Chương 4.Bài 11: Tích vô hướng của hai vecto (1) | Giáo án điện tử môn Toán 10 | Kết nối tri thức với cuộc sống
Giáo án PowerPoint Toán 10 Kết nối tri thức với cuộc sống là tài liệu cực kì hữu ích mà muốn giới thiệu đến quý thầy cô tham khảo. Bài giảng điện tử môn Toán 10 Kết nối tri thức bao gồm đầy đủ các bài giảng trong cả năm học được thiết kế dưới dạng file trình chiếu PowerPoint với nhiều hiệu ứng rất đẹp mắt. Với nội dung bài học trình bày chi tiết cho từng phần học và bám sát chương trình SGK Toán 10 Kết nối tri thức.
Chủ đề: Bài giảng điện tử Toán 10
Môn: Toán 10
Sách: Kết nối tri thức
Thông tin:
Tác giả:
Preview text:
CHƯƠNG I CHƯƠNG IV. VECTƠ
§7. Các khái niệm mở đầu
§8. Tổng và hiệu của hai vectơ
§9. Tích của một vectơ với một số
§10. Vectơ trong mặt phẳng tọa độ
§11. Tích vô hướng của hai vectơ
Bài tập cuối chương 4 CHƯƠNG I CHƯƠNG IV. VECTƠ TOÁN ĐẠI SỐ ➉ 11
TÍCH VÔ HƯỚNG CỦA HAI VECTƠ 1 GÓC GIỮA HAI VECTƠ 2
TÍCH VÔ HƯỚNG CỦA HAI VECTƠ 3
BIỂU THỨC TỌA ĐỘ VÀ TÍNH CHẤT CỦA TÍCH VÔ HƯỚNG 1. GÓC GIỮA HAI VECTƠ
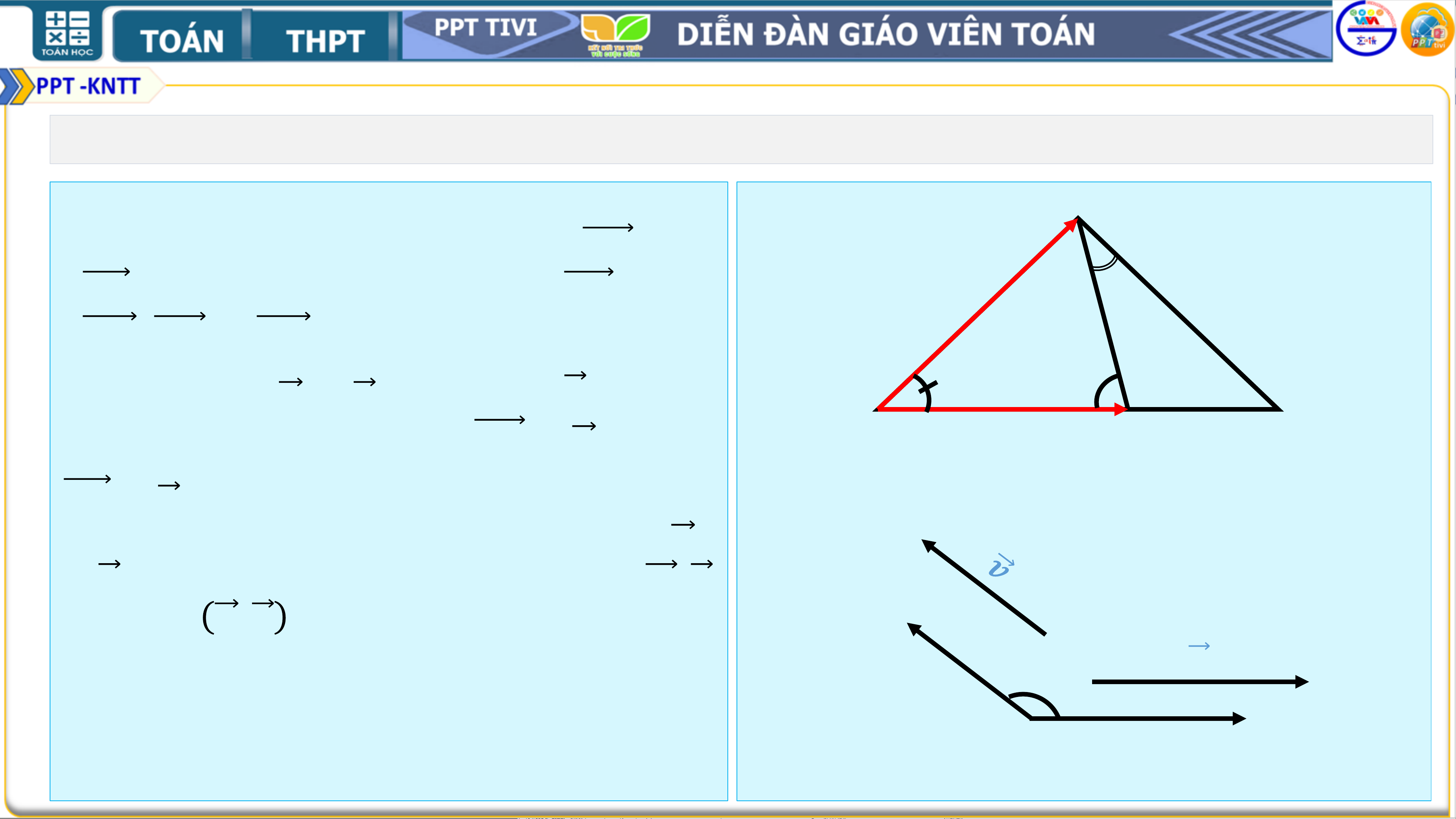
• HĐ1. Trong hình 4.39 , số đo góc BAC cũng 𝑩
được gọi là số đo góc giữa vectơ𝑨𝑩 và
𝑨𝑪 . Hãy tìm số đo các góc giữa 𝑩𝑪 và 𝟑𝟎𝟎
𝑩𝑫, 𝑫𝑨 và 𝑫𝑩.
Cho hai vectơ 𝒖 và 𝒗 khác vec tơ 𝟎. Từ một 𝟖𝟎𝟎 điểm 𝑫
A tuỳ ý , vẽ các vec tơ 𝑨𝑩 = 𝒖 và 𝑨 𝑪 Hình 4.39
𝑨𝑪 = 𝒗 (H 4.40). Khi đó, số đo của góc BAC
được gọi là số đo của góc giữa hai vectơ 𝒖
và 𝒗 hay đơn giản là góc giữa hai vectơ 𝒖, 𝒗,
kí hiệu là 𝒖, 𝒗 . 𝑪 𝒖 𝑨 𝑩 Hình 4.40 Chú ý
•Quy ước rằng góc giữa hai vectơ 𝒖 và 𝟎 có thể nhận một giá trị tuỳ ý từ
𝟎∘đến 𝟏𝟖𝟎∘.
•Nếu vectơ 𝒖, 𝒗 = 𝟗𝟎∘thì ta nói rằng 𝒖 và 𝒗 vuông góc với nhau, kí hiệu
là 𝒖 ⊥ 𝒗 hoặc 𝒗 ⊥ 𝒖.
• Đặc biệt vectơ 𝟎được coi là vuông góc với mọi véctơ.
? Khi nào thì góc giữa hai vec tơ bằng 𝟎∘, bằng 𝟏𝟖𝟎∘? Giải:
• Góc giữa hai vec tơ bằng 𝟎∘khi hai vec tơ cùng hướng.
• Góc giữa hai vec tơ bằng 𝟏𝟖𝟎∘khi hai vec tơ ngược hướng.
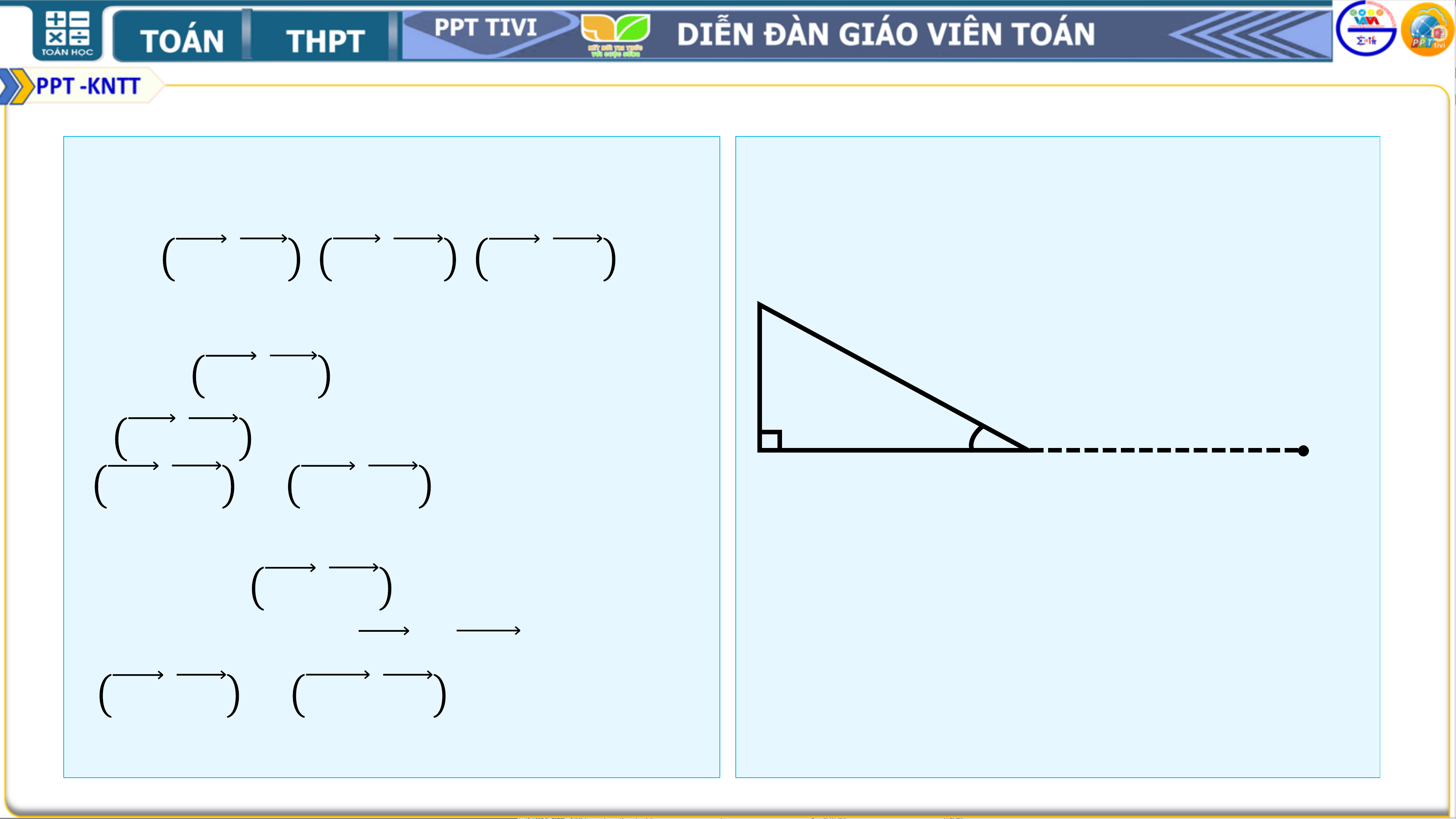
• Ví dụ 1. Cho tam giác ABC vuông
tại A và 𝑩 = 𝟑𝟎∘.
Tính 𝑨𝑩, 𝑨𝑪 , 𝑪𝑨, 𝑪𝑩 , 𝑨𝑩, 𝑩𝑪 . 𝑪 Giải ( H 4. 41)
Ta có: 𝑨𝑩, 𝑨𝑪 = 𝑩𝑨𝑪 = 𝟗𝟎°, 𝑪𝑨, 𝑪𝑩 =
𝑨𝑪𝑩 = 𝟔𝟎°, 𝟑𝟎𝟎
𝑨𝑩, 𝑩𝑪 = 𝑩𝑫, 𝑩𝑪 = 𝑫𝑩𝑪 = 𝟏𝟓𝟎°. 𝑨 𝑩 𝑫
Luyện tập 1. Cho tam giác đều Hình 4.41
ABC, tính 𝑨𝑩, 𝑩𝑪 .
• Giải: Vẽ vectơ 𝑨𝑩 = 𝑩𝑩′. Ta có
𝑨𝑩, 𝑩𝑪 = 𝑩𝑩′, 𝑩𝑪 = 𝑩′𝑩𝑪 = 𝟏𝟐𝟎°.
2. TÍCH VÔ HƯỚNG CỦA HAI VECTƠ
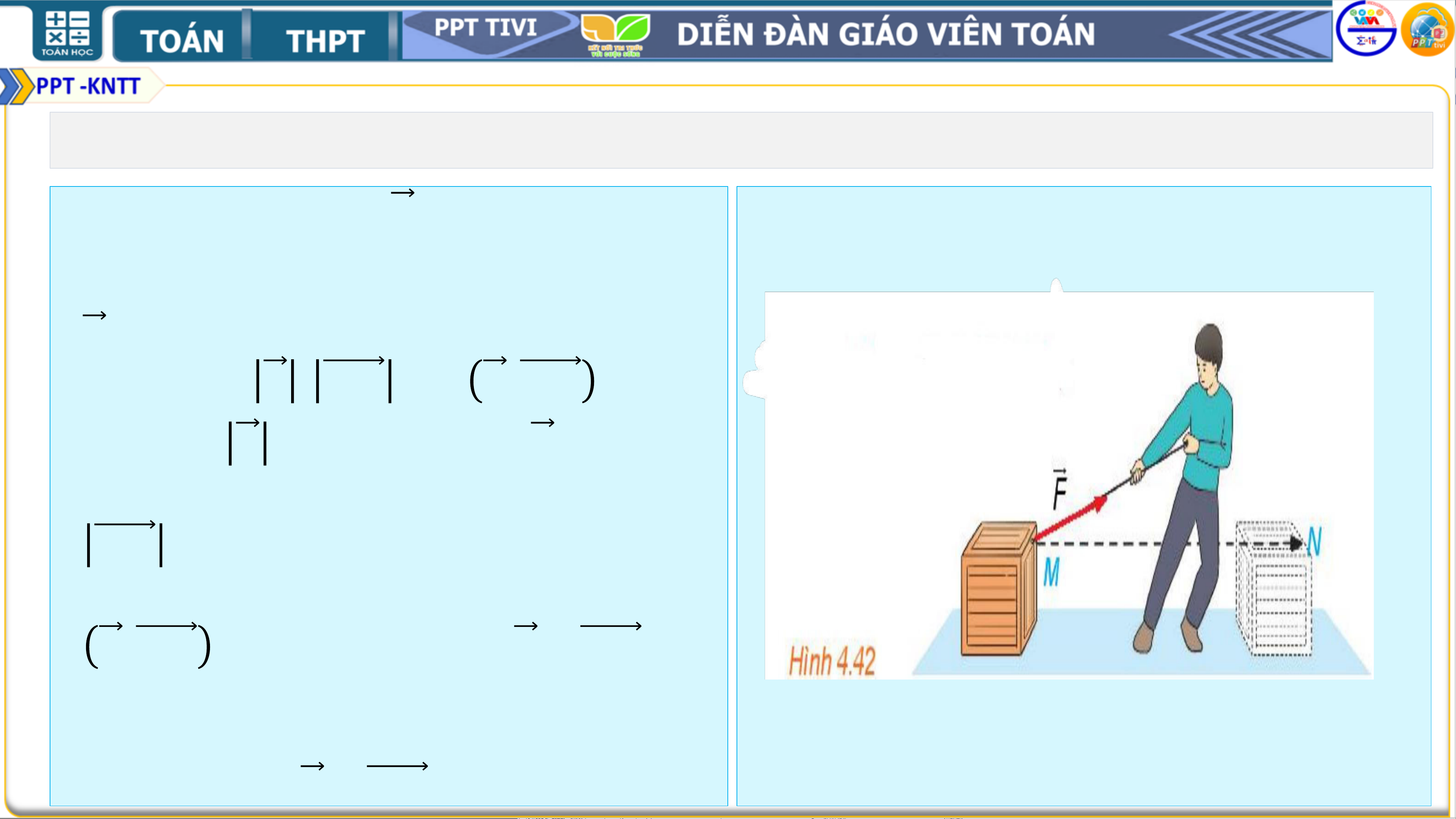
• Trong Vật lí, nếu lực 𝑭không đổi tác dụng
vào một vật và điểm đặt của lực chuyển
động thẳng từ M tới N, thì công A của lực
𝑭được tính theo công thức:
𝑨 = 𝑭 . 𝑴𝑵 . 𝒄𝒐𝒔 𝑭, 𝑴𝑵
• Trong đó 𝑭 là độ lớn của lực 𝑭 (theo đơn vị Newton);
• 𝑴𝑵 là độ dài của vectơ MN (theo đơn vị mét);
• 𝑭, 𝑴𝑵 góc giữa hai vec tơ 𝑭và 𝑴𝑵.
• Toán học gọi giá trị A (không kể đơn vị đo)
trong biểu thức nói trên là tích vô hướng
của hai vec tơ 𝑭và 𝑴𝑵.
• Tích vô hướng của hai vectơ 𝒖 và 𝒗 là một
số , kí hiệu là 𝒖. 𝒗, được xác định bởi công
thức sau: 𝒖.𝒗 = 𝒖 . 𝒗 .𝒄𝒐𝒔 𝒖,𝒗 .
? Khi nào tích vô hướng của hai vectơ 𝒖, 𝒗 là
một số dương? Là một số âm? Giải:
• Tích vô hướng của hai vectơ 𝒖, 𝒗 là một số
dương khi góc giữa hai vectơ đó là góc
nhọn ( hoặc bằng 𝟎∘).
• Tích vô hướng của hai vectơ 𝒖, 𝒗 là một số
âm khi góc giữa hai vectơ đó là góc tù
( hoặc bằng 𝟏𝟖𝟎∘). Chú ý
• 𝒖 ⊥ 𝒗 ⇔ 𝒖. 𝒗 = 𝟎.
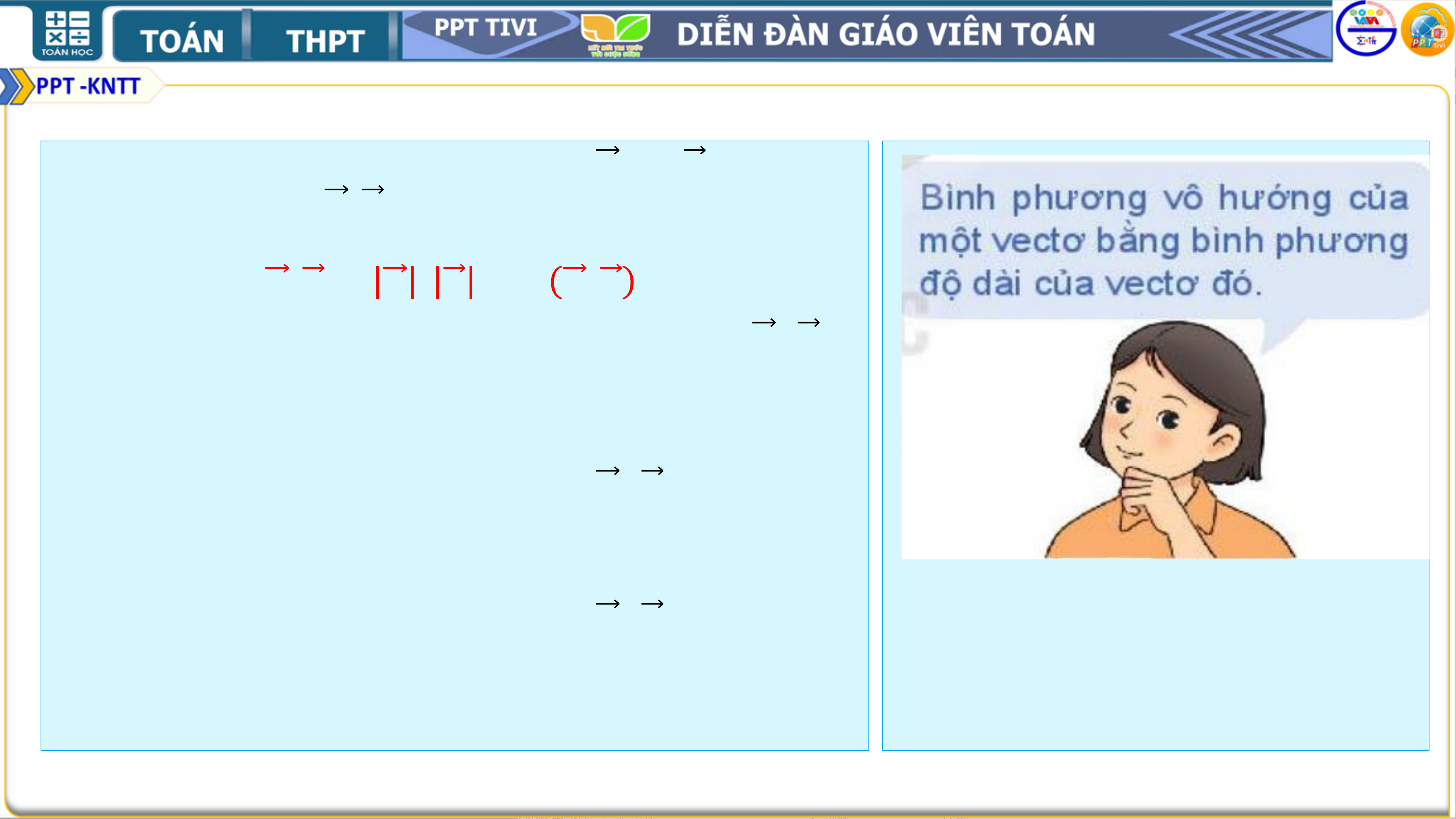
• 𝒖. 𝒖 còn được viết là 𝒖𝟐 và được gọi là bình phương vô hướng của vectơ 𝒖 .
Ta có 𝒖𝟐 = 𝒖 . 𝒖 . 𝒄𝒐𝒔𝟎∘ = 𝒖 𝟐.
? Khi nào thì 𝒖. 𝒗 𝟐 = 𝒖𝟐. 𝒗𝟐?
• Giải: 𝒖. 𝒗 𝟐 = 𝒖𝟐. 𝒗𝟐 ⇔ ቈ 𝒖, 𝒗 = 𝟎∘ 𝒖, 𝒗 = 𝟏𝟖𝟎∘
• Ví dụ 2. Cho hình vuông ABCD có cạnh
bằng.Tính các tích vô hướng sau: 𝑨 𝑩
𝑨𝑩. 𝑨𝑫, 𝑨𝑩. 𝑨𝑪, 𝑨𝑩. 𝑩𝑫.
• Giải: Vì 𝑨𝑩. 𝑨𝑫 = 𝟗𝟎∘ nên 𝑨𝑩. 𝑨𝑫 = 𝟎.
Hình vuông có cạnh bằng 𝒂 nên có đường
chéo là 𝒂 𝟐.
Mặt khác, 𝑨𝑩, 𝑨𝑪 = 𝟒𝟓∘, 𝑨𝑩, 𝑩𝑫 = 𝟏𝟑𝟓∘, do đó 𝑪 𝑫 Hình 4.43
𝑨𝑩. 𝑨𝑪 = 𝑨𝑩. 𝑨𝑪. 𝒄𝒐𝒔 𝟒 𝟓∘ = 𝒂. 𝒂 𝟐. 𝟐 𝟐 Chú ý = 𝒂𝟐;
Hình vuông có cạnh bằng a nên
𝑨𝑩. 𝑩𝑫 = 𝑨𝑩. 𝑩𝑫. 𝒄𝒐𝒔 𝟏 𝟑𝟓∘
đường chéo là 𝒂 𝟐 𝟐
= 𝒂. 𝒂 𝟐. − 𝟐 = −𝒂𝟐.
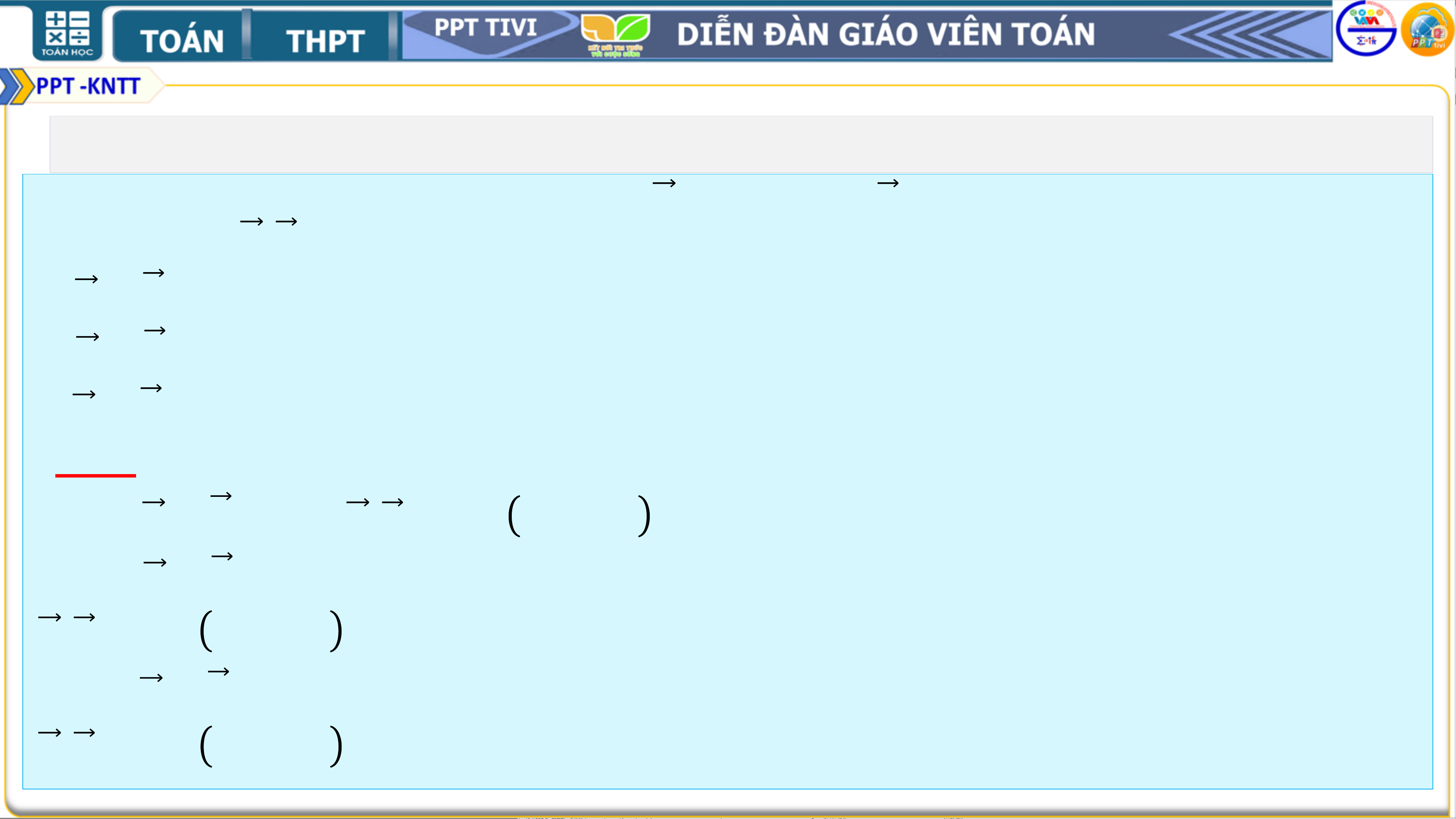
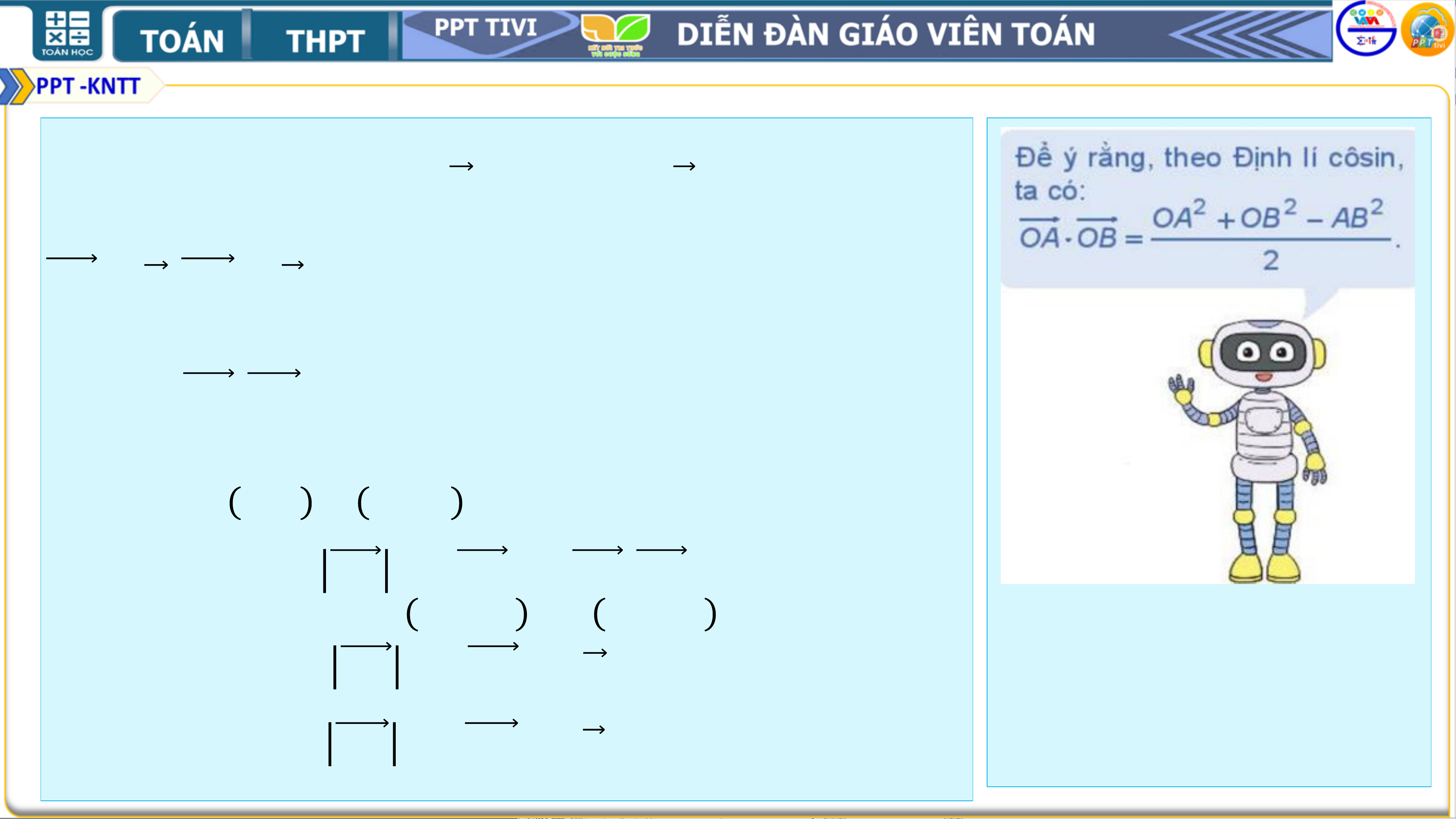
• Luyện tập 2. Cho tam giác ABC có
𝑩𝑪 = 𝒂, 𝑪𝑨 = 𝒃, 𝑨𝑩 = 𝒄.
Hãy tính 𝑨𝑩. 𝑨𝑪 theo 𝒂, 𝒃, 𝒄. • Giải:
Từ định lí Cô sin trong tam giác ABC , suy ra
𝒃𝟐 + 𝒄𝟐 − 𝒂𝟐 𝒄𝒐𝒔𝑨 = 𝟐𝒃𝒄 Ta có:
𝑨𝑩. 𝑨𝑪 = 𝑨𝑩 𝑨𝑪 𝒄𝒐𝒔𝑨 = 𝒄. 𝒃. 𝒄𝒐𝒔 𝑨
= 𝒄. 𝒃. 𝒃𝟐+𝒄𝟐−𝒂𝟐 = 𝒃𝟐+𝒄𝟐−𝒂𝟐 . 𝟐𝒃𝒄 𝟐
3. BIỂU THỨC TOẠ ĐỘ VÀ TÍNH CHẤT CỦA TÍCH VÔ HƯỚNG
• HĐ2: Cho hai vectơ cùng phương 𝒖 = (𝒙; 𝒚) và 𝒗 = (𝒌 𝒙 ; 𝒌 𝒚). Hãy kiểm tra
công thức 𝒖. 𝒗 = 𝒌(𝒙𝟐 + 𝒚𝟐) theo từng trường hợp sau: a) 𝒖 = 𝟎;
b) 𝒖 ≠ 𝟎 và 𝒌 ≥ 𝟎;
c) 𝒖 ≠ 𝟎 và 𝒌 < 𝟎. • Giải:
a) Khi 𝒖 = 𝟎; ta có 𝒖. 𝒗 = 𝟎; 𝒌 𝒙𝟐 + 𝒚𝟐 = 𝟎. Vậy công thức đã cho đúng.
b) Khi 𝒖 ≠ 𝟎 và 𝒌 ≥ 𝟎 thì công thức đã cho không đúng vì sẽ xảy ra trường hợp
𝒖. 𝒗 ≠ 𝟎; 𝒌 𝒙𝟐 + 𝒚𝟐 = 𝟎.
c) Khi 𝒖 ≠ 𝟎 và 𝒌 < 𝟎 thì công thức đã cho không đúng vì sẽ xảy ra trường hợp
𝒖. 𝒗 > 𝟎; 𝒌 𝒙𝟐 + 𝒚𝟐 < 𝟎.
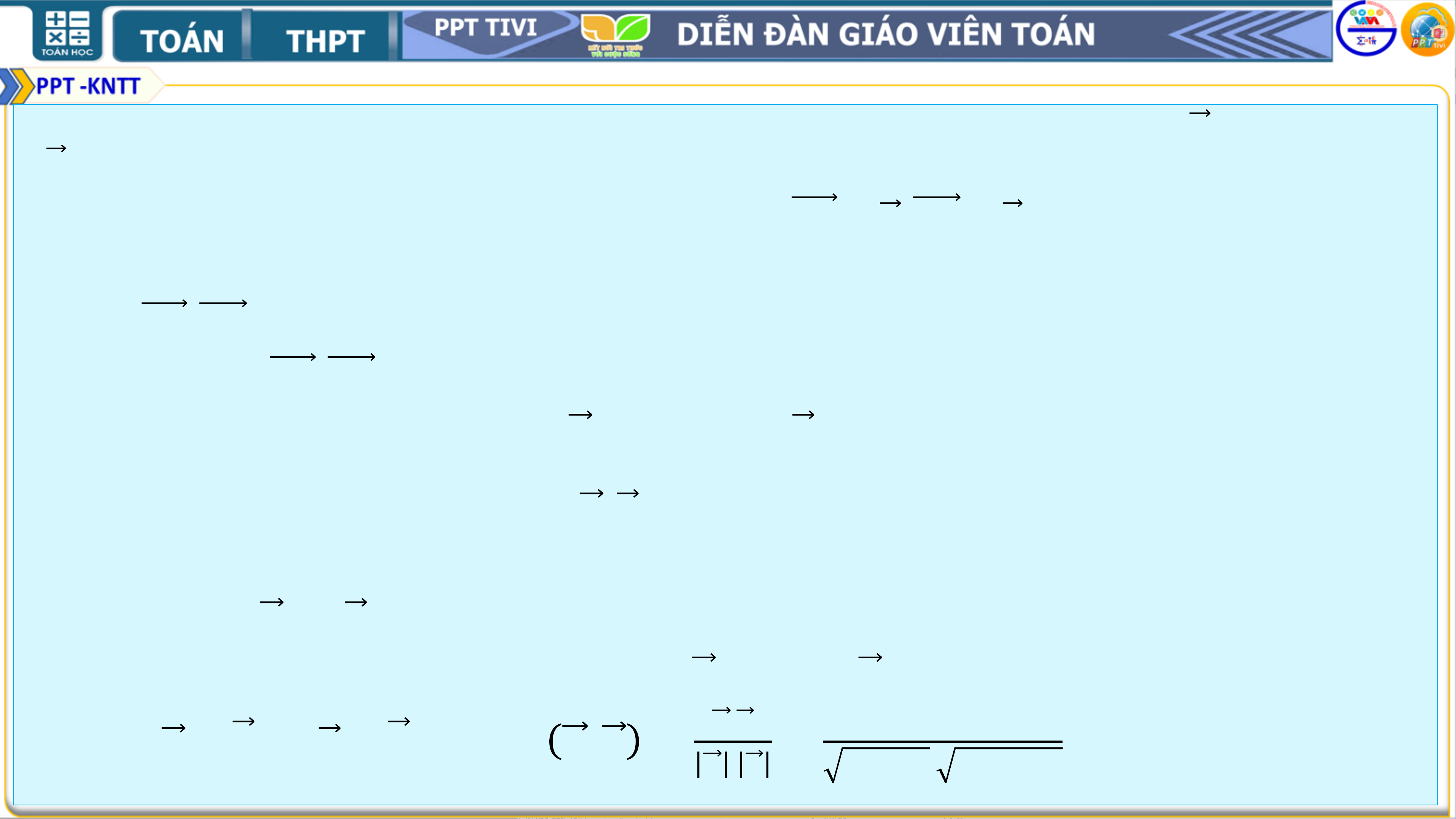
• HĐ3: Trong mặt phẳng toạ độ Ox𝒚, cho hai vectơ
không cùng phương 𝒖 = (𝒙; 𝒚) và 𝒗 = (𝒙′; 𝒚′)
a) Xác định toạ độ của các điểm A và B sao cho
𝑶𝑨 = 𝒖, 𝑶𝑩 = 𝒗.
b) Tính 𝑨𝑩𝟐, 𝑶𝑨𝟐, 𝑶𝑩𝟐 theo toạ độ của A và B.
c) Tính 𝑶𝑨. 𝑶𝑩 theo toạ độ của A, B. Giải:
a) Ta có 𝑨 𝒙; 𝒚 , 𝑩 𝒙′; 𝒚′ . 𝟐
b) Ta có 𝑨𝑩𝟐 = 𝑨𝑩 = 𝑨𝑩𝟐 = 𝑨𝑩. 𝑨𝑩
= 𝒙′ − 𝒙 𝟐 + 𝒚′ − 𝒚 𝟐. 𝟐
𝑶𝑨𝟐 = 𝑶𝑨 = 𝑶𝑨𝟐 = 𝒖𝟐 = 𝒙𝟐 + 𝒚𝟐. 𝟐
𝑶𝑩𝟐 = 𝑶𝑩 = 𝑶𝑩𝟐 = 𝒗𝟐 = 𝒙′𝟐 + 𝒚′𝟐.
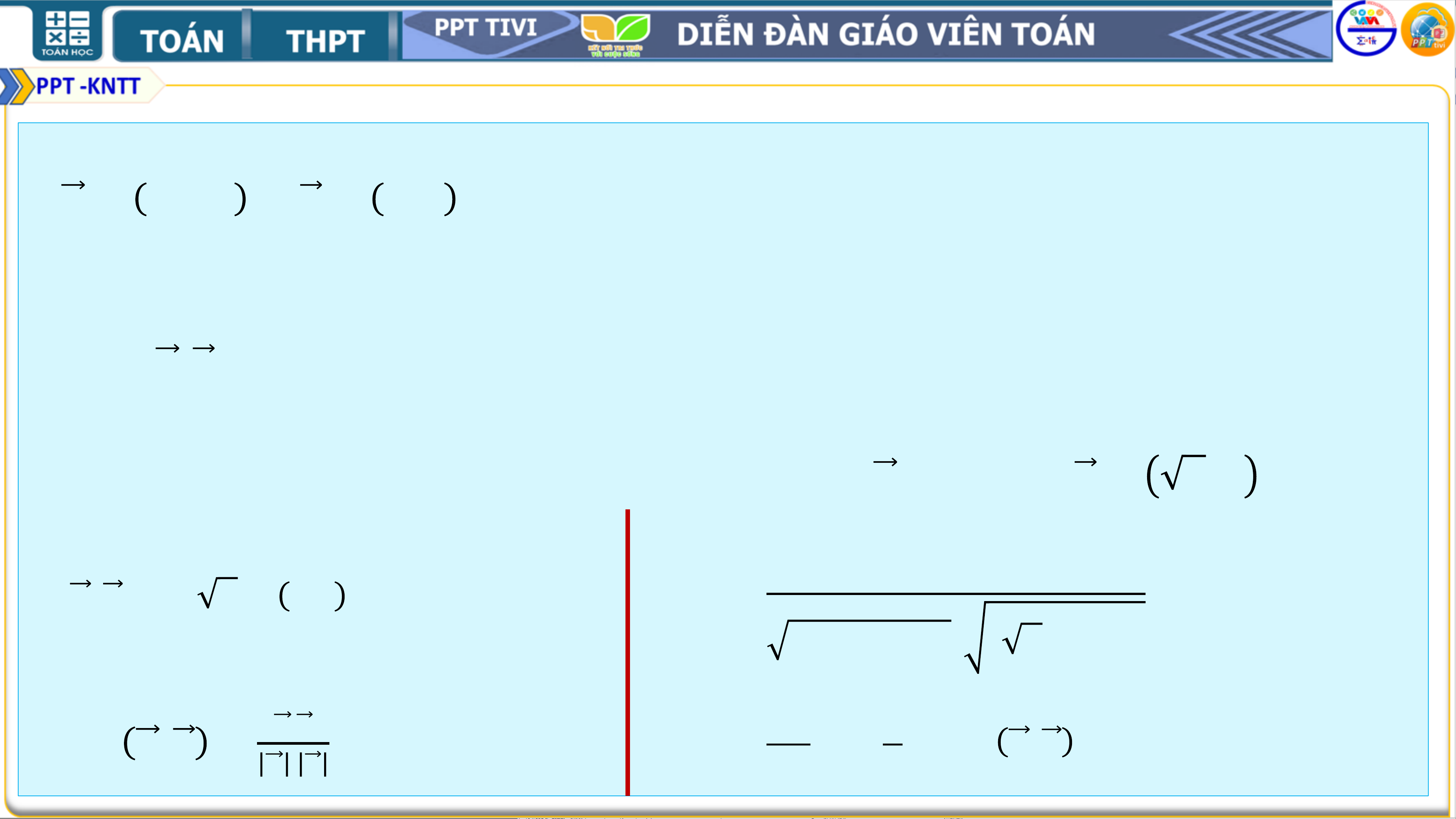
• HĐ3: Trong mặt phẳng toạ độ Ox𝒚, cho hai vectơ không cùng phương 𝒖 = (𝒙; 𝒚) và 𝒗 = (𝒙′; 𝒚′)
a) Xác định toạ độ của các điểm A và B sao cho 𝑶𝑨 = 𝒖, 𝑶𝑩 = 𝒗.
b) Tính 𝑨𝑩𝟐, 𝑶𝑨𝟐, 𝑶𝑩𝟐 theo toạ độ của A và B.
c) Tính 𝑶𝑨. 𝑶𝑩 theo toạ độ của A, B.
Giải: c) Ta có 𝑶𝑨. 𝑶𝑩 = 𝒙. 𝒙′ + 𝒚. 𝒚′.
• Tích vô hướng của hai vectơ 𝒖 = (𝒙; 𝒚) và 𝒗 = (𝒙′; 𝒚′) được tính theo công thức:
𝒖. 𝒗 = 𝒙. 𝒙′ + 𝒚. 𝒚′. • Nhận xét:
•Hai vectơ 𝒖 và 𝒗 vuông góc với nhau khi và chỉ khi 𝒙𝒙′ + 𝒚𝒚′ = 𝟎.
•Bình phương vô hướng của vectơ 𝒖(𝒙; 𝒚) là 𝒖𝟐 = 𝒙𝟐 + 𝒚𝟐.
•Nếu 𝒖 ≠ 𝟎 và 𝒗 ≠ 𝟎 thì cos 𝒖, 𝒗 = 𝒖.𝒗 = 𝒙𝒙′+𝒚𝒚′ . 𝒖 . 𝒗
𝒙𝟐+𝒚𝟐. 𝒙′𝟐+𝒚′𝟐
• Ví dụ 3. Trong mặt phẳng toạ độ Oxy, tính tích vô hướng của các cặp vectơ sau:
a) 𝒖 = 𝟐; −𝟑 và 𝒗 = 𝟓; 𝟑 ;
b) Hai vec tơ đơn vị Ԧ𝒊 và Ԧ𝒋 tương ứng của các trục Ox, Oy. • Giải
a) Ta có: 𝒖. 𝒗 = 𝟐. 𝟓 + (−𝟑). 𝟑 = 𝟏𝟎 − 𝟗 = 𝟏.
b) Vì Ԧ𝒊 = (𝟏; 𝟎) và Ԧ𝒋 = (𝟎; 𝟏) nên Ԧ𝒊. Ԧ𝒋 = 𝟏. 𝟎 + 𝟎. 𝟏 = 𝟎.
• Luyện tập 3. Tính tích vô hướng và góc giữa hai vec tơ 𝒖 = (𝟎; −𝟓), 𝒗 = 𝟑; 𝟏 • Giải: Ta có: −𝟓
* 𝒖. 𝒗 = 𝟎. 𝟑 + −𝟓 . 𝟏 =
𝟎𝟐 + (−𝟓)𝟐. ( 𝟑)𝟐 + 𝟏𝟐
= 𝟎 − 𝟓 = −𝟓. −𝟓 𝟏
* cos 𝒖, 𝒗 = 𝒖.𝒗 =
⇒ 𝒖, 𝒗 = 𝟏𝟐𝟎∘. 𝒖 . 𝒗 𝟏𝟎 = − 𝟐
• HĐ4: Cho ba vectơ 𝒖 = (𝒙𝟏; 𝒚𝟏), 𝒗 = 𝒙𝟐; 𝒚𝟐 , 𝒘 = 𝒙𝟑; 𝒚𝟑 .
a) Tính 𝒖. (𝒗 + 𝒘), 𝒖. 𝒗 + 𝒖. 𝒘 theo toạ độ của các vectơ 𝒖, 𝒗, 𝒘.
b) So sánh 𝒖. (𝒗 + 𝒘) và 𝒖. 𝒗 + 𝒖. 𝒘.
c) So sánh 𝒖. 𝒗 và 𝒗. 𝒖. • Giải:
a) Ta có 𝒗 + 𝒘 = 𝒙𝟐 + 𝒙𝟑; 𝒚𝟐 + 𝒚𝟑 .
Suy ra: 𝒖. (𝒗 + 𝒘) = 𝒙𝟏. 𝒙𝟐 + 𝒙𝟑 + 𝒚𝟏 𝒚𝟐 + 𝒚𝟑 .
b) Ta có 𝒖. 𝒗 + 𝒖. 𝒘 = 𝒙𝟏𝒙𝟐 + 𝒚𝟏𝒚𝟐 + 𝒙𝟏𝒙𝟑 + 𝒚𝟏𝒚𝟑
= 𝒙𝟏 𝒙𝟐 + 𝒙𝟑 + 𝒚𝟏 𝒚𝟐 + 𝒚𝟑 .
Suy ra: 𝒖. (𝒗 + 𝒘) = 𝒖. 𝒗 + 𝒖. 𝒘.
c)Ta có 𝒖. 𝒗 = 𝒙𝟏𝒙𝟐 + 𝒚𝟏𝒚𝟐 và 𝒗. 𝒖 = 𝒙𝟏𝒙𝟐 + 𝒚𝟏𝒚𝟐.
Suy ra: 𝒖. 𝒗 = 𝒗. 𝒖.
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15