CHƯƠNG I CHƯƠNG IV. VECTƠ
§7. Các khái niệm mở đầu
§8. Tổng và hiệu của hai vectơ
§9. Tích của một vectơ với một số
§10. Vectơ trong mặt phẳng tọa độ
§11. Tích vô hướng của hai vectơ
Bài tập cuối chương 4 CHƯƠNG I CHƯƠNG IV. VECTƠ TOÁN HÌNH HỌC ➉ 11
TÍCH VÔ HƯỚNG CỦA HAI VECTƠ 1 GÓC GIỮA HAI VECTƠ 2
TÍCH VÔ HƯỚNG CỦA HAI VECTƠ 3
BIỂU THỨC TỌA ĐỘ VÀ TÍNH CHẤT CỦA TÍCH VÔ HƯỚNG
3. Tính chất của tích vô hướng
• Với ba vectơ 𝒖, 𝒗, 𝒘 bất kì và mọi số thực k, • Chú ý: Từ các tính chất trên, ta có thể ta có: chứng minh được:
• 𝒖. 𝒗 = 𝒗. 𝒖 (tính chất giao hoán); • 𝒖. 𝒗 − 𝒘 = 𝒖. 𝒗 − 𝒖. 𝒘 (tính chất phân
• 𝒖. 𝒗 + 𝒘 = 𝒖. 𝒗 + 𝒖. 𝒘 phối (tính chất phân
đối với phép trừ);
phối đối với phép cộng);
• 𝒖 + 𝒗 𝟐 = 𝒖𝟐 + 𝟐𝒖. 𝒗 + 𝒗𝟐;
• 𝒌𝒖 . 𝒗 = 𝒌 𝒖. 𝒗 = 𝒖. 𝒌𝒗 .
• 𝒖 − 𝒗 𝟐 = 𝒖𝟐 − 𝟐𝒖. 𝒗 + 𝒗𝟐;
• 𝒖 + 𝒗 . 𝒖 − 𝒗 = 𝒖𝟐 − 𝒗𝟐.
Ví dụ 4. ( Ứng dụng của vectơ trong bài toán hình học)
Cho điểm M thay đổi trên đường tròn tâm Do đó 𝒙𝑨 + 𝒙𝑩 + 𝒙𝑪 = 𝟎 và 𝒚𝑨 + 𝒚𝑩 + 𝒚𝑪 = 𝟎.
O ngoại tiếp tam giác đều ABC cho trước. Chứng
Vì 𝑶𝑴𝟐 = 𝑶𝑨𝟐 = 𝑹𝟐 nên
minh rằng 𝑴𝑨𝟐 + 𝑴𝑩𝟐 + 𝑴𝑪𝟐không đổi 𝟐 𝟐 .
𝒙𝟐 + 𝒚𝟐 = 𝒙𝑨 + 𝒚𝑨 = 𝑹𝟐. Lời giải
Vậy 𝑴𝑨𝟐 = (𝒙 − 𝒙𝑨)𝟐 + (𝒚 − 𝒚𝑨)𝟐 Cách 𝟐 𝟐
1: (Dùng tọa độ).
= (𝒙𝟐 + 𝒚𝟐) + (𝒙𝑨 + 𝒚𝑨) − 𝟐𝒙𝒙𝑨 − 𝟐𝒚𝒚𝑨
Xét hệ trục tọa độ có gốc trùng với
= 2R𝟐 − 𝟐𝒙𝒙𝑨 − 𝟐𝒚𝒚𝑨.
tâm O của đường tròn ngoại tiếp tam
Tương tự 𝑴𝑩𝟐 = 𝟐𝑹𝟐 − 𝟐𝒙𝒙𝑩 − 𝟐𝒚𝒚𝑩 và
giác ABC. Gọi tọa độ của các điểm
𝑴𝑪𝟐 = 𝟐𝑹𝟐 − 𝟐𝒙𝒙𝑪 − 𝟐𝒚𝒚𝑪.
là 𝑨(𝒙𝑨; 𝒚𝑨) , 𝑩( 𝒙𝑩; 𝒚𝑩) , 𝑪( 𝒙𝑪; 𝒚𝑪) , 𝑴( 𝒙; 𝒚) .
Do đó 𝑴𝑨𝟐 + 𝑴𝑩𝟐 + 𝑴𝑪𝟐 =
=𝟔𝑹𝟐 − 𝟐𝒙 𝒙
Vì tam giác ABC đều nên tâm đường
𝑨 + 𝒙𝑩 + 𝒙𝑪 − 𝟐𝒚 𝒚𝑨 + 𝒚𝑩 + 𝒚𝑪
tròn ngoại tiếp 𝑶( 𝟎; 𝟎) đồng thời là
= 𝟔𝑹𝟐 (không đổi).
trọng tâm của tam giác.
Ví dụ 4. ( Ứng dụng của vectơ trong bài toán hình học)
Cho điểm M thay đổi trên đường tròn tâm A
O ngoại tiếp tam giác đều ABC cho trước. M
Chứng minh rằng 𝑴𝑨𝟐 + 𝑴𝑩𝟐 + 𝑴𝑪𝟐không đổi. Hình 4.44 Lời giải R O
Cách 2: (Dùng tích vô hướng). (H.4.44) B C
Vì tam giác ABC đều nên tâm O của
đường tròn ngoại tiếp đồng thời là trọng
= 𝟑𝑴𝑶 + 𝟐𝑴𝑶. 𝑶𝑨 + 𝟐𝑴𝑶. 𝑶𝑩 + 𝟐𝑴𝑶. 𝑶𝑪
tâm của tam giác. Vậy 𝑶𝑨 + 𝑶𝑩 + 𝑶𝑪 = 𝟎.
+ 𝟎𝑨𝟐 + 𝟎𝑩𝟐 + 𝟎𝑪𝟐
Giả sử (O) có bán kính R. Ta có:
= 𝟑𝑴𝑶 + 𝟐𝑴𝑶. 𝑶𝑨 + 𝑶𝑩 + 𝑶𝑪 + 𝟑𝑹𝟐
𝑴𝑨𝟐 + 𝑴𝑩𝟐 + 𝑴𝑪𝟐 = 𝑴𝑨𝟐 + 𝑴𝑩𝟐 + 𝑴𝑪𝟐
= 𝟑𝑹𝟐 + 𝟐𝑴𝑶. 𝟎 + 𝟑𝑹𝟐 = 𝟔𝑹𝟐 𝟐 𝟐 𝟐
= 𝑴𝑶 + 𝑶𝑨 + 𝑴𝑶 + 𝑶𝑩 + 𝑴𝑶 + 𝑶𝑪
Vậy 𝑴𝑨𝟐 + 𝑴𝑩𝟐 + 𝑴𝑪𝟐 không đổi khi M thay đổi trên (O). Luyện tập 4.
Cho tam giác ABC với A(-1; 2), B(8; -1), A K
C(8; 8). Gọi H là trực tâm của tam giác.
a) Chứng minh rằng 𝑨𝑯. 𝑩𝑯 = 𝟎 và Hình 4.45 𝑩𝑯. 𝑪𝑨 = 𝟎. B C H
b) Tìm tọa độ điểm H.
b) Giả sử 𝑯 𝒙; 𝒚 ta có
c) Giải tam giác ABCLời giải
𝑨𝑯 = 𝒙 + 𝟏; 𝒚 − 𝟐 , 𝑩𝑪 = 𝟎; 𝟗 ,
a) Vì 𝑯 là trực tâm tam giác 𝑨𝑩𝑪 nên
𝑩𝑯 = 𝒙 − 𝟖; 𝒚 + 𝟏 , 𝑪𝑨 = −𝟗; −𝟔 Vì 𝑨𝑯 ⊥ 𝑩𝑪
𝑯 là trực tâm tam giác 𝑨𝑩𝑪 nên
và 𝑩𝑯 ⊥ 𝑪𝑨
do đó 𝑨𝑯 ⊥ 𝑩𝑪 và 𝑩𝑯 ⊥ 𝑪𝑨 suy ra
ቊ𝑨𝑯 ⋅ 𝑩𝑪 = 𝟎 ⇔ ቊ 𝒙 + 𝟏 . 𝟎 + 𝒚 − 𝟐 . 𝟗 = 𝟎 𝑩𝑯 ⋅ 𝑪𝑨 = 𝟎
−𝟗 𝒙 − 𝟖 − 𝟔 𝒚 + 𝟏 = 𝟎
𝑨𝑯 ⋅ 𝑩𝑪 = 𝟎 và 𝑩𝑯 ⋅ 𝑪𝑨 = 𝟎 ⇔ ቊ𝒙 = 𝟔
𝒚 = 𝟐 ⇒ 𝑯 𝟔; 𝟐 Luyện tập 4.
Cho tam giác ABC với A(-1; 2), B(8; -1), A K
C(8; 8). Gọi H là trực tâm của tam giác.
a) Chứng minh rằng 𝑨𝑯. 𝑩𝑯 = 𝟎và Hình 4.45 𝑩𝑯. 𝑪𝑨 = 𝟎. B C H
b) Tìm tọa độ điểm H.
c) Giải tam giác ABCLời giải 𝑨𝑪 =
𝟖 + 𝟏 𝟐 + 𝟖 − 𝟐 𝟐
= 𝟏𝟏𝟕 = 𝟑 𝟏𝟑 c) 𝑨𝑩 =
𝟖 + 𝟏 𝟐 + −𝟏 − 𝟐 𝟐 𝑩𝑪 =
𝟖 − 𝟖 𝟐 + 𝟖 + 𝟏 𝟐 = 𝟗𝟎 = 𝟗 = 𝟑 𝟏𝟎 Vận dụng
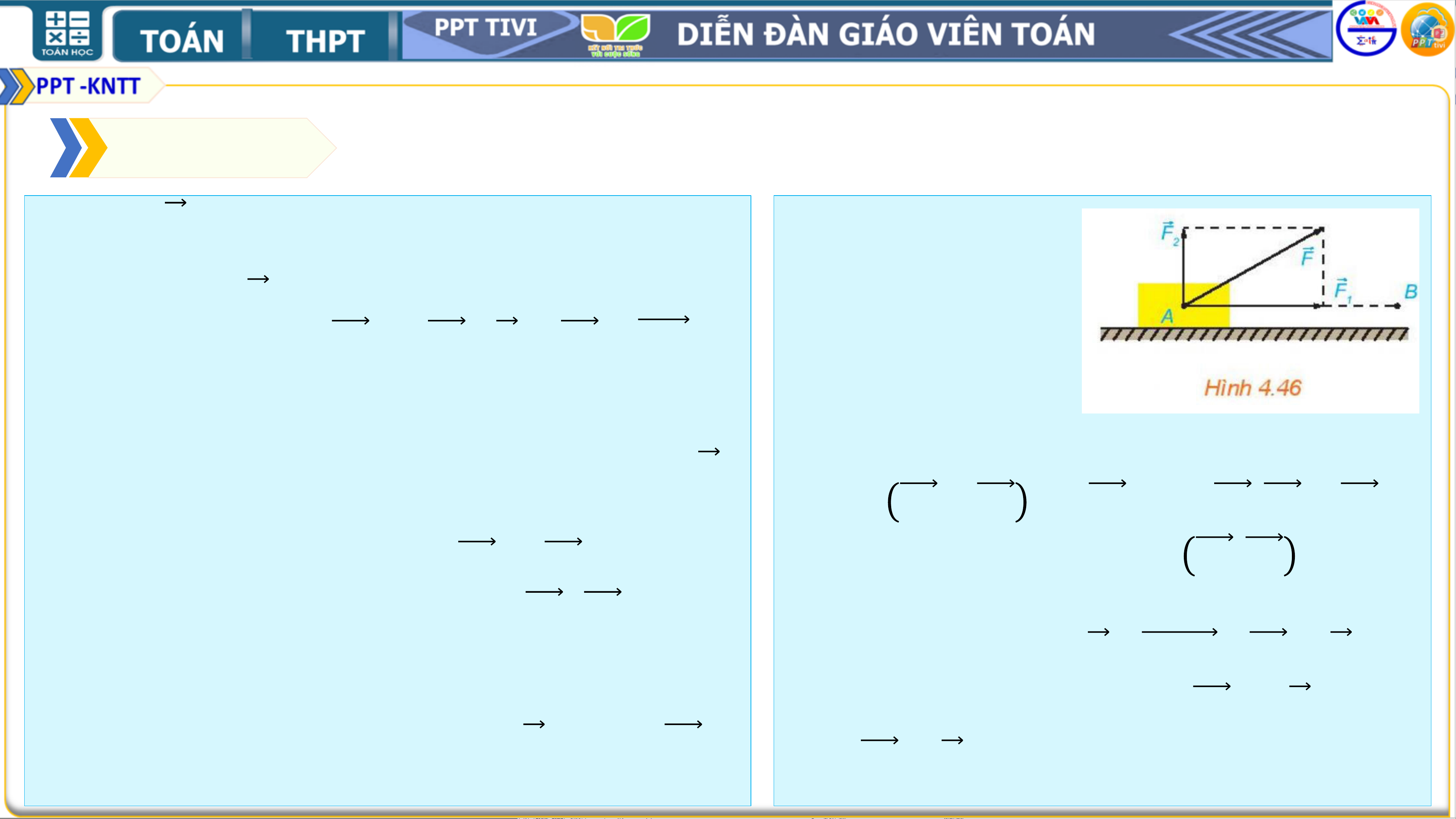
Một lực 𝑭 không đổi tác động vào một vật
và điểm đặt của lực chuyển động thẳng từ
A đến B. Lực 𝑭 được phân tích thành hai
lực thành phần là 𝑭𝟏 và 𝑭𝟐 (𝑭 = 𝑭𝟏 + 𝑭𝟐). Lời giải
a) Dựa vào tính chất của tích vô hướng, a)Ta có:
hãy giải thích vì sao công sinh bởi lực 𝑭 𝟐 𝟐 𝟐 ( 𝑭
đã được đề cập ở trên) bằng tổng của 𝟏 + 𝑭𝟐
= 𝑭𝟏 + 𝟐. 𝑭𝟏. 𝑭𝟐 + 𝑭𝟐
các công sinh bởi các lực 𝑭 = 𝑭𝟐 𝟐 𝟏và 𝑭𝟐.
𝟏 + 𝟐. 𝑭𝟏. 𝑭𝟐. 𝒄𝒐𝒔 𝑭𝟏, 𝑭𝟐 + 𝑭𝟐
b) Giả sử các lực thành phần 𝑭 = 𝑭𝟐 𝟐
𝟏, 𝑭𝟐tương
𝟏 + 𝟐. 𝑭𝟏. 𝑭𝟐. 𝒄𝒐𝒔 𝟗 𝟎° + 𝑭𝟐
ứng cùng phương, vuông góc với phương = 𝑭𝟐 𝟐
𝟏 + 𝑭𝟐 = 𝑭𝟐 = 𝑭𝟐 ⇒ 𝑭𝟏+ 𝑭𝟐 = 𝑭.
chuyển động của vật. Hãy tìm mối quan
b) Gọi 𝜶 là góc tạo bởi 𝑭𝟏 và 𝑭
hệ giữa các công sinh bởi lực 𝑭 và lực 𝑭𝟏.
⇒ 𝑭𝟏 = 𝑭. 𝒄𝒐𝒔 𝜶. BÀI TẬP
4.21. Trong mặt phẳng tọa độ Oxy, hãy
a) 𝒄𝒐𝒔 𝒂, 𝒃 = −𝟑.𝟐+𝟏.𝟔 = 𝟎
tính góc giữa hai vectơ 𝒂 và 𝒃
−𝟑 𝟐+𝟏𝟐. 𝟐𝟐+𝟔𝟐
trong mỗi trường hợp sau: ⇒ 𝒂, 𝒃 = 𝟗𝟎𝒐
a) 𝒂 = (−𝟑; 𝟏), 𝒃 = (𝟐; 𝟔);
b) 𝒂 = (𝟑; 𝟏), 𝒃 = (𝟐; 𝟒);
b) 𝒄𝒐𝒔 𝒂, 𝒃 = 𝟑.𝟐+𝟏.𝟒 = 𝟏𝟎 = 𝟏
𝟑𝟐+𝟏𝟐. 𝟐𝟐+𝟒𝟐 𝟏𝟎 𝟐 𝟐
c) 𝒂 = (− 𝟐; 𝟏), 𝒃 = (𝟐; − 𝟐). ⇒ 𝒂, 𝒃 = 𝟒𝟓𝒐 Lời giải
c) 𝒄𝒐𝒔 𝒂, 𝒃 = − 𝟐.𝟐−𝟏. 𝟐
Vận dụng công thức tính góc giữa hai
− 𝟐 𝟐+𝟏𝟐. 𝟐𝟐+ − 𝟐 𝟐
véc tơ 𝒄𝒐𝒔 𝒂, 𝒃 = 𝒂. 𝒃 −𝟑 𝟐 𝒂 . 𝒃 =
= −𝟏 ⇒ 𝒂, 𝒃 = 𝟏𝟖𝟎𝒐 𝟑 𝟐 BÀI TẬP
4.22. Tìm điều kiện của 𝒖, 𝒗 để:
4.23. Trong mặt phẳng tọa độ Oxy,
a) 𝒖. 𝒗 = 𝒖 . 𝒗 ;
cho hai điểm 𝑨(𝟏; 𝟐), 𝑩( − 𝟒; 𝟑). Gọi
b) 𝒖. 𝒗 = − 𝒖 . 𝒗 .
𝑴( 𝒕; 𝟎) là một điểm thuộc trục hoành. Lời giải
a) Tính 𝑨𝑴. 𝑩𝑴 theo t.
a) Ta có 𝒖 ⋅ 𝒗 = |𝒖| ⋅ |𝒗|𝒄𝒐𝒔 𝒖, 𝒗 do đó b) Tìm t để ෣ 𝑨𝑴𝑩 = 𝟗𝟎𝟎.
để 𝒖 ⋅ 𝒗 = |𝒖| ⋅ |𝒗| thì 𝒄𝒐𝒔 𝒖, 𝒗 = 𝟏 hay Lời giải
𝒖 và 𝒗 cùng hướng.
a) Ta có 𝑨𝑴 = 𝒕 − 𝟏; −𝟐 ,
b) Ta có 𝒖 ⋅ 𝒗 = |𝒖| ⋅ |𝒗|𝒄𝒐𝒔 𝒖, 𝒗 do đó
để 𝒖 ⋅ 𝒗 = −|𝒖| ⋅ |𝒗|
𝑩𝑴 = 𝒕 + 𝟒; −𝟑
thì 𝒄𝒐𝒔 𝒖, 𝒗 = −𝟏
hay 𝒖và 𝒗ngược hướng.
⇒ 𝑨𝑴. 𝑩𝑴 = 𝒕 − 𝟏 𝒕 + 𝟒 + 𝟐. 𝟑
= 𝒕𝟐 + 𝟑𝒕 − 𝟒 BÀI TẬP
4.23. Trong mặt phẳng tọa độ Oxy,
4.24. Trong mặt phẳng tọa độ Oxy,
cho hai điểm 𝑨(𝟏; 𝟐), 𝑩( − 𝟒; 𝟑). Gọi
cho ba điểm không thẳng hàng
𝑴( 𝒕; 𝟎) là một điểm thuộc trục hoành. 𝑨(−𝟒; 𝟏), 𝑩( 𝟐; 𝟒), 𝑪( 𝟐; −𝟐).
a) Tính 𝑨𝑴. 𝑩𝑴 theo t.
a) Giải tam giác ABC. b) Tìm t để ෣ 𝑨𝑴𝑩 = 𝟗𝟎𝟎.
b) Tìm tọa độ trực tâm H của tam giác ABC. Lời giải Lời giải b) Để ෣
𝑨𝑴𝑩 = 𝟗𝟎° thì 𝑨𝑴 ⊥ 𝑩𝑴 ⇔ a)
𝑨𝑴. 𝑩𝑴 = 𝟎 ⇔ 𝒕𝟐 + 𝟑𝒕 − 𝟒 = 𝟎 ⇔ 𝑨𝑩 =
𝟐 + 𝟒 𝟐 + 𝟒 − 𝟏 𝟐 = 𝟒𝟓
ቈ𝒕 = 𝟏 . Vậy với 𝒕 = −𝟒 ቈ𝒕 = 𝟏 𝒕 = −𝟒 𝑨𝑪 =
𝟐 + 𝟒 𝟐 + −𝟐 − 𝟏 𝟐 = 𝟒𝟓 thì ෣ 𝑨𝑴𝑩 = 𝟗𝟎° 𝑩𝑪 =
𝟐 − 𝟐 𝟐 + −𝟐 − 𝟒 𝟐 = 𝟔 BÀI TẬP Lời giải
b) Giả sử 𝑯 𝒙; 𝒚 ta có
𝑨𝑯 = 𝒙 + 𝟒; 𝒚 − 𝟏 , 𝑩𝑪 = 𝟎; −𝟔 ,
𝑨𝑩𝟐 + 𝑨𝑪𝟐 − 𝑩𝑪𝟐 𝟒𝟓 + 𝟒𝟓 + 𝟑𝟔 𝒄𝒐𝒔 𝑨 =
𝑩𝑯 = 𝒙 − 𝟐; 𝒚 − 𝟒 , 𝑪𝑨 = −𝟔; 𝟑 𝟐. 𝑨𝑩. 𝑨𝑪 = 𝟐. 𝟒𝟓. 𝟒𝟓
Vì 𝑯 là trực tâm tam giác 𝑨𝑩𝑪 𝟑 =
nên ቊ𝑨𝑯 ⋅ 𝑩𝑪 = 𝟎
𝟓 ⇒ ෡𝑨 ≈ 𝟓𝟑𝟎 𝑩𝑯 ⋅ 𝑪𝑨 = 𝟎
𝑨𝑩𝟐 + 𝑩𝑪𝟐 − 𝑨𝑪𝟐 𝟒𝟓 + 𝟑𝟔 − 𝟒𝟓 𝟏𝟑 𝒄𝒐𝒔 𝑩 = 𝟐. 𝑨𝑩. 𝑩𝑪 = 𝟐. 𝟒𝟓. 𝟑𝟔
⇔ ቊ 𝒙 + 𝟒 . 𝟎 + 𝒚 − 𝟏 . −𝟔 = 𝟎 𝟏
−𝟔 𝒙 − 𝟖 + 𝟑 𝒚 − 𝟒 = 𝟎 ⇔ ቐ𝒙 = 𝟐 𝒚 = 𝟏
= 𝟗 ⇒ ෡𝑩 ≈ 𝟖𝟗𝟎 𝟏𝟑
෡𝑪 = 𝟏𝟖𝟎𝟎 − (𝟓𝟑𝟎 + 𝟖𝟗𝟎) ≈ 𝟑𝟖𝟎 ⇒ 𝑯 𝟐 ; 𝟏 BÀI TẬP
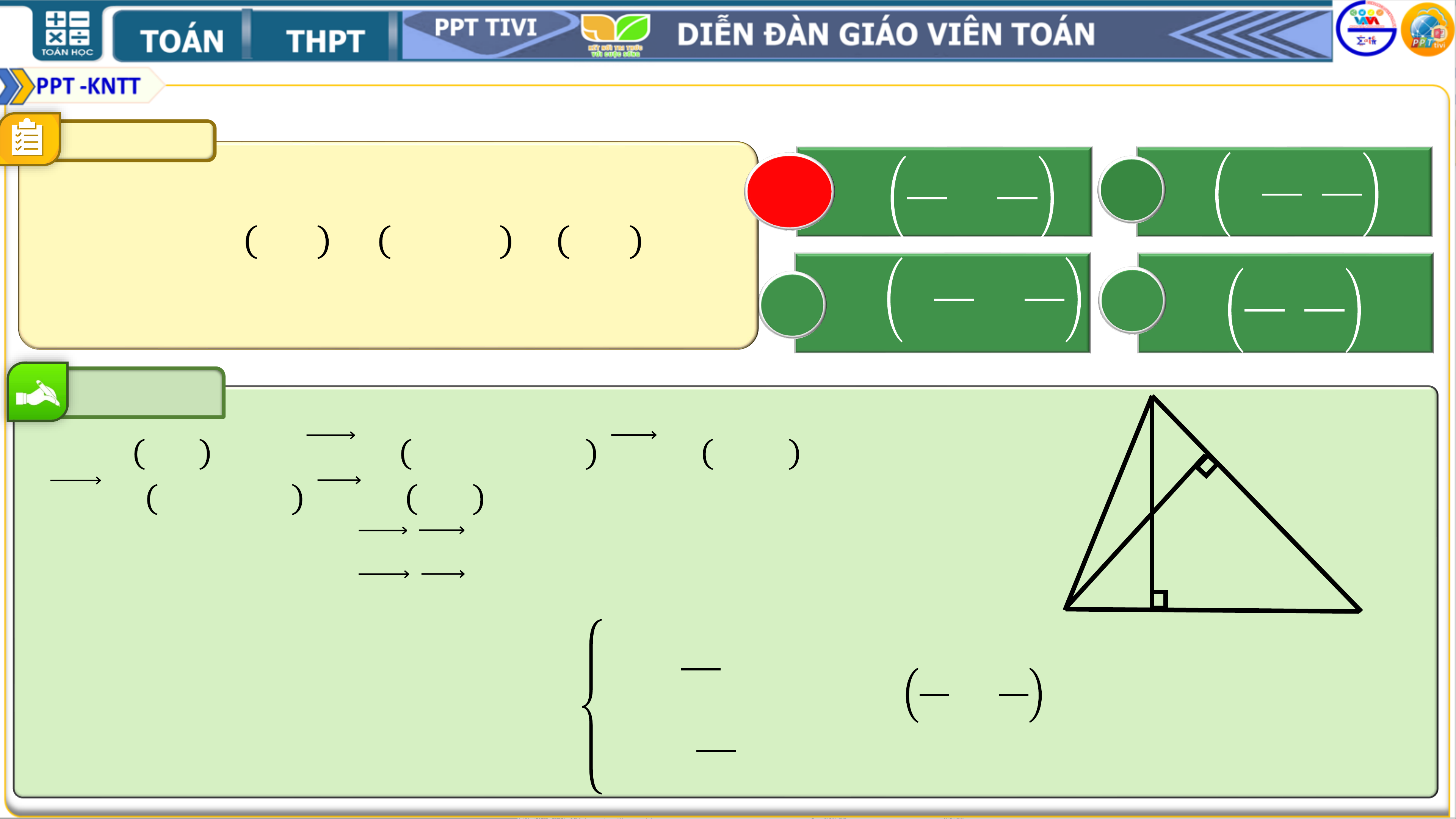
4.25. Chứng minh rằng với mọi tam
4.26. Cho tam giác ABC có trọng tâm G. giác ABC, ta có:
Chứng minh rằng với mọi điểm M, ta có: 𝟐
𝑴𝑨𝟐 + 𝑴𝑩𝟐 + 𝑴𝑪𝟐 = 𝟑𝑴𝑮𝟐 + 𝑮𝑨𝟐 +
𝑺𝑨𝑩𝑪 = 𝟏 𝑨𝑩𝟐. 𝑨𝑪𝟐 − 𝑨𝑩. 𝑨𝑪 . 𝑮𝑩𝟐 + 𝑮𝑪𝟐. 𝟐 Lời giải Lời giải
Ta có 𝑺 = 𝟏 𝑨𝑩. 𝑨𝑪. 𝒔𝒊𝒏 𝑨 𝟐 𝟏
𝐌𝑨𝟐 + 𝐌𝑩𝟐 + 𝐌𝑪𝟐 = 𝑴𝑨𝟐 + 𝑴𝑩𝟐 + 𝑴𝑪𝟐 ⇒ 𝑺𝟐 = 𝟐 𝟐 𝟐
𝟒 𝑨𝑩𝟐. 𝑨𝑪𝟐 𝟏 − 𝒄𝒐𝒔𝟐𝑨
= 𝑴𝑮 + 𝑮𝑨 + 𝑴𝑮 + 𝑮𝑩 + 𝑴𝑮 + 𝑮𝑪 𝟐
Hay 𝑺𝟐 = 𝟏 𝑨𝑩𝟐. 𝑨𝑪𝟐 𝟏 − 𝑨𝑩.𝑨𝑪
= 𝟑𝐌𝑮𝟐 + 𝟐𝑴𝑮 𝑮𝑨 + 𝑮𝑩 + 𝑮𝑪 + 𝑮𝑨𝟐 + 𝑮𝑩𝟐 𝟒 𝑨𝑩𝟐.𝑨𝑪𝟐 𝟏 𝟐 + 𝑮𝑪𝟐 =
= 𝟑𝐌𝑮𝟐 + 𝐆𝑨𝟐 + 𝐆𝑩𝟐 + 𝐆𝑪𝟐
𝟒 𝑨𝑩𝟐. 𝑨𝑪𝟐 − 𝑨𝑩. 𝑨𝑪
Vậy 𝑺𝑨𝑩𝑪 = 𝟏 𝑨𝑩𝟐 ⋅ 𝑨𝑪𝟐 − 𝑨𝑩 ⋅ 𝑨𝑪 𝟐 𝟐 III
BÀI TẬP TRẮC NGHIỆM CỦNG CỐ CÂU 1
Trong mặt phẳng tọa độ, độ dài của 𝒂 = 𝟏; 𝟐 là 𝟑. A B 𝟑. C 𝟓. D 𝟓. Bài giải
Áp dụng công thức: Độ dài của vectơ 𝒂 = 𝒂𝟏; 𝒂𝟐 được tính theo
công thức 𝒂 = 𝒂𝟐 𝟐 𝟏 + 𝒂𝟐.
Ta có: 𝒂 = 𝟏; 𝟐
⇒ 𝒂 = 𝟏𝟐 + 𝟐𝟐 = 𝟓. III
BÀI TẬP TRẮC NGHIỆM CỦNG CỐ CÂU 2
Trong mặt phẳng tọa độ, khoảng cách giữa hai điểm 𝑴 𝟏; 𝟐 và 𝑵 𝟒; 𝟔 là 𝟖𝟗. A B 𝟖𝟗. C 𝟓. D 𝟓. Bài giải
Áp dụng công thức: Khoảng cách giữa hai điểm 𝑨 𝒙𝑨; 𝒚𝑨 và 𝑩 𝒙𝑩; 𝒚𝑩 được
tính theo công thức 𝑨𝑩 = 𝒙 𝟐 𝟐 𝑩 − 𝒙𝑨
+ 𝒚𝑩 − 𝒚𝑨 .
Ta có: 𝑴 𝟏; 𝟐 và 𝑵 𝟒; 𝟔 ⇒ 𝑴𝑵 =
𝟒 − 𝟏 𝟐 + 𝟔 − 𝟐 𝟐 = 𝟓. III
BÀI TẬP TRẮC NGHIỆM CỦNG CỐ CÂU 3
Trong mặt phẳng tọa độ, góc giữa hai vectơ 𝒂 = −𝟐; −𝟏 và 𝒃 = 𝟑; −𝟏 là A 𝟏𝟑𝟓°. A B 𝟒𝟓°. C 𝟗𝟎°. D 𝟔𝟎°. Bài giải
Áp dụng công thức: Nếu 𝒂 = 𝒂𝟏; 𝒂𝟐 và 𝒃 = 𝒃𝟏; 𝒃𝟐 đều khác 𝟎 thì ta có
𝒄𝒐𝒔 𝒂; 𝒃 = 𝒂.𝒃 = 𝒂𝟏𝒃𝟏+𝒂𝟐𝒃𝟐 . 𝒂 . 𝒃 𝒂𝟐 𝟐 𝟐 𝟐
𝟏+𝒂𝟐. 𝒃𝟏+𝒃𝟐
Ta có: 𝒄𝒐𝒔 𝒂; 𝒃 = 𝒂.𝒃 = −𝟐.𝟑+ −𝟏 −𝟏
= −𝟔+𝟏 = − 𝟐. 𝒂 . 𝒃
−𝟐 𝟐+ −𝟏 𝟐. 𝟑𝟐+ −𝟏 𝟐 𝟓. 𝟏𝟎 𝟐
Vậy: 𝒂; 𝒃 = 𝟏𝟑𝟓°. Câu 4 𝐚𝟐
Cho hình vuông 𝑨𝑩𝑪𝑫 có độ dài cạnh A B 𝑎2 2 𝟐
bằng 𝒂. Tính 𝑨𝑩. 𝑨𝑪 theo 𝒂. C D 𝐚𝟐 𝟐 𝐚𝟐 𝟐 Bài giải
Ta có 𝑨𝑩. 𝑨𝑪 = 𝑨𝑩. 𝑨𝑪. 𝒄𝒐𝒔 𝑨𝑩, 𝑨𝑪 = 𝒂. 𝒂 𝟐. 𝟐 𝟐 = 𝒂𝟐. Câu 5 𝟐𝟓 𝟓𝟖 𝟐𝟓 𝟓𝟖
Trong mặt phẳng tọa độ 𝑶𝒙𝒚, cho tam A 𝐇 B 𝐇 − giác 𝟑 ; − 𝟑 𝟑 ; 𝟑
𝑨𝑩𝑪 có 𝑨 𝟑; 𝟐 , 𝑩 −𝟏𝟏; 𝟎 , 𝑪 𝟓; 𝟒 . Xác 𝟐𝟓 𝟓𝟖
định tọa độ trực tâm 𝑯 của tam giác 𝑨𝑩𝑪. C 𝐇 − D 𝟐𝟓 𝟓𝟖 𝟑 ; − 𝟑 𝐇 𝟑 ; 𝟑 Bài giải A
Gọi 𝑯 𝒙; 𝒚 . Ta có 𝑨𝑯 = 𝒙 − 𝟑; 𝒚 − 𝟐 , 𝑩𝑪 = 𝟏𝟔; 𝟒 ,
𝑩𝑯 = 𝒙 + 𝟏𝟏; 𝒚 , 𝑨𝑪 = 𝟐; 𝟐 . H
Vì 𝑯 là trực tâm nên ቊ𝑨𝑯. 𝑩𝑪 = 𝟎 ⇔ ቊ𝟒𝒙 + 𝒚 = 𝟏𝟒 𝑩𝑯. 𝑨𝑪 = 𝟎 𝒙 + 𝒚 = −𝟏𝟏 B C 𝟐𝟓 𝒙 = ⇔ 𝟑
. Vậy 𝑯 𝟐𝟓 ; − 𝟓𝟖 . 𝟓𝟖 𝟑 𝟑 𝒚 = − 𝟑 III
BÀI TẬP TRẮC NGHIỆM CỦNG CỐ CÂU 6
Cho tam giác 𝑨𝑩𝑪 vuông tại 𝑨 và 𝑨𝑩. 𝑪𝑩 = 𝟗; 𝑨𝑪. 𝑩𝑪 = 𝟑. Độ dài cạnh 𝑩𝑪 bằng? A 𝟔. B 𝟑 𝟐. C 𝟐 𝟑. D 𝟏𝟓. Bài giải 𝟐
𝑨𝑩. 𝑨𝑩 − 𝑨𝑪 = 𝟗 𝑨𝑩 = 𝟗
Ta có ቊ𝑨𝑩. 𝑪𝑩 = 𝟗 ⇔ ቐ ⇔ ቐ 𝑨𝑪. 𝑩𝑪 = 𝟑
𝑨𝑪. 𝑨𝑪 − 𝑨𝑩 = 𝟑 𝟐 𝑨𝑪 = 𝟑
⇒ 𝑩𝑪 = 𝟗 + 𝟑 = 𝟐 𝟑. III
BÀI TẬP TRẮC NGHIỆM CỦNG CỐ CÂU 7
Cho 2 vectơ 𝒂, 𝒃 biết |𝒂| = 𝟐, |𝒃| = 𝟏 và |𝒂 + 𝟐𝒃| = 𝟐. Tính góc giữa 2
vectơ 𝒂 + 𝒃 và 𝒂 − 𝟐𝒃. 𝟑𝟎°. A B 𝟔𝟎°. C 𝟏𝟐𝟎°. D 𝟏𝟓𝟎°. Bài giải
Ta có: • 𝒂 + 𝟐𝒃 = 𝟐 ⇔ 𝒂𝟐 + 𝟒𝒂. 𝒃 + 𝟒𝒃𝟐 = 𝟒 ⇒ 𝒂. 𝒃 = −𝟏. 𝟐
• 𝒂 + 𝒃 . 𝒂 − 𝟐𝒃 = 𝒂𝟐 − 𝒂. 𝒃 − 𝟐𝒃𝟐 = 𝟑. • 𝒂 + 𝒃 = 𝒂𝟐 + 𝟐𝒂. 𝒃 + 𝒃𝟐 = 𝟑 ⇒ |𝒂 + 𝒃| = 𝟑. 𝟐
• 𝒂 − 𝟐𝒃 = 𝒂𝟐 − 𝟒𝒂. 𝒃 + 𝟒𝒃𝟐 = 𝟏𝟐 ⇒ |𝒂 − 𝟐𝒃| = 𝟐 𝟑.
Mà: 𝒄𝒐𝒔 𝒂 + 𝒃, 𝒂 − 𝟐𝒃 = 𝒂+𝒃 . 𝒂−𝟐𝒃 = 𝟑 = 𝟏 . Nên góc giữa 2 vectơ 𝒂 + 𝒃 và 𝒂 − 𝟐𝒃 bằng |𝒂+𝒃|.|𝒂−𝟐𝒃| 𝟑.𝟐 𝟑 𝟐 𝟔𝟎°. Câu 8
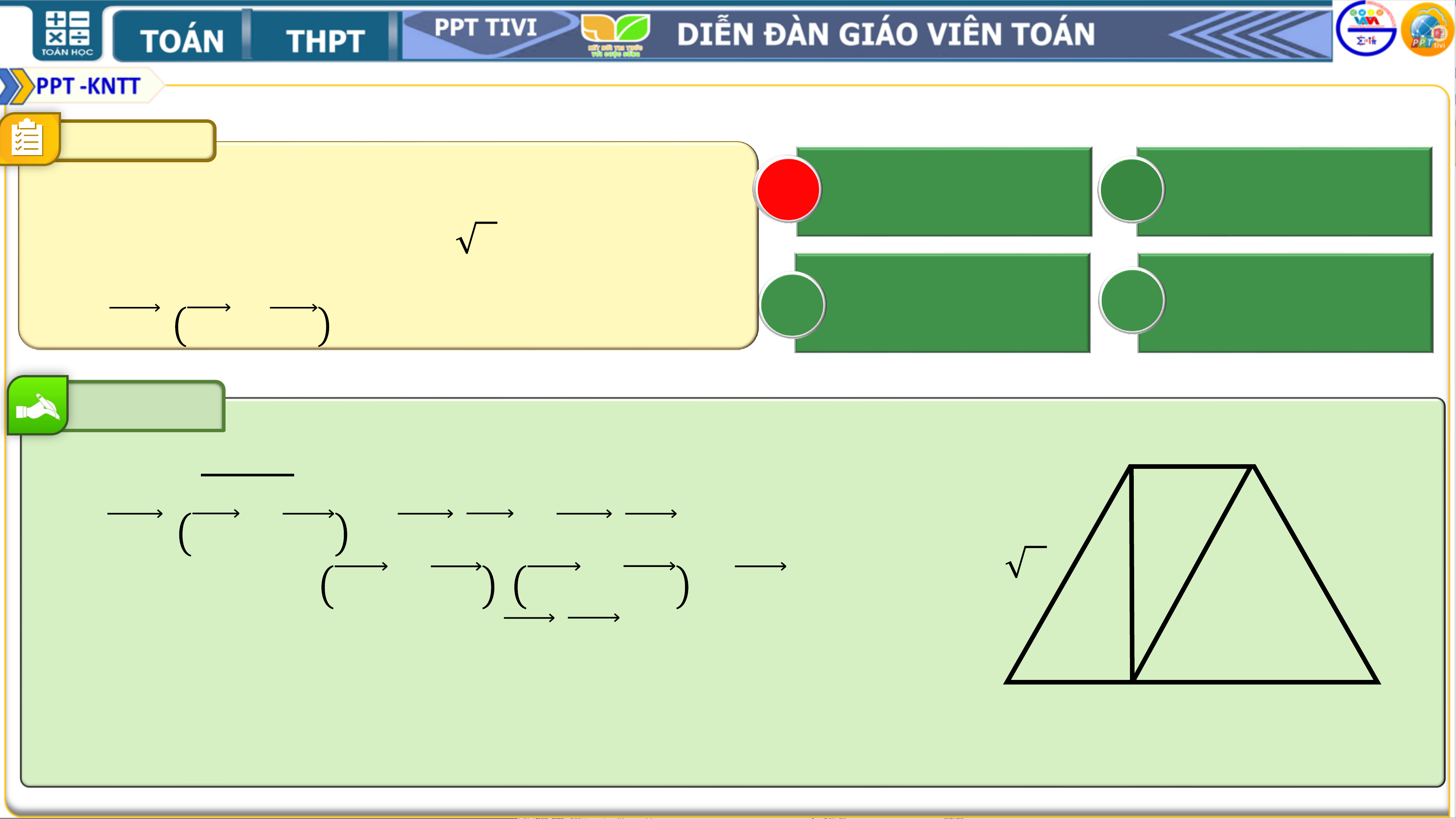
Cho hình thang cân 𝑨𝑩𝑪𝑫 biết đáy lớn A B 𝟓𝐚𝟐 𝐚𝟐 A
𝑪𝑫 = 𝟑𝒂, 𝑨𝑩 = 𝒂 và 𝑩𝑪 = 𝒂 𝟐. Gọi 𝑯 là
hình chiếu vuông góc của 𝑨 lên cạnh 𝑪𝑫. C −𝐚𝟐 D −𝟓𝐚𝟐
Tính 𝑩𝑯. 𝑨𝑪 + 𝑨𝑫 . Bài giải 𝑨 𝒂 𝑩
Có 𝑫𝑯 = 𝑪𝑫−𝑨𝑫 = 𝒂 ⇒ 𝑨𝑩𝑯𝑫 là hình bình hành và 𝑨𝑯 = 𝒂 𝟐
Có: 𝑩𝑯. 𝑨𝑪 + 𝑨𝑫 = 𝑩𝑯. 𝑨𝑪 + 𝑩𝑯. 𝑨𝑫
= 𝑨𝑯 − 𝑨𝑩 . 𝑨𝑯 + 𝑯𝑪 + 𝑨𝑫𝟐 𝒂 𝟐
= 𝑨𝑯𝟐 − 𝑨𝑩. 𝑯𝑪 + 𝑨𝑫𝟐
= 𝒂𝟐 − 𝒂. 𝟐𝒂. 𝒄𝒐𝒔 𝟎𝟎 + 𝟐𝒂𝟐 = 𝒂𝟐 𝑫 𝑯 𝑪 III
BÀI TẬP TRẮC NGHIỆM CỦNG CỐ CÂU 9
Cho ba điểm 𝑨(𝟑; 𝟒), 𝑩(𝟐; 𝟏) và 𝑪(−𝟏; −𝟐). Tìm điểm 𝑴 trên đường
thẳng 𝑩𝑪 để góc ෣
𝑨𝑴𝑩 = 𝟒𝟓𝟎. A 𝐌 𝟓; 𝟒 . A B 𝐌 𝟐; 𝟑 . C 𝐌 −𝟓; 𝟒 . D 𝐌 𝟐; −𝟑 . Bài giải
Giả sử 𝑴 𝒙; 𝒚 suy ra 𝑴𝑨 𝟑 − 𝒙; 𝟒 − 𝒚 , 𝑴𝑩 𝟐 − 𝒙; 𝟏 − 𝒚 , 𝑩𝑪 −𝟑; −𝟑 Vì ෣
𝑨𝑴𝑩 = 𝟒𝟓𝟎 suy ra 𝒄𝒐𝒔 ෣
𝑨𝑴𝑩 = 𝒄𝒐𝒔 𝑴𝑨; 𝑩𝑪 ⇔ 𝒄𝒐𝒔 𝟒 𝟓𝟎 = 𝑴𝑨.𝑩𝑪 ⇔ 𝟐 = −𝟑 𝟑−𝒙 −𝟑 𝟒−𝒚 𝑴𝑨 . 𝑩𝑪 𝟐
𝟑−𝒙 𝟐+ 𝟒−𝒚 𝟐 𝟗+𝟗 ⇔
𝟑 − 𝒙 𝟐 + 𝟒 − 𝒚 𝟐 = 𝒙 + 𝒚 − 𝟕 (*) Mặt 𝟐−𝒙
khác M thuộc đường thẳng BC nên hai vectơ 𝑴𝑩, 𝑩𝑪 cùng phương. Suy ra
= 𝟏−𝒚 ⇔ 𝒙 = 𝒚 + 𝟏 thế vào (*) ta −𝟑 −𝟑 được
𝟐 − 𝒚 𝟐 + 𝟒 − 𝒚 𝟐 = 𝟐𝒚 − 𝟔 ⇔ 𝒚𝟐 − 𝟔𝒚 + 𝟖 = 𝟎 ⇔ 𝒚 = 𝟐 hoặc 𝒚 = 𝟒
+ Với 𝒚 = 𝟐 ⇒ 𝒙 = 𝟑, ta có 𝑴𝑨 𝟎; 𝟐 , 𝑴𝑩 −𝟏; −𝟏 ⇒ 𝒄𝒐𝒔 ෣
𝑨𝑴𝑩 = 𝒄𝒐𝒔 𝑴𝑨; 𝑴𝑩 = − 𝟏𝟐 Khi đó ෣
𝑨𝑴𝑩 = 𝟏𝟑𝟓𝟎 (không thỏa mãn)
+ Với 𝒚 = 𝟒 ⇒ 𝒙 = 𝟓, 𝑴𝑨 −𝟐; 𝟎 , 𝑴𝑩 −𝟑; −𝟑 ⇒ 𝒄𝒐𝒔 ෣
𝑨𝑴𝑩 = 𝒄𝒐𝒔 𝑴𝑨; 𝑴𝑩 = 𝟏 . Khi đó ෣
𝑨𝑴𝑩 = 𝟒𝟓𝟎. Vậy 𝑴 𝟓; 𝟒 là điểm 𝟐 cần tìm.
Câu 10 Cho điểm 𝑨 𝟐;𝟏 . Lấy điểm 𝑩 𝟐𝟓 𝟓𝟖 𝟐𝟓 𝟓𝟖
nằm trên trục hoành có hoành độ không A 𝐇 B 𝐇 − âm 𝟑 ; − 𝟑 𝟑 ; 𝟑
và điểm 𝑪 trên trục tung có tung độ
dương sao cho tam giác 𝑨𝑩𝑪 vuông tại 𝑨. 𝟐𝟓 𝟓𝟖 C 𝐇 − D 𝟐𝟓 𝟓𝟖
Tìm toạ độ điểm 𝑪 để tam giác 𝑨𝑩𝑪 có 𝟑 ; − 𝟑 D 𝐇 𝟑 ; 𝟑
diện tích lớn nhất. Bài giải
Gọi 𝑩 𝒃; 𝟎 , 𝑪 𝟎; 𝒄 với 𝒃 ≥ 𝟎, 𝒄 > 𝟎. Suy ra 𝑨𝑩 𝒃 − 𝟐; −𝟏 , 𝑨𝑪 −𝟐; 𝒄 − 𝟏
Theo giả thiết ta có tam giác 𝑨𝑩𝑪 vuông tại 𝑨 nên 𝑨𝑩. 𝑨𝑪 = 𝟎
⇔ 𝒃 − 𝟐 −𝟐 − 𝟏. 𝒄 − 𝟏 = 𝟎 ⇔ 𝒄 = −𝟐𝒃 + 𝟓
Ta có 𝑺𝜟𝑨𝑩𝑪 = 𝟏 𝑨𝑩. 𝑨𝑪 = 𝟏 (𝒃 − 𝟐)𝟐 + 𝟏. 𝟐𝟐 + (𝒄 − 𝟏)𝟐 = (𝒃 − 𝟐)𝟐 + 𝟏 = 𝒃𝟐 − 𝟒𝒃 + 𝟓 𝟐 𝟐
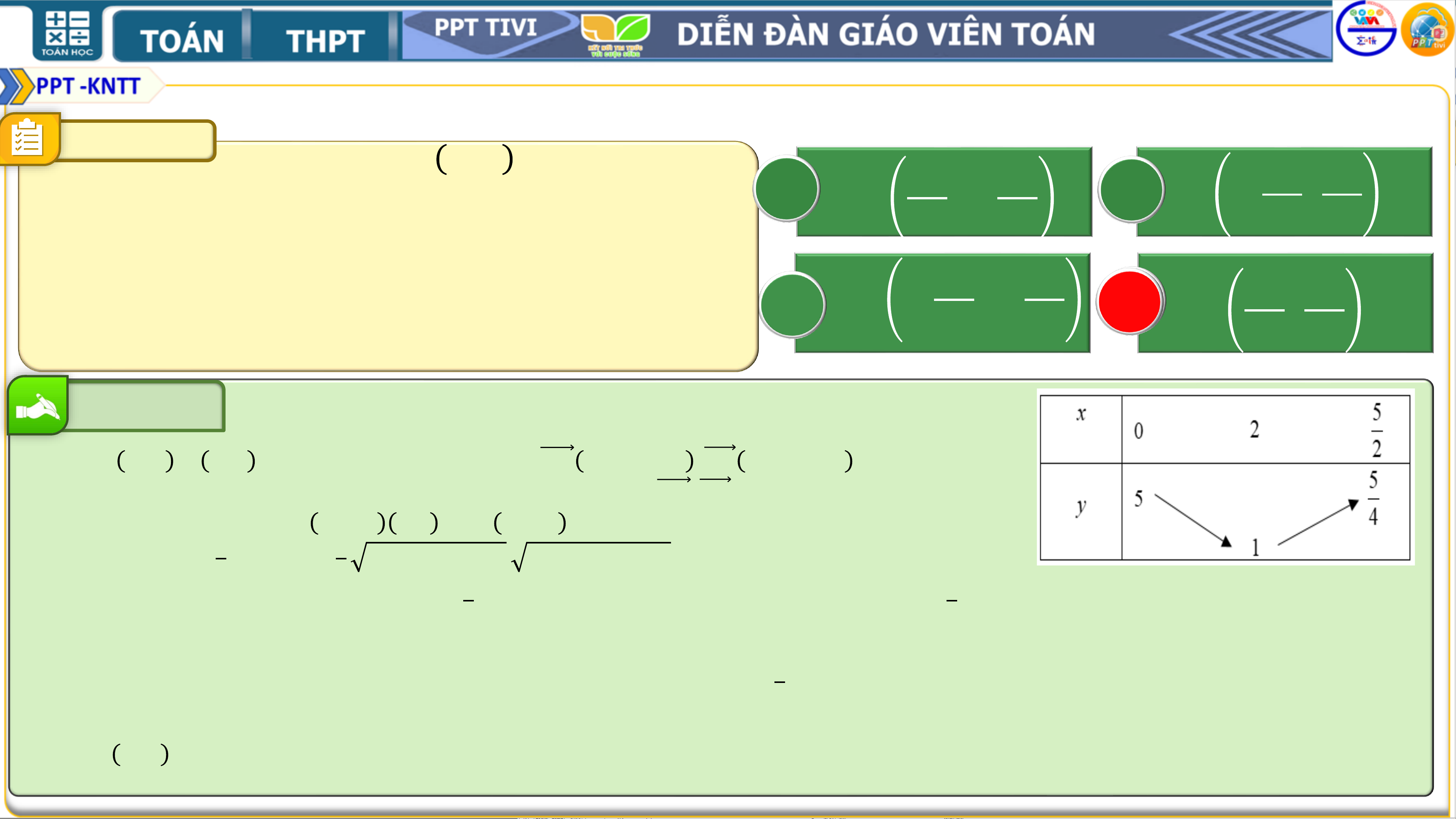
Vì 𝒄 > 𝟎 nên −𝟐𝒃 + 𝟓 > 𝟎 ⇒ 𝟎 ≤ 𝒃 < 𝟓. Xét hàm số 𝒚 = 𝒙𝟐 − 𝟒𝒙 + 𝟓 với 𝟎 ≤ 𝒙 < 𝟓 𝟐 𝟐 Bảng biến thiên
Suy ra giá trị lớn nhất của hàm số 𝒚 = 𝒙𝟐 − 𝟒𝒙 + 𝟓 với 𝟎 ≤ 𝒙 < 𝟓 là 𝒚 = 𝟓 khi 𝒙 = 𝟎. Do đó diện tích tam giác 𝑨𝑩𝑪 𝟐
lớn nhất khi và chỉ khi 𝒃 = 𝟎, suy ra 𝒄 = 𝟓.
Vậy 𝑪 𝟎; 𝟓 là điểm cần tìm.
Document Outline

• Slide 1
• Slide 2
• Slide 3
• Slide 4
• Slide 5
• Slide 6
• Slide 7
• Slide 8
• Slide 9
• Slide 10
• Slide 11
• Slide 12
• Slide 13
• Slide 14
• Slide 15
• Slide 16
• Slide 17
• Slide 18
• Slide 19
• Slide 20
• Slide 21
• Slide 22
• Slide 23