Chương 5: Bài 12: Số gần đúng và sai số | Giáo án điện tử môn Toán 10 | Kết nối tri thức với cuộc sống
Giáo án PowerPoint Toán 10 Kết nối tri thức với cuộc sống là tài liệu cực kì hữu ích mà muốn giới thiệu đến quý thầy cô tham khảo. Bài giảng điện tử môn Toán 10 Kết nối tri thức bao gồm đầy đủ các bài giảng trong cả năm học được thiết kế dưới dạng file trình chiếu PowerPoint với nhiều hiệu ứng rất đẹp mắt. Với nội dung bài học trình bày chi tiết cho từng phần học và bám sát chương trình SGK Toán 10 Kết nối tri thức.
Chủ đề: Bài giảng điện tử Toán 10
Môn: Toán 10
Sách: Kết nối tri thức
Thông tin:
Tác giả:
Preview text:
CHƯƠNG I CHƯƠNG IV. VECTƠ
§7. Các khái niệm mở đầu
§8. Tổng và hiệu của hai vectơ
§9. Tích của một vectơ với một số
§10. Vectơ trong mặt phẳng tọa độ
§11. Tích vô hướng của hai vectơ
Bài tập cuối chương 4 C C H H Ư Ư Ơ Ơ N N G G I V.I VECTƠ TOÁN HÌNH HỌC ➉ ÔN CHƯƠNG IV 1 BÀI TẬP SKG 2 BÀI TẬP THÊM 3
BÀI TẬP TRẮC NGHIỆM 1. BÀI TẬP
4.34. Cho hình bình hành
. Hướng dẫn:
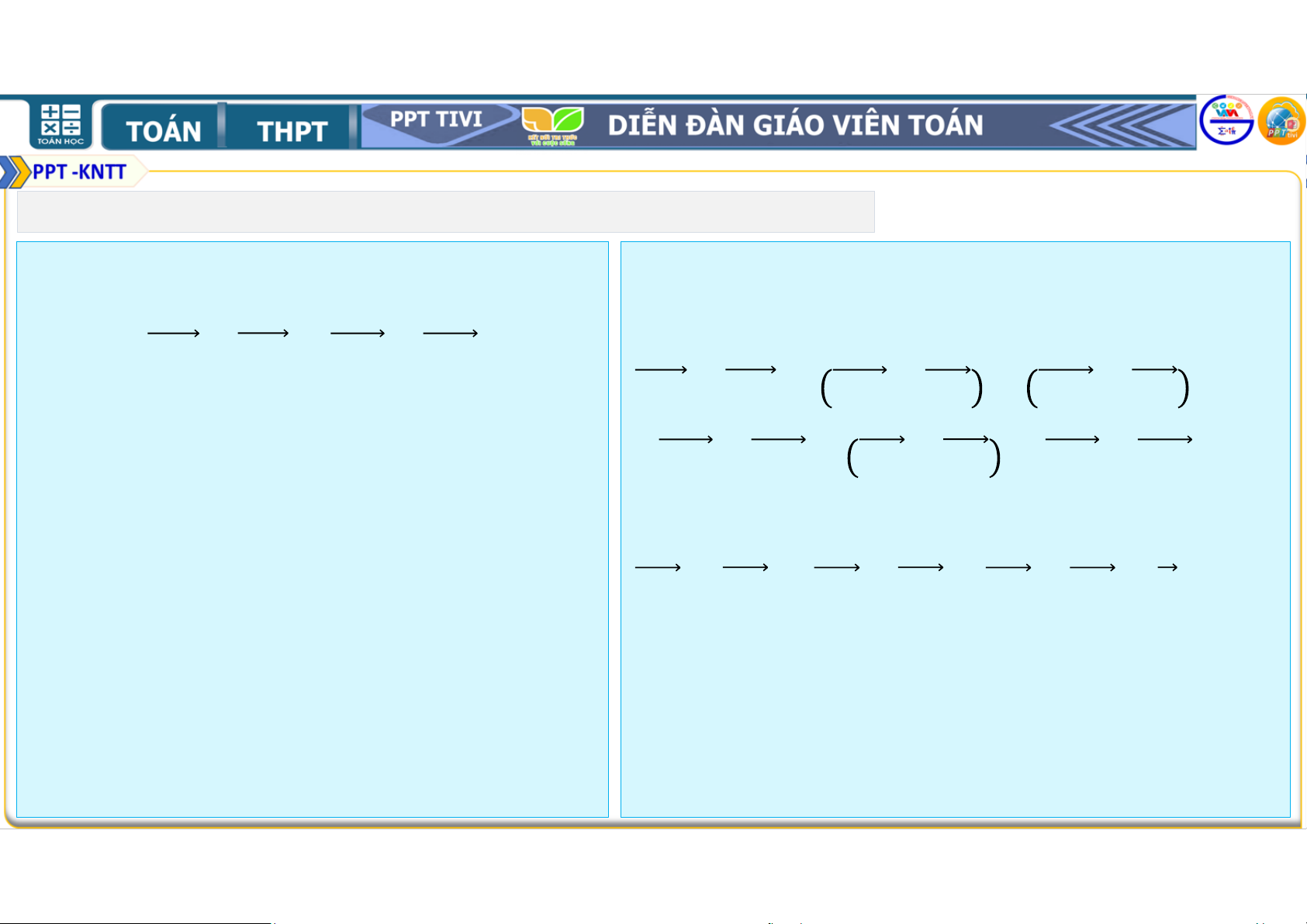
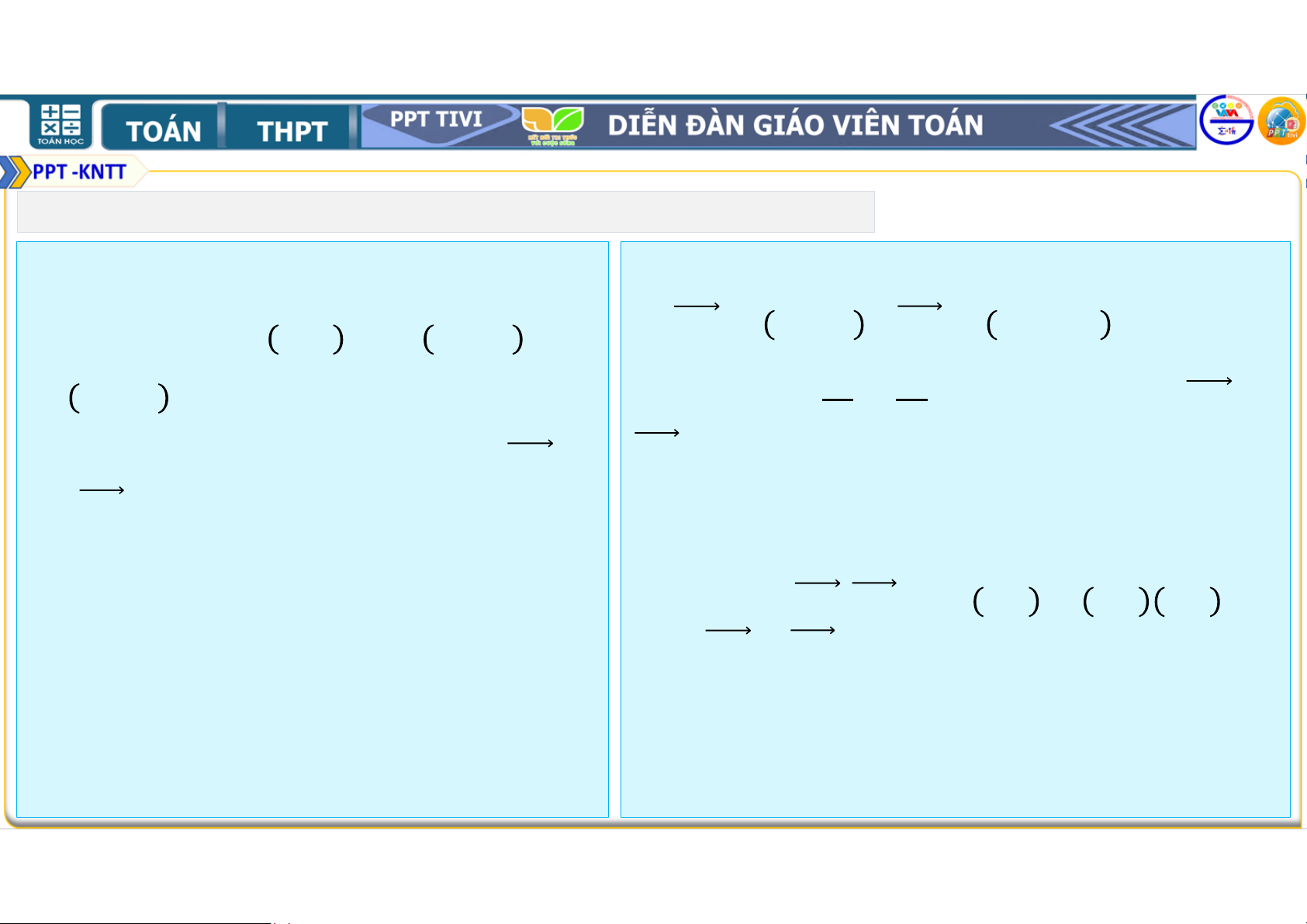
Chứng minh rằng với mọi điểm Ta có: ta có: + = + . + = + + + = + + + = + . Vì
là hình bình hành nên = ⇒ + = + = 1. BÀI TẬP
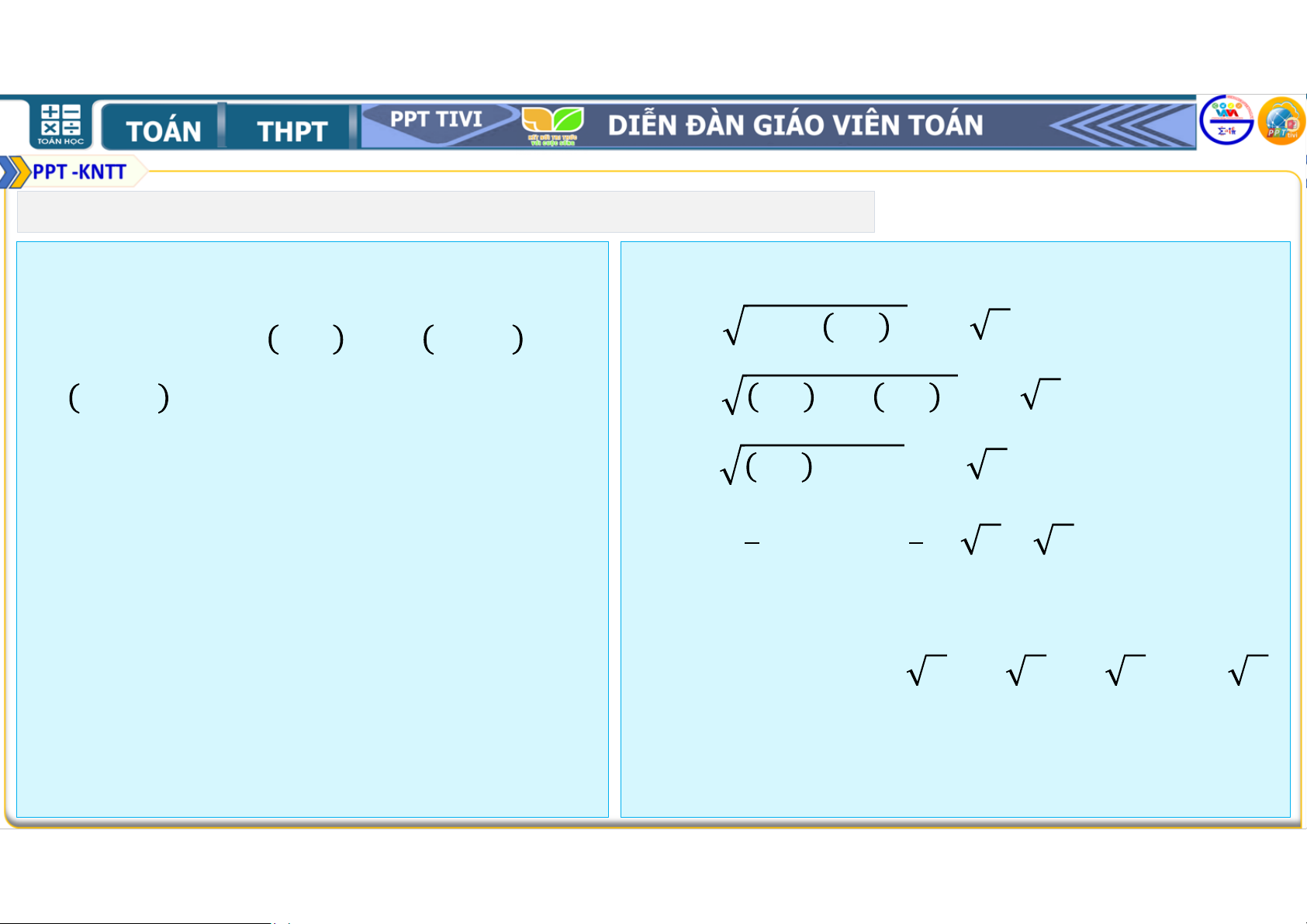
4.35. Trong mặt phẳng tọa độ Hướng dẫn: , cho ; ; − ; và a. = ; − ; = − ; − . − ; b. Ta thấy ≠ nên 2 vec-tơ và .
a. Tìm tọa độ của các vectơ và
không cùng phương suy ra 3 điểm . , ,
không thẳng hàng do đó chúng
là 3 đỉnh của 1 tam giác.
b. Chứng minh rằng , , là ba
đỉnh của một tam giác vuông. Lại có: . = . − + − − =
Tính diện tích và chu vi của tam nên ⊥ suy ra vuông tại . giác đó. 1. BÀI TẬP
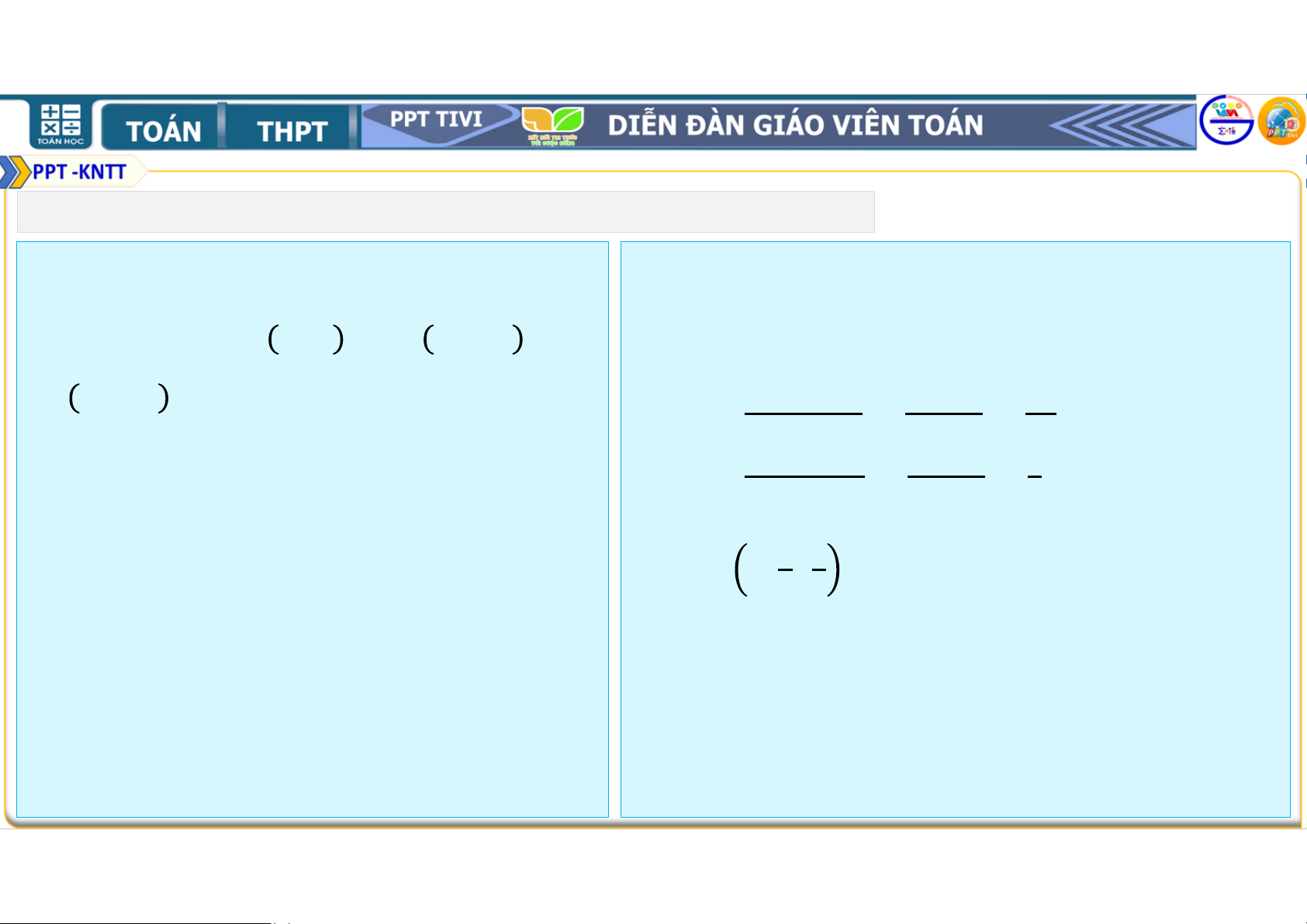
4.35. Trong mặt phẳng tọa độ Hướng dẫn: , cho ; ; − ; và = + − = ; − ; = − + − = ; .
a. Tìm tọa độ trọng tâm của = − + = ∆ . .
b. Tìm tọa độ của điểm sao cho = . = . . = (đvdt) tứ giác là một hình bình Chu vi tam giác bằng hành. + + = + + = (đvcv). 1. BÀI TẬP
4.35. Trong mặt phẳng tọa độ Hướng dẫn: , cho ; ; − ;
và c. là trọng tâm của tam giác nên − ; . = = =
c. Tìm tọa độ trọng tâm của ∆ = = = .
d. Tìm tọa độ của điểm sao cho Vậy − ; . tứ giác là một hình bình hành. 1. BÀI TẬP
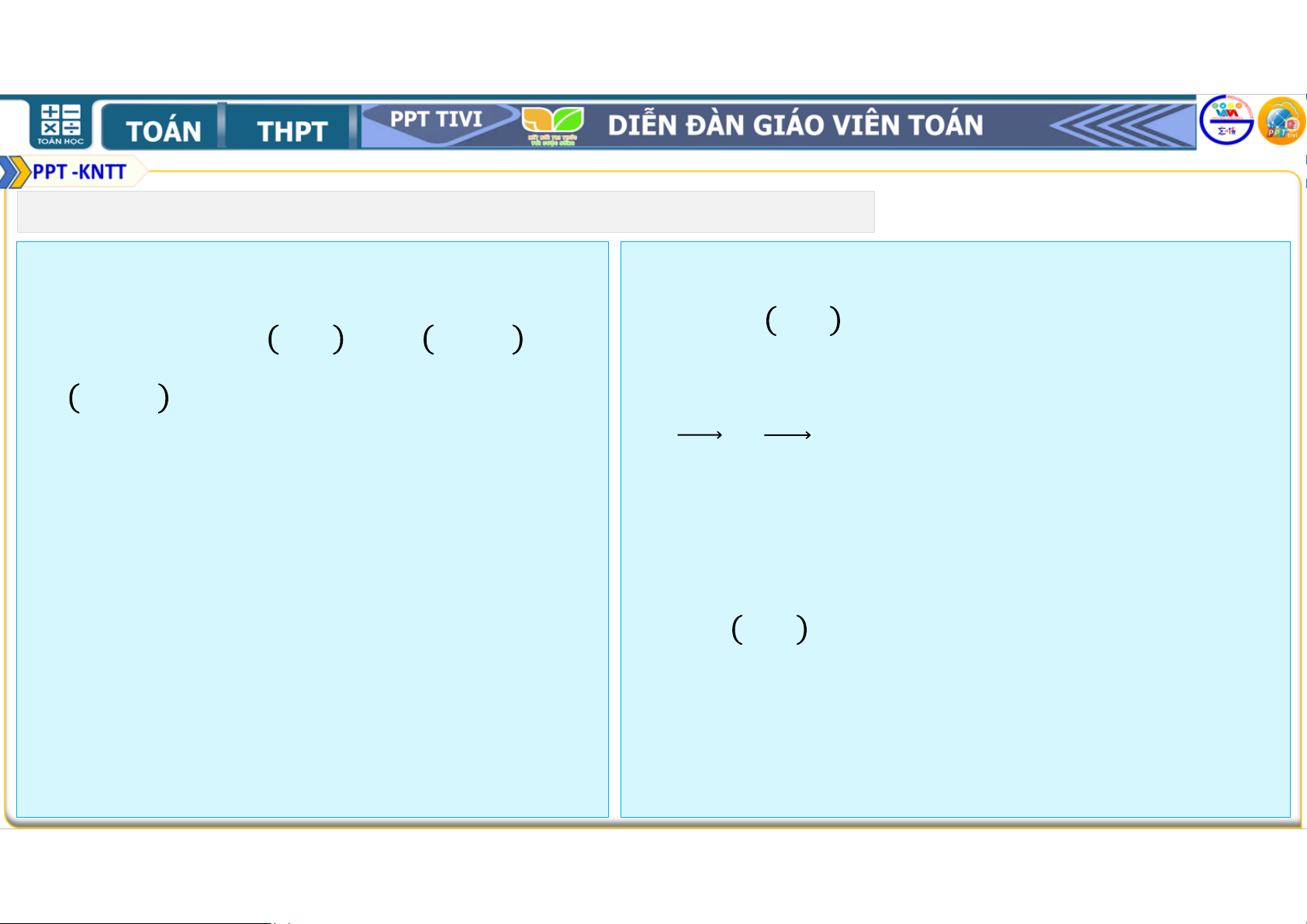
4.35. Trong mặt phẳng tọa độ Hướng dẫn: , cho ; ; − ;
và d. Gọi !, # Do là một tam giác . nên tứ giác là hình bình hành − ; . − = −
c. Tìm tọa độ trọng tâm của ⇔ = ⇔ % − = − ∆ .
d. Tìm tọa độ của điểm sao cho ⇔ % − = − ! − = − # ⇔ % ! = # = . tứ giác là một hình bình hành. Vậy ; . 1. BÀI TẬP
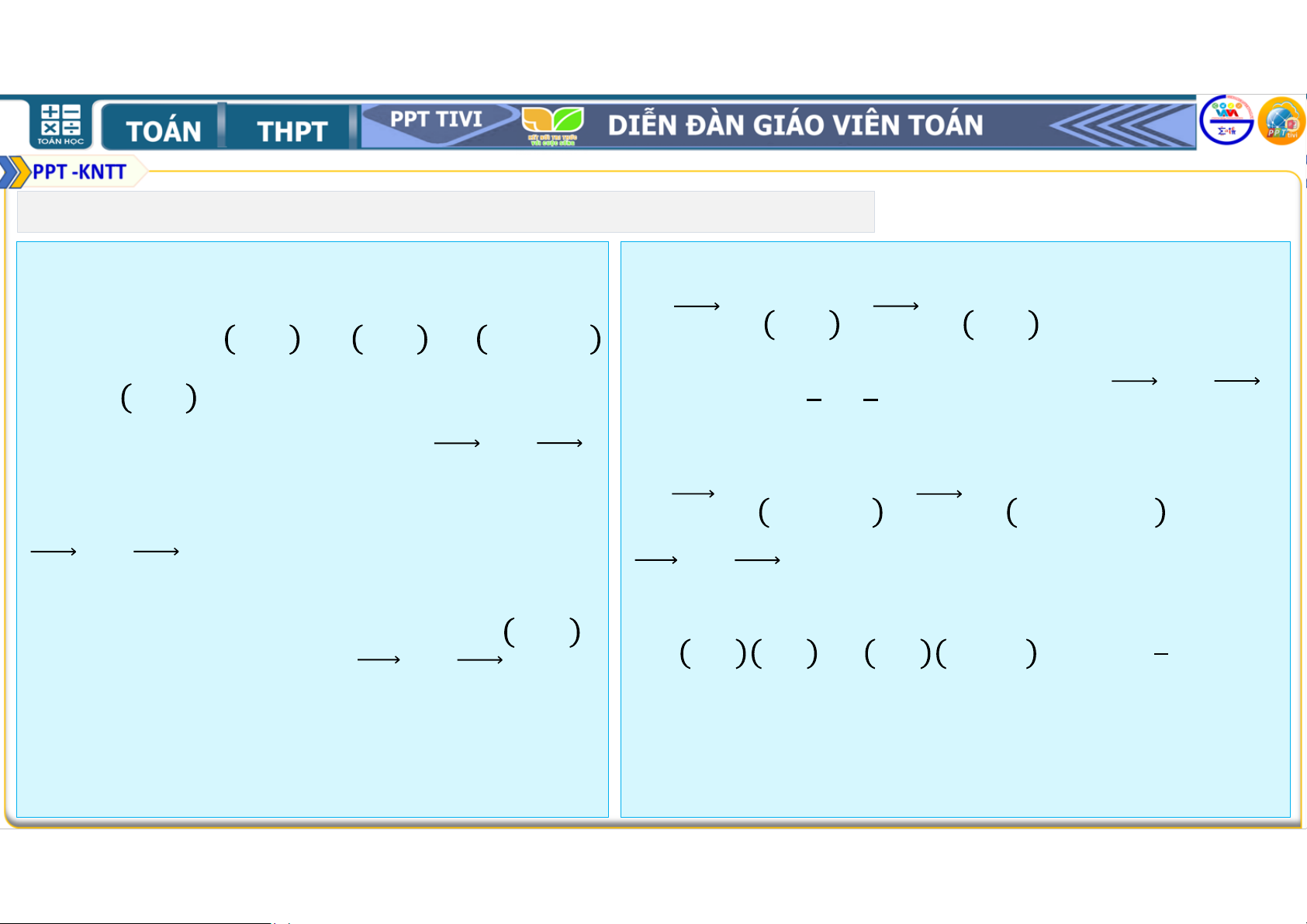
4.36. Trong mặt phẳng tọa độ Hướng dẫn: , cho ; ; ; ; − ; − a. = ; ; = ; . và &;
b. Ta thấy = nên 2 vec-tơ và .
a. Tìm tọa độ của vec-tơ và . cùng phương.
b. Hãy giải thích vì sao các vec-tơ c.
= − ; − ; ' = ! − ; − . và cùng phương.
và ' cùng phương
c. Giả sử ' là điểm có tọa độ !; . ⇔ − − = − ! − ⇔ ! = .
Tìm ! để các vec-tơ và ' cùng phương. 1. BÀI TẬP
4.36. Trong mặt phẳng tọa độ Hướng dẫn: , cho ; ; ; ; − ; −
d. Khi ! = thì ' ; . và &;
Giả sử tồn tại bộ (, ) ∈ ℝ thỏa mãn .
c. Giả sử ' là điểm có tọa độ !; . ' = ( + )
Tìm ! để các vec-tơ và ' cùng phương. ( =
⇔ , = ( − ) ⇔ , ) = .
d. Với ! vừa tìm được, hãy biểu thị − = ( − )
vec-tơ ' theo các vectơ và Vậy ' = + . . 1. BÀI TẬP
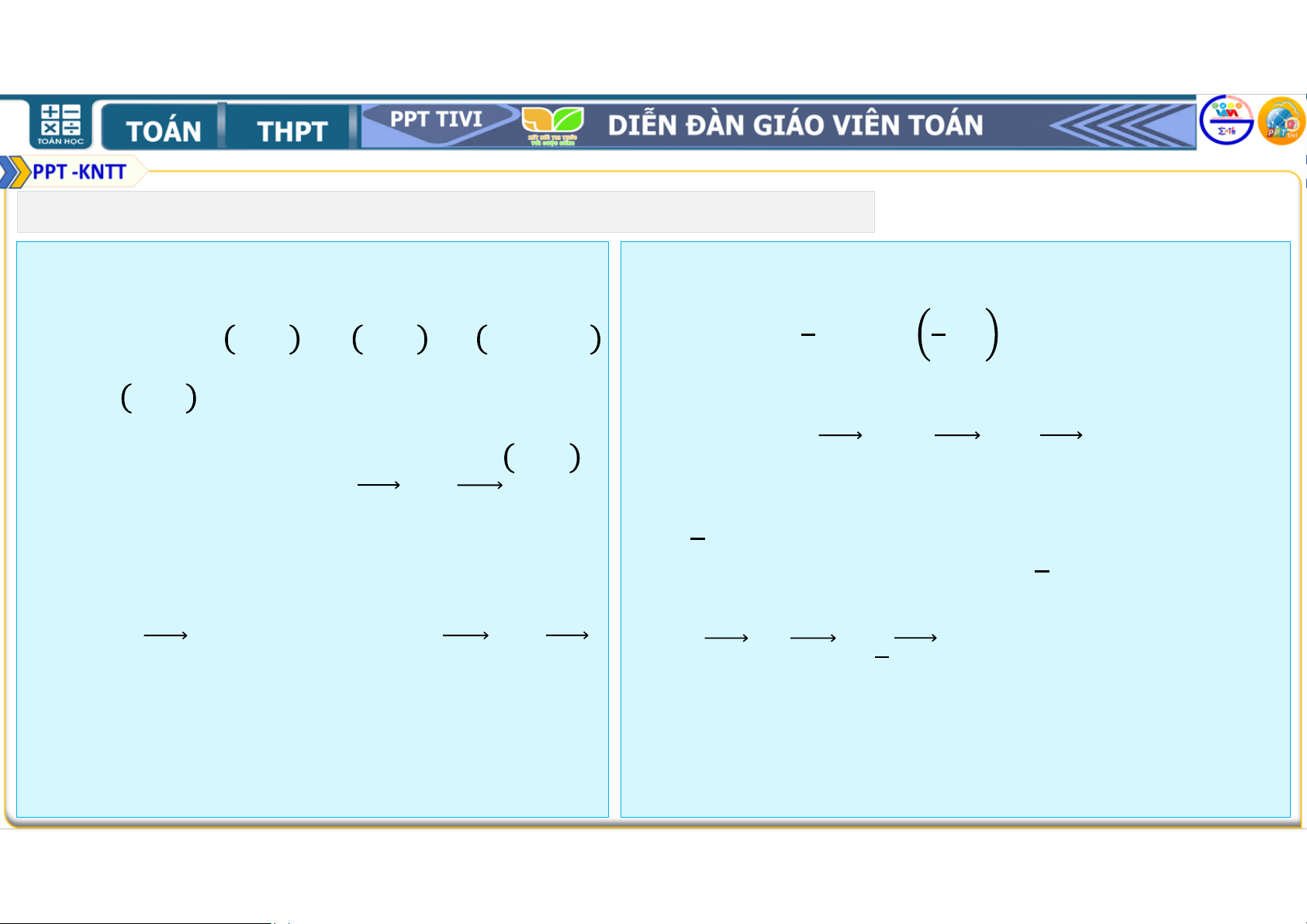
4.37. Cho vectơ ! ≠
. Chứng Hướng dẫn: Ta có: ! =
! = và > nên minh rằng
! (hay còn được viết ! ! ! !
! là một vectơ đơn vị, cùng hướng !
là ! ) là một vectơ đơn vị, cùng với vectơ !. !
hướng với vectơ !. 1. BÀI TẬP
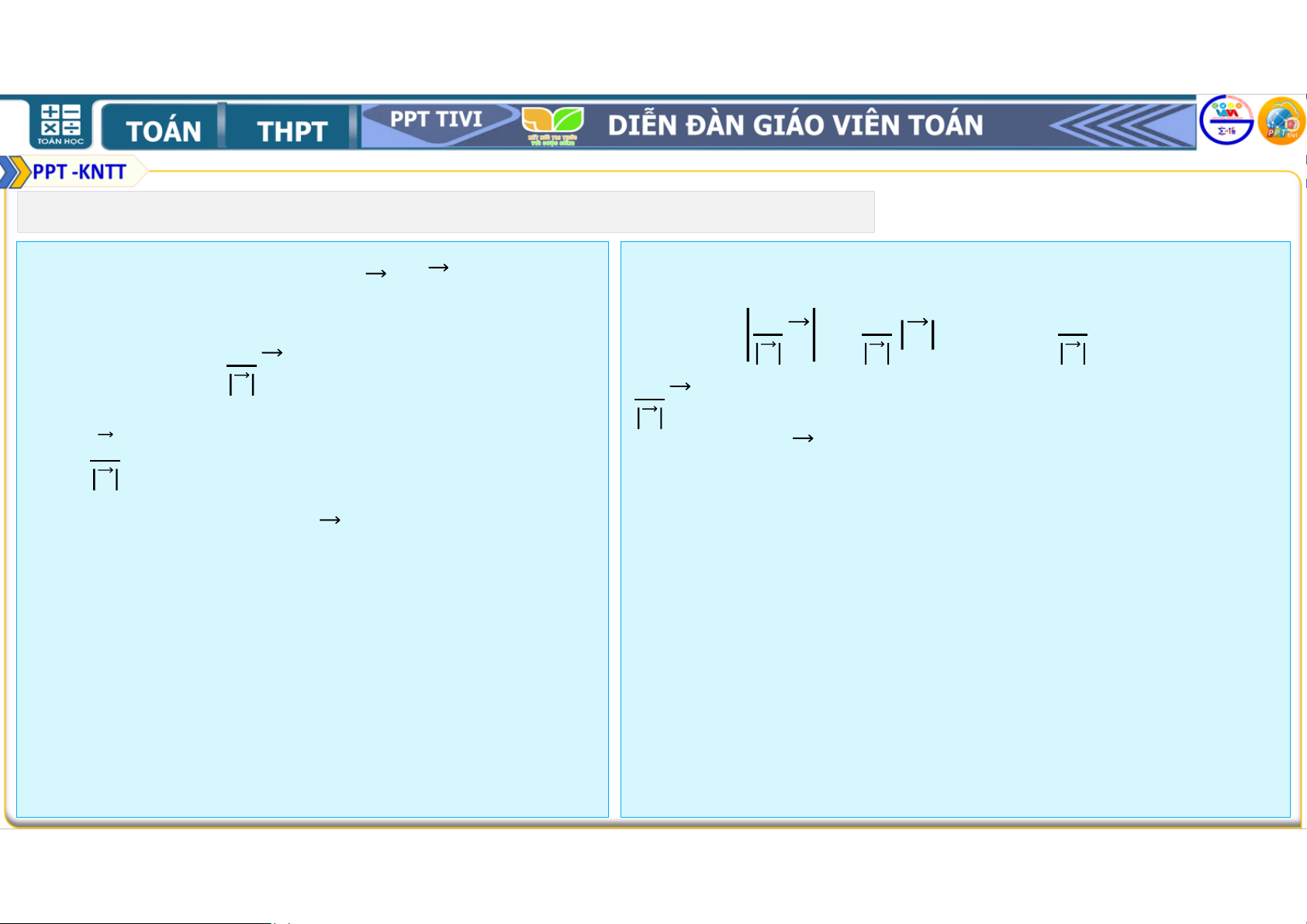
4.38. Cho ba vectơ !, #, . với Hướng dẫn: ! = # =
và ! ⊥ #. Xét một hệ Giả sử: . = ! + #, , ∈ ℝ . trục
với các vectơ đơn vị /⃗ = Ta có:
!, 1⃗ = #. Chứng minh rằng:
. = . . 345 ., ! ! + . . 345 ., # #
a) Vectơ . có toạ độ là . ⋅ !; . ⋅ # .
= . . ! . 345 ., ! ! + . . # . 345 ., # #
b) . = . ⋅ ! ! + . ⋅ # #. = . ⋅ ! ! + . ⋅ # #
Vậy vectơ . có toạ độ là . ⋅ !; . ⋅ # và
. = . ⋅ ! ! + . ⋅ # #. 1. BÀI TẬP
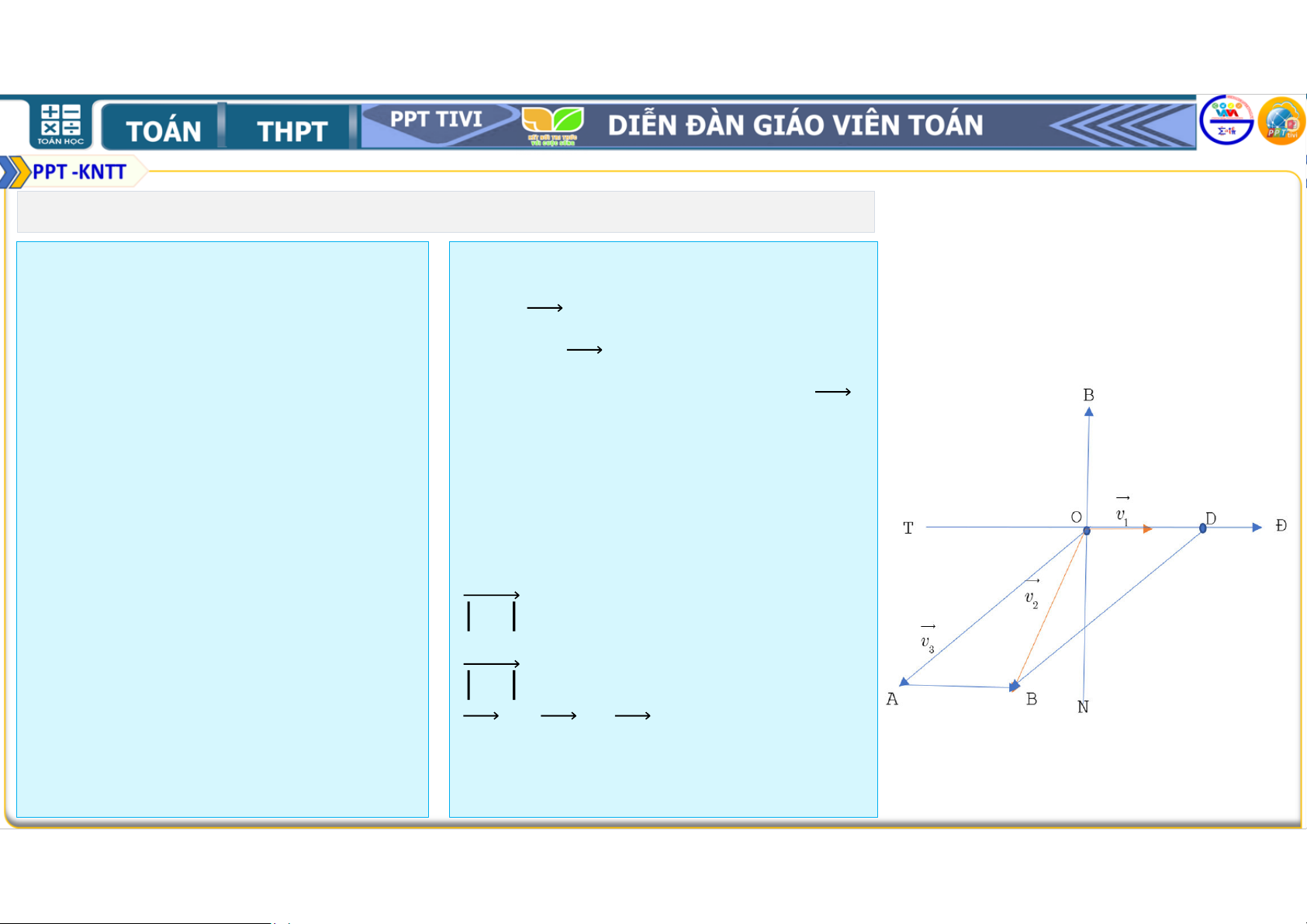
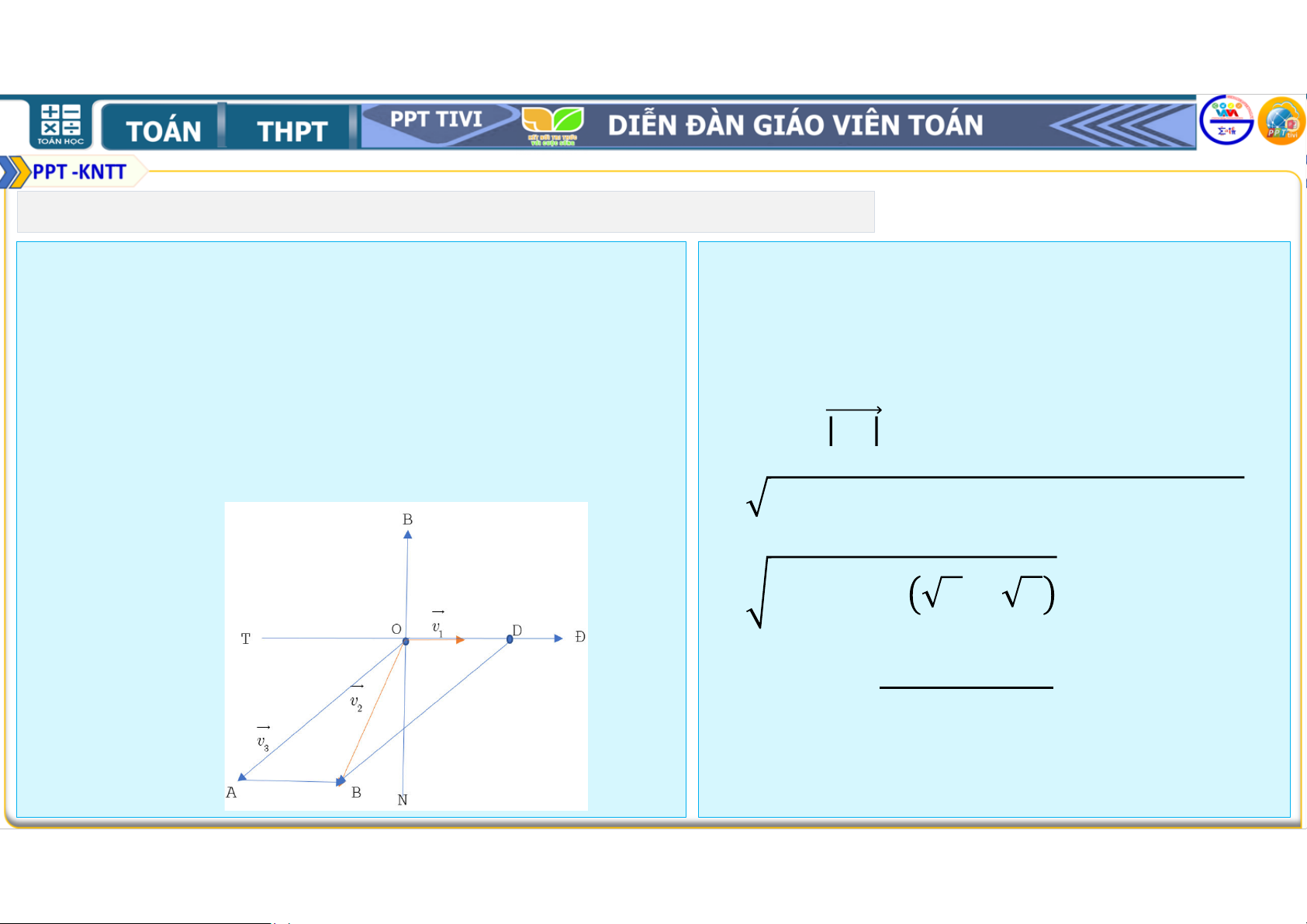
4.39. Trên sông, một Hướng dẫn: ca nô chuyển động
Gọi 9 là vận tốc dòng
thẳng đều theo hướng
nước; 9 là vận tốc ca nô
∘' với vận tốc có độ có sức cản của nước; 9 lớn bằng
km/8 . là vận tốc riêng của ca
Tính vận tốc riêng của nô.
ca nô, biết rằng, nước trên sông chảy về Từ đề bài ta có
hướng đông với vận 9 = = :(/8;
tốc có độ lớn bằng km/8. 9 = = :(/8 và 9 = 9 + 9 . 1. BÀI TẬP
4.39. Trên sông, một ca nô chuyển Hướng dẫn:
động thẳng đều theo hướng
∘' với Ca nô chuyển động thẳng đều theo
vận tốc có độ lớn bằng
km/8. Tính hướng °' thì < = °.
vận tốc riêng của ca nô, biết rằng,
nước trên sông chảy về hướng đông Suy ra 9 = =
với vận tốc có độ lớn bằng km/8. = + − . . 345 ° = = + & − . >?@ < = ≈ . == . . Suy ra < ≈ °. 1. BÀI TẬP
4.39. Trên sông, một ca nô chuyển Hướng dẫn:
động thẳng đều theo hướng
∘' với Suy ra < ≈ °
vận tốc có độ lớn bằng km/8. Tính .
vận tốc riêng của ca nô, biết rằng, Vậy Cano đi một mình theo hướng
nước trên sông chảy về hướng đông °' với vận tốc:
với vận tốc có độ lớn bằng km/8. = + & − :(/8. 2. BÀI TẬP THÊM
Bài 1. Chứng minh rằng điểm B là Hướng dẫn:
trung điểm của đoạn thẳng
• Nếu B là trung điểm của đoạn thẳng thì B = B và hai vec tơ B , B
khi và chỉ khi B = −B .
ngược hướng. Vậy B = −B .
• Ngược lại, nếu B
= −B thì B = B và
hai vec tơ B , B ngược hướng. Do đó , B, thẳng hàng.
Vậy B là trung điểm của đoạn thẳng .