lOMoAR cPSD| 27879799
Chương 5: Tích Phân Mặt Mục lục I
TÍCH PHÂN MẶT LOẠI MỘT 2 1
Định nghĩa tích phân mặt loại I . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 2
Cách tính tích phân mặt loại I . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 2.1
Mặt S cho bởi phương trình tham số . . . . . . . . . . . . . . . . . . . . . . . . 3 2.2
Mặt S được cho bởi phương trình z = z(x,y) . . . . . . . . . . . . . . . . . . . 3 3
Ứng dụng tích phân mặt loại I
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
II TÍCH PHÂN MẶT LOẠI HAI 6 1
Định nghĩa tích phân mặt loại II
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 2
Cách tính tích phân mặt loại II
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7 2.1
Mặt S được cho bởi phương trình tham số . . . . . . . . . . . . . . . . . . . . . 7 2.2
Mặt S được cho bởi phương trình f(x,y,z) = 0 . . . . . . . . . . . . . . . . . . 7 2.3
Liên hệ giữa tích phân mặt loại I và loại II . . . . . . . . . . . . . . . . . . . . . 9 3
Công thức Ostrogradsky và công thức Stokes
. . . . . . . . . . . . . . . . . . . . . . . 9 3.1
Công thức Ostrogradsky . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9 3.2
Công thức Stokes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10 lOMoAR cPSD| 27879799
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập I
TÍCH PHÂN MẶT LOẠI MỘT 1
Định nghĩa tích phân mặt loại I
Cho mặt cong S → → → →
r ( u,v ) = x ( u,v ) . i + y ( u,v ) . j + z ( u,v ) . k
( u,v ) ∈ D ⊂ 2 − − − − và f S f → →
( x ( u,v ) ,y ( u,v ) ,z ( u,v )) . | r u r v − ∧ | dudv − D f S
f ( x,y,z ) dS S Với → ∂x → ∂y → ∂z → r u . i+ . j+ . k − = ∂u − ∂u − ∂u − → ∂x → ∂y → ∂z → r v . i+ . j+ . k − = ∂v − ∂v − ∂v −
Công thức 1. Cho mặt cong S trơn cho bởi phương trình tham số như trên. Mặt S chỉ được phủ một
lần khi (u,v) biến thiên trên miền D. Diện tích mặt cong
S được xác định bởi:
Ví dụ 1. Tính diện tích mặt cầu x2 + y2 + z2 = R2.
[Hướng dẫn giải] +) Đặt +) Khi đó ta có 1 lOMoAR cPSD| 27879799
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập 2
Cách tính tích phân mặt loại I S S → → → →
r ( u,v ) = x ( u,v ) . i + y ( u,v ) . j + z ( u,v ) . k , với ( u,v ) ∈ D ⊂ 2 − − − − f → → ( x,y,z ) dS =
f ( x ( u,v ) ,y ( u,v ) ,z ( u,v )) . | r u r v − ∧ | dudv − S D x2 dS S
x 2 + y 2 + z 2 = 1 S +) Đặt +) Ta thấy . Từ đó ta có : 2.2
Mặt S được cho bởi phương trình z = z(x,y) S
z = z ( x,y ) , ( x,y ) ∈ D ⊂ 2 x = u S y = v
z = z ( u,v ) |→ → p r u r v 1+( z ′ − ∧ | =
u ) 2 +( z ′ v ) 2 = » 1+( z ′ x ) 2 +( z ′ y ) 2 −
Miền xác định của ( u,v ) cũng chính là miền xác định của ( x,y ) S phẳng Oxy f ( x,y,z ) dS =
f ( x,y,z ( x,y )) » 1+( z ′ x ) 2 +( z ′ y ) 2 dxdy S D 2 lOMoAR cPSD| 27879799
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập S A » =
1+( z ′ x ) 2 +( z ′ y ) 2 dxdy D z
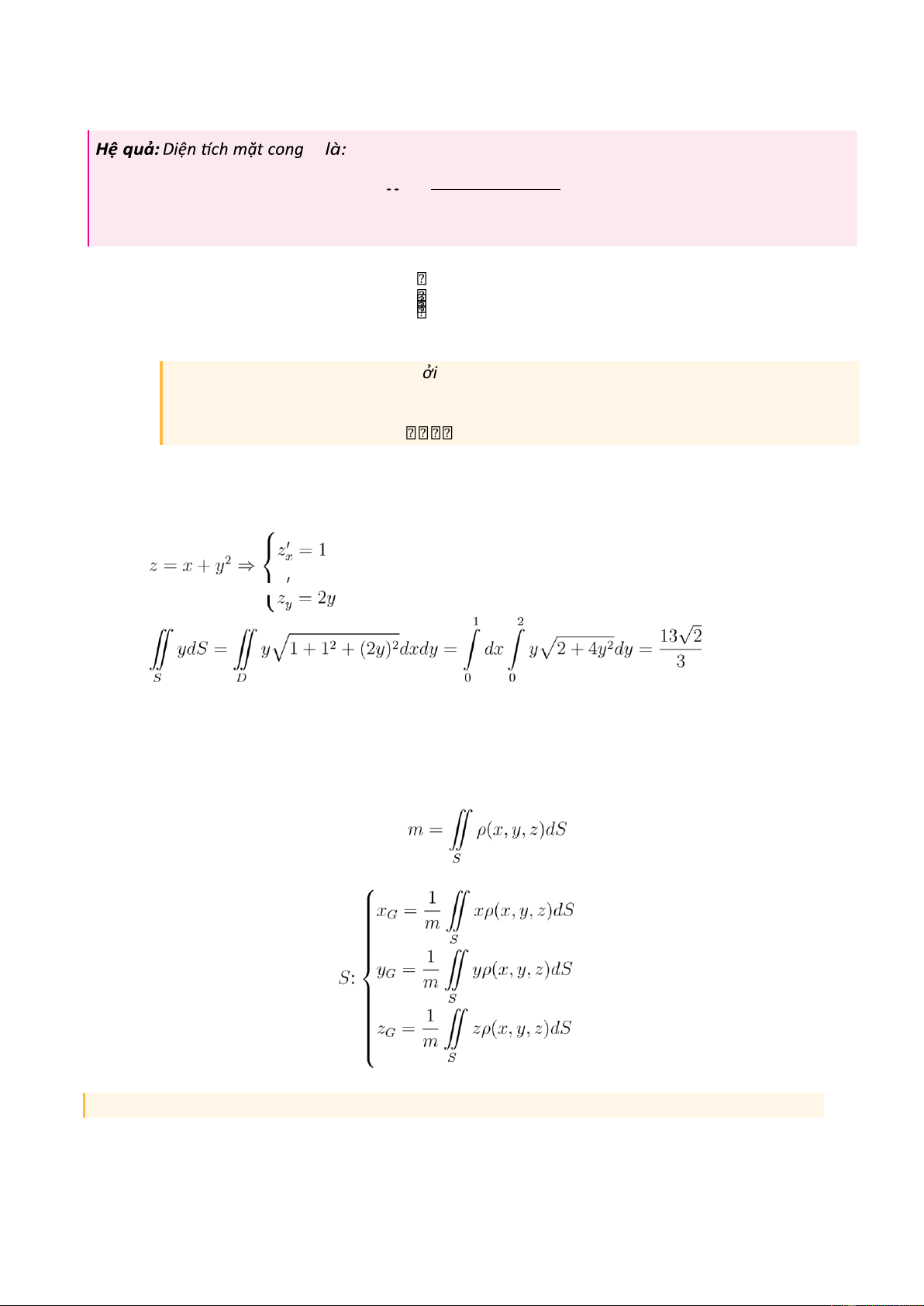
= x + y 2 S
Ví dụ 3. Tính ¨ ydS với S giới hạn bởi 0 ≤ x ≤ 1 0 ≤ y ≤ 2
[Hướng dẫn giải] +) Ta có: +) Ta có: . 3
Ứng dụng tích phân mặt loại I
▶ Khối lượng của mặt S với khối lượng riêng ρ(x,y,z)
▶ Toạ độ trọng tâm G của mặt
Ví dụ 4. Xác định trọng tâm của nửa mặt cầu x2 + y2 + z2 = a2,z ≥ 0 và khối lượng riêng là k 3 lOMoAR cPSD| 27879799
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
[Hướng dẫn giải]
+) Phương trình nửa mặt cầu S: z = pa2 − (x2 + y2) (x2 + y2 ≤ a2) +) Khối lượng mặt cầu là:
+) Toạ độ trọng tâm G của mặt cầu là: = 0; = 0; . 4 lOMoAR cPSD| 27879799
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập II
TÍCH PHÂN MẶT LOẠI HAI 1
Định nghĩa tích phân mặt loại II
Định nghĩa 2. Cho S là mặt cong trơn, giới hạn bởi một đường cong trơn từng khúc C. Lấy điểm M ∈
S và dựng pháp tuyến →−n của S tại M. Nếu xuất phát từ điểm M di chuyển theo một đường cong
kín, quay về điểm xuất phát M mà pháp tuyến →−n không đổi hướng, thì ta nói S định hướng được.
Nếu mặt S định hướng được thì ta chọn một hướng làm hướng dương và hướng còn lại được gọi là hướng âm.
▶ Các mặt xác định bởi z = f(x,y) là các mặt định hướng được và có hai hướng:
+) Hướng →−n tạo với trục Oz một góc nhọn ((→−n ;−Oz→) ≤ 90◦),
+) Hướng →−n tạo với trục Oz một góc tù ((→−n ;−Oz→) ≥ 90◦)
▶ Các mặt kín như mặt cầu, ellipsoid,... là các mặt định hướng được và có hai hướng:
→−n hướng ra ngoài và →−n hướng vào trong.
Định nghĩa 3. Cho mặt cong S trơn, định hướng được, cho bởi phương trình tham số:
⃗r(u,v) = x(u,v)⃗i + y(u,v)⃗j + z(u,v)⃗k, (u,v) ∈ D ⊂ R2,
và ⃗n = (cosα,cosβ,cosγ) là vector pháp tuyến đơn vị tại M(x,y,z) theo hướng dương đã chọn của S. Giả sử
là một hàm vector xác định trên S. Nếu tồn tại tích phân loại I:
¨ →−F · →−n dS = ¨ (Pcosα + Qcosβ + Ccosγ)dS S S
thì giá trị đó được gọi là tích phân mặt loại II của hàm vector →−F lấy theo hướng đã chọn của
mặt S và kí hiệu là:
¨ Pdydz + Qdzdx + Rdxdy S 5 lOMoAR cPSD| 27879799
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
Lưu ý 2. Tính chất của tích phân mặt loại II:
▶ Nếu S đổi hướng thì tích phân đổi dấu;
▶ Nếu P,Q,R liên tục trên mặt S định hướng, trơn thì tồn tại tích phân mặt loại II;
▶ Có tính chất tương tự như tích phân kép: tuyến tính, cộng tính,... 2
Cách tính tích phân mặt loại II
2.1 Mặt S được cho bởi phương trình tham số
– Mặt cong S trơn, được cho bởi phương trình tham số
r(u,v) = x(u,v).→−i + y(u,v).→−j + z(u,v).→−k với (u,v) ∈ D ⊂ R2 –
Một vector pháp tuyến của S tại điểm M chính quy là → → −N ↑↑ n − A B C cos α = √ ; cos β = √ ; cos γ = √
A 2 + B 2 + C 2
A 2 + B 2 + C 2
A 2 + B 2 + C 2 √
dS = A 2 + B 2 + C 2 dudv ⇒
Pdydz + Qdzdx + Rdxdy =
( AP + BQ + CR ) dudv S D → → −N ↑↓ n − − − − cos A B C α = √ ; cos β = √ ; cos γ = √
A 2 + B 2 + C 2
A 2 + B 2 + C 2
A 2 + B 2 + C 2 ⇒
Pdydz + Qdzdx + Rdxdy = −
( AP + BQ + CR ) dudv S D 6 lOMoAR cPSD| 27879799
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập 2.2
Mặt S được cho bởi phương trình f(x,y,z) = 0 I I ,I ,I 1 2 3 I = Pdydz + Qdzdx + Rdxdy S S S | { z } | {z } | { z } I 1 I 2 I 3 I
z = z ( x,y ) z ( x,y ) cùng với các đạo hàm riêng của 3 D S Oxy →
( n ,Oz ) < 90 o : Rdxdy =
R ( x,y,z ( x,y )) dxdy − S D →
( n ,Oz ) > 90 o : Rdxdy = −
R ( x,y,z ( x,y )) dxdy − S D
I 1 và I 2
Ví dụ 5. Tính ¨ z(x2 + y2)dxdy, trong đó S là nửa mặt cầu x2 + y2 + z2 = 1,z ≥ 0 hướng ra S
phía ngoài mặt cầu.
[Hướng dẫn giải] z → n ( x,y,z ) − y O
D : x 2 + y 2 ≤ a 2 x
+) Ta có: z = p1 − x2 − y2, hình chiếu S lên Oxy là D : x2 + y2 ≤ 1 +) Do
Ví dụ 6. Tính ¨ x2y2zdxdy, trong đó S là mặt dưới nửa mặt cầu x2 + y2 + z2 = R2,z ≤ 0. S 7 lOMoAR cPSD| 27879799
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập z y O x
[Hướng dẫn giải]
+) Ta có: S : z = −pR2 − x2 −2y2 2 2
+) Hình chiếu S lên Oxy là D : x + y ≤ R . Ta có nên
+) Đổi biến toạ độ cực, ta được: [
Pcosα + Qcosβ + Rcosγ ] dS =
Pdydz + Qdzdx + Rdxdy S S cosα,cosβ,cosγ → n S −
Ví dụ 7. Gọi S là phần mặt cầu x2 + y2 + z2 = 1 nằm trong mặt trụ x2 + x + z2 = 0,y ≥ 0 và hướng của
S là phía ngoài của mặt cầu.
Chứng minh rằng: ¨ (x − y)dxdy + (y − z)dydz + (z − x)dzdx = 0. S
[Hướng dẫn giải] +) Ta có: +) Do suy ra ã 8 lOMoAR cPSD| 27879799
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
+) Từ đó ta tính được 3
Công thức Ostrogradsky và công thức Stokes P,Q,R
V ⊂ 3 V giới hạn bởi mặt S Å ∂Q ∂R ã Pdydz ∂P
+ Qdzdx + Rdxdy = + + dxdydz, ∂x ∂y ∂z S V Lưu ý 3.
• Nếu tích phân ở vế trái lấy theo hướng pháp tuyến trong: • Nếu mặt cong S không kín, có thể
bổ sung thành mặt cong S′ kín để áp dụng công thức Ostrogradsky, rồi trừ đi phần bổ sung.
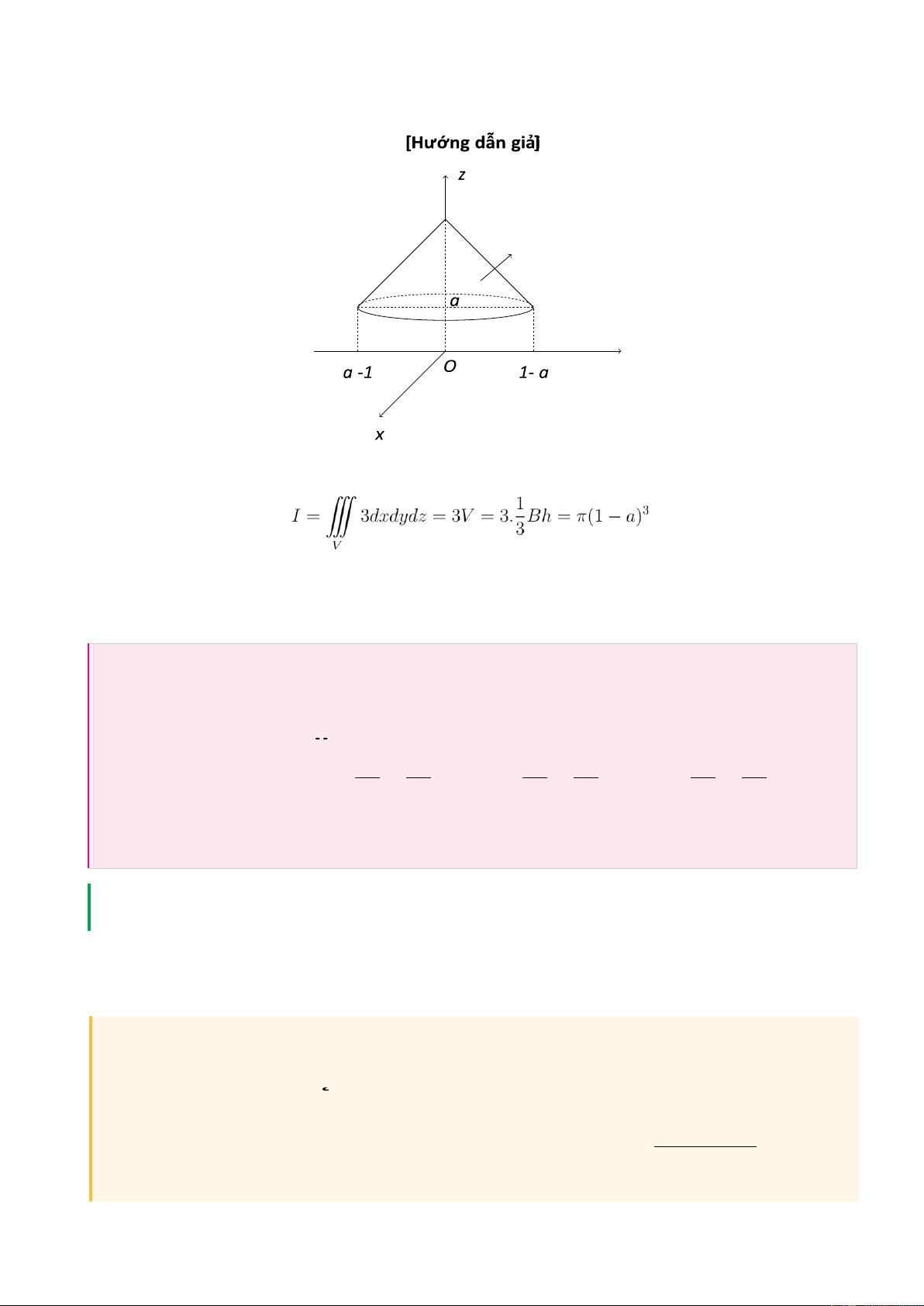
(z − 1) ≤ x + y2
Ví dụ 8. Tính ¨S xdydz + ydzdx + zdxdy, với S là phía ngoài của miền a ≤ z ≤2 1 2 a > 0 9 lOMoAR cPSD| 27879799
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập → n − y
+) Áp dụng công thức Ostrogradsky ta có:
3.2 Công thức Stokes
Công thức 8. Công thức Stokes:
Giả sử S là mặt cong trơn, có biên ∂S là đường cong trơn. Giả thiết P,Q,R là các hàm số liên tục và có
đạo hàm riêng liên tục trong một tập mở nào đó chứa S. Khi đó: ∂R ∂Q ∂P ∂R ∂Q ∂P
ˆ Pdx + Qdy + Rdz =Å ∂y −
∂z ã dydz + Å ∂z − ∂x ã dzdx + Å ∂x − ∂y ã dxdy ∂S S
Trong đó tích phân đường ở vế trái lấy theo hướng dương của ∂S phù hợp với hướng dương của mặt S. Lưu ý 4.
Hướng dương của ∂S phù hợp hướng dương của S được xác định theo quy tắc nắm tay phải.
Ví dụ 9. Tính tích phân đường
(y2 + z2)dx + (z2 + x2)dy +
(x2 + y2)dz, C
trong đó C là giao của mặt cầu x2 + y2 + z2 = 4 với mặt nón z = −px2 + (y − 1)2, với hướng cùng
chiều kim đồng hồ khi nhìn từ gốc O.
[Hướng dẫn giải]
+) Áp dụng công thức Stokes: 10 lOMoAR cPSD| 27879799
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
I = ¨S 2(y − z)dydz + 2(z − x)dzdx + 2(x − y)dxdy
Trong đó S là phần mặt cầu phía trên hướng theo trục Oz.
+) Ta có phương trình mặt S là: z = p4 − x2 − y2 +) Do suy ra ã
+) Từ đó ta tính được
I = ¨S(x(y − z) + y(z − x) + z(x − y))dS = 0 11