Chương 6 Thanh thẳng chịu uốn phẳng: Tóm tắt lý thuyết và ứng dụng | Môn Sức bền vật liệu - Đại học Xây Dựng Hà Nội

lOMoAR cPSD| 58970315 09-Aug-22
TRƯỜNG ĐẠI HỌC XÂY DỰNG HÀ NỘI
KHOA XÂY DỰNG DÂN DỤNG VÀ CÔNG NGHIỆP
www: xaydung.huce.edu.vn
Sức bền Vật liệu
Bộ môn Sức bền Vật liệu – Khoa Xây dựng Dân dụng và Công nghiệp
TRƯỜNG ĐẠI HỌC XÂY DỰNG HÀ NỘI 1
CHƯƠNG 6: THANH THẲNG CHỊU UỐN PHẲNG 6.1 . Kháiniệmchung
6.2 . Thanh thẳng chịu uốn thuầntúy
6.3 . Thanh thẳng chịu uốn ngangphẳng
6.4 . Biếndạngcủadầm chịu uốn: độvõngvàgóc xoay
6.5 *. Điều kiện cứng của dầm chịu uốn 2 lOMoAR cPSD| 58970315 09-Aug-22 6.1. Khái niệm chung
Thanh chịu uốn ( thường gọi là dầm) là thanh mà dưới tác
dụng của ngoại lực, trục thanh thay đổi độ cong.
Ví dụ: Dầm (thép, bê tông) trong
khungnhà;dầmcầu…làcáccấukiện
chịuuốnđiểnhình 3 6.1 . Khái niệm chung lOMoAR cPSD| 58970315 09-Aug-22 6.1. Khái niệm chung
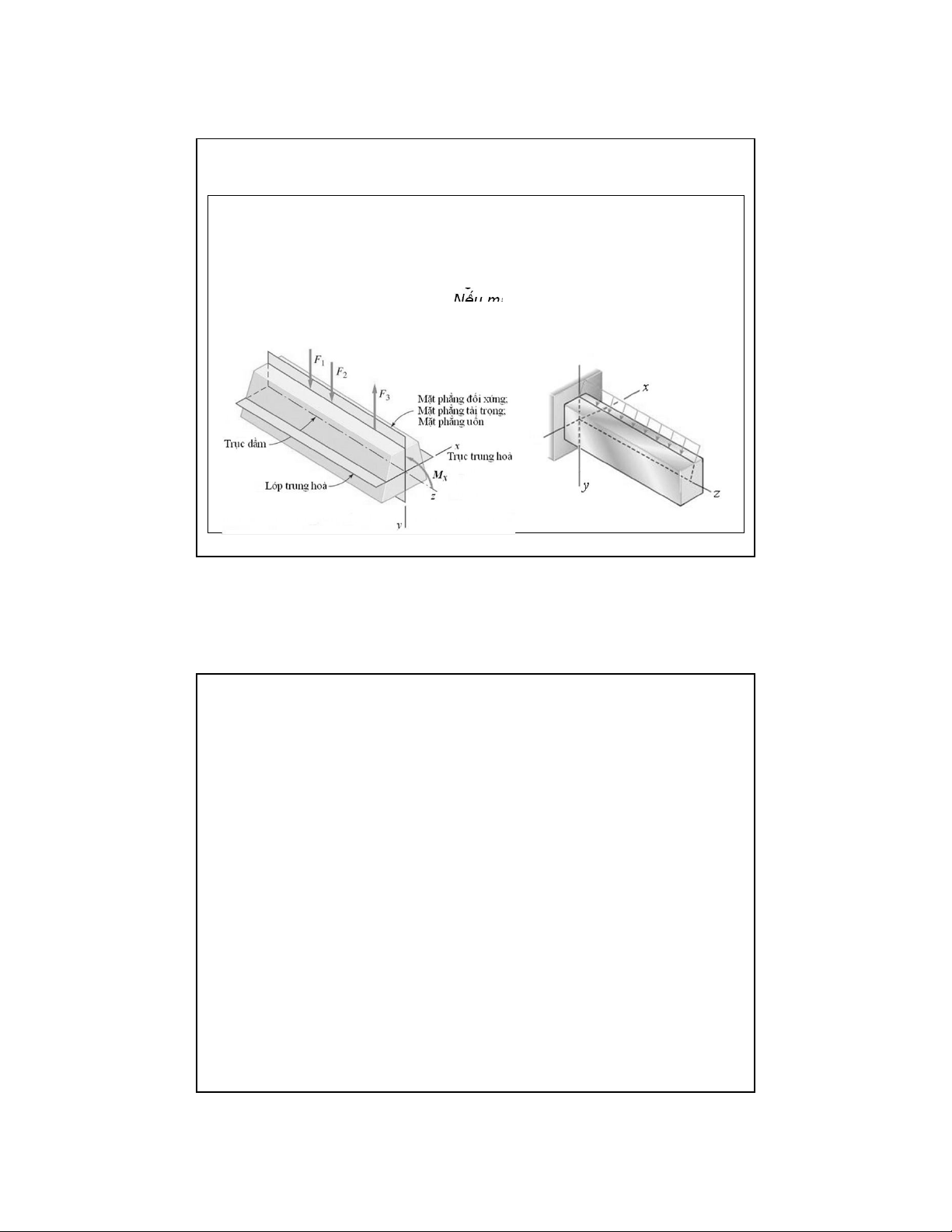
❖ Giới hạn nghiên cứu: Tiết diện có 1 trục đối xứng (chữ nhật, chữ I, chữ
T, hình tròn...); ngoại lực nằm trong mặt phẳng đối xứng
❖ Mặt phẳng tải trọng (mặt phẳng uốn): Chứa tải trọng và trục dầm
❖ Mặt phẳng quán tính chính trung tâm: chứa trục dầm và trục quán tính
chính trung tâm của tiết diện. Nếu mặt phẳng uốn trùng với mặt phẳng
quán tính chính trung tâm thì dầm chịu uốn phẳng Uốn xiên 4 5 lOMoAR cPSD| 58970315 09-Aug-22 6.1. Khái niệm chung 6.1 . Khái niệm chung 6 7 lOMoAR cPSD| 58970315 09-Aug-22 6.1. Khái niệm chung Giànmáigỗtruyền thống–cácthanh xà gồ chịu uốn xiên 6.1. Khái niệm chung Phân loại uốn phẳng:
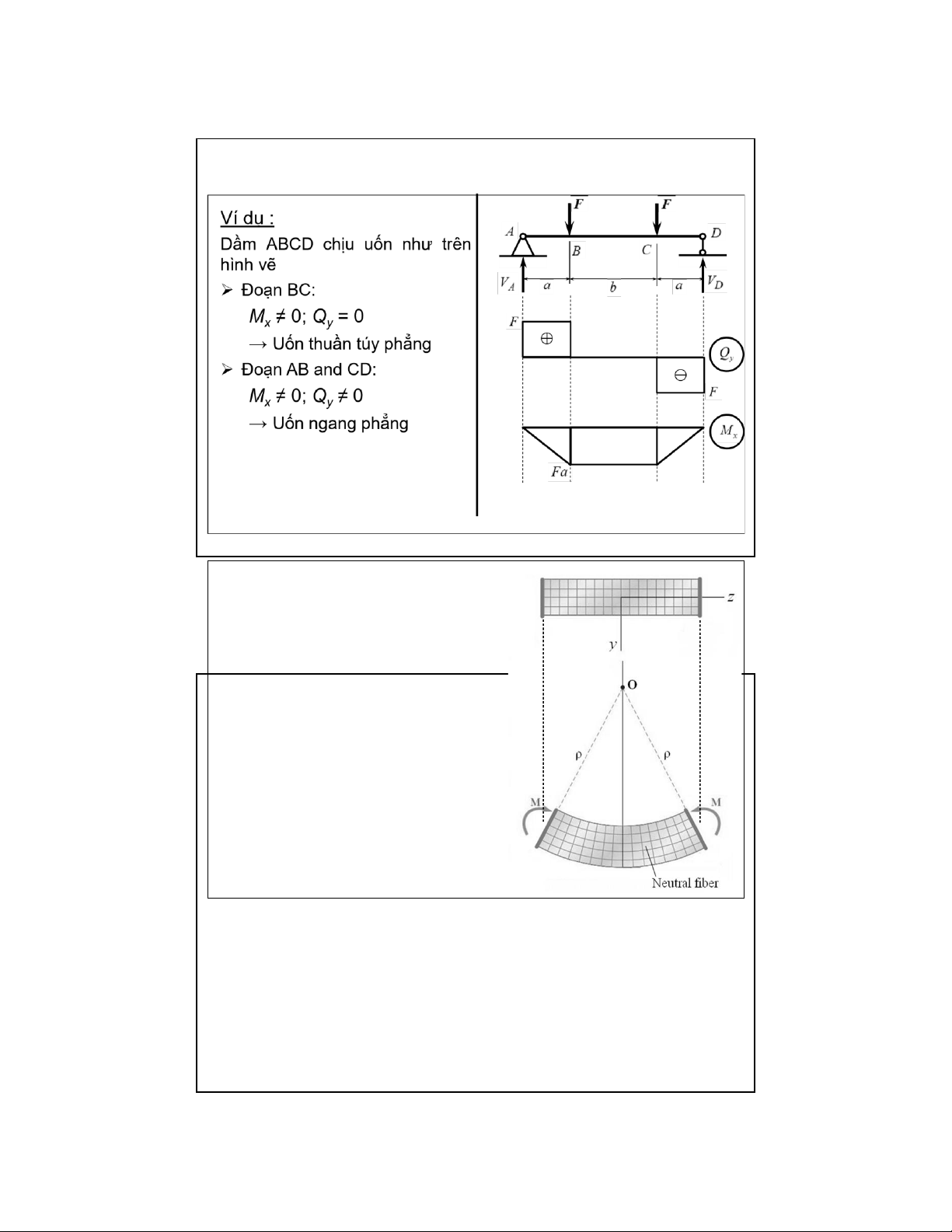
❖ Uốn thuần túy phẳng:
M ≠ 0; Q = 0 x y ❖ Uốn ngang phẳng :
M ≠ 0; Q ≠ 0 x y 8 9 lOMoAR cPSD| 58970315 09-Aug-22 6.1. Khái niệm chung
6.2. Thanh thẳng chịu uốn thuần túy
Thí nghiệm: Trước khi thí nghiệm, vẽ lên bề mặt thanh :
- Những đường thẳng song song với trục thanh
- Những đường thẳng vuông góc với trục thanh
→ Tạo thành lưới ô vuông Quan sát biến dạng:
- Những đường thẳng song song
trở thành những đường cong,
nhưng vẫn song song trục dầm.
Khoảng cách giữa chúng không đổi.
- Những đường thẳng vuông góc
vẫn thẳng và vuông góc với trục dầm 10 lOMoAR cPSD| 58970315 09-Aug-22
6.2. Thanh thẳng chịu uốn thuần túy
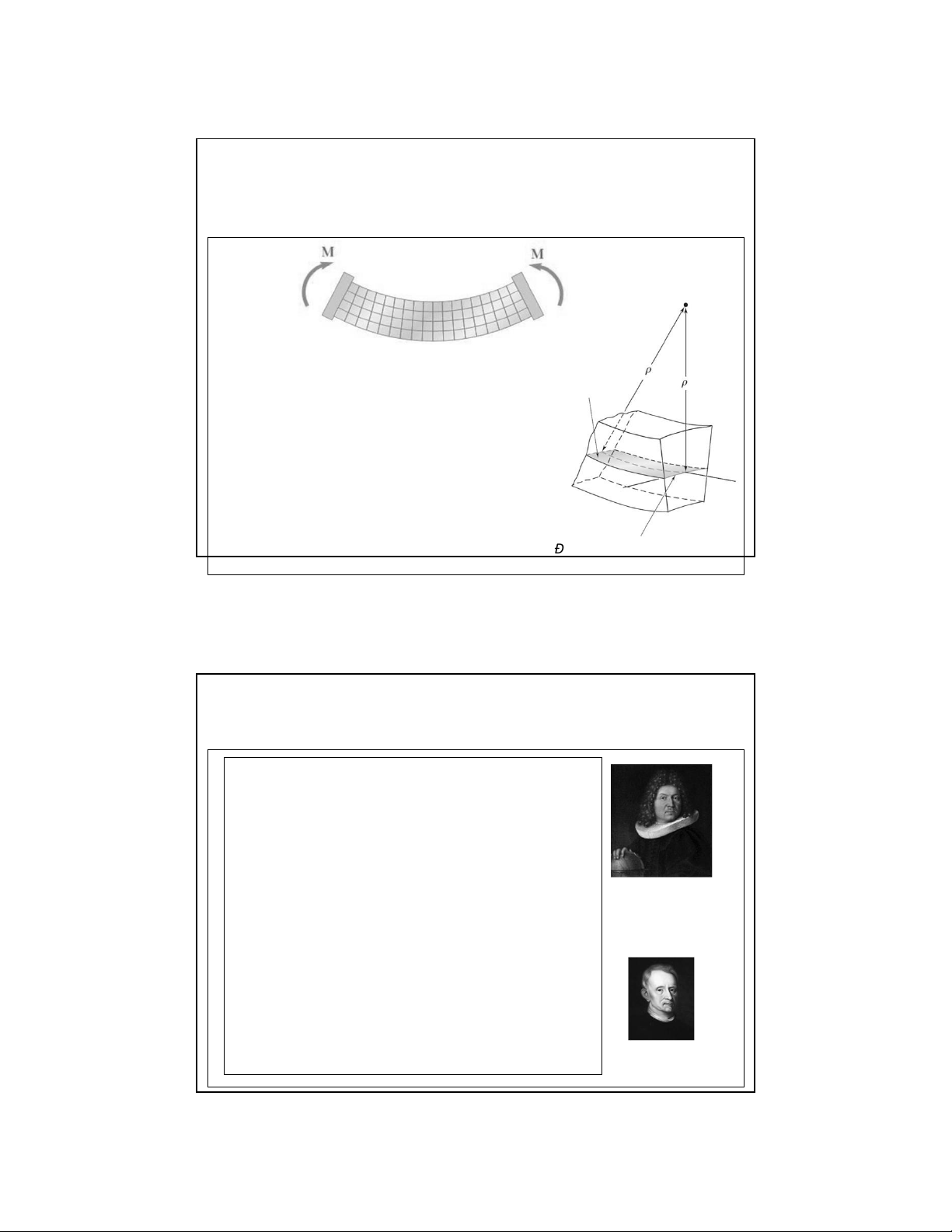
Quan sát biến dạng (tiếp): Lớp trung hòa
- Các thớ dọc phía dưới bị kéo giãn ra,
các thớ dọc phía trên bị nén co lại
❖ Tồn tại những thớ vật liệu không
chịu kéo cũng không chịu nén – thớ trung hoà
❖ Tập hợp của các thớ trung hòa – mặt trung hòa
❖ Đường trung hoà: giao tuyến của
mặt trung hoà với mặt cắt ngang Đường trung hòa 11
6.2. Thanh thẳng chịu uốn thuần túy
Các giả thuyết về biến dạng:
Giả thuyết 1: Giả thuyết về mặt cắt ngang phẳng (Bernoulli)
Mặt cắt ngang trước biến dạng là phẳng và vuông góc với trục
thanh, sau biến dạng vẫn phẳng và vuông góc với trục thanh.
Jacob Bernoulli(1654-1705)
Giả thuyết 2: Giả thuyết về các thớ dọc
Các lớp vật liệu dọc trục không có tác dụng
tương hỗ với nhau (không chèn ép, xô đẩy lẫn nhau).
Chú ý: Ứng xử của vật liệu tuân theo Định luật Robert Hooke Hooke (ứng
suất tỷ lệ thuận với biến dạng) (1635 -1703) lOMoAR cPSD| 58970315 09-Aug-22
6.2. Thanh thẳng chịu uốn thuần túy 12 13 lOMoAR cPSD| 58970315 09-Aug-22
6.2. Thanh thẳng chịu uốn thuần túy
6.2.1 Ứng suất pháp trên mặt cắt ngang
• Giả thuyết 1 → t = 0
• Giả thuyết 2 → σ = σ = 0 x y
→ chỉ tồn tại duy nhất thành phần
ứngsuấtphápσ z
• Đường trung hòa đi qua trọng tâm mặt cắt ngang (trùng trục x),
chia mặt cắt ngang làm 2 phần: chịu kéo và chịu nén
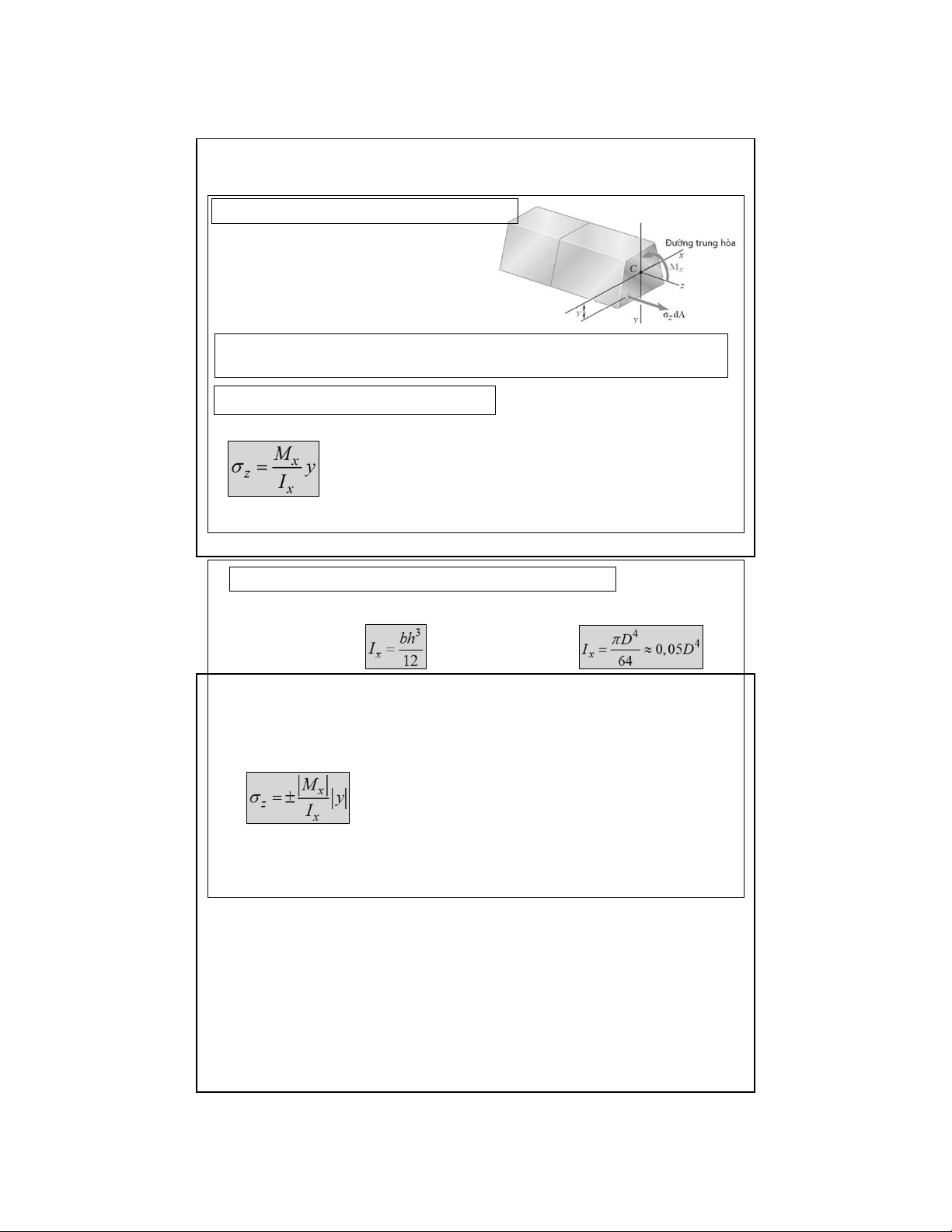
• Công thức tính ứng suất pháp
M x mô men uốnnộilựctrênmặt cắt ngang.
I x là mô men quán tính của mặt cắt ngang đối với trục x
ylà tọa độ của điểm tính ứngsuất
6.2. Thanh thẳng chịu uốn thuần túy
6.2.1 Ứng suất pháp trên mặt cắt ngang ( tiếp theo ) ✓ Hìnhchữnhật ✓ Hìnhtròn:
Đểthuậnlợichoviệctínhtoán,người
ta thường áp dụng công thức kỹ thuật:
➢ Lấy dấu “+” nếu điểm đang xét thuộc vùng chịu kéo
➢ Lấy dấu “–” nếu điểm đang xét thuộc vùng chịu nén 14 15 lOMoAR cPSD| 58970315 09-Aug-22
6.2. Thanh thẳng chịu uốn thuần túy
6.2.1 Ứng suất pháp trên mặt cắt ngang ( tiếp theo )
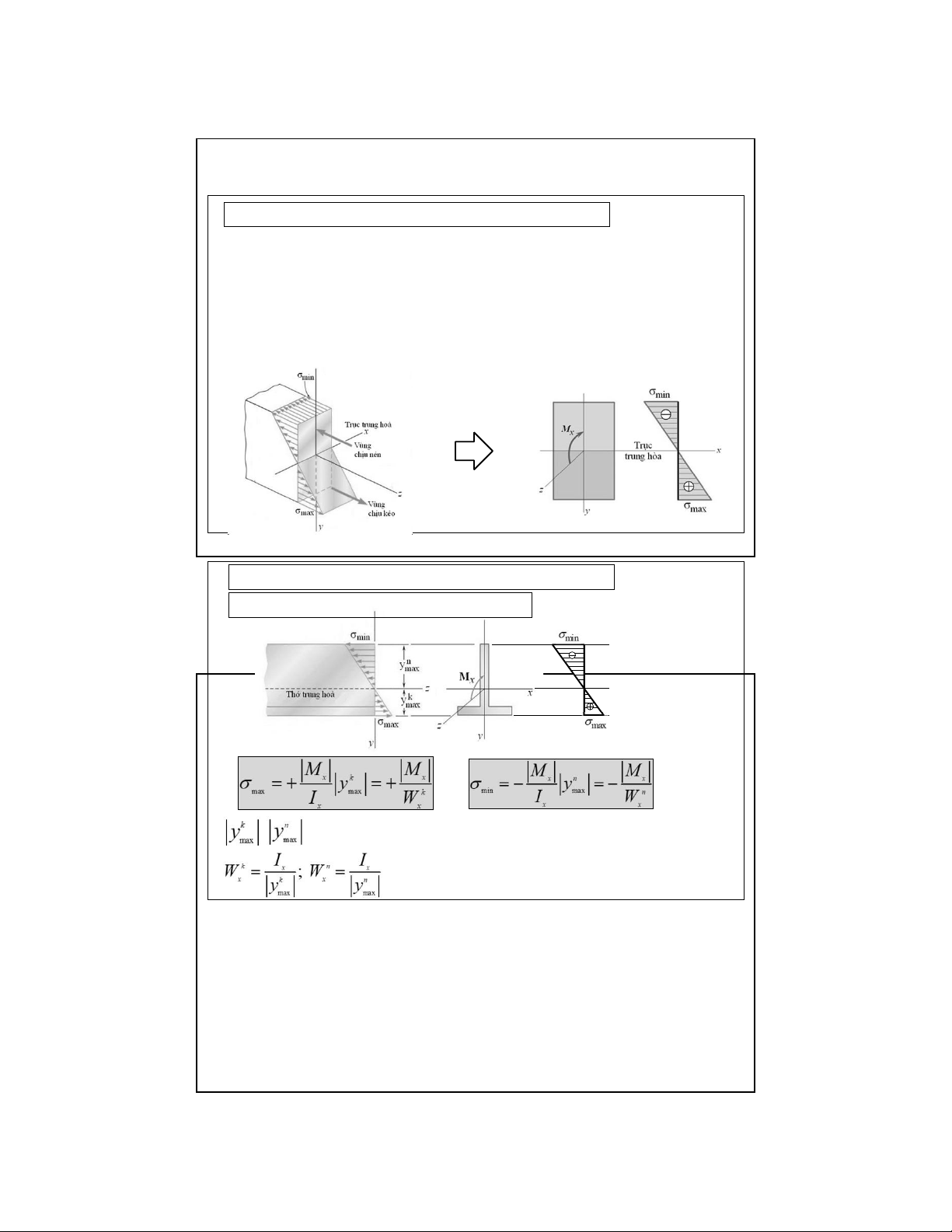
❖ Phân bố ứng suất pháp trên mặt cắt ngang
- Ứng suất pháp σ phân bố bậc nhất theo khoảng cách y đến trục trung z
hoà, những điểm cùng nằm trên đường thẳng song song với đường trung
hòa có ứng suất như nhau.
- Đạt cực trị tại các mép biên trên và dưới của mặt cắt ngang và bằng 0 trên trục trung hòa
6.2. Thanh thẳng chịu uốn thuần túy
6.2.1 Ứng suất pháp trên mặt cắt ngang ti ( ếp theo )
✓ Mặt cắt ngang có 1 trục đối xứng
Khoảng cáchđiểmxaĐTH nhấtthuộcvùngchịu kéo, và chịu nén
Mô men chống uốn của mặt cắt ngang 16 17 lOMoAR cPSD| 58970315 09-Aug-22
6.2. Thanh thẳng chịu uốn thuần túy
✓ Mặt cắt ngang có 2 trục đối xứng
–Mômenchốnguốncủamặt cắtngang
6.2. Thanh thẳng chịu uốn thuần túy
Mặtcắtngangcó2trụcđốixứng
Mômenchốnguốncủa1sốhìnhđơngiản Tiết diện chữ nhật: Tiết diện tròn: Tiết diện tròn rỗng: 18 19 lOMoAR cPSD| 58970315 09-Aug-22
6.2. Thanh thẳng chịu uốn thuần túy
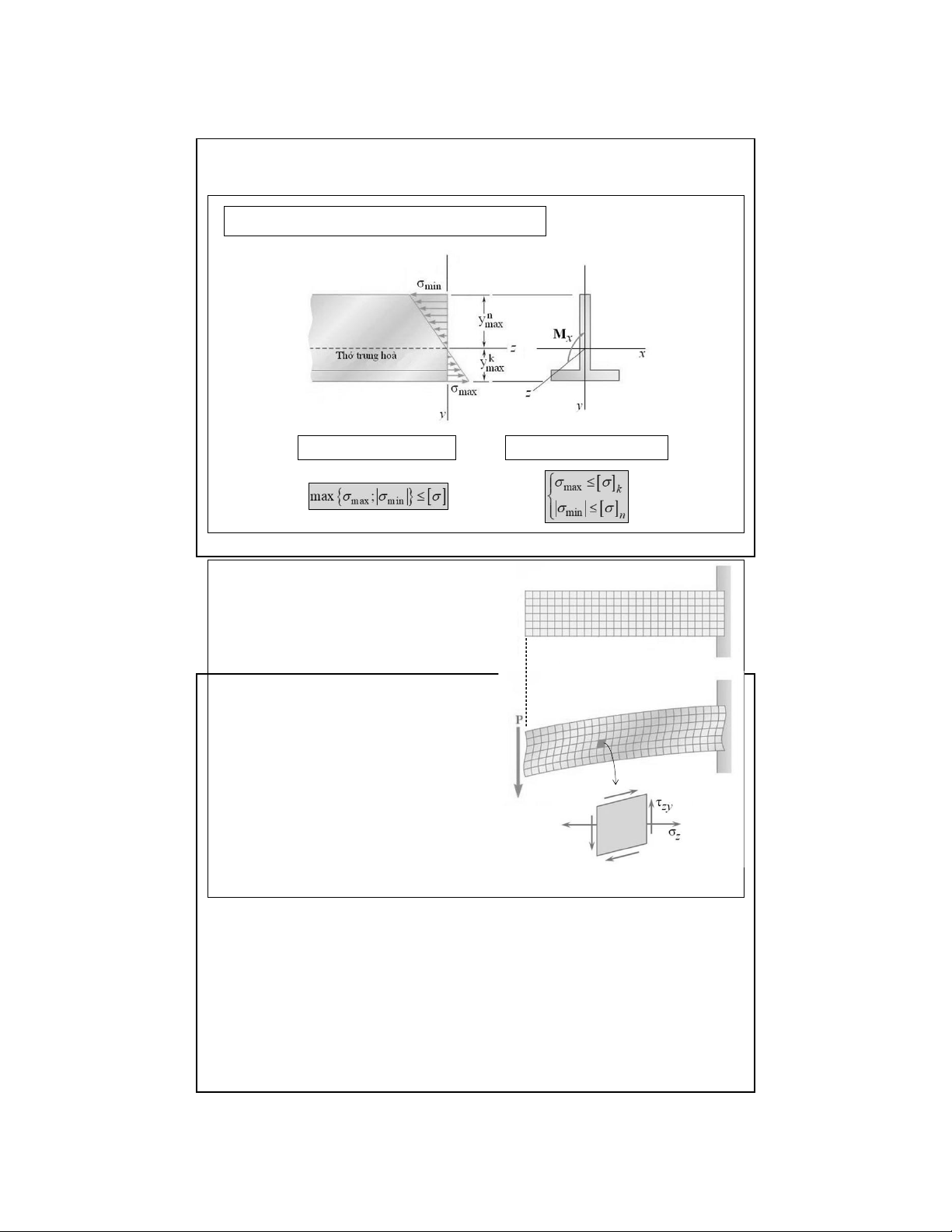
6.2.2 Điều kiện bền ứng suất pháp
Đối với vật liệu dẻo:
Đối với vật liệu giòn:
6.3. Thanh thẳng chịu uốn ngang phẳng
Thí nghiệm: Uốn dầm như hình vẽ.
Trước khi uốn, kẻ trên bề mặt dầm:
- Hệ những đường thẳng song song với trục dầm
- Hệ những đường thẳng vuông góc với trục dầm
→ Tạo thành một lưới ô vuông Quan sát biến dạng:
- Sau biến dạng, ô vuông trở thành
ô bình hành → có biến dạng góc
- Mặt cắt ngang không còn phẳng
→ giả thiết về mặt cắt ngang
phẳng của Bernoul i không còn chính xác 20 lOMoAR cPSD| 58970315 09-Aug-22
6.3. Thanh thẳng chịu uốn ngang phẳng
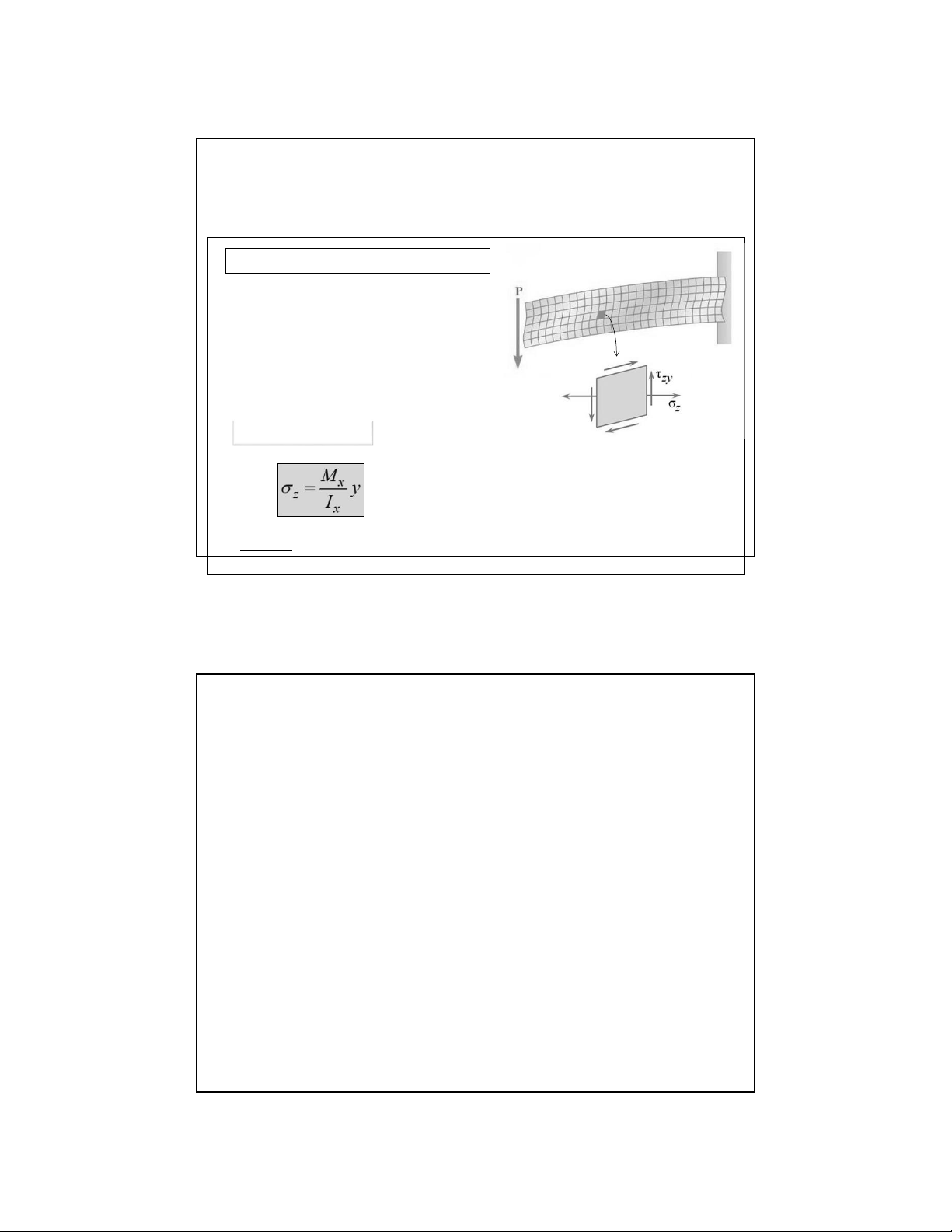
6.3.1 Ứng suất trên mặt cắt ngang
Trênmặtcắtngangcóhaithànhphần ứnglực:
➢ Mômenuốn M x → Ứngsuấtpháp σ z
➢ Lựccắt Q y → Ứngsuấttiếp τ zy a.Ứngsuấtpháp
M x – Mômen uốn nội lực trên mặt cắt ngang
I x – Mômen quán tính của mặt cắt ngang đối
vớitrụcquántínhchínhtrungtâm Ox
y – Tung độ của điểm tính ứng suất
Ghi chú: M > 0 khi làm căng các thớ dưới của dầm; x
M < 0 khi làm căng các thớ trên của dầm x 21 lOMoAR cPSD| 58970315 09-Aug-22
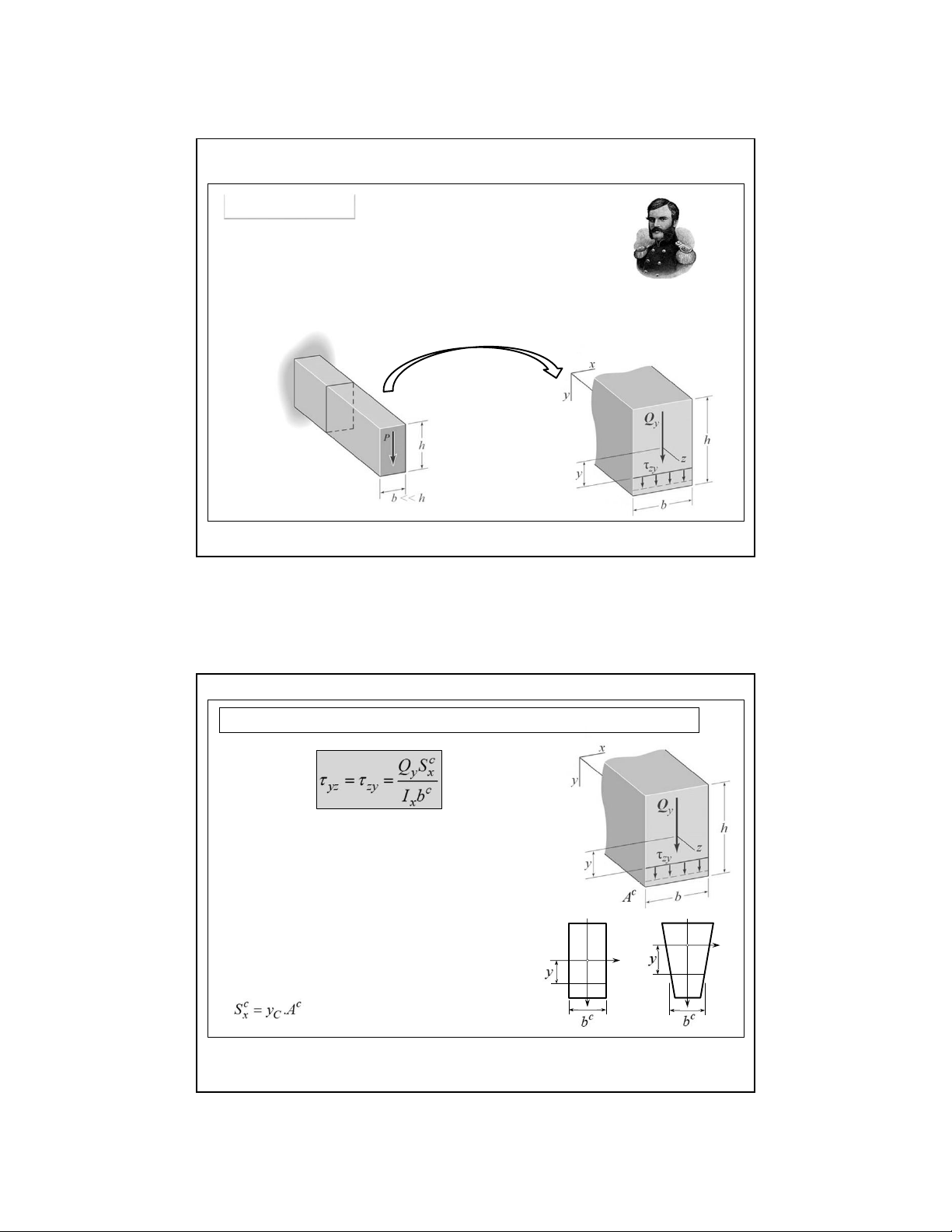
6.3. Thanh thẳng chịu uốn ngang phẳng b. Ứng suất tiếp
Với mặt cắt ngang hình chữ nhật hẹp (b<ứng suất tiếp tuân theo giả thiết Zhuravski :
• Có phương song song với lực cắt Q , cùng y
chiều lực cắt Q Dmitrii Ivanovich Zhuravskii y (1821 -1891)
• Phân bố đều trên bề rộng mặt cắt ngang 22
6.3. Thanh thẳng chịu uốn ngang phẳng
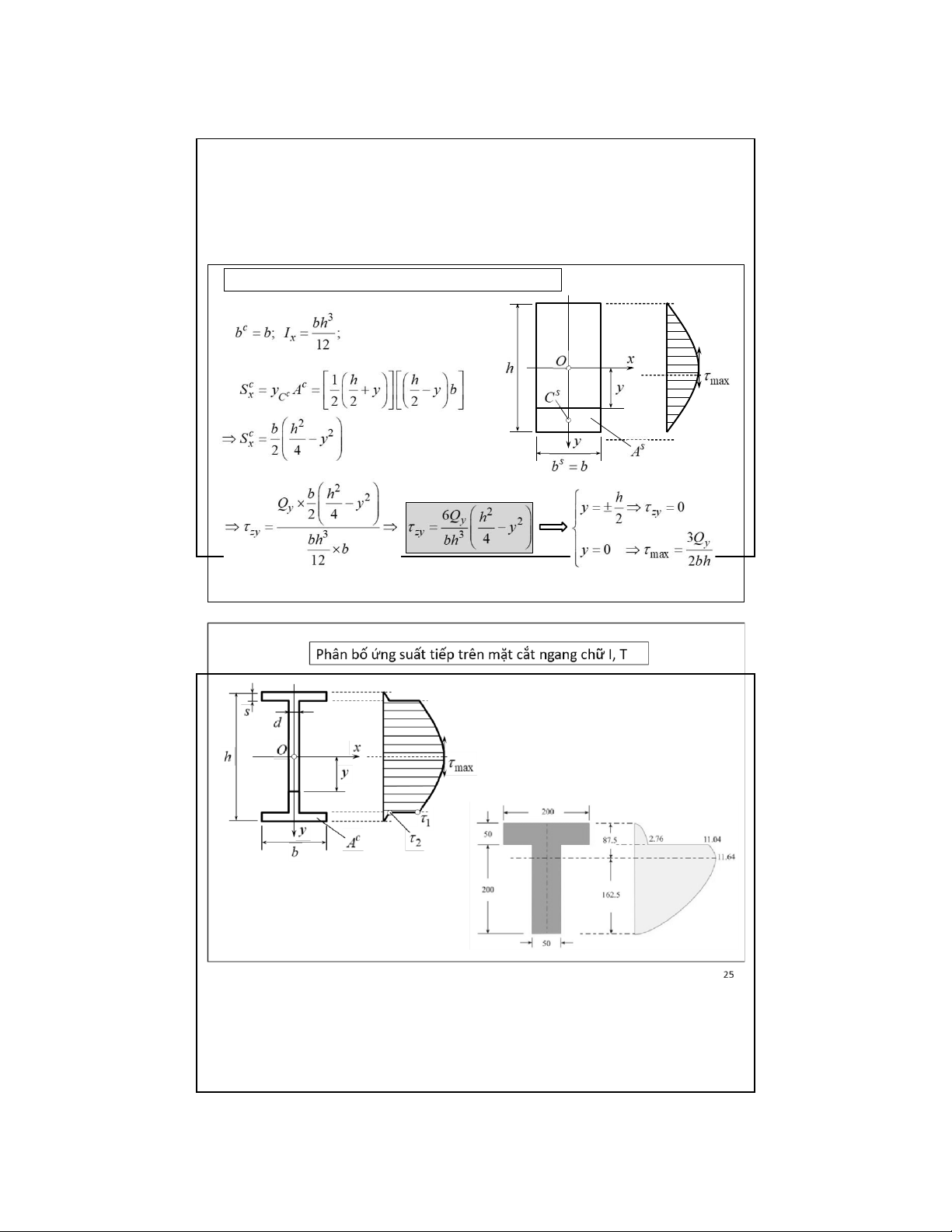
6.3.2 Ứng suất tiếp trên mặt cắt ngang – Công thức Zhuravskii
Q y –Lựccắttrênmặtcắtngangđangxét
A c –Phầndiệntíchbịcắt
S x c –Mômentĩnhcủadiệntích A c đốivớitrục Ox
I x –Mômenquántínhcủamặtcắtngangđối
vớitrụcquántínhchínhtrungtâm Ox
b c –Chiềurộngcủamặtcắtngangtạiđiểm tínhứngsuất
y C –tọađộtrọngtâmphầndiệntích A c 23 lOMoAR cPSD| 58970315 09-Aug-22
6.3. Thanh thẳng chịu uốn ngang phẳng
6.3. Thanh thẳng chịu uốn ngang phẳng
Phân bố ứng suất tiếp trên mặt cắt ngang chữ nhật 24 lOMoAR cPSD| 58970315 09-Aug-22
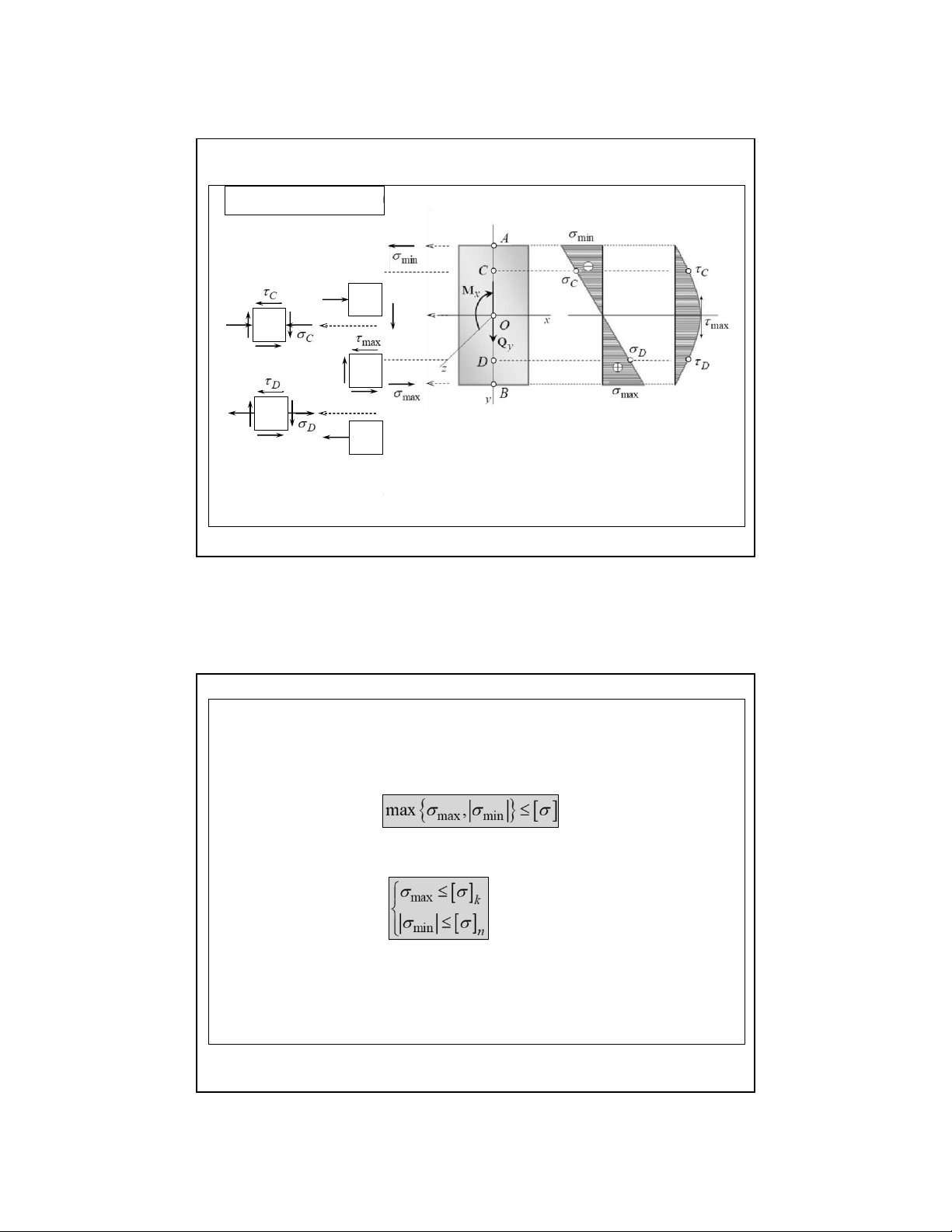
6.3. Thanh thẳng chịu uốn ngang phẳng 6.3.3 X Đi ét dề ầu m ki ti ệ ế n b t di ề ệ n n
chữ nhật chịu uốn ngang phẳng. Ta có phân bố ứng
suất trên tiết diện dầm: A, B – TTUS đơn
O – TTUS trượt thuần túy
C, D – TTUS phẳng đặc biệt 26
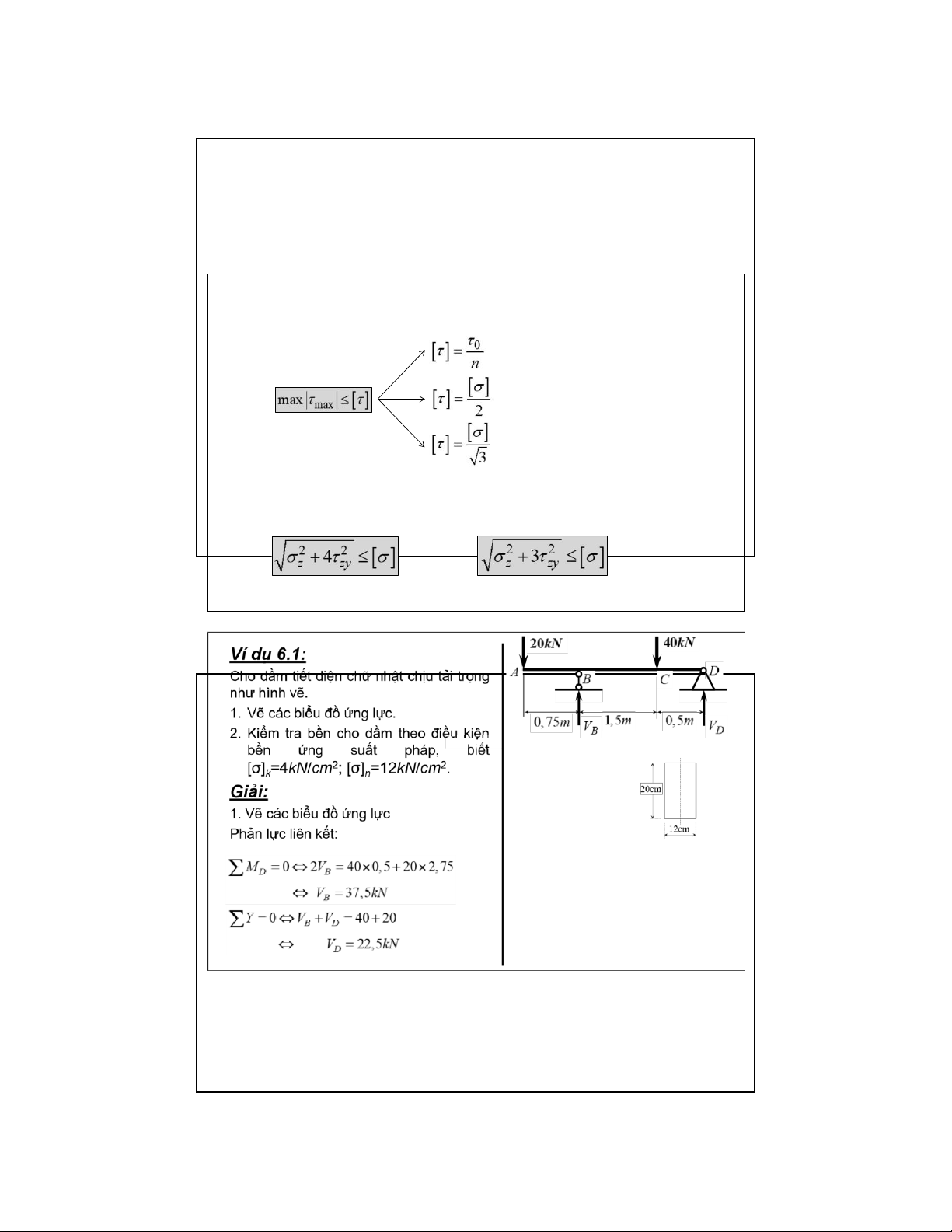
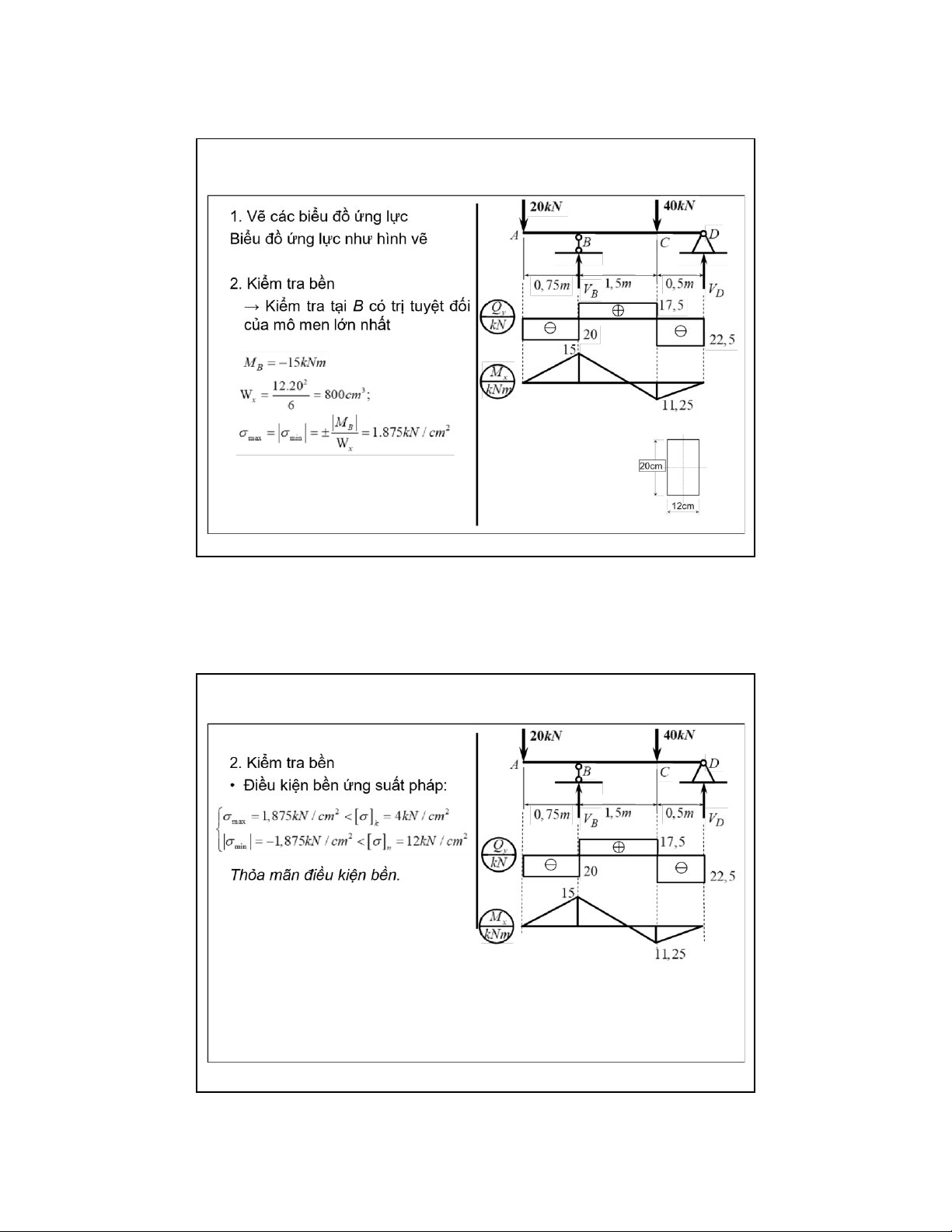
6.3. Thanh thẳng chịu uốn ngang phẳng
❖ Điều kiện bền cho điểm ở TTUS đơn (đk bền ứng suất pháp): Với vật liệu dẻo:
Kiểm tra tai mặt cắt có trị tuyệt đối của mô men là lớn nhất Với vật liệu giòn:
Tiết diện có 2 trục đối xứng, kiểm tra tai mặt cắt có trị tuyệt đối của mô men là lớn nhất
Tiết diện có 1 trục đối xứng, kiểm tra tại tiết diện có mô men âm lớn nhất
và mô men dương lớn nhất 27 lOMoAR cPSD| 58970315 09-Aug-22
6.3. Thanh thẳng chịu uốn ngang phẳng
6.3 . Thanh thẳng chịu uốn ngang phẳng
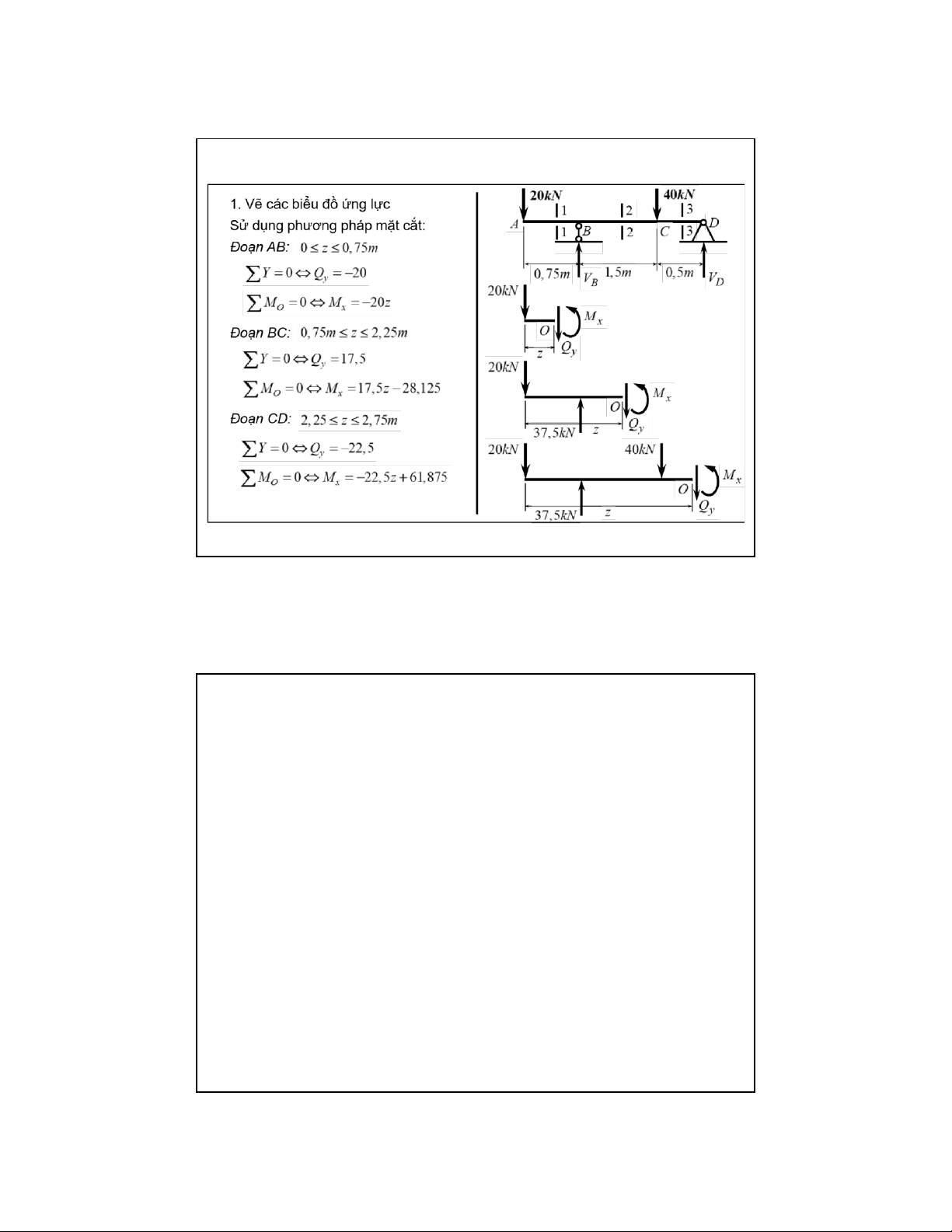
❖ Điều kiện bền cho điểm ở TTUS trượt thuần túy:
Kiểm tra tại tiết diện có lực cắt lớn nhất
: τ 0 được xác định từ thí nghiệm : Thuyết bền 3 : Thuyết bền 4
❖ Điều kiện bền cho điểm ở TTUS phẳng đặc biệt
Kiểm tra tại tiết diện có mô men và lực cắt cùng lớn Thuyết bền 3 Thuyết bền 4 28 29 lOMoAR cPSD| 58970315 09-Aug-22
6.3. Thanh thẳng chịu uốn ngang phẳng 30 lOMoAR cPSD| 58970315 09-Aug-22
6.3. Thanh thẳng chịu uốn ngang phẳng 31
6.3. Thanh thẳng chịu uốn ngang phẳng 32 lOMoAR cPSD| 58970315 09-Aug-22
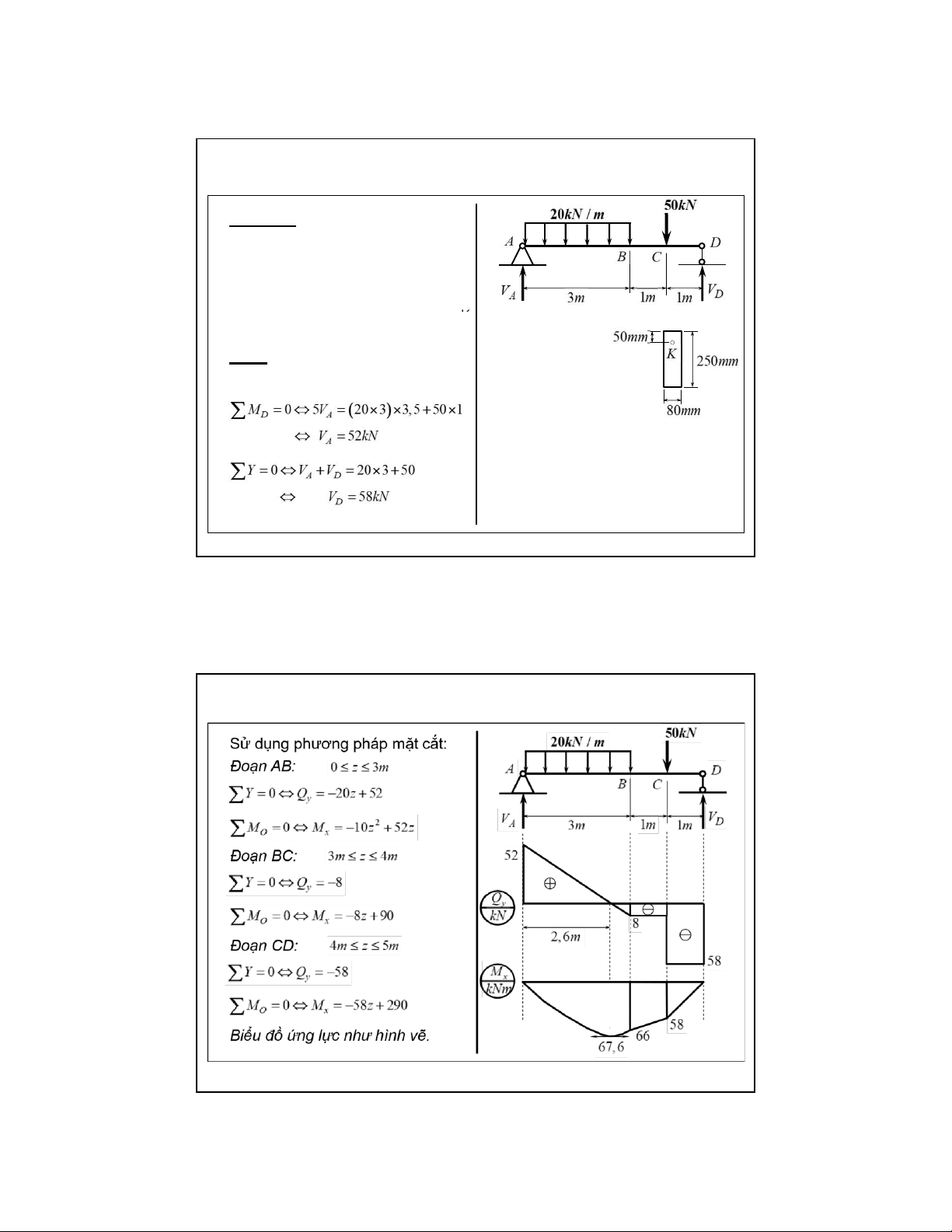
6.3. Thanh thẳng chịu uốn ngang phẳng Vídụ6.2:
Dầmtiếtdiệnchữnhậtchịulựcnhư
hìnhvẽ.Biếtứngsuấtchophép
[σ]=16 kN / cm 2 . ▪ Vẽbiểuđồứnglực
▪ XácđịnhcácứngsấttạiđiểmK
thuộctiếtdiệnchínhgiữađoạnAB Giải: Phảnlực: 33
6.3. Thanh thẳng chịu uốn ngang phẳng 34