











Preview text:
CHÖÔNG 7
PHAÂN BOÁ TAÛI TROÏNG PHAÙP TUYEÁN,
KHAÛ NAÊNG BAÙM VAØ TÍNH OÅN ÑÒNH CUÛA OÂ TOÂ. Muïc tieâu :
Sau khi hoïc xong chöông naøy caùc sinh vieân coù khaû naêng:
1. Xaùc ñònh ñöôïc phaûn löïc thaúng goùc taùc duïng leân caùc baùnh xe trong nhöõng ñieàu kieän
chuyeån ñoäng khaùc nhau cuûa oâ toâ.
2. Xaùc ñònh ñöôïc heä soá phaân boá taûi troïng leân caùc baùnh xe cuûa oâ toâ.
3. Ñònh nghóa ñöôïc heä soá thay ñoåi taûi troïng leân caùc baùnh xe cuûa oâ toâ.
4. Ñònh nghóa ñöôïc tính oån ñònh cuûa oâ toâ, tính oån ñònh doïc tónh, tính oån ñònh doïc ñoäng.
5. Xaùc ñònh ñöôïc goùc doác giôùi haïn maø taïi ñoù oâ toâ bò laät ñoå hay bò tröôït trong nhöõng
ñieàu kieän chuyeån ñoäng khaùc nhau.
6. Xaùc ñònh ñöôïc vaän toác giôùi haïn maø taïi ñoù oâ toâ bò laät ñoå hay bò tröôït trong nhöõng
ñieàu kieän chuyeån ñoäng khaùc nhau. 104
7.1. PHAÂN BOÁ TAÛI TROÏNG VAØ KHAÛ NAÊNG BAÙM CUÛA OÂ TOÂ:
7.1.1. Xaùc ñònh phaûn löïc thaúng goùc cuûa ñöôøng taùc duïng leân caùc baùnh xe trong maët phaúng doïc:
Nhö chuùng ta ñaõ bieát: Tính oån ñònh cuûa oâ toâ phuï thuoäc vaøo söï phaân boá taûi troïng leân
caùc caàu vaø khaû naêng baùm giöõa caùc baùnh xe vôùi maët ñöôøng. Trong ñoù khaû naêng baùm laïi phuï
thuoäc vaøo phaûn löïc thaúng goùc cuûa ñöôøng taùc duïng caùc baùnh xe vaø heä soá baùm giöõa baùnh xe vôùi maët ñöôøng.
Khi xe chuyeån ñoäng, caùc phaûn löïc thaúng goùc taùc duïng leân caùc baùnh xe luoân thay ñoåi
tuyø thuoäc vaøo traïng thaùi vaø ñieàu kieän chuyeån ñoäng. Giaù trò cuûa caùc phaûn löïc naøy coù aûnh
höôûng tröïc tieáp ñeán caùc chæ tieâu kyõ thuaät cuûa oâ toâ nhö: khaû naêng keùo vaø baùm, chaát löôïng
phanh, tính oån ñònh vaø tuoåi thoï cuûa caùc chi tieát. Bôûi vaäy, chuùng ta seõ xaùc ñònh caùc phaûn löïc
ñoù trong caùc tröôøng hôïp cuï theå sau:
7.1.1.1. Tröôøng hôïp chuyeån ñoäng toång quaùt:
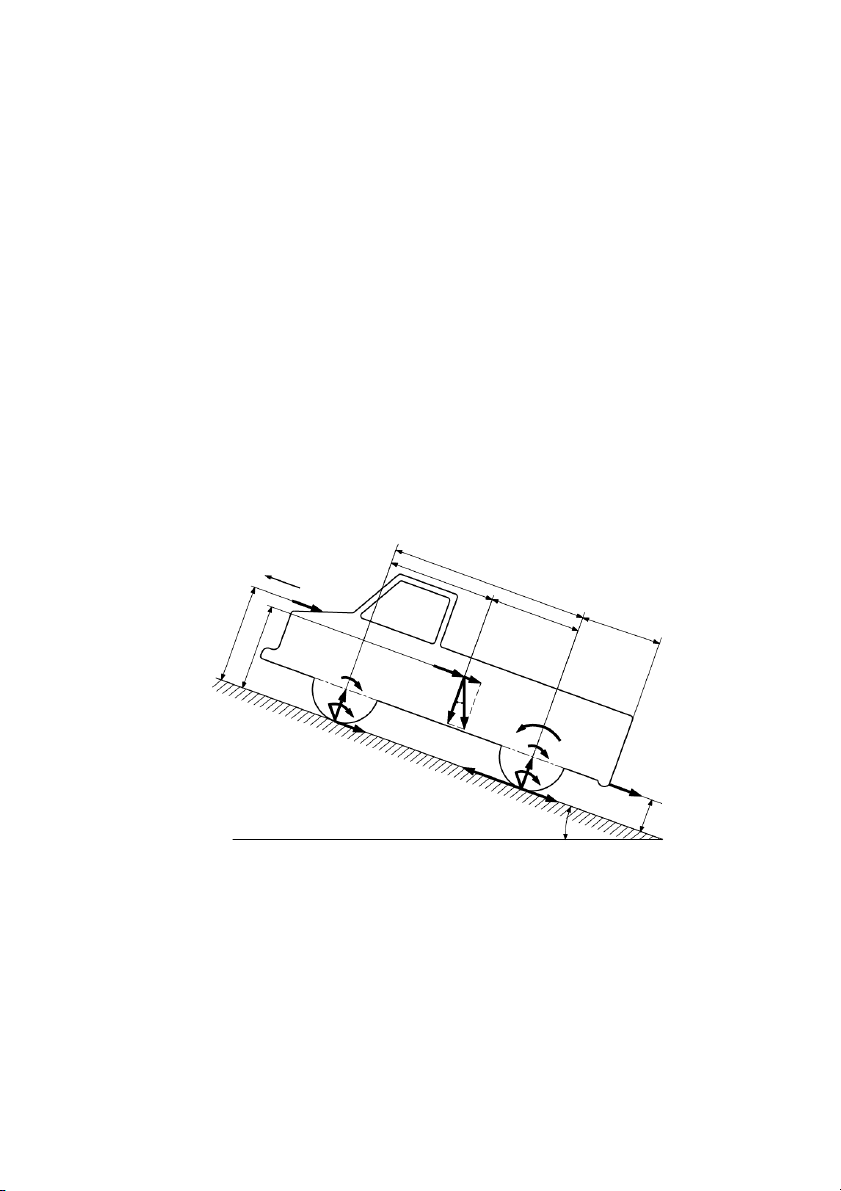
Xeùt oâ toâ chuyeån ñoäng leân doác khoâng oån ñònh coù keùo rômoùc: v a L F b h l m hg F M j T j1 Gsin Z1 Gcos Mf1 M k G O1 Ff1 Mj2 Z2 Mf2 Fm F k O2 h m Ff2
Hình 7.1: Sô ñoà caùc löïc vaø moâmen taùc duïng leân oâtoâ khi chuyeån ñoäng leân doác. 105
Treân hình 7.1 trình baøy sô ñoà caùc löïc vaø moâmen taùc duïng leân oâtoâ ñang chuyeån ñoäng
taêng toác ôû treân doác. YÙ nghóa cuûa caùc kyù hieäu ôû treân hình veõ nhö sau:
G – Troïng löôïng toaøn boä cuûa oâtoâ. F k L
– öïc keùo tieáp tuyeán ôû caùc baùnh xe chuû ñoäng. Ff 1
– Löïc caûn laên ôû caùc baùnh xe caàu tröôùc. Ff 2
– Löïc caûn laên ôû caùc baùnh xe caàu sau. F
– Löïc caûn khoâng khí.
Fi – Löïc caûn leân doác.
Fj – Löïc caûn quaùn tính khi xe chuyeån ñoäng khoâng oån ñònh (coù gia toác).
Fm – Löïc caûn ôû moùc keùo. Mf1 M –
oâmen caûn laên ôû caùc baùnh xe caàu tröôùc. Mf2 M –
oâmen caûn laên ôû caùc baùnh xe caàu sau. G
– oùc doác cuûa maët ñöôøng. f – Heä soá caûn laên. r b B
– aùn kính tính toaùn cuûa baùnh xe. hg T
– oïa ñoä troïng taâm cuûa xe theo chieàu cao. hm K
– hoaûng caùch töø ñieåm ñaët löïc keùo moùc ñeán maët ñöôøng. L C
– hieàu daøi cô sôû cuûa oâ toâ. lm K
– hoaûng caùch töø taâm baùnh xe sau ñeán ñieåm ñaët löïc keùo moùc.
Z1, Z2 – Phaûn löïc phaùp tuyeán cuûa maët ñöôøng taùc duïng leân caùc baùnh xe ôû caàu tröôùc vaø caàu sau. Mj , M 1 j 2 M –
oâmen caûn quaùn tính cuûa baùnh xe, thoâng thöôøng trò soá naøy nhoû neân coù theå boû qua.
Qua vieäc laáy moâmen laàn löôït ñoái vôùi ñieåm O , 2 O1 (O , 1 O
2 laø giao ñieåm cuûa maët
ñöôøng vôùi maët phaúng thaúng ñöùng qua truïc cuûa baùnh xe caàu tröôùc, caàu sau) vaø ruùt goïn ta ñöôïc: G cos (
b fr ) (Gsin F F )h F h b j g m m Z = (7.1) 1 L G cos (
a fr ) (Gsin F F )h F h Z b j g m m (7.2) 2 L
7.1.1.2. Tröôøng hôïp xe chuyeån ñoäng oån ñònh treân ñöôøng naèm ngang, khoâng keùo rômoùc:
Trong tröôøng hôïp naøy thì: Xe chuyeån ñoäng oån ñònh neân Fj = 0; khoâng keùo rômoùc
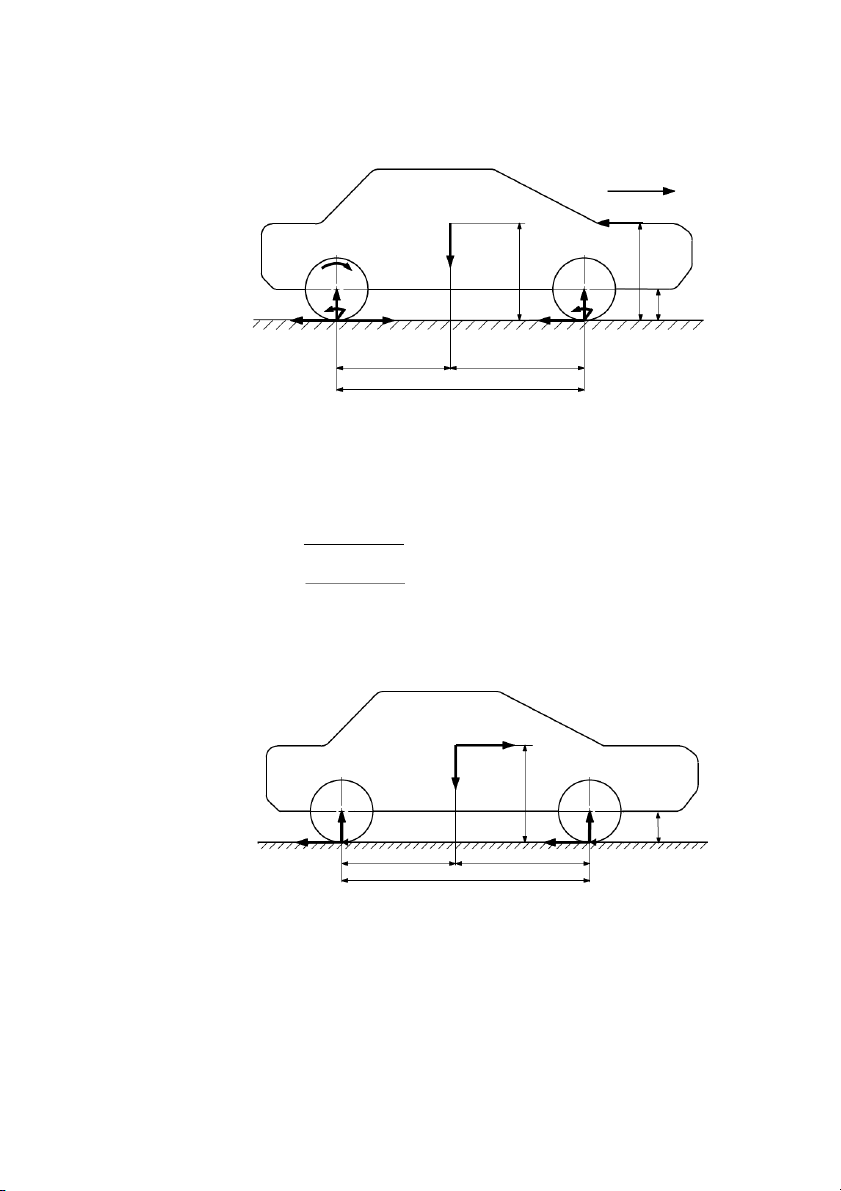
neân Fm = 0, vaø xe chuyeån ñoäng treân ñöôøng baèng α = 0 neân Fi = Gsin α = 0. 106 v F T Mk G h h g M M f2 Z2 F f1 Z1 k rb O2 F O f2 1 Ff1 b a L
Hình 7.2: Sô ñoà moâmen vaø löïc taùc duïng leân oâ toâ chuyeån ñoäng treân ñöôøng naèm ngang.
Ñeå xaùc ñònh caùc löïc Z ,
1k Z2k ta laäp phöông trình moâmen ñoái vôùi ñieåm O2 vaø
O1 roài ruùt goïn, ta ñöôïc: G(b fr ) F h Z b g (7.3) k 1 L G a ( fr ) F h Z b g 2k L
7.1.1.3. Tröôøng hôïp xe ñang phanh treân ñöôøng naèm ngang, khoâng keùo rômoùc: Fj T G h g Z2p Z1p rb Ff2 Ff1 F F p2 O2 b a p1 O1 L
Hình 7.3: Sô ñoà löïc taùc duïng leân oâ toâ khi phanh treân ñöôøng naèm ngang, khoâng keùo rômoùc. 107
Trong tröôøng hôïp naøy ta coi löïc caûn khoâng khí F 0 , moâmen caûn laên Mf 0, löïc
quaùn tính cuøng chieàu chuyeån ñoäng cuûa xe.
Töông töï nhö treân ta cuõng xaùc ñònh ñöôïc Z
1p vaø Z2p thoâng qua vieäc laáy moâmen ñoái vôùi ñieåm O va 2 ø O , r 1
oài ruùt goïn ta ñöôïc: Gb F h j g Z 1p L (7.4) Ga F h j g Z 2p L
7.1.1.4. Tröôøng hôïp xe ñöùng yeân treân ñöôøng naèm ngang, khoâng keùo rômoùc:
Trong tröôøng hôïp naøy chæ coøn ba löïc taùc duïng leân xe: Troïng löôïng toaøn boä cuûa xe G
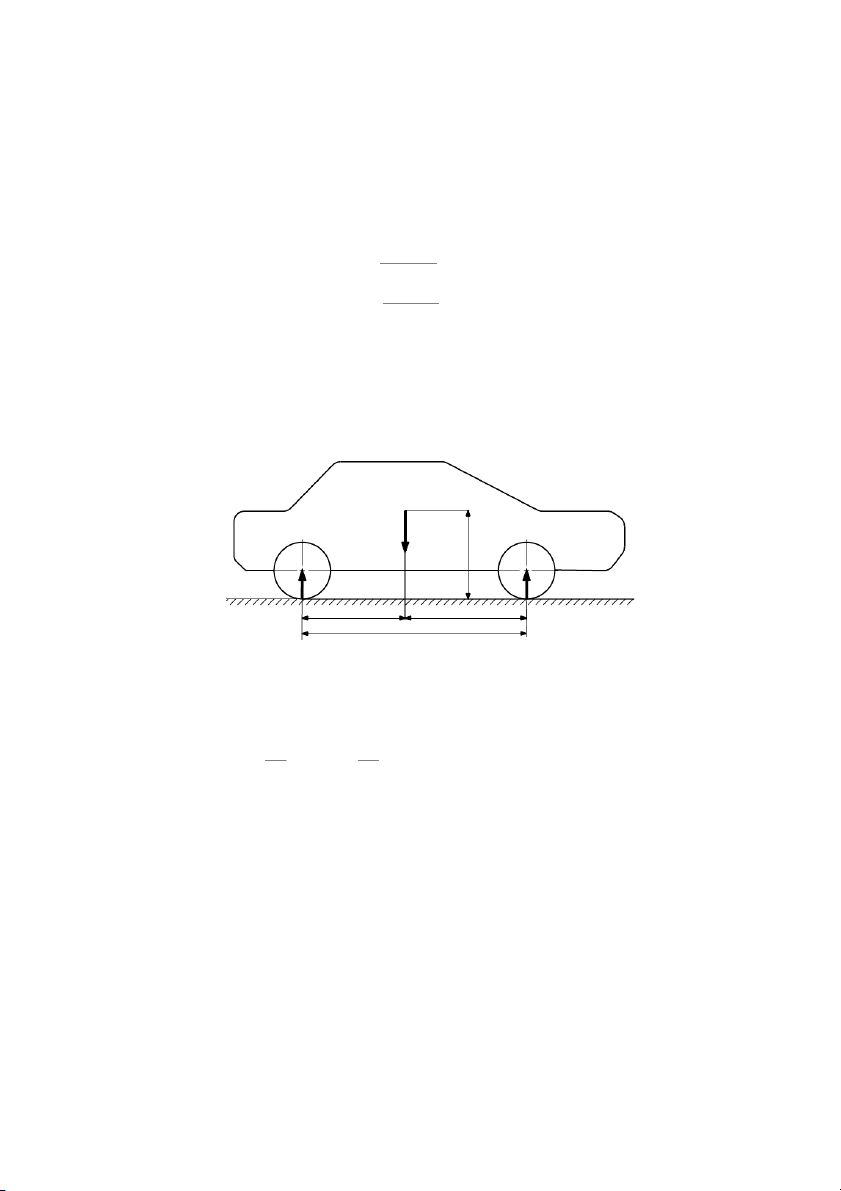
vaø caùc phaûn löïc thaúng ñöùng taùc duïng leân caùc baùnh xe cuûa caàu tröôùc vaø caàu sau ôû traïng thaùi tónh Z1t vaø Z2t . T G h g Z Z 2t 1t O b a 2 O1 L
Hình 7.4: Sô ñoà löïc taùc duïng leân xe khi ñöùng yeân.
Z1t vaø Z2t cuõng ñöôïc xaùc ñònh baèng caùch laáy moâmen ñoái vôùi ñieåm O va 2 ø O1: Gb Ga Z = ; Z = (7.5) 1t 2t L L
7.1.1.5. Heä soá phaân boá taûi troïng leân caùc baùnh xe cuûa oâ toâ:
Trong thöïc teá, oâ toâ laøm vieäc ôû nhöõng ñieàu kieän khaùc nhau tuyø thuoäc vaøo ñieàu kieän
ñöôøng xaù vaø söï ñieàu khieån cuûa ngöôøi laùi. Do ñoù trò soá caùc phaûn löïc thaúng goùc töø ñöôøng taùc
duïng leân caùc baùnh xe cuõng bò thay ñoåi theo. Tuy nhieân, caùc hôïp löïc Z 1+ Z 2vaãn luoân baèng
troïng löôïng cuûa xe. Nghóa laø khi chuyeån ñoäng tieán, thì troïng löôïng phaân ra caàu tröôùc seõ
giaûm ñi vaø troïng löôïng phaân ra caàu sau seõ taêng leân. Khi phanh oâ toâ, troïng löôïng phaân ra
caàu sau giaûm ñi, coøn phaàn troïng löôïng phaân ra caàu tröôùc seõ taêng leân. 108
Ñeå ñaùnh giaù söï phaân boá taûi troïng ngöôøi ta ra ñöa khaùi nieäm heä soá phaân boá taûi troïng
vaø ñöôïc ñaëc tröng bôûi tæ soá : Z1 n = 1 G (7.6) Z2 n = 2 G Trong ñoù: n1, n -
2 Heä soá phaân boá taûi troïng leân caùc baùnh xe caàu tröôùc vaø caàu sau.
G - Troïng löôïng toaøn boä cuûa oâ toâ.
Heä soá phaân boá taûi troïng ñöôïc xaùc ñònh öùng vôùi töøng tröôøng hôïp cuï theå sau:
7.1.1.5.1. Xe ñöùng yeân treân ñöôøng naèm ngang, khoâng keùo rômoùc:
Thay caùc giaù trò cuûa Z va 1 ø Z ô
2 û (7.5) vaøo (7.6) ta ñöôïc: Z Gb b 1t n = = = 1t G GL L (7.7) Z Ga a 2t n = = = 2t G GL L Trong ñoù :
n1t , n2t - Heä soá phaân boá taûi troïng tónh leân caùc baùnh xe caàu tröôùc vaø caàu sau.
7.1.1.5.2. Xe chuyeån ñoäng oån ñònh treân ñöôøng naèm ngang, khoâng keùo rômoùc: Thay caùc giaù trò Z va 1
ø Z2 ôû bieåu thöùc (7.3) vaøo (7.6) ta ñöôïc: Z k 1 Gb Gfr F h Gfr F h n b g n b g k 1 G GL GL t 1 GL (7.8) Z Ga Gfr F h Gfr F h b g b g 2k n n t 2k 2 G GL GL GL Trong ñoù : n1k , n -
2k Heä soá phaân boá taûi troïng leân caùc baùnh xe tröôùc vaø sau khi xe
chuyeån ñoäng tònh tieán. 109
7.1.1.5.3. Xe ñang phanh treân ñöôøng naèm ngang khoâng keùo rômoùc: Thay caùc giaù trò Z va 1p
ø Z2p ôû bieåu thöùc (7.4) vaøo (7.6) ta ñöôïc: 1 Z p Gb j F hg j F hg n n 1p 1t G GL GL GL (7.9) Z 2p Ga Fjh g Fjh g n n 2p 2t G GL GL GL Trong ñoù : n , n 1p
2p - Heä soá phaân boá taûi troïng ra caàu tröôùc vaø caàu sau khi phanh xe.
F - Löïc quaùn tính cuûa oâ toâ khi phanh. j
Qua caùc tröôøng hôïp nghieân cöùu treân ta coù nhaän xeùt sau:
- Söï phaân boá taûi troïng leân caùc baùnh xe phuï thuoäc vaøo toïa ñoä troïng taâm cuûa xe.
- Toïa ñoä troïng taâm cuûa xe aûnh höôûng tôùi chaát löôïng baùm cuûa baùnh xe vôùi maët
ñöôøng, cuõng nhö tính oån ñònh vaø tính daãn höôùng cuûa xe.
- Khi phanh oâ toâ, löïc quaùn tính höôùng veà phía tröôùc neân phaûn löïc taùc duïng leân
caàu tröôùc lôùn hôn caàu sau .
- Ñoái vôùi oâ toâ du lòch, thoâng thöôøng : Z = 1 Z = 2 0,5G.
- Ñoái vôùi xe taûi, thoâng thöôøng : Z = 2 (0,7 0,75)G.
7.1.1.6. Heä soá thay ñoåi taûi troïng leân caùc baùnh xe cuûa oâ toâ:
Khi xe chuyeån ñoäng, do traïng thaùi vaø ñieàu kieän chuyeån ñoäng luoân thay ñoåi, bôûi vaäy
taûi troïng taùc duïng leân caùc baùnh xe ôû caàu tröôùc vaø caàu sau cuõng luoân thay ñoåi so vôùi xe
ñöùng yeân treân ñöôøng naèm ngang. Ñeå thaáy ñöôïc taûi troïng ñoäng thay ñoåi taêng hay giaûm so
vôùi taûi troïng tónh, chuùng ta seõ ñöa ra khaùi nieäm: Heä soá thay ñoåi taûi troïng ( hoaëc laø: heä soá
thay ñoåi phaûn löïc) leân caùc baùnh xe vaø ñöôïc tính nhö sau: m1 = Z1ñ / Z1t (7.10) m2 = Z2ñ / Z2t (7.11) ÔÛ ñaây: m1, m 2 H –
eä soá thay ñoåi taûi troïng leân caùc baùnh xe ôû caàu tröôùc vaø caàu sau. Z1ñ, Z2ñ T –
aûi troïng ñoäng taùc duïng leân caùc baùnh xe ôû caàu tröôùc vaø caàu sau.
Z1t, Z2t – Taûi troïng tónh taùc duïng leân caùc baùnh xe ôû caàu tröôùc vaø caàu sau.
Khi xe taêng toác ( hoaëc leân doác, hoaëc chuyeån ñoäng ngöôïc chieàu gioù) thì m < 1 1,
m2 >1 vaø seõ ñöôïc kí hieäu laø m , m 1k . 2k
Khi xe ñang phanh (hoaëc xuoáng doác, hoaëc chuyeån ñoäng thuaän chieàu gioù) thì m1 > 1,
m2 < 1 vaø seõ ñöôïc kyù hieäu laø m , m . 1p 2p Caùc heä soá m , 1 m
2 ñöôïc söû duïng thöôøng xuyeân khi tính toaùn caùc heä thoáng phanh,
treo, laùi vaø caùc caàu xe. 110
7.1.2. Xaùc ñònh phaûn löïc thaúng goùc cuûa ñöôøng taùc duïng leân caùc baùnh xe oâ toâ trong maët phaúng ngang:
7.1.2.1. Tröôøng hôïp chuyeån ñoäng toång quaùt: Xe chuyeån ñoäng quay voøng treân ñöôøng
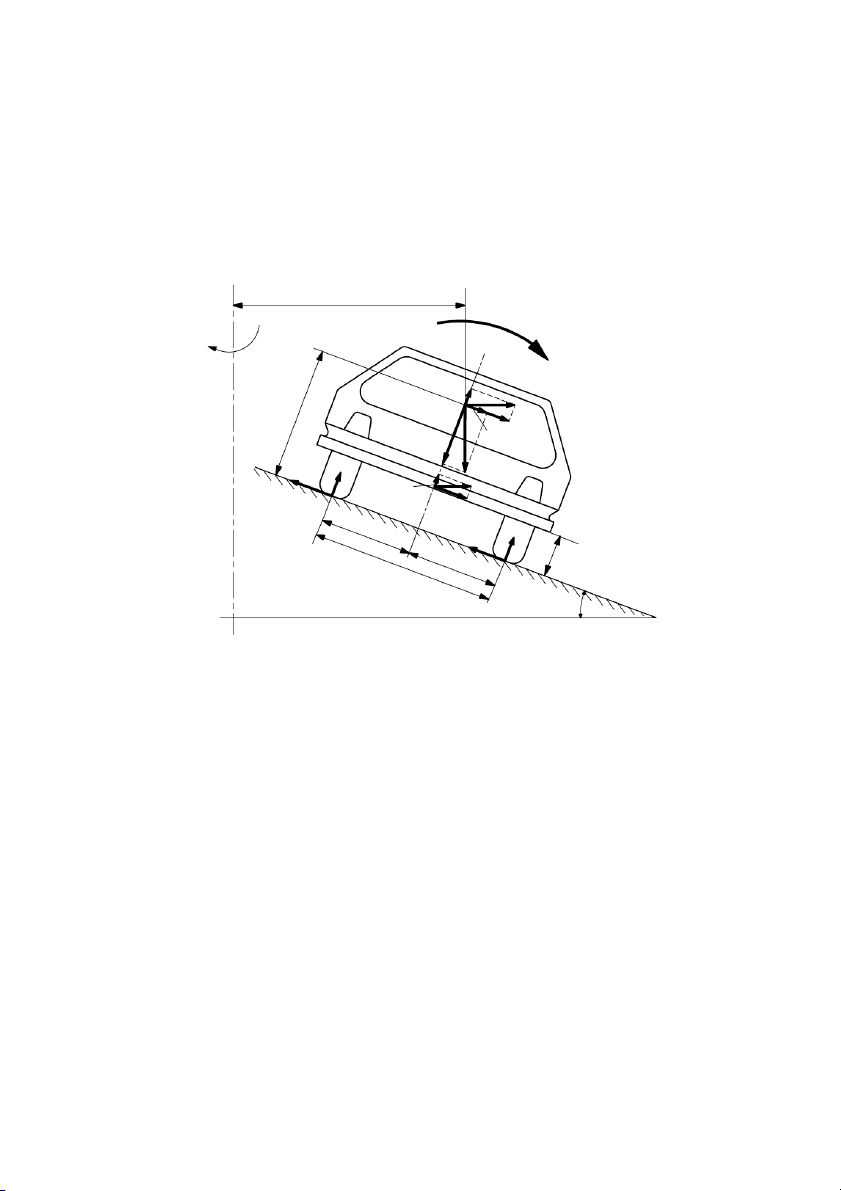
nghieâng ngang: R Y Mjn Flsin h â toâ g Fl T uûa o Flcos Gcos Gsin øng c Z” G F B msin F ay vo D m Y” Fmcos ruïc qu c/2 Z’ T A c c/2 hm Y’ Y
Hình 7.5: Sô ñoà löïc vaø moâmen taùc duïng leân oâ toâ khi quay voøng
treân ñöôøng nghieâng ngang.
Trong tröôøng hôïp naøy ta giaû thuyeát raèng veát cuûa baùnh xe tröôùc vaø sau truøng nhau,
troïng taâm cuûa xe naèm trong maët phaúng ñoái xöùng doïc, löïc vaø moâmen taùc duïng leân oâ toâ goàm:
G – Troïng löôïng toaøn boä cuûa oâ toâ vaø ñöôïc phaân ra caùc thaønh phaàn theo goùc nghieâng ngang β .
M – Moâmen cuûa caùc löïc quaùn tính tieáp tuyeán cuûa caùc phaàn quay cuûa ñoäng cô jn
vaø heä thoáng truyeàn löïc taùc duïng trong maët phaúng ngang khi xe chuyeån ñoäng khoâng oån ñònh.
Fm – Löïc keùo ôû moùc keùo ( phöông cuûa löïc Fm truøng vôùi phöông naèm ngang cuûa maët ñöôøng). Fl – Löïc ly taâm 111 2 ÔÛ ñaây: Gv F 1 gR v V
– aän toác chuyeån ñoäng cuûa xe.
R – Baùn kính quay voøng cuûa oâ toâ. g G
– ia toác troïng tröôøng. Z’1, Z” va 1 ø Z’ , Z 2
”2 – Caùc phaûn löïc thaúng goùc cuûa ñöôøng taùc duïng leân baùnh xe
beân phaûi vaø beân traùi ôû caàu tröôùc vaø caàu sau. Y’1, Y”1 va ø Y’2 va
ø Y”2 – Caùc phaûn löïc ngang töø ñöôøng taùc duïng leân baùnh xe
beân phaûi vaø beân traùi ôû caàu tröôùc vaø caàu sau.
c – Chieàu roäng cô sôû cuûa oâ toâ.
YY – Truïc quay voøng cuûa oâ toâ. β G
– oùc nghieâng ngang cuûa ñöôøng.
Ñeå xaùc ñònh trò soá caùc phaûn löïc beân traùi, ta laäp phöông trình caân baèng moâmen ñoái
vôùi ñöôøng thaúng ñi qua hai ñieåm tieáp xuùc ( hai ñieåm A – hình 7.5 ) cuûa caùc baùnh xe beân
phaûi vôùi maët ñöôøng, ta ñöôïc: Z” = Z”1 + Z” 2 = = 1 c c c G( co s h si n ) F (h co s sin) M F (h co s sin ) (7.12) g m m jn 1 g c 2 2 2
Töông töï, ta laäp phöông trình caân baèng moâmen ñoái vôùi ñöôøng thaúng ñi qua hai ñieåm
tieáp xuùc ( hai ñieåm B ) cuûa caùc baùnh xe beân traùi vôùi maët ñöôøng, ta xaùc ñònh ñöôïc trò soá caùc phaûn löïc beân phaûi: Z’ = Z’1 + Z’ = 2 =1 c c c G( co s h si n ) F (h co s sin ) M F (h co s sin ) (7.13) g m m jn 1 g c 2 2 2
Muoán xaùc ñònh phaûn löïc ngang Y ,1 ta cuõng laäp phöông trình moâmen ñoái vôùi ñöôøng
thaúng ñi qua hai ñieåm tieáp xuùc ( hai ñieåm O2
– hình 7.1 ) cuûa caùc baùnh xe sau vôùi maët ñöôøng, ta ñöôïc: Y
Gbsin F bcos F l cos 1 = Y’ 1 + Y” = 1 1 m m (7.14) L
Töông töï nhö treân, ta laäp phöông trình moâmen ñoái vôùi ñöôøng thaúng ñi qua hai ñieåm
tieáp xuùc ( hai ñieåm O 1) cuûa caùc baùnh xe tröôùc vôùi maët ñöôøng ñeå xaùc ñònh phaûn löïc ngang Y2: Y
Ga sin F a cos F (l L) cos 2 = Y’ 2 + Y”2 = 1 m m (7.15) L 112 Trong ñoù: Y1 P
– haûn löïc ngang cuûa ñöôøng taùc duïng leân caùc baùnh xe tröôùc. Y2 P
– haûn löïc ngang cuûa ñöôøng taùc duïng leân caùc baùnh xe sau. lm K
– hoaûng caùch töø ñieåm ñaët löïc keùo moùc ñeán ñieåm O 2 (xem hình 7.1). 7. .
1 2.2. Tröôøng hôïp xe ñöùng yeân treân doác nghieâng ngang, khoâng keùo rômoùc:
Trong tröôøng hôïp naøy thì löïc ly taâm Fl = 0 vaø löïc keùo moùc Fm = 0.
Ruùt goïn bieåu thöùc (7.12) vaø (7.13) ta xaùc ñònh ñöôïc caùc phaûn löïc thaúng goùc cuûa
ñöôøng taùc duïng leân caùc baùnh xe beân traùi vaø beân phaûi nhö sau: Z” = G c ( cosβ - h sinβ) g c 2 (7.16) G c Z’ = ( cosβ + h sinβ) g c 2
Töø caùc bieåu thöùc tính toaùn treân, ta coù nhaän xeùt sau:
- Trò soá cuûa caùc phaûn löïc thaúng goùc cuõng nhö caùc phaûn löïc ngang töø ñöôøng taùc
duïng leân caùc baùnh xe phuï thuoäc vaøo trò soá, ñieåm ñaët vaø chieàu taùc duïng cuûa caùc
ngoaïi löïc taùc duïng trong maët phaúng cuûa oâ toâ.
- Caùc phaûn löïc naøy aûnh höôûng ñeán tính oån ñònh vaø tính naêng daãn höôùng cuûa oâ toâ.
7.2. TÍNH OÅN ÑÒNH CUÛA OÂ TOÂ :
Tính oån ñònh cuûa oâ toâ laø khaû naêng ñaûm baûo giöõ cho quyõ ñaïo chuyeån ñoäng theo yeâu
caàu trong moïi ñieàu kieän chuyeån ñoäng khaùc nhau. Tuyø thuoäc ñieàu kieän söû duïng, oâ toâ coù theå
ñöùng yeân, chuyeån ñoäng treân ñöôøng doác ( ñöôøng coù goùc nghieâng doïc hoaëc nghieâng ngang)
coù theå phanh hoaëc quay voøng ôû caùc loaïi ñöôøng khaùc nhau ( ñöôøng xaáu, ñöôøng toát…).
Trong nhöõng ñieàu kieän phöùc taïp nhö vaäy, oâ toâ phaûi giöõ ñöôïc quyõ ñaïo cuûa noù sao cho
khoâng bò laät ñoå, khoâng bò tröôït hoaëc thuøng xe khoâng bò nghieâng, caàu xe bò quay leäch trong
giôùi haïn cho pheùp ñeå ñaûm baûo chuùng chuyeån ñoäng an toaøn, naâng cao vaän toác chuyeån ñoäng
cuûa xe coù nghóa laø taêng tính kinh teá vaø tính oån ñònh cuûa oâ toâ trong moïi ñieàu kieän laøm vieäc.
Trong phaàn naøy, chuùng ta nghieân cöùu tính oån ñònh cuûa oâ toâ ñeå ñaûm baûo khaû naêng
khoâng bò laät ñoå hoaëc bò tröôït trong nhöõng ñieàu kieän chuyeån ñoäng khaùc nhau.
7.2.1. Tính oån ñònh doïc cuûa oâ toâ:
7.2.1.1 Tính oån ñònh doïc tónh:
Tính oån ñònh doïc tónh cuûa oâ toâ laø khaû naêng ñaûm baûo cho xe khoâng bò laät ñoå hoaëc bò
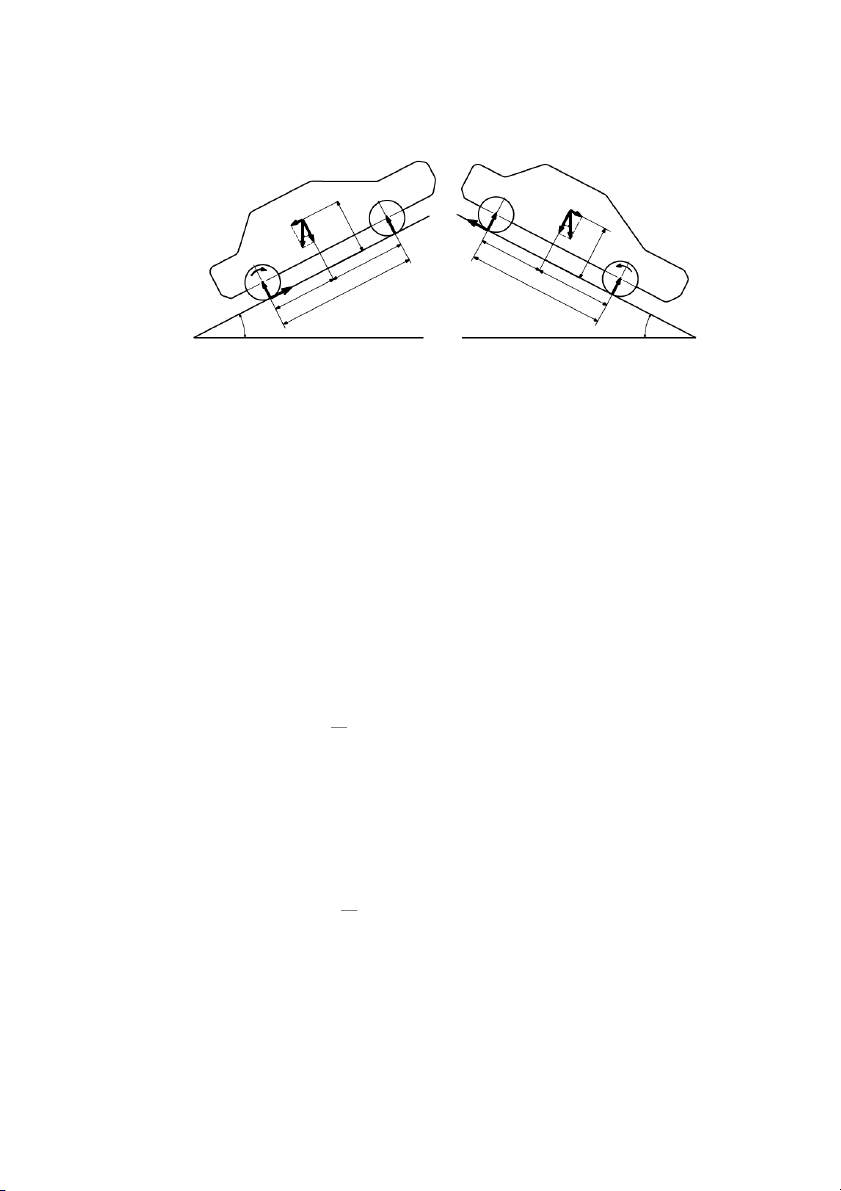
tröôït khi ñöùng yeân treân ñöôøng doác doïc. 113 T F GsinT p Z2 Gsin Z1 Gcos Gcos O ' O2 1 α t G G t M a b Mf f Fp b L a L Z Z 2 1 O O1 2 ' t αt a) b)
Hình 7.6: Sô ñoà löïc vaø moâmen taùc duïng leân oâ toâ khi ñöùng yeân.
a- OÂ toâ ñöùng quay ñaàu treân doác.
b- OÂ toâ ñöùng quay ñaàu xuoáng doác.
*Xeùt oån ñònh theo ñieàu kieän laät ñoå :
+ Xe ñaäu treân doác ñaàu höôùng leân (hình 7.6a):
- Xu höôùng laät ñoå: Xe coù xu höôùng laät quanh truïc naèm trong maët phaúng cuûa ñöôøng
vaø ñi qua ñieåm tieáp xuùc cuûa hai baùnh xe caàu sau vôùi maët ñöôøng (ñieåm O ) 2 theo phöông doïc.
- Traïng thaùi giôùi haïn laät ñoå: Khi goùc α taêng daàn ñeán goùc α (goùc giôùi haïn maø xe t
bò laät khi ñöùng quay ñaàu leân doác) thì caùc baùnh xe caàu tröôùc nhaác khoûi maët ñöôøng: Z = 1 0
Ta laäp phöông trình moâmen ñoái vôùi ñieåm O : 2 M = Gh sinα - Gbcosα = 0 iO g t t 2 b tgα = (7.17) t h g
+ Töông töï khi oâ toâ quay ñaàu xuoáng doác (hình 7.6b), thì xe coù xu höôùng laät quanh
truïc naèm trong maët phaúng cuûa ñöôøng vaø ñi qua ñieåm tieáp xuùc cuûa hai baùnh xe caàu tröôùc vôùi
maët ñöôøng (ñieåm O1) , khi goùc α taêng daàn ñeán goùc 'α (goùc giôùi haïn maø xe bò laät khi ñöùng t
quay ñaàu xuoáng doác) thì caùc baùnh xe caàu sau nhaác khoûi maët ñöôøng: Z2 = 0 , laáy moâmen ñoái vôùi ñieåm O va 1
ø ruùt goïn thì ta ñöôïc : a ' tgα = (7.18) t h g 114
* Chuù yù :
Trong caùc phöông trình treân ñaõ boû qua moâmen caûn laên nhaèm taêng tính oån ñònh tónh cuûa oâ toâ.
* Nhaän xeùt : Goùc doác giôùi haïn laät ñoå tónh chæ phuï thuoäc vaøo toïa ñoä troïng taâm cuûa xe.
Moät soá goùc doác giôùi haïn ôû moät soá loaïi oâ toâ khi ñöùng treân doác: + Ñoái vôùi xe du lòch: ' o α = α = 60 . t t + Xe taûi khi ñaày taûi: o ' o α = (35÷40) , α 60 . t t
+ Xe töï ñoå khi khoâng taûi: o ' o α = (20÷35) , α > 60 t t
*Xeùt oån ñònh theo ñieàu kieän tröôït:
Söï maát oån ñònh doïc tónh cuûa oâ toâ khoâng chæ do söï laät ñoå doïc maø coøn do tröôït treân
doác do khoâng ñuû löïc phanh hoaëc do löïc baùm khoâng toát giöõa caùc baùnh xe vaø maët ñöôøng.
+ Tröôøng hôïp thöù nhaát: Neáu phanh tay laø phanh heä thoáng truyeàn löïc vaø xe chæ coù caàu sau chuû ñoäng:
Khi löïc phanh ñaït tôùi giôùi haïn baùm, xe coù theå bò tröôït xuoáng doác, goùc doác khi xe bò
tröôït ñöôïc xaùc ñònh nhö sau: F Gsin Z (7.19) pmax 2 Trong ñoù:
Fpmax – Löïc phanh lôùn nhaát ñaët ôû caùc baùnh xe sau. φ H
– eä soá baùm doïc cuûa baùnh xe vôùi ñöôøng. Z2 H
– ôïp löïc cuûa caùc phaûn löïc thaúng goùc töø ñöôøng taùc duïng leân caùc baùnh xe sau.
Khi α taêng tôùi goùc α (goùc doác giôùi haïn maø oâ toâ baét ñaàu bò tröôït khi ñöùng quay ñaàu tφ
treân doác ) thì luùc ñoù löïc phanh ñaït tôùi giôùi haïn baùm.
M = Gh sinα + Gacosα - Z L = 0 iO g tφ tφ 2 1 Gacosα + Gh sinα tφ g tφ Z = (7.20) 2 L
Khi oâ toâ ñöùng treân doác quay ñaàu leân, ta thay giaù trò Z2 vaøo (7.19), ta ñöôïc : aφ tgα = (7.21) tφ L - φh g 115
Khi oâ toâ ñöùng treân doác quay ñaàu xuoáng, laøm töông töï ta ñöôïc: aφ ' tgα = (7.22) tφ L + φh g Trong ñoù: '
α , α - Goùc doác giôùi haïn bò tröôït khi xe ñöùng yeân treân doác quay ñaàu tφ tφ leân vaø xuoáng.
+ Tröôøng hôïp thöù hai: neáu phanh tay söû duïng chung cô caáu phanh vôùi phanh chaân,
luùc ñoù taát caû caùc baùnh xe ñeàu ñöôïc phanh. F G cos (7.23) pmax
Töông töï ta coù ñieàu kieän ñeå oâ toâ treân doác bò tröôït nhö sau: ' tgα = tgα = φ (7.24) tφ tφ
Ñeå ñaûm baûo an toaøn khi oâ toâ ñöùng yeân treân doác thì hieän töôïng tröôït phaûi xaûy ra
tröôùc khi laät ñoå, ñöôïc xaùc ñònh baèng bieåu thöùc: tgα < tgα tφ t
- Neáu xe chæ phanh ôû caàu sau thì: aφ b < L - φh h g g (7.25)
- Neáu xe phanh ôû taát caû caùc baùnh xe thì : b φ < hg * Nhaän xeùt:
Goùc giôùi haïn khi oâ toâ ñöùng treân doác bò tröôït hoaëc bò laät ñoå chæ phuï thuoäc vaøo toïa ñoä
troïng taâm cuûa xe vaø chaát löôïng maët ñöôøng.
7.2.1.2. Tính oån ñònh doïc ñoäng:
Khi oâ toâ chuyeån ñoäng treân ñöôøng doác coù theå bò maát oån ñònh (laät ñoå hoaëc tröôït) döôùi
taùc duïng cuûa caùc löïc vaø moâmen hoaëc bò laät ñoå khi oâ toâ chuyeån ñoäng ôû toác ñoä cao treân ñöôøng baèng.
7.2.1.2.1 Tröôøng hôïp chuyeån ñoäng toång quaùt:
Xeùt oâ toâ chuyeån ñoäng leân doác khoâng oån ñònh coù keùo rômoùc (sô ñoà moâmen vaø löïc nhö ôû hình 7.1)
Khi taêng goùc doác α ñeán giaù trò giôùi haïn thì xe seõ laät ñoå öùng vôùi Z = 1 0, caùc baùnh xe
tröôùc bò nhaác khoûi maët ñöôøng. Laøm töông töï nhö phaàn oån ñònh doïc tónh, ta xaùc ñònh ñöôïc
goùc doác giôùi haïn maø xe bò laät ñoå khi chuyeån ñoäng leân doác hoaëc xuoáng doác.
Ñeå ñôn giaûn, ta xeùt tröôøng hôïp oâ toâ chuyeån ñoäng oån ñònh leân doác, khoâng keùo rômoùc nghóa laø: F = 0, Fm = 0. j 116
Vì α nhoû neân ta coù theå coi cos α = 1
Sau khi ruùt goïn bieåu thöùc (7.1) ta ñöôïc goùc doác giôùi haïn khi xe bò laät ñoå laø: tg b fr F α ñ= b (7.26) h g G
7.2.1.2.2. Tröôøng hôïp xe chuyeån ñoäng leân doác vôùi vaän toác nhoû, khoâng keùo rômoùc vaø
chuyeån ñoäng oån ñònh:
ÔÛ tröôøng hôïp naøy ta coù: Fj = 0 , Fm = 0, F 0, Ff 0 (löïc caûn laên nhoû coù theå boû qua).
*Xeùt oån ñònh theo ñieàu kieän laät ñoå:
OÂ toâ coù xu höôùng laät ñoå quanh truïc qua ñieåm tieáp xuùc cuûa hai baùnh xe ôû caàu sau vôùi maët ñöôøng.
Theá caùc giaù trò treân vaøo (7.1) vaø laøm töông töï nhö ôû tröôøng hôïp oån ñònh doïc tónh ta
xaùc ñònh ñöôïc goùc doác giôùi haïn maø xe bò laät ñoå khi xe chuyeån ñoäng leân doác: tg b α ñ = (7.27) hg
Khi xe chuyeån ñoäng xuoáng doác ta cuõng xaùc ñònh ñöôïc goùc doác giôùi haïn maø xe bò laät ñoå laø: tg a α' ñ = (7.28) h g
*Xeùt oån ñònh theo ñieàu kieän tröôït:
Khi löïc keùo chuû ñoäng ñaït tôùi giôùi haïn baùm thì xe baét ñaàu tröôït( xeùt tröôøng hôïp chæ
coù caàu sau chuû ñoäng): F F Z G (7.29) k max sin 2 Maët khaùc ta coù: φG α α
F = φ Z2 = (acos φ ñ + hgsin φ ñ) (7.30) L Vôùi Z ñ
2 öôïc xaùc ñònh baèng caùch laáy moâmen ñoái vôùi ñieåm O . 1
Töø (7.29) vaø (7.30) : Ta xaùc ñònh ñöôïc goùc doác giôùi haïn maø xe bò tröôït: tg φa α (7.31) φ ñ = L - φhg Trong ñoù :
Fkmax – Löïc keùo tieáp tuyeán lôùn nhaát ôû baùnh xe chuû ñoäng.
F – Löïc baùm cuûa baùnh xe chuû ñoäng.
φ – Heä soá baùm doïc cuûa baùnh xe vôùi maët ñöôøng.
Ñieàu kieän ñeå ñaûm baûo cho oâ toâ tröôït tröôùc khi bò laät ñoå laø : tg α φ ñ < tg α ñ 117
7.2.1.2.3. Tröôøng hôïp xe keùo rômoùc chuyeån ñoäng leân doác vôùi vaän toác nhoû vaø oån ñònh:
ÔÛ tröôøng hôïp naøy ta coù: Fj = 0, F , Ff 0 , cos 0 α 1.
*Xeùt oån ñònh theo ñieàu kieän laät ñoå:
Xe coù xu höôùng laät ñoå quanh truïc qua ñieåm tieáp xuùc cuûa hai baùnh xe caàu sau vôùi
maët ñöôøng (ñieåm O2).
Khi taêng goùc doác α ñeán giaù trò giôùi haïn thì baùnh xe caàu tröôùc nhaác khoûi maët ñöôøng: Z1 = 0
Theá caùc giaù trò treân vaøo (7.1) ta ñöôïc: tg b F h α m m ñ = (7.32) h Gh g g Trong ñoù : Fm – Löïc keùo rômoùc.
hm – Chieàu cao töø ñieåm ñaët moùc keùo ñeán maët ñöôøng.
* Xeùt oån ñònh theo ñieàu kieän tröôït:
Xe coù xu höôùng tröôït töø treân doác xuoáng döôùi doác.
Khi löïc keùo tieáp tuyeán ñaït tôùi giaù trò giôùi haïn baùm thì oâ toâ tröôït doïc. F F Z (7.33) k max 2
Maët khaùc ta coù : F Gsin F (G G )sin (7.34) k m m Vôùi: Fm = Gm s n i α
Theá caùc giaù trò F = 0, Ff 0 vaøo (7.2) vaø keát hôïp vôùi (7.33),(7.34) ta ñöôïc: m φ (G + G)sinα =
(Gsinα hg + Gcosα a + G h sinα ) m φ φ φ m m φ L Gaφ tgα = (7.35) φ G(L - φh ) + G (L - φh ) g m m
7.2.1.2.4. Tröôøng hôïp xe chuyeån ñoäng oån ñònh vôùi vaän toác cao treân ñöôøng naèm ngang khoâng keùo rômoùc:
Trong tröôøng hôïp naøy (thöôøng laø oâ toâ du lòch) ta coù: Fj = 0 , Fm = 0 , α = 0, boû qua
aûnh höôûng cuûa löïc caûn laên.
Sô ñoà moâmen vaø löïc taùc duïng leân oâ toâ nhö hình 7.2 118
Khi ñoù xe coù khaû naêng bò laät do löïc caûn khoâng khí gaây ra neáu chuyeån ñoäng vôùi toác
ñoä raát lôùn. Löïc caûn khoâng khí taêng tôùi giaù trò giôùi haïn, xe seõ bò laät quanh ñieåm O 2( O 2laø
giao ñieåm cuûa maët phaúng qua truïc baùnh xe sau vôùi ñöôøng), luùc ñoù phaûn löïc Z1 = 0.
Ñeå xaùc ñònh vaän toác giôùi haïn maø xe bò laät ñoå, ta söû duïng coâng thöùc (7.3): G(b fr ) F h Z b g 1 L
Ta coi Mf 0 vì trò soá cuûa noù raát nhoû so vôùi vaø ruùt goïn ta F , thay giaù trò 2 F Wv 0
ñöôïc vaän toác nguy hieåm maø xe bò laät ñoå: Gb v = (7.36) n Wh g Trong ñoù:
vn – Vaän toác giôùi haïn maø xe bò laät ñoå (m/s).
W – Nhaân toá caûn khoâng khí: W = 0,625C S
x coù ñôn vò laø Ns2/m2, vôùi C x
laø heä soá caûn khoâng khí coù ñôn vò Ns2/m va 4
ø S laø dieän tích caûn khoâng khí coù ñôn vò laø m2.
Ñeå thuaän tieän ta ñoåi sang ñôn vò km/h: Gb v =3,6 (7.37) n Wh g * Nhaän xeùt:
+ Söï maát oån ñònh cuûa xe phuï thuoäc vaøo toïa ñoä troïng taâm cuûa xe vaø moùc keùo, nhaân
toá caûn khoâng khí, heä soá baùm cuûa xe vôùi maët ñöôøng…
+ Ñoái vôùi nhöõng xe thöôøng chuyeån ñoäng vôùi vaän toác cao hoaëc thöôøng hoaït ñoäng
treân nhöõng ñòa hình phöùc taïp neân haï thaáp troïng taâm ñeå taêng tính oån ñònh cho oâ toâ.
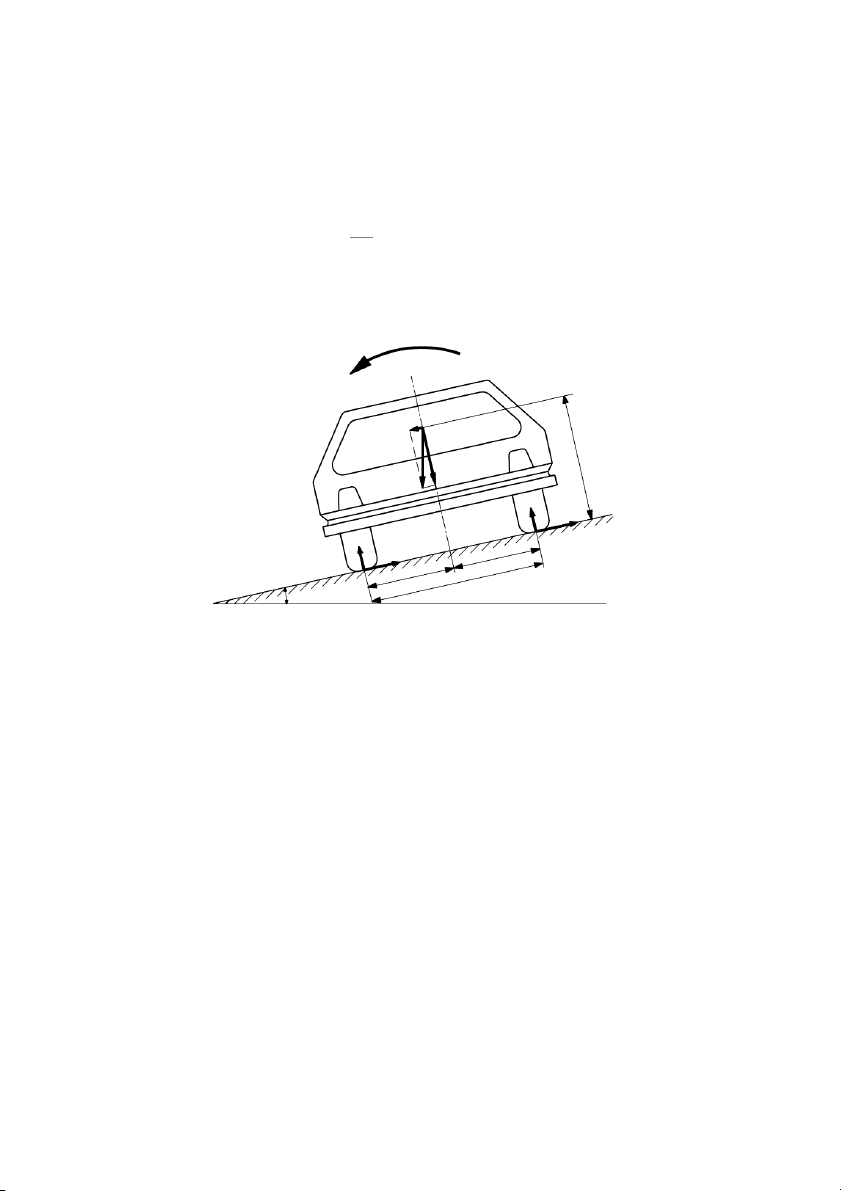
7.2.2. Tính oån ñònh ngang cuûa oâ toâ khi chuyeån ñoäng thaúng treân ñöôøng nghieâng ngang:
7.2.2.1. Xeùt oån ñònh theo ñieàu kieän laät ñoå:
OÂtoâ coù xu höôùng laät ñoå quanh truïc naèm trong maët phaúng cuûa ñöôøng vaø ñi qua ñieåm
tieáp xuùc cuûa hai baùnh xe beân traùi vôùi maët ñöôøng (ñieåm B) nhö hình 7.7.
Laáy moâmen ñoái vôùi ñieåm B vaø ruùt goïn ta ñöôïc : c G cosβ - Gh sinβ - M g jn Z’= 2 (7.38) c
Khi goùc β taêng tôùi giaù trò giôùi haïn β ñ thì xe bò laät quanh truïc ñi qua B. Luùc ñoù Z’= 0. 119
Thoâng thöôøng giaù trò Mj nho n
û neân coù theå coi Mjn 0 , xe khoâng keùo rômoùc neân Fm = 0.
Ta xaùc ñònh ñöôïc goùc giôùi haïn laät ñoå khi xe chuyeån ñoäng treân ñöôøng nghieâng ngang laø: tg c βñ = (7.39) 2hg Trong ñoù :
β ñ - Goùc doác giôùi haïn maø xe bò laät ñoå. Mjn T Gsin hg Gcos G Z’ Y’ A Z” Y” B c/2 c/2 c
Hình 7.7: Sô ñoà löïc vaø moâmen taùc duïng leân oâ toâ khi chuyeån ñoäng thaúng
treân ñöôøng nghieâng ngang. Trong ñoù:
Y’ , Y” - Caùc phaûn löïc ngang taùc duïng leân caùc baùnh xe beân phaûi vaø beân traùi.
β - Goùc nghieâng ngang cuûa ñöôøng.
Z’ , Z” - Caùc phaûn löïc thaúng goùc töø ñöôøng taùc duïng leân caùc baùnh xe beân phaûi vaø beân traùi.
M - Moâmen cuûa caùc löïc quaùn tính tieáp tuyeán taùc duïng trong maët phaúng jn
ngang khi oâ toâ chuyeån ñoäng khoâng oån ñònh.
7.2.2.2.Xeùt oån ñònh theo ñieàu kieän tröôït:
Khi chaát löôïng baùm cuûa baùnh xe vôùi ñöôøng keùm thì xe coù xu höôùng tröôït khi chuyeån
ñoäng treân ñöôøng nghieâng ngang.
Ñeå xaùc ñònh goùc giôùi haïn khi xe bò tröôït, ta laäp phöông trình hình chieáu caùc löïc leân
maët phaúng song song vôùi maët ñöôøng :
Gsinβ = Y’ + Y” = φ (Z’+ Z”) = φ Gcosβ (7.40) φ y y φ 120 Trong ñoù:
β - Goùc doác giôùi haïn maø oâ toâ bò tröôït. φ
φ - Heä soá baùm ngang giöõa baùnh xe vaø maët ñöôøng. y
Ruùt goïn bieåu thöùc (7.40) ta ñöôïc: tg β = φ (7.41) φ y
Ñeå ñaûm baûo an toaøn thì xe phaûi bò tröôït tröôùc khi laät ñoå, nghóa laø: tg c β < tgβ ñ hay φ < (7.42) φ y 2hg
Khi oâ toâ ñöùng yeân treân ñöôøng nghieâng ngang, ta cuõng xaùc ñònh ñöôïc goùc nghieâng
giôùi haïn maø taïi ñoù xe bò laät ñoå hoaëc bò tröôït.
ÔÛ tröôøng hôïp naøy, oâ toâ chæ chòu taùc duïng cuûa troïng löôïng. Phöông phaùp xaùc ñònh
cuõng töông töï nhö phaàn treân, ta coù ngay goùc giôùi haïn maø xe bò laät ñoå: tg c β t = (7.43) 2hg
Cuõng töông töï ta coù goùc giôùi haïn maø xe bò tröôït laø: tg β = φ tφ y
Ñieàu kieän ñeå xe tröôït tröôùc khi laät ñoå laø: tg c β < tgβ t hay φ < (7.44) tφ y 2hg 121




