Chương I Hàm số 1 - Giải tích 1| Trường đại học Bách Khoa, Đại học Đà Nẵng
Chương I Hàm số 1 - Giải tích 1| Trường đại học Bách Khoa, Đại học Đà Nẵng được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn sinh viên cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Môn: Giải tích 1(GT 1) 40 tài liệu
Trường: Trường Đại học Bách khoa, Đại học Đà Nẵng 410 tài liệu
Tác giả:
Preview text:
Giơí thiệu môn học : Giải tích 1 Tài liệu tham khảo :
- Toán cao cấp ( chủ biên Nguyễn Đình Trí )
- Giải tích ( Thái Xuân Tiên – Đặng Ngọc Dục )
- Bài tập toán cao cấp ( ĐHBK ĐN )
Chương I : Hàm số - giới hạn – liên tục
Chương II : Đạo hàm và vi phân Chương III : Tích phân
Chương IV : Hàm nhiều biến
Chương V : Hình vi phân
-------------------------------------
CHƯƠNG I : HÀM SỐ - GIỚI HẠN – LIÊN TỤC
BÀI I : HÀM SỐ :
I) Bổ sung về số phức :
1) Dạng đại số của số phức:
1.1) Số ảo : là số I có i 2 = -1.
1.2) Số phức dạng đại số : z = a+bi , với a,b là số thực.
Trong đó a gọi là phần thực , b là phần ảo . Tập hợp các
số phức ký hiệu là C. Ta có mỗi số thực đều là số phức .
Ví dụ : Phương trình bậc 2 2 2
x x 1 0 có 3
3i trong tập C có 2 nghiệm phức 1 3 1 3 x i , . 1 x2 i 2 2 2 2
1.3) Số phức liên hợp của z = a+bi là z = a-bi.
1.4) Số phức bằng nhau : z = a+bi , t = c+di ta có
z = t khi và chỉ khi a = c , b = d
1.5) Các phép toán số phức dưới dạng đại số : a) Tổng 2 số phức :
Định lý : Cho 2 số phức z = a+bi , t = c+di thì z + t = (a+c)+(b+d)i.
Tính chất : Cho 3 số phức z , t , r thì
- Tính giao hoán : z+t = t+z.
- Tính kết hợp : (z+t)+r = z+(t+r). - z+0 = z với 0 = 0+0i.
- z+(-z) = 0 với –z = -a –bi là số phức đối của z. b) Tích 2 số phức :
Định lý : Cho z = a+bi và t = c+di thì : z.t = (ac-bd)+(ad+bc)i.
* Tính chất : Cho 3 số phức z , t , r thì :
- Tính giao hoán : z.t = t.z.
- Tính kết hợp : (z.t).r = z.(t.r) - z.1 = z với 1 = 1 + 0i.
- Số phức đảo của z là 1 1 Z sao cho . z z 1 - 2 2 .
z z a b . c) Thương 2 số phức :
* Định lý : Cho z = a+bi và t = c+di thì : z a bi
(a bi)(c di) ac bd bc ad i , t 0 2 2 2 2 t c di
(c di)(c di) c d c d
2) Dạng lượng giác của số phức : b M(a,b) o a x
2.1) Định nghĩa :Mỗi số phức z = a +bi tương ứng 1-1 với
điểm M(a,b) trong mặt phẳng .Gọi r OM và (O .xOM). Ta có : 2 2 b
a r cos, b r sin và r a b
, tan z r(cos i sin) gọi là a
dạng lượng giác của số phức z , trong đó r là modun và
là acgumen của z Ký hiệu r z , acg(z)
2.2) Số phức bằng nhau dạng lượng giác : Cho
z r (cos i sin ) và z r (cos i sin )thì z z r r và 2 1 1 1 1 2 2 2 2 1 2 1 2 1 2 k Ví dụ : 1 3 z
i có r 1.tan 3
z cos i sin . 2 2 3 3 3
2.3) Các phép toán số phức dạng lượng giác:
a) Phép nhân: Cho 2 số phức dạng lượng giác sau :
z r (cos i sin ) và z r (cos isin )thì z .z r r [cos(
) isin( i sin )] 1 1 1 1 2 2 2 2 1 2 1 2 1 2 1 2
b) Phép chia : z1 1r
[cos( ) i sin( )], z 0. 1 2 1 2 2 z2 2 r
c) Phép lũy thừa : (cos sin) n n z r i
thì z r [cos(n) i sin(n)] . d) Căn bâc n : 2k 2k z r(cos isin ) n n thì z r[cos isin
] , k 0,1, 2,..., n 1 n n
e) Công thức Euler : ixe cos xisin x. Ví dụ : z 2 2 z 3(cos
i sin ), z 2(cos i sin ) z z 6(cos i sin ), (cos i sin ) 1 2 1 2 6 6 3 3 2 2 z 3 6 6 1 3 / 3 2k / 3 2k 3 3 z 27(cos
isin ) , z 2(cos i sin ), k 0,1, 2 1 2 2 2 2 3 II)
CÁC KHÁI NIỆM VỀ HÀM SỐ:
1) ĐỊNH NGHĨA HÀM SỐ : Cho X ,Y CR . Một hàm số từ X vào Y
là một quy tắc ứng với m i
ỗ phần tử x thuôc X ta có phần tử duy
nhất y thuộc Y . Ký hiệu :
f : X------------ Y hoặc X------ f------ Y
x I--------- y =f(x) x I----------- y = f(x)
Để đơn giản ta thường viết hàm số là y = f(x).
2) Miền xác định ( MXĐ) của hàm số : là tập hợp D gồm các phần tử
x thuộc X để cho hàm số có nghĩa . Ví dụ :
a) y = 3x + 5 có MXĐ là D = R
b) y = x3 MXÐ x 3
3) Các đặc tính của hàm số : 3.1) Hàm bị chặn :
a) Hàm bị chặn trên : Hàm y = f(x) gọi là bị chặn trên trong tập D nếu t n t ồ ại s M sa ố
o cho f (x) M , x D
b) Hàm bị chặn dưới : Hàm y = f(x) gọi là bị chặn dưới trong tập D nếu t n t ồ ại s m
ố sao cho f (x) m, x . D c) Hàm s v
ố ừa bị chặn trên vừa bị chặn dưới ta g i ọ chung là hàm bị chặn Ví d :
ụ hàm y = sinx , y = cosx bị chặn trên R. (Vì 1 sin ,
x cos x 1 , x ) R 3.2) Hàm đơn điệu :
a) Hàm đơn điệu tăng ( đồng biến ) : Hàm y = f(x) gọi là đơn
điệu tăng trong tập D nếu x
, x D mà x x f (x ) f (x ) 1 2 1 2 1 2
b) Hàm đơn điệu giảm ( nghịch biến ) : hàm y = f(x) gọi là đơn
điệu giảm trong tập D nếu x
, x D mà x x f (x ) f (x ). x 2 1 2 1 2 c) Hàm số c
luôn tăng hoặ luôn giảm trong tập D ta gọi là hàm đơn
điệu tăng hoặc đơn điệu giảm trong D. 3.3) Hàm chẳn , lẽ :
a) Hàm chẳn : Hàm y = f(x) gọi là chẳn trong tập đối xứng D
nếu : ,xxD f (x) f (x)( đồ thị hàm chẳn đối xứng qua trục tung )
b) Hàm lẽ : Hàm y = f(x) gọi là lẽ trong tập đối xứng D nếu : ,
x x D f ( ) x f ( )
x ( đồ thị hàm lẽ đối xứng qua gốc tọa độ ) Ví d :
ụ Hàm y = cosx là hàm chẳn trên R ( cos(-x) = cosx
Hàm y = sinx , tanx , cotx là các hàm lẽ ( sin(-x) = -sinx,
tan(-x) = - tanx, cot(-x) = -cotx.
3.4) Hàm tuần hoàn : Hàm y = f(x) gọi là tuần hoàn nếu : ,
x x L D f (x ) L f ( )
x . Số dương T nhỏ nhất trong các s L ố ở trên g i
ọ là chu kỳ của hàm tuần hoàn. Ví d :
ụ Hàm y = sinx , y = cosx tuần hoàn chu kỳ T = 2.
Hàm y = tanx , y = tuần hoàn chu kỳ T =
4) Các phép toán trên hàm số : ( tham khảo SGK ).
III) Hàm hợp và hàm ngược :
1) Hàm Hợp : Cho 2 hàm s f và ố g sau : X ----f-- Y ---g- Z
xI----- y=f(x)----- z=g[f(x)] Hàm h : X-------- Z
xI------ z = h(x) gọi là hàm hợp của f và g . Ký hiệu h = . 0
g f (đọc là g rông f ) . Ta có h(x) = g f (x) [ g f (x)] 0 Ví d ụ 2 2
f (x) 2x 1 , g(x) x 2 g f ( ) x [ g f ( )
x ] g(2x 1) (2x 1) 2 0
2) Hàm ngược : Cho hàm số f : X------- Y xI----- y = f(x)
là phép tương ứng 1-1 (song ánh)
Hàm ngược của f là hàm số f 1 : YI------- X yI------ x = f 1(y) Ta có quan hệ y = f(x) 1
x f (y) .( Đồ thị 2 hàm ngược nhau đối xứng qua đường y = x ).
IV) Một số hàm sơ cấp cơ bản :
1) Hàm lũy thừa : y x, . R
MXĐ tùy thuộc vào . Chẳng hạn : 1 2 2 2
y x : MXÐ D R , y x : MXÐ x
0, y x x :MXÐ x 0.
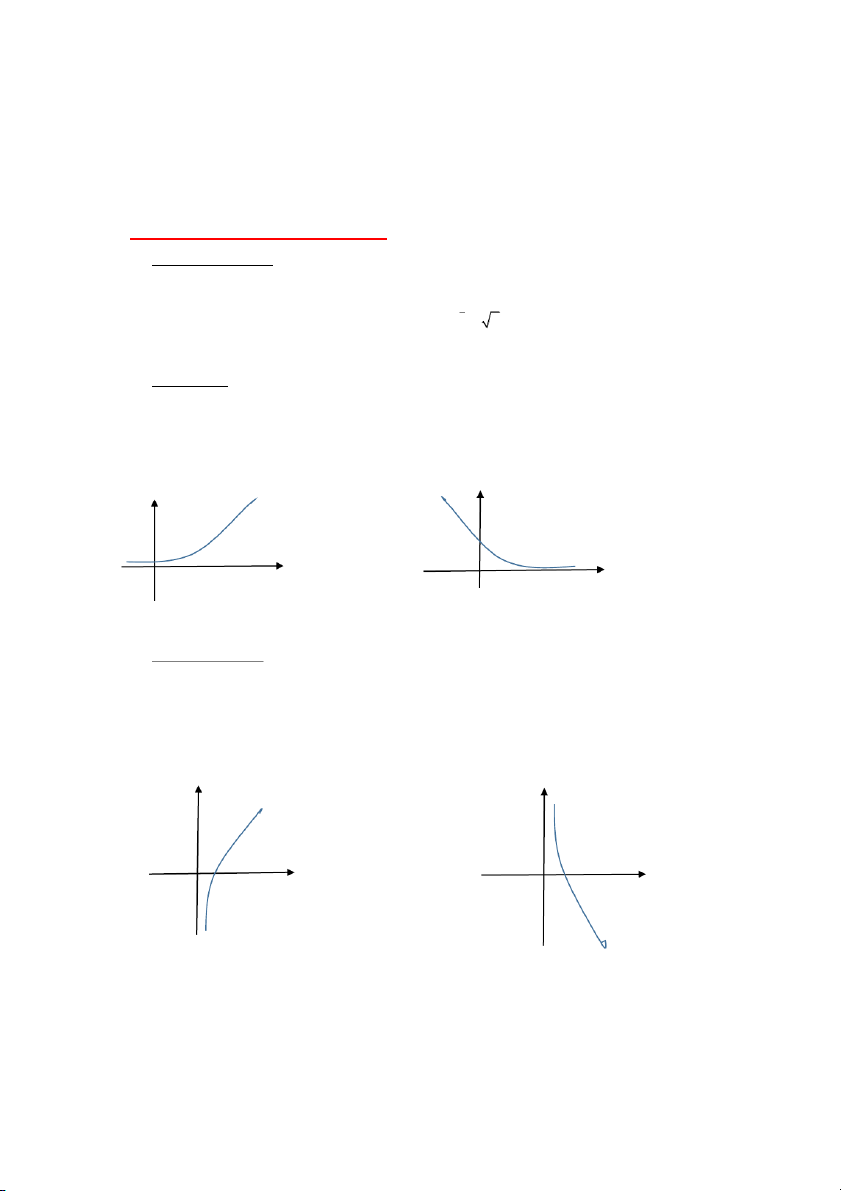
Đồ thị đi qua điểm I(1,1) và O(0,0) với o. 2) Hàm mũ : x
y a , a 0, a 1.( a gọi là cơ s ). ố MXĐ D = R
Đồ thị hàm số nằm phía trên trục hoành , đi qua điểm I(0,1):
Khi a > 1 hàm số luôn tăng , khi 0 < a < 1 hàm số luôn giảm
Hình Dạng Đồ Thị : 1 x 1 x
a>1 (Hinh dạng đồ thị) 0 < a < 1
Tính chất ( tham khảo SGK )
3) Hàm logarit : y log x,a 0,a 1.là hàm ngược của hàm mũ a y log y
x x a . a MXĐ x 0
Đồ thị nằm bên phải trục tung , đi qua điểm J(1,0)
Khi a > 1 hàm số luôn tăng, khi 0 < a < 1 hàm s l ố uôn giảm. 0 1 x o 1 x
a > 1 ( Dạng đồ thị ) 0 < a < 1
Các tính chất ( tham khảo SGK ).
Đặc biệt log x lgx , log x x ( logarit thập phân và logarit nepe e ln 10 ) 4) Các hàm lượng giác :
a) y =sinx : MXĐ D = R . Là hàm lẽ ,bị chặn ( 1
sin x 1 ) , đi
qua O(0,0), tuần hoàn chu kỳ T = 2
b) y = cosx : MXĐ D = R , là hàm chẳn , bị chặn ( 1
cos x 1 ) ,
đi qua I(0,1) , tuần hoàn chu kỳ T = 2 c) y = tanx = sin x :MXÐx
k (k Z) , là hàm lẽ , không bị chặn , cos x 2 tuần hoàn chu kỳ T =
d) y = cotx = cosx:MXÐ x
k ,k Z , là hàm lẽ , không bị chặn , tuần sin x hoàn chu kỳ T = .
5) Các hàm lượng giác ngược :
a) y = arcsinx : là hàm ngược c a ủ y = sinx với x [
, ], y arcsin x x sin y 2 2
Là hàm lẽ , bị chặn , không tuần hoàn.
b) y = arccosx : là hàm ngược của y = cosx với x [
0, ], y arccos x x cos y
Là hàm không chẳn , lẽ , bị chặn , không tuần hoàn.
c) y= arctanx : là hàm ngược của y = tanx với
x ( , ): y arctan x x tan y 2 2
Là hàm lẽ , bị chặn , không tuần hoàn.
d) y = arccotx : là hàm ngược của y = cotx với x (
0,): y arccot x x cot y
Là hàm không chẳn , lẽ , bị chặn , không tuần hoàn ( Ta có :
arcsinx arccosx ,arctan x arccot x ). 2 2
Chú thích : Các hàm sơ cấp là các phép toán trên các hàm sơ cấp cơ bản. BÀI TẬP :
1) Tìm MXĐ của các hàm số sau : a) y = 2 2
4x x lg(x 9) Hàm số xác định khi 2 4
x x 0 0 x 4
3 x 4 MXÐ D (3,4] 2 x 9 0
x 3Ux 3 b) y = 3 2 3 arcsin x x 5 Hàm số xác định khi 3 x 0 x 3 3 2 1
x 3 MXÐ D [ 1 ,3] x 1 1 1 x 4 5
2) Xét tính chẳn , lẽ của các hàm sau : a) f(x) = xa 1 x x a 1
MXĐ D =R ( tập đối xứng ) x a 1 x a 1
f (x) x x f ( ) x , ,
x x D x a 1 x a 1
Vậy f(x) là hàm chẳn trên D = R b) f(x) = 2
ln(x 1 x )
MXĐ D = R ( tập đối xứng) 2 1 2 f ( )
x ln(x (x) 1) ln
ln( x x 1 ) f ( ) x 2 x x 1
Vậy f(x) là hàm lẽ trên D = R
BÀI 2 : GIỚI HẠN HÀM SỐ
I) Các định nghĩa về giới hạn hàm số
Lân cận của 1 điểm trên 1 trục : (---------x ---------) 0 0 x 0 x
a) Lân cận tại 1 điểm x :U(x ) (x ,x ). , 0 khá bé 0 0 0 0
b) Lân cận bên trái tại x :U(x 0) (x ,x ) , 0 khá bé 0 0 0 0
c) Lân cận bên phải tại x :U(x 0)(x ,x ), 0 khá bé 0 0 0 0
1) Giới hạn hàm số tại 1 điểm : Cho hàm y = f(x) xác
định trong lân cận của x . Ta nói L là giới hạn của 0 hàm s khi ố
x tiến về x nếu với mọi 0 cho trước , 0
tồn tại 0phụ thuộc sao cho : 0 x x f (x) L 0 . Ký hiệu
f (x) L hay f (x) lim L x x xx 0 0
Ta có thể mô tả dưới ngôn ngữ toán học như sau : 2) Giới hạn một phía :
a) Giới hạn bên trái : x tiến về 0x bên trái
lim f (x) L ( 0, ( ) 0 : x x x f (x) L ) 0 0 x 0 x 0
b) Giới hạn bên phải: x tiến về ả 0 x bên ph i
lim f (x) L ( 0, ( ) 0: x x x f (x) L ) 0 0 x 0 x 0 Ta còn viết
x x 0 là x x
và x x 0 0 0 0 là x 0 x
c) Định Lý : Hàm số có giới hạn tại x khi và chỉ khi 0
nó có giới hạn bên trái và phải tại đó và các giới
hạn đó bằng nhau(lim f ( )x L lim f ( )x lim f ( )x ) L x x x x 0 0 0 x x 0 0 3) Giới hạn vô tận:
a) lim f ( )x (M 0,(M) 0:0 x x f ( )x M) 0 x 0 x
b) lim f (x) L ( 0, (
A ) 0 : x A f (x) L ) x
c) lim f (x) (M 0, (
A M ) 0 : x A f (x) M ) x
II) Các tính chất về giới hạn :
1)Tính chất 1: lim C C ( C là hằng số ) x 0 x
2)Tính chất 2: lim f ( )x Lthì L là duy nhất. x 0 x
3)Tính chất 3: lim f ( )x L. Nếu L > 0 ( hoặc L < 0 ) thì x 0 x
f(x) > 0 (hoặc f(x) < 0 ) , x U
(x ), x x . 0 0
4)Tính chất 4: Nếu f(x) > 0 ( hoặc f(x) < 0 ) x
U(x ), x x L 0(hay L 0). 0 0
5)Tính chất 5:lim f ( )x L , lim g( ) . Nếu 1 x L2 x 0 x x 0 x
L L f ( ) x g( ) x , x
U(x ), x x 1 2 0 0
6)Tính chất 6: lim f (x) L lim f (x) L. x 0 x x 0 x
7)Tính chất 7: Nếu lim f (x) L ( L hữu hạn) thì f(x) bị x 0 x
chặn trong lân cận của x . 0
III) Các phép toán về giới hạn:
1) lim[ f (x) g(x)] lim f ( )x lim g( )x. x 0 x x 0 x x 0 x
2) lim[ f (x).g( )x] lim f ( )x.lim g( )x. x 0 x x 0 x x 0 x 3) f ( ) x lim lim f ( ) x / lim ( g ) x . x 0 x g(x) x 0 x x 0 x 4) Nếu lim ( u )
x u , lim f ( )
u L lim f[ ( u ) x ] . L 0 x 0 x u 0 u xx0
5) Nếu f(x) là hàm sơ cấp thì lim f( )x f( x ). 0 x 0 x IV)Các tiêu chu n t ẩ n t ồ i
ạ giới hạn của hàm s : ố
1.Tiêu chuẩn 1: Nếu f(x) g(x)và h(x) cùng xác định trong U(x ) sao cho : 0 f (x) ( h ) x g( ) x , x U
(x ), x x saocho lim f ( )
x lim g( ) 0 0 x L x 0 x x 0 x
lim h(x) L. x 0 x Áp d ng : ụ Ta có sin cos x x 1 x (0, ) x 2 sin x
lim cos x lim1 1 lim 1 x 0 x 0 x 0 x
Hệ quả : tan x lim 1 x 0 x Ví d : ụ a) tan 5x tan 5x 3x 5 5 Lim Lim . . x 0 x 0 sin 3x 5x sin 3x 3 3 tan3 3 x 5 b) tan3x 5x 2 3 lim lim x x 0 x 0 sin 2x 3 sin 2 x x 5 2 3 2x
2) Tiêu chuẩn 2 : Nếu f(x) là hàm không giảm và bị chặn trên với m i
ọ x>0 khá lớn thi t n t
ồ ại lim f (x) L . x * Áp d 1 ụng : 1 lim(1 ) x ,
e lim(1 x) x e 2,718 x x 0 x * H 1 ệ qu : ả a u (x ) a u (x ) Lim [1 ]
e , lim [1 a ( u ) x ] a e . ( u ) x ( u ) x 0 u(x) Ví d : ụ 1) 3 1 x x 3 3 sin sin lim(1 sin x) lim[1 sin x) ] e x 0 x 0 3sin x x 3sin sin x sin x x x ( ) x sinx sin 3 2)lim( ) lim(1 ) x x x e x 0 x 0 x x x1 x 1 1 3x 4 6 x 1 2 3 2 2(3x 2 ) 6 6 3)lim( ) lim[(1 ) ] (e )
x 3x 2 x 3x 2 e
Bài III) VÔ CÙNG BÉ VÀ VÔ CÙNG LỚN
I) Vô cùng bé ( VCB :
1) Định nghĩa : Hàm (x) được gọi là VCB khi
x x lim (x) 0 0 x 0 x Ví d :
ụ (x) sin x là VCB khi x 0 , 1
(x) làVCB khi x x
2) Liên hệ giữa VCB và giới hạn hàm s : ố
* Định lý: lim f ( )x L f ( )x LlàVCBkhi x 0 x x 0 x 3) Các: tính chất c a ủ VCB :
a) Tính chất 1) Nếu (x)và (x)là các VCB khi x x , hằng số 0 C là
thì C( )x,( )x. ( )x,( )x. ( )xlàVCBkhi x 0 x
b) Tính chất 2) Nếu (x)làVCBkhi x bị chặn trong lân cận 0 x và f (x)
của x thì(x).f (x) . 0 làVCB khi x x 0 Ví d : ụ sin x sin ( ). ( ) lim x x f x làVCB khi x 0 (vì x x x 1 cosx
(x) làVCB khi x , f (x) sin x bị chặn trên R) tương tự lim 0 x x x
4)So sánh các VCB : Cho (x),(x)là2VCBkhi x x khi đó: 0 a) Nếu (x) lim 0 thì( )
x làVCB bậc cao hơn (x) ( hoăc (x) là VCB x 0 x (x)
bậc thấp hơn (x))khi x x . 0 b) Nếu (x) lim
L( L 0, L )
ta nói chúng là các VCB ngang cấp ( cùng x 0 x (x)
bậc) trong quá trình đó. Đặc biệt nếu ( ) lim
x 1thì( )xvà ( ) x là 2VCB x x ( ) 0 x
tương đương trong quá trình đó . Ký hiệu : (x) i x x 0 c) Nếu (x) lim
L ( L 0,L ,k 0) ta nói (x)làVCB bậc k so với 0 [ (x)]k x x
(x)khi x x . 0
Một số ng g VCB tương đương thườ p khi ặ x 0 sau : sin x 2 x 1cos x x 0 2
5)Quy tắc ngắt bỏ VCB bậc cao và sử dụng VCB tương đương:
a) Ngắt bỏ VCB bậc cao : Nếu ( )
x là VCB bâc cao hon ( )
x khi x x thì lim[ ( ) x ( ) x ] Lim ( ) . 0 x x x 0 x x 0 Ví d : ụ 3 2
3x 4x 2x 2x lim lim 0,5 2 x 0 x 0 3x 4x 4x
b) Sử dụng VCB tương đương : Nếu ( ) x
i x x thì lim[(x). (x)] lim[ (x). ( ) x ]và 0 1 1 x 0 x x 0 x (x) (x) 1 lim lim x 0 x (x)
xx (x) 1 c) Ví d : ụ 2 2 ln(1 ax ) ax a 1) lim lim ,( a 0) 2 2 x 0 x 0 sin 3x (3 ) x 9 2
( vìln(1 ax ) ) 2) 2
1 cos(x cos 2x) (x cos 2x) 1 lim lim 2 2 x 0 x 0 3x 2.3x 6 3) 2 2 1 cos x 1cos x x 1 lim lim lim 2 2 2 x 0 x 0 x 0 tan x ( 2 1 cos ) x tan x 2.2 2 x 4 2 4) 2 2 2 x 2 x 2 2 e cos3x e 1 1 cos3x 2x (3 ) x 2 3 13 lim lim lim lim lim 2 2 x 0 x 0 x 0 x 0 x 0 x tan 2x x tan 2x x tan 3x 3x 2.3x 3 2 6
II) Vô cùng lớn ( VCL )
1) Định nghĩa : Hàm f(x) được gọi là VCL khi
x x nêu lim f ( ) 0 x x x 0
2)Quan hệ giữa VCL và VCB: f(x) là VCL khi 1 x x
làVCB khi x x . 0 0 f ( ) x 3) Tính chất VCL:
3.1) Tính chất 1:Nếu f(x) và g(x) là 2 VCL khi x . Thì : 0 x
a) Cf(x) , f(x).g(x) cũng là các VCL trong quá trình trên , C khác 0.
b) f(x)+g(x) là VCL nều f(x) , g(x) cùng dấu trong quá trình đó
c) f(x)-g(x)-----------------------------khác dấu----------------------
3.2) Tính chất 2: Nếu f(x) là VCL khi x x và g(x) bị chặn 0
trong lân cận x thì f(x)+g(x) là VCL trong quá trình đó. 0
4) So sánh các VCL: Cho f(x) và g(x) là 2 VCL khi x . Khi 0 x đó: a) Nếu f (x) lim
, ta nói f(x) là VCL bậc cao hơn g(x) ( hoặc x 0 x g (x )
g(x) là VCL bậc thấp hơn f(x) ) trong quá trình đó. b) Nếu f (x) lim (
L L 0, L ) , ta nói f(x) và g(x) là 2 VCL ngang x 0 x g(x) cấp ( cùng b ậc ) trong quá trình đó. c) Nếu f ( ) x lim (
L 0,L ,
k 0) , ta nói f(x) là VCL bậc k so với
0 [g(x)]k x x g(x) trong quá trình đó. 5) Quy tắc ngắt b VC ỏ
L bậc thấp : Cho g(x) là VCL bậc thấp
hơn f(x) khi x x thì lim[f (x) g(x)] lim f (x) 0 x 0 x x 0 x Ví d : ụ 3 2 3 5x 2x 3 5x 5 lim lim 3 3 x 4x 3 x x 4x 4
III)Một số dạng vô định của giới hạn: 0 1) Dạng ,
0 : Để khử dạng vô định này ta có các phương pháp sau: Áp d ng bi ụ
ến đổi sơ cấp để rút g n bi ọ ểu thức
Sử dụng VCB tương đương. Sử dụng quy t ắc Lopital ( Chươn II )
2) Dang 0. : Sử d ng bi ụ p c ến đổi sơ cấ huyển về dạng 1) 3) Dang 1 : Áp d ng c ụ
ác công thức ở tiêu chuẩn 2 c a ủ giới hạn. 4) Dạng 0 0
0 ,0 , : Thường gặp ở dạng I = u x v x v x ln[ ( )] 0 ( ) ( ) lim[u(x)]
,tacó ln I lim ln[u(x)] lim ( , ) A
A I e x x x x x x 1 0 0 0 0 ( v ) x Các ví dụ : 1) I =
x 1 1 x 0 2x 1 lim ( ) lim x 0 x 0 3x 0 3 ( x x 1 1 x) 3
2sin x(sin x cos ) x 2) I =
1 sin x cos x
1 cos x sin x 0 2 2 2 lim lim ( ) lim 1 x 0 x 0 x 0
1 sin x cos x
1 cos x sin x 0
2sin x(sin x cos x) 2 2 2 3) I = 2 1 1 1 cos lim( )( ) lim
x lim x 0 x 0 x 0 x 0 sin x tan x sin x 2x 4) I = u cos
lim( ) tan (0.) lim tan( ) lim u x x u u 1 u 0 u 0 x 2 2 sin u 2 2 1 5) I= 1 tan x 2 2 2x 2 tan x 2 lim (1 tan ) x (1 ) lim[(1 tan ) x ] x e x 0 x 0 6) I = x 1 x x 1 x) lim (sin x 1 sin ) x lim 2cos( )sin( 0 x x 2 2
III) HÀM LIÊN TỤC VÀ GIÁN ĐOẠN
1) Hàm liên tục: 1.1) Các định nghĩa : a) Hàm liên t c
ụ tại 1 điểm : Hàm y = f(x) gọi là liên tục tại x 0
nếu : f(x) xác định tại x và lân cận c a ủ ng th i 0 0 x , đồ ờ lim f ( )
x f ( x ) . 0 x 0 x b) Hàm f(x) g i ọ là liên t c
ụ bên trái tại 0x nếu f(x) xác định tại
x vàU (x 0) , đồng thời lim f (x) f (x ). 0 0 0 x 0 x 0 c) Hàm f(x) g i ọ là liên t ,b)c ụ
bên phải tại x nếu f(x) xác định 0
tại x vàU(x 0), đồng thời lim f (x) f (x ) 0 0 0 x 0 x 0
Định lý 1 : f(x) liên tục tại ụ ả ạ 0
x f(x) liên t c bên trái và ph i t i đó d) Hàm f(x) g i ọ là liên t c
ụ trong (a,b) nếu nó liên tục tại m i ọ x thuôc khoảng đó e) Hàm f(x) g i
ọ là liên tuc trên [a,b] nó liên t c ụ trong (a,b), liên t c
ụ bên phải tại a , bên trái tại b.
Định lý 2: Tất cả các hàm sơ cấp đều luôn liên tục trên MXĐ của nó.
1.2) Các phép toán về hàm liên tục:
a) Định lý 3: Nếu f(x) , g(x) liên tục tại 0x thì Cf(x) , f(x)+g(x),
f(x).g(x) cũng liên tục tại đó , đồng thời f(x)/g(x) cũng liên
tục tại x ,trongdóg(x ) 0. 0 0
b) Định lý 4: Nếu u = u(x) liên t c ụ tại ụ ạ 9
x và y = f(u) liên t c t i
u u(x ) thì y=f[u(x)] cũng liên tục tại x . 0 0 0
1.3) Các tính chất hàm liên tục trên 1 đoạn
1) Tính chất 1: Nếu f(x) liên t c ụ trên [a,b]
thì f(x) bị chặn và tồn tại GTLN, GTNN trên đó.
2) Tính chất 2 : Nếu f(x) liên t c ụ trên [a,b] và f(a).f(b)<0 thì t n t ồ ại c nằm trong [a,b] có f(c) = 0
3)Tính chất 3 : Nếu f(x) liên t c
ụ trên [a,b] có M ,m là GTLN ,GTNN và [ ,
m M ]thìc[ , a ] b có f ( ) c sin x Các ví d : ụ 1) Cho f(x) = khi x 0 x Chứng minh f(x) liên 1 khi x 0 tục trên R Ta có x
0thì f(x) là hàm sơ cấp nên nó liên tục và sin x
lim f (x) lim
1 f (0) f (x) liên t c
ụ tại x = 0 . Vậy f(x) liên t c ụ x 0 x 0 x trên R 2) Cho f(x) = x 1 khi x 1 Tìm a để f(x) liên t c ụ trên R 2 3 ax khi x 1
Khi x < 1 hoặc x > 1 thì f(x) là hàm sơ cấp nên nó luôn liên tục
, để f(x) liên tục trên R thì nó phải liên tục tại x = 1. Lúc đó
lim f (x) lim f (x) f (1) 2 3 a a 1 x 1 0 x 1 0 2)Hàm gián đoạn:
2.1) Định nghĩa : Hàm f(x) gọi là bị gián đoạn tại ế 0 x n u nó không liên t c ụ tại đó. 2.2) ng h Các trườ ợp hàm gián đoạn:
a) Nếu f(x) không xác định tại điểm nào thì bị gián đoạn tại đó . Chẳng hạn :
* f(x) = sin x bị gián đoạn tại x = 0. x
* f(x) = 1 bị gián đoạn tại x = 3 x 3
b) Nếu lim f ( )x f (x ) thì f(x) bị gián đoạn tại x 0 0 x 0 x ví d :
ụ Cho hàm f(x) = giánTa có sin x
lim f (x) lim
1 f (0) 2, Vây x 0 x 0 x
f(x) bị gián đoạn tại x = 0 2.3) Phân lo n :
ại điểm gián đoạ Nếu f(x) bị gián đoạn tại
x và lim f ( )
x L , lim f ( )
x L ( hữu hạn ) ta nói đó là điểm gián 0 1 2 x 0 x 0 x x0 0
đoạn loại 1 có bước nhảy là L L ( nếu bước nhảy bằng 0 ta nói 2 1
đó là gián đoạn bỏ đươc ). Các điểm gián đoạn ngoài loại 1 thì
đó là điểm gián đoạn loại 2 Ví dụ n
: Tìm điểm gián đoạ đoạn và phân loại
1) f(x) = x bị gián đoạn khi x = k ,k Z sin x Khi k = 0 thì x x lim 1và lim 1. V m ậy x = 0 là điể gián x 0 0 x 0 0 sin x sin x đoạn lọai 1 bỏ đ ợ ư c Khi x k 0 thì lim
, Vậy đó là đỉể n l m gián đoạ oại 2 x k sin x
2) f(x) = 7 x 3 bị gián đoạn tại x = -2 và x = 2 2 x 4 Ta có 7 x 3 x 2 lim lim .Vậy x = - m 2 là điể 2 x 2 x 2 x 4
(x 2)(x 2)( 7 x 3) gián đoạn loại 2 Và x 2 1 1
lim f (x) lim , lim f (x) . Vây x= 2 là x 2 0 x20 x 2 0
(x 2)(x 2)( 7 x 3) 24 24
điểm gián đoạn loại 1 bỏ được
3) f)x) = tan x bị gián đoạn khi x = k,k Z và x x 2 khi x
k f ( )
x . Đó là điểm gián đoạn loại 2 2
Khi x = lim f (x) lim f ( )x 1
x là điểm gián đoạn loại 1 bỏ x 0 x 0 được.
4) f(x) = cot x ( Tương tự như bài 3) x k là điểm gián đoạn 2 x loại 2 . x
là điểm gián đoạn loaij1 b ỏ được ) 2 BÀI TẬP 2 1 1 x
(1 x )sin(x 1) ln(1 2x)sin 3 1) lim ; 2) lim ;3) lim x I I I 2 2 x 1 x 0 x 1 x 0 3x sin 2x (e 1)ln x
1 1 x tan 2x 2 3x tan 2 x 4) I lim ; x 0 sin 3 ( x 1 cos 2 x) 2x 3 2x 3 5) I lim( ) ; x 2x 5 2 1 x 2x 1 6)I lim(
)x ;7) lim(cos x)x ;8) I lim [ x ln( x ) a ln ] x 2 x x0 x 4x 2 x x 1 khi x 1 9) Xét tính liên t c ụ c a ủ f(x) = cos x khi x 1 2
10) Tim A,B để f(x) sau liên tục trên R : 2 sin x khi x 2 f(x) =
Asin x B khi x 2 2 cosx khi x 2
11) Tìm điển gián đoạn và phân loại : a) f(x) = x 2x x 6 x 3 , ) b f ( ) x , ) c f ( ) x , d) f ( ) x 2 tan x cot x sin 2x x 9