Chuyên đề bất đẳng thức ôn thi vào lớp 10

Tài liệu gồm 109 trang, hướng dẫn phương pháp giải và tuyển chọn các bài tập chuyên đề bất đẳng thức, có đáp án và lời giải chi tiết, giúp học sinh lớp 9 ôn tập chuẩn bị cho kì thi tuyển sinh vào lớp 10 môn Toán

Chủ đề:

Tài liệu ôn thi vào 10 môn Toán 110 tài liệu

Môn:

Môn Toán 1.3 K tài liệu

Thông tin:
109 trang 1 năm trước
Tác giả:
N
Nguyễn Vân
docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Chuyên đề bất đẳng thức ôn thi vào lớp 10

Tài liệu gồm 109 trang, hướng dẫn phương pháp giải và tuyển chọn các bài tập chuyên đề bất đẳng thức, có đáp án và lời giải chi tiết, giúp học sinh lớp 9 ôn tập chuẩn bị cho kì thi tuyển sinh vào lớp 10 môn Toán

145 73 lượt tải Tải xuống

Chủ đề: Tài liệu ôn thi vào 10 môn Toán 110 tài liệu

Môn: Môn Toán 1.3 K tài liệu

Thông tin:

109 trang 1 năm trước

Tác giả:

Profile Nguyễn Vân
THCS.TOANMATH.com
BẤT ĐẲNG THỨC
Phần 1: BẤT ĐẲNG THỨC CAUCHY (CÔ SI)
Cho các số thực không âm
,,abc
khi đó ta có:
1.
2a b ab+≥
. Dấu đẳng thức xảy ra khi và chỉ khi
ab=
.
2.
3
3a b c abc++≥
. Dấu đẳng thức xảy ra khi và chỉ khi
abc= =
.
Các bất đẳng thức 1, 2 gọi là bất đẳng thức Cauchy cho 2 và 3 số thực
không âm. (Còn gọi là bất đẳng thức Cô si hay bất đẳng thức AM- GM)
Để vận dụng tốt bất đẳng thức Cauchy . Ta cần nắm chắc những kết quả
sau:
1)
22
1 1 4 22
a b ab
ab
+≥ ≥
+
+
;
( )
2
22
xy
xy
a b ab
+
+≥
+
2)
222
1 1 1 9 33
a b c abc
abc
++≥ ≥
++
++
3)
4)
22 2 2 2
131
() () ()
444
a abb ab ab ab−+= + + − ≥ +
5)
( )
2
222
3
abc
ab bc ca a b c
++
++≤ ≤++
6)
( )
2
2 22
xyz
xyz
a b c abc
++
++≥
++
7)
( )
3
33
4
ab
ab
+
+≥
THCS.TOANMATH.com
8)
( )
( )
2
2
44
2
44 22 44
() ()
2( )
24 8
ab
ab ab
ab ab ab

+
++
+ ≥ + ≥ = ⇒+≥



9) Với
,0ab≥
thì
1
()
2
mn mn m m
a b ab
++
+≥ +
(*)
Thật vậy BĐT cần chứng minh tương đương với
( )( )( ) 0
n nm mn n
a ba ba b+ − −≥
điều này là hiển nhiên đúng.
(**) Tổng quát ta có
22
n
nn
a b ab++

≥


Thật vậy áp dụng (*) ta có
11
......
22 2 2
n
nn n n
a b ab a b ab
−−

++ + +
 
≥≥

 
 

10) Với
,, 0abc≥
thì
1
( )( )
3
mn mn mn m m m n n n
a b c a b cabc
+++
+ + ≥ ++ ++
(*)
Thật vậy ta có bất đẳng thức cần chứng minh tương đương với:
( )( ) ( )( ) ( )( ) 0
m m n n m mn n m mn n
a bab b cbc c aca− −+ − −+− −≥
mà điều
này là hiển nhiên đúng.
Tổng quát ta có:
33
n
nnn
a b c abc+ + ++

≥


. Thật vậy áp dụng (*) ta có:
2
111 2 2 2
.
33 3 3 3
nnn n n n n n n
a b c abc a b c abc a b c
−−− − − −

+ + ++ + + ++ + +
 
≥≥

 
 

Áp dụng bất đẳng thức này ta có:
3 3 33
n
nnn
nnn
nnn nnn
n
a b b abc abc abc

+ + ++ ++ ++
≥ ⇔≤



Tương tự ta có:
1 1 1 111
33
n
nnn
a b c abc

+ + ++

≥



Do
111 9
a b c abc
++≥
++
suy ra
111 3
3
n
nnn
a b c abc

++≥

++

.
11)
11 2
11
1
ab
ab
+≥
++
+
với mọi
,1
ab≥
THCS.TOANMATH.com
Tổng quát: với
,1ab≥
ta có
( )
11 2
(1 ) (1 )
1
n
nn
ab
ab
+≥
++
+
12) Với
0,1ab≤≤
thì
11 2
11
1
ab
ab
+≤
++
+
Tổng quát: Với
[ ]
, 0;1ab∈
ta có:
11 2
11
1
nn
n
ab
ab
+≤
++
+
13) Một số kết quả được suy ra từ bất đẳng thức Cô si.
+
( )
( )( )
( )
3
333 3 33
a b x y m n axm byn+ + +≥ +
(*)
Áp dụng BĐT Cauchy ta có:
( )
( )
( )
33 3
33 3 3 33
333 3 33
3
3a x m axm
ab x y mn
abx ymn
++ ≥
++ +
++ +
( )
( )
( )
333
33 3 3 33
333 3 33
3
3b y n byn
ab x y mn
abx ymn
++ ≥
++ +
++ +
Cộng hai bất đẳng thức cùng chiều ta suy ra:
( )( )( )
333 3 33
3
33
3
axm byn
abx ymn
+
≥⇔
++ +
( )( )( )
( )
3
333 3 33
a b x y m n axm byn+ + +≥ +
.
+ Hoàn toàn tương tự ta cũng chứng minh được:
( )( )( )
( )
3
3333 33 33 3
a b c x y z m n p axm byn czp++ ++ ++ ≥ + +
.
Ví dụ 1: Cho các số thực không âm
,,abc
. Chứng minh rằng:
a)
( )
33
a b ab a b+≥ +
.
THCS.TOANMATH.com
b)
33 33 33
1 1 11
a b abc b c abc c a abc abc
++≤
++ ++ ++
. Với
( , , 0)abc>
c)
(
)(
)(
)
8
a b b c c a abc+ + +≥
.
d)
( )
( )
(
) ( )( )
8
9
abbcca abcabbcca
+ + + ≥ ++ + +
.
e) Cho
( )( )( )
1abbcca+ + +=
. Chứng minh:
3
4
ab bc ca++≤
( Trích
đề tuyển sinh lớp 10 chuyên Toán TP Hà Nội năm 2015)
Lời giải:
a) Ta có :
( )
( )
33 2 2
a b a b a ab b+=+ −+
. Suy ra
(
) ( )
( )
(
)( )
2
33 2 2
20a b abab aba abb abab+− +=+ − + =+ − ≥
suy ra
đpcm.
b) Áp dụng bất đẳng thức ở câu a ta có:
( ) ( )
33
a b abc ab a b abc ab a b c+ + ≥ + + = ++
. Suy ra
( )
33
11
a b abc ab a b c
≤
+ + ++
. Tương tự ta có:
(
) ( )
33 33
1 11 1
;
b c abc bc a b c c a abc ca a b c
≤≤
+ + ++ + + ++
. Cộng ba bất
đẳng thức cùng chiều ra suy ra:
33 33 33
1 1 11
a b abc b c abc c a abc abc
++≤
++ ++ ++
. Dấu bằng xảy ra khi và
chỉ khi
abc= =
.
c)
( )
( )( )
8
a b b c c a abc+ + +≥
.
Cách 1: Ta có:
( )( )( )
2, 2, 2 8a b ab b c bc c a ca a b b c c a abc+≥ +≥ +≥ ⇒ + + + ≥
.
Cách 2:
( )(
)( ) ( )( )
a b b c c a a b c ab bc ca abc+ + + = ++ + + −
. Theo bất
đẳng thức Cauchy ta có:
3
222
3
3, 3a b c abc ab bc ca a b c++≥ + + ≥ ⇒
THCS.TOANMATH.com
(
)(
)
9a b c ab bc ca abc
++ + + ≥
. Suy ra
( )
( )(
)
( )( )
8a b b c c a a b c ab bc ca abc abc+ + + = ++ + + − ≥
.
Chú ý:
( )( )( ) (
)
( )
a b b c c a a b c ab bc ca abc+ + + = ++ + + −
là một biến đổi
được sử dụng rất nhiều trong chứng minh bất đẳng thức:
d)
(
)( )( )
( )(
)
8
9
abbcca abcabbcca
+ + + ≥ ++ + +
.
Chú ý rằng:
( )( )( ) ( )( )
a b b c c a a b c ab bc ca abc+ + + = ++ + + −
. Áp dụng
câu c ta có đpcm.
e) Ta chú ý:
( )( )( ) ( )( )
a b b c c a a b c ab bc ca abc+ + + = ++ + + −
. Suy
ra
1 abc
ab bc ca
abc
+
++=
++
.
Theo bất đẳng thức Cô si ta có:
( )(
)
( )
3
3
33
2
abbcca abbcca abc
+++++≥ + + + =⇒++≥
.Mặt
khác sử dụng:
( )( )( )
1
8
8
a b b c c a abc abc+ + +≥ ⇒ ≤
. Từ đó suy ra:
1
1
13
8
3
4
2
abc
ab bc ca
abc
+
+
++= ≤ =
++
. Dấu ‘’=’’ xảy ra khi và chỉ khi
1
2
abc= = =
.
Ví dụ 2:
a) Cho các số thực dương
,,abc
sao cho
6a b c ab bc ca+++++=
.
Chứng minh rằng:
222
6abc++≥
. Trích đề tuyển sinh lớp 10- TP
Hà Nội 2013.
THCS.TOANMATH.com
b) Cho các số thực dương
,ab
sao cho :
11
2
ab
+=
. Chứng minh:
42 2 42 2
1 11
2 22
Q
a b ab b a a b
=+≤
++ ++
Trích đề tuyển sinh lớp 10
chuyên Nguyễn Trãi- Hải Dương 2013).
c) Cho các số thực dương
,ab
sao cho
2ab+=
. Chứng minh:
( )
22
22
11
2 6 9 10
ab
ab
ba a b

+− ++ + ≥


.
d) Cho các số thực dương
,,abc
thỏa mãn
2abc++=
. Tìm giá trị
nhỏ nhất của
222
P a bc b ac c ab= ++ ++ +
. Trích đề tuyển
sinh lớp 10- TP Hà Nội 2014.
e) Cho các số thực không âm
,ab
sao cho
22
4
ab
+=
. Tìm GTLN của
2
ab
P
ab
=
++
. Trích đề tuyển sinh lớp 10- TP Hà Nội 2015.
Lời giải:
a) Dự đoán dấu bằng xảy ra khi
1abc= = =
. Ta có cách giải như sau:
Áp dụng bất đẳng thức Cô si ta có:
2222222 2 2
2, 2, 2, 12, 12, 12
a b ab b c bc c a ac a a b b c c+ ≥ + ≥ + ≥ +≥ +≥ +≥
.
Cộng 6 bất đẳng thúc cùng chiều ta suy ra
(
)
(
)
222 222
3 3 2 12 3abc abbccaabc abc+ + +≥ + + +++ = ⇒ + + ≥
. Dấu
bằng xảy ra khi và chỉ khi
1abc= = =
.
b) Dự đoán khi
1ab= =
thì bất đẳng thức xảy ra dấu bằng. Từ đó ta có
cách áp dụng BĐT Cô si như sau:
Ta có:
4 2 24 2 2
2, 2a b a b b a ab+≥ +≥
. Từ đó suy ra
( ) ( ) ( )
2 22 2
1 1 1 11
22 22 2 2
Q
a b ab b a a b ab a b ab a b ab a b
≤ + =+=
+ + + ++
. Từ
giả thiết
11
2 22
ab
a b ab
a b ab
+
+ =⇒ =⇒+=
suy ra
( )
2
2
Q
ab
≤
+
. Do
THCS.TOANMATH.com
11 4 1 1
2
2a b ab ab
=+≥ ⇒ ≤
++
. Suy ra
1
2
Q ≤
. Dấu bằng xảy ra khi và chỉ
khi
1ab= =
.
c) Ta viết lại bất đẳng thức cần chứng minh thành:
( )
( )
( )
22
2
22
22
2 2 6 9 10
a b ab a b ab
a b ab
ab a b
+− +−

+− − + ≥

. Hay
22 33 22
22
42 42
8 4 6 9 10 0 2 4 24 12 36 18
ab ab
ab a b a b ab a b ab
ab a b
−−
−−+−≥⇔−−−++−≥
22 33 22 3 2
2 4 24 12 36 18 0 4 10 42 36 0a b a b ab a b ab t t t⇔− − − + + − ≥ ⇔ − + − ≤
(*) với
( )
2
01
4
ab
t ab
+
<= ≤ =
. Ta có (*) tương đương với:
32
2 5 21 18 0tt t− + −≤
( )
( )
2
1 2 3 18 0t tt⇔− −+ ≤
. Do
2
2 3 18 0tt−+ >
và
10
t −≤
nên
( )
( )
2
1 2 3 18 0t tt− −+ ≤
. Dấu bằng xảy ra khi và chỉ khi
11t ab=⇔==
.
d)
( )
2abc aabc bc+ = ++ +
. Áp dụng bất đẳng thức Cô si
( )( )
2
abac
abac
+++
+ +≤
, tương tự ta có:
( )
( )
( )
2
2
babc
bac babc ac babc
+++
+ = ++ + ≤ + + ≤
,
2
2
cacb
c ab
+++
+≤
. Từ đó suy ra
222
2 2 2 2( )
222
abc bca cab
P a bc b ac c ab a b c
++ ++ ++
= + + + + + ≤ + + = ++
.Dấu bằng xảy ra khi
2
3
abc
= = =
.
Ta viết lại
2
ab
P
ab
= ⇒
++
. Đặt
22ab t t
++ =⇒>
(
)
2
22 2
2 2 2 22a b ab t ab t t⇔ ++ =− ⇒ =−+
( ) ( )
22
2ab t+=−
.Ta có :
( )
( ) ( )
22
22
2 8 22 2 22 2a b ab ab ab t+ ≥ + ⇒ + ≤⇔ +≤ ⇒ <≤ +
. Ta sẽ
THCS.TOANMATH.com
chứng minh:
2
22
2
ab t t
P
ab t
−+
= =
++
.Dự đoán dấu bằng xảy ra khi
2 22 2ab t= = ⇒= +
nên ta chứng minh:
( )
( )
2
2
1 22 1
2 1 22 3 22 2 0
21 21
tt
P tt
t
−+
≤⇔ ≤⇔+−+++≤
++
.
Hay
(
)
(
)
(
)
2
21 20 222 21 0
ttt t
− + +≤⇔ − − − + ≤
. Bất đẳng thức
này luôn đúng do
2 22 2t<≤ +
. Dấu bằng xảy ra khi và chỉ khi
22 2 2t ab= +⇔==
.
MỘT SỐ KỸ THUẬT VẬN DỤNG BẤT ĐẲNG THỨC CÔ SI.
1. Dự đoán dấu bằng để phân tích số hạng và vận dụng bất đẳng
thức Cô si.
Đối với các bài toán bất đẳng thức đối xứng thông thường dấu bằng xảy ra
khi các biến bằng nhau đây là cơ sở để ta phân tích các số hạng sao cho khi
áp dụng bất đẳng thức Cô si thì dấu bằng phải đảm bảo.
Ta xét các ví dụ sau:
Ví dụ 1: Cho
,xy
là các số dương thỏa mãn
2xy+=
. Chứng minh
(
)
22 2 2
2xy x y+≤
(Đề thi tuyển sinh lớp 10 Chu Văn An, Hà Nội – Amsterdam 2006-2007)
Lời giải:
Ta dự đoán dấu bằng xảy ra khi
1xy= =
. Khi đó
1xy =
,
22
2xy+=
Mặt khác để tận dụng giả thiết
2xy+=
ta sẽ đưa về hằng đẳng thức
( )
2
xy+
. Vì vậy ta phân tích bài toán như
sau:
( ) ( )
2222 22
1
. .2
2
x y x y xy xy x y+= +
. Theo bất đẳng thức Cauchy thì
THCS.TOANMATH.com
(
)
2
1
4
xy
xy
+
≤=
,
( )
( )
2
4
22
22
2
24
24
xy
xy x y
xy x y
+

++
+≤ = =


. Từ đó
suy ra
(
)
22 2 2
2xy x y+≤
. Dấu bằng xảy ra khi
1xy= =
.
Ngoài cách làm trên ta có thể giải bài toán bằng cách đưa về một biến:
txy= +
hoặc
t xy
=
với chú ý:
( )
2
4x y xy+≥
,
( )
( )
2
22
2
x y xy
+ ≥+
. Thật
vậy: Đặt
( )
2
22
;2t xy x y x y xy= + =++
.
22 22
4 2 42xy t xy t⇒= + + ⇔ + =−
. Do
( )
2
10 1
4
xy
xy t
+
≤ =⇒ <≤
. Ta
cần chứng minh:
( ) ( )
( )
2 32 2
42 2 2 10 1 1 0t t t t t tt− ≤ ⇔ − +≥ ⇔ − −− ≤
.
Bất đẳng thức này luôn đúng với mọi giá trị
01
t<≤
.
Ví dụ 2:
a) Cho
,ab
là các số không âm thỏa mãn
22
2ab+≤
. Chứng minh
rằng:
( )
( )
3 2 3 26a aa b b bb a++ +≤
. (Đề thi tuyển sinh lớp 10 chuyên Ngoại
Ngữ ĐHQGHN năm 2008-2009).
b) Với ba số dương
,,xyz
thỏa mãn
1xyz++=
, tìm giá trị lớn nhất
của biểu thức:
xyz
Q
x x yz y y zx z z xy
=++
++ ++ ++
. (Đề thi tuyển
sinh lớp 10 chuyên Toán TP Hà Nội 2014)
Lời giải:
a) Dự đoán dấu bằng xảy ra khi
1ab= =
. Khi đó
3 2 ,3 2a a bb b a=+=+
nên ta có thể áp dụng bất đẳng thức Cauchy trực
tiếp cho biểu thức trong dấu căn.
THCS.TOANMATH.com
Sử dụng bất đẳng thức Cauchy dạng
2
xy
xy
+
≤
, dễ thấy
( )
2
32
32 2
2
aa b
a a a b a a ab
++
+≤ =+
,
( )
2
32
32 2
2
bb a
b b b a b b ab
++
+≤ =+
.
Cộng hai bất đẳng thức này lại vế theo vế, ta được:
( )
( )
( )
22
3 2 3 2 2 2 42
M a a a b b b b a a b ab ab= + + + ≤ ++ =+
. Tiếp tục
sử dụng bất đẳng thức Cauchy kết hợp với giả thiết, ta có:
22
42 4 6ab a b+ ≤+ + =
. Từ đó ta có ngay
6M
≤
. Dấu bằng xảy ra
1ab
⇔==
.
b) Ta có:
(
)
( )
( )
( )
22
x x x y z yz x
x x yz x
x
x yz x x x y z yz x
x x yz
++ + −
+−
= =
+− +++−
++
.
Áp dụng bất đẳng thức Cauchy co hai số thực dương
2
ab
ab
+
≤
ta có:
( )( )
( )
( )
2
2
xyxz
xx
x xyxz x
xy xz
xy yz xz xy yz xz xy yz xz
+++

+−

+ +−
+

≤=
++ ++ ++
. Chứng
minh tương tự rồi cộng vế, ta suy ra
1Q
≤
.Đẳng thức xảy ra khi
1
3
xyz
= = =
. Vậy
Q
lớn nhất bằng
1
khi
1
3
xyz= = =
Ví dụ 3: Cho
0c >
và
,ab c≥
. Chứng minh rằng
( ) (
)
c a c c b c ab−+ −≤
.
Lời giải:Dự đoán dấu bằng xảy ra khi
ab=
. Bất đẳng thức cần chứng minh
có thể viết thành:
THCS.TOANMATH.com
. .1
ca c cb c
P
ba ab
−−
=+≤
. Sử dung bất đẳng thức Cauchy dạng:
2
xy
xy
+
≤
, ta có:
11
1
22 2
caccbccccc
b a a b b aa b
P
−−
+ + +− + +−
≤+= =
. Bài
toán được giải quyết hoàn toàn. Đẳng thức xảy ra khi và chỉ khi
111
c ac
ba
c bc
abc
ab
−
=
⇔+=
−
=
. Ngoài ra ta cũng có thể chứng minh bài toán bằng
biến đổi tương đương.
Ví dụ 4: Cho
,,xyz
là các số thực dương. Chứng minh rằng:
2 22
2 22
1
2 22
xyz
x yz y zx z xy
++≥
+ ++
.
Lời giải:
Sử dụng bất đẳng thức Cauchy dạng:
22
2
ab a b≤+
, dễ thấy:
2 22 2 2 2
2 2 2 2 22 222 22 2
1
2 22
xyz x y z
P
x yz y zx z xy x y z y z x z x y
=++≥ + + =
+ + + ++ ++ ++
Đẳng thức xảy ra khi và chỉ khi
xyz= =
.
Ví dụ 5: Cho
,0xy>
và
1xy+≤
. Chứng minh rằng
( )
44
1
85xy
xy
+ +≥
.
Giải:
Dự đoán dấu bằng xảy ra khi
1
2
xy= =
. Ta đánh giá
44
xy+
để đưa về
xy
.
Theo bất đẳng thức Cô si ta có:
4 4 22
2x y xy+≥
suy ra
( )
4 4 22
8 16x y xy+≥
.
THCS.TOANMATH.com
Suy ra
( )
4 4 22
11
8 16
x y xy
xy xy
+ +≥ +
Để ý rằng dấu bằng xảy ra thì
22
16 1xy =
nên ta phân tích như
sau:
22 22
1 111
16 16
442
xy xy
xy xy xy xy
+= +++
. Áp dụng bất đẳng thức Cô si
3
3a b c abc++≥
ta có:
22
11
16 3
44
xy
xy xy
++≥
,
( )
2
1
41
4
xy x y xy≤+ =⇒≤
. Suy ra
22
111
16 3 2 5
442
xy
xy xy xy
+++≥+=
.
Đẳng thức xảy ra khi và chỉ khi
1
2
xy= =
.
Ví dụ 6) Cho
,,abc
là các số dương thỏa mãn
3abc++=
. Chứng minh
rằng:
222
222
222
9
12
abc
ab bc ca
abc
++≥
+
.
Lời giải:
Bất đẳng thức cần chứng minh được viết lại thành:
( )
222
222
1
29ab bc ca
abc

++ + ≥


(
)
222
222
111
29ab bc ca
ab bc ca
⇔ ++ + + + ≥
. Mặt khác sử dụng bất đẳng
thức Cauchy bộ ba số, ta có:
2 2 22
3
22
11
3 .. 3
ab ab abab a
ab ab
++ ≥ =
,
2 2 22
3
22
11
3 .. 3
bc bc bcbc b
bc bc
++ ≥ =
2 2 22
3
22
11
3 .. 3ca ca caca c
ca ca
++ ≥ =
THCS.TOANMATH.com
Cộng ba bất đẳng thức trên lại vế theo vế, ta được:
( )
222
222
111
29ab bc ca
ab bc ca
++ + + + ≥
. Dấu đẳng thức xảy ra khi và hcir
khi
1abc= = =
.
Ví dụ 7) Cho
,1xy
>
. Chứng minh rằng:
( ) (
)
( )( )
33 22
8
11
xy xy
xy
+−+
≥
−−
.
Giải:
Sử dụng bất đẳng thức Cauchy, ta có:
( )( )
2 2 22
2
2.
1 1 11
11
x y x y xy
P
y x yx
xy
=+≥ =
− − −−
−−
(1). Mặt khác, lại để ý
rằng nếu sử dụng bất đẳng thức Cauchy bộ hai số dạng
2
ab
ab
+
≤
, thì:
( )
( )
21 11
1 1. 1 ; 1 1. 1
22 22
xx yy
xx yy
+− +−
−= − ≤ = −= − ≤ =
. Nhân
hai bất đẳng thức trên lại theo vế, ta thu
được:
( )(
)
( )( )
2
11 8
4
11
xy xy
xy
xy
− −≤ ⇔ ≥
−−
(2). Từ (1) và (2) suy
ra điều phải chứng minh. Dấu đẳng thức xảy ra khi và chỉ khi
22
2
11
2, 2
xy
xy
yx
xy
=
⇔==
−−
= =
.
Đối với các bài toán mà dấu bằng không xảy ra khi các biến bằng nhau.
Ta cần chú ý tính đối xứng của từng bộ phận , để dự đoán sau đó liên
kết các dữ liệu của bài toán để tìm ra điểm rơi. Từ đó áp dụng bất đẳng
thức Cauchy để thu được kết quả:
Ta xét các ví dụ sau:
THCS.TOANMATH.com
Ví dụ 8: Cho
,, 0xyz>
thỏa mãn:
1xy yz zx++=
. Tìm GTNN của
22 2
2
Px y z
=++
Giải:
Ta dự đoán dấu bằng xảy ra khi
x y az= =
và mong muốn biến đổi được :
22 2
2( )P x y z k xy yz zx
=++ ≥ ++
để tận dụng giả thiết
1xy yz zx++=
và
dấu bằng xảy ra khi
x y az= =
. Để có tích
.
xy
ta áp dụng
22
2x y xy
+≥
.
Để tạo ra
yz
ta áp dụng:
2 22
2y a z ayz+≥
. Để tạo ra
zx
ta áp dụng:
22 2
2a z x azx+≥
.
Vì hệ số của
,yz zx
là
a
nên ta nhân
a
vào bất đẳng thức đầu tiên rồi cộng
lại theo vế ta thu
được
( ) ( ) ( )
( )
( )
2 2 2 22 22 2 2 2 22
12
()
22
ax y y az az x a x y az
a xy yz zx
+++ + + + ++
++ ≤ =
Hay
2 2 22
2 ( 1)( ) 2a a x y az≤+ + +
. Để tạo ra
22 2
2Px y z=++
ta cần có tỷ
lệ:
22
15
( 1):2 1:2 1 0
2
a a aa a
+
+ = ⇒ − −= ⇒ =
.
Từ đó ta tìm được:
2
51
1
a
P
a
≥=−
+
. Các em học sinh tự hoàn thiện lời
giải.
Ví dụ 9) Cho
,, 0xyz>
thỏa mãn:
3
xyz
++=
. Tìm GTNN của
2 23
Px y z=++
Lời giải:
THCS.TOANMATH.com
Ta dự đoán dấu bằng có khi
,x y az b
= = =
; và
23ab+=
. Theo bất đẳng
thức Cô si ta có:
22
22
333 2
2
2
3
x a ax
y a ay
z b b bz
+≥
+≥
++≥
. Cộng ba bất đẳng thức cùng chiều ta
có:
2 23 2 3 2
222()3
x y z a b ax y bz+ ++ + ≥ ++
.Tức là:
2 23 2 2 3
2( ) 3 2 2x y z ax y bz a b+ +≥ ++ − −
Bây giờ ta cần chọn a, b sao cho
2
2 :3 1:1ab=
2
23
23
ab
ab
=
⇔
+=
. Giải hệ tìm
được:
19 37 37 1
;
12 6
xya zc
−−
= = = = =
Từ đó bạn đọc tự hoàn thiện lời giải:
Ví dụ 10) Cho các số thực dương
,,abc
thỏa mãn:
222
231abc++=
.
Tìm GTNN của
333
234Pa b c= ++
Lời giải:
Dự đoán dấu bằng xảy ra khi
;;
a xb yc z= = =
với
,, 0xyz>
và
2 22
231xyz++=
Ta có:
333 2
3a a x ax++≥
;
333 2
3b b y by++≥
;
333 2
3c c z cz++≥
, suy ra
3 23
23
a ax x≥−
333 2
3b b y by++≥
3 23
93
3
22
b yb y⇔≥ −
,
3332 323
3 23c c z cz c cz z++≥ ⇔ ≥ −
( )
3 23
4 23c cz z⇒≥ −
. Cộng ba bất
đẳng thức cùng chiều suy ra:
2 2 23 33
33
32 2
22
P xa yb zc x y z

≥ + + −− −


.
THCS.TOANMATH.com
Ta cần chọn
,,xyz
để:
3
: :2 1:2:3
2
x yz
=
và
2 22
231xyz
++=
. Áp dụng
tính chất dãy tỷ số bằng nhau ta dễ dàng tìm được:
689
;;
407 407 407
xyz= = =
. Học sinh tự hoàn thiện lời giải.
Ví dụ 11) Cho các số thực dương
,,,abcd
thỏa mãn:
1abc bcd cda dab+++=
. Tìm GTNN của
(
)
333 3
49P abc d= ++ +
.(Trích
đề thi vào lớp 10 chuyên Trường chuyên KHTN- ĐHQG Hà Nội 2012)
Lời giải:
Biểu thức
P
cho ta dự đoán dấu bằng xảy ra khi và chỉ khi
,abcxd= = =
Để giảm ẩn trong bài toán ta sẽ áp dụng bất đẳng thức Cô si
theo cách:
Khi đó
333
3a b c abc++≥
,
3 3 33
3b c x d xbcd++ ≥
,
3 3 33
3c a x d xcad++ ≥
,
3 3 33
3a b x d xabd++ ≥
Suy ra
( )
333
3 3 33
3 3 33
3 3 33
3
3
3
3
x a b c xabc
b c x d xbcd
c a x d xcad
a b x d xabd
++ ≥
++ ≥
++ ≥
++ ≥
. Cộng bốn bất đẳng thức cùng chiều ta có:
( ) ( ) ( ) ( )
3 3 3 33
2 2 23 3 3x a x b x c x d x abc bcd cda dab x+ ++ ++ + ≥ + + + =
.
Bây giờ ta chọn
x
sao cho
( )
33
3
24
2 :3 4:9 4 3 6
39
x
x x xx
x
+
+ = ⇔ =⇔ −=
.
Đặt
11
2
xy
y

= +


thay vào ta tìm được
(
)
3 3 33
1
6 35, 6 35 6 35 6 35
2
yy x= + = − ⇒= + + −
. Bạn đọc tự
hoàn thiện lời giải.
2. Kỹ thuật ghép đối xứng
THCS.TOANMATH.com
Trong nhiều bài toán mà biểu thức ở hai vế tương đối phức tạp, việc chứng
minh trực tiếp trở nên khó khăn thì ta có thể sử dụng kỹ thuật ghép đối xứng
để bài toán trở nên đơn giản hơn.
ở các bài toán bất đẳng thức, thông thường chúng ta hay gặp hai dạng sau:
Dạng 1: Chứng minh
XY Z ABC++≥++
ý tưởng: Nếu ta chứng minh được
2XY A+≥
. Sau đó, tương tự hóa đẻ chỉ
ra
2
YZ B+≥
và
2ZX C+≥
(nhờ tính đối xứng của bài toán). Sau đó cộng
ba bất đẳng thức trên lại theo vế rồi rút gọn cho 2, ta có ngay điều phải
chứng minh.
Dạng 2: Chứng minh
XYZ ABC≥
với
,, 0
XYZ
≥
Ý tưởng: Nếu ta chứng minh được
2
XY A≥
. Sau đó, tương tự hóa để chỉ ra
2
YZ B≥
và
2
ZX C
=
(nhờ tính chất đối xứng của bài toán). Sau đó nhân ba
bất đẳng thức trên lại theo vế rồi lấy căn bậc hai, ta có:
222
XYZ A B C ABC ABC= = ≥
.
Ví dụ 1. Cho ba số dương
,,xyz
thỏa mãn
1xyz++=
. Chứng minh rằng
2 2 2 22 2
2 22 22 25
x xy y y yz z z zx x++ + ++ + ++ ≥
(Đề thi tuyển sinh lớp 10 tỉnh Thái Bình năm 2005-2006)
Giải:
Ta cần một đánh giá dạng :
( )
2
22
22x xy y mx ny++ ≥ +
sao cho dấu bằng xảy
ra khi
xy=
. Để có được đánh giá này thông thường ta viết lại
( ) ( ) ( ) ( ) ( )
22
22 2 2
22 2x xy y axy bx y abx baxy aby++ = − + + =+ + − ++
.
Từ đó suy ra
3
2
4
1
5
2
4
ab
a
ba
b
+=
=

⇒

−=

=
. Từ đó ta
THCS.TOANMATH.com
có:
( )
(
)
( )
( )
22 2
22 22
355 5
22 22
444 2
x xy y xy xy xy x xy y xy
++ = − + + ≥ + ⇒ ++ ≥ +
tương tự ta có 2 bất đẳng thức và cộng lại ta
có:
( )
2 2 2 22 2
2 22 22 25 5x xy y y yz z z zx x x y z++ + ++ + ++ ≥ ++=
dấu bằng xảy ra khi
1
3
xyz= = =
. Ta cũng có thể chứng minh trực tiếp:
(
)
( )
2
22 22
5
5
22 22
24
xy
x xy y x xy y x y
+
++ ≥ ⇔ ++ ≥ +
( ) ( )
( )
2
22
5
23
44
xy
x y xy x y xy
+
⇔ +−≥ +⇔ ≥
(đúng theo Cauchy)
Ví dụ 2. Cho các số thực dương
,,abc
sao cho
1ab bc ca++=
. Chứng
minh rằng:
(
)
42 42 4 2
5
2
9
abc a b c a b b c c a
++ ≤ + + +
. (Trích đề tuyển sinh
vào lớp 10- Trường Chuyên KHTN- ĐHQG Hà Nội 2014).
Lời giải:
Áp dụng bất đẳng thức Cauchy cho 3 số thực dương ta có:
( )
42 2 2
42 2 2 42 42 42
42 2 2
11
39
11 2 1
39 3 9
11
39
a b abc ca a bc
bc abc ab bca abc a b c ab bc ca
c a ab c bc c ab
+ +≥
+ + ≥ ⇒ ++ ≤ + + +
+ +≥
(1).
Mặt khác ta cũng có:
( )
( )
2
11
...
33
abc a b c ab ac bc ba ca cb ab bc ca++=++≤++=
. Suy ra
( )
44
39
abc a b c++ ≤
(2). Cộng theo vế (1) và (2) ta có đpcm.
THCS.TOANMATH.com
Ví dụ 3) Cho ba số dương
,,xyz
thỏa
111
2
111xyz
++≥
+++
. Chứng minh
rằng
1
8
xyz
≤
.
Giải:
Từ giả thiết
111
2
111xyz
++≥
+++
, ta suy ra:
( )( )
11 1
11 2
1 1 1 1 1 11
y z yz
x y z y z yz


≥− +− = + ≥


+ + + + + ++


( )
( )
1
2
1 11
yz
x yz
⇒≥
+ ++
.
Hoàn toàn tương tự ta cũng
có:
( )( ) ( )( )
11
2 ;2
1 111 11
zx xy
y zxz xy
≥≥
+ +++ ++
Nhân ba bất đẳng thức trên lại theo vế, ta thu
được:
( )( )( )
( )( )( )
18 1
111 111 2
xyz
xyz
xyz xyz
≥ ⇒=
+++ +++
.
Ví dụ 4. Cho
,, 2xyz>
và
111
1
xyz
++=
. Chứng minh rằng
( )( )( )
2 2 21xyz− − −≤
(Đề thi tuyển sinh lớp 10 chuyên Lam Sơn Thanh Hóa năm 2005-2006).
Lời giải:
Với giả thiết
,, 2xyz>
, ta nghĩ đến việc đặt ẩn phụ để đưa bài toán về dạng
đơn giản và quen thuộc hơn. Đặt
2; 2; 2
xa yb zc=+=+=+
với
,, 0abc>
.
Bài toán quay về chứng minh
1abc ≤
THCS.TOANMATH.com
Với
,, 0abc>
thỏa mãn:
111
11
222 222
abc
abc abc
++=⇔++=
+++ +++
.
Ta có:
1 1 1 11 11
1
2 222222c ab a b

=− − =− +−

+ ++ + +

( ) ( ) ( )( )
2 22 2 2 2
a b ab
a b ab
=+≥
+ + ++
Tương tự:
(
)( ) ( )( )
11
;
2 22 2 22
ca bc
bcaabc
≥≥
+ ++ + ++
Nhân ba bất đẳng thức trên lại theo vế, ta được:
( )( )( )
( )( )( )
1
1
222 222
abc
abc
abc abc
≥ ⇒≤
+++ +++
.
Ví dụ 5) Cho
,,xyz
là các số dương. Tìm giá trị nhỏ nhất của biểu thức
111
222
xyz
P
yz zx xy


=+++


+++


.
Giải:
Ta có
( ) ( )( )
( )( )( )
2 22
8
xyz yzx zxy
P
xyyzzx
++ + ++ ++
=
+ ++
(1)
Theo bất đẳng thức Cô si ta có:
( )( ) ( )( )
22
xyz xyxz xyxz++=++≥ ++
(2)
( )( ) ( )( )
22yzx yzyx yzxy++= + + ≥ + +
(3)
( )( ) ( )( )
22zxy zxzy zxzy++=++≥ ++
(4)
Nhân từng vế của (2),(3),(4) và từ (1) suy ra
1P ≥
THCS.TOANMATH.com
Dấu bằng trong (5) xảy ra
⇔
đồng thời có dấu bằng trong (2),(3),(4)
0
xy xz
yz yx x yz
zxzy
+=+
⇔ +=+⇔= =>
+=+
.Từ đó suy ra
min 1P =
.
3. Kỹ thuật cô si ngược dấu:
Ví dụ 1. Cho
,, 0
abc>
và
3
abc++=
. Chứng minh
rằng:
333
3
2
abc
b ab c bc a ca
++≥
+++
.
Giải:
Áp dụng bất đẳng thức Cauchy ta có:
32
2
1 1 1 1 1 11
1
4
2
2
abb
b ab b a b b b b a
a
ab

=− ≥− =− ≥− +

++

. Tương tự:
33
1 11 1 11
1; 1
44
bc
c bc c b a ca a c

≥− + ≥− +

++

Cộng ba bất đẳng thức này lại vế theo vế, ta được:
333
31 1 1 3
44
abc
b abc bca ca abc

+ + ≥ ++ −

+++

Bài toán được quy về chứng
minh:
3111 3 3 111
3
4 42abc abc

++ −≥⇔++≥


111
36a b c abc
abc
 
⇔ + + + + + ≥+++=
 
 
. Bất đẳng thức cuối cùng
hiển nhiên đúng vì theo bất đẳng thức Cauchy, ta
có:
1 11
2, ; 2; 2a bc
a bc
+≥ = +≥ +≥
Bài toán được chứng minh xong. Đẳng thức xảy ra khi và chỉ khi
1abc= = =
.
THCS.TOANMATH.com
Ví dụ 2) Cho
, , 0, 9abc a b c> ++=
. Chứng minh:
33 33 3 3
9
999
ab bc ca
ab bc ac
+++
++≥
+++
.
Ta chứng minh
được
( )
3
33
33 3 2
22
1 1 36( )
(), ()
4 4 9 ( ) 36 ( ) 36
ab
a b ab
a b ab ab ab ab
ab ab ab
+
++
+≥+ ≤+⇒ ≥ =+−
+ ++ ++
Mặt khác ta có:
2
( ) 36 12( )ab ab+ +≥ +
. Suy ra
33
3
9
ab
ab
ab
+
≥+−
+
. Cộng ba
bất đẳng thức cùng chiều suy ra đpcm.
Ví dụ 3) Cho
,, 0
xyz
>
và
3xyz++=
.Tìm giá trị nhỏ nhất của biểu thức
222
111
xyz
P
yzx
=++
+++
.
Lời giải:
Ta có:
2
22
11
x xy
x
yy
= −
++
. Theo bất đẳng thức Cô si thì
2
12
yy
+≥
Suy
ra
2
12
x xy
x
y
≥−
+
Tương tự, ta có:
2
12
y yz
y
z
≥−
+
,
2
12
z zx
z
x
≥−
+
Cộng từng vế ba bất đẳng thức trên ta có
( )
( )
1
2
P x y z xy yz zx
≥ ++ − + +
.
Mặt khác theo bất đẳng thức Cô si, ta có:
(
) ( )
2
3 xy yz zx x y z
+ + ≤ ++
. Vì
33x y z xy yz zx++=⇒ + + ≤
. Như vậy
3
min 1
2
P xyz=⇔===
4. Phương pháp đặt ẩn phụ:
Kỹ thuật đặt ẩn phụ là một kỹ thuật rất đặc biệt trong chứng minh bất đẳng
thức:
Việc chọn ẩn phụ thích hợp sẽ giúp bài toán trở nên đơn giản hơn:
Một số kỹ thuật hay gặp như sau:
THCS.TOANMATH.com
1. Khi có giả thiết :
a b c abc++=
ta có thể biến đổi thành:
111
1
ab bc ca
++=
đặt
111
;; 1x y z xy yz zx
abc
= = =⇒++=
.
2. Khi gặp giả thiết
1abc++=
ta có thể viết thành:
. . .1
ab ac bc ba ac cb
cb ac ba
++=
. Đặt
,, 1
ab bc ca
x y z xy yz zx
cab
= = =⇒++=
.
3. Khi gặp giả thiết:
4
ab bc ca abc+++ =
. Ta có thể viết thành:
111
1
222abc
++=
+++
. Đặt
111
;; 1
222
x y z xyz
abc
= = = ⇒++=
+++
.
4. Từ điều hiển nhiên:
+
111
11
111
xyz
yz zx xy
xyz xyz xyz
xyz
++=⇒++=
+++
++ ++ ++
+++
. Đặt
;;
yz zx xy
abc
xyz
+++
= = =
ta suy ra
111
12
111
abc a b c
abc
+ + =⇔ =+++
+++
. Từ đó suy ra khi gặp
giả thiết:
2abc a b c=+++
ta có thể đặt:
;;
yz zx xy
abc
xyz
+++
= = =
+ Nếu đổi
( )
111
,, ; ;abc
abc

→


ta có:
2abc a b c=+++
tương
đương với
21ab bc ca abc+++ =
. Vì vậy khi gặp giả thiết
21ab bc ca abc+++ =
ta có thể đặt
;;
xyz
abc
yz zx xy
= = =
+++
.
Một cách tổng quát: Khi gặp giả thiết:
111
1
ka kb kc
++=
+++
khi
khai triển thu gọn ta có:
THCS.TOANMATH.com
( )
( ) ( )( )
322
32 1 0k k k k a b c k ab bc ca abc−+− +++− +++ =
. Suy
ra tồn tại các số
,,xyz
sao cho
111
;;
xyz
ka xyzkb xyzkc xyz
= = =
+ ++ + ++ + ++
. Như vậy: Với
các số thực dương
,,abc
thỏa mãn:
111
1
ka kb kc
++=
+++
. Thì tồn
tại các số
,, 0mn p>
sao cho:
;;
mn p mn p mn p
a kb kc k
mn p
++ ++ ++
= −= −= −
.
+ Nếu
,, 0abc>
và
4ab bc ca abc+++ =
thì ta có thể đặt
2 22
;;
mn p
ab c
n p pm mn
= = =
+++
.
+ Nếu
,, 0abc>
và
14a b c abc+++=
thì ta có thể đặt
;;
2 22
n p pm mn
ab c
mn p
+++
= = =
..
5. Khi gặp giả thiết:
1xyz =
. Ta có thể chọn các phép đặt:
222
; ; 1;
abc
x y z abc
bca
= = =⇒=
22 2
;;
ab c
xyz
bc ac ab
= = =
hoặc
;;
xyz
abc
yzx
= = =
…
6. Đặt:
;;x abcy bcaz cab=+− =+− =+−
hoặc đặt
;;x aby bcz ca=+=+=+
…
Ví dụ 1: Cho
,,xyz
là các số thực dương và thỏa mãn điều kiện
x y z xyz++=
. Tìm giá trị lớn nhất của biểu thức
2 22
111
111
P
xyz
=++
+++
.
Lời giải:
THCS.TOANMATH.com
Từ giả thiết
x y z xyz++=
, ta có
111
1
xy yz zx
++=
. Đặt
111
; ;c , , 0
a b abc
xyz
===⇒>
Giả thiết trở thành:
1ab bc ca++=
,
222
111
abc
P
abc
=++
+++
Để
ý rằng:
(
)( )
( )(
) ( )( )
222
1 ;1 ,1
a abacb babcc cacb+= + + += + + += + +
Lúc này
P
có dạng
( )( ) ( )( ) ( )( )
abc
P
abac babc cacb
=++
++ ++ ++
aabbcc
abac abbc cacb
=++
++ ++ ++
. Theo bất đẳng thức Cô si,
ta có:
13
22
aabbcc
P
ab ac ba bc ca cb

≤ +++++ =

++++++

hay
3
2
P
≤
.
Dấu = xảy ra
1
3
3
abc x yz=== ⇔===
. Vậy
3
max
2
P =
. Giá trị lớn
nhất đạt được khi và chỉ khi
3xyz= = =
.
Ví dụ 2) Cho
,, 0
xyz>
và
3x y z xyz++=
.Chứng minh:
( ) (
)
( )
3 33
1
222
yz zx xy
xz y yx z zy x
++≥
+++
.
Lời Giải:
Đặt
( ) ( ) ( )
3 33
222
yz zx xy
P
xz y yx z zy x
=++
+++
, đặt
111
;;abc
xyz
= = =
. Từ
giả thiết ta có
,, 0abc>
và
3ab bc ca++=
. Lúc này dễ thấy
333
22 2
abc
P
bccaab
=++
++ +
. Theo bất đẳng thức Cô si ta có:
( )
3
2
9
26
2
a
b ca a
bc
++ ≥
+
,
( )
3
2
9
26
2
b
c ab b
ca
++ ≥
+
,
THCS.TOANMATH.com
(
)
3
2
9
26
2
c
a bc c
ab
++ ≥
+
. Cộng từng vế ba bất đẳng thức cùng chiều ta có
(
)
( )
222
93 6P ab bc ca a b c
+ ++ ≥ ++
. Mặt khác ta có kết quả quen thuộc:
222
a b c ab bc ca
++≥ ++
kết hợp với
3ab bc ca++=
suy ra
1P ≥
. Vậy
min 1
P
=
. Giá trị nhỏ nhất đạt được khi
1xyz= = =
.
Ví dụ 3: Cho
,,abc
là độ dài 3 cạnh một tam giác. Chứng minh rằng:
( )( )( )
a b c b c a c a b abc+− +− +− ≤
.
Lời giải:
Đặt
,,
2
xyz
x abcy bcaz cab abc
++
=+− =+− =+−⇒++=
. Từ đó ta
suy ra
;;
222
zx xy yz
abc
+++
= = =
. Bất đẳng thức cần chứng minh có
dạng:
( )
( )(
)
8
x y y z z x xyz
+ + +≥
. Đây là bất đẳng thức quen thuộc ( xem
ở 1).
Ví dụ 4. Cho
,, 2xyz>
và
111
1
xyz
++=
. Chứng minh rằng
( )( )( )
2 2 21xyz− − −≤
(Đề thi tuyển sinh lớp 10 chuyên Lam Sơn Thanh Hóa năm 2005-2006).
Giải:
Với giả thiết
,, 2xyz>
, ta nghĩ đến việc đặt ẩn phụ để đưa bài toán về dạng
đơn giản và quen thuộc hơn.
Đặt
2; 2; 2xa yb zc=+=+=+
với
,, 0abc>
. Bài toán quay về chứng
minh
1abc ≤
Với
,, 0abc>
thỏa mãn:
THCS.TOANMATH.com
111
11
222 222
abc
abc abc
++=⇔++=
+++ +++
.Đến đây ta đặt tiếp
;; 1
222
ab c
m n p mn p
ab c
= = = ⇒ ++ =
+++
. Ta có:
1 2 2 21 2
11
a np m
a
m a a a m m np
++
= =+ ⇒ = −= ⇒ =
+
. Tương tự:
22
;
np
bc
pm mn
= =
++
Do đó bất đẳng thức trở
thành:
( )
( )
( )
2 22
.. 1 8
mn p
m n n p p m mnp
n p p mm n
≤⇔ + + + ≥
++ +
Sử dụng bất đẳng thức Cauchy, ta
có:
( )
( )(
)
2 .2 .2 8m n n p p m mn np pm mnp
+ + +≥ =
.
Bài toán được giải quyết xong. Đẳng thức xảy ra
13mn p abc x yz
⇔ ==⇔===⇔===
.
Ví dụ 5. Cho
,,abc
là các số thực dương thỏa mãn
4
ab bc ca abc+++ =
Chứng minh rằng:
3ab bc ca++≤
.
Lời giải:
Ta có:
(
) ( )
4248124
ab bc ca abc abc ab bc ca a b c ab bc ca+++ =⇔ + ++ + +++=++++
( )( )( ) ( )( )( ) ( )( )
222 222 22abc abc ca⇔+++=++++++
111
1
222
abc
⇔= + +
+++
.
Suy ra tồn tại các số dương
,,mn p
sao cho:
2 22
,,
mn p
ab c
n p pm mn
= = =
+++
.
Thay vào bất đẳng thức cần chứng minh ta
THCS.TOANMATH.com
được:
2 2 22 22
. . .3
m n n p pm
n ppm pmmn mnn p
+ +≤
+ + + + ++
2 . 2. 2. 3
m n n p pm
m pn p m nm p n pm n
⇔ + +≤
++ ++ + +
. Sử dụng bất
đẳng thức Cauchy, ta
có:
2.
mn m n
mpnp mpnp
≤+
++ + +
2.
np n p
mnm p mn m p
≤+
++ + +
,
2.
pm p m
n pmn n p mn
≤+
++ + +
Cộng ba bất đẳng thức này lại theo vế, ta được:
2 . 2. 2. 3
m n n p p m mn n p m p
m pn p mnm p n pmn mn n p m p
++ +
+ + ≤++ =
++ ++ + + + + +
BẤT ĐẲNG THỨC SCHUR
Cho
,,
xyz
là các số thực không âm và số thực dương
t
. Khi đó ta có:
( )( ) ( )( ) ( )( ) 0
ttt
xx yx z yy zy x zz yz x−−+−−+−−≥
(*)
Đây là bất đẳng thức có khá nhiều ứng dụng và tương đối chặt nhiều bài
toán Bđt chỉ là hệ quả của BĐT này. Việc chứng minh (*) khá đơn giản:
Giả sử:
( )
(*) ( ) ( ) ( )( ) 0
tt t
x y z x y xx z yy x zz yz x

≥≥⇒ ⇔ − − − − + − − ≥

. Điều
này là hiển nhiên. Dấu bằng xảy ra khi cả 3 số bằng nhau hoặc hai số bằng
nhau, một số bằng 0.
Các bất đẳng thức suy ra từ BĐT SCHUR khi
1t =
là:
1)
333
3 ()()()a b c abc ab a b bc b c ca c a+++ ≥ ++ ++ +
.
2)
( )
3
9 4( )( )a b c abc a b c ab bc ca++ + ≥ ++ + +
.
THCS.TOANMATH.com
3)
()()()abc a b c b c a c a b≥ +− +− +−
.
4)
222
9
2( )
abc
a b c ab bc ca
abc
+++ ≥ ++
++
.
5)
4
2
( )( )( )
a b c abc
bc ca ab abbcca
+++ ≥
+ + + +++
.
Các BĐT (4) (5) còn gọi là BĐT SCHUR dạng phân thức khi
1t =
.
Ngoài ra cần chú ý biến đổi:
( ) ( ) ( )
2
333
33a b c abc a b c a b c ab bc ca

+ + − = ++ ++ − + +

.Hoặc:
(
) ( )
333 2 22
3
a b c abc a b c a b c ab bc ca

+ + − = ++ + + − + +

Ta xét các ví dụ sau:
Ví dụ 1) Cho
,,abc
là ba số thực không âm và
1abc++=
. Chứng minh
rằng:
( )
94 1
abc ab bc ca≥ ++ −
.
Lời giải:
Áp dụng bất đẳng thức Schur dạng:
( )
3
9 4( )( )a b c abc a b c ab bc ca
++ + ≥ ++ + +
.Thay
1abc++=
ta có:
( )
19 4abc ab bc ca
+ ≥ ++
. Dấu đẳng thức xảy ra khi và chỉ khi có hai số
bằng
1
2
và 1 số bằng 0 hoặc
1
3
abc= = =
Ví dụ 2) Cho các số thực dương
,,abc
sao cho
4ab bc ca abc+++ ≤
.
Chứng minh:
( )
222
2a b c a b c ab bc ca+ + +++≥ + +
.(Trích đề tuyển sinh
vào lớp 10- Trường Chuyên KHTN- ĐHQG Hà Nội 2015).
Lời giải:
Áp dụng BĐT Schur dạng phân số ta có:
222
9
2( )
abc
a b c ab bc ca
abc
+++ ≥ ++
++
. Để chứng minh bài toán ta chỉ cần
THCS.TOANMATH.com
chỉ ra:
(
)
2
9
9
abc
abc abc abc
abc
++≥ ⇔ ++ ≥
++
. Theo bất đẳng thức Cô si
ta có:
( )
( )
2
2
33
39a b c abc a b c abc++≥ ⇒ ++ ≥
. Ta chứng minh:
1abc ≤
. Thật vậy từ giả thiết ta có:
4ab bc ca abc+++ ≤
mà
3
222
3ab bc ca a b c
++≥
. Đặt
3
t abc=
ta suy ra:
( )
( )
2
32
3 40 1 2 0 1tt t t t+ −≤⇔ − + ≤⇔≤
. Suy ra
1abc ≤
hay
(
)
2
3
abc abc≥
suy ra đpcm. Dấu bằng xảy ra khi và chỉ khi
1abc= = =
.
Ví dụ 3) Cho
,,abc
là các số thực không âm sao cho
1abc++=
. Chứng
minh rằng
( )
333
4 15 1a b c abc++ + ≥
.
Lời giải:
Ta có:
(
) ( ) ( )
( )
2
333
3 3 13a b c abc a b c a b c ab bc ca ab bc ca

+ + − = ++ ++ − + + =− + +

Suy ra
( )
( )
333
4 15 27 4 12a b c abc abc ab bc ca+ + + = +− + +
( ) ( )
3 4 1 4 12 1ab bc ca ab bc ca≥ ++ −+− ++ =


. Theo ví dụ 1 ta có:
( )
94 1
abc ab bc ca≥ ++ −
. Từ đó suy ra:
( ) ( ) ( )
27 4 12 3 4 1 4 12 1abc ab bc ca ab bc ca ab bc ca+− ++ ≥ ++ −+− ++ =


Hay
( )
333
4 15 1a b c abc++ + ≥
. Dấu đẳng thức xảy ra khi và chỉ khi có hai
số bằng
1
2
và 1 số bằng 0 hoặc
1
3
abc= = =
Ví dụ 4) Cho các số thực không âm
,,
abc
. Chứng minh rằng:
( )
( )
2
222
3
3a b c abc ab bc ca+++ ≥ ++
(Trích đề tuyển sinh vào lớp 10
Trường chuyên Phan Bội Châu – Nghệ An 2014)
Lời giải:
Đặt
333
222
;;a xb yc z= = =
THCS.TOANMATH.com
Suy ra:
2 32 32 3 3 3 3
;; ; ;a xb yc z a xb y c z= = = ⇒= = =
và
,, 0xyz≥
.Bất đẳng thức đã cho thành:
(
)
3 3 3 3 3 33 33
32x y z xyz x y y z z x+++ ≥ + +
(1)
Áp dụng bất đẳng thức Schur ta suy ra:
( ) ( ) ( )
3 33
3x y z xyz xy x y yz y z zx z x+++ ≥ ++ ++ +
Mặt khác theo bất đẳng thức Cauchy ta có:
( )
33
22xy x y xy xy x y+≥ =
.
Tương tự ta có:
( )
33
2yz y z y z+≥
,
( )
33
2zx z x z x+≥
Cộng vế theo vế
các bất đẳng thức trên ta thu được:
( ) ( ) ( )
(
)
3 3 33 33
2xy x y yz y z zx z x x y y z z x++ ++ +≥ + +
(2)
Từ (1) và (2) ta có:
(
)
3 3 3 3 3 33 33
32x y z xyz x y y z z x+++ ≥ + +
Hay
( ) ( )
2
222
3
3a b c abc ab bc ca+++ ≥ ++
. Đẳng thức xảy ra khi
xyz= =
hay
abc= =
.
Ví dụ 5) Cho
,,abc
là các số thực dương có tổng bằng 1.Chứng minh rằng
( ) ( )
333 222
6 15abc abc+ + +≥ + +
.
Lời giải:
Ta có:
( )
( ) ( ) ( )
2
333
3 3 13a b c abc a b c a b c ab bc ca ab bc ca

+ + − = ++ ++ − + + =− + +

suy ra
( )
( )
333
6 1 6 1 3 18 1a b c ab bc ca abc+ + += − + + + +


( ) ( )
2
1 18 6 18abc a b c ab bc ca
=+ + ++ − + + =
( ) ( ) ( )
22
1 18 5 18abc a b c a b c ab bc ca+ + ++ + ++ − + +
( )
( ) ( )
2
222
1 5 18 8a b c abc a b c ab bc ca=+ + + + + ++ − + +
( )
( )
222
5 29 1 4a b c abc ab bc ca= + + + +− + +


.Theo ví dụ 1 ta có:
THCS.TOANMATH.com
( ) ( )
9 4 1 9 14 0abc ab bc ca abc ab bc ca≥ ++ −⇒ +− ++ ≥
. Suy ra
( )
(
)
333 222
6 15abc abc+ + +≥ + +
.
Ví dụ 6) Cho
,,abc
là các số thực dương.
Chứng minh rằng
( )
222
2 12a b c abc ab bc ca
+ + + +≥ + +
.
Lời giải:
Bất đẳng thức cần chứng minh tương đương với:
( ) ( )
2
2 14a b c abc ab bc ca++ + +≥ + +
(
) ( )
2
2 14
abc ab bc ca a b c⇔ +≥ + + − ++
, Áp dụng bất đẳng thức Schur
dạng phân số ta có:
( )
222
9
2
abc
a b c ab bc ca
abc
+++ ≥ ++
++
Hay :
( ) ( )
2
9
4
abc
ab bc ca a b c
abc
≥ + + − ++
++
. Do đó ta chỉ cần chứng minh
9
21
abc
abc
abc
+≥
++
hay
9
21abc
abc

−≤

++

.
Nếu
9
2
S ≥
thì hiển nhiên bất đẳng thức đúng. Nếu
9
2
abc++≤
, áp dụng
bất đẳng thức AM-GM, ta
được:
( )
3
3
92
9 92 1
2. 1
27 27 3
ss s
ss
abc
abc s
++ −

−

−≤ ≤ =


++


với
s abc=++
Ví dụ 7) Cho
,,abc
là các số thực không âm thỏa mãn điều kiện
1
ab bc ca++=
. Chứng minh rằng
333
6a b c abc a b c+ + + ≥++
.
Lời giải:
THCS.TOANMATH.com
Ta có:
( ) ( )
333 2 22
3a b c abc a b c a b c ab bc ca

+ + − = ++ + + − + +

( )
222
1abca b c

= ++ + + −

. Suy ra
( )
( )
333 222
69 1a b c abc abc a b c a b c+ + + = + ++ + + −
. Áp dụng bất đẳng
thức Schur dạng:
(
)
3
9 4( )( )
a b c abc a b c ab bc ca++ + ≥ ++ + +
. Ta suy ra:
( )
( ) ( )
222 3 222
9 14abcabcabc ss abcss
+++ ++−≥−+ ++ −
( )
2222
3s sabc s
= −+++ =
với
s abc=++
.Dấu bằng xảy ra khi và chỉ
khi
1
3
abc= = =
hoặc có hai số bằng 1, một số bằng 0.
BÀI TẬP RÈN LUYỆN CƠ BẢN
Câu 1) Cho
13
44
x−≤≤
. Chứng minh rằng:
34 14 2xx−++ ≥
.
Câu 2) Chứng minh rằng với mọi số thực khác không
,xy
, ta có:
22
22
x y xy
y x yx
+ ≥+
.
Câu 3). Chứng minh rằng với mọi số thực khác không
,xy
ta có:
22
22
43
x y xy
y x yx

+ +≥ +


.
Câu 4) Cho
1, 1xy≥≥
. Chứng minh rằng
11x y y x xy−+ −≤
.
Câu 5) Cho hai số thực
,xy
khác
0
. Chứng minh rằng:
( )
22 2 2
2
22
22
4
3
xy x y
yx
xy
++≥
+
.
Câu 6. Cho các số thực dương
,ab
. Chứng minh bất đẳng thức sau:
THCS.TOANMATH.com
22
33 22
22
2 32
a b a ab
ab ab
+
+≥
++
Câu 7) Cho các số thực dương
,
ab
. Chứng minh bất đẳng thức
22
2
22
ab a b a b
ab
ab
++
+ ≥+
+
.
Câu 8) Cho
[ ]
, , 1; 2abc∈−
và
0abc++=
. Chứng minh rằng:
a)
222
6abc++≤
;
b)
222
2 2 2;abc a b c abc≤++≤ +
c)
222
8a b c abc+ + ≤−
.
Câu 9) Cho các số thực không âm
,,
abc
.
Chứng minh rằng
( )
3
333
24a b c a b c abc++ ≥ + + +
.
Câu 10) Cho
,,
abc
+
∈
thỏa mãn
1abc++=
.
Chứng minh rằng
3
2
a bc b ca c ab
a bc b ca c ab
−−−
++≤
+++
Câu 11) Cho các số thực dương
,,abc
.
Chứng minh rằng
(
)
( )
2
333
222
2
9
33
abc
abc
abc a b c
++
++
+≥
++
.
Câu 12) Cho các số thực
,,abc
. Chứng minh rằng
( ) ( )
2
222 3 3 3
3a b c ab bc ca++ ≥ + +
.
Câu 13) Cho các số
,, 0xyz≥
và
1xyz++=
.
Chứng minh rằng
( )( )( )
2 41 1 1x yz x y z+ +≥ − − −
.
THCS.TOANMATH.com
Câu 14) Cho các số thực dương
a,b
. Chứng minh:
2
22 22
23
432 5
ab b
abab
+≤
++
Câu 15) Cho các số thực dương
,
ab
. Chứng minh bất đẳng thức
22
16 1 1
5
ab
b a ab a b

++ ≥ +

+

.
Câu 16) Cho các số thực dương
,
ab
. Chứng minh bất đẳng thức sau:
( )
22
22
323
22
a ab b
ab
ab
++
≥+
+
.
Câu 17) Giả sử
,xy
là những số thực không âm thỏa mãn:
33 22
x y xy x y++=+
. Tìm giá trị nhỏ nhất của biểu thức:
12
21
xx
P
yy
++
= +
++
.
Câu 18) Cho
,,abc
dương thỏa mãn:
632a b c abc++=
.Tìm giá trị lớn
nhất của
22 2
123
149
B
ab c
=++
++ +
.
Câu 19) Cho các số
,,abc
không âm. Chứng minh rằng
( )
( )
2
222
3
3a b c abc ab bc ca+++ ≥ ++
.Đẳng thức xảy ra khi nào?
Câu 20) Cho các số thực dương
,ab
sao cho
1ab b+≤
. Tìm GTNN của
2
2
11
Pa b
ab
=+ ++
.
HƯỚNG DẪN GIẢI;
Câu 1) Bất đẳng thức cần chứng minh tương đương với:
( )
2
34 14 4xx−++ ≥
THCS.TOANMATH.com
4234 14 4 34 14 0xx xx⇔+ − +≥⇔− +≥
.
Bất đẳng thức được chứng minh.
Câu 2) Bất đẳng thức đã cho tương đương với:
2
22
2
x y xy xy xy
y x yx yx yx

+ ≥+⇔ + −≥+


( )
( )
2
22
22
2 10 0
x y x xy y
xy xy
yx yx xy
− ++

⇔ +− ++≥⇔ ≥


Mà
( )
( )
2
2 2 22
2 0, , 0x xy y x y x y x y+ + = + + + >∀ ≠
nên ta có điều phải
chứng minh.
Đẳng thức xảy ra khi và chỉ khi
0xy= ≠
.
Câu 3) Bất đẳng thức đã cho tương đương với:
2
22
22
43 23
x y xy xy
y x yx yx
 
+ +≥ + +≥ +
 
 
( )
( )
2
22
22
2 10 0
x y x xy y
xy xy
yx yx xy
− −+

+− + +−≥⇔ ≥


Mà
(
)
( )
2
2 2 22
20x xy y x y x y−+ =++− >
với mọi số thực
,xy
khác
0
nên ta có điều phải chứng minh.
Đẳng thức xảy ra khi và chỉ khi
0xy= ≠
.
Câu 4)
Đặt
1, 1a xb y=−=−
thì
0, 0ab≥≥
. Bất đẳng thức cần chứng minh
tương đương với:
( ) ( ) ( ) ( )
22 22
11 11a bb a a bb+++≤+++
THCS.TOANMATH.com
( ) ( ) ( ) ( )( ) ( )
222 222
1 12 1 1 12 1 0abb aba b ba⇔ + + +− + ++ + +− + ≥
(
)
( )
( )
(
)
2
2 22
1 1 1 10a bb b a⇔+++++ −≥
.
Bất đẳng thức cuối cùng đúng nên ta có điều phải chứng minh.
Dấu đẳng thức xảy ra khi
1
ab= =
hay
2
xy= =
.
Câu 5) Bất đẳng thức đã cho tương đương với:
( )
( )
(
)
2
22 2 2
22 2 2 4 22 4
22
2 2 22
22 22
4
42
1 20 0
xy x y
xy x y x xy y
y x xy
xy xy
−+
−+
−++−≥⇔ + ≥
++
( )
( )
( )
( )
( )
22
22 22
2
22
22
22 22
22 22
11
0. 0
xy xy
xy
xy xy
xy xy

−− −

⇔ + ≥⇔ − − ≥

++

( )
( )
( )
( )
( )
2
2 2 22
4 4 22
22
22 22
22
22 2 2 22 2 2
00
x y xy
x y xy
xy xy
xy x y xy x y
−−
++
⇔− ≥⇔− ≥
++
Bất đẳng thức cuối cùng đúng nên ta có điều phải chứng minh.
Đẳng thức xảy ra khi và chỉ khi
xy= ±
.
Câu 6)
Dấu đẳng thức xảy ra với
ab=
khi và chỉ khi:
22
33 22
12
;1
2 32
a b a ab
ab ab
+
= =
++
.
Ta có biến đổi sau:
22 22
33 22 33 22
22 12
1
2 32 2 32
a b a ab a b a ab
ab ab ab ab
++
+≥ ⇔ −≥ −
+ ++ +
THCS.TOANMATH.com
( )
( )
( )
(
)
( )
(
)
22
2
22 22
33 33
2
12
0
22
32 32
ab ab ab
ab
ab
ab ab
ab ab

−− + −−
−

⇔ ≥ ⇔− − ≥
++
++


(
)
(
)
(
)
(
)
2
33 22
32 2 2 0
ab a b a b ab

⇔− + − + + ≥

(
)
( )
( )( )
24
332 2
222 2 0 0ab a b ab ab abab⇔− + − − ≥⇔+ − ≥
(đpcm).
Câu 7) Ta có:
( )
( )
2
2
22
ab
a b ab
ab ab
−
+
−=
++
( )
22
2
22
22
22
2
2
2
2
2
ab
ab
ab
ab
ab
ab
ab
ab
ab
+
−
−
+
−= =

+
+
+
+



Do đó bất đẳng thức cần chứng minh tương đương với:
(
)
2
22
22
2 11
0
22 2
2
ab
a b a b ab
ab
ab ab
ab
ab


−
++

−≥−⇔ −≥

++
+
+


( )
( )
2
22
22 2 2 0
a b a b a b ab

⇔− +− + − ≥


Vì
( )
2
0ab−≥
nên ta chỉ cần chứng minh:
( )
22
22 2 2 0a b a b ab+− + − ≥
(*)
( )
( )
( )
( )
2
22
22
2
2
ab
ab a b
a b ab
−
+− + =−
+ ++
THCS.TOANMATH.com
( )
( )
( )
2
2
2
ab
a b ab a b
ab
−
+− = − =
−
Do vậy bất đẳng thức (*) tương đương với:
( )
(
)
(
)
( )
2
2
22
11
0
2
ab
a b ab
ab


−− ≥

+ ++
+


( )
(
)
(
)
2
2
22
20
ab a b ab a b

⇔ − + ++− + ≥


( )
( )
2
22
2 20a b a b ab

⇔− + − ≥


( )
( )
( )
( )
( )
4
22
2
22 22
24
2
00
22 22
a b ab
ab
ab
a b ab a b ab
+−
−
⇔ − ≥⇔ ≥
++ ++
.
Bất đẳng thức này hiển nhiên đúng, ta có điều phải chứng minh.
Đẳng thức xảy ra khi và chỉ khi
ab=
.
Câu 8) Vì
[ ]
, , 1; 2abc∈−
nên có một số bất đẳng thức hiển nhiên đúng
( )( ) ( )( )( ) ( )( )( )
1 2 0, 1 1 1 0, 2 2 2 0aa abc a b c+ −≤ + + +≥ − − −≤
.
a) Do
[
]
, , 1; 2abc∈−
nên
( )( )
2
1 20 2a a aa+ − ≤⇔ ≤+
.
Tương tự ta suy ra:
222
66a b c abc+ + ≤+++=
(do
0abc++=
).
b) Vì
[ ]
, , 1; 2abc∈−
nên
( )( )( )
1 1 10abc+ + +≥
, hay
10abc ab bc ca a b c+ + + + +++≥
10abc ab bc ca⇔ + + + +≥
(do
0abc++=
) (1)
Mặt khác cũng vì
0
abc++=
nên
( )
2
0abc++ =
, tức là
THCS.TOANMATH.com
222
2
abc
ab bc ca
++
++=−
(2)
Từ (1) và (2) ta có:
222
222
10 22
2
abc
abc a b c abc
++
− +≥ ⇔ + + ≤ +
Dấu đẳng thức có, chẳng hạn
1, 1, 0a bc=−==
Ta còn phải chứng minh
222
2a b c abc++≥
Không mất tính tổng quát, giả sử
abc≥≥
Từ đó suy ra
1 01
3
abc
cc
++
−≤ ≤ ≤ ⇒ ≤
Sử dụng đánh giá này, ta được
2 2.. 2.abc abc ab≤≤
Suy ra
( )
2
222 222 2
2 2. 0abc abcabc ab ab c++− ≥++− = − +≥
Dấu đẳng thức có khi
0abc= = =
.
c) Vì
[ ]
, , 1; 2abc∈−
nên
( )
( )( )
2 2 20abc− − −≤
, hay
( ) ( )
2 4 80abc ab bc ca a b c− + + + ++ −≤
( )
2 80
abc ab bc ca⇔ − + + −≤
(do
0
abc++=
) (3)
Từ (3) và (2) ta có:
222 222
80 8abc a b c a b c abc+++−≤⇔++≤−
Dấu đẳng thức có, chẳng hạn
2, 1, 1ab c= =−=−
.
Câu 12. Cho
[ ]
, , 0; 2abc
∈
và
3abc++=
.
Chứng minh rằng
( )( )( )
333
3 3 1 1 19abc a b c≤ + +− − − −≤
.
Giải:
Đặt
1, 1, 1ax by cz=+=+=+
thì
[ ]
, , 1;1xyz∈−
và
0xyz++=
Ta có
( )( )( )
333
31 1 1Pabc a b c=++− − − −
(
) ( ) ( )
3 33
1 1 13x y z xyz=+++++−
( )
( )
3 33 2 22
33 3 3x y z xyz x y z x y z= + + − + + + + ++ +
THCS.TOANMATH.com
Mà
0xyz++=
nên
( )
(
)
3 33 2 22
30
x y z xyz x y z x y z xy yz zx++− =++ ++−−− =
Do đó
( )
2 22
33P xyz
= ++ +
Vậy ta có
2 22
02xyz≤++≤
nên
39
P
≤≤
.
Câu 9)
Giải:
Ta có:
( ) (
)
( )
( )
3
333
3abc a b c abbcca++ ≥ + + + + + +
Nên bất đẳng thức đã cho tương đương với:
( )(
)( )
8a b b c c a abc
+ + +≥
222222
6ab ac bc ba ca cb abc⇔+++++≥
2 22 22 2
2 2 20ab abc ac bc abc ba ca abc cb⇔−++−++−+≥
(
) (
) ( )
222
0ab c bc a ca b⇔ −+−+ −≥
Vậy ta có điều phải chứng minh.
Đẳng thức xảy ra khi và chỉ khi
abc= =
.
Câu 10)
Ta có
( ) ( )( )
abc aabc bc abac+= +++=+ +
nên bất đẳng thức cần
chứng minh tương đương với:
( )
( )( )
( )
( )( )
( )
( )( )
3
2
aabc bc babc ca cabc ab
abac bcba cacb
++ − ++ − ++ −
++≤
++ ++ ++
( )
( )
( )
( )
22
a ab ac bc b c b ba bc ca c a⇔ + +− ++ + +− ++
THCS.TOANMATH.com
( )
(
)
( )
( )
(
)
2
3
2
c cacaabab abbcca++− +≤ + + +
222222
6
ab ac bc ba ca cb abc⇔+++++≥
( ) ( ) ( )
222
0ab c bc a ca b⇔ −+−+ −≥
Vậy bài toán được chứng minh.
Đẳng thức xảy ra khi và chỉ khi
1
3
abc
= = =
.
Câu 11)
Bất đẳng thức đã cho tương đương với:
( )
( )
2
333
222
2
9
6 27 0
abc
abc
abc a b c
++
++
−+ − ≥
++
( )
( ) ( )
222 222
222
2 18
0
a b c a b c ab bc ca a b c ab bc ca
abc a b c
++ ++−−− ++−−−
⇔ −≥
++
( )
222
222
9
20
abc
a b c ab bc ca
abc a b c
++

⇔ ++−−− − ≥

++

( ) ( )
( ) ( )
( )
222
222
90a b b c c a a b c a b c abc


⇔ − + − + − ++ + + − ≥


Do
(
) ( ) ( )
222
ab bc ca− +− +−
nên ta chỉ cần chứng minh
( )
( )
222
90
a b c a b c abc++ + + − ≥
( )
( ) ( )
333 22 2 2 22
3 60a b c abc a b c b c a c a b abc⇔ ++− + + + + + + − ≥
Bất đẳng thức này đúng vì ta có:
THCS.TOANMATH.com
( )
( )
333 222
3a b c abc a b c a b c ab bc ca+ + − = ++ + + − − −
( ) ( ) ( ) ( )
222
0
2
abc ab bc ca

++ − + − + −

= ≥
Và
( ) ( ) ( )
(
) ( ) ( )
222
22 2 2 22
60a b c b c a c a b abc a b c b c a c a b++ ++ +− = −+−+ −≥
Đẳng thức xảy ra khi và chỉ khi
abc= =
.
Câu 12) Giải:
Từ hằng đẳng thức:
( ) ( ) ( )
22
222 3 3 3 22
1
32
2
a b c a b b c c a a b bc ab ac++ − + + = −+ −− +
(
)
( )
22
22 22
11
22
22
b c ca bc ba c a ab ca cb
+−+−−+−+−−
Suy ra ta có điều phải chứng minh.
Câu 13)
Do
1xyz++=
nên bất đẳng thức cần chứng minh có thể viết lại thành:
( )(
) ( )( )( )
2
24x yzxyz xyyzzx+ + ++ ≥ + + +
Do vai trò của
x
và
z
trong bất đẳng thức trên là như nhau nên ta hoàn toàn
có thể giả sử
xz≥
.
Áp dụng bất đẳng thức Cauchy dạng
( )
2
4a b ab+≥
, ta có
( ) ( )
2
4xyz xyz++ ≥ +
.
Sử dụng đánh giá này, dễ thấy chứng minh sẽ hoàn tất nếu ta chỉ ra được
THCS.TOANMATH.com
( ) ( )( )
( )
20xx yz xyzx yxz+ +≥+ +⇔ −≥
, hiển nhiên đúng theo giả sử
xz
≥
.
Bài toán được chứng minh xong.
Đẳng thức xảy ra khi và chỉ khi
1
;0
2
xz y= = =
.
Câu 14) Viết lại bất đẳng thức thành:
2
22 22
23
432 5
ab b
abab
+≤
++
2 2 2 22
22 22 22 22
2 2 1 2 10 8 3 3
00
5 4532 4 32
ab b a ab b a b
ab ab ab ab
−+ −
⇔− +− ≥⇔ + ≥
++ + +
( )( )
( )(
)
22 22
2 43
0
4 32
aba b abab
ab ab
−− −+
⇔ +≥
++
( ) ( )
( )
(
)
( )
22 22
2 43 2 3 4 0ab abab abab

⇔− − + + + + ≥

( )
(
)
(
) (
)
22
3 2 23
9 21 16 4 0 3 2 0
ab a ab ab b ab a b⇔− − + − ≥⇔− − ≥
Ta có điều phải chứng minh.Đẳng thức xảy ra khi và chỉ khi
ab=
hoặc
2
3
ab=
.
Câu 15) Vì
,0ab>
nên bất đẳng thức đã cho tương đương với:
22
1 1 4 11
40
ab
b b a a ab a b

−+ −+ −− ≥

+

( )
( )
2
22
4
40
ab a b
ab ba
b a a b ab
−+
−−
⇔++ ≥
++
THCS.TOANMATH.com
(
) (
)
(
)
(
)
22
22
4
0
ab ab ab
a b a b ab
−+ −
⇔ −≥
+
( ) ( )
(
)
22 4
40 0ab ab ab ab

⇔− + − ≥⇔− ≥

.
Bất đẳng thức cuối đúng nên có điều phải chứng minh.
Dấu đẳng thức xảy ra khi
0ab= >
.
Câu 16) Bài toán này có chứa căn nên để xuất hiện nhân tử chung dạng
( )
2
ab−
ta cần chú ý đến phép biến đổi
( )
( )
( )
( )
( )
2
22
22
2
2
ab
a b ab
a b ab
−
+ −+=
+ ++
Khi đó:
( )
22
22
323
22
a ab b
ab
ab
++
≥+
+
( )
( )
( )
22
22
323
2 22 2
a ab b
ab a b ab
ab
++
⇔ −+≥ +−+
+
( )
( )
(
)
(
)
22
22
2
2
ab ab
ab
a b ab
−−
⇔≥
+
+ ++
(
)
(
)
( ) ( )
2
22
2 20ab a b ab ab

⇔− + −+− + ≥


( )
( )
( )
( )
( )
4
2
22
22
20 0
2
ab
ab a b ab
a b ab
−

⇔ − + − + ≥⇔ ≥


+ ++
Bất đẳng
thức cuối cùng đúng do
,ab
dương.Đẳng thức xảy ra khi và chỉ khi
ab=
.
Câu 17)
( ) ( ) (
)
32
33 22
32
x y xy x y x y xy x y xy x y xy++=+⇔+ − ++=+ −
Đặt
;xyaxyb+= =
, ta có:
( ) ( )
3 22
3 3 0 13 1 0a ab b a a a b a− + − =⇔ −− −=
THCS.TOANMATH.com
( )
( )
( )
2
2
2
1
1
1 30
3
3
xy
a
a ab
ab
x y xy
+=
=
⇔− − =⇔ ⇔
=
+=
Vì
( )
2
4; , 0x y xy x y+ ≥ ∀≠
suy ra
0xy= =
hoặc
1xy
+=
Với
0xy
= =
thì
5
2
P =
Nếu
x
hoặc
y
khác
0
, ta có
01
1
01
x
xy
y
≤≤
+=⇒
≤≤
,
( ) ( )
10
4
min ; max 4
01
3
yy
PP
xx
= =

=⇔=⇔

= =

Vậy
( )
4
min
3
P =
khi
(
)
0, 1; max 4x yP= = =
khi
1; 0xy= =
.
Câu 18) Đặt
,,
23
bc
x ay z= = =
thì
,,xyz
là các số dương và
x y z xyz++=
.
Khi đó:
2 22
111
111
A
xyz
=++
+++
Ta có:
( ) ( )( ) ( ) ( )
2
2
1
22
1
xyz yz y z
xxyz xyz xyxz xy xz
x
= = ≤+
++ + + + + +
+
Tương tự ta có:
( ) ( ) ( ) ( )
22
11
;
22 22
11
xz xy
xy yz xz yz
yz
≤+ ≤+
++ ++
++
( ) ( ) ( )
3
222 2
xy xz yz
A
xy xz yz
+++
⇒≤ + + =
+++
. Dấu đẳng thức xảy ra khi và chỉ
khi:
3 3, 2 3, 3 3xyz a b c=== ⇒= = =
.Vậy giá trị lớn nhất của
biểu thức
A
là
3
2
đạt được khi và chỉ khi
3, 2 3, 3 3ab c= = =
.
Câu 19) Đặt
333
222
;;
a xb yc z= = =
Suy ra:
2 32 32 3 3 3 3
;; ; ;a xb yc z a xb y c z= = = ⇒= = =
và
,, 0xyz≥
.
Bất đẳng thức đã cho thành:
THCS.TOANMATH.com
(
)
3 3 3 3 3 33 33
32x y z xyz x y y z z x
+++ ≥ + +
(1)
Vì vai trò của
,,xyz
bình đẳng nên có thể giả sử
0xyz
≥≥≥
Khi đó:
(
)
( )
( )( )( )
22
0xxy zyz zxyxyyz− + − + +− − − ≥
Suy ra:
( ) ( ) ( )
3 33
3x y z xyz xy x y yz y z zx z x
+++ ≥ ++ ++ +
(2)
Áp dụng bất đẳng thức Cô si ta có:
( )
33
22
xy x y xy xy x y+≥ =
(3)
Tương tự ta có:
( )
33
2yz y z y z+≥
(4)
( )
33
2zx z x z x+≥
(5). Cộng vế theo vế các bất đẳng thức (3),(4),(5) ta
được:
( ) ( ) ( )
(
)
3 3 33 33
2xy x y yz y z zx z x x y y z z x++ ++ +≥ + +
(6)
Từ (2) và (6) ta có:
(
)
3 3 3 3 3 33 33
32
x y z xyz x y y z z x+++ ≥ + +
Hay
( )
( )
2
222
3
3a b c abc ab bc ca+++ ≥ ++
Đẳng thức xảy ra khi
xyz= =
hay
abc= =
.
Câu 20) Giả thiết ta suy ra
1
1a
b
+≤
.Ta có
2
2
11
22
ab
Pa b
ba b a
=++ + ≥ +
.
Đặt
1
1
22
a
a
b
t
b
+
=≤≤
. Ta chứng minh:
9P ≥
. Thật vậy ta có:
( )
( )
2
32
22 2
21 42
2 292
29 0
t tt
tt
t
tt t
− −−
−+
+ −= = ≥
. Do
1
0
2
t<≤
, dấu đẳng
thức xảy ra khi và chỉ khi
4
1
1
2
1
ba
t
a
b
=
= ⇔
+=
.
BÀI TẬP RÈN LUYỆN NÂNG CAO
Câu 1) Cho
,,xyz
là các số thực dương thỏa mãn điều kiện
1xyz++=
.
Tìm giá trị lớn nhất của biểu thức
P x yz y zx z xy= ++ ++ +
.
Câu 2) Cho
,,xyz
là ba số thực dương và
1xyz =
.
THCS.TOANMATH.com
Tìm giá trị nhỏ nhất của biểu thức
2 2 22
22
11
1
xy yz
zx
P
xy yz zx
++ ++
++
=++
.
Câu 3) Cho
2, 3, 4xyz≥ ≥≥
. Tìm giá trị lớn nhất của biểu thức sau:
423
xy z yz x zx y
P
xyz
−+ −+ −
=
Câu 4) Cho
,,xyz
là các số dương sao cho
1xyz
++=
. Tìm giá trị lớn
nhất của biểu thức
3
P x xy xyz=++
.
Câu 5) Cho
,0xy>
và thỏa mãn điều kiện
3
23 6
x y xy
++ =
. Tìm giá trị nhỏ
nhất của biểu thức
33
27 8P xy= +
.
Câu 6) Cho
,,xyz
là các số thực dương và
1xyz
=
. Tìm giá trị nhỏ nhất
của biểu thức:
( )( )
( )( )
( )( )
333
11 11 11
xyz
P
xy zx xy
=++
++ ++ ++
.
Câu 7) Cho
,,xyz
là 3 số dương và thỏa mãn điều kiện
3xyz++=
.
Tìm giá trị nhỏ nhất của biểu thức
(
)
3 33
333
2
8 8 8 27
xyz
P xy yz zx
yzx
= + + − ++
+++
.
Câu 8) Cho
,,xyz
là ba số dương và
3
xyz++=
.
Tìm giá trị nhỏ nhất của biểu thức
222
111
111
xyz
P
yzx
+++
=++
+++
Câu 9) Cho
,,xyz
là ba số thực dương thỏa mãn điều kiện
3xyz++=
.
Tìm giá trị nhỏ nhất của biểu thức
222
111
xyz
P
yzx
=++
+++
.
THCS.TOANMATH.com
Câu 10) Cho
,,xyz
là ba số thực dương thỏa mãn điều kiện
3xyz++=
.
Tìm giá trị nhỏ nhất của biểu thức
2 22
333
2 22
xyz
P
xyyzzx
=++
+ ++
.
Câu 11) Cho
,, 0xyz≥
thỏa mãn điều kiện
3xyz++=
.
Tìm giá trị bé nhất của biểu thức
22 2
22
22 2
xy z
P
x yy z z x
=++
++ +
.
Câu 12) Cho
,,xyz
là ba số thực dương và
3xyz++=
.
Tìm giá trị nhỏ nhất của biểu thức
2 22
111
111
P
xyz
=++
+++
.
Câu 13) Cho
,,xyz
là ba số thực dương thỏa mãn điều kiện
8xyz
=
.
Tìm giá trị lớn nhất của biểu thức
222
111
xyz
P
xyz
−−−
=++
+++
Câu 14) Cho
,,
xyz
là các số thực dương thỏa mãn điều kiện
1xyz =
.
Tìm giá trị nhỏ nhất của biểu thức
( ) ( ) ( )
3 33
111
1
P
xyz yz zxy
= ++
+ ++
Câu 15) Cho
,, 0xyz>
và thỏa mãn điều kiện
1xyz++=
.
Tìm giá trị lớn nhất của biểu thức
111
2
111
x y z yzx
P
x y z xyz

+++
= + + − ++

−−−

.
Câu 16) Cho
,,xyz
là các số thực dương.
Tìm giá trị lớn nhất của biểu thức:
( )( )
( )( )
( )( )
xyz
P
x xyxz y yzyx z zxzy
=++
++ + ++ + ++ +
.
THCS.TOANMATH.com
Câu 17) Cho
,,xyz
là ba số dương và
1xyz =
. Tìm giá trị lớn nhất của biểu
thức:
52 52 52
111
36 36 36
P
x x xy y y yz z z xy
=++
−++ −++ −++
(1)
Câu 18) Cho
,, 0xyz≥
và thỏa mãn điều kiện
3xyz++=
. Tìm giá trị nhỏ
nhất của biểu thức
( )
P x y z xy yz zx= + + − ++
.
Câu 19) Cho
,,xyz
là các số thực không âm và thỏa mãn điều kiện
2 22
3xyz
++=
.
Tìm giá trị lớn nhất của biểu thức
2 22
23 23 23
xyz
P
xy yz zx
=++
++ ++ ++
.
Câu 20) Cho
,,
xyz
là các số thực dương và thỏa mãn điều kiện
8xyz =
.
Tìm giá trị nhỏ nhất của biểu thức
( )( )
( )( )
( )( )
2 23
3 3 33 33
11 11 11
xyz
P
xy yz zx
=++
++ ++ ++
Câu 21) Cho
,,xyz
là các số thực dương..
Tìm giá trị nhỏ nhất của biểu thức:
( )
( )
( )
333
333
3 33
xyz
P
xyz yzx zxy
=++
+++
.
Câu 22) Cho
,, 0xyz≥
và thỏa mãn điều kiện
1xY z++=
. Tìm giá trị nhỏ
nhất của biểu thức
22 22 2 2
111
xyz
P
yz zx xy
=++
++ ++ ++
.
THCS.TOANMATH.com
Câu 23) Cho
,,xyz
là các số thực dương thỏa mãn điều kiện
1xyz =
.
Tìm giá trị lớn nhất của biểu thức
3 3 33 33
111
26 26 26
P
xy yz zx
=++
++ ++ ++
.
Câu 24) Cho
,,xyz
là các số thực dương sao cho
1xyz =
.
Tìm giá trị nhỏ nhất của biểu thức
( )
( ) ( )
2 22
222
xyz yzx zxy
P
yy zz zz xx xx yy
+++
= ++
+++
.
Câu 25) Cho
,,xyz
là các số thực dương và thỏa mãn điều kiện
6xyz++=
.
Tìm giá trị nhỏ nhất của biểu thức
333
111
xyz
P
yzx
=++
+++
.
Câu 26) Cho
,,xyz
là ba số dương và thảo mãn điều kiện
111
1
xyz
++≤
.
1) Tìm giá trị nhỏ nhất của biểu thức
222
2 2 22 22
8 14 3 8 14 3 8 14
xy z
P
x y xy y z yz z x zx
=++
++ ++ ++
.
2) Tìm giá trị nhỏ nhất của biểu thức
111
xy yz zx
Q
xyz
+ ++
=++
+++
.
Câu 27) Cho
,,xyz
là các số thực dương sao cho
3xyz++=
. Tìm giá trị
nhỏ nhất của biểu thức
2 22
P x y z xyz=+++
.
Câu 28) Cho
,, 0xyz>
và thỏa mãn
1xyz =
.
THCS.TOANMATH.com
Tìm giá trị nhỏ nhất của biểu thức
(
)(
)( ) ( )
2P xyyzzx xyz= + + + − ++
.
Câu 29) Cho các số thực dương
,,abc
.
Chứng minh rằng:
( )
( ) ( )
33 33 3 3
3 33
2
444
ab bc ca
c ab a bc b ca
+++
++≤
++ ++ ++
Câu 30) Cho các số thực dương
,,abc
sao cho
1
abc++=
. Tìm GTLN của
( ) ( ) (
) ( )
222
6P abbcca aab bbc cca= ++ + − + − + −
.
LỜI GIẢI BÀI TẬP RÈN LUYỆN
Câu 1)
Từ điều kiện
1xyz
++=
, ta có
( ) ( )( )
xyzxxyz yz xyxz+= +++=+ +
.
Tương tự, ta cũng có
( )( )
( )(
)
( )( )
P xyxz yzyx zxzy
= + ++ + ++ + +
Áp dụng bất đẳng thức Cô si, ta có:
( )( )
( )( )
(
)( )
222
xyxz yzyx zxzy
P
++ ++ ++
≤++
hay
( )
22P xyz≤ ++ =
Như vậy
2P ≤
. Dấu bằng trong xảy ra khi
1
3
1
xy xz
yz yx
xyz
zxzy
xyz
+=+
+=+
⇔ ⇔===
+=+
++=
. Từ đó ta có
1
max 2
3
P xyz=⇔===
.
Câu 2) Áp dụng bất đẳng thức Cô si, ta có:
2 2 22
3
22
33
33
3
xy yz
zx
P
xy yz zx
≥++
THCS.TOANMATH.com
Hay
333
P
xy yz zx
≥++
. Lại theo bất đẳng thức Cô si, ta có:
3
2 22
3 3 3 33
3
xy yz zx
xyz
++≥
. Do
1xyz =
, nên suy ra
33P ≥
. Vậy
min 3 3 1
P xyz
= ⇔===
.
Câu 3)
Đưa biểu thức về dạng
3
42
y
zx
P
zxy
−
−−
=++
. Áp dụng bất đẳng
thức Cô si ta có:
(
)
( )
44
1 1 3 41
4 4 .4
2 22 4 4
z
z
zz
z
−+
−
−= − ≤ =⇒ ≤
( )
( )
22
1 1 21
2 2 .2
2
2 2 22 22
x
xx
xx
x
−+
−
−= − ≤ = ⇒ ≤
(
)
( )
33
3
11 1
3 3 .3
2
3 3 23 23
y
y
y
yy
y
−+
−
−= − ≤ = ⇒ ≤
Cộng từng vế ba bất đẳng thứctrên ta có
11 1 1
22
23
P

≤ ++


. Vậy
1111
max 4, 6, 8
2
234
P xyz

= + + ⇔= = =


.
Câu 4)
Viết lại biểu thức trên dưới dạng:
3
11
.4 .4 .16
24
P x xy xy z=++
.
Áp dụng bất đẳng thức Cô si ta có:
THCS.TOANMATH.com
4 4 16
4 12
xyxy z
Px
+ ++
≤+ +
hay
( )
4
3
xyz
P
++
≤
. Từ
1xyz++=
và (2)
suy ra
4
3
P ≤
. Vậy
4
max
3
P =
Câu 5) Theo bất đẳng thức Cô si, ta có:
3
11 3
82
xx
++≥
;
3
11 3
27 3
yy
++≥
;
33
13
8 27 6
x y xy
+ +≥
. Cộng từng vế ta có:
33
2 53
8 27 2 3 6
x y x y xy


+ +≥ + +




.
Do
3
23 6
x y xy
++ =
, ta có:
33
2
8 27
xy

+≥


. Suy ra
33
27 8 432P xy= +≥
(4)
Dấu bằng trong (4) xảy ra khi
2, 3xy
= =
. Vậy
min 432P =
, giá trị nhỏ
nhất đạt được khi
2, 3xy= =
.
Câu 6) Theo bất đẳng thức Cô si, ta có:
( )( ) ( )( )
33
1 1 11
3
11 8 8 11 88
x x y x xy
xy xy
+ + ++
++≥
++ ++
Hay
( )( )
3
11 3
11 8 84
x x yx
xy
++
++≥
++
. Lập luận tương tự ta có:
( )( )
3
11 3
11 8 84
y z xy
zx
++
++≥
++
( )( )
3
11 3
11 8 84
z x yz
xy
++
++≥
++
Cộng
từng vế ta có
( )
31
42
P xyz+≥ ++
.Dấu = xảy ra
1xyz⇔===
. Lại
theo bất đẳng thức Cô si, ta có:
3
33x y z xyz++≥ =
Từ đó suy ra
33 3
42 4
PP+≥⇒≥
. Dấu bằng trong (5) xảy ra
1
xyz⇔===
(do
1xyz =
) . Như vậy
3
min
4
P =
. Giá trị nhỏ nhất đạt được
1xyz⇔===
.
Câu 7) Theo bất đẳng thức Cô si, ta có:
32
3
2 24
8 27 27 3
x y yy x
P
y
+ −+
= ++ ≥
+
THCS.TOANMATH.com
32
3
96
8 27
x xyy
y
+− −
⇒≥
+
(1). Dấu bằng trong (1) xảy
32
3
2 24
8 27 27
x y yy
P
y
+ −+
⇔= + =
+
3
3
3
3
2
1;
1
8 27
4
2;
2
2;
3
8 27
xy
y
xy
y
yx
xy
y
y
+
= =
= =
+
⇔⇔
= =
+
= =
+
. Lập luận tương tự ta có:
32
3
96
8 27
y yzz
z
+− −
≥
+
(2)
32
3
96
8 27
z zxx
x
+− −
≥
+
(3). Cộng từng vế (1),(2),(3) và có:
( )
( )
2 22
3 33
333
10 18
8 8 8 27
xyz x y z
xyz
yzx
++ − + + −
⇔ ++≥
+++
(4)
Do
3xyz
++=
nên (4) có
( ) ( )
2
3 33
333
30 2 18
8 8 8 27
x y z xy yz zx
xyz
yzx

− ++ − + + −

++≥
+++
( )
3 33
333
21
8 8 8 27 9
xyz
xy yz zx
yzx
⇒ + + − ++ ≥
+++
hay
1
9
P ≥
(5)
Dấu bằng trong (5) xảy ra
⇔
đồng thời có dấu bằng trong (1),(2),(3)
1xyz⇔===
Vậy
1
min
9
P =
1xyz⇔===
.
THCS.TOANMATH.com
Câu 8) Ta có:
(
)
2
22
1
1
1
11
xy
x
x
yy
+
+
= +−
++
. Theo bất đẳng thức Cô si ta có:
2
12yy+≥
Suy ra
( )
2
2
1
1
11
12 2
xy
x xy y
xx
yy
+
++
≥ +− = +−
+
. Chứng minh tương tự, ta
có:
2
1
1
12
y yz z
y
z
++
≥ +−
+
;
2
1
1
12
z zx x
z
x
++
≥ +−
+
suy ra
(
)
3
2
x y z xy yz zx
P
++− + +
≥+
Do
( )
( )
3
93 3x y z xy yz zx xy yz zx=++ ≥ ++ ⇒++≤
. Vậy
min 3 3P xyz=⇔===
.
Câu 9) Giải:
Ta có:
2
22
11
x xy
x
yy
= −
++
. Theo bất đẳng thức Cô si, ta có:
2
12yy+≥
, khi
đó
22
2
1 22
xy xy xy
yy
≤=
+
suy ra:
2
12
x xy
x
y
≥−
+
Tương tự ta có:
2
;
12
y yz
y
z
≥−
+
2
12
z zx
z
x
≥−
+
. Cộng từng vế ta có
2
xy yz zx
Pxyz
++
≥++−
1xyz
⇔===
.Do
( ) ( )
2
2 22
39 2x y z x y z x y z xy yz zx++=⇒= ++ = + + + + +
( ) ( )
92 3
xy yz zx xy yz zx xy yz zx⇒≥ ++ + ++ ⇒++≤
(7). Vậy
3
min 1
2
P xyz=⇔===
.
Câu 10)
THCS.TOANMATH.com
Ta có:
23
33
2
22
x xy
x
xy xy
= −
++
. Theo bất đẳng thức Cô si, thì
3 33 6 2
3
3
2 33x y x y y xy y x+ =++≥ =
suy ra
23
3
2
3
2
3
22
23
2
x xy
x x yx
xy
yx
≥− =−
+
. Tương tự, có:
2
3
2
3
2
23
y
y zz
yz
≥−
+
,
2
3
2
3
2
23
z
z xz
zx
≥−
+
. Cộng từng vế ta có:
( )
(
)
3
3
22 2
3
2
3
P x y z zy xz yx≥ ++ − + +
, hay
(
)
3
3
22 2
3
2
3
3
P zy xz yx
≥− + +
. Theo bất đẳng thức cô si ta có:
3
2
3x xz xz x z++≥
,
3
2
3y yx yx y x
++≥
2
3
3z zy zy z y++≥
Cộng từng vế ba bất đẳng thức trên ta có:
(
) (
)
(
)
3
3
222
3
23
x y z xy yz zx x z y x z y++ + + + ≥ + +
vì
( ) ( )
2
93 3x y z xy yz zx xy yz zx=++ ≥ ++ ⇒++≤
. Do
3xyz++=
, suy ra
(
)
3
33
222 222
33 3
3 2.3 3 3 1xz yx zy xy yx zy P+≥ ++ ⇒++≤⇒≥
Vậy
min 1 1
P xyz=⇔===
.
Câu 11) Ta có:
22
22
2
22
x xy
x
xy xy
= −
++
. Áp dụng bất đẳng thức Cô si, ta có:
2 22 4
3
23x y x y y xy
+ =++≥
. Suy ra
( )
22
2
3
2
4
3
22
23
3
x xy
x x xy
xy
xy
≥− =−
+
.
Tương tự, ta có:
( )
2
2
3
2
2
23
y
y yz
yz
≥−
+
,
(
)
2
2
3
2
2
23
z
z zx
zx
≥−
+
. Cộng theo vế
ta có:
( ) ( ) ( ) ( )
222
333
2
3
P x y z xy yz zx

≥ ++ − + +


. Theo bất đẳng thức Cô si,
ta có:
22
3
3x xy y x y+ +≥
22
3
,3y yz z y z+ +≥
3
22
,3z zx x z x+ +≥
. Từ đó
THCS.TOANMATH.com
suy ra
( ) ( ) ( )
( )
( )
222
333
23x y z xy yz zx xy yz zx

++ + + + ≥ + +


(7) Dễ
thấy dấu bằng trong (7) xảy ra
1xyz⇔===
. Kết hợp với
1xyz++=
, ta
có:
( )
( ) (
)
( )
( ) ( )
222 222
333 333
633 3
xy yz zx xy yz zx

+≥ ++ ⇒++≤


. Vậy
2
3 .3 1
3
PP
≥− ⇒ ≥
hay
min 1 1P xyz
=⇔===
.
Câu 12) Ta có:
2
22
1
1
11
x
xx
= −
++
. Theo bất đẳng thức Cô si, thì
2
12xx+≥
2
2
1
11
12 2
xx
xx
⇒ ≥− =−
+
Tương tự, ta có:
2
1
1
12
y
y
≥−
+
,
2
1
1
12
z
z
≥−
+
. Suy ra
3
3
22
xyz
P
++
≥− =
(do
3
xyz++=
).
Từ đó suy ra
min 3 1P xyz=⇔===
.
Câu 13) Viết lại
P
dưới dạng:
11
33
111
y
P
xyz

=− ++

+++

. Đặt
2 22
;;
XYZ
x yz
Y ZX
= = =
Khi đó có
,, 0XYZ>
(vì
8xyz =
) Lúc này:
111 1 1 1
2 22
111
111
XYZ
xyz
Y ZX
++= + +
+++
+++
22 2
22 2
2 22 2 2 2
YZX Y Z X
X Y Y Z Z X XY Y YZ Z ZX X
= ++ = + +
+++ + + +
. Áp
dụng bất đẳng thức Cauchy- Schwarz
THCS.TOANMATH.com
( ) ( )
( )
22
2
22 2
111
1
1 1 12 2 2
XYZ XYZ
x y z XY Y YZ Z ZX X
XYZ
++ ++
++≥ = =
+ + + ++ ++ +
++
,
suy ra
0P ≤
. Vậy
max 0 2P xyz=⇔===
.
Câu 14) Ta có:
( ) ( ) ( )
2
2
2
1
1
1
1
y
x
z
P
xy z yz zx y
= ++
+ ++
. Áp dụng bất đẳng thức
Cauchy- Schwarz
(
)
( )
(
)
2
2
2 22
111
22
xy yz zx
xyz
P
xy yz zx xy yz zx x y z

++

++

≥=
++ ++
. Do
1xyz =
, nên ta có:
2
xy yz zx
P
++
≥
Lại theo bất đẳng thức Cô si ta có:
( )
2
3
33
xy yz zx xyz
++≥ =
(do
1xyz =
.
Suy ra
3
2
P
≥
Vậy
3
min 1
2
P xyz=⇔===
.
Câu 15) Viết lại biểu thức
P
dưới dạng:
2 2 2 11 11
11 2 2 2 2
111 111
x y z yzx
P xyz
x y z xyz xz yx


=+ ++ + − + + = − + − +


−−− −−−


Do
1xyz++=
, nên ta có:
11 11 11
2223Px y z
yz z zx x xy y


=−+−+−+


+++


( ) ( ) ( ) ( ) ( ) ( )
22 2
332
xy yz zx xy yz zx
zy z xz x yx y zy z xz x yx y

−
= − − +=− + +


+++ +++

. Áp dụng bất đẳng thức Bunhiacopski, ta có:
THCS.TOANMATH.com
( ) ( ) ( )
2
2
xy yz zx xy yz zx
yz zx xy
z x y zxy xzx yxy


+ + = ++ ++ +




+++


( ) ( ) ( )
(
)
( )( )
xy yz zx
yzzxxy
zx z xz x yx y

≤ + + +++



+++

Rõ ràng, ta lại có:
( )
2
3
xy yz zx
xyz
zxy

+ + ≥ ++



.Dựa vào bất đẳng
thức hiển nhiên
( ) ( )
2
3a b c ab bc ca++ ≥ + +
suy ra:
(
)
( )
(
)
( )
(
)
32
xy yz zx
xyz xyz
zy z xz x yx y

++ ≤ + + ++

+++

Từ
1xyz++=
ta có:
( )
( )
( )
23
xy yz zx
zy z xz x yx y

++ ≥

+++

suy ra
0P ≤
.
Vậy
1
max 0
3
P xyz=⇔===
.
Câu 16)
Áp dụng bất đẳng thức Bunhiacopski, ta có:
(
)( )
( )
( )
( )
(
)
( )
2 2 22 2
..xyxz x y x z xx yz

+ += + + ≥ +


( )( )
( )
2
x y x z x yz⇒+ +≥+
. Suy ra:
( )( )
2
xx
x yz
x xyxz
≤
+
++ +
.
Tương tự, ta có:
( )( )
2
yy
y zx
y yzyx
≤
+
++ +
,
( )( )
2
zz
z xy
z zxzy
≤
+
++ +
. Suy ra
THCS.TOANMATH.com
222
xyz
P
x yz y zx z xy
≤++
+ ++
111
2.2. 2.
P
yz zx xy
xx yy zz
⇒≤ + +
+++
. Đặt
.; .; .
yz zx xy
abc
xx yy zz
= = =
, thì
,, 0abc>
và
1abc =
.
111
222
PQ
abc
≤= + +
+++
( )( ) ( )( ) ( )(
)
(
)( )( )
22 22 22
222
bc ca ab
abc
+ +++ +++ +
=
+++
(
) ( )
( ) ( )
12 4
84 2
a b c ab bc ca
a b c ab bc ca abc
+ ++ + + +
=
+ ++ + + + +
. Theo bất đẳng thức Cô si
thì :
( )
2
33
ab bc ca abc++≥ =
suy ra
1P ≤
. Vậy
max 1 0P xyz=⇔==>
.
Câu 17) Ta có:
(
)
( )
( )
52 52 22
633 33 13 1xx x xx x xx x−+− +=−−+= −− −
(
)
(
)
( )
( )
2 432
1 13 1 3x xx x xxx

= − ++ − = − + + −

( )
( ) ( ) ( )
( )
( )
2
432 32
1 1 1 1 1 2 33x x x x x xxx

= − −+ −+ − = − + + +

Do
32
0 2 30x xxx>⇒ + + >
, nên từ (2) suy ra
52
63 3
xx x− +≥ +
THCS.TOANMATH.com
( )
( )
52
52
11
63 3 1
31
63
x x xy xy x
xy x
x x xy
⇒ − ++ ≥ ++ ⇒ ≤
++
− ++
.
Tương tự, ta có:
( )
52
11
31
36
yz y
y y xyz
≤
++
−+ +
,
( )
52
11
31
36
zx z
z z xyz
≤
++
−+ +
Suy ra
11 1 1
31 1 1
P
xy x yz y zx z

≤ ++


++ ++ ++

. Áp dụng bất đẳng
thức Bunhiacopski, ta
có:
( )
111 1 1 1
111
1 11
1 11
xy x yz y zx z
xy x yz y zx z

+ + ++ ≥ + +

++ ++ ++
++ ++ ++

1 1 1 111
3
1 11
1 11
xy x yz y zx z
xy x yz y zx z

⇒ + + ≤ ++

++ ++ ++
++ ++ ++

111
1
1 11
P
xy x yz y zx z
⇒≤ + + =
++ ++ ++
. Vậy
max 1 1P xyz=⇔===
.
Câu 18) Ta có:
( )
( )
2
2 22
2 22
9
22
xyz x y z
xyz
xy yz zx
++ − + +
−−−
++= =
.
Vậy
P
có dạng:
( )
2 22
9
2
xyz
Pxyz
− ++
=++=
( )
22
2 92 9Px y x y z⇒ = + ++ + + −
Áp dụng bất đẳng thức Cô si, ta có:
2
2
2
3
3
3
x x xx
y y yy
z z zz
++≥
++≥
++≥
THCS.TOANMATH.com
Suy ra :
(
)
( )
2 22
2 39x y z x y z xyz+ + + + + ≥ ++ =
.Vậy
min 0 1P xyz=⇔===
.
Câu 19)
Vì
222
12; 12; 12x xy yz z+≥ +≥ +≥
, nên ta có:
( ) ( ) ( )
2 12 12 1
xyz
P
xy yz zx
≤++
++ ++ ++
.Ta có:
111
111
111 1 1 1
xyz y z x
xy yz zx xy yz zx

+++

+ + =− +− +−


++ ++ ++ ++ ++ ++


111
3
111
yzx
xy yz zx

+++
=− ++

++ ++ ++

31 1 1 1
22 1 1 1
yzx
P
xy yz zx

+++
⇒≤− + +

++ ++ ++

( )
( )( )
( )
( )( )
( )
( )( )
222
111
31
22 1 1 1 1 1 1
yzx
y xy z yz x zx

+++
≤− + +

+ ++ + ++ + ++


. Áp dụng
bất đẳng thức Cauchy- Schwarz :
( )
( )( )
( )
( )( )
( )
( )( )
222
111
1 11 11 1
yzx
y xy z yz x zx
+++
++≥
+ ++ + ++ + ++
(
)
( )( ) ( )(
) ( )( )
2
111
1 11 11 1
yzx
y xy z yz x zx
++ ++ +
≥
+ +++ + +++ + ++
. Để ý rằng do:
2 22
3xyz++=
, nên ta
có:
( )( )(
)( ) ( )( )
1 11 1 1 1
yxyzyz xzx++++++++++
( )
2 22
33x y z xy yz zx x y z= +++++++++
(
)
( )
2
2 22
11
9666222 3
22
x y z x y z xy yz zx x y z= +++++++++ = +++
.
THCS.TOANMATH.com
( )
( )
( )
( )
(
)
( )
(
)
( )( )
222
111
2
1 11 11 1
yzx
y xy z yz x zx
+++
++≥
+ ++ + ++ + ++
. Vậy
1
max 1
2
P xyz=⇔===
.
Câu 20) Nhận xét:
a∀
thì
(
) (
)
2
32
41 2
aa+≤+
. Thật vậy,
(
)
2
34 2 4 3 2 2
44 4 4 4 4 0 1 0a a a a a a aa
⇔+ ≤ + +⇔ − + ≥⇔ − ≥
. Cũng có
thể chứng minh bằng bất đẳng thức Cauchy:
( )
( )
( )
( )
2
2
2
2
32
2
11
1 11
24
a
a aa
a a aa
+

+ +− +
+ = + −+ ≤ =


. Áp dụng vào
bài toán ta có:
( )(
)
( ) (
)
( )(
)
2 22
33 3 3 33
444
41 1 1 41 41 1
xyz
P
xy y z zx
=++
++ + + ++
( )( )
( )( ) ( )( )
2 22
2 2 22 22
444
22 22 22
xyz
xy yz zx
≥++
++ ++ ++
. Đặt
2 22
;;
444
xyz
abc
= = =
.
Khi đó do
,, 0xyz>
và
8 ,, 0xyz a b c=⇒>
và
1abc
=
.
Suy ra:
( )( )
( )( )
( )( )
16 16 16
24 24 24 24 24 24
abc
P
ab bc ca
≥++
++ ++ ++
. Hay
( )( ) ( )
( ) ( )(
)
4
12 12 1 12 12 12
abc
P
ab abc ca

≥ ++

++ ++ ++

( ) ( ) ( )
( )( )( )
( )
( ) ( )
12 12 12 2
44
12 12 12 12 4 8
a c b a c b a b c ab bc ca
PP
a b c a b c ab bc ca
+ + + + + +++ + +
⇒≥ ⇒≥
+ + + + ++ + + + +
. Ta có:
3
33a b c abc++≥ =
( )
2 918a b c ab bc ca abc⇒+++ + + ≥=+
THCS.TOANMATH.com
( ) (
) ( ) ( ) ( )
18 2 4 3 2abc a b c ab bc ca a b c ab bc ca⇒ + + ++ + + + ≤ ++ + + +


. Suy ra
4
3
P ≥
. Vậy
4
min 2
3
P xyz=⇔===
.
Câu 21) Ta có nhận xét sau: với mọi
,,xyz
là các số thực dương, ta
có:
( )
32
3
2 22
3
xx
xyz
x yz
≥
++
++
(1) . Thật vậy, (1)
( )
( )
34
32
3
2 22
xx
xyz
xyz
⇔≥
+
++
(
)
( )
(
)
2
3
34 222 22 74
2xx xyz yz xxxz

⇔ + + + + ≥+ +


( ) ( )
(
)
2
3
2 22 22
2x yz yz xyz⇔++++ ≥ +
..Theo bất đẳng thức Cô si, ta có:
( ) ( ) ( )
23
2 222 22 222
2 2 22x xyz yz xyz+ +++ ≥ +
. (3). Rõ ràng:
(
)
( )
2
22
2
y z yz+ ≥+
(4)
Từ (3),(4) suy ra:
(
)
(
)
(
)
(
)
2
63
222 22 2
2xy z y z xyz xyz
+++ ≥ + = +
(5)
Tương tự (1), ta có:
( )
32
3
2 22
3
yy
xyz
y zx
≥
++
++
(6),
( )
32
3
2 22
3
zz
xyz
z xy
≥
++
++
(7)
Cộng từng vế (1),(6),(7) và có
1P ≥
(8)
Vậy
min 1 0P xyz=⇔==>
.
Chú ý: Ta có thể chứng minh:
( )
32
3
2 22
3
xx
xyz
x yz
≥
++
++
nhanh hơn bằng
cách áp dụng bất đẳng thức Cau chy
THCS.TOANMATH.com
( )
(
)
2
32
2
3
21 2
11 1
22
1
a
a a aa
a
a
+
+= + −+ ≤ ⇒ ≥
+
+
thay
yz
a
x
+
=
suy ra
( )
( )
32
32
32
2
2
xx
x yz x yz
≥
++ ++
. Lại có
( )
( )
2
22
2
xy x y+≤ +
suy
ra
( )
32
3
2 22
3
xx
xyz
x yz
≥
++
++
Câu 22) Áp dụng bất đẳng thức Bunhiacopski, ta có:
( ) ( ) ( )
22 22 2 2
22 22 2 2
1 11
111
xyz
x yz y zx z xy
yz zx xy


++ + ++ + ++ + +

++ ++ ++

Từ (1) và do
1xyz++=
, ta có:
( )
( )
( )
22 22 2 2
1
1 11
P
x yz y zx z xy
≥
++ + ++ + ++
. Đặt
( ) ( ) ( )
22 22 2 2
1 11Qx y z y z x z x y= ++ + ++ + ++
( ) ( ) ( ) ( )
x y z xy x y yz z y zx z x=+++ ++ ++ +
( ) ( ) ( )
1 xy x y yz z y zx z x=+ ++ ++ +
( ) ( ) ( )
2 22
1 xyz yzx zxy=+ ++ ++ +
. Có thể thấy rằng:
( ) ( ) (
)
2 22
1
4
xyz yzx zxy++ ++ + ≤
Từ đó có:
5
4
Q
≤⇒
4
5
P ≥
.Vậy
4
min
5
P =
. Giá trị nhỏ nhất đạt được khi
1
;0
2
xy z= = =
.
Câu 23) Áp dụng bất đẳng thức Bunhiacopski ta có:
THCS.TOANMATH.com
3 3 33 33
111
26 26 26xy yz zx


++ ≤

++ ++ ++

3 3 33 33
111
3
26 26 26xy yz zx

++

++ ++ ++

Hay
3 3 33 33
111
3
26 26 26
P
xy yz zx

≤ ++

++ ++ ++

. Áp dụng bất đẳng
thức Cô si ta có:
(
)
(
)
3 3 33 3
2 6 1 11 3 3 3 3
x y x y y xy y+ += + ++ +++≥ + +
( )
33
2 63 1x y xy y⇒ + +≥ ++
Tương tự, có:
( )
33
2 63 1y z yz z+ +≥ ++
,
( )
33
2 63 1z x zx x+ +≥ ++
Suy ra :
111
111
P
xy y yz z zx x
≤ ++
++ ++ ++
. Do
1xyz =
, nên dễ
thấy
111 1
1
111111
xy y
xy y yz z zx x xy y xy y xy y
++=++ =
++ ++ ++ ++ ++ ++
suy ra
1P ≤
Vậy
max 1 1
P xyz=⇔===
.
Câu 24) Theo bất đẳng thức Cô si, ta có:
1
22y z yz
x
+≥ =
(do
1xyz =
)
Từ đó suy ra:
( )
( )
2
22
12
22
22
xyz
xx
x y z x xx
x
yy zz yy zz
+
+≥ = ⇒ ≥
++
(1)
Lập luận tương tự, có:
( )
2
2
22
yzx
yy
zz xx zz xx
+
≥
++
,
( )
2
2
22
zxy
zz
xx yy xx yy
+
≥
++
. Cộng từng vế
THCS.TOANMATH.com
2
222
yy
xx zz
P
yy zz zz xx xx yy

≥ ++


+++

. Đặt
;;
X x xY y yZ z z= = =
thì
,, 0XYZ>
và
1XYZ =
.
Khi đó (4) có dạng
2
22 2
XY Z
P
Y ZZ X X Y

≥ ++

++ +

222
2
22 2
XYZ
P
XY ZX YZ XY XZ YZ

⇒≥ + +

++ +

. Áp dụng bất đẳng thức
Cauchy- Schwarz ta có:
( )
( )
2
2
3
XYZ
P
XY YZ ZX
++
≥
++
do
( ) ( )
2
3X Y Z XY YZ ZX++ ≥ + +
3P⇒≥
và
31P XYZ
=⇔===
. Vậy
min 3 1P xyz=⇔===
.
Câu 25)
Áp dụng bất đẳng thức Cô si, ta có:
( )
( )
( )
(
)
2
32
11
11 1
2
y yy
y y yy
++ −+
+= + −+ ≤
2
3
2
1
2
y
y
+
⇒ +≤
2
3
2
2
1
xx
y
y
⇒≥
+
+
tương tự, ta có:
2
3
2
2
1
yy
z
z
≥
+
+
,
2
3
2
2
1
zz
x
x
≥
+
+
222
2
222
xyz
P
yzx

⇒≥ + +

+++

. Dấu bằng trong (5) xảy ra
⇔
đồng thời
có dấu bằng trong
2xyz⇔===
. Ta sẽ chứng minh
222
222
2
222
xyz
yzx
++≥
+++
222
222
4
222
x yz
x yz
yzx


⇔− +− +− ≤


+++


(do
6xyz++=
)
2 22
22 2
4
22
xy yz zx
yz x
⇔ + +≤
++
. Áp dụng bất đẳng thức Cô si, ta
có:
2 22 4
3
3
2 4 4 34 3 4y yy y yy+= + +≥ =
2
3
3
24
2
y yy
⇒ +≥
Tương
THCS.TOANMATH.com
tự có:
2
3
3
24
2
z zz
+≥
,
2
3
3
24
2
x xz+≥
VT
2 22
3
3
3
3 33
44 4
2 22
xy yz zx
yy z xx
≤ ++
.Áp dụng bất đẳng thức Cô si, ta có:
3
2
2. .
3
x xy xy
x xy xy
++
≤
,
3
2
2. .
3
y yz yz
y yz yz
++
≤
3
2
2. .
3
z zx zx
z zx zx
++
≤
. VT
( )
(
)
1
22
9
x y z xy yz zx
≤ ++ + + +


Mặt khác, ta có:
(
) ( )
2
3 xy yz zx x y z+ + ≤ ++
12xy yz zx⇒++≤
. Từ đó
suy ra
2P ≥
.
Vậy
min 2 2P xyz
=⇔===
.
Câu 26)
Giải:
1)Ta có theo bất đẳng thức Cô si:
( )( )
( )( )
22
432
3 8 14 432 23
2
xyxy
x y xy xyxy xy
++
++ = + + ≤ =+
Như vậy suy ra
22
22
23
3 8 14
xx
xy
x y xy
≥
+
++
. Tương tự ta có:
22
22
23
3 8 14
yy
yz
y z yz
≥
+
++
22
22
23
3 8 16
zz
zx
z x zx
≥⇒
+
++
2 22
23 23 23
xyz
P
xy yz zx
≥++
+ ++
. Theo bất
đẳng thức Cauchy- Schwarz ta
có:
( )
2 22
1
2323235
xyz
xyz
xy yz zx
+ + ≥ ++
+ ++
. Theo bất đẳng thức Cô si cơ
THCS.TOANMATH.com
bản, ta có:
( )
111
9
xyz
xyz

++ + + ≥


. Do
111
01
xyz
<++≤
, nên có:
9xyz++≥
vậy
9
5
P
≥
. Vậy
9
min 3
5
P xyz=⇔===
.
Câu 27) Do tính bình đẳng giữa
,,xyz
nên có thể giả sử
xyz≥≥
Kết hợp với
3xyz++=
suy ra
01
z
<≤
. Ta có
2 22
P x y z xyz
=+++
(
) (
)
2
2x y z xyz xy yz zx= ++ + − + +
( )
( )
9 22xy z z y x=+ −− +
( ) ( )
9 2 23xy z z z=+ −− −
(1)
Hiển nhiên ta có:
22
3
22
xy z
xy
+−

≤=


. Do
0 1 20zz<≤⇒−<
, vậy từ
(1) có:
(
) ( )
2
3
9 2 23
2
z
P z zz
−

≥+ − − −


. Ta có
VP(2)
( ) ( )( )
33 3
9249238
22 2
zz z
z z z zz
−− −

=+−−=+−−−




( ) ( )
23 2
3 11
9 3 6 3 18 3 2 16
2 44
z
zz zz zz
−


=+ −−−= −+ = −++


( ) ( )
2
1
1 2 16
4
zz

= − ++

. Do
01x<≤
nên suy ra
4P⇒≥
. Vậy
min 4 1
P xyz=⇔===
.
Câu 28) Áp dụng đồng nhất thức
( )( )( ) ( )(
)
x y y z z x x y z xy yz zx xyz+ + + = ++ + + −
(*)
Ta có:
( )( ) (
)
2P x y z xy yz zx xyz x y z
= ++ + + − − ++
. Theo bất đẳng
thức Cô si ta có:
3
33x y z xyz++≥ =
(do
1xyz =
).Lại có:
THCS.TOANMATH.com
2 22
3
33xy yz zx x y z++≥ =
(do
2 22
1xyz =
) suy ra:
( )
( )
3 12P xyz xyz≥ ++ −− ++
(
)
1 31 2
P xyz⇒ ≥ + + −≥−=
.
2)Trước hết ta chứng minh rằng
( )( )( ) ( )(
)(
)
111xyyzzx x y z+ + +≥+ + +
Thật vậy, dựa vào (*) suy ra:
( )
( )
1
x y z xy yz zx xyz xy yz zx x y z
⇔ ++ + + − ≥ + + ++++
( )( )
22x y z xy yz zx xy yz zx x y z⇔ ++ + + −≥ + + ++++
(do
1xyz =
)
(
)( )
3x y z xy yz zx xy yz zx x y z
⇔ ++ + + ≥ + + ++++
Do
13xyz x y z
=⇒++≥
và
3xy yz zx++≥
. Ta có
( )( ) ( ) ( )
33
x y z xy yz zx
x y z xy yz zx xy yz zx x y z
++ + +
++ + + = + + + ++ +
( )
( )
3
x y z xy yz zx++ + +
+
suy ra
( )( )
3x y z xy yz zx xy yz zx x y z++ + + ≥ + + ++++
.Theo bất đẳng thức Cô
si ta có:
( )( )( )
( )( )( )
3
33
111
xyyzzx
Q
xyz
+ ++
≥≥
+++
. Vậy
min 3 1Q xyz=⇔===
.
Câu 29) Giải:
Ta có:
( )
( )
( )
( ) ( )
3
33 33 2 2 33
43 3a b a b aba abb a b abab ab+ =++ + −+ ≥++ + =+
Suy ra
( ) ( )
33 33
33
44a b ab c a b abc+ ≥+⇒+ + ≥++
. Do đó
( )
33
3
4
ab ab
abc
c ab
++
≤
++
++
, đẳng thức xảy ra khi và chỉ khi
ab=
. Tương
THCS.TOANMATH.com
tự cũng có
( ) ( )
33 33
33
44
bc bc ca ca
abc abc
a ca b ca
+ ++ +
≤+ ≤
++ ++
++ ++
. Suy ra
( ) ( ) (
)
33 33 33
3 33
2
444
ab bc ca
c ab a bc b ca
+++
++≤
++ ++ ++
Đẳng thức xảy ra khi và chỉ khi
abc= =
.
Câu 30) Ta có:
0 ,, 1abc<<
suy ra
( ) ( )
( )
22 2
22
2ab aab a b abaab− ≥ − ⇔+≥ + −
. Tương tự 3 bất đẳng thức
nữa ta có:
(
) (
)
( ) (
)
222
6P abbcca aab bbc cca= ++ + − + − + −
( )
( )
222
42ab bc ca a b c≤ ++ + ++
hay
2P ≤
. Dấu bằng xảy ra khi và chỉ
khi
2
3
abc= = =
.
BẤT ĐẲNG THỨC ABEL VÀ ỨNG DỤNG
CÔNG THỨC ABEL VÀ ỨNG DỤNG.
1. Công thức tổng Abel:
Giả sử
12
, ,...,
n
aa a
và
12
, ,....,
n
bb b
là hai dãy số thực. Khi đó ta có:
11 2 2 1 2 1 2 3 2
... ( ) ( ) ...
nn n n
ab ab ab b b S b b S bS+ ++ = − + − ++
trong đó
12
...
kk
S aa a= + ++
.
Chứng minh: Thật vậy thay
1k kk
aSS
−
= −
với
2,3,...
kn=
ta có vế trái
bằng:
11 2 2 1 3 3 2 1
( ) ( ) ... ( )
nn n
b S b S S b S S b S S VP
−
+ − + − ++ − =
.
THCS.TOANMATH.com
Trường hợp
3n =
ta
có:
(
)
(
) (
)
()
axbycz x ya yzab zabc
+ + = − + − + + ++
đây là đẳng thức
quan trọng có nhiều ứng dụng trong giải toán.
2. Bất đẳng thức Abel:
Cho hai dãy số thực:
12
, ,....,
n
aa a
và
123
......
n
bbb b≥≥≥ ≥
. Đặt
12
...
kk
S aa a= + ++
với
{ }
1, 2,3,...kn∈
và
{ } { }
12 12
min , ,...., , max , ,....,
nn
m SS S M SS S= =
. Khi đó ta có:
1 11 2 2 1
...
nn
mb A a b a b a b Mb
≤= + ++ ≤
,
Chứng minh:
Ta có:
11 2 2 1 2 1 2 3 2
... ( ) ( ) ...
nn n n
ab ab ab b b S b b S bS+ ++ = − + − ++
mà
1
0
kk
bb
+
−≥
nên
12 23 12 23
( ) ( ) ... ( ) ( ) ...
nn
bbm bbm bmA bbM b bM bM− + − ++ ≤ ≤ − + − ++
hay
11
mb A Mb≤≤
.
MỘT SỐ VÍ DỤ:
Ví dụ 1: Cho
0xyz≥≥≥
thỏa mãn:
3, 5, 6x xy xyz≥ +≥ ++≥
. Chứng
minh:
2 22
14xyz++≥
.
Lời giải:
Ta có:
( )( ) ( )( ) ( )( )
2 22
14 3 3 2 1 1 1xyz x x y y z z+ + − = − ++ − ++ − +
. Áp
dụng công thức Abel ta có:
2 22
14 ( 3 2)( 3) ( 2 1) ( 1)( 3 2 1)xyz xyx yz zxyz
+ + − = +−− − + +−−+ + −+−+−
( ) ( ) ( )( )
1( 3) 1( 5) 1 6 0xy x yz xy z xyz= −+ − + −+ +− + + ++− ≥
. Dấu
bằng xảy ra khi và chỉ khi
3; 2; 1
xyz= = =
.
THCS.TOANMATH.com
Ví dụ 2) Cho các số thực dương
,,
xyz
sao cho
3, 6, 6x xy xyz≥≥ ≥
.
Chứng minh:
6xyz
++≥
.
Lời giải:
Ta có:
( )
( )
6 3 1 2 1 1 1 32 1 21 2
3 2 1 3 32
x y z x xy
xyz
 
++−= −+ −+ −=− −+− +− +
 
 
1. 1 1 1 1 2 3
3 2 1 3 32 321
x y z x xy xyz
 
−+−+−= −+ +− + ++−
 
 
. Áp dụng
bất đẳng thức Cô si ta có:
2 2;
32 6
x y xy
+≥ ≥
3
33
3 2 1 3.2.1
x y z xyz
++≥ ≥
. Suy
ra đpcm. Dấu bằng xảy ra khi và chỉ khi
3, 2, 1xyz
= = =
.
Ví dụ 5: Cho
,, 0xyz
>
sao cho
23xyz
<<
và
1, 3, 6x xy xyz
≥ +≥ ++≥
. Chứng minh:
(
)
6 11
xy yz zx xyz++ ≤
.
Lời giải:
Ta cần chứng minh:
1 1 1 11
6xyz
++≤
.Ta có:
11 111 11111 1 2 3
1
6 2 3 23
xy z
xyz x y z x y z

−−−
− ++ =−+−+−= + + =


( ) ( ) ( )
11 1 1 1
1 3 60
2 23 3
x xy xyz
xy yz z

− −+ − +− + ++− ≥


Dấu bằng xảy ra khi và chỉ khi
3, 2, 1xyz= = =
.
Ví dụ 3: Cho các số thực không âm
,,xyz
sao cho
1, 5, 14x xy xyz≤ +≤ ++≤
. Chứng minh:
6
xyz++≤
.
Lời giải:
THCS.TOANMATH.com
Tacó:
(
)
(
)
11 11 1
1 23 12 23 3
xyz
x xy xyz

+ += − + − + + ++ ≤


11 11 1
.1 .5 .14 1 2 3
12 23 3

−+−+=++


. Ta suy ra
( )
( ) ( )
2
2
123 123 36
123
xyz
xyz

+ + ≤ ++ + + ≤ ++ =


.
Ví dụ 4: Cho các số thực dương
1,3,6,6a b a ab ab c≥≥ ≤ ≤ ≤
. Chứng
minh:
4
abc+−≤
.
Lời giải:
Ta cần chứng minh:
132ab c++≤++
.
Ta có:
( ) ( )
( ) ( )
3
32 32 3 6 6 3
3 2 1 3 12
1
cc
c b ab b ab
a b a b a ab ab a

++= ++ +− + +− ≥ +− +−


( )
3 2( 1) 1
b ab ab≥+ − + − =++
. Dấu bằng xảy ra khi và chỉ khi
3, 2, 1abc= = =
.
Ví dụ 5: Cho các số thực dương
,,abc
sao cho
0 ,9
9
3
4
9
2
4
abcc
b
a
c
b
c
<≤≤ ≥
++≤
+≤
.
Chứng minh:
abc+≤
.
Lời giải:
Ta có:
( )
99 9
91 2
44
bb
ab a c
cc c

++= +++++−



THCS.TOANMATH.com
(
)
99
9
44
3 2 2 32 23
32 2
bb
a
cc
c cc

++ +


≤ + + − =++ −=+



.
Ví dụ 6) Cho các số thực
,,abc
sao cho
10
2
2
32
3
ab c
c
b
c
ab
≥ ≥≥ >
+≤
+ +≤
. Chứng minh:
111 1
6
abc
+−≤−
.
Lời giải:
Ta cần chứng minh:
11 111
1
32
ab c
++≤++
. Tacó:
1 1 1 1 1 1 1 1 11
1
32 32 2
1111 11 11 11
1
32 2
ab b
c a c b a c bc
a c b a c bc
ab b
 
++= ++ + − + + −
 
 



= +++− ++−





Áp dụng bất đẳng thức Cauchy- Schwarz. Ta có:
111 9 11 4
3, 2
3 2 32 2 2
cc
cc
a b ab b b
+ +≥ ≥ +≥ ≥
++ +
, ta có
111 3 11 1 11
21 1
32c a ba b ab

++≥+ − + − =++


.
THCS.TOANMATH.com
Ví dụ 7) Giả sử
,,abc
là các số thực dương thỏa mãn:
3
1
ab c
cb
abc
≤≤≤
≥+
+≥
.
Tìm GTNN của
2 ( 1)
( 1)( 1)( 1)
ab a b c ab
Q
abc
+++ −
=
+++
.
(Trích đề thi vào lớp 10 Trường chuyên KHTN- ĐHQG Hà Nội)
Lời giải:
Ta có:
( ) ( ) ( )
( 1)( 1)( 1) 1 1 1
abc ab ac a abc bc ba b abc ca cb c
abc
Q
abc a b c
++++ +++− +++
= =+−
+++ + + +
Ta chứng minh:
1 2 35 3 2 1
0
1 1 1 1 1 1 2 1 3 12 3(1 ) 3( 1) 2(1 )
a b c cb a
abc cb a
−− −
+−≥+−=⇔ + + ≥
+ + + ++ + + + +
Hay
11 11
(3 ) (3 2)
4( 1) 3( 1) 3( 1) 2( 1)
c cb
cb ba

− − + ++− −

++ ++

( )
1
3 21 0
2(1 )
cb a
a
+ −+−+− ≥
+
. Rút gọn ta thu được:
( )
( )
( )
2 31
(3 4 1) 1
(3 ) 1 0
12( 1)( 1) 6( 1)( 1) 2( 1)
ab
bc
c b c abc
bc ba a
−−
−−
− + +− + + − ≥
++ ++ +
.
Điều này là hiển nhiên đúng.
BẤT ĐẲNG THỨC BUNHIACOPXKI
Một số kết quả quan trọng:
Cho các số thực dương
,,,,,abcx yz
.
a)
222
a b c ab bc ca++≥ ++
.
THCS.TOANMATH.com
b)
( )
2
222
3( )a b c abc+ + ≥ ++
.
c)
( )
( )
( )
2
222 2
ax by a b x y+ ≤+ +
.
d)
( )
( )(
)
2
2222 22
ax by cz a b c x y z++ ≤ ++ ++
e)
(
)(
) ( )( )( )
89
abcabbcca abbcca
++ + + ≤ + + +
f)
22 22 22
()b c a c a b abc a b c+ + ≥ ++
g)
( ) (
)
22
2
111
a bc
ab ac
+≥
+
++
.
h)
( )
2
22
xy
xy
a b ab
+
+≥
+
.
i)
( )
2
2 22
xyz
xyz
a b c abc
++
++≥
++
.
Chứng minh:
a)
( )
( ) ( ) (
2
222 222
22a b c ab bc ca a b c ab bc ca a b b++≥ ++⇔ ++ ≥ ++ ⇔− +
Bất đẳng thức này luôn đúng. Dấu đẳng thức xảy ra khi và chỉ khi
abc
= =
.
b) Khai triển hai vế và thu gọn ta quy về câu a.
c) Khai triển hai vế rồi thu gọn ta đưa bất đẳng thức về dạng:
( )
2
0ay bx−≥
. Dấu đẳng thức xảy ra khi và chỉ khi
ab
xy
=
.
d) Khai triển hai vế rồi thu gọn ta đưa bất đẳng thức về dạng:
( ) ( ) ( )
222
0ay bx bz cy cx az− +− +− ≥
. Dấu đẳng thức xảy ra khi và chỉ khi
abc
xyz
= =
. Các bất đẳng thức c, d còn được gọi là bất đẳng thức
Bunhiacopxki cho 2 số, 3 số.
e) Khai triển hai vế rồi thu gọn ta đưa bất đẳng thức về dạng:
( )( )(
)
8a b b c c a abc+ + +≥
bất đẳng thức này luôn đúng theo AM- GM
(xem chứng minh ở phần Bất đẳng thức Cô si).
f) Theo bất đẳng thức Cô si thì:
22 22 2
2b c a c abc+≥
Tương tự ta có 2
bất đẳng thức nữa và cộng lại suy ra đpcm.
THCS.TOANMATH.com
g) Theo bất đẳng thức Bunhiacopxki cho 2 số ta có:
( )
(
)
(
)
2
2
22
.1
b b bc
a b a bc a bc a bc
c cc

+

+ =+ ≤ + += +





suy ra
( )
(
)
( )
2
2
1 c
a bc b c
ab
≥
++
+
. Tương tự
( )
( )
( )
2
2
1
b
a bc b c
ac
≥
++
+
. Cộng hai
bất đẳng thức cùng chiều ta suy ra đpcm.
h) Quy đồng và rút gọn đưa bất đẳng thức cần chứng minh về dạng:
( )
2
0
ay bx−≥
.
i) Áp dụng bất đẳng thức h) ta có:
( )
( )
22
2 22 2
xy xyz
xyz z
a b c ab c abc
+ ++
++≥ +≥
+ ++
.
Bất đẳng thức này còn được gọi là bất đẳng thức Cauchy-Chwarz.
1. Những kỹ năng vận dụng cơ bản:
Ví dụ 1: Cho các số thực dương
,,abc
sao cho
3abc++=
. Chứng minh
rằng:
1
222
abc
a bc b ac c ab
++≥
+++
.
Giải:
2 222
2 222
2 2 222 2 2 2
aa abcabc
a bc a abc a bc b ac c ab a abc b abc c ab
= ⇒++= + +
+ + +++ + + +
Áp dụng bất đẳng thức Cauchy- Schwarz ta có:
( )
2
222
2 2 2 222
222 6
abc
abc
a abc b abc c abc a b c abc
++
++≥
+ + + +++
. Ta cần chứng
minh:
( )
2
222
1
6
abc
a b c abc
++
≥
+++
( )( )
39ab bc ca abc a b c ab bc ca abc⇔++≥ ⇔++ ++ ≥
. Theo bất đẳng
thức Cô si ta có:
3
222
3
3, 3a b c abc ab bc ca a b c++≥ + + ≥
nhân 2 vế các
THCS.TOANMATH.com
bất đẳng thức dương cùng chiều ta có đpcm. Dấu bằng xảy ra khi và chỉ khi
1abc= = =
.
Ví dụ 2: Cho các số thực dương
,,abc
. Chứng minh rằng:
3 3 3 222
222 3
a b c abc
abbcca
++
++≥
+++
.
Giải:
Ta có:
( )
( )
2
222
34 4 4 4
2
2 2 22
22 2 2 2
abc
aa a b c
VT
a b a ab a ab b bc c ca
abc
++
= ⇒= + + ≥
++ + + +
++
.
Ta cần chứng
minh:
( )
( )
2
222
222
222
2
3
abc
abc
a b c ab bc ca
abc
++
++
≥ ⇔++≥ ++
++
. Điều này
là hiển nhiên.
Ví dụ 3: Cho các số thực dương
,,abc
. Chứng minh:
( )( )(
)
( )
2
222
2 2 23a b c abc+ + + ≥ ++
.
Giải:
Ta có:
( )
( )
( )
2
2
2
2
2. 2 1
2
2
bc
bc
abc a a

+

+

++ = + ≤ + +







.Suy ra:
( )
( )
( )
2
2
2
3 3 21
2
bc
abc a

+
++ ≤ + +



. Ta cần chứng minh:
( )
( )
( )
( )( )
2
2 222
3 21 2 2 2
2
bc
a abc

+
+ + ≤+ + +



hay
( )
( )( )
2
22
31 2 2
2
bc
bc

+
+ ≤+ +



. Sau khi khai triển và thu gọn ta được:
THCS.TOANMATH.com
22
22
3 10
2
bc
b c bc
+
+ − +≥
. Để ý rằng:
22
2
bc
bc
+
≥
nên bất đẳng thức trở
thành:
( )
2
22
2 10 1 0b c bc bc− +≥ ⇔ − ≥
.
Ví dụ 4: Cho các số thực dương
,,abc
. Chứng minh:
( )( ) ( )( )
( )( )
333
22 22 22 2 2 2 2 22
1
22 22 22
abc
abc
ab ac bc ba ca cb
++≤
++
++ ++ ++
Giải:
Ta mong muốn xuất hiện lượng:
abc++
Ta có:
( )( ) ( )( ) ( )
( )
2
2
22 22 22 2 2 22 2 2
22ab ac abaaac aabac aabc+ + = + + + + ≥ + + = ++
Từ đó suy ra:
( )( )
( )
3
2
22 22
22
aa
ab ac
abc
≤
++
++
. Tương tự ta có 2 bất đẳng
thức nữa và cộng lại thì suy ra điều phải chứng minh.
Ví dụ 5: Cho các số thực dương
,,abc
sao cho
4ab bc ca abc+++ ≤
.
Chứng minh:
( )
222
2
a b c a b c ab bc ca+ + +++≥ + +
. (Trích đề tuyển sinh
vào lớp 10- Trường Chuyên KHTN- ĐHQG Hà Nội 2015).
Lời giải:
Ta viết lại giả thiết bài toán thành:
( )
( ) ( ) ( )
12 4 8 4 2
ab bc ca a b c a b c ab bc ca abc+ + + + ++ ≥+ ++ + + + +
hay
( )( ) ( )( ) ( )( ) ( )( )( )
22 22 22 222ab bc ca abc+ +++ +++ +≥+ + +
111
1
222abc
⇔++≥
+++
Ta có:
( )
( )
( )
22 22
2
22
1
2
11
ab c ab c
a
a ab c
abc
++ ++
= ≤
+
++ + +
++
, Tương tự ta
THCS.TOANMATH.com
có:
( )
( )
22 22
22
11
;
22
bc a aa b
bc
abc abc
++ ++
≤≤
++
++ ++
. Suy ra
( )
(
)
222
2
2
111
1
222
abc a b c
abc
abc
+++ + +
≤++≤
+++
++
( )
( )
2
222
2abc a b c abc⇔+++ + + ≥ ++
hay
( )
222
2a b c a b c ab bc ca+ + +++≥ + +
. Dấu bằng xảy ra khi và chỉ khi
1abc= = =
.
Ví dụ 6) Cho các số thực dương
,,abc
sao cho
1ab bc ca++=
. Chứng
minh rằng:
( )
42 42 4 2
5
2
9
abc a b c a b b c c a++ ≤ + + +
. (Trích đề tuyển sinh
vào lớp 10- Trường Chuyên KHTN- ĐHQG Hà Nội 2014).
Lời giải:
Sử dụng bất đẳng thức
2 22
x y z xy yz zx++≥++
. Ta có:
( )
42 42 4 2 2 2 2 2 2 2 2 2 2
...ab bc ca abbc bcca caab abc ab bc ca+ + ≥ + + = ++
.
Tiếp tục sử dụng bất đẳng thức: Cauchy- Shwarz và giá thiết
1ab bc ca++=
ta có:
( )
( )
2
222
2
222
1 1 1 111
abc
bca
ab bc ca abc a b c
a b c abc
++
+ + = + + ≥ = ++
++
. Từ đó suy ra
( )
2
42 42 4 2
a b b c c a abc a b c+ + ≥ ++


. Bây giờ ta sẽ chứng minh:
( ) ( ) (
)( )
2
2
5
2 0 6 50 1 5 0
9
abc a b c abc a b c t t t t++ − ++ + ≥⇔ − +≥⇔ − − ≥


với
( )
t abc a b c= ++
. Mặt khác ta có:
( ) ( )
2
11
. . . 01
33
abc a b c ab ac bc ba ca cb ab bc ca t++=++≤++=⇒<≤
.
Suy ra đpcm. Dấu đẳng thức xảy ra khi và chỉ khi
1
3
abc= = =
.
THCS.TOANMATH.com
Ví dụ 7: Cho các số thực dương
,,
abc
. Chứng minh:
2
2 22
111abc
a ab bc b bc ca c ca ab ab bc ca
++

++≤

++ ++ ++ ++

Lời giải:
Ta muốn làm xuất hiện:
ab bc ca++
Ta có:
( )( )
( )
22
2
2
22
1 c ab bc c ab bc
a ab bc
a ab bc c ab bc
ac ab bc
++ ++
= ≤
++
++ ++
++
. Tương
tự với 2 số hạng còn lại ta có:
( )
( )
( )
2
2
22
2
1
abc
c ab bc
a ab bc
ac ab bc ac ab bc
++
++
∑ ≤∑ =
++
++ ++
Ví dụ 8: Cho các số thực dương
,,abc
. Chứng minh:
222
222
ab bc ca a b c
a bc ca b ca ab c ab bc ab bc ca
++
++≤
++ ++ ++ ++
Giải:
Ta muốn làm xuất hiện:
ab bc ca++
( )( )
( )
22
2
2
22
()()ab ab b bc ca ab b bc ca
a bc ca
a bc ca b bc ca
ab bc ca
++ ++
= ≤
++
++ ++
++
Từ đó suy ra:
( ) ( ) ( )
22 2
222
( )( )( )ab b bc ca bc c ca ab ca a ab bc
VT
ab bc ca ab bc ca ab bc ca
++ ++ ++
≤++
++ ++ ++
.
Ta chỉ cần chứng minh:
( )
( )
2 2 2 222
( )( )( )ab b bc ca bc c ca ab ca a ab bc a b c ab bc ca++ + ++ + ++ ≤ ++ ++
333
()a b b c c a abc a b c⇔ + + ≥ ++
222
abc
abc
cab
⇔ + + ≥++
. Nhưng bất
đẳng thức này là hiển nhiên đúng theo bất đẳng thức Cauchy- Shwarz
THCS.TOANMATH.com
Ví dụ 9: Cho các số thực dương
,,
abc
sao cho
1abc++=
. Chứng minh
rằng:
32 32 3 2
1
abc
abcbcacab
++≤
++ ++ ++
Giải:
Ta muốn làm xuất hiện
abc++
.
( )
( )
2
32
32
11
11
1
1
9
1
ac ac
a a ca
aa
abc
abc
abc c
a
 
++ ++
 
++
 
= ≤=
++

++
+ + ++


. Từ đó suy
ra:
32 32 3 2
111
999
a b c a ca b ab c bc
abcbcacab
++ ++ ++
+ + ≤++
++ ++ ++
Ta cần chứng minh:
111
13
999
a ca b ab c bc
ab bc ca
++ ++ ++
+ + ≤⇔ + + ≤
.
Nhưng điều này là hiển nhiên đúng do:
(
)
2
3
3
abc
ab bc ca
++
++≤ =
Ví dụ 10: Cho các số thực dương
,,abc
sao cho
1abc =
. Chứng minh rằng:
222
111
1
111ab bc ca
++≤
++ ++ ++
Giải:
Ta đặt
3 33
, ,,1a x b y c z xyz
= = = =
. Bất đẳng thức cần chứng minh trở
thành:
3 6 36 36
111
1
111
xy yz zx
++≤
++ ++ ++
.
Ta có:
( )
( ) ( )
4
4
2
4 2 22
2
22
36
2 22 2 22
364
2
1
1
1
1
1
1
zx
zx
y
z x yz z x
y
xy
xyz xyz
xyzx
y

++
++

++

= ≤=
++

++ ++
+ + ++


THCS.TOANMATH.com
Ta cần chứng minh:
(
) (
)
2
4 2 22 2 2 2 22 22 22
()
z x yz z x x y z x y y z z x xyz x y z
∑ + + ≤ + + ⇔ + + ≥ ++
.
Điều này là hiển nhiên đúng theo bất đẳng thức
222
a b c ab bc ca++≥ ++
Ví dụ 11: Cho các số thực dương
,,abc
. Chứng minh rằng:
33 33 3 3
1 1 11
a b abc b c abc c a abc abc
++≤
++ ++ ++
.
Do bất đẳng thức thuần nhất nên ta chuẩn hóa:
1abc =
. Bất đẳng thức cần
chứng minh trở thành:
33 33 3 3
111
1
111ab bc ca
++≤
++ ++ ++
.
Ta có:
( )
(
) (
)
22
2
22
33
33 2
11 11
1
11
1
1
cc
bc ca c c
ab ab
a b abc
abc abc
ab c
ab

++ ++

++

= ≤==
+ + ++

++ ++
+ + ++


Tương tự với 2 số hạng còn lại và cộng ba bất đẳng thức cùng chiều suy ra
đpcm.
Ví dụ 12) Với ba số dương
,,xyz
thỏa mãn
1xyz++=
, tìm giá trị lớn
nhất của biểu thức:
xyz
Q
x x yz y y zx z z xy
=++
++ ++ ++
.(Trích đề
tuyển sinh vào lớp 10 chuyên Toán TP Hà Nội – 2014)
Lời giải:
Ta có:
( ) ( )( )
xyz xxyz yz xyxz+= +++= + +
. Chú ý rằng: Theo
bất đẳng thức Bunhiacopxki thì:
( )( )
( )
( )( )
2
.. ..xyxz xy zx xyxz xy zx++≥ + ⇒++≥ +
.
Từ đó suy ra:
( )
xx x
x x yz x y z
x xy z
≤=
++ + +
++
. Tương tự
THCS.TOANMATH.com
ta có:
;
y
y zz
yyzx xyzzzxyxyz
≤
++ ++ ++ ++
. Cộng 3 bất
đẳng thức cùng chiều ta suy ra
1Q
≤
. Dấu đẳng thức xảy ra khi và chỉ khi
1
3
xyz= = =
Ví dụ 13) Cho các số thực không âm
,,abc
sao cho
0, 0a bc> +>
và
222
1abc++=
. Chứng minh:
3 33
2 22
2
a bc
b bc c a
+
+≥
−+
.
Lời giải:
Ta có:
( )
( )
( )
( )
2
222
4 44
22
22
22 2222
1
abc
a bc
ab ac
a b bc c a b c
a b bc c a b bc c a b a c
++
++≥ =

−++ +
−+ −+ + +

Theo bất đẳng thức Cauchy ta có:
( )
( )
2
2
2
a bc
ab c
++
+≤ ⇒
( )
( )
22 2
2
22
11
2
a b bc c a b c
a bc
a b bc c
≥

−++ +
++

−++



( ) ( )
222 2
22
3 3 32aabc a a
= =
++ −
. Bây giờ ta chứng minh :
( )
(
)
23
2
2 22
2 32 2 2 3
22
32
aa a a
aa
≥⇔ − ≤⇔ ++≥
−
. Theo bất đẳng
thức Cauchy cho 3 số ta có:
3
22
23
22
aa++≥
. Dấu bằng xảy ra khi và
chỉ khi
2
,0
2
ab c= = =
. Ta cũng có thể chứng minh:
THCS.TOANMATH.com
( )
( )
2
23
1
32 2 2 3 2 0 2 2 0
2
a a aa a a

− ≤ ⇔ − + ≥⇔ − + ≥


. Bất đẳng
thức này luôn đúng.
Ví dụ 14) Cho các số thực
,xy
sao cho
22
2 10xy y+ +=
. Tìm GTNN,
GTLN của
31
xy
P
y
=
+
(Trích đề tuyển sinh vào lớp 10 chuyên Trường
chuyên – KHTN- ĐHQG Hà Nội 2015).
Lời giải:
Từ giả thiết ta suy ra
0y ≠
.
2
22 2 2
2
12 1
2 10 1 1 1xy y x x
yy y

+ += ⇒ + + =⇔ + + =


. Đặt
1
1a
y
= +
. Ta
được
22
1xa+=
. Ta có:
( )
2
2
24
1
2
3
xx
P P x Pa P x Pa
a
y
= = ⇒=−⇒ =−
+
+
. Theo bất đẳng thức
Bunhiacopxki ta có:
( )
( )
( )
2
222 2
11x Pa P x a a− ≤+ + =+
. Suy ra
2 22
33
41 31
33
P PP P≤ + ⇔ ≤ ⇔− ≤ ≤
. Với
32 3
;
23 3
xy P
= =⇒=
,
32 3
;
23 3
xy P
−
= =−⇒ =−
. Vậy GTLN của
P
là
3
3
, GTNN của
P
là
3
3
−
2. Kỹ thuật tách ghép
Để giải quyết những bài toán dạng này người giải cần linh hoạt trong việc
tách các nhóm số hạng sao cho đảm bảo dấu bằng và tạo ra các bất đẳng
thức phụ quen thuộc.
THCS.TOANMATH.com
Ta cần chú ý các bất đẳng thức quen thuộc sau:
1 11 1
4ab a b

≤+

+

và
1 11 1 1
9abc a b c

≤ ++

++

.
Ví dụ 1: Cho các số thực dương
,,abc
. Chứng minh:
222 4
bc ca ab a b c
abc bca cab
++
++≤
++ ++ ++
Giải:
Ta có:
1 1 4 11 1
2 4( ) ( ) 4abc ab ac ab ac

= ≤+

++ + + + + +

Từ đó suy ra:
( )
11
24 4
bc bc bc
abc
abc ab ac

∑ ≤ ∑ + = ++

++ + +

Ví dụ 2: Cho các số thực dương
,,abc
. Chứng minh:
222
22 22 22
()()()
3
()()()
bc ca ab
bcabccabca abcab
++ +
++≤
++ + ++ + ++ +
Giải:
Ta có:
2 2 22
22
() ()
()()()()()
bc bc b c b c
b c abc bba cca bba cca ba ca
++
= ≤+=+
++ + ++ + + + + +
.
Từ đó suy ra
2
22
()
3
()
bc b c
b c ab c b a c a
+

∑ ≤∑ + =

++ + + +

Ví dụ 3: Cho các số thực dương
,,abc
sao cho
3abc++=
. Chứng minh
rằng:
222 22 2 222
1111
4442abc bca cab
++≤
++ ++ ++
.
Giải:
THCS.TOANMATH.com
Ta có:
( )
2
22 2
222 2 22 22 2 22 22
9
4 2()()2()()
abc
ab c
abc a ab ac a ab ac
++
= ≤+ +
++ ++++ + +
Suy ra
22 2
222 2 22 22
99
4 2 ( )( ) 2
ab c
abc a ab ac

∑ ≤∑ + + =

++ + +

Ví dụ 4: Cho các số thực
,,abc
sao cho
222
1abc++=
.Chứng minh rằng:
222
3
1 1 14
bc ca ab
abc
++≤
+++
Giải:
Ta có:
( ) ( ) ( )
222
222 2 2 2
1
1 1 14 1 1 1
bc ca ab
bc ca ab
abc a b c

++ +
++≤ + +

+++ + + +


Mặt khác ta có:
( ) ( )
( ) ( ) ( ) ( )
22
22
2222
22 22 22 22
bc bc
bc
aabc
ab ac ab ac
++
= ≤+
+++
+++ + +
. Từ đó suy ra
( )
( ) ( )
2
22
2
22 22
3
1
bc
bc
a
ab ac

+

∑ ≤∑ + =
+
++


. Suy ra điều phải chứng minh.
Ví dụ 5:
Cho các số thực dương
,,abc
. Chứng minh rằng:
222
111bc ca ab
a bc b ac c ab a b c
+++
+ + ≤++
+++
.
Giải:
Ta có:
( )
( )
( )
( )
( ) ( ) ( ) ( )
22
22
2
2 22 22 22 22
bc bc
bc b c
a bc
abcbc cab bac cab bac
++
+
= = ≤+
+
+ + ++ + + +
THCS.TOANMATH.com
. Từ đó suy ra :
(
)
( )
( )
( )
22 22
2
22 22 22 22
1bc b c b a
a bc c
ca b ba c ca b ca b

+

∑≤∑+=∑+=∑
+
++ ++


Chú ý: Nếu ta thay
( )
111
,, , ,abc
abc

→


thì thu được bất đẳng thức mới là:
222
222
()()()abc bc a cab
abc
a bc b ca c ab
+++
+ + ≤++
+++
Nếu phân tích:
2
22
() ()
abc bcbc
bc
a bc a bc
++
=+−
++
thì thu được bất đẳng thức mới:
222
() () ()bc b c ca c a ab a b
abc
a bc b ca c ab
++ +
+ + ≥++
+++
. Đây là các bất đẳng thức đẹp
và khó.
Ví dụ 6: Cho các số thực dương
,,abc
. Chứng minh rằng:
222
222
1
222
abc
a bc b ac c ab
++≥
+++
Giải: Ta có:
(
)
2
222
2 2 2 222
1
2 2 2 222
abc
abc
a bc b ac c ab a bc b ac c ab
++
++≥ =
+++ +++++
Thay
( )
111
,, , ,abc
abc

→


ta thu được kết quả:
222
1
222
bc ca ab
bc a ca b ab c
++≥
+++
Mặt khác ta có:
2
22
2
1
22
bc a
bc a a bc
= −
++
nên bất đẳng thức trên có thể viết lại
thành:
THCS.TOANMATH.com
222
222
1
222
abc
a bc b ac c ab
++≤
+++
. Thay
( )
111
,, , ,
abc
abc

→


ta lại thu
được:
222
1
222
bc ca ab
a bc b ac c ab
++≤
+++
Những bất đẳng thức này có ứng dụng rất quan trọng.
Ví dụ 7: Cho các số thực dương
,,abc
. Chứng minh rằng:
222
1
(2 )(2 ) (2 )(2 ) (2 )(2 ) 3
abc
ab ac bc ba ca cb
++≤
++ ++ ++
Giải:
Ta có
( )
2
22 2
22
2
1 14
(2 )(2 ) 2( ) 2 92( ) 2 9 2(
aa
aa a
ab ac aabc a bc aabc a bc aab
+
= = ≤
+ + ++ + + ++ + + ++
Từ đó suy ra:
2 22 2
22
1 4 12
(2 )(2 ) 9 2 ( ) 2 9 2
a a a aa
ab ac aabc a bc abc a bc

∑ ≤∑ + =∑ +


+ + ++ + ++ +

. Áp dụng kết quả của VD 6 ta suy ra điều phải chứng minh.
Ví dụ 8: Cho các số thực dương
,,abc
sao cho
3ab bc ca++=
. Chứng
minh rằng:
222
1 1 13
1 1 12abc
++≥
+++
Giải:
Ta có:
2
22
1
1
11
a
aa
= −
++
nên bất đẳng thức tương đương với
222
222
3
1 1 12
abc
abc
++≤
+++
.
THCS.TOANMATH.com
222
222
1
3 33 33 3 2
abc
abc
⇔++≤
+++
. Ta có:
(
)
2
2 2 22
22 2 2
44
333 ()2 ()2
aa
a a aa
a a ab bc ca a a b c a bc a a b c a bc
+
= = ≤+
+ + + + ++ + + ++ +
2
2
( )2
aa
abc a bc
= +
++ +
Tương tự với 2 số hạng còn lại ta có:
22
22
11
3 34 2 2
a aa
a abc a bc

∑ ≤∑ + ≤

+ ++ +

Ở đây ta đã sử dụng kết quả:
2
2
1
2
a
a bc
∑≤
+
Ví dụ 9: Cho các số thực dương
,,abc
. Chứng minh:
222
2 22 22 2
1
5 ( )5 ( )5 ( )3
abc
a bc b ca c ab
++≤
++ ++ ++
Giải:
Ta có:
( )
( )
( )
2
22
22
222 2 222 2
2
99
5()
2(2 ) 2(2 )
aa
aa
a bc
abc abc abc abc
+
= =
++
++ + + ++ + +
( ) ( )
2 2 22
22
222 222
42
2(2 ) 2
a a aa
a bc a bc
abc abc
≤ += +
++
++ ++
Từ đó suy ra:
2 22
2 2 222 2
1 21
5 ( )9 2 3
a aa
a bc abc abc

∑ ≤∑ + ≤

++ ++ +

Ví dụ 10: Cho các số thực dương
,,abc
thỏa mãn:
1abc++=
. Chứng
minh:
1
32 32 32 4
ab bc ca
ab b c bc c a ca a b
++≤
++ ++ ++
Giải:
THCS.TOANMATH.com
Ta có:
( )
( )
2
32 32( ) 2 2ab b c ab b c a b c ab bc ca c ab b++= ++ ++= ++ + + +
Từ đó ta có:
( )
( )
( )
2
2
2
112
1 11
22
22
ab bc ca c ab b
ab bc ca c ab b
++
≤ ++
++ +
++ + + +
Như vậy:
22
11
3 2 16 2 2 16 2 2
ab ab ab ab ab ab a
ab b c ab bc ca c ab b ab bc ca c ab

≤ ++= ++

++ ++ + ++ +

Từ đó suy ra:
2
11
3 2 16 2 2 4
ab ab ab a
ab b c ab bc ca c ab

∑ ≤∑ + + ≤

++ ++ +

.
3. Kỹ thuật thêm bớt.
Ví dụ 1: Cho các số thực dương
,,abc
sao cho
222
3abc
++=
. Chứng
minh rằng:
111
3
222abc
++≥
−−−
Phân tích: Nếu ta áp dụng trực tiếp bất đẳng thức:
( )
2
2 22
xyz
xyz
a b c abc
++
++≥
++
thì phần sau sẽ bị ngược dấu. Để khắc phục ta
thêm bớt như sau:
Xét
1 12
22
m ma
m
aa
−+
−=
−−
ta chọn
m
sao cho
12 0m ma−+>
và
12m ma−+
chỉ còn đơn giản một số hạng. Điều này làm ta nghỉ đến
1
2
m =
.
Từ đó ta có cách chứng minh như sau:
1111113
3
2 22 22 22 2 2 2
abc
a b c abc
−+ −+ −≥⇔ + + ≥
− − − −−−
THCS.TOANMATH.com
222
222
3
222
abc
aabbcc
⇔ ++≥
−−−
.Áp dụng bất đẳng thức:
( )
2
2 22
xyz
xyz
A B C ABC
++
++≥
++
ta có:
(
)
( )
2
222
2( )
abc
VT
abc a b c
++
≥
++ − + +
Ta cần chứng minh:
( )
( )
( )
22
222
33
2( ) 3
2( )
abc abc
abc
abc a b c
++ ++
≥⇔ ≥
++ −
++ − + +
(
)
2
6( ) 9 0
abc abc
⇔ ++ − ++ +≥
(
)
2
30
abc⇔ ++− ≥
Ví dụ 2: Cho các số thực dương
,,abc
sao cho
3ab bc ca++=
. Chứng
minh rằng:
222
111
1
222abc
++≤
+++
Phân tích:
Xét:
2
22
1 12
22
m ma
m
aa
−−
−=
++
ta nghỉ đến chọn
1
2
m =
. Khi đó ta có:
222
2 2 2 222
1111111
1
22 22 22 2 2 2 2
abc
a b c abc
−+ −+ −≤−⇔ + + ≥
+ + + +++
.
Áp dụng bất đẳng thức:
( )
2
2 22
xyz
xyz
A B C ABC
++
++≥
++
ta có:
(
)
2
222
2 2 2 222
222 6
abc
abc
a b c abc
++
++≥
+ + + +++
. Ta cần chứng minh:
( )
( )
( )
22
222 222
11
62
abc abc
abc abc abbcca
++ ++
≥⇔ ≥
+++ +++ ++
. Nhưng đây là một
đẳng thức. Suy ra điều phải chứng minh.
Ngoài ra ta có thể giải bằng cách khác như sau:
THCS.TOANMATH.com
(
)
( )
(
)
( )
( )
22
2
2
2
2
11
1
22
2
21
2
bc bc
a
abc
bc
a
++
++
= ≤
+

++
+
++



. Từ đó cộng các bất đẳng thức
cùng chiều ta suy ra điều phải chứng minh:
Chú ý: Với các giả thiết
,,abc
là độ dài ba cạnh một tam giác ta cần chú ý
biến đổi để sử dụng điều kiện:
0, 0, 0abc bca cab+−> +−> +−>
Ví dụ 3: Cho
,,abc
là độ dài ba cạnh một tam giác. Chứng minh rằng:
1
333
abc
abc bca cab
++≥
−+ −+ −+
Phân tích:
Ta viết lại:
(3 )
33
a amabc
m
abc abc
− −+
−=
−+ −+
. Ta chọn
1
4
m
=
khi đó:
1
3 4 4(3 )
a abc
abc abc
+−
−=
−+ −+
. Từ đó ta có bất đẳng thức cần chứng minh
được viết lại thành:
1111
3434344
abc
abc bca cab
−+ −+ −≥⇔
−+ −+ −+
1
333
abc bca cab
abc bca cab
+− +− +−
++≥
−+ −+ −+
.
Ta có
( )
( )( )
( )
22
222
1
3 2( )
abcbcaacb abc
VT
abc abc a b c abbcca
+−++−++− ++
≥==
∑ +− −+ + + + + +
Đối với các bất đẳng thức dạng
()()()fa fb fc M++≤
. Ta thường thêm
bớt vào một số
m
để tử số có dạng bình phương.
THCS.TOANMATH.com
Ví dụ 4: Cho các số thực dương
,,
abc
sao cho
1abc =
.Chứng minh rằng:
222
111
3
111aabbcc
++≤
−+ −+ −+
.
Phân tích:
Ta lấy
2
22
11
11
m ma ma
m
aa aa
−− +
−=
−+ −+
để
2
1 m ma ma−− +
phân tích
được thành:
2
()xa y+
thì
2
10m ma ma−− + =
có nghiệm kép. Hay
( )
2
4
4 (1 ) 0 4 3 0
3
m mm m m m
∆= + − = ⇔ − = ⇔ =
. Ta viết lại bất đẳng
thức thành:
222
141414
1
13 13 13aabbcc
−+ −+ −≤−
−+ −+ −+
hay
222
222
(2 1) (2 1) (2 1)
3
111
abc
aabbcc
−−−
++≥
−+ −+ −+
. Áp dụng bất đẳng thức:
( )
2
2 22
xyz
xyz
A B C ABC
++
++≥
++
ta thu được:
[ ]
( )
2
222
2( ) 3
( )3
abc
VT
a b c abc
++ −
≥
+ + − ++ +
. Ta cần chứng minh:
[
]
(
)
2
222
2()33 ()3
abc a b c abc

++ − ≥ + + − ++ +

hay
( ) ( )
2
6( ) 9abc abbcca abc++ + + + ≥ ++
Ta có:
2 22 22 2 2
( ) 2( )ab bc ca a b b c c a abc a b c+ + = + + + ++
222
2()3()3()
a bc b ca c ab abc a b c abc a b c a b c≥ + + + ++ = ++ = ++
. Ta quy
bài toán về chứng minh:
( ) ( )
2
6 3( ) 9abc abc abc++ + ++ ≥ ++
. Đặt
3( ) 3t abc t= ++ ⇒≥
. Ta có bất đằng thức trở thành:
( )
4
24 2 3 2
6 3 27 54 0 27 54 ( 3) ( 6) 0
9
t
t t t t t t t t tt t+ ≥ ⇔ − + ≥⇔ − + = − + ≥
.
Điều này là hiển nhiên. Dấu bằng xảy ra khi và chỉ khi
1abc= = =
.
THCS.TOANMATH.com
Cho các số thực dương
,,abc
sao cho
222
3abc
++=
. Chứng minh rằng:
222
1
2 3 2 3 2 32
abc
ab bc ca
++≤
++ ++ ++
.
Một số cách thêm bớt không mẫu mực:
Ví dụ 5: Cho các số thực dương
,,abc
sao cho
1.abc++=
Chứng minh:
222
1
3 13 13 118( )
abc
a b c ab bc ca
++≤
+ + + ++
Giải:
Ta có:
22
13 1
.
313313 31
aa a
a
aa a

= = −

++ +

. Vì vậy ta quy bài toán về chứng
minh:
1
1
3 13 13 16( )
abc
a b c ab bc ca
+++ ≥
+ + + ++
Ta có:
( )
( ) ( ) ( )
( )
2
222
1
31 31 31 31
31
abc
a
aaabbcc
abc
++
∑≥ =
+ ++ ++ +
++ +
Suy ra
(
)
( )
2
222
1 14
1
6( )
31
31
VT
ab bc ca
abc
abc
≥ +≥ =
++
++ +
++ +
Ví dụ 6: Cho các số thực dương
,,abc
sao cho
1.abc
++=
Chứng minh:
111
2
111
bca abc
abc abc
+++

++ ≥ + +

−−−

Giải:
Do
12
1
1
aa
a bc
+
= +
−+
nên ta viết lại bất đẳng thức thành:
3
2
bca a b c
a b c bc ca ab
++≥+++
++ +
. Lại có:
()
a a ab
c bc cbc
−=
++
nên ta sẽ
THCS.TOANMATH.com
chứng minh:
3
( )2
ab
cb c
∑≥
+
. Áp dụng bất đẳng thức Cauchy Shwarz ta có:
( )
( )
2
22
() ()2
ab bc ca
ab a b
c b c abc b c abc a b c
++
∑=∑ ≥
+ + ++
Ta cần chứng minh:
( )
( )
2
3
22
ab bc ca
abc a b c
++
≥
++
nhưng đây là bài toán quen thuộc.
Ví dụ 7: Cho các số thực dương
,,abc
sao cho
1.ab bc ca++=
Chứng
minh:
33
2
ab bc ca
abc
bc ca ab
+++ + + ≥
++ +
Giải:
Nhân 2 vế với
abc++
và chú ý:
( )
2
ab a b
abc ab
bc bc
++ = +
++
. Ta viết bất
đẳng thức cần chứng minh thành:
( ) ( )
222
2
33
1
2
ab bc ca
abc abc
bc ca ab
++ ++ + + ≥ ++
++ +
Ta có:
( )
( )
2
222
2
1
( )( )( )
1
ab bc ca
ab bc ca
bc ca ab bbc cca aab
abc
++
++≥ =
+ + + ++ ++ +
++ −
.
Cuối cùng ta chứng minh:
(
)
( )
(
)
2
2
1 33
1
2
1
abc abc
abc
++ ++ ≥ ++
++ −
.
Nhưng
( ) ( )
2
33 3
3
24
abc abc

++ ≤ ++ +

nên ta quy về:
( )
( )
( )
22
2
13
13
4
1
abc abc
abc

++ ++ ≥ ++ +

++ −
. Dành cho học sinh.
4). PHƯƠNG PHÁP ĐẶT ẨN PHỤ.
Tùy theo bài toán ta có thể chọn một trong các cách đặt ẩn phụ sau:
THCS.TOANMATH.com
1).
(
)
111
,, , ,
abc
abc

→


2).
( )
,, , ,
ka kb kc
abc
bca

→


3).
(
)
,, , ,
kb kc ka
abc
abc

→


4).
( )
222
,, , ,
ka kb kc
abc
bc ac ab

→


5).
( )
222
,, , ,
kbc kca kab
abc
abc

→


Ví dụ 1: Cho các số thực dương
,,xyz
sao cho
1xyz =
. Chứng minh rằng:
222
111
1
1 11xx yy zz
++≥
++ ++ ++
.
Phân tích: Nếu áp dụng trực tiếp bất đẳng thức:
( )
2
222
XYZ
XYZ
A B C ABC
++
++≥
++
thì bất đẳng thức tiếp theo bị ngược dấu.
Để không bị ngược dấu ta thay
( )
222
,, , ,
bc ca ab
xyz
abc

→


thì bất đẳng thức
cần chứng minh trở thành:
444
4 2 22 4 2 22 4 2 22
1
abc
a a bc b c b b ac a c c c ab a b
++≥
++ ++ ++
. (*)
Bây giờ áp dụng bất đẳng thức:
( )
2
222
XYZ
XYZ
A B C ABC
++
++≥
++
ta có:
THCS.TOANMATH.com
( )
2
222
4 2 22 4 2 22 4 2 22
abc
VT
a a bc b c b b ac a c c c ab a b
++
≥
++++++++
. Ta cần chứng
minh:
( )
2
222
4 2 22 4 2 22 4 2 22
1
abc
a a bc b c b b ac a c c c ab a b
++
≥
++++++++
22 22 22
()b c a c a b abc a b c
⇔ + + ≥ ++
. Nhưng đây là kết quả quen thuộc.
Ví dụ 2: Cho các số thực dương
,,xyz
sao cho
1xyz =
. Chứng minh rằng:
1 1 11
( 1)( 2) ( 1)( 2) ( 1)( 2) 2xx yy zz
++≥
++ ++ ++
.
Phân tích:
Đặt
222
;;
bc ac ab
xyz
abc
= = =
bất đẳng thức cần chứng minh trở thành:
4
22
1
(2 )( ) 2
a
a bc a bc
∑≥
++
. Áp dụng bất đẳng thức:
( )
2
222
XYZ
XYZ
A B C ABC
++
++≥
++
ta có:
(
)
2
222
22
(2 )( )
abc
VT
a bc a bc
∑ ++
≥
∑+ +
. Ta cần chứng minh:
( )
2
222 2 2
2 (2 )( )abc abcabc∑ + + ≥∑ + +
22 22 2 2
()a b b c c a abc a b c
⇔ + + ≥ ++
. Đây là kết quả quen thuộc.
Ví dụ 3: Cho 3 số thực dương
,,xyz
. Chứng minh rằng:
222
3
xyz
xy yz zx
++≤
+ ++
Giải:
THCS.TOANMATH.com
Đặt
;;
abc
xyz
bca
= = =
. Bất đẳng thức cần chứng minh trở thành:
222
222
3
2
abc
a bc b ac c ab
++≤
+++
. Áp dụng bất đẳng thức
Bunhiacopxki ta có:
2
222
222 2
( )( )
( )( )
a b c a aa b a c
a bc b ac c ab a b a c a bc


++

∑ + + ≤∑ ∑




+++ ++ +



Mặt khác ta có:
( )( ) ( )( )( )
89abcabbcca abbcca++ + + ≤ + + +
. Mặt
khác ta có:
( )
2
9
( )( ) ( )( )( ) 4( )
ab bc ca
a
abac abbcca abc
++
∑= ≤
+ + + + + ++
. Ta quy bài
toán về chứng minh:
( )
2
( )( )
2
aa b a c
abc
a bc
++
∑ ≤ ++
+
. Mặt khác ta có:
2
22
( )( ) ( )aabac abc
a
a bc a bc
++ +
= +
++
. Ta quy bài toán về chứng minh:
2
2
()
abc
abc
a bc
+
∑ ≤++
+
KỸ THUẬT ĐỐI XỨNG HÓA.
Ví dụ 1: Cho các số thực dương
,,abc
. Chứng minh:
222
3
abc
ab bc ca
++≤
+++
Giải:
THCS.TOANMATH.com
Ta có:
( )
( )
( )
( )
2
22
2
() ()
aa c aa c
a
ab
abac abac

++

= ⇒∑ ≤

+
++ ++

( )
( ) ( )
2( ) 2.
() () ()
abc
abc
abac bcba cacb

++ + +

++ ++ ++

( )( )
( )( )( )
8 a b c ab bc ca
abbcca
++ + +
=
+++
Bây giờ ta cần chứng minh:
( )( )
( )( )( )
( )( ) ( )( )( )
8
98 9
a b c ab bc ca
abcabbcca abbcca
abbcca
++ + +
≤⇔ ++ + + ≤ + + +
+++
Nhưng đây là kết quả quen thuộc:
Ví dụ 2: Cho các số thực dương
,,abc
. Chứng minh:
3
2 2 22
abc
ab c bc a ca b
++≤
++ ++ ++
Giải:
Ta có:
( )
( )
( )
( )
(
)( )
2
22
2
22 22
aa b c aa b c
a
ab c
ab ca bc ab ca bc

++ ++

= ⇒∑ ≤

++
++ + + ++ + +

(
)
( )
( )
( )
( )
( )(
)
2
43
1
2
22 22(2)
a ab a
aa b c
ab ca bc ab ca bcb ac
∑ +∑ ∑

∑ ++ ∑ =



++ + + ++ + + + +

Ta cần chứng minh:
( )
( )
( )( )
2
43
9
2 2 ( 2 )4
a ab a
ab ca bcb ac
∑ +∑ ∑
≤
++ + + + +
. Sau khi khai
triển và thu gọn thì được:
( )
333
2 ()()()a b c ab a b bc b c ca c a++ ≥ ++ ++ +
.
Đây là bài toán quen thuộc.
Ví dụ 3: Cho các số thực dương
,,abc
sao cho
1abc++=
THCS.TOANMATH.com
Chứng minh:
2
2
ab bc ca
ab bc bc ca ca ab
++≤
+++
Giải:
Ta có:
( )
( )( )
2
2
ab a b
ab a b
ac acab
ab bc
+
= =
+ ++
+
suy ra
( )
( )( )
( )
( )( )
( )
( )( )
2
22
2
2
2
()
a a b abc a
ab a b
ab
ab
acab acab abbcca


∑∑ + ∑

+


∑ ≤∑ + ∑ =




++ ++ +++


Ta cần chứng minh:
( )
( )( )
( )
22
22
2
1
4
() 2
a a b abc a
a a b abc a
abbcca

∑∑ + ∑


≤⇔ ∑ ∑ + ∑

+++
( )( )( )
()abcabbcca≤ ++ + + +
. Khai triển và thu gọn ta quy về:
( ) ( ) ( ) ( )
22 22 2 2 222222
2ab a b bc b c ca c a a b b c c a++ ++ +≥ + +
. Nhưng bất
đẳng thức này là hiển nhiên đúng theo BĐT cô si:
BÀI TẬP RÈN LUYỆN.
Cho các số thực dương
,,abc
. Chứng minh rằng:
1)
2 22 22 2
a b c abc
b bc c c ca a c ca a ab bc ca
++
++≥
++ ++ ++ ++
2)
2 2 2 2 2 2 222
a b c abc
a ab b b bc c c ca a a b c
++
++≥
++ ++ ++ ++
3)
( )( )( )
( )
2
222
3 3 34 1a b c abc+ + + ≥ +++
4)
333
222
()
111 1
a b b c c a abc a b c
ab bc ca abc
++
++≥
+++ +
5)
222
222
1
222
abc
abbcca
++≥
+++
với
3abc++=
6)
( )
1
32 32 32 6
ab bc ca
abc
abcbcacab
+ + ≤ ++
++ ++ ++
THCS.TOANMATH.com
7)
222
2 22 2 2 2 2 22
2 2 24
ab bc ca a b c
a bc b ca c ab
++
++≤
++ ++ ++
8)
222
111
1
2 12 12 1ab bc ca
++≥
+++
với
3
abc
++=
.
9)
333
4
222
ab bc ca
ac ba cb
+++
++≥
+++
. Với
,,
abc
là độ dài 3 cạnh tam giác
10) 10)
222
5
2
a b c ab bc ca
bc ca ab a b c
++
+++ ≤
+ + + ++
. Với
,,abc
là độ dài 3
cạnh tam giác
11)
22 22 2 2
1
2
ab bc ca
ab bc ca
++≥
+++
biết
,, 0
abc≥
sao cho không
có 2 số nào đồng thời bằng
0
và
222
2( )a b c ab bc ca++= ++
.
12)
1
43 43 43
abc
a bc b ca c ab
++≤
+++
biết
,, 0abc
≥
sao cho
không có 2 số nào đồng thời bằng
0
và
2abc++=
.
HƯỚNG DẪN GIẢI BÀI TẬP
1)
2 22 22 2
a b c abc
b bc c c ca a c ca a ab bc ca
++
++≥
++ ++ ++ ++
Ta có:
2
2 22 2
aa
b bc c ab abc ac
=
++ + +
. Suy ra
( )
2
2
2 2 2222
3
abc
a
ab abc ac ab ac bc ba abc
++
∑≥
++ ++++
Ta cần chứng minh:
( )
2
2222
3
abc
abc
ab ac bc ba abc ab bc ca
++
++
≥
+ + + + ++
( )( )
2222
3
ab bc ca a b c ab ac bc ba abc⇔ + + ++ ≥ + + + +
(Nhưng đây là
hằng đẳng thức)
2) Ta có:
222
ab bc ca a b c++≤++
THCS.TOANMATH.com
Suy ra
2 22 22 2 222
a b c abc
b bc c c ca a c ca a a b c
++
++≥
++ ++ ++ ++
3)
( )
( )
( )
2
2
2
2
1
1
1 3 31
3
3
bc
bc
abc a a

++

++

+++ = + ≤ + +







Từ đó suy ra
( )
( )
( )
2
2
2
1
4 1 4 31
3
bc
abc a

++
+++ ≤ + +



. Ta chứng minh:
( )
( )
( )( )( )
( )
( )(
2
2
2 222 2
1
4 3 1 3 3 3 43 1 3 3
3
bc
a abc bc b

++

+ + ≤ + + + ⇔ + ++ ≤ +




Bất đẳng thức này tương đương với:
( )
( )( )
2
2 2 22 2 2
43 1 3 3 3 44 2 2 2 9 9 3b c b c b c bc b c b c b


+ ++ ≤ + + ⇔ + + + + + ≤ + +


( )
2 2 22
5 3 8( ) 8 13 0b c b c b c bc⇔ + + − +− +≥
. Ta viết lại bất đẳng thức trên
thành:
(
)
( )
2
22
5 2 8( ) 8 3 1 0b c bc b c bc+ − − + ++ − ≥
.
Ta có
22
2,b c bc+≥
( )
( )
( )
( )
22
22 22
2 42b c bc b c bc+≥+⇒ +≥ +
. Nên
( )
( )
2
22 2
5 28()83 12()8()8223(1b c bc b c bc b c b c bc bc bc+ − − + ++ − ≥ + − + ++ − + −
( )
2
2
2 2 3( 1) 0b c bc= +− + − ≥
. Dấu bằng xảy ra khi và chỉ khi
1abc= = =
4)
333
222
()
111 1
a b b c c a abc a b c
ab bc ca abc
++
++≥
+++ +
THCS.TOANMATH.com
Ta có:
3 422
2 2 232
1
ab abc
ab abc a b c
=
++
Suy ra
( )
2
222
3 422
2 2 232 2 232 2 232 2 2 32
1
a bc b ac c ab
ab abc
ab abc a b c abc a b c bca b c a cab c a b
++
∑=∑ ≥
+ + + ++ ++
(
)
2
222
2 232 2 232 2 2 32
abc a b c
abc a b c bca b c a cab c a b
++
=
+ ++ ++
Ta chứng minh:
( )
2
222
2 232 2 232 2 2 32
()
1
abc a b c
abc a b c
abc a b c bca b c a cab c a b abc
++
++
≥
+ ++ ++ +
( )
2 232 2 23 2 2 2 32
1 ()
abc abc a b c abc a b c bca b c a cab c a b+ ++≥+ ++ ++
. Đây
là đẳng thức.Dấu bằng xảy ra khi và chỉ khi
abc
= =
.
5)
24
2 2 22
22
aa
a b a ab
=
++
.
Suy ra
( )
2
222
24
2 3 22 3 22
22 2
abc
aa
a b a ab a ab
++
∑=∑ ≥
+ + ∑ +∑
. Ta chứng minh:
( )
2
222
3 22
1
2
abc
a ab
++
≥
∑ +∑
Hay
( )
2
222
444 333
3 22
1
2
abc
abc abc
a ab
++
≥⇔ + + ≥ + +
∑ +∑
Ta cần chứng minh:
444 333
abc abc
++≥++
với
3abc++=
. Ta chứng
minh:
( ) ( )
( )
( ) ( ) (
444 333 444 22 22
32abc abcabc abc abab bcbc++ ≥ ++ ++⇔ ++ ≥ + + +
Để ý rằng:
( ) ( ) ( )(
) ( ) ( )
2
44 22 2222 22 44 22
22ab ab abab abab ababab+=+ =+ +≥ +⇔+≥ +
. Cộng ba bất đẳng thức cùng chiều ta suy ra điều phải chứng minh:
6) Ta có:
THCS.TOANMATH.com
1 1 11 1 1 1
32 ( )( )2 9 2 32 9
ab ab
a b c ac bc b ab bc b a b c ab

= ≤++⇒ ≤+

++ ++++ + + ++ +

Tương tự ta có 2 bất đẳng thức nữa và cộng lại thì thu được:
11 1
32 32 32 9 2 2
ab bc ca ab ab bc bc c
ab
a b c b c a c a b ac bc ba ca c
+ + ≤ + ++ + ++
+++++++++++
( )
1
32 32 32 6
ab bc ca
abc
abcbcacab
⇔ + + ≤ ++
++ ++ ++
7) Ta có
222
2 22 2 2 2 2 22
2 2 24
ab bc ca a b c
a bc b ca c ab
++
++≤
++ ++ ++
( )
2
2 22
2 22 2222 22 22
24 4
ab
ab b b a b
a bc abbc ab bc

+

≤ ≤+


+ + +++ + +



Suy ra
22 22 22
22 22 22 2 2 22 2 2
444 4
b a b c b c a a c abc
VT
ab bc bc ca ab ca

++
≤ ++ ++ +=

++ ++ ++

8)
222
111
1
2 12 12 1ab bc ca
++≥
+++
Ta có:
2
2 22 2
1
2 12
c
ab ab c c
=
++
suy ra
( )
2
2 2 2 22 2 2 22
222
abc
VT
a b c abc abc abc
++
≥
+++ + +
. Ta chứng minh:
( )
2
22 2 2 22
2 2 2 22 2 2 22
1
222
abc
ab bc ca a b c a bc ab c
a b c abc abc abc
++
≥⇔ + + ≥ + +
+++ + +
() 1ab bc ca abc a b c abc⇔ + + ≥ ++ ⇔ ≤
. Theo bất đẳng thức Cô si ta có:
3
3 33 1a b c abc abc=++≥ =⇒ ≤
là điều phải chứng minh.
THCS.TOANMATH.com
9) Ta xét:
3 (3 2 )
22
ab a m bmc
m
ac ac
+ − +−
−=
++
Chọn
1m =
để xuất hiện:
3
1
22
ab abc
ac ac
+ +−
−=
++
Khi đó ta có: Bất đẳng thức cần chứng minh có dạng:
1
222
abc bca cab
ac ba cb
+− +− +−
++≥
+++
Suy ra
( ) (
)
( )
22
2
1
( )(2 )
abcbcacab abc
VT
abc ac
abc
+−++−++− ++
≥==
∑ +− +
++
. Đpcm
10) Ta viết lại bất đẳng thức thành:
222
1
111
2
a b c ab bc ca
bc ca ab a b c
++
− +− +− ≥ +
+ + + ++
( )
( )
2
222
2
abc
bca acb abc
bc ca ab
abc
++
+− +− +−
⇔++≥
+++
++
Ta có
( )
( )( )
( )
( )
22
222
4
2
abc abc
VT
bcabc
abc
++ ++
≥=
∑ +− +
++
11) Ta có:
22
22 22 22
2ab ab a b ab
ab ab ab
+
= ≥
+++
.
Ta quy bài toán về chứng minh:
22 22 2 2
222
1
ab bc ca
ab bc ca
++≥
+++
. Hay
(
) (
) ( )
222
22 22 2 2
4
ab bc ca
ab bc ca
+++
++≥
+++
. Thật vậy ta có:
THCS.TOANMATH.com
( )
( )
( )
( )
22
222 222
44
4
2 222
abc abc
VT
abc abc abbcca
++ ++
≥= =
++ ++ + + +
. Dấu bằng xảy
ra khi và chỉ khi
,0a bc= =
và các hoán vị.
12) Ta có:
(
)
2
43 43 43
abc
VT abc
a bc b ca c ab

≤ ++ + +

+++

2
43 43 43
abc
a bc b ca c ab

= ++

+++

. Ta chứng minh:
1
43 43 43 2
abc
a bc b ca c ab
++≤
+++
1111
44 3 44 3 44 3 4
abc
a bc b ca c ab
⇔− +− +− ≥
+++
1
43 43 43 3
bc ca ab
a bc b ca c ab
⇔++≥
+++
.
Ta có:
( )
( )
( )
( )
( )
22
22 22 2 2 22 22 2 2
1
3
3432
ab bc ca ab bc ca
VT
a b b c c a abc a b b c c a abc a b c
++ ++
≥= =
+++ +++ ++
| 1/109

Tài liệu khác của Môn Toán

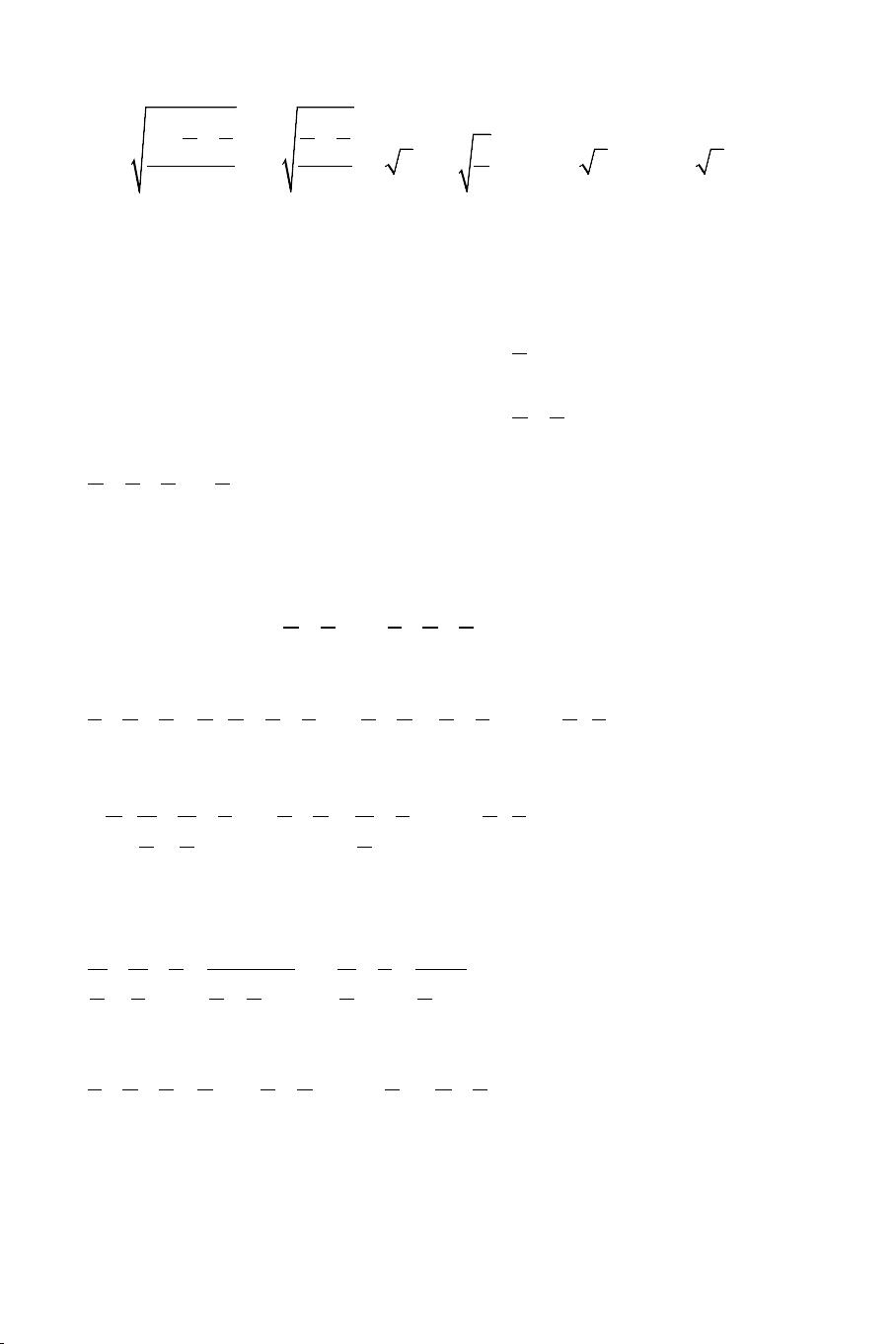
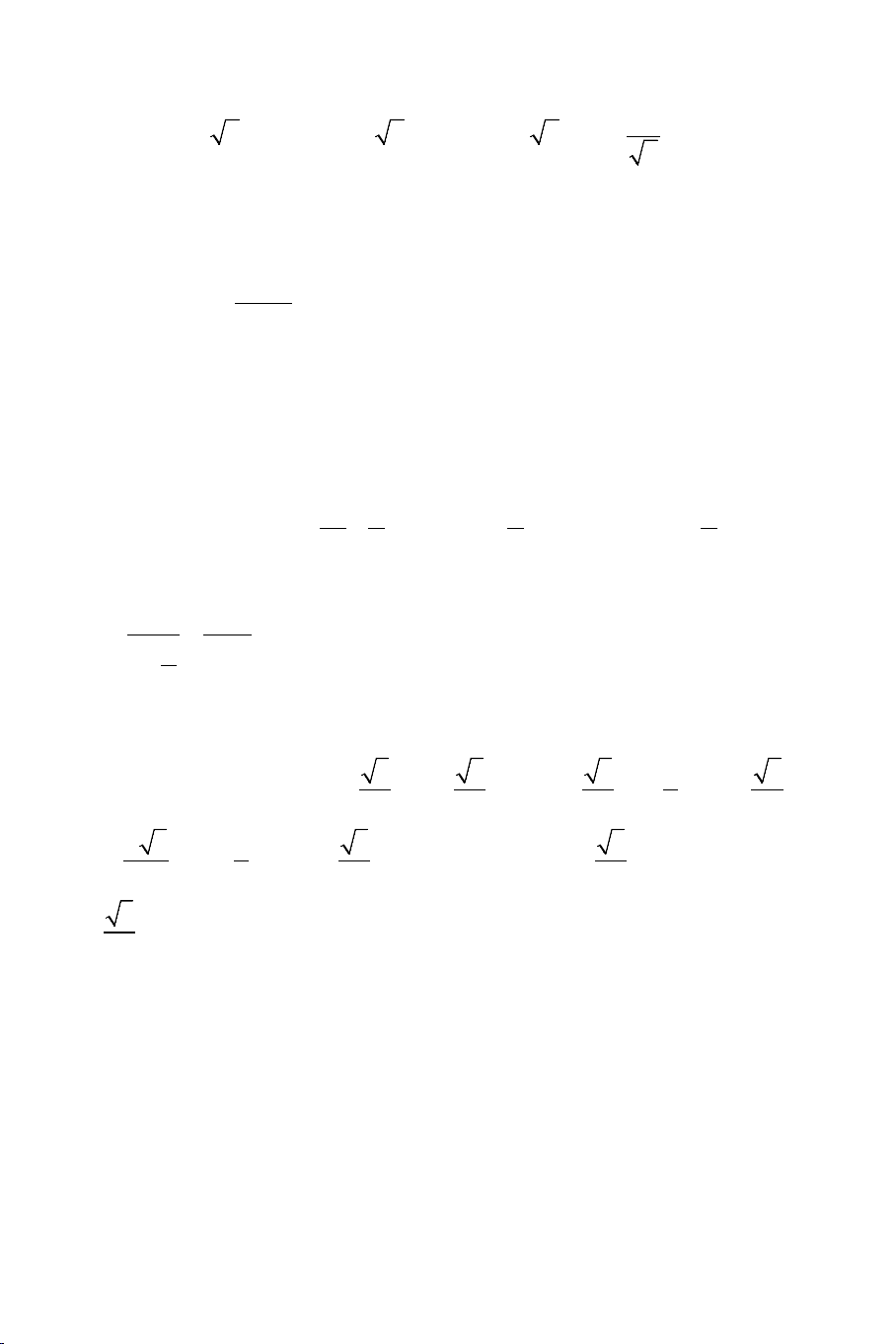
Preview text:

BẤT ĐẲNG THỨC
Phần 1: BẤT ĐẲNG THỨC CAUCHY (CÔ SI)
Cho các số thực không âm a,b,c khi đó ta có:
1. a + b ≥ 2 ab . Dấu đẳng thức xảy ra khi và chỉ khi a = b . 2. 3
a + b + c ≥ 3 abc . Dấu đẳng thức xảy ra khi và chỉ khi a = b = c .
Các bất đẳng thức 1, 2 gọi là bất đẳng thức Cauchy cho 2 và 3 số thực
không âm. (Còn gọi là bất đẳng thức Cô si hay bất đẳng thức AM- GM)
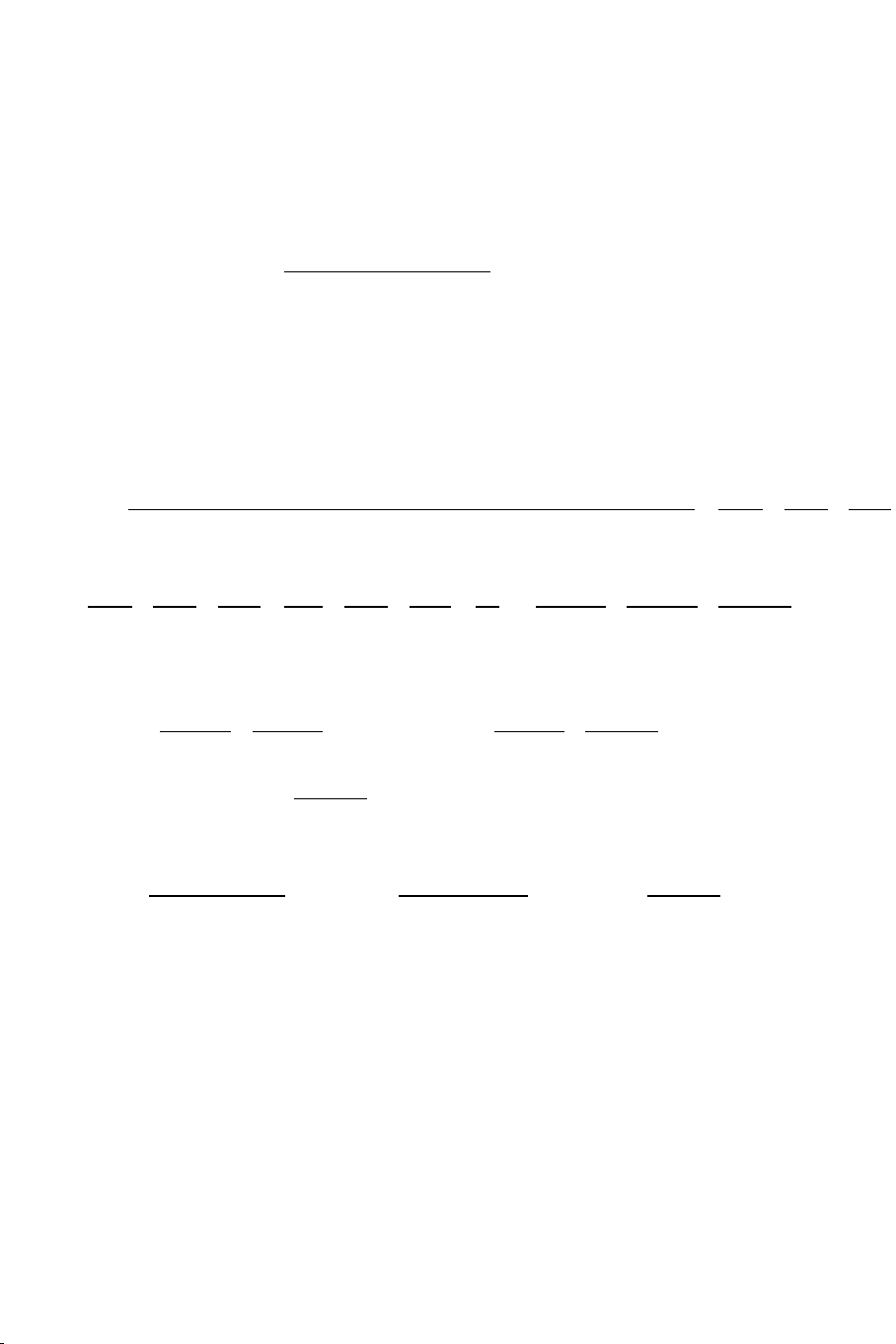
Để vận dụng tốt bất đẳng thức Cauchy . Ta cần nắm chắc những kết quả sau: x y ( + )2 2 2 x y 1) 1 1 4 2 2 + ≥ ≥ ; + ≥ 2 2 a b a + b a + b a b a + b 2) 1 1 1 9 3 3 + + ≥ ≥ 2 2 2
a b c a + b + c a + b + c 3) 2 2 3 2 1 2 3 2
a + ab + b = (a + b) + (a − b) ≥ (a + b) 4 4 4 4) 2 2 1 2 3 2 1 2
a − ab + b = (a + b) + (a − b) ≥ (a + b) 4 4 4
(a +b + c)2 5) 2 2 2
ab + bc + ca ≤
≤ a + b + c 3 x y z ( + + )2 2 2 2 x y z 6) + + ≥ a b c a + b + c a + b 3 3 ( )3 7) a + b ≥ 4 THCS.TOANMATH.com a + b  + +
8) a + b ≥ (a + b ) ( ) 2 2 4 4 2 4 4 2 2 (a b) 4 4 (a b) 2( ) ≥   = ⇒ a + b ≥  2  4 8  
9) Với a,b ≥ 0 thì m+n m+n 1 + ≥ ( m m a b a + b ) (*) 2
Thật vậy BĐT cần chứng minh tương đương với ( n n + )( m m − )( n n a b a
b a − b ) ≥ 0 điều này là hiển nhiên đúng. n n n +  +
(**) Tổng quát ta có a b a b  ≥ 2  2    n n n 1 − n 1 − n +  +  +   +
Thật vậy áp dụng (*) ta có a b a b a b   ...... a b  ≥ ≥ 2 2  2   2     
10) Với a,b,c ≥ 0 thì m+n m+n m+n 1 + + ≥ ( m m m + + )( n n n a b c a b
c a + b + c ) (*) 3
Thật vậy ta có bất đẳng thức cần chứng minh tương đương với: ( m m − )( n n − ) + ( m m − )( n n − ) + ( m m − )( n n a b a b b c b c c
a c − a ) ≥ 0 mà điều
này là hiển nhiên đúng. n n n n + +  + + Tổng quát ta có: a b c a b c  ≥
. Thật vậy áp dụng (*) ta có: 3  3    n n n n− n− n− 2 1 1 1 n−2 n−2 n−2 a + b + c
a + b + c  a + b + c   a + b + c   a + b + c  ≥    ≥    . 3  3  3   3   3 
Áp dụng bất đẳng thức này ta có: n n n n n n n n n n n n n + +  + +  + + + + a b b a b c a b c a b c ≥   ⇔ ≤ n 3  3  3 3   1 1 1  1 1 1 n  + + + + n n n   Tương tự ta có: a b c a b c ≥ 3  3      n Do 1 1 1 9 + + ≥ suy ra 1 1 1  3 3  + + ≥ .
a b c a + b + c n n n a b c   a b c  + +  11) 1 1 2 + ≥
với mọi a,b ≥1
a +1 b +1 1+ ab THCS.TOANMATH.com
Tổng quát: với a,b ≥1 ta có 1 1 2 + ≥ (1+ )n (1+ )n a b ( n 1+ ab )
12) Với 0 ≤ a,b ≤1 thì 1 1 2 + ≤
a +1 b +1 1+ ab
Tổng quát: Với a,b∈[0; ] 1 ta có: 1 1 2 + ≤ n 1 n + 1 n a + b 1+ ab
13) Một số kết quả được suy ra từ bất đẳng thức Cô si. + ( 3 3 + )( 3 3 + )( 3 3 a b x
y m + n ) ≥ (axm + byn)3 (*)
Áp dụng BĐT Cauchy ta có: 3 3 3 a x m 3axm + + ≥ 3 3 3 3 3 3 a + b x + y m + n ( 3 3 a + b )( 3 3 x + y )( 3 3 3 m + n ) 3 3 3 b y n 3byn + + ≥ 3 3 3 3 3 3 a + b x + y m + n ( 3 3 a + b )( 3 3 x + y )( 3 3 3 m + n )
Cộng hai bất đẳng thức cùng chiều ta suy ra: 3 + 3 3 axm byn ≥ ( ⇔ 3 3 a + b )( 3 3 x + y )( 3 3 3 m + n ) ( 3 3 + )( 3 3 + )( 3 3 a b x
y m + n ) ≥ (axm + byn)3 .
+ Hoàn toàn tương tự ta cũng chứng minh được: ( 3 3 3 + + )( 3 3 3 + + )( 3 3 3 a b c x y z
m + n + p ) ≥ (axm + byn + czp)3 .
Ví dụ 1: Cho các số thực không âm a,b,c . Chứng minh rằng: a) 3 3
a + b ≥ ab(a + b). THCS.TOANMATH.com b) 1 1 1 1 + + ≤
. Với (a,b,c > 0) 3 3 3 3 3 3
a + b + abc b + c + abc c + a + abc abc
c) (a + b)(b + c)(c + a) ≥ 8abc .
d) (a + b)(b + c)(c + a) 8
≥ (a + b + c)(ab + bc + ca) . 9
e) Cho (a + b)(b + c)(c + a) =1. Chứng minh: 3
ab + bc + ca ≤ ( Trích 4
đề tuyển sinh lớp 10 chuyên Toán TP Hà Nội năm 2015) Lời giải: a) Ta có : 3 3 + = ( + )( 2 2 a b
a b a − ab + b ). Suy ra 3 3
a + b − ab(a + b) = (a + b)( 2 2
a − 2ab + b ) = (a + b)(a −b)2 ≥ 0 suy ra đpcm.
b) Áp dụng bất đẳng thức ở câu a ta có: 3 3
a + b + abc ≥ ab(a + b) + abc = ab(a + b + c) . Suy ra 1 1 ≤ . Tương tự ta có: 3 3
a + b + abc ab(a + b + c) 1 1 1 1 ≤ ; ≤ . Cộng ba bất 3 3
b + c + abc bc(a + b + c) 3 3
c + a + abc ca(a + b + c)
đẳng thức cùng chiều ra suy ra: 1 1 1 1 + + ≤
. Dấu bằng xảy ra khi và 3 3 3 3 3 3
a + b + abc b + c + abc c + a + abc abc
chỉ khi a = b = c .
c) (a + b)(b + c)(c + a) ≥ 8abc . Cách 1: Ta có:
a + b ≥ 2 ab,b + c ≥ 2 bc,c + a ≥ 2 ca ⇒ (a + b)(b + c)(c + a) ≥ 8abc .
Cách 2: (a + b)(b + c)(c + a) = (a + b + c)(ab + bc + ca) − abc . Theo bất đẳng thức Cauchy ta có: 3 3 2 2 2
a + b + c ≥ 3 abc,ab + bc + ca ≥ 3 a b c ⇒ THCS.TOANMATH.com
(a +b + c)(ab +bc + ca) ≥ 9abc . Suy ra
(a +b)(b + c)(c + a) = (a +b + c)(ab +bc + ca)− abc ≥ 8abc .
Chú ý: (a + b)(b + c)(c + a) = (a + b + c)(ab + bc + ca) − abc là một biến đổi
được sử dụng rất nhiều trong chứng minh bất đẳng thức:
d) (a + b)(b + c)(c + a) 8
≥ (a + b + c)(ab + bc + ca) . 9
Chú ý rằng: (a + b)(b + c)(c + a) = (a + b + c)(ab + bc + ca) − abc . Áp dụng câu c ta có đpcm.
e) Ta chú ý: (a + b)(b + c)(c + a) = (a + b + c)(ab + bc + ca) − abc . Suy + ra 1 abc
ab + bc + ca = . a + b + c
Theo bất đẳng thức Cô si ta có: 3 3
a + b + b + c + c + a ≥ 3 (a + b)(b + c)(c + a) = 3 ⇒ a + b + c ≥ .Mặt 2
khác sử dụng: (a + b)(b + c)(c + a) 1
≥ 8abc ⇒ abc ≤ . Từ đó suy ra: 8 1 1 1 abc + + 8 3
ab + bc + ca = ≤
= . Dấu ‘’=’’ xảy ra khi và chỉ khi a + b + c 3 4 2 1
a = b = c = . 2 Ví dụ 2:
a) Cho các số thực dương a,b,c sao cho a + b + c + ab + bc + ca = 6. Chứng minh rằng: 2 2 2
a + b + c ≥ 6 . Trích đề tuyển sinh lớp 10- TP Hà Nội 2013. THCS.TOANMATH.com
b) Cho các số thực dương a,b sao cho : 1 1 + = 2. Chứng minh: a b 1 1 1 Q = +
≤ Trích đề tuyển sinh lớp 10 4 2 2 4 2 2
a + b + 2ab
b + a + 2a b 2
chuyên Nguyễn Trãi- Hải Dương 2013).
c) Cho các số thực dương a,b sao cho a + b = 2 . Chứng minh: ( 2 2
a b )  a b   1 1 2 6 9  + − + + + ≥     10 . 2 2  b a   a b
d) Cho các số thực dương a,b,c thỏa mãn a + b + c = 2 . Tìm giá trị
nhỏ nhất của P = 2a + bc + 2b + ac + 2c + ab . Trích đề tuyển
sinh lớp 10- TP Hà Nội 2014.
e) Cho các số thực không âm a,b sao cho 2 2
a + b = 4 . Tìm GTLN của ab P =
. Trích đề tuyển sinh lớp 10- TP Hà Nội 2015. a + b + 2 Lời giải:
a) Dự đoán dấu bằng xảy ra khi a = b = c =1. Ta có cách giải như sau:
Áp dụng bất đẳng thức Cô si ta có: 2 2 2 2 2 2 2 2 2 a + b ≥ 2 ,
ab b + c ≥ 2bc,c + a ≥ 2ac,a +1≥ 2a,b +1≥ 2 , b c +1≥ 2c .
Cộng 6 bất đẳng thúc cùng chiều ta suy ra ( 2 2 2
a + b + c ) + ≥ (ab + bc + ca + a + b + c) 2 2 2 3 3 2
= 12 ⇒ a + b + c ≥ 3. Dấu
bằng xảy ra khi và chỉ khi a = b = c =1.
b) Dự đoán khi a = b =1 thì bất đẳng thức xảy ra dấu bằng. Từ đó ta có
cách áp dụng BĐT Cô si như sau: Ta có: 4 2 2 4 2 2
a + b ≥ 2a b,b + a ≥ 2ab . Từ đó suy ra 1 1 1 1 1 Q ≤ + = + = . Từ 2 2 2 2 2a b + 2ab
2b a + 2a b 2ab(a + b) 2ab(a + b) ab(a + b) + giả thiết 1 1 + = 2 a b ⇒
= 2 ⇒ a + b = 2ab suy ra 2 Q ≤ . Do a b ab (a +b)2 THCS.TOANMATH.com 1 1 4 1 1 2 = + ≥ ⇒ ≤ . Suy ra 1
Q ≤ . Dấu bằng xảy ra khi và chỉ a b a + b a + b 2 2
khi a = b =1.
c) Ta viết lại bất đẳng thức cần chứng minh thành: 2 2 ( + − + −  a + b)2 (a b) 2ab (a b) 2ab 2 − 2ab − 6 + 9 ≥ 10 2 2   . Hay ab a b 4 − 2ab 4 − 2ab 2 2 3 3 2 2 8 − 4ab − 6 + 9 −10 ≥ 0 ⇔ 2
− a b − 4a b − 24ab +12a b + 36 −18ab ≥ 2 2 ab a b 2 2 3 3 2 2 3 2 ⇔ 2
− a b − 4a b − 24ab +12a b + 36 −18ab ≥ 0 ⇔ 4t −10t + 42t − 36 ≤ 0 (a +b)2
(*) với 0 < t = ab ≤
= 1. Ta có (*) tương đương với: 4 3 2
2t − 5t + 21t −18 ≤ 0 ⇔ (t − )( 2
1 2t − 3t +18) ≤ 0 . Do 2
2t − 3t +18 > 0 và
t −1≤ 0 nên (t − )( 2
1 2t − 3t +18) ≤ 0 . Dấu bằng xảy ra khi và chỉ khi
t =1 ⇔ a = b =1.
d) 2a + bc = a(a + b + c) + bc . Áp dụng bất đẳng thức Cô si ( )( ) a b a c a b a c + + + + + ≤ , tương tự ta có: 2 2 ( ) ( )( ) b a b c b ac b a b c ac b a b c + + + + = + + + ≤ + + ≤ , 2 2 c a c b c ab + + + + ≤ . Từ đó suy ra 2
2a + b + c 2b + c + a 2 + + = 2 + + 2 + + 2 c a b P a bc b ac c + ab ≤ + +
= 2(a + b + c) 2 2 2 .Dấu bằng xảy ra khi 2
a = b = c = . 3 Ta viết lại ab P =
⇒ . Đặt a + b + 2 = t ⇒ t > 2 a + b + 2 2 2
⇔ a + b + ab = (t − )2 2 2
2 ⇒ 2ab = t − 2t + 2 (a + b)2 = (t − )2 2 .Ta có : ( 2 2
2 a + b ) ≥ (a + b)2 ⇒ (a + b)2 ≤ 8 ⇔ a + b ≤ 2 2 ⇒ 2 < t ≤ 2 2 + 2 . Ta sẽ THCS.TOANMATH.com 2 − + chứng minh: ab t 2t 2 P = =
.Dự đoán dấu bằng xảy ra khi a + b + 2 t
a = b = 2 ⇒ t = 2 2 + 2 nên ta chứng minh: 2 1 t − 2t + 2 1 P ≤ ⇔ ≤ ⇔ ( 2 + ) 2
1 t − (2 2 +3)t + 2 2 + 2 ≤ 0 . 2 +1 t 2 +1 Hay 2t − ( 2 + )
1 t + 2 ≤ 0 ⇔ (t − 2 2 − 2)(t − 2 + )
1 ≤ 0 . Bất đẳng thức
này luôn đúng do 2 < t ≤ 2 2 + 2 . Dấu bằng xảy ra khi và chỉ khi
t = 2 2 + 2 ⇔ a = b = 2 .
MỘT SỐ KỸ THUẬT VẬN DỤNG BẤT ĐẲNG THỨC CÔ SI.
1. Dự đoán dấu bằng để phân tích số hạng và vận dụng bất đẳng thức Cô si.
Đối với các bài toán bất đẳng thức đối xứng thông thường dấu bằng xảy ra
khi các biến bằng nhau đây là cơ sở để ta phân tích các số hạng sao cho khi
áp dụng bất đẳng thức Cô si thì dấu bằng phải đảm bảo.
Ta xét các ví dụ sau:
Ví dụ 1: Cho x, y là các số dương thỏa mãn x + y = 2 . Chứng minh 2 2 x y ( 2 2
x + y ) ≤ 2
(Đề thi tuyển sinh lớp 10 Chu Văn An, Hà Nội – Amsterdam 2006-2007) Lời giải:
Ta dự đoán dấu bằng xảy ra khi x = y =1. Khi đó xy =1, 2 2
x + y = 2
Mặt khác để tận dụng giả thiết x + y = 2 ta sẽ đưa về hằng đẳng thức ( + )2
x y . Vì vậy ta phân tích bài toán như sau: 2 2 x y ( 2 2 x + y ) 1 = .x .2 y xy ( 2 2
x + y ) . Theo bất đẳng thức Cauchy thì 2 THCS.TOANMATH.com (x + y)2 2 4 2 2
xy + x + y x + y xy ≤ = 1, 2xy ( 2 2 x + y ) 2 ( ) ≤   = = 4 . Từ đó 4  2  4 suy ra 2 2 x y ( 2 2
x + y ) ≤ 2 . Dấu bằng xảy ra khi x = y =1.
Ngoài cách làm trên ta có thể giải bài toán bằng cách đưa về một biến:
t = x + y hoặc t = xy với chú ý: (x + y)2 ≥ 4xy , ( 2 2
2 x + y ) ≥ (x + y)2 . Thật
vậy: Đặt t = xy (x + y)2 2 2 ;
= x + y + 2xy . (x + y)2 2 2 2 2
⇒ 4 = x + y + 2t ⇔ x + y = 4 − 2t . Do xy ≤
= 1⇒ 0 < t ≤1. Ta 4
cần chứng minh: 2t ( − t) 3 2
≤ ⇔ t − t + ≥ ⇔ (t − )( 2 4 2 2 2 1 0 1 t − t − ) 1 ≤ 0 .
Bất đẳng thức này luôn đúng với mọi giá trị 0 < t ≤1. Ví dụ 2:
a) Cho a,b là các số không âm thỏa mãn 2 2
a + b ≤ 2 . Chứng minh rằng:
a 3a(a + 2b) + b 3b(b + 2a) ≤ 6. (Đề thi tuyển sinh lớp 10 chuyên Ngoại
Ngữ ĐHQGHN năm 2008-2009).
b) Với ba số dương x, y, z thỏa mãn x + y + z =1, tìm giá trị lớn nhất của biểu thức: x y z Q = + + . (Đề thi tuyển
x + x + yz y + y + zx z + z + xy
sinh lớp 10 chuyên Toán TP Hà Nội 2014) Lời giải:
a) Dự đoán dấu bằng xảy ra khi a = b =1. Khi đó
3a = a + 2b,3b = b + 2a nên ta có thể áp dụng bất đẳng thức Cauchy trực
tiếp cho biểu thức trong dấu căn. THCS.TOANMATH.com
Sử dụng bất đẳng thức Cauchy dạng x y xy + ≤ , dễ thấy 2 a + +
3a(a + 2b) 3a a 2b 2 ≤ a = 2a + ab , 2 b + +
3b(b + 2a) 3b b 2a 2 ≤ b
= 2b + ab . 2
Cộng hai bất đẳng thức này lại vế theo vế, ta được:
M = a a(a + b) + b b(b + a) ≤ ( 2 2 3 2 3 2
2 a + b ) + 2ab = 4 + 2ab. Tiếp tục
sử dụng bất đẳng thức Cauchy kết hợp với giả thiết, ta có: 2 2
4 + 2ab ≤ 4 + a + b = 6 . Từ đó ta có ngay M ≤ 6 . Dấu bằng xảy ra
⇔ a = b =1.
x( x + yz − x x
) x( x(x+ y+ z)+ yz −x) b) Ta có: = = . 2
x + x + yz
x + yz − x
x(x + y + z) 2 + yz − x
Áp dụng bất đẳng thức Cauchy co hai số thực dương a b ab + ≤ ta có: 2 (
x + y + x + z  ( + )( + ) − ) x+ −  x x x y x z x  2   xy + xz ≤ = . Chứng
xy + yz + xz
xy + yz + xz
2(xy + yz + xz)
minh tương tự rồi cộng vế, ta suy ra Q ≤1.Đẳng thức xảy ra khi 1
x = y = z = . Vậy Q lớn nhất bằng 1 khi 1
x = y = z = 3 3
Ví dụ 3: Cho c > 0 và a,b ≥ c . Chứng minh rằng
c(a − c) + c(b − c) ≤ ab .
Lời giải:Dự đoán dấu bằng xảy ra khi a = b . Bất đẳng thức cần chứng minh
có thể viết thành: THCS.TOANMATH.com c − − = . a c c + .b c P
≤1. Sử dung bất đẳng thức Cauchy dạng: b a a b
c a − c c b − c c c c c x y + + +1− + +1− xy + ≤ , ta có: b a a b b a a b P ≤ + = =1. Bài 2 2 2 2
toán được giải quyết hoàn toàn. Đẳng thức xảy ra khi và chỉ khi c a − c = b a 1 1 1 
⇔ + = . Ngoài ra ta cũng có thể chứng minh bài toán bằng c b − c a b c  = a b
biến đổi tương đương.
Ví dụ 4: Cho x, y, z là các số thực dương. Chứng minh rằng: 2 2 2 x y z + + ≥1. 2 2 2
x + 2yz y + 2zx z + 2xy Lời giải:
Sử dụng bất đẳng thức Cauchy dạng: 2 2
2ab ≤ a + b , dễ thấy: 2 2 2 2 2 2 x y z x y z P = + + ≥ + + =1 2 2 2 2 2 2 2 2 2 2 2 2
x + 2yz y + 2zx z + 2xy x + y + z y + z + x z + x + y
Đẳng thức xảy ra khi và chỉ khi x = y = z .
Ví dụ 5: Cho x, y > 0 và x + y ≤1. Chứng minh rằng ( 4 4 x + y ) 1 8 + ≥ 5 . xy Giải:
Dự đoán dấu bằng xảy ra khi 1
x = y = . Ta đánh giá 4 4
x + y để đưa về xy . 2
Theo bất đẳng thức Cô si ta có: 4 4 2 2
x + y ≥ 2x y suy ra ( 4 4 x + y ) 2 2 8 ≥ 16x y . THCS.TOANMATH.com Suy ra ( 4 4 x + y ) 1 2 2 1 8 + ≥ 16x y +
Để ý rằng dấu bằng xảy ra thì xy xy 2 2
16x y =1 nên ta phân tích như sau: 2 2 1 2 2 1 1 1 16x y + = 16x y + + +
. Áp dụng bất đẳng thức Cô si xy
4xy 4xy 2xy 3
a + b + c ≥ 3 abc ta có: 2 2 1 1 16x y + + ≥ 3, 4xy 4xy
xy ≤ (x + y)2 1 4 = 1⇒ xy ≤ . Suy ra 2 2 1 1 1 16x y + + + ≥ 3+ 2 = 5. 4
4xy 4xy 2xy
Đẳng thức xảy ra khi và chỉ khi 1
x = y = . 2
Ví dụ 6) Cho a,b,c là các số dương thỏa mãn a + b + c = 3. Chứng minh 2 2 2 rằng: 2 2 2 9a b c
a b + b c + c a ≥ . 2 2 2 1+ 2a b c Lời giải:
Bất đẳng thức cần chứng minh được viết lại thành: ( 2 2 2 a b b c c a) 1 2  + + + ≥   9 2 2 2  a b c  ⇔ ( 2 2 2
a b + b c + c a) 1 1 1 2 + + +
≥ 9 . Mặt khác sử dụng bất đẳng 2 2 2 ab bc ca 1 1
thức Cauchy bộ ba số, ta có: 2 2 2 2 + + ≥ 3 a b a b 3 a . b a . b = 3a , 2 2 ab ab 2 2 1 2 2 1 + + ≥ 3 b c b c 3 b . c b .c = 3b 2 2 bc bc 2 2 1 2 2 1 + + ≥ 3 c a c a 3 c . a c . a = 3c 2 2 ca ca THCS.TOANMATH.com
Cộng ba bất đẳng thức trên lại vế theo vế, ta được: ( 2 2 2
a b + b c + c a) 1 1 1 2 + + +
≥ 9. Dấu đẳng thức xảy ra khi và hcir 2 2 2 ab bc ca
khi a = b = c =1. ( 3 3 x + y ) −( 2 2 x + y )
Ví dụ 7) Cho x, y >1. Chứng minh rằng: ( ≥ . x − )( y − ) 8 1 1 Giải:
Sử dụng bất đẳng thức Cauchy, ta có: 2 2 2 2 x y x y 2 = + ≥ 2 . xy P =
(1). Mặt khác, lại để ý y −1 x −1 y −1 x −1
(x − )1( y − )1
rằng nếu sử dụng bất đẳng thức Cauchy bộ hai số dạng a b ab + ≤ , thì: 2 − =
( − ) 2+ x −1 x ≤ = − = ( − ) 1+ y −1 1 1. 1 ; 1 1. 1 y x x y y ≤ = . Nhân 2 2 2 2
hai bất đẳng thức trên lại theo vế, ta thu
được: ( − )( − ) xy 2 1 1 xy x y ≤ ⇔
≥ 8 (2). Từ (1) và (2) suy 4
(x − )1( y − )1
ra điều phải chứng minh. Dấu đẳng thức xảy ra khi và chỉ khi 2 2  x y  =
y −1 x −1 ⇔ x = y = 2 .  x = 2, y = 2
Đối với các bài toán mà dấu bằng không xảy ra khi các biến bằng nhau.
Ta cần chú ý tính đối xứng của từng bộ phận , để dự đoán sau đó liên
kết các dữ liệu của bài toán để tìm ra điểm rơi. Từ đó áp dụng bất đẳng
thức Cauchy để thu được kết quả:
Ta xét các ví dụ sau: THCS.TOANMATH.com
Ví dụ 8: Cho x, y, z > 0 thỏa mãn: xy + yz + zx =1. Tìm GTNN của 2 2 2
P = x + y + 2z Giải:
Ta dự đoán dấu bằng xảy ra khi x = y = az và mong muốn biến đổi được : 2 2 2
P = x + y + 2z ≥ k(xy + yz + zx) để tận dụng giả thiết xy + yz + zx =1 và
dấu bằng xảy ra khi x = y = az . Để có tích . x y ta áp dụng 2 2
x + y ≥ 2xy .
Để tạo ra yz ta áp dụng: 2 2 2
y + a z ≥ 2ayz . Để tạo ra zx ta áp dụng: 2 2 2
a z + x ≥ 2azx .
Vì hệ số của yz, zx là a nên ta nhân a vào bất đẳng thức đầu tiên rồi cộng lại theo vế ta thu được a( 2 2 x + y )+( 2 2 2
y + a z )+( 2 2 2
a z + x ) (a + )( 2 2 x + y ) 2 2 1 + 2a z
a(xy + yz + zx) ≤ = 2 2 Hay 2 2 2 2
2a ≤ (a +1)(x + y ) + 2a z . Để tạo ra 2 2 2
P = x + y + 2z ta cần có tỷ lệ: 2 2 1 5 (a 1) : 2a 1: 2 a a 1 0 a + + = ⇒ − − = ⇒ = . 2 Từ đó ta tìm được: 2a P ≥
= 5 −1. Các em học sinh tự hoàn thiện lời 1+ a giải.
Ví dụ 9) Cho x, y, z > 0 thỏa mãn: x + y + z = 3. Tìm GTNN của 2 2 3
P = x + y + z Lời giải: THCS.TOANMATH.com
Ta dự đoán dấu bằng có khi x = y = a, z = b ; và 2a + b = 3. Theo bất đẳng 2 2
x + a ≥ 2ax  thức Cô si ta có:  2 2
y + a ≥ 2ay
. Cộng ba bất đẳng thức cùng chiều ta  3 3 3 2
z + b + b ≥ 3b z  có: 2 2 3 2 3 2
x + y + z + 2a + 2b ≥ 2a(x + y) + 3b z .Tức là: 2 2 3 2 2 3
x + y + z ≥ 2a(x + y) + 3b z − 2a − 2b 2 
Bây giờ ta cần chọn a, b sao cho 2 2a :3b =1:1 2a = 3b ⇔  . Giải hệ tìm 2a + b = 3 − − được: 19 37 37 1
x = y = a = ; z = c = 12 6
Từ đó bạn đọc tự hoàn thiện lời giải:
Ví dụ 10) Cho các số thực dương a,b,c thỏa mãn: 2 2 2
a + 2b + 3c =1. Tìm GTNN của 3 3 3
P = 2a + 3b + 4c Lời giải:
Dự đoán dấu bằng xảy ra khi a = ;
x b = y;c = z với x, y, z > 0 và 2 2 2
x + 2y + 3z =1 Ta có: 3 3 3 2
a + a + x ≥ 3a x ; 3 3 3 2
b + b + y ≥ 3b y ; 3 3 3 2
c + c + z ≥ 3c z , suy ra 3 2 3
2a ≥ 3a x − x 3 3 3 2
b + b + y ≥ 3b y 3 9 2 3 3
⇔ 3b ≥ yb − y , 2 2 3 3 3 2 3 2 3
c + c + z ≥ 3c z ⇔ 2c ≥ 3c z − z 3 ⇒ c ≥ ( 2 3 4
2 3c z − z ). Cộng ba bất
đẳng thức cùng chiều suy ra:  2 3 2 2  3 3 3 3
P ≥ 3 xa + yb + 2zc − x − y −   2z .  2  2 THCS.TOANMATH.com
Ta cần chọn x, y, z để: 3
x : y : 2z =1: 2 :3 và 2 2 2
x + 2y + 3z =1. Áp dụng 2
tính chất dãy tỷ số bằng nhau ta dễ dàng tìm được: 6 8 9 x = ; y = ; z =
. Học sinh tự hoàn thiện lời giải. 407 407 407
Ví dụ 11) Cho các số thực dương a,b,c,d thỏa mãn:
abc + bcd + cda + dab =1. Tìm GTNN của P = ( 3 3 3
a + b + c ) 3 4 + 9d .(Trích
đề thi vào lớp 10 chuyên Trường chuyên KHTN- ĐHQG Hà Nội 2012) Lời giải:
Biểu thức P cho ta dự đoán dấu bằng xảy ra khi và chỉ khi
a = b = c = xd,Để giảm ẩn trong bài toán ta sẽ áp dụng bất đẳng thức Cô si theo cách: Khi đó 3 3 3
a + b + c ≥ 3abc , 3 3 3 3
b + c + x d ≥ 3xbcd , 3 3 3 3
c + a + x d ≥ 3xcad , 3 3 3 3
a + b + x d ≥ 3xabd x( 3 3 3
a + b + c ) ≥ 3xabc  3 3 3 3 
Suy ra b + c + x d ≥ 3xbcd
. Cộng bốn bất đẳng thức cùng chiều ta có: 3 3 3 3
c + a + x d ≥ 3xcad  3 3 3 3
a + b + x d ≥ 3xabd (x + ) 3 a + (x + ) 3 b + (x + ) 3 3 3 2 2
2 c + 3x d ≥ 3x(abc + bcd + cda + dab) = 3x . +
Bây giờ ta chọn x sao cho (x + 2) 3 x 2 4 3 :3x = 4 :9 ⇔
= ⇔ 4x − 3x = 6 . 3 3x 9   Đặt 1 1 x =  y + thay vào ta tìm được 2 y    3 3 1
y = 6 + 35, y = 6 − 35 ⇒ x = (3 3
6 + 35 + 6 − 35 ). Bạn đọc tự 2
hoàn thiện lời giải.
2. Kỹ thuật ghép đối xứng THCS.TOANMATH.com
Trong nhiều bài toán mà biểu thức ở hai vế tương đối phức tạp, việc chứng
minh trực tiếp trở nên khó khăn thì ta có thể sử dụng kỹ thuật ghép đối xứng
để bài toán trở nên đơn giản hơn.
ở các bài toán bất đẳng thức, thông thường chúng ta hay gặp hai dạng sau:
Dạng 1: Chứng minh X +Y + Z ≥ A + B + C
ý tưởng: Nếu ta chứng minh được X +Y ≥ 2A. Sau đó, tương tự hóa đẻ chỉ
ra Y + Z ≥ 2B và Z + X ≥ 2C (nhờ tính đối xứng của bài toán). Sau đó cộng
ba bất đẳng thức trên lại theo vế rồi rút gọn cho 2, ta có ngay điều phải chứng minh.
Dạng 2: Chứng minh XYZ ≥ ABC với X ,Y, Z ≥ 0
Ý tưởng: Nếu ta chứng minh được 2
XY ≥ A . Sau đó, tương tự hóa để chỉ ra 2 YZ ≥ B và 2
ZX = C (nhờ tính chất đối xứng của bài toán). Sau đó nhân ba
bất đẳng thức trên lại theo vế rồi lấy căn bậc hai, ta có: 2 2 2
XYZ = A B C = ABC ≥ ABC .
Ví dụ 1. Cho ba số dương x, y, z thỏa mãn x + y + z =1. Chứng minh rằng 2 2 2 2 2 2
2x + xy + 2y + 2y + yz + 2z + 2z + zx + 2x ≥ 5
(Đề thi tuyển sinh lớp 10 tỉnh Thái Bình năm 2005-2006) Giải:
Ta cần một đánh giá dạng : 2 2
2x + xy + 2y ≥ (mx + ny)2 sao cho dấu bằng xảy
ra khi x = y . Để có được đánh giá này thông thường ta viết lại 2 2
x + xy + y = a(x − y)2 + b(x + y)2 = (a + b) 2
x + (b − a) xy + (a + b) 2 2 2 2 y .  3 a + b = 2 a =  Từ đó suy ra   4  1 ⇒  . Từ đó ta b −  a = 5  2 b  =  4 THCS.TOANMATH.com có: 2 2 3
x + xy + y = (x − y)2 5 + (x + y)2 5 ≥ (x + y)2 2 2 5 2 2
⇒ 2x + xy + 2y ≥ (x + y) 4 4 4 2
tương tự ta có 2 bất đẳng thức và cộng lại ta có: 2 2 2 2 2 2
2x + xy + 2y + 2y + yz + 2z + 2z + zx + 2x ≥ 5 (x + y + z) = 5 dấu bằng xảy ra khi 1
x = y = z = . Ta cũng có thể chứng minh trực tiếp: 3 5 x + y 2 2 ( ) 2 2 5
2x + xy + 2y ≥
⇔ 2x + xy + 2y ≥ (x + y)2 2 4 ( + ⇔ x + y) 5 x y 2
− 3xy ≥ (x + y) ( )2 2 2 ⇔
≥ xy (đúng theo Cauchy) 4 4
Ví dụ 2. Cho các số thực dương a,b,c sao cho ab + bc + ca =1. Chứng
minh rằng: 2abc(a + b + c) 5 4 2 4 2 4 2
≤ + a b + b c + c a . (Trích đề tuyển sinh 9
vào lớp 10- Trường Chuyên KHTN- ĐHQG Hà Nội 2014). Lời giải:
Áp dụng bất đẳng thức Cauchy cho 3 số thực dương ta có:  4 2 1 2 1 2
a b + abc + ca ≥ a bc  3 9   4 2 1 2 1 2 2 b
c + a bc + ab ≥ b ca ⇒ abc(a + b + c) 4 2 4 2 4 2 1
≤ a b + b c + c a + (1). 3 9 3 9   4 2 1 2 1 2
c a + ab c + bc ≥ c ab  3 9 Mặt khác ta cũng có:
abc(a + b + c) 1
= ab ac + bc ba + ca cb ≤ (ab + bc + ca)2 1 . . . = . Suy ra 3 3
4 abc(a+b+c) 4
≤ (2). Cộng theo vế (1) và (2) ta có đpcm. 3 9 THCS.TOANMATH.com
Ví dụ 3) Cho ba số dương x, y, z thỏa 1 1 1 + + ≥ 2 . Chứng minh
1+ x 1+ y 1+ z rằng 1 xyz ≤ . 8 Giải: Từ giả thiết 1 1 1 + + ≥ 2 , ta suy ra:
1+ x 1+ y 1+ z 1  1   1 ≥ 1− + 1  y z − = + ≥     2 yz
1+ x  1+ y   1+ z  1+ y 1+ z (1+ y)(1+ z) 1 ⇒ ≥ 2 yz . 1+ x (1+ y)(1+ z)
Hoàn toàn tương tự ta cũng có: 1 zx 1 ≥ 2 xy ≥ + y ( + z)( + x); 2 1 1 1 1+ z (1+ x)(1+ y)
Nhân ba bất đẳng thức trên lại theo vế, ta thu 1 8xyz 1 được: ( ≥ ⇒ xyz = .
1+ x)(1+ y)(1+ z) (1+ x)(1+ y)(1+ z) 2
Ví dụ 4. Cho x, y, z > 2 và 1 1 1 + + = 1. Chứng minh rằng x y z
(x − 2)( y − 2)(z − 2) ≤1
(Đề thi tuyển sinh lớp 10 chuyên Lam Sơn Thanh Hóa năm 2005-2006). Lời giải:
Với giả thiết x, y, z > 2, ta nghĩ đến việc đặt ẩn phụ để đưa bài toán về dạng
đơn giản và quen thuộc hơn. Đặt x = a + 2; y = b + 2; z = c + 2 với a,b,c > 0 .
Bài toán quay về chứng minh abc ≤1 THCS.TOANMATH.com Với a a b c
,b,c > 0 thỏa mãn: 1 1 1 + + = 1 ⇔ + + = 1.
a + 2 b + 2 c + 2
a + 2 b + 2 c + 2 Ta có: 1 1 1  1 1   1 1 1  = − − = − + − c 2
a 2 b 2  2 a 2     2 b 2  + + + + +  a b ab = + ≥
2(a + 2) 2(b + 2) (a + 2)(b + 2) Tương tự: 1 ca 1 bc ≥ ≥ b + (c + )(a + ); 2 2 2 a + 2 (b + 2)(c + 2)
Nhân ba bất đẳng thức trên lại theo vế, ta được: 1 abc ( ≥ ⇒ ≤ .
a + )(b + )(c + ) (a + )(b + )(c + ) abc 1 2 2 2 2 2 2
Ví dụ 5) Cho x, y, z là các số dương. Tìm giá trị nhỏ nhất của biểu thức  x 1  y 1  z 1  P = + + +  .
y + z 2 
 z + x 2 
 x + y 2  Giải:
(2x + y + z)+(2y + z + x)(2z + x + y) Ta có P = (1)
8(x + y)( y + z)(z + x)
Theo bất đẳng thức Cô si ta có:
2x + y + z = (x + y)(x + z) ≥ 2 (x + y)(x + z) (2)
2y + z + x = ( y + z)( y + x) ≥ 2 ( y + z)(x + y) (3)
2z + x + y = (z + x)(z + y) ≥ 2 (z + x)(z + y) (4)
Nhân từng vế của (2),(3),(4) và từ (1) suy ra P ≥1 THCS.TOANMATH.com
Dấu bằng trong (5) xảy ra ⇔ đồng thời có dấu bằng trong (2),(3),(4)
x + y = x + z
⇔ y + z = y + x ⇔ x = y = z > 0 .Từ đó suy ra min P =1.
z + x = z +  y
3. Kỹ thuật cô si ngược dấu:
Ví dụ 1. Cho a,b,c > 0 và a + b + c = 3. Chứng minh rằng: a b c 3 + + ≥ . 3 3 3
b + ab c + bc a + ca 2 Giải:
Áp dụng bất đẳng thức Cauchy ta có: a 1 b 1 b 1 1 1 1  1  1 = − ≥ − = − ≥ − + . Tương tự: 3 2  2
b + ab b a + b b 2 ab
b 2 a b 4  a b 1 1  1  c 1 1  1  1;  1 ≥ − + ≥ − + 3 3 c bc c 4  ba ca a 4  c  + + 
Cộng ba bất đẳng thức này lại vế theo vế, ta được: a b c 3  1 1 1  3 + + ≥ + + − 3 3 3
b ab c bc a ca 4  a b c  + + +   4
Bài toán được quy về chứng minh: 3  1 1 1  3 3 1 1 1 + + − ≥ ⇔ + + ≥   3 4  a b c  4 2 a b c  1   1   1 a b c ⇔ + + + + +
≥ 3+ a + b + c =      
6. Bất đẳng thức cuối cùng  a   b   c
hiển nhiên đúng vì theo bất đẳng thức Cauchy, ta có: 1 1 1 + a ≥ 2, ;
= + b ≥ 2; + c ≥ 2 a b c
Bài toán được chứng minh xong. Đẳng thức xảy ra khi và chỉ khi
a = b = c =1. THCS.TOANMATH.com
Ví dụ 2) Cho a,b,c > 0,a + b + c = 9 . Chứng minh: 3 3 3 3 3 3 a + b b + c c + a + + ≥ 9.
ab + 9 bc + 9 ac + 9 Ta chứng minh được 1 1 a + b (a +b)3 3 3 36(a + b) 3 3 3 2
a + b ≥ (a + b) ,ab ≤ (a + b) ⇒ ≥ = a + b − 2 2 4 4
ab + 9 (a + b) + 36 (a + b) + 36 3 3 a + b Mặt khác ta có: 2
(a + b) + 36 ≥12(a + b) . Suy ra
≥ a + b − 3 . Cộng ba ab + 9
bất đẳng thức cùng chiều suy ra đpcm.
Ví dụ 3) Cho x, y, z > 0 và x + y + z = 3.Tìm giá trị nhỏ nhất của biểu thức x y z P = + + . 2 2 2 1+ y 1+ z 1+ x Lời giải: 2 Ta có: x xy = x −
. Theo bất đẳng thức Cô si thì 2
1+ y ≥ 2y Suy 2 2 1+ y 1+ y y yz z zx ra x xy ≥ x − Tương tự, ta có: ≥ y − , ≥ z − 2 1+ y 2 2 1+ z 2 2 1+ x 2
Cộng từng vế ba bất đẳng thức trên ta có P ≥ (x + y + z) 1
− (xy + yz + zx) . 2
Mặt khác theo bất đẳng thức Cô si, ta có: ( + + ) ≤ ( + + )2 3 xy yz zx x y z . Vì
x + y + z = 3 ⇒ xy + yz + zx ≤ 3 . Như vậy 3
min P = ⇔ x = y = z =1 2
4. Phương pháp đặt ẩn phụ:
Kỹ thuật đặt ẩn phụ là một kỹ thuật rất đặc biệt trong chứng minh bất đẳng thức:
Việc chọn ẩn phụ thích hợp sẽ giúp bài toán trở nên đơn giản hơn:
Một số kỹ thuật hay gặp như sau: THCS.TOANMATH.com
1. Khi có giả thiết : a + b + c = abc ta có thể biến đổi thành: 1 1 1 + + = 1 đặt 1 1 1 = ;
x = y; = z ⇒ xy + yz + zx =1. ab bc ca a b c
2. Khi gặp giả thiết a + b + c =1 ta có thể viết thành: ab .ac bc + .ba ac + . cb =1. Đặt c b a c b a
ab = , bc = , ca x y
= z ⇒ xy + yz + zx =1. c a b
3. Khi gặp giả thiết: ab + bc + ca + abc = 4. Ta có thể viết thành: 1 1 1 + + = 1. Đặt
a + 2 b + 2 c + 2 1 1 1 x = ; y = ; z =
⇒ x + y + z =1. a + 2 b + 2 c + 2
4. Từ điều hiển nhiên: + x y z 1 1 1 + + = 1⇒ + + = 1
x + y + z x + y + z x + y + z 1 y + z + 1 z + x + 1 x + y + x y z . Đặt y + z + + = ; z x = ; x y a b c = ta suy ra x y z 1 1 1 + +
= 1 ⇔ abc = a + b + c + 2 . Từ đó suy ra khi gặp
a +1 b +1 c +1
giả thiết: abc = a + b + c + 2 ta có thể đặt: y + z + + = ; z x = ; x y a b c = x y z
+ Nếu đổi (a b c)  1 1 1 , , ; ;  → 
ta có: abc = a + b + c + 2 tương a b c   
đương với ab + bc + ca + 2abc =1. Vì vậy khi gặp giả thiết
ab + bc + ca + 2abc =1 ta có thể đặt x = ; y = ; z a b c = . y + z z + x x + y
Một cách tổng quát: Khi gặp giả thiết: 1 1 1 + + = 1 khi
k + a k + b k + c
khai triển thu gọn ta có: THCS.TOANMATH.com 3 2 k − k + ( 2 3
k − 2k )(a + b + c) + (k − )
1 (ab + bc + ca) + abc = 0 . Suy
ra tồn tại các số x, y, z sao cho 1 x 1 y 1 = ; = ; z = . Như vậy: Với
k + a x + y + z k + b x + y + z k + c x + y + z
các số thực dương a,b,c thỏa mãn: 1 1 1 + + = 1. Thì tồn
k + a k + b k + c tại các số , m , n p > 0 sao cho: m + n + p + + + + = − ; m n p = − ; m n p a k b k c = − k . m n p
+ Nếu a,b,c > 0 và ab + bc + ca + abc = 4 thì ta có thể đặt 2m 2n 2 = ; = ; p a b c = . n + p p + m m + n
+ Nếu a,b,c > 0 và a + b + c +1 = 4abc thì ta có thể đặt n + p + + = ; p m = ; m n a b c = .. 2m 2n 2 p
5. Khi gặp giả thiết: xyz =1. Ta có thể chọn các phép đặt: 2 2 2 a 2 2 2 = ; b = ; c x y
= z ⇒ abc =1; a = ; b = ; c x y = z hoặc b c a bc ac ab x = ; y = ; z a b c = … y z x
6. Đặt: x = a + b − ;
c y = b + c − a; z = c + a − b hoặc đặt x = a + ; b y = b + ;
c z = c + a …
Ví dụ 1: Cho x, y, z là các số thực dương và thỏa mãn điều kiện
x + y + z = xyz . Tìm giá trị lớn nhất của biểu thức 1 1 1 P = + + . 2 2 2 1+ x 1+ y 1+ z Lời giải: THCS.TOANMATH.com
Từ giả thiết x + y + z = xyz , ta có 1 1 1 + + = 1. Đặt xy yz zx 1 1 1
a = ;b = ;c = ⇒ a,b,c > 0 x y z
Giả thiết trở thành: ab + bc + ca =1 , a b c P = + + Để 2 2 2 1+ a 1+ b 1+ c ý rằng: 2
a + = (a + b)(a + c) 2
b + = (b + a)(b + c) 2 1 ; 1
,c +1 = (c + a)(c + b)
Lúc này P có dạng a b c P = + +
(a +b)(a + c)
(b + a)(b + c)
(c + a)(c +b) a a b b c c = + +
. Theo bất đẳng thức Cô si,
a + b a + c
a + b b + c
c + a c + b ta có: 1  a a b b c c  3 P ≤ + + + + + = hay 3 P ≤ .
2  a b a c b a b c c a c b  + + + + + +  2 2 Dấu = xảy ra 1
a = b = c =
⇔ x = y = z = 3 . Vậy 3
max P = . Giá trị lớn 3 2
nhất đạt được khi và chỉ khi x = y = z = 3 .
Ví dụ 2) Cho x, y, z > 0 và x + y + z = 3xyz .Chứng minh: yz zx xy + + ≥1. 3
x (z + 2y) 3
y (x + 2z) 3
z ( y + 2x) Lời Giải: Đặt yz zx xy P = + + , đặt 1 1 1
a = ;b = ;c = . Từ 3 3 3
x (z + 2y) y (x + 2z) z ( y + 2x) x y z
giả thiết ta có a,b,c > 0 và ab + bc + ca = 3. Lúc này dễ thấy 3 3 3 a b c P = + +
. Theo bất đẳng thức Cô si ta có:
b + 2c c + 2a a + 2b 3 9a 3 + (b + 2c) 2
a ≥ 6a , 9b + (c + 2a) 2 b ≥ 6b , b + 2c c + 2a THCS.TOANMATH.com 3
9c +(a+2b) 2
c ≥ 6c . Cộng từng vế ba bất đẳng thức cùng chiều ta có a + 2b
P + (ab + bc + ca) ≥ ( 2 2 2 9 3
6 a + b + c ) . Mặt khác ta có kết quả quen thuộc: 2 2 2
a + b + c ≥ ab + bc + ca kết hợp với ab + bc + ca = 3 suy ra P ≥1. Vậy
min P =1. Giá trị nhỏ nhất đạt được khi x = y = z =1.
Ví dụ 3: Cho a,b,c là độ dài 3 cạnh một tam giác. Chứng minh rằng:
(a +b −c)(b + c − a)(c + a −b) ≤ abc . Lời giải: Đặt , , x y z x a b c y b c a z c a b a b c + + = + − = + − = + − ⇒ + + = . Từ đó ta 2 + + + suy ra z x = ; x y = ; y z a b c =
. Bất đẳng thức cần chứng minh có 2 2 2
dạng: (x + y)( y + z)(z + x) ≥ 8xyz . Đây là bất đẳng thức quen thuộc ( xem ở 1).
Ví dụ 4. Cho x, y, z > 2 và 1 1 1 + + = 1. Chứng minh rằng x y z
(x − 2)( y − 2)(z − 2) ≤1
(Đề thi tuyển sinh lớp 10 chuyên Lam Sơn Thanh Hóa năm 2005-2006). Giải:
Với giả thiết x, y, z > 2, ta nghĩ đến việc đặt ẩn phụ để đưa bài toán về dạng
đơn giản và quen thuộc hơn.
Đặt x = a + 2; y = b + 2; z = c + 2 với a,b,c > 0 . Bài toán quay về chứng minh abc ≤1
Với a,b,c > 0 thỏa mãn: THCS.TOANMATH.com 1 1 1 + + = 1 a b c ⇔ + +
= 1.Đến đây ta đặt tiếp
a + 2 b + 2 c + 2
a + 2 b + 2 c + 2 a = ; b = ; c m n p =
⇒ m + n + p =1. Ta có: a + 2 b + 2 c + 2 1 a + 2 2 2 1 n + p 2 = = 1+ ⇒ = −1 m = ⇒ a = . Tương tự: m a a a m m n + p 2n 2 = ; p b c = p + m m + n
Do đó bất đẳng thức trở thành: 2m 2n 2 .
. p ≤1 ⇔ (m + n)(n + p)( p + m) ≥ 8mnp
n + p p + m m + n
Sử dụng bất đẳng thức Cauchy, ta
có:(m + n)(n + p)( p + m) ≥ 2 mn.2 np.2 pm = 8mnp .
Bài toán được giải quyết xong. Đẳng thức xảy ra
⇔ m = n = p ⇔ a = b = c =1 ⇔ x = y = z = 3.
Ví dụ 5. Cho a,b,c là các số thực dương thỏa mãn ab + bc + ca + abc = 4
Chứng minh rằng: ab + bc + ca ≤ 3. Lời giải: Ta có:
ab + bc + ca + abc = 4 ⇔ abc + 2(ab + bc + ca) + 4(a + b + c) +8 =12 + ab + bc + ca + 4
⇔ (a + 2)(b + 2)(c + 2) = (a + 2)(b + 2)(c + 2) + (c + 2)(a + 2) 1 1 1 ⇔ 1 = + + .
a + 2 b + 2 c + 2
Suy ra tồn tại các số dương m n p , m , n p sao cho: 2 2 2 a = ,b = ,c = . n + p p + m m + n
Thay vào bất đẳng thức cần chứng minh ta THCS.TOANMATH.com được: 2m 2n 2n 2 p 2 p 2 . + . + . m ≤ 3
n + p p + m
p + m m + n
m + n n + p ⇔ 2
m . n +2 n . p +2 p . m ≤ 3. Sử dụng bất
m + p n + p
m + n m + p
n + p m + n đẳng thức Cauchy, ta có: 2 m . n m n ≤ + 2 n . p n p ≤ + ,
m + p n + p m + p n + p
m + n m + p m + n m + p 2 p . m p m ≤ +
n + p m + n n + p m + n
Cộng ba bất đẳng thức này lại theo vế, ta được: + + + 2
m . n +2 n . p +2 p . m m n n p m p ≤ + + = 3
m + p n + p
m + n m + p
n + p m + n m + n n + p m + p
BẤT ĐẲNG THỨC SCHUR
Cho x, y, z là các số thực không âm và số thực dương t . Khi đó ta có: t ( − )( − ) t + ( − )( − ) t x x y x z
y y z y x + z (z − y)(z − x) ≥ 0 (*)
Đây là bất đẳng thức có khá nhiều ứng dụng và tương đối chặt nhiều bài
toán Bđt chỉ là hệ quả của BĐT này. Việc chứng minh (*) khá đơn giản: Giả sử:
≥ ≥ ⇒ (*) ⇔ ( − ) t  ( − ) t − ( − ) t x y z x y x x z
y y x  + z (z − y)(z − x) ≥ 0   . Điều
này là hiển nhiên. Dấu bằng xảy ra khi cả 3 số bằng nhau hoặc hai số bằng nhau, một số bằng 0.
Các bất đẳng thức suy ra từ BĐT SCHUR khi t =1 là: 1) 3 3 3
a + b + c + 3abc ≥ ab(a + b) + bc(b + c) + ca(c + a) . 2)
(a +b + c)3 +9abc ≥ 4(a +b + c)(ab +bc + ca). THCS.TOANMATH.com 3)
abc ≥ (a + b − c)(b + c − a)(c + a − b) . 4) 2 2 2 9abc
a + b + c +
≥ 2(ab + bc + ca) . a + b + c 5) a b c 4abc + + + ≥ 2.
b + c c + a a + b (a + b)(b + c)(c + a)
Các BĐT (4) (5) còn gọi là BĐT SCHUR dạng phân thức khi t =1.
Ngoài ra cần chú ý biến đổi: 3 3 3
a + b + c − 3abc = (a + b + c) (a + b + c)2 −3(ab + bc + ca)   .Hoặc: 3 3 3
a + b + c − abc = (a + b + c) 2 2 2 3
a + b + c − (ab + bc + ca)   Ta xét các ví dụ sau:
Ví dụ 1) Cho a,b,c là ba số thực không âm và a + b + c =1 . Chứng minh
rằng: 9abc ≥ 4(ab + bc + ca) −1. Lời giải:
Áp dụng bất đẳng thức Schur dạng:
(a +b + c)3 +9abc ≥ 4(a +b + c)(ab +bc + ca).Thay a +b + c =1 ta có:
1+ 9abc ≥ 4(ab + bc + ca). Dấu đẳng thức xảy ra khi và chỉ khi có hai số
bằng 1 và 1 số bằng 0 hoặc 1
a = b = c = 2 3
Ví dụ 2) Cho các số thực dương a,b,c sao cho ab + bc + ca + abc ≤ 4 . Chứng minh: 2 2 2
a + b + c + a + b + c ≥ 2(ab + bc + ca).(Trích đề tuyển sinh
vào lớp 10- Trường Chuyên KHTN- ĐHQG Hà Nội 2015). Lời giải:
Áp dụng BĐT Schur dạng phân số ta có: 2 2 2 9abc
a + b + c +
≥ 2(ab + bc + ca) . Để chứng minh bài toán ta chỉ cần a + b + c THCS.TOANMATH.com chỉ ra: 9abc
a + b + c ≥
⇔ (a + b + c)2 ≥ 9abc . Theo bất đẳng thức Cô si a + b + c
ta có: a + b + c ≥
abc ⇒ (a + b + c) ≥ ( abc)2 2 3 3 3 9 . Ta chứng minh:
abc ≤1. Thật vậy từ giả thiết ta có: ab + bc + ca + abc ≤ 4 mà 3 2 2 2
ab + bc + ca ≥ 3 a b c . Đặt 3
t = abc ta suy ra: 3 2
t + 3t − 4 ≤ 0 ⇔ (t − )
1 (t + 2)2 ≤ 0 ⇔ t ≤1. Suy ra abc ≤1 hay ( )2
3 abc ≥ abc suy ra đpcm. Dấu bằng xảy ra khi và chỉ khi a = b = c =1.
Ví dụ 3) Cho a,b,c là các số thực không âm sao cho a + b + c =1. Chứng minh rằng ( 3 3 3
4 a + b + c ) +15abc ≥1. Lời giải: Ta có: 3 3 3
a + b + c − 3abc = (a + b + c) (a + b + c)2 −3(ab + bc + ca) =1− 3(ab + bc + ca)   Suy ra ( 3 3 3
4 a + b + c ) +15abc = 27abc + 4 −12(ab + bc + ca) ≥ 34
 (ab + bc + ca) −1 + 4 −12 
(ab +bc + ca) =1. Theo ví dụ 1 ta có:
9abc ≥ 4(ab + bc + ca) −1 . Từ đó suy ra:
27abc + 4 −12(ab + bc + ca) ≥ 34
 (ab + bc + ca) −1 + 4 −12 
(ab +bc + ca) =1 Hay ( 3 3 3
4 a + b + c ) +15abc ≥1. Dấu đẳng thức xảy ra khi và chỉ khi có hai
số bằng 1 và 1 số bằng 0 hoặc 1
a = b = c = 2 3
Ví dụ 4) Cho các số thực không âm a,b,c . Chứng minh rằng: 2 2 2 3
a + b + c + 3 (abc)2 ≥ (ab + bc + ca) (Trích đề tuyển sinh vào lớp 10
Trường chuyên Phan Bội Châu – Nghệ An 2014) Lời giải: Đặt 3 2 3 2 3 2 a = ;
x b = y; c = z THCS.TOANMATH.com Suy ra: 2 3 2 3 2 3 3 3 3
a = x ;b = y ;c = z ⇒ a = x ;b = y ;c = z và
x, y, z ≥ 0 .Bất đẳng thức đã cho thành: 3 3 3
x + y + z + xyz ≥ ( 3 3 3 3 3 3 3
2 x y + y z + z x ) (1)
Áp dụng bất đẳng thức Schur ta suy ra: 3 3 3
x + y + z + 3xyz ≥ xy(x + y) + yz ( y + z) + zx(z + x)
Mặt khác theo bất đẳng thức Cauchy ta có: xy (x + y) 3 3
≥ 2xy xy = 2 x y .
Tương tự ta có: yz ( y + z) 3 3
≥ 2 y z , zx(z + x) 3 3
≥ 2 z x Cộng vế theo vế
các bất đẳng thức trên ta thu được:
xy (x + y) + yz ( y + z) + zx(z + x) ≥ ( 3 3 3 3 3 3
2 x y + y z + z x ) (2) Từ (1) và (2) ta có: 3 3 3
x + y + z + xyz ≥ ( 3 3 3 3 3 3 3
2 x y + y z + z x ) Hay 2 2 2 3
a + b + c + 3 (abc)2 ≥ (ab + bc + ca). Đẳng thức xảy ra khi
x = y = z hay a = b = c .
Ví dụ 5) Cho a,b,c là các số thực dương có tổng bằng 1.Chứng minh rằng ( 3 3 3
a + b + c ) + ≥ ( 2 2 2 6
1 5 a + b + c ) . Lời giải: Ta có: 3 3 3
a + b + c − 3abc = (a + b + c) (a + b + c)2 −3(ab + bc + ca) =1− 3(ab + bc + ca)   suy ra ( 3 3 3
6 a + b + c ) +1= 6 1  − 3 
(ab +bc + ca) +18abc +1 
= + abc + (a + b + c)2 1 18 6
−18(ab + bc + ca) =
+ abc + (a + b + c)2 + (a + b + c)2 1 18 5
−18(ab + bc + ca) = + ( 2 2 2
1 5 a + b + c ) +18abc + (a + b + c)2 −8(ab + bc + ca) = ( 2 2 2
5 a + b + c ) + 29abc +1− 4(ab + bc + ca)   .Theo ví dụ 1 ta có: THCS.TOANMATH.com
9abc ≥ 4(ab + bc + ca) −1⇒ 9abc +1− 4(ab + bc + ca) ≥ 0 . Suy ra ( 3 3 3
a + b + c ) + ≥ ( 2 2 2 6
1 5 a + b + c ) .
Ví dụ 6) Cho a,b,c là các số thực dương. Chứng minh rằng 2 2 2
a + b + c + 2abc +1≥ 2(ab + bc + ca) . Lời giải:
Bất đẳng thức cần chứng minh tương đương với:
(a +b + c)2 + 2abc +1≥ 4(ab +bc + ca)
⇔ abc + ≥ (ab + bc + ca) − (a + b + c)2 2 1 4
, Áp dụng bất đẳng thức Schur dạng phân số ta có: 2 2 2 9abc
a + b + c +
≥ 2(ab + bc + ca) a + b + c
Hay : 9abc ≥ 4(ab + bc + ca) − (a + b + c)2 . Do đó ta chỉ cần chứng minh a + b + c 9 2 +1 abc abc ≥ hay  9 2 − abc ≤   1. a + b + c
a + b + c  Nếu 9
S ≥ thì hiển nhiên bất đẳng thức đúng. Nếu 9
a + b + c ≤ , áp dụng 2 2
bất đẳng thức AM-GM, ta  9  9 − 2s s
1  s + s + ( − s) 3 3 9 2  được: −  2abc ≤ . ≤   =1 với
a + b + cs 27 27  3 
s = a + b + c
Ví dụ 7) Cho a,b,c là các số thực không âm thỏa mãn điều kiện
ab + bc + ca =1. Chứng minh rằng 3 3 3
a + b + c + 6abc ≥ a + b + c . Lời giải: THCS.TOANMATH.com Ta có: 3 3 3
a + b + c − abc = (a + b + c) 2 2 2 3
a + b + c − (ab + bc + ca)  
= (a + b + c) 2 2 2
a + b + c −1   . Suy ra 3 3 3
a + b + c + abc = abc + (a + b + c)( 2 2 2 6 9
a + b + c − ) 1 . Áp dụng bất đẳng
thức Schur dạng: (a + b + c)3 + 9abc ≥ 4(a + b + c)(ab + bc + ca). Ta suy ra:
abc + (a + b + c)( 2 2 2
a + b + c − ) 3
≥ s − s + ( 2 2 2 9 1 4
a + b + c )s − s = s( 2 2 2 2
3− s + a + b + c ) = s với s = a + b + c .Dấu bằng xảy ra khi và chỉ khi 1
a = b = c =
hoặc có hai số bằng 1, một số bằng 0. 3
BÀI TẬP RÈN LUYỆN CƠ BẢN Câu 1) Cho 1 3
− ≤ x ≤ . Chứng minh rằng: 3− 4x + 1+ 4x ≥ 2 . 4 4
Câu 2) Chứng minh rằng với mọi số thực khác không x, y , ta có: 2 2 x y x y + ≥ + . 2 2 y x y x
Câu 3). Chứng minh rằng với mọi số thực khác không x, y ta có: 2 2 x y   + + 4 ≥ 3 x y + . 2 2 y xy x   
Câu 4) Cho x ≥1, y ≥1. Chứng minh rằng x y −1 + y x −1 ≤ xy .
Câu 5) Cho hai số thực x, y khác 0 . Chứng minh rằng: 2 2 2 2 4x y x y ( + + ≥ . x + y ) 3 2 2 2 2 2 y x
Câu 6. Cho các số thực dương a,b . Chứng minh bất đẳng thức sau: THCS.TOANMATH.com 2 2 a b 2 a + 2ab + ≥ 3 3 2 2 2a + b 3 2a + b
Câu 7) Cho các số thực dương a,b . Chứng minh bất đẳng thức 2 2 2ab a + b a + b + ≥ ab + . a + b 2 2
Câu 8) Cho a,b,c ∈[ 1;
− 2] và a + b + c = 0 . Chứng minh rằng: a) 2 2 2
a + b + c ≤ 6 ; b) 2 2 2
2abc ≤ a + b + c ≤ 2abc + 2; c) 2 2 2
a + b + c ≤ 8 − abc .
Câu 9) Cho các số thực không âm a,b,c .
Chứng minh rằng (a + b + c)3 3 3 3
≥ a + b + c + 24abc .
Câu 10) Cho a,b,c +
∈  thỏa mãn a + b + c =1.
Chứng minh rằng a − bc b − ca c − ab 3 + + ≤
a + bc b + ca c + ab 2
Câu 11) Cho các số thực dương a,b,c . 2( 3 3 3
a + b + c ) 9(a + b + c)2 Chứng minh rằng + ≥ 33. 2 2 2 abc a + b + c
Câu 12) Cho các số thực a,b,c . Chứng minh rằng
(a +b +c )2 2 2 2 ≥ ( 3 3 3
3 a b + b c + c a).
Câu 13) Cho các số x, y, z ≥ 0 và x + y + z =1.
Chứng minh rằng x + 2y + z ≥ 4(1− x)(1− y)(1− z) . THCS.TOANMATH.com
Câu 14) Cho các số thực dương a,b . Chứng minh: 2 2ab b 3 + ≤ 2 2 2 2 a + 4b 3a + 2b 5
Câu 15) Cho các số thực dương a,b . Chứng minh bất đẳng thức a b 16  1 1 5  + + ≥ + . 2 2 b a a ba b  +  
Câu 16) Cho các số thực dương a,b . Chứng minh bất đẳng thức sau: 2 2
3a + 2ab + 3b ≥ 2 2( 2 2 a + b ) . a + b
Câu 17) Giả sử x, y là những số thực không âm thỏa mãn: 3 3 2 2
x + y + xy = x + y . Tìm giá trị nhỏ nhất của biểu thức: 1+ x 2 + x P = + . 2 + y 1+ y
Câu 18) Cho a,b,c dương thỏa mãn: 6a + 3b + 2c = abc .Tìm giá trị lớn nhất của 1 2 3 B = + + . 2 2 2 a +1 b + 4 c + 9
Câu 19) Cho các số a,b,c không âm. Chứng minh rằng 2 2 2 3
a + b + c + 3 (abc)2 ≥ (ab + bc + ca).Đẳng thức xảy ra khi nào?
Câu 20) Cho các số thực dương a,b sao cho ab +1≤ b . Tìm GTNN của 1 2 1 P = a + + b + . 2 a b HƯỚNG DẪN GIẢI;
Câu 1) Bất đẳng thức cần chứng minh tương đương với: ( − x + + x)2 3 4 1 4 ≥ 4 THCS.TOANMATH.com
⇔ 4 + 2 3− 4x 1+ 4x ≥ 4 ⇔ 3− 4x 1+ 4x ≥ 0.
Bất đẳng thức được chứng minh.
Câu 2) Bất đẳng thức đã cho tương đương với: 2 2 2 x y x yx y  + ≥ + ⇔ + −   2 x y ≥ + y x y xy x y xx y  x y  (x − y)2 ( 2 2
x + xy + y ) ⇔ + − 2 + +1 ≥ 0 ⇔ ≥    0 2 2  y x  y xx y Mà ( 2 2
x + xy + y ) 2 2 2
= x + y + (x + y)2 > 0, x
∀ , y ≠ 0 nên ta có điều phải chứng minh.
Đẳng thức xảy ra khi và chỉ khi x = y ≠ 0 .
Câu 3) Bất đẳng thức đã cho tương đương với: 2 2 2 x y     + + 4 ≥ 3 x y + +   2 ≥ 3 x y + 2 2 y x y xy x       x y   x y  (x − y)2 ( 2 2
x − xy + y ) + − 2 + + −1 ≥ 0 ⇔ ≥     0 2 2  y x   y xx y Mà ( 2 2
x − xy + y ) 2 2 2
= x + y + (x − y)2 > 0 với mọi số thực x, y khác 0
nên ta có điều phải chứng minh.
Đẳng thức xảy ra khi và chỉ khi x = y ≠ 0 . Câu 4)
Đặt a = x −1,b = y −1 thì a ≥ 0,b ≥ 0. Bất đẳng thức cần chứng minh tương đương với:
( 2a + )b+( 2b + )a ≤ ( 2a + )b+( 2 1 1 1 b + ) 1 THCS.TOANMATH.com ⇔ ( 2 a + )b + ( 2 b + ) − ( 2 a + )b + +( 2 a + )( 2 b + ) − ( 2 1 1 2 1 1 1 2 b + ) 1 a ≥ 0 ⇔ ( 2 a + )b + ( 2 b + ) + ( 2 1 1 b + ) 1 (a − )2 1 ≥ 0 .
Bất đẳng thức cuối cùng đúng nên ta có điều phải chứng minh.
Dấu đẳng thức xảy ra khi a = b =1 hay x = y = 2 .
Câu 5) Bất đẳng thức đã cho tương đương với: 4x y x y
4x y − (x + y )2 2 2 2 2 2 2 2 2 4 2 2 4
x − 2x y + y ( − + + − ≥ ⇔ + ≥ x + y ) 1 2 0 0 2 2 2 y x (x + y )2 2 2 2 2 2 2 x y (x y )2 (x y )2 2 2 2 2  1 1  − − − ⇔ +
≥ 0 ⇔ x − y . −  ≥ 0 2 2 2 ( )2 2 2 (x y ) 2 2 2 2 x yx y ( 2 2 x y )2  + +   2 2 2 2 2 (
) (x − y ) − x y + + ⇔ − ≥ 0 x y x y x y ⇔ x − y ≥ 0 2 ( ) 4 4 2 2 2 2 2 2 2 2
x y (x + y )
x y (x + y )2 2 2 2 2 2 2 2 2
Bất đẳng thức cuối cùng đúng nên ta có điều phải chứng minh.
Đẳng thức xảy ra khi và chỉ khi x = ± y . Câu 6) 2 2 +
Dấu đẳng thức xảy ra với a = b khi và chỉ khi: a b 1 a 2 = ; ab =1. 3 3 2 2 2a + b 3 2a + b Ta có biến đổi sau: 2 2 2 2 a b 2 a + 2ab a b 1 a + 2ab + ≥ ⇔ − ≥ −1 3 3 2 2 3 3 2 2 2a + b 3 2a + b 2a + b 3 2a + b THCS.TOANMATH.com (a b)2 (2a b) (a b)2   − − + − − 2 1 2a − b ⇔ ≥ ⇔ a − b  −  ≥ 3( 0 3 3 2a + b ) 2 2 ( ) 2 2 2a + b 2a + b 3( 3 3 2a + b )  
⇔ (a − b)2  ( 3 3 a + b ) −( 2 2 3 2
2a + b )(2a + b) ≥ 0 
⇔ (a − b)2 ( 3 3 2 2
2a + 2b − 2a b − 2ab ) ≥ 0 ⇔ (a + b)(a −b)4 ≥ 0 (đpcm). a + b 2ab (a −b)2 Câu 7) Ta có: − = 2
a + b 2(a + b) 2 2
a + b −ab a + b (a −b)2 2 2 2 − ab = = 2 2 +  2 2 2 a b  + + 2 a b ab  + ab  2  2   
Do đó bất đẳng thức cần chứng minh tương đương với:   a + b a + b 2ab (a b)2 2 2  1 1  − − ab ≥ − ⇔  − ≥ 0 2 2 2 2 a + b 2  a + b a + b   + ab   2  (a b)2  a b ( 2 2 2 2 2 a b ) 2 ab ⇔ − + − + − ≥ 0   
Vì (a − b)2 ≥ 0 nên ta chỉ cần chứng minh: a + b − ( 2 2 2 2
2 a + b ) − 2 ab ≥ 0 (*) 2 a − b a + b − 2( 2 2 a + b ) ( ) = − 2( 2 2
a + b ) + (a + b) THCS.TOANMATH.com a − b
a + b − 2 ab = ( a − b)2 ( ) = ( a − b )2
Do vậy bất đẳng thức (*) tương đương với:   (a b)2  1 1  − ( − ≥  a + b) 0 2 2( 2 2 a b ) (a b) + + + 
(a b)  (a b ) a b  ( a b)2 2 2 2 2  ⇔ − + + + − + ≥ 0   (a b)2  ( 2 2 2 a b ) 2 ab ⇔ − + − ≥ 0    2( 2 2
a + b − 4ab 2 ) 4 ( − ⇔ a − b) 2(a b) ≥ ⇔ ≥ . 2( 0 0 2 2
a + b ) + 2 ab 2( 2 2
a + b ) + 2 ab
Bất đẳng thức này hiển nhiên đúng, ta có điều phải chứng minh.
Đẳng thức xảy ra khi và chỉ khi a = b .
Câu 8) Vì a,b,c ∈[ 1;
− 2] nên có một số bất đẳng thức hiển nhiên đúng (a + )
1 (a − 2) ≤ 0,(a + ) 1 (b + ) 1 (c + )
1 ≥ 0,(a − 2)(b − 2)(c − 2) ≤ 0 .
a) Do a,b,c ∈[ 1;
− 2] nên (a + )(a − ) 2 1
2 ≤ 0 ⇔ a ≤ a + 2. Tương tự ta suy ra: 2 2 2
a + b + c ≤ a + b + c + 6 = 6 (do a + b + c = 0 ).
b) Vì a,b,c ∈[ 1; − 2] nên (a + ) 1 (b + ) 1 (c + ) 1 ≥ 0 , hay
abc + ab + bc + ca + a + b + c +1≥ 0
⇔ abc + ab + bc + ca +1≥ 0 (do a + b + c = 0 ) (1)
Mặt khác cũng vì a + b + c = 0 nên (a + b + c)2 = 0 , tức là THCS.TOANMATH.com 2 2 2 a b c ab bc ca + + + + = − (2) 2 Từ (1) và (2) ta có: 2 2 2 a + b + c 2 2 2 abc −
+1≥ 0 ⇔ a + b + c ≤ 2 + 2abc 2
Dấu đẳng thức có, chẳng hạn a = 1, − b =1,c = 0 Ta còn phải chứng minh 2 2 2
a + b + c ≥ 2abc
Không mất tính tổng quát, giả sử a ≥ b ≥ c Từ đó suy ra + + 1 a b c − ≤ c ≤ ≤ 0 ⇒ c ≤1 3
Sử dụng đánh giá này, ta được 2abc ≤ 2 a . b . c ≤ 2 a . b
Suy ra a + b + c − abc ≥ a + b + c − a b = ( a − b )2 2 2 2 2 2 2 2 2 2 . + c ≥ 0
Dấu đẳng thức có khi a = b = c = 0 .
c) Vì a,b,c ∈[ 1;
− 2] nên (a − 2)(b − 2)(c − 2) ≤ 0 , hay
abc − 2(ab + bc + ca) + 4(a + b + c) −8 ≤ 0
⇔ abc − 2(ab + bc + ca) −8 ≤ 0 (do a + b + c = 0 ) (3) Từ (3) và (2) ta có: 2 2 2 2 2 2
abc + a + b + c −8 ≤ 0 ⇔ a + b + c ≤ 8 − abc
Dấu đẳng thức có, chẳng hạn a = 2,b = 1, − c = 1 − .
Câu 12. Cho a,b,c ∈[0;2] và a + b + c = 3. Chứng minh rằng 3 3 3
3 ≤ a + b + c − 3(a − ) 1 (b − ) 1 (c − ) 1 ≤ 9. Giải:
Đặt a = x +1,b = y +1,c = z +1 thì x, y, z ∈[ 1; − ]
1 và x + y + z = 0 Ta có 3 3 3
P = a + b + c − 3(a − ) 1 (b − ) 1 (c − ) 1
= (x + )3 + ( y + )3 + (z + )3 1 1 1 − 3xyz 3 3 3
= x + y + z − xyz + ( 2 2 2 3
3 x + y + z ) + 3(x + y + z) + 3 THCS.TOANMATH.com
Mà x + y + z = 0 nên 3 3 3
x + y + z − xyz = (x + y + z)( 2 2 2 3
x + y + z − xy − yz − zx) = 0 Do đó P = ( 2 2 2
3 x + y + z ) + 3 Vậy ta có 2 2 2
0 ≤ x + y + z ≤ 2 nên 3 ≤ P ≤ 9. Câu 9) Giải:
Ta có: (a + b + c)3 3 3 3
≥ a + b + c + 3(a + b)(b + c)(c + a)
Nên bất đẳng thức đã cho tương đương với: (a + b)(b + c)(c + a) ≥ 8abc 2 2 2 2 2 2
⇔ ab + ac + bc + ba + ca + cb ≥ 6abc 2 2 2 2 2 2
⇔ ab − 2abc + ac + bc − 2abc + ba + ca − 2abc + cb ≥ 0
⇔ a(b − c)2 + b(c − a)2 + c(a − b)2 ≥ 0
Vậy ta có điều phải chứng minh.
Đẳng thức xảy ra khi và chỉ khi a = b = c . Câu 10)
Ta có a + bc = a(a + b + c) + bc = (a + b)(a + c) nên bất đẳng thức cần
chứng minh tương đương với:
a(a + b + c) − bc b(a + b + c) − ca c(a + b + c) − ab 3 ( + + ≤
a + b)(a + c)
(b + c)(b + a)
(c + a)(c +b) 2 ⇔ ( 2 + + − )( + ) + ( 2 a ab ac bc b c
b + ba + bc − ca)(c + a) + THCS.TOANMATH.com ( 2
c + ca + ca − ab)(a + b) 3
≤ (a + b)(b + c)(c + a) 2 2 2 2 2 2 2
⇔ ab + ac + bc + ba + ca + cb ≥ 6abc
⇔ a(b − c)2 + b(c − a)2 + c(a − b)2 ≥ 0
Vậy bài toán được chứng minh.
Đẳng thức xảy ra khi và chỉ khi 1
a = b = c = . 3 Câu 11)
Bất đẳng thức đã cho tương đương với: 2( 3 3 3
a + b + c )
9(a + b + c)2 − 6 + − 27 ≥ 0 2 2 2 abc a + b + c
2(a + b + c)( 2 2 2
a + b + c − ab − bc − ca) 18( 2 2 2
a + b + c − ab − bc − ca) ⇔ − ≥ 0 2 2 2 abc a + b + c ( 2 2 2
a b c ab bc ca) a + b + c 9 2  ⇔ + + − − − − ≥   0 2 2 2  abc
a + b + c
⇔ (a − b)2 + (b − c)2 + (c − a)2  (a + b + c)    ( 2 2 2
a + b + c ) −9abc ≥ 0 
Do ( − )2 + ( − )2 + ( − )2 a b b c
c a nên ta chỉ cần chứng minh
(a +b + c)( 2 2 2
a + b + c ) −9abc ≥ 0 3 3 3
⇔ a + b + c − abc + a( 2 2
b + c ) + b( 2 2
c + a ) + c( 2 2 3
a + b ) − 6abc ≥ 0
Bất đẳng thức này đúng vì ta có: THCS.TOANMATH.com 3 3 3
a + b + c − abc = (a + b + c)( 2 2 2 3
a + b + c − ab − bc − ca)
(a +b + c)(a −b)2 +(b −c)2 +(c − a)2   = ≥ 0 2 Và a( 2 2
b + c ) + b( 2 2
c + a ) + c( 2 2
a + b ) − 6abc = a(b − c)2 + b(c − a)2 + c(a −b)2 ≥ 0
Đẳng thức xảy ra khi và chỉ khi a = b = c . Câu 12) Giải: Từ hằng đẳng thức:
(a +b +c )2 − (a b+b c+c a) 1 3
= (a −b + 2bc − ab − ac)2 2 2 2 3 3 3 2 2 + 2 1
+ (b − c + ca −bc −ba)2 1 2
+ (c − a + 2ab − ca − cb)2 2 2 2 2 2 2
Suy ra ta có điều phải chứng minh. Câu 13)
Do x + y + z =1 nên bất đẳng thức cần chứng minh có thể viết lại thành:
(x + y + z)(x + y + z)2 2
≥ 4(x + y)( y + z)(z + x)
Do vai trò của x và z trong bất đẳng thức trên là như nhau nên ta hoàn toàn
có thể giả sử x ≥ z .
Áp dụng bất đẳng thức Cauchy dạng (a + b)2 ≥ 4ab , ta có
(x + y + z)2 ≥ 4x( y + z) .
Sử dụng đánh giá này, dễ thấy chứng minh sẽ hoàn tất nếu ta chỉ ra được THCS.TOANMATH.com
x(x + 2y + z) ≥ (x + y)(z + x) ⇔ y(x − z) ≥ 0, hiển nhiên đúng theo giả sử x ≥ z .
Bài toán được chứng minh xong.
Đẳng thức xảy ra khi và chỉ khi 1
x = z = ; y = 0 . 2
Câu 14) Viết lại bất đẳng thức thành: 2 2ab b 3 + ≤ 2 2 2 2 a + 4b 3a + 2b 5 2 2 2 2 2 2 2ab 1 b
2a −10ab + 8b 3a − 3 ⇔ − + − ≥ 0 b ⇔ + ≥ 0 2 2 2 2 2 2 2 2 5 a + 4b 5 3a + 2b a + 4b 3a + 2b
2(a − b)(a − 4b) 3(a − b)(a + b) ⇔ + ≥ 0 2 2 2 2 a + 4b 3a + 2b
⇔ (a − b)  (a − b)  ( 2 2
a + b ) + (a + b)( 2 2 2 4 3 2 3
a + 4b ) ≥ 0  ⇔ (a − b)( 3 2 2 3
9a − 21a b +16ab − 4b ) ≥ 0 ⇔ (a −b)2 (3a − 2b)2 ≥ 0
Ta có điều phải chứng minh.Đẳng thức xảy ra khi và chỉ khi a = b hoặc 2 a = b . 3
Câu 15) Vì a,b > 0 nên bất đẳng thức đã cho tương đương với: a 1 b 1  4 1 1 4  − + − + − − ≥   0 2 2 b b a a
a + b a b
a − b b − a
4ab − (a + b)2 ⇔ + + 4 ≥ 0 2 2 b + a (a +b)ab THCS.TOANMATH.com
(a −b)2 (a +b) 4(a −b)2 ⇔ − ≥ 0 2 2 a b (a +b)ab
⇔ (a − b)2 (a + b)2 − ab ≥ ⇔ (a − b)4 4 0 ≥ 0   .
Bất đẳng thức cuối đúng nên có điều phải chứng minh.
Dấu đẳng thức xảy ra khi a = b > 0 .
Câu 16) Bài toán này có chứa căn nên để xuất hiện nhân tử chung dạng ( − )2
a b ta cần chú ý đến phép biến đổi 2 a − b 2( 2 2
a + b ) −(a + b) ( ) = 2( 2 2
a + b ) + (a + b) Khi đó: 2 2
3a + 2ab + 3b ≥ 2 2( 2 2 a + b ) a + b 2 2
3a + 2ab + 3b ⇔
− 2(a + b) ≥ 2 2( 2 2
a + b ) − 2(a + b) a + b (a −b)2 2(a − b)2 ⇔ ≥ a + b 2( 2 2
a + b ) + (a + b) (a b)2  ( 2 2
2 a b ) (a b) 2(a b) ⇔ − + − + − + ≥ 0   4 ⇔ ( − )2 a − b a b  2( 2 2
a + b ) −(a + b) ( ) ≥ 0 ⇔ ≥  Bất đẳng   2( 0 2 2
a + b ) + a + b
thức cuối cùng đúng do a,b dương.Đẳng thức xảy ra khi và chỉ khi a = b . Câu 17) 3 3 2 2
x + y + xy = x + y ⇔ (x + y)3 − 3xy(x + y) + xy = (x + y)2 − 2xy
Đặt x + y = a; xy = b , ta có: 3 2 2
a − 3ab + 3b − a = 0 ⇔ a (a − ) 1 − 3b(a − ) 1 = 0 THCS.TOANMATH.com a =1 x + y =1 ⇔ (a − ) 1 ( 2
a − 3b) = 0 ⇔  ⇔  2 a = 3b
(x + y)2 = 3xy
Vì (x + y)2 ≥ 4xy; x
∀ , y ≠ 0 suy ra x = y = 0 hoặc x + y =1
Với x = y = 0 thì 5 P = 2 0 ≤ x ≤1
Nếu x hoặc y khác 0 , ta có x + y =1⇒  , 0 ≤ y ≤ 1 ( y = y = P min) 4 1 = ⇔  ; P(max) 0 = 4 ⇔ 3 x 0  = x = 1 Vậy P( ) 4
min = khi x = 0, y =1; P(max) = 4 khi x =1; y = 0 . 3 Câu 18) Đặt = , b = , c x a y
z = thì x, y, z là các số dương và 2 3
x + y + z = xyz . Khi đó: 1 1 1 A = + + 2 2 2 1+ x 1+ y 1+ z Ta có: 1 xyz yz y z = = ≤ + 2 2 x +1
x (x + y + z) + xyz
(x + y)(x + z) 2(x + y) 2(x + z) Tương tự ta có: 1 x z 1 ≤ + ; x y ≤ + 2
y +1 2( x + y) 2( y + z) 2
z +1 2( x + z) 2( y + z) x + y x + z y + z 3 ⇒ A ≤ + +
= . Dấu đẳng thức xảy ra khi và chỉ
2(x + y) 2(x + z) 2( y + z) 2
khi: x = y = z = 3 ⇒ a = 3,b = 2 3,c = 3 3 .Vậy giá trị lớn nhất của
biểu thức A là 3 đạt được khi và chỉ khi a = 3,b = 2 3,c = 3 3 . 2 Câu 19) Đặt 3 2 3 2 3 2 a = ;
x b = y; c = z Suy ra: 2 3 2 3 2 3 3 3 3
a = x ;b = y ;c = z ⇒ a = x ;b = y ;c = z và x, y, z ≥ 0 .
Bất đẳng thức đã cho thành: THCS.TOANMATH.com 3 3 3
x + y + z + xyz ≥ ( 3 3 3 3 3 3 3
2 x y + y z + z x ) (1)
Vì vai trò của x, y, z bình đẳng nên có thể giả sử x ≥ y ≥ z ≥ 0
Khi đó: x(x − y)2 + z ( y − z)2 + (z + x − y)(x − y)( y − z) ≥ 0 Suy ra: 3 3 3
x + y + z + 3xyz ≥ xy(x + y) + yz ( y + z) + zx(z + x) (2)
Áp dụng bất đẳng thức Cô si ta có: xy (x + y) 3 3
≥ 2xy xy = 2 x y (3)
Tương tự ta có: yz ( y + z) 3 3 ≥ 2 y z (4) zx(z + x) 3 3
≥ 2 z x (5). Cộng vế theo vế các bất đẳng thức (3),(4),(5) ta
được: xy (x + y) + yz ( y + z) + zx(z + x) ≥ ( 3 3 3 3 3 3
2 x y + y z + z x ) (6) Từ (2) và (6) ta có: 3 3 3
x + y + z + xyz ≥ ( 3 3 3 3 3 3 3
2 x y + y z + z x ) Hay 2 2 2 3
a + b + c + 3 (abc)2 ≥ (ab + bc + ca)
Đẳng thức xảy ra khi x = y = z hay a = b = c .
Câu 20) Giả thiết ta suy ra 1 a a b + ≤ 1.Ta có 1 1 2 P = a + + + b ≥ 2 + 2 . b 2 b a b a 1 a + Đặt a b 1 t = ≤
≤ . Ta chứng minh: P ≥ 9 . Thật vậy ta có: b 2 2 2
2t − 9t + 2 (2t − ) 1 ( 2 3 2 t − 4t − 2) 2t + − 9 = = ≥ 0 . Do 1
0 < t ≤ , dấu đẳng 2 2 2 t t t 2 b  = 4a
thức xảy ra khi và chỉ khi 1 t  = ⇔  1 . 2 a + =  1  b
BÀI TẬP RÈN LUYỆN NÂNG CAO
Câu 1) Cho x, y, z là các số thực dương thỏa mãn điều kiện x + y + z =1.
Tìm giá trị lớn nhất của biểu thức P = x + yz + y + zx + z + xy .
Câu 2) Cho x, y, z là ba số thực dương và xyz =1. THCS.TOANMATH.com
Tìm giá trị nhỏ nhất của biểu thức 2 2 2 2 2 2 1+ x + y 1+ y + z 1+ z + x P = + + . xy yz zx
Câu 3) Cho x ≥ 2, y ≥ 3, z ≥ 4 . Tìm giá trị lớn nhất của biểu thức sau:
xy z − 4 + yz x − 2 + zx y − 3 P = xyz
Câu 4) Cho x, y, z là các số dương sao cho x + y + z =1. Tìm giá trị lớn nhất của biểu thức 3
P = x + xy + xyz .
Câu 5) Cho x, y > 0 và thỏa mãn điều kiện x y xy + + = 3 . Tìm giá trị nhỏ 2 3 6 nhất của biểu thức 3 3
P = 27x + 8y .
Câu 6) Cho x, y, z là các số thực dương và xyz =1. Tìm giá trị nhỏ nhất 3 3 3 của biểu thức: x y z P = ( + + .
1+ x)(1+ y) (1+ z)(1+ x) (1+ x)(1+ y)
Câu 7) Cho x, y, z là 3 số dương và thỏa mãn điều kiện x + y + z = 3.
Tìm giá trị nhỏ nhất của biểu thức 3 3 3 x y z 2 P = + + −
xy + yz + zx . 3 3 3 ( )
y + 8 z + 8 x + 8 27
Câu 8) Cho x, y, z là ba số dương và x + y + z = 3.
Tìm giá trị nhỏ nhất của biểu thức x +1 y +1 z +1 P = + + 2 2 2
y +1 z +1 x +1
Câu 9) Cho x, y, z là ba số thực dương thỏa mãn điều kiện x + y + z = 3.
Tìm giá trị nhỏ nhất của biểu thức x y z P = + + . 2 2 2 1+ y 1+ z 1+ x THCS.TOANMATH.com
Câu 10) Cho x, y, z là ba số thực dương thỏa mãn điều kiện x + y + z = 3. 2 2 2
Tìm giá trị nhỏ nhất của biểu thức x y z P = + + . 3 3 3 x + 2y y + 2z z + 2x
Câu 11) Cho x, y, z ≥ 0 thỏa mãn điều kiện x + y + z = 3. 2 2 2
Tìm giá trị bé nhất của biểu thức x y z P = + + . 2 2
x + 2y y + 2z z + 2x
Câu 12) Cho x, y, z là ba số thực dương và x + y + z = 3.
Tìm giá trị nhỏ nhất của biểu thức 1 1 1 P = + + . 2 2 2
x +1 y +1 z +1
Câu 13) Cho x, y, z là ba số thực dương thỏa mãn điều kiện xyz = 8.
Tìm giá trị lớn nhất của biểu thức
x − 2 y − 2 z − 2 P = + +
x +1 y +1 z +1
Câu 14) Cho x, y, z là các số thực dương thỏa mãn điều kiện xyz =1.
Tìm giá trị nhỏ nhất của biểu thức 1 1 1 P = + + 3
x ( y + z) 3 y (z + ) 3 1
z (x + y)
Câu 15) Cho x, y, z > 0 và thỏa mãn điều kiện x + y + z =1. + + +  
Tìm giá trị lớn nhất của biểu thức
1 x 1 y 1 z = + + − 2 y z x P + + .
1 x 1 y 1 zx y z  − − −  
Câu 16) Cho x, y, z là các số thực dương.
Tìm giá trị lớn nhất của biểu thức: x y z P = + + .
x + (x + y)(x + z) y + ( y + z)( y + x) z + (z + x)(z + y) THCS.TOANMATH.com
Câu 17) Cho x, y, z là ba số dương và xyz =1. Tìm giá trị lớn nhất của biểu thức: 1 1 1 P = + + (1) 5 2 5 2 5 2
x − x + 3xy + 6
y − y + 3yz + 6
z − z + 3xy + 6
Câu 18) Cho x, y, z ≥ 0 và thỏa mãn điều kiện x + y + z = 3. Tìm giá trị nhỏ
nhất của biểu thức
P = x + y + z − (xy + yz + zx).
Câu 19) Cho x, y, z là các số thực không âm và thỏa mãn điều kiện 2 2 2
x + y + z = 3 .
Tìm giá trị lớn nhất của biểu thức x y z P = + + . 2 2 2
x + 2y + 3 y + 2z + 3 z + 2x + 3
Câu 20) Cho x, y, z là các số thực dương và thỏa mãn điều kiện xyz = 8.
Tìm giá trị nhỏ nhất của biểu thức 2 2 3 x y z P = ( + + 3 + x )( 3 + y ) ( 3 + y )( 3 + z ) ( 3 + z )( 3 1 1 1 1 1 1+ x )
Câu 21) Cho x, y, z là các số thực dương..
Tìm giá trị nhỏ nhất của biểu thức: 3 3 3 x y z P = + + . 3
x ( y + z)3 3
y (z + x)3 3
z (x + y)3
Câu 22) Cho x, y, z ≥ 0 và thỏa mãn điều kiện x +Y + z =1. Tìm giá trị nhỏ
nhất của biểu thức x y z P = + + . 2 2 2 2 2 2 1+ y + z 1+ z + x 1+ x + y THCS.TOANMATH.com
Câu 23) Cho x, y, z là các số thực dương thỏa mãn điều kiện xyz =1.
Tìm giá trị lớn nhất của biểu thức 1 1 1 P = + + . 3 3 3 3 3 3 x + 2y + 6 y + 2z + 6 z + 2x + 6
Câu 24) Cho x, y, z là các số thực dương sao cho xyz =1.
Tìm giá trị nhỏ nhất của biểu thức 2
x ( y + z) 2 y (z + x) 2 z (x + y) P = + + .
y y + 2z z z z + 2x x x x + 2y y
Câu 25) Cho x, y, z là các số thực dương và thỏa mãn điều kiện
x + y + z = 6 .
Tìm giá trị nhỏ nhất của biểu thức x y z P = + + . 3 3 3 y +1 z +1 x +1
Câu 26) Cho x, y, z là ba số dương và thảo mãn điều kiện 1 1 1 + + ≤ 1. x y z
1) Tìm giá trị nhỏ nhất của biểu thức 2 2 2 x y z P = + + . 2 2 2 2 2 2
x + 8y +14xy
3y + 8z +14yz
3z + 8x +14zx + + +
2) Tìm giá trị nhỏ nhất của biểu thức x y y z z x Q = + + . x +1 y +1 z +1
Câu 27) Cho x, y, z là các số thực dương sao cho x + y + z = 3. Tìm giá trị
nhỏ nhất của biểu thức 2 2 2
P = x + y + z + xyz .
Câu 28) Cho x, y, z > 0 và thỏa mãn xyz =1. THCS.TOANMATH.com
Tìm giá trị nhỏ nhất của biểu thức P = (x + y)( y + z)(z + x) − 2(x + y + z) .
Câu 29) Cho các số thực dương a,b,c . Chứng minh rằng: a + b b + c c + a + + ≤ c + 4( 2 3 3
a + b ) a + 4( 3 3
b + c ) b + 4( 3 3 3 3 3 c + a )
Câu 30) Cho các số thực dương a,b,c sao cho a + b + c =1. Tìm GTLN của
P = (ab + bc + ca) + a(a − b)2 + b(b − c)2 + c(c − a)2 6 .
LỜI GIẢI BÀI TẬP RÈN LUYỆN Câu 1)
Từ điều kiện x + y + z =1, ta có x + yz = x(x + y + z) + yz = (x + y)(x + z) . Tương tự, ta cũng có
P = (x + y)(x + z) + ( y + z)( y + x) + (z + x)(z + y)
Áp dụng bất đẳng thức Cô si, ta có:
(x + y)(x + z) ( y + z)( y + x) (z + x)(z + y) P ≤ + + hay 2 2 2
P ≤ 2(x + y + z) = 2
Như vậy P ≤ 2 . Dấu bằng trong xảy ra khi
x + y = x + z
y + z = y + x 1 ⇔ 
⇔ x = y = z = . Từ đó ta có 1
max P = 2 ⇔ x = y = z = .
z + x = z + y 3  3
x + y + z =1
Câu 2) Áp dụng bất đẳng thức Cô si, ta có: 3 2 2 3 2 2 3 2 2 3 x y 3 y z 3 z x P ≥ + + xy yz zx THCS.TOANMATH.com Hay 3 3 3 P ≥ + +
. Lại theo bất đẳng thức Cô si, ta có: xy yz zx 3 3 3 3 3 + + ≥ 33
. Do xyz =1, nên suy ra P ≥ 3 3 . Vậy 2 2 2 xy yz zx x y z
min P = 3 3 ⇔ x = y = z =1. Câu 3) z − 4 x − 2 y − 3
Đưa biểu thức về dạng P = + + . Áp dụng bất đẳng z x y thức Cô si ta có: 1 − + z − = (z − ) 1 ( z 4) 4 3 z − 4 1 4 4 .4 ≤ = ⇒ ≤ 2 2 2 4 z 4 1 − + x − = (x − ) 1 ( x 2) 2 x x − 2 1 2 2 .2 ≤ = ⇒ ≤ 2 2 2 2 2 x 2 2 1 − + − y − = ( y − ) 1 ( y 3) 3 y y 3 1 3 3 .3 ≤ = ⇒ ≤ 3 3 2 2 3 y 2 3
Cộng từng vế ba bất đẳng thứctrên ta có 1 1 1 1 P   ≤ + + . Vậy 2  2 2 3    1  1 1 1 max P  = + +
⇔ x = 4, y = 6, z =   8 . 2  2 3 4  Câu 4)
Viết lại biểu thức trên dưới dạng: 1 1 3 P = x + .4 x y + .4 x .16 y z . 2 4
Áp dụng bất đẳng thức Cô si ta có: THCS.TOANMATH.com
x 4y x 4y 16z
4(x + y + z) P x + + + ≤ + + hay P ≤
. Từ x + y + z =1 và (2) 4 12 3 suy ra 4 P ≤ . Vậy 4 max P = 3 3 3 3
Câu 5) Theo bất đẳng thức Cô si, ta có: x 1 1 3 x + + ≥ ; y 1 1 3 y + + ≥ ; 8 2 27 3 3 3 x y 3 3   1 3 xy + + ≥
. Cộng từng vế ta có: 2 x y   5 3 x y xy  + + ≥ + + . 8 27 6  8 27   2 3 6    3 3   Do x y xy + + = 3 , ta có: x y  +  ≥ 2 . Suy ra 3 3
P = 27x + 8y ≥ 432 2 3 6  8 27  (4)
Dấu bằng trong (4) xảy ra khi x = 2, y = 3 . Vậy min P = 432, giá trị nhỏ
nhất đạt được khi x = 2, y = 3.
Câu 6) Theo bất đẳng thức Cô si, ta có: 3 3 x 1+ x 1+ y x 1+ x 1+ y ( + + ≥ Hay + x)( + y) 3 1 1 8 8 (1+ x)(1+ y) 8 8 3 x
1+ x 1+ y 3x ( + + ≥
. Lập luận tương tự ta có: 1+ x)(1+ y) 8 8 4 3 y
1+ z 1+ x 3y 3 z
1+ x 1+ y 3z ( + + ≥ + + ≥ Cộng 1+ z)(1+ x) 8 8 4 (1+ x)(1+ y) 8 8 4 từng vế ta có 3 1
P + ≥ (x + y + z) .Dấu = xảy ra ⇔ x = y = z =1. Lại 4 2
theo bất đẳng thức Cô si, ta có: 3
x + y + z ≥ 3 xyz = 3 Từ đó suy ra 3 3 3
P + ≥ ⇒ P ≥ . Dấu bằng trong (5) xảy ra ⇔ x = y = z =1 (do 4 2 4 xyz =1) . Như vậy 3
min P = . Giá trị nhỏ nhất đạt được ⇔ x = y = z =1. 4 3 2 Câu 7) + − +
Theo bất đẳng thức Cô si, ta có: x y 2 y 2y 4 x P = + + ≥ 3 y + 8 27 27 3 THCS.TOANMATH.com 3 2 x
9x + y − y − 6 ⇒ ≥
(1). Dấu bằng trong (1) xảy 3 y + 8 27 3 2 x
y + 2 y − 2y + 4 ⇔ P = + = 3 y + 8 27 27 3  x y + 2  y = 1; = 3 x = y =1 y + 8 27   ⇔ ⇔
4 . Lập luận tương tự ta có: 3  x y + 2  y = 2; x =  y = 2; =  3 3  y + 8 27 3 2 y
9y + z − z − 6 ≥ (2) 3 z + 8 27 3 2 z
9z + x − x − 6 ≥
(3). Cộng từng vế (1),(2),(3) và có: 3 x + 8 27 x y z
10(x + y + z) − ( 2 2 2 3 3 3
x + y + z ) −18 ⇔ + + ≥ (4) 3 3 3
y + 8 z + 8 x + 8 27
Do x + y + z = 3 nên (4) có
30 − (x + y + z)2 3 3 3
− 2(xy + yz + zx) −18 x y z   + + ≥ 3 3 3
y + 8 z + 8 x + 8 27 3 3 3 x y z 2 1 ⇒ + + −
xy + yz + zx ≥ hay 1 P ≥ (5) 3 3 3 ( )
y + 8 z + 8 x + 8 27 9 9
Dấu bằng trong (5) xảy ra ⇔ đồng thời có dấu bằng trong (1),(2),(3)
⇔ x = y = z =1 Vậy 1
min P = ⇔ x = y = z =1. 9 THCS.TOANMATH.com x +1 (x + ) 2 1 y Câu 8) Ta có: = x +1−
. Theo bất đẳng thức Cô si ta có: 2 2 y +1 y +1 2
y +1≥ 2y x +1 (x + ) 2 1 y + Suy ra ≥ +1− = +1 xy y x x −
. Chứng minh tương tự, ta 2 y +1 2y 2 + + + +
có: y 1 ≥ +1 yz z y −
; z 1 ≥ +1 zx x z − suy ra 2 z +1 2 2 x +1 2
x + y + z − (xy + yz + zx) P ≥ 3+ 2
Do = (x + y + z)3 9
≥ 3(xy + yz + zx) ⇒ xy + yz + zx ≤ 3. Vậy
min P = 3 ⇔ x = y = z = 3. Câu 9) Giải: 2 Ta có: x xy = x −
. Theo bất đẳng thức Cô si, ta có: 2
1+ y ≥ 2y , khi 2 2 1+ y 1+ y 2 2 đó xy xy xy ≤ = suy ra: x xy ≥ x − Tương tự ta có: 2 1+ y 2y 2 2 1+ y 2 y yz ≥ y − ; z zx ≥ z − . Cộng từng vế ta có 2 1+ z 2 2 1+ x 2 xy yz zx P x y z + + ≥ + + − 2
⇔ x = y = z =1.Do
x + y + z = ⇒ = (x + y + z)2 2 2 2 3 9
= x + y + z + 2(xy + yz + zx)
⇒ 9 ≥ (xy + yz + zx) + 2(xy + yz + zx) ⇒ xy + yz + zx ≤ 3 (7). Vậy 3
min P = ⇔ x = y = z =1. 2 Câu 10) THCS.TOANMATH.com 2 3 Ta có: x 2xy = x −
. Theo bất đẳng thức Cô si, thì 3 3 x + 2y x + 2y 3 3 3 3 6 2 3
x + 2y = x + y + y ≥ 3 xy = 3y x suy ra 2 3 x 2xy 2 2 3 2 ≥ x −
= x − y x . Tương tự, có: y 2 3 2
≥ y − z z , 3 2 3 x + 2y 2y x 3 3 y + 2z 3 2 z 2 3 2
≥ z − x z . Cộng từng vế ta có: 3 z + 2x 3
P ≥ (x + y + z) 2 − ( 3 2 3 2 3 2
z y + x z + y x ), hay 3 2 P ≥ 3− ( 3 2 3 2 3 2
z y + x z + y x ). Theo bất đẳng thức cô si ta có: 3 3 2
x + xz + xz ≥ 3x z , 3 2
y + yx + yx ≥ 3y x 3 2
z + zy + zy ≥ 3z y
Cộng từng vế ba bất đẳng thức trên ta có:
(x + y + z)+ 2(xy + yz + zx) ≥ 3( 3 2 3 2 3 2
x z + y x + z y ) vì
= (x + y + z)2 9
≥ 3(xy + yz + zx) ⇒ xy + yz + zx ≤ 3 . Do x + y + z = 3, suy ra 3+ 2.3 ≥ 3( 3 2 3 2 3 2
x z + y x + z y ) 3 2 3 2 3 2
⇒ x y + y x + z y ≤ 3 ⇒ P ≥1
Vậy min P =1 ⇔ x = y = z =1. 2 2
Câu 11) Ta có: x 2xy = x −
. Áp dụng bất đẳng thức Cô si, ta có: 2 2 x + 2y x + 2y 2 2 2 2 2 2 x 2xy 2 3 4
x + 2y = x + y + y ≥ 3 xy . Suy ra ≥ x − = x − (xy)3 . 2 x + 2y 3 4 3 xy 3 2 2 2 2 Tương tự, ta có: y 2 ≥ y − ( yz) z 2 3 , ≥ z − zx . Cộng theo vế 2 ( )3 2 y + 2z 3 z + 2x 3 2 2 2
ta có: P (x y z) 2 (xy)  ≥ + + −
3 + ( yz)3 + ( zx)3 . Theo bất đẳng thức Cô si, 3     ta có: 3 2 2
x + xy + y ≥ 3 x y 3 2 2
, y + yz + z ≥ 3 y z 3 2 2
, z + zx + x ≥ 3 z x . Từ đó THCS.TOANMATH.com 2 2 2
suy ra (x y z) (xy yz zx) (xy)  + + + + + ≥
3 + ( yz)3 + ( zx)3 2 3  (7) Dễ  
thấy dấu bằng trong (7) xảy ra ⇔ x = y = z =1. Kết hợp với x + y + z =1, ta 2 2 2 2 2 2 có: (xy)  + ≥
3 + ( yz)3 + ( zx)3 ⇒ ( xy)3 + ( yz)3 + ( zx)3 6 3 3 ≤ 3   . Vậy   2
P ≥ 3− .3 ⇒ P ≥1 hay min P =1 ⇔ x = y = z =1. 3 2 Câu 12) Ta có: 1 =1 x −
. Theo bất đẳng thức Cô si, thì 2 x +1≥ 2x 2 2 x +1 x +1 2 1 ⇒ ≥ 1 x − = 1 x − 2 x +1 2x 2
Tương tự, ta có: 1 ≥1 y − , 1 ≥1 z − . Suy ra x y z 3 P + + ≥ 3− = 2 y +1 2 2 z +1 2 2 2
(do x + y + z = 3).
Từ đó suy ra min P = 3 ⇔ x = y = z =1.  
Câu 13) Viết lại P dưới dạng: 1 y 1 P = 3− 3 + +  . Đặt
x 1 y 1 z 1 + + +  2X 2Y 2 = ; = ; Z x y z = Y Z X
Khi đó có X ,Y, Z > 0 (vì xyz = 8) Lúc này: 1 1 1 1 1 1 + + = + +
x +1 y +1 z +1 2X 2Y 2 +1 +1 Z +1 Y Z X 2 2 2 Y Z X Y Z X = + + = + + . Áp 2 2 2
2X +Y 2Y + Z 2Z + X 2XY +Y 2YZ + Z 2ZX + X
dụng bất đẳng thức Cauchy- Schwarz THCS.TOANMATH.com 1 1 1
( X +Y + Z )2
( X +Y + Z )2 + + ≥ = = 1, 2 2 2
x +1 y +1 z +1 2XY +Y + 2YZ + Z + 2ZX + X
( X +Y + Z )2
suy ra P ≤ 0. Vậy max P = 0 ⇔ x = y = z = 2 . 1 1 1 2 2 2 Câu 14) Ta có: x y z P = + +
. Áp dụng bất đẳng thức
x( y + z) y(z + ) 1 z (x + y) 2  1 1 1  + +  x y z  (xy + yz +   zx)2 Cauchy- Schwarz P ≥ = . Do 2 2 2
2(xy + yz + zx) 2(xy + yz + zx) x y z xyz =1, nên ta có: xy yz zx P + + ≥ 2
Lại theo bất đẳng thức Cô si ta có: xy + yz + zx ≥ (xyz)2 3 3 = 3 (do xyz =1. Suy ra 3 P ≥ Vậy 3
min P = ⇔ x = y = z =1. 2 2
Câu 15) Viết lại biểu thức P dưới dạng: 2x 2y 2zy z x   1 1   1 1   P =1+ +1+ + − 2 + + = 2x − +   2y − +     2z 1− x 1− y 1− zx y z  1− x z  1− y x   1−
Do x + y + z =1, nên ta có:  1 1   1 1   1 1  P = 2x − + 2y − +   2z − +     3 y + z z   z + x x   x + y y  2 − xy 2yz 2zxxy yz zx  = − − + = −  + + 
z ( y z) x(z x) y(x y) 3 3 2 z ( y z) x(z x) y(x y)  + + + + + +  
. Áp dụng bất đẳng thức Bunhiacopski, ta có: THCS.TOANMATH.com 2 2  xy yz zx   xy yz zx   + +  =    
( + ) y + z + ( + ) z + x + ( +   ) x + y z x y z x y x z x y x y    xy yz zx  ≤  + +   + + + 
z (x z) x(z x) y(x y) ( y z)(z x)(x y) + + +   2   Rõ ràng, ta lại có: xy yz zx  + +
 ≥ 3( x + y + z)  .Dựa vào bất đẳng z x y   
thức hiển nhiên (a + b + c)2 ≥ 3(ab + bc + ca) suy ra:   3( + + ) ≤ 2 xy yz zx x y z  + +  + + Từ z
 ( y + z) x( z + x) y ( x + y) ( x y z)   
x + y + z =1 ta có: 2 xy yz zx  + +
 ≥ suy ra P ≤ 0. z
 ( y + z) x( z + x) y ( x + y) 3  Vậy 1
max P = 0 ⇔ x = y = z = . 3 Câu 16)
Áp dụng bất đẳng thức Bunhiacopski, ta có:
(x y)(x z) ( x)2 ( y)2 
 ( x )2 ( z )2  + + = + + ≥ 
 ( x x + y z )2 . .  ⇒ ( + )( + ) ≥ ( + )2 x y x z x yz . Suy ra: x x ≤ .
x + (x + y)(x + z) 2x + yz Tương tự, ta có: y y ≤ ,
y + ( y + z)( y + x) 2y + zx z z ≤ . Suy ra
z + (z + x)(z + y) 2z + xy THCS.TOANMATH.com x y z P ≤ + +
2x + yz 2y + zx 2z + xy 1 1 1 ⇒ P ≤ + + . Đặt 2 y + . z 2 z + . x 2 x + . y x x y y z z y = . z ; z = . x ; x = . y a b c
, thì a,b,c > 0 và x x y y z z abc =1. 1 1 1 P ≤ Q = + +
2 + a 2 + b 2 + c
(2+b)(2+ c)+(2+ c)(2+ a)+(2+ a)(2+b) =
(2+ a)(2+b)(2+ c)
12 + 4(a + b + c) + (ab + bc + ca)
= 8+4(a+b+c)+2(ab+bc+ca)+abc
9 + 4(a + b + c)(ab + bc + ca) + 3 =
. Theo bất đẳng thức Cô si
9 + 4(a + b + c)(ab + bc + ca) + (ab + bc + ca)
thì : ab + bc + ca ≥ (abc)2 3
= 3 suy ra P ≤1. Vậy
max P =1 ⇔ x = y = z > 0 . Câu 17) Ta có: 5 2
x − x + − ( x + ) 5 2 2
= x − x − x + = x ( 2 6 3 3 3 3 x − ) 1 − 3(x − ) 1
= (x − ) ( 2x + x + )−  = (x − )  ( 4 3 2 1 1 3
1 x + x + x − 3)
= (x − ) ( 4x − )+( 3x − )+( 2x − ) = (x − )2  ( 3 2 1 1 1 1
1 x + 2x + 3x + 3) Do 3 2
x > 0 ⇒ x + 2x + 3x > 0 , nên từ (2) suy ra 5 2
x − x + 6 ≥ 3x + 3 THCS.TOANMATH.com 5 2
⇒ x − x + + xy ≥ (xy + x + ) 1 1 6 3 3 1 ⇒ ≤ . 5 2
x − x + 6 + 3xy 3(xy + x + ) 1 Tương tự, ta có: 1 1 ≤ , 5 2
y − y + 3xyz + 6 3( yz + y + ) 1 1 1 ≤ 5 2
z − z + 3xyz + 6 3(zx + z + ) 1   Suy ra 1 1 1 1 P ≤  + +
 . Áp dụng bất đẳng 3  xy x 1 yz y 1 zx z 1  + + + + + +   thức Bunhiacopski, ta có:  1 1 1  + +  ( + + )  1 1 1 1 1 1 ≥  + +
xy x 1 yz y 1 zx z 1  + + + + + +   xy + x +1 yz + y +1 zx + z +1 1 1 1  1 1 1  ⇒ + + ≤ 3 + + xy + x +1 yz + y +1 zx + z +1 
xy x 1 yz y 1 zx z 1 + + + + + +  1 1 1 ⇒ P ≤ + + = 1. Vậy
xy + x +1 yz + y +1 zx + z +1
max P =1 ⇔ x = y = z =1.
(x + y + z)2 −( 2 2 2
x + y + z ) 2 2 2 Câu 18) − − − Ta có: 9 x y z
xy + yz + zx = = . 2 2 Vậy P có dạng: − ( 2 2 2
9 x + y + z )
P = x + y + z = 2 2 2
⇒ 2P = x + y + 9 + 2( x + y + z )−9 2
x + x + x ≥ 3x
Áp dụng bất đẳng thức Cô si, ta có:  2
y + y + y ≥ 3y  2
z + z + z ≥  3zTHCS.TOANMATH.com Suy ra : 2 2 2
x + y + z + 2( x + y + z ) ≥ 3(x + y + z) = 9 .Vậy
min P = 0 ⇔ x = y = z =1. Câu 19) Vì 2 2 2 x +1≥ 2 ;
x y +1≥ 2y; z +1≥ 2z , nên ta có: x y z P ≤ + + .Ta có: 2(x + y + ) 1 2( y + z + ) 1 2(z + x + ) 1 x y zy +1   z +1   x +1 1  1  1  + + = − + − + −
x y 1 y z 1 z x 1  x y 1 
y z 1  z x 1 + + + + + + + + + + + +  y +1 z +1 x +1  = 3− + + 
x y 1 y z 1 z x 1 + + + + + +  3 1  y +1 z +1 x +1  ⇒ P ≤ − + +
2 2  x y 1 y z 1 z x 1 + + + + + +  3 1  ( y + )2 (z + )2 (x + )2 1 1 1  ≤ −  + +  . Áp dụng 2 2 ( y + ) 1 (x + y + ) 1 (z + ) 1 ( y + z + ) 1
(x + )1(z + x + )1  
bất đẳng thức Cauchy- Schwarz : ( y + )2 (z + )2 (x + )2 1 1 1 ( + + ≥ y + ) 1 (x + y + ) 1
(z + )1( y + z + )1 (x + )1(z + x + )1
( y + + z + + x + )2 1 1 1 ≥ ( . Để ý rằng do: y + ) 1 (x + y + ) 1 + (z + ) 1 ( y + z + ) 1 + (x + ) 1 (z + x + ) 1 2 2 2
x + y + z = 3 , nên ta có:( y + ) 1 (x + y + ) 1 (z + ) 1 ( y + z + ) 1 + (x + ) 1 (z + x + ) 1
= (x + y + z) 2 2 2 3
+ xy + yz + zx + x + y + z + 3 1 = ( 2 2 2
x + y + z + + x + y + z + xy + yz + zx) 1 9 6 6 6 2 2 2
= (x + y + z + 3)2 . 2 2 THCS.TOANMATH.com ( y + )2 (z + )2 (x + )2 1 1 1 ( + + ≥ . Vậy
y + )(x + y + ) (z + )( y + z + ) (x + )(z + x + ) 2 1 1 1 1 1 1 1
max P = ⇔ x = y = z =1. 2
Câu 20) Nhận xét: a
∀ thì ( + a ) ≤ (a + )2 3 2 4 1 2 . Thật vậy, 3 4 2 4 3 2 2
⇔ 4 + 4a ≤ a + 4a + 4 ⇔ a − 4a + 4a ≥ 0 ⇔ a (a − )2 1 ≥ 0 . Cũng có
thể chứng minh bằng bất đẳng thức Cauchy: (
 + a + − a + a a +
1+ a ) = (1+ a)(1− a + a ) 1 1 ( 2)2 2 2 2 3 2 ≤   = . Áp dụng vào  2  4 bài toán ta có: 2 2 2 4x 4y 4z P = + + 4( 3 1+ x )( 3 1+ y ) ( 3 1+ y )4( 3 1+ z ) 4( 3 1+ z )( 3 1+ x ) 2 2 2 4x 4y 4z ≥ ( + + . Đặt 2 2 + x )( 2 2 + y ) ( 2 2 + y )( 2 2 + z ) ( 2 2 + z )( 2 2 + x ) 2 2 2 x = ; y = ; z a b c = . 4 4 4
Khi đó do x, y, z > 0 và xyz = 8 ⇒ a,b,c > 0 và abc =1. Suy ra: 16a 16b 16c P ≥ ( + + . Hay
2 + 4a)(2 + 4b) (2 + 4b)(2 + 4c) (2 + 4c)(2 + 4a)   ≥ 4 a b c P ( + +
1 2a)(1 2b) (1 ab)(1 2c) (1 2c)(1 2a) + + + + + +  
a(1+ 2c) + b(1+ 2a) + c(1+ 2b)
a + b + c + 2(ab + bc + ca) ⇒ P ≥ 4 ( ⇒ ≥
+ a)( + b)( + c) P 4 1 2 1 2 1 2
1+ 2(a + b + c) + 4(ab + bc + ca) + 8 . Ta có: 3
a + b + c ≥ 3 abc = 3 ⇒ a + b + c + 2(ab + bc + ca) ≥ 9 =1+8abc THCS.TOANMATH.com
⇒ (1+ 8abc) + 2(a + b + c) + 4(ab + bc + ca) ≤ 3(a + b + c) + 2(ab + bc + ca)     . Suy ra 4 P ≥ . Vậy 4
min P = ⇔ x = y = z = 2. 3 3
Câu 21) Ta có nhận xét sau: với mọi x, y, z là các số thực dương, ta 3 2 có: x x ≥ (1) . Thật vậy, (1) 3
x + ( y + z)3 2 2 2 x + y + z 3 4 x x ⇔ ≥ 3
x ( y + z)3 ( 2 2 2
x + y + z )2 3  4 2 ⇔ x x + x ( 2 2 y + z ) + ( 2 2 y + z )2 7 4 2
≥ x + x (x + z)3   2 ⇔ + ( 2 2 + ) + ( 2 2 2x y z
y + z )2 ≥ x( y + z)3..Theo bất đẳng thức Cô si, ta có:
x + x ( y + z ) + ( y + z )2 ≥
x ( y + z )3 2 2 2 2 2 2 2 2 2 2 2 2 2 . (3). Rõ ràng: ( 2 2
2 y + z ) ≥ ( y + z)2 (4) Từ (3),(4) suy ra: 2 ( 2 2 + ) + ( 2 2 + )2 2 2x y z y z
≥ x ( y + z)6 = x( y + z)3 (5) 3 2 Tương tự (1), ta có: y y ≥ (6), 3
y + (z + x)3 2 2 2 x + y + z 3 2 z z ≥ (7) 3
z + (x + y)3 2 2 2 x + y + z
Cộng từng vế (1),(6),(7) và có P ≥1 (8)
Vậy min P =1 ⇔ x = y = z > 0 . 3 2
Chú ý: Ta có thể chứng minh: x x ≥ nhanh hơn bằng 3
x + ( y + z)3 2 2 2 x + y + z
cách áp dụng bất đẳng thức Cau chy THCS.TOANMATH.com a +
+ = (a + )(a − a + ) 2 3 2 a + 2 1 2 1 1 1 ≤ ⇒ ≥ thay y z a = 2 3 2 a +1 a + 2 x 3 2 suy ra x 2x ≥
. Lại có (x + y)2 ≤ ( 2 2 2 x + y ) suy 3
x + ( y + z)3 2
2x + ( y + z)2 3 2 ra x x ≥ 3
x + ( y + z)3 2 2 2 x + y + z
Câu 22) Áp dụng bất đẳng thức Bunhiacopski, ta có:  (   2 2 1+ + ) + ( 2 2 1+ + ) + ( 2 2 1+ + ) x y z x y z y z x z x y  + +   2 2 2 2 2 2 1+ y + z 1+ z + x 1+ x + y
Từ (1) và do x + y + z =1, ta có: 1 P ≥ . Đặt x( 2 2
1+ y + z ) + y( 2 2
1+ z + x ) + z( 2 2 1+ x + y ) Q = x( 2 2
+ y + z ) + y( 2 2
+ z + x ) + z( 2 2 1 1 1+ x + y )
= (x + y + z) + xy(x + y) + yz (z + y) + zx(z + x)
= 1+ xy (x + y) + yz (z + y) + zx(z + x) 2 = + ( + ) 2 + ( + ) 2 1 x y z
y z x + z (x + y) . Có thể thấy rằng: 2
x ( y + z) 2
+ y (z + x) 2
+ z (x + y) 1 ≤ 4 Từ đó có: 5 Q ≤ ⇒ 4 P ≥ .Vậy 4
min P = . Giá trị nhỏ nhất đạt được khi 4 5 5 1
x = y = ; z = 0 . 2
Câu 23) Áp dụng bất đẳng thức Bunhiacopski ta có: THCS.TOANMATH.com  1 1 1   + +  ≤  3 3 3 3 3 3 x 2y 6 y 2z 6 z 2x 6  + + + + + +    1 1 1  3 + +  3 3 3 3 3 3  x 2y 6 y 2z 6 z 2x 6  + + + + + +    Hay 1 1 1 P ≤ 3 + +  . Áp dụng bất đẳng 3 3 3 3 3 3  x 2y 6 y 2z 6 z 2x 6  + + + + + +  thức Cô si ta có: 3 3 x + y + = ( 3 3 x + y + ) + ( 3 2 6 1 y +1+ )
1 + 3 ≥ 3xy + 3y + 3 3 3
⇒ x + 2y + 6 ≥ 3(xy + y + ) 1 Tương tự, có: 3 3
y + 2z + 6 ≥ 3( yz + z + ) 1 , 3 3
z + 2x + 6 ≥ 3(zx + x + ) 1 Suy ra : 1 1 1 P ≤ + +
. Do xyz =1, nên dễ
xy + y +1 yz + z +1 zx + x +1 thấy 1 1 1 1 xy y + + = + + = 1
xy + y +1 yz + z +1 zx + x +1 xy + y +1 xy + y +1 xy + y +1 suy ra P ≤1
Vậy max P =1 ⇔ x = y = z =1.
Câu 24) Theo bất đẳng thức Cô si, ta có: 1
y + z ≥ 2 yz = 2 (do xyz =1) x 2 x y + z Từ đó suy ra: 2 ( + ) 2 1 ( ) 2 ≥ 2 = 2 x x x y z x x x ⇒ ≥ x y y + 2z z y y + 2z z (1)
Lập luận tương tự, có: 2 y (z + x) 2y y 2 z (x + y) ≥ , 2z z ≥ . Cộng từng vế
z z + 2x x z z + 2x x x x + 2y y x x + 2y y THCS.TOANMATH.com x x y y  ≥ 2 z z P  + +   . Đặt
y y 2z z z z 2x x x x 2y y  + + +  
X = x x;Y = y y;Z = z z thì X ,Y, Z > 0 và XYZ =1. Khi đó (4) có dạng 2 X Y Z P  ≥ + + 
Y 2Z Z 2X X 2Y  + + +  2 2 2   ⇒ ≥ 2 X Y Z P  + +
. Áp dụng bất đẳng thức
XY 2ZX YZ 2XY XZ 2YZ  + + + 
( X +Y + Z )2
Cauchy- Schwarz ta có: P ≥ 2 do
3( XY +YZ + ZX )
( X +Y + Z )2 ≥ 3( XY +YZ + ZX ) ⇒ P ≥ 3 và P = 3 ⇔ X = Y = Z =1. Vậy
min P = 3 ⇔ x = y = z =1. Câu 25)
Áp dụng bất đẳng thức Cô si, ta có: 2
y +1 + y − y +1 2 3 y +1 = ( y + ) 1 ( 2 y − y + ) ( ) ( ) 1 ≤ 3 y 2 y + ⇒ +1 ≤ 2 2 x 2x ⇒ ≥ tương tự, ta có: y 2y ≥ , z 2z ≥ 2 3 y +1 y + 2 2 3 z +1 z + 2 2 3 x +1 x + 2   ⇒ ≥ 2 x y z P + + 
. Dấu bằng trong (5) xảy ra ⇔ đồng thời 2 2 2  y 2 z 2 x 2  + + + 
có dấu bằng trong ⇔ x = y = z = 2 . Ta sẽ chứng minh 2x 2y 2z + + ≥ 2 2 2 2
y + 2 z + 2 x + 2  2x   2y   2z x y z  ⇔ − + − + − ≤       4 (do 2 2 2  y + 2   z + 2   x + 2  2 2 2
x + y + z = 6 ) xy yz zx ⇔ + +
≤ 4. Áp dụng bất đẳng thức Cô si, ta 2 2 2
y + 2 z + 2 x có: 2 2 2 3 3 4 3
2y + 4 = y + y + 4 ≥ 3 4y = 3y 4y 2 3
⇒ y + 2 ≥ y 4y Tương 2 THCS.TOANMATH.com tự có: 2 3 3
z + 2 ≥ z 4z , 2 3 3
x + 2 ≥ x 4z 2 2 2 2 2 VT xy yz zx ≤ + + 3 3 3
.Áp dụng bất đẳng thức Cô si, ta có: 3 3 3 y 4y 4z x 4x 2 2 2 2x xy xy 3 2 . x x . y xy + + ≤ , 3 2y yz yz z zx zx 3 2 . y yz.yz + + ≤ 3 2 2z. . zx zx + + ≤ . VT 3 3 1 ≤ 2
 ( x + y + z) + 2( xy + yz + zx) 9 
Mặt khác, ta có: ( + + ) ≤ ( + + )2 3 xy yz zx
x y z ⇒ xy + yz + zx ≤12 . Từ đó
suy ra P ≥ 2 . Vậy min P = 2 ⇔ x = y = z = 2 . Câu 26) Giải:
1)Ta có theo bất đẳng thức Cô si:
x + 4y 3x + 2y 2 2
3x + 8y +14xy = (x + 4y)(3x + 2y) ( )( ) ≤
= 2x + 3y 2 2 2 Như vậy suy ra x x ≥ . Tương tự ta có: 2 2
3x + 8y +14xy 2x + 3y 2 2 y y ≥ 2 2
3y + 8z +14yz 2y + 3z 2 2 z z 2 2 2 ≥ ⇒ x y z P ≥ + + . Theo bất 2 2
3z + 8x +16zx 2z + 3x
2x + 3y 2y + 3z 2z + 3x
đẳng thức Cauchy- Schwarz ta 2 2 2 có: x y z 1 + +
≥ (x + y + z) . Theo bất đẳng thức Cô si cơ
2x + 3y 2y + 3z 2z + 3x 5 THCS.TOANMATH.com  
bản, ta có: (x + y + z) 1 1 1 + + ≥   9 . Do 1 1 1 0 < + + ≤1, nên có:  x y z x y z
x + y + z ≥ 9 vậy 9 P ≥ . Vậy 9
min P = ⇔ x = y = z = 3. 5 5
Câu 27) Do tính bình đẳng giữa x, y, z nên có thể giả sử x ≥ y ≥ z
Kết hợp với x + y + z = 3 suy ra 0 < z ≤1. Ta có 2 2 2
P = x + y + z + xyz
= (x + y + z)2 + xyz − 2(xy + yz + zx) = 9 + xy(z − 2) − 2z ( y + x)
= 9 + xy (z − 2) − 2z (3− z) (1) 2 2 Hiển nhiên ta có:  x y   3 z xy + −  ≤ = 
. Do 0 < z ≤1⇒ z − 2 < 0 , vậy từ 2   2      (1) có: 2 ( ) 3− 9 2 z P z  ≥ + − − 2z (3−   z) . Ta có  2  −  −  − VP(2) 3 z = + ( − ) 3 z 3 9 2 − 4 = 9 z z z +   
( z − 2)(3 − z) − 8z 2  2  2  3− z 2 1 = +
−z − z −  =   ( 3z − z + ) 1 9 3 6
3 18 = ( 2z −3z + 2)+16 2 4 4  1 = (z − )2 1 (z + 2) +16
< x ≤ nên suy ra ⇒ P ≥ 4 . Vậy 4   . Do 0 1
min P = 4 ⇔ x = y = z =1.
Câu 28) Áp dụng đồng nhất thức
(x + y)( y + z)(z + x) = (x + y + z)(xy + yz + zx)− xyz (*)
Ta có: P = (x + y + z)(xy + yz + zx) − xyz − 2(x + y + z) . Theo bất đẳng thức Cô si ta có: 3
x + y + z ≥ 3 xyz = 3 (do xyz =1).Lại có: THCS.TOANMATH.com 3 2 2 2
xy + yz + zx ≥ 3 x y z = 3 (do 2 2 2 x y z =1) suy ra:
P ≥ 3(x + y + z) −1− 2(x + y + z)
⇒ P ≥ (x + y + z) −1≥ 3−1 = 2 .
2)Trước hết ta chứng minh rằng (x + y)( y + z)(z + x) ≥ (x + ) 1 ( y + ) 1 (z + ) 1
Thật vậy, dựa vào (*) suy ra:
⇔ (x + y + z)(xy + yz + zx) − xyz ≥ xy + yz + zx + x + y + z +1
⇔ (x + y + z)(xy + yz + zx) − 2 ≥ xy + yz + zx + x + y + z + 2 (do xyz =1)
⇔ (x + y + z)(xy + yz + zx) ≥ xy + yz + zx + x + y + z + 3 Do
xyz =1⇒ x + y + z ≥ 3 và xy + yz + zx ≥ 3. Ta có
( + + )( + + ) x + y + z =
( + + )+( + + ) xy + yz + zx x y z xy yz zx xy yz zx x y z + 3 3
(x + y + z)(xy + yz + zx) + suy ra 3
(x + y + z)(xy + yz + zx) ≥ xy + yz + zx + x + y + z +3.Theo bất đẳng thức Cô
(x + y)( y + z)(z + x) si ta có: Q ≥ 33 ( ≥ . Vậy
x + )( y + )(z + ) 3 1 1 1
min Q = 3 ⇔ x = y = z =1.
Câu 29) Giải: Ta có: ( 3 3 a + b ) 3 3
= a + b + (a + b)( 2 2
a − ab + b ) 3 3 4 3
≥ a + b + 3(a + b)ab = (a + b)3 Suy ra ( 3 3
a + b ) ≥ a + b ⇒ c + ( 3 3 3 3 4
4 a + b ) ≥ a + b + c . Do đó a + b a + b = ( ≤
, đẳng thức xảy ra khi và chỉ khi a b . Tương 3 3 3 4 ) a+b+ + + c c a b THCS.TOANMATH.com tự cũng có b + c b + c c + a c + a ( ≤ + ≤ . Suy ra 3
3 ) a + b + c ( 3 3 3 3 4 4 ) a+b+ + + + + c a c a b c a a + b b + c c + a + + ≤ c + 4( 2 3 3
a + b ) a + 4( 3 3
b + c ) b + 4( 3 3 3 3 3 c + a )
Đẳng thức xảy ra khi và chỉ khi a = b = c .
Câu 30) Ta có: 0 < a,b,c <1 suy ra
(a −b)2 ≥ a(a −b)2 2 2
⇔ a + b ≥ 2ab + a(a − b)2 . Tương tự 3 bất đẳng thức nữa ta có:
P = (ab + bc + ca) + a(a − b)2 + b(b − c)2 + c(c − a)2 6
≤ (ab + bc + ca) + ( 2 2 2 4
2 a + b + c ) hay P ≤ 2 . Dấu bằng xảy ra khi và chỉ khi 2
a = b = c = . 3
BẤT ĐẲNG THỨC ABEL VÀ ỨNG DỤNG
CÔNG THỨC ABEL VÀ ỨNG DỤNG.
1. Công thức tổng Abel:
Giả sử a ,a ,...,a và b ,b ,....,b là hai dãy số thực. Khi đó ta có: 1 2 n 1 2 n
a b + a b +...+ a b = b − b S + b − b S + + b S trong đó n n ( ) ( ) ... 1 1 2 2 1 2 1 2 3 2 n n
S = a + a + + a . k ... 1 2 k
Chứng minh: Thật vậy thay a = S − S với k = n ta có vế trái k k k 2,3,... 1 − bằng:
b S + b (S − S ) + b (S − S ) +...+ b S − S = . − VP n ( n n ) 1 1 2 2 1 3 3 2 1 THCS.TOANMATH.com
Trường hợp n = 3 ta
có: ax + by + cz = (x − y)a + ( y − z)(a + b) + z (a + b + c) đây là đẳng thức
quan trọng có nhiều ứng dụng trong giải toán.
2. Bất đẳng thức Abel:
Cho hai dãy số thực: a ,a ,....,a và b ≥ b ≥ b ≥ ...... ≥ b . Đặt 1 2 n 1 2 3 n
S = a + a + + a với k ∈{1,2,3,... } n và k ... 1 2 k
m = min{S , S ,...., S M = S S S . Khi đó ta có: n , max , ,...., 1 2 } { 1 2 n}
mb ≤ A = a b + a b +...+ a b ≤ Mb , 1 1 1 2 2 n n 1 Chứng minh:
Ta có: a b + a b +...+ a b = b − b S + b − b S + + b S mà n n ( ) ( ) ... 1 1 2 2 1 2 1 2 3 2 n n
b − b ≥ nên k k+ 0 1
(b − b )m + (b − b )m +...+ b m ≤ A ≤ b − b M + b − b M + + b M hay n ( ) ( ) ... 1 2 2 3 1 2 2 3 n
mb ≤ A ≤ Mb . 1 1 MỘT SỐ VÍ DỤ:
Ví dụ 1: Cho x ≥ y ≥ z ≥ 0 thỏa mãn: x ≥ 3, x + y ≥ 5, x + y + z ≥ 6 . Chứng minh: 2 2 2
x + y + z ≥14 . Lời giải: Ta có: 2 2 2
x + y + z −14 = (x − 3)(x + 3) + ( y − 2)( y + ) 1 + (z − ) 1 (z + ) 1 . Áp
dụng công thức Abel ta có: 2 2 2
x + y + z −14 = (x + 3− y − 2)(x − 3) + (y + 2 − z −1) + (z +1)(x − 3+ y − 2 + z −1) = (x − y + )
1 (x − 3) + ( y − z + )
1 (x + y − 5) + (z + )
1 (x + y + z − 6) ≥ 0 . Dấu
bằng xảy ra khi và chỉ khi x = 3; y = 2; z =1 . THCS.TOANMATH.com
Ví dụ 2) Cho các số thực dương x, y, z sao cho x ≥ 3, xy ≥ 6, xyz ≥ 6 .
Chứng minh: x + y + z ≥ 6 . Lời giải: Ta có: 6 3 x 1 2 y  1 1 z  1 (3 2) x  1 (2 ) 1 x y x y z           2 + + − = − + − + − = − − + − + − +  3 2 1 3 3 2           
1. x 1 y 1 z 1  x   1  x y   2  x y z   3 − + − + − = − + + − + + + −  . Áp dụng 3 2 1 3 3 2 3 2 1         
bất đẳng thức Cô si ta có: x y 2 xy + ≥ ≥ 2; x y z xyz + + ≥ 3 3 ≥ 3 . Suy 3 2 6 3 2 1 3.2.1
ra đpcm. Dấu bằng xảy ra khi và chỉ khi x = 3, y = 2, z =1 .
Ví dụ 5: Cho x, y, z > 0 sao cho x < 2y < 3z và
x ≥1, x + y ≥ 3, x + y + z ≥ 6 . Chứng minh: 6(xy + yz + zx) ≤11xyz . Lời giải:
Ta cần chứng minh: 1 1 1 11 + + ≤ .Ta có: x y z 6 11  1 1 1 
1 1 1 1 1 x −1 y − 2 z − 3 − + + =   1− + − + − = + + = 6  x y z x 2 y 3 z x 2y 3z  1 1 (   − x − ) 1 1 + − (x + y − ) 1 1 3 +
(x + y + z −6) ≥     0  x 2y   2y 3z  3z
Dấu bằng xảy ra khi và chỉ khi x = 3, y = 2, z =1 .
Ví dụ 3: Cho các số thực không âm x, y, z sao cho
x ≤1, x + y ≤ 5, x + y + z ≤14 . Chứng minh: x + y + z ≤ 6 . Lời giải: THCS.TOANMATH.com Tacó: x y z 1 1   1 1   x  + + = − + −  ( x + y) 1
+ (x + y + z) ≤ 1 2 3 1 2   2 3  3 1 1   1 1  1 − .1+ − .5 + .14 =1+ 2 +     3 . Ta suy ra 1 2   2 3  3 ( )2 ( ) x y z x y z   + + ≤ + + + + ≤ ( + + )2 1 2 3 1 2 3 =   36 .  1 2 3 
Ví dụ 4: Cho các số thực dương a ≥ b ≥1,a ≤ 3,ab ≤ 6,ab ≤ 6c . Chứng
minh: a + b − c ≤ 4 . Lời giải:
Ta cần chứng minh: a + b +1≤ 3+ 2 + c . Ta có:  3 2 3 2 c c  (b ) 3 2 1  + + = + + + − + + (a − b) 3 6c 6 3 ≥ 3 3 + (b − ) 1 2 + (a −     b)  a b 1   a b a ab ab a
≥ 3+ 2(b −1) + (a − b) = a + b +1. Dấu bằng xảy ra khi và chỉ khi
a = 3,b = 2,c =1 . 
0 < a ≤ b ≤ c,c ≥ 9 
Ví dụ 5: Cho các số thực dương  b a 9
,b,c sao cho a + + ≤ 3 . 4 c  b 9 + ≤ 2 4 c
Chứng minh: a + b ≤ c . Lời giải:     Ta có: b 9 b 9 a + b + =  a + +  +  +  +     ( c − ) 9 9 1 2 4 c 4 c c     THCS.TOANMATH.com b 9  b 9  a + +  + 4 c 4 ≤ 3  + 2
c +( c −2) 9 = 3+2+ c −2 = 3+ c .  3  2 2     
a ≥ b ≥1≥ c > 0 
Ví dụ 6) Cho các số thực a 2
,b,c sao cho  + c ≤ 2 . Chứng minh: b  3 2 + + c ≤ 3 a b 1 1 1 1 + − ≤ − . a b c 6 Lời giải: Ta cần chứng minh: 1 1 1 1 1 + +1≤ + + . Tacó: a b 3 2 c
1 1 1 1  a b 1   1 1  b 1   1  1 + + = + + + − + +      1− 3 2 c a 3 2 c b a 2 c b         c    
1  1 1 1   1 1  1 1   1  1 =  + +  + −   +  + 1− a 3 2 c b a 2 c b         ca b   b
Áp dụng bất đẳng thức Cauchy- Schwarz. Ta có: 1 1 1 9 1 1 4 + + ≥ ≥ 3, + ≥ ≥ 2 3 2 , ta có c 3 2 2 c 2 + + c + c a b a b b b 1 1 1 3  1 1   1  1 1 + + ≥ + 2 − + 1− = + +     1. 3 2 c ab a   b a b THCS.TOANMATH.com
a ≤ b ≤ 3 ≤ c
Ví dụ 7) Giả sử a
,b,c là các số thực dương thỏa mãn: c ≥ b +1 . a +b ≥  c + + + − Tìm GTNN của 2ab a b c(ab 1) Q = .
(a +1)(b +1)(c +1)
(Trích đề thi vào lớp 10 Trường chuyên KHTN- ĐHQG Hà Nội) Lời giải: Ta có:
(abc + ab + ac + a)+(abc +bc +ba +b)−(abc + ca + cb + c) a b c Q = = + −
(a +1)(b +1)(c +1)
a +1 b +1 c +1 Ta chứng minh: a b c 1 2 3 5 3− c b − 2 a −1 + − ≥ + − = ⇔ + + ≥ 0
1+ a 1+ b 1+ c 1+1 1+ 2 1+ 3 12
3(1+ c) 3(b +1) 2(1+ a) Hay  1 1   1 1  (3− c) − +
 (3 + c + b − 2) − 
 4(c 1) 3(b 1)  
 3(b 1) 2(a 1)  + + + + 
+ ( − c + b − + a − ) 1 3 2 1
≥ 0 . Rút gọn ta thu được: 2(1+ a) (3b − 4c −1) − − − c
+ (b + − c) (2a 3b )
1 +(a+b−c) 1 (3 ) 1 ≥ 0 . 12(b +1)(c +1) 6(b +1)(a +1) 2(a +1)
Điều này là hiển nhiên đúng.
BẤT ĐẲNG THỨC BUNHIACOPXKI
Một số kết quả quan trọng:
Cho các số thực dương a,b,c, x, y, z . a) 2 2 2
a + b + c ≥ ab + bc + ca . THCS.TOANMATH.com b) 2 2 2
3(a + b + c ) ≥ (a + b + c)2 . c) ( + )2 ≤ ( 2 2 + )( 2 2 ax by a b x + y ). d) ( + + )2 ≤ ( 2 2 2 + + )( 2 2 2 ax by cz a b c
x + y + z )
e) 8(a + b + c)(ab + bc + ca) ≤ 9(a + b)(b + c)(c + a) f) 2 2 2 2 2 2
b c + a c + a b ≥ abc(a + b + c) g) 1 1 1 + ≥ .
(a +b)2 (a + c)2 2 a + bc x y ( + )2 2 2 x y h) + ≥ . a b a + b x y z ( + + )2 2 2 2 x y z i) + + ≥ . a b c a + b + c Chứng minh: a) 2 2 2
a + b + c ≥ ab + bc + ca ⇔ ( 2 2 2
2 a + b + c ) ≥ 2(ab + bc + ca) ⇔ (a −b)2 + (b
Bất đẳng thức này luôn đúng. Dấu đẳng thức xảy ra khi và chỉ khi a = b = c .
b) Khai triển hai vế và thu gọn ta quy về câu a.
c) Khai triển hai vế rồi thu gọn ta đưa bất đẳng thức về dạng:
(ay −bx)2 ≥ 0. Dấu đẳng thức xảy ra khi và chỉ khi a b = . x y
d) Khai triển hai vế rồi thu gọn ta đưa bất đẳng thức về dạng:
(ay −bx)2 +(bz −cy)2 +(cx − az)2 ≥ 0 . Dấu đẳng thức xảy ra khi và chỉ khi a b c
= = . Các bất đẳng thức c, d còn được gọi là bất đẳng thức x y z
Bunhiacopxki cho 2 số, 3 số.
e) Khai triển hai vế rồi thu gọn ta đưa bất đẳng thức về dạng:
(a +b)(b + c)(c + a) ≥ 8abc bất đẳng thức này luôn đúng theo AM- GM
(xem chứng minh ở phần Bất đẳng thức Cô si).
f) Theo bất đẳng thức Cô si thì: 2 2 2 2 2
b c + a c ≥ 2abc Tương tự ta có 2
bất đẳng thức nữa và cộng lại suy ra đpcm. THCS.TOANMATH.com
g) Theo bất đẳng thức Bunhiacopxki cho 2 số ta có: 2 ( )2  b      ( 2 ) b   ( 2  + . 1 ) b c a b a bc a bc a bc  + = + ≤ + + = + suy ra c    c    c  1 c ≥ . Tương tự 1 b ≥ . Cộng hai (a +b)2 ( 2
a + bc)(b + c) (a + c)2 ( 2
a + bc)(b + c)
bất đẳng thức cùng chiều ta suy ra đpcm.
h) Quy đồng và rút gọn đưa bất đẳng thức cần chứng minh về dạng:
(ay −bx)2 ≥ 0.
i) Áp dụng bất đẳng thức h) ta có: x y z ( + )2 z ( + + )2 2 2 2 2 x y x y z + + ≥ + ≥ . a b c a + b c a + b + c
Bất đẳng thức này còn được gọi là bất đẳng thức Cauchy-Chwarz.
1. Những kỹ năng vận dụng cơ bản:
Ví dụ 1: Cho các số thực dương a,b,c sao cho a + b + c = 3. Chứng minh rằng: a b c + + ≥ 1.
a + 2bc b + 2ac c + 2ab Giải: 2 2 2 2 a a a b c a b c = ⇒ + + = + + 2 2 2 2
a + 2bc a + 2abc
a + 2bc b + 2ac c + 2ab a + 2abc b + 2abc c + 2ab
Áp dụng bất đẳng thức Cauchy- Schwarz ta có: a b c
(a +b + c)2 2 2 2 + + ≥ . Ta cần chứng 2 2 2 2 2 2
a + 2abc b + 2abc c + 2abc a + b + c + 6abc
(a +b + c)2 minh: ≥1 2 2 2
a + b + c + 6abc
⇔ ab + bc + ca ≥ 3abc ⇔ (a + b + c)(ab + bc + ca) ≥ 9abc . Theo bất đẳng thức Cô si ta có: 3 3 2 2 2
a + b + c ≥ 3 abc,ab + bc + ca ≥ 3 a b c nhân 2 vế các THCS.TOANMATH.com
bất đẳng thức dương cùng chiều ta có đpcm. Dấu bằng xảy ra khi và chỉ khi
a = b = c =1.
Ví dụ 2: Cho các số thực dương a,b,c . Chứng minh rằng: 3 3 3 2 2 2 a b c a + b + c + + ≥ .
a + 2b b + 2c c + 2a 3 Giải: Ta có: a a a b c
(a +b +c )2 2 2 2 3 4 4 4 4 = ⇒ VT = + + ≥ . 2 2 2 2
a + 2b a + 2ab
a + 2ab b + 2bc c + 2ca
(a +b + c)2 Ta cần chứng
(a +b +c )2 2 2 2 2 2 2 + + minh: a b c 2 2 2 ≥
⇔ a + b + c ≥ ab + bc + ca . Điều này
(a +b + c)2 3 là hiển nhiên.
Ví dụ 3: Cho các số thực dương a,b,c . Chứng minh:
( 2a + )( 2b + )( 2 2
2 c + 2) ≥ 3(a + b + c)2 . Giải: 2 2   b + c   b + c
Ta có: (a + b + c)2 = a + ≤   ( 2 2. a + 2) ( ) 1  +  .Suy ra:   2   2     + 
(a +b + c) ≤ (a + ) (b c)2 2 2 3 3 2 1  +  . Ta cần chứng minh:  2    2 (  b + c  2 a + ) ( )  +  ≤ ( 2 a + )( 2 b + )( 2 3 2 1 2 2 c + 2) hay  2     (b + c)2   +  ≤ ( 2 b + )( 2 3 1
2 c + 2). Sau khi khai triển và thu gọn ta được:  2    THCS.TOANMATH.com 2 2 b + c 2 2 2 2 +
+ b c − 3bc +1≥ 0. Để ý rằng: b
c ≥ bc nên bất đẳng thức trở 2 2 thành: 2 2
b c − 2bc +1≥ 0 ⇔ (bc − )2 1 ≥ 0 .
Ví dụ 4: Cho các số thực dương a,b,c . Chứng minh: 3 3 3 a b c 1 ( + + ≤ 2 2 2a + b )( 2 2 2a + c ) ( 2 2 2b + c )( 2 2 2b + a ) ( 2 2 2c + a )( 2 2
2c + b ) a + b + c Giải:
Ta mong muốn xuất hiện lượng: a + b + c Ta có: ( 2 2 a + b )( 2 2 a + c ) = ( 2 2 2
a + b + a )( 2 2 2
a + a + c ) ≥ ( 2
a + ab + ac)2 2 2 2
= a (a + b + c)2 3 Từ đó suy ra: a a ( ≤
. Tương tự ta có 2 bất đẳng 2 2 a + b )( 2 2 2
2a + c ) (a + b + c)2
thức nữa và cộng lại thì suy ra điều phải chứng minh.
Ví dụ 5: Cho các số thực dương a,b,c sao cho ab + bc + ca + abc ≤ 4 . Chứng minh: 2 2 2
a + b + c + a + b + c ≥ 2(ab + bc + ca). (Trích đề tuyển sinh
vào lớp 10- Trường Chuyên KHTN- ĐHQG Hà Nội 2015). Lời giải:
Ta viết lại giả thiết bài toán thành:
12 + (ab + bc + ca) + 4(a + b + c) ≥ 8 + 4(a + b + c) + 2(ab + bc + ca) + abc
hay (a + 2)(b + 2) + (b + 2)(c + 2) + (c + 2)(a + 2) ≥ (a + 2)(b + 2)(c + 2) 1 1 1 ⇔ + + ≥1Ta có:
a + 2 b + 2 c + 2 2 2 2 2 1 a + b + c a + b + c = ≤ , Tương tự ta a + 2 (a +1+ ) 1 ( 2 2
a + b + c ) (a + b + c)2 THCS.TOANMATH.com 2 2 2 2 + + + + có: 1 b c a 1 ≤ ; a a b ≤ . Suy ra
b + 2 (a + b + c)2 c + 2 (a + b + c)2 1 1 1
a + b + c + 2( 2 2 2
a + b + c ) 1≤ + + ≤
a + 2 b + 2 c + 2
(a +b + c)2
⇔ a + b + c + ( 2 2 2
2 a + b + c ) ≥ (a + b + c)2 hay 2 2 2
a + b + c + a + b + c ≥ 2(ab + bc + ca). Dấu bằng xảy ra khi và chỉ khi
a = b = c =1.
Ví dụ 6) Cho các số thực dương a,b,c sao cho ab + bc + ca =1. Chứng
minh rằng: 2abc(a + b + c) 5 4 2 4 2 4 2
≤ + a b + b c + c a . (Trích đề tuyển sinh 9
vào lớp 10- Trường Chuyên KHTN- ĐHQG Hà Nội 2014). Lời giải:
Sử dụng bất đẳng thức 2 2 2
x + y + z ≥ xy + yz + zx . Ta có: 4 2 4 2 4 2 2 2 2 2 2 2
a b + b c + c a ≥ a b b c + b c c a + c a a b = abc( 2 2 2 . . .
ab + bc + ca ).
Tiếp tục sử dụng bất đẳng thức: Cauchy- Shwarz và giá thiết
ab + bc + ca =1ta có: b c a a + b + c 2 2 2 ( )2 2 2 2
ab + bc + ca = + + ≥
= abc(a + b + c)2 1 1 1 1 1 1 . Từ đó suy ra + + a b c a b c + + ≥  ( + + ) 2 4 2 4 2 4 2 a b b c c a abc a b c  
 . Bây giờ ta sẽ chứng minh: abc
(a +b + c) 2 − 2abc
(a +b + c) 5 2
+ ≥ 0 ⇔ t − 6t + 5 ≥ 0 ⇔ (t − ) 1 (t − 5) ≥ 0 9
với t = abc(a + b + c) . Mặt khác ta có:
abc(a + b + c) 1
= ab ac + bc ba + ca cb ≤ (ab + bc + ca)2 1 . . . = ⇒ 0 < t ≤1. 3 3
Suy ra đpcm. Dấu đẳng thức xảy ra khi và chỉ khi 1
a = b = c = . 3 THCS.TOANMATH.com
Ví dụ 7: Cho các số thực dương a,b,c . Chứng minh: 2 1 1 1
a + b + c  + + ≤ 2 2 2 a
ab bc b bc ca c ca ab  ab bc ca  + + + + + + + +  Lời giải:
Ta muốn làm xuất hiện: ab + bc + ca 2 2 + + + + Ta có: 1 c ab bc c ab bc = ≤ . Tương 2
a + ab + bc ( 2
a + ab + bc)( 2
c + ab + bc) (ac + ab + bc)2
tự với 2 số hạng còn lại ta có: 1
c + ab + bc
(a +b + c)2 2 ∑ ≤ ∑ = 2
a + ab + bc
(ac + ab +bc)2 (ac + ab +bc)2
Ví dụ 8: Cho các số thực dương a,b,c . Chứng minh: 2 2 2 ab bc ca a + b + c + + ≤ 2 2 2
a + bc + ca b + ca + ab c + ab + bc ab + bc + ca Giải:
Ta muốn làm xuất hiện: ab + bc + ca 2 2 ab
ab(b + bc + ca)
ab(b + bc + ca) = ≤ 2
a + bc + ca ( 2
a + bc + ca)( 2
b + bc + ca) (ab + bc + ca)2 2 2 2 + + + + + + Từ đó suy ra:
ab(b bc ca) bc(c ca ab) ca(a ab bc) VT ≤ + + .
(ab +bc + ca)2 (ab +bc + ca)2 (ab +bc + ca)2 Ta chỉ cần chứng minh: 2 2 2
ab b + bc + ca + bc c + ca + ab + ca a + ab + bc ≤ ( 2 2 2 ( ) ( ) ( )
a + b + c )(ab + bc + ca) 2 2 2 3 3 3
⇔ a b + b c + c a ≥ abc(a + b + c) a b c ⇔ + +
≥ a + b + c . Nhưng bất c a b
đẳng thức này là hiển nhiên đúng theo bất đẳng thức Cauchy- Shwarz THCS.TOANMATH.com
Ví dụ 9: Cho các số thực dương a,b,c sao cho a + b + c =1. Chứng minh rằng: a b c + + ≤1 3 2 3 2 3 2
a + b + c b + c + a c + a + b Giải:
Ta muốn làm xuất hiện a + b + c .  1   1 a 1 ca 1 c + + + + aa   a   1+ a + ca = ≤ = . Từ đó suy 3 2
a + b + c ( 3 2
a + b + c) 1 
(a +b + c)2 9 +1+  c a    + + + + + + ra: a b c
1 a ca 1 b ab 1 c bc + + ≤ + + 3 2 3 2 3 2
a + b + c b + c + a c + a + b 9 9 9 + + + + + +
Ta cần chứng minh: 1 a ca 1 b ab 1 c bc + +
≤1 ⇔ ab + bc + ca ≤ 3 . 9 9 9
(a +b + c)2
Nhưng điều này là hiển nhiên đúng do: ab + bc + ca ≤ = 3 3
Ví dụ 10: Cho các số thực dương a,b,c sao cho abc =1. Chứng minh rằng: 1 1 1 + + ≤1 2 2 2 1+ a + b 1+ b + c 1+ c + a Giải: Ta đặt 3 3 3
a = x ,b = y ,c = z , xyz =1. Bất đẳng thức cần chứng minh trở thành: 1 1 1 + + ≤ 1. 3 6 3 6 3 6 1+ x + y 1+ y + z 1+ z + x Ta có:   4 1 4 1  z + x +  z + x + 2 2 4 2 2 2 1  y y
z + x yz + z x = ≤ = 3 6 1+ x + y ( + + ) 1  1 + + ( 2 2 2
x + y + z )2 ( 2 2 2 3 6 4 x + y + z x y z x )2 2 y    THCS.TOANMATH.com Ta cần chứng minh:
∑(z + x yz + z x ) ≤ (x + y + z )2 4 2 2 2 2 2 2 2 2 2 2 2 2
⇔ x y + y z + z x ≥ xyz(x + y + z) .
Điều này là hiển nhiên đúng theo bất đẳng thức 2 2 2
a + b + c ≥ ab + bc + ca
Ví dụ 11: Cho các số thực dương a,b,c . Chứng minh rằng: 1 1 1 1 + + ≤ . 3 3 3 3 3 3
a + b + abc b + c + abc c + a + abc abc
Do bất đẳng thức thuần nhất nên ta chuẩn hóa: abc =1. Bất đẳng thức cần chứng minh trở thành: 1 1 1 + + ≤1. 3 3 3 3 3 3
a + b +1 b + c +1 c + a +1 Ta có:  1 1 2   1 1 2 c c  + + + +     2 1  a b   a b
bc + ca + c c = ≤ = = 3 3 a + b +1 ( 3 3
a + b + ) 1 1 2  (a + b + c)2
(a +b + c)2 1 a + b + c + +  c a b   
Tương tự với 2 số hạng còn lại và cộng ba bất đẳng thức cùng chiều suy ra đpcm.
Ví dụ 12) Với ba số dương x, y, z thỏa mãn x + y + z =1, tìm giá trị lớn nhất của biểu thức: x y z Q = + + .(Trích đề
x + x + yz y + y + zx z + z + xy
tuyển sinh vào lớp 10 chuyên Toán TP Hà Nội – 2014) Lời giải:
Ta có: x + yz = x(x + y + z) + yz = (x + y)(x + z) . Chú ý rằng: Theo
bất đẳng thức Bunhiacopxki thì:
(x + y)(x + z) ≥ ( x y + z x)2 . .
⇒ (x + y)(x + z) ≥ x. y + z. x . Từ đó suy ra: x x x ≤ = . Tương tự
x + x + yz x + x ( y + z ) x + y + z THCS.TOANMATH.com y y ta có: ≤ ; z z . Cộng 3 bất
y + y + zx
x + y + z z + z + xy x + y + z
đẳng thức cùng chiều ta suy ra Q ≤1. Dấu đẳng thức xảy ra khi và chỉ khi 1
x = y = z = 3
Ví dụ 13) Cho các số thực không âm a,b,c sao cho a > 0,b + c > 0 và 3 3 3 2 2 2 +
a + b + c =1. Chứng minh: a b c + ≥ 2 . 2 2 2
b − bc + c a Lời giải: Ta có: a b c
(a +b +c )2 2 2 2 4 4 4 1 + + ≥ = a( 2 2
b − bc + c ) 2 2 a b a c a( 2 2
b − bc + c ) 2 2 2 2
+ a b + a c a b − bc + c + a(b + c)  
Theo bất đẳng thức Cauchy ta có: 2 + +
a(b + c) a (b c)2 ≤ ⇒ 2 1 1 ≥ 2 2
a b − bc + c + a(b + c) 2    
a + b + c  2 2 ( )2
a b − bc + c +   2   2 2 = =
. Bây giờ ta chứng minh : a( 2 2 2
a + 3b + 3c ) a( 2 3− 2a ) 2 2 3 2 2 ≥ ⇔ − ≤ ⇔ + + ≥ . Theo bất đẳng a( 2 a 3 2a 2 2a 3a 2 3− 2a ) ( ) 2 2
thức Cauchy cho 3 số ta có: 3 2 2 2a + +
≥ 3a . Dấu bằng xảy ra khi và 2 2 chỉ khi 2 a = b =
,c = 0 . Ta cũng có thể chứng minh: 2 THCS.TOANMATH.com a( a ) a a ( a )2 2 3  1 3 2 2 2 3 2 0 2 2 a  − ≤ ⇔ − + ≥ ⇔ − + ≥   0 . Bất đẳng  2 
thức này luôn đúng.
Ví dụ 14) Cho các số thực x, y sao cho 2 2
x y + 2y +1 = 0. Tìm GTNN, GTLN của xy P =
(Trích đề tuyển sinh vào lớp 10 chuyên Trường 3y +1
chuyên – KHTN- ĐHQG Hà Nội 2015). Lời giải:
Từ giả thiết ta suy ra y ≠ 0 . 2   2 2 2 1 2 2 1
x y + 2y +1 = 0 ⇒ x + + =1 ⇔ x + +1 =   1. Đặt 1 a = +1. Ta 2 y yyy được 2 2
x + a =1. Ta có: x x 2 P = =
⇒ 2P = x − Pa ⇒ 4P = (x − Pa)2 1 . Theo bất đẳng thức a + 2 3+ y
Bunhiacopxki ta có: (x − Pa)2 ≤ ( 2 + P )( 2 2 x + a ) 2 1 =1+ a . Suy ra 2 2 2 3 3
4P ≤1+ P ⇔ 3P ≤1 ⇔ − ≤ P ≤ . Với 3 2 3 x = ; y = ⇒ P = , 3 3 2 3 3 − 3 2 3 x =
; y = − ⇒ P = −
. Vậy GTLN của P là 3 , GTNN của P là 2 3 3 3 3 − 3
2. Kỹ thuật tách ghép
Để giải quyết những bài toán dạng này người giải cần linh hoạt trong việc
tách các nhóm số hạng sao cho đảm bảo dấu bằng và tạo ra các bất đẳng thức phụ quen thuộc. THCS.TOANMATH.com
Ta cần chú ý các bất đẳng thức quen thuộc sau: 1 1  1 1  ≤ + và
a b 4  a b  +   1 1  1 1 1  ≤ + + .
a b c 9  a b c  + +  
Ví dụ 1: Cho các số thực dương a,b,c . Chứng minh: bc ca ab a + b + c + + ≤
2a + b + c 2b + c + a 2c + a + b 4 Giải: Ta có: 1 1 4 1  1 1  = ≤ +
2a b c 4 (a b) (a c) 4  a b a c  + + + + + + +  Từ đó suy ra: bc 1  bc bc  1 ∑ ≤ ∑ + = (a + b +   c)
2a + b + c 4  a + b a + c  4
Ví dụ 2: Cho các số thực dương a,b,c . Chứng minh: 2 2 2 (b + c) (c + a) (a + b) + + ≤ 3 2 2 2 2 2 2
b + c + a(b + c) c + a + b(c + a) a + b + c(a + b) Giải: Ta có: 2 2 2 2 (b + c) (b + c) b c b c = ≤ + = + . 2 2
b + c + a(b + c) b(b + a) + c(c + a) b(b + a) c(c + a) b + a c + a 2 + Từ đó suy ra (b c)  b c  ∑ ≤ ∑ + =   3 2 2
b + c + a(b + c)
b + a c + a
Ví dụ 3: Cho các số thực dương a,b,c sao cho a + b + c = 3. Chứng minh rằng: 1 1 1 1 + + ≤ . 2 2 2 2 2 2 2 2 2
4a + b + c
4b + c + a
4c + a + b 2 Giải: THCS.TOANMATH.com Ta có: 9
(a +b + c)2 2 2 2 a b c = ≤ + + 2 2 2 2 2 2 2 2 2 2 2 2 2
4a + b + c
2a + (a + b ) + (a + c ) 2a
(a + b ) (a + c ) 2 2 2   Suy ra 9 a b c 9 ∑ ≤ ∑ + + = 2 2 2  2 2 2 2 2 4a b c 2a (a b ) (a c ) + + + +  2
Ví dụ 4: Cho các số thực a,b,c sao cho 2 2 2
a + b + c =1.Chứng minh rằng: bc ca ab 3 + + ≤ 2 2 2
a +1 b +1 c +1 4 Giải: bc ca ab
1 (b + c)2 (c + a)2 (a + b)2  Ta có: + + ≤  + +  2 2 2 2 2 2
a +1 b +1 c +1 4  a +1 b +1 c +1    Mặt khác ta có: (b + c)2 (b + c)2 2 2 b c = ≤ + . Từ đó suy ra 2 2 2 2
a + a + b + c ( 2 2 a + b ) + ( 2 2 a + c ) ( 2 2 a + b ) ( 2 2 a + c ) (b c)2  2 2 b c  + ∑ ≤ ∑  +
 = 3 . Suy ra điều phải chứng minh. 2 a +1 ( 2 2 a + b ) ( 2 2 a + c )   Ví dụ 5:
Cho các số thực dương a,b,c . Chứng minh rằng: b + c c + a a + b 1 1 1 + + ≤ + + . 2 2 2
a + bc b + ac c + ab a b c Giải: Ta có: b + c (b + c)2 (b + c)2 2 2 b c = = ≤ + 2 a + bc ( 2
a + bc)(b + c) c( 2 2
a + b ) + b( 2 2
a + c ) c( 2 2
a + b ) b( 2 2 a + c ) THCS.TOANMATH.com . Từ đó suy ra :  2 2   2 2 b c b c b a  + 1 ∑ ≤ ∑  +  = ∑  +  = ∑ 2 a + bcc  ( 2 2
a + b ) b( 2 2 a + c ) c   ( 2 2
a + b ) c( 2 2 a + b ) c
Chú ý: Nếu ta thay (a b c)  1 1 1 , , , ,  → 
thì thu được bất đẳng thức mới là: a b c    2 2 2
a (b + c) b (c + a) c (a + b) + +
≤ a + b + c 2 2 2 a + bc b + ca c + ab 2 + +
Nếu phân tích: a (b c) bc(b c) = b + c −
thì thu được bất đẳng thức mới: 2 2 a + bc a + bc
bc(b + c) ca(c + a) ab(a + b) + +
≥ a + b + c . Đây là các bất đẳng thức đẹp 2 2 2 a + bc b + ca c + ab và khó.
Ví dụ 6: Cho các số thực dương a,b,c . Chứng minh rằng: 2 2 2 a b c + + ≥ 1 2 2 2
a + 2bc b + 2ac c + 2ab Giải: Ta có: a b c
(a +b + c)2 2 2 2 + + ≥ =1 2 2 2 2 2 2
a + 2bc b + 2ac c + 2ab a + 2bc + b + 2ac + c + 2ab Thay (a b c)  1 1 1 , , , ,  →  ta thu được kết quả: a b c    bc ca ab + + ≥1 2 2 2 bc + 2a ca + 2b ab + 2c 2 Mặt khác ta có: bc 2 = 1 a −
nên bất đẳng thức trên có thể viết lại 2 2 bc + 2a 2a + bc thành: THCS.TOANMATH.com 2 2 2 a b c + + ≤ 1 . Thay (a b c)  1 1 1 , ,  , ,  → ta lại thu 2 2 2
2a + bc 2b + ac 2c + ab a b c    được: bc ca ab + + ≤1 2 2 2
a + 2bc b + 2ac c + 2ab
Những bất đẳng thức này có ứng dụng rất quan trọng.
Ví dụ 7: Cho các số thực dương a,b,c . Chứng minh rằng: 2 2 2 a b c 1 + + ≤
(2a + b)(2a + c) (2b + c)(2b + a) (2c + a)(2c + b) 3 Giải: Ta có a a 1 (2a + a)2 2 2 2 1  4a = = ≤ 2 2
(2a b)(2a c) 2a(a b c) 2a bc 9 2a(a b c) 2a bc 9  + + + + + + + + + +
2a(a + b + Từ đó suy ra: 2 2 2 2 a 1  4a a  1  2a a  ∑ ≤ ∑ +  = ∑ + 2  2
(2a b)(2a c) 9  2a(a b c) 2a bc  9 a b c 2a bc + + + + + + + + 
. Áp dụng kết quả của VD 6 ta suy ra điều phải chứng minh.
Ví dụ 8: Cho các số thực dương a,b,c sao cho ab + bc + ca = 3. Chứng minh rằng: 1 1 1 3 + + ≥ 2 2 2
a +1 b +1 c +1 2 Giải: 2 Ta có: 1 =1 a −
nên bất đẳng thức tương đương với 2 2 a +1 a +1 2 2 2 a b c 3 + + ≤ . 2 2 2
a +1 b +1 c +1 2 THCS.TOANMATH.com 2 2 2 a b c 1 ⇔ + + ≤ . Ta có: 2 2 2
3a + 3 3b + 3 3c + 3 2 4a 4a (a + a)2 2 2 2 2 a a = = ≤ + 2 2 2 2
3a + 3 3a + ab + bc + ca a(a + b + c) + 2a + bc a(a + b + c) 2a + bc 2 a a = +
Tương tự với 2 số hạng còn lại ta có: 2
(a + b + c) 2a + bc 2 2 a 1  a a  1 ∑ ≤ ∑ +  ≤ 2 2
3a + 3 4  a + b + c 2a + bc  2 2
Ở đây ta đã sử dụng kết quả: a ∑ ≤ 1 2 2a + bc
Ví dụ 9: Cho các số thực dương a,b,c . Chứng minh: 2 2 2 a b c 1 + + ≤ 2 2 2 2 2 2
5a + (b + c)
5b + (c + a)
5c + (a + b) 3 Giải: Ta có: 9a 9a (a + 2a)2 2 2 = = 2 2
5a + (b + c) ( 2 2 2
a + b + c ) 2 + 2(2a + bc) ( 2 2 2
a + b + c ) 2 + 2(2a + bc) 2 2 2 2 a 4a a 2a ≤ ( + = + 2 2 2
a + b + c ) 2
2(2a + bc) ( 2 2 2
a + b + c ) 2 2a + bc 2 2 2   Từ đó suy ra: a 1 a 2a 1 ∑ ≤ ∑ + ≤ 2 2  2 2 2 2 5a (b c) 9 a b c 2a bc  + + + + +  3
Ví dụ 10: Cho các số thực dương a,b,c thỏa mãn: a + b + c =1. Chứng minh: ab bc ca 1 + + ≤
3ab + 2b + c 3bc + 2c + a 3ca + 2a + b 4 Giải: THCS.TOANMATH.com Ta có:
ab + b + c = ab + b + c a + b + c = (ab + bc + ca) + ( 2 3 2 3 2 ( )
c + 2ab) + 2b (1+1+ 2)2 Từ đó ta có: 1 1 1 ( ≤ + +
ab + bc + ca) + ( 2 c + 2ab) 2
+ 2b ab + bc + ca c + 2ab 2b Như vậy: ab 1  ab ab ab 1  ab ab a  ≤ + + = + +  2   2
3ab 2b c 16 ab bc ca c
2ab 2b  16 ab bc ca c 2ab 2 + + + + + + + +  Từ đó suy ra: ab 1  ab ab a  1 ∑ ≤ ∑ + + ≤  . 2 3ab 2b c 16 ab bc ca c 2ab 2 + + + + +  4
3. Kỹ thuật thêm bớt.
Ví dụ 1: Cho các số thực dương a,b,c sao cho 2 2 2
a + b + c = 3. Chứng minh rằng: 1 1 1 + + ≥ 3
2 − a 2 − b 2 − c
Phân tích: Nếu ta áp dụng trực tiếp bất đẳng thức: x y z ( + + )2 2 2 2 x y z + + ≥
thì phần sau sẽ bị ngược dấu. Để khắc phục ta a b c a + b + c thêm bớt như sau: − + Xét 1 1 2m ma − m =
ta chọn m sao cho 1− 2m + ma > 0 và 2 − a 2 − a
1− 2m + ma chỉ còn đơn giản một số hạng. Điều này làm ta nghỉ đến 1 m = . 2
Từ đó ta có cách chứng minh như sau: 1 1 1 1 1 1 3 a b c − + − + − ≥ ⇔ + + ≥ 3
2 − a 2 2 − b 2 2 − c 2 2
2 − a 2 − b 2 − c THCS.TOANMATH.com 2 2 2 a b c ⇔ + +
≥ 3 .Áp dụng bất đẳng thức: 2 2 2 2a − a 2b − b 2c − c x y z ( + + )2 2 2 2 x y z
(a +b + c)2 + + ≥ ta có: VT ≥ A B C A + B + C
a + b + c − ( 2 2 2 2(
) a + b + c )
(a +b + c)2
(a +b + c)2 Ta cần chứng minh: ≥ ⇔ ≥
2(a + b + c) − ( 3 3 2 2 2
a + b + c )
2(a + b + c) − 3
⇔ (a + b + c)2 − 6(a + b + c) + 9 ≥ 0 ⇔ (a + b + c − )2 3 ≥ 0
Ví dụ 2: Cho các số thực dương a,b,c sao cho ab + bc + ca = 3. Chứng minh rằng: 1 1 1 + + ≤1 2 2 2
a + 2 b + 2 c + 2 Phân tích: 2 − − Xét: 1 1 2m ma − m = ta nghỉ đến chọn 1
m = . Khi đó ta có: 2 2 a + 2 a + 2 2 2 2 2 1 1 1 1 1 1 1 a b c − + − + − ≤ − ⇔ + + ≥ 1. 2 2 2 2 2 2
a + 2 2 b + 2 2 c + 2 2 2
a + 2 b + 2 c + 2 x y z ( + + )2 2 2 2 x y z
Áp dụng bất đẳng thức: + + ≥ ta có: A B C A + B + C a b c
(a +b + c)2 2 2 2 + + ≥ . Ta cần chứng minh: 2 2 2 2 2 2
a + 2 b + 2 c + 2 a + b + c + 6
(a +b + c)2
(a +b + c)2 ≥1 ⇔ ≥1. Nhưng đây là một 2 2 2 2 2 2
a + b + c + 6
a + b + c + 2(ab + bc + ca)
đẳng thức. Suy ra điều phải chứng minh.
Ngoài ra ta có thể giải bằng cách khác như sau: THCS.TOANMATH.com (b + c)2 (b + c)2 1+ 1 1 + 2 2 = ≤
. Từ đó cộng các bất đẳng thức 2 2 2 a + 2 (  b + c a + b + c 2 a + 2) ( ) ( ) 1  +   2  
cùng chiều ta suy ra điều phải chứng minh:
Chú ý: Với các giả thiết a,b,c là độ dài ba cạnh một tam giác ta cần chú ý
biến đổi để sử dụng điều kiện: a + b − c > 0,b + c − a > 0,c + a − b > 0
Ví dụ 3: Cho a,b,c là độ dài ba cạnh một tam giác. Chứng minh rằng: a b c + + ≥ 1
3a − b + c 3b − c + a 3c − a + b Phân tích: − − + Ta viết lại: a a m(3a b c) − m = . Ta chọn 1 m = khi đó:
3a − b + c
3a − b + c 4 a 1
a + b − c − =
. Từ đó ta có bất đẳng thức cần chứng minh
3a − b + c 4 4(3a − b + c) được viết lại thành: a 1 b 1 c 1 1 − + − + − ≥ ⇔
3a − b + c 4 3b − c + a 4 3c − a + b 4 4
a + b − c
b + c − a
c + a − b + + ≥1.
3a − b + c 3b − c + a 3c − a + b Ta có
(a +b −c +b + c − a + a + c −b)2
(a +b + c)2 VT ≥ ( = =
∑ a + b − c)(3a − b + c) 1 2 2 2
a + b + c + 2(ab + bc + ca)
Đối với các bất đẳng thức dạng f (a) + f (b) + f (c) ≤ M . Ta thường thêm
bớt vào một số m để tử số có dạng bình phương. THCS.TOANMATH.com
Ví dụ 4: Cho các số thực dương a,b,c sao cho abc =1.Chứng minh rằng: 1 1 1 + + ≤ 3. 2 2 2
a − a +1 b − b +1 c − c +1 Phân tích: 2 − − + Ta lấy 1 1 m ma ma − m = để 2
1− m − ma + ma phân tích 2 2 a − a +1 a − a +1 được thành: 2 (xa + y) thì 2
1− m − ma + ma = 0 có nghiệm kép. Hay 2
∆ = m + m − m = ⇔ m( − m) 4 4 (1 ) 0
4 3 = 0 ⇔ m = . Ta viết lại bất đẳng 3 thức thành: 1 4 1 4 1 4 − + − + − ≤ 1 − hay 2 2 2
a − a +1 3 b − b +1 3 c − c +1 3 2 2 2 (2a −1) (2b −1) (2c −1) + +
≥ 3. Áp dụng bất đẳng thức: 2 2 2
a − a +1 b − b +1 c − c +1 x y z ( + + )2 2 2 2 x y z + + ≥ ta thu được: A B C A + B + C
[2(a +b + c) − ]2 3 VT ≥ ( . Ta cần chứng minh: 2 2 2
a + b + c ) − (a + b + c) + 3
[ a +b + c − ]2 ≥ ( 2 2 2 2( ) 3
3 a + b + c ) − (a + b + c) + 3 hay
(a +b + c)2 + 6(ab +bc + ca) ≥ 9(a +b + c) Ta có: 2 2 2 2 2 2 2
(ab + bc + ca) = a b + b c + c a + 2abc(a + b + c) 2 2 2
≥ a bc + b ca + c ab + 2abc(a + b + c) = 3abc(a + b + c) = 3(a + b + c) . Ta quy
bài toán về chứng minh: (a + b + c)2 + 6 3(a + b + c) ≥ 9(a + b + c) . Đặt
t = 3(a + b + c) ⇒ t ≥ 3. Ta có bất đằng thức trở thành: 4 t 2 4 2
+ t ≥ t ⇔ t − t + t ≥ ⇔ t ( 3t − t + ) 2 6 3 27 54 0
27 54 = t(t − 3) (t + 6) ≥ 0 . 9
Điều này là hiển nhiên. Dấu bằng xảy ra khi và chỉ khi a = b = c =1. THCS.TOANMATH.com
Cho các số thực dương a,b,c sao cho 2 2 2
a + b + c = 3. Chứng minh rằng: a b c 1 + + ≤ . 2 2 2
a + 2b + 3 b + 2c + 3 c + 2a + 3 2
Một số cách thêm bớt không mẫu mực:
Ví dụ 5: Cho các số thực dương a,b,c sao cho a + b + c =1. 2 2 2 Chứng minh: a b c 1 + + ≤
3a +1 3b +1 3c +1 18(ab + bc + ca) Giải: 2 2 Ta có: a 1 3a 1 .  aa  = = −
. Vì vậy ta quy bài toán về chứng
3a 1 3 3a 1 3  3a 1 + + +  minh: a b c 1 + + + ≥ 1
3a +1 3b +1 3c +1 6(ab + bc + ca) a
(a +b + c)2 Ta có: 1 ∑ ≥ =
3a +1 a(3a + ) 1 + b(3b + ) 1 + c(3c + ) 1 3( 2 2 2
a + b + c ) +1 Suy ra 1 1 4 VT ≥ + ≥ = 3( 1 2 2 2
a + b + c ) +1 6(ab + bc + ca) 3(a + b + c)2 +1
Ví dụ 6: Cho các số thực dương a,b,c sao cho a + b + c =1.Chứng minh:
b c a  1+ a 1+ b 1+ 2 c + + ≥ + + 
a b c  1− a 1− b 1− c Giải: + Do 1 a 2a =
+1 nên ta viết lại bất đẳng thức thành: 1− a b + c b c a a b c 3 + + ≥ + + + . Lại có: a a ab − = nên ta sẽ
a b c b + c c + a a + b 2
c b + c c(b + c) THCS.TOANMATH.com chứng minh: ab 3 ∑
≥ . Áp dụng bất đẳng thức Cauchy Shwarz ta có:
c(b + c) 2 ab a b
(ab +bc + ca)2 2 2 ∑ = ∑ ≥ c(b + c)
abc(b + c) 2abc(a + b + c)
(ab +bc + ca)2 Ta cần chứng minh: 3
≥ nhưng đây là bài toán quen thuộc.
2abc(a + b + c) 2
Ví dụ 7: Cho các số thực dương a,b,c sao cho ab + bc + ca =1.Chứng minh: ab bc ca 3 3
a + b + c + + + ≥
b + c c + a a + b 2 Giải: 2
Nhân 2 vế với a + b + c và chú ý: ab ( + + ) a b a b c = ab + . Ta viết bất b + c b + c
đẳng thức cần chứng minh thành: 2 2 2
(a +b + c)2 a b b c c a 3 3 +1+ + + ≥
(a +b + c)
b + c c + a a + b 2 a b b c c a
(ab +bc + ca)2 2 2 2 Ta có: 1 + + ≥ = .
b + c c + a a + b b(b + c) + c(c + a) + a(a + b) (a + b + c)2 −1
Cuối cùng ta chứng minh: (a + b + c)2 1 3 3 +1+ ≥
a + b + c . 2 ( )
(a +b + c) −1 2
Nhưng 3 3 (a + b + c) 3
≤ (a + b + c)2 + 3 2 4   nên ta quy về:
(a +b + c)2 1 3 +1+
≥  a + b + c + 3 . Dành cho học sinh. 2 ( )2 (a b c) 1 4   + + −
4). PHƯƠNG PHÁP ĐẶT ẨN PHỤ.
Tùy theo bài toán ta có thể chọn một trong các cách đặt ẩn phụ sau: THCS.TOANMATH.com 1). (a b c)  1 1 1 , , , ,  →  a b c    2). ( , , )
ka , kb , kc a b c  →  b c a    3). ( , , )
kb , kc , ka a b c  →  a b c    2 2 2   4). ( , , ) ka →  , kb , kc a b c bc ac ab   
5). ( , , )  kbc , kca , kab a b c  →  2 2 2 a b c   
Ví dụ 1: Cho các số thực dương x, y, z sao cho xyz =1. Chứng minh rằng: 1 1 1 + + ≥ 1. 2 2 2
x + x +1 y + y +1 z + z +1
Phân tích: Nếu áp dụng trực tiếp bất đẳng thức: X Y Z ( + + )2 2 2 2 X Y Z + + ≥
thì bất đẳng thức tiếp theo bị ngược dấu. A B C A + B + C
Để không bị ngược dấu ta thay ( , , )  bc , ca , ab x y z  →  thì bất đẳng thức 2 2 2 a b c   
cần chứng minh trở thành: 4 4 4 a b c + + ≥ 1. (*) 4 2 2 2 4 2 2 2 4 2 2 2
a + a bc + b c
b + b ac + a c
c + c ab + a b X Y Z ( + + )2 2 2 2 X Y Z
Bây giờ áp dụng bất đẳng thức: + + ≥ ta có: A B C A + B + C THCS.TOANMATH.com
(a +b +c )2 2 2 2 VT ≥ . Ta cần chứng 4 2 2 2 4 2 2 2 4 2 2 2
a + a bc + b c + b + b ac + a c + c + c ab + a b minh:
(a +b +c )2 2 2 2 ≥1 4 2 2 2 4 2 2 2 4 2 2 2
a + a bc + b c + b + b ac + a c + c + c ab + a b 2 2 2 2 2 2
⇔ b c + a c + a b ≥ abc(a + b + c) . Nhưng đây là kết quả quen thuộc.
Ví dụ 2: Cho các số thực dương x, y, z sao cho xyz =1. Chứng minh rằng: 1 1 1 1 + + ≥ .
(x +1)(x + 2) (y +1)(y + 2) (z +1)(z + 2) 2 Phân tích: Đặt bc = ; ac = ; ab x y z =
bất đẳng thức cần chứng minh trở thành: 2 2 2 a b c 4 a 1 ∑
≥ . Áp dụng bất đẳng thức: 2 2
(2a + bc)(a + bc) 2 X Y Z ( + + )2 2 2 2 X Y Z + + ≥ ta có: A B C A + B + C
∑(a + b + c )2 2 2 2 VT ≥ . Ta cần chứng minh: 2 2
∑(2a + bc)(a + bc)
∑(a + b + c )2 2 2 2 2 2 2
≥ ∑(2a + bc)(a + bc) 2 2 2 2 2 2
⇔ a b + b c + c a ≥ abc(a + b + c) . Đây là kết quả quen thuộc.
Ví dụ 3: Cho 3 số thực dương x, y, z . Chứng minh rằng: 2x 2y 2z + + ≤ 3 x + y y + z z + x Giải: THCS.TOANMATH.com Đặt a = ; b = ; c x y
z = . Bất đẳng thức cần chứng minh trở thành: b c a 2 2 2 a b c 3 + + ≤
. Áp dụng bất đẳng thức 2 2 2 a + bc b + ac c + ab 2 Bunhiacopxki ta có: 2  2 2 2 a b c   a
 a(a + b)(a + c)  ∑ + +  ≤ ∑ ∑ 2 2 2   2 a + bc b + ac c + ab  
 (a + b)(a + c)  a + bc    
Mặt khác ta có: 8(a + b + c)(ab + bc + ca) ≤ 9(a + b)(b + c)(c + a). Mặt a
2(ab + bc + ca) khác ta có: 9 ∑ = ≤ . Ta quy bài
(a + b)(a + c) (a + b)(b + c)(c + a) 4(a + b + c) + +
toán về chứng minh: a(a b)(a c) ∑
≤ 2 a + b + c . Mặt khác ta có: 2 ( ) a + bc 2
a(a + b)(a + c) a (b + c) = a +
. Ta quy bài toán về chứng minh: 2 2 a + bc a + bc 2 a (b + c) ∑
≤ a + b + c 2 a + bc
KỸ THUẬT ĐỐI XỨNG HÓA.
Ví dụ 1: Cho các số thực dương a,b,c . Chứng minh: 2a 2b 2c + + ≤ 3 a + b b + c c + a Giải: THCS.TOANMATH.com 2a a(a + c)  a(a + c) 2 2 2  Ta có: = ⇒  ∑  ≤ a + b
(a +b)(a + c) 
(a +b)(a + c)      2( + + ) 2. a b c a b c ( + +
a b)(a c) (b c)(b a) (c a)(c b) + + + + + +  
8(a + b + c)(ab + bc + ca) = (
a + b)(b + c)(c + a)
Bây giờ ta cần chứng minh:
8(a + b + c)(ab + bc + ca) ( ≤ ⇔ + + + + ≤ + + +
a + b)(b + c)(c + a) 9
8(a b c)(ab bc ca) 9(a b)(b c)(c a)
Nhưng đây là kết quả quen thuộc:
Ví dụ 2: Cho các số thực dương a,b,c . Chứng minh: a b c 3 + + ≤
a + b + 2c
b + c + 2a
c + a + 2b 2 Giải: Ta có: a
a(a + b + c) 
a(a + b + c) 2 2 2  = ⇒  ∑  ≤
a + b + 2c
(a +b + 2c)(a + 2b + c) 
(a +b + 2c)(a + 2b + c)     1  ( 2
4 ∑ a + 3∑ ab)(∑a) ∑ a
(a + 2b + c)∑  (  =
a + b + 2c)(a + 2b + c) (a +b + 2c)(a + 2b + c)(b + 2a + c) ( 2
4 ∑ a + 3∑ ab)(∑a) Ta cần chứng minh: 9 ( ≤ . Sau khi khai
a + b + 2c)(a + 2b + c)(b + 2a + c) 4
triển và thu gọn thì được: ( 3 3 3
2 a + b + c ) ≥ ab(a + b) + bc(b + c) + ca(c + a) .
Đây là bài toán quen thuộc.
Ví dụ 3: Cho các số thực dương a,b,c sao cho a + b + c =1 THCS.TOANMATH.com ab bc ca 2 Chứng minh: + + ≤ ab + bc bc + ca ca + ab 2 Giải: 2 2 ab a b
a b(a + b) Ta có: = = suy ra ab + bc a + c
(a + c)(a +b)  2
a b(a + b) 2  2  a b  2(∑ a) 2 2
∑ a b + abc ∑ a    ∑  (  ≤ ∑ +    ∑  =
a + c)(a + b) (a b)   
 (a + c)(a + b)
(a +b)(b + c)(c + a) Ta cần chứng minh: 2(∑ a) 2 2
∑ a b + abc ∑ a   1 2 2 ( )( )
≤ ⇔ 4(∑ a) ∑ a b + abc ∑ aa b b c (c a) 2   + + +
≤ (a + b + c)(a + b)(b + c)(c + a) . Khai triển và thu gọn ta quy về: ab( 2 2
a + b ) + bc( 2 2
b + c ) + ca( 2 2
c + a ) ≥ ( 2 2 2 2 2 2
2 a b + b c + c a ). Nhưng bất
đẳng thức này là hiển nhiên đúng theo BĐT cô si:
BÀI TẬP RÈN LUYỆN.
Cho các số thực dương a,b,c . Chứng minh rằng: + + 1) a b c a b c + + ≥ 2 2 2 2 2 2
b + bc + c
c + ca + a
c + ca + a
ab + bc + ca + + 2) a b c a b c + + ≥ 2 2 2 2 2 2 2 2 2
a + ab + b
b + bc + c
c + ca + a a + b + c 3)
( 2a + )( 2b + )( 2 3
3 c + 3) ≥ 4(a + b + c + )2 1 3 3 3 4) a b b c c a
abc(a + b + c) + + ≥ 2 2 2 1+ ab 1+ bc 1+ ca 1+ abc 2 2 2 5) a b c + +
≥ 1 với a + b + c = 3 2 2 2 a + 2b b + 2c c + 2a 6) ab bc ca 1 + +
≤ (a + b + c)
a + 3b + 2c b + 3c + 2a c + 3a + 2b 6 THCS.TOANMATH.com 2 2 2 7) ab bc ca a + b + c + + ≤ 2 2 2 2 2 2 2 2 2
a + 2b + c
b + 2c + a
c + 2a + b 4 8) 1 1 1 + +
≥1 với a + b + c = 3. 2 2 2
2ab +1 2bc +1 2ca +1 + + + 9)
3a b 3b c 3c a + +
≥ 4. Với a,b,c là độ dài 3 cạnh tam giác
2a + c 2b + a 2c + b + + 10) 10) a b c ab bc ca 5 + + +
≤ . Với a,b,c là độ dài 3 2 2 2
b + c c + a a + b a + b + c 2 cạnh tam giác 11) ab bc ca 1 + + ≥
biết a,b,c ≥ 0 sao cho không 2 2 2 2 2 2 a + b b + c c + a 2
có 2 số nào đồng thời bằng 0 và 2 2 2
a + b + c = 2(ab + bc + ca) . 12) a b c + +
≤ 1 biết a,b,c ≥ 0 sao cho 4a + 3bc 4b + 3ca 4c + 3ab
không có 2 số nào đồng thời bằng 0 và a + b + c = 2 .
HƯỚNG DẪN GIẢI BÀI TẬP + + 1) a b c a b c + + ≥ 2 2 2 2 2 2
b + bc + c
c + ca + a
c + ca + a
ab + bc + ca 2 Ta có: a a = . Suy ra 2 2 2 2
b + bc + c
ab + abc + ac a
(a +b + c)2 2 ∑ ≥ 2 2 2 2 2 2
ab + abc + ac
ab + ac + bc + ba + 3abc
(a +b + c)2 + + Ta cần chứng minh: a b c ≥ 2 2 2 2
ab + ac + bc + ba + 3abc ab + bc + ca
⇔ (ab + bc + ca)(a + b + c) 2 2 2 2
≥ ab + ac + bc + ba + 3abc (Nhưng đây là hằng đẳng thức) 2) Ta có: 2 2 2
ab + bc + ca ≤ a + b + c THCS.TOANMATH.com + + Suy ra a b c a b c + + ≥ 2 2 2 2 2 2 2 2 2
b + bc + c
c + ca + a
c + ca + a a + b + c 2 2 
b + c +1  b + c +1 
3) (a + b + c + )2 1 = a + 3 ≤   ( 2a +3) ( ) 1  +    3   3     b + c +1 
Từ đó suy ra 4(a + b + c + ) 1 ≤ 4(a + 3) ( )2 2 2 1  +  . Ta chứng minh:  3    2  b + c +  4( 1 2 a + 3) ( ) 1  +  ≤ ( 2 a + 3)( 2 b + 3)( 2
c + 3) ⇔ 43+ (b + c + )2 1  ≤ 3( 2 b + 3)( 3      
Bất đẳng thức này tương đương với:
 + (b + c + )2 ≤ ( 2b + )( 2c + ) 2 2 2 2 4 3 1 3 3
3 ⇔ 4 4 + b + c + 2bc + 2b + 2c ≤ 9b + 9c + 3b     ⇔ ( 2 2 b + c ) 2 2 5
+ 3b c −8(b + c) −8bc +13 ≥ 0 . Ta viết lại bất đẳng thức trên thành: ( 2 2
5 b + c ) − 2bc −8(b + c) +8+ 3(bc − )2 1 ≥ 0 . Ta có 2 2
b + c ≥ 2bc, ( 2 2
b + c ) ≥ (b + c)2 ⇒ ( 2 2 2
4 b + c ) ≥ 2(b + c)2 . Nên ( 2 2
b + c ) − bc − b + c + + (bc − )2 2 5 2 8( ) 8 3
1 ≥ 2(b + c) −8(b + c) + 8 + 2bc − 2bc + 3(bc −1 = (b + c − )2 2 2
2 + 3(bc −1) ≥ 0 . Dấu bằng xảy ra khi và chỉ khi a = b = c =1 3 3 3 4) a b b c c a
abc(a + b + c) + + ≥ 2 2 2 1+ ab 1+ bc 1+ ca 1+ abc THCS.TOANMATH.com 3 4 2 2 Ta có: a b a b c = Suy ra 2 2 2 3 2 1+ ab abc + a b c a b a b c
(a bc+b ac+c ab)2 2 2 2 3 4 2 2 ∑ = ∑ ≥ 2 2 2 3 2 2 2 3 2 2 2 3 2 2 2 3 2 1+ ab abc + a b c
abc + a b c + bca + b c a + cab + c a b 2 2 2
a b c (a + b + c)2 = 2 2 3 2 2 2 3 2 2 2 3 2
abc + a b c + bca + b c a + cab + c a b Ta chứng minh: 2 2 2
a b c (a + b + c)2
abc(a + b + c) ≥ 2 2 3 2 2 2 3 2 2 2 3 2
abc + a b c + bca + b c a + cab + c a b 1+ abc ( + abc) 2 2 3 2 2 2 3 2 2 2 3 2 1
abc(a + b + c) ≥ abc + a b c + bca + b c a + cab + c a b . Đây
là đẳng thức.Dấu bằng xảy ra khi và chỉ khi a = b = c . 2 4 5) a a = . 2 2 2 2 a + 2b a + 2a b a a
(a +b +c )2 2 2 2 2 4 Suy ra ∑ = ∑ ≥ . Ta chứng minh: 2 3 2 2 3 2 2 a + 2b a + 2a b ∑ a + 2∑ a b
(a +b +c )2 2 2 2 ≥1 3 2 2 ∑ a + 2∑ a b
(a +b +c )2 2 2 2 Hay 4 4 4 3 3 3
≥1 ⇔ a + b + c ≥ a + b + c 3 2 2 ∑ a + 2∑ a b Ta cần chứng minh: 4 4 4 3 3 3
a + b + c ≥ a + b + c với a + b + c = 3. Ta chứng minh: ( 4 4 4
a + b + c ) ≥ ( 3 3 3
a + b + c )(a + b + c) ⇔ ( 4 4 4
a + b + c ) ≥ ab( 2 2
a + b ) + bc( 2 2 3 2 b + c Để ý rằng:
(a +b ) = (a +b )2 4 4 2 2 = ( 2 2 a + b )( 2 2
a + b ) ≥ ab( 2 2 a + b ) 4 4
⇔ a + b ≥ ab( 2 2 2 2 a + b )
. Cộng ba bất đẳng thức cùng chiều ta suy ra điều phải chứng minh: 6) Ta có: THCS.TOANMATH.com 1 1 1  1 1 1  ab 1  ab = ≤ + + ⇒ ≤ +
a 3b 2c (a c) (b c) 2b 9  a b b c 2b 
a 3b 2c 9  + + + + + + + + + +  a + b
Tương tự ta có 2 bất đẳng thức nữa và cộng lại thì thu được: ab bc ca 1  ab ab 1 bc bc 1 c + + ≤ + +  a + + + b +
a + 3b + 2c b + 3c + 2a c + 3a + 2b 9  a + c b + c 2
b + a c + a 2 c + ab bc ca 1 ⇔ + +
≤ (a + b + c)
a + 3b + 2c b + 3c + 2a c + 3a + 2b 6 2 2 2 7) + + Ta có ab bc ca a b c + + ≤ 2 2 2 2 2 2 2 2 2
a + 2b + c
b + 2c + a
c + 2a + b 4 ab b  (a +b)2 2  2 2 b a b  ≤   ≤ + 2 2 2 2 2 2 2  2 2 2 2 a 2b c 4 a b b c  4   a b b c  + + + + + + +  Suy ra 2 2 2 2 2 2 b a bc b ca a c
a + b + c VT ≤  +  +  +  +  +  = 2 2 2 2 2 2 2 2 2 2 2 2
4  a + b b + c  4  b + c
c + a  4  a + b c + a  4 8) 1 1 1 + + ≥1 2 2 2
2ab +1 2bc +1 2ca +1 2 Ta có: 1 c = suy ra 2 2 2 2
2ab +1 2ab c + c
(a +b + c)2 VT ≥ . Ta chứng minh: 2 2 2 2 2 2 2 2 2
a + b + c + 2a b c + 2a bc + 2ab c
(a +b + c)2 2 2 2 2 2 2
≥1 ⇔ ab + bc + ca ≥ a b c + a bc + ab c 2 2 2 2 2 2 2 2 2
a + b + c + 2a b c + 2a bc + 2ab c
⇔ ab + bc + ca ≥ abc(a + b + c) ⇔ abc ≤1. Theo bất đẳng thức Cô si ta có: 3
3 = a + b + c ≥ 3 abc = 3 ⇒ abc ≤1 là điều phải chứng minh. THCS.TOANMATH.com + − + − 9) Ta xét: 3a b
a(3 2m) b mc − m = 2a + c 2a + c + + −
Chọn m =1 để xuất hiện: 3a b −1 a b c = 2a + c 2a + c
Khi đó ta có: Bất đẳng thức cần chứng minh có dạng:
a + b − c b + c − a c + a − b + + ≥ 1 2a + c 2b + a 2c + b
(a +b −c +b + c − a + c + a −b)2 (a +b + c)2 Suy ra VT ≥ = = 1. Đpcm
∑(a + b − c)(2a + c)
(a +b + c)2
10) Ta viết lại bất đẳng thức thành: a b c 1 + + 1− +1− +1 ab bc ca − ≥ + 2 2 2 b + c c + a
a + b 2 a + b + c
b + c − a a + c − b a + b − c
(a +b + c)2 ⇔ + + ≥ b + c c + a a + b ( 2 2 2
2 a + b + c )
4(a + b + c)2
(a +b + c)2 Ta có VT ≥ ( =
∑ b + c − a)(b + c) 2( 2 2 2
a + b + c ) 2 2 + 11) Ta có: ab ab a b 2ab = ≥ . 2 2 2 2 2 2 a + b a + b a + b
Ta quy bài toán về chứng minh: 2ab 2bc 2ca + + ≥1. Hay 2 2 2 2 2 2 a + b b + c c + a
(a +b)2 (b + c)2 (c + a)2 + +
≥ 4 . Thật vậy ta có: 2 2 2 2 2 2 a + b b + c c + a THCS.TOANMATH.com
4(a + b + c)2
4(a + b + c)2 VT ≥ = = . Dấu bằng xảy 2( 4 2 2 2
a + b + c ) ( 2 2 2
a + b + c ) + 2ab + 2bc + 2ca
ra khi và chỉ khi a = ,
b c = 0 và các hoán vị. 12) Ta có: 2 ( ) a b c VT a b c  ≤ + + + + 
 4a 3bc 4b 3ca 4c 3ab  + + +  2 a b c  = + +  . Ta chứng minh:
 4a 3bc 4b 3ca 4c 3ab  + + +  a b c 1 + + ≤
4a + 3bc 4b + 3ca 4c + 3ab 2 1 a 1 b 1 c 1 ⇔ − + − + − ≥
4 4a + 3bc 4 4b + 3ca 4 4c + 3ab 4 bc ca ab 1 ⇔ + + ≥ .
4a + 3bc 4b + 3ca 4c + 3ab 3 Ta có:
(ab +bc + ca)2
(ab +bc + ca)2 1 VT ≥ = = 3( 2 2 2 2 2 2
a b + b c + c a + 4abc) 3( 2 2 2 2 2 2
a b + b c + c a + 2abc(a + b + c)) 3 THCS.TOANMATH.com