





















Preview text:
BẤT ĐẲNG THỨC HÌNH HỌC
I). SỬ DỤNG CÁC TÍNH CHẤT HÌNH HỌC ĐƠN GIẢN.
1) Bất đẳng thức liên hệ giữa độ dài các cạnh một tam giác. AB AC BC AB BC Chú ý rằng: a). Với 3 điểm , A ,
B C bất kỳ ta luôn có: AB BC
AC . Dấu bằng xảy ra khi và chỉ khi , A ,
B C thẳng hàng và điểm B nằm giữa hai điểm , A C . b) Với 3 điểm , A ,
B C bất kỳ ta luôn có: AB AC
BC . Dấu bằng xảy ra khi và chỉ khi , A ,
B C thẳng hàng và điểm B nằm giữa hai điểm , A C . c) Cho hai điểm ,
A B nằm về một phía đường thẳng (d). Điểm M chuyển
động trên đường thẳng (d). Gọi A' là điểm đối xứng với A qua (d). Ta có kết quả sau: B A M (d) 0 M1 M A' + MA MB MA' MB
A'B . Dấu bằng xảy ra khi và chỉ khi M là
giao điểm cuả A'B và đường thẳng (d).( M trùng với M ) 0 THCS.TOANMATH.com + MA MB
AB . Dấu bằng xảy ra khi và chỉ khi M là giao điểm cuả
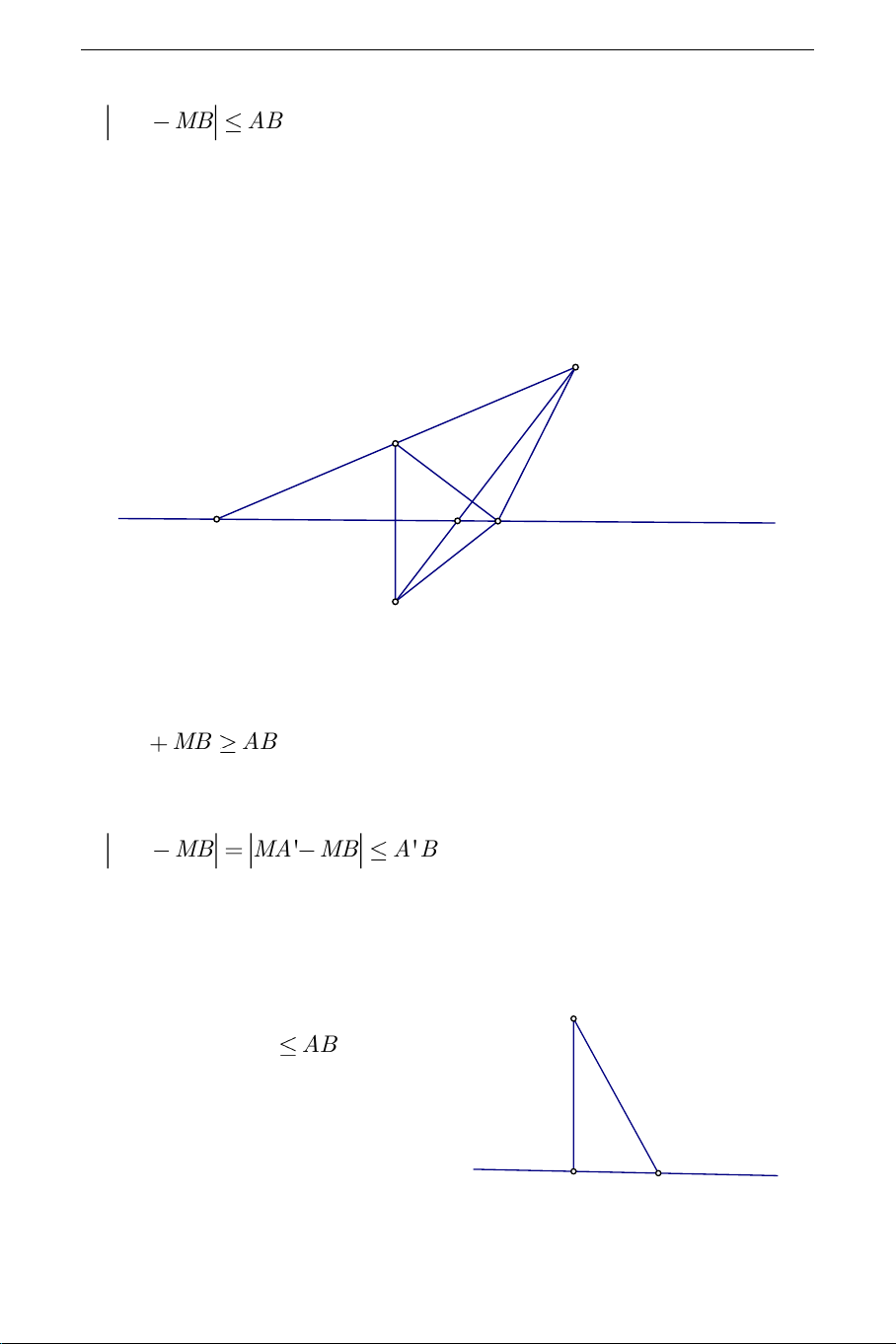
AB và đường thẳng (d)( M trùng với M ). 1 d) Cho hai điểm ,
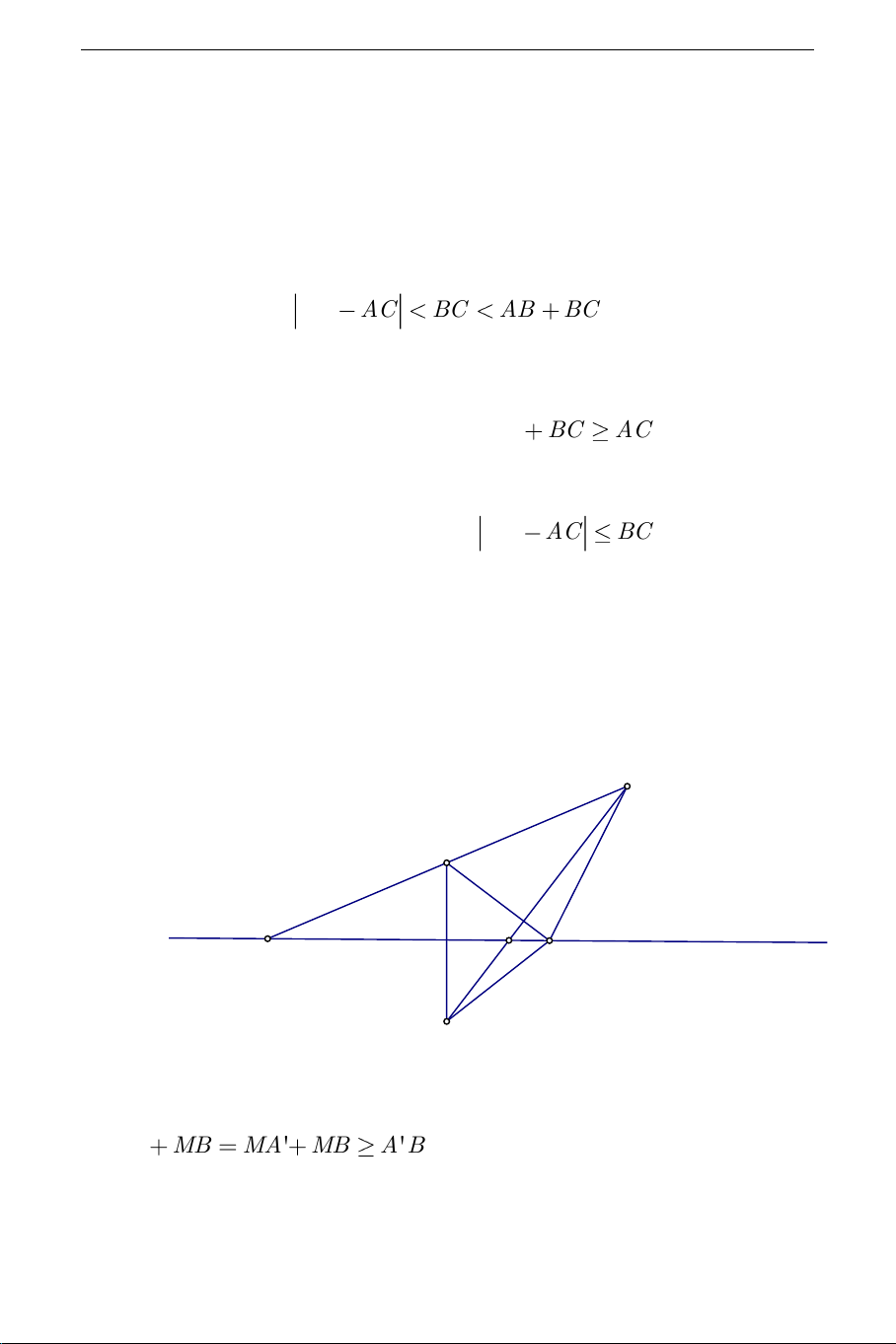
A B nằm về hai phía đường thẳng (d). Điểm M chuyển
động trên đường thẳng (d). Gọi A' là điểm đối xứng với A qua (d). Ta có kết quả sau: B A' M (d) 0 M1 M A + MA MB
AB . Dấu bằng xảy ra khi và chỉ khi M là giao điểm cuả
AB và đường thẳng (d).( M trùng với M ) 0 + MA MB MA' MB
A'B . Dấu bằng xảy ra khi và chỉ khi M là
giao điểm cuả A'B và đường thẳng (d)( M trùng với M ). 1
e) Trong quá trình giải toán ta cần lưu ý tính chất: Đường vuông góc luôn
nhỏ hơn hoặc bằng đường xiên. A Trong hình vẽ: AH AB H B THCS.TOANMATH.com
2) Trong một đường tròn, đường kính là dây cung lớn nhất
3) Cho đường tròn ( ; O )
R và một điểm A . Đường thẳng AO cắt đường
tròn tại hai điểm M ,M . Giả sử AM
AM . Khi đó với mọi điểm M 1 2 1 2
nằm trên đường tròn ta luôn có: AM AM AM 1 2
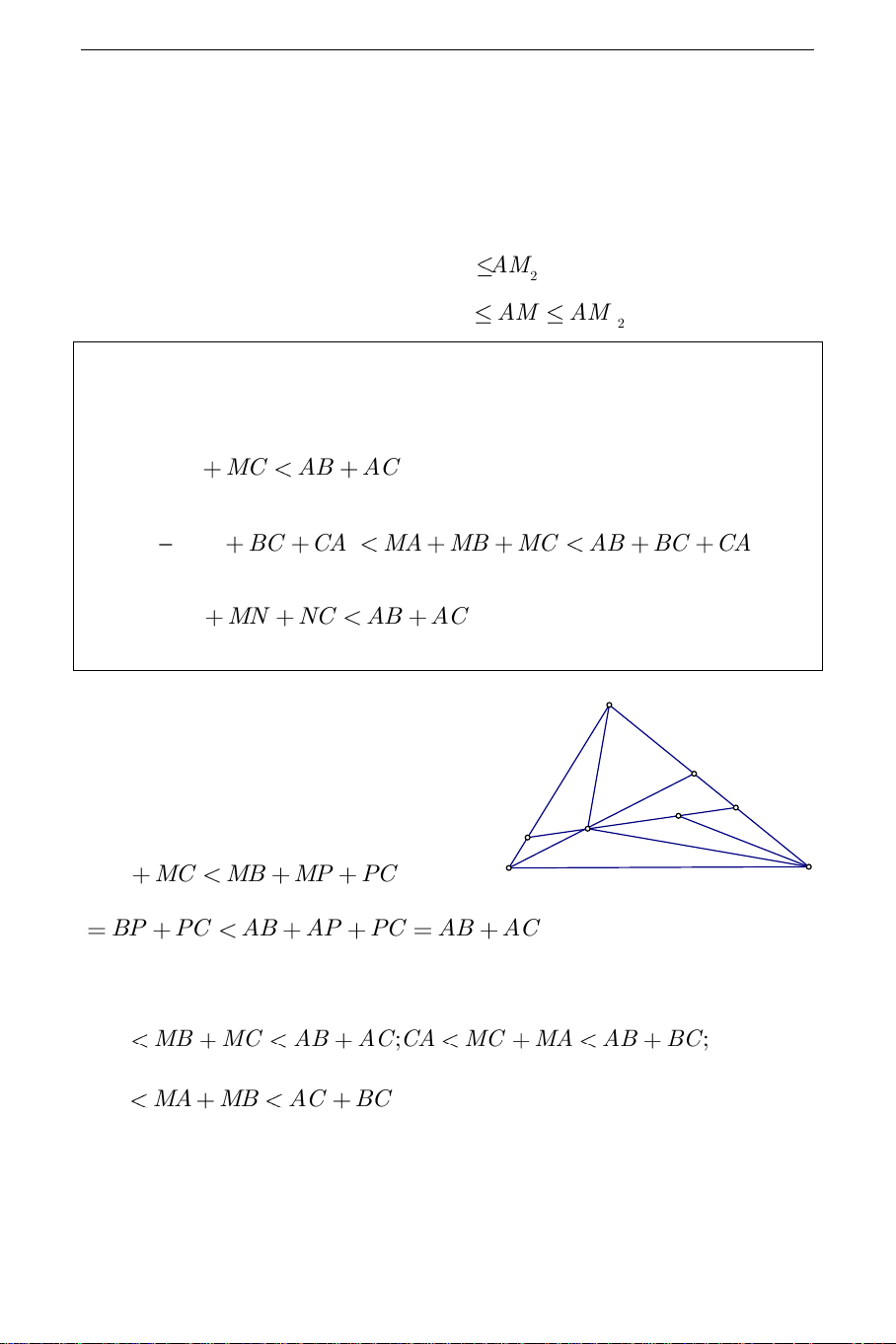
Ví dụ 1:Cho tam giác ABC và điểm M nằm trong tam giác . Chứng minh rằng: a) MB MC AB AC 1 b) AB BC CA MA MB MC AB BC CA 2 c) BM MN NC AB
AC trong đó điểm N nằm trong tam
giác sao cho MN cắt hai cạnh , AB AC A Hướng dẫn giải:
a) Đường thẳng BM cắt AC ở P . P N F
Áp dụng BĐT(1) ta có: M E MB MC MB MP PC B C BP PC AB AP PC AB AC b) Theo trên ta có: BC MB MC AB AC;CA MC MA AB BC; AB MA MB AC
BC . Cộng theo từng vế các BĐT trên ta có điều phải chứng minh. THCS.TOANMATH.com
c) Áp dụng câu 1) ta có: BM MN NC BE EM MN NF FC BE EF FC BE EA AF FC AB AC .
Ví dụ 2: Cho tam giác ABC và 3 trung tuyến AM,BN,CP . Chứng minh rằng: AB AC BC AB AC a) AM 2 2 3 AB BC CA b) AM BN CP AB BC CA 4 c) Giả sử AB AC . Gọi A ,
D AM theo thứ tự là đường phân giác,
đường trung tuyến của tam giác ABC . Chứng minh rằng: AB AC BC AB AC AD AM 2 2 Hướng dẫn giải: B D
a). + Xét các tam giác M , AB MAC ta có: M AM AB BM,AM AC MC Suy ra 2AM AB AC (MC MC ) A C 2AM AB AC BC
+ Gọi D là điểm đối xứng với A qua M thì ABDC là hình bình hành nên AB CD và AD
2AM . Trong tam giác ACD ta có: AD AC CD 2AM AB AC AB AC BC AB AC Như vậy: AM . 2 2 THCS.TOANMATH.com
b). Áp dụng bất đẳng thức ở câu a) Cho 3 đường trung tuyến AM, BN,CP AB AC BC AB AC ta có: AM , 2 2 BC AB AC AC BC BN , 2 2 BC AC AB AC BC CP
. Cộng ba bất đẳng thức cùng chiều 2 2 3 AB BC CA ta có: AM BN CP AB BC CA . 4
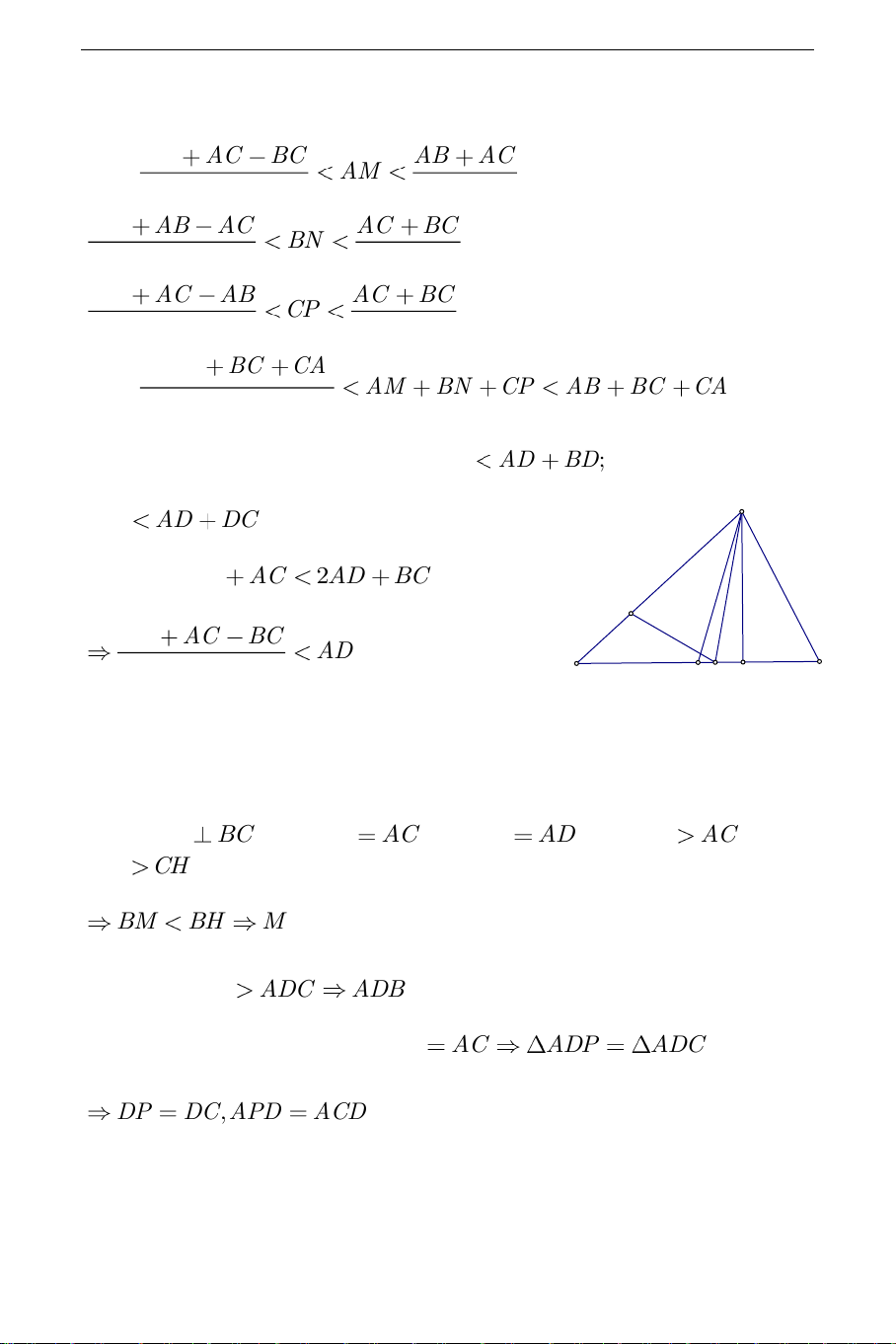
c). Trong tam giác AB , D ADC có AB AD B ; D A AC AD
DC . Cộng theo từng vế hai BĐT trên được: AB AC 2AD BC . P AB AC BC AD 2 C B M D H
Kết quả này vẫn đúng với D là điểm
bất kỳ nằm bên trong đoạn BC . Dựng AH BC . Với AB AC thì AM AD . Với AB AC thì BH CH BM BH
M thuộc đoạn BH . Hơn nữa ADB ADC
ADB tù. Do đó D thuộc đoạn BH .
Lấy điểm P trên AB sao cho AP AC ADP ADC (c.g.c) DP DC,APD ACD . THCS.TOANMATH.com + Nếu 0 ACB 90 (hình) thì 0 APD ACB 90 0 BPD 90 ACB PBD BD PD CD BM BD MH DH AM AD . + Nếu 0 ACB 90 (hình) thì BPD ACH ADC ABC BD PD CD BM BD MH DH AM AD .
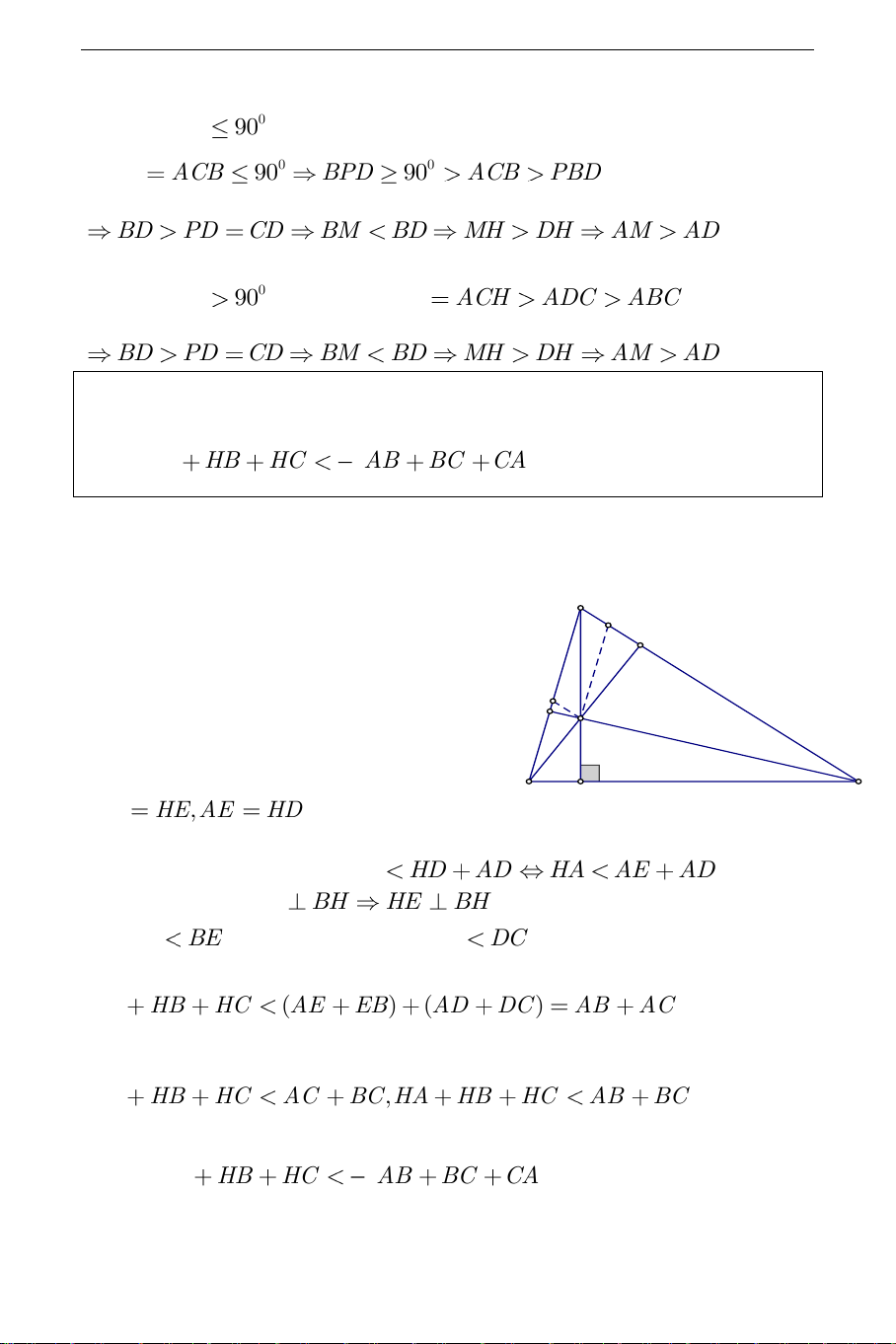
Ví dụ 3: a) Cho tam giác nhọn ABC có trực tâm là điểm H . Chứng minh 2 rằng: HA HB HC AB BC CA 3 Hướng dẫn giải:
Dựng đường thẳng qua H song song với A D
AB cắt AC tại D . Dựng đường thẳng
qua H song song AC cắt AB tại E . E H
Tứ giác AEHD là hình bình hành nên B C AD HE,AE HD A'
Xét tam giác AHD ta có: HA HD AD HA AE AD (1) . Vì
HE / /AC mà AC BH HE
BH . Trong tam giác vuông HBE ta có: HB
BE (2) Tương tự ta có: HC
DC (3). Cộng các bất đẳng thức
cùng chiều (1),(2),(3) ta suy ra HA HB HC (AE EB) (AD DC ) AB AC Tương tự ta cũng có: HA HB HC AC BC,HA HB HC AB BC 2 Suy ra HA HB HC AB BC CA . 3 THCS.TOANMATH.com
Ví dụ 4) Cho tam giác đều ABC có cạnh bằng 3a . M là một điểm tùy ý
trên cạnh BC , gọi P,Q lần lượt là hình chiếu vuông góc của M lên ,
AB AC . Tìm vị trí điểm M để:
a) PQ có độ dài nhỏ nhất
b) Dựng một đường thẳng song song với BC cắt ,
AB AC tại E,F sao cho AE
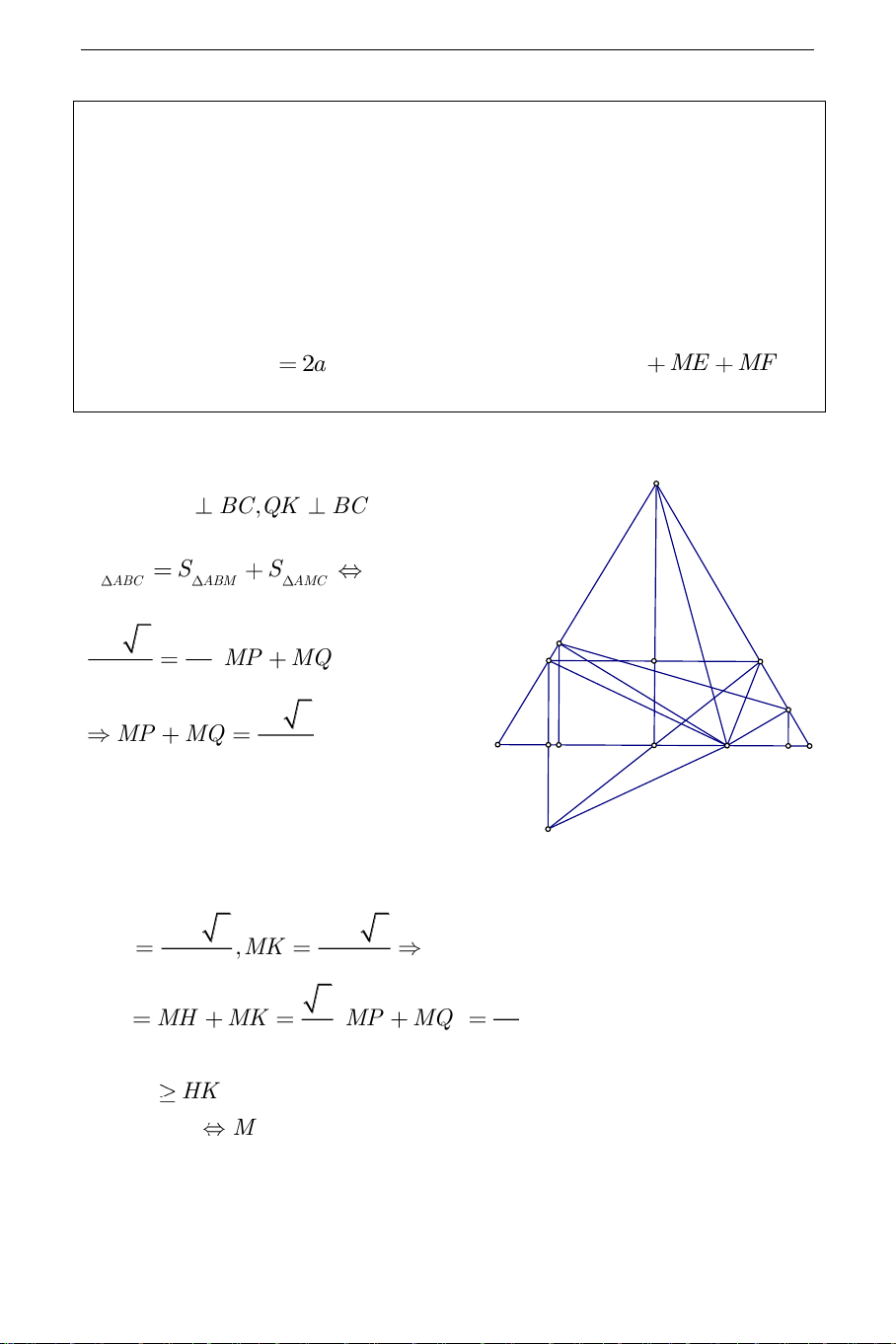
2a .Tìm vị trí điểm M sao cho MA ME MF nhỏ nhất. Hướng dẫn giải: A a). Hạ PH BC,QK BC . Ta có S S S ABC ABM AMC 2 9a 3 3a P MP MQ E F 4 2 Q 3a 3 MP MQ 2 B C H I M K
Áp dụng hệ thức lượng trong các tam giác R vuông MP ,
B MQC ta tính được: MP 3 MQ 3 HM ,MK 2 2 3 9a HK MH MK MP MQ . 2 4 Vì PQ
HK . Nên PQ nhỏ nhất bằng HK khi và chỉ khi PQ / /HK
M là trung điểm của BC THCS.TOANMATH.com
b). Gọi R là điểm đối xứng với E qua BC , I là trung điểm của BC . Ta dễ chứng minh được ,
R I,F thẳng hàng. 2 1 3a 3 Ta tính đươc.: 2 RF 2IF 2 a . 7a . Ta có: 3 2 ME MF MR MF RF
a 7 . Dấu bằng xảy ra khi và chỉ khi 3a 3 M
I . Ta cũng có MA AI
. Dấu bằng xảy ra khi và chỉ khi 2 3a 3 2 7 3 3 M I . Suy ra ME MF MA a 7 a . Dấu 2 2
bằng xảy ra khi và chỉ khi M I.
Ví dụ 5: Cho đường tròn ( ; O )
R và điểm A nằm ngoài đường tròn đó. Một
đường thẳng thay đổi quanh A cắt ( ; O )
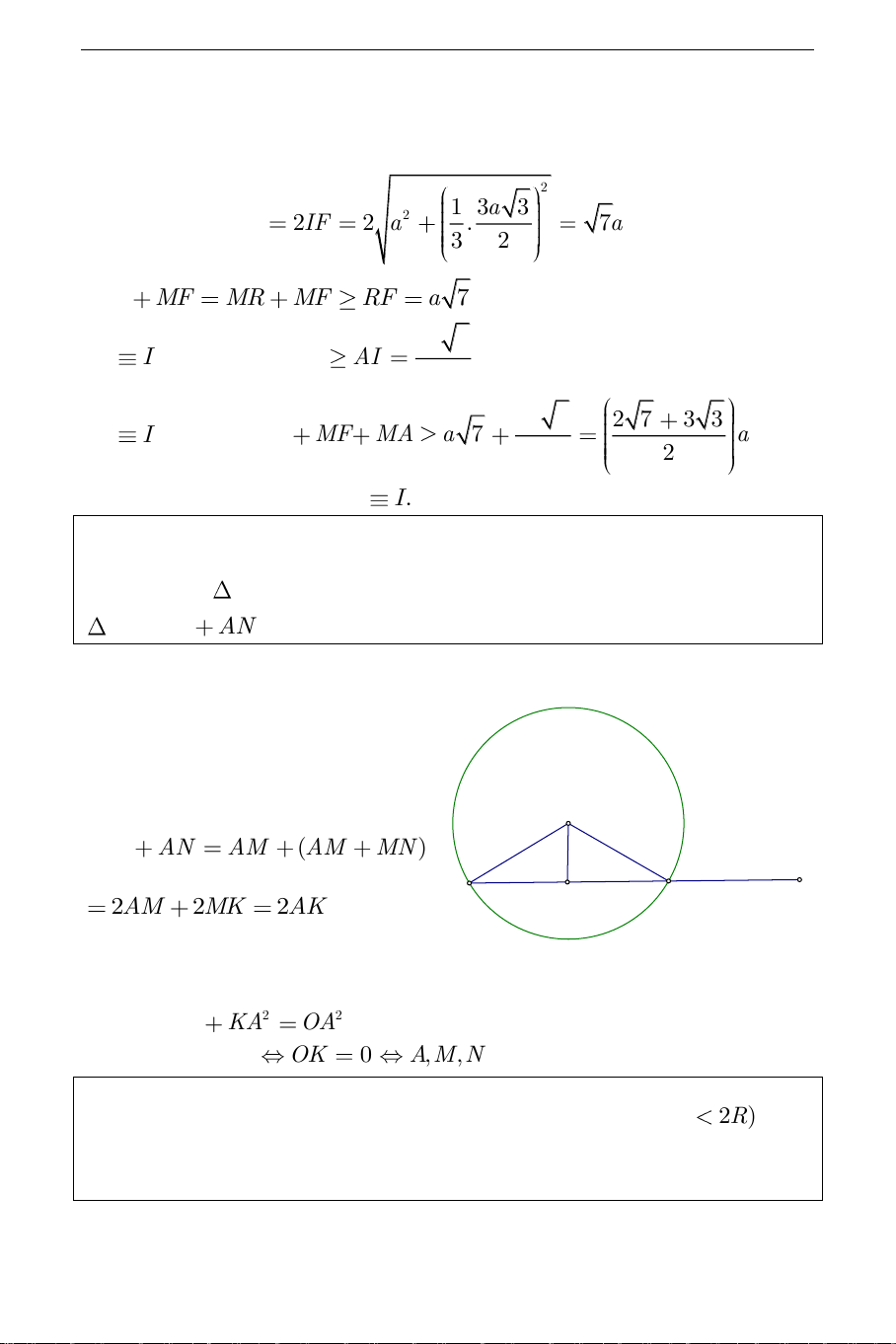
R tại hai điểm M,N . Tìm vị trí để AM AN lớn nhất. Hướng dẫn giải:
Gọi K là trung điểm của dây cung MN ta có: O AM AN AM (AM MN ) A N K M 2AM 2MK 2AK
Xét tam giác vuông OKA Ta có: 2 2 2 OK KA
OA không đổi . Như vậy AK lớn nhất khi và chỉ khi OK nhỏ nhất OK 0 ,
A M,N,O nhỏ nhất.
Ví dụ 6: Cho đường tròn ( ; O )
R và dây cung AB cố định (AB 2 ) R .
Trên cung lớn AB lấy điểm M . Tìm vị trí điểm M để chu vi tam giác
MAB lớn nhất. THCS.TOANMATH.com Hướng dẫn giải:
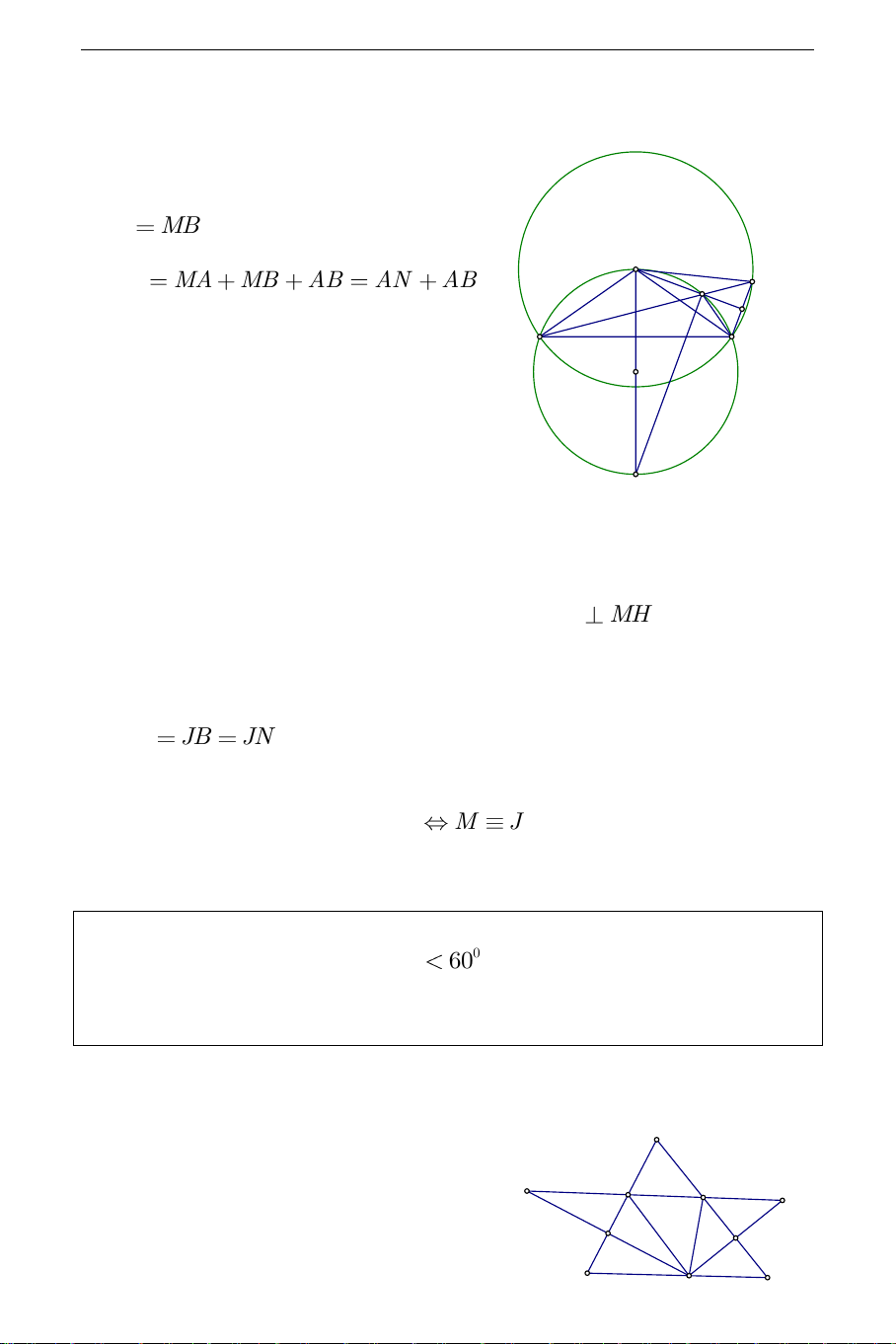
Trên tia đối của AM lấy điểm N sao cho MN
MB . Khi đó chu vi tam giác MAB J Là 2p MA MB AB AN AB . N M H
Do AB không đổi nên chu vi tam giác A B O
MAB lớn nhất khi và chỉ khi AN lớn
nhất.Tam giác BMN cân tại M và MH I
là phân giác của góc BMN đồng thời
cũng là phân giác ngoài của góc AMB . Phân giác trong của góc AMB là
MI với I là trung điểm cung lớn AB . Suy ra MI
MH . Do đó MH cắt đường tròn ( ; O )
R tại điểm J và IJ là đường kính của ( ; O ) R .
Tam giác MBN cân tại M nên MJ là đường trung trực của BN . Từ đó ta có: JA JB
JN . Hay điểm N thuộc đường tròn tâm J cố định bán
kính JA . Vì AN là dây cung của đường tròn J nên AN lớn nhất khi và
chỉ khi AN là đường kính của J M
J . Như vậy chu vi tam giác
MAB lớn nhất khi và chỉ khi M trùng với trung điểm J của cung nhỏ AB .
Ví dụ 7: Cho tam giác ABC có 0 A
60 . Trên cạnh BC lấy điểm I cố định. Tìm trên cạnh ,
AB AC lấy hai điểm M,N để chu vi tam giác
IMN đạt giá trị nhỏ nhất. Hướng dẫn giải: A
Gọi E,F lần lượt là các điểm đối xứng của M N I qua ,
AB AC . Do tam giác ABC cố E F THCS.TOANMATH.com B C I
định nên E,F cố định:
Ta có: Chu vi tam giác IMN là 2p IM IN MN ME MN NF
EF . Dấu bằng xảy ra khi
và chỉ khi E,M,N,F thẳng hàng. Hay M, N là các giao điểm của EF với các cạnh , AB AC
Ví dụ 8: Cho tam giác ABC vuông tại A có AB
AC ngoại tiếp đường tròn tâm O . Gọi ,
D E,F lần lượt là tiếp điểm của O với các cạnh A ,
B AC,BC ; M là điểm di chuyển trên đoạn CE . Gọi N là giao điểm
của BM với cung nhỏ EF của O , P và Q lần lượt là hình chiếu của
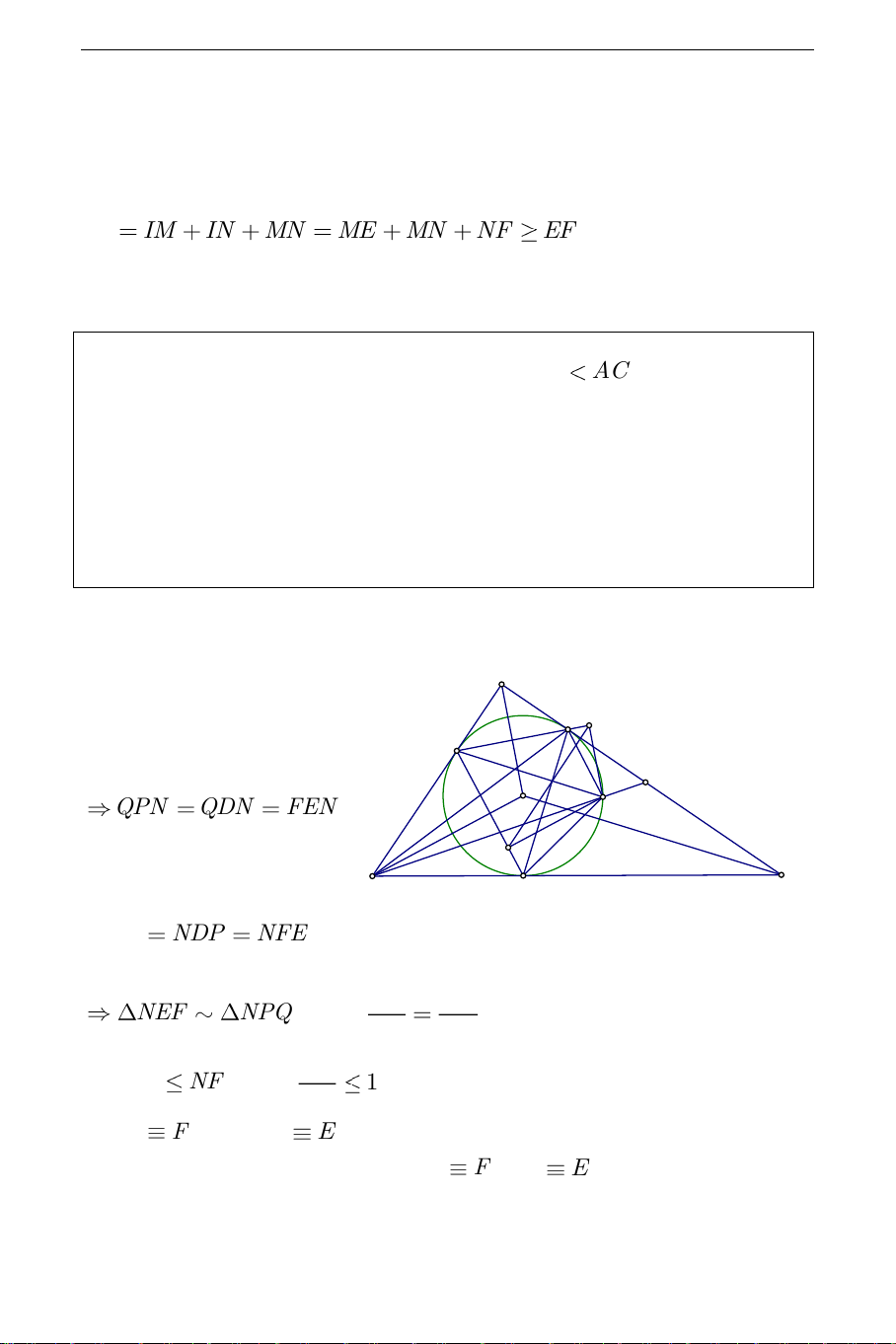
N trên các đường thẳng DE,DF . Xác định vị trí của điểm M để PQ lớn nhất. Hướng dẫn giải: A
Ta có tứ giác PNQD , E P EDFN nội tiếp D M O QPN QDN FEN . N Tương tự Q có ta có: B C F NQP NDP NFE . PQ NQ NEF NPQ Suy ra
. Trong tam giác vuông NQF ta EF NF PQ có: NQ NF do đó
1. Như vậy PQ lớn nhất bằng EF khi và chỉ EF khi Q F khi đó P
E , do P và Q lần lượt là hình chiếu của N trên
các đường thẳng DE,DF nên khi Q F , P
E thì DN là đường THCS.TOANMATH.com
kính của (O) . Từ đó suy ra cách xác định M như sau: Dựng đường kính
DN cuả (O) , M là giao điểm của BN và AC .
Ví dụ 9: Cho hai đường tròn (O ;R ),(O ;R ) cắt nhau tại 2 điểm , A B . 1 1 2 2
Một đường thẳng (d) bất kỳ qua A cắt (O ;R ),(O ;R ) lần lượt tại M, N . 1 1 2 2
Tiếp tuyến tại M của (O ;R ) và tiếp tuyến tại N của (O ;R ) cắt nhau tại 1 1 2 2
I . Tìm giá trị lớn nhất của bán kính đường tròn ngoại tiếp tam giác IMN
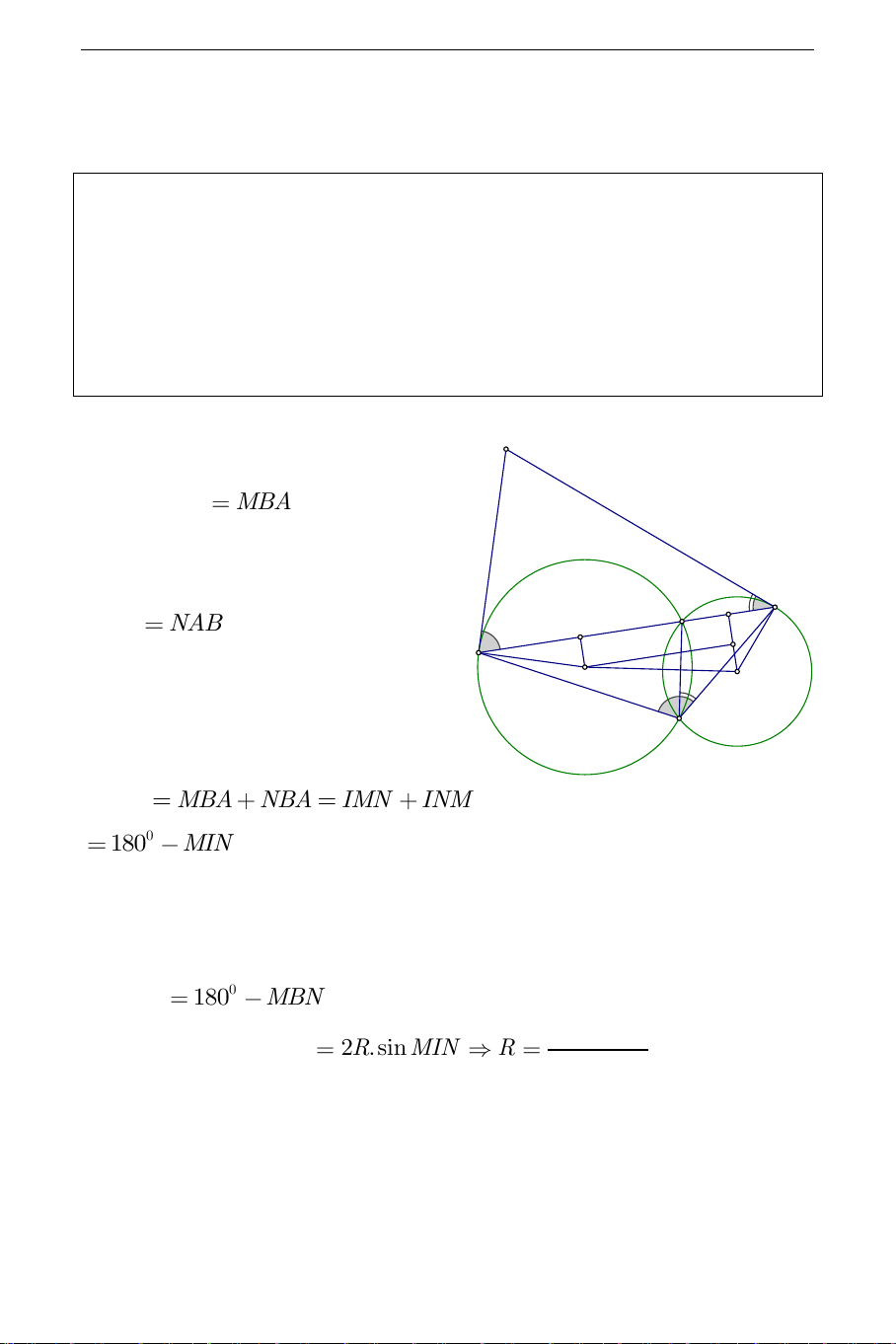
khi (d) quay quanh A . Hướng dẫn giải: I Ta có: IMN MBA(Tính chất góc
giữa tiếp tuyến và dây cung) A F N INM
NAB (Tính chất góc E K M
giữa tiếp tuyến và dây cung) O O 2 1
Xét tứ giác IMBN ta có: B MBN MBA NBA IMN INM 0 180
MIN . Suy ra tứ giác IMBN nội tiếp. Các góc AM ,
B ANB là những góc nội tiếp chắn cung AB cố định của
(O ;R ),(O ;R ) nên AM ,
B ANB không đối. Suy ra MBN không đổi. Suy 1 1 2 2 ra 0 MIN 180
MBN không đổi. Gọi R bán kính vòng tròn ngoại tiếp MN
tam giác MIN thì MN 2 . R sin MIN R . Do đó R lớn 2 sin MIN
nhất khi và chỉ khi MN lớn nhất. Gọi E,F là hình chiếu vuông góc của
O ,O lên (d) , K là hình chiếu vuông góc của O lên O F thì 1 2 1 2 THCS.TOANMATH.com MN 2EF 2O K
2OO . Dấu bằng xảy ra khi và chỉ khi 1 1 2 EF / /OO (d) / /OO . 1 2 1 2
Ví dụ 10) Trên các cạnh A , B BC,C ,
D DA của hình chữ nhật ABCD lần
lượt lấy các điểm M,N,E,F . Tìm vị trí bốn điểm đó để chu vi tứ giác
MNEF đạt giá trị nhỏ nhất. Giải:
Ta chứng minh kết quả phụ sau:Cho điểm M cố định. Khi chu M A B
vi tứ giác MNEF đạt giá trị nhỏ I N
nhất ta có MNEF là hình bình F J K
hành có các cạnh song song với D C E
các đường chéo của hình chữ nhật
ABCD . Thật vậy, gọi I,J,K lần lượt là trung điểm MN,ME,EF ta có: 1 1 1 1 IB MN,IJ NE;JK MF;DK
EF (hệ thức lượng trong 2 2 2 2 tam giác vuông).
Vậy chu vi tứ giác MNEF : 2p 2 BI IJ JK KD 2BD . Dấu
“=” xảy ra khi và chỉ khi ,
B I,J,K,D theo thứ tự nằm trên một đường thẳng
MF / /NE / /BD .
Tương tự ta có để chu vi tứ giác MNEF đạt giá trị nhỏ nhất thì MNEF là
hình bình hành có cạnh song song với đường chéo của hình chữ nhật
ABCD (kết quả phụ được chứng minh).
Từ chứng minh trên ta thấy, nếu tứ giác MNEF có các cạnh song song với
các đường chéo của hình chữ nhật ABCD thì chu vi của nó là p 2BD
const , không phụ thuộc vào cách lấy điểm M trên cạnh AB . THCS.TOANMATH.com
Vậy chu vi tứ giác MNEF đạt giá trị nhỏ nhất bằng 2BD khi MNEF là
hình bình hành có các cạnh song song với với các đường chéo của hình chữ nhật ABCD .
Ta có bài toán tổng quát sau: Cho tứ giác ABCD . Gọi M,N,P,Q lần
lượt là trung điểm của A , B BC,C , D DA . Khi đó: AB BC CD DA 2 MP NQ (*)
Thật vậy: Dựng E đối xứng với B qua P thì tứ giác BCED là hình bình hành nên BC DE . C N Ta có: BC AD DE AD AE 2MP B . Tương tự AB CD 2NQ . Cộng hai bất P M
đẳng thức cùng chiều ta suy ra điều A E phải chứng minh. Q D
Dấu bằng xảy ra khi và chỉ khi
AD / /BC,AB / /CD hay ABCD là hình bình hành.
Ví dụ 11) Cho hình thoi ABCD . Đường chéo AC không nhỏ hơn đường
chéo BD . M là một điểm tùy ý trên AC . Đường thẳng qua M song song
với AB cắt AD tại E, cắt BC tại G Đường thẳng qua M song song với
AD cắt AB tại F cắt CD tại H . Biết hình thoi ABCD có độ dài hai
đường chéo là d và d . Xác định M sao cho chu vi tứ giác EFGH là nhỏ 1 2
nhất?Tính chu vi đó theo d ,d . 1 2 Hướng dẫn giải: B
Ta dễ dàng chứng minh được F I EFGH G là hình thang cân, J A C L O M THCS.TOANMATH.com H K E D
AFME , MGCH là hình thoi,
Các tứ giác BFMG, EDHM là
hình bình hành. Do đó các đường chéo
AM, EF cắt nhau tại L , MC,GH cắt nhau tại J , BM,FG cắt nhau tại
I , DM,EH cắt nhau tại K thì ,
L I,J,K lần lượt là trung điểm của EF,F , G GH,HE .
Áp dụng bài toán (*) ta có chu vi tứ giác EFGH là 2p EF GH FG EH 2IK 2FG 2IK 2LJ BD 2LJ . 1 Nhưng LJ LM MJ AC 2p AC
BD . Dấu bằng xảy ra 2
khi và chỉ khi FG / /AC
FGHE là hình chữ nhật. Tức điểm M O là
giao điểm của hai đường chéo của hình thoi ABCD
SỬ DỤNG BẤT ĐẲNG THỨC CỔ ĐIỂN ĐỂ GIẢI BÀI TOÁN CỰC TRỊ
Ở cấp THCS, các em học sinh được làm quen với bất đẳng thức Cauchy dạng 2 số hoặc 3 số:
Để giải quyết tốt các bài toán hình học: Ta cần nắm chắc một số kết quả quan trọng sau:
Trước hết ta cần nắm được các kết quả cơ bản sau:
1). Cho các số thực dương , a b : 2 a b 2 + a b 2 ab ab a b
4ab . Dấu bằng xảy ra khi 2 và chỉ khi a b THCS.TOANMATH.com 2 1 1 4 2 2 2 2 x y x y + ; 2 2 a b a b a b a b a b 3 1 3 + 2 2 2 2 2 a ab b (a b) (a b) (a b) 4 4 4 1 3 1 + 2 2 2 2 2 a ab b (a b) (a b) (a b) 4 4 4
2). Cho các số thực dương a, , b c : 3 a b c + 3 a b c 3 abc abc
Dấu bằng xảy ra khi và chỉ khi 3 a b c 1 1 1 9 3 3 + 2 2 2 a b c a b c a b c 2 a b c 4) 2 2 2 ab bc ca a b c 3 2 2 2 2 x y z x y z 5) a b c a b c
Ngoài ra các em học sinh cần nắm chắc các công thức về diện tích tam
giác ,liên hệ độ dài các cạnh và góc như: 1 + S a.h 2 1 1 1 + S ab sinC ab sinC bc sinA 2 2 2 a b c + S ( p p a)(p b)(p
c) với p 2 THCS.TOANMATH.com + a
2R sinA, b 2R sin , B c 2R sinC …
+ Diện tích hình chữ nhật: S ab 1
+ Diện tích hình thang: S a b h . 2 + Diện tích hình vuông: 2 S a .
Ví dụ 1) Cho tam giác ABC có BC , a CA , b AB
c . M là một
điểm thuộc miền trong ABC . Gọi E,F,K lần lượt là hình chiếu vuông
góc của M trên BC,C ,
A AB . Xác định vị trí điểm M để tích M .
E MF.MK đạt giá trị lớn nhất. Hướng dẫn giải: A Ta có: F 2S 2 S S S K . ABC MBC MCA MAB M . a ME . b MF . c MK B E C
Do đó áp dụng bất đẳng thức Cô-si
với bộ 3 số a.ME, . b MF, . c MK . Ta có: . a . b .
c ME.MF.MK a.ME . . b MF . . c MK 1 3 3 8S 3 . a ME . b MF . c MK 8S ME.MF. ABC MK . 27 ABC abc
Dấu “=” xảy ra khi và chỉ khi . a ME . b MF . c MK S S S
M là trọng tâm tam giác ABC . MBC MCA MAB 3 8S Vậy max ME.MF. ABC MK
khi M là trọng tâm tam giác ABC . abc THCS.TOANMATH.com
Ví dụ 2) Cho tam giác ABC cân đỉnh A . Gọi O là trung điểm của BC .
Đường tròn O tiếp xúc với AB ở E tiếp xúc với AC ở F . Điểm H
chạy trên cung nhỏ EF tiếp tuyến của đường tròn tại H cắt , AB AC lần
lượt tại M,N . Xác định vị trí của điểm H để diện tích tam giác AMN đạt giá trị lớn nhất. Hướng dẫn giải:
Dễ thấy OM,ON lần lượt là phân giác EOM,FOH . Từ đó ta có: 0 180 BAC MON ABC MBO OCN 2 2 MB BO BC (g.g) BM.CN O . BOC const (1) OC CN 4 A Ta lại có S S S AMN ABC BMNC N nên S
đạt giá trị lớn nhất AMN H M khi và chỉ khi S đạt giá trị BMNC E F
nhỏ nhất. Gọi R là bán kính B C O
của đường tròn O , ta có: S S S S BMNC BOM MON NOC 1 1 R BM MN NC R BE CF 2 EM FN Vì 2 2 MN EM FN R BE EM FN vì BE CF R BE BM CN 2BE R BM CN BE (2) THCS.TOANMATH.com
Áp dụng bất đẳng thức Cô-si, từ (1) và (2) suy ra: BC S R BM.CN BE R
BE . Dấu “=” xảy ra khi và chỉ BMNC 2 khi BM CN
MN / /BC khi và chỉ khi H là giao điểm của đường
trung trực của BC với đường tròn O . Vậy diện tích tam giác AMN đạt
giá trị lớn nhất khi H là giao của đường trung trực của BC với đường tròn O .
Ví dụ 3) Cho tam giác ABC trên trung tuyến AD lấy điểm I cố định.
Đường thẳng d đi qua I lần lượt cắt cạnh ,
AB AC tại M,N . Tìm vị trí
của đường thẳng d để diện tích tam giác AMN đạt giá trị nhỏ nhất. Hướng dẫn giải: Từ ,
B C dựng các đường thẳng song song với d , lần lượt cắt tia AD tại E,F . A h N M d Dễ thấy BED CFD M I nên DE DF hay hB E AE AF 2AD . C B D AE AF AB AC AD F 2 AM AN AI AI AB AE AC AF Ta có: ; . AM AI AN AI AE AF AB AC AD 2 const AM AN AI AI THCS.TOANMATH.com
Gọi h ,h là khoảng cách từ B, M đến AC . Áp dụng định lý Talet, ta có B M 2 1 AC AB h AB AC.h 2 S B AC AB AD B ; ABC 2 . AN AM h AM 2 S 1 AN AM 2 AI M AMN AN.h 2 M 2 AD S S .
Dấu “=” xảy ra khi và chỉ khi AMN ABC 2 AI AB AC 2 AD
MN / /BC . Vậy min S S . khi d là AM AN AMN ABC 2 AI
đường thẳng đi qua I và song song với BC .
Ví dụ 4) Cho góc nhọn xOy và điểm I cố định nằm ở trong các góc đó.
Đường thẳng d đi qua I và cắt Ox,Oy lần lượt tại M,N . Xác định đường
thẳng d để diện tích tam giác OMN đạt giá trị nhỏ nhất. Giải:
Trước hết ta dựng đường thẳng đi qua I cắt Ox,Oy tại E,F sao cho IE IF (*). y Ta dựng đường thẳng như sau:
Lấy O ' là điểm đối xứng của F d O'
O qua I . Từ O ' kẻ đường N
thẳng song song với Ox cắt x O E M
Oy tại F , song song với Oy
cắt Ox tại E . Vì OEO ' F là hình bình hành nên OO ' EF I là trung
điểm của E . Lấy là đường thẳng EF , ta có thỏa mãn điều kiện (*), cố định. THCS.TOANMATH.com
Giả sử d là đường thẳng bất kỳ qua I cắt Ox ở M , cắt Oy ở N . Ta dễ OE OF OI chứng minh được: 2 2 . OM ON OI OE OF 1 OE OF
Áp dụng bất đẳng thức Cô si ta có: . 1 . OM ON 2 OM ON OE OF
Dấu “=” xảy ra khi và chỉ khi 1 OE OM,OF ON OM ON hay M E,N
F . Vậy đường thẳng d trùng với thì diện tích
OMN đạt giá trị nhỏ nhất.
Ví dụ 5). Cho ba điểm ,
A I,B thẳng hàng theo thứ tự. Gọi d ,d là hai nửa 1 2
đường thẳng vuông góc với AB tại ,
A B và nằm về cùng một phía đối với
đường thẳng AB . Góc vuông xIy quay xung quanh đỉnh I sao cho hai
cạnh của góc tương ứng cắt d ở M cắt d ở N . Tìm vị trí của M, N để 1 2
diện tích tam giác IMN đạt giá trị nhỏ nhất. Giải: d1 d2 Ta có: M 0 0 AMI AIM 90 ,BIN AIM 90 N AMI BIN MAI IBN (g.g) AI AM B (*) A I BN BI AM.BN AI.BI const .Mặt khác, 1 1 2 2 2 2 S IM.IN AI AM BI
BN . Áp dụng bất đẳng IMN 2 2
thức Bu-nhi-a-côp-xki ta có: THCS.TOANMATH.com 2 2 2 2 2 AI AM BI BN AI.BI
AM.BN . Dấu “=” xảy ra khi và AI AM AI BI chỉ khi BI BN AM BN
Kết hợp với (*) suy ra diện tích
IMN đạt giá trị nhỏ nhất khi và chỉ khi BI BN AI 1 hay BI BN,AI AM . BN BI AM
Khi đó AIM, BIN vuông cân tại các đỉnh , A B
IM,IN hợp với AB các góc bằng 0
45 . Vậy diện tích tam giác IMN đạt giá trị nhỏ nhất khi
IM,IN cùng hợp với AB các góc bằng 0 45 .
Ví dụ 6) Cho tam giác ABC và một điểm M tùy ý trong tam giác đó. Gọi
khoảng cách từ M đến các cạnh BC,C ,
A AB theo thứ tự là , m , n p và các
đường cao hạ từ các đỉnh , A ,
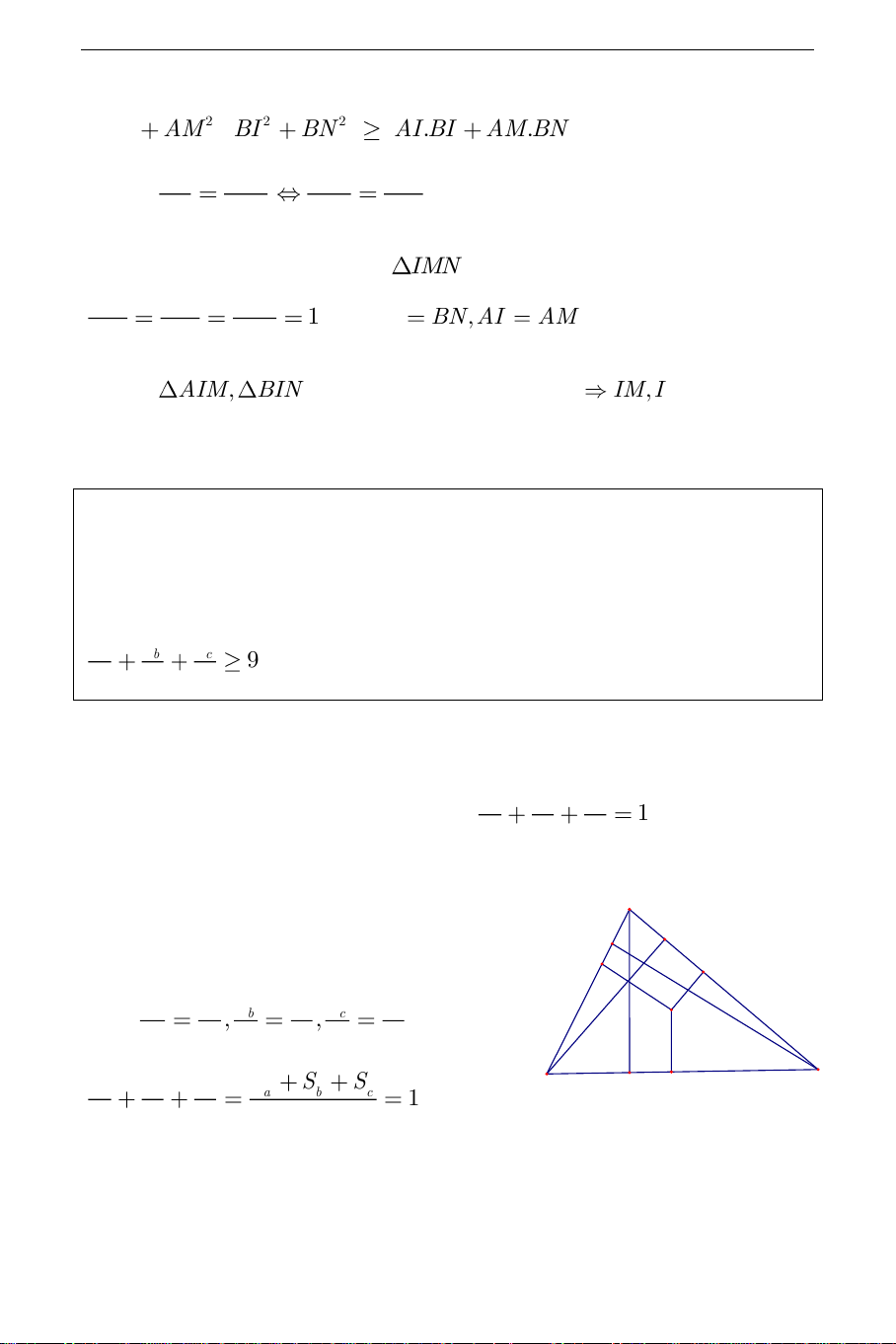
B C là h ,h ,h . Chứng minh: a b c h h h a b c 9 m n p Hướng dẫn giải: m n p
Trước hết ta chứng minh kết quả sau: 1 h h h a b c
Kí hiệu S ,S ,S ,S lần lượt là diện tích a b c A
tam giác MBC,MAC,MA , B ABC T S F E H n S m S n S p p ta có: a , b , c suy ra M S h S h S h hb h a b c c ha m B C m n p S S S a b c 1 R D h h h S a b c THCS.TOANMATH.com
Sử dụng bất đẳng thức Cô si ta dễ chứng minh được kết quả sau(với 1 1 1 (x, , y z 0): x y z 9 . x y z h h h 9
Áp dụng vào bài toán ta có: a b c 9 .Dấu bằng m n p m n p h h h a b c h h h
xảy ra khi và chỉ khi a = b = c = 3 . Hay M là trọng tâm của tam giác m n n ABC.
Ví dụ 7) Cho tam giác ABC và một điểm M tùy ý trong tam giác đó. Các
đường thẳng AM,BM,CM cắt các cạnh BC,C ,
A AB tại các giao điểm
tương ứng là: A ,B ,C . Kí hiệu S ,S ,S ,S lần lượt là diện tích tam giác 1 1 1 a b c
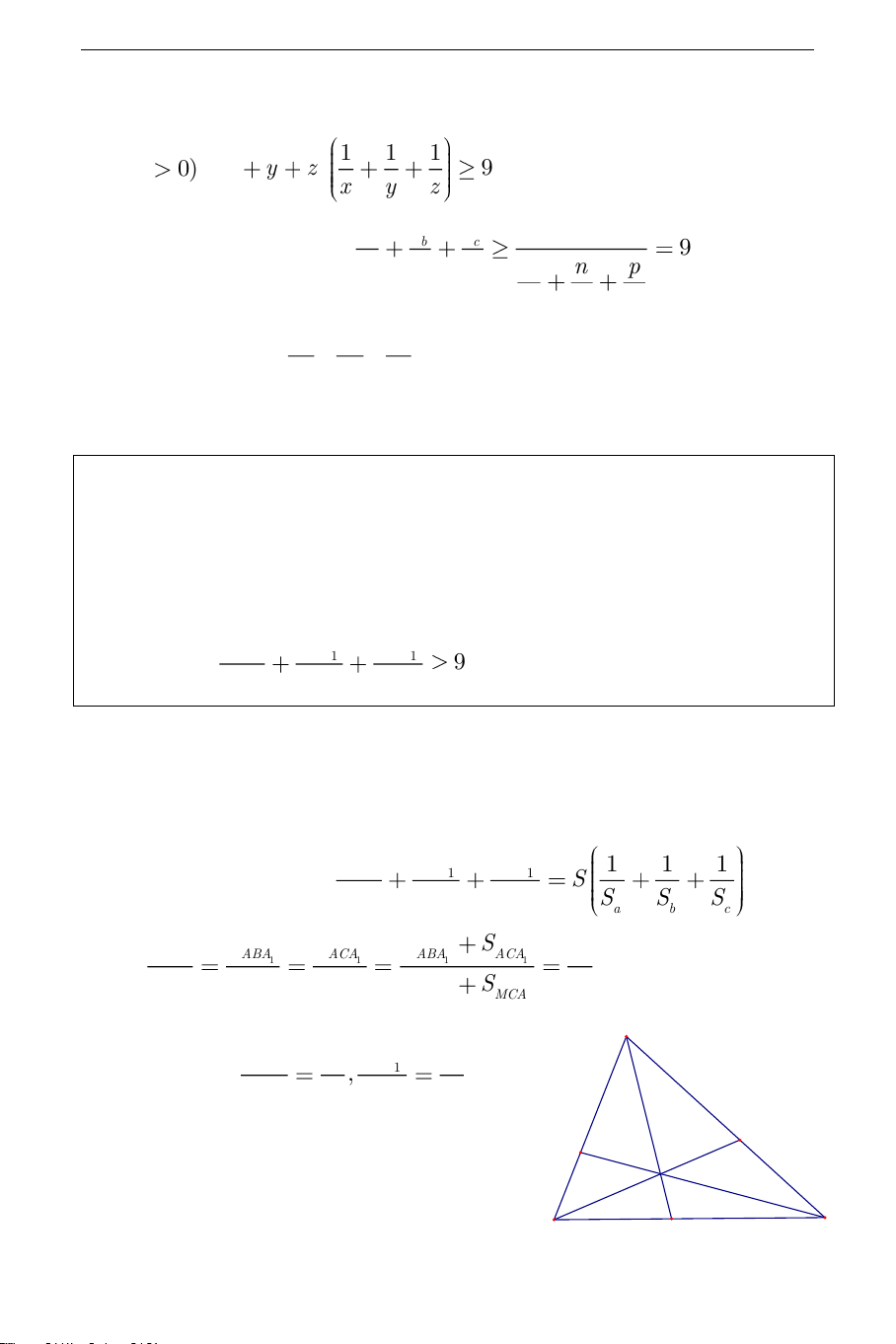
MBC,MAC,MA , B ABC . AA BB CC Chứng minh: 1 1 1 9 MA MB MC 1 1 1 Hướng dẫn giải: AA BB CC 1 1 1
Trước hết ta chứng minh : 1 1 1 S . MA MB MC S S S 1 1 1 a b c AA S S S S ABA ACA ABA ACA S Ta có 1 1 1 1 1 , MA S S S S S 1 MBA MCA MBA MCA a 1 1 1 1 A BB S CC S Tương tự ta có: 1 1 , . MB S MC S 1 b 1 c B1 C
Cộng ba đẳng thức ta có: 1 M A1 B C THCS.TOANMATH.com AA BB CC 1 1 1 1 1 1 S MA MB MC S S S 1 1 1 a b c 1 1 1
Áp dụng bất đẳng thức: x y z 9 với (x, , y z 0) . Để x y z 1 1 1 9 9 ý rằng: S S S S ta có: ta có: a b c S S S S S S S a b c a b c 1 1 1 S
9. Dấu bằng xảy ra khi và chỉ khi S S S a b c 1 S S S
S . Hay M là trọng tâm của tam giác ABC . a b c 3
Chú ý rằng: Từ bài toán trên ta cũng có: MA S S S S S 1 MBA MCA MBA MCA 1 1 1 1
a . Tương tự ta có: AA S S S S S 1 ABA ACA ABA ACA 1 1 1 1 MB S MC S MA MB MC S S S 1 b 1 , c . Suy ra 1 1 1 a b c 1 BB S CC S AA BB CC S 1 1 1 1 1 Nếu ta thay: MA AA MA MA MB MB MC MC 1 1 1 1 1 , 1 , 1 , thì ta AA AA AA BB BB CC CC 1 1 1 1 1 1 1 MA MB MC thu được đẳng thức:
2 .Qua đó ta cũng tạo ra được AA BB CC 1 1 1
nhiều bất đẳng thức đẹp khác.
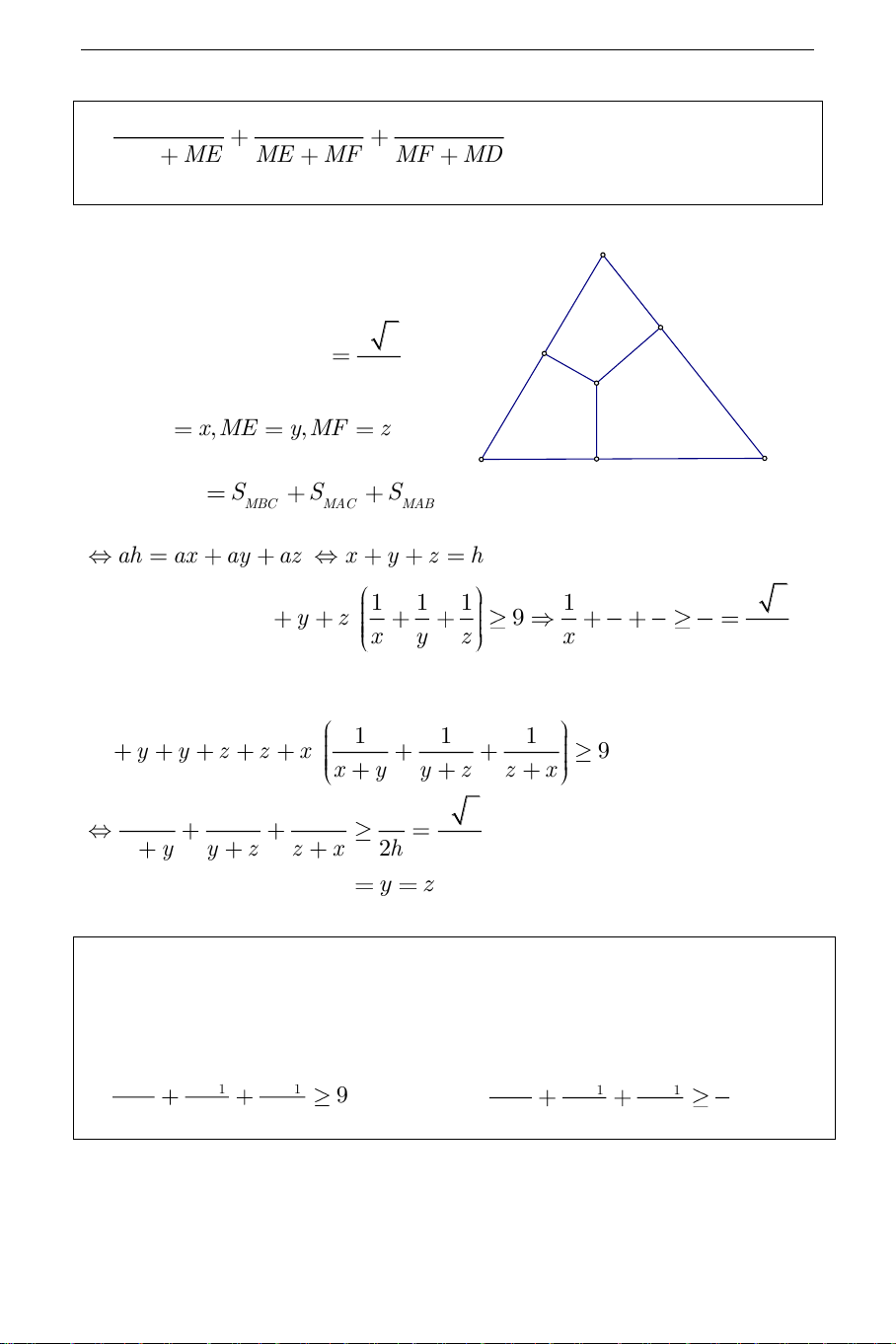
Ví dụ 8. Cho tam giác đều ABC có cạnh bằng a . Gọi đường vuông góc từ
điểm M nằm trong tam giác đến các cạnh BC,C ,
A AB lần lượt là M ,
D ME,MF . Xác định vị trí điểm M để: 1 1 1 a)
đạt giá trị nhỏ nhất. Tính giá trị đó. MD ME MF THCS.TOANMATH.com 1 1 1 b)
đạt giá trị nhỏ nhất. Tính giá MD ME ME MF MF MD trị đó. Hướng dẫn giải: A
Gọi h là độ dài đường cao của E a 3
tam giác đều ABC thì h . F z y 2 M Đặt MD x,ME , y MF z . x B D C Ta có S S S S ABC MBC MAC MAB ah ax ay az x y z h không đổi. 1 1 1 1 1 1 9 6 3 Áp dụng BĐT : x y z 9 . x y z x y z h a b) Ta có: 1 1 1 x y y z z x 9 x y y z z x 1 1 1 9
3 3 . Trong cả hai trường hợp đẳng x y y z z x 2h a
thức xảy ra khi và chỉ khi x y
z , lúc đó M là tâm của tam giác đều ABC .
Ví dụ 9. Gọi H là trực tâm của tam giác ABC có ba góc nhọn với ba đường
cao AA ,BB ,CC . Chứng minh rằng: 1 1 1 AA BB CC HA HB HC 3 a) 1 1 1 9 . b) 1 1 1 . HA HB HC HA HB HC 2 1 1 1 Hướng dẫn giải: THCS.TOANMATH.com
Gọi diện tích các tam giác ABC,HBC,HAC,HAB lần lượt là S,S ,S ,S 1 2 3 HA S HB S HC S thì S S S S . Dễ thấy 1 1 1 2 1 3 ; ; . 1 2 3 AA S BB S CC S 1 1 1 A HA HB HC Do đó 1 1 1 1 . AA BB CC B1 1 1 1 C1 1 1 1 H Áp dụng BĐT x y z 9 . x y z C B A1 AA BB CC Ta được: 1 1 1
9 . Đẳng thức xảy ra khi và chỉ khi HA HB HC 1 1 1 HA HB HC 1 S 1 1 1 S S S
. Lúc đó H vừa là trực 1 2 3 AA BB CC 3 3 1 1 1
tâm, vừa là trọng tâm của tam giác ABC , nên ABC là tam giác đều. HA S HA HA S S b) Từ 1 1 có 1 1 1 1 . AA S HA AA HA S S S S 1 1 1 1 2 3 HB S HC S Tương tự 1 2 1 3 ; . Áp dụng BĐT HB S S HC S S 1 3 1 2 a b c 3 HA HB HC 3 (*). Ta có 1 1 1 . b c c a a b 2 HA HB HC 2
Lập luận như trên đẳng thức xảy ra khi và chỉ khi tam giác ABC đều.
Bất đẳng thức (*) có tên là bất đẳng thức Netbis là bất đẳng thức đơn giản
nhưng có rất nhiều ứng dụng. Ta có thể chứng minh nó như sau: a b c b c c a a b 9 . Nhưng b c c a a b a b c THCS.TOANMATH.com b c c a a b a b b c c a 2 2 2 6 . a b c b a c b a c a b c Suy ra
. Dấu bằng xảy ra khi và chỉ khi a = b = c . b c c a a b
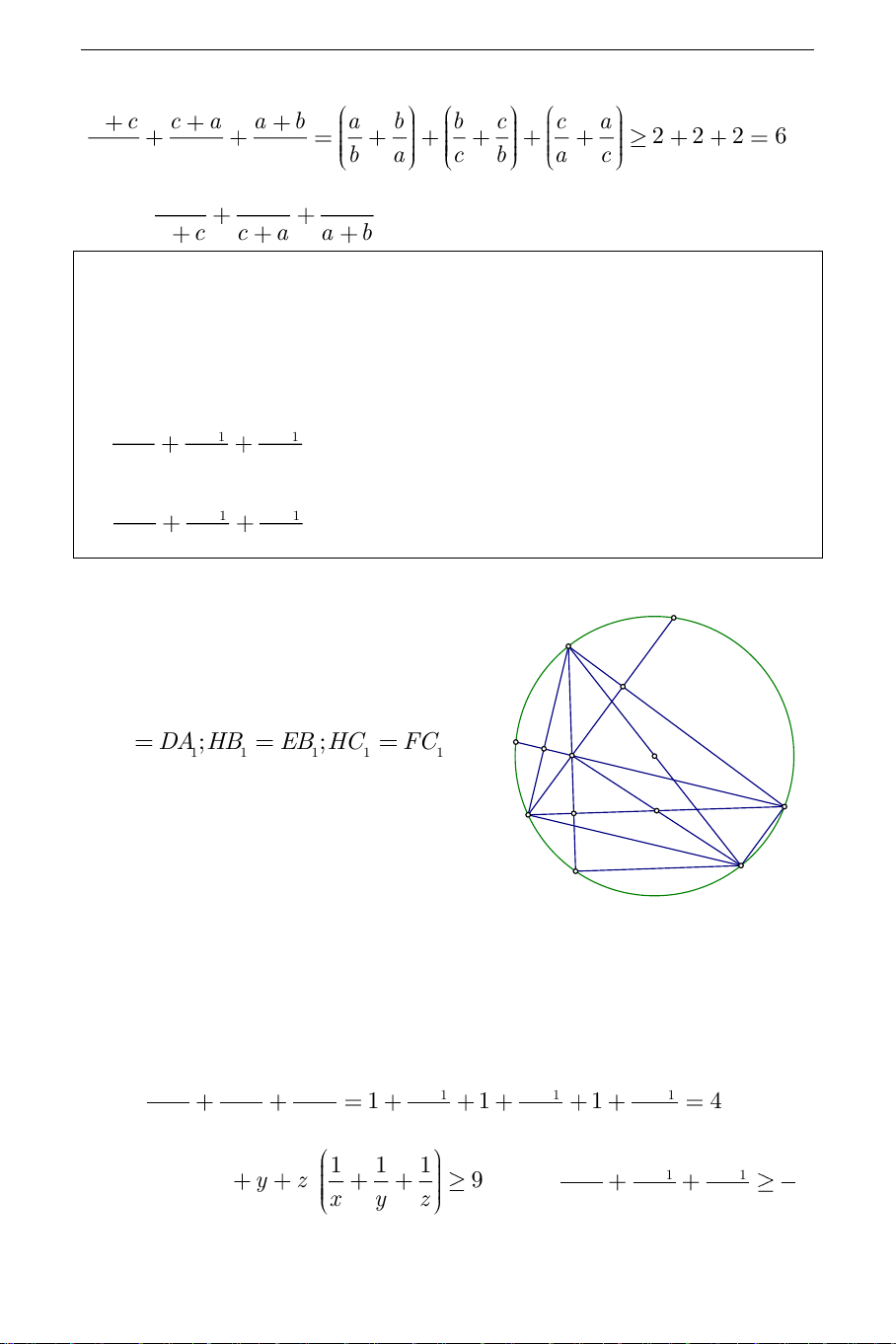
Ví dụ 10. Xét tam giác ABC có ba góc nhọn nội tiếp đường tròn O với
ba đường cao AA,BB ,CC lần lượt cắt đường tròn O lần nữa tại 1 1 1 ,
D E,F . Xác định dạng của tam giác ABC sao cho: AA BB CC a) 1 1
1 đạt giá trị nhỏ nhất. Tính giá trị nhỏ nhất đó. DA EB FC 1 1 1 AA BB CC b) 1 1
1 đạt giá trị nhỏ nhất. Tính giá trị nhỏ nhất đó. AD BE CF Hướng dẫn giải: E A
Gọi H là trực tâm của tam giác ABC .
Dễ dàng chứng minh được B1 HA DA ;HB EB ;HC FC . F 1 1 1 1 1 1 C1 O H
(Xem phần đường thẳng Ơ le- Đường A M 1 C B tròn Ơ le) A' D
Áp dụng ví dụ 9. Tổng đang xét đạt
giá trị nhỏ nhất là 9 khi và chỉ khi tam giác ABC đều. AD BE CF HA HB HC b) Từ 1 1 1 1 1 1 4 , áp AA BB CC AA BB CC 1 1 1 1 1 1 1 1 1 AA BB CC 4 dụng BĐT: x y z 9 suy ra 1 1 1 . x y z AD BE CF 9 THCS.TOANMATH.com
Đẳng thức xảy ra khi và chỉ khi ABC là tam giác đều.
Ví dụ 11. Trong các tam giác ngoại tiếp đường tròn tâm O bán kính r hãy
các định dạng của tam giác sao cho tổng độ dài ba đường cao đạt giá trị nhỏ
nhất. Tính giá trị đó. Hướng dẫn giải:
Gọi h ,h ,h là độ dài các đường cao tương ứng với các cạnh a, , b c của tam a b c
giác ABC ngoại tiếp đường tròn O . Ta dễ chứng minh được: r r r 1 1 1
1 .Áp dụng bất đẳng thức x y z 9 ta h h h x y z a b c 1 1 1 có h h h h h h r
9r . Đẳng thức xảy ra a b c a b c h h h a b c khi h h h 3r,h h h
9r , lúc đó tam giác ABC đều. a b c a b c
Ví dụ 12. Cho tam giác ABC và M là điểm nằm trong tam giác. Kẻ
AM,BM,CM cắt các cạnh BC,C ,
A AB lần lượt tại A ,B ,C . Xác định vị 1 1 1 MA MB MC
trí của điểm M để: . .
đạt giá trị nhỏ nhất. Tính giá trị nhỏ MA MB MC 1 1 1 nhất đó. Giải:
Gọi diện tích các tam giác ABC,MBC,MAC,MAB lần lượt là AA BB CC
S,S ,S ,S thì S S S S . Đặt 1 1 1 x, , y z thì 1 2 3 1 2 3 MA MB MC 1 1 1 MA AA MB BB 1 1 x 1; 1 1 y 1, MA MA MB MB 1 1 1 1 MC CC1 1 z 1.Theo ví dụ 7 ta có: MC MC 1 1 THCS.TOANMATH.com MA MB MC 1 1 1 1 1 1 1 xy yz zx xyz . Từ đó AA BB CC x y z 1 1 1 MA MB MC suy ra . . x 1 y 1 z 1 MA MB MC 1 1 1 xyz xy yz zx x y z 1 x y z 1 1 1 1 x y z 1 9 1
8 . Đẳng thức xảy ra khi x y z x y
z , lúc đó M là trọng tâm của tam giác ABC .
BẤT ĐẲNG THỨC ERDOS – MORDELL
Cho tam giác ABC và M là một điểm bất kỳ nằm trong tam giác đó. Gọi
R ,R ,R theo thứ tự là khoảng cách từ M đến các đỉnh , A , B C . Còn a b c
d ,d ,d lần lượt là khoảng cách từ M đến các cạnh BC,C , A AB . Khi đó ta a b c
có bất đẳng thức R R R 2 d d
d .Đẳng thức xảy ra khi và a b c a b c
chỉ khi tam giác ABC đều và M là tâm của tam giác.
Chứng minh bất đẳng thức: A Đặt BC , a CA , b AB c .
Lấy điểm M đối xứng với 1 M
điểm M qua đường phân M1 K D B C
giác trong của BAC . Dựng H BH AM và CK AM . 1 1 THCS.TOANMATH.com
Giả sử AM cắt BC tại D . Khi đó BD BH,DC CK . Đẳng thức 1
xảy ra khi và chỉ khi AD BC hay AM BC . Từ đó ta có: 1 a BH CK aR 2S 2S (chú ý rằng AM AM R ) a ABM ACM 1 a 1 1 c b hay aR cd bd . Từ đó R d
d (1). Tương tự ta có a b c a b c a a a c a b R d d (2); R d
d (3). Cộng theo vế các bất đẳng b c a b b c b a c c
thức (1),(2),(3) ta thu được: b c a c a b R R R d d d 2 d d d a b c a b c a b c c b c a b a
(Sử dụng bất đẳng thức Cauchy cho các biểu thức trong ngoặc).
Đẳng thức xảy ra khi và chỉ khi a b
c đồng thời M là trực tâm của 1
tam giác ABC . Nói cách khác, M (và do đó cả M ) là tâm của tam giác 1
đều ABC . Từ cách chứng minh trên chúng ta còn có một số kết quả sau:
Hệ quả 1. (Bất đẳng thức Erdos –Mordell dạng tích).
Cho tam giác ABC và M là điểm bất kỳ nằm trong tam giác đó. Gọi
R ,R ,R thứ tự là khoảng cách từ M đến các đỉnh , A ,
B C . Còn d ,d ,d a b c a b c
lần lượt là khoảng cách từ M đến các cạnh BC,C ,
A AB . Khi đó ta có bất
đẳng thức R .R .R 8d d d . a b c a b c Chứng minh:
Từ cách chứng minh bất đẳng thức Erdos – Mordell, ta có: c b a c a b R d d (1); R d d (2); R d d (3) a b c a a b c a b b c b a c c
Nhân theo vế ba bất đẳng thức trên ta được: THCS.TOANMATH.com c b a c a b R .R .R d d d d d d a b c b c c a b a a a b b c c c b a c a b 2 d . d .2 d . d .2 d . d 8d d d (đpcm). b c c a b a a b c a a b b c c
Hệ quả 2. (Bất đẳng thức Erdos –Mordell dạng căn thức). Cho tam giác
ABC và M là một điểm bất kỳ nằm trong tam giác đó. Gọi R ,R ,R thứ a b c
tự là khoảng cách từ M đến các đỉnh , A ,
B C . Còn d ,d ,d lần lượt là a b c
khoảng cách từ M đến các cạnh BC,C ,
A AB . Khi đó ta có bất đẳng thức R R R 2 d d d . a b c a b c Chứng minh:
Từ các bất đẳng thức (1),(2) và (3) theo bất đẳng thức Cauchy ta có: c b . d . d b c c b a a R d d
(4). Tương tự ta cũng có: a b c a a 2 a c . d . d c a a c b b R d d (5) b c a b b 2 a b . d . d b a a b c c R d d
(6). Cộng theo vế các bất c b a c c 2
đẳng thức (4),(5) và (6) ta được: R R R a b c 1 b c 1 c a 1 a b d d d 2 a c b 2 b a c 2 c b a 2 d d
d . Áp dụng bất đẳng thức Cauchy cho các biểu a b c
thức trong ngoặc của bất đẳng thức trên. Ta có điều cần chứng minh. THCS.TOANMATH.com
Một số ứng dụng của bất đẳng thức Erdos – Mordell
Ví dụ 1. Gọi I là tâm r là bán kính đường tròn nội tiếp tam giác ABC .
Chứng minh rằng điều kiện cần và đủ để tam giác ABC đều và IA IB IC 6r . Giải: A
Kẻ IH, IJ,IK theo thứ tự vuông góc
với các cạnh BC,C , A AB . Ta có J K IH IJ IK r . Áp dụng bất I
đẳng thức Erdos – Mordell cho điểm B C H
I trong tam giác ABC , ta thấy IA IB IC 2 IH IJ IK 6r .
Đẳng thức xảy ra khi và chỉ khi tam giác ABC đều. Nói cách khác, điều
kiện cần và đủ để tam giác ABC đều là IA IB IC 6r (đpcm)
Ví dụ 2. Giả sử M là một điểm bất kỳ nằm trong tam giác ABC . Gọi r là
bán kính đường tròn nội tiếp tam giác. Chứng minh rằng MA MB MC
6r . Đẳng thức xảy ra khi nào? Giải: A Gọi x, ,
y z lần lượt là khoảng cách
từ M đến các cạnh BC,C , A AB . M x
Kẻ AH vuông góc với BC,MA 1 B C H A1
vuông góc với BC . Khi đó ta có THCS.TOANMATH.com 2S AM MA AH . Từ đó ABC AM x . 1 BC 2S 2S Tương tự, ABC BM ; ABC y CM
z . Cộng theo vế ba bất đẳng CA AB thức này ta được: 1 1 1 MA MB MC 2S x y z ABC BC CA AB 1 1 1 r BC CA AB x y z (1). BC CA AB
Áp dụng bất đẳng thức Cauchy ta được: 1 1 1 BC CA AB
9 (2). Áp dụng bất đẳng thức BC CA AB
Erdos – Mordell cho điểm M đối với tam giác ABC ta có: MA MB MC 2 x y z (3). MA MB MC
Từ (1),(2), (3) suy ra MA MB MC 9r hay 2 MA MB MC
6r . Đẳng thức xảy ra khi và chỉ khi tam giác ABC đều (đpcm).
Ví dụ 3. Chứng minh rằng với mọi tam giác ABC nhọn ta có các bất đẳng thức: 3 a) cos A cosB cosC 2 1 b) cos . A cos . B cosC
. Đẳng thức xảy ra khi nào? 8 Giải: A a). Gọi ;
O R theo thứ tự là tâm và bán
kính đường tròn ngoại tiếp tam giác ABC ; K I O THCS.TOANMATH.com B C H
thứ tự là hình chiếu vuông góc kẻ từ O đến
các cạnh BC,C ,
A AB . Từ giả thiết tam giác 1
ABC nhọn, ta nhận thấy BAC BOC 2
(góc nội tiếp bằng nửa góc ở tâm cùng chắn một cung) hay BAC
HOC . Tương tự có ABC AOI;ACB BOK . Từ đó cosA cosB cosC cosHOC cosAOI cosBOK OH OI OK OH OI
OK (1). Nhưng theo bất đẳng thức OC OA OB R
Erdos – Mordell cho điểm O nằm trong tam giác ABC ta có OA OB OC OH OI OK (2) 2 3
Từ (1) và (2) suy ra cos A cosB cosC
. Đẳng thức xảy ra khi và 2
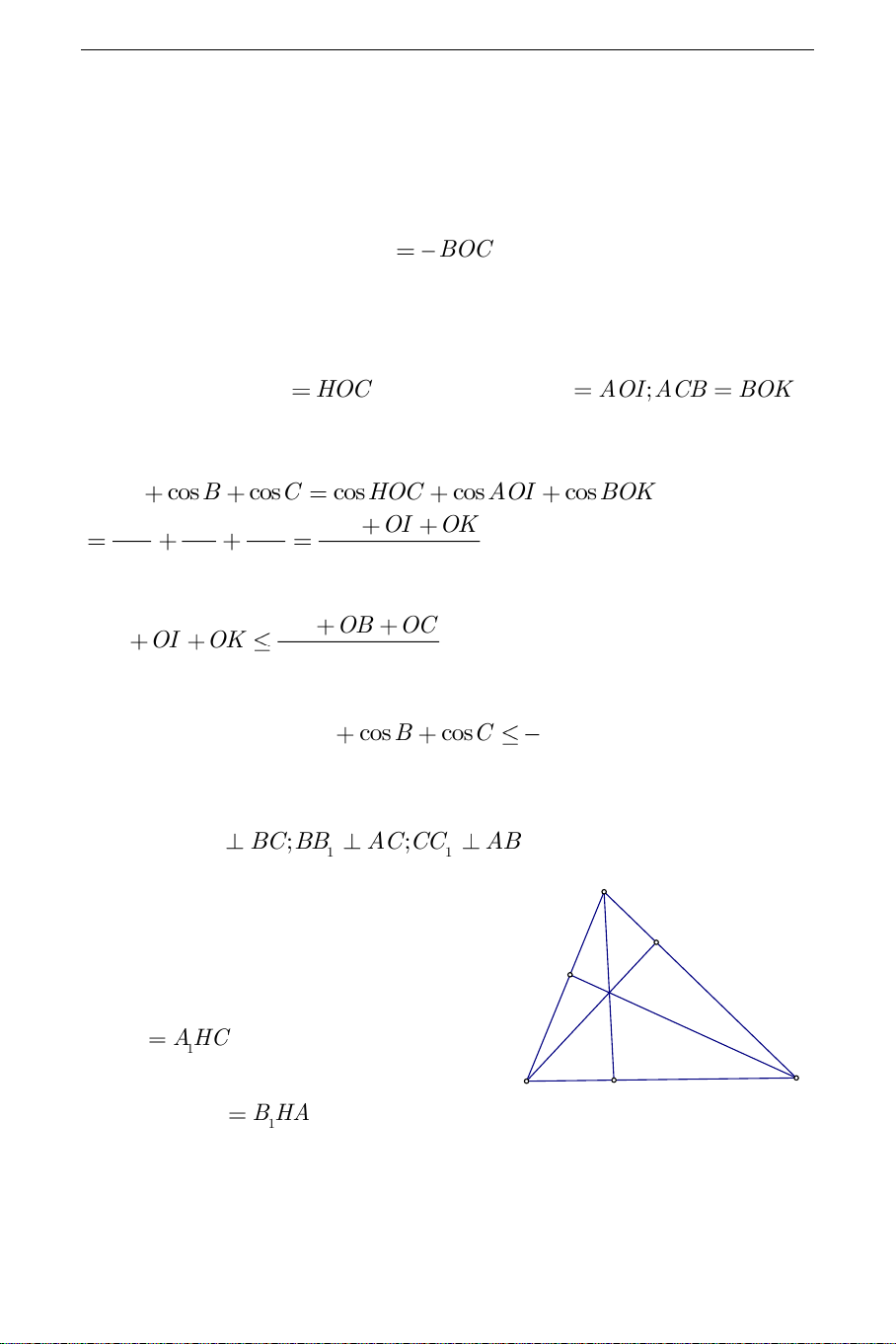
chỉ khi tam giác ABC đều. b). Dựng AA BC;BB AC;CC AB . 1 1 1 A
Gọi H là trực tâm của tam giác ABC . B1
Do đó tứ giác BC HA nội tiếp nên 1 1 C1 H ABC
A HC . Tứ giác CA HB nội 1 1 1 C B A1 tiếp nên ACB B HA . Tứ giác 1 THCS.TOANMATH.com
AC HB nội tiếp nên BAC C HB . Do đó 1 1 1
HA .HB .HC 1 1 1 cos . A cos . B cosC cosAHC.cosB H . A cosC HB (3) 1 1 1 H . AH . B HC
Sử dụng bất đẳng thức Erdos – Mordell dạng tích ta có: 1 H . AH . B HC
8HA .HB .HC . Từ (3) suy ra cos . A cos . B cosC . 1 1 1 8
Đẳng thức xảy ra khi và chỉ khi tam giác ABC đều.
Chú ý: Do tam giác ABC nhọn nên cosA,cos B,cosC 0 . Áp dụng bất đẳng thức Cô si ta có: 3 cosA cosB cosC 3 cos . A cos . B cosC . Theo 3
chứng minh trên ta có: cos A cosB cosC suy ra 2 3 3 1 3 cos . A cos . B cosC cos . A cos . B cosC 2 8
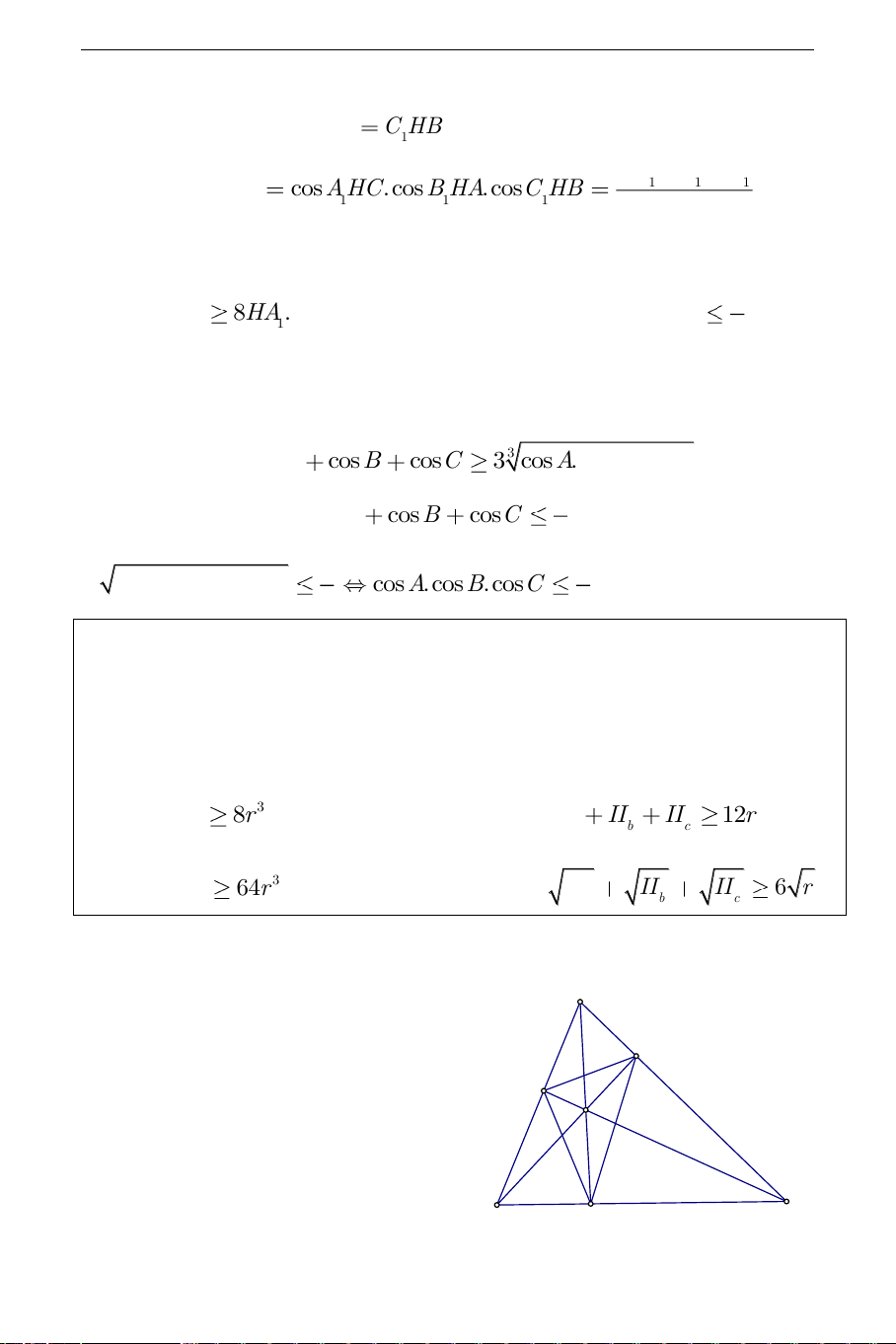
Ví dụ 4. Cho tam giác ABC nhọn, gọi I,I ,I ,I theo thứ tự là tâm đường a b c
tròn nội tiếp, tâm các đường tròn bàng tiếp tương ứng với các đỉnh , A , B C của
tam giác đó; r là bán kính của đường tròn I . Chứng minh rằng: a) 3 I . AI . B IC 8r . b) II II II 12r . a b c c) 3
II .II .II 64r . d) II II II 6 r . a b c a b c Hướng dẫn giải: Ia
a). Gọi H,J,K lần lượt là tiếp điểm B
của đường tròn I với các cạnh C I BC,C ,
A AB . Sử dụng bất đẳng
thức Erdos – Mordell dạng tích ta có: I I c b A THCS.TOANMATH.com I . AI . B IC
8IH.IJ.IK , hay 3 I . AI . B IC
8r (đpcm). Đẳng thức xảy ra khi và chỉ khi tam giác ABC đều.
Lưu ý: Bất đẳng thức ở câu a) cũng đúng cho tam giác ABC bất kỳ.
b) Nhận xét rằng điểm I là trực tâm của tam giác I I I . Áp dụng bất đẳng a b c
thức Erdos – Mordell cho điểm I đối với tam giác I I I ta nhận a b c được:II II II 2 IA IB IC
12r (theo kết quả của ví dụ 1). a b c
Đẳng thức xảy ra khi và chỉ khi tam giác ABC đều.
c) Áp dụng bất đẳng thức Erdos – Mordell dạng tích cho điểm I đối với
tam giác I I I ta nhận được 3
II .II .II 8I . AI . B IC 64r (theo kết quả a b c a b c
câu a). đẳng thức xảy ra khi và chỉ khi tam giác ABC đều.
d) Áp dụng bất đẳng thức Erdos – Mordell dạng căn thức cho điểm I trong
tam giác I I I ta có II II II 2 IA IB IC (1). a b c a b c
Tiếp tục áp dụng bất đẳng thức Erdos – Mordell dạng căn thức cho điểm I
đối với tam giác ABC ta được: IA IB IC 2 IH IJ IK 3 2. r (2)
Từ (1) và (2) suy ra II II II
6 r (đpcm). Đẳng thức xảy ra a b c
khi và chỉ khi tam giác ABC đều.
Ví dụ 5. Cho tam giác ABC với BC , a C , A , b AB
c . Gọi r là bán
kính đường tròn nội tiếp tam giác đó. Chứng minh bất đẳng thức 3 abc
24 3r . Đẳng thức xảy ra khi nào? Hướng dẫn giải: THCS.TOANMATH.com
Gọi p là nửa chu vi tam giác ABC . Từ công thức Heron 2 S p p a p b p c và S . p r . (1) ABC ABC
Gọi I là tâm đường tròn nội tiếp tam giác ABC . Theo định lý Pythagore và từ (1) ta có: 2 2 2 2 2 2 2 2 2
IA .IB .IC r p a r p b r p c p a bc p b ac p c ab (2). p p p
Áp dụng bất đẳng thức Cauchy ta có: p a p b p c p 3 p a p b p c hay 3 3 3 p p a p b p c (3). Từ (2) và (3) suy ra 27 2 2 2 a b c abc 2 2 2
IA .IB .IC . IA IB.IC
(4). Áp dụng bất đẳng thức 27 3 3
Erdos – Mordell dạng tích ta có 3 I . AI . B IC 8r (5) Từ (4) và (5) ta suy ra 3 abc
24 3r (đpcm). Đẳng thức xảy ra khi và chỉ
khi tam giác ABC đều.
Chú ý: Các bạn nếu đã quen làm với định lí sin trong tam giác ABC thì thấy a 2R sin ; A b 2R sin ; B c
2R sinC (R là bán kính đường tròn
ngoại tiếp tam giác ABC ). Khi đó từ bất đẳng thức 3 abc 24 3r ta nhận
được bất đẳng thức: 3 3 8R sin . A sin . B sinC
24 3r ta nhận được bất đẳng thức. THCS.TOANMATH.com
Hệ quả. Với mọi tam giác ABC ta có bất đẳng thức 3 r sin . A sin . B sinC 3 3
. Đẳng thức xảy ra khi và chỉ khi tam giác R ABC đều.
Ví dụ 6. Giả sử đường tròn tâm I bán kính r nội tiếp tam giác ABC tiếp
xúc với các cạnh BC,C ,
A AB theo thứ tự tại A ,B ,C . Chứng minh bất 1 1 1 đẳng thức A . B BC.CA
8AB .BC .C A . Đẳng thức xảy ra khi nào? 1 1 1 1 1 1 Hướng dẫn giải: Đặt BC , a AC , b AB
c và p là nửa chu vi tam giác ABC . Sử dụng
định lý Ptolemy cho các tứ giác nội tiếp IC AB ;IC BA ;IACB ta thấy 1 1 1 1 1 1 I . ABC IB .AC IC .AB 1 1 1 1 1 1 A hay I . AB C 2r p a (1) 1 1 B1 C1 Tương tự I . B AC 2r p b (2); 1 1 I IC.AB 2r p c B C (3) 1 1 A1
Nhân các đẳng thức (1),(2) và (3) 3 8r p a p b p c
theo vế ta được: I . AI . B IC (4). Sử dụng bất
B C .C A .AB 1 1 1 1 1 1
đẳng thức Cauchy cho hai số dương ta có: THCS.TOANMATH.com 2 2 p a p b c p a p b ; 2 4 2 2 p b p c a p b p c 2 4 2 2 p c p a b p c p a
. Nhân ba bất đẳng thức theo vế 2 4 abc
ta thu được p a p b p c
(5). Áp dụng bất đẳng thức Erdos 8
– Mordell dạng tích ta có 3 I . AI . B IC
8r (6). Từ (4),(5),(6) suy ra A . B BC.CA
8AB .BC .C A (đpcm). Đẳng thức xảy ra khi và chỉ khi 1 1 1 1 1 1
tam giác ABC đều. Từ (1),(2) và (3) suy ra PA PB PC 2 d d
d . Điều này mâu thuẫn với bất đẳng thức a b c
Erdos – Mordell. Từ đây ta có đpcm.
Ví dụ 7. Giả sử H là trực tâm của tam giác nhọn ABC . Gọi , D E,F lần
lượt là trung điểm của BC,C ,
A AB; R là bán kính đường tròn ngoại tiếp 3
tam giác ABC . Chứng minh bất đẳng thức HD HE HF R 2 Hướng dẫn giải:
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC , là tâm đường tròn
Euler của tam giác ABC . Ta có các kết quả sau: A +)
là trung điểm của OH .
+) Bán kính đường tròn Euler F E H
của tam giác ABC bằng nửa bán w O
kính đường tròn ngoại tiếp tam B C D THCS.TOANMATH.com
giác đó.(Xem them phần đường
thẳng Ơle, đường tròn Ơ le).
Sử dụng hai kết quả trên ta có: HD OD 2 D R ; HE OE 2 E R ;HF OF 2 F
R . Cộng theo vế ba bất đẳng thức ta được: HD HE HF 3R OD OE OF (1)
Áp dụng bất đẳng thức Erdos – Mordell cho điểm O nằm trong tam giác OA OB OC 3R ABC ta có: OD OE OF (2). Từ (1) và (2) 2 2 3 suy ra HD HE HF
R (đpcm). Đẳng thức xảy ra khi và chỉ khi 2 tam giác ABC đều.
Ví dụ 8. Cho tam giác nhọn ABC nội tiếp đường tròn O bán kính R . Các
đường cao AA,BB ,CC đồng quy tại H . Kẻ OO vuông góc với 1 1 1 1
BC,OO vuông góc với AC,OO vuông góc với AB . Chứng minh rằng: 2 3 3R HA HB HC OO OO OO . 1 1 1 1 2 3 2 Hướng dẫn giải: Nhận xét rằng HA 2OO ;HB 2OO ;HC 2OO 1 2 3 A
Xem thêm phần đường tròn B1 Ơ le C - Đường thẳng Ơ le 1 O O H 2 3
(Áp dụng đẳng thức Erdos – Mordell O C cho điể B
m H trong tam giác ABC , ta có: A O 1 1 HA HB HC HA HB HC OO OO OO . 1 1 1 1 2 3 2 THCS.TOANMATH.com
Áp dụng bất đẳng thức Erdos – Mordell cho điểm O trong tam giác ABC OA OB OC 3R ta có: OO OO OO (đpcm) 1 2 3 2 2
Ví dụ 9. Cho tam giác ABC và M là một điểm bất kỳ nằm trong tam giác
đó. Gọi R ,R ,R theo thứ tự là khoảng cách từ điểm M đến các đỉnh a b c , A ,
B C . Còn d ,d ,d lần lượt là khoảng cách từ điểm M đến các cạnh a b c BC,C ,
A AB . Chứng minh bất đẳng thức d d d d d d d d d 2 a c c a a b . a b c R R R a b c Giải: A
Gọi A ,B ,C theo thứ tự là 1 1 1 B1
chân các đường vuông góc A2 C1
kẻ từ M lên các cạnh BC,C , A AB . H C2 B O 2 Ta có B C M . A sinA R .sin ; A 1 1 a B C A1 C A M . B sinB R .sinB 1 1 b AB MC.sinC
R .sinC . Kẻ MA vuông góc với BC ; MB vuông 1 1 c 2 1 1 2
góc với C A ; MC vuông góc với AB . Khi đó 1 1 2 1 1 MB .MC d .d 1 1 MA MB .sin MB A MB .sin b c MAC (1) 2 1 1 2 1 1 MA Ra MA .MC d d 1 1 MB MC .sin MC B MC .sin a c MBA (2) 2 1 1 2 1 1 MB Rb MB .MA d .d 1 1 MC MA .sin MAC MA .sin b a MCB (3) 2 1 1 2 1 1 MC Rc THCS.TOANMATH.com
Áp dụng bất đẳng thức Erdos – Merdell cho điểm M trong tam giác A B C 1 1 1 ta có: MA MB MC 2 MA MB MC (4) 1 1 1 2 2 2 d d d d d d
Từ (1),(2),(3),(4) ta suy ra: d d d 2 a c c a a b (đpcm). a b c R R R a b c Chọn x R ,y R ,z R ta nhận được: a b c R R R R R R c b c a a b R R R d d d a b c a b c R R R R R R b c a c b a 2 d d d a b c THCS.TOANMATH.com




