Chuyên đề cơ bản số phức và các phép toán ôn thi TN THPT môn Toán

Chuyên đề cơ bản số phức và các phép toán ôn thi TN THPT môn Toán được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

29 15 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 4: Số phức

Môn: Toán 12

Thông tin:

36 trang 7 tháng trước

Tác giả:

Profile Mai Nguyệt
SỐ PHỨC VÀ CÁC PHÉP TOÁN
Dành cho học sinh mất gốc Toán
LÊ BÁ BẢO
Trường THPT Đặng Huy Trứ, Huế
Admin CLB Giáo viên trẻ TP Huế
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chủ đề:
SỐ PHỨC
I. TÓM TẮT LÝ THUYẾT
A. SỐ PHỨC VÀ CÁC PHÉP TOÁN
1. Số i
Ta đã biết các phương trình bậc hai với biệt số âm không có nghiệm thực. Ví dụ phương trình
2
10x 
không có nghiệm trên tập
.
Nhằm mở rộng tập hợp số thực để mọi phương trình bậc
n
đều có nghiệm, người ta đưa ra
một số mới, kí hiệu là
và xem nó là nghiệm của phương trình
2
1 0.x 
Như vậy:
2
1i 
.
2. Định nghĩa số phức
Mỗi biểu thức dạng
,a bi
trong đó
,ab
,
2
1i 
được gọi là một số phức.
Đối với số phức
,z a bi
ta nói
a
là phần thực,
b
là phần ảo của
z
.
Tập hợp các số phức kí hiệu là
.
3. Số phức bằng nhau
Hai số phức là bằng nhau nếu phần thực và phần ảo của chúng tương ứng bằng nhau.
ac
a bi c di
bd

;
, , ,a b c d
Chú ý:
+ Mỗi số thực
a
được xem là một số phức với phần ảo bằng 0:
0.a a i
Như vậy, mỗi số thực cũng là một số phức. Ta có:
.
+ Số phức
0z bi
được gọi là số thuần ào và viết đơn giản là
.bi
Đặc biệt:
01ii
. Vậy số
được gọi là đơn vị ảo.
4. Biểu diễn hình học số phức
Mỗi số phức hoàn toàn xác định bởi cặp số thực
;.ab
Điểm
;M a b
trong hệ tọa độ vuông góc của mặt
phẳng được gọi là điểm biểu diễn số phức
.z a bi
x
y
b
a
M
O
5. Môđun của số phức
Giả sử số phức
z a bi
được biểu diễn bởi
điểm
;M a b
trên mặt phẳng tọa độ.
Độ dài của vectơ
OM
được gọi là mô đun của số
phức
z
và kí hiệu là
.z
Vậy
z OM OM
hay
a bi OM
.
Suy ra:
22
a bi a b
x
y
M
a
b
O
6. Số phức liên hợp
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Cho số phức
.z a bi
Ta gọi
a bi
là số phức
liên hợp của
z
và kí hiệu
z a bi
.
Nhận xét:
+
zz
+
zz
x
y
-b
z = a - bi
z = a+bi
a
b
O
7. Cộng và trừ số phức
Cho
//
;z a bi z a b i
/ / / / / /
;z z a a b b i z z a a b b i
8. Nhân hai số phức:
Cho
//
;z a bi z a b i
/ / / / /
.z z aa bb ab a b i
9. Chia hai số phức
Với
vµ
1 1 1 2 2 2 2
0z a b i z a b i z
Lúc đó:
1 1 2 2 1 1 2 2
1 1 1 1 1 2
2 2 2
2 2 2 2
2 2 2 2
22
2
.
a b i a b i a b i a b i
z a b i z z z
z a b i z
a b i a b i
ab
z





Lưu ý: 1)
z a bi
là số thực
0b
2)
z a bi
là số thuần ảo
0.a
B. PHƯƠNG TRÌNH BẬC HAI VỚI HỆ SỐ THỰC
1. Căn bậc hai của số thực âm
2
22
Do 1 nªn ta nãi lµ mét c¨n bËc hai cña 1 vµ còng lµ mét c¨n bËc hai cña 1
do ( ) 1. T¬ng tù, c¨n bËc hai cña 5 lµ 5 do ( 5) 5
i i i
i i i
Tæng qu¸t: C¨n bËc hai cña sè thùc ©m lµ: a i a
2. Phương trình bậc hai với hệ số thực
2
2
Cho ph¬ng tr×nh: 0 (*) víi , , , 0.
XÐt 4
ax bx c a b c a
b ac
0
TH 1: 0, ph¬ng tr×nh (*) cã mét nghiÖm .
2
b
thùc x
a
1,2
TH 2: 0, ph¬ng tr×nh (*) cã hai nghiÖm
2
TH 3: 0, ph¬ng tr×nh (*) « nghiÖm . Nhng nÕu gi¶i (*) trªn
tËp th× cã hai c¨n bËc hai lµ:

b
thùc x
a
kh ng cã thùc
i nªn (*) cã hai nghiÖm phøc lµ:
1,2
2
bi
x
a
II. BÀI TẬP TRẮC NGHIỆM MINH HỌA
A. SỐ PHỨC VÀ CÁC PHÉP TOÁN
Dạng 1: Số phức và các khái niệm liên quan
Câu 1: Kí hiệu là tập số thực, là tập số phức. Khẳng định nào sau đây sai?
A.
.
B.
1.i
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
C.
1z 
không phải là số phức. D.
2
1.i 
Câu 2: Số phức có phần thực bằng
1
và phần ảo bằng
3
là
A.
1 3 .i
B.
1 3 . i
C.
1 3 .i
D.
1 3 . i
Câu 3: Số phức nào sau đây là số thuần ảo?
A.
1.i
B.
3.i
C.
3.
D.
1 2 .i
Câu 4: Số phức nào dưới đây là số thuần ảo?
A.
23zi
. B.
3zi
. C.
2z 
. D.
3zi
.
Câu 5: Cho số phức
2
1 1 , .z m m i m
Tập hợp tất cả các giá trị của tham số
m
để số phức
z
là số thuần ảo là
A.
1.
B.
.
C.
1;1 .
D.
1.
Câu 6: Phần thực của số phức
42zi
bằng
A.
2
. B.
4
. C.
4
. D.
2
.
Câu 7: Cho số phức
1 3 .zi
Phần thực của số phức
z
là
A.
1.
B.
3.
C.
3.i
D.
0.
Câu 8: Biết các số thực
;ab
thỏa mãn
1 2 3 3 .a b a b i i
Tính
.ab
A.
1.
B.
3.
C.
2.
D.
0.
Câu 9: Cho số phức
1 3 .zi
Phần ảo của số phức
z
là
A.
1.
B.
3.
C.
3.i
D.
0.
Câu 10: Cho số phức
32zi
. Tìm phần thực và phần ảo của số phức
z
.
A. Phần thực bằng
3
và Phần ảo bằng
2i
. B. Phần thực bằng
3
và Phần ảo bằng
2
.
C. Phần thực bằng
3
và Phần ảo bằng
2i
. D. Phần thực bằng
3
và Phần ảo bằng
2
.
Câu 11: Cho số phức
2 3 .zi
Tìm phần thực
a
và phần ảo
b
của số phức
.z
A.
2; 3.ab
B.
2; 3.ab
C.
2; 3 .a b i
D.
2; 3 .a b i
Câu 12: Cho số phức bất kì
, ; .z a bi a b
Khẳng định nào sau đây đúng?
A.
.z a bi
B.
.z a bi
C.
.z b ai
D.
.z b ai
Câu 13: Số phức liên hợp của số phức
12zi
là
A.
1 2 .zi
B.
1 2 .zi
C.
1 2 .zi
D.
1 2 .zi
Câu 14: Số phức liên hợp của số phức
35zi
A.
35 zi
. B.
35zi
. C.
35 zi
. D.
35zi
.
Câu 15: Tìm
1 2 .i
A.
1 2 .i
B.
1 2 .i
C.
1 2 .i
D.
1 2 .i
Câu 16: Cho số phức
1 3 .zi
Phần ảo của số phức
z
là
A.
1.
B.
3.
C.
3.i
D.
3.
Câu 17: Tìm số phức liên hợp của số phức
31z i i
.
A.
3zi
. B.
3 zi
. C.
3zi
. D.
3 zi
.
Câu 18: Cho số phức
3
1z i i
. Tìm phần thực
a
và phần ảo
b
của
z
.
A.
0, 1.ab
B.
2, 1. ab
C.
1, 0.ab
D.
1, 2. ab
Câu 19: Khẳng định nào sau đây đúng?
A.
,z z z
luôn là số thực. B.
, 0.zz
C.
,.z z z
luôn là số thực. D.
2
22
,.z z z z
Câu 20: Số phức đối của số phức
12zi
là
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
A.
1 2 .i
B.
12
.
55
i
C.
1 2 .i
D.
1 2 .i
Câu 21: Mệnh đề nào dưới đây sai?
A.
:zz
là số thực. B.
:zz
là số phức.
C.
:zz
là số thực dương. D.
:zz
là số thực không âm.
Câu 22: Môđun của số phức
12zi
là
A.
5.z
B.
5.z
C.
2.z
D.
3.z
Câu 23: Cho số phức
2zi
. Tính
z
.
A.
3z
. B.
5z
. C.
2z
. D.
5z
.
Câu 24: Với
là số thực bất kì, tính
sin cos .i

A.
0.
B.
1.
C.
2.
D.
3.
Câu 25: Cho số phức bất kì
, ; .z a bi a b
Khẳng định nào sau đây đúng?
A.
22
.z a b
B.
22
.z a b
C.
.z a b
D.
.z a b
Câu 26: Cho số phức
12.z m m i m
. Tất cả các giá trị của
m
để
5z
là
A.
6
2
m
m

. B.
30 m
. C.
03 m
. D.
3
0
m
m

.
Câu 27: Cho số phức
1 3 .zi
Khẳng định nào sau đây sai?
A.
1 3 .zi
B.
10.z
C.
10.z
D.
1 3 .zi
Câu 28: Biết các số thực
;ab
thỏa mãn
2 3 6 .a b i a b i i
Tính
.ab
A.
1.
B.
3.
C.
2.
D.
0.
Câu 29: Biết các số thực
;xy
thỏa mãn
1 3 2 .x y i i x yi
Tính
2.xy
A.
1.
B.
3.
C.
2.
D.
8.
Câu 30: Tìm hai số thực
x
và
y
thỏa mãn
2 3 3 5 4x yi i x i
với
i
là đơn vị ảo.
A.
1; 1xy
B.
1; 1xy
C.
1; 1xy
D.
1; 1xy
Câu 31: Tìm các số thực
a
và
b
thỏa mãn
2 1 2a b i i i
với
i
là đơn vị ảo.
A.
0, 2ab
. B.
1
,1
2
ab
. C.
0, 1ab
. D.
1, 2ab
.
Câu 32: Tìm hai số thực
x
và
y
thỏa mãn
3 2 2 2 3x yi i x i
với
i
là đơn vị ảo.
A.
2; 2xy
. B.
2; 1xy
. C.
2; 2xy
. D.
2; 1xy
Dạng 2: Tìm số phức thỏa mãn yêu cầu
Câu 33: Cho hai số phức
1
1zi
và
2
3 2 .zi
Khẳng định nào sau đây đúng?
A.
12
4 3 .z z i
B.
12
4 3 .z z i
C.
12
4 3 .z z i
D.
12
2 3 .z z i
Câu 34: Cho hai số phức
1
12zi
và
2
2
3 6 ; .z m m i m
Tìm tập hợp tất cả các giá trị
m
để
12
zz
là số thực.
A.
2; 2 .
B.
2.
C.
1.
D.
6; 6 .
Câu 35: Cho hai số phức
1
2zi
và
2
3 2 .zi
Phần ảo của số phức
12
2zz
là
A.
4.i
B.
3.
C.
4.
D.
3.
Câu 36: Cho hai số phức
1
3zi
và
2
1 2 .zi
Phần thực của số phức
12
.zz
là
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
A.
7.
B.
1.
C.
7.
D.
3.
Câu 37: Cho hai số phức
32zi
và
14wi
. Số phức
zw
bằng
A.
42i
. B.
42i
. C.
26i
. D.
26i
.
Câu 38: Cho hai số phức
3zi
và
23wi
. Số phức
zw
bằng
A.
14i
. B.
12i
. C.
54i
. D.
52i
.
Câu 39: Cho số phức
32zi
, số phức
1 iz
bằng.
A.
15i
B.
5 i
C.
15i
D.
5 i
Câu 40: Cho số phức
2zi
, số phức
23iz
bằng
A.
18i
. B.
74i
. C.
74i
. D.
18i
.
Câu 41: Cho số phức
3.zi
Phần thực của số phức
12zz
là
A.
10.
B.
1.
C.
7.
D.
3.
Câu 42: Tính
1 2 3 2 .ii
A.
10.
B.
25.
C.
50.
D.
5 2.
Câu 43: Cho hai số phức
1
1zi
và
2
23zi
. Tính môđun của số phức
12
.zz
A.
12
13zz
. B.
12
5zz
. C.
12
1zz
. D.
12
5zz
.
Câu 44: Cho hai số phức
1
3zi
và
2
, ; .z m ni m n
Khẳng định nào sau đây đúng?
A.
12
3 3 .z z m n m n i
B.
12
3 3 .z z m n m n i
C.
12
3 3 .z z m n m n i
D.
12
3 3 .z z m n m n i
Câu 45: Cho số phức
,z m i m
là tham số. Tìm tập hợp giá trị
m
để
2
z
là số thuần ảo.
A.
0.
B.
1.
C.
1;1 .
D.
.
Câu 46: Cho hai số phức
1
3zi
và
2
1.zi
Phần thực của số phức
1
2
z
z
là
A.
7.
B.
1.
C.
2.
D.
2.
Câu 47: Cho hai số phức
1
1zi
và
2
, ; .z a bi a b
Phần ảo của số phức
2
1
z
z
là
A.
.
2
ab
B.
2
ab
C.
.ab
D.
.ab
Câu 48: Tìm số phức nghịch đảo của số phức
1 2 .i
A.
1 2 .i
B.
51
.
22
i
C.
12
.
55
i
D.
1 2 .i
Câu 49: Cho số phức
z
thỏa mãn
32iz i
. Số phức liên hợp của
z
là:
A.
23zi
. B.
23zi
. C.
23zi
. D.
23zi
.
Câu 50: Số phức
z
thỏa mãn
65iz i
. Số phức liên hợp của
z
là
A.
56zi
. B.
56zi
. C.
56zi
. D.
56zi
.
Câu 51: Tìm số phức
z
thỏa mãn
1 3 2 0.i z i
A.
51
.
22
zi
B.
51
.
22
zi
C.
51
.
22
zi
D.
51
.
22
zi
Câu 52: Cho số phức
2 5 .zi
Tìm số phức
w iz z
A.
73wi
. B.
33wi
. C.
3 7 .wi
D.
77wi
Câu 53: Tìm số phức
z
thỏa mãn
1 3 5 0.i z i
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
A.
1 4 .zi
B.
1 4 .zi
C.
1 2 .zi
D.
2.zi
Câu 54: Tính môđun của số phức
z
thỏa mãn
2 13 1z i i
.
A.
34z
B.
34z
C.
5 34
3
z
D.
34
3
z
Câu 55: Biết số phức
z
thỏa mãn
2 1 5 0.i z i
Tính
1.zi
A.
2 5.
B.
2.
C.
3.
D.
85
.
5
Câu 56: Biết số phức
,;z a bi a b
thỏa mãn
1 2 6 3 .i z i z i
Tính
.ab
A.
0.
B.
2.
C.
3.
D.
2.
Câu 57: Biết số phức
,;z a bi a b
thỏa mãn
1 3 2 10 2 .i z i z i
Tính
.ab
A.
17
.
11
B.
2.
C.
3.
D.
32
.
11
Câu 58: Cho số phức
z
thỏa mãn
2 2 3 2 .i z i z i
Tìm tọa độ của điểm biểu diễn của số phức
liên hợp với
.z
A.
11 5
;.
88



B.
11 5
;.
88



C.
11 5
;.
88



D.
11 5
;.
88




Câu 59: Có bao nhiêu số phức
z
thỏa mãn điều kiện
.2z z z
và
2?z
A.
1.
B.
2.
C.
3.
D.
4.
Câu 60: Biết số phức
,;z a bi a b
thỏa mãn
1 2 1 6 .i z i z i
Tính
3.ab
A.
2.
B.
2.
C.
3.
D.
5.
Câu 61: Biết số phức
,;z a bi a b
thỏa mãn
2 1 4 3 .i z i z i
Tính
.ab
A.
1.
B.
2.
C.
3.
D.
2.
Câu 62: Biết số phức
,;z a bi a b
thỏa mãn
1 2 1 2 .i z i z i
Tính
.ab
A.
2.
B.
1.
C.
1.
D.
4.
Câu 63: Biết số phức
,;z a bi a b
thỏa mãn
3 4 1 .i z i z i
Tính
7.ab
A.
2.
B.
0.
C.
3.
D.
2.
Câu 64: Biết số phức
,;z a bi a b
thỏa mãn
2 3 2 1 4 .i z i z i
Tính
8 8 .ab
A.
12.
B.
8.
C.
3.
D.
10.
Câu 65: Biết số phức
,;z a bi a b
thỏa mãn
1 3 5 4 .i z i z i
Tính
4.ab
A.
7.
B.
2.
C.
3.
D.
5.
Câu 66: Biết số phức
,;z a bi a b
thỏa mãn
2 4 1 3 .i z i z i
Tính
6 3 .ab
A.
3.
B.
2.
C.
3.
D.
5.
Câu 67: Biết số phức
,;z a bi a b
thỏa mãn
1 3 3 4 .i z i z i
Tính
4.ab
A.
3.
B.
5.
C.
3.
D.
5.
Câu 68: Biết số phức
,;z a bi a b
thỏa mãn
2 3 4 1 2 .i z i z i
Tính
2.ab
A.
7.
B.
5.
C.
3.
D.
5.
Câu 69: Biết số phức
,;z a bi a b
thỏa mãn
3 2 3 3 .i z i z i
Tính
.ab
A.
7.
B.
5.
C.
3.
D.
2.
Câu 70: Biết số phức
,;z a bi a b
thỏa mãn
1 5 3 4 1 7 .i z i z i
Tính
4.ab
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
A.
1.
B.
1.
C.
3.
D.
2.
Câu 71: Biết số phức
,;z a bi a b
thỏa mãn
2 3 4 1 2 .i z i z i
Tính
5.ab
A.
7.
B.
5.
C.
3.
D.
2.
Câu 72: Biết số phức
,;z a bi a b
thỏa mãn
21
3 2 .
11
ii
z z i
ii


Tính
.ab
A.
4.
B.
5.
C.
3.
D.
2.
Câu 73: Biết số phức
,;z a bi a b
thỏa mãn
12
3 5 .
21
ii
z z i
ii


Tính
.ab
A.
2
.
7
B.
11
.
5
C.
3
.
4
D.
21
.
11
Câu 74: Cho số phức
z
thỏa
2 3 16 2 i z i z i
. Môđun của
z
bằng
A.
5
. B.
13
. C.
13
. D.
5
.
Câu 75: Cho số phức
z
thỏa
( 2 ) 4( ) 8 19i z z i i
. Môđun của
z
bằng
A.
13
. B.
5
. C.
13
. D.
5
.
Câu 76: Cho số phức
,z a bi a b
thoả mãn
2z i z
. Tính
4S a b
.
A.
4.S
B.
2.S
C.
2.S 
D.
4.S 
Câu 77: Cho số phức
z a bi
( , )ab
thỏa mãn
1 3 0z i z i
. Tính
3.S a b
A.
7
.
3
S
B.
5.S 
C.
5.S
D.
7
.
3
S 
Câu 78: Cho số phức
z
thỏa mãn
35z
và
2 2 2 z i z i
. Tính
z
.
A.
17z
. B.
17z
. C.
10z
. D.
10z
.
Câu 79: Có bao nhiêu số phức
z
thỏa mãn
2z
và
22z i z
là số thuần ảo?
A.
1
. B.
0
. C.
2
. D.
4
.
Dạng 3: Biểu diễn số phức
Câu 80: Kí hiệu điểm
M
là điểm biểu diễn số phức,
M
là điểm biểu diễn số phức
.z
Khẳng định nào
sau đây đúng?
A.
,MM
đối xứng nhau qua trục tung. B.
,MM
đối xứng nhau qua trục hoành.
C.
,MM
đối xứng nhau qua gốc tọa độ. D.
,MM
đối xứng nhau qua
.yx
Câu 81: Cho số phức
1 3 .zi
Điểm biểu diễn số phức
z
trên mặt phẳng tọa độ là
A.
1; 3 .M
B.
1;3 .N
C.
1; 3 .P 
D.
1;3 .Q
Câu 82: Trên mặt phẳng tọa độ, điểm biểu diễn số phức
32i
có tọa độ là
A.
2;3
. B.
2;3
. C.
3;2
. D.
3; 2
.
Câu 83: Cho số phức
1 3 .zi
Điểm biểu diễn số phức
z
trên mặt phẳng tọa độ là
A.
1; 3 .M
B.
1;3 .N
C.
1; 3 .P 
D.
1;3 .Q
Câu 84: Cho hai số phức
12
2 , 1z i z i
. Trên mặt phẳng tọa độ Oxy, điểm biểu diễn số phức
12
2zz
có tọa độ là:
A.
5; 1
. B.
1;5
. C.
5;0
. D.
0;5
.
Câu 85: Trên mặt phẳng tọa độ, điểm biểu diễn số phức
2
12zi
là điểm nào dưới đây?
A.
3;4P
B.
5;4Q
. C.
4; 3N
. D.
5;4M
.
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Câu 86: Cho hai số phức
1
1zi
và
2
2zi
. Trên mặt phẳng
Oxy
, điểm biểu diễn số phức
12
2zz
có tọa độ là
A.
2;5
. B.
3;5
. C.
5;2
. D.
5;3
.
Câu 87: Cho số phức
12zi
. Điểm nào dưới đây là điểm biểu diễn của số phức
w iz
trên mặt
phẳng tọa độ?
A.
(1;2)Q
B.
(2;1)N
C.
(1; 2)M
D.
( 2;1)P
Câu 88: Điểm
1; 2A
là biểu diễn trên mặt phẳng tọa độ số phức
z
nào trong các số phức sau?
A.
1 2 .zi
B.
1 2 .zi
C.
1 2 .zi
D.
1 2 .zi
Câu 89: Trên mặt phẳng tọa độ, điểm
( 2;3)M
là điểm biểu diễn số phức nào dưới đây?
A.
3
23zi
. B.
4
23zi
. C.
1
23zi
. D.
2
23zi
.
Câu 90: Số phức nào dưới đây có điểm biểu diễn trên mặt phẳng tọa độ là điểm
M
như hình bên?
A.
4
2.zi
B.
2
1 2 .zi
C.
3
2. zi
D.
1
1 2 .zi
Câu 91: Điểm
M
trong hình vẽ bên dưới là điểm biểu diễn của số phức nào trong 4 số phức được cho
ở các phương án A, B, C, D?
x
y
M
-3
2
O
A.
3 2 .zi
B.
2 3 .zi
C.
3 2 .zi
D.
3 2 .zi
Câu 92: Điểm biểu diễn số phức
32zi
là điểm nào trong 4 điểm
, , ,M N P Q
trong hình vẽ bên
dưới?
x
y
Q
P
N
M
-3
-2
2
3
O
A.
.M
B.
.N
C.
.P
D.
.Q
Câu 93: Cho hai số phức
1
12zi
và
2
3 2 .zi
Gọi
,AB
là hai điểm lần lượt biểu diễn số phức
12
,zz
trên mặt phẳng tọa độ. Tính độ dài
.AB
A.
10.
B.
5.
C.
2 5.
D.
3.
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Câu 94: Cho số phức
3 2 .zi
Gọi
,AB
là hai điểm lần lượt biểu diễn số phức
,zz
trên mặt phẳng
tọa độ. Tính diện tích tam giác
OAB
(
O
là gốc tọa độ).
A.
6.
B.
5.
C.
2 5.
D.
3.
Câu 95: Biết số phức
z
thỏa mãn
1 3 3 .z i z i
Tập hợp điểm biểu diễn số phức
z
trên mặt
phẳng tọa độ là đường thẳng có phương trình
A.
2 4 0.xy
B.
2 4 0.xy
C.
2 4 0.xy
D.
4 0.xy
Câu 96: Biết số phức
z
thỏa mãn
1 3 3 5 .z i z i
Tập hợp điểm biểu diễn số phức
z
trên mặt
phẳng tọa độ là đường thẳng có phương trình
A.
2 4 0.xy
B.
4 6 0.xy
C.
2 6 0.xy
D.
4 0.xy
Câu 97: Biết số phức
z
thỏa mãn
2 2 4 .z i z i
Tập hợp điểm biểu diễn số phức
z
trên mặt
phẳng tọa độ là đường thẳng có phương trình
A.
2 4 0.xy
B.
4 6 0.xy
C.
2 6 0.xy
D.
4 0.xy
Câu 98: Biết số phức
z
thỏa mãn
1 3.zi
Tập hợp điểm biểu diễn số phức
z
trên mặt phẳng tọa
độ là đường tròn có phương trình
A.
22
1 1 9.xy
B.
22
1 1 9.xy
C.
22
1 1 9.xy
D.
22
1 1 9.xy
Câu 99: Biết số phức
z
thỏa mãn
3 4 4.zi
Biết tập hợp điểm biểu diễn số phức
z
trên mặt phẳng
tọa độ là đường tròn
.C
Tìm tâm
I
và tính bán kính
R
của đường tròn
.C
A.
3;4 , 16.IR
B.
3;4 , 4.IR
C.
3; 4 , 4.IR
D.
3; 4 , 16.IR
Câu 100: Biết số phức
z
thỏa mãn
1 2.zi
Biết tập hợp điểm biểu diễn số phức
z
trên mặt phẳng
tọa độ là đường tròn
.C
Tìm tâm
I
và tính bán kính
R
của đường tròn
.C
A.
1;1 , 2.IR
B.
1; 1 , 4.IR
C.
1; 1 , 2.IR
D.
1;1 , 4.IR
Câu 101: Xét các số phức
z
thỏa mãn
22z i z
là số thuần ảo. Biết rằng tập hợp tất cả các
điểm biểu diễn của
z
là một đường tròn, tâm của đường tròn đó có tọa độ là
A.
1; 1
. B.
1;1
. C.
1;1
. D.
1; 1
.
Câu 102: Xét các số phức
z
thỏa mãn
22z i z
là số thuần ảo. Trên mặt phẳng tọa độ, tập hợp
tất cả các điểm biểu diễn các số phức
z
là một đường tròn có bán kính bằng
A.
2 2.
B.
2.
C.
2.
D.
4.
Câu 103: Cho các số phức
z
thỏa mãn
4z
. Biết rằng tập hợp các điểm biểu diễn các số
phức
(3 4 )w i z i
là một đường tròn. Tính bán kính
r
của đường tròn đó.
A.
4r
. B.
5r
. C.
20r
. D.
22r
.
B. PHƯƠNG TRÌNH BẬC HAI VỚI HỆ SỐ THỰC
Câu 104: Phương trình
2
0ax bx c
,,a b c
có hai nghiệm phức phân biệt khi và chỉ khi
A.
2
40b ac
. B.
2
0
40
a
b ac

. C.
2
0
40
a
b ac

. D.
2
0
40
a
b ac

.
Câu 105: Trên tập số phức, phương trình nào sau đây có nghiệm thực?
A.
2
1 0.x 
B.
2
1 0.x 
C.
2
4 0.x 
D.
2
2 1 0.x 
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Câu 106: Kí hiệu
1
z
,
2
z
là hai nghiệm phức của phương trình
2
3z 
. Giá trị của
12
zz
bằng
A.
6
. B.
23
. C.
3
. D.
3.
Câu 107: Trên tập số phức, tập nghiệm của phương trình
2
2 2 0zz
là
A.
1 ;1 .ii
B.
1 ;1 .ii
C.
1 ; 1 .ii
D.
; 1 .ii
Câu 108: Trên tập số phức, gọi
12
,zz
là hai nghiệm của phương trình
2
2 2 0.zz
Tính
12
.zz
A.
2 2.
B.
2.
C.
42
D.
4.
Câu 109: Phương trình nào dưới đây nhận hai số phức
12i
và
12i
là nghiệm?
A.
2
2 3 0. zz
B.
2
2 3 0 . zz
C.
2
2 3 0. zz
D.
2
2 3 0 . zz
Câu 110: Trên tập số phức, gọi
12
,zz
là hai nghiệm của phương trình
2
4 2 0.zz
Tính
22
12
.zz
A.
2 2.
B.
2.
C.
8.
D.
4.
Câu 111: Gọi
12
,zz
là hai nghiệm phức của phương trình
2
4 5 0zz
. Giá trị của
22
12
zz
bằng
A.
6
. B.
8
. C.
16
. D.
26
.
Câu 112: Gọi
12
,zz
là 2 nghiệm phức của phương trình
2
6 14 0 zz
. Giá trị của
22
12
zz
bằng:
A. 36. B. 8. C.
28
. D. 18.
Câu 113: Kí hiệu
12
,zz
là hai nghiệm của phương trình
2
40z 
. Gọi
,MN
lần lượt là điểm biểu
diển của
12
,zz
trên mặt phẳng tọa độ. Tính
T OM ON
với
O
là gốc tọa độ.
A.
2T
. B.
2T
. C.
8T
. D.
4T
.
Câu 114: Ký hiệu
12
,zz
là hai nghiệm phức của phương trình
2
60zz
Tính
12
11
P
zz

.
A.
1
6
P
. B.
1
12
P
. C.
1
6
P 
. D.
6P
.
Câu 115: Gọi
0
z
là nghiệm phức có phần ảo âm của phương trình
2
2 5 0zz
. Môđun của số
phức
0
zi
bằng
A. 2. B.
2
. C.
10
. D.
10
.
Câu 116: Kí hiệu
0
z
là nghiệm phức có phần ảo dương của phương trình
2
4 16 17 0zz
. Trên mặt
phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn của số phức
0
w iz
?
A.
1
1
;2
2
M



. B.
2
1
;2
2
M



. C.
3
1
;1
4
M



. D.
4
1
;1
4
M



.
Câu 117: Trên tập số phức, cho phương trình
2
2 0,z z m m
là tham số. Tìm tập hợp tất cả các giá trị
của tham số
m
để phương trình đã cho không có nghiệm thực.
A.
.
B.
1; .
C.
1; .

D.
.
Câu 118: Gọi
0
z
là nghiệm phức có phần ảo dương của phương trình
2
6 34 0zz
. Tính
0
2.zi
A.
17
. B.
17
. C.
2 17
. D.
37
.
Câu 119: Ký hiệu
12
,zz
là hai nghiệm phức của phương trình
2
60zz
Tính
12
11
P
zz

.
A.
1
6
P
. B.
1
12
P
. C.
1
6
P 
. D.
6P
.
Câu 120: Gọi
0
z
là nghiệm phức có phần ảo dương của phương trình
2
6 13 0zz
. Trên mặt
phẳng tọa độ, điểm biểu diễn
0
1 z
là:
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
A.
2;2M
. B.
4; 2Q
. C.
4;2N
. D.
2; 2P 
.
Câu 121: Gọi
1
z
là nghiệm phức có phần ảo âm của phương trình
2
2 5 0zz
. Tìm tọa độ điểm biểu
diễn số phức
1
74i
z
trên mặt phẳng phức?
A.
3; 2P
. B.
1; 2N
. C.
3; 2Q
. D.
1; 2M
.
Câu 122: Trên tập số phức, số nghiệm thực của phương trình
42
3 4 0zz
là
A.
0.
B.
1.
C.
4.
D.
2.
Câu 123: Trên tập số phức, tập nghiệm của phương trình
42
2 3 0zz
là
A.
3.
B.
;3i
C.
; 3 .i
D.
; 3 .ii
Câu 124: Trên tập số phức, tập nghiệm của phương trình
42
4 3 0zz
là
A.
1; 3 .
B.
.
C.
; 3 .ii
D.
; 3 .ii
Câu 125: Trên tập số phức, gọi
1 2 3 4
, , ,z z z z
là bốn nghiệm của phương trình
42
2 3 0.zz
Tính
1 2 3 4
.z z z z
A.
2 2 3.
B.
2 3.
C.
4 2 3.
D.
4 4 3.
Câu 126: Kí hiệu
1 2 3
,,z z z
và
4
z
là bốn nghiệm phức của phương trình
42
12 0zz
. Tính
tổng
1 2 3 4
T z z z z
.
A.
4.T
B.
2 3.T
C.
4 2 3.T
D.
2 2 3.T
Câu 127: Trên tập số phức, tổng môđun các nghiệm của phương trình
22
1 4 0zz
là
A.
6.
B.
1.
C.
4.
D.
2.
Câu 128: Trên tập số phức, gọi
12
,zz
là hai nghiệm của phương trình
2
2 2 0.zz
Biết
,AB
lần lượt là
hai điểm biểu diễn
12
,zz
trên mặt phẳng. Tính độ dài đoạn thẳng
.AB
A.
2 2.
B.
2.
C.
1.
D.
4.
Câu 129: Trên tập số phức, tìm giá trị tham số thực
m
để phương trình
2
40z mz m
có một
nghiệm là
1.zi
A.
2.m 
B.
1.m
C.
3.m
D.
4.m
Câu 130: Trên tập số phức, gọi
12
,zz
là hai nghiệm của phương trình
2
2 2 0.zz
Biết
,AB
lần lượt là
hai điểm biểu diễn
12
,zz
trên mặt phẳng. Tọa độ trung điểm của đoạn thẳng
AB
là
A.
1;0
B.
1;0 .
C.
0;1 .
D.
0; 1 .
Câu 131: Trên tập số phức, gọi
12
,zz
là hai nghiệm của phương trình
2
2 5 0.zz
Biết
,AB
lần lượt là
hai điểm biểu diễn
12
,zz
trên mặt phẳng. Tính
cos ,AOB
(với
O
là gốc tọa độ).
A.
3
5
B.
3
.
5
C.
1
.
5
D.
1
.
5
Câu 132: Trên tập số phức, gọi
12
,zz
là hai nghiệm của phương trình
2
4 8 0.zz
Biết
,AB
lần lượt là
hai điểm biểu diễn
12
,zz
trên mặt phẳng. Tính
,OAB
(với
O
là gốc tọa độ).
A.
o
30
B.
o
60
C.
o
135
D.
o
45 .
Câu 133: Gọi
12
,zz
là hai nghiệm của phương trình
2
4 13 0zz
và
A
,
B
lần lượt là hai điểm biểu
diễn cho hai số phức
1
z
,
2
z
trong mặt phẳng tọa độ
Oxy
. Diện tích tam giác
OAB
bằng
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
A.
13
. B.
12
. C.
13
2
. D.
6
.
Câu 134: Gọi
1
z
,
2
z
,
3
z
là ba nghiệm của phương trình
32
5 7 0z z z
. Tính
1 2 3
M z z z
.
A.
1 2 7M 
. B.
1 7 2M 
. C.
27M 
. D.
3M
.
Câu 135: Gọi
A
,
B
,
C
là các điểm biểu diễn các số phức
1
z
,
2
z
,
3
z
là nghiệm của phương trình
32
6 12 7 0z z z
. Tính diện tích
S
của tam giác
ABC
.
A.
33S
. B.
33
2
S
. C.
1S
. D.
33
4
S
.
Câu 136: Trên tập hợp các số phức, xét phương trình
22
2 1 0z m z m
. Có bao nhiêu giá trị
của
m
để phương trình đó có nghiệm
o
z
thõa mãn
8?
o
z
A.
4
. B.
3
. C.
2
. D.
1
.
III. LỜI GIẢI CHI TIẾT
A. SỐ PHỨC VÀ CÁC PHÉP TOÁN
Dạng 1: Số phức và các khái niệm liên quan
Câu 1: Kí hiệu là tập số thực, là tập số phức. Khẳng định nào sau đây sai?
A.
.
B.
1.i
C.
1z 
không phải là số phức. D.
2
1.i 
Câu 2: Số phức có phần thực bằng
1
và phần ảo bằng
3
là
A.
1 3 .i
B.
1 3 . i
C.
1 3 .i
D.
1 3 . i
Câu 3: Số phức nào sau đây là số thuần ảo?
A.
1.i
B.
3.i
C.
3.
D.
1 2 .i
Câu 4: Số phức nào dưới đây là số thuần ảo?
A.
23zi
. B.
3zi
. C.
2z 
. D.
3zi
.
Câu 5: Cho số phức
2
1 1 , .z m m i m
Tập hợp tất cả các giá trị của tham số
m
để số phức
z
là số thuần ảo là
A.
1.
B.
.
C.
1;1 .
D.
1.
Lời giải:
Số phức
z
là số thuần ảo
2
1
1 0 .
1
m
m
m

Chọn đáp án C.
Câu 6: Phần thực của số phức
42zi
bằng
A.
2
. B.
4
. C.
4
. D.
2
.
Câu 7: Cho số phức
1 3 .zi
Phần thực của số phức
z
là
A.
1.
B.
3.
C.
3.i
D.
0.
Câu 8: Biết các số thực
;ab
thỏa mãn
1 2 3 3 .a b a b i i
Tính
.ab
A.
1.
B.
3.
C.
2.
D.
0.
Lời giải:
Ta có:
1 3 1
1 2 3 3 .
2 3 1
a b a
a b a b i i
a b b



Vậy
2.ab
Chọn đáp án C.
Câu 9: Cho số phức
1 3 .zi
Phần ảo của số phức
z
là
A.
1.
B.
3.
C.
3.i
D.
0.
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Câu 10: Cho số phức
32zi
. Tìm phần thực và phần ảo của số phức
z
.
A. Phần thực bằng
3
và Phần ảo bằng
2i
. B. Phần thực bằng
3
và Phần ảo bằng
2
.
C. Phần thực bằng
3
và Phần ảo bằng
2i
. D. Phần thực bằng
3
và Phần ảo bằng
2
.
Câu 11: Cho số phức
2 3 .zi
Tìm phần thực
a
và phần ảo
b
của số phức
.z
A.
2; 3.ab
B.
2; 3.ab
C.
2; 3 .a b i
D.
2; 3 .a b i
Lời giải:
Ta có:
Chọn đáp án A.
Câu 12: Cho số phức bất kì
, ; .z a bi a b
Khẳng định nào sau đây đúng?
A.
.z a bi
B.
.z a bi
C.
.z b ai
D.
.z b ai
Câu 13: Số phức liên hợp của số phức
12zi
là
A.
1 2 .zi
B.
1 2 .zi
C.
1 2 .zi
D.
1 2 .zi
Câu 14: Số phức liên hợp của số phức
35zi
A.
35 zi
. B.
35zi
. C.
35 zi
. D.
35zi
.
Câu 15: Tìm
1 2 .i
A.
1 2 .i
B.
1 2 .i
C.
1 2 .i
D.
1 2 .i
Lời giải:
Kí hiệu
12i
là số phức liên hợp của
12i
.
Chọn đáp án A.
Câu 16: Cho số phức
1 3 .zi
Phần ảo của số phức
z
là
A.
1.
B.
3.
C.
3.i
D.
3.
Lời giải:
Ta có:
1 3 .zi
Chọn đáp án D.
Câu 17: Tìm số phức liên hợp của số phức
31z i i
.
A.
3zi
. B.
3 zi
. C.
3zi
. D.
3 zi
.
Lời giải:
3 1 3z i i i
nên suy ra
3zi
.
Câu 18: Cho số phức
3
1z i i
. Tìm phần thực
a
và phần ảo
b
của
z
.
A.
0, 1.ab
B.
2, 1. ab
C.
1, 0.ab
D.
1, 2. ab
Lời giải:
Ta có:
32
1 1 . 1 1 2z i i i i i i i i
Suy ra phần thực của
z
là
1a
, phần ảo của
z
là
2b 
.
Câu 19: Khẳng định nào sau đây đúng?
A.
,z z z
luôn là số thực. B.
, 0.zz
C.
,.z z z
luôn là số thực. D.
2
22
,.z z z z
Lời giải:
Ta có:
2
, . 0.z z z z
Chọn đáp án C.
Câu 20: Số phức đối của số phức
12zi
là
A.
1 2 .i
B.
12
.
55
i
C.
1 2 .i
D.
1 2 .i
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Lời giải:
Số phức đối của số phức
12zi
là
1 2 1 2 .ii
Chọn đáp án C.
Câu 21: Mệnh đề nào dưới đây sai?
A.
:zz
là số thực. B.
:zz
là số phức.
C.
:zz
là số thực dương. D.
:zz
là số thực không âm.
Câu 22: Môđun của số phức
12zi
là
A.
5.z
B.
5.z
C.
2.z
D.
3.z
Lời giải:
Ta có:
22
1 2 5.z
Chọn đáp án B.
Câu 23: Cho số phức
2zi
. Tính
z
.
A.
3z
. B.
5z
. C.
2z
. D.
5z
.
Câu 24: Với
là số thực bất kì, tính
sin cos .i

A.
0.
B.
1.
C.
2.
D.
3.
Lời giải:
Ta có:
22
sin cos sin cos 1.i
Chọn đáp án B.
Câu 25: Cho số phức bất kì
, ; .z a bi a b
Khẳng định nào sau đây đúng?
A.
22
.z a b
B.
22
.z a b
C.
.z a b
D.
.z a b
Lời giải:
Ta có:
Chọn đáp án B.
Câu 26: Cho số phức
12.z m m i m
. Tất cả các giá trị của
m
để
5z
là
A.
6
2
m
m

. B.
30 m
. C.
03 m
. D.
3
0
m
m

.
Lời giải:
Ta có:
12
22
22
5 2 6 5 5 2 6 0 0;3 .z m m m m m m m


Chọn đáp án B.
Câu 27: Cho số phức
1 3 .zi
Khẳng định nào sau đây sai?
A.
1 3 .zi
B.
10.z
C.
10.z
D.
1 3 .zi
Lời giải:
Ta có:
1 3 10z i z
hoặc nhận xét
.zz
Vậy C sai.
Chọn đáp án C.
Câu 28: Biết các số thực
;ab
thỏa mãn
2 3 6 .a b i a b i i
Tính
.ab
A.
1.
B.
3.
C.
2.
D.
0.
Lời giải:
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Ta có:
32
2 3 6 2 1 3 6 .
2 1 6 1
a b a
a b i a b i i a b a b i i
a b b



Vậy
3.ab
Chọn đáp án B.
Câu 29: Biết các số thực
;xy
thỏa mãn
1 3 2 .x y i i x yi
Tính
2.xy
A.
1.
B.
3.
C.
2.
D.
8.
Lời giải:
Ta có:
1 3 2 5 4 3 2x y i i x yi x y x y i x yi
32
.
23
x y x x
x y y y




Vậy
2 8.xy
Chọn đáp án D.
Câu 30: Tìm hai số thực
x
và
y
thỏa mãn
2 3 3 5 4x yi i x i
với
i
là đơn vị ảo.
A.
1; 1xy
B.
1; 1xy
C.
1; 1xy
D.
1; 1xy
Lời giải:
2 3 5 1
2 3 3 5 4 2 3 3 1 5 4
3 1 4 1
x x x
x yi i x i x y i x i
yy



.
Chọn đáp án D.
Câu 31: Tìm các số thực
a
và
b
thỏa mãn
2 1 2a b i i i
với
i
là đơn vị ảo.
A.
0, 2ab
. B.
1
,1
2
ab
. C.
0, 1ab
. D.
1, 2ab
.
Lời giải:
Ta có
2 1 2 2 1 1 2a b i i i a bi i
2 1 1 1
22
aa
bb





.
Vậy
1, 2ab
.
Chọn đáp án D.
Câu 32: Tìm hai số thực
x
và
y
thỏa mãn
3 2 2 2 3x yi i x i
với
i
là đơn vị ảo.
A.
2; 2xy
. B.
2; 1xy
. C.
2; 2xy
. D.
2; 1xy
Lời giải:
Ta có:
3 2 2 2 3x yi i x i
3 2 2 1 2 3x y x i
3 2 2 2
2 1 3 2
x x x
yy




.
Chọn đáp án A.
Dạng 2: Tìm số phức thỏa mãn yêu cầu
Câu 33: Cho hai số phức
1
1zi
và
2
3 2 .zi
Khẳng định nào sau đây đúng?
A.
12
4 3 .z z i
B.
12
4 3 .z z i
C.
12
4 3 .z z i
D.
12
2 3 .z z i
Lời giải:
Ta có:
12
1 3 2 4 3 .z z i i i
Chọn đáp án A.
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Câu 34: Cho hai số phức
1
12zi
và
2
2
3 6 ; .z m m i m
Tìm tập hợp tất cả các giá trị
m
để
12
zz
là số thực.
A.
2; 2 .
B.
2.
C.
1.
D.
6; 6 .
Lời giải:
Ta có:
2
12
1 4 .z z m m i
Yêu cầu bài toán
2
2
4 0 .
2
m
m
m

Chọn đáp án A.
Câu 35: Cho hai số phức
1
2zi
và
2
3 2 .zi
Phần ảo của số phức
12
2zz
là
A.
4.i
B.
3.
C.
4.
D.
3.
Lời giải:
Ta có:
12
2 2 2 3 2 4 3 .z z i i i
Chọn đáp án D.
Câu 36: Cho hai số phức
1
3zi
và
2
1 2 .zi
Phần thực của số phức
12
.zz
là
A.
7.
B.
1.
C.
7.
D.
3.
Lời giải:
Ta có:
2
12
. 3 1 2 3 6 2 1 7 .z z i i i i i i
Chọn đáp án B.
Câu 37: Cho hai số phức
32zi
và
14wi
. Số phức
zw
bằng
A.
42i
. B.
42i
. C.
26i
. D.
26i
.
Lời giải:
Ta có:
3 2 1 4 4 2z w i i i
.
Chọn đáp án B.
Câu 38: Cho hai số phức
3zi
và
23wi
. Số phức
zw
bằng
A.
14i
. B.
12i
. C.
54i
. D.
52i
.
Lời giải:
3 2 3 1 2 . z w i i i
Chọn đáp án B.
Câu 39: Cho số phức
32zi
, số phức
1 iz
bằng.
A.
15i
B.
5 i
C.
15i
D.
5 i
Lời giải:
Ta có:
1 1 3 2 5 . i z i i i
Chọn đáp án D.
Câu 40: Cho số phức
2zi
, số phức
23iz
bằng
A.
18i
. B.
74i
. C.
74i
. D.
18i
.
Lời giải:
Ta có:
2 3 2 3 2 7 4i z i i i
.
Chọn đáp án C.
Câu 41: Cho số phức
3.zi
Phần thực của số phức
12zz
là
A.
10.
B.
1.
C.
7.
D.
3.
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Lời giải:
Ta có:
1 2 1 3 2 3 10 .z z i i i
Chọn đáp án A.
Câu 42: Tính
1 2 3 2 .ii
A.
10.
B.
25.
C.
50.
D.
5 2.
Lời giải:
Ta có:
1 2 3 2 5 5 25 25 5 2.i i i
Chọn đáp án D.
Câu 43: Cho hai số phức
1
1zi
và
2
23zi
. Tính môđun của số phức
12
.zz
A.
12
13zz
. B.
12
5zz
. C.
12
1zz
. D.
12
5zz
.
Lời giải:
12
1 2 3 3 2z z i i i
nên ta có:
2
2
12
3 2 3 2 13 z z i
.
Chọn đáp án A.
Câu 44: Cho hai số phức
1
3zi
và
2
, ; .z m ni m n
Khẳng định nào sau đây đúng?
A.
12
3 3 .z z m n m n i
B.
12
3 3 .z z m n m n i
C.
12
3 3 .z z m n m n i
D.
12
3 3 .z z m n m n i
Lời giải:
Ta có:
2
12
3 3 3 3 3 .z z i m ni m ni mi ni m n m n i
Chọn đáp án D.
Câu 45: Cho số phức
,z m i m
là tham số. Tìm tập hợp giá trị
m
để
2
z
là số thuần ảo.
A.
0.
B.
1.
C.
1;1 .
D.
.
Lời giải:
Ta có:
2
2 2 2 2
2 1 2 .z m i m mi i m mi
Yêu cầu bài toán
2
1
1 0 .
1
m
m
m

Chọn đáp án C.
Câu 46: Cho hai số phức
1
3zi
và
2
1.zi
Phần thực của số phức
1
2
z
z
là
A.
7.
B.
1.
C.
2.
D.
2.
Lời giải:
Ta có:
2
1
2
31
3 3 3
1 2 .
1 2 2
ii
z
i i i i
i
zi

Chọn đáp án B.
Câu 47: Cho hai số phức
1
1zi
và
2
, ; .z a bi a b
Phần ảo của số phức
2
1
z
z
là
A.
.
2
ab
B.
2
ab
C.
.ab
D.
.ab
Lời giải:
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Ta có:
2
2
1
1
.
1 2 2 2 2
a bi i
z
a bi a ai bi bi a b a b
i
zi




Chọn đáp án A.
Câu 48: Tìm số phức nghịch đảo của số phức
1 2 .i
A.
1 2 .i
B.
51
.
22
i
C.
12
.
55
i
D.
1 2 .i
Lời giải:
Số phức nghịch đảo của số phức
12i
là
1 1 2
.
1 2 5 5
i
i

Chọn đáp án C.
Câu 49: Cho số phức
z
thỏa mãn
32iz i
. Số phức liên hợp của
z
là:
A.
23zi
. B.
23zi
. C.
23zi
. D.
23zi
.
Lời giải:
Ta có:
3 2 2 3iz i z i
. Nên
23zi
.
Chọn đáp án A.
Câu 50: Số phức
z
thỏa mãn
65iz i
. Số phức liên hợp của
z
là
A.
56zi
. B.
56zi
. C.
56zi
. D.
56zi
.
Lời giải:
Ta có:
65
6 5 5 6
i
iz i z i
i
. Vậy
56zi
.
Chọn đáp án C.
Câu 51: Tìm số phức
z
thỏa mãn
1 3 2 0.i z i
A.
51
.
22
zi
B.
51
.
22
zi
C.
51
.
22
zi
D.
51
.
22
zi
Lời giải:
Ta có:
3 2 5 1
1 3 2 0 1 3 2 .
1 2 2
i
i z i i z i z i
i

Chọn đáp án A.
Câu 52: Cho số phức
2 5 .zi
Tìm số phức
w iz z
A.
73wi
. B.
33wi
. C.
3 7 .wi
D.
77wi
Lời giải:
Ta có
(2 5 ) (2 5 ) 2 5 2 5 3 3 . w iz z i i i i i i
Chọn đáp án B.
Câu 53: Tìm số phức
z
thỏa mãn
1 3 5 0.i z i
A.
1 4 .zi
B.
1 4 .zi
C.
1 2 .zi
D.
2.zi
Lời giải:
Ta có:
35
1 3 5 0 1 3 5 1 4 1 4 .
1
i
i z i i z i z i z i
i

Chọn đáp án B.
Câu 54: Tính môđun của số phức
z
thỏa mãn
2 13 1z i i
.
A.
34z
B.
34z
C.
5 34
3
z
D.
34
3
z
Lời giải:
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
2 13 1z i i
1 13 2
1 13
35
2 2 2
ii
i
z z z i
i i i

.
2
2
3 5 34.z
Chọn đáp án A.
Câu 55: Biết số phức
z
thỏa mãn
2 1 5 0.i z i
Tính
1.zi
A.
2 5.
B.
2.
C.
3.
D.
85
.
5
Lời giải:
Ta có:
1 5 3 11 3 11 8 6
2 1 5 0 1 1 .
2 5 5 5 5 5 5
i
i z i z i z i i i i
i




Vậy
1 2.zi
Chọn đáp án B.
Câu 56: Biết số phức
,;z a bi a b
thỏa mãn
1 2 6 3 .i z i z i
Tính
.ab
A.
0.
B.
2.
C.
3.
D.
2.
Lời giải:
Ta có:
1 2 6 3 1 2 6 3i z i z i i a bi i a bi i
22
2 2 6 3
3 6 2
3 2 6 3 .
2 3 1
a bi ai bi a bi ai bi i
aa
a a b i i
a b b




Vậy
3.ab
Chọn đáp án C.
Câu 57: Biết số phức
,;z a bi a b
thỏa mãn
1 3 2 10 2 .i z i z i
Tính
.ab
A.
17
.
11
B.
2.
C.
3.
D.
32
.
11
Lời giải:
Ta có:
1 3 2 10 2 1 3 2 10 2i z i z i i a bi i a bi i
22
3 3 2 2 10 2
14
4 3 10
11
4 3 2 6 3 .
2 2 18
11
a bi ai bi a bi ai bi i
a
ab
a b a b i i
ab
b


Vậy
32
.
11
ab
Chọn đáp án D.
Câu 58: Cho số phức
z
thỏa mãn
2 2 3 2 .i z i z i
Tìm tọa độ của điểm biểu diễn của số phức
liên hợp với
.z
A.
11 5
;.
88



B.
11 5
;.
88



C.
11 5
;.
88



D.
11 5
;.
88




Lời giải:
Gọi
; ; .z a bi a b
Ta có:
2 2 3 2 2 2 3 2i z i z i i a bi i a bi i
2 2 2 3 2 2 3 1a b b a i a b a b i
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
11
2 2 3 2 2
11 5
8
.
2 2 3 1 3 5 1 5
88
8
a
a b a b a b
zi
b a a b a b
b



Vậy
11 5
.
88
zi
Chọn đáp án B.
Câu 59: Có bao nhiêu số phức
z
thỏa mãn điều kiện
.2z z z
và
2?z
A.
1.
B.
2.
C.
3.
D.
4.
Lời giải:
Gọi
; ; .z a bi a b
Để ý:
2
..z z z
Ta có hệ:
2
22
2
22
22
8 12 2
44
.
0
4
4
a b a a
ab
b
ab
ab




Vậy tồn tại duy nhất 1 số phức thỏa yêu cầu bài toán.
Lưu ý: Hoặc ta có thể biến đổi
. 2 1 2 1 2.z z z z z z z
Chọn đáp án A.
BÀI TẬP TƯƠNG TỰ:
Câu 60: Biết số phức
,;z a bi a b
thỏa mãn
1 2 1 6 .i z i z i
Tính
3.ab
A.
2.
B.
2.
C.
3.
D.
5.
Đáp số:
11
6.
3
zi
Câu 61: Biết số phức
,;z a bi a b
thỏa mãn
2 1 4 3 .i z i z i
Tính
.ab
A.
1.
B.
2.
C.
3.
D.
2.
Đáp số:
13
.
22
zi
Câu 62: Biết số phức
,;z a bi a b
thỏa mãn
1 2 1 2 .i z i z i
Tính
.ab
A.
2.
B.
1.
C.
1.
D.
4.
Đáp số:
14
.
33
zi
Câu 63: Biết số phức
,;z a bi a b
thỏa mãn
3 4 1 .i z i z i
Tính
7.ab
A.
2.
B.
0.
C.
3.
D.
2.
Đáp số:
1
.
7
zi
Câu 64: Biết số phức
,;z a bi a b
thỏa mãn
2 3 2 1 4 .i z i z i
Tính
8 8 .ab
A.
12.
B.
8.
C.
3.
D.
10.
Đáp số:
11 21
.
88
zi
Câu 65: Biết số phức
,;z a bi a b
thỏa mãn
1 3 5 4 .i z i z i
Tính
4.ab
A.
7.
B.
2.
C.
3.
D.
5.
Đáp số:
9
2.
4
zi
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Câu 66: Biết số phức
,;z a bi a b
thỏa mãn
2 4 1 3 .i z i z i
Tính
6 3 .ab
A.
3.
B.
2.
C.
3.
D.
5.
Đáp số:
14
.
63
zi
Câu 67: Biết số phức
,;z a bi a b
thỏa mãn
1 3 3 4 .i z i z i
Tính
4.ab
A.
3.
B.
5.
C.
3.
D.
5.
Đáp số:
7
2.
4
zi
Câu 68: Biết số phức
,;z a bi a b
thỏa mãn
2 3 4 1 2 .i z i z i
Tính
2.ab
A.
7.
B.
5.
C.
3.
D.
5.
Đáp số:
3
4.
2
zi
Câu 69: Biết số phức
,;z a bi a b
thỏa mãn
3 2 3 3 .i z i z i
Tính
.ab
A.
7.
B.
5.
C.
3.
D.
2.
Đáp số:
17
.
33
zi
Câu 70: Biết số phức
,;z a bi a b
thỏa mãn
1 5 3 4 1 7 .i z i z i
Tính
4.ab
A.
1.
B.
1.
C.
3.
D.
2.
Đáp số:
5 19 .zi
Câu 71: Biết số phức
,;z a bi a b
thỏa mãn
2 3 4 1 2 .i z i z i
Tính
5.ab
A.
7.
B.
5.
C.
3.
D.
2.
Đáp số:
71
.
20 4
zi
Câu 72: Biết số phức
,;z a bi a b
thỏa mãn
21
3 2 .
11
ii
z z i
ii


Tính
.ab
A.
4.
B.
5.
C.
3.
D.
2.
Đáp số:
75
.
33
zi
Câu 73: Biết số phức
,;z a bi a b
thỏa mãn
12
3 5 .
21
ii
z z i
ii


Tính
.ab
A.
2
.
7
B.
11
.
5
C.
3
.
4
D.
21
.
11
Đáp số:
94 88
.
21 21
zi
Câu 74: Cho số phức
z
thỏa
2 3 16 2 i z i z i
. Môđun của
z
bằng
A.
5
. B.
13
. C.
13
. D.
5
.
Lời giải:
Gọi
z x yi
với
( , )xy
.
Khi đó:
(2 ) 3 16 2( ) ( 3) ( 2 16) (2 2 )i z i z i y x y i y i
.
3 0 2
2 3 13
2 16 2 2 3
yx
z i z
x y y y



.
Chọn đáp án C.
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Câu 75: Cho số phức
z
thỏa
( 2 ) 4( ) 8 19i z z i i
. Môđun của
z
bằng
A.
13
. B.
5
. C.
13
. D.
5
.
Lời giải:
Gọi
z x yi
với
( , )xy
.
Khi đó:
( 2 ) 4( ) 8 19 2 ( 6 4) 8 19i z z i i x y x y i i
.
2 8 3
3 2 13
6 15 2
x y x
z i z
x y y



.
Chọn đáp án C.
Câu 76: Cho số phức
,z a bi a b
thoả mãn
2z i z
. Tính
4S a b
.
A.
4.S
B.
2.S
C.
2.S 
D.
4.S 
Lời giải:
Ta có
(1)
(2)
22
22
2
2 2 1
10
a a b
z i z a b i a b
b

Từ (2) ta có:
1b 
. Thay vào (1):
2
22
20
3
12
4
1 ( 2)
a
a a a
aa

Vậy
4 4.S a b
Chọn đáp án D.
Câu 77: Cho số phức
z a bi
( , )ab
thỏa mãn
1 3 0z i z i
. Tính
3.S a b
A.
7
.
3
S
B.
5.S 
C.
5.S
D.
7
.
3
S 
Lời giải:
2 2 2 2
1 3 0 1 3 0 1 3 0z i z i a bi i a b i a b a b i
2 2 2
2
2
11
1
1 0 1
33
4
3 0 1 3
4
3
13
3
aa
a
aa
bb
b
b a b b b
bb
b







4
3 1 3. 5
3
S a b
Chọn đáp án B.
Câu 78: Cho số phức
z
thỏa mãn
35z
và
2 2 2 z i z i
. Tính
z
.
A.
17z
. B.
17z
. C.
10z
. D.
10z
.
Lời giải:
Gọi
( , ) z a bi a b
.
Ta có:
2
2
3 5 3 5 3 25 z a bi a b
(1).
Ta lại có:
2 2 2 2
22
2 2 2 2 2 2
( 2) ( 2) ( 2)
2
( 2) 1
2

z i z i a bi i a bi i
a b a b
aa
a a a
aa
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Thế vào (1)
22
16 25 9 bb
.
Vậy
2 2 2
1 9 10 z a b
.
Chọn đáp án C.
Câu 79: Có bao nhiêu số phức
z
thỏa mãn
2z
và
22z i z
là số thuần ảo?
A.
1
. B.
0
. C.
2
. D.
4
.
Lời giải:
Đặt
z x yi
,xy
.
Theo đề ta có:
+)
2 2 2 2
2 2 2z x y x y
.
1
+)
2
2 2 2 2 4 2 2 4z i z zz z zi i z x yi x yi i i
2
2 2 2 2 2 4 2 2 2 2 2 4x yi xi y i x y x y i
.
Vì
22z i z
là số thuần ảo nên
2 2 2 0 1x y y x
.
Thay
1yx
vào
1
, ta được:
2
22
13
2
1 2 2 2 1 0
13
2
x
x x x x
x
.
Vậy có hai số phức thỏa để là
1 3 1 3
22
zi

và
1 3 1 3
22
zi

.
Chọn đáp án C.
Dạng 3: Biểu diễn số phức
Câu 80: Kí hiệu điểm
M
là điểm biểu diễn số phức,
M
là điểm biểu diễn số phức
.z
Khẳng định nào
sau đây đúng?
A.
,MM
đối xứng nhau qua trục tung. B.
,MM
đối xứng nhau qua trục hoành.
C.
,MM
đối xứng nhau qua gốc tọa độ. D.
,MM
đối xứng nhau qua
.yx
Lời giải:
Số phức
; ; ;z a bi z a bi a b
có điểm biểu diễn lần lượt là
; , ; .M a b M a b
Dễ thấy,
,MM
đối xứng nhau qua trục hoành.
Chọn đáp án B.
Câu 81: Cho số phức
1 3 .zi
Điểm biểu diễn số phức
z
trên mặt phẳng tọa độ là
A.
1; 3 .M
B.
1;3 .N
C.
1; 3 .P 
D.
1;3 .Q
Câu 82: Trên mặt phẳng tọa độ, điểm biểu diễn số phức
32i
có tọa độ là
A.
2;3
. B.
2;3
. C.
3;2
. D.
3; 2
.
Câu 83: Cho số phức
1 3 .zi
Điểm biểu diễn số phức
z
trên mặt phẳng tọa độ là
A.
1; 3 .M
B.
1;3 .N
C.
1; 3 .P 
D.
1;3 .Q
Lời giải:
Ta có:
1 3 .zi
Chọn đáp án B.
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Câu 84: Cho hai số phức
12
2 , 1z i z i
. Trên mặt phẳng tọa độ Oxy, điểm biểu diễn số phức
12
2zz
có tọa độ là:
A.
5; 1
. B.
1;5
. C.
5;0
. D.
0;5
.
Lời giải:
Ta có
12
25z z i
. Nên điểm biểu diễn là
5; 1
.
Chọn đáp án A.
Câu 85: Trên mặt phẳng tọa độ, điểm biểu diễn số phức
2
12zi
là điểm nào dưới đây?
A.
3;4P
B.
5;4Q
. C.
4; 3N
. D.
5;4M
.
Lời giải:
Ta có
2
2
1 2 1 4 4 3 4z i i i i
điểm biểu diễn số phức
2
12zi
là điểm
3;4P
.
Chọn đáp án A.
Câu 86: Cho hai số phức
1
1zi
và
2
2zi
. Trên mặt phẳng
Oxy
, điểm biểu diễn số phức
12
2zz
có tọa độ là
A.
2;5
. B.
3;5
. C.
5;2
. D.
5;3
.
Lời giải:
Ta có
12
2 (1 ) 2(2 ) 5 3z z i i i
.
Vậy điểm biểu diễn số phức
12
2zz
có tọa độ
5;3 .
Chọn đáp án D.
Câu 87: Cho số phức
12zi
. Điểm nào dưới đây là điểm biểu diễn của số phức
w iz
trên mặt
phẳng tọa độ?
A.
(1;2)Q
B.
(2;1)N
C.
(1; 2)M
D.
( 2;1)P
Lời giải:
1 2 2w iz i i i
. Điểm biểu diễn số phức
w
là
2;1N
.
Chọn đáp án B.
Câu 88: Điểm
1; 2A
là biểu diễn trên mặt phẳng tọa độ số phức
z
nào trong các số phức sau?
A.
1 2 .zi
B.
1 2 .zi
C.
1 2 .zi
D.
1 2 .zi
Câu 89: Trên mặt phẳng tọa độ, điểm
( 2;3)M
là điểm biểu diễn số phức nào dưới đây?
A.
3
23zi
. B.
4
23zi
. C.
1
23zi
. D.
2
23zi
.
Câu 90: Số phức nào dưới đây có điểm biểu diễn trên mặt phẳng tọa độ là điểm
M
như hình bên?
A.
4
2.zi
B.
2
1 2 .zi
C.
3
2. zi
D.
1
1 2 .zi
Câu 91: Điểm
M
trong hình vẽ bên dưới là điểm biểu diễn của số phức nào trong 4 số phức được cho
ở các phương án A, B, C, D?
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
x
y
M
-3
2
O
A.
3 2 .zi
B.
2 3 .zi
C.
3 2 .zi
D.
3 2 .zi
Câu 92: Điểm biểu diễn số phức
32zi
là điểm nào trong 4 điểm
, , ,M N P Q
trong hình vẽ bên
dưới?
x
y
Q
P
N
M
-3
-2
2
3
O
A.
.M
B.
.N
C.
.P
D.
.Q
Câu 93: Cho hai số phức
1
12zi
và
2
3 2 .zi
Gọi
,AB
là hai điểm lần lượt biểu diễn số phức
12
,zz
trên mặt phẳng tọa độ. Tính độ dài
.AB
A.
10.
B.
5.
C.
2 5.
D.
3.
Lời giải:
Ta có:
1;2
2; 4 4 16 2 5.
3; 2
A
AB AB
B
Chọn đáp án C.
Câu 94: Cho số phức
3 2 .zi
Gọi
,AB
là hai điểm lần lượt biểu diễn số phức
,zz
trên mặt phẳng
tọa độ. Tính diện tích tam giác
OAB
(
O
là gốc tọa độ).
A.
6.
B.
5.
C.
2 5.
D.
3.
Lời giải:
x
y
H
-2
2
3
B
A
O
Ta có:
3 2 .zi
Suy ra:
3;2 , 3; 2 4.A B AB
Vậy
1
; . 6.
2
OAB
S d O AB AB
Chọn đáp án A.
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Câu 95: Biết số phức
z
thỏa mãn
1 3 3 .z i z i
Tập hợp điểm biểu diễn số phức
z
trên mặt
phẳng tọa độ là đường thẳng có phương trình
A.
2 4 0.xy
B.
2 4 0.xy
C.
2 4 0.xy
D.
4 0.xy
Lời giải:
Gọi
; ; .z x yi x y
Điểm
;M x y
biểu diễn số phức
z
trên mặt phẳng tọa độ.
Ta có:
1 3 3 1 3 3z i z i x yi i x yi i
1 1 3 3x y i x y i
2 2 2 2
1 1 3 3x y x y
2 2 2 2
2 1 2 1 6 9 6 9 2 4 0.x x y y x x y y x y
Vậy tập hợp điểm biểu diễn số phức
z
trên mặt phẳng tọa độ là đường thẳng
: 2 4 0.d x y
Chọn đáp án A.
Câu 96: Biết số phức
z
thỏa mãn
1 3 3 5 .z i z i
Tập hợp điểm biểu diễn số phức
z
trên mặt
phẳng tọa độ là đường thẳng có phương trình
A.
2 4 0.xy
B.
4 6 0.xy
C.
2 6 0.xy
D.
4 0.xy
Lời giải:
Gọi
; ; .z x yi x y
Điểm
;M x y
biểu diễn số phức
z
trên mặt phẳng tọa độ.
Ta có:
1 3 3 5 1 3 3 5z i z i x yi i x yi i
1 3 3 5x y i x y i
2 2 2 2
1 3 3 5x y x y
2 2 2 2
2 1 6 9 6 9 10 25 4 6 0.x x y y x x y y x y
Vậy tập hợp điểm biểu diễn số phức
z
trên mặt phẳng tọa độ là đường thẳng
: 4 6 0.d x y
Chọn đáp án B.
Câu 97: Biết số phức
z
thỏa mãn
2 2 4 .z i z i
Tập hợp điểm biểu diễn số phức
z
trên mặt
phẳng tọa độ là đường thẳng có phương trình
A.
2 4 0.xy
B.
4 6 0.xy
C.
2 6 0.xy
D.
4 0.xy
Lời giải:
Gọi
; ; .z x yi x y
Điểm
;M x y
biểu diễn số phức
z
trên mặt phẳng tọa độ.
Ta có:
2 2 4 2 2 4z i z i x yi i x yi i
2 2 4x y i x y i
2 2 2
2
2 2 4x y x y
2 2 2 2
4 4 4 4 8 16 4 0.x y y x x y y x y
Vậy tập hợp điểm biểu diễn số phức
z
trên mặt phẳng tọa độ là đường thẳng
: 4 0.d x y
Chọn đáp án D.
Câu 98: Biết số phức
z
thỏa mãn
1 3.zi
Tập hợp điểm biểu diễn số phức
z
trên mặt phẳng tọa
độ là đường tròn có phương trình
A.
22
1 1 9.xy
B.
22
1 1 9.xy
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
C.
22
1 1 9.xy
D.
22
1 1 9.xy
Lời giải:
Gọi
; ; .z x yi x y
Điểm
;M x y
biểu diễn số phức
z
trên mặt phẳng tọa độ.
Ta có:
1 3 1 3 1 1 3z i x yi i x y i
2 2 2 2
1 1 3 1 1 9.x y x y
Vậy tập hợp điểm biểu diễn số phức
z
trên mặt phẳng tọa độ là đường tròn
22
: 1 1 9.C x y
Chọn đáp án C.
Câu 99: Biết số phức
z
thỏa mãn
3 4 4.zi
Biết tập hợp điểm biểu diễn số phức
z
trên mặt phẳng
tọa độ là đường tròn
.C
Tìm tâm
I
và tính bán kính
R
của đường tròn
.C
A.
3;4 , 16.IR
B.
3;4 , 4.IR
C.
3; 4 , 4.IR
D.
3; 4 , 16.IR
Lời giải:
Gọi
; ; .z x yi x y
Điểm
;M x y
biểu diễn số phức
z
trên mặt phẳng tọa độ.
Ta có:
3 4 4 3 4 4 3 4 4z i x yi i x y i
2 2 2 2
3 4 4 3 4 16.x y x y
Vậy tập hợp điểm biểu diễn số phức
z
trên mặt phẳng tọa độ là đường tròn
C
có tâm
3;4 ,I
bán kính
4.R
Chọn đáp án B.
Câu 100: Biết số phức
z
thỏa mãn
1 2.zi
Biết tập hợp điểm biểu diễn số phức
z
trên mặt phẳng
tọa độ là đường tròn
.C
Tìm tâm
I
và tính bán kính
R
của đường tròn
.C
A.
1;1 , 2.IR
B.
1; 1 , 4.IR
C.
1; 1 , 2.IR
D.
1;1 , 4.IR
Lời giải:
Gọi
; ; .z x yi x y
Điểm
;M x y
biểu diễn số phức
z
trên mặt phẳng tọa độ.
Ta có:
3 4 4 3 4 4 3 4 4z i x yi i x y i
2 2 2 2
3 4 4 3 4 16.x y x y
Vậy tập hợp điểm biểu diễn số phức
z
trên mặt phẳng tọa độ là đường tròn
C
có tâm
3;4 ,I
bán kính
4.R
Chọn đáp án C.
Câu 101: Xét các số phức
z
thỏa mãn
22z i z
là số thuần ảo. Biết rằng tập hợp tất cả các
điểm biểu diễn của
z
là một đường tròn, tâm của đường tròn đó có tọa độ là
A.
1; 1
. B.
1;1
. C.
1;1
. D.
1; 1
.
Lời giải:
+ Gọi
z x yi
,
,xy
.
+ Ta có
2 2 2 2z i z x yi i x yi
22x y i x yi
2 2 2 2x x y y x y xy i


.
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
+
22z i z
là số thuần ảo
2 2 0x x y y
22
1 1 2xy
.
+ Vậy tập hợp các điểm biểu diễn của số phức
z
là đường tròn tâm
1; 1I 
.
Chọn đáp án D.
Câu 102: Xét các số phức
z
thỏa mãn
22z i z
là số thuần ảo. Trên mặt phẳng tọa độ, tập hợp
tất cả các điểm biểu diễn các số phức
z
là một đường tròn có bán kính bằng
A.
2 2.
B.
2.
C.
2.
D.
4.
Lời giải:
Gọi
z a bi
,
,ab
Ta có:
22
2 2 2 2 2 2 2 2z i z a bi i a bi a a b b a b i
Vì
22z i z
là số thuần ảo nên ta có
22
22
2 2 0 1 1 2a a b b a b
.
Trên mặt phẳng tọa độ, tập hợp tất cả các điểm biểu diễn các số phức
z
là một đường tròn có bán
kính bằng
2
.
Chọn đáp án B.
Câu 103: Cho các số phức
z
thỏa mãn
4z
. Biết rằng tập hợp các điểm biểu diễn các số
phức
(3 4 )w i z i
là một đường tròn. Tính bán kính
r
của đường tròn đó.
A.
4r
. B.
5r
. C.
20r
. D.
22r
.
Lời giải:
Giả sử
; ; , , ,z a bi w x yi a b x y
Theo đề
3 4 3 4w i z i x yi i a bi i
3 4 3 4
3 4 3 4 1
3 4 1 1 3 4
x a b x a b
x yi a b b a i
y b a y b a



Ta có
2 2 2
2 2 2 2 2
1 3 4 4 3 25 25 25x y a b a b a b a b
Mà
22
4 16z a b
. Vậy
2
2
1 25.16 400xy
Bán kính đường tròn là
400 20r 
.
Chọn đáp án C.
B. PHƯƠNG TRÌNH BẬC HAI VỚI HỆ SỐ THỰC
Câu 104: Phương trình
2
0ax bx c
,,a b c
có hai nghiệm phức phân biệt khi và chỉ khi
A.
2
40b ac
. B.
2
0
40
a
b ac

. C.
2
0
40
a
b ac

. D.
2
0
40
a
b ac

.
Câu 105: Trên tập số phức, phương trình nào sau đây có nghiệm thực?
A.
2
1 0.x 
B.
2
1 0.x 
C.
2
4 0.x 
D.
2
2 1 0.x 
Lời giải:
Ta có:
2
1
1 0 .
1
x
x
x

Chọn đáp án B.
Câu 106: Kí hiệu
1
z
,
2
z
là hai nghiệm phức của phương trình
2
3z 
. Giá trị của
12
zz
bằng
A.
6
. B.
23
. C.
3
. D.
3.
Lời giải:
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Ta có:
2
12
3
3 2 3.
3
zi
z z z
zi

Chọn đáp án B.
Câu 107: Trên tập số phức, tập nghiệm của phương trình
2
2 2 0zz
là
A.
1 ;1 .ii
B.
1 ;1 .ii
C.
1 ; 1 .ii
D.
; 1 .ii
Lời giải:
Ta có:
2
1
2 2 0 .
1
zi
zz
zi
Chọn đáp án C.
Câu 108: Trên tập số phức, gọi
12
,zz
là hai nghiệm của phương trình
2
2 2 0.zz
Tính
12
.zz
A.
2 2.
B.
2.
C.
42
D.
4.
Lời giải:
Ta có:
2
1
2
1
2 2 0 .
1
zi
zz
zi


Vậy
12
2 2.zz
Chọn đáp án A.
Câu 109: Phương trình nào dưới đây nhận hai số phức
12i
và
12i
là nghiệm?
A.
2
2 3 0. zz
B.
2
2 3 0 . zz
C.
2
2 3 0. zz
D.
2
2 3 0 . zz
Câu 110: Trên tập số phức, gọi
12
,zz
là hai nghiệm của phương trình
2
4 2 0.zz
Tính
22
12
.zz
A.
2 2.
B.
2.
C.
8.
D.
4.
Lời giải:
Ta có:
2
1
2
13
2 4 0 .
13
zi
zz
zi


Vậy
22
12
8.zz
Chọn đáp án C.
Câu 111: Gọi
12
,zz
là hai nghiệm phức của phương trình
2
4 5 0zz
. Giá trị của
22
12
zz
bằng
A.
6
. B.
8
. C.
16
. D.
26
.
Lời giải:
2
22
1 2 1 2 1 2
2 16 10 6z z z z z z
.
Chọn đáp án A.
Câu 112: Gọi
12
,zz
là 2 nghiệm phức của phương trình
2
6 14 0 zz
. Giá trị của
22
12
zz
bằng:
A. 36. B. 8. C.
28
. D. 18.
Lời giải:
Ta có:
2
2
22
1 2 1 2 1 2
6 14
2 2 8
11



z z z z z z
.
Chọn đáp án B.
Câu 113: Kí hiệu
12
,zz
là hai nghiệm của phương trình
2
40z 
. Gọi
,MN
lần lượt là điểm biểu
diển của
12
,zz
trên mặt phẳng tọa độ. Tính
T OM ON
với
O
là gốc tọa độ.
A.
2T
. B.
2T
. C.
8T
. D.
4T
.
Lời giải:
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Ta có:
1
2
2
2
40
2
zi
z
Zi

Suy ra
0; 2 ; 0;2MN
nên
2
2
2 2 4T OM ON
.
Chọn đáp án D.
Câu 114: Ký hiệu
12
,zz
là hai nghiệm phức của phương trình
2
60zz
Tính
12
11
P
zz

.
A.
1
6
P
. B.
1
12
P
. C.
1
6
P 
. D.
6P
.
Lời giải:
Ta có
2
1 23
22
60
1 23
22
zi
zz
zi


suy ra
12
1 1 1
6
P
zz
.
Chọn đáp án A.
Câu 115: Gọi
0
z
là nghiệm phức có phần ảo âm của phương trình
2
2 5 0zz
. Môđun của số
phức
0
zi
bằng
A. 2. B.
2
. C.
10
. D.
10
.
Lời giải:
Xét phương trình:
2
2 5 0zz
có
40
Phương trình có hai nghiệm phức
12zi
và
12zi
0
z
là nghiệm phức có phần ảo âm nên
0
12zi
nên
00
12z i i z i
.
Chọn đáp án B.
Câu 116: Kí hiệu
0
z
là nghiệm phức có phần ảo dương của phương trình
2
4 16 17 0zz
. Trên mặt
phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn của số phức
0
w iz
?
A.
1
1
;2
2
M



. B.
2
1
;2
2
M



. C.
3
1
;1
4
M



. D.
4
1
;1
4
M



.
Lời giải:
Xét phương trình
2
4 16 17 0zz
có
2
64 4.17 4 2i
.
Phương trình có hai nghiệm
12
8 2 1 8 2 1
2 , 2
4 2 4 2
ii
z i z i

.
Do
0
z
là nghiệm phức có phần ảo dương nên
0
1
2
2
zi
.
Ta có
0
1
2
2
w iz i
. Vậy điểm biểu diễn
0
w iz
là
2
1
;2
2
M



.
Chọn đáp án B.
Câu 117: Trên tập số phức, cho phương trình
2
2 0,z z m m
là tham số. Tìm tập hợp tất cả các giá trị
của tham số
m
để phương trình đã cho không có nghiệm thực.
A.
.
B.
1; .
C.
1; .

D.
.
Lời giải:
Phương trình đã cho không có nghiệm thực
0 1 0 1.mm
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chọn đáp án C.
Câu 118: Gọi
0
z
là nghiệm phức có phần ảo dương của phương trình
2
6 34 0zz
. Tính
0
2.zi
A.
17
. B.
17
. C.
2 17
. D.
37
.
Lời giải:
2
6 34 0zz
35
.
35
zi
zi
Do đó
0
35zi
0
2 1 4 17z i i
.
Chọn đáp án A.
Câu 119: Ký hiệu
12
,zz
là hai nghiệm phức của phương trình
2
60zz
Tính
12
11
P
zz

.
A.
1
6
P
. B.
1
12
P
. C.
1
6
P 
. D.
6P
.
Lời giải:
Ta có
2
1 23
22
60
1 23
22
zi
zz
zi


suy ra
12
1 1 1
6
P
zz
.
Chọn đáp án A.
Câu 120: Gọi
0
z
là nghiệm phức có phần ảo dương của phương trình
2
6 13 0zz
. Trên mặt
phẳng tọa độ, điểm biểu diễn
0
1 z
là:
A.
2;2M
. B.
4; 2Q
. C.
4;2N
. D.
2; 2P 
.
Lời giải:
Xét phương trình
2
6 13 0zz
.
Ta có
2
9 13 4 2i
.
Suy ra phương trình (1) có 2 nghiệm phức phân biệt là
32
32
zi
zi


.
0
z
là nghiệm phức có phần ảo dương của phương trình
2
6 13 0zz
nên
32
o
zi
.
0
1 1 3 2 2 2z i i
.
Vậy điểm biểu diễn số phức
0
1 z
là điểm
2; 2P 
.
Chọn đáp án D.
Câu 121: Gọi
1
z
là nghiệm phức có phần ảo âm của phương trình
2
2 5 0zz
. Tìm tọa độ điểm biểu
diễn số phức
1
74i
z
trên mặt phẳng phức?
A.
3; 2P
. B.
1; 2N
. C.
3; 2Q
. D.
1; 2M
.
Lời giải:
Ta có
2
12
2 5 0 .
12
zi
zz
zi


Theo yêu cầu bài toán chọn
1
12zi
. Khi đó
22
1
7 4 1 2
7 4 7 4
3 2 .
12
12
ii
ii
i
zi


Vậy điểm biểu diễn của số phức là
3; 2P
.
Chọn đáp án A.
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Câu 122: Trên tập số phức, số nghiệm thực của phương trình
42
3 4 0zz
là
A.
0.
B.
1.
C.
4.
D.
2.
Lời giải:
Ta có:
2
42
2
1
3 4 0 .
42
z z i
zz
zz
Chọn đáp án D.
Câu 123: Trên tập số phức, tập nghiệm của phương trình
42
2 3 0zz
là
A.
3.
B.
;3i
C.
; 3 .i
D.
; 3 .ii
Lời giải:
Ta có:
2
42
2
1
2 3 0 .
33
z z i
zz
zz
Chọn đáp án C.
Câu 124: Trên tập số phức, tập nghiệm của phương trình
42
4 3 0zz
là
A.
1; 3 .
B.
.
C.
; 3 .ii
D.
; 3 .ii
Lời giải:
Ta có:
2
42
2
1
4 3 0 .
33
z z i
zz
z z i
Chọn đáp án D.
Câu 125: Trên tập số phức, gọi
1 2 3 4
, , ,z z z z
là bốn nghiệm của phương trình
42
2 3 0.zz
Tính
1 2 3 4
.z z z z
A.
2 2 3.
B.
2 3.
C.
4 2 3.
D.
4 4 3.
Lời giải:
Ta có:
2
42
2
11
2 3 0 .
33
zz
zz
zz
Suy ra:
1 2 3 4
2 2 3.z z z z
Chọn đáp án A.
Câu 126: Kí hiệu
1 2 3
,,z z z
và
4
z
là bốn nghiệm phức của phương trình
42
12 0zz
. Tính
tổng
1 2 3 4
T z z z z
.
A.
4.T
B.
2 3.T
C.
4 2 3.T
D.
2 2 3.T
Lời giải:
2
42
2
3
3
12 0
2
4
z
zi
zz
z
z



1 2 3 4
3 3 2 2 2 3 4. T z z z z i i
Chọn đáp án C.
Câu 127: Trên tập số phức, tổng môđun các nghiệm của phương trình
22
1 4 0zz
là
A.
6.
B.
1.
C.
4.
D.
2.
Lời giải:
Ta có:
2
22
2
1
1 4 0 2 2 6.
42
z z i
z z i i
zz
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Chọn đáp án A.
Câu 128: Trên tập số phức, gọi
12
,zz
là hai nghiệm của phương trình
2
2 2 0.zz
Biết
,AB
lần lượt là
hai điểm biểu diễn
12
,zz
trên mặt phẳng. Tính độ dài đoạn thẳng
.AB
A.
2 2.
B.
2.
C.
1.
D.
4.
Lời giải:
Ta có:
1
2
2
1 1;1
2 2 0 .
1 1; 1
z i A
zz
z i B
Ta có:
0; 2 2.AB AB
Chọn đáp án B.
Câu 129: Trên tập số phức, tìm giá trị tham số thực
m
để phương trình
2
40z mz m
có một
nghiệm là
1.zi
A.
2.m 
B.
1.m
C.
3.m
D.
4.m
Lời giải:
Ta có:
2
42
1 1 4 0 2 2 4 0 2.
2
i
i m i m i i m m
i

Chọn đáp án A.
Câu 130: Trên tập số phức, gọi
12
,zz
là hai nghiệm của phương trình
2
2 2 0.zz
Biết
,AB
lần lượt là
hai điểm biểu diễn
12
,zz
trên mặt phẳng. Tọa độ trung điểm của đoạn thẳng
AB
là
A.
1;0
B.
1;0 .
C.
0;1 .
D.
0; 1 .
Lời giải:
Ta có:
1
2
2
1 1;1
2 2 0 .
1 1; 1
z i A
zz
z i B
I
là trung điểm
1;0 .AB I
Chọn đáp án B.
Câu 131: Trên tập số phức, gọi
12
,zz
là hai nghiệm của phương trình
2
2 5 0.zz
Biết
,AB
lần lượt là
hai điểm biểu diễn
12
,zz
trên mặt phẳng. Tính
cos ,AOB
(với
O
là gốc tọa độ).
A.
3
5
B.
3
.
5
C.
1
.
5
D.
1
.
5
Lời giải:
x
y
B
A
-2
2
O
1
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Ta có:
1
2
2
1 2 1;2
2 5 0 .
1 2 1; 2
z i A
zz
z i B
Ta có:
1;2
.3
cos .
.5
1; 2
OA
OA OB
AOB
OA OB
OB

Chọn đáp án B.
Câu 132: Trên tập số phức, gọi
12
,zz
là hai nghiệm của phương trình
2
4 8 0.zz
Biết
,AB
lần lượt là
hai điểm biểu diễn
12
,zz
trên mặt phẳng. Tính
,OAB
(với
O
là gốc tọa độ).
A.
o
30
B.
o
60
C.
o
135
D.
o
45 .
Lời giải:
x
y
B
A
-2
2
O
Ta có:
1
2
2
2 2 2;2
4 8 0 .
2 2 2; 2
z i A
zz
z i B
Ta có:
o
2; 2
.2
cos 45 .
.2
0; 4
AO
AO AB
AOB AOB
AO AB
AB

Chọn đáp án D.
Câu 133: Gọi
12
,zz
là hai nghiệm của phương trình
2
4 13 0zz
và
A
,
B
lần lượt là hai điểm biểu
diễn cho hai số phức
1
z
,
2
z
trong mặt phẳng tọa độ
Oxy
. Diện tích tam giác
OAB
bằng
A.
13
. B.
12
. C.
13
2
. D.
6
.
Lời giải:
Ta có
2
4 13 0zz
2
29z
22
23zi
23
23
zi
zi


.
2;3 ,A
2; 3B
.
13OA OB
OAB
cân tại
O
. Gọi
H
là trung điểm của
AB
2;0H
và
OH AB
,
2OH
,
6AB
. Vậy
11
. .2.6 6
22
OAB
S OH AB
.
Chọn đáp án D.
Câu 134: Gọi
1
z
,
2
z
,
3
z
là ba nghiệm của phương trình
32
5 7 0z z z
. Tính
1 2 3
M z z z
.
A.
1 2 7M 
. B.
1 7 2M 
. C.
27M 
. D.
3M
.
Lời giải:
Ta có:
3 2 2
1
5 7 0 1 2 7 0 1 6
16
z
z z z z z z z i
zi
.
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Suy ra:
1 2 3
1 1 6 1 6 1 2 7M z z z i i
.
Chọn đáp án A.
Câu 135: Gọi
A
,
B
,
C
là các điểm biểu diễn các số phức
1
z
,
2
z
,
3
z
là nghiệm của phương trình
32
6 12 7 0z z z
. Tính diện tích
S
của tam giác
ABC
.
A.
33S
. B.
33
2
S
. C.
1S
. D.
33
4
S
.
Lời giải:
Sử dụng MTCT ta có phương trình
32
6 12 7 0z z z
có
3
nghiệm
1
1z
;
2
53
22
zi
,
3
53
22
zi
. Suy ra:
1;0A
,
53
;
22
B




,
53
;
22
C




.
93
3
44
AB AB
;
93
3
44
AC AC
;
3BC BC
.
ABC
đều cạnh
3
. Vậy
2
33
33
44
ABC
S 
.
Chọn đáp án D.
Câu 136: Trên tập hợp các số phức, xét phương trình
22
2 1 0z m z m
. Có bao nhiêu giá trị
của
m
để phương trình đó có nghiệm
o
z
thõa mãn
8?
o
z
A.
4
. B.
3
. C.
2
. D.
1
.
Lời giải:
Ta có
84m
.
Trường hợp 1:
1
0
2
m
suy ra phương trình có 2 nghiệm thực
o
z
là nghiệm
thực.
8
8
8
o
o
o
z
z
z


thay vào phương trình
2
2
4
16 48 0 /
12
16 80 0( )
m
m m T M
m
m m VN

.
Trường hợp 2:
1
0
2
m
suy ra phương trình sẽ có 2 nghiệm phức, vì
o
z
là nghiệm
nên suy ra
o
z
cũng là nghiệm
2
2
8
8 64 . 64 64
8
o o o o
m
z z z z m
m

.
Kết hợp điều kiện nên ta nhận
8m 
.
Vậy có 3 giá trị
m
thỏa mãn.
Chọn đáp án B.
_____________________HẾT_____________________
Huế, 08h30’ Ngày 18 tháng 02 năm 2023
| 1/36
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỐ PHỨC VÀ CÁC PHÉP TOÁN
Dành cho học sinh mất gốc Toán LÊ BÁ BẢO
Trường THPT Đặng Huy Trứ, Huế
Admin CLB Giáo viên trẻ TP Huế
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia Chủ đề: SỐ PHỨC I. TÓM TẮT LÝ THUYẾT
A. SỐ PHỨC VÀ CÁC PHÉP TOÁN 1. Số i
Ta đã biết các phương trình bậc hai với biệt số âm không có nghiệm thực. Ví dụ phương trình 2
x  1  0 không có nghiệm trên tập .
Nhằm mở rộng tập hợp số thực để mọi phương trình bậc n đều có nghiệm, người ta đưa ra
một số mới, kí hiệu là i và xem nó là nghiệm của phương trình 2
x  1  0. Như vậy: 2 i   1 .
2. Định nghĩa số phức
Mỗi biểu thức dạng a bi, trong đó a, b  , 2
i  1 được gọi là một số phức.
Đối với số phức z a bi, ta nói a là phần thực, b là phần ảo của z .
Tập hợp các số phức kí hiệu là .
3. Số phức bằng nhau
Hai số phức là bằng nhau nếu phần thực và phần ảo của chúng tương ứng bằng nhau. a c
a bi c di  
; a, b, c, d   b   d Chú ý:
+ Mỗi số thực a được xem là một số phức với phần ảo bằng 0: a a  0i.
Như vậy, mỗi số thực cũng là một số phức. Ta có:  .
+ Số phức z  0  bi được gọi là số thuần ào và viết đơn giản là bi.
Đặc biệt: i  0  1i . Vậy số i được gọi là đơn vị ảo.
4. Biểu diễn hình học số phức
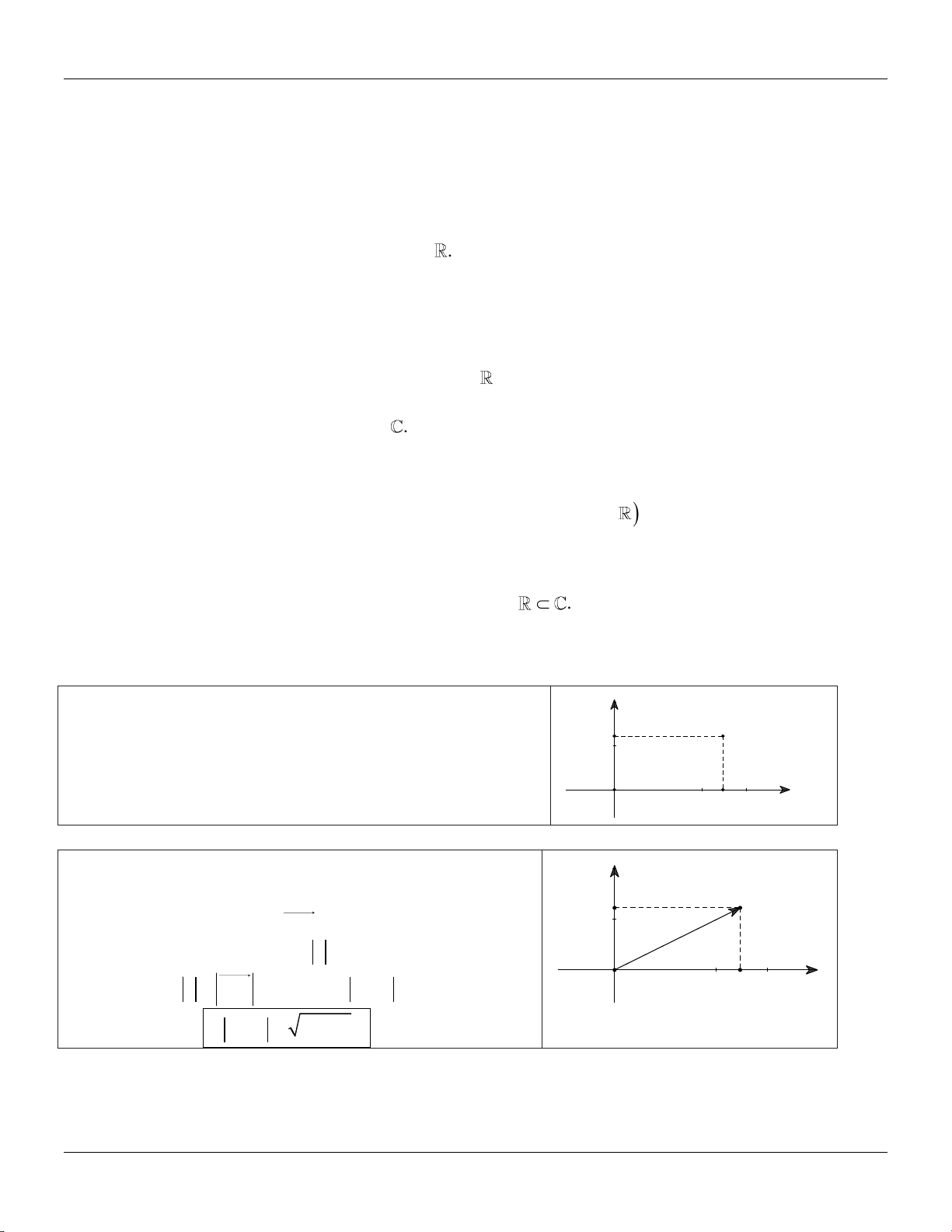
Mỗi số phức hoàn toàn xác định bởi cặp số thực ya;b. b M
Điểm M a; b trong hệ tọa độ vuông góc của mặt
phẳng được gọi là điểm biểu diễn số phức O a x
z a bi.
5. Môđun của số phức
Giả sử số phức z a bi được biểu diễn bởi y
điểm M a; b trên mặt phẳng tọa độ. M b
Độ dài của vectơ OM được gọi là mô đun của số
phức z và kí hiệu là z .
Vậy z OM OM hay a bi OM . O a x Suy ra: 2 2
a bi a b
6. Số phức liên hợp
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Cho số phức z a bi. Ta gọi a bi là số phức y
liên hợp của z và kí hiệu z a bi . z = a+bi Nhận xét: b + z z O a x + z z -b z = a - bi
7. Cộng và trừ số phức
Cho z a bi / /
; z a b i / z z   /
a a    / b b  /
i z z   /
a a    / ;
b b i
8. Nhân hai số phức:
Cho z a bi / /
; z a b i /   / /   / / . z z aa bb
ab a bi
9. Chia hai số phức
Với z a b i vµ z a b i z  0 1 1 1 2 2 2  2    z a b i
a b i a b i
a b i a b i z z .z 1 1 1 1 1   2 2   1 1  2 2  Lúc đó:       z a b i
a b i a b i a bz  2 2   2 2  1 1 2 2 2 2 2 2 2 2 2 2 z  2 
Lưu ý: 1) z a bi là số thực  b  0
2) z a bi là số thuần ảo  a  0.
B. PHƯƠNG TRÌNH BẬC HAI VỚI HỆ SỐ THỰC
1. Căn bậc hai của số thực âm 2 Do i  1
 nªn ta nãi i lµ mét c¨n bËc hai cña 1 vµ  i còng lµ mét c¨n bËc hai cña 1 2 2 do (i)  1.
 T­¬ng tù, c¨n bËc hai cña  5 lµ  i 5 do (  i 5)  5
Tæng qu¸t: C¨n bËc hai cña sè thùc a ©m lµ:  i a
2. Phương trình bậc hai với hệ số thực 2
Cho ph­¬ng tr×nh: ax bx c  0 (*) víi , a ,
b c  , a  0. 2
XÐt   b  4ac
TH 1:   0, ph­¬ng tr×nh (*) cã mét nghiÖm   b thùc x . 0 2ab  
TH 2:   0, ph­¬ng tr×nh (*) cã hai nghiÖm thùc x  1,2 2a
TH 3:   0, ph­¬ng tr×nh (*) k «
h ng cã nghiÖm .
thùc Nh­ng nÕu gi¶i (*) trªn
tËp th×  cã hai c¨n bËc hai lµ:  i  nªn (*) cã hai nghiÖm phøc lµ: b i x  1,2 2a
II. BÀI TẬP TRẮC NGHIỆM MINH HỌA
A. SỐ PHỨC VÀ CÁC PHÉP TOÁN Dạng 1:
Số phức và các khái niệm liên quan Câu 1: Kí hiệu là tập số thực,
là tập số phức. Khẳng định nào sau đây sai? A.  .
B. 1  i  .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
C. z  1 không phải là số phức. D. 2 i  1.
Câu 2: Số phức có phần thực bằng 1 và phần ảo bằng 3 là A. 1 3 . i B. 1 3 . i C. 1 3 . i D. 1 3 . i
Câu 3: Số phức nào sau đây là số thuần ảo?
A. 1  i. B. 3i. C. 3.
D. 1  2i.
Câu 4: Số phức nào dưới đây là số thuần ảo? A. z  2   3i .
B. z  3i . C. z  2 .
D. z  3  i .
Câu 5: Cho số phức 2
z m  1  m  
1 i, m . Tập hợp tất cả các giá trị của tham số m để số phức z là số thuần ảo là A.   1 . B. .  C.  1  ;  1 . D.   1 .
Câu 6: Phần thực của số phức z  4  2i bằng A. 2 . B. 4  . C. 4 . D. 2  .
Câu 7: Cho số phức z  1  3i. Phần thực của số phức z là A. 1. B. 3. C. 3i. D. 0.
Câu 8: Biết các số thực a; b thỏa mãn a b  1  2a bi  3  3i. Tính a  . b A. 1. B. 3. C. 2. D. 0.
Câu 9: Cho số phức z  1  3i. Phần ảo của số phức z là A. 1. B. 3. C. 3i. D. 0.
Câu 10: Cho số phức z  3  2i . Tìm phần thực và phần ảo của số phức z .
A. Phần thực bằng 3
 và Phần ảo bằng 2i .
B. Phần thực bằng 3  và Phần ảo bằng 2  .
C. Phần thực bằng 3 và Phần ảo bằng 2i .
D. Phần thực bằng 3 và Phần ảo bằng 2 .
Câu 11: Cho số phức z  2  3i. Tìm phần thực a và phần ảo b của số phức . z
A. a  2; b  3. 
B. a  2; b  3.
C. a  2; b  3i.
D. a  2; b  3i.
Câu 12: Cho số phức bất kì z a bi, a;b . Khẳng định nào sau đây đúng?
A. z a bi.
B. z a bi.
C. z b ai.
D. z b ai.
Câu 13: Số phức liên hợp của số phức z  1  2i là
A. z  1  2i.
B. z  1  2i.
C. z  1  2i.
D. z  1  2i.
Câu 14: Số phức liên hợp của số phức z  3  5i
A. z  3  5i .
B. z  3  5i .
C. z  3  5i .
D. z  3  5i .
Câu 15: Tìm 1  2i.
A. 1  2i.
B. 1  2i.
C. 1  2i.
D. 1  2i.
Câu 16: Cho số phức z  1  3i. Phần ảo của số phức z là A. 1. B. 3. C. 3i. D. 3.
Câu 17: Tìm số phức liên hợp của số phức z i 3i   1 .
A. z  3  i .
B. z  3  i .
C. z  3  i .
D. z  3  i .
Câu 18: Cho số phức 3
z  1 i i . Tìm phần thực a và phần ảo b của z .
A. a  0,b  1.
B. a  2,b  1.
C. a  1,b  0.
D. a  1,b  2.
Câu 19: Khẳng định nào sau đây đúng? A. z
  ,z z luôn là số thực. B. z   , z  0. 2 C. z   , .
z z luôn là số thực. D. 2 2 z
  ,z z z .
Câu 20: Số phức đối của số phức z  1  2i là
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia 1 2
A. 1  2i.
B. i.
C. 1  2i.
D. 1  2i. 5 5
Câu 21: Mệnh đề nào dưới đây sai? A. z
  : z là số thực. B. z
  : z là số phức. C. z
  : z là số thực dương. D. z
  : z là số thực không âm.
Câu 22: Môđun của số phức z  1  2i là
A. z  5.
B. z  5.
C. z  2.
D. z  3.
Câu 23: Cho số phức z  2  i . Tính z . A. z  3 . B. z  5 . C. z  2 . D. z  5 .
Câu 24: Với  là số thực bất kì, tính sin  cos i . A. 0. B. 1. C. 2. D. 3.
Câu 25: Cho số phức bất kì z a bi, a;b . Khẳng định nào sau đây đúng? A. 2 2
z a b . B. 2 2
z a b .
C. z a  . b
D. z a b.
Câu 26: Cho số phức z  m  
1  m  2.i m  . Tất cả các giá trị của m để z  5 là m  6  m  3  A. .
B. 0  m  3 .
C. 3  m  0 . D. . m  2 m   0
Câu 27: Cho số phức z  1  3i. Khẳng định nào sau đây sai?
A. z  1  3i.
B. z  10.
C. z  10.
D. z  1  3i.
Câu 28: Biết các số thực a; b thỏa mãn a b i  2a bi  3  6 .i Tính a  . b A. 1. B. 3. C. 2. D. 0.
Câu 29: Biết các số thực x; y thỏa mãn x y1  i  3  2i x yi. Tính x  2y. A. 1. B. 3. C. 2. D. 8.
Câu 30: Tìm hai số thực x và y thỏa mãn 2x  3yi  3  i  5x  4i với i là đơn vị ảo.
A. x  1; y  1
B. x  1; y  1
C. x  1; y  1
D. x  1; y  1
Câu 31: Tìm các số thực a và b thỏa mãn 2a  b ii  1 2i với i là đơn vị ảo. 1
A. a  0,b  2 .
B. a  ,b  1.
C. a  0,b  1 .
D. a  1,b  2 . 2
Câu 32: Tìm hai số thực x và y thỏa mãn 3x  2 yi  2  i  2x  3i với i là đơn vị ảo.
A. x  2; y  2 .
B. x  2; y  1.
C. x  2; y  2 .
D. x  2; y  1  Dạng 2:
Tìm số phức thỏa mãn yêu cầu
Câu 33: Cho hai số phức z  1  i và z  3  2 .i Khẳng định nào sau đây đúng? 1 2
A. z z  4  3i.
B. z z  4  3i.
C. z z  4  3i.
D. z z  2  3i. 1 2 1 2 1 2 1 2
Câu 34: Cho hai số phức z  1  2i và z m  3   2
m  6 i; m
. Tìm tập hợp tất cả các giá trị m 2    1
để z z là số thực. 1 2 A. 2;  2 . B.   2 . C.   1 .
D.  6; 6.
Câu 35: Cho hai số phức z  2  i và z  3  2 .i Phần ảo của số phức z  2z là 1 2 1 2
A. 4i. B. 3. C. 4. D. 3.
Câu 36: Cho hai số phức z  3  i và z  1  2i. Phần thực của số phức z .z là 1 2 1 2
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia A. 7. B. 1. C. 7. D. 3.
Câu 37: Cho hai số phức z  3  2i và w  1 4i . Số phức z w bằng
A. 4  2i .
B. 4  2i .
C. 2  6i . D. 2  6i .
Câu 38: Cho hai số phức z  3  i và w  2  3i . Số phức z w bằng
A. 1 4i . B. 1 2i .
C. 5  4i . D. 5  2i .
Câu 39: Cho số phức z  3  2i , số phức 1 iz bằng.
A. 1 5i
B. 5  i
C. 1 5i D. 5  i
Câu 40: Cho số phức z 2
i , số phức 2 3i z bằng
A. 1 8i . B. 7 4i .
C. 7 4i . D. 1 8i .
Câu 41: Cho số phức z  3  i. Phần thực của số phức 1  z  2z là A. 10. B. 1. C. 7. D. 3.
Câu 42: Tính 1  i  23  2i . A. 10. B. 25. C. 50. D. 5 2.
Câu 43: Cho hai số phức z  1  i và z  2  3i . Tính môđun của số phức z z . 1 2 1 2
A. z z  13 .
B. z z  5 .
C. z z  1 .
D. z z  5 . 1 2 1 2 1 2 1 2
Câu 44: Cho hai số phức z  3  i và z m ni, m;n
. Khẳng định nào sau đây đúng? 2   1
A. z z  3m n m  3n i.
B. z z  3m n m  3n i. 1 2   1 2  
C. z z  3m n m  3n i.
D. z z  3m n m  3n i. 1 2   1 2  
Câu 45: Cho số phức z m i,m là tham số. Tìm tập hợp giá trị m để 2
z là số thuần ảo. A.   0 . B.   1 . C.  1  ;  1 . D. .  z
Câu 46: Cho hai số phức z  3  i và z  1  i. Phần thực của số phức 1 là 1 2 z2 A. 7. B. 1. C. 2. D. 2. z
Câu 47: Cho hai số phức z  1  i và z a bi, a;b
. Phần ảo của số phức 2 là 2   1 z1 a b a b A. . B. C. a  . b D. a  . b 2 2
Câu 48: Tìm số phức nghịch đảo của số phức 1  2i. 5 1 1 2
A. 1  2i.
B. i.
C. i.
D. 1  2i. 2 2 5 5
Câu 49: Cho số phức z thỏa mãn iz  3  2i . Số phức liên hợp của z là:
A. z  2  3i . B. z  2   3i . C. z  2   3i .
D. z  2  3i .
Câu 50: Số phức z thỏa mãn iz  6  5i . Số phức liên hợp của z là
A. z  5  6i .
B. z  5  6i .
C. z  5  6i .
D. z  5  6i .
Câu 51: Tìm số phức z thỏa mãn 1  iz  3  2i  0. 5 1 5 1 5 1 5 1
A. z    i. B. z   . i
C. z    i. D. z   . i 2 2 2 2 2 2 2 2
Câu 52: Cho số phức z  2  5 .i Tìm số phức w iz z
A. w  7  3i .
B. w  3  3i .
C. w  3  7i.
D. w  7  7i
Câu 53: Tìm số phức z thỏa mãn 1  iz  3  5i  0.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
A. z  1  4i.
B. z  1  4i.
C. z  1  2i.
D. z  2  i.
Câu 54: Tính môđun của số phức z thỏa mãn z 2  i 13i  1. 5 34 34 A. z  34 B. z  34 C. z D. z  3 3
Câu 55: Biết số phức z thỏa mãn 2  iz  1  5i  0. Tính z  1  i . 8 5 A. 2 5. B. 2. C. 3. D. . 5
Câu 56: Biết số phức z a bi,a;b  thỏa mãn 1  iz  2  iz  6  3i. Tính a  . b A. 0. B. 2. C. 3. D. 2.
Câu 57: Biết số phức z a bi,a;b  thỏa mãn 1  iz  3  2iz  10  2i. Tính a  . b 17 32 A. . B. 2. C. 3. D. . 11 11
Câu 58: Cho số phức z thỏa mãn 2  2  iz  3  2iz  .i Tìm tọa độ của điểm biểu diễn của số phức liên hợp với . z  11 5   11 5   11 5   11 5  A. ;   . B.  ; . C.   ; . D.  ;   .  8 8   8 8   8 8   8 8 
Câu 59: Có bao nhiêu số phức z thỏa mãn điều kiện .
z z z  2 và z  2? A. 1. B. 2. C. 3. D. 4.
Câu 60: Biết số phức z a bi,a;b  thỏa mãn 1  iz  2  iz  1  6i. Tính 3a  . b A. 2. B. 2. C. 3. D. 5.
Câu 61: Biết số phức z a bi,a;b  thỏa mãn 2  iz  1  4iz  3  i. Tính a  . b A. 1. B. 2. C. 3. D. 2.
Câu 62: Biết số phức z a bi,a;b  thỏa mãn 1  iz  2  iz  1  2i. Tính a  . b A. 2. B. 1. C. 1. D. 4.
Câu 63: Biết số phức z a bi,a;b  thỏa mãn 3  iz  4  iz  1  .i Tính 7a  . b A. 2. B. 0. C. 3. D. 2.
Câu 64: Biết số phức z a bi,a;b  thỏa mãn 2  iz  3  2iz  1  4i. Tính 8a  8 . b A. 12. B. 8. C. 3. D. 10.
Câu 65: Biết số phức z a bi,a;b  thỏa mãn 1  iz  3  iz  5  4i. Tính 4a  . b A. 7. B. 2. C. 3. D. 5.
Câu 66: Biết số phức z a bi,a;b  thỏa mãn 2  iz  4  iz  1  3i. Tính 6a  3 . b A. 3. B. 2. C. 3. D. 5.
Câu 67: Biết số phức z a bi,a;b  thỏa mãn 1  iz  3  iz  3  4i. Tính 4a  . b A. 3. B. 5. C. 3. D. 5.
Câu 68: Biết số phức z a bi,a;b  thỏa mãn 2  3iz  4  iz  1  2i. Tính 2a  . b A. 7. B. 5. C. 3. D. 5.
Câu 69: Biết số phức z a bi,a;b  thỏa mãn 3  iz  2  3iz  3  .i Tính a  . b A. 7. B. 5. C. 3. D. 2.
Câu 70: Biết số phức z a bi,a;b  thỏa mãn 1  5iz  3  4iz  1  7 .i Tính 4a  . b
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia A. 1. B. 1. C. 3. D. 2.
Câu 71: Biết số phức z a bi,a;b  thỏa mãn 2  iz  3  4iz  1  2i. Tính 5a  . b A. 7. B. 5. C. 3. D. 2. 2  i 1  i
Câu 72: Biết số phức z a bi,a;b  thỏa mãn z
z  3  2i. Tính a  . b 1  i 1  i A. 4. B. 5. C. 3. D. 2. 1  i 2  i
Câu 73: Biết số phức z a bi,a;b  thỏa mãn z
z  3  5i. Tính a  . b 2  i 1  i 2 11 3 21 A. . B. . C. . D. . 7 5 4 11
Câu 74: Cho số phức z thỏa 2  iz  3 16i  2 z i . Môđun của z bằng A. 5 . B. 13 . C. 13 . D. 5 .
Câu 75: Cho số phức z thỏa (2  i)z  4(z i)  8
 19i . Môđun của z bằng A. 13 . B. 5 . C. 13 . D. 5 .
Câu 76: Cho số phức z a bia, b  thoả mãn z  2  i z . Tính S  4a b .
A. S  4.
B. S  2.
C. S  2.
D. S  4.
Câu 77: Cho số phức z a bi (a,b  ) thỏa mãn z  1  3i z i  0 . Tính S a  3 . b 7 7
A. S  .
B. S  5.
C. S  5.
D. S   . 3 3
Câu 78: Cho số phức z thỏa mãn z  3  5 và z  2i z  2  2i . Tính z . A. z  17 . B. z  17 . C. z  10 . D. z  10 .
Câu 79: Có bao nhiêu số phức z thỏa mãn z  2 và  z  2i z  2 là số thuần ảo? A. 1. B. 0 . C. 2 . D. 4 . Dạng 3:
Biểu diễn số phức
Câu 80: Kí hiệu điểm M là điểm biểu diễn số phức, M là điểm biểu diễn số phức z. Khẳng định nào sau đây đúng?
A. M, M đối xứng nhau qua trục tung.
B. M, M đối xứng nhau qua trục hoành.
C. M, M đối xứng nhau qua gốc tọa độ.
D. M, M đối xứng nhau qua y  . x
Câu 81: Cho số phức z  1  3i. Điểm biểu diễn số phức z trên mặt phẳng tọa độ là A. M 1; 3  .
B. N 1; 3. C. P 1  ; 3  .
D. Q 1; 3.
Câu 82: Trên mặt phẳng tọa độ, điểm biểu diễn số phức 3  2i có tọa độ là A. 2;3 . B. 2;3 . C. 3; 2 . D. 3; 2 .
Câu 83: Cho số phức z  1  3i. Điểm biểu diễn số phức z trên mặt phẳng tọa độ là A. M 1; 3  .
B. N 1; 3. C. P 1  ; 3  .
D. Q 1; 3.
Câu 84: Cho hai số phức z  2  i, z  1 i . Trên mặt phẳng tọa độ Oxy, điểm biểu diễn số phức 1 2
2z z có tọa độ là: 1 2 A. 5;   1 . B. 1;5 . C. 5;0 . D. 0;5 .
Câu 85: Trên mặt phẳng tọa độ, điểm biểu diễn số phức z    i2 1 2
là điểm nào dưới đây?
A. P 3; 4
B. Q 5; 4 . C. N 4; 3   .
D. M 5; 4 .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Câu 86: Cho hai số phức z  1  i và z  2  i . Trên mặt phẳng Oxy , điểm biểu diễn số phức z  2z 1 2 1 2 có tọa độ là A. 2;5 . B. 3;5 . C. 5;2 . D. 5;3 .
Câu 87: Cho số phức z  1  2i . Điểm nào dưới đây là điểm biểu diễn của số phức w iz trên mặt phẳng tọa độ?
A. Q(1; 2)
B. N (2;1)
C. M (1; 2) D. P(2;1)
Câu 88: Điểm A1; 2 là biểu diễn trên mặt phẳng tọa độ số phức z nào trong các số phức sau?
A. z  1  2i.
B. z  1  2i. C. z  1   2i. D. z  1   2i.
Câu 89: Trên mặt phẳng tọa độ, điểm M (2;3) là điểm biểu diễn số phức nào dưới đây?
A. z  2  3i . B. z  2   3i . C. z  2   3i .
D. z  2  3i . 3 4 1 2
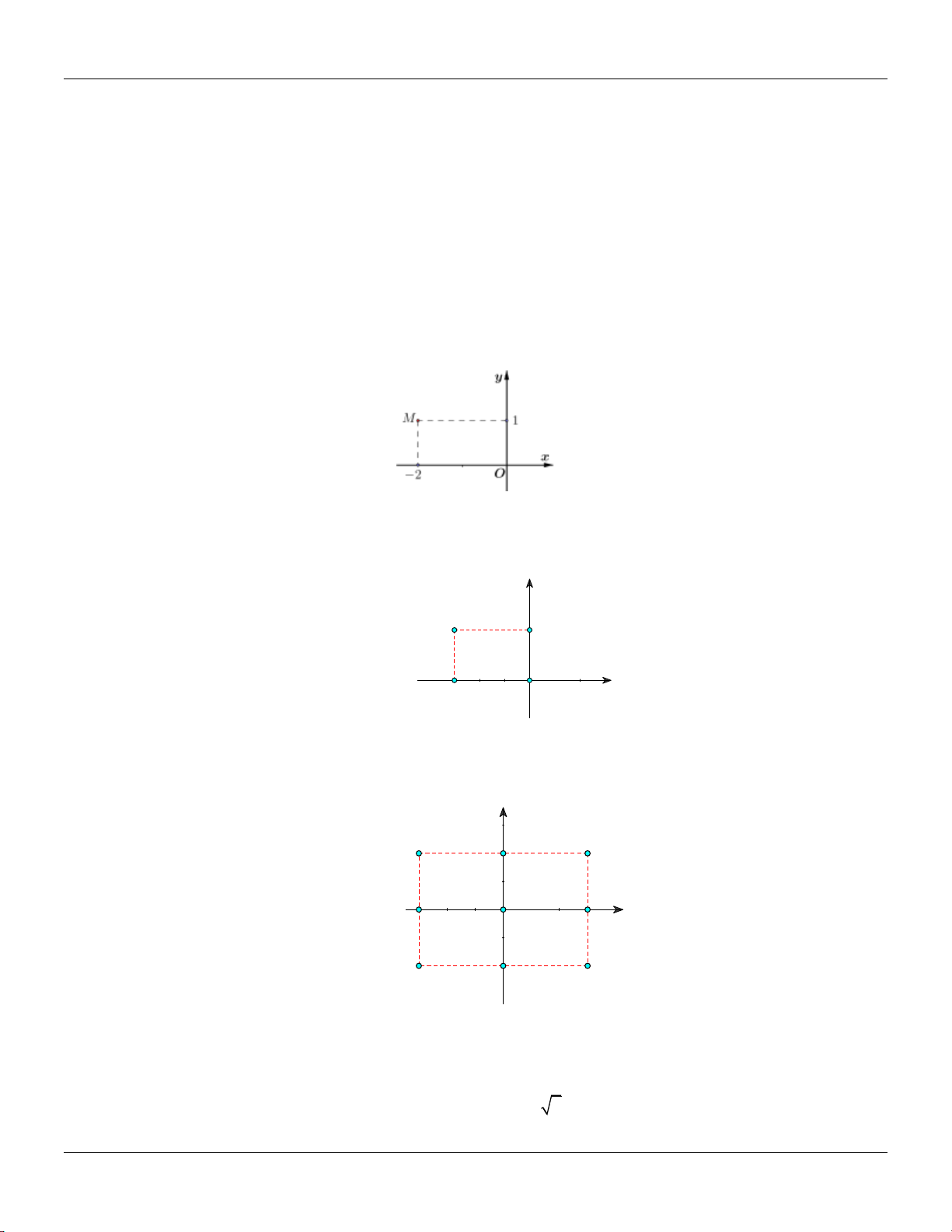
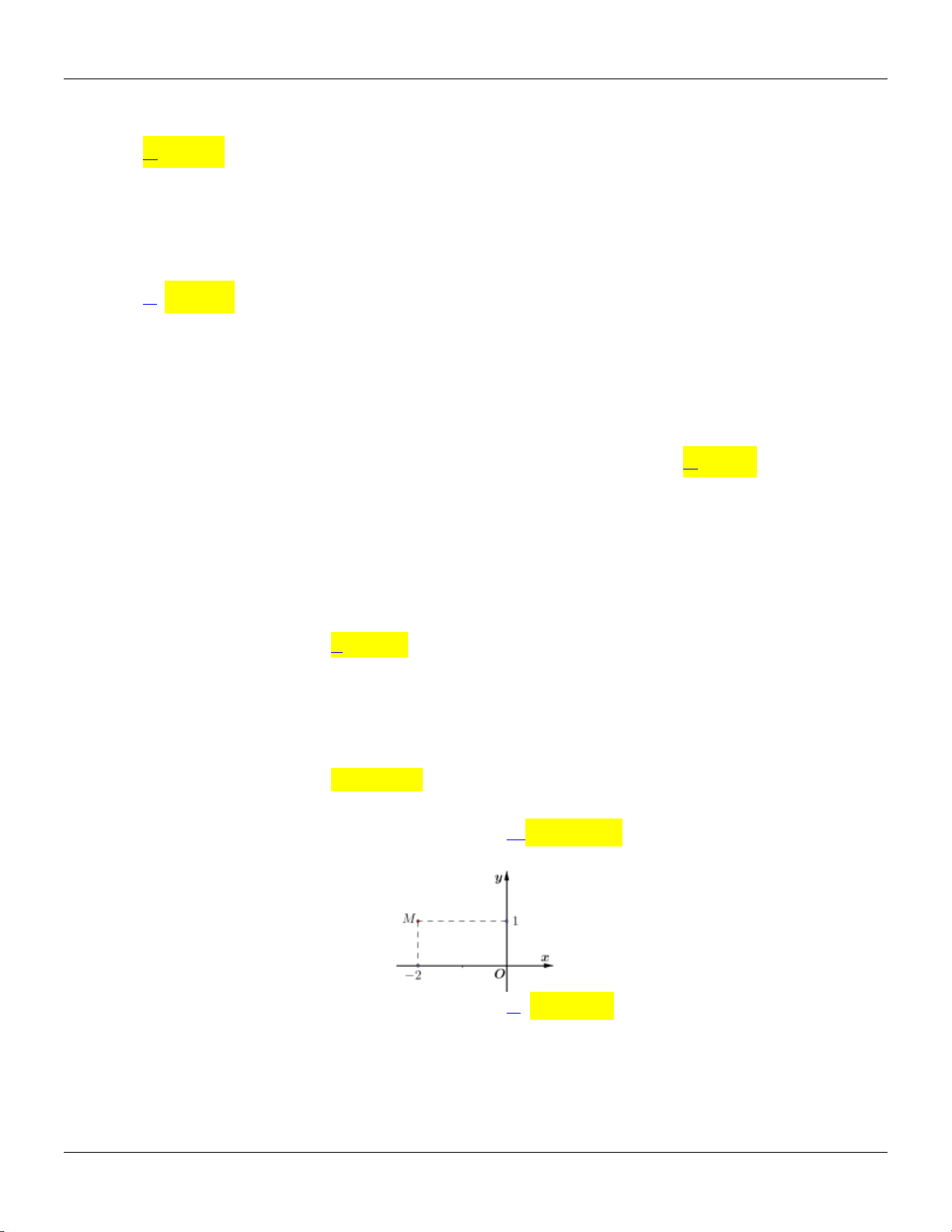
Câu 90: Số phức nào dưới đây có điểm biểu diễn trên mặt phẳng tọa độ là điểm M như hình bên? A. z  2  . i
B. z  1 2 . i C. z  2   .i
D. z  1 2 . i 4 2 3 1
Câu 91: Điểm M trong hình vẽ bên dưới là điểm biểu diễn của số phức nào trong 4 số phức được cho
ở các phương án A, B, C, D? y M 2 x -3 O
A. z  3  2i.
B. z  2  3i.
C. z  3  2i.
D. z  3  2i.
Câu 92: Điểm biểu diễn số phức z  3  2i là điểm nào trong 4 điểm M, N, P, Q trong hình vẽ bên dưới? y M 2 N -3 x 3 O Q -2 P A. M. B. N. C. P. D. Q.
Câu 93: Cho hai số phức z  1  2i và z  3  2i. Gọi A, B là hai điểm lần lượt biểu diễn số phức 1 2
z , z trên mặt phẳng tọa độ. Tính độ dài . AB 1 2 A. 10. B. 5. C. 2 5. D. 3.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
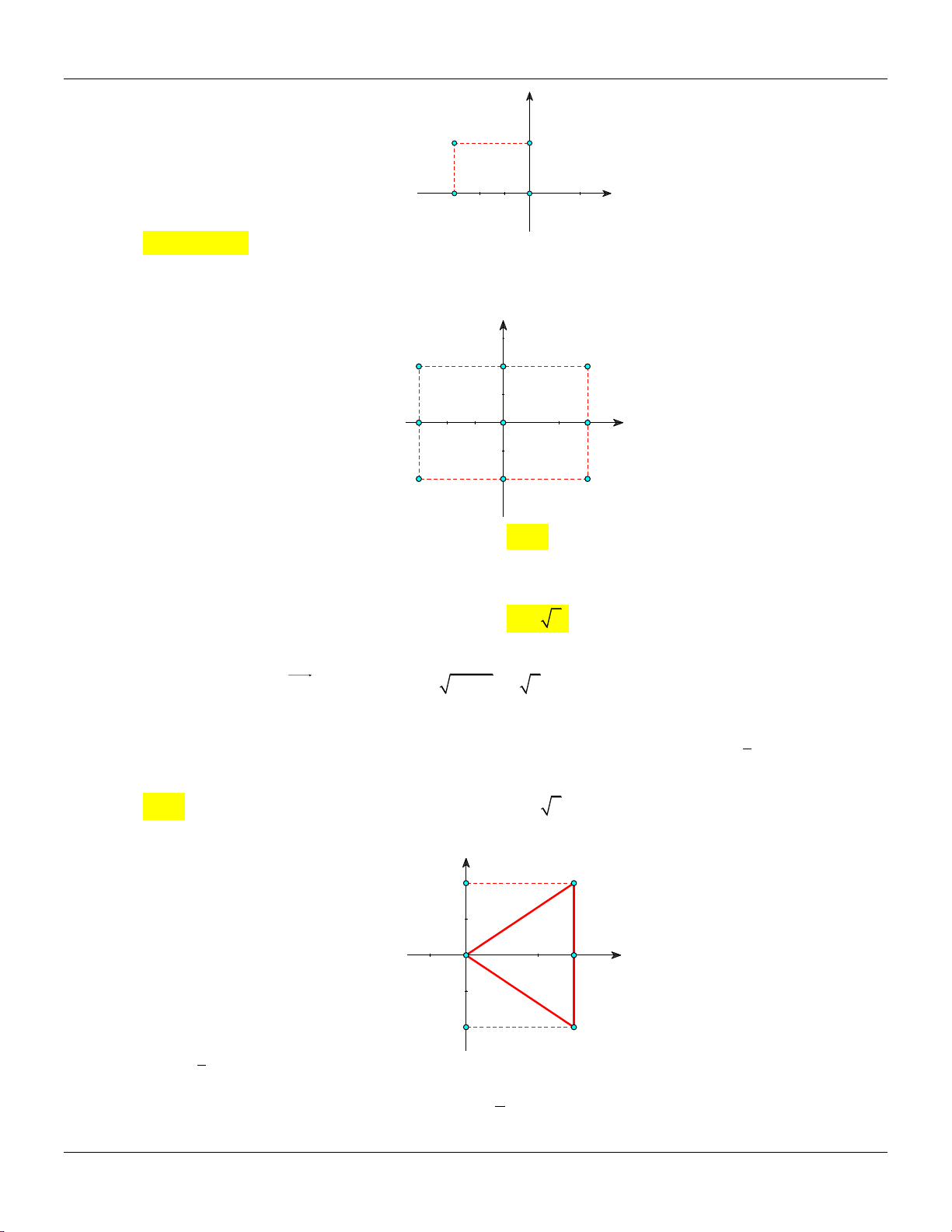
Câu 94: Cho số phức z  3  2i. Gọi A, B là hai điểm lần lượt biểu diễn số phức z, z trên mặt phẳng
tọa độ. Tính diện tích tam giác OAB ( O là gốc tọa độ). A. 6. B. 5. C. 2 5. D. 3.
Câu 95: Biết số phức z thỏa mãn z  1  i z  3  3i . Tập hợp điểm biểu diễn số phức z trên mặt
phẳng tọa độ là đường thẳng có phương trình
A. x  2y  4  0.
B. x  2y  4  0.
C. x  2y  4  0.
D. x y  4  0.
Câu 96: Biết số phức z thỏa mãn z  1  3i z  3  5i . Tập hợp điểm biểu diễn số phức z trên mặt
phẳng tọa độ là đường thẳng có phương trình
A. x  2y  4  0.
B. x  4y  6  0.
C. x  2y  6  0.
D. x y  4  0.
Câu 97: Biết số phức z thỏa mãn z  2i z  2  4i . Tập hợp điểm biểu diễn số phức z trên mặt
phẳng tọa độ là đường thẳng có phương trình
A. x  2y  4  0.
B. x  4y  6  0.
C. x  2y  6  0.
D. x y  4  0.
Câu 98: Biết số phức z thỏa mãn z  1  i  3. Tập hợp điểm biểu diễn số phức z trên mặt phẳng tọa
độ là đường tròn có phương trình 2 2 2 2
A. x  1  y  1  9.
B. x  1  y  1  9. 2 2 2 2
C. x  1  y  1  9.
D. x  1  y  1  9.
Câu 99: Biết số phức z thỏa mãn z  3  4i  4. Biết tập hợp điểm biểu diễn số phức z trên mặt phẳng
tọa độ là đường tròn C. Tìm tâm I và tính bán kính R của đường tròn C. A. I  3;
 4,R  16. B. I  3;
 4,R  4. C. I 3; 4
 ,R  4. D. I 3; 4
 ,R  16.
Câu 100: Biết số phức z thỏa mãn z  1  i  2. Biết tập hợp điểm biểu diễn số phức z trên mặt phẳng
tọa độ là đường tròn C. Tìm tâm I và tính bán kính R của đường tròn C. A. I  1
 ;1,R  2. B. I 1; 1
 ,R  4. C. I 1; 1
 ,R  2. D. I  1
 ;1,R  4.
Câu 101: Xét các số phức z thỏa mãn  z  2i z  2 là số thuần ảo. Biết rằng tập hợp tất cả các
điểm biểu diễn của z là một đường tròn, tâm của đường tròn đó có tọa độ là A. 1;  1  . B. 1  ;1 . C. 1;  1 . D. 1;   1 .
Câu 102: Xét các số phức z thỏa mãn  z  2i z  2 là số thuần ảo. Trên mặt phẳng tọa độ, tập hợp
tất cả các điểm biểu diễn các số phức z là một đường tròn có bán kính bằng A. 2 2. B. 2. C. 2. D. 4.
Câu 103: Cho các số phức z thỏa mãn z  4 . Biết rằng tập hợp các điểm biểu diễn các số
phức w  (3  4i)z i là một đường tròn. Tính bán kính r của đường tròn đó. A. r  4 . B. r  5 . C. r  20 .
D. r  22 .
B. PHƯƠNG TRÌNH BẬC HAI VỚI HỆ SỐ THỰC Câu 104: Phương trình 2
ax bx c  0 a,b,c   có hai nghiệm phức phân biệt khi và chỉ khi a  0 a  0 a  0 A. 2
b  4ac  0 . B. . C. . D. . 2
b  4ac  0 2
b  4ac  0 2
b  4ac  0
Câu 105: Trên tập số phức, phương trình nào sau đây có nghiệm thực? A. 2 x  1  0. B. 2 x  1  0. C. 2 x  4  0. D. 2
2x  1  0.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Câu 106: Kí hiệu z , z là hai nghiệm phức của phương trình 2
z  3 . Giá trị của z z bằng 1 2 1 2 A. 6 . B. 2 3 . C. 3 . D. 3.
Câu 107: Trên tập số phức, tập nghiệm của phương trình 2
z  2z  2  0 là A.  1   i;1  i . B.  1   i;1   i . C.  1   i;1  i . D. i; 1    i .
Câu 108: Trên tập số phức, gọi z , z là hai nghiệm của phương trình 2
z  2z  2  0. Tính z z . 1 2 1 2 A. 2 2. B. 2. C. 4 2 D. 4.
Câu 109: Phương trình nào dưới đây nhận hai số phức 1  2i và 1  2i là nghiệm? A. 2
z  2z  3  0. B. 2
z  2z  3  0. C. 2
z  2z  3  0. D. 2
z  2z  3  0. 2 2
Câu 110: Trên tập số phức, gọi z , z là hai nghiệm của phương trình 2
z  4z  2  0. Tính zz . 1 2 1 2 A. 2 2. B. 2. C. 8. D. 4.
Câu 111: Gọi z , z là hai nghiệm phức của phương trình 2
z  4z  5  0 . Giá trị của 2 2 z z bằng 1 2 1 2 A. 6 . B. 8 . C. 16 . D. 26 . 2 2
Câu 112: Gọi z , z z z   z z 1
2 là 2 nghiệm phức của phương trình 2 6 14 0 . Giá trị của 1 2 bằng: A. 36. B. 8. C. 28 . D. 18.
Câu 113: Kí hiệu z , z là hai nghiệm của phương trình 2
z  4  0 . Gọi M , N lần lượt là điểm biểu 1 2
diển của z , z trên mặt phẳng tọa độ. Tính T OM ON với O là gốc tọa độ. 1 2 A. T  2 . B. T  2 . C. T  8 . D. T  4 . 1 1
Câu 114: Ký hiệu z , z là hai nghiệm phức của phương trình 2
z z  6  0 Tính   . 1 2 P z z 1 2 1 1 1 A. P  . B. P  . C. P   . D. P  6 . 6 12 6
Câu 115: Gọi z là nghiệm phức có phần ảo âm của phương trình 2 z 2z 5 0 . Môđun của số 0 phức z i bằng 0 A. 2. B. 2 . C. 10 . D. 10 .
Câu 116: Kí hiệu z là nghiệm phức có phần ảo dương của phương trình 2
4z  16z  17  0 . Trên mặt 0
phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn của số phức w iz ? 0  1   1   1   1 
A. M  ;2 . B. M   ; 2  . C. M   ;1 .
D. M  ;1 . 1  2  2  2  3  4  4  4 
Câu 117: Trên tập số phức, cho phương trình 2
z  2z m  0,m là tham số. Tìm tập hợp tất cả các giá trị
của tham số m để phương trình đã cho không có nghiệm thực. A. .
B. 1; . C. 1;   . D. . 
Câu 118: Gọi z là nghiệm phức có phần ảo dương của phương trình 2
z  6z  34  0 . Tính z  2  i . 0 0 A. 17 . B. 17 . C. 2 17 . D. 37 . 1 1
Câu 119: Ký hiệu z , z là hai nghiệm phức của phương trình 2
z z  6  0 Tính P   . 1 2 z z 1 2 1 1 1
A. P . B. P .
C. P   .
D. P  6 . 6 12 6
Câu 120: Gọi z là nghiệm phức có phần ảo dương của phương trình 2
z  6z 13  0 . Trên mặt 0
phẳng tọa độ, điểm biểu diễn 1 z là: 0
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia A. M  2  ;2.
B. Q 4; 2 .
C. N 4; 2 . D. P  2  ; 2   .
Câu 121: Gọi z là nghiệm phức có phần ảo âm của phương trình 2
z  2z  5  0 . Tìm tọa độ điểm biểu 1 7  4i diễn số phức trên mặt phẳng phức? z1
A. P 3; 2 .
B. N 1;  2 . C. Q3; 2   .
D. M 1; 2 .
Câu 122: Trên tập số phức, số nghiệm thực của phương trình 4 2
z  3z  4  0 là A. 0. B. 1. C. 4. D. 2.
Câu 123: Trên tập số phức, tập nghiệm của phương trình 4 2
z  2z  3  0 là A.  3.
B. i; 3
C. i; 3.
D. i;i 3.
Câu 124: Trên tập số phức, tập nghiệm của phương trình 4 2
z  4z  3  0 là A. 1;   3 . B. . 
C. i;i 3.
D. i;i 3.
Câu 125: Trên tập số phức, gọi z , z , z , z là bốn nghiệm của phương trình 4 2
z  2z  3  0. Tính 1 2 3 4
z z z z . 1 2 3 4 A. 2  2 3. B. 2 3. C. 4  2 3. D. 4  4 3.
Câu 126: Kí hiệu z , z , z và z là bốn nghiệm phức của phương trình 4 2
z z 12  0 . Tính 1 2 3 4
tổngT z z z z . 1 2 3 4
A. T  4. B. T  2 3.
C. T  4  2 3.
D. T  2  2 3.
Câu 127: Trên tập số phức, tổng môđun các nghiệm của phương trình  2 z   2
1 z  4  0 là A. 6. B. 1. C. 4. D. 2.
Câu 128: Trên tập số phức, gọi z , z là hai nghiệm của phương trình 2
z  2z  2  0. Biết A, B lần lượt là 1 2
hai điểm biểu diễn z , z trên mặt phẳng. Tính độ dài đoạn thẳng . AB 1 2 A. 2 2. B. 2. C. 1. D. 4.
Câu 129: Trên tập số phức, tìm giá trị tham số thực m để phương trình 2
z mz m  4  0 có một
nghiệm là z  1  i.
A. m  2.
B. m  1.
C. m  3.
D. m  4.
Câu 130: Trên tập số phức, gọi z , z là hai nghiệm của phương trình 2
z  2z  2  0. Biết A, B lần lượt là 1 2
hai điểm biểu diễn z , z trên mặt phẳng. Tọa độ trung điểm của đoạn thẳng AB là 1 2 A. 1;0
B. 1;0. C. 0;1. D. 0; 1  .
Câu 131: Trên tập số phức, gọi z , z là hai nghiệm của phương trình 2
z  2z  5  0. Biết A, B lần lượt là 1 2
hai điểm biểu diễn z , z trên mặt phẳng. Tính cos AOB, (với O là gốc tọa độ). 1 2 3 3  1 1  A. B. . C. . D. . 5 5 5 5
Câu 132: Trên tập số phức, gọi z , z là hai nghiệm của phương trình 2
z  4z  8  0. Biết A, B lần lượt là 1 2
hai điểm biểu diễn z , z trên mặt phẳng. Tính OAB, (với O là gốc tọa độ). 1 2 A. o 30 B. o 60 C. o 135 D. o 45 .
Câu 133: Gọi z , z là hai nghiệm của phương trình 2
z  4z  13  0 và A , B lần lượt là hai điểm biểu 1 2
diễn cho hai số phức z , z trong mặt phẳng tọa độ Oxy . Diện tích tam giác OAB bằng 1 2
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia 13 A. 13 . B. 12 . C. . D. 6 . 2
Câu 134: Gọi z , z , z là ba nghiệm của phương trình 3 2
z z  5z  7  0 . Tính M z z z . 1 2 3 1 2 3
A. M  1  2 7 .
B. M  1  7 2 .
C. M  2  7 .
D. M  3 .
Câu 135: Gọi A , B , C là các điểm biểu diễn các số phức z , z , z là nghiệm của phương trình 1 2 3 3 2
z  6z  12z  7  0 . Tính diện tích S của tam giác ABC . 3 3 3 3
A. S  3 3 . B. S .
C. S  1 . D. S . 2 4
Câu 136: Trên tập hợp các số phức, xét phương trình 2
z  m   2 2
1 z m  0 . Có bao nhiêu giá trị
của m để phương trình đó có nghiệm z thõa mãn z  8? o o A. 4 . B. 3 . C. 2 . D. 1.
III. LỜI GIẢI CHI TIẾT
A. SỐ PHỨC VÀ CÁC PHÉP TOÁN Dạng 1:
Số phức và các khái niệm liên quan Câu 1: Kí hiệu là tập số thực,
là tập số phức. Khẳng định nào sau đây sai? A.  .
B. 1  i  .
C. z  1 không phải là số phức. D. 2 i  1.
Câu 2: Số phức có phần thực bằng 1 và phần ảo bằng 3 là A. 1 3 . i B. 1 3 . i C. 1 3 . i D. 1 3 . i
Câu 3: Số phức nào sau đây là số thuần ảo?
A. 1  i. B. 3i. C. 3.
D. 1  2i.
Câu 4: Số phức nào dưới đây là số thuần ảo? A. z  2   3i .
B. z  3i . C. z  2 .
D. z  3  i .
Câu 5: Cho số phức 2
z m  1  m  
1 i, m  . Tập hợp tất cả các giá trị của tham số m để số phức z là số thuần ảo là A.   1 . B. .  C.  1  ;  1 . D.   1 . Lời giải: m  1 
Số phức z là số thuần ảo 2
m  1  0   . m   1
Chọn đáp án C.
Câu 6: Phần thực của số phức z  4  2i bằng A. 2 . B. 4  . C. 4 . D. 2  .
Câu 7: Cho số phức z  1  3i. Phần thực của số phức z là A. 1. B. 3. C. 3i. D. 0.
Câu 8: Biết các số thực a; b thỏa mãn a b  1  2a bi  3  3i. Tính a  . b A. 1. B. 3. C. 2. D. 0. Lời giải:
a b   a
Ta có: a b    a b 1 3 1 1 2
i  3  3i    
. Vậy a b  2. 2a b  3 b    1
Chọn đáp án C.
Câu 9: Cho số phức z  1  3i. Phần ảo của số phức z là A. 1. B. 3. C. 3i. D. 0.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Câu 10: Cho số phức z  3  2i . Tìm phần thực và phần ảo của số phức z .
A. Phần thực bằng 3
 và Phần ảo bằng 2i .
B. Phần thực bằng 3  và Phần ảo bằng 2  .
C. Phần thực bằng 3 và Phần ảo bằng 2i .
D. Phần thực bằng 3 và Phần ảo bằng 2 .
Câu 11: Cho số phức z  2  3i. Tìm phần thực a và phần ảo b của số phức . z
A. a  2; b  3. 
B. a  2; b  3.
C. a  2; b  3i.
D. a  2; b  3i. Lời giải: Ta có:
Chọn đáp án A.
Câu 12: Cho số phức bất kì z a bi, a;b . Khẳng định nào sau đây đúng?
A. z a bi.
B. z a bi.
C. z b ai.
D. z b ai.
Câu 13: Số phức liên hợp của số phức z  1  2i là
A. z  1  2i.
B. z  1  2i.
C. z  1  2i.
D. z  1  2i.
Câu 14: Số phức liên hợp của số phức z  3  5i
A. z  3  5i .
B. z  3  5i .
C. z  3  5i .
D. z  3  5i .
Câu 15: Tìm 1  2i.
A. 1  2i.
B. 1  2i.
C. 1  2i.
D. 1  2i. Lời giải:
Kí hiệu 1  2i là số phức liên hợp của 1  2i .
Chọn đáp án A.
Câu 16: Cho số phức z  1  3i. Phần ảo của số phức z là A. 1. B. 3. C. 3i. D. 3. Lời giải:
Ta có: z  1  3i.
Chọn đáp án D.
Câu 17: Tìm số phức liên hợp của số phức z i 3i   1 .
A. z  3  i .
B. z  3  i .
C. z  3  i .
D. z  3  i . Lời giải:
z i 3i   1  3
  i nên suy ra z  3   i .
Câu 18: Cho số phức 3
z  1 i i . Tìm phần thực a và phần ảo b của z .
A. a  0,b  1.
B. a  2,b  1.
C. a  1,b  0.
D. a  1,b  2. Lời giải: Ta có: 3 2
z  1 i i  1 i i .i  1 i i  1 2i
Suy ra phần thực của z là a  1 , phần ảo của z là b  2 .
Câu 19: Khẳng định nào sau đây đúng? A. z
  ,z z luôn là số thực. B. z   , z  0. 2 C. z   , .
z z luôn là số thực. D. 2 2 z
  ,z z z . Lời giải: 2 Ta có: z   , .
z z z  0.
Chọn đáp án C.
Câu 20: Số phức đối của số phức z  1  2i là 1 2
A. 1  2i.
B. i.
C. 1  2i.
D. 1  2i. 5 5
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia Lời giải:
Số phức đối của số phức z  1  2i là 1  2i  1   2 .i
Chọn đáp án C.
Câu 21: Mệnh đề nào dưới đây sai? A. z
  : z là số thực. B. z
  : z là số phức. C. z
  : z là số thực dương. D. z
  : z là số thực không âm.
Câu 22: Môđun của số phức z  1  2i là
A. z  5.
B. z  5.
C. z  2.
D. z  3. Lời giải: Ta có: 2 2 z  1  2  5.
Chọn đáp án B.
Câu 23: Cho số phức z  2  i . Tính z . A. z  3 . B. z  5 . C. z  2 . D. z  5 .
Câu 24: Với  là số thực bất kì, tính sin  cos i . A. 0. B. 1. C. 2. D. 3. Lời giải: Ta có:      2 2 sin cos
i  sin   cos   1.
Chọn đáp án B.
Câu 25: Cho số phức bất kì z a bi, a;b . Khẳng định nào sau đây đúng? A. 2 2
z a b . B. 2 2
z a b .
C. z a  . b
D. z a b. Lời giải: Ta có:
Chọn đáp án B.
Câu 26: Cho số phức z  m  
1  m  2.i m  . Tất cả các giá trị của m để z  5 là m  6  m  3  A. .
B. 0  m  3 .
C. 3  m  0 . D. . m  2 m   0 Lời giải: 2 2 Ta có: z   m   1  m  2 2 2 5
 2m  6m  5  5  2m  6m  0  m 0;3.  
Chọn đáp án B.
Câu 27: Cho số phức z  1  3i. Khẳng định nào sau đây sai?
A. z  1  3i.
B. z  10.
C. z  10.
D. z  1  3i. Lời giải:
Ta có: z  1  3i z  10 hoặc nhận xét z z . Vậy C sai.
Chọn đáp án C.
Câu 28: Biết các số thực a; b thỏa mãn a b i  2a bi  3  6 .i Tính a  . b A. 1. B. 3. C. 2. D. 0. Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia a b  a
Ta có: a b i   a bi   i a b   a b   3 2 2 3 6 2
1 i  3  6i     .
2a b  1  6 b    1
Vậy a b  3.
Chọn đáp án B.
Câu 29: Biết các số thực x; y thỏa mãn x y1  i  3  2i x yi. Tính x  2y. A. 1. B. 3. C. 2. D. 8. Lời giải:
Ta có: x y1  i  3  2i  5x  4yi x y  3  x y  2i x yi
x y  3  xx  2      .
x y  2  y y  3   
Vậy x  2y  8. 
Chọn đáp án D.
Câu 30: Tìm hai số thực x và y thỏa mãn 2x  3yi  3  i  5x  4i với i là đơn vị ảo.
A. x  1; y  1
B. x  1; y  1
C. x  1; y  1
D. x  1; y  1 Lời giải:      
x yi    i  x i   x     y   2x 3 5x x 1 2 3 3 5 4 2 3 3
1 i  5x  4i     . 3  y 1  4 y 1
Chọn đáp án D.
Câu 31: Tìm các số thực a và b thỏa mãn 2a  b ii  1 2i với i là đơn vị ảo. 1
A. a  0,b  2 .
B. a  ,b  1.
C. a  0,b  1 .
D. a  1,b  2 . 2 Lời giải: a   a
Ta có 2a  b ii  1 2i  2a 1 bi  1 2 1 1 1 2i     . b   2 b   2
Vậy a  1,b  2 .
Chọn đáp án D.
Câu 32: Tìm hai số thực x và y thỏa mãn 3x  2 yi  2  i  2x  3i với i là đơn vị ảo.
A. x  2; y  2 .
B. x  2; y  1.
C. x  2; y  2 .
D. x  2; y  1  Lời giải:
Ta có: 3x  2 yi  2  i  2x  3i 3
x  2  2xx  2 
 3x  2  2y  
1  2x  3i     . 2y 1  3  y  2 
Chọn đáp án A. Dạng 2:
Tìm số phức thỏa mãn yêu cầu
Câu 33: Cho hai số phức z  1  i và z  3  2 .i Khẳng định nào sau đây đúng? 1 2
A. z z  4  3i.
B. z z  4  3i.
C. z z  4  3i.
D. z z  2  3i. 1 2 1 2 1 2 1 2 Lời giải:
Ta có: z z  1  i  3  2i  4  3 .i 1 2    
Chọn đáp án A.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Câu 34: Cho hai số phức z  1  2i và z m  3   2
m  6 i; m
. Tìm tập hợp tất cả các giá trị m 2    1
để z z là số thực. 1 2 A. 2;  2 . B.   2 . C.   1 .
D.  6; 6. Lời giải:
Ta có: z z m  1   2 m  4 i. 1 2  m  2 Yêu cầu bài toán 2
m  4  0   . m  2  
Chọn đáp án A.
Câu 35: Cho hai số phức z  2  i và z  3  2 .i Phần ảo của số phức z  2z là 1 2 1 2
A. 4i. B. 3. C. 4. D. 3. Lời giải:
Ta có: z  2z  2  i  2 3  2i  4   3 .i 1 2    
Chọn đáp án D.
Câu 36: Cho hai số phức z  3  i và z  1  2i. Phần thực của số phức z .z là 1 2 1 2 A. 7. B. 1. C. 7. D. 3. Lời giải:
Ta có: z .z  3  i1  2i 2
 3  6i i  2i  1 7 .i 1 2
Chọn đáp án B.
Câu 37: Cho hai số phức z  3  2i và w  1 4i . Số phức z w bằng
A. 4  2i .
B. 4  2i .
C. 2  6i . D. 2  6i . Lời giải:
Ta có: z w  3  2i 1 4i  4  2i .
Chọn đáp án B.
Câu 38: Cho hai số phức z  3  i và w  2  3i . Số phức z w bằng
A. 1 4i . B. 1 2i .
C. 5  4i . D. 5  2i . Lời giải:
z w  3  i  2  3i  1 2 . i
Chọn đáp án B.
Câu 39: Cho số phức z  3  2i , số phức 1 iz bằng.
A. 1 5i
B. 5  i
C. 1 5i D. 5  i Lời giải:
Ta có: 1 iz  1 i 3   2i  5   .i
Chọn đáp án D.
Câu 40: Cho số phức z 2
i , số phức 2 3i z bằng
A. 1 8i . B. 7 4i .
C. 7 4i . D. 1 8i . Lời giải: Ta có: 2 3i z 2 3i 2 i 7 4i .
Chọn đáp án C.
Câu 41: Cho số phức z  3  i. Phần thực của số phức 1  z  2z là A. 10. B. 1. C. 7. D. 3.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia Lời giải:
Ta có: 1  z  2z  1  3  i  23  i  10  .i
Chọn đáp án A.
Câu 42: Tính 1  i  23  2i . A. 10. B. 25. C. 50. D. 5 2. Lời giải:
Ta có: 1  i  23  2i  5
  5i  25  25  5 2.
Chọn đáp án D.
Câu 43: Cho hai số phức z  1  i và z  2  3i . Tính môđun của số phức z z . 1 2 1 2
A. z z  13 .
B. z z  5 .
C. z z  1 .
D. z z  5 . 1 2 1 2 1 2 1 2 Lời giải:
z z  1 i  2  3i  3  2i nên ta có: z z  3  2i  3  2   13 . 1 2  2 2 1 2  
Chọn đáp án A.
Câu 44: Cho hai số phức z  3  i và z m ni, m;n
. Khẳng định nào sau đây đúng? 2   1
A. z z  3m n m  3n i.
B. z z  3m n m  3n i. 1 2   1 2  
C. z z  3m n m  3n i.
D. z z  3m n m  3n i. 1 2   1 2   Lời giải:
Ta có: z z  3  im ni 2
 3m  3ni mi ni  3m n m  3n i. 1 2  
Chọn đáp án D.
Câu 45: Cho số phức z m i,m là tham số. Tìm tập hợp giá trị m để 2
z là số thuần ảo. A.   0 . B.   1 . C.  1  ;  1 . D. .  Lời giải:
Ta có: z  m i2 2 2 2 2
m  2mi i m  1 2mi. m  1 Yêu cầu bài toán 2
m  1  0   . m  1  
Chọn đáp án C. z
Câu 46: Cho hai số phức z  3  i và z  1  i. Phần thực của số phức 1 là 1 2 z2 A. 7. B. 1. C. 2. D. 2. Lời giải: z 3  i
3i1i 2
3  3i i i Ta có: 1     1 2 .i z 1  i 2 2 2
Chọn đáp án B. z
Câu 47: Cho hai số phức z  1  i và z a bi, a;b
. Phần ảo của số phức 2 là 2   1 z1 a b a b A. . B. C. a  . b D. a  . b 2 2 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia z a bi
abi1i 2
a ai bi bi
a b a b  Ta có: 2        .i z 1  i 2 2 2  2  1
Chọn đáp án A.
Câu 48: Tìm số phức nghịch đảo của số phức 1  2i. 5 1 1 2
A. 1  2i.
B. i.
C. i.
D. 1  2i. 2 2 5 5 Lời giải: 1 1 2
Số phức nghịch đảo của số phức 1  2i là   i. 1  2i 5 5
Chọn đáp án C.
Câu 49: Cho số phức z thỏa mãn iz  3  2i . Số phức liên hợp của z là:
A. z  2  3i . B. z  2   3i . C. z  2   3i .
D. z  2  3i . Lời giải:
Ta có: iz  3  2i z  2  3i . Nên z  2  3i .
Chọn đáp án A.
Câu 50: Số phức z thỏa mãn iz  6  5i . Số phức liên hợp của z là
A. z  5  6i .
B. z  5  6i .
C. z  5  6i .
D. z  5  6i . Lời giải: 6  5i
Ta có: iz  6  5i z
 5  6i . Vậy z  5  6i . i
Chọn đáp án C.
Câu 51: Tìm số phức z thỏa mãn 1  iz  3  2i  0. 5 1 5 1 5 1 5 1
A. z    i. B. z   . i
C. z    i. D. z   . i 2 2 2 2 2 2 2 2 Lời giải:   i
Ta có:   iz   i     i 3 2 5 1 1 3 2 0 1 z  3
  2i z     . i 1  i 2 2
Chọn đáp án A.
Câu 52: Cho số phức z  2  5 .i Tìm số phức w iz z
A. w  7  3i .
B. w  3  3i .
C. w  3  7i.
D. w  7  7i Lời giải:
Ta có w iz z i(2  5i)  (2  5i)  2i  5  2  5i  3   3 .i
Chọn đáp án B.
Câu 53: Tìm số phức z thỏa mãn 1  iz  3  5i  0.
A. z  1  4i.
B. z  1  4i.
C. z  1  2i.
D. z  2  i. Lời giải:   i
Ta có:   iz   i     i 3 5 1 3 5 0 1 z  3
  5i z
 1 4i z  1 4 .i 1  i
Chọn đáp án B.
Câu 54: Tính môđun của số phức z thỏa mãn z 2  i 13i  1. 5 34 34 A. z  34 B. z  34 C. z D. z  3 3 Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia 113i
113i2i
z 2  i 13i  1  z   z      z     i  i  .  2 2 3 5 34. iz 3 5i 2 2 2
Chọn đáp án A.
Câu 55: Biết số phức z thỏa mãn 2  iz  1  5i  0. Tính z  1  i . 8 5 A. 2 5. B. 2. C. 3. D. . 5 Lời giải:   i   Ta có:   i 1 5 3 11 3 11 8 6 2
z  1  5i  0  z   
i z  1  i  
i  1  i     . i 2  i 5 5  5 5  5 5
Vậy z  1  i  2.
Chọn đáp án B.
Câu 56: Biết số phức z a bi,a;b  thỏa mãn 1  iz  2  iz  6  3i. Tính a  . b A. 0. B. 2. C. 3. D. 2. Lời giải:
Ta có: 1  iz  2  iz  6  3i  1  ia bi  2  ia bi  6  3i 2 2
a bi ai bi  2a  2bi ai bi  6  3i    
a   a b 3a 6 a 2 3 2
i  6  3i     . 2a b  3 b    1
Vậy a b  3.
Chọn đáp án C.
Câu 57: Biết số phức z a bi,a;b  thỏa mãn 1  iz  3  2iz  10  2i. Tính a  . b 17 32 A. . B. 2. C. 3. D. . 11 11 Lời giải:
Ta có: 1  iz  3  2iz  10  2i  1  ia bi  3  2ia bi  10  2i 2 2
a bi ai bi  3a  3bi  2ai  2bi  10  2i  14 a     
a b  a b 4a 3b 10 11 4 3
2 i  6  3i     . a  2b  2   18 b   11 32
Vậy a b  . 11
Chọn đáp án D.
Câu 58: Cho số phức z thỏa mãn 2  2  iz  3  2iz  .i Tìm tọa độ của điểm biểu diễn của số phức liên hợp với . z  11 5   11 5   11 5   11 5  A. ;   . B.  ; . C.   ; . D.  ;   .  8 8   8 8   8 8   8 8  Lời giải:
Gọi z a bi; a;b .
Ta có: 2  2  iz  3  2iz i  2  2  ia bi  3  2ia bi  i
 2  2a b  2b ai  3a  2b   2
a  3b  1i
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia  11  2  2   3  2    2 a a b a b a b  8 11 5        z   . i 2b a  2
a  3b  1 3a  5b    1 5 8 8 b    8 11 5 Vậy z   i. 8 8
Chọn đáp án B.
Câu 59: Có bao nhiêu số phức z thỏa mãn điều kiện .
z z z  2 và z  2? A. 1. B. 2. C. 3. D. 4. Lời giải: 2
Gọi z a bi;a;b . Để ý: . z z z . a  42 2 2 2  b  4
a b  8a  12 a  2 Ta có hệ:      . 2 2 2 2
a b  4
a b  4 b  0
Vậy tồn tại duy nhất 1 số phức thỏa yêu cầu bài toán.
Lưu ý: Hoặc ta có thể biến đổi .
z z z  2  z z  1  2  z z  1  2.
Chọn đáp án A.
BÀI TẬP TƯƠNG TỰ:
Câu 60: Biết số phức z a bi,a;b  thỏa mãn 1  iz  2  iz  1  6i. Tính 3a  . b A. 2. B. 2. C. 3. D. 5. 11 Đáp số: z    6i. 3
Câu 61: Biết số phức z a bi,a;b  thỏa mãn 2  iz  1  4iz  3  i. Tính a  . b A. 1. B. 2. C. 3. D. 2. 1 3
Đáp số: z    i. 2 2
Câu 62: Biết số phức z a bi,a;b  thỏa mãn 1  iz  2  iz  1  2i. Tính a  . b A. 2. B. 1. C. 1. D. 4. 1 4 Đáp số: z   . i 3 3
Câu 63: Biết số phức z a bi,a;b  thỏa mãn 3  iz  4  iz  1  .i Tính 7a  . b A. 2. B. 0. C. 3. D. 2. 1
Đáp số: z    .i 7
Câu 64: Biết số phức z a bi,a;b  thỏa mãn 2  iz  3  2iz  1  4i. Tính 8a  8 . b A. 12. B. 8. C. 3. D. 10. 11 21 Đáp số: z    . i 8 8
Câu 65: Biết số phức z a bi,a;b  thỏa mãn 1  iz  3  iz  5  4i. Tính 4a  . b A. 7. B. 2. C. 3. D. 5. 9
Đáp số: z    2i. 4
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Câu 66: Biết số phức z a bi,a;b  thỏa mãn 2  iz  4  iz  1  3i. Tính 6a  3 . b A. 3. B. 2. C. 3. D. 5. 1 4 Đáp số: z   . i 6 3
Câu 67: Biết số phức z a bi,a;b  thỏa mãn 1  iz  3  iz  3  4i. Tính 4a  . b A. 3. B. 5. C. 3. D. 5. 7
Đáp số: z   2i. 4
Câu 68: Biết số phức z a bi,a;b  thỏa mãn 2  3iz  4  iz  1  2i. Tính 2a  . b A. 7. B. 5. C. 3. D. 5. 3
Đáp số: z   4 . i 2
Câu 69: Biết số phức z a bi,a;b  thỏa mãn 3  iz  2  3iz  3  .i Tính a  . b A. 7. B. 5. C. 3. D. 2. 1 7
Đáp số: z    i. 3 3
Câu 70: Biết số phức z a bi,a;b  thỏa mãn 1  5iz  3  4iz  1  7 .i Tính 4a  . b A. 1. B. 1. C. 3. D. 2.
Đáp số: z  5  19 .i
Câu 71: Biết số phức z a bi,a;b  thỏa mãn 2  iz  3  4iz  1  2i. Tính 5a  . b A. 7. B. 5. C. 3. D. 2. 7 1 Đáp số: z   i. 20 4 2  i 1  i
Câu 72: Biết số phức z a bi,a;b  thỏa mãn z
z  3  2i. Tính a  . b 1  i 1  i A. 4. B. 5. C. 3. D. 2. 7 5
Đáp số: z    i. 3 3 1  i 2  i
Câu 73: Biết số phức z a bi,a;b  thỏa mãn z
z  3  5i. Tính a  . b 2  i 1  i 2 11 3 21 A. . B. . C. . D. . 7 5 4 11 94 88 Đáp số: z   i. 21 21
Câu 74: Cho số phức z thỏa 2  iz  3 16i  2 z i . Môđun của z bằng A. 5 . B. 13 . C. 13 . D. 5 . Lời giải:
Gọi z x yi với ( , x y  ) .
Khi đó: (2  i)z  3 16i  2(z i)  ( y  3)  (x  2 y 16)i  (2  2 y)i . y  3  0 x  2    
z  2  3i z  13 .
x  2y 16  2  2yy  3 
Chọn đáp án C.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Câu 75: Cho số phức z thỏa (2  i)z  4(z i)  8
 19i . Môđun của z bằng A. 13 . B. 5 . C. 13 . D. 5 . Lời giải:
Gọi z x yi với ( , x y  ) .
Khi đó: (2  i)z  4(z i)  8  19i  2
x y  (x  6y  4)i  8  19i .  2
x y  8  x  3    
z  3 2i z  13 .
x  6y 15 y  2
Chọn đáp án C.
Câu 76: Cho số phức z a bia, b  thoả mãn z  2  i z . Tính S  4a b .
A. S  4.
B. S  2.
C. S  2.
D. S  4. Lời giải:  2 2
a   a b
Ta có z  2  i z  a  2  b   2 2 2 (1)
1 i a b   b  1  0 (2) a  2  0 3 
Từ (2) ta có: b  1 . Thay vào (1): 2
a  1  a  2    a 2 2
a  1  (a  2) 4
Vậy S  4a b  4.
Chọn đáp án D.
Câu 77: Cho số phức z a bi (a,b  ) thỏa mãn z  1  3i z i  0 . Tính S a  3 . b 7 7
A. S  .
B. S  5.
C. S  5.
D. S   . 3 3 Lời giải: 2 2
z   i z i   a bi   i a b i   a    2 2 1 3 0 1 3 0 1
b  3  a b i  0  a  1  a  1  a  1  a  1  0 a  1          b  3
 b  3   4 2 2 2
b  3  a b  0
 b  1  b  3   b   b  1   b  32 2 4  3 b    3 4 
S a  3b  1   3.  5  3
Chọn đáp án B.
Câu 78: Cho số phức z thỏa mãn z  3  5 và z  2i z  2  2i . Tính z . A. z  17 . B. z  17 . C. z  10 . D. z  10 . Lời giải:
Gọi z a bi(a,b  ) . Ta có: z
  a bi    a  2 2 3 5 3 5 3  b  25(1). Ta lại có:
z  2i z  2  2i a bi  2i a bi  2  2i 2 2 2 2
a  (b  2)  (a  2)  (b  2) a  2  a 2 2
a  (a  2)   a  1 
a  2  a
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia Thế vào (1) 2 2
 16  b  25  b  9 . Vậy 2 2 2
z a b  1  9  10 .
Chọn đáp án C.
Câu 79: Có bao nhiêu số phức z thỏa mãn z  2 và  z  2i z  2 là số thuần ảo? A. 1. B. 0 . C. 2 . D. 4 . Lời giải:
Đặt z x yi x , y   . Theo đề ta có: +) 2 2 2 2 z  2  x y
2  x y  2 .   1 2
+)  z  2iz  2  zz  2z  2zi  4i z  2x yi  2x yii  4i   2 2
 2x  2yi  2xi  2y  4i  2  2x  2y  2x  2y  4i .
Vì  z  2i z  2 là số thuần ảo nên 2  2x  2y  0  y x 1.
Thay y x 1 vào   1 , ta được:  1 3 x
x   x  2 2 2 2 1
 2  2x  2x 1  0   .  1 3 x   2 1 3 1   3 1 3 1   3
Vậy có hai số phức thỏa để là z   i và z   i . 2 2 2 2
Chọn đáp án C. Dạng 3:
Biểu diễn số phức
Câu 80: Kí hiệu điểm M là điểm biểu diễn số phức, M là điểm biểu diễn số phức z. Khẳng định nào sau đây đúng?
A. M, M đối xứng nhau qua trục tung.
B. M, M đối xứng nhau qua trục hoành.
C. M, M đối xứng nhau qua gốc tọa độ.
D. M, M đối xứng nhau qua y  . x Lời giải:
Số phức z a bi; z a bi;a;b  có điểm biểu diễn lần lượt là M a;b , Ma; b.
Dễ thấy, M, M đối xứng nhau qua trục hoành.
Chọn đáp án B.
Câu 81: Cho số phức z  1  3i. Điểm biểu diễn số phức z trên mặt phẳng tọa độ là A. M 1; 3  .
B. N 1; 3. C. P 1  ; 3  .
D. Q 1; 3.
Câu 82: Trên mặt phẳng tọa độ, điểm biểu diễn số phức 3  2i có tọa độ là A. 2;3 . B. 2;3 . C. 3; 2 . D. 3; 2 .
Câu 83: Cho số phức z  1  3i. Điểm biểu diễn số phức z trên mặt phẳng tọa độ là A. M 1; 3  .
B. N 1; 3. C. P 1  ; 3  .
D. Q 1; 3. Lời giải:
Ta có: z  1  3i.
Chọn đáp án B.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Câu 84: Cho hai số phức z  2  i, z  1 i . Trên mặt phẳng tọa độ Oxy, điểm biểu diễn số phức 1 2
2z z có tọa độ là: 1 2 A. 5;   1 . B. 1;5 . C. 5;0 . D. 0;5 . Lời giải:
Ta có 2z z  5  i . Nên điểm biểu diễn là 5;   1 . 1 2
Chọn đáp án A.
Câu 85: Trên mặt phẳng tọa độ, điểm biểu diễn số phức z    i2 1 2
là điểm nào dưới đây?
A. P 3; 4
B. Q 5; 4 . C. N 4; 3   .
D. M 5; 4 . Lời giải:
Ta có z    i2 2 1 2
1 4i  4i  3
  4i  điểm biểu diễn số phức z    i2 1 2
là điểm P 3; 4 .
Chọn đáp án A.
Câu 86: Cho hai số phức z  1  i và z  2  i . Trên mặt phẳng Oxy , điểm biểu diễn số phức z  2z 1 2 1 2 có tọa độ là A. 2;5 . B. 3;5 . C. 5;2 . D. 5;3 . Lời giải:
Ta có z  2z  (1  i)  2(2  i)  5  3i . 1 2
Vậy điểm biểu diễn số phức z  2z có tọa độ 5;3. 1 2
Chọn đáp án D.
Câu 87: Cho số phức z  1  2i . Điểm nào dưới đây là điểm biểu diễn của số phức w iz trên mặt phẳng tọa độ?
A. Q(1; 2)
B. N (2;1)
C. M (1; 2) D. P(2;1) Lời giải:
w iz i 1 2i  2  i . Điểm biểu diễn số phức w là N   2;1 .
Chọn đáp án B.
Câu 88: Điểm A1; 2 là biểu diễn trên mặt phẳng tọa độ số phức z nào trong các số phức sau?
A. z  1  2i.
B. z  1  2i. C. z  1   2i. D. z  1   2i.
Câu 89: Trên mặt phẳng tọa độ, điểm M (2;3) là điểm biểu diễn số phức nào dưới đây?
A. z  2  3i . B. z  2   3i . C. z  2   3i .
D. z  2  3i . 3 4 1 2
Câu 90: Số phức nào dưới đây có điểm biểu diễn trên mặt phẳng tọa độ là điểm M như hình bên? A. z  2  . i
B. z  1 2 . i C. z  2   .i
D. z  1 2 . i 4 2 3 1
Câu 91: Điểm M trong hình vẽ bên dưới là điểm biểu diễn của số phức nào trong 4 số phức được cho
ở các phương án A, B, C, D?
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia y M 2 x -3 O
A. z  3  2i.
B. z  2  3i.
C. z  3  2i.
D. z  3  2i.
Câu 92: Điểm biểu diễn số phức z  3  2i là điểm nào trong 4 điểm M, N, P, Q trong hình vẽ bên dưới? y M 2 N -3 x 3 O Q -2 P A. M. B. N. C. P. D. Q.
Câu 93: Cho hai số phức z  1  2i và z  3  2i. Gọi A, B là hai điểm lần lượt biểu diễn số phức 1 2
z , z trên mặt phẳng tọa độ. Tính độ dài . AB 1 2 A. 10. B. 5. C. 2 5. D. 3. Lời giải: A1;2 Ta có:         B  
AB 2; 4 AB 4 16 2 5. 3; 2
Chọn đáp án C.
Câu 94: Cho số phức z  3  2i. Gọi A, B là hai điểm lần lượt biểu diễn số phức z, z trên mặt phẳng
tọa độ. Tính diện tích tam giác OAB ( O là gốc tọa độ). A. 6. B. 5. C. 2 5. D. 3. Lời giải: y 2 A 3 x O H -2 B
Ta có: z  3  2i. 1
Suy ra: A3; 2 ,B3; 2
   AB  4. Vậy Sd O AB AB OAB  ; . 6. 2
Chọn đáp án A.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Câu 95: Biết số phức z thỏa mãn z  1  i z  3  3i . Tập hợp điểm biểu diễn số phức z trên mặt
phẳng tọa độ là đường thẳng có phương trình
A. x  2y  4  0.
B. x  2y  4  0.
C. x  2y  4  0.
D. x y  4  0. Lời giải:
Gọi z x yi;x; y  . Điểm M x; y biểu diễn số phức z trên mặt phẳng tọa độ.
Ta có: z  1  i z  3  3i x yi  1  i x yi  3  3i
 x  1  y 1i  x  3  y  3i
 x  2  y  2  x  2  y  2 1 1 3 3 2 2 2 2
x  2x  1 y  2y  1  x  6x  9  y  6y  9  x  2y  4  0.
Vậy tập hợp điểm biểu diễn số phức z trên mặt phẳng tọa độ là đường thẳng d : x  2y  4  0.
Chọn đáp án A.
Câu 96: Biết số phức z thỏa mãn z  1  3i z  3  5i . Tập hợp điểm biểu diễn số phức z trên mặt
phẳng tọa độ là đường thẳng có phương trình
A. x  2y  4  0.
B. x  4y  6  0.
C. x  2y  6  0.
D. x y  4  0. Lời giải:
Gọi z x yi;x; y  . Điểm M x; y biểu diễn số phức z trên mặt phẳng tọa độ.
Ta có: z  1  3i z  3  5i x yi  1  3i x yi  3  5i
 x  1  y  3i  x  3  y  5i
 x  2  y  2  x  2  y  2 1 3 3 5 2 2 2 2
x  2x  1 y  6y  9  x  6x  9  y  10y  25  x  4y  6  0.
Vậy tập hợp điểm biểu diễn số phức z trên mặt phẳng tọa độ là đường thẳng d : x  4y  6  0.
Chọn đáp án B.
Câu 97: Biết số phức z thỏa mãn z  2i z  2  4i . Tập hợp điểm biểu diễn số phức z trên mặt
phẳng tọa độ là đường thẳng có phương trình
A. x  2y  4  0.
B. x  4y  6  0.
C. x  2y  6  0.
D. x y  4  0. Lời giải:
Gọi z x yi;x; y  . Điểm M x; y biểu diễn số phức z trên mặt phẳng tọa độ.
Ta có: z  2i z  2  4i x yi  2i x yi  2  4i
x  y  2i  x  2  y  4i
x  y  2  x  2  y  2 2 2 2 4 2 2 2 2
x y  4y  4  x  4x  4  y  8y  16  x y  4  0.
Vậy tập hợp điểm biểu diễn số phức z trên mặt phẳng tọa độ là đường thẳng d : x y  4  0.
Chọn đáp án D.
Câu 98: Biết số phức z thỏa mãn z  1  i  3. Tập hợp điểm biểu diễn số phức z trên mặt phẳng tọa
độ là đường tròn có phương trình 2 2 2 2
A. x  1  y  1  9.
B. x  1  y  1  9.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia 2 2 2 2
C. x  1  y  1  9.
D. x  1  y  1  9. Lời giải:
Gọi z x yi;x; y  . Điểm M x; y biểu diễn số phức z trên mặt phẳng tọa độ.
Ta có: z  1  i  3  x yi  1  i  3  x  1  y  1i  3
 x  2  y  2   x  2  y  2 1 1 3 1 1  9.
Vậy tập hợp điểm biểu diễn số phức z trên mặt phẳng tọa độ là đường tròn
C x  2 y  2 : 1 1  9.
Chọn đáp án C.
Câu 99: Biết số phức z thỏa mãn z  3  4i  4. Biết tập hợp điểm biểu diễn số phức z trên mặt phẳng
tọa độ là đường tròn C. Tìm tâm I và tính bán kính R của đường tròn C. A. I  3;
 4,R  16. B. I  3;
 4,R  4. C. I 3; 4
 ,R  4. D. I 3; 4
 ,R  16. Lời giải:
Gọi z x yi;x; y  . Điểm M x; y biểu diễn số phức z trên mặt phẳng tọa độ.
Ta có: z  3  4i  4  x yi  3  4i  4  x  3  y  4i  4
 x  2  y  2   x  2  y  2 3 4 4 3 4  16.
Vậy tập hợp điểm biểu diễn số phức z trên mặt phẳng tọa độ là đường tròn C có tâm
I 3; 4 , bán kính R  4.
Chọn đáp án B.
Câu 100: Biết số phức z thỏa mãn z  1  i  2. Biết tập hợp điểm biểu diễn số phức z trên mặt phẳng
tọa độ là đường tròn C. Tìm tâm I và tính bán kính R của đường tròn C. A. I  1
 ;1,R  2. B. I 1; 1
 ,R  4. C. I 1; 1
 ,R  2. D. I  1
 ;1,R  4. Lời giải:
Gọi z x yi;x; y  . Điểm M x; y biểu diễn số phức z trên mặt phẳng tọa độ.
Ta có: z  3  4i  4  x yi  3  4i  4  x  3  y  4i  4
 x  2  y  2   x  2  y  2 3 4 4 3 4  16.
Vậy tập hợp điểm biểu diễn số phức z trên mặt phẳng tọa độ là đường tròn C có tâm
I 3; 4 , bán kính R  4.
Chọn đáp án C.
Câu 101: Xét các số phức z thỏa mãn  z  2i z  2 là số thuần ảo. Biết rằng tập hợp tất cả các
điểm biểu diễn của z là một đường tròn, tâm của đường tròn đó có tọa độ là A. 1;  1  . B. 1  ;1 . C. 1;  1 . D. 1;   1 . Lời giải:
+ Gọi z x yi , x, y  .
+ Ta có  z  2iz  2  x yi  2ix yi  2  x   y  2i  x  2  yi    
xx  2  yy  2  x  2 y  2 xyi  .
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia +  2 2
z  2i z  2 là số thuần ảo  xx  2  y y  2  0   x   1   y   1  2 .
+ Vậy tập hợp các điểm biểu diễn của số phức z là đường tròn tâm I  1  ;  1 .
Chọn đáp án D.
Câu 102: Xét các số phức z thỏa mãn  z  2i z  2 là số thuần ảo. Trên mặt phẳng tọa độ, tập hợp
tất cả các điểm biểu diễn các số phức z là một đường tròn có bán kính bằng A. 2 2. B. 2. C. 2. D. 4. Lời giải:
Gọi z a bi , a, b
Ta có:  z i z    a bi ia bi   2 2 2 2 2
2  a  2a b  2b  2 a b  2i 2 2
Vì  z  2i z  2 là số thuần ảo nên ta có 2 2
a  2a b  2b  0  a   1  b   1  2 .
Trên mặt phẳng tọa độ, tập hợp tất cả các điểm biểu diễn các số phức z là một đường tròn có bán kính bằng 2 .
Chọn đáp án B.
Câu 103: Cho các số phức z thỏa mãn z  4 . Biết rằng tập hợp các điểm biểu diễn các số
phức w  (3  4i)z i là một đường tròn. Tính bán kính r của đường tròn đó. A. r  4 . B. r  5 . C. r  20 .
D. r  22 . Lời giải:
Giả sử z a bi ; w x yi ;a,b, x, y  
Theo đề w  3  4iz i x yi  3  4ia bi  i          
a b   b a   x 3a 4b x 3a 4b x yi 3 4 3 4 1 i     Ta có
y  3b  4a 1
y 1  3b  4a
x   y  2   a b2   a b2 2 2 2  a b   2 2 1 3 4 4 3 25 25 25 a b  Mà 2 2
z  4  a b  16 . Vậy x   y  2 2 1  25.16  400
Bán kính đường tròn là r  400  20 .
Chọn đáp án C.
B. PHƯƠNG TRÌNH BẬC HAI VỚI HỆ SỐ THỰC Câu 104: Phương trình 2
ax bx c  0 a,b,c   có hai nghiệm phức phân biệt khi và chỉ khi a  0 a  0 a  0 A. 2
b  4ac  0 . B. . C. . D. . 2
b  4ac  0 2
b  4ac  0 2
b  4ac  0
Câu 105: Trên tập số phức, phương trình nào sau đây có nghiệm thực? A. 2 x  1  0. B. 2 x  1  0. C. 2 x  4  0. D. 2
2x  1  0. Lời giải: x  1  Ta có: 2 x  1  0   . x   1
Chọn đáp án B.
Câu 106: Kí hiệu z , z là hai nghiệm phức của phương trình 2
z  3 . Giá trị của z z bằng 1 2 1 2 A. 6 . B. 2 3 . C. 3 . D. 3. Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia z  i 3 Ta có: 2 z  3   
z z  2 3. 1 2 z   i 3
Chọn đáp án B.
Câu 107: Trên tập số phức, tập nghiệm của phương trình 2
z  2z  2  0 là A.  1   i;1  i . B.  1   i;1   i . C.  1   i;1  i . D. i; 1    i . Lời giải: z  1   i Ta có: 2
z  2z  2  0   . z  1    i
Chọn đáp án C.
Câu 108: Trên tập số phức, gọi z , z là hai nghiệm của phương trình 2
z  2z  2  0. Tính z z . 1 2 1 2 A. 2 2. B. 2. C. 4 2 D. 4. Lời giải: z  1 i Ta có: 2 1
z  2z  2  0  
. Vậy z z  2 2. z  1   i 1 2 2
Chọn đáp án A.
Câu 109: Phương trình nào dưới đây nhận hai số phức 1  2i và 1  2i là nghiệm? A. 2
z  2z  3  0. B. 2
z  2z  3  0. C. 2
z  2z  3  0. D. 2
z  2z  3  0. 2 2
Câu 110: Trên tập số phức, gọi z , z là hai nghiệm của phương trình 2
z  4z  2  0. Tính zz . 1 2 1 2 A. 2 2. B. 2. C. 8. D. 4. Lời giải: z  1 3i 2 2 Ta có: 2 1
z  2z  4  0   . Vậy zz  8.  1 2 z  1   3i 2
Chọn đáp án C.
Câu 111: Gọi z , z là hai nghiệm phức của phương trình 2
z  4z  5  0 . Giá trị của 2 2 z z bằng 1 2 1 2 A. 6 . B. 8 . C. 16 . D. 26 . Lời giải:
z z   z z 2 2 2
 2z z 16 10  6 . 1 2 1 2 1 2
Chọn đáp án A. 2 2
Câu 112: Gọi z , z z z   z z 1
2 là 2 nghiệm phức của phương trình 2 6 14 0 . Giá trị của 1 2 bằng: A. 36. B. 8. C. 28 . D. 18. Lời giải: 2  6  14
Ta có: z z   z z 2 2 2  2z z   2  8 . 1 2 1 2 1 2    1  1
Chọn đáp án B.
Câu 113: Kí hiệu z , z là hai nghiệm của phương trình 2
z  4  0 . Gọi M , N lần lượt là điểm biểu 1 2
diển của z , z trên mặt phẳng tọa độ. Tính T OM ON với O là gốc tọa độ. 1 2 A. T  2 . B. T  2 . C. T  8 . D. T  4 . Lời giải:
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia z  2  i Ta có: 2 1 z  4  0   Z  2i  2 Suy ra M 0; 2
 ; N 0;2 nên T OM ON   2 2 2  2  4 .
Chọn đáp án D. 1 1
Câu 114: Ký hiệu z , z là hai nghiệm phức của phương trình 2
z z  6  0 Tính   . 1 2 P z z 1 2 1 1 1 A. P  . B. P  . C. P   . D. P  6 . 6 12 6 Lời giải:  1 23 z   i 2 2 1 1 1 Ta có 2
z z  6  0   suy ra    .  P 1 23 z z 6 z   i 1 2  2 2
Chọn đáp án A.
Câu 115: Gọi z là nghiệm phức có phần ảo âm của phương trình 2 z 2z 5 0 . Môđun của số 0 phức z i bằng 0 A. 2. B. 2 . C. 10 . D. 10 . Lời giải:
Xét phương trình: 2
z  2z  5  0 có   4  0
Phương trình có hai nghiệm phức z  1  2i và z  1  2i
z là nghiệm phức có phần ảo âm nên z  1  2i nên z i  1  i z i  2 . 0 0 0 0
Chọn đáp án B.
Câu 116: Kí hiệu z là nghiệm phức có phần ảo dương của phương trình 2
4z  16z  17  0 . Trên mặt 0
phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn của số phức w iz ? 0  1   1   1   1 
A. M  ;2 . B. M   ; 2  . C. M   ;1 .
D. M  ;1 . 1  2  2  2  3  4  4  4  Lời giải: Xét phương trình 2
4z  16z  17  0 có        2 64 4.17 4 2i . 8  2i 1 8  2i 1
Phương trình có hai nghiệm z
 2  i, z   2  i . 1 2 4 2 4 2 1
Do z là nghiệm phức có phần ảo dương nên z  2  i . 0 0 2 1  1 
Ta có w iz    2i . Vậy điểm biểu diễn w iz là M   ; 2 . 0  2 0 2  2 
Chọn đáp án B.
Câu 117: Trên tập số phức, cho phương trình 2
z  2z m  0,m là tham số. Tìm tập hợp tất cả các giá trị
của tham số m để phương trình đã cho không có nghiệm thực. A. .
B. 1; . C. 1;   . D. .  Lời giải:
Phương trình đã cho không có nghiệm thực    0  1  m  0  m  1.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Chọn đáp án C.
Câu 118: Gọi z là nghiệm phức có phần ảo dương của phương trình 2
z  6z  34  0 . Tính z  2  i . 0 0 A. 17 . B. 17 . C. 2 17 . D. 37 . Lời giải:
z    i 2
z  6z  34  3 5 0   . Do đó z  3
  5i z  2  i  1
  4i  17 . z  3    5i 0 0
Chọn đáp án A. 1 1
Câu 119: Ký hiệu z , z là hai nghiệm phức của phương trình 2
z z  6  0 Tính P   . 1 2 z z 1 2 1 1 1
A. P . B. P .
C. P   .
D. P  6 . 6 12 6 Lời giải:  1 23 z   i 1 1 1 Ta có 2      2 2 z z 6 0 suy ra P    .  1 23 z z 6 z   i 1 2  2 2
Chọn đáp án A.
Câu 120: Gọi z là nghiệm phức có phần ảo dương của phương trình 2
z  6z 13  0 . Trên mặt 0
phẳng tọa độ, điểm biểu diễn 1 z là: 0 A. M  2  ;2.
B. Q 4; 2 .
C. N 4; 2 . D. P  2  ; 2   . Lời giải: Xét phương trình 2
z  6z 13  0 . Ta có        2 9 13 4 2i . z  3 2i
Suy ra phương trình (1) có 2 nghiệm phức phân biệt là  . z  3 2i
z là nghiệm phức có phần ảo dương của phương trình 2
z  6z 13  0 nên z  3  2i . 0 o
1 z  1 3  2i  2   2i . 0  
Vậy điểm biểu diễn số phức 1 z là điểm P  2  ; 2   . 0
Chọn đáp án D.
Câu 121: Gọi z là nghiệm phức có phần ảo âm của phương trình 2
z  2z  5  0 . Tìm tọa độ điểm biểu 1 7  4i diễn số phức trên mặt phẳng phức? z1
A. P 3; 2 .
B. N 1;  2 . C. Q3; 2   .
D. M 1; 2 . Lời giải:
z  1 2i Ta có 2
z  2z  5  0   . z  1   2i 7  4i 7  4i
7 4i1 2i
Theo yêu cầu bài toán chọn z  1  2i . Khi đó    3  2 .i 1 2 2 z 1  2i 1  2 1
Vậy điểm biểu diễn của số phức là P 3; 2 .
Chọn đáp án A.
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Câu 122: Trên tập số phức, số nghiệm thực của phương trình 4 2
z  3z  4  0 là A. 0. B. 1. C. 4. D. 2. Lời giải: 2 z  1
  z  i Ta có: 4 2
z  3z  4  0   . 2
z  4  z  2 
Chọn đáp án D.
Câu 123: Trên tập số phức, tập nghiệm của phương trình 4 2
z  2z  3  0 là A.  3.
B. i; 3
C. i; 3.
D. i;i 3. Lời giải: 2 z  1
  z  i Ta có: 4 2
z  2z  3  0   . 2
z  3  z   3
Chọn đáp án C.
Câu 124: Trên tập số phức, tập nghiệm của phương trình 4 2
z  4z  3  0 là A. 1;   3 . B. . 
C. i;i 3.
D. i;i 3. Lời giải: 2 z  1
  z  i Ta có: 4 2
z  4z  3  0   . 2 z  3
  z  i 3
Chọn đáp án D.
Câu 125: Trên tập số phức, gọi z , z , z , z là bốn nghiệm của phương trình 4 2
z  2z  3  0. Tính 1 2 3 4
z z z z . 1 2 3 4 A. 2  2 3. B. 2 3. C. 4  2 3. D. 4  4 3. Lời giải: 2
z  1  z  1  Ta có: 4 2
z  2z  3  0  
. Suy ra: z z z z  2  2 3. 2  1 2 3 4 z  3   z   3
Chọn đáp án A.
Câu 126: Kí hiệu z , z , z và z là bốn nghiệm phức của phương trình 4 2
z z 12  0 . Tính 1 2 3 4
tổngT z z z z . 1 2 3 4
A. T  4. B. T  2 3.
C. T  4  2 3.
D. T  2  2 3. Lời giải: 2 z  3  z  i 3 4 2
z z 12  0     2 z  4 z  2 
T z z z z i 3  i 3  2   2  2 3  4. 1 2 3 4
Chọn đáp án C.
Câu 127: Trên tập số phức, tổng môđun các nghiệm của phương trình  2 z   2
1 z  4  0 là A. 6. B. 1. C. 4. D. 2. Lời giải: z  1
  z  i Ta có: z   1 z  4 2 2 2  0  
i  i  2   2  6. 2
z  4  z  2 
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Chọn đáp án A.
Câu 128: Trên tập số phức, gọi z , z là hai nghiệm của phương trình 2
z  2z  2  0. Biết A, B lần lượt là 1 2
hai điểm biểu diễn z , z trên mặt phẳng. Tính độ dài đoạn thẳng . AB 1 2 A. 2 2. B. 2. C. 1. D. 4. Lời giải:
z  1 i A 1;1 2 1  
Ta có: z  2z  2  0   .
z  1 i B 1; 1   2   Ta có: AB  0; 2    AB  2.
Chọn đáp án B.
Câu 129: Trên tập số phức, tìm giá trị tham số thực m để phương trình 2
z mz m  4  0 có một
nghiệm là z  1  i.
A. m  2.
B. m  1.
C. m  3.
D. m  4. Lời giải: 2 4   2i
Ta có: 1  i  m1  i  m  4  0  2i  2  im  4  0  m   2  . 2  i
Chọn đáp án A.
Câu 130: Trên tập số phức, gọi z , z là hai nghiệm của phương trình 2
z  2z  2  0. Biết A, B lần lượt là 1 2
hai điểm biểu diễn z , z trên mặt phẳng. Tọa độ trung điểm của đoạn thẳng AB là 1 2 A. 1;0
B. 1;0. C. 0;1. D. 0; 1  . Lời giải: z  1
  i A 1  ;1 2 1  
Ta có: z  2z  2  0   . z  1
  i B 1  ; 1   2  
I là trung điểm AB I  1  ;0.
Chọn đáp án B.
Câu 131: Trên tập số phức, gọi z , z là hai nghiệm của phương trình 2
z  2z  5  0. Biết A, B lần lượt là 1 2
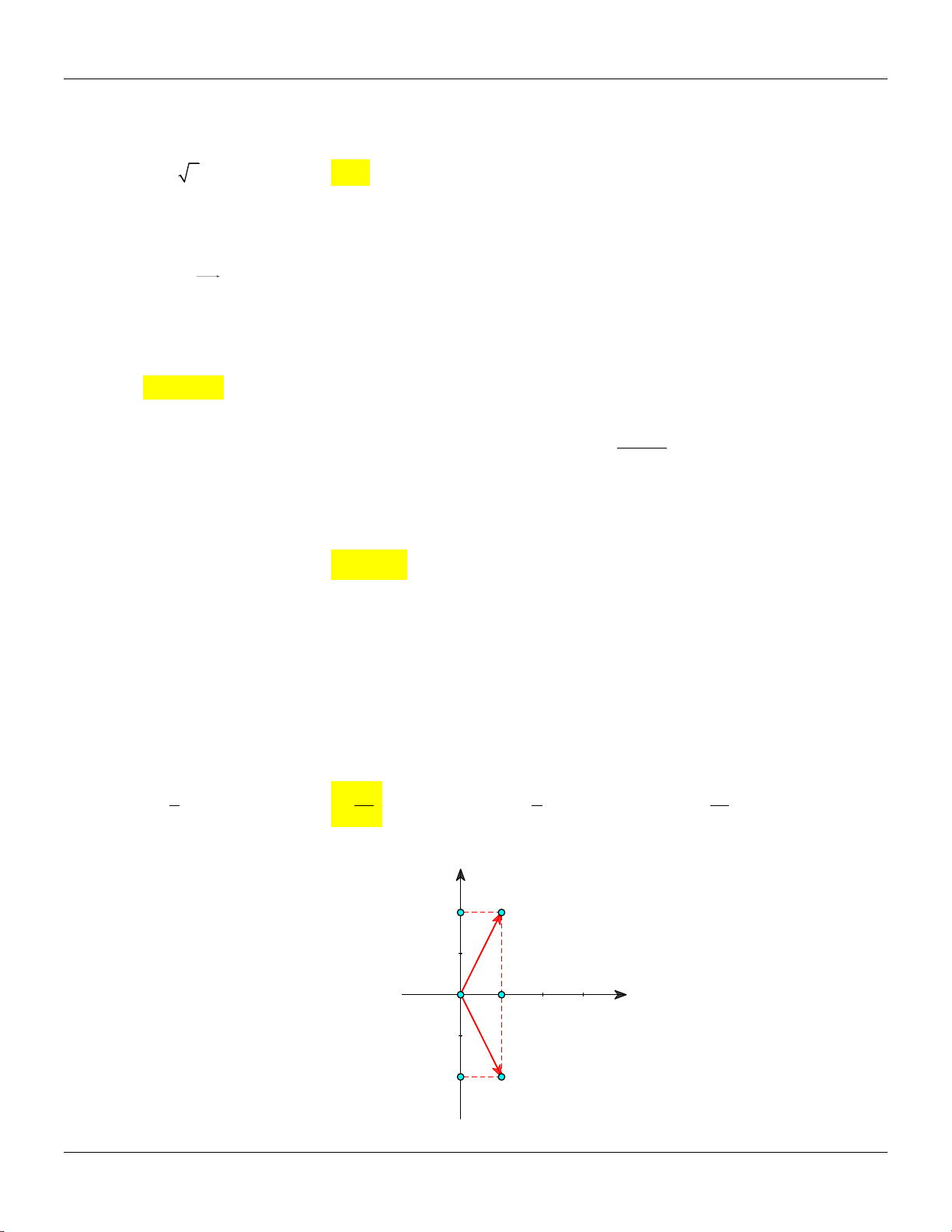
hai điểm biểu diễn z , z trên mặt phẳng. Tính cos AOB, (với O là gốc tọa độ). 1 2 3 3  1 1  A. B. . C. . D. . 5 5 5 5 Lời giải: y A 2 x 1 O -2 B
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
z  1 2i A 1;2 2 1  
Ta có: z  2z  5  0   .
z  1 2i B 1; 2   2   OA    1;2 O . A OB 3  Ta có:     OB     AOB 1; 2   cos . O . A OB 5
Chọn đáp án B.
Câu 132: Trên tập số phức, gọi z , z là hai nghiệm của phương trình 2
z  4z  8  0. Biết A, B lần lượt là 1 2
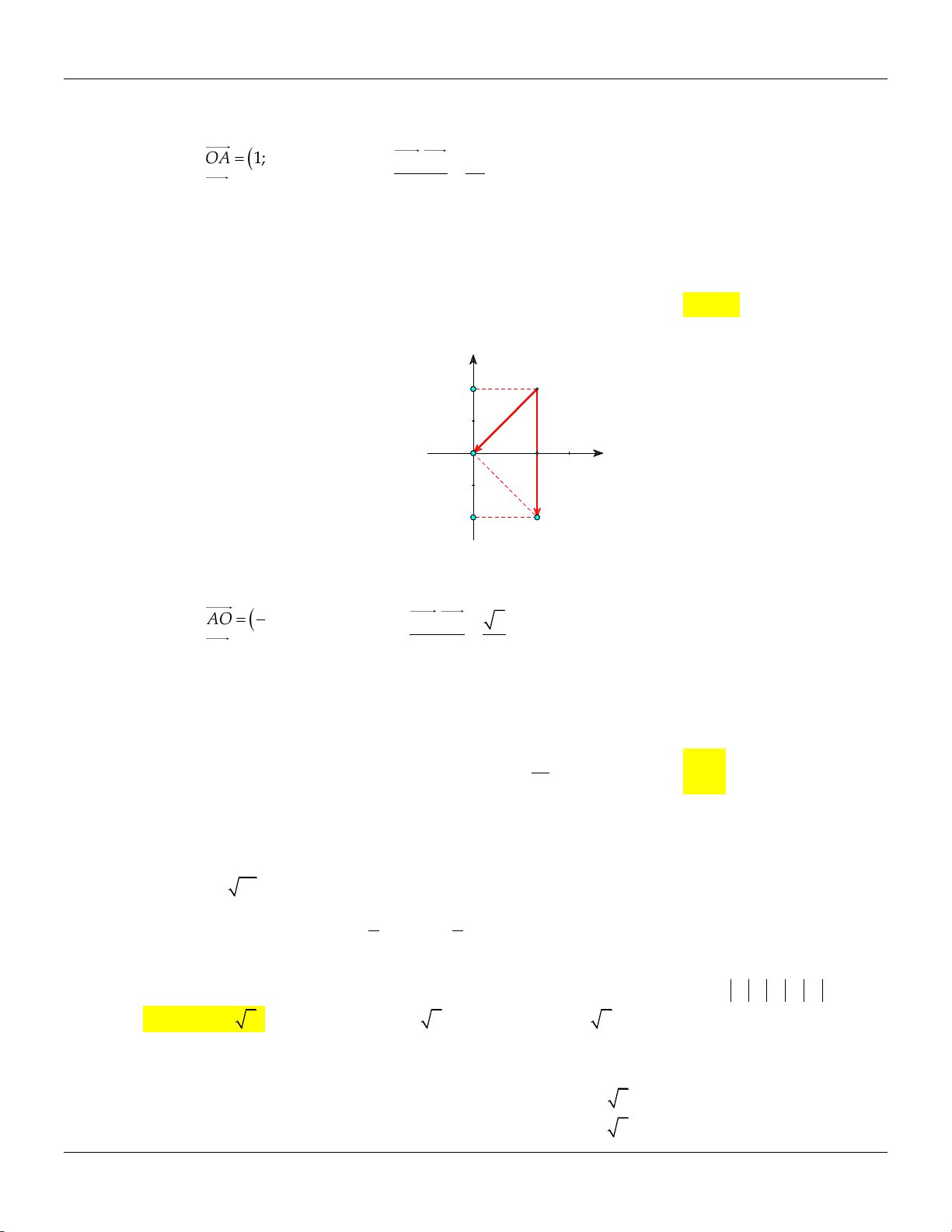
hai điểm biểu diễn z , z trên mặt phẳng. Tính OAB, (với O là gốc tọa độ). 1 2 A. o 30 B. o 60 C. o 135 D. o 45 . Lời giải: y A 2 x O -2 B
z  2  2i A 2;2 2 1  
Ta có: z  4z  8  0   .
z  2  2i B 2; 2   2   AO  2; 2    . AO AB 2 Ta có: o       AB    AOB AOB 0; 4   cos 45 . . AO AB 2
Chọn đáp án D.
Câu 133: Gọi z , z là hai nghiệm của phương trình 2
z  4z  13  0 và A , B lần lượt là hai điểm biểu 1 2
diễn cho hai số phức z , z trong mặt phẳng tọa độ Oxy . Diện tích tam giác OAB bằng 1 2 13 A. 13 . B. 12 . C. . D. 6 . 2 Lời giải:    2 2 z 2 3i Ta có 2
z  4z  13  0  z  2 2
 9  z  2  3i  
.  A2; 3 , B2;  3 . z  2   3i
OA OB  13  O
AB cân tại O . Gọi H là trung điểm của AB H 2;0 và OH AB , 1 1
OH  2 , AB  6 . Vậy S
OH.AB  .2.6  6 . OAB 2 2
Chọn đáp án D.
Câu 134: Gọi z , z , z là ba nghiệm của phương trình 3 2
z z  5z  7  0 . Tính M z z z . 1 2 3 1 2 3
A. M  1  2 7 .
B. M  1  7 2 .
C. M  2  7 .
D. M  3 . Lời giải: z  1  Ta có: 3 2
z z  5z  7  0  z  1 2
z  2z  7   0  z  1   i 6 . z  1   i 6 
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115
Bài giảng PHƯƠNG TRÌNH MẶT PHẲNG Ôn thi Tốt nghiệp THPT Quốc gia
Suy ra: M z z z  1  1   i 6  1
  i 6  1 2 7 . 1 2 3
Chọn đáp án A.
Câu 135: Gọi A , B , C là các điểm biểu diễn các số phức z , z , z là nghiệm của phương trình 1 2 3 3 2
z  6z  12z  7  0 . Tính diện tích S của tam giác ABC . 3 3 3 3
A. S  3 3 . B. S .
C. S  1 . D. S . 2 4 Lời giải: 5 3
Sử dụng MTCT ta có phương trình 3 2
z  6z  12z  7  0 có 3 nghiệm z  1 ; z   i , 1 2 2 2 5 3  5 3   5 3  z  
i . Suy ra: A1;0 , B ;  , C ;  . 3 2 2  2 2      2 2   9 3 9 3 AB AB
  3 ; AC AC
  3 ; BC BC  3 . 4 4 4 4  2 3 3  3 3 ABC
đều cạnh 3 . Vậy S   . ABC 4 4
Chọn đáp án D.
Câu 136: Trên tập hợp các số phức, xét phương trình 2
z  m   2 2
1 z m  0 . Có bao nhiêu giá trị
của m để phương trình đó có nghiệm z thõa mãn z  8? o o A. 4 . B. 3 . C. 2 . D. 1. Lời giải:
Ta có   8m  4 . 1
Trường hợp 1:   0  m   suy ra phương trình có 2 nghiệm thực  z là nghiệm 2 o thực.  m  4 z  8 2
m 16m  48  0   T / M z  8 o
thay vào phương trình   m 12 . oz  8   o  2
m 16m  80  0(VN) 1
Trường hợp 2:   0  m   suy ra phương trình sẽ có 2 nghiệm phức, vì z là nghiệm 2 o
nên suy ra z cũng là nghiệm o   2 m 8 2 z  8  z
 64  z .z  64  m  64  . o o o o  m  8 
Kết hợp điều kiện nên ta nhận m  8 .
Vậy có 3 giá trị m thỏa mãn.
Chọn đáp án B.
_____________________HẾT_____________________
Huế, 08h30’ Ngày 18 tháng 02 năm 2023
Lớp Toán thầy Lê Bá Bảo TP Huế 0935785115