Chuyên đề cực trị số phức Toán 12

Chuyên đề cực trị số phức Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

15 8 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 4: Số phức

Môn: Toán 12

Thông tin:

60 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
toanthaycu.com
CHUYÊN ĐỀ CỰC TRỊ SỐ PHỨC
(TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH GIỎI MỨC 9-10 ĐIỂM)
A. MỘT SỐ TÍNH CHẤT CẦN NHỚ.
1. Môđun của số phức:Số phức
z a bi
được biểu diễn bởi điểm M(a; b) trên mặt phẳng Oxy. Độ
dài của véctơ
OM
được gọi là môđun của số phức z. Kí hiệu
2 2
z = a + bi = a + b
 Tính chất
2 2
z a b zz OM
z z z z
. ' . '
z z z z
, ' 0
' '
z z
z
z z
' ' '
z z z z z z
. ,kz k z k
 Chú ý:
2
2
2 2 2 2 2 2 2 2 2 2
2 ( ) 4 .
z a b abi a b a b a b z z z z
.
Lưu ý:
1 2 1 2
z z z z
dấu bằng xảy ra
1 2
0
z kz k
1 2 1 2
z z z z
dấu bằng xảy ra
1 2
0
z kz k
.
1 2 1 2
z z z z
dấu bằng xảy ra
1 2
0
z kz k
1 2 1 2
z z z z
dấu bằng xảy ra
1 2
0
z kz k
2 2 2 2
1 2 1 2 1 2
2
z z z z z z
2
2
z z z z
z
2.Một số quỹ tích nên nhớ
Biểu thức liên hệ
,
x y
Quỹ tích điểm M
ax 0
by c
(1)
z a bi z c di
(2)
(1)Đường thẳng
:ax 0
by c
(2) Đường trung trực đoạn AB với
, , ,
A a b B c d
2 2
2
x a y b R
hoặc
z a bi R
Đường tròn tâm
;
I a b
, bán kính
R
2 2
2
x a y b R
hoặc
z a bi R
Hình tròn tâm
;
I a b
, bán kính
R
2 2
2 2
r x a y b R
hoặc
r z a bi R
Hình vành khăn giới hạn bởi hai đường tròn
đồng tâm
;
I a b
, bán kính lần lượt là
,
r R
2
2
0
y ax bx c
c
x ay by c
Parabol
2 2
2 2
1 1
x a y c
b d
hoặc
1 1 2 2
2
z a b i z a b i a
1
Elip
2
Elip nếu
1 1 2 2
2 , , , ,
a AB A a b B a b
Đoạn AB nếu
2
a AB
Trang 2
2 2
2 2
1
x a y c
b d
Hypebol
B. MỘT SỐ DẠNG TOÁN THƯỜNG GẶP
Dạng 1: Quỹ tích điểm biểu diễn số phức là đường thẳng.
TQ1: Cho số phức
z
thỏa mãn
z a bi z
, tìm
Min
z
. Khi đó ta có
 Quỹ tích điểm
;
M x y
biểu diễn số phức
z
là đường trung trực đoạn
OA
với
;
A a b
2 2
0
1 1
2 2
2 2
Min
z z a b
a b
z i
TQ2: Cho số phức thỏa mãn điều kiện
.
z a bi z c di
Tìm
min
z
. Ta có
 Quỹ tích điểm
;
M x y
biểu diễn số phức
z
là đường trung trực đoạn
AB
với
; , ;
A a b B c d
2 2 2 2
2 2
,
2
Min
a b c d
z d O AB
a c b d
Lưu ý: Đề bài có thể suy biến bài toán thành 1 số dạng, khi đó ta cần thực hiện biến đổi để đưa về dạng cơ
bản.
Ví dụ 1:
 Cho số phức thỏa mãn điều kiện
.
z a bi z c di
Khi đó ta biến đổi
.
z a bi z c di z a bi z c di
 Cho số phức thỏa mãn điều kiện
.
iz a bi z c di
Khi đó ta biến đổi
.
a bi c di
iz a bi iz c di z z z b ai z d ci
i i
Dạng 2: Quỹ tích điểm biểu diễn số phức là đường tròn.
TQ: Cho số phức
z
thỏa mãn điều kiện
0
0
z a bi R z z R
. Tìm ,
Max Min
z z
. Ta có
 Quỹ tích điểm
;
M x y
biểu diễn số phức
z
là đường tròn tâm
;
I a b
bán kính
R
2 2
0
2 2
0
Max
Min
z OI R a b R z R
z OI R a b R z R
Lưu ý: Đề bài có thể cho ở dạng khác, ta cần thực hiện các phép biến đổi để đưa về dạng cơ bản.
Ví dụ 1: Cho số phức
z
thỏa mãn điều kiện
a bi R
iz a bi R z
i i
(Chia hai vế cho
i
)
z b ai R
Ví dụ 2: Cho số phức
z
thỏa mãn điều kiện
z a bi R z a bi R
(Lấy liên hợp 2 vế)
Ví dụ 3: Cho số phức
z
thỏa mãn điều kiện
2 2
a bi R R
c di z a bi R z
c di c di
c d
Hay viết gọn
1
0 1
0 0
z
R
z z z R z
z z
(Chia cả hai vế cho
0
z
)
Dạng 3: Quỹ tích điểm biểu diễn số phức là Elip.
Toanthaycu.com
Trang 3
TQ1: (Elip chính tắc). Cho số phức
z
thỏa mãn điều kiện
2 ,
z c z c a a c
Khi đó ta có
 Quỹ tích điểm
;
M x y
biểu diễn số phức
z
là Elip:
2 2
2 2 2
1
x y
a a c
2 2
Max
Min
z a
z a c
TQ2: (Elip không chính tắc). Cho số phức
z
thỏa mãn điều kiện
1 2
2
z z z z a
Thỏa mãn
1 2
2
a z z
.
Khi đó ta thực hiện phép biến đổi để đưa Elip về dạng chính tắc
Ta có
Khi đề cho Elip dạng không chính tắc
1 2 1 2
2 , 2
z z z z a z z a
và
1 2
, ,
z z c ci
). Tìm
Max, Min của
0
P z z
.
Đặt
1 2
2 2 2
2
z z c
b a c
Nếu
1 2
0
0
2
z z
z
Max
Min
P a
P b
(dạng chính tắc)
Nếu
1 2
0
0 1 0 2
2
z z
z a
z z k z z
1 2
0
1 2
0
2
2
Max
Min
z z
P z a
z z
P z a
Nếu
1 2
0
0 1 0 2
2
z z
z a
z z k z z
1 2
0
2
Max
z z
P z a
Nếu
0 1 0 2
z z z z
1 2
0
2
Min
z z
P z b
C. BÀI TẬP ÁP DỤNG
Câu 1: Cho số phức
z
thoả mãn
2 3 1
z i
. Tìm giá trị lớn nhất của
1
z i
.
A.
13 3
. B.
13 5
. C.
13 1
. D.
13 6
.
Lời giải
Chọn C
Ta có
2
1 2 3 2 3 . 2 3 2 3 2 3
z i z i z i z i z i
1 2 3 2 3 2 3 1 1 3 2 1(*)
z i z i z i z i i
.
+Đặt
w 1
z i
, khi đó
w 3 2 1
i
.
Trang 4
Tập hợp các điểm biểu diễn số phức
w 1
z i
là đường tròn
;1
I
và
w
là khoảng cách từ
gốc tọa độ đến 1 điểm trên đường tròn. Do đó giá trị lớn nhất của
w
chính là đoạn
OQ
2 2
max
w 1 3 2 1 13
.
Nhận xét: Ở đây ta sử dụng kiến thức sau:
2
1 2 1 2
. , . .
z z z z z z z
Câu 2: (Chuyên Hạ Long 2019) Cho số phức
z
thỏa mãn
6 6 20
z z
. Gọi
M
,
n
lần lượt là
môđun lớn nhất và nhỏ nhất của z. Tính
M n
A.
2
M n
. B.
4
M n
. C.
7
M n
. D.
14
M n
.
Lời giải
Gọi , . Theo giả thiết, ta có
6 6 20
z z
.
6 6 20
x yi x yi
2 2
2 2
6 6 20x y x y
.
Gọi
;
M x y
,
1
6;0
F và
2
6;0
F .
Khi đó
1 2 1 2
20 12
MF MF F F
nên tập hợp các điểm
E
là đường elip có hai
tiêu điểm
1
F
và
2
F
. Và độ dài trục lớn bằng
20
.
Ta có
6
c
;
2 20 10
a a
và
2 2 2
64 8
b a c b
.
Do đó, phương trình chính tắc của là
2 2
1
100 64
x y
.
Suy ra
'
max 10
z OA OA
khi
10
z
và
'
min 8
z OB OB
khi
8
z i
.
Vậy
2
M n
.
* Nhận xét: Ở trên ta đã sử dụng định nghĩa (E) để nhận dạng được phưng trình elip
Câu 3: (Đề Tham Khảo 2018) Xét số phức
z a bi
,a b
thỏa mãn
4 3 5
z i . Tính
P a b
khi
1 3 1
z i z i
đạt giá trị lớn nhất.
A.
8
P
B.
10
P
C.
4
P
D.
6
P
Lời giải
Chọn B
Gọi
;
M a b
là điểm biểu diễn của số phức z.
Theo giả thiết ta có:
2 2
4 3 5 4 3 5
z i a b
Tập hợp điểm biểu diễn số
phức
z
là đường tròn tâm
4;3
I
bán kính
5
R
Gọi:
1;3
1 3 1
1; 1
A
Q z i z i MA MB
B
z x yi
,x y
E
E
Toanthaycu.com
Trang 5
Gọi E là trung điểm của AB, kéo dài EI cắt đường tròn tại D
Ta có:
2 2 2
2 .
MA MBQ
MA MB
2 2 2 2 2 2 2
2
Q MA MB MA MB MA MB
Vì
ME
là trung tuyến trong
MAB
2 2 2 2
2 2 2 2
2
2 4 2
MA MB AB AB
ME MA MB ME
2
2 2 2 2
2 2 4
2
AB
Q ME ME AB
. Mặt khác
2 5 5 3 5
ME DE EI ID
2
2
4. 3 5 20 200
Q
10 2 10 2
4 2( 4) 6
2 6;4 10
2 2( 3) 4
max
D D
D D
MA MB
Q Q
M D
x x
EI ID M P a b
y y

Cách 2:Đặt
.
z a bi
Theo giả thiết ta có:
2 2
4 5 5.
a b
Đặt
4 5 sin
3 5 cos
a t
b t
. Khi đó:
2 2 2 2
1 3 1 1 3 1 1
Q z i z i a b a b
2 2 2
2
5 sin 5 5cos 5 sin 3 5 cos 4
t t t t
30 10 5 sin 30 2 5 3sin 4cos
t t t
Áp dụng BĐT Bunhiacopski ta có:
2 60 8 5 2sin cos 2 60 8 5. 5 200 10 2
Q t t
10 2 10 2
max
Q Q
Dấu bằng xảy ra khi
2
sin
6
5
10.
1 4
cos
5
t
a
P a b
b
t
Câu 4: (Đề Tham Khảo 2017) Xét số phức
z
thỏa mãn
2 4 7 6 2.
z i z i Gọi
,
m M
lần
lượt là giá trị nhỏ nhất và giá trị lớn nhất của
1 .
z i
Tính
.
P m M
A.
5 2 2 73
2
P
B.
5 2 73
P
C.
5 2 73
2
P
D.
13 73
P
Lời
giải
Chọn
A
Trang 6
Gọi
A
là điểm biểu diễn số phức
z
,
2;1 , 4;7
E F và
1; 1 .
N
Từ
2 4 7 6 2
AE A F z i z i và
6 2
EF nên ta có
A
thuộc đoạn thẳng
EF
.
Gọi
H
là hình chiếu của
N
lên
EF
, ta có
3 3
;
2 2
H
. Suy ra
5 2 2 73
.
2
P NH NF
Câu 5: (THPT Cẩm Giàng 2 2019) Cho số phức
z
thỏa mãn
2 2 1
z i
. Số phức
z i
có môđun
nhỏ nhất là:
A.
5 2
. B.
5 1
. C.
5 1
. D.
5 2
.
Lời giải
Cách 1:
Đặt
w z i z w i
.
Gọi
;
M x y
là điểm biểu diễn hình học của số phức
.
w
Từ giả thiết
2 2 1
z i
ta được:
2 2 1
w i i
2 1
w i
2 1 1
x y i
2 2
2 1 1
x y
.
Suy ra tập hợp những điểm
;
M x y
biểu diễn cho số phức
w
là đường tròn
C
có tâm
2;1
I
bán kính
1
R
.
Giả sử
OI
cắt đường tròn
C
tại hai điểm
,
A B
với
A
nằm trong đoạn thẳng
OI
.
Ta có
w OM
Mà
OM MI OI
OM MI OA AI
OM OA
5
8
6
4
2
2
H
E
N
D
A
Toanthaycu.com
Trang 7
Nên
w
nhỏ nhất bằng
5 1
OA OI IA
khi
.
M A
Cách 2:
Từ
2 2 1
z i
2 2
2 2 1
a b
với
,z a bi a b
2 sin ; 2 cos
a x b x
2 sin , 2 cos
a x b x
Khi đó:
2 sin 2 cos
z i x x i i
2 2
2 sin 1 cos
x x
6 4sin 2cos
x x
2 2 2 2
6 4 2 sin cos
x x
2
6 2 5 5 1 5 1
Nên
z i
nhỏ nhất bằng
5 1
khi
4cos 2sin
4sin 2cos 2 5
x x
x x
2 5
sin
5
5
cos
5
x
x
Ta được
2 5 5
2 2
5 5
z i
Cách 3:
Sử dụng bất đẳng thức
1 2 1 2 1 2
z z z z z z
2 2 2 2 2 2 5 1
z i z i i z i i
Câu 6: (THPT Gia Lộc Hải Dương 2019) Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất
của
2
z i
P
z
với
z
là số phức khác
0
và thỏa mãn
2
z
. Tính tỉ số
M
m
.
A.
3
M
m
. B.
4
3
M
m
. C.
5
3
M
m
. D.
2
M
m
.
Lời giải
Ta có
2 2 2
2 1 1 3 5
2 2
2 2
z i z i z i
z i
P P P P
z z z z z z
.
Vậy
5
3
M
m
.
Câu 7: Xét tất cả các số phức
z
thỏa mãn
3 4 1
z i
. Giá trị nhỏ nhất của
2
7 24
z i
nằm trong
khoảng nào?
A.
0;1009
. B.
1009;2018
. C.
2018;4036
. D.
4036;

.
Lời giải
Chọn B
Ta có
1 3 4 3 4 5 1 5 1 4 6
z i z i z z z
.
Đặt
2
0 0 0
4 3 5, 7 24
z i z z i
.
Ta có
2 2
2 2
2 2 2 2 2
7 24
o o o
A z i z z z z z z
2
4 4 2
. . 2 .
o o o o
z z z z z z z z
Trang 8
Mà
2 2
1 . . 1
o o o o o
z z z z z z z z z z
Suy ra
2
2
4 4 2 2 4 2
1 2 . 2 2 1201
o o o
A z z z z z z z z
.
Hàm số
4 2
2 2 1201
y t t
đồng biến trên
4;6
nên
4 2
2.4 2.4 1201 1681
A .
Dấu bằng xảy ra khi và chỉ khi
4
4 3 1
z
z i
.
Do đó
2
7 24
z i
nằm trong khoảng
1009;2018
.
Câu 8: (Chuyen Phan Bội Châu Nghệ An 2019) Cho số phức z thỏa mãn
4
z z z z
. Gọi M, m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
2 2
P z i
. Đặt
A M m
. Mệnh đề nào
sau đây là đúng?
A.
34;6
A
. B.
6; 42
A
. C.
2 7; 33
A
. D.
4;3 3
A
.
Lời giải
Chọn A
Giả sử:
, , ;
z x yi x y N x y
: điểm biểu diễn của số phức z trên mặt phẳng tọa độ
Oxy
.
Ta có:
• 4 2
z z z z x y N
thuộc các cạnh của hình vuông BCDF (hình vẽ).
•
2 2
2 2 2 2 ;
P z i P x y P d I N
với
2;2
I
Từ hình ta có:
1;1
E
2 2
max
4 2 2 5
M P ID
và
2 2
min
2 1 2 1 2
m P IE
Vậy,
2 2 5 34;6
A M m
.
Câu 9: (THPT Quang Trung Đống Đa Hà Nội 2019) Cho số phức
z
thỏa mãn
3 4 2
z i
và
w 2 1
z i
. Khi đó
w
có giá trị lớn nhất bằng
x
y
1
1
-2 2
-2
2
O
D
F
C
I
B
E
Toanthaycu.com
Trang 9
A.
4 74
. B.
2 130
. C.
4 130
. D.
16 74
.
Lời giải
Chọn C
Theo bất đẳng thức tam giác ta có
w 2 1 2 6 8 7 9 2 6 8 7 9 4 130
z i z i i z i i
.
Vậy giá trị lớn nhất của
w
là
4 130
.
Câu 10: (THPT Quang Trung Đống Đa Hà Nội 2019) Xét số phức
z
và số phức liên hợp của nó có
điểm biểu diễn là
M
và
M
. Số phức
4 3
z i
và số phức liên hợp của nó có điểm biểu diễn
là
N
và
N
. Biết rằng
M
,
M
,
N
,
N
là bốn đỉnh của hình chữ nhật. Tìm giá trị nhỏ nhất của
4 5
z i
.
A.
5
34
. B.
2
5
. C.
1
2
. D.
4
13
.
Lời giải
Chọn C
Gọi
z x yi
, trong đó
,x y
. Khi đó
z x yi
,
;
M x y
,
;
M x y
.
Ta đặt
4 3 4 3 4 3 3 4 4 3 ;3 4
w z i x yi i x y x y i N x y x y
. Khi đó
4 3 4 3 3 4 4 3 ; 3 4
w z i x y x y i N x y x y
.
Ta có
M
và
M
;
N
và
N
từng cặp đối xứng nhau qua trục
Ox
. Do đó, để chúng tạo thành
một hình chữ nhật thì
M N
y y
hoặc
M N
y y
. Suy ra
3 4
y x y
hoặc
3 4
y x y
. Vậy tập
hợp các điểm
M
là hai đường thẳng:
1
: 0
d x y
và
2
:3 5 0
d x y
.
Đặt
2 2
4 5 5 4
P z i x y
. Ta có
P MA
với
5; 4
A
.
min min 1
;
P MA MA d A d
hoặc
2
;
MA d A d
. Mà
1
1
;
2
d A d
,
2
5
;
34
d A d
,
vậy
min 1
1
;
2
P d A d
.
Câu 11: Biết số phức
z
thỏa mãn
3 2
iz z i
và
z
có giá trị nhỏ nhất. Phần thực của số phức
z
bằng:
A.
2
5
. B.
1
5
. C.
2
5
. D.
1
5
.
Lời giải
Chọn D
Trang 10
Đặt
z x yi
(
x
,
y
).
Khi đó
3 2
iz z i
2 2 2
2
3 2 1
x y x y
2 1 0
x y
2 1
x y
1
.
Lại có
2 2
z x y
2
.
Thay
1
vào
2
ta được:
2 2
z x y
2
2
2 1
y y
2
5 4 1
y y
2
2 1 5
5
5 5 5
y
Dấu đẳng thức xảy ra khi
2
0
5
y
2
5
y
.
Thay
2
5
y
vào
1
suy ra
1
5
x
.
Vậy phần thực của số phức
z
là
1
5
.
Câu 12: (Chuyên Nguyễn Trãi Hải Dương -2019) Xét các số phức
z
thỏa mãn
1 3 2
z i
. Số phức
z
mà
1
z
nhỏ nhất là
A.
1 5
z i
. B.
1
z i
. C.
1 3
z i
. D.
1
z i
.
Lời giải
Gọi
z x yi
,
,x y
. Khi đó
;
M x y
là điểm biểu diễn của số phức
z
.
Theo bài ra ta có
2 2
1 3 2 1 3 4
z i x y
.
Suy ra tập hợp điểm
M
là đường tròn tâm
1; 3
I
bán kính
2
R
.
Khi đó
2
2
1 1
z x y I M
với
1; 0
I
.
1
z
nhỏ nhất khi
I M
ngắn nhất hay
I
,
M
,
I
thẳng hàng,
M
nằm giữa
I
và
I
.
Toanthaycu.com
Trang 11
Phương trình đường thẳng
II
là
1x
.
Tọa độ giao điểm của đường thẳng
II
với đường tròn tâm
I
bán kính
2R
là
1
1; 1M
và
1
1; 5M
.
Thử lại ta thấy
1
1; 1M
thỏa mãn. Vậy
1z i
.
Câu 13: (Chuyên Phan Bội Châu -2019) Cho số phức
z
thỏa mãn
4.z z z z
Gọi
,M m
lần
lượt là giá trị lớn nhất và giá trị nhỏ nhất của
2 2 .P z i
Đặt
.A M m
Mệnh đề nào sau
đây là đúng?
A.
34;6A
. B.
6; 42A
. C.
2 7; 33A
. D.
4;3 3A
.
Lời giải
Chọn A
Đặt
z x iy
và gọi
;M x y
là điểm biểu diễn của
z x iy
ta có:
4 2z z z z x y
Gọi
2;2A
và
P MA
* Theo hình vẽ,
min , ,P d A
với
: 2x y
và
2 2 2
min 2
2
P
2 2
max 2 4 2 5,P AE
với
0; 2E
Vậy
2 2 5 5,88M m
Câu 14: (Chuyên Lê Quý Đôn Điện Biên 2019) Trong các số phức
z
thỏa mãn
1 1 2z i z i
,
số phức
z
có mô đun nhỏ nhất có phần ảo là
A.
3
10
. B.
3
5
. C.
3
5
. D.
3
10
.
Lời giải
Gọi
z x yi
,
,x y
được biểu diễn bởi điểm
;M x y
.
1 1 2 1 1 1 2z i z i x y i x y i
2 2 2 2
3
1 1 1 2 4 2 3 0 2
2
x y x y x y y x
.
Cách 1:
Trang 12
2 2
2 2 2 2
3 9 3 9 3 5
2 5 6 5 ,
2 4 5 20 10
z x y x x x x x x
.
Suy ra
3 5
10
min z
khi
3 3
;
5 10
x y
.
Vậy phần ảo của số phức
z
có mô đun nhỏ nhất là
3
10
.
Cách 2:
Trên mặt phẳng tọa độ
Oxy
, tập hợp điểm biểu diễn số phức
z
là đường thẳng
: 4 2 3 0
d x y
.
Ta có
z OM
.
z
nhỏ nhất
OM
nhỏ nhất
M
là hình chiếu của
O
trên
d
.
Phương trình đường thẳng
OM
đi qua
O
và vuông góc với
d
là:
2 0
x y
.
Tọa độ của
M
là nghiệm của hệ phương trình:
3
4 2 3 0
5
2 0 3
10
x
x y
x y
y
3 3
;
5 10
M
. Hay
3 3
5 10
z i
.
Vậy phần ảo của số phức
z
có mô đun nhỏ nhất là
3
10
.
Nhận xét: Ta có thể tìm tập hợp điểm biểu diễn số phức
z
như sau:
1 1 2 1 1 2
z i z i z i z i
*
Gọi
M
biểu diễn số phức
z
, điểm
1; 1
A
biểu diễn số phức
1
i
, điểm
1; 2
B
biểu
diễn số phức
1 2
i
.
Khi đó
*
MA MB
. Suy ra tập hợp điểm biểu diễn số phức
z
là đường trung trực của
đoạn thẳng
AB
có phương trình
: 4 2 3 0
d x y
.
Câu 15: Cho hai số phức
1 2
,
z z
thỏa mãn
1 2
1 2
1; 2
2 3 1
z i z i
z i z i
. Giá trị nhỏ nhất của
1 2
z z
là
A.
2 2
. B.
2
. C.
1
. D.
2 1
.
Lời giải
Chọn A
Giả sử
1 1 1
z x y i
với
1 1
;x y
. Khi đó:
1
1 1 1 1 1 1
1
1 2 3 1 2 3
2 3
z i
z i z i x y i x y i
z i
1
2 2 2
2
1 1 1 1 2
1 2 3 3 0
x y x y x y
.
Quỹ tích điểm
M
biểu diễn số phức
1
z
là đường thẳng
: 3 0
x y
.
Giả sử
2 2 2
z x y i
với
2 2
;x y
. Ta có:
2
2 2 2 2 2 2
2
2 2 1 1 2 1 1
1
z i
z i z i x y i x y i
z i
Toanthaycu.com
Trang 13
2 2 2
2 2 2
2 2 2 2 2 2 2 2
1 2 1 1 4 2 3 0
x y x y x y x y
.
Quỹ tích điểm
N
biểu diễn số phức
2
z
là đường tròn
2 2
: 4 2 3 0
C x y x y
có tâm
2; 1
I
và bán kính
2
2
2 1 3 2
R
.
Khoảng cách từ
I
đến
là:
2
2
2 1 3
; 3 2
1 1
d I R
đường thẳng
và đường
tròn
C
không có điểm chung.
Quỹ tích các điểm biểu diễn số phức
1 2
z z
là đoạn thẳng
MN
.
1 2
z z
nhỏ nhất khi và chỉ
khi
MN
nhỏ nhất.
Dễ thấy
min
3 2 2 2 2
MN .
Câu 16: (Sở Bình Phước 2019) Gọi
S
là tập hợp các số phức
z
thỏa mãn
1 34
z và
1 2
z mi z m i
, (trong đó
m
). Gọi
1
z
,
2
z
là hai số phức thuộc
S
sao cho
1 2
z z
lớn nhất, khi đó giá trị của
1 2
z z
bằng
A.
2
B.
10
C.
2
D.
130
Lời giải
Chọn A
Đặt
z x yi
,
,x y
. Khi đó
1 34
z
2
2
1 34
x y
;
1 2
z mi z m i
2 1 2 2 3 0
m x m y
.
Do đó tập hợp các điểm
M
biểu diễn số phức
z
là giao điểm của đường tròn
2
2
: 1 34
C x y
và đường thẳng
: 2 1 2 2 3 0
d m x m y
.
Gọi
A
,
B
là hai điểm biểu diễn
1
z
và
2
z
. Suy ra
,
C d A B
.
Mặt khác
1 2
2 2 34
z z AB R
do đó
1 2
max 2 34 2 1;0
z z AB R I d
.
Từ đó ta có
1
2
m
nên
:3 5 3 0
d x y
1
2
6 3
4 3
z i
z i
.
Vậy
1 2
2
z z
.
N
M
I
N'
M'
Trang 14
Câu 17: Cho hai số phức
,
z w
thỏa mãn
3 2 2
z
,
4 2 2 2
w i
. Biết rằng
z w
đạt giá trị
nhỏ nhất khi
0
z z
,
0
w w
. Tính
0 0
3
z w
.
A.
2 2
. B.
4 2
. C. 1. D.
6 2
.
Lời giải
Ta có: +
3 2 2
z
, suy ra tập hợp điểm biểu diễn
M
biểu diễn số phức
z
là đường tròn có
tâm
3 2 ;0
I
, bán kính
2
r .
+
4 2 2 2
w i
, suy ra tập hợp điểm biểu diễn
N
biểu diễn số phức
w
là đường tròn có tâm
0;4 2
J
, bán kính
2 2
R
.
Ta có
min min
z w MN
.
+
5 2; 2; 2 2
IJ IM r NJ R
.
Mặt khác
IM MN NJ IJ
MN IJ IM NJ
hay
5 2 2 2 2 2 2
MN .
Suy ra
min 2 2
MN khi
, , ,
I M N J
thẳng hàng và
,
M N
nằm giữa
,
I J
(Hình vẽ).
Cách 1:
Khi đó ta có:
0 0
3 3
z w OM ON
và
3 2
IN
1 3
;
5 5
IM IJ IN IJ
 
.
Mặt khác
ON OI IN
3
5
OI IJ
;
3 3OM OI IM
 
1 3
3 3
5 5
OI IJ OI IJ
.
Suy ra
0 0
3 3
z w OM ON

3 3
3 2
5 5
OI IJ OI IJ OI
6 2
.
Cách 2:
Ta có
3 3 0
IN IM IM IN
.
Do đó
0 0
3 3 3 2 2. 2.3 2 6 2.
z w OM ON OI IM OI IN OI OI

Cách 3:
+)
0
12 2
1 12 2 4 2
5
5 5 5
4 2
5
M
M
x
IM
IM IJ IM IJ z i
IJ
y
.
Toanthaycu.com
Trang 15
+)
0
6 2
3 6 2 12 2
5
5 5 5
12 2
5
N
N
x
IN
IN IJ IN IJ w i
IJ
y
.
Suy ra
0 0
3 6 2 6 2
z w
.
Câu 18: Cho hai số phức
z
và
w
thỏa mãn
2 8 6
z w i
và
4.
z w
Giá trị lớn nhất của biểu thức
z w
bằng
A.
4 6.
B.
2 26.
C.
66.
D.
3 6.
Lời giải
Chọn C
Giả sử
,
M N
lần lượt là các điểm biểu diễn cho
z
và
.
w
Suy ra
2 ,
OM ON OF OI
 
4
z w MN
và
2 10.
OF OI
Đặt
; .
2
a
z ON w OM b
Dựng hình bình hành
OMFE
Ta có
2 2 2
2 2
2 2 2
25
264
2 4
2
3
16
2 4
a b ME
a b
b ME a
2
2
2 2
1 1
2 66
2 4 2
a
z w b a b
Suy ra
66,
a b
dấu “=” xảy ra khi
2 66
.
3
a b
Vậy
max
66.
a b
Câu 19: Cho số phức
z
thoả mãn
1
z
. Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
biểu thức
2
1 1
P z z z
. Tính
.
M m
A.
13 3
4
. B.
39
4
. C.
3 3
. D.
13
4
.
Lời giải
Chọn A
Thay
2
1
z
vào
P
ta có
a
b
I
F
E
N
M
O
Trang 16
2
1 1
P z z z
2
2
1
z z z z
2
1 .
z z z z z
1 1
z z z z
1 1
z z z
.
Mặt khác
2
1 1 1 2
z z z z z
.
Đặt
t z z
do
1
z
nên điều kiện
2;2
t
.
Suy ra
2 1
P t t
.
Xét hàm số
2 1
f t t t
với
2;2
t
.
1
1
2 2
f t
t
với
1
t
. Suy ra
0
f t
với
1
t
.
1
1
2 2
f t
t
với
1
t
. Suy ra
0
f x
7
4
x
.
Ta có bảng biến thiên
Từ bảng biến thiên suy ra
13
4
M
tại
7
4
t
và
3
m tại
2
t
.
Vậy
13 3
.
4
M m
.
Câu 20: (THPT Yên Khánh - Ninh Bình - 2019) Cho hai số phức
z
và
a bi
thỏa mãn
5 5 6
z z
;
5 4 20 0
a b
. Giá trị nhỏ nhất của
z
là
A.
3
41
. B.
5
41
. C.
4
41
. D.
3
41
.
Lời giải
Chọn A
Đặt
1
5 ;0
F
,
2
5 ;0
F
, vì
5 3
nên tập hợp các điểm
M
biểu diễn số phức
z
thuộc elip
có
2 2 2
3
4
5
a
b a c
c
suy ra
2 2
: 1
9 4
x y
E
.
Tập hợp các điểm
N
biểu diễn số phức
thuộc đường thẳng
: 5 4 20 0
x y
.
Yêu cầu bài toán trở thành tìm điểm
M E
và
N
sao cho
MN
nhỏ nhất.
Toanthaycu.com
Trang 17
Đường thẳng
d
song song với
có dạng
: 5 4 0
d x y c
,
20
c
.
d
tiếp xúc với
E
khi và chỉ khi
2
2 2
17
5 .9 4 .4 289
17
c
c
c
.
Với
17
c
2
2
20 17
37
,
41
5 4
d d
.
Với
17
c
2
2
20 17
3
,
41
5 4
d d
.
Vậy
3
min
41
MN
.
Câu 21: (KTNL GV THPT Lý Thái Tổ 2019) Gọi
z a bi
,a b
là số phức thỏa mãn điều kiện
1 2 2 3 10
z i z i
và
có mô đun nhỏ nhất. Tính
7 ?
S a b
A.
7
. B.
0
. C.
5
. D.
12
.
Lời giải
Chọn A
Gọi
;
M a b
là điểm biểu diễn số phức
z a bi
1;2
A
là điểm biểu diễn số phức
1 2
i
2;3
B
là điểm biểu diễn số phức
2 3
i
,
10
AB
4
2
2
4
O
M
H
B
A
Trang 18
1 2 2 3 10z i z i
trở thành
MA MB AB
, ,M A B
thẳng hàng và M ở giữa A và B
Gọi
H
là điểm chiếu của
O
lên AB, phương trình
: 3 7 0AB x y
,
:3 0OH x y
Tọa độ điểm
7 21
;
10 10
H
, Có
3 1
;
10 10
AH
,
27 9
;
10 10
BH
và
9BH AH
Nên
H
thuộc đoạn
AB
z
nhỏ nhất
OM
nhỏ nhât, mà
M
thuộc đoạn AB
7 21
;
10 10
M H
Lúc đó
49 21
7 7
10 10
S a b
.
Câu 22: (KTNL GV Thuận Thành 2 Bắc Ninh 2019) Cho số phức thỏa mãn
. Gọi lần lượt là giá trị lớn nhất, nhỏ nhất của biểu thức . Tính .
A. . B. . C. . D. .
Giải:
Chọn D
Gọi
, ,z x yi x y
, ta có
4
2 8 2 4
2
x
z z z z x y
y
, tập hợp
;K x y
biểu diễn số phức
z
thuộc cạnh các cạnh của trong hình thoi
ABCD
như hình vẽ.
đạt giá trị lớn nhất khi
KM
lớn nhất, theo hình vẽ ta có
KM
lớn nhất khi
K D
hay
4;0K
suy ra
49 9 58M
đạt giá trị nhỏ nhất khi
KM
nhỏ nhất, theo hình vẽ ta có
KM
nhỏ nhất khi
K F
(
F
là hình chiếu của
E
trên
AB
.
Suy ra
2;1F
do
AE AB
nên
F
là trung điểm của
AB
.
Suy ra
1 4 5m
. Vậy
58 5M m
Câu 23: (Chuyên Bắc Giang -2019) Cho số phức z có
1z
. Tìm giá trị lớn nhất của biểu thức
2 2
1P z z z z
.
z
2 8
z z z z
,
M m
3 3
P z i
M m
10 34
2 10
10 58
5 58
3 3
P z i
3 3
P z i
Toanthaycu.com
Trang 19
A.
13
4
B. 3 C.
3
D.
11
4
Lời giải
Chọn A
2 2 2 2
1 1 1 1 1
P z z z z z z z z z z z
Do
1
z
nên ta đặt
cos .sin
z x i x
. Khi đó
2
2 2 2
2
2
1 1 cos .sin 1 cos 2 sin 2 cos sin 1
cos 1 sin cos 2 cos 1 sin 2 sin
2 2cos 3 4cos 2cos2
2 2cos 4cos 4cos 1
2 2cos 2cos 1
P z z z x i x x i x x i x
x x x x x x
x x x
x x x
x x
Đặt
cos , 1;1
t x t
. Xét hàm
2 2 2 1
y t t
Với
1
2
t
thì
1
2 2 2 1, ' 2
2 2
y t t y
t
1 7
' 0 2 0
8
2 2
y t
t
7 13
1 3;
8 4
y y
;
1
3
2
y
Với
1
2
t
thì
1
2 2 2 1, ' 2
2 2
y t t y
t
1 1
' 0 2 0 2 2
2
2 2
y t
t
(phương trình vô nghiệm)
1 3
y
;
1
3
2
y
Vậy
1;1
13
max
4
y
. Do đó giá trị lớn nhất của
2 2
1
P z z z z
là
13
4
.
Câu 24: (Chuyên Đại Học Vinh -2019) Giả sử
1 2
,
z z
là hai trong các số phức thỏa mãn
6 8
z zi
là
số thực. Biết rằng
1 2
4
z z
, giá trị nhỏ nhất của
1 2
3
z z
bằng
A.
5 21
B.
20 4 21
C.
20 4 22
D.
5 22
Lời giải
Chọn C
Trang 20
Giả sử z x yi ,
,x y
.Gọi
,A B
lần lượt là điểm biểu diễn cho các số phức
1 2
,z z
. Suy ra
1 2
4AB z z
.
* Ta có
6 8z zi
6 . 8x yi y xi
2 2
8 6 48 6 8x y x y x y i
.
Theo giả thiết
6 8z zi
là số thực nên ta suy ra
2 2
6 8 0x y x y
. Tức là các điểm
,A B
thuộc đường tròn
C
tâm
3;4I
, bán kính
5R
.
* Xét điểm
M
thuộc đoạn
AB
thỏa
3 0 3 4MA MB OA OB OM
.Gọi
H
là trung điểm
AB
. Ta tính được
2 2 2 2 2
21; 22HI R HB IM HI HM
, suy ra điểm
M
thuộc
đường tròn
C
tâm
3;4I
, bán kính
22r
.
* Ta có
1 2
3 3 4 4z z OA OB OM OM
, do đó
1 2
3z z
nhỏ nhất khi
OM
nhỏ nhất.
Ta có
0
min
5 22OM OM OI r
.
Vậy
1 2 0
min
3 4 20 4 22z z OM
.
Câu 25: Trong các số phức
z
thỏa mãn
3 4 2z i
có hai số phức
1 2
,z z
thỏa mãn
1 2
1z z
. Giá trị
nhỏ nhất của
2 2
1 2
z z
bằng
A.
10
B.
4 3 5
C.
5
D.
6 2 5
Lời giải
Chọn A
Đặt
1 1 1 1 1
, ,z x y i x y
và
2 2 2 2 2
, ,z x y i x y
.
Khi đó
2 2
1 1
2 2
2 2
3 4 4
3 4 4
x y
x y
và
2 2
1 2 1 2
1x x y y
.
Ta có
2 2 2 2
1 1 2 2
3 4 3 3x y x y
2 2 2 2
1 1 2 2 1 2 1 2
6 8x y x y x x y y
.
Suy ra
2 2 2 2
2 2
1 2 1 2 1 2 1 2 1 2
2 3 4 2. 3 4 10z z x x y y x x y y
.
Do đó
2 2
1 2
10 10z z
.
Toanthaycu.com
Trang 21
Câu 26: (Chuyên Lê Hồng Phong Nam Định 2019) Cho hai số phức
1 2
,
z z
thoả mãn
1 1
2 4 7 6 2
z i z i
và
2
1 2 1
iz i
. Tìm giá trị nhỏ nhất của biểu thức
1 2
T z z
.
A.
2 1
. B.
2 1
. C.
2 2 1
. D.
2 2 1
.
Lời giải
Gọi
M
là điểm biểu diễn số phức
1
z
và
2;1
A
;
4;7
B
lần lượt là hai điểm biểu diễn hai số
phức
2
i
,
4 7
i
. Ta có
6 2
AB
. Phương trình đường thẳng
AB
là
: 3 0
d x y
.
+)
1 1
2 4 7 6 2
z i z i
6 2
MA MB
MA MB AB
. Do đó tập hợp các
điểm biểu diễn số phức
1
z
là đoạn thẳng
AB
.
+)
2 2 2
1 2 1 1 2 1 2 1
iz i iz i i z i
.
Gọi
N
là điểm biểu diễn số phức
2
z
và
2;1
I
là điểm biểu diễn số phức
2
i
. Ta có
1
IN
Suy ra tập hợp các điểm biểu diễn số phức
2
z
là đường tròn
C
có phương trình:
2 2
2 1 1
x y
.
, 2 2 1
d I AB
, suy ra
AB
không cắt đường tròn.
Gọi
K
là hình chiếu của
2;1
I
lên
AB
. Dễ thấy
K
nằm trên đoạn thẳng
AB
.
Gọi
H
là giao điểm của đoạn
IK
với đường tròn
C
.
Ta có
1 2
, 2 2 1
z z MN KH d I AB R
.
Suy ra
1 2
2 2 1.
min z z
Câu 27: (Chuyên Nguyễn Tất Thành Yên Bái 2019) Cho
z
là số phức thỏa mãn
2
z z i
. Giá trị
nhỏ nhất của
1 2 1 3
z i z i
là
A.
5 2
. B.
13
. C.
29
. D.
5
.
Lời giải
Đặt
,z a bi a b
.
Trang 22
Ta có:
2
2 2 2
2 2
z z i a b a b
4 4 0 1
b b
z a i
.
Xét:
1 2 1 3 1 1 2
z i z i a i a i
2 2
2 2
1 1 1 2
a a
.
Áp dụng BĐT Mincôpxki:
2 2 2 2
2 2
1 1 1 2 1 1 1 2
a a a a
4 9 13
.
Suy ra:
1 2 1 3
z i z i
đạt GTNN là
13
khi
1
2 1 1
3
a a a
.
Nhận xét: Bài toán trên có thể được giải quyết bằng cách đưa về bài toán hình học phẳng.
Câu 28: (Chuyên Hạ Long - 2018) Cho các số phức
1
2
z i
,
2
2
z i
và số phức
z
thay đổi thỏa
mãn
2 2
1 2
16
z z z z
. Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
z
.
Giá trị biểu thức
2 2
M m
bằng
A.
15
. B.
7
. C.
11
. D.
8
.
Lời giải
Giả sử
,z x yi x y
.
Ta có:
2 2
1 2
16
z z z z
2 2
2 2 16
x yi i x yi i
2
2
1 4
x y
.
Suy ra tập hợp điểm biểu diễn của số phức
z
là đường tròn tâm số phức
0;1
I bán kính
2
R
.
Do đó
1
m
,
3
M
.
Vậy
2 2
8
M m
.
Câu 29: (Chuyên Quang Trung - 2018) Cho số phức
z
thỏa mãn
2 4
z i z i
và
3 3 1
z i
. Giá
trị lớn nhất của biểu thức
2
P z
là:
A.
13 1
. B.
10 1
. C.
13
. D.
10
.
Lời giải
Toanthaycu.com
Trang 23
Gọi
;M x y
là điểm biểu diễn số phức
z
ta có:
2 4z i z i
2 2
2 2
2 4x y x y
3y
;
3 3 1z i
điểm M nằm trên đường tròn tâm
3;3I
và bán kính bằng 1. Biểu
thức
2P z AM
trong đó
2;0A
, theo hình vẽ thì giá trị lớn nhất của
2P z
đạt
được khi
4;3M
nên
2 2
max 4 2 3 0 13P
.
Câu 30: Xét số phức
z
thỏa mãn
2 2 2z i
. Giá trị nhỏ nhất của biểu thức
1 5 2P z i z i
bằng
A.
1 10
. B.
4
. C.
17
D.
5
.
Lời giải
Gọi
;M x y
là điểm biểu diễn số phức
z
. Do
2 2 2z i
nên tập hợp điểm
M
là đường
tròn
2 2
: 2 2 4C x y
.
Các điểm
1;1A
,
5;2B
là điểm biểu diễn các số phức
1 i
và
5 2i
. Khi đó,
P MA MB
.
Nhận thấy, điểm
A
nằm trong đường tròn
C
còn điểm
B
nằm ngoài đường tròn
C
, mà
17MA MB AB
. Đẳng thức xảy ra khi
M
là giao điểm của đoạn
AB
với
C
.
Ta có, phương trình đường thẳng
: 4 3 0AB x y
.
Tọa độ giao điểm của đường thẳng
AB
và đường tròn
C
là nghiệm của hệ với
1 5y
Trang 24
2 2 2 2
2 2 4 4 5 2 4
4 3 0 4 3
x y y y
x y x y
Ta có
2 2
2
22 59
17
4 5 2 4 17 44 25 0
22 59
17
y N
y y y y
y L
Vậy
min 17
P khi
37 4 59 22 59
17 17
z i
Câu 31: (SGD Cần Thơ - 2018) Cho số phức
z
thỏa mãn
3 4 5
z i . Gọi
M
và
m
lần lượt là giá
trị lớn nhất và giá trị nhỏ nhất của biểu thức
2 2
2
P z z i
. Môđun của số phức
w M mi
là
A.
3 137
w
. B.
1258
w
. C.
2 309
w
. D.
2 314
w
.
Lời giải
Chọn B
- Đặt
z x yi
, với ,x y
.
Ta có:
3 4 5
z i
3 4 5
x y i
2 2
3 4 5
x y
, hay tập hợp các
điểm biểu diễn số phức
z
là đường tròn
C
có tâm
3;4
I , bán kính
5
r
.
- Khi đó :
2 2
2
P z z i
2 2
2 2
2 1
x y x y
4 2 3
x y
4 2 3 0
x y P
, kí hiệu là đường thẳng
.
- Số phức
z
tồn tại khi và chỉ khi đường thẳng
cắt đường tròn
C
;
d I r
23
5
2 5
P
23 10
P
13 33
P
Suy ra
33
M
và
13
m
33 13
w i
.
Vậy
1258
w .
Câu 32: (THPT Hậu Lộc 2 - 2018) Cho hai số phức
1 2
,
z z
thỏa mãn
1
1 2
z i
và
2 1
z iz
. Tìm giá
trị nhỏ nhất
m
của biểu thức
1 2
z z
?
A.
2 1
m
. B.
2 2
m
. C.
2
m
. D.
2 2 2
m
.
Lời giải
Chọn D
Đặt
1
; ,z a bi a b
2
z b ai
1 2
z z a b b a i
.
Nên
2 2
1 2 1
2.
z z a b b a z
Ta lại có
1 1 1
2 1 1 2
z i z i z
1
2 2
z
. Suy ra
1 2 1
2. 2 2 2
z z z
.
Dấu
" "
xảy ra khi
0
1 1
a b
.
Toanthaycu.com
Trang 25
Vậy
1 2
min 2 2 2
m z z
.
Câu 33: (SGD Bắc Giang - 2018) Hcho hai số phức
,w
z
thỏa mãn
3 2 1
w 1 2 w 2
z i
i i
. Tìm giá trị
nhỏ nhất
min
P
của biểu thức
w
P z
.
A.
min
3 2 2
2
P
. B.
min
2 1
P
. C.
min
5 2 2
2
P
. D.
min
3 2 2
2
P
.
Lời giải
Chọn C
Giả sử
z a bi
,a b
,
w
x yi
,x y
.
3 2 1
z i
2 2
3 2 1
a b
(1)
w 1 2 w 2
i i
2 2 2 2
1 2 2 1
x y x y
.
Suy ra
0
x y
.
2 2 2 2
w
P z a x b y a x b x
.
Từ (1) ta có
3;2
I , bán kính
1
r
. Gọi
H
là hình chiếu của
I
trên :
d y x
.
Đường thẳng
HI
có PTTS
3
2
x t
y t
.
3 ;2
M HI M t t
2
2 1
M C t
1
2
1
2
t
t
1 1
2 3 ;2
2 2
t M
,
5 2
2
MH
1 1
3 3 ;2
2 2
t M
,
5 2
2
MH
Vậy
min
5 2 2
2
P
.
Câu 34: (Chuyên Lê Hồng Phong - TPHCM - 2018) Cho số phức
z
thỏa
1
z
. Gọi
m
,
M
lần lượt
là giá trị nhỏ nhất, giá trị lớn nhất của biểu thức
5 3 4
6 2 1
P z z z z
. Tính
M m
.
A.
4
m
,
3
n
. B.
4
m
,
3
n
C.
4
m
,
4
n
. D.
4
m
,
4
n
.
Lời giải
Vì
1
z
và
2
.
z z z
nên ta có
1
z
z
.
Trang 26
Từ đó,
5 3 4
6 2 1
P z z z z
4 4 4
6 2 1
z z z z
4 4 4
6 2 1
z z z
.
Đặt
4
z x iy
, với ,x y
. Do
1
z
nên
4 2 2
1
z x y
và
1 , 1
x y
.
Khi đó
6 2 1
P x iy x iy x iy
2
2
2 6 2 1
x x y
2 6 2 2 2
x x
2
2 2 1 3
x
.
Do đó
3
P
. Lại có
1 1
x
0 2 2 2
x
1 2 2 1 1
x
4
P
.
Vậy
4
M
khi
4
1
z
và
3
m
khi
4
1 3
i
2 2
z . Suy ra
1
M m
.
Câu 35: (Chuyên Đh Vinh - 2018) Cho các số phức
w
,
z
thỏa mãn
3 5
w i
5
và
5w 2 i 4
z
. Giá trị lớn nhất của biểu thức
1 2i 5 2i
P z z
bằng
A.
6 7
. B.
4 2 13
. C.
2 53
. D.
4 13
.
Lời giải
Chọn C
Gọi
i
z x y
, với ,x y
. Khi đó
;
M x y
là điểm biểu diễn cho số phức
z
.
Theo giả thiết,
5w 2 i 4
z
5 w i 2 i 4 5i
z
2 i w i 3 2i
z
3 2i 3
z
. Suy ra
;
M x y
thuộc đường tròn
2 2
: 3 2 9
C x y
.
Ta có
1 2i 5 2i
P z z
MA MB
, với
1;2
A và
5;2
B .
Gọi
H
là trung điểm của
AB
, ta có
3;2
H
và khi đó:
P MA MB
2 2
2
MA MB
hay
2 2
4
P MH AB
.
Mặt khác,
MH KH
với mọi
M C
nên
2 2
4
P KH AB
2
2
4
IH R AB
2 53
.
Vậy
max
2 53
P
khi
M K
MA MB
hay
3 5i
z
và
3 11
w i
5 5
.
Câu 36: (Kim Liên - Hà Nội - 2018) Xét các số phức
z a bi
(
,a b
) thỏa mãn
3 2 2
z i
.
Tính
a b
khi
1 2 2 2 5
z i z i
đạt giá trị nhỏ nhất.
V
Toanthaycu.com
Trang 27
A.
4 3
. B.
2 3
. C.
3
. D.
4 3
.
Lời giải
Cách 1:
Đặt
3 2
z i w
với
w x yi
,x y
. Theo bài ra ta có
2 2
2 4
w x y
.
Ta có
2 2 2
2
1 2 2 2 5 4 2 1 3 4 2 1 3
P z i z i w w i x y x y
2 2 2 2
20 8 2 1 3 2 5 2 2 1 3
x x y x x y
2 2 2 2 2
2 2 2
2 2 1 1 3 2 1 1 3
x y x x y x y x y
2 3 2 3 6
y y y y
.
2 2
1
1
6 3 0
3
4
x
x
P y y
y
x y
.
Vậy GTNN của
P
là bằng
6
đạt được khi
2 2 3
z i
.
Cách 2:
3 2 2
z i
2
MI
;2
M I
với
3;2
I .
1 2 2 2 5 2
P z i z i MA MB
với
1;2
A ,
2;5
B .
Ta có
2
IM
;
4
IA
. Chọn
2;2
K thì
1
IK
. Do đó ta có
2
.
IA IK IM
IA IM
IM IK
IAM
và
IMK
đồng dạng với nhau
2
AM IM
MK IK
2
AM MK
.
Từ đó
2
P MA MB
2
MK MB
2
BK
.
Dấu bằng xảy ra khi và chỉ khi
M
,
K
,
B
thẳng hàng và
M
thuộc đoạn thẳng
BK
.
Từ đó tìm được
2;2 3
M
.
Cách 3:
Gọi
;
M a b
là điểm biểu diễn số phức
.
z a bi
Đặt
3;2
I ,
1;2
A và
2;5
B .
Ta xét bài toán: Tìm điểm M thuộc đường tròn
C
có tâm
I
, bán kính
2
R
sao cho biểu thức
2
P MA MB
đạt giá trị nhỏ nhất.
Trước tiên, ta tìm điểm
;
K x y
sao cho
2
MA MK
M C
.
Ta có
2 2
2 2
2 4 4
MA MK MA MK MI IA MI IK
Trang 28
2 2 2 2 2 2 2
2 . 4 2 . 2 4 3 4
MI IA MI IA MI IK MI IK MI IA IK R IK IA
  
*
.
*
luôn đúng
2 2 2
4 0
3 4 0
IA IK
M C
R IK IA
.
4 3 4
2
4 0
2
4 2 0
x
x
IA IK
y
y

.
Thử trực tiếp ta thấy
2;2
K thỏa mãn
2 2 2
3 4 0
R IK IA
.
Vì
2 2 2 2
1 3 10 4
BI R
nên
B
nằm ngoài
C
.
Vì
2 2
1 4
KI R
nên
K
nằm trong
C
.
Ta có
2 2 2 2 2
MA MB MK MB MK MB KB
.
Dấu bằng trong bất đẳng thức trên xảy ra khi và chỉ khi
M
thuộc đoạn thẳng
BK
.
Do đó
2
MA MB
nhỏ nhất khi và chỉ khi M là giao điểm của
C
và đoạn thẳng
.
BK
Phương trình đường thẳng
: 2
BK x
.
Phương trình đường tròn
2 2
: 3 2 4
C x y
.
Tọa độ điểm
M
là nghiệm của hệ
2 2
2
2
3 2 4
2 3
x
x
x y
y
hoặc
2
2 3
x
y
.
Thử lại thấy
2;2 3
M
thuộc đoạn
BK
.
Vậy
2
a
,
2 3
b
4 3
a b .
Câu 37: (Liên Trường - Nghệ An - 2018) Biết rằng hai số phức
1
z
,
2
z
thỏa mãn
1
3 4i 1
z
và
2
1
3 4i
2
z
. Số phức
z
có phần thực là
a
và phần ảo là
b
thỏa mãn
3 2 12
a b
. Giá trị
nhỏ nhất của
1 2
2 2
P z z z z
bằng:
A.
min
9945
11
P . B.
min
5 2 3
P
. C.
min
9945
13
P . D.
min
5 2 5
P
.
Lời giải
Chọn C
Gọi
1
M
,
2
M
,
M
lần lượt là điểm biểu diễn cho số phức
1
z
,
2
2
z
,
z
trên hệ trục tọa độ
Oxy
.
Khi đó quỹ tích của điểm
1
M
là đường tròn
1
C
tâm
3;4
I , bán kính
1
R
;
quỹ tích của điểm
2
M
là đường
2
C
tròn tâm
6;8
I
, bán kính
1
R
;
quỹ tích của điểm
M
là đường thẳng
:3 2 12 0
d x y
.
Bài toán trở thành tìm giá trị nhỏ nhất của
1 2
2
MM MM
.
Toanthaycu.com
Trang 29
Gọi
3
C
có tâm
3
138 64
;
13 13
I
,
1
R
là đường tròn đối xứng với
2
C
qua
d
. Khi đó
1 2 1 3
min 2 min 2
MM MM MM MM
với
3 3
M C
.
Gọi
A
,
B
lần lượt là giao điểm của đoạn thẳng
1 3
I I
với
1
C
,
3
C
. Khi đó với mọi điểm
1 1
M C
,
3 3
M C
,
M d
ta có
1 3
2 2
MM MM AB
, dấu "=" xảy ra khi
1 3
,
M A M B
. Do đó
min 1 3
2 2 2
P AB I I
1 3
9945
13
I I .
Câu 38: (Chuyên Lê Quý Đôn – Điện Biên - 2019) Trong các số phức thỏa mãn:
1 1 2
z i z i
, số phức
z
có mô đun nhỏ nhất có phần ảo là
A.
3
10
. B.
3
5
. C.
3
5
. D.
3
10
.
Lời giải
Chọn D
+ Gọi số phức cần tìm là
, ( , )
z a bi a b
.
z a b i
+
1 1 2
z i z i
1 1 2
a bi i a bi i
1 1 1 2
a b i a b i
.
2 2 2 2
1 1 1 2
a b a b
4 3 3
4 2 3 0 2
2 2
a
a b b a
+
2
2 2 2 2 2
3 9 6 9 9
2 5 6 5
2 4 5 25 20
z a b a a a a a a
2
3 9 9 3 5
5
5 20 20 10
a
z
nhỏ nhất bằng
3 5
10
khi
3 3
5 10
a b
.
Câu 39: (Chuyên Bắc Giang 2019) Cho số phức
z
thỏa mãn
1
z
. Gọi
,
M m
lần lượt là giá trị lớn
nhất, giá trị lớn nhất của
5 3 4
6 2 1
P z z z z
. Tính
M m
.
I
3
I
2
I
1
M
8
6
4
3
O
y
x
B
A
Trang 30
A.
1
M m
. B.
7
M m
. C.
6
M m
. D.
3
M m
.
Lời giải
Chọn A
Ta có:
2
1
1zz z z
z
.
Suy ra
5 4 8 4 4 8 4 4
3
3
1 1
6 2 1 1 6 2 1 6 1 2 1
P z z z z z z z z z
z
z
Đặt
4
1
w z w
, ta được
2
6 1 2 2
P w w w
.
Gọi
w x yi
, vì
2 2
1
1 1
1
x
w x y
y
.
2 2 2
6 1 2 3 2 1 2 6 2 3 2 1
P x x y y x i x yi x x y x i x yi
2
2
2 3 2 1 2 3 2 2 2
x x yi x y x x yi x
2 3 2 2 2
x x
Xét hàm số
2 3 2 2 2
f x x x
trên đoạn
1;1
.
1 1 1
2 2 ; 0 2 2 0 2 2 1
2
2 2 2 2
f x f x x x
x x
.
Ta có:
1
1 4; 3; 1 4
2
f f f
Vậy
4, 3 1
M m M m
.
Câu 40: (Bình Giang-Hải Dương 2019) Cho số phức
z
thỏa mãn
1
z
. Giá trị lớn nhất của biểu thức
1 2 1
P z z
bằng
A.
6 5
. B.
4 5
. C.
2 5
. D.
5
.
Lời giải
Chọn C
Gọi
; ;
z x yi x y
.
2 2 2 2
1 1 1 1;1 .
z x y y x x
Ta có:
2 2
2 2
1 3 1 1 3 1 2 1 2 2 1
P z z x y x y x x
.
Xét hàm số
2 1 2 2 1 ; 1;1 .
f x x x x
Hàm số liên tục trên
1;1
và với
1;1
x
ta có:
1 2
.
2 1 2 1
f x
x x
1 2 3
0 0 1;1 .
5
2 1 2 1
f x x
x x
3
1 2; 1 4; 2 5
5
f f f
.
1;1
max 2 5
x
f x .
Toanthaycu.com
Trang 31
Vậy giá trị lớn nhất của biểu thức
1 31
P z z
bằng
2 5
khi
3
5
x
,
4
5
y
.
Câu 41: (SGD Hưng Yên 2019) Cho số phức
z
thoả mãn
1
z
. Gọi
M
và
m
lần lượt là giá trị lớn
nhất và giá trị nhỏ nhất của biểu thức
2
1 1
P z z z
. Tính
.
M m
A.
13 3
4
. B.
39
4
. C.
3 3
. D.
13
4
.
Lời giải
Chọn A
Thay
2
1
z
vào
P
ta có
2
1 1
P z z z
2
2
1
z z z z
2
1 .
z z z z z
1 1
z z z z
1 1
z z z
.
Mặt khác
2
1 1 1 2
z z z z z
.
Đặt
t z z
do
1
z
nên điều kiện
2;2
t .
Suy ra
2 1
P t t
.
Xét hàm số
2 1
f t t t
với
2;2
t .
1
1
2 2
f t
t
với
1
t
. Suy ra
0
f t
với
1
t
.
1
1
2 2
f t
t
với
1
t
. Suy ra
0
f x
7
4
x
.
Ta có bảng biến thiên
Từ bảng biến thiên suy ra
13
4
M
tại
7
4
t
và
3
m
tại
2
t
.
Vậy
13 3
.
4
M m
.
Câu 42: (Chuyên - KHTN - Hà Nội - 2019) Cho số phức
z
thỏa mãn :
2
z z i
. Giá trị nhỏ nhất của
biểu thức
4
P z i z
là
A.
5.
B.
4.
C.
3 3.
D.
6.
Lời giải
Chọn A
Trang 32
Gọi
( ; )
M x y
là điểm biểu diễn số phức
.
z
Ta có
2 1 0,
z z i y
tức biểu diễn hình học
của số phức thỏa mãn giả thiết là đường thẳng
1 0.
y
Xét điểm
(0;1)
A
và
(4;0)
B
thì
4 .
P z i z MA MB
Dễ thấy
,
A B
cùng phía với đường thẳng
1 0
y
nên
MA MB
nhỏ nhất bằng
BA
trong đó
(0; 3)
A
đối xứng với
A
qua đường thẳng
1 0.
y
Do đó
MA MB
nhỏ nhất bằng
5.
BA
Câu 43: (SGD Bến Tre 2019) Cho các số phức
1
1 3
z i
,
2
5 3
z i
. Tìm điểm
;
M x y
biểu diễn
số phức
3
z
, biết rằng trong mặt phẳng phức điểm
M
nằm trên đường thẳng
2 1 0
x y
và mô
đun số phức
3 2 1
3 2
w z z z
đạt gí trị nhỏ nhất.
A.
3 1
;
5 5
M
. B.
3 1
;
5 5
M
. C.
3 1
;
5 5
M
. D.
3 1
;
5 5
M
.
Lời giải
Chọn A
Trắc nghiệm: Thay tọa độ điểm M vào vế trái phương trình đường thẳng kết quả bằng 0 thỏa
ta được đáp án A
Tự luận:
Ta có
3 2 1 3 3 3
3 2 3 3 3 3 1 3 1 3
w z z z z i z i w z i AM
với
1;3
A
;
M x y
biểu diễn số phức
3
z
nằm trên đường thẳng
: 2 1 0
d x y
và
1;3
A d
.
Khi đó
3
3 1 3
w z i AM
đạt giá trị nhỏ nhất khi
AM
ngắn nhất
AM d
AM d
nên
AM
có phương trình:
2 1 0
x y
.
Khi đó
M AM d
nên
3 1
; .
5 5
M
.
Câu 44: (SGD Cần Thơ 2019) Cho số phức
z
thoả mãn
1 2 5
z i
. Giá trị lớn nhất của
1
z i
bằng
A.
5
. B.
5 2
. C.
20
. D.
2 5
.
Lời giải
Chọn D
Cách 1.
Ta có
1 1 2 2 1 2 2 2 5
z i z i i z i i
.
Đẳng thức xảy ra khi
3 3
z i
.
Vậy
max 1 2 5
z i
.
Cách 2.
M'
A
B
A'
M
Toanthaycu.com
Trang 33
Đặt
, ,z x yi x y
thì từ điều kiện ta có:
2 2
1 2 5
x y
.
Gọi
;
M x y
là điểm biểu diễn cho
z
và
1; 1
A
là điểm biểu diễn cho số phức
1
i
, khi
đó
1
z i AM
với
M
thuộc đường tròn
C
tâm
1; 2
I
bán kính
5
R
.
Dễ thấy
A C
, do đó
2 2 5
AM R .
Suy ra
max 1 2 5
z i
, đẳng thức xảy ra khi
M K
.
Cách 3.
1 2 5
z i
*
Đặt
z x yi
,
x y
, khi ấy, ta có
* 1 2 5
x yi i
1 2 5
x y i
2 2
1 2 5
x y
.
Đặt
1 5 sin
2 5 cos
x a
y a
. Ta có
1 1 1
z i x y i
2 2
1 1
x y
2 2
5 sin 2 5 cos 1
a a
10 4 5 sin 2 5 cos
a a
2 5 5
10 10 sin cos
5 5
a a
10 10sin
a
với
2 5
cos
5
5
sin
5
.
Vì
1 sin 1
a
với mọi
;
a
10 10 1 10 10
z i
0 1 2 5
z i
.
Vậy giá trị lớn nhất của
1
z i
là
2 5
. Dấu
" "
xảy ra khi
sin 1
a
2
2
a k
5
cos cos 2 sin
2 5
2 5
sin sin 2 cos
2 5
a k
a k
1 5 sin
2 5 cos
x a
y a
1 2
2 1
x
y
3
3
x
y
3 3
z i
.
Câu 45: (Thi thử hội 8 trường chuyên 2019) Cho số phức
z
thỏa mãn
2 2 2
i z i z i
. Giá trị
nhỏ nhất của
z
bằng
Trang 34
A.
1
. B.
2 5
5
. C.
2
. D.
5
5
.
Lời giải
Chọn D
Giả sử
z x yi
,x y
. Ta có
2 2 2
i z i z i
2 2 2
i x yi i x yi i
2 2 2 2 2
x y y x i x y y x i i
4 2 2
y x i i
4 2 2
y x
2 1
x y
.
Do đó
2
2 2
2 2 2 2
2 1 1
2 1 5 4 1 5 , .
5 5
5
z x y y y y y y y
Suy ra
1 5
min
5 5
z
khi
2
5
y
,
1
5
x
.
Câu 46: (Chuyên Nguyễn Du-ĐăkLăk 2019) Số phức
z
có môđun nhỏ nhất thoả mãn
2 3
i z z i
là
A.
6 3
5 5
i
. B.
3 6
5 5
i
. C.
3 6
5 5
i
. D.
6 3
5 5
i
.
Lời giải
Chọn C
Đặt
, ; .
z x yi x y z x yi
Khi đó
2 3 2 3 1
i z z i x y i x y i
2 2 2
2
2 3 1 2 3 0
x y x y x y
.
Do đó tập hợp điểm biểu diễn của
z
là đường thẳng
: 2 3 0
x y
.
Ta có
min d ,
z O
. Gọi
d
là đường thẳng qua
O
và vuông góc với
:2 0
d x y
.
Gọi
2 0
3 6
: ;
2 3 0
5 5
x y
H d H H
x y
.
Khi đó
z
có môđun nhỏ nhất thoả mãn có điểm biểu diễn là
H
, tức là
3 6
5 5
z i
.
Câu 47: (Sở GD Nam Định - 2019) Trong các số phức
z
thỏa mãn
12 5 17 7
13
2
i z i
z i
. Tìm giá
trị nhỏ nhất của
z
.
A.
3 13
26
. B.
5
5
. C.
1
2
. D.
2
.
Lời giải
Chọn A
Điều kiện:
2
z i
.
Phương trình đã cho
17 7
12 5 . 13 2 1 2
12 5
i
i z z i z i z i
i
1
.
Toanthaycu.com
Trang 35
Gọi
;
M x y
là điểm biểu diễn số phức
z x yi
. Vì
2
z i
nên
2;1
M N
.
Khi đó,
2 2 2 2
1 1 1 2 1 6 4 3 0
x y x y x y
.
Ta thấy đường thẳng
: 6 4 3 0
d x y
không đi qua điểm
2;1
N
nên tập hợp điểm
M
là
đường thẳng
d
.
Ngoài ra,
z OM
nên
z
nhỏ nhất khi
OM
nhỏ nhất, tức là
2 2
3 3 13
d ,
26
6 4
OM O d
.
Vậy
3 13
min
26
z
.
Câu 48: (Chuyên Nguyễn Huệ-HN-2019) Cho số phức
z
thỏa mãn
2
2 5 1 2 3 1
z z z i z i
. Tính
min ,
w
với
2 2
w z i
.
A.
1
min
2
w
. B.
min 1
w
. C.
3
min
2
w
. D.
min 2
w
.
Lời giải
Chọn B
Theo giả thiết,
2
2 5 1 2 3 1
z z z i z i
1 2 1 2 1 2 3 1
z i z i z i z i
1 2 . 1 2 1 3 0
z i z i z i
1 2 0 1
1 2 1 3 2
z i
z i z i
.
1 1 2 0 1 2
z i z i
. Khi đó,
1 2 2 2 1
w i i
3
.
Đặt
z x yi
(
, x y
). Khi đó,
2 1 2 1 3
x y i x y i
2 2 2 2 2 2
1 1
1 2 1 3 2 3
2 2
x y x y y y y z x i
.
2
3 9 9 3
2 2
2 4 4 2
w x i x
x
.
4
.
Từ
3
và
4
min 1
w
.
Câu 49: (Kim Liên - Hà Nội 2019) Xét các số phức
z
thỏa mãn
3 2 3 3 5
z i z i
. Gọi
M
,
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
2 1 3
P z z i
. Tìm
M
,
m
.
A.
17 5
M ;
3 2
m . B.
26 2 5
M ;
2
m .
C.
26 2 5
M ;
3 2
m
. D.
17 5
M ;
3
m .
Lời giải
Chọn C
Trang 36
Gọi
M
là điểm biểu diễn số phức
z
,
1
3;2
F
,
2
3; 1
F
,
2;0
A
và
1;3
B
.
Ta có
3 2 3 3 5
z i z i và
1 2
3 5
F F
1 2 1 2
MF MF F F
.
Do đó tập hợp các điểm
M
là đoạn thẳng
1 2
F F
.
Dựa vào hình vẽ, ta thấy:
+
max 2 2
26 2 5
M P M A M B
.
+
min 1 1
3 2
m P M A M B AB
.
Vậy
26 2 5
M ;
3 2
m .
Câu 50: (Chuyên Nguyễn Trãi Hải Dương 2019) Xét các số phức
z
thỏa mãn
1 3 2
z i
. Số phức
z
mà
1
z
nhỏ nhất là
A.
1 5
z i
. B.
1
z i
. C.
1 3
z i
. D.
1
z i
.
Lời giải
Chọn B
Giả sử
;z x yi x y
.
Ta có
1 3 2
z i
2 2
1 3 2
x y
2
2
1 6 5
x y y
Vì
2
2
1 0 6 5 0 1 5
x y y y
2
2
1 1 6 5
z x y y
Vì
1 5 1 6 5 25 1 1 5
y y z
Vậy
1
z
nhỏ nhất khi
1
1
x
y
khi đó
1
z i
Câu 51: (Chuyên Ngữ Hà Nội 2019) Cho các số phức
, ,
z z z
1 2
thay đổi thỏa mãn các điều kiện sau:
iz i
2 4 3
, phần thực của
z
1
bằng 2, phần ảo của
z
2
bằng 1. Tìm giá trị nhỏ nhất của biểu
thức
T z z z z
2 2
1 2
.
A.
.
9
B.
.
2
C.
.
5
D.
.
4
Lời giải
Chọn D
Đặt
, ,z x yi x y
, ta có
;
M z M x y
Khi đó:
iz i i x yi i y x i
2 4 3 2 4 3 4 2 3
Toanthaycu.com
Trang 37
x y
2 2
2 4 9
Suy ra tập hợp điểm
M
là đường tròn
C
tâm
;
I
2 4
, bán kính
.
R
3
Mặt khác:
;z bi A z A b
1 1
2 2
Tập hợp điểm
A
là đường thẳng
: .
d x
1
2
;z a i B z B a
2 2
1
Tập hợp điểm
B
là đường thẳng
: .
d y
2
1
Giao điểm của
d
1
và
d
2
là
;
P
2 1
.
Gọi
H
và
K
lần lượt là hình chiếu của
M
trên
d
1
và
.
d
2
Ta có:
T z z z z MA MB MH MK MP
2 2
2 2 2 2 2
1 2
.
T
đạt giá trị nhỏ nhất khi
,
A H B K
và
, ,
I M P
thẳng hàng (theo thứ tự đó).
Phương trình đường thẳng
: ;
x t
IP M t t
y t
2 4
2 4 1 3
1 3
(vì
M IP
).
Mà
M C
nên ta có
t
t t t
t
2 2 2
2
9
5
4 4 3 3 9 1
8
25
5
- Với
;t M
8 22 29
5 5 5
(loại)
- Với
; , .
t M z i z i z i
1 2
2 2 11 2 11 11 2
2
5 5 5 5 5 5 5
Suy ra
min
MP IP IM IP R
2
2
4 3 3 2
.
Vậy
min
T
2
2 4
khi
, , .
z i z i z i
1 2
2 11 11 2
2
5 5 5 5
Câu 52: (Chuyên Bắc Giang 2019) Cho số phức
z
thỏa mãn
3 4 5
z i và biểu thức
2 2
2
P z z i
đạt giá trị lớn nhất. Tính
z i
.
A.
5 3
. B.
41
. C.
61
. D.
3 5
.
Lời giải
Chọn C
Giả sử
z x yi
, (
,x y
).
Trang 38
+) Ta có:
2 2
3 4 5 3 4 5 1
z i x y
.
+)
2 2 2 2
2 2
2 2 1 4 2 3
P z z i x y x y x y
2 2
2 2
4 3 2 4 23 4 2 3 4 23 33
x y x y
.
3 4
33 3 2 4 2
4 2
x y
P x y
.
Từ
1
và
2
suy ra
5
5
x
y
hoặc
1
3
x
y
.
Với
5
33
5
x
P
y
; Với
1
13
3
x
P
y
.
Vậy số phức
z
thỏa mãn
3 4 5
z i
và biểu thức
2 2
2
P z z i
đạt giá trị lớn nhất là
5 5
z i
. Khi đó
61
z i
.
Câu 53: (Đại học Hồng Đức –Thanh Hóa –2019) Cho số phức
,z a bi a b
thỏa mãn
1 1
z i
. Giá trị nhỏ nhất của biểu thức
5
P a b
là
A.
3 2
. B.
2 2
. C.
3 2 2
. D.
2 2
.
Lời giải
Chọn A
Cách 1:
Theo giả thiết ta có
2 2
1 1 1 1 1
z i a b
.
Đặt
1 sin , 1 cos 0 2
a t b t t
.
Khi đó 5 sin cos 3 2 sin 3 3 2 sin
4 4
P a b t t t t
.
Ta có:
1 sin 1 2 2 sin 2 3 2 3 2
4 4
t t P
.
Do đó giá trị nhỏ nhất của
P
là
3 2
.
Cách 2:
Theo giả thiết ta có
2 2
1 1 1 1 1 , 0; 2
z i a b a b
.
Khi đó
5 5 3 1 1
P a b a b a b
.
Theo BĐT Bunhia ta có:
2 2
2 2
1 1 1 1 . 1 1 2
a b a b
Do đó
3 2
P .
Câu 54: (Đại học Hồng Đức –Thanh Hóa 2019) Cho số phức
z a bi
(
a
,
b
) thỏa mãn
1
z
.
Tìm giá trị lớn nhất của biểu thức
2 2 2
A z z
.
A.
10
. B.
5 2
. C.
10 2
. D.
7
.
Toanthaycu.com
Trang 39
Lời giải
Chọn B
Ta có:
2 2
2
2 2z a b
;
2 2
2
2 2z a b
.
Suy ra:
2 2
2 2z z
2 2
2 8a b
2
2 8z
10
.
Ta có:
2
2 2
2 2 2
2 2 2 1 2 2 2 50A z z z z
.
Vì
0A
nên từ đó suy ra
50 5 2A
.
Vậy giá trị lớn nhất của
A
là
5 2
.
Câu 55: (THPT Thăng Long-Hà Nội- 2019) Cho số thực
a
thay đổi và số phức
z
thỏa mãn
2
1 2
1
z i a
a a i
a
. Trên mặt phẳng tọa độ, gọi
M
là điểm biểu diễn số phức
z
. Khoảng
cách nhỏ nhất giữa hai điểm
M
và
3;4I
(khi
a
thay đổi) là
A.
6
. B.
5
. C.
4
. D.
3
.
Lời giải
Chọn C
Ta có:
2
2
2 2
2
1 2
1 2
1 1
1
i a a ai
z i a z
a a i
a a
a
3 2
2
2 2
2
1
1.
1 1
1
a a a i
z a i
z z
a a
a
Vậy tập hợp các điểm biểu diễn của số phức
z
là đường tròn tâm
O
bán kính
1R
.
Ta có:
5OI
. Do đó:
min 1
5 1 4OM OM OI R
.
Câu 56: (Chuyên Lê Hồng Phong-Nam Định- 2019) Xét số phức
z
thỏa mãn
2 4 5z i
. Gọi
a
và
b
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
z
. Giá trị biểu thức
2 2
a b
bằng
A.
40
. B.
4 5
. C.
20
. D.
2 5
.
Lời giải
Trang 40
Chọn A
Gọi
;M x y
là điểm biểu diễn số phức z x yi với
,x y
.
Ta có
2 2
2 4 5 2 4 5z i x y
tập hợp điểm biểu diễn số phức
z
là một
đường tròn có tâm
2;4I
và bán kính
5R
.
Kẻ đường thẳng đi qua
2
điểm
O
và
I
cắt đường tròn tại
2
điểm
M
và
N
như hình vẽ.
2 2
2 4 2 5OI
;
5IM IN R
.
Từ hình vẽ ta thấy:
min
2 5 5 5z OM OI IM b
.
max
2 5 5 3 5z ON OI IN a
.
Vậy
2 2
40a b
.
Câu 57: (Hậu Lộc 2-Thanh Hóa- 2019) Cho
1 2
, z z
là hai trong các số phức thỏa mãn
3 3 2z i
và
1 2
4z z
. Giá trị lớn nhất của
1 2
z z
bằng
A.
8
. B.
4 3
. C.
4
. D.
2 2 3
.
Lời giải
Chọn A
Gọi
, M N
lần lượt là điểm biểu diễn của hai số phức
1 2
, z z
.
Do
1 2
1 2
3 3 3 3 2
4
z i z i
z z
nên
2
2
2
, N : 3 3 2
4 2.2
M C x y
MN
.
Như vậy
MN
là đường kính của đường tròn
C
với tâm
3; 3I
, bán kính
2R
, do đó
I
là trung điểm
MN
,
O 12I
.
Toanthaycu.com
Trang 41
Ta có
2
2 2 2
1 2
1 1 2 2O 8
2
MN
z z OM ON OM ON I
.
Dấu
" "
xảy ra khi và chỉ khi
OM ON MN
là đường kính của
C
vuông góc với
OI
.
Câu 58: (Chuyên Đại học Vinh - 2019) Giả sử
1 2
,
z z
là hai trong các số phức thỏa mãn
6 8
z zi
là số thực. Biết rằng
1 2
4
z z
. Giá trị nhỏ nhất của
1 2
3
z z
bằng
A.
5 21
. B.
20 4 21
. C.
20 4 22
. D.
5 22
.
Lời giải
Chọn C
Giả sử số phức
z x yi
thỏa mãn
6 8
z zi
là số thực. Ta có:
6 8 6 (8 ) 6 8 8 8 6 8
z zi x yi x yi i x y xy x x y y i
Để là
6 8
z zi
số thực thì
2 2
2
8 6 8 0 3 4 5
x x y y x y
Vậy điểm biểu diễn số phức
1 2
,
z z
thuộc đường tròn tâm
3, 4
I , bán kính
5
R
Giả sử
1 1 1
z x y i
có điểm biểu diễn
1 1
,
A x y
;
2 2 2
z x y i
có điểm biểu diễn
2 2
,
B x y
.
Vì
2 2
1 2 1 2 1 2
4 4 4
z z x x y y AB
Ta xét
1 2
3 3
z z OA OB
 
Gọi
H
là trung điểm
,
AB
K
là trung điểm
HB
, khi đó ta có:
1 2
3 3 2 4 4
z z OA OB OH OB OK OK
Ta có
5; 4;AH HB 2; 1
OI IB IA AB HK
Suy ra
21 22
IH IK
.
Theo bất đẳng thức tam giác ta có
5 22
OK KI OI OK OI KI OK .
Trang 42
Suy ra
1 2
3 4 20 4 22
z z OK
Câu 59: (Chuyên Hoàng Văn Thụ-Hòa Bình-2019)Trong các số phức
z
thỏa mãn
2
1 2
z z
gọi
1
z
và
2
z
lần lượt là các số phức có môđun nhỏ nhất và lớn nhất. Giá trị của biểu thức
2 2
1 2
z z
bằng
A.
6.
B.
2 2.
C.
4 2.
D.
2.
Lời giải
Chọn A
Áp dụng bất đẳng thức mô đun :
1 2 1 2
.
z z z z
Dấu bằng xảy ra
1 2
, 0 .
z kz k
Ta có:
2 2 2
2 1 1 2 1 2
z z z z z z
Với
2 2
1 2 2 1 0 1 2
z z z z z
Dấu bằng xảy ra khi và chỉ khi:
2
max
2
3 2 2
1 2
1 2
1 2
k
z
z z
z i
z k
Với
2 2
1 2 2 1 0 1 2
z z z z z
Dấu bằng xảy ra khi và chỉ khi:
1
min
2
3 2 2
2 1
2 1
2 1
m
z
z z
z i
z m
Vậy
2 2
2 2
1 2
2 1 2 1 6.
z z
Câu 60: (SGD Đà Nẵng 2119) Gọi
z
là số phức có môđun nhỏ nhất thỏa mãn điều kiện
2 8 17
z i
. Biết
,z a bi a b
, tính
2
2 3
m a b
A.
18
m
. B.
54
m
. C.
10
m
. D.
14
m
.
Lời giải
Chọn C
Gọi
;
M a b
là điểm biểu diễn số phức
,z a bi a b
.
Ta có:
2 2
2 8 17 2 8 17 17
z i a b IM
với
2;8
I
.
Suy ra:
M
thuộc đường tròn
C
có tâm
I
bán kính
17
R
.
Lại có:
2 2
2 8 2 17
OI R
nên
O
nằm ngoài
C
.
GTNN của môđun
z
là
min
min
z OM
17
OI R
1
.
Đẳng thức xảy ra khi
M OI C
và
M
nằm giữa
O
và
I
2
.
Từ
1
và
2
ta có
M
là trung điểm
OI
nên
1;4
M
.
Suy ra
1; 4
a b
. Khi đó:
2
2 3 2 12 10
m a b
.
Câu 61: (Nho Quan A - Ninh Bình - 2019) Xét các số phức
,z a bi a b
thỏa mãn
2 3 2 2
z i . Tính
2
P a b
khi
1 6 7 2
z i z i
đạt giá trị lớn nhất.
Toanthaycu.com
Trang 43
A.
3
P
. B.
3
P
. C.
1
P
. D.
7
P
.
Lời giải
Chọn B
Đặt
1; 6 , 7;2 8;8
A B AB
và trung điểm của
AB
là
3; 2
K
.
Gọi
;
M a b
là điểm biểu diễn số phức
z
ta có:
2 2
2 3 8
a b
.
M
thuộc đường tròn
C
có tâm
2;3
I
, bán kính
8
R .
Ta thấy
5; 5 . 0
IK IK AB I
nằm trên đường thẳng trung trực của
AB
.
Xét tam giác
2
2 2 2
2
2
AB
MAB MA MB MK
.
2
2 2 2 2 2 2
2 4 4
MA MB MK AB MA MB MA MB MK AB
.
Ta có
1 6 7 2
z i z i
là tổng khoảng cách từ điểm
M
trên đường tròn
C
tới hai điểm
A
và
B
.
Vậy
MA MB
lớn nhất khi:
max
MA MB
MK
. Điều này xảy ra khi
M
là giao điểm của
IK
với
đường tròn
C
và
M
nằm ngoài đoạn
IK
.
Ta có phương trình của đường thẳng
2
:
3
x t
IK
y t
.
Tọa độ giao điểm của
IK
với đường tròn
C
là nghiệm của hệ:
2
2 2
2
3 2 8 2
2 3 8
x t
y t t t
x y
.
Vậy điểm
M
cần tìm ứng với
2
t
khi đó
4
4;5 2 8 5 3
5
a
M P a b
b
Câu 62: (SGD Bắc Ninh 2019) Cho số phức
z
thỏa mãn
1 1 3 3 2
i z i
. Giá trị lớn nhất của biểu
thức
2 6 2 3
P z i z i
bằng
A.
5 6
. B.
15 1 6
. C.
6 5
. D.
10 3 15
.
Lời giải
Chọn C
(C)
A
B
I
N
K
M
Trang 44
Cách 1
1 1 3 3 2
i z i
1 3
1 3 2
1
i
i z
i
1 2 3 1
z i
.
Gọi
;
OM x y
,
1; 2
OI
là vec-tơ biểu diễn cho các số phức
z x iy
,
w 1 2
i
.
Từ
1
có
3
OM OI
3
MI
.
Suy ra
M
thuộc đường tròn
C
tâm
1;2
I
bán kính
3
R
,
2 3
: 1 2 9
C x y
Gọi
2; 1
OA
,
2;3
OB
lần lượt là vec-tơ biểu diễn cho số phức
2
a i
,
2 3
b i
.
Có
3; 3
IA
,
1;1
IB
. Suy ra
3 3 0
IA IB IA IB
.
Lúc đó 6 2. 3
P MA MB MA MB
2 2
3 3
MA MB
.
Có
2 2
2 2
3 3
MA MB IA IM IB IM
2 2 2
4 3
IM IA IB
.
Có
2
9
IM
,
2
18
IA
,
2
2
IB
, nên
2 2
3 60
MA MB
.
Suy ra
3.60 6 5
P .
Có
6 5
P
3
1
2
MA MB
.
Vậy giá trị lớn nhất của
P
là
6 5
P .
Cách 2.
Giả sử
;
M x y
là điểm biểu diễn của số phức
z
khi đó
2 2
1 1 3 3 2 1 3 3 2 2 4 4 0
i z i x y x y i x y x y
2 2
1 2 9
x y
. Do đó
M
thuộc đường tròn tâm
1;2
I
, bán kính
3
R
.
Đặt
1
2
a x
b y
Ta có
2 2
9
a b
. Gọi
2; 1
A
,
2;3
B
2 2 2 2
2 6 2 3 6 2 1 6 2 3
P z i z i MA MB x y x y
2 2 2 2
3 3 6 1 1 6 27 6 2 11
a b a b a b a b
6 27 2 6 33 1 2 27 33 6 5
a b a b
.
Toanthaycu.com
Trang 45
Câu 63: (Lômônôxốp - Hà Nội 2019) Cho số phức
z
thay đổi thỏa mãn
1 3
z i
. Giá trị nhỏ nhất
của biểu thức
2 4 5 1 7
A z i z i
bằng
a b
(với
,
a b
là các số nguyên tố). Tính
S a b
?
A.
20
. B.
18
. C.
24
. D.
17
.
Lời giải
Chọn B
Gọi
, ,z x yi x y
.
Ta có:
2 2
1 3 1 1 9
z i x y C
;
Suy ra, tập hợp tất cả các điểm biểu diễn số phức
z
là đường tròn
C
, có tâm là
1;1
I
và
bán kính
3
R
.
Ta có:
2 2 2 2
2 4 5 1 7 2 4 5 1 7
A z i z i x y x y
2 2 2 2 2 2
2 4 5 1 7 3 1 1 9
x y x y x y
2 2
2 2
2 4 5 4 8 4 20 29
x y x x y y
2 2
2 2
29
2 4 5 2 2 10
4
x y x x y y
2
2 2 2
5
2 4 5 1
2
x y x y
.
Gọi
;
M x y C
.
2 4 5 1 7 2 , 4; 5 ; 1;7
A z i z i MA MB A B
.
Trang 46
5
2 2 , 1;
2
A MA MB MA MC C
.
Ta có:
3 3
0;
2 2
C
IC IC R
.
Suy ra, điểm
C
nằm trong đường tròn
C
.
Vậy, đường thẳng
AC
cắt đường tròn
C
tại hai điểm.
Do đó, để
2
A MA MC
đạt giá trị nhỏ nhất thì
M
phải nằm giữa hai điểm
A
và
C
.
5 13
2 2 ,
2
A MA MC AC AC
.
5 13
A a b
.
Vậy,
18
a b
.
Câu 64: (Nguyễn Huệ- Ninh Bình- 2019)Cho
1 2
,
z z
là nghiệm phương trình
6 3 2 6 9
i iz z i
và thỏa mãn
1 2
8
5
z z
. Giá trị lớn nhất của
1 2
z z
bằng
A.
56
5
. B.
28
5
. C.
6
. D.
5
.
Lời giải
Chọn A
Gọi
1 1 1 2 2 2
,
z x y i z x y i
, với
1 1 2 2
, , ,x y x y
.
Do
1 2
8
5
z z
1 2 1 2
8
5
x x y y i
2 2
1 2 1 2
8
5
x x y y
Gọi
1 1 1
;
M x y
,
2 2 2
;
M x y
2 2
1 2 1 2 1 2
8
5
M M x x y y
.
Mà
1
z
là nghiệm phương trình
6 3 2 6 9
i iz z i
1 1 1 1
6 3 2 6 2 9
y x i x y i
2 2 2 2
1 1 1 1
6 3 2 6 2 9
y x x y
2 2
1 1 1 1
6 8 24 0
x y x y
1 1 1
;M x y
đường tròn
2 2
( ) : 6 8 24 0
C x y x y
.
Tương tự
2 2 2
;
M x y C
.
Đường tròn
( )
C
có tâm
3; 4
I
, bán kính
1
R
.
Goị
M
là trung điểm
1 2
M M
1 2
IM M M
,
2
2 2
1
4 3
1
5 5
IM R M M
, và
1 2
2
z z OM
.
Mà
OM OI IM
, dấu bằng xảy ra khi
, ,
O I M
thẳng hàng. Khi đó
1 2
OM M M
, và
28
5
OM OI IM
.
Toanthaycu.com
Trang 47
1 2
z z
đạt giá trị lớn nhất bằng
2 OI IM
, bằng
56
5
.
Hoặc đánh giá chọn đáp án như sau:
Gọi
2 2
;N x y
2 2
1 1 2 1 2 1 2
NM x x y y z z
Và
N
đối xứng với
2
M
qua gốc tọa độ
O
,
N
đường tròn
2 2
1
( ): 6 8 24 0C x y x y
.
1
( )C
có tâm
1
3; 4I
, bán kính
1
1R
,
1
( )C
đối xứng với
C
qua gốc tọa độ
O
.
Có
1
10I I
1 1
8I I R R
.
Nhận xét: với mọi điểm
1
M C
,
1
N C
thì
1 1 1
M N I I R R
. Loại các đáp án B,C,D
1 2 1
z z M N
đạt giá trị lớn nhất bằng
56
5
.
Câu 65: Cho các số phức
z
và
w
thỏa mãn
3 1
1
z
i z i
w
. Tìm giá trị lớn nhất
T w i
Trang 48
A.
2
2
. B.
3 2
2
. C.
2
. D.
1
2
.
Lời giải
Chọn B
3 1
1
z
i z i
w
3 1 1
1
z
z z i
w
2 2
3 1 1 .
1
z
z z
w
.
Đặt
t z
;
0
t
(vì
0
z
không thỏa phương trình trên).
(1) trở thành:
2 2
3 1 1
1
t
t t
w
2
1 .
10 8 2
t
w
t t
.
2
2
1 1 1
1 ; 0.
8 2 2
1
10
2 2 2
w t
t
t
t
.
Ta luôn có:
1
1 1 2
2
w i w i
3 2
.
2
w i
.
Dấu = xảy ra
1
2
1 1
3 2
2
t z
w k i
w i
1
2
3 1
2 2
z i
w i
.
Vậy: Giá trị lớn nhất của
3 2
.
2
T
.
Câu 66: Cho các số phức
z
thỏa mãn
2 2 2 3
z z
. Tìm giá trị nhỏ nhất của biểu thức
2 3 3 3 2 3
P z i z i z i
.
A.
12
. B.
6
. C.
8
. D.
10
.
Lời giải
Chọn A
Toanthaycu.com
Trang 49
Gọi
;
M x y
,
1
2;0
F
,
2
2;0
F
, lần lượt là điểm biểu diễn cho các số phức
z x yi
,
2
,
2
.
Có
2 2 2 3
z z
1 2
2 3
MF MF , có
1 2
2 3 2 2
F F .
Suy ra
;
M x y
chạy trên
E
có tiêu cự
2 2 2
c , độ dài trục lớn
2 2 3
a , độ dài trục nhỏ
2 2
b
và phương trình chính tắc của
E
là
2 2
1
3 1
x y
.
Có
3 3
;
1 1
x
M x y E
y
.
Có
2 3 3 3 2 3
P z i z i z i
.
2 2
2 2 2
2
2 3 1 3 3 2 3
x y x y x y .
2 2
2 2 2
2 3 1 3 3 2 3
x y x y y .
2
2
2 3 3 3 2 3 3 1
x x y y
(Bất đẳng thức tam giác).
2
4 12 84 3
y y y
.
Đặt
2
2 3 21 3
f y y y y
, với
1 1
y
.
Có
2
2 3
1
3 21
y
f y
y y
.
0
f y
2
3 21 2 3 1
y y y
,
Có
1 1 1
y
2
3 9 12 0
y y
1 nhaän
4 loaïi
y
y
.
Có
1 4 2 19
f
,
1 12
f
.
Suy ra
1;1
12
y
Min f y
12
P
.
Đẳng thức
1
xảy ra khi
0, 1
2 3 1
0
2
3 3
x y
x y
y
x
0, 1
x y
.
Thử lại: Khi
0, 1
x y
có
12
P
.
Vậy
12
MinP
khi
0, 1
x y
.
Câu 67: Cho số phức
z x yi
,
,x y
thỏa mãn
2
2
3 16
z y
. Biểu thức
2
P z i z
đạt giá
trị lớn nhất tại
0 0
;
x y
với
0 0
0, 0
x y
. Khi đó:
2 2
0 0
x y
bằng
A.
20 3 6
2
. B.
20 3 7
2
. C.
20 3 6
2
. D.
20 3 7
2
.
Lời giải
Trang 50
Chọn D
Ta có:
2
2 2 2
3 16 4 16
z y x y
.
2 2 2 2 2
2 2 2
1 2 1 2
P x y x y x y x y
2 2
2 1 5
x x y y
.
2
2
max
2 2
2 2
2 2
. 2 1
2 2 0
2 0
2 2 4 16 0
. 2 0
1 . 0
2 0
1 . 0
5
4 16
1 . 0
4 16
0
0
0
0
0
0
x y
x y x y
x y
x x
y y
x x
y y
x x
y y
P
x y
y y
x y
x
x
x
y
y
y
0
2 2
0 0
0
1 7
1 7
20 3 7
2
1 7
2
1 7
2
x
y
x y
y
x
.
Nhận xét: Bài này ta dùng bất đẳng thức véc tơ như sau
Cho
1 2 1 2 1 1 2 2
; , ; ;
a a a b b b a b a b a b
, ta có:
2 2
2 2 2 2
1 1 2 2 1 2 1 2
a b a b a b a b a a b b
.
Dấu “ = ” xãy ra
,
a b
ngược hướng
1 2 2 1
1 1
2 2
0
0
a b a b
a b
a b
.
Câu 68: Cho số phức
z a bi
,a b
thỏa mãn
4 4 10
z z
và
6
z
lớn nhất. Tính
S a b
.
A.
11
S
. B.
5
S
. C.
3
S
. D.
5
S
.
Lời giải
Chọn B
Trong mp tọa độ
Oxy
, Ta gọi các điểm biểu diễn của các số phức:
z x yi
là
;
M x y
;
4 0
z i
là
1
4;0
F
;
4 0
z i
là
2
4;0
F
.
Ta có:
4 4 10
z z
1 2
10
MF MF
. (1)
2
2 2
1
2 2
1 2 1 2
2
2 2
2
4
8
16
5
4
MF x y
x
MF MF x MF MF
MF x y
.(2)
Từ (1) và (2), suy ra
1
4
5
5
x
MF
.
Mặt khác
2
2 2
1
4
MF x y
2
2 2
2
2
4
5 4 1
5 25 9
x x y
x y
.
Vậy, tập hợp các điểm biểu diễn của số phức thỏa mãn
4 4 10
z z
là Elip có phương
trình
2 2
: 1
25 9
x y
E
.
Toanthaycu.com
Trang 51
Theo đề, ta cần tìm điểm thuộc
E
sau cho
6
z
lớn nhất.
Ta gọi các điểm biểu diễn số phức:
6 0
z i
là
6;0
A
;
z a bi
là
;
M a b E
;
5 0
z i
là
5;0
C
.
Do đó,
6
z
lớn nhất khi và chỉ khi
MA
lớn nhất.
Dựa, vào hình vẽ trên ta thấy để
MA
lớn nhất khi
5;0 5; 0 5
M C a b S
.
Câu 69: Cho số phức
,z a bi a b
thỏa
4 4 10
z z
và
6
z
lớn nhất. Tính
S a b
?
A.
3
S
. B.
5
S
. C.
5
S
. D.
11
S
.
Lời giải
Chọn C
Gọi
;
M a b
là điểm biểu diễn số phức
,z a bi a b
.
2 2
2 2
4 4 10 4 4 10
4 4 10 *
z z a bi a bi
a b a b
Xét
1
4;0
F
và
2
4;0
F
. Khi đó
1 2
* 10
MF MF
Suy ra
M
thuộc Elip có
2 2
4
3
2 10 5
c
b a c
a a
Ta có:
2
2
6 6 , 6;0
z a b IM I
, suy ra
max 6
z IA
hay điểm
5;0 5 0 5
M A z i S
.
Câu 70: Cho số phức
z
thỏa mãn
1
z
,
,
M m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu
thức
1 2 1
A z z
. Giá trị của biểu thức
M m
bằng
A.
2 5 2
. B.
6
. C.
2 5 4
. D.
7
.
Lời giải
Trang 52
Chọn A
Gọi
z x yi
với
,x y
.
2 2 2 2
1 1 1
z x y x y
2 2
2 2
1 2 1 1 2 1 2 2 2 2 2
A z z x y x y x x
.
Xét hàm số
2 2 2 2 2
f x x x
với
1;1
x
.
Hàm số
f x
liên tục trên đoạn
1;1
và
2
1 2 1 2 1
2 2 2 2
2 1
x x
f x
x x
x
.
3
0 1 2 1 0 1;1
5
f x x x x
.
Khi đó
1 4
f
;
3
2 5
5
f
;
1 2
f
.
Do đó
1;1
1;1
3
max 2 5 ; min 1 2
5
M f x f m f x f
. Suy ra
2 5 2
M m
.
Câu 71: Xét tập hợp
S
các số phức
,z x yi x y
thỏa mãn điều kiện
3 1 2 2
z z i i
.
Biểu thức
2
Q z z x
đạt giá trị lớn nhất là
M
và đạt được tại
0 0 0
z x y i
( khi
z
thay
đổi trong tập
S
). Tính giá trị
2
0 0
. .
T M x y
A.
9 3
2
T
. B.
9 3
4
T
. C.
9 3
2
T
. D.
9 3
4
T
.
Lời giải
Chọn D
Ta có:
2 2 2 2 2 2
3 1 2 2 4 16 16 4 4 4 4
z z i i x y x y y x
Do đó,
2 2
2 4 2 4 2 , 2 2 .
Q z z x y x x x f x x
2
2
2 2 4
, 2 2 .
4
1
0 1.
2 2 ; 2
x x
f x x
x
x
f x x
x
Mặt khác,
2 0, 2 0, 1 3 3.
f f f
Suy ra
3 3
M
tại
2
0 0
3
1, .
4
x y
Vậy
9 3
.
4
T
Câu 72: (THPT Hậu Lộc 2 2019) Cho
1 2
,
z z
là hai trong các số phức thỏa mãn
3 3 2
z i
và
1 2
4
z z
. Giá trị lớn nhất của
1 2
z z
bằng
A.
8
. B.
4 3
. C.
4
. D.
2 2 3
.
Toanthaycu.com
Trang 53
Lời giải
Chọn A
Gọi
, M N
lần lượt là điểm biểu diễn của hai số phức
1 2
, z z
.
Do
1 2
1 2
3 3 3 3 2
4
z i z i
z z
nên
2
2
2
, N : 3 3 2
4 2.2
M C x y
MN
.
Như vậy
MN
là đường kính của đường tròn
C
với tâm
3; 3I
, bán kính
2R
, do đó
I
là trung điểm
MN
,
O 12I
.
Ta có
2
2 2 2
1 2
1 1 2 2O 8
2
MN
z z OM ON OM ON I
.
Dấu
" "
xảy ra khi và chỉ khi
OM ON MN
là đường kính của
C
vuông góc với
OI
.
Câu 73: (Chuyên Lê Hồng Phong Nam Định 2019) Cho hai số phức
1
z
,
2
z
thỏa mãn
1 1
2 4 7 6 2z i z i
và
2
1 2 1iz i
. Tìm giá trị nhỏ nhất của biểu thức
1 2
T z z
.
A.
2 2 1
. B.
2 1
. C.
2 2 1
. D.
2 1
.
Lời giải
Chọn C
Trên mặt phẳng
Oxy
, gọi
;M a b
là điểm biểu diễn cho số phức
1
z
;
2;1A
,
4;7B
lần lượt
là điểm biểu cho các số phức
2 i
và
4 7i
6 2AB
.
Từ đó ta được
6 2MA MB AB
nên tập hợp các điểm
M
biểu diễn cho số phức
1
z
là đoạn
thẳng
AB
nằm trên đường thẳng
: 3 0d x y
.
Đặt
3 2
z z
, khi đó
Trang 54
2 3 3
1 2 1 1 2 1 2 1
iz i iz i z i
. Gọi
;
N c d
là điểm biểu diễn cho
3
z
;
2;1
I
là điểm biểu diễn cho số phức
2
i
, khi đó
1
IN
nên tập hợp các điểm biểu diễn cho số
phức
3
z
là đường tròn
2 2
: 2 1 1
C x y
.
1 2 1 3
z z z z MN
.
Dễ thấy hình chiếu vuông góc của điểm
2;1
I
trên đường thẳng
d
là điểm
0;3
K
thuộc
đoạn
AB
suy ra
MN KH
với
H
là giao điểm của
IK
với
C
và thuộc đoạn
IK
.
Do đó
min , 2 2 1
MN KH d I AB R
. Vậy
1 2
min 2 2 1
z z
Câu 74: (Trường Thpt Hàm Rồng 2019) Cho số phức
1 2
, ,
z z z
thỏa mãn
1 2
4 5 1 1
z i z
và
4 8 4
z i z i
. Tính
1 2
z z
khi
1 2
P z z z z
đạt giá trị nhỏ nhất
A.
8
B.
6
. C.
41
. D.
2 5
.
Lời giải
Chọn D
Gọi
A
là điểm biểu diễn của số phức
1
z
. Suy ra
A
thuộc đường tròn
1
C
tâm
1
4;5 , 1
I R
.
Gọi
B
là điểm biểu diễn của số phức
2
z
. Suy ra
B
thuộc đường tròn
2
C
tâm
2
1;0 , 1
I R
.
Gọi
;
M x y
là điểm biểu diễn của số phức
z x yi
Theo giả thiết
4 8 4
z i z i
4
x y
. Suy ra M thuộc đường thẳng
4 0
d x y
Gọi
2
'
C
có tâm
2
' 4; 3 , 1
I R
là đường tròn đối xứng với đường tròn
2
C
tâm
2 2
1;0 , 1
I R
qua đường thẳng d. Gọi
'
B
là điểm đối xứng với đối xứng với
B
qua đường
thẳng d. Ta có
1 2 1 2 1 2
' ' ' 6
P z z z z MA MB MA MB AB I I R R
.
Toanthaycu.com
Trang 55
Dấu = xảy ra khi và chỉ khi
1 2
, ', , ',
A B I I M
thẳng hàng. Khi đó
1 1 2
1
'
8
I A I I
suy ra
4;4
A
và
2 2 1
1
' '
8
I B I I
suy ra
' 4; 2 2;0
B B
.
2 5
AB
.
Vậy
1 2
2 5
z z
.
Câu 75: (Chuyên ĐH Vinh- 2019) Cho các số phức
z
và
thỏa mãn
2 1 .
z
i z i
Tìm giá trị
lớn nhất của
1
T i
A.
4 2
3
B.
2
3
C.
2 2
3
D.
2
Lời giải
Chọn A
2
2 2
2
2 2
2 2
2
2 1 2 1 .
2 1 1 2 1 1
5 2 2
2 4
0 ' ' 0 0 2
5 2 2
5 2 2
z z
i z i i z i
z
z z
z z i z z
z z
t t t
f t t f t f t t t
t t
t t
Bảng biến thiên
Ta có
2 4 2
1 1 2
9 3
T i z i
Câu 76: Cho số phức
z
và gọi
1
z
,
2
z
là hai nghiệm phức của phương trình
2
8 0
z i
(
1
z
có phần thực
dương). Giá trị nhỏ nhất của biểu thức
2
1 2 1
2
2
z
P z z z z z z
được viết dưới dạng
m n p q
(trong đó
,n p
;
m
,
q
là các số nguyên tố). Tổng
m n p q
bằng
A.
3
. B.
4
. C.
0
. D.
2
.
Lời giải
Chọn A
2
8 0
z i
1
2 2
z i
và
2
2 2
z i
.
Trang 56
1 2 11 2 1
2 2
2
2
2
2
P z z z z z z z z z MA MB M
z z
z
C
z z
.
Trong đó ,
2; 2
A
,
2;2
B ,
3; 3
C
lần lượt là điểm biểu diễn cho các số phức
z
,
1
z
,
2
z
,
2
1
2 3 3
2
i
z
z
.
Gọi
H
là hình chiếu vuông góc của
M
trên
OC
.
Ta có
MA MB HA HB
MA MB MC HA HB HC
.
Do đó
min
min
P MA MB MC HA HB HC
M H
:
M OC y x
.
Gỉa sử
;
M x x
3;0
x
2
2 3 2 2 4
P MA MB MC x x
2
2 2 2.
4
x
P
x
0
P
2 3
3;0
3
x
.
Vậy
2
min
2 3 2 3
2 3 2 2 4 2 6 3 2
3 3
P
.
Suy ra
2
m
,
6
n
,
3
p
,
2
q
3
m n p q
.
Câu 77: Trong các số phức
z
thỏa mãn
2
1 2
z z
gọi
1
z
và
2
z
lần lượt là các số phức có môđun nhỏ
nhất và lớn nhất. Giá trị của biểu thức
2 2
1 2
z z
bằng
A.
6
. B.
2 2
. C.
4 2
. D.
2
.
Lời giải
Chọn A
Đặt
; ,z a bi a b
.
2
2 2 2 2 2 2 2
1 1 2 1 4
z a b abi a b a b
;
2 2
2 2
z a b
.
Ta có
2
2 2 2 2 2 2 2
1 2 1 4 4
z z a b a b a b
2 2
2 2 2 2 2 2 2 2 2 2 2 2
4 2 1 4 0 2 6 1 0
a b a b a b a b a b a b
2
2 2 2 2 2
6 1 4
a b a b a
.
Vì
2
4 0,a a
nên
2
2 2 2 2 2 2
6 1 0 3 2 2 3 2 2
a b a b a b
.
M
Toanthaycu.com
Trang 57
Suy ra
2 2 2 2
2 1
2 1 2 1 6.
2 1
m
a b m M
M
2 2
0
0
2 1 .
1 2
3 2 2
a
a
M
b
a b
2 2
0
0
2 1 .
2 1
3 2 2
a
a
m
b
a b
Câu 78: (Sở Nam Định - 2019) Xét các số phức
w
,
z
thỏa mãn
3 5
w
5
i
và
5 2 4
w i z
.
Tìm giá trị lớn nhất của biểu thức
2 6 2
P z i z i
.
A.
7
. B.
2 53
. C.
2 58
. D.
4 13
.
Lời giải
Chọn C
Cách 1.
Ta có:
5 2 4 5 5 2 4 5
w i z w i i z i
5 5 2 4 5 5 1 2 4 1 2 5 3 2
w i i z i w i i z i z i
3 5
5. 5 3 2 3 2 3
5
z i z i
.
Ta có:
2 2 2 2
1 1 1 1
2 ; ,
z z z z z z z z
. (1)
2
2 2
1
1 1
; ,
2
z z
z z z z
. (2)
Ta có:
2 6 2 3 2 3 3 2 3
P z i z i z i z i
.
Áp dụng (1) và (2), ta có:
2 2 2
3 2 3 3 2 3 2 3 2 9
z i z i z i
.
2 2
2 2
3 2 3 3 2 3 2 6 2
3 2 3 3 2 3
2 2
z i z i z i z i
z i z i
.
Vậy, ta có:
2
2
2 2
2 6 2
2 3 2 9 2 6 2 4 3 2 9
2
z i z i
z i z i z i z i
.
2
2
4 3 2 9
P z i
.
Do
2 2
4 3 2 9 4 3 2 4 9
z i z i i
nên
2
2
4 3 2 4 9
P z i i
Trang 58
2 2
4 7 9 232 2 58
P P
.
Cách 2.
Ta có:
5 2 4
w i z
thay
3 5
w
5
i
3 2 3
z i
.
Suy ra, tập hợp các điểm biểu diễn số phức
z
là đường tròn
2 2
: 3 2 9
C x y
.
Gọi
M C
.
Ta có:
2 6 2 ; 0;2 , 6;2
P z i z i AM BM A B
.
Suy ra
2 2
2P AM BM .
Gọi
H
là trung điểm của cạnh
AB
.
Ta có:
2
2 2 2 2 2
2 2 2 4
2
AB
P AM BM MH MH AB
.
Vậy,
2 6 2
P z i z i
đạt giá trị lớn nhất khi
2
MH
đạt giá trị lớn nhất.
Dựa vào hình vẽ sau
Suy ra,
2
MH
đạt giá trị lớn nhất khi
'
M M
2
232 2 58
P P
.
Câu 79: Cho các số phức
1
z
,
2
z
,
3
z
thỏa mãn
1 2 3
1
z z z
.
Tính giá trị lớn nhất của biểu thức
2 2 2
1 2 2 3 3 1
P z z z z z z
.
A.
9
P
. B.
10
P
. C.
8
P
. D.
12
P
.
Lời giải
Chọn A
Gọi
1 1
;
A x y
;
2 2
;
B x y
;
3 3
;
C x y
là các điểm lần lượt biễu diễn các số phức
1
z
;
2
z
;
3
z
.
Toanthaycu.com
Trang 59
vì
1 2 3
1
z z z
suy ra
A
;
B
;
C
thuộc đường tròn tâm
O
bán kính bằng 1.
Ta có
1 2
z z AB
;
2 3
z z BC
3 1
z z AC
.
Suy ra
2 2 2
1 2 2 3 3 1
P z z z z z z
2 2 2
AB BC AC
2 2 2
AO OB BO OC AO OC
6 2 . . .
OA OB OB OC OA OC
2
9
OA OB OC
2
9 3
OG
2
9 9
OG
( với
G
là trọng tâm tam giác
ABC
).
Dấu “ = “ xảy ra khi
G O
, hay
ABC
đều.
Câu 80: Cho số phức
z
thỏa mãn
3 2 12.
z z z z
Gọi
,
M m
lần lượt là giá trị lớn nhất, nhỏ nhất
của
4 3 .
z i
Giá trị của
.
M m
bằng:
A.
28
. B.
24
. C.
26 .
D.
20
.
Lời giải
Chọn B
Gọi
; ; .
z x yi x y
Xét
3 2 12 3 2 6. (1)
z z z z x y
Ta có:
2 2
4 3 4 3 2
P z i x y
Tập hợp những điểm biểu diễn
; ; .
z x yi x y
thỏa mãn (1) là miền trong (tính cả biên)
của hình thoi
ABCD
với
0;3
A
;
2;0
B
;
0; 3
C
;
2;0
D
tạo bởi 4 đường thẳng
3 2 6.
x y
Điểm biểu diễn
z
thỏa mãn (2) là đường tròn tâm
4; 3
I
bán kính
0
R P
.
Trang 60
P
đạt min, max khi bán kính đường tròn đạt min, max khi xét sự tương giao với miền hình thoi
.
ABCD
Ta có đường tròn giao với miền hình thoi điểm gần tâm nhất khi đường tròn tiếp xúc cạnh CD:
3 2 6 0
x y
tương ứng có
2 2
3.4 2.3 6
12
.
13
3 2
m
Điểm giao xa nhất là đỉnh
0;3
A
của hình thoi. Do đó
2 2
4 6 2 13.
M
. 24.
M m
| 1/60
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

toanthaycu.com
CHUYÊN ĐỀ CỰC TRỊ SỐ PHỨC
(TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH GIỎI MỨC 9-10 ĐIỂM)
A. MỘT SỐ TÍNH CHẤT CẦN NHỚ.
1. Môđun của số phức:Số phức z  a  bi được biểu diễn bởi điểm M(a; b) trên mặt phẳng Oxy. Độ 
dài của véctơ OM được gọi là môđun của số phức z. Kí hiệu 2 2 z = a + bi = a + b  Tính chất   2 2
z  a  b  zz  OM  z  0, z
  , z  0  z  0  z z z.z '  z . z '  
, z '  0  z  z '  z  z '  z  z ' z ' z '  kz  k . z , k   2  Chú ý: 2 2 2 2 2 2 2 2 2 2 2
z  a  b  2abi  (a  b )  4a b  a  b  z  z  z.z . Lưu ý:
 z  z  z  z dấu bằng xảy ra  z  kz k  0 1 2   1 2 1 2
 z  z  z  z dấu bằng xảy ra  z  kz k  0 . 1 2   1 2 1 2
 z  z  z  z dấu bằng xảy ra  z  kz k  0 1 2   1 2 1 2
 z  z  z  z dấu bằng xảy ra  z  kz k  0 1 2   1 2 1 2  2 2 z  z  z  z  2 2 2 z  z 1 2 1 2 1 2  2  2 z  z z  z z  
2.Một số quỹ tích nên nhớ Biểu thức liên hệ x, y Quỹ tích điểm M ax  by  c  0 (1) (1)Đường thẳng :  ax  by  c  0
z  a  bi  z  c  di (2)
(2) Đường trung trực đoạn AB với Aa,b,Bc,d   2   2 2 x a y b  R hoặc Đường tròn tâm I  ; a b , bán kính R z  a  bi  R   2   2 2 x a y b  R hoặc Hình tròn tâm I  ; a b , bán kính R z  a  bi  R
   2    2 2 2 r x a y b  R hoặc
Hình vành khăn giới hạn bởi hai đường tròn đồng tâm I  ;
a b , bán kính lần lượt là r, R r  z  a  bi  R 2  y  ax  bx  c Parabol  c  0 2 x  ay  by  c x  a2  y  c2  1 Elip  1 1 hoặc 2 2   b d
2 Elip nếu 2a  AB , Aa ,b ,B a ,b 1 1   2 2
z  a  b i  z  a  b i  2a 1 1 2 2 Đoạn AB nếu 2a  AB x  a2  y  c2 Hypebol  1 2 2 b d
B. MỘT SỐ DẠNG TOÁN THƯỜNG GẶP
Dạng 1: Quỹ tích điểm biểu diễn số phức là đường thẳng.
TQ1: Cho số phức z thỏa mãn z  a  bi  z , tìm z . Khi đó ta có Min
 Quỹ tích điểm M  ;
x y biểu diễn số phức z là đường trung trực đoạn OA với A ; a b  1 1 2 2 z  z  a  b  0 Min   2 2  a b z   i  2 2
TQ2: Cho số phức thỏa mãn điều kiện z  a  bi  z  c  di . Tìm z . Ta có min
 Quỹ tích điểm M  ;
x y biểu diễn số phức z là đường trung trực đoạn AB với A ; a b, B ; c d  2 2 2 2 a  b  c  d  z  d O, AB  Min
2 a  c2  b  d 2
Lưu ý: Đề bài có thể suy biến bài toán thành 1 số dạng, khi đó ta cần thực hiện biến đổi để đưa về dạng cơ bản. Ví dụ 1:
 Cho số phức thỏa mãn điều kiện z  a  bi  z  c  di . Khi đó ta biến đổi
z  a  bi  z  c  di  z  a  bi  z  c  di .
 Cho số phức thỏa mãn điều kiện iz  a  bi  z  c  di . Khi đó ta biến đổi a  bi c  di
iz  a  bi  iz  c  di  z   z 
 z  b  ai  z  d  ci . i i
Dạng 2: Quỹ tích điểm biểu diễn số phức là đường tròn.
TQ: Cho số phức z thỏa mãn điều kiện z  a  bi  R  0 z  z  R . Tìm z , z . Ta có 0  Max Min
 Quỹ tích điểm M  ;
x y biểu diễn số phức z là đường tròn tâm I  ; a b bán kính R 2 2  z
 OI  R  a  b  R  z  R 0   Max  2 2  z
 OI  R  a  b  R  z  R 0 Min 
Lưu ý: Đề bài có thể cho ở dạng khác, ta cần thực hiện các phép biến đổi để đưa về dạng cơ bản. a  bi R
Ví dụ 1: Cho số phức z thỏa mãn điều kiện iz  a  bi  R  z   (Chia hai vế cho i ) i i  z  b  ai  R
Ví dụ 2: Cho số phức z thỏa mãn điều kiện z  a  bi  R  z  a  bi  R (Lấy liên hợp 2 vế) a  bi R R
Ví dụ 3: Cho số phức z thỏa mãn điều kiện c  di z  a  bi  R  z    2 2 c  di c  di c  d z R Hay viết gọn 1 z z  z  R  z   (Chia cả hai vế cho z ) 0 1 z z 0 0 0
Dạng 3: Quỹ tích điểm biểu diễn số phức là Elip. Trang 2 Toanthaycu.com
TQ1: (Elip chính tắc). Cho số phức z thỏa mãn điều kiện z  c  z  c  2a ,a  c Khi đó ta có 2 2 x y
 Quỹ tích điểm M  ;
x y biểu diễn số phức z là Elip:  1 2 2 2 a a  c  z  a   Max  2 2  z  a  c  Min
TQ2: (Elip không chính tắc). Cho số phức z thỏa mãn điều kiện z  z  z  z  2a 1 2 Thỏa mãn 2a  z  z . 1 2
Khi đó ta thực hiện phép biến đổi để đưa Elip về dạng chính tắc Ta có
Khi đề cho Elip dạng không chính tắc z  z  z  z  2a , z  z  2a và z , z  c, ci ). Tìm 1 2  1 2  1 2
Max, Min của P  z  z . 0  z  z  2c Đặt 1 2  2 2 2 b   a  c z  z P  a Nếu 1 2 z   0 Max 0 (dạng chính tắc) 2 P  b  Min  z  z  z  z 1 2 z   a  1 2 P  z   a Nếu 0   2 Max 0  2   z  z  k z  z  z  z 0 1  0 2  1 2 P  z   a Min 0  2  z  z z  z 1 2 z   a  1 2 P  z   a Nếu 0  2 Max 0 2 z  z  k z  z  0 1  0 2 Nếu z  z  z  z z  z 0 1 0 2 1 2 P  z   b Min 0 2 C. BÀI TẬP ÁP DỤNG
Câu 1: Cho số phức z thoả mãn z  2  3i  1. Tìm giá trị lớn nhất của z 1 i . A. 13  3. B. 13  5. C. 13 1. D. 13  6 . Lời giải Chọn C Ta có 2
1  z  2  3i   z  2  3i . z  2  3i   z  2  3i z  2  3i
 1  z  2  3iz  2  3i  z  2  3i 1  z 1 i  3 2i 1(*) .
+Đặt w  z 1 i , khi đó  w  3  2i  1 . Trang 3
Tập hợp các điểm biểu diễn số phức w  z 1 i là đường tròn I; 
1 và w là khoảng cách từ
gốc tọa độ đến 1 điểm trên đường tròn. Do đó giá trị lớn nhất của w chính là đoạn OQ 2 2  w
 1 3  2  1 13 . max
Nhận xét: Ở đây ta sử dụng kiến thức sau: 2 z.z  z , z .z  z . z 1 2 1 2
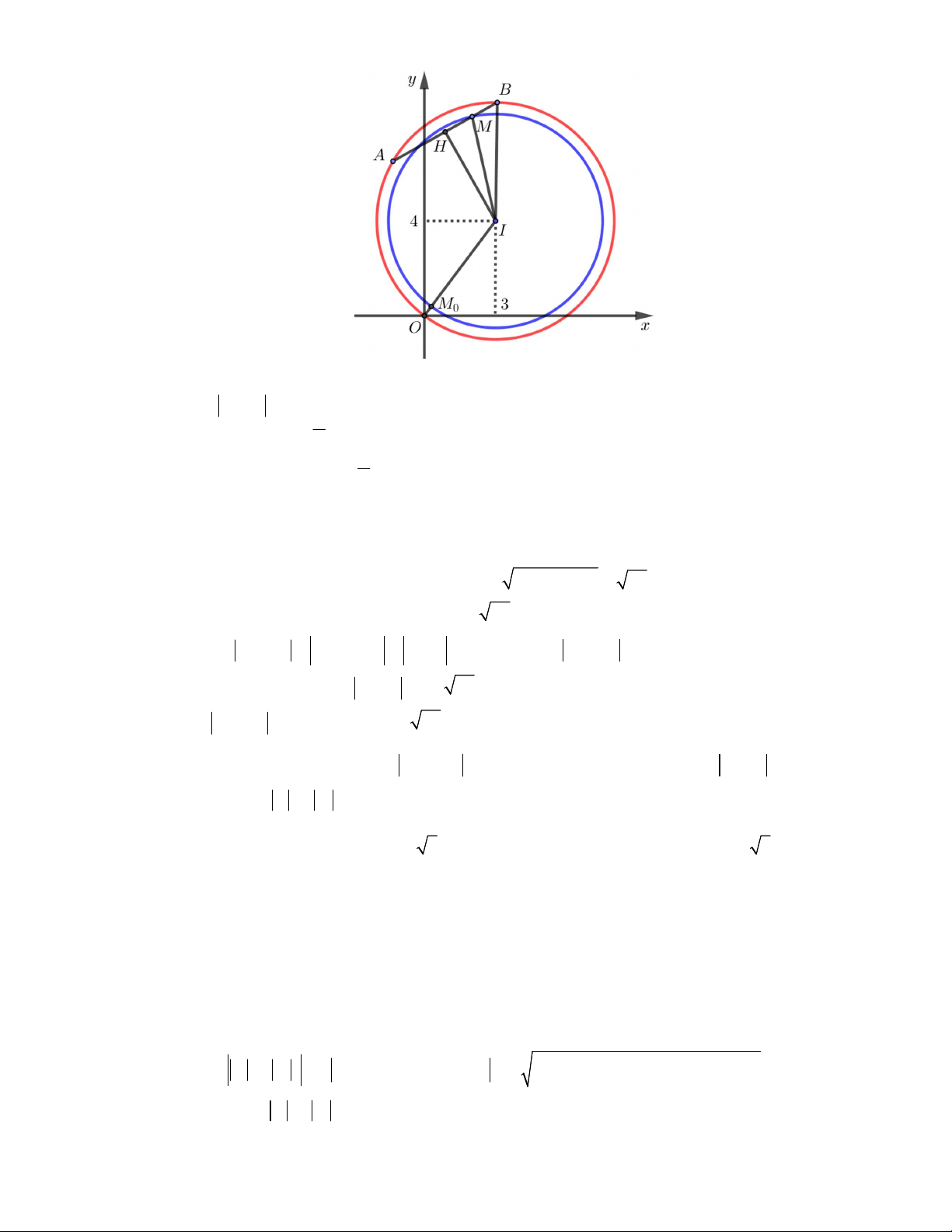
Câu 2: (Chuyên Hạ Long 2019) Cho số phức z thỏa mãn z  6  z  6  20 . Gọi M , n lần lượt là
môđun lớn nhất và nhỏ nhất của z. Tính M  n A. M  n  2 . B. M  n  4 . C. M  n  7 . D. M  n  14 . Lời giải
Gọi z  x  yi ,  x, y   . Theo giả thiết, ta có z  6  z  6  20 .
 x  6  yi  x  6  yi  20  x  2  y  x  2 2 2 6 6  y  20    .
Gọi M  x; y , F 6;0 và F 6;0 . 2   1   Khi đó  
  MF  MF  20  F F  12 nên tập hợp các điểm E là đường elip E có hai 1 2 1 2
tiêu điểm F và F . Và độ dài trục lớn bằng 20 . 1 2
Ta có c  6 ; 2a  20  a  10 và 2 2 2
b  a  c  64  b  8. 2 2 x y
Do đó, phương trình chính tắc của E là   1. 100 64 Suy ra '
max z  OA  OA  10 khi z  10 và '
min z  OB  OB  8 khi z  8i . Vậy M  n  2 .
* Nhận xét: Ở trên ta đã sử dụng định nghĩa (E) để nhận dạng được phưng trình elip
Câu 3: (Đề Tham Khảo 2018) Xét số phức z  a  bi  ,
a b thỏa mãn z  4  3i  5 . Tính
P  a  b khi z 1 3i  z 1 i đạt giá trị lớn nhất. A. P  8 B. P  10 C. P  4 D. P  6 Lời giải Chọn B Gọi M  ;
a b là điểm biểu diễn của số phức z.
Theo giả thiết ta có: z   i 
 a  2  b  2 4 3 5 4
3  5  Tập hợp điểm biểu diễn số
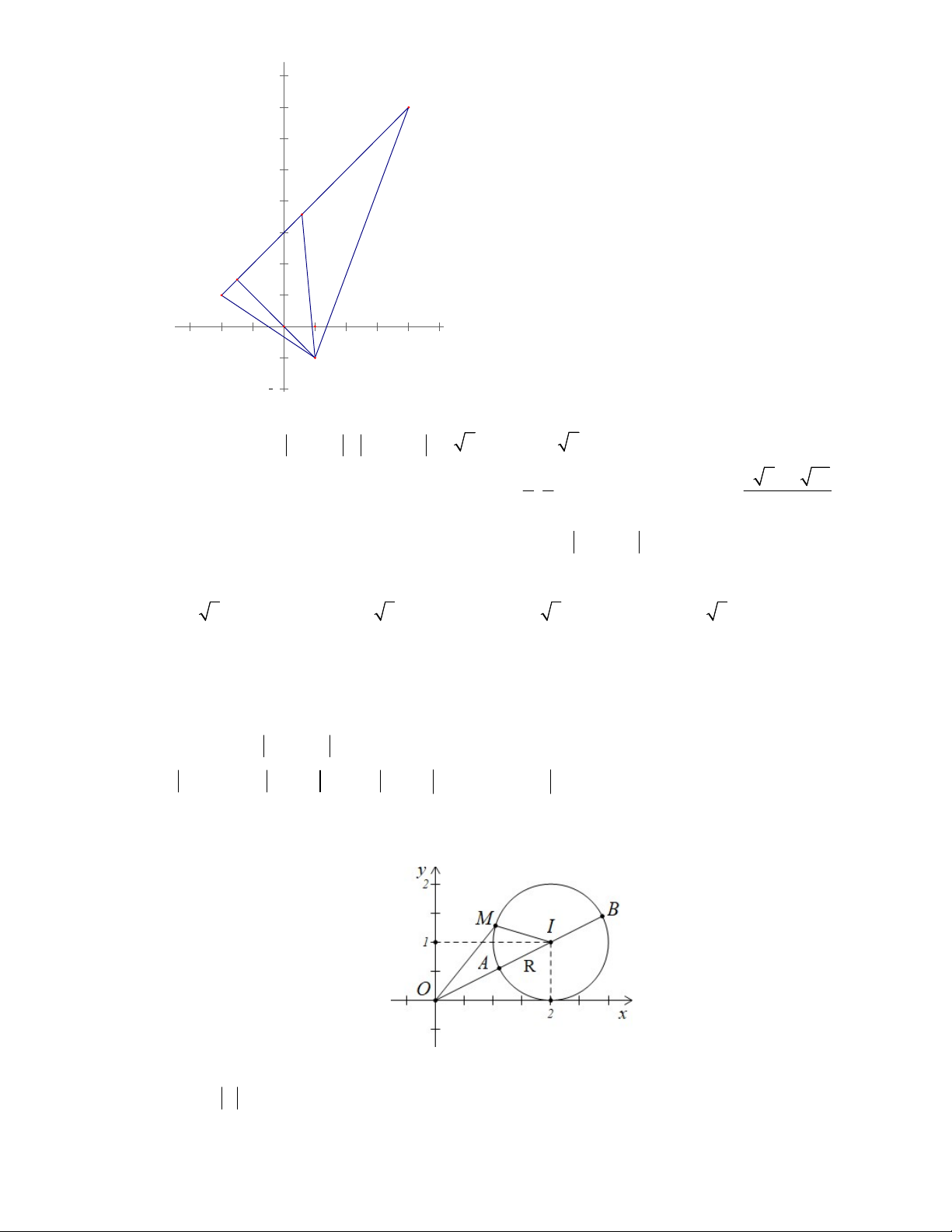
phức z là đường tròn tâm I 4;  3 bán kính R  5 A  1;3 Gọi: 
     Q  z 1 3i  z 1 i  MA  MB B 1; 1 Trang 4 Toanthaycu.com
Gọi E là trung điểm của AB, kéo dài EI cắt đường tròn tại D Ta có: 2 2 2 Q  MA  MB  2M . A MB 2 2 2 2 2
 Q  MA  MB  MA  MB   2 2 2 MA  MB 
Vì ME là trung tuyến trong MAB 2 2 2 2 MA  MB AB AB 2 2 2 2  ME    MA  MB  2ME  2 4 2 2   2 2 AB 2 2  Q  22ME 
  4ME  AB . Mặt khác ME  DE  EI  ID  2 5  5  3 5 2    Q   2 2 4. 3 5  20  200 MA  MB  Q 10 2  Q 10 2  max M   D   4  2(x  4) x  6  EI  2 D D ID    
 M 6;4  P  a  b 10 2  2(y  3) y  4  D  D
Cách 2:Đặt z  a  b .i Theo giả thiết ta có: a  2  b  2 4 5  5. a  4  5 sint Đặt  . Khi đó: b   3  5 cost
Q  z   i  z   i  a  2  b  2  a  2  b  2 1 3 1 1 3 1 1   t  2  t   t  2   t  2 2 5 sin 5 5cos 5 sin 3 5 cos 4
 30 10 5 sin t  30  2 5 3sin t  4cost
Áp dụng BĐT Bunhiacopski ta có:
Q  260  8 5 2sint  cost  260  8 5. 5  200 10 2  Q 10 2  Q 10 2 max  2 sin t   5 a  6 Dấu bằng xảy ra khi     P  a  b 10. 1 b    4 cost   5
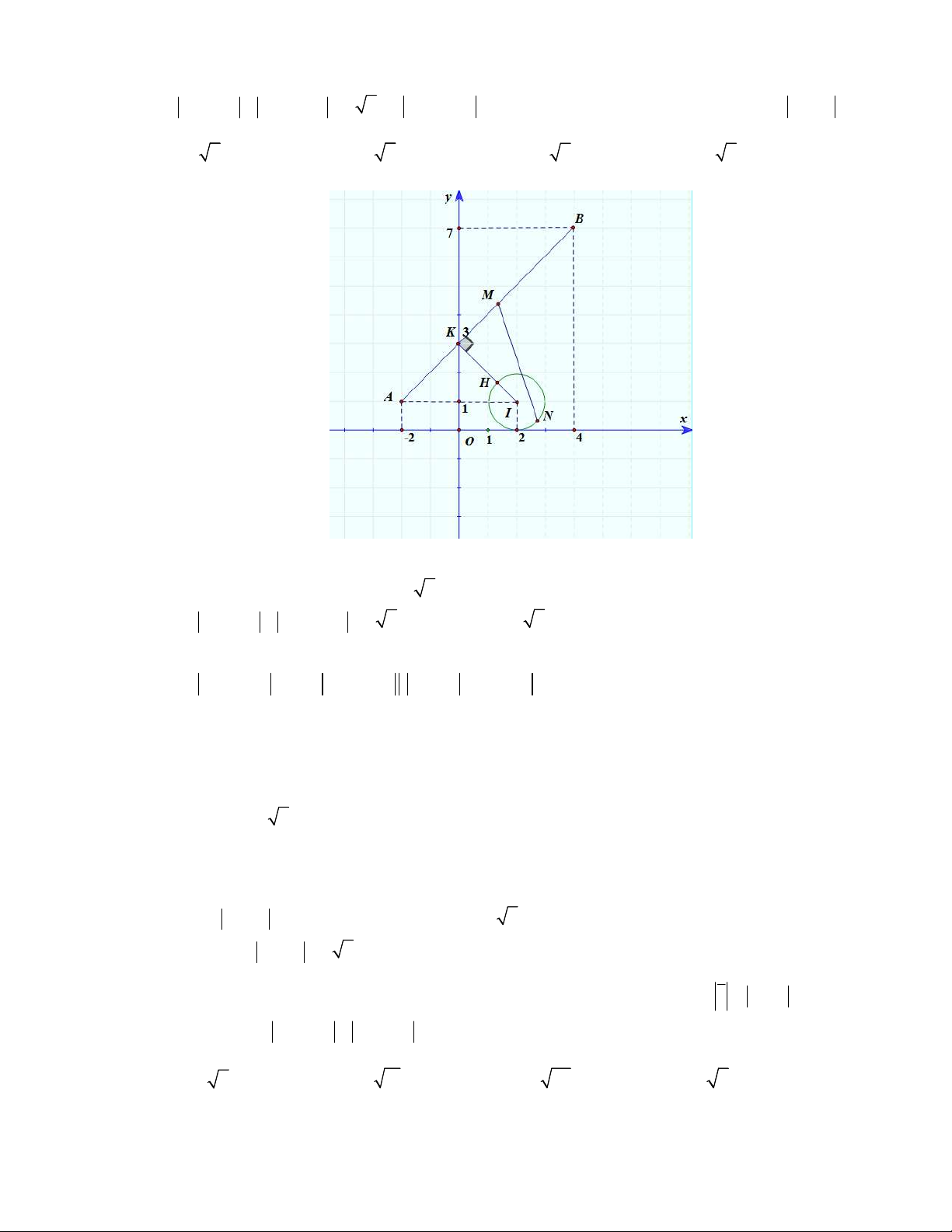
Câu 4: (Đề Tham Khảo 2017) Xét số phức z thỏa mãn z  2  i  z  4  7i  6 2. Gọi m, M lần
lượt là giá trị nhỏ nhất và giá trị lớn nhất của z 1 i . Tính P  m  M . 5 2  2 73 5 2  73 A. P  B. P  5 2  73 C. P  D. P  13  73 2 2 Lời giải Chọn A Trang 5 8 D 6 4 A 2 H E 5 N 2
Gọi A là điểm biểu diễn số phức z , E  2  ; 
1 , F 4;7 và N 1;  1 .
Từ AE  A F  z  2  i  z  4  7i  6 2 và EF  6 2 nên ta có A thuộc đoạn thẳng EF .  3 3  5 2  2 73
Gọi H là hình chiếu của N lên EF , ta có H  ; 
 . Suy ra P  NH  NF  .  2 2  2
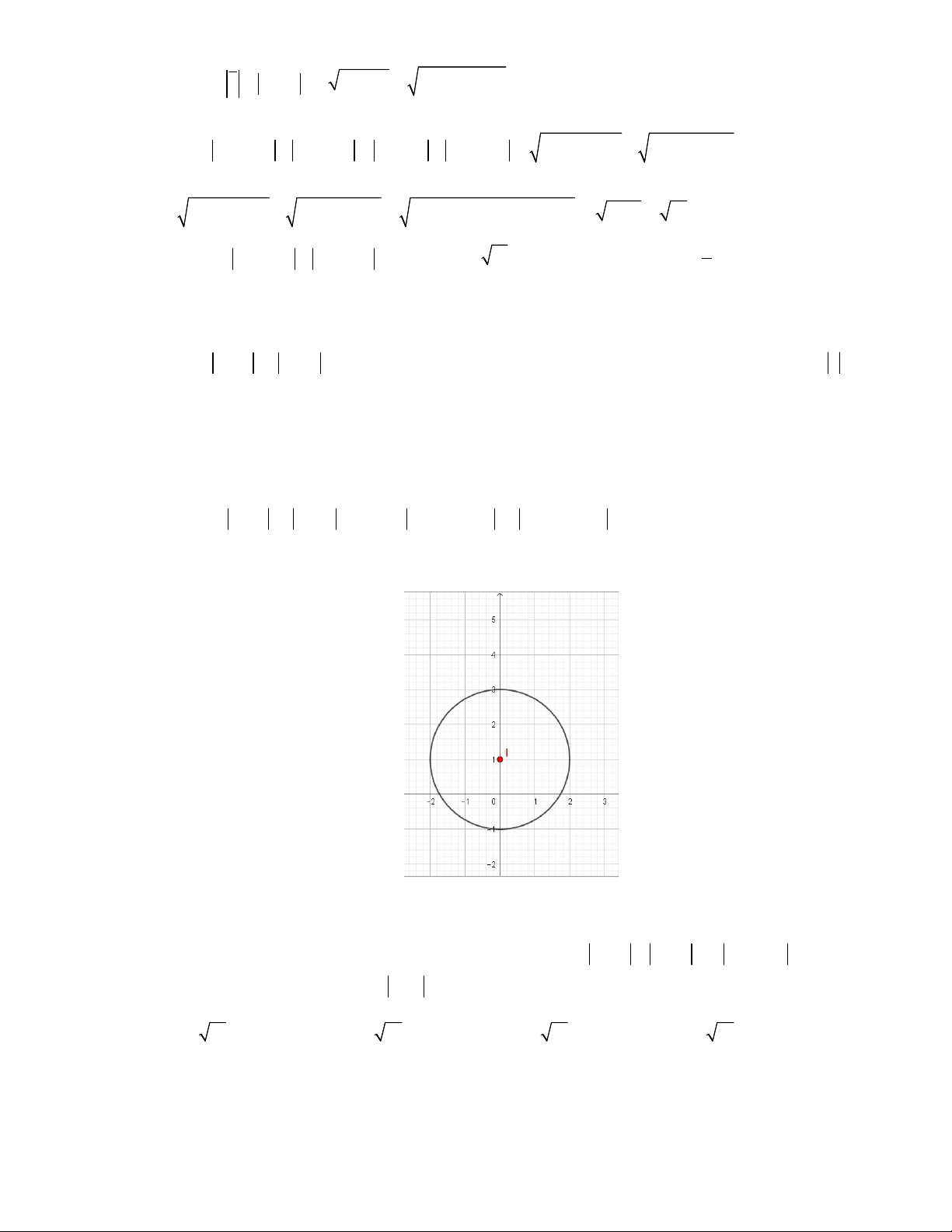
Câu 5: (THPT Cẩm Giàng 2 2019) Cho số phức z thỏa mãn z  2  2i 1. Số phức z  i có môđun nhỏ nhất là: A. 5  2 . B. 5 1. C. 5 1. D. 5  2 . Lời giải Cách 1:
Đặt w  z  i  z  w  i . Gọi M  ;
x y là điểm biểu diễn hình học của số phức . w
Từ giả thiết z  2  2i  1 ta được:
w  i  2  2i 1  w  2  i  1  x  2   y  
1 i  1   x  2   y  2 2 1  1.
Suy ra tập hợp những điểm M  ;
x y biểu diễn cho số phức w là đường tròn C có tâm I 2;  1 bán kính R 1.
Giả sử OI cắt đường tròn C tại hai điểm ,
A B với A nằm trong đoạn thẳng OI . Ta có w  OM
Mà OM  MI  OI  OM  MI  OA  AI  OM  OA Trang 6 Toanthaycu.com
Nên w nhỏ nhất bằng OA  OI  IA  5 1 khi M  . A Cách 2:
Từ z  2  2i 1  a  2  b  2 2
2  1 với z  a  bi a,b a  2  sin ;
x b  2  cos x  a  2  sin , x b  2  cos x
Khi đó: z  i  2  sin x  2  cos xi  i    x2    x2 2 sin 1 cos
 6  4sin x  2cos x    2 2   2 2 6 4 2 sin x  cos x      2 6 2 5 5 1  5 1  2 5 4cos x  2sin x s  in x    
Nên z  i nhỏ nhất bằng 5 1 khi 5   
4sin x  2cos x  2 5   5 cos x   5  2 5   5  Ta được z   2     2  i  5   5      Cách 3:
Sử dụng bất đẳng thức z  z  z  z  z  z 1 2 1 2 1 2
z  i   z  2  2i  2  i  z  2  2i  2  i  5 1
Câu 6: (THPT Gia Lộc Hải Dương 2019) Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất 2z  i M của P  với z z  . Tính tỉ số . z
là số phức khác 0 và thỏa mãn 2 m M M 4 M 5 M A.  3 . B.  . C.  . D.  2 . m m 3 m 3 m Lời giải 2z  i 2z  i 2z  i 2z  i 1 1 3 5 Ta có P     P   2   P  2    P  . z z z z z z 2 2 M 5 Vậy  . m 3
Câu 7: Xét tất cả các số phức z thỏa mãn z 3i  4 1. Giá trị nhỏ nhất của 2 z  7  24i nằm trong khoảng nào? A. 0;1009 . B. 1009;2018 . C. 2018;4036 . D. 4036; . Lời giải Chọn B
Ta có 1  z  3i  4  z  3i  4  z  5  1
  z  5 1 4  z  6 . Đặt 2
z  4  3i  z  5, z  7  24i . 0 0 0 2 2 2 2 Ta có 2 2 2 A  z   i  z  z   2 2 7 24 z  z z  z
 z  z  z z  z z  z z o  o o 2 4 4 2 . . 2 . o o   o  o Trang 7
Mà  z  z z  z  2 2
 1 z.z  z .z  1 z  z o o o o o Suy ra A  z  z    z  z 2 2 4 4 2 2 4 2 1  2 . z z  2 z  2 z 1201. o o o Hàm số 4 2
y  2t  2t 1201 đồng biến trên 4;6 nên 4 2
A  2.4  2.4 1201  1681.  z  4 
Dấu bằng xảy ra khi và chỉ khi  .  z  4  3i  1  Do đó 2
z  7  24i nằm trong khoảng 1009;2018 .
Câu 8: (Chuyen Phan Bội Châu Nghệ An 2019) Cho số phức z thỏa mãn z  z  z  z  4 . Gọi M, m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của P  z  2  2i . Đặt A  M  m . Mệnh đề nào sau đây là đúng? A. A 34;6. B. A6; 42 .
C. A2 7; 33. D. A4;3 3. Lời giải Chọn A
Giả sử: z  x  yi, , x y    N  ;
x y : điểm biểu diễn của số phức z trên mặt phẳng tọa độ Oxy . Ta có:
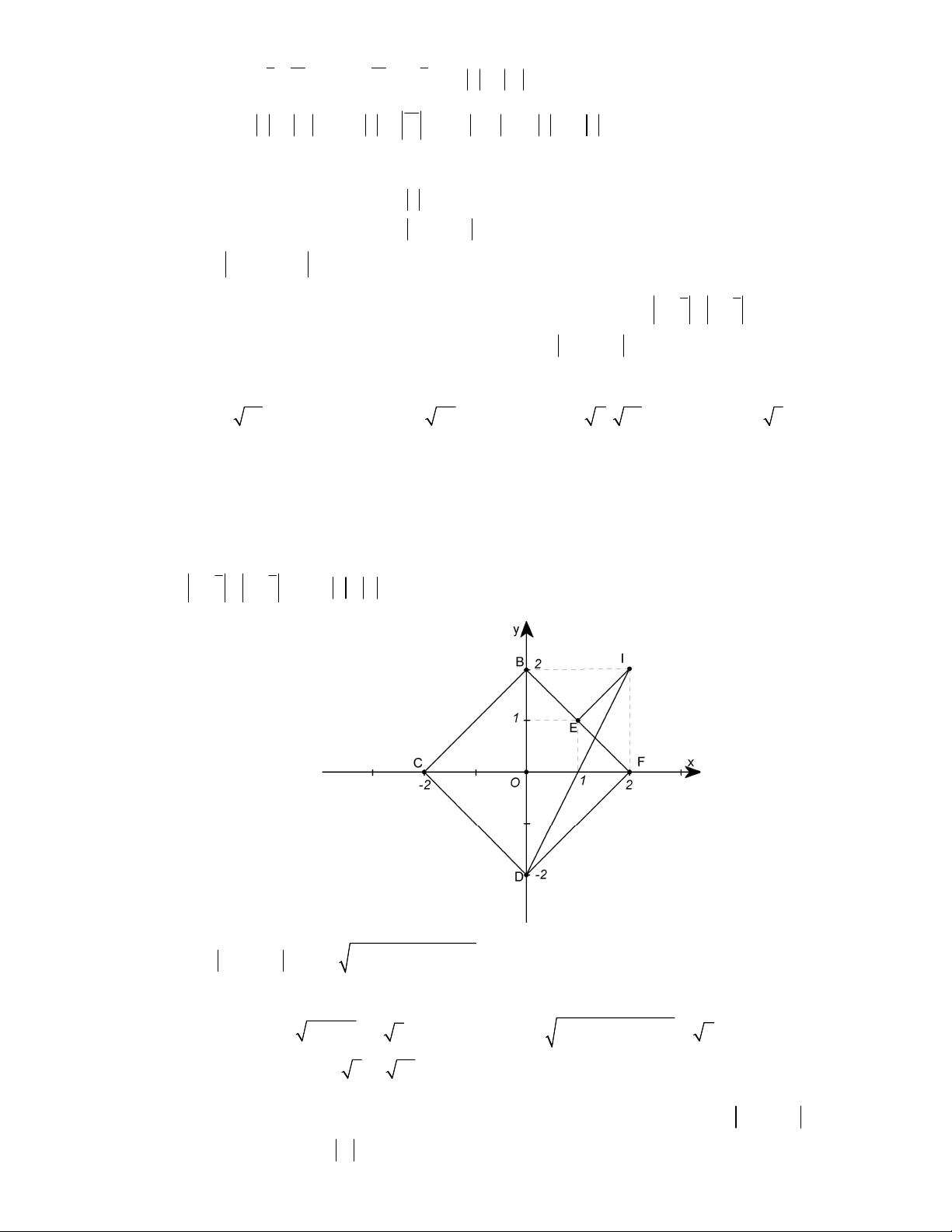
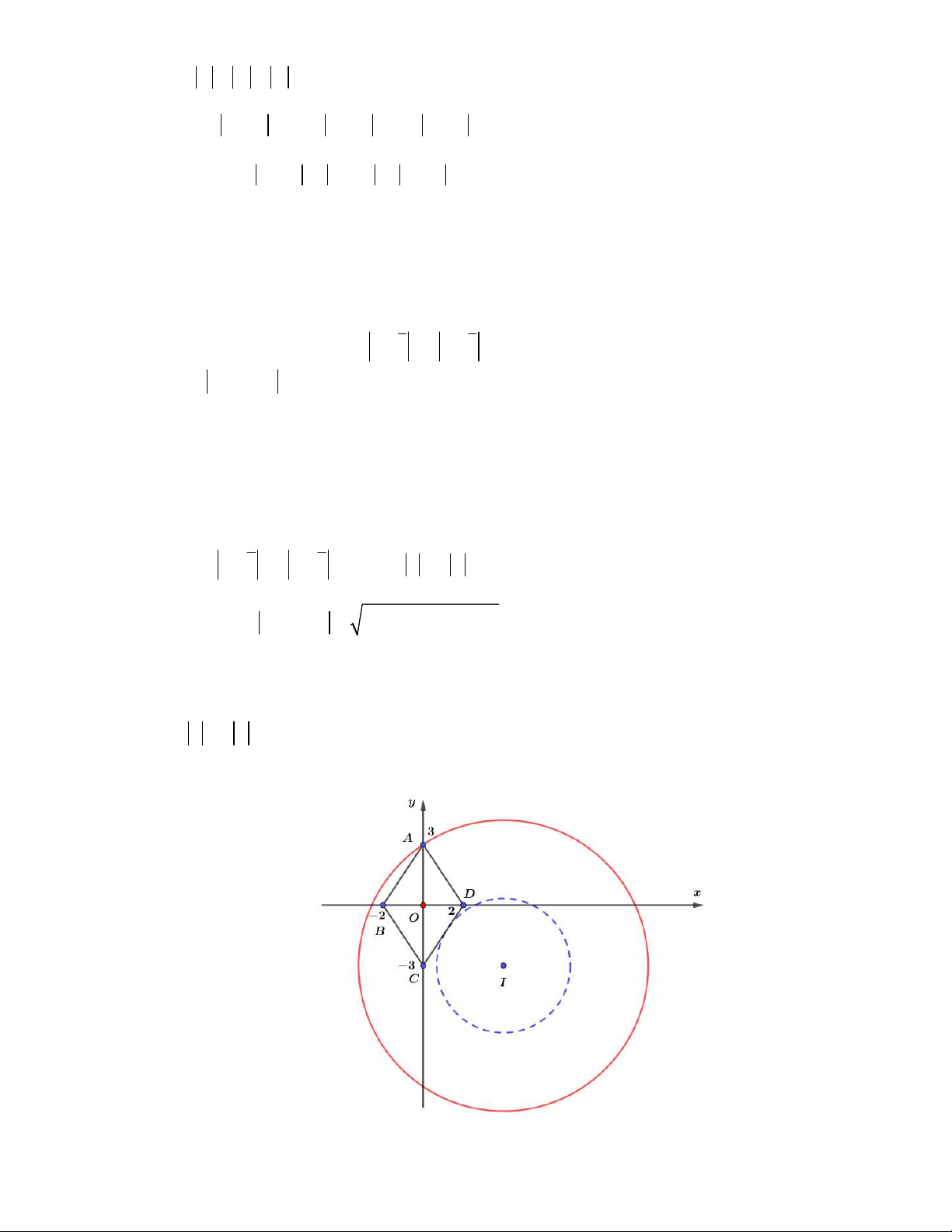
• z  z  z  z  4  x  y  2 N thuộc các cạnh của hình vuông BCDF (hình vẽ). y 2 I B 1 E C F x O 1 -2 2 D -2
• P  z   i  P   x  2   y  2 2 2 2
2  P  d I; N  với I 2;2 Từ hình ta có: E 1;  1 2 2 M  P
 ID  4  2  2 5 và m  P  IE  2 1  2 1  2 min  2  2 max
Vậy, A  M  m  2  2 5  34;6.
Câu 9: (THPT Quang Trung Đống Đa Hà Nội 2019) Cho số phức z thỏa mãn z  3  4i  2và
w  2z 1 i . Khi đó w có giá trị lớn nhất bằng Trang 8 Toanthaycu.com A. 4  74 . B. 2  130 . C. 4  130 . D. 16  74 . Lời giải Chọn C
Theo bất đẳng thức tam giác ta có
w  2z 1 i  2z  6  8i  7  9i  2z  6  8i  7  9i  4  130 .
Vậy giá trị lớn nhất của w là 4 130 .
Câu 10: (THPT Quang Trung Đống Đa Hà Nội 2019) Xét số phức z và số phức liên hợp của nó có
điểm biểu diễn là M và M . Số phức z 4  3i và số phức liên hợp của nó có điểm biểu diễn
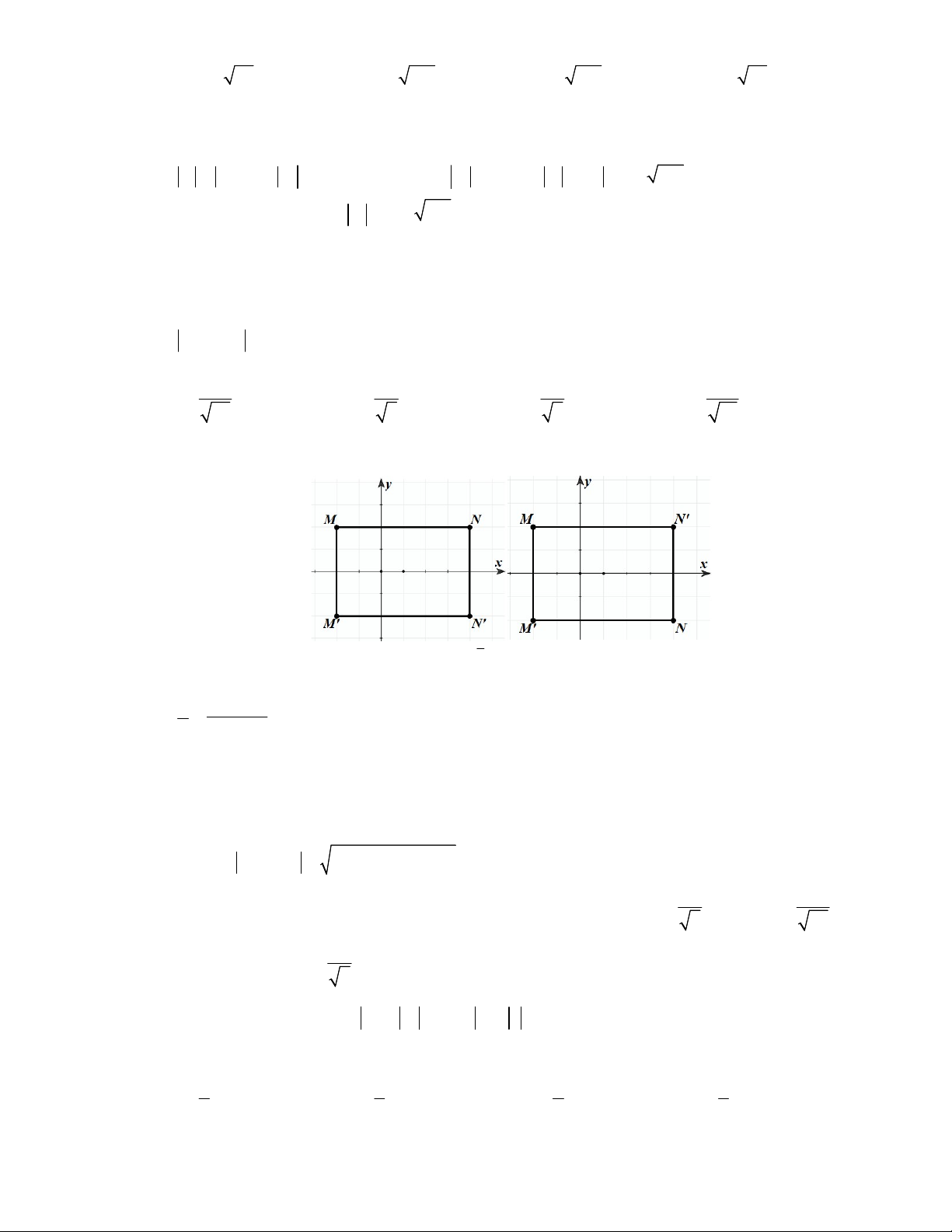
là N và N. Biết rằng M , M , N , N là bốn đỉnh của hình chữ nhật. Tìm giá trị nhỏ nhất của z  4i  5 . 5 2 1 4 A. . B. . C. . D. . 34 5 2 13 Lời giải Chọn C
Gọi z  x  yi , trong đó x, y   . Khi đó z  x yi, M  ;
x y , M  x; y .
Ta đặt w  z 4  3i   x  yi4  3i  4x  3y  3x  4yi  N 4x  3 ; y 3x  4y. Khi đó
w  z 4  3i  4x  3 y   3x  4 yi  N 4x  3y; 3x  4 y  .
Ta có M và M ; N và N từng cặp đối xứng nhau qua trục Ox . Do đó, để chúng tạo thành
một hình chữ nhật thì y  y y  y      M N hoặc M N . Suy ra y 3x 4 y hoặc y 3x 4 y . Vậy tập
hợp các điểm M là hai đường thẳng: d : x  y  0 d :3x 5y  0 1 và 2 .
Đặt P  z  i    x  2   y  2 4 5 5
4 . Ta có P  MA với A5; 4   . 1 5 P  MA  MA  d ; A d hoặc MA  d  ; A d . Mà d  ; A d  d ; A d  1  ,  2  , 2  min min  1 2 34 1 vậy P  d ; A d  min  1 . 2
Câu 11: Biết số phức z thỏa mãn iz 3  z  2 i và z có giá trị nhỏ nhất. Phần thực của số phức z bằng: 2 1 2 1 A. . B. . C.  . D.  . 5 5 5 5 Lời giải Chọn D Trang 9
Đặt z  x  yi ( x , y ). Khi đó
iz 3  z  2 i  x  y  2  x  2   y  2 2 3 2
1  x  2y 1 0  x  2  y 1   1 . Lại có 2 2 z  x  y 2 . Thay   1 vào 2 ta được: 2  2  1 5 2 2
z  x  y   y  2 2 2 1  y 2  5y  4y 1  5 y       5  5 5 2
Dấu đẳng thức xảy ra khi y   2 0  y   . 5 5 2 1 Thay y   vào   1 suy ra x   . 5 5 1
Vậy phần thực của số phức z là  . 5
Câu 12: (Chuyên Nguyễn Trãi Hải Dương -2019) Xét các số phức z thỏa mãn z 1 3i  2 . Số phức z mà z 1 nhỏ nhất là A. z 1 5i . B. z 1 i . C. z 1 3i . D. z 1 i . Lời giải
Gọi z  x  yi , x, y   . Khi đó M  ;
x y là điểm biểu diễn của số phức z .
Theo bài ra ta có z   i    x  2   y  2 1 3 2 1 3  4 .
Suy ra tập hợp điểm M là đường tròn tâm I 1;  3 bán kính R  2 .
Khi đó z    x  2 2 1 1  y  I M  với I1; 0 . z 1 nhỏ nhất khi I M
 ngắn nhất hay I , M , I thẳng hàng, M nằm giữa I và I . Trang 10 Toanthaycu.com
Phương trình đường thẳng II  là x  1.
Tọa độ giao điểm của đường thẳng II với đường tròn tâm I bán kính R  2 là M 1; 1 và 1   M 1; 5 . 1  
Thử lại ta thấy M 1; 1 thỏa mãn. Vậy z 1 i . 1  
Câu 13: (Chuyên Phan Bội Châu -2019) Cho số phức z thỏa mãn z  z  z  z  4. Gọi M , m lần
lượt là giá trị lớn nhất và giá trị nhỏ nhất của P  z  2  2i . Đặt A  M  . m Mệnh đề nào sau đây là đúng? A. A  34;6. B. A6; 42 .
C. A 2 7; 33. D. A 4;3 3  . Lời giải Chọn A
Đặt z  x  iy và gọi M  ;
x y là điểm biểu diễn của z  x  iy
ta có: z  z  z  z  4  x  y  2 Gọi A2;2 và P  MA
* Theo hình vẽ, min P  d  ,
A , với  : x  y  2 2  2  2 và min P   2 2 2 2
max P  AE  2  4  2 5, với E 0; 2  
Vậy M  m  2  2 5  5,88
Câu 14: (Chuyên Lê Quý Đôn Điện Biên 2019) Trong các số phức z thỏa mãn z 1 i  z  1 2i ,
số phức z có mô đun nhỏ nhất có phần ảo là 3 3 3 3 A. . B. . C.  . D.  . 10 5 5 10 Lời giải
Gọi z  x  yi ,  x, y   được biểu diễn bởi điểm M  x; y.
z 1 i  z 1 2i   x   1   y   1 i   x   1   y  2i
 x  2   y  2   x  2   y  2 3 1 1 1 2
 4x  2y  3  0  y  2  x  . 2 Cách 1: Trang 11 2 2  3  9  3  9 3 5 2 2 2 2 z  x  y  x  2  x   5x  6x   5 x    , x      .  2  4  5  20 10 3 5 3 3 Suy ra min z  khi x   ; y   . 10 5 10 3
Vậy phần ảo của số phức z có mô đun nhỏ nhất là  . 10 Cách 2:
Trên mặt phẳng tọa độ Oxy , tập hợp điểm biểu diễn số phức z là đường thẳng d : 4x  2y  3  0 .
Ta có z  OM . z nhỏ nhất  OM nhỏ nhất  M là hình chiếu của O trên d .
Phương trình đường thẳng OM đi qua O và vuông góc với d là: x  2y  0 .  3 x   4x  2y  3  0 
Tọa độ của M là nghiệm của hệ phương trình: 5    x  2y  0 3 y    10  3 3   3 3 M  ;    . Hay z    i .  5 10  5 10 3
Vậy phần ảo của số phức z có mô đun nhỏ nhất là  . 10
Nhận xét: Ta có thể tìm tập hợp điểm biểu diễn số phức z như sau:
z 1 i  z 1 2i  z  1 i  z   1   2i   *
Gọi M biểu diễn số phức z , điểm A1; 
1 biểu diễn số phức 1  i , điểm B 1  ; 2 biểu
diễn số phức 1  2i . Khi đó  
*  MA  MB . Suy ra tập hợp điểm biểu diễn số phức z là đường trung trực của
đoạn thẳng AB có phương trình d : 4x  2y  3  0 . z  i z  i
Câu 15: Cho hai số phức z , z thỏa mãn 1 2  1;
 2 . Giá trị nhỏ nhất của z  z là 1 2 z  2  3i z 1 i 1 2 1 2 A. 2 2 . B. 2 . C. 1. D. 2 1. Lời giải Chọn A
Giả sử z  x  y i với x ; y   . Khi đó: 1 1 1 1 1 z  i 1
 1  z  i  z  2  3i  x  y 1 i  x  2  y  3 i 1 1 1  1   1   1  z  2  3i 1
 x   y 1  x  2  y  3  x  y  3  0 . 1 2  1 2  1 2 2 1 1 2
 Quỹ tích điểm M biểu diễn số phức z là đường thẳng  : x  y  3  0 . 1
Giả sử z  x  y i với x ; y   . Ta có: 2 2 2 2 2 z  i 2
 2  z  i  2 z 1 i  x  y 1 i  2 x 1  y 1 i 2 2 2  2   2   2  z 1 i 2 Trang 12 Toanthaycu.com  x   y  2 1  2  x  2 1   y  2 2 2 2
1  x  y  4x  2 y  3  0 . 2 2 2 2 2 2 2 2
 Quỹ tích điểm N biểu diễn số phức z là đường tròn C 2 2
: x  y  4x  2y  3  0 có tâm 2 I 2;  1 và bán kính R    2 2 2 1  3  2 . 2  1   3
Khoảng cách từ I đến  là: d I;   
 3 2  R  đường thẳng  và đường 1   2 2 1
tròn C không có điểm chung.
Quỹ tích các điểm biểu diễn số phức z  z là đoạn thẳng MN .  z  z nhỏ nhất khi và chỉ 1 2 1 2 khi MN nhỏ nhất. I N' N M M' Dễ thấy MN  3 2  2  2 2 . min
Câu 16: (Sở Bình Phước 2019) Gọi S là tập hợp các số phức z thỏa mãn z 1  34 và
z 1 mi  z  m  2i , (trong đó m   ). Gọi z , z là hai số phức thuộc S sao cho z  z 1 2 1 2
lớn nhất, khi đó giá trị của z  z bằng 1 2 A. 2 B. 10 C. 2 D. 130 Lời giải Chọn A
Đặt z  x  yi ,  x, y  . Khi đó
z 1  34   x  2 2
1  y  34 ; z 1 mi  z  m  2i  2m  
1 x  22  m y  3  0 .
Do đó tập hợp các điểm M biểu diễn số phức z là giao điểm của đường tròn C x  2 2 :
1  y  34 và đường thẳng d : 2m  
1 x  22  m y  3  0.
Gọi A, B là hai điểm biểu diễn z và z . Suy ra C  d   , A  B . 1 2
Mặt khác z  z  AB  2R  2 34 do đó max z  z  2 34  AB  2R  I 1;0  d . 1 2   1 2 1 z  6  3i
Từ đó ta có m   nên d :3x  5y  3  0 1   . 2 z  4  3i  2 Vậy z  z  2 . 1 2 Trang 13
Câu 17: Cho hai số phức z , w thỏa mãn z  3 2  2 , w  4 2i  2 2 . Biết rằng z  w đạt giá trị
nhỏ nhất khi z  z , w  w . Tính 3z  w . 0 0 0 0 A. 2 2 . B. 4 2 . C. 1. D. 6 2 . Lời giải
Ta có: + z  3 2  2 , suy ra tập hợp điểm biểu diễn M biểu diễn số phức z là đường tròn có
tâm I 3 2 ;0, bán kính r  2 .
+ w  4 2i  2 2 , suy ra tập hợp điểm biểu diễn N biểu diễn số phức w là đường tròn có tâm
J 0;4 2  , bán kính R  2 2 .
Ta có min z  w  min MN .
+ IJ  5 2; IM  r  2; NJ  R  2 2 .
Mặt khác IM  MN  NJ  IJ  MN  IJ  IM  NJ hay MN  5 2  2  2 2  2 2 .
Suy ra min MN  2 2 khi I , M , N, J thẳng hàng và M , N nằm giữa I , J (Hình vẽ). Cách 1:  
 1   3 
Khi đó ta có: 3z  w  3OM  ON và IN  3 2  IM  IJ; IN  IJ . 0 0 5 5
    3       1    3 
Mặt khác ON  OI  IN  OI  IJ ; 3OM  3OI  IM   3 OI  IJ  3OI  IJ   . 5  5  5  
 3   3  
Suy ra 3z  w  3OM  ON  3OI  IJ  OI  IJ  2OI  6 2 . 0 0   5  5  Cách 2:     
Ta có IN  3IM  3IM  IN  0 .       
Do đó 3z  w  3OM  ON  3 OI  IM  OI  IN  2OI  2.OI  2.3 2  6 2. 0 0     Cách 3:  12 2 x   IM   1 M   5 12 2 4 2 +) IM  IJ  IM  IJ    z   i . 0 IJ 5  4 2 5 5 y  M  5 Trang 14 Toanthaycu.com  6 2 x   IN   3 N   5 6 2 12 2 +) IN  IJ  IN  IJ    w   i . 0 IJ 5  12 2 5 5 y  N  5
Suy ra 3z  w  6 2  6 2 . 0 0
Câu 18: Cho hai số phức z và w thỏa mãn z  2w  8  6i và z  w  4. Giá trị lớn nhất của biểu thức z  w bằng A. 4 6. B. 2 26. C. 66. D. 3 6. Lời giải Chọn C
   
Giả sử M , N lần lượt là các điểm biểu diễn cho z và .
w Suy ra OM  ON  OF  2OI,
z  w  MN  4 và OF  2OI 10. a
Đặt z  ON  ; w  OM  .
b Dựng hình bình hành OMFE 2 E F I N a O b M 2 2 2 a  b ME   25  2 4 264 Ta có 2 2   a  2b  2 2 2 b   ME a 3  16  2 4 2   2  a    z w   b     1 1 2 2 a  2b    66    2   4 2  2 66
Suy ra a  b  66, dấu “=” xảy ra khi a  b  . 3 Vậy a  b  66. max
Câu 19: Cho số phức z thoả mãn z  1. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 2
P  z 1  z  z 1 . Tính M.m 13 3 39 13 A. . B. . C. 3 3 . D. . 4 4 4 Lời giải Chọn A Thay 2 z  1 vào P ta có Trang 15 2 P  z 1  z  z 1 2 2  z 1  z  z  z 2  z 1  z  z  .
z z  z 1  z z  z 1  z 1  z  z 1 . Mặt khác 2 z 1   z   1 z   1  2  z  z .
Đặt t  z  z do z  1 nên điều kiện t 2;2.
Suy ra P  t  2  t 1 .
Xét hàm số f t  t  2  t 1 với t 2;2. f t 1 
1 với t 1. Suy ra f t  0 với t 1. 2 t  2 7 f t 1 
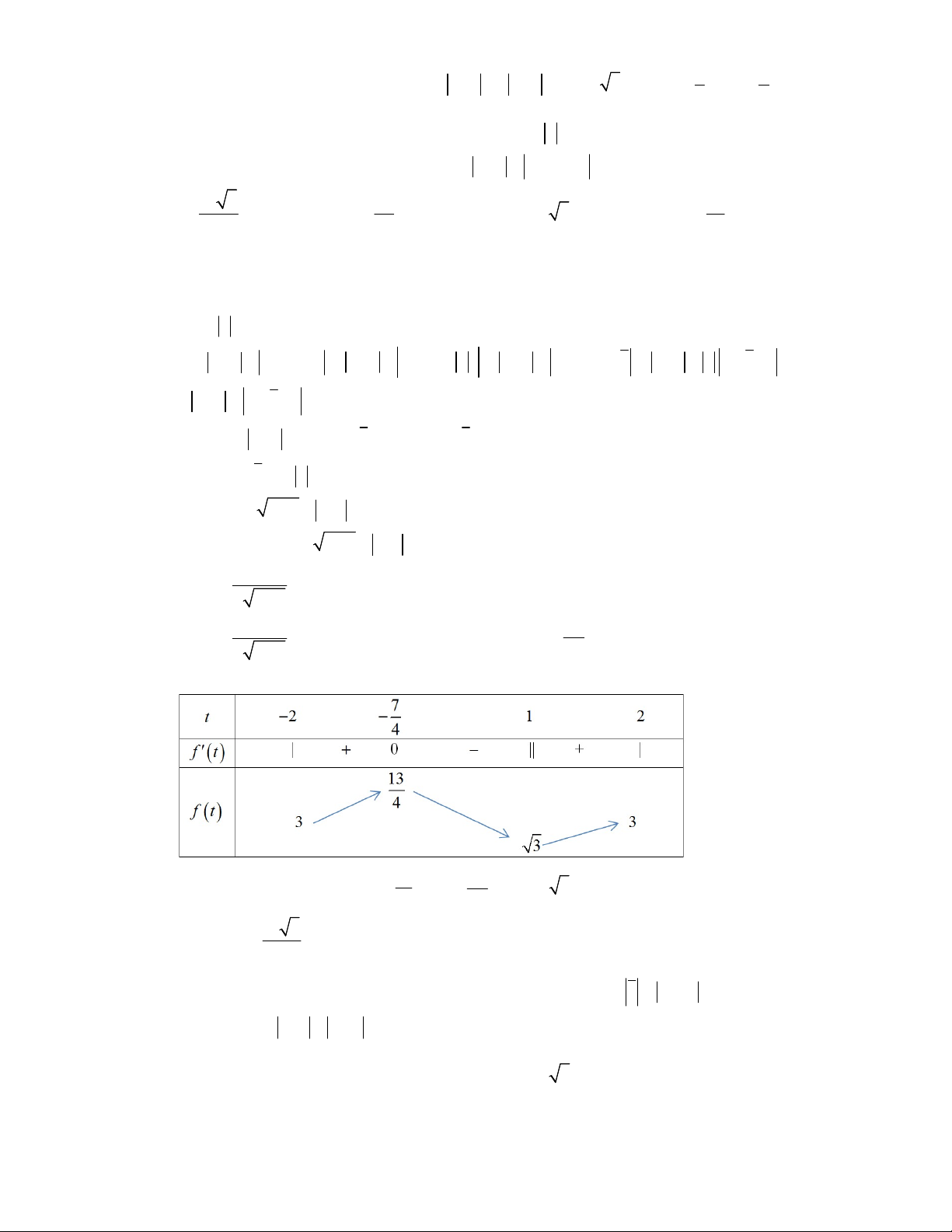
1 với t 1. Suy ra f x  0  x  . 2 t  2 4 Ta có bảng biến thiên 13 7 
Từ bảng biến thiên suy ra M  tại t  và m  3 tại t  2. 4 4 13 3 Vậy M .m  . 4
Câu 20: (THPT Yên Khánh - Ninh Bình - 2019) Cho hai số phức z và   a  bi thỏa mãn
z  5  z  5  6 ; 5a  4b  20  0 . Giá trị nhỏ nhất của z  là 3 5 4 3 A. . B. . C. . D. . 41 41 41 41 Lời giải Chọn A Đặt F  5 ;0 , F
5 ;0 , vì 5  3 nên tập hợp các điểm M biểu diễn số phức z thuộc elip 2   1   a  3  2 2 x y có 2 2 2 
 b  a  c  4 suy ra E:  1. c  5 9 4
Tập hợp các điểm N biểu diễn số phức  thuộc đường thẳng  : 5x  4 y  20  0 .
Yêu cầu bài toán trở thành tìm điểm M E và N   sao cho MN nhỏ nhất. Trang 16 Toanthaycu.com
Đường thẳng d song song với  có dạng d : 5x  4 y  c  0 , c  2  0 . c 17
d tiếp xúc với E khi và chỉ khi c  5 .9   4  2 2 2 .4  289   . c  17 20 17 37
Với c 17  d d,    .   2 2 41 5 4 20 17 3 Với c  1  7  d d,   .   2 2 41 5 4 Vậy MN 3 min  . 41
Câu 21: (KTNL GV THPT Lý Thái Tổ 2019) Gọi z  a  bi a,b  là số phức thỏa mãn điều kiện
z  1 2i  z  2  3i  10 và
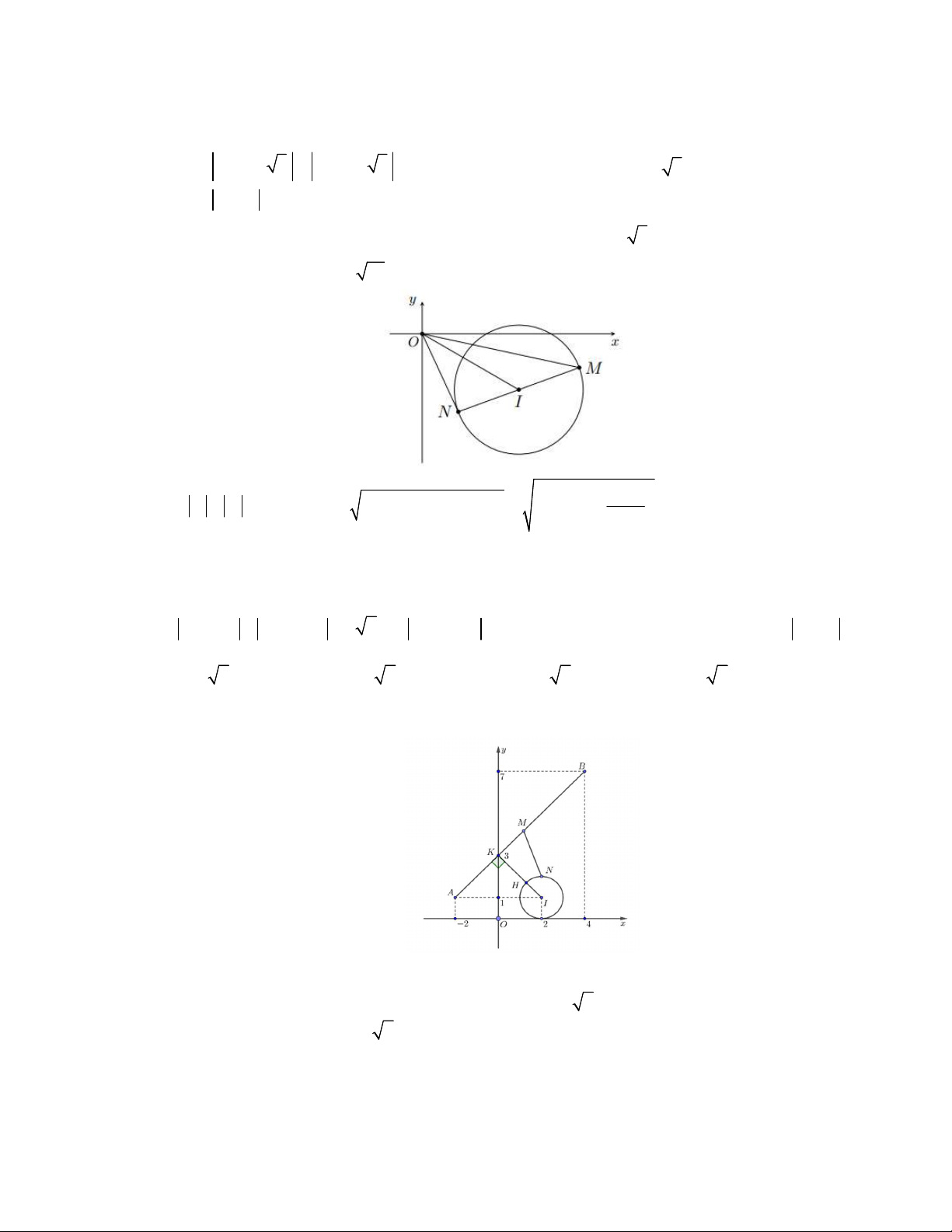
có mô đun nhỏ nhất. Tính S  7a b ? A. 7 . B. 0 . C. 5 . D. 12 . Lời giải Chọn A 4 B M H 2 A O 2 4 Gọi M  ;
a b là điểm biểu diễn số phức z  a bi
A1;2 là điểm biểu diễn số phức 12i
B 2;3 là điểm biểu diễn số phức 2  3i, AB  10 Trang 17
z 1 2i  z  2  3i  10 trở thành MA  MB  AB  M, ,
A B thẳng hàng và M ở giữa A và B
Gọi H là điểm chiếu của O lên AB, phương trình  AB : x  3y  7  0, OH  : 3x  y  0 7 21  3 1   27 9    Tọa độ điểm H  ;  , Có AH    ; , BH   ; và BH  9  AH 10 10         10 10   10 10  Nên H thuộc đoạn AB
z nhỏ nhất  OM nhỏ nhât, mà M thuộc đoạn AB  7 21  M  H  ; 10 10    49 21 Lúc đó S  7a  b    7 . 10 10
Câu 22: (KTNL GV Thuận Thành 2 Bắc Ninh 2019) Cho số phức z thỏa mãn z  z  2 z  z  8
. Gọi M,m lần lượt là giá trị lớn nhất, nhỏ nhất của biểu thức P  z  3  3i . Tính M  m . A. 10  34 . B. 2 10 . C. 10  58 . D. 5  58 . Giải: Chọn D x  4
Gọi z  x  yi, x, y   , ta có z z 2 z z 8 x 2 y 4           , tập hợp y  2  K  ;
x y biểu diễn số phức z thuộc cạnh các cạnh của trong hình thoi ABCD như hình vẽ.
P  z  3  3i đạt giá trị lớn nhất khi KM lớn nhất, theo hình vẽ ta có KM lớn nhất khi K  D hay K  4
 ;0 suy ra M  499  58
P  z  3  3i đạt giá trị nhỏ nhất khi KM nhỏ nhất, theo hình vẽ ta có KM nhỏ nhất khi
K  F ( F là hình chiếu của E trên AB . Suy ra F 2; 
1 do AE  AB nên F là trung điểm của AB .
Suy ra m  1 4  5 . Vậy M  m  58  5
Câu 23: (Chuyên Bắc Giang -2019) Cho số phức z có z  1. Tìm giá trị lớn nhất của biểu thức 2 2
P  z  z  z  z 1 . Trang 18 Toanthaycu.com 13 11 A. B. 3 C. 3 D. 4 4 Lời giải Chọn A 2 2 2 2
P  z  z  z  z 1  z z 1  z  z 1  z 1  z  z 1
Do z  1 nên ta đặt z  cos x  .isin x . Khi đó 2
P  z 1  z  z 1  cos x  .isin x 1  cos 2x  i sin 2x  cos x  i sin x 1  cos x  2
1  sin x  cos 2x  cos x  2 1  sin 2x  sin x2 2
 2  2cos x  3  4cos x  2cos 2x 2
 2  2cos x  4cos x  4cos x 1
 2  2cos x  2cos x 1 Đặt t  cos x, t  1  ; 
1 . Xét hàm y  2  2t  2t 1 1 1
Với t   thì y  2  2t  2t 1, y '   2 2 2  2t 1 7 y '  0   2  0  t  2  2t 8    1  y   7 13 1  3; y    ; y   3    8  4  2  1 1 
Với t   thì y  2  2t  2t 1, y '   2 2 2  2t 1 1 y '  0   2  0  2  2t 
(phương trình vô nghiệm) 2  2t 2  1 y   1  3  ; y   3    2  13 13 Vậy max y 
. Do đó giá trị lớn nhất của 2 2
P  z  z  z  z 1 là . 1; 1 4 4
Câu 24: (Chuyên Đại Học Vinh -2019) Giả sử z , z là hai trong các số phức thỏa mãn  z  68 zi là 1 2
số thực. Biết rằng z  z  4 , giá trị nhỏ nhất của z  3z bằng 1 2 1 2 A. 5  21 B. 20  4 21 C. 20  4 22 D. 5  22 Lời giải Chọn C Trang 19 Giả sử z  x  yi , , x y  .Gọi ,
A B lần lượt là điểm biểu diễn cho các số phức z , z . Suy ra 1 2 AB  z  z  4 . 1 2
* Ta có  z  68 zi  x 6  yi.
 8  y  xi   x  y     2 2 8 6 48 x  y  6x  8yi .
Theo giả thiết  z  68  zi là số thực nên ta suy ra 2 2
x  y 6x 8y  0. Tức là các điểm ,
A B thuộc đường tròn Ctâm I 3;4 , bán kính R  5.      
* Xét điểm M thuộc đoạn AB thỏa MA  3MB  0  OA  3OB  4OM .Gọi H là trung điểm AB . Ta tính được 2 2 2 2 2
HI  R  HB  21; IM  HI  HM  22 , suy ra điểm M thuộc
đường tròn C tâm I 3;4 , bán kính r  22 .   
* Ta có z  3z  OA  3OB  4OM  4OM , do đó z  3z nhỏ nhất khi OM nhỏ nhất. 1 2 1 2 Ta có OM 
 OM  OI  r  5  22 . 0 min Vậy z  3z  4OM  20  4 22 . 1 2 0 min
Câu 25: Trong các số phức z thỏa mãn z  3 4i  2 có hai số phức z , z thỏa mãn z  z  1. Giá trị 1 2 1 2 nhỏ nhất của 2 2 z  z bằng 1 2 A. 1  0 B. 4  3 5 C. 5  D. 6  2 5 Lời giải Chọn A
Đặt z  x  y i, x , y   và z  x  y i, x , y   . 2 2 2  2 2  1 1 1  1 1    x  3  y  4  4  1 2  1 2 Khi đó  và  x  x  y  y  1. 1 2 2  1 2 2   x  3  2   y  42  4 2 2
Ta có  x  32   y  42   x  32   y  32 2 2  x  y   2 2 x  y  6 x  x  8 y  y . 1 1 2 2   1 2   1 2  1 1 2 2 Suy ra 2 2 z  z
 2 3 x  x   4 y  y   2. 3  4 x  x 2   y  y 2 2 2  10 1 2 1 2 1 2 1 2 1 2   . Do đó 2 2 10  z  z  10 . 1 2 Trang 20 Toanthaycu.com
Câu 26: (Chuyên Lê Hồng Phong Nam Định 2019) Cho hai số phức z , z thoả mãn 1 2
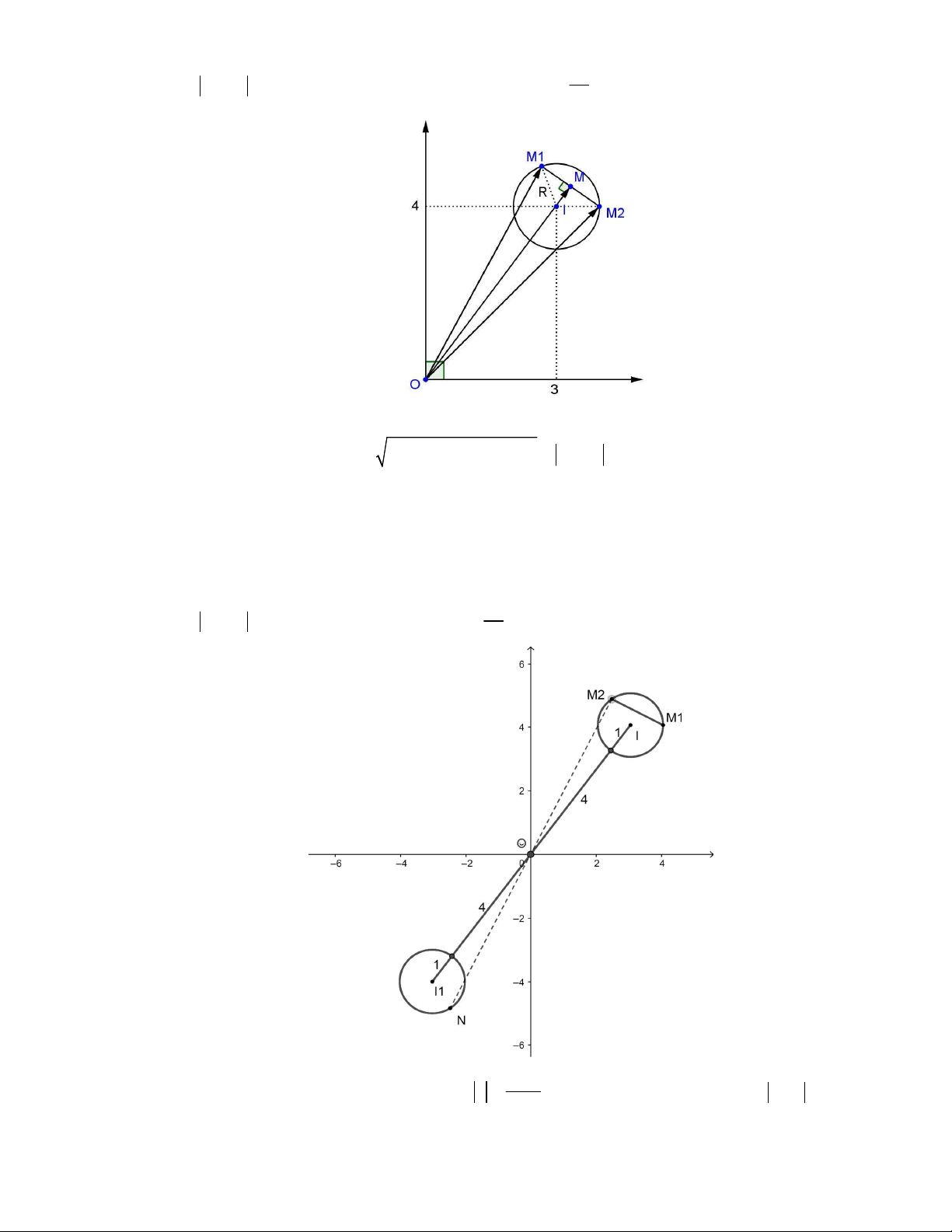
z  2  i  z  4  7i  6 2 và iz 1 2i 1. Tìm giá trị nhỏ nhất của biểu thức T  z  z . 1 1 2 1 2 A. 2 1. B. 2 1. C. 2 2 1. D. 2 2 1. Lời giải
Gọi M là điểm biểu diễn số phức z và A 2  ; 
1 ; B4;7 lần lượt là hai điểm biểu diễn hai số 1
phức 2  i , 4  7i . Ta có AB  6 2 . Phương trình đường thẳng AB là d : x  y  3  0 .
+) z  2  i  z  4  7i  6 2  MA  MB  6 2  MA  MB  AB . Do đó tập hợp các 1 1
điểm biểu diễn số phức z là đoạn thẳng AB . 1
+) iz 1 2i 1  iz 1 2i i 1  z  2  i 1. 2 2 2
Gọi N là điểm biểu diễn số phức z và I 2; 
1 là điểm biểu diễn số phức 2  i . Ta có IN  1 2
Suy ra tập hợp các điểm biểu diễn số phức z là đường tròn C có phương trình: 2
x  2  y  2 2 1  1 .
d I, AB  2 2  1, suy ra AB không cắt đường tròn.
Gọi K là hình chiếu của I 2; 
1 lên AB . Dễ thấy K nằm trên đoạn thẳng AB .
Gọi H là giao điểm của đoạn IK với đường tròn C.
Ta có z  z  MN  KH  d I, AB  R  2 2 1. 1 2  
Suy ra min z  z  2 2 1. 1 2
Câu 27: (Chuyên Nguyễn Tất Thành Yên Bái 2019) Cho z là số phức thỏa mãn z  z  2i . Giá trị
nhỏ nhất của z 1 2i  z 1 3i là A. 5 2 . B. 13 . C. 29 . D. 5 . Lời giải
Đặt z  a  bi a, b . Trang 21
Ta có: z  z  i  a  b  a  b  2 2 2 2 2 2  4b  4  0  b  1   z  a  i .
Xét: z 1 2i  z 1 3i  a 1 i  a 1 2i    a2     a2 2 2 1 1 1  2 . Áp dụng BĐT Mincôpxki:
  a2     a2     a   a2   2 2 2 1 1 1 2 1 1 1 2  49  13 .
Suy ra: z 1 2i  z 1 3i đạt GTNN là 13 khi   a 1 2 1 1 a  a  . 3
Nhận xét: Bài toán trên có thể được giải quyết bằng cách đưa về bài toán hình học phẳng.
Câu 28: (Chuyên Hạ Long - 2018) Cho các số phức z  2
  i , z  2  i và số phức z thay đổi thỏa 1 2 mãn 2 2 z  z  z  z
 16 . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của z . 1 2 Giá trị biểu thức 2 2 M  m bằng A. 15 . B. 7 . C. 11. D. 8 . Lời giải
Giả sử z  x  yi  x, y  . Ta có: 2 2 z  z  z  z  16 2 2
 x  yi  2  i  x  yi  2  i  16  x   y  2 2 1  4 . 1 2
Suy ra tập hợp điểm biểu diễn của số phức z là đường tròn tâm số phức I 0;  1 bán kính R  2 . Do đó m  1, M  3. Vậy 2 2 M  m  8 .
Câu 29: (Chuyên Quang Trung - 2018) Cho số phức z thỏa mãn z  2i  z  4i và z  3  3i  1. Giá
trị lớn nhất của biểu thức P  z  2 là: A. 13 1. B. 10 1. C. 13 . D. 10 . Lời giải Trang 22 Toanthaycu.com Gọi M  ;
x y là điểm biểu diễn số phức z ta có: z  2i  z  4i
 x   y  2  x   y  2 2 2 2 4
 y  3; z  3  3i  1  điểm M nằm trên đường tròn tâm I 3;3 và bán kính bằng 1. Biểu
thức P  z  2  AM trong đó A2;0 , theo hình vẽ thì giá trị lớn nhất của P  z  2 đạt được khi M 4;3 nên
P    2    2 max 4 2 3 0  13 .
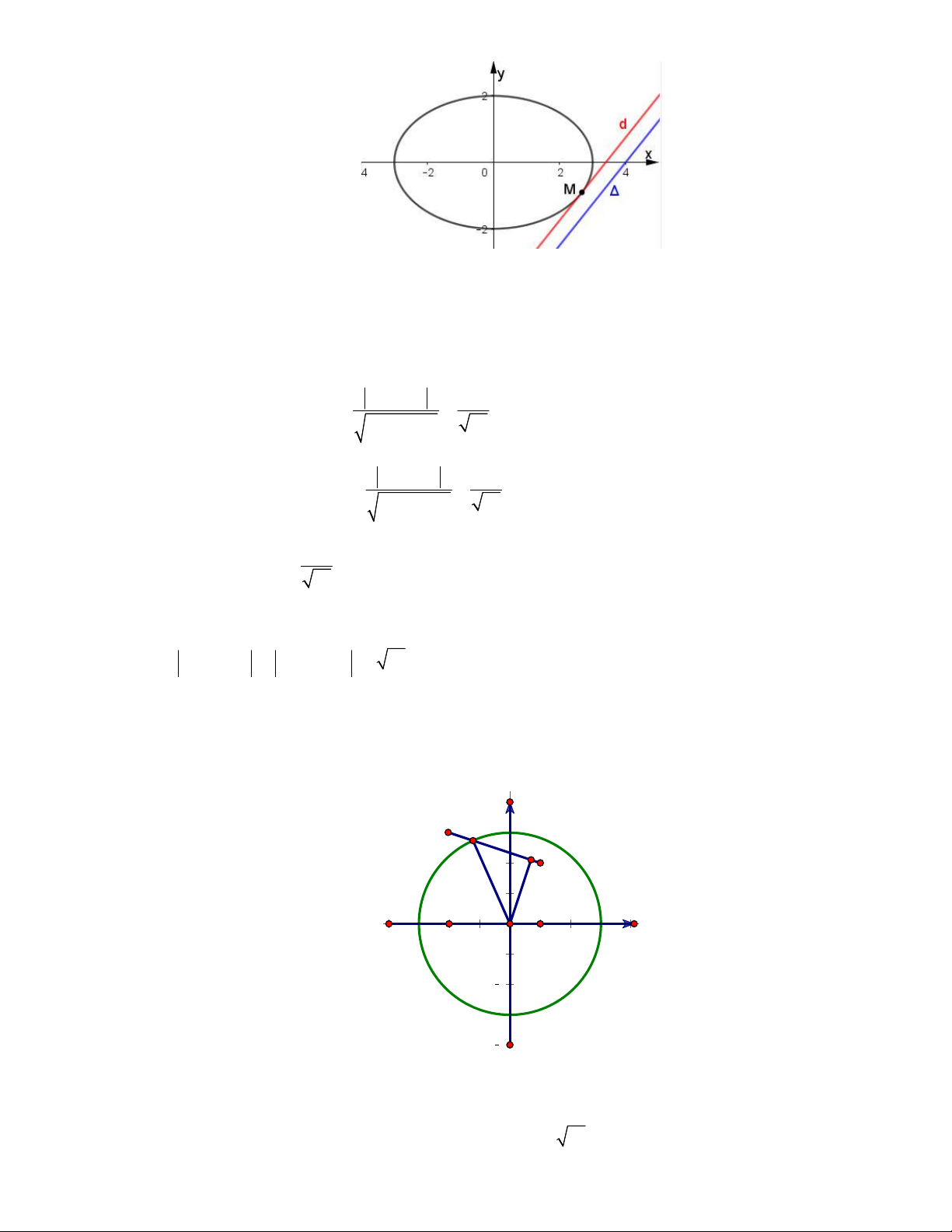
Câu 30: Xét số phức z thỏa mãn z  2  2i  2 . Giá trị nhỏ nhất của biểu thức P  z 1 i  z  5  2i bằng A. 1 10 . B. 4 . C. 17 D. 5 . Lời giải
Gọi M x; y là điểm biểu diễn số phức z . Do z  2  2i  2 nên tập hợp điểm M là đường
tròn C   x  2   y  2 : 2 2  4 . Các điểm A1; 
1 , B 5;2 là điểm biểu diễn các số phức 1 i và 5  2i . Khi đó, P  MA  MB .
Nhận thấy, điểm A nằm trong đường tròn C  còn điểm B nằm ngoài đường tròn C , mà
MA  MB  AB  17 . Đẳng thức xảy ra khi M là giao điểm của đoạn AB với C  .
Ta có, phương trình đường thẳng AB : x  4y  3  0 .
Tọa độ giao điểm của đường thẳng AB và đường tròn C  là nghiệm của hệ với 1 y  5 Trang 23 
 x  2  y  2  
 y  2  y  2 2 2 4 4 5 2  4    x  4y  3  0 x  4y 3  22  59  y  N 
Ta có  y  2   y  2 2 17 4 5
2  4  17 y  44 y  25  0    22  59  y  L  17 37  4 59 22  59 Vậy min P  17 khi z   i 17 17
Câu 31: (SGD Cần Thơ - 2018) Cho số phức z thỏa mãn z  3  4i  5 . Gọi M và m lần lượt là giá
trị lớn nhất và giá trị nhỏ nhất của biểu thức 2 2
P  z  2  z  i . Môđun của số phức w  M  mi là A. w  3 137 . B. w  1258 . C. w  2 309 . D. w  2 314 . Lời giải Chọn B
- Đặt z  x  yi , với , x y   .
Ta có: z  3  4i  5   x  3   y  4i  5   x  2   y  2 3
4  5 , hay tập hợp các
điểm biểu diễn số phức z là đường tròn C có tâm I 3;4 , bán kính r  5 . - Khi đó : 2 2
P  z  2  z  i   x  2  y  x   y  2 2 2 2 1  4x  2y  3
 4x  2y  3 P  0, kí hiệu là đường thẳng .
- Số phức z tồn tại khi và chỉ khi đường thẳng  cắt đường tròn C  23  P  d I;  r 
 5  P  23  10  13  P  33 2 5
Suy ra M  33 và m  13  w  33 13i . Vậy w  1258 .
Câu 32: (THPT Hậu Lộc 2 - 2018) Cho hai số phức z , z thỏa mãn z 1 i  2 và z  iz . Tìm giá 1 2 1 2 1
trị nhỏ nhất m của biểu thức z  z ? 1 2 A. m  2 1. B. m  2 2 . C. m  2 . D. m  2 2  2 . Lời giải Chọn D Đặt z  a  b ; i , a b  z  b   ai 1 2
 z  z  a  b  b  a i . 1 2    
Nên z  z  a  b2  b  a2  2. z 1 2 1
Ta lại có 2  z 1 i  z  1 i  z  2 1 1 1
 z  2  2 . Suy ra z  z  2. z  2 2  2 . 1 1 2 1 a b Dấu "  " xảy ra khi   0 . 1 1  Trang 24 Toanthaycu.com
Vậy m  min z  z  2 2  2 . 1 2  z  3  2i  1 
Câu 33: (SGD Bắc Giang - 2018) Hcho hai số phức z, w thỏa mãn  . Tìm giá trị
 w 1 2i  w  2  i 
nhỏ nhất P của biểu thức P  z  w . min 3 2  2 5 2  2 3 2  2 A. P  . B. P  2 1. C. P  . D. P  . min 2 min min 2 min 2 Lời giải Chọn C
Giả sử z  a  bi a,b   , w  x  yi  x, y  .
z  3  2i  1  a  2  b  2 3 2  1 (1)
w 1 2i  w  2  i   x  2   y  2   x  2   y  2 1 2 2 1 . Suy ra x  y  0. P  z 
 a  x2  b  y2  a  x2  b  x2 w .
Từ (1) ta có I 3;2 , bán kính r 1. Gọi H là hình chiếu của I trên d : y  x . x  3  t
Đường thẳng HI có PTTS  .  y  2  t
M  HI  M 3 t;2  t  1 t   M C 2  2t 1 2    1 t    2  1 1  5  2 t  2  M 3  ; 2    , MH   2 2  2  1 1  5  2 t  3  M 3  ;2    , MH   2 2  2 5 2  2 Vậy P  . min 2
Câu 34: (Chuyên Lê Hồng Phong - TPHCM - 2018) Cho số phức z thỏa z 1. Gọi m , M lần lượt
là giá trị nhỏ nhất, giá trị lớn nhất của biểu thức 5 3 4
P  z  z  6z  2 z 1 . Tính M  m . A. m  4 , n  3 . B. m  4 , n  3 C. m  4 , n  4 . D. m  4 , n  4 . Lời giải 1 Vì z  1 và 2 . z z  z nên ta có z  . z Trang 25 Từ đó, 5 3 4
P  z  z  6z  2 z 1 4 4 4
 z z  z  6  2 z 1 4 4 4
 z  z  6  2 z 1 . Đặt 4 z  x  iy , với , x y   . Do z 1 nên 4 2 2 z  x  y  1 và 1   , x y  1.
Khi đó P  x  iy  x  iy  6  2 x  iy 1  x   x  2 2 2 6 2 1  y
 2x  6  2 2x  2   x   2 2 2 1  3 .
Do đó P  3 . Lại có 1  x  1  0  2x  2  2  1
  2x  2 1 1  P  4 . 1 3 Vậy M  4 khi 4 z  1  và m  3 khi 4 z    i . Suy ra M  m  1. 2 2 3 5
Câu 35: (Chuyên Đh Vinh - 2018) Cho các số phức w , z thỏa mãn w  i  và 5
5w  2  i z  4 . Giá trị lớn nhất của biểu thức P  z 1 2i  z  5  2i bằng A. 6 7 . B. 4  2 13 . C. 2 53 . D. 4 13 . Lời giải Chọn C Gọi z  x  yi , với , x y   . Khi đó M  ;
x y là điểm biểu diễn cho số phức z .
Theo giả thiết, 5w  2  i z  4  5w  i  2  i z  4  5i  2  iw  i  z  3  2i
 z  3  2i  3. Suy ra M  ;
x y thuộc đường tròn C   x  2   y  2 : 3 2  9 .
Ta có P  z 1 2i  z  5  2i  MA  MB , với A1;2 và B5;2 .
Gọi H là trung điểm của AB , ta có H 3;2 và khi đó: P  MA  MB   2 2 2 MA  MB  hay 2 2 P  4MH  AB .
Mặt khác, MH  KH với mọi M C nên 2 2 P  4KH  AB    2 2 4 IH R  AB  2 53 . M  K 3 11 Vậy P  2 53 khi
hay z  3  5i và w   i . max  MA  MB 5 5
Câu 36: (Kim Liên - Hà Nội - 2018) Xét các số phức zV a  bi ( a,b ) thỏa mãn z  3 2i  2.
Tính a  b khi z 1 2i  2 z  2  5i đạt giá trị nhỏ nhất. Trang 26 Toanthaycu.com A. 4  3 . B. 2  3 . C. 3 . D. 4  3 . Lời giải Cách 1:
Đặt z  3  2i  w với w  x  yi  x, y   . Theo bài ra ta có 2 2 w  2  x  y  4 .
Ta có P  z   i  z   i  w   w   i   x  2  y 
x  2   y  2 2 1 2 2 2 5 4 2 1 3 4 2 1 3   x 
x  2   y  2   x 
x  2   y  2 20 8 2 1 3 2 5 2 2 1 3
  x  y  x   x  2 y  2    x  2  y  x  2 y  2 2 2 2 2 2 1 1 3 2 1 1 3 
 2 y  y 3   2 y  3 y  6 . x  1       P   y   y x 1 6 3  0   .  y  3 2 2 x  y  4
Vậy GTNN của P là bằng 6 đạt được khi z  2  2 3i . Cách 2:
z  3  2i  2  MI  2  M I;2 với I  3;2 .
P  z 1 2i  2 z  2  5i  MA  2MB với A  1;2 , B  2;5 .
Ta có IM  2 ; IA  4 . Chọn K 2;2 thì IK 1. Do đó ta có 2 I . A IK  IA IM IM   IM IK AM IM  IAM và I
 MK đồng dạng với nhau    2  AM  2MK . MK IK
Từ đó P  MA  2MB  2MK  MB  2BK .
Dấu bằng xảy ra khi và chỉ khi M , K , B thẳng hàng và M thuộc đoạn thẳng BK .
Từ đó tìm được M  2;2  3. Cách 3:
Gọi M a;b là điểm biểu diễn số phức z  a  b .i Đặt I  3;2 , A 1  ;2 và B2;5.
Ta xét bài toán: Tìm điểm M thuộc đường tròn C  có tâm I , bán kính R  2 sao cho biểu thức
P  MA  2MB đạt giá trị nhỏ nhất.
Trước tiên, ta tìm điểm K  ; x y sao cho MA  2MK M  C .   2   2 Ta có 2 2
MA  2MK  MA  4MK  MI  IA  4MI  IK  Trang 27        2 2
 MI  IA  MI IA   2 2
MI  IK  MI IK   MI IA  IK  2 2 2 2 . 4 2 . 2 4  3R  4IK  IA   * .      IA 4IK  0 * luôn đúng M  C   . 2 2 2 3  R  4IK  IA  0    4   x  3  4  x  2 IA  4IK  0     . 4   y  2  0 y  2
Thử trực tiếp ta thấy K 2;2 thỏa mãn 2 2 2 3R  4IK  IA  0 . Vì 2 2 2 2
BI 1  3 10  R  4 nên B nằm ngoài C . Vì 2 2
KI  1  R  4 nên K nằm trong C .
Ta có MA  2MB  2MK  2MB  2MK  MB  2KB .
Dấu bằng trong bất đẳng thức trên xảy ra khi và chỉ khi M thuộc đoạn thẳng BK .
Do đó MA  2MB nhỏ nhất khi và chỉ khi M là giao điểm của C và đoạn thẳng BK.
Phương trình đường thẳng BK : x  2 .
Phương trình đường tròn C   x  2   y  2 : 3 2  4 . x  2  x  2  x  2 
Tọa độ điểm M là nghiệm của hệ     hoặc  .  x  3 
2  y  22  4 y  2 3 y  2  3
Thử lại thấy M 2;2  3 thuộc đoạn BK .
Vậy a  2 , b  2  3  a  b  4  3 .
Câu 37: (Liên Trường - Nghệ An - 2018) Biết rằng hai số phức z , z thỏa mãn z  3  4i  1 và 1 2 1 1
z  3  4i  . Số phức z có phần thực là a và phần ảo là b thỏa mãn 3a  2b  12 . Giá trị 2 2
nhỏ nhất của P  z  z  z  2z  2 bằng: 1 2 9945 9945 A. P  . B. P  5  2 3 . C. P  . D. P  5  2 5 . min 11 min min 13 min Lời giải Chọn C
Gọi M , M , M lần lượt là điểm biểu diễn cho số phức z , 2z , z trên hệ trục tọa độ Oxy . 1 2 1 2
Khi đó quỹ tích của điểm M là đường tròn C tâm I 3;4 , bán kính R  1; 1  1
quỹ tích của điểm M là đường C tròn tâm I 6;8 , bán kính R 1; 2  2
quỹ tích của điểm M là đường thẳng d : 3x  2y 12  0 .
Bài toán trở thành tìm giá trị nhỏ nhất của MM  MM  2 . 1 2 Trang 28 Toanthaycu.com y I2 8 I3 B I A 1 M 4 O 3 6 x 138 64  Gọi C có tâm I ;
, R  1 là đường tròn đối xứng với C qua d . Khi đó 2  3  3    13 13 
min MM  MM  2  min MM  MM  2 với M  C . 3  3 1 2   1 3 
Gọi A , B lần lượt là giao điểm của đoạn thẳng I I với C , C . Khi đó với mọi điểm 3  1  1 3
M  C , M  C , M  d ta có MM  MM  2  AB  2 , dấu "=" xảy ra khi 3  3 1  1 1 3 9945 M  ,
A M  B . Do đó P  AB  2  I I  2  2  I I  . 1 3 min 1 3 1 3 13
Câu 38: (Chuyên Lê Quý Đôn – Điện Biên - 2019) Trong các số phức thỏa mãn: z  1  i  z  1  2i
, số phức z có mô đun nhỏ nhất có phần ảo là 3 3 3 3 A. . B. . C.  . D.  . 10 5 5 10 Lời giải Chọn D
+ Gọi số phức cần tìm là z  a  bi, (a, b   ) .  z  a  b i
+ z  1  i  z  1  2i
 a  bi 1 i  a bi 1 2i
 a 1  b 1i  a 1 b  2i .
 a  2 b 2  a  2 b  2 1 1 1 2 4a 3 3
 4a  2b3 0 b    2  a  2 2 2  3  9  6 9  9 + 2 2 2 2 2 z  a  b  a  2a 
 5a  6a   5 a  a        2  4  5 25  20 2  3  9 9 3 5  5 a        5  20 20 10 3 5 3 3 z nhỏ nhất bằng khi a   b   . 10 5 10
Câu 39: (Chuyên Bắc Giang 2019) Cho số phức z thỏa mãn z  1. Gọi M , m lần lượt là giá trị lớn
nhất, giá trị lớn nhất của 5 3 4
P  z  z  6z  2 z 1 . Tính M  m . Trang 29 A. M  m 1. B. M  m  7 . C. M  m  6 . D. M  m  3. Lời giải Chọn A Ta có: 2 1 zz  z  1  z  . z 1 1 Suy ra 5 4 8 4 4 8 4 4 P  z   6z  2 z 1 
z 1 6z  2 z 1  z  6z 1  2 z 1 3 3 z z Đặt 4
w  z  w 1, ta được 2
P  w  6w 1  2w  2 .  x 1  Gọi w  x  yi , vì 2 2
w  1  x  y  1  .  y  1  2 2
P  x  x   y  y  x   2 6 1 2
3 i  2 x 1 yi  2x  6x  2y  x  3i  2 x 1 yi
 x   x  yi  x  2 2 2 3 2
1  y  2  x  3 x  yi  2 2x  2
 2x  3  2 2x  2
Xét hàm số f  x  2 x  3  2 2x  2 trên đoạn  1  ;  1 . f  x 1   f  x 1 1 2 2 ;  0  2  2
 0  2x  2 1 x   . 2x  2 2x  2 2  1  Ta có: f   1  4; f   3; f    1  4  2 
Vậy M  4,m  3  M  m 1.
Câu 40: (Bình Giang-Hải Dương 2019) Cho số phức z thỏa mãn z  1. Giá trị lớn nhất của biểu thức
P  1 z  2 1 z bằng A. 6 5 . B. 4 5 . C. 2 5 . D. 5 . Lời giải Chọn C Gọi z  x  y ; i  ; x y  . 2 2 2 2
z  1  x  y  1  y  1 x  x  1  ;  1 . Ta có: P   z 
 z    x2  y    x2 2 2 1 3 1 1 3 1
 y  21 x  2 21 x .
Xét hàm số f  x  21 x  2 21 x; x  1  ;  1 . 1 2
Hàm số liên tục trên  1  ;  1 và với x  1  ;  1 ta có: f x   . 21 x 21 x f  x 1 2 3  0    0  x    1  ;  1 . 21 x 21 x 5 f    f    3  1 2; 1  4; f   2 5   .  5   max f x  2 5 . x   1  ;  1 Trang 30 Toanthaycu.com 3 4
Vậy giá trị lớn nhất của biểu thức P  1 z  3 1 z bằng 2 5 khi x   , y   . 5 5
Câu 41: (SGD Hưng Yên 2019) Cho số phức z thoả mãn z  1. Gọi M và m lần lượt là giá trị lớn
nhất và giá trị nhỏ nhất của biểu thức 2
P  z 1  z  z 1 . Tính M.m 13 3 39 13 A. . B. . C. 3 3 . D. . 4 4 4 Lời giải Chọn A Thay 2 z  1 vào P ta có 2 P  z 1  z  z 1 2 2  z 1  z  z  z 2
 z 1  z  z  z.z  z 1  z z  z 1  z 1  z  z 1 . Mặt khác 2 z 1   z   1 z   1  2  z  z .
Đặt t  z  z do z  1 nên điều kiện t  2  ;2.
Suy ra P  t  2  t 1 .
Xét hàm số f t  t  2  t 1 với t  2  ;2. f t  1 
1 với t 1. Suy ra f t  0 với t 1. 2 t  2 7  f t  1 
1 với t 1. Suy ra f x  0  x  . 2 t  2 4 Ta có bảng biến thiên 13 7
Từ bảng biến thiên suy ra M  tại t  và m  3 tại t  2. 4 4 13 3 Vậy M .m  . 4
Câu 42: (Chuyên - KHTN - Hà Nội - 2019) Cho số phức z thỏa mãn : z  z  2i . Giá trị nhỏ nhất của
biểu thức P  z  i  z  4 là A. 5. B. 4. C. 3 3. D. 6. Lời giải Chọn A Trang 31 Gọi M ( ;
x y) là điểm biểu diễn số phức z. Ta có z  z  2i  y 1  0, tức biểu diễn hình học
của số phức thỏa mãn giả thiết là đường thẳng y 1  0. Xét điểm ( A 0;1) và B(4;0) thì
P  z  i  z  4  MA M . B Dễ thấy ,
A B cùng phía với đường thẳng y 1  0 nên MA  MB
nhỏ nhất bằng BA trong đó A (  0; 3
 ) đối xứng với A qua đường thẳng y 1 0. B A M' M A'
Do đó MA  MB nhỏ nhất bằng BA  5.
Câu 43: (SGD Bến Tre 2019) Cho các số phức z  1 3i , z  5
  3i . Tìm điểm M x; y biểu diễn 1 2
số phức z , biết rằng trong mặt phẳng phức điểm M nằm trên đường thẳng x  2y 1 0 và mô 3
đun số phức w  3z  z  2z đạt gí trị nhỏ nhất. 3 2 1  3 1   3 1   3 1   3 1  A. M  ;   . B. M ;   . C. M  ;    . D. M ;    .  5 5   5 5   5 5   5 5  Lời giải Chọn A
Trắc nghiệm: Thay tọa độ điểm M vào vế trái phương trình đường thẳng kết quả bằng 0 thỏa ta được đáp án A Tự luận:
Ta có w  3z  z  2z  3z  3  3i  3 z 1 i  w  3 z 1 i  3AM với A1;3 3 2 1 3  3  3
M  x; y biểu diễn số phức z nằm trên đường thẳng d : x  2y 1 0 và A1;3d . 3
Khi đó w  3 z 1 i  3AM đạt giá trị nhỏ nhất khi AM ngắn nhất  AM  d 3
AM  d nên AM có phương trình: 2x  y 1 0 .  3 1 
Khi đó M  AM  d nên M  ; .   .  5 5 
Câu 44: (SGD Cần Thơ 2019) Cho số phức z thoả mãn z 1 2i  5 . Giá trị lớn nhất của z 1 i bằng A. 5 . B. 5 2 . C. 20 . D. 2 5 . Lời giải Chọn D Cách 1.
Ta có z 1 i  z 1 2i  2  i  z 1 2i  2  i  2 5 .
Đẳng thức xảy ra khi z  3  3i .
Vậy max z 1 i  2 5 . Cách 2. Trang 32 Toanthaycu.com
Đặt z  x  yi, x, y thì từ điều kiện ta có:  x  2   y  2 1 2  5 . Gọi M  ;
x y là điểm biểu diễn cho z và A 1  ; 
1 là điểm biểu diễn cho số phức 1 i , khi
đó z 1 i  AM với M thuộc đường tròn C tâm I 1; 2   bán kính R  5 .
Dễ thấy AC , do đó AM  2R  2 5 .
Suy ra max z 1 i  2 5 , đẳng thức xảy ra khi M  K . Cách 3. z 1 2i  5   *
Đặt z  x  yi  x, y  , khi ấy, ta có *  x  yi 1 2i  5  x   1   y  2i  5
 x  2   y  2 1 2  5 . x 1 5sin a Đặt 
. Ta có z 1 i   x 1   y  
1 i   x  2   y  2 1 1 y  2  5 cos a   a  2   a  2 5 sin 2 5 cos
1  10  4 5 sin a  2 5 cos a  2 5  cos  2 5 5    10 10 sin a  cos a  5 
 10 10sin a   với  . 5 5     5 sin   5 Vì 1
  sin a  1 với mọi ;
a    10 10  z 1 i  10 10
 0  z 1 i  2 5 . 
Vậy giá trị lớn nhất của z 1 i là 2 5 . Dấu "  " xảy ra khi sina  1  a    k2 2     5 cos a  cos
 k2   sin       2  5 x 1 5sin a x 1  2 x  3             2 5 y  2  5 cos a  y  2  1 y  3  sin a  sin
 k2   cos       2  5  z  3  3i .
Câu 45: (Thi thử hội 8 trường chuyên 2019) Cho số phức z thỏa mãn 2  i z  2  i z  2i . Giá trị nhỏ nhất của z bằng Trang 33 2 5 5 A. 1. B. . C. 2 . D. . 5 5 Lời giải Chọn D
Giả sử z  x  yi  x, y  . Ta có
2i z 2i z  2i  2ix  yi2ix  yi  2i
 2x  y  2 y  xi  2x  y  2y  xi  2i 
 4y  2xi  2i  4y  2x  2  x  2 y 1. 2  2  1 1 Do đó 2
z  x  y  2y  2 2 2 2 2 1  y  5y  4y 1  5y    , y   .     5  5 5 1 5 2 1 Suy ra min z   khi y  , x   . 5 5 5 5
Câu 46: (Chuyên Nguyễn Du-ĐăkLăk 2019) Số phức z có môđun nhỏ nhất thoả mãn 2
  3i  z  z  i là 6 3 3 6 3 6 6 3 A.  i . B.  i . C.  i . D.  i . 5 5 5 5 5 5 5 5 Lời giải Chọn C Đặt z  x  yi, ;
x y    z  x  y .i
Khi đó 2  3i  z  z  i   x  2   y  3i  x   y   1 i
 x  2   y  2  x   y  2 2 2 3 1  x  2y  3  0 .
Do đó tập hợp điểm biểu diễn của z là đường thẳng  : x  2y 3  0 . Ta có min z  d ,
O  . Gọi d là đường thẳng qua O và vuông góc với   d : 2x  y  0. 2x  y  0  3 6 
Gọi H  d    H :   H ;  . x 2y 3 0       5 5  3 6
Khi đó z có môđun nhỏ nhất thoả mãn có điểm biểu diễn là H , tức là z   i . 5 5 12 5i z 17  7i
Câu 47: (Sở GD Nam Định - 2019) Trong các số phức z thỏa mãn  13. Tìm giá z  2  i trị nhỏ nhất của z . 3 13 5 1 A. . B. . C. . D. 2 . 26 5 2 Lời giải Chọn A
Điều kiện: z  2  i . 17  7i
Phương trình đã cho  12  5i . z 
13 z  2 i  z 1 i  z  2  i   1 . 12  5i Trang 34 Toanthaycu.com
Gọi M x; y là điểm biểu diễn số phức z  x  yi . Vì z  2  i nên M  N 2;  1 .
Khi đó,     x  2   y  2   x  2   y  2 1 1 1 2
1  6x  4 y  3  0 .
Ta thấy đường thẳng d : 6x  4 y  3  0 không đi qua điểm N 2; 
1 nên tập hợp điểm M là đường thẳng d .
Ngoài ra, z  OM nên z nhỏ nhất khi OM nhỏ nhất, tức là OM  O d  3 3 13 d ,   . 2 2 6  4 26 3 13 Vậy min z  . 26
Câu 48: (Chuyên Nguyễn Huệ-HN-2019) Cho số phức z thỏa mãn 2
z  2z  5   z 1 2i z  3i   1
. Tính min w , với w  z  2  2i . 1 3 A. min w  . B. min w 1. C. min w  . D. min w  2 . 2 2 Lời giải Chọn B Theo giả thiết, 2
z  2z  5   z 1 2i z  3i   1
 z 1 2i z 1 2i  z 1 2i z  3i   1
 z 1 2i . z 1 2i  z 1 3i   0  z 1 2i  0   1   .
 z 1 2i  z 1 3i  2
 1  z 1 2i  0  z 12i . Khi đó, w  12i 2 2i 1 3.
Đặt z  x  yi ( x, y   ). Khi đó, 2   x  
1   y  2i   x   1   y  3i
 x  2   y  2  x  2   y  2   y  2   y  2 1 1 1 2 1 3 2
3  y    z  x  i . 2 2  w  x   3  i  x  2 9 9 3 2 2    x   . 4 . 2 4 4 2
Từ 3 và 4  min w 1.
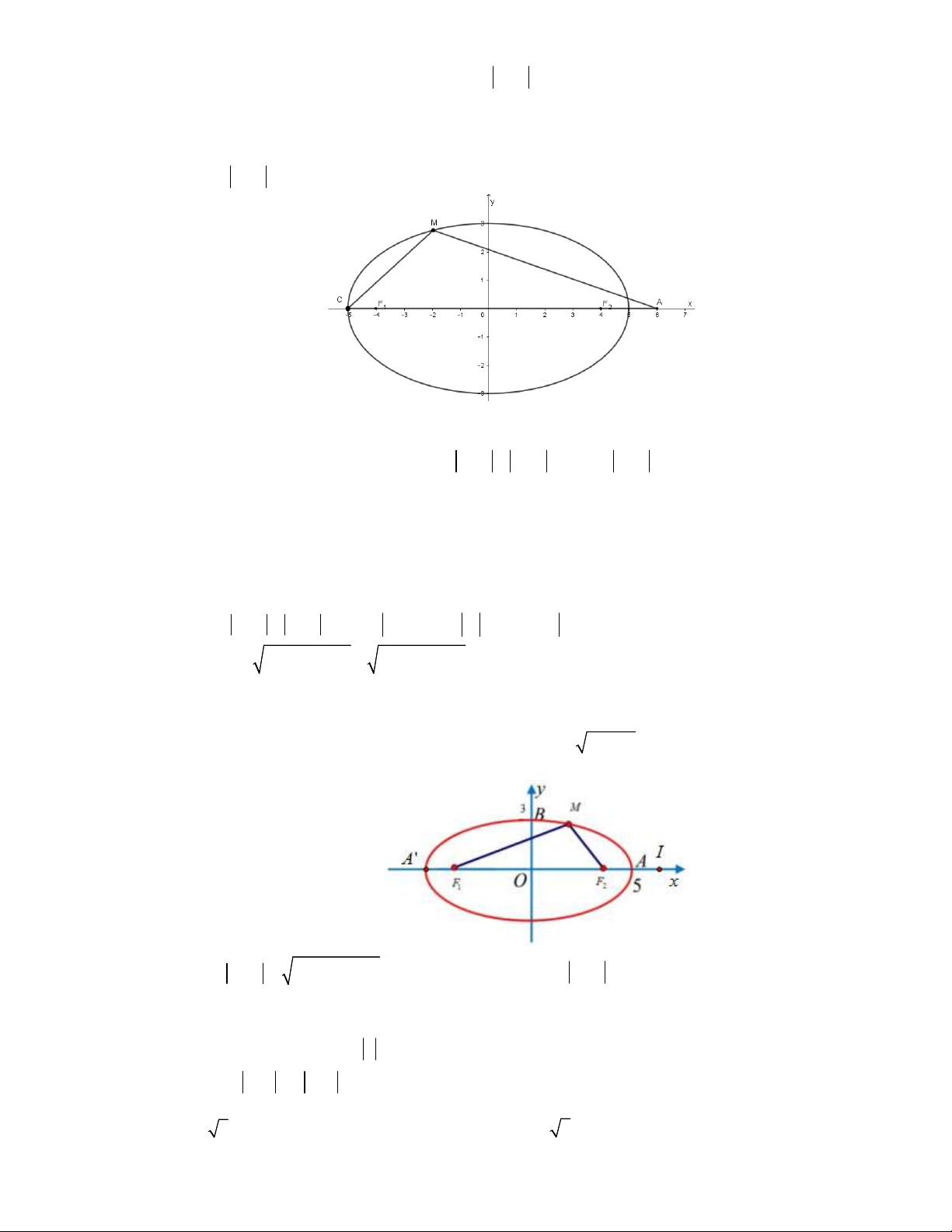
Câu 49: (Kim Liên - Hà Nội 2019) Xét các số phức z thỏa mãn z  3  2i  z  3  i  3 5 . Gọi M ,
m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P  z  2  z 1 3i . Tìm M , m .
A. M  17  5 ; m  3 2 .
B. M  26  2 5 ; m  2 .
C. M  26  2 5 ; m  3 2 . D. M  17  5 ; m  3 . Lời giải Chọn C Trang 35
Gọi M là điểm biểu diễn số phức z , F 3  ;2 , F 3;1 , A 2  ;0 và B1;3 . 2   1  
Ta có z  3  2i  z  3  i  3 5 và F F  3 5  MF  MF  F F . 1 2 1 2 1 2
Do đó tập hợp các điểm M là đoạn thẳng F F . 1 2
Dựa vào hình vẽ, ta thấy: + M  P
 M A  M B  26  2 5 . max 2 2
+ m  P  M A  M B  AB  3 2 . min 1 1
Vậy M  26  2 5 ; m  3 2 .
Câu 50: (Chuyên Nguyễn Trãi Hải Dương 2019) Xét các số phức z thỏa mãn z 1 3i  2 . Số phức z mà z 1 nhỏ nhất là A. z 1 5i . B. z 1 i . C. z 1 3i . D. z 1 i . Lời giải Chọn B
Giả sử z  x  yi  ; x y  .
Ta có z 1 3i  2   x  2   y  2 1 3  2   x  2 2 1   y  6 y  5 Vì  x  2 2
1  0   y  6 y  5  0  1  y  5 z    x  2 2 1 1  y  6y  5
Vì 1  y  5  1  6y  5  25  1  z 1  5 x  1
Vậy z 1 nhỏ nhất khi  khi đó z 1 i  y  1
Câu 51: (Chuyên Ngữ Hà Nội 2019) Cho các số phức z, z , z
1 2 thay đổi thỏa mãn các điều kiện sau: iz  i
2 4  3 , phần thực của z1 bằng 2, phần ảo của z2 bằng 1. Tìm giá trị nhỏ nhất của biểu
thức T  z  z 2  z  z 2 1 2 . A. 9. B. 2. C. . 5 D. 4. Lời giải Chọn D Đặt z  x y ,i ,
x y  , ta có M z M  ;x y Khi đó: iz  i
2 4  3  ix yi i2 4  3  y 4x2i  3 Trang 36 Toanthaycu.com
 x  2 y  2 2 4  9
Suy ra tập hợp điểm M là đường tròn C tâm I  ; 2 4, bán kính R  3.
Mặt khác: z1 2bi  Az1 A ;
2 b Tập hợp điểm A là đường thẳng d : x 1  2.
z2  a i  Bz2 B ; a 
1  Tập hợp điểm B là đường thẳng d : y 2 1.
Giao điểm của d1 và d2 là P ; 2  1 .
Gọi H và K lần lượt là hình chiếu của M trên d1 và d .2
Ta có: T  z  z 2  z  z 2  MA2  MB2  MH 2  MK 2  MP2 1 2 .
T đạt giá trị nhỏ nhất khi A  H, B  K và I,M, P thẳng hàng (theo thứ tự đó). x 2 t4
Phương trình đường thẳng IP :  M 2 t4;1 t3  (vì M  IP ). y  1 t  3  2 t   9
Mà M C nên ta có  2 2 2 
 t   t    t    5 4 4 3 3 9 1 25  8 t    5 8  22 29
- Với t    M  ;    (loại) 5   5 5  2 2 11 2 11 11 2
- Với t    M  ;  
 z   i  z  2 i, z   .i 5   5 5  1 2 5 5 5 5 Suy ra M 2 2 m
P in  IP  IM  IP  R  4 3 3  2 . 2 11 11 2 Vậy 2 m
T in 2  4 khi z   i, z1  2 i, z2   .i 5 5 5 5
Câu 52: (Chuyên Bắc Giang 2019) Cho số phức z thỏa mãn z  3  4i  5 và biểu thức 2 2
P  z  2  z  i đạt giá trị lớn nhất. Tính z  i . A. 5 3 . B. 41 . C. 61 . D. 3 5 . Lời giải Chọn C
Giả sử z  x  yi , ( x, y   ). Trang 37 +) Ta có: z   i 
 x  2   y  2 3 4 5 3 4  5   1 . +) 2 2 P  z 
 z  i   x  2  y   x   y  2 2 2 2 2 1   4x  2 y  3    
 x     y       x  2   y  2 2 2 4 3 2 4 23 4 2 3 4   23  33   . x  3 y  4 P  33  
 x  3  2 y  4 2 . 4 2 x  5 x 1 Từ   1 và 2 suy ra  hoặc  . y  5 y  3 x  5 x 1 Với   P  33 ; Với   P 13. y  5 y  3
Vậy số phức z thỏa mãn z  3 4i  5 và biểu thức 2 2
P  z  2  z  i đạt giá trị lớn nhất là
z  5  5i . Khi đó z  i  61 .
Câu 53: (Đại học Hồng Đức –Thanh Hóa –2019) Cho số phức z  a  bi a,b thỏa mãn
z 1 i  1. Giá trị nhỏ nhất của biểu thức P  a  b 5 là A. 3  2 . B. 2  2 . C. 3 2 2 . D. 2  2 . Lời giải Chọn A Cách 1:
Theo giả thiết ta có z   i   a  2  b  2 1 1 1 1  1.
Đặt a 1 sin t , b 1 cos t 0  t  2  .      
Khi đó P  a  b  5  sin t  cost  3  2 sin t   3  3  2 sin t      .  4   4        Ta có: 1  sin t 
 1   2   2 sin t 
 2  3  2  P  3 2     .  4   4 
Do đó giá trị nhỏ nhất của P là 3  2 . Cách 2:
Theo giả thiết ta có z   i   a  2  b  2 1 1 1 1  1  a,b 0;2.
Khi đó P  a  b  5  5  a  b  3  a   1  b   1    . Theo BĐT Bunhia ta có:
a   b       a  2 b  2 2 2 1 1 1 1 . 1 1   2   Do đó P  3 2 .
Câu 54: (Đại học Hồng Đức –Thanh Hóa 2019) Cho số phức z  a  bi ( a , b  ) thỏa mãn z 1.
Tìm giá trị lớn nhất của biểu thức A  z  2  2 z  2 . A. 10 . B. 5 2 . C. 10 2 . D. 7 . Trang 38 Toanthaycu.com Lời giải Chọn B Ta có: 2 z   a  2 2 2 2  b ; 2 z   a  2 2 2 2  b . Suy ra: 2 2 z  2  z  2   2 2 2 a  b   8 2  2 z  8 10 . 2
Ta có: A   z   z       2 2 2 2 2 2 2 2 1 2
z  2  z  2   50.
Vì A  0 nên từ đó suy ra A  50  5 2 .
Vậy giá trị lớn nhất của A là 5 2 .
Câu 55: (THPT Thăng Long-Hà Nội- 2019) Cho số thực a thay đổi và số phức z thỏa mãn z i  a 
. Trên mặt phẳng tọa độ, gọi M là điểm biểu diễn số phức z . Khoảng 2 a 1 1 a a  2i
cách nhỏ nhất giữa hai điểm M và I  3
 ;4 (khi a thay đổi) là A. 6 . B. 5. C. 4. D. 3. Lời giải Chọn C z i  a z i a 2 1 a  2ai Ta có:    a 1 1 a a  2i a 1 a  2 2 2 2 1 3 z a  a   2 a   1 i a  i    z   z  a 1  1. 2 a  2 2 2 1 a 1
Vậy tập hợp các điểm biểu diễn của số phức z là đường tròn tâm O bán kính R  1 . Ta có: OI  5 . Do đó: OM
 OM  OI  R  5 1  4 . min 1
Câu 56: (Chuyên Lê Hồng Phong-Nam Định- 2019) Xét số phức z thỏa mãn z  2  4i  5 . Gọi a
và b lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của z . Giá trị biểu thức 2 2 a  b bằng A. 40 . B. 4 5 . C. 20 . D. 2 5 . Lời giải Trang 39 Chọn A
Gọi M  x; y là điểm biểu diễn số phức z  x  yi với x, y   . Ta có z   i 
 x  2   y  2 2 4 5 2
4  5  tập hợp điểm biểu diễn số phức z là một
đường tròn có tâm I 2;4 và bán kính R  5 .
Kẻ đường thẳng đi qua 2 điểm O và I cắt đường tròn tại 2 điểm M và N như hình vẽ. 2 2
OI  2  4  2 5 ; IM  IN  R  5 . Từ hình vẽ ta thấy: z
 OM  OI  IM  2 5  5  5  b . min z
 ON  OI  IN  2 5  5  3 5  a . max Vậy 2 2 a  b  40 .
Câu 57: (Hậu Lộc 2-Thanh Hóa- 2019) Cho z , z là hai trong các số phức thỏa mãn z  3  3i  2 1 2
và z  z  4 . Giá trị lớn nhất của z  z bằng 1 2 1 2 A. 8 . B. 4 3 . C. 4 . D. 2  2 3 . Lời giải Chọn A
Gọi M , N lần lượt là điểm biểu diễn của hai số phức z , z . 1 2
 z 3 3i  z 3 3i  2 
M C x   y 2 2 2 , N : 3 3  2 Do 1 2  nên  .  z  z  4     1 2 MN 4 2.2
Như vậy MN là đường kính của đường tròn C với tâm I 3; 3 , bán kính R  2 , do đó I
là trung điểm MN , OI  12 . Trang 40 Toanthaycu.com  MN 
Ta có z  z  OM  ON  1  1 OM  ON  2 2 2 2  2 2OI     8. 1 2  2 
Dấu "  " xảy ra khi và chỉ khi OM  ON  MN là đường kính của C vuông góc với OI .
Câu 58: (Chuyên Đại học Vinh - 2019) Giả sử z , z là hai trong các số phức thỏa mãn  z  68  zi 1 2
là số thực. Biết rằng z  z  4 . Giá trị nhỏ nhất của z  3z bằng 1 2 1 2 A. 5  21 . B. 20  4 21 . C. 20  4 22 . D. 5  22 . Lời giải Chọn C
Giả sử số phức z  x  yi thỏa mãn  z  68  zi là số thực. Ta có:
z  68  zi  x  yi  6(8 x  yii)  x 68 y8xy  8x 
x  6  y8  yi 
Để là  z  68  zi số thực thì  xx    y   y   x  2   y  2 2 8 6 8 0 3 4  5
Vậy điểm biểu diễn số phức z , z thuộc đường tròn tâm I 3, 4 , bán kính R  5 1 2
Giả sử z  x  y i có điểm biểu diễn Ax , y ; z  x  y i có điểm biểu diễn B x , y . 2 2  1 1  1 1 1 2 2 2
Vì z  z  4   x  x 2   y  y 2  4  AB  4 1 2 1 2 1 2  
Ta xét z  3z  OA  3OB 1 2 Gọi H là trung điểm A ,
B K là trung điểm HB , khi đó ta có:     
z  3z  OA  3OB  2 OH  OB  4OK  4OK 1 2  
Ta có OI  IB  IA  5; AB  4;AH  HB  2; HK 1 Suy ra IH  21  IK  22 .
Theo bất đẳng thức tam giác ta có OK  KI  OI  OK  OI  KI  OK  5  22 . Trang 41
Suy ra z  3z  4OK  20  4 22 1 2
Câu 59: (Chuyên Hoàng Văn Thụ-Hòa Bình-2019)Trong các số phức z thỏa mãn 2 z 1  2 z gọi z 1
và z lần lượt là các số phức có môđun nhỏ nhất và lớn nhất. Giá trị của biểu thức 2 2 z  z 2 1 2 bằng A. 6. B. 2 2. C. 4 2. D. 2. Lời giải Chọn A
Áp dụng bất đẳng thức mô đun : z  z  z  z . Dấu bằng xảy ra z  kz , k  0 . 1 2   1 2 1 2 Ta có: 2 2 2
2 z  z 1  z 1  2  z  z 1  2 z Với 2 2
z 1  2 z  z  2 z 1  0  z  1 2  z 1 2 k  3   2 2 
Dấu bằng xảy ra khi và chỉ khi:     z  1 2  z 2 z   k z     1 2 max 2 i Với 2 2 z 1  2
 z  z  2 z 1  0  z  1 2
 z  2 1 m  3 2 2 
Dấu bằng xảy ra khi và chỉ khi:     z  2 1  z 2 z   m z      2   min 1 1 i 2 2 Vậy 2 2 z  z  2 1  2 1  6. 1 2    
Câu 60: (SGD Đà Nẵng 2119) Gọi z là số phức có môđun nhỏ nhất thỏa mãn điều kiện z  2 8i  17 . Biết z  a  bi , a b , tính 2 m  2a  3b A. m  18 . B. m  54 . C. m  10 . D. m  14 . Lời giải Chọn C Gọi M  ;
a b là điểm biểu diễn số phức z  a bi , a b . Ta có: z   i 
 a  2  b  2 2 8 17 2
8  17  IM  17 với I 2;8 .
Suy ra: M thuộc đường tròn C có tâm I bán kính R  17 . Lại có: 2 2
OI  2 8  2 17  R nên O nằm ngoài C . GTNN của môđun z là z
 OM  OI  R  17   1 . min min
Đẳng thức xảy ra khi M  OI C và M nằm giữa O và I 2 . Từ  
1 và 2 ta có M là trung điểm OI nên M 1;4 .
Suy ra a  1;b  4 . Khi đó: 2
m  2a  3b  2 12  10 .
Câu 61: (Nho Quan A - Ninh Bình - 2019) Xét các số phức z  a  bi a,b  thỏa mãn
z  2  3i  2 2 . Tính P  2a  b khi z 1 6i  z  7  2i đạt giá trị lớn nhất. Trang 42 Toanthaycu.com A. P  3 . B. P  3  . C. P  1. D. P  7 . Lời giải Chọn B M (C) I B N K A  Đặt A 1
 ; 6, B7;2  AB  8;8 và trung điểm của AB là K 3; 2. Gọi M  ;
a b là điểm biểu diễn số phức z ta có: a  2  b  2 2 3  8 .
 M thuộc đường tròn C có tâm I  2
 ;3, bán kính R  8 .   
Ta thấy IK  5; 5  IK.AB  0  I nằm trên đường thẳng trung trực của AB . 2 AB Xét tam giác 2 2 2 MAB  MA  MB  2MK  . 2
 MA  MB   MK  AB  MA MB2 2 2 2 2 2 2 2 4
 MA  MB  4MK  AB .
Ta có z 1 6i  z  7  2i là tổng khoảng cách từ điểm M trên đường tròn C tới hai điểm A và B . MA  MB
Vậy MA  MB lớn nhất khi: 
. Điều này xảy ra khi M là giao điểm của IK với MK max
đường tròn C và M nằm ngoài đoạn IK . x  2  t
Ta có phương trình của đường thẳng IK : . y  3 t
Tọa độ giao điểm của IK với đường tròn C  là nghiệm của hệ: x  2   t  2  y  3  t  2t  8  t  2.    x  2  2   y 32  8
Vậy điểm M cần tìm ứng với t  2  khi đó    M   a 4 4;5    P  2a  b  8   5  3  b   5
Câu 62: (SGD Bắc Ninh 2019) Cho số phức z thỏa mãn 1 i z 1 3i  3 2 . Giá trị lớn nhất của biểu
thức P  z  2  i  6 z  2  3i bằng A. 5 6 . B. 15 1 6. C. 6 5 . D. 10  3 15 . Lời giải Chọn C Trang 43 Cách 1  1 3i
1 i z 1 3i  3 2  1 i z 
 3 2  z  1 2i  3   1 . 1 i   Gọi OM   ;
x y , OI  1; 2 là vec-tơ biểu diễn cho các số phức z  x  iy , w 1 2i .   Từ  
1 có OM  OI  3  MI  3.
Suy ra M thuộc đường tròn C tâm I 1;2 bán kính R  3, C   x  2   y  3 : 1 2  9   Gọi OA   2  ; 
1 , OB  2;3 lần lượt là vec-tơ biểu diễn cho số phức a  2  i , b  2  3i .        Có IA   3
 ;3 , IB  1;  1 . Suy ra IA  3  IB  IA 3IB  0 .
Lúc đó P  MA  6MB  MA  2. 3MB   2 2 3 MA  3MB  .   2   2 Có 2 2
MA  3MB  IA IM   3IB  IM  2 2 2  4IM  IA  3IB . Có 2 IM  9 , 2 IA  18 , 2 IB  2 , nên 2 2 MA  3MB  60 . Suy ra P  3.60  6 5 . MA 3MB Có P  6 5   . 1 2
Vậy giá trị lớn nhất của P là P  6 5 . Cách 2. Giả sử M  ;
x y là điểm biểu diễn của số phức z khi đó   i z   i 
 x  y   x  y   2 2 1 1 3 3 2 1
3 i  3 2  x  y  2x  4 y  4  0
  x  2   y  2 1
2  9 . Do đó M thuộc đường tròn tâm I 1;2 , bán kính R  3. a  x 1 Đặt  Ta có 2 2
a  b  9 . Gọi A   2  ;  1 , B  2;3 b   y  2 P  z   i  z   i  MA 
MB   x  2   y  2 
x  2   y  2 2 6 2 3 6 2 1 6 2 3   
 a  2  b  2 
a  2 b  2 3 3 6 1
1   6a  b  27  6 2a  b 11  
 6a  b  27  2 6a  b  33  1 227  33  6 5 . Trang 44 Toanthaycu.com
Câu 63: (Lômônôxốp - Hà Nội 2019) Cho số phức z thay đổi thỏa mãn z 1 i  3. Giá trị nhỏ nhất
của biểu thức A  2 z  4  5i  z 1 7i bằng a b (với ,
a b là các số nguyên tố). Tính S  a  b ? A. 20 . B. 18 . C. 24 . D. 17 . Lời giải Chọn B
Gọi z  x  yi,  x, y . Ta có:
z   i    x  2   y  2 1 3 1 1  9 C  ;
Suy ra, tập hợp tất cả các điểm biểu diễn số phức z là đường tròn C , có tâm là I  1  ;  1 và bán kính R  3 . Ta có:
A  z   i  z   i 
x  2  y  2  x  2  y  2 2 4 5 1 7 2 4 5 1 7 
x  2   y  2  x  2  y  2   x  2 y  2 2 4 5 1 7 3 1 1  9 
x  2   y  2 2 2 2 4
5  4x  8x  4y  20y  29
 2 x  42   y  52 29 2 2
 2 x  2x  y 10y  4 2       
x  2   y  2   x  2 5 2 4 5 1  y     .   2    
Gọi M  x; yC.
 A  2 z  4  5i  z 1 7i  2MA  M , B A4;5; B 1  ;7 . Trang 45  
 A  MA  MB  MA  MC 5 2 2 , C 1;   .  2 
  3   3 Ta có: IC  0;  IC      R  .  2  2 C
Suy ra, điểm C nằm trong đường tròn C .
Vậy, đường thẳng AC cắt đường tròn C tại hai điểm.
Do đó, để A  2MA MC đạt giá trị nhỏ nhất thì M phải nằm giữa hai điểm A và C .  A  MA  MC 5 13 2  2AC, AC  . 2  A  5 13  a b . Vậy, a  b  18 .
Câu 64: (Nguyễn Huệ- Ninh Bình- 2019)Cho z , z là nghiệm phương trình 6  3i  iz  2z  6  9i 1 2 8
và thỏa mãn z  z  . Giá trị lớn nhất của z  z bằng 1 2 5 1 2 56 28 A. . B. . C. 6 . D. 5. 5 5 Lời giải Chọn A
Gọi z  x  y i, z  x  y i , với x , y , x , y . 1 1 1 2 2 2 1 1 2 2 8 8 8 Do z  z 
 x  x  y  y i   x  x  y  y  1 2 2  1 2 2 1 2   1 2 1 2 5 5 5 8
Gọi M x ; y , M x ; y  M M  x  x  y  y  . 1 2  1 2 2  1 2 2 2  2 2  1  1 1  5
Mà z là nghiệm phương trình 6  3i  iz  2z  6  9i 1
 6  y  x 3 i  2x  6  2y 9 i 1   1   1   1 
 6  y 2   x 32  2x  62  2y 92 2 2
 x  y  6x 8y  24  0 1 1 1 1 1 1 1 1
 M x ; y  đường tròn 2 2
(C) : x  y  6x  8 y  24  0 . 1  1 1  Tương tự M x ; y  C . 2  2 2   
Đường tròn (C) có tâm I 3; 4 , bán kính R  1 . 2 Goị  4  3
M là trung điểm M M  IM  M M , 2 2 IM  R  M M  1   , và 1 2 1 2 1    5  5 z  z  2OM . 1 2
Mà OM  OI  IM , dấu bằng xảy ra khi O, I , M thẳng hàng. Khi đó OM  M M , và 1 2 28 OM  OI  IM  . 5 Trang 46 Toanthaycu.com 56
 z  z đạt giá trị lớn nhất bằng 2 OI  IM  , bằng . 1 2 5
Hoặc đánh giá chọn đáp án như sau:
Gọi N x ;  y  NM  x  x  y  y  z  z 1  1 22  1 22 2 2  1 2
Và N đối xứng với M qua gốc tọa độ O , N đường tròn 2 2
(C ) : x  y  6x  8y  24  0 . 2 1
(C ) có tâm I 3; 4 , bán kính R  1, (C ) đối xứng với C  qua gốc tọa độ O . 1   1 1 1
Có I I  10  I I  R  R  8 . 1 1 1
Nhận xét: với mọi điểm M  C , N C thì M N  I I  R  R . Loại các đáp án B,C,D 1  1   1 1 1 56
 z  z  M N đạt giá trị lớn nhất bằng . 1 2 1 5 z
Câu 65: Cho các số phức z và w thỏa mãn 3 i z 
1 i . Tìm giá trị lớn nhất T  w  i w 1 Trang 47 2 3 2 1 A. . B. . C. 2 . D. . 2 2 2 Lời giải Chọn B  z z z 3  i z  1 i 
 3 z 1 1 z i 
  z  2    z 2 3 1 1 . . w 1 w 1 w 1
Đặt t  z ; t  0 (vì z  0 không thỏa phương trình trên). t t (1) trở thành:
  t  2    t2 3 1 1  w 1  . . w 1 2 10t  8t  2 1 1 1  w 1    ; t   0. . 8 2 2 2 10   1  2 2  2  2 t t    t  1
Ta luôn có: w  i  w 1  1 i   3 2 2  w  i  .. 2 2  1 t   z  2  1  z  i  
Dấu = xảy ra  w 1  k 1 i 2   .  3 1  3 2 w   i  w i   2 2  2 3 2
Vậy: Giá trị lớn nhất của T  . . 2
Câu 66: Cho các số phức z thỏa mãn z  2  z  2  2 3 . Tìm giá trị nhỏ nhất của biểu thức
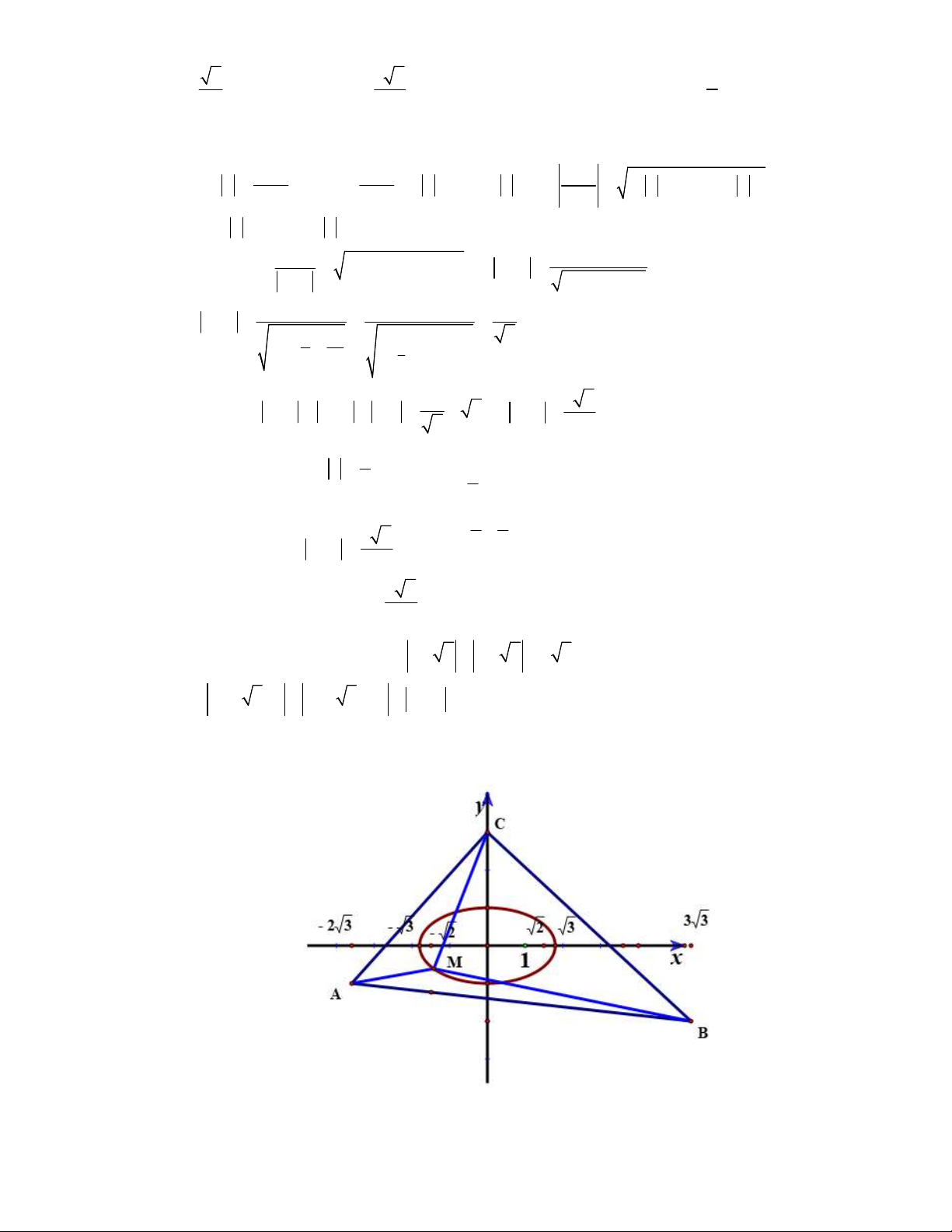
P  z  2 3  i  z  3 3  2i  z  3i . A. 12 . B. 6 . C. 8. D. 10 . Lời giải Chọn A Trang 48 Toanthaycu.com
Gọi M x; y , F  2;0 , F
2;0 , lần lượt là điểm biểu diễn cho các số phức z  x  yi , 2   1    2 , 2 .
Có z  2  z  2  2 3  MF  MF  2 3 , có 2 3  F F  2 2 . 1 2 1 2
Suy ra M x; y chạy trên E  có tiêu cự 2c  2 2 , độ dài trục lớn 2a  2 3 , độ dài trục nhỏ 2 2 2b x y
 2 và phương trình chính tắc của E là   1. 3 1   x  Có M x yE 3 3 ;   . 1  y  1
Có P  z  2 3  i  z  3 3  2i  z  3i .  x 
2 y   x 2 2
 y  2  x y  2 2 2 3 1 3 3 2 3 . 2 2  x 
 y 2   x y 2  y 2 2 3 1 3 3 2 3 .  x    x2  y  2 2 3 3 3 2 3  y  3  
1 (Bất đẳng thức tam giác). 2
 4y 12y  84  3  y . Đặt f y 2
 2 y  3y  21  3  y , với 1  y  1. 2y  3 Có f y  1. 2 y  3y  21 f y  0  2
y  3y  21  2y  3   1 , y 1 nhaän
Có 1  y  1   1 2
 3y  9y 12  0   . y  4   loaïi Có f   1  4  2 19 , f   1  12 .
Suy ra Min f y  12  P  12 . y   1;    1 x  0, y  1 
Đẳng thức 1 xảy ra khi  x  2 3 y 1  x  0, y  1.   0  3 3  x y  2
Thử lại: Khi x  0, y  1 có P  12 .
Vậy MinP  12 khi x  0, y  1.
Câu 67: Cho số phức z  x  yi , x, y  thỏa mãn 2 2
z  3y 16. Biểu thức P  z  i  z  2 đạt giá
trị lớn nhất tại  x ; y với x  0, y  0 . Khi đó: 2 2 x  y bằng 0 0  0 0 0 0 20  3 6 20  3 7 20  3 6 20  3 7 A. . B. . C. . D. . 2 2 2 2 Lời giải Trang 49 Chọn D Ta có: 2 2 2 2
z  3y 16  x  4y 16. P 
x   y  2   x  2  y  x   y  2    x2  y2 2 2 2 1 2 1 2
  x   x2   y   y2 2 1  5 .  .
x  y  2  x y   1 x  2y  2  0 x  2  2y     . x 2  x  0 x 2  x  0  2  2y2 2  4y 16  0      y   1 .y  0   y   1 .y  0 x2  x  0 P  5      max  2 2 2 2 x  4y  16 x  4y 16  y   1 . y  0    x  0 x  0 x  0    y   0 y  0 y  0  1 7 x 1 7 0  y   20  3 7 2 2   2    x  y  . 0 0 1 7 2   y  0 x  1 7  2
Nhận xét: Bài này ta dùng bất đẳng thức véc tơ như sau    
Cho a  a ;a ,b  b ;b  a  b  a  b ;a  b , ta có: 1 2   1 2  1 1 2 2    
a  b  a  b  a  b 2  a  b 2 2 2 2 2  a  a  b  b . 1 1 2 2 1 2 1 2   a b  a b 1 2 2 1 
Dấu “ = ” xãy ra  a ,b ngược hướng  a b  0 . 1 1 a b  0  2 2
Câu 68: Cho số phức z  a  bi  ,
a b thỏa mãn z  4  z  4 10 và z  6 lớn nhất. Tính S  a b . A. S 11. B. S  5  . C. S  3  . D. S  5. Lời giải Chọn B
Trong mp tọa độ Oxy , Ta gọi các điểm biểu diễn của các số phức:
z  x  yi là M  x; y ; z  4   0i là F 4
 ;0 ; z  4  0i là F 4;0 . 2   1  
Ta có: z  4  z  4 10  MF  MF  10 . (1) 1 2 MF   x  42 2 2  y 1 8x 2 2 
 MF  MF  16x  MF  MF  .(2) MF   x   1 2 1 2 2 2 2 5 4  y 2 4x
Từ (1) và (2), suy ra MF  5  . 1 5 2 2 2  4x  x y
Mặt khác MF  x  42 2 2  y  5     x  42 2  y    1. 1  5  25 9
Vậy, tập hợp các điểm biểu diễn của số phức thỏa mãn z  4  z  4 10 là Elip có phương 2 2 x y trình E :  1. 25 9 Trang 50 Toanthaycu.com
Theo đề, ta cần tìm điểm thuộc  E sau cho z  6 lớn nhất.
Ta gọi các điểm biểu diễn số phức: z  6  0i là A6;0 ; z  a  bi là M a;bE; z  5   0i là C  5  ;0 .
Do đó, z  6 lớn nhất khi và chỉ khi MA lớn nhất.
Dựa, vào hình vẽ trên ta thấy để MA lớn nhất khi M  C  5  ;0  a  5  ;b  0  S  5  .
Câu 69: Cho số phức z  a  bi a,b thỏa z  4  z  4 10 và z  6 lớn nhất. Tính S  a  b ? A. S  3  . B. S  5. C. S  5  . D. S  11. Lời giải Chọn C
Gọi M a;b là điểm biểu diễn số phức z  a  bia,b  .
z  4  z  4  10  a  4  bi  a  4  bi  10
 a  42  b  a  42 2 2  b  10* Xét F 4
 ;0 và F 4;0 . Khi đó   *  MF  MF  10 2   1   1 2 c  4 Suy ra M thuộc Elip có 2 2   b  a  c  3 2a 10  a  5
Ta có: z   a  2 2 6
6  b  IM , I 6;0 , suy ra max z  6  IA hay điểm M  A 5  ;0  z  5   0i  S  5  .
Câu 70: Cho số phức z thỏa mãn z  1, M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu
thức A  1 z  2 1 z . Giá trị của biểu thức M  m bằng A. 2 5  2 . B. 6 . C. 2 5  4 . D. 7 . Lời giải Trang 51 Chọn A
Gọi z  x  yi với x, y  . 2 2 2 2
z  1 x  y  1  x  y  1  A   z 
 z  x  2  y    x2 2 2 1 2 1 1 2 1
 y  2  2x  2 2  2x .
Xét hàm số f  x  2  2x  2 2  2x với x  1  ;  1 . 1 2 1 x  2 1 x
Hàm số f  x liên tục trên đoạn  1  ;  1 và f  x    . 2  2x 2  2x 2 2 1 x  f  x 3
 0  1 x  2 1 x  0  x    1  ;  1 . 5  3  Khi đó f   1  4; f   2 5   ; f   1  2 .  5   3 
Do đó M  max f  x  f   2 5 ; m  min f   x  f  
1  2 . Suy ra M  m  2 5  2 .  1  ;  1  5  1  ;  1 
Câu 71: Xét tập hợp S các số phức z  x  yi  ,
x y  thỏa mãn điều kiện 3z  z  1 i2  2i .
Biểu thức Q  z  z 2  x đạt giá trị lớn nhất là M và đạt được tại z  x  y i ( khi z thay 0 0 0
đổi trong tập S ). Tính giá trị 2 T  M .x y . 0 0 9 3 9 3 9 3 9 3 A. T   . B. T  . C. T  . D. T   . 2 4 2 4 Lời giải Chọn D
Ta có: z  z    i  i 2 2 2 2 2 2 3 1 2 2
 4x 16 y  16  x  4 y  4  4 y  4  x
Do đó, Q  z  z   x 2  y   x 2 2 4 2
 4  x 2  x  f x, 2  x  2. 2   f  x 2x 2x 4  , 2   x  2. 2 4  x    f  x x 1  0      x     x 1. 2 2 ; 2 Mặt khác, f  2
   0, f 2  0, f   1  3 3. 3 Suy ra M  3 3 tại 2 x  1  , y  . 0 0 4 9  3 Vậy T  . 4
Câu 72: (THPT Hậu Lộc 2 2019) Cho z , z là hai trong các số phức thỏa mãn z  3  3i  2 và 1 2
z  z  4. Giá trị lớn nhất của z  z bằng 1 2 1 2 A. 8. B. 4 3 . C. 4. D. 2  2 3 . Trang 52 Toanthaycu.com Lời giải Chọn A
Gọi M , N lần lượt là điểm biểu diễn của hai số phức z , z . 1 2
 z 3 3i  z 3 3i  2 
M C x   y 2 2 2 , N : 3 3  2 Do 1 2  nên  .  z  z  4     1 2 MN 4 2.2
Như vậy MN là đường kính của đường tròn C với tâm I 3; 3 , bán kính R  2 , do đó I
là trung điểm MN , OI  12 .  MN 
Ta có z  z  OM  ON  1  1 OM  ON  2 2 2 2  2 2OI     8. 1 2 2  
Dấu "  " xảy ra khi và chỉ khi OM  ON  MN là đường kính của C vuông góc với OI .
Câu 73: (Chuyên Lê Hồng Phong Nam Định 2019) Cho hai số phức z , z thỏa mãn 1 2
z  2  i  z  4  7i  6 2 và iz 1 2i  1. Tìm giá trị nhỏ nhất của biểu thức T  z  z . 1 1 2 1 2 A. 2 2 1. B. 2 1. C. 2 2 1. D. 2 1. Lời giải Chọn C
Trên mặt phẳng Oxy , gọi M  ;
a b là điểm biểu diễn cho số phức z ; A 2  ;  1 , B4;7 lần lượt 1
là điểm biểu cho các số phức 2
  i và 4  7i  AB  6 2 .
Từ đó ta được MA  MB  6 2  AB nên tập hợp các điểm M biểu diễn cho số phức z là đoạn 1
thẳng AB nằm trên đường thẳng d : x  y  3  0. Đặt z  z , khi đó 3 2 Trang 53 iz 1 2i 1  i
 z 1 2i 1 z  2 i 1. Gọi N  ;
c d  là điểm biểu diễn cho z ; 2 3 3 3 I 2; 
1 là điểm biểu diễn cho số phức 2  i , khi đó IN 1 nên tập hợp các điểm biểu diễn cho số
phức z là đường tròn C   x  2   y  2 : 2 1  1. 3 z  z  z  z  MN . 1 2 1 3
Dễ thấy hình chiếu vuông góc của điểm I 2; 
1 trên đường thẳng d  là điểm K 0;3 thuộc
đoạn AB suy ra MN  KH với H là giao điểm của IK với C và thuộc đoạn IK .
Do đó min MN  KH  d I, AB  R  2 2 1. Vậy min z  z  2 2 1 1 2
Câu 74: (Trường Thpt Hàm Rồng 2019) Cho số phức z, z , z thỏa mãn z  4  5i  z 1 1 và 1 2 1 2
z  4i  z  8  4i . Tính z  z
khi P  z  z  z  z đạt giá trị nhỏ nhất 1 2 1 2 A. 8 B. 6 . C. 41 . D. 2 5. Lời giải Chọn D
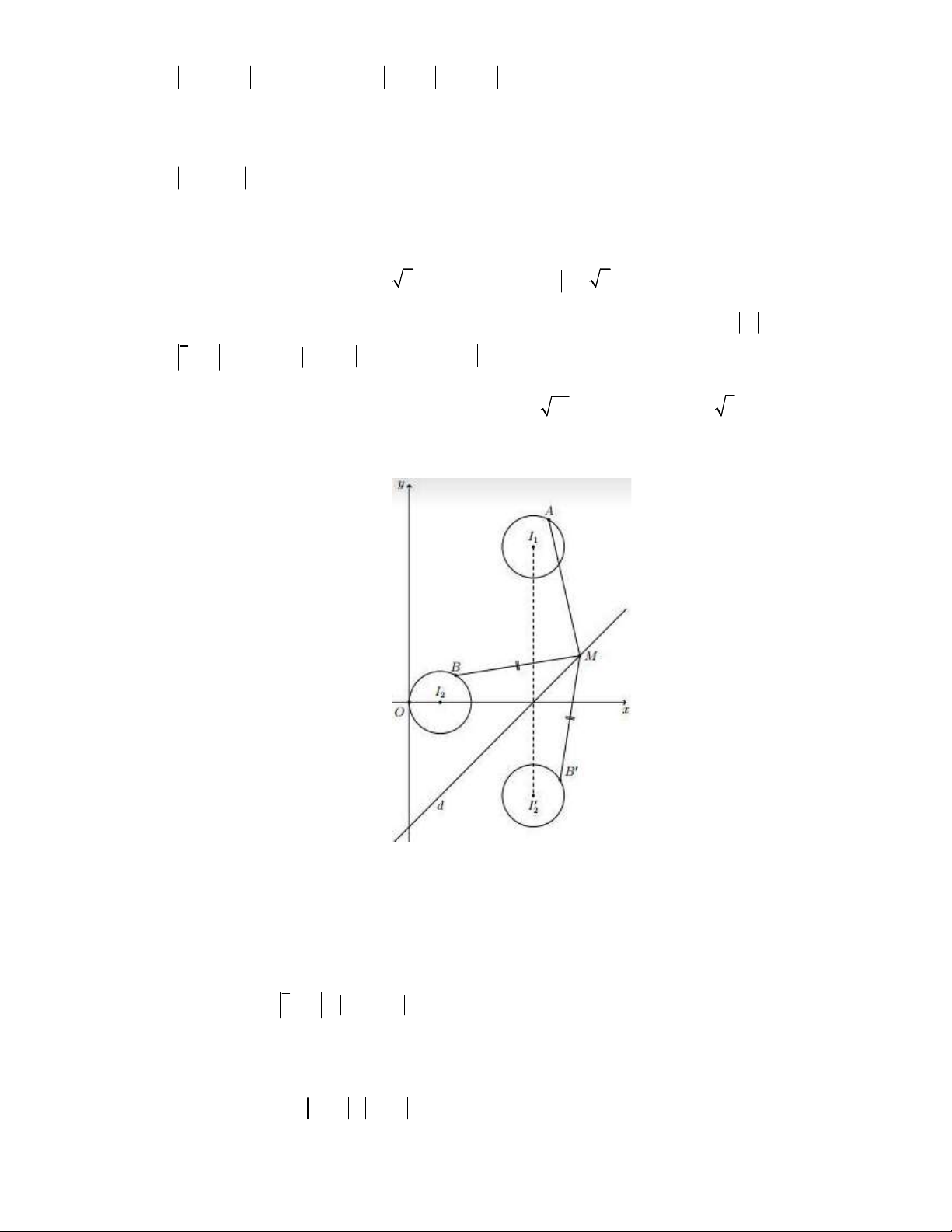
Gọi A là điểm biểu diễn của số phức z . Suy ra A thuộc đường tròn C tâm 1  1 I 4;5 , R  1. 1  
Gọi B là điểm biểu diễn của số phức z . Suy ra B thuộc đường tròn C tâm I 1;0 , R 1. 2   2  2 Gọi M  ;
x y là điểm biểu diễn của số phức z  x  yi
Theo giả thiết z  4i  z  8  4i  x  y  4 . Suy ra M thuộc đường thẳng d  x  y  4  0 Gọi C ' có tâm I ' 4; 3
 , R 1 là đường tròn đối xứng với đường tròn C tâm 2  2   2 
I 1; 0 , R  1qua đường thẳng d. Gọi B ' là điểm đối xứng với đối xứng với B qua đường 2   2
thẳng d. Ta có P  z  z  z  z  MA  MB  MA  MB '  AB '  I I ' R  R  6 . 1 2 1 2 1 2 Trang 54 Toanthaycu.com  1 
Dấu = xảy ra khi và chỉ khi ,
A B ', I , I ', M thẳng hàng. Khi đó I A  I I ' suy ra A4;4 và 1 2 1 1 2 8
 1 
I B'  I ' I suy ra B'4; 2    B2;0. AB  . 2 2 1 8 2 5 Vậy z  z  2 5 . 1 2 z
Câu 75: (Chuyên ĐH Vinh- 2019) Cho các số phức z và  thỏa mãn 2  i z   1 i. Tìm giá trị 
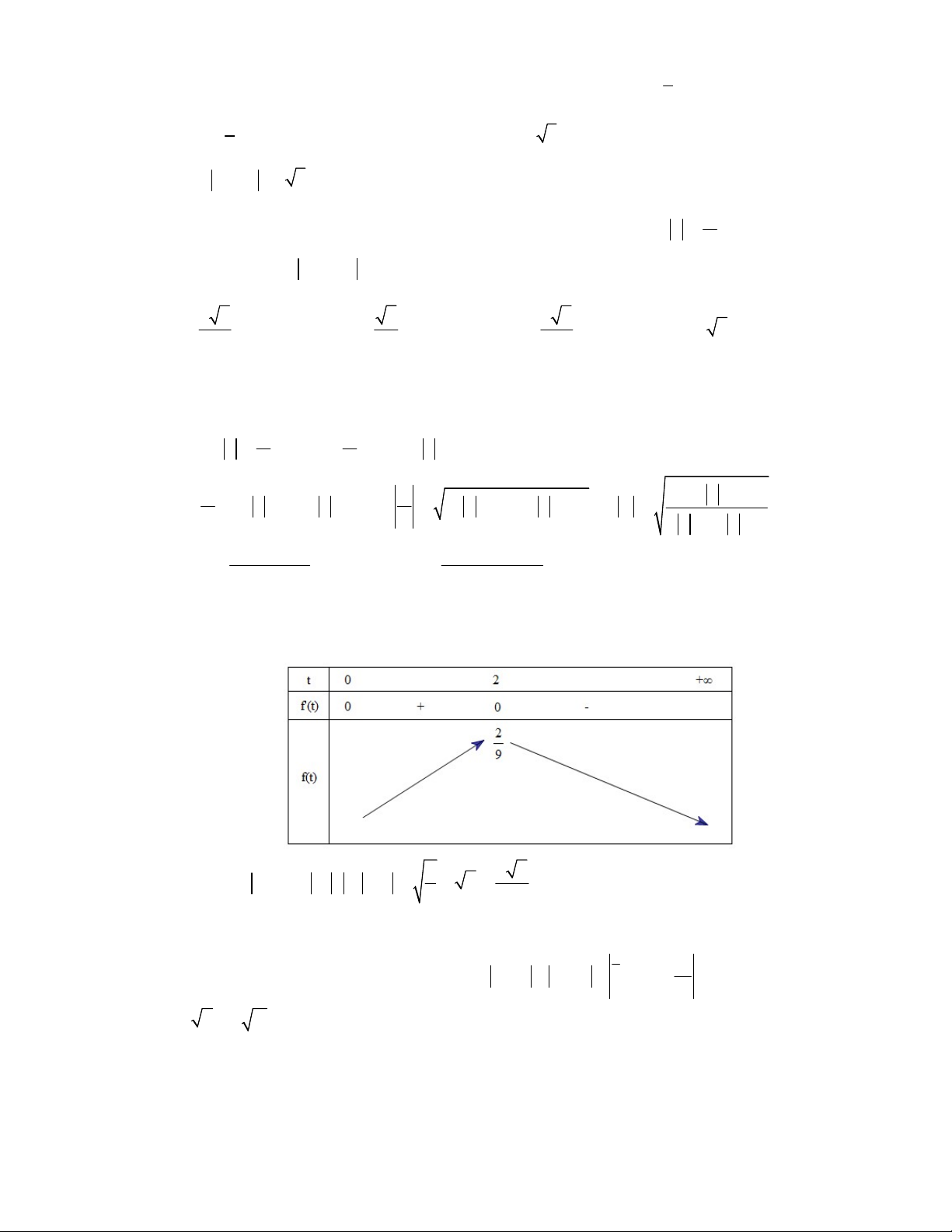
lớn nhất của T   1 i 4 2 2 2 2 A. B. C. D. 2 3 3 3 Lời giải Chọn A  z z 2  i z   1 i   2  i z 1 .i   2 z    z z 2 z   1   z   1 i   2 z  2 1   z  2 1    2   5 z  2 z  2 2 2   t 2  t  4t f t  t  0  f ' t 
 f ' t  0  t  0  t  2 2     2   5t  2t  2  2 5t  2t  2 Bảng biến thiên 2 4 2
Ta có T   1 i  z  1 i   2  9 3
Câu 76: Cho số phức z và gọi z , z là hai nghiệm phức của phương trình 2
z 8i  0 ( z có phần thực 1 2 1 z
dương). Giá trị nhỏ nhất của biểu thức 2
P  z  z  z  z  z  2z 
được viết dưới dạng 1 2 1 2 m n  p q (trong đó ,
n p  ; m , q là các số nguyên tố). Tổng m  n  p  q bằng A. 3 . B. 4 . C. 0 . D. 2 . Lời giải Chọn A 2
z 8i  0  z  2  2i và z  2   2i . 1 2 Trang 55 z z 2 2
P  z  z  z  z  z  2z 
 z  z  z  z  z  2z   MA  MB  MC . 1 2 1 1 2 1 2 2
Trong đó M , A2;2 , B  2
 ;2, C 3;3 lần lượt là điểm biểu diễn cho các số phức z , z1 z , z , 2   2  z   3  3i . 2 1 2
Gọi H là hình chiếu vuông góc của M trên OC .
Ta có MA MB  HA HB  MA  MB  MC  HA  HB  HC . Do đó P  MA  MB  MC
 HA  HB  HC  M  H  M OC : y  x. min  min
Gỉa sử M  x; x  x  3
 ;0  P  MA  MB  MC  x     2 2 3 2 2 x  4 x 2 3  P  2  2 2.  P  0  x    3  ;0 . 2 x  4 3 2 2 3  2 3      Vậy P  2    3  2 2 
  4  2 6  3 2 . min  3   3        
Suy ra m  2 , n  6 , p  3, q  2  m  n  p  q  3.
Câu 77: Trong các số phức z thỏa mãn 2
z 1  2 z gọi z và z lần lượt là các số phức có môđun nhỏ 1 2
nhất và lớn nhất. Giá trị của biểu thức 2 2 z  z bằng 1 2 A. 6 . B. 2 2 . C. 4 2 . D. 2 . Lời giải Chọn A
Đặt z  a  bi ; a ,b   .
z   a  b   abi  a  b  2 2 2 2 2 2 2 2 1 1 2 1  4a b ; 2 2 2 z  2 a  b . 2 Ta có 2 z   z   2 2 a  b   2 2  a b   2 2 1 2 1 4 4 a  b 
 a  b 2  a b  a b    a  b    a  b 2 2 2 2 2 2 2 2 2 2 2 2 2 4 2 1 4 0  2a  6b 1  0  a  b 2 2 2   2 2 a  b  2 6 1  4a . 2 Vì 2 4  a  0, a   nên  2 2 a  b    2 2 a  b  2 2 6
1 0  3  2 2  a  b  3  2 2 . Trang 56 Toanthaycu.com m  2 1 Suy ra 2 2 2 2
2 1  a  b  2 1   m  M  6. M  2 1   a  0 a 0   M  2 1     . 2 2 a  b  3 2 2 b    1 2   a  0 a 0   m  2 1     . 2 2 a  b  3 2 2 b     2  1 3 5
Câu 78: (Sở Nam Định - 2019) Xét các số phức w , z thỏa mãn w  i 
và 5w  2  i z  4 . 5
Tìm giá trị lớn nhất của biểu thức P  z  2i  z  6  2i . A. 7 . B. 2 53 . C. 2 58 . D. 4 13 . Lời giải Chọn C Cách 1.
Ta có: 5w  2  i z  4  5w 5i  2  i z  4  5i
 5w  5i  2  iz  4  5i  5 w  i  1 2iz  4 1 2i  5 z  3  2i 3 5  5.
 5 z  3 2i  z  3 2i  3. 5 Ta có: 2 2 z  z  z  z  2 2 2 z  z ; z  , z . (1) 1 1 1  1  z  z 2 2 2 1 z  z  ; z  , z . (2) 1 1 2
Ta có: P  z  2i  z  6  2i  z  3 2i  3  z  3  2i  3 .
Áp dụng (1) và (2), ta có: 2 2 z   i   z   i    2 3 2 3 3 2 3 2 z  3  2i  9 .
 z 3 2i 3  z 3 2i 3 2  z  2i  z 6 2i 2 2 2
z  3  2i  3  z  3  2i  3   2 2 . Vậy, ta có:
 z 2i  z 6 2i 2  2 2
z  3  2i  9   z  2i  z  6  2i 2  4 2 z  3  2i  9 . 2  P   2 2 4 z  3  2i  9. 2 Do  2 z   i     2 4 3 2 9
4 z  3  2i  4i  9 nên 2 P  4 z 3 2i  4  i   9 Trang 57 2  P   2
4 7  9  232  P  2 58 . Cách 2. 3 5
Ta có: 5w  2  i z  4 thay w  i  5  z 3 2i  3 .
Suy ra, tập hợp các điểm biểu diễn số phức z là đường tròn C   x  2   y  2 : 3 2  9 . Gọi M C .
Ta có: P  z  2i  z  6  2i  AM  BM ; A0;2, B6;2 . Suy ra P   2 2 2 AM  BM  .
Gọi H là trung điểm của cạnh AB .  AB  Ta có: P  AM  BM  2 2 2 2 2 2 2  2 2MH     4MH  AB .  2 
Vậy, P  z  2i  z  6  2i đạt giá trị lớn nhất khi 2
MH đạt giá trị lớn nhất. Dựa vào hình vẽ sau Suy ra, 2
MH đạt giá trị lớn nhất khi M  M ' 2
 P  232  P  2 58 .
Câu 79: Cho các số phức z , z , z thỏa mãn z  z  z 1. Tính giá trị lớn nhất của biểu thức 1 2 3 1 2 3 2 2 2 P  z  z  z  z  z  z . 1 2 2 3 3 1 A. P  9 . B. P  10 . C. P  8 . D. P  12 . Lời giải Chọn A
Gọi A x ; y ; B x ; y ; C  x ; y là các điểm lần lượt biễu diễn các số phức z ; z ; z . 3 3  2 2  1 1  1 2 3 Trang 58 Toanthaycu.com
vì z  z  z  1 suy ra 1 2 3
A ; B ; C thuộc đường tròn tâm O bán kính bằng 1.
Ta có z  z  AB ; z  z  BC z  z  AC . 1 2 2 3 3 1 Suy ra 2 2 2 P  z  z  z  z  z  z 2 2 2  AB  BC  AC 1 2 2 3 3 1      
        
2   2   2 AO OB BO OC AO OC  6  2O . A OB  O . B OC  O . A OC 
         2 9 OA OB OC    2 9 3OG 2
 9  OG  9 ( với G là trọng tâm tam giác ABC ).
Dấu “ = “ xảy ra khi G  O , hay ABC đều.
Câu 80: Cho số phức z thỏa mãn 3 z  z  2 z  z  12. Gọi M , m lần lượt là giá trị lớn nhất, nhỏ nhất
của z  4  3i . Giá trị của M .m bằng: A. 28 . B. 24 . C. 26 . D. 20 . Lời giải Chọn B Gọi z  x  yi; ; x y  . 
Xét 3 z  z  2 z  z  12  3 x  2 y  6. (1)
Ta có: P  z   i   x  2   y  2 4 3 4 3 2
Tập hợp những điểm biểu diễn z  x  yi; ; x y  .
 thỏa mãn (1) là miền trong (tính cả biên)
của hình thoi ABCD với A0;  3 ; B 2  ;0; C0; 3
 ; D2;0 tạo bởi 4 đường thẳng
3 x  2 y  6. Điểm biểu diễn z thỏa mãn (2) là đường tròn tâm I 4; 3
  bán kính R  P  0 . Trang 59
P đạt min, max khi bán kính đường tròn đạt min, max khi xét sự tương giao với miền hình thoi ABC . D
Ta có đường tròn giao với miền hình thoi điểm gần tâm nhất khi đường tròn tiếp xúc cạnh CD: 3.4  2.3  6 12
3x  2 y  6  0 tương ứng có m  
. Điểm giao xa nhất là đỉnh A0;  3 2 2 3  2 13 của hình thoi. Do đó 2 2 M  4  6  2 13.  M.m  24. Trang 60