Chuyên đề đạo hàm – Nguyễn Bảo Vương

Tài liệu gồm 185 trang gồm lý thuyết, công thức đạo hàm cơ bản và mở rộng, phân dạng và hướng dẫn giải các dạng toán chuyên đề đạo hàm, các bài tập có đáp án.

64 32 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 9: Đạo hàm (KNTT)

Môn: Toán 11

Thông tin:

185 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
CHƯƠNG V.
ĐẠO HÀM –
TẬP 1.
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 hoặc Liên hệ qua
Facebook: https://web.facebook.com/phong.baovuong
Website: http://tailieutoanhoc.vn/
Email: baovuong7279@gmail.com
Page Facebook: https://web.facebook.com/tracnghiemtoanthpt489/
ALBA – CHƯ SÊ- GIA LAI
NGUYỄN BẢO VƯƠNG
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
1
CHƯƠNG V. ĐẠO HÀM
TẬP 1. KHÁI NIỆM ĐẠO HÀM VÀ CÁC
PHƯƠNG PHÁP TÍNH ĐẠO HÀM
NGUYỄN BẢO VƯƠNG
Mục Lục
KHÁI NIỆM ĐẠO HÀM .................................................................................................................................... 2
Vấn đề 1. Tính đạo hàm bằng định nghĩa .................................................................................................. 2
CÁC BÀI TOÁN LUYỆN TẬP .................................................................................................................. 4
CÁC QUY TẮC TÍNH ĐẠO HÀM ................................................................................................................... 8
Vấn đề 1. Tính đạo hàm bằng công thức .................................................................................................... 8
CÁC BÀI TOÁN LUYỆN TẬP ................................................................................................................ 11
Vấn đề 2. Sử dụng đạo hàm để tìm giới hạn ........................................................................................... 24
CÁC BÀI TOÁN LUYỆN TẬP ................................................................................................................ 25
Vấn đề 3. Đạo hàm cấp vao và vi phân ..................................................................................................... 27
CÁC BÀI TOÁN LUYỆN TẬP ................................................................................................................ 29
ĐẠO HÀM TỔNG HỢP .................................................................................................................................. 33
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
2
CHỦ ĐỀ: ĐẠO HÀM
KHÁI NIỆM ĐẠO HÀM
1. Đạo hàm tại một điểm
Hàm số
()y f x
liên tục trên
, được gọi là có đạo hàm tại
0
( ; )x a b
nếu giới hạn sau tồn tại (hữu
hạn):
0
0
0
( ) ( )
lim
xx
f x f x
xx
và giá trị của giới hạn đó gọi là giá trị đạo hàm của hàm số tại điểm
0
x
.Ta kí hiệu
0
'( )fx
.
Vậy
0
0
0
0
( ) ( )
'( ) lim
xx
f x f x
fx
xx
2. Đạo hàm bên trái, bên phải
0
0
0
0
( ) ( )
'( ) lim
xx
f x f x
fx
xx
.
0
0
0
0
( ) ( )
'( ) lim
xx
f x f x
fx
xx
.
Hệ quả : Hàm
()fx
có đạo hàm tại
00
( )x f x
và
0
'( )fx
đồng thời
00
'( ) '( )f x f x
.
3. Đạo hàm trên khoảng, trên đoạn
Hàm số
()fx
có đạo hàm (hay hàm khả vi) trên
nếu nó có đạo hàm tại mọi điểm thuộc
.
Hàm số
()fx
có đạo hàm (hay hàm khả vi) trên
[ ; ]ab
nếu nó có đạo hàm tại mọi điểm thuộc
( ; )ab
đồng thời tồn tại đạo hàm trái
'( )fb
và đạo hàm phải
'( )fa
.
4. Mối liên hệ giữa đạo hàm và tính liên tục
Định lí: Nếu hàm số
()fx
có đạo hàm tại
0
x
thì
()fx
liên tục tại
0
x
.
Chú ý: Định lí trên chỉ là điều kiện cần, tức là một hàm có thể liên tục tại điểm
0
x
nhưng hàm đó không
có đạo hàm tại
0
x
.
Chẳng hạn: Xét hàm
()f x x
liên tục tại
0x
nhưng không liên tục tại điểm đó.
Vì
0
( ) (0)
lim 1
x
f x f
x
, còn
0
( ) (0)
lim 1
x
f x f
x
.
Vấn đề 1. Tính đạo hàm bằng định nghĩa
Phương pháp:
0
0
0
0
( ) ( )
'( ) lim
xx
f x f x
fx
xx
0
0
0
0
( ) ( )
'( ) lim
xx
f x f x
fx
xx
0
0
0
0
( ) ( )
'( ) lim
xx
f x f x
fx
xx
Hàm số
()y f x
có đạo hàm tại điểm
0 0 0
'( ) '( )x x f x f x
Hàm số
()y f x
có đạo hàm tại điểm thì trước hết phải liên tục tại điểm đó.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
3
Các ví dụ
Ví dụ 1. Tính đạo hàm của các hàm số sau tại các điểm đã chỉ:
1.
3
( ) 2 1f x x
tại
2x
3.
32
11
khi 0
()
0 khi 0
xx
x
fx
x
x
tại
0x
2.
2
( ) 1f x x
tại
1x
Lời giải.
1. Ta có
3
2
2 2 2
( ) (2)
2 16
lim lim lim2( 2 4) 24
22
x x x
f x f
x
xx
xx
'(2) 24f
.
2. Ta có :
2
11
( ) (1)
12
'(1) lim lim
11
xx
f x f
x
f
xx
1
2
( 1)( 1) 1
lim
2
( 1)( 1 2)
x
xx
xx
.
3. Ta có
(0) 0f
, do đó:
32
2
0 0 0
32
( ) (0)
1 1 1 1
lim lim lim
2
11
x x x
f x f
x x x
x
x
xx
Vậy
1
'(0)
2
f
.
Ví dụ 2. Chứng minh rằng hàm số
2
21
()
1
xx
fx
x
liên tục tại
1x
nhưng không có đạo hàm tại
điểm đó.
Lời giải.
Vì hàm
()fx
xác định tại
1x
nên nó liên tục tại đó.
Ta có:
11
( ) ( 1)
2
'( 1 ) lim lim 1
11
xx
f x f
x
f
xx
11
( ) ( 1)
'( 1 ) lim lim 2 2
1
xx
f x f
f
x
'( 1 ) '( 1 ) ( )f f f x
không có đạo hàm tại
1x
.
Ví dụ 3. Tìm
a
để hàm số
2
1
khi 1
1
khi 1
x
x
fx
x
ax
có đạo hàm tại
1x
Lời giải.
Để hàm số có đạo hàm tại
1x
thì trước hết
()fx
phải liên tục tại
1x
Hay
2
11
1
lim ( ) lim 2 (1)
1
xx
x
f x f a
x
.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
4
Khi đó, ta có:
2
11
1
2
( ) (1)
1
lim lim 1
11
xx
x
f x f
x
xx
.
Vậy
2a
là giá trị cần tìm.
CÁC BÀI TOÁN LUYỆN TẬP
Bài 1 Tính đạo hàm của các hàm số sau tại các điểm đã chỉ ra
Câu 1.
( ) 2 1f x x
tại
0
1x
A.2 B.3 C.4 D.5
Bài làm 1. Ta có:
0
'( ) 2fx
Câu 2.
1
()
1
x
fx
x
tại
0
2x
A.
2
B.2 C.3 D.4
Bài làm 2 .
0
'( ) 2fx
Câu 3.
2
( ) 1f x x x
tại điểm
0
2x
A.
2
B.
C.
8
3
D.
41
Bài làm 3.
2
22
2
1 7 ( 2)( 3) 5
'(2) lim lim
2
27
( 2)( 1 7)
xx
x x x x
f
x
x x x
Câu 4.
2
( ) sinf x x
tại
2
x
A. 0 B.1 C.2 D.3
Bài làm 4.
'( ) 0
2
f
Câu 5.
32
2 1 1
khi 1
()
1
0 khi 1
x x x
x
fx
x
x
tại điểm
0
1x
.
A.
1
3
B.
1
5
C.
1
2
D.
1
4
Bài làm 5.
32
2
1 1 1
32
( ) (1)
2 1 1 1
lim lim lim
12
( 1)
2 1 1
x x x
f x f
x x x x
x
x
x x x
Vậy
1
'(1)
2
f
.
Bài 2 Tính đạo hàm của các hàm số sau tại điểm chỉ ra
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
5
Câu 1.
( ) sin2f x x
tại
0
2
x
A.
1
B.
2
C.
3
D.
4
Bài làm 1. Ta có:
( ) ( ) sin2 sin 2cos sin
2 2 2
f x f x x x
22
cos .sin
( ) ( )
22
2
lim 2 lim 2
22
xx
xx
f x f
xx
Vậy
'1
2
f
.
Câu 2.
( ) tanf x x
tại
4
x
A.
2
B.
4
C.
5
D.
31
Bài làm 2. Ta có
( ) tan tan 1 tan .tan
4 4 4
f x f x x x
Suy ra
44
(1 tan )tan
( ) ( )
4
4
lim lim 2
44
xx
xx
f x f
xx
Vậy
'2
4
f
.
Câu 3.
2
1
sin khi 0
()
0 khi 0
xx
fx
x
x
tại
0x
.
A.
0
B.
1
2
C.
2
3
D.
7
Bài làm 3. Ta có:
00
( ) (0)
1
lim lim sin 0
xx
f x f
x
xx
Vậy
'(0) 0f
.
Bài 3 Tính đạo hàm các hàm số sau tại các điểm chỉ ra
Câu 1.
3
()f x x
tại
0
1x
A.
4
B.
3
C.
5
D.6
Bài làm 1. Ta có:
32
( ) (1) 1 ( 1)( 1)f x f x x x x
Suy ra:
2
11
( ) (1)
lim lim 1 3
1
xx
f x f
xx
x
Vậy
'(1) 3f
.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
6
Câu 2.
32
2 3 1
()
2 7 4
khi 1
1
x khi x
fx
x x x
x
x
tại
0
1x
.
A.
0
B.
4
C.
5
D. Đáp án khác
Bài làm 2. Ta có
11
lim ( ) lim 2 3 5
xx
f x x
32
2
1 1 1
2 7 4
lim ( ) lim lim( 3 4) 0
1
x x x
x x x
f x x x
x
Dẫn tới
11
lim ( ) lim ( )
xx
f x f x
hàm số không liên tục tại
1x
nên hàm số không có đạo hàm tại
0
1x
.
Câu 3.
2
2
sin
khi 0
()
khi 0
x
x
fx
x
x x x
tại
0
0x
A.1 B.2 C.3 D.5
Bài làm 3. Ta có
2
0 0 0
sin sin
lim ( ) lim lim .sin 0
x x x
xx
f x x
xx
2
00
lim ( ) lim 0
xx
f x x x
nên hàm số liên tục tại
0x
2
2
00
( ) (0)
sin
lim lim 1
xx
f x f
x
x
x
và
2
00
( ) (0)
lim lim 1
xx
f x f
xx
xx
Vậy
'(0) 1f
.
Câu 4.
2
1
()
xx
fx
x
tại
0
1x
.
A.2 B.0 C.3 D.đáp án khác
Bài làm 4. Ta có hàm số liên tục tại
0
1x
và
2
1
( ) ( 1)
1 ( 1)
x x x
f x f
x x x
Nên
2
11
( ) ( 1)
21
lim lim 0
1 ( 1)
xx
f x f
xx
x x x
2
11
( ) ( 1)
1
lim lim 2
1 ( 1)
xx
f x f
x
x x x
Do đó
11
( ) ( 1) ( ) ( 1)
lim lim
11
xx
f x f f x f
xx
Vậy hàm số không có đạo hàm tại điểm
0
1x
.
Nhận xét: Hàm số
()y f x
có đạo hàm tại
0
xx
thì phải liên tục tại điểm đó.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
7
Bài 4
Câu 1. Tìm
,ab
để hàm số
2
1
()
1
x x khi x
fx
ax b khi x
có đạo hàm tại
1x
.
A.
23
1
a
b
B.
3
11
a
b
C.
33
31
a
b
D.
3
1
a
b
Bài làm 1. Ta có:
2
11
lim ( ) lim( ) 2
xx
f x x x
;
11
lim ( ) lim( )
xx
f x ax b a b
Hàm có đạo hàm tại
1x
thì hàm liên tục tại
1x
2ab
(1)
2
1 1 1
( ) (1)
2
lim lim lim ( 2) 3
11
x x x
f x f
xx
x
xx
1 1 1
( ) (1)
2
lim lim lim
1 1 1
x x x
f x f
ax b ax a
a
x x x
(Do
2ba
)
Hàm có đạo hàm tại
1x
3
1
a
b
.
Câu 2. Tìm a,b để hàm số
2
2
1 0
()
2 0
x khi x
fx
x ax b khi x
có đạo hàm trên .
A.
10, 11ab
B.
0, 1ab
C.
0, 1ab
D.
20, 1ab
Bài làm 2. Ta thấy với
0x
thì
()fx
luôn có đạo hàm. Do đó hàm số có đạo hàm trên khi và chỉ
khi hàm có đạo hàm tại
0x
.
Ta có:
00
lim ( ) 1; lim ( )
xx
f x f x b
()fx
liên tục tại
01xb
.
Khi đó:
00
( ) (0) ( ) (0)
'(0 ) lim 0; '(0 ) lim
xx
f x f f x f
f f a
xx
'(0 ) '(0 ) 0f f a
.
Vậy
0, 1ab
là những giá trị cần tìm.
Câu 3. Tìm
,ab
để hàm số
2
1
khi 0
()
1
khi 0
x
x
fx
x
ax b x
có đạo hàm tại điểm
0x
.
A.
11, 11ab
B.
10, 10ab
C.
12, 12ab
D.
1, 1ab
Bài làm 3. Ta có
00
lim ( ) 1 (0); lim ( )
xx
f x f f x b
Hàm số liên tục tại
01xb
00
( ) (0)
1
lim lim 1
1
xx
f x f
x
xx
,
00
( ) (0)
lim lim
xx
f x f
aa
x
Hàm số có đạo hàm tại điểm
01xa
Vậy
1, 1ab
là giá trị cần tìm.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
8
CÁC QUY TẮC TÍNH ĐẠO HÀM
1. Quy tắc tính đạo hàm
1.1. Đạo hàm của tổng, hiệu, tích, thương của hàm số
' ' '
1 2 1 2
( ... )' ...
nn
u u u u u u
( . ( ))' . '( )k u x k u x
( )' ' ' 'uvw u vw uv w uvw
1
( ( ))' ( ). '( )
nn
u x nu x u x
'
2
( ) '( ) ( ) '( ) ( )
()
()
u x u x v x v x u x
vx
vx
2
. '( )
'
()
()
c c u x
ux
ux
.
1.2. Đạo hàm của hàm số hợp
Cho hàm số
( ( )) ( )y f u x f u
với
()u u x
. Khi đó
' ' . '
x u x
y y u
.
2. Bảng công thức đạo hàm các hàm sơ cấp cơ bản
Đạo hàm
Hàm hợp
( )' 0c
( )' 1x
1
( )'xx
1
'
2
x
x
1
1
'
n
n
n
x
nx
(sin )' cosxx
(cos )' sinxx
2
1
(tan )'
cos
x
x
2
1
(cot )'
sin
x
x
1
' . 'u u u
'
'
2
u
u
u
1
'
'
n
n
n
u
u
nu
(sin )' '.cosu u u
(cos )' 'sinu u u
2
'
tan '
cos
u
u
u
2
'
cot '
sin
u
u
u
Vấn đề 1. Tính đạo hàm bằng công thức
Phương pháp: Sử dụng các quy tắc tính đạo hàm
Các ví dụ
Ví dụ 1. Tính đạo hàm các hàm số sau:
1.
32
3 2 1y x x x
2.
3
31y x x
3.
4
2
1
4
x
yx
4.
42
3
21
2
y x x
5.
21
3
x
y
x
6.
2
22
1
xx
y
x
Lời giải.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
9
1. Ta có:
'
32
' 3 1 3 6 2y x x x x
2. Ta có:
'
32
' 3 1 3 3y x x x
3. Ta có:
'
4
23
' 1 2
4
x
y x x x
4. Ta có:
'
4 2 3
3
' 2 1 8 3
2
y x x x x
5. Ta có:
22
(2 1)'( 3) ( 3)'(2 1) 7
'
( 3) ( 3)
x x x x
y
xx
6. Ta có:
22
2
( 2 2)'( 1) ( 2 2)( 1)'
'
( 1)
x x x x x x
y
x
22
22
(2 2)( 1) ( 2 2) 2 4
( 1)
1
x x x x x x
x
x
.
Nhận xét: Với hàm số
ax b
y
cx d
ta có:
2
'
()
ad bc
y
cx d
.
Ví dụ 2. Giải bất phương trình
'( ) 0fx
biết:
1.
2
( ) 4f x x x
2.
2
( ) 2 12f x x x
3.
22
( ) 1 1f x x x x x
4.
4
2
( ) 1f x x x
Lời giải.
1. TXĐ:
2;2D
Ta có:
22
2
22
42
'( ) 4
44
xx
f x x
xx
Do đó:
2
'( ) 0 4 2 0 2 2f x x x
.
2. TXĐ:
D
Ta có:
2
22
2 12 2
'( ) 1
12 12
x x x
fx
xx
Suy ra:
2
'( ) 0 12 2f x x x
(1)
Với
0x
thì (1) luôn đúng
Với
0x
thì
22
0
(1) 0 2
12 4
x
x
xx
Vậy bất phương trình
'( ) 0fx
có nghiệm
2x
.
3. TXĐ:
D
Ta có:
22
2 1 2 1
'( )
2 1 2 1
xx
fx
x x x x
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
10
Suy ra
22
'( ) 0 1 2 1 1 2 1f x x x x x x x
22
2
2
(1 2 )(1 2 ) 0
1 3 1 3
(1 2 ) 1 2
2 4 2 4
xx
x x x x
22
11
0
22
(1 2 ) (1 2 )
x
x
xx
.
4. TXĐ:
0; D
Ta có:
23
4
1
'( )
2
2 ( 1)
x
fx
x
x
.
2 3 6 2 3
4
'( ) 0 ( 1) ( 1)f x x x x x x
22
1xx
bất phương trình này vô nghiệm
Ví dụ 3. Tính đạo hàm các hàm số sau:
1.
2
2 3 1y x x
2.
5
2
2 1 3 2y x x
3.
2
2sin (2 1) cosy x x
4.
2 2 3
tan(sin 3 ) cot (1 2 ) 3y x x
5.
3
sin(tan ) cos(cot )y x x
Lời giải.
1. Ta có:
2
22
(2 3 1)' 4 3
'
2 2 3 1 2 2 3 1
x x x
y
x x x x
.
2. Ta có
2
5
24
1
' ( 2 1 3 2)'
5. ( 2 1 3 2)
y x x
xx
2
5
24
12
( 3)
21
5. ( 2 1 3 2)
x
x
xx
.
3. Ta có:
2
22
1
2sin(4 2) sin
(2sin (2 1) cos )'
2
'
2 2sin (2 1) cos 2 2sin (2 1) cos
xx
xx
x
y
x x x x
2
4 sin(4 2) sin
4 2 sin (2 1) cos
x x x
x x x x
.
4. Ta có:
23
2 2 2
23
[cot (1 2 ) 3]'
' [1 tan (sin 3 )](sin 3 )'
2 cot (1 2 ) 3
x
y x x
x
2 2 3 3
22
23
6 [1 cot (1 2 )]cot(1 2 )
3[1 tan (sin 3 )]sin6
cot (1 2 ) 3
x x x
xx
x
.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
11
5. Ta có:
2
[sin(tan ) cos(cot )]'
'
3 [sin(tan ) cos(cot )]
xx
y
xx
22
2
(1 tan )cos(tan ) (1 cot )sin(cot )
3 [sin(tan ) cos(cot )]
x x x x
xx
.
Ví dụ 4. Tính đạo hàm các hàm số sau :
1.
2
3 1 khi 1
()
2 2 khi 1
x x x
fx
xx
2.
2
1
cos khi 0
()
2
0 khi 0
xx
fx
x
x
Lời giải.
1. Với
2
1 ( ) 3 1 '( ) 2 3x f x x x f x x
Với
1 ( ) 2 2 '( ) 2x f x x f x
Với
1x
ta có:
2
11
lim ( ) lim 3 1 1 (1)
xx
f x x x f
hàm số không liên tục tại
1x
, suy ra hàm
số không có đạo hàm tại
1x
Vậy
2 3 khi 1
'( )
2 khi 1
xx
fx
x
.
2. Với
2
1 1 1 1
0 ( ) cos '( ) 2 cos cos
2 2 2 2
x f x x f x x
x x x
Với
0x
ta có:
00
( ) (0)
1
lim lim cos 0 '(0) 0
2
xx
f x f
xf
xx
Vậy
11
2 cos khi 0
'( )
22
0 khi 0
xx
fx
x
x
.
CÁC BÀI TOÁN LUYỆN TẬP
Bài 1 Tính đạo hàm các hàm số sau
Câu 1.
42
3 2 1y x x x
A.
3
' 4 6 3y x x
B.
4
' 4 6 2yxx
C.
3
' 4 3 2y x x
D.
3
' 4 6 2y x x
Bài làm 1. Ta có:
3
' 4 6 2y x x
Câu 2.
3
2
21
3
x
y x x
A.
2
' 2 4 1y x x
B.
2
' 3 4 1y x x
C.
2
1
' 4 1
3
y x x
D.
2
' 4 1y x x
Bài làm 2. Ta có
2
' 4 1y x x
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
12
Câu 3.
21
2
x
y
x
A.
2
3
2x
B.
3
2x
C.
2
3
2x
D.
2
2
2x
Bài làm 3. Ta có
22
(2 1)'( 2) ( 2)'(2 1) 3
'
( 2) ( 2)
x x x x
y
xx
Câu 4.
2
1
1
xx
y
x
A.
2
2
2
1
xx
x
B.
2
2
2
1
xx
x
C.
2
2
2
1
xx
x
D.
2
22
1
x
x
Bài làm 4. Ta có
22
22
(2 1)( 1) ( 1) 2
'
( 1) ( 1)
x x x x x x
y
xx
Câu 5.
, 0
ax b
y ac
cx d
A.
a
c
B.
2
ad bc
cx d
C.
2
ad bc
cx d
D.
ad bc
cx d
Bài làm 5. Ta có
22
'
( ) ( )
ab
cd
ad cb
y
cx d cx d
Câu 6.
2
, ' 0
''
ax bx c
y aa
a x b
.
A.
2
' 2 ' ' '
( ' ')
aa x ab x bb a c
a x b
B.
2
2
' 2 ' ' '
( ' ')
aa x ab x bb a c
a x b
C.
2
2
' 2 ' ' '
( ' ')
aa x ab x bb a c
a x b
D.
2
2
' 2 ' ' '
( ' ')
aa x ab x bb a c
a x b
Bài làm 6. Ta có:
2
2
(2 )( ' ') '( )
'
( ' ')
ax b a x b a ax bx c
y
a x b
2
2
' 2 ' ' '
( ' ')
aa x ab x bb a c
a x b
.
Bài 2 Tính đạo hàm các hàm số sau
Câu 1.
2
1y x x
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
13
A.
2
2
21
21
x
x
B.
2
2
1
1
x
x
C.
2
2
41
1
x
x
D.
2
2
21
1
x
x
Bài làm 1. Ta có:
2
2 2 2
2
( 1)'
' ' 1 1 ' 1 .
21
x
y x x x x x x
x
22
2
22
21
1
11
xx
x
xx
.
Câu 2.
2
3
(2 5)
y
x
A.
4
12
25x
B.
3
12
25x
C.
3
6
25x
D.
3
12
25x
Bài làm 2. Ta có:
'
2
4 4 3
3 (2 5)
12(2 5) 12
'
(2 5) (2 5) (2 5)
x
x
y
x x x
Câu 3.
2
2
22
1
xx
y
x
A.
2
2
2
2 6 2
1
xx
x
B.
2
4
2
2 6 2
1
xx
x
C.
2
2
2
2 6 2
1
xx
x
D.
2
2
2
2 6 2
1
xx
x
Bài làm 3. Ta có
2 2 2
2 2 2 2
(2 2)( 1) 2 ( 2 2) 2 6 2
'
( 1) ( 1)
x x x x x x x
y
xx
Câu 4.
3 2tany x x
A.
2
5 2 tan
2 3 2tan
x
xx
B.
2
5 2tan
2 3 2tan
x
xx
C.
2
5 2 tan
2 3 2tan
x
xx
D.
2
5 2tan
2 3 2tan
x
xx
Bài làm 4. Ta có:
22
(3 2tan )' 3 2(1 tan ) 5 2tan
'
2 3 2tan 2 3 2tan 2 3 2tan
x x x x
y
x x x x x x
Câu 5.
2
sin (3 1)yx
A.
3sin(6 2)x
B.
sin(6 2)x
C.
3sin(6 2)x
D.
3cos(6 2)x
Bài làm 5. Ta có:
'
' 2sin(3 1). sin(3 1) 2sin(3 1).3cos(3 1)y x x x x
3sin(6 2)x
.
Câu 6.
2
( 1) 1y x x x
.
A.
2
2
4 5 3
21
xx
xx
B.
2
2
4 5 3
21
xx
xx
C.
2
2
4 5 3
1
xx
xx
D.
2
2
4 5 3
21
xx
xx
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
14
Bài làm 6. Ta có
2
2
22
2 1 4 5 3
' 1 ( 1)
2 1 2 1
x x x
y x x x
x x x x
Bài 3. Tính đạo hàm các hàm số sau
Câu 1.
2
7
y x x
A.
76
' ( )(7 1)y x x x
B.
7
' 2( )y x x
C.
6
' 2(7 1)yx
D.
76
' 2( )(7 1)y x x x
Bài làm
1.Đáp án D
Câu 2.
22
1 5 3y x x
A.
3
'4y x x
B.
3
'4y x x
C.
3
' 12 4y x x
D.
3
' 12 4y x x
Bài làm
2. Ta có: Đáp án D
Câu 3.
2
2
1
x
y
x
A.
2
22
22
( 1)
x
x
B.
2
22
2 343
( 1)
x
x
C.
2
22
22
( 1)
x
x
D.
2
22
22
( 1)
x
x
Bài làm
22
2 2 2 2
2( 1) 2 .2 2 2
'
( 1) ( 1)
x x x x
y
xx
Câu 4.
2
2 1 5 3y x x x
A.
22
' 40 3 6y x x x
B.
32
' 40 3 6y x x x
C.
32
' 40 3 6y x x x
D.
32
' 40 3y x x x
Bài làm
4 3 2 3 2
10 3 ' 40 3 6y x x x y x x x
Câu 5.
3
2
5
4yx
x
A.
2
32
10 5
' 3 4 4yx
xx
B.
2
32
10 5
' 3 4 4yx
xx
C.
2
2
5
'4yx
x
D.
2
32
10 5
' 3 4 4yx
xx
Bài làm
2
32
10 5
' 3 4 4yx
xx
Câu 6.
32
( 2) ( 3)y x x
A.
2 3 3
' 3( 5 6) 2( 3)( 2)y x x x x
B.
2 2 3
' 2( 5 6) 3( 3)( 2)y x x x x
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
15
C.
2
' 3( 5 6) 2( 3)( 2)y x x x x
D.
2 2 3
' 3( 5 6) 2( 3)( 2)y x x x x
Bài làm
2 2 3
' 3( 5 6) 2( 3)( 2)y x x x x
Câu 7.
32
32y x x
A.
2
32
36
'
32
xx
y
xx
B.
2
32
36
'
2 3 2
xx
y
xx
C.
2
32
36
'
2 3 2
xx
y
xx
D.
2
32
36
'
2 3 2
xx
y
xx
Bài làm
2
32
36
'
2 3 2
xx
y
xx
Câu 8.
2
1y x x x
A.
' 2 1
21
x
y x x
x
B.
' 2 1
21
x
y x x
x
C.
'
21
x
y
x
D.
' 2 1
21
x
y x x
x
Bài làm
' 2 1
21
x
y x x
x
Câu 9.
22
x
y
ax
A.
2
2 2 3
'
()
a
y
ax
B.
2
2 2 3
'
()
a
y
ax
C.
2
2 2 3
2
'
()
a
y
ax
D.
2
2 2 3
'
()
a
y
ax
Bài làm
2
22
2
22
22
2 2 3
'
()
()
x
ax
a
ax
y
ax
ax
Câu 10.
1
y
xx
A.
2
31
'
2
y
xx
B.
2
1
'y
xx
C.
2
1
'y
xx
D.
2
31
'
2
y
xx
Bài làm
3
2
( )' 3 1
'
2
xx
y
x
xx
Câu 11.
1
1
x
y
x
A.
3
13
'
(1 )
x
y
x
B.
3
13
'
3 (1 )
x
y
x
C.
3
1 1 3
'
3
2 (1 )
x
y
x
D.
3
13
'
2 (1 )
x
y
x
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
16
Bài làm
3
1
1
13
21
'
1
2 (1 )
x
x
x
x
y
x
x
Câu 12.
2
sin 3yx
A.
' sin6yx
B.
' 3sin3yx
C.
' 2sin6yx
D.
' 3sin6yx
Bài làm
' 3sin6yx
Câu 13.
2
3tan cot2y x x
A.
22
2
3tan (1 tan ) (1 cot 2 )
'
3 3tan cot2
x x x
y
xx
B.
22
2
3tan (1 tan ) (1 cot 2 )
'
2 3tan cot 2
x x x
y
xx
C.
22
2
3tan (1 tan ) (1 cot 2 )
'
3tan cot2
x x x
y
xx
D.
22
2
3tan (1 tan ) (1 cot 2 )
'
3tan cot2
x x x
y
xx
Bài làm
22
2
3tan (1 tan ) (1 cot 2 )
'
3tan cot2
x x x
y
xx
Câu 14.
34
3
cos (2 )
3
y x x
A.
23
3
34
3
3 8cos (2 )sin(2 )
44
'
3 cos (2 )
3
x x x
y
xx
B.
23
3
34
3
3 8cos (2 )sin(2 )
44
'
4 cos (2 )
3
x x x
y
xx
C.
23
3
34
3
6 8cos (2 )sin(2 )
44
'
3 cos (2 )
3
x x x
y
xx
D.
23
3
34
3
3 8cos (2 )sin(2 )
44
'
3 cos (2 )
3
x x x
y
xx
Bài làm
23
3
34
3
3 8cos (2 )sin(2 )
44
'
3 cos (2 )
3
x x x
y
xx
Câu 15.
2
2sin 2yx
A.
2
' cos( 2)y x x
B.
2
' 4cos( 2)yx
C.
2
' 2 cos( 2)y x x
D.
2
' 4 cos( 2)y x x
Bài làm
2
' 4 cos( 2)y x x
Câu 16.
23
cos sinyx
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
17
A.
32
' sin(2sin )sin cosy x x x
B.
32
' 6sin(2sin )sin cosy x x x
C.
32
' 7sin(2sin )sin cosy x x x
D.
32
' 3sin(2sin )sin cosy x x x
Bài làm
32
' 3sin(2sin )sin cosy x x x
Câu 17.
sin
x
y
x
A.
2
sin cos
'
sin
xx
y
x
B.
sin cos
'
sin
x x x
y
x
C.
sin cos
'
sin
xx
y
x
D.
2
sin cos
'
sin
x x x
y
x
Bài làm
2
sin cos
'
sin
x x x
y
x
Câu 18.
3
cos 4
cot
3
3sin
x
yx
x
A.
3
' cot 1yx
B.
4
' 3cot 1yx
C.
4
' cot 1yx
D.
4
' cotyx
Bài làm
23
1 4 1
cot (1 cot ) cot cot cot
3 3 3
y x x x x x
Suy ra
2 2 2 4
' cot (1 cot ) 1 cot cot 1y x x x x
Câu 19.
3
1
sin khi 0
()
0 khi 0
xx
fx
x
x
A.
2
11
sin cos khi 0
'( )
0 khi 0
x x x
fx
xx
x
B.
2
11
3 sin cos khi 0
'( )
0 khi 0
x x x
fx
xx
x
C.
2
11
3 sin cos khi 0
'( )
0 khi 0
x x x
fx
xx
x
D.
2
11
3 sin cos khi 0
'( )
0 khi 0
xx
fx
xx
x
Bài làm
2
11
0 '( ) 3 sin cosx f x x x
xx
Với
0
( ) (0)
0 '(0) lim 0
x
f x f
xf
x
Vậy
2
11
3 sin cos khi 0
'( )
0 khi 0
x x x
fx
xx
x
.
Bài 4. Tính
'1
'0
f
. Biết rằng :
2
()f x x
và
( ) 4 sin
2
x
xx
.
A.
'(1)
4
'(0) 8
f
B.
'(1)
2
'(0) 8
f
C.
'(1)
4
'(0)
f
D.
'(1)
4
'(0) 8
f
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
18
Bài làm Bài 4.
'( ) 2 '(1) 2; '( ) 4 cos '(0) 4
2 2 2
x
f x x f x
Suy ra
'(1)
4
'(0) 8
f
.
Bài 6. Tìm
m
để các hàm số
Câu 1.
32
( 1) 3( 2) 6( 2) 1y m x m x m x
có
' 0, yx
A.
3m
B.
1m
C.
4m
D.
42m
Bài làm 1. Ta có:
2
' 3 ( 1) 2( 2) 2( 2)y m x m x m
Do đó
2
' 0 ( 1) 2( 2) 2( 2) 0y m x m x m
(1)
1m
thì (1)
6 6 0 1xx
nên
1m
(loại)
1m
thì (1) đúng với
10
'0
am
x
1
4
( 1)(4 ) 0
m
m
mm
Vậy
4m
là những giá trị cần tìm.
Câu 2.
3
2
(3 1) 1
3
mx
y mx m x
có
' 0, yx
.
A.
2m
B.
2m
C.
0m
D.
0m
Bài làm 2. Ta có:
2
' 2 3 1y mx mx m
Nên
2
' 0 2 3 1 0y mx mx m
(2)
0m
thì (1) trở thành:
10
đúng với
x
0m
, khi đó (1) đúng với
0
'0
am
x
00
0
(1 2 ) 0 1 2 0
mm
m
m m m
Vậy
0m
là những giá trị cần tìm.
Bài 7. Tính đạo hàm của các hàm số sau
Câu 1.
2
1
sin khi 0
()
0 khi 0
xx
fx
x
x
A.
11
sin cos khi 0
'( )
0 khi 0
xx
fx
xx
x
B.
11
sin cos khi 0
'( )
0 khi 0
x x x
fx
xx
x
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
19
C.
11
2 sin cos khi 0
'( )
0 khi 0
x x x
fx
xx
x
D.
11
2 sin cos khi 0
'( )
0 khi 0
xx
fx
xx
x
Bài làm 1. Với
0x
ta có:
11
'( ) 2 sin cosf x x
xx
Tại
0x
ta có:
00
( ) (0)
1
lim lim sin 0
xx
f x f
x
xx
Vậy
11
2 sin cos khi 0
'( )
0 khi 0
xx
fx
xx
x
.
Câu 2.
2
1 khi 1
()
1 3 khi 1
x x x
fx
xx
A.
2 khi 1
'( )
1
khi 1
21
xx
fx
x
x
B.
2 1 khi 1
'( )
1
khi 1
1
xx
fx
x
x
C.
2 1 khi 1
'( )
1
khi 1
1
xx
fx
x
x
D.
2 1 khi 1
'( )
1
khi 1
21
xx
fx
x
x
Bài làm 2. Với
1x
ta có:
'( ) 2 1f x x
Với
1x
ta có:
1
'( )
21
fx
x
Tại
1x
ta có:
2
11
( ) (1)
2
lim lim 3
11
xx
f x f
xx
xx
11
( ) (1)
1
lim lim
11
xx
f x f
x
xx
suy ra hàm số không có đạo
hàm tại
1x
Vậy
2 1 khi 1
'( )
1
khi 1
21
xx
fx
x
x
.
Bài 8. Tìm
,ab
để các hàm số sau có đạo hàm trên
Câu 1. .
2
2
1 khi 1
()
khi 1
x x x
fx
x ax b x
A.
13
1
a
b
B.
3
11
a
b
C.
23
21
a
b
D.
3
1
a
b
Bài làm 1 Với
1x
thì hàm số luôn có đạo hàm
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
20
Do đó hàm số có đạo hàm trên hàm số có đạo hàm tại
1x
.
Ta có
11
lim ( ) 1; lim ( ) 1
xx
f x f x a b
Hàm số liên tục trên
1 1 2a b a b
Khi đó:
1
( ) (1)
lim 1;
1
x
f x f
x
2
11
( ) (1)
1
lim lim 2
11
xx
f x f
x ax a
a
xx
Nên hàm số có đạo hàm trên thì
23
2 1 1
a b a
ab
.
Câu 2.
2
2
1
khi 0
()
1
khi 0
xx
x
fx
x
x ax b x
.
A.
0, 11ab
B.
10, 11ab
C.
20, 21ab
D.
0, 1ab
Bài làm 2. Tương tự như ý 1. ĐS:
0, 1ab
.
Bài 9. Tính đạo hàm các hàm số sau
Câu 1.
33
( 2 )y x x
A.
3 2 2
' ( 2 ) (3 2)y x x x
B.
3 2 2
' 2( 2 ) (3 2)y x x x
C.
3 2 2
' 3( 2 ) (3 2)y x x x
D.
3 2 2
' 3( 2 ) (3 2)y x x x
Bài làm 1.Ta có:
'
3 2 3 3 2 2
' 3( 2 ) 2 3( 2 ) (3 2)y x x x x x x x
Câu 2.
23
( 1)(3 2 )y x x x
A.
42
' 3 2y x x
B.
42
' 5 3 2y x x
C.
42
' 15 3y x x
D.
42
' 15 3 2y x x
Bài làm 2. Ta có:
3 2 2 4 2
' 2 (3 2 ) ( 1)(9 2) 15 3 2y x x x x x x x
Câu 3.
2
2
2
3
yx
x
A.
23
24
'1
33
yx
xx
B.
23
24
' 2 1
33
yx
xx
C.
23
24
'1
33
yx
xx
D.
23
24
' 2 1
33
yx
xx
Bài làm 3.Ta có:
23
24
' 2 1
33
yx
xx
Câu 4.
32
2sin 2 tan 3 cos4y x x x x
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
21
A.
22
' 12sin 2 cos2 6tan3 1 2tan 3 cos4 4 sin4y x x x x x x x
B.
22
' 12sin 2 cos2 6tan3 1 tan 3 cos4 sin4y x x x x x x x
C.
22
' 12sin 2 cos2 tan3 1 tan 3 cos4 4 sin4y x x x x x x x
D.
22
' 12sin 2 cos2 6tan3 1 tan 3 cos4 4 sin4y x x x x x x x
Bài làm 4. Ta có:
22
' 12sin 2 cos2 6tan3 1 tan 3 cos4 4 sin4y x x x x x x x
Câu 5.
sin2
cos3
xx
y
xx
A.
22
2 cos2 sin2 cos3 3 sin3
'
cos 3
x x x x x x
y
xx
B.
22
2 cos2 sin2 cos3 3 sin3
'
cos 3
x x x x x x
y
xx
C.
22
2 cos2 sin2 cos3 3 sin3
'
cos 3
x x x x x x
y
xx
D.
22
2 cos2 sin2 cos3 3 sin3
'
cos 3
x x x x x x
y
xx
Bài làm 5. Ta có:
'
2
sin2 2 cos2 sin2x x x x
x
x
,
'
2
cos3 3 sin3
cos3
cos 3
x x x x
x
x
Nên
22
2 cos2 sin2 cos3 3 sin3
'
cos 3
x x x x x x
y
xx
.
Câu 6.
32
sin2 1y x x x x
A.
2
32
32
' sin2 2 cos2
21
xx
y x x x
xx
B.
2
32
32
' sin2 2 cos2
1
xx
y x x x
xx
C.
2
32
32
' sin2 2 cos2
21
xx
y x x x
xx
D.
2
32
32
' sin2 2 cos2
21
xx
y x x x
xx
Bài làm 6.Ta có:
2
32
32
' sin2 2 cos2
21
xx
y x x x
xx
Câu 7.
23
2sin 1y x x
A.
2
23
2sin2 3
'
2sin 1
xx
y
xx
B.
2
23
2sin2 3
'
2 2sin 1
xx
y
xx
C.
2
23
sin2 3
'
2sin 1
xx
y
xx
D.
2
23
2sin2 3
'
2 2sin 1
xx
y
xx
Bài làm 7. Ta có:
2
23
2sin2 3
'
2 2sin 1
xx
y
xx
Câu 8.
2
1 2 1y x x
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
22
A.
2
22
21
'
( 1) 1 2 1
xx
y
x x x
B.
2
22
1
'
( 1) 1 2 1
xx
y
x x x
C.
2
22
1
'
2 ( 1) 1 2 1
xx
y
x x x
D.
2
22
21
'
2 ( 1) 1 2 1
xx
y
x x x
Bài làm 8. Ta có:
2
2
2
22
2
21
1
'
2 1 2 1
2 ( 1) 1 2 1
x
xx
x
y
xx
x x x
.
Câu 9.
1
tan2
cot
x
y x x
x
A.
22
' tan2 2 1 tan 2 tan ( 1)(tan 1)y x x x x x
B.
22
' tan2 1 tan 2 tan ( 1)(tan 1)y x x x x x
C.
22
' tan2 2 1 tan 2 tan 2( 1)(tan 1)y x x x x x
D.
22
' tan2 2 1 tan 2 tan ( 1)(tan 1)y x x x x x
Bài làm 9. Ta có:
'
2
tan2 tan2 2 1 tan 2x x x x x
'
'
2
1
( 1)tan tan ( 1)(tan 1)
cot
x
x x x x
x
Nên
22
' tan2 2 1 tan 2 tan ( 1)(tan 1)y x x x x x
Câu 10.
3
sin 2 1
3
yx
A.
2
3
3sin 2 cos 2
33
'
2 sin 2 1
3

xx
y
x
B.
2
3
sin 2 cos 2
33
'
2 sin 2 1
3

xx
y
x
C.
2
3
sin 2 cos 2
33
'
sin 2 1
3

xx
y
x
D.
2
3
3sin 2 cos 2
33
'
sin 2 1
3

xx
y
x
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
23
Bài làm 10. Ta có:
2
3
3sin 2 cos 2
33
'
sin 2 1
3

xx
y
x
.
Bài 10. Giải bất phương trình :
Câu 1.
'( ) 0fx
với
32
( ) 2 3 1f x x x
A.
0
1
x
x
B.
1x
C.
0x
D.
01x
Bài làm 1. TXĐ:
D
Ta có:
2
'( ) 6 6f x x x
, suy ra
0
'( ) 0
1
x
fx
x
Câu 2.
'( ) 0fx
với
42
( ) 2 4 1f x x x
A.
10
1
x
x
B.
10x
C.
1x
D.
0x
Bài làm 2. TXĐ:
D
Ta có:
3
'( ) 8 8f x x x
, suy ra
10
'( ) 0
1
x
fx
x
Câu 3.
2 '( ) ( ) 0xf x f x
với
2
( ) 1f x x x
A.
1
3
x
B.
1
3
x
C.
1
3
x
D.
2
3
x
Bài làm 3. TXĐ:
D
Ta có:
22
()
'( ) 1
11
fx
x
fx
xx
Mặt khác:
2
( ) 0, f x x x x x x
Nên
2
2 ( )
2 '( ) ( ) 0 ( ) 0
1
xf x
xf x f x f x
x
2
2
0
1
21
31
3
x
x x x
x
.
Câu 4.
'( ) 0fx
với
2
( ) 4f x x x
.
A.
22x
B.
2x
C.
2 x
D.
0x
Bài làm 4. TXĐ:
2;2D
Ta có:
2
2
'( ) 1 '( ) 0 4
4
x
f x f x x x
x
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
24
22
20
20
0
22
02
4
x
x
x
x
x
xx
.
Vấn đề 2. Sử dụng đạo hàm để tìm giới hạn
Từ định nghĩa đạo hàm
0
0
0
0
( ) ( )
'( ) lim
xx
f x f x
fx
xx
,ta thấy có thể sử dụng đạo hàm để tìm giới hạn của
hàm số. Cụ thể
Để tính
0
0
()
lim
xx
gx
A
xx
, biết
0
( ) 0gx
.
Ta viết
0
( ) ( ) ( )g x f x f x
. Khi đó nếu
()fx
có đạo hàm tại
0
x
thì :
0
0
0
0
( ) ( )
lim '( )
xx
f x f x
A f x
xx
.
Để tính:
0
()
lim
()
xx
Fx
B
Gx
, biết
00
( ) ( ) 0F x G x
.
Ta viết
0
( ) ( ) ( )F x f x f x
và
0
( ) ( ) ( )G x g x g x
.
Nếu hai hàm số
( ), ( )f x g x
có đạo hàm tại
0
xx
và
0
'( ) 0gx
thì:
0
0
00
0
0
0
( ) ( )
'( )
lim
( ) ( )
'( )
xx
f x f x
x x f x
B
g x g x
gx
xx
.
Các ví dụ
Ví dụ 1. Tính các giới hạn sau :
1.
3
0
11
lim
x
x
A
x
2.
3
2
1
2 1 3 2
lim
1
x
xx
B
x
3.
0
1 3 1
lim
n
x
x
C
x
4.
3
2
4
2
0
1 1 2
lim
x
xx
D
xx
Lời giải.
1. Đặt
3
2
3
1
( ) 1 '( )
3 (1 )
f x x f x
x
và
(0) 1f
0
( ) (0)
1
lim '(0)
03
x
f x f
Af
x
.
2. Đặt
3
( ) 2 1 3 2f x x x
2
3
23
'( )
2 3 2
3. (2 1)
fx
x
x
và
(1) 0f
.
1 1 1
( ) (0) ( ) (0)
11
lim . lim .lim
1 1 1 1
x x x
f x f f x f
B
x x x x
1 2 3 5
. '(1)
2 3 2 9
f
.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
25
3. Đặt
0
( ) (0)
3
( ) 1 3 lim '(0)
n
x
f x f
f x x C f
xn
.
4. Đặt
3
2
4
( ) 1 1 2f x x x
2 2 3
3
4
21
'( )
3. (1 ) 2. (1 2 )
x
fx
xx
00
( ) (0)
11
lim .lim '(0)
12
xx
f x f
Df
xx
.
Ví dụ 2. Tính giới hạn sau :
3
22
0
1 2 1 3
lim
1 cos
x
xx
A
x
Lời giải.
Ta có:
3
22
2
00
22
22
1 2 1 3
()
lim lim
2sin 2sin
22
xx
xx
fx
x
A
xx
xx
.
Mà
2
2
2
00
2sin sin
11
22
lim lim
22
2
xx
xx
x
x
.
Đặt
3
2
00
1 2 1 3
lim ( ) lim 0
xt
tt
t x f x
t
.
Vậy
0A
.
CÁC BÀI TOÁN LUYỆN TẬP
Bài 1. Tìm các giới hạn sau
Câu 1.
34
0
(1 3 ) (1 4 )
lim
x
xx
A
x
A.25 B.26 C.27 D.28
Bài làm 1 Xét hàm số
34
( ) (1 3 ) (1 4 ) '(0) 25f x x x A f
Câu 2.
0
(1 )(1 2 )(1 3 ) 1
lim
x
x x x
B
x
A.6 B.4 C.3 D.2
Bài làm 2. Xét hàm số
( ) (1 )(1 2 )(1 3 ) 1 '(0) 6f x x x x B f
Câu 3.
0
11
lim ( , ; . 0)
11
n
m
x
ax
C m n a b
bx
A.
a
C
b
B.
m
C
n
C.
ma
C
nb
D.
ma
C
nb
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
26
Bài làm 3. Xét hai hàm số
( ) 1 1, ( ) 1 1
nm
f x ax g x bx
Suy ra
'(0)
'(0)
f
ma
C
g nb
.
Câu 4.
2
1
21
lim
1
x
xx
D
x
A.0 B.1 C.2 D.3
Bài làm 4. Xét hàm số
1
1
( ) 2 1 lim . '(1) 0
1
x
f x x x D f
x
Bài 2 Tìm các giới hạn sau
Câu 1.
3
1
2
2 1 1
lim
12
x
x
A
x
A.
2
3
B.1 C.2 D.
3
2
Bài làm 1. Đặt
3
2
3
22
( ) 2 1 1 '( ) '(1)
3
3. (2 1)
f x x f x f
x
và
2
2
( ) 1 2 '( ) '(1) 1
2
x
g x x g x g
x
.
Khi đó:
1 1 1
( ) (1)
( ) ( ) (1) '(1)
2
1
lim lim lim
( ) (1)
( ) ( ) (1) '(1) 3
1
x x x
f x f
f x f x f f
x
A
g x g
g x g x g g
x
.
Câu 2.
3
2
0
2 1 1
lim
sin
x
xx
B
x
A.1 B.2 C.3 D.4
Bài làm 2. Đặt
3
2
22
3
12
( ) 2 1 1 '( )
21
3. ( 1)
x
f x x x f x
x
x
.
'(0) 1f
. Và
( ) sin '( ) cos '(0) 1g x x g x x g
.
Khi đó:
00
( ) (0)
( ) '(0)
lim lim 1
( ) (0)
( ) '(0)
xx
f x f
f x f
x
B
g x g
g x g
x
.
Câu 3.
3
4
34
1
26 1 80 1
lim
1
x
xx
C
x
A.
4
27
B.1 C.2 D.
4
27
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
27
Bài làm 3. Đặt
11
( ) 1 '( ) '(1)
2
2
g x x g x g
x
và
3
3
4
34
3 2 4 3
3
4
26 80
( ) 26 1 80 1 '( )
(26 1) (80 1)
x
f x x x f x
xx
2
'(1)
27
f
.
Khi đó:
10
( ) (1)
( ) '(1)
4
1
lim lim
( ) (1)
( ) '(1) 27
1
xx
f x f
f x f
x
C
g x g
g x g
x
.
Câu 4.
33
22
0
4 2 4 2
lim
22
x
x x x x
E
xx
A.
3
4. 2
3
B.
3
4. 2
3
C.
3
4
3
D.1
Bài làm 4. Xét hai hàm số
33
22
( ) 4 2 4 2f x x x x x
( ) 2 2g x x x
Ta có:
3
'(0)
4. 2
'(0) 3
f
E
g
.
Vấn đề 3. Đạo hàm cấp vao và vi phân
Phương pháp:
Vi phân của hàm số
Tích
0
'( ).f x x
được gọi là vi phân của hàm số
()y f x
tại điểm
0
x
(ứng với số gia
x
) được kí hiệu
là
00
( ) '( )df x f x x
.
Nếu hàm số
f
có đạo hàm
'f
thì tích
'( )f x x
được gọi là vi phân hàm số
()y f x
, kí hiệu là:
( ) '( )df x f x x
.
Đặc biệt:
'dx x x x
nên ta viết
( ) '( )df x f x dx
.
Đạo hàm cấp n
Đạo hàm cấp hai: Cho hàm số
f
có đạo hàm
'f
. Nếu
'f
cũng có đạo hàm thì đạo hàm của nó được
gọi là đạo hàm cấp hai của
f
và được kí hiệu là:
''f
, tức là:
'' ( ')'ff
.
Đạo hàm cấp
n
: Cho hàm số
f
có đạo hàm cấp
(với
,2nn
) là
( 1)n
f
. Nếu
( 1)n
f
cũng có
đạo hàm thì đạo hàm của nó được gọi là đạo hàm cấp
n
của
f
và được kí hiệu là
()n
f
, tức là:
( ) ( 1)
( )'
nn
ff
.
Các ví dụ
Ví dụ 1. Tính đạo hàm cấp
n
của hàm số sau:
31
2
x
y
x
Lời giải.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
28
Ta có:
2
7
'
( 2)
y
x
,
3
7.2
''
( 2)
y
x
,
4
7.2.3
'''
( 2)
y
x
Bằng quy nạp ta chứng minh:
()
1
( 1) .7. !
( 2)
n
n
n
n
y
x
(2)
Với
1n
ta thấy (2) đúng
Giả sử (2) đúng với
nk
, tức là:
()
1
( 1) .7. !
( 2)
k
k
k
k
y
x
Ta có:
'
( 1)
12
( 1) .7. ! ( 1) .7. !.( 1)
( 2) ( 2)
kk
k
kk
k k k
y
xx
1
2
( 1) .7.( 1)!
( 2)
k
k
k
x
Nên (2) đúng với mọi số tự nhiên
n
.
Ví dụ 2. Cho đa thức
32
( ) 5 1f x x x
. Viết
()fx
dưới dạng lũy thừa của
2x
Lời giải.
Ta có:
(3) ''
32
(2) (2) '(2)
( ) ( 2) ( 2) ( 2) (2)
3! 2! 1!
f f f
f x x x x f
Mà
2
'( ) 3 10 , ''( ) 6 10, '''( ) 6f x x x f x x f x
Nên
32
( ) ( 2) ( 2) 8( 2) 11f x x x x
.
Ví dụ 3. Tìm vi phân của của hàm số:
1.
4
21y x x
2.
3
( 2)( 1)y x x
3.
2
2 6 5
24
xx
y
x
4.
sin3 cos5y x x
5.
2
4 tany x x
Lời giải.
1. Ta có
43
( 2 1)' (4 2)dy x x dx x dx
2. Ta có
4 3 3 2
2 1 (4 3 2)y x x x dy x x dx
3. Ta có
22
22
(4 6)(2 4) 2(2 6 5) 4 16 34
'
(2 4) (2 4)
x x x x x x
y
xx
Suy ra
2
2
4 16 34
(2 4)
xx
dy dx
x
.
4. Ta có
11
sin8 sin2 4cos8 cos2
22
y x x dy x x dx
5. Ta có:
22
22
8 1 tan 8 1 tan
'
2 4 tan 2 4 tan
x x x x
y dy dx
x x x x
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
29
CÁC BÀI TOÁN LUYỆN TẬP
Bài 1. Cho hàm số
sin2yx
Câu 1. Tính
''y
A.
'' sin2yx
B.
'' 4sinyx
C.
'' sin2yx
D.
'' 4sin2yx
Bài làm 1. Ta có
' 2cos2 '' 4sin2y x y x
Câu 2. Tính
'''( )
3
y
,
(4)
()
4
y
A. 4 và 16 B. 5 và 17 C. 6 và 18 D. 7 và 19
Bài làm 2. Ta có
(4)
''' 8cos2 , 16sin2y x y x
Suy ra
(4)
2
'''( ) 8cos 4; ( ) 16sin 16
3 3 4 2
yy
.
Câu 3. Tính
()n
y
A.
()
2 sin(2 )
3
nn
y x n
B.
()
2 sin(2 )
2
nn
yx
C.
()
2 sin( )
2
nn
yx
D.
()
2 sin(2 )
2
nn
y x n
Bài làm 3. Ta có
2
' 2sin(2 ), '' 2 sin(2 2 )
22
y x y x
,
3
''' 2 sin(2 3 )
2
yx
Bằng quy nạp ta chứng minh
()
2 sin(2 )
2
nn
y x n
Với
1
1 ' 2 sin(2 )
2
n y x
đúng
Giả sử
()
2 sin(2 )
2
kk
y x k
,
suy ra
( 1) ( ) 1 1
' 2 cos(2 ) 2 sin 2 ( 1)
22
k k k k
y y x k x k
Theo nguyên lí quy nạp ta có điều phải chứng minh.
Bài 2. Tính đạo hàm cấp n của các hàm số sau
Câu 1.
21
2
x
y
x
A.
1
()
1
(1) .3. !
( 2)
n
n
n
n
y
x
B.
1
()
1
( 1) . !
( 2)
n
n
n
n
y
x
C.
1
()
1
( 1) .3. !
( 2)
n
n
n
n
y
x
D.
1
()
1
( 1) .3. !
( 2)
n
n
n
n
y
x
Bài làm 1. Ta có
'
2
2 4 3
3 ( 2)
3 3.2
' , ''
( 2) ( 2) ( 2)
x
yy
x x x
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
30
4
3.2.3
'''
( 2)
y
x
. Ta chứng minh
1
()
1
( 1) .3. !
( 2)
n
n
n
n
y
x
Với
0
22
( 1) .3 3
1'
( 2) ( 2)
ny
xx
đúng
Giả sử
1
()
1
( 1) .3. !
( 2)
k
k
k
k
y
x
11
( 1) ( )
2 2 2
( 1) .3. !. ( 2) '
( 1) .3.( 1)!
'
( 2) ( 2)
kk
k
kk
kk
kx
k
yy
xx
Theo nguyên lí quy nạp ta có điều phải chứng minh.
Câu 2.
1
,0ya
ax b
A.
()
1
(2) . . !
()
nn
n
n
an
y
ax b
B.
()
1
( 1) . . !
( 1)
nn
n
n
an
y
x
C.
()
1
( 1) . !
()
n
n
n
n
y
ax b
D.
()
1
( 1) . . !
()
nn
n
n
an
y
ax b
Bài làm 2. Ta có
23
2 3 4
.2 .2.3
' , '' , '''
( ) ( ) ( )
a a a
y y y
ax b ax b ax b
Ta chứng minh:
()
1
( 1) . . !
()
nn
n
n
an
y
ax b
Với
11
22
( 1) . .1!
1'
( ) ( )
aa
ny
ax b ax b
đúng
Giả sử
()
1
( 1) . . !
()
kk
k
k
ak
y
ax b
1
11
( 1) ( )
2 2 2
( 1) . . !. ( ) '
( 1) . .( 1)!
'
( ) ( 2)
k k k
kk
kk
kk
a k ax b
ak
yy
ax b x
Theo nguyên lí quy nạp ta có điều phải chứng minh.
Câu 3.
2
21
56
x
y
xx
A.
()
11
(2) .7. ! (1) .5. !
( 2) ( 3)
nn
n
nn
nn
y
xx
B.
11
()
11
( 1) .7. ! ( 1) .5. !
( 2) ( 3)
nn
n
nn
nn
y
xx
C.
()
( 1) .7. ! ( 1) .5. !
( 2) ( 3)
nn
n
nn
nn
y
xx
D.
()
11
( 1) .7. ! ( 1) .5. !
( 2) ( 3)
nn
n
nn
nn
y
xx
Bài làm 3. Ta có:
2 1 7( 2) 5( 3)x x x
;
2
5 6 ( 2)( 3)x x x x
Suy ra
75
32
y
xx
.
Mà
( ) ( )
1 1 1
1 ( 1) .1 . ! ( 1) . ! 1 ( 1) . !
,
22
( 2) ( 2) ( 3)
nn
n n n n
n n n
n n n
xx
x x x
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
31
Nên
()
11
( 1) .7. ! ( 1) .5. !
( 2) ( 3)
nn
n
nn
nn
y
xx
.
Câu 4.
cos2yx
A.
()
1 cos 2
2
n
n
y x n
B.
()
2 cos 2
2
nn
yx
C.
( ) 1
2 cos 2
2
nn
y x n
D.
()
2 cos 2
2
nn
y x n
Bài làm 4. Ta có
2
' 2cos 2 , '' 2 cos 2 2 ,
22
y x y x
3
''' 2 cos 2 3
2
yx
.
Bằng quy nạp ta chứng minh được
()
2 cos 2
2
nn
y x n
.
Câu 5.
21yx
A.
1
()
21
( 1) .3.5...(3 1)
(2 1)
n
n
n
n
y
x
B.
1
()
21
( 1) .3.5...(2 1)
(2 1)
n
n
n
n
y
x
C.
1
()
21
( 1) .3.5...(2 1)
(2 1)
n
n
n
n
y
x
D.
1
()
21
( 1) .3.5...(2 1)
(2 1)
n
n
n
n
y
x
Bài làm 5. Ta có
35
1 1 3
' , '' , '''
21
(2 1) (2 1)
y y y
x
xx
Bằng quy nạp ta chứng minh được:
1
()
21
( 1) .3.5...(2 1)
(2 1)
n
n
n
n
y
x
Câu 6.
2
21
32
x
y
xx
A.
()
11
5.( 1) . ! 3.( 1) . !
( 2) ( 1)
nn
n
nn
nn
y
xx
B.
()
11
5.( 1) . ! 3.( 1) . !
( 2) ( 1)
nn
n
nn
nn
y
xx
C.
()
11
5.( 1) . ! 3.( 1) . !
:
( 2) ( 1)
nn
n
nn
nn
y
xx
D.
()
11
5.( 1) . ! 3.( 1) . !
( 2) ( 1)
nn
n
nn
nn
y
xx
Bài làm 6. Ta có:
53
21
y
xx
Bằng quy nạp ta chứng minh được:
()
11
5.( 1) . ! 3.( 1) . !
( 2) ( 1)
nn
n
nn
nn
y
xx
.
Bài 4. Tìm vi phân của các hàm số sau
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
32
Câu 1.
32
2y x x
A.
2
(3 4 )dy x x dx
B.
2
(3 )dy x x dx
C.
2
(3 2 )dy x x dx
D.
2
(3 4 )dy x x dx
Bài làm 1.
2
(3 4 )dy x x dx
Câu 2.
32yx
A.
3
32
dy dx
x
B.
1
2 3 2
dy dx
x
C.
1
32
dy dx
x
D.
3
2 3 2
dy dx
x
Bài làm 2.
3
2 3 2
dy dx
x
Câu 3.
3
sin2 siny x x
A.
2
cos2 3sin cosdy x x x dx
B.
2
2cos2 3sin cosdy x x x dx
C.
2
2cos2 sin cosdy x x x dx
D.
2
cos2 sin cosdy x x x dx
Bài làm 3.
2
2cos2 3sin cosdy x x x dx
Câu 4.
tan2yx
A.
2
(1 tan 2 )dy x dx
B.
2
(1 tan 2 )dy x dx
C.
2
2(1 tan 2 )dy x dx
D.
2
2(1 tan 2 )dy x dx
Bài làm 4.
2
2(1 tan 2 )dy x dx
Câu 5.
3
1yx
A.
2
3
1
( 1)
dy dx
x
B.
2
3
3
( 1)
dy dx
x
C.
2
3
2
( 1)
dy dx
x
D.
2
3
1
3 ( 1)
dy dx
x
Bài làm 5.
2
3
1
3 ( 1)
dy dx
x
Câu 6.
10
(3 1)yx
A.
9
10(3 1)dy x dx
B.
10
30(3 1)dy x dx
C.
10
9(3 1)dy x dx
D.
9
30(3 1)dy x dx
Bài làm 6.
9
30(3 1)dy x dx
.
Bài 6. Tính đạo hàm cấp
n
của các hàm số sau
Câu 1.
2
56
x
y
xx
A.
()
11
( 1) .3. ! ( 1) .2. !
( 3) ( 2)
nn
n
nn
nn
y
xx
B.
()
( 1) .3. ! ( 1) .2. !
( 3) ( 2)
nn
n
nn
nn
y
xx
C.
()
11
( 1) .3. ! ( 1) .2. !
( 3) ( 2)
nn
n
nn
nn
y
xx
D.
()
11
( 1) .3. ! ( 1) .2. !
( 3) ( 2)
nn
n
nn
nn
y
xx
Bài làm 1. Ta có:
3( 2) 2( 3)x x x
;
2
5 6 ( 2)( 3)x x x x
Suy ra
32
32
y
xx
.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
33
Mà
( ) ( )
1 1 1
1 ( 1) .1 . ! ( 1) . ! 1 ( 1) . !
,
23
( 2) ( 2) ( )
nn
n n n n
n n n
n n n
xx
x x x
Nên ta có:
()
11
( 1) .3. ! ( 1) .2. !
( 3) ( 2)
nn
n
nn
nn
y
xx
.
Câu 2.
cos2yx
A.
( ) 1
2 cos 2
2
nn
y x n
B.
( ) 1
2 cos 2
2
nn
y x n
C.
()
2 cos 2
2
nn
yx
D.
()
2 cos 2
2
nn
y x n
Bài làm 2. Ta có :
2
' 2cos 2 , '' 2 cos 2 2 ,
22
y x y x
3
''' 2 cos 2 3
2
yx
.
Bằng quy nạp ta chứng minh được
()
2 cos 2
2
nn
y x n
.
ĐẠO HÀM TỔNG HỢP
Bài 1. Tính đạo hàm của các hàm số sau:
Câu 1:
5 4 3 2
1 2 3
45
2 3 2
y x x x x x
A.
4 3 2
18
' 3 3 4.
23
y x x x x
B.
4 3 2
52
' 3 3 4.
23
y x x x x
C.
4 3 2
58
' 3 4.
23
y x x x x
D.
4 3 2
58
' 3 3 4.
23
y x x x x
Bài làm:
/
5 4 3 2
1 2 3
' 4 5
2 3 2
y x x x x x
/ / /
/
/
5 4 3 2 /
1 2 3
' 4 5
2 3 2
y x x x x x
4 3 2
58
' 3 3 4.
23
y x x x x
Câu 2:
24
11
0,5
43
y x x x
A.
3
1
' 2 .
3
y x x
B.
3
1
' 2 .
3
y x x
C.
3
1
' 2 .
3
y x x
D.
3
1
' 2 2 .
3
y x x
Bài làm
/
/ 2 4
11
0,5
43
y x x x
//
//
/ 2 4
11
0,5
43
y x x x
3
1
' 2 2 .
3
y x x
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
34
Câu 3:
43
1
2 2 5
3
y x x x
A.
32
1
' 8 .y x x
x
B.
32
1
' 8 .y x x
x
C.
32
1
' 2 .y x x
x
D.
32
1
' 8 .y x x
x
Bài làm
/
43
1
' 2 2 5
3
y x x x
/
/
/
4 3 /
1
' 2 2 5
3
y x x x
32
1
' 8 .y x x
x
Câu 4:
43
2
1
4 3 2
xx
y x x a
(a là hằng số)
A.
32
1
'1
3
y x x x
B.
32
' 4 1y x x x
C.
32
1
'1
4
y x x x
D.
32
'1y x x x
Bài làm
/
43
2
1
'
4 3 2
xx
y x x a
32
'1y x x x
.
Câu 5:
2
32
3
y x x x
x
A.
3
61
.
2
x
x
x
B.
3
61
.x
x
x
C.
3
61
.x
x
x
D.
3
61
.
2
x
x
x
Bài làm
/
2
32
'
3
y x x x
x
//
/
2
2
' 3.
3
y x x x x
/
3/
12
' 3. 2 . . .
3
2
y x x x x x
x
3
6 1 2 1
'.
3
22
y x x
x
xx
33
6 1 2 6 1
'.
32
22
x
y x x
xx
xx
Câu 6:
43
1
2 2 5
3
y x x x
A.
32
1
' 2 .y x x
x
B.
32
1
'.y x x
x
C.
32
1
' 8 3 .y x x
x
D.
32
1
' 8 .y x x
x
Bài làm
/
43
1
' 2 2 5
3
y x x x
/
/
/
4 3 /
1
' 2 2 5
3
y x x x
32
1
' 8 .y x x
x
Câu 7:
53
4 2 3y x x x x
A.
4
3
' 4 12 2 .
2
y x x
x
B.
4
3
' 5 12 2 .
2
y x x
x
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
35
C.
4
3
' 5 4 2 .
2
y x x
x
D.
42
3
' 5 12 2 .
2
y x x
x
Bài làm
/
53
' 4 2 3y x x x x
/
//
5 3 /
' 4 2. 3y x x x x
4
3
' 5 12 2 .
2
y x x
x
Bài 2. Tính đạo hàm của các hàm số sau;
Câu a).
2
3 2 .y x x x
A.
2
3 6.xx
B.
2
3 2 6.xx
C.
2
3 2 .xx
D.
2
3 2 6.xx
Bài làm
/
/
/
2 2 2
' 3 2 3 . 2 3 . 2y x x x x x x x x x
22
2 3 2 3 1 3 2 6.x x x x x x
Câu b).
5
2 3 2y x x x
A.
54
12 15 8 6.x x x
B.
54
12 5 8 6.x x x
C.
54
12 15 6.x x x
D.
54
12 6.x x x
Bài làm
/
/
/
5 5 5
' 2 3 2 2 3 2 2 2 3y x x x x x x x x x
5 4 5 4
2 2 5 2 2 3 12 15 8 6.x x x x x x x
Câu c).
22
1 5 3y x x
A.
3
12 4 .xx
B.
3
12 4 .xx
C.
3
6 4 .xx
D.
3
12 .xx
Bài làm
/
//
2 2 2 2 2 2
' 1 5 3 1 5 3 5 3 1y x x x x x x
2 2 3 3 3
2 5 3 6 1 10 6 6 6 12 4 .x x x x x x x x x x
Câu d).
2
2 1 3 2 2 3 2y x x x x x x
A.
2
18 2xx
B.
2
18 2.xx
C.
2
8 2 2.xx
D.
2
18 2 2.xx
Bài làm
/
/
/
2 2 2
' 2 3 2 2 3 2 3 2 . 2y x x x x x x x x x
22
4 1 3 2 3 2 18 2 2.x x x x x x
Câu e).
22
2 3 2 3y x x x
A.
32
12 4 4 6.x x x
B.
32
2 4 24 6.x x x
C.
32
12 24 6.x x x
D.
32
12 4 24 6.x x x
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
36
Bài làm
/
//
2 2 2 2 2 2
' 2 3 2 3 2 3 2 3 2 3 2 3y x x x x x x x x x
2 2 3 2
4 2 2 3 4 2 3 12 4 24 6.x x x x x x x x
Câu f)
2
y x x
A.
.
2
xx
B.
5
.
2
x
C.
5
.
3
xx
D.
5
.
2
xx
Bài làm
//
/
2 2 2 2
1 1 5
' . . 2 . . 2 .
22
2
xx
y x x x x x x x x x x x x x
x
Câu g)
21
43
x
y
x
A.
2
2
.
43x
B.
2
2
.
3x
C.
2
.
43x
D.
2
2
.
43x
Bài làm
/
21
'
43
x
y
x
//
2 2 2
2 1 4 3 4 3 2 1 2 4 3 4 2 1
2
.
4 3 4 3 4 3
x x x x x x
x x x
Câu h)
2 10
43
x
y
x
A.
2
46
43x
B.
2
4
43x
C.
46
43x
D.
2
46
43x
Bài làm
/
2 10
'
43
x
y
x
//
2 2 2
2 10 . 4 3 4 3 . 2 10 2 4 3 4 2 10
46
4 3 4 3 4 3
x x x x x x
x x x
Câu k).
3
21
y
x
A.
2
6
.
21x
B.
2
16
.
21x
C.
2
26
.
21x
D.
2
36
.
21x
Bài làm
/
/
22
21
16
' 3. 3. .
21
2 1 2 1
x
y
x
xx
Câu l).
21
13
x
y
x
A.
2
15
.
13x
B.
2
5
.
13x
C.
2
25
.
13x
D.
2
5
.
13x
Bài làm
/
21
'
13
x
y
x
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
37
//
2 2 2
2 1 1 3 1 3 2 1 2 1 3 3 2 1
5
'.
1 3 1 3 1 3
x x x x x x
y
x x x
Câu m).
2
2
1
1
xx
y
xx
A.
22
2
2
1 2 1 1 2 1
1
x x x x x x
xx
B.
22
2
2
1 2 1 1 2 1
1
x x x x x x
xx
C.
22
2
2
1 2 1 2 1
1
x x x x x x
xx
D.
22
2
2
1 2 1 1 2 1
1
x x x x x x
xx
Bài làm
/
2
2
1
'
1
xx
y
xx
//
2 2 2 2
2
2
1 1 1 1
1
x x x x x x x x
xx
22
2
2
1 2 1 1 2 1
1
x x x x x x
xx
Câu n).
2
33
1
xx
y
x
A.
2
2
.
1
xx
x
B.
2
2
2
.
1
xx
x
C.
2
2
2
.
1
x
x
D.
2
2
2
.
1
xx
x
Bài làm
/
/
22
2
3 3 1 1 3 3
'
1
x x x x x x
y
x
2
2
22
2 3 1 3 3
2
.
11
x x x x
xx
xx
Câu o).
2
2 4 1
3
xx
y
x
A.
2
2
2 2 11
.
3
xx
x
B.
2
2
2 11
.
3
xx
x
C.
2
2
12 11
.
3
xx
x
D.
2
2
2 12 11
.
3
xx
x
Bài
làm
/
/
22
2
2 4 1 3 3 2 4 1
'
3
x x x x x x
y
x
2
2
22
4 4 3 2 4 1
2 12 11
.
33
x x x x
xx
xx
Bài 3. Tính đạo hàm của các hàm số sau:
Câu a).
2
7
y x x
.
A.
76
71x x x
B.
6
2 7 1x
C.
76
21x x x
D.
76
2 7 1x x x
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
38
Bài làm Sử dụng công thức
/
1
. . 'u u u
(với
7
u x x
)
/
7 7 7 6
' 2 . 2 7 1y x x x x x x x
Câu b).
2
32
2 3 6 1y x x x
.
A.
3 2 2
2 2 6 1 6 6 6 .x x x x x
B.
3 2 2
2 2 3 1 6 6 .x x x x x
C.
3 2 2
2 2 3 6 1 6 6 .x x x x x
D.
3 2 2
2 2 3 6 1 6 6 6 .x x x x x
Bài làm Sử dụng công thức
/
u
với
32
2 3 6 1u x x x
/
3 2 3 2 3 2 2
' 2 2 3 6 1 2 3 6 1 2 2 3 6 1 6 6 6 .y x x x x x x x x x x x
Câu c).
3
2
1 2 .yx
A.
2
2
12 1 2 .xx
B.
2
2
12 1 2 .xx
C.
2
2
24 1 2 .xx
D.
2
2
24 1 2 .xx
Bài làm: Sử dụng công thức
/
u
với
2
12ux
2 / 2 2
2 2 2 2
' 3 1 2 1 2 3 1 2 4 12 1 2 .y x x x x x x
Câu d).
32
2
y x x
.
A.
31
2
. 1 2x x x
B.
31
2
32 xx
C.
31
2
32 1 x
D.
31
2
32 . 1 2x x x
Bài làm: Sử dụng công thức
/
u
với
2
u x x
31 / 31
2 2 2
' 32 . 32 . 1 2y x x x x x x x
Câu e).
4
2
1y x x
.
A.
3
2
4 1 .xx
B.
3
2
1 . 2 1x x x
C.
3
2
1.xx
D.
3
2
4 1 . 2 1x x x
Bài làm: Sử dụng công thức
/
u
với
2
1u x x
3 / 3
2 2 2
' 4 1 . 1 4 1 . 2 1y x x x x x x x
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
39
Câu f).
32
22
1 . 1y x x x x
A.
2
2 2 2
' 1 3 2 1 1 2 2 1 1y x x x x x x x x
B.
2
2 2 2 2
' 1 1 3 2 1 1 1y x x x x x x x x x
C.
2
2 2 2 2
' 1 1 3 2 1 1 2 2 1 1y x x x x x x x x x x
D.
2
2 2 2 2
' 1 1 3 2 1 1 2 2 1 1y x x x x x x x x x x
Bài làm: Đầu tiên sử dụng quy tắc nhân.
//
3 2 2 3
2 2 2 2
' 1 1 1 1 .y x x x x x x x x
Sau đó sử dụng công thức
/
u
2 / / 3
2 2 2 2 2 2
' 3 1 1 1 2 1 1 1y x x x x x x x x x x x x
2 2 3
2 2 2 2
' 3 1 2 1 1 2 1 2 1 1y x x x x x x x x x x
2
2 2 2 2
' 1 1 3 2 1 1 2 2 1 1y x x x x x x x x x x
.
Câu g)
3
21
1
x
y
x
A.
2
4
3 2 1
.
1
x
x
B.
2
4
21
.
1
x
x
C.
2
4
21
.
1
x
x
D.
2
4
3 2 1
.
1
x
x
Bài làm: Bước đầu tiên sử dụng
/
u
, với
21
1
x
u
x
2
2 / 2
24
3 2 1
2 1 2 1 2 1 1
' 3. . 3. . .
1 1 1
11
x
x x x
y
x x x
xx
Câu h).
5
2
1
1
y
xx
A.
6
2
5 2 1
1
x
xx
B.
6
2
5 2 1
1
x
xx
C.
6
2
21
1
x
xx
D.
6
2
21
1
x
xx
Bài làm: Đầu tiên sử dụng công thức
/
1
u
với
5
2
1u x x
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
40
/
5
2
4/
22
2 10 6
5 2 2
2
1
5 1 . 1
5 2 1
'
11
1
xx
x x x x
x
y
x x x x
xx
Câu k).
23
2
23
1
xx
y
xx
A.
4 2 2 2 3
2
2
5 6 1 1 2 2 3
'
1
x x x x x x x x
y
xx
B.
4 2 2 2 3
2
2
5 6 1 1 2 2 3
'
1
x x x x x x x x
y
xx
C.
4 2 2 2 3
2
2
5 1 1 2 3
'
1
x x x x x x x x
y
xx
D.
4 2 2 2 3
2
2
5 6 6 1 1 2 2 3
'
1
x x x x x x x x
y
xx
Bài làm: Đầu tiên sử dụng
/
u
v
/
/
2 3 2 2 2 3
2
2
2 3 . 1 1 2 3
'
1
x x x x x x x x
y
xx
Tính
/
//
2 3 2 3 3 2
2 3 2 3 3 2x x x x x x
3 2 2 4 2
2 3 3 2 5 6 6 .x x x x x x x
Vậy
4 2 2 2 3
2
2
5 6 6 1 1 2 2 3
'
1
x x x x x x x x
y
xx
Câu l).
23
1 2 2 3 3 4y x x x
A.
2 3 3 2 2
' 2 3 3 4 1 2 6 3 4 1 2 2 3 12y x x x x x x x x
B.
2 3 3 2 2
' 4 2 3 3 4 1 2 6 3 4 1 2 2 3 12y x x x x x x x x
C.
2 3 3 2 2
' 2 2 3 3 4 1 2 6 3 4 1 2 2 3 12y x x x x x x x x
D.
2 3 3 2 2
' 2 2 3 3 4 1 2 6 3 4 1 2 2 3 12y x x x x x x x x
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
41
Bài làm:
//
/
2 3 2 3 2 3
' 1 2 2 3 3 4 1 2 2 3 3 4 1 2 2 3 3 4y x x x x x x x x x
2 3 3 2 2
' 2 2 3 3 4 1 2 6 3 4 1 2 2 3 12y x x x x x x x x
.
Bài 4. Tính đạo hàm các hàm số sau
Câu a).
2
1y x x x
A.
3
.
2
x
x
B.
2.
2
x
x
C.
.
2
x
x
D.
3
2.
2
x
x
Bài làm:
/. /
/
2/
13
' 1 2 '. . 2 . 2 .
2
2
x
y x x x x x x x x x x x x
x
Câu b).
2
12y x x
.
A.
2
12
x
xx
B.
2
1
12xx
C.
2
1
1
x
xx
D.
2
1
12
x
xx
Bài làm: Sử dụng công thức
/
u
với
2
12u x x
/
2
22
12
1
'
1 2 1 2
xx
x
y
x x x x
.
Câu c).
22
11y x x
A.
22
1
.
11
x
xx
B.
22
1
.
11
x
xx
C.
22
11
.
11xx
D.
22
.
11
xx
xx
Bài làm:
//
22
//
22
2 2 2 2
11
' 1 1 .
2 1 2 1 1 1
xx
xx
y x x
x x x x
Câu d).
2
1x
y
x
.
A.
2
2
11
1
1
x
x
x
B.
2
1
1
2
x
x
C.
2
2
31
1
1
2
x
x
x
D.
2
2
11
1
1
2
x
x
x
Bài làm: Sử dụng công thức
/
u
với
2
1x
u
x
/
2
2
22
1 1 1 1
' . 1
11
22
x
y
x
x
xx
xx
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
42
Câu e).
1
1
x
y
x
.
A.
2
11
' 2 .
1
1
x
y
x
x
B.
2
11
' 2 .
1
1
x
y
x
xx
C.
2
11
'.
1
1
x
y
x
xx
D.
2
11
' 2 .
1
1
x
y
x
xx
Bài làm: Đầu tiên sử dụng công thức
/
u
với
1
1
x
u
x
/
11
' 2 .
11
xx
y
xx
Tính
//
/
2
1 1 1 1
1
1
1
x x x x
x
x
x
22
11
11
1
22
11
xx
xx
x x x
Vậy
2
11
' 2 .
1
1
x
y
x
xx
.
Câu f).
1
1
1
yx
x
A.
11
.
1 2 1 1x x x
B.
11
.
2 1 2 1xx
C.
11
.
1 1 1x x x
D.
11
.
2 1 2 1 1x x x
Bài làm:
/
/
/
2
1
1 1 1 1
' 1 .
1 2 1 2 1 2 1 1
1
x
yx
x x x x x
x
Câu g).
5
1
yx
x
.
A.
4
1 1 1
5
2 2 .
x
x x x x
B.
4
1 1 1
5
.
x
x x x x
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
43
C.
4
1 1 1
2 2 .
x
x x x x
D.
4
1 1 1
5
2 2 .
x
x x x x
Bài làm: Bước đầu tiên sử dụng
/
u
với
1
ux
x
/
4 / 4
2
1 1 1 1
' 5 . 5 .
2
x
y x x x
x x x x
x
4
1 1 1
5
2 2 .
x
x x x x
Câu h).
1
1
x
y
x
.
A.
.
2 1 1
x
xx
B.
3
.
11
x
xx
C.
3
.
2 1 1xx
D.
3
.
2 1 1
x
xx
Bài làm: Sử dụng
/
u
v
được:
/
/
2
1 1 1 1
'
1
x x x x
y
x
/
1
1 . 1
21
1
x
xx
x
x
2 1 1
3
.
2 1 . 1 2 1 1
xx
x
x x x x
Câu i)
.y x x x
A.
1 1 1
. 1 . 1 .
2
2
2
x
xx
xxx
B.
1 1 1
. 1 . 1 .
x
xx
xxx
C.
1 1 1
. 1 . 1 .
2
2
x
xx
xxx
D.
1 1 1
. 1 . 1 .
2
2
2
x
xx
xxx
Bài làm: Đầu tiên áp dụng
u
với
u x x x
/
/
1 1 1
' 1 .
2
22
y x x x x x
xx
x x x x x x
1 1 1
. 1 . 1 .
2
2
2
x
xx
xxx
Câu k).
2
41
2
x
y
x
(áp dụng u chia v đạo hàm)
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
44
A.
22
22
x
xx
B.
22
8
22
x
xx
C.
22
8
32
x
xx
D.
22
8
22
x
xx
Bài làm:
/
2
/
2
/
22
2
2
2
2
2
4. 2 . 4 1
4 1 2 2 . 4 1
22
'
2
2
x
xx
x x x x
x
y
x
x
2
2
2
2
2 2 2 2
4 2 4 1
4 2 4 1
8
2
2
2 2 2 2
x
xx
x x x
x
x
x
x x x x
Câu l).
3
1
x
y
x
(Áp dụng căn bặc hai của u đạo hàm).
A.
32
2
3
13
' . .
1
2
1
xx
y
x
x
x
B.
32
2
3
12
' . .
1
2
1
xx
y
x
x
x
C.
32
2
3
1 2 3
' . .
1
1
xx
y
x
x
x
D.
32
2
3
1 2 3
' . .
1
2
1
xx
y
x
x
x
Bài làm:
/
3
3
1
'.
1
2
1
x
y
x
x
x
Ta có:
/
/
/
33
23
3 3 2
2 2 2
1 1 .
31
23
1
1 1 1
x x x x
x x x
x x x
x
x x x
Vậy
32
2
3
1 2 3
' . .
1
2
1
xx
y
x
x
x
Câu m).
3
2.yx
A.
2
.
22
x
x
B.
2
.
2
x
x
C.
32
.
2
x
x
D.
32
.
22
x
x
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
45
Bài làm: Đầu tiên áp dụng
/
u
với
3
2ux
/
32
33
32
11
' . 2 .3. 2 .
22
2 2 2 2
x
y x x
x
xx
Câu n)
3
1 1 2yx
.
A.
2
6 1 1 2
.
12
x
x
B.
2
1 1 2
.
2 1 2
x
x
C.
2
1 1 2
.
12
x
x
D.
2
6 1 1 2
.
2 1 2
x
x
Bài làm: Bước đầu tiên áp dụng
/
u
với
1 1 2ux
2
/
2 / 2
6 1 1 2
12
' 3 1 1 2 . 1 1 2 3 1 1 2 . .
2 1 2 2 1 2
x
x
y x x x
xx
Bài 5. Tính đạo hàm các hàm số sau:
Câu a).
cosy x x
.
A.
cos sin .xx
B.
sin .xx
C.
sin .xx
D.
cos sin .x x x
Bài làm: Ta áp dụng đạo hàm tích.
/
' 'cos . cos cos sin .y x x x x x x x
Câu b)
3
sin
1 cos
x
y
x
.
A.
2
3
sin
1 cos
x
x
B.
2
2
3sin
1 cos
x
x
C.
2
2
2sin
1 cos
x
x
D.
2
3
3sin
1 cos
x
x
Bài làm: Bước đầu tiên ta áp dụng công thức
/
u
với
sin
1 cos
x
u
x
2/
sin sin
' 3 .
1 cos 1 cos
x
y
xx
Tính :
//
/
2
22
sin 1 cos 1 cos .sin cos 1 cos sin
sin
1 cos
1 cos 1 cos
x x x x x x x
x
x
xx
22
2
cos cos sin 1
1 cos
1 cos
x x x
x
x
.
Vậy
2
2
3
sin 1 3sin
' 3 .
1 cos 1 cos
1 cos
xx
y
xx
x
.
Câu c).
3
sin 2 1yx
.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
46
A.
2
sin 2 1 cos 2 1 .xx
B.
2
12sin 2 1 cos 2 1 .xx
C.
2
3sin 2 1 cos 2 1 .xx
D.
2
6sin 2 1 cos 2 1 .xx
Bài làm: Bước đầu tiên áp dung công thức
/
u
với
sin 2 1ux
Vậy
/
/
32
' sin 2 1 3sin 2 1 . sin 2 1 .y x x x
Tính
/
sin 2 1x
: Áp dụng
/
sinu
, với
21ux
Ta được:
/
/
sin 2 1 cos 2 1 . 2 1 2cos 2 1 .x x x x
22
' 3.sin 2 1 .2cos 2 1 6sin 2 1 cos 2 1 .y x x x x
Câu d).
2
sin 2yx
.
A.
2
cos 2 .x
B.
2
2
1
.cos 2 .
2
x
x
C.
2
1
.cos 2 .
2
x
D.
2
2
.cos 2 .
2
x
x
x
Bài làm: Áp dụng công thức
/
sinu
với
2
2ux
/
2
/
2 2 2 2
22
2
' cos 2 . 2 cos 2 . .cos 2 .
2 2 2
x
x
y x x x x
xx
Câu e).
sin 2y x x
.
A.
cos 2
.
2 sin 2
x
xx
B.
cos 2
.
sin 2
x
xx
C.
2
.
2 sin 2xx
D.
cos
.
2 sin 2
x
xx
Bài làm: Áp dụng
/
u
, với
sin 2u x x
/
sin 2
cos 2
'.
2 sin 2 2 sin 2
xx
x
y
x x x x
Câu f).
23
2sin 4 3cos 5y x x
.
A.
45
' sin8 cos5 .sin10
2
y x x x
B.
5
' 8sin8 cos5 .sin10
2
y x x x
C.
45
' 8sin cos5 .sin10
2
y x x x
D.
45
' 8sin8 cos5 .sin10
2
y x x x
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
47
Bài làm: Bước đầu tiên áp dụng
/
uv
//
23
' 2sin 4 3 cos 5y x x
Tính
/
2
sin 4x
: Áp dụng
/
u
, với
sin4 ,ux
ta được:
/
//
2
sin 4 2sin4 . sin4 2sin4 .cos4 4 4sin8 .x x x x x x x
Tương tự:
/
//
3 2 2
cos 5 3cos 5 . cos5 3cos 5 . sin5 . 5x x x x x x
2
15
15cos 5 .sin5 cos5 .sin10 .
2
x x x x
Kết luận:
45
' 8sin8 cos5 .sin10
2
y x x x
Câu h).
3
2
2 sin 2yx
.
A.
3
2
' 6sin4 2 sin 2 .y x x
B.
2
2
' 3sin4 2 sin 2 .y x x
C.
2
2
' in4 2 sin 2 .y s x x
D.
2
2
' 6sin4 2 sin 2 .y x x
Bài làm: Áp dụng
/
u
, với
2
2 sin 2 .ux
2 / 2 /
2 2 2 2
' 3 2 sin 2 2 sin 2 3 2 sin 2 sin 2 .y x x x x
Tính
/
2
sin 2 ,x
áp dụng
/
,u
với
sin2 .ux
/
//
2
sin 2 2.sin2 sin2 2.sin2 .cos2 2 2sin4 .x x x x x x x
2
2
' 6sin4 2 sin 2 .y x x
Câu i).
22
sin cos .tany x x
.
A.
2 2 2
' cos cos .tan sin2 tan 2tany x x x x x
B.
2 2 2
' cos cos .tan sin2 tan tany x x x x x
C.
2 2 2
' cos cos .tan sin2 tan tany x x x x x
D.
2 2 2
' cos cos .tan sin2 tan 2tany x x x x x
Bài làm: Áp dụng
/
sin ,u
với
22
cos tanu x x
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
48
/
2 2 2 2
' cos cos .tan . cos .tan .y x x x x
Tính
/
22
cos .tan ,xx
bước đầu sử dụng
/
.,uv
sau đó sử dụng
/
.u
/ / /
2 2 2 2 2 2
cos .tan cos .tan tan .cosx x x x x x
//
22
2cos cos tan 2tan tan cosx x x x x x
2 2 2
2
1
2sin cos tan 2tan cos sin2 tan 2tan .
cos
x x x x x x x x
x
Vậy
2 2 2
' cos cos .tan sin2 tan 2tany x x x x x
Câu j).
2
1
cos
1
x
y
x
.
A.
2
11
' .sin .
1
1
x
y
x
xx
B.
2
11
' .cos 2. .
1
1
x
y
x
xx
C.
2
11
' .sin 2. .
1
1
x
y
x
xx
D.
2
11
' .sin 2. .
1
1
x
y
x
xx
Bài làm: Áp dụng
/
,u
với
1
cos
1
x
u
x
/
/
1 1 1 1 1
' 2.cos . cos 2.cos .sin .
1 1 1 1 1
x x x x x
y
x x x x x
/
11
' sin 2 . .
11
xx
y
xx
Tính
//
/
22
1 . 1 1 . 1
11
.
1
11
x x x x
x
x
x x x
Vậy
2
11
' .sin 2. .
1
1
x
y
x
xx
Câu k).
sin2 cos2
.
2sin2 cos2
xx
y
xx
A.
2
6
2sin2 cos2xx
B.
2
6
sin2 cos2xx
C.
2
6
2sin2 cosxx
D.
2
6
2sin2 cos2xx
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
49
Bài làm:
//
2
sin2 cos2 . 2sin2 cos2 2sin2 cos2 . sin2 cos2
'
2sin2 cos2
x x x x x x x x
y
xx
2
2cos2 2sin2 2sin2 cos2 4cos2 2sin2 sin2 cos2
'
2sin2 cos2
x x x x x x x x
y
xx
22
22
6cos 2 6sin 2 6
'
2sin2 cos2 2sin2 cos2
xx
y
x x x x
.
Câu l).
22
11
cos2
cos sin
y
x
xx
.
A.
2
sin2
.
cos 2
x
x
B.
2
sin
.
cos 2
x
x
C.
2
2cos2
.
sin 2
x
x
D.
2
2sin2
.
cos 2
x
x
Bài làm: Áp dụng
/
1
u
.
//
2 2 2
cos2 sin2 . 2
2sin2
'.
cos 2 cos 2
cos2
x x x
x
y
xx
x
Câu m).
sin .cos2y x x
.
A.
5
cos2 .x
B.
4
cos2 .x
C.
5
4 cos2 .x
D.
5
2 cos2 .x
Bài làm: Áp dụng
/
.uv
/ / /
' sin .cos2 cos2 .sin cos .cos2 sin2 . 2 .siny x x x x x x x x x
' cos .cos2 2sin2 .sin .y x x x x
Câu n).
5
44
cos siny x x
A.
4
10cos 2 .x
B.
4
cos 2 .sin2 .xx
C.
4
10cos 2 .sin .xx
D.
4
10cos 2 .sin2 .xx
Bài làm:
5
5
2 2 2 2
cos sin cos sin cos2 .x x x x x
Áp dụng
/
u
, với
cos2ux
//
4 4 4
' 5.cos 2 . cos2 5.cos 2 . sin2 . 2 10cos 2 .sin2 .y x x x x x x x
Câu o).
24
sin cos tan 3yx
A.
4 4 3 3
' sin 2cos tan 3 . sin tan 3 .4tan 3 . 1 tan 3 .3y x x x x
B.
4 4 3 3
' sin 2cos tan 3 . sin tan 3 .tan 3 . 1 tan 3 .y x x x x
C.
4 4 3 3
' sin 2cos tan 3 . sin tan 3 .4tan 3 . 1 tan 3y x x x x
D.
4 4 3 3
' sin 2cos tan 3 . sin tan 3 .4tan 3 . 1 tan 3 .3y x x x x
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
50
Bài làm: Đầu tiên áp dụng
/
,u
với
4
sin cos tan 3ux
/
44
' 2sin cos tan 3 . sin cos tan 3y x x
Sau đó áp dụng
/
sin ,u
với
4
cos tan 3ux
/
4 4 4
' 2sin cos tan 3 .cos cos tan 3 . cos tan 3y x x x
Áp dụng
/
cos ,u
với
4
tan 3 .ux
/
4 4 4
' sin 2cos tan 3 . sin tan 3 . tan 3 .y x x x
Áp dụng
/
,u
với
tan3ux
/
4 4 3
' sin 2cos tan 3 . sin tan 3 .4tan 3 . tan3 .y x x x x
/
4 4 3 2
' sin 2cos tan 3 . sin tan 3 .4tan 3 . 1 tan 3 . 3 .y x x x x x
4 4 3 3
' sin 2cos tan 3 . sin tan 3 .4tan 3 . 1 tan 3 .3y x x x x
.
Câu p)
33
sin 2 .cos 2y x x
A.
2
sin 4 .cos4 .xx
B.
2
3
sin .cos .
2
xx
C.
2
sin .cos4 .xx
D.
2
3
sin 4 .cos4 .
2
xx
Bài làm:
3
3
3 3 3
11
sin 2 .cos 2 sin2 .cos2 sin4 .sin 4
28
y x x x x x x
. Áp dụng
/
, sin4 .u u x
//
2 2 2
1 1 3
' .3sin 4 sin4 .3sin 4 .cos4 . 4 sin 4 .cos4 .
8 8 2
y x x x x x x x
Câu q)
3
sin cosy x x
.
A.
2
3 sin cos cos sin .x x x x
B.
2
3 sin os cos sin .x c x x x
C.
2
sin cos cos sin .x x x x
D.
2
3 sin cos cos sin .x x x x
Bài làm: Áp dụng
/
,u
với
sin cosu x x
2 / 2
' 3 sin cos . sin cos 3 sin cos cos sin .y x x x x x x x x
Câu r).
5sin 3cosy x x
A.
5cos 3sin .xx
B.
cos 3sin .xx
C.
cos sin .xx
D.
5cos 3sin .xx
Bài làm:
//
' 5sin 3cos 5cos 3sin .y x x x x
Câu s).
2
sin 3 2y x x
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
51
A.
2
cos 3 2xx
B.
2
2 3 .sin 3 2x x x
C.
2
3 .cos 3 2x x x
D.
2
2 3 .cos 3 2x x x
Bài làm: Áp dụng
/
sin ,u
với
2
32u x x
/
2 2 2
' cos 3 2 . 3 2 2 3 .cos 3 2y x x x x x x x
Bài 6. Tính đạo hàm các hàm số sau:
Câu a).
sinyx
.
A.
1
.cos .x
x
B.
1
.cos .x
x
C.
1
.sin .x
x
D.
1
.cos .
2
x
x
Bài làm: Áp dụng
/
sin ,u
với
ux
//
1
' sin cos . .cos .
2
y x x x x
x
Câu b).
2
cosyx
.
A.
sin2 .x
B.
in2 .sx
C.
cos2 .x
D.
2sin2 .x
Bài làm: Áp dụng công thức
/
,u
với
cosux
/
/
2
' cos 2.cos cos 2cos . sin sin2 .y x x x x x
Câu c).
cos 2 1yx
.
A.
1
.sin 2 1.
21
x
x
B.
1
.sin 2 1.
21
x
x
C.
sin 2 1.x
D.
1
.cos 2 1.
21
x
x
Bài làm: Áp dụng
/
cos ,u
với
21ux
Câu
/
//
21
' cos 2 1 sin 2 1 2 1 sin 2 1.
2 2 1
x
y x x x x
x
21
sin 2 1. .sin 2 1.
2 2 1 2 1
xx
xx
Câu d).
sin3 .cos5y x x
11
sin 2 sin8 sin2 sin8
22
x x x x
A.
4cos8 cos2xx
B.
cos8 cos2xx
C.
4cos8 cos2xx
D.
4cos8 cos2xx
Bài làm:
/ / / / /
1 1 1 1 1
' sin8 sin2 sin8 sin2 cos8 8 cos2 . 2
2 2 2 2 2
y x x x x x x x x
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
52
4cos8 cos2xx
Câu e).
sin cos
sin cos
xx
y
xx
.
A.
2
sin2
.
sin cos
x
xx
B.
2
3sin 2
.
sin cos
x
xx
C.
2
sin2
.
sin cos
x
xx
D.
2
2sin2
.
sin cos
x
xx
Bài làm: Áp dụng
/
u
v
//
2
sin cos sin cos sin cos . sin cos
'
sin cos
x x x x x x x x
y
xx
2
cosx sin sin cos cos sin sin cos
'
sin cos
x x x x x x x
y
xx
22
22
sin cos sin cos
2sin2
'.
sin cos sin cos
x x x x
x
y
x x x x
Câu f).
cos2yx
.
A.
sin2
.
cos2
x
x
B.
sin
.
cos2
x
x
C.
sin2
.
2 cos2
x
x
D.
sin2
.
cos2
x
x
Bài làm: Áp dụng
/
,u
với
cos2ux
//
cos2 sin2 . 2
sin2
'.
2 cos2 2 cos2 cos2
x x x
x
y
x x x
Câu g)
sin
sin
xx
y
xx
A.
22
cos sin sin cos
.
sin
x x x x x
xx
B.
22
cos sin sin cos
.
sin
x x x x x x
xx
C.
22
cos sin sin cos
.
sin
x x x x x
xx
D.
22
cos sin sin cos
.
sin
x x x x x x
xx
Bài làm:
//
sin
'
sin
xx
y
xx
//
//
2 2 2 2
sin . .sin .sin sin .
cos sin sin cos
.
sin sin
x x x x x x x x
x x x x x x
x x x x
h)
Câu Câu h).
sin cos cos siny x x
A.
sin cosxx
B.
sin cosxx
C.
sin cosx
D.
sin x
Bài làm: Bước đầu tiên sử dụng đạo hàm tổng, sau đó sử dụng
//
sin , cosuu
.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
53
//
//
' sin cos cos sin cos cos . cos sin sin . siny x x x x x x
sin .cos cos cos .sin sin sin .cos cos cos .sin sinx x x x x x x x
sin cosxx
Câu i).
sin
sin
xx
y
xx
.
A.
2
2sin 2 cos
.
sin
x x x
xx
B.
2
2sin cos
.
sin
x x x
xx
C.
2
sin cos
.
sin
x x x
xx
D.
2
2sin 2 cos
.
sin
x x x
xx
Bài làm: Sử dụng
/
u
v
//
2
sin . sin sin . sin
'
sin
x x x x x x x x
y
xx
2
1 cos sin 1 cos sin
sin
x x x x x x
xx
2
2sin 2 cos
.
sin
x x x
xx
Câu k).
2
1 cos2
1 cos2
x
y
x
.
A.
2
1 cos2 4sin2
2.
1 cos2
1 cos2
xx
x
x
B.
2
1 cos2 4sin 2
.
1 cos2
1 cos2
xx
x
x
C.
2
1 cos2 sin2
2.
1 cos2
1 cos2
xx
x
x
D.
2
1 cos2 4sin2
2.
1 cos2
1 cos2
xx
x
x
Bài làm: Sử dụng
/
u
với
1 cos2
1 cos2
x
u
x
/
1 cos2 1 cos2
' 2 .
1 cos2 1 cos2
xx
y
xx
//
2
1 cos2 1 cos2 1 cos2 1 cos2
1 cos2
2.
1 cos2
1 cos2
x x x x
x
x
x
2
2sin2 1 cos2 2sin2 1 cos2
1 cos2
2.
1 cos2
1 cos2
x x x x
x
x
x
2
1 cos2 4sin2
2.
1 cos2
1 cos2
xx
x
x
.
Câu l).
44
sin cosy x x
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
54
A.
sin4 .x
B.
2 sin4 .x
C.
cos4 sin4 .xx
D.
sin4 .x
Bài làm:
2
1 3 1
1 sin 2 cos4 .
2 4 4
xx
/
//
3 1 1 1
' cos4 cos4 sin4 . 4 sin4 .
4 4 4 4
y x x x x x
Câu m).
2
cos 2
4
yx
.
A.
2
4 .sin 2 .
44
xx
B.
2
2 .sin 2 .
44
xx
C.
2
4 2 .sin .
44
xx
D.
2
4 2 .sin 2 .
44
xx
Bài làm: Áp dụng
/
cosu
với
2
2
4
ux
/
2 2 2 /
' sin 2 . 2 sin 2 .2 2 . 2
4 4 4 4 4
y x x x x x
2
4 2 .sin 2 .
44
xx
Câu n).
sin cos
cos sin
x x x
y
x x x
A.
2
2
.
cos sin
x
xx
B.
2
2
.
cos sin
x
xx
C.
2
2
2
.
cos sin
x
x x x
D.
2
2
.
cos sin
x
x x x
Bài làm:
//
2
sin cos cos sin cos sin sin cos
'
cos sin
x x x x x x x x x x x x
y
x x x
Tính
/ / /
sin cos cos cos cos '.cos . cosx x x x x x x x x x x
cos cos sin sinx x x x x x
Tính
//
cos sin sin '.sin . sinx x x x x x x x
sin sin cos cosx x x x x x
2
22
sin cos sin cos sin cos
'.
cos sin cos sin
x x x x x x x x x x
x
y
x x x x x x
Bài 7. Cho
23
1 2 3
fx
x
xx
. Tính
'1f
.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489
55
A.-14 B.12 C.13 D.10
Bài làm: Bước đầu tiên tính đạo hàm sử dụng công thức
/
1
1
xx
/
2 3 2 3 4
1 2 3 1 4 9
'fx
x
x x x x x
' 1 1 4 9 14f
Bài 8. Cho
2
11
f x x
x
x
. Tính
'1f
A.
1
2
B.1 C.2 D.3
Bài làm: Ta có
/
/
2
22
1 1 1 1 1
' 2 2
2
x
f x x x x
xx
xx
x x x
Vậy
11
' 1 1 2
22
f
Bài 9. Cho
53
23f x x x x
. Tính
' 1 ' 1 4 0f f f
A.4 B.5 C.6 D.7
Bài làm: Ta có
/
5 3 4 2
' 2 3 5 3 2f x x x x x x
' 1 ' 1 4 0 (5 3 2) (5 3 2) 4.( 2) 4f f f
Bài 10. Cho
2
4
x
fx
x
. Tính
'0f
A.
1
4
B.1 C.2 D.3
Bài làm:
2
/
2
22
/
2
2
2
2 2 2
2
4
' 4 4
4
4
'
4
4 4 4
4
x
x
x x x x
x
x
fx
x
x x x
x
Vậy
1
'0
4
f
.
CHƯƠNG V.
ĐẠO HÀM
TẬP 2A. VIẾT PHƯƠNG TRÌNH TIẾP TUYẾN CỦA
ĐỒ THỊ HÀM SỐ KHI BIẾT TIẾP ĐIỂM.
Giáo viên muốn mua file word liên hệ 0946798489 để gặp thầy Vương. Hoc liên h qua:
Facebook: https://web.facebook.com/phong.baovuong
Page : https://web.facebook.com/tracnghiemtoanthpt489/
Email: baovuong7279@gmail.com
Website: http://tailieutoanhoc.vn/
0946798489
NGUYỄN BẢO VƯƠNG
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
1
MỤC LỤC
P TUYN C TH HÀM S......................................................................................... 1
Vấn đề 1. Viết phương trình tiếp tuyến của đồ thị hàm số khi biết tiếp điểm................................................ 2
CÁC BÀI TOÁN LUYN TP ............................................................................................................................. 13
LỜI TÂM SỰ
Ở tài liệu tiếp tuyến này, tôi chia thành 3 tập nhỏ, vì đảm bảo chất lượng bố cục, và công tác trình bày, vì
vậy mong quý vị bạn đọc theo dõi một cách thường xuyên để luôn được cập nhật tài liệu hay và chất lượng
của chúng tôi. Thân ái.
GIÁO VIÊN NÀO MUỐN MUA FILE WORD VUI LÒNG
LIÊN HỆ 0946798489 ĐỂ ĐẶT MUA NHÉ. THÂN ÁI.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
2
PHƯƠNG TRÌNH TIẾP TUYẾN CỦA ĐỒ THỊ HÀM SỐ
Ý nghĩa hình học của đạo hàmo hàm ca hàm s
y f(x)
tm
0
x
là h s góc
ca tip tuyn v th (C) ca hàm s tm
0 0 0
M x ;f(x )
.
Khi p tuyn ca (C) tm
0 0 0
M x ;f(x )
là:
0 0 0
  )
00
y f(x )
u kin c  ng
1
): yC f(x
và
2
): yC g(x
tip xúc nhau
tm c
0
x
là h 
00
00
xx
x
f( ) g( )
f'( ) g'( )x

có nghim
0
x
Nghim ca h  ca tim c
Nu

1
(C : y px) q
và
2
2
y ax c C : bx
thì
và
2
C
ip xúc nhau 
2
ax bx c px q
có nghim kép.
Các dạng tiếp tuyến của đồ thị hàm số thường gặp
- Vip tuyn khi bit t tim
00
M x ;y
, ho 
0
x
, ho
0
y
.
- Vip tuyn khi bit tip tuym
AA
A x ;y
c.
- Vip tuyn khi bit h s góc ca nó.
Phương pháp:
Cho hàm s
y f x
 th
C
và
00
M x ;y
m trên
C
. Tip tuyn v th
C
ti
00
M x ;y
có:
- H s góc:
0
k f' x
- 
00
y y k x x
, hay
0 0 0
y y f' x x x
V vip tuyn ti
00
M x ;y
chúng ta c ba yu t sau:
-  tim:
0
x
-  tim:
0
y
(N i tính bng cách thay
0
x
vào hàm s
00
y f x
)
- H s góc
0
k f' x
Vấn đề 1. Viết phương trình tiếp tuyến của đồ thị hàm số khi biết tiếp điểm.
Phương pháp:
Bài toán 1 :
ng cong
C : y f x
và
C' : y g x
tip xúc nhau ti
00
M x ;y
m
M C C'
và
tip tuyn ti
M
ca
C
trùng vi tip tuyn ti
M
ca
C'
ch khi h 
00
00
f x g x
f' x g' x
có nghim
0
x
.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
3
Lưu ý : M mng hp:
C : y f x
d : y ax b

tip xúc nhau
f x ax b 0
có nghim kép .
Hàm
nhn
0
x
làm nghim bi
k
nu
k1
0 0 0
f x f' x ... f x 0
và
k
0
f x 0
. Nghim bi
lc bng
2
ch không phải nghiệm kép.
Phép bio toàn s bi ca nghim.
Ví dụ 1. ng cong
yx
không tip xúc vi trc hoành ti
0
, t
x0
không nhn
0
làm nghim bi lc bng
2
  th
3
C : y x
ca hàm s tip xúc vi trc hoành
ti
x0

3
x0
nhn
0
làm nghim bi
3
.
Ví dụ 2.  th
C : y sinx
ca hàm s tip xúc vng thng
d : y x
ti
x0

trình
sinx x 0
thì không th có nghim kép.
y, bi bo toàn tp nghim, ch không chc bo toàn s bi
các nghilà sai lm d mc phi khi gii quyt bài toán tip tuyn.
Bài toán 2 :
*
ng cong
C : y f x
có tip tuyn t
0
x
khi và ch khi hàm s
y f x
kh vi
ti
0
x
ng hp
C
có tip tuyn t
0
x
thì tip tuy s góc
0
f' x
.
*
p tuyn ca  th
C : y f x
tm
00
M x ;f x
có dng :
0 0 0
y f' x x x f x
Bài toán 3. Vip tuyn c th hàm s
y f x
tm
00
M(x ;f(x ))
.
Giải. Tip tuyn ca  th hàm s
y f(x)
ti
00
M(x ;y )
là:
0 0 0
y f'(x )(x x ) y
.
Bài toán 4. Vip tuyn c th hàm s
y f x
bi tim
0
xx
.
Giải:
Tính

0 0 0
y f(x ),y'(x )
 p tuyn:
0 0 0
y f'(x )(x x ) y
Bài toán 5. Vip tuyn c th hàm s
y f x
bi tim bng
0
y
.
Giải. Gi
00
M(x ;y )
là tim
Gi
0
f(x) y
c các nghim
0
x
.
Tính
0
y'(x )

Các ví dụ
Ví dụ 1 : Cho hàm s
32
y x 3x 1
 th là (C). Vi p tuyn ca (C) :
1. Tm
M 1;3
; 2. T bng 2 ;
3. T bng 1 ;. 4. Tm (C) vi trc tung ;
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
4
5. Có h s góc là 9 ;
6. Song song vng thng (d ):
27x 3y 5 0
;
7. Vuông góc vng thng (d) :
x 9y 2013 0
.
Lời giải.
Hàm s nh
D
Ta có:
2
y' 3x 6x
1. p tuyn
t
ti
M 1;3
 :
y y' 1 x 1 3
Ta có:
y' 1 3

t
là:
y 3x 6
Chú ý:
Vip tuyn c th hàm s
y f x
tm
00
M x ;f x
.
Tip tuyn c th hàm s
y f x
ti
00
M x ;y
là:
0 0 0
y f' x x x y
2. Thay
x2
 th ca (C) c
y 21
.
 câu 1, 
t
là:
y 24x 27
Chú ý:
Vip tuyn c th hàm s
y f x
bi tim
0
xx
,
00
y f x ,
0
y' x
 p tuyn:
0 0 0
y f' x x x y
3. Thay
y1
 th ca (C) c
2
x x 3 0 x 0
hoc
x3
.
 câu 1, 
t
là:
y1
,
y 9x 28
Chú ý: Vip tuyn c th hàm s
y f x
bi tim bng
0
y
. Gi
00
M x ;y
là tim
Gi  
0
f x y
c các nghim
0
x
.
Tính
0
y' x
 p tuyn:
0 0 0
y f' x x x y
4. Trc tung Oy :
x 0 y 1
. câu 1, 
t
là:
y1
5. Gi
00
x ;y
là t tim c th (C ) ca hàm s và tip tuyn
t
.
Ta có :
2
0 0 0
y' x 3x 6x
, theo gi thit
0
y' x 9
, tc là
2
00
3x 6x 9
0
x3
hoc
0
x1

t câu 1
6. Gi
00
x ;y
là t tim c th (C ) ca hàm s và tip tuyn
t
.
Theo bài toán:
td
:
5
y 9x
3
0
y' x 9
 câu 1
7. Gi
00
x ;y
là t tim c th (C ) ca hàm s và tip tuyn
t
.
Theo bài toán:
t d'
:
1 2013
yx
99
0
y' x 9
 câu 1
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
5
Ví dụ 2 .
1. Cho hàm s:
32
y x m 1 x 3m 1 x m 2
. Tìm
m
 tip tuyn c th hàm s tm có
 bng
1
m
A 2; 1
.
2. Gi (Cm)  th ca hàm s
32
y x (2m 1)x (m 3)x 3
và (d) là tip tuyn ca (C) t m có
  khong cách t gc t n (d) bng
7
17
.
Lời giải.
1. Hàm s nh vi
x
.
Ta có:
2
y' 3x 2 m 1 x 3m 1
Vi
x 1 y 1 3m 1 y' 1 m 6
p tuyn tm có
x1
:
y m 6 x 1 3m 1
Tip tuy
A 2; 1
nên có:
1 m 6 3m 1 m 2
Vy,
m2
là giá tr cn tìm.
2. Hàm s nh vi
x
.
Ta có:
2
y' 3x 2 2m 1 x m 3.
p tuyn (d) :
y y'(2)(x 2) y(2)
      
22
2
8m 15
7
d(0,(d)) 17(8m 15) 49[(11 7m) 1]
17
(11 7m) 1

2
1313m 3466m 2153 0 m 1,
2153
m
1313
Ví dụ 3 :
1. Vip tuyn c th
C
:
42
y x x 6
, bit tip tuyn vuông góc vng thng
1
y x 1
6

.
2. Cho hàm s
3
12
y x x
33
 th là (C).    

12
yx
33
.
Lời giải.
1. Hàm s nh
D
Gi
t
là tip tuyn c th
C
ca hàm s và
t
vuông góc vng thng
1
y x 1
6

ng
thng
t
có h s góc bng
6
.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
6
Cách 1: Gi
00
M x ;y
là t tim ca tip tuyn
t
 th
C
ca hàm s . Khi 

3
0 0 0
y' x 6 4x 2x 6
2
0 0 0
x 1 2x 2x 3 0
. Vì
2
0 0 0
2x 2x 3 0, x

00
x 1 y y 1 4 M 1;4
.
p tuyn cn tìm là:
y 6 x 1 4 6x 10
.
Cách 2: 
t
có dng
y 6x m
t
tip xúc
C
tm
00
M x ;y
khi h   m
0
x
42
0 0 0
3
00
x x 6 6x m
4x 2x 6
có nghim
0
0
x1
x
m 10

2. Hàm s nh
D
Ta có:
2
y' x 1
Gi
3
0 0 0 0 0
12
M(x ;y ) (C) y x x
33
,
T
2
00
y'(x ) x 1

12
yx
33

2
1
k
3

22
1 2 0 0
1
d k .k 1 (x 1) 1 x 4
3



00
00
4
x 2 y
3
x 2 y 0
Vm
4
M 2;0 , 2;
3



là t cn tìm.
Ví dụ 4
1. Cho hàm s
3x
y
x2
(1). Vip tuyn (d) ca (C) bim
A 1; 2
và
B 1;0 .
2. Cho hàm s
32
y x 6x 9x 1
(1). Vi p tuyn (d) ca (C) bi m
A 2;7
và
B 2;7 .
Lời giải.
1. Cách 1. p tuyn (d) có dng
0 0 0
y f'(x )(x x ) f(x )
(
0
x
 tim ca (d) và (C)).
=
2
0 0 0
0
2 2 2
0
0 0 0
3 x ( x 6x 6)
55
(x x ) x
x2
(x 2) (x 2) (x 2)
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
7
22
0 0 0
5x (x 2) y x 6x 6 0
2 2 2
0 0 0 0 0
44
00
5 2(x 2) x 6x 6 5 x 6x 6
d(A,(d)) d(B,(d))
25 (x 2) 25 (x 2)
22
22
0 0 0 0
0 0 0 0
22
0 0 0 0
x 14x 19 x 6x 1
x 14x 19 x 6x 1
x 14x 19 x 6x 1
0
0
2
00
x1
x 1.
x 4x 9 0

V

Cách 2. Tip tuym A, B suy ra hoc (d) song song vng thng AB ho
m I(0; - 1) cn AB.
ng hp 1: (d) //AB.
H s góc cng thng AB:
AB
AB
AB
yy
k1
xx

.
(d) // AB suy ra h s góc ca (d) :
0
2
0
5
(x 2)
ng
hp này không xy ra.
ng hp 2: m I cn AB.
ng y = kx 1.
(d) tip xúc (C) t
0
x
0
0
0
2
0
3x
kx 1 (2)
x2
5
k (3)
(x 2)



có nghim
0
x
.
Thay
2
0
5
k
(x 2)


0
2
0
0
3x
5
1
x2
(x 2)
0
0
0
2
0
0 0 0
x2
x2
x1
x1
(3 x )(x 2) 5 (x 2)




Thay
0
x1
 c
k5
.
V

2. p tuyn (D) có dng :
2 3 2
0 0 0 0 0 0
y (3x 12x 9)(x x ) x 6x 9x 1
2 3 2
0 0 0 0
(3x 12x 9)x 2x 6x 1
2 3 2
0 0 0 0
(3x 12x 9)x y 2x 6x 1 0
(*)
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
8
d(A,(D)) d(B,(D))
2 3 2 2 3 2
0 0 0 0 0 0 0 0
2 2 2 2
0 0 0 0
2(3x 12x 9) 7 2x 6x 1 2(3x 12x 9) 7 2x 6x 1
(3x 12x 9) 1 (3x 12x 9) 1

3 2 3
0 0 0 0 0
2x 12x 24x 10 2x 24x 26
3 2 3
0 0 0 0 0
3 2 3
0 0 0 0 0
2x 12x 24x 10 2x 24x 26 (1)
2x 12x 24x 10 2x 24x 26 (2)
2
0 0 0 0
32
00
00
12x 48x 36 0 x 3 x 1
x 1 x 2
4x 12x 16 0

Lt thay
0 0 0 0
x 3 x 1 x 1 x 2
p tuyn (D) là
y 1 0, y 3 0, y 24x 7, y 3x 7.
Ví dụ 5 Vip tuyn
d
v th
C
:
1.
32
y x 3x 2
, bit
d
ct các trc
Ox,
Oy
l t ti
A,
B
tha mãn:
OB 9OA
.
2. Vip tuyn v th
C
:
32
y x 6x 9x 2
tm
M,
bit
M
cùng
2
m cc
tr ca
C
to thành tam giác có din tích bng
6.
Lời giải.
1. Gi
00
M x ;y x
là to  tim.
ng thng
d
ng th
2
m phân bit
A,B
.
Gi
là góc to bi gia
d
và
Ox

d
có h s góc
k tan
D thy, tam giác
AOB
vuông ti
O
, suy ra
OB
tan 9
OA
Nói khác  ng thng
d
có h s góc là
9

2
0
00
2
0
00
y' x 9
3x 6x 9 0
y' x 9
3x 6x 9 0

2
0 0 0
x 2x 3 0 x 1
hoc
0
x3
vì
2
0 0 0
x 2x 3 0, x
.
Vi
0
x1
p tuyn
y 9x 7
Vi
0
x3
p tuyn
y 9x 25
Vy, có
2
tip tuyn
y 9x 7
,
y 9x 25
th bài .
2. Hàm s 
2
m cc tr
A 1;2 ,
B 3; 2
ng th
2
cc tr là
2x y 4 0
.
Gi
00
M x ;y
là t tim c  th
C
ca hàm s và tip tuyn
d
c  
32
0 0 0 0
y x 6x 9x 2
Ta có:
AB 2 5
,
00
2x y 4
d M;AB
5

Gi thit
MAB
1
S 6 .AB.d M;AB 6
2
00
2x y 4 6
00
2x y 10
hoc
00
2x y 2
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
9
TH1: T
M
tha mãn h:
00
32
0 0 0 0
2x y 2
y x 6x 9x 2
00
0
2
0 0 0
0
y 2 2x
y2
x x 6x 11 0
x0



hay
M 0; 2
Tip tuyn ti
M
là:
y 9x 2
.
TH2: T
M
tha mãn h:
00
32
0 0 0 0
2x y 10
y x 6x 9x 2

00
0
2
0 0 0
0
y 10 2x
y2
x 4 x 6x 11 0
x4





hay
M 4;2
Tip tuyn ti
M
là:
y 9x 34
.
Vy, có
2
tip tuyn th bài:
y 9x 2
và
y 9x 34
Ví dụ 6 Gi (C)  th ca hàm s
x1
y
x3
.
1. Gi M là mm thuc (C) có khon tr bng 5. Vip tuyn ca
(C) ti M
2. Gi (d) là mt tip tuyn ca (C) , (d) cng tim cng ca (C) ti A , cng tim cn ngang
ca (C) ti B và gi xng ca (C) . Vit p tuyn (d) bit:
i) IA = 4IB. ii) IA + IB nh nht
Lời giải.
1. Khong cách t n trc Ox bng 5
M
y5
.
TH1:
M
M
M
M
M
M
y5
7
M (C)
x
x1
3
5
y5
y5
x3








TH2:
M
M
M
M
M
M
y5
x4
M (C)
x1
5
y5
y5
x3


p tuyn ca (C) tm
7
M ; 5
3




là
y 9x 16.
p tuyn ca (C) tm
M 4;5
là
y 4x 21.
2. i) Ta có
ABI
bng góc hình hc hp bi tip tuyn (d) vi trc hoành suy ra h s góc ca (d) là
IA
k tanABI 4
IB
p tuyn
d : y 4x 5
hoc
y 4x 21.
ii) p tuyn (d) có dng :
2
0 0 0
0
2 2 2
0
0 0 0
x 1 x 2x 3
44
y (x x ) x .
x3
(x 3) (x 3) (x 3)
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
10
Tim cng ca (C) :
1
D : x 3
Tim cn ngang ca (C) :
2
D : y 1.
m ca (d) và
1
D
2
00
A
2
0
x 2x 15
y
(x 3)


 m ca (C) vi
2
D
B0
x 2x 3
.
2
00
A I B I 0 0
2
0
0
x 2x 15
8
IA IB y y x x 1 2x 6 2x 6
x3
(x 3)

Áp dng bng thc Cauchy ,ta có
0
0
8
IA IB 2 2x 6 8
x3
.
2
0
00
0
0
x1
8
IA IB 8 2x 6 (x 3) 4
x5
x3

min IA IB 8 d: y x, y x 8
Ví dụ 7
1. Bit r th
32
y x m 1 x 4m 2 x 1
,
m
C
tn t 
1
m mà t  c tip
tuyn vuông góc vng thng
x 10y 2013 0
.Vip tuyn ca
m
C
tm

2. Lp tuyn c th
C
:
2x 3
y
x1
ti nhm thu th có khon
ng thng
d:
3x 4y 2 0
bng
2.
Lời giải.
1. Gi tim là
M a;b
, tip tuyn ti
M
có h s góc là
2
k y' a 3a 2 m 1 a 4m 2
, theo gi
thit suy ra
k 10
 th ch có
1

2
3a 2 m 1 a 4m 8 0
có nghim kép hay
'0
tc
m5
 c
a 2 M 2;29
.
Vy, tip tuyn cn tìm là
y 10x 9
2. Gi
00
M x ;y
m thu th
C
 
0
00
0
2x 3
y y x
x1

Ta có:
00
00
22
3x 4y 2
d M, d 2 2 3x 4y 12 0
34



hoc
00
3x 4y 8 0
TH1:
0
0 0 0
0
2x 3
3x 4y 12 0 3x 4 12 0
x1




2
00
3x x 0
0
x0
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
11
hoc
0
1
x
3
TH2:
00
3x 4y 8 0
0
0
0
2x 3
3x 4 8 0
x1




2
00
3x 19x 20 0
0
x5
hoc
0
4
x
3

p tuyn
d
ti
M
thu th
C
có dng:
0 0 0
y y' x x x y x
trong  
0
2
0
1
y' x ,
x1
0
x1
.
p tuyn
ti
1
M 0;3
là
y x 3
.
p tuyn
2
d
ti
2
1 11
M;
34



là
9 47
yx
16 16
.
p tuyn
3
d
ti
3
7
M 5;
4



là
1 23
yx
16 16
.
p tuyn
4
d
ti
4
4
M ; 1
3




là
y 9x 13
.
Vy, có
4
tip tuyn th bài:
y x 3,
9 47
y x ,
16 16
1 23
y x ,
16 16
y 9x 13
.
Ví dụ 8
1. Cho hàm s
x3
yC
x2
vng thng

m
d : y 2x m.
Tìm
m
 ng thng
m
d
ct
C
ti
m phân bit
A, B
  i xng
I
ca
C
u hai tip tuyn vi
C
tm
A, B.
2. Cho hàm s
32
y x 3x 1
 th là
C
 th m
A, B
sao cho tip tuyn ti
A
và
B
song song vi nhau và khong cách t
O
n ng th m
A, B
bng
10
5
.
Lời giải.
1.
D \ 2 .
 m cng thng
m
d
và
C
là nghim c

2
x3
2x m 2x m 5 x 2m 3 0
2
x
x
2

m
d
ct
C
tm phân bit
A, B
khi và ch m phân bit
khác
2
nên phi có:
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
12




2
2
2
0
m 5 4.2. 2m 3 0
m 3 40 0
g 2 0
15 0
2.2 2 m 5 2
m
m 3 0
Các tip tuyn:


21 1 1
2
12
1 2
2
5 5 5 5
: y x x 1 , : y x x 1
x 2 x 2
x 2 x 2
22
12
1
22
1
2
2
x 2 x 2 25
d I; d I; m 3.
x 2 x 2
Vy,
m3
là giá tr cn tìm.
2. Gi
32
1 1 1 1
A x ;y x 3x 1
,
32
2 2 2 2
B x ;y x 3x 1
là
2
m cn tìm vi
12
xx
Ta có

2
y' 3x 6x
H s góc ca các tip tuyn ca
C
ti
A
và
B
lt là
22
1 1 1 2 2 2
k 3x 6x ,k 3x 6x
Tip tuyn ca
C
ti
A
và
B
song song vi nhau nên
22
1 2 1 1 2 2
k k 3x 6x 3x 6x
1 2 1 2 1 2
3(x x ) x x 6(x x ) 0
12
x x 2 0
21
x 2 x
H s góc cng thng
AB
là


3 3 2 2
2 1 1 2 1 2
2 1 2 1
y y x x 3(x x )
k
x x x x
2
1 2 1 2 1 2 1 1 1
k x x x x 3 x x 4 x (2 x ) 6 2x 2
tng thng
AB
là
32
1 1 1 1
y ( 2x 2)(x x ) x 3x 1
11
( 2x 2)x y 2x 1 0
22
1 1 1 1
22
22
1 1 1 1
x 2x 1 x 2x 1
10 2
d O,AB
5
5
x 2x 2 1 x 2x 1 1 1
2
22
1 1 1 1
5 x 2x 1 2 x 2x 1 1 1
. 
2
v và rút g c:
2
22
1 1 1 1
3 x 2x 1 4 x 2x 1 4 0
2
11
x 2x 1 2 1
hoc
2
11
2
x 2x 1 2
3
Gii
1
c
12
x 1 x 1
Gii
2
c
1
3 2 6
x
3
hoc
1
3 2 6
x
3
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
13
Vy, m cn tìm là
3 2 6 9 2 6 3 2 6 9 2 6
A ; ,B ;
3 9 3 9
hoc li.

Bài 1. Cho hàm s
32
y x 3x 6x 1
(C)
Vip tuyn c th (C) bit
Câu 1.  tim bng 1
A.
y 3x 6
B.
y 3x 7
C.
y 3x 4
D.
y 3x 5
Bài làm 1. Gi
00
M x ;y
là tim
Ta có:
2
y' 3x 6x 6
.
Ta có:
00
x 1 y 1,y'(1) 3
p tuyn là:
0 0 0
y y'(x )(x x ) y 3(x 1) 1 3x 4
Câu 2.  tim bng
9
A.
18 81
9
9 27
yx
yx
yx


B.
81
9
92
yx
yx
yx

C.
18 1
9
97
yx
yx
yx


D.
81
9
92
yx
yx
yx


Bài làm 2. Gi
00
M x ;y
là tim
Ta có:
2
y' 3x 6x 6
.
Ta có:
32
0 0 0 0
y 9 x 3x 6x 8 0
0 0 0
x 1,x 2,x 4
.
00
x 4 y'(x ) 18
 p tuyn là:
y 18(x 4) 9 18x 81
00
x 1 y'(x ) 9
 p tuyn là:
y 9(x 1) 9 9x
00
x 2 y'(x ) 18
 p tuyn là:
y 18(x 2) 9 18x 27
.
Câu 3. Tip tuyn vuông góc vng thng
1
y x 1
18
A. :
y 18x 8
và
y 18x 27
. B. :
y 18x 8
và
y 18x 2
.
C. :
y 18x 81
và
y 18x 2
. D. :
y 18x 81
và
y 18x 27
.
Bài làm 3. Gi
00
M x ;y
là tim
Ta có:
2
y' 3x 6x 6
.
Vì tip tuyn vuông góc vng thng
1
y x 1
18
nên
Ta có:
2
0 0 0 0 0
y'(x ) 15 x 2x 8 0 x 4,x 2
T c hai tip tuyn:
y 18x 81
và
y 18x 27
.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
14
Câu 4. Tip tuym
N(0;1)
.
A.
33
y x 11
4
B.
33
y x 12
4
C.
33
y x 1
4
D.
33
y x 2
4
Bài làm 4. Gi
00
M x ;y
là tim
Ta có:
2
y' 3x 6x 6
.
p tuyn có dng:
2 3 2
0 0 0 0 0 0
y (3x 6x 6)(x x ) x 3x 6x 1
Vì tip tuy
N(0;1)
nên ta có:
2 3 2
0 0 0 0 0 0
1 (3x 6x 6)( x ) x 3x 6x 1
32
0 0 0 0
3
2x 3x 0 x 0,x
2
00
x 0 y'(x ) 6
 tip tuyn:
y 6x 1
.
0 0 0
3 107 33
x y ,y'(x )
2 8 4
p tuyn



33 3 107 33
y' x x 1
4 2 8 4
.
Bài 2. Cho hàm s
3
y x 3x 1
(C). Vi p tuyn c th (C), bit:
Câu 1.  tim bng
0
A.
y 3x 12
B.
y 3x 11
C.
y 3x 1
D.
y 3x 2
Bài làm 1. Ta có:

2
y' 3x 3
. Gi
00
M x ;y
là tim
Ta có:
0 0 0
x 0 y 1,y'(x ) 3
p tuyn:
y 3x 1
.
Câu 2.  tim bng
3
A.
y 9x 1
hay
y3
B.
y 9x 4
hay
y3
C.
y 9x 3
hay
y3
D.
y 9x 13
hay
y2
Bài làm 2. Ta có:

2
y' 3x 3
. Gi
00
M x ;y
là tiim
Ta có:
3
0 0 0 0 0
y 3 x 3x 2 0 x 2,x 1
00
x 1 y'(x ) 0
 p tuyn:
y3
00
x 2 y'(x ) 9
 p tuyn:
y 9(x 2) 3 9x 13
.
Câu 3. H s góc ca tip tuyn bng
9
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
15
A.
y 9x 1
hay
y 9x 17
B.
y 9x 1
hay
y 9x 1
C.
y 9x 13
hay
y 9x 1
D.
y 9x 13
hay
y 9x 17
Bài làm 3. Ta có:

2
y' 3x 3
. Gi
00
M x ;y
là tim
Ta có:
2
0 0 0
y'(x ) 9 3x 3 9 x 2
00
x 2 y 3
. Ph p tuyn:
y 9(x 2) 3 9x 13
.
00
x 2 y 1
p tuyn:
y 9(x 2) 1 9x 17
.
Câu 4. Tip tuyn vuông góc vi trc Oy.
A.
y 2,y 1
B.
y 3,y 1
C.
y 3,y 2
D.
x 3,x 1
Bài làm 4. Ta có:

2
y' 3x 3
. Gi
00
M x ;y
là tim
Vì tip tuyn vuông góc vi Oy nên ta có:
0
y'(x ) 0
Hay

0
x1
. T c hai tip tuyn:
y 3,y 1
.
Bài 3. Vip tuyn c th hàm s:
42
y 2x 4x 1
bit:
Câu 1.  tim bng
1
A.
1
8 2 5
8 2 5
y
yx
yx


B.
1
8 2 15
8 2 15
y
yx
yx


C.
1
8 2 1
8 2 1
y
yx
yx


D.
1
8 2 10
8 2 10
y
yx
yx


Bài làm 1. . Ta có:

3
y' 8x 8x
Gi
00
M x ;y
là tim.
Ta có:
42
0 0 0 0 0
y 1 2x 4x 0 x 0,x 2
00
x 0 y'(x ) 0
 p tuyn là:
y1
00
x 2 y'(x ) 8 2
 p tuyn
y 8 2 x 2 1 8 2x 15
00
x 2 y'(x ) 8 2
 trình tip tuyn
y 8 2 x 2 1 8 2x 15
.
Câu 2. Tip tuyn song song vng thng
y 48x 1
.
A.
y 48x 9
B.
y 48x 7
C.
y 48x 10
D.
y 48x 79
Bài làm 2. . Ta có:

3
y' 8x 8x
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
16
Gi
00
M x ;y
là tim.
Vì tip tuyn song song vng thng
y 48x 1
Nên ta có:
3
0 0 0 0
y'(x ) 48 x x 6 0 x 2
Suy ra
0
y 17
p tuyn là:
y 48(x 2) 17 48x 79
.
Bài 4. Cho hàm s
42
y x x 1
(C). Vi p tuyn c th (C), bit:
Câu 1.  tim bng 1
A.
y2
B.
y1
C.
y3
D.
y4
Bài làm 1. Ta có:

3
y' 4x 2x
. Gi
00
M x ;y
là tim
Ta có
42
0 0 0 0
y 1 x x 0 x 0
,
0
y'(x ) 0
p tuyn:
y1
Câu 2. Tip tuyn song song vng thng
y 6x 1
A.
y 6x 2
B.
y 6x 7
C.
y 6x 8
D.
y 6x 3
Bài làm 2. Ta có:

3
y' 4x 2x
. Gi
00
M x ;y
là tim
Vì tip tuyn song song vng thng
y 6x 1
nên ta có:
3
0 0 0 0 0
y'(x ) 6 4x 2x 6 x 1 y 3
 p tuyn:
y 6x 3
.
Câu 3. Tip tuym
M 1;3
.
A.
y 6x 2
B.
y 6x 9
C.
y 6x 3
D.
y 6x 8
Bài làm 3. Ta có:

3
y' 4x 2x
. Gi
00
M x ;y
là tim
p tuyn có dng:
3 4 2
0 0 0 0 0
y 4x 2x x x x x 1
Vì tip tuy
M 1;3
nên ta có:
3 4 2
0 0 0 0 0
3 4x 2x 1 x x x 1
4 3 2
0 0 0 0
3x 4x x 2x 2 0
22
0 0 0 0 0 0
(x 1) (3x 2x 2) 0 x 1 y 3,y'(x ) 6
p tuyn:
y 6x 3
.
Bài 5. Cho hàm s
2x 2
y
x1
(C). Vip tuyn ca (C), bit:
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
17
Câu 1.  tim bng
2
.
A.
7
1
yx
yx
B.
7
21
yx
yx
C.
27
21
yx
yx
D.
27
1
yx
yx
0
0
2
0
0
2x 2
4
: y (x x )
x1
(x 1)
.
Bài làm 1. Hàm s nh vi mi
x1
. Ta có:
2
4
y'
(x 1)
Gi
00
M(x ;y )
là tip tuyn ca (C):
Vì tip tuyn có h s góc bng
1
nên ta có
00
2
0
4
1 x 3,x 1
(x 1)
00
x 2 y 4 : y x 7
00
x 1 y 0 : y x 1
Câu 2. Tip tuyn song song vng thng
d: y 4x 1
.
A.
42
4 14
yx
yx
B.
4 21
4 14
yx
yx
C.
42
41
yx
yx
D.
4 12
4 14
yx
yx
Bài làm 2. Hàm s nh vi mi
x1
. Ta có:
2
4
y'
(x 1)
Gi
00
M(x ;y )
là tip tuyn ca (C):
Vì tip tuyn song vng thng
d: y 4x 1
nên ta có:
0 0 0
2
0
4
y'(x ) 4 4 x 0,x 2
(x 1)
.
00
x 0 y 2 : y 4x 2
00
x 2 y 6 : y 4x 14
.
Câu 3. Tip tuyim
A(4;3)
A.
11
99
11
44
yx
yx
B.
1 31
99
1 31
44
yx
yx
C.
11
99
1 31
44
yx
yx
D.
1 31
99
11
44
yx
yx
Bài làm 3. Hàm s nh vi mi
x1
. Ta có:
2
4
y'
(x 1)
Gi
00
M(x ;y )
là ti  p tuyn ca (C):
Vì tip tuy
A(4;3)
nên ta có:
0
0
2
0
0
2x 2
4
3 4 x
x1
(x 1)
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
18
22
0 0 0
3(x 1) 4(x 4) 2(x 1)
2
0 0 0 0
x 10x 21 0 x 3,x 7
0 0 0
81
x 7 y ,y'(x )
39
p tuyn
1 8 1 31
y x 7 x
9 3 9 9
.
0 0 0
1
x 3 y 1,y'(x )
4
p tuyn
1 1 1
y x 3 1 x
4 4 4
.
Câu 4. Vip tuyn ca (C), bit tip tuyn to vi hai trc t mt tam giác vuông cân.
A.
11
7
yx
yx
B.
11
17
yx
yx
C.
1
17
yx
yx
D.
1
7
yx
yx
Bài làm 4. Hàm s nh vi mi
x1
. Ta có:
2
4
y'
(x 1)
Gi
00
M(x ;y )
là tip tuyn ca (C):
Vì tip tuyn to vi hai trc t mt tam giác vuông cân nên tip tuyn phi vuông góc vi mt trong
ng phân giác
yx
,  s góc ca tip tuyn bng
1
hay

0
y'(x ) 1
. Mà
y' 0, x 1
nên ta có
0
y'(x ) 1
00
2
0
4
1 x 1,x 3
(x 1)
00
x 1 y 0 : y x 1
00
x 3 y 4 : y x 7
.
Bài 6. Cho hàm s
2x 1
y
x1
(C). Vip tuyn ca (C) bit:
Câu 1. Tip tuyn vuông góc vng thng

1
y x 2
3
A.
y 3x 11
hay
y 3x 11
B.
y 3x 11
hay
y 3x 1
C.
y 3x 1
hay
y 3x 1
D.
y 3x 1
hay
y 3x 11
Bài làm 1. Ta có
2
3
y'
(x 1)
. Gi
00
M x ;y
là tim. Vì tip tuyn vuông góc vng thng

1
y x 2
3
nên ta có
0 0 0
2
0
3
y'(x ) 3 3 x 0,x 2
(x 1)
00
x 0 y 1
 p tuyn là:
y 3x 1
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
19
00
x 2 y 5
 p tuyn là:
y 3(x 2) 5 3x 11
.
Câu 2. Tip tuyn ct Ox, Oy lt ti A, B sao cho tam giác OAB có din tích bng
1
6
A.
41
y 3x 1,y 3x 1,y 12x 2,y x
33
B.
42
y 3x 1,y 3x 11,y 12x 2,y x
33
C.
43
y 3x 11,y 3x 11,y 12x,y x
34
D.
42
y 3x 1,y 3x 11,y 12x 2,y x
33
Bài làm 2. Ta có
2
3
y'
(x 1)
. Gi
00
M x ;y
là tim.  p tuyn
có dng:
0
0
2
0
0
2x 1
3
y x x
x1
(x 1)
.
0
0
2
0
0
y0
2x 1
3
Ox A :
(x x ) 0
x1
(x 1)
Suy ra





2
00
2x 2x 1
A ;0
3
.

00
2
0
0
x0
3x 2x 1
Oy B :
y
x1
(x 1)
Suy ra:





2
00
2
0
2x 2x 1
B 0;
(x 1)
Din tích tam giác
OAB
:






2
2
00
0
2x 2x 1
11
S OA.OB
2 6 x 1
Suy ra





2
2
00
OAB
0
2x 2x 1
1
S1
6 x 1





22
0 0 0 0 0
22
0 0 0 0 0
2x 2x 1 x 1 2x x 0
2x 2x 1 x 1 2x 3x 2 0
00
00
1
x 0,x
2
1
x ,x 2
2
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
20
T c các tip tuyn là:
42
y 3x 1,y 3x 11,y 12x 2,y x
33
.
Câu 3. Tip tuy
A 7;5
.
A.
3 1 3 29
y x , y x
4 4 16 16
B.
3 1 3 2
y x , y x
4 2 16 16
C.
3 1 3 9
y x , y x
4 4 16 16
D.
3 1 3 29
y x , y x
4 4 16 16
Bài làm 3. Ta có
2
3
y'
(x 1)
. Gi
00
M x ;y
là tim. Do tip tuy
A 7;5
nên ta có:
2
0
0
0 0 0
2
0
0
0
x1
2x 1
3
5 7 x x 4x 5 0
x5
x1
(x 1)
T c các tip tuyn là:
3 1 3 29
y x , y x
4 4 16 16
.
Bài 7. Cho hàm s
42
y x 8x m 1
m
(C )
. Gi s rng tip tuyn c th (Cm) t m có hoành 
0
x1
luôn c th (Cm) t  m phân bit. Tìm t  m.
A.
A(1;m 6), B 1 3;m 18 3
B.
A(1;m 6), B 1 7;m 18 7
C.
A(1;m 6), B 1 2;m 18 2
D.
A(1;m 6), B 1 6;m 18 6
Ta có:

3
y' 4x 16x
Vì
0 0 0
x 1 y m 6, y'(x ) 12
 p tuyn d ca (Cm) t 
0
x1
là:
y 12(x 1) m 6 12x m 6
.
   m ca (Cm) vi d
4 2 4 2
x 8x m 1 12x m 6 x 8x 12x 5 0
22
(x 1) (x 2x 5) 0 x 1,x 1 6
Vy d và (Cm) luôn ct nhau tm phân bit
A(1;m 6), B 1 6;m 18 6
Bài 8. Cho hàm s

2x m 1
y
x1
(Cm). Tìm
m
 tip tuyn ca (Cm)
Câu 1. T 
0
x0

A(4;3)
A.
16
m
5

B.
6
m
5

C.
1
m
5

D.
16
m
15

Bài làm 1. Ta có:

2
m3
y'
(x 1)
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
21
Vì
0 0 0
x 0 y m 1, y'(x ) m 3
p tuyn d ca (Cm) t
0
x0
là:
y ( m 3)x m 1
Tip tuy khi:
16
3 ( m 3)4 m 1 m
5
.
Câu 2. T
0
x2
to vi hai trc t mt tam giác có din tích bng
25
2
.
A.
23
m 2;m
9
28
m 7;m
9
B.
23
m 2;m
9
28
m 7;m
9

C.
23
m 2;m
9
28
m 7;m
9

D.
23
m 2;m
9
28
m 7;m
9
Bài làm 2. Ta có:

2
m3
y'
(x 1)
Ta có
0 0 0
x 2 y m 5, y'(x ) m 3
 p tuyn
ca (Cm) t 
0
x2
là:
y ( m 3)(x 2) m 5 ( m 3)x 3m 11
.


3m 11
Ox A A ;0
m3
, vi
m 3 0
Oy B B 0;3m 11
Suy ra din tích tam giác OAB là:

2
1 1 (3m 11)
S OA.OB
22
m3
Theo gi thit bài toán ta suy ra:
2
1 (3m 11) 25
22
m3
2
2
2
9m 66m 121 25m 75
(3m 11) 25 m 3
9m 66m 121 25m 75

2
2
23
m 2;m
9m 41m 46 0
9
28
9m 91m 196 0
m 7;m
9
.
Bài 9. Gi s tip tuyn c th
f(x)
y f(x),y g(x),y
g(x)
tm c
x0
bng nhau.
Kht.
A.
1
f(0)
4
B.
1
f(0)
4
C.
1
f(0)
4
D.
1
f(0)
4
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
22
Theo gi thit ta có:

2
f'(0).g(0) g'(0)f(0)
f'(0) g'(0)
g (0)



2
2
2
f'(0) g'(0)
1 1 1
g(0) f(0)
f(0) g(0) g (0) g(0)
1
4 2 4
g (0)
Bài 10:
Câu 1. Tìm trên (C) :
32
y 2x 3x 1
nhm M sao cho tip tuyn ca (C) ti M ct trc tung t m
 bng 8.
A.
M( 1; 4)
B.
M( 2; 27)
C.
M(1;0)
D.
M(2;5)
Bài làm 1. Gi s
00
M(x ;y ) (C)
32
0 0 0
y 2x 3x 1
. Ta có:

2
y 3x 6x
.
p tuyn ti M:
2 3 2
0 0 0 0 0
y (6x 6x )(x x ) 2x 3x 1
.
a
P(0;8)
32
00
8 4x 3x 1

0
x1
. Vy
M( 1; 4)
.
Câu 2. Vit phng trình tip tuyn c th hàm s
32
y x 6x 11x 1
t bng 5.
A.
y 2x 1
;
y x 2
;
y 2x 1
B.
y 2x 3
;
y x 7
;
y 2x 2
C.
y 2x 1
;
y x 2
;
y 2x 2
D.
y 2x 3
;
y x 7
;
y 2x 1
Bài làm 2. Ta có:
32
y 5 x 6x 11x 6 0 x 1;x 2;x 3
p tuyn:
y 2x 3
;
y x 7
;
y 2x 1
Câu 3. Vip tuyn c th hàm s
32
1 1 4
y x x 2x
3 2 3
, bit tip tuyn vuông góc
vng thng
x 4y 1 0
.
A.
7
y 4x
6

;
2
y 4x
3

B.
73
y 4x
6

;
26
y 4x
3

C.
73
y 4x
6

;
2
y 4x
3

D.
7
y 4x
6

;
26
y 4x
3

Bài làm 3. Tip tuyn vuông góc vng thng
x 4y 1 0
11
yx
44
Tip tuyn có h s góc
k4
2
y' 4 x x 6 0 x 3;x 2
*
x3
p tuyn
1 73
y 4(x 3) 4x
66
*
x2
 p tuyn
2 26
y 4(x 2) 4x
33
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
23
Câu 4. Vip tuyn
d
c th
C
:
2x 1
y
x1
bit
d
u
2
m
A 2;4
và
B 4; 2
.
A.
11
yx
44

,
y x 3
,
y x 1
B.
15
yx
42

,
y x 5
,
y x 4
C.
15
yx
44

,
y x 4
,
y x 1
D.
15
yx
44

,
y x 5
,
y x 1
Bài làm 4. Gi
00
M x ;y x
,
0
x1
là t tim ca
d
và
C

d
có h s góc
0
2
0
1
y' x
x1

0
2
0
0
11
y x x 2
x1
x1
Vì
d
u
A,
B
nên
d
m
I 1;1
ca
AB
hoi
AB
.
TH1:
d
m
I 1;1
, thì ta luôn có:
0
2
0
0
11
1 1 x 2
x1
x1
, phm
0
x1
Vi
0
x1
p tuyn
d
:
15
yx
44

.
TH2:
d
i
AB
, tc là
d
và
AB
có cùng h s 
BA
0 AB
BA
yy
y' x k 1
xx
hay
2
0
1
1
x1

0
x2
hoc
0
x0
Vi
0
x2
tip tuyn
d
:
y x 5
.
Vi
0
x0
p tuyn
d
:
y x 1
.
Vy, có
3
tip tuyn th bài:
15
yx
44

,
y x 5
,
y x 1
Câu 5. Tìm
m
 t m
M 1;2
k c
2
tip tuy th
32
m
C : y x 2x m 1 x 2m
.
A.
10
m ,m 3
81
B.
100
m ,m 3
81

C.
10
m ,m 3
81

D.
100
m ,m 3
81
Bài làm 5. Gi
00
N x ;y C
 p tuyn
d
ca
A
ti
N
là:
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
24
2 3 2
0 0 0 0 0 0
y 3x 4x m 1 x x x 2x m 1 x 2m
32
0 0 0
M d 2x 5x 4x 3 3m
D thy
 m c th
y 3 3m
và
32
0 0 0 0
f x 2x 5x 4x
.
Xét hàm s
32
0 0 0 0
f x 2x 5x 4x
có
2
0 0 0
f' x 6x 10x 4
00
f' x 0 x 2
hoc
0
1
x
3
.
Lp bng bin thiên, suy ra
100
m ,m 3
81
Câu 6. Cho hàm s
2
3m 1 x m m
y
xm
 th là
m
C
,
m
và
m0
.Vi giá tr nào ca
m
thì
t th vi trc hoành, tip tuyn c th s song song vng thng
x y 10 0
.
A.
m1
;
1
m
5

B.
m1
;
1
m
5

C.
m1
;
1
m
5
D.
m1
;
1
m
5
Bài làm 6.  giao m c th vi trc hoành là nghi
2
2
x m,m 0
3m 1 x m m
0,m 0
xm
3m 1 x m m 0
22
11
x m,m 0,m m 0,m
33
m m m m
x x m
3m 1 3m 1










. Mà
2
2
4m
y'
xm
22
2
2
m m 4m
y'
3m 1
mm
m
3m 1









.
Tip tuyn song song vng thng
x y 10 0
nên
2
mm
y' 1
3m 1




m1
hoc
1
m
5

m1
 m là
A 1;0
, tip tuyn là
y x 1
.
1
m
5
 m là
3
B ;0
5



, tip tuyn là
3
yx
5

.
Câu 7. Tìm
m
 tip tuyn có h s góc nh nht ca
m
C
:
32
y x 2x m 1 x 2m
vuông góc
vng thng
yx
A.
10
m
3
B.
1
m
3
C.
10
m
13
D.
m1
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
25
Bài làm 7.
2
2
2 7 7
y' 3x 4x m 1 3 x m m
3 3 3



7
y' m
3
7
y' m
3
khi
2
x
3
.Theo
bài toán ta có:
7 10
y' 1 1 m 1 1 m
33



.
Câu 8. Tìm
m
  th :
32
1
y mx m 1 x 3m 4 x 1
3
m mà tip tuyn t
vng thng
x y 2013 0
.
A.
m1
B.
1
m
2

C.
1
m1
2
D.
1
m1
2
Bài làm 8.  tip tuyn c th vuông góc vng
x y 2012 0
khi và ch khi
y'.1 1
hay
2
mx m 1 x 3m 3 0
có nghim

. Đáp số:
1
m1
2
.
Câu 9. Cho hàm s
3
y x 3x 1
 th là
C.
Gi s
d
là tip tuyn ca
C
t
x2
ng thi
d
c th
C
ti
N,
tìm t
N
.
A.
N 1; 1
B.
N 2;3
C.
N 4; 51
D.
N 3;19
Bài làm 9. Tip tuyn
d
tm
M
c th
C

00
x 2 y 3
Ta có
2
0
y'(x) 3x 3 y'(x ) y'(2) 9
p tuyn
d
tm
M
c th
C
là
0 0 0
y y'(x )(x x ) y y 9(x 2) 3 y 9x 15

3 3 2
x 3x 1 9x 15 x 12x 16 0 x 2 x 2x 8 0
x4
hoc
x2
( không tha )
Vy
N 4; 51
m cn tìm
Bài 11:
Câu 1. Cho hàm s
32
y x 2x 8x 5
 th là
C.
Kh   nht ?
A. Không có bt k hai tip tuyn nào c th hàm s li vuông góc vi nhau
B. Luôn có bt k hai tip tuyn nào c th hàm s li vuông góc vi nhau
C. Hàm s m
1;17M
D. C u sai
Bài làm 1. Ta có
2
y'(x) 3x 4x 8
Gi s trái li có hai tip tuyn v th
C
vuông góc vi nhau.
Gi
12
x ,x
 ca hai tim ca hai tip tuy
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
26
Gi
12
k ,k
lt là các h s góc ca hai tip tuyn tm trên
C

12
x ,x
.

' ' 2 2
1 2 1 2 1 1 2 2
k ,k 1 y x .y x 1 3x 4x 8 3x 4x 8 1
1
Tam thc
2
f t 3t 4t 8
có
'0
nên
f t 0 t
t  
1
suy ra mâu thun.
Vy, gi thit phn ch)
Câu 2. Cho hàm s
42
y x 2x 3
 p tuyn ca hàm s có khom
M 0; 3
bng
5
65
.
A.
21yx
B.
32yx
C.
76yx
D.
Bài làm 2. Gi
AC
42
A a;a 2a 3
Ta có:
33
y' 4x 4x y' a 4a 4a
p tuyn
t
:
3 4 2
4a 4a x y 3a 2a 3 0
5
d M; t
65
hay
42
2
3
3a 2a 5
65
4a 4a 1

hay
6 4 2
5 a 1 a 1 117a 193a 85a 5 0
Gi p tuyn cn tìm.
Câu 3. Tìm
m
  th
3
y x 3mx 2
có tip tuyn to vng thng
d:
x y 7 0
góc
sao
cho
1
cos
26

.
A.
2m
B.
3m
C.
1, 4mm
D. 
Bài làm 3. Gi
k
là h s góc ca tip tuyn
tip tuyn
1
n k; 1
,
d
 
pháp tuyn
2
n 1;1
Ta có
12
2
12
nn
k1
13
cos k
2
26
nn
2 k 1
hoc
2
k
3
Yêu cu bài toán
ít nht m
1
y' k
hoc
2
y' k
có nghim
x
tc
2
2
3
3x 2 1 2m x 2 m có nghiêm
2
2
3x 2 1 2m x 2 m có nghiêm
3
. Tìm điều kiện có nghiệm suy ra m. Bạn tự giải tiếp, hí hí.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
27
Câu 4.  hai tip tuyn c th
42
y x 2mx 2m 1
ti
A 1;0
và
B 1;0
hp vi
nhau mt góc
sao cho
15
cos
17

.
A.
m 0,
m 2,
5
m,
16
7
m
6
. B.
m 0,
m 2,
15
m,
16
17
m
16
.
C.
m 0,
m 2,
15
m,
16
7
m
16
. D.
m 0,
m 2,
5
m,
6
7
m
6
.
Bài làm 4. D thy,
A,
B
là
2
m thu th vi
m
.
Tip tuyn
1
d
ti
A
:
4m 4 x y 4m 4 0
Tip tuyn
2
d
ti
B
:
4m 4 x y 4m 4 0
Đáp số:
m 0,
m 2,
15
m,
16
17
m
16
.
Bài 12. Cho hàm s:
2x 2
y
x1
 th
C
.
Vip tuyn c th (C) .
Câu a. Tip tuyn có h s góc bng
1
.
A.
y x 2,
y x 7
. B.
y x 5,
y x 6
.
C.
y x 1,
y x 4
. D.
y x 1,
y x 7
.
Bài làm a. Hàm s nh vi
x1
. Ta có:
2
4
y'
x1
Gi
00
M x ;y
là t ti p tuyn ca
C:
0
0
2
0
0
2x 2
4
y x x
x1
x1
vi
0
2
0
4
y' x
x1
và
0
0
0
2x 2
y
x1
Tip tuyn có h s góc bng
1
Nên có:
0
2
4
1 x 3,
x1
0
x1
Vi
00
x 1 y 0 : y x 1
Vi
00
x 2 y 4 : y x 7
Vy, có
2
tip tuyn th bài:
y x 1,
y x 7
.
Câu b. Tip tuyn song song vng thng
d: y 4x 1
.
A.
y 4x 3,
y 4x 4
. B.
y 4x 2,
y 4x 44
.
C.
y 4x 2,
y 4x 1
. D.
y 4x 2,
y 4x 14
.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
28
Bài làm b. Hàm s nh vi
x1
. Ta có:
2
4
y'
x1
Gi
00
M x ;y
là t ti p tuyn ca
C:
0
0
2
0
0
2x 2
4
y x x
x1
x1
vi
0
2
0
4
y' x
x1
và
0
0
0
2x 2
y
x1
Tip tuyn song song vng thng
d: y 4x 1
.
Nên có:
00
2
0
4
y' x 4 4 x 0
x1
hoc
0
x2
Vi
00
x 0 y 2 : y 4x 2
Vi
00
x 2 y 6 : y 4x 14
Vy, có
2
tip tuyn th bài:
y 4x 2,
y 4x 14
.
Câu c. Tip tuyn to vi
2
trc t lp thành mt tam giác cân.
A.
y x 1,
y x 6
. B.
y x 2
y x 7
.
C.
y x 1,
y x 5
. D.
y x 1,
y x 7
.
Bài làm c. Hàm s nh vi
x1
. Ta có:
2
4
y'
x1
Gi
00
M x ;y
là t ti p tuyn ca
C:
0
0
2
0
0
2x 2
4
y x x
x1
x1
vi
0
2
0
4
y' x
x1
và
0
0
0
2x 2
y
x1
Tip tuyn to vi
2
trc t lp thành mt tam giác cân nên h s góc ca tip tuyn bng
1
. Mt
khác:
0
y' x 0
, nên có:
0
y' x 1
Tc
0
2
0
4
1 x 1
x1
hoc
0
x3
.
Vi
00
x 1 y 0 : y x 1
Vi
00
x 3 y 4 : y x 7
Vy, có
2
tip tuyn th bài:
y x 1,
y x 7
.
Câu d. Tip tuyn tm thu th có khon trc
Oy
bng
2
.
A.
41
y x ,
99
y 4x 14
. B.
42
y x ,
99
y 4x 1
.
C.
41
y x ,
99
y 4x 1
. D.
42
y x ,
99
y 4x 14
.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
29
Bài làm d. Hàm s nh vi
x1
. Ta có:
2
4
y'
x1
Gi
00
M x ;y
là t ti p tuyn ca
C:
0
0
2
0
0
2x 2
4
y x x
x1
x1
vi
0
2
0
4
y' x
x1
và
0
0
0
2x 2
y
x1
Khong cách t
00
M x ;y
n trc
Oy
bng
2
suy ra
0
x2
, hay
2
M 2;
3



,
M 2;6
.
p tuyn ti
2
M 2;
3



là:
42
yx
99
p tuyn ti
M 2;6
là:
y 4x 14
Vy, có
2
tip tuyn th bài:
42
y x ,
99
y 4x 14
.
Bài 13. Vip tuyn v th hàm s:
2x
y,
x1
bit:
Câu a. H s góc ca tip tuyn bng
2
A.
y 2x 1,y 2x
B.
y 2x 2,y 2x 4
C.
y 2x 9,y 2x
D.
y 2x 8,y 2x
Bài làm a. Ta có:
22
2 x 1 2x
2
y'
x 1 x 1



. Gi
00
x ;y
là t tim, h s góc
tip tuyn ti
00
x ;y
bng
0
2
0
2
y' x
x1
Theo gii thit, ta có:
0
2
0
2
y' x 2 2
x1
2
0 0 0
0
0 0 0
x 1 1 x 2 y 4
x 1 1
x 1 1 x 0 y 0


Vy, có
2
tip tuyn tha  bài:
y 2x 8,y 2x
Câu b. Tip tuyn song song vng thng
d : x 2y 0
A.
1 7 1 7
y x ,y x
2 4 2 4
B.
1 27 1 7
y x ,y x
2 4 2 4
C.
1 2 1 7
y x ,y x
2 4 2 4
D.
1 27 1 7
y x ,y x
2 4 2 4
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
30
Bài làm b. Ta có:
22
2 x 1 2x
2
y'
x 1 x 1



. Gi
00
x ;y
là t tim, h s góc
tip tuyn ti
00
x ;y
bng
0
2
0
2
y' x
x1
Theo gii thit, ta có:
2
0
2
0
2 1 1
x1
24
x1
Vy, có
2
tip tuyn th bài:
1 27 1 7
y x ,y x
2 4 2 4
Câu c. Tip tuyn vuông góc vng thng
:9x 2y 1 0
A.
2 2 2 8
y x ,y x
9 9 9 9
B.
2 32 2 8
y x ,y x
9 9 9 9
C.
2 1 2 8
y x ,y x
9 9 9 9
D.
2 32 2 4
y x ,y x
9 9 9 9
Bài làm c. Ta có:
22
2 x 1 2x
2
y'
x 1 x 1



. Gi
00
x ;y
là t tim, h s góc
tip tuyn ti
00
x ;y
bng
0
2
0
2
y' x
x1
Theo gii thit, ta có:
2
0
2
0
2 2 1
x1
99
x1
Vy, có
2
tip tuyn th bài:
2 32 2 8
y x ,y x
9 9 9 9
Câu d. To vng thng
d' : 4x 3y 2012 0
góc
0
45
A.
23yx
B.
1
3
4
yx
C.
2
3
3
yx
D. 
Bài làm d. Ta có:
22
2 x 1 2x
2
y'
x 1 x 1



. Gi
00
x ;y
là t tim, h s góc
tip tuyn ti
00
x ;y
bng
0
2
0
2
y' x
x1
Tip tuyn c
00
y k x x y x
vi
0
k y' x 0
, có
n là
n k; 1
,
d'
n là
m 4;3
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
31
0
2
n.m
4k 3
11
cos45 k
7
2
nm
k 1.5
th bài.
Câu e. To vi chia trc hoành mt góc
sao cho
2
cos
5
A.
13
54
yx
B.
13
54
yx
C.
1 13
54
yx
D. 
Bài làm e. Ta có:
22
2 x 1 2x
2
y'
x 1 x 1



. Gi
00
x ;y
là t tim, h s góc
tip tuyn ti
00
x ;y
bng
0
2
0
2
y' x
x1
Tip tuyn to vi chin ti
0; 


tan 0
và
2
0
2
tan
x1

. Ta có:
2
2
1 1 1
tan 1 tan
42
cos
, nên có:
2
0
2
0
21
x 1 4
2
x1
Câu f. Tm
M
thu th và vuông góc vi
IM
(
I
m
2
tim cn )
A.
13
54
yx
B.
13
54
yx
C.
1 13
54
yx
D. 
Bài làm f. Ta có:
22
2 x 1 2x
2
y'
x 1 x 1



. Gi
00
x ;y
là t tim, h s góc
tip tuyn ti
00
x ;y
bng
0
2
0
2
y' x
x1
IM
2
0
2
k
x1
, theo bài toán nên có:
IM 0
k .y' x 1
2
0
x 1 4
Bài 14: Cho hàm s
42
xx
y2
42
 th (C).
Câu 1. Vi trình tip tuyn ca (C) song song vng thng :
y 2x 2
.
A.
3
2
4
yx
B.
1
2
4
yx
C.
3
2
4
yx
D.
21yx
Bài làm 1.
0
y'(x ) 2
ó
0
x
 tim ca (t) vi (C)).
33
0 0 0 0 0
x x 2 x x 2 0 x 1.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
32
P (t):
11 3
y y'(1)(x 1) y(1) 2(x 1) 2x
44
Câu 2. Vip tuyn (d) ca (C) bit khong cách t n (d) bng
9
45
.
A.
13
y 2x ,y 2x
44
B.
33
y 2x ,y 2x
4 14
C.
33
y 2x ,y 2x
44
D.
33
y 2x ,y 2x
14 4
Bài làm 2. p tuyn (d) có dng :
0 0 0
y y'(x )(x x y(x )

0
x
 tim ca (d) vi (C)).
P (d):
42
3 3 4 2
00
0 0 0 0 0 0 0
xx
31
y (x x )(x x ) 2 (x x )x x x 2
4 2 4 2
3 4 2
0 0 0 0
31
(x x )x y x x 2 0.
42
42
00
32
00
31
x x 1
42
99
d(A;(d))
4 5 4 5
(x x ) 1

4 2 2 2 2
0 0 0 0
3x 2x 4 5 9 x (x 1) 1
4 2 2 2 2 2
0 0 0 0
5(3x 2x 4) 81[x (x 1) 1]
t
2
0
t x , t 0
  thành:
2 2 2
5(3t 2t 4) 81[t(t 1) 1]
4 2 3 2 3 2
5(9t 4t 16 12t 24t 16t) 81t 162t 81t 81
4 3 2 3 2
45t 21t 22t t 1 0 (t 1)(45t 24t 2t 1) 0
32
t 1 (do t 0 nên 45t 24t 2t 1 0)
Vi
t1
,ta có
2
00
x 1 x 1
.
p tuyn (d):
33
y 2x ,y 2x
44
Bài 15:
Câu 1. Cho hàm s
ax b
y
x2
 th là
C
. Tìm
a,b
bit tip tuyn c th
C
tm ca
C
và tr
1
y x 2
2
A.
a 1, b 1
B.
a 1, b 2
C.
a 1, b 3
D.
a 1, b 4
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
33
Bài làm 1. m ca tip tuyn
d
:
1
y x 2
2
vi trc Ox là
A 4;0 ,
h s góc ca
1
d : k
2

và
A 4;0 ,
4a b
(C) 0 4a b 0
2
.
Ta có:
2
2a b 2a b
y' y 4
4
(x 2)
Theo bài toán thì:
1 1 2a b 1
k y'(4) 2a b 2
2 2 4 2

Gii h
4a b 0
2a b 2

c
a 1, b 4
Câu 2. Cho hàm s
42
y ax bx c (a 0)
 th là
C
. Tìm
a,b,c
bit
C
 m cc tr m
cc tiu ca
C
có t là
0;3
và tip tuyn d ca
C
tm ca
C
vi trc Ox có

y 8 3x 24
.
A.
a 1, b 2, c 3
B.
a 1, b 21, c 3
C.
a 1, b 21, c 13
D.
a 12, b 22, c 3
Bài làm 2.
C
m cc tr m cc tiu ca
C
có t là
0;3
a 0,b 0
c3
m ca tip tuyn d và trc Ox là
B 3;0
và h s góc ca d là
83
3
9a 3b c 0
B (C)
9a 3b c 0
.
y' 3 8 3
6a b 4
4a 3 2b 3 8 3




Gii h
c3
9a 3b c 0
6a b 4

c
42
a 1, b 2, c 3 y x 2x 3
Bài 16: Cho hàm s
42
y 2x 4x 1
 th là (C).
Câu 1. Vip tuyn ca (C), bit tip tuyn vuông góc vng thng
x 48y 1 0
.
A.
: y 48x 81
B.
: y 48x 81
C.
: y 48x 1
D.
: y 48x 8
Bài làm 1. Ta có
3
y' 8x 8x
Gi
00
M(x ;y )
. Tip tuyn
t
3 4 2
0 0 0 0 0
y (8x 8x )(x x ) 2x 4x 1
.Vì tip tuyn vuông góc vng thng
x 48y 1 0
Nên ta có:
00
1
y'(x ). 1 y'(x ) 48
48
3
0 0 0 0
x x 6 0 x 2 y 15
.

: y 48(x 2) 15 48x 81
.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
34
Câu 2. Vip tuyn ca (C), bit tip tuy
A(1; 3)
.
A.
: y 3
hay
64 1
: y x
27 81
B.
: y 3
hay
64 1
: y x
27 8
C.
: y 3
hay
64 51
: y x
27 2
D.
: y 3
hay
64 51
: y x
27 81
Bài làm 2. Ta có
3
y' 8x 8x
Gi
00
M(x ;y )
. Tip tuyn
t
3 4 2
0 0 0 0 0
y (8x 8x )(x x ) 2x 4x 1
.Vì tip tuyn

A(1; 3)
nên ta có
3 4 2
0 0 0 0 0
3 (8x 8x )(1 x ) 2x 4x 1
4 3 2
0 0 0 0
3x 4x 2x 4x 1 0
2
0 0 0
(x 1) (x 1)(3x 1) 0
0
x 1 : y 3
0
1 64 51
x : y x
3 27 81
.
Câu 3. Vip tuyn ca (C), bit tip tuyn tip xúc vi (C) tm phân bit.
A.
: y 3
B.
: y 4
C.
: y 3
D.
: y 4
Bài làm 3. Ta có
3
y' 8x 8x
Gi
00
M(x ;y )
. Tip tuyn
trình:
3 4 2
0 0 0 0 0
y (8x 8x )(x x ) 2x 4x 1
.Gi s
tip xúc vi (C) t m th hai
42
N(n;2n 4n 1)
Suy ra:
3 4 2
: y (8n 8n)(x n) 2n 4n 1
Nên ta có:
33
00
4 2 4 2
00
8x 8x 8n 8n
6x 4x 1 6n 4n 1
22
00
22
00
x nx n 1 0
(x n)(3x 3n 2) 0
22
00
0
x x n n 1 0
x n 0

(I) hoc
22
00
22
0
x x n n 1 0
3x 3n 2 0
(II)
Ta có (I)
0
xn
n1

;
22
0
0
2
xn
3
(II)
1
xn
3

vô nghim. Vy
: y 3
.
Bài 17: G th ca hàm s
3
2
x
y x 2x 1
3
.
Câu 1. Vi p tuyn ca (C) t  m ca (C) vi trc tung.
A.
21yx
B.
22 1yx
C.
23yx
D.
24yx
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
35
Câu 2. Vip tuyn ca (C) vuông góc vng thng
x
y2
5
.
A. y = 5x +
2
3
hoc y = 5x 8 B. y = 5x +
8
3
hoc y = 5x 9
C. y = 5x +
8
3
hoc y = 5x 5 D. y = 5x +
8
3
hoc y = 5x 8
Bài làm 2. Cách 1. Tip tuyn (d) ca (C) vuông góc vng thng
x
y2
5
 
có dng : y = 5x + m.
(d) tip xúc vi (C)
3
2
2
x
x 2x 1 5x m (1)
3
x 2x 2 5 (2)
có nghim.
Gii h trên, (2)
x = -1
x = 3.
Thay x = - c m =
8
3
.
 c m = - 8 .
Vp tuyn cn tìm là y = 5x +
8
3
hoc y = 5x 8 .
Cách 2. Tip tuyn (d) vuông góc vng thng
x
y2
5
suy ra h s góc ca (d) : k = 5.
Gi
0
x
 tim ca (d) vi (C) ,ta có :
2
0 0 0 0 0
k f'(x ) 5 x 2x 2 x 1,x 3
.

8
y 5(x 1) f(1) 5x
3
y 5(x 3) f(3) 5x 8
.
Câu 3.Vip tuyn ca (C) bit tip tuyt trc hoành , trc tung lt ti A, B sao
cho tam giác OAB vuông cân (O là gc t ).
A. y = x +
1
3
. B. y = x +
4
3
. C. y = x +
4
13
. D. y = x -
4
3
.
Bài làm 3. Vì tam giác OAB là tam giác vuông ti O nên nó ch có th vuông cân ta
tip tuyn (D) và trc Ox là
0
45
,suy ra h s góc ca (D) là
D
k1
ng hp
D
k1
   
0)
(D) tip xúc (C)
3
2
2
x
x 2x 1 x a (3)
3
x 2x 2 1 (4)
có nghim.
2
(4) x 2x 1 0 x 1
.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
36
c a =
4
3
.
Vng h
4
x
3
ng hp
D
k1
- x + a .
(D) tip xúc vi (C)
3
2
2
x
x 2x 1 x a (5)
3
x 2x 2 1 (6)
có nghim
(6)
2
x 2x 3 0
.P/t này vô nghim nên h (5), (6) vô nghim ,suy ra (D) : y = - x + a không tip xúc vi
(C).
Vp tuyn cn tìm là y = x +
4
3
.
Bài 18: Cho hàm s
32
y x 2x (m 1)x 2m
 th là
m
(C )
.
Câu 1. Tìm
m
 tip tuyn c th
m
(C )
t
x1
song song vng thng
y 3x 10
.
A.
2m
B.
4m
C.
0m
D.Không tn ti m
Bài làm 1. Ta có:
2
y' 3x 4x m 1
. Tip tuyn ca
m
(C )
t
x1
 
y (m 2)(x 1) 3m 2 (m 2)x 2m
Yêu cu bài toán
m 2 3
2m 10
vô nghim.
Vy không tn ti
m
tha yêu cu bài toán.
Câu 2. Tìm
m
 tip tuyn có h s góc nh nht c th
m
(C )
vuông góc vi ng thng
: y 2x 1
.
A.
1m
B.
2m
C.
11
6
m
D.
6
11
m
Bài làm 2. Ta có:
2
y' 3x 4x m 1
.Ta có:
2
2
4 4 7 2 7
y' 3 x x m 3 x m
3 9 3 3 3
7
y' m
3
.
Tip tuyn t
2
x
3
có h s góc nh nht và h s góc có giá tr :
7
km
3

.
Yêu cu bài toán
7 11
k.2 1 m .2 1 m
36



.
Câu 3. Tìm
m
 t m
M(1;2)
v n
m
(C )
p tuyn.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
37
A.
m3
10
m
81

B.
m3
100
m
81
C.
m3
10
m
81
D.
m3
100
m
81

Bài làm 3. Ta có:
2
y' 3x 4x m 1
. Gi
00
A(x ;y )
là t tim.
p tuyn
ti A:
2 3 2
0 0 0 0 0 0
y 3x 4x m 1 (x x ) x 2x (m 1)x 2m
2 3 2
0 0 0 0 0 0
M 2 3x 4x m 1 (1 x ) x 2x (m 1)x 2m
32
0 0 0
2x 5x 4x 3m 3 0
(*)
Yêu cu bài toán
(*)
i nghim phân bit (1)
Xét hàm s:
32
h(t) 2t 5t 4t, t
Ta có:
2
1
h'(t) 6t 10t 4 h'(t) 0 t ,t 2
3
Bng bin thiên
x

2
1
3

y'
0
0
y
12


19
27
Da vào bng bin thiên, suy ra
3 3m 12
(1)
19
3 3m
27
m3
100
m
81

là nhng giá tr cn tìm.
Bài 19: Tìm
m
  th :
Câu 1.
32
1
y mx m 1 x 4 3m x 1
3
tn t
2
 p tuyn t
vuông góc vng thng
x 2y 3 0
.
A.
1 1 2
m 0; ;
4 2 3

B.
1 1 7
m 0; ;
4 2 3

C.
1 1 8
m 0; ;
2 2 3

D.
1 1 2
m 0; ;
2 2 3

Bài làm 1. Hàm s  nh trên .
Ta có:
2
y' mx 2 m 1 x 4 3m
.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
38
T yêu cu bái toán d
1
y1
2




2
nghit, tc
2
mx 2 m 1 x 2 3m 0

2
t
m0
'0
S0
P0


m0
1
m
2
0 m 1
2
0m
3


hay
1 1 2
m 0; ;
2 2 3

.
Câu 2.
22
x 2mx 2m 1
y
x1
ct trc hoành tm phân bit và các tip tuyn vi
m
C
ti hai
m này vuông góc vi nhau.
A.
2
m
3
B.
m1
C.
2
m , m 1
3
D.
m0
Bài làm 2. Hàm s nh trên
\1
.
 m ca
m
C
và trc hoành:
22
22
x 2mx 2m 1
0 x 2mx 2m 1 0, x 1
x1
1

m
C
ct trc hoành tm phân bit

1
phi có hai nghim phân bit
khác
1
. Tc là ta phi có:
22
2
' m 2m 1 0
1 2m 2m 1 0
hay
1 m 1 m 0
2m m 1 0

tc
1 m 1
m0

2
.
Gi
12
x ;x
là hai nghim ca
1
nh lý Vi ét , ta có:
12
x x 2m,
2
12
x .x 2m 1
Gi s
0
I x ;0
 m ca
m
C
và trc hoành. Tip tuyn ca
m
C
ti m
I
có h s góc
22
0 0 0 0
0
0
2
0
0
2x 2m x 1 x 2mx 2m 1
2x 2m
y' x
x1
x1

y, tip tuyn ti
lt có h s góc là
1
1
1
2x 2m
y' x
x1
,
2
2
2
2x 2m
y' x
x1
.
Tip tuyn ti
vuông góc nhau khi và ch khi
12
y' x y' x 1
hay
12
12
2x 2m 2x 2m
1
x 1 x 1



2
1 2 1 2
5x .x 4m 1 x x 4m 1 0
tc
2
3m m 2 0
m1
hoc
2
m
3
i chiu kin ch có
2
m
3
tha mãn.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
39
Bài 20: m
M
 th
2x 1
y
x1
sao cho khong cách t
M
ng thng
:
x 3y 3 0
t giá tr nh nht.
A.
M 2;1
B.
M 2;5
C.
1
M 1;
2



D.
7
M 3;
2



Bài làm: Gi
2m 1
M m;
m1


là t m cn tìm
m1
.
Khong cách t
M
ng thng
là:
22
2m 1
m 3 3
m1
d
13



hay
2
1 m 2m 6
d.
m1
10

Xét hàm s:
2
2
2
m 2m 6
khi m 1
m 2m 6
m1
fm
m1
m 2m 6
khi m 1
m1






Ta có:
f' m 0 m 2
tha
m1
hoc
m4
tha
m1
.
Lp bng bin thiên suy ra
2
mind
10
khi
m2
tc
M 2;1
.
Tip tuyn ti
M
là
11
yx
33
, tip tuyn này song song vi
.
CHƯƠNG V.
ĐẠO HÀM.
TẬP 2B. VIẾT PHƯƠNG TRÌNH TIẾP TUYẾN
KHI BIẾT HỆ SỐ GÓC
GIÁO VIÊN MUN MUA FILE WORD LIÊN H 0946798489 hoc
Facebook: https://web.facebook.com/phong.baovuong
Page: https://web.facebook.com/tracnghiemtoanthpt489/
Website: http://tailieutoanhoc.vn/
Email: baovuong7279@gmail.com
0946798489
NGUYỄN BẢO VƯƠNG
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM.
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
1
MỤC LỤC
V 2. Vip tuyn c th hàm s khi bit h s góc ca tip tuyn. ......................... 2
CÁC BÀI TOÁN LUYN TP ................................................................................................................................. 10
GIÁO VIÊN NÀO MUN MUA FILE WORD LIÊN H  GP TH
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM.
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
2
V 2. Vip tuyn c th hàm s khi bit h s góc
ca tip tuyn.

Gi
'( )f x k
gic các nghim
12
, ,...,
n
x x x
.
p tuyn:
'( )( ) ( ) ( 1,2,..., )
i i i
y f x x x f x i n
.


'( )f x k
.

1 1 1
:d y k x b

2 2 2
:d y k x b

i)
12
12
tan
1.
kk
kk

12
( , )dd
.
ii)
12
12
12
//
kk
dd
bb
iii)
1 2 1 2
.1d d k k
.
Nng thng d ct các trc Ox, Oy lt ti A, B thì
tan
OB
OAB
OA

 s góc cc
nh bi
' tany x OAB
Ví d 1 : Cho hàm s
21
1
x
y
x
 th (C)
1. Gii b
'4y 
;
2. Vip tuyn vi (C) bit tip tuyn này ct các trc Ox, Oy lt ti A, B mà
4OA OB
.
Li gii.
1. Ta có
2
1
'
( 1)
y
x
.
B
2
2
1 1 1 3
( 1) 1
1
' 4 4
4 2 2 2
( 1)
1 1 1
x x x
y
x
x x x
2. Cách 1:
Ta có
1
tan
4
OB
OAB
OA

nên h s góc ca tip tuyn
1
4
k
hoc
1
4
k 
.

2
1
' 0, 1
( 1)
yx
x
nên h s góc ca tip tuyn là
1
4
k 
.
 tim nghi
2
3
11
1
4
( 1)
x
x
x



.
T c hai tip tuyn tha mãn:
1 5 1 13
;
4 4 4 4
y x y x
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM.
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
3
Cách 2:
p tuyn vi (C) tm
0
00
0
21
; ( 1)
1
x
M x x
x




là:
0
0
2
0
0
21
1
()
1
( 1)
x
y x x
x
x
hay
2
00
22
00
2 2 1
( 1) ( 1)
xx
x
y
xx



c t m ca tip tuyn vi các trc t:
2
2
00
00
2
0
2 2 1
(2 2 1;0), 0;
( 1)
xx
A x x B
x






T gi thit
4OA OB
, ta có:
2
22
0
00
0 0 0
2
0
0
3
2 2 1
2 2 1 4 ( 1) 4
1
( 1)
x
xx
x x x
x
x


Cách 3: Gi s
( ;0), (0; )A a B b
vi
0ab
.
Vi gi thit
1
4 4 4
4
b
OA OB a b a b
a
ng thm A, B có dng
:1
y
x
ab
hay
:
b
y x b
a
ng
:
b
y x b
a
tip xúc (C) t 
0
x
khi và ch khi h sau có nghim
0
x
:
2
0
0
0
0
1
(*)
( 1)
21
(**)
1
b
a
x
x
b
xb
xa

(I). T (*) suy ra
1
0
4
bb
aa
.
H (I) tr thành
0
2
0
0
0
0
0
0
0
3
11
13
4
( 1)
1
4
21
5
1
21
1
4
14
14
x
b
x
x
x
x
b
xb
bx
x
x








Do vy có hai tip tuyn tha mãn:
1 5 1 13
;
4 4 4 4
y x y x
Ví d 2 G th ca hàm s
2
2x mx m
y
xm

, m là tham s khác 0 và khác
1
3
1.Chng minh rng nu (C) ct Ox t 
0
x
thì h s góc ca tip tuyn ca (C) ti M là :
0
0
22xm
k
xm
2. (C) ct Ox tm và hai tip tuyn ca (C) ti nhau.
Li gii.
1. Ta có
2
3
3
mm
y x m
xm
Khi m
0 và m
1
3
 c t không chia h c m th hàm s không suy bin
ng thng.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM.
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
4
H s góc ca tip tuyn (d) ca (C) ti M là
2
0 0 0 0
0
2
0
(2 2 )( ) ( 2 )
'( ) .
()
x m x m x mx m
k y x
xm

Vì M thuc Ox nên
2
2
00
0 0 0
0
2
( ) 0 2 0
x mx m
y x x mx m
xm

.
0 0 0
2
0
0
(2 2 )( ) 2 2
()
x m x m x m
k
xm
xm

2. m ca (C) và Ox
2
2
2
0
( ) 2 0 (1)
xm
x mx m
xm
g x x mx m



(C) ct Ox tm phân bit M,N
(1) có hai nghim x1, x2 khác m .
2
2
01
01
'0
.
1
( ) 0 3 0
3
mm
mm
mm
g m m m
m




(*)
 s góc ca hai tip tuyn ca (C) ti M, N là
12
12
12
2 2 2 2
,
x m x m
kk
x m x m



.
Hai tip tuyn này vuông góc
12
.1kk
12
12
2 2 2 2
1
x m x m
x m x m


22
1 2 1 2 1 2 1 2
4[ ( ) ] ( ) (2)x x m x x m x x m x x m
Li có
1 2 1 2
x x 2m , x .x m
:
2
(2) 5 0 0 5m m m m
.
So vu kin (*) nhn m = 5.
Ví d 3 : Cho hàm s
1
x
y
x
 th là (C). Tìm t m M thuc (C), bit rng tip tuyn ca (C) ti
M vuông góc vng thm
I 1;1
.
Li gii.
Vi
0
1x
, tip tuyn (d) vi (C) ti
0
0
0
M x ;
1
x
x




 :
0
0
2
0
0
1
()
1
( 1)
x
y x x
x
x
2
0
22
00
1
0
( 1) ( 1)
x
xy
xx

(d) có vec  
2
0
1
1;
( 1)
u
x




,
0
0
1
1;
1
IM x
x




 u kin là :
0
0
2
0
0
0
0
11
. 0 1.( 1) 0
2
1
( 1)
x
u IM x
x
x
x
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM.
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
5
Vi
0
0x
c
0;0M
Vi
0
2x
c
2;2M
Vy,
0;0M
và
2;2M
là t cn tìm.
Ví d 4 : Cho hàm s
32
3 9 5y x x x
 th là (C). 
.
Li gii.
Hàm s nh
D

2
' 3 6 9y x x
.
G
00
( ; ) ( )M x y C
32
0 0 0 0
3 9 5y x x x
.

22
0 0 0 0
'( ) 3 6 9 3( 1) 12 12k y x x x x
mink 12,

00
1 y 16.x

M 1;16 .

plà:
y 12x + 4
Ví d 5. G th ca hàm s
32
2 6 5y x x
.
1. Vip tuyn (d) ca (C) tm A thu 
x3
 m khác A ca (d) và (C).
2. nh tham s  tn ti ít nht mt tip tuyn ca (C) có h s góc là a.
3. Chng minh rng ch có duy nht mt tip tuyn cm  th
'' 0y
ca (C).
Li gii.
1. p tuyn (d) ca (C) tm A:
'(3)( 3) (3) 18 49y y x y x
.
   m ca (d) và (C):
3 2 3 2
2 6 5 18 49 2 6 18 54 0 3 3x x x x x x x x
Suy ra gm ca (d) và (C) khác A là
B 3;103 .
2. Tn ti ít nht mt tip tuyn ca (C) có h s góc là a
00
, '( )x y x a
2
0 0 0
: 6 12x x x a
.
Bài toán quy v  - 6x
2
+12x = a (1) có nghim.
(1)
6x
2
12x + a = 0 . (1) có nghim
' 36 6 0 6.aa
Vy a
6.
3. T gi thi 
'' 0 1yx
I 1; 1 .
p tuyn (D) ca (
I 1; 1 .
có dng :
(D) tip xúc (C) t 
0
x
32
0 0 0
2
00
2 6 5 ( 1) 1 (1)
6 12 (2)
x x k x
x x k
có nghim
0
x
.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM.
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
6
Thay
(2)
c
3 2 2 3
0 0 0 0 0 0 0
2 6 5 ( 6 12 )( 1) 1 ( 1) 0 1x x x x x x x


Ví d 6 : Cho hàm s
32
25
( 1) (3 2)
33
y x m x m x
 th là (C). Tìm
m
 trên
()C
 m
phân bit
1 1 1 2 2 2
( ; ), ( ; )M x y M x y
tha mãn
12
.0xx
và tip tuyn ca
()C
ti m i
ng thng
: 3 1 0.d x y
Li gii.
Hàm s nh
D

2
' 2 2( 1) 3 2y x m x m
.
H s góc ca
: 3 1 0d x y
là
1
3
d
k
.
Tip tuyn tm
1 1 1 2 2 2
( ; ), ( ; )M x y M x y
vuông góc vi
d
thì phi có:
'3y 
Trong 
12
,xx
là các nghim c:
2
2 2( 1) 3 2 3x m x m
2
2 2( 1) 3 1 0x m x m
(1)
Yêu cu bài toán
m
12
,xx
tha mãn
12
.0xx
2
3
' ( 1) 2(3 1) 0
1
31
1.
0
3
2
m
mm
m
m



Vy,
3m 
hoc
1
1
3
m
tha mãn bài toán.
Ví d 7 Vip tuyn v th
C
:
32
6 9 2y x x x
tm
,M
bit
M
cùng
2
m
cc tr ca
C
to thành tam giác có din tích bng
6.
Li gii.
Hàm s 
2
m cc tr
1;2 ,A
3; 2B
 ng th
2
cc tr là
:AB
2 4 0xy
.
Gi
00
;M x y
là t tim c  th
C
ca hàm s và tip tuyn
d
c  
32
0 0 0 0
6 9 2y x x x
Ta có:
25AB
,
00
24
;
5
xy
d M AB

Gi thit
1
6 . . ; 6
2
MAB
S AB d M AB
00
2 4 6xy
00
2 10xy
hoc
00
22xy
TH1: T
M
tha mãn h:
00
32
0 0 0 0
22
6 9 2
xy
y x x x
00
0
2
0 0 0
0
22
2
6 11 0
0
yx
y
x x x
x




hay
0; 2M
Tip tuyn ti
M
là:
92yx
.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM.
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
7
TH2: T
M
tha mãn h:
00
32
0 0 0 0
2 10
6 9 2
xy
y x x x

00
0
2
0 0 0
0
10 2
2
4 6 11 0
4
yx
y
x x x
x



hay
4;2M
Tip tuyn ti
M
là:
9 34yx
.
Vy, có
2
tip tuyn th bài:
92yx
và
9 34yx
Ví d 8 : Cho hàm s
1
2( 1)
x
y
x
 th là (C). Tìm nhm M trên (C) sao cho tip tuyn vi (C) ti
M to vi hai trc t mt tam giác có trng tâm nng thng 4x + y = 0.
Li gii.
Hàm s nh
\1D
Gi M(
0
0
0
1
;
2( 1)
x
x
x
)
()C
m cn tìm.
Gi
tip tuyn vi (C) ti M 
:
'
0
00
0
1
( )( )
2( 1)
x
y f x x x
x
0
0
2
0
0
1
1
()
2( 1)
1
x
y x x
x
x
Gi
A Ox
2
00
21
;0
2
xx
A





,
B Oy
2
00
2
0
21
0;
2( 1)
xx
B
x





.
OAB có trng tâm là: G(
22
0 0 0 0
2
0
2 1 2 1
;
6
6( 1)
x x x x
x




.
Do G thuc ng thng: 4x + y = 0
22
0 0 0 0
2
0
2 1 2 1
4. 0
6
6( 1)
x x x x
x
2
0
1
4
1x
(vì A, B
O nên
2
00
2 1 0xx
)
00
00
11
1
22
13
1
22
xx
xx







Vi
0
1 1 3
;
2 2 2
xM



Vi
0
3 3 5
;
2 2 2
xM



.
Ví d 9 :
1. Tìm
m
 tip tuyn c th
32
3y x x m
t bng
1
ct các trc
Ox
,
Oy
lt
ti
A
và
B
sao cho din tích tam giác
OAB
có din tích bng
1,5
2. Tìm các giá tr a
m

:
m
C
42
3 1 3 2y x m x m
ct trc hoành ti
4
m phân bit và
tip tuyn t ln nht cùng vi
2
trc t to thành tam giác có din tích bng
24
.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM.
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
8
Li gii.
1.
1 1 2x y m
suy ra
1; 2Mm
. Tip tuyn ti
M
là
:d
32y x m
.
d
ct
Ox
ti
A
nên
;0
A
Ax
và
Ad
suy ra
2
;0
3
m
A


d
ct
Oy
ti
B
nên
0;
B
By
và
Bd
suy ra
0; 2Bm
Din tích tam giác
OAB
có din tích bng
1,5
khi và ch khi
13
..
22
OA OB
hay
.3OA OB 
2
. 2 3
3
m
m

hay
2
29m 
 
2
nghim
5m 
hoc
1m
.
Vy,
5m 
hoc
1m
là giá tr cn tìm.
2 m
m
C
và trc hoành :
4 2 2 2
3 1 3 2 0 1 3 2 0x m x m x x m


Vi
0m
thì
m
C
ct trc hoành ti
4
m phân bit và
32xm
 ln nht.
Ga s
3 2;0Am
 ln nht và tip tuyn
d
ti
A
 trình:
2 3 1 3 2. 2 3 1 3 2y m m x m m
Gi
B
m ca
d
và
Oy
suy ra
0; 2 3 1 3 2B m m
Theo gi thit, tam giác
OAB
vuông ti
O
và
24
OAB
S
. 48OAOB
hay
2
3 2 18 22 4 48m m m
Xét
2
3 2 18 22 4 48,f m m m m
0m
.
Ta có:
'0fm
vi mi
0m
, suy ra
fm
ng bin vi mi
0m
và
2
0
3
f




có nghim duy nht
2
3
m
.
Vy,
2
3
m
th  bài.
Ví d 10 Tìm
m
 tip tuyn c th hàm s :
3
1y x mx m
t  bng
1
ct
ng tròn
22
1
23
5
xy
theo
1
dây cung  dài nh nht.
Li gii.
2
' 3 ' 1 3y x m y m
. Vi
1 1 0 1;0x y M
.
 p tuyn ti
M
:
' 1 1y y x
3 3 0m x y m d
.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM.
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
9
ng tròn có tâm
2;3I
và bán kính
1
5
R
. Vì
IM R
 dài cung nh nht khi
d
tip xúc vi
ng tròn, tc là
;d I d R
2
3 2 3 3
1
5
31
mm
m


hay
2
1
5
6 10
m
mm

ng hai v
và rút g
2
2 3 5 0mm
, gi   c
1m
hoc
5
2
m
tha bài
toán.
Ví d 11 : Tì tip tuyn c th
32
3y x x m
tm  bng 1 ct các trc Ox, Oy
lt tng tròn ngoi tip tam giác OAB có chu vi
5
2
18
.
Li gii.
Vi
00
x y m
Tip tuyn ti M là d:
2
0 0 0
(3 6 )( ) 2y x x x x m
d : y 3x m 1
d ct trc Ox ti A:
11
0 3 1 ; 0
33
AA
mm
x m x A


d ct trc Oy ti B :
1 (0 ; 1)
B
y m B m
Tam giác vuông tm I ci tip I
11
;
62
mm


BK OI=
5
1
18
m
Gi thit có
0
5
2 2 1 1
2
18
m
OI m
m


Ví d 12. G th ca hàm s
1
1
x
y
x
. Vip tuyn (t) ca (C), bit:
1. (t) tip xúc vng tròn:
22
( ) :( 2) ( 6) 45xy
.
2. Khong cách t (tm I(1;1) ln nht.
Li gii.
1. Tnh tin
OI
vi I(1;1), h trc Oxy
h trc IXY.
Công thc chuyn h t :
1
1
I
I
x X x X
y Y y Y
i vi h trc IXY thì A có t là
1 2 1 1
1 6 1 5
Xx
Yy
Hàm s cho tr thành :
1 1 2 2
1 ( ).
( 1) 1
XX
Y Y F X
X X X

ng tròn
()
là
22
( 1) ( 5) 45,XY
(
) có tâm A(1;5) , bán kính R = 3
5
.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM.
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
10
p tuyn (D) ca (C) ti 
0
X
là
0 0 0 0
22
00
00
2 2 2 4
'( )( ) ( ) ( )Y F X X X F X X X X
XX
XX
2
00
2 4 0.X X Y X
(D) tip xúc (C)
d A, D R
2
22
00
2
00
4
4
0
0
2 5 4
(5 4 2)
[ ,( )) 3 5 [( ( ,( ))] 45
4
4
Xx
XX
d A D d A D
X
X


4 2 3 2 4
0 0 0 0 0 0
25 16 4 40 20 16 180 45X X X X X X
4 3 2
0 0 0 0
5 10 9 4 44 0X X X X
22
0 0 0 0
( 2) (5 10 11) 0 2X X X X
V   
1
2
2
YX
,s     i vi h trc xut phát Oxy là :
1 1 1
1 ( 1) 2
2 2 2
y x x
.
2. i vi h t p tuyn (d) có dng :
2
00
2 4 0X X Y X
,
0
4
0
4
( ,( ))
4
X
d I d
X
Áp dng bng thc Cauchy ,ta có :
4 4 2
0 0 0
4 2 4 4X X X
00
4
00
2
0
0
44
( ,( )) 2 ( ,( )) 2 4 2
2
4
XX
d I d d I d X X
X
X
p tuyn (d):
2 2, 2 2Y X Y X
.
i vi h trc Oxy là
2 2 2yx
.
CÁC BÀI TOÁN LUYỆN TẬP
Bài 1. Cho hàm s
21
y
1
x
x
 th là
C.
L trình tip tuyn c th
C
sao cho tip
tuyn này ct các trc
O , Oxy
l t t m
A,B
tho mãn
OA 4OB.
A.
15
44
1 13
44
yx
yx
B.
15
44
1 13
44
yx
yx
C.
15
44
1 13
44
yx
yx
D.
15
44
1 13
44
yx
yx
Bài làm 1. Gi s tip tuyn
d
ca
C
ti
00
( ; ) ( )M x y C
ct
Ox
ti
,A
Oy
ti
B
sao cho
4OOA B
.
Do
OAB
vuông ti
O
nên
1
tan
4
OB
A
OA

H s góc ca
d
bng
1
4
hoc
1
4
.
H s góc ca
d
là
0
22
00
1 1 1
( ) 0
4
( 1) ( 1)
yx
xx

NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM.
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
11
00
00
3
1
2
5
3
2
xy
xy








2
tip tuyn tho mãn là:
1 3 1 5
( 1)
4 2 4 4
1 5 1 13
( 3)
4 2 4 4
y x y x
y x y x






.
Bài 2:
Câu 1. Cho hàm s
23
2
x
y
x
 th là
C.
Vi tip tuyn tm
M
thuc
C
bit tip
tuy t tim c ng và tim cn ngang l t ti
A,B
sao cho côsin góc
ABI
bng
4
17
, vi
I 2;2
.
A.
13
42
yx
;
17
42
yx
B.
13
42
yx
;
17
42
yx
C.
13
42
yx
;
17
42
yx
D.
13
42
yx
;
17
42
yx
Bài làm 1.
I 2; 2
, gi
0
0
0
23
; ( )
2
x
M x C
x


,
0
2x
p tuyn
ti
M
:
0
0
2
0
0
23
1
()
2
( 2)
x
y x x
x
x
m ca
vi các tim cn:
0
0
22
2;
2
x
A
x


,
0
(2 2;2)Bx
.
Do
4
cos
17
ABI
nên
1
tan
4
IA
ABI
IB

2 2 4
0
16. ( 2) 16IB IA x
0
0x
hoc
0
4x
Ti
3
0;
2
M



 trình tip tuyn:
13
42
yx
Ti
5
4;
3
M



p tuyn:
17
42
yx
Câu 2. Cho hàm s
21
1
x
y
x
.Tìm trên hai nhánh c th m M, N sao cho các tip tuyn ti M
và N cng tim cn tm lp thành mt hình thang.
A.
2;5 , 0; 1MN
B.
71
3; , 1;
22
MN
C.
1
2;5 , 1;
2
MN



D. Vi mi M, N
Bài làm 2. Gi
( ; ), ( ; )
MN
M m y N n y
m thuc 2 nhánh ca (C).
Tip tuyn ti M ct hai tim cn ti A, B. Tip tuyn ti N ct hai tim cn ti C, D.
p tuyn ti M có dng:
( ).( )
M
y y m x m y
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM.
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
12
24
1; , (2 1;2)
1
m
A B m
m


. :
24
1; , (2 1;2)
1
n
C D n
n


.
ng thng AD và u có h s góc:
3
( 1)( 1)
k
mn

nên AD // BC.
Vy mm M, N thuc 2 nhánh cu tho mãn bài toán.
Bài 3:
Câu 1. Bit vi mm
M
tùy ý thuc
C
:
2
33
2
xx
y
x

, tip tuyn ti
M
ct
C
tm
A,B
to
vi
I 2; 1
mt tam giác có dii , Di.
A. 2 B.4 C.5 D. 7
Bài làm 1.
2
3 3 1
1
22
xx
yx
xx


. Ta có :
2
1
'1
2
y
x

.
Gi
0 0 0 0
0
1
; ( ) 1
2
M x y C y x
x
Tip tuyn vi
()C
ti
M
là
00
2
0
0
11
: 1 1
2
2
y x x x
x
x




Nu
2x
tm
A
, thì
0
0
2
A
x
y
x

0
0
2;
2
x
A
x




Nu
ct tim cn xin tm
B
thì
0 0 0 0
2
0
0
11
1 1 1 2 2 1 2 3
2
2
B B B B B
x x x x x x y x x
x
x




00
2 2;2 3B x x
Nu
I
là giao hai tim cn , thì
I
có t
I 2; 1 .
Gi
H
là hình chiu vuông góc ca
B
trên tim cng
2x 
suy ra
0
H( 2;2 3)x
Din tích tam giác
0
0
0
1 1 1
AIB: . . 1 2 2 2
2 2 2 2
A I B H
x
S AI BH y y x x x
x
Hay
0
0
12
.2 2 2
2
2
Sx
x

Chng t
S
là mt hng s , không ph thuc vào v trí cm
M
.
Câu 2. Cho hàm s
3
1
x
y
x
 th là (C).Tìm trên ng thng
: 2 1d y x
m t  c duy
nht mt tip tuyn ti (C).
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM.
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
13
A.
(0;1)
( 1; 1)
(2; 5)
(1;3)
M
M
M
M

B.
(5;11)
( 1; 1)
(7;15)
(1;3)
M
M
M
M

C.
(4;9)
( 1; 1)
(2; 5)
(1;3)
M
M
M
M

D.
(0;1)
( 1; 1)
(3;7)
( 2; 3)
M
M
M
M


Bài làm 2. Gi
( ;2 1)M m m d
.
ng thng qua M có h s góc k có dng:
( ) 2 1y k x m m
  m ca và (C):
3
( ) 2 1
1
x
k x m m
x
2
( 1) 2 (2 4) 0kx m k m x mk m
(*)
tip xúc vi (C) (*) có nghim kép
2
0
( 1) 2 4 (2 4) 0
k
m k m k mk m

2 2 2 2
0
( ) ( 1) 4( 4) 4 0
k
g k m k m m k m

Qua
( ;2 1)M m m d
k p tuyn (C)
( ) 0gk
m
0k
22
22
32( 2) 0; (0) 4 0
32( 2) 0; (0) 4 0
1
1 0 16 4 0
4
m m g m
m m g m
m k k
0 (0;1)
1 ( 1; 1)
2 (2; 5)
1 (1;3)
mM
mM
mM
mM


Bài 4: Cho hàm s
3
32y x x
 th là (C).
Câu 1.  th (C) tip xúc vi trc hoành t bng?
A. 1 B.2 C.3 D.
1
Bài làm 1. Xét h p
3
2
3 2 0
1
3 3 0
xx
x
x
Vy (C) tip xúc vi Ox t
1x 
.
Câu 2.Vip tuyn ca (C) tm ca (C) vi trc hoành.
A.
0y
;
9 18yx
B.
0y
;
93yx
C.
0y
;
98yx
D.
0y
;
91yx
Bài làm 2 m ca (C) và Ox.
3
3 2 0 1, 2x x x x
.
*
1 0, '(1) 0x y y
 p tuyn:
0y
.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM.
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
14
*
2 0, '(2) 9x y y
 p tuyn:
9( 2) 9 18y x x
.
Câu 3. Tìm nhm trên trc hoành sao cho t  c ba tip tuy th hàm s 
có hai tip tuyn vuông góc vi nhau.
A.
8
;0
27
M



B.
28
;0
7
M



C.
8
;0
7
M



D.
28
;0
27
M



Bài làm 3m
( ;0)M m Ox
.
Cách 1: ng th s góc k có ptrình:
()y k x m
.
d là tip tuyn ca (C)
h
3
2
3 2 ( )
3 3
x x k x m
xk
có nghim
x
Th  nh
23
3( 1)( ) ( 3 2) 0x x m x x
22
( 1)(3 3(1 ) 3 ) ( 1)( 2) 0x x m x m x x x
2
( 1)[2 (3 2) 3 2] 0x x m x m
1
1x
hoc
2
2 (3 2) 3 2 0 2x m x m
 t M k c ba tip tuyn thì
1
phi có nghim
x
ng thi phi có
3
giá tr
k
 
2
phi có hai nghim phân bit khác
1
ng thi phi có
2
giá tr
k
khác nhau và khác
0
2
phi có hai nghim phân bit khác
1
khi và ch khi :
2
(3 2)(3 6) 0
, 2
3
3 3 0
1
mm
mm
m
m



3
Vu kin
3
, gi
12
,xx
là hai nghim ca
2
  s góc ca ba tip tuyn là
22
1 1 2 2 3
3 3, 3 3, 0k x k x k
.
 hai trong ba tip tuyn này vuông góc vi nhau
12
.1kk
và
12
kk
12
.1kk
2 2 2 2 2
1 2 1 2 1 2 1 2
9( 1)( 1) 1 9 9( ) 18 10 0 ( )x x x x x x x x i
Mnh lí Viet
1 2 1 2
3 2 3 2
;
22
mm
x x x x

.

28
( ) 9(3 2) 10 0
27
i m m
thu kin
3
, kim tra li ta thy
12
kk
Vy,
28
;0
27
M



m cn tìm.
Cách 2: Gi
00
( ; ) ( )N x y C
. Tip tuyn
ca (C) t 
2
0 0 0
3 3 ( )y x x x y
.

2
0 0 0
0 3 3 ( )M x m x y
2
0 0 0 0 0
3( 1)( 1)( ) ( 1) ( 2) 0x x x m x x
2
0 0 0
( 1) 2 (3 2) 3 2 0x x m x m


0
2
00
1
2 (3 2) 3 2 0 (a)
x
x m x m

NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM.
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
15
T M v n (C) ba tip tuyn
()a
có hai nghim phân bit khác
1
, và có hai giá tr
2
0
33kx
khác nhau và khác
0
y ra khi và ch khi:
2
(3 2)(3 6) 0
(3 2) 8(3 2) 0
3 3 0
2 2(3 2) 0
mm
mm
m
m


1
2
,2
3
m
mm

()b
.
Vì tip tuyn t
1x 
có h s góc bng 0 nên yêu cu bài toán
22
( 3 3)( 3 3) 1pq

,pq
là hai nghim c 
()a
)
2 2 2 2
9 9( ) 10 0p q p q
2 2 2
9 9( ) 18 10 0p q p q pq
22
9(3 2) 9(3 2)
9(3 2) 10 0
44
mm
m

28
27
m
. Vy
28
;0
27
M



.
Bài 5. Cho hàm s
42
21y x x
 th là (C).
Câu 1. Vip tuyn ca (C), bit tip tuyn song song vng thng
: 24 1 0d x y
.
A.
: 24 4yx
B.
: 24 42yx
C.
: 24 23yx
D.
: 4 42yx
Bài làm 1. Ta có
3
' 4 4y x x
Gi
00
( ; ) ( )A x y C
. Tip tuyn ca (C) t 
3
0 0 0 0
: (4 4 )( )y x x x x y
Tip tuyn song song vi
: 24 1d y x
nên ta có:
3
00
4 4 24xx
3
0 0 0 0
6 0 2 7x x x y
.Vy
: 24 42yx
.
Câu 2. Tìm
M Oy
sao cho t M v p tuyn.
A.
(0; 2)M
B.
(0; 1)M
C.
(0; 5)M
D.
(0; 9)M
Bài làm 2. Ta có
3
' 4 4y x x
Gi
00
( ; ) ( )A x y C
. Tip tuyn ca (C) t 
3
0 0 0 0
: (4 4 )( )y x x x x y
Vì (C) nhn Oy làm tri xng nên nu
d
là mt tip tuyn cng thng
'd
i xng vi d
p tuyn c t M v c ba tip tuyn (C) thì trong ba tip tuy
phi có mt tip tuyn vuông góc vi Oy. Mà (C) có hai tip tuyi Ox là:
2y 
và
1y 
.
ng thng này ct Oy ti
12
(0; 2), (0; 1)MM
.
Ta kic qua
1
M
ch v c mt tip tuyn, còn t
2
M
v c ba tip tuyn.
Vy
(0; 1)M
m cn tìm.
Câu 3. Vip tuyn ca (C), bit tip tuyn tip xúc vi (C) tm phân bit.
A.
2yx
B.
21yx
C.
2y 
D.
4y 
Bài làm 3. Ta có
3
' 4 4y x x
Gi
00
( ; ) ( )A x y C
. Tip tuyn ca (C) t 
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM.
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
16
3
0 0 0 0
: (4 4 )( )y x x x x y
Gi s
là tip tuyn tip xúc vi (C) tm phân bit
42
( ; 2 1)M m m m
và
42
( ; 2 1)N n n n
vi
mn
.

: '( )( ) ( )y y m x m y m
: '( )( ) ( )y y n x n y n
Suy ra
'( ) '( )
. '( ) ( ) . '( ) ( )
y m y n
m y m y m n y n y n
33
4 2 4 2
4 4 4 4
3 2 1 3 2 1
n n m m
m m n n
22
2 2 2 2 2 2
( )( ) ( ) 0
3( )( ) 2( ) 0
n m n mn n n m
n m n m n m
22
22
10
( ) 3( ) 2 0 (*)
n mn n
n m n m


T (*) ta có:
0mn
hoc
22
2
3
nm
.
2
0 1 1m n m n n n
22
2
1
2
3
4
3
()
3
mn
mn
mn

vô nghim.
Vy
2y 
là tip tuyn cn tìm.
Bài 6 Cho hàm s
32
3 9 1y x x x
 th là (C).
1. Vip tuyn ca (C), bit tip tuyn có h s góc nh nht.
A.
22yx
B.
2yx
C.
12 7yx
D.
12 2yx
Bài làm 1. Ta có:
2
' 3( 2 3)y x x
. Do
2
' 3 ( 1) 4 12 min ' 12y x y


c khi
1x
.
p tuyn cn tìm là:
12 2yx
.
Câu 2. Vip tuyn ca (C), bit tip tuyn to vng thng
:1d y x
mt góc
tha
5
cos
41
.
A.
1 9 321
9
99
yx




B.
1 9 321
34
99
yx




C.
1 9 321
7
99
yx




D. 
Bài làm 2. Ta có:
2
' 3( 2 3)y x x
. Gi
00
( ; )M x y
là tim
p tuyn
ti M:
0 0 0
'( )( )y y x x x y
Hay
0kx y b
, Vi
0
'( )k y x
Theo bài ra ta có:
2
1
5
cos
41
1. 2
k
k

NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM.
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
17
2 2 2
41( 1) 50( 1) 9 82 9 0k k k k
1
9,
9
kk
.
2
0 0 0 0
9 2 0 0, 2k x x x x
T c hai tip tuyn:
91yx
và
93yx
2
0 0 0
1 9 321
27 54 80 0
99
k x x x
T c hai tip tuyn là:
0
1 9 321
()
99
y x y x




.
Câu 3. Vip tuyn ca (C), bit tip tuym
( 1;6)A
.
A.
7; 9 3y y x
B.
6; 9 7y y x
C.
6; 2 3y y x
D.
6; 9 3y y x
Bài làm 3. Ta có:
2
' 3( 2 3)y x x
. Gi
00
( ; )M x y
là ti  p tuyn
ti M:
0 0 0
'( )( )y y x x x y
.
Do tip tuy
2 3 2
0 0 0 0 0 0
6 3( 2 3)( 1 ) 3 9 1x x x x x x
32
0 0 0 0 0 0
3 2 0 ( 1) ( 2) 0 1, 2x x x x x x
0
16xy
0
2 9 3x y x
Bài 7:
Câu 1. Cho hàm s
32
21y x x x
m thu th hàm s mà tip tuyn ti
mt tip tuyn khác c th.
A.
1;5M
B.
1;1N
C.
0;1E
D. 
Bài làm 1. Gi
( ; ( ))A a f a
m thu th.
p tuyn ti
A
có h s góc
2
3 4 1k a a
* Nu
1
;1
3
aa
hin nhiên không có tip tuyn nào vuông góc vi tip tuyn ti A.
* Nu
0k

2
2
1
3 4 1
3 4 1
xx
aa

2
2
1
3 4 1 0
3 4 1
xx
aa

(1).
 tn ti tip tuyn vuông góc vi tip tuyn ti
A
thì (1) phi có nghim
2
1
' 4 3(1 ) 0
3 4 1aa

2
22
1 1 3 4 2
00
3
3 4 1 3 4 1
aa
a a a a

2 10 1 2 10
; 1; ;
3 3 3
a
 






.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM.
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
18
Câu 2. Cho hàm s
3
32y x x
 th là (C). Tìm to  m
M
thuc
2: 3yxd
sao cho t
M
k
n
()C
hai tip tuyn và hai tip tuyi nhau.
A.
(1; 1)M
B.
(3; 7)M
C.
( 1;5)M
D.
(0;2)M
Bài làm 2. Gi
( ; 3 2)M m m d
p tuyn
ca (C) ti
00
( ; )A x y
:
23
0 0 0 0
(3 3)( ) 3 2y x x x x x
Tip tuy
23
0 0 0 0
3 2 (3 3)( ) 3 2m x m x x x
2
00
(2 3 ) 0x x m
.Yêu cu bài toán
0m
. Vy
(0;2)M
.
Bài 8:
Câu 1. G th ca hàm s y =
2
2
xm
x
,m là tham s khác 4 và (d) là mt tip tuyn ca (C) .Tìm
 (d) to vng tim cn ca (C) mt tam giác có din tích bng 2.
A.
6
5
m
m


B.
3
5
m
m
C.
3
6
m
m

D.
3
5
m
m


Bài làm 1. ng tim cng và ngang ct là x = 2, y = 2 ,suy ra giao
m ca chúng là I(2;2).
Tnh tin
OI
. H trc Oxy
H trc IXY.
Công thc chuyn h t :
2
2
I
I
x X x X
y Y y Y
i vi h trc IXY .
ng tim cng và ngang ct là X = 0 , Y = 0.
 
2( 2) 4
2 ( )
22
X m m
Y Y F X
XX

.
Gi X0  tim ca tip tuyn (d) v
0
22
00
00
4 4 4 2 8
()
m m m m
Y X X X
XX
XX
.
Gm ca (C) vng tim cng ca nó thì
0
28
0;
m
A
X




Gm ca (C) vng tim cn ngang ca nó thì B(
0
2X
; 0)
Din tích tam giác vuông IAB do (d) to vng tim cn là
0
0
1 1 1 2 8
. 2 2 8
2 2 2
AB
m
S IA IB Y X X m
X
.
2 8 2 3
2 2 8 2
2 8 2 5
mm
Sm
mm



.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM.
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
19
Câu 2. Cho hàm s
3
1 ( 1)y x m x
 th là
. Có bao nhiêu giá tr
m
 tip tuyn ca
ti
m ca nó vi trc tung to vi hai trc t mt tam giác có din tích bng
8
.
A. 1 B.2 C.3 D. 4
Bài làm 2. Ta có
(0;1 )Mm
m ca
vi trc tung
2
' 3 '(0)y x m y m
h tip tuyn vi
tm
m
là
1y mx m
Gi
A, B
lm ca tip tuyn này vi trc hoanh và trc tung, ta có t
1
;0
m
A
m


và
(0;1 )Bm
Nu
0m
thì tip tuyn song song vi
Ox
nên loi kh 
Nu
0m
ta có
2
1
9 4 5
1 1 1
8 . 8 1 8 16
22
7 4 3
OAB
m
m
m
S OA OB m
m
m
m

Vy có 4 giá tr cn tìm
Bài 9:
Câu 1. Cho hàm s
1
21
x
y
x
.Tìm giá tr nh nht ca m sao cho tn ti ít nht mm M (C) mà tip
tuyn ca (C) ti M to vi hai trc to  mt tam giác có trng tâm nng thng
: 2 1d y m
.
A.
1
3
B.
3
3
C.
2
3
D.
2
3
Bài làm 1. Gi
00
( ; ) ( )M x y C
. P p tuyn ti M :
00
2
0
3
()
(2 1)
y x x y
x
Gm ca tip tuyn vi trc hoành và trc tung
2
00
2
0
2 4 1
(2 1)
B
xx
y
x

.
T ng tâm G ca OAB có:
2
00
2
0
2 4 1
3(2 1)
G
xx
y
x

.
Vì G d nên
2
00
2
0
2 4 1
21
3(2 1)
xx
m
x


Mt khác:
2 2 2 2
0 0 0 0 0
2 2 2
0 0 0
2 4 1 6 (2 1) 6
11
(2 1) (2 1) (2 1)
x x x x x
x x x
 tn ti ít nht mm M tho bài toán thì
11
21
33
mm
.
Vy GTNN ca m là
1
3
.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM.
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
20
Câu 2. Cho hàm s
23mx
y
xm
.Gm ca hai tim cn ca (C). Tìm m  tip tuyn ti mt
dim bt kì ca (C) ct hai tim cn ti A và B sao cho IAB có din tích
22S
.
A.
5m 
B.
6m 
C.
7m 
D.
4m 
Bài làm 2. (C) có tim cng
xm
, tim cn ngang
2ym
.
m 2 tim cn là
( ;2 )I m m
và
0
0
0
23
; ( )
mx
M x C
xm


.
Pp tuyn ca (C) ti M:
2
0
0
2
0
0
23
23
()
()
mx
m
y x x
xm
xm
.
ci
2
0
0
2 2 6
;
mx m
Am
xm





, ct TCN ti
0
(2 ;2 )B x m m
.
Ta có:
2
0
46m
IA
xm
;
0
2IB x m
2
1
. 4 6 22
2
IAB
S IA IB m
4m 
.
Câu 3. Gi
d
là tip tuyn c th
23
:
2
x
Cy
x
ti
M
cng tim cn tm phân bit
,AB
. Tìm t m
M
  ng tròn ngoi tip tam giác
IAB
có din tích nh nht , vi
I
là giao
m hai tim cn .
A.
1;1M
5
1;
3
M



B.
5
4;
3
M



3;3M
C.
1;1M
5
4;
3
M



D.
1;1M
3;3M
Bài làm 3. Gi
0
0 0 0
0
23
;
2
x
M x y C y
x
và
0
2
0
1
'
2
y
x

p tuyn
d
ca
C
ti
M
:
0
0
2
0
0
23
1
2
2
x
y x x
x
x
d
c ng tim cn t m phân bit
0
0
22
2; ,
2
x
A
x




0
2 2;2Bx
.
D thy
M
m
AB
và
2;2I
ng tim cn.
Tam giác
IAB
vuông ti
I
ng tròn ngoi tip tam giác
IAB
có din tích
2
22
2
0
00
2
0
0
23
1
2 2 2 2
2
2
x
S IM x x
x
x












Dng thc xy ra khi
2
0
2
0
1
2
2
x
x

00
00
11
33
xy
xy
Vy
1;1M
3;3M
tha mãn bài toán.
Bài toán có thể mở rộng : Tìm nhm trên
C

2x
sao cho tip tuyn to vi hai
ng tim cn mt tam giác có chu vi nh nht.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM.
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
21
HD: theo trên ta có :
0
0
0
22
2; , 2 2;2 ,
2
x
A B x IA IB
x





.Chu vi tam giác
AIB
là
22
2 . 2. .P IA IB AB IA IB IA IB IA IB IA IB
ng thc xy ra khi
IA IB
Nng hp tam giác
AIB
không vuông thì
P IA IB AB
 tính
AB
ta cnh lý hàm s
cosin
2 2 2
2 . cos ,AB IA IB IA IB IA IB
.
2 2 2
2 . 2 . cos ,P IA IB AB IA IB IA IB IA IB IA IB
2 . 2 . 2 . cos ,P IA IB IA IB IA IB IA IB
ng thc xy ra khi
IA IB
.
Bài 10: Cho hàm s
2
1
x
y
x
 th là
C
. Có bao nhiêu m
M
thuc
C
sao cho tip tuyn ti
M
ca
C
ct
,Ox
Oy
ti
,A
B
sao cho din tích tam giác
OAB
bng
1
4
,
O
là gc t.
A. 1 B.2 C.3 D. 4
Bài làm 1. Gi
0
0 0 0 0
2
0
0
2
2
;'
1
1
x
M x y C y y
x
x
nh tip tuyn
t
ca
C
ti
M
là :
2
0
0
22
00
2
2
11
x
yx
xx


.
Tip tuyn
t
ct hai trc t
,Ox Oy
tm phân bit
2
0
;0Ax
,
2
0
2
0
2
0;
1
x
B
x




sao cho din tích tam giác
AOB
có din tích bng
1
4

2
2
22
0
0 0 0
2
0
2
1 1 1 1
. . . . 4 1 0
2 4 2 2
1
x
OA OB OA OB x x x
x
2
0
00
2
00
0
11
;2
2 1 0
22
2 1 0
1 1;1
xM
xx
xx
xM




.
Bài 12: Cho hàm s
22
1
x
y
x
 th là (C).
Câu 1. Vi p tuyn ca (C), bit tip tuyn song song vng thng
: 4 1d y x
.
A.
: 4 2yx
;
: 4 1yx
B.
: 4 2yx
;
: 4 7yx
C.
: 4 6yx
;
: 4 14yx
D.
: 4 2yx
;
: 4 14yx
Bài làm 1. Hàm s nh vi mi
1x
.
Ta có:
2
4
'
( 1)
y
x
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM.
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
22
Tim cng:
1x
; tim cn ngang:
2y
i xng
(1;2)I
Gi
00
( ; )M x y
là tip tuyn ca (C):
0
0
2
0
0
22
4
: ( )
1
( 1)
x
y x x
x
x
.
Vì tip tuyn song vng thng
: 4 1d y x
nên ta có:
0 0 0
2
0
4
'( ) 4 4 0, 2
( 1)
y x x x
x
.
*
00
0 2 : 4 2x y y x
*
00
2 6 : 4 14x y y x
.
Câu 2. Vip tuyn ca (C), bit tip tuyn to vi hai trc t mt tam giác vuông cân.
A.
:7yx
;
:1yx
B.
: 2 7yx
;
: 11yx
C.
: 78yx
;
: 11yx
D.
:9yx
;
:1yx
Bài làm 2. Hàm s nh vi mi
1x
.
Ta có:
2
4
'
( 1)
y
x
Tim c ng:
1x
; tim cn ngang:
2y
 i xng
(1;2)I
Gi
00
( ; )M x y
là tiình tip tuyn ca (C):
0
0
2
0
0
22
4
: ( )
1
( 1)
x
y x x
x
x
.
Vì tip tuyn to vi hai trc t mt tam giác vuông cân nên h s góc ca tip tuyn bng
1
.
00
2
0
4
1 1, 3
( 1)
xx
x
*
00
1 0 : 1x y y x
*
00
3 4 : 7x y y x
Câu 3. Vip tuyn ca (C), bit tip tuyn to vi hai tim cn mt tam giác có chu vi nh
nht.
A.
: 21yx
và
:7yx
. B.
:3yx
và
:2yx
.
C.
:1yx
và
: 17yx
. D.
:1yx
và
:7yx
.
Bài làm 3. Hàm s nh vi mi
1x
.
Ta có:
2
4
'
( 1)
y
x
Tim c ng:
1x
; tim cn ngang:
2y
 i xng
(1;2)I
Gi
00
( ; )M x y
là tip tuyn ca (C):
0
0
2
0
0
22
4
: ( )
1
( 1)
x
y x x
x
x
.
Tip tuyn ct tim cng ti
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM.
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
23
0
0
0
2
0
0
0
1
26
22
: 1;
4
(1 )
1
1
( 1)
x
x
x
AA
yx
x
x
x





Tip tuyn ct tim ngang ti
0
0
0
2
0
0
2
22
: (2 1;2)
4
2 ( )
1
( 1)
y
x
B B x
xx
x
x


Suy ra:
0
0
8
; 2 1 . 16
1
IA IB x IA IB
x
Chu vi tam giác
:IAB
22
P IA IB AB IA IB IA IB
Mà
22
2 . 8; 2 . 32IA IB IA IB IA IB IA IB
Nên
8 32 8 4 2P
ng thc xy ra
2
0 0 0
( 1) 4 3, 1IA IB x x x
Vy ta có hai tip tuyn tha yêu cu bài toán:
:1yx
và
:7yx
.
Bài 13 Cho hàm s
2
2
x
y
x
 th (C).
Câu 1 th (C) tn tm mà tip tuyn ca (C) tng thng
43yx
.
A. 1 B.2 C.3 D. 4
Bài làm 1. Hàm s nh vi mi
2x 
.
Ta có:
2
4
'
( 2)
y
x
Gi
00
( ; ) ( )M x y C
. Tip tuyn
ca (C) t 
2
00
0
2 2 2
0
0 0 0
22
44
()
2
( 2) ( 2) ( 2)
xx
y x x x
x
x x x
Tip tuyn
song song vng thng
43yx
khi và ch khi
2
0
00
2
0
2
0
4
4
( 2)
1; 3
2
3
( 2)
x
xx
x
x
.
Vm tha yêu cu bài toán.
Câu 2. Vip tuyn ca (C), bit tip tuyn to vi hai trc t mt tam giác có din tích
bng
1
18
.
A.
91
:
42
yx
;
41
:
99
yx
B.
9 31
:
42
yx
;
42
:
99
yx
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM.
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
24
C.
91
:
42
yx
;
44
:
99
yx
D.
91
:
42
yx
;
42
:
99
yx
Bài làm 2. Hàm s nh vi mi
2x 
.
Ta có:
2
4
'
( 2)
y
x
Gi
00
( ; ) ( )M x y C
. Tip tuyn
ca (C) t 
2
00
0
2 2 2
0
0 0 0
22
44
()
2
( 2) ( 2) ( 2)
xx
y x x x
x
x x x
Gi A, B lm ca tip tuyn
vi Ox, Oy
Suy ra
2
2
0
0
22
00
0
1
:
2
4
0
2
( 2) ( 2)
0
y
A
x
xx
x
xx
y




2
0
1
( ;0)
2
Ax
2
2
0
0
2
2
0
0
0
2
: 0;
2
( 2)
( 2)
x
x
BB
x
y
x
x





Vì
0
,0A B O x
.
Tam giác AOB vuông ti O nên
4
0
2
0
11
.
22
( 2)
AOB
x
S OA OB
x

Suy ra
4
42
0
00
2
0
1
9 9 ( 2)
18
( 2)
AOB
x
S x x
x
2
0
00
2
0
00
1
3 2 0 (vn)
2
3 2 0
3
x
xx
x
xx



.
*
0 0 0
24
1 , '( )
39
x y y x

42
:
99
yx
*
0 0 0
29
1, '( )
34
x y y x

9 2 9 1
: ( ) 1
4 3 4 2
y x x
.
Câu 3. Gi s tn ti p tuyn ca (C), bit khong cách t i xn tip tuyn ln
nht. tim lúc này là:
A.
00
0, 4xx
B.
00
0, 3xx
C.
00
1, 4xx
D.
00
1, 3xx
Bài làm 3. Hàm s nh vi mi
2x 
.
Ta có:
2
4
'
( 2)
y
x
Gi
00
( ; ) ( )M x y C
. Tip tuyn
ca (C) t 
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM.
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
25
2
00
0
2 2 2
0
0 0 0
22
44
()
2
( 2) ( 2) ( 2)
xx
y x x x
x
x x x
i xng
( 2;2)I
Khong cách t n tip tuyn
2
0
22
00
2
4
:0
( 2) ( 2)
x
xy
xx

:
0
2
4
0
82
8
16
( 2) 16
x
t
d
t
x


, vi
2
0
( 2) 0tx
Do
2
2
1
2
16
16
2 16
tt
d
t
t
ng thc xy ra khi
22
0
16 4 ( 2) 4t t x
00
0, 4xx
.
Bài 14: Cho hàm s
32
y x ax bx c
,
 th (C) ct Oy
A
m chung vi trc
Ox là
M
và
N
. Tip tuyn v th ti
M

A
. Tìm
;;a b c

1
AMN
S
.
A.
4, 5, 2a b c
B.
4, 5, 2a b c
C.
4, 6, 2a b c
D.
4, 5, 2a b c
Bài làm Gi s (C) ct Ox ti
( ;0)Mm
và
( ;0)Nn
ct Oy ti
(0; )Ac
Tip tuyn t
2
(3 2 )( )y m am b x m
.
Tip tuy
32
3 2 0m am bm c
32
20
2
a
m am m
(do
32
0am cm bm
)
Mà (C) ct Ox t m nên (C) tip xúc vi Ox.
Nu M là ti     p xúc
vi Ox t
3 2 2
( ) ( )y x ax bx c x n x m
Suy ra
23
22
,
2
24
2 32
5 16
aa
mn
m n a
mn n b a c
mn c a b


(1).
Mt khác
1 2 8
AMN
S c n m c a
0a
ta có:
3
2
32
8
5 16
ac
ac
ab

vô nghim.
0a
ta có:
3
2
32
8 4, 5, 2
5 16
ac
ac a b c
ab
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM.
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
26
Bài 15: Cho hàm s
21
1
x
y
x
 th là (C).
Câu 1. Vip tuyn ca (C), bit tip tuyn có h s góc bng
1
4
.
A. :
13
44
yx
và
13
44
yx
. B. :
13
42
yx
và
15
42
yx
.
C. :
11
44
yx
và
15
44
yx
. D. :
1 13
44
yx
và
15
44
yx
.
Bài làm 1. : Gi
00
( ; )M x y
là ti  p tuyn
ti M
0
0
2
0
0
21
1
()
1
( 1)
x
y x x
x
x
.
H s góc ca tip tuyn bng
1
4
nên suy ra
00
2
0
11
3, 1
4
( 1)
xx
x
.
T c tip tuyn là:
1 13
44
yx
và
15
44
yx
.
Câu 2. Vip tuyn ca (C), bit tip tuyn to vi hai tim cn mt tam giác có chu vi nh
nht.
A.
13
44
yx
và
15
44
yx
. B.
1
3
4
yx
và
1
1
4
yx
.
C.
1 13
44
yx
và
1
1
4
yx
. D.
1 13
44
yx
và
15
44
yx
.
Bài làm 2. : Gi
00
( ; )M x y
là ti rình tip tuyn
ti M
0
0
2
0
0
21
1
()
1
( 1)
x
y x x
x
x
.
Tip tuyn
ct tim cng ti
0
0
2
(1; ),
1
x
A
x
cng tim cn ngang ti
0
(2 1;2)Bx
 i xng
(1;2)I
Suy ra
0
0
2
, 2 1 . 4
1
IA IB x IA IB
x
Chu vi tam giác IAB :
22
p AB IA IB IA IB IA IB
Mt khác:
22
2 . 8; 2 . 4IA IB IA IB IA IB IA IB
Nên
2 2 4p 
ng thc xy ra
IA IB
2
0 0 0
( 1) 4 3, 1x x x
.
T c tip tuyn là:
1 13
44
yx
và
15
44
yx
.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM.
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
27
Câu 3. Vip tuyn ca (C), bit khong cách t i xn tip tuyn to ln nht.
A.
13
44
yx
và
15
44
yx
. B.
1
1
4
yx
và
1
5
4
yx
.
C.
1 13
44
yx
và
13
44
yx
. D.
1 13
44
yx
và
15
44
yx
.
Bài làm 3. : Gi
00
( ; )M x y
là ti rình tip tuyn
ti M
0
0
2
0
0
21
1
()
1
( 1)
x
y x x
x
x
.
Gi H là hình chiu ca I lên
. Ta có
( , )d I IH
Trong tam giác vuông IAB ta có:
2 2 2
1 1 1 2 1
.2IA IB
IH IA IB
Suy ra
2IH
ng thc xy ra
IA IB
.
T c tip tuyn là:
1 13
44
yx
và
15
44
yx
.
Câu 4. m M thuc (C) sao cho tip tuyn ca (C) ti M vuông góc vi IM.
A.
1, 4y x y x
B.
3, 5y x y x
C.
1, 3y x y x
D.
1, 5y x y x
Bài làm 4. : Gi
00
( ; )M x y
là ti  p tuyn
ti M
0
0
2
0
0
21
1
()
1
( 1)
x
y x x
x
x
.
ng thng
có VTCP
2
0
1
1;
( 1)
u
x



,
0
0
1
( 1; )
1
IM x
x

.
0 0 0
3
0
1
1 0 0, 2
( 1)
IM x x x
x
.
T c tip tuyn:
1, 5y x y x
.
Bài 16:
Câu 1. G th ca hàm s
4
y1x
và (d) là mt tip tuyn ca (C) , (d) ct hai trc t ti A và
B. Vip tuyn (d) khi tam giác OAB có din tích nh nht ( O là gc t ).
A.
4
48
5
15
yx
B.
4
48
5
12
yx
C.
4
47
5
5
yx
D.
4
48
5
125
yx
Bài làm 1. p tuyn (d) có dng :
3 4 3 4
0 0 0 0 0
4 ( ) 1 4 3 1y x x x x x x x
0 là
 tim ca (d) vi (C).
m ca (d) vi trc Ox
4
0
3
0
31
;0
4
x
A
x




m ca (C) vi trc Oy
4
0
(0; 3 1)Bx
.
Din tích ca tam giác vuông OAB:
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM.
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
28
4 2 4 2
00
33
0
0
(3 1) (3 1)
1 1 1 1
.
2 2 2 8
4
AB
xx
S OA OB x y
x
x

ng hp
0
x0
 
42
0
3
0
(3 1)
1
S .
8
x
x
.
Xét hàm s
42
0
00
3
0
(3 1)
( ) , (0; ).
x
f x x
x

4 3 3 4 2 2 4 4
0 0 0 0 0 0 0
0
64
00
2(3 1)12 . (3 1) .3 3(3 1)(5 1)
'( ) .
x x x x x x x
fx
xx

4
0 0 0 0
4
11
'( ) 0 ( 0)
5
5
f x x x do x
Bng bin thiên ca
0
()fx
T bng bin thiên suy ra
0
4
64
min ( )
55
fx
c khi và ch khi
0
4
1
5
x
Suy ra
4
8
minS
55
0
4
1
5
x
.
a (d) là
4
48
5
125
yx
.
Vì trc Oy là tri xng cng hp x0 a (d) là
4
48
5
125
yx
.
Vp tuyn cn tìm là
4
48
5
125
yx
.
Câu 2. G th ca hàm s
42
y x 3 m 1 .x 3m 2
, m là tham s
Tìm các giá tr dương ca tham s  (Cm) ct trc hoành ti bm phân bit và tip tuyn ca (Cm) ti
 ln nht hp vi hai trc to  mt tam giác có din tích bng 24.
A.
m 1
B.
1
m
3
C.
2
m
3
D.
m 7
Bài làm 2.  m ca (Cm) và trc hoành là
42
x 3 m 1 .x 3m 2 0
(1)
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM.
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
29
t
2
t x ,t 0
 thành :
2
t 3 m 1 .t 3m 2 0
(2)
(Cm) ct trc Ox ti bm phân bit
m phân bit

hai nghit .
Vì (2) luôn có hai nghim là
t 1, t 3m 2
vi mi m và vì m > 0 (gi thit) nên ta có
1 3m 2
,suy ra
vi mi tham s m > 0 , (Cm) ct Ox ti 4 dim phân bit và nu g ln nht thì
 A là
A
x 3 2m
.
Gi
42
f(x) x 3 m 1 .x 3m 2
 p tuyn d ca (Cm) ti A là
3
'( )( ) ( ) [4 6( 1) ]( )
A A A A A A
y f x x x f x x m x x x
( vì
( ) 0
A
fx
)
[4(3 2) 3 2 6( 1) 3 2]( 3 2)m m m m x m
6m 2 3 2 3 2)m x m
Gm ca tip tuyn d vi trc Oy thì
B 0 ; 6m 2 3m 2
. Tam giác mà tip tuyn d to
vi hai trc to  là tam giác vuông OAB ( vuông tiO) ,theo gi thit ta có :
24 . 48 48
OAB A B
S OAOB x y
3 2(6 2)(3 2) 48m m m
(3).
Gi
2
f m 3 2(6 2)(3 2) 3 2(18 22 4)m m m m m m
2
3
'( ) (18 22 4) (36 22) 3 2 0
2 3 2
f m m m m m
m
vi mi m >0.
Suy ra hàm s ng bin trên (0;+
)
và vì
2
24
3
f



 có mt nghim là
2
m
3
trên (0;+
)
Bài 18:
Câu 1. Cho hàm s
2
2
x
y
x
 th là
C.
Vi trình tip tuyn c th
C
 khong cách
t i xng c th
C
n tip tuyn là ln nht.
A.
2yx
và
8yx
. B.
yx
và
9yx
. C.
3yx
và
8yx
. D.
yx
và
8yx
.
Bài làm 1. Tip tuyn
d
c th
C
tm
M

2a 
thuc
C

22
2
42
( ) 4 ( 2) 2 0
2
( 2)
a
y x a x a y a
a
a
 i xng ca
C
là
2;2I
.
42
8 2 8 2 8 2
( , ) 2 2
2 2 2
16 ( 2) 2.4.( 2)
a a a
d I d
a
aa
( , )d I d
ln nht khi
2
( 2) 4 4aa
hoc
0a
.
T p tuyn
yx
và
8yx
.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM.
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
30
Câu 2. Cho hàm s
23
2
x
y
x
 th
C.
Tìm trên
C
nhm
M
sao cho tip tuyn ti
M
ca
C
ct hai tim cn ca
C
ti
A,B
sao cho
AB
ngn nht.
A.
(3;3)M
hoc
5
( 1; )
3
M
B.
5
( 1; )
3
M
hoc
(1;1)M
C.
5
(4; )
2
M
hoc
5
( 1; )
3
M
D.
(3;3)M
hoc
(1;1)M
Bài làm 2. Lm
1
;2
2
Mm
m



C
. Ta có:
2
1
()
( 2)
ym
m

Tip tuyn
d
ti
M

2
11
( ) 2
2
( 2)
y x m
m
m
m ca
d
vi tim cng là:
2
2;2
2
A
m



m ca
d
vi tim cn ngang là:
 Bm
Ta có:
22
2
1
4 ( 2) 8
( 2)
AB m
m



. ng thc xy ra khi
1m
hoc
3m
.
Vy, m
M
cn tìm có t là:
(3;3)M
hoc
(1;1)M
Bài 19 : Tìm m  tip tuyn c th
3
1y x mx m
t
1x 
cng tròn (C)

22
( 2) ( 3) 4xy
theo m dài nh nht.
A.
3m
B.
6m
C.
8m
D.
2m
Bài làm : Ta có:
2
3y x m

( 1) 3ym
;
( 1) 2 2ym
. (C) có tâm
(2;3)I
, R = 2.
ng thng d ti
( 1;2 2)Mm
:
(3 ) 1y m x m
(3 ) 1 0m x y m
2
2 2 2
1 (3 ) 2. (3 ) 1
4
( , ) 2
(3 ) 1 (3 ) 1 (3 ) 1
mm
m
d I d R
m m m
Du "=" xy ra
2m

( , )d I d
t ln nht
2m
Tip tuyn d ct (C) tm A, B sao cho AB ngn nht
( , )d I d
t ln nht
2m
, suy ra d:
3yx
.
CHƯƠNG V.
ĐẠO HÀM
TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN ĐI QUA
ĐIỂM CHO TRƯỚC
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 HOẶC
Facebook: https://web.facebook.com/phong.baovuong
Page: https://web.facebook.com/tracnghiemtoanthpt489/
Website: http://tailieutoanhoc.vn/
Email: baovuong7279@gmail.com
0946798489
NGUYỄN BẢO VƢƠNG
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
1
MỤC LỤC
Vấn đề 3. Viết phƣơng trình tiếp tuyến của đồ thị hàm số khi tiếp tuyến đi qua điểm cho trƣớc. ............................ 2
CÁC BÀI TOÁN LUYN TP .............................................................................................................................................. 8
GIÁO VIÊN MUA FILE WORD LIÊN HỆ 0946798489
BC MUN NHN FILE PDF, HÃY THEO DÕI PAGE
https://web.facebook.com/tracnghiemtoanthpt489/
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
2
Vấn đề 3. Viết phƣơng trình tiếp tuyến của đồ thị hàm số khi tiếp tuyến đi qua
điểm cho trƣớc.
Phƣơng pháp:
p tuyn c th
:C y f x
m
11
;M x y
Cách 1 :
ng thng
d
m
M
có h s góc là
k
có dng :
11
y k x x y
.
d
tip xúc v th
C
ti
00
;N x y
khi h:
0 0 1 1
0
'
f x k x x y
f x k
có nghim
0
x
.
Cách 2 :
Gi
00
;N x y
là t tim c th
C
và tip tuyn
d
m
M
, nên
d
ng
0 0 0
'y y x x y
.
d
 m
M
h :
1 0 1 0 0
'*y y x x y
T 
*
c t m
00
;N x y
, t  ng thng
d
.
Các ví dụ
Ví dụ 1 :
1. Vip tuyn
d
v th
C
:
32
3
34
xx
yx
, bit
d
ng thng
80xy
.
2. Cho hàm s
32
2 3 5y x x
 th là (C).   
19
;4
12
A





Lời giải.
1. Hàm s nh
D
Cách 1: Tip tuyn
d
song song vng thng
80xy
nên
d
có dng
y x b
.
d
tip xúc vi
C
t
0
x
khi và ch khi h ph
32
00
00
2
0
0
3
1
34
3
1 1 2
2
xx
x x b
x
x
có nghim
0
x
.

2
00
2 2 3 0xx
0
0x
hoc
0
3
2
x 
.
Vi
0
0x

1
c
0b
 
d
:
yx
.
Vi
0
3
2
x 

1
c
9
16
b

d
:
9
16
yx
.
Cách 2: Gi
00
;x y x
là t tim ca tip tuyn
d
và
C
, vi
32
00
00
3
34
xx
y x x
, tip tuyn
d
có h s góc
2
0
00
3
'1
2
x
y x x
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
3
0
|| 8 0 ' 1d x y y x
tc
2
0
0
3
11
2
x
x
hay nghim
0
0x
hoc
0
3
2
x 
. Phn còn li giành cho bn
c.
2. Hàm s nh
D
Ta có:
2
' 6 6y x x

32
0 0 0 0 0
( ; ) ( ) 2 3 5M x y C y x x
và
2
0 0 0
'( ) 6 6y x x x

0 0 0
'( )( )y y y x x x
3 2 2 2 3 2
0 0 0 0 0 0 0 0 0
(2 3 5) (6 6 )( ) (6 6 ) 4 3 5y x x x x x x y x x x x x
2 3 2 3 2
0 0 0 0 0 0 0 0
19
4 (6 6 ). 4 3 5 8 25 19 2 0 1
12
A x x x x x x x x
hoc
0
2x
hoc
0
1
8
x
Vi
0
1 : 4xy
Vi
0
2 : 12 15x y x
Vi
0
1 21 645
:
8 32 128
x y x
Ví dụ 2 :
1. Cho hàm s
42
13
3
22
y x x
 th là
C.
Vi p tuyn c  th
C
bit tip tuy
m
3
0;
2
M



.
2. Cho hàm s:
2
1
x
y
x
 th là
C
m
0;Am
nh
m
 t
A
k c 2 tip tuyn
C
sao cho hai ting nm v i vi trc
Ox
.
Lời giải.
1. ng thng
0x
m
3
0;
2
M



không phi là tip tuyn c th
C
.
d
ng th m
3
0;
2
M



có h s góc
k

3
2
y kx
ng thng
d
là tip tuyn c th
C
 là
0
x
thì
0
x
là nghim ca h  :
42
0 0 0
3
00
1 3 3
31
2 2 2
2 6 2
x x kx
x x k

Thay
2
vào
1
ri rút gc
22
0 0 0
2 0 0x x x
hoc
0
2x 
Khi
0
0x
thì
0k
  p tuyn là
3
2
y
Khi
0
2x 
thì
22k
  p tuyn là
3
22
2
yx
Khi
0
2x
thì
22k 
  p tuyn là
3
22
2
yx
Vy, có ba tip tuyn là
3
2
y
,
3
22
2
yx
,
3
22
2
yx
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
4
2. Cách 1: Gm
1
1
2
m
. Tip tuyn
ti M ca
C
  
2
0 0 0 0
1 3 2 1 0m x x x x
(vi
0
1x
)
2
00
1 2 2 2 0m x m x m
.
Yêu cu bài toán

có hai nghim
,ab
khác
1
sao cho
2 2 2 4
0
1 1 1
a b ab a b
a b ab a b

hay là:
1
2
3
m
m

.
Vy
2
1
3
m
là nhng giá tr cn tìm.
Cách 2: ng thng
d

A
, h s góc
k
:
y kx m
.
d tip xúc vi
C
t
0
x
h
0
0
0
2
0
2
1
3
1
x
kx m
x
k
x


có nghim
0
x
.
Th
k
vào  nh
2
0
00
2
0
0
2
3
1 2 2 2 0
1
1
x
x
m m x m x m
x
x
 t
A
k c hai tip tuyn thì
có hai nghim phân bit khác 1
' 3 2 0
2
1
1
1 2 2 2 0
m
m
mi
m
m m m


 hai tim là:
1 1 1 2 2 2
; , ;M x y M x y
vi x1,x2 là nghim ca
và
12
12
12
22
;
11
xx
yy
xx



 M1, M2 nm v hai phía
Ox
thì
1 2 1 2
12
1 2 1 2
24
. 0 0 1
1
x x x x
yy
x x x x
Áp dnh lí Viet:
1 2 1 2
22
2
;
11
m
m
x x x x
mm

.
9 6 2
10
33
m
m
.
Kt hp vi
i
c
2
1
3
m
là nhng giá tr cn tìm.
Ví dụ 3 :
1. Tìm tt c ng thng
:d
5 61
4 24
x
y 
 t   th
32
7
2
3 2 3
xx
yx
có
3
tip
tuyng vi
3
ti
1 2 3
,,x x x
tha mãn:
1 2 3
0x x x
2. Tìm tt c các giá tr ca
k
 tn ti
2
tip tuyn vi
C
:
32
6 9 3y x x x
phân bit và có cùng h s góc
k
ng thng thm ca
2
tip tuyi
C
ct các trc
,Ox Oy
 ng ti
,AB
sao cho
2012.OB OA
.
Lời giải.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
5
1.
5 61
;
4 24
m
M m d




, tip tuyn
t
tm
00
;N x y

M
:
32
0 0 0
2 1 3 5
0
3 2 4 24
m
x m x mx



0
2
00
1
0
2
2 5 5 3
0
3 6 12 2
x
m
x m x





có hai nghim phân bit âm, tc là :
2
7 5 5 1
0;
3 12 2 6
55
0
18 18
3 5 5
0
2 4 6
m
m m m
mm
mm









Vy, nhm
M
tha bài toán là:
5
2
M
x 
hoc
15
6 18
M
x
2.  tim
0
x
ca tip tuyn dng
y kx m
vi
C
là nghim c g trình
2
0 0 0
' 3 12 9 0 1f x k x x k
 tn ti
2
tip tuyn vi
C
phân bi
1
có hai nghim phân bi
' 9 3 0k
hay
32k 
.
 tim
00
;xy
ca
2
tip tuyn vi
C
là nghim h 
32
0 0 0 0
2
00
6 9 3
3 12 9
y x x x
x x k
2
0 0 0 0 0
2
00
1
2 3 12 9 2 3
3
3 12 9
y x x x x
x x k
0 0 0 0
2
00
1 6 2 9
2 2 3
3 3 3
3 12 9
kk
y x k x x
x x k
Vy ng thm là
d
:
6 2 9
33
kk
yx


.
Do
d
ct trc
,Ox Oy
 ng ti
A
và
B
sao cho
2012.OB OA
nên có th xy ra:
Nu
AO
thì
BO
ng hp này ch tha nu
d

O

9
2
k
.
Nu
AO

AOB
vuông ti
O
sao cho
6
tan 2012 2012 6042
3
OB k
OAB k
OA
hoc
6030k 
( không tha
2
).
Vy
9
2
k
,
6042k
tha bài toán.
Ví dụ 4 : Cho hàm s
3
3 2,y x x
 th là
.C
Tìm t ng thng
4y 
mà t 
th k  th
C
p tuyn.
Lời giải.
Hàm s nh và liên tc trên
.
Gi
A
m nng thng
4y 
nên
; 4 .Aa
ng thng
qua
A
vi h s góc
k

4y k x a
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
6
ng thng
tip xúc v th
C
khi và ch khi h nghim:
32
3
2
2
3 2 3 1
3 2 4
33
33
x x x x a
x x k x a
xk
xk


2
2
1 2 3 2 3 2 0 1
3 3 2
x x a x a
xk



1
i:
2
1
2 3 2 3 2 0
x
g x x a x a
Qua
A
k c hai tip tuyn
C
khi và ch khi
2
có
2
giá tr
k

1

nghim phân bit
12
,xx
ng thi tha
22
1 1 2 2
3 3, 3 3k x k x
có
2
giá tr
k
khác nhau
Trƣờng hợp 1:
gx
phi tha mãn có mt nghim bng
1
và nghim khác
1
hay
10
6 6 0
1
32
0
1
2
g
a
a
a
a



kim tra
2
thy tha.
Trƣờng hợp 2:
gx
phi tha mãn có mt nghim kép khác
1
hay
2
3 2 8 3 2 0
3 3 2 2 0
32
3 2 2
1
2
aa
aa
a
a



2
3
a
hoc
2,a
kim tra
2
thy tha.
Vm cn tìm là
1; 4 , 2; 4AA
hoc
2
; 4 .
3
A




Ví dụ 5 Cho hàm s
3
3y x x
 th là
C.
ng thng (d):
yx
m M mà t  c
p tuyn phân bit v th (C).
Lời giải.
Gi
( ; )M m m d
.
P ng thng qua M có h s góc
k
có dng:
()y k x m m
.
là tip xúc (C) ti 
0
x
khi h sau có nghim
0
x
:
3
0 0 0
2
0
3 ( ) (1)
3 3 (2)
x x k x m m
xk

()
c:
32
00
2 3 4 0x mx m
3
0
2
0
2
34
x
m
x
()
T M k p tuyn vi (C)
()
có nghim
0
x
ng thi (2) tn t  
k
khác nhau

()
có nghim
0
x
phân bit tha mãn (2) có 2 giá tr
k
khác nhau .
Xét hàm s
3
0
0
2
0
2
()
34
x
fx
x
.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
7
Tnh
23
\ 1;
3
D


Ta có:
42
00
0
22
0
6 24
()
(3 4)
xx
fx
x
và
00
( ) 0 0f x x
hoc
0
2x 
Da vào bng bin thiên suy ra
2m 
. Kim tra (2) , ta thy tha mãn.
Vy:
( 2;2)M
hoc
(2; 2)M
.
Ví dụ 6 Lm
M
thu th
32
: 2 3 3C y x x
. Chng minh rng có nhiu nh ng th
m
M
và tip xúc vi
C
Lời giải.
Gi
32
; 2 3 3M a a a
m thu th
C
ca hàm sng thng
d

M
có h s góc
k
, có

32
2 3 3y k x a a a
.
ng thng
d
tip xúc v  th
C
ti
00
;N x y
khi h  
3 2 3 2
0 0 0
2
00
2 3 3 2 3 3 1
6 6 2
x x k x a a a
x x k
có nghim
0
x
. Thay
2
vào
1
, bii và rút g c

2
00
4 2 3 0x a x a
tc
0
xa
hoc
0
23
4
a
x

.
Vy h 
1
,
2
có nhiu nht
2
nghim, tc có nhiu nht
2
ng th
M
và tip
xúc v th
C
.
Ví dụ 7: Cho hàm s
32
2 4 1y x x
 th là
C
1. Gi
d
ng th
0;1A
có h s góc là
k
. Tìm
k

d
ct
C
ti
2
m phân bit
,BC
khác
A
sao cho
B
nm gia
A
và
C
ng thi
3AC AB
;
2. Tìm trên trc tung nhm mà t  
2
tip tuyn
C
Lời giải.
1.
:1d y kx
. Vi
2k
thì
d
ct
C
ti
2
m phân bit
B
và
C
khác
A
  
; 1 ,
BB
B x kx
;1
CC
C x kx
,
BC
xx
vi
,
BC
xx
là nghim c 
2
2 4 0x x k
.
3AC AB
tc
3
CB
xx
và
2, .
2
B C B C
k
x x x x
suy ra
3
2
k
.
2. Gi
0;Mm
và
t
qua
M
có h s góc là
a
nên
t
:
y ax m
.
t
tip xúc
C
t
0
x
khi
h
32
0 0 0
2
0 0 0
2 4 1
68
x x kx m
x x x
có nghim
0
x
suy ra
32
00
4 4 1 0x x m
có nghim
0
x
  
trình

2
nghim, t c
11
27
m
hoc
1m
.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
8
CÁC BÀI TOÁN LUYỆN TẬP
Bài 1: Cho hàm s
32
1
23
3
y x x x
 th là (C).   
44
;
93
A





A.
:
4
:
3
58
:
9 81
yx
yx
yx


B.
:3
4
:1
3
5 128
:
9 81
yx
yx
yx

C.
:
4
:
3
51
:
9 81
yx
y
yx


D.
:3
4
:
3
5 128
:
9 81
yx
y
yx


Bài làm: 
44
93
y k x




x

32
2
1 4 4
2 3 (1)
3 9 3
4 3 (2)
x x x k x
x x k




x
c:
3 2 2 2
1 4 4
2 3 ( 4 3) (3 11 8) 0
3 9 3
x x x x x x x x x



(2)
(2)
(2)
0 3 : 3
4
1 0 :
3
8 5 5 128
:
3 9 9 81
x k y x
x k y
x k y x
Bài 2
42
13
3
22
y x x

3
0;
2
A




(C).
A.
3
:
2
3
: 2 2
2
3
: 2 2
2
y
yx
yx

B.
3
:
2
3
:2
2
3
:2
2
yx
yx
yx

C.
3
:1
2
1
:2
2
1
:2
2
yx
yx
yx

D.
3
:
2
3
:2
2
3
:2
2
y
yx
yx


Bài làm: 
3
2
y kx
.

x

42
3
1 3 3
3 (1)
2 2 2
2 6 (2)
x x kx
x x k


x

4 2 3 2 2
1 3 3
3 (2 6 ) ( 2) 0
2 2 2
x x x x x x x
(2)
(2)
(2)
3
0 0 :
2
3
2 2 2 : 2 2
2
3
2 2 2 : 2 2
2
x k y
x k y x
x k y x
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
9
Bài 3: Vip tuyn ca
C:
Câu 1.
3
2
31
3
x
y x x
 m
1
0;
3
A



A.
1
y 3x-
3
B.
2
y 3x
3

C.
1
yx
3

D.
1
y 3x
3

Bài làm: 
D
Ta có:
2
' 2 3y x x
p tuyn
d
ca
C
có dng :
0 0 0
'( )( ) ( )y y x x x y x

0
x
 tim ca
d
vi
C
)
3
2 2 2 3 2
0
0 0 0 0 0 0 0 0 0
2
( 2 3)( ) 3 1 ( 2 3) 1
33
x
y x x x x x x x x x x x
3 2 3 2
0 0 0 0 0
1 1 2
0; 1 2 3 4 0 2.
3 3 3
A d x x x x x



p tuyn cn tìm là
1
y 3x
3

.
Câu 2.
42
43y x x
 m cc tiu c th.
A.
y3
;
16 59
y
9
3
x
B.
y3
;
16 5
y
9
33
x
C.
y9
;
16 5
y
9
3
x
D.
y3
;
16 59
y
9
33
x
Bài làm: 2. m cc tiu ca
C
là
A 0; 3 .
p tuyn
d
ca
C
có dng :
0 0 0
'( )( ) ( )y y x x x y x

0
x
 tim ca
d
vi
C
)
3 4 2
0 0 0 0 0
( 4 8 )( ) 4 3y x x x x x x
3 4 2
0 0 0 0
( 4 8 ) 3 4 3x x x x x
4 2 4 2
0 0 0 0
(0; 3) 3 3 4 3 3 4 0A d x x x x
0
0x
hoc
0
2
3
x 
Vi
0
0x
 
d:
y3
Vi
0
2
3
x 

d:
16 59
y
9
33
x
Vi
0
2
3
x

d:
16 59
y
9
33
x
Vy, tip tuyn cn tìm là:
y3
,
16 59
y
9
33
x
,
16 59
y
9
33
x
Câu 3.
32
32y x x
 m
23
;2
9
A



.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
10
A.
2
9 25
5 61
3 27
y
yx
yx



B.
2
25
51
3 27
y
yx
yx


C.
2
92
5 61
32
y
yx
yx



D.
2
5
61
27
y
yx
yx



Bài làm: 3. Gi
0 0 0
;M x y C
p tuyn
d
ca
C
ti
0
M
là
3 2 2
0 0 0 0 0 0 0 0
' 3 2 3 6y y y x x x y x x x x x x
Do
d
m
23
;2
9
A



nên
3 2 2 3 2
0 0 0 0 0 0 0 0
23
2 3 2 3 6 6 32 46 12 0
9
x x x x x x x x



0
2
0 0 0 0
0
22
2 3 10 3 0 3 9 25
1 5 61
3 3 27
xy
x x x x y x
x y x
Câu 4.
32
24y x x x
 m
4; 24 .M 
A.
3 508; 8; 5 4.y x y x y x
B.
13 5; 8 8; 5 4.y x y x y x
C.
133 508; 8; 4.y x y x y x
D.
133 508; 8 8; 5 4.y x y x y x
Bài làm: 4. Hàm s nh và liên tc trên
.
Gi s tip tuyn cn tìm tip xúc v th
C
t
0
x
   p tuyn
có
dng:
2
0 0 0
3
000 0 0
2
0
' 3 4 1 2 4y y x x x y x x x x x x x x
Vì
m
4; 24M 
nên:
2
32
000000
24 3 4 1 4 2 4x x x x x x
0
32
000
5 8 12 0 6x x x x
hoc
0
1x 
hoc
0
2.x
- Vi
0
6x 
p tuyn là
133 508yx
- Vi
0
1x 
p tuyn là
88yx
- Vi
0
2x
p tuyn là
54yx
Vp tuyn cn tìm là:
133 508; 8 8; 5 4.y x y x y x
Bài 4:
Câu 1. Vip tuyn c th hàm s
2
21
2
xx
y
x

, bit tip tuym
(6;4)M
.
A.
5y
và
1
2
yx
. B.
4y
và
11
42
yx
. C.
5y
và
3
6
4
yx
. D.
4y
và
31
42
yx
.
Bài làm: 1. ng thng

(6;4)M
vi h s góc
k

( 6) 4y k x
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
11
ti th t
0
x
2
1
( 6) 4 (1)
2
1
1 (2)
( 2)
x k x
x
k
x


có nghim
0
x
Thay (2) vào (1) và bic:
0 0 0 0
2
0
0
11
1 ( 6) 4 0, 3
2
( 2)
x x x x
x
x




Tahy vào (2) ta có:
3
,0
4
kk
.
Vy tip tuyn cn tìm là:
4y
và
31
42
yx
.
Câu 2. Vip tuyn
d
v th
C
:
2
2
x
y
x
, bit
d
m
6;5 .A
A.
1yx
,
7
42
x
y 
. B.
1yx
,
5
42
x
y
.
C.
1yx
,
7
42
x
y
. D.
1yx
,
7
42
x
y 
.
Bài làm: 2. Cách 1: Gi
00
;x y x
là t tim ca tip tuyn
d
và
C
, vi
0
0
0
2
2
x
yx
x
, tip tuyn
d
có h s góc
0
2
0
4
'
2
yx
x
,
0
2x
và
d
 
0
0
2
0
0
2
4
2
2
x
y x x
x
x
d
 m
6;5A
nên có
0
0
2
0
0
2
4
56
2
2
x
x
x
x
i
2
00
60xx
0
0x
hoc
0
6x
Vi
0
0x

1yx
Vi
0
6x

7
42
x
y
Vy, có
2
tip tuyn th bài
1yx
,
7
42
x
y
.
Cách 2
d
 qua
6;5A
có h s góc
k

d
 :
65y k x
d
tip xúc
C
t
0
x
khi và ch khi h :
0
0
0
2
0
2
65
2
4
2
x
kx
x
k
x


có nghim
0
x
hay
2
00
2
0
4 24 0
4
2
xx
k
x


có nghim
0
x
0
0
0, 1 : 1
17
6, :
4 4 2
x k d y x
x
x k d y
Vy, có
2
tip tuyn tha bài
1yx
,
7
42
x
y
.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
12
Câu 3. Cho hàm s
32
3 9 11y x x x
 th là
.C
Lp tuyn c th hàm s bit tip
tuym
29
;184 .
3
I



A.
8 36; 36 14; 15 9y x y x y x
B.
40 76; 36 14; 15 9y x y x y x
C.
420 76; 164; 39y x y x y x
D.
420 3876; 36 164; 15 39y x y x y x
Bài làm: 3. Gi s tip tuyn cn tìm tip xúc v th
C
t
0
x
 
p tuyn
có dng:
23
0 0 0 0
2
0 0000
' 3 6 9 3 9 11y y x x x y x x x x x x x x
Vì
m
29
;184
3
I



nên:
23
0 0 0
2
0 0 0
29
184 3 6 9 3 9 11
3
x x x x x x



32
0000
2 32 58 260 0 13x x x x
hoc
0
5x
hoc
0
2.x 
- Vi
0
13x
p tuyn là
420 3876yx
- Vi
0
5x
p tuyn là
36 164yx
- Vi
0
2x 
p tuyn là
15 39yx
Vp tuyn cn tìm là:
420 3876; 36 164; 15 39y x y x y x
Bài 5: G th ca hàm s
32
32y x x
Câu 1. Vip tuyn ca (C) song song vng thng y = 9x 7 .
A. y = 9x + 25 B. y = 7x + 2 C. y = 9x + 5 D. y = 9x + 2
Bài làm: 1. Tip tuyn (d) ca (C) song song vng thng y = 9x ng : y = 9x
+ m (m
- 7)
(d) tip xúc vi (C) t
0
x
khi h
32
0 0 0
2
00
3 2 9 (1)
3 6 9 (2)
x x x m
xx

có nghim
0
x
(2)
0
x
= 1
0
x
= - 3 .
Lt thay
0
x
= 1 ,
0
x
= - c m = - 7 , m = 25 và m = - 7 b loi
Vp tuyn (d): y = 9x + 25.
Câu 2. Vip tuyn cm A(- 2;7).
A. y = 9x + 25 B. y = 9x + 9 C. y = 9x + 2 D. y = x + 25
Bài làm: 2. p tuy-2;7) có dng y = k(x+2) +7 .
(D) tip xúc (C) t
0
x
khi h
32
0 0 0
2
00
3 2 ( 2) 7 (3)
3 6 (4)
x x k x
x x k

có nghim
0
x
c:
3 2 2
0 0 0 0 0
3 2 (3 6 )( 2) 7x x x x x
32
0 0 0 0
2 9 12 9 0 3x x x x
Thay
0
x
= -  
Bài 6: Cho hàm s
22
(2 )y x x
 th (C).
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
13
Câu 1. Vip tuyn tm ca (C) vi Parabol
2
yx
.
A.
0y
;
1y
;
24 6yx
B.
9y
;
1y
;
24 6yx
C.
0y
;
5y
;
24 63yx
D.
0y
;
1y
;
24 63yx
Bài làm: 1. Ta có:
4 3 2 3 2
4 4 ' 4 12 8y x x x y x x x
    m ca (C) và Parabol
2
yx
4 3 2 2 2 2
4 4 ( 4 3) 0 0, 1, 3x x x x x x x x x x
.
0x
 p tuyn là:
0y
.
1x
 p tuyn là:
1y
3x
 p tuyn là:
24 63yx
.
Câu 2. Vip tuyn ca (C), bit tip tuym
(2;0)A
.
A.
26
27 27
yx
B.
32
9
27
yx
C.
32 4
27 27
yx
D.
32 64
27 27
yx
Bài làm: 2. Ta có:
4 3 2 3 2
4 4 ' 4 12 8y x x x y x x x
Cách 1: Gi
00
( ; ) ( )M x y C
.
Tip tuyn
ca (C) t
32
0 0 0 0 0
(4 12 8 )( )y x x x x x y
.
3 2 2 2
0 0 0 0 0 0
0 (4 12 8 )(2 ) ( 2)A x x x x x x
32
0 0 0 0 0 0 0
4
(2 )(3 10 8 ) 0 0, 2,
3
x x x x x x x
.
*
0 0 0
0 '( ) 0, 0x y x y
p tuyn
0y
*
0 0 0
2 '( ) 0, 0x y x y
p tuyn
0y
*
00
4 32 64
'( ) ,
3 27 81
x y x y
p tuyn:
32 64
27 27
yx
.
Cách 2: Gng th s góc k
: ( 2)d y k x
d ti th t
0
x
khi h
22
0 0 0
0 0 0
(2 ) ( 2)
4 ( 2)( 1)
x x k x
x x x k
có nghim
0
x
 nhc:
4 3 2 3 2 2
0 0 0 0 0 0 0 0 0 0
4 4 ( 2)(4 12 8 ) (3 4)( 2) 0x x x x x x x x x x
0 0 0
4
0, 2,
3
x x x
.
*
0
00xk
Php tuyn
0y
*
0
20xk
p tuyn
0y
*
0
4 32
3 27
xk
p tuyn
32 64
27 27
yx
.
Bài 7:
Câu 1.  (Cm):
3
2
1
( 2) 2 1
32
x
y m x mx
tip xúc vng thng y = 1
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
14
A.
2
0; ;2
3
m



B.
2
4; ;6
3
m



C.
0;4;6m
D.
2
0; ;6
3
m



Bài làm: 1. (Cm) ting thng y = 1 t
0
x
khi h sau
3
2
0
00
2
00
1
( 2) 2 1 1 ( )
32
( 2) 2 0 ( )
x
m x mx a
x m x m b
có nghim
0
x
.
00
( ) 2 .b x x m
Thay
0
2x
  c
2
m
3
.
Thay
0
xm
  c
3
2
0 0 6.
6
m
m m m
Vy (Cm) ting thng y = 1
2
0; ;6
3
m




Câu 2. G th ca hàm s y =
2
21
x
x
. M(0;m) là mm thuc trc Oy .Vi giá tr nào ca m thì luôn tn
ti ít nht mt tip tuyn cM và tim ca tip tuyn này v 
A. m
0 B. m
0 C. m<0 D. m
0
Bài làm: 2. ng th s góc k : y = kx + m.
(d) tip xúc (C) t
0
x
khi h sau
0
0
0
2
0
2
(1)
21
3
(2)
(2 1)
x
kx m
x
k
x

có
nghim
0
x
.
c :
00
2
0
0
23
21
(2 1)
xx
m
x
x

2
0 0 0
( 2)(2 1) 3 (2 1)x x x m x
(3) (do
0
x
=
1
2
không phi là
nghim ca (3))
2
00
(4 2) 4( 2) 2 0m x m x m
(4)
Yêu cu ca bài toán
t mt nghii mi m
0. Vì m
0
nên 4m 2 < 0 suy ra
(4) có nghim
2
' 4( 2) (4 2)( 2) 0m m m
20m
. Bng thi mi m
0.
i
12
,xx
là hai nghim c  4).
Ta có
12
12
4( 2)
0
42
0,
2
0
42
m
xx
m
m
m
xx
m


,suy ra
12
0, 0xx
Vy, vi mi m
0 luôn tn ti ít nht mt tip tuyn c tim ca tip tuyn vi
(C) là s 
Bài 8:
Câu 1. Cho hàm s
3
32y x x
 ng thng
:4dy
m mà t  p tuyn vi
(C).
A.
( 1;4)
;
7;4
;
(2;4)
. B.
( 1;4)
;
7;4
;
(9;4)
.
C.
( 2;4)
;
5;4
;
(2;4)
. D.
( 1;4)
;
2
;4
3



;
(2;4)
.
Bài làm: 1. Gi
( ;4)M m d
. P ng thng qua M có dng:
( ) 4y k x m
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
15
là tip tuyn ca (C) h  sau có nghim x:
3
2
3 2 ( ) 4 (1)
3 3 (2)
x x k x m
xk

(*)
c:
2
( 1) 2 (3 2) 3 2 0 (3)x x m x m


1x 
hoc
2
2 (3 2) 3 2 0 (4)x m x m
Theo bài toán (*) có nghing thi
(2)
có 2 giá tr k khác nhau, t(3) có nghim x phân
bit tha mãn 2 giá tr k khác nhau.
+ TH1: (4) có 2 nghim phân bim bng 1
1m 
+ TH2: (4) có nghim kép khác 1
2
3
m 
hoc
2m
Vm cn tìm là:
( 1;4)
;
2
;4
3



;
(2;4)
.
Câu 2. Cho hàm s
32
32y x x
ng thng (d): y m mà t  c 3 tip tuyn phân
bit v th (C).
A. M(m; 2) (d) vi
1
2
3
2
mm
m
B. M(m; 2) (d) vi
7m 
C. M(m; 2) (d) vi
4
3
3
2
mm
m
D. M(m; 2) (d) vi
5
1
3
2
mm
m
Bài làm: 2. Gi
( ;2) ( )M m d
.
 ng thng  m M có dng :
( ) 2y k x m
là tip tuyn ca (C) h m x:
32
2
3 2 ( ) 2 (1)
3 6 (2)
x x k x m
x x k
(*).
c:
32
2 3( 1) 6 4 0x m x mx
2
( 2) 2 (3 1) 2 0x x m x


2x
hoc
2
( ) 2 (3 1) 2 0 (3)f x x m x
T M k c 3 tip tuy th (C)
h (*) có nghim x phân bing thi
(2) có 3 giá tr k khác nhau
(3) có hai nghim phân bit khác 2 và có giá tr x tha
 k khác nhau
5
0
1
3
(2) 0
2
mm
f
m



.
Vy ,M(m; 2) (d) vi
5
1
3
2
mm
m
có th k c 3 tip tuyn vi (C).
Câu 3. Vip tuyn
d
tip xúc v th
H
:
2
2
1yx
ca hàm s t
2
m phân
bit.
A.
2yx
B.
0y
C.
21yx
D.
1y
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
16
Bài làm: 4. Gi s
d
ng thng tip xúc vi
H
tm
2
2
;1M m m
ng thng
d
có

2
22
2 1 1y m m x m m
ng thng
d
tip xúc vi
H
ti
2
m phân bit khi và ch khi h 
22
2 2 2
22
1 2 1 1
2 1 2 1
x m m x m m
x x m m
t nghim khác
m
tc h
2 2 3
22
20
10
x m x x mx m m x
x m x mx m


t nghim khác
m
hay
3
22
10
xm
x mx m

có nghim
1, 1xm
hoc
1, 1xm
.
Vy
0y
th bài.
Bài 9. Cho hàm s
42
23y x x
 th là
C
Câu  th
C
m
B
mà tip tuyn vi
C
ti tip tuyn vi
C
tm
1;2A
.
A.
1;2B
B.
0;3B
C.
1;3B
D.
2;3B
Bài làm:
0;3B
,
3y
.
Câu ng thng
2y
nh c
4
tip tuyn phân bit v th
C
.
A.
,0;2 1;2MM
B.
,0;2 3;2MM
C.
,5;2 1;2MM
D. Không tn ti
Bài làm: b. Gi
;2Mm
m thung thng
2y
ng th
;2Mm
có h s
góc là
k
và
d
:
2y k x m
.
d
tip xúc
C
tm có hoành 
0
x
khi h
42
0 0 0
3
00
2 3 2 1
4 4 2
x x k x m
x x k

có nghim
0
x

22
0 0 0
1 3 4 1 0x x ax
có nghim
0
x
.
Qua
M
k c
4
tip tuyn
C

có
4
nghim phân bi
2
có
4
giá
tr
k
khác nhau.
D thy
2
0
1 0 1 1x k k
  tn ti
4
giá tr
k
 tha bài toán. Tóm li, không
có t
M
tha bài toán.
Bài 10 . Cho hàm s :
42
2y x x
 th là
C
.
Câu a. Vip tuyn ca
C
bit tip tuyc t.
A.
1 2 3
66
: 0; : ; :
99
t y t y x t y x
B.
1 2 3
4 6 4 6
: 0; : ; :
77
t y t y x t y x
C.
1 2 3
44
: 0; : ; :
99
t y t y x t y x
D.
1 2 3
4 6 4 6
: 0; : ; :
99
t y t y x t y x
Bài làm: a. Gi
00
;A x y C
 p tuyn
t
ca
C
ti
A
là:
4 2 3
0 0 0 0 0
2 4 4y x x x x x x
.
t

0;0O
nên
4 2 4 4 2
0 0 0 0 0 0 0 0 0
6
2 4 4 3 2 0 0,
3
x x x x x x x x x
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
17
Thay các giá tr ca
0
x
a
t
c
3
tip tuyn ca
C
k t
0;0O
là:
1 2 3
4 6 4 6
: 0; : ; :
99
t y t y x t y x
Câu b..Tìm nhm
M
trên trc
Oy
 t
M
k c
4
tip tuyn
C
.
A.
0;Mm
vi
01m
B.
0;Mm
vi
1
1
3
m
C.
0;Mm
vi
2
0
3
m
D.
0;Mm
vi
1
0
3
m
Bài làm: b.
00
0; ; ;M Oy M m B C B x y
p tuyn
T
ca
C
ti
B
là
4 2 3
0 0 0 0 0
2 4 4y x x x x x x
.
T

0;Mm
nên
4 2 4 4 2
0 0 0 0 0 0 0
2 4 4 3 2 0 *m x x x x x x x m
Do h s góc ca tip tuyn là
3
00
44k x x
nên hai giá tr khác nhau ca
0
x
cho hai giá tr khác nhau ca
k
nên
cho hai tip tuyn khác nhau
Vy t
0;Mm
k c
4
tip tuy th
C
khi và ch 
*
có
4
nghim phân bit.
t
2
0
Xx
ta có p
2
3 2 0 * *X X m

*
có
4
nghim phân bit khi và ch khi
**
có
2
nghim phân bit
,
1 3 0
1
00
33
2
0
3
m
m
Pm
S

. Vy t nhm
0;Mm
vi
1
0
3
m
k c
4
tip tuy th
C
ca hàm s 
Câu c. Tìm nhm
N
ng thng
:3dy
 t
N
k c
4
tip tuyn
C
.
A.
;3 , 3N n n
B.
;3 , 3N n n
C.
;3 , 2N n n
D.
;3 , 13N n n
Bài làm: c.
00
: 3 ;3 ; ;N d y N n I C I x y
p tuyn
ca
C
ti
I
là:
4 2 3
0 0 0 0 0
2 4 4y x x x x x x
.

;3Nn
nên
4 2 4 4 2 2
0 0 0 0 0 0 0 0 0
3 2 4 4 3 4 2 4 3 0x x x x n x x nx x nx
4 3 2
0 0 0 0
3 1 4 2 0 *x n x x x
.Do
0
0x
không phi là nghim ca
*

2
00
2
0
0
11
* 3 4 2 0 * *x n x
x
x








t
2
0 0 0
0
1
10t x x tx
x
luôn có hai nghim phân bit vi mi
t

2
* * 3 4 4 0 * * *t nt
Do h s góc ca tip tuyn là
3
00
44k x x
nên hai giá tr khác nhau ca
0
x
cho hai giá tr khác nhau ca
k
nên
cho hai tip tuyn khác nhau
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
18
Vy t
N
k c
4
tip tuy th
C
khi và ch 
*
có
4
nghim phân bit khi và ch
khi
**
có
4
nghim phân bit khi và ch 
***
có
2
nghim phân bit
2
' 4 12 0n
2
3 0 3nn
. Vy t nhm
N
ng thng
3y
vi
3n
k c
4
tip tuy
th
C
ca hàm s 
Bài 10:
Câu 1. Cho hàm s
32
1
( 1) (4 3 ) 1
3
y mx m x m x
 th là
m
C.
Tìm các giá tr
m
 th
m
C.
tn ti m m duy nh   âm mà tip tuyn t     ng thng
d : 2 3 0xy
.
A.
12m
hoc
2
3
m
. B.
0m
hoc
1m
C.
1m
hoc
1
3
m
D.
0m
hoc
2
3
m
Bài làm: 1.
d
có h s góc
1
2
tip tuyn có h s góc
2k
. Gi
x
 tim thì:
22
' 2 2( 1) (4 3 ) 2 2( 1) 2 3 0y mx m x m mx m x m
Theo  
t nghim âm.
Nu
0m
thì
2 2 1xx
(không tha)
Nu
0m
thì d th
có
2
nghim là
23
1 hay x
m
x
m


có mt nghim âm thì
23
00
m
m
m
hoc
2
3
m
.
Câu 2. Cho hàm s
32
1
( 1) (4 3 ) 1
3
y mx m x m x
 th là
m
C.
Tìm các giá tr
m
 th
m
C.
tn ti   m      p tuyn t     ng thng
d : 2 3 0xy
.
A.
1 1 2
0; ;
3 2 3
m

B.
1 1 5
0; ;
2 2 3
m





C.
1 1 8
0; ;
2 2 3
m





D.
1 1 2
0; ;
2 2 3
m





Bài làm: 2. Ta có:
2
2( 1) 4 3y mx m x m
;
13
:
22
d y x
.
Theo yêu cu bài toán 
2y
 2 nghit
2
2( 1) 2 3 0mx m x m
 t
0
0
0
0
m
S
P


1
0
2
12
23
m
m


.
Vy, vi
1 1 2
0; ;
2 2 3
m





tha mãn bài toán
Câu 3. Cho hàm s:
2
1
x
y
x
có  th là
C.
m
(0; )Aa
. Tìm
a
 t
A
k c
2
tip tuyn t th
C
sao cho
2
ti ng nm v
2
phía ca trc hoành.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
19
A.
1
1
3
a
B.
2
2
3
a
C.
11a
D.
2
1
3
a
Bài làm: 3. ng thng
d

(0; )Aa
và có h s góc
k : y kx a
d
tip xúc
C
t
x
khi h:
2
2
1
3
( 1)
x
kx a
x
k
x



có nghim
x
2
(1 ) 2( 2) ( 2) 0a x a x a
1
có nghim
1x
.
 qua
A
có
2
tip tuyn thì
1
phi có
2
nghim phân bit
12
,xx
1
1
2
3a 6 0
a
a
a





2

1 2 1 2
2( 2) 2
,
11
aa
x x x x
aa


và
12
12
33
1 , 1
11
yy
xx


2
tim nm v
2
i vi trc hoành thì
12
.0yy
12
33
1 . 1 0
11xx

1 2 1 2
1 2 1 2
. 2( ) 4
0
. ( ) 1
x x x x
x x x x

3 2 0a
2
3
a 
i chiu vu kin
2
c:
2
1
3
a
.
Bài 11: Cho hàm s
3
2
2
42
3
x
y x x
, g th ca hàm s là (C).
Câu 1. Vi p tuyn ca (C) có h s góc ln nht.
A.
9 25
2 12
yx
B.
25
5
12
yx
C.
9 25
4 12
yx
D.
75
2 12
yx
Bài làm: 1. Gi (d) là tip tuyn c
0
x
 tim ca (d) vi (C) thì h s góc
ca (d):
2
2
0 0 0 0
9 1 9
'( ) 2 2 4
2 2 2
k y x x x x



0
91
.
22
kx
Vy
9
maxk
2
c khi và ch khi
0
1
2
x
.
p tuyn (d) :
9 1 1 9 25
2 2 2 2 12
y x y x
.
Câu 2. Vip tuyn cm A(2;9).
A. y = - x + 2 B. y = - 8x + 5 C. y = x + 25 D. y = - 8x + 25
Bài làm: 2. ng thm A(2;9) có h s góc k là
( 2) 9y k x
(D) tip xúc vi (C) t
0
x
khi h
3
2
0
0 0 0
2
00
2
4 2 ( 2) 9 (1)
3
2 2 4 (2)
x
x x k x
x x k
có nghim
0
x
.
Thay c :
3
22
0
0 0 0 0 0
2
4 2 ( 2 2 4)( 2) 9
3
x
x x x x x
32
0 0 0 0
4 15 12 9 0 3x x x x
Thay
0
x
c k = - 8 .
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
20
Vp tuyn (D) là y = - 8x + 25.
Bài 12: G th ca hàm s
2
2
x
y
x
.
Câu 1. Vip tuyn ca (C) vuông góc vng thng
4
y 1
3
x
.
A.
3 7 3 1
d : y ,
4 2 4 2
x y x
B.
33
d : y , 1
44
x y x
C.
3 9 3 1
d : y ,
4 2 4 2
x y x
D.
3 9 3 1
d : y ,
4 2 4 2
x y x
Bài làm: 1. Tip tuyn (d) c    ng thng
4
y1
3
x
      ng :
3
4
y x m
.
(d) tip xúc (C) t    
0
x
khi h
2
0
0
0
2
00
2
0
3
24
4
3
4
(2 )
x
xm
x
xx
x


có nghim
0
x
2
00
2
0
4
3
4
(2 )
xx
x

00
62xx
3 9 3 1
d : y ,
4 2 4 2
x y x
.
Câu 2. Vip tuyn cm A(2; - 2).
A.
31
42
yx
B.
31
42
yx
C.
37
42
yx
D.
35
42
yx
Bài làm:
2. p tuyn (d) c- 2) có dng : y = k(x 2) 2 .
(d) tip xúc (C) t
0
x
khi h
2
0
0
0
2
00
2
0
( 2) 2 (1)
2
4
(2 )
x
kx
x
xx
k
x

có nghim
0
x
22
0 0 0
0
2
0
0
4
( 2) 2
2
(2 )
x x x
x
x
x

0
31
2
42
x y x
Câu 3. Gi M là mm thuc (C) có khong cách t n trc hoành bng hai ln khong cách t n trc
tung, M không trùng vi gc t O. Vip tuyn ca (C) ti M.
A.
9y 
B.
64y 
C.
12y 
D.
8y 
Bài làm: 3.
2
2
()
2
.
2
( , ) 2 ( , )
2
2
M
M
M
M
M
M
MM
MM
x
x
y
y
MC
x
x
d M Ox d M Oy
yx
yx



2
2
2
4
2
2
0
3
(*)
2
08
2
3 4 0
22
3
MM
M
M
MM
M
M
M
M
M
M
MM
M
M M M
yx
x
x
yx
x
y
x
x
y
x
xx
y
y x x





Vì M không trùng vi gc t O nên ch nhn
48
;
33
M



.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
21
p tuyn ca (C) ti M là y = 8x 8.
2
2
2
2
2
4
(*)
2
8
2
40
22
MM
M
MM
M
M
M
M
M
M
MM
M M M
yx
x
yx
x
y
x
x
y
x
xx
y x x










(do M
O).
p tuyn ca (C) ti M là
8y 
.
Bài 13: G th ca hàm s y =
32
2 3( 1) 1x m x mx m
và (d) là tip tuyn ca (Cm) t m có
 x = - 
Câu 1. m A(0;8).
A.
0m
B.
1m
C.
2m
D.
3m
Bài làm: 1.
Ta có
2
' 6 6( 1)y x m x m
 p tuyn (d) là
'( 1)( 1) ( 1)y y x y
(12+7m)(x+1) 3m 4
y
(12+7m)x +4m+8
(0;8) ( )Ad
8 = 4m +8
0m
.
Câu 2. (d) to vi hai trc t mt tam giác có din tích bng
8
.
3
A.
5
0
3
.
9 73
6
mm
m

B.
5
0
3
.
19 73
6
mm
m

C.
5
0
3
.
93
6
mm
m

D.
5
0
3
.
19 73
6
mm
m

Bài làm: 2. Ta có
2
' 6 6( 1)y x m x m
ng trình tip tuyn (d) là
'( 1)( 1) ( 1)y y x y
(12+7m)(x+1) 3m 4
y
(12+7m)x +4m+8
Gi P,Q lm ca (d) vi trc Ox và Oy thì
48
;0
12 7
m
P
m


, Q(0; 4m+8).
Din tích: OPQ:
2
8 32 32
1 1 4 8
. 4 8
2 2 12 7
12 7
mm
m
S OP OQ m
m
m

2
88
8 32 32 12 7
33
S m m m
2
2
2
2
5
8
5
0
8 32 32 (12 7 )
0
3
3
.
3
8
19 73
3 19 24 0
8 32 32 (12 7 )
3
6
mm
m m m
mm
mm
m m m
m


Bài 14: Cho hàm s
4
2
24
4
x
yx
 th là ( C ).
Câu 1. Tìm tham s   th (C) tip xúc vi parabol
2
P : y xm
.
A.
4; 20mm
B.
124; 2mm
C.
14; 20mm
D.
4; 2mm
Bài làm: 1. (C) tip xúc (P) t
0
x
khi h sau có nghim
0
x
4
22
0
00
00
3
0 0 0
06
24
4
4 20
42
x
xx
x x m
mm
x x x





Câu 2. Gi (d) là tip tuyn ca (C) t  (d) ct li (C) tm E, F khác M
m I cn E, F n
2
y 4x
.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
22
A. a = 0 B. a = -1 C. a = 2 D. a = 1
Bài làm:.p tuyn (d):
44
2 3 2
'( )( ) 2 4 ( 4 )( ) 2 4
44
aa
y y a x a a a a x a a
4
32
3
( 4 ) 2 4
4
a
a a x a
   m ca (C) và (d):
44
2 3 2 4 2 3 4 2
3
2 4 ( 4 ) 2 4 8 4( 4 ) 3 8 0
44
xa
x a a x a x x a a x a a
2 2 2
22
( ) ( 2 3 8) 0
2 3 8 0 (3)
xa
x a x ax a
x ax a
(d) ct (C) t  m E,F khác M
    i nghim phân bit khác a
22
2
22
' 3 8 0
.
2
6 8 0
3
a
aa
a
a






(*)
T m I ca E,F :
4
4
2
32
2
7
3
64
( 4 )( ) 2 4 ( ( ))
4
4
EF
I
I
I
I
xx
xa
xa
a
a
ya
y a a a a do I d




42
2 2 2 2
0
7
( ) : 4 6 4 4 7 (1 ) 0 .
2
44
a
aa
I P y x a a a
a

So vu kin (*) nhn a = 0.
Bài 15:
Câu 1.   th hàm s
2
1
1
xx
y
x

tip xúc vi Parabol
2
y x m
.
A.
2m 
B.
0m
C.
1m 
D.
3m
Bài làm: 1. p xúc nhau t
0
x
h  
2
2
00
0
0
2
00
0
2
0
1
(1)
1
2
2 (2)
( 1)
xx
xm
x
xx
x
x


có nghim
0
x
.
Ta có:
2
0 0 0
(2) (2 5 4) 0 0x x x x
 c
1m 
.
Vy
1m 
là giá tr cn tìm.
Câu 2.   th hai hàm s sau tip xúc vi nhau
32
1
( ) : (1 2 ) 2C y mx m x mx
và
3
2
( ) : 3 3(1 2 ) 4 2C y mx m x m
.
A.
1 3 6
,
22
mm

B.
1 8 6
,
2 12
mm

C.
5 3 6
,
2 12
mm

D.
1 3 6
,
2 12
mm

Bài làm: 2.
1
()C
và
2
()C
tip xúc nhau t 
0
x
h m
0
x
:
3 2 3
0 0 0 0 0
22
0 0 0
(1 2 ) 2 3 3(1 2 ) 4 2
3 2(1 2 ) 2 9 3(1 2 )
mx m x mx mx m x m
mx m x m mx m
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
23
32
0 0 0
2
00
2 (1 2 ) (3 8 ) 4 2 0 (1)
6 2(1 2 ) 3 8 0 (2)
mx m x m x m
mx m x m
có nghim
0
x
Ta có :
2
0 0 0
(1) ( 1)(2 (1 4 ) 4 2) 0x mx m x m
0
2
00
1
2 (1 4 ) 4 2 0
x
mx m x m
Vi
0
1x
thay vào (2), ta có:
1
2
m
.
Vi
2
00
2 (1 4 ) 4 2 0mx m x m
(*) ta có :
0
2
00
0
1
(2) 4 1 4 0 ( 0
14
4
x
mx x m m
m
x
m

vì
0m
h vô nghim)
Thay
0
14
4
m
x
m
  c:
22
(1 4 ) (1 4 )
2 4 0
84
mm
m
mm

2
36
48 24 1 0
12
m m m
.
Vy
1 3 6
,
2 12
mm

là nhng giá tr cn tìm.
Câu 3. Tìm tham s   th (Cm) ca hàm s
32
4 7 3y x mx mx m
tip xúc vi parabol
2

A.
2; 7;1m
B.
1
5; ;78
4
m




C.
3
2; ;1
4
m




D.
1
2; ;1
4




Bài làm: 3. (Cm) tip xúc vi (P) t
0
x
khi h
3 2 2
0 0 0 0 0
2
0 0 0
4 7 3 1 (1)
()
3 8 7 2 1
x mx mx m x x
A
x mx m x
có
nghim
0
x
.
Gii h (A),
32
0 0 0
(1) (4 1) (7 1) 3 1 0x m x m x m
0
2
0 0 0
2
00
1
( 1)( 4 3 1) 0
4 3 1 0
x
x x mx m
x mx m
Vy (A)
2
0
00
2
2
00
00
1
4 3 1 0
3 2(4 1) 7 1 0 (2)
3 2(4 1) 7 1 0 (2)
x
x mx m
x m x m
x m x m



Thay
0
x
c m = 2.
H
22
0 0 0 0
22
0 0 0 0
3 2(4 1) 7 1 0 (2) 3 2(4 1) 7 1 0 (2)
4 3 1 0 (3) 3 12 9 3 0 (4)
x m x m x m x m
x mx m x mx m





Tr  vi v c.
4m
0
x
2
0
x
2m 2 = 0
0
(2 1) 1 (5)m x m
.
Khi m =
1
2
thì (5) tr 
0
1
21
m
x
m

.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
24
Thay
0
x
=
1
21
m
m
c
2
11
4 3 1 0
2 1 2 1
mm
mm
mm

32
1
4 11 5 2 0 2 1.
4
m m m m m m
Vy các giá tr m cn tìm là m
1
2; ;1
4




.
Bài 16: 
2
1
1
xx
y
x


Câu 1   
: 3 4 1 0xy
.
A.
33
44
yx
;
3
1
4
yx
B.
3
3
4
yx
;
35
44
yx
C.
3
9
4
yx
;
3
7
4
yx
D.
33
44
yx
;
35
44
yx
Ta có
2
2
2
'
( 1)
xx
y
x
.
Gi
00
( ; )M x y
là t tim ca tip tuyn
d
vi (C)
22
0 0 0 0
0
2
0
0
21
: ( )
1
( 1)
x x x x
d y x x
x
x
.
Bài làm: 1. Vì d song song vng thng
31
:
44
yx
, nên ta có:
2
2
00
0 0 0 0
2
0
2
3
2 3 0 1, 3
4
( 1)
xx
x x x x
x
.
0
1x 
 p tuyn:
33
44
yx
.
0
3x 
 p tuyn:
35
44
yx
.
Câu 2
( 1;3)M
.
A.
31yx
;
3yx
B.
13y
;
3yx
C.
3y
;
31yx
D.
3y
;
3yx
Bài làm: 2. Ta có
2
2
2
'
( 1)
xx
y
x
.
Gi
00
( ; )M x y
là t tim ca tip tuyn
d
vi (C)
22
0 0 0 0
0
2
0
0
21
: ( )
1
( 1)
x x x x
d y x x
x
x
Cách 1:
22
0 0 0 0
0
2
0
0
21
3 ( 1 )
1
( 1)
x x x x
M d x
x
x
2 2 2
0 0 0 0 0 0 0
3( 1) ( 2 )( 1) ( 1)( 1)x x x x x x x
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
25
2
0 0 0 0
1
2 5 2 0 2,
2
x x x x
.
Vi
0
2x 
 p tuyn
3y
.
Vi
0
1
2
x 
p tuyn
3yx
.
Cách 2: Gng th
( 1;3)M
, có h s   ng:
( 1) 3y k x
d ti th t
0
x
khi h  m
0
x
:
2
00
0
0
2
00
2
0
1
( 1) 3 (1)
1
2
(2)
( 1)
xx
kx
x
xx
k
x

Th c:
22
0 0 0 0
0
2
0
0
12
( 1) 3
1
( 1)
x x x x
x
x
x
2
0 0 0 0
1
2 5 2 0 2,
2
x x x x
.
Vi
0
20xk
ng trình tip tuyn
3y
.
Vi
0
1
3
2
xk
p tuyn
3yx
.
Câu 3 (C).
A.
21yx
B.
32yx
C.
43yx
D.Không tn ti
Bài làm: 3. Ta có
2
2
2
'
( 1)
xx
y
x
.
Gi
00
( ; )M x y
là t tim ca tip tuyn
d
vi (C)
22
0 0 0 0
0
2
0
0
21
: ( )
1
( 1)
x x x x
d y x x
x
x
 th có hai tim cn
1x
và
yx
m ca hai tim cn là
(1;1)I
.
Cách 1:
22
0 0 0 0
0
2
0
0
21
1 (1 )
1
( 1)
x x x x
I d x
x
x
22
0 0 0 0 0
1 2 1 2 0x x x x x
vô nghim.
Vy không có tip tuy
I
.
Cách 2: Gng th s góc k
: ( 1) 1d y k x
d là tip xúc v th t
0
x
khi h
2
00
0
0
2
00
2
0
1
( 1) 1
1
2
( 1)
xx
kx
x
xx
k
x

có nghim
0
x
Th  c:
22
0 0 0 0
00
12
1
11
x x x x
xx


22
0 0 0 0 0
1 2 1x x x x x
  m
Vy qua I không có tip tuyn nào k n (C).
Bài 17:
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
26
Câu 1. Cho hàm s:
2
1
x
y
x
 th  m
0;Am
nh
m
 t A k c 2 tip tuyn (C)
sao cho hai ting nm v i vi trc Ox.
A.
1
1
3
m
m

B.
1
2
5
m
m

C.
1
1
m
m

D.
1
2
3
m
m

Bài làm: Cách 1: Gm
00
( ; ) ( )M x y C
. Tip tuyn
ti M c 
0
0
2
0
0
2
3
()
1
( 1)
x
y x x
x
x
.
00
2
0
0
32
1
( 1)
xx
Am
x
x
2
0 0 0 0
( 1) 3 ( 2)( 1) 0m x x x x
(vi
0
1x
)
2
00
( 1) 2( 2) 2 0m x m x m
(*).
Yêu cu bài toán
(*)
có hai nghim
,ab
khác
1
sao cho
( 2)( 2) 2( ) 4
0
( 1)( 1) ( ) 1
a b ab a b
a b ab a b

hay là:
' 3( 2) 0
1
10
2
3 2 0
3
m
m
m
m
m





.
Vy
1
2
3
m
m

là nhng giá tr cn tìm.
Cách 2: ng th s 
y kx m
.
d là ti th t
0
x
khi h
0
0
0
2
0
2
1
3
( 1)
x
kx m
x
k
x

có nghim
0
x
. Th   
nh
2
00
00
2
0
0
23
( 1) 2( 2) 2 0
1
( 1)
xx
m m x m x m
x
x

(*).
 t A k c hai tip tuyn thì (*) có hai nghim phân bit khác 1
' 3( 2) 0
2
1 ( )
1
1 2( 2) 2 0
m
m
mi
m
m m m



 hai tim là:
1 1 1 2 2 2
( ; ), ( ; )M x y M x y
vi x1,x2 là nghim ca (*) và
12
12
12
22
;
11
xx
yy
xx



 M1, M2 nm v hai phía Ox thì
1 2 1 2
12
1 2 1 2
2( ) 4
. 0 0 (1)
( ) 1
x x x x
yy
x x x x
Áp dnh lí Viet:
1 2 1 2
2( 2) 2
;
11
mm
x x x x
mm


.
9 6 2
(1) 0
33
m
m
.
Kt hp vi (i) ta có
2
3
1
m
m

là nhng giá tr cn tìm.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
27
Câu 2. Tìm tham s   th (C) :
32
2( 1) 5 2y x m x mx m
ca hàm s tip xúc vi trc hoành.
A.
4
0;1;
3
m



B.
0;1;2m
C.
4
1;2;
3
m



D.
4
0;1;2;
3
m



Bài làm: 2. (C) tip xúc vi trc hoành t
0
x
khi h
32
0 0 0
2
00
2( 1) 5 2 0
3 4( 1) 5 0
x m x mx m
x m x m
(A) có
nghim
0
x
.
Gii h (A).
2
0
0 0 0
2
2
00
00
2
( 2)( 2 ) 0
()
3 4( 1) 5 0 (1)
3 4( 1) 5 0
x
x x mx m
A
x m x m
x m x m



Hoc
2
00
2
00
20
3 4( 1) 5 0
x mx m
x m x m
Thay
0
x
c
4
3
m
.
H
22
0 0 0 0
22
0 0 0 0
2 0 (2) 3 6 3 0 (3)
3 4( 1) 5 0 3 4( 1) 5 0 (1)
x mx m x mx m
x m x m x m x m





Tr  vi v c
00
( 2)
2
m
m x m x
m
.
Thay
0
2
m
x
m

vào (1), ta c :
22
2
2
0
2
( 2)
mm
m
m
m
32
3 2 0 0 1 2m m m m m m
.Vy m
4
0;1;2;
3



.
Câu 3. Gi
m
C
 th ca hàm s y =
42
( 1) 4x m x m
. Tìm tham s 
m
C
tip xúc vng thng
(d): y = 3 tm phân bit .
A. m = 1
m = 3. B. m = 1
m = 16. C. m = 2
m = 13. D. m = 1
m = 13.
Bài làm: 3.
m
C
tip xúc vi (d) t
0
x
khi h
42
00
3
00
( 1) 4 3 (1)
4 2( 1) 0 (2)
x m x m
x m x
(A) có nghim
0
x
.
Gii h (A),
0
(2) 0x
hoc
2
0
1
2
m
x
Thay
0
x
= 0 vào c m =
3
4
.
Thay
2
0
1
2
m
x
 c
2
2
1 ( 1)
43
22
mm
m


2
14 13 0 1 13.m m m m
Khi
3
m
4
thì
m
C
tip xúc vi (d) ti ch mm (0;3) nên
3
m
4
không tha mãn yêu cu ca bài toán.
Khi m= 1 thì
2
00
x 1 1x
,suy ra
m
C
tip xúc vi (d) tm (
).
Khi m = 13 thì
2
00
x 7 7x
,suy ra
m
C
tip xúc vi (d) tm (
7;3)
. Vy các giá tr m cn tìm là
m = 1
m = 13.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
28
Bài 18: Tìm tt c m trên Oy sao cho t  v c ít nht mt tip tuy th hàm s
2
4 2 1y x x x
.
A. M(0;m) vi
21m
B. M(0;m) vi
1
5
2
m
C. M(0;m) vi
1
1
2
m
D. M(0;m) vi
15m
Bài làm:: Xét
(0; )M m Oy
ng th   s  
y kx m
.
d là ti th t
0
x
khi h
2
0 0 0 0
0
2
00
4 2 1
41
1
4 2 1
x x x kx m
x
k
xx


có nghim
0
x
.
 nhc:
2
2
00
0 0 0 0
2
00
4
4 2 1
4 2 1
xx
x x x x m
xx

2 2 2
0 0 0 0 0 0
4 2 1 4 4 2 1x x x x m x x
0
0
2
00
1
()
4 2 1
x
m f x
xx

(*)
 t M k c ít nht mt tip tuy th
(*)
có ít nht mt nghim.
Xét hàm s f(
0
x
), ta có:
0
0 0 0
23
00
3
'( ) '( ) 0 0
( 4 2 1)
x
f x f x x
xx

Mt khác:
00
11
lim ( ) ; lim ( )
22
xx
f x f x
 
Bng bin thiên:
0
x

0

0
'( )fx
0
0
()fx
1
1
2
1
2
(*) có nghim
1
1
2
m
.
Vy M(0;m) vi
1
1
2
m
là nhm cn tìm.
Bài 19: Cho hàm s:
3
4 3 2y x x
 th là
C
.
Câu 1. Tìm
a
 
32
4 3 2 3 0x x a a
có hai nghim âm và mt nghi
A.
1
0
2
a
hoc
15a
. B.
02a
hoc
29a
.
C.
1
0
2
a
hoc
3
1
2
a
. D.
04a
hoc
6 89a
.
Bài làm: 1.  
32
4 3 2 3 0x x a a
     
32
4 3 2 2 3 2x x a a
.
o có hai nghim âm và mt nghi ng thng
2
2 3 2y a a
c th
3
4 3 2y x x
t   âm và m   th suy
ra:
2
1 2 3 2 2aa
tc ta có h:
2
2
0 2 3 1
2 3 0
aa
aa

hay
1
0
2
a
hoc
3
1
2
a
.
NGUYỄN BẢO VƯƠNG
CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
29
Câu 2. Tìm nhng thng
3y
 t  v ng thng tip xúc v th
C
.
A.
1m 
hoc
1
2
3
m
B.
1m 
hoc
11
32
m
C.
2m 
hoc
11
32
m
D.
3m 
hoc
1
1
2
m
Bài làm: 2. Gi s
;3Mm
m cn tìm và
d
ng thng qua
M
có h s góc là
k

dng:
3y k x m
.
ng thng
d
tip xúc v th
C
tm
00
;N x y
khi h :
3
0 0 0
3
0 0 0
4 3 2 3
4 3 2 ' 3 '
x x k x m
x x k x m


có nghim
0
x
, t h suy ra
2
0 0 0
2 1 4 2 3 1 3 1 0 1x x m x m


có nghim
0
x
.
Qua
M
k c
3
ng thng tip xúc vi
C
khi và ch 
1
có
3
nghim
0
x
, t
trình
2
00
4 2 3 1 3 1 0 2x m x m
có hai nghim phân bit khác
1
2
hay
1m 
hoc
11
32
m
.
Bài 20:
Câu 1. Tìm tham s
m
  th hàm s
m
C
:
2
1
x x m
y
x

vi
0m
ct trc hoành ti
2
m phân bit
,AB
sao cho tip tuyn ti
2
im
,AB
vuông góc vi nhau.
A.
1
5
m 
B.
1
3
m 
C.
1
5
m
D.
4
7
m 
Bài làm: 1. Hàm s ct trc hoành thm phân bit
,AB
có h s góc là
21
1
x
k
x
.
Ta có:
2
2
21
'
1
x x m
y
x
t
2
21g x x x m
.
Theo bài toán,
0gx
có hai nghim phân bit khác
1
.
, tip tuyn ti
A
và
B
vuông góc nhau tc
.1
AB
kk
 c
1
5
m 
.
Câu 2. Cho hàm s
2
2
2
x
y
x
 th là
C
ng thng
yx
nhm mà t  k c
2
tip tuyn
C
ng thi
2
tip tuyi nhau.
A.
53m
B.
5 53m
C.
6 23m
D.
5 23m
Bài làm: 2ng thng
d
m
;M m m
có h s góc là
k
ng:
y k x m m
.
d
tip xúc
C
t    
0
x
khi h :
2
0
0
0
2
00
2
0
2
2
28
2
x
k x m m
x
xx
k
x
có nghim
0
x
, t    c
5 23m
250 BÀI TẬP TRẮC
NGHIỆM ĐẠO HÀM TỰ
LUYỆN
TẬP 3. CHƯƠNG V. ĐẠO HÀM LỚP 11
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 ĐỂ GẶP THẦY VƯƠNG,
HOẶC LIÊN HỆ QUA:
LINK FACEBOOK Nguyễn Vương: https://www.facebook.com/phong.baovuong
TÀI LIỆU CHIA SẺ TẠI: http://tailieutoanhoc.vn/
Page: https://web.facebook.com/tracnghiemtoanthpt489/?ref=bookmarks
Gmail: baovuong7279@gmail.com
[ALBA – CHƯ SÊ – GIA LAI]
NGUYỄN BẢO VƯƠNG
TỔNG BIÊN SOẠN VÀ TỔNG HỢP
NGUYỄN BẢO VƢƠNG
CHƯƠNG V. ĐẠO HÀM
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
1
Mục lục
Tổng hợp lần 1. CHƯƠNG V: ĐẠO HÀM ......................................................... 2
BÀI 1: ĐỊNH NGHĨA VÀ Ý NGHĨA CỦA ĐẠO HÀM ............................................................... 2
BÀI 2: QUY TẮC TÍNH ĐẠO HÀM ...................................................................................... 3
BÀI 3: ĐẠO HÀM CỦA HÀM SỐ LƯỢNG GIÁC ................................................................... 6
BÀI 4: VI PHÂN ............................................................................................................... 8
BÀI 5: ĐẠO HÀM CẤP CAO .............................................................................................. 9
Tổng hợp lần 2. CHƯƠNG V. ĐẠO HÀM ......................................................... 11
Tổng hợp lần 3. CHƯƠNG V. ĐẠO HÀM ......................................................... 24
NGUYỄN BẢO VƢƠNG
CHƯƠNG V. ĐẠO HÀM
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
2
Tổng hợp lần 1. CHƯƠNG V: ĐẠO HÀM
BÀI 1: ĐỊNH NGHĨA VÀ Ý NGHĨA CỦA ĐẠO HÀM
Câu 1. Cho hàm số f(x) liên tục tại x
0
. Đạo hàm của f(x) tại x
0
là:
A. f(x
0
) B.
h
xfhxf )()(
00
C.
00
0
( ) ( )
h
f x h f x
lim
h

(nếu tồn tại giới hạn) D.
00
0
( ) ( )
h
f x h f x h
lim
h
(nếu tồn tại giới hạn)
Câu 2. Cho hàm số f(x) là hàm số trên R định bởi f(x) = x
2
và x
0
R. Chọn câu đúng:
A. f
/
(x
0
) = x
0
B. f
/
(x
0
) = x
0
2
C. f
/
(x
0
) = 2x
0
D. f
/
(x
0
) không tồn
tại.
Câu 3. Cho hàm số f(x) xác định trên
0;
bởi f(x) =
1
x
. Đạo hàm của f(x) tại x
0
=
2
là:
A.
1
2
B–
1
2
C.
1
2
D. –
1
2
Câu 4. Phƣơng trình tiếp tuyến của đồ thị của hàm số y = (x+1)
2
(x–2) tại điểm có hoành độ x = 2 là:
A. y = –8x + 4 B. y = –9x + 18 C. y = –4x + 4 D. y = –8x + 18
Câu 5. Phƣơng trình tiếp tuyến của đồ thị của hàm số y = x(3–x)
2
tại điểm có hoành độ x = 2 là
A. y = –12x + 24 B. y = –12x + 26 C. y = 12x –24 D. y = 12x –26
Câu 6. Điểm M trên đồ thị hàm số y = x
3
– 3x
2
– 1 mà tiếp tuyến tại đó có hệ số góc k bé nhất trong tất cả các tiếp
tuyến của đồ thị thì M, k là:
A. M(1; –3), k = –3 B. M(1; 3), k = –3 C. M(1; –3), k = 3 D. M(–1; –3), k = –3
Câu 7. Cho hàm số y =
1
ax b
x
có đồ thị cắt trục tung tại A(0; –1), tiếp tuyến tại A có hệ số góc k = –3. Các giá trị
của a, b là:
A. a = 1; b=1 B. a = 2; b=1 C. a = 1; b=2 D. a = 2; b=2
Câu 8. Cho hàm số y =
2
2
1
x mx m
x

. Giá trị m để đồ thị hàm số cắt trục Ox tại hai điểm và tiếp tuyến của đồ thị
tại hai điểm đó vuông góc là:
A. 3 B. 4 C. 5 D. 7
Câu 9. Cho hàm số y =
2
31
2
xx
x

và xét các phƣơng trình tiếp tuyến có hệ số góc k = 2 của đồ thị hàm số là:
A. y = 2x–1, y = 2x–3 B. y = 2x–5, y = 2x–3 C. y = 2x–1, y = 2x–5 D. y = 2x–1, y =
2x+5
Câu 10. Cho hàm số y =
2
33
2
xx
x

, tiếp tuyến của đồ thị hàm số vuông góc với đƣờng thẳng
3y – x + 6 là:
A. y = –3x – 3; y= –3x– 4 B. y = –3x – 3; y= –3x + 4 C. y = –3x + 3; y= –3x–4 D. y = –3x–3; y=3x–
4
NGUYỄN BẢO VƢƠNG
CHƯƠNG V. ĐẠO HÀM
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
3
Câu 11. Tìm m để tiếp tuyến của đồ thị hàm số y = (2m – 1)x
4
– m +
5
4
tại điểm có hoành độ x = –1 vuông góc với
đƣờng thẳng 2x – y – 3 = 0
A.
2
3
B.
1
6
C.
1
6
D.
5
6
Câu 12. Cho hàm số
2
2
x
y
x
, tiếp tuyến của đồ thị hàm số kẻ từ điểm (–6; 4) là:
A. y = –x–1, y =
17
42
x
B. y= –x–1, y =–
17
42
x
C. y = –x+1, y =–
17
42
x
D. y= –x+1, y =
17
42
x
Câu 13. Tiếp tuyến kẻ từ điểm (2; 3) tới đồ thị hàm số
34
1
x
y
x
là:
A. y = 3x; y = x+1 B. y = –3x; y = x+1 C. y = 3; y = x–1 D. y = 3–x; y = x+1
Câu 14. Cho hàm số y = x
3
– 6x
2
+ 7x + 5 (C), trên (C) những điểm có hệ số góc tiếp tuyến tại điểm nào bằng 2?
A. (–1; –9); (3; –1) B. (1; 7); (3; –1) C. (1; 7); (–3; –97) D. (1; 7); (–1; –9)
Câu 15. Tìm hệ số góc của tiếp tuyến với đồ thị y = tanx tại điểm có hoành độ x =
4
:
A. k = 1 B. k =
1
2
C. k =
2
2
D. 2
Câu 16. Cho đƣờng cong (C): y = x
2
. Phƣơng trình tiếp tuyến của (C) tại điểm M(–1; 1) là:
A. y = –2x + 1 B. y = 2x + 1 C. y = –2x – 1 D. y = 2x – 1
Câu 17. Cho hàm số
2
2
xx
y
x
. Phƣơng trình tiếp tuyến tại A(1; –2) là:
A. y = –4(x–1) – 2 B. y = –5(x–1) + 2 C. y = –5(x–1) – 2 D. y = –3(x–1) – 2
Câu 18. Cho hàm số y =
1
3
x
3
– 3x
2
+ 7x + 2. Phƣơng trình tiếp tuyến tại A(0; 2) là:
A. y = 7x +2 B. y = 7x – 2 C. y = –7x + 2 D. y = –7x –2
Câu 19. Gọi (P) là đồ thị hàm số y = 2x
2
– x + 3. Phƣơng trình tiếp tuyến với (P) tại điểm mà (P) cắt trục tung là:
A. y = –x + 3 B. y = –x – 3 C. y = 4x – 1 D. y = 11x + 3
Câu 20. Đồ thị (C) của hàm số
31
1
x
y
x
cắt trục tung tại điểm A. Tiếp tuyến của (C) tại A có phƣơng trình là:
A. y = –4x – 1 B. y = 4x – 1 C. y = 5x –1 D. y = – 5x –1
Câu 21. Gọi (C) là đồ thị của hàm số y = x
4
+ x. Tiếp tuyến của (C) vuông góc với đƣờng thẳng d: x + 5y = 0 có
phƣơng trình là:
A. y = 5x – 3 B. y = 3x – 5 C. y = 2x – 3 D. y = x + 4
BÀI 2: QUY TẮC TÍNH ĐẠO HÀM
Câu 22. Cho hàm số
2
2
xx
y
x
đạo hàm của hàm số tại x = 1 là:
A. y
/
(1) = –4 B. y
/
(1) = –5 C. y
/
(1) = –3 D. y
/
(1) = –2
NGUYỄN BẢO VƢƠNG
CHƯƠNG V. ĐẠO HÀM
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
4
Câu 23. Cho hàm số
2
4
x
y
x
. y
/
(0) bằng:
A. y
/
(0)=
1
2
B. y
/
(0)=
1
3
C. y
/
(0)=1 D. y
/
(0)=2
Câu 24. Cho hàm số f(x) xác định trên R bởi f(x) =
2
x
. Giá trị f
/
(0) bằng:
A. 0 B. 2 C. 1 D. Không tồn tại
Câu 25. Đạo hàm cấp 1của hàm số y = (1–x
3
)
5
là:
A. y
/
= 5(1–x
3
)
4
B. y
/
= –15(1–x
3
)
4
C. y
/
= –3(1–x
3
)
4
D. y
/
= –5(1–x
3
)
4
Câu 26. Đạo hàm của hàm số f(x) = (x
2
+ 1)
4
tại điểm x = –1 là:
A. –32 B. 30 C. –64 D. 12
Câu 27. Hàm số
21
1
x
y
x
có đạo hàm là:
A. y
/
= 2 B.
/
2
1
( 1)
y
x

C.
/
2
3
( 1)
y
x

D.
/
2
1
( 1)
y
x
Câu 28. Hàm số
3
1
3
xx
có đạo hàm là:
A.
2
/
2
2
(1 )
xx
y
x

B.
2
/
2
2
(1 )
xx
y
x
C. y
/
= –2(x – 2) D.
2
/
2
2
(1 )
xx
y
x
Câu 29. Cho hàm số f(x) =
2
1
1
x
x




. Đạo hàm của hàm số f(x) là:
A.
/
3
2(1 )
()
(1 )
x
fx
x

B.
/
3
2(1 )
()
(1 )
x
fx
xx

C.
/
2
2(1 )
()
(1 )
x
fx
xx
D.
/
2(1 )
()
(1 )
x
fx
x
Câu 30. Cho hàm số y = x
3
– 3x
2
– 9x – 5. Phƣơng trình y
/
= 0 có nghiệm là:
A. {–1; 2} B. {–1; 3} C. {0; 4} D. {1; 2}
Câu 31. Cho hàm số f(x) xác định trên R bởi f(x) = 2x
2
+ 1. Giá trị f
/
(–1) bằng:
A. 2 B. 6 C. –6 D. 3
Câu 32. Cho hàm số f(x) xác định trên R bởi f(x)
3
x
.Giá trị f
/
(–8) bằng:
A.
1
12
B. –
1
12
C.
1
6
D. –
1
6
Câu 33. Cho hàm số f(x) xác định trên R \{1} bởi
2
()
1
x
fx
x
. Giá trị f
/
(–1) bằng:
A.
1
2
B. –
1
2
C. –2 D. Không tồn tại
NGUYỄN BẢO VƢƠNG
CHƯƠNG V. ĐẠO HÀM
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
5
Câu 34. Cho hàm số f(x) xác định bởi
2
11
( 0)
()
0 ( 0)
x
x
fx
x
x

. Giá trị f
/
(0) bằng:
A. 0 B. 1 C.
1
2
D. Không tồn tại.
Câu 35. Cho hàm số f(x) xác định trên R bởi f(x) = ax + b, với a, b là hai số thực đã cho. chọn câu đúng:
A. f
/
(x) = a B. f
/
(x) = –a C. f
/
(x) = b D. f
/
(x) = –b
Câu 36. Cho hàm số f(x) xác định trên R bởi f(x) = –2x
2
+ 3x. Hàm số có đạo hàm f
/
(x) bằng:
A. –4x – 3 B. –4x +3 C. 4x + 3 D. 4x – 3
Câu 37. Cho hàm số f(x) xác định trên
0;D
cho bởi f(x) = x
x
có đạo hàm là:
A. f
/
(x) =
1
2
x
B. f
/
(x) =
3
2
x
C. f
/
(x) =
1
2
x
x
D. f
/
(x) =
2
x
x
Câu 38. Cho hàm số f(x)=
3
()k x x k R
. Để f
/
(1)=
3
2
thì ta chọn:
A. k = 1 B. k = –3 C. k = 3 D. k =
9
2
Câu 39. Hàm số f(x) =
2
1
x
x



xác định trên
0;D 
. Có đạo hàm của f là:
A. f
/
(x) = x +
1
x
–2 B. f
/
(x) = x –
2
1
x
C. f
/
(x) =
1
x
x
D. f
/
(x) = 1 +
2
1
x
Câu 40. Hàm số f(x) =
3
1
x
x



xác định trên
0;D 
. Đạo hàm của hàm f(x) là:
A. f
/
(x) =
2
3 1 1 1
2
x
x x x x x



B. f
/
(x) =
2
3 1 1 1
2
x
x x x x x



C. f
/
(x) =
2
3 1 1 1
2
x
x x x x x



D. f
/
(x) =
31
3x x x
x x x
Câu 41. Cho hàm số f(x) = –x
4
+ 4x
3
– 3x
2
+ 2x + 1 xác định trên R. Giá trị f
/
(–1) bằng:
A. 4 B. 14 C. 15 D. 24
Câu 42. Cho hàm số f(x) =
21
1
x
x
xác định R\{1}. Đạo hàm của hàm số f(x) là:
A. f
/
(x) =
2
2
1x
B. f
/
(x) =
2
3
1x
C. f
/
(x) =
2
1
1x
D. f
/
(x) =
2
1
1x
Câu 43. Cho hàm số f(x) =
3
1
1
x

xác định R
*
. Đạo hàm của hàm số f(x) là:
A. f
/
(x) =
3
1
3
xx
B. f
/
(x) =
3
1
3
xx
C. f
/
(x) =
3
1
3xx
D. f
/
(x) =
3
2
1
3xx
Câu 44. Với
2
25
()
1
xx
fx
x

. f
/
(x) bằng:
NGUYỄN BẢO VƢƠNG
CHƯƠNG V. ĐẠO HÀM
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
6
A. 1 B. –3 C. –5 D. 0
Câu 45. Cho hàm số
2
()
4
x
y f x
x

. Tính y
/
(0) bằng:
A. y
/
(0)=
1
2
B. y
/
(0)=
1
3
C. y
/
(0)=1 D. y
/
(0)=2
Câu 46. Cho hàm số y =
2
2
xx
x
, đạo hàm của hàm số tại x = 1 là:
A. y
/
(1)= –4 B. y
/
(1)= –3 C. y
/
(1)= –2 D. y
/
(1)= –5
BÀI 3: ĐẠO HÀM CỦA HÀM SỐ LƯỢNG GIÁC
Câu 47. Hàm số y = sinx có đạo hàm là:
A. y
/
= cosx B. y
/
= – cosx C. y
/
= – sinx D.
/
1
cos
y
x
Câu 48. Hàm số y = cosx có đạo hàm là:
A. y
/
= sinx B. y
/
= – sinx C. y
/
= – cosx D.
/
1
sin
y
x
Câu 49. Hàm số y = tanx có đạo hàm là:
A. y
/
= cotx B. y
/
=
2
1
cos x
C. y
/
=
2
1
sin x
D. y
/
= 1 – tan
2
x
Câu 50. Hàm số y = cotx có đạo hàm là:
A. y
/
= – tanx B. y
/
= –
2
1
cos x
C. y
/
= –
2
1
sin x
D. y
/
= 1 + cot
2
x
Câu 51. Hàm số y =
1
2
(1+ tanx)
2
có đạo hàm là:
A. y
/
= 1+ tanx B. y
/
= (1+tanx)
2
C. y
/
= (1+tanx)(1+tanx)
2
D. y
/
= 1+tan
2
x
Câu 52. Hàm số y = sin
2
x.cosx có đạo hàm là:
A. y
/
= sinx(3cos
2
x – 1) B. y
/
= sinx(3cos
2
x + 1) C. y
/
= sinx(cos
2
x + 1) D. y
/
= sinx(cos
2
x –
1)
Câu 53. Hàm số y =
sin x
x
có đạo hàm là:
A.
/
2
cos sinx x x
y
x
B.
/
2
cos sinx x x
y
x
C.
/
2
sin cosx x x
y
x
D.
/
2
sin cosx x x
y
x
Câu 54. Hàm số y = x
2
.cosx có đạo hàm là:
A. y
/
= 2xcosx – x
2
sinx B. y
/
= 2xcosx + x
2
sinx C. y
/
= 2xsinx – x
2
cosx D. y
/
= 2xsinx +
x
2
cosx
Câu 55. Hàm số y = tanx – cotx có đạo hàm là:
A. y
/
=
2
1
cos 2x
B. y
/
=
2
4
sin 2x
C. y
/
=
2
4
cos 2x
D. ) y
/
=
2
1
sin 2x
NGUYỄN BẢO VƢƠNG
CHƯƠNG V. ĐẠO HÀM
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
7
Câu 56. Hàm số y =
2 sin 2 cosxx
có đạo hàm là:
A.
/
11
sin cos
y
xx

B.
/
11
sin cos
y
xx

C.
/
cos sin
sin cos
xx
y
xx

D.
/
cos sin
sin cos
xx
y
xx

Câu 57. Hàm số y = f(x) =
2
cos( )x
có f
/
(3) bằng:
A.
2
B.
8
3
C.
43
3
D. 0
Câu 58. Hàm số y = tan
2
2
x
có đạo hàm là:
A.
/
2
sin
2
cos
2
x
y
x
B.
/
3
2sin
2
cos
2
x
y
x
C.
/
3
sin
2
2cos
2
x
y
x
D. y
/
= tan
3
2
x
Câu 59. Hàm số y =
cot2x
có đạo hàm là:
A.
2
/
1 cot 2
cot2
x
y
x
B.
2
/
(1 cot 2 )
cot2
x
y
x

C.
2
/
1 tan 2
cot2
x
y
x
D.
2
/
(1 tan 2 )
cot2
x
y
x

Câu 60. Cho hàm số y = cos3x.sin2x. y
/
3



bằng:
A. y
/
3



= –1 B. y
/
3



= 1 C. y
/
3



= –
1
2
D. y
/
3



=
1
2
Câu 61. Cho hàm số y =
cos2
1 sin
x
x
. y
/
6



bằng:
A. y
/
6



= 1 B. y
/
6



= –1 C. y
/
6



=2 D. y
/
6



=–2
Câu 62. Xét hàm số f(x) =
3
cos2x
. Chọn câu sa i:
A.
1
2
f




B.
/
3
2
2sin2
()
3 cos 2
x
fx
x
C.
/
1
2
f



D. 3.y
2
.y
/
+ 2sin2x =
0
Câu 63. Cho hàm số y = f(x) =
sin cosxx
. Giá trị
2
/
16
f



bằng:
A. 0 B.
2
C.
2
D.
22
Câu 64. Cho hàm số
( ) tan coty f x x x
. Giá trị
/
4
f



bằng:
NGUYỄN BẢO VƢƠNG
CHƯƠNG V. ĐẠO HÀM
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
8
A.
2
B.
2
2
C. 0 D.
1
2
Câu 65. Cho hàm số
1
()
sin
y f x
x

Giá trị
/
2
f



bằng:
A. 1 B.
1
2
C. 0 D. Không tồn tại.
Câu 66. Xét hàm số
5
( ) 2sin
6
y f x x



Giá trị
/
6
f



bằng:
A. –1 B. 0 C. 2 D. –2
Câu 67. Cho hàm số
2
( ) tan
3
y f x x



Giá trị
/
0f
bằng:
A. 4 B.
3
C. –
3
D. 3
Câu 68. Cho hàm số
( ) 2siny f x x
. Đạo hàm của hàm số y là:
A.
/
2cosyx
B.
/
1
cosyx
x
C.
/
1
2 cosyx
x
D.
/
1
cos
y
xx
Câu 69. Cho hàm số y = cos3x.sin2x. Tính
/
3
y



bằng:
A.
/
1
3
y




B.
/
1
32
y



C.
/
1
32
y




D.
/
1
3
y



Câu 70. Cho hàm số
cos
()
1 sin
x
y f x
x

Tính
/
6
y



bằng:
A.
/
6
y



=1 B.
/
6
y



=–1 C.
/
6
y



=2 D.
/
6
y



=–2
BÀI 4: VI PHÂN
Câu 71. Cho hàm số y = f(x) = (x – 1)
2
. Biểu thức nào sau đây chỉ vi phân của hàm số f(x)?
A. dy = 2(x – 1)dx B. dy = (x–1)
2
dx C. dy = 2(x–1) D. dy = (x–1)dx
Câu 72. Xét hàm số y = f(x) =
2
1 cos 2x
. Chọn câu đúng:
A.
2
sin4
()
2 1 cos 2
x
df x dx
x
B.
2
sin4
()
1 cos 2
x
df x dx
x
C.
2
cos2
()
1 cos 2
x
df x dx
x
D.
2
sin2
()
2 1 cos 2
x
df x dx
x
Câu 73. Cho hàm số y = x
3
– 5x + 6. Vi phân của hàm số là:
A. dy = (3x
2
– 5)dx B. dy = –(3x
2
– 5)dx C. dy = (3x
2
+ 5)dx D. dy = (–3x
2
+ 5)dx
Câu 74. Cho hàm số y =
3
1
3x
. Vi phân của hàm số là:
A.
1
4
dy dx
B.
4
1
dy dx
x
C.
4
1
dy dx
x

D.
4
dy x dx
NGUYỄN BẢO VƢƠNG
CHƯƠNG V. ĐẠO HÀM
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
9
Câu 75. Cho hàm số y =
2
1
x
x
. Vi phân của hàm số là:
A.
2
1
dx
dy
x
B.
2
3
1
dx
dy
x
C.
2
3
1
dx
dy
x
D.
2
1
dx
dy
x

Câu 76. Cho hàm số y =
2
1
1
xx
x

. Vi phân của hàm số là:
A.
2
2
22
( 1)
xx
dy dx
x


B.
2
21
( 1)
x
dy dx
x
C.
2
21
( 1)
x
dy dx
x

D.
2
2
22
( 1)
xx
dy dx
x

Câu 77. Cho hàm số y = x
3
– 9x
2
+ 12x–5. Vi phân của hàm số là:
A. dy = (3x
2
– 18x+12)dx B. dy = (–3x
2
– 18x+12)dx
C. dy = –(3x
2
– 18x+12)dx D. dy = (–3x
2
+ 18x–12)dx
Câu 78. Cho hàm số y = sinx – 3cosx. Vi phân của hàm số là:
A. dy = (–cosx+ 3sinx)dx B. dy = (–cosx–3sinx)dx
C. dy = (cosx+ 3sinx)dx D. dy = –(cosx+ 3sinx)dx
Câu 79. Cho hàm số y = sin
2
x. Vi phân của hàm số là:
A. dy = –sin2xdx B. dy = sin2xdx C. dy = sinxdx D. dy = 2cosxdx
Câu 80. Vi phân của hàm số
tan x
y
x
là:
A.
2
2
4 cos
x
dy dx
x x x
B.
2
sin(2 )
4 cos
x
dy dx
x x x
C.
2
2 sin(2 )
4 cos
xx
dy dx
x x x
D.
2
2 sin(2 )
4 cos
xx
dy dx
x x x

Câu 81. Hàm số y = xsinx + cosx có vi phân là:
A. dy = (xcosx – sinx)dx B. dy = (xcosx)dx
C. dy = (cosx – sinx)dx D. dy = (xsinx)dx
Câu 82. Hàm số y =
2
1
x
x
. Có vi phân là:
A.
2
22
1
( 1)
x
dy dx
x
B.
2
2
( 1)
x
dy dx
x
C.
2
2
1
( 1)
x
dy dx
x
D.
22
1
( 1)
dy dx
x
BÀI 5: ĐẠO HÀM CẤP CAO
Câu 83. Hàm số
2
x
y
x
có đạo hàm cấp hai là:
A. y
//
= 0 B.
//
2
1
2
y
x
C.
//
2
4
2
y
x

D.
//
2
4
2
y
x
Câu 84. Hàm số y = (x
2
+ 1)
3
có đạo hàm cấp ba là:
A. y
///
= 12(x
2
+ 1) B. y
///
= 24(x
2
+ 1) C. y
///
= 24(5x
2
+ 3) D. y
///
= –12(x
2
+ 1)
NGUYỄN BẢO VƢƠNG
CHƯƠNG V. ĐẠO HÀM
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
10
Câu 85. Hàm số y =
25x
có đạo hàm cấp hai bằng:
A.
//
1
(2 5) 2 5
y
xx

B.
//
1
25
y
x
C.
//
1
(2 5) 2 5
y
xx


D.
//
1
25
y
x

Câu 86. Hàm số y =
2
1
1
xx
x

có đạo hàm cấp 5 bằng:
A.
(5)
5
120
( 1)
y
x

B.
(5)
5
120
( 1)
y
x
C.
(5)
5
1
( 1)
y
x
D.
(5)
5
1
( 1)
y
x

Câu 87. Hàm số y =
2
1xx
có đạo hàm cấp hai bằng:
A.
3
//
22
23
11
xx
y
xx


B.
2
//
2
21
1
x
y
x
C.
3
//
22
23
11
xx
y
xx

D.
2
//
2
21
1
x
y
x

Câu 88. Cho hàm số f(x) = (2x+5)
5
. Có đạo hàm cấp 3 bằng:
A. f
///
(x) = 80(2x+5)
3
B. f
///
(x) = 480(2x+5)
2
C. f
///
(x) = –480(2x+5)
2
D. f
///
(x) = –80(2x+5)
3
Câu 89. Đạo hàm cấp 2 của hàm số y = tanx bằng:
A.
//
3
2sin
cos
x
y
x

B.
//
2
1
cos
y
x
C.
//
2
1
cos
y
x

D.
//
3
2sin
cos
x
y
x
Câu 90. Cho hàm số y = sinx. Chọn câu sai:
A.
/
sin
2
yx




B.
//
sinyx

C.
///
3
sin
2
yx




D.
(4)
sin 2yx

Câu 91. Cho hàm số y = f(x) =
2
23
1
xx
x

. Đạo hàm cấp 2 của f(x) là:
A.
//
2
1
2
(1 )
y
x

B.
//
3
2
(1 )
y
x
C.
//
3
2
(1 )
y
x
D.
//
4
2
(1 )
y
x
Câu 92. Xét hàm số y = f(x) =
cos 2
3
x



. Phƣơng trình f
(4)
(x) = –8 có nghiệm x
0;
2



là:
A. x =
2
B. x = 0 và x =
6
C. x = 0 và x =
3
D. x = 0 và x =
2
Câu 93. Cho hàm số y = sin2x. Hãy chọn câu đúng:
A. 4y – y
//
= 0 B. 4y + y
//
= 0 C. y = y
/
tan2x D. y
2
= (y
/
)
2
= 4
Câu 94. Cho hàm số y = f(x) =
1
x
xét 2 mệnh đề:
NGUYỄN BẢO VƢƠNG
CHƯƠNG V. ĐẠO HÀM
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
11
(I): y
//
= f
//
(x) =
3
2
x
(II): y
///
= f
///
(x) =
4
6
x
.
Mệnh đề nào đúng:
A. Chỉ (I) B. Chỉ (II) đúng C. Cả hai đều đúng D. Cả hai đều sai.
Câu 95. Nếu
//
3
2sin
()
cos
x
fx
x
, thì f(x) bằng:
A.
1
cos x
B. –
1
cos x
C. cotx D. tanx
Câu 96. Cho hàm số f(x) =
2
2
1
xx
x
xác định trên D = R\{1}. Xét 2 mệnh đề:
(I): y
/
= f
/
(x) =
2
2
1 0, 1
( 1)
x
x
, (II): y
//
= f
//
(x) =
2
4
0, 1
( 1)
x
x
Chọn mệnh đề đúng:
A. Chỉ có (I) đúng B. Chỉ có (II) đúng C. Cả hai đều đúng D. Cả hai đều sai.
Câu 97. Cho hàm số f(x) = (x+1)
3
. Giá trị f
//
(0) bằng:
A. 3 B. 6 C. 12 D. 24
Câu 98. Với
32
( ) sinf x x x
thì
//
2
f



bằng:
A. 0 B. 1 C. –2 D. 5
Câu 99. Giả sử h(x) = 5(x+1)
3
+ 4(x + 1). Tập nghiệm của phƣơng trình h
//
(x) = 0 là:
A. [–1; 2] B. (–; 0] C. {–1} D.
Câu 100. Cho hàm số
1
3
y
x
. Tính
3
1y
có kết quả bằng:
A.
3
3
(1)
8
y
B.
3
1
(1)
8
y
C.
3
3
(1)
8
y 
D.
3
1
(1)
4
y 
Câu 101. Cho hàm số y = f(x) = (ax+b)
5
(a, b là tham số). Tính f
(10)
(1)
A. f
(10)
(1)=0 B. f
(10)
(1) = 10a + b C. f
(10)
(1) = 5a D. f
(10)
(1)= 10a
Câu 102. Cho hàm số y = sin2x.cosx. Tính y
(4)
6



có kết quả là:
A.
4
11
3
22



B.
4
11
3
22



C.
4
11
3
22




D.
4
11
3
22




Tổng hợp lần 2. CHƯƠNG V. ĐẠO HÀM
Câu 1. Số gia của hàm số
2
2yx
tại điểm
0
2x
ứng với số gia
1x
bằng bao nhiêu?
A. 13 B. 9 C. 5 D. 2
Câu 2. Số gia của hàm số
2
1yx
tại điểm
0
2x
ứng với số gia
0,1x
bằng bao nhiêu?
A. – 0, 01 B. 0,21 C. 0,99 D. 11,1
Câu 3. Đạo hàm của hàm số
32
2 (4 3)y x x
bằng biểu thức nào sau đây?
A.
2
6 8 3xx
. B.
2
6 8 3xx
.
C.
2
2(3x 4 )x
. D.
2
2(3x 8 )x
NGUYỄN BẢO VƢƠNG
CHƯƠNG V. ĐẠO HÀM
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
12
Câu 4. Cho hàm số
32
( ) 3f x x x x
. Giá trị
( 1)f
bằng bao nhiêu?
A.
2
. B.
1
.
C.
0
. D.
2
.
Câu 5. Cho hàm số
2
3
g( ) 9
2
x x x
. Đạo hàm của hàm số g(x) dương trong trường hợp nào?
A.
3x
. B.
6x
.
C.
3x
. D.
3x 
.
Câu 6. Cho hàm số
32
( ) 3 3f x x x
. Đạo hàm của hàm số f(x) dương trong trường hợp nào?
A.
01xx
. B.
02xx
.
C.
02x
. D.
.
Câu 7. Cho hàm số
5
4
( ) 6
5
f x x
. Số nghiệm của phương trình
(x) 4f
là bao nhiêu?
A.
0
. B.
1
.
C.
2
. D. Nhiều hơn
2
nghiệm.
Câu 8. Cho hàm số
3
2
( ) 1
3
f x x
. Số nghiệm của phương trình
(x) 2f

là bao nhiêu?
A. 0. B. 1. C. 2. D. 3.
Câu 9. Cho hàm số
4
( ) 2f x x x
. Phương trình
(x) 2f
có bao nhiêu nghiệm?
A. 0. B. 1. C. 2. D. 3.
Câu 10. Cho hai hàm số
2
( ) 5f x x
;
2
3
( ) 9
2
g x x x
. Giá trị của x là bao nhiêu để
(x) ( )f g x

?
A.
4
. B. 4. C.
4
5
. D.
5
4
.
Câu 11. Hàm số nào sau đây có đạo hàm bằng
2(3 1)x
?
A.
3
22xx
. B.
2
3 2 5xx
.
C.
2
3x 5x
. D.
2
(3x 1)
Câu 12. Hàm số nào sau đây có đạo hàm bằng
3(2 1)x
?
A.
2
3
(2 1)
2
x
. B.
2
3xx
.
C.
3x( 1)x
. D.
3
23xx
Câu 13. Cho hàm số
32
( ) 2 3 36 1f x x x x
. Để
( ) 0fx
thì x có giá trị thuộc tập hợp nào?
A.
3;2
. B.
3; 2
.
C.
6;4
. D.
4; 6
.
Câu 14. Cho hàm số
32
( ) 2 7 5f x x x x
. Để
( ) 0fx
thì x có giá trị thuộc tập hợp nào?
A.
7
;1
3



. B.
7
1;
3



.
C.
7
;1
3



. D.
7
1;
3



.
Câu 15. Cho hàm số
32
( ) 2 7 3f x x x x
. Để
( ) 0fx
thì x có giá trị thuộc tập hợp nào?
NGUYỄN BẢO VƢƠNG
CHƯƠNG V. ĐẠO HÀM
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
13
A.
7
;1
3



. B.
7
1;
3



.
C.
7
;1
3



. D.
7
;1
3



.
Câu 16. Cho hàm số
32
1
( ) 2 2 8 1
3
f x x x x
. Để
( ) 0fx
thì x có giá trị thuộc tập hợp nào?
A.
22
. B.
22
.
C.
2; 2
. D.
.
Câu 17. Đạo hàm của hàm số
5
2
23yx
x
bằng biểu thức nào sau đây?
A.
4
2
2
10x
x
. B.
4
2
2
10x
x
.
C.
4
2
2
10 3x
x

. D.
2
2
10x
x
.
Câu 18. Đạo hàm của hàm số
5
4
( ) 2 5f x x
x
tại
1x 
bằng số nào sau đây?
A. 21. B. 14. C. 10. D. – 6 .
Câu 19. Cho
2
( ) 5f x x
;
2
( ) 2(8 )g x x x
. Bất phương trình
(x) ( )f g x

có nghiệm là?
A.
8
7
x
. B.
6
7
x
. C.
8
7
x
. D.
8
7
x 
.
Câu 20. Phương trình tiếp tuyến với đồ thị
32
21y x x x
tại điểm có hoành độ
0
1x 
là:
A.
83yx
. B.
87yx
.
C.
88yx
. D.
8 11yx
.
Câu 21. Tiếp tuyến với đồ thị
32
1y x x
tại điểm có hoành độ
0
1x
có phương trình là:
A.
yx
. B.
2yx
.
C.
21yx
. D.
2yx
.
Câu 22. Hệ số góc của tiếp tuyến với đồ thị
32
2 3 2y x x
tại điểm có hoành độ
0
2x
là:
A. 18. B. 14.
C. 12. D. 6.
Câu 23. Tiếp tuyến với đồ thị
32
y x x
tại điểm có hoành độ
0
2x 
có phương trình là:
A.
48yx
. B.
20 56yx
.
C.
20 14yx
. D.
20 24yx
.
Câu 24. Hệ số góc của tiếp tuyến với đồ thị hàm số
32
2 3 5y x x
tại điểm có hoành độ
2
là:
A. 38. B. 36. C. 12. D. – 12.
Câu 25. Hệ số góc của tiếp tuyến với đồ thị hàm số
4 3 2
21y x x x
tại điểm có hoành độ
1
là:
A. 11. B. 4. C. 3. D. – 3.
Câu 26. Tiếp tuyến với đồ thị hàm số
32
1y x x
tại điểm có hoành độ
0
1x 
có hệ số góc bằng:
A. 7. B. 5. C. 1. D. – 1.
NGUYỄN BẢO VƢƠNG
CHƯƠNG V. ĐẠO HÀM
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
14
Câu 27. Cho hàm số
42
( ) 2 3f x x x
. Với giá trị nào của x thì
()fx
dương?
A.
0x
. B.
0x
.
C.
1x 
. D.
10x
.
Câu 28. Cho hàm số
32
( ) 5f x x x x
. Với giá trị nào của x thì
()fx
âm?
A.
1
1
3
x
. B.
1
1
3
x
.
C.
1
1
3
x
. D.
2
2
3
x
.
Câu 29. Cho hàm số
3
1
()
3
f x mx x
. Với giá trị nào của m thì
1x 
là nghiệm của bất phương trình
( ) 2fx
?
A.
3m
. B.
3m
.
C.
3m
. D.
1m
.
Câu 30. Cho hàm số
3
( ) 2f x mx mx
. Với giá trị nào của m thì
1x
là nghiệm của bất phương trình
( ) 1fx
?
A.
1m 
. B.
1m 
.
C.
11m
. D.
1m
.
Câu 31. Cho hàm số
2
3
( ) 2
2
f x x x
. Đạo hàm của hàm số f(x) nhận giá trị dương khi x nhận giá trị thuộc
tập hợp nào dưới đây?
A.
2
;
3



. B.
2
;
3




.
C.
3
;
2



. D.
3
;
2




.
Câu 32. Cho hàm số
2
2
1
()
1
x
fx
x
. Đạo hàm của hàm số f(x) nhận giá trị âm khi x nhận giá trị thuộc tập
hợp nào dưới đây?
A.
;0
. B.
0;
.
C.
;1 1; 

. D.
1;1

.
Câu 33. Cho hàm số
32
1
( ) 3 2 18 2
3
f x x x x
. Để
(x) 0f
thì x có giá trị thuộc tập hợp nào dưới đây?
A.
3 2;
. B.
3 2;

. C.
. D. .
Câu 34. Cho hàm số
32
11
( ) 6 5
32
f x x x x
. Để
(x) 0f
thì x có giá trị thuộc tập hợp nào dưới đây?
A.
; 3 2; 
. B.
3;2
.
C.
2;3
. D.
; 4 3; 

.
Câu 35. Cho hàm số
32
11
( ) 12 1
32
f x x x x
. Để
(x) 0f
thì x có giá trị thuộc tập hợp nào dưới đây?
A.
; 3 4; 

. B.
3;4

.
NGUYỄN BẢO VƢƠNG
CHƯƠNG V. ĐẠO HÀM
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
15
C.
4;3

. D.
; 2 3; 
.
Câu 36. Cho hàm số
2
( ) 2 3f x x x
. Để
(x) 0f
thì x có giá trị thuộc tập hợp nào dưới đây?
A.
1
;
3




. B.
1
0;
3



.
C.
12
;
33



. D.
1
;
3




.
Câu 37. Đạo hàm của hàm số
2
( ) 5f x x x
bằng biểu thức nào sau đây?
A.
2
1
25xx
. B.
2
25
5
x
xx
.
C.
2
25
25
x
xx
. D.
2
25
5
x
xx
.
Câu 38. Đạo hàm của hàm số
2
( ) 2 3f x x
bằng biểu thức nào sau đây?
A.
2
6
23
x
x
. B.
2
2
6
2 2 3
x
x
.
C.
2
3
23
x
x
. D.
2
3
23
x
x
.
Câu 39. Đạo hàm của hàm số
( ) ( 2)( 3)f x x x
bằng biểu thức nào sau đây?
A.
25x
. B.
27x
.
C.
21x
. D.
25x
.
Câu 40. Đạo hàm của hàm số
23
()
21
x
fx
x
bằng biểu thức nào sau đây?
A.
2
12
21x
. B.
2
8
21x
.
C.
2
4
21x
. D.
2
4
21x
.
Câu 41. Đạo hàm của hàm số
4
()
21
x
fx
x
bằng biểu thức nào sau đây?
A.
2
7
21x
. B.
2
7
21x
.
C.
2
9
21x
. D.
2
9
21x
.
Câu 42. Đạo hàm của hàm số
4
()
25
x
fx
x
bằng biểu thức nào sau đây?
A.
2
18
25x
. B.
2
13
25x
.
C.
2
3
25x
. D.
2
22
25x
.
NGUYỄN BẢO VƢƠNG
CHƯƠNG V. ĐẠO HÀM
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
16
Câu 43. Đạo hàm của hàm số
23
()
21
x
fx
x
bằng biểu thức nào sau đây?
A.
2
7
21x
. B.
2
4
21x
.
C.
2
8
21x
. D.
2
1
21x
.
Câu 44. Hàm số nào sau đây có đạo hàm luôn dương với mọi giá trị thuộc tập xác định của hàm số đó?
A.
32
51
x
y
x
. B.
32
51
x
y
x
.
C.
2
21
x
y
x

. D.
2
1
x
y
x

.
Câu 45. Hàm số nào sau đây có đạo hàm luôn âm với mọi giá trị thuộc tập xác định của hàm số đó?
A.
2
1
x
y
x

. B.
2
1
x
y
x
.
C.
32
1
x
y
x
. D.
32
1
x
y
x
.
Câu 46. Tiếp tuyến với đồ thị hàm số
32
()
23
x
fx
x
tại điểm có hoành độ
0
1x
có hệ số góc bằng bao
nhiêu?
A.
13
B.
1
. C.
5
. D.
13
.
Câu 47. Tiếp tuyến với đồ thị hàm số
5
()
2
x
fx
x
tại điểm có hoành độ
0
3x
có hệ số góc bằng bao
nhiêu?
A.
3
B.
3
. C.
7
. D.
10
.
Câu 48. Đạo hàm của hàm số
35
()
3
x
f x x
x

tại điểm
1x
bằng bao nhiêu?
A.
3
B.
4
. C.
7
2
. D.
1
2
.
Câu 49. Đạo hàm của hàm số
3
( ) 4
3
x
f x x
x

tại điểm
1x
bằng bao nhiêu?
A.
5
8
B.
5
8
. C.
25
16
. D.
11
8
.
Câu 50. Đạo hàm của hàm số
1
( ) 4
1
x
f x x
x

tại điểm
1x
bằng bao nhiêu?
A.
1
2
B.
1
2
. C.
3
4
. D.
3
2
.
Câu 51. Đạo hàm của hàm số
4
( ) 2f x x x
tại điểm
1x
bằng bao nhiêu?
A.
17
2
B.
9
2
. C.
9
4
. D.
3
2
.
Câu 52. Đạo hàm của hàm số
3
( ) 5f x x x
tại điểm
1x
bằng bao nhiêu?
A.
7
2
B.
5
2
. C.
7
4
. D.
3
2
.
NGUYỄN BẢO VƢƠNG
CHƯƠNG V. ĐẠO HÀM
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
17
Câu 53. Đạo hàm của hàm số
2
1
()
1
fx
x
bằng biểu thức nào sau đây?
A.
2
2
1
x
x
. B.
2
2
2
1
x
x
.
C.
2
2
2
1
x
x
. D.
2
2
2
1
x
x
.
Câu 54. Đạo hàm của hàm số
2
1
()
1
fx
x
bằng biểu thức nào sau đây?
A.
2
2
2
2
1
x
x
. B.
2
2
2
1
x
x
.
C.
2
2
1
1x
. D.
2
2
2
1
x
x
.
Câu 55. Đạo hàm của hàm số
2
2
1
()
1
x
fx
x
bằng biểu thức nào sau đây?
A.
2
2
2
4
1
x
x
. B.
2
2
4
1
x
x
.
C.
2
2
2
1x
. D.
2
2
4
1
x
x
.
Câu 56. Đạo hàm của hàm số
2
1
()
2
fx
x
bằng biểu thức nào sau đây?
A.
2
2
2
2
x
x
. B.
2
2
2
2
x
x
.
C.
2
2
2
2 x
. D.
2
2
1
2 x
.
Câu 57. Đạo hàm của hàm số
2
2
1
2
x
y
x
bằng biểu thức nào sau đây?
A.
2
2
2
2
x
x
. B.
2
2
2
2
x
x
.
C.
2
2
2
2 x
. D.
2
2
1
2 x
.
Câu 58. Đạo hàm của hàm số
2
1
1
y
xx

bằng biểu thức nào sau đây?
A.
2
2
(2 1)
1
x
xx


. B.
2
2
2( 1)
1
x
xx


.
C.
2
2
(2 1)
1
x
xx


. D.
2
2
2(2 1)
1
x
xx

.
Câu 59. Đạo hàm của hàm số
2
2
1
1
xx
y
xx


bằng biểu thức nào sau đây?
NGUYỄN BẢO VƢƠNG
CHƯƠNG V. ĐẠO HÀM
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
18
A.
2
2
2(2 1)
1
x
xx

. B.
2
2
2(2 2)
1
x
xx

.
C.
2
2
2(2 1)
1
x
xx

. D.
2
2
2(2 1)
1
x
xx

.
Câu 60. Đạo hàm của hàm số
2
2
3
1
xx
y
xx


bằng biểu thức nào sau đây?
A.
2
2
2(2 1)
1
x
xx

. B.
2
2
4(2 1)
1
x
xx

.
C.
2
2
4(2 1)
1
x
xx

. D.
2
2
4(2 4)
1
x
xx

.
Câu 61. Đạo hàm của hàm số
2
1
21
y
xx

bằng biểu thức nào sau đây?
A.
2
2
(4 1)
21
x
xx

. B.
2
2
41
21
x
xx

.
C.
2
2
(4 1)
21
x
xx

. D.
2
2
1
21xx

.
Câu 62. Đạo hàm của hàm số
2
2
25
22
xx
y
xx


bằng biểu thức nào sau đây?
A.
2
2
3(4 1)
22
x
xx


. B.
2
2
3(4 1)
22
x
xx


.
C.
2
2
3
22xx

. D.
2
2
(4 1)
22
x
xx


.
Câu 63. Đạo hàm của hàm số
3 2 2
()y x x
bằng biểu thức nào sau đây?
A.
53
64xx
. B.
54
6 10 4x x x
.
C.
5 4 3
6 10 4x x x
. D.
5 4 3
6 10 4x x x
.
Câu 64. Đạo hàm của hàm số
5 2 2
( 2 )y x x
bằng biểu thức nào sau đây?
A.
93
10 16xx
. B.
9 6 3
10 14 16x x x
.
C.
9 6 3
10 28 16x x x
. D.
9 6 3
10 28 8x x x
.
Câu 65. Đạo hàm của hàm số
3 2 3
()y x x
bằng biểu thức nào sau đây?
A.
3 2 2
3( )xx
. B.
3 2 2 2
3( ) (3 2 )x x x x
.
C.
3 2 2 2
3( ) (3 )x x x x
. D.
3 2 2
3( )(3 2 )x x x x
.
Câu 66. Đạo hàm của hàm số
2
32
y x x x
bằng biểu thức nào sau đây?
A.
2
3 2 2
2 3 2 1x x x x x
.
B.
3 2 2 2
2 3 2x x x x x x
.
C.
3 2 2
2 3 2x x x x x
.
NGUYỄN BẢO VƢƠNG
CHƯƠNG V. ĐẠO HÀM
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
19
D.
3 2 2
2 3 2 1x x x x x
.
Câu 67. Đạo hàm của hàm số
2
23
21
x
y
x


bằng biểu thức nào sau đây?
A.
2
14 2 3
.
21
21
x
x
x

. B.
2
4 2 3
.
21
21
x
x
x

.
C.
2
16 2 3
.
21
21
x
x
x
. D.
23
2
21
x
x


.
Câu 68. Đạo hàm của hàm số
22
(2 1)y x x
bằng biểu thức nào sau đây?
A.
2
(4 1)x
. B.
22
2(2 1)(4 )x x x x
.
C.
22
2(2 1) (4 1)x x x
. D.
2
2(2 1)(4 1)x x x
.
Câu 69. Đạo hàm của hàm số
2
3 2 12y x x
bằng biểu thức nào sau đây?
A.
2
1
2 3 2 12xx
. B.
2
4
2 3 2 12
x
xx
.
C.
2
31
2 3 2 12
x
xx

. D.
2
6
2 3 2 12
x
xx
.
Câu 70. Đạo hàm của hàm số
23
4y x x
bằng biểu thức nào sau đây?
A.
23
1
24xx
. B.
2
23
6
24
xx
xx
.
C.
2
23
12
24
xx
xx
. D.
2
23
2
24
xx
xx
.
Câu 71. Cho hàm số
22yx
. Biểu thức
(1) (1)ff
có giá trị là bao nhiêu?
A.
1
2
. B.
3
2
.
C.
9
4
. D.
5
2
.
Câu 72. Cho
2
2
( ) 3 3f x x x
. Biểu thức
có giá trị là bao nhiêu?
A.
1
B.
1
. C.
2
. D.
12
.
Câu 73. Cho
2
2
( ) 3 4 1f x x x
. Biểu thức
(2)f
có giá trị là bao nhiêu?
A.90 B. 80. C. 40. D.10.
Câu 74. Đạo hàm của hàm số
tan3yx
bằng biểu thức nào sau đây?
A.
2
3
cos 3
x
x
. B.
2
3
cos 3x
.
C.
2
3
cos 3x
. D.
2
3
sin 3x
.
Câu 75. Đạo hàm của hàm số
tan2yx
tại x = 0 là số nào sau đây?
A.
2
B.
0
. C.
1
. D.
2
.
Câu 76. Đạo hàm của hàm số
cosyx
bằng biểu thức nào sau đây?
NGUYỄN BẢO VƢƠNG
CHƯƠNG V. ĐẠO HÀM
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
20
A.
os
2 cos
cx
x
. B.
sin
2 cos
x
x
.
C.
sin
2 cos
x
x
. D.
sin
cos
x
x
.
Câu 77. Đạo hàm của hàm số
cos2yx
bằng biểu thức nào sau đây?
A.
sin2
2 cos2
x
x
. B.
sin2
cos2
x
x
.
C.
sin2
cos2
x
x
. D.
sin2
2 cos
x
x
.
Câu 78. Đạo hàm của hàm số
sinyx
bằng biểu thức nào sau đây?
A.
os
2 sin
cx
x
. B.
cos
2 sin
x
x
.
C.
cos
sin
x
x
. D.
1
2 sin x
.
Câu 79. Đạo hàm của hàm số
sin3yx
bằng biểu thức nào sau đây?
A.
os3
2 sin 3
cx
x
. B.
3cos3
2 sin 3
x
x
.
C.
3cos3
2 sin3
x
x
. D.
os3
2 sin 3
cx
x
.
Câu 80. Đạo hàm của hàm số
tan5yx
bằng biểu thức nào sau đây?
A.
2
1
cos 5x
. B.
2
5
sin 5x
.
C.
2
3
cos 5x
. D.
2
5
cos 5x
.
Câu 81. Đạo hàm của hàm số
tan3yx
tại x = 0 có giá trị là bao nhiêu?
A.
3
. B.
0
.
C.
3
. D. Không xác định.
Câu 82. Đạo hàm của hàm số
2
tan 5yx
bằng biểu thức nào sau đây?
A.
2tan5x
. B.
3
10sin5
cos 5
x
x
.
C.
3
10sin5
cos 5
x
x
. D.
3
5sin 5
cos 5
x
x
.
Câu 83. Hàm số nào sau đây có đạo hàm
siny x x
?
A.
cosxx
. B.
sinx cosxx
.
C.
sinx oscx
. D.
cos sinxxx
.
Câu 84. Đạo hàm của hàm số
cos 3
3
yx




bằng biểu thức nào sau đây?
A.
sin 3
3
x



. B.
sin 3
3
x




.
NGUYỄN BẢO VƢƠNG
CHƯƠNG V. ĐẠO HÀM
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
21
C.
3sin 3
3
x




. D.
3sin 3
3
x



.
Câu 85. Đạo hàm của hàm số
sin 2
2
yx




bằng biểu thức nào sau đây?
A.
cos 2
2
x



. B.
cos 2
2
x




.
C.
2cos 2
2
x




. D.
2cos 2
2
x



.
Câu 86. Đạo hàm của hàm số
10
2
( ) 3f x x
bằng biểu thức nào sau đây?
A.
9
2
10 3xx
. B.
9
2
10 3 x
.
C.
9
2
20 3xx
. D.
9
2
20 3xx
.
Câu 87. Đạo hàm số của hàm số
2sin2 os2xy x c
bằng biểu thức nào nào sau đây?
A.
4cos2 2sin2xx
. B.
4cos2 2sin2xx
.
C.
2cos2 2sin2xx
. D.
4cos2 2sin2xx
.
Câu 88. Đạo hàm số của hàm số
sin3 4 os2xy x c
bằng biểu thức nào nào sau đây?
A.
cos3 4sin2xx
. B.
3cos3 4sin2xx
.
C.
3cos3 8sin2xx
. D.
3cos3 8sin2xx
.
Câu 89. Đạo hàm của hàm số
sin5yx
bằng biểu thức nào sau đây?
A.
5 os5
2 sin 5
cx
x
. B.
5 os5
sin5
cx
x
.
C.
os5
2 sin 5
cx
x
. D.
5 os5
2 sin 5
cx
x
.
Câu 90. Đạo hàm của hàm số
( ) cos4f x x
bằng biểu thức nào sau đây?
A.
2sin4
cos4
x
x
. B.
2cos4
cos4
x
x
.
C.
sin4
2 cos4
x
x
. D.
2sin4
cos4
x
x
.
Câu 91. Cho
22
( ) cos sinf x x x
. Biểu thức
4
f



có giá trị là bao nhiêu?
A.
2
B.
0
. C.
1
. D.
2
.
Câu 92. Cho
( ) sin2f x x
. Biểu thức
4
f



có giá trị là bao nhiêu?
A.
1
. B.
0
.
C.
1
. D. Không xác định.
Câu 93. Đạo hàm số của hàm số
3
os 4xyc
bằng biểu thức nào nào sau đây?
A.
2
3sin 4x
. B.
2
3cos 4x
.
C.
2
12cos 4 .sin4xx
. D.
2
3cos 4 .sin4xx
.
Câu 94. Đạo hàm số của hàm số
2
sin 3xy
bằng biểu thức nào nào sau đây?
NGUYỄN BẢO VƢƠNG
CHƯƠNG V. ĐẠO HÀM
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
22
A.
6sin6x
. B.
3sin6x
.
C.
sin6x
. D.
2sin3x
.
Câu 95. Đạo hàm số của hàm số
(x) sin3 os2xf x c
bằng biểu thức nào nào sau đây?
A.
cos3 sin2xx
. B.
cos3 sin2xx
.
C.
3cos3 2sin2xx
. D.
3cos3 2sin2xx
.
Câu 96. Cho
( ) tan4f x x
. Giá trị
(0)f
bằng số nào sau đây?
A.
4
B.
1
. C.
1
. D.
4
.
Câu 97. Đạo hàm của hàm số
cot2yx
bằng biểu thức nào sau đây?
A.
2
1
sin 2x
. B.
2
2
sin 2x
.
C.
2
2
cos 2x
. D.
2
2
cos 2x
.
Câu 98. Đạo hàm của hàm số
4
cot 2yx
bằng biểu thức nào sau đây?
A.
3
5
8cos 2
sin 2
x
x
. B.
3
6
8cos 2
sin 2
x
x
.
C.
3
2
8cos 2
sin 2
x
x
. D.
3
5
4cos 2
sin 2
x
x
.
Câu 99. Đạo hàm của hàm số
cotyx
bằng biểu thức nào sau đây?
A.
1
2 cot x
. B.
sinx
2 cot x
.
C.
2
1
sin cotxx
. D.
2
1
2sin cotxx
.
Câu 100. Cho
66
( ) sin osf x x c x
và
22
g( ) 3sin . osx x c x
. Tổng
( ) g (x)fx

bằng biểu thức nào sau đây?
A.
55
6(sin os sinx.cosx)x c x
.
B.
55
6(sin os sinx.cosx)x c x
.
C. 6.
D. 0.
Câu 101. Vi phân của hàm số
5
2
25yx
x
là biểu thức nào sau đây?
A.
4
2
2
10 5x dx
x




. B.
4
2
2
10x dx
x



.
C.
4
2
2
10x dx
x



. D.
2
2
10x dx
x



.
Câu 102. Vi phân của hàm số
2
5y x x
là biểu thức nào sau đây?
A.
2
1
25
dx
xx
. B.
2
25
5
x
dx
xx
.
C.
2
25
25
x
dx
xx
. D.
2
25
25
x
dx
xx
.
NGUYỄN BẢO VƢƠNG
CHƯƠNG V. ĐẠO HÀM
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
23
Câu 103. Vi phân của hàm số
23
21
x
y
x
là biểu thức nào sau đây?
A.
2
7
(2 1)
dx
x
. B.
2
8
(2 1)
dx
x
.
C.
2
4
(2 1)
dx
x
. D.
2
4
(2 1)
dx
x
.
Câu 104. Vi phân của hàm số
tan3yx
là biểu thức nào sau đây?
A.
2
3
cos 3
dx
x
. B.
2
3
cos 3
x
dx
x
.
C.
2
3
cos 3
dx
x
. D.
2
3
sin 3
dx
x
.
Câu 105. Vi phân của hàm số
( ) cosf x x
là biểu thức nào sau đây?
A.
cos
2 cos
x
dx
x
. B.
sin
2 cos
x
dx
x
.
C.
sin
cos
x
dx
x
. D.
sin
2 cos
x
dx
x
.
Câu 106. Vi phân của hàm số
sin 2
2
yx




bằng biểu thức nào sau đây?
A.
cos 2
2
x dx



. B.
2cos 2
2
x dx




.
C.
2cos 2
2
x dx




. D.
2cos 2
2
x dx



.
Câu 107. Đạo hàm cấp hai của hàm số
52
4
( ) 6 7
5
f x x x x
bằng biểu thức nào sau đây?
A.
3
16 12x
. B.
3
16 12xx
.
C.
3
4 12x
. D.
2
16 12x
.
Câu 108. Đạo hàm cấp hai của hàm số
5
4
( ) 2 5f x x
x
bằng biểu thức nào sau đây?
A.
3
3
4
40x
x
. B.
3
3
4
40x
x
.
C.
3
3
8
40x
x
. D.
3
3
8
40x
x
.
Câu 109. Đạo hàm cấp hai của hàm số
os2xyc
bằng biểu thức nào nào sau đây?
A.
2sin2x
. B.
4cos2x
.
C.
4sin2x
. D.
4cos2x
.
Câu 110. Đạo hàm cấp hai của hàm số
sin2yx
bằng biểu thức nào nào sau đây?
A.
sin2x
. B.
4sinx
.
C.
4sin2x
. D.
2sin2x
.
Câu 111. Một chuyển động thẳng xác định bởi phương trình
32
3 5 2S t t t
, trong đó tính t bằng giây
và tính S bằng mét. Gia tốc của chuyển động khi t = 3 là:
A. 24
2
( / )ms
. B.17
2
( / )ms
.
NGUYỄN BẢO VƢƠNG
CHƯƠNG V. ĐẠO HÀM
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
24
C.14
2
( / )ms
. D.12
2
( / )ms
.
Câu 112. Cho hàm số
32
11
( ) 12 1
32
f x x x x
. Tập hợp các giá trị x để đạo hàm cấp 2 của f(x) không âm
là:
A.
1
;
2



. B.
1
;
2




.
C.
1
;
2



. D.
1
;
2



.
Tổng hợp lần 3. CHƯƠNG V. ĐẠO HÀM
Câu 1. Cho hàm số
2
1
1
2
yx
, Đặt
2
'' 2y 1A x y
. Chọn câu trả lời đúng:
A.
2
Ax
B.
1A 
C.
0A
D. Tất cả đều sai
Câu 2. Cho hàm số
32
21y x x
. Nếu đặt
2
'' ' 3M xy y x
, thì ta có.
A.
0M
B.
1M
C.
1M 
D.
2M
Câu 3. Đạo hàm của hàm số
13 13
13 13 1y x x
tại
0
1x 
bằng:
A. 676 B. 13 C. 26 D.0
Câu 4. Phương trình tiếp tuyến của đồ thị (C) của hàm số
2
24y f x x x
tại điểm có hoành độ
0
1x 
là:
A.
44yx
B.
23yx
C.
35yx
D.
43yx
Câu 5. Đạo hàm của hàm số
24
3
x
y
x
là:
A.
10
'
3
y
x
B.
5
'
2 3 2 4 3
y
x x x
C.
2
5
'
2 4 3
y
xx

D.
3
'2
24
x
y
x
Câu 6. Cho hàm số
3
tan
6
x
fx
. Giá trị của
'2f
bằng:
A.
6
B.
12
C.
63
D.
36
Câu 7. Cho hàm số
2
2cos 4 1f x x
.Miền giá trị của
'fx
là:
A.
8;8

B.
4;4

C.
1;1

D.
;
Câu 8. Cho hàm số
2
fx
x
Tính giá trị của
'1f
là:
A.
1
B.
0
C.
2
D.
2
Câu 9. Cho hàm số
yx
là:
A.
'0y
B.
1
'2y x x

C.
1
'y x x

D.
1
2
'yx

NGUYỄN BẢO VƢƠNG
CHƯƠNG V. ĐẠO HÀM
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
25
Câu 10. Đạo hàm của hàm số
32
2
5
2
xx
yx
xx

là:
A. 1 B. 5 C. 6 D.
51x
Câu 11. Đạo hàm của hàm số
32
2
3
2
3
xx
yx
x

là:
A.
2
x
B.
2x
C.
4x
D.
6x
Câu 12. Đạo hàm của hàm số
3
sin 4
2
yx




là:
A.
4sin4x
B.
4cos4x
C.
4sin4x
D.
4cos4x
Câu 13. Đạo hàm của hàm số
sinxtan
2
yx




là:
A.
cosx
B.
sinx
C.
sinx
D.
cosx
Câu 14. Đạo hàm của hàm số
5
5
1k
y f x kx

là:
A.
B.
4
75x
C.
D.
3
75x
Câu 15. Hàm số có đạo hàm bằng
2
1
2x
x
là:
A.
3
1x
y
x
B.
3
51xx
y
x

C.
3
33xx
y
x
D.
2
21xx
y
x

Câu 16. Cho hàm số
3
sin 1f x x
. Với mọi
x
, hàm số có đạo hàm bằng:
A.
3
cos 1 x
B.
3
cos 1 x
C.
2
3sin 1 cos 1xx
D.
2
3sin 1 cos 1xx
Câu 17. Cho hàm số
32
2 2 3y x x x
có đồ thị (C) . Phương trình tiếp tuyến của đồ thị (C) tại điểm M có
hoành đồ
0
1x
là:
A.
2
3 4 2 1 2y x x x
B.
0 1 2yx
C.
12yx
D.
12yx
Câu 18. Tại mọi điểm
4x
, hàm số
23
4
x
y
x
có đạo hàm là:
A.
2
10
'
4
y
x
B.
2
10
'
4
y
x

C.
5
'
4
y
x
D.
2
5
'
4
y
x
Câu 19. Hàm số
sin cosy x x x
có đạo hàm là:
A.
' cos sinxyx
B.
'' siny x x
C.
' sinx 2cosxy 
D.
'' cosy x x
Câu 20. Cho hàm số
2
2 1, 1
3, 1
2, 1
xx
f x x
xx



.Kết luận nào sau đây SAI?
NGUYỄN BẢO VƢƠNG
CHƯƠNG V. ĐẠO HÀM
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
26
A.
fx
liên tục tại
1x
B.
fx
có đạo hàm tại
1x
C.
fx
liên tục va có đạo hàm tại
1x
D.
fx
liên tục tại
1x
nhưng không có đạo hàm tại
1x
Câu 21. Cho hàm số
sin2 2, 0
3 2, 0
xx
fx
xx


.Khẳng định nào sau đây là đúng
A.
fx
không liên tục tại
0x
B.
fx
co đạo hàm tại
0x
C.
fx
liên tục tại
0x
và co đạo hàm tại
0x
D.
fx
liên tục tại
0x
và nhưng không có đạo hàm tại
0x
Câu 22. Cho hàm số
2
2 3 3
3
x khi x
fx
x khi x

Khẳng định nào sau đây đúng?
A.
fx
có đạo hàm trên
B.
fx
có đạo hàm trong khoảng
3;
C.
fx
có đạo hàm trong khoảng
;3
D.
fx
có đạo hàm trên
\3
Câu 23. Cho hàm số
cos sinxf x x x
. Giá trị của
''
22
ff

bằng:
A.
2
B.
1
C.
1
D.
2
Câu 24. Cho hàm số
cos sinxy x x
có đồ thị (C). Hệ số của tiếp tuyến của đồ thị (C) tại điểm có hoành độ
2
x

lằ:
A.
2
B.
2
C.
2
D.
2
Câu 25. Cho hàm số
32
31y x x
có đồ thị là (C). Phương trình tiếp tuyến của đồ thị (C), song song với
đường thẳng
( ) : 9 10yx
là:
A.
9 6 9 26y x hay y x
B.
9 6 9 28y x hay y x
C.
9 6 9 26y x hay y x
D.
9 6 9 28y x hay y x
Câu 26. Đạo hàm cấp 2010 của hàm số
20
cosy x x
là:
A.
sinx
B.
sinx
C.
D.
cosx
Câu 27. Cho hàm số
2
1
f x x x
x
. giá trị của
'1f
bằng:
A.
1
B.
2
C.
3
D.
4
NGUYỄN BẢO VƢƠNG
CHƯƠNG V. ĐẠO HÀM
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489
27
Câu 28. Cho hàm số
2
1
4f x x
x

. Giá trị của
' 2 ' 1ff
bằng:
A.
15
4
B.
23
4
C.
13
2
D.
15
2
Câu 29. Đạo hàm của hàm số
2
1y x x
bằng:
A.
2
1
x
x
B.
2
1
x
x
C.
2
2
21
1
x
x
D.
2
2
21
21
x
x
Câu 30. Cho hàm số
và
có đạo hàm là
'u
và
'v
Khẳng định nào sau đây là sai>
A.
' ' 'uv u v v u
B.
' ' 'u v u v
C.
2
''
'
u u v uv
v
v


D.
2
''
'
u u v uv
v
v


ĐÁP ÁN
1B
2A
3D
4D
5C
6A
7A
8C
9D
10C
11D
12A
13B
14B
15B
16C
17C
18D
19D
20D
21D
22D
23D
24A
25A
26C
27B
28B
29C
30D
| 1/185
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1.
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 hoặc Liên hệ qua
Facebook: https://web.facebook.com/phong.baovuong
Website: http://tailieutoanhoc.vn/ Email: baovuong7279@gmail.com
Page Facebook: https://web.facebook.com/tracnghiemtoanthpt489/
ALBA – CHƯ SÊ- GIA LAI
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1.
CHƯƠNG V. ĐẠO HÀM
TẬP 1. KHÁI NIỆM ĐẠO HÀM VÀ CÁC
PHƯƠNG PHÁP TÍNH ĐẠO HÀM NGUYỄN BẢO VƯƠNG Mục Lục
KHÁI NIỆM ĐẠO HÀM .................................................................................................................................... 2
Vấn đề 1. Tính đạo hàm bằng định nghĩa .................................................................................................. 2
CÁC BÀI TOÁN LUYỆN TẬP .................................................................................................................. 4
CÁC QUY TẮC TÍNH ĐẠO HÀM ................................................................................................................... 8
Vấn đề 1. Tính đạo hàm bằng công thức .................................................................................................... 8
CÁC BÀI TOÁN LUYỆN TẬP ................................................................................................................ 11
Vấn đề 2. Sử dụng đạo hàm để tìm giới hạn ........................................................................................... 24
CÁC BÀI TOÁN LUYỆN TẬP ................................................................................................................ 25
Vấn đề 3. Đạo hàm cấp vao và vi phân ..................................................................................................... 27
CÁC BÀI TOÁN LUYỆN TẬP ................................................................................................................ 29
ĐẠO HÀM TỔNG HỢP .................................................................................................................................. 33
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 1
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1.
CHỦ ĐỀ: ĐẠO HÀM KHÁI NIỆM ĐẠO HÀM
1. Đạo hàm tại một điểm Hàm số y f ( )
x liên tục trên (a; )
b , được gọi là có đạo hàm tại x ( ; a )
b nếu giới hạn sau tồn tại (hữu 0 f (x) f (x ) hạn): 0 lim
và giá trị của giới hạn đó gọi là giá trị đạo hàm của hàm số tại điểm x .Ta kí hiệu 0 x x0 x x0 f '(x ) . 0 f (x) f (x ) Vậy 0 f '(x ) lim 0 x x0 x x0
2. Đạo hàm bên trái, bên phải f (x) f (x ) f (x) f (x ) 0 f '(x ) lim . 0 f '(x ) lim . 0 0 x x x x x x x x 0 0 0 0
Hệ quả : Hàm f (x) có đạo hàm tại x
f (x ) và f '(x ) đồng thời f '(x ) f '(x ) . 0 0 0 0 0
3. Đạo hàm trên khoảng, trên đoạn
Hàm số f (x) có đạo hàm (hay hàm khả vi) trên (a; )
b nếu nó có đạo hàm tại mọi điểm thuộc (a; ) b .
Hàm số f (x) có đạo hàm (hay hàm khả vi) trên [a; ]
b nếu nó có đạo hàm tại mọi điểm thuộc (a; ) b
đồng thời tồn tại đạo hàm trái f '(b ) và đạo hàm phải f '(a ) .
4. Mối liên hệ giữa đạo hàm và tính liên tục
 Định lí: Nếu hàm số f (x) có đạo hàm tại x thì f (x) liên tục tại x . 0 0
Chú ý: Định lí trên chỉ là điều kiện cần, tức là một hàm có thể liên tục tại điểm x nhưng hàm đó không 0
có đạo hàm tại x . 0
Chẳng hạn: Xét hàm f (x)
x liên tục tại x
0 nhưng không liên tục tại điểm đó. f (x) f (0) f (x) f (0) Vì lim 1 , còn lim 1 . x 0 x x 0 x
Vấn đề 1. Tính đạo hàm bằng định nghĩa Phương pháp: f (x) f (x ) 0 f '(x ) lim 0 x x0 x x0 f (x) f (x ) 0 f '(x ) lim 0 x x x x 0 0 f (x) f (x ) 0 f '(x ) lim 0 x x x x 0 0 Hàm số y f ( )
x có đạo hàm tại điểm x x f '(x ) f '(x ) 0 0 0 Hàm số y f ( )
x có đạo hàm tại điểm thì trước hết phải liên tục tại điểm đó.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 2
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1. Các ví dụ
Ví dụ 1. Tính đạo hàm của các hàm số sau tại các điểm đã chỉ: 3 2 x x 1 1 1. 3 f ( ) x 2x 1 tại x 2 3. khi x 0 f (x) x tại x 0 0 khi x 0 2. 2 f ( ) x x 1 tại x 1 Lời giải. 3 f (x) f (2) 2x 16 1. Ta có 2 lim lim lim 2(x 2x 4) 24 f '(2) 24 . x 2 x 2 x 2 x 2 x 2 2 f (x) f (1) x 1 2
2. Ta có : f '(1) lim lim x 1 x 1 x 1 x 1 (x 1)(x 1) 1 lim . x 1 2 (x 1)( x 1 2) 2 3 2 f (x) f (0) x x 1 1 x 1 1 3. Ta có f (0) 0 , do đó: lim lim lim 2 x 0 x x 0 x 0 3 2 x 2 x x 1 1 1 Vậy f '(0) . 2 2 2x x 1
Ví dụ 2. Chứng minh rằng hàm số f (x) liên tục tại x
1 nhưng không có đạo hàm tại x 1 điểm đó. Lời giải.
Vì hàm f (x) xác định tại x
1 nên nó liên tục tại đó. f ( ) x f ( 1) 2x Ta có: f '( 1 ) lim lim 1 x 1 x 1 x 1 x 1 f (x) f ( 1) f '( 1 ) lim lim 2 2 x 1 x 1 x 1 f '( 1 ) f '( 1 ) f ( )
x không có đạo hàm tại x 1 . 2 x 1 khi x 1
Ví dụ 3. Tìm a để hàm số f x x 1
có đạo hàm tại x 1 a khi x 1 Lời giải.
Để hàm số có đạo hàm tại x
1 thì trước hết f (x) phải liên tục tại x 1 2 x 1 Hay lim f (x) lim 2 f (1) a . x 1 x 1 x 1
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 3
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1. 2 x 1 2 f (x) f (1) Khi đó, ta có: x 1 lim lim 1 . x 1 x 1 x 1 x 1 Vậy a 2 là giá trị cần tìm.
CÁC BÀI TOÁN LUYỆN TẬP
Bài 1 Tính đạo hàm của các hàm số sau tại các điểm đã chỉ ra Câu 1. f ( ) x 2x 1 tại x 1 0 A.2 B.3 C.4 D.5
Bài làm 1. Ta có: f '(x ) 2 0 x 1
Câu 2. f (x) tại x 2 x 1 0 A. 2 B.2 C.3 D.4
Bài làm 2 . f '(x ) 2 0 Câu 3. 2 f ( ) x x
x 1 tại điểm x 2 0 5 8 A. 2 B. C. D. 41 2 7 3 2  x x 1 7 (x 2)(x 3) 5
Bài làm 3. f '(2) lim lim x 2 x 2 x 2 2 (x 2)( x x 1 7 ) 2 7 Câu 4. 2 f ( ) x sin x tại x 2 A. 0 B.1 C.2 D.3
Bài làm 4. f '( ) 0 2 3 2 x 2x x 1 1 Câu 5. khi x 1 f (x) x 1 tại điểm x 1 . 0 0 khi x 1 1 1 1 1 A. B. C. D. 3 5 2 4 3 2 f (x) f (1)  x 2x x 1 1 x 1 Bài làm 5. lim lim lim 2 x 1 x 1 x 1 x 1 3 2 (x 1) 2 x 2x x 1 1 1 Vậy f '(1) . 2
Bài 2 Tính đạo hàm của các hàm số sau tại điểm chỉ ra
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 4
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1. Câu 1. f ( ) x sin 2x tại x0 2 A. 1 B. 2 C. 3 D. 4
Bài làm 1. Ta có: f (x) f ( ) sin 2x sin 2 cos x sin x 2 2 2 cos x .sin ( ) ( ) x f x f 2 2 2 lim 2 lim 2 x x 2 x 2 x 2 2 Vậy f ' 1 . 2 Câu 2. f ( ) x tan x tại x 4 A. 2 B. 4 C. 5 D. 31
Bài làm 2. Ta có f (x) f tan x tan 1 tan x .tan x 4 4 4 (1 tan x) tan ( ) ( ) x f x f 4 Suy ra 4 lim lim 2 x x 4 x 4 x 4 4 Vậy f ' 2 . 4 2 1 x sin khi x 0
Câu 3. f (x) x tại x 0 . 0 khi x 0 1 2 A. 0 B. C. D. 7 2 3 f (x) f (0)  1
Bài làm 3. Ta có: lim lim x sin 0 x 0 x x 0 x Vậy f '(0) 0 .
Bài 3 Tính đạo hàm các hàm số sau tại các điểm chỉ ra Câu 1. 3 f (x) x tại x 1 0 A. 4 B. 3 C. 5 D.6
Bài làm 1. Ta có: 3 2 f ( ) x f (1) x 1 (x 1)(x x 1) f (x) f (1) Suy ra: 2 lim lim x x 1 3 x 1 x 1 x 1 Vậy f '(1) 3 .
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 5
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1. 2x 3 khi x 1 Câu 2. 3 2 f (x) x 2x 7x 4 tại x 1 . 0 khi x 1 x 1 A. 0 B. 4 C. 5 D. Đáp án khác
Bài làm 2. Ta có lim f ( ) x lim 2x 3 5 x 1 x 1 3 2 x 2x 7x 4 2 lim f ( ) x lim lim (x 3x 4) 0 x 1 x 1 x 1 x 1 Dẫn tới lim f ( ) x lim f ( ) x
hàm số không liên tục tại x
1 nên hàm số không có đạo hàm tại x 1 . 0 x 1 x 1 2 sin x khi x 0
Câu 3. f (x) x tại x 0 0 2 x x khi x 0 A.1 B.2 C.3 D.5 2  sin x sin x
Bài làm 3. Ta có lim f ( ) x lim lim .sin x 0 x 0 x 0 x x 0 x 2 lim f (x) lim x x
0 nên hàm số liên tục tại x 0 x 0 x 0 2 f (x) f (0) sin x lim lim 1 và 2 x 0 x x 0 x 2 f (x) f (0) x x lim lim 1 x 0 x x 0 x Vậy f '(0) 1 . 2 x x 1
Câu 4. f (x) tại x 1. x 0 A.2 B.0 C.3 D.đáp án khác
Bài làm 4. Ta có hàm số liên tục tại x 1 và 0 2 f (x) f ( 1) x x x 1 x 1 ( x x 1) 2 f (x) f ( 1) x 2x 1 Nên lim lim 0 x 1 x 1 x 1 ( x x 1) 2 f (x) f ( 1) x 1 lim lim 2 x 1 x 1 x 1 ( x x 1) f (x) f ( 1) f (x) f ( 1) Do đó lim lim x 1 x 1 x 1 x 1
Vậy hàm số không có đạo hàm tại điểm x 1. 0
Nhận xét: Hàm số y f ( )
x có đạo hàm tại x
x thì phải liên tục tại điểm đó. 0
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 6
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1. Bài 4 2 x x khi x 1
Câu 1. Tìm a,b để hàm số f (x)
có đạo hàm tại x 1 . ax b khi x 1 a 23 a 3 a 33 a 3 A. B. C. D. b 1 b 11 b 31 b 1 Bài làm 1. Ta có: 2 lim f ( ) x lim (x ) x 2 ; lim f ( ) x lim (ax ) b a b x 1 x 1 x 1 x 1
Hàm có đạo hàm tại x
1 thì hàm liên tục tại x 1 a b 2 (1) 2 f (x) f (1) x x 2 lim lim lim (x 2) 3 x 1 x 1 x 1 x 1 x 1 f (x) f (1) ax b 2 ax a lim lim lim a (Do b 2 a ) x 1 x 1 x 1 x 1 x 1 x 1 a 3
Hàm có đạo hàm tại x 1 . b 1 2 x 1 khi x 0
Câu 2. Tìm a,b để hàm số f (x) có đạo hàm trên . 2 2x ax b khi x 0 A. a 10,b 11 B. a 0,b 1 C. a 0,b 1 D. a 20,b 1
Bài làm 2. Ta thấy với x 0 thì f (x) luôn có đạo hàm. Do đó hàm số có đạo hàm trên khi và chỉ
khi hàm có đạo hàm tại x 0 . Ta có: lim f ( ) x 1; lim f ( ) x b
f (x) liên tục tại x 0 b 1. x 0 x 0 f (x) f (0) f (x) f (0) Khi đó: f '(0 ) lim 0; f '(0 ) lim a x 0 x x 0 x f '(0 ) f '(0 ) a 0 . Vậy a 0,b
1 là những giá trị cần tìm. 2 x 1 khi x 0
Câu 3. Tìm a,b để hàm số f (x) x 1
có đạo hàm tại điểm x 0 . ax b khi x 0 A. a 11,b 11 B. a 10,b 10 C. a 12,b 12 D. a 1,b 1
Bài làm 3. Ta có lim f (x) 1 f (0); lim f ( ) x b x 0 x 0
Hàm số liên tục tại x 0 b 1 f (x) f (0) x 1 f (x) f (0) lim lim 1 , lim lim a a x 0 x x 0 x 1 x 0 x x 0
Hàm số có đạo hàm tại điểm x 0 a 1 Vậy a 1,b 1 là giá trị cần tìm.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 7
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1.
CÁC QUY TẮC TÍNH ĐẠO HÀM 1. Quy tắc tính đạo hàm
1.1. Đạo hàm của tổng, hiệu, tích, thương của hàm số ' ' ' (u u ... u )' u u ... u ( . k ( u ) x )' . k u'(x) 1 2 n 1 2 n (uv ) w '
u' vw uv' w uvw' n n 1 (u ( ) x )' nu (x).u'(x) ' ( u x) u'(x) (
v x) v'(x) ( u x) c . c u'(x) ' . 2 ( v x) v (x) 2 ( u x) u (x)
1.2. Đạo hàm của hàm số hợp Cho hàm số y f ( ( u ) x ) f ( ) u với u ( u ) x . Khi đó y' y' .u' . x u x
2. Bảng công thức đạo hàm các hàm sơ cấp cơ bản Đạo hàm Hàm hợp (c)' 0 ( ) x ' 1 1 1 (x )' x u ' u .u' 1 x ' u' u ' 2 x 2 u n 1 x ' n u' u ' n n 1 n x n n 1 n u (sin ) x ' cos x (sin ) u ' u'.cosu (cos ) x ' sin x (cos ) u ' u'sinu 1 (tan x)' u' 2 tan u ' cos x 2 cos u 1 (cot ) x ' u' cot u ' 2 sin x 2 sin u
Vấn đề 1. Tính đạo hàm bằng công thức
Phương pháp: Sử dụng các quy tắc tính đạo hàm Các ví dụ
Ví dụ 1. Tính đạo hàm các hàm số sau: 1. 3 2 y x 3x 2x 1 2. 3 y x 3x 1 4 x 3 3. 2 y x 1 4. 4 2 y 2x x 1 4 2 2x 1 2 x 2x 2 5. y 6. y x 3 x 1 Lời giải.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 8
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1. ' 1. Ta có: 3 2 y' x 3x 1 3x 6x 2 ' 2. Ta có: 3 2 y' x 3x 1 3x 3 ' 4 x 3. Ta có: 2 3 y' x 1 x 2x 4 ' 3 4. Ta có: 4 2 3 y' 2x x 1 8x 3x 2
(2x 1)'(x 3) (x 3)'(2x 1) 7 5. Ta có: y' 2 2 (x 3) (x 3) 2 2 (x 2x 2)'(x 1) (x 2x 2)(x 1)' 6. Ta có: y' 2 (x 1) 2 2 (2x 2)(x 1) (x 2x 2) x 2x 4 . 2 2 (x 1) x 1 ax b ad bc
Nhận xét: Với hàm số y ta có: y' . cx d 2 (cx d)
Ví dụ 2. Giải bất phương trình f '( ) x 0 biết: 1. 2 f ( ) x x 4 x 2. 2 f ( ) x x 2 x 12 3. 2 2 f ( ) x x x 1 x x 1 4. 4 2 f ( ) x x 1 x Lời giải. 1. TXĐ: D 2; 2 2 2 x 4 2x Ta có: 2 f '(x) 4 x 2 2 4 x 4 x Do đó: 2 f '( ) x 0 4 2x 0 2 x 2 . 2. TXĐ: D 2 2x x 12 2x Ta có: f '(x) 1 2 2 x 12 x 12 Suy ra: 2 f '( ) x 0 x 12 2x (1) Với x 0 thì (1) luôn đúng x 0 Với x 0 thì (1) 0 x 2 2 2 x 12 4x
Vậy bất phương trình f '( ) x 0 có nghiệm x 2 . 3. TXĐ: D 2x 1 2x 1 Ta có: f '(x) 2 2 2 x x 1 2 x x 1
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 9
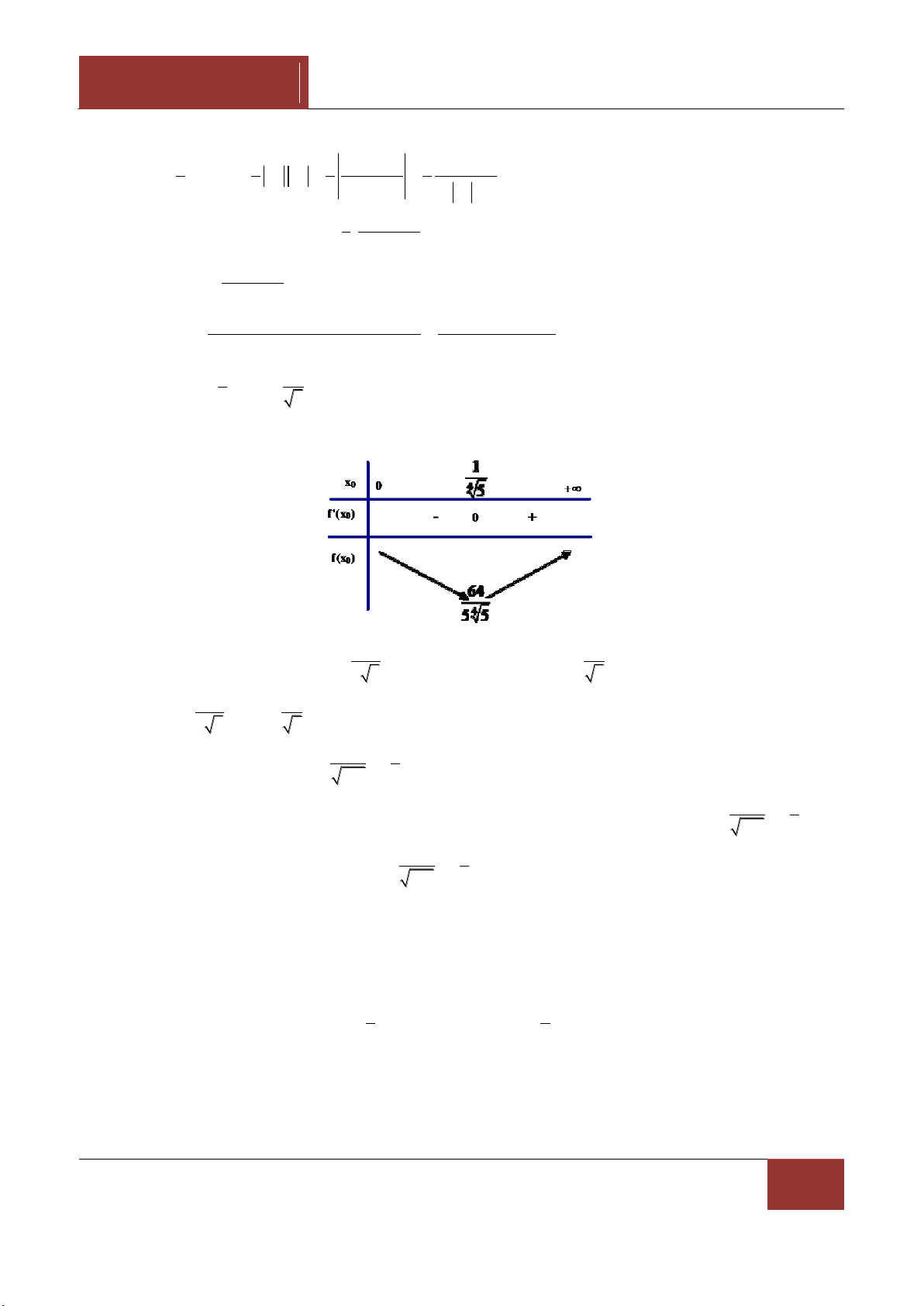
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1. Suy ra 2 2 f '( ) x 0 1 2x x x 1 1 2x x x 1 (1 2x)(1 2x) 0 2 2 1 3 2 2 1 3 (1 2x) x 1 2x x 2 4 2 4 1 1 x 2 2 x 0 . 2 2 (1 2x) (1 2x) 4. TXĐ: D 0;  x 1 Ta có: f '(x) . 4 2 3 2 (x 1) 2 x 4 2 3 6 2 3 f '( ) x 0 x x (x 1) x (x 1) 2 2 x x
1 bất phương trình này vô nghiệm
Ví dụ 3. Tính đạo hàm các hàm số sau: 1. 2 y 2x 3x 1 2. 5 2 y 2x 1 3x 2 3. 2 y 2 sin (2x 1) cos x 4. 2 2 3 y tan(sin 3 ) x cot (1 2x ) 3 5. 3 y sin(tan ) x cos(cot ) x Lời giải. 2 (2x 3x 1)' 4x 3 1. Ta có: y' . 2 2 2 2x 3x 1 2 2x 3x 1 1 2. Ta có 2 y' ( 2x 1 3x 2)' 5 2 4 5. ( 2x 1 3x 2) 1 2x ( 3) . 2 5 2 4 2x 1 5. ( 2x 1 3x 2) 1 2 sin(4x 2) sin x 2 (2 sin (2x 1) cos x)' 3. Ta có: 2 ' x y 2 2 2 2 sin (2x 1) cos x 2 2 sin (2x 1) cos x 4 x sin(4x 2) sin x . 2 4 2x sin (2x 1) x cos x 2 3 [cot (1 2x ) 3]' 4. Ta có: 2 2 2 y'
[1 tan (sin 3x)](sin 3 ) x ' 2 3 2 cot (1 2x ) 3 2 2 3 3 2 2
6x [1 cot (1 2x )]cot(1 2x )
3[1 tan (sin 3x)]sin 6x . 2 3 cot (1 2x ) 3
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 10
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1. [sin(tan x) cos(cot x)]' 5. Ta có: y' 2 3 [sin(tan x) cos(cot x)] 2 2
(1 tan x)cos(tan x) (1 cot x)sin(cot x) . 2 3 [sin(tan x) cos(cot x)]
Ví dụ 4. Tính đạo hàm các hàm số sau : 2 x 3x 1 khi x 1 2 1 x cos khi x 0 1. f (x) 2. f (x) 2x 2x 2 khi x 1 0 khi x 0 Lời giải. 1. Với 2 x 1 f ( ) x x 3x 1 f '(x) 2x 3 Với x 1 f ( ) x 2x 2 f '(x) 2 Với x 1 ta có: 2 lim f ( ) x lim x 3x 1 1 f (1)
hàm số không liên tục tại x 1 , suy ra hàm x 1 x 1
số không có đạo hàm tại x 1 2x 3 khi x 1 Vậy f '( ) x . 2 khi x 1 2. Với 2 1 1 1 1 x 0 f ( ) x x cos f '(x) 2x cos cos 2x 2x 2 2x f (x) f (0) 1 Với x 0 ta có: lim lim x cos 0 f '(0) 0 x 0 x x 0 2x 1 1 2x cos khi x 0 Vậy f '(x) 2 2x . 0 khi x 0
CÁC BÀI TOÁN LUYỆN TẬP
Bài 1 Tính đạo hàm các hàm số sau Câu 1. 4 2 y x 3x 2x 1 A. 3 y' 4x 6x 3 B. 4 y' 4x 6x 2 C. 3 y' 4x 3x 2 D. 3 y' 4x 6x 2
Bài làm 1. Ta có: 3 y' 4x 6x 2 3 x Câu 2. 2 y 2x x 1 3 1 A. 2 y' 2x 4x 1 B. 2 y' 3x 4x 1 C. 2 y' x 4x 1 D. 2 y' x 4x 1 3 Bài làm 2. Ta có 2 y' x 4x 1
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 11
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1. 2x 1 Câu 3. y x 2 3 3 3 2 A. B. C. D. 2 2 2 x 2 x 2 x 2 x 2  (2x 1)'(x 2) (x 2)'(2x 1) 3
Bài làm 3. Ta có y' 2 2 (x 2) (x 2) 2 x x 1 Câu 4. y x 1 2 x 2x 2 x 2x 2 x 2x 2x 2 A. B. C. D. 2 2 2 2 x 1 x 1 x 1 x 1 2 2 
(2x 1)(x 1) (x x 1) x 2x
Bài làm 4. Ta có y' 2 2 (x 1) (x 1) ax b Câu 5. y , ac 0 cx d a ad bc ad bc ad bc A. B. C. D. c 2 2 cx d cx d cx d a b ad cb c d
Bài làm 5. Ta có y' 2 2 (cx d) (cx d) 2 ax bx c Câu 6. y , aa' 0 . a' x b' 2 aa' x 2ab' x bb' a' c 2 aa' x 2ab' x bb' a' c A. B. (a' x b') 2 (a' x b') 2 aa' x 2ab' x bb' a' c 2 aa' x
2ab' x bb' a' c C. D. 2 (a' x b') 2 (a' x b') 2  (2ax ) b (a' x b') a'(ax bx c)
Bài làm 6. Ta có: y' 2 (a' x b') 2 aa' x 2ab' x
bb' a' c . 2 (a' x b')
Bài 2 Tính đạo hàm các hàm số sau Câu 1. 2 y x x 1
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 12
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1. 2 2x 1 2 x 1 2 4x 1 2 2x 1 A. B. C. D. 2 2 x 1 2 x 1 2 x 1 2 x 1 2  (x 1)' Bài làm 1. Ta có: 2 2 2 y' x' x 1 x 1 ' x x 1 .x 2 2 x 1 2 2 2 x 2x 1 x 1 . 2 2 x 1 x 1 3 Câu 2. y 2 (2x 5) 12 12 6 12 A. B. C. D. 4 3 3 3 2x 5 2x 5 2x 5 2x 5 ' 2 3 (2x 5)  12(2x 5) 12
Bài làm 2. Ta có: y' 4 4 3 (2x 5) (2x 5) (2x 5) 2 2 2x x Câu 3. y 2 x 1 2 2x 6x 2 2 2x 6x 2 2 2x 6x 2 2 2x 6x 2 A. B. C. D. 2 4 2 2 2 x 1 2 x 1 2 x 1 2 x 1 2 2 2  (2x 2)(x 1) 2 ( x x 2x 2) 2x 6x 2
Bài làm 3. Ta có y' 2 2 2 2 (x 1) (x 1) Câu 4. y 3x 2 tan x 2 5 2 tan x 2 5 2 tan x 2 5 2 tan x 2 5 2 tan x A. B. C. D. 2 3x 2 tan x 2 3x 2 tan x 2 3x 2 tan x 2 3x 2 tan x 2 2  (3x 2 tan ) x ' 3 2(1 tan ) x 5 2 tan x
Bài làm 4. Ta có: y' 2 3x 2 tan x 2 3x 2 tan x 2 3x 2 tan x Câu 5. 2 y sin (3x 1) A. 3sin(6x 2) B. sin(6x 2) C. 3sin(6x 2) D. 3cos(6x 2)  '
Bài làm 5. Ta có: y'
2 sin(3x 1). sin(3x 1)
2 sin(3x 1).3cos(3x 1) 3sin(6x 2) . Câu 6. 2 y (x 1) x x 1 . 2 4x 5x 3 2 4x 5x 3 2 4x 5x 3 2 4x 5x 3 A. B. C. D. 2 2 x x 1 2 2 x x 1 2 x x 1 2 2 x x 1
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 13
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1. 2  2x 1 4x 5x 3 Bài làm 6. Ta có 2 y' x x 1 (x 1) 2 2 2 x x 1 2 x x 1
Bài 3. Tính đạo hàm các hàm số sau 2 Câu 1. 7 y x x A. 7 6 y' (x ) x (7x 1) B. 7 y' 2(x ) x C. 6 y' 2(7x 1) D. 7 6 y' 2(x ) x (7x 1)
Bài làm 1.Đáp án D Câu 2. 2 2 y x 1 5 3x A. 3 y' x 4x B. 3 y' x 4x C. 3 y' 12x 4x D. 3 y' 12x 4x
Bài làm 2. Ta có: Đáp án D 2x Câu 3. y 2 x 1 2 2x 2 2 2x 343 2 2x 2 2 2x 2 A. B. C. D. 2 2 (x 1) 2 2 (x 1) 2 2 (x 1) 2 2 (x 1) 2 2  2(x 1) 2 . x 2x 2x 2 Bài làm y' 2 2 2 2 (x 1) (x 1) Câu 4. 2 y
x 2x 1 5x 3 A. 2 2 y' 40x 3x 6x B. 3 2 y' 40x 3x 6x C. 3 2 y' 40x 3x 6x D. 3 2 y' 40x 3x xBài làm 4 3 2 3 2 y 10x x 3x y' 40x 3x 6x 3 5 Câu 5. y 4x 2 x 2 2 10 5 10 5 A. y' 3 4 4x B. y' 3 4 4x 3 2 x x 3 2 x x 2 2 5 10 5 C. y ' 4x D. y' 3 4 4x 2 x 3 2 x x 2  10 5 Bài làm y' 3 4 4x 3 2 x x Câu 6. 3 2 y (x 2) (x 3) A. 2 3 3 y' 3(x 5x 6) 2(x 3)(x 2) B. 2 2 3 y' 2(x 5x 6) 3(x 3)(x 2)
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 14
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1. C. 2 y' 3(x 5x 6) 2(x 3)(x 2) D. 2 2 3 y' 3(x 5x 6) 2(x 3)(x 2) Bài làm 2 2 3 y' 3(x 5x 6) 2(x 3)(x 2) Câu 7. 3 2 y x 3x 2 2 3x 6x 2 3x 6x 2 3x 6x 2 3x 6x A. y' B. y' C. y' D. y' 3 2 x 3x 2 3 2 2 x 3x 2 3 2 2 x 3x 2 3 2 2 x 3x 2 2  3x 6x Bài làm y' 3 2 2 x 3x 2 Câu 8. 2 y x x x 1 x x A. y' 2x x 1 B. y' 2x x 1 2 x 1 2 x 1 x x C. y' D. y' 2x x 1 2 x 1 2 x 1  x Bài làm y' 2x x 1 2 x 1 x Câu 9. y 2 2 a x 2 a 2 a 2 2a 2 a A. y ' B. y ' C. y ' D. y ' 2 2 3 (a x ) 2 2 3 (a x ) 2 2 3 (a x ) 2 2 3 (a x ) 2 2 2 x a x 2 2 2  a x a Bài làm y ' 2 2 2 2 3 (a x ) (a x ) 1 Câu 10. y x x 3 1 1 1 3 1 A. y ' B. y ' C. y ' D. y' 2 2 x x 2 x x 2 x x 2 2 x x  (x x)' 3 1 Bài làm y' 3 2 x 2 x x 1 x Câu 11. y 1 x 1 3x 1 3x 1 1 3x 1 3x A. y ' B. y' C. y' D. y' 3 (1 x) 3 3 (1 x) 3 3 2 (1 x) 3 2 (1 x)
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 15
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1. 1 x 1 x  2 1 x 1 3x Bài làm y ' 1 x 3 2 (1 x) Câu 12. 2 y sin 3x A. y' sin 6x B. y' 3sin 3x C. y' 2sin 6x D. y' 3sin 6x
Bài làm y' 3sin6x Câu 13. 2 y 3 tan x cot 2x 2 2 3 tan ( x 1 tan ) x (1 cot 2 ) x 2 2 3 tan ( x 1 tan ) x (1 cot 2 ) x A. y' B. y' 2 3 3 tan x cot 2x 2 2 3 tan x cot 2x 2 2 3 tan ( x 1 tan ) x (1 cot 2 ) x 2 2 3 tan ( x 1 tan ) x (1 cot 2 ) x C. y' D. y' 2 3 tan x cot 2x 2 3 tan x cot 2x 2 2  3 tan ( x 1 tan ) x (1 cot 2 ) x Bài làm y' 2 3 tan x cot 2x Câu 14. 3 4 3 y x cos (2x ) 3 2 3 3x 8 cos (2x )sin(2x ) 2 3 3x 8 cos (2x )sin(2x ) A. 4 4 y ' B. 4 4 y ' 3 3 3 4 3 3 x cos (2x ) 3 4 3 4 x cos (2x ) 3 3 2 3 6x 8 cos (2x )sin(2x ) 2 3 3x 8 cos (2x )sin(2x ) C. 4 4 y ' D. 4 4 y ' 3 3 3 4 3 3 x cos (2x ) 3 4 3 3 x cos (2x ) 3 3 2 3 3x 8 cos (2x )sin(2x ) Bài làm 4 4 y ' 3 3 4 3 3 x cos (2x ) 3 Câu 15. 2 y 2 sin x 2 A. 2 y' x cos(x 2) B. 2 y' 4 cos(x 2) C. 2 y' 2xcos(x 2) D. 2 y' 4xcos(x 2) Bài làm 2 y' 4xcos(x 2) Câu 16. 2 3 y cos sin x
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 16
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1. A. 3 2 y' sin(2sin )
x sin xcos x B. 3 2 y' 6sin(2sin )
x sin xcos x C. 3 2 y' 7 sin(2sin )
x sin xcos x D. 3 2 y' 3sin(2sin )
x sin xcos xBài làm 3 2 y' 3sin(2sin )
x sin xcos x x Câu 17. y sin x sin x cos x sin x x cos x sin x cos x sin x x cos x A. y' B. y' C. y' D. y' 2 sin x sin x sin x 2 sin x  sin x x cos x Bài làm y' 2 sin x cos x 4 Câu 18. y cot x 3 3sin x 3 A. 3 y' cot x 1 B. 4 y' 3cot x 1 C. 4 y' cot x 1 D. 4 y' cot x  1 4 1 Bài làm 2 3 y cot ( x 1 cot ) x cot x cot x cot x 3 3 3 2 2 2 4 Suy ra y' cot ( x 1 cot ) x 1 cot x cot x 1 3 1 x sin khi x 0
Câu 19. f (x) x 0 khi x 0 2 1 1 x sin x cos khi x 0 2 1 1 3x sin x cos khi x 0 A. f '(x) x x B. f '(x) x x 0 khi x 0 0 khi x 0 2 1 1 3x sin x cos khi x 0 2 1 1 3x sin cos khi x 0 C. f '(x) x x D. f '(x) x x 0 khi x 0 0 khi x 0 Bài làm 2 1 1 x 0 f '( ) x 3x sin x cos x x f (x) f (0) Với x 0 f '(0) lim 0 x 0 x 2 1 1 3x sin x cos khi x 0 Vậy f '(x) x x . 0 khi x 0 f ' 1 x Bài 4. Tính . Biết rằng : 2 f (x) x và (x) 4x sin . ' 0 2 f '(1) 4 f '(1) 2 f '(1) 4 f '(1) 4 A. B. C. D. '(0) 8 '(0) 8 '(0) '(0) 8
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 17
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1.x
Bài làm Bài 4. f '( ) x 2x f '(1) 2; '( ) x 4 cos '(0) 4 2 2 2 f '(1) 4 Suy ra '(0) 8 .
Bài 6. Tìm m để các hàm số Câu 1. 3 2 y (m 1)x 3(m 2)x 6(m 2)x 1 có y' 0, x A. m 3 B. m 1 C. m 4 D. m 4 2
Bài làm 1. Ta có: 2 y' 3 (m 1)x 2(m 2)x 2(m 2) Do đó 2 y' 0 (m 1)x 2(m 2)x 2(m 2) 0 (1) m 1 thì (1) 6x 6 0 x 1 nên m 1 (loại) a m 1 0 m
1 thì (1) đúng với x ' 0 m 1 m 4 (m 1)(4 ) m 0 Vậy m
4 là những giá trị cần tìm. 3 mx Câu 2. 2 y mx
(3m 1)x 1 có y' 0, x . 3 A. m 2 B. m 2 C. m 0 D. m 0
Bài làm 2. Ta có: 2 y' mx 2mx 3m 1 Nên 2 y' 0 mx 2mx 3m 1 0 (2) m 0 thì (1) trở thành: 1 0 đúng với x a m 0 m
0 , khi đó (1) đúng với x ' 0 m 0 m 0 m 0 ( m 1 2 ) m 0 1 2m 0 Vậy m
0 là những giá trị cần tìm.
Bài 7. Tính đạo hàm của các hàm số sau 2 1 x sin khi x 0
Câu 1. f (x) x 0 khi x 0 1 1 1 1 x sin cos khi x 0 x sin x cos khi x 0 A. f '(x) x x B. f '(x) x x 0 khi x 0 0 khi x 0
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 18
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1. 1 1 1 1 2x sin x cos khi x 0 2x sin cos khi x 0 C. f '(x) x x D. f '(x) x x 0 khi x 0 0 khi x 0  1 1
Bài làm 1. Với x 0 ta có: f '(x) 2x sin cos x x f (x) f (0) 1 Tại x 0 ta có: lim lim x sin 0 x 0 x x 0 x 1 1 2x sin cos khi x 0 Vậy f '(x) x x . 0 khi x 0 2 x x 1 khi x 1
Câu 2. f (x) x 1 3 khi x 1 2x khi x 1 2x 1 khi x 1 A. f '(x) 1 B. f '(x) 1 khi x 1 khi x 1 2 x 1 x 1 2x 1 khi x 1 2x 1 khi x 1 C. f '(x) 1 D. f '(x) 1 khi x 1 khi x 1 x 1 2 x 1
Bài làm 2. Với x 1 ta có: f '( ) x 2x 1 1 Với x 1 ta có: f '(x) 2 x 1 Tại x 1 ta có: 2 f (x) f (1) x x 2 lim lim 3 x 1 x 1 x 1 x 1 f (x) f (1) x 1 lim lim
 suy ra hàm số không có đạo x 1 x 1 x 1 x 1 hàm tại x 1 2x 1 khi x 1 Vậy f '(x) 1 . khi x 1 2 x 1
Bài 8. Tìm a,b để các hàm số sau có đạo hàm trên 2 x x 1 khi x 1
Câu 1. . f (x) 2 x ax b khi x 1 a 13 a 3 a 23 a 3 A. B. C. D. b 1 b 11 b 21 b 1
Bài làm 1 Với x 1 thì hàm số luôn có đạo hàm
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 19
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1.
Do đó hàm số có đạo hàm trên
hàm số có đạo hàm tại x 1 . Ta có lim f ( ) x 1; lim f ( ) x a b 1 x 1 x 1 Hàm số liên tục trên a b 1 1 a b 2 f (x) f (1) Khi đó: lim 1; x 1 x 1 2 f (x) f (1) x ax 1 a lim lim a 2 x 1 x 1 x 1 x 1 a b 2 a 3
Nên hàm số có đạo hàm trên thì . a 2 1 b 1 2 x x 1 khi x 0
Câu 2. f (x) x 1 . 2 x ax b khi x 0 A. a 0,b 11 B. a 10,b 11 C. a 20,b 21 D. a 0,b 1
Bài làm 2. Tương tự như ý 1. ĐS: a 0,b 1 .
Bài 9. Tính đạo hàm các hàm số sau Câu 1. 3 3 y (x 2 ) x A. 3 2 2 y' (x 2x) (3x 2) B. 3 2 2 y' 2(x 2 ) x (3x 2) C. 3 2 2 y' 3(x 2 ) x (3x 2) D. 3 2 2 y' 3(x 2 ) x (3x 2) ' Bài làm 1.Ta có: 3 2 3 3 2 2 y' 3(x 2 ) x x 2x 3(x 2 ) x (3x 2) Câu 2. 2 3 y (x 1)(3x 2 ) x A. 4 2 y' x 3x 2 B. 4 2 y' 5x 3x 2 C. 4 2 y' 15x 3x D. 4 2 y' 15x 3x 2
Bài làm 2. Ta có: 3 2 2 4 2 y' 2 ( x 3x 2 ) x (x 1)(9x 2) 15x 3x 2 2 2 Câu 3. y x 2 3x 2 4 2 4 A. y' x 1 B. y' 2 x 1 2 3 3x 3x 2 3 3x 3x 2 4 2 4 C. y' x 1 D. y' 2 x 1 2 3 3x 3x 2 3 3x 3x  2 4
Bài làm 3.Ta có: y' 2 x 1 2 3 3x 3x Câu 4. 3 2 y 2sin 2x tan 3x x cos 4x
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 20
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1. A. 2 2 y' 12 sin 2x cos 2x
6 tan 3x 1 2 tan 3x
cos 4x 4xsin 4x B. 2 2 y' 12 sin 2xcos 2x
6 tan 3x 1 tan 3x cos 4x xsin 4x C. 2 2 y' 12 sin 2xcos 2x tan 3x 1 tan 3x
cos 4x 4xsin 4x D. 2 2 y' 12 sin 2xcos 2x
6 tan 3x 1 tan 3x
cos 4x 4xsin 4x
Bài làm 4. Ta có: 2 2 y' 12 sin 2xcos 2x
6 tan 3x 1 tan 3x
cos 4x 4xsin 4x sin 2x x Câu 5. y x cos 3x 2x cos 2x sin 2x cos 3x 3x sin 3x 2x cos 2x sin 2x cos 3x 3x sin 3x A. y' B. y' 2 2 x cos 3x 2 2 x cos 3x
2x cos 2x sin 2x cos 3x 3x sin 3x
2x cos 2x sin 2x cos 3x 3x sin 3x C. y' D. y' 2 2 x cos 3x 2 2 x cos 3x ' '  sin 2x
2x cos 2x sin 2x x cos 3x 3x sin 3x Bài làm 5. Ta có: , 2 x x 2 cos 3x cos 3x
2x cos 2x sin 2x cos 3x 3x sin 3x Nên y' . 2 2 x cos 3x Câu 6. 3 2 y x sin 2x x x 1 2 3x 2x 2 3x 2x A. y'
sin 2x 2x cos 2x B. y' sin 2x 2x cos 2x 3 2 2 x x 1 3 2 x x 1 2 3x 2x 2 3x 2x C. y' sin 2x 2x cos 2x D. y' sin 2x 2x cos 2x 3 2 2 x x 1 3 2 2 x x 1 2  3x 2x
Bài làm 6.Ta có: y' sin 2x 2x cos 2x 3 2 2 x x 1 Câu 7. 2 3 y 2 sin x x 1 2 2 sin 2x 3x 2 2 sin 2x 3x A. y ' B. y ' 2 3 2 sin x x 1 2 3 2 2 sin x x 1 2 sin 2x 3x 2 2 sin 2x 3x C. y ' D. y ' 2 3 2 sin x x 1 2 3 2 2 sin x x 1 2  2 sin 2x 3x
Bài làm 7. Ta có: y ' 2 3 2 2 sin x x 1 Câu 8. 2 y x 1 2x 1
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 21
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1. 2 x 2 x 1 2 x x 1 A. y ' B. y ' 2 2 (x 1) x 1 2x 1 2 2 (x 1) x 1 2x 1 2 x x 1 2 x 2 x 1 C. y ' D. y ' 2 2 2 (x 1) x 1 2x 1 2 2 2 (x 1) x 1 2x 1 x 2 2 2  x 1 x 2 x 1
Bài làm 8. Ta có: y ' . 2 2 2 2 x 1 2x 1 2 (x 1) x 1 2x 1 x 1 Câu 9. y x tan 2x cot x A. 2 2 y'
tan 2x 2x 1 tan 2x tan x (x 1)(tan 1) B. 2 2 y' tan 2x x 1 tan 2x tan x (x 1)(tan 1) C. 2 2 y' tan 2x 2x 1 tan 2x tan x 2(x 1)(tan 1) D. 2 2 y' tan 2x 2x 1 tan 2x tan x (x 1)(tan 1)  ' Bài làm 9. Ta có: 2 x tan 2x tan 2x 2x 1 tan 2x ' x 1 ' 2 (x 1) tan x tan x (x 1)(tan 1) cot x Nên 2 2 y' tan 2x 2x 1 tan 2x tan x (x 1)(tan 1)  Câu 10. 3 y sin 2x 1 3     2 3 sin 2x cos 2x 2 sin 2x cos 2x 3 3 3 3 A. y ' B. y '   3 2 sin 2x 1 3 2 sin 2x 1 3 3     2 sin 2x cos 2x 2 3 sin 2x cos 2x 3 3 3 3 C. y ' D. y '   3 sin 2x 1 3 sin 2x 1 3 3
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 22
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1.   2 3 sin 2x cos 2x  3 3
Bài làm 10. Ta có: y ' .  3 sin 2x 1 3
Bài 10. Giải bất phương trình : Câu 1. f '( ) x 0 với 3 2 f ( ) x 2x 3x 1 x 0 A. B. x 1 C. x 0 D. 0 x 1 x 1
Bài làm 1. TXĐ: D x 0 Ta có: 2 f '( ) x 6x
6x , suy ra f '(x) 0 x 1 Câu 2. f '( ) x 0 với 4 2 f ( ) x 2x 4x 1 1 x 0 A. B. 1 x 0 x 1 C. x 1 D. x 0
Bài làm 2. TXĐ: D 1 x 0 Ta có: 3 f '( ) x 8x
8x , suy ra f '(x) 0 x 1 Câu 3. 2xf '( ) x f ( ) x 0 với 2 f ( ) x x x 1 1 1 1 2 A. x B. x C. x D. x 3 3 3 3
Bài làm 3. TXĐ: D x f (x) Ta có: f '(x) 1 2 2 x 1 x 1 Mặt khác: 2 f ( ) x x x x x 0, x 2xf (x) Nên 2xf '(x) f (x) 0 f (x) 0 2 x 1 x 0 2 1 2x x 1 x . 2 3x 1 3 Câu 4. f '( ) x 0 với 2 f ( ) x x 4 x . A. 2 x 2 B. x 2 C. 2 x D. x 0
Bài làm 4. TXĐ: D 2; 2 x Ta có: 2 f '(x) 1 f '(x) 0 4 x x 2 4 x
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 23
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1. 2 x 0 2 x 0 x 0 2 x 2 . 2 2 0 x 2 4 x x
Vấn đề 2. Sử dụng đạo hàm để tìm giới hạn f (x) f (x )
Từ định nghĩa đạo hàm 0 f '(x ) lim
,ta thấy có thể sử dụng đạo hàm để tìm giới hạn của 0 x x0 x x0 hàm số. Cụ thể ( g x) Để tính A lim , biết ( g x ) 0 . 0 x x0 x x0 Ta viết ( g ) x f ( ) x
f (x ) . Khi đó nếu f (x) có đạo hàm tại x thì : 0 0 f (x) f (x ) 0 A lim f '(x ) . 0 x x0 x x0 F(x) Để tính: B lim , biết ( F x ) ( G x ) 0 . 0 0 x x0 ( G x) Ta viết ( F ) x f ( ) x f (x ) và ( G ) x ( g ) x ( g x ) . 0 0 f (x) f (x ) 0 x x f '(x )
Nếu hai hàm số f ( ) x , ( g )
x có đạo hàm tại x
x và g'(x ) 0 thì: 0 0 B lim . 0 0 x x ( g x) ( g x ) 0 0 g '(x ) 0 x x0 Các ví dụ
Ví dụ 1. Tính các giới hạn sau : 3 1 x 1 3 2x 1 3x 2 1. A lim 2. B lim x 0 x 2 x 1 x 1 n 1 3x 1 3 2 4 1 x 1 2x 3. C lim 4. D lim x 0 x 2 x 0 x x Lời giải. 1 1. Đặt 3 f (x) 1 x f '(x) và f (0) 1 3 2 3 (1 ) x f (x) f (0) 1 A lim f '(0) . x 0 x 0 3 2. Đặt 3 f ( ) x 2x 1 3x 2 2 3 f '(x) và f (1) 0 . 3 2 3. (2x 1) 2 3x 2 1 f (x) f (0) 1 f ( ) x f (0) 1 2 3 5 B lim . lim .lim . f '(1) . x 1 x 1 x 1 x 1 x 1 x 1 x 1 2 3 2 9
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 24
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1. f ( ) x f (0) 3
3. Đặt f (x) n 1 3x C lim f '(0) . x 0 x n 2x 1 4. Đặt 3 2 4 f ( ) x 1 x 1 2x f '(x) 3 2 2 4 3 3. (1 x ) 2. (1 2 ) x 1 f (x) f (0) 1 D lim .lim f '(0) . x 0 x 1 x 0 x 2 2 3 2 1 2x 1 3x
Ví dụ 2. Tính giới hạn sau : A lim x 0 1 cos x Lời giải. 2 3 2 1 2x 1 3x 2 f (x) Ta có: lim x A lim . x 0 x x 0 2 2 x 2 sin 2 sin 2 2 2 2 x x 2 2 x x 2 sin sin 1 1 Mà 2 2 lim lim . 2 x 0 x 2 x 0 x 2 2 3 1 2t 1 3t Đặt 2 t x lim f (x) lim 0 . x 0 t 0 t Vậy A 0 . CÁC BÀI TOÁN LUYỆN TẬP
Bài 1. Tìm các giới hạn sau 3 4 (1 3x) (1 4x) Câu 1. A lim x 0 x A.25 B.26 C.27 D.28
Bài làm 1 Xét hàm số 3 4 f ( ) x (1 3 ) x (1 4 ) x A f '(0) 25
(1 x)(1 2x)(1 3x) 1 Câu 2. B lim x 0 x A.6 B.4 C.3 D.2
Bài làm 2. Xét hàm số f ( ) x (1 ) x (1 2 ) x (1 3 ) x 1 B f '(0) 6 n 1 ax 1 Câu 3. C lim (m,n ; . a b 0) 0 m x 1 bx 1 a m m a ma A. C B. C C. C D. C b n n b nb
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 25
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1.
Bài làm 3. Xét hai hàm số ( ) n 1 1, ( ) m f x ax g x 1 bx 1 f '(0) ma Suy ra C . g'(0) nb 2x 1 x Câu 4. D lim 2 x 1 x 1 A.0 B.1 C.2 D.3  1
Bài làm 4. Xét hàm số f (x) 2x 1 x D lim . f '(1) 0 x 1 x 1
Bài 2 Tìm các giới hạn sau 3 2x 1 1 Câu 1. A lim x 1 2 1 2 x 2 3 A. B.1 C.2 D. 3 2  2 2 Bài làm 1. Đặt 3 f ( ) x 2x 1 1 f '( ) x f '(1) 3 2 3 3. (2x 1) x và 2 ( g x) 1 2 x g'(x) g'(1) 1 . 2 2 x f (x) f (1) f (x) f (x) f (1) f '(1) 2 Khi đó: x 1 A lim lim lim . x 1 ( g x) x 1 ( g x) ( g 1) x 1 ( g x) ( g 1) g'(1) 3 x 1 3 2 2x 1 x 1 Câu 2. B lim x 0 sin x A.1 B.2 C.3 D.4  1 2x Bài làm 2. Đặt 3 2 f (x) 2x 1 x 1 f '(x) . 3 2 2 2x 1 3. (x 1) f '(0) 1 . Và ( g ) x sin x g'( ) x cos x g'(0) 1. f (x) f (0) f (x) f '(0) Khi đó: lim lim x B 1 . x 0 ( g x) x 0 ( g x) ( g 0) g '(0) x 3 3 4 4 26x 1 80x 1 Câu 3. C lim x 1 x 1 4 4 A. B.1 C.2 D. 27 27
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 26
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1.  1 1 Bài làm 3. Đặt ( g x) x 1 g'(x) g'(1) và 2 x 2 3 3 3 4 4 26 80x f (x) 26x 1 80x 1 f '(x) 3 3 2 4 4 3 (26x 1) (80x 1) 2 f '(1) . 27 f (x) f (1) f (x) f '(1) 4 Khi đó: x 1 C lim lim . x 1 ( g x) x 0 ( g x) ( g 1) g '(1) 27 x 1 3 2 3 2 4 2x x 4 2x x Câu 4. E lim x 0 2 x 2 x 3 4. 2 3 4. 2 3 4 A. B. C. D.1 3 3 3
Bài làm 4. Xét hai hàm số 3 2 3 2 f ( ) x 4 2x x 4 2x x ( g ) x 2 x 2 x 3 f '(0) 4. 2 Ta có: E . g'(0) 3
Vấn đề 3. Đạo hàm cấp vao và vi phân Phương pháp:
Vi phân của hàm số
Tích f '(x ).x được gọi là vi phân của hàm số y f ( )
x tại điểm x (ứng với số gia x ) được kí hiệu 0 0 là df (x )
f '(x )x . 0 0
Nếu hàm số f có đạo hàm f ' thì tích f '( )
x x được gọi là vi phân hàm số y f ( ) x , kí hiệu là: df ( ) x f '( ) x x . Đặc biệt: dx x' x
x nên ta viết df ( ) x f '( ) x dx .
Đạo hàm cấp n
Đạo hàm cấp hai: Cho hàm số f có đạo hàm f ' . Nếu f ' cũng có đạo hàm thì đạo hàm của nó được
gọi là đạo hàm cấp hai của f và được kí hiệu là: f '' , tức là: f ' ( f ')' .
Đạo hàm cấp n : Cho hàm số f có đạo hàm cấp n 1 (với n ,n 2 ) là (n 1) f . Nếu (n 1) f cũng có
đạo hàm thì đạo hàm của nó được gọi là đạo hàm cấp n của f và được kí hiệu là (n) f , tức là: (n) (n 1) f ( f )' . Các ví dụ 3x 1
Ví dụ 1. Tính đạo hàm cấp n của hàm số sau: y x 2 Lời giải.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 27
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1. 7 7.2 7.2.3 Ta có: y' , y'' , y''' 2 (x 2) 3 (x 2) 4 (x 2) ( 1)n n .7.n!
Bằng quy nạp ta chứng minh: ( ) y (2) n 1 (x 2) Với n 1 ta thấy (2) đúng ( 1)k k .7.k!
Giả sử (2) đúng với n k , tức là: ( ) y k 1 (x 2) ' ( 1)k .7.k! ( 1)k k .7.k!.(k 1) Ta có: ( 1) y k 1 k 2 (x 2) (x 2) k 1 ( 1) .7.(k 1)! k 2 (x 2)
Nên (2) đúng với mọi số tự nhiên n .
Ví dụ 2. Cho đa thức 3 2 f ( ) x x 5x
1 . Viết f (x) dưới dạng lũy thừa của x 2 Lời giải. (3) ' f (2) f (2) f '(2) Ta có: 3 2 f ( ) x (x 2) (x 2) (x 2) f (2) 3! 2! 1! Mà 2 f '( ) x 3x 10x, f ''( ) x 6x 10, f '''( ) x 6 Nên 3 2 f ( ) x (x 2) (x 2) 8(x 2) 11 .
Ví dụ 3. Tìm vi phân của của hàm số: 1. 4 y x 2x 1 2. 3 y (x 2)(x 1) 2 2x 6x 5 3. y 4. y sin 3xcos 5x 2x 4 5. 2 y 4x tan x Lời giải. 1. Ta có 4 3 dy (x 2x 1)'dx (4x 2)dx 2. Ta có 4 3 3 2 y x x 2x 1 dy (4x 3x 2)dx 2 2 (4x 6)(2x 4) 2(2x 6x 5) 4x 16x 34 3. Ta có y' 2 2 (2x 4) (2x 4) 2 4x 16x 34 Suy ra dy dx . 2 (2x 4) 1 1 4. Ta có y sin 8x sin 2x dy
4 cos 8x cos 2x dx 2 2 2 2 8x 1 tan x 8x 1 tan x 5. Ta có: y' dy dx 2 2 2 4x tan x 2 4x tan x
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 28
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1.
CÁC BÀI TOÁN LUYỆN TẬP
Bài 1. Cho hàm số y sin 2x
Câu 1. Tính y '' A. y'' sin 2x B. y'' 4sin x C. y'' sin 2x D. y'' 4sin 2x
Bài làm 1. Ta có y' 2cos2x y'' 4sin 2x
Câu 2. Tính y ' '( ) , (4) y ( ) 3 4 A. 4 và 16 B. 5 và 17 C. 6 và 18 D. 7 và 19 Bài làm 2. Ta có (4) y''' 8cos 2x, y 16sin 2x 2 Suy ra (4) y'''( ) 8 cos 4; y ( ) 16 sin 16 . 3 3 4 2
Câu 3. Tính (n) y A. (n) 2n y sin(2x
n ) B. (n) 2n y sin(2x ) 3 2 C. (n) 2n y sin(x ) D. (n) 2n y sin(2x n ) 2 2 Bài làm 3. Ta có 2 y' 2 sin(2x ), y' 2 sin(2x 2 ) , 3 y''' 2 sin(2x 3 ) 2 2 2
Bằng quy nạp ta chứng minh (n) 2n y sin(2x n ) 2 Với 1 n 1 y' 2 sin(2x ) đúng 2 Giả sử (k) 2k y sin(2x k ) , 2 suy ra (k 1) (k) k 1 k 1 y y ' 2 cos(2x k ) 2 sin 2x (k 1) 2 2
Theo nguyên lí quy nạp ta có điều phải chứng minh.
Bài 2. Tính đạo hàm cấp n của các hàm số sau 2x 1 Câu 1. y x 2 n 1 n 1 n (1) .3.n! n ( 1) .n! A. ( ) y B. ( ) y n 1 (x 2) n 1 (x 2) n 1 n 1 n ( 1) .3.n! n ( 1) .3.n! C. ( ) y D. ( ) y n 1 (x 2) n 1 (x 2) ' 2 3 (x 2)  3 3.2
Bài làm 1. Ta có y' , y'' 2 4 3 (x 2) (x 2) (x 2)
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 29
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1. 3.2.3 n 1 n ( 1) .3.n! y''' . Ta chứng minh ( ) y 4 (x 2) n 1 (x 2) 0 ( 1) .3 3 Với n 1 y' đúng 2 2 (x 2) (x 2) k 1 k ( 1) .3.k! Giả sử ( ) y k 1 (x 2) k 1 k 1 ( 1) .3.k!. (x 2) ' k (k 1) (k) ( 1) .3.(k 1)! y y ' 2k 2 k 2 (x 2) (x 2)
Theo nguyên lí quy nạp ta có điều phải chứng minh. 1 Câu 2. y , a 0 ax b (2)n. n n n n n n n a .n! n ( 1) .a .n! n ( 1) .n! n ( 1) .a .n! A. ( ) y B. ( ) y C. ( ) y D. ( ) y n 1 (ax ) b n 1 (x 1) n 1 (ax ) b n 1 (ax ) b 2 3  a a .2 a .2.3
Bài làm 2. Ta có y' , y'' , y''' 2 3 4 (ax ) b (ax ) b (ax ) b ( 1)n. n n a .n! Ta chứng minh: ( ) y n 1 (ax ) b 1 1 ( 1) .a .1! a Với n 1 y' đúng 2 2 (ax ) b (ax ) b ( 1)k . k k a .k! Giả sử ( ) y k 1 (ax ) b k k k 1
( 1) .a .k!. (ax ) b ' k 1 k 1 (k 1) (k) ( 1) .a .(k 1)! y y ' 2k 2 k 2 (ax ) b (x 2)
Theo nguyên lí quy nạp ta có điều phải chứng minh. 2x 1 Câu 3. y 2 x 5x 6 (2)n.7.n! (1)n n 1 n 1 n .5.n! n ( 1) .7.n! ( 1) .5.n! A. ( ) y B. ( ) y n 1 n 1 (x 2) (x 3) n 1 n 1 (x 2) (x 3) n n n n ( 1)n.7.n! ( 1)n n .5.n! C. (n) ( 1) .7. ! ( 1) .5. ! y D. ( ) y (x 2)n (x 3)n n 1 n 1 (x 2) (x 3)
Bài làm 3. Ta có: 2x 1 7(x 2) 5(x 3) ; 2 x 5x 6 (x 2)(x 3) 7 5 Suy ra y . x 3 x 2 (n) (n) 1
( 1)n.1n.n! ( 1)n.n! 1 ( 1)n.n! Mà , n 1 n 1 n 1 x 2 (x 2) (x 2) x 2 (x 3)
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 30
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1. ( 1)n.7.n! ( 1)n n .5.n! Nên ( ) y . n 1 n 1 (x 2) (x 3) Câu 4. y cos 2x n A. (n) y 1 cos 2x n B. (n) 2n y cos 2x 2 2 C. (n) n 1 y 2 cos 2x n D. (n) 2n y cos 2x n 2 2 Bài làm 4. Ta có 2 y' 2 cos 2x , y'' 2 cos 2x 2 , 2 2 3 y' ' 2 cos 2x 3 . 2
Bằng quy nạp ta chứng minh được (n) 2n y cos 2x n . 2 Câu 5. y 2x 1 n 1 n 1 n ( 1) .3.5...(3n 1) n ( 1) .3.5...(2n 1) A. ( ) y B. ( ) y 2n 1 (2x 1) 2n 1 (2x 1) n 1 n 1 n ( 1) .3.5...(2n 1) n ( 1) .3.5...(2n 1) C. ( ) y D. ( ) y 2n 1 (2x 1) 2n 1 (2x 1)  1 1 3
Bài làm 5. Ta có y' , y'' , y''' 3 5 2x 1 (2x 1) (2x 1) n 1 n ( 1) .3.5...(2n 1)
Bằng quy nạp ta chứng minh được: ( ) y 2n 1 (2x 1) 2x 1 Câu 6. y 2 x 3x 2 5.( 1)n.n! 3.( 1)n n n n .n! n 5.( 1) .n! 3.( 1) .n! A. ( ) y B. ( ) y n 1 n 1 (x 2) (x 1) n 1 n 1 (x 2) (x 1)
5.( 1)n.n! 3.( 1)n n n n .n! n 5.( 1) .n! 3.( 1) .n! C. ( ) y : D. ( ) y n 1 n 1 (x 2) (x 1) n 1 n 1 (x 2) (x 1)  5 3
Bài làm 6. Ta có: y x 2 x 1 5.( 1)n.n! 3.( 1)n n .n!
Bằng quy nạp ta chứng minh được: ( ) y . n 1 n 1 (x 2) (x 1)
Bài 4. Tìm vi phân của các hàm số sau
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 31
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1. Câu 1. 3 2 y x 2x A. 2 dy (3x 4 ) x dx B. 2 dy (3x ) x dx C. 2 dy (3x 2 ) x dx D. 2 dy (3x 4 ) x dxBài làm 1. 2 dy (3x 4 ) x dx Câu 2. y 3x 2 3 1 1 3 A. dy dx B. dy dx C. dy dx D. dy dx 3x 2 2 3x 2 3x 2 2 3x 2  3 Bài làm 2. dy dx 2 3x 2 Câu 3. 3 y sin 2x sin x A. 2 dy cos 2x 3sin x cos x dx B. 2 dy 2 cos 2x 3sin x cos x dx C. 2 dy 2 cos 2x sin x cos x dx D. 2 dy cos 2x sin x cos x dxBài làm 3. 2 dy 2 cos 2x 3sin xcos x dx Câu 4. y tan 2x A. 2 dy (1 tan 2x)dx B. 2 dy (1 tan 2x)dx C. 2 dy 2(1 tan 2 ) x dx D. 2 dy 2(1 tan 2 ) x dxBài làm 4. 2 dy 2(1 tan 2 ) x dx Câu 5. 3 y x 1 1 3 2 1 A. dy dx B. dy dx C. dy dx D. dy dx 3 2 (x 1) 3 2 (x 1) 3 2 (x 1) 3 2 3 (x 1)  1 Bài làm 5. dy dx 3 2 3 (x 1) Câu 6. 10 y (3x 1) A. 9 dy 10(3x 1) dx B. 10 dy 30(3x 1) dx C. 10 dy 9(3x 1) dx D. 9 dy 30(3x 1) dxBài làm 6. 9 dy
30(3x 1) dx .
Bài 6. Tính đạo hàm cấp n của các hàm số sau x Câu 1. y 2 x 5x 6 ( 1)n.3.n! ( 1)n n n n .2.n! n n A. ( ) y B. (n) ( 1) .3. ! ( 1) .2. ! y n 1 n 1 (x 3) (x 2) (x 3)n (x 2)n ( 1)n.3.n! ( 1)n n n n .2.n! n ( 1) .3.n! ( 1) .2.n! C. ( ) y D. ( ) y n 1 n 1 (x 3) (x 2) n 1 n 1 (x 3) (x 2)
Bài làm 1. Ta có: x 3(x 2) 2(x 3) ; 2 x 5x 6 (x 2)(x 3) 3 2 Suy ra y . x 3 x 2
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 32
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1. (n) (n) 1 ( 1)n.1 . n n! ( 1)n.n! 1 ( 1)n.n! Mà , n 1 n 1 n 1 x 2 (x 2) (x 2) x 3 (x ) ( 1)n.3.n! ( 1)n n .2.n! Nên ta có: ( ) y . n 1 n 1 (x 3) (x 2) Câu 2. y cos 2x A. (n) n 1 y 2 cos 2x n B. (n) n 1 y 2 cos 2x n 2 2 C. (n) 2n y cos 2x D. (n) 2n y cos 2x n 2 2
Bài làm 2. Ta có : 2 y' 2 cos 2x , y'' 2 cos 2x 2 , 3 y' ' 2 cos 2x 3 . 2 2 2
Bằng quy nạp ta chứng minh được (n) 2n y cos 2x n . 2 ĐẠO HÀM TỔNG HỢP
Bài 1. Tính đạo hàm của các hàm số sau: 1 2 3 Câu 1: 5 4 3 2 y x x x x 4x 5 2 3 2 1 8 5 2 A. 4 3 2 y' x x 3x 3x 4. B. 4 3 2 y' x x 3x 3x 4. 2 3 2 3 5 8 5 8 C. 4 3 2 y' x x x 3x 4. D. 4 3 2 y' x x 3x 3x 4. 2 3 2 3 / / / / /  1 2 3 1 2 3 / Bài làm: 5 4 3 2 y' x x x x 4x 5 5 4 3 2 / y' x x x x 4x 5 2 3 2 2 3 2 5 4 8 3 2 y' x x 3x 3x 4. 2 3 1 1 Câu 2: 2 4 y x x 0, 5x 4 3 1 1 1 1 A. 3 y' x 2x . B. 3 y' 2x x . C. 3 y' x 2x . D. 3 y' 2x 2x . 3 3 3 3 /  1 1 Bài làm / 2 4 y x x 0, 5x 4 3 / / / / / 1 1 2 4 y x x 0, 5x 4 3 1 3 y' 2x 2x . 3
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 33
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1. 1 Câu 3: 4 3 y 2x x 2 x 5 3 A. 3 2 1 y' 8x x . B. 3 2 1 y' 8x x . C. 3 2 1 y' 2x x . D. 3 2 1 y' 8x x . x x x x / / / /  1 1 Bài làm 4 3 y' 2x x 2 x 5 4 3 / y' 2x x 2 x 5 3 2 1 y' 8x x . 3 3 x 4 3 x x 1 Câu 4: 2 y x x a (a là hằng số) 4 3 2 1 1 A. 3 2 y' x x x 1 B. 3 2 y' 4x x x 1 C. 3 2 y' x x x 1 D. 3 2 y' x x x 1 3 4 / 4 3  x x 1 Bài làm 2 y' x x a 3 2 y' x x x 1 . 4 3 2 3 2 Câu 5: y x x x 2 x 3 6 1 6 1 6 1 6 1 A. x. B. x. C. x. D. x. 3 x 2 x 3 x x 3 x x 3 x 2 x / / / /  3 2 Bài làm y ' x x x 2 2 y' 3.x x x x 2 x 3 3 / 3 1 2 / 6 1 2 1 y' 3. 2 .x x . x x .x y' x .x 2 x 3 3 x 2 x 3 2 x 6 1 2 x 6 1 y' x x. 3 3 x 2 x 3 2 x 2 x 1 Câu 6: 4 3 y 2x x 2 x 5 3 A. 3 2 1 y' 2x x . B. 3 2 1 y' x x . C. 3 2 1 y' 8x 3x . D. 3 2 1 y' 8x x . x x x x / / / /  1 1 Bài làm 4 3 y' 2x x 2 x 5 4 3 / y' 2x x 2 x 5 3 2 1 y' 8x x . 3 3 x Câu 7: 5 3 y x 4x 2x 3 x A. 4 3 y' 4x 12x 2 . B. 4 3 y' 5x 12x 2 . 2 x 2 x
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 34
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1. C. 4 3 y' 5x 4x 2 . 2 x D. 4 2 3 y' 5x 12x 2 . 2 x / / / / Bài làm 5 3 y' x 4x 2x 3 x 5 3 / y' x 4 x 2.x 3 x 4 3 y' 5x 12x 2 . 2 x
Bài 2. Tính đạo hàm của các hàm số sau; Câu a). 2 y x 3x 2 x . A. 2 3x x 6. B. 2 3x 2x 6. C. 2 3x 2 . x D. 2 3x 2x 6. / /  / Bài làm 2 2 2 y' x 3x 2 x x 3x . 2 x x 3x . 2 x 2 2 2x 3 2 x x 3x 1 3x 2x 6. Câu b). 5 y 2x 3 x 2x A. 5 4 12x 15x 8x 6. B. 5 4 12x 5x 8x 6. C. 5 4 12x 15x x 6. D. 5 4 12x x x 6. / /  / Bài làm 5 5 5 y' 2x 3 x 2x 2x 3 x 2x x 2x 2x 3 5 4 5 4 2 x 2x 5x 2 2x 3 12x 15x 8x 6. Câu c). 2 2 y x 1 5 3x A. 3 12x 4 . x B. 3 12x 4 . x C. 3 6x 4 . x D. 3 12x . x / / / Bài làm 2 2 2 2 2 2 y' x 1 5 3x x 1 5 3x 5 3x x 1 2 2 3 3 3 2x 5 3x 6x x 1 10x 6x 6x 6x 12x 4 . x Câu d). 2 y x 2x 1 3x 2 2x x 3x 2 A. 2 18x 2x B. 2 18x x 2. C. 2 8x 2x 2. D. 2 18x 2x 2. / /  / Bài làm 2 2 2 y' 2x x 3x 2 2x x 3x 2 3x 2 . 2x x 2 2 4x 1 3x 2 3 2x x 18x 2x 2. Câu e). 2 2 y x 2x 3 2x 3 A. 3 2 12x 4x 4x 6. B. 3 2 2x 4x 24x 6. C. 3 2 12x x 24x 6. D. 3 2 12x 4x 24x 6.
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 35
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1. / / / Bài làm 2 2 2 2 2 2 y' x 2x 3 2x 3 x 2x 3 2x 3 2x 3 x 2x 3 2 2 3 2 4x 2 2x 3 4x x 2x 3 12x 4x 24x 6. Câu f) 2 y x x x x 5 x 5x x 5x x A. . B. . C. . D. . 2 2 3 2 / / /  1 1 5x x Bài làm 2 2 2 2 y' x x x . x x .x 2 . x x .x 2x x x x . 2 x 2 2 2x 1 Câu g) y 4x 3 2 2 2 2 A. . B. . C. . D. . 2 2 2 4x 3 x 3 4x 3 4x 3 / / / 2x 1 4x 3 4x 3 2x 1 2 4x 3 4 2x 1  2x 1 2 Bài làm y ' . 4x 3 2 2 2 4x 3 4x 3 4x 3 2x 10 Câu h) y 4x 3 46 4 46 46 A. B. C. D. 2 2 2 4x 3 4x 3 4x 3 4x 3 / / / 2x 10 . 4x 3 4x 3 . 2x 10 2 4x 3 4 2x 10  2x 10 46 Bài làm y' 4x 3 2 2 2 4x 3 4x 3 4x 3 3 Câu k). y 2x 1 6 16 26 36 A. . B. . C. . D. . 2 2 2 2 2x 1 2x 1 2x 1 2x 1 / / 1 2x 1  6 Bài làm y' 3. 3. . 2 2 2x 1 2x 1 2x 1 2x 1 Câu l). y 1 3x 15 5 25 5 A. . B. . C. . D. . 2 2 2 2 1 3x 1 3x 1 3x 1 3x /  2x 1 Bài làm y ' 1 3x
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 36
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1. / / 2x 1 1 3x 1 3x 2x 1 2 1 3x 3 2x 1 5 y' . 2 2 2 1 3x 1 3x 1 3x 2 1 x x Câu m). y 2 1 x x 2 2 1 2x 1 x x 1 2x 1 x x 2 2 1 2x 1 x x 1 2x 1 x x A. B. 2 2 2 1 x x 2 1 x x 2 2 1 2x 1 x x 2x 1 x x 2 2 1 2x 1 x x 1 2x 1 x x C. D. 2 2 2 1 x x 2 1 x x / / / 2 2 2 2 2 1 x x 1 x x 1 x x 1 x x  1 x x Bài làm y ' 2 1 x x 2 2 1 x x 2 2 1 2x 1 x x 1 2x 1 x x 2 2 1 x x 2 x 3x 3 Câu n). y x 1 2 x x 2 x 2x 2 x 2 2 x 2x A. . B. . C. . D. . 2 2 2 2 x 1 x 1 x 1 x 1 / / 2 2 x 3x 3 x 1 x 1 x 3x 3 2 2x 3 x 1 x 3x 3 2  x 2x Bài làm y' . 2 2 2 x 1 x 1 x 1 2 2x 4x 1 Câu o). y x 3 2 2x 2x 11 2 2x x 11 2 x 12x 11 2 2x 12x 11 A. . B. . C. . D. . 2 2 2 2 x 3 x 3 x 3 x 3 Bài / / 2 2 2x 4x 1 x 3 x 3 2x 4x 1 2 4x 4 x 3 2x 4x 1 2 2x 12x 11 làm y' . 2 2 2 x 3 x 3 x 3
Bài 3. Tính đạo hàm của các hàm số sau: 2 Câu a). 7 y x x . A. 7 6 x x 7x 1 B. 6 2 7x 1 C. 7 6 2 x x x 1 D. 7 6 2 x x 7x 1
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 37
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1. /
Bài làm Sử dụng công thức 1 u .u .u' (với 7 u x x ) / 7 7 7 6 y' 2 x x . x x 2 x x 7x 1 2 Câu b). 3 2 y 2x 3x 6x 1 . A. 3 2 2 2 2x x 6x 1 6x 6x 6 . B. 3 2 2 2 2x 3x x 1 x 6x 6 . C. 3 2 2 2 2x 3x 6x 1 x 6x 6 . D. 3 2 2 2 2x 3x 6x 1 6x 6x 6 . /
Bài làm Sử dụng công thức u với 3 2 u 2x 3x 6x 1 / 3 2 3 2 3 2 2 y' 2 2x 3x 6x 1 2x 3x 6x 1 2 2x 3x 6x 1 6x 6x 6 . 3 Câu c). 2 y 1 2x . 2 2 2 2 A. 2 12x 1 2x . B. 2 12x 1 2x . C. 2 24x 1 2x . D. 2 24x 1 2x . /
Bài làm: Sử dụng công thức u với 2 u 1 2x 2 / 2 2 2 2 2 2 y' 3 1 2x 1 2x 3 1 2x 4x 12x 1 2x . 32 Câu d). 2 y x x . 31 31 31 A. 2 x x . 1 2x B. 2 32 x x C. 2 32 1 x 31 D. 2 32 x x . 1 2x /
Bài làm: Sử dụng công thức u với 2 u x x 31 / 31 2 2 2 y' 32 x x . x x 32 x x . 1 2x 4 Câu e). 2 y x x 1 . 3 3 3 A. 2 4 x x 1 . B. 2 x x 1 . 2x 1 C. 2 x x 1 . 3 D. 2 4 x x 1 . 2x 1 /
Bài làm: Sử dụng công thức u với 2 u x x 1 3 / 3 2 2 2 y' 4 x x 1 . x x 1 4 x x 1 . 2x 1
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 38
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1. 3 2 Câu f). 2 2 y x x 1 . x x 1 2 A. 2 2 2 y' x x 1 3 2x 1 x x 1 2 2x 1 x x 1 2 B. 2 2 2 2 y' x x 1 x
x 1 3 2x 1 x x 1 x x 1 2 C. 2 2 2 2 y' x x 1 x
x 1 3 2x 1 x x 1 2 2x 1 x x 1 2 D. 2 2 2 2 y' x x 1 x
x 1 3 2x 1 x x 1 2 2x 1 x x 1
Bài làm: Đầu tiên sử dụng quy tắc nhân. / / 3 2 2 3 2 2 2 2 y' x x 1 x x 1 x x 1 x x 1 . /
Sau đó sử dụng công thức u 2 / / 3 2 2 2 2 2 2 y' 3 x x 1 x x 1 x x 1 2 x x 1 x x 1 x x 1 2 2 3 2 2 2 2 y' 3 x x 1 2x 1 x x 1 2 x
x 1 2x 1 x x 1 2 2 2 2 2 y' x x 1 x
x 1 3 2x 1 x x 1 2 2x 1 x x 1 . 3 2x 1 Câu g) y x 1 2 2 2 2 3 2x 1 2x 1 2x 1 3 2x 1 A. . B. . C. . D. . 4 4 4 4 x 1 x 1 x 1 x 1 /  2x 1
Bài làm: Bước đầu tiên sử dụng u , với u x 1 2 2 / 2 2x 1 2x 1 2x 1 1 3 2x 1 y' 3. . 3. . . 2 4 x 1 x 1 x 1 x 1 x 1 1 Câu h). y 5 2 x x 1 5 2x 1 5 2x 1 2x 1 2x 1 A. B. C. D. 6 6 6 6 2 x x 1 2 x x 1 2 x x 1 2 x x 1 / 5  1
Bài làm: Đầu tiên sử dụng công thức với 2 u x x 1 u
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 39
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1. / 5 2 4 / x x 1 2 2 5 x x 1 . x x 1 5 2x 1 y ' 2 10 6 5 2 2 2 x x 1 x x 1 x x 1 2 3 2 x 3 x Câu k). y 2 1 x x 4 2 2 2 3 5x 6x x 1 x x 1 2x 2 x 3 x A. y' 2 2 1 x x 4 2 2 2 3 5x 6x x 1 x x 1 2x 2 x 3 x B. y' 2 2 1 x x 4 2 2 2 3 5x x x 1 x x 1 x 2 x 3 x C. y' 2 2 1 x x 4 2 2 2 3 5x 6x 6x 1 x x 1 2x 2 x 3 x D. y' 2 2 1 x x /  u
Bài làm: Đầu tiên sử dụng v / / 2 3 2 2 2 3 2 x 3 x . 1 x x 1 x x 2 x 3 x y ' 2 2 1 x x / / / Tính 2 3 2 3 3 2 2 x 3 x 2 x 3 x 3 x 2 x 3 2 2 4 2 2x 3 x 3x 2 x 5x 6x 6 . x 4 2 2 2 3 5x 6x 6x 1 x x 1 2x 2 x 3 x Vậy y' 2 2 1 x x Câu l). 2 3 y 1 2x 2 3x 3 4x A. 2 3 3 2 2 y' 2 3x 3 4x
1 2x 6x 3 4x 1 2x 2 3x 12x B. 2 3 3 2 2 y' 4 2 3x 3 4x
1 2x 6x 3 4x 1 2x 2 3x 12x C. 2 3 3 2 2 y' 2 2 3x 3 4x
1 2x 6x 3 4x 1 2x 2 3x 12x D. 2 3 3 2 2 y' 2 2 3x 3 4x
1 2x 6x 3 4x 1 2x 2 3x 12x
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 40
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1.Bài làm: / / / 2 3 2 3 2 3 y' 1 2x 2 3x 3 4x 1 2x 2 3x 3 4x 1 2x 2 3x 3 4x 2 3 3 2 2 y' 2 2 3x 3 4x
1 2x 6x 3 4x 1 2x 2 3x 12x .
Bài 4. Tính đạo hàm các hàm số sau Câu a). 2 y x x x 1 3 x x x 3 x A. x . B. 2x . C. x . D. 2x . 2 2 2 2 / /. /  x Bài làm: 2 / 1 3 y' x x x 1 2x x'. x x .x 2x x .x 2x . 2 x 2 Câu b). 2 y 1 2x x . x 1 1 x 1 x A. B. C. D. 2 1 2x x 2 1 2x x 2 1 x x 2 1 2x x /
Bài làm: Sử dụng công thức u với 2 u 1 2x x / 2 1 2x x 1 x y ' . 2 2 1 2x x 1 2x x Câu c). 2 2 y x 1 1 x 1 x x 1 1 1 x x A. . B. . C. . D. . 2 2 x 1 1 x 2 2 x 1 1 x 2 2 x 1 1 x 2 2 x 1 1 x / / 2 2 / / x 1 1 xx x Bài làm: 2 2 y' x 1 1 x . 2 2 2 2 2 x 1 2 1 x x 1 1 x 2 x 1 Câu d). y . x 1 1 1 3 1 1 1 A. 1 B. C. 1 D. 1 2 2 2 2 1 x x 2 x 1 2 1 x x 2 1 x x 2 2 2 x x x x / 2  x 1
Bài làm: Sử dụng công thức u với u x / 2 1 x 1 1 1 y ' . 1 2 2 x 2 1 1 x x x 2 2 x x
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 41
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1. 1 x Câu e). y . 1 x 1 x 1 1 x 1 A. y' 2 . B. y' 2 . 2 1 x 2 1 x 1 x x 1 x 1 x 1 1 x 1 C. y' . D. y' 2 . 2 1 x 2 x 1 x 1 x x 1 x /  1 x
Bài làm: Đầu tiên sử dụng công thức u với u 1 x / 1 x 1 x y' 2 . 1 x 1 x / / / 1 x 1 x 1 x 1 1 x x Tính 2 1 x 1 x 1 1 1 x 1 x 2 x 2 x 1 2 2 1 x x 1 x 1 x 1 Vậy y' 2 . . 2 1 x x 1 x 1 Câu f). y x 1 x 1 1 1 1 1 A. . B. . x 1 2 x 1 x 1 2 x 1 2 x 1 1 1 1 1 C. . D. . x 1 x 1 x 1 2 x 1 2 x 1 x 1 / / / x 1  1 1 1 1 Bài làm: y' x 1 . 2 x 1 2 x 1 2 x 1 2 x 1 x 1 x 1 5 1 Câu g). y x . x 4 4 1 1 1 1 1 1 A. 5 x B. 5 x x 2 x 2 x.x x x x.x
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 42
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1. 4 4 1 1 1 1 1 1 C. x D. 5 x x 2 x 2 x.x x 2 x 2 x.x /  1
Bài làm: Bước đầu tiên sử dụng u với u x x / 4 / 4 1 1 1 1 x y ' 5 x . x 5 x . 2 x x x 2 x x 4 1 1 1 5 x x 2 x 2 x.x 1 x Câu h). y . 1 x x 3 x 3 3 x A. . B. . C. . D. . 2 1 x 1 x 1 x 1 x 2 1 x 1 x 2 1 x 1 x / / / 1 x 1 x 1 x 1 xu
Bài làm: Sử dụng được: y' v 2 1 x / 1 x 1 x . 1 x 2 1 x 2 1 x 1 x 3 x . 1 x 2 1 x. 1 x 2 1 x 1 x Câu i) y x x x . 1 1 1 1 1 1 A. . 1 . 1 . B. . 1 . 1 . 2 2 2 x x x x x x x x x x x x 1 1 1 1 1 1 C. . 1 . 1 . D. . 1 . 1 . 2 2 x x x x x x 2 2 2 x x x x x x
Bài làm: Đầu tiên áp dụng u với u x x x / / 1 1 1 y' x x x 1 . x x 2 2 2 x x x x x x x x 1 1 1 . 1 . 1 . 2 2 2 x x x x x x 4x 1 Câu k). y
(áp dụng u chia v đạo hàm) 2 x 2
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 43
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1. x x 8 x 8 x 8 A. B. C. D. 2 2 x 2 x 2 2 2 x 2 x 2 2 2 x 3 x 2 2 2 x 2 x 2 / 2 x 2 / 2 / 2 2 4. x 2 . 4x 1 4x 1 x 2 x 2 . 4x 1 2  2 x 2 Bài làm: y' 2 2 2 x 2 x 2 2 x 4 x 2 4x 1 2 2 4 x 2 x 4x 1 x 2 x 8 2 2 2 2 2 x 2 x 2 x 2 x 2 x 2 3 x Câu l). y
(Áp dụng căn bặc hai của u đạo hàm). x 1 3 2 1 x 3x A. y ' . . 2 3 x x 1 2 x 1 3 2 1 2x x B. y ' . . 2 3 x x 1 2 x 1 3 2 1 2x 3x 3 2 1 2x 3x C. y ' . . D. y ' . . 2 3 2 x x 1 3 x x 1 2 x 1 x 1 / 3  1 x Bài làm: y ' . 3 x 1 x 2 x 1 / / / 3 3 2 3 3 x x 1 x 1 .x 3 2 x 3x x 1 x 2x 3x Ta có: 2 2 2 x 1 x 1 x 1 x 1 3 2 1 2x 3x Vậy y ' . . 2 3 x x 1 2 x 1 3 Câu m). y x 2 . x 2 x 2 3 x 2 3 x 2 A. . B. . C. . D. . 2 x 2 x 2 x 2 2 x 2
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 44
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1. /  3
Bài làm: Đầu tiên áp dụng u với u x 2 / 1 3 1 2 3 x 2 y' . x 2 .3. x 2 . 3 3 2 x 2 2 x 2 2 x 2 3 Câu n) y 1 1 2x . 2 2 2 2 6 1 1 2x 1 1 2x 1 1 2x 6 1 1 2x A. . B. . C. . D. . 1 2x 2 1 2x 1 2x 2 1 2x /
Bài làm: Bước đầu tiên áp dụng u với u 1 1 2x 2 / 2 / 2 6 1 1 2 1 2 x x y' 3 1 1 2x . 1 1 2x 3 1 1 2x . . 2 1 2x 2 1 2x
Bài 5. Tính đạo hàm các hàm số sau: Câu a). y
xcos x . A. cos x sin . x B. xsin . x C. xsin . x D. cos x xsin . x
Bài làm: Ta áp dụng đạo hàm tích. / y' x'cos x . x cos x cos x x sin . x 3 sin x Câu b) y . 1 cos x 2 sin x 2 3 sin x 2 2 sin x 2 3 sin x A. B. C. D. 3 2 2 3 1 cos x 1 cos x 1 cos x 1 cos x /  sin x
Bài làm: Bước đầu tiên ta áp dụng công thức u với u 1 cos x 2 / sin x sin y' 3 . 1 cos x 1 cos x / / / 2 sin x sin x 1 cos x 1 cos x .sin x cos x 1 cos x sin x Tính : 2 2 1 cos x 1 cos x 1 cos x 2 2 cos x cos x sin x 1 . 2 1 cos 1 cos x x 2 2 sin x 1 3sin x Vậy y' 3 . . 3 1 cos x 1 cos x 1 cos x Câu c). 3 y sin 2x 1 .
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 45
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1. A. 2 sin 2x 1 cos 2x 1 . B. 2
12 sin 2x 1 cos 2x 1 . C. 2
3sin 2x 1 cos 2x 1 . D. 2
6 sin 2x 1 cos 2x 1 . /
Bài làm: Bước đầu tiên áp dung công thức u với u sin 2x 1 / / Vậy 3 2 y' sin 2x 1
3sin 2x 1 . sin 2x 1 . / / Tính sin 2x 1
: Áp dụng sin u , với u 2x 1 / / Ta được: sin 2x 1 cos 2x 1 . 2x 1 2 cos 2x 1 . 2 2 y'
3.sin 2x 1 .2cos 2x 1
6sin 2x 1 cos 2x 1 . Câu d). 2 y sin 2 x . 1 1 A. 2 cos 2 x . B. 2 .cos 2 x . C. 2 .cos 2 x . 2 2 x 2 x D. 2 .cos 2 x . 2 2 x  /
Bài làm: Áp dụng công thức sin u với 2 u 2 x / 2 / 2 x 2 2 2 x 2 y' cos 2 x . 2 x cos 2 x . .cos 2 x . 2 2 2 2 x 2 x Câu e). y sin x 2x . cos x 2 cos x 2 2 cos x A. . B. . C. . D. . 2 sin x 2x sin x 2x 2 sin x 2x 2 sin x 2x /
Bài làm: Áp dụng u , với u sinx 2x / sin x 2x cos x 2 y' . 2 sin x 2x 2 sin x 2x Câu f). 2 3 y
2sin 4x 3cos 5x . 45 5 A. y' sin 8x cos 5 . x sin10x B. y' 8 sin 8x cos 5 . x sin10x 2 2 45 45 C. y' 8 sin x cos 5 . x sin10x D. y' 8 sin 8x cos 5 . x sin10x 2 2
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 46
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1.  /
Bài làm: Bước đầu tiên áp dụng u v / / 2 3 y' 2 sin 4x 3 cos 5x / / Tính 2
sin 4x : Áp dụng u , với u sin 4x, ta được: / / / 2 sin 4x 2 sin 4 . x sin 4x 2 sin 4 .
x cos 4x 4x 4 sin 8 . x / / / Tương tự: 3 2 2 cos 5x 3cos 5 . x cos 5x 3cos 5 . x sin 5x . 5x 2 15 15cos 5 . x sin 5x cos 5 . x sin10 . x 2 45 Kết luận: y' 8 sin 8x cos 5 . x sin10x 2 3 Câu h). 2 y 2 sin 2x . 3 2 A. 2 y' 6 sin 4x 2 sin 2x . B. 2 y' 3sin 4x 2 sin 2x . 2 2 C. 2 y' sin 4x 2 sin 2x . D. 2 y' 6 sin 4x 2 sin 2x . /
Bài làm: Áp dụng u , với 2 u 2 sin 2x. 2 / 2 / 2 2 2 2 y' 3 2 sin 2x 2 sin 2x 3 2 sin 2x sin 2x . / / Tính 2
sin 2x , áp dụng u , với u sin 2 . x / / / 2 sin 2x 2.sin 2x sin 2x 2.sin 2 .
x cos 2x 2x 2 sin 4 . x 2 2 y' 6 sin 4x 2 sin 2x . Câu i). 2 2 y sin cos .
x tan x . A. 2 2 2 y' cos cos .
x tan x sin 2x tan x 2 tanx B. 2 2 2 y' cos cos .
x tan x sin 2x tan x tan x C. 2 2 2 y' cos cos . x tan x sin 2x tan x tan x D. 2 2 2 y' cos cos . x tan x sin 2x tan x 2 tan x  /
Bài làm: Áp dụng sin u , với 2 2 u cos x tan x
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 47
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1. / 2 2 2 2 y' cos cos . x tan x . cos . x tan x . / / / Tính 2 2 cos .
x tan x , bước đầu sử dụng .
u v , sau đó sử dụng u . / / / 2 2 2 2 2 2 cos . x tan x cos x .tan x tan x .cos x / / 2 2
2 cos x cos x tan x
2 tan x tan x cos x 2 1 2 2
2 sin x cos x tan x 2 tan x cos x sin 2x tan x 2 tan . x 2 cos x Vậy 2 2 2 y' cos cos . x tan x sin 2xtan x 2 tan x x Câu j). 2 1 y cos . x 1 1 x 1 1 x 1 A. y' .sin . B. y' .cos 2. . 2 x 1 2 x x 1 x 1 x x 1 1 x 1 1 x 1 C. y' .sin 2. . D. y' .sin 2. . 2 x 1 2 x x 1 x 1 x x 1 /  x 1
Bài làm: Áp dụng u , với u cos x 1 / / x 1 x 1 x 1 x 1 x 1 y' 2.cos . cos 2.cos .sin . x 1 x 1 x 1 x 1 x 1 / x 1 x 1 y' sin 2 . . x 1 x 1 / / / x 1 . x 1 x 1 . x 1 x 1 1 Tính . 2 2 x 1 x 1 x x 1 1 x 1 Vậy y' .sin 2. . 2 x 1 x x 1 sin 2x cos 2x Câu k). y . 2 sin 2x cos 2x 6 6 6 6 A. B. C. D. 2 2 2 2 2 sin 2x cos 2x sin 2x cos 2x 2 sin 2x cos x 2 sin 2x cos 2x
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 48
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1. / / sin 2x
cos 2x . 2 sin 2x cos 2x
2 sin 2x cos 2x . sin 2x cos 2xBài làm: y' 2 2 sin 2x cos 2x
2 cos 2x 2 sin 2x 2 sin 2x cos 2x 4 cos 2x 2 sin 2x sin 2x cos 2x y' 2 2 sin 2x cos 2x 2 2
6 cos 2x 6 sin 2x 6 y' . 2 2 2 sin 2x cos 2x 2 sin 2x cos 2x 1 1 Câu l). y . 2 2 cos x sin x cos 2x sin 2x sin x 2 cos 2x 2 sin 2x A. . B. . C. . D. . 2 cos 2x 2 cos 2x 2 sin 2x 2 cos 2x /  1
Bài làm: Áp dụng . u / / cos 2x sin 2 . x 2x 2 sin 2x y' . 2 2 2 cos 2x cos 2 cos 2 x x Câu m). y sin .
x cos 2x . 5 4 5 5 A. cos 2x . B. cos 2x . C. 4 cos 2x . D. 2 cos 2x .  /
Bài làm: Áp dụng . u v / / / y' sin x .cos 2x cos 2x .sin x cos . x cos 2x sin 2 .
x 2x .sin x y' cos .
x cos 2x 2sin 2 . x sin . x 5 Câu n). 4 4 y cos x sin x A. 4 10 cos 2 . x B. 4 cos 2 . x sin 2 . x C. 4 10cos 2 . x sin . x D. 4 10cos 2 . x sin 2 . x 5 /  5 Bài làm: 2 2 2 2
cos x sin x cos x sin x
cos 2x . Áp dụng u , với u cos 2x / / 4 4 4 y' 5.cos 2 . x cos 2x 5.cos 2 . x sin 2x . 2x 10 cos 2 . x sin 2 . x Câu o). 2 4 y sin cos tan 3x A. 4 4 3 3 y'
sin 2 cos tan 3x . sin tan 3x .4 tan 3x. 1 tan 3x .3 B. 4 4 3 3 y'
sin 2 cos tan 3x . sin tan 3x .tan 3 . x 1 tan 3x . C. 4 4 3 3 y'
sin 2 cos tan 3x . sin tan 3x .4 tan 3 . x 1 tan 3x D. 4 4 3 3 y'
sin 2 cos tan 3x . sin tan 3x .4 tan 3 . x 1 tan 3x .3
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 49
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1. /
Bài làm: Đầu tiên áp dụng u , với 4 u sin cos tan 3x / 4 4 y'
2 sin cos tan 3x . sin cos tan 3x /
Sau đó áp dụng sin u , với 4 u cos tan 3x / 4 4 4 y'
2 sin cos tan 3x .cos cos tan 3x . cos tan 3x /
Áp dụng cosu , với 4 u tan 3 . x / 4 4 4 y'
sin 2 cos tan 3x . sin tan 3x . tan 3x . / Áp dụng u , với u tan 3x / 4 4 3 y'
sin 2 cos tan 3x . sin tan 3x .4 tan 3 . x tan 3x . / 4 4 3 2 y'
sin 2 cos tan 3x . sin tan 3x .4 tan 3 .
x 1 tan 3x . 3x . 4 4 3 3 y'
sin 2 cos tan 3x . sin tan 3x .4 tan 3 . x 1 tan 3x .3 . Câu p) 3 3 y sin 2 . x cos 2x 3 3 A. 2 sin 4 . x cos 4x. B. 2 sin . x cos . x C. 2 sin . x cos 4 . x D. 2 sin 4 . x cos 4 . x 2 2 3 /  3 1 1 Bài làm: 3 3 3 y sin 2 . x cos 2x sin 2 . x cos 2x sin 4x
.sin 4x . Áp dụng u ,u sin 4 . x 2 8 1 / 1 / 2 2 3 2 y' .3sin 4x sin 4x .3sin 4 . x cos 4 . x 4x sin 4 . x cos 4 . x 8 8 2 3 Câu q) y sin x cos x . 2 2 A. 3 sin x cos x cos x sin x .
B. 3 sin x c os x cos x sin x . 2 2 C. sin x cos x cos x sin x . D. 3 sin x cos x cos x sin x . /
Bài làm: Áp dụng u , với u sin x cosx 2 / 2 y' 3 sin x cos x . sin x cos x 3 sin x cos x cos x sin x . Câu r). y
5sin x 3cos x A. 5cos x 3sin . x B. cos x 3sin . x C. cos x sin . x D. 5cos x 3sin . x  / / Bài làm: y' 5sin x 3cos x 5cos x 3sin . x Câu s). 2 y sin x 3x 2
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 50
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1. A. 2 cos x 3x 2 B. 2 2x 3 .sin x 3x 2 C. 2 x 3 .cos x 3x 2 D. 2 2x 3 .cos x 3x 2  /
Bài làm: Áp dụng sin u , với 2 u x 3x 2 / 2 2 2 y' cos x 3x 2 . x 3x 2 2x 3 .cos x 3x 2
Bài 6. Tính đạo hàm các hàm số sau: Câu a). y sin x . 1 1 1 1 A. .cos x. B. .cos x. C. .sin x. D. .cos x. x x x 2 x  /
Bài làm: Áp dụng sin u , với u x / / 1 y' sin x cos x. x .cos x. 2 x Câu b). 2 y cos x . A. sin 2 . x B. sin 2 . x C. cos 2 . x D. 2sin 2 . x /
Bài làm: Áp dụng công thức u , với u cos x / / 2 y' cos x 2.cos cos x 2 cos . x sin x sin 2 . x Câu c). y cos 2x 1 . 1 1 A. .sin 2x 1. B. .sin 2x 1. C. sin 2x 1. 2x 1 2x 1 1 D. .cos 2x 1. 2x 1  /
Bài làm: Áp dụng cosu , với u 2x 1 / / / 2x 1 Câu y' cos 2x 1 sin 2x 1 2x 1 sin 2x 1. 2 2x 1 2 1 sin 2x 1. .sin 2x 1. 2 2x 1 2x 1 1 1 Câu d). y sin 3 .
x cos 5x sin 2x sin 8x sin 2x sin 8x 2 2
A. 4cos8x cos 2x
B. cos8x cos 2x C. 4cos8x cos 2x
D. 4cos8x cos 2x  1 / 1 / 1 / 1 / 1 / Bài làm: y' sin 8x sin 2x sin 8x sin 2x cos 8x 8x cos 2 . x 2x 2 2 2 2 2
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 51
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1. 4cos8x cos 2x sin x cos x Câu e). y . sin x cos x sin 2x 3 sin 2x sin 2x 2 sin 2x A. . B. . C. . D. . 2 2 2 2 sin x cos x sin x cos x sin x cos x sin x cos x /  u
Bài làm: Áp dụng v / / sin x cos x sin x cos x
sin x cos x . sin x cos x y' 2 sin x cos x
cosx sin x sin x cos x cos x sin x sin x cos x y' 2 sin x cos x 2 2 sin x cos x sin x cos x 2 sin 2x y' . 2 2 sin x cos x sin x cos x Câu f). y cos 2x . sin 2x sin x sin 2x sin 2x A. . B. . C. . D. . cos 2x cos 2x 2 cos 2x cos 2x /
Bài làm: Áp dụng u , với u cos 2x / / cos 2x sin 2 . x 2x sin 2x y' . 2 cos 2x 2 cos 2x cos 2x sin x x Câu g) y x sin x cos x sin x sin x x cos x
x cos x sin x sin x x cos x A. . B. . 2 2 x sin x 2 2 x sin x
x cos x sin x sin x cos x
x cos x sin x sin x x cos x C. . D. . 2 2 x sin x 2 2 x sin xBài làm: / / / / / / sin x x
sin x .x x .sin x x .sin x sin x .x
x cos x sin x sin x x cos x y' . h) x sin x 2 2 2 2 x sin x x sin x Câu Câu h). y sin cos x cos sin x A. sin x cos x B. sin x cos x C. sin cos x D. sin x  / /
Bài làm: Bước đầu tiên sử dụng đạo hàm tổng, sau đó sử dụng sinu , cosu .
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 52
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1. / / / / y' sin cos x cos sin x
cos cos x . cos x
sin sin x . sin x sin . x cos cos x cos . x sin sinx sinx.cos cosx cosx.sin sinx sin x cos x x sin x Câu i). y . x sin x 2 sin x 2x cos x 2 sin x x cos x sin x x cos x 2 sin x 2x cos x A. . B. . C. . D. . 2 2 2 2 x sin x x sin x x sin x x sin x /  u
Bài làm: Sử dụng v / / x
sin x . x sin x
x sin x . x sin x y' 2 x sin x 1 cos x x sin x 1 cos x x sin x 2 sin x 2x cos x . 2 2 x sin x x sin x 2 1 cos 2x Câu k). y . 1 cos 2x 1 cos 2x 4 sin 2x 1 cos 2x 4 sin 2x A. 2 . B. . 2 1 cos 2x 2 1 cos 2x 1 cos 2x 1 cos 2x 1 cos 2x sin 2x 1 cos 2x 4 sin 2x C. 2 . D. 2 . 2 1 cos 2x 2 1 cos 2x 1 cos 2x 1 cos 2x /  1 cos 2x
Bài làm: Sử dụng u với u 1 cos 2x / 1 cos 2x 1 cos 2x y' 2 . 1 cos 2x 1 cos 2x / / 1 cos 2x 1 cos 2x 1 cos 2x 1 cos 2x 1 cos 2x 2 . 2 1 cos 2x 1 cos 2x 1 cos 2x
2 sin 2x 1 cos 2x
2 sin 2x 1 cos 2x 2 . 2 1 cos 2x 1 cos 2x 1 cos 2x 4 sin 2x 2 . . 2 1 cos 2x 1 cos 2x Câu l). 4 4 y sin x cos x
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 53
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1. A. sin 4 . x B. 2 sin 4 . x
C. cos 4x sin 4 . x D. sin 4 . x  1 3 1 Bài làm: 2 1 sin 2x cos 4 . x 2 4 4 / 3 1 1 / 1 / y' cos 4x cos 4x sin 4x . 4x sin 4 . x 4 4 4 4 2 Câu m). y cos 2x . 4 2 2 A. 4 x .sin 2x . B. 2x .sin 2x . 4 4 4 4 2 2 C. 4 2x .sin x . D. 4 2x .sin 2x . 4 4 4 4 2 /
Bài làm: Áp dụng cosu với u 2x 4 / 2 2 2 / y' sin 2x . 2x sin 2x .2 2x . 2x 4 4 4 4 4 2 4 2x .sin 2x . 4 4 sin x x cos x Câu n). y cos x x sin x 2 x 2 x 2 2x 2 x A. . B. . C. . D. . 2 2 2 2 cos x sin x cos x sin x cos x x sin x cos x x sin x / / sin x x cos x cos x x sin x cos x x sin x sin x x cos xBài làm: y' 2 cos x x sin x / / /
Tính sin x x cos x cos x x cos x cos x x'.cos x . x cos x cos x cos x x sin x x sin x / / Tính cos x x sin x sin x x'.sin x . x sin x sin x sin x x cos x x cos x 2
x sin x cos x x sin x
x cos x sin x x cos x x y' . 2 2 cos x x sin x cos x x sin x 1 2 3 Bài 7. Cho f x . Tính f ' 1 . 2 3 x x x
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 54
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM – TẬP 1. A.-14 B.12 C.13 D.10 /  1
Bài làm: Bước đầu tiên tính đạo hàm sử dụng công thức 1 x x / 1 2 3 1 4 9 f ' x f ' 1 1 4 9 14 2 3 2 3 4 x x x x x x 1 1 Bài 8. Cho 2 f x x . Tính f ' 1 x x 1 A. B.1 C.2 D.3 2 / / x  1 1 1 1 1
Bài làm: Ta có 2 f ' x x 2x 2x 2 2 x x x x x 2x x 1 1 Vậy f ' 1 1 2 2 2 Bài 9. Cho 5 3 f x x x
2x 3 . Tính f ' 1 f ' 1 4 f 0 A.4 B.5 C.6 D.7 /
Bài làm: Ta có 5 3 4 2 f ' x x x 2x 3 5x 3x 2 f ' 1 f ' 1 4 f 0 (5 3 2) (5 3 2) 4.( 2) 4 x Bài 10. Cho f x . Tính f ' 0 2 4 x 1 A. B.1 C.2 D.3 4 2 / 2 x / 2 2 4 ' 4 4 x x x x x 2  x 4 x 4
Bài làm: f ' x 2 2 2 2 2 4 x 2 4 x 4 x 4 4 x x 1 Vậy f ' 0 . 4
GIÁO VIÊN MUỐ N MUA FILE WORD LIÊN HỆ 0946798489 55 NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM
TẬP 2A. VIẾT PHƯƠNG TRÌNH TIẾP TUYẾN CỦA
ĐỒ THỊ HÀM SỐ KHI BIẾT TIẾP ĐIỂM.
Giáo viên muốn mua file word liên hệ 0946798489 để gặp thầy Vương. Hoặc liên hệ qua:
Facebook: https://web.facebook.com/phong.baovuong
Page : https://web.facebook.com/tracnghiemtoanthpt489/ Email: baovuong7279@gmail.com
Website: http://tailieutoanhoc.vn/ 0946798489
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN MỤC LỤC
PHƢƠNG TRÌNH TIẾP TUYẾN CỦA ĐỒ THỊ HÀM SỐ......................................................................................... 1
Vấn đề 1. Viết phương trình tiếp tuyến của đồ thị hàm số khi biết tiếp điểm................................................ 2
CÁC BÀI TOÁN LUYỆN TẬP ............................................................................................................................. 13 LỜI TÂM SỰ
Ở tài liệu tiếp tuyến này, tôi chia thành 3 tập nhỏ, vì đảm bảo chất lượng bố cục, và công tác trình bày, vì
vậy mong quý vị bạn đọc theo dõi một cách thường xuyên để luôn được cập nhật tài liệu hay và chất lượng
của chúng tôi. Thân ái.
GIÁO VIÊN NÀO MUỐN MUA FILE WORD VUI LÒNG
LIÊN HỆ 0946798489 ĐỂ ĐẶT MUA NHÉ. THÂN ÁI.
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 1
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
PHƯƠNG TRÌNH TIẾP TUYẾN CỦA ĐỒ THỊ HÀM SỐ
Ý nghĩa hình học của đạo hàm: Đạo hàm của hàm số y  f(x) tại điểm x0 là hệ số góc
của tiếp tuyến với đồ thị (C) của hàm số tại điểm 0 M x0;f(x0) .
Khi đó phƣơng trình tiếp tuyến của (C) tại điểm 0 M x0;f(x0) là: y – y  f 0 (x0).(x – x0) y  0 f(x0)
 Điều kiện cần và đủ để hai đƣờng    1 C  : y f( ) x và  2 C  : y g( ) x tiếp xúc nhau  f(x )  g(x )
tại điểm có hoành độ x0 là hệ phƣơng trình 0 0  có nghiệm x f'(x   0 0 ) g'(x0)
Nghiệm của hệ là hoành độ của tiếp điểm của hai đƣờng đó.  Nếu (C ) : y  px  2    1 q và  2 C  : y ax bx c thì 2 1
(C ) và C2  iếp xúc nhau  phƣơng trình ax  bx  c  px  q có nghiệm kép.
Các dạng tiếp tuyến của đồ thị hàm số thường gặp -
Viết phƣơng trình tiếp tuyến khi biết tọa độ tiếp điểm Mx0; y0  , hoặc hoành độ x0 , hoặc tung độ y0 . -
Viết phƣơng trình tiếp tuyến khi biết tiếp tuyến đi qua điểm AxA; yA  cho trƣớc. -
Viết phƣơng trình tiếp tuyến khi biết hệ số góc của nó. Phương pháp:
Cho hàm số y  f x có đồ thị C và Mx0; y0  là điểm trên C . Tiếp tuyến với đồ thị C tại Mx0; y0  có: -
Hệ số góc: k  f 'x0  - Phƣơng trình: y  y      0
kx x0  , hay y y0 f'x0 x x0 
Vậy, để viết đƣợc phƣơng trình tiếp tuyến tại Mx0; y0  chúng ta cần đủ ba yếu tố sau: -
Hoành độ tiếp điểm: x0 - Tung độ tiếp điểm: y 
0 (Nếu đề chƣa cho, ta phải tính bằng cách thay x0 vào hàm số y0 f x0  ) -
Hệ số góc k  f 'x0 
Vấn đề 1. Viết phương trình tiếp tuyến của đồ thị hàm số khi biết tiếp điểm. Phương pháp: Bài toán 1 :
Hai đƣờng cong C : y  f x và C' : y  gx tiếp xúc nhau tại Mx   0 ; y0  .Khi điểm M C C' và
tiếp tuyến tại M của C trùng với tiếp tuyến tại M của C' chỉ khi hệ phƣơng trình sau: f x   0  g x0   có nghiệm x . f 'x   0  0  g'x0 
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 2
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
Lưu ý : Mệnh đề sau đây không đúng cho mọi trƣờng hợp: C: y   f x 
tiếp xúc nhau  f x  ax  b  0 có nghiệm kép . d   : y  ax   b k 1  Hàm f x nhận x     k 
0 làm nghiệm bội k nếu f x0  f 'x0    ... f
x0 0và f x0 0. Nghiệm bội
lớn hơn hoặc bằng 2 chứ không phải nghiệm kép.
Phép biến đổi tƣơng đƣơng của phƣơng trình nói chung không bảo toàn số bội của nghiệm.
Ví dụ 1. Đƣờng cong y  x không tiếp xúc với trục hoành tại 0 , tức là phƣơng trình x  0 không nhận
0 làm nghiệm bội lớn hơn hoặc bằng 2 . Khi đó đồ thị   3
C : y  x của hàm số tiếp xúc với trục hoành
tại x  0 nhƣng phƣơng trình 3
x  0 nhận 0 làm nghiệm bội 3 .
Ví dụ 2. Đồ thị C : y  sin x của hàm số tiếp xúc với đƣờng thẳng d : y  x tại x  0 nhƣng phƣơng
trình sin x  x  0 thì không thể có nghiệm kép.
Nhƣ vậy, biến đổi tƣơng đƣơng của phƣơng trình chỉ bảo toàn tập nghiệm, chứ không chắc bảo toàn số bội
các nghiệm. Đây cũng là sai lầm dễ mắc phải khi giải quyết bài toán tiếp tuyến. Bài toán 2 :
* Đƣờng cong C : y  f x có tiếp tuyến tại điểm có hoành độ x 
0 khi và chỉ khi hàm số y f x khả vi
tại x0 . Trong trƣờng hợp C có tiếp tuyến tại điểm có hoành độ x0 thì tiếp tuyến đó có hệ số góc f 'x0  .
* Phƣơng trình tiếp tuyến của đồ thị C : y  f x tại điểm Mx0;f x0  có dạng : y  f '   0 x x x0  f x0 
Bài toán 3. Viết phƣơng trình tiếp tuyến của đồ thị hàm số y  f x tại điểm M(x0;f(x0)) .
Giải. Tiếp tuyến của đồ thị hàm số y  f(x) tại M(x0; y0) là: y  f '(x )(x  x )  0 0 y0 .
Bài toán 4. Viết phƣơng trình tiếp tuyến của đồ thị hàm số y  f x biết hoành độ tiếp điểm x  x0 . Giải: Tính y  f(x ), y'(x )  0 0 0
phƣơng trình tiếp tuyến: y  f '(x )(x  x )  0 0 0 y
Bài toán 5. Viết phƣơng trình tiếp tuyến của đồ thị hàm số y  f x biết tung độ tiếp điểm bằng y0 .
Giải. Gọi M(x0; y0) là tiếp điểm
Giải phƣơng trình f(x)  y0 ta tìm đƣợc các nghiệm x0 .
Tính y'(x0) và thay vào phƣơng trình (1). Các ví dụ
Ví dụ 1 : Cho hàm số 3 2
y  x  3x  1 có đồ thị là (C). Viết phƣơng trình tiếp tuyến của (C) : 1. Tại điểm M 1  ;3 ;
2. Tại điểm có hoành độ bằng 2 ;
3. Tại điểm có tung độ bằng 1 ;. 4. Tại giao điểm (C) với trục tung ;
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 3
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
5. Có hệ số góc là 9 ;
6. Song song với đƣờng thẳng (d ): 27x  3y  5  0 ;
7. Vuông góc với đƣờng thẳng (d’ ) : x  9y  2013  0 . Lời giải.
Hàm số đã cho xác định D  Ta có: 2 y'  3x  6x
1. Phƣơng trình tiếp tuyến t tại M 1
 ; 3 có phƣơng trình : y  y'  1 x   1  3 Ta có: y'  1  3
 , khi đó phƣơng trình t là: y  3  x  6 Chú ý:
Viết phƣơng trình tiếp tuyến của đồ thị hàm số y  f x tại điểm Mx0;f x0  .
Tiếp tuyến của đồ thị hàm số y  f x tại Mx    0 ; y0  là: y f ' 0 x x x0  y0
2. Thay x  2 vào đồ thị của (C) ta đƣợc y  21 .
Tƣơng tự câu 1, phƣơng trình t là: y  24x  27 Chú ý:
Viết phƣơng trình tiếp tuyến của đồ thị hàm số y  f x biết hoành độ tiếp điểm x  x  0 , y0 f x0 , y'x     0 
phƣơng trình tiếp tuyến: y f ' 0 x x x0  y0
3. Thay y  1 vào đồ thị của (C) ta đƣợc 2
x x  3  0  x  0 hoặc x  3  .
Tƣơng tự câu 1, phƣơng trình t là: y  1 , y  9x  28
Chú ý: Viết phƣơng trình tiếp tuyến của đồ thị hàm số y  f x biết tung độ tiếp điểm bằng y0 . Gọi
Mx0; y0  là tiếp điểm
Giải phƣơng trình f x  y0 ta tìm đƣợc các nghiệm x0 . Tính y'x     0 
phƣơng trình tiếp tuyến: y f ' 0 x x x0  y0
4. Trục tung Oy : x  0  y  1.Tƣơng tự câu 1, phƣơng trình t là: y  1
5. Gọi x0; y0  là tọa độ tiếp điểm của đồ thị (C ) của hàm số và tiếp tuyến t . Ta có : y'x  2          0 3 0 x 6 0
x , theo giả thiết y'x0  9 , tức là 2 3x0 6x0 9 x0 3 hoặc x0 1 . Tƣơng tự câu 1
6. Gọi x0; y0  là tọa độ tiếp điểm của đồ thị (C ) của hàm số và tiếp tuyến t . 5
Theo bài toán: t d : y  9x   y'  0
x  9 . Tƣơng tự câu 1 3
7. Gọi x0; y0  là tọa độ tiếp điểm của đồ thị (C ) của hàm số và tiếp tuyến t . 1 2013
Theo bài toán: t  d' : y   x   y'  0
x  9 . Tƣơng tự câu 1 9 9
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 4
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN Ví dụ 2 . 1. Cho hàm số: 3      2 y x m 1 x  3m  
1 x  m  2 . Tìm m để tiếp tuyến của đồ thị hàm số tại điểm có
hoành độ bằng 1 đi qua điểm A2; 1  .
2. Gọi (Cm) là đồ thị của hàm số 3 2
y  x  (2m  1)x  (m  3)x  3 và (d) là tiếp tuyến của (C) tại điểm có 7
hoành độ x = 2. Tìm m để khoảng cách từ gốc tọa độ O đến (d) bằng . 17 Lời giải.
1. Hàm số đã cho xác định với x   . Ta có: 2 y'  3x  2m   1 x  3m  1 Với x  1  y  1  3m  1  y'  1  m  6
Phƣơng trình tiếp tuyến tại điểm có x  1: y  m  6x   1  3m  1
Tiếp tuyến này đi qua A2; 1  nên có: 1
  m  6  3m  1  m  2  Vậy, m  2
 là giá trị cần tìm.
2. Hàm số đã cho xác định với x   . Ta có: 2 y'  3x  22m   1 x  m  3.
Phƣơng trình tiếp tuyến (d) : y  y'(2)(x  2)  y(2)
y  11 – 7mx – 2  7 – 6m  11 – 7mx  8m – 15  (11  7m)x  y  8m  15  0 8m  15 7 2 2 d(0,(d))  
 17(8m  15)  49[(11  7m)  1] 2   17 (11 7m) 1 2  2153
1313m  3466m  2153  0  m  1, m  1313 Ví dụ 3 :
1. Viết phƣơng trình tiếp tuyến của đồ thị C     : 4 2 y x x
6 , biết tiếp tuyến vuông góc với đƣờng thẳng 1 y  x  1. 6 1 2 2. Cho hàm số 3 y  x  x 
có đồ thị là (C). Tìm tr n đồ thị (C) điểm mà tại đó tiếp tuyến của đồ thị 3 3 1 2
vuông góc với đƣờng thẳng y   x  . 3 3 Lời giải.
1. Hàm số đã cho xác định D  1
Gọi t là tiếp tuyến của đồ thị C của hàm số và t vuông góc với đƣờng thẳng y  x  1, n n đƣờng 6
thẳng t có hệ số góc bằng 6  .
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 5
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
Cách 1: Gọi Mx0; y0  là tọa độ tiếp điểm của tiếp tuyến t và đồ thị C của hàm số . Khi đó, ta có phƣơng trình: y'x  3        0 6 4x0 2x0 6  x   1  2          0 2x0 2x0 3 0   . Vì 2 2x0 2x0 3 0, x0 n n phƣơng trình          0 x 1 y0 y  1 4 M1; 4 .
Phƣơng trình tiếp tuyến cần tìm là: y  6  x   1  4  6  x  10 .
Cách 2: Phƣơng trình t có dạng y  6  x  m
t tiếp xúc C tại điểm Mx0;y0 khi hệphƣơngtrình sau có nghiệm x0  4 2 x        0 x0 6 6x0 m x 1  có nghiệm 0 x   3  0 4  x     m  10 0 2x0 6
2. Hàm số đã cho xác định D  Ta có: 2 y'  x  1 1 2 Gọi 3 M(x      0 ; y0 ) (C) y0 x0 x0 , 3 3
Tiếp tuyến tại điểm M có hệ số góc: 2 y'(x   0 ) x0 1 1 2 1
Đƣờng thẳng d: y   x  có hệ số góc k   3 3 2 3    4    2 1 2   x 2 y d           0 0  1 k .k2 1 (x0 1)  1 x0 4 3  3   x      0 2 y0 0   Vậy, có 2 điểm   4 M 2; 0 , 
2;  là tọa độ cần tìm.  3  Ví dụ 4 3  x
1. Cho hàm số y  x  (1). Viết phƣơng trình tiếp tuyến (d) của (C) biết (d) cách đều hai điểm 2 A 1
 ;  2 và B1;0. 2. Cho hàm số 3 2
y  x  6x  9x  1 (1). Viết phƣơng trình tiếp tuyến (d) của (C) biết (d) cách đều hai điểm
A2;7 và B 2;7. Lời giải.
1. Cách 1. Phƣơng trình tiếp tuyến (d) có dạng y  f '(   0
x )(x x0) f(x0) ( x0 là hoành độ tiếp điểm của (d) và (C)). 2 5 3  x 5 (x  6x  6) = 0 0 0  (x  x     0 ) x 2 2 2 (x  2) x  0 2   0 (x0 2) (x0 2)
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 6
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN 2 2  5x  (x      0 2) y x0 6x0 6 0 2 2 2 5   2(x        0 2) x0 6x0 6 5 x0 6x0 6 d(A,(d))  d(B,(d))   4 4 25  (x    0 2) 25 (x0 2)  2 2      x  1  2 2 x0 14x0 19 x0 6x0 1  0 x             0 14x0 19 x0 6x0 1 x 1. 2 2  2 0 x        x  4x  9  0 0 14x0 19 x0 6x0 1  0 0
Vậy phƣơng trình d : y   5x – 1
Cách 2. Tiếp tuyến (d) cách đều hai điểm A, B suy ra hoặc (d) song song với đƣờng thẳng AB hoặc (d) đi qua
trung điểm I(0; - 1) của đoạn AB. * Trƣờng hợp 1: (d) //AB. y  y
Hệ số góc của đƣờng thẳng AB: A B k   AB 1 x  . A xB 5
(d) // AB suy ra hệ số góc của (d) : f’x     0  1
1 (*) . Phƣơng trình (*) vô nghiệm do đó trƣờng 2 (x  0 2) hợp này không xảy ra.
* Trƣờng hợp 2: (d) qua trung điểm I của đoạn AB.
Phƣơng trình (d) có dạng y = kx – 1. 3  x0   kx  0 1 (2) x  2
(d) tiếp xúc (C) tại điểm có hoành độ x 0  0  có nghiệm x . 5  0   k (3)  2 (x   0 2) 5 3  x 5 Thay k   vào (2) ta đƣơc 0    1 2 (x  2 x  2  0 2) 0 (x0 2) x      0 2 x0 2      x  1  2 0 (  3  x )(x  2)  5   (x  2) x  1   0 0 0  0 Thay x     0 1 vào (2) ta đƣợc k 5 .
Vậy phƣơng trình d : y   5x – 1
2. Phƣơng trình tiếp tuyến (D) có dạng : 2 3 2 y  (3x        2 3 2       0
12x0 9)(x x0) x0 6x0 9x0 1 (3 0 x 12 0 x 9)x 2 0 x 6x0 1 2 3 2  (3        0 x 12x0 9)x y 2x0 6x0 1 0 (*)
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 7
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN 2 3 2 2 3 2 2(3x              0 12x0 9) 7 2x0 6x0 1 2(3x0 12x0 9) 7 2x0 6x0 1 d(A,(D))  d(B,(D))   2 2 2 2 (3x       0 12x0 9) 1 (3x0 12x0 9) 1  3 2 3         3 2 3  2x 12x 24x 10 2x 24x 26 (1) 2  x        0 0 0 0 0   0 12x0 24x0 10 2x0 24x0 26 3 2 3  2  x        0 12x0 24x0 10 2x0 24x0 26 (2)  2 12x        0 48x0 36 0 x0 3 x0 1     3 2     x 12x 16 0      0 1 x0 2 4x  0 0 Lần lƣợt thay         0 x 3 0 x 1 0 x 1 0 x
2 vào (*) ta đƣợc phƣơng trình tiếp tuyến (D) là
y  1  0, y  3  0, y  24x  7, y   3x  7.
Ví dụ 5 Viết phƣơng trình tiếp tuyến d với đồ thị C : 1. 3 2
y  x  3x  2 , biết d cắt các trục Ox, Oy lần lƣợt tại A, B thỏa mãn: OB  9OA .
2. Viết phƣơng trình tiếp tuyến với đồ thị C : 3 2
y  x  6x  9x  2 tại điểm M, biết M cùng 2 điểm cực
trị của C tạo thành tam giác có diện tích bằng 6. Lời giải.
1. Gọi Mx0; yx0  là toạ độ tiếp điểm.
Theo bài toán, đƣờng thẳng d chính là đƣờng thẳng đi qua 2 điểm phân biệt A, B .
Gọi  là góc tạo bởi giữa d và Ox , do đó d có hệ số góc k   tan OB
Dễ thấy, tam giác AOB vuông tại O , suy ra tan   9 OA  y'x      0  2 9 3x 6x 9 0
Nói khác hơn đƣờng thẳng d có hệ số góc là 9
 , nghĩa là ta luôn có: 0 0    y'  x  2    0 9 3x     0 6x0 9 0 2              0 x 2x0 3 0 x0 1 hoặc x0 3 vì 20 x 2x0 3 0, x0 . Với x     0
1 suy ra phƣơng trình tiếp tuyến y 9x 7 Với x    0
3 suy ra phƣơng trình tiếp tuyến y 9x 25
Vậy, có 2 tiếp tuyến y  9x  7 , y  9x  25 thỏa đề bài .
2. Hàm số đã cho có 2 điểm cực trị A1; 2 , B3; 2
  và đƣờng thẳng đi qua 2 cực trị là AB : 2x  y  4  0 .
Gọi Mx0; y0  là tọa độ tiếp điểm của đồ thị C của hàm số và tiếp tuyến d cần tìm. Khi đó 3 2 y     0 0 x 6x0 9x0 2 2x  y  4
Ta có: AB  2 5 , dM; AB 0 0  5 1 Giả thiết S        MAB 6 .AB.dM; AB 6 2x y 4 6 2 0 0  2      0 x y0 10 hoặc 2 0 x y0 2
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 8
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN 2x     y  2   2x     0 y0 2 0 0 y 2
TH1: Tọa độ M thỏa mãn hệ:  0     hay 3 2  2 y     x       0  x0 6x0 1   1 0 x 0 0 x0 6x0 9x0 2  0 M0; 2  
Tiếp tuyến tại M là: y  9x  2 . 2x    0 y0 10
TH2: Tọa độ M thỏa mãn hệ:  3 2 y      0 x0 6x0 9x0 2 y    0 10 2x0 y  0 2     hay M4; 2 x  4     2      0 x0 6x0 11 0 x  0 4
Tiếp tuyến tại M là: y  9x  34 .
Vậy, có 2 tiếp tuyến thỏa đề bài: y  9x  2 và y  9x  34 x  1
Ví dụ 6 Gọi (C) là đồ thị của hàm số y  x  . 3
1. Gọi M là một điểm thuộc (C) có khoảng cách đến trục hoành độ bằng 5. Viết phƣơng trình tiếp tuyến của (C) tại M
2. Gọi (d) là một tiếp tuyến của (C) , (d) cắt đƣờng tiệm cận đứng của (C) tại A , cắt đƣờng tiệm cận ngang
của (C) tại B và gọi I là tâm đối xứng của (C) . Viết phƣơng trình tiếp tuyến (d) biết: i) IA = 4IB.
ii) IA + IB nhỏ nhất Lời giải.
1. Khoảng cách từ M đến trục Ox bằng 5  y   M 5 . y   M 5  7 M(C)  x   TH1: M    x    M 1 3 y      M 5 5   x  3 y     M 5 M y  M 5 M(C)  x  4  TH2: M    x    M 1 y       M 5 5 y  M 5 x   M 3  7 
Phƣơng trình tiếp tuyến của (C) tại điểm M  ; 5    là y  9x  16.  3 
Phƣơng trình tiếp tuyến của (C) tại điểm M 4; 5 là y  4x  21.
2. i) Ta có ABI bằng góc hình học hợp bởi tiếp tuyến (d) với trục hoành suy ra hệ số góc của (d) là IA k  tan ABI    4  IB
Phƣơng trình tiếp tuyến d : y  4x  5 hoặc y  4x  21. 2 4 x  1 4 x  2x  3
ii) Phƣơng trình tiếp tuyến (d) có dạng : 0 0 0 y  (x  x    0 ) x . 2 2 2 (x  3) x  0 3   0 (x0 3) (x0 3)
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 9
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
Tiệm cận đứng của (C) :    1 D  : x 3
Tiệm cận ngang của (C) :   2 D  : y 1. 2 x  2x  15
A là giao điểm của (d) và  0 0   1 D  yA 2 (x  0 3)
B là giao điểm của (C) với D    2  xB 2x0 3 . 2 x   0 2x0 15 8 IA  IB  y           A yI xB xI 1 2x0 6 2x0 6 2 (x  3) x  0 3 0
Áp dụng bất đẳng thức Cauchy ,ta có 8 IA  IB  2 2x   0 6 8 x  . 0 3 8    2 x0 1 IA  IB  8   2x      0 6 (x0 3) 4  x    0 3 x  0 5
minIA  IB  8  d: y  x, y  x  8 Ví dụ 7
1. Biết rằng tr n đồ thị 3      2 y x
m 1 x  4m  2x  1, Cm  tồn tại đúng 1 điểm mà từ đó kẻ đƣợc tiếp
tuyến vuông góc với đƣờng thẳng x  10y  2013  0 .Viết phƣơng trình tiếp tuyến của Cm  tại điểm đó 2x  3
2. Lập phƣơng trình tiếp tuyến của đồ thị C : y  x  tại những điểm thuộc đồ thị có khoảng cách đến 1
đƣờng thẳng d : 3x  4y  2  0 bằng 2. Lời giải.
1. Gọi tiếp điểm là Ma; b , tiếp tuyến tại M có hệ số góc là    2 k y' a  3a  2m   1 a  4m  2 , theo giả thiết suy ra k  10
Tr n đồ thị chỉ có 1 điểm n n phƣơng trình 2 3a  2m  
1 a  4m  8  0 có nghiệm kép hay '  0 tức
m  5 , thay vào ta đƣợc a  2  M2; 29 .
Vậy, tiếp tuyến cần tìm là y  10x  9 2x  3 2. Gọi Mx  
0 ; y0  là điểm thuộc đồ thị C , khi đó: y yx  0 0 0 x  0 1 3x  4y  2 Ta có: d M,d 0 0   2   2  3x      0 4y0 12 0 hoặc 2 2 3  4 3    0 x 4y0 8 0  2x  3  TH1: 0 3x           2     0 4y0 12 0 3 0 x 4 12 0  3x x 0 x 0 x    0 0 0 0 1 
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 10
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN 1 hoặc x  0 3  2x  3  TH2: 3    0       2     0 x 4y0 8 0 3x0 4 8 0  3x 19x 20 0 x    0 0 0 1   4 x     0 5 hoặc x0 3
Phƣơng trình tiếp tuyến d tại M thuộc đồ thị C có dạng: 1  y  y'      0
x x x0  yx0  trong đó và y'x0  , x 1  0 . x  2 0 1
Phƣơng trình tiếp tuyến     1 d  tại 1 M 0; 3 là y x 3 .  1 11 9 47
Phƣơng trình tiếp tuyến d    2  tại M2  ;  là y x .  3 4  16 16  7  1 23
Phƣơng trình tiếp tuyến d     3  tại M3  5;  là y x .  4  16 16  4 
Phƣơng trình tiếp tuyến d      4  tại M4  ; 1 là y 9x 13 .  3 
Vậy, có 4 tiếp tuyến thỏa đề bài: y  x  9 47 3, y   x  1 23 , y   x  , y  9  x 13 . 16 16 16 16 Ví dụ 8 x  3 1. Cho hàm số y 
C và đƣờng thẳng dm: y  2xm. Tìm m để đƣờng thẳng dm cắt C tại x  2
hai điểm phân biệt A, B sao cho tâm đối xứng I của C cách đều hai tiếp tuyến với C tại các điểm A, B. 2. Cho hàm số  3  2 y x
3x  1 có đồ thị là C . Tìm tr n đồ thị hai điểm A, B sao cho tiếp tuyến tại A và 10
B song song với nhau và khoảng cách từ O đến đƣờng thẳng đi qua hai điểm A, B bằng . 5 Lời giải. 1. D   \  2 .
Hoành độ giao điểm của đƣờng thẳng dm  và C là nghiệm của phƣơng trình x  3  2x  m  2
2x  m  5x  2m  3  0 x  2 x  2
Để dm  cắt C tại hai điểm phân biệt A, B khi và chỉ khi phƣơng trình tr n có hai nghiệm phân biệt khác 2 nên phải có:
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 11
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN    0
m  52  4.2.2m  3  0
m  32  40  0 m  g2    0  2 2.2   2m  5     2m  3  0 15   0 Các tiếp tuyến:  5 5 5 5 1  : y   x  1x1 , 1 : y   x x21 x 22 x  1 2 x 22 x    2 2 1 2  2 2  x 2 x 2 25 d I; 1  dI; 2    1    2         m    3. x  1 22  x  2  2 2
Vậy, m  3 là giá trị cần tìm.
2. Gọi Ax ; y  3 x  2 3x  B x ; y  3 x  2 3x  1 1 1 1
1,  2 2 2 2 1 là 2 điểm cầntìm với x  1 x2 Ta có  2 y' 3x  6x
Hệ số góc của các tiếp tuyến của C tại A và B lần lƣợt là k  2 3x  6x ,k  2 3x  1 1 1 2 2 6x2
Tiếp tuyến của C tại A và B song song với nhau nên k  k  2 3x  6x  2 3x  1 2 1 1 2 6x2
 3(x  x )x  x   6(x  x )  1 2 1 2 1 2 0  x  x  2  1 2 0  x  2  2 1 x y  3 y x  3 x  2 3(x  2 x )
Hệ số góc của đƣờng thẳng AB là k  2 1  1 2 1 2 x  x x  2 1 2 1 x k  x  1 x2 2  x x  1 2 3x  1
x2   4  x (2  x )  6  2x  1 1 1 2
Phƣơng trình đƣờng thẳng AB là y  (2x  2)(x  x )  3 x  2 3x  1 1 1 1 1
 (2x  2)x  y   2x  1  1 1 0  2 x  2x  1  2 x  2x  1     1 1  1 1  10  2 d O,AB  2 2 5 2 x  2x  5 1 1 2  1  2x 2x 1 1 1 1  1 2  5  2 x  2x  1  1 1 2  2 x  2x  1  1 1
1 1.Bìnhphƣơng 2 vếvà rút gọn đƣợc: 3 2  2 x  2x  1 1 1 4 2x 2x  1 1 1  4  0   2 2 x  2x  1   2 x  2x  1   1 1 2   1 hoặc 1 1 2 3
Giải 1 ta đƣợc x  1  x  1 2 1 3  2 6 3  2 6
Giải 2 ta đƣợc x  x  1 hoặc 3 1 3
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 12
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN  3  2 6 9    2 6 3  2 6 9   2 6
Vậy, các điểm cần tìm là A ;   ,B ;      hoặc ngƣợc lại.  3 9   3 9  CÁC BÀI TOÁN LUYỆN TẬP Bài 1. Cho hàm số  3  2 y x 3x  6x  1 (C)
Viết phƣơng trình tiếp tuyến của đồ thị (C) biết
Câu 1. Hoành độ tiếp điểm bằng 1 A. y  3x  6 B. y  3x  7 C. y  3x  4 D. y  3x  5
Bài làm 1. Gọi Mx0;y0  là tiếp điểm Ta có:  2 y' 3x  6x  6 .
Ta có: x  1  y  1, y'(1)  0 0 3
Phƣơng trình tiếp tuyến là: y  y'(x )(x  x )  y  3(x  1)  1  3x  0 0 0 4
Câu 2. Tung độ tiếp điểm bằng 9
y  18x  81
y x  81
y  18x  1
y x  81     A. y  9  x
B. y  9xC. y  9  xD. y  9  x
y  9x  27 
y  9x  2  y  9x 7 
y  9x  2 
Bài làm 2. Gọi Mx0;y0  là tiếp điểm Ta có:  2 y' 3x  6x  6 . Ta có: y  9  3 x  2 3x  6x  8  0 0 0 0
0  x  1,x  2,x   0 0 0 4 .  x  4  y'(x )  0 0
18 . Phƣơng trình tiếp tuyến là: y  18(x  4)  9  18x  81
 x  1 y'(x )   0 0
9 . Phƣơng trình tiếp tuyến là: y  9(x  1)  9  9x  x  2  y'(x )  0 0
18 . Phƣơng trình tiếp tuyến là: y  18(x  2)  9  18x  27 . 1
Câu 3. Tiếp tuyến vuông góc với đƣờng thẳng y   x  1 18
A. : y  18x  8 và y  18x  27 .
B. : y  18x  8 và y  18x  2 .
C. : y  18x  81 và y  18x  2 .
D. : y  18x  81 và y  18x  27 .
Bài làm 3. Gọi Mx0;y0  là tiếp điểm Ta có:  2 y' 3x  6x  6 . 1
Vì tiếp tuyến vuông góc với đƣờng thẳng y   x  1 nên 18 Ta có: y'(x )  15  2
x  2x  8  0  x  4,x  0 0 0 0 0 2
Từ đó ta tìm đƣợc hai tiếp tuyến: y  18x  81 và y  18x  27 .
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 13
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
Câu 4. Tiếp tuyến đi qua điểm N(0;1) . 33 33 33 33 A. y   x  11 B. y   x  12 C. y   x  1 D. y   x  2 4 4 4 4
Bài làm 4. Gọi Mx0;y0  là tiếp điểm Ta có:  2 y' 3x  6x  6 .
Phƣơng trình tiếp tuyến có dạng: y  2
(3x  6x  6)(x  x )  3 x  2 3x  6x  0 0 0 0 0 0 1
Vì tiếp tuyến đi qua N(0;1) nên ta có: 1  2 (3x  6x  6)(x )  3 x  2 3x  6x  0 0 0 0 0 0 1  3  2
3x  0  x  0,x   3 2x0 0 0 0 2  x  0  y'(x )   0 0
6 . Phƣơng trình tiếp tuyến: y  6x  1 . 
  3  y  107 ,y'(x )   33 x0 0 0
. Phƣơng trình tiếp tuyến 2 8 4 33  3      107   33 y' x x    1 . 4  2  8 4 Bài 2. Cho hàm số  3
y x  3x  1 (C). Viết phƣơng trình tiếp tuyến của đồ thị (C), biết:
Câu 1. Hoành độ tiếp điểm bằng 0 A. y  3  x  12 B. y  3  x  11 C. y  3x  1 D. y  3  x  2
Bài làm 1. Ta có:  2
y' 3x  3 . Gọi Mx0; y0  là tiếp điểm
Ta có: x  0  y  1, y'(x )   0 0 0 3
Phƣơng trình tiếp tuyến: y  3x  1 .
Câu 2. Tung độ tiếp điểm bằng 3
A. y  9x  1 hay y  3
B. y  9x  4 hay y  3
C. y  9x  3 hay y  3
D. y  9x  13 hay y  2
Bài làm 2. Ta có:  2
y' 3x  3 . Gọi Mx0; y0  là tiếp điểm Ta có: y  3  3
x  3x  2  0  x  2,x   0 0 0 0 0 1  x  1 y'(x )  0 0
0 . Phƣơng trình tiếp tuyến: y  3  x  2  y'(x )  0 0
9 . Phƣơng trình tiếp tuyến:
y  9(x  2)  3  9x  13 .
Câu 3. Hệ số góc của tiếp tuyến bằng 9
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 14
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
A. y  9x  1 hay y  9x  17
B. y  9x  1 hay y  9x  1
C. y  9x  13 hay y  9x  1
D. y  9x  13 hay y  9x  17
Bài làm 3. Ta có:  2
y' 3x  3 . Gọi Mx0; y0  là tiếp điểm Ta có: y'(x )  9  2 3x  3  9  x   0 0 0 2  x  2  y  0 0
3 . Phƣơng trình tiếp tuyến:
y  9(x  2)  3  9x  13 .  x  2  y   0 0
1. Phƣơng trình tiếp tuyến:
y  9(x  2)  1  9x  17 .
Câu 4. Tiếp tuyến vuông góc với trục Oy. A. y  2, y  1  B. y  3, y  1 C. y  3, y  2  D. x  3,x  1 
Bài làm 4. Ta có:  2
y' 3x  3 . Gọi Mx0; y0  là tiếp điểm
Vì tiếp tuyến vuông góc với Oy nên ta có: y'(x )  0 0 Hay x   0
1 . Từ đó ta tìm đƣợc hai tiếp tuyến: y  3, y  1.
Bài 3. Viết phƣơng trình tiếp tuyến của đồ thị hàm số:  4  2 y 2x 4x  1 biết:
Câu 1. Tung độ tiếp điểm bằng 1 y  1 y  1 y  1 y  1    
A. y  8 2x  5
B. y  8 2x  15
C. y  8 2x  1
D. y  8 2x  10     y  8  2x  5  y  8  2x 15  y  8  2x 1  y  8  2x 10 
Bài làm 1. . Ta có:  3 y' 8x  8x
Gọi Mx0; y0  là tiếp điểm. Ta có: y  1  4 2x  2 4x  0  x  0,x   0 0 0 0 0 2  x  0  y'(x )  0 0
0 . Phƣơng trình tiếp tuyến là: y  1  x  2  y'(x )  0 0
8 2 . Phƣơng trình tiếp tuyến
y  8 2 x  2  1  8 2x 15
 x   2  y'(x )   0 0
8 2 . Phƣơng trình tiếp tuyến y  8  2 x  2 1 8  2x 15.
Câu 2. Tiếp tuyến song song với đƣờng thẳng y  48x  1 . A. y  48x  9 B. y  48x  7 C. y  48x  10 D. y  48x  79
Bài làm 2. . Ta có:  3 y' 8x  8x
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 15
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
Gọi Mx0; y0  là tiếp điểm.
Vì tiếp tuyến song song với đƣờng thẳng y  48x  1
Nên ta có: y'(x )  48  3 x  x  6  0  x  0 0 0 0 2 Suy ra y  0
17 . Phƣơng trình tiếp tuyến là:
y  48(x  2)  17  48x  79 . Bài 4. Cho hàm số  4  2 y x
x  1 (C). Viết phƣơng trình tiếp tuyến của đồ thị (C), biết:
Câu 1. Tung độ tiếp điểm bằng 1 A. y  2 B. y  1 C. y  3 D. y  4
Bài làm 1. Ta có:  3
y' 4x  2x . Gọi Mx0; y0  là tiếp điểm Ta có y  1  4 x  2 x  0  x  0 0 0 0 0 , y'(x )  0 0
Phƣơng trình tiếp tuyến: y  1
Câu 2. Tiếp tuyến song song với đƣờng thng y  6x  1 A. y  6x  2 B. y  6x  7 C. y  6x  8 D. y  6x  3
Bài làm 2. Ta có:  3
y' 4x  2x . Gọi Mx0; y0  là tiếp điểm
Vì tiếp tuyến song song với đƣờng thẳng y  6x  1 nên ta có: y'(x )  6  3
4x  2x  6  x  1  y  0 0 0 0 0 3
Phƣơng trình tiếp tuyến: y  6x  3 .
Câu 3. Tiếp tuyến đi qua điểm M1; 3 . A. y  6  x  2 B. y  6  x  9 C. y  6x  3 D. y  6  x  8
Bài làm 3. Ta có:  3
y' 4x  2x . Gọi Mx0; y0  là tiếp điểm
Phƣơng trình tiếp tuyến có dạng: y   3 4x  0 2x0 x  x0   4 x  2 x  0 0 1
Vì tiếp tuyến đi qua M1; 3 nên ta có: 3   3 4x  4 3 2 0 2x0 1 x0   4 x  2 x  0 0
1  3x  4x  x  2x  2  0 0 0 0 0  (x  2 2
1) (3x  2x  2)  0  x  1  y  3, y'(x )   0 0 0 0 0 0 6
Phƣơng trình tiếp tuyến: y  6x  3 . 2x  2
Bài 5. Cho hàm số y 
(C). Viết phƣơng trình tiếp tuyến của (C), biết: x  1
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 16
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
Câu 1. Tung độ tiếp điểm bằng 2 .
y  x  7
y  x  7
y  x  27
y  x  27 A. B. C. D. y  x   1 y  x   21 y  x   21 y  x   1 4 2x   : y  (x  x )  0 2 . (x  0 2 1) x  0 1 0   4
Bài làm 1. Hàm số xác định với mọi x  1. Ta có: y'  (x  2 1)
Gọi M(x0; y0) là tiếp điểm, suy ra phƣơng trình tiếp tuyến của (C):
Vì tiếp tuyến có hệ số góc bằng 1 nên ta có  4
 1  x  3,x  1 (x  0 0 2 0 1)
 x  2  y  4   : y  x  0 0 7
 x  1 y  0   : y  x  0 0 1
Câu 2. Tiếp tuyến song song với đƣờng thẳng d : y  4x  1. y  4  x  2 y  4  x  21 y  4  x  2 y  4  x  12 A. B. C. D. y  4  x   14 y  4  x   14 y  4  x   1 y  4  x   14   4
Bài làm 2. Hàm số xác định với mọi x  1. Ta có: y'  (x  2 1)
Gọi M(x0; y0) là tiếp điểm, suy ra phƣơng trình tiếp tuyến của (C):
Vì tiếp tuyến song với đƣờng thẳng d : y  4x  1 nên ta có:     4 y'(x ) 4  4  x  0,x  0 2 . (x  0 0 2 0 1)
 x  0  y  2   : y  4x  0 0 2
 x  2  y  6   : y  4x  0 0 14 .
Câu 3. Tiếp tuyến đi qua điểm A(4; 3)  1 1  1 31  1 1  1 31 y   x   y   x   y   x   y   x   A. 9 9  B. 9 9  C. 9 9  D. 9 9   1 1  1 31  1 31  1 1 y   x   y   x y   x y   x   4 4  4 4  4 4  4 4   4
Bài làm 3. Hàm số xác định với mọi x  1. Ta có: y'  (x  2 1)
Gọi M(x0; y0) là tiếp điểm, suy ra phƣơng trình tiếp tuyến của (C): 4 2x 2
Vì tiếp tuyến đi qua A(4; 3) nên ta có: 3  4  x0   0 (x  2 1) x  0 1 0
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 17
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN  3(x  2 1)  4(x  4)  2 2(x  2 0 0 0
1)  x  10x  21  0  x  3,x  0 0 0 0 7  8 1 x  7  y  , y'(x )   0 0 0
. Phƣơng trình tiếp tuyến 3 9
  1     8   1  31 y x 7 x . 9 3 9 9  1
x  3  y  1, y'(x )   0 0 0
. Phƣơng trình tiếp tuyến 4
  1       1  1 y x 3 1 x . 4 4 4
Câu 4. Viết phƣơng trình tiếp tuyến của (C), biết tiếp tuyến tạo với hai trục tọa độ một tam giác vuông cân.
y  x 11
y  x 11
y  x 1
y  x 1 A. B. C. D. y  x   7 y  x   17 y  x   17 y  x   7   4
Bài làm 4. Hàm số xác định với mọi x  1. Ta có: y'  (x  2 1)
Gọi M(x0; y0) là tiếp điểm, suy ra phƣơng trình tiếp tuyến của (C):
Vì tiếp tuyến tạo với hai trục tọa độ một tam giác vuông cân nên tiếp tuyến phải vuông góc với một trong
hai đƣờng phân giác y  x , do đó hệ số góc của tiếp tuyến bằng 1 hay y'(x )   0 1. Mà y'  0,  x  1 nên ta có 4 y'(x )  1   1  x  1,x  0 3 (x  0 0 2 0 1)
 x  1 y  0   : y  x  0 0 1
 x  3  y  4   : y  x  0 0 7 . 2x  1
Bài 6. Cho hàm số y 
(C). Viết phƣơng trình tiếp tuyến của (C) biết: x  1 1
Câu 1. Tiếp tuyến vuông góc với đƣờng thẳng y  x  2 3 A. y  3  x 11 hay y  3  x  11 B. y  3  x 11 hay y  3  x  1
C. y  3x  1 hay y  3  x  1
D. y  3x  1 hay y  3  x  11   3
Bài làm 1. Ta có y' 
. Gọi Mx0; y0  là tiếp điểm. Vì tiếp tuyến vuông góc với đƣờng thẳng (x  2 1)  1 y x  2 nên ta có 3     3 y'(x ) 3  3  x  0,x  0 2 (x  0 0 2 0 1)  x  0  y   0 0
1, phƣơng trình tiếp tuyến là: y  3x  1
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 18
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN  x  2  y  0 0
5 , phƣơng trình tiếp tuyến là:
y  3(x  2)  5  3x  11. 1
Câu 2. Tiếp tuyến cắt Ox, Oy lần lƣợt tại A, B sao cho tam giác OAB có diện tích bằng 6 4 1 A. y  3x   1,y  3x   1,y  1  2x  2,y   x  3 3 4 2 B. y  3x   1,y  3x   11,y  1  2x  2,y   x  3 3 4 3 C. y  3x   11,y  3x   11,y  1  2x,y   x  3 4 4 2
D. y  3x  1, y  3x  11, y  12x  2, y   x  3 3   3
Bài làm 2. Ta có y' 
. Gọi Mx0; y0  là tiếp điểm. Phƣơng trình tiếp tuyến  có dạng: (x  2 1)   3 y x  2x 1 x0    0 . (x  2 1) x  0 1 0 y  0 
   Ox  A :  3 2x  (x  x )  0 1   0 (x  0 2 1) x   0 1 0  2  2x  2x  1 Suy ra A 0 0 ; 0   . 3    x  0     Oy  B : 3x 2x  y  0  0 1  (x  2 1) x   0 1 0  2  2x  2x  1 Suy ra: B 0 0 0;   2  (x   0 1)   2 2 1 1 2x  2x  1
Diện tích tam giác OAB : S  OA.OB   0 0  2 6  x  1   0   2 2 1 2x  2x  1 Suy ra S    0 0   OAB  1 6 x  1   0   1  2  x  0,x   2x  2x  1  x  2 1 2x  x   0 0   0 0 0   0 0 0   2  2 2x  2x  1  x  1  2 2x  3x  2    1 0 0 0  0 0 0 x  ,x    2  0 0 2
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 19
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
Từ đó ta tìm đƣợc các tiếp tuyến là:            4  2 y 3x 1, y 3x 11, y 12x 2, y x . 3 3
Câu 3. Tiếp tuyến đi qua A7; 5 . 3 1 3 29 3 1 3 2 A. y   x  , y  x  B. y   x  , y  x  4 4 16 16 4 2 16 16 3 1 3 9 3 1 3 29 C. y   x  , y  x  D. y   x  , y  x  4 4 16 16 4 4 16 16   3
Bài làm 3. Ta có y'  . Gọi Mx A 
0 ; y0  là tiếp điểm. Do tiếp tuyến đi qua  7;5 nên ta có: (x  2 1)   3 5 7  2x 1 x 1 x0       0  2 x  4x  5  0  0 0  0 (x  2 1) x  1 x  0  0 5 0 3 1 3 29
Từ đó ta tìm đƣợc các tiếp tuyến là: y   x  , y  x  . 4 4 16 16 Bài 7. Cho hàm số  4  2 y x
8x  m  1 (Cm ) . Giả sử rằng tiếp tuyến của đồ thị (Cm) tại điểm có hoành độ x  0
1 luôn cắt đồ thị (Cm) tại ba điểm phân biệt. Tìm tọa độ các giao điểm.
A. A(1; m  6), B 1   3;m  18  3
B. A(1; m  6), B 1   7;m  18 7 
C. A(1; m  6), B 1   2;m  18  2 
D. A(1; m  6), B1 6;m  18 6  Ta có:  3 y' 4x  16x
Vì x  1  y  m  6, y'(x )   0 0 0
12 . Phƣơng trình tiếp tuyến d của (Cm) tại điểm có hoành độ x  0 1 là:
y  12(x  1)  m  6  12x  m  6 .
Phƣơng trình hoành độ giao điểm của (Cm) với d 4  2        4  2 x 8x m 1 12x m 6 x 8x  12x  5  0   2 2
(x 1) (x  2x  5)  0  x  1,x  1  6
Vậy d và (Cm) luôn cắt nhau tại ba điểm phân biệt
A(1; m  6), B1 6;m  18 6  2x  m  1
Bài 8. Cho hàm số y 
(Cm). Tìm m để tiếp tuyến của (Cm) x  1
Câu 1. Tại điểm có hoành độ x  0 0 đi qua A(4; 3) 16 6 1 16 A. m   B. m   C. m   D. m   5 5 5 15 m   3
Bài làm 1. Ta có: y'  (x  2 1)
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 20
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
Vì x  0  y  m  1, y'(x )  m  0 0 0
3 . Phƣơng trình tiếp tuyến d của (Cm) tại điểm có hoành độ x  0 0 là:
y  (m  3)x  m  1
Tiếp tuyến đi qua A khi và chỉ khi:         16 3 ( m 3)4 m 1 m . 5 25
Câu 2. Tại điểm có hoành độ x  0
2 tạo với hai trục tọa độ một tam giác có diện tích bằng . 2  23  23  23  23 m  2  ;m    m  2; m   m  2  ;m    m  2; m    A. 9  B. 9  C. 9  D. 9   28  28  28  28 m  7  ;m    m  7  ;m   m  7; m  m  7  ;m   9  9  9  9 m   3
Bài làm 2. Ta có: y'  (x  2 1)
Ta có x  2  y  m  5, y'(x )  m  0 0 0
3 . Phƣơng trình tiếp tuyến  của (Cm) tại điểm có hoành độ x  0 2 là:
y  (m  3)(x  2)  m  5  (m  3)x  3m  11 .  3m  11     Ox  A  A ; 0 , với m  3  0  m  3 
   Oy  B  B0;3m 1  1  2 1 1 (3m 11)
Suy ra diện tích tam giác OAB là: S  OA.OB  2 2 m  3  2 1 (3m 11) 25
Theo giả thiết bài toán ta suy ra:  2 m  3 2  2 9m  66m  121  25m    2     75 (3m 11) 25 m 3  2
9m  66m  121  25m   75  23 2 m  2; m   9m  41m  46     0   9 .  2      m  7; m   28 9m 91m 196 0  9
Bài 9. Giả sử tiếp tuyến của ba đồ thị    f(x) y f(x), y g(x), y
tại điểm của hoành độ x  0 bằng nhau. g(x)
Khẳng định nào sau đây là đúng nhất. 1 1 1 A. f(0)  B.  1 f(0) C. f(0)  D. f(0)  4 4 4 4
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 21
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN f '(0).g(0)  g'(0)f(0)
Theo giả thiết ta có: f '(0)  g'(0)  2 g (0) f'(0)  g'(0)  1  1 2  1 
g(0)  f(0)  f(0)  g(0)  2 g (0)   g(0)     1   4  2  4  2 g (0) Bài 10:
Câu 1. Tìm trên (C) :  3  2 y 2x
3x  1 những điểm M sao cho tiếp tuyến của (C) tại M cắt trục tung tại điểm có tung độ bằng 8. A. M( 1  ; 4  ) B. M( 2  ; 2  7) C. M(1; 0) D. M(2; 5)
Bài làm 1. Giả sử M(x ; y ) 3 2 2 0 0 (C)  y  2x  3x  0 0 0 1. Ta có:  y  3x  6x .
Phƣơng trình tiếp tuyến  tại M: y  2 (6x  6x )(x  x )  3 2x  2 3x  0 0 0 0 0 1 .
 đi qua P(0;8)  8   3 4x  2 3x  0 0 1  x   0 1 . Vậy M(1; 4) .
Câu 2. Viết phƣơng trình tiếp tuyến của đồ thị hàm số 3 2
y  x  6x  11x  1 tại điểm có tung độ bằng 5.
A. y  2x  1 ; y  x  2 ; y  2x  1
B. y  2x  3 ; y  x  7 ; y  2x  2
C. y  2x  1 ; y  x  2 ; y  2x  2
D. y  2x  3 ; y  x  7 ; y  2x  1
Bài làm 2. Ta có: 3 2
y  5  x  6x  11x  6  0  x  1; x  2; x  3
Phƣơng trình các tiếp tuyến: y  2x  3 ; y  x  7 ; y  2x  1 1 1 4
Câu 3. Viết phƣơng trình tiếp tuyến của đồ thị hàm số 3 2 y  x  x  2x 
, biết tiếp tuyến vuông góc 3 2 3
với đƣờng thẳng x  4y  1  0 . 7 2 73 26 A. y  4x  ; y  4x  B. y  4x  ; y  4x  6 3 6 3 73 2 7 26 C. y  4x  ; y  4x  D. y  4x  ; y  4x  6 3 6 3
Bài làm 3. Tiếp tuyến vuông góc với đƣờng thẳng x  4y  1  0 1 1
 y   x   Tiếp tuyến có hệ số góc k  4 4 4 2
 y'  4  x  x  6  0  x  3  ;x  2 1 73 * x  3
 Phƣơng trình tiếp tuyến y  4(x  3)   4x  6 6 2 26
* x  2  Phƣơng trình tiếp tuyến y  4(x  2)   4x  3 3
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 22
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN 2x  1
Câu 4. Viết phƣơng trình tiếp tuyến d của đồ thị C : y  A 2; 4 và x 
biết d cách đều 2 điểm   1 B 4;  2   . 1 1 1 5 A. y  x 
, y  x  3 , y  x  1 B. y  x 
, y  x  5 , y  x  4 4 4 4 2 1 5 1 5 C. y 
x  , y  x  4 , y  x  1 D. y  x 
, y  x  5 , y  x  1 4 4 4 4
Bài làm 4. Gọi Mx   0 ; y x0  , x0
1 là tọa độ tiếp điểm của d và C 1
Khi đó d có hệ số góc y'x  0  
và có phƣơng trình là : x  2 0 1 1   1 y x  x   0  2  2 x   1 0 1 x0
Vì d cách đều A, B nên d đi qua trung điểm I  1
 ;1 của AB hoặc cùng phƣơng với AB.
TH1: d đi qua trung điểm I  1  ;1, thì ta luôn có: 1   1 1 1   x    0  2 x 1  
, phƣơng trình này có nghiệm 2 x  0  1 0 1 x0 1 5 Với x    0
1 ta có phƣơng trình tiếp tuyến d : y x . 4 4 y  y
TH2: d cùng phƣơng với AB , tức là d và AB có cùng hệ số góc, khi đó y'x  B A    0 kAB 1 x  hay B xA 1  1  x  2  x  0  0 hoặc 0 x  2 0 1 Với x     0
2 ta có phƣơng trình tiếp tuyến d : y x 5 . Với x    0
0 ta có phƣơng trình tiếp tuyến d : y x 1. 1 5
Vậy, có 3 tiếp tuyến thỏa mãn đề bài: y  x 
, y  x  5 , y  x  1 4 4 Câu 5. Tìm m 
để từ điểm M1; 2 kẻ đƣợc 2 tiếp tuyến đến đồ thị   3 2      m C : y x 2x m 1x 2m . 10 100 10 100 A. m  ,m  3  B. m  ,m  3 C. m  ,m  3 D. m  ,m  3  81 81 81 81
Bài làm 5. Gọi N  0
x ; y0  C . Phƣơng trình tiếp tuyến d của A tại N là:
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 23
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN y   2 3x  4x  m   1 x  x  3 2      0 0 0 x0 2x0 m 1x0 2m Md 3 2  2      0 x 5 0 x 4x0 3 3m  
Dễ thấy  là phƣơng trình hoành độ giao điểm của đồ thị y  3  3m và f x  3 2    0 2 0 x 5 0 x 4x0 . Xét hàm số f x  3 2       0 2 0 x 5 0 x 4x0 có f'x  2 0 6x0 10x0 4 1 f 'x      0  0 x0 2 hoặc x0 . 3 100
Lập bảng biến thiên, suy ra m  ,m  3  81    2 3m 1 x  m  m
Câu 6. Cho hàm số y  C , m 
và m  0 .Với giá trị nào của m thì x  có đồ thị là  m  m
tại giao điểm đồ thị với trục hoành, tiếp tuyến của đồ thị sẽ song song với đƣờng thẳng x  y  10  0 . 1 1 1 1 A. m  1  ; m  
B. m  1; m   C. m  1  ; m  D. m  1; m  5 5 5 5
Bài làm 6. Hoành độ giao điểm của đồ thị với trục hoành là nghiệm phƣơng trình: 3m   2 1 x  m  m x  m,m  0   0,m  0   x  m 3m    2 1 x  m  m   0  1  1 x  m,m  0,m   m  0,m      3  3 2  2  2   4m m m 4m    . Mà y'   y'   . 2 2  m  m  m  m     2 x  m2 3m 1    2  x  x   m   m m  3m 1    3m  1   m  3m  1     2 m m   1
Tiếp tuyến song song với đƣờng thẳng x  y  10  0 nên y'   1   m  1  hoặc m   3m  1    5  m  1  giao điểm là A 1
 ;0 , tiếp tuyến là y  x  1. 1    3 3 m  
giao điểm là B ;0 , tiếp tuyến là y  x  . 5  5  5 Câu 7. Tìm m 
để tiếp tuyến có hệ số góc nhỏ nhất của C 3 2      m  : y x 2x m 1x 2m vuông góc
với đƣờng thẳng y  x  10 1 10 A. m  B. m  C. m  D. m  1 3 3 13
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 24
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN 2    7 2
Bài làm 7. 2 2 7 7
y'  3x  4x  m  1  3 x   m   m     y'  m  7  y'  m  khi x  .Theo  3  3 3 3 3 3  7  10
bài toán ta có: y'  1  1   m   1  1   m    .  3  3 1
Câu 8. Tìm m để đồ thị : 3 y  mx  m   2
1 x  3m  4x  1 có điểm mà tiếp tuyến tại đó vuông góc 3
với đƣờng thẳng x  y  2013  0 . 1 1 1 A. m  1 B.   m C.   m  1 D.   m  1 2 2 2
Bài làm 8. Để tiếp tuyến của đồ thị vuông góc với đthẳng x  y  2012  0 khi và chỉ khi y'.1  1  hay 2 1 mx  m  
1 x  3m  3  0 có nghiệm  . Đáp số:   m  1 . 2 Câu 9. Cho hàm số 3
y  x  3x  1 có đồ thị là C. Giả sử d là tiếp tuyến của C tại điểm có hoành độ
x  2 , đồng thời d cắt đồ thị C tại N, tìm tọa độ N . A. N1; 1  B. N2; 3 C. N 4;  5   1 D. N3;19
Bài làm 9. Tiếp tuyến d tại điểm M của đồ thị C có hoành độ    0 x 2 y0 3 Ta có 2 y'(x)  3x  3  y'(x   0 ) y'(2) 9
Phƣơng trình tiếp tuyến d tại điểm M của đồ thị C là y  y'(          0 x )(x 0 x ) y0 y 9(x 2) 3 y 9x 15 Xét phƣơng trình 3 3             2 x 3x 1 9x 15 x 12x 16 0 x 2 x  2x  8  0  x  4
 hoặc x  2 ( không thỏa ) Vậy N 4;  5   1 là điểm cần tìm Bài 11: Câu 1. Cho hàm số 3 2
y  x  2x  8x  5 có đồ thị là C. Khẳng định nào sau đây đúng nhất ?
A. Không có bất kỳ hai tiếp tuyến nào của đồ thị hàm số lại vuông góc với nhau
B. Luôn có bất kỳ hai tiếp tuyến nào của đồ thị hàm số lại vuông góc với nhau
C. Hàm số đi qua điểm M 1;17
D. Cả A, B, C đều sai
Bài làm 1. Ta có 2 y'(x)  3x  4x  8
Giả sử trái lại có hai tiếp tuyến với đồ thị C vuông góc với nhau. Gọi 1
x ,x2 tƣơng ứng là các hoành độ của hai tiếp điểm của hai tiếp tuyến đó.
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 25
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN Gọi 1
k ,k2 lần lƣợt là các hệ số góc của hai tiếp tuyến tại các điểm trên C có hoành độ 1 x ,x2 . Khi đó ' k ,k  1   y x  ' .y x   1    2 3x  4x  8 2     1 1 2 1 2 1 1 3x2 4x2 8 1 Tam thức   2
f t  3t  4t  8 có '  0 nên f t  0 t  
từ đó và từ 1 suy ra mâu thuẫn.
Vậy, giả thiết phản chứng là sai, suy ra (đpcm) Câu 2. Cho hàm số 4 2
y  x  2x  3 . Tìm phƣơng trình tiếp tuyến của hàm số có khoảng cách đến điểm 5 M0; 3   bằng . 65
A. y  2x  1
B. y  3x  2
C. y  7x  6 D.Đáp án khác
Bài làm 2. Gọi AC   4 2 A a;a  2a  3 Ta có: 3      3 y' 4x 4x y' a  4a  4a
Phƣơng trình tiếp tuyến t :  3   4 2 4a
4a x  y  3a  2a  3  0    5 4 2 3a  2a 5 d M; t  hay  hay 65   2 3 65 4a 4a  1      6 4 2
5 a 1 a 1 117a  193a  85a  5  0
Giải tìm a, sau đó thế vào phƣơng trình (t) suy ra các phƣơng trình tiếp tuyến cần tìm.
Câu 3. Tìm m để đồ thị 3
y  x  3mx  2 có tiếp tuyến tạo với đƣờng thẳng d : x  y  7  0 góc  sao 1 cho cos  . 26 A. m  2 B. m  3
C. m  1, m  4 D. Đáp án khác
Bài làm 3. Gọi k là hệ số góc của tiếp tuyến  tiếp tuyến có vectơ pháp tuyến   1 n k; 1 , d có vec tơ pháp tuyến n  2 1;1 1 n n2 1 k  1 3 2 Ta có cos      k  hoặc k  2 n n 26 2  3 1 2 2 k 1
Yêu cầu bài toán  ít nhất một trong hai phƣơng trình y'   1
k hoặc y' k2 có nghiệm x tức  2      3 3x 2 1 2m x  2  m  có nghiêm 2 
. Tìm điều kiện có nghiệm suy ra m. Bạn tự giải tiếp, hí hí.  2     2 3x 2 1 2m x  2  m  có nghiêm  3
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 26
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
Câu 4. Xác định m để hai tiếp tuyến của đồ thị 4 2
y  x  2mx  2m  1 tại A1; 0 và B 1  ;0 hợp với 15
nhau một góc  sao cho cos  . 17 5 7 15 17
A. m  0, m  2, m  , m  .
B. m  0, m  2, m  , m  . 16 6 16 16 15 7 5 7
C. m  0, m  2, m  , m  .
D. m  0, m  2, m  , m  . 16 16 6 6
Bài làm 4. Dễ thấy, A, B là 2 điểm thuộc đồ thị với m   . Tiếp tuyến d      1 tại A : 4m 4x y 4m 4 0 Tiếp tuyến d       2 tại B :  4m 4x y 4m 4 0 15 17
Đáp số: m  0, m  2, m  , m  . 16 16 2x  2
Bài 12. Cho hàm số: y  C . x  có đồ thị   1
Viết phƣơng trình tiếp tuyến của đồ thị (C) .
Câu a. Tiếp tuyến có hệ số góc bằng 1  .
A. y  x  2, y  x  7 .
B. y  x  5, y  x  6 .
C. y  x  1, y  x  4 .
D. y  x  1, y  x  7 .   4
Bài làm a.
Hàm số đã cho xác định với x
  1. Ta có: y'  x 21
Gọi Mx0; y0  là tọa độ tiếp điểm, suy ra phƣơng trình tiếp tuyến của C : 4   4  2x  2 y   2x 2 x  x    0  0 y' x   với  0 và 0 y 2 x  0  2  1 0 1 x x  x 1 0 1 0 0
Tiếp tuyến có hệ số góc bằng 1  4  Nên có:  1   x  3, x  1   0 x   0 2 1  Với          0 x 1 0 y 0 : y x 1  Với         0 x 2 0 y 4 : y x 7
Vậy, có 2 tiếp tuyến thỏa mãn đề bài: y  x  1, y  x  7 .
Câu b. Tiếp tuyến song song với đƣờng thẳng d : y  4  x  1. A. y  4  x  3, y  4  x  4 . B. y  4  x  2, y  4  x  44 . C. y  4  x  2, y  4  x  1 . D. y  4  x  2, y  4  x  14 .
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 27
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN   4
Bài làm b.
Hàm số đã cho xác định với x
  1. Ta có: y'  x 21
Gọi Mx0; y0  là tọa độ tiếp điểm, suy ra phƣơng trình tiếp tuyến của C : 4   4  2x  2 y   2x 2 x  x    0  0   với y' 0 x  và 0 y 2 x   2 0  1 0 1 x x  x 1 0 1 0 0
Tiếp tuyến song song với đƣờng thẳng d : y  4  x  1. 4  Nên có: y'x         0  4 4 x 0 x 2  hoặc 0 x   0 2 0 1  Với         0 x 0 y0 2 : y 4x 2  Với         0 x 2 0 y 6 : y 4x 14
Vậy, có 2 tiếp tuyến thỏa mãn đề bài: y  4  x  2, y  4  x  14 .
Câu c. Tiếp tuyến tạo với 2 trục tọa độ lập thành một tam giác cân.
A. y  x  1, y  x  6 .
B. y  x  2 y  x  7 .
C. y  x  1, y  x  5 .
D. y  x  1, y  x  7 .   4
Bài làm c.
Hàm số đã cho xác định với x
  1. Ta có: y'  x 21
Gọi Mx0; y0  là tọa độ tiếp điểm, suy ra phƣơng trình tiếp tuyến của C : 4   4  2x  2 y   2x 2 x  x    0  0 y' x   với  0 và 0 y 2 x  0  2  1 0 1 x x  x 1 0 1 0 0
Tiếp tuyến tạo với 2 trục tọa độ lập thành một tam giác cân nên hệ số góc của tiếp tuyến bằng 1  . Mặt khác: y'x    0  0 , nên có: y'x0  1 4  Tức  1   x  1  x  3  hoặc 0 . x   0 2 0 1  Với          0 x 1 0 y 0 : y x 1  Với         0 x 3 y0 4 : y x 7
Vậy, có 2 tiếp tuyến thỏa mãn đề bài: y  x  1, y  x  7 .
Câu d. Tiếp tuyến tại điểm thuộc đồ thị có khoảng cách đến trục Oy bằng 2 . 4 1 4 2
A. y   x  , y  4x  14 . B. y   x  , y  4x  1 . 9 9 9 9 4 1 4 2
C. y   x  , y  4x  1 . D. y   x  , y  4x  14 . 9 9 9 9
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 28
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN   4
Bài làm d. Hàm số đã cho xác định với x
  1. Ta có: y'  x 21
Gọi Mx0; y0  là tọa độ tiếp điểm, suy ra phƣơng trình tiếp tuyến của C : 4   4  2x  2 y   2x 2 x  x    0  0   với y' 0 x  và 0 y 2 x   2 0  1 0 1 x x  x 1 0 1 0 0  2  Khoảng cách từ Mx   
0 ; y0  đến trục Oy bằng 2 suy ra x0
2 , hay M 2;  , M2;6 .  3   2  4 2
Phƣơng trình tiếp tuyến tại M 
 2;  là: y   x   3  9 9
Phƣơng trình tiếp tuyến tại M2; 6 là: y  4x  14 4 2
Vậy, có 2 tiếp tuyến thỏa đề bài: y   x  , y  4x  14 . 9 9 2x
Bài 13. Viết phƣơng trình tiếp tuyến với đồ thị hàm số: y  , x  biết: 1
Câu a. Hệ số góc của tiếp tuyến bằng 2  A. y  2x   1,y  2x  B. y  2x   2,y  2x   4 C. y  2  x  9,y  2  x D. y  2  x  8,y  2  x 2x   1  2x   2
Bài làm a. Ta có: y'   x ; y  .
Gọi  0 0  là tọa độ tiếp điểm, hệ số góc x  2 1 x  2 1 2  tiếp tuyến tại x 
0 ; y0  bằng y ' x0  x  2 0 1 2 
Theo giải thiết, ta có: y'x      0  2 2 x  2 0 1    2 x       0 1 1 x0 2 y0 4 x     0 1 1  x        0 1 1 x  0 0 y0 0
Vậy, có 2 tiếp tuyến thỏa đề bài: y  2  x  8,y  2  x
Câu b. Tiếp tuyến song song với đƣờng thẳng d : x  2y  0 1 7 1 7 1 27 1 7 A. y   x  , y   x  B. y   x  , y   x  2 4 2 4 2 4 2 4 1 2 1 7 1 27 1 7 C. y   x  , y   x  D. y   x  , y   x  2 4 2 4 2 4 2 4
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 29
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN 2x   1  2x   2
Bài làm b. Ta có: y'   x ; y  .
Gọi  0 0  là tọa độ tiếp điểm, hệ số góc x  2 1 x  2 1 2  tiếp tuyến tại x 
0 ; y0  bằng y ' x0  x  2 0 1 2  1 1 Theo giải thiết, ta có:    x   0 2 1   2 2 4 x0 1 1 27 1 7
Vậy, có 2 tiếp tuyến thỏa đề bài: y   x  , y   x  2 4 2 4
Câu c. Tiếp tuyến vuông góc với đƣờng thẳng  : 9x  2y  1  0 2 2 2 8 2 32 2 8 A. y   x  , y   x  B. y   x  , y   x  9 9 9 9 9 9 9 9 2 1 2 8 2 32 2 4 C. y   x  , y   x  D. y   x  , y   x  9 9 9 9 9 9 9 9 2x   1  2x   2
Bài làm c. Ta có: y'   x ; y  .
Gọi  0 0  là tọa độ tiếp điểm, hệ số góc x  2 1 x  2 1 2  tiếp tuyến tại x 
0 ; y0  bằng y ' x0  x  2 0 1 2  2 1 Theo giải thiết, ta có:    x   0 2 1   2 9 9 x0 1 2 32 2 8
Vậy, có 2 tiếp tuyến thỏa đề bài: y   x  , y   x  9 9 9 9
Câu d. Tạo với đƣờng thẳng d' : 4x  3y  2012  0 góc 0 45 1 2
A. y  2x  3 B. y x  3 C. y x  3 D. Đáp án khác 4 3 2x   1  2x   2
Bài làm d. Ta có: y'   x ; y 
. Gọi  0 0  là tọa độ tiếp điểm, hệ số góc x  2 1 x  2 1 2  tiếp tuyến tại x 
0 ; y0  bằng y ' x0  x  2 0 1
Tiếp tuyến cần tìm có phƣơng trình: y  kx  x    0  yx0  với k y' 0 x  0, có
vectơ pháp tuyến là n  k;  
1 , d' có vectơ pháp tuyến là m  4; 3
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 30
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN n.m 4k  3 0 1 1 cos 45   
 k   thỏa đề bài. 2 n m  2 7 k 1.5 2
Câu e. Tạo với chiều dƣơng của trục hoành một góc  sao cho cos    5 1 3 1 3 1 13 A. y x B. y x C. y x D. Đáp án khác 5 4 5 4 5 4 2x   1  2x   2
Bài làm e. Ta có: y'   x ; y 
. Gọi  0 0  là tọa độ tiếp điểm, hệ số góc x  2 1 x  2 1 2  tiếp tuyến tại x 
0 ; y0  bằng y ' x0  x  2 0 1
Tiếp tuyến tạo với chiều dƣơng trục hoành ,khi đó tồn tại   0;     để tan  0 2  1 1 1 và tan   tan    1   tan    . Ta có: 2 , nên có: 2 x  2 cos  4 2 0 1 2  1    x   0 2 1 4   2 2 x0 1
Câu f. Tại điểm M thuộc đồ thị và vuông góc với IM ( I là giao điểm 2 tiệm cận ) 1 3 1 3 1 13 A. y x B. y x C. y x D. Đáp án khác 5 4 5 4 5 4 2x   1  2x   2
Bài làm f. Ta có: y'   x ; y 
. Gọi  0 0  là tọa độ tiếp điểm, hệ số góc x  2 1 x  2 1 2  tiếp tuyến tại x 
0 ; y0  bằng y ' x0  x  2 0 1 2 k     x   0 2 IM k .y' x 1 1 4  , theo bài toán nên có: IM  0 x  2 0 1 4 2 x x
Bài 14: Cho hàm số y    2 có đồ thị (C). 4 2
Câu 1. Viết phƣơng trình tiếp tuyến của (C) song song với đƣờng thẳng : y  2x  2 . 3 1 3
A. y  2x
B. y  2x
C. y  2x
D. y  2x  1 4 4 4
Bài làm 1. y'(x  0 )
2 (trong đó x0 là hoành độ tiếp điểm của (t) với (C)).  3 3         0 x 0 x 2 0 x 0 x 2 0 0 x 1.
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 31
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN 11 3
Phƣơng trình (t): y  y'(1)(x  1)  y(1)  2(x  1)   2x  4 4 9
Câu 2. Viết phƣơng trình tiếp tuyến (d) của (C) biết khoảng cách từ điểm A(0;3) đến (d) bằng . 4 5 1 3 3 3 A. y  2x  , y  2  x  B. y  2x  , y  2  x  4 4 4 14 3 3 3 3 C. y  2x  , y  2  x  D. y  2x  , y  2  x  4 4 14 4
Bài làm 2. Phƣơng trình tiếp tuyến (d) có dạng : y  y'(    0 x )(x x0 y(x0)
(trong đó x0 là hoành độ tiếp điểm của (d) với (C)). 4 2 x x 3 1 Phƣơng trình (d): 3 0 0 3 4 2 y  (x           0 x0)(x x0) 2 (x0 x0)x x0 x0 2 4 2 4 2 3 3 4 1 2  (x       0 x0)x y x0 x0 2 0. 4 2 3 4 1 2  x   0 x0 1 9 4 2 9 d(A;(d))    3 2 4 5   4 5 (x0 x0) 1 4 2 2 2 2       4 2 2 2 2 2       0 3x 2x0 4 5 9 x0(x0 1) 1 5(3x0 2x0 4) 81[x0(x0 1) 1] Đặt 2 t  x       0 , t
0 . Phƣơng trình (1) trở thành: 2 2 2 5(3t 2t 4) 81[t(t 1) 1] 4 2 3 2 3 2
 5(9t  4t  16  12t  24t  16t)  81t  162t  81t  81 4 3 2 3 2
 45t  21t  22t  t 1  0  (t 1)(45t  24t  2t  1)  0 3 2
 t  1 (do t  0 nên 45t  24t  2t  1  0)
Với t  1 ,ta có 2     0 x 1 x0 1 . 3 3
Suy ra phƣơng trình tiếp tuyến (d): y  2x  , y  2  x  4 4 Bài 15: ax  b
Câu 1. Cho hàm số y 
C . Tìm a, b biết tiếp tuyến của đồ thị C tại giao điểm của x  , có đồ thị là   2  1
C và trục Ox có phƣơng trình là y   x  2 2 A. a   1, b  1 B. a   1, b  2 C. a   1, b  3 D. a   1, b  4
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 32
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN  1 1
Bài làm 1. Giao điểm của tiếp tuyến d : y   x  2 với trục Ox là A4;0 , hệ số góc của d : k   và 2 2 4a  b A4;0 , (C)   0  4a  b  0 . 2 2  a  b 2  a  b Ta có: y'   y4  2 (x  2) 4 1 1 2  a  b 1
Theo bài toán thì: k    y'(4)       2a  b  2 2 2 4 2 4a  b  0 Giải hệ 
ta đƣợc a   1, b  4 2a  b   2 Câu 2. Cho hàm số 4 2
y  ax  bx  c (a  0) , có đồ thị là C . Tìm a,b,c biết C có ba điểm cực trị , điểm
cực tiểu của C có tọa độ là 0; 3 và tiếp tuyến d của C tại giao điểm của C với trục Ox có phƣơng trình là y  8  3x  24 . A. a  1  , b  2, c  3
B. a  1, b  21, c  3 C. a  1  , b  21, c  13 D. a  1  2, b  22, c  3 a   0 ,b  0
Bài làm 2. C có ba điểm cực trị , điểm cực tiểu của C có tọa độ là 0;3  c   3
Giao điểm của tiếp tuyến d và trục Ox là B 3;0 và hệ số góc của d là 8  3 B(C) 9a  3b  c  0           9a 3b c 0       4a   33 . y' 3 8 3  2b 3  8  3 6a  b  4  c  3 
Giải hệ 9a  3b  c  0 ta đƣợc 4 2 a  1
 , b  2, c  3  y  x   2x  3 6a  b  4   Bài 16: Cho hàm số 4 2
y  2x  4x  1 có đồ thị là (C).
Câu 1. Viết phƣơng trình tiếp tuyến của (C), biết tiếp tuyến vuông góc với đƣờng thẳng x  48y  1  0 . A.  : y  4  8x  81 B.  : y  4  8x  81 C.  : y  4  8x 1 D.  : y  4  8x  8
Bài làm 1. Ta có 3 y'  8x  8x
Gọi M(x0; y0) . Tiếp tuyến  tại M có phƣơng trình: 3 4 2 y  (8x         0
8x0)(x x0) 2x0 4x0 1.Vì tiếp tuyến vuông góc với đƣờng thẳng x 48y 1 0 1 Nên ta có: y'(x      0 ). 1 y'(x0) 48 48 3         0 x 0 x 6 0 0 x 2 y0 15 . Phƣơng trình  : y  4  8(x  2)  15  4  8x  81 .
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 33
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN
Câu 2. Viết phƣơng trình tiếp tuyến của (C), biết tiếp tuyến đi qua A(1; 3  ). 64 1 64 1 A.  : y  3  hay  : y   x  B.  : y  3  hay  : y   x  27 81 27 8 64 51 64 51 C.  : y  3  hay  : y   x  D.  : y  3  hay  : y   x  27 2 27 81
Bài làm 2. Ta có 3 y'  8x  8x
Gọi M(x0; y0) . Tiếp tuyến  tại M có phƣơng trình: 3 4 2 y  (8x       0
8x0)(x x0) 2x0 4x0 1.Vì tiếp tuyến  đi qua A(1; 3)nên ta có 3 4 2 3   (8x      0 8x0)(1 x0) 2x0 4x0 1 4 3 2  3      2      0 x 4x0 2x0 4x0 1 0 ( 0 x 1) ( 0 x 1)(3 0 x 1) 0        0 x 1 : y 3  1 64 51 x       0 : y x . 3 27 81
Câu 3. Viết phƣơng trình tiếp tuyến của (C), biết tiếp tuyến tiếp xúc với (C) tại hai điểm phân biệt. A.  : y  3  B.  : y  4 C.  : y  3 D.  : y  4 
Bài làm 3. Ta có 3 y'  8x  8x
Gọi M(x0; y0) . Tiếp tuyến  tại M có phƣơng trình: 3 4 2 y  (8x        0
8x0)(x x0) 2x0 4x0 1.Giả sử  tiếp xúc với (C) tại điểm thứ hai 4 2 N(n; 2n 4n 1) Suy ra: 3 4 2
 : y  (8n  8n)(x  n)  2n  4n 1  3 3 8x  8x  8n  8n  2 2 x  nx  n  1  0 Nên ta có: 0 0  0 0   4 2 4 2  6  x        2 2      0 4x0 1 6n 4n 1 (x  0 n)(3x0 3n 2) 0  2 2   2 2 x     x  x n  n  1  0 0 x0n n 1 0   (I) hoặc 0 0   (II) x    2 2     0 n 0 3x  0 3n 2 0  2 2 2    x  n x  0 n  Ta có (I) 0   ; 3 (II)  
vô nghiệm. Vậy  : y  3  . n  1  1 x  0n  3 3 x
Bài 17: Gọi (C) là đồ thị của hàm số 2 y   x  2x  1 . 3
Câu 1. Viết phƣơng trình tiếp tuyến của (C) tại giao điểm của (C) với trục tung.
A. y  2x  1
B. y  22x  1
C. y  2x  3
D. y  2x  4
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 34
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN x
Câu 2. Viết phƣơng trình tiếp tuyến của (C) vuông góc với đƣờng thẳng y    2 . 5 2 8 A. y = 5x + hoặc y = 5x – 8 B. y = 5x + hoặc y = 5x – 9 3 3 8 8 C. y = 5x + hoặc y = 5x – 5 D. y = 5x + hoặc y = 5x – 8 3 3  x
Bài làm 2. Cách 1. Tiếp tuyến (d) của (C) vuông góc với đƣờng thẳng y  
 2 ,suy ra phƣơng trình (d) 5 có dạng : y = 5x + m.  3 x 2 
 x  2x  1  5x  m (1)
(d) tiếp xúc với (C)   3 có nghiệm.  2 x  2x  2   5 (2)
Giải hệ trên, (2)  x = -1  x = 3. 8
Thay x = - 1 vào (1) ta đƣợc m = . 3
Thay x = 3 vào (1) ta đƣợc m = - 8 . 8
Vậy phƣơng trình tiếp tuyến cần tìm là y = 5x + hoặc y = 5x – 8 . 3 x
Cách 2. Tiếp tuyến (d) vuông góc với đƣờng thẳng y  
 2 suy ra hệ số góc của (d) : k = 5. 5 Gọi x         
0 là hoành độ tiếp điểm của (d) với (C) ,ta có : 2 k f '(x0) 5 x0 2x0 2 x0 1,x0 3 .  8
y  5(x  1)  f(1)  5x   Suy ra phƣơng trình (d): 3  .
y  5(x  3)  f(3)  5x  8
Câu 3.Viết phƣơng trình tiếp tuyến của (C) biết tiếp tuyến đó cắt trục hoành , trục tung lần lƣợt tại A, B sao
cho tam giác OAB vuông cân (O là gốc tọa độ ). 1 4 4 4 A. y = x + . B. y = x + . C. y = x + . D. y = x - . 3 3 13 3
Bài làm 3. Vì tam giác OAB là tam giác vuông tại O nên nó chỉ có thể vuông cân tại O , khi đó góc giữa
tiếp tuyến (D) và trục Ox là 0
45 ,suy ra hệ số góc của (D) là k   D 1 Trƣờng hợp k   D
1 ,khi đó phƣơng trình (D) : y = x + a. (a 0)  3 x 2 
 x  2x  1  x  a (3) (D) tiếp xúc (C)   3 có nghiệm.  2 x  2x  2   1 (4) 2
(4)  x  2x  1  0  x  1 .
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 35
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN 4
Thay x = 1 vaò phƣơng trình (3) ta đƣợc a = . 3 4
Vậy trong trƣờng hợp này ,phƣơng trình (D): y = x  3 Trƣờng hợp k   D
1 , khi đó phƣơng trình (D): y = - x + a .  3 x 2 
 x  2x  1  x  a (5)
(D) tiếp xúc với (C)   3 có nghiệm  2 x  2x  2  1   (6) (6) 2
 x  2x  3  0 .P/t này vô nghiệm nên hệ (5), (6) vô nghiệm ,suy ra (D) : y = - x + a không tiếp xúc với (C). 4
Vậy phƣơng trình tiếp tuyến cần tìm là y = x + . 3 Bài 18: Cho hàm số 3 2
y  x  2x  (m  1)x  2m có đồ thị là (Cm ) .
Câu 1. Tìm m để tiếp tuyến của đồ thị (C 
m ) tại điểm có hoành độ x
1 song song với đƣờng thẳng y  3x  10 . A. m  2 B. m  4 C. m  0 D.Không tồn tại m
Bài làm 1. Ta có: 2
y'  3x  4x  m  1 . Tiếp tuyến của (C 
m ) tại điểm có hoành độ x 1 có phƣơng trình
y  (m  2)(x  1)  3m  2  (m  2)x  2m m  2  3 Yêu cầu bài toán   vô nghiệm. 2m   10
Vậy không tồn tại m thỏa yêu cầu bài toán.
Câu 2. Tìm m để tiếp tuyến có hệ số góc nhỏ nhất của đồ thị (Cm ) vuông góc với đƣờng thẳng  : y  2x  1. 11 6 A. m  1 B. m  2 C. m D. m  6 11
Bài làm 2. Ta có: 2
y'  3x  4x  m  1 .Ta có: 2     2 4 4 7 2 7 7 y'  3 x  x   m   3 x   m       y'  m  .  3 9  3  3  3 3 2 7
Tiếp tuyến tại điểm có hoành độ x 
có hệ số góc nhỏ nhất và hệ số góc có giá trị : k  m  . 3 3  7  11
Yêu cầu bài toán  k.2  1   m  .2  1   m    .  3  6
Câu 3. Tìm m để từ điểm M(1; 2) vẽ đến (Cm ) đúng hai tiếp tuyến.
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 36
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN m  3  m  3 m  3 m  3      A. 10  B. 100 C. 10 D. 100 m         m m m  81  81  81  81
Bài làm 3. Ta có: 2
y'  3x  4x  m  1 . Gọi A(x0; y0) là tọa độ tiếp điểm.
Phƣơng trình tiếp tuyến  tại A: y   2 3x  4x  m   3 2       0 0 1 (x x0) x0 2x0 (m 1)x0 2m M   2   2 3x  4x  m   3 2       3 2       0 0 1 (1 x0) x0 2x0 (m 1)x0 2m 2x0 5x0 4x0 3m 3 0 (*)
Yêu cầu bài toán  (*) có đúng hai nghiệm phân biệt (1) Xét hàm số: 3 2
h(t)  2t  5t  4t, t  Ta có: 2 1
h'(t)  6t  10t  4  h'(t)  0  t  ,t  2  3 Bảng biến thiên x  2  1  3 y'  0  0  12  y  19  27 3  3m  12 m  3   
Dựa vào bảng biến thiên, suy ra (1)  19  
100 là những giá trị cần tìm. 3  3m      m  27  81
Bài 19: Tìm m để đồ thị : 1 Câu 1. 3 y  mx  m   2
1 x  4  3mx  1 tồn tại đúng 2 điểm có hoành độ dƣơng mà tiếp tuyến tại đó 3
vuông góc với đƣờng thẳng x  2y  3  0 .  1   1 2   1   1 7  A. m  0;     ;  B. m  0;     ;   4   2 3   4   2 3   1   1 8   1   1 2  C. m  0;     ;  D. m  0;     ;   2   2 3   2   2 3 
Bài làm 1. Hàm số đã cho xác định trên . Ta có: 2 y'  mx  2m   1 x  4  3m .
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 37
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN  1 
Từ yêu cầu bái toán dẫn đến phƣơng trình y   1   
có đúng 2 nghiệm dƣơng phân biệt, tức  2  m  0 m  0   1     m 2 ' 0  mx  2m  
1 x  2  3m  0 có đúng 2 dƣơng phân biệt   2   hay S  0  0  m  1  P   0  2 0  m   3  1   1 2  m  0;     ;  .  2   2 3  2 2 x  2mx  2m  1 Câu 2. y 
cắt trục hoành tại hai điểm phân biệt và các tiếp tuyến với Cm  tại hai x  1
điểm này vuông góc với nhau. 2 2 A. m  B. m  1  C. m  , m  1  D. m  0 3 3
Bài làm 2. Hàm số đã cho xác định trên  \  1 .
Xét phƣơng trình hoành độ giao điểm của Cm  và trục hoành: 2 2 x  2mx  2m  1 2 2
 0  x  2mx  2m  1  0, x  1 1 x  1
Để Cm  cắt trục hoành tại hai điểm phân biệt A,B thì phƣơng trình 1 phải có hai nghiệm phân biệt  2 2
'  m  2m  1  0
1 m1 m   0  1   m  1
khác 1 . Tức là ta phải có:  hay  tức  2. 2 1    2m  2m  1  0 2m  m  1   0 m   0 Gọi    2   1
x ; x2 là hai nghiệm của 1 . Theo định lý Vi – ét , ta có: 1 x x2 2m, 1 x .x2 2m 1
Giả sử I x0;0 là giao điểm của Cm  và trục hoành. Tiếp tuyến của Cm  tại điểm I có hệ số góc
2x  2mx  1  2 2    0 0 x0 2mx0 2m 1   2x  0 2m y' x   0  2 x   1 0 1 x0 2x  2m 2x  2m
Nhƣ vậy, tiếp tuyến tại A, B lần lƣợt có hệ số góc là y'x  1   1 y' x  ,   2 2  . 1 x 1 x2 1
Tiếp tuyến tại A, B vuông góc nhau khi và chỉ khi y'   1 x y'x2  1 hay  2     1 x 2m 2x2 2m     1      5             1 x .x2 4m 1 1x x2 2 4m 1 0 m 1   tức 2 3m m 2 0  1 x 1 x  2 1  2 2 hoặc m 
. Đối chiếu điều kiện chỉ có m  thỏa mãn. 3 3
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 38
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. TẬP 2A. PHƯƠNG TRÌNH TIẾP TUYẾN 2x  1
Bài 20: Tìm điểm M tr n đồ thị C : y 
sao cho khoảng cách từ M đến đƣờng thẳng  : x  1
x  3y  3  0 đạt giá trị nhỏ nhất.  1   7  A. M 2;  1 B. M2; 5 C. M 1   ;  D. M  3;   2   2      2m 1
Bài làm: Gọi M m;
 là tọa độ điểm cần tìm m   1 .  m  1   2m  1 m  3    3  m  1  2 1 m  2m  6
Khoảng cách từ M đến đƣờng thẳng  là: d  hay d  . 2 2  1  3 10 m 1  2 m  2m  6  khi m  1 2 m  2m  6   m  1 Xét hàm số: f m      m  1 2 m  2m  6  khi m  1  m  1
Ta có: f 'm  0  m  2
 thỏa m  1 hoặc m  4 thỏa m  1. 2
Lập bảng biến thiên suy ra min d  khi m  2  tức M 2;  1. 10 1 1
Tiếp tuyến tại M là y   x 
, tiếp tuyến này song song với  . 3 3
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 39 NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM.
TẬP 2B. VIẾT PHƯƠNG TRÌNH TIẾP TUYẾN
KHI BIẾT HỆ SỐ GÓC
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 hoặc
Facebook: https://web.facebook.com/phong.baovuong
Page: https://web.facebook.com/tracnghiemtoanthpt489/
Website: http://tailieutoanhoc.vn/ Email: baovuong7279@gmail.com 0946798489
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. MỤC LỤC
Vấn đề 2. Viết phƣơng trình tiếp tuyến của đồ thị hàm số khi biết hệ số góc của tiếp tuyến. ......................... 2
CÁC BÀI TOÁN LUYỆN TẬP ................................................................................................................................. 10
GIÁO VIÊN NÀO MUỐN MUA FILE WORD LIÊN HỆ 0946798489 ĐỂ GẶP THẦY VƢƠNG.
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 1
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM.
Vấn đề 2. Viết phƣơng trình tiếp tuyến của đồ thị hàm số khi biết hệ số góc của tiếp tuyến. Phƣơng pháp:
 Giải phương trình f '( )
x k giải phương trình này ta tìm được các nghiệm x , x ,..., x . 1 2 n
 Phương trình tiếp tuyến: y f '(x )(x x )  f (x ) (i  1,2,..., ) n . i i i
h : ối v i ài to n này ta ần ưu m t số v n đ sau
 ố tiếp tuyến a đ th h nh à số nghiệm a phương trình f '( ) x k .
 Cho hai đư ng th ng d : y k x b và d : y k x b hi đ 1 1 1 2 2 2 k k i) 1 2 tan 
trong đ   (d ,d ) . 1  k .k 1 2 1 2 k k ii) 1 2 d / /d   1 2 b b 1 2
iii) d d k .k  1  . 1 2 1 2 OB
Nếu đư ng th ng d cắt các trục Ox, Oy lần ượt tại A, B thì tanOAB  
trong đ hệ số góc c a d được OA
x đ nh bởi y'x  tanOAB 2x  1
Ví dụ 1 : Cho hàm số y  đ th (C) x  1
1. Giải b t phương trình y'  4  ;
2. Viết phương trình tiếp tuyến v i (C) biết tiếp tuyến này cắt các trục Ox, Oy lần ượt tại A, B mà OA  4OB . Lời giải. 1 
1. Ta có y '  . 2 (x  1)    2 1 1 1 3 1  (  x 1)   x 1    x
B t phương trình y'  4    4    4   2  2 2 2 (x  1) x  1 x  1 x     1 2. Cách 1: OB 1 1 1 Ta có tanOAB  
nên hệ số góc c a tiếp tuyến k  hoặc k   . OA 4 4 4 1  1 Nhưng do y'   0, x
  1 nên hệ số góc c a tiếp tuyến là k   . 2 (x  1) 4 1  1  x  3
Hoành đ tiếp điểm nghiệm phương trình    . 2 (x  1) 4 x  1  1 5 1 13
Từ đ ta x đ nh được hai tiếp tuyến thỏa mãn: y   x  ; y   x  4 4 4 4
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 2
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. Cách 2:  2x  1 
Phương trình tiếp tuyến v i (C) tại điểm 0 M x ;  (x  1)  là: 0  0 x   1 0  1  2x  1 2 x 2x  2x  1 0 y  (x x )  hay 0 0 y   2 0 (x  1) x  1 2 2 (x  1) (x  1) 0 0 0 0
Ta x đ nh được tọa đ giao điểm c a tiếp tuyến v i các trục tọa đ : 2
 2x  2x 1 2 0 0 (
A 2x  2x  1; 0), B 0;  0 0  2 (x 1)    0  2 2x  2x  1 x  3
Từ giả thiết OA  4OB , ta có: 2 0 0 2 0
2x  2x  1  4
 (x 1)  4   0 0 2 0 (x  1) x  1   0 0 Cách 3: Giả sử ( A ; a 0), ( B 0; )
b v i ab  0 . b 1
V i giả thiết OA  4OB a  4 b a  4  b    a 4 x y b
ư ng th ng đi qua hai điểm A, B có dạng  :
  1 hay  : y   x b a b a b
ư ng  : y   x b tiếp xúc (C) tại điểm hoành đ x khi và chỉ khi hệ sau có nghiệm x : a 0 0  1  b    (*) 2 (x  1) a 0 b b 1 
(I). Từ (*) suy ra   0   . 2x  1  b a a 4 0
  x b (**) 0  x   1 a 0  1  1 x  3 0    13   2  (  1) 4   1  b x x  Hệ (I) trở thành 0 0 4      2x  1  1  2x  1 1  5 0 0   x b b   x b     0 x 1 4   x  1 4  4 0  0 1 5 1 13
Do vậy có hai tiếp tuyến thỏa mãn: y   x  ; y   x  4 4 4 4 2
x  2mx m 1
Ví dụ 2 Gọi (C) à đ th c a hàm số y
, m là tham số khác 0 và khác  x m 3
1.Chứng minh rằng nếu (C) cắt Ox tại điểm M hoành đ x thì hệ số góc c a tiếp tuyến c a (C) tại M là : 0 2x  2m 0
k x m 0
2.Tìm m để (C) cắt Ox tại hai điểm và hai tiếp tuyến c a (C) tại hai điêm đ vuông g v i nhau. Lời giải. 2 3m m
1. Ta có y x  3m xm Khi m  0 và m  1 
thì đa thức tử không chia hết ho đa thức mẫu do đ đ th hàm số không suy biến 3 thành đư ng th ng.
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 3
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM.
Hệ số góc c a tiếp tuyến (d) c a (C) tại M là 2 (2x  2 ) m (x  )
m  (x  2mx m) 0 0 0 0
k y'(x )  . 0 2 (x  ) m 0 2
x  2mx m Vì M thu c Ox nên 0 0 2 ( y x ) 
 0  x  2mx m  0 . 0 0 0 x m 0 (2x  2 ) m (x  ) m 2x  2m 0 0 0  k   (đp m) 2 (x  ) m x m 0 0
2.Phương trình hoành đ giao điểm c a (C) và Ox 2
x  2mx m x  m  0   2 x m  (
g x)  x  2mx m  0 (1)
(C) cắt Ox tại hai điểm phân biệt M,N  (1) có hai nghiệm x1, x2 khác – m .     2 m 0 m 1
'  m m  0
m  0  m  1        . (*) 2 1  ( g  ) m  0
3m m  0 m    3
hi đ hệ số góc c a hai tiếp tuyến c a (C) tại M, N là 2x  2m 2x  2m 1 2 k  , k  . 1 2 x m x m 1 2
Hai tiếp tuyến này vuông góc  k .k  1  1 2
 2x  2m  2x  2m  1 2      1  x m x    m 1 2  2 2  4[x x  (
m x x )  m ]  x x  (
m x x )  m (2) 1 2 1 2 1 2 1 2
Lại có x  x  2m , x .x  m Do đ : 2 (2)  m
 5m  0  m  0  m  5 . 1 2 1 2
So v i đi u kiện (*) nhận m = 5. x
Ví dụ 3 : Cho hàm số y
đ th là (C). Tìm tọa đ điểm M thu c (C), biết rằng tiếp tuyến c a (C) tại x  1
M vuông góc v i đư ng th ng đi qua điểm M và điểm I 1;1 . Lời giải. x
V i x  1 , tiếp tuyến (d) v i (C) tại 0 M  x ;  phương trình : 0  0 x 1   0  1 x 2 1 x 0 y   (x x )  0  x y   0 2 0 (x  1) x  1 2 2 (x  1) (x  1) 0 0 0 0  1   1  (d)
có vec tơ hỉ phương u   1;   
, IM   x  1;  2   (x 1)    0 x   1  0  0
ể (d) vuông g IM đi u kiện là : 1 1 x  0 0 . u IM  0  1  .(x 1)   0   0 2
(x  1) x  1 x  2 0 0 0
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 4
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM.
V i x  0 ta được M 0; 0 0
V i x  2 ta được M 2; 2 0
Vậy, M 0; 0 và M 2; 2 là tọa đ cần tìm.
Ví dụ 4 : Cho hàm số 3 2
y x  3x  9x  5 đ th là (C). Trong t t ả tiếp tuyến a đ th (C) h y tìm
tiếp tuyến hệ số g nhỏ nh t. Lời giải.
Hàm số đ ho x đ nh D  Ta 2
y'  3x  6x  9 . Gọi (
M x ; y ) (C) 3 2
y x  3x  9x  5 . 0 0 0 0 0 0
Tiếp tuyến tại điểm M hệ số g 2 2
k y'(x )  3x  6x  9  3(x  1) 12  1  2 0 0 0 0 mink  1
 2, đạt đượ hi x  1   y  16. 0 0
ậy trong t t ả tiếp tuyến a đ th hàm số tiếp tuyến tại M  1
 ;16. hệ số g nhỏ nh t và phương trình là: y  1  2x + 4
Ví dụ 5. Gọi (C) à đ th c a hàm số 3 2 y  2
x  6x  5 .
1. Viết phương trình tiếp tuyến (d) c a (C) tại điểm A thu (C) hoành đ
x  3 Tìm giao điểm khác A c a (d) và (C).
2. X đ nh tham số a để t n tại ít nh t m t tiếp tuyến c a (C) có hệ số góc là a.
3. Chứng minh rằng chỉ có duy nh t m t tiếp tuyến c a (C) đi qua điểm hoành đ thỏa m n phương trình y'  0 c a (C). Lời giải.
1. Phương trình tiếp tuyến (d) c a (C) tại điểm A:
y y'(3)(x  3)  ( y 3)  1  8x  49 .
Phương trình hoành đ giao điểm c a (d) và (C): 3 2 3 2
 2x  6x  5  1
 8x  49  2x  6x 18x  54  0  x  3  x  3 
Suy ra giao điểm c a (d) và (C) khác A là B 3;103.
2. T n tại ít nh t m t tiếp tuyến c a (C) có hệ số góc là a  x
  , y'(x )  a 0 0 2  x  : 6
x 12x a . 0 0 0
Bài toán quy v Tìm a để phương trình - 6x2 +12x = a (1) có nghiệm.
(1)  6x2 – 12x + a = 0 . (1) có nghiệm  '  36  6a  0  a  6. Vậy a  6.
3. Từ giả thiết suy ra hoành đ phương trình y'  0  x  1  I 1;   1 .
Phương trình tiếp tuyến (D) c a (C) đi qua I 1;  
1 . có dạng : y  x –  1 – 1 3 2  2
x  6x  5  ( k x  1)  1 (1)
(D) tiếp xúc (C) tại điểm hoành đ x 0 0 0   có nghiệm x . 0 2  6
x  12x k (2) 0  0 0
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 5
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. Thay (2) vào (1) ta được 3 2 2 3
 2x  6x  5  ( 6
x 12x )(x 1) 1  (x 1)  0  x  1 0 0 0 0 0 0 0
uy ra phương trình d y  6x – 7 2 5
Ví dụ 6 : Cho hàm số 3 2
y   x  (m  1)x  (3m  2)x
đ th là (C). Tìm m để trên (C) hai điểm 3 3
phân biệt M (x ; y ), M (x ; y ) thỏa mãn x .x  0 và tiếp tuyến c a (C) tại mỗi điểm đ vuông g v i 1 1 1 2 2 2 1 2
đư ng th ng d : x  3y  1  0. Lời giải.
Hàm số đ ho x đ nh D  Ta 2 y'  2
x  2(m1)x  3m 2 . 1
Hệ số góc c a d : x  3y  1  0 là k  . d 3
Tiếp tuyến tại điểm M (x ; y ), M (x ; y ) vuông góc v i d thì phải có: y'  3  1 1 1 2 2 2
Trong đ x , x là các nghiệm c a phương trình: 1 2 2 2
x  2(m1)x  3m 2  3  2
 2x  2(m1)x  3m1  0 (1)
Yêu cầu bài toán  phương trình (1) hai nghiệm x , x thỏa mãn x .x  0 1 2 1 2 2
'  (m 1)  2(3m  1)  0 m  3      3  m 1  1   0  1   m   .  2  3 1 Vậy, m  3  hoặc 1
  m   thỏa mãn bài toán. 3
Ví dụ 7 Viết phương trình tiếp tuyến v i đ th C : 3 2
y x  6x  9x  2 tại điểm M, biết M cùng 2 điểm
cực tr c a C tạo thành tam giác có diện tích bằng 6. Lời giải.
Hàm số đ ho 2 điểm cực tr A1; 2 , B3; 2
  và đư ng th ng đi qua 2 cực tr là AB : 2x y  4  0 .
Gọi M x ; y
là tọa đ tiếp điểm c a đ th C c a hàm số và tiếp tuyến d cần tìm hi đ 0 0  3 2
y x  6x  9x  2 0 0 0 0 2x y  4
Ta có: AB  2 5 , dM; AB 0 0  5 1 Giả thiết S  6  .A .
B d M AB   2x y  4  6 MAB  ;  6 2 0 0
 2x y  10 hoặc 2x y  2  0 0 0 0
2x y  2  y  2   2x     0 0 y 2
TH1: Tọa đ M thỏa mãn hệ: 0 0  0     hay M 0; 2   3 2
y x  6x  9x  2  x   2
x  6x  11  0 x  0 0 0 0   0 0 0 0 0
Tiếp tuyến tại M là: y  9x  2 .
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 6
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM.
2x y  10
TH2: Tọa đ M thỏa mãn hệ: 0 0  3 2
y x  6x  9x  2  0 0 0 0
y  10  2x    0 0 y 2     hay M 4; 2 x  4   
x 6x 1  0 2 1  0 x  4 0 0 0  0
Tiếp tuyến tại M là: y  9x  34 .
Vậy, có 2 tiếp tuyến thỏa đ bài: y  9x  2 và y  9x  34 x  1
Ví dụ 8 : Cho hàm số y
đ th là (C). Tìm những điểm M trên (C) sao cho tiếp tuyến v i (C) tại 2(x  1)
M tạo v i hai trục tọa đ m t tam giác có trọng tâm nằm trên đư ng th ng 4x + y = 0. Lời giải.
Hàm số đ ho x đ nh D   \   1 x  1 Gọi M( 0 x ;
) (C) à điểm cần tìm. 0 2(x  1) 0
Gọi  tiếp tuyến v i (C) tại M ta phương trình  : x  1 1 x  1 ' 0
y f (x )(x x )  0  y  (x x )  0 0 2(x  1) x 2 0 2(x   1) 0 1 0 0 2
x  2x 1  2
x  2x 1
Gọi A   Ox  0 0 A  ; 0  0 0 
, B   Oy B 0;  . 2      2 2(x  1)  0  2 2        x 2x 1 x 2x 1 OAB có trọng tâm là: G( 0 0 0 0   ;   . 2 6 6(x 1)    0  2 2
x  2x  1 x  2x  1
Do G thu c đư ng th ng: 4x + y = 0  0 0 0 0 4  .   0 2 6 6(x  1) 0  1  1 x  1  x    0 0  1 4     2 2      (vì A, B  O nên 2 x 2x 1 0 ) 0 0 x  2 1  1  3 0 x  1   x   0 0  2    2 1  1 3 
V i x    M  ;    0 2  2 2  3  3 5 
V i x    M   ;  . 0 2  2 2  Ví dụ 9 :
1. Tìm m để tiếp tuyến c a đ th 3 2
y x  3x m tại điểm hoành đ bằng 1 cắt các trục Ox , Oy lần ượt
tại A và B sao cho diện tích tam giác OAB có diện tích bằng 1, 5
2. Tìm các giá tr dương a m để C  : 4
y x  m   2 3
1 x  3m  2 cắt trục hoành tại 4 điểm phân biệt và m
tiếp tuyến tại điểm hoành đ l n nh t cùng v i 2 trục tọa đ tạo thành tam giác có diện tích bằng 24 .
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 7
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. Lời giải.
1. x  1  y  
1  m  2 suy ra M 1; m  2 . Tiếp tuyến tại M là d : y  3
x m 2 .  m  2 
d cắt Ox tại A nên Ax ; 0 và Ad suy ra A ; 0  A   3 
d cắt Oy tại B nên B0; y
và B d suy ra B0; m  2 B  1 3
Diện tích tam giác OAB có diện tích bằng 1, 5 khi và chỉ khi . OA . OB  hay 2 2 m
OA . OB  3 
2 . m 2  3 hay m 2 2
 9 phương trình này 2 nghiệm m  5  hoặc m  1. 3 Vậy, m  5
 hoặc m  1 là giá tr cần tìm.
2 Phương trình hoành đ giao điểm C và trục hoành : m  4
x  m   2
x m     2 x   2 3 1 3 2 0 1 x   3m2  0  
V i m  0 thì C
cắt trục hoành tại 4 giao điểm phân biệt và x  3m  2 à hoành đ l n nh t. m
Gỉa sử A 3m  2;0 à giao điểm hoành đ l n nh t và tiếp tuyến d tại A phương trình:
y  23m   1
3m  2.x  23m   1 3m  2
Gọi B à giao điểm c a d và Oy suy ra B0; 2  3m  1 3m  2
Theo giả thiết, tam giác OAB vuông tại O và S  24  O . A OB  48 hay m   2 3
2 18m  22m  4  48 OAB 
Xét f m  m   2 3
2 18m  22m  4  48, m  0 .  2 
Ta có: f 'm  0 v i mọi m  0 , suy ra f m đ ng biến v i mọi m  0 và f
  0 do đ phương trình  3   2
có nghiệm duy nh t m  . 3 2 Vậy, m  thỏa m n đ bài. 3
Ví dụ 10 Tìm m
để tiếp tuyến c a đ th hàm số : 3
y x mx m 1 tại điểm hoành đ bằng 1 cắt 2 2 1
đư ng tròn x  2  y  3 
theo 1 dây cung đ dài nhỏ nh t. 5 Lời giải. 2
y'  3x m y' 
1  3  m . V i x  1  y  
1  0  M 1;0 .
Phương trình tiếp tuyến tại M : y y'  1 x  
1  3  mx y  3  m  0d .
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 8
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. 1
ư ng tròn có tâm I 2; 3 và bán kính R
. Vì IM R nên đ dài cung nhỏ nh t khi d tiếp xúc v i 5
3m233 m 1 m 1
đư ng tròn, tức là dI;d  R   hay  ình phương hai vế   2 m2 5 3  1 m  6m  10 5 5
và rút gọn ta đượ phương trình 2
2m  3m  5  0 , giải phương trình này ta được m  1 hoặc m  thỏa bài 2 toán.
Ví dụ 11 : Tìm m để tiếp tuyến c a đ th 3 2
y x  3x m tại điểm hoành đ bằng 1 cắt các trục Ox, Oy 5
lần ượt tại điểm A và B sao ho đư ng tròn ngoại tiếp tam giác OAB có chu vi 2 . 18 Lời giải.
V i x  1  y m  2  M 1; m – 2 0 0   Tiếp tuyến tại M là d: 2
y  (3x  6x )(x x )  m  2  d : y  3  x  m 1 0 0 0 m  1  m  1 
d cắt trục Ox tại A: 0  3
x m  1  x   A ; 0  A A 3  3 
d cắt trục Oy tại B : y m  1  ( B 0 ; m  1) B
m  1 m  1
Tam giác vuông tại O Trung điểm I c a AB à tâm đt ngoại tiếp I  ;   6 2  5 BK OI= m  1 18 5 m  0
Giả thiết có 2OI  2
m  1  1   18 m  2   x  1
Ví dụ 12. Gọi (C) à đ th c a hàm số y
. Viết phương trình tiếp tuyến (t) c a (C), biết: x  1
1. (t) tiếp xúc v i đư ng tròn: 2 2
( ) : (x  2)  (y  6)  45 .
2. Khoảng cách từ (t) đến điểm I(1;1) l n nh t. Lời giải.
1. T nh tiến OI v i I(1;1), hệ trục Oxy  hệ trục IXY.
x X x X 1
Công thức chuyển hệ tọa đ : I
y Y y Y  1 I
X x 1  2 1  1
ối v i hệ trục IXY thì A có tọa đ là Y y 1  61   5 X  1 1 X  2 2
Hàm số cho trở thành : Y  1    Y   F(X). (X  1)  1 X X
Phương trình a đư ng tròn ( ) là 2 2
(X 1)  (Y  5)  45, (  ) có tâm A(1;5) , bán kính R = 3 5 .
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 9
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM.
Phương trình tiếp tuyến (D) c a (C) tại điểm hoành đ X là 0 2 2 2 4
Y F '(X )(X X )  F(X )   (X X )    X  2
 2X X Y  4X  0. 0 0 0 2 0 2 X X X X 0 0 0 0 0 0
(D) tiếp xúc (C)  dA,D  R 2 2 2 2  5X  4x   0 0 (5X 4X 2) 2 0 0  [ d A,( ) D )   3 5  [( ( d A,(D))]   45 4 4  4 4  X X 0 0 4 2 3 2 4
 25X 16X  4  40X  20X 16X  180  45X 0 0 0 0 0 0 4 3 2
 5X 10X  9X  4X  44  0 2 2
 (X  2) (5X 10X 11)  0  X  2  0 0 0 0 0 0 0 0 1 Vậy phương trình (D)
Y   X  2 ,suy ra phương trình (D) đối v i hệ trục xu t phát Oxy là : 2 1 1 1
y  1   (x  1)  2   x  . 2 2 2
2. ối v i hệ tọa đ IXY phương trình tiếp tuyến (d) có dạng : 4X 2
2X X Y  4X  0 , 0 ( d I,(d))  0 0 4 4  X0
Áp dụng b t đ ng thức Cauchy ,ta có : 4 4 2
4  X  2 4X  4X 0 0 0 4X 4X 0 0 4  ( d I,(d))    2  ( d I,( )
d )  2  X  4  X   2 0 0 2 2 4 X X 0 0
hi đ phương trình tiếp tuyến (d): Y X
  2 2,Y  X  2 2 .
uy ra phương trình (d) đối v i hệ trục Oxy là y  x  2  2 2 .
CÁC BÀI TOÁN LUYỆN TẬP 2x  1
Bài 1. Cho hàm số y 
đ th là C. Lập phương trình tiếp tuyến c a đ th C sao cho tiếp x  1
tuyến này cắt các trục Ox, Oy lần ượt tại điểm A,B thoả mãn OA  4OB.  1 5  1 5  1 5  1 5 y   x   y   x   y   x   y   x   A. 4 4  B. 4 4  C. 4 4  D. 4 4   1 13  1 13  1 13  1 13 y   x   y   x y   x y   x   4 4  4 4  4 4  4 4
Bài làm 1. Giả sử tiếp tuyến d c a C tại (
M x ; y ) (C) cắt Ox tại A, Oy tại B sao cho OA  4OB . 0 0 OB 1 1 1 Do O
 AB vuông tại O nên tan A  
 Hệ số góc c a d bằng hoặc  . OA 4 4 4 1 1 1
Hệ số góc c a d là y (  x )    0     0 2 2 (x  1) (x  1) 4 0 0
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 10
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM.   3  x  1   y   0 0   2     5  x  3  y   0 0   2   1 3  1 5
y   (x  1)  y   x   
hi đ 2 tiếp tuyến thoả mãn là: 4 2 4 4    .  1 5  1 13
y   (x  3)  y   x   4 2    4 4 Bài 2: 2x  3
Câu 1. Cho hàm số y
đ th là C. Viết phương trình tiếp tuyến tại điểm M thu c C biết tiếp x  2 4
tuyến đ ắt tiệm cận đứng và tiệm cận ngang lần ượt tại A,B sao cho côsin góc ABI bằng , v i 17 I 2; 2 . 1 3 1 7 1 3 1 7
A. y   x
; y   x
B. y   x
; y   x  4 2 4 2 4 2 4 2 1 3 1 7 1 3 1 7
C. y   x
; y   x
D. y   x
; y   x  4 2 4 2 4 2 4 2     2x 3
Bài làm 1. I 2; 2 , gọi 0 M x ;
 (C) , x  2 0 x   2 0 0  1 2x  3
Phương trình tiếp tuyến  tại M : 0 y   (x x )  2 0 (x  2) x  2 0 0  2x  2 
Giao điểm c a  v i các tiệm cận: 0 A 2;  , (
B 2x  2; 2) . x   2 0 0  4 1 IA Do cos ABI  nên tan ABI   2 2 4
IB  16.IA  (x  2)  16  x  0 hoặc x  4 0 0 0 17 4 IB  3  1 3
Tại M  0;  phương trình tiếp tuyến: y   x   2  4 2  5  1 7
Tại M  4;  phương trình tiếp tuyến: y   x   3  4 2 2x  1
Câu 2. Cho hàm số y
.Tìm trên hai nhánh c a đ th (C) điểm M, N sao cho các tiếp tuyến tại M x  1
và N cắt hai đư ng tiệm cận tại 4 điểm lập thành m t hình thang.  7   1   
A. M 2; 5 , N 0;   1 B. M 3; , N 1     ;  C. M   1 2; 5 , N 1   ;  D. V i mọi M, N  2   2   2 
Bài làm 2. Gọi ( M ;
m y ), N(n;y ) à 2 điểm thu c 2 nhánh c a (C). M N
Tiếp tuyến tại M cắt hai tiệm cận tại A, B. Tiếp tuyến tại N cắt hai tiệm cận tại C, D.
Phương trình tiếp tuyến tại M có dạng: y y (  ) m .(x  ) m y M
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 11
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM.  2m  4   2n  4   A1;  , (
B 2m  1; 2) . Tương tự: C 1;  , (
D 2n  1; 2) .  m  1   n  1  3 
Hai đư ng th ng AD và BC đ u có hệ số góc: k  nên AD // BC.
(m  1)(n  1)
Vậy mọi điểm M, N thu c 2 nhánh c a (C) đ u thoả mãn bài toán. Bài 3: 2 x  3x  3
Câu 1. Biết v i m t điểm M tùy ý thu c C : y
, tiếp tuyến tại M cắt C tại hai điểm A,B tạo x  2 v i I  2;   
1 m t tam giác có diện t h hông đổi , Diện t h tam gi đ à?. A. 2( đvdt ) B.4( đvdt ) C.5( đvdt ) D. 7( đvdt ) 2    x 3x 3 1 1
Bài làm 1. y   x  1 . Ta có : y'  1  . x  2 x  2 x 22 1
Gọi M x ; y (C)  y x 1   0 0  0 0   x  2 0   1 1
Tiếp tuyến v i (C) tại M là  : y  1  
 x x x 1 2 0    x  0  x   2 2 0 0  xx  Nếu   x  2
 tại điểm A , thì 0 y   0  A 2;    A x  2   x 2   0 0 
Nếu  cắt tiệm cận xiện tại điểm B thì   1     1 1
x x x  1 
x  1  x  2x  2  y x  1  2x  3 2 B 0    x  0 B B 0 B B 0  x   2 2 0 0 
B2x  2;2x  3 0 0 
Nếu I là giao hai tiệm cận , thì I có tọa đ I  2;    1 .
Gọi H là hình chiếu vuông góc c a B trên tiệm cận đứng x  2  suy ra H( 2  ; 2x  3) 0 1 1 1 x Diện tích tam giác 0 AIB : S AI.BH
y y . x x    1 2x  2  2 A I B H 0 2 2 2 x  2 0 1 2 Hay S
.2 x  2  2 ( đvdt ) 0 2 x  2 0
Chứng tỏ S là m t hằng số , không phụ thu c vào v trí c a điểm M . x  3
Câu 2. Cho hàm số y
đ th là (C).Tìm trên đư ng th ng d : y  2x  1 điểm từ đ ẻ được duy x  1
nh t m t tiếp tuyến t i (C).
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 12
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. M(0;1) M(5;11) M(4;9) M(0;1)     M( 1  ; 1  ) M( 1  ; 1  ) M( 1  ; 1  ) M( 1  ; 1  ) A.      B. C. D. M(2; 5)  M(7;15)  M(2;5)  M(3;7)     M(1; 3) M(1; 3) M(1; 3) M( 2  ; 3) 
Bài làm 2. Gọi ( M ;
m 2m  1) d .
Phương trình đư ng th ng  qua M có hệ số góc k có dạng: y  ( k x  ) m  2m  1 x  3
Phương trình hoành đ giao điểm c a  và (C): ( k x  )
m  2m  1  x1  2
kx (m  1)k  2 
m x  mk (2m  4)  0 (*)
 tiếp xúc v i (C)  (*) có nghiệm kép k  0     
(m1)k 2m2 4kmk (2m 4)  0    k 0  2 2 2 2  (
g k)  (m  1) k  4(m m  4)k  4m  0 Qua ( M ;
m 2m  1) d kẻ đượ đúng 1 tiếp tuyến đến (C) 2 2   3
 2(m m  2)  0; (
g 0)  4m  0   (
g k)  0 đúng 1 nghiệm k  0  2 2   3
 2(m m  2)  0; (
g 0)  4m  0  1
m 1  0  16k  4  0  k    4 m  0  M(0;1)        m 1 M( 1; 1)
m  2 M(2;5) 
m  1  M(1;3) Bài 4: Cho hàm số 3
y  x  3x  2 đ th là (C).
Câu 1. th (C) tiếp xúc v i trục hoành tại điểm hoành đ bằng? A. 1 B.2 C.3 D. 1  3
x  3x  2  0
Bài làm 1. Xét hệ phương trình   x  1  2  3  x  3  0
Vậy (C) tiếp xúc v i Ox tại điểm hoành đ x  1  .
Câu 2.Viết phương trình tiếp tuyến c a (C) tại giao điểm c a (C) v i trục hoành.
A. y  0 ; y  9  x 18
B. y  0 ; y  9  x  3
C. y  0 ; y  9  x  8
D. y  0 ; y  9  x 1
Bài làm 2 Phương trình hoành đ giao điểm c a (C) và Ox. 3
x  3x  2  0  x  1  ,x  2 . * x  1
  y  0, y'(1)  0 phương trình tiếp tuyến: y  0 .
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 13
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM.
* x  2  y  0, y'(2)  9
 phương trình tiếp tuyến: y  9  (x  2)  9  x 18 .
Câu 3. Tìm những điểm trên trục hoành sao cho từ đ ẻ được ba tiếp tuyến đến đ th hàm số và trong đ
có hai tiếp tuyến vuông góc v i nhau.  8   28   8   28  A. M   ; 0  B. M   ; 0  C. M   ; 0  D. M   ; 0   27   7   7   27 
Bài làm 3 Xét điểm ( M ; m 0) Ox .
Cách 1: ư ng th ng d đi qua M hệ số góc k có phương trình: y  ( k x  ) m . 3
x  3x  2  k(x  ) m
d là tiếp tuyến c a (C)  hệ  có nghiệm x 2  3
x  3  k
Thế vào phương trình thứ nh t ta đươ 2 3
3(x 1)(x  )
m  (x  3x  2)  0 2 2
 (x 1)(3x  3(1 ) m x  3 )
m (x  1)(x x  2)  0 2
 (x 1)[2x (3m 2)x  3m 2]  0 1  x  1  hoặc 2
2x  (3m  2)x  3m  2  0 2
ể từ M kẻ được ba tiếp tuyến thì 1 phải có nghiệm x đ ng th i phải có 3 giá tr k h nhau hi đ
2 phải có hai nghiệm phân biệt khác 1
 đ ng th i phải có 2 giá tr k khác nhau và khác 0  2 
  (3m  2)(3m  6)  0
m   , m  2
2 phải có hai nghiệm phân biệt khác 1  khi và chỉ khi :    3 3 3m  3   0 m  1  
V i đi u kiện 3 , gọi x , x là hai nghiệm c a 2 hi đ hệ số góc c a ba tiếp tuyến là 1 2 2 2 k  3
x  3, k  3
x  3, k  0 . 1 1 2 2 3
ể hai trong ba tiếp tuyến này vuông góc v i nhau k .k  1  và k k 1 2 1 2 k .k  1  2 2 2 2 2
 9(x 1)(x 1)  1
  9x x 9(x x ) 18x x 10  0 (i) 1 2 1 2 1 2 1 2 1 2 3m  2 3m  2
Mặt h theo nh lí Viet x x  ; x x  . 1 2 1 2 2 2 28
Do đ (i)  9(3m  2)  10  0  m  
thỏa đi u kiện 3 , kiểm tra lại ta th y k k 27 1 2  28  Vậy, M  
; 0  à điểm cần tìm.  27 
Cách 2: Gọi N(x ; y ) (C) . Tiếp tuyến  c a (C) tại N phương trình y   2 3
x  3 (x x )  y . 0  0 0 0 0
 đi qua M  0   2 3
x  3 (m x )  y 0  0 0 2
 3(x 1)(x 1)(x  )
m (x  1) (x  2)  0 0 0 0 0 0 x  1  2
 (x 1)2x (3m  2)x  3m 2  0 0   0  0 0  2
2x (3m  2)x  3m  2  0 (a)  0 0
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 14
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM.
Từ M vẽ đượ đến (C) ba tiếp tuyến  ( )
a có hai nghiệm phân biệt khác 1  , và có hai giá tr 2 k  3
x  3 khác nhau và khác 0 đi u đ xảy ra khi và chỉ khi: 0    2   m 1
(3m  2)  8(3m  2)  0 (
 3m  2)(3m  6)  0       (b) .  2
2  2(3m  2)  0 3m  3  0
m   , m   2  3
Vì tiếp tuyến tại điểm hoành đ x  1
 có hệ số góc bằng 0 nên yêu cầu bài toán 2 2  ( 3  p  3)( 3  q  3)  1
 (trong đ p,q là hai nghiệm c a phương trình (a) ) 2 2 2 2
 9p q  9(p q ) 10  0 2 2 2
 9p q  9(p  )
q  18pq  10  0 2 2 9(3m  2) 9(3m  2)      28 9(3m  2)  10  28 0  m   . Vậy M   ; 0  . 4 4 27  27  Bài 5. Cho hàm số 4 2
y x  2x  1 đ th là (C).
Câu 1. Viết phương trình tiếp tuyến c a (C), biết tiếp tuyến song song v i đư ng th ng d : 24x y  1  0 .
A.  : y  24x  4
B.  : y  24x  42
C.  : y  24x  23
D.  : y  4x  42
Bài làm 1. Ta có 3
y'  4x  4x Gọi (
A x ; y ) (C) . Tiếp tuyến c a (C) tại A phương trình 0 0 3
 : y  (4x  4x )(x x )  y 0 0 0 0
Tiếp tuyến song song v i d : y  24x  1 nên ta có: 3 4x  4x  24 0 0 3
x x  6  0  x  2  y  7 .Vậy  : y  24x  42 . 0 0 0 0
Câu 2. Tìm M Oy sao cho từ M vẽ đến (C) đúng a tiếp tuyến. A. ( M 0; 2  ) B. ( M 0; 1  ) C. ( M 0; 5  ) D. ( M 0; 9  )
Bài làm 2. Ta có 3
y'  4x  4x Gọi (
A x ; y ) (C) . Tiếp tuyến c a (C) tại A phương trình 0 0 3
 : y  (4x  4x )(x x )  y 0 0 0 0
Vì (C) nhận Oy làm trụ đối xứng nên nếu d là m t tiếp tuyến c a (C) thì đư ng th ng d' đối xứng v i d
qua Oy ũng à tiếp tuyến c a (C) Do đ để từ M vẽ được ba tiếp tuyến đến (C) thì trong ba tiếp tuyến đ
phải có m t tiếp tuyến vuông góc v i Oy. Mà (C) có hai tiếp tuyến ùng phương v i Ox là: y  2  và y  1  .
ư ng th ng này cắt Oy tại M (0; 2  ), M (0; 1  ) . 1 2
Ta kiểm tra được qua M chỉ vẽ đến (C) được m t tiếp tuyến, còn từ M vẽ đến (C) được ba tiếp tuyến. 1 2 Vậy ( M 0; 1  ) à điểm cần tìm.
Câu 3. Viết phương trình tiếp tuyến c a (C), biết tiếp tuyến tiếp xúc v i (C) tại hai điểm phân biệt. A. y  2  x B. y  2  x 1 C. y  2  D. y  4 
Bài làm 3. Ta có 3
y'  4x  4x Gọi (
A x ; y ) (C) . Tiếp tuyến c a (C) tại A phương trình 0 0
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 15
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. 3
 : y  (4x  4x )(x x )  y 0 0 0 0
Giả sử  là tiếp tuyến tiếp xúc v i (C) tại hai điểm phân biệt 4 2 ( M ;
m m  2m 1) và 4 2 ( N ;
n n  2n  1) v i m n .
Ta phương trình  : y y'( ) m (x  ) m  ( y ) m
 : y y'( ) n (x  ) n  ( y ) ny'( ) m y'( ) n 3 3
4n  4n  4m  4m Suy ra     . m y'( ) m  ( y ) m   . n y'( ) n   ( y ) n 4 2 4 2  3
m  2m 1  3
n  2n 1 2 2 (  n )
m (n mn n )  (n  ) m  0 2 2
n mn n 1   0     2 2 2 2 2 2
3(n m )(n m )  2(n m )  0 2 2 (n  )
m 3(n m )  2  0 (*)   
Từ (*) ta có: m n  0 hoặc 2 2 2 n m  . 3  2
m n  0  m n
  n  1  n  1   1 mn    2  2 2 3 m n    vô nghiệm. 3  2 4 (m  ) n   3 Vậy y  2
 là tiếp tuyến cần tìm. Bài 6 Cho hàm số 3 2
y x  3x  9x  1 đ th là (C).
1. Viết phương trình tiếp tuyến c a (C), biết tiếp tuyến có hệ số góc nhỏ nh t. A. y  2  x  2
B. y  x  2 C. y  1  2x  7 D. y  1  2x  2
Bài làm 1. Ta có: 2
y'  3(x  2x  3) . Do 2 y'  3 (
x 1)  4  1  2  min y'  1  2  
đạt được khi x  1 .
Phương trình tiếp tuyến cần tìm là: y  1  2x  2 .
Câu 2. Viết phương trình tiếp tuyến c a (C), biết tiếp tuyến tạo v i đư ng th ng d : y  x  1 m t góc  5 thỏa cos  . 41 1  9  321  1  9  321 
A. y    x    9
B. y    x    34 9  9      9 9   1  9  321 
C. y    x    7 D. đ p n h 9  9   
Bài làm 2. Ta có: 2
y'  3(x  2x  3) . Gọi (
M x ; y ) là tiếp điểm 0 0
Phương trình tiếp tuyến  tại M: y y'(x )(x x )  y 0 0 0
Hay kx y b  0 , V i k y'(x ) 0 k  1 5
Theo bài ra ta có: cos   2 k  1. 2 41
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 16
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. 2 2 2
 41(k 1)  50(k 1)  9k  82k  9  1 0  k  9,  k   . 9  2 k  9
  x  2x  0  x  0,x  2 0 0 0 0
Từ đ ta tìm được hai tiếp tuyến: y  9
x 1 và y  9  x  3   1 9 321 2
k    27x  54x  80  0  x  0 0 0 9 9 1  9  321 
Từ đ ta tìm được hai tiếp tuyến là: y    x    ( y x ) . 0 9  9   
Câu 3. Viết phương trình tiếp tuyến c a (C), biết tiếp tuyến đi qua điểm ( A 1  ;6) .
A. y  7; y  9  x  3
B. y  6; y  9  x 7
C. y  6; y  2  x  3
D. y  6; y  9  x  3
Bài làm 3. Ta có: 2
y'  3(x  2x  3) . Gọi (
M x ; y ) là tiếp điểm Phương trình tiếp tuyến  tại M: 0 0
y y'(x )(x x )  y . 0 0 0
Do tiếp tuyến đi qua A nên ta phương trình 2 3 2
6  3(x  2x  3)( 1
  x )  x  3x  9x 1 0 0 0 0 0 0 3 2
x  3x  2  0  (x 1) (x  2)  0  x  1  ,x  2 0 0 0 0 0 0  x  1   y  6 0
x  2  y  9  x  3 0 Bài 7: Câu 1. Cho hàm số 3 2
y x  2x x  1 Tìm điểm thu đ th hàm số mà tiếp tuyến tại đ vuông g v i
m t tiếp tuyến khác c a đ th . A. M 1; 5 B. N  1  ;  1 C. E0;  1 D. p n h
Bài làm 1. Gọi ( A ; a f ( )
a ) à điểm thu đ th .
hi đ tiếp tuyến tại A có hệ số góc 2
k  3a  4a  1 1
* Nếu a   ; a  1
 hiển nhiên không có tiếp tuyến nào vuông góc v i tiếp tuyến tại A. 3 1
* Nếu k  0 Ta xét phương trình 2
3x  4x  1   2 3a  4a  1 2 1
3x  4x  1   0 (1). 2 3a  4a  1
ể t n tại tiếp tuyến vuông góc v i tiếp tuyến tại A thì (1) phải có nghiệm 1 2     1 1 3a 4a 2 '  4  3(1  )  0    0   0 2 3a  4a  1 2 2
3a  4a  1 3 3a  4a  1  2   10   1   2   10   a;   1  ;    ;    . 3   3   3     
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 17
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. Câu 2. Cho hàm số 3
y x  3x  2 đ th là (C). Tìm toạ đ điểm M thu c d : y  3
x  2 sao cho từ M kẻ
đượ đến (C) hai tiếp tuyến và hai tiếp tuyến đ vuông g v i nhau. A. ( M 1; 1  ) B. ( M 3; 7  ) C. ( M 1  ;5) D. ( M 0; 2)
Bài làm 2. Gọi ( M ; m 3
m 2)d
Phương trình tiếp tuyến  c a (C) tại ( A x ; y ) : 0 0 2 3
y  (3x  3)(x x )  x  3x  2 0 0 0 0 Tiếp tuyến đi qua M 2 3  3
m 2  (3x  3)(mx )  x  3x  2 0 0 0 0 2
x (2x  3 )
m  0 .Yêu cầu bài toán  m  0 . Vậy ( M 0; 2) . 0 0 Bài 8: 2x m
Câu 1. Gọi (C) à đ th c a hàm số y =
,m là tham số khác – 4 và (d) là m t tiếp tuyến c a (C) .Tìm x  2
m để (d) tạo v i hai đư ng tiệm cận c a (C) m t tam giác có diện tích bằng 2. m  6  m  3 m  3  m  3  A. B. C. D. m  5   m   5 m   6 m  5  
Bài làm 1. Hai đư ng tiệm cận đứng và ngang c a (C) phương trình ần ượt là x = 2, y = 2 ,suy ra giao
điểm c a chúng là I(2;2).
T nh tiến OI . Hệ trục Oxy  Hệ trục IXY.
x X x X  2
Công thức chuyển hệ tọa đ : I
y Y y Y  2 I ối v i hệ trục IXY .
Hai đư ng tiệm cận đứng và ngang c a (C) phương trình ần ượt là X = 0 , Y = 0. 2(X  2)  m 4  m
(C) phương trình à Y  2 
Y F(X)  . X  2  2 X
Gọi X0 à hoành đ tiếp điểm c a tiếp tuyến (d) v i (C) thì phương trình (d) à m  4 m  4 m  4 2m  8 Y   (X X )    X  . 2 0 2 X X X X 0 0 0 0  2m  8 
Gọi A à giao điểm c a (C) v i đư ng tiệm cận đứng c a nó thì A 0;   X   0 
Gọi B à giao điểm c a (C) v i đư ng tiệm cận ngang c a nó thì B( 2X ; 0) 0
Diện tích tam giác vuông IAB do (d) tạo v i hai đư ng tiệm cận là 1 1 1 2m  8 S I . A IB Y X
2X  2m  8 . A B 0 2 2 2 X0 2m  8  2 m  3 
S  2  2m  8  2     . 2m  8  2  m  5   
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 18
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. Câu 2. Cho hàm số 3
y x 1  (
m x 1) đ th là (C ) . Có bao nhiêu giá tr m để tiếp tuyến c a (C ) tại m m
giao điểm c a nó v i trục tung tạo v i hai trục tọa đ m t tam giác có diện tích bằng 8 . A. 1 B.2 C.3 D. 4
Bài làm 2. Ta có ( M 0;1 )
m à giao điểm c a (C ) v i trục tung m 2
y'  3x m y'(0)  m
Phương trình tiếp tuyến v i (C ) tại điểm m là y mx 1 m m  1 m
Gọi A, B lần ượt à giao điểm c a tiếp tuyến này v i trục hoanh và trục tung, ta có tọa đ A ; 0  và  m  ( B 0;1 ) m
Nếu m  0 thì tiếp tuyến song song v i Ox nên loại khả năng này Nếu m  0 ta có 1 1 1  m  m2 1 m  9  4 5 S  8  O . A OB  8  1  m  8   16   OAB 2 2 m mm  7    4 3
Vậy có 4 giá tr cần tìm Bài 9: x  1
Câu 1. Cho hàm số y
.Tìm giá tr nhỏ nh t c a m sao cho t n tại ít nh t m t điểm M  (C) mà tiếp 2x  1
tuyến c a (C) tại M tạo v i hai trục toạ đ m t tam giác có trọng tâm nằm trên đư ng th ng d : y  2m 1. 1 3 2 2 A. B. C. D. 3 3 3 3   3
Bài làm 1. Gọi (
M x ; y ) (C) . Phương trình tiếp tuyến tại M : y
(x x )  y 0 0 2 0 0 (2x  1) 0
Gọi A B à giao điểm c a tiếp tuyến v i trục hoành và trục tung 2    2x 4x 1 0 0 y  . B 2 (2x  1) 0 2 2x  4x  1
Từ đ trọng tâm G c a OAB có: 0 0 y  . G 2 3(2x  1) 0 2 2x  4x  1 Vì G  d nên 0 0  2m 1 2 3(2x  1) 0 2 2 2 2 2x  4x  1
6x  (2x  1) 6x Mặt khác: 0 0 0 0 0   1  1  2 2 2 (2x  1) (2x  1) (2x  1) 0 0 0 1 1
Do đ để t n tại ít nh t m t điểm M thoả bài toán thì 2m  1    m  . 3 3 1 Vậy GTNN c a m là . 3
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 19
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. 2mx  3
Câu 2. Cho hàm số y
.Gọi I à giao điểm c a hai tiệm cận c a (C). Tìm m để tiếp tuyến tại m t x m
diểm b t kì c a (C) cắt hai tiệm cận tại A và B sao cho IAB có diện tích S  22 . A. m  5  B. m  6  C. m  7  D. m  4 
Bài làm 2. (C) có tiệm cận đứng x m, tiệm cận ngang y  2m .  2mx  3 
Giao điểm 2 tiệm cận là I( ; m 2 ) m và 0 M x ;  (C) . 0 x   m 0  2 2m  3 2mx  3
Phương trình tiếp tuyến  c a (C) tại M: 0 y  (x x )  . 2 0 (x  ) m x m 0 0 2      2mx 2m 6 cắt TC tại 0 A ; m   , cắt TCN tại ( B 2x  ; m 2 ) m . x m    0 0  2 4m  6 1 Ta có: IA
; IB  2 x m  2 SI .
A IB  4m  6  22  m  4  . x m 0 IAB 2 0 x
Câu 3. Gọi d là tiếp tuyến c a đ th C 2 3 : y
tại M cắt đư ng tiệm cận tại hai điểm phân biệt x  2
A, B . Tìm tọa đ điểm M sao ho đư ng tròn ngoại tiếp tam giác IAB có diện tích nhỏ nh t , v i I là giao điểm hai tiệm cận .  5   5   5  A. M 1;  1 M 1;   
B. M  4;  M 3; 3 C. M 1;  1 M  4;  D. M 1;  1 M 3; 3  3   3   3    2x 3 1
Bài làm 3. Gọi M x ; y C 0  y  và y'   0 0 0 x  2 0 x 2 0 2 0 1  2x  3
Phương trình tiếp tuyến d c a C tại M : y  xx  2 0  0 xx   2 2 0 0   2x  2 
d cắt hai đư ng tiệm cận tại hai điểm phân biệt 0 A 2;  , 
B2x  2; 2 . 0  x 2    0 
Dễ th y M à trung điểm AB và I 2; 2 à giao điểm hai đư ng tiệm cận.
Tam giác IAB vuông tại I nên đư ng tròn ngoại tiếp tam giác IAB có diện tích 2             x S IM x  22 2 3    2 
   x  22 2 1 0    2 0   0  x  2        x 22  0 0      2 1 x 1 y 1
D u đ ng thức xảy ra khi x  2  0 0   0
 x 22 x 3y 3  0 0 0 Vậy M 1; 
1 M 3; 3 thỏa mãn bài toán.
Bài toán có thể mở rộng : Tìm những điểm trên C hoành đ x  2 sao cho tiếp tuyến tại đ tạo v i hai
đư ng tiệm cận m t tam giác có chu vi nhỏ nh t.
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 20
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM.  2x  2  HD: theo trên ta có : 0 A 2;
 ,B2x  2; 2  IA,IB   .Chu vi tam giác AIB 0  x   2 0  là 2 2
P IA IB AB IA IB IA IB  2 I . A IB  2.I . A IB
ng thức xảy ra khi IA IB
Nếu trư ng hợp tam giác AIB không vuông thì P IA IB AB để tính AB ta cần đến đ nh lý hàm số cosin 2 2 2
AB IA IB  2I .
A IBcosIA,IB . 2 2 2
P IA IB AB  2 I .
A IB IA IB  2I .
A IBcosIA,IBP  2 I . A IB  2I . A IB  2I .
A IBcosIA,IB ng thức xảy ra khi IA IB . 2x
Bài 10: Cho hàm số y
đ th là C . Có bao nhiêu điểm M thu c C sao cho tiếp tuyến tại M x  1 1
c a C cắt Ox, Oy tại A, B sao cho diện tích tam giác OAB bằng , O là gốc tọa đ . 4 A. 1 B.2 C.3 D. 4  2x 2
Bài làm 1. Gọi M x ; y  C 0  y   y'  0 0 0 0 x  1 x 12 0 0 2 2 2x
Phương trình tiếp tuyến t c a C tại M là : 0 y x  . 0 x  2 1 x  2 1 0 0
Tiếp tuyến t cắt hai trục tọa đ Ox,Oy tại hai điểm phân biệt A 2 x ;0 , 0   2  2x  1 0 B 0;  
sao cho diện tích tam giác AOB có diện tích bằng hi đ    x  12 4 0  2 1 1 1 2x 1 0 .O . A OB   O . A OB   x .
  4x x  1  0 0 2 0  0 2 2 2 2 4 2   2 x 1 0   1  1  2
2x x 1  0
x    M   ; 2   0 0 0   2   2  . 2
2x x 1  0  0 0
x  1  M 1;1  0   2x  2
Bài 12: Cho hàm số y  đ th là (C). x  1
Câu 1. Viết phương trình tiếp tuyến c a (C), biết tiếp tuyến song song v i đư ng th ng d : y  4  x 1 . A.  : y  4
x  2 ;  : y  4  x 1 B.  : y  4
x  2 ;  : y  4  x 7 C.  : y  4
x  6 ;  : y  4  x 14 D.  : y  4
x  2 ;  : y  4  x 14
Bài làm 1. Hàm số x đ nh v i mọi x  1 . 4  Ta có: y '  2 (x  1)
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 21
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM.
Tiệm cận đứng: x  1 ; tiệm cận ngang: y  2 ; tâm đối xứng I(1; 2) Gọi (
M x ; y ) là tiếp điểm suy ra phương trình tiếp tuyến c a (C): 0 0 4  2x  2 0  : y  (x x )  . 2 0 (x  1) x  1 0 0
Vì tiếp tuyến song v i đư ng th ng d : y  4
x 1 nên ta có: 4  y'(x )  4    4
  x  0,x  2 . 0 2 0 0 (x  1) 0
* x  0  y  2   : y  4  x  2 0 0
* x  2  y  6   : y  4  x 14 . 0 0
Câu 2. Viết phương trình tiếp tuyến c a (C), biết tiếp tuyến tạo v i hai trục tọa đ m t tam giác vuông cân.
A.  : y  x  7 ;  : y  x  1 B.  : y  2
x 7 ;  : y  x 11
C.  : y  x  78 ;  : y  x 11
D.  : y  x  9 ;  : y  x  1
Bài làm 2. Hàm số x đ nh v i mọi x  1 . 4  Ta có: y '  2 (x  1)
Tiệm cận đứng: x  1 ; tiệm cận ngang: y  2 ; tâm đối xứng I(1; 2) Gọi (
M x ; y ) là tiếp điểm suy ra phương trình tiếp tuyến c a (C): 0 0 4  2x  2 0  : y  (x x )  . 2 0 (x  1) x  1 0 0
Vì tiếp tuyến tạo v i hai trục tọa đ m t tam giác vuông cân nên hệ số góc c a tiếp tuyến bằng 1  . 4   1   x  1  ,x  3 2 0 0 (x  1) 0 * x  1
  y  0   : y  x 1 0 0
* x  3  y  4   : y  x  7 0 0
Câu 3. Viết phương trình tiếp tuyến c a (C), biết tiếp tuyến tạo v i hai tiệm cận m t tam giác có chu vi nhỏ nh t.
A.  : y  x  21 và  : y  x  7 .
B.  : y  x  3 và  : y  x  2 .
C.  : y  x  1 và  : y  x  17 .
D.  : y  x  1 và  : y  x  7 .
Bài làm 3. Hàm số x đ nh v i mọi x  1 . 4  Ta có: y '  2 (x  1)
Tiệm cận đứng: x  1 ; tiệm cận ngang: y  2 ; tâm đối xứng I(1; 2) Gọi (
M x ; y ) là tiếp điểm suy ra phương trình tiếp tuyến c a (C): 0 0 4  2x  2 0  : y  (x x )  . 2 0 (x  1) x  1 0 0
Tiếp tuyến cắt tiệm cận đứng tại
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 22
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. x  1   2x  6  0 A :  4 
2x  2  A1;  0 y  (1  x )   x  1   2 0  0  (x  1) x  1  0 0
Tiếp tuyến cắt tiệm ngang tại y  2  B :  4  2x  2  ( B 2x  1; 2) 0 0 2  (x x )   2 0 (x  1) x  1  0 0 8 Suy ra: IA
; IB  2 x  1  I . A IB  16 0 x  1 0 Chu vi tam giác IAB : 2 2
P IA IB AB IA IB IA IB Mà 2 2
IA IB  2 I .
A IB  8; IA IB  2I . A IB  32
Nên P  8  32  8  4 2 ng thức xảy ra 2
IA IB  (x 1)  4  x  3,x  1  0 0 0
Vậy ta có hai tiếp tuyến thỏa yêu cầu bài toán:  : y  x  1 và  : y  x  7 . 2x
Bài 13 Cho hàm số y  đ th (C). x  2
Câu 1 Trên đ th (C) t n tại ao nhiêu điểm mà tiếp tuyến c a (C) tại đ song song v i đư ng th ng
y  4x  3 . A. 1 B.2 C.3 D. 4
Bài làm 1. Hàm số x đ nh v i mọi x  2  . 4 Ta có: y '  2 (x  2) Gọi (
M x ; y ) (C) . Tiếp tuyến  c a (C) tại M phương trình 0 0 2 4 2x 4 2x 0 0 y  (x x )   x  2 0 2 2 (x  2) x  2 (x  2) (x  2) 0 0 0 0
Tiếp tuyến  song song v i đư ng th ng y  4x  3 khi và chỉ khi  4   4 2 (x   2) 0   x  1  ; x  3 . 2 0 0 2x  0  3  2 (x  2)  0
Vậy trên (C) hai điểm thỏa yêu cầu bài toán.
Câu 2. Viết phương trình tiếp tuyến c a (C), biết tiếp tuyến tạo v i hai trục tọa đ m t tam giác có diện tích 1 bằng . 18 9 1 4 1 9 31 4 2 A.  : y x  ;  : y x B.  : y x  ;  : y x  4 2 9 9 4 2 9 9
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 23
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. 9 1 4 4 9 1 4 2 C.  : y x  ;  : y x D.  : y x  ;  : y x  4 2 9 9 4 2 9 9
Bài làm 2. Hàm số x đ nh v i mọi x  2  . 4 Ta có: y '  2 (x  2) Gọi (
M x ; y ) (C) . Tiếp tuyến  c a (C) tại M phương trình 0 0 2 4 2x 4 2x 0 0 y  (x x )   x  2 0 2 2 (x  2) x  2 (x  2) (x  2) 0 0 0 0
Gọi A, B lần ượt à giao điểm c a tiếp tuyến  v i Ox, Oy y  0   1 1 Suy ra 2 2 A :  4 2xx   x 2  ( A x ; 0) 0 0 x   0    2 0 2 2 2 (x  2) (x  2)  0 0 y    0 x  0 2   2x  2 0 B :  2xB0;  0   2 y (x   2)  2  0  (x  2)  0
Vì A, B O x  0 . 0 4 1 1 x
Tam giác AOB vuông tại O nên 0 SO . A OB AOB 2 2 2 (x  2) 0 4 1 x Suy ra 0 4 2 S  
 9  9x  (x  2) AOB 2 0 0 18 (x  2) 0   2 x 1  0
3x x  2  0 (vn) 0 0     2 . 2
3x x  2  0 x    0 0 0  3 2 4 4 2
* x  1  y  , y'(x ) 
Phương trình  : y x  0 0 0 3 9 9 9 2 9
* x    y  1  , y'(x )  0 0 0 3 4 9 2 9 1
Phương trình  : y  (x  )  1  x  . 4 3 4 2
Câu 3. Giả sử t n tại phương trình tiếp tuyến c a (C), biết khoảng cách từ tâm đối xứng đến tiếp tuyến l n
nh t. thì hoành đ tiếp điểm lúc này là:
A. x  0, x  4 
B. x  0, x  3 
C. x  1, x  4 
D. x  1, x  3  0 0 0 0 0 0 0 0
Bài làm 3. Hàm số x đ nh v i mọi x  2  . 4 Ta có: y '  2 (x  2) Gọi (
M x ; y ) (C) . Tiếp tuyến  c a (C) tại M phương trình 0 0
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 24
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. 2 4 2x 4 2x 0 0 y  (x x )   x  2 0 2 2 (x  2) x  2 (x  2) (x  2) 0 0 0 0
Ta tâm đối xứng I( 2;  2) 2 4 2x
Khoảng cách từ I đến tiếp tuyến 0  : x y   0 : 2 2 (x  2) (x  2) 0 0 8 x  2 0 t d   8 , v i 2
t  (x  2)  0 2 0 4   t  16 (x 2) 16 0 t t 1 Do    d  2 2 2 t  16 16 2 16t ng thức xảy ra khi 2 2
t  16  t  4  (x  2)  4  x  0, x  4  . 0 0 0 Bài 14: Cho hàm số 3 2
y x ax bx c , c  0 đ th (C) cắt Oy ở A và đúng hai điểm chung v i trục
Ox là M và N . Tiếp tuyển v i đ th tại M đi qua A . Tìm ; a ; b c để S  1. AMN
A. a  4,b  5,c  2 
B. a  4,b  5,c  2 C. a  4
 ,b  6,c  2  D. a  4
 ,b  5,c  2 
Bài làm Giả sử (C) cắt Ox tại ( M ; m 0) và N( ; n 0) cắt Oy tại ( A 0;c)
Tiếp tuyến tại M phương trình 2
y  (3m  2am  ) b (x  ) m .
Tiếp tuyến đi qua A nên ta 3 2
3m  2am bm c  0 3 2 a
 2m am  0  m   (do 3 2
m am bm c  0 ) 2
Mà (C) cắt Ox tại hai điểm nên (C) tiếp xúc v i Ox.
Nếu M là tiếp điểm thì suy ra Ox đi qua A vô nên ta (C) tiếp xúc v i Ox tại N Do đ 3 2 2
y x ax bx c  (x  ) n (x  ) ma a m   ,     2 n m n  a  2 4   Suy ra 2 3
2mn n b  a  32c (1).  2  2 mn  c 5a  16b    Mặt khác S  1  c
nm  2  ca  8 AMN 3 a  32c
a  0 ta có: ac  8  vô nghiệm.  2 5a  16b  3 a  32c
a  0 ta có: ac  8  a  4
 ,b  5,c  2   2 5a  16b
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 25
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. 2x  1
Bài 15: Cho hàm số y  đ th là (C). x  1 1
Câu 1. Viết phương trình tiếp tuyến c a (C), biết tiếp tuyến có hệ số góc bằng  . 4 1 3 1 3 1 3 1 5
A. : y   x
và y   x  .
B. : y   x
và y   x  . 4 4 4 4 4 2 4 2 1 1 1 5 1 13 1 5
C. : y   x
và y   x  .
D. : y   x
và y   x  . 4 4 4 4 4 4 4 4
Bài làm 1. : Gọi (
M x ; y ) là tiếp điểm Phương trình tiếp tuyến  tại M 0 0 1  2x  1 0 y  (x x )  . 2 0 (x  1) x  1 0 0 1
Hệ số góc c a tiếp tuyến bằng  nên suy ra 4 1 1 
   x  3,x  1  . 2 0 0 (x  1) 4 0 1 13 1 5
Từ đ ta tìm được tiếp tuyến là: y   x
và y   x  . 4 4 4 4
Câu 2. Viết phương trình tiếp tuyến c a (C), biết tiếp tuyến tạo v i hai tiệm cận m t tam giác có chu vi nhỏ nh t. 1 3 1 5 1 1
A. y   x
và y   x  .
B. y   x  3 và y   x  1 . 4 4 4 4 4 4 1 13 1 1 13 1 5
C. y   x
và y   x  1 .
D. y   x
và y   x  . 4 4 4 4 4 4 4
Bài làm 2. : Gọi (
M x ; y ) là tiếp điểm Phương trình tiếp tuyến  tại M 0 0 1  2x  1 0 y  (x x )  . 2 0 (x  1) x  1 0 0 2x
Tiếp tuyến  cắt tiệm cận đứng tại 0 ( A 1;
), cắt đư ng tiệm cận ngang tại (
B 2x  1; 2) Tâm đối xứng x  1 0 0 I(1; 2) 2 Suy ra IA
, IB  2 x  1  I . A IB  4 0 x  1 0 Chu vi tam giác IAB : 2 2
p AB IA IB IA IB IA IB Mặt khác: 2 2
IA IB  2I .
A IB  8; IA IB  2 I . A IB  4
Nên p  2 2  4 ng thức xảy ra  IA IB 2
 (x 1)  4  x  3,x  1  . 0 0 0 1 13 1 5
Từ đ ta tìm được tiếp tuyến là: y   x
và y   x  . 4 4 4 4
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 26
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM.
Câu 3. Viết phương trình tiếp tuyến c a (C), biết khoảng cách từ tâm đối xứng I đến tiếp tuyến tạo l n nh t. 1 3 1 5 1 1
A. y   x
và y   x  .
B. y   x  1 và y   x  5 . 4 4 4 4 4 4 1 13 1 3 1 13 1 5
C. y   x
và y   x  .
D. y   x
và y   x  . 4 4 4 4 4 4 4 4
Bài làm 3. : Gọi (
M x ; y ) là tiếp điểm Phương trình tiếp tuyến  tại M 0 0 1  2x  1 0 y  (x x )  . 2 0 (x  1) x  1 0 0
Gọi H là hình chiếu c a I lên  . Ta có ( d I, )   IH 1 1 1 2 1
Trong tam giác vuông IAB ta có:     2 2 2 IH IA IB I . A IB 2
Suy ra IH  2 ng thức xảy ra  IA IB . 1 13 1 5
Từ đ ta tìm được tiếp tuyến là: y   x
và y   x  . 4 4 4 4
Câu 4. Tìm điểm M thu c (C) sao cho tiếp tuyến c a (C) tại M vuông góc v i IM.
A. y  x  1, y  x  4
B. y  x  3, y  x  5 C. y  x  1, y  x  3 D. y  x  1, y  x  5
Bài làm 4. : Gọi (
M x ; y ) là tiếp điểm Phương trình tiếp tuyến  tại M 0 0 1  2x  1 0 y  (x x )  . 2 0 (x  1) x  1 0 0  1   1
ư ng th ng  có VTCP u  1;  
, IM  (x  1; ) . 2 (x 1)    0 x  1 0  0 1
IM    x  1
 0  x  0,x  2 . 0 3 0 0 (x  1) 0
Từ đ ta tìm được tiếp tuyến: y  x  1, y  x  5 . Bài 16:
Câu 1. Gọi (C) à đ th c a hàm số 4
y  x  1 và (d) là m t tiếp tuyến c a (C) , (d) cắt hai trục tọa đ tại A và
B. Viết phương trình tiếp tuyến (d) khi tam giác OAB có diện tích nhỏ nh t ( O là gốc tọa đ ). 4 8 4 8 4 7 4 8 A. y   x B. y   x C. y   x D. y   x  4 15 5 4 12 5 4 5 5 4 125 5
Bài làm 1. Phương trình tiếp tuyến (d) có dạng : 3 4 3 4
y  4x (x x )  x  1  4x x  3x 1 trong đ x0 là 0 0 0 0 0
hoành đ tiếp điểm c a (d) v i (C). 4  3x 1 
A à giao điểm c a (d) v i trục Ox  0 A ; 0   3 4x   0 
B à giao điểm c a (C) v i trục Oy 4  ( B 0; 3  x 1) . 0
Diện tích c a tam giác vuông OAB:
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 27
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. 4 2 4 2 1 1 1 (3x  1) 1 (3x  1) 0 0 S O . A OB x y   A B 3 3 2 2 2 4x 8 0 x0 4 2 1 (3x  1)
Xét trư ng hợp x  0 hi đ 0 S  . . 0 3 8 x0 4 2 (3x  1) 0
Xét hàm số f (x )  , x (0;  )  . 0 3 0 x0 4 3 3 4 2 2 4 4
2(3x  1)12x .x  (3x  1) .3x
3(3x  1)(5x  1) 0 0 0 0 0 0 0 f '(x )   . 0 6 4 x x 0 0 4 1 1
f '(x )  0  x   x  (do x  0) 0 0 0 0 4 5 5
Bảng biến thiên c a f (x ) 0 64 1
Từ bảng biến thiên suy ra min f (x ) 
đạt được khi và chỉ khi x  0 4 0 5 5 4 5 8 1 Suy ra minS   x  . 4 0 5 5 4 5 4 8
hi đ phương trình a (d) là y x  . 4 125 5 4 8
Vì trục Oy là trụ đối xứng c a (C) nên trong trư ng hợp x0 < 0 phương trình a (d) là y   x  . 4 125 5 4 8
Vậy phương trình tiếp tuyến cần tìm là y   x  . 4 125 5
Câu 2. Gọi (Cm) à đ th c a hàm số 4      2 y x
3 m 1 .x  3m  2 , m là tham số
Tìm các giá tr dương c a tham số m để (Cm) cắt trục hoành tại bốn điểm phân biệt và tiếp tuyến c a (Cm) tại
giao điểm hoành đ l n nh t hợp v i hai trục toạ đ m t tam giác có diện tích bằng 24. 1 2 A. m  1 B. m  C. m  D. m  7 3 3
Bài làm 2. Phương trình hoành đ giao điểm c a (Cm) và trục hoành là 4     2 x
3 m 1 .x  3m  2  0 (1)
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 28
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. ặt 2
t  x ,t  0 Phương trình (1) trở thành : 2 t  3m   1 .t  3m  2  0 (2)
(Cm) cắt trục Ox tại bốn điểm phân biệt  Phương trình (1) 4 nghiệm phân biệt  Phương trình (2)
hai nghiệm dương phân iệt .
Vì (2) luôn có hai nghiệm là t  1, t  3m  2 v i mọi m và vì m > 0 (giả thiết) nên ta có 1  3m  2 ,suy ra
v i mọi tham số m > 0 , (Cm) cắt Ox tại 4 diểm phân biệt và nếu gọi A à giao điểm hoành đ l n nh t thì
hoành đ A là x  3m  2 . A Gọi 4      2 f(x) x
3 m 1 .x  3m  2 phương trình tiếp tuyến d c a (Cm) tại A là 3
y f '(x )(x x )  f (x )  [4x  6(m  1)x ](x x ) ( vì f (x )  0 ) A A A A A A A
 [4(3m 2) 3m 2 6(m1) 3m 2](x  3m 2)
 6m  2 3m 2 x 3m2)
Gọi B à giao điểm c a tiếp tuyến d v i trục Oy thì B0 ;6m  23m  2 . Tam giác mà tiếp tuyến d tạo
v i hai trục toạ đ là tam giác vuông OAB ( vuông tạiO) ,theo giả thiết ta có : S  24  O .
A OB  48  x y  48 OAB A B
 3m 2(6m 2)(3m 2)  48 (3). Gọi   2
f m  3m  2(6m  2)(3m  2)  3m  2(18m  22m  4) 3 2 f '( ) m
(18m  22m  4)  (36m  22) 3m  2  0 v i mọi m >0. 2 3m  2  2 
Suy ra hàm số f(m) đ ng biến trên (0;+ ) và vì f
  24 do đ phương trình (3) hỉ có m t nghiệm là  3  2 m  trên (0;+ ) 3 Bài 18: 2x
Câu 1. Cho hàm số y
đ th là C. Viết phương trình tiếp tuyến c a đ th C để khoảng cách x  2
từ tâm đối xứng c a đ th C đến tiếp tuyến là l n nh t.
A. y  2x và y x  8 .
B. y x và y x  9 .
C. y  3x và y x  8 . D. y x và y x  8 .
Bài làm 1. Tiếp tuyến d c a đ th C tại điểm M hoành đ a  2
 thu c C phương trình 4 2a 2 2 y  (x  ) a
 4x (a  2) y  2a  0 2 (a  2) a  2
Tâm đối xứng c a C là I  2;  2 . 8 a  2 8 a  2 8 a  2 ( d I,d)     2 2 4 2 16  (a  2) 2.4.(a  2) 2 2 a  2 ( d I, ) d l n nh t khi 2
(a  2)  4  a  4  hoặc a  0 .
Từ đ suy ra hai tiếp tuyến y x và y x  8 .
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 29
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM. 2x  3
Câu 2. Cho hàm số y
đ th C. Tìm trên C những điểm M sao cho tiếp tuyến tại M c a x  2
C cắt hai tiệm cận c a C tại A,B sao cho AB ngắn nh t. 5 5 A. (
M 3; 3) hoặc M( 1  ; ) B. M( 1  ; ) hoặc ( M 1;1) 3 3 5 5
C. M(4; ) hoặc M( 1  ; ) D. ( M 3; 3) hoặc ( M 1;1) 2 3    1 1
Bài làm 2. L y điểm M ; m 2  
 C . Ta có: y( ) m    m  2  2 (m  2) 1 1
Tiếp tuyến d tại M phương trình y   (x  ) m  2  2 (m  2) m  2  2 
Giao điểm c a d v i tiệm cận đứng là: A 2; 2     m  2 
Giao điểm c a d v i tiệm cận ngang là: ( B 2m – 2; 2)  1  Ta có: 2 2 AB  4 (  m  2) 
  8 . ng thức xảy ra khi m  1 hoặc m  3 . 2  (m  2) 
Vậy, điểm M cần tìm có tọa đ là: ( M 3; 3) hoặc ( M 1;1)
Bài 19 : Tìm m để tiếp tuyến c a đ th 3
y x mx m  1 tại điểm M hoành đ x  1  cắt đư ng tròn (C) phương trình 2 2
(x  2)  (y  3)  4 theo m t dây ung đ dài nhỏ nh t. A. m  3 B. m  6 C. m  8 D. m  2
Bài làm : Ta có: 2
y  3x m y (  1  )  3  m ; ( y 1
 )  2m 2 . (C) có tâm I(2; 3) , R = 2.
Phương trình đư ng th ng d tại ( M 1
 ; 2m 2) : y  (3  ) m x m  1  (3  )
m x y m  1  0 2 4  m 1  (3  ) m 2. (3  ) m  1 ( d I,d)     2  R 2 2 2 (3  ) m  1 (3  ) m  1 (3  ) m  1
D u "=" xảy ra  m  2 D đ ( d I, )
d đạt l n nh t  m  2
Tiếp tuyến d cắt (C) tại 2 điểm A, B sao cho AB ngắn nh t  ( d I, )
d đạt l n nh t  m  2 , suy ra d: y x  3 .
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 30 NGUYỄN BẢO VƢƠNG CHƯƠNG V. ĐẠO HÀM
TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN ĐI QUA ĐIỂM CHO TRƯỚC
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 HOẶC
Facebook: https://web.facebook.com/phong.baovuong
Page: https://web.facebook.com/tracnghiemtoanthpt489/
Website: http://tailieutoanhoc.vn/ Email: baovuong7279@gmail.com 0946798489
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN MỤC LỤC
Vấn đề 3. Viết phƣơng trình tiếp tuyến của đồ thị hàm số khi tiếp tuyến đi qua điểm cho trƣớc. ............................ 2
CÁC BÀI TOÁN LUYỆN TẬP .............................................................................................................................................. 8
GIÁO VIÊN MUA FILE WORD LIÊN HỆ 0946798489
BẠN ĐỌC MUỐN NHẬN FILE PDF, HÃY THEO DÕI PAGE
https://web.facebook.com/tracnghiemtoanthpt489/
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 1
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN
Vấn đề 3. Viết phƣơng trình tiếp tuyến của đồ thị hàm số khi tiếp tuyến đi qua điểm cho trƣớc. Phƣơng pháp:
Phương trình tiếp tuyến của đồ thị C : y f x đi qua điểm M x ; y 1 1  Cách 1 :
 Phương trình đường thẳng d đi qua điểm M có hệ số góc là k có dạng : y kx x y . 1  1
f x k x x   y 0   0 1
 d tiếp xúc với đồ thị C tại Nx ; y khi hệ: 1  có nghiệm x . 0 0  f ' 0  x   k 0  Cách 2 :
 Gọi N x ; y là tọa độ tiếp điểm của đồ thị C và tiếp tuyến d qua điểm M , nên d cũng có dạng 0 0 
y y' x x y . 0  0  0
 d đi qua điểm M nên có phương trình : y y' x x y * 1 0  1 0  0  
 Từ phương trình * ta tìm được tọa độ điểm Nx ; y , từ đây ta tìm được phương trình đường thẳng d . 0 0  Các ví dụ Ví dụ 1 : 3 2 x 3x
1. Viết phương trình tiếp tuyến d với đồ thị C : y  
x , biết d song song đường thẳng x y  8  0 . 3 4  19  2. Cho hàm số 3 2
y  2x  3x  5 có đồ thị là (C). ìm phương trình c c đường thẳng đi qua điểm A ; 4  v tiếp  12 
c với đồ thị của h m số Lời giải.
1. Hàm số đã cho c định D
Cách 1: Tiếp tuyến d song song với đường thẳng x y  8  0 nên d có dạng y  x b . 3 2 x 3x 0 0  
x  x b 1 0 0   
d tiếp xúc với C tại điểm có ho nh độ x khi và chỉ khi hệ phương trình 3 4  có nghiệm 0  3x 2 0 x   1  1  2 0    2 x . 0 3 Phương trình 2 2
 2x  3x  0  x  0 hoặc x   . 0 0 0 0 2
Với x  0 thay v o phương trình 1 , ta được b  0 khi đó d : y  x . 0 3 9 9 Với x  
thay v o phương trình 1 , ta được b
khi đó d : y  x  . 0 2 16 16
Cách 2: Gọi x ; y x
là tọa độ tiếp điểm của tiếp tuyến d và C , với 0  0  3x y x  3 2 x 3x 0 0  
x , tiếp tuyến d có hệ số góc y'x x  1 0  2 0 0 0 3 4 0 2
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 2
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN 3x 3 d | | x
y  8  0  y'x  1  tức 2 0 x  1  1
 hay nghiệm x  0 hoặc x   . Phần còn lại giành cho bạn 0  0 2 0 0 2 đọc.
2. Hàm số đã cho c định D  Ta có: 2
y'  6x  6x ọi 3 2 (
M x ; y ) (C)  y  2x  3x  5 và 2
y'(x )  6x  6x 0 0 0 0 0 0 0 0
Phương trình tiếp tuyến của tại có dạng y y y'(x )(x x ) 0 0 0 3 2 2 2 3 2
y (2x  3x  5)  (6x  6x )(x x )  y  (6x  6x )x  4x  3x  5 0 0 0 0 0 0 0 0 0 2 19 3 2 3 2 1
A    4  (6x  6x ).
 4x  3x  5  8x  25x 19x  2  0  x  1 hoặc x  2 hoặc x  0 0 0 0 0 0 0 0 12 0 0 8
Với x  1   : y  4 0
Với x  2   : y  12x  15 0 1 21 645 Với x    : y   x  0 8 32 128 Ví dụ 2 : 1 3 1. Cho hàm số 4 2 y x  3x
có đồ thị là C. Viết phương trình tiếp tuyến của đồ thị C biết tiếp tuyến đó đi 2 2  3 
qua điểm M 0;  .  2  x  2
2. Cho hàm số: y
có đồ thị là C v điểm A0; m X c định m để từ A kẻ được 2 tiếp tuyến đến Cx  1
sao cho hai tiếp điểm tương ứng nằm về hai phía đối với trục Ox . Lời giải.  3 
1. Đường thẳng x  0 đi qua điểm M 0;  không phải là tiếp tuyến của đồ thị C .  2   3  3
d l đường thẳng đi qua điểm M 0;  có hệ số góc k có phương trình y kx   2  2
Đường thẳng d là tiếp tuyến của đồ thị C tai điểm có ho nh độ là x thì x là nghiệm của hệ phương trình : 0 0 1 4 2 3 3
x  3x   kx  1 0 0 0   2 2 2 3
2x  6x k 2  0 0  
Thay 2 vào 1 rồi rút gọn ta được 2 x  2
x  2  0  x  0 hoặc x   2 0 0  0 0 3
Khi x  0 thì k  0 l c đó phương trình tiếp tuyến là y  0 2 3
Khi x   2 thì k  2 2 l c đó phương trình tiếp tuyến là y  2 2x  0 2 3
Khi x  2 thì k  2
 2 l c đó phương trình tiếp tuyến là y  2  2x  0 2 3 3 3
Vậy, có ba tiếp tuyến là y  , y  2 2x  , y  2  2x  2 2 2
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 3
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN 1
2. Cách 1: Gọi điểm  
m  1 . Tiếp tuyến  tại M của C có phương trình 2 mx  2
1  3x x  2 x  1  0 (với x  1 )  m   2
1 x  2 m  2 x m  2  0  . 0   0 0  0  0  0 0
Yêu cầu bài toán   có hai nghiệm a,b khác 1 sao cho   
a  2b  2
ab  2a b  4 m 1     hay là:  2 .
a  b  
ab  a b 0 1 1  1 m    3 2 Vậy 
m  1 là những giá trị cần tìm. 3
Cách 2: Đường thẳng d đi qua A , hệ số góc k có phương trình: y kx m . x  2 0   kx m 0 x  1 
d tiếp xúc với C tại điểm có ho nh độ x  hệ 0  có nghiệm x . 0 3   0    k x  1 2 0
Thế k vào phương trình thứ nhất, ta đươc x  2 3  x 0 
m  m   2
1 x  2 m  2 x m  2  0  2 0   x  1  0 x 1 0  0
Để từ A kẻ được hai tiếp tuyến thì  có hai nghiệm phân biệt khác 1
'  3m  2  0  m  2   m  1   i   
m   m   m 1 1 2 2  m  2  0  x  2 x  2
Khi đó tọa độ hai tiếp điểm là: M x ; y , M x ; y với x1,x2 là nghiệm của  và 1 2 y  ; y  1  1 1  2  2 2  1 2 x  1 x  1 1 2
x x  2 x x  4 1 2  1 2 
Để M1, M2 nằm về hai phía Ox thì y .y  0   0 1 1 2
x x x x  1 1 2  1 2    2m  2 m  2
Áp dụng định lí Viet: x x  ; x x  . 1 2 1 2 m  1 m  1    9m  6 2 1   0  m   . 3  3 2
Kết hợp với i ta được   m  1 là những giá trị cần tìm. 3 Ví dụ 3 : 5x 61 3 2 x x 7
1. Tìm tất cả c c điểm trên đường thẳng d : y  
để từ đó kẻ đến đồ thị y     2x  có 3 tiếp 4 24 3 2 3
tuyến tương ứng với 3 tiếp điểm có ho nh độ x , x , x thỏa mãn: x x  0  x 1 2 3 1 2 3
2. Tìm tất cả các giá trị của k để tồn tại 2 tiếp tuyến với C : 3 2
y x  6x  9x  3 phân biệt và có cùng hệ số góc
k , đồng thời đường thẳng đi qua c c tiếp điểm của 2 tiếp tuyến đó với C cắt các trục Ox,Oy tương ứng tại
A, B sao cho OB  2012.OA . Lời giải.
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 4
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN  5m 61  2  1  3m 5 1. M ; m   
d , tiếp tuyến t tại điểm N x ; y đi qua M : 3 2 x
m x mx      0 0 0   4 24  0 0 0 3  2  4 24  1 x    0 0 2  2   2 5 5 3m x   m x    0     0 0    3  6  12 2   2 7m 5 5 1 m    0 m   ; m    3 12 2 6    5  5
heo b i to n, phương trình  có hai nghiệm phân biệt âm, tức là :   m  0  m  18 18   3 5  5 m   0 m    2 4  6 5 1 5
Vậy, những điểm M thỏa bài toán là: x   hoặc  x M 2 6 M 18
2. Ho nh độ tiếp điểm x của tiếp tuyến dạng y kx m với C là nghiệm của phương trình 0 f 'x  2
k  3x 12x  9  k  0 1 0 0 0  
Để tồn tại 2 tiếp tuyến với C phân biệt nhau thì phương trình 1 có hai nghiệm phân biệt, khi đó
'  9  3k  0 hay k  3  2 . 3 2
y x  6x  9x  3
Khi đó tọa độ tiếp điểm x ; y
của 2 tiếp tuyến với C là nghiệm hệ phương trình 0 0 0 0  0 0  2
3x  12x  9  k  0 0  1     1 k 6 2k 9
y  x  2 2
3x  12x  9  2x  3 y
x  2 k  2x  3  x  0  0  0 0 0 0  0   3 0 0   3 3 3  2
3x  12x  9  k   2
3x  12x  9  k 0 0  0 0 k  6 2k  9
Vậy phương trình đường thẳng đi qua c c tiếp điểm là d : y x  . 3 3
Do d cắt trục Ox,Oy tương ứng tại A và B sao cho OB  2012.OA nên có thể xảy ra:  9
Nếu A O thì B O , trường hợp này chỉ thỏa nếu d cũng qua O Khi đó k  . 2
 Nếu A O , khi đó trong tam gi c AOB vuông tại O sao cho OB k  6 tanOAB   2012   2
 012  k  6042 hoặc k  6030  ( không thỏa 2 ). OA 3 9 Vậy k
, k  6042 thỏa bài toán. 2
Ví dụ 4 : Cho hàm số 3
y  x  3x  2, có đồ thị là C. Tìm tọa độ c c điểm trên đường thẳng y  4  mà từ đó có
thể kẻ đến đồ thị C đ ng hai tiếp tuyến. Lời giải.
Hàm số đã cho c định và liên tục trên .
Gọi A l điểm nằm trên đường thẳng y  4  nên A ; a 4  .
Đường thẳng  qua A với hệ số góc k có phương trình y k x a  4
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 5
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN
Đường thẳng  tiếp xúc với đồ thị C khi và chỉ khi hệ phương trình sau có nghiệm: 3
x  3x  2  kx a 3  4
x  3x  2  3 2x  1xa    2 2  3
x  3  k  3
x  3  k x  2 1 2x  
3a2x3a2   0  1   2  3
x  3  k  2 x  1
Phương trình 1 tương đương với: g  x 2
 2x  3a  2x  3a  2   0
Qua A kẻ được hai tiếp tuyến đến C khi và chỉ khi 2 có 2 giá trị k kh c nhau , khi đó 1 có đ ng 2
nghiệm phân biệt x , x , đồng thời thỏa 2 2 k  3
x  3, k  3
x  3 có 2 giá trị k khác nhau 1 2 1 1 2 2 Trƣờng hợp 1:
g x phải thỏa mãn có một nghiệm bằng 1  và nghiệm khác 1  hay g  1  0  6a  6  0      a  1 3a 2
 kiểm tra 2 thấy thỏa.   1  a  0  2 Trƣờng hợp 2:  a 2 3
2  8 3a  2  0  
33a  2a  2  0
g x phải thỏa mãn có một nghiệm kép khác 1  hay   3a 2     1  3a  2  2   2 2
a   hoặc a  2, kiểm tra 2 thấy thỏa. 3  2 
Vậy, c c điểm cần tìm là A 1  ; 4  , A2; 4
  hoặc A  ; 4   .  3 
Ví dụ 5 Cho hàm số 3
y  3x x có đồ thị là C. ìm trên đường thẳng (d): y  x c c điểm M mà từ đó kẻ được
đ ng 2 tiếp tuyến phân biệt với đồ thị (C). Lời giải. Gọi ( M ; m  ) m d .
Phương trình đường thẳng  qua M có hệ số góc k có dạng: y  ( k x  ) m m .
 là tiếp xúc (C) tại điểm có ho nh độ x khi hệ sau có nghiệm x : 0 0 3
3x x  ( k x  ) m m (1) 0 0 0  ( )  2
3  3x k (2)  0 3 2x hay 2 v o 1 ta được: 3 2
2x  3mx  4m  0  0 m  ( )  0 0 2 3x  4 0
Từ M kẻ được đ ng 2 tiếp tuyến với (C)  ( )
 có nghiệm x đồng thời (2) tồn tại đ ng 2 gi trị k khác nhau 0 Khi đó ( )
 có nghiệm x phân biệt thỏa mãn (2) có 2 giá trị k khác nhau . 0 3 2x Xét hàm số 0 f (x )  . 0 2 3x  4 0
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 6
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN  2 3  Tập c định D  \ 1  ;    3  4 2 6x  24x Ta có: 0 0 f (  x )  và f (
x )  0  x  0 hoặc x  2  0 2 2 (3x  4) 0 0 0 0
Dựa vào bảng biến thiên suy ra  m  2
 . Kiểm tra (2) , ta thấy thỏa mãn. Vậy: ( M 2  ;2) hoặc ( M 2; 2  ) .
Ví dụ 6 Lấy điểm M thuộc đồ thị C 3 2 : y  2
x  3x  3 . Chứng minh rằng có nhiều nhất hai đường thẳng đi qua
điểm M và tiếp xúc với CLời giải. Gọi M  3 2 ; a 2
a  3a  3 l điểm thuộc đồ thị C của hàm số Đường thẳng d đi qua M có hệ số góc k , có phương trình
y k x a 3 2
 2a  3a  3 . Đường thẳng
d tiếp xúc với đồ thị C tại Nx ;y khi hệ phương trình 0 0  3 2  2
x  3x  3  kx a 3 2
 2a  3a   3 1 0 0 0   
có nghiệm x . Thay 2 vào 1 , biến đổi và rút gọn ta được 2 6  x  6x   k 2 0  0 0   phương trình  2  a  3
x a2 4x  2a  3  0 tức x a hoặc x  . 0  0  0 0 4
Vậy hệ phương trình 1 , 2 có nhiều nhất 2 nghiệm, tức có nhiều nhất 2 đường thẳng đi qua M và tiếp
xúc với đồ thị C .
Ví dụ 7: Cho hàm số 3 2 y  2
x  4x 1 , có đồ thị là C
1. Gọi d l đường thẳng đi qua A0; 
1 có hệ số góc là k . Tìm k để d cắt C tại 2 điểm phân biệt B,C khác A
sao cho B nằm giữa A và C đồng thời AC  3AB ;
2. Tìm trên trục tung những điểm mà từ đó kẻ được đ ng 2 tiếp tuyến đến CLời giải. 1.
d : y kx  1 . Với k  2 thì d cắt C tại 2
điểm phân biệt B và C khác A Khi đó Bx ; kx   1 , B B
C x ; kx  
1 , x x với x , x là nghiệm của phương trình 2
2x  4x k  0 . C C B C B C k 3
AC  3AB tức x  3x và x x  2, x .x  suy ra k  . C B B C B C 2 2
2. Gọi M 0; m và t qua M có hệ số góc là a nên t : y ax m . t tiếp xúc C tại điểm có ho nh độ x khi 0 3 2  2
x  4x  1  kx m hệ 0 0 0  có nghiệm x suy ra 3 2
4x  4x  1 m  0 có nghiệm x  heo b i to n thì phương 2  6
x  8x x 0 0  0 0 0 0 0 11
trình  có đ ng 2 nghiệm, từ đó có được m  hoặc m  1 . 27
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 7
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN
CÁC BÀI TOÁN LUYỆN TẬP 1  4 4  Bài 1: Cho hàm số 3 2 y
x  2x  3x có đồ thị là (C). ìm phương trình c c đường thẳng đi qua điểm A ;  v 3  9 3 
tiếp c với đồ thị của h m số      : y x
 : y  3x  : y x
 : y  3x     4 4 4 4
A.  : y x         B. : y x 1 C. : y D. : y 3  3  3  3     5 8  5 128 5 1 5 128
: y   x
 : y   x
 : y   x
 : y   x   9 81  9 81  9 81  9 81    4 4
Bài làm: Phương trình đường thẳng đi qua với hệ số góc k có dạng y k x      9  3 1   3 2 4 4
x  2x  3x k x    (1)
tiếp c với tại điểm có ho nh độ x khi hệ phương trình 3  9  3 có nghiệm x  2
x  4x  3   k (2) 1  4  4 hế 2 v o 1 , được: 3 2 2 2
x  2x  3x  (x  4x  3) x    (
x 3x  11x  8)    0 3  9  3  (2)
x  0 k  3   : y  3x  (2) 4 
x  1 k  0   : y   3  (2) 8 5 5 128
x   k     : y   x   3 9 9 81 1 3  3  Bài 2 ho h m số 4 2 y x  3x
ìm phương trình tiếp tuyến đi qua điểm A  0;  v tiếp c với đồ thị 2 2  2  (C).  3     3 3 3 : y    : y x
 : y x  1   : y   2  2  2  2   3  3  1  3 A.  : y  2  2x  
B.  : y   2x
C.  : y  2x
D.  : y   2x  2     2  2  2  3  3 1 3 : y  2 2x            : y 2x : y 2x : y 2x  2  2  2  2  3
Bài làm: Phương trình đường thẳng đi qua điểm v có hệ số góc k có đạng y kx  . 2 1 4 2 3 3
x  3x   kx  (1)
tiếp c với tại điểm có ho nh độ x khi hệ phương trình 2 2 2 có nghiệm x  3 2x  6x   k (2) (2)  3
x  0  k  0   : y   2  1 3 3 (2)  3 hế 2 v o 1 , ta có 4 2 3 2 2 x  3x   (2x  6 ) x x
x (x  2)  0  x  2  k  2  2   : y  2  2x   2 2 2 2  (2)  3
x   2  k  2 2   : y  2 2x   2
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 8
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN
Bài 3: Viết phương trình tiếp tuyến của C : 3 x  1  Câu 1. 2 y
x  3x 1 đi qua điểm A0;  3  3  1 2 1 1 A. y  3x- B. y  3x  C. y  x  D. y  3x  3 3 3 3
Bài làm: XĐ D  Ta có: 2
y'  x  2x  3
Phương trình tiếp tuyến d của C có dạng : y y'(x )(x x )  ( y x ) 0 0 0
trong đó x l ho nh độ tiếp điểm của d với C ) 0 3 x 2 2 0 2 2 3 2
y  (x  2x  3)(x x ) 
x  3x 1  (x  2x  3)x x x 1 0 0 0 0 0 0 0 0 0 3 3  1  1 2 3 2 3 2 A 0;
d    x x 1 2x  3x  4  0 x  2    . 0 0 0 0 0  3  3 3 1
Suy ra phương trình tiếp tuyến cần tìm là y  3x  . 3 Câu 2. 4 2
y  x  4x  3 đi qua điểm cực tiểu của đồ thị. 16 59 16 5 A. y  3  ; y   x B. y  3  ; y   x  3 9 3 3 9 16 5 16 59 C. y  9  ; y   x D. y  3  ; y   x  3 9 3 3 9
Bài làm: 2. Điểm cực tiểu của C là A0; 3  .
Phương trình tiếp tuyến d của C có dạng : y y'(x )(x x )  ( y x ) 0 0 0
trong đó x l ho nh độ tiếp điểm của d với C ) 0 3 4 2 y  ( 4
x  8x )(x x )  x  4x  3 3 4 2  ( 4
x  8x )x  3x  4x  3 0 0 0 0 0 0 0 0 0 4 2 4 2 2 ( A 0; 3  )d  3
  3x  4x  3  3x  4x  0  x  0 hoặc x   0 0 0 0 0 0 3
Với x  0 thì phương trình d: y  3  0 2 16 59 Với x  
thì phương trình d: y   x  0 3 3 3 9 2 16 59 Với x  thì phương trình d: y  x  0 3 3 3 9 16 59 16 59
Vậy, tiếp tuyến cần tìm là: y  3  , y   x  , y  x  3 3 9 3 3 9  23  Câu 3. 3 2
y x  3x  2 đi qua điểm A ; 2    .  9 
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 9
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN     y  2  y  2 y  2 y  2     
A. y  9x   25
B. y x   25
C. y  9x   2
D. y x   5  5 61     5 1 5 61 61 y x  y x  y x  y x   3 27  3 27  3 2  27
Bài làm: 3. Gọi M x ; y C Phương trình tiếp tuyến d của C tại M là 0  0 0    0
y y y'x x x   y   3 2
x  3x  2   2 3x  6x x x 0 0 0 0 0 0 0   0   23 
Do d đi qua điểm A ; 2    nên  9    2    3 2
x  3x  2   2 3x  6x  23 3 2
x  6x  32x  46x 12    0 0 0 0 0 0 0 0 0  9  
x  2  y  2   
x  23x 10x  3 0 2
 0  x  3  y  9x  25 0 0 0 0  1 5 61
x   y x  0  3 3 27 Câu 4. 3 2
y x  2x x  4 đi qua điểm M  4  ; 2  4.
A. y  3x  508; y x  8; y  5x  4.
B. y  13x  5; y  8x  8; y  5x  4.
C. y  133x  508; y x  8; y x  4.
D. y  133x  508; y  8x  8; y  5x  4.
Bài làm: 4. Hàm số đã cho c định và liên tục trên .
Giả sử tiếp tuyến cần tìm tiếp xúc với đồ thị C tại điểm có ho nh độ x khi đó phương trình tiếp tuyến  có 0 dạng:
y y'x x x   yx    2 3 2
3x  4x  1 x x x  2x x  4 0 0 0 0 0  0 0 0 0 2
Vì  đi qua điểm M  4;  2  4 nên: 2
 4  3x 4x 1 4
  x x  2x x  4 0  0  3 2 0 0 0 0 3 2
x  5x  8x 12  0  x  6  hoặc x  1  hoặc x  2. 0 0 0 0 0 0 - Với x  6
 thì phương trình tiếp tuyến là y  133x  508 0 - Với x  1
 thì phương trình tiếp tuyến là y  8x  8 0
- Với x  2 thì phương trình tiếp tuyến là y  5x  4 0
Vậy, có ba phương trình tiếp tuyến cần tìm là: y  133x  508; y  8x  8; y  5x  4. Bài 4: 2 x  2x  1
Câu 1. Viết phương trình tiếp tuyến của đồ thị hàm số y
, biết tiếp tuyến đi qua điểm ( M 6; 4) . x  2 1 1 1 3 3 1
A. y  5 và y x  .
B. y  4 và y x
. C. y  5 và y
x  6 . D. y  4 và y x  . 2 4 2 4 4 2
Bài làm: 1. Đường thẳng  đi qua (
M 6; 4) với hệ số góc k có phương trình y  ( k x  6)  4
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 10
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN  1 x
k(x  6)   4 (1)   x  2
tiếp c đồ thị tại điểm có ho nh độ x  có nghiệm x 0 1 0 1    k (2) 2  (x  2) 1  1 
Thay (2) vào (1) và biến đổi, ta được: x   1
(x  6)  4  x  0,x  3 0  2 0 0 0 x 2 (x 2)    0  0  3
Tahy vào (2) ta có: k  , k  0 . 4 3 1
Vậy tiếp tuyến cần tìm là: y  4 và y x  . 4 2 x  2
Câu 2. Viết phương trình tiếp tuyến d với đồ thị C : y
, biết d đi qua điểm A 6;  5. x  2 x 7 x 5
A. y x  1 , y   .
B. y  x  1 , y    . 4 2 4 2 x 7 x 7
C. y  x  1 , y    . D. y x  1 , y   . 4 2 4 2
Bài làm: 2. Cách 1: Gọi x ; y x
là tọa độ tiếp điểm của tiếp tuyến d và C , với 0  0   4 
y x x 2 0 
, tiếp tuyến d có hệ số góc y'x
, x  2 và d có phương trình 0  0 x  2  0 x  2 0 2 0 4   y   x 2 x x  2 0  0 xx   2 2 0 0 4  x  2
d đi qua điểm A 6;  5 nên có 5   6   x
phương trình n y tương đương với 2 0  0 xx   2 2 0 0 2
x  6x  0  x  0 hoặc x  6 0 0 0 0
Với x  0 , ta có phương trình y  x  1 0 x 7
Với x  6 , ta có phương trình y    0 4 2 x 7
Vậy, có 2 tiếp tuyến thỏa đề bài y  x  1 , y    . 4 2
Cách 2 Phương trình d đi qua A 6;
 5 có hệ số góc k , khi đó d có phương trình l : y kx  6  5
d tiếp xúc C tại điểm có ho nh độ x khi và chỉ khi hệ : 0    x k x  6 2 0  5  2
4x  24x  0 0         x  2  0 0  x 0, k 1 d : y x 1 0 0   có nghiệm x hay  4 có nghiệm x  4 1 x 7  0 k   0         k    2 x 6, k d : y 0   x 2  4 4 2 0   x 22 0 x 7
Vậy, có 2 tiếp tuyến thỏa đề bài y  x  1 , y    . 4 2
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 11
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN Câu 3. Cho hàm số 3 2
y x  3x  9x  11 có đồ thị là C. Lập phương trình tiếp tuyến của đồ thị hàm số biết tiếp  29 
tuyến đi qua điểm I  ;184 .  3 
A. y  8x  36; y  36x 14; y  15x  9
B. y  40x  76; y  36x 14; y  15x  9
C. y  420x  76; y x 164; y x  39
D. y  420x  3876; y  36x 164; y  15x  39
Bài làm: 3. Giả sử tiếp tuyến cần tìm tiếp xúc với đồ thị C tại điểm có ho nh độ x khi đó 0
phương trình tiếp tuyến  có dạng:
y y'x x x   yx    2
3x  6x  9 x x x  3x  9x  11 0  0 3 2 0 0 0 0 0 0 0  29    2 3 29
Vì  đi qua điểm I  ;184  nên: 184   2 3x  6x  9
x x  3x  9x    11 0 0   3  0 0 0 0  3  3 2
 2x  32x  58x  260  0  x  13 hoặc x  5 hoặc x  2.  0 0 0 0 0 0
- Với x  13 thì phương trình tiếp tuyến là y  420x  3876 0
- Với x  5 thì phương trình tiếp tuyến là y  36x 164 0 - Với x  2
 thì phương trình tiếp tuyến là y  15x  39 0
Vậy, có ba phương trình tiếp tuyến cần tìm là:
y  420x  3876; y  36x 164; y  15x  39
Bài 5: Gọi l đồ thị của hàm số 3 2
y x  3x  2
Câu 1. Viết phương trình tiếp tuyến của (C) song song với đường thẳng y = 9x – 7 . A. y = 9x + 25 B. y = 7x + 2 C. y = 9x + 5 D. y = 9x + 2
Bài làm: 1. Tiếp tuyến (d) của (C) song song với đường thẳng y = 9x – 7 ,suy ra phương trình d có dạng : y = 9x + m (m  - 7) 3 2
x  3x  2  9x m (1)
(d) tiếp xúc với (C) tại điểm có ho nh độ x khi hệ 0 0 0  có nghiệm x 0 2
3x  6x  9 (2) 0  0 0
(2)  x = 1  x = - 3 . 0 0
Lần lượt thay x = 1 , x = - 3 v o 1 ta được m = - 7 , m = 25 và m = - 7 bị loại 0 0
Vậy phương trình tiếp tuyến (d): y = 9x + 25.
Câu 2. Viết phương trình tiếp tuyến của đi qua điểm A(- 2;7). A. y = 9x + 25 B. y = 9x + 9 C. y = 9x + 2 D. y = x + 25
Bài làm: 2. Phương trình tiếp tuyến D đi qua -2;7) có dạng y = k(x+2) +7 . 3 2
x  3x  2  ( k x  2)  7 (3)
(D) tiếp xúc (C) tại điểm có ho nh độ x khi hệ 0 0 0  có nghiệm x 0 2
3x  6x k (4) 0  0 0 hay 4 v o 3 ta được: 3 2 2
x  3x  2  (3x  6x )(x  2)  7 3 2
 2x  9x 12x  9  0  x  3  0 0 0 0 0 0 0 0 0
Thay x = - 3 v o 4 ta được k = 9 Suy ra phương trình D y = 9 + 25 0 Bài 6: Cho hàm số 2 2 y  (2  )
x x , có đồ thị (C).
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 12
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN
Câu 1. Viết phương trình tiếp tuyến tại giao điểm của (C) với Parabol 2 y x .
A. y  0 ; y  1 ; y  24x  6
B. y  9 ; y  1 ; y  24x  6
C. y  0 ; y  5 ; y  24x  63
D. y  0 ; y  1 ; y  24x  63
Bài làm: 1. Ta có: 4 3 2 3 2
y x  4x  4x y'  4x  12x  8x Phương trình ho nh độ giao điểm của (C) và Parabol 2 y x 4 3 2 2 2 2
x  4x  4x x x (x  4x  3)  0  x  0, x  1, x  3 .
x  0 ta có phương trình tiếp tuyến là: y  0 .
x  1 ta có phương trình tiếp tuyến là: y  1
x  3 ta có phương trình tiếp tuyến là: y  24x  63 .
Câu 2. Viết phương trình tiếp tuyến của (C), biết tiếp tuyến đi qua điểm ( A 2; 0) . 2 6 32 32 4 32 64 A. y   x B. y   x  9 C. y   x D. y   x  27 27 27 27 27 27 27
Bài làm: 2. Ta có: 4 3 2 3 2
y x  4x  4x y'  4x  12x  8x Cách 1: Gọi (
M x ; y ) (C) . 0 0
Tiếp tuyến  của (C) tại có phương trình 3 2
y  (4x  12x  8x )(x x )  y . 0 0 0 0 0 3 2 2 2
A    0  (4x 12x  8x )(2  x )  x (x  2) 0 0 0 0 0 0 3 2 4
 (2  x )(3x 10x  8x )  0  x  0,x  2,x  . 0 0 0 0 0 0 0 3
* x  0  y'(x )  0, y  0  Phương trình tiếp tuyến y  0 0 0 0
* x  2  y'(x )  0, y  0  Phương trình tiếp tuyến y  0 0 0 0 4 32 64 32 64 * x
y'(x )   , y
 Phương trình tiếp tuyến: y   x  . 0 0 3 27 81 27 27
Cách 2: Gọi d l đường thẳng đi qua , có hệ số góc k  d : y  ( k x  2) 2 2 (
 2  x ) x  ( k x  2)
d tiếp c đồ thị tại điểm có ho nh độ x khi hệ 0 0 0  có nghiệm x 0
4x (x  2)(x 1)  k  0 0 0 0
hay k v o phương trình thứ nhất ta được: 4 3 2 3 2 2
x  4x  4x  (x  2)(4x 12x  8x )  x (3x  4)(x  2)  0 0 0 0 0 0 0 0 0 0 0 4
x  0,x  2,x  . 0 0 0 3
* x  0  k  0  Phương trình tiếp tuyến y  0 0
* x  2  k  0  Phương trình tiếp tuyến y  0 0 4 32 32 64 * x   k  
 Phương trình tiếp tuyến y   x  . 0 3 27 27 27 Bài 7: 3 x 1
Câu 1. ìm m để (Cm): 2 y
 (m  2)x  2mx  1 tiếp xúc với đường thẳng y = 1 3 2
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 13
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN  2   2   2 
A. m  0; ; 2
B. m  4; ; 6
C. m 0; 4;  6
D. m  0; ; 6  3   3   3 
Bài làm: 1. (Cm) tiếp c đường thẳng y = 1 tại điểm có ho nh độ x khi hệ sau 0 3 x 1 0 2 
 (m  2)x  2mx  1  1 ( ) a 0 0  3 2 có nghiệm x .  0 2
x  (m  2)x  2m  0 ( ) b  0 0 ( )
b x  2  x  . m 0 0 2
Thay x  2 v o a ta được m  . 0 3 3 m
Thay x m v o a ta được 2 
m  0  m  0  m  6. 0 6  2 
Vậy (Cm) tiếp c đường thẳng y = 1  m  0; ; 6  3  x  2
Câu 2. Gọi l đồ thị của hàm số y =
. M(0;m) là một điểm thuộc trục Oy .Với giá trị nào của m thì luôn tồn 2x  1
tại ít nhất một tiếp tuyến của đi qua M và tiếp điểm của tiếp tuyến này với có ho nh độ dương A. m  0 B. m  0 C. m<0 D. m  0
Bài làm: 2. Phương trình của đường thẳng d đi qua có hệ số góc k : y = kx + m.  x  2 0   kx m (1) 0 2x  1
(d) tiếp xúc (C) tại điểm có ho nh độ x khi hệ sau 0  x . 0 3 có nghiệm  0  k (2) 2 (2x   1) 0 x  2 3x 1 0 0 2 hay 2 v o 1 ta được : 
m  (x  2)(2x 1)  3x  ( m 2x 1) (3) (do x = không phải là 2 2x  1 (2x  1) 0 0 0 0 2 0 0 nghiệm của (3)) 2
 (4m 2)x  4(m 2)x m 2  0 (4) 0 0
Yêu cầu của bài toán  Phương trình 4 có ít nhất một nghiệm dương với mọi m  0. Vì m  0 nên 4m – 2 < 0 suy ra (4) có nghiệm  2
'  4(m 2) (4m 2)(m2)  0  m 2  0 . Bất đẳng thức n y đ ng với mọi m  0.
Khi đó gọi x , x là hai nghiệm của phương trình 4). 1 2  4(m  2) x x    0 1 2   Ta có 4m 2 m   0 , 
,suy ra x  0, x  0 m  2  1 2 x x   0 1 2  4m  2
Vậy, với mọi m  0 luôn tồn tại ít nhất một tiếp tuyến của đi qua v ho nh độ tiếp điểm của tiếp tuyến với (C) là số dương Bài 8: Câu 1. Cho hàm số 3
y x  3x  2 ìm trên đường thẳng d : y  4 c c điểm mà từ đó kẻ được đ ng 2 tiếp tuyến với (C). A. ( 1
 ; 4) ; 7; 4 ; (2; 4) . B. ( 1
 ; 4) ; 7; 4 ; (9; 4) .  2  C. ( 2;  4) ;  5  ; 4 ; (2; 4) . D. ( 1
 ; 4) ;  ; 4 ; (2;4) .  3 
Bài làm: 1. Gọi ( M ;
m 4) d . Phương trình đường thẳng  qua M có dạng: y  ( k x  ) m  4
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 14
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN
 là tiếp tuyến của (C)  hệ phương trình sau có nghiệm x: 3
x  3x  2  ( k x  ) m  4 (1)  (*) 2
3x  3  k (2) hay 2 v o 1 ta được: 2
(x  1) 2x (3m  2)x  3m  2  0 (3)  x  1  hoặc 2
2x (3m  2)x  3m  2  0 (4)
Theo bài toán  (*) có nghiệm , đồng thời (2) có 2 giá trị k khác nhau, tức l phương trình (3) có nghiệm x phân
biệt thỏa mãn 2 giá trị k khác nhau.
+ TH1: (4) có 2 nghiệm phân biệt, trong đó có 1 nghiệm bằng –1  m  1  2
+ TH2: (4) có nghiệm kép khác –1  m   hoặc m  2 3  2 
Vậy c c điểm cần tìm là: ( 1
 ; 4) ;  ; 4 ; (2;4) .  3  Câu 2. Cho hàm số 3 2
y  x  3x  2 ìm trên đường thẳng (d): y = 2 c c điểm mà từ đó kẻ được 3 tiếp tuyến phân biệt với đồ thị (C).  1 m  2   m
A. M(m; 2)  (d) với  3
B. M(m; 2)  (d) với m  7  m   2  4   5 m  3   m  m  1   m
C. M(m; 2)  (d) với  3
D. M(m; 2)  (d) với  3 m   2 m   2
Bài làm: 2. Gọi ( M ; m 2) (d) .
Phương trình đường thẳng  đi qua điểm M có dạng : y  ( k x  ) m  2
 là tiếp tuyến của (C)  hệ phương trình sau có nghiệm x: 3 2
x  3x  2  ( k x  ) m  2 (1)  (*). 2  3
x  6x k (2) hay 2 v 1 ta được: 3 2
2x  3(m  1)x  6mx  4  0 2
 (x  2)2x (3m1)x  2  0  x  2 hoặc 2 f ( )
x  2x (3m  1)x  2  0 (3)
Từ M kẻ được 3 tiếp tuyến đến đồ thị (C)  hệ (*) có nghiệm x phân biệt đồng thời
(2) có 3 giá trị k khác nhau
 (3) có hai nghiệm phân biệt khác 2 và có giá trị x thỏa  5   0 m  1   m
phương trình 2 có 3 gi trị k khác nhau     3 . f (2)   0 m   2  5 m  1   m
Vậy ,M(m; 2)  (d) với 
3 có thể kẻ được 3 tiếp tuyến với (C). m   2
Câu 3. Viết phương trình tiếp tuyến d tiếp xúc với đồ thị H  : y  x  2 2 1
của hàm số tại đ ng 2 điểm phân biệt.
A. y  2x B. y  0
C. y  2x  1 D. y  1
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 15
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN 2
Bài làm: 4. Giả sử d l đường thẳng tiếp xúc với H tại điểm Mm  2 ; m  
1  Khi đó đường thẳng d có
phương trình y mm  x m  m  2 2 2 2 1 1
Đường thẳng d tiếp xúc với H  tại 2 điểm phân biệt khi và chỉ khi hệ phương trình x  2 1
 2mm  
1 x m  m   12 2 2 2 
có đ ng một nghiệm khác m tức hệ 2x   2 x   1  2m 2 m  1 xm  x   2 2
x mx m  3
m  2x  0  3 x  m 
có đ ng một nghiệm khác m hay  có nghiệm  2 2 x m        2 2
x mx m   1  0 x mx m 1 0 x  1,m  1  hoặc x  1  ,m  1 .
Vậy y  0 thỏa đề bài. Bài 9. Cho hàm số 4 2
y x  2x  3 , có đồ thị là C
Câu a ìm trên đồ thị C điểm B mà tiếp tuyến với C tại điểm đó song song với tiếp tuyến với C tại điểm A1; 2 . A. B1; 2 B. B0; 3 C. B 1  ; 3 D. B 2;3
Bài làm: B0; 3 , y  3 .
Câu b ìm trên đường thẳng y  2 những điểm m qua đó ta kẻ được 4 tiếp tuyến phân biệt với đồ thị C .
A. M 0; 2 , M 1; 2
B. M 0; 2 , M3; 2
C. M 5; 2 , M1; 2 D. Không tồn tại
Bài làm: b. Gọi M  ;
m 2 l điểm thuộc đường thẳng y  2 Phương trình đường thẳng đi qua M  ; m 2 có hệ số 4 2
x  2x  3  k x m   2 1 0 0  0   
góc là k và d : y kx m  2 . d tiếp xúc C tại điểm có hoành độ x khi hệ  0 3 4x  4x   k 2  0 0  
có nghiệm x suy ra phương trình  2 x   1  2
3x  4ax  1  0  có nghiệm x . 0 0 0  0 0
Qua M kẻ được 4 tiếp tuyến đến C khi phương trình  có 4 nghiệm phân biệt v phương trình 2 có 4 giá trị k khác nhau. Dễ thấy 2
x  1  0  k 1
  k 1 , do đó không thể tồn tại 4 giá trị k kh c nhau để thỏa bài toán. Tóm lại, không 0    
có tọa độ M thỏa bài toán.
Bài 10 . Cho hàm số : 4 2
y x  2x có đồ thị là C .
Câu a. Viết phương trình tiếp tuyến của C biết tiếp tuyến đi qua gốc tọa độ. 6 6 4 6 4 6
A. t : y  0; t : y  
x; t : y x
B. t : y  0; t : y  
x; t : y x 1   2  3 1   2   3 9 9 7 7 4 4 4 6 4 6
C.t : y  0; t : y   x; t : y x
D.t : y  0; t : y  
x; t : y x 1   2  3 1   2  3 9 9 9 9
Bài làm: a. Gọi Ax ; y C Phương trình tiếp tuyến t của C tại A là: 0 0    y   4 2
x  2x    3 4x  4x
x x . t đi qua O0; 0 nên 0 0 0 0   0   4 2
x x    4
x x x  4 2 6 2 4 4
 3x  2x  0  x  0,x   0 0 0 0 0 0 0 0 0 3
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 16
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN
Thay các giá trị của x v o phương trình của t ta được 3 tiếp tuyến của C kẻ từ O0; 0 là: 0  4 6 4 6
t : y  0; t : y  
x; t : y x 1   2  3 9 9
Câu b..Tìm những điểm M trên trục Oy để từ M kẻ được 4 tiếp tuyến đến C . 1
A. M 0; m với 0  m  1 B. M 0; m với 1   m  3 2 1
C. M 0; m với 0  m
D. M 0; m với 0  m  3 3
Bài làm: b. M Oy M0;m; BC  Bx ; y 0 0 
Phương trình tiếp tuyến T  của C tại B là y   4 2
x  2x    3 4x  4x
x x . T  đi qua M 0; m nên 0 0 0 0   0  m   4 2
x  2x    4
4x  4x x  4 2
 3x  2x m  0 * 0 0 0 0 0 0 0  
Do hệ số góc của tiếp tuyến là 3
k  4x  4x nên hai giá trị khác nhau của x cho hai giá trị khác nhau của k nên 0 0 0
cho hai tiếp tuyến khác nhau
Vậy từ M 0; m kẻ được 4 tiếp tuyến đến đồ thị C khi và chỉ khi phương trình * có 4 nghiệm phân biệt. Đặt 2
X x ta có phương trình 2
3X  2X m  0  * * 0
Phương trình * có 4 nghiệm phân biệt khi và chỉ khi * * có 2 nghiệm phân biệt  ,
  1 3m  0   m 1  1 P   0
 0  m  . Vậy từ những điểm M0;m với 0  m  kẻ được 4 tiếp tuyến đến đồ thị 3 3  3  2 S   0  3
Ccủa hàm số đã cho
Câu c. Tìm những điểm N trên đường thẳng d : y  3 để từ N kẻ được 4 tiếp tuyến đến C . A. N  ;
n 3 , n  3 B. N  ;
n 3 , n  3 C. N  ;
n 3 , n  2 D. N  ;
n 3 , n  13
Bài làm: c. N d : y  3  N ;
n 3; I C  I x ; y 0 0 
Phương trình tiếp tuyến  của C tại I là: y   4 2
x  2x    3 4x  4x
x x .  đi qua N  ; n 3 nên 0 0 0 0   0  3   4 2
x  2x    4
4x  4x n x  4 2 2
 3x  4nx  2x  4nx  3  0 0 0 0 0 0 0 0 0 0  3 4 x   1  4n 3 x x  2
 2x  0 * .Do x  0 không phải là nghiệm của * Phương trình 0 0 0 0   0       2 1 1 *  3 x
  4nx    2  0 * * 0  2   0    x    x  0 0 1 Đặt 2 t x
x tx 1  0 luôn có hai nghiệm phân biệt với mọi t 0 0 0 x0 a có phương trình   2
* *  3t  4nt  4  0 * * *
Do hệ số góc của tiếp tuyến là 3
k  4x  4x nên hai giá trị khác nhau của x cho hai giá trị khác nhau của k nên 0 0 0
cho hai tiếp tuyến khác nhau
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 17
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN
Vậy từ N kẻ được 4 tiếp tuyến đến đồ thị C khi và chỉ khi phương trình * có 4 nghiệm phân biệt khi và chỉ
khi * * có 4 nghiệm phân biệt khi và chỉ khi phương trình * * * có 2 nghiệm phân biệt 2
 '  4n 12  0 2
n  3  0  n  3 . Vậy từ những điểm N trên đường thẳng y  3 với n  3 kẻ được 4 tiếp tuyến đến đồ
thị C của hàm số đã cho Bài 10: 1 Câu 1. Cho hàm số 3 2 y
mx  (m  1)x  (4  3 )
m x  1 có đồ thị là C . Tìm các giá trị m sao cho trên đồ thị m  3
C . tồn tại một điểm duy nhất có ho nh độ âm mà tiếp tuyến tại đó vuông góc với đường thẳng m 
d: x2y3  0. 2 1 2
A. m  12 hoặc m  .
B. m  0 hoặc m  1
C. m  1 hoặc m
D. m  0 hoặc m  3 3 3  1
Bài làm: 1. d có hệ số góc 
 tiếp tuyến có hệ số góc k  2 . Gọi x l ho nh độ tiếp điểm thì: 2 2 2
y'  2  mx  2(m 1)x  (4  3 )
m  2  mx  2(m 1)x  2  3m  0 
Theo b i to n, phương trình  có đ ng một nghiệm âm.
Nếu m  0 thì   2  x  2
  x  1 (không thỏa) 2  3m
Nếu m  0 thì dễ thấy phương trình  có 2 nghiệm là x  1 hay x  m 2  3m 2
Do đó để  có một nghiệm âm thì
 0  m  0 hoặc m  . m 3 1 Câu 2. Cho hàm số 3 2 y
mx  (m  1)x  (4  3 )
m x  1 có đồ thị là C . Tìm các giá trị m sao cho trên đồ thị m  3
C . tồn tại đ ng hai điểm có ho nh độ dương m tiếp tuyến tại đó vuông góc với đường thẳng m 
d: x2y3  0.  1   1 2   1   1 5   1   1 8   1   1 2 
A. m  0;   ; 
B. m  0;   ; 
C. m  0;   ; 
D. m  0;   ;   3   2 3   2   2 3   2   2 3   2   2 3   1 3
Bài làm: 2. Ta có: 2
y  mx  2(m  1)x  4  3m ; d : y   x  . 2 2
Theo yêu cầu bài toán  phương trình y  2 có đ ng 2 nghiệm dương phân biệt  2
mx  2(m 1)x  2  3m  0 có đ ng 2 nghiệm dương phân biệt m  0   1     0 m  0   2  . S  0   1 2    mP   0  2 3  1   1 2 
Vậy, với m  0;   ;  thỏa mãn bài toán  2   2 3  x  2
Câu 3. Cho hàm số: y
có đồ thị là C. ho điểm ( A 0; )
a . Tìm a để từ A kẻ được 2 tiếp tuyến tới đồ thị x  1
C sao cho 2 tiếp điểm tương ứng nằm về 2 phía của trục hoành.
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 18
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN 1 2 2
A.   a  1 B.   a  2 C. 1   a  1 D.   a  1 3 3 3
Bài làm: 3. Phương trình đường thẳng d đi qua ( A 0; )
a và có hệ số góc k : y kx a
x  2  kx  a   x  1
d tiếp xúc C tại điểm có ho nh độ x khi hệ:  có nghiệm x 3  k  2  (x  1) 2  (1 )
a x  2(a  2)x (a  2)  0 1 có nghiệm x  1 .
Để qua A có 2 tiếp tuyến thì 1 phải có 2 nghiệm phân biệt x , x 1 2 a  1 a  1     2     3a  6  0 a  2  2(a  2) a  2 3 3
Khi đó ta có x x  , x x  và y  1  , y  1 1 2 1 2 a  1 a  1 1 2 x  1 x  1 1 2
Để 2 tiếp điểm nằm về 2 phía đối với trục hoành thì y .y  0 1 2  3   3      x .x 2(x x ) 4 2 1  . 1       0 1 2 1 2 
 0  3a  2  0  a   x  1 x     1
x .x  (x x )  1 3 1 2  1 2 1 2 2
Đối chiếu với điều kiện 2 ta được:   a  1 . 3 3 2x Bài 11: Cho hàm số 2 y  
x  4x  2 , gọi đồ thị của hàm số là (C). 3
Câu 1. Viết phương trình tiếp tuyến của (C) có hệ số góc lớn nhất. 9 25 25 9 25 7 5 A. y x
B. y  5x C. y x D. y x  2 12 12 4 12 2 12
Bài làm: 1. Gọi (d) là tiếp tuyến cần tìm phương trình v x l ho nh độ tiếp điểm của (d) với (C) thì hệ số góc 0 2 9  1  9 9 1 của (d): 2
k y'(x )  2
x  2x  4   x     k   x  . 0 0 0 0 2  2  2 0 2 2 9 1 Vậy maxk 
đạt được khi và chỉ khi x  . 2 0 2 9  1   1  9 25
Suy ra phương trình tiếp tuyến (d) : y x   yx      . 2  2   2  2 12
Câu 2. Viết phương trình tiếp tuyến của đi qua điểm A(2;9). A. y = - x + 2 B. y = - 8x + 5 C. y = x + 25 D. y = - 8x + 25
Bài làm: 2. Phương trình đường thẳng D đi qua điểm A(2;9) có hệ số góc k là y  ( k x  2)  9 3  2x0 2 
x  4x  2  k(x  2)  9 (1)
(D) tiếp xúc với (C) tại điểm có ho nh độ x khi hệ 0 0 0  có nghiệm x . 0 3  0 2 2
x  2x  4  k (2)  0 0 3 2x Thay 2 v o 1 ta được : 0 2 2 
x  4x  2  ( 2
x  2x  4)(x  2)  9 0 0 0 0 0 3 3 2
 4x 15x 12x  9  0  x  3 0 0 0 0
Thay x = 3 v o 2 ta được k = - 8 . 0
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 19
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN
Vậy phương trình tiếp tuyến (D) là y = - 8x + 25. 2 x
Bài 12: Gọi l đồ thị của hàm số y  . 2  x 4
Câu 1. Viết phương trình tiếp tuyến của (C) vuông góc với đường thẳng y  x  1 . 3 A.   3 7 3 1
d : y   x  , y   x B.   3 3
d : y   x, y   x  1 4 2 4 2 4 4 C.   3 9 3 1 d : y  x  , y x D.   3 9 3 1
d : y   x  , y   x  4 2 4 2 4 2 4 2  4
Bài làm: 1. Tiếp tuyến (d) của vuông góc đường thẳng y 
x  1 suy ra phương trình d có dạng : 3 3
y   x m . 4 2  x 3 0    x m 0 2  x 4 2 x  4x 3
(d) tiếp xúc (C) tại điểm có ho nh độ x khi hệ 0  có nghiệm x 0 0    0 2 x   4x 0 3 2 (2  x ) 4 0 0   0  2 (2  x ) 4  0
x  6  x  2     3 9 3 1
d : y   x  , y   x  0 0 . 4 2 4 2
Câu 2. Viết phương trình tiếp tuyến của đi qua điểm A(2; - 2). 3 1 3 1
A. y   x
B. y   x  4 2 4 2 3 7 3 5
C. y   x
D. y   x  4 2 4 2
Bài làm: 2. Phương trình tiếp tuyến (d) của đi qua 2 ; - 2) có dạng : y = k(x – 2) – 2 . 2  x0 
k(x  2)  2 (1) 0 2  x0
(d) tiếp xúc (C) tại điểm có ho nh độ x  0 khi hệ 2  có nghiệm x   4x 0 0  k  2 (2  x )  0 2 2 xx  4x 3 1 x 0 0 0  
(x  2)  2  x  2
  y   x  0 2 0 2  x (2  x ) 0 4 2 0 0
Câu 3. Gọi M là một điểm thuộc (C) có khoảng cách từ đến trục hoành bằng hai lần khoảng cách từ đến trục
tung, M không trùng với gốc tọa độ O. Viết phương trình tiếp tuyến của (C) tại M. A. y  9  B. y  64  C. y  12  D. y  8  2 2  xxM (C) M My  y
Bài làm: 3. M    2 Mx    x M 2 . ( d M,Ox)   2 ( d M,Oy) M   y  2 x y  2  xM MM M 2  4  xy  2xM M My   y  2x
x  0 xMM 2 M M M 3 (*)  2  x   x       M M 2 2x   
3x  4x  0  y  0 8  y  2 M x 2 M M Mx y    M M M M  3  4 8 
Vì M không trùng với gốc tọa độ O nên chỉ nhận M  ;  .  3 3 
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 20
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN
Phương trình tiếp tuyến của (C) tại M là y = 8x – 8. 2  xy  2  x M M My   y  2  x x  4 M 2 (*)  2 M M Mx   x     (do M  O). M M 2 2  x   
x  4x  0  y  8   y  2 Mx 2 M M MxM MM
Phương trình tiếp tuyến của (C) tại M là y  8  .
Bài 13: Gọi m l đồ thị của hàm số y = 3 2
2x  3(m  1)x mx m  1 và (d) là tiếp tuyến của (Cm) tại điểm có
ho nh độ x = - 1 ìm m để
Câu 1. d đi qua điểm A(0;8). A. m  0 B. m  1 C. m  2 D. m  3
Bài làm: 1. Ta có 2
y'  6x  6(m  1)x m , suy ra phương trình tiếp tuyến (d) là y y'( 1  )(x 1)  ( y 1
 )  (12+7m)(x+1) – 3m – 4  y  (12+7m)x +4m+8 ( A 0; 8) ( )
d  8 = 4m +8  m  0 . 8
Câu 2. (d) tạo với hai trục tọa độ một tam giác có diện tích bằng . 3  5  5  5  5
m  0  m   
m  0  m  
m  0  m   
m  0  m    3 3 3 3 A.  . B.  . C.  . D.  .  9   73  19   73  9   3  19   73 m   m  m  m   6  6  6  6
Bài làm: 2. Ta có 2
y'  6x  6(m  1)x m , suy ra phương trình tiếp tuyến (d) là y y'( 1  )(x 1)  ( y 1
 )  (12+7m)(x+1) – 3m – 4  y  (12+7m)x +4m+8  4m  8 
Gọi P,Q lần lượt l giao điểm của (d) với trục Ox và Oy thì P   ; 0  , Q(0; 4m+8).  12  7m  2 8m  32   32 1 1 4 8 m m
Diện tích: OPQ: S O . P OQ   4m  8  2 2 12  7m 12  7m 8 2 8 S
 8m  32m  32  12  7m 3 3  8  5 2
8m  32m  32  (12  7 ) m      2 5 m 0 m m m   0 3 3    3   .      2 8 2 19 73
8m  32m  32   (12  7 ) m  
3m  19m  24  0 m   3  6 4 x Bài 14: Cho hàm số 2 y
 2x  4 , có đồ thị là ( C ). 4
Câu 1. Tìm tham số m để đồ thị (C) tiếp xúc với parabol   2
P : y  x m .
A. m  4; m  20
B. m  124; m  2
C. m  14; m  20
D. m  4; m  2
Bài làm: 1. (C) tiếp xúc (P) tại điểm có ho nh độ x khi hệ sau có nghiệm x 0 0 4 x0 2 2 
 2x  4  x m
x  0 x  6 0 0 0 0  4     
m  4 m  20 3 x  4x   2x 0 0 0
Câu 2. Gọi (d) là tiếp tuyến của (C) tại điểm có ho nh độ = a ìm a để (d) cắt lại (C) tại hai điểm E, F khác M
v trung điểm I của đoạn E, F nằm trên parabol P’ 2
y  x  4 .
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 21
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN A. a = 0 B. a = -1 C. a = 2 D. a = 1
Bài làm:.Phương trình tiếp tuyến (d): 4 4 a 4 2 3 a 2 3a y y'( ) a (x  ) a
 2a  4 (a  4 ) a (x  ) a   2a  4 3 2  (a  4 ) a x   2a  4 4 4 4
Phương trình ho nh độ giao điểm của (C) và (d): 4 4 x 2 3 3a 2 4 2 3 4 2
 2x  4  (a  4 ) a x
 2a  4  x  8x  4(a  4 )
a x  3a  8a  0 4 4 x a 2 2 2  (x  )
a (x  2ax  3a  8)  0   2 2
x  2ax  3a  8   0 (3)
(d) cắt (C) tại hai điểm E,F khác M  Phương trình 3 có hai nghiệm phân biệt khác a  2   a  2 2 2
'  a  3a  8  0      2 . (*) 2 6a  8  0 a     3
Tọa độ trung điểm I của E,F :  x x E Fx   ax  a I  2 I    4  4 7a 2       3 3a 2 y 6a 4
y  (a  4a)(a) 
 2a  4 (do I (d)) II 4  4 4 2 7a aa  0 2 2 2 2
I (P) : y  x  4  
 6a  4  a  4  7a (1 )  0   . 4 4 a  2  
So với điều kiện (*) nhận a = 0. Bài 15: 2 x x  1
Câu 1. ìm m để đồ thị hàm số y  tiếp xúc với Parabol 2
y x m . x  1 A. m  2  B. m  0 C. m  1  D. m  3
Bài làm: 1. Hai đường cong đã cho tiếp xúc nhau tại điểm có ho nh độ x  hệ phương trình 0 2 x x  1 0 0 2   x m (1) 0  x  1 0 
có nghiệm x . 2 x   2x 0 0 0  2x (2)  2 0 (x  1)  0 Ta có: 2
(2)  x (2x  5x  4)  0  x  0 thay v o 1 ta được m  1  . 0 0 0 Vậy m  1
 là giá trị cần tìm.
Câu 2. ìm m để đồ thị hai hàm số sau tiếp xúc với nhau 3 2
(C ) : y mx  (1 2 ) m x  2mx và 3
(C ) : y  3mx  3(1 2 )
m x  4m  2 . 1 2 1 3  6 1 8  6 5 3  6 1 3  6 A. m  , m B. m  , m C. m  , m D. m  , m  2 2 2 12 2 12 2 12
Bài làm: 2. (C ) và (C ) tiếp xúc nhau tại điểm có ho nh độ x  hệ phương trình sau có nghiệm 1 2 0 3 2 3 mx (1 2 )
m x  2mx  3mx  3(1  2 ) m x  4m  2 x : 0 0 0 0 0  0 2 2 3mx  2(1 2 )
m x  2m  9mx  3(1  2 ) m  0 0 0
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 22
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN 3 2 2mx (1 2 ) m x  (3  8 )
m x  4m  2  0 (1) 0 0 0   có nghiệm x 2 6mx  2(1 2 )
m x  3  8m  0 (2) 0  0 0 Ta có : 2
(1)  (x 1)(2mx (1 4 )
m x  4m  2)  0 0 0 0 x  1 0   2 2mx (1 4 )
m x  4m  2  0  0 0  1
Với x  1 thay vào (2), ta có: m  . 0 2  Với 2 2mx (1 4 )
m x  4m  2  0 (*) ta có : 0 0 x  1 0 2 
(2)  4mx x  1  4m  0  
(m  0 vì m  0 hệ vô nghiệm) 0 0 1 4mx  0  4m 1  4m Thay x  v o * ta được: 0 4m 2 2 (1 4 ) m (1  4 ) m   2  4m  0 8m 4m  2 3 6
 48m  24m  1  0  m  . 12 1 3  6 Vậy m  , m
là những giá trị cần tìm. 2 12
Câu 3. Tìm tham số m để đồ thị (Cm) của hàm số 3 2
y x  4mx  7mx  3m tiếp xúc với parabol   2 P y  –  1  1   3   1  A. m 2; 7  ;  1
B. m 5;  ;78
C. m  2;  ;1 D.  2;  ;1  4   4   4  3 2 2
x  4mx  7mx  3m x x 1 (1)
Bài làm: 3. (Cm) tiếp xúc với (P) tại điểm có ho nh độ x khi hệ 0 0 0 0 0  ( ) A có 0 2
3x  8mx  7m  2x 1  0 0 0 nghiệm x . 0 Giải hệ (A), 3 2
(1)  x  (4m  1)x  (7m  1)x  3m  1  0 0 0 0 x  1 2 0
 (x 1)(x  4mx  3m  1)  0   0 0 0 2
x  4mx  3m  1  0  0 0 2 x  1
x  4mx  3m1  0 Vậy (A) 0 0 0     2 2
3x  2(4m  1)x  7m  1  0 (2) 
3x  2(4m  1)x  7m  1  0 (2) 0 0  0 0
Thay x = 1 v o 2 ta được m = 2. 0 2 2
3x  2(4m1)x 7m1  0 (2)
3x  2(4m1)x 7m1  0 (2) Hệ 0 0 0 0    2 2
x  4mx  3m  1  0 (3) 
3x 12mx  9m  3  0 (4) 0 0  0 0
Trừ hai phương trình 2 v 4 ,vế với vế ta được. 4m x x
 (2m1)x m1 (5) 0 – 2 0 – 2m – 2 = 0 0 . 1 m  1 Khi m =
thì (5) trở th nh 0 = 3/2 sai do đó 5  x  2 0 2m  . 1
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 23
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN m  1
Thay x0 = 2m  v o phương trình 3 ,ta được 1 2  m  1   m  1   4m  3m 1      0  2m 1  2m 1 3 2 1
 4m 11m  5m  2  0  m  2  m    m  1. 4  1 
Vậy các giá trị m cần tìm là m 2;  ;1  4  . 2 x x  1
Bài 16: ho h m số y  có đồ thị x  1
Câu 1 iết phương trình tiếp tuyến của , biết tiếp tuyến song song với đường thẳng  : 3x  4y  1  0 . 3 3 3 3 3 5 A. y x  ; y
x  1 B. y x  3 ; y x  4 4 4 4 4 4 3 3 3 3 3 5 C. y x  9 ; y x  7 D. y x  ; y x  4 4 4 4 4 4 2 x  2x Ta có y '  . 2 (x  1) Gọi (
M x ; y ) là tọa độ tiếp điểm của tiếp tuyến d với (C) 0 0 2 2 x  2x x x  1 0 0 0 0 d : y  (x x )  . 2 0 (x  1) x  1 0 0  3 1
Bài làm: 1. Vì d song song với đường thẳng  : y x  , nên ta có: 4 4 2 x  2x 3 0 0 2
  x  2x  3  0  x  1  ,x  3 . 2 0 0 0 0 (x  1) 4 0  3 3 x  1
 phương trình tiếp tuyến: y x  . 0 4 4  3 5
x  3  phương trình tiếp tuyến: y x  . 0 4 4
Câu 2 iết phương trình tiếp tuyến của uất ph t từ ( M 1  ;3) .
A. y  3x  1; y  3  x
B. y  13 ; y  3  x
C. y  3 ; y  3  x 1
D. y  3 ; y  3  x 2   x 2x
Bài làm: 2. Ta có y '  . 2 (x  1) Gọi (
M x ; y ) là tọa độ tiếp điểm của tiếp tuyến d với (C) 0 0 2 2 x  2x x x  1 0 0 0 0 d : y  (x x )  2 0 (x  1) x  1 0 0 2 2 x  2x x x  1 Cách 1: 0 0 0 0
M d  3  ( 1   x )  2 0 (x  1) x  1 0 0 2 2 2
 3(x 1)  (x  2x )(x 1) (x 1)(x x 1) 0 0 0 0 0 0 0
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 24
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN 2 1
 2x  5x  2  0  x  2,x  . 0 0 0 0 2
 Với x  2  Phương trình tiếp tuyến y  3 . 0  1 Với x
 Phương trình tiếp tuyến y  3  x . 0 2
Cách 2: Gọi d l đường thẳng đi qua ( M 1
 ;3) , có hệ số góc k, khi đó phương trình d có dạng: y  ( k x  1)  3 2 x x  1 0 0 
k(x  1)  3 (1) 0  x  1
d tiếp c đồ thị tại điểm có ho nh độ x khi hệ phương trình sau có nghiệm x : 0  0 0 2 x   2x 0 0  k (2)  2 (x  1)  0 2 2 x x  1 x  2x Thế 2 v o 1 ta được: 0 0 0 0  (x  1)  3 2 0 x  1 (x  1) 0 0 2 1
 2x  5x  2  0  x  2,x  . 0 0 0 0 2
 Với x  2  k  0  Phương trình tiếp tuyến y  3 . 0  1 Với x   k  3
  Phương trình tiếp tuyến y  3  x . 0 2
Câu 3 iết phương trình tiếp tuyến của đi qua giao điểm hai đường tiệm cận của (C).
A. y  2x  1
B. y  3x  2
C. y  4x  3 D.Không tồn tại 2   x 2x
Bài làm: 3. Ta có y '  . 2 (x  1) Gọi (
M x ; y ) là tọa độ tiếp điểm của tiếp tuyến d với (C) 0 0 2 2 x  2x x x  1 0 0 0 0 d : y  (x x ) 
Đồ thị có hai tiệm cận x  1 và y x suy ra giao điểm của hai tiệm cận là I(1;1) . 2 0 (x  1) x  1 0 0 2 2 x  2x x x  1 Cách 1: 0 0 0 0
I d  1  (1  x )  2 0 (x  1) x  1 0 0 2 2
x 1  x  2x x x 1  2  0 vô nghiệm. 0 0 0 0 0
Vậy không có tiếp tuyến n o đi qua I .
Cách 2: Gọi d l đường thẳng đi qua I, có hệ số góc k  d : y  ( k x 1)  1 2 x x  1 0 0 
k(x 1)  1 0  x  1
d là tiếp xúc với đồ thị tại điểm có ho nh độ x khi hệ 0  có nghiệm x 0 2 x   2x 0 0 0  k  2 (x  1)  0 2 2 x x  1 x  2x
Thế k v o phương trình thứ hai ta được: 0 0 0 0   1 x  1 x  1 0 0 2 2
x x 1  x  2x x 1 phương trình vô nghiệm 0 0 0 0 0
Vậy qua I không có tiếp tuyến nào kẻ đến (C). Bài 17:
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 25
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN x  2
Câu 1. Cho hàm số: y
có đồ thị l v điểm A0; m X c định m để từ A kẻ được 2 tiếp tuyến đến (C) x  1
sao cho hai tiếp điểm tương ứng nằm về hai phía đối với trục Ox. m  1      m 1   m 1 m  1  A.  1 B.  2 C.D.  2 m    m   m  1  m    3  5  3
Bài làm: Cách 1: Gọi điểm (
M x ; y ) (C) . Tiếp tuyến  tại M của có phương trình 0 0 3  x  2 0 y  (x x )  . 2 0 (x  1) x  1 0 0 3x x  2 0 0
A    m   2  (
m x  1)  3x  (x  2)(x  1)  0 (với x  1 ) 2
 (m1)x  2(m 2)x m 2  0 2 (x  1) x  1 0 0 0 0 0 0 0 0 0 (*).
Yêu cầu bài toán  (*) có hai nghiệm a,b khác 1 sao cho
'  3(m  2)  0 m  1
(a  2)(b  2) ab  2(a  ) b  4    
0 hay là: m  1  0   2 .
(a  1)(b  1) ab  (a  ) b  1 m     3  m  2  0   3 m  1  Vậy 
2 là những giá trị cần tìm. m    3
Cách 2: Đường thẳng d đi qua , hệ số góc k có phương trình y kx m . x  2 0   kx m 0  x  1
d là tiếp c đồ thị tại điểm có ho nh độ x khi hệ 0 
có nghiệm x . Thế k v o phương trình thứ 0 3   0  k 2 (x   1) 0 nhất, ta đươc x  2 3  x 0 0 2 
m  (m 1)x  2(m  2)x m  2  0 (*). 2 0 0 x  1 (x  1) 0 0
Để từ A kẻ được hai tiếp tuyến thì (*) có hai nghiệm phân biệt khác 1
'  3(m  2)  0  m  2   m  1   (i) m    1
m  1  2(m  2)  m  2  0  x  2 x  2
Khi đó tọa độ hai tiếp điểm là: M (x ; y ), M (x ; y ) với x1,x2 là nghiệm của (*) và 1 2 y  ; y  1 1 1 2 2 2 1 2 x  1 x  1 1 2
x x  2(x x )  4
Để M1, M2 nằm về hai phía Ox thì 1 2 1 2 y .y  0   0 (1) 1 2
x x  (x x )  1 1 2 1 2 2(m  2) m  2
Áp dụng định lí Viet: x x  ; x x  . 1 2 1 2 m  1 m  1 9m  6 2  (1)   0  m   . 3  3  2 m  
Kết hợp với (i) ta có 
3 là những giá trị cần tìm. m   1
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 26
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN
Câu 2. Tìm tham số m để đồ thị (C) : 3 2
y  x  2(m  1)x  5mx  2m của hàm số tiếp xúc với trục hoành.  4   4   4 
A. m  0;1; 
B. m 0;1;  2 C. m  1  ; 2; 
D. m  0;1; 2;   3   3   3  3 2
x  2(m 1)x  5mx  2m  0
Bài làm: 2. (C) tiếp xúc với trục hoành tại điểm có ho nh độ x khi hệ 0 0 0  (A) có 0 2  3
x  4(m  1)x  5m  0  0 0 nghiệm x . 0 Giải hệ (A). 2 (
 x  2)(x  2mx  ) m  0 x  2 0 0 0 0 ( ) A     2 2
3x  4(m  1)x  5m  0 
3x  4(m  1)x  5m  0 (1)  0 0 0 0 2
x  2mx m  0 4 Hoặc 0 0 
Thay x = 2 v o 1 ta được m  . 2
3x  4(m  1)x  5m  0 0  3 0 0 2 2
x  2mx m  0 (2)
3x 6mx  3m  0 (3) Hệ 0 0 0 0    2 2
3x  4(m  1)x  5m  0 
3x  4(m  1)x  5m  0 (1) 0 0  0 0
Trừ hai phương trình 1 v 3 , vế với vế ta được m
(m  2)x  m x   . 0 0 m  2 m 2 2 m 2m Thay x   vào (1), ta được :   m  0 0 m  2 2 (m  2) m  2   3 2  4
m  3m  2m  0  m  0  m  1 m  2 .Vậy m 0;1; 2;  .  3  Câu 3. Gọi C
l đồ thị của hàm số y = 4 2
x  (m  1)x  4m . Tìm tham số m để C
tiếp xúc với đường thẳng m  m 
(d): y = 3 tại hai điểm phân biệt . A. m = 1  m = 3. B. m = 1  m = 16. C. m = 2  m = 13. D. m = 1  m = 13. 4 2
x (m 1)x  4m  3 (1)
Bài làm: 3. C tiếp xúc với (d) tại điểm có ho nh độ x khi hệ 0 0  (A) có nghiệm x . m  0 3
4x  2(m  1)x  0 (2) 0  0 0 m  1
Giải hệ (A), (2)  x  0 hoặc 2 x  0 0 2 3
Thay x = 0 vào 1 ta được m = . 0 4 2 m  1 2  m  1 (m  1) Thay 2 x  v o 1 ta được   4m    3 0 2  2  2 2
m 14m13  0  m  1  m  13. 3 3 Khi m  thì C
tiếp xúc với (d) tại chỉ một điểm (0;3) nên m 
không thỏa mãn yêu cầu của bài toán. m  4 4 Khi m= 1 thì 2 x  1  x  1
 ,suy ra C tiếp xúc với (d) tại hai điểm ( 1  ; 3 ). m  0 0 Khi m = 13 thì 2
x  7  x   7 ,suy ra C
tiếp xúc với (d) tại hai điểm (  7 ; 3) . Vậy các giá trị m cần tìm là m  0 0 m = 1  m = 13.
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 27
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN
Bài 18: Tìm tất cả c c điểm trên Oy sao cho từ đó ta có thể vẽ được ít nhất một tiếp tuyến đến đồ thị hàm số 2
y x  4x  2x  1 . 1 A. M(0;m) với 2   m  1 B. M(0;m) với   m  5 2 1 C. M(0;m) với 
m  1 D. M(0;m) với 1   m  5 2
Bài làm:: Xét ( M 0; )
m Oy Đường thẳng d đi qua , hệ số góc k có phương trình y kx m .  2
x  4x  2x  1  kx m 0 0 0 0 
d là tiếp c đồ thị tại điểm có ho nh đồ x khi hệ  4x  1 có nghiệm x . 0 0 1   k  0 2  4x  2x  1  0 0
hay k v o phương trình thứ nhất ta được: 2 4x x x  1 2 0 0
x  4x  2x  1  x   m 2 2 2
 4x  2x 1  4x x m 4x  2x 1 0  m   f (x ) 0 0 0 0 0 0 0 0 0 0 0 2 4x  2x  1 2 4x  2x  1 0 0 0 0 (*)
Để từ M kẻ được ít nhất một tiếp tuyến đến đồ thị  (*) có ít nhất một nghiệm. 3  x
Xét hàm số f( x ), ta có: 0 f '(x ) 
f '(x )  0  x  0 0 0 0 0 2 3
( 4x  2x  1) 0 0 1 1
Mặt khác: lim f (x ) 
; lim f (x )   0 0 x 2 x 2 Bảng biến thiên: x  0  0 f '(x )  0  0 1 f (x ) 0 1  1 2 2 1 (*) có nghiệm    m  1 . 2 1 Vậy M(0;m) với 
m  1 là những điểm cần tìm. 2
Bài 19: Cho hàm số: 3 y  4
x  3x  2 , có đồ thị là C .
Câu 1. Tìm a để phương trình 3 2
4x  3x  2a  3a  0 có hai nghiệm âm và một nghiệm dương; 1 A. 0  a
hoặc 1  a  5 .
B. 0  a  2 hoặc 2  a  9 . 2 1 3 C. 0  a  hoặc 1  a  .
D. 0  a  4 hoặc 6  a  89 . 2 2
Bài làm: 1. Phương trình 3 2
4x  3x  2a  3a  0 tương đương với phương trình 3 2 4
x  3x  2  2a  3a  2 .
Phương trình đã cho có hai nghiệm âm và một nghiệm dương khi v chỉ khi đường thẳng 2
y  2a  3a  2 cắt đồ thị 3 y  4
x  3x  2 tại ba điểm trong đó có hai điểm có ho nh độ âm và một điểm có ho nh độ dương ừ đồ thị suy 2
0  2a  3a 1 1 3 ra: 2
1  2a  3a  2  2 tức ta có hệ:  hay 0  a  hoặc 1  a  . 2
2a  3a  0 2 2
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 28
NGUYỄN BẢO VƯƠNG CHƯƠNG V. ĐẠO HÀM- TẬP 2C. PHƯƠNG TRÌNH TIẾP TUYẾN
Câu 2. Tìm những điểm trên đường thẳng y  3 để từ đó có thể vẽ được ba đường thẳng tiếp xúc với đồ thị C . 1 1 1 A. m  1
 hoặc  m  2 B. m  1  hoặc  m  3 3 2 1 1 1 C. m  2  hoặc  m D. m  3  hoặc 1  m  3 2 2
Bài làm: 2. Giả sử M  ;
m 3 l điểm cần tìm và d l đường thẳng qua M có hệ số góc là k , phương trình có
dạng: y k x m  3 .
Đường thẳng d tiếp xúc với đồ thị C tại điểm N x ; y khi hệ : 0 0  3  4
x  3x  2  k x m  3  0 0  0  
có nghiệm x , từ hệ suy ra 3 4
x  3x  2 '  k x m   3 ' 0 0 0     0   2x   2
1 4x  2 3m  1 x  3m  1  0 1 có nghiệm x . 0  0   0    0
Qua M kẻ được 3 đường thẳng tiếp xúc với C khi và chỉ khi phương trình 1 có 3 nghiệm x , tức phương 0 1 1 1 trình 2
4x  2 3m 1 x  3m  1  0 2 có hai nghiệm phân biệt khác hay m  1  hoặc  m  . 0   0   2 3 2 Bài 20: 2
x x m
Câu 1. Tìm tham số m để đồ thị hàm số C : y
với m  0 cắt trục hoành tại 2 điểm phân biệt A, B m x  1
sao cho tiếp tuyến tại 2 điểm A, B vuông góc với nhau. 1 1 1 4 A. m   B. m   C. m D. m   5 3 5 7   2x 1
Bài làm: 1. Hàm số cắt trục hoành thại hai điểm phân biệt A, B có hệ số góc là k  . x  1 2
x  2x m  1 Ta có: y'      
, đặt g x 2 x 2x m 1 . x  2 1
Theo bài toán, g x  0 có hai nghiệm phân biệt khác 1  . 1
heo đề, tiếp tuyến tại A và B vuông góc nhau tức k .k  1
 , tìm được m   . A B 5 2 2x
Câu 2. Cho hàm số y
có đồ thị là C ìm trên đường thẳng y x những điểm mà từ đó có thể kẻ được x  2
2 tiếp tuyến đến C , đồng thời 2 tiếp tuyến đó vuông góc với nhau. A. m  5   3 B. m  5   53 C. m  6   23 D. m  5   23
Bài làm: 2 Đường thẳng d đi qua điểm M ;
m m có hệ số góc là k , phương trình có dạng: y k x m  m . 2  2x0 
k x m m 0   x   2 0
d tiếp xúc C tại điểm có ho nh độ x khi hệ : 
có nghiệm x , từ đây ta tìm được 0 2 2x  8x  0 0 0     k x  22 0 m  5   23
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 29 NGUYỄN BẢO VƯƠNG
TỔNG BIÊN SOẠN VÀ TỔNG HỢP 250 BÀI TẬP TRẮC NGHIỆM ĐẠO HÀM TỰ LUYỆN
TẬP 3. CHƯƠNG V. ĐẠO HÀM LỚP 11
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 ĐỂ GẶP THẦY VƯƠNG, HOẶC LIÊN HỆ QUA:
LINK FACEBOOK Nguyễn Vương: https://www.facebook.com/phong.baovuong
TÀI LIỆU CHIA SẺ TẠI: http://tailieutoanhoc.vn/
Page: https://web.facebook.com/tracnghiemtoanthpt489/?ref=bookmarks Gmail: baovuong7279@gmail.com
[ALBA – CHƯ SÊ – GIA LAI]
NGUYỄN BẢO VƢƠNG CHƯƠNG V. ĐẠO HÀM Mục lục
Tổng hợp lần 1. CHƯƠNG V: ĐẠO HÀM ......................................................... 2
BÀI 1: ĐỊNH NGHĨA VÀ Ý NGHĨA CỦA ĐẠO HÀM ............................................................... 2
BÀI 2: QUY TẮC TÍNH ĐẠO HÀM ...................................................................................... 3
BÀI 3: ĐẠO HÀM CỦA HÀM SỐ LƯỢNG GIÁC ................................................................... 6
BÀI 4: VI PHÂN ............................................................................................................... 8
BÀI 5: ĐẠO HÀM CẤP CAO .............................................................................................. 9
Tổng hợp lần 2. CHƯƠNG V. ĐẠO HÀM ......................................................... 11
Tổng hợp lần 3. CHƯƠNG V. ĐẠO HÀM ......................................................... 24
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 1
NGUYỄN BẢO VƢƠNG CHƯƠNG V. ĐẠO HÀM
Tổng hợp lần 1. CHƯƠNG V: ĐẠO HÀM
BÀI 1: ĐỊNH NGHĨA VÀ Ý NGHĨA CỦA ĐẠO HÀM
Câu 1. Cho hàm số f(x) liên tục tại x . Đạ 0
o hàm của f(x) tại x0 là:
f (x h)  f (x ) A. f(x 0 0 0) B. h
f (x h)  f (x )
f (x h)  f (x h) C. 0 0 lim
(nếu tồn tại giới hạn) D. 0 0 lim
(nếu tồn tại giới hạn) h0 h h0 h
Câu 2. Cho hàm số f(x) là hàm số trên R định bởi f(x) = x2 và x0 R. Chọn câu đúng: A. f/(x 2 0) = x0 B. f/(x0) = x0 C. f/(x0) = 2x0 D. f/(x0) không tồn tại. 1
Câu 3. Cho hàm số f(x) xác định trên 0;  bởi f(x) = . Đạo hàm của f(x) tại x0 = 2 là: x 1 1 1 A. B– C. D. – 1 2 2 2 2
Câu 4. Phƣơng trình tiếp tuyến của đồ thị của hàm số y = (x+1)2(x–2) tại điểm có hoành độ x = 2 là: A. y = –8x + 4 B. y = –9x + 18 C. y = –4x + 4 D. y = –8x + 18
Câu 5. Phƣơng trình tiếp tuyến của đồ thị của hàm số y = x(3–x)2 tại điểm có hoành độ x = 2 là A. y = –12x + 24 B. y = –12x + 26 C. y = 12x –24 D. y = 12x –26
Câu 6. Điểm M trên đồ thị hàm số y = x3 – 3x2 – 1 mà tiếp tuyến tại đó có hệ số góc k bé nhất trong tất cả các tiếp
tuyến của đồ thị thì M, k là: A. M(1; –3), k = –3 B. M(1; 3), k = –3 C. M(1; –3), k = 3
D. M(–1; –3), k = –3 ax b
Câu 7. Cho hàm số y =
có đồ thị cắt trục tung tại A(0; –1), tiếp tuyến tại A có hệ số góc k = –3. Các giá trị x  1 của a, b là: A. a = 1; b=1 B. a = 2; b=1 C. a = 1; b=2 D. a = 2; b=2 2
x  2mx m
Câu 8. Cho hàm số y =
. Giá trị m để đồ thị hàm số cắt trục Ox tại hai điểm và tiếp tuyến của đồ thị x  1
tại hai điểm đó vuông góc là: A. 3 B. 4 C. 5 D. 7 2 x  3x  1
Câu 9. Cho hàm số y =
và xét các phƣơng trình tiếp tuyến có hệ số góc k = 2 của đồ thị hàm số là: x  2
A. y = 2x–1, y = 2x–3
B. y = 2x–5, y = 2x–3
C. y = 2x–1, y = 2x–5 D. y = 2x–1, y = 2x+5 2 x  3x  3
Câu 10. Cho hàm số y =
, tiếp tuyến của đồ thị hàm số vuông góc với đƣờng thẳng x  2 3y – x + 6 là:
A. y = –3x – 3; y= –3x– 4
B. y = –3x – 3; y= –3x + 4
C. y = –3x + 3; y= –3x–4
D. y = –3x–3; y=3x– 4
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 2
NGUYỄN BẢO VƢƠNG CHƯƠNG V. ĐẠO HÀM 5
Câu 11. Tìm m để tiếp tuyến của đồ thị hàm số y = (2m – 1)x4 – m +
tại điểm có hoành độ x = –1 vuông góc với 4
đƣờng thẳng 2x – y – 3 = 0 2 1 1 5 A. B. C. D. 3 6 6 6 x  2
Câu 12. Cho hàm số y
, tiếp tuyến của đồ thị hàm số kẻ từ điểm (–6; 4) là: x  2 1 7 A. y = –x–1, y = x
B. y= –x–1, y =– 1 7 x  4 2 4 2 1 7 C. y = –x+1, y =– 1 7 x D. y= –x+1, y =  x  4 2 4 2 3x  4
Câu 13. Tiếp tuyến kẻ từ điểm (2; 3) tới đồ thị hàm số y  là: x  1 A. y = 3x; y = x+1 B. y = –3x; y = x+1 C. y = 3; y = x–1 D. y = 3–x; y = x+1
Câu 14. Cho hàm số y = x3 – 6x2 + 7x + 5 (C), trên (C) những điểm có hệ số góc tiếp tuyến tại điểm nào bằng 2?
A. (–1; –9); (3; –1) B. (1; 7); (3; –1)
C. (1; 7); (–3; –97) D. (1; 7); (–1; –9) 
Câu 15. Tìm hệ số góc của tiếp tuyến với đồ thị y = tanx tại điểm có hoành độ x = : 4 1 2 A. k = 1 B. k = C. k = D. 2 2 2
Câu 16. Cho đƣờng cong (C): y = x2. Phƣơng trình tiếp tuyến của (C) tại điểm M(–1; 1) là: A. y = –2x + 1 B. y = 2x + 1 C. y = –2x – 1 D. y = 2x – 1 2 x x
Câu 17. Cho hàm số y
. Phƣơng trình tiếp tuyến tại A(1; –2) là: x  2
A. y = –4(x–1) – 2 B. y = –5(x–1) + 2
C. y = –5(x–1) – 2
D. y = –3(x–1) – 2 1
Câu 18. Cho hàm số y = x3 – 3x2 + 7x + 2. Phƣơng trình tiếp tuyến tại A(0; 2) là: 3 A. y = 7x +2 B. y = 7x – 2 C. y = –7x + 2 D. y = –7x –2
Câu 19. Gọi (P) là đồ thị hàm số y = 2x2 – x + 3. Phƣơng trình tiếp tuyến với (P) tại điểm mà (P) cắt trục tung là: A. y = –x + 3 B. y = –x – 3 C. y = 4x – 1 D. y = 11x + 3 3x  1
Câu 20. Đồ thị (C) của hàm số y
cắt trục tung tại điểm A. Tiếp tuyến của (C) tại A có phƣơng trình là: x  1 A. y = –4x – 1 B. y = 4x – 1 C. y = 5x –1 D. y = – 5x –1
Câu 21. Gọi (C) là đồ thị của hàm số y = x4 + x. Tiếp tuyến của (C) vuông góc với đƣờng thẳng d: x + 5y = 0 có phƣơng trình là: A. y = 5x – 3 B. y = 3x – 5 C. y = 2x – 3 D. y = x + 4
BÀI 2: QUY TẮC TÍNH ĐẠO HÀM 2 x x
Câu 22. Cho hàm số y
đạo hàm của hàm số tại x = 1 là: x  2 A. y/(1) = –4 B. y/(1) = –5 C. y/(1) = –3 D. y/(1) = –2
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 3
NGUYỄN BẢO VƢƠNG CHƯƠNG V. ĐẠO HÀM x
Câu 23. Cho hàm số y  . y/(0) bằng: 2 4  x 1 1 A. y/(0)= B. y/(0)= C. y/(0)=1 D. y/(0)=2 2 3
Câu 24. Cho hàm số f(x) xác định trên R bởi f(x) = 2
x . Giá trị f/(0) bằng: A. 0 B. 2 C. 1 D. Không tồn tại
Câu 25. Đạo hàm cấp 1của hàm số y = (1–x3)5 là: A. y/ = 5(1–x3)4 B. y/ = –15(1–x3)4 C. y/ = –3(1–x3)4 D. y/ = –5(1–x3)4
Câu 26. Đạo hàm của hàm số f(x) = (x2 + 1)4 tại điểm x = –1 là: A. –32 B. 30 C. –64 D. 12 2x  1
Câu 27. Hàm số y  có đạo hàm là: x  1 1 3 1 A. y/ = 2 B. / y   C. / y   D. / y  2 (x  1) 2 (x  1) 2 (x  1) 1 Câu 28. Hàm số 3
x x có đạo hàm là: 3 2 x  2x 2 x  2x 2 x  2x A. / y B. / y C. y/ = –2(x – 2) D. / y  2 (1  x) 2 (1  x) 2 (1  x) 2  1 x
Câu 29. Cho hàm số f(x) =   
 . Đạo hàm của hàm số f(x) là:  1 x  2  (1 x) 2  (1 x) 2(1  x) A. / f (x)  B. / f (x)  C. / f (x)  D. 3 (1  x) 3 x(1  x) 2 x(1  x)  / 2(1 x)
f (x)  (1 x)
Câu 30. Cho hàm số y = x3 – 3x2 – 9x – 5. Phƣơng trình y/ = 0 có nghiệm là: A. {–1; 2} B. {–1; 3} C. {0; 4} D. {1; 2}
Câu 31. Cho hàm số f(x) xác định trên R bởi f(x) = 2x2 + 1. Giá trị f/(–1) bằng: A. 2 B. 6 C. –6 D. 3
Câu 32. Cho hàm số f(x) xác định trên R bởi f(x) 3
x .Giá trị f/(–8) bằng: 1 1 A. B. – 1 C. D. – 1 12 12 6 6 2x
Câu 33. Cho hàm số f(x) xác định trên R \{1} bởi f (x)  . Giá trị f/(–1) bằng: x  1 1 A. B. – 1 C. –2 D. Không tồn tại 2 2
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 4
NGUYỄN BẢO VƢƠNG CHƯƠNG V. ĐẠO HÀM  2 x  1  1   Câu 34. (x 0)
Cho hàm số f(x) xác định bởi f (x)   x . Giá trị f/(0) bằng: 0 (x   0) 1 A. 0 B. 1 C. D. Không tồn tại. 2
Câu 35. Cho hàm số f(x) xác định trên R bởi f(x) = ax + b, với a, b là hai số thực đã cho. chọn câu đúng: A. f/(x) = a B. f/(x) = –a C. f/(x) = b D. f/(x) = –b
Câu 36. Cho hàm số f(x) xác định trên R bởi f(x) = –2x2 + 3x. Hàm số có đạo hàm f/(x) bằng: A. –4x – 3 B. –4x +3 C. 4x + 3 D. 4x – 3
Câu 37. Cho hàm số f(x) xác định trên D  0;  
 cho bởi f(x) = x x có đạo hàm là: 1 3 1 x x A. f/(x) = x B. f/(x) = x C. f/(x) = D. f/(x) = x  2 2 2 x 2 3
Câu 38. Cho hàm số f(x)= 3
k x x (k  ) R . Để f/(1)= thì ta chọn: 2 9 A. k = 1 B. k = –3 C. k = 3 D. k = 2 2  1 
Câu 39. Hàm số f(x) =  x
 xác định trên D  0;  . Có đạo hàm của f là:  x  1 1 1 1 A. f/(x) = x + –2 B. f/(x) = x – C. f/(x) = x D. f/(x) = 1 + x 2 x x 2 x 3  1 
Câu 40. Hàm số f(x) =  x
 xác định trên D  0;  . Đạo hàm của hàm f(x) là:  x  3  1 1 1  3  1 1 1  A. f/(x) =  x     B. f/(x) =  x     2 2  x x x x x  2 2  x x x x x  3  1 1 1  3 1 C. f/(x) =   x    
D. f/(x) = x x  3 x   2 2  x x x x x x x x
Câu 41. Cho hàm số f(x) = –x4 + 4x3 – 3x2 + 2x + 1 xác định trên R. Giá trị f/(–1) bằng: A. 4 B. 14 C. 15 D. 24 2x  1
Câu 42. Cho hàm số f(x) =
xác định R\{1}. Đạo hàm của hàm số f(x) là: x  1 2 3 1 1  A. f/(x) =  B. f/(x) = C. f/(x) = D. f/(x) = x  12 x12 x12 x12 1
Câu 43. Cho hàm số f(x) = 1  
xác định R*. Đạo hàm của hàm số f(x) là: 3 x 1 1 1 1 A. f/(x) = 3  x x B. f/(x) = 3 x x C. f/(x) =  D. f/(x) =  3 3 3 3x x 3 2 3x x 2 x  2x  5
Câu 44. Với f (x)  . f/(x) bằng: x  1
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 5
NGUYỄN BẢO VƢƠNG CHƯƠNG V. ĐẠO HÀM A. 1 B. –3 C. –5 D. 0 x
Câu 45. Cho hàm số y f (x)  . Tính y/(0) bằng: 2 4  x 1 1 A. y/(0)= B. y/(0)= C. y/(0)=1 D. y/(0)=2 2 3 2 x x
Câu 46. Cho hàm số y =
, đạo hàm của hàm số tại x = 1 là: x  2 A. y/(1)= –4 B. y/(1)= –3 C. y/(1)= –2 D. y/(1)= –5
BÀI 3: ĐẠO HÀM CỦA HÀM SỐ LƯỢNG GIÁC
Câu 47. Hàm số y = sinx có đạo hàm là: A. y/ = cosx B. y/ = – cosx C. y/ = – sinx D. / 1 y  cosx
Câu 48. Hàm số y = cosx có đạo hàm là: A. y/ = sinx B. y/ = – sinx C. y/ = – cosx D. / 1 y  sinx
Câu 49. Hàm số y = tanx có đạo hàm là: 1 1 A. y/ = cotx B. y/ = C. y/ = D. y/ = 1 – tan2x 2 cos x 2 sin x
Câu 50. Hàm số y = cotx có đạo hàm là: 1 1 A. y/ = – tanx B. y/ = – C. y/ = – D. y/ = 1 + cot2x 2 cos x 2 sin x 1 Câu 51. Hàm số y =
(1+ tanx)2 có đạo hàm là: 2 A. y/ = 1+ tanx B. y/ = (1+tanx)2
C. y/ = (1+tanx)(1+tanx)2 D. y/ = 1+tan2x
Câu 52. Hàm số y = sin2x.cosx có đạo hàm là:
A. y/ = sinx(3cos2x – 1)
B. y/ = sinx(3cos2x + 1) C. y/ = sinx(cos2x + 1) D. y/ = sinx(cos2x – 1) sin x Câu 53. Hàm số y = có đạo hàm là: x
x cos x  sin x
x cos x  sin x
x sin x  cos x A. / y B. / y C. / y D. 2 x 2 x 2 x  /
x sin x cos x y  2 x
Câu 54. Hàm số y = x2.cosx có đạo hàm là:
A. y/ = 2xcosx – x2sinx B. y/ = 2xcosx + x2sinx
C. y/ = 2xsinx – x2cosx D. y/ = 2xsinx + x2cosx
Câu 55. Hàm số y = tanx – cotx có đạo hàm là: 1 4 4 1 A. y/ = B. y/ = C. y/ = D. ) y/ = 2 cos 2x 2 sin 2x 2 cos 2x 2 sin 2x
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 6
NGUYỄN BẢO VƢƠNG CHƯƠNG V. ĐẠO HÀM
Câu 56. Hàm số y = 2 sin x  2 cos x có đạo hàm là: A. / 1 1 y   B. / 1 1 y   sin x cos x sin x cos x x x x x C. / cos sin y   D. / cos sin y   sin x cos x sin x cos x 2
Câu 57. Hàm số y = f(x) = cos( có f/(3) bằng: x) 8 4 3 A. 2 B. C. D. 0 3 3 x
Câu 58. Hàm số y = tan2 2 có đạo hàm là: x x x sin 2 sin sin x A. / 2 y B. / 2 y C. / 2 y D. y/ = tan3 2 2 x x x cos 3 cos 3 2 cos 2 2 2
Câu 59. Hàm số y = cot 2x có đạo hàm là: 2  x 2   x 2  x A. / 1 cot 2 y B. / (1 cot 2 ) y C. / 1 tan 2 y D. cot 2x cot 2x cot 2x 2   / (1 tan 2x) y  cot 2x   
Câu 60. Cho hàm số y = cos3x.sin2x. y/    3  bằng:             1 A. y/          3  = –1 B. y/  3  = 1 C. y/  3  = – 1 D. y/ 2  3  = 2    cos 2x
Câu 61. Cho hàm số y = . y/   1  sin x  6  bằng:             A. y/          6  = 1 B. y/  6  = –1 C. y/  6  =2 D. y/  6  =–2
Câu 62. Xét hàm số f(x) = 3 cos 2x . Chọn câu sai:    2  sin 2x    A. f  1    B. / f (x)  C. / f    1 D. 3.y2.y/ + 2sin2x =  2  3 2 3 cos 2x  2  0 2   
Câu 63. Cho hàm số y = f(x) = sin x  cos x . Giá trị / f   bằng:  16  2 2 2 A. 0 B. 2 C. D.    
Câu 64. Cho hàm số y f ( )
x  tan x  cot x . Giá trị / f   bằng:  4 
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 7
NGUYỄN BẢO VƢƠNG CHƯƠNG V. ĐẠO HÀM 2 1 A. 2 B. C. 0 D. 2 2 1   
Câu 65. Cho hàm số y f (x)  Giá trị / f   bằng: sin x  2  1 A. 1 B. C. 0 D. Không tồn tại. 2  5    
Câu 66. Xét hàm số y f (x)  2 sin   x  Giá trị / f   bằng:  6   6  A. –1 B. 0 C. 2 D. –2  2 
Câu 67. Cho hàm số y f (x)  tan x    Giá trị / f 0 bằng:  3  A. 4 B. 3 C. – 3 D. 3
Câu 68. Cho hàm số y f ( )
x  2 sin x . Đạo hàm của hàm số y là: A. / y  2 cos x B. / 1 y  cos x C. / 1 y  2 x cos D. / 1 y x x x cos x   
Câu 69. Cho hàm số y = cos3x.sin2x. Tính / y   bằng:  3              A. / y  1    B. / 1 y    C. / 1 y     D. / y    1  3   3  2  3  2  3  cos x   
Câu 70. Cho hàm số y f (x)  Tính / y   bằng: 1  sin x  6              A. / y   =1 B. / y   =–1 C. / y   =2 D. / y   =–2  6   6   6   6  BÀI 4: VI PHÂN
Câu 71. Cho hàm số y = f(x) = (x – 1)2. Biểu thức nào sau đây chỉ vi phân của hàm số f(x)? A. dy = 2(x – 1)dx B. dy = (x–1)2dx C. dy = 2(x–1) D. dy = (x–1)dx
Câu 72. Xét hàm số y = f(x) = 2
1 cos 2x . Chọn câu đúng: sin 4x sin 4x
A. df (x) 
dx B. df (x)  dx 2 2 1  cos 2x 2 1  cos 2x cos 2x sin 2x
C. df (x)  dx
D. df (x)  dx 2 1  cos 2x 2 2 1  cos 2x
Câu 73. Cho hàm số y = x3 – 5x + 6. Vi phân của hàm số là: A. dy = (3x2 – 5)dx
B. dy = –(3x2 – 5)dx C. dy = (3x2 + 5)dx D. dy = (–3x2 + 5)dx 1
Câu 74. Cho hàm số y =
. Vi phân của hàm số là: 3 3x 1 1 1 A. dy dx B. dy dx C. dy   dx D. 4 dy x dx 4 4 x 4 x
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 8
NGUYỄN BẢO VƢƠNG CHƯƠNG V. ĐẠO HÀM x  2
Câu 75. Cho hàm số y =
. Vi phân của hàm số là: x  1 dx 3dx 3  dx dx A. dy       B. dy C. dy D. dy x  2 1 x 2 1 x 2 1 x 2 1 2 x x  1
Câu 76. Cho hàm số y =
. Vi phân của hàm số là: x  1 2 x  2x  2 2x  1 2x  1 A. dy   dx B. dy dx C. dy   dx D. 2 (x  1) 2 (x  1) 2 (x  1) 2 x  2x  2 dy dx 2 (x  1)
Câu 77. Cho hàm số y = x3 – 9x2 + 12x–5. Vi phân của hàm số là:
A. dy = (3x2 – 18x+12)dx
B. dy = (–3x2 – 18x+12)dx
C. dy = –(3x2 – 18x+12)dx
D. dy = (–3x2 + 18x–12)dx
Câu 78. Cho hàm số y = sinx – 3cosx. Vi phân của hàm số là:
A. dy = (–cosx+ 3sinx)dx
B. dy = (–cosx–3sinx)dx C. dy = (cosx+ 3sinx)dx
D. dy = –(cosx+ 3sinx)dx
Câu 79. Cho hàm số y = sin2x. Vi phân của hàm số là: A. dy = –sin2xdx B. dy = sin2xdx C. dy = sinxdx D. dy = 2cosxdx tan x
Câu 80. Vi phân của hàm số y  là: x 2 x sin(2 x) A. dy dx B. dy dx 2 4x x cos x 2 4x x cos x 2 x  sin(2 x) 2 x  sin(2 x) C. dy
dx D. dy   dx 2 4x x cos x 2 4x x cos x
Câu 81. Hàm số y = xsinx + cosx có vi phân là:
A. dy = (xcosx – sinx)dx B. dy = (xcosx)dx
C. dy = (cosx – sinx)dx D. dy = (xsinx)dx x Câu 82. Hàm số y = . Có vi phân là: 2 x  1 2 1  x 2x 2 1  x 1 A. dy dx B. dy dx C. dy dx D. dy dx 2 2 (x  1) 2 (x  1) 2 (x  1) 2 2 (x  1)
BÀI 5: ĐẠO HÀM CẤP CAO x
Câu 83. Hàm số y
có đạo hàm cấp hai là: x  2 1 4 4 A. y// = 0 B. // y  / /   / /   C. y D. y 2 2 x  22 x2 x2
Câu 84. Hàm số y = (x2 + 1)3 có đạo hàm cấp ba là: A. y/// = 12(x2 + 1) B. y/// = 24(x2 + 1) C. y/// = 24(5x2 + 3) D. y/// = –12(x2 + 1)
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 9
NGUYỄN BẢO VƢƠNG CHƯƠNG V. ĐẠO HÀM
Câu 85. Hàm số y = 2x  5 có đạo hàm cấp hai bằng: A. // 1 y B. // 1 y
(2x  5) 2x  5 2x  5 C. // 1 y   D. // 1 y  
(2x  5) 2x  5 2x  5 2 x x  1 Câu 86. Hàm số y =
có đạo hàm cấp 5 bằng: x  1 120 120 1 1 A. (5) y   B. (5) yC. (5) yD. (5) y   5 (x  1) 5 (x  1) 5 (x  1) 5 (x  1) Câu 87. Hàm số y = 2
x x  1 có đạo hàm cấp hai bằng: 3 2x  3x 2 2x  1 A. // y   / /  B. y  2 1  x  2 1  x 2 1  x 3 2x  3x 2 2x  1 C. // y  / /  D. y   2 1  x  2 1  x 2 1  x
Câu 88. Cho hàm số f(x) = (2x+5)5. Có đạo hàm cấp 3 bằng: A. f///(x) = 80(2x+5)3
B. f///(x) = 480(2x+5)2
C. f///(x) = –480(2x+5)2
D. f///(x) = –80(2x+5)3
Câu 89. Đạo hàm cấp 2 của hàm số y = tanx bằng: 2 sin x 1 1 2 sin x A. // y   B. // y C. // y   D. // y  3 cos x 2 cos x 2 cos x 3 cos x
Câu 90. Cho hàm số y = sinx. Chọn câu sai:       A. / y  sin x    B. / /
y  sinx   C. /// 3 y  sin x    D.  2   2  (4) y  sin2  x 2 2  x  3x
Câu 91. Cho hàm số y = f(x) =
. Đạo hàm cấp 2 của f(x) là: 1  x 1 2 2  2 A. // y  2  B. // y C. // y D. // y  2 (1  x) 3 (1  x) 3 (1  x) 4 (1  x)      
Câu 92. Xét hàm số y = f(x) = cos 2x  
 . Phƣơng trình f(4)(x) = –8 có nghiệm x 0;   là:  3   2      A. x = B. x = 0 và x = C. x = 0 và x = D. x = 0 và x = 2 6 3 2
Câu 93. Cho hàm số y = sin2x. Hãy chọn câu đúng: A. 4y – y// = 0 B. 4y + y// = 0 C. y = y/tan2x D. y2 = (y/)2 = 4 1
Câu 94. Cho hàm số y = f(x) =  xét 2 mệnh đề: x
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 10
NGUYỄN BẢO VƢƠNG CHƯƠNG V. ĐẠO HÀM 2 6 (I): y// = f//(x) = (II): y/// = f///(x) =  . 3 x 4 x Mệnh đề nào đúng: A. Chỉ (I) B. Chỉ (II) đúng
C. Cả hai đều đúng D. Cả hai đều sai. 2 sin x Câu 95. Nếu // f (x)  , thì f(x) bằng: 3 cos x 1 A. B. – 1 C. cotx D. tanx cos x cos x 2 x x  2
Câu 96. Cho hàm số f(x) =
xác định trên D = R\{1}. Xét 2 mệnh đề: x  1 2 4 (I): y/ = f/(x) = 1    0, x
  1, (II): y// = f//(x) =  0, x   1 2 (x  1) 2 (x  1) Chọn mệnh đề đúng: A. Chỉ có (I) đúng
B. Chỉ có (II) đúng
C. Cả hai đều đúng D. Cả hai đều sai.
Câu 97. Cho hàm số f(x) = (x+1)3. Giá trị f//(0) bằng: A. 3 B. 6 C. 12 D. 24    Câu 98. Với 3 2 f ( )
x  sin x x thì // f    bằng:  2  A. 0 B. 1 C. –2 D. 5
Câu 99. Giả sử h(x) = 5(x+1)3 + 4(x + 1). Tập nghiệm của phƣơng trình h//(x) = 0 là: A. [–1; 2] B. (–; 0] C. {–1} D.  1 3
Câu 100. Cho hàm số y  . Tính y
 1có kết quả bằng: x  3 3 3 3 1 3 3 3 1 A. y (1)  B. y (1)  C. y (1)   D. y (1)   8 8 8 4
Câu 101. Cho hàm số y = f(x) = (ax+b)5 (a, b là tham số). Tính f(10)(1) A. f(10)(1)=0 B. f(10)(1) = 10a + b C. f(10)(1) = 5a D. f(10)(1)= 10a   
Câu 102. Cho hàm số y = sin2x.cosx. Tính y(4)  
 6  có kết quả là: 1  1  1  1  1  1  1  1  A. 4 3    B. 4 3    C. 4 3     D. 4  3    2  2  2  2  2  2  2  2 
Tổng hợp lần 2. CHƯƠNG V. ĐẠO HÀM Câu 1. Số gia của hàm số 2
y x  2 tại điểm x  2 ứng với số gia x   1 bằng bao nhiêu? 0 A. 13 B. 9 C. 5 D. 2 Câu 2. Số gia của hàm số 2
y x  1 tại điểm x  2 ứng với số gia x
  0,1 bằng bao nhiêu? 0 A. – 0, 01 B. 0,21 C. 0,99 D. 11,1 Câu 3. Đạo hàm của hàm số 3 2
y  2x  (4x  3) bằng biểu thức nào sau đây? A. 2
6x  8x  3 . B. 2
6x  8x  3 . C. 2 2(3 x  4 ) x . D. 2 2(3 x  8x)
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 11
NGUYỄN BẢO VƢƠNG CHƯƠNG V. ĐẠO HÀM Câu 4. Cho hàm số 3 2 f ( )
x x x  3x . Giá trị f (  1  ) bằng bao nhiêu? A. 2  . B. 1  . C. 0 . D. 2 . 3 Câu 5. Cho hàm số 2
g(x)  9x x . Đạo hàm của hàm số g(x) dương trong trường hợp nào? 2 A. x  3 . B. x  6 . C. x  3 . D. x  3  . Câu 6. Cho hàm số 3 2 f ( )
x x  3x  3 . Đạo hàm của hàm số f(x) dương trong trường hợp nào?
A. x  0  x  1 .
B. x  0  x  2 .
C. 0  x  2 . D. x  1. 4 Câu 7. Cho hàm số 5 f (x) 
x  6 . Số nghiệm của phương trình f (  x)  4 là bao nhiêu? 5 A. 0 . B. 1 . C. 2 .
D. Nhiều hơn 2 nghiệm. 2 Câu 8. Cho hàm số 3 f (x) 
x  1 . Số nghiệm của phương trình f (  x)  2  là bao nhiêu? 3 A. 0. B. 1. C. 2. D. 3. Câu 9. Cho hàm số 4 f ( )
x x  2x . Phương trình f (
 x)  2 có bao nhiêu nghiệm? A. 0. B. 1. C. 2. D. 3. 3 Câu 10. Cho hai hàm số 2 f ( ) x x  5 ; 2 (
g x)  9x x . Giá trị của x là bao nhiêu để f (  x)  g ( ) x ? 2 4 5 A. 4  . B. 4. C. . D. . 5 4 Câu 11.
Hàm số nào sau đây có đạo hàm bằng 2(3x  1) ? A. 3 2x  2x . B. 2
3x  2x  5 . C. 2 3x  x  5 . D. 2 (3 x 1) Câu 12.
Hàm số nào sau đây có đạo hàm bằng 3(2x  1) ? 3 A. 2 (2x  1) . B. 2 3x x . 2
C. 3 x(x  1) . D. 3 2x  3x Câu 13. Cho hàm số 3 2 f ( )
x  2x  3x  36x 1 . Để f (  )
x  0 thì x có giá trị thuộc tập hợp nào? A.  3  ;  2 . B. 3;  2  . C.  6  ;  4 . D. 4;  6  . Câu 14. Cho hàm số 3 2 f ( )
x x  2x  7x  5 . Để f (  )
x  0 thì x có giá trị thuộc tập hợp nào?  7   7  A.  ;1   . B.  1;   .  3   3   7   7  C.   ;1 . D. 1;    .  3   3  Câu 15. Cho hàm số 3 2 f ( )
x x  2x  7x  3 . Để f (  )
x  0 thì x có giá trị thuộc tập hợp nào?
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 12
NGUYỄN BẢO VƢƠNG CHƯƠNG V. ĐẠO HÀM  7   7  A.  ;1   . B. 1;    .  3   3   7   7  C.   ;1 . D.  ;1 .  3   3  1 Câu 16. Cho hàm số 3 2 f (x) 
x  2 2x  8x  1 . Để f (  )
x  0 thì x có giá trị thuộc tập hợp nào? 3 A. 2 2 . B.  2  2. C. 2; 2 . D.  . Câu 17. Đạo hàm của hàm số 5 2
y  2x   3 bằng biểu thức nào sau đây? x 2 2 A. 4 10x  . B. 4 10x  . 2 x 2 x 2 2 C. 4 10x   3 . D. 10x  . 2 x 2 x Câu 18. Đạo hàm của hàm số 5 4
f (x)  2x   5 tại x  1
 bằng số nào sau đây? x A. 21. B. 14. C. 10. D. – 6 . Câu 19. Cho 2 f ( ) x  5x ; 2 ( g )
x  2(8x x ) . Bất phương trình f (  x)  g ( ) x có nghiệm là? 8 6 8 8 A. x  . B. x  . C. x  . D. x   . 7 7 7 7 Câu 20.
Phương trình tiếp tuyến với đồ thị 3 2
y x  2x x  1 tại điểm có hoành độ x  1  là: 0
A. y  8x  3 .
B. y  8x  7 .
C. y  8x  8 .
D. y  8x  11. Câu 21.
Tiếp tuyến với đồ thị 3 2
y x x  1 tại điểm có hoành độ x  1 có phương trình là: 0
A. y x .
B. y  2x .
C. y  2x  1.
D. y x  2 . Câu 22.
Hệ số góc của tiếp tuyến với đồ thị 3 2
y  2x  3x  2 tại điểm có hoành độ x  2 là: 0 A. 18. B. 14. C. 12. D. 6. Câu 23.
Tiếp tuyến với đồ thị 3 2
y x x tại điểm có hoành độ x  2  có phương trình là: 0
A. y  4x  8 .
B. y  20x  56 .
C. y  20x  14 .
D. y  20x  24 . Câu 24.
Hệ số góc của tiếp tuyến với đồ thị hàm số 3 2
y  2x  3x  5 tại điểm có hoành độ 2  là: A. 38. B. 36. C. 12. D. – 12. Câu 25.
Hệ số góc của tiếp tuyến với đồ thị hàm số 4 3 2
y x x  2x  1 tại điểm có hoành độ 1  là: A. 11. B. 4. C. 3. D. – 3. Câu 26.
Tiếp tuyến với đồ thị hàm số 3 2
y x x  1 tại điểm có hoành độ x  1  có hệ số góc bằng: 0 A. 7. B. 5. C. 1. D. – 1.
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 13
NGUYỄN BẢO VƢƠNG CHƯƠNG V. ĐẠO HÀM Câu 27. Cho hàm số 4 2 f ( )
x x  2x  3 . Với giá trị nào của x thì f (  x) dương? A. x  0 . B. x  0 . C. x  1  . D. 1   x  0 . Câu 28. Cho hàm số 3 2 f ( )
x x x x  5 . Với giá trị nào của x thì f (  x) âm? 1 1 A. 1   x  . B.x  1. 3 3 1 2
C.   x  1 . D.   x  2 . 3 3 1 Câu 29. Cho hàm số 3
f (x)  mx x . Với giá trị nào của m thì x  1
 là nghiệm của bất phương trình 3 f (  ) x  2 ? A. m  3 . B. m  3 . C. m  3 . D. m  1 . Câu 30. Cho hàm số 3 f ( )
x  2mx mx . Với giá trị nào của m thì x  1 là nghiệm của bất phương trình f (  ) x  1 ? A. m  1  . B. m  1  . C. 1   m  1. D. m  1 . 3 Câu 31. Cho hàm số 2
f (x)  2x x . Đạo hàm của hàm số f(x) nhận giá trị dương khi x nhận giá trị thuộc 2
tập hợp nào dưới đây?  2   2  A.   ;  . B.   ;  .  3   3   3   3  C.   ;  . D.   ;  .  2   2  2 x  1 Câu 32.
Cho hàm số f (x) 
. Đạo hàm của hàm số f(x) nhận giá trị âm khi x nhận giá trị thuộc tập 2 x  1 hợp nào dưới đây? A. ; 0 . B. 0;  . C.  ;  1  1  ;    . D.  1  ;1   . 1 Câu 33. Cho hàm số 3 2 f (x) 
x  3 2x  18x  2 . Để f (
 x)  0 thì x có giá trị thuộc tập hợp nào dưới đây? 3 A. 3 2;  . B. 3 2;   . C.  . D. . 1 1 Câu 34. Cho hàm số 3 2 f (x) 
x x  6x  5 . Để f (
 x)  0 thì x có giá trị thuộc tập hợp nào dưới đây? 3 2 A.  ;  3   2; . B.  3  ; 2 . C.  2  ; 3 . D.  ;  4    3;   . 1 1 Câu 35. Cho hàm số 3 2 f (x) 
x x  12x  1 . Để f (
 x)  0 thì x có giá trị thuộc tập hợp nào dưới đây? 3 2 A.  ;  3    4;    . B.  3  ; 4   .
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 14
NGUYỄN BẢO VƢƠNG CHƯƠNG V. ĐẠO HÀM C.  4  ; 3   . D.  ;  2  3; . Câu 36. Cho hàm số 2 f ( )
x  2x  3x . Để f (
 x)  0 thì x có giá trị thuộc tập hợp nào dưới đây?  1   1  A.   ;  . B.  0;  .  3   3   1 2   1  C.  ;  . D. ;    .  3 3   3  Câu 37. Đạo hàm của hàm số 2 f ( )
x x  5x bằng biểu thức nào sau đây? 1 2x  5 A. . B. . 2 2 x  5x 2 x  5x 2x  5 2x  5 C. . D.  . 2 2 x  5x 2 x  5x Câu 38. Đạo hàm của hàm số 2 f ( )
x  2  3x bằng biểu thức nào sau đây? 6  x 2 6  x A. . B. . 2 2  3x 2 2 2  3x 3x 3  x C. . D. . 2 2  3x 2 2  3x Câu 39.
Đạo hàm của hàm số f ( )
x  (x  2)(x  3) bằng biểu thức nào sau đây? A. 2x  5 . B. 2x  7 . C. 2x  1. D. 2x  5 . 2x  3 Câu 40.
Đạo hàm của hàm số f (x) 
bằng biểu thức nào sau đây? 2x  1 12 8 A.    . B. . 2x  12 2x12 4 4 C.   . D. . 2x  12 2x12 x  4 Câu 41.
Đạo hàm của hàm số f (x) 
bằng biểu thức nào sau đây? 2x  1 7 7 A.   . B. . 2x  12 2x12 9 9 C.   . D. . 2x  12 2x12 x  4 Câu 42.
Đạo hàm của hàm số f (x) 
bằng biểu thức nào sau đây? 2  5x 18 13 A.    . B. . 2  5x2 25x2 3 22 C.  . D. . 2  5x2 25x2
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 15
NGUYỄN BẢO VƢƠNG CHƯƠNG V. ĐẠO HÀM 2  3x Câu 43.
Đạo hàm của hàm số f (x) 
bằng biểu thức nào sau đây? 2x  1 7 4 A.    . B. . 2x  12 2x12 8 1 C.  . D. . 2x  12 2x12 Câu 44.
Hàm số nào sau đây có đạo hàm luôn dương với mọi giá trị thuộc tập xác định của hàm số đó? 3x  2 3x  2 A. y  . B. y  . 5x  1 5x  1 x  2 x  2 C. y  . D. y  . 2x  1 x  1 Câu 45.
Hàm số nào sau đây có đạo hàm luôn âm với mọi giá trị thuộc tập xác định của hàm số đó? x  2 x  2 A. y  . B. y  . x  1 x  1 3x  2 3x  2 C. y  . D. y  . x  1 x  1 3x  2 Câu 46.
Tiếp tuyến với đồ thị hàm số f (x) 
tại điểm có hoành độ x  1 có hệ số góc bằng bao 2x  3 0 nhiêu? A. 13 B. 1  . C. 5  . D. 13  . x  5 Câu 47.
Tiếp tuyến với đồ thị hàm số f (x) 
tại điểm có hoành độ x  3 có hệ số góc bằng bao x  2 0 nhiêu? A. 3 B. 3  . C. 7  . D. 10  . 3x  5 Câu 48.
Đạo hàm của hàm số f (x) 
x tại điểm x  1 bằng bao nhiêu? x  3 7 1 A. 3  B. 4 . C. . D. . 2 2 x  3 Câu 49.
Đạo hàm của hàm số f (x) 
 4x tại điểm x  1 bằng bao nhiêu? x  3 5 5 25 11 A. B. . C. . D. . 8 8 16 8 x  1 Câu 50.
Đạo hàm của hàm số f (x) 
 4x tại điểm x  1 bằng bao nhiêu? x  1 1 1 3 3 A. B. . C. . D. . 2 2 4 2 Câu 51. Đạo hàm của hàm số 4 f ( )
x x x  2 tại điểm x  1 bằng bao nhiêu? 17 9 9 3 A. B. . C. . D. . 2 2 4 2 Câu 52. Đạo hàm của hàm số 3 f ( )
x x x  5 tại điểm x  1 bằng bao nhiêu? 7 5 7 3 A. B. . C. . D. . 2 2 4 2
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 16
NGUYỄN BẢO VƢƠNG CHƯƠNG V. ĐẠO HÀM 1 Câu 53.
Đạo hàm của hàm số f (x) 
bằng biểu thức nào sau đây? 2 x  1 x 2x A.   . B. . x  2 2 1 x 12 2 2x 2x C.   . D. . x  12 2 x 12 2 1 Câu 54.
Đạo hàm của hàm số f (x) 
bằng biểu thức nào sau đây? 2 x  1 2 2x 2  x A.  . B. . x  12 2 x 12 2 1 2x C.   . D. . x  12 2 x 12 2 2 x  1 Câu 55.
Đạo hàm của hàm số f (x) 
bằng biểu thức nào sau đây? 2 x  1 2 4x 4x A.  . B. . x  12 2 x 12 2 2  4  x C.  . D. . x  12 2 x 12 2 1 Câu 56.
Đạo hàm của hàm số f (x) 
bằng biểu thức nào sau đây? 2 2  x 2x 2x A.   . B. . 2  x 2 2 2x 2 2 2 1 C.    . D. . 2  x 2 2 2x 2 2 2 1  x Câu 57.
Đạo hàm của hàm số y
bằng biểu thức nào sau đây? 2 2  x 2x 2x A.   . B. . 2  x 2 2 2x 2 2 2 1 C.    . D. . 2  x 2 2 2x 2 2 1 Câu 58.
Đạo hàm của hàm số y
bằng biểu thức nào sau đây? 2 x x  1 (  2x  1) 2  (x  1) A.  . B. .
x x  12 2
x x12 2 (  2x 1) 2(2x  1) C.  . D. .
x x  12 2
x x12 2 2 x x  1 Câu 59.
Đạo hàm của hàm số y
bằng biểu thức nào sau đây? 2 x x  1
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 17
NGUYỄN BẢO VƢƠNG CHƯƠNG V. ĐẠO HÀM 2(2x  1) 2(2x  2) A.    . B. .
x x  12 2
x x12 2 2(2x  1) 2(2x  1) C.   . D. .
x x  12 2
x x12 2 2 x x  3 Câu 60.
Đạo hàm của hàm số y
bằng biểu thức nào sau đây? 2 x x  1 2(2x  1) 4(2x  1) A.    . B. .
x x  12 2
x x12 2 4(2x  1) 4(2x  4) C.    . D. .
x x  12 2
x x12 2 1 Câu 61.
Đạo hàm của hàm số y
bằng biểu thức nào sau đây? 2 2x x  1 (4x  1) 4x  1 A.   . B. .
2x x  12 2
2x x12 2 (4x  1) 1  C.   . D. .
2x x  12 2
2x x12 2 2 2x x  5 Câu 62.
Đạo hàm của hàm số y
bằng biểu thức nào sau đây? 2 2x x  2 3  (4x 1) 3  (4x  1) A.   . B. .
2x x  22 2
2x x22 2 3  (  4x  1) C.   . D. .
2x x  22 2
2x x22 2 Câu 63. Đạo hàm của hàm số 3 2 2
y  (x x ) bằng biểu thức nào sau đây? A. 5 3 6x  4x . B. 5 4
6x 10x  4x . C. 5 4 3
6x 10x  4x . D. 5 4 3
6x 10x  4x . Câu 64. Đạo hàm của hàm số 5 2 2
y  (x  2x ) bằng biểu thức nào sau đây? A. 9 3 10x  16x . B. 9 6 3
10x 14x  16x . C. 9 6 3
10x  28x  16x . D. 9 6 3
10x  28x  8x . Câu 65. Đạo hàm của hàm số 3 2 3
y  (x x ) bằng biểu thức nào sau đây? A. 3 2 2 3(x x ) . B. 3 2 2 2
3(x x ) (3x  2 ) x . C. 3 2 2 2
3(x x ) (3x  ) x . D. 3 2 2
3(x x )(3x  2 ) x . Câu 66.
Đạo hàm của hàm số     2 3 2 y x x x
bằng biểu thức nào sau đây? 2 A.  3 2
x x x  2 2
3x  2x   1 . B.  3 2
x x x 2 2 2
3x  2x x . C.  3 2
x x x 2 2 3x  2x .
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 18
NGUYỄN BẢO VƢƠNG CHƯƠNG V. ĐẠO HÀM D.  3 2
x x x 2 2
3x  2x   1 . 2  2  3x Câu 67.
Đạo hàm của hàm số y  
 bằng biểu thức nào sau đây?  2x  1  1  4 2  3x 4  2  3x A.  . B. . . x  .2 2x  1 2 1  x 2 2x  1 2 1 16 2  3x  2  3x C.  . D. 2   . x  .2 2x  1 2 1  2x  1  Câu 68. Đạo hàm của hàm số 2 2
y  (2x x  1) bằng biểu thức nào sau đây? A. 2 (4x  1) . B. 2 2
2(2x x  1)(4x  ) x . C. 2 2
2(2x x  1) (4x 1) . D. 2
2(2x x  1)(4x  1) . Câu 69. Đạo hàm của hàm số 2
y  3x  2x  12 bằng biểu thức nào sau đây? 1 4x A. . B. . 2
2 3x  2x  12 2
2 3x  2x  12 3x  1 6x C. . D. . 2
2 3x  2x  12 2
2 3x  2x  12 Câu 70. Đạo hàm của hàm số 2 3
y x  4x bằng biểu thức nào sau đây? 1 2 x  6x A. . B. . 2 3 2 x  4x 2 3 2 x  4x 2 x  12x 2 x  2x C. . D. . 2 3 2 x  4x 2 3 2 x  4x Câu 71.
Cho hàm số y  2x  2 . Biểu thức f (1)  f (
 1) có giá trị là bao nhiêu? 1 3 A. . B. . 2 2 9 5 C. . D. . 4 2 Câu 72.
Cho f x  x x  2 2 ( ) 3 3 . Biểu thức f (
 1) có giá trị là bao nhiêu? A. 1 B. 1  . C. 2  . D. 12  . Câu 73.
Cho f x   x x  2 2 ( ) 3 4 1 . Biểu thức f (
 2) có giá trị là bao nhiêu? A.90 B. 80. C. 40. D.10. Câu 74.
Đạo hàm của hàm số y  tan 3x bằng biểu thức nào sau đây? 3x 3 A. . B. . 2 cos 3x 2 cos 3x 3 3 C.  . D.  . 2 cos 3x 2 sin 3x Câu 75.
Đạo hàm của hàm số y  tan 2x tại x = 0 là số nào sau đây? A. 2  B. 0 . C. 1 . D. 2 . Câu 76.
Đạo hàm của hàm số y  cos x bằng biểu thức nào sau đây?
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 19
NGUYỄN BẢO VƢƠNG CHƯƠNG V. ĐẠO HÀM os c x sinx A. . B. . 2 cos x 2 cos x sinx sinx C.  . D.  . 2 cos x cos x Câu 77.
Đạo hàm của hàm số y  cos 2x bằng biểu thức nào sau đây? sin2x sin2x A. . B.  . 2 cos 2x cos 2x sin2x sin2x C. . D.  . cos 2x 2 cos x Câu 78.
Đạo hàm của hàm số y  sin x bằng biểu thức nào sau đây? os c x cosx A. . B.  . 2 sin x 2 sin x cosx 1 C. . D. . sin x 2 sin x Câu 79.
Đạo hàm của hàm số y  sin 3x bằng biểu thức nào sau đây? o c s3x 3cos3x A. . B. . 2 sin 3x 2 sin 3x 3cos3x  o c s3x C.  . D. . 2 sin 3x 2 sin 3x Câu 80.
Đạo hàm của hàm số y  tan 5x bằng biểu thức nào sau đây? 1 5  A. . B. . 2 cos 5x 2 sin 5x 3  5 C. . D. . 2 cos 5x 2 cos 5x Câu 81.
Đạo hàm của hàm số y  tan 3x tại x = 0 có giá trị là bao nhiêu? A. 3  . B. 0 . C. 3 . D. Không xác định. Câu 82. Đạo hàm của hàm số 2
y  tan 5x bằng biểu thức nào sau đây? 10 sin 5x A. 2 tan 5x . B. . 3 cos 5x 1  0sin 5x 5 sin 5x C. . D. . 3 cos 5x 3 cos 5x Câu 83.
Hàm số nào sau đây có đạo hàm y  x sin x ?
A. xcos x .
B. sinx  xcos x . C. sinx o c sx .
D. xcos x  sinx .    Câu 84.
Đạo hàm của hàm số y  cos  
3x  bằng biểu thức nào sau đây?  3        A. sin   3x  . B.  sin   3x  .  3   3 
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 20
NGUYỄN BẢO VƢƠNG CHƯƠNG V. ĐẠO HÀM       C. 3  sin   3x  . D. 3sin   3x  .  3   3     Câu 85.
Đạo hàm của hàm số y  sin  
2x  bằng biểu thức nào sau đây?  2        A. cos   2x  . B.  cos   2x  .  2   2        C. 2  cos   2x  . D. 2 cos   2x  .  2   2  Câu 86.
Đạo hàm của hàm số f x    x 10 2 ( ) 3
bằng biểu thức nào sau đây? A. x  x 9 2 10 3 . B.   9 2 10 3 x . C. x  x 9 2 20 3 . D. x  x 9 2 20 3 . Câu 87.
Đạo hàm số của hàm số y  2sin 2x  o
c s2x bằng biểu thức nào nào sau đây?
A. 4cos 2x  2sin 2x .
B. 4cos 2x  2sin 2x .
C. 2cos 2x  2sin 2x . D. 4
 cos2x  2sin2x . Câu 88.
Đạo hàm số của hàm số y  sin 3x  4 o
c s2x bằng biểu thức nào nào sau đây?
A. cos 3x  4sin 2x .
B. 3cos 3x  4sin 2x .
C. 3cos 3x  8sin 2x .
D. 3cos 3x  8sin 2x . Câu 89.
Đạo hàm của hàm số y  sin 5x bằng biểu thức nào sau đây? 5  o c s5x 5 o c s5x A. . B. . 2 sin 5x sin 5x o c s5x 5 o c s5x C. . D. . 2 sin 5x 2 sin 5x Câu 90.
Đạo hàm của hàm số f ( )
x  cos 4x bằng biểu thức nào sau đây? 2sin4x 2cos4x A.  . B.  . cos 4x cos 4x sin4x 2sin4x C.  . D. . 2 cos 4x cos 4x    Câu 91. Cho 2 2 f ( )
x  cos x  sin x . Biểu thức f   có giá trị là bao nhiêu?  4  A. 2  B. 0 . C. 1 . D. 2 .    Câu 92. Cho f ( )
x  sin 2x . Biểu thức f   có giá trị là bao nhiêu?  4  A. 1 . B. 0 . C. 1  . D. Không xác định. Câu 93.
Đạo hàm số của hàm số 3 y  o
c s 4x bằng biểu thức nào nào sau đây? A. 2 3sin 4x . B. 2 3cos 4x . C. 2 1  2cos 4 . x sin 4x . D. 2 3  cos 4 . x sin 4x . Câu 94.
Đạo hàm số của hàm số 2
y  sin 3x bằng biểu thức nào nào sau đây?
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 21
NGUYỄN BẢO VƢƠNG CHƯƠNG V. ĐẠO HÀM A. 6sin 6x . B. 3sin 6x . C. sin 6x . D. 2sin 3x . Câu 95.
Đạo hàm số của hàm số f (x)  sin 3x  o
c s2x bằng biểu thức nào nào sau đây?
A. cos 3x  sin 2x .
B. cos 3x  sin 2x .
C. 3cos 3x  2sin 2x . D. 3
 cos3x  2sin2x . Câu 96. Cho f ( )
x  tan 4x . Giá trị f (
 0) bằng số nào sau đây? A. 4  B. 1  . C. 1 . D. 4 . Câu 97.
Đạo hàm của hàm số y  cot 2x bằng biểu thức nào sau đây? 1  2  A. . B. . 2 sin 2x 2 sin 2x 2  2 C. . D. . 2 cos 2x 2 cos 2x Câu 98. Đạo hàm của hàm số 4
y  cot 2x bằng biểu thức nào sau đây? 3 8  cos 2x 3 8  cos 2x A. . B. . 5 sin 2x 6 sin 2x 3 8  cos 2x 3 4  cos 2x C. . D. . 2 sin 2x 5 sin 2x Câu 99.
Đạo hàm của hàm số y  cot x bằng biểu thức nào sau đây? 1 s inx A. . B.  . 2 cot x 2 cot x 1  1  C. . D. . 2 sin x cot x 2 2 sin x cot x Câu 100. Cho 6 6 f ( )
x  sin x  o c s x và 2 2 g( ) x  3sin . x o
c s x . Tổng f (  ) x  g (
 x) bằng biểu thức nào sau đây? A. 5 5 6(sin x  o
c s x  sinx.cosx) . B. 5 5 6(sin x  o
c s x  sinx.cosx) . C. 6. D. 0.
Câu 101. Vi phân của hàm số 5 2 y  2x
 5 là biểu thức nào sau đây? x  2   2  A. 4 10x    5dx . B. 4 10x   dx . 2  x  2  x   2   2  C. 4 10x   dx . D. 10x   dx . 2  x  2  x
Câu 102. Vi phân của hàm số 2
y x  5x là biểu thức nào sau đây? 1 2x  5 A. dx . B. dx . 2 2 x  5x 2 x  5x 2x  5 2x  5 C.dx . D. dx . 2 2 x  5x 2 2 x  5x
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 22
NGUYỄN BẢO VƢƠNG CHƯƠNG V. ĐẠO HÀM 2x  3
Câu 103. Vi phân của hàm số y
là biểu thức nào sau đây? 2x  1 7 8 A.dx . B.dx . 2 (2x  1) 2 (2x  1) 4 4 C.dx . D. dx . 2 (2x  1) 2 (2x  1) Câu 104.
Vi phân của hàm số y  tan 3x là biểu thức nào sau đây? 3 3x A. dx . B. dx . 2 cos 3x 2 cos 3x 3 3 C.dx . D.dx . 2 cos 3x 2 sin 3x Câu 105.
Vi phân của hàm số f ( )
x  cos x là biểu thức nào sau đây? cosx sinx A. dx . B. dx . 2 cos x 2 cos x sinx sinx C. dx . D. dx . cos x 2 cos x   
Câu 106. Vi phân của hàm số y  sin  
2x  bằng biểu thức nào sau đây?  2        A. cos   2x dx . B. 2  cos   2x dx .  2   2        C. 2  cos   2x dx . D. 2 cos   2x dx .  2   2  4
Câu 107. Đạo hàm cấp hai của hàm số 5 2 f (x) 
x  6x  7x bằng biểu thức nào sau đây? 5 A. 3 16x  12 . B. 3 16x  12x . C. 3 4x  12 . D. 2 16x  12 .
Câu 108. Đạo hàm cấp hai của hàm số 5 4
f (x)  2x   5 bằng biểu thức nào sau đây? x 4 4 A. 3 40x  . B. 3 40x  . 3 x 3 x 8 8 C. 3 40x  . D. 3 40x  . 3 x 3 x
Câu 109. Đạo hàm cấp hai của hàm số y  o
c s2x bằng biểu thức nào nào sau đây? A. 2  sin2x . B. 4  cos2x . C. 4  sin2x . D. 4cos 2x .
Câu 110. Đạo hàm cấp hai của hàm số y  sin 2x bằng biểu thức nào nào sau đây? A. sin 2x . B. 4  sin x . C. 4  sin2x . D. 2  sin2x .
Câu 111. Một chuyển động thẳng xác định bởi phương trình 3 2
S t  3t  5t  2 , trong đó tính t bằng giây
và tính S bằng mét. Gia tốc của chuyển động khi t = 3 là: A. 24 2 (m / s ) . B.17 2 (m / s ) .
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 23
NGUYỄN BẢO VƢƠNG CHƯƠNG V. ĐẠO HÀM C.14 2 (m / s ) . D.12 2 (m / s ) . 1 1
Câu 112. Cho hàm số 3 2 f (x) 
x x  12x  1 . Tập hợp các giá trị x để đạo hàm cấp 2 của f(x) không âm 3 2 là:  1   1  A. ;    . B. ;    .  2   2   1   1  C. ;    . D.  ;    . 2   2 
Tổng hợp lần 3. CHƯƠNG V. ĐẠO HÀM 1 Câu 1. Cho hàm số 2 y x  1 , Đặt 2
A x y'  2 y 1 . Chọn câu trả lời đúng: 2 A. 2 A x B. A  1  C. A  0
D. Tất cả đều sai Câu 2. Cho hàm số 3 2
y x  2x  1 . Nếu đặt 2
M xy'  y' 3x , thì ta có. A. M  0 B. M  1 C. M  1  D. M  2
Câu 3. Đạo hàm của hàm số y   13 x   13 13
13 1 x  tại x  1  bằng: 0 A. 676 B. 13 C. 26 D.0
Câu 4. Phương trình tiếp tuyến của đồ thị (C) của hàm số y f x 2
x  2x  4 tại điểm có hoành độ x  1  0 là: A. y  4  x  4 B. y  2  x  3
C. y  3x  5 D. y  4  x  3 2x  4
Câu 5. Đạo hàm của hàm số y  là: x  3 10 5 A. y '  B. y'  x  3
2x  3 2x  4x  3 5 x  3 C. y'  D. y'  2  
2x  4x  32 2x 4  x
Câu 6. Cho hàm số f x 3  tan
. Giá trị của f '2 bằng: 6 A. 6 B. 12 C. 63 D. 36
Câu 7. Cho hàm số f x 2  2cos 4x  
1 .Miền giá trị của f 'x là: A.  8  ;8   B.  4  ; 4   C.  1  ;1   D. ; 
Câu 8. Cho hàm số   2 f x
Tính giá trị của f '  1 là: x A. 1  B. 0 C. 2  D. 2 
Câu 9. Cho hàm số y   x là:    A. y'  0 B. yx   x 1 ' 2 C. yx   x 1 ' D. y     x 1 2 '
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 24
NGUYỄN BẢO VƢƠNG CHƯƠNG V. ĐẠO HÀM 3 2 x  2x
Câu 10. Đạo hàm của hàm số y   là:    5x x x 2 A. 1 B. 5 C. 6 D. 5x  1 3 2 x x
Câu 11. Đạo hàm của hàm số 2 3 y  2x  là: x  3 A. 2 x B. 2x C. 4x D. 6x  3 
Câu 12. Đạo hàm của hàm số y  sin   4x  là:  2  A. 4sin 4x B. 4  cos4x C. 4  sin4x D. 4cos 4x   
Câu 13. Đạo hàm của hàm số y  sinxtan   x là:  2  A. cos x B. sinx C. sinx D. cos x
Câu 14. Đạo hàm của hàm số y f x 5 5  kx là: k1 A. 3 60x B. 4 75x C. 4 60x D. 3 75x 1
Câu 15. Hàm số có đạo hàm bằng 2x  là: 2 x 3 x  1 3 x  5x  1 3 3x  3x 2 2x x  1 A. y B. y C. y D. y x x x x
Câu 16. Cho hàm số f x 3
 sin 1 x . Với mọi x , hàm số có đạo hàm bằng: A. 3 cos 1 xB. 3 cos 1 xC. 2 3
 sin 1 xcos1 xD. 2
3sin 1 xcos1 xCâu 17. Cho hàm số 3 2
y x  2x  2x  3 có đồ thị (C) . Phương trình tiếp tuyến của đồ thị (C) tại điểm M có
hoành đồ x  1 là: 0 A. y   2
3x  4x  2x   1  2
B. y  0x   1  2
C. y  x   1  2
D. y  x   1  2 2x  3
Câu 18. Tại mọi điểm x  4 , hàm số y  có đạo hàm là: 4  x 10 10 5 5 A. y '       B. y ' C. y ' D. y ' 4  x2 x42 4 x x42
Câu 19. Hàm số y xsin x  cos x có đạo hàm là:
A. y'  cos x  sinx
B. y''  x sin x
C. y'  sinx 2cosx
D. y''  xcos x
2x  1, x  1 
Câu 20. Cho hàm số f x  3, x  1
.Kết luận nào sau đây SAI?  2 x  2, x   1
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 25
NGUYỄN BẢO VƢƠNG CHƯƠNG V. ĐẠO HÀM
A. f x liên tục tại x  1
B. f x có đạo hàm tại x  1
C. f x liên tục va có đạo hàm tại x  1
D. f x liên tục tại x  1 nhưng không có đạo hàm tại x  1  x x
Câu 21. Cho hàm số f x sin 2 2, 0  
.Khẳng định nào sau đây là đúng 3x  2, x   0
A. f x không liên tục tại x  0
B. f x co đạo hàm tại x  0
C. f x liên tục tại x  0 và co đạo hàm tại x  0
D. f x liên tục tại x  0 và nhưng không có đạo hàm tại x  0
2x  3 khi x  3
Câu 22. Cho hàm số f x  
Khẳng định nào sau đây đúng? 2 x khi x  3
A. f x có đạo hàm trên
B. f x có đạo hàm trong khoảng 3; 
C. f x có đạo hàm trong khoảng ; 3
D. f x có đạo hàm trên  \  3      
Câu 23. Cho hàm số f x  xcos x  sinx . Giá trị của f
  f ''  bằng:  2   2  A. 2 B. 1 C. 1  D. 2 
Câu 24. Cho hàm số y xcos x  sinx có đồ thị (C). Hệ số của tiếp tuyến của đồ thị (C) tại điểm có hoành độ  x   lằ: 2   A. B. 2 C. 2  D. 2 2 Câu 25. Cho hàm số 3 2
y x  3x  1 có đồ thị là (C). Phương trình tiếp tuyến của đồ thị (C), song song với đường thẳng ( )
 : y  9x 10 là:
A. y  9x  6 hay y  9x  26
B. y  9x  6 hay y  9x  28
C. y  9x  6 hay y  9x  26
D. y  9x  6 hay y  9x  28
Câu 26. Đạo hàm cấp 2010 của hàm số 20
y  cos x x là: A. sin x B. s inx C. cosx D. cos x
Câu 27. Cho hàm số   2 1 f x x
x . giá trị của f '  1 bằng: x A. 1 B. 2 C. 3 D. 4
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 26
NGUYỄN BẢO VƢƠNG CHƯƠNG V. ĐẠO HÀM 1
Câu 28. Cho hàm số f x  4x
. Giá trị của f '2  f '  1 bằng: 2 x 15 23 13 15 A. B. C. D. 4 4 2 2
Câu 29. Đạo hàm của hàm số 2
y x x  1 bằng: x x 2 2x  1 2 2x  1 A. B. C. D. 2 2 x  1 x  1 2 x  1 2 2 x  1
Câu 30. Cho hàm số ux và vx có đạo hàm là u' và v' Khẳng định nào sau đây là sai>  u
u' v uv'  u
u' v uv'
A. uv'  u'v v'u
B. u v'  u' v' C. '    D. '    2  v v 2  v v ĐÁP ÁN 1B 2A 3D 4D 5C 6A 7A 8C 9D 10C 11D 12A 13B 14B 15B 16C 17C 18D 19D 20D 21D 22D 23D 24A 25A 26C 27B 28B 29C 30D
GIÁO VIÊN MUỐN MUA FILE WORD LIÊN HỆ 0946798489 27
Document Outline

  • Binder1.pdf
    • TẬP 1. KHÁI NIỆM ĐẠO HÀM, PHƯƠNG PHÁP TÍNH ĐẠO HÀM
    • VIẾT-PHƯƠNG-TRÌNH-TIẾP-TUYẾN-KHI-BIẾT-ĐIỂM-ĐI-QUA
    • TẬP-2B.-PHUONG-TRÌNH-TIẾP-TUYẾN-KHI-BIẾT-HỆ-SỐ-GÓC-1
    • TẬP-2C.-PHƯƠNG-TRÌNH-TIẾP-TUYẾN-ĐI-QUA-ĐIỂM-CHO-TRƯỚC
  • TẬP 3. 250 BÀI TẬP TRẮC NGHIỆM ĐẠO HÀM. CHƯƠNG V.LỚP 11. pdf.pdf