Chuyên đề đạo hàm Toán 11 – Lê Minh Tâm

Tài liệu gồm 98 trang, được biên soạn bởi thầy giáo Lê Minh Tâm, bao gồm lý thuyết và các dạng bài tập chuyên đề đạo hàm trong chương trình môn Toán 11, có đáp án và lời giải chi tiết.

130 65 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

 Biên soạn: LÊ MINH TÂM – 093.337.6281 1

Chương VII.

ĐẠO HÀM

 Bài 01. ĐẠO HÀM

A. Lý thuyết

1. Đạo hàm. .......................................................................................................................................2

2. Ý nghĩa hình học của đạo hàm ............................................................................................... 3

3. Ý nghĩa vật lý của đạo hàm ................................................................................................... 4

4. Số e............................................................................................................................................... 4

B. Bài tập

 Dạng 1. Tính đạo hàm tại 1 điểm bằng định nghĩa...........................................................5

 Dạng 2. Tính đạo hàm tại 1 điểm bất kỳ trên (a;b) bằng định nghĩa .........................8

 Dạng 3. Ý nghĩa hình học của đạo hàm ............................................................................ 10

 Dạng 4. Ý nghĩa vật lý của đạo hàm................................................................................. 12

 Dạng 5. Tìm tham số để hàm số có đạo hàm tại x

...................................................... 13

C. Luyện tập

 Bài 02. CÁC QUY TẮC TÍNH ĐẠO HÀM

A. Lý thuyết

1. Đạo hàm hàm số

yx

........................................................................................................... 19

2. Đạo hàm hàm số

yx

........................................................................................................ 19

3. Đạo hàm hàm số lượng giác ................................................................................................. 19

4. Đạo hàm của hàm số mũ và hàm số logarit ................................................................... 19

5. Các quy tắc tính đạo hàm .................................................................................................... 20

6. Đạo hàm của hàm hợp .......................................................................................................... 20

7. Đạo hàm cấp hai ...................................................................................................................... 21

B. Bài tập

 Dạng 1. Tính đạo hàm đa thức – hữu tỉ – căn thức........................................................ 22

 Dạng 2. Tính đạo hàm lượng giác ..................................................................................... 24

 Dạng 3. Tính đạo hàm mũ – logarit .................................................................................. 26

C. Luyện tập

Mục lục

 Biên soạn: LÊ MINH TÂM – 093.337.6281 2

Chương VII.

ĐẠO HÀM

1. Đạo hàm.

 Tính đạo hàm bằng định nghĩa:

Để tính đạo hàm của hàm số

 

y f x

tại

 

;x a b

, ta thực hiện theo các bước sau:

 Bước 1. Tính

   

f x f x

 Bước 2. Lập và rút gọn tỉ số

   

f x f x



với

 

;,x a b x x

 Bước 3. Tính giới hạn

   

lim

f x f x





Lý thuyết

Định nghĩa:

Cho hàm số xác định trên khoảng và .



Nếu tồn tại giới hạn hữu hạn thì giới hạn đó được gọi là đạo hàm

của tại điểm , tức là:

 Kí hiệu là hay .

Trong định nghĩa & quy tắc trên đây, thay bởi ta sẽ có định nghĩa và quy tắc tính

đạo hàm của hàm số tại điểm .

Chú ý

ĐẠO HÀM

 Biên soạn: LÊ MINH TÂM – 093.337.6281 3

Chương VII.

ĐẠO HÀM

2. Ý nghĩa hình học của đạo hàm

 Lời giải

........................................................................................................................

 Trong mặt phẳng tọa độ

Oxy

, cho đồ thị

 

của hàm số

 

y f x

và điểm

   

;M x y C

Xét

 

;M x f x

là một diểm di chuyển trên

 

Đường thẳng

là một cát tuyến của

 

Hệ số góc của cát tuyến

được tính bởi công thức

   

tan

f x f x







Khi cho

dần tới

thì

di chuyển trên

 

tới

Giả sử cát tuyến

có vị trí giới hạn là

thì

được gọi là tiếp tuyến của

 

tại

và

được gọi là tiếp điểm

Ta có hệ số góc của tiếp tuyến

là

 

   

 

tan lim tan lim

x x x x

f x f x

k f x







   



Ví dụ 2.1.

Cho hàm số và điểm

⑴ Vẽ đồ thị và tính .

⑵ Vẽ đường thẳng qua có hệ số góc . Nhận xét về vị trí tương đối

giữa và

 Biên soạn: LÊ MINH TÂM – 093.337.6281 4

Chương VII.

ĐẠO HÀM

3. Ý nghĩa vật lý của đạo hàm

4. Số e

Đạo hàm của đồ thị hàm số tại điểm là hệ số góc của tiếp tuyến của

tại điểm

Tiếp tuyến có phương trình:

 Nếu hàm số biểu thị quãng đường di chuyển của vật theo thời gian thì

biểu thị tốc độ tức thời của chuyển động tại thời điểm .

 Nếu hàm số biểu thị nhiệt độ

theo thời gian thì biểu thị tốc độ thay

đổi nhiệt độ theo thời gian tại thời điểm .

Người ta còn biết rằng là số vô tỉ và (Số thập phân vô hạn không tuần hoàn).

 Biên soạn: LÊ MINH TÂM – 093.337.6281 5

Chương VII.

ĐẠO HÀM

 Dạng 1. Tính đạo hàm tại 1 điểm bằng định nghĩa

 Lời giải

.......................................................................................................................................................

Bài tập

 Để tính đạo hàm của hàm số tại , ta thực hiện theo các bước sau:

 Bước 1. Tính .

 Bước 2. Lập và rút gọn tỉ số với và

 Bước 3. Tính giới hạn .

⑴ ⑵ ⑶

 Hàm số có đạo hàm tại điểm .

 Hàm số có đạo hàm tại điểm thì trước hết phải liên tục tại điểm đó.

Phương pháp

Ví dụ 1.1.

Tính đạo hàm bằng định nghĩa tại một điểm của các hàm số sau:

⑴ tại ⑵ tại

 Biên soạn: LÊ MINH TÂM – 093.337.6281 6

Chương VII.

ĐẠO HÀM

 Lời giải

.......................................................................................................................................................

 Lời giải

.......................................................................................................................................................

Ví dụ 1.2.

Tính đạo hàm bằng định nghĩa tại một điểm của các hàm số sau:

⑴ tại ⑵ tại

Ví dụ 1.3.

Tính đạo hàm bằng định nghĩa tại một điểm của các hàm số sau:

⑴ tại

⑵ tại

 Biên soạn: LÊ MINH TÂM – 093.337.6281 7

Chương VII.

ĐẠO HÀM

 Lời giải

.......................................................................................................................................................

Ví dụ 1.4.

Tìm để hàm số có đạo hàm tại

 Biên soạn: LÊ MINH TÂM – 093.337.6281 8

Chương VII.

ĐẠO HÀM

 Dạng 2. Tính đạo hàm tại 1 điểm bất kỳ trên (a;b) bằng định nghĩa

 Lời giải

.......................................................................................................................................................

 Để tính đạo hàm của hàm số tại , ta thực hiện theo các bước sau:

 Bước 1. Tính .

 Bước 2. Lập và rút gọn tỉ số với và

 Bước 3. Tính giới hạn .

 Hàm số có đạo hàm tại điểm thì trước hết phải liên tục tại điểm đó.

Phương pháp

Ví dụ 2.1.

Tính đạo hàm bằng định nghĩa của các hàm số sau:

⑴ ⑵

⑶ ⑷

⑸ ⑹

 Biên soạn: LÊ MINH TÂM – 093.337.6281 9

Chương VII.

ĐẠO HÀM

.......................................................................................................................................................

 Biên soạn: LÊ MINH TÂM – 093.337.6281 10

Chương VII.

ĐẠO HÀM

 Dạng 3. Ý nghĩa hình học của đạo hàm

 Lời giải

.......................................................................................................................................................

 Ý nghĩa hình học: (Phương trình tiếp tuyến)

Cho hàm số có đồ thị , .

Phương trình tiếp tuyến tại có dạng: .

Trong đó: hoành độ tiếp điểm.

tung độ tiếp điểm.

hệ số góc tiếp tuyến.

Bài toán: Viết phương trình tiếp tuyến của đồ thị hàm số tại .

 Bước 1. Tính .

 Bước 2. Từ .

 Bước 3. Hoàn thiện phương trình tiếp tuyến cần tìm .

Phương pháp

Ví dụ 3.1.

Viết phương trình tiếp tuyến của

⑴ Đồ thị hàm số tại điểm có hoành độ .

⑵ Đồ thị hàm số tại điểm có hoành độ .

⑶

Đồ thị hàm số tại điểm có tung độ .

 Biên soạn: LÊ MINH TÂM – 093.337.6281 11

Chương VII.

ĐẠO HÀM

.......................................................................................................................................................

 Biên soạn: LÊ MINH TÂM – 093.337.6281 12

Chương VII.

ĐẠO HÀM

 Dạng 4. Ý nghĩa vật lý của đạo hàm

 Lời giải

.......................................................................................................................................................

 Lời giải

.......................................................................................................................................................

 Ý nghĩa vật lý: (quãng đường, nhiệt độ, điện lượng)

 Nếu hàm số biểu thị quãng đường

di chuyển của vật theo thời gian thì biểu

thị tốc độ tức thời của chuyển động tại thời điểm .

 Nếu hàm số biểu thị nhiệt độ

theo thời gian thì biểu thị tốc độ thay đổi

nhiệt độ theo thời gian tại thời điểm .

Phương pháp

Ví dụ 4.1.

Một chất điểm chuyển động có phương trình chuyển động là (t

được tính bằng giây, s được tính bằng mét).

⑴ Tính đạo hàm của hàm số tại điểm .

⑵ Tính vận tốc tức thời của chuyển động tại thời điểm .

Ví dụ 4.2.

Cho biết điện lượng trong một dây dẫn theo thời gian biểu thị bởi hàm số

(t được tính bằng giây, Q được tính bằng Coulomb). Tính cường độ của dòng điện

trong dây dẫn tại thời điểm

 Biên soạn: LÊ MINH TÂM – 093.337.6281 13

Chương VII.

ĐẠO HÀM

 Dạng 5. Tìm tham số để hàm số có đạo hàm tại x

 Lời giải

.......................................................................................................................................................

 Lời giải

.......................................................................................................................................................

 Cho hàm số hoặc . Tìm tham số m để hàm

số có đạo hàm tại

 Bước 1. Xác định .

 Bước 2. Hàm số liên tục tại

 Bước 3. Tính ; .

 Bước 4. Hàm số có đạo hàm tại .

Phương pháp

Ví dụ 5.1.

Cho hàm số . Tìm

để hàm số có đạo hàm tại .

Ví dụ 5.2.

Cho hàm số . Tìm

, thì hàm số có đạo hàm tại ?

 Biên soạn: LÊ MINH TÂM – 093.337.6281 14

Chương VII.

ĐẠO HÀM

Câu 1. Tính đạo hàm của các hàm số sau tại các điểm đã chỉ:

⑴

 

21f x x

tại

2x 

⑵

 

2024 2023f x x

tại

1x 

⑶

 

21f x x x  

tại

1x 

⑷

 

21f x x

tại

2x 

⑸

 

21f x x x  

tại

1x 

⑹

 







tại

2x 

⑺

 





tại

2x 

⑻

 







tại

3x 

⑼

 

1f x x

tại

1x 

⑽

 

2023f x x

tại

2x 

Câu 2. Tính đạo hàm của các hàm số sau tại các điểm (nếu có):

⑴

 

2 3 3

khi

















. Tính

 



. ⑵

 

1 2 0

khi

















. Tính

 



⑶

 

f x x

. Tính

 



. ⑷

 

f x x x

. Tính

 



⑸

 

21f x x x  

. Tính

 



. ⑹

 

f x x x

. Tính

 



⑺

 

2023f x x

. Tính

 



. ⑻

 

2f x x x

. Tính

 



⑼





. Tính

 



. ⑽

 

1xx





. Tính

 





Câu 3. Tính đạo hàm của các hàm số sau tại các điểm đã chỉ (nếu có):

⑴

 

khi

x x x

















. Tính

 



⑵

 

khi

x x x





















. Tính

 



⑶

 

2 3 1

2 7 4

khi

x x x











  









. Tính

 



⑷

 

7 12

khi





















. Tính

 



⑸

 

khi

















. Tính

 



⑹

 

3 4 0

khi



  













. Tính

 



Luyện tập

 Biên soạn: LÊ MINH TÂM – 093.337.6281 15

Chương VII.

ĐẠO HÀM

⑺

 

2 1 1

khi

x x x



   

















. Tính

 



⑻

 

khi





















. Tính

 



⑼

 

khi





















. Tính

 



⑽

 

khi



















. Tính

 



Câu 4. Tính đạo hàm của các hàm số sau tại các điểm đã chỉ (nếu có):

⑴

 

khi





















. Tính

 



⑵

 

khi



















. Tính

 



⑶

 

3 1 2

khi























. Tính

 



⑷

 

4 8 8 4

khi



  















. Tính

 



Câu 5. Tìm tham số để hàm số có đạo hàm tại

⑴ Tìm

để hàm số

 

khi





















có đạo hàm tại điểm

1x 

⑵ Tìm

;ab

để hàm số

 

1 khi 0

ax bx x

ax b x



  







  





có đạo hàm tại điểm

0x 

⑶ Tìm

;ab

để hàm số

 

khi

ax b x





















có đạo hàm tại điểm

0x 

 Biên soạn: LÊ MINH TÂM – 093.337.6281 16

Chương VII.

ĐẠO HÀM

⑷ Tìm

;ab

để hàm số

 

2 1 1

3 2 1

khi

ax x x

x bx x



  







  





có đạo hàm tại điểm

1x 

Câu 6. Cho hàm số

24y x x  

có đồ thị

 

⑴ Tìm hệ số góc của tiếp tuyến của

 

tại điểm có hoành độ

1x 

thuộc

 

⑵ Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có

0x 

thuộc

 

⑶ Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có

1y 

thuộc

 

⑷ Viết phương trình tiếp tuyến của đồ thị hàm số biết hệ số góc tiếp tuyến bằng

4

⑸ Viết phương trình tiếp tuyến của đồ thị hàm số, biết tiếp tuyến đó song song với

đường thẳng

13yx

Câu 7. Cho hàm số





có đồ thị

 

⑴ Viết phương trình tiếp tuyến của đồ thị hàm số tại giao điểm của

 

với trục

⑵ Viết phương trình tiếp tuyến của đồ thị hàm số tại giao điểm của

 

với trục

⑶ Viết phương trình tiếp tuyến của đồ thị hàm số tại giao điểm của

 

với đường

thẳng

1yx

⑷ Viết phương trình tiếp tuyến của đồ thị hàm số biết hệ số góc của tiếp tuyến bằng

k 

⑸ Viết phương trình tiếp tuyến của đồ thị hàm số, biết tiếp tuyến đó song song với

đường thẳng

13yx

Câu 8. Cho hàm số

21y x x  

có đồ thị

 

⑴ Tìm hệ số góc của tiếp tuyến của hàm số trên tại điểm có

0x 

⑵ Viết phương trình tiếp tuyến của hầm số biết nó có

2.k 

⑶ Viết phương trình tiếp tuyến của hàm số trên, biết nó tạo với hai trục

Oxy

một tam

giác vuông cân tại

Câu 9. Một chất điểm chuyển động thẳng biến đổi đều với phương trình

 

21 s t t m  

⑴ Tìm vận tốc tức thời của vật tại thời điểm

2ts

⑵ Tìm vận tốc trung bình của chất điểm trong khoảng thời gian từ

0t 

tới

2ts

Câu 10. Một vật chuyển động thẳng xác định bởi phương trình

 

s s t

trong đó

được tính

bằng giây và

được tính bằng mét. Thực hiện các yêu cầu dưới đây:

⑴ Với

 

3s s t t t  

thì vận tốc của vật tại thời điểm

3st 

là bao nhiêu?

⑵ Với

 

7s s t t t  

thì vận tốc của vật tại thời điểm

4st 

là bao nhiêu?

 Biên soạn: LÊ MINH TÂM – 093.337.6281 17

Chương VII.

ĐẠO HÀM

⑶ Với

 

s s t t t   

thì vận tốc của vật tại thời điểm

10st 

là bao nhiêu?

⑷ Với

 

3 2

64s s t t t 

thì vận tốc của vật tại thời điểm

3st 

là bao nhiêu?

⑸ Với

 

2 10s s t t t   

thì vận tốc của vật tại thời điểm

3st 

là bao nhiêu?

⑹ Với

 

34s s t t t t   

thì vận tốc của vật tại thời điểm

4st 

là bao nhiêu?

⑺ Với

 

2 3 7s s t t t   

thì vận tốc của vật tại thời điểm

6st 

là bao nhiêu?

⑻ Với

 

coss s t t



  





thì vận tốc của vật tại thời điểm

2st 

là bao nhiêu?

⑼ Với

 

s s t t t  

thì vận tốc của vật tại thời điểm

4st 

là bao nhiêu?

⑽ Với

 

39s s t t t t   

thì vận tốc của vật tại thời điểm

5st 

là bao nhiêu?

Câu 11. Một chất điểm chuyển động theo phương trình

 

s s t

trong đó

được tính bằng giây

và

được tính bằng mét. Thời gian để vận tốc của chất điểm đạt giá trị lớn nhất

⑴ Với

 

10 9s t t t t   

trong khoảng 10 giây đầu tiên.

⑵ Với

 

9 10s tt tt   

trong 12 giây đầu tiên.

⑶ Với

 

6s t t t  

trong 10 giây đầu tiên.

⑷ Với

 

s t t t  

trong 10 giây đầu tiên.

⑸ Với

 

s t t t  

trong 10 giây đầu tiên.

⑹ Với

 

s t t t  

trong 9 giây đầu tiên.

⑺ Với

 

s t t t

trong 5 giây đầu tiên.

⑻ Với

3 20

s t t   

trong 10 giây đầu tiên.

Câu 12. Một vật chuyển động thẳng xác định bởi phương trình

 

s s t

trong đó

được tính

bằng giây và

được tính bằng mét.

⑴ Với

 

2 6 3 1s s t t t t    

thì gia tốc của vật tại thời điểm

3st 

là bao nhiêu?

⑵ Với

 

4 10 9s s t t t   

thì gia tốc của vật tại thời điểm vận tốc bằng

là bao

nhiêu?

⑶ Với

 

35s s t t t   

thì gia tốc của vật tại tại giây thứ

là bao nhiêu?

⑷ Với

 

3 9 1s s t t t t    

thì gia tốc của vật tại tại thời điểm vật dừng lại là bao

nhiêu?

 Biên soạn: LÊ MINH TÂM – 093.337.6281 18

Chương VII.

ĐẠO HÀM

⑸ Với

 

3 5 2s s t t t t    

thì gia tốc của vật tại giây thứ

là bao nhiêu?

⑹ Với

 

3 3 10s s t t t t    

thì gia tốc của vật tại thời điểm vật dừng lại là bao

nhiêu?

⑻ Với

 

s s t t t t    

thì gia tốc của vật tại thời điểm

2st 

là bao nhiêu?

Câu 13. Một vật chuyển động thẳng xác định bởi phương trình

 

s s t

trong đó

được tính

bằng giây và

được tính bằng mét. Hỏi:

⑴ Gia tốc tại thời điểm vận tốc triệt tiêu với

 

39s s t t t t   

là bao nhiêu?

⑵ Gia tốc tại thời điểm vận tốc triệt tiêu với

 

3 9 27s s t t t t    

là bao nhiêu?

⑶ Vận tốc tại thời điểm gia tốc triệt tiêu với

 

39s s t t t t    

là bao nhiêu?

⑷ Vận tốc tại thời điểm gia tốc triệt tiêu với

 

3s s t t t  

là bao nhiêu?

⑸ Vận tốc tại thời điểm gia tốc bằng không với

 

2 3 4 ,s s t t t t   

là bao nhiêu?

⑹ Vận tốc tại thời điểm gia tốc triệt tiêu với

 

3 36

s s t t t t   

là bao nhiêu?

⑺ Gia tốc tại thời điểm vận tốc triệt tiêu với

 

3 9 2020s s t t t t     

là bao nhiêu?

⑻ Vận tốc tại thời điểm gia tốc triệt tiêu với

 

2 3 4s s t t t t   

là bao nhiêu?

⑼ Vận tốc tại thời điểm gia tốc triệt tiêu với

 

3 9 2024s s t t t t    

là bao nhiêu?

⑽ Vận tốc tại thời điểm gia tốc của vật đạt giá trị nhỏ nhất trong 20 giây đầu tiên với

 

4 3 2

6 10

s t t t t t   

là bao nhiêu?

--------------------Hết--------------------

 Biên soạn: LÊ MINH TÂM – 093.337.6281 19

Chương VII.

ĐẠO HÀM

1. Đạo hàm hàm số

yx

2. Đạo hàm hàm số

yx

3. Đạo hàm hàm số lượng giác

⑴ Hàm số

sinyx

có đạo hàm trên và

 

sin cosxx





⑵ Hàm số

cosyx

có đạo hàm trên và

 

cos sinxx





⑶ Hàm số

tanyx

có đạo hàm tại mọi

xk

và

 

tan

cos





⑷ Hàm số

cotyx

có đạo hàm tại mọi

xk

và

 

cot

sin





4. Đạo hàm của hàm số mũ và hàm số logarit

⑴ Hàm số

ye

có đạo hàm trên

 





⑵ Hàm số

ya

có đạo hàm trên

 

.ln

a a a





⑶ Hàm số

log

yx

có đạo hàm tại mọi

0x 

 

log





⑷ Hàm số

lnyx

có đạo hàm tại mọi

0x 

 

ln x





Lý thuyết

Hàm số có đạo hàm trên và .

CÁC QUY TẮC TÍNH ĐẠO HÀM

ĐẠO HÀM

 Biên soạn: LÊ MINH TÂM – 093.337.6281 20

Chương VII.

ĐẠO HÀM

5. Các quy tắc tính đạo hàm

6. Đạo hàm của hàm hợp

6.1 Khái niệm hàm số hợp

6.2 Đạo hàm của hàm số hợp

Giả sử các hàm số có đạo hàm trên khoảng .

Khi đó: ⑴

⑵

⑶

⑷

Giả sử là hàm số xác định trên khoảng , có tập giá trị chứa khoảng

và là hàm số xác định trên . Hàm số được gọi là hàm

số hợp của hàm số với .

Nếu hàm số có đạo hàm tại và hàm số có đạo hàm tại

thì hàm số hợp có đạo hàm tại là

 Biên soạn: LÊ MINH TÂM – 093.337.6281 21

Chương VII.

ĐẠO HÀM

Từ đó ta có các kết quả sau:

⑴

 

x n x







⑵











⑶

 





 

u n u u



















 

.uu





⑷

 

sin cosxx





⑸

 

cos sinxx





⑹

 

tan

cos





⑺

 

cot

sin





 

sin .cosu u u





 

cos .sinu u u





 

tan .

cos





 

cot .

sin





⑻

 





⑼

 

.ln

a a a





 

e u e





 

. .ln

a u a a





⑽

 

ln x





⑾

 

log





 

ln .uu





 

log .





7. Đạo hàm cấp hai

 Ý nghĩa cơ học của đạo hàm cấp hai

Một chuyển động có phương trình

 

s f t

thì đạo hàm cấp hai (nếu có) của hàm số

 

s f t

là gia tốc tức thời của chuyển động

 

s s t

tại thời điểm

. Ta có

   

a t f t





Cho hàm số có đạo hàm tại mọi điểm .

Nếu hàm số lại có đạo hàm tại thì ta gọi đạo hàm của là đạo

hàm cấp hai của hàm số tại , kí hiệu là hoặc .

Khi đó: .

 Biên soạn: LÊ MINH TÂM – 093.337.6281 22

Chương VII.

ĐẠO HÀM

 Dạng 1. Tính đạo hàm đa thức – hữu tỉ – căn thức

 Lời giải

.......................................................................................................................................................

Bài tập

 Áp dụng quy tắc đạo hàm:

Khi đó: ⑴

⑵

⑶

⑷

 Áp dụng công thức đạo hàm:

⑴ ⑵

⑶ ⑷

Phương pháp

Ví dụ 1.1.

Tính đạo hàm các hàm số sau:

⑴ ⑵

⑶ ⑷

⑸ ⑹

⑺ ⑻

⑼

⑽

 Biên soạn: LÊ MINH TÂM – 093.337.6281 23

Chương VII.

ĐẠO HÀM

.......................................................................................................................................................

 Biên soạn: LÊ MINH TÂM – 093.337.6281 24

Chương VII.

ĐẠO HÀM

 Dạng 2. Tính đạo hàm lượng giác

 Lời giải

.......................................................................................................................................................

 Áp dụng quy tắc đạo hàm:

Khi đó: ⑴

⑵

⑶

⑷

 Để tính đạo hàm của hàm số tại , ta thực hiện theo các bước sau:

⑴ ⑵

⑶ ⑷

Phương pháp

Ví dụ 2.1.

Tính đạo hàm các hàm số sau:

⑴ ⑵

⑶ ⑷

⑸ ⑹

⑺ ⑻

⑼

⑽

 Biên soạn: LÊ MINH TÂM – 093.337.6281 25

Chương VII.

ĐẠO HÀM

.......................................................................................................................................................

 Biên soạn: LÊ MINH TÂM – 093.337.6281 26

Chương VII.

ĐẠO HÀM

 Dạng 3. Tính đạo hàm mũ – logarit

 Lời giải

.......................................................................................................................................................

 Áp dụng quy tắc đạo hàm:

Khi đó: ⑴

⑵

⑶

⑷

 Để tính đạo hàm của hàm số tại , ta thực hiện theo các bước sau:

⑴ ⑵

⑶ ⑷

Phương pháp

Ví dụ 3.1.

Tính đạo hàm các hàm số sau:

⑴ ⑵

⑶ ⑷

⑸ ⑹

⑺ ⑻

⑼

⑽

 Biên soạn: LÊ MINH TÂM – 093.337.6281 27

Chương VII.

ĐẠO HÀM

.......................................................................................................................................................

 Biên soạn: LÊ MINH TÂM – 093.337.6281 28

Chương VII.

ĐẠO HÀM

Câu 14. Tính đạo hàm của các hàm số sau:

⑴

24y x x  

⑵

 

31yx

⑶

2 4 1y x x   

⑷

2 2 8 1

y x x x   

⑸







⑹







⑺







⑻

 

  





⑼

  

2 1 5 3y x x x  

⑽

  

1 5 3y x x  

Câu 15. Tính đạo hàm của các hàm số sau:

⑴







⑵





⑶







⑷







⑸

2 4 1







⑹







⑺

y x x

⑻

 

2 3 2y x x x  

⑼

  

2 1 3 2y x x x  

⑽

  

2 3 2 3y x x x   

Câu 16. Tính đạo hàm của các hàm số sau:

⑴

1y x x  

⑵

 

1y x x  

⑶





⑷

 

21y x x  

⑸

5 2 1y x x  

⑹













⑺







⑻

4y x x  

⑼













⑽

y x x x  

Câu 17. Tính đạo hàm của các hàm số sau:

⑴

cos2x





⑵

cos .siny x x

⑶

2sin siny x x

⑷

12cosyx

Luyện tập

 Biên soạn: LÊ MINH TÂM – 093.337.6281 29

Chương VII.

ĐẠO HÀM

⑸

3cosyx

⑹

sin cos







⑺

tan coty x x

⑻

sin













⑼

cos







⑽

sin cos

cos sin

x x x







Câu 18. Tính đạo hàm cấp 2 của các hàm số sau:

⑴

1y x x

⑵

sinyx









⑶

2sinyx

⑷

2sin siny x x

⑸

22sin cosy x x x  

⑹







⑺

1y x x  

⑻

 

31yx

⑼







⑽

 

sin sinyx

Câu 19. Tính đạo hàm cấp 3 tại các điểm được chỉ ra dưới đây

⑴ Cho hàm số

3 3 5y x x x    

. Tính giá trị của

 

2017y

⑵ Cho hàm số





. Tính giá trị của

 

⑶ Cho hàm số





. Tính giá trị của

 

⑷ Cho hàm số

cosyx

. Tính giá trị của

 







Câu 20. Chứng minh rằng:

⑴ Với hàm số

2y x x

ta có

10.yy





⑵ Với hàm số

1y x x  

ta có

 

10.y x y



  

⑶ Với hàm số

siny x x

ta có

 

20sinxy y x xy

 

   

⑷ Với hàm số







ta có

 

21y y y

 



⑸ Với hàm số

2cotyx

ta có

2 2 0yy



  

⑹ Với hàm số

tany x x

ta có

 

2 2 2

2 1 0x y x y y



   

⑺ Với hàm số

tanyx

ta có

10yy



  

⑻ Với hàm số

1yx

ta có

.y y xy y

 



⑼ Với hàm số

1yx 

ta có

y y xy y

 



 Biên soạn: LÊ MINH TÂM – 093.337.6281 30

Chương VII.

ĐẠO HÀM

⑽ Với hàm số

1yx

ta có

0.y y xy y

 

  

Câu 21. Cho

 

43f x x x  

và

 

3 10 7g x x x  

. Giải phương trình

   

0f x g x

 



Câu 22. Cho hàm số

 

3 4 6f x x x x   

. Giải bất phương trình

   

1f x f x

 



Câu 23. Cho hàm số

3 4 6y x x x   

. Giải bất phương trình





Câu 24. Cho hàm số

     

5 1 4 1y f x x x    

. Giải phương trình

 

0fx





Câu 25. Cho hàm số

 

cosy f x x



  





. Tìm các nghiệm thuộc đoạn





của phương

trình

 

8fx

--------------------Hết--------------------

 Biên soạn: LÊ MINH TÂM – 093.337.6281 1

Chương VII.

ĐẠO HÀM

 Bài 01. ĐẠO HÀM

A. Lý thuyết

1. Đạo hàm. ...................................................................................................................................... 2

2. Ý nghĩa hình học của đạo hàm ............................................................................................... 3

3. Ý nghĩa vật lý của đạo hàm ................................................................................................... 4

4. Số e ............................................................................................................................................... 4

B. Bài tập

 Dạng 1. Tính đạo hàm tại 1 điểm bằng định nghĩa .......................................................... 5

 Dạng 2. Tính đạo hàm tại 1 điểm bất kỳ trên (a;b) bằng định nghĩa ........................ 8

 Dạng 3. Ý nghĩa hình học của đạo hàm ............................................................................ 10

 Dạng 4. Ý nghĩa vật lý của đạo hàm ................................................................................. 12

 Dạng 5. Tìm tham số để hàm số có đạo hàm tại x

...................................................... 13

C. Luyện tập

 Bài 02. CÁC QUY TẮC TÍNH ĐẠO HÀM

A. Lý thuyết

1. Đạo hàm hàm số

yx

.......................................................................................................... 39

2. Đạo hàm hàm số

yx

....................................................................................................... 39

3. Đạo hàm hàm số lượng giác ................................................................................................ 39

4. Đạo hàm của hàm số mũ và hàm số logarit .................................................................. 39

5. Các quy tắc tính đạo hàm ................................................................................................... 40

6. Đạo hàm của hàm hợp ......................................................................................................... 40

7. Đạo hàm cấp hai ..................................................................................................................... 41

B. Bài tập

 Dạng 1. Tính đạo hàm đa thức – hữu tỉ – căn thức ........................................................ 42

 Dạng 2. Tính đạo hàm lượng giác .................................................................................... 44

 Dạng 3. Tính đạo hàm mũ – logarit .................................................................................. 46

C. Luyện tập

Mục lục

 Biên soạn: LÊ MINH TÂM – 093.337.6281 2

Chương VII.

ĐẠO HÀM

1. Đạo hàm.

 Tính đạo hàm bằng định nghĩa:

Để tính đạo hàm của hàm số

 

y f x

tại

 

;x a b

, ta thực hiện theo các bước sau:

 Bước 1. Tính

   

f x f x

 Bước 2. Lập và rút gọn tỉ số

   

f x f x



với

 

;,x a b x x

 Bước 3. Tính giới hạn

   

lim

f x f x





Lý thuyết

Định nghĩa:

Cho hàm số xác định trên khoảng và .



Nếu tồn tại giới hạn hữu hạn thì giới hạn đó được gọi là đạo hàm

của tại điểm , tức là:

 Kí hiệu là hay .

Trong định nghĩa & quy tắc trên đây, thay bởi ta sẽ có định nghĩa và quy tắc tính

đạo hàm của hàm số tại điểm .

Chú ý

ĐẠO HÀM

 Biên soạn: LÊ MINH TÂM – 093.337.6281 3

Chương VII.

ĐẠO HÀM

2. Ý nghĩa hình học của đạo hàm

 Lời giải

⑴ Vẽ đồ thị

 

và tính

 



 

      

 

1 1 1 1

1 1 1

1 1 2

1 1 1

lim lim lim lim

x x x x

f x f x x

x x x

   

  





     

  

⑵ Vẽ đường thẳng

qua

có hệ số góc

 



. Nhận xét về vị trí tương đối giữa

và

 

Đường thẳng

cắt

 

tại hai điểm

 

00;O

và

 

24;M

 Trong mặt phẳng tọa độ

Oxy

, cho đồ thị

 

của hàm số

 

y f x

và điểm

   

;M x y C

Xét

 

;M x f x

là một diểm di chuyển trên

 

Đường thẳng

là một cát tuyến của

 

Hệ số góc của cát tuyến

được tính bởi công thức

   

tan

f x f x







Khi cho

dần tới

thì

di chuyển trên

 

tới

Ví dụ 2.1.

Cho hàm số và điểm

⑴ Vẽ đồ thị và tính .

⑵ Vẽ đường thẳng qua có hệ số góc . Nhận xét về vị trí tương đối

giữa và

 Biên soạn: LÊ MINH TÂM – 093.337.6281 4

Chương VII.

ĐẠO HÀM

Giả sử cát tuyến

có vị trí giới hạn là

thì

được gọi là tiếp tuyến của

 

tại

và

được gọi là tiếp điểm

Ta có hệ số góc của tiếp tuyến

là

 

   

 

tan lim tan lim

x x x x

f x f x

k f x







   



3. Ý nghĩa vật lý của đạo hàm

4. Số e

Đạo hàm của đồ thị hàm số tại điểm là hệ số góc của tiếp tuyến của

tại điểm

Tiếp tuyến có phương trình:

 Nếu hàm số biểu thị quãng đường di chuyển của vật theo thời gian thì

biểu thị tốc độ tức thời của chuyển động tại thời điểm .

 Nếu hàm số biểu thị nhiệt độ

theo thời gian thì biểu thị tốc độ thay

đổi nhiệt độ theo thời gian tại thời điểm .

Người ta còn biết rằng là số vô tỉ và (Số thập phân vô hạn không tuần hoàn).

 Biên soạn: LÊ MINH TÂM – 093.337.6281 5

Chương VII.

ĐẠO HÀM

 Dạng 1. Tính đạo hàm tại 1 điểm bằng định nghĩa

 Lời giải

⑴

 

21y f x x x   

tại

0x 

Tại

0x 

ta có

         

 

3 3 2

0 2 1 1 2 2 1f x f x f x f x x x x x x           

       

 

f x f x f x f

x x x x





    



 

   

 

0 2 1 1lim lim

x x x

f x f x







    



⑵

 

21y f x x x   

tại

1x 

Tại

0x 

ta có

         

0 2 1 2 2 3f x f x f x f x x x x         

          

0 1 3

1 1 1

f x f x f x f x x

x x x x x

   



     

   

Bài tập

 Để tính đạo hàm của hàm số tại , ta thực hiện theo các bước sau:

 Bước 1. Tính .

 Bước 2. Lập và rút gọn tỉ số với và

 Bước 3. Tính giới hạn .

⑴ ⑵ ⑶

 Hàm số có đạo hàm tại điểm .

 Hàm số có đạo hàm tại điểm thì trước hết phải liên tục tại điểm đó.

Phương pháp

Ví dụ 1.1.

Tính đạo hàm bằng định nghĩa tại một điểm của các hàm số sau:

⑴ tại ⑵ tại

 Biên soạn: LÊ MINH TÂM – 093.337.6281 6

Chương VII.

ĐẠO HÀM

 

   

 

1 3 4lim lim

x x x

f x f x







    



 Lời giải

⑴

 

y f x





tại

2x 

Tại

2x 

ta có

       

2f x f x f x f   

  

2 2 2 2

1 1 1 3 1 1 2 1

4 2 1 3 3 3

1 1 1 1

. . .

x x x x

x x x x x x x x



     

     



       

            

2 1 2 1

1 1 1

2 3 2 3

. . .

f x f x f x f x x x

x x x x

     

     

  

   

 

       

   

1 2 1

1 1 1

3 3 3

2 2 1

lim lim . .

x x x

f x f x x

 



   



       









   



⑵

 

y f x







tại

3x 

Tại

3x 

ta có

       

 

  

 

3 5 2

3 9 5 13 6

2 1 5

5 2 1 5 2 1

x x x x

f x f x f x f



   

      





          

 

3 3 5 2 5 2

5 2 1 5 2 1

f x f x f x f x x x

x x x x

    

   

  



 

         

 

3 5 2

3 25

5 2 1

lim lim lim

x x x x

f x f x f x f x

x x x

  

  



    





 Lời giải

Ví dụ 1.2.

Tính đạo hàm bằng định nghĩa tại một điểm của các hàm số sau:

⑴ tại ⑵ tại

Ví dụ 1.3.

Tính đạo hàm bằng định nghĩa tại một điểm của các hàm số sau:

⑴ tại

⑵ tại

 Biên soạn: LÊ MINH TÂM – 093.337.6281 7

Chương VII.

ĐẠO HÀM

⑴

 

khi





















tại

1x 

Ta có:

 

13f 

Do đó:

      

1 1 1 1

1 4 1

3 1 3 3 4

1 1 1 1

lim lim lim lim

x x x x

f x f x x

x x x x

   

  

    

   

   

Vậy

 

05f





⑵

 

khi



  















tại

0x 

Ta có

 

00f 

Do đó:

   

0 0 0

1 1 1 1

lim lim lim

x x x

f x f

x x x

  



   

  

  

Vậy

 





 Lời giải

Để hàm số có đạo hàm tại

1x 

thì trước hết

 

phải liên tục tại

1x 

Hay

   

lim lim

f f a





   



Khi đó, ta có:

   

lim lim

f x f









Vậy

2a 

là giá trị cần tìm.

Ví dụ 1.4.

Tìm để hàm số có đạo hàm tại

 Biên soạn: LÊ MINH TÂM – 093.337.6281 8

Chương VII.

ĐẠO HÀM

 Dạng 2. Tính đạo hàm tại 1 điểm bất kỳ trên (a;b) bằng định nghĩa

 Lời giải

⑴

 

43y f x x  

Tại

x 

tùy ý, ta có:

     

0 0 0

4 3 4 3 4f x f x x x x x      

     

f x f x x x

x x x x



  



   

4 4 4lim lim

x x x x

f x f x







    



⑵

 

2024 2025y f x x  

Tại

x 

tùy ý, ta có:

     

0 0 0

2024 2025 2024 2025 2024f x f x x x x x      

     

2024

f x f x x x

x x x x



  



   

2024 2024 2024lim lim

x x x x

f x f x







    



⑶

 

2 2024y f x x  

Tại

x 

tùy ý, ta có:

 Để tính đạo hàm của hàm số tại , ta thực hiện theo các bước sau:

 Bước 1. Tính .

 Bước 2. Lập và rút gọn tỉ số với và

 Bước 3. Tính giới hạn .

 Hàm số có đạo hàm tại điểm thì trước hết phải liên tục tại điểm đó.

Phương pháp

Ví dụ 2.1.

Tính đạo hàm bằng định nghĩa của các hàm số sau:

⑴ ⑵

⑶ ⑷

⑸ ⑹

 Biên soạn: LÊ MINH TÂM – 093.337.6281 9

Chương VII.

ĐẠO HÀM

      

2 2 2 2

0 0 0 0 0

2 2024 2 2024 2 2 2f x f x x x x x x x x x         

      

 

0 0 0

f x f x x x x x

x x x x

  

   



   

 

2 4 4lim lim

x x x x

f x f x

x x x y x







     



⑷

 

31y f x x x   

Tại

x 

tùy ý, ta có:

      

0 0 0 0 0

3 1 3 1 3f x f x x x x x x x x x          

      

0 0 0

f x f x x x x x

x x x x

   

    



   

 

3 2 3 2 3lim lim

x x x x

f x f x

x x x y x







        



⑸

 

2y f x x x  

Tại

x 

tùy ý, ta có:

     

 

3 3 2 2

0 0 0 0 0 0

2 2 2.f x f x x x x x x x x x x x         

   

 

0 0 0

x x x x x x

f x f x

x x x x

   



     



   

 

2 2 2 2

0 0 0

2 3 2 3 2lim lim .

x x x x

f x f x

x x x x x y x







         



⑹

 

22y f x x x   

Tại

x 

tùy ý, ta có:

     

 

4 2 4 2 3 2 2 3

0 0 0 0 0 0 0 0

2 2 2 2 2 2f x f x x x x x x x x x x x x x x             

   

 

3 2 2 3

0 0 0 0 0

3 2 2 3

0 0 0 0

x x x x x x x x x

f x f x

x x x x x x x

x x x x

     



       



   

lim

f x f x









 

3 2 2 3

0 0 0 0

22lim

x x x x x x x



     

3 3 3 3 3

0 0 0 0 0 0 0 0

2 2 4 4x x x x x x x x       

44y x x



  

 Biên soạn: LÊ MINH TÂM – 093.337.6281 10

Chương VII.

ĐẠO HÀM

 Dạng 3. Ý nghĩa hình học của đạo hàm

 Lời giải

⑴ Đồ thị hàm số

24y x x  

 

tại điểm có hoành độ

0x 

Gọi

 

;Z x y

là tiếp điểm.

Tại

x 

tùy ý, ta có:

      

0 0 0 0 0

2 4 2 4 2f x f x x x x x x x x x          

      

0 0 0

f x f x x x x x

x x x x

   

    



   

 

2 2 2 2 2lim lim

x x x x

f x f x

x x x y x







        



Hệ số góc của tiếp tuyến của

 

tại điểm có hoành độ

0x 

là

 

02ky





Tung độ tiếp điểm tại điểm có hoành độ

0x 

là

 

4yx 

 Ý nghĩa hình học: (Phương trình tiếp tuyến)

Cho hàm số có đồ thị , .

Phương trình tiếp tuyến tại có dạng: .

Trong đó: hoành độ tiếp điểm.

tung độ tiếp điểm.

hệ số góc tiếp tuyến.

Bài toán: Viết phương trình tiếp tuyến của đồ thị hàm số tại .

 Bước 1. Tính .

 Bước 2. Từ .

 Bước 3. Hoàn thiện phương trình tiếp tuyến cần tìm .

Phương pháp

Ví dụ 3.1.

Viết phương trình tiếp tuyến của

⑴ Đồ thị hàm số tại điểm có hoành độ .

⑵ Đồ thị hàm số tại điểm có hoành độ .

⑶ Đồ thị hàm số tại điểm có tung độ .

 Biên soạn: LÊ MINH TÂM – 093.337.6281 11

Chương VII.

ĐẠO HÀM

Phương trình tiếp tuyến cần tìm là

    

0 0 0 2 4y y x y y x



     

⑵ Đồ thị hàm số

1yx

 

tại điểm có hoành độ

1x 

Gọi

 

;C x y

là tiếp điểm.

Tại

x 

tùy ý, ta có:

     

 

3 3 2 2

0 0 0 0 0

11 .f x f x x x x x x x x x        

   

 

0 0 0

x x x x x x

f x f x

x x x x

  



    



   

 

2 2 2 2

0 0 0

33lim lim .

x x x x

f x f x

x x x x x y x







      



Hệ số góc của tiếp tuyến của

 

tại điểm có hoành độ

1x 

là

 

13ky





Tung độ tiếp điểm tại điểm có hoành độ

1x 

là

 

2yx 

Phương trình tiếp tuyến cần tìm là

    

1 1 1 3 1y y x y y x



     

⑶ Đồ thị hàm số

23yx

 

tại điểm có tung độ

1y 

Gọi

 

;T x y

là tiếp điểm.

Tại

x 

tùy ý, ta có:

      

0 0 0 0

2 1 2 1 2f x f x x x x x x x       

      

 

0 0 0

f x f x x x x x

x x x x

  

   



   

 

2 4 4lim lim

x x x x

f x f x

x x x y x







     



Ta có

0 0 0

2 2 3 1 2 2

y x x





        







● Với

1x 

Hệ số góc của tiếp tuyến của

 

tại điểm có hoành độ

1x 

là

 

14ky





Phương trình tiếp tuyến cần tìm là

    

1 1 1 4 5y y x y y x



     

● Với

1x 

Hệ số góc của tiếp tuyến của

 

tại điểm có hoành độ

1x 

là

 

14ky



   

Phương trình tiếp tuyến cần tìm là

    

1 1 1 4 5y y x y y x



        

 Biên soạn: LÊ MINH TÂM – 093.337.6281 12

Chương VII.

ĐẠO HÀM

 Dạng 4. Ý nghĩa vật lý của đạo hàm

 Lời giải

⑴ Tính đạo hàm của hàm số

 

tại điểm

Ta có

 

   

lim

f t f t











 

  

 

0 0 0

4 6 4 6

4 2 4lim lim lim

t t t t t t

t t t t

t t t

t t t t

  



    



  



      









⑵ Tính vận tốc tức thời của chuyển động tại thời điểm

5t 

Vận tốc tức thời của chuyển động tại thời điểm

5t 

 





5 2 5 4 14.



  

 Lời giải

Ta có

 

6 5 6Q t Q t



   

Cường độ dòng điện trong dây dẫn tại thời điểm

10t 

là

 

10 6IQ





 Ý nghĩa vật lý: (quãng đường, nhiệt độ, điện lượng)

 Nếu hàm số biểu thị quãng đường

di chuyển của vật theo thời gian thì biểu

thị tốc độ tức thời của chuyển động tại thời điểm .

 Nếu hàm số biểu thị nhiệt độ

theo thời gian thì biểu thị tốc độ thay đổi

nhiệt độ theo thời gian tại thời điểm .

Phương pháp

Ví dụ 4.1.

Một chất điểm chuyển động có phương trình chuyển động là (t

được tính bằng giây, s được tính bằng mét).

⑴ Tính đạo hàm của hàm số tại điểm .

⑵ Tính vận tốc tức thời của chuyển động tại thời điểm .

Ví dụ 4.2.

Cho biết điện lượng trong một dây dẫn theo thời gian biểu thị bởi hàm số

(t được tính bằng giây, Q được tính bằng Coulomb). Tính cường độ của dòng điện

trong dây dẫn tại thời điểm

 Biên soạn: LÊ MINH TÂM – 093.337.6281 13

Chương VII.

ĐẠO HÀM

 Dạng 5. Tìm tham số để hàm số có đạo hàm tại x

 Lời giải

Ta có

 

2lim

x x a a



  

 

00f 

Hàm số có đạo hàm tại

0x 

 

fx

liên tục tại

0x 

 

2 0 0lim

x x a f a



     

 

     

 

0 0 0 0

0 2 1

0 2 1 1

lim lim lim lim

x x x x

f x f x x

x x x

   





      



 Lời giải

Ta có

 





 

lim ; lim ;

ax b a b f





    

.Hàm số liên tục tại

1x 

nên

ab

Đạo hàm phải

 

       

1 1 1 1

1 1 1

lim lim lim lim

x x x x

f x f ax b a b a x

f a a

x x x

   



   

    



    

  

Đạo hàm trái

 

      

 

1 1 1 1

1 1 2

lim lim lim lim

x x x x

f x f x x x

   



   



   



    





Hàm số có đạo hàm tại

1x 

   

1 1 1f f a





  

Vậy

1 0 5;,ab  

 Cho hàm số hoặc . Tìm tham số m để hàm

số có đạo hàm tại

 Bước 1. Xác định .

 Bước 2. Hàm số liên tục tại

 Bước 3. Tính ; .

 Bước 4. Hàm số có đạo hàm tại .

Phương pháp

Ví dụ 5.1.

Cho hàm số . Tìm

để hàm số có đạo hàm tại .

Ví dụ 5.2.

Cho hàm số . Tìm

, thì hàm số có đạo hàm tại ?

 Biên soạn: LÊ MINH TÂM – 093.337.6281 14

Chương VII.

ĐẠO HÀM

Câu 1. Tính đạo hàm của các hàm số sau tại các điểm đã chỉ:

⑴

 

21f x x

tại

2x 

⑵

 

2024 2023f x x

tại

1x 

⑶

 

21f x x x  

tại

1x 

⑷

 

21f x x

tại

2x 

⑸

 

21f x x x  

tại

1x 

⑹

 







tại

2x 

⑺

 





tại

2x 

⑻

 







tại

3x 

⑼

 

1f x x

tại

1x 

⑽

 

2023f x x

tại

2x 

Lời giải

⑴

 

21f x x

tại

2x 

Ta có

 

     

2 2 2

2 2 1 4 1

2 2 2

lim lim lim

x x x

f x f x

x x x

  

     





    

  

⑵

 

2024 2023f x x

tại

1x 

Ta có

 

     

1 1 1

1 2024 2023 1

2023 2023

1 2023

1 1 1

lim lim lim

x x x

f x f x

x x x

  

  





    

  

⑶

 

21f x x x  

tại

1x 

Ta có

 

      

 

1 1 1 1

2 1 2

1 3 4

lim lim lim lim

x x x x

f x f x x x

x x x x

   

  

  



     

  

⑷

 

21f x x

tại

2x 

Ta có

 

   

 

2 2 2

2 16

2 2 2 4 24

lim lim lim

x x x

f x f

f x x

  





     



⑸

 

21f x x x  

tại

1x 

Ta có

 

      

 

1 1 1 1

1 1 2 3

2 1 4

1 2 3 5

1 1 1

lim lim lim lim

x x x x

f x f x x

x x x

   

  

  



     

  

⑹

 







tại

2x 

Ta có

 

   

2 2 2 2

1 1 3 3

2 2 2 1

lim lim lim lim

x x x x

x x x

f x f

x x x x

   

   







     

   

⑺

 





tại

2x 

Luyện tập

 Biên soạn: LÊ MINH TÂM – 093.337.6281 15

Chương VII.

ĐẠO HÀM

Ta có

 

   

2 2 2 2

2 2 2 1 2 1

lim lim lim lim

x x x x

f x f

x x x x

   







      

    

⑻

 







tại

3x 

Ta có

 

   

3 3 3 3

2 1 2 1 7 14

3 3 3 2 3 2

lim lim lim lim

x x x x

x x x

f x f

x x x x

   

   







      

    

⑼

 

1f x x

tại

1x 

Ta có

   

 

1 1 1 1

1 2 1 1 1

1 2 2 2

1 1 2

lim lim lim lim

x x x x

f x f

   



  

   





  

⑽

 

2023f x x

tại

2x 

Ta có

   

lim

f x f





2023 2025

lim









 

2023 2025 1 1

2023 2025 2 2025

2 2023 2025

lim lim





  



  

Câu 2. Tính đạo hàm của các hàm số sau tại các điểm (nếu có):

⑴

 

2 3 3

khi

















. Tính

 



. ⑵

 

1 2 0

khi

















. Tính

 



⑶

 

f x x

. Tính

 



. ⑷

 

f x x x

. Tính

 



⑸

 

21f x x x  

. Tính

 



. ⑹

 

f x x x

. Tính

 



⑺

 

2023f x x

. Tính

 



. ⑻

 

2f x x x

. Tính

 



⑼





. Tính

 



. ⑽

 

1xx





. Tính

 





Lời giải

⑴

 

2 3 3

khi

















. Tính

 



Đạo hàm phải

 

     

3 3 3

3 2 3 2 3 3

3 2 2

lim lim lim

x x x

f x f x

  



  

   



   



Đạo hàm trái

 

     

 

3 3 3

3 2 3 3

3 3 6

lim lim lim

x x x

f x f x

  



  

  



    



Suy ra

   

33ff









Hàm số không tồn tại đạo hàm tại

3x 

 Biên soạn: LÊ MINH TÂM – 093.337.6281 16

Chương VII.

ĐẠO HÀM

⑵

 

1 2 0

khi

















. Tính

 



Đạo hàm phải

 

   

 

0 0 0

lim lim lim

x x x

f x f

  



  







   



Đạo hàm trái

 

   

 

0 0 0

1 2 1

0 2 2

lim lim lim .

x x x

f x f

  



  







     



Suy ra

   

00ff









Hàm số không tồn tại đạo hàm tại

0x 

⑶

 

f x x

. Tính

 



Ta có:

 

khi

y f x













Đạo hàm phải

 

   

lim lim

f x f











  



Đạo hàm trái

 

   

lim lim

f x f













   



Suy ra

   

00ff









Hàm số không tồn tại đạo hàm tại

0x 

⑷

 

f x x x

. Tính

 



Ta có:

 

khi

y f x













Đạo hàm phải

 

   

0 0 0

2 0 2

lim lim lim

x x x

f x f

x x x

  



  





   



Đạo hàm trái

 

   

0 0 0

lim lim lim

x x x

f x f

x x x

  



  





   



Suy ra

   

00ff









Hàm số không tồn tại đạo hàm tại

0x 

⑸

 

21f x x x  

. Tính

 



Ta có:

 

3 1 1

khi

y f x













Đạo hàm phải

 

     

1 1 1

1 3 1

3 1 2

1 1 1

lim lim lim

x x x

f x f x

x x x

  



  





   

  

Đạo hàm trái

 

   

1 1 1

1 2 1

1 1 1

lim lim lim

x x x

f x f

x x x

  



  



  



   

  

Suy ra

   

11ff









Hàm số không tồn tại đạo hàm tại

1x 

⑹

 

f x x x

. Tính

 



Ta có:

 

3 1 1

khi

y f x













 Biên soạn: LÊ MINH TÂM – 093.337.6281 17

Chương VII.

ĐẠO HÀM

Đạo hàm phải

 

     

1 1 1

1 3 1

3 1 2

1 1 1

lim lim lim

x x x

f x f x

x x x

  



  





   

  

Đạo hàm trái

 

   

1 1 1

1 2 1

1 1 1

lim lim lim

x x x

f x f

x x x

  



  



  



   

  

Suy ra

   

11ff









Hàm số không tồn tại đạo hàm tại

1x 

⑺

 

2023f x x

. Tính

 



Ta có

 

2023 0

khi

y f x













Đạo hàm phải

 

     

0 0 0

0 2023 2023

lim lim lim

x x x

f x f x

x x x

  



  

   



   



Đạo hàm trái

 

     

0 0 0

0 2023 2023

lim lim lim

x x x

f x f x

x x x

  



  

   





    



Suy ra

   

00ff









Hàm số không tồn tại đạo hàm tại

0x 

⑻

 

2f x x x

. Tính

 



Ta có

 

2 2 0

khi ;

khi

x x x x

x x x



   







    





Đạo hàm phải

 

   

 

0 0 0

0 2 2lim lim lim

x x x

f x f

  



  







    

Đạo hàm trái

 

   

 

0 0 0

0 2 2lim lim lim

x x x

f x f

  



  







      

Suy ra

   

00ff









Hàm số không tồn tại đạo hàm tại

0x 

⑼





. Tính

 



Ta có

 

khi

























Đạo hàm phải

 

   

0 0 0

lim lim lim

x x x

f x f

x x x

  



  







   



Đạo hàm trái

 

   

0 0 0

lim lim lim

x x x

f x f

x x x

  



  







    



Suy ra

   

00ff









Hàm số không tồn tại đạo hàm tại

0x 

 Biên soạn: LÊ MINH TÂM – 093.337.6281 18

Chương VII.

ĐẠO HÀM

⑽

 

1xx





. Tính

 





Ta có

 

khi























Đạo hàm phải

 

1 1 1 1

lim lim lim lim

x x x x

   



   









    





Đạo hàm trái

 

1 1 1

lim lim lim

x x x

  



  









   



Suy ra

   

11ff









Hàm số không tồn tại đạo hàm tại

1x 

Câu 3. Tính đạo hàm của các hàm số sau tại các điểm đã chỉ (nếu có):

⑴

 

khi

x x x

















. Tính

 



⑵

 

khi

x x x





















. Tính

 



⑶

 

2 3 1

2 7 4

khi

x x x











  









. Tính

 



⑷

 

7 12

khi





















. Tính

 



⑸

 

khi

















. Tính

 



⑹

 

3 4 0

khi



  













. Tính

 



⑺

 

2 1 1

khi

x x x



   

















. Tính

 



⑻

 

khi





















. Tính

 



 Biên soạn: LÊ MINH TÂM – 093.337.6281 19

Chương VII.

ĐẠO HÀM

⑼

 

khi





















. Tính

 



⑽

 

khi



















. Tính

 



Lời giải

⑴

 

khi

x x x

















. Tính

 



Thấy

 

lim lim

f x x x





   













Hàm số liên tục tại

1x 

Ta có

 

   

lim

f x f











lim









  

lim









 

2lim





1

⑵

 

khi

x x x





















. Tính

 



Thấy

 

  

 

1 1 1 1

1 3 3

lim lim lim lim

x x x x

x x x x x

x x x

   



  



   



















   

1lim

f x f







Hàm số không liên tục tại

1x 

nên hàm số không có đạo hàm tại điểm

1x 

⑶

 

2 3 1

2 7 4

khi

x x x











  









. Tính

 



Thấy

   

 

1 1 1

2 3 5

2 7 4

3 4 0

lim lim

lim lim lim

x x x

f x x

x x x

f x x x



  



  



  





  

    









   

lim lim

f x f x









Hàm số không liên tục tại

1x 

nên hàm số không có đạo hàm tại điểm

1x 

⑷

 

7 12

khi





















. Tính

 



 Biên soạn: LÊ MINH TÂM – 093.337.6281 20

Chương VII.

ĐẠO HÀM

Thấy

 

   

3 3 3

7 12

lim lim lim

x x x

f x x

  











    









Hàm số liên tục tại

3x 



Đạo hàm của hàm số tại

3x 

 

   

7 12 0

lim lim

f x f





  



   



⑸

 

khi

















. Tính

 



Thấy

 

lim lim

f x x



























Hàm số liên tục tại

1x 

Đạo hàm trái

 

   

 

1 1 1

1 1 1 1 2

lim lim lim

x x x

f x f

  



  





      



Đạo hàm phải

 

   

1 1 1

1 1 2

lim lim lim

x x x

f x f

  



  





   





Suy ra

   

11ff









Hàm số không tồn tại đạo hàm tại

1x 

⑹

 

3 4 0

khi



  













. Tính

 



Thấy

 

3 4 1

lim lim

f x x





   













Hàm số liên tục tại

1x 

Ta có

 

   

lim

f x f











3 4 1

lim



  



lim







  

 

2 4 2 4

lim



   





 

   

000

1 1 1

2 4 2 4 0

2 4 2 4

lim lim lim

xxx

x x x x





    

   

⑺

 

2 1 1

khi

x x x



   

















. Tính

 



Thấy

 

10f 

 Biên soạn: LÊ MINH TÂM – 093.337.6281 21

Chương VII.

ĐẠO HÀM

 

2 1 1

lim lim

x x x



   





 





1 2 1 1

lim

x x x

x x x x







    

 





 

2 1 1

1 2 1 1

lim lim

x x x x

x x x

x x x x





  

   

    



Hàm số liên tục tại

1x 

Ta có

 

   

 

1 1 1

2 1 1 1

2 1 1

lim lim lim

x x x

f x f

x x x x

x x x

  



   



   



   



⑻

 

khi





















. Tính

 



Thấy

 

0 0 0 0

1 1 1 1 1 1

lim lim lim lim

x x x x

   







   



   











Hàm số liên tục tại

0x 

Ta có

 

   

lim lim

f x f













lim







⑼

 

khi





















. Tính

 



Thấy

 

3 4 1

lim lim























Hàm số liên tục tại

0x 

Ta có

 

   

lim

f x f











3 4 1

lim









lim







 

4 2 4

lim









 

4 2 4

lim









 

4 2 4 0





⑽

 

khi



















. Tính

 



 Biên soạn: LÊ MINH TÂM – 093.337.6281 22

Chương VII.

ĐẠO HÀM

Thấy

 

   

0 0 0 0

1 1 1 1

0lim lim lim lim

x x x x

f x x

   









   

   







Hàm số liên tục tại

0x 

Ta có

 

   









0 0 0 0

2 2 2

1 1 1 1

lim lim lim lim

x x x x

f x f

x x x

   







    



   

Câu 4. Tính đạo hàm của các hàm số sau tại các điểm đã chỉ (nếu có):

⑴

 

khi





















. Tính

 



⑵

 

khi



















. Tính

 



⑶

 

3 1 2

khi























. Tính

 



⑷

 

4 8 8 4

khi



  















. Tính

 



Lời giải

⑴

 

khi





















. Tính

 



Thấy

 

0 0 0

1 1 1

lim lim lim

x x x

  





  

















Hàm số không liên tục tại

0x 



   

0lim

f x f







Hàm số không liên tục tại

0x 

nên hàm số không có đạo hàm tại điểm

0x 

⑵

 

khi



















. Tính

 



Thấy

 





 

0 0 0 0

lim lim lim lim

x x x x

x x x

   





   















 Biên soạn: LÊ MINH TÂM – 093.337.6281 23

Chương VII.

ĐẠO HÀM



Hàm số liên tục tại

0x 

Ta có

 

   

lim

f x f















1 0 0 0

1 1 1 1

lim lim lim lim

x x x x

   







    



⑶

 

3 1 2

khi























. Tính

 



Thấy

 

3 1 2

lim lim









 

111

4 1 4

4 3 1 5

3 1 2

1 3 1 2 1 3 1 2

lim lim lim

xxx

x x x

x x x x x x



   

    

   

  

   

    



     

Và

 

f 



Hàm số liên tục tại

1x 

Ta có

 

   

lim

f x f











 

3 1 2 5

4 3 1 3 5

lim lim







  







  

 

4 3 1 3 5 4 3 1 3 5

4 1 4 3 1 3 5

lim

x x x x

x x x



     



   

   

 

16 3 1 3 5

4 1 4 3 1 3 5

lim

x x x



  



   

 

9 18 9

4 1 4 3 1 3 5

lim

x x x



  



   

 

4 4 3 1 3 5

4 1 4 3 1 3 5

lim lim

x x x







   

  

   

 Biên soạn: LÊ MINH TÂM – 093.337.6281 24

Chương VII.

ĐẠO HÀM

⑷

 

4 8 8 4

khi



  















. Tính

 



Thấy

 

4 8 8 4

lim lim



  



4 8 2 8 4 2

lim lim



   







 













2 2 2

4 8 2 4 8 4 8 2 4

8 4 2 8 4 2

8 4 2

4 8 4 8 2 4

lim lim

x x x





     



   









   





 









4 4 8 4 8 2 4

8 8 4 2

0 0 0

8 4 2

4 8 4 8 2 4

lim lim

x x x





   







    





   





Và

 

00f 



Hàm số liên tục tại

0x 

Ta có

 

   

4 8 8 4

0 lim lim

f x f





  





Thừa nhận kết quả bên trên, ta được

 

   

00lim

f x f









Câu 5. Tìm tham số để hàm số có đạo hàm tại

⑴ Tìm

để hàm số

 

khi





















có đạo hàm tại điểm

1x 

⑵ Tìm

;ab

để hàm số

 

1 khi 0

ax bx x

ax b x



  







  





có đạo hàm tại điểm

0x 

⑶ Tìm

;ab

để hàm số

 

khi

ax b x





















có đạo hàm tại điểm

0x 

⑷ Tìm

;ab

để hàm số

 

2 1 1

3 2 1

khi

ax x x

x bx x



  







  





có đạo hàm tại điểm

1x 

Lời giải

⑴ Tìm

để hàm số

 

khi





















có đạo hàm tại điểm

1x 

 Biên soạn: LÊ MINH TÂM – 093.337.6281 25

Chương VII.

ĐẠO HÀM

Ta có

 

  

 

1 1 1 1

lim lim lim lim

x x x x

f x x

   





    



 

1fa

Hàm số có đạo hàm tại

1x 

 

fx

liên tục tại

1x 

   

12lim

f x f a



   

 

   

1 1 1 1

1 2 2 2 1

lim lim lim lim

x x x x

f x f

x x x x

   



    





    



⑵ Tìm

;ab

để hàm số

 

1 khi 0

ax bx x

ax b x



  







  





có đạo hàm tại điểm

0x 

Ta có

 

   

lim lim

f x ax bx

f x ax b b













   





     





Hàm số liên tục tại

0x 

nên

1 1 2bb     

Đạo hàm phải

 

   

 

0 0 0

2 1 1

0 2 2lim lim lim

x x x

f x f

ax x

f ax

  



  



  



     

Đạo hàm trái

 

   

 

0 0 0

0 lim lim lim

x x x

f x f

f a a

  



  







   

Hàm số có đạo hàm tại

0x 

   

0 0 2f f a





    

Vậy với

2a 

2b 

thì hàm số có đạo hàm tại

0x 

⑶ Tìm

;ab

để hàm số

 

khi

ax b x





















có đạo hàm tại điểm

0x 

Ta có

 

   

0 0 0

lim lim lim

lim lim

x x x

f x x

f x ax b b

  



  













   







  





Hàm số liên tục tại

0x 

nên

     

01lim lim

f x f x f b





   

Đạo hàm phải

 

   

 

0 0 0 0

0 1 1

lim lim lim lim

x x x x

f x f

   



   





    



Đạo hàm trái

 

   

0 0 0 0 0

lim lim lim lim lim .

x x x x x

f x f

ax b b ax ax

f a a

x x x x

    



    



   



     



Hàm số có đạo hàm tại điểm

0x 

   

0 0 1.f f a





   

Vậy với

11;ab

thì hàm số có đạo hàm tại

0x 

 Biên soạn: LÊ MINH TÂM – 093.337.6281 26

Chương VII.

ĐẠO HÀM

⑷ Tìm

;ab

để hàm số

 

2 1 1

3 2 1

khi

ax x x

x bx x



  







  





có đạo hàm tại điểm

1x 

Ta có

 

2 1 1

3 2 1

lim lim

f x ax x a

f x x bx b













    





    



Hàm số liên tục tại

1x 

nên

     

1 1 1 2lim lim

f x f x f a b b a





        

Đạo hàm phải

 

   

 

1 1 1

1 2 2 2

lim lim lim

x x x

f x f

ax x a

f ax a a

  



  



  



      



Đạo hàm trái

 

   

lim

f x f













 

3 2 2 1

3 2 1

lim lim

x a x a

x bx a





    

   





3 2 1

lim







    







Hàm số có đạo hàm tại điểm

1x 

   

1 1 2 2 3 1f f a a a





        

Vậy với

13;ab  

thì hàm số có đạo hàm tại

1x 

Câu 6. Cho hàm số

24y x x  

có đồ thị

 

⑴ Tìm hệ số góc của tiếp tuyến của

 

tại điểm có hoành độ

1x 

thuộc

 

⑵ Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có

0x 

thuộc

 

⑶ Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có

1y 

thuộc

 

⑷ Viết phương trình tiếp tuyến của đồ thị hàm số biết hệ số góc tiếp tuyến bằng

4

⑸ Viết phương trình tiếp tuyến của đồ thị hàm số, biết tiếp tuyến đó song song với

đường thẳng

13yx

Lời giải

 Tính đạo hàm bằng định nghĩa:

Tại

x 

tùy ý, ta có:

      

0 0 0 0 0

2 4 2 4 2f x f x x x x x x x x x          

            

0 0 0 0 0

0 0 0 0 0 0

f x f x x x f x f x x x x x

x x x x x x x x x x x x

      



      

   

   

 

2 2 2 2 2lim lim

x x x x

f x f x

x x x y x







        



 Tính đạo hàm bằng công thức:

   

2 2 2

2 4 2 4 2 4 2 2y x x y x x x x x





            

 Gọi

 

;M x y

là tiếp điểm.

 Biên soạn: LÊ MINH TÂM – 093.337.6281 27

Chương VII.

ĐẠO HÀM

⑴ Tìm hệ số góc của tiếp tuyến của

 

tại điểm có hoành độ

1x 

thuộc

 

Hệ số góc của tiếp tuyến của

 

tại điểm có hoành độ

1x 

thuộc

 

là

 

14ky





⑵ Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có

0x 

thuộc

 

Ta có

   

y x y











  





Phương trình tiếp tuyến cần tìm là

    

0 0 0 2 4y y x y y x



     

⑶ Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có

1y 

thuộc

 

Ta có

0 0 0

1 2 4 1

y x x





       







Với

















Phương trình tiếp tuyến là

    

1 1 1 4 5y y x y y x



     

Với

















Phương trình tiếp tuyến là

    

3 3 3 4 13y y x y y x



        

⑷ Viết phương trình tiếp tuyến của đồ thị hàm số biết hệ số góc của tiếp tuyến bằng

4

Gọi

 

;M x y

là tiếp điểm của tiếp tuyến của đồ thị

 

với hệ số góc

4k 

 

0 0 0 0

4 2 2 4 3 1y x x x y



            



Phương trình tiếp tuyến với hệ số góc

4k 

là

 

4 3 1 4 13y x y x       

⑸ Viết phương trình tiếp tuyến của đồ thị hàm số, biết tiếp tuyến đó song song với đường thẳng

13yx

Vì tiếp tuyến song song với đưởng thẳng

13yx

nên tiếp tuyến có hệ số góc

3k 

Gọi

 

;M x y

là tiếp điểm của tiếp tuyến của đồ thị

 

với hệ số góc

4k 

 

0 0 0 0

5 11

3 2 2 3

y x x x y



            



Phương trình tiếp tuyến với hệ số góc

3k 

là

5 11 41

2 4 4

y x y x



       





Câu 7. Cho hàm số





có đồ thị

 

⑴ Viết phương trình tiếp tuyến của đồ thị hàm số tại giao điểm của

 

với trục

⑵ Viết phương trình tiếp tuyến của đồ thị hàm số tại giao điểm của

 

với trục

⑶ Viết phương trình tiếp tuyến của đồ thị hàm số tại giao điểm của

 

với đường

thẳng

1yx

 Biên soạn: LÊ MINH TÂM – 093.337.6281 28

Chương VII.

ĐẠO HÀM

⑷ Viết phương trình tiếp tuyến của đồ thị hàm số biết hệ số góc của tiếp tuyến bằng

k 

⑸ Viết phương trình tiếp tuyến của đồ thị hàm số, biết tiếp tuyến đó song song với

đường thẳng

13yx

Lời giải

 Tính đạo hàm bằng định nghĩa:

Tại

 

0\x 

tùy ý, ta có:

   

 

3 3 3 .

f x f x

x x x x





   

     

0 0 0 0

f x f x x x

x x x x x x x x

  



  



   

1 1 1

lim lim

x x x x

f x f x

x x x x









     



 Tính đạo hàm bằng công thức:

 

1 1 3 1





  



     





 Gọi

 

;M x y

là tiếp điểm.

⑴ Viết phương trình tiếp tuyến của đồ thị hàm số tại giao điểm của

 

với trục

Vì

 

không cắt

nên không tồn tại tiếp tuyến thỏa YCBT.

⑵ Viết phương trình tiếp tuyến của đồ thị hàm số tại giao điểm của

 

với trục

Tọa độ giao điểm của

 

với trục

là

 

10;



Phương trình tiếp tuyến cần tìm là

  

1 1 0

y y x y x



       

⑶ Viết phương trình tiếp tuyến của đồ thị hàm số tại giao điểm của

 

với đường thẳng

1yx

Tọa độ giao điểm của

 

với

1yx

là nghiệm của

1 3 2 1 0

x x x



   





      



  





Với

















Phương trình tiếp tuyến là

  

1 1 0

y y x y x



       

 Biên soạn: LÊ MINH TÂM – 093.337.6281 29

Chương VII.

ĐẠO HÀM

Với



















Phương trình tiếp tuyến là

1 1 4 7

3 3 3 3

y y x y x

  



      

  

  

⑷ Viết phương trình tiếp tuyến của đồ thị hàm số biết hệ số góc của tiếp tuyến bằng

k 

Gọi

 

;M x y

là tiếp điểm của tiếp tuyến của đồ thị

 

với hệ số góc

k 

 

1 1 1



  





       



   





Với

















Phương trình tiếp tuyến là

 

1 2 1

3 3 3

y x y x       

Với

















Phương trình tiếp tuyến là

 

1 1 1

3 3 3

y x y x      

⑸ Viết phương trình tiếp tuyến của đồ thị hàm số, biết tiếp tuyến đó vuông góc với đưởng thẳng

34yx

Tiếp tuyến đó vuông góc với đưởng thẳng

34yx



Tiếp tuyến hệ số góc

k 

 

1 1 1



  





       



   





Với

















Phương trình tiếp tuyến là

 

1 2 1

3 3 3

y x y x       

Với

















Phương trình tiếp tuyến là

 

1 1 1

3 3 3

y x y x      

Câu 8. Cho hàm số

21y x x  

có đồ thị

 

⑴ Tìm hệ số góc của tiếp tuyến của hàm số trên tại điểm có

0x 

⑵ Viết phương trình tiếp tuyến của hầm số biết nó có

2.k 

⑶ Viết phương trình tiếp tuyến của hàm số trên, biết nó tạo với hai trục

Oxy

một tam

giác vuông cân tại

Lời giải

 Tính đạo hàm bằng công thức:

 Biên soạn: LÊ MINH TÂM – 093.337.6281 30

Chương VII.

ĐẠO HÀM

 

3 3 2

2 1 2 1 3 2y x x y x x x



        

 Gọi

 

;M x y

là tiếp điểm.

⑴ Tìm hệ số góc của tiếp tuyến của hàm số trên tại điểm có

0x 

Hệ số góc của tiếp tuyến của hàm số tại điểm có

0x 

là

 

0 3 0 2 2.ky



    

⑵ Viết phương trình tiếp tuyến của hầm số biết nó có

2.k 

Ta có

 

0 0 0

2 2 3 2 2 0k f x x x



          



Phương trình tiếp tuyến tại điểm

 

01;M

có dạng:

2 0 1 2 1()y x y x       

⑶ Viết phương trình tiếp tuyến của hàm số trên, biết nó tạo với hai trục

Oxy

một tam giác vuông

cân tại

Cách 1: Gọi phương trình đoạn chắn cắt 2 trục tọa độ và tạo với 2 trục 1 tam giác

vuông cân tại O có dạng

 

1 1 0. , . ;

x x b

y b x b a b a b d

a b a a



         





 

là tiếp tuyến của

 

thì

  

Vì

3 2 1

3 9 5 3

3 2 1

3 9 5 3



  



   











  



  

  











  





Có 4 phương trình tiếp tuyến ứng với các điểm tiếp xúc và hệ số góc trên như sau

 

1 1 0 1.y x y x     

 

1 1 2 3.y x y x     

3 9 5 3 9 2 3

3 9 9

.y x y x





       





3 9 5 3 9 2 3

3 9 9

.y x y x





       





Cách 2: Gọi phương trình tiếp tuyến của

(C)

thỏa mãn YCBT có dạng

 

:d y kx b

Ta có

32kx

Có giao điểm của

với

tại









; với trục Oy tại

 

0;b

Vì

tạo với hai trục

Oxy

một tam giác vuông cân tại

 Biên soạn: LÊ MINH TÂM – 093.337.6281 31

Chương VII.

ĐẠO HÀM

 

b loai

b b k









       

















3 2 1

3 9 5 3

3 2 1

3 9 5 3



  



   















  



  



  

















  





Có 4 phương trình tiếp tuyến ứng với các điểm tiếp xúc và hệ số góc trên như sau

 

1 1 0 1.y x y x     

 

1 1 2 3.y x y x     

3 9 5 3 9 2 3

3 9 9

.y x y x





       





3 9 5 3 9 2 3

3 9 9

.y x y x





       





Câu 9. Một chất điểm chuyển động thẳng biến đổi đều với phương trình

 

21 s t t m  

⑴ Tìm vận tốc tức thời của vật tại thời điểm

2ts

⑵ Tìm vận tốc trung bình của chất điểm trong khoảng thời gian từ

0t 

tới

2ts

Lời giải

Ta có:

41v s t



  

⑴ Tìm vận tốc tức thời của vật tại thời điểm

2ts

Vận tốc tức thời của vật tại thời điểm

2ts

là:

 

4 2 1 9./ms

⑵ Tìm vận tốc trung bình của chất điểm trong khoảng thời gian từ

0t 

tới

2ts

Trong khoảng thời gian từ

02t s t s  

thì chất điểm di chuyển được quãng đường:

 

4 2 2 1 9. m  



Vận tốc trung bình của chất điểm trong khoảng thời gian

kể từ thời điểm

0t 

là:

 

, / .

v m s



  



Câu 10. Một vật chuyển động thẳng xác định bởi phương trình

 

s s t

trong đó

được tính

bằng giây và

được tính bằng mét. Thực hiện các yêu cầu dưới đây:

⑴ Với

 

3s s t t t  

thì vận tốc của vật tại thời điểm

3st 

là bao nhiêu?

⑵ Với

 

7s s t t t  

thì vận tốc của vật tại thời điểm

4st 

là bao nhiêu?

⑶ Với

 

s s t t t   

thì vận tốc của vật tại thời điểm

10st 

là bao nhiêu?

 Biên soạn: LÊ MINH TÂM – 093.337.6281 32

Chương VII.

ĐẠO HÀM

⑷ Với

 

3 2

64s s t t t 

thì vận tốc của vật tại thời điểm

3st 

là bao nhiêu?

⑸ Với

 

2 10s s t t t   

thì vận tốc của vật tại thời điểm

3st 

là bao nhiêu?

⑹ Với

 

34s s t t t t   

thì vận tốc của vật tại thời điểm

4st 

là bao nhiêu?

⑺ Với

 

2 3 7s s t t t   

thì vận tốc của vật tại thời điểm

6st 

là bao nhiêu?

⑻ Với

 

coss s t t



  





thì vận tốc của vật tại thời điểm

2st 

là bao nhiêu?

⑼ Với

 

s s t t t  

thì vận tốc của vật tại thời điểm

4st 

là bao nhiêu?

⑽ Với

 

39s s t t t t   

thì vận tốc của vật tại thời điểm

5st 

là bao nhiêu?

Lời giải

⑴ Với

 

3s s t t t  

thì vận tốc của vật tại thời điểm

3st 

là bao nhiêu?

Ta có

   

36'v t S t t t  

. Từ đó:

   

39m/sv 

⑵ Với

 

7s s t t t  

thì vận tốc của vật tại thời điểm

4st 

là bao nhiêu?

Ta có

   

27'v t S t t  

. Từ đó:

   

4 2 4 7 15. m/sv   

⑶ Với

 

s s t t t   

thì vận tốc của vật tại thời điểm

10st 

là bao nhiêu?

Ta có

       

3 3 100

24 10 240 90

m/s .v t s t t t v





       

⑷ Với

 

3 2

64s s t t t 

thì vận tốc của vật tại thời điểm

3st 

là bao nhiêu?

Ta có

       

3 12 3 3 3 12 3 9. . m/s .v t s t t t v



        

⑸ Với

 

2 10s s t t t   

thì vận tốc của vật tại thời điểm

3st 

là bao nhiêu?

Ta có

       

6 1 3 6 3 1 53. m/s .v t s t t v



      

⑹ Với

 

34s s t t t t   

thì vận tốc của vật tại thời điểm

4st 

là bao nhiêu?

Ta có

       

9 8 1 4 9 4 8 4 1 175. . m/s .v t s t t t v



        

⑺ Với

 

2 3 7s s t t t   

thì vận tốc của vật tại thời điểm

6st 

là bao nhiêu?

Ta có

       

4 3 6 4 6 3 27. m/s .v t s t t v



      

⑻ Với

 

coss s t t



  





thì vận tốc của vật tại thời điểm

2st 

là bao nhiêu?

Ta có

       

6 2 2 6 4 16 32

sin sin . m/s .v t s t t v

   



         

   

   

⑼ Với

 

s s t t t  

thì vận tốc của vật tại thời điểm

4st 

là bao nhiêu?

 Biên soạn: LÊ MINH TÂM – 093.337.6281 33

Chương VII.

ĐẠO HÀM

Ta có

       

2 3 4 2 4 3 4 140. . m/s .v t s t t t v



      

⑽ Với

 

39s s t t t t   

thì vận tốc của vật tại thời điểm

5st 

là bao nhiêu?

Ta có

       

3 6 9 5 3 5 6 5 9 36. . m/s .v t s t t t v



        

Câu 11. Một chất điểm chuyển động theo phương trình

 

s s t

trong đó

được tính bằng giây

và

được tính bằng mét. Thời gian để vận tốc của chất điểm đạt giá trị lớn nhất

Lời giải

⑴ Với

 

10 9s t t t t   

trong khoảng 10 giây đầu tiên.

Vận tốc tại thời điểm

là

   

3 18 1v t s t t t



    

trên đoạn

0 10;





   

 

   

3 18 1 3 6 9 9 1 3 3 8 3 3 24 24v t s t t t t t t t





                   





Vậy vận tốc đạt được giá trị lớn nhất bằng

 

3 0 3t t s    

⑵ Với

 

9 10s tt tt   

trong 12 giây đầu tiên.

Vận tốc tại thời điểm

là

   

3 18 1'v t S t t t    

trên đoạn

0 12;





   

 

343 18 6 9 9 1 3 3 241 2'v t S t t ttt t            

Vậy vận tốc đạt được giá trị lớn nhất bằng

 

3 0 3t t s    

⑶ Với

 

6s t t t  

trong 10 giây đầu tiên.

Vận tốc tại thời điểm

là

   

3 12v t s t t t



   

trên đoạn

0 10;





   

 

3 12 3 4 4 12 3 2 12 12v t s t t t t t t



             

Vậy vận tốc đạt được giá trị lớn nhất bằng

 

2 0 2t t s    

⑷ Với

 

s t t t  

trong 10 giây đầu tiên.

Vận tốc tại thời điểm

là

   

v t s t t t



   

trên đoạn

0 10;





   

 

   

3 3 3

8 16 16 4 16 4 24 24

2 2 2

v t s t t t t t





              





Vậy vận tốc đạt được giá trị lớn nhất bằng

 

4 0 4t t s    

⑸ Với

 

s t t t  

trong 10 giây đầu tiên.

Vận tốc tại thời điểm

là

   

v t s t t t



   

trên đoạn

0 10;





   

 

   

3 3 3

12 36 36 6 36 6 54 54

2 2 2

v t s t t t t t





              





Vậy vận tốc đạt được giá trị lớn nhất bằng

 

6 0 6t t s    

 Biên soạn: LÊ MINH TÂM – 093.337.6281 34

Chương VII.

ĐẠO HÀM

⑹ Với

 

s t t t  

trong 9 giây đầu tiên.

Vận tốc tại thời điểm

là

   

12v t s t t t



   

trên đoạn

09;





       

12 6 36 6 36 36v t s t t t t t





            





Vậy vận tốc đạt được giá trị lớn nhất bằng

 

6 0 6t t s    

⑺ Với

 

s t t t

trong 5 giây đầu tiên.

Vận tốc tại thời điểm

là

   

v t s t t t



  

trên đoạn

05;





   

 

   

1 1 1

4 4 4 2 4 2 2 2

2 2 2

v t s t t t t t





              





Vậy vận tốc đạt được giá trị lớn nhất bằng

 

2 0 2t t s    

⑻ Với

3 20

s t t   

trong 10 giây đầu tiên.

Vận tốc tại thời điểm

là

   

v t s t t t





  

trên đoạn

05;





   

 

   

3 3 3

4 4 4 2 4 2 6 6

2 2 2

v t s t t t t t

  





           





Vậy vận tốc đạt được giá trị lớn nhất bằng

 

2 0 2t t s    

Câu 12. Một vật chuyển động thẳng xác định bởi phương trình

 

s s t

trong đó

được tính

bằng giây và

được tính bằng mét.

⑴ Với

 

2 6 3 1s s t t t t    

thì gia tốc của vật tại thời điểm

3st 

là bao nhiêu?

⑵ Với

 

4 10 9s s t t t   

thì gia tốc của vật tại thời điểm vận tốc bằng

là bao

nhiêu?

⑶ Với

 

35s s t t t   

thì gia tốc của vật tại tại giây thứ

là bao nhiêu?

⑷ Với

 

3 9 1s s t t t t    

thì gia tốc của vật tại tại thời điểm vật dừng lại là bao

nhiêu?

⑸ Với

 

3 5 2s s t t t t    

thì gia tốc của vật tại giây thứ

là bao nhiêu?

⑹ Với

 

3 3 10s s t t t t    

thì gia tốc của vật tại thời điểm vật dừng lại là bao

nhiêu?

⑻ Với

 

s s t t t t    

thì gia tốc của vật tại thời điểm

2st 

là bao nhiêu?

Lời giải

⑴ Với

 

2 6 3 1s s t t t t    

thì gia tốc của vật tại thời điểm

3st 

là bao nhiêu?

 Biên soạn: LÊ MINH TÂM – 093.337.6281 35

Chương VII.

ĐẠO HÀM

Vận tốc của chuyển động là:

   

 

4 2 3

2 6 3 1 8 12 3v t s t t t t t t



       

Gia tốc của chuyển động là:

   

24 12a t v t t



  

Gia tốc của chuyển động tại thời điểm

3st 

là:

 

3 24 9 12 228

. m/sa   

⑵ Với

 

4 10 9s s t t t   

thì gia tốc của vật tại thời điểm vận tốc bằng

là bao nhiêu?

Vận tốc của chuyển động là:

   

12 10v t s t t



  

Gia tốc của chuyển động là:

   

24a t v t t





Mà

 

2 12 10 2

v t t





    







. Do

0t 

nên

1t 

suy ra

 

2 24m/ sa 

⑶ Với

 

35s s t t t   

thì gia tốc của vật tại tại giây thứ

là bao nhiêu?

Vận tốc của chuyển động là:

   

36v t s t t t



  

Gia tốc của chuyển động là:

   

66a t v t t



  

Gia tốc của chuyển động tại thời điểm

10st 

là:

 

10 6 10 6 54

. m/sa   

⑷ Với

 

3 9 1s s t t t t    

thì gia tốc của vật tại tại thời điểm vật dừng lại là bao nhiêu?

Vận tốc của chuyển động là:

   

3 6 9v t s t t t



   

Gia tốc của chuyển động là:

   

66a t v t t



  

Tại thời điểm chất điểm dừng lại thì

0v 

 

3 6 9 0





    









Gia tốc của chất điểm tại thời điểm chất điểm dừng lại là

 

3 6 3 6 12.a   

⑸ Với

 

3 5 2s s t t t t    

thì gia tốc của vật tại giây thứ

là bao nhiêu?

Vận tốc của chuyển động là:

   

3 6 5v t s t t t



   

Gia tốc của chuyển động là:

   

66a t v t t



  

Gia tốc của chuyển động tại thời điểm

3st 

là:

 

3 6 3 6 12

. m/sa   

⑹ Với

 

3 3 10s s t t t t    

thì gia tốc của vật tại thời điểm vật dừng lại là bao nhiêu?

Vận tốc của chuyển động là:

   

3 6 3'v t s t t t   

Gia tốc của chuyển động là:

   

66a t v t t



  

Tại thời điểm chất điểm dừng lại thì

0v 

3 6 3 0 1t t t     

Gia tốc của chất điểm tại thời điểm chất điểm dừng lại là

 

1 6 1 6 0.a   

⑺ Với

 

83v t t t

thì gia tốc của vật khi vận tốc của vật là

 

/ms

.là bao nhiêu?

Gia tốc của chuyển động là:

   

86'a t v t t  

 Biên soạn: LÊ MINH TÂM – 093.337.6281 36

Chương VII.

ĐẠO HÀM

Mà

 

11 8 3 11

v t t t







    









. Do

0t 

nên

1t 

suy ra

 

1 14m/ sa 

⑻ Với

 

s s t t t t    

thì gia tốc của vật tại thời điểm

2st 

là bao nhiêu?

Vận tốc của chuyển động là:

   

2 4 1'v t s t t t   

Gia tốc của chuyển động là:

   

44a t v t t



  

Gia tốc của chuyển động tại thời điểm

10st 

là:

 

2 4 2 4 12

. m/sa   

Câu 13. Một vật chuyển động thẳng xác định bởi phương trình

 

s s t

trong đó

được tính

bằng giây và

được tính bằng mét. Hỏi:

⑴ Gia tốc tại thời điểm vận tốc triệt tiêu với

 

39s s t t t t   

là bao nhiêu?

⑵ Gia tốc tại thời điểm vận tốc triệt tiêu với

 

3 9 27s s t t t t    

là bao nhiêu?

⑶ Vận tốc tại thời điểm gia tốc triệt tiêu với

 

39s s t t t t    

là bao nhiêu?

⑷ Vận tốc tại thời điểm gia tốc triệt tiêu với

 

3s s t t t  

là bao nhiêu?

⑸ Vận tốc tại thời điểm gia tốc bằng không với

 

2 3 4 ,s s t t t t   

là bao nhiêu?

⑹ Vận tốc tại thời điểm gia tốc triệt tiêu với

 

3 36

s s t t t t   

là bao nhiêu?

⑺ Gia tốc tại thời điểm vận tốc triệt tiêu với

 

3 9 2020s s t t t t     

là bao nhiêu?

⑻ Vận tốc tại thời điểm gia tốc triệt tiêu với

 

2 3 4s s t t t t   

là bao nhiêu?

⑼ Vận tốc tại thời điểm gia tốc triệt tiêu với

 

3 9 2024s s t t t t    

là bao nhiêu?

⑽ Vận tốc tại thời điểm gia tốc của vật đạt giá trị nhỏ nhất trong 20 giây đầu tiên với

 

4 3 2

6 10

s t t t t t   

là bao nhiêu?

Lời giải

⑴ Gia tốc tại thời điểm vận tốc triệt tiêu với

 

39s s t t t t   

là bao nhiêu?

Vận tốc của chuyển động là:

   

3 6 9'v t s t t t   

Gia tốc của chuyển động là:

   

66a t v t t



  

Khi vận tốc triệt tiêu ta có

 

0 3 6 9 0 3v t t t t      

(vì

0t 

)

Khi đó gia tốc là

 

3 6 3 6 1. 2m/sa   

⑵ Gia tốc tại thời điểm vận tốc triệt tiêu với

 

3 9 27s s t t t t    

là bao nhiêu?

Vận tốc của chuyển động là:

   

3 6 9'v t s t t t   

Gia tốc của chuyển động là:

   

66a t v t t



  

 Biên soạn: LÊ MINH TÂM – 093.337.6281 37

Chương VII.

ĐẠO HÀM

Khi vận tốc triệt tiêu ta có

 

0 3 6 9 0

v t t t





     







(vì

0t 

)

Khi đó gia tốc là

 

1 6 1 6 12. m/sa   

⑶ Vận tốc tại thời điểm gia tốc triệt tiêu với

 

39s s t t t t    

là bao nhiêu?

Vận tốc của chuyển động là:

   

3 6 9'v t s t t t    

Gia tốc của chuyển động là:

   

66a t v t t



   

Khi gia tốc triệt tiêu ta có

 

0 6 6 0 1a t t t      

Khi đó vận tốc là

 

1 3 1 6 1 9 12. . m/sv     

⑷ Vận tốc tại thời điểm gia tốc triệt tiêu với

 

3s s t t t  

là bao nhiêu?

Vận tốc của chuyển động là:

   

36'v t s t t t  

Gia tốc của chuyển động là:

   

66a t v t t



  

Khi gia tốc triệt tiêu ta có

 

0 6 6 0 1a t t t     

Khi đó vận tốc là

 

1 3 1 6 1 3. . m/sv    

⑸ Vận tốc tại thời điểm gia tốc bằng không với

 

2 3 4 ,s s t t t t   

là bao nhiêu?

Vận tốc của chuyển động là:

   

6 6 4'v t s t t t   

Gia tốc của chuyển động là:

   

12 6a t v t t



  

Khi gia tốc triệt bằng 0 có

 

0 12 6 0

a t t t     

Khi đó vận tốc là

1 1 1 5

6 6 4

2 2 2 2

. . m/sv

     

   

     

     

⑹ Vận tốc tại thời điểm gia tốc triệt tiêu với

 

3 36

s s t t t t   

là bao nhiêu?

Vận tốc của chuyển động là:

   

6 36v t s t t t



   

Gia tốc của chuyển động là:

   

26a t v t t



  

Khi gia tốc triệt tiêu ta có

 

0 2 6 0 3a t t t     

Khi đó vận tốc là

 

3 3 6 3 36 27. m/sv    

⑺ Gia tốc tại thời điểm vận tốc triệt tiêu với

 

3 9 2020s s t t t t     

là bao nhiêu?

Vận tốc của chuyển động là:

   

3 6 9v t s t t t



    

Gia tốc của chuyển động là:

   

66a t v t t



   

Khi vận tốc triệt tiêu ta có

 

0 3 6 9 0

loait

v t t t





      









(vì

0t 

)

 Biên soạn: LÊ MINH TÂM – 093.337.6281 38

Chương VII.

ĐẠO HÀM

Khi đó gia tốc là

 

6 3 6 12. m/ sa v t



     

⑻ Vận tốc tại thời điểm gia tốc triệt tiêu với

 

2 3 4s s t t t t   

là bao nhiêu?

Vận tốc của chuyển động là:

   

6 6 4v t s t t t



   

Gia tốc của chuyển động là:

   

12 6a t v t t



  

Khi gia tốc triệt tiêu ta có

 

0 12 6 0

a t t t     

Khi đó vận tốc là

, m/sv









⑼ Vận tốc tại thời điểm gia tốc triệt tiêu với

 

3 9 2024s s t t t t    

là bao nhiêu?

Vận tốc của chuyển động là:

   

69v t s t t t



   

Gia tốc của chuyển động là:

   

66'.a t v t t  

Khi gia tốc triệt tiêu ta có

 

0 6 6 0 1a t t t     

Khi đó vận tốc là

 

1 12

m/sv 

⑽ Vận tốc tại thời điểm gia tốc của vật đạt giá trị nhỏ nhất trong 20 giây đầu tiên với

 

4 3 2

6 10

s t t t t t   

là bao nhiêu?

Vận tốc của chuyển động là:

   

3 12 10

v t s t t t t



    

Gia tốc của chuyển động là:

     

6 12 3 3a t v t t t t



      

Thấy rằng

   

3 3 3a t t   

Gia tốc đạt được giá trị bé nhất bằng

 

3 0 3t t s    

Khi đó vận tốc của vật bằng

   

3 28 m/sv 

--------------------Hết--------------------

 Biên soạn: LÊ MINH TÂM – 093.337.6281 39

Chương VII.

ĐẠO HÀM

1. Đạo hàm hàm số

yx

2. Đạo hàm hàm số

yx

3. Đạo hàm hàm số lượng giác

⑴ Hàm số

sinyx

có đạo hàm trên và

 

sin cosxx





⑵ Hàm số

cosyx

có đạo hàm trên và

 

cos sinxx





⑶ Hàm số

tanyx

có đạo hàm tại mọi

xk

và

 

tan

cos





⑷ Hàm số

cotyx

có đạo hàm tại mọi

xk

và

 

cot

sin





4. Đạo hàm của hàm số mũ và hàm số logarit

⑴ Hàm số

ye

có đạo hàm trên

 





⑵ Hàm số

ya

có đạo hàm trên

 

.ln

a a a





⑶ Hàm số

log

yx

có đạo hàm tại mọi

0x 

 

log





⑷ Hàm số

lnyx

có đạo hàm tại mọi

0x 

 

ln x





Lý thuyết

Hàm số có đạo hàm trên và .

CÁC QUY TẮC TÍNH ĐẠO HÀM

ĐẠO HÀM

 Biên soạn: LÊ MINH TÂM – 093.337.6281 40

Chương VII.

ĐẠO HÀM

5. Các quy tắc tính đạo hàm

6. Đạo hàm của hàm hợp

6.1 Khái niệm hàm số hợp

6.2 Đạo hàm của hàm số hợp

Giả sử các hàm số có đạo hàm trên khoảng .

Khi đó: ⑴

⑵

⑶

⑷

Giả sử là hàm số xác định trên khoảng , có tập giá trị chứa khoảng

và là hàm số xác định trên . Hàm số được gọi là hàm

số hợp của hàm số với .

Nếu hàm số có đạo hàm tại và hàm số có đạo hàm tại

thì hàm số hợp có đạo hàm tại là

 Biên soạn: LÊ MINH TÂM – 093.337.6281 41

Chương VII.

ĐẠO HÀM

Từ đó ta có các kết quả sau:

⑴

 

x n x







⑵











⑶

 





 

u n u u



















 

.uu





⑷

 

sin cosxx





⑸

 

cos sinxx





⑹

 

tan

cos





⑺

 

cot

sin





 

sin .cosu u u





 

cos .sinu u u





 

tan .

cos





 

cot .

sin





⑻

 





⑼

 

.ln

a a a





 

e u e





 

. .ln

a u a a





⑽

 

ln x





⑾

 

log





 

ln .uu





 

log .





7. Đạo hàm cấp hai

 Ý nghĩa cơ học của đạo hàm cấp hai

Một chuyển động có phương trình

 

s f t

thì đạo hàm cấp hai (nếu có) của hàm số

 

s f t

là gia tốc tức thời của chuyển động

 

s s t

tại thời điểm

. Ta có

   

a t f t





Cho hàm số có đạo hàm tại mọi điểm .

Nếu hàm số lại có đạo hàm tại thì ta gọi đạo hàm của là đạo

hàm cấp hai của hàm số tại , kí hiệu là hoặc .

Khi đó: .

 Biên soạn: LÊ MINH TÂM – 093.337.6281 42

Chương VII.

ĐẠO HÀM

 Dạng 1. Tính đạo hàm đa thức – hữu tỉ – căn thức

 Lời giải

⑴

 

1f x x

Ta có

 

     

3 3 2 3

5 1 1 15 1f x x x x x



    

⑵

 

200f x x x x   

Bài tập

 Áp dụng quy tắc đạo hàm:

Khi đó: ⑴

⑵

⑶

⑷

 Áp dụng công thức đạo hàm:

⑴ ⑵

⑶ ⑷

Phương pháp

Ví dụ 1.1.

Tính đạo hàm các hàm số sau:

⑴ ⑵

⑶ ⑷

⑸ ⑹

⑺ ⑻

⑼ ⑽

 Biên soạn: LÊ MINH TÂM – 093.337.6281 43

Chương VII.

ĐẠO HÀM

Ta có

 

200f x x x x



   

   

200x x x





   

4 2 1xx  

⑶

 

3 2021f x x x x   

Ta có

 

4 3 3 2

3 2021 12 3 1f x x x x x x



      

⑷

 

27f x x x

   

Ta có

 

   

 

3 2 3 2 2

5 5 5

2 7 2 7 3 4f x x x x x x x



   





           

   

   

⑸

 

f x x



Ta có

 

4 4 4

f x x









    





⑹

 

7 5 3

23f x x x x   

Ta có

 

7 5 3 6 4 2

2 3 7 10 9f x x x x x x x



       

⑺

    

12f x x x  

Ta có

        

1 2 1 2 2 1 2 1f x x x x x x x x





           

⑻

 







Ta có

 

      

 

   

2 2 2

3 5 2 1 3 5 2 1 3 2 1 2 3 5

2 1 2 1 2 1

.x x x x x x

x x x



       





  

  

⑼

 







Ta có.

 

      

     

2 2 2

2 1 2 1

1 1 1

x x x x

x x x





    



   



   







  

⑽

 







Ta có

 

      

 

   

2 2 2

1 1 1 1 1 1

1 1 1

x x x x x x

x x x





       







   







  

 Biên soạn: LÊ MINH TÂM – 093.337.6281 44

Chương VII.

ĐẠO HÀM

 Dạng 2. Tính đạo hàm lượng giác

 Lời giải

⑴

sinyx









3 3 3 3

6 6 6

.cos cosy x x x



     



      

     

     

⑵

sinyx



  







 

2 2 2 2

2 3 3 2 3 3

. .cos . .cos .cosy x x x x x x



       



         

       

       

 Áp dụng quy tắc đạo hàm:

Khi đó: ⑴

⑵

⑶

⑷

 Để tính đạo hàm của hàm số tại , ta thực hiện theo các bước sau:

⑴ ⑵

⑶

⑷

Phương pháp

Ví dụ 2.1.

Tính đạo hàm các hàm số sau:

⑴ ⑵

⑶ ⑷

⑸ ⑹

⑺ ⑻

⑼

⑽

 Biên soạn: LÊ MINH TÂM – 093.337.6281 45

Chương VII.

ĐẠO HÀM

⑶

2cosyx



   

2 2 2

24. . sin .siny x x x x



   

⑷

tan





1 1 1 1 1 1

2 2 2 2 2

. . tan tan

cos

x x x x



       

   



     

       



       

⑸

2sinyx





2 2 2 2

2 2 2

.cos cos cos

y x x x x



       



⑹

 

sin sinyx

     

sin .cos sin cos .cos siny x x x x



  

⑺

22sin cosy x x x  

2 2 2 2 1 2 2 2 2 1 4 2 1. .cos .sin sin sin sin siny x x x x x x



        

⑻

 

21cosyx

 

3 2 1 2 1. cos .cosy x x



   

 

3 2 2 1 2 1. sin .cosxx   

   

6 2 1 2 1sin cosxx   

⑼

2tan coty x x

 

3 2 2

2 2 2

2 1 2

2 3 3

tan cot . tan .tan tan

sin cos sin

y x x x x x

x x x



      

⑽

 

32siny x x  



   

 

2 2 2

3 2 3 2 2 3 3 2.cos cosy x x x x x x x



        

 Biên soạn: LÊ MINH TÂM – 093.337.6281 46

Chương VII.

ĐẠO HÀM

 Dạng 3. Tính đạo hàm mũ – logarit

 Lời giải

⑴

 

21logyx

Ta có

 

   

2 1 3 2 1 3ln ln











⑵

 

1 2007logyx

Ta có

 

   

1 2007

2007

1 2007 3 1 2007 3.ln ln











⑶





Ta có

 

2 1 2 1

2 1 5 5 2 5 5. .ln . .ln





  

 Áp dụng quy tắc đạo hàm:

Khi đó: ⑴

⑵

⑶

⑷

 Để tính đạo hàm của hàm số tại , ta thực hiện theo các bước sau:

⑴ ⑵

⑶ ⑷

Phương pháp

Ví dụ 3.1.

Tính đạo hàm các hàm số sau:

⑴ ⑵

⑶ ⑷

⑸ ⑹

⑺ ⑻

⑼ ⑽

 Biên soạn: LÊ MINH TÂM – 093.337.6281 47

Chương VII.

ĐẠO HÀM

⑷

2025





Ta có

 

2025 2025

2025 2025 2025.ln







  

⑸

 

3lny x x  

Ta có

 







   



⑹

sin

y 

Ta có

 

sin

sin .e





sin

cos .e

x

⑺

2 3 2025





Ta có

 

2 3 2025 2 3 2 3

2 3 2e e .e .e

x x x

  



    

⑻

 

2logy x x

Ta có

 

   

2 2 2 2ln ln

x x x x











⑼

 

21logy x x  

Ta có

 

   

2 1 3 2 1 3

log

ln ln

y x x

x x x x









    

   

⑽

 

32log

y x x  

Ta có

 

   

3 2 3 3 3 3

2 3 2 3

log ln ln

ln ln

x x x

y x x

x x x x







      



 Biên soạn: LÊ MINH TÂM – 093.337.6281 48

Chương VII.

ĐẠO HÀM

Câu 14. Tính đạo hàm của các hàm số sau:

⑴

24y x x  

⑵

 

31yx

⑶

2 4 1y x x   

⑷

2 2 8 1

y x x x   

⑸







⑹







⑺







⑻

 

  





⑼

  

2 1 5 3y x x x  

⑽

  

1 5 3y x x  

Lời giải

⑴

24y x x  



 

2 4 6y x x x



     

⑵

 

31yx



       

2 2 2 2

3 1 2 3 1 3 1 12 3 1.y x x x x x







      





⑶

2 4 1y x x   



 

4 2 3

2 4 1 8 8y x x x x



      

⑷

2 2 8 1

y x x x   

3 2 2

2 2 8 1 4 2 8

y x x x x x







       





⑸







      

   

2 1 2 2 1 2

2 1 3

x x x x





    







   









⑹























Luyện tập

 Biên soạn: LÊ MINH TÂM – 093.337.6281 49

Chương VII.

ĐẠO HÀM

 

1 1 1 1

x x x x x x



      





  

 

2 1 1 1

x x x x

    





   

2 2 2

2 3 1 1 2

x x x x x x

     





⑺







Cách 1:















      

 

2 2 2 2

3 1 3 1

x x x x x x x x



        







 

   

 

2 1 1 3 2 1

x x x x x x

      





 

2 1 1 3

x x x x x

     





 

4 2 1







Cách 2:

Ta có:







  





1xx





















1xx













1xx















 









 

4 2 1







⑻

 

  









  











 

3 3 2 2 3 3 2 2

x x x x x x



        





  

 

2 3 2 2 2 3 3

x x x x

      





 

4 10 6 2 6 6

x x x x

     





 







 







⑼

  

2 1 5 3y x x x  

Cách 1:

  

2 1 5 3y x x x







   



 

         

2 2 2

2 1 5 3 2 1 5 3 2 1 5 3x x x x x x x x x





        

 

   

2 2 2

2 10 3 2 5 3 5 2 1x x x x x x x      

3 2 3 2 3 2

20 2 6 10 6 10 5x x x x x x x      

40 3 6x x x  

Cách 2:

Ta có

  

 

2 2 2 4 3 2

2 1 5 3 10 3 10 3y x x x x x x x x x        

 Biên soạn: LÊ MINH TÂM – 093.337.6281 50

Chương VII.

ĐẠO HÀM

  

 

2 4 3 2

2 1 5 3 10 3y x x x x x x







      



40 3 6x x x  

⑽

  

1 5 3y x x  

      

2 2 2 2

1 5 3 1 5 3y x x x x





      

   

2 2 3 3 3

2 5 3 6 1 10 6 6 6 12 4x x x x x x x x x x          

Câu 15. Tính đạo hàm của các hàm số sau:

⑴

4 3 1y x x  

⑵

3y x x  

⑶







⑷

 

23y x x  

⑸

21yx

⑹

 

72 3yxx 

⑺

13yx

⑻

 

21y x x x  

⑼







⑽

47y x x  

Lời giải

⑴

4 3 1y x x  





 

4 3 1

2 4 3 1 2 4 3 1

y x x

x x x x











    

   

⑵

3y x x  

 

2 3 2 3

x x x x











   

⑶







Cách 1.

       

 

   

2 2 2

2 1 2 2 1 2 2 2 2 1 1

2 2 2

. . . .x x x x x x

x x x



       



  

  

Cách 2.

 

   

2 2 1 1









⑷

 

23y x x  

 

   

 

5 2 3 2 2 10 1 2 3y x x x x x x



       

⑸

21yx





21yx





 

2 2 1









2 2 1









 Biên soạn: LÊ MINH TÂM – 093.337.6281 51

Chương VII.

ĐẠO HÀM

⑹

 

72 3yxx 

   

73 2 1033xy x x 



⑺

13yx

2 1 3 1 3









⑻

 

21 .y x x x  

   





2 1 2 1..y x x x x x x



     

  

2 1 2 1

x x x x





     



⑼







       

 

   

2 2 2

3 4 2 2 3 4 3 2 3 4

2 2 2

.x x x x x x

x x x



           



  

  

⑽

47y x x  

 

4 2 4 2

2 4 7 4 7

x x x x









   

Câu 16. Tính đạo hàm của các hàm số sau:

⑴







⑵





⑶







⑷







⑸

2 4 1







⑹







⑺

y x x

⑻

 

2 3 2y x x x  

⑼

  

2 1 3 2y x x x  

⑽

  

2 3 2 3y x x x   

Lời giải

⑴







      

 

   

     

2 2 2 2

4 3 2 1 4 3 2 1 2 4 3 4 2 1

8 6 8 4 10

4 3 4 3 4 3 4 3

x x x x x x

x x x x



       

   



   

   

⑵





 Biên soạn: LÊ MINH TÂM – 093.337.6281 52

Chương VII.

ĐẠO HÀM

   

3 2 1 2 1 3

2 1 2 1

..xx



  





  



⑶







       

 

   

2 1 1 3 1 3 2 1 2 1 3 3 2 1

1 3 1 3

x x x x x x



       



   







⑷







 

3 3 1 3 3 1

x x x x x x



      







  

 

2 3 1 3 3

x x x x

    





 

2 5 3 3 3

x x x x

    





 







⑸

2 4 1







2xx





 



   

7 2 12 11





   



⑹







       

 

2 2 2 2

1 1 1 1

.x x x x x x x x



        







 

   

 

1 2 1 1 2 1

x x x x x x

      





 

1 2 1 1

2 1 2

x x x x x

x x x x

     





   

⑺

y x x

 

2 2 2

. . . .y x x x x x x x



    

x x x x  

⑻

 

2 3 2y x x x  

 Biên soạn: LÊ MINH TÂM – 093.337.6281 53

Chương VII.

ĐẠO HÀM

 

2 3 2 2 3 2y x x x x x x



     

 

2 2 2 3 5 2x x x x    

5 5 4

2 4 10 4 15 6x x x x x     

12 15 8 6x x x   

⑼

  

2 1 3 2y x x x  

  

 

2 3 2

2 1 3 2 6 2 6 2y x x x x x x x x x        

 

3 2 2

6 2 18 2 2y x x x x x



     

⑽

  

2 3 2 3y x x x   

      

2 2 2 2

2 3 2 3 2 3 2 3y x x x x x x





       

 

   

 

2 2 2 3 2 3 4x x x x x     

3 2 3 2

4 6 4 6 4 8 12x x x x x x      

8 12 18 6x x x   

Câu 17. Tính đạo hàm của các hàm số sau:

⑴

1y x x  

⑵

 

1y x x  

⑶





⑷

 

21y x x  

⑸

5 2 1y x x  

⑹













⑺







⑻

4y x x  

⑼













⑽

y x x x  

Lời giải

⑴

1y x x  





 

2 1 2 1

y x x

x x x x











      

   

⑵

 

1y x x  

 

1 5 2 1 1y x x x x x







      





⑶













 

2 2 2 2

1 1 2

1 2 1 1 1

x x x x











     





   





 Biên soạn: LÊ MINH TÂM – 093.337.6281 54

Chương VII.

ĐẠO HÀM

⑷

 

21y x x  

 

2 2 2

2 2 2 1

2 1 1 1

x x x

y x x

x x x

  





     

  

⑸

5 2 1y x x  





 

2 2 2

5 2 1

10 2 5 1

5 2 1

2 5 2 1 2 5 2 1 5 2 1

y x x

x x x x x x











     

     

⑹













 

4 3 3

2 2 2 2 2

1 1 1 1 2

1 1 1 1

x x x x x x x x x x

x x x x





       

        





  

       



   



       



⑺







   









1 1 1 1

x x x x



    







 

  







 

1 1 2

x x x

  





 

   

1 1 2

x x x

  

  





⑻

4y x x  

2 4 4

x x x

  



  



⑼













   

2 1 2 1 2 1 3 12 6

1 1 1

x x x x

x x x



    

    



   

    

  

    



⑽

y x x x  

y x x x   

 Biên soạn: LÊ MINH TÂM – 093.337.6281 55

Chương VII.

ĐẠO HÀM

 







  



 

2 2 2 2..

y x x y x x







    



1 2 1

x x x x x x x x





    

Câu 18. Tính đạo hàm của các hàm số sau:

⑴

cos2x





⑵

cos .siny x x

⑶

2sin siny x x

⑷

12cosyx

⑸

3cosyx

⑹

sin cos







⑺

tan coty x x

⑻

sin













⑼

cos







⑽

sin cos

cos sin

x x x







Lời giải

⑴

cos2x





     

 

2 3 1 2 3 1 2 3 1 2 3 2

3 1 3 1

cos . cos . sin cosx x x x x x x



     







⑵

cos .siny x x

 

2 2 3 2

cos .sin cos . sin sin +2cos .siny x x x x x x x



   

⑶

2sin siny x x

 

2 2 2 2sin sin sin cos cosy x x x x x



   

⑷

12cosyx





 

2 2 2

2 2 2 4

2 1 2 1 2 1 2

cos

.sin cos sin

cos

cos cos cos

x x x











    

  

⑸

3cosyx

 

3 6 3 3cos sin cosy x x x



  

 Biên soạn: LÊ MINH TÂM – 093.337.6281 56

Chương VII.

ĐẠO HÀM

⑹

sin cos







      

 

sin cos sin cos sin cos sin cos

sin cos

x x x x x x x x



    







     

 

cos sin sin cos sin cos sin cos

sin cos

x x x x x x x x

    





   

 

sin cos sin cos

sin cos

x x x x

  





 

2 2 2 2

22sin sin cos cos sin sin cos cos

sin cos

x x x x x x x

    





 

sin cos

(sin cos )

sin cos



   



⑺

tan coty x x

 

tan cot

y x x







  



cos sin

sin cos

tan cot sin .cos tan cot

x x x x x x







2 2 2 2

cos sin cos sin

sin cos

sin .cos

cos sin

sin .cos

x x x x







cos sin

sin .cos sin .cos

x x x x





⑻

sin













2 1 2 1

sin

sin sin















   









   











     

   





   



   



   

 Biên soạn: LÊ MINH TÂM – 093.337.6281 57

Chương VII.

ĐẠO HÀM

 

3 1 1

1 1 1

2 1 2 1

2 1 2 1 2 1

2 1 2 1

sin cos

sin sin

x x x



   



     

  



   

     



   



  

     



   



   



   

 

2 1 2 1

sin cos

sin

   





   



   















⑼

cos







2 3 2 3

cos cos

















1 1 1

2 3 2 3 2 3

cos sin

x x x





  





  



2 3 2 3

cos sin























 

2 3 2 3

cos sin













 

15 1 1

2 3 2 3

2 2 3

cos sin











⑽

sin cos

cos sin

x x x







     

 

sin cos sin cos sin sin cos cos sin cos

cos sin

x x x x x x x x x x x x x x

x x x

      





    

 

cos cos sin sin cos sin

cos sin

x x x x x x x x x x

x x x

   





 

2 2 2

cos sin cos sin cos sin

cos sin

x x x x x x x x x

x x x

  





cos sin

x x x











Câu 19. Tính đạo hàm cấp 2 của các hàm số sau:

⑴

1y x x

⑵

sinyx









 Biên soạn: LÊ MINH TÂM – 093.337.6281 58

Chương VII.

ĐẠO HÀM

⑶

2sinyx

⑷

2sin siny x x

⑸

22sin cosy x x x  

⑹







⑺

1y x x  

⑻

 

31yx

⑼







⑽

 

sin sinyx

Lời giải

⑴

1y x x







 

11y x x x x



   

  



   





   









2 2 2 2

2 1 1 2 1 1

x x x x



    

















 

   

 

2 2 3

4 1 2 1

x x x

x x x x

  



  







⑵

sinyx











sinyx



















cosxx



   

  

   

   

cos x



  







cosyx









  









3 3 3 9 3

6 6 6

sin sinx x x



     

     

     

     

⑶

2sinyx











2 2 2

2 2 2sin . cosy x x x





    

. cos







. cos























. cos cos







   



















2 2 2

cos sin

x x x







    



 Biên soạn: LÊ MINH TÂM – 093.337.6281 59

Chương VII.

ĐẠO HÀM

 





3 2 2

cos . sin

   





 





cos .sin .

   



⑷

2sin siny x x



   

 

2 2 2 2 2 2 2 2sin sin sin sin sin .cos cos sin cosy x x x x x x x x x





       



 

2 2 2sin cosy x x







   

2 2 2sin cosxx





2 2 4 2cos sinxx

⑸

22sin cosy x x x  



 

22sin cosy x x x



  

 

   

2 2 4 2 2 1 2 2 2 2 1 4 2 1sin cos sin cos sin sin sin sinx x x x x x x x x





          



 

4 2 1 8 2sin cosy x x





  

⑹









      

 

   

2 2 2

3 1 2 3 1 2 1 2 2 3

1 2 1 2 1 2

x x x x x x

x x x



       



  

  



 

   

2 4 4 3

2 2 1 2

7 28

1 2 1 2 1 2 1 2

x x x x







   









      



   



⑺

1y x x  







 

2 1 2 1

y x x

x x x x











    

   







 





 





 

2 1 2 1 2 1 2 1

x x x x x x





        

















 

4 1 2 2 1

x x x



    







 

4 1 1x x x x



   

⑻

 

31yx

 Biên soạn: LÊ MINH TÂM – 093.337.6281 60

Chương VII.

ĐẠO HÀM



      

2 2 2 2

3 1 2 3 1 3 1 12 3 1y x x x x x







        







   

2 2 2

12 3 1 12 3 1 12 6 108 12y x x x x x x







        



⑼









       

 

2 2 2 2

3 1 3 1

x x x x x x x x



          







 

   

 

2 1 1 3 2 1

x x x x x x

        





 

4 2 1

  







 

   

 

   

2 4 3

2 2 2

8 1 4 2 1 2 2 1 1

4 2 1

24 24 16

1 1 1

x x x x x x





         

  







  



     





⑽

 

sin sinyx



       

sin sin sin cos sin cos cos siny x x x x x







    





         

 

cos cos sin cos cos sin cos cos siny x x x x x x







     



       

 

sin cos sin cos cos sin sinx x x x x      

   

sin cos sin cos sin sinx x x x    

Câu 20. Tính đạo hàm cấp 3 tại các điểm được chỉ ra dưới đây

⑴ Cho hàm số

3 3 5y x x x    

. Tính giá trị của

 

2017y

⑵ Cho hàm số





. Tính giá trị của

 

⑶ Cho hàm số





. Tính giá trị của

 

⑷ Cho hàm số

cosyx

. Tính giá trị của

 







Lời giải

⑴ Cho hàm số

3 3 5y x x x    

. Tính giá trị của

 

2017y

Ta có:

9 6 1'y x x   

18 6''yx  

18'''y 

 

2017 18y  

 Biên soạn: LÊ MINH TÂM – 093.337.6281 61

Chương VII.

ĐẠO HÀM

⑵ Cho hàm số





. Tính giá trị của

 

Cách 1:Ta có:

 

   

2 3 12

   



 

y  

Cách 2: Ta có:

 





 

   

2 2 1







 

   

3 6 4

12 1

4 12

1 1 1

x x x









    



  



 

y  

⑶ Cho hàm số





. Tính giá trị của

 

Ta có:

 







   

 

   

2 2 2 2

4 3 3

2 2 2

2 1 2 2 1 2 2 1 8

1 1 1

x x x x x x

x x x

      



  

  

 

     

 

   

2 2 2 2 2

6 4 4

2 2 2

12 1 6 1 6 2 12 1 6 6 2

24 24

1 1 1

.x x x x x x x x x

x x x

      



  

  

 

y  

⑷ Cho hàm số

cosyx

. Tính giá trị của

 







Ta có:

22' sin .cos siny x x x   

2'' cos2yx

 

4sin2yx

 









Câu 21. Chứng minh rằng:

⑴ Với hàm số

2y x x

ta có

10.yy





 Biên soạn: LÊ MINH TÂM – 093.337.6281 62

Chương VII.

ĐẠO HÀM

⑵ Với hàm số

1y x x  

ta có

 

10.y x y



  

⑶ Với hàm số

siny x x

ta có

 

20sinxy y x xy

 

   

⑷ Với hàm số







ta có

 

21y y y

 



⑸ Với hàm số

2cotyx

ta có

2 2 0yy



  

⑹ Với hàm số

tany x x

ta có

 

2 2 2

2 1 0x y x y y



   

⑺ Với hàm số

tanyx

ta có

10yy



  

⑻ Với hàm số

1yx

ta có

.y y xy y

 



⑼ Với hàm số

1yx 

ta có

y y xy y

 



⑽ Với hàm số

1yx

ta có

0.y y xy y

 

  

Lời giải

⑴ Với hàm số

2y x x

ta có

10.yy





Ta có

 

.yx











   

1 2 1

x x x



   









 

22.

x x x

x x x x

  









2xx







Khi đó:









1 2 1

..y y x x





   



1 1 0   

Vậy

10.yy





⑵ Với hàm số

1y x x  

ta có

 

10.y x y



  

Ta có





















 

11.















Khi đó:

 









1 1 1

..y x y x x x



      











1 1 1 1 0

     



Vậy

 

10.y x y



  

⑶ Với hàm số

siny x x

ta có

 

20sinxy y x xy

 

   

Ta có

sin cosy x x x





 Biên soạn: LÊ MINH TÂM – 093.337.6281 63

Chương VII.

ĐẠO HÀM

cos cos siny x x x x



   

2cos sinx x x

Khi đó:

 

2 sinxy y x xy

 

  

     

22. cos sin sin cos sin . .sinx x x x x x x x x x x     

22cos sin cos sinx x x x x x x x   

 

2 2 0cos cos sin sinx x x x x x x x    

Vậy

 

20sinxy y x xy

 

   

⑷ Với hàm số







ta có

 

21y y y

 



Ta có







, điều kiện:

4x 

 







 









Khi đó:

 

21y y y

 





   

7 3 14



















   

98 7 14









   

98 98

44xx





Vậy

 

21y y y

 



⑸ Với hàm số

2cotyx

ta có

2 2 0yy



  

Ta có

2cotyx

, điều kiện:

sin

xx  

k

2sin



  

Khi đó:

22yy





2 2 2

cot

sin

   

 

2 1 2 2 2 2 0cot cotxx     

Vậy

2 2 0yy



  

⑹ Với hàm số

tany x x

ta có

 

2 2 2

2 1 0x y x y y



   

Ta có

tany x x

, điều kiện:

cosx x k   

k

tan tan tan

cos

y x x x x x



     

21tan tan

cos cos

y x x x



    

Khi đó:

 

2 2 2

21x y x y y



  

 

2 2 2 2 2

2 1 2 1. tan tan tan tan

cos cos

x x x x x x x x x



      





   

 

2 2 2 2 2 2

1 2 2 1 1 2 1. tan tan tan tan tanx x x x x x x x x x



       



 Biên soạn: LÊ MINH TÂM – 093.337.6281 64

Chương VII.

ĐẠO HÀM

2 2 2 3 3 3 2 3 2 2 3 3

2 2 2 2 2 2 2 2tan tan tan tan tan tanx x x x x x x x x x x x x x       

0

Vậy

 

2 2 2

2 1 0x y x y y



   

⑺ Với hàm số

tanyx

ta có

10yy



  

Ta có

tany x x

, điều kiện:

cosx x k   

k

 

1tan tan

cos

y x x



    

Khi đó:

2 2 2

1 1 1 0tan tany y x x



      

Vậy

10yy



  

⑻ Với hàm số

1yx

ta có

.y y xy y

 







2 1 1

x x x



    



x y x y y













  





 

3 3 3

y y y





  

Khi đó:

1 1 1

. . .

x x x

y y xy y x y

y y y y y



 

       

Vậy

.y y xy y

 



⑼ Với hàm số

1yx 

ta có

y y xy y

 



Ta có:







;

 













;

Khi đó:

 

2 2 2 2

.y y

x x x

y xy x









      

   

Vậy

y y xy y

 



⑽ Với hàm số

1yx

ta có

0.y y xy y

 

  

Ta có

 









2 3 3

;

y x y y



  

  





 

      





Khi đó

 





 

2 2 2

. . .

y y xy y x x x



 

       



2 2 2 2

2 2 2

1 1 1 1 0

1 1 1

x x x x

x x x



              

  

(ĐPCM)

 Biên soạn: LÊ MINH TÂM – 093.337.6281 65

Chương VII.

ĐẠO HÀM

Câu 22. Cho

 

43f x x x  

và

 

3 10 7g x x x  

. Giải phương trình

   

0f x g x

 



Lời giải

Ta có

     

4 2 3 2

4 3 4 8 12 8;f x x x f x x x f x x

 

       

   

3 10 7 10 14 .g x x x g x x



     

Khi đó

   

0 12 8 10 14 0 12 14 2 0

f x g x x x x x







 

           









Vậy tập nghiệm của phương trình là









Câu 23. Cho hàm số

 

3 4 6f x x x x   

. Giải bất phương trình

   

1f x f x

 



Lời giải

Ta có

     

3 2 2

3 4 6 3 6 4 6 6;f x x x x f x x x f x x

 

         

Khi đó

   

1 6 6 3 6 4 1 3 12 9 0

f x f x x x x x x





 

            







Vậy tập nghiệm của bất phương trình là

13( ; ] [ ; )S    

Câu 24. Cho hàm số

3 4 6y x x x   

. Giải bất phương trình





Lời giải

Ta có

3 6 4 6 6;y x x y x

 

    

Do đó

0 6 6 0 1y x x



     

Vậy tập nghiệm của bất phương trình là

 

1;T  

Câu 25. Cho hàm số

     

5 1 4 1y f x x x    

. Giải phương trình

 

0fx





Lời giải

Ta có

       

15 1 4 30 1 4;f x x x f x x

 

     

Do đó

   

2 17

0 30 1 4 0 1

15 15

f x x x x



           

Vậy tập nghiệm của phương trình là









Câu 26. Cho hàm số

 

cosy f x x



  





. Tìm các nghiệm thuộc đoạn





của phương

trình

 

8fx

Lời giải

Ta có

   

2 2 4 2

sin ; cosf x x f x x

   

 

     

   

   

 Biên soạn: LÊ MINH TÂM – 093.337.6281 66

Chương VII.

ĐẠO HÀM

 

8 2 16 2

sin ; cosf x x f x x

   



   

   

   

Do đó

 

8 16 2 8 2

3 3 2

cos cosf x x x

   

         

   

   

 



  





  



  

   





0;x







Xét

xk

. Ta có

2 2 2 2

k k k x



          

Xét

xk  

. Ta có

1 7 5

6 6 6 6

k k k x



          

Vậy tập nghiệm của phương trình là









--------------------Hết--------------------

Bấm Tải xuống để xem toàn bộ.

| 1/98

| | Tải xuống

Preview text:

Chương VII. ĐẠO HÀM Mục lục
 Bài 01. ĐẠO HÀM A. Lý thuyết
1. Đạo hàm. .......................................................................................................................................2
2. Ý nghĩa hình học của đạo hàm ............................................................................................... 3
3. Ý nghĩa vật lý của đạo hàm ................................................................................................... 4
4. Số e............................................................................................................................................... 4 B. Bài tập
 Dạng 1. Tính đạo hàm tại 1 điểm bằng định nghĩa...........................................................5
 Dạng 2. Tính đạo hàm tại 1 điểm bất kỳ trên (a;b) bằng định nghĩa .........................8
 Dạng 3. Ý nghĩa hình học của đạo hàm ............................................................................ 10
 Dạng 4. Ý nghĩa vật lý của đạo hàm................................................................................. 12
 Dạng 5. Tìm tham số để hàm số có đạo hàm tại x0 ...................................................... 13 C. Luyện tập
 Bài 02. CÁC QUY TẮC TÍNH ĐẠO HÀM A. Lý thuyết
1. Đạo hàm hàm số n
y  x ........................................................................................................... 19
2. Đạo hàm hàm số y  x ........................................................................................................ 19
3. Đạo hàm hàm số lượng giác ................................................................................................. 19
4. Đạo hàm của hàm số mũ và hàm số logarit ................................................................... 19
5. Các quy tắc tính đạo hàm .................................................................................................... 20
6. Đạo hàm của hàm hợp .......................................................................................................... 20
7. Đạo hàm cấp hai ...................................................................................................................... 21 B. Bài tập
 Dạng 1. Tính đạo hàm đa thức – hữu tỉ – căn thức........................................................ 22
 Dạng 2. Tính đạo hàm lượng giác ..................................................................................... 24
 Dạng 3. Tính đạo hàm mũ – logarit .................................................................................. 26 C. Luyện tập
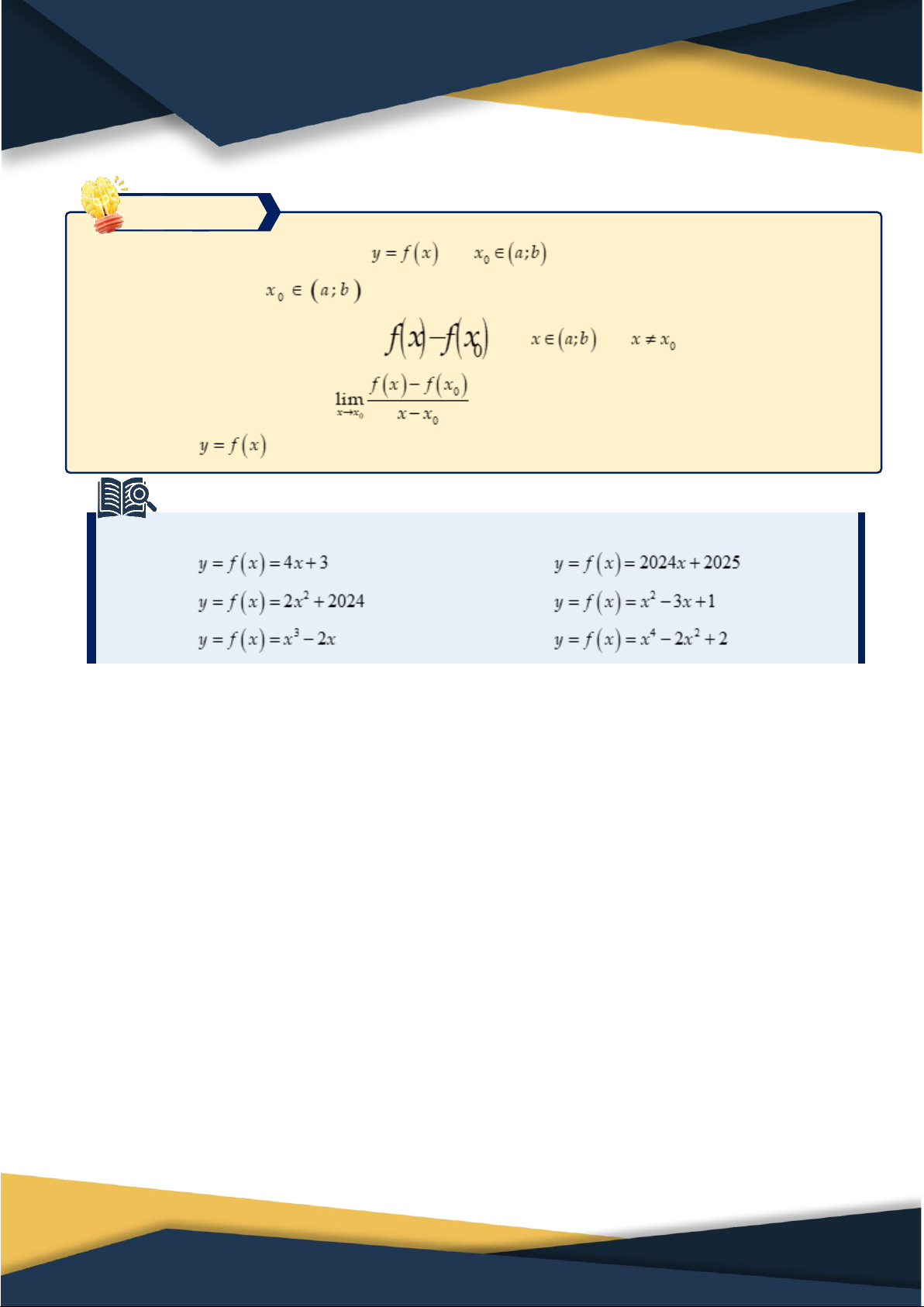
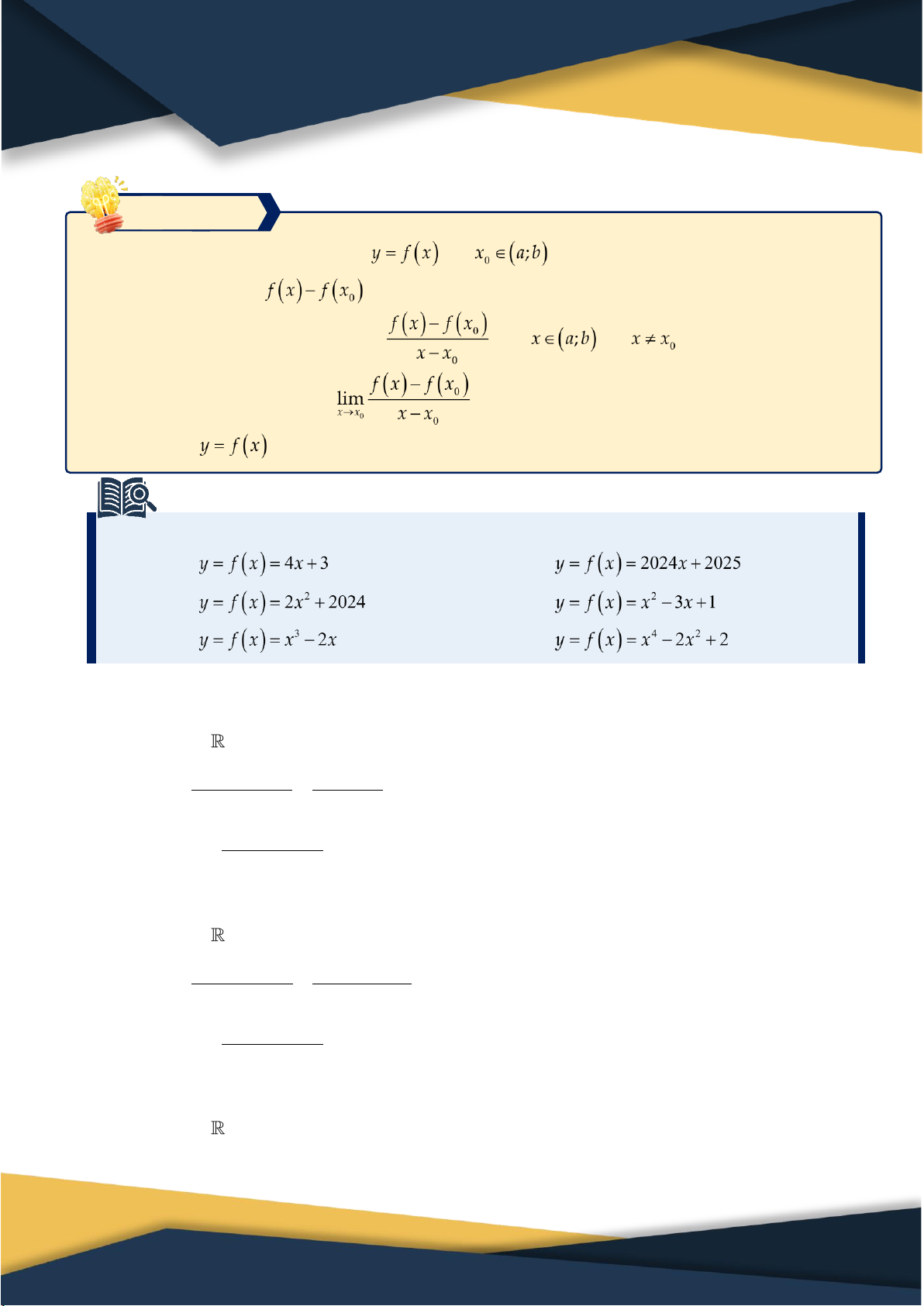
 Biên soạn: LÊ MINH TÂM – 093.337.6281 1 Chương VII. ĐẠO HÀM ĐẠO HÀM ĐẠO HÀM A Lý thuyết 1. Đạo hàm. Định nghĩa: Cho hàm số xác định trên khoảng và .
 Nếu tồn tại giới hạn hữu hạn
thì giới hạn đó được gọi là đạo hàm của tại điểm , tức là:  Kí hiệu là hay .
 Tính đạo hàm bằng định nghĩa:
Để tính đạo hàm của hàm số y  f x tại x  ;
a b , ta thực hiện theo các bước sau: 0  
 Bước 1. Tính f x  f x . 0 
f x  f x0 
 Bước 2. Lập và rút gọn tỉ số x ;
a b , x  x x  với   x 0 0
f x  f x0 
 Bước 3. Tính giới hạn lim xx  . 0 x x0 Chú ý
Trong định nghĩa & quy tắc trên đây, thay
bởi ta sẽ có định nghĩa và quy tắc tính đạo hàm của hàm số tại điểm .
 Biên soạn: LÊ MINH TÂM – 093.337.6281 2 Chương VII. ĐẠO HÀM
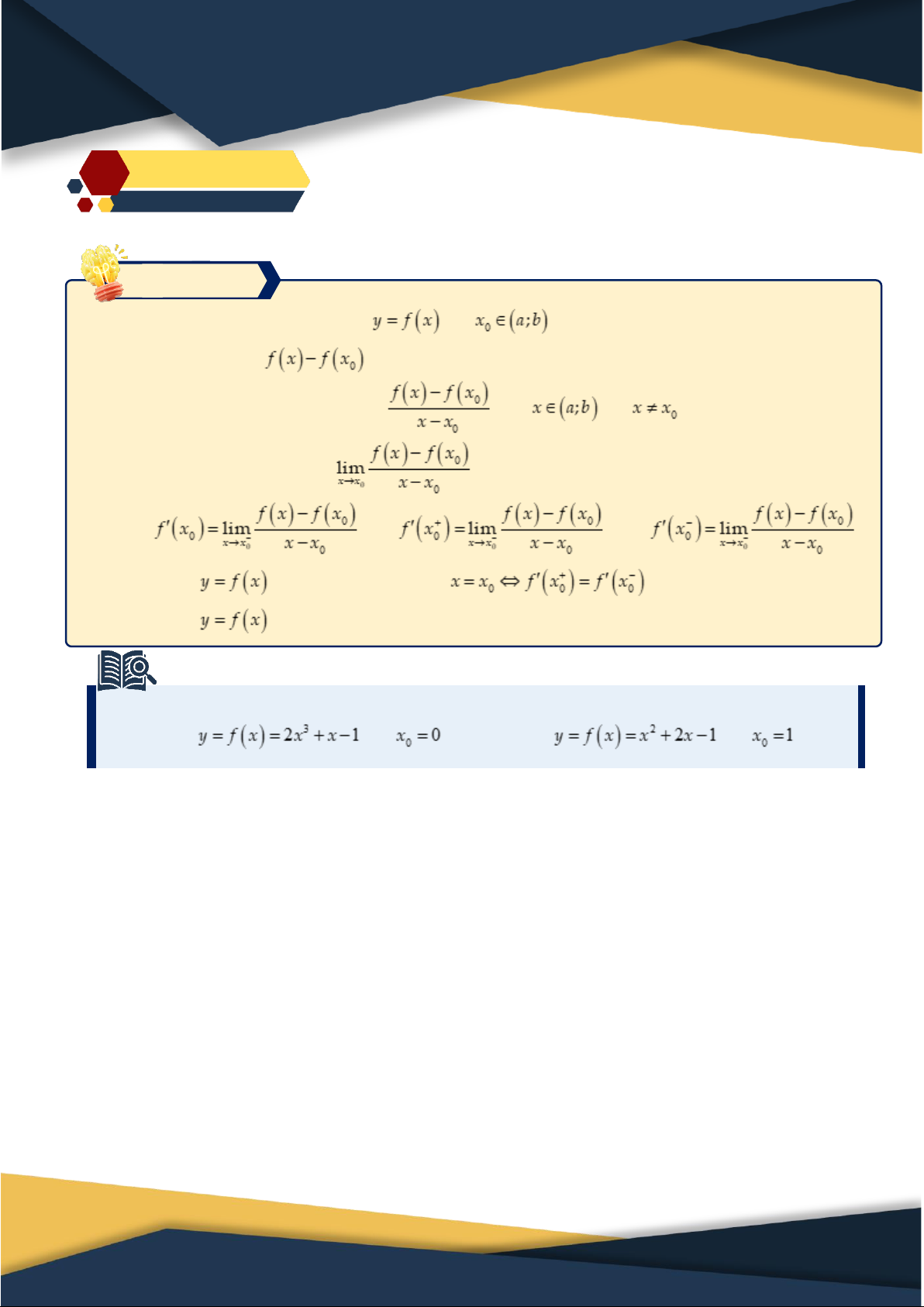
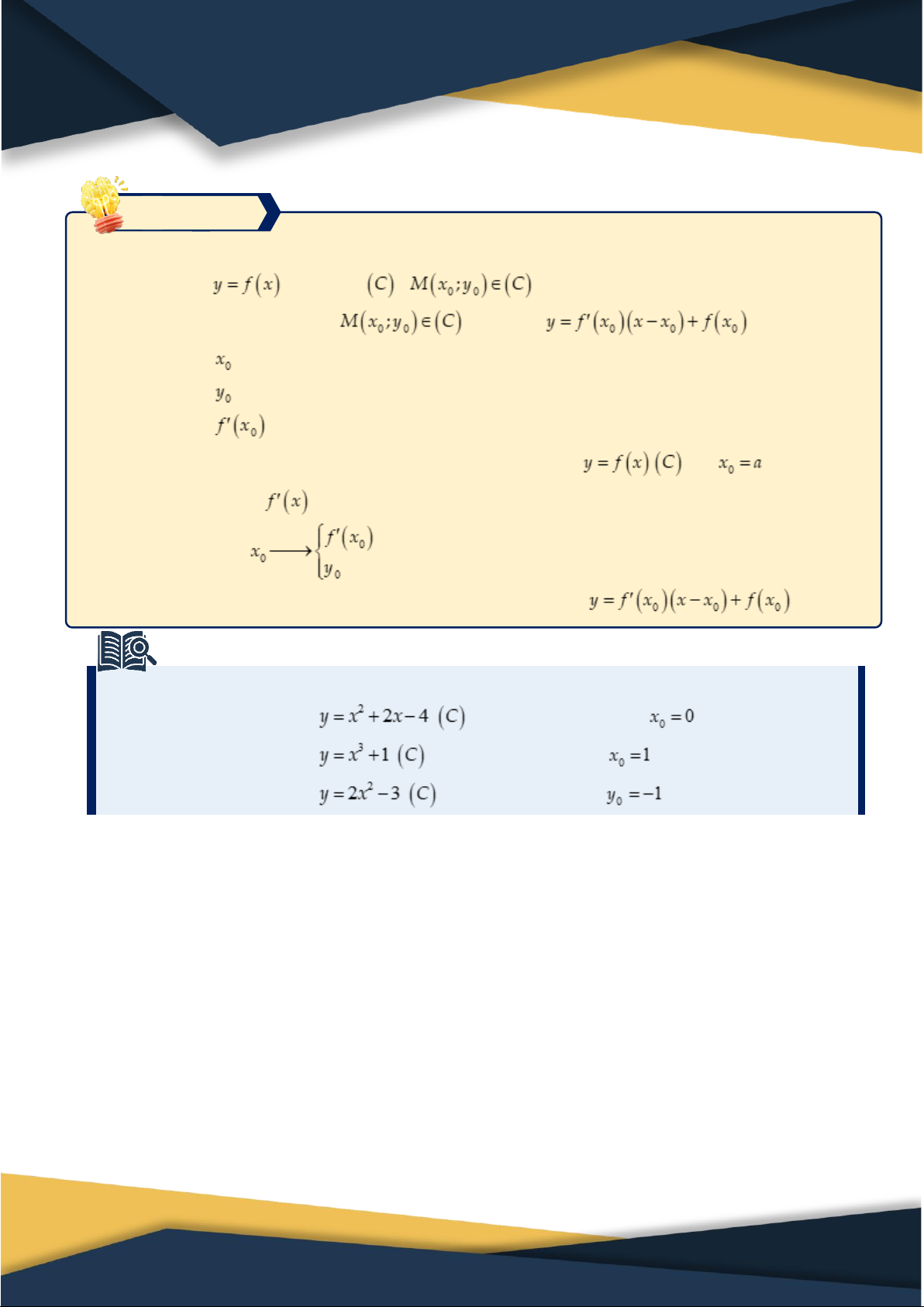
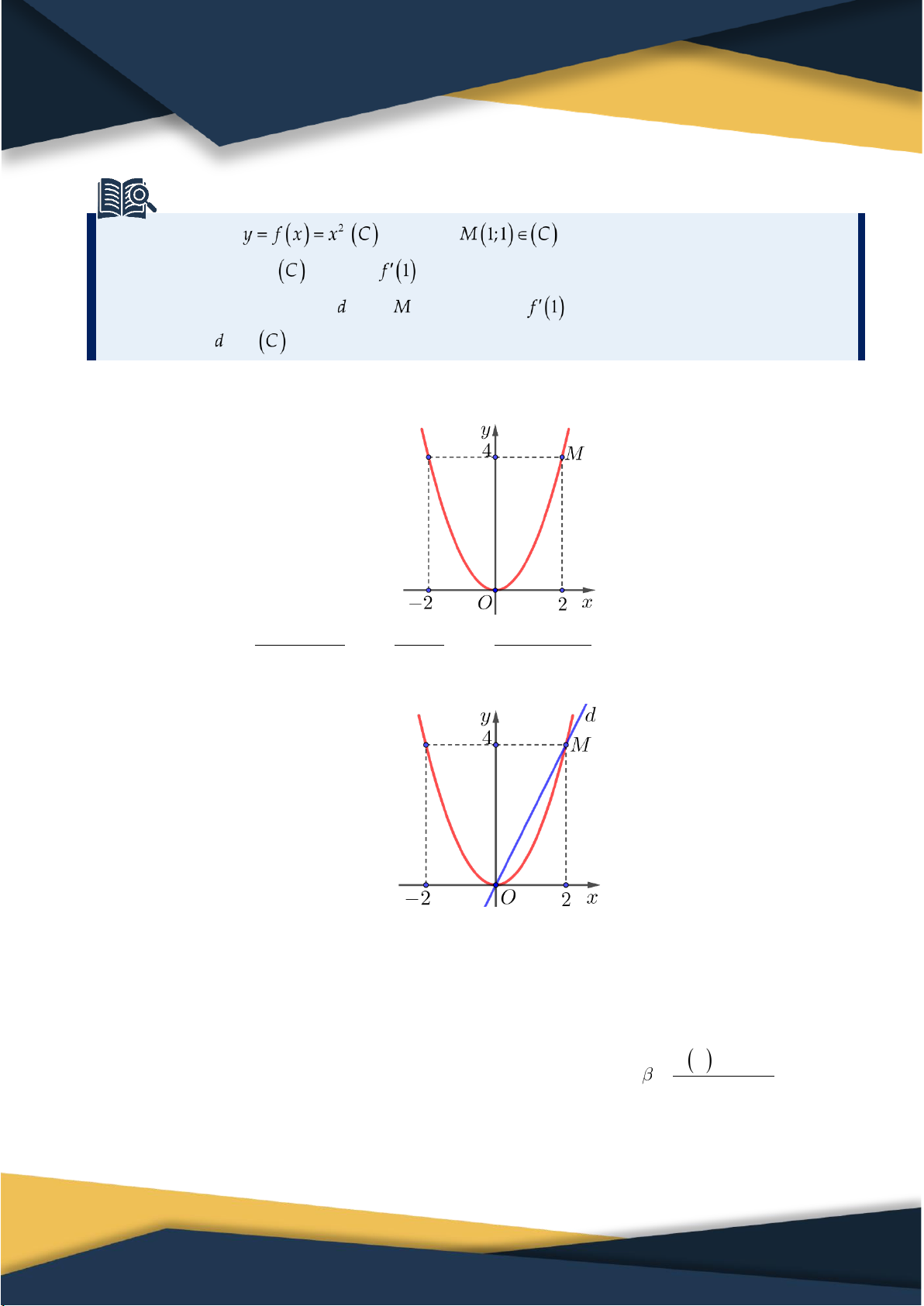
2. Ý nghĩa hình học của đạo hàm Ví dụ 2.1. Cho hàm số và điểm ⑴ Vẽ đồ thị và tính .
⑵ Vẽ đường thẳng qua có hệ số góc
. Nhận xét về vị trí tương đối giữa và
 Lời giải
........................................................................................................................
........................................................................................................................
........................................................................................................................
........................................................................................................................
........................................................................................................................
........................................................................................................................
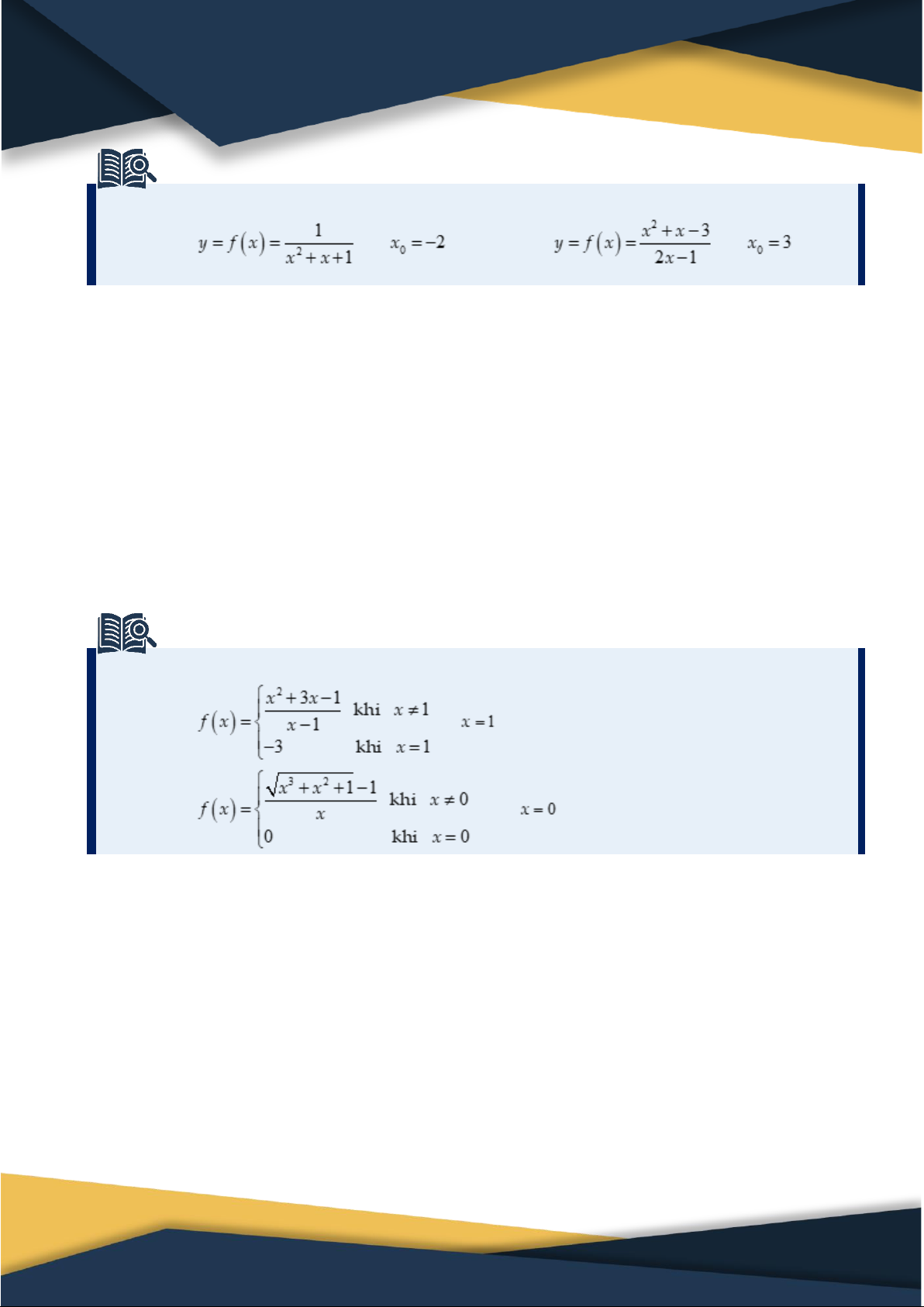
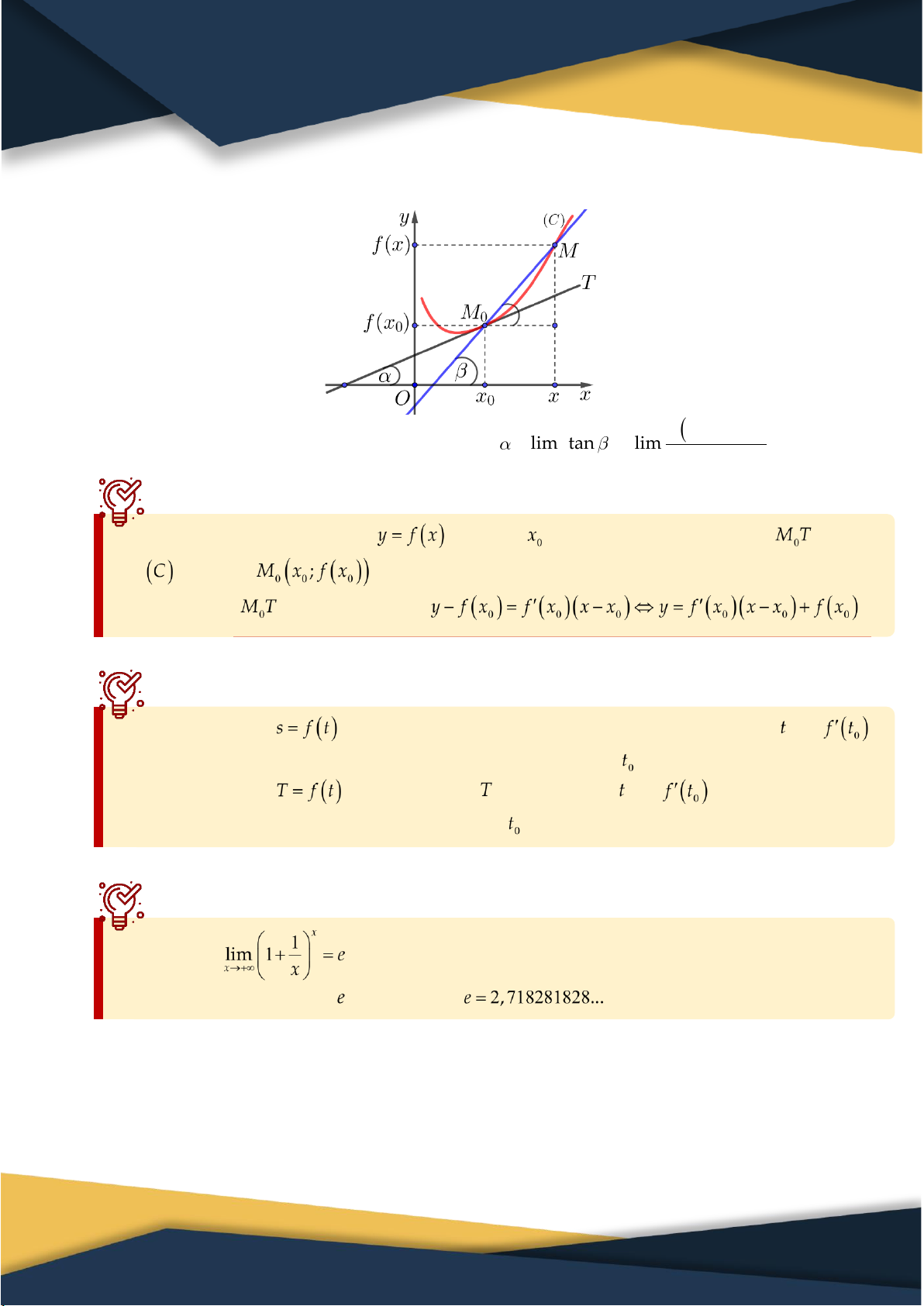
 Trong mặt phẳng tọa độ Oxy , cho đồ thị C của hàm số y  f x và điểm Mx ; y  C . 0 0   
Xét M x; f x là một diểm di chuyển trên C .
Đường thẳng MM là một cát tuyến của C . 0
f x  f x0 
Hệ số góc của cát tuyến MM được tính bởi công thức k  tan  0 MM0 x  . x0
Khi cho x dần tới x thì M di chuyển trên C tới M . 0 0
Giả sử cát tuyến MM có vị trí giới hạn là M T thì M T được gọi là tiếp tuyến của C tại 0 0 0
M và M được gọi là tiếp điểm 0 0 f x  f x
Ta có hệ số góc của tiếp tuyến M T là k  tan  lim tan     0  lim  f  x M T  0 0 0 xx xx  0 0 x x0
 Biên soạn: LÊ MINH TÂM – 093.337.6281 3 Chương VII. ĐẠO HÀM
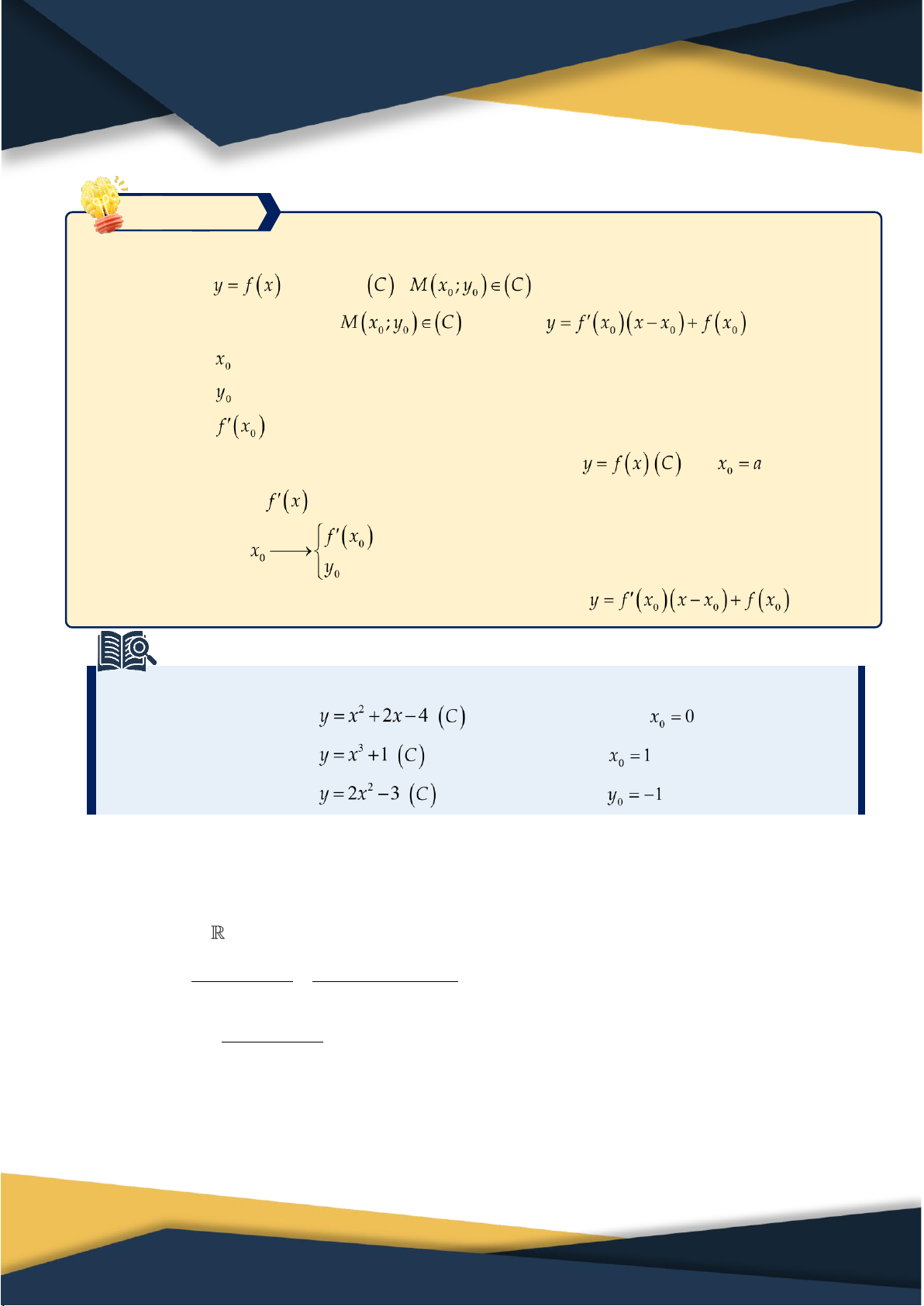
Đạo hàm của đồ thị hàm số tại điểm
là hệ số góc của tiếp tuyến của tại điểm Tiếp tuyến có phương trình: 3. Ý nghĩa
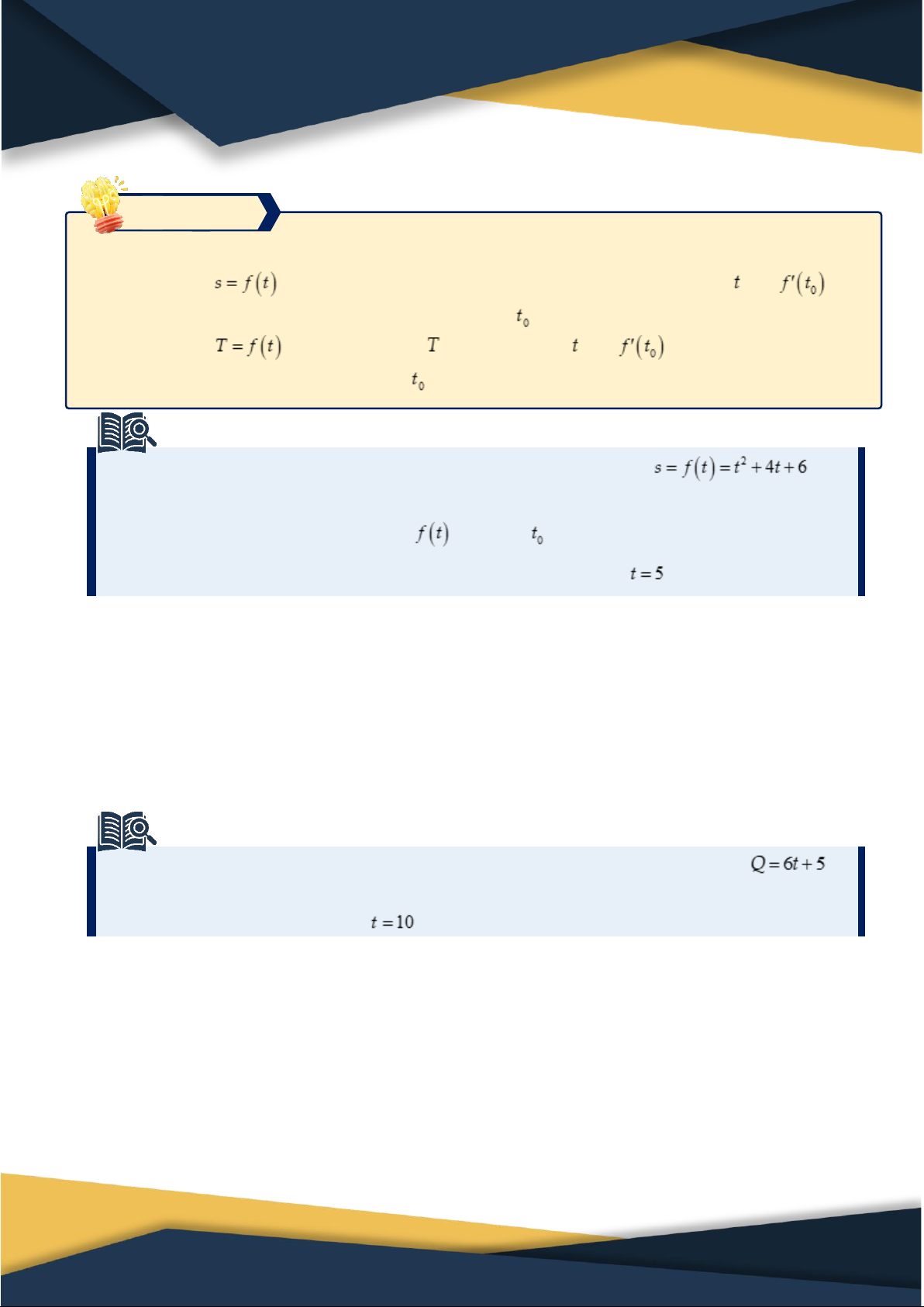
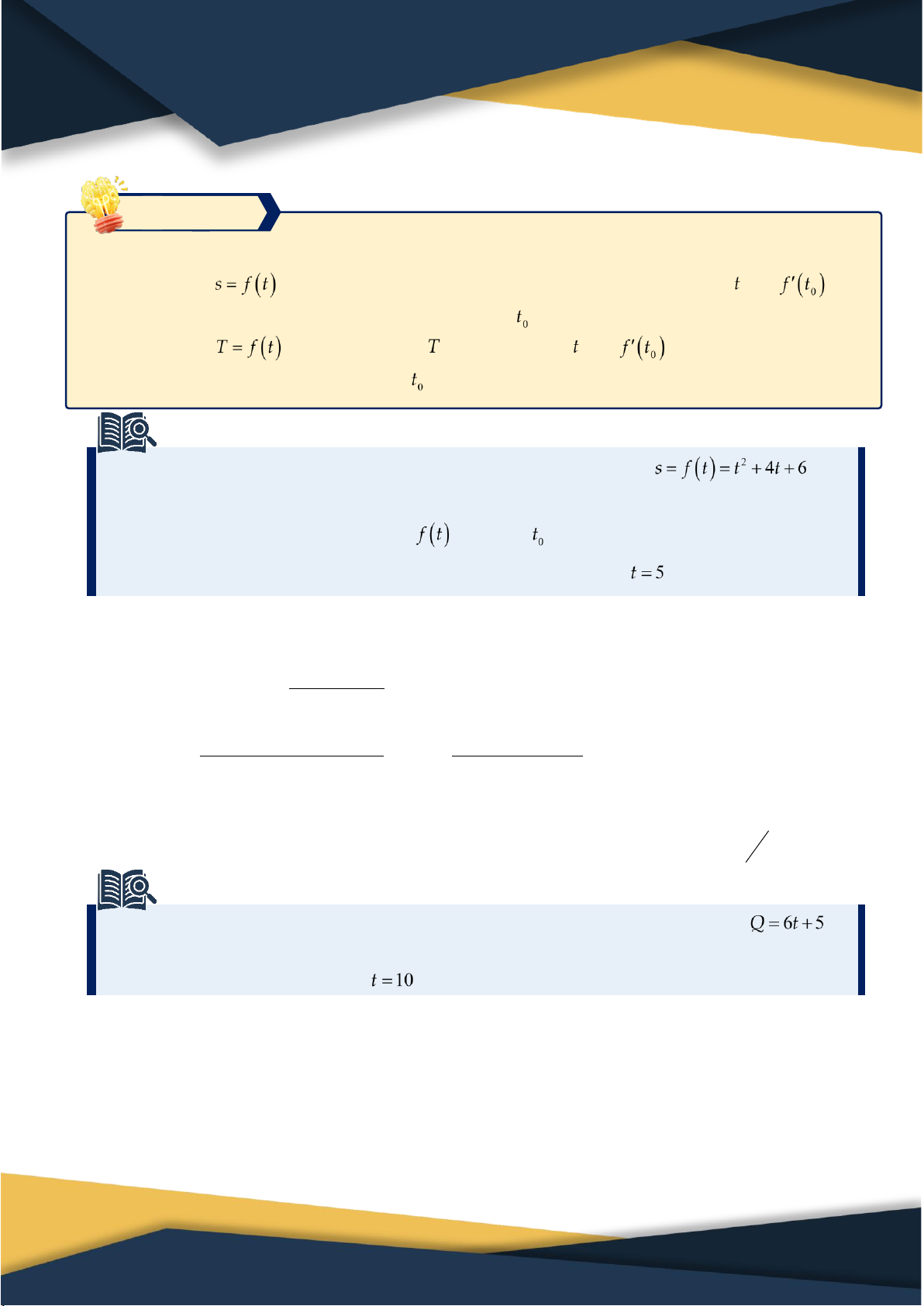
vật lý của đạo hàm  Nếu hàm số
biểu thị quãng đường di chuyển của vật theo thời gian thì
biểu thị tốc độ tức thời của chuyển động tại thời điểm .  Nếu hàm số
biểu thị nhiệt độ theo thời gian thì
biểu thị tốc độ thay
đổi nhiệt độ theo thời gian tại thời điểm . 4. Số e
Người ta còn biết rằng là số vô tỉ và
(Số thập phân vô hạn không tuần hoàn).
 Biên soạn: LÊ MINH TÂM – 093.337.6281 4 Chương VII. ĐẠO HÀM B Bài tập
 Dạng 1. Tính đạo hàm tại 1 điểm bằng định nghĩa Phương pháp
 Để tính đạo hàm của hàm số tại
, ta thực hiện theo các bước sau:  Bước 1. Tính .
 Bước 2. Lập và rút gọn tỉ số với và
 Bước 3. Tính giới hạn . ⑴ ⑵ ⑶  Hàm số
có đạo hàm tại điểm .  Hàm số
có đạo hàm tại điểm thì trước hết phải liên tục tại điểm đó. Ví dụ 1.1.
Tính đạo hàm bằng định nghĩa tại một điểm của các hàm số sau: ⑴ tại ⑵ tại
 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: LÊ MINH TÂM – 093.337.6281 5 Chương VII. ĐẠO HÀM Ví dụ 1.2.
Tính đạo hàm bằng định nghĩa tại một điểm của các hàm số sau: ⑴ tại ⑵ tại
 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
....................................................................................................................................................... Ví dụ 1.3.
Tính đạo hàm bằng định nghĩa tại một điểm của các hàm số sau: ⑴ tại ⑵ tại
 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: LÊ MINH TÂM – 093.337.6281 6 Chương VII. ĐẠO HÀM Ví dụ 1.4. Tìm để hàm số có đạo hàm tại
 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: LÊ MINH TÂM – 093.337.6281 7 Chương VII. ĐẠO HÀM
 Dạng 2. Tính đạo hàm tại 1 điểm bất kỳ trên (a;b) bằng định nghĩa Phương pháp
 Để tính đạo hàm của hàm số tại
, ta thực hiện theo các bước sau:  Bước 1. Tính .
 Bước 2. Lập và rút gọn tỉ số với và
 Bước 3. Tính giới hạn .  Hàm số
có đạo hàm tại điểm thì trước hết phải liên tục tại điểm đó. Ví dụ 2.1.
Tính đạo hàm bằng định nghĩa của các hàm số sau: ⑴ ⑵ ⑶ ⑷ ⑸ ⑹
 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: LÊ MINH TÂM – 093.337.6281 8 Chương VII. ĐẠO HÀM
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: LÊ MINH TÂM – 093.337.6281 9 Chương VII. ĐẠO HÀM
 Dạng 3. Ý nghĩa hình học của đạo hàm Phương pháp
 Ý nghĩa hình học: (Phương trình tiếp tuyến) Cho hàm số có đồ thị , .
Phương trình tiếp tuyến tại có dạng: . Trong đó: hoành độ tiếp điểm. tung độ tiếp điểm.
hệ số góc tiếp tuyến.
Bài toán: Viết phương trình tiếp tuyến của đồ thị hàm số tại .  Bước 1. Tính .  Bước 2. Từ .
 Bước 3. Hoàn thiện phương trình tiếp tuyến cần tìm . Ví dụ 3.1.
Viết phương trình tiếp tuyến của
⑴ Đồ thị hàm số
tại điểm có hoành độ .
⑵ Đồ thị hàm số
tại điểm có hoành độ .
⑶ Đồ thị hàm số tại điểm có tung độ .
 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: LÊ MINH TÂM – 093.337.6281 10 Chương VII. ĐẠO HÀM
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: LÊ MINH TÂM – 093.337.6281 11 Chương VII. ĐẠO HÀM
 Dạng 4. Ý nghĩa vật lý của đạo hàm Phương pháp
 Ý nghĩa vật lý: (quãng đường, nhiệt độ, điện lượng)  Nếu hàm số
biểu thị quãng đường di chuyển của vật theo thời gian thì biểu
thị tốc độ tức thời của chuyển động tại thời điểm .  Nếu hàm số
biểu thị nhiệt độ theo thời gian thì
biểu thị tốc độ thay đổi
nhiệt độ theo thời gian tại thời điểm . Ví dụ 4.1.
Một chất điểm chuyển động có phương trình chuyển động là (t
được tính bằng giây, s được tính bằng mét).
⑴ Tính đạo hàm của hàm số tại điểm .
⑵ Tính vận tốc tức thời của chuyển động tại thời điểm .
 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
....................................................................................................................................................... Ví dụ 4.2.
Cho biết điện lượng trong một dây dẫn theo thời gian biểu thị bởi hàm số
(t được tính bằng giây, Q được tính bằng Coulomb). Tính cường độ của dòng điện
trong dây dẫn tại thời điểm
 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: LÊ MINH TÂM – 093.337.6281 12 Chương VII. ĐẠO HÀM
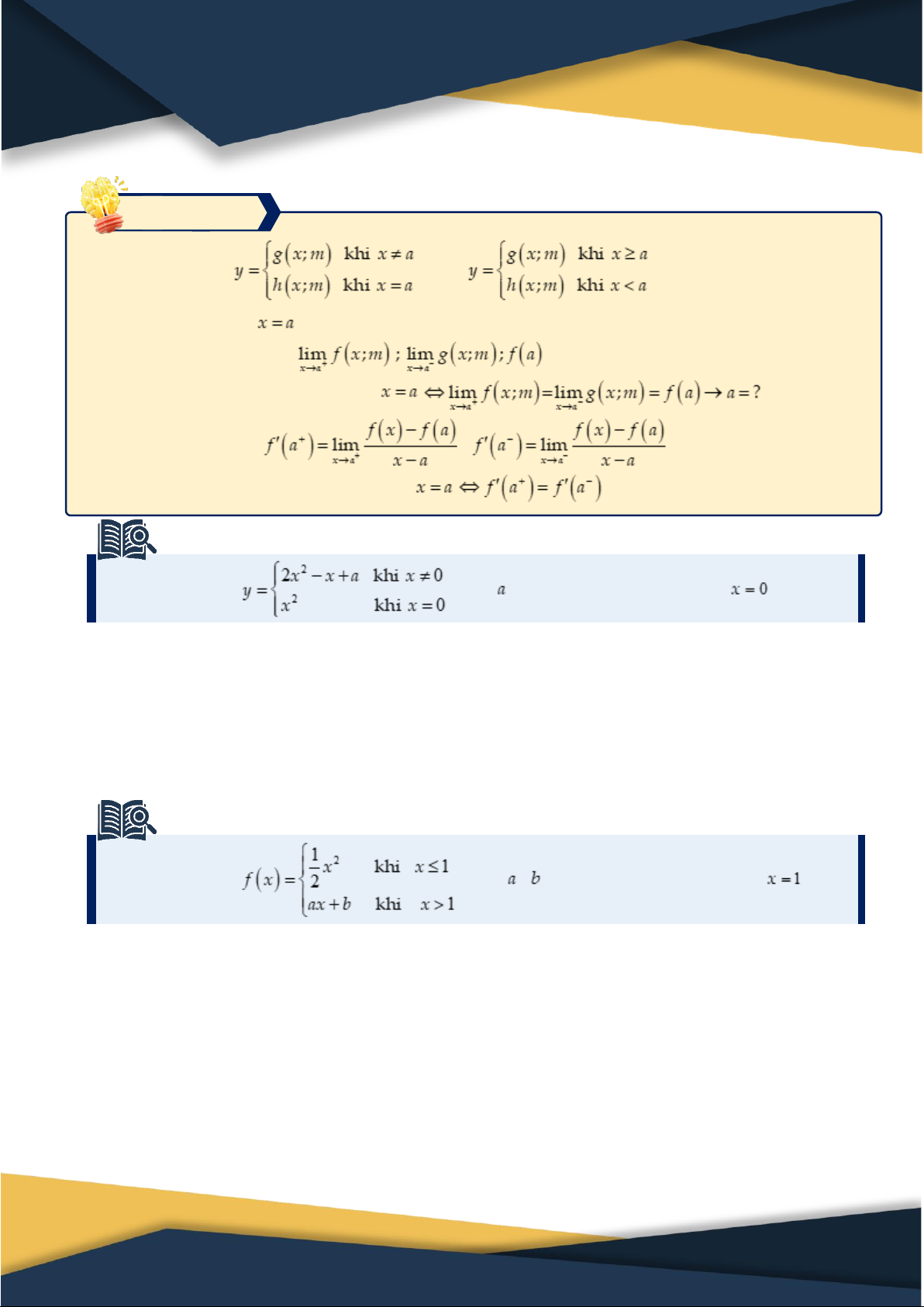
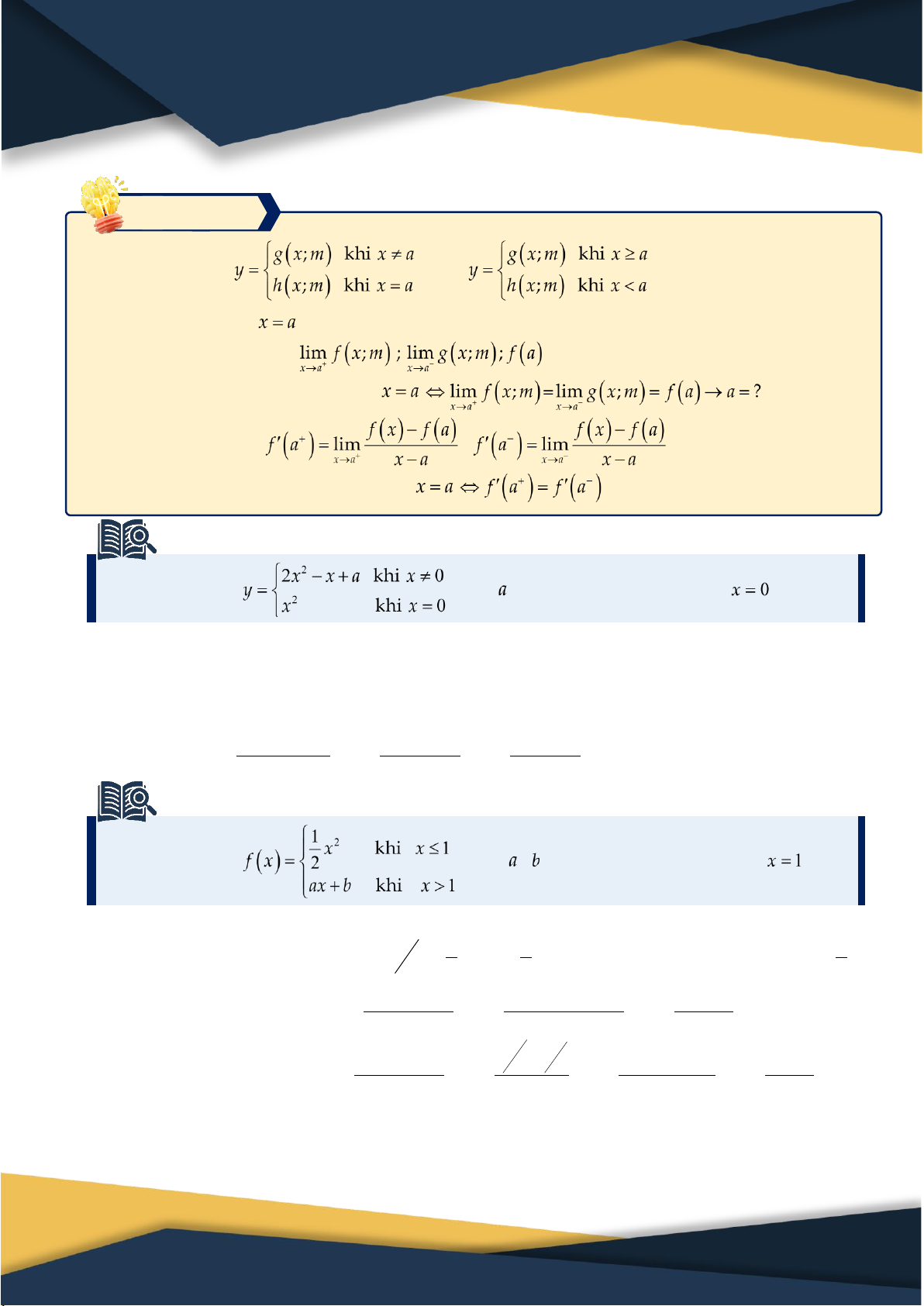
 Dạng 5. Tìm tham số để hàm số có đạo hàm tại x0 Phương pháp  Cho hàm số hoặc
. Tìm tham số m để hàm số có đạo hàm tại
 Bước 1. Xác định .
 Bước 2. Hàm số liên tục tại  Bước 3. Tính ; .
 Bước 4. Hàm số có đạo hàm tại . Ví dụ 5.1. Cho hàm số
. Tìm để hàm số có đạo hàm tại .
 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
....................................................................................................................................................... Ví dụ 5.2. Cho hàm số
. Tìm , thì hàm số có đạo hàm tại ?
 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: LÊ MINH TÂM – 093.337.6281 13 Chương VII. ĐẠO HÀM C Luyện tập
Câu 1. Tính đạo hàm của các hàm số sau tại các điểm đã chỉ:
⑴ f x  2x 1 tại x  2 
⑵ f x  20242023x tại x 1
⑶ f x 2
 x  2x 1 tại x 1
⑷ f x 3
 2x 1 tại x  2  ⑸ x f x 2
 2x  x 1 tại x 1
⑹ f x 1  tại x  2 x 1  ⑺ x f x 1  tại x  2
⑻ f x 2 1  tại x  3 x 1 x  2
⑼ f x  x 1 tại x 1
⑽ f x  2023 x tại x  2
Câu 2. Tính đạo hàm của các hàm số sau tại các điểm (nếu có):     ⑴
x  khi x  f x 2x 3 khi x 3   . Tính f 3 .
⑵ f x 2 1 0   . Tính f 0 . 2
x khi x  3 1   2  x khi x  0
⑶ f x  x . Tính f 0.
⑷ f x  x x . Tính f 0.
⑸ f x  2x  x 1 . Tính f   1 .
⑹ f x  x  x . Tính f   1 .
⑺ f x  x  2023. Tính f 0.
⑻ f x 2
 x  2x . Tính f 0 . x 2 x  x 1 ⑼ y  f  0 .
⑽ f x  . Tính f   1 . x  . Tính   1 x
Câu 3. Tính đạo hàm của các hàm số sau tại các điểm đã chỉ (nếu có):  ⑴    f x 2 x 3x khi x 1   . Tính f   1  2   khi x 1 3 2
 x  4x  3x  
⑵ f x khi x 1 2
  x 3x  2 . Tính f   1 0  khi x  1 2x  3 khi x  1 ⑶  f x 3 2
 x  2x  7x  4 . Tính f   1 . khi x   1  x 1 2
 x  7x 12  
⑷ f x khi x 3   x  3
. Tính f 3 1  khi x  3
 x khi x 1
⑸ f x   . Tính f   1 2 x khi x  1    
⑹ f x 3 4 x khi x 0  
. Tính f 0 1  khi x  0
 Biên soạn: LÊ MINH TÂM – 093.337.6281 14 Chương VII. ĐẠO HÀM  3 2
x  2x  x 1 1  ⑺  f x khi x 1   x 1 . Tính f   1 0  khi x  1  x 1 1  
⑻ f x khi x 0   x
. Tính f 0 0  khi x  0 3 4  x  khi x  0 
⑼ f x 4  
. Tính f 0 1  khi x  0 4  2 x 1 1  
⑽ f x khi x 0   x
. Tính f 0 0  khi x  0
Câu 4. Tính đạo hàm của các hàm số sau tại các điểm đã chỉ (nếu có):  x 1 1 ⑴   f x khi x 0   x . Tính f 0 0  khi x  0  2 x 1 1 ⑵   f x khi x 0   x . Tính f 0 0  khi x  0
 3x 1  2x  khi x  1 ⑶  f x x 1   . Tính f   1 .  5  khi x 1  4  3 2 2
4x  8  8x  4 ⑷   f x khi x 0   x
. Tính f 0 0  khi x  0
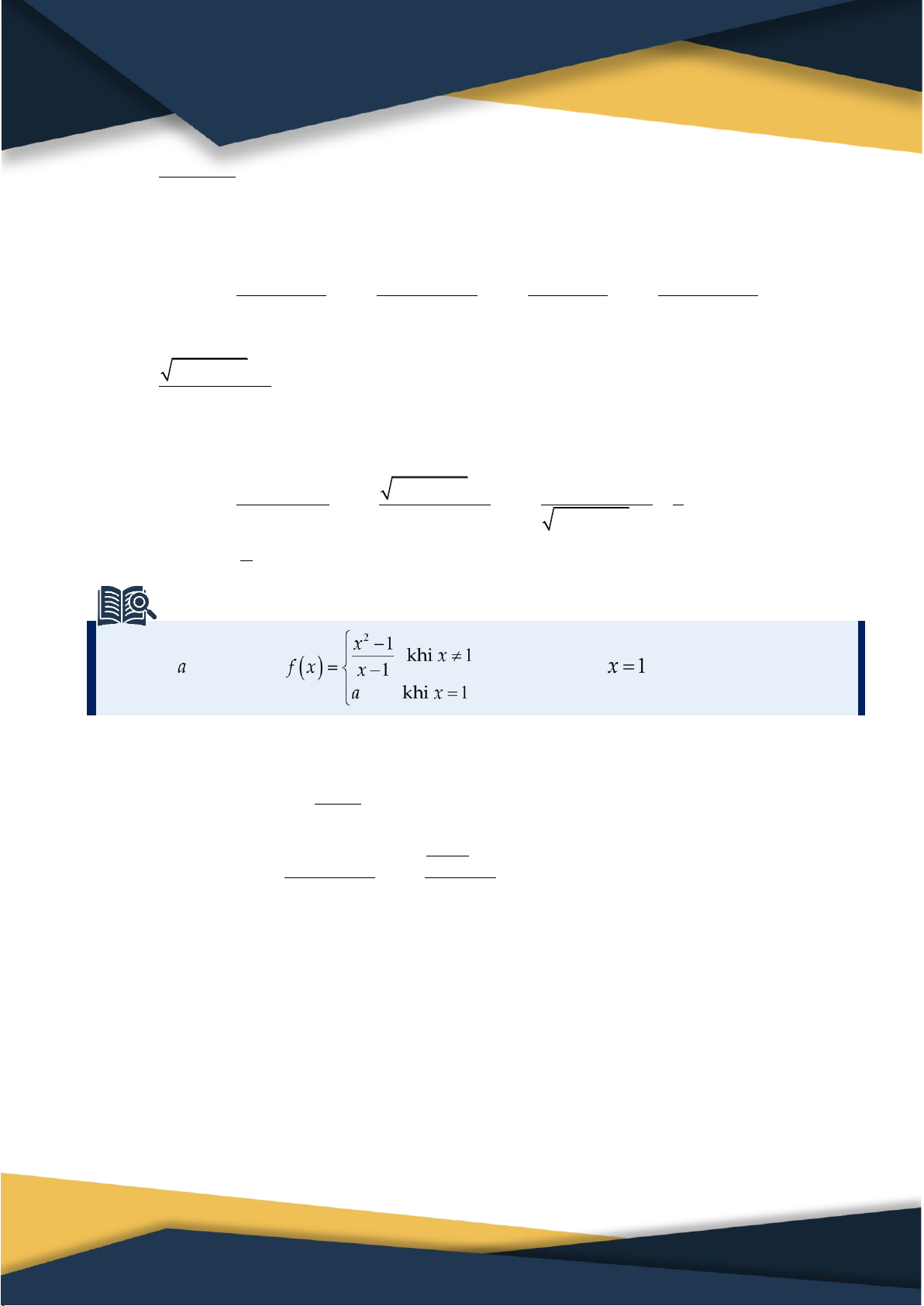
Câu 5. Tìm tham số để hàm số có đạo hàm tại x 0 2  x 1   ⑴ khi x 1
Tìm a để hàm số f x   x 1
có đạo hàm tại điểm x 1.
a khi x 1     ⑵ ax bx x
Tìm a; b để hàm số f x 2 1 khi 0  
có đạo hàm tại điểm x  0 .
ax  b 1 khi x  0 2  x 1   ⑶ khi x 0
Tìm a; b để hàm số f x   x 1
có đạo hàm tại điểm x  0 .
axb khi x  0
 Biên soạn: LÊ MINH TÂM – 093.337.6281 15 Chương VII. ĐẠO HÀM     ⑷ ax x khi x
Tìm a; b để hàm số f x 2 2 1 1  
có đạo hàm tại điểm x 1.  3 2 
x  bx khi x  1 Câu 6. Cho hàm số 2
y  x  2x  4 có đồ thị C
⑴ Tìm hệ số góc của tiếp tuyến của C tại điểm có hoành độ x 1 thuộc C . 0
⑵ Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có x  0 thuộc C . 0
⑶ Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có y  1 thuộc C . 0
⑷ Viết phương trình tiếp tuyến của đồ thị hàm số biết hệ số góc tiếp tuyến bằng 4  .
⑸ Viết phương trình tiếp tuyến của đồ thị hàm số, biết tiếp tuyến đó song song với
đường thẳng y 1 3x .  Câu 7. x 1
Cho hàm số y 
có đồ thị C 3x
⑴ Viết phương trình tiếp tuyến của đồ thị hàm số tại giao điểm của C với trục Oy .
⑵ Viết phương trình tiếp tuyến của đồ thị hàm số tại giao điểm của C với trục Ox .
⑶ Viết phương trình tiếp tuyến của đồ thị hàm số tại giao điểm của C với đường
thẳng y  x 1.
⑷ Viết phương trình tiếp tuyến của đồ thị hàm số biết hệ số góc của tiếp tuyến bằng 1 k   . 3
⑸ Viết phương trình tiếp tuyến của đồ thị hàm số, biết tiếp tuyến đó song song với
đường thẳng y  1 3x . Câu 8. Cho hàm số 3
y  x  2x 1 có đồ thị C
⑴ Tìm hệ số góc của tiếp tuyến của hàm số trên tại điểm có x  0 .
⑵ Viết phương trình tiếp tuyến của hầm số biết nó có k  2  .
⑶ Viết phương trình tiếp tuyến của hàm số trên, biết nó tạo với hai trục Oxy một tam
giác vuông cân tại O .
Câu 9. Một chất điểm chuyển động thẳng biến đổi đều với phương trình 2
s  2t  t 1 m
⑴ Tìm vận tốc tức thời của vật tại thời điểm t  2s .
⑵ Tìm vận tốc trung bình của chất điểm trong khoảng thời gian từ t  0 tới t  2s .
Câu 10. Một vật chuyển động thẳng xác định bởi phương trình s  st trong đó t được tính
bằng giây và S được tính bằng mét. Thực hiện các yêu cầu dưới đây:
⑴ Với s  st 3 2
 t 3t thì vận tốc của vật tại thời điểm t  3s là bao nhiêu?
⑵ Với s  st 2
 t  7t thì vận tốc của vật tại thời điểm t  4s là bao nhiêu?
 Biên soạn: LÊ MINH TÂM – 093.337.6281 16 Chương VII. ĐẠO HÀM ⑶ 1
Với s  st 3 2
  t 12t thì vận tốc của vật tại thời điểm t 10s là bao nhiêu? 2
⑷ Với s  st 3 2  t
  6t  4 thì vận tốc của vật tại thời điểm t  3s là bao nhiêu?
⑸ Với s  st 3
 2t t 10 thì vận tốc của vật tại thời điểm t  3s là bao nhiêu?
⑹ Với s  st 3 2
 3t  4t t thì vận tốc của vật tại thời điểm t  4s là bao nhiêu?
⑺ Với s  st 2
 2t  3t  7 thì vận tốc của vật tại thời điểm t  6s là bao nhiêu? ⑻  
Với s  st  3cos 2 t  
 thì vận tốc của vật tại thời điểm t  2s là bao nhiêu?  3  ⑼ 1
Với s  st   4 2
t  3t  thì vận tốc của vật tại thời điểm t  4s là bao nhiêu? 2
⑽ Với s  st 3 2
 t 3t 9t thì vận tốc của vật tại thời điểm t  5s là bao nhiêu?
Câu 11. Một chất điểm chuyển động theo phương trình s  st trong đó t được tính bằng giây
và S được tính bằng mét. Thời gian để vận tốc của chất điểm đạt giá trị lớn nhất
⑴ Với st 2 3
10  t  9t t trong khoảng 10 giây đầu tiên.
⑵ Với st 3 2  t
  9t  t 10 trong 12 giây đầu tiên.
⑶ Với st 3 2  t
  6t trong 10 giây đầu tiên. ⑷ 1
Với st 3 2
  t  6t trong 10 giây đầu tiên. 2 ⑸ 1 Với st 3 2
  t  9t trong 10 giây đầu tiên. 2 ⑹ 1 Với st 3 2
  t  6t trong 9 giây đầu tiên. 3 ⑺ 1 Với st 2 3
 t  t trong 5 giây đầu tiên. 6 ⑻ 1 Với 3 2
s   t  3t  20 trong 10 giây đầu tiên. 2
Câu 12. Một vật chuyển động thẳng xác định bởi phương trình s  st trong đó t được tính
bằng giây và S được tính bằng mét.
⑴ Với s  st 4 2
 2t  6t 3t 1 thì gia tốc của vật tại thời điểm t  3s là bao nhiêu?
⑵ Với s  st 3
 4t 10t  9 thì gia tốc của vật tại thời điểm vận tốc bằng 2 là bao nhiêu?
⑶ Với s  st 3 2
 t 3t 5 thì gia tốc của vật tại tại giây thứ 10 là bao nhiêu?
⑷ Với s  st 3 2
 t 3t 9t 1 thì gia tốc của vật tại tại thời điểm vật dừng lại là bao nhiêu?
 Biên soạn: LÊ MINH TÂM – 093.337.6281 17 Chương VII. ĐẠO HÀM
⑸ Với s  st 3 2
 t 3t  5t  2 thì gia tốc của vật tại giây thứ 3 là bao nhiêu?
⑹ Với s  st 3 2
 t 3t  3t 10 thì gia tốc của vật tại thời điểm vật dừng lại là bao nhiêu? ⑻ 2
Với s  st 3 2
 t  2t t  4 thì gia tốc của vật tại thời điểm t  2s là bao nhiêu? 3
Câu 13. Một vật chuyển động thẳng xác định bởi phương trình s  st trong đó t được tính
bằng giây và S được tính bằng mét. Hỏi:
⑴ Gia tốc tại thời điểm vận tốc triệt tiêu với s  st 3 2
 t 3t 9t là bao nhiêu?
⑵ Gia tốc tại thời điểm vận tốc triệt tiêu với s  st 3 2
 t  3t 9t  27 là bao nhiêu?
⑶ Vận tốc tại thời điểm gia tốc triệt tiêu với s  st 3 2  t
  3t  9t là bao nhiêu?
⑷ Vận tốc tại thời điểm gia tốc triệt tiêu với s  st 3 2
 t 3t là bao nhiêu?
⑸ Vận tốc tại thời điểm gia tốc bằng không với s  st 3 2
 2t 3t  4t, là bao nhiêu? ⑹ 1
Vận tốc tại thời điểm gia tốc triệt tiêu với s  st 3 2
 t 3t  36t là bao nhiêu? 3
⑺ Gia tốc tại thời điểm vận tốc triệt tiêu với s  st 3 2  t
  3t  9t  2020 là bao nhiêu?
⑻ Vận tốc tại thời điểm gia tốc triệt tiêu với s  st 3 2
 2t 3t  4t là bao nhiêu?
⑼ Vận tốc tại thời điểm gia tốc triệt tiêu với s  st  t  2
t  3t  9  2024 là bao nhiêu?
⑽ Vận tốc tại thời điểm gia tốc của vật đạt giá trị nhỏ nhất trong 20 giây đầu tiên với st 1 4 3 2 
t  t  6t 10t là bao nhiêu? 12
--------------------Hết--------------------
 Biên soạn: LÊ MINH TÂM – 093.337.6281 18 Chương VII. ĐẠO HÀM ĐẠO HÀM
CÁC QUY TẮC TÍNH ĐẠO HÀM A Lý thuyết
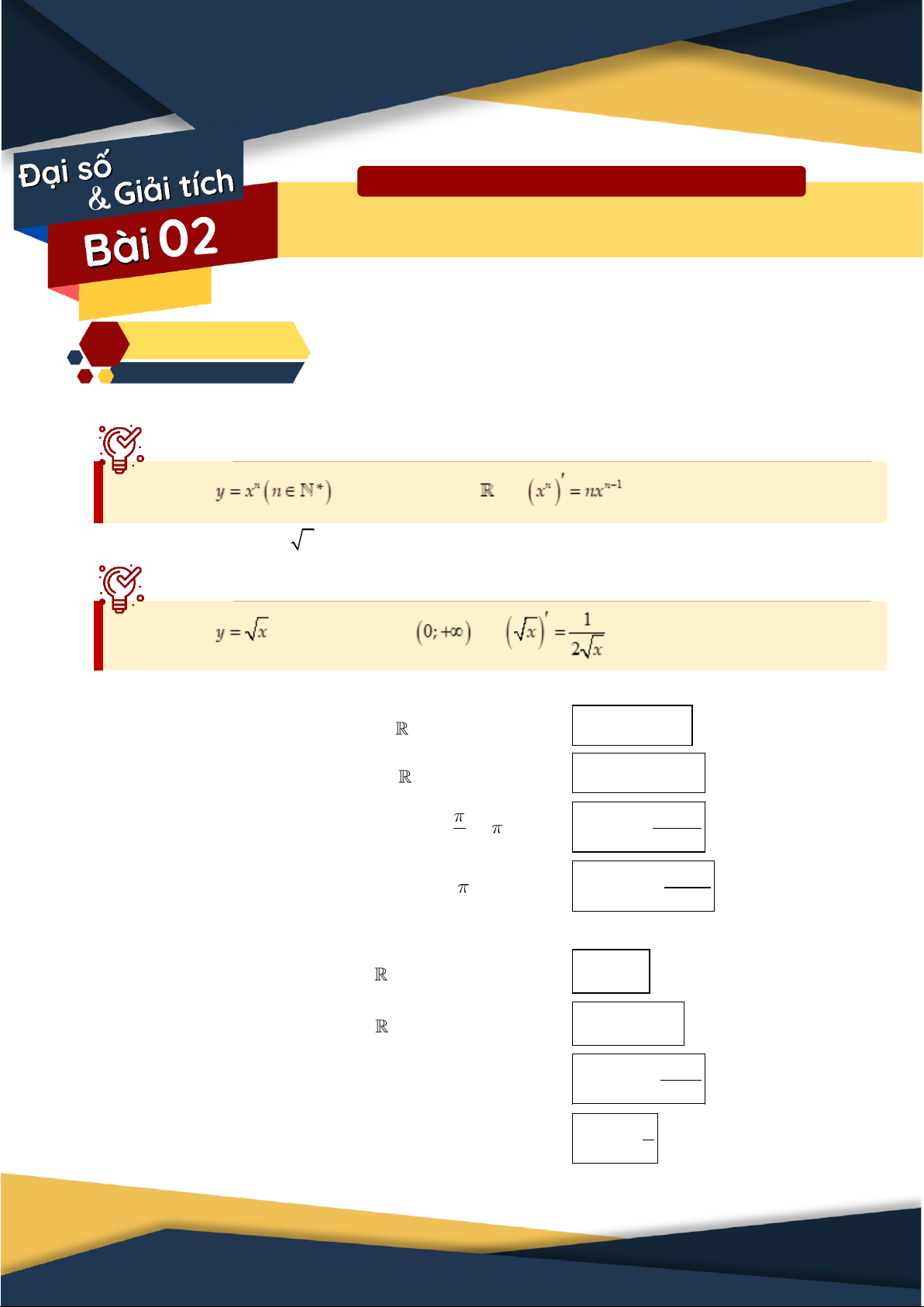
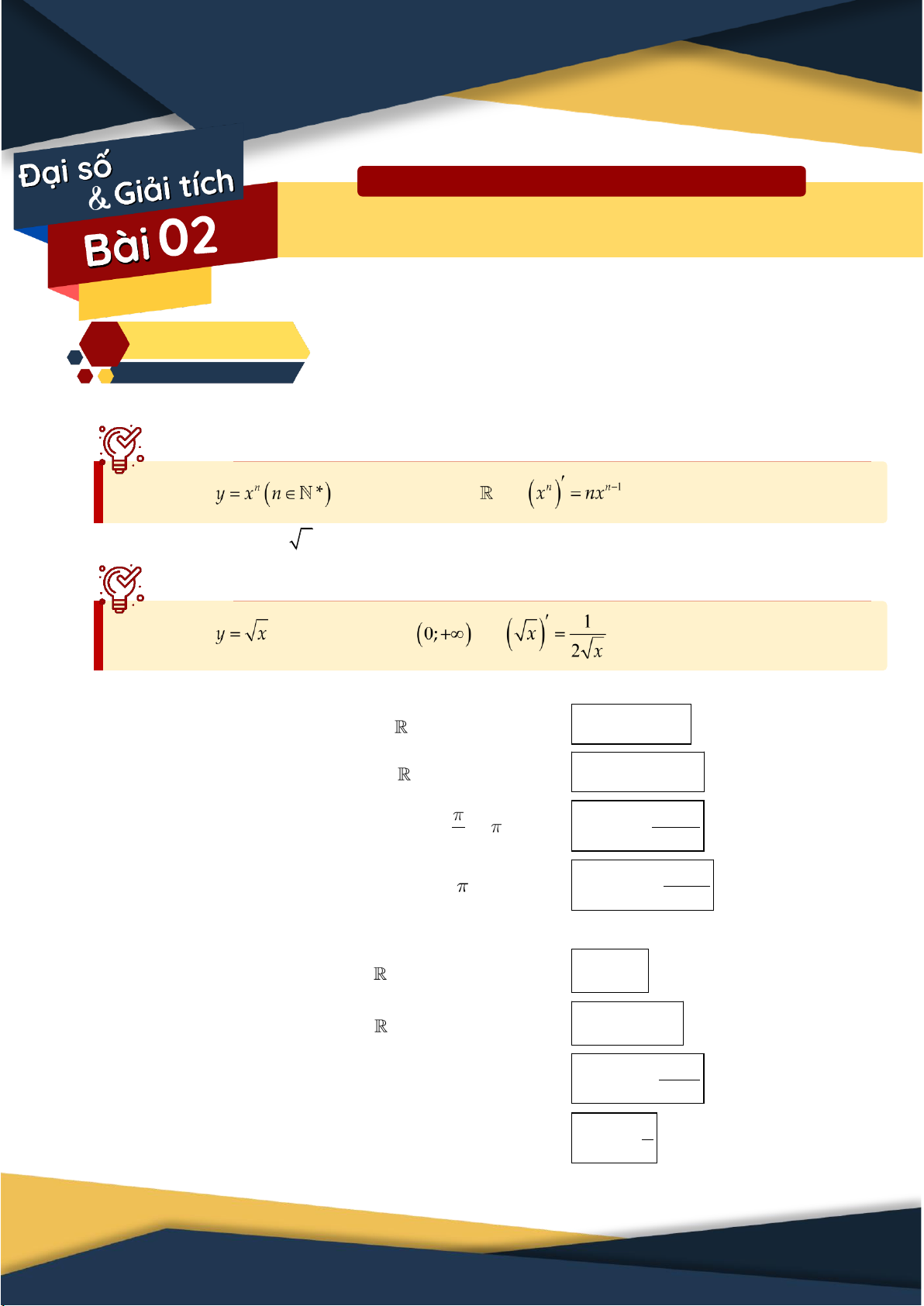
1. Đạo hàm hàm số n y  x Hàm số có đạo hàm trên và .
2. Đạo hàm hàm số y  x Hàm số có đạo hàm trên và .
3. Đạo hàm hàm số lượng giác ⑴ 
Hàm số y  sin x có đạo hàm trên và
sinx  cosx . ⑵ 
Hàm số y  cos x có đạo hàm trên và
cosx  sinx . ⑶  1
Hàm số y  tan x có đạo hàm tại mọi x   k và tanx  . 2 2 cos x ⑷  1
Hàm số y  cot x có đạo hàm tại mọi x  k và cotx   . 2 sin x
4. Đạo hàm của hàm số mũ và hàm số logarit ⑴  Hàm số x
y  e có đạo hàm trên  x x e  e . ⑵  Hàm số x
y  a có đạo hàm trên  x x a  a .ln a . ⑶ 
Hàm số y  log x có đạo hàm tại mọi x  0  x  . a  1 log a x ln a ⑷ 
Hàm số y  ln x có đạo hàm tại mọi x  0   1 ln x  . x
 Biên soạn: LÊ MINH TÂM – 093.337.6281 19 Chương VII. ĐẠO HÀM
5. Các quy tắc tính đạo hàm Giả sử các hàm số
có đạo hàm trên khoảng . Khi đó: ⑴ ⑵ ⑶ ⑷
6. Đạo hà m của hàm hợp
6.1 Khái niệm hàm số hợp Giả sử
là hàm số xác định trên khoảng
, có tập giá trị chứa khoảng và
là hàm số xác định trên . Hàm số được gọi là hàm số hợp của hàm số với .
6.2 Đạo hàm của hàm số hợp Nếu hàm số có đạo hàm tại và hàm số có đạo hàm tại thì hàm số hợp có đạo hàm tại là
 Biên soạn: LÊ MINH TÂM – 093.337.6281 20 Chương VII. ĐẠO HÀM
Từ đó ta có các kết quả sau: ⑴    n x  n 1  . n x   nu n 1  . n u  .u   ⑵  1  1  1  1         .u 2  x  x 2  u  u ⑶    x  1   u 1  .u 2 x 2 u ⑷  
sin x  cosx
sinu  u.cosu ⑸  
cosx  sin x cosu  u  .sinu ⑹  1  1 tan x  tanu  .u 2 cos x 2 cos u ⑺  1  1
cotx   cotx   .u 2 sin x 2 sin x   ⑻  x  x e  e u u
e   u.e   ⑼  x  x a  a .ln a u u
a   u.a .lna ⑽     1 ln x   u 1 ln  .u x u ⑾    x   u  u a  1 log . a  1 log x ln a uln a
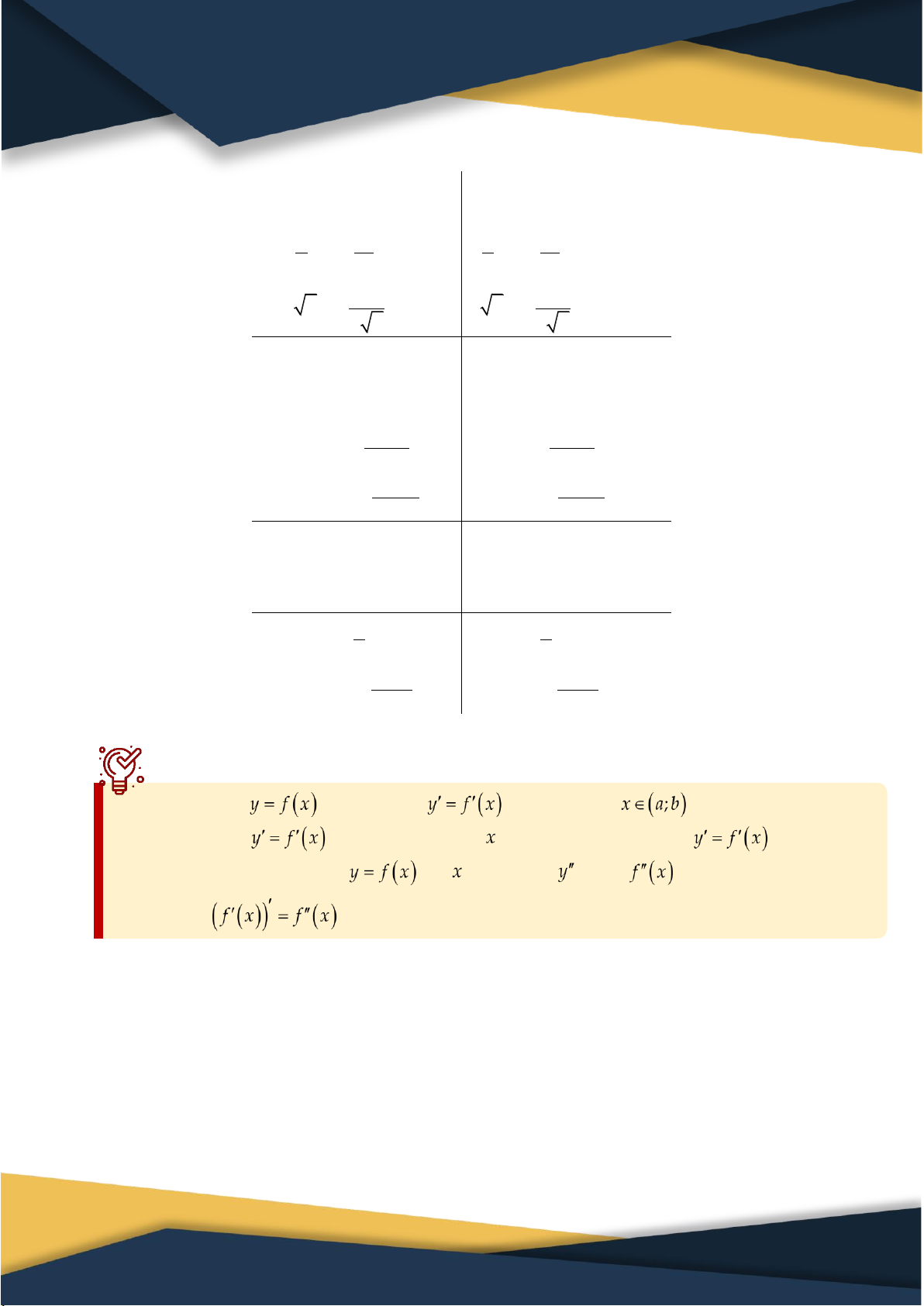
7. Đạo hàm cấp hai Cho hàm số có đạo hàm tại mọi điểm . Nếu hàm số
lại có đạo hàm tại thì ta gọi đạo hàm của là đạo
hàm cấp hai của hàm số tại , kí hiệu là hoặc . Khi đó: .
 Ý nghĩa cơ học của đạo hàm cấp hai
Một chuyển động có phương trình s  f t thì đạo hàm cấp hai (nếu có) của hàm số
s  f t là gia tốc tức thời của chuyển động s  st tại thời điểm t . Ta có at  f  t
 Biên soạn: LÊ MINH TÂM – 093.337.6281 21 Chương VII. ĐẠO HÀM B Bài tập
 Dạng 1. Tính đạo hàm đa thức – hữu tỉ – căn thức Phương pháp
 Áp dụng quy tắc đạo hàm: Khi đó: ⑴ ⑵ ⑶ ⑷
 Áp dụng công thức đạo hàm: ⑴ ⑵ ⑶ ⑷ Ví dụ 1.1.
Tính đạo hàm các hàm số sau: ⑴ ⑵ ⑶ ⑷ ⑸ ⑹ ⑺ ⑻ ⑼ ⑽
 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: LÊ MINH TÂM – 093.337.6281 22 Chương VII. ĐẠO HÀM
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: LÊ MINH TÂM – 093.337.6281 23 Chương VII. ĐẠO HÀM
 Dạng 2. Tính đạo hàm lượng giác Phương pháp
 Áp dụng quy tắc đạo hàm: Khi đó: ⑴ ⑵ ⑶ ⑷
 Để tính đạo hàm của hàm số tại
, ta thực hiện theo các bước sau: ⑴ ⑵ ⑶ ⑷ Ví dụ 2.1.
Tính đạo hàm các hàm số sau: ⑴ ⑵ ⑶ ⑷ ⑸ ⑹ ⑺ ⑻ ⑼ ⑽
 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: LÊ MINH TÂM – 093.337.6281 24 Chương VII. ĐẠO HÀM
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: LÊ MINH TÂM – 093.337.6281 25 Chương VII. ĐẠO HÀM
 Dạng 3. Tính đạo hàm mũ – logarit Phương pháp
 Áp dụng quy tắc đạo hàm: Khi đó: ⑴ ⑵ ⑶ ⑷
 Để tính đạo hàm của hàm số tại
, ta thực hiện theo các bước sau: ⑴ ⑵ ⑶ ⑷ Ví dụ 3.1.
Tính đạo hàm các hàm số sau: ⑴ ⑵ ⑶ ⑷ ⑸ ⑹ ⑺ ⑻ ⑼ ⑽
 Lời giải
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: LÊ MINH TÂM – 093.337.6281 26 Chương VII. ĐẠO HÀM
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
 Biên soạn: LÊ MINH TÂM – 093.337.6281 27 Chương VII. ĐẠO HÀM C Luyện tập
Câu 14. Tính đạo hàm của các hàm số sau: ⑴ 3
y  2x  4 x
⑵ y   x  2 2 3 1 ⑶ 1 4 2 y  2
 x  4x 1 ⑷ 3 2
y  x  2 2x  8x 1 3  2   ⑸ 2x 1 x x 1 y  ⑹ y  x  2 x 1 2   2    ⑺ x x 3 x 3x 3 y  ⑻ y  2 x  x 1 2x   1 ⑼ 2
y  x 2x   1 5x  3 ⑽ y   2 x   2 1 5  3x 
Câu 15. Tính đạo hàm của các hàm số sau: ⑴ 2x 1 y  ⑵ 3 y  4x  3 2x 1 2 ⑶ 2x 1 x  3x  3 y  ⑷ y  1 3x x 1 2   2   ⑸ 2x 4x 1 1 x x y  ⑹ y  x  3 2 1 x  x ⑺ 2 y  x x
⑻ y   x   5 2
3 x  2x
⑼ y  x2x   1 3x  2 ⑽ y   2
x  x   2 2 3 2x  3 .
Câu 16. Tính đạo hàm của các hàm số sau: ⑴ 2
y  x  x 1
⑵ y  x  x 5 2 1 ⑶ 1 y 
⑷ y  x   2 2 x 1 2 x 1 4 2
 x  x 1 ⑸ 2
y  5x  2x 1 ⑹ y     x 1  x 1 ⑺ y  ⑻ 2
y  x  4  x 4 x 1 2  2x 1 ⑼ y   
⑽ y  x  x  x  x 1 
Câu 17. Tính đạo hàm của các hàm số sau: ⑴ cos2x y  y  x x 3x  ⑵ 2 cos .sin 1 ⑶ 2
y  sin x  sin 2x ⑷ 2
y  1 cos 2x
 Biên soạn: LÊ MINH TÂM – 093.337.6281 28 Chương VII. ĐẠO HÀM  ⑸ x x 2 y  cos 3x ⑹ sin cos y  sin x  cos x 2    ⑺ 1 x
y  tan x  cot x
⑻ y  sin    2x 1   ⑼ 1 x 3 x x x y  cos ⑽ sin cos y  2x  3
x cos x  sin x
Câu 18. Tính đạo hàm cấp 2 của các hàm số sau: ⑴   2
y  x 1 x ⑵ y  sin  3  x   6  ⑶ 2
y  sin 2  x ⑷ 2
y  sin x  sin 2x  ⑸ x 2
y  2sin x  cos 2x  x ⑹ 3 y  1 2x ⑺ 2
y  x  x 1
⑻ y   x  2 2 3 1 2   ⑼ x x 3 y 
⑽ y  sinsin x 2 x  x 1
Câu 19. Tính đạo hàm cấp 3 tại các điểm được chỉ ra dưới đây ⑴ 3 Cho hàm số 3 2 y  3
 x  3x  x  5. Tính giá trị của y 2017 . ⑵ 2 3 Cho hàm số y 
. Tính giá trị của y   1 . 1 x ⑶ 1 3 Cho hàm số y 
. Tính giá trị của y 2 . 2 x 1 ⑷    3 Cho hàm số 2
y  cos x . Tính giá trị của y   .  3 
Câu 20. Chứng minh rằng: ⑴ Với hàm số 2
y  2x  x ta có 3
y .y 1  0 . ⑵ Với hàm số 2
y  x  x 1 ta có y  x3 .y 1  0 .
⑶ Với hàm số y  xsin x ta có xy  2ysinx xy  0.  ⑷ x 3 Với hàm số y  2
2y  y 1 y . x  ta có   4
⑸ Với hàm số y  cot 2x ta có 2
y  2y  2  0 .
⑹ Với hàm số y  x tan x ta có 2 x y   2 2
2 x  y 1 y  0 .
⑺ Với hàm số y  tan x ta có 2
y  y 1  0 . ⑻ Với hàm số 2
y  x 1 ta có 2
y .y  xy  y . ⑼ Với hàm số 2
y  x 1 ta có 2
y y   xy  y .
 Biên soạn: LÊ MINH TÂM – 093.337.6281 29 Chương VII. ĐẠO HÀM ⑽ Với hàm số 2
y  1 x ta có 2
y .y  xy  y  0 .
Câu 21. Cho f x 4 2
 x  4x  3 và gx 2
 310x  7x . Giải phương trình f  x  gx  0
Câu 22. Cho hàm số f x 3 2
 x 3x  4x  6 . Giải bất phương trình f  x  f x 1 Câu 23. Cho hàm số 3 2
y  x  3x  4x  6 . Giải bất phương trình y  0 . Câu 24. 3
Cho hàm số y  f x  5x   1  4x  
1 . Giải phương trình f x  0 .  
Câu 25. Cho hàm số y  f x  cos 2x  
 . Tìm các nghiệm thuộc đoạn 0;     của phương 3  4 trình f x  8.
--------------------Hết--------------------
 Biên soạn: LÊ MINH TÂM – 093.337.6281 30 Chương VII. ĐẠO HÀM Mục lục
 Bài 01. ĐẠO HÀM A. Lý thuyết
1. Đạo hàm. ...................................................................................................................................... 2
2. Ý nghĩa hình học của đạo hàm ............................................................................................... 3
3. Ý nghĩa vật lý của đạo hàm ................................................................................................... 4
4. Số e ............................................................................................................................................... 4 B. Bài tập
 Dạng 1. Tính đạo hàm tại 1 điểm bằng định nghĩa .......................................................... 5
 Dạng 2. Tính đạo hàm tại 1 điểm bất kỳ trên (a;b) bằng định nghĩa ........................ 8
 Dạng 3. Ý nghĩa hình học của đạo hàm ............................................................................ 10
 Dạng 4. Ý nghĩa vật lý của đạo hàm ................................................................................. 12
 Dạng 5. Tìm tham số để hàm số có đạo hàm tại x0 ...................................................... 13 C. Luyện tập
 Bài 02. CÁC QUY TẮC TÍNH ĐẠO HÀM A. Lý thuyết
1. Đạo hàm hàm số n
y  x .......................................................................................................... 39
2. Đạo hàm hàm số y  x ....................................................................................................... 39
3. Đạo hàm hàm số lượng giác ................................................................................................ 39
4. Đạo hàm của hàm số mũ và hàm số logarit .................................................................. 39
5. Các quy tắc tính đạo hàm ................................................................................................... 40
6. Đạo hàm của hàm hợp ......................................................................................................... 40
7. Đạo hàm cấp hai ..................................................................................................................... 41 B. Bài tập
 Dạng 1. Tính đạo hàm đa thức – hữu tỉ – căn thức ........................................................ 42
 Dạng 2. Tính đạo hàm lượng giác .................................................................................... 44
 Dạng 3. Tính đạo hàm mũ – logarit .................................................................................. 46 C. Luyện tập
 Biên soạn: LÊ MINH TÂM – 093.337.6281 1 Chương VII. ĐẠO HÀM ĐẠO HÀM ĐẠO HÀM A Lý thuyết 1. Đạo hàm. Định nghĩa: Cho hàm số xác định trên khoảng và .
 Nếu tồn tại giới hạn hữu hạn
thì giới hạn đó được gọi là đạo hàm của tại điểm , tức là:  Kí hiệu là hay .
 Tính đạo hàm bằng định nghĩa:
Để tính đạo hàm của hàm số y  f x tại x  ;
a b , ta thực hiện theo các bước sau: 0  
 Bước 1. Tính f x  f x . 0 
f x  f x0 
 Bước 2. Lập và rút gọn tỉ số x  ;
a b , x  x x  với   x 0 0
f x  f x0 
 Bước 3. Tính giới hạn lim xx  . 0 x x0 Chú ý
Trong định nghĩa & quy tắc trên đây, thay
bởi ta sẽ có định nghĩa và quy tắc tính đạo hàm của hàm số tại điểm .
 Biên soạn: LÊ MINH TÂM – 093.337.6281 2 Chương VII. ĐẠO HÀM
2. Ý nghĩa hình học của đạo hàm Ví dụ 2.1. Cho hàm số và điểm ⑴ Vẽ đồ thị và tính .
⑵ Vẽ đường thẳng qua có hệ số góc
. Nhận xét về vị trí tương đối giữa và
 Lời giải
⑴ Vẽ đồ thị C và tính f  1 .      f  
f x f   2 2 1 x 1
x 1x 1 1  lim  lim  lim lim x   1  2 x 1  x 1  x 1  x 1 x 1 x 1 x 1 
⑵ Vẽ đường thẳng d qua M có hệ số góc f  
1 . Nhận xét về vị trí tương đối giữa d và C .
Đường thẳng d cắt C tại hai điểm O0;0 và M2; 4 .
 Trong mặt phẳng tọa độ Oxy , cho đồ thị C của hàm số y  f x và điểm Mx ; y  C . 0 0   
Xét M x; f x là một diểm di chuyển trên C .
Đường thẳng MM là một cát tuyến của C . 0
f x  f x0 
Hệ số góc của cát tuyến MM được tính bởi công thức k  tan  0 MM0 x  . x0
Khi cho x dần tới x thì M di chuyển trên C tới M . 0 0
 Biên soạn: LÊ MINH TÂM – 093.337.6281 3 Chương VII. ĐẠO HÀM
Giả sử cát tuyến MM có vị trí giới hạn là M T thì M T được gọi là tiếp tuyến của C tại 0 0 0
M và M được gọi là tiếp điểm 0 0 f x  f x
Ta có hệ số góc của tiếp tuyến M T là k  tan  lim tan     0  lim  f  x M T  0 0 0 xx xx  0 0 x x0
Đạo hàm của đồ thị hàm số tại điểm
là hệ số góc của tiếp tuyến của tại điểm Tiếp tuyến có phương trình: 3. Ý nghĩa
vật lý của đạo hàm  Nếu hàm số
biểu thị quãng đường di chuyển của vật theo thời gian thì
biểu thị tốc độ tức thời của chuyển động tại thời điểm .  Nếu hàm số
biểu thị nhiệt độ theo thời gian thì
biểu thị tốc độ thay
đổi nhiệt độ theo thời gian tại thời điểm . 4. Số e
Người ta còn biết rằng là số vô tỉ và
(Số thập phân vô hạn không tuần hoàn).
 Biên soạn: LÊ MINH TÂM – 093.337.6281 4 Chương VII. ĐẠO HÀM B Bài tập
 Dạng 1. Tính đạo hàm tại 1 điểm bằng định nghĩa Phương pháp
 Để tính đạo hàm của hàm số tại
, ta thực hiện theo các bước sau:  Bước 1. Tính .
 Bước 2. Lập và rút gọn tỉ số với và
 Bước 3. Tính giới hạn . ⑴ ⑵ ⑶  Hàm số
có đạo hàm tại điểm .  Hàm số
có đạo hàm tại điểm thì trước hết phải liên tục tại điểm đó. Ví dụ 1.1.
Tính đạo hàm bằng định nghĩa tại một điểm của các hàm số sau: ⑴ tại ⑵ tại
 Lời giải
⑴ y  f x 3
 2x  x 1 tại x  0 0
Tại x  0 ta có f x  f x   f x  f 0 3
 2x  x 1   3
1  2x  x  x  2 2x 1 0  0
f x  f x 
f x  f 0 x 2 2x 1 0  2      2x 1 x  x x  0 x 0   f x  f x f 0    0  lim  lim  2 2x   1  1 xx x0  0 x x0
⑵ y  f x 2
 x  2x 1 tại x  1 0
Tại x  0 ta có f x  f x  f x  f 0  x  2x 1 2  x  2x 3 0      2   2 0
f x  f x 
f x  f 0 2 x  2x  3 x 1 x  3 0          x  3 x  x x 1 x 1 x  1 0
 Biên soạn: LÊ MINH TÂM – 093.337.6281 5 Chương VII. ĐẠO HÀM   f  
f x f x0  1  lim
 lim x  3  4 xx x 1   0 x x0 Ví dụ 1.2.
Tính đạo hàm bằng định nghĩa tại một điểm của các hàm số sau: ⑴ tại ⑵ tại
 Lời giải
⑴ y  f x 1  tại x  2 2 x  x 1 0
Tại x  2 ta có f x  f x  f x  f 2  0      0 2 2 1 1
1 3  x  x 1
1 x  x  2 1 x   1 x  2    .  .   . 2 2 2 2
x  x 1 4  2 1 3 x  x 1 3 x  x 1 3 x  x 1
f x  f x f x  f 2 1 x 1 x  2 1 1 x 1 0                . .   . 2 2 x  x x  2 3 x  x 1 x  2 3 x  x 1 0        f  
f x f x 1 x 1 1 2 1 0      1 2  lim  lim  .    .  2 2 xx x 2      0 x x 3 x x 1 3 3       0  2  2 1 ⑵  
y  f x 2 x x 3  tại x  3 2x 1 0 Tại x  3 ta có 0      
f x  f  x x 3 9 5x 13x 6 x 3 5x 2
x  f x  f 3     0      2 2    2x 1 5 52x   1 52x   1
f x  f x f x  f 3 x  3 5x  2 1 5x  2 0               .  x  x x  3 5 2x 1 x  3 5 2x 1 0         f  
f x f x f x f 3 5x 2 0        17 3  lim  lim  lim  xx x3 x3    0 x x x 3 5 2x 1 25 0   Ví dụ 1.3.
Tính đạo hàm bằng định nghĩa tại một điểm của các hàm số sau: ⑴ tại ⑵ tại
 Lời giải
 Biên soạn: LÊ MINH TÂM – 093.337.6281 6 Chương VII. ĐẠO HÀM 2
 x  3x 1 ⑴   f x khi x 1   x 1 tại x 1 3  khi x  1 Ta có: f   1  3 
f x  f   2 2 1
x  3x 1 3 x  3x  4
x4x 1 Do đó: lim  lim  lim  lim  5 x 1  x 1  x 1  x 1 x 1 x 1 x 1  x 1
Vậy f 0  5.  3 2
x  x 1 1 ⑵   f x khi x 0   x tại x  0 0  khi x  0 Ta có f 0  0
f x  f 0 3 2
x  x 1 1 x 1 1 Do đó: lim  lim  lim  2 x0 x0 x0 3 2 x x 2
x  x 1 1 1
Vậy f 0  . 2 Ví dụ 1.4. Tìm để hàm số có đạo hàm tại
 Lời giải
Để hàm số có đạo hàm tại x 1 thì trước hết f x phải liên tục tại x 1 2 x 1
Hay lim f x  lim  2  f   1  a x 1  x 1  x  . 1 2  
f x  f   x 1 2 1  Khi đó, ta có: x 1 lim  lim 1. x 1  x 1 x 1  x 1
Vậy a  2 là giá trị cần tìm.
 Biên soạn: LÊ MINH TÂM – 093.337.6281 7 Chương VII. ĐẠO HÀM
 Dạng 2. Tính đạo hàm tại 1 điểm bất kỳ trên (a;b) bằng định nghĩa Phương pháp
 Để tính đạo hàm của hàm số tại
, ta thực hiện theo các bước sau:  Bước 1. Tính .
 Bước 2. Lập và rút gọn tỉ số với và
 Bước 3. Tính giới hạn .  Hàm số
có đạo hàm tại điểm thì trước hết phải liên tục tại điểm đó. Ví dụ 2.1.
Tính đạo hàm bằng định nghĩa của các hàm số sau: ⑴ ⑵ ⑶ ⑷ ⑸ ⑹
 Lời giải
⑴ y  f x  4x 3 Tại x 
tùy ý, ta có: f x  f x  4x  3 4x  3  4 x  x 0  0  0  0
f x  f x 4 x  x 0   0      4 x  x x  x 0 0
f x  f x0    lim
 lim 4  4  y  4 xx xx  0 0 x x0
⑵ y  f x  2024x  2025 Tại x 
tùy ý, ta có: f x  f x  2024x  2025 2024x  2025  2024 x  x 0  0  0  0
f x  f x 2024 x  x 0   0      2024 x  x x  x 0 0
f x  f x0   lim
 lim 2024  2024  y  2024 xx xx  0 0 x x0
⑶ y  f x 2  2x  2024 Tại x  tùy ý, ta có: 0
 Biên soạn: LÊ MINH TÂM – 093.337.6281 8 Chương VII. ĐẠO HÀM
f x  f x  2 2 2 2
 2x  2024 2x  2024  2x  2x  2 x  x x  x 0 0 0  0   0 
f x  f x 2 x  x x  x 0   0   0    
 2x  x0  x  x x  x 0 0
f x  f x0    lim
 lim 2x  x  4x  y  4x 0  0 xx xx  0 0 x x0
⑷ y  f x 2
 x 3x 1 Tại x 
tùy ý, ta có: f x  f x  2 2
 x 3x 1 x  3x 1 x  x x  x 3 0 0 0  0   0  0
f x  f x x  x x  x  3 0   0   0    
 x  x  3 0 x  x x  x 0 0
f x  f x0    lim
 lim x  x  3  2x 3  y  2x 3 0  0 xx xx  0 0 x x0
⑸ y  f x 3  x  2x Tại x 
tùy ý, ta có: f x  f x  3 3
 x  2x  x  2x  x  x  2 2 x  . x x  x  2 0 0 0 0 0 0  0
f x  f x x  x x  . x x  x  2 0    2 2 0 0 0       2 2 x  . x x  x  2 0 0  x  x x  x 0 0
f x  f x0   lim  lim  2 2 x  .
x x  x  2 2 2
 3x  2  y  3x  2 0 0 0 xx xx  0 0 x x0
⑹ y  f x 4 2
 x  2x  2 Tại x  tùy ý, ta có: 0
f x  f x  4 2 4 2
 x  2x  2  x  2x  2  x  x  3 2
x  x x  x  2 x  2 3  x  2x 0 0 0 0 0 0 0 0 
f x  f x  x  x  3 2
x  x x  x  2 x  2 3  x  2x 0 0 0 0 0 0  3 2   
 x  x x  x 2 x  2 3  x  2x 0 0 0 0 x  x x  x 0 0
f x  f x0    lim xx  0 x x0  lim      3 3 3 3 3
 x  x  x  2x  x  2x  4x  4x   3 2 x x x x  2 x 2 3 x 2x 0 0 0 0  0 0 0 0 0 0 0 0 x x0 3
 y  4x  4x
 Biên soạn: LÊ MINH TÂM – 093.337.6281 9 Chương VII. ĐẠO HÀM
 Dạng 3. Ý nghĩa hình học của đạo hàm Phương pháp
 Ý nghĩa hình học: (Phương trình tiếp tuyến) Cho hàm số có đồ thị , .
Phương trình tiếp tuyến tại có dạng: . Trong đó: hoành độ tiếp điểm. tung độ tiếp điểm.
hệ số góc tiếp tuyến.
Bài toán: Viết phương trình tiếp tuyến của đồ thị hàm số tại .  Bước 1. Tính .  Bước 2. Từ .
 Bước 3. Hoàn thiện phương trình tiếp tuyến cần tìm . Ví dụ 3.1.
Viết phương trình tiếp tuyến của
⑴ Đồ thị hàm số
tại điểm có hoành độ .
⑵ Đồ thị hàm số
tại điểm có hoành độ .
⑶ Đồ thị hàm số tại điểm có tung độ .
 Lời giải
⑴ Đồ thị hàm số 2
y  x  2x  4 C tại điểm có hoành độ x  0 . 0
Gọi Zx ; y là tiếp điểm. 0 0  Tại x 
tùy ý, ta có: f x  f x  2 2
 x  2x  4 x  2x  4  x  x x  x  2 0 0 0  0   0  0
f x  f x x  x x  x  2 0   0   0    
 x  x  2 0 x  x x  x 0 0
f x  f x0   lim
 lim x  x  2  2x  2  y  2x  2 0  0 xx xx  0 0 x x0
Hệ số góc của tiếp tuyến của C tại điểm có hoành độ x  0 là k  y0  2 0
Tung độ tiếp điểm tại điểm có hoành độ x  0 là y x  4  0  0
 Biên soạn: LÊ MINH TÂM – 093.337.6281 10 Chương VII. ĐẠO HÀM
Phương trình tiếp tuyến cần tìm là y  y0x  0  y0  y  2x  4
⑵ Đồ thị hàm số 3
y  x 1 C tại điểm có hoành độ x  1. 0
Gọi C x ; y là tiếp điểm. 0 0  Tại x 
tùy ý, ta có: f x  f x  3 3
 x 1 x 1  x  x  2 2 x  . x x  x 0 0 0 0 0  0
f x  f x x  x x  . x x  x 0    2 2 0 0 0  2 2     x  . x x  x 0 0 x  x x  x 0 0
f x  f x0    lim  lim  2 2 x  . x x  x  2 2
 3x  y  3x 0 0 0 xx xx  0 0 x x0
Hệ số góc của tiếp tuyến của C tại điểm có hoành độ x  1 là k  y  1  3 0
Tung độ tiếp điểm tại điểm có hoành độ x  1 là y x  2 0  0
Phương trình tiếp tuyến cần tìm là y  y  1 x   1  y  
1  y  3x 1
⑶ Đồ thị hàm số 2
y  2x  3 C tại điểm có tung độ y  1. 0
Gọi T x ; y là tiếp điểm. 0 0  Tại x 
tùy ý, ta có: f x  f x  2 2
 2x 1 2x 1 2 x  x x  x 0 0  0   0  0
f x  f x 2 x  x x  x 0   0   0    
 2x  x0  x  x x  x 0 0
f x  f x0    lim
 lim 2x  x  4x  y  4x 0   0 xx xx  0 0 x x0 x 1 Ta có 2 2 0 y  2   2x 3  1
  2x  2   . 0 0 0 x  1   0 ● Với x  1: 0
Hệ số góc của tiếp tuyến của C tại điểm có hoành độ x  1 là k  y  1  4 0
Phương trình tiếp tuyến cần tìm là y  y  1 x   1  y  
1  y  4x  5 . ● Với x  1: 0
Hệ số góc của tiếp tuyến của C tại điểm có hoành độ x  1 là k  y  1  4  0
Phương trình tiếp tuyến cần tìm là y  y  1 x   1  y   1  y  4  x 5.
 Biên soạn: LÊ MINH TÂM – 093.337.6281 11 Chương VII. ĐẠO HÀM
 Dạng 4. Ý nghĩa vật lý của đạo hàm Phương pháp
 Ý nghĩa vật lý: (quãng đường, nhiệt độ, điện lượng)  Nếu hàm số
biểu thị quãng đường di chuyển của vật theo thời gian thì biểu
thị tốc độ tức thời của chuyển động tại thời điểm .  Nếu hàm số
biểu thị nhiệt độ theo thời gian thì
biểu thị tốc độ thay đổi
nhiệt độ theo thời gian tại thời điểm . Ví dụ 4.1.
Một chất điểm chuyển động có phương trình chuyển động là (t
được tính bằng giây, s được tính bằng mét).
⑴ Tính đạo hàm của hàm số tại điểm .
⑵ Tính vận tốc tức thời của chuyển động tại thời điểm .
 Lời giải
⑴ Tính đạo hàm của hàm số f t tại điểm t . 0 f t  f t
Ta có f t  lim 0     0 tt  0 t t0 2
 t  4t  6 2t  4t 6 
 t t t  t  4  0 0   0 0   lim   lim
  lim t  t  4  2t  4 . 0  0 tt tt       tt 0 0 0 t t t t 0    0 
⑵ Tính vận tốc tức thời của chuyển động tại thời điểm t  5.
Vận tốc tức thời của chuyển động tại thời điểm t  5: 5  2 5 .  4  14 m f . s  Ví dụ 4.2.
Cho biết điện lượng trong một dây dẫn theo thời gian biểu thị bởi hàm số
(t được tính bằng giây, Q được tính bằng Coulomb). Tính cường độ của dòng điện
trong dây dẫn tại thời điểm
 Lời giải
Ta có Q  6t  5  Qt  6 .
Cường độ dòng điện trong dây dẫn tại thời điểm t 10 là I  Q10  6 .
 Biên soạn: LÊ MINH TÂM – 093.337.6281 12 Chương VII. ĐẠO HÀM
 Dạng 5. Tìm tham số để hàm số có đạo hàm tại x0 Phương pháp  Cho hàm số hoặc
. Tìm tham số m để hàm số có đạo hàm tại
 Bước 1. Xác định .
 Bước 2. Hàm số liên tục tại  Bước 3. Tính ; .
 Bước 4. Hàm số có đạo hàm tại . Ví dụ 5.1. Cho hàm số
. Tìm để hàm số có đạo hàm tại .
 Lời giải Ta có lim  2
2x  x  a  a , f 0  0. x0
Hàm số có đạo hàm tại x  0  f x liên tục tại x  0  lim 2
2x  x  a  f 0  a  0 x 0      f  f x f x x x x 0   0 2 2 0 2 1  lim  lim  lim  lim2x   1  1  x0 x0 x0 x0 x  . 0 x x Ví dụ 5.2. Cho hàm số
. Tìm , thì hàm số có đạo hàm tại ?
 Lời giải 2 1 1 1 Ta có lim    
 .Hàm số liên tục tại x 1 nên a  b  .    ; lim x ax b a b ; f 1  x 1  x 1   2    2 2 2 f x  f 1
ax  b  a 1 .  b a x 1
Đạo hàm phải f 1           lim  lim  lim  lim a  a     x 1   x 1   x 1   . x 1 x 1 x 1 x 1  2 x 1 f x  f 1  x 1 x 1   x 1
Đạo hàm trái f          2 2 1  lim  lim  lim  lim  1.     x 1   x 1   x 1 x 1 x 1  2 x   x 1 1  2
Hàm số có đạo hàm tại x   
1 f 1   f 1   a  1
Vậy a 1; b  0  ,5 .
 Biên soạn: LÊ MINH TÂM – 093.337.6281 13 Chương VII. ĐẠO HÀM C Luyện tập
Câu 1. Tính đạo hàm của các hàm số sau tại các điểm đã chỉ:
⑴ f x  2x 1 tại x  2 
⑵ f x  20242023x tại x 1
⑶ f x 2
 x  2x 1 tại x 1
⑷ f x 3
 2x 1 tại x  2  ⑸ x f x 2
 2x  x 1 tại x 1
⑹ f x 1  x  x  tại 2 1  ⑺ x f x 1  x 
⑻ f x 2 1  x  x  tại 2 1 x  tại 3 2
⑼ f x  x 1 tại x 1
⑽ f x  2023 x tại x  2 Lời giải
⑴ f x  2x 1 tại x  2  f x  f 2  2x 1 4  1 2x  4 Ta có f  2          lim  lim  lim  2 x 2  x 2  x 2 x  2 x  2  x  . 2
⑵ f x  20242023x tại x 1 f x  f 1 2024  2023x  1 2  023x  2023 Ta có f         1  lim  lim  lim  2  023 x 1  x 1  x 1 x 1 x 1  x  . 1
⑶ f x 2
 x  2x 1 tại x 1 2 f x  f x
x  2x 1 2 x 1 x  3 Ta có f      0    1  lim  lim  lim
 lim x  3  4 x 1  x 1  x 1  x 1 x  x x 1 x  1  0
⑷ f x 3
 2x 1 tại x  2 3 f x  f 2 2x 16 Ta có f 2      lim  lim  lim 2 2
x  2x  4  24 x2 x2 x2 x  2 x  . 2
⑸ f x 2
 2x  x 1 tại x 1 2 f x  f 1
2x  x 1 4 x 1 2x  3 Ta có f          1  lim  lim  lim
 lim2x  3  5 x 1  x 1  x 1  x 1 x 1 x 1 x  1  
⑹ f x x 1  x  x  tại 2 1 x 1
x 1 3x  3  3 f x  f 2   2  Ta có f       x 1 x 1 2  lim  lim  lim  lim  2 x2 x2 x2 x2 x  2 x  2 x  2 x  . 1
⑺ f x 1  x  x  tại 2 1
 Biên soạn: LÊ MINH TÂM – 093.337.6281 14 Chương VII. ĐẠO HÀM 1 2  x 1 f x  f 2   1  1  Ta có f       x 1 x 1 2  lim  lim  lim  lim   1  x2 x2 x2 x2 x  2 x  2 x  2 x 1 2  . 1 
⑻ f x 2x 1  x  x  tại 3 2 2x 1
2x 1 7x 14  7 f x  f 3   5  5  Ta có f       x 2 x 2 3  lim  lim  lim  lim   5 x3 x3 x3 x3 x  3 x  3 x  3 x  2 3  . 2
⑼ f x  x 1 tại x 1
f x  f   1 x 1  2 x 1 1 1 Ta có lim  lim  lim  lim  x 1  x 1  x 1 x 1 x 1  x  
1  x 1  2  x 1  x 1  2 2 2
⑽ f x  2023 x tại x  2
f x  f 2 Ta có lim x2 x  2 2023  x  2025  lim x2 x  2 2023  x  2025 1 1  lim  lim 
x2 x  2 2023 x  2025 x2 2023 x  2025 2 2025
Câu 2. Tính đạo hàm của các hàm số sau tại các điểm (nếu có):       ⑴ x khi x f x 2x 3 khi x 3   . Tính f 3 .
⑵ f x 2 1 0   . Tính f 0 . 2
x khi x  3 1   2  x khi x  0
⑶ f x  x . Tính f 0.
⑷ f x  x  x . Tính f 0.
⑸ f x  2x  x 1 . Tính f   1 .
⑹ f x  x  x . Tính f   1 .
⑺ f x  x  2023 . Tính f 0.
⑻ f x 2
 x  2x . Tính f 0. x 2 x  x 1 ⑼ y  f  0 .
⑽ f x  . Tính f   1 . x  . Tính   1 x Lời giải   
⑴ f x 2x 3 khi x 3   . Tính f 3 . 2
x khi x  3 f x  f 3 2x  3  2 3 .  3
Đạo hàm phải f 3         lim  lim  lim 2  2    x 3   x 3   . x 3 x 3 x 3  2 f x  f 3 x  2 3 .  3
Đạo hàm trái f 3         lim  lim  lim       x 3 6 x 3   x 3   . x 3 x 3 x 3 
Suy ra f 3   f 3  
 Hàm số không tồn tại đạo hàm tại x 3.
 Biên soạn: LÊ MINH TÂM – 093.337.6281 15 Chương VII. ĐẠO HÀM  ⑵    f x 2 x 1 khi x 0   . Tính f 0 . 1   2  x khi x  0 2 f x  f 0  x 11
Đạo hàm phải f 0       lim  lim  lim  .     x  0 x0  x0 x0 x 0 x f x  f 0  1 2x 1
Đạo hàm trái f 0       lim  lim  lim    .     2 2. x0  x0 x0 x 0 x
Suy ra f 0   f 0  
 Hàm số không tồn tại đạo hàm tại x0.
⑶ f x  x . Tính f 0. x khi x 
Ta có: y  f x 0  
 x khi x  0 f x  f 0  x  0
Đạo hàm phải f 0       lim  lim 1   x0  . x0 x 0 x f x  f 0  x  0
Đạo hàm trái f 0       lim  lim  1    x0  . x0 x 0 x
Suy ra f 0   f 0  
 Hàm số không tồn tại đạo hàm tại x0.
⑷ f x  x  x . Tính f 0.  x khi x 
Ta có: y  f x 2 0   0  khi x  0 f x  f 0  2x  0 2x
Đạo hàm phải f 0       lim  lim  lim  2    x0  . x0 x0 x 0 x x f x  f 0  0  0 0
Đạo hàm trái f 0       lim  lim  lim  0    x0  . x0 x0 x 0 x x
Suy ra f 0   f 0  
 Hàm số không tồn tại đạo hàm tại x0.
⑸ f x  2x  x 1 . Tính f   1 .
 x  khi x 
Ta có: y  f x 3 1 1  
x 1 khi x 1 f x  f 1     3x 1 2 3 x 1
Đạo hàm phải f 1         lim  lim  lim  3    x 1   x 1   x 1 x 1 x 1  x  . 1 f x  f 1  x 1 2 x 1
Đạo hàm trái f 1       lim  lim  lim 1    x 1   x 1   x 1 x 1 x 1  x  . 1
Suy ra f 1   f 1  
 Hàm số không tồn tại đạo hàm tại x1.
⑹ f x  x  x . Tính f   1 .
 x  khi x 
Ta có: y  f x 3 1 1  
x 1 khi x 1
 Biên soạn: LÊ MINH TÂM – 093.337.6281 16 Chương VII. ĐẠO HÀM f x  f 1     3x 1 2 3 x 1
Đạo hàm phải f 1         lim  lim  lim  3 .    x 1   x 1   x 1 x 1 x 1  x 1 f x  f 1  x 1 2 x 1
Đạo hàm trái f 1       lim  lim  lim 1.    x 1   x 1   x 1 x 1 x 1  x 1
Suy ra f 1   f 1  
 Hàm số không tồn tại đạo hàm tại x1.
⑺ f x  x  2023 . Tính f 0. x  khi x 
Ta có y  f x 2023 0   2023   x khi x  0 f x  f 0 x  2023  2  023  x
Đạo hàm phải f 0         lim  lim  lim 1    x0  . x0 x0 x 0 x x f x  f 0 2023  x  2  023  x
Đạo hàm trái f 0         lim  lim  lim  1     x0  . x0 x0 x 0 x x
Suy ra f 0   f 0  
 Hàm số không tồn tại đạo hàm tại x0.
⑻ f x 2
 x  2x . Tính f 0. 2 x  2x
khi x  2; x  0
Ta có f x   .    2
x  2x khi  2  x  0 2 f x  f 0  x  2x
Đạo hàm phải f 0       lim  lim  lim   .     x 2 2 x0 x0 x0 x x 2 f x  f 0  x  2x
Đạo hàm trái f 0         lim  lim  lim     .     x 2 2 x0 x0 x0 x x
Suy ra f 0   f 0  
 Hàm số không tồn tại đạo hàm tại x0. x ⑼ y  f  0 . x  . Tính   1  x khi x  0   Ta có f x x 1    x  khi x  0 x 1 x 0 f x  f 0   1
Đạo hàm phải f       x 1 0  lim  lim  lim 1    x0  x0 x0 x 0 x x  . 1 x 0 f x  f 0   1 
Đạo hàm trái f       x 1 0  lim  lim  lim  1     x0  x0 x0 x 0 x x  . 1
Suy ra f 0   f 0  
 Hàm số không tồn tại đạo hàm tại x0.
 Biên soạn: LÊ MINH TÂM – 093.337.6281 17 Chương VII. ĐẠO HÀM 2 x  x 1
⑽ f x  . Tính f   1 . x 2  x  x 1  khi x  1   Ta có   x f x   2
 x  x 1 khi x  1   x 2
x  x 1 1      x 2x 1 x 2 2 1 x 1
Đạo hàm phải 1   lim x f  lim  lim  lim  0     x 1   x 1 x 1  xx   x 1 1 
xx   x 1 1  x 2
x  x 1 1 2  x 1 x 1
Đạo hàm trái 1   lim x f  lim  lim  2    x 1   x 1 x 1 
xx   x 1 1  x
Suy ra f 1   f 1  
 Hàm số không tồn tại đạo hàm tại x1.
Câu 3. Tính đạo hàm của các hàm số sau tại các điểm đã chỉ (nếu có):  ⑴    f x 2 x 3x khi x 1   . Tính f   1  2   khi x 1 3 2
 x  4x  3x  
⑵ f x khi x 1 2
  x 3x  2 . Tính f   1 0  khi x  1 2x  3 khi x  1 ⑶  f x 3 2
 x  2x  7x  4 . Tính f   1 . khi x   1  x 1 2
 x  7x 12  
⑷ f x khi x 3   x  3
. Tính f 3 1  khi x  3
 x khi x 1
⑸ f x   . Tính f   1 2 x khi x  1    
⑹ f x 3 4 x khi x 0  
. Tính f 0 1  khi x  0  3 2
x  2x  x 1 1  ⑺  f x khi x 1   x 1 . Tính f   1 0  khi x  1  x 1 1  
⑻ f x khi x 0   x
. Tính f 0 0  khi x  0
 Biên soạn: LÊ MINH TÂM – 093.337.6281 18 Chương VII. ĐẠO HÀM 3 4  x  khi x  0 
⑼ f x 4  
. Tính f 0 1  khi x  0 4  2 x 1 1  ⑽  f x khi x 0   x
. Tính f 0 0  khi x  0 Lời giải  ⑴    f x 2 x 3x khi x 1   . Tính f   1  2   khi x 1
lim f x  lim 2x 3x  2   Thấy x 1  x 1  
 Hàm số liên tục tại x 1  f    1  2  f x  f 1 2 x  3x  2
x 1x2 Ta có f       1  lim  lim  lim
 lim x  2  1  x 1  x 1 x 1  x 1 x 1  x 1 x 1  3 2
 x  4x  3x  
⑵ f x khi x 1 2
  x 3x  2 . Tính f   1 0  khi x  1 
x  x  x x x  x  x x  lim f x 3 2 4 3  1 3  3  lim  lim  lim  2 Thấy 2 x 1  x 1  x 1  x  3x  2 
x 1x2 x 1 x2  f    1  0
 lim f x  f   1 x 1 
 Hàm số không liên tục tại x 1 nên hàm số không có đạo hàm tại điểm x 1 2x  3 khi x  1 ⑶  f x 3 2
 x  2x  7x  4 . Tính f   1 . khi x   1  x 1 lim f    
x lim2x 3 5 x 1  x 1   Thấy 
x  x  x  lim f       x 3 2 2 7 4 lim lim    2 x 3x 4 0 x 1  x 1   x 1 x 1 
 lim f x  lim f x    x 1  x 1 
 Hàm số không liên tục tại x 1 nên hàm số không có đạo hàm tại điểm x 1 2
 x  7x 12  
⑷ f x khi x 3   x  3
. Tính f 3 1  khi x  3
 Biên soạn: LÊ MINH TÂM – 093.337.6281 19 Chương VII. ĐẠO HÀM  f 3  1   Thấy  x  x  lim f x 2 7 12  lim
 lim x  4  1 x3 x3 x3  x  3
 Hàm số liên tục tại x  3 f x  f 3     x 7x 12 0
Đạo hàm của hàm số tại x  3 : f 3     2  lim  lim  1  0 x 3  x 3 x  3  x  3
 x khi x 1
⑸ f x   . Tính f   1 2 x khi x  1 lim f    x lim x 1  x 1  x 1   Thấy lim f 
  Hàm số liên tục tại x 1  x lim x 1  x 1  x 1    f   1  1  2 f x  f 1  x 1
Đạo hàm trái f 1       lim  lim  lim         x 1 1 1 2 x 1   x 1   x 1 x 1 x 1  f x  f 1  x 1 1 1
Đạo hàm phải f 1       lim  lim  lim  . x    1   x 1   x 1 x 1 x 1  x 1 2
Suy ra f 1   f 1  
 Hàm số không tồn tại đạo hàm tại x1.    
⑹ f x 3 4 x khi x 0  
. Tính f 0 1  khi x  0
lim f x  lim 3 4x 1 x0 x0   Thấy 
 Hàm số liên tục tại x 1  f  0 1 f x  f 0 3  4  x 1 Ta có f 0      lim  lim x0 x  0 x0 x
2 4x2 4x 2  4  x  lim  lim x0 x x0
x2  4  x  4  4  x x 1 1 1  lim  lim  lim  
x0 x2 4 x x0 x2 4 x x0 2  4  x 2  4 0 4  3 2
x  2x  x 1 1  ⑺  f x khi x 1   x 1 . Tính f   1 0  khi x  1 Thấy f   1  0
 Biên soạn: LÊ MINH TÂM – 093.337.6281 20 Chương VII. ĐẠO HÀM
x  x  x   3 2
x  2x  x lim f x 3 2 2 1 1  lim  lim x 1  x 1  x 1 x 1  x   1  3 2
x  2x  x 1   1 xx  2 1 x x   1  lim  lim  0 x 1    x   1  3 2
x  2x  x 1   x 1 3 2 1
x  2x  x 1 1
 Hàm số liên tục tại x 1 3 2 f x  f 1
x  2x  x 1 1 x 1 Ta có f       1  lim  lim  lim  x x 1 x x 2 1 1 x 1  3 2 2 1
x  2x  x 1 1  x 1 1  
⑻ f x khi x 0   x
. Tính f 0 0  khi x  0  f 0  0  Thấy  x   x   lim f x 1 1 1 1 1 1  lim  lim  lim   x0 x0 x0 x x  x 1    x0 1 x 1 1 2
 Hàm số liên tục tại x  0 f x  f 0 x 1 1 1 1 Ta có f 0      lim  lim  lim  . x0 x0 x  0 x x0 x 1 1 2 3 4  x  khi x  0 
⑼ f x 4  
. Tính f 0 1  khi x  0 4  f   1 0   4 Thấy 
 Hàm số liên tục tại x  0    x lim f x 3 4 1  lim   x0 x0  4 4 3  4  x 1 f x  f  0 Ta có f 0      lim 4 4  lim x0 x  0 x0 x 2  4  x 4  4  x  1 1 1 lim  lim  lim   . x0 4x
x0 4x2  4  x x0 42 4 x     16 4 2 4 0  2 x 1 1  
⑽ f x khi x 0   x
. Tính f 0 0  khi x  0
 Biên soạn: LÊ MINH TÂM – 093.337.6281 21 Chương VII. ĐẠO HÀM  f 0  0  Thấy   x   x  
Hàm số liên tục tại x  0 lim f x 2 2 1 1 1 1  lim  lim  lim x  0 x0 x0 x0 x0  x x 2 2 f x  f 0 x 1 1 x 1 1 Ta có f 0      lim  lim  lim  lim  . 2 x0 x0 x0  2 x 0 x  x  2
x    x 0  2 x    2 1 1 1 1
Câu 4. Tính đạo hàm của các hàm số sau tại các điểm đã chỉ (nếu có):  x 1 1 ⑴   f x khi x 0   x . Tính f 0 0  khi x  0  2 x 1 1 ⑵   f x khi x 0   x . Tính f 0 0  khi x  0
 3x 1  2x  khi x  1 ⑶  f x x 1   . Tính f   1 .  5  khi x 1  4  3 2 2
4x  8  8x  4 ⑷   f x khi x 0   x
. Tính f 0 0  khi x  0 Lời giải  x 1 1 ⑴   f x khi x 0   x . Tính f 0 0  khi x  0  x   x lim f x 1 1 1  lim  lim   Thấy x0 x0 x0 x 
x  x    2 1 1
 Hàm số không liên tục tại x  0   f  0  0
 lim f x  f 0 x0
 Hàm số không liên tục tại x  0 nên hàm số không có đạo hàm tại điểm x  0  2 x 1 1 ⑵   f x khi x 0   x . Tính f 0 0  khi x  0  x   x x lim f x 2 2 1 1  lim  lim  lim  0      Thấy x 0 x 0 x 0 x  x  2
x 1   x 0 2 1 x 1 1   f  0  0
 Biên soạn: LÊ MINH TÂM – 093.337.6281 22 Chương VII. ĐẠO HÀM
 Hàm số liên tục tại x  0 f x  f 0 Ta có f 0      lim x0 x  0 2 x 1 1 0 2 2 x 1 1 x 1 1  lim x  lim  lim  lim  2 x 1  x0 x0 2 x x  x  2
x 1   x 0 2 2 1 x 1 1
 3x 1  2x  khi x  1 ⑶  f x x 1   . Tính f   1 .  5  khi x 1  4 3x 1  2x
Thấy lim f x  lim x 1  x 1  x  1  1   1  4  x 1 x  4  x      2   4
 x  3x 1  4   4  5  lim  lim  lim   x 1  x  
1  3x 1  2x x 1  x  
1  3x 1  2x x 1  3x 1  2 4 x Và f   5 1   4
 Hàm số liên tục tại x 1 f x  f 1 Ta có f       1  lim x 1  x 1 3x 1  2x 5  
4 3x 1  3x  5 x 1 4  lim  lim x x 1 x 4 x  2 1 1 1
4 3x13x54 3x13x5  lim x 4x  2 1
1 4 3x 1  3x  5 16 3x   1  3x  52  lim x 4 x  2 1
1 4 3x 1  3x  5 2 9
 x 18x  9  lim x 4 x  2 1
1 4 3x 1  3x  5 9  x  2 1 9  9  lim  lim   . x  4 x  2 1
1 4 3x 1  3x  5 x 1 
x   x   64 4 4 3 1 3 5
 Biên soạn: LÊ MINH TÂM – 093.337.6281 23 Chương VII. ĐẠO HÀM  3 2 2
4x  8  8x  4 ⑷   f x khi x 0   x
. Tính f 0 0  khi x  0
4x  8  8x  4
Thấy lim f x 3 2 2  lim x0 x0 x 3 2 2 4x  8  2 8x  4  2  lim  lim x0 x0 x x    2
4x  8  2  2 4x  82 3 3 2 3  4x  8 2 .  4    2 8x  4  2 2 8x  4  2  lim  lim x0      x  x 2 x  2 0 3 2 3  x  . x     2 8x 4 2 4 8 4 8 2 4      4x   2 4x  82 3 2 3  4x 8 2 .  4 8x    2 8x  4  2  lim  lim  0  0  0 x0   x  2   x  2 0 3 2 3  x  .     2 8x 4 2 4 8 4 8 2 4    Và f 0  0
 Hàm số liên tục tại x  0 f x  f 0
4x  8  8x  4 Ta có f 0     3 2 2  lim  lim x0 x0 x x f x  f 0
Thừa nhận kết quả bên trên, ta được f 0      lim  0 . x0 x
Câu 5. Tìm tham số để hàm số có đạo hàm tại x 0 2  x 1   ⑴ khi x 1
Tìm a để hàm số f x   x 1
có đạo hàm tại điểm x 1.
a khi x 1     ⑵ ax bx x
Tìm a; b để hàm số f x 2 1 khi 0  
có đạo hàm tại điểm x  0 .
ax  b 1 khi x  0 2  x 1   ⑶ khi x 0
Tìm a; b để hàm số f x   x 1
có đạo hàm tại điểm x  0 .
axb khi x  0     ⑷ ax x khi x
Tìm a; b để hàm số f x 2 2 1 1  
có đạo hàm tại điểm x 1.  3 2 
x  bx khi x  1 Lời giải 2  x 1   ⑴ khi x 1
Tìm a để hàm số f x   x 1
có đạo hàm tại điểm x 1.
a khi x 1
 Biên soạn: LÊ MINH TÂM – 093.337.6281 24 Chương VII. ĐẠO HÀM 2 x 1 x 1 x 1
Ta có lim f x     lim  lim  limx   1  2 , f   1  a . x 1  x 1  x 1  x 1 x 1 x 1 
Hàm số có đạo hàm tại x 1  f x liên tục tại x 1  lim f x  f   1  a  2 x 1  2 x 1  2        f  
f x f   2 2 1 x 1 2x 2 x 2x 1 x 1 1  lim  lim  lim  lim  . x x 1 x x 1 x x  1 2  1 x x 2 1 1 1 1 1  ⑵ ax  bx  x 
Tìm a; b để hàm số f x 2 1 khi 0  
có đạo hàm tại điểm x  0 .
ax  b 1 khi x  0  f 0 1   Ta có lim f     .  x lim 2 ax bx 1 1 x0 x0  lim f       
x limax b 1 b 1 x0 x0
Hàm số liên tục tại x  0 nên b  11 b  2  . 2 f x  f 0 
ax  2x 11
Đạo hàm phải f 0       lim  lim  lim    .     ax 2 2 x0 x0 x0 x x f x  f 0  ax 11
Đạo hàm trái f 0       lim  lim  lim  .     a  a x0 x0 x0 x x
Hàm số có đạo hàm tại x   
0  f 0   f 0   a  2 Vậy với a  2  , b  2
 thì hàm số có đạo hàm tại x  0 . 2  x 1   ⑶ khi x 0
Tìm a; b để hàm số f x   x 1
có đạo hàm tại điểm x  0 .
axb khi x  0  f 0 1  2  x 1 Ta có lim f      x lim lim    x 1 1 x0 x0  x0 x 1  lim f    
x limax b b x0 x0
Hàm số liên tục tại x  0 nên lim f     .  x lim f 
x f 0 b 1 x 0  x 0  2 x 1 1 2 f x  f 0   x  x
Đạo hàm phải f       x 1 0  lim  lim  lim  lim11.     x0  x0 x0 x 0 x
xx   x0 1 f x  f 0 
ax  b  b ax 11 ax
Đạo hàm trái f 0       lim  lim  lim  lim  lim a  . a      x0  x0 x0 x0 x0 x 0 x x x
Hàm số có đạo hàm tại điểm x  0  f 0   f 0     a 1.
Vậy với a 1; b 1 thì hàm số có đạo hàm tại x  0 .
 Biên soạn: LÊ MINH TÂM – 093.337.6281 25 Chương VII. ĐẠO HÀM     ⑷ ax x khi x
Tìm a; b để hàm số f x 2 2 1 1  
có đạo hàm tại điểm x 1.  3 2 
x  bx khi x  1   f   1  a 1  Ta có lim f      .  x lim 2 ax 2x 1  a 1 x 1  x 1   lim f      
x lim 3 2x bx  1 b x 1  x 1 
Hàm số liên tục tại x 1 nên lim f x  lim f x  f  
1  a 1  1 b  b  2  a .   x 1  x 1  2 f x  f 1 
ax  2x  a  2
Đạo hàm phải f 1       lim  lim  lim         ax a 2 2a 2 x 1   x 1   . x 1 x 1 x 1  f x  f 1
Đạo hàm trái f 1       lim  x 1  x 1
3  2x  bx  a 1
3  2x  2  a x  a 1    2 lim  lim  lima  2    a  3  x   1   x 1 x 1  x 1 x 1   3  2x 1 
Hàm số có đạo hàm tại điểm x 1  f 1   f 1  
  2a2  a3 a  1 Vậy với a  1
 ;b  3 thì hàm số có đạo hàm tại x 1. Câu 6. Cho hàm số 2
y  x  2x  4 có đồ thị C
⑴ Tìm hệ số góc của tiếp tuyến của C tại điểm có hoành độ x 1 thuộc C . 0
⑵ Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có x  0 thuộc C . 0
⑶ Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có y  1 thuộc C . 0
⑷ Viết phương trình tiếp tuyến của đồ thị hàm số biết hệ số góc tiếp tuyến bằng 4  .
⑸ Viết phương trình tiếp tuyến của đồ thị hàm số, biết tiếp tuyến đó song song với
đường thẳng y  1 3x . Lời giải
 Tính đạo hàm bằng định nghĩa: Tại x 
tùy ý, ta có: f x  f x  2 2
 x  2x  4 x  2x  4  x  x x  x  2 0 0 0  0   0  0
f x  f x  x  x 1 1  f x  f x x  x x  x  2 0   0     0  0   0     .  
 x  x  2 0 x  x 3 . x x x  x 3 . x x x  x x  x 0 0 0 0 0 0
f x  f x0   lim
 lim x  x  2  2x  2  y  2x  2 0  0 xx xx  0 0 x x0
 Tính đạo hàm bằng công thức:   2  
y  x  x   y   2
x  x     2 2 4 2 4
x   2x  4  2x  2
 Gọi M x ; y là tiếp điểm. 0 0 
 Biên soạn: LÊ MINH TÂM – 093.337.6281 26 Chương VII. ĐẠO HÀM
⑴ Tìm hệ số góc của tiếp tuyến của C tại điểm có hoành độ x 1 thuộc C . 0
Hệ số góc của tiếp tuyến của C tại điểm có hoành độ x  1 thuộc C là k  y  1  4 0
⑵ Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có x  0 thuộc C . 0
yx  y 0  2 0    Ta có  y
 x  y 0  4 0   
Phương trình tiếp tuyến cần tìm là y  y0x  0  y0  y  2x  4
⑶ Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có y  1 thuộc C . 0 x 1 Ta có 2 0 y  1
  x  2x  4  1    . 0 0 0 x  3   0 x 1 Với 0 
Phương trình tiếp tuyến là y  y  1 x   1  y  
1  y  4x  5 . y  1   0 x  3  Với 0 
Phương trình tiếp tuyến là y  y 
3 x  3  y 3    y  4  x 13 . y  1   0
⑷ Viết phương trình tiếp tuyến của đồ thị hàm số biết hệ số góc của tiếp tuyến bằng 4  .
Gọi M x ; y là tiếp điểm của tiếp tuyến của đồ thị C với hệ số góc k  4  0 0 
 yx  4   2x  2  4   x  3   y  1  0  0 0 0
Phương trình tiếp tuyến với hệ số góc k  4  là y  4
 x 31 y  4  x 13.
⑸ Viết phương trình tiếp tuyến của đồ thị hàm số, biết tiếp tuyến đó song song với đường thẳng
y 1 3x .
Vì tiếp tuyến song song với đưởng thẳng y  1 3x nên tiếp tuyến có hệ số góc k  3 
Gọi M x ; y là tiếp điểm của tiếp tuyến của đồ thị C với hệ số góc k  4  0 0   y 5 11 x  3   2x  2  3
  x    y   0  0 0 0 2 4    5 11 41
Phương trình tiếp tuyến với hệ số góc k  3
 là y  3 x  
 y  3x    .  2  4 4  Câu 7. x 1
Cho hàm số y 
có đồ thị C 3x
⑴ Viết phương trình tiếp tuyến của đồ thị hàm số tại giao điểm của C với trục Oy .
⑵ Viết phương trình tiếp tuyến của đồ thị hàm số tại giao điểm của C với trục Ox .
⑶ Viết phương trình tiếp tuyến của đồ thị hàm số tại giao điểm của C với đường
thẳng y  x 1.
 Biên soạn: LÊ MINH TÂM – 093.337.6281 27 Chương VII. ĐẠO HÀM
⑷ Viết phương trình tiếp tuyến của đồ thị hàm số biết hệ số góc của tiếp tuyến bằng 1 k   . 3
⑸ Viết phương trình tiếp tuyến của đồ thị hàm số, biết tiếp tuyến đó song song với
đường thẳng y  1 3x . Lời giải
 Tính đạo hàm bằng định nghĩa:
Tại x  \ 0 tùy ý, ta có: 0      
f x  f x  x 1 x 1 x x0 0    0 3x 3x 3 . x x 0 0
f x  f x  x  x  0   0  1 1    .  x  x 3 . x x x  x 3 . x x 0 0 0 0
f x  f x   0  1 1 1  lim  lim   y   2 2 xx xx  0 0 x x 3 . x x 3x 3x 0 0 0
 Tính đạo hàm bằng công thức:  x 1  x 1 3  1 y   y       3x  3x   2 2 3 3 x x
 Gọi M x ; y là tiếp điểm. 0 0 
⑴ Viết phương trình tiếp tuyến của đồ thị hàm số tại giao điểm của C với trục Oy .
Vì C không cắt Oy nên không tồn tại tiếp tuyến thỏa YCBT.
⑵ Viết phương trình tiếp tuyến của đồ thị hàm số tại giao điểm của C với trục Ox .
Tọa độ giao điểm của C với trục Ox là  1  ;0
Phương trình tiếp tuyến cần tìm là y  y x   1 1 1
1  0  y   x  3 3
⑶ Viết phương trình tiếp tuyến của đồ thị hàm số tại giao điểm của C với đường thẳng y  x1
Tọa độ giao điểm của C với y  x 1 là nghiệm của x  1   y  0 x 1 2 
 x 1  3x  2x 1  0  1 4 3x
x   y   3 3 x  1  Với 0 
 Phương trình tiếp tuyến là y  y x   1 1 1
1  0  y   x  . y  0  3 3 0
 Biên soạn: LÊ MINH TÂM – 093.337.6281 28 Chương VII. ĐẠO HÀM  1 x   0   1  1  4 7 Với 3 
 Phương trình tiếp tuyến là y  y x 
  y  3x     . 4   3  3  3 3 y  0  3 ⑷ 1
Viết phương trình tiếp tuyến của đồ thị hàm số biết hệ số góc của tiếp tuyến bằng k   . 3 1
Gọi M x ; y là tiếp điểm của tiếp tuyến của đồ thị C với hệ số góc k   0 0  3  2      yx  1 1 1 x 1 y 0 0        3 0 3   x 2 3 3      0 x 1 y 0  0 0 x 1 0  1 2 1 Với 
2  Phương trình tiếp tuyến là y   x   1 
 y   x 1. y   3 3 3 0  3 x 1 1 1 1 Với 0 
Phương trình tiếp tuyến là y   x  
1  y   x  . y  0  3 3 3 0
⑸ Viết phương trình tiếp tuyến của đồ thị hàm số, biết tiếp tuyến đó vuông góc với đưởng thẳng
y  3x  4 .
Tiếp tuyến đó vuông góc với đưởng thẳng y  3x  4 .  1
Tiếp tuyến hệ số góc k   . 3  2      yx  1 1 1 x 1 y 0 0        3 0 3   x 2 3 3      0 x 1 y 0  0 0 x 1 0  1 2 1 Với 
2  Phương trình tiếp tuyến là y   x   1 
 y   x 1. y   3 3 3 0  3 x 1 1 1 1 Với 0 
Phương trình tiếp tuyến là y   x  
1  y   x  . y  0  3 3 3 0 Câu 8. Cho hàm số 3
y  x  2x 1 có đồ thị C
⑴ Tìm hệ số góc của tiếp tuyến của hàm số trên tại điểm có x  0.
⑵ Viết phương trình tiếp tuyến của hầm số biết nó có k  2  .
⑶ Viết phương trình tiếp tuyến của hàm số trên, biết nó tạo với hai trục Oxy một tam
giác vuông cân tại O . Lời giải
 Tính đạo hàm bằng công thức:
 Biên soạn: LÊ MINH TÂM – 093.337.6281 29 Chương VII. ĐẠO HÀM  3
y  x  x   y   3 x  x   2 2 1 2 1  3x  2
 Gọi M x ; y là tiếp điểm. 0 0 
⑴ Tìm hệ số góc của tiếp tuyến của hàm số trên tại điểm có x  0 .
Hệ số góc của tiếp tuyến của hàm số tại điểm có x  0 là k  y0  3 0 .  2  2 
⑵ Viết phương trình tiếp tuyến của hầm số biết nó có k  2  . Ta có k  2
  f x  2  2   3x  2  2   x  0 0 0 0
Phương trình tiếp tuyến tại điểm M0;  1 có dạng: y  2
 (x 0)1 y  2  x 1
⑶ Viết phương trình tiếp tuyến của hàm số trên, biết nó tạo với hai trục Oxy một tam giác vuông cân tại O .
Cách 1: Gọi phương trình đoạn chắn cắt 2 trục tọa độ và tạo với 2 trục 1 tam giác x y  x  b
vuông cân tại O có dạng  1 y  . b 1
  x  b, .ab  0; a    b d a b  a  a  b
d là tiếp tuyến của C thì 2 3x  2   0 a
x 1 y  0 0 0 x  1   y  2  0 0 2 3x  2 1  Vì 0 3 9  5 3 a  b        2 x y 0 0 3x  2  1   0  3 9   3 9  5 3 x   y  0 0  3 9
Có 4 phương trình tiếp tuyến ứng với các điểm tiếp xúc và hệ số góc trên như sau
y 1.x  
1  0  y  x 1
y 1.x  
1  2  y  x  3  3  9  5 3 9  2 3 y  1  . x   
 y  x   3  9 9    3  9  5 3 9  2 3 y  1  . x   
 y  x   3  9 9  
Cách 2: Gọi phương trình tiếp tuyến của (C) thỏa mãn YCBT có dạng d : y  kx  b Ta có 2 k  3x  2 0  b 
Có giao điểm của d với Ox tại 
; 0  ; với trục Oy tại 0;b  k 
Vì d tạo với hai trục Oxy một tam giác vuông cân tại O .
 Biên soạn: LÊ MINH TÂM – 093.337.6281 30 Chương VII. ĐẠO HÀM b  1 
b  0 loai   b  b .   0    k  1  k  k 1   k  1 
x 1 y  0 0 0 x  1   y  2 2  0 0   2 x 1  0 3x  2  1  0  3 9  5 3         2 1  2 x y 0 0 3x  2  1   x  0  0 3 9  3   3 9  5 3 x   y  0 0  3 9
 Có 4 phương trình tiếp tuyến ứng với các điểm tiếp xúc và hệ số góc trên như sau
y 1.x  
1  0  y  x 1
y  1.x  
1  2  y  x  3  3  9  5 3 9  2 3 y  1  . x   
 y  x   3  9 9    3  9  5 3 9  2 3 y  1  . x   
 y  x   3  9 9  
Câu 9. Một chất điểm chuyển động thẳng biến đổi đều với phương trình 2
s  2t  t 1 m
⑴ Tìm vận tốc tức thời của vật tại thời điểm t  2s .
⑵ Tìm vận tốc trung bình của chất điểm trong khoảng thời gian từ t  0 tới t  2s . Lời giải
Ta có: v  s  4t 1
⑴ Tìm vận tốc tức thời của vật tại thời điểm t  2s .
Vận tốc tức thời của vật tại thời điểm t  2s là: 4 2
. 1  9m / s
⑵ Tìm vận tốc trung bình của chất điểm trong khoảng thời gian từ t  0 tới t  2s .
Trong khoảng thời gian từ t  0s  t  2sthì chất điểm di chuyển được quãng đường: 4 2
.  2 1  9m
 Vận tốc trung bình của chất điểm trong khoảng thời gian 2s kể từ thời điểm t  0 s 9  0 là: v  
 4,5m / s. t 2  0
Câu 10. Một vật chuyển động thẳng xác định bởi phương trình s  st trong đó t được tính
bằng giây và S được tính bằng mét. Thực hiện các yêu cầu dưới đây:
⑴ Với s  st 3 2
 t 3t thì vận tốc của vật tại thời điểm t  3s là bao nhiêu?
⑵ Với s  st 2
 t  7t thì vận tốc của vật tại thời điểm t  4s là bao nhiêu? ⑶ 1
Với s  st 3 2
  t 12t thì vận tốc của vật tại thời điểm t 10s là bao nhiêu? 2
 Biên soạn: LÊ MINH TÂM – 093.337.6281 31 Chương VII. ĐẠO HÀM
⑷ Với s  st 3 2  t
  6t  4 thì vận tốc của vật tại thời điểm t  3s là bao nhiêu?
⑸ Với s  st 3
 2t t 10 thì vận tốc của vật tại thời điểm t  3s là bao nhiêu?
⑹ Với s  st 3 2
 3t  4t t thì vận tốc của vật tại thời điểm t  4s là bao nhiêu?
⑺ Với s  st 2
 2t  3t  7 thì vận tốc của vật tại thời điểm t  6s là bao nhiêu? ⑻  
Với s  st  3cos 2 t  
 thì vận tốc của vật tại thời điểm t  2s là bao nhiêu?  3  ⑼ 1
Với s  st   4 2
t  3t  thì vận tốc của vật tại thời điểm t  4s là bao nhiêu? 2
⑽ Với s  st 3 2
 t 3t 9t thì vận tốc của vật tại thời điểm t  5s là bao nhiêu? Lời giải
⑴ Với s  st 3 2
 t 3t thì vận tốc của vật tại thời điểm t  3s là bao nhiêu?
Ta có vt  S't 2
 3t  6t . Từ đó: v3  9m/s.
⑵ Với s  st 2
 t  7t thì vận tốc của vật tại thời điểm t  4s là bao nhiêu?
Ta có vt  S't  2t  7 . Từ đó: v4  2 4
.  7 15m/s . ⑶ 1
Với s  st 3 2
  t 12t thì vận tốc của vật tại thời điểm t 10s là bao nhiêu? 2 3 3  1 . 00
Ta có vt  st 2
  t  24t  v10   240  90m/s. 2 2
⑷ Với s  st 3 2  t
  6t  4 thì vận tốc của vật tại thời điểm t  3s là bao nhiêu?
Ta có vt  st 2
  t  t  v  2 3 12 3  3  3 . 12 3 .  9m/s.
⑸ Với s  st 3
 2t t 10 thì vận tốc của vật tại thời điểm t  3s là bao nhiêu?
Ta có vt  st 2
 t   v  2 6 1 3  6 3 . 1 53m/s.
⑹ Với s  st 3 2
 3t  4t t thì vận tốc của vật tại thời điểm t  4s là bao nhiêu?
Ta có vt  st 2
 t  t   v  2 9 8 1 4  9 4 . 8 4 . 1 175m/s.
⑺ Với s  st 2
 2t  3t  7 thì vận tốc của vật tại thời điểm t  6s là bao nhiêu?
Ta có vt  st  4t  3  v6  4 6 .  3  27m/s. ⑻  
Với s  st  3cos 2 t  
 thì vận tốc của vật tại thời điểm t  2s là bao nhiêu?  3     
Ta có v t  st  6  sin 2  t    v 2  6  sin 4   16  32   . m/s.  3   3  ⑼ 1
Với s  st   4 2
t  3t  thì vận tốc của vật tại thời điểm t  4s là bao nhiêu? 2
 Biên soạn: LÊ MINH TÂM – 093.337.6281 32 Chương VII. ĐẠO HÀM
Ta có vt  st 3
 t  t  v  3 2 3 4  2 4 .  3 4 . 140m/s.
⑽ Với s  st 3 2
 t 3t 9t thì vận tốc của vật tại thời điểm t  5s là bao nhiêu?
Ta có vt  st 2
 t  t   v  2 3 6 9 5  3 5 .  6 5 .  9  36m/s.
Câu 11. Một chất điểm chuyển động theo phương trình s  st trong đó t được tính bằng giây
và S được tính bằng mét. Thời gian để vận tốc của chất điểm đạt giá trị lớn nhất Lời giải
⑴ Với st 2 3
10  t  9t t trong khoảng 10 giây đầu tiên.
Vận tốc tại thời điểm t là vt  st 2  3
 t 18t 1 trên đoạn 0;10   .
vt  s t   t  t    t  t        t  2      t  2 2 2 3 18 1 3 6 9 9 1 3 3 8 3 3  24  24  
Vậy vận tốc đạt được giá trị lớn nhất bằng 24  t  3  0  t  3s
⑵ Với st 3 2  t
  9t  t 10 trong 12 giây đầu tiên.
Vận tốc tại thời điểm t là vt  S't 2  3
 t 18t 1 trên đoạn 0;12   .
v t  S't 2  3
 t 18t 1   t  6t  99 
1  3t  32 2 3  24  4 2
Vậy vận tốc đạt được giá trị lớn nhất bằng 24  t  3  0  t  3s
⑶ Với st 3 2  t
  6t trong 10 giây đầu tiên.
Vận tốc tại thời điểm t là vt  st 2  3
 t 12t trên đoạn 0;10   .
v t  st   t  t   t  t      t  2 2 2 3 12 3 4 4 12 3 2 12  12
Vậy vận tốc đạt được giá trị lớn nhất bằng 12  t  2  0  t  2s ⑷ 1
Với st 3 2
  t  6t trong 10 giây đầu tiên. 2 3
Vận tốc tại thời điểm t là vt  st 2
  t 12t trên đoạn 0;10   . 2
vt  s t 3
  t  t    3   t  2 3   8 16 16 4
16   t  42 2  24  24 2 2   2
Vậy vận tốc đạt được giá trị lớn nhất bằng 24  t  4  0  t  4s ⑸ 1 Với st 3 2
  t  9t trong 10 giây đầu tiên. 2 3
Vận tốc tại thời điểm t là vt  st 2
  t 18t trên đoạn 0;10   . 2
vt  s t 3
  t  t    3    t  2 3   12 36 36 6
 36   t 62 2  54  54 2 2   2
Vậy vận tốc đạt được giá trị lớn nhất bằng 54  t  6  0  t  6s
 Biên soạn: LÊ MINH TÂM – 093.337.6281 33 Chương VII. ĐẠO HÀM ⑹ 1 Với st 3 2
  t  6t trong 9 giây đầu tiên. 3
Vận tốc tại thời điểm t là vt  st 2  t
 12t trên đoạn 0;9   .
vt  s t  t   t    t  2     t  2 2 12 6 36 6  36  36  
Vậy vận tốc đạt được giá trị lớn nhất bằng 36  t  6  0  t  6s ⑺ 1 Với st 2 3
 t  t trong 5 giây đầu tiên. 6 1
Vận tốc tại thời điểm t là vt  st 2
 2t  t trên đoạn 0;5   . 2
vt  s t 1
  t  t    1   t  2 1   4 4 4 2
 4   t  22 2  2  2 2 2   2
Vậy vận tốc đạt được giá trị lớn nhất bằng 2  t  2  0  t  2s ⑻ 1 Với 3 2
s   t  3t  20 trong 10 giây đầu tiên. 2 3 
Vận tốc tại thời điểm t là vt  st 2 
t  6t trên đoạn 0; 5   . 2   
vt  s t 3 
t  t   3  t  2 3   4 4 4 2  4  t 22 2  6  6 2 2   2
Vậy vận tốc đạt được giá trị lớn nhất bằng 6  t  2  0  t  2s
Câu 12. Một vật chuyển động thẳng xác định bởi phương trình s  st trong đó t được tính
bằng giây và S được tính bằng mét.
⑴ Với s  st 4 2
 2t  6t 3t 1 thì gia tốc của vật tại thời điểm t  3s là bao nhiêu?
⑵ Với s  st 3
 4t 10t  9 thì gia tốc của vật tại thời điểm vận tốc bằng 2 là bao nhiêu?
⑶ Với s  st 3 2
 t 3t 5 thì gia tốc của vật tại tại giây thứ 10 là bao nhiêu?
⑷ Với s  st 3 2
 t 3t 9t 1 thì gia tốc của vật tại tại thời điểm vật dừng lại là bao nhiêu?
⑸ Với s  st 3 2
 t 3t  5t  2 thì gia tốc của vật tại giây thứ 3 là bao nhiêu?
⑹ Với s  st 3 2
 t 3t  3t 10 thì gia tốc của vật tại thời điểm vật dừng lại là bao nhiêu? ⑻ 2
Với s  st 3 2
 t  2t t  4 thì gia tốc của vật tại thời điểm t  2s là bao nhiêu? 3 Lời giải
⑴ Với s  st 4 2
 2t  6t 3t 1 thì gia tốc của vật tại thời điểm t  3s là bao nhiêu?
 Biên soạn: LÊ MINH TÂM – 093.337.6281 34 Chương VII. ĐẠO HÀM 
Vận tốc của chuyển động là: v t  st   4 2
t  t  t   3 2 6 3
1  8t 12t  3 .
Gia tốc của chuyển động là: at  vt 2  24t 12.
Gia tốc của chuyển động tại thời điểm t  3s 2
là: a 3  24 9 . 12  228m/s  .
⑵ Với s  st 3
 4t 10t  9 thì gia tốc của vật tại thời điểm vận tốc bằng 2 là bao nhiêu?
Vận tốc của chuyển động là: vt  st 2 12t 10 .
Gia tốc của chuyển động là: at  vt  24t . t 1 Mà v t 2
 2  12t 10  2  
. Do t  0 nên t 1 suy ra a  2 2  24m/ s . t  1  
⑶ Với s  st 3 2
 t 3t 5 thì gia tốc của vật tại tại giây thứ 10 là bao nhiêu?
Vận tốc của chuyển động là: vt  st 2  3t  6t .
Gia tốc của chuyển động là: at  vt  6t  6 .
Gia tốc của chuyển động tại thời điểm t 10s là: a 10  6 10  6  54 2 . m/s  .
⑷ Với s  st 3 2
 t 3t 9t 1 thì gia tốc của vật tại tại thời điểm vật dừng lại là bao nhiêu?
Vận tốc của chuyển động là: vt  st 2
 3t  6t 9.
Gia tốc của chuyển động là: at  vt  6t  6 . t  1  L 2  
Tại thời điểm chất điểm dừng lại thì v  0  3t  6t  9  0   t  3
Gia tốc của chất điểm tại thời điểm chất điểm dừng lại là a3  6 3 .  6 12 .
⑸ Với s  st 3 2
 t 3t  5t  2 thì gia tốc của vật tại giây thứ 3 là bao nhiêu?
Vận tốc của chuyển động là: vt  st 2
 3t  6t  5.
Gia tốc của chuyển động là: at  vt  6t  6 .
Gia tốc của chuyển động tại thời điểm t  3s 2
là: a 3  6.3  6  12 m/s  .
⑹ Với s  st 3 2
 t 3t  3t 10 thì gia tốc của vật tại thời điểm vật dừng lại là bao nhiêu?
Vận tốc của chuyển động là: vt  s't 2
 3t  6t  3 .
Gia tốc của chuyển động là: at  vt  6t  6 .
Tại thời điểm chất điểm dừng lại thì v  0 2
 3t 6t 3  0  t 1
Gia tốc của chất điểm tại thời điểm chất điểm dừng lại là a  1  6 1 .  6  0 .
⑺ Với vt 2
 8t  3t thì gia tốc của vật khi vận tốc của vật là 11 m / s.là bao nhiêu?
Gia tốc của chuyển động là: at  v't  8 6t .
 Biên soạn: LÊ MINH TÂM – 093.337.6281 35 Chương VII. ĐẠO HÀM t 1  Mà v t 2
11  8t  3t 11 11 
. Do t  0 nên t 1 suy ra a  2 1  14m/ s . t    3 ⑻ 2
Với s  st 3 2
 t  2t t  4 thì gia tốc của vật tại thời điểm t  2s là bao nhiêu? 3
Vận tốc của chuyển động là: vt  s't 2
 2t  4t 1.
Gia tốc của chuyển động là: at  vt  4t  4.
Gia tốc của chuyển động tại thời điểm t 10s là: a 2  4 2  4  12 2 . m/s  .
Câu 13. Một vật chuyển động thẳng xác định bởi phương trình s  st trong đó t được tính
bằng giây và S được tính bằng mét. Hỏi:
⑴ Gia tốc tại thời điểm vận tốc triệt tiêu với s  st 3 2
 t 3t 9t là bao nhiêu?
⑵ Gia tốc tại thời điểm vận tốc triệt tiêu với s  st 3 2
 t  3t 9t  27 là bao nhiêu?
⑶ Vận tốc tại thời điểm gia tốc triệt tiêu với s  st 3 2  t
  3t  9t là bao nhiêu?
⑷ Vận tốc tại thời điểm gia tốc triệt tiêu với s  st 3 2
 t 3t là bao nhiêu?
⑸ Vận tốc tại thời điểm gia tốc bằng không với s  st 3 2
 2t 3t  4t, là bao nhiêu? ⑹ 1
Vận tốc tại thời điểm gia tốc triệt tiêu với s  st 3 2
 t 3t  36t là bao nhiêu? 3
⑺ Gia tốc tại thời điểm vận tốc triệt tiêu với s  st 3 2  t
  3t  9t  2020 là bao nhiêu?
⑻ Vận tốc tại thời điểm gia tốc triệt tiêu với s  st 3 2
 2t 3t  4t là bao nhiêu?
⑼ Vận tốc tại thời điểm gia tốc triệt tiêu với s  st  t  2
t  3t  9  2024 là bao nhiêu?
⑽ Vận tốc tại thời điểm gia tốc của vật đạt giá trị nhỏ nhất trong 20 giây đầu tiên với st 1 4 3 2 
t  t  6t 10t là bao nhiêu? 12 Lời giải
⑴ Gia tốc tại thời điểm vận tốc triệt tiêu với s  st 3 2
 t 3t 9t là bao nhiêu?
Vận tốc của chuyển động là: vt  s't 2
 3t  6t 9 .
Gia tốc của chuyển động là: at  vt  6t  6 .
Khi vận tốc triệt tiêu ta có vt 2
 0  3t  6t 9  0  t  3 (vì t  0 )
Khi đó gia tốc là a  2 3  6 3 .  6 12m/s .
⑵ Gia tốc tại thời điểm vận tốc triệt tiêu với s  st 3 2
 t  3t 9t  27 là bao nhiêu?
Vận tốc của chuyển động là: vt  s't 2
 3t  6t 9 .
Gia tốc của chuyển động là: at  vt  6t  6 .
 Biên soạn: LÊ MINH TÂM – 093.337.6281 36 Chương VII. ĐẠO HÀM t 1
Khi vận tốc triệt tiêu ta có v t 2
 0  3t  6t  9  0   (vì t  0 ) t  3  
Khi đó gia tốc là a  2 1  6 1 .  6 12m/s .
⑶ Vận tốc tại thời điểm gia tốc triệt tiêu với s  st 3 2  t
  3t  9t là bao nhiêu?
Vận tốc của chuyển động là: vt  s't 2  3
 t  6t  9 .
Gia tốc của chuyển động là: at  vt  6  t  6 .
Khi gia tốc triệt tiêu ta có at  0  6
 t  6  0  t 1
Khi đó vận tốc là v  2 1  3  1 .  6 1 .  9 12m/s .
⑷ Vận tốc tại thời điểm gia tốc triệt tiêu với s  st 3 2
 t 3t là bao nhiêu?
Vận tốc của chuyển động là: vt  s't 2  3t  6t .
Gia tốc của chuyển động là: at  vt  6t  6 .
Khi gia tốc triệt tiêu ta có at  0  6t  6  0  t 1
Khi đó vận tốc là v  2 1  3 1 .  6 1 .  3  m/s .
⑸ Vận tốc tại thời điểm gia tốc bằng không với s  st 3 2
 2t 3t  4t, là bao nhiêu?
Vận tốc của chuyển động là: vt  s't 2
 6t  6t  4.
Gia tốc của chuyển động là: at  vt 12t  6 .
Khi gia tốc triệt bằng 0 có at 1
 0 12t  6  0  t  2 2  1   1   1  5
Khi đó vận tốc là v  6.  6.  4        m/s .  2   2   2  2 ⑹ 1
Vận tốc tại thời điểm gia tốc triệt tiêu với s  st 3 2
 t 3t  36t là bao nhiêu? 3
Vận tốc của chuyển động là: vt  st 2
 t  6t  36 .
Gia tốc của chuyển động là: at  vt  2t  6 .
Khi gia tốc triệt tiêu ta có at  0  2t  6  0  t  3
Khi đó vận tốc là v  2 3  3  6 3 .  36  27m/s .
⑺ Gia tốc tại thời điểm vận tốc triệt tiêu với s  st 3 2  t
  3t  9t  2020 là bao nhiêu?
Vận tốc của chuyển động là: vt  st 2  3
 t  6t  9.
Gia tốc của chuyển động là: at  vt  6  t  6 . t  1  loai
Khi vận tốc triệt tiêu ta có vt 2    0  3
 t  6t  9  0   (vì t  0 ) t  3
 Biên soạn: LÊ MINH TÂM – 093.337.6281 37 Chương VII. ĐẠO HÀM
Khi đó gia tốc là a  vt   .     2 6 3 6 12 m/ s  .
⑻ Vận tốc tại thời điểm gia tốc triệt tiêu với s  st 3 2
 2t 3t  4t là bao nhiêu?
Vận tốc của chuyển động là: vt  st 2
 6t  6t  4 .
Gia tốc của chuyển động là: at  vt 12t  6 .
Khi gia tốc triệt tiêu ta có at 1
 0 12t  6  0  t  2  1  5
Khi đó vận tốc là v   2   ,5m/s .  2  2
⑼ Vận tốc tại thời điểm gia tốc triệt tiêu với s  st  t  2
t  3t  9  2024 là bao nhiêu?
Vận tốc của chuyển động là: vt  st 2
 t  6t 9 .
Gia tốc của chuyển động là: at  v't  6t  6.
Khi gia tốc triệt tiêu ta có at  0  6t  6  0  t 1
Khi đó vận tốc là v  1  1  2 2 m/s .
⑽ Vận tốc tại thời điểm gia tốc của vật đạt giá trị nhỏ nhất trong 20 giây đầu tiên với st 1 4 3 2 
t  t  6t 10t là bao nhiêu? 12 1
Vận tốc của chuyển động là: vt  st 3 2
 t 3t 12t 10. 3
Gia tốc của chuyển động là: at  vt  t  t   t  2 2 6 12 3  3
Thấy rằng at  t  2 3  3  3
Gia tốc đạt được giá trị bé nhất bằng 3  t  3  0  t  3s
Khi đó vận tốc của vật bằng v3  28m/s .
--------------------Hết--------------------
 Biên soạn: LÊ MINH TÂM – 093.337.6281 38 Chương VII. ĐẠO HÀM ĐẠO HÀM
CÁC QUY TẮC TÍNH ĐẠO HÀM A Lý thuyết
1. Đạo hàm hàm số n y  x Hàm số có đạo hàm trên và .
2. Đạo hàm hàm số y  x Hàm số có đạo hàm trên và .
3. Đạo hàm hàm số lượng giác ⑴ 
Hàm số y  sin x có đạo hàm trên và
sinx  cosx . ⑵ 
Hàm số y  cos x có đạo hàm trên và
cosx  sinx . ⑶  1
Hàm số y  tan x có đạo hàm tại mọi x   k và tanx  . 2 2 cos x ⑷  1
Hàm số y  cot x có đạo hàm tại mọi x  k và cotx   . 2 sin x
4. Đạo hàm của hàm số mũ và hàm số logarit ⑴  Hàm số x
y  e có đạo hàm trên  x x e  e . ⑵  Hàm số x
y  a có đạo hàm trên  x x a  a .ln a . ⑶ 
Hàm số y  log x có đạo hàm tại mọi x  0  x  . a  1 log a x ln a ⑷ 
Hàm số y  ln x có đạo hàm tại mọi x  0   1 ln x  . x
 Biên soạn: LÊ MINH TÂM – 093.337.6281 39 Chương VII. ĐẠO HÀM
5. Các quy tắc tính đạo hàm Giả sử các hàm số
có đạo hàm trên khoảng . Khi đó: ⑴ ⑵ ⑶ ⑷
6. Đạo hà m của hàm hợp
6.1 Khái niệm hàm số hợp Giả sử
là hàm số xác định trên khoảng
, có tập giá trị chứa khoảng và
là hàm số xác định trên . Hàm số được gọi là hàm số hợp của hàm số với .
6.2 Đạo hàm của hàm số hợp Nếu hàm số có đạo hàm tại và hàm số có đạo hàm tại thì hàm số hợp có đạo hàm tại là
 Biên soạn: LÊ MINH TÂM – 093.337.6281 40 Chương VII. ĐẠO HÀM
Từ đó ta có các kết quả sau: ⑴    n x  n 1  . n x    nu n 1  . n u .u   ⑵  1  1  1  1         .u 2  x  x 2  u  u   ⑶  x 1   u 1  .u 2 x 2 u ⑷  
sin x  cosx
sinu  u.cosu ⑸  
cosx   sin x cosu  u  .sinu ⑹  1  1 tan x  tanu  .u 2 cos x 2 cos u ⑺  1  1
cotx   cotx   .u 2 sin x 2 sin x   ⑻  x  x e  e u u
e   u.e   ⑼  x  x a  a .ln a  u  . u a
u a .ln a ⑽     1 ln x   u 1 ln  .u x u ⑾    x   u  u a  1 log . a  1 log x ln a uln a
7. Đạo hàm cấp hai Cho hàm số có đạo hàm tại mọi điểm . Nếu hàm số
lại có đạo hàm tại thì ta gọi đạo hàm của là đạo
hàm cấp hai của hàm số tại , kí hiệu là hoặc . Khi đó: .
 Ý nghĩa cơ học của đạo hàm cấp hai
Một chuyển động có phương trình s  f t thì đạo hàm cấp hai (nếu có) của hàm số
s  f t là gia tốc tức thời của chuyển động s  st tại thời điểm t . Ta có at  f  t
 Biên soạn: LÊ MINH TÂM – 093.337.6281 41 Chương VII. ĐẠO HÀM B Bài tập
 Dạng 1. Tính đạo hàm đa thức – hữu tỉ – căn thức Phương pháp
 Áp dụng quy tắc đạo hàm: Khi đó: ⑴ ⑵ ⑶ ⑷
 Áp dụng công thức đạo hàm: ⑴ ⑵ ⑶ ⑷ Ví dụ 1.1.
Tính đạo hàm các hàm số sau: ⑴ ⑵ ⑶ ⑷ ⑸ ⑹ ⑺ ⑻ ⑼ ⑽
 Lời giải
⑴ f x    x 5 3 1 4 4 
Ta có f x   3  x   3  x  2  x  3 5 1 1 15 1 x  .
⑵ f x 4 2
 x  x  x  200
 Biên soạn: LÊ MINH TÂM – 093.337.6281 42 Chương VII. ĐẠO HÀM   
Ta có f x   4 2
x  x  x  200   4 x    2
x   x  200 3
 4x  2x 1.
⑶ f x 4 3
 3x  x  x  2021 
Ta có f x   4 3
x  x  x   3 2 3
2021  12x  3x 1.
⑷ f x 5 3 2
 x  2x   7 x    5     5   5
Ta có f x 3 2
 x  2x   7   3 x    2 2x    7 2
 3x  4x      2  x   x  x ⑸   4
f x  x  x   4  4 x  4
Ta có f x 2  x   1    . 2 2  x  x x
⑹ f x 7 5 3
 x  2x  3x 
Ta có f x   7 5 3
x  x  x  6 4 2 2 3
 7x 10x  9x .
⑺ f x  x  
1 x  2  
Ta có f x  x  
1 x  2  x  
1 x  2  x  2  x 1  2x 1 . 
⑻ f x 3x 5  1   2x  
3x  5 . 2x 1  3x  5 2x 1 32x   1  2 3x  5 13 
Ta có f x            2x  2 1 2x 2 1 2x 2 1 
⑼ f x x 2  x 1     x  2  x  2
x 1  x  2 x 1
x 1 x  2 1
Ta có. f x              .  x 1  x 2 1 x 2 1 x 2 1 
⑽ f x x 1  x 1     x 1 x 1
x 1  x 1 x 1
x 1x 1 2
Ta có f x              .  x 1 x 2 1 x 2 1 x 2 1
 Biên soạn: LÊ MINH TÂM – 093.337.6281 43 Chương VII. ĐẠO HÀM
 Dạng 2. Tính đạo hàm lượng giác Phương pháp
 Áp dụng quy tắc đạo hàm: Khi đó: ⑴ ⑵ ⑶ ⑷
 Để tính đạo hàm của hàm số tại
, ta thực hiện theo các bước sau: ⑴ ⑵ ⑶ ⑷ Ví dụ 2.1.
Tính đạo hàm các hàm số sau: ⑴ ⑵ ⑶ ⑷ ⑸ ⑹ ⑺ ⑻ ⑼ ⑽
 Lời giải ⑴   y  sin  3  x   6          y   3  x  .cos  3  x  3   cos  3  x  .  6   6   6  ⑵ 1   2 y   sin   x  2  3            1 1 2 2 y   .  x .cos  x   . 2  x 2 2 .cos  x  . x cos         x  . 2  3   3  2  3   3 
 Biên soạn: LÊ MINH TÂM – 093.337.6281 44 Chương VII. ĐẠO HÀM ⑶ 2
y  2 cos x   y  . 2 x  . 2  sin x  2 2  4 .
x sin x . ⑷ x 1 y  tan 2    x 1 1  x 1  x 1  1  x 1  2 2  y  .  . 1 tan  1        tan   2  x 1 2  2   2  2  2  cos 2 ⑸ 2
y  sin 2  x   y   2x x 2 2  x  2 2 2 .cos 2  x  cos 2  x  cos 2  x 2 2 2 2  x 2  x
⑹ y  sinsin x 
 y  sin x .cossin x  cos .
x cossin x ⑺ 2
y  2sin x  cos 2x  x  y  2 2 . .cos .
x sin x  2sin 2x 1  2sin 2x  2sin 2x 1  4sin 2x 1 ⑻ 3
y  cos 2x   1 
 y  .cos x   2 3 2 1 .cos 2x   1
 . sin x   2 3 2 2 1 .cos 2x  
1   sin x   2 6 2 1 cos 2x   1 ⑼ 3
y  tan x  cot 2x    y   2 1 2 3
tan x  cot 2x  3.tan x 2 2 .tan x   3 tan x  2 2 2 sin 2x cos x sin 2x
⑽ y  sin  2
x  3x  2   y   2
x  x   .cos 2
x  x     x  cos 2 3 2 3 2 2 3
x  3x  2 .
 Biên soạn: LÊ MINH TÂM – 093.337.6281 45 Chương VII. ĐẠO HÀM
 Dạng 3. Tính đạo hàm mũ – logarit Phương pháp
 Áp dụng quy tắc đạo hàm: Khi đó: ⑴ ⑵ ⑶ ⑷
 Để tính đạo hàm của hàm số tại
, ta thực hiện theo các bước sau: ⑴ ⑵ ⑶ ⑷ Ví dụ 3.1.
Tính đạo hàm các hàm số sau: ⑴ ⑵ ⑶ ⑷ ⑸ ⑹ ⑺ ⑻ ⑼ ⑽
 Lời giải
⑴ y  log 2x 1 3     2x   1 2 Ta có y    . 2x   1 ln 3 2x 1ln3
⑵ y  log 1 2007x 3     1 2007x 2007  Ta có y    .
1 2007x.ln 3 1 2007xln3 ⑶ 2 1 5 x y   
Ta có y   x   2x 1 2x 1 2 1 5 . .ln5  2 5 .  .ln5.
 Biên soạn: LÊ MINH TÂM – 093.337.6281 46 Chương VII. ĐẠO HÀM ⑷ 2025 2025x y    Ta có y   x2025  x2025 2025  y  2025 .ln 2025 .
⑸ y  x  lnx   3   x  3 1 Ta có y  1 1 . x  3 x  3 ⑹ sin e x y   Ta có     sin sin .e x y x sin  cos .e x x . ⑺ 2x3 2025 y  e  e  
Ta có y   2x3 2025 e  e
   x  2x3 2x3 2 3 .e  2.e .
⑻ y  log  2
x  2x 2    2 x  2x 2x  2 Ta có y    . 2
x  2xln 2  2 x  2xln 2
⑼ y  log  2
2x  x 1 3   2 2  x  x 1 2x 1
Ta có y  log  2 2x  x 1   . 3     2 2x  x   1 ln 3  2 2x  x   1 ln 3 ⑽  3x y  log  2 x  2x 3   2  x  2x 1 4x
Ta có y  3x  log  2 x  2x  3x ln3  3x ln3 . 3     2 x  2x ln3  2 x  2x ln3
 Biên soạn: LÊ MINH TÂM – 093.337.6281 47 Chương VII. ĐẠO HÀM C Luyện tập
Câu 14. Tính đạo hàm của các hàm số sau: ⑴ 3
y  2x  4 x
⑵ y   x  2 2 3 1 ⑶ 1 4 2 y  2
 x  4x 1 ⑷ 3 2
y  x  2 2x  8x 1 3  2   ⑸ 2x 1 x x 1 y  ⑹ y  x  2 x 1 2   2    ⑺ x x 3 x 3x 3 y  ⑻ y  2 x  x 1 2x   1 ⑼ 2
y  x 2x   1 5x  3 ⑽ y   2 x   2 1 5  3x  Lời giải ⑴ 3
y  2x  4 x   y   2 3 2
 x  4 x  2  6  x  . x
⑵ y   x  2 2 3 1     
y   x  2 2    2 x  . 2
x    x 2 3 1 2 3 1 3 1 12 3x   1 .   ⑶ 4 2 y  2
 x  4x 1   y   4 2
 x  x   3 2 4
1  8x  8x . ⑷ 1 3 2
y  x  2 2x  8x 1 3   1  3 2 2
 y   x  2 2x 8x 1  
x  4 2x  8 .  3   ⑸ 2x 1 y  x  2     2x 1
2x 1 x22x 1x2 3  y      .  x  2  x22 x22 2   ⑹ x x 1 y  x  1  2
 x  x 1  y     x 1 
 Biên soạn: LÊ MINH TÂM – 093.337.6281 48 Chương VII. ĐẠO HÀM   2  x  x   1 x   1   2 x  x   1 x   1   x  2 1
2x 1x 1 2x x 1 2 2 2        2x 3x 1 x x 1 x 2x    2 2 x  2 1 x 1 x 1 2   ⑺ x x 3 y  2 x  x 1   2 
 2x x3  2x x 1 2x x3 2x x 
x  x  3  1
Cách 1:  y     2
 x  x 1 
x x 2 2 1
2x 1 2x  x 1 2x  x32x 1 2x 1 2 2
x  x 1 x  x  3 42x   1     2 x  x  2 2 1
 2x  x 1
x  x 2 2 1 Cách 2: 2 x  x  3 2
x  x 1 4 4 Ta có: y   1 2 x  x 1 2 x  x 1 2 x  x 1     2 2 
4 x  x  
x  x  3      1 42x   1  4 4 y     1    1       2
 x  x 1  2  x  x 1  2
 x  x 1
x x 2 2 1
x  x 2 2 1 2    ⑻ x 3x 3 y  2x   1   2 2  2  
x 3x3 2x2x 3x32x2
x  3x  3   y     2  x  2  2x22  2
 x  32x  2  2 2
x  3x  3 2 2       2   2    4x 10x 6 2x 6x 6  2x 4x  x 2x   2 2 2 2x  22 2x2 4 x   1 2 x   1 ⑼ 2
y  x 2x  
1 5x  3 Cách 1:  2
 y  x  2x   1 5x  3  2  
 x   x   x   2
 x  x    x   2 2 1 5 3 2 1 5
3  x 2x   1 5x  3  x 2 x  x   2
 x  x   2 2 10 3 2 5
3  5x 2x   1 3 2 3 2 3 2
 20x  2x 6x 10x 6x 10x 5x 3 2
 40x 3x 6x Cách 2: Ta có 2
y  x  x   x   2  x  2 x  x   4 3 2 2 1 5 3 10
3  10x  x  3x
 Biên soạn: LÊ MINH TÂM – 093.337.6281 49 Chương VII. ĐẠO HÀM   2
 y  x 3 2
  x   x      4 3 2 2 1 5 3
10x  x  3x   40x 3x  6x ⑽ y   2 x   2 1 5  3x     y   2 x    2  x   2 x   2 1 5 3 1 5  3x   x 2
 x   x 2 x   3 3 3 2 5 3 6
1  10x  6x  6x  6x  12x  4x
Câu 15. Tính đạo hàm của các hàm số sau: ⑴ 2
y  4x  3x 1 ⑵ 2
y  x  x  3 ⑶ 2x 1 y 
⑷ y  x  x 5 2 2 3 x  2 ⑸ 2 y  2x 1
⑹ y  2x 3x  3 5 7 ⑺ 2 y  1 3x
⑻ y   x   2 2 1 x  x   ⑼ 3x 4 y  ⑽ 4 2
y  x  4x  7 x  2 Lời giải ⑴ 2
y  4x  3x 1      x  x  x  y
4x  3x 1  2 4 3 1 8 3 2    . 2 2 2 4x  3x 1 2 4x  3x 1 ⑵ 2
y  x  x  3   2 x  x  3 2x 1 y   . 2 2 2 x  x  3 2 x  x  3 ⑶ 2x 1 y  x  2    2x  
1 .x  2  2x   1 .x  2
2.x  2  2x   1 1 . 5
Cách 1. y     . x  22 x22 x22 2 2 . 1.  1 5
Cách 2. y    . x  22 x22
⑷ y  x  x 5 2 2 3
y  x  x  4 2
 x   x  2 5 2 3 2 2 10
1 x  2x  3 ⑸ 2
y  2x 1    2 2x   1 4x 2x y   2 2x 1    . 2 2 2x 1 2 2 2x 1 2 2x 1
 Biên soạn: LÊ MINH TÂM – 093.337.6281 50 Chương VII. ĐẠO HÀM
⑹ y  2x 3x  3 5 7
y  32x 3x  2 5  4 7 10x  3 . ⑺ 2
y  1 3x 6  x 3  x y   . 2 2 2 1 3x 1 3x
⑻ y   x   2 2 1
x  x.  
y   x   2
. x  x   x  . 2 2 1 2 1 x  x 
2x 12x  2 1 4x 1 2 2
 2. x  x 
 2 x  x  . 2 2 2 x  x 2 x  x   ⑼ 3x 4 y  x  2    3
 x  4 x  2 x  2  3  x  4 3
 .x  2  3  x  4 2 y     . x  22 x22 x22 ⑽ 4 2
y  x  4x  7   4 2 x  4x  3 2x  4x y   . 4 2 4 2 2 x  4x  7 x  4x  7
Câu 16. Tính đạo hàm của các hàm số sau: ⑴ 2x 1 y  ⑵ 3 y  4x  3 2x 1 2 ⑶ 2x 1 x  3x  3 y  ⑷ y  1 3x x 1 2   2   ⑸ 2x 4x 1 1 x x y  ⑹ y  x  3 2 1 x  x ⑺ 2 y  x x
⑻ y   x   5 2
3 x  2x
⑼ y  x2x   1 3x  2 ⑽ y   2
x  x   2 2 3 2x  3. Lời giải ⑴ 2x 1 y  4x  3   
4x  32x  
1  4x  3 2x   1
2 4x  3  42x   1
8x  6  8x  4 1  0 y      4x  32 4x32 4x32 4x32 ⑵ 3 y  2x 1
 Biên soạn: LÊ MINH TÂM – 093.337.6281 51 Chương VII. ĐẠO HÀM  3.2x   1  2x   1 3 . 6   y    . 2x  2 1 2x 2 1 ⑶ 2x 1 y  1 3x    2x  
1 1 3x  1 3x 2x   1
2 1 3x  32x   1 5  y    .    x 13x2 13 1 3 x2 2 ⑷ x  3x  3 y  x 1   2 
x  3x  3 x   1   2
x  3x  3x   1  y   x  2 1
2x3x 1 2x 3x3 2 2      2   2x 5x 3 x 3x 3  x 2x   . 2 2 x  2 1 x 1 x 1 2   ⑸ 2x 4x 1 y  x  3 2 2x  4x 1 7 2 7 2x 12x 11 y   2x  2   y  2   . x  3 x  3 x32 x32 2   ⑹ 1 x x y  2 1 x  x    2
1 x  x   2
1 x  x    2
1 x  x . 2 1 x  x   y  
1 x  x 2 2 12x 2
1 x  x    2
1 x  x 2x   1  
1 x  x 2 2 12x 2 2
1 x  x 1 x  x  2 1 2x    .
1 x  x 2
1xx 2 2 2 ⑺ 2 y  x x    y   1 2 x  2
. x  x . x  2  2 . x x  x . 2 x x x 5  2x x   x x . 2 2
⑻ y   x   5 2
3 x  2x
 Biên soạn: LÊ MINH TÂM – 093.337.6281 52 Chương VII. ĐẠO HÀM  
y   x    5
x  x   x   5 2 3 2 2 3 x  2x   5
x  x   x   4 2 2 2 3 5x  2 5 5 4
 2x  4x 10x  4x 15x 6 5 4
12x 15x 8x  6 .
⑼ y  x2x  
1 3x  2
y  x  x   x    x  2 x  x   3 2 2 1 3 2 6
2  6x  x  2x  y   3 2
x  x  x 2 6 2
 18x  2x  2 . ⑽ y   2
x  x   2 2 3 2x  3.   y   2
x  x    2 x     2
x  x   2 2 3 2 3 2
3 2x  3   x   2 x     2 2 2 2 3
x  2x  34x 3 2 3 2
 4x  6x  4x 6 4x 8x 12x 3 2
 8x 12x 18x 6.
Câu 17. Tính đạo hàm của các hàm số sau: ⑴ 2
y  x  x 1
⑵ y  x  x 5 2 1 ⑶ 1 y 
⑷ y  x   2 2 x 1 2 x 1 4 2
 x  x 1 ⑸ 2
y  5x  2x 1 ⑹ y     x 1   ⑺ x 1 y  ⑻ 2
y  x  4  x 4 x 1 2    ⑼ 2x 1 y   
⑽ y  x  x  x  x 1  Lời giải ⑴ 2
y  x  x 1      x  x  x  y x  x 1  2 1 2 1 2      . 2 2 2 x  x 1 2 x  x 1
⑵ y  x  x 5 2 1   
y  x  x  5   x  x  x    4 2 2 1 5 2 1 1 .   ⑶ 1 y  2 x 1      2 x 1 1  1 2x x y            x     x   . 2 2 2 2 x 1 1 2 x 1  2x   2 2 1 x 1 1
 Biên soạn: LÊ MINH TÂM – 093.337.6281 53 Chương VII. ĐẠO HÀM
⑷ y  x   2 2 x 1 x
x   x x  x  x 
y  x 1  x  2 2 2 1  2 2 2 2 1 2   . 2 2 2 2 x 1 x 1 x 1 ⑸ 2
y  5x  2x 1      x  x  x  x  y
5x  2x 1  2 5 2 1 10 2 5 1 2     . 2 2 2 2 5x  2x 1 2 5x  2x 1 5x  2x 1 4 2
 x  x 1 ⑹ y     x 1   4 3 3    2 2 2 2 2
 x  x 1
 x  x 1  x  x 1
 x  x 1 x  2x y       4  .   4  .  .  x 1  
 x 1   x 1   x 1    x 2 1  ⑺ x 1 y  4 x 1    x   4 1
x 1  x   1  4 x 1 y   x 12 4 x
x 1  x   3 4 4 1 4 3 4 3 4
x 1 x  
x 1 x   4 3 2 x 1 1 2 1 2  x x     x 2x 1   . 4 x 1  3 3 x  3 4 1  4x  1  4x  1 ⑻ 2
y  x  4  x 2 2  x 4  x  x y  1  . 2 2 2 4  x 4  x 2    ⑼ 2x 1 y     x 1  
 2x 1 2x 1  2x 1 3  12x  6 y  2  2        .
 x 1  x 1 
 x 1  x  2 1 x 3 1
⑽ y  x  x  x
y  x  x  x 2
 y  x  x  x
 Biên soạn: LÊ MINH TÂM – 093.337.6281 54 Chương VII. ĐẠO HÀM   x  x   2 . y y  1 2 x  x    x  x  1 1 1 1 2 x  y     2y 2 2 2 . y y x  x 2y 2 . x  x 1 2 x 1   2 3
2 x  x  x
8 x  x  x x  x
Câu 18. Tính đạo hàm của các hàm số sau: ⑴ cos2x y  ⑵ 2 y  cos . x sin x 3x 1 ⑶ 2
y  sin x  sin 2x ⑷ 2
y  1 cos 2x  ⑸ x x 2 y  cos 3x ⑹ sin cos y  sin x  cos x 2    ⑺ 1 x
y  tan x  cot x
⑻ y  sin    2x 1   ⑼ 1 x x x x 3 y  cos ⑽ sin cos y  2x  3
x cos x  sin x Lời giải ⑴ cos2x y  3x 1   
cos 2x .3x   1  cos 2 . x 3x   1 2  3x  
1 sin 2x  3cos 2x y    3x  2 1 3x 2 1 ⑵ 2 y  cos . x sin x  y   x 2 x  x  2 x 3 2 cos .sin cos . sin  sin x+2cos . x sin x ⑶ 2
y  sin x  sin 2x  y   2
sin x  sin 2x  2sin x cos x  2cos 2x ⑷ 2
y  1 cos 2x       cos x  .sin xcos x sin x y 1 cos 2x   2 1 2 2 2 2 4 2     . 2 2 2 2 1 cos 2x 1 cos 2x 1 cos 2x ⑸ 2
y  cos 3x  y   2
cos 3x  6sin 3xcos3x
 Biên soạn: LÊ MINH TÂM – 093.337.6281 55 Chương VII. ĐẠO HÀM  ⑹ sin x cos x y  sin x  cos x   
sin x  cos x sin x  cos x  sin x  cos xsin x  cos x y  
sin x  cos x2
cosxsinxsinxcosxsinxcosxsinxcosx  
sin x  cos x2
sinxcosx2 sinxcosx2   
sin x  cos x2 2 2 2 2
sin x  2 sin x cos x  cos x  sin  2sin x cos x  cos x   
sin x  cos x2 2  2 2
sin x  cos x 2      . x  x2 2
(sin x  cos x) sin cos
⑺ y  tan x  cot x      x  x y
tan x  cot x  tan cot  
2 tan x  cot x 1 1  2 2 2 2 cos x  sin sin cos x x x   2 2
2 tan x  cot x 2 sin .
x cos x tan x  cot x 2 2 2 2 cos x  sin x cos x  sin x   2 2  2 2 sin x cos x 2 2 sin x cos x 2 sin . x cos x  2 sin . x cos x cos x sin x sin . x cos x 2 2 cos x  sin x  2 sin . x cos x sin . x cos x 2    ⑻ 1 x y  sin    2x 1  2    1 x      1 x    1  sin x   2   2x 1 sin    sin       2x 1   2x 1 y   2 2  1 x   1 x  2 sin 2   sin    2x 1  2x 1
 Biên soạn: LÊ MINH TÂM – 093.337.6281 56 Chương VII. ĐẠO HÀM  3  1 x   1   1   1   1 x x x  x   sin  cos sin cos                       2x 1 2x 1 2x 1   x 2 2x 1 2x 1 2 1    2 2  1 x   1 x  sin   sin    2x 1  2x 1  1 x   1 x  3  sin cos   2x 1  2x 1  2     x  2 1 x 2 1 sin    2x 1  ⑼ 1 x 3 y  cos 2x  3  1 x  1 x  2 y  3cos cos  2x  3  2x  3      1 x  1 x 1 x 2  3    cos sin  2x  3  2x  3 2x  3     1 x     2x  3  1 x 1 x 2  3  cos sin 1 2 x x  3 2x  3 2 2x3 15 2x32 1 x 1 x 15 1 x 1 x 2   cos sin 2   cos sin 1 2 x x  3 2x  3    2 1 2 x x 3 2x 3 2 2 2x  3 2x  3 2x  3  ⑽
x sin x cos x y 
x cos x  sin x
sinx xcosxsinxxcosxsinxxsinxcosxcosxxsinxcosx y '  
x cos x  sin x2
x cos x x cos x  sin x  x sin x  cos xx sin x  
x cos x  sin x2 2 x  2 2
cos x  sin x  x cos x sin x  x cos x sin x 2    x     .
x cos x  sin x2
 x cos x  sin x 
Câu 19. Tính đạo hàm cấp 2 của các hàm số sau: ⑴   2
y  x 1 x ⑵ y  sin  3  x   6 
 Biên soạn: LÊ MINH TÂM – 093.337.6281 57 Chương VII. ĐẠO HÀM ⑶ 2
y  sin 2  x ⑷ 2
y  sin x  sin 2x  ⑸ x 2
y  2sin x  cos 2x  x ⑹ 3 y  1 2x ⑺ 2
y  x  x 1
⑻ y   x  2 2 3 1 2   ⑼ x x 3 y 
⑽ y  sinsin x 2 x  x 1 Lời giải ⑴ 2
y  x 1 x  2 2    2x x 2x 1 y  x  2
 x  x 2 1 1 x 2  x  1 x 2   1 x  . 2 2 1 x 2 2 1 x 1 x       2 2x   2 1 1 x   2 2x   1   x  2 2 1 x 2 1   y        1 x   1x 2 2 2 2 x
4x 1 x   2 2x   1 4    1 x  x  2 1 x  x 2 2x  3 2 1 2x  3x    . 2 1 x  2 1 x  2 1 x 1x 3 2 ⑵   y  sin  3  x   6              y  sin  3  x    3  x  cos  3  x   3cos  3  x    6   6   6   6              y   3  cos  3  x   3  3  x  sin  3  x  9   sin  3  x  .   6   6   6   6  ⑶ 2
y  sin 2  x    x y   2 sin  x    2  x  2 2 2 . cos 2  x 2  . cos 2  x 2 2  x     x 2 y   . cos 2  x    2  2  x    x  x     . cos    2 2  x    2 cos 2  x 2 2   2  x  2  x 2 x 2  x  . x 2 2 x x   2  cos 2  x   2 2  x  sin 2 2  x 2 2   2   2  2 x x
 Biên soạn: LÊ MINH TÂM – 093.337.6281 58 Chương VII. ĐẠO HÀM 2 x x 2  cos 2  x  . sin  2 2  x 3 2 2   2   2  x 2  2 x x 2 2 x 2  cos 2  x  .sin  2 2  x . 2 3    2  x  2 x 2 ⑷ 2
y  sin x  sin 2x     y   2
sin x  sin x   2 2
sin x  sin 2x  2sin .
x cos x  2cos 2x  sin 2x  2cos 2x    
y  sin 2x  2cos 2x  sin 2x  2cos 2x  2cos2x  4sin2x . ⑸ 2
y  2sin x  cos 2x  x   y   2
2 sin x  cos 2x  x   2  
 2sin x cos2x  x  4sin xcos x  2sin 2x 1 2sin 2x  2sin 2x 1 4sin 2x 1  
y  4sin 2x   1  8cos 2x .  ⑹ x 3 y  1 2x   
x  3 1 2x  x  31 2x
1 2x  2x  3  7 y     1 2x2 12x2 12x2        1 2x2 7   2    2  1 2x  28 y           1 2x 7 7 2    12x4 12x4 12x3 ⑺ 2
y  x  x 1  2  x  x 1   2x 1 y   2
x  x 1     2 2 2 x  x 1 2 x  x 1       2x   1  2         x  
 2x x 1 2x 1 2 2x x 1 2 1   y       x  x    4   2 2 x  x   1 2 1  2x 1 2
4 x  x 1  22x   1  2 2 x  x 1  3  4  2 x  x   1 4  2 x  x   2 1 x  x 1
⑻ y   x  2 2 3 1
 Biên soạn: LÊ MINH TÂM – 093.337.6281 59 Chương VII. ĐẠO HÀM      2 y   2 x     2 x   2
x    x 2 3 1 2 3 1 3 1 12 3x    1   
 y   x    2x      2x   2 12 3 1 12 3
1 12x  6x  108x 12 2   ⑼ x x 3 y  2 x  x 1    2
x  x  3  2 x  x   1   2
x  x  3 2 x  x   1  y   x  x  2 2 1
2x 1 2x  x 1 2x  x32x 1 42x 1    x  x  2 2 1
x  x 2 2 1    4    2x 1 8  
x x 2 2
1  4  2x   1  2 2x   1  2 x  x   2 1    24x 24x 16 y       x  x  2 1 
x x 4 1 x x   3 2 2 2 1
⑽ y  sinsin x    y  sin  sinx  
sinx cossin x  cosxcossin x   
 y  cos x cossin x  cos x cossin x  cos x   cossinx
  sin xcossin x  cos xcos xsinsin x   x   x 2 sin cos sin
 cos xsinsinx
Câu 20. Tính đạo hàm cấp 3 tại các điểm được chỉ ra dưới đây ⑴ 3 Cho hàm số 3 2 y  3
 x  3x  x  5. Tính giá trị của y 2017 . ⑵ 2 3 Cho hàm số y 
. Tính giá trị của y   1 . 1 x ⑶ 1 3 Cho hàm số y 
. Tính giá trị của y 2 . 2 x 1 ⑷    3 Cho hàm số 2
y  cos x . Tính giá trị của y   .  3  Lời giải ⑴ 3 Cho hàm số 3 2 y  3
 x  3x  x  5. Tính giá trị của y 2017 . Ta có: 2 y'  9
 x  6x 1 y''  1  8x  6 y'''  18  3  y 2017  1  8 .
 Biên soạn: LÊ MINH TÂM – 093.337.6281 60 Chương VII. ĐẠO HÀM ⑵ 2 3 Cho hàm số y 
. Tính giá trị của y   1 . 1 x 3 3 2 3 . ! 12 Cách 1:Ta có: y    1    1 x4 1 x4 3  y   3 1   . 4 2
Cách 2: Ta có: y'    1 x2 2 2 . 1 x 4 y ''    . 1 x4 1 x3  2    4 12 1 x 3   12 y            1 x3  1 x6 1 x4 3  y   3 1   . 4 ⑶ 1 3 Cho hàm số y 
. Tính giá trị của y 2 . 2 x 1 2  x Ta có: y '   . x  2 2 1 2  x  2 2 1  2 2 . x 2 x   1 2 . x 2   2 x   2 2 1  8x 6x  2 y''     . x  4 1 x  3 1 x  3 2 2 2 1
12x x  3
1  6x x  2 2 2 1 . 2
6x  2 12x 2 x   1  6x  2 6x  2   3   3 24x 24x y     x  6 1 x  4 1 x  4 2 2 2 1  3  y   80 2   . 3 ⑷    3 Cho hàm số 2
y  cos x . Tính giá trị của y   .  3  Ta có: y'  2  sin .
x cosx  sin 2x . y'  2  cos2x .  3 y  4sin2x .    3  y  2 3   .  3 
Câu 21. Chứng minh rằng: ⑴ Với hàm số 2
y  2x  x ta có 3
y .y 1  0 .
 Biên soạn: LÊ MINH TÂM – 093.337.6281 61 Chương VII. ĐẠO HÀM ⑵ Với hàm số 2
y  x  x 1 ta có y  x3 .y 1  0 .
⑶ Với hàm số y  xsin x ta có xy  2ysinx xy  0. ⑷ x  3 Với hàm số y  ta có 2
2y  y   1 y . x  4
⑸ Với hàm số y  cot 2x ta có 2
y  2y  2  0 .
⑹ Với hàm số y  x tan x ta có 2 x y   2 2
2 x  y 1 y  0 .
⑺ Với hàm số y  tan x ta có 2
y  y 1  0 . ⑻ Với hàm số 2
y  x 1 ta có 2
y .y  xy  y . ⑼ Với hàm số 2
y  x 1 ta có 2
y y   xy  y . ⑽ Với hàm số 2
y  1 x ta có 2
y .y  xy  y  0 . Lời giải ⑴ Với hàm số 2
y  2x  x ta có 3
y .y 1  0 . 1 1 x Ta có y  .2  2x  2 2 2x  x 2 2x  x   1 2 x 1 . 2x  x  .1 x 2 2 2
x  2x  1 x 2x  x   1 y    2 2x  x  2 2x  x  2 . 2x  x  2xx 32 3 1  Khi đó: 3
y .y 1   2
2x  x  .   1  1 0 . 2x  x  1 3 2 Vậy 3
y .y 1  0 . ⑵ Với hàm số 2
y  x  x 1 ta có y  x3 .y 1  0 . 2x x Ta có y  1  1 2 2 x 1 2 x 1 2 x x 1  . x 2 2 2 x 1    x 1 x 1 y    2 x 1 2 x 1. 2 x   1  x 13 2 3 3 3 1 1
Khi đó: y  x .y 1   2
x  x 1  x .   2x 1   . 1 11  0 3 x 1 1 3 2  2x1
Vậy y  x3 .y 1  0 .
⑶ Với hàm số y  xsin x ta có xy  2ysinx xy  0.
Ta có y  sin x  xcos x
 Biên soạn: LÊ MINH TÂM – 093.337.6281 62 Chương VII. ĐẠO HÀM
 y  cosx  cosx  xsinx  2cosxxsinx
Khi đó: xy  2y  sin x  xy  .
x 2cos x  xsin x  2sin x  xcos x  sin x  . x  . x sin x 2 2
 2xcosx  x sin x  2xcosx  x sinx   xcos x  xcos x   2 2 2 2
x sin x  x sin x  0
Vậy xy  2y  sin x  xy  0 . ⑷ x  3 Với hàm số y  ta có 2
2y  y   1 y . x  4 x  3 Ta có y 
, điều kiện: x  4  . x  4 7   14 y      y . x  42 x43 Khi đó: 2
2y  y   1 y 2        7 x 3 14 98 7  1  4 98 98 2       .   . 4 3  4 4      x   1 2   x  4 4   x 43 x  x 4 4 x4
x4 x4 Vậy 2
2y  y   1 y .
⑸ Với hàm số y  cot 2x ta có 2
y  2y  2  0 . k
Ta có y  cot 2x , điều kiện: sin 2x  0  x  , k  . 2 2  y   . 2 sin 2x 2 Khi đó: 2
y  2y  2 2  
 2cot 2x  2    2  cot x 2 2 1 2
 2cot 2x  2  0 . 2 sin 2x Vậy 2
y  2y  2  0 .
⑹ Với hàm số y  x tan x ta có 2 x y   2 2
2 x  y 1 y  0 .
Ta có y  x tan x , điều kiện: cos x  0  x   k , k . 2 x 2
 y  tan x 
 tan x  xtan x  x . 2 cos x 1 1 2  y 
 tan x  2xtan x 1. 2 2 cos x cos x Khi đó: 2 x y   2 2
2 x  y 1 y  1 1  2 2  x .
 tan x  2x tan x 1  2 2 2 2
x  x tan x 1   x tan x 2 2    cos x cos x  2 2
 x .  tan x  x tan x   2  tan x     2 2 2 1 2 2 1 1
2 x  x tan x1 x tan x
 Biên soạn: LÊ MINH TÂM – 093.337.6281 63 Chương VII. ĐẠO HÀM 2 2 2 3 3 3 2 3 2 2 3 3
 2x  2x tan x  2x tan x  2x tan x  2x  2x tanx  2x tan x  2x tan x  0 Vậy 2 x y   2 2
2 x  y 1 y  0 .
⑺ Với hàm số y  tan x ta có 2
y  y 1  0 .
Ta có y  x tan x , điều kiện: cos x  0  x   k , k . 2 
 y  tan x 1 2  1 tan x 2 cos x Khi đó: 2 2 2
y  y 1  1 tan x  tan x 1  0 . Vậy 2
y  y 1  0 . ⑻ Với hàm số 2
y  x 1 ta có 2
y .y  xy  y .  y   2x x x 2 x 1    . 2 2 2 1 1 y x x x y   . x  2 2  2x   2 x  x .y  . x y y 1   x y x 1 y         . 2 2  y  y y 3 3 3 y y y 2 2 2 1 x 1 x 1 x y Khi đó: 2 2
y .y  xy  y .  . x      y . 3 y y y y y y Vậy 2
y .y  xy  y . ⑼ Với hàm số 2
y  x 1 ta có 2
y y   xy  y . 2 2 x x 1  x 2 x 1 1 Ta có: y  ; y   ; 2 2 x 1 x 1  2x   2 1 x 1 2 1 x x 1 Khi đó: 2
y y  xy   2 x   2 1   . x 
 x 1  y . 2 x   2 2 2 1 x 1 x 1 x 1 Vậy 2
y y   xy  y . ⑽ Với hàm số 2
y  1 x ta có 2
y .y  xy  y  0 .  2 x  1 x  . x  1   1 x x x  1  2 x  2 2 2
Ta có y  1 x  y  ; y    2  1 1  x x
 1x 3  1x 3 2 2 2 1 x 2 2  
Khi đó y .y  xy  y  1 x  2 .     .x  1 x 3 2 2 1 1 x x 2 2 1 x 1 x 2 2 2 2     1 x  
 1 x   1 x  1 x  0 (ĐPCM) 2 2 2 1 x 1 x 1 x
 Biên soạn: LÊ MINH TÂM – 093.337.6281 64 Chương VII. ĐẠO HÀM
Câu 22. Cho f x 4 2
 x  4x  3 và gx 2
 310x  7x . Giải phương trình f  x  gx  0 Lời giải Ta có f x 4 2
 x  x   f x 3  x  ; x f  x 2 4 3 4 8 12x 8. g x 2
 310x  7x  gx 1014 . x  x 1 Khi đó 
f  x  gx 2 2
 0  12x 8 10 14x  0 12x 14x  2  0  1  x   6  1 
Vậy tập nghiệm của phương trình là S  1  ;  .  6
Câu 23. Cho hàm số f x 3 2
 x 3x  4x  6 . Giải bất phương trình f  x  f x 1 Lời giải Ta có f x 3 2
 x  x  x   f x 2 3 4 6
 3x  6x  4; f  x  6x 6. x 1
Khi đó f  x  f x 2 2
1  6x  6  3x  6x  4 1  3x 12x  9  0   x  3
Vậy tập nghiệm của bất phương trình là S  (;1] 3 [ ; ) . Câu 24. Cho hàm số 3 2
y  x  3x  4x  6 . Giải bất phương trình y  0 . Lời giải Ta có 2
y  3x  6x  4; y  6x  6 .
Do đó y  0  6x  6  0  x 1
Vậy tập nghiệm của bất phương trình là T   ;   1 . Câu 25. 3
Cho hàm số y  f x  5x   1  4x  
1 . Giải phương trình f x  0 . Lời giải 2
Ta có f x 15x  
1  4x; f  x  30x   1  4 .
Do đó f x   x  2 17 0 30
1  4  0  x 1    x   15 15  17 
Vậy tập nghiệm của phương trình là T    .  15   
Câu 26. Cho hàm số y  f x  cos 2x  
 . Tìm các nghiệm thuộc đoạn 0;     của phương 3  4 trình f x  8. Lời giải    
Ta có f x  2  sin 2x 
; f  x  4  cos 2x      .  3   3 
 Biên soạn: LÊ MINH TÂM – 093.337.6281 65 Chương VII. ĐẠO HÀM    
f x 4  8sin 2x  ; f
x 16cos 2x      3   3       4 1 Do đó f x  8   16cos 2x   8  cos 2x         3   3  2  2  2x    k2 x   k   3 3 2     k  .  2  2x     k2 x    k  3 3  6 Do x  0;    1 1 Xét x   k . Ta có 0 k k k         
k  0  x  . 2 2 2 2 2 1 7  5 Xét x    k . Ta có 0 k
   k    k  
k 1 x  . 6 6 6 6 6 5 
Vậy tập nghiệm của phương trình là T   ;  .  6 2 
--------------------Hết--------------------
 Biên soạn: LÊ MINH TÂM – 093.337.6281 66
Document Outline

Pages from C7-ĐẠO HÀM-GHÉP TỔNG HỢP HS-đã nén

Chuyên đề đạo hàm Toán 11 – Lê Minh Tâm

Thông tin :

Tài liệu liên quan:

Toán 11 Bài 33: Đạo hàm cấp hai - sách Kết Nối Tri Thức

Toán 11 Bài 31: Định nghĩa và ý nghĩa của đạo hàm - Sách Kết Nối Tri Thức

Chuyên đề đạo hàm – Lư Sĩ Pháp

Top 7 chuyên đề đạo hàm

Các dạng toán trắc nghiệm đạo hàm thường gặp – Nguyễn Bảo Vương