Chuyên đề hàm số và đồ thị ôn thi vào lớp 10 môn Toán – Nguyễn Đăng Tuấn

Tài liệu gồm 52 trang, được biên soạn bởi thầy giáo ThS. Nguyễn Đăng Tuấn, tuyển tập 105 bài tập chuyên đề hàm số và đồ thị ôn thi vào lớp 10 môn Toán, có đáp án và lời giải chi tiết.

71 36 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 1

HÀM SỐ VÀ ĐỒ THỊ

I. Hàm số bậc nhất

Bài 1. TS Lớp 10 Bắc Giang 2017-2018

Tìm

để đồ thị hàm số

y x m

 

đi qua điểm





2;3

Lời giải:

+ Đồ thị hàm số

y x m

 

đi qua điểm

(2;3)

K 3 4

  

  

+ Vậy

 

Bài 2. TS Lớp 10 Gia Lai 2017-2018

Tìm tất cả các giá trị của

để hàm số

( 2017) 2018

y m m x    đồng biến trên



Lời giải:

Hàm số đồng biến trên



khi và chỉ khi



2017 0,

m m

   

với mọi

1 8067

2 4

 

   

 

 

với mọi

Điều này luôn thỏa mãn.

Vậy khi với mọi giá trị của

thì hàm số luôn đồng biến trên



Bài 3. TS Lớp 10 Hải Dương 2017-2018

Cho hai đường thẳng





y x m

   

v à







( 2) 3

y m x

  

. Tìm

để





và







song song với nhau.

Lời giải:

Điều kiện để hai đồ thị song song là

1 2

2 3

 



  





 



 



Loại



, chọn

 

Bài 4. TS Lớp 10 Phú Thọ 2016-2017

Cho hàm số

(2 1) 4

y m x m

   

(m là tham số) có đồ thị là đường thẳng (d).

a) Tìm m để (d) đi qua điểm

( 1;2)



b) Tìm m để (d) song song với đường thẳng (Δ) có phương trình:

5 1

y x

 

c) Chứng minh rằng khi m thay đổi thì đường thẳng (d) luôn đi qua một điểm cố định.

Lời giải:

a) Ta có (d) đi qua điểm

( 1;2)



2 (2 1)( 1) 4

m m

     

2 3 1.

m m

     

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 2

b) Ta có

2 1 5

( )//( )

4 1

 



 



 



 

c) Giả sử

0 0

( ; )

M x y

là điểm cố định của đường thẳng (d).

Khi đó ta có:

0 0

(2 1) 4

y m x m m

    

0 0 0

(2 1) 4 0

x m x y m

      

0 0

2 1 0

4 0

x y

 







  





 















Vậy khi m thay đổi đường thẳng (d) luôn đi qua điểm cố định

1 7

;

2 2

 



 

 

Bài 5. TS Lớp 10 Quãng Ninh 2016-2017

Tìm giá trị của

để hai đường thẳng

( ) : 1

d mx y

 

và

( ) : 6

d x my m

  

cắt nhau tại một

điểm

thuộc đường thẳng

( ) : 2 8.

d x y

 

Lời giải:

Để hai đường thẳng (d

), (d

) cắt nhau thì

   



luôn T/M với mọi

( ) : 2 8 8 2

d x y x y

    

(1)

( ) : 1

d mx y m



   

( ) : 6

d x my m m



    



(2)

Do đó

2 2

1 6

y x

y x x

x y

 

    



2 2

6 1 0

x x y

    

(3)

Thay (1) vào (3) ta được tung độ giao điểm

là nghiệm PT:

   

8 – 2 – 6 8 2 1

y y y

  

5 – 20 15 0

y y

  

 

hoặc



ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 3

Với

1 1

1 6

y x

  

thay (6; 1) vào (2) ta được



(TMĐK)

Với

2 2

y x

  

2 thay (2; 3) vào (2) ta được

 

(TMĐK)

Vậy với



hoặc

 

thì hai đường thẳng





và

(

) cắt nhau tại một điểm

thuộc

đường thẳng





Bài 6. TS Lớp 10 Hà Tĩnh 2016-2017

Trong mặt phẳng tọa độ

Oxy

cho hai đường thẳng





: 1

d y ax a

  

và









: – 3 3 3 – .

d y a a x a



  

a) Tìm

để





đi qua





1;3

A .

b) Tìm

để





song song với







Lời giải:

a) * Nếu



thì đường thẳng



không đi qua điểm





1;3

* Nếu



thì





đi qua





1;3

3 .1 1 1

a a a

     









d d



3 3 0( )

1 3

3 3 0

3 3

1 3

a a Loai

a a

a a a

a a

 







  









  





  









  







  









  





Vậy



thì









d d



Bài 7. TS lớp 10 Hưng Yên 2016– 2017

Tìm

để hàm số bậc nhất





2 1,

( )

y m x m

   

đồng biến trên



Lời giải:

Để hàm số





– 2 –1

y m x

 đồng biến thì

– 2 0 2.

m m

  

Vậy



Bài 8. TS lớp 10 Hải Dương 2015– 2016

Cho hai hàm số

(3 2) 5

y m x

  

với

 

và

y x

  

có đồ thị cắt nhau tại điểm





; .

A x y

Tìm các giá trị của

để biểu thức

2 3

P y x

  

đạt giá trị nhỏ nhất.

Lời giải:

Với

 

hai đồ thị cắt nhau tại điểm

2 2

; 1

1 1

m m



 



 

 

 

2 2

2 3 1 2 3

1 1

P y x

m m



   

      

   

 

   

Đặt





ta được

 

4 2 2 6 6

P t t t

       

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 4

6 2 2 0

P t m

       



Vậy



thì biểu thức

2 3

P y x

  

đạt giá trị nhỏ nhất

Bài 9. TS lớp 10 Hưng Yên 2015– 2016

Xác định toạ độ các điểm

và

thuộc đồ thị hàm số

2 6

y x

 

, biết điểm

có hoành độ bằng

và điểm

có tung độ bằng

Lời giải:

Điểm

thuộc đường thẳng

2 6

y x

 

, mà hoành độ



Suy ra tung độ

 

Vậy điểm

có toạ độ

( )

0; 6 .



Điểm

thuộc đường thẳng

2 6

y x

 

, mà tung độ



Suy ra hoành độ



Vậy điểm

có toạ độ

(

3;0

)

Bài 10. TS lớp 10 Thái Nguyên 2015 - 2016

Tìm giá trị của tham số

để đường thẳng

: 2

d y x

  

cắt đường thẳng

: 2 3

d y x k

  

tại

một điểm nằm trên trục hoành.

Lời giải:

Ta thấy hai đường thẳng

1 2

;

d d

luôn cắt nhau:

+ Đường thẳng

cắt trục hoành tại điểm





2;0

+ Đường thẳng

cắt trục hoành tại điểm



 

 

 

+ Để hai đường thẳng

1 2

;

d d

cắt nhau tại một điểm trên trục hoành thì

2 7



  

Bài 11. TS lớp 10 Quãng Bình 2015 - 2016

Cho hàm số:





1 3

y m x m

   

với

 

(

là tham số)

a) Tìm giá trị của

để đồ thị của hàm số đi qua điểm





1; 4



b) Tìm giá trị của

để đồ thị của hàm số song song với đường thẳng





: 2 1

d y x

  

Lời giải:

a) Cho phương trình:





2 2

– 2 1 2 0

x m x m m

    

(1) (

là tham số).

Ta có





1; 4



thuộc đồ thị hàm số

1; 4

x y

   

thay vào hàm số đã cho ta có:





4 1 .1 3

m m

    

4 1 3

m m

     

4 2 2

   

6 2

  





3m TM

ĐK

  

Với

 

thì đồ thị hàm số đã cho đi qua điểm





1; 4



b) Để đồ thị hàm số đã cho song song với đường thẳng





: 2 1

d y x

  

khi và chỉ khi

' 1 2 1

' 3 1 2

a a m m

b b m m

     

  

    

  

    

  

Vậy với

 

thì đồ thị hàm số





1 3

y m x m

   

song song với đường thẳng





: 2 1

d y x

  

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 5

Bài 12. TS lớp 10 TPHCM 06 – 07

Viết phương trình đường thẳng





song song với đường thẳng

3 1

y x

 

và cắt trục tung tại

điểm có tung độ bằng

Lời giải:

đường thẳng





song song với đường thẳng

3 1

y x

 

nên





có dạng





3y x b b  







cắt trục tung tại điểm có tung độ bằng

nên





đi qua điểm





0,4

A hay

4 3.0 4

b b

   

Vậy phương trình đường thẳng





3 4

y x

 

Bài 13. TS lớp 10 Bắc Giang 11 – 12

Tìm các giá trị của tham số

để hàm số bậc nhất





– 2 3

y m x

 

đồng biến trên



Lời giải:

Để hàm số bậc nhất





– 2 3

y m x

 

đồng biến trên



thì

2 0 2

m m

   

Bài 14. TS lớp 10 Bình Thuận 11 – 12

Cho hàm số bậc nhất

– – 2

y x



có đồ thị là đường thẳng





a) Trong mặt phẳng tọa độ

Oxy

, hãy vẽ đường thẳng





b) Hàm số: 2

y mx n

 

có đồ thị là đường thẳng







. Tìm

và

để hai đường thẳng





và







song song với nhau.

Lời giải:

a) Ta có





đi qua





0, 2



;





2,0

B  nên đô thị hàm số là :





và







song song với nhau khi và chỉ khi

2 1





 









 

 





 



Bài 15. TS lớp 10 Cần Thơ 11 – 12

Xác định

để đường thẳng





2 – 3 –

y m x m m

  tạo với trục hoành một góc

 

Lời giải:

Để đường thẳng





2 – 3 –

y m x m m

  tạo với trục hoành một góc

 

thì

o o

2 tan 60 2 tan 60 2 3

m m       .

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 6

Bài 16. TS lớp 10 Đăk Lăk 11 – 12

Với giá trị nào của

thì đồ thị của hai hàm số





12 7 –

y x m

  và





2 3

y x m

   cắt nhau tại

một điểm nằm trên trục tung?

Lời giải:

Để đồ thị của hai hàm số





12 7 –

y x m

  và





2 3

y x m

   cắt nhau tại một điểm nằm trên

trục tung thì





 

12.0 7 –

2.0 3

7 3 2 4 2

y m

m m m m





       







 

  

Bài 17. TS lớp 10 Hải Phòng 11 – 12

Xác định các hệ số

của hàm số





y ax b a

  

biết đồ thị





của hàm số đi qua





1;1

và song song với đường thẳng

–3 2011

y x

 

Lời giải:

Để đồ thị





của hàm số song song với đường thẳng

–3 2011

y x

 

thì





–3 2011

y x b b   .

Đồ thị





đi qua





1;1

A nên

1 3.1 4

b b

    

. Vậy

3 4

y x

  

Bài 18. TS lớp 10 Hải Dương 11 – 12

Cho hai đường thẳng





2 5

y x

 

;





–4 1

y x

 

cắt nhau tại

. Tìm

để đường thẳng









1 2 –1

y m x m   đi qua điểm

Lời giải:

Tọa độ

là nghiệm của hệ

2 5

–4

y x















 







 













đi qua điểm

nên

 

11 2

1 2 –1 4

3 3

m m m



    

Bài 19. TS lớp 10 Kiên Giang 11 – 12

Cho hàm số





2 – – 3

y m x m

 

(1) (

là tham số).

a) Vẽ đồ thị





của hàm số khi



b) Tìm giá trị của tham số

để đồ thị hàm số (1) đồng biến.

Lời giải:

a) Khi



ta có

y x

 

đi qua





0,2

A ;





2,0

B  có đồ thị :

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 7

b) Để đồ thị hàm số (1) đồng biến thì

2 0 2

m m

   

Bài 20. TS lớp 10 Quảng Trị 11 – 12

a) Vẽ đồ thị





của hàm số

– 3

y x

 

;

b) Tìm trên





điểm có hoành độ và tung độ bằng nhau.

Lời giải:

a) Ta có

– 3

y x

 

đi qua





0,3

A ;





3,0

B có đồ thị :

b) Trên





điểm có hoành độ và tung độ bằng nhau khi

3 2 3

x x x x y

       

Vậy

3 3

2 2

 

 

 

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 8

Bài 21. TS lớp 10 Ninh Bình 11 – 12

Cho hàm số:

 

y mx

(1), trong đó

là tham số.

a) Tìm

để đồ thị hàm số (1) đi qua điểm





1; 4

A . Với giá trị

vừa tìm được, hàm số (1)

đồng biến hay nghịch biến trên



b) Tìm

để đồ thị hàm số (1) song song với đường thẳng





có phương trình:

3 0

  

x y .

Lời giải:

a) Ta có

 

y mx

đi qua





1; 4

A khi và chỉ khi

4 1 3

   

m m . Khi đó

3 1

 

y x

đồng biến

trên



b) Ta có

3 0 3

      

x y y x

, đồ thị hàm số (1) song song với đường thẳng





khi

1 3

 





 



Vậy

 

m .

Bài 22. TS lớp 10 Quảng Ngãi 11 – 12

Trong cùng một hệ toạ độ

Oxy

cho ba điểm:





2;4

A ;





–3; –1

B và





–2; 1

C . Chứng minh ba

điểm

không thẳng hàng.

Lời giải:

Ta có đường thẳng đi qua





2;4

A và





–3; –1

B có phương trình là

 

y x không đi qua





–2; 1

C vì

1 2 2

  

hay ba điểm

không thẳng hàng.

Bài 23. TS lớp 10 Quảng Ninh 11 – 12

Biết rằng đồ thị của hàm số

– 4



y ax đi qua điểm





2; 5

M . Tìm

Lời giải:

Ta có đồ thị của hàm số

– 4



y ax đi qua điểm





2; 5

M nên

5 2.a 4 a

   

Bài 24. TS lớp 10 An Giang 12 – 13

Tìm giá trị của

, biết đồ thị hàm số

–1



y ax

đi qua điểm





1;5

A .

Lời giải:

Ta có đồ thị của hàm số

–1



y ax

đi qua điểm





1;5

A nên

5 –1 6

  

a a .

Bài 25. TS lớp 10 Đăk Lăk 12 – 13

Tìm hàm số

 

y ax b

, biết đồ thị hàm số của nó đi qua hai điểm





2;5

A và





–2; –3 .

Lời giải:

Ta có đồ thị của hàm số đi qua hai điểm





2;5

A và





–2; –3

B nên

5 2 2

3 2 1

a b a

a b b

  

 



 

    

 

Vậy hàm số

2 1

 

y x

Bài 26. TS lớp 10 Đồng Tháp 12 – 13

Xác định hệ số

của hàm số 2

 

y x b

, biết khi



x thì



y .

Lời giải:

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 9

Ta có 2

 

y x b

khi



x thì



y nên

3 2.2 1

    

b b .

Bài 27. TS lớp 10 Hà Tĩnh 12 – 13

Trong mặt phẳng tọa độ

Oxy

, đường thẳng





 

y ax b

đi qua điểm





–1;2

M và song song

với đường thẳng







2 1

 

y x

. Tìm

Lời giải:

Ta có đường thẳng





 

y ax b

song song với đường thẳng







2 1

 

y x

nên



a và đi

qua điểm





–1;2

M nên

2 2 4

    

b b .

Vậy

2; 4

 

a b .

Bài 28. TS lớp 10 Hà Nam 12 – 13

Tìm

để các đường thẳng 2

 

y x m

và

– 2 3

 

y x m cắt nhau tại một điểm nằm trên trục

tung.

Lời giải:

Để các đường thẳng 2

 

y x m

và

– 2 3

 

y x m cắt nhau tại một điểm nằm trên trục tung thì

2 3 1

2 3





     



  



y m

m m m

y m

Bài 29. TS lớp 10 Hưng Yên 12 – 13

Cho đường thẳng





2 –1

 

y x m

a) Khi



m , tìm

để điểm





; –4

A a thuộc đường thẳng





b) Tìm

để đường thẳng





cắt các trục tọa độ

lần lượt tại

và

sao cho tam

giác

OMN

có diện tích bằng

Lời giải:

a) Khi



m để điểm





; –4

A a thuộc đường thẳng





thì

4 2. 3 –1 3

     

a a .

b) Đường thẳng





cắt các trục tọa độ

lần lượt tại

và

thì



 

 

 

và





0, 1



N m nên

 

1 1 1

. 1 .

2 2 2



 

  

 

 

MNO

S MO NO m .

Mà

   

1 1

1 1 . 1 1 4

2 2







 

       

 



 

 



MNO

S m m

Bài 30. TS lớp 10 Hòa Bình 12 – 13

a) Vẽ đồ thị hàm số

3 2

 

y x (1)

b) Gọi

là giao điểm của đồ thị hàm số (1) với trục tung và trục hoành. Tính diện tích tam

giác

OAB

Lời giải:

a) Vẽ đồ thị hàm số

3 2

 

y x (1)

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 10

Đồ thị đi qua





0,2

A và



 

 

 

b) Ta có

1 1 2 2

. 2.

2 2 3 3



  

OAB

S OAOB

Bài 31. TS lớp 10 Ninh Bình 12 – 13

Hàm số bậc nhất

2 1

 

y x

đồng biến hay nghịch biến trên



? Vì sao?

Lời giải:

2 0

 

a nên hàm số bậc nhất

2 1

 

y x

đồng biến trên



Bài 32. TS lớp 10 Lâm Đồng 12 – 13

Cho 2 đường thẳng













3 16 3

   

y m x m và

( )



 

y x m

. Tìm

để





( )



cắt

nhau tại một điểm nằm trên trục tung.

Lời giải:

Để





( )



cắt nhau tại một điểm nằm trên trục tung thì

16 4





    







m m

y m

Khi



m thì





d d

loại

Vậy

 

m .

Bài 33. TS lớp 10 Nam Định 12 – 13

Tìm các giá trị của tham số

để hai đường thẳng





1 2

   

y m x m và

5 2

 

y x song song

với nhau.

Lời giải:

Để hai đường thẳng





1 2

   

y m x m và

5 2

 

y x song song với nhau thì

1 5

2 2

 



 





 



 



ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 11

Bài 34. TS lớp 10 Kiên Giang 12 – 13

Cho đường thẳng





(1 )( 2)



   



y x m m

(

là tham số)

a) Với giá trị nào của

thì đường thẳng





vuông góc với đường thẳng





 

y x

b) Với giá trị nào của

thì





là hàm số đồng biến ?

Lời giải:

a) Để đường thẳng





vuông góc với đường thẳng





thì

4 8 1 0

1 1

. 1 3

2 4

   





     









m m

b) Để hàm số

  

1 2



   



y x m m

đồng biến thì

0 2 1



    



Bài 35. TS lớp 10 Bắc Giang 13 – 14

Tìm

để đường thẳng





 

2 1 1,

 

   

 

 

y m x m và







3 2

 

y x song song với nhau.

Lời giải:

Để





song song







thì

2 1 3

1 2

 



 



 



Bài 36. TS lớp 10 Bắc Ninh 13- 14

Cho hàm số:

y mx

 

(1), trong đó

là tham số.

a) Tìm

để đồ thị hàm số (1) đi qua điểm





1; 4

A . Với giá trị

vừa tìm được, hàm số (1)

đồng biến hay nghịch biến trên



b) Tìm

để đồ thị hàm số (1) song song với đường thẳng





có phương trình

  

y m x m .

Lời giải:

a) Ta có

y mx

 

đi qua





1; 4

A khi và chỉ khi

4 1 3

m m

   

. Khi đó

3 1

y x

 

đồng biến

trên



b) Ta có

y mx

 

đồ thị hàm số (1) song song với đường thẳng





khi

1 1

m m





 



 



Vậy



Bài 37. TS lớp 10 Bình Định 13 – 14

Cho hàm số ( 1)

  

y m x m

. Tìm

để đồ thị hàm số vuông góc với đường thẳng

3 2013 0

x y

  

Lời giải:

Để đồ thị hàm số vuông góc với đường thẳng

3 2013 0 671

x y y x



      thì

 

1 . 1 1 3 4



 

       

 

 

m m m

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 12

Bài 38. TS lớp 10 Đà Nẵng 13 - 14

Cho hàm số bậc nhất

– 2

y ax



(1). Hãy xác định hệ số

, biết rằng



và đồ thị của hàm số

(1) cắt trục hoành

, trục tung

lần lượt tại hai điểm

sao cho

OB OA



(với

là gốc

tọa độ).

Lời giải:

Ta có

 

 

 





0, 2



, để

2 4 4. 4 2

OB OA a a

      

Bài 39. TS lớp 10 Hà Tĩnh 13 – 14

Trong mặt phẳng tọa độ

Oxy

cho đường thẳng

( 2)

  

y m x m

và đường thẳng

6 2

y x

 

. Tìm

để hai đường thẳng đó song song với nhau.

Lời giải:

Để hai đường thẳng đó song song với nhau thì

2 6

 



 



   

 





Bài 40. TS lớp 10 Lâm Đồng 13 – 14

Cho hàm số bậc nhất





– 3 2014

y m x  . Tìm giá trị của

để hàm số đồng biến trên



Lời giải:

Để hàm số đồng biến trên



thì

3 0 3

m m

   

Bài 41. TS lớp 10 Lào Cai 13 – 14

Cho hai hàm số bậc nhất





5 1

y x m

   

và





4 7

y x m

   (với

là tham số). Với giá trị nào

của

thì đồ thị hai hàm số trên cắt nhau tại một điểm trên trục tung. Tìm tọa độ giao điểm đó.

Lời giải:





5 1

y x m

   

cắt trục tung tại điểm của tung độ bằng







4 7

y x m

   cắt trục tung tại điểm của tung độ bằng



Để hai đồ thị hàm số cắt nhau tại một điểm trên trục tung thì

1 7 3

m m m

    

Khi đó tọa độ giao điểm là





0;4

Bài 42. TS lớp 10 Ninh Thuận 13 – 14

Viết phương trình đường thẳng





có hệ số góc bằng 7 và đi qua điểm





2;1 .

Lời giải:

Do đường thẳng





có hệ số góc bằng 7 và đi qua điểm





2;1

M , Gọi phương trình





là

y ax b

 

ta có

7 7

1 7.2 13

a a

b b

 

 



 

   

 

Vậy

7 13

y x

 

Bài 43. TS lớp 10 Quảng Ngãi 13 – 14

Cho hàm số bậc nhất:





2 1 – 6

y m x

 

a) Với giá trị nào của

thì hàm số dã cho nghịch biến trên



ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 13

b) Tìm

để đồ thị của hàm số đã cho đi qua điểm





1; 2 .

Lời giải:

a) Để hàm số đã cho nghịch biến trên



thì

2 1 0

m m



    .

b) Để đồ thị của hàm số đã cho đi qua điểm





1; 2

A thì

 

2 2 1 – 6 2 1. 8

1m m m

      

Bài 44. TS lớp 10 Quảng Ninh 13 – 14

Xác định hệ số a để hàm số

– 5

y ax



cắt trục hoành tại điểm có hoành độ bằng

1,5

Lời giải:

Để hàm số

– 5

y ax



cắt trục hoành tại điểm có hoành độ bằng

1,5

thì

3 10

0 . – 5

2 3

a a

  

Bài 45. TS lớp 10 Tây Ninh 13 – 14

Tìm

và

để đường thẳng

( ) : ( 2) b

d y a x

  

có hệ số góc bằng

và đi qua điểm





M 1;

 

Lời giải:

Để đường thẳng

( ) : ( 2) b

d y a x

  

có hệ số góc bằng

và đi qua điểm





M 1;

 

thì

2 4 6

3 ( 2) b 7

a a

a b

  

 



 

     

 

II. Hàm số bậc hai

Bài 46. TS LỚP 10 Vĩnh Long 2017 – 2018

Trong mặt phẳng tọa độ

Oxy

, cho Parabol





y x

 . Vẽ đồ thị parabol





Lời giải:

Vẽ Parabol





y x



Bảng giá trị giữa

và



0 1 2

Vẽ đúng đồ thị

Bài 47. TS LỚP 10 Hưng Yên 2016– 2017

Tìm tọa dộ điểm

thuộc đồ thị hàm số

y x

 , biết hoành độ của điểm

bằng

Lời giải:

Vì

có hoành độ bằng

và thuộc đồ thị hàm số

y x

 nên

2.2 8.

 

Vậy





2;8

A .

Bài 48. TS LỚP 10 Bắc Giang 2015– 2016

Biết đồ thị của hàm số

y ax

 , (



) đi qua điểm





3; 6



. Hãy xác định giá trị của

Lời giải:

y=2x

-2

-1

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 14

Đồ thị hàm số

y ax

 , (



) đi qua điểm





3; 6



khi

.3–

6 3 2

a a a

     



Vậy

 

là giá trị cần tìm.

Bài 49. TS LỚP 10 Hòa Bình 2015– 2016

Cho hàm số

y x

 có đồ thị là





Tìm trên





các điểm có tung độ bằng 4, vẽ đồ thị





Lời giải:

Thay



ta có

2 2

4 2 2 2

x x x

     

Vậy các điểm cần tìm là





2;4

và





2;4

 .

Bảng giá trị



0 1 2

y x



8 2 0 2 8

Đồ thị

Bài 50. TS LỚP 10 Hưng Yên 2015– 2016

Xác định tham số

để đồ thị hàm số

y mx

 đi qua điểm

( )

1; 2 .



Lời giải:

Đồ thị hàm số

y mx

 đi qua điểm

(

)



suy ra

2 . mm

  



Vậy

 

Bài 51. TS LỚP 10 Sơn La 2015– 2016

Tìm hàm số

y ax

 biết đồ thị của nó đi qua điểm





1;2 .

A  Với hàm số tìm được hãy tìm các

điểm trên đồ thị có tung độ là

Lời giải:

+ Ta có đồ thị hàm số

y ax

 đi qua điểm





1;2

A  nên ta có:

2 .( 1) 2

a a

   

Vậy hàm số cần tìm là

2 .

y x



+ Các điểm trên đồ thị có tung độ là 8.

Gọi điểm cần tìm là





0 0

;

M x y

Ta có:

2 2

0 0 0 0

8 8 2. 4 2

y x x x

       

Vậy các điểm cần tìm trên đồ thị có tung độ là 8 là :









2;8 ; 2;8 .

M M

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 15

Bài 52. TS LỚP 10 Tây Ninh 2015– 2016

Vẽ đồ thị hàm số

y x

 

Lời giải:

Vẽ đồ thị hàm số

y x

 



0 1 2



1,5



1,5



-2

-1

0 1

Bài 53. TS LỚP 10 Đông Nai 2015– 2016

Vẽ đồ thị





của hàm số

y  . Tìm tọa độ giao điểm của





và đường thẳng



Lời giải:

Bảng giá trị:



0 1 2

y 

2 1/2 0 1/2 2





cắt





nên





  



 



hay tọa đô giao điểm là





2;2

 và





2;2

Bài 54. TS LỚP 10 Thừa Thiên Huế 2008– 2009

Biết đường cong trong Hình 1 là một parabol

y ax

 . Tính hệ số

và tìm tọa độ các điểm thuộc

parabol có tung độ

 

Lời giải:

Từ Hình 1, ta có parabol

y ax

 đi qua điểm





2; 2



-2

-1

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 16

nên

2 .2

a a

    

Gọi điểm trên parabol có tung độ

 

là





; 9



ta có:

2 2

9 18 18 3 2

x x x          .

Vậy có 2 điểm trên parabol có tung độ bằng



là





3 2; 9



Bài 55. TS LỚP 10 Hưng Yên 2014- 2015

Tìm hoành độ của điểm

trên parabol

y x

 ,

biết tung độ



Lời giải:

A A

y x





  







Bài 56. TS LỚP 10 Thái nguyên

Trong mặt phẳng tọa độ

Oxy

cho các điểm

   

1 1

2;1 ; 0;2 ; 2; ; 1;

2 4

A B C D



   

 

   

   

Đồ thị hàm số

y  đi qua những điểm nào trong các điểm đã cho? Giải thích.

Lời giải:

Hai điểm

và

thuộc đồ thì hàm số

y 

Thật vậy thay vào ta có:

Tại

có:

 

1 1

1 2 .4

4 4

  

Tại

có:





1 1 1

2 .2

2 4 4

 

Bài 57. TS lớp 10 Cần Thơ 11 – 12

Cho parabol





y ax

 . Tìm

biết rằng parabol





đi qua điểm





3; –3 .

A Vẽ





với

vừa

tìm được.

Lời giải:





đi qua điểm





3; –3

A nên ta có

3 3 .

a a



   

Vậy

P x

  .

Bài 58. TS lớp 10 Hải Phòng 12 – 13

Xác định hàm số





y a x

  , biết đồ thị hàm số đi qua điểm





1; –2 .

Lời giải:





y a x

  đi qua điểm





1; –2

A nên





2 1 1 1 2 3

a a a

         

Bài 59. TS lớp 10 Đà Nẵng 13 – 14

Vẽ đồ thị hàm số

y x

 .

Hình 1

-2

-1

0 1

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 17

Lời giải:

Bài 60. TS lớp 10 Ninh Thuận 13 - 14

Trong mặt phẳng tọa độ

Oxy

, vẽ đồ thị





của hàm số

2 .

y x



Lời giải:

III. Sự tương giao giữa parabol (P) và đường thẳng (d)

Bài 61. TS LỚP 10 Bình Định 2017 - 2018

Cho Parabol





P y x



và đường thẳng





: 2 1 2

d y m x m

   

(

là tham số)

a) Chứng minh rằng với mọi

đường thẳng

luôn cắt





tại hai điểm phân biệt.

b) Tìm các giá trị của

để đường thẳng

luôn cắt





tại hai điểm phân biệt





1 1

; ,

A x y





2 2

;

B x y

thỏa

1 1 2 2

x y x y

 

Lời giải:

a) Phương trình hoành độ giao điểm













2 2

2 1 2 2 1 2 0 *

x m x m x m x m         

Ta có

     

2 2

2 1 4.1. 2 4 8 9 4 1 5 5 0

m m m m m

            

Vậy Parabol luông cắt đường thẳng tại hai điểm phân biệt.

b) Vì

1 2

x x

là nghiệm của phương trình





nên

1 2

2 1

x x m

  





 



. Mặt khác

1 1

2 2

y x















Ta có









3 3 2 2

1 1 2 2 1 2 1 2 1 1 2 2

0 0 0

x y x y x x x x x x x x

         

 

1 2

2 2

1 1 2 2

1 2 1 2

2 1 0

3 0

4 7 7 0

x x

x x x x

m m vn



 



 







  



  

  





  





Vậy



Bài 62. TS LỚP 10 Bình Dương 2017 - 2018

Cho Parabol





P y x



và đường thẳng





: 4 9

d y x

 

a) Vẽ đồ thị





b) Viết phương trình đường thẳng





biết





song song với đường thẳng (d) và





tiếp xúc





Lời giải:

a) Vẽ đồ thị





P y x





Ta có đồ thị hàm số

b) Gọi phương trình đường thẳng





có dạng:

y ax b

 

Vì





song song với





nên ta có:

 

: 4

d y x b





  







Phương trình hoành độ giao điểm của





và





là:

-2 2-1

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 18





2 2

4 4 0 *

x x b x x b     

Vì





tiếp xúc với





nên (*) có nghiệm kép



        

0 4 0 4 (tmñk)

b b

Vậy phương trình đường thẳng





là:

4 – 4

y x



Bài 63. TS LỚP 10 Bình Phước 2017 - 2018

Cho parabol





: 2

P y x

 và đường thẳng

: 1.

d y x

 

a) Vẽ parabol





và đường thẳng

trên cùng một trục tọa độ.

b) Viết phương trình đường thẳng song song với đường thẳng

và đi qua





1;2 .

A 

Lời giải:

a) Cho parabol





: 2

P y x

 và đường thẳng

: 1

d y x

 

Bảng giá trị

b) Phương trình đường thẳng

song song với đường

thẳng

có dạng

y x b

 

đi qua điểm





1;2

A  nên ta có

1 2 3 : 3

b b d y x

       

Bài 64. TS LỚP 10 Cần Thơ 2017 - 2018

Trong mặt phẳng với hệ tọa độ

Oxy

, cho parabol

 

P y x

 và đường thẳng

 

1 3

4 2

d y x

 

a) Vẽ đồ thị của





b) Gọi





1 1

;

A x y

và





2 2

;

B x y

lần lượt là các giao điểm của





với





. Tính giá trị biểu thức

1 2

x x

y y







Lời giải:

a) HS tự vẽ.

b) Phương trình hoành độ giao điểm của





và





1 1 3

2 4 2

x x

 





2 2 2;2

3 9 3 9

;

2 8 2 8

x y A

x y B

   







 



    

 



 



. Vậy

1 2

x x

y y

 

 

 



 

  





0 1 2

y x



2 0 2



y x

 

y=x+1

y=2x

-2

-1

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 19

Bài 65. TS LỚP 10 Chuyên ĐHSP Hà Nội 2017 - 2018

Cho parabol





P y x



và đường thẳng





2 4

y ax a

  

(với

là tham số )

a) Tìm tọa độ giao điểm của





và





khi

 

b) Tìm tất cả các giá trị của

để đường thẳng





cắt





taị hai điểm phân biệt có hoành độ

1 2

;

x x

thỏa mãn

1 2

x x

 

Lời giải:

a) Phương trình hoành độ





và





là

2 4 0

x ax a

  

Khi

 

thì phương trình trở thành

2 0

x x

  

Có

a b c

  

nên phương trình có 2 nghiệm là

 

;



b) Phương trình hoành độ





và





là

2 4 0

x ax a

  

(*)

để đường thẳng





cắt





tại hai điểm phân biệt thì phương trình (*) phải có 2 nghiệm phân

biệt

 

4 0

a a







     







Với











theo Viét

1 2

x x a

  













 

1 2 1 2 1 2 1 2 1 2

3 9 2 2 9

x x x x x x x x x x

         

4 8 8 9

a a a

   

Với



2 2

4 8 8 9 4 16 9 0

a a a a a a



        

Với



2 2

4 8 8 9 4 9

a dk

a a a a

a dk



 



     







 





Vậy

 

Bài 66. TS LỚP 10 Đà Nẵng 2017 - 2018

Cho hai hàm số

y x



và

y mx

 

, với

là tham số.

a) Khi



, tìm tọa độ các giao điểm của hai đồ thị hàm số trên.

b) Chứng minh rằng với mọi giá trị

, đồ thị của hai hàm số đã cho luôn cắt nhau tại hai điểm

phân biệt





1 1 1

;

A x y

và





2 2 2

; .

A x y

Tìm tất cả các giá trị của

sao cho









2 2

1 2

y y

 

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 20

Lời giải:

a) Phương trình hoành độ giao điểm của

y x



và

y mx

 

là

4 0

x mx

  

(1)

Thay



vào phương trình (1) ta có:

3 4 0

x x

  

Ta có:









– 1– 3 4 0

a b c

     

Vậy phương trình

3 4 0

x x

  

có hai nghiệm



 







Với

1 1 ( 1;1)

x y A

     

Với





4 16 4;16

x y B   

Vậy với



thì hai đồ thị hàm số giao nhau tại 2 điểm

( 1;1)



và





4;16

b) Ta có số giao điểm của hai đồ thị hàm số đã cho là số nghiệm của phương trình (1)

Phương trình (1) có:





2 2

4. 4 16 0m m m

        



Do đó (1) luôn có hai nghiệm phân biệt

1 2

;

x x

Vậy đồ thị của hai hàm số đã cho luôn cắt nhau tại hai điểm phân biệt





1 1 1

;

A x y

và





2 2 2

;

A x y

với

mọi

Theo hệ thức Vi-et ta có:

1 2

. 4

x x m

x x



 





 





Ta lại có:

1 1

2 2

y x















Theo đề, ta có:









   

     

 

   

 

2 2

1 2

2 2

1 2

2 2

2 2 2 2 2 2

1 1 2 2 1 2

2 2

1 2 1 2

2 2

1 2 1 2 1 2

2 2

2 2 49

2 49

2 2 49

2. 4 2 4 49

8 81

8 9

8 9 do 8 0

8 9

y y

x x

x x x x x x

x x x x

x x x x x x

m m m

 

  

    

   

 

    

 

 

 

     

 

  



 

      



  



  

Vậy với

1; 1

m m

  

thì









2 2

1 2

y y

 

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 21

Bài 67. TS LỚP 10 Phú Thọ 2017 - 2018

Trong mặt phẳng tọa độ

Oxy

cho parabol





có phương trình

y x

 và hai điểm

A B

thuộc





có hoành độ lần lượt là

1, 2.

A B

x x

  

a) Tìm tọa độ của hai điểm

A B

b) Viết phương trình đường thẳng





đi qua hai điểm

A B

c) Tính khoảng cách từ điểm

(gốc tọa độ) tới đường thẳng





a) Vì

A B

thuộc





nên:

 

1 1

2 2

A A

x y

     

2 2 2

B B

x y

   

Vậy

 

1; , 2;2

A B

 



 

 

b) Gọi phương trình của đường thẳng

là

y ax b

 

Ta có hệ phương tình:

1 3 1

2 2 2

2 2 2 2 1

a b a a

a b a b b

  

    

  

 

  

  

    

  

Vậy

: 1

d y x

 

cắt trục

tại điểm





0;1

C và cắt trục

tại điểm





2;0

D 

 

và



Gọi

là khoảng cách từ

tới

Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông

OCD

, ta có:

2 2 2 2 2

1 1 1 1 1 5 2 5

1 2 4 5

h OC OD

       .

Bài 68. TS LỚP 10 Quãng Ngãi 2017 – 2018

Cho hàm số

y x



có đồ thị là





và hàm số

y x

  

có đồ thị là





a) Vẽ





và





trên cùng một mặt phẳng tọa độ

Oxy

b) Bằng phép tính, tìm tọa độ các giao điểm

A B

của





và





; (hoành độ của

nhỏ hơn

hoành độ của

). Gọi

và

lần lượt là hình chiếu vuông góc của

và

trên trục hoành, tính

diện tích của tứ giác

ABDC

Lời giải:

Phương trình hđgđ của





và





x x

  

2 0

x x

  

2 2 0

x x x

    









1 2 0

x x

   

1 2

x x

    



1 1.

x y

  



2 4

x y

   

Vậy









2;4 , 1;1 .

A B

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 22

ABDC

là hình thang vuông có 2 đáy

1; 4.

B A

BD y AC y

   

Đường cao

B A

CD x x

  

Vậy

 

1 4 .3 7,5

ABDC

S   

(đvdt).

Bài 69. TS LỚP 10 Thừa Thiên Huế 2017 – 2018

Cho hàm số

y x

  có đồ thị





a) Vẽ đồ thị





của hàm số.

b) Cho đường thẳng





y mx n

  

. Tìm

m n

để đường thẳng







song song với đường thẳng





2 5

y x d

   và có duy nhất một điểm chung với đồ thị





Lời giải:

a) Đồ thị hàm số

y x

  là một parabol có đỉnh là gốc tọa độ, bề lõm hướng xuống và đi qua

các điểm





















0;0 , 2; 2 ; 2; 2 ; 4; 8 ; 4; 8

     

Đồ thị

y x

  :



song song với

2 5

y x

  

suy ra

 









Phương trình hoành độ giao điểm của



và





x x n

   

4 2 0

x x n

   

(*)

Để



và





có một điểm chung duy nhất thì phương trình (*) có nghiệm duy nhất thì

0 4 2 0 2

n n



      

(thỏa mãn)

Vậy

2; 2

m n

  

Bài 70. TS LỚP 10 Tiền Giang 2017 – 2018

Cho parabol





: 2

P y x

 và đường thẳng





: 1

d y x

 

a) Vẽ đồ thị của





và





trên cùng hệ trục tọa độ.

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 23

b) Bằng phép tính, xác định tọa độ giao điểm

và

của





và





Tính độ dài đoạn thẳng

Lời giải:

a) Vẽ đồ thị: (như hình vẽ bên)

Tọa độ giao điểm của





và





Phương trình hoành độ giao điểm:

2 – –1 0

x x



Ta có

a b c

  

nên phương trình có hai nghiệm



; 1 suy ra tọa độ hai giao điểm là:

1 1

;

2 2

 



 

 

và





1;2

b) Tính độ dài

   

2 2

1 1

1 2

2 2

3 3 3 2

2 2 2

B A B A

AB x x y y

 

   

        

   

 

   

 

   

  

   

   

Bài 71. TS LỚP 10 HCM 2017 – 2018

Trong mặt phẳng tọa độ

Oxy

a) Vẽ đồ thị





của hàm số:

y x



b) Cho đường thẳng





y x m

 

đi qua điểm





6;7 .

C Tìm tọa độ giao điểm của





và





Lời giải:

a) Vẽ





học sinh tự vẽ.





y x m

 

đi qua điểm





6;7

C nên

.6 7 2

m m

    

Phương trình hoành độ giao điểm giữa





và





2 1

4 4

4 2

x y

  



  



  



Vậy tọa độ giao điểm là









2;1 , 4;4

Bài 72. TS LỚP 10 Yên Bái 2016 – 2017

Cho đường thẳng





có phương trình

y x

 

và parabol





có phương trình

y x



a) Vẽ đường thẳng





và parabol





trên cùng hệ trục tọa độ

Oxy

b) Đường thẳng





cắt





tại hai điểm

và

(với

có hoành độ âm,

có hoành độ

dương). Bằng tính toán hãy tìm tọa độ các điểm

và

Lời giải:

a) Vẽ đường thẳng





và parabol





trên cùng hệ trục tọa độ

Oxy

Bảng giá trị

y=x+1

y=2x

-2

-1

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 24

-2 -1 0 1 2

y x

 

0 2

y x



4 1 0 1 4

Đồ thị

b) Phương trình hoành độ giao điểm của (d) và (P):









2 2

2 – – 2 0 – 2 1 0 2

x x x x x x x

        

hoặc

–1



Với





2 4 2;4

x y B    (vì

có hoành độ dương)

Với





–1 1 –1;1

x y A    (vì

có hoành độ âm)

Vậy









–1;1 , 2;4

A B .

Bài 73. TS LỚP 10 Bình Dương 2016 – 2017

Vẽ đồ thị hàm số





: 2

P y x

 trên hệ trục tọa độ. Tìm giao điểm của





: 2

P y x

 với





: – 3

d y x

 

bằng phép tính.

Lời giải:

Vẽ đồ thị





: 2

P y x



Bảng giá trị

-2 -1 0 1 2

8 2 0 2 8

Vẽ đồ thị:

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 25

Phương trình hoành độ giao điểm của





và





là:

2 2

2 3 2 3 0

1 4.2.( 3) 25 0

x x x x

      

     

Phương trình đã cho có 2 nghiệm phân biệt:

1 2

1 5 3 1 5

; 1

4 2 4

x x

    

   

Hoặc học sinh có thể làm theo cách: ta có





2 1 3 0

a b c

      

Với



ta có:



Với

x 



ta có:



Vậy tọa độ giao điểm là





1;2

và

3 9

;

2 2

 



 

 

Bài 74. TS LỚP 10 Cần Thơ 2016 – 2017

Trong mặt phẳng với hệ tọa độ

Oxy

, cho parabol





y x

 

a) Vẽ đồ thị của





b) Tìm tọa độ các giao điểm của





với đường thẳng

2 1

3 3

y x

  

Lời giải:

(P):

y x

 

Bảng giá trị

x -4 -2 0 2 4

y -4 -1 0 -1 -4

Vẽ

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 26

Xét phương trình hoành độ giao điểm của





và đường thẳng

là

2 2 2

1 2 1 1 2 1

0 3 8 4 0

4 3 3 4 3 3

( 4) 3.4 4 0

4 2 2

3 3

4 2

x x x x x x



          



     





 











 





Với



ta có

y 



2 1

;

3 9



 



 

 

Với



ta có

 





2; 1

 

Vậy tọa độ giao điểm của





và là

2 1

;

3 9



 

 

 

và





2; 1



Bài 75. TS LỚP 10 Đà Nẵng 2016 – 2017

Cho hai hàm số

y x

 và đồ thị hàm số





và

y x

 

có đồ thị





a) Vẽ đồ thị





b) Gọi

A B

là các giao điểm của hai đồ thị





và





Biết rằng đơn vị đo trên các trục tọa độ

là xentimét, tìm tất cả các điểm

trên tia

sao cho diện tích tam giác

MAB

bằng

Lời giải:

a) Vẽ đồ thị





y x



Bảng giá trị



0 1 2

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 27

b) Xét phương trình hoành độ giao điểm của





và





là:

2 2

4 2 8 0

( 1) ( 8) 9 0

x x x x

     



      

Phương trình có 2 nghiệm phân biệt:

4; 2

x x

  

Với

 

ta có





2 2;2

y A  

Với



ta có





8 4;8

y B 

Gọi





M m thuộc tia





0 .

Ox m  Gọi









–2;0 , 4;0 .

C D

Xét hai trường hợp:

Trường hợp 1:

thuộc đoạn

: Ta có

AMB ABDC ACM BDM

S S S S  

Có

ABDC

là hình thang,

2 , 8 , 6

AC cm BD cm CD cm

  

⇒

(2 8).6

30(cm )

ABDC



 

Suy ra

AMB

< 30cm

(loại)

Trường hợp 2:

thuộc tia





Dx M D m

  

Ta có :

AMB ABDC ACM BDM

S S S S  

Có









30 , 2 , – 4

ABCD

S cm MC m cm MD m cm

   

Suy ra

(thỏa mãn)

Vậy





6;0

M là điểm cần tìm.

Bài 76. TS LỚP 10 Hà Nội 2016 – 2017

1 1

. .2.( 2) 2( )

2 2

1 1

. .8.(m 4) 4(m 4)( )

2 2

S 30 2 4( 4) 6

ACM

BDM

AMB ACM BDM

S AC CM m m cm

S BD DM cm

cm S S m m m

    

    

         

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 28

Trong mặt phẳng tọa độ

Oxy

cho đường thẳng





: 3 –1

d y x m  và parabol





P y x



a) Chứng minh





luôn cắt





tại hai điểm phân biệt với mọi

b) Gọi

1 2

x x

là hoành độ các giao điểm của





và





Tìm

để









1 2

1 1

) 1a x x

  

Lời giải:

a) Xét phương trình hoành độ giao điểm của





và









2 2 2 2

3 1 3 1 0 *

x x m x x m       

2 2

9 1 8 0

m m m

       

Suy ra phương trình (*) luôn có hai nghiệm phân biệt với mọi

hay





luôn cắt





tại hai

điểm phân biệt với mọi

b) Ta có:

1 2 1 2 1 1

( 1)( 1) 1 ( ) 0

x x x x x x

      

Áp dụng hệ thức Vi-et cho (*):

1 2

x x

x x m

 





  



2 2

(**) 1 3 0 4 2

m m m

         

Vậy

 

Bài 77. TS LỚP 10 HCM 2016 – 2017

a) Vẽ đồ thị





của hàm số

 

và đường thẳng





 

trên cùng một hệ trục tọa

độ.

b) Tìm tọa độ các giao điểm của (P) và (D) ở câu trên bằng phép tính.

Lời giải:

a) Vẽ đồ thị hai hàm số.

Bảng giá trị



0 1 2







 



Đồ thị

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 29

b) Tìm tọa độ giao điểm của





và





bằng phép tính

Xét phương trình hoành độ giao điểm của





và





2 2 8 0

4 2

x x



     



 

Phương trình trên có hai nghiệm phân biệt:

1 2

2; 4

x x

  

Với



ta có





1, 2; 1

y A

  

Với

 

ta có





4, 4; 4

y A

   

Vậy





cắt





tại hai điểm phân biệt









2; 1 ; 4; 4

A B

  

Bài 78. TS LỚP 10 Bến Tre 2015 – 2016

Trong mặt phẳng tọa độ

Oxy

cho parabol





P y x

 

và đường thẳng





: 2 – 3

d y x



a) Vẽ đồ thị Parabol





b) Bằng phương pháp đại số, hãy tìm tọa độ giao điểm của





và





c) Viết phương trình đường thẳng





song song với đường thẳng





và có điểm chung với

parabol





tại điểm có hoành độ bằng



Lời giải:

a) Bảng một số giá trị của







y x

 



ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 30

b) Phương trình hoành độ giao điểm của





và





2 – 3

x x

 

2 – 3 0

x x

  

1 1

3 9

x y

y y

   







    



Vậy giao điểm của





và









1; 1



và





3; 9

 

c) Phương trình đường thẳng





có dạng:

y ax b

 













// 2 2 3

d d a y x b b

      

Gọi

là điểm thuộc





có





1 1 1; 1

A A

x y A

       





có chung với





điểm





1; 1

 

nên:





1 2. 1 1

b b

     

Vậy





có phương trình:

2 1

y x

 

Bài 79. TS LỚP 10 Bình Dương 2015 – 2016

a) Vẽ đồ thị





hàm số

y 

b) Xác định

a b

để đường thẳng

y ax b

 

đi qua gốc tọa độ và cắt





tại điểm

có hoành độ bằng

–3

Lời giải:

a) Vẽ đồ thị (P) hàm số

y 

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 31

b) Gọi





là đường thẳng có phương trình

y ax b

 

Vì





đi qua gốc tọa độ





0;0

O nên



Phương trình hoành độ giao điểm của





và





=ax

Vì





cắt





tại điểm

có hoành độ là



nên:

9 3

( 3)

4 4

a a



   

Vậy:



 ;



Bài 80. TS LỚP 10 Bình Thuận 2015 – 2016

a) Vẽ đồ thị





của hàm số

y x



b) Chứng minh rằng đường thẳng





d y kx

 

luôn cắt đồ thị





tại hai điểm phân biệt với

mọi

Lời giải:

a) Vẽ đồ thị





của hàm số

y x



b) PT hoành độ giao điểm của





và





x kx

 

1 0

x kx

   

  

Vì



với mọi giá trị

Nên

4 0

 

với mọi giá trị

  

với mọi giá trị

Vậy đường thẳng





d y kx

 

luôn cắt đồ thị





tại hai điểm phân biệt với mọi

Bài 81. TS LỚP 10 Đà Nẵng 2015 – 2016

Cho hàm số

y x



có đồ thị





a) Vẽ đồ thị





-2 2-1

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 32

b) Cho các hàm số

y x

 

và

y x m

  

(với

là tham số) lần lượt có đồ thị là





và





Tìm tất cả các giá trị của

để trên một mặt phẳng tọa độ các đồ thị của









P d

và





cùng đi qua một điểm.

Lời giải:

a) Lập bảng giá trị và vẽ đồ thị:

y x



0 1 2

0 1 4

b) Phương trình hoành độ giao điểm của





và









2 2

2 2 0 *

x x x x     

Phương trình (*) có dạng :

a b c

  

nên có 2 nghiệm :

 









 





Ta có





cắt





tại hai điểm





1;1

A  và





2;4 .

Để









P d

và





cùng đi qua một điểm thì hoặc





A d

 hoặc





B d



+ Với









1;1

A d

  , ta có :





1 1 0

m m

     

+ Với









2;4

B d

 , ta có :

4 2 6

m m

    

Vậy khi



hoặc



thì









P d

và





cùng đi qua một điểm.

Bài 82. TS LỚP 10 Khánh Hòa 2015 – 2016

Trong mặt phẳng toạ độ

Oxy

, cho parabol





P y x

 

a) Vẽ parabol





b) Xác định toạ độ các giao điểm

A B

của đường thẳng





: 2

d y x

  

và





Tìm toạ điểm

trên





sao cho tam giác

MAB

cân tại

Lời giải:

a) Vẽ đồ thị





P y x

 

TXĐ:





Tọa độ đỉnh:





0;0

Trục đối xứng:



Tính biến thiên:

Hàm số đồng biến trên





 và nghịch biến trên





0; .



BBT:

-2 2-1

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 33

Bảng giá trị



0 1



-1

-4

-2

-1

b) Viết phương trình đường trung trực







của

, tìm giao điểm của







và





ta tìm được

hai điểm

Hoành độ các giao điểm

A B

của đường thẳng





: – 2

d y x  và





là nghiệm của phương

trình:

2 2

2 2 0

x x x x

       

  

hoặc



+ Với

 

, thay vào





ta có:





1 1

    

, ta có:





1; 1

 

+ Với



, thay vào





ta có:





2 4

   

, ta có:





2; 4



Suy ra trung điểm của

là:

1 5

;

2 2



 

 

 

Đường thẳng







vuông góc với





có dạng:

;

y x b

 

Vì







đi qua

nên:

5 1

2 2



    

b b

Vậy





: 3

d y x



 

Phương trình hoành độ của







và





là:

3 0

x x

  

1 13

 

 x

+ Với

1 13 7 13

2 2

   

  x y

+Với

1 13 7 13

2 2

   

  x y

Vậy có hai điểm

cần tìm là:

1 13 7 13

;

2 2

 

   

 

 

và

1 13 7 13

;

2 2

 

   

 

 

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 34

Bài 83. TS LỚP 10 Kiên Giang 2015 – 2016

Cho parabol







y x

và đường thẳng





: 2 1

a y x

  

c) Vẽ





và

trên cùng một hệ trục toạ độ.

d) Xác định đường thẳng





biết đường thẳng





song song với đường thẳng





và cắt

parabol





tại điểm có hoành độ bằng



Lời giải:

a) Parabol có đỉnh gốc

đi qua hai điểm









2;2 , 2;2 ,

A B đường thẳng đi qua hai điểm









1; 1 , 0;1

C D

y=-2x+1

-2

-1

b) Vì









d a





: 2

d y x b

   

(

khác

)

Gọi





0 0

;

N x y

là giao điểm của





và





ta có

 

( ) 2

N P y

  

( ) 2 2( 2) 2( )

        

N d b b TM

0,25

Vậy





: 2 2

d y x

  

Bài 84. TS LỚP 10 Lạng Sơn 2015 – 2016

a) Vẽ đồ thị của các hàm số

y x



và

3 2

y x

 

trên cùng một hệ trục tọa độ

b) Xác định tọa độ các giao điểm của hai đồ thị trên.

Lời giải:

a) Vẽ đồ thị trên cùng một hệ trục

Vẽ

y x





y x



Vẽ

3 2

y x

 

Cho

0 2

x y

   

; cho

1 1

x y

  

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 35

-2 2-1

b) Tính tọa độ giao điểm

Ta có phương trình hoành độ giao điểm:

3 2

x x

 

3 2 0

x x

   

có

1 3 2 0

a b c

     

nên phương trình có nghiệm

1 2

1; 2

x x

 

Tại



ta có



, tọa độ thứ nhất là





1;1

Tại



ta có



, tọa độ thứ 2 là





2;4

Bài 85. TS LỚP 10 Long An 2015 – 2016

Cho các hàm số





P y x

 

và





: 2 3.

d y x

 

a) Vẽ đồ thị của hai hàm số đã cho trên cùng một mặt phẳng tọa độ

Oxy

b) Tìm tọa độ giao điểm của hai đồ thị trên bằng phép tính .

c) Viết phương trình đường thẳng





d y ax b

 

, biết rằng





song song với





và





cắt

trục tung tại điểm có tung độ bằng



Lời giải:

a) Vẽ đồ thị của hai hàm số đã cho trên cùng một mặt phẳng tọa độ

Oxy

y=-x

-1

-2 -1

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 36

b) Tìm tọa độ giao điểm của hai đồ thị bằng phép tính.

Phương trình hoành độ giao điểm của





và





là:

2 2

1 2

2 3 2 3 0

1; 3

      

   

x x x x

x x

* Với

1 1

x y

    

giao diểm thứ nhất là





1; 1



* Với

3 9

x y

     

giao diểm thứ hai là





3; 9

 

c) Viết phương trình đường thẳng





d y ax b

 

, biết rằng





song song với





và





cắt

trục tung tại điểm có tung độ bằng



Đường thẳng





d y ax b

 

song song đường thẳng





: 2 3

d y x

 









 



 Phương trình đường thẳng





: 2

d y x b

 

Vì đường thẳng





: 2

d y x b

 

cắt trục tung tại điểm có tung độ bằng



  

(thỏa mãn)

Suy ra phương trình đường thẳng





là

2 4.

y x

 

Bài 86. TS LỚP 10 Thái Bình 2015 – 2016

Cho parabol





P y x



và điểm

A B

thuộc





có hoành độ lần lượt là

1;2.



Đường thẳng





có phương trình

y mx n

 

e) Tìm toạ độ điểm

A B

. Tìm

m n

biết

( )

đi qua điểm

và

f) Tính độ dài đường cao

của tam giác

OAB

(điểm

là gốc tọa độ).

Lời giải:

a) Ta có:

( ; ) ( )



A A

A x y P

có hoành độ

1 1 1

1 .( 1) 1;

2 2 2

 

       

 

 

A A

x y A

( ; ) ( )



B B

B x y P

có hoành độ

 

2 .2 2 2;2

    

B B

x y B

Vì đường thẳng

y mx n

 

đi qua 2 điểm

và

nên ta có hệ:

1 3 1

2 2 2

2 2 2 2 1

2. 2





  



    

   

  

   

   

    

 

  





m n m m

m n m n n

Vậy với

, 1

m n

 

thì





đi qua 2 điểm

 

1; ; 2;2

 



 

 

A B

b) Vẽ





và





trên cùng 1 hệ trục tạo độ như hình vẽ

Dễ thấy





cắt

tại





2;0

C  và cắt

tại





0;1 2; 1

D OC OD

  

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 37

Độ dài đường cao

của tam giác

OAB

chính là độ dài đường cao

của tam giác

OCD

Áp dụng hệ thức lượng trong tam giác vuông

OCD

ta có:

2 2 2

1 1 1 1 1 5

4 1 4

4 2 5

( )

5 5

    

   

OH OC OD

OH OH dvdt

Vậy

2 5

( )

OH dvdt



Bài 87. TS LỚP 10 Thanh Hóa 2015 – 2016

Trong mặt phẳng tọa độ

Oxy

cho đường thẳng





: 1

d y x m

  

và parabol





P y x



a) Tìm

để





đi qua điểm





0;1

b) Tìm

để đường thẳng





cắt parabol





tại hai điểm phân biệt có hoành độ lần lượt là

thỏa mãn:

1 2

1 1

4 3 0

 

   

 

 

x x

Lời giải:

a) Thay

0; 1

x y

 

vào phương trình đường thẳng





ta được:



b) Phương trình hoành độ giao điểm của





và





là:









1 0 *

x x m  

Để





cắt parabol





tại hai điểm phân biệt thì phương trình (*) phải có 2 nghiệm phân biệt

4 3 0

      

m m

Khi đó theo định lý Vi-ét ta có:

1 2

( 1)

x x

x x m

 





  



Theo đề bài:

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 38

1 2

1 2 1 2

1 1

4 3 0 4 3 0

2 0

6 0 ( : m 1)

3( )

2( )

   



       

   

   

   

 

    

 











x x

x x x x

m m DK

m L

m TM

Vậy



là giá trị cần tìm.

Bài 88. TS LỚP 10 Tiền Giang 2015 – 2016

Cho parabol

( ) :

P y x



và đường thẳng

( ) :d y x

  

g) Vẽ đồ thị của





và





trên cùng mặt phẳng tọa độ.

h) Bằng phép tính, xác định tọa độ các giao điểm

A B

của





và





i) Tìm tọa độ điểm

trên cung

của đồ thị





sao cho tam giác

AMB

có diện tích lớn

nhất.

Lời giải:

a) Vẽ đồ thị





và





như hình vẽ

b) Phương trình hoành độ giao điểm của





và





2 2

2 2 0

x x x x

      

 

hoặc

 

Nếu

 

thì







2;4

A 

Nếu



thì





1 1;1

y B 

c) Gọi





;

M M

M x y

là điểm thuộc parabol





cung

sao cho diện tích tam giác

AMB

lớn

nhất.

Điều kiện:

2 1

  

và

0 4

 

Từ

, kẻ

MH AB



tại

, ta có:

+ Phương trình đường thẳng

: – 2.

AB y x

 

+ Phương trình đường thẳng

có dạng:

y ax b

 

. Đường thẳng này vuông góc với

Suy ra





. 1 1

  

. Suy ra:



, đường thẳng

có phương trình

y x b

 

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 39

+ Phương trình hoành độ giao điểm giữa





và

2 2

: 0.

MH x x b x x b

    



( 1) 4.1.( ) 1 4

0 1 4 0

      



      

b b

Do đó:

có phương trình:

y x

 

+ phương trình hoành độ giao điểm giữa

và

1 9

4 8

     

x x x

Khi đó:

9 1 7

8 4 8

  

và

9 7

;

8 8

 

 

 

+ Phương trình hoành độ giao điểm giữa (P) và MH:

2 2

1 1

4 4

x x x x

     

phương trình có nghiệm kép:



(thỏa điều kiện)

Khi đó:

1 1 1 1

4 2 4 4

y x

    

(thỏa điều kiện)

Vậy:

1 1

;

2 4

 

 

 

Khi đó:

2 2

1 9 1 7 25 5

( ) ( ) 2

2 8 4 8 32 8

   

         

   

   

M H M H

MH x x y y

2 2

3 3 3 2

AB   

Diện tích tam giác

AMB

là

1 1 5 15

. . .3 2. 2 ( )

2 2 8 8

AMB

S AB MH dvdt

  

Bài 89. TS LỚP 10 Hà Nam 2015 – 2016

Trong mặt phẳng tọa độ

Oxy

cho Parabol





P y x

 

và đường thẳng





: 3 3

d y mx

 

(với

là tham số).

a) Tìm

để đường thẳng





đi qua điểm





1;3 .

b) Xác định các giá trị của

để





cắt





tại hai điểm phân biệt sao cho tổng 2 tung độ của

hai giao điểm đó bằng

10.



Lời giải:

a) Đường thẳng





đi qua





1;3

A nên

3 3 .1 3 2.

m m

   

b) Phương trình hoành độ giao điểm của đường thẳng





và Parabol





là:





2 2

3 3 3 3 0 *

x mx x mx      

Ta có

9 12 0

   

, với mọi

nên phương trình (*) có hai nghiệm phân biệt.

Do đó, đường thẳng





và Parabol





cắt nhau tại hai điểm





1 1

;

x y

và





2 2

;

x y

Theo định lý Vi-ét ta có:

1 2 1 2

3 ; . 3.

x x m x x

    

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 40

Theo bài ra ta có:

2 2

1 2 1 2

10 10

( ) 2 10

9 6 10

       

   

  

  

y y x x

x x x x

Bài 90. TS LỚP 10 Trà Vinh 2015 – 2016

Cho hai hàm số

2 3

y x

 

và

y x



có đồ thị lần lượt là





và





j) Vẽ





và





trên cùng một hệ trục tọa độ

Oxy

k) Tìm tọa độ giao điểm của





và





bằng phép toán.

Lời giải:

a) Bảng giá trị:



0 1 2

2 3

y x

 

3 5

y x



4 1 0 1 4

Đồ thị

b) Phương trình hoành độ giao điểm của





và





2 2

2 3 2 3 0

x x x x

     









1 3 0 1

x x x

      

hoặc



Với





1 1 1

x y

     

; với

3 3 9

x y

   

Vậy tọa độ giao điểm của





và





là





–1;1

và





3;9

Bài 91. TS LỚP 10 Vĩnh Long 2015 – 2016

Trong mặt phẳng tọa độ

Oxy

, cho parabol

( ) :

P y x



và đường thẳng





: 2 1( )

5 2

d y m x m

    (

là tham số)

l) Vẽ đồ thị parabol





ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 41

m) Biết đường thẳng





luôn cắt parabol





tại hai điểm phân biệt. Gọi hoành độ giao điểm của

đường thẳng





và parabol





là

1 2

x x

. Tìm

để

2 2

1 2

x x

 

Lời giải:

a) Vẽ đồ thị

Bảng giá trị:



0 1 2

y x



4 1 0 1 4

Đồ thị:

-2 2-1

Phương trình hoành độ giao điểm của





và





2 2

2( 1) 5 2 2( 1) 2 5 0

         

x m x m x m x m

Theo định lý Vi-ét:

1 2

2 2

2 5

  





 



x x m

Theo đề bài, ta có:

     

2 2

2 2 2

1 2 1 2 1 2

6 2 6 2 2 2 2 5 6 4 12 8 0





               







x x x x x x m m m m

Vậy:



hoặc



Bài 92. TS LỚP 10 Phú Thọ 2015 – 2016

Cho parabol





P y x



và đường thẳng





có phương trình:





2 1 3 2

y m x m

   

a) Tìm tọa độ giao điểm của





và





với



b) Chứng minh





và





luôn cắt nhau tại 2 điểm phân biệt

và

với mọi

c) Gọi

1 2

;

x x

là hoành độ giao điểm của

và

. Tìm

để

2 2

1 2

x x

 

Lời giải:

a) (1 điểm)

Thay



ta được





: 8 7

d y x

 

Phương trình hoành độ giao điểm





và





khi



là

2 2

8 7 8 7 0

x x x x

     

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 42

Giải phương trình ta được

1 2

1; 7

x x

 

Tọa độ giao điểm của





và





là









1;1 ; 7;49

b) (0,5 điểm)

Xét phương trình hoành độ giao điểm của





và





là:





2 1 3 2 0

x m x m

    

(1)

2 2

1 11

2 1 3 2 3 0

2 4

 



             

 

 

m m m m m m m

Nên phương trình (1) có hai nghiệm phân biệt



suy ra





và





luôn cắt nhau tại 2 điểm

phân biệt

A B

với mọi

c) (0,5 điểm)

Ta có:

1 2

;

x x

là nghiệm phương trình (1) vì



 



. Theo Vi-et ta có:

1 2

2 2

3 2

x x m

  





 



2 2 2 2

1 2 1 2 1 2

20 ( ) 2 20 (2 2) 2(3 2) 20

2 6 0 ( 2)(2 3)

          







       

 







x x x x x x m m

m m m m

Bài 93. TS LỚP 10 An Giang 2015 – 2016

Cho hàm số

y x



có đồ thị là Parabol





a) Vẽ đồ thị hàm số đã cho trên mặt phẳng tọa độ

Oxy

b) Viết phương trình đường thẳng





đi qua điểm nằm trên Parabol





có hoành độ



và

có hệ số góc

Với giá trị

nào thì





tiếp xúc





Lời giải:

Bảng giá trị:



0 1 2

y x



4 1 0 1 4

Đồ thị hàm số là hình vẽ

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 43

-2 2-1

b) Đường thẳng





có hệ số góc

nên có dạng

y kx b

 

Điểm thuộc





có hoành độ

2 4

x y

  





qua





2;4 4 .2 2 4

k b b k

      

Suy ra





: 2 4

d y kx k

  

Đường thẳng





tiếp xúc





khi đó phương trình sau có nghiệm kép

2 4

x kx k

  

2 4 0

x kx k

    

8 16

k k

   

Phương trình có nghiệm kép khi

0 8 16 0 4

k k k

       

Vậy



Bài 94. TS LỚP 10 Cần Thơ 2015 – 2016

Trong mặt phẳng với hệ tọa độ

Oxy

, cho





y x





a) Vẽ đồ thị của





b) Gọi





1 1

A x y

và





2 2

;

B x y

là hoành độ giao điểm của





và





: 4

d y x

 

. Chứng minh:





1 2 1 2

5 0

   

y y x x

Lời giải:





y x





Phương trình hoành độ giao điểm của





và





2 2

4 2 8 0



     

x x x x

Giải phương trình ta được:

2; 4

x x

  

Tọa độ giao điểm là:





2; 2



và





4; 8

 

Khi đó:













1 2 1 2

5 2 8 5 2 4 0

         

y y x x .

-2

-1

0 1

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 44

Bài 95. TS LỚP 10 Bình Phước 2014– 2015

Cho parabol





P y x

 

và đường thẳng

: 3 2

d y x

 

a) Vẽ parabol





và đường thẳng

trên cùng một hệ trục toạ độ.

b) Viết phương trình đường thẳng



vuông góc với đường thẳng

và tiếp xúc với





Lời giải:

a) + Bảng một số giá trị của







0 1 2

y x









đi qua 2 điểm





0;2

và





1; 1

 

+ Đồ thị:



có dạng :

y a x b

 

 

;

. 1

 

   

d d a a

với



1 1

3 3

 

  

    

a d y x b

Phương trình hoành độ giao điểm của





và



2 2

1 1

(*)

3 3



 

    x b x x bx

PT (*) có



  

tiếp xúc với





khi

4 0



   



 b

Vậy



có phương trình:

1 1

3 36



 y x

Bài 96. TS LỚP 10 Đà Nẵng 2014– 2015

Cho hàm số

y x



có đồ thị





và hàm số 4

y x m

 

có đồ thị





a) Vẽ đồ thị





b) Tìm tất cả các giá trị của

sao cho





và





cắt nhau tại hai điểm phân biệt, trong đó

tung độ của một trong hai giao điểm đó bằng 1.

Lời giải:

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 45

a) Vẽ đồ thị





-2 2-1

b) Phương trình hoành độ giao điểm của

y x



và đường thẳng 4

y x m

 

là :





2 2

4 4 0 1

x x m x x m     

(1) có

  

Để





và





cắt nhau tại hai điểm phân biệt thì

0 4 0 4

m m



       

4 1

y x m

  

 



Yêu cầu của bài toán tương đương với

4 4 4

1 7 7

2 4 4 4

4 4 4

4 4

7 ( ) 7

4 4 7

2 15 0

3 5

     

  

  



  

    

       

  

  



 

   

 

    

 

 

 

  





 



 







  



 





    

 















m m m

hay

m m m

m m

m L hay m

m m

m hay m

Bài 97. TS LỚP 10 Hà Nam 2014– 2015

Trong mặt phẳng tọa độ

Oxy

cho Parabol





có phương trình

y x



và đường thẳng





có

phương trình: 2

y x m

  

(với

là tham số).

a) Tìm giá trị của

để





cắt





tại điểm có hoành độ là 2.

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 46

b) Tìm giá trị của

để





cắt tại hai điểm phân biệt có hoành độ

1 2

;

x x

thỏa mãn hệ thức

2 2 2 2

1 2 1 2

6 

x x x x

Lời giải:

a) Điểm thuộc Parabol





P y x



có hoành độ



nên tung độ

2 4

 





cắt





tại điểm có hoành độ bằng 2

4 2.2 8

m m

     

Vậy



là giá trị cần tìm

b) Phương trình hoành độ giao điểm của





và





là:





2 2

2 2 0 *

x x m x x m      





cắt





tại hai điểm phân biệt

1 0 1

m m



       

Với

 

thì





cắt





tại hai điểm phân biệt có hoành độ

1 2

;

x x

Nên theo hệ thức Vi-ét:

1 2

  





 



x x

x x m

mà

2 2 2 2 2

1 1 1 2 1 2 1 2

( ) 2 6    

x x x x x x x x

2 2 2

1 2

( 2) 2( ) 6( ) 3 2 0 1;



            m m m m m m

Vậy

1 2



 m m là các giá trị cần tìm.

Bài 98. TS LỚP 10 Hà Nội 2014– 2015

Trên mặt phẳng tọa độ

Oxy

cho đường thẳng





: 6

d y x

  

và parabol





: .

P y x



a) Tìm tọa độ các giao điểm của





và





b) Gọi

A B

là hai giao điểm của





và





Tính diện tích tam giác

OAB

Lời giải:

a) Phương trình hoành độ giao điểm của





và





là:

6 0

x x

  

25 0

   

phương trình có 2 nghiệm phân biệt

2; 3

x x

  

Với





2 4 2;4

x y A   

Với





3 9 3;9

x y B     

Vậy

cắt





tại 2 điểm phân biệt





2;4

và





3;9

 .

b) Gọi

A B

 

lần lượt là hình chiếu của

và

xuống trục hoành.

Ta có

   

  

  

OAB AA B B OAA OBB

S S S S

Ta có :

| | 5, 9; 4

   

        

B A B A A B

A B x x x x AA y BB y

Diện tích hình thang :

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 47

9 4 65

. .5 ( )

2 2 2

1 27

. ( )

2 2

. 4( )

65 27

4 15( )

2 2

 









   

  

 

 

 

  

 

 

 

 

      

AA B B

OAA

OBB

OAB AA B OAA OBB

AA BB

S A B dvdt

S A A A O dvdt

S B B B O dvdt

S S S S dvdt

Bài 99. TS LỚP 10 Kon Tum 2014– 2015

a) Vẽ đồ thị hai hàm số:

y x



và

y x

 

trên cùng hệ trục tọa độ

Oxy

b) Xác định đường thẳng

y ax b

 

biết rằng đường thẳng này song song với đường thẳng

3 5

y x

  

và cắt Parabol

y x

 tại điểm

có hoành độ bằng



Lời giải:

a) Gọi





và





là đồ thị của 2 hàm số :

y x



và

y x

 

y x



x -1 0

y 1 0

y x

 

x 0 -2

y 2 0

y=x

-2 2-1

b) Phương trình đường thẳng







có dạng

y ax b

 

Vì







songsong với đường thẳng

3 5

y x

  

  

và





5 ' : 3

b d y x b

    

thuộc Parabol:

y x







2 1 2

   

Suy ra tọa độ









1;2

A d



 









2 3 . 1

    





1 ' : 3 – 1

b d y x     

Bài 100. TS LỚP 10 Long An 2014– 2015

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 48

Trong mặt phẳng tọa độ

Oxy

cho Parabol





P y x



và đường thẳng





: 2.

d y x

  

a) Hãy vẽ





và





trên cùng một mặt phẳng tọa độ

Oxy

b) Tìm tọa độ giao điểm của





và





c) Viết phương trình đường thẳng





d y ax b

 

. Biết rằng





song song với





và cắt





tại điểm

có hoành độ là

Lời giải:

a) Hãy vẽ





và





b) Tìm tọa độ giao điểm của





và





Dựa vào đồ thị hàm số ta có: hai giao điểm





1;1

và





2;4





song song với





d a

  

Ta có





2;4

A thuộc





2 4 6

P a b b

    

Vậy





y x

  

Bài 101. TS LỚP 10 Thái Bình 2014– 2015

Cho parabol





P y x



và đường thẳng









: 2 3 2 2

d y m x m

   

(

là tham số).

a) Với

 

, tìm tọa độ giao điểm của parabol





và đường thẳng





b) Chứng minh rằng: với mọi

parabol





và đường thẳng





cắt nhau tại hai điểm phân

biệt. Tìm

sao cho hai giao điểm đó có hoành độ dương.

c) Tìm điểm cố định mà đường thẳng





luôn đi qua với mọi

Lời giải:

a) Với

 





có phương trình

4 12

y x

  

Hoành độ giao điểm của





và





là nghiệm phương trình:

2 2

4 12 4 12 0 ( 6)( 2) 0

 



           







x x x x x x

6 36

2 4

    

   

x y

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 49

Vậy với

 

thì





và





cắt nhau tại hai điểm









6;36 , 2;4 .



b) Hoành độ giao điểm của





và





là nghiệm phương trình:









2 2

2 3 2 2 2 3 2 2 0(1)

         x m x m x m x m

2 2 2

( 3) (2 2) 4 11 ( 2) 6 0



            

m m m m m m

Do đó (1) có hai nghiệm phân biệt với mọi

suy ra





và





cắt nhau tại hai điểm phân biệt

1 2

;

x x

là hai nghiệm của phương trình (1), áp dụng định lý Viet ta có:

1 2

2( 3)

2 2

x x m

  





 



Hai giao điểm đó có hoành độ dương khi và chỉ khi





1 2

2 3 0

0 1

2 2 0

 

 

 





   

  

 

 





x x

x x m

Vậy với



thì





và





cắt nhau tại hai điểm phân biệt với hoành độ dương.

c) Gọi điểm cố định mà đường thẳng





đi qua với mọi

là





0 0

;

x y

ta có:





 

0 0

0 0 0

0 0

0 0 0

2 3 2 2

2 2 6 2 0

2 2 0 1

6 2 0 8

    

      

  

 

 

 

   

 

y m x m m

m x x y m

x x

x y y

Vậy với mọi

thì đường thẳng





luôn đi qua





1;8 .

Bài 102. TS LỚP 10 Thanh HÓa 2014– 2015

Trong mặt phẳng tọa độ

Oxy

cho đường thẳng





: 3

d y mx

 

tham số

và Parabol





: .

P y x



a) Tìm

để đường thẳng





đi qua điểm





1;0 .

b) Tìm

để đường thẳng





cắt Parabol





tại hai điểm phân biệt có hoành độ lần lượt là

1 2

;

x x

thỏa mãn

1 2

x x

 

Lời giải:

a) Đường thẳng





đi qua điểm





1;0

A nên có

0 .1 3 3

m m

   

b) Xét phương trình hoành độ giao điểm giữa





và





3 0

x mx

  

Có

  





cắt





tại hai điểm phân biệt có hoành độ lần lượt là

1 2

x x

khi

2 2

2 3

12 0 12

2 3





      



 





m m

Áp dụng hệ thức Vi – Ét ta có:

1 2

 









x x m

x x

Theo bài ra ta có

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 50









2 2

1 2 1 2 1 2 1 2

2 2

2 4 4 4

4.3 4 16 4

        

       

x x x x x x x x

m m m

Vậy

 

m là giá trị cần tìm.

Bài 103. TS LỚP 10 Thừa Thiên Huế 2014– 2015

Cho hàm số

y ax

 có đồ thị





và đường thẳng





: – 3

d y mx m 

a) Tìm

để đồ thị





đi qua điểm





2; 2



b) Chứng minh rằng đường thẳng





luôn cắt đồ thị





tại hai điểm phân biệt

và

với

mọi giá trị của

c) Gọi

và

lần lượt là hoành độ của hai điểm

và

Tìm các giá trị của

sao cho

2 2

2 20 0

C D C D

x x x x

   

Lời giải:





đi qua điểm





2; 2



nên ta có:

2 .2



   a a

Vậy





y x





b) Phương trình hoành độ giao điểm của





và





là:

   

2 2

3 2 2 6 0(*)

2 6 2 6 1 5 0



       



           

x mx m x mx m

m m m m m m

Do đó, đường thẳng





luôn cắt đồ thị





tại hai điểm phân biệt

và

với mọi giá trị của

c) Áp dụng định lí Vi-ét ta có:

2 6

C D

x x m

  





 



Theo giả thiết

 

2 2

2 20 0 4 20 0

( 2 ) 4(2 6) 20 0 4 8 4 0

4( 1) 0 1

        

         

    

C D C D C D C D

x x x x x x x x

m m m m

m m

Vậy với



thỏa mãn yêu cầu bài toán.

Bài 104. TS LỚP 10 Tiền Giang 2014– 2015

Trong mặt phẳng tọa độ cho Paradol





P y x



và đường thẳng





: 2

d y x

 

a) Vẽ





và





trên cùng một hệ trục tọa độ.

b) Tìm tọa độ giao điểm

và

của





và





bằng phép tính.

c) Tính độ dài đoạn

Lời giải:

a) Vẽ





và





Lập bảng giá trị (có ít nhất 5 giá trị)



0 1 2

4 1 0 1 4

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 51

y=x

-2 2-1

Phương trình hoành độ giao điểm của





và





là:

2 2

2 2 0

     

x x x x

Ta có:





1 1 2 0

a b c    

 

nên phương trình có nghiệm 2 nghiệm

1 2

1; 2

x x

  

Từ đó tính được:

1 2

1; 4

y y

 

Vậy tọa độ giao điểm giữa





và





là:









1;1 ; 2;4

A B

Áp dụng công thức tính khoảng cách ta có:

   

2 2

3 3 18 3 2( )

       

B A B A

AB x x y y dvdt

Bài 105. TS LỚP 10 Bà Rịa Vũng Tàu 2014– 2015

Cho parabol





: 2

P y x

 và đường thẳng





: 1

d y x m

  

(với

là tham số)

a) Vẽ Parabol





b) Tìm tất cả các giá trị của

để





cắt





có đúng một điểm chung.

c) Tìm tọa độ các điểm thuộc





có hoành độ bằng hai lần tung độ.

Lời giải:

a) Vẽ đồ thị hàm số:



0 1 2

y x



8 2 0 2 8

ThS.Nguyễn Đăng Tuấn Chuyên đề luyện thi vào lớp 10

Trang 52

b) Xét phương trình hoành độ giao điểm cả





và





   

2 2

2 1 2 1 0

1 4.2. 1 9 8

       

      

x x m x x m

m m

Để





và





có một điểm chung thì :

0 9 8 0

m m

      

Vậy với



thì





và





có một điểm chung.

c) Điểm thuộc





mà hoành độ bằng hai lần tung độ nghĩa là

x y



nên ta có:

 

2 2 8







   









y y y y

Vậy điểm thuộc





mà hoành độ bằng hai lần tung độ là

 

1 1

;

4 8

0;0 ;

 

 

 

__________ THCS.TOANMATH.com __________

Bấm Tải xuống để xem toàn bộ.

| 1/52

| | Tải xuống

Preview text:

ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10 HÀM SỐ VÀ ĐỒ THỊ I. Hàm số bậc nhất Bài 1.
TS Lớp 10 Bắc Giang 2017-2018
Tìm m để đồ thị hàm số y  2x  m đi qua điểm K 2;3 . Lời giải:
+ Đồ thị hàm số y  2x  m đi qua điểm K (2;3)  3  4  m  m  1 + Vậy m  1  . Bài 2. TS Lớp 10 Gia Lai 2017-2018
Tìm tất cả các giá trị của m để hàm số 2
y  (m  m  2017)x  2018 đồng biến trên  . Lời giải:
Hàm số đồng biến trên  khi và chỉ khi a  0 2
 m  m  2017  0, với mọi m 2  1  8067  m    0,   với mọi m  2  4
Điều này luôn thỏa mãn.
Vậy khi với mọi giá trị của m thì hàm số luôn đồng biến trên  . Bài 3.
TS Lớp 10 Hải Dương 2017-2018
Cho hai đường thẳng d  : y  x  m  2 v à d : 2
y  (m  2)x  3. T ìm m để d  và
d song song với nhau. Lời giải:
Điều kiện để hai đồ thị song song là 2 1  m  2 m  1    m  2  3 m  1 Loại m  1, chọn m  1  . Bài 4.
TS Lớp 10 Phú Thọ 2016-2017
Cho hàm số y  (2m  1)x  m  4 (m là tham số) có đồ thị là đường thẳng (d).
a) Tìm m để (d) đi qua điểm ( A 1;2) .
b) Tìm m để (d) song song với đường thẳng (Δ) có phương trình: y  5x  1.
c) Chứng minh rằng khi m thay đổi thì đường thẳng (d) luôn đi qua một điểm cố định. Lời giải:
a) Ta có (d) đi qua điểm ( A 1  ;2)  2  (2m 1)( 1  )  m  4 .
 2  m  3  m  1. Trang 1 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10 2m 1  5 b) Ta có (d )//()   m  4  1  m  2 .
c) Giả sử M (x ; y ) là điểm cố định của đường thẳng (d). 0 0 Khi đó ta có:
y  (2m 1)x  m  4 m
  (2x 1)m  x  y  4  0 m  0 0 0 0 0  1    2x 1  0 x  0 0   2    x  y  4  0  7 0 0 y  0  2  1 7 
Vậy khi m thay đổi đường thẳng (d) luôn đi qua điểm cố định M  ;   .  2 2  Bài 5.
TS Lớp 10 Quãng Ninh 2016-2017
Tìm giá trị của m để hai đường thẳng (d ) : mx  y  1 và (d ) : x  my  m  6 cắt nhau tại một 1 2
điểm M thuộc đường thẳng (d) : x  2 y  8. Lời giải: m 1
Để hai đường thẳng (d1), (d2) cắt nhau thì 2   m  1  luôn T/M với mọi m . 1 m
(d) : x  2 y  8  x  8  2 y (1) 1 y
(d ) : mx  y  1  m  1 x x  6
(d ) : x  my  m  6  m  (2) 2 1 y 1 y x  6 Do đó 2 2  1 y  x  6x x 1 y 2 2  x  6x  y 1  0 (3)
Thay (1) vào (3) ta được tung độ giao điểm M là nghiệm PT:  y2   y 2 8 – 2 – 6 8 2  y 1 2  5y – 20y 15  0  y  1 hoặc y  6 1 2 Trang 2 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10
Với y  1 x  6 thay (6; 1) vào (2) ta được m  0 (TMĐK) 1 1
Với y  3  x  2 thay (2; 3) vào (2) ta được m  1  (TMĐK) 2 2
Vậy với m  0 hoặc m  1
 thì hai đường thẳng d và (d ) cắt nhau tại một điểm M thuộc 1  2 đường thẳng d  . Bài 6.
TS Lớp 10 Hà Tĩnh 2016-2017
Trong mặt phẳng tọa độ Oxy cho hai đường thẳng d  : y  ax  a 1 và d y   2 :
a – 3a  3 x  3 – . a
a) Tìm a để d  đi qua A1;3 .
b) Tìm a để d  song song với d. Lời giải:
a) * Nếu a  0 thì đường thẳng y  1 không đi qua điểm A1;3
* Nếu a  0 thì d  đi qua A1;3  3  . a 1 a 1  a  1 a  0  2
a  3a  3  0(Loai) a 1 3 a  
b) d  // d  a  0  a  3  2 a  3a  3  0  2 a  3a  3  a  a 1  3  a
Vậy a  3 thì d  // d . Bài 7.
TS lớp 10 Hưng Yên 2016– 2017
Tìm m để hàm số bậc nhất y  m  2 x 1, (m  2) đồng biến trên  . Lời giải:
Để hàm số y  m – 2 x –1 đồng biến thì m – 2  0  m  2. Vậy m  2. Bài 8.
TS lớp 10 Hải Dương 2015– 2016
Cho hai hàm số y  (3m  2)x  5 với m  1 và y  x 1 có đồ thị cắt nhau tại điểm A ; x y.
Tìm các giá trị của m để biểu thức 2
P  y  2x  3 đạt giá trị nhỏ nhất. Lời giải:  2 2 
Với m  1 hai đồ thị cắt nhau tại điểm A ; 1    m 1 m 1  2  2   2 2  P  y  2x  3  1  2  3      m 1   m 1 2 Đặt t 
ta được P  t  t   t  2 2 4 2 2  6  6  m 1 Trang 3 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10 2 P  6  t  2   2  m  0 m 1
Vậy m  0 thì biểu thức 2
P  y  2x  3 đạt giá trị nhỏ nhất Bài 9.
TS lớp 10 Hưng Yên 2015– 2016
Xác định toạ độ các điểm A và B thuộc đồ thị hàm số y  2x  6 , biết điểm A có hoành độ bằng
0 và điểm B có tung độ bằng 0 . Lời giải:
Điểm A thuộc đường thẳng y  2x  6 , mà hoành độ x  0 Suy ra tung độ y  6.
Vậy điểm A có toạ độ ( A 0;  ) 6 .
Điểm B thuộc đường thẳng y  2x  6 , mà tung độ y  0 Suy ra hoành độ x  3.
Vậy điểm B có toạ độ B(3;0 . )
Bài 10. TS lớp 10 Thái Nguyên 2015 - 2016
Tìm giá trị của tham số k để đường thẳng d : y  x  2 cắt đường thẳng d : y  2x  3  k tại 1 2
một điểm nằm trên trục hoành. Lời giải:
Ta thấy hai đường thẳng d ; d luôn cắt nhau: 1 2
+ Đường thẳng d cắt trục hoành tại điểm A2;0 1  k  3 
+ Đường thẳng d cắt trục hoành tại điểm B ;0 2    2  k  3
+ Để hai đường thẳng d ; d cắt nhau tại một điểm trên trục hoành thì  2  k  7 . 1 2 2
Bài 11. TS lớp 10 Quãng Bình 2015 - 2016
Cho hàm số: y  m  
1 x  m  3 với m  1 ( m là tham số)
a) Tìm giá trị của m để đồ thị của hàm số đi qua điểm M 1; 4   .
b) Tìm giá trị của m để đồ thị của hàm số song song với đường thẳng d  : y  2  x 1. Lời giải: a) Cho phương trình: 2 x  m   2 – 2
1 x  m  m  2  0 (1) ( m là tham số). Ta có M 1; 4
  thuộc đồ thị hàm số  x 1; y  4 thay vào hàm số đã cho ta có: 4  m  
1 .1 m  3  4  m 1 m  3  4  2  2m  6  2m  m  3TMĐK 
Với m  3 thì đồ thị hàm số đã cho đi qua điểm M 1; 4   .
b) Để đồ thị hàm số đã cho song song với đường thẳng d  : y  2  x 1 khi và chỉ khi a  a ' m 1  2  m  1       m  1  b   b ' m  3  1 m  2 Vậy với m  1
 thì đồ thị hàm số y  m  
1 x  m  3 song song với đường thẳng d: y  2  x 1 . Trang 4 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10
Bài 12. TS lớp 10 TPHCM 06 – 07
Viết phương trình đường thẳng d  song song với đường thẳng y  3x 1 và cắt trục tung tại
điểm có tung độ bằng 4 . Lời giải:
đường thẳng d  song song với đường thẳng y  3x 1nên d  có dạng y  3x  bb 
d  cắt trục tung tại điểm có tung độ bằng 4 nên d  đi qua điểm A0,4 hay 4  3.0  b  b  4
Vậy phương trình đường thẳng d  y  3x  4
Bài 13. TS lớp 10 Bắc Giang 11 – 12
Tìm các giá trị của tham số m để hàm số bậc nhất y  m – 2 x  3 đồng biến trên  . Lời giải:
Để hàm số bậc nhất y  m – 2 x  3 đồng biến trên  thì m  2  0  m  2 .
Bài 14. TS lớp 10 Bình Thuận 11 – 12
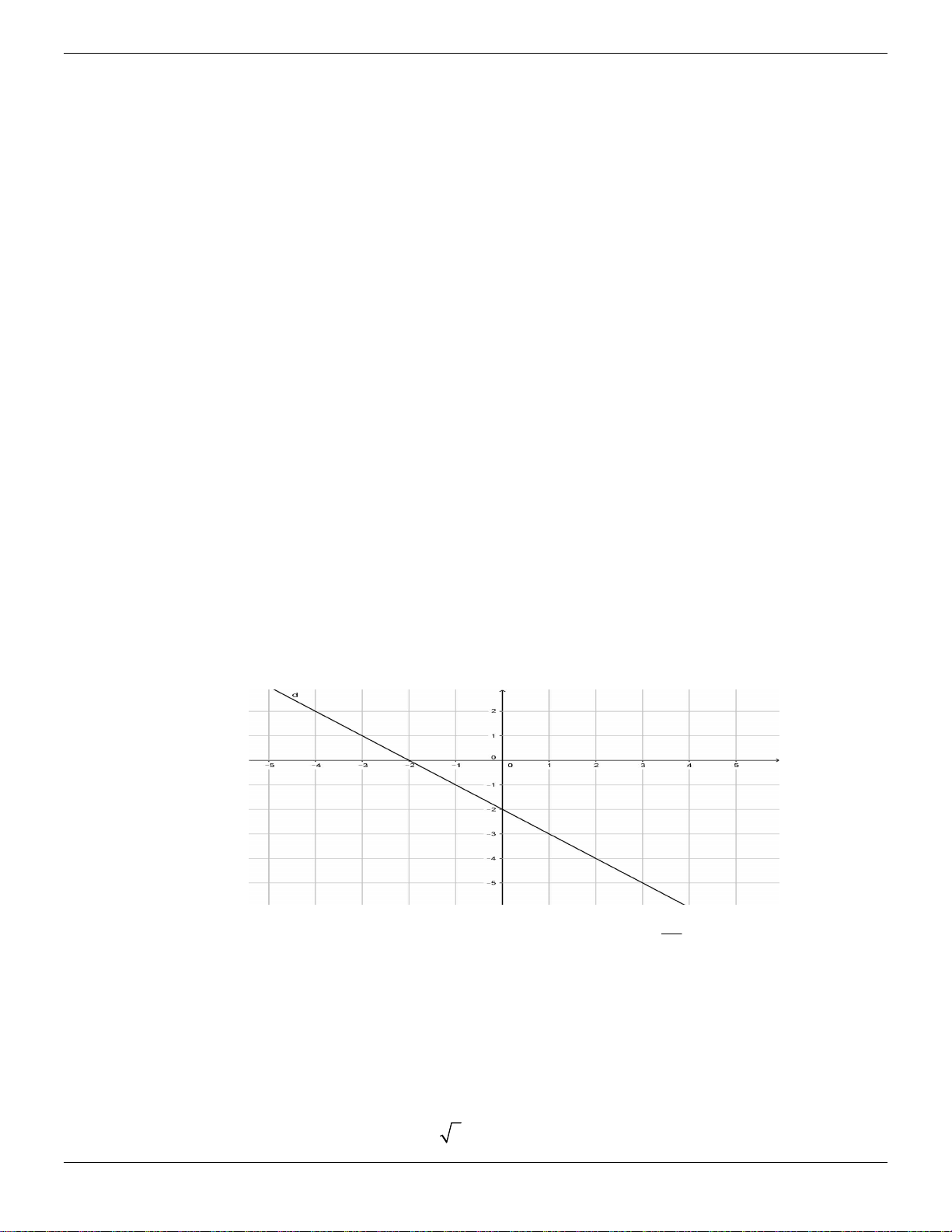
Cho hàm số bậc nhất y  – x – 2 có đồ thị là đường thẳng d 
a) Trong mặt phẳng tọa độ Oxy , hãy vẽ đường thẳng d 
b) Hàm số: y  2mx  n có đồ thị là đường thẳng d . Tìm m và n để hai đường thẳng d  và
d song song với nhau. Lời giải:
a) Ta có d  đi qua A0,2 ; B 2,0 nên đô thị hàm số là :  1 2m  1 m 
b) d  và d song song với nhau khi và chỉ khi    2 n  2 n  2
Bài 15. TS lớp 10 Cần Thơ 11 – 12
Xác định m để đường thẳng y   m 2 2 –
x  3m – m tạo với trục hoành một góc a  60 . Lời giải:
Để đường thẳng y   m 2 2 –
x  3m – m tạo với trục hoành một góc a  60 thì o o
2  m  tan 60  m  2  tan 60  2  3 . Trang 5 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10
Bài 16. TS lớp 10 Đăk Lăk 11 – 12
Với giá trị nào của m thì đồ thị của hai hàm số y  12x  7 – m và y  2x  3  m cắt nhau tại
một điểm nằm trên trục tung? Lời giải:
Để đồ thị của hai hàm số y  12x  7 – m và y  2x  3  m cắt nhau tại một điểm nằm trên  y  12.0   7 – m trục tung thì 
 7  m  3 m  2m  4  m  2 .  y  2.0   3  m
Bài 17. TS lớp 10 Hải Phòng 11 – 12
Xác định các hệ số a , b của hàm số y  ax  ba  0 biết đồ thị d  của hàm số đi qua A1;  1
và song song với đường thẳng y  –3x  2011 . Lời giải:
Để đồ thị d  của hàm số song song với đường thẳng y  –3x  2011 thì y  –3x  bb  201  1 .
Đồ thị d  đi qua A1; 
1 nên 1  3.1 b  b  4 . Vậy y  3  x  4
Bài 18. TS lớp 10 Hải Dương 11 – 12
Cho hai đường thẳng d : y  2x  5 ;d : y  –4x 1 cắt nhau tại I . Tìm m để đường thẳng 2  1 
d : y  m  1 x  2m –1 đi qua điểm I ? 3  Lời giải:  2 x   y  2x  5 
Tọa độ I là nghiệm của hệ 3     y  –4x 1 11  y   3 11 2
Do d đi qua điểm I nên  m   1  2m –1  m  4 . 3  3 3
Bài 19. TS lớp 10 Kiên Giang 11 – 12
Cho hàm số y  2 – m x – m  3 (1) ( m là tham số).
a) Vẽ đồ thị d  của hàm số khi m  1.
b) Tìm giá trị của tham số m để đồ thị hàm số (1) đồng biến. Lời giải:
a) Khi m  1 ta có y  x  2 đi qua A0,2 ; B 2,0 có đồ thị : Trang 6 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10
b) Để đồ thị hàm số (1) đồng biến thì 2  m  0  m  2 .
Bài 20. TS lớp 10 Quảng Trị 11 – 12
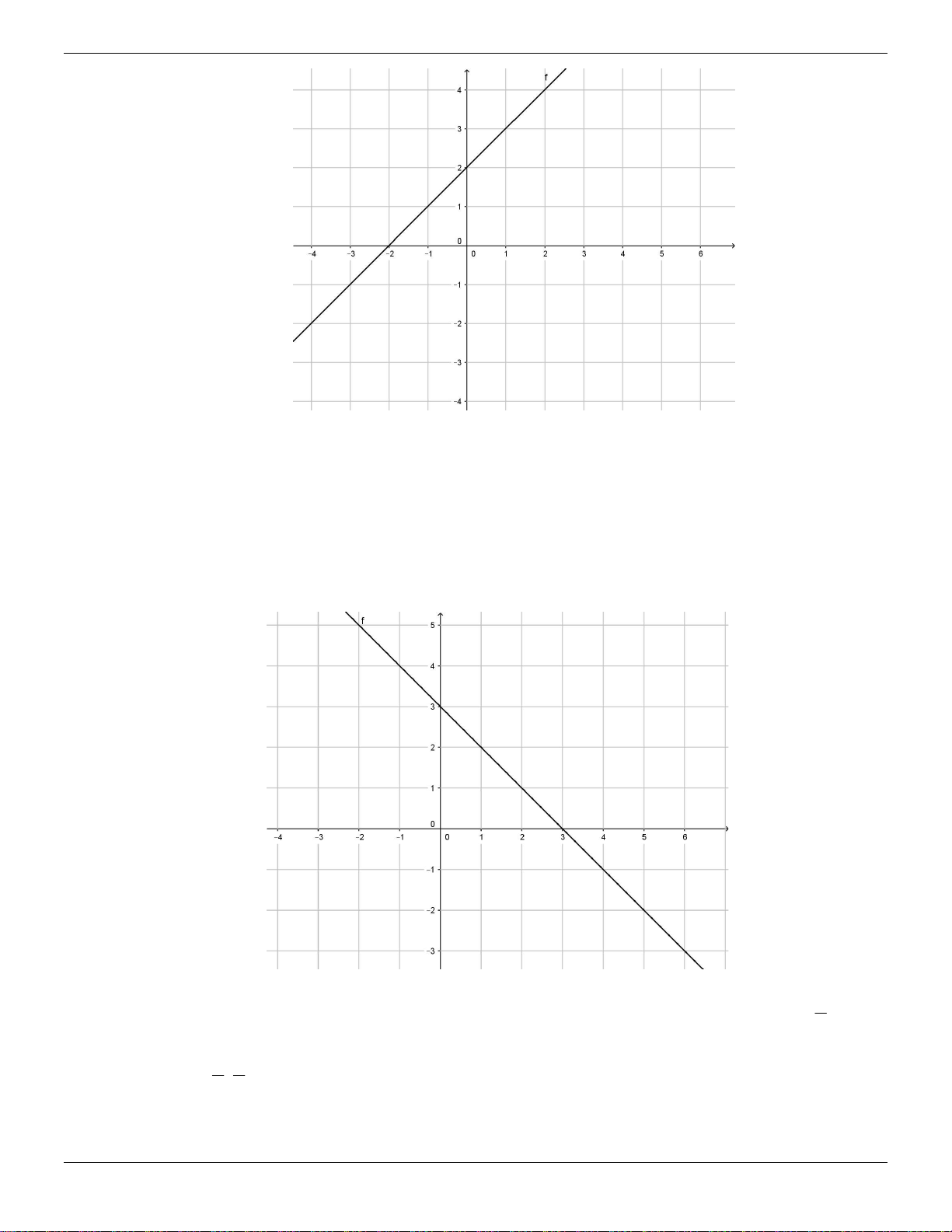
a) Vẽ đồ thị d  của hàm số y  –x  3 ;
b) Tìm trên d  điểm có hoành độ và tung độ bằng nhau. Lời giải:
a) Ta có y  – x  3 đi qua A0,3 ; B 3,0 có đồ thị : 3
b) Trên d  điểm có hoành độ và tung độ bằng nhau khi x  x  3  2x  3  x  y  2  3 3  Vậy M ,   .  2 2  Trang 7 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10
Bài 21. TS lớp 10 Ninh Bình 11 – 12
Cho hàm số: y  mx 1 (1), trong đó m là tham số.
a) Tìm m để đồ thị hàm số (1) đi qua điểm A1; 4 . Với giá trị m vừa tìm được, hàm số (1)
đồng biến hay nghịch biến trên  ?
b) Tìm m để đồ thị hàm số (1) song song với đường thẳng d  có phương trình: x  y  3  0 . Lời giải:
a) Ta có y  mx 1 đi qua A1; 4 khi và chỉ khi 4  m 1  m  3. Khi đó y  3x 1 đồng biến trên  .
b) Ta có x  y  3  0  y  x  3, đồ thị hàm số (1) song song với đường thẳng d  khi m  1   1   3 Vậy m  1  .
Bài 22. TS lớp 10 Quảng Ngãi 11 – 12
Trong cùng một hệ toạ độ Oxy cho ba điểm: A2;4 ; B –3; –  1 và C –2;  1 . Chứng minh ba
điểm A , B , C không thẳng hàng. Lời giải:
Ta có đường thẳng đi qua A2;4 và B –3; – 
1 có phương trình là y  x  2 không đi qua C –2;  1 vì 1  2
  2 hay ba điểm A , B ,C không thẳng hàng.
Bài 23. TS lớp 10 Quảng Ninh 11 – 12
Biết rằng đồ thị của hàm số y  ax – 4 đi qua điểm M 2; 5 . Tìm a . Lời giải: 9
Ta có đồ thị của hàm số y  ax – 4 đi qua điểm M 2; 5 nên 5  2.a 4  a  2
Bài 24. TS lớp 10 An Giang 12 – 13
Tìm giá trị của a , biết đồ thị hàm số y  ax –1 đi qua điểm A1;5 . Lời giải:
Ta có đồ thị của hàm số y  ax –1 đi qua điểm A1;5 nên 5  a –1  a  6 .
Bài 25. TS lớp 10 Đăk Lăk 12 – 13
Tìm hàm số y  ax  b , biết đồ thị hàm số của nó đi qua hai điểm A2;5 và B –2; –3. Lời giải: 5   2a  b a  2
Ta có đồ thị của hàm số đi qua hai điểm A2;5 và B –2; –3 nên    3  2a  b b  1
Vậy hàm số y  2x 1.
Bài 26. TS lớp 10 Đồng Tháp 12 – 13
Xác định hệ số b của hàm số y  2x  b , biết khi x  2 thì y  3 . Lời giải: Trang 8 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10
Ta có y  2x  b khi x  2 thì y  3 nên 3  2.2  b  b  1.
Bài 27. TS lớp 10 Hà Tĩnh 12 – 13
Trong mặt phẳng tọa độ Oxy , đường thẳng d  : y  ax  b đi qua điểm M –1;2 và song song
với đường thẳng  : y  2x 1 . Tìm a , b . Lời giải:
Ta có đường thẳng d  : y  ax  b song song với đường thẳng  : y  2x 1 nên a  2 và đi
qua điểm M –1;2 nên 2  2  b  b  4 . Vậy a  2;b  4 .
Bài 28. TS lớp 10 Hà Nam 12 – 13
Tìm m để các đường thẳng y  2x  m và y  x – 2m  3 cắt nhau tại một điểm nằm trên trục tung. Lời giải:
Để các đường thẳng y  2x  m và y  x – 2m  3 cắt nhau tại một điểm nằm trên trục tung thì  y  m   m  2  m  3  m 1.  y  2m  3
Bài 29. TS lớp 10 Hưng Yên 12 – 13
Cho đường thẳng d  : y  2x  m –1
a) Khi m  3 , tìm a để điểm A ;
a –4 thuộc đường thẳng d  .
b) Tìm m để đường thẳng d  cắt các trục tọa độ Ox , Oy lần lượt tại M và N sao cho tam
giác OMN có diện tích bằng 1. Lời giải:
a) Khi m  3 để điểm A ;
a –4 thuộc đường thẳng d  thì 4  2.a  3 –1  a  3. 1 m 
b) Đường thẳng d  cắt các trục tọa độ Ox , Oy lần lượt tại M và N thì M ,0   và  2  1 1 1 m  N 0, m   1 nên S  M . O NO  m . MNO    1 .  2 2  2  1 1 m  m  Mà S  1  m m . MNO    1 .  1    2 3 1  4    2  2   m  1
Bài 30. TS lớp 10 Hòa Bình 12 – 13
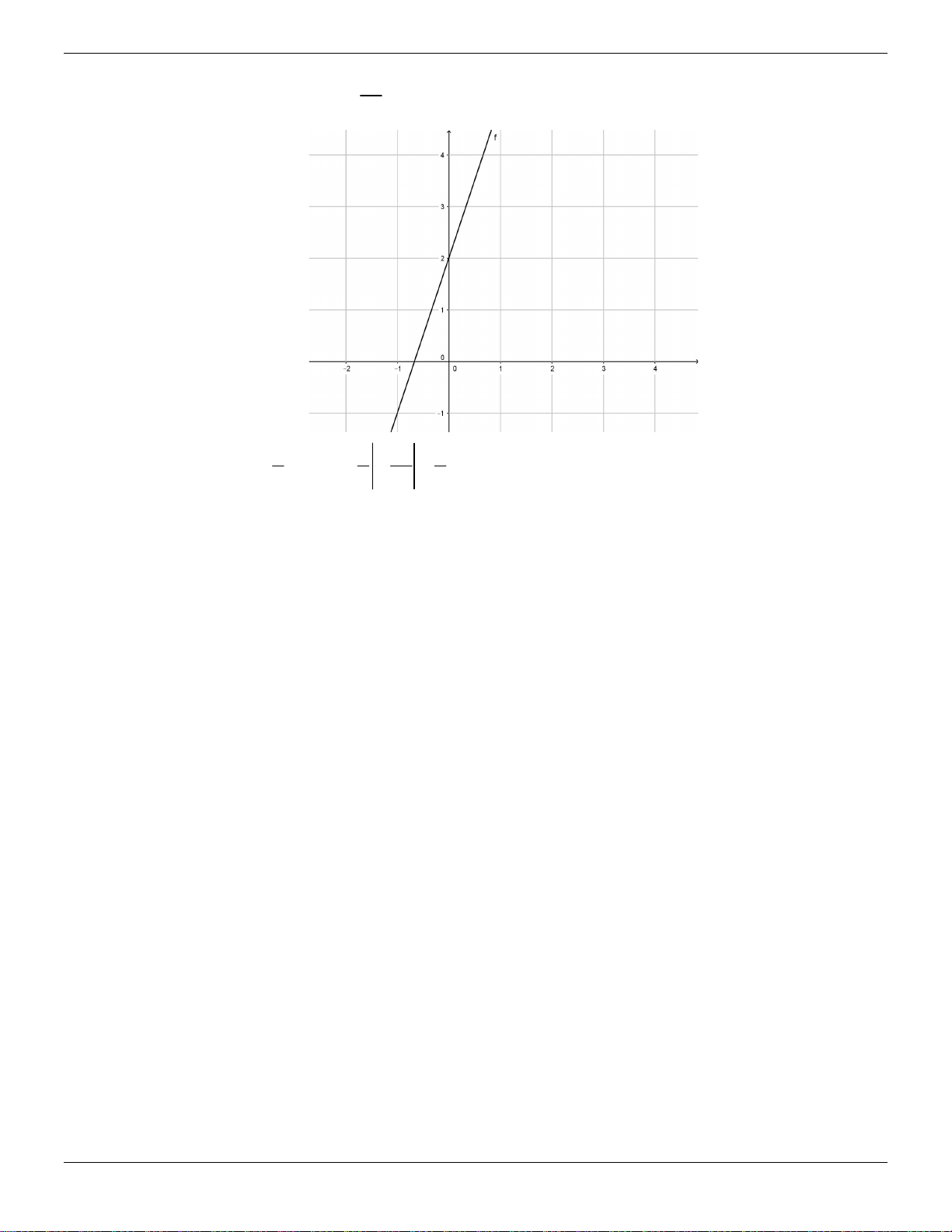
a) Vẽ đồ thị hàm số y  3x  2 (1)
b) Gọi A , B là giao điểm của đồ thị hàm số (1) với trục tung và trục hoành. Tính diện tích tam giác OAB . Lời giải:
a) Vẽ đồ thị hàm số y  3x  2 (1) Trang 9 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10  2  
Đồ thị đi qua A0,2 và B ,0    3  1 1 2 2 b) Ta có S  O . A OB  2.  . OAB 2 2 3 3
Bài 31. TS lớp 10 Ninh Bình 12 – 13
Hàm số bậc nhất y  2x 1 đồng biến hay nghịch biến trên  ? Vì sao? Lời giải:
Do a  2  0 nên hàm số bậc nhất y  2x 1 đồng biến trên  .
Bài 32. TS lớp 10 Lâm Đồng 12 – 13
Cho 2 đường thẳng d  : y  m  3 x 16 m  3 và (d ) : 2
y  x  m . Tìm m để d  , (d ) cắt
nhau tại một điểm nằm trên trục tung. Lời giải:  y  16
Để d  , (d ) cắt nhau tại một điểm nằm trên trục tung thì 2   m  16  m  4  2  y  m
Khi m  4 thì d  d loại Vậy m  4 .
Bài 33. TS lớp 10 Nam Định 12 – 13
Tìm các giá trị của tham số m để hai đường thẳng y   2 m  
1 x  m  2 và y  5x  2 song song với nhau. Lời giải:
Để hai đường thẳng y   2 m  
1 x  m  2 và y  5x  2 song song với nhau thì 2 m 1  5 m  2     . m  2  2 m  0 Trang 10 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10
Bài 34. TS lớp 10 Kiên Giang 12 – 13 1 m
Cho đường thẳng d y 
x  (1 m)(m  2) ( m là tham số) m  m  2 1
a) Với giá trị nào của m thì đường thẳng d vuông góc với đường thẳng d  : y  x  3 ? m  4
b) Với giá trị nào của m thì d là hàm số đồng biến ? m  Lời giải: a) Để đường thẳng
d vuông góc với đường thẳng d thì m  1 m 1 4m  8 1 m  0 .  1     m  3  m  2 4 m  2 1 m 1 m b) Để hàm số y 
x  1 mm  2 đồng biến thì  0  2  m  1. m  2 m  2
Bài 35. TS lớp 10 Bắc Giang 13 – 14
Tìm m để đường thẳng d  : y  m    1   2 1 x 1, m  
 và d : y  3x  2 song song với nhau.  2  Lời giải: 2m 1  3
Để d  song song d thì   m  2 1   2
Bài 36. TS lớp 10 Bắc Ninh 13- 14
Cho hàm số: y  mx 1 (1), trong đó m là tham số.
a) Tìm m để đồ thị hàm số (1) đi qua điểm A1; 4 . Với giá trị m vừa tìm được, hàm số (1)
đồng biến hay nghịch biến trên  ?
b) Tìm m để đồ thị hàm số (1) song song với đường thẳng d  có phương trình 2 y  m x  m 1 . Lời giải:
a) Ta có y  mx 1 đi qua A1; 4 khi và chỉ khi 4  m 1  m  3. Khi đó y  3x 1 đồng biến trên  . 2 m  m
b) Ta có y  mx 1 đồ thị hàm số (1) song song với đường thẳng d  khi   m  1 1   m 1 Vậy m  1.
Bài 37. TS lớp 10 Bình Định 13 – 14
Cho hàm số y  (m 1)x  m . Tìm m để đồ thị hàm số vuông góc với đường thẳng x  3y  2013  0 . Lời giải: 1
Để đồ thị hàm số vuông góc với đường thẳng x  3y  2013  0  y  x  671 thì 3 m   1   1 .  1
  m 1  3  m  4   .  3  Trang 11 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10
Bài 38. TS lớp 10 Đà Nẵng 13 - 14
Cho hàm số bậc nhất y  ax – 2 (1). Hãy xác định hệ số a , biết rằng a  0 và đồ thị của hàm số
(1) cắt trục hoành Ox , trục tung Oy lần lượt tại hai điểm A , B sao cho OB  2OA (với O là gốc tọa độ). Lời giải:  2  4 Ta có A ,0   , B 0,2 , để 2 OB  2OA  4  4.  a  4  a  2 .  a  2 a
Bài 39. TS lớp 10 Hà Tĩnh 13 – 14
Trong mặt phẳng tọa độ Oxy cho đường thẳng 2
y  (m  2)x  m và đường thẳng y  6x  2 . Tìm
m để hai đường thẳng đó song song với nhau. Lời giải: 2 m  2  6 m  2 
Để hai đường thẳng đó song song với nhau thì     m  2  . m  2 m  2
Bài 40. TS lớp 10 Lâm Đồng 13 – 14
Cho hàm số bậc nhất y  m – 3 x  2014 . Tìm giá trị của m để hàm số đồng biến trên  . Lời giải:
Để hàm số đồng biến trên  thì m  3  0  m  3.
Bài 41. TS lớp 10 Lào Cai 13 – 14
Cho hai hàm số bậc nhất y  5  x  m  
1 và y  4x  7  m (với m là tham số). Với giá trị nào
của m thì đồ thị hai hàm số trên cắt nhau tại một điểm trên trục tung. Tìm tọa độ giao điểm đó. Lời giải: y  5  x  m  
1 cắt trục tung tại điểm của tung độ bằng m 1
y  4x  7  m cắt trục tung tại điểm của tung độ bằng 7  m
Để hai đồ thị hàm số cắt nhau tại một điểm trên trục tung thì m 1  7  m  m  3.
Khi đó tọa độ giao điểm là 0;4 .
Bài 42. TS lớp 10 Ninh Thuận 13 – 14
Viết phương trình đường thẳng d  có hệ số góc bằng 7 và đi qua điểm M 2;  1 . Lời giải:
Do đường thẳng d  có hệ số góc bằng 7 và đi qua điểm M 2; 
1 , Gọi phương trình d  là a  7 a  7 y  ax  b ta có    . 1   7.2  b b   13 Vậy y  7x 13 .
Bài 43. TS lớp 10 Quảng Ngãi 13 – 14
Cho hàm số bậc nhất: y  2m   1 x – 6
a) Với giá trị nào của m thì hàm số dã cho nghịch biến trên  ? Trang 12 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10
b) Tìm m để đồ thị của hàm số đã cho đi qua điểm A1; 2. Lời giải: 1
a) Để hàm số đã cho nghịch biến trên  thì 2m 1 0  m  . 2
b) Để đồ thị của hàm số đã cho đi qua điểm A1; 2 thì   m   7 2 2
1 .1 – 6  2m 1  8  m  . 2
Bài 44. TS lớp 10 Quảng Ninh 13 – 14
Xác định hệ số a để hàm số y  ax – 5 cắt trục hoành tại điểm có hoành độ bằng 1,5 . Lời giải: 3 10
Để hàm số y  ax – 5 cắt trục hoành tại điểm có hoành độ bằng 1,5 thì 0  . a – 5  a  . 2 3
Bài 45. TS lớp 10 Tây Ninh 13 – 14
Tìm a và b để đường thẳng (d) : y  (a  2)x  b có hệ số góc bằng 4 và đi qua điểm M1;  . Lời giải:
Để đường thẳng (d) : y  (a  2)x  b có hệ số góc bằng 4 và đi qua điểm M1;  thì a  2  4 a  6    .  3   (a  2)  b b   7  II. Hàm số bậc hai
Bài 46. TS LỚP 10 Vĩnh Long 2017 – 2018
Trong mặt phẳng tọa độ Oxy , cho Parabol P 2
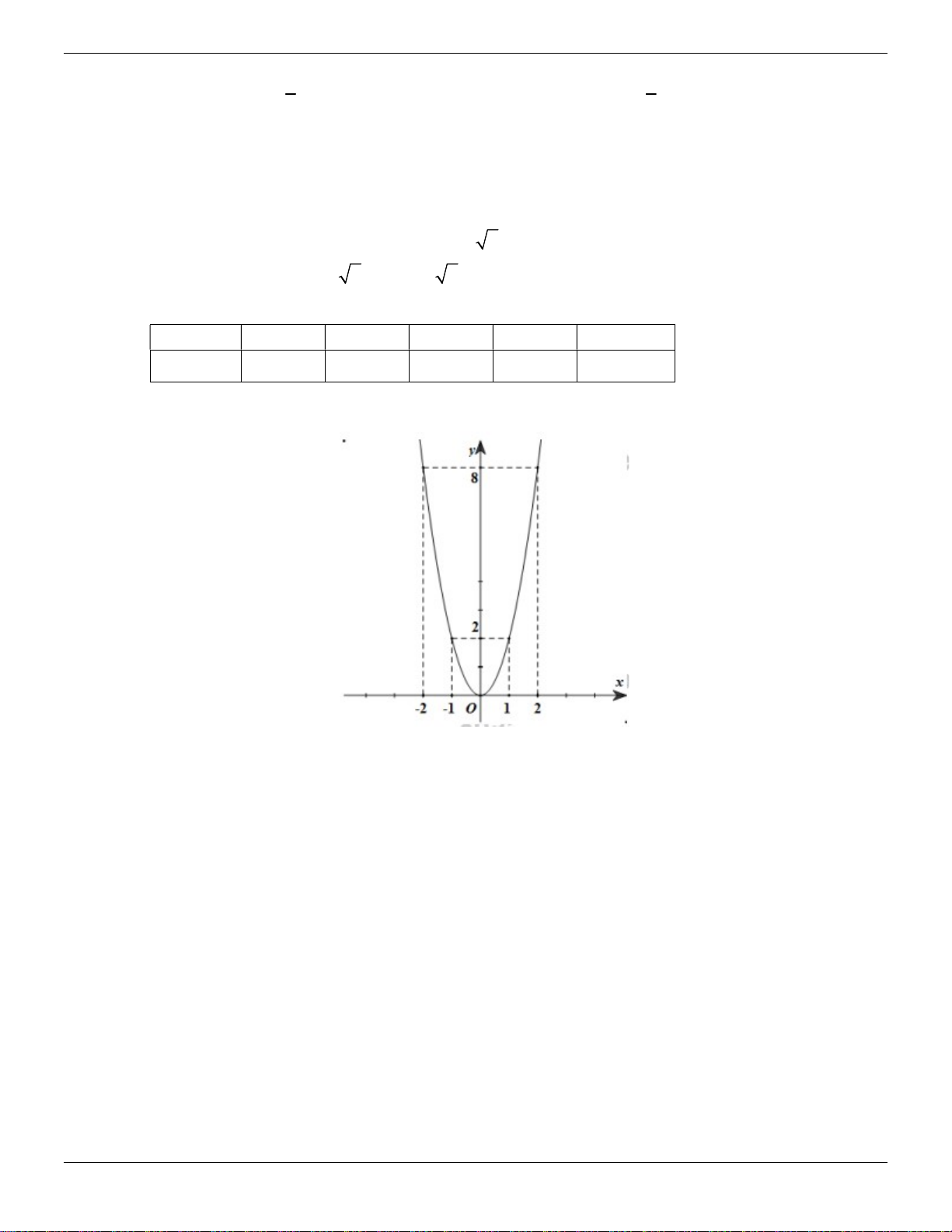
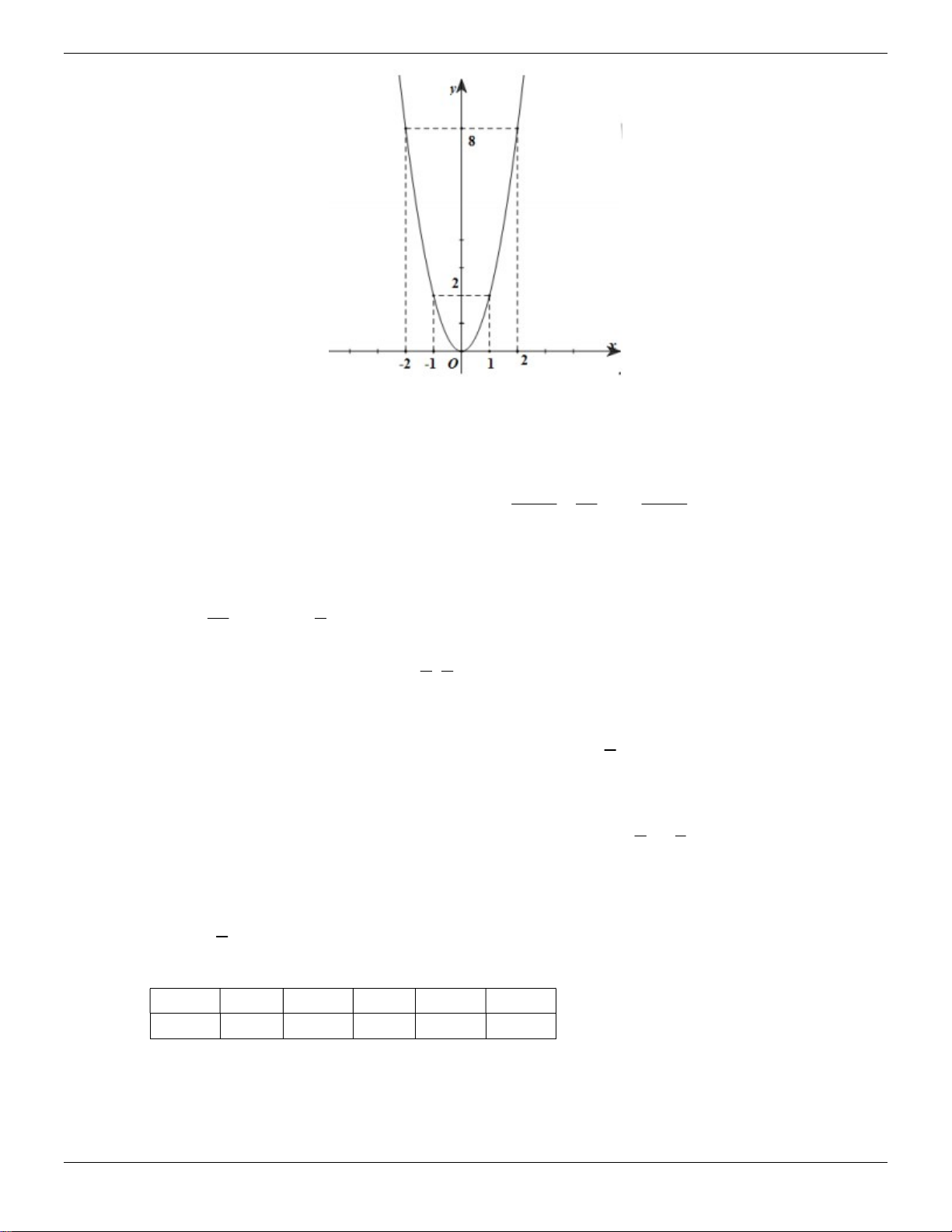
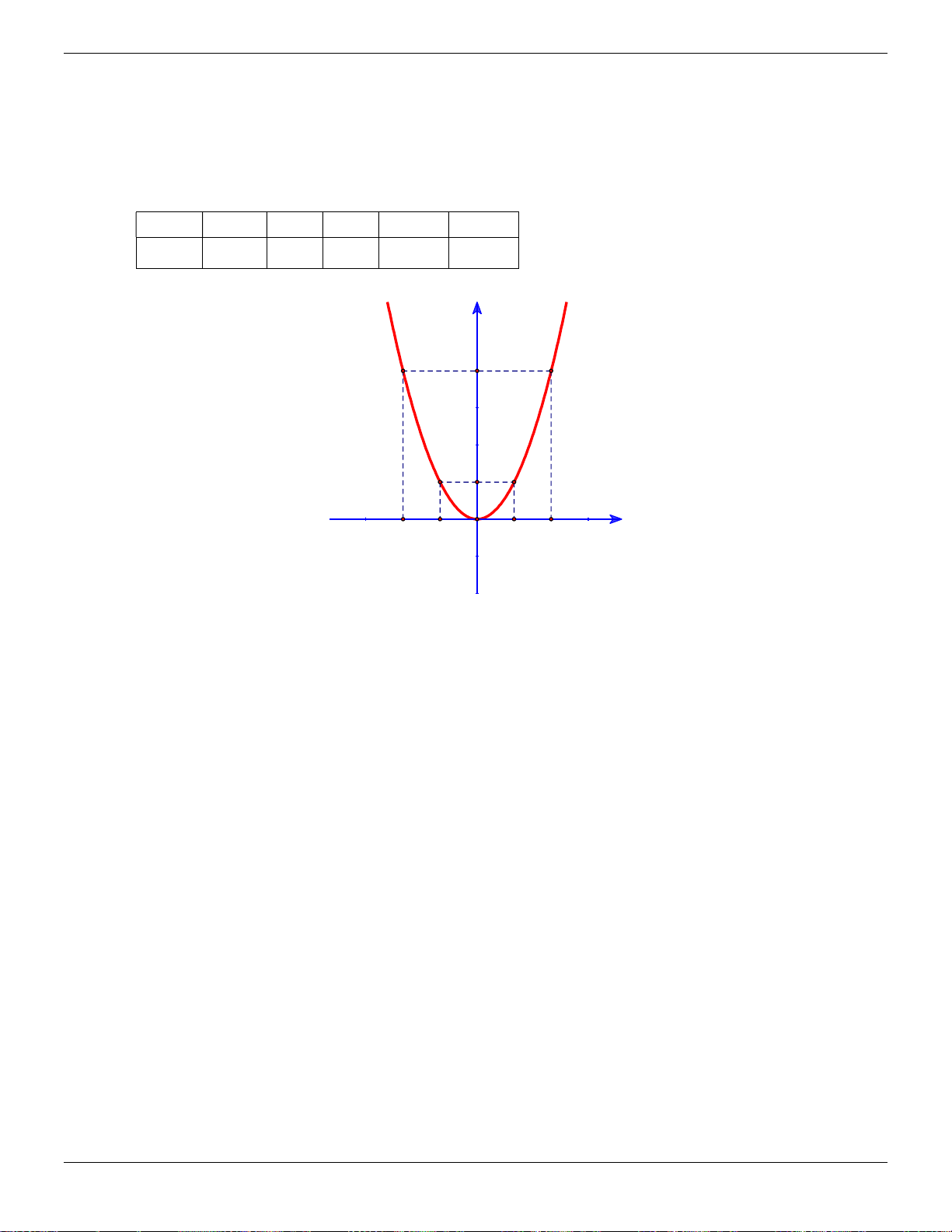
: y  2x . Vẽ đồ thị parabol P. Lời giải: y Vẽ Parabol P 2 : y  2x y=2x2
Bảng giá trị giữa x và y : x 2 1 0 1 2 y 8 2 0 2 8 Vẽ đúng đồ thị -2 -1 0 1 x
Bài 47. TS LỚP 10 Hưng Yên 2016– 2017
Tìm tọa dộ điểm A thuộc đồ thị hàm số 2
y  2x , biết hoành độ của điểm A bằng 2. Lời giải:
Vì A có hoành độ bằng 2 và thuộc đồ thị hàm số 2 y  2x nên 2 y  2.2  8. Vậy A2;8 .
Bài 48. TS LỚP 10 Bắc Giang 2015– 2016 1
Biết đồ thị của hàm số 2
y  ax , ( a  0 ) đi qua điểm M 3; 6
  . Hãy xác định giá trị của . a 3 Lời giải: Trang 13 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10 1 1 Đồ thị hàm số 2
y  ax , ( a  0 ) đi qua điểm M 3; 6   khi 2 – 6  .
a 3  6  3a  a  2 3 3
Vậy a  2 là giá trị cần tìm.
Bài 49. TS LỚP 10 Hòa Bình 2015– 2016 Cho hàm số 2
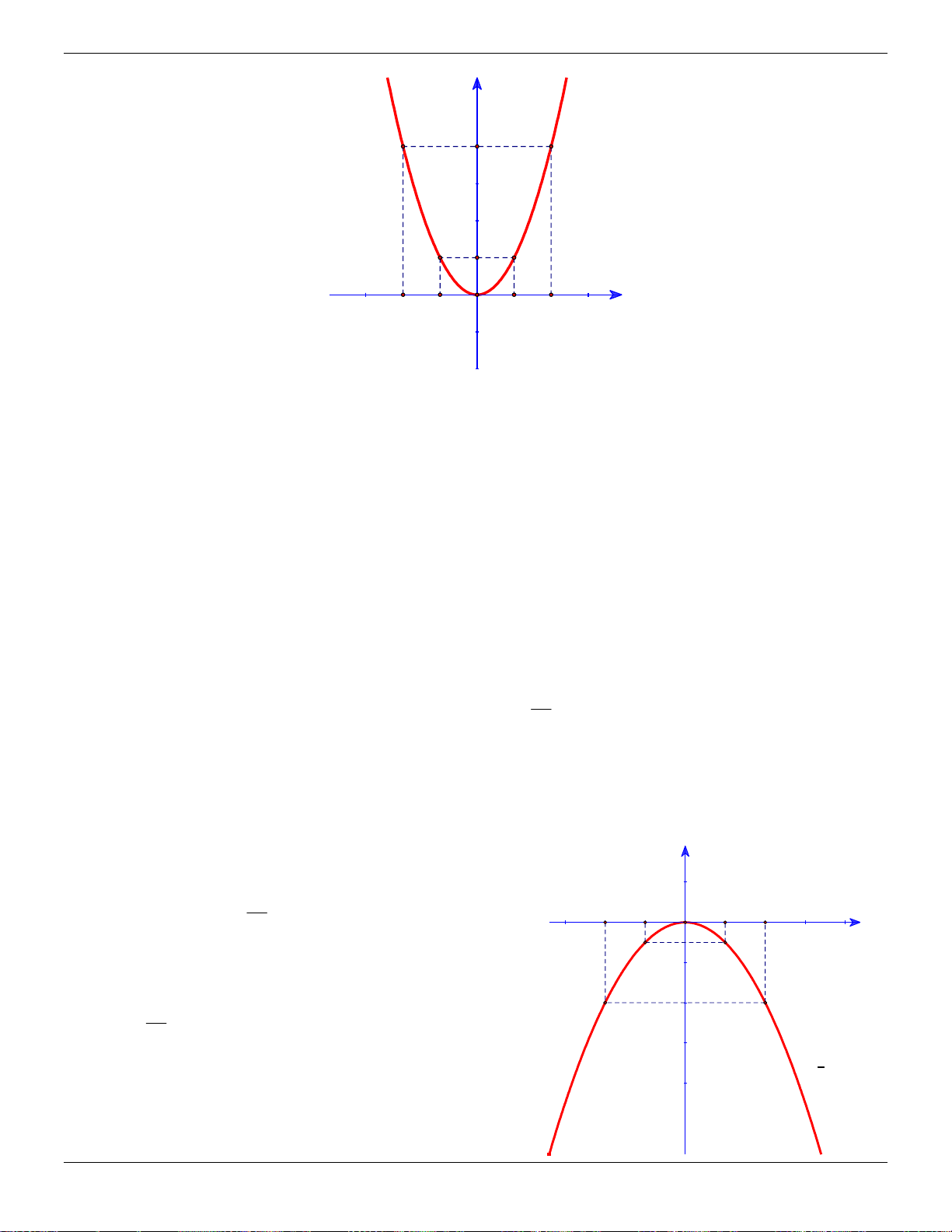
y  2x có đồ thị là P. Tìm trên P các điểm có tung độ bằng 4, vẽ đồ thị P. Lời giải: Thay y  4 ta có 2 2
4  2x  x  2  x   2
Vậy các điểm cần tìm là  2;4 và  2;4. Bảng giá trị x 2 1 0 1 2 2 y  2x 8 2 0 2 8 Đồ thị
Bài 50. TS LỚP 10 Hưng Yên 2015– 2016
Xác định tham số m để đồ thị hàm số 2
y  mx đi qua điểm P(1;  ) 2 . Lời giải: Đồ thị hàm số 2
y  mx đi qua điểm P(1; 2  ) suy ra 2 2  . m 1  m  2 Vậy m  2 .
Bài 51. TS LỚP 10 Sơn La 2015– 2016 Tìm hàm số 2
y  ax , biết đồ thị của nó đi qua điểm A1;2. Với hàm số tìm được hãy tìm các
điểm trên đồ thị có tung độ là 8. Lời giải:
+ Ta có đồ thị hàm số 2
y  ax đi qua điểm A1;2 nên ta có: 2 2  . a (1)  a  2
Vậy hàm số cần tìm là 2 y  2x .
+ Các điểm trên đồ thị có tung độ là 8.
Gọi điểm cần tìm là M  x ; y 0 0  Ta có: 2 2
y  8  8  2.x  x  4  x  2 0 0 0 0
Vậy các điểm cần tìm trên đồ thị có tung độ là 8 là : M 2;8; M 2;8. Trang 14 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10
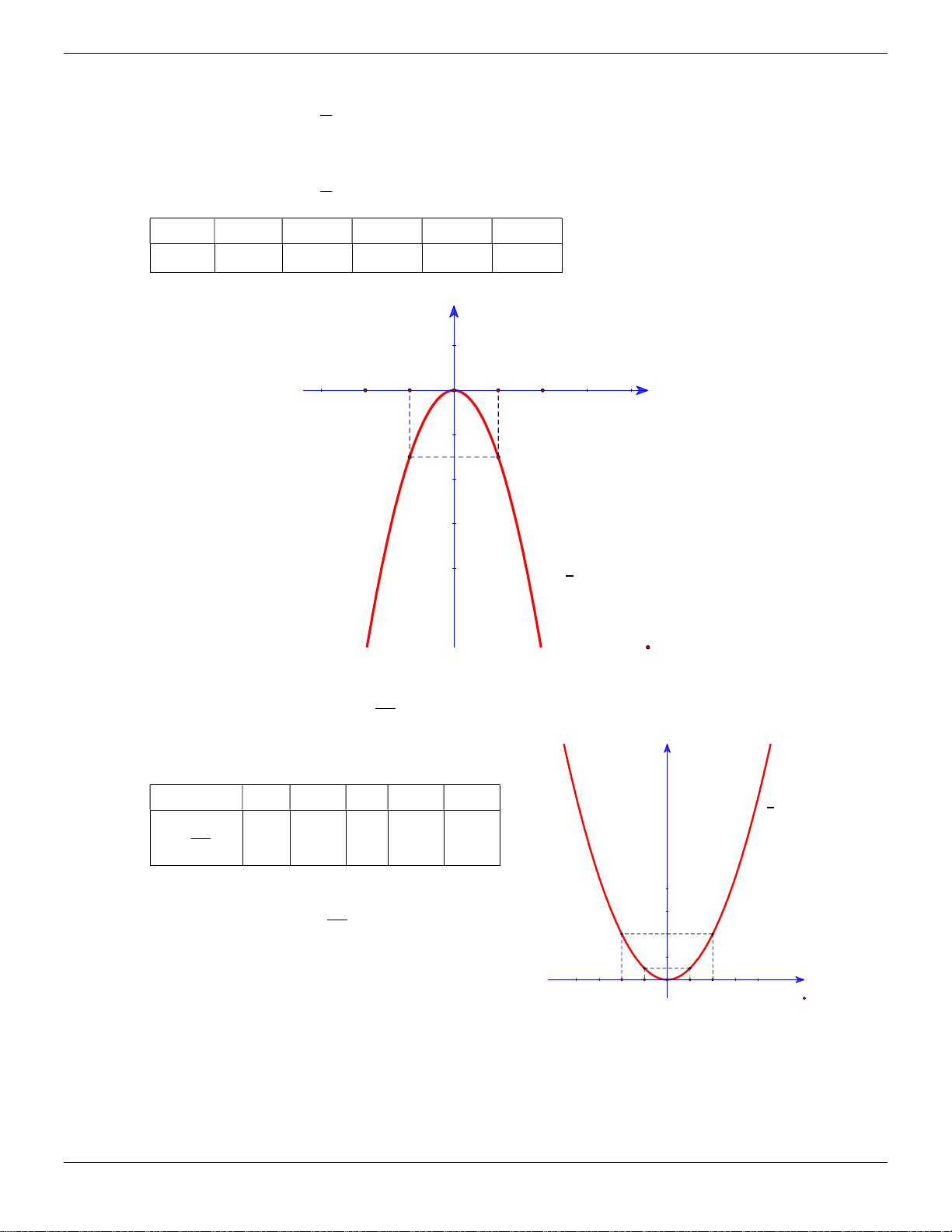
Bài 52. TS LỚP 10 Tây Ninh 2015– 2016 3 Vẽ đồ thị hàm số 2 y   x 2 Lời giải: 3 Vẽ đồ thị hàm số 2 y   x 2 x 2 1 0 1 2 y 6 1,5 0 1,5 6 y -2 -1 0 1 2 x 3 y=- x2 2
Bài 53. TS LỚP 10 Đông Nai 2015– 2016 2 x
Vẽ đồ thị P của hàm số y 
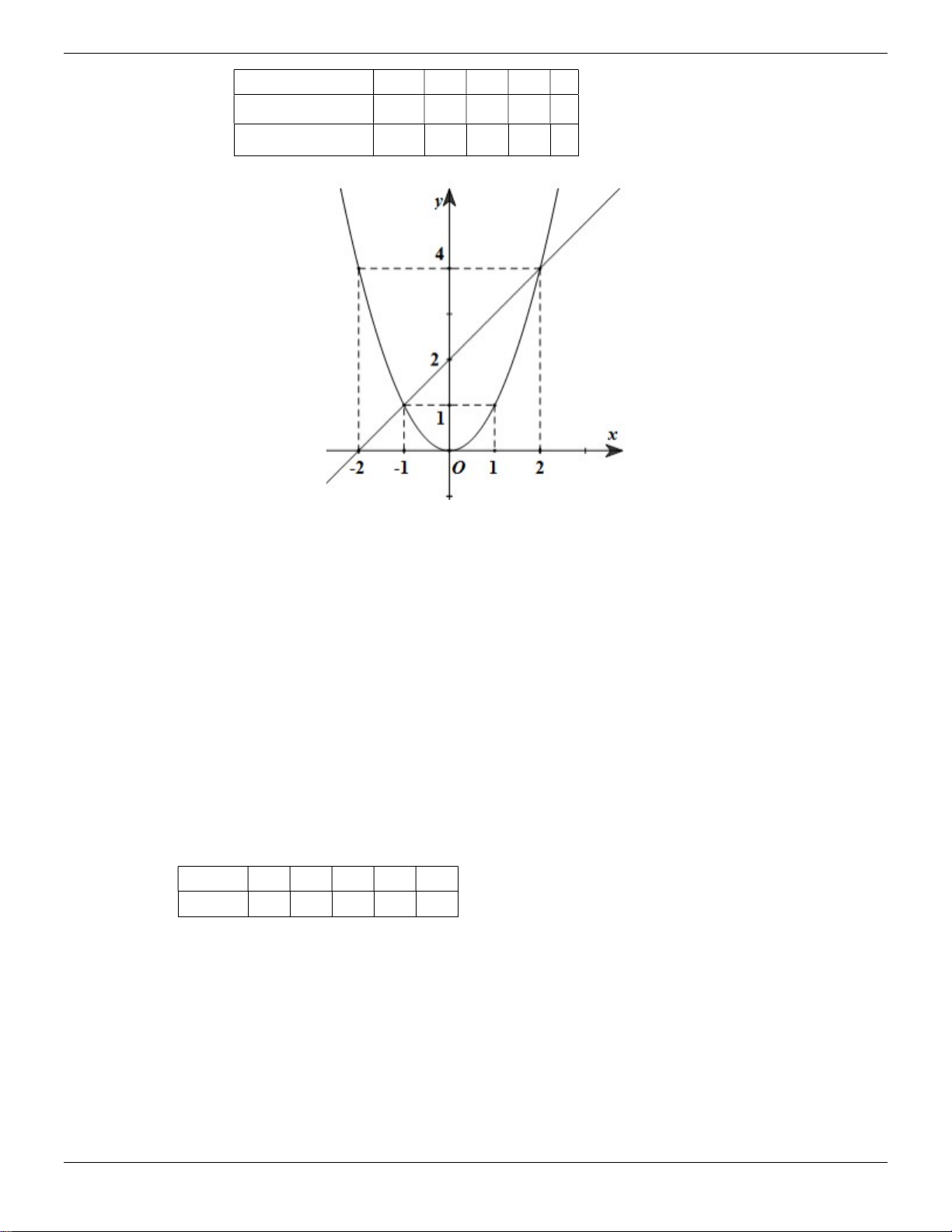
. Tìm tọa độ giao điểm của P và đường thẳng y  2. 2 Lời giải: y Bảng giá trị: x 2 1 0 1 2 1 y= x2 2 x 2 1/2 0 1/2 2 2 y  2 2  x x  2 P cắt d  nên 1  2    2 x  2  2
hay tọa đô giao điểm là 2;2 và 2;2 -2 -1 0
Bài 54. TS LỚP 10 Thừa Thiên Huế 2008– 2009 1 x
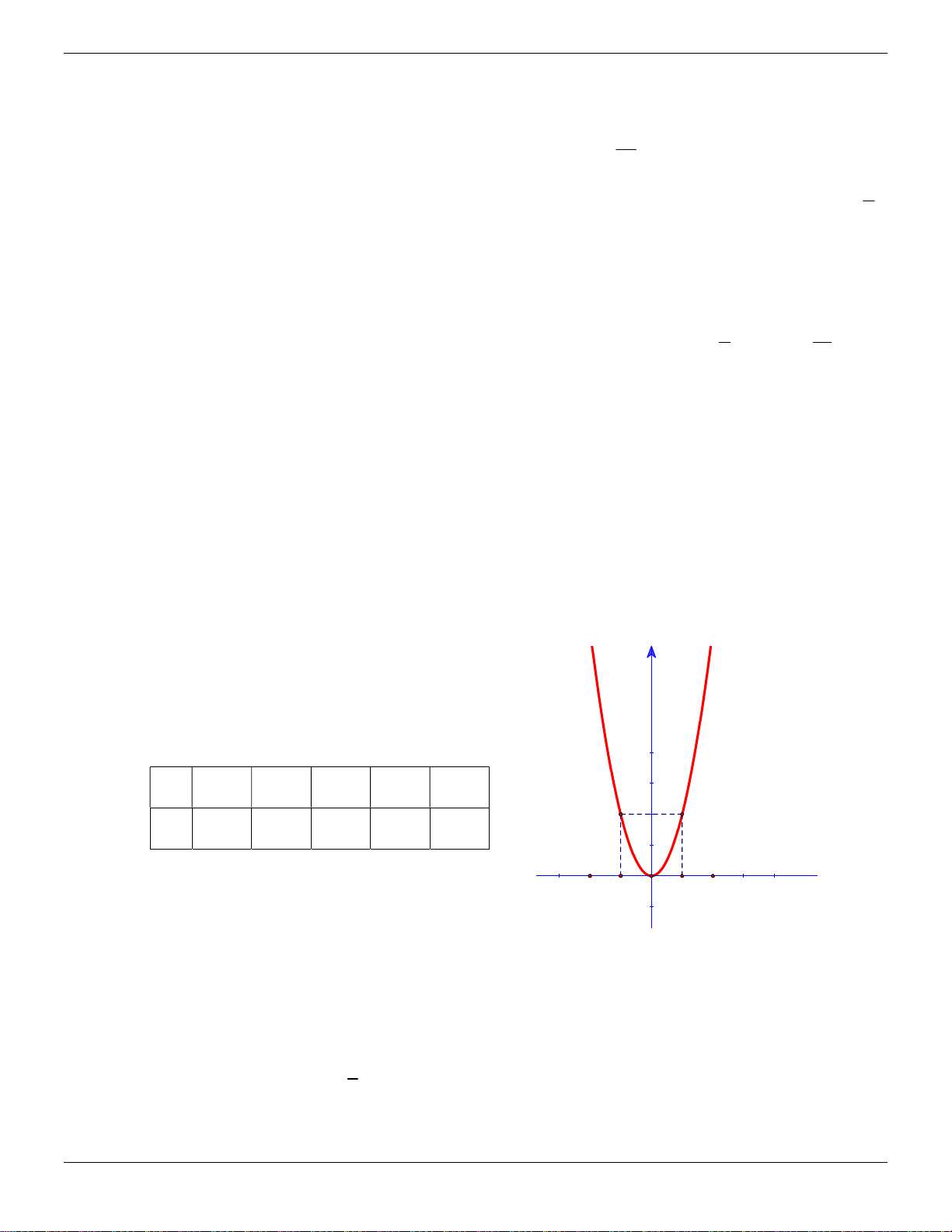
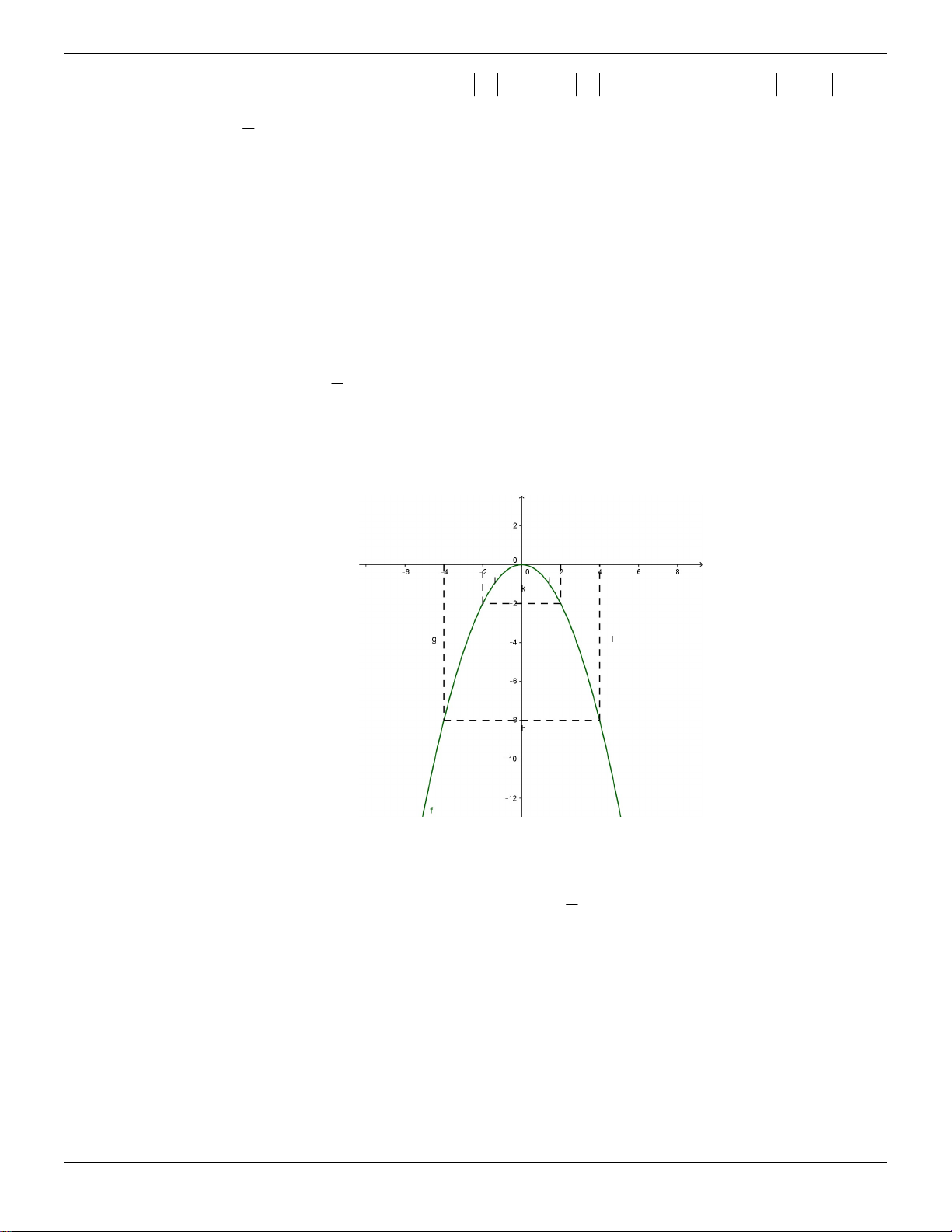
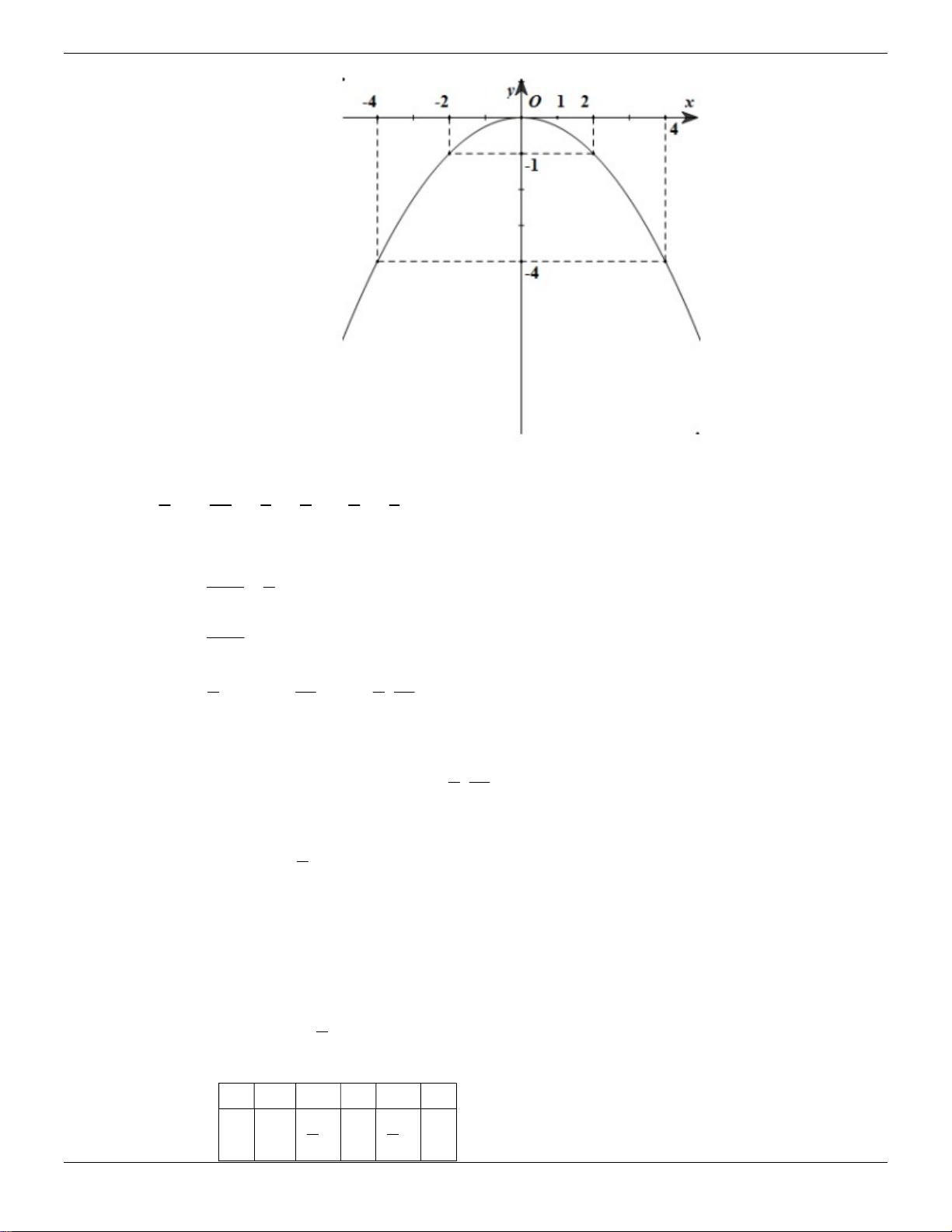
Biết đường cong trong Hình 1 là một parabol 2
y  ax . Tính hệ số a và tìm tọa độ các điểm thuộc parabol có tung độ y  9  . Lời giải: Từ Hình 1, ta có parabol 2
y  ax đi qua điểm 2; 2 Trang 15 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10 1 nên 2 2  . a 2  a   . y 2
Gọi điểm trên parabol có tung độ y  9 là  ; x  9 , -2 -1 0 1 2 1 x ta có: 2 2
9   x  x  18  x   18  3 2 . 2
Vậy có 2 điểm trên parabol có tung độ bằng 9 là 3 2; 9
Bài 55. TS LỚP 10 Hưng Yên 2014- 2015 Hình 1
Tìm hoành độ của điểm A trên parabol 2 y  2x , 1 y=- x2 biết tung độ y  18 . 2 Lời giải:  y  18 A   x   3 2 y  2 A x  A A
Bài 56. TS LỚP 10 Thái nguyên     
Trong mặt phẳng tọa độ Oxy, cho các điểm A  B   1 1 2;1 ; 0; 2 ;C 2; ; D 1  ;      2   4  2 x Đồ thị hàm số y 
đi qua những điểm nào trong các điểm đã cho? Giải thích. 4 Lời giải: 2 x
Hai điểm A và C thuộc đồ thì hàm số y  4
Thật vậy thay vào ta có: 1 1 Tại A có: 1   2  2  .4 4 4 Tại C có:   2 1 1 1 2  .2 2 4 4
Bài 57. TS lớp 10 Cần Thơ 11 – 12 Cho parabol P : 2
y  ax . Tìm a biết rằng parabol P đi qua điểm A3; –3. Vẽ P với a vừa tìm được. Lời giải:  1
P đi qua điểm A3; –3 nên ta có 2 3  3 .a  a  3 1 Vậy 2 P   x . 3
Bài 58. TS lớp 10 Hải Phòng 12 – 13
Xác định hàm số y  a   2
1 x , biết đồ thị hàm số đi qua điểm A1; –2. Lời giải: y  a   2
1 x đi qua điểm A1; –2 nên   a   2 2
1 1  a 1  2  a  3  .
Bài 59. TS lớp 10 Đà Nẵng 13 – 14 1 Vẽ đồ thị hàm số 2 y  x . 2 Trang 16 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10 Lời giải:
Bài 60. TS lớp 10 Ninh Thuận 13 - 14
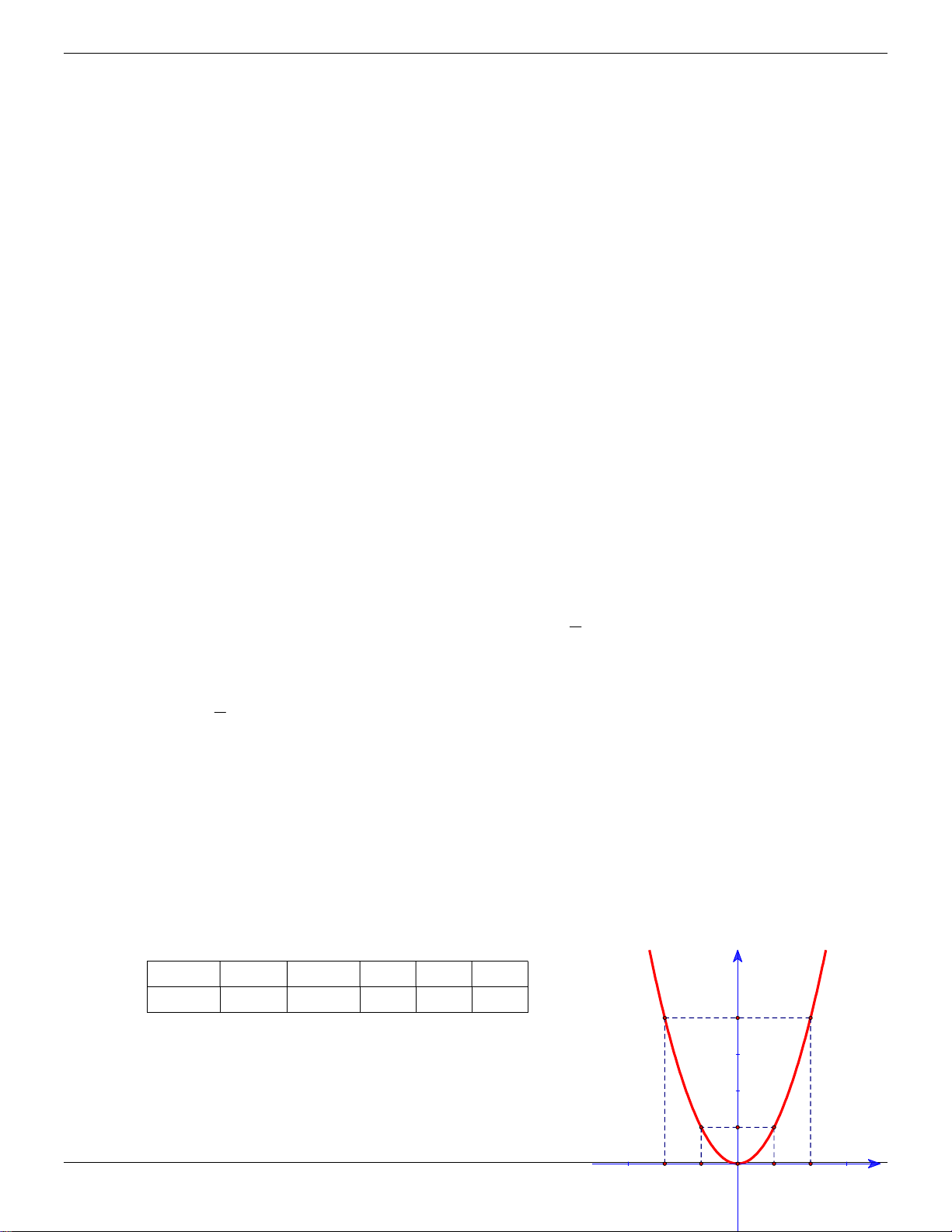
Trong mặt phẳng tọa độ Oxy , vẽ đồ thị P của hàm số 2 y  2x . Lời giải:
III. Sự tương giao giữa parabol (P) và đường thẳng (d)
Bài 61. TS LỚP 10 Bình Định 2017 - 2018 Cho Parabol P 2
: y  x và đường thẳng d : y  2m  
1 x  m  2 ( m là tham số)
a) Chứng minh rằng với mọi m đường thẳng d luôn cắt P tại hai điểm phân biệt.
b) Tìm các giá trị của m để đường thẳng d luôn cắt P tại hai điểm phân biệt A x ; y , 1 1 
B  x ; y thỏa x y  x y  0 . 2 2  1 1 2 2 Lời giải:
a) Phương trình hoành độ giao điểm 2 x   m   2 2
1 x  m  2  x  2m   1 x  m  2  0  *
Ta có    m  2 
m    m  m   m  2 2 2 1 4.1. 2 4 8 9 4 1  5  5  0
Vậy Parabol luông cắt đường thẳng tại hai điểm phân biệt. x  x  2m 1 2 y  x
b) Vì x , x là nghiệm của phương trình * nên 1 2 . Mặt khác 1 1 . 1 2   x x  m  2  2   1 2 y x  2 2 Ta có 3 3
x y  x y  0  x  x  0   x  x  2 2 x  x x  x  0 1 1 2 2 1 2 1 2 1 1 2 2   1 x  x  0 2m 1  0 m  1 2       x x x x 0   x x  2 2 2 2 3x x 0        2 1 1 2 2 1 2 1 2 4m  7m  7  0  vn 1 Vậy m  . 2
Bài 62. TS LỚP 10 Bình Dương 2017 - 2018 Cho Parabol P 2
: y  x và đường thẳng d  : y  4x  9 . a) Vẽ đồ thị P.
b) Viết phương trình đường thẳng d biết d song song với đường thẳng (d) và d tiếp xúc 1  1  1  P. Lời giải: a) Vẽ đồ thị P 2 : y  x y x 2 1 0 1 2 y 4 1 0 1 4 Ta có đồ thị hàm số 4
b) Gọi phương trình đường thẳng d có dạng: y  ax  b 1  a  4
Vì d song song với d  nên ta có:   d : y  4x  b 1  1  b  9
Phương trình hoành độ giao điểm của P và d là: 1 1  Trang 17 -2 -1 2 0 1 x ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10 2 2
x  4x  b  x  4x  b  0*
Vì d tiếp xúc với P nên (*) có nghiệm kép 1 
   0  4  b  0  b  4 (tmñk)
Vậy phương trình đường thẳng d là: y  4x – 4 . 1 
Bài 63. TS LỚP 10 Bình Phước 2017 - 2018 Cho parabol P 2
: y  2x và đường thẳng d : y  x  1.
a) Vẽ parabol P và đường thẳng d trên cùng một trục tọa độ.
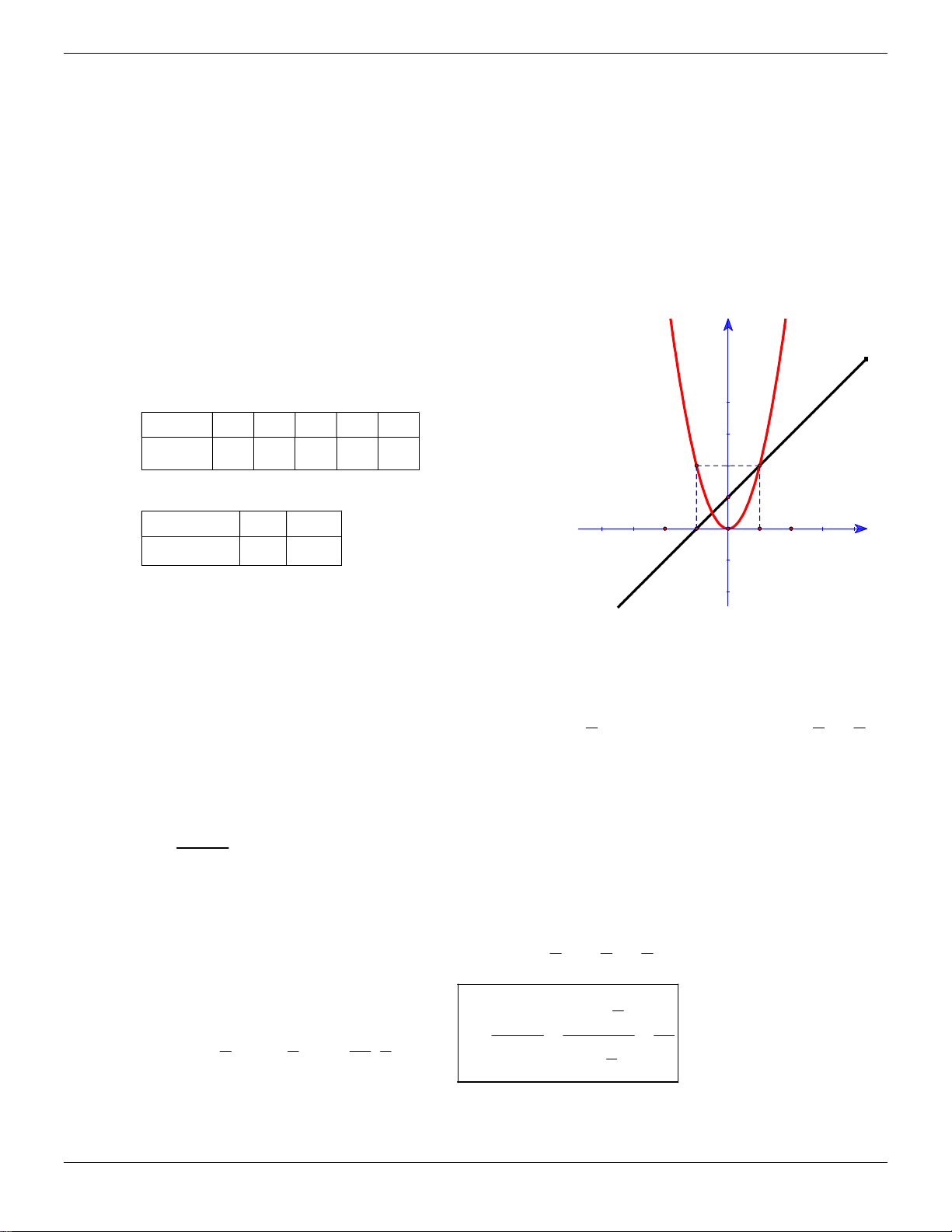
b) Viết phương trình đường thẳng song song với đường thẳng d và đi qua A1;2. Lời giải: y y=2x2 a) Cho parabol P 2
: y  2x và đường thẳng d : y  x 1. Bảng giá trị x  y=x+1 2 1 0 1 2 2  8 2 0 2 8 y 2x x 0 1 -2 y  x 1 1 0 -1 0 1 x
b) Phương trình đường thẳng d song song với đường 1
thẳng d có dạng y  x  b .
d đi qua điểm A1;2 nên ta có 1 b  2  b  3  d : y  x  3 . 1 1
Bài 64. TS LỚP 10 Cần Thơ 2017 - 2018 1
Trong mặt phẳng với hệ tọa độ Oxy , cho parabol P 2
: y  x và đường thẳng d  1 3 : y  x  2 4 2
a) Vẽ đồ thị của P.
b) Gọi A x ; y và B  x ; y lần lượt là các giao điểm của P với d  . Tính giá trị biểu thức 2 2  1 1  x  x 1 2 T  . y  y 1 2 Lời giải: a) HS tự vẽ. 1 1 3
b) Phương trình hoành độ giao điểm của P và d  : 2 x  x  2 4 2
x  2  y  2  A2;2  3  2        x x  2  4  3 9  3 9  . Vậy 1 2 T    . x    y   B ;   y  y 9  25  2 8  2 8  1 2 2  8 Trang 18 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10
Bài 65. TS LỚP 10 Chuyên ĐHSP Hà Nội 2017 - 2018 Cho parabol P 2
: y  x và đường thẳng d  : y  2ax  4a (với a là tham số ) 1
a) Tìm tọa độ giao điểm của d  và P khi a   . 2
b) Tìm tất cả các giá trị của a để đường thẳng d  cắt P taị hai điểm phân biệt có hoành độ
x ; x thỏa mãn x  x  3. 1 2 1 2 Lời giải:
a) Phương trình hoành độ d  và P là 2 x  2ax  4a  0 1
Khi a   thì phương trình trở thành 2 x  x  2  0 2
Có a  b  c  0 nên phương trình có 2 nghiệm là x  1  ; x  2 .
b) Phương trình hoành độ d  và P là 2 x  2ax  4a  0 (*)
để đường thẳng d  cắt P tại hai điểm phân biệt thì phương trình (*) phải có 2 nghiệm phân a 
biệt    a a   0 4  0   a  4 a  0 Với  theo Viét a  4 x  x  2a 1 2  x x  4a  1 2
x  x  3   x  x 2  9   x  x 2  2x x  2 x x  9 1 2 1 2 1 2 1 2 1 2 2  4a  8a  8a  9  Với a  0 : 2 2 1
4a  8a  8a  9  4a 16a  9  0  a  2  3 a   dk  2 Với a  4 : 2 2
4a  8a  8a  9  4a  9   3  a  dk  2 1 Vậy a   . 2
Bài 66. TS LỚP 10 Đà Nẵng 2017 - 2018 Cho hai hàm số 2
y  x và y  mx  4 , với m là tham số.
a) Khi m  3 , tìm tọa độ các giao điểm của hai đồ thị hàm số trên.
b) Chứng minh rằng với mọi giá trị m , đồ thị của hai hàm số đã cho luôn cắt nhau tại hai điểm 2 2
phân biệt A x ; y và A x ; y . Tìm tất cả các giá trị của m sao cho y  y  7 . 1   2 2 2  2 2  1  1 1  Trang 19 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10 Lời giải:
a) Phương trình hoành độ giao điểm của 2
y  x và y  mx  4 là 2 x  mx  4  0 (1)
Thay m  3 vào phương trình (1) ta có: 2 x 3x  4  0
Ta có: a – b  c  1– 3  4  0 x  1  Vậy phương trình 2
x 3x  4  0 có hai nghiệm  x  4
Với x  1  y  1  A(1;1)
Với x  4  y  16  B 4;16
Vậy với m  3 thì hai đồ thị hàm số giao nhau tại 2 điểm A(1;1) và B 4;16 .
b) Ta có số giao điểm của hai đồ thị hàm số đã cho là số nghiệm của phương trình (1) Phương trình (1) có: 2   m    2 4. 4  m 16  0 m   
Do đó (1) luôn có hai nghiệm phân biệt x ; x 1 2
Vậy đồ thị của hai hàm số đã cho luôn cắt nhau tại hai điểm phân biệt A x ; y và A x ; y với 2  2 2  1  1 1  mọi . m x  x  m
Theo hệ thức Vi-et ta có: 1 2  x .x  4   1 2 2 y  x Ta lại có: 1 1  2 y  x  2 2 Theo đề, ta có: y 2 y 2 2  7 1 2  x 2  x 2 2 2  49 1 2
 x 2  2x x  x 2 2 2 2 2  2 2 2 x x  49 1 1 2 2 1 2 
 x  x 2 2x x 2 2 2  49 1 2 1 2 x x  2 2 2x x      2x x 2  49 1 2 1 2 1 2    m  2.  4 2 2  42 2  49  m 82 2  81 2 m  8  9 2    m  8  9 2 do m  8  0 m  2  m  8  9  m  1  2 2
Vậy với m  1; m  1 thì y   y  2  7 . 1 2 Trang 20 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10
Bài 67. TS LỚP 10 Phú Thọ 2017 - 2018 1
Trong mặt phẳng tọa độ Oxy cho parabol P có phương trình 2 y  x và hai điểm , A B thuộc 2
P có hoành độ lần lượt là x  1  , x  2. A B
a) Tìm tọa độ của hai điểm , A B .
b) Viết phương trình đường thẳng d  đi qua hai điểm , A B .
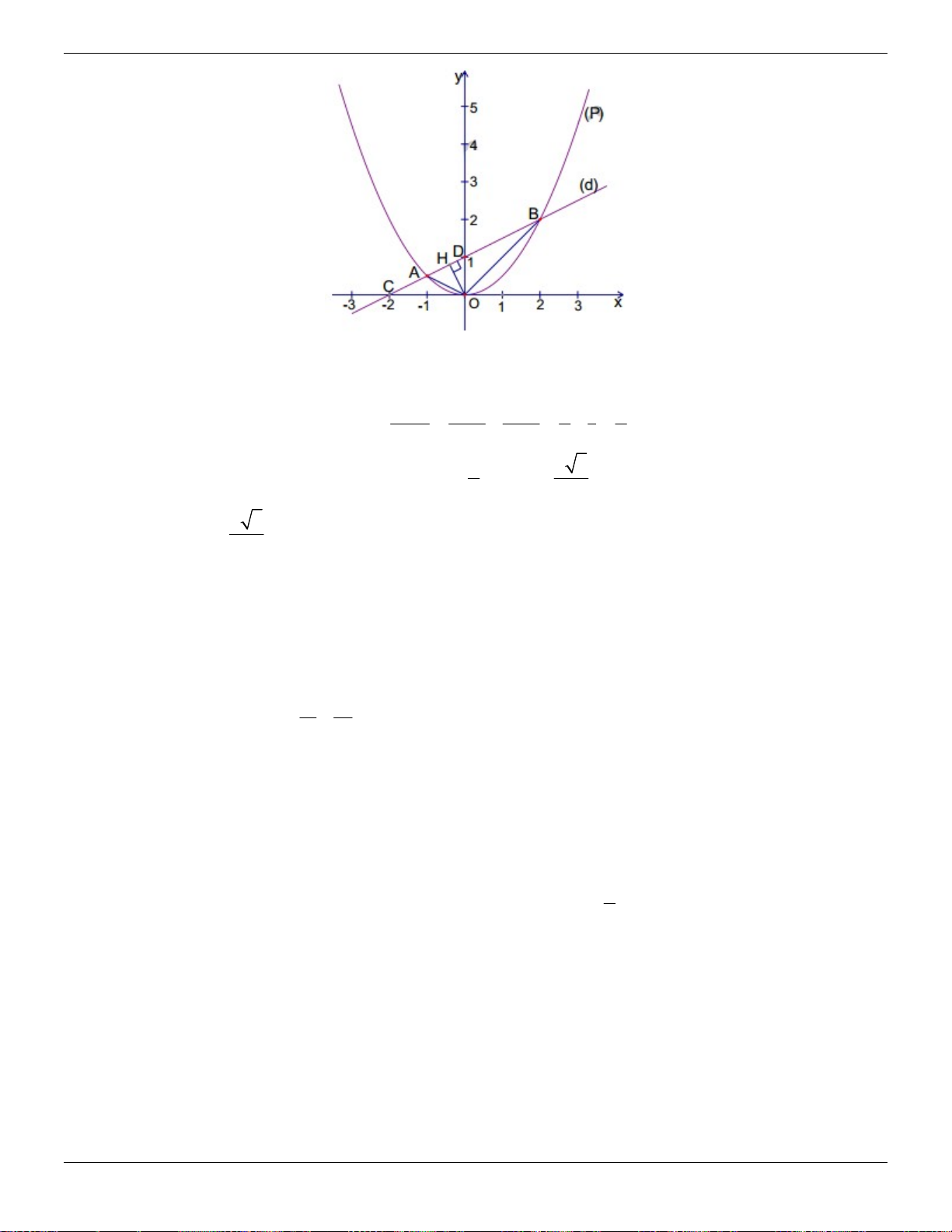
c) Tính khoảng cách từ điểm O (gốc tọa độ) tới đường thẳng d  . a) Vì , A B thuộc P nên: 1 x    y    A A  2 1 1 1 2 2 1 2 x  2  y  2  2 B B 2  1  Vậy A 1  ; , B   2;2.  2 
b) Gọi phương trình của đường thẳng d là y  ax  b .  1  3  1 a  b  3  a  a 
Ta có hệ phương tình:  2   2   2 2a b 2 2a b 2      b  1 1 Vậy d : y  x 1 . 2
c) d cắt trục Oy tại điểm C 0; 
1 và cắt trục Ox tại điểm D2;0  OC  1 và OD  2 .
Gọi h là khoảng cách từ O tới d
Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông OCD , ta có: 1 1 1 1 1 5 2 5       h  . 2 2 2 2 2 h OC OD 1 2 4 5
Bài 68. TS LỚP 10 Quãng Ngãi 2017 – 2018 Cho hàm số 2
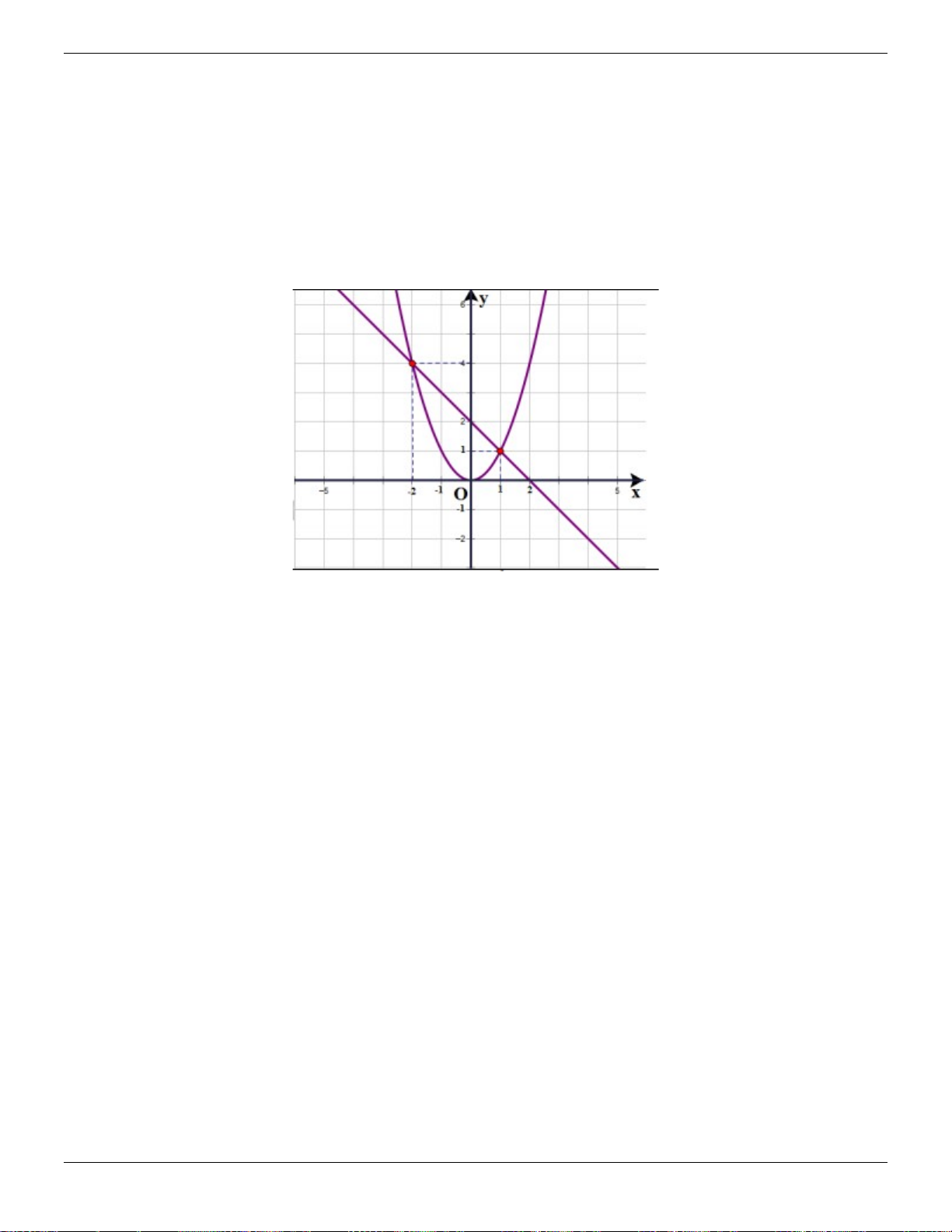
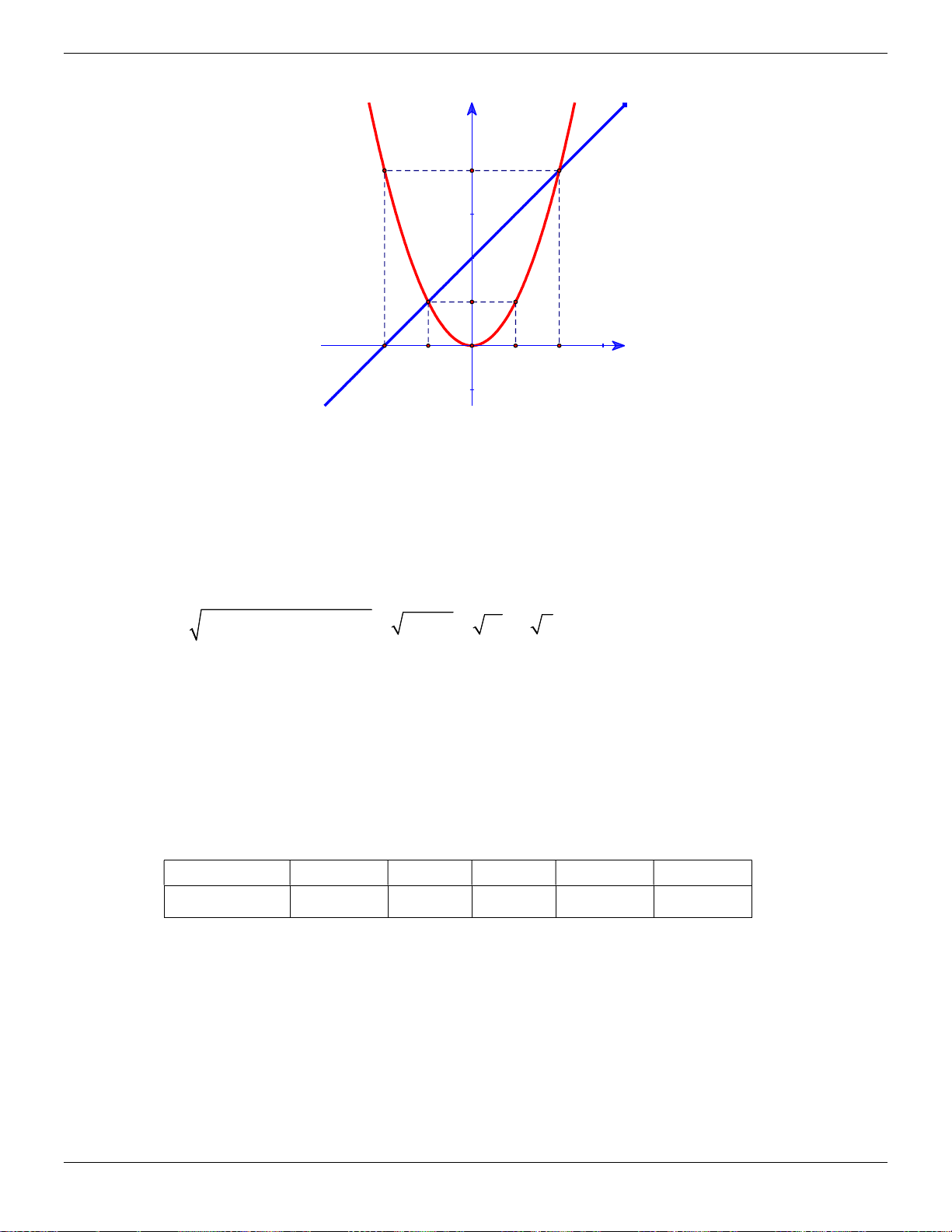
y  x có đồ thị là P và hàm số y  x  2 có đồ thị là d .
a) Vẽ P và d  trên cùng một mặt phẳng tọa độ Ox . y
b) Bằng phép tính, tìm tọa độ các giao điểm ,
A B của  P và d  ; (hoành độ của A nhỏ hơn
hoành độ của B ). Gọi C và D lần lượt là hình chiếu vuông góc của A và B trên trục hoành, tính
diện tích của tứ giác ABD . C Lời giải:
Phương trình hđgđ của P và d  : 2 x  x  2 2 x  x  2  0 2
 x  x  2x  2  0  x  
1  x  2  0  x 1 x  2   x  1  y  1.  x  2  y  4 Vậy A 2  ;4, B1;  1 . Trang 21 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10
ABDC là hình thang vuông có 2 đáy BD  y  1; AC  y  4. Đường cao CD  x  x  3. B A B A 1 Vậy S    (đvdt). ABDC 1 4.3 7,5 2
Bài 69. TS LỚP 10 Thừa Thiên Huế 2017 – 2018 1 Cho hàm số 2
y   x có đồ thị P . 2
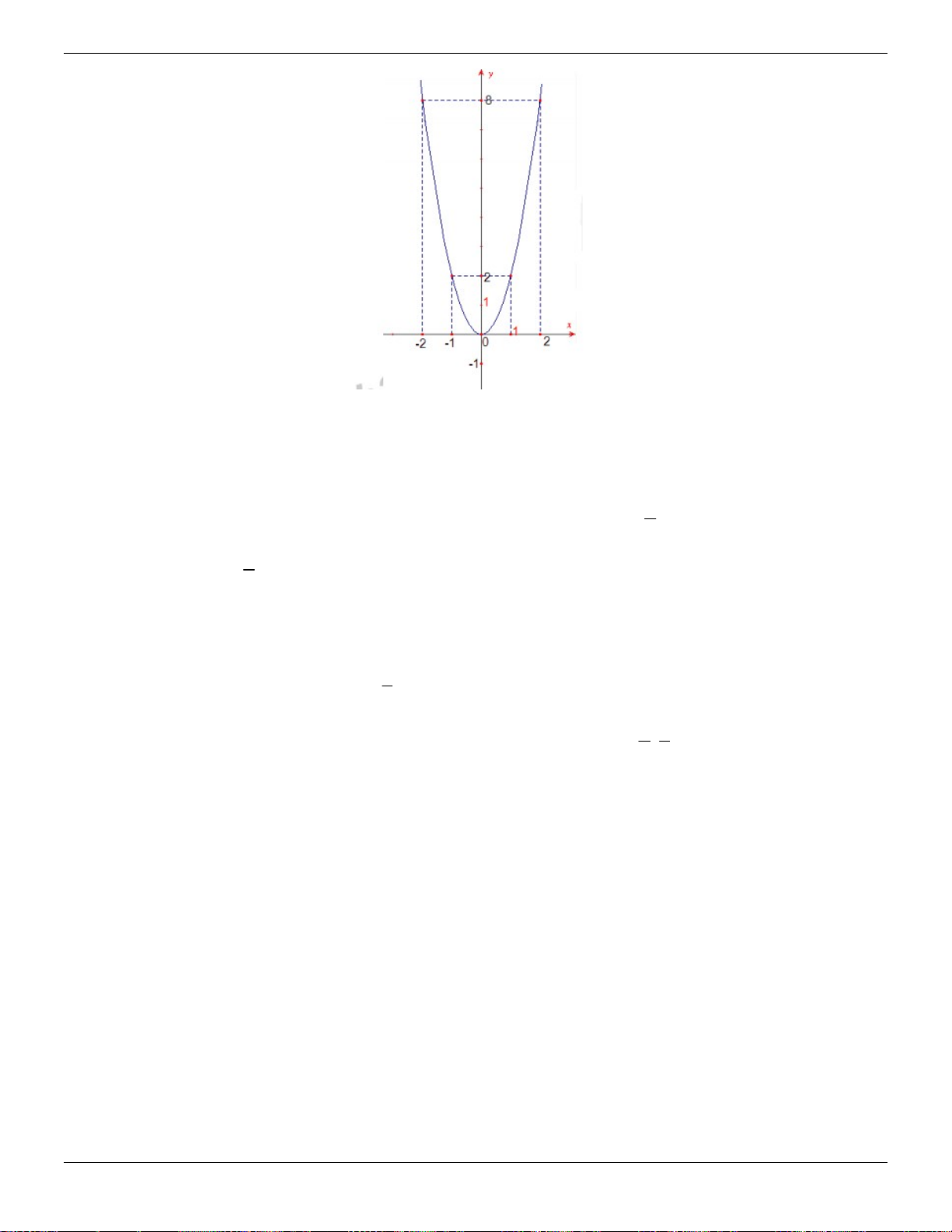
a) Vẽ đồ thị P của hàm số.
b) Cho đường thẳng y  mx  n . Tìm m, n để đường thẳng  song song với đường thẳng
y  2x  5d  và có duy nhất một điểm chung với đồ thị P . Lời giải: 1 a) Đồ thị hàm số 2
y   x là một parabol có đỉnh là gốc tọa độ, bề lõm hướng xuống và đi qua 2
các điểm 0;0,2; 2;2; 2;4;8;4;8 . 1 Đồ thị 2 y   x : 2 m  2 b)  song song với y  2  x  5 suy ra  n  5 1
Phương trình hoành độ giao điểm của  và P : 2  x  2x  n 2 2  x  4x  2n  0 (*)
Để  và P có một điểm chung duy nhất thì phương trình (*) có nghiệm duy nhất thì
  0  4  2n  0  n  2 (thỏa mãn) Vậy m  2  ;n  2 .
Bài 70. TS LỚP 10 Tiền Giang 2017 – 2018 Cho parabol P 2
: y  2x và đường thẳng d  : y  x 1.
a) Vẽ đồ thị của P và d  trên cùng hệ trục tọa độ. Trang 22 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10
b) Bằng phép tính, xác định tọa độ giao điểm A và B của P và d . Tính độ dài đoạn thẳng A . B y Lời giải: y=2x2
a) Vẽ đồ thị: (như hình vẽ bên)
Tọa độ giao điểm của P và d  y=x+1
Phương trình hoành độ giao điểm: 2 2x – x –1  0
Ta có a  b  c  0 nên phương trình có hai nghiệm 1   1 1 
; 1 suy ra tọa độ hai giao điểm là: A  ;   và B1;2 2  2 2  b) Tính độ dài AB : -2 -1 0 1 x 2 2      AB   x  x  y  y      B A 2  B A2 1 1 1 2        2   2  2 2  3   3  3 2         2   2  2
Bài 71. TS LỚP 10 HCM 2017 – 2018
Trong mặt phẳng tọa độ Oxy. 1 2
a) Vẽ đồ thị P của hàm số: y  x 4 3
b) Cho đường thẳng D : y  x  m đi qua điểm C 6;7. Tìm tọa độ giao điểm của D và 2 P. Lời giải:
a) Vẽ P học sinh tự vẽ. 3 3
b) D : y  x  m đi qua điểm C 6;7 nên .6  m  7  m  2  2 2 2 x 3 x  2  y  1
Phương trình hoành độ giao điểm giữa D và P :  x  2  4 2  x  4  y  4
Vậy tọa độ giao điểm là 2;  1 ,4;4 .
Bài 72. TS LỚP 10 Yên Bái 2016 – 2017
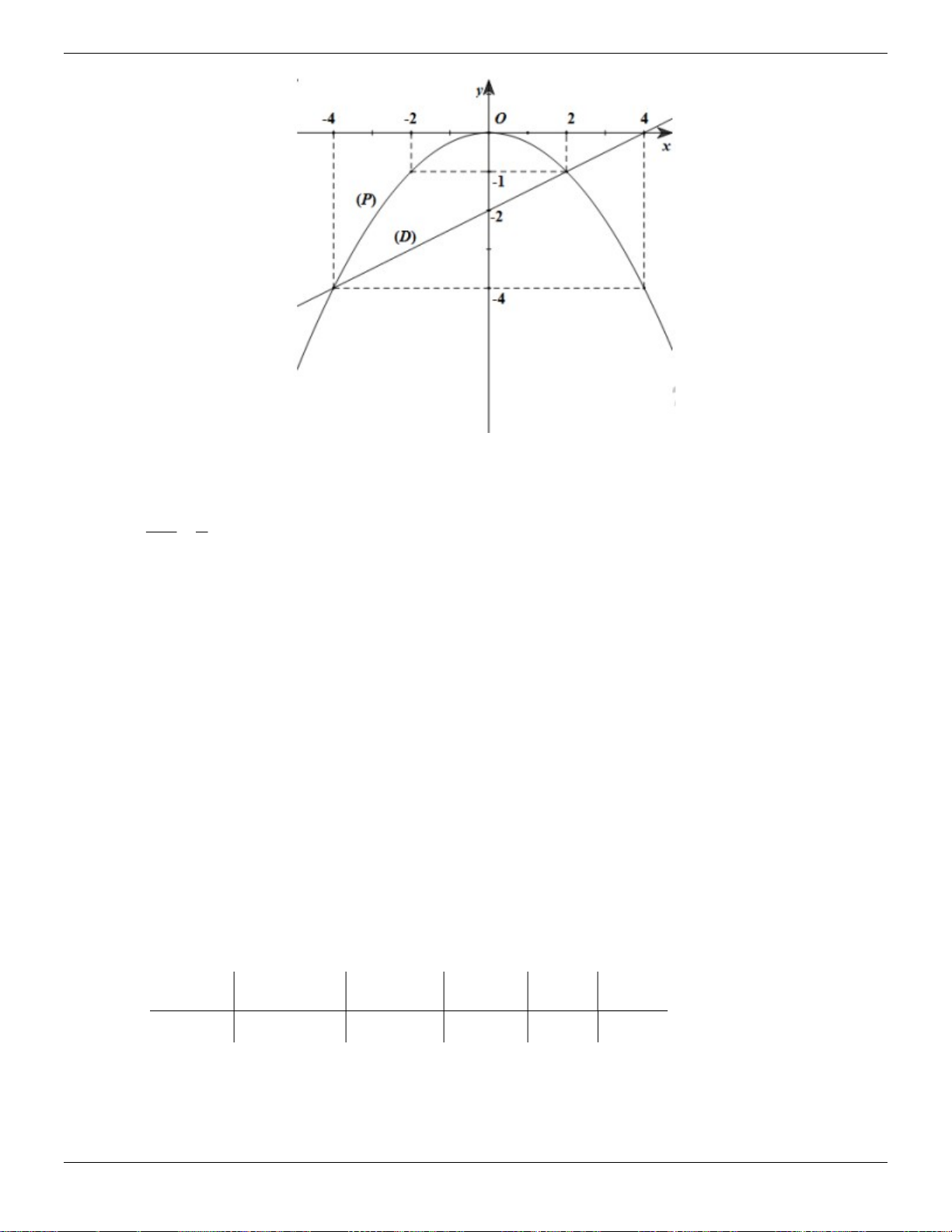
Cho đường thẳng d  có phương trình y  x  2 và parabol P có phương trình 2 y  x .
a) Vẽ đường thẳng d  và parabol P trên cùng hệ trục tọa độ Oxy .
b) Đường thẳng d  cắt P tại hai điểm A và B (với A có hoành độ âm, B có hoành độ
dương). Bằng tính toán hãy tìm tọa độ các điểm A và B . Lời giải:
a) Vẽ đường thẳng d  và parabol P trên cùng hệ trục tọa độ Oxy . Bảng giá trị Trang 23 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10 x -2 -1 0 1 2 y  x  2 0 2 2 y  x 4 1 0 1 4 Đồ thị
b) Phương trình hoành độ giao điểm của (d) và (P): 2 2
x  x  2  x – x – 2  0   x – 2 x  
1  0  x  2 hoặc x  –1
Với x  2  y  4  B 2;4 (vì B có hoành độ dương)
Với x  –1 y  1 A–1; 
1 (vì A có hoành độ âm) Vậy A–1;  1 , B 2;4 .
Bài 73. TS LỚP 10 Bình Dương 2016 – 2017
Vẽ đồ thị hàm số P 2
: y  2x trên hệ trục tọa độ. Tìm giao điểm của P 2 : y  2x với
d: y  –x  3 bằng phép tính. Lời giải: Vẽ đồ thị P 2 : y  2x Bảng giá trị x -2 -1 0 1 2 y 8 2 0 2 8 Vẽ đồ thị: Trang 24 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10
Phương trình hoành độ giao điểm của P và d  là: 2 2
2x  x  3  2x  x  3  0 2
  1  4.2.(3)  25  0 1   5 3  1 5
Phương trình đã cho có 2 nghiệm phân biệt: x   ; x   1 1 2 4 2 4
Hoặc học sinh có thể làm theo cách: ta có a  b  c  2 1  3    0 Với x  1 ta có: y  2 3  9 Với x  ta có: y  2 2  3 9 
Vậy tọa độ giao điểm là 1;2 và  ;   .  2 2 
Bài 74. TS LỚP 10 Cần Thơ 2016 – 2017 1
Trong mặt phẳng với hệ tọa độ Oxy , cho parabol P : 2 y   x 4
a) Vẽ đồ thị của P 2 1
b) Tìm tọa độ các giao điểm của P với đường thẳng d : y   x  3 3 Lời giải: 1 (P): 2 y   x 4 Bảng giá trị x -4 -2 0 2 4 y -4 -1 0 -1 -4 Vẽ Trang 25 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10
Xét phương trình hoành độ giao điểm của P và đường thẳng d là 1 2  1 1 2 1 2 2 2  x 
x   x  x   0  3x  8x  4  0 4 3 3 4 3 3 2
  (4)  3.4  4  0  4  2 2 x    3 3   4  2 x   2  3 2 1   2 1 Với x  ta có y   A ;   3 9  3 9  Với x  2 ta có y  1   B 2;  1  2 1
Vậy tọa độ giao điểm của P và là A ;   và B 2;  1 .  3 9 
Bài 75. TS LỚP 10 Đà Nẵng 2016 – 2017 1 Cho hai hàm số 2
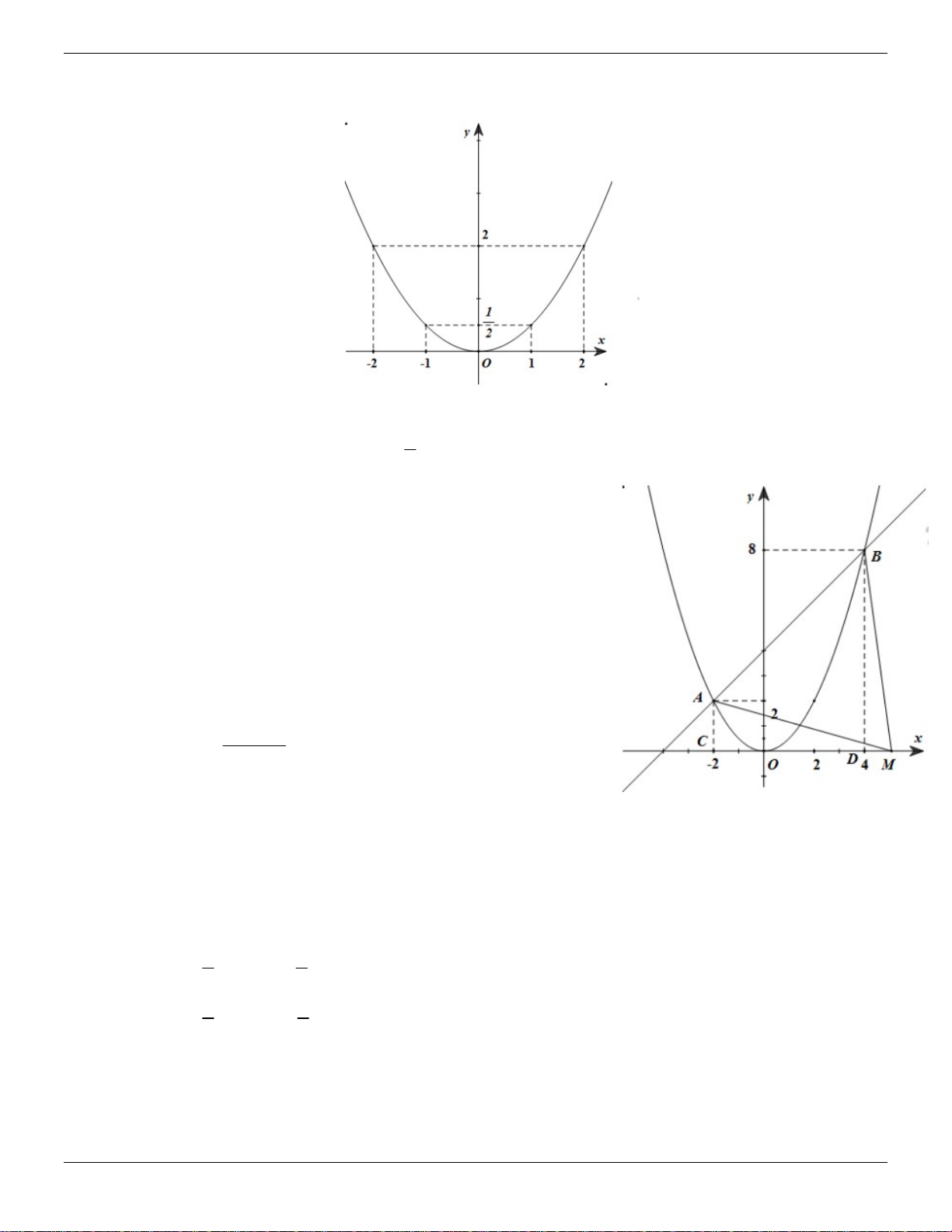
y  x và đồ thị hàm số P và y  x  4 có đồ thị d  2 a) Vẽ đồ thị P. b) Gọi ,
A B là các giao điểm của hai đồ thị P và d . Biết rằng đơn vị đo trên các trục tọa độ
là xentimét, tìm tất cả các điểm M trên tia Ox sao cho diện tích tam giác MAB bằng 30 cm2. Lời giải: 1 a) Vẽ đồ thị P : 2 y  x 2 Bảng giá trị x 2 1 0 1 2 y 2 1 0 1 2 2 2 Trang 26 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10
b) Xét phương trình hoành độ giao điểm của P và d  là: 1 2 2
x  x  4  x  2x  8  0 2 2   ( 1  )  ( 8  )  9  0
Phương trình có 2 nghiệm phân biệt: x  4; x  2 Với x  2
 ta có y  2  A2;2
Với x  4 ta có y  8  B 4;8 Gọi M  ;
m 0 thuộc tia Oxm  0. Gọi C –2;0, D4;0. Xét hai trường hợp:
Trường hợp 1: M thuộc đoạn OD : Ta có S  S  S  S AMB ABDC ACM BDM
Có ABDC là hình thang, AC  2cm, BD  8c , m CD  6cm (2  8).6 ⇒ 2 S   30(cm ) ABDC 2 Suy ra S < 30cm2 (loại) AMB
Trường hợp 2: M thuộc tia Dx M  D  m  4 Ta có : S  S  S  S AMB ABDC ACM BDM Có 2 S
 30cm , MC  m  2cm, MD  m – 4 cm ABCD   Suy ra 1 1 2 S
 AC.CM  .2.(m  2)  m  2(cm ) ACM 2 2 1 1 2 S  B .
D DM  .8.(m 4)  4(m 4)(cm ) BDM 2 2 (thỏa mãn) 2  S  30cm  S  S
 m  2  4(m  4)  m  6 AMB ACM BDM
Vậy M 6;0 là điểm cần tìm.
Bài 76. TS LỚP 10 Hà Nội 2016 – 2017 Trang 27 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10
Trong mặt phẳng tọa độ Oxy cho đường thẳng d  : y  3x  m –1 và parabol P 2 : y  x
a) Chứng minh d  luôn cắt P tại hai điểm phân biệt với mọi m .
b) Gọi x , x là hoành độ các giao điểm của d  và P. Tìm m để a )  x 1 x 1 1 1  2  1 2 Lời giải:
a) Xét phương trình hoành độ giao điểm của d  và P : 2 2 2 2
x  3x  m 1  x  3x  m 1  0* 2 2
  9  m 1  8  m  0 m 
Suy ra phương trình (*) luôn có hai nghiệm phân biệt với mọi m hay d  luôn cắt P tại hai
điểm phân biệt với mọi m .
b) Ta có: (x 1)(x 1)  1  x x  (x  x )  0 1 2 1 2 1 1 x  x  3
Áp dụng hệ thức Vi-et cho (*): 1 2  2 x x  m 1  1 2 2 2
(**)  m 1 3  0  m  4  m  2  Vậy m  2 .
Bài 77. TS LỚP 10 HCM 2016 – 2017 2 x x
a) Vẽ đồ thị P của hàm số y  
và đường thẳng D : y   2 trên cùng một hệ trục tọa 4 2 độ.
b) Tìm tọa độ các giao điểm của (P) và (D) ở câu trên bằng phép tính. Lời giải:
a) Vẽ đồ thị hai hàm số. Bảng giá trị x 2 1 0 1 2 2 x y  4 1 0 1 4 4 x y   2 2 0 2 Đồ thị Trang 28 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10
b) Tìm tọa độ giao điểm của d  và P bằng phép tính
Xét phương trình hoành độ giao điểm của d  và P 2 x x 2
  2  x  2x  8  0 4 2   9
Phương trình trên có hai nghiệm phân biệt: x  2; x  4 1 2
Với x  2 ta có y  1, A 2; 1 1   1
Với x  4 ta có y  4  , A 4;4 2   2
Vậy d  cắt P tại hai điểm phân biệt A2;  1 ; B 4;4 .
Bài 78. TS LỚP 10 Bến Tre 2015 – 2016
Trong mặt phẳng tọa độ Oxy cho parabol P 2
: y  x và đường thẳng d  : y  2x – 3
a) Vẽ đồ thị Parabol P.
b) Bằng phương pháp đại số, hãy tìm tọa độ giao điểm của P và d .
c) Viết phương trình đường thẳng d song song với đường thẳng d  và có điểm chung với 1 
parabol P tại điểm có hoành độ bằng 1. Lời giải:
a) Bảng một số giá trị của P : x 2 1 0 1 2 2 y  x 4 1 0 1 4 Trang 29 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10
b) Phương trình hoành độ giao điểm của P và d  : 2 x  2x – 3 2  x  2x – 3  0 x  1 y  1     y  3   y  9
Vậy giao điểm của P và d  : 1;  1 và 3; 9  
c) Phương trình đường thẳng d có dạng: y  ax  b 1 
d // d  a  2  y  2x b b  3 1     
Gọi A là điểm thuộc P có x  1 y  1 A1;  1 A A
d có chung với Pđiểm A 1  ;  1 nên: 1  2.  1  b  b  1 1 
Vậy d có phương trình: y  2x 1 1 
Bài 79. TS LỚP 10 Bình Dương 2015 – 2016 2 x
a) Vẽ đồ thị P hàm số y  4
b) Xác định a,b để đường thẳng y  ax  b đi qua gốc tọa độ và cắt P tại điểm
A có hoành độ bằng –3 . Lời giải: 2 x
a) Vẽ đồ thị (P) hàm số y  4 Trang 30 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10 y 1 0 x
b) Gọi d  là đường thẳng có phương trình y  ax  . b
Vì d  đi qua gốc tọa độ O0;0 nên b  0. 2 x
Phương trình hoành độ giao điểm của P vàd  : =ax 4 9 3 
Vì d  cắt P tại điểm A có hoành độ là 3 nên:  a( 3  )  a  4 4 3 Vậy: a  ; b  0 4
Bài 80. TS LỚP 10 Bình Thuận 2015 – 2016
a) Vẽ đồ thị P của hàm số 2 y  x .
b) Chứng minh rằng đường thẳng d  y  kx 1 luôn cắt đồ thị P tại hai điểm phân biệt với mọi k. y Lời giải:
a) Vẽ đồ thị P của hàm số 2 y  x . 4
b) PT hoành độ giao điểm của P và d  2 x  kx 1 2  x  kx 1  0 2   k  4 Vì 2
k  0 với mọi giá trị k 1 Nên 2
k  4  0 với mọi giá trị k    -2 -1 2 0 với mọi giá trị k 0 1 x
Vậy đường thẳng d  y  kx 1 luôn cắt đồ thị P tại hai điểm phân biệt với mọi k .
Bài 81. TS LỚP 10 Đà Nẵng 2015 – 2016 Cho hàm số 2
y  x có đồ thị P a) Vẽ đồ thị P . Trang 31 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10
b) Cho các hàm số y  x  2 và y  x  m (với m là tham số) lần lượt có đồ thị là d  và
d . Tìm tất cả các giá trị của m để trên một mặt phẳng tọa độ các đồ thị của P,d và m
d cùng đi qua một điểm. y m  Lời giải:
a) Lập bảng giá trị và vẽ đồ thị: 2 y  x 4 x 0 1 2 y 0 1 4
b) Phương trình hoành độ giao điểm của P và d : 1 2 2
x  x  2  x  x  2  0* -2 -1 2 0 1 x x  1 1 
Phương trình (*) có dạng : a  b  c  0 nên có 2 nghiệm :    c x  2  2  a
Ta có d cắt P tại hai điểm A1;  1 và B 2;4.
Để P,d và d cùng đi qua một điểm thì hoặc Ad hoặc B d m  m  m  + Với A1; 
1 d , ta có : 1    1  m  m  0 m 
+ Với B 2;4d , ta có : 4  2   m  m  6 m 
Vậy khi m  0 hoặc m  6 thì P,d và d cùng đi qua một điểm. m 
Bài 82. TS LỚP 10 Khánh Hòa 2015 – 2016
Trong mặt phẳng toạ độ Oxy , cho parabol P 2 : y  x a) Vẽ parabol P.
b) Xác định toạ độ các giao điểm ,
A B của đường thẳng d : y  x  2 và P. Tìm toạ điểm
M trên P sao cho tam giác MAB cân tại M . Lời giải: a) Vẽ đồ thị P 2 : y  x TXĐ: D  
Tọa độ đỉnh: I 0;0 Trục đối xứng: x  0 Tính biến thiên:
Hàm số đồng biến trên  ;
 0 và nghịch biến trên 0;. BBT: Trang 32 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10 Bảng giá trị x 1 0 1 y 1 0 1 y -2 -1 2 0 1 x -1 -4
b) Viết phương trình đường trung trực d của AB , tìm giao điểm của d và P, ta tìm được hai điểm M.
Hoành độ các giao điểm ,
A B của đường thẳng d : y  x – 2 và P là nghiệm của phương trình: 2 2
x  x  2  x  x  2  0  x  1 hoặc x  2 + Với x  1
 , thay vào P, ta có: y   2 1  1 , ta có: A 1  ;  1
+ Với x  2 , thay vào P, ta có: y   2 2  4  , ta có: B2;4  1 5 
Suy ra trung điểm của AB là: I ;    2 2 
Đường thẳng d vuông góc với d có dạng: y  x  ; b 5 1
Vì d đi qua I nên:   b  b  3  2 2
Vậy d : y  x  3. 1 13
Phương trình hoành độ của d và P là: 2 x  x  3  0  x  2 1   13 7   13 + Với x   y  2 2 1   13 7  13 +Với x   y  2 2  1 13 7  13   1 13 7   13 
Vậy có hai điểm M cần tìm là:  ;   và  ;  . 2 2      2 2   Trang 33 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10
Bài 83. TS LỚP 10 Kiên Giang 2015 – 2016 1 Cho parabol P : 2
y  x và đường thẳng a : y  2x 1 2
c) Vẽ P và a trên cùng một hệ trục toạ độ.
d) Xác định đường thẳng d biết đường thẳng d song song với đường thẳng a và cắt
parabol P tại điểm có hoành độ bằng 2 . Lời giải:
a) Parabol có đỉnh gốc O đi qua hai điểm A2;2, B2;2, đường thẳng đi qua hai điểm C 1;  1 , D0;  1 y y=-2x+1 1 y= x2 2 -2 -1 0 1 x
b) Vì d // a  d : y  2  x  b ( b khác 1)
Gọi N  x ; y là giao điểm của d và P ta có x  2 0 0  0 N  (P)  y  2 0
N  (d)  2  2(2)  b  b  2  (TM ) 0,25
Vậy d : y  2x  2 .
Bài 84. TS LỚP 10 Lạng Sơn 2015 – 2016
a) Vẽ đồ thị của các hàm số 2
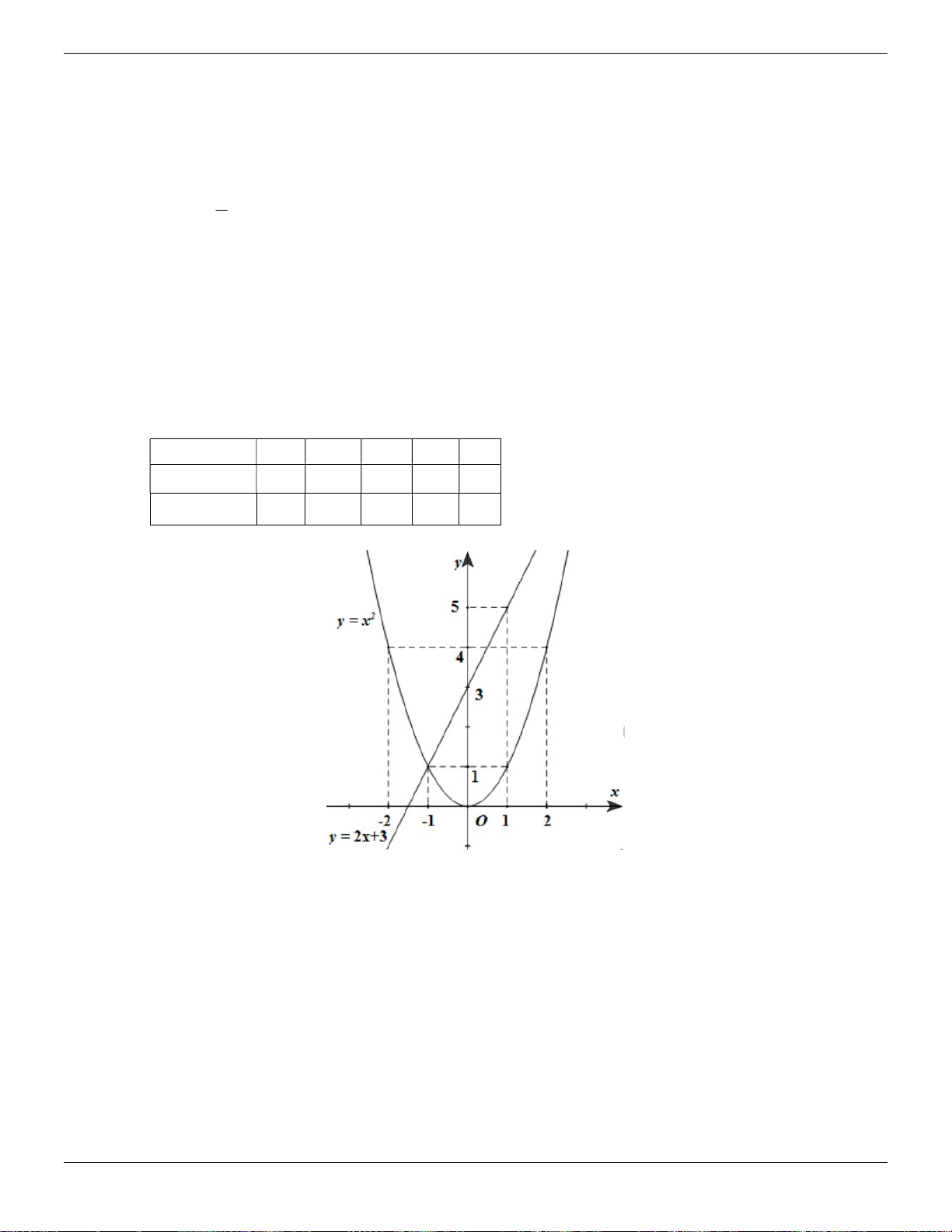
y  x và y  3x  2 trên cùng một hệ trục tọa độ
b) Xác định tọa độ các giao điểm của hai đồ thị trên. Lời giải:
a) Vẽ đồ thị trên cùng một hệ trục Vẽ 2 y  x x 2 1 0 1 2 2 y  x 4 1 0 1 4 Vẽ y  3x  2 Cho x  0  y  2  ; cho x  1  y  1 Trang 34 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10 y 4 1 -2 -1 2 0 1 x
b) Tính tọa độ giao điểm
Ta có phương trình hoành độ giao điểm: 2 x  3x  2 2  x  3x  2  0
có a  b  c  1 3  2  0 nên phương trình có nghiệm x  1; x  2 1 2
Tại x  1 ta có y  1, tọa độ thứ nhất là 1;  1
Tại x  2 ta có y  4 , tọa độ thứ 2 là 2;4
Bài 85. TS LỚP 10 Long An 2015 – 2016 Cho các hàm số P 2
: y  x và d : y  2x  3.
a) Vẽ đồ thị của hai hàm số đã cho trên cùng một mặt phẳng tọa độ Ox . y
b) Tìm tọa độ giao điểm của hai đồ thị trên bằng phép tính .
c) Viết phương trình đường thẳng d : y  ax  b , biết rằng d song song với d và d cắt 1  1  1 
trục tung tại điểm có tung độ bằng 4 . Lời giải:
a) Vẽ đồ thị của hai hàm số đã cho trên cùng một mặt phẳng tọa độ Ox . y y y=2x-3 -2 -1 2 0 1 x -1 y=-x2 Trang 35 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10
b) Tìm tọa độ giao điểm của hai đồ thị bằng phép tính.
Phương trình hoành độ giao điểm của P và d là: 2 2
x  2x  3  x  2x  3  0  x  1; x  3  1 2
* Với x  1  y  1  giao diểm thứ nhất là 1;  1 * Với x  3  y  9
  giao diểm thứ hai là 3; 9  
c) Viết phương trình đường thẳng d : y  ax  b , biết rằng d song song với d và d cắt 1  1  1 
trục tung tại điểm có tung độ bằng 4 .
Đường thẳng d : y  ax  b song song đường thẳng d : y  2x  3 1  a  3   b  3
 Phương trình đường thẳng d : y  2x  b 1 
Vì đường thẳng d : y  2x  b cắt trục tung tại điểm có tung độ bằng 4 1   b  4 (thỏa mãn)
Suy ra phương trình đường thẳng d là y  2x  4. 1 
Bài 86. TS LỚP 10 Thái Bình 2015 – 2016 Cho parabol P 2 : y  x và điểm ,
A B thuộc P có hoành độ lần lượt là 1;2. Đường thẳng d
có phương trình y  mx  . n e) Tìm toạ độ điểm , A B . Tìm ,
m n biết (d) đi qua điểm A và B .
f) Tính độ dài đường cao OH của tam giác OAB (điểm O là gốc tọa độ). Lời giải: 1 1  1  a) Ta có: (
A x ; y )  (P) có hoành độ 2
x  1  y  .(1)   A 1  ; A A A A   2 2  2  1
B(x ; y )  (P) có hoành độ 2
x  2  y  .2  2  B B B 2;2 B B 2
Vì đường thẳng y  mx  n đi qua 2 điểm A và B nên ta có hệ:  1  1  3 m   1 m  n  3  m   2 m   2   2     2 1 2m  n  2
2m  n  2 2.  n  2 n 1  2 1  1 
Vậy với m  ,n  1 thì d đi qua 2 điểm A 1  ; ;   B 2;2 2  2 
b) Vẽ P và d trên cùng 1 hệ trục tạo độ như hình vẽ
Dễ thấy d cắt Ox tại C2;0 và cắt Oy tại D0;  1  OC  2;OD  1 Trang 36 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10
Độ dài đường cao OH của tam giác OAB chính là độ dài đường cao OH của tam giác OCD
Áp dụng hệ thức lượng trong tam giác vuông OCD ta có: 1 1 1 1 1 5      2 2 2 OH OC OD 4 1 4 4 2 5 2  OH   OH  (dvdt) 5 5 2 5 Vậy OH  (dvdt) 5
Bài 87. TS LỚP 10 Thanh Hóa 2015 – 2016
Trong mặt phẳng tọa độ Oxy cho đường thẳng d : y  x  m 1 và parabol P 2 : y  x
a) Tìm m để d đi qua điểm A0;  1
b) Tìm m để đường thẳng d cắt parabol P tại hai điểm phân biệt có hoành độ lần lượt là x , 1  1 1 
x thỏa mãn: 4    x x  3  0 . 2 1 2  x x 1 2  Lời giải:
a) Thay x  0; y  1 vào phương trình đường thẳng d ta được: m  2
b) Phương trình hoành độ giao điểm của d và P là: 2 x  x  m   1  0*
Để d cắt parabol P tại hai điểm phân biệt thì phương trình (*) phải có 2 nghiệm phân biệt 3
   4m  3  0  m  4 x  x  1
Khi đó theo định lý Vi-ét ta có: 1 2  x x  (m 1)  1 2 Theo đề bài: Trang 37 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10  1 1   x  x  1 2 4 
  x x  3  0  4   x x  3  0 1 2 1 2  x x x x 1 2   1 2  4   m  2  0 m 1 2
 m  m  6  0 (DK : m  1) m  3  (L)  m  2(TM)
Vậy m  2 là giá trị cần tìm.
Bài 88. TS LỚP 10 Tiền Giang 2015 – 2016 Cho parabol 2
(P) : y  x và đường thẳng (d) : y  x  2
g) Vẽ đồ thị của P và d trên cùng mặt phẳng tọa độ.
h) Bằng phép tính, xác định tọa độ các giao điểm ,
A B của P và d.
i) Tìm tọa độ điểm M trên cung AB của đồ thị P sao cho tam giác AMB có diện tích lớn nhất. Lời giải:
a) Vẽ đồ thị P và d như hình vẽ
b) Phương trình hoành độ giao điểm của P và d : 2 2
x  x  2  x  x  2  0  x  1 hoặc x  2.
Nếu x  2 thì y  4  A 2  ;4
Nếu x  1 thì y  1  B 1;  1
c) Gọi M  x ; y là điểm thuộc parabol P, cung AB sao cho diện tích tam giác AMB lớn M M  nhất.
Điều kiện: 2  x  1 và 0  y  4 M M
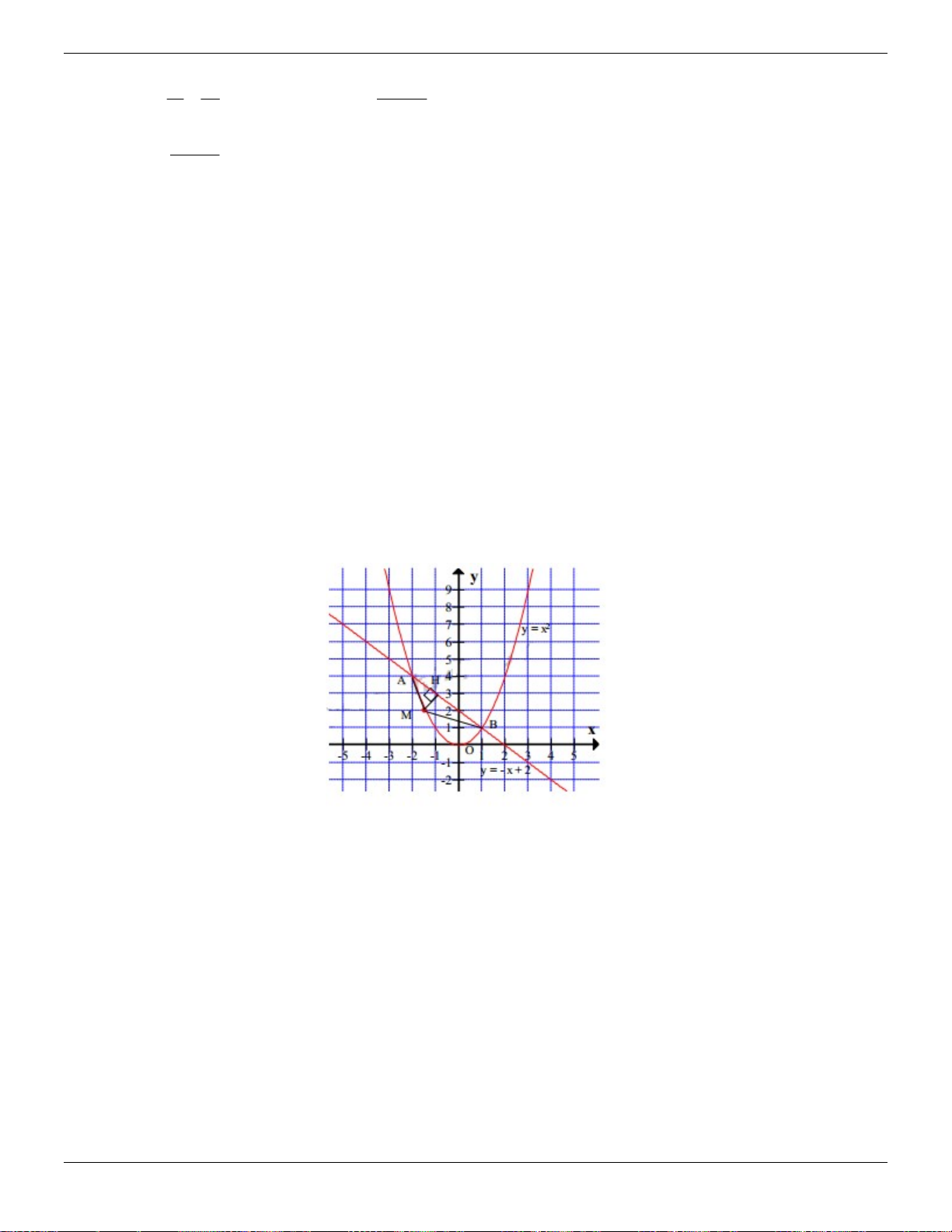
Từ M , kẻ MH  AB tại H , ta có:
+ Phương trình đường thẳng AB : y  – x  2.
+ Phương trình đường thẳng MH có dạng: y  ax  b . Đường thẳng này vuông góc với AB Suy ra . a  
1  1 . Suy ra: a  1, đường thẳng MH có phương trình y  x  b Trang 38 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10
+ Phương trình hoành độ giao điểm giữa P và 2 2
MH : x  x  b  x  x  b  0. 2   ( 1
 )  4.1.(b) 1 4b 1 
  0  1 4b  0  b  4 1
Do đó: MH có phương trình: y  x  4 1 9
+ phương trình hoành độ giao điểm giữa AB và MH : x   x  2  x  4 8 9 1 7  9 7  Khi đó: y    và H ;   8 4 8  8 8  1 1
+ Phương trình hoành độ giao điểm giữa (P) và MH: 2 2
x  x   x  x   0 4 4 1
phương trình có nghiệm kép: x  (thỏa điều kiện) 2 1 1 1 1
Khi đó: y  x     (thỏa điều kiện) 4 2 4 4  1 1  Vậy: M ;    2 4  Khi đó: 2 2  1 9   1 7  25 5 2 2
MH  (x  x )  ( y  y )       2 M H M H      2 8   4 8  32 8 2 2 AB  3  3  3 2 1 1 5 15
Diện tích tam giác AMB là S  .A . B MH  .3 2. 2  (dvdt) AMB 2 2 8 8
Bài 89. TS LỚP 10 Hà Nam 2015 – 2016
Trong mặt phẳng tọa độ Oxy cho Parabol P 2
: y  x và đường thẳng d : y  3mx  3 (với m là tham số).
a) Tìm m để đường thẳng d đi qua điểm A1;3.
b) Xác định các giá trị của m để d cắt P tại hai điểm phân biệt sao cho tổng 2 tung độ của
hai giao điểm đó bằng 10. Lời giải:
a) Đường thẳng d đi qua A1;3 nên 3  3 . m 1 3  m  2.
b) Phương trình hoành độ giao điểm của đường thẳng d và Parabol P là: 2 2
x  3mx  3  x  3mx  3  0* Ta có 2
  9m 12  0 , với mọi m nên phương trình (*) có hai nghiệm phân biệt.
Do đó, đường thẳng d và Parabol P cắt nhau tại hai điểm  x ;y và  x ; y . 2 2  1 1 
Theo định lý Vi-ét ta có: x  x  3  ; m x .x  3. 1 2 1 2 Trang 39 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10 Theo bài ra ta có: 2 2 y  y  1  0  x  x  1  0 1 2 1 2 2  (x  x )  2x x 10 1 2 1 2 2  9m  6  10 2  m   3
Bài 90. TS LỚP 10 Trà Vinh 2015 – 2016
Cho hai hàm số y  2x  3 và 2
y  x có đồ thị lần lượt là d và P
j) Vẽ d và P trên cùng một hệ trục tọa độ Oxy .
k) Tìm tọa độ giao điểm của d và P bằng phép toán. Lời giải: a) Bảng giá trị: x 2 1 0 1 2 y  2x  3 3 5 2 y  x 4 1 0 1 4 Đồ thị
b) Phương trình hoành độ giao điểm của d và P : 2 2
2x  3  x  x  2x  3  0  x  
1  x  3  0  x  1 hoặc x  3
Với x    y   2 1 1  1 ; với 2 x  3  y  3  9
Vậy tọa độ giao điểm của d và P là –1;  1 và 3;9 .
Bài 91. TS LỚP 10 Vĩnh Long 2015 – 2016
Trong mặt phẳng tọa độ Oxy , cho parabol 2
(P) : y  x và đường thẳng (d) : y  2m  
1 x  5  2m ( m là tham số)
l) Vẽ đồ thị parabol P. Trang 40 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10
m) Biết đường thẳng d luôn cắt parabol P tại hai điểm phân biệt. Gọi hoành độ giao điểm của
đường thẳng d và parabol P là x , x . Tìm m để 2 2 x  x  6 . 1 2 1 2 Lời giải: a) Vẽ đồ thị Bảng giá trị: x 2 1 0 1 2 2 y  x 4 1 0 1 4 Đồ thị: y 4 1 -2 -1 2 0 1 x
Phương trình hoành độ giao điểm của P và d : 2 2
x  2(m 1)x  5  2m  x  2(m 1)x  2m  5  0 x  x  2m  2 Theo định lý Vi-ét: 1 2  x x  2m  5  1 2 Theo đề bài, ta có: m 
x  x  6   x  x 2  2x x  6  2m  22 1 2 2  22m  5 2
 6  4m 12m  8  0  1 2 1 2 1 2  m  2
Vậy: m  1 hoặc m  2 .
Bài 92. TS LỚP 10 Phú Thọ 2015 – 2016 Cho parabol P 2
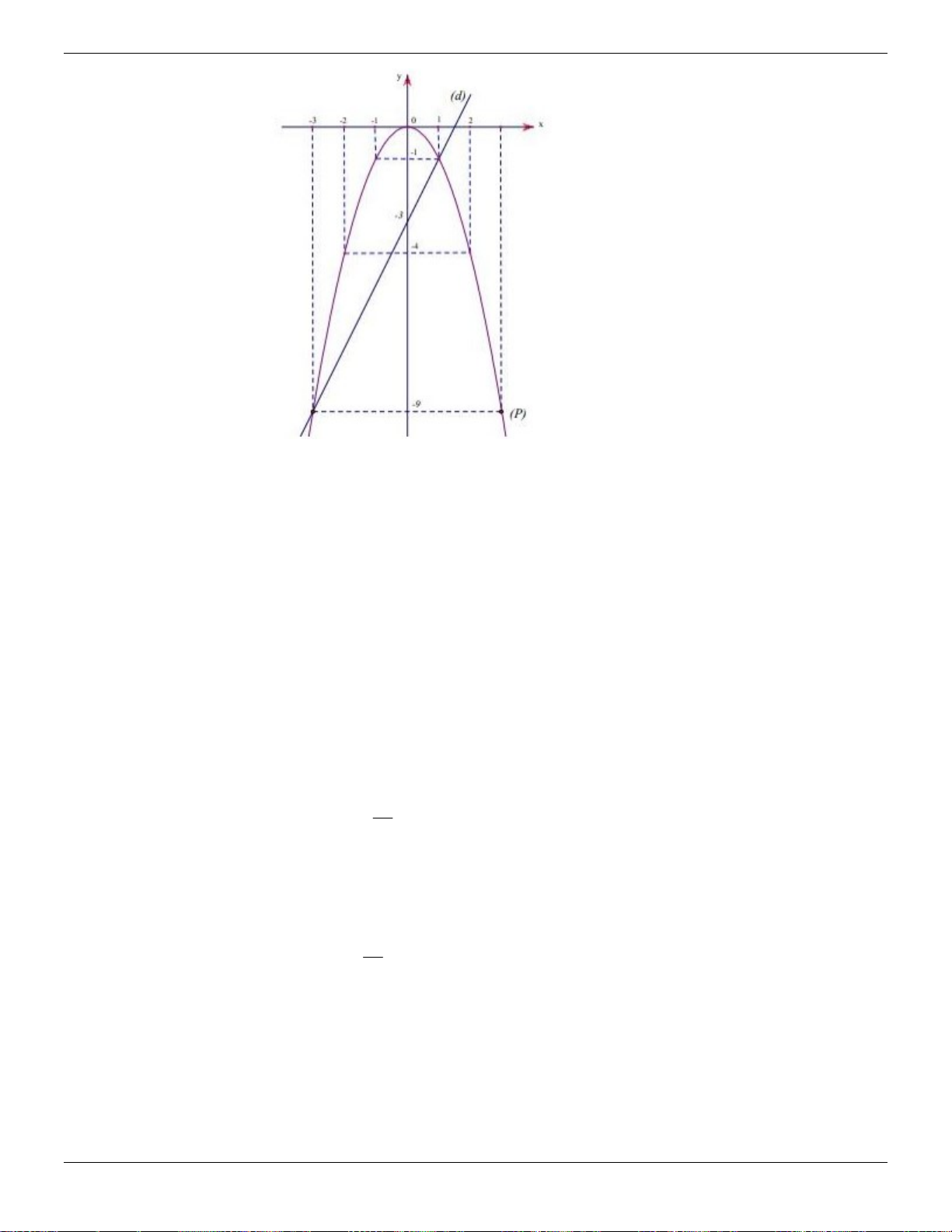
: y  x và đường thẳng d có phương trình: y  2m   1 x  3m  2
a) Tìm tọa độ giao điểm của P và d với m  3 .
b) Chứng minh P và d luôn cắt nhau tại 2 điểm phân biệt A và B với mọi m .
c) Gọi x ; x là hoành độ giao điểm của A và B . Tìm m để 2 2 x  x  20 . 1 2 1 2 Lời giải: a) (1 điểm)
Thay m  3 ta được d : y  8x  7
Phương trình hoành độ giao điểm P và d khi m  3 là 2 2
x  8x  7  x  8x  7  0 Trang 41 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10
Giải phương trình ta được x  1; x  7 1 2
Tọa độ giao điểm của P và d là 1;  1 ;7;49 b) (0,5 điểm)
Xét phương trình hoành độ giao điểm của P và d là: 2 x  2m   1 x  3m  2  0 (1) 2  1  11 2 2
  m  2m 1 3m  2  m  m  3  m    0   m  2  4
Nên phương trình (1) có hai nghiệm phân biệt m suy ra P và d luôn cắt nhau tại 2 điểm phân biệt , A B với mọi m . c) (0,5 điểm)
Ta có: x ; x là nghiệm phương trình (1) vì   0 m . Theo Vi-et ta có: 1 2 x  x  2m  2 1 2 x x  3m2  1 2 2 2 2 2
x  x  20  (x  x )  2x x  20  (2m  2)  2(3m  2)  20 1 2 1 2 1 2 m  2  2
 2m  m  6  0  (m  2)(2m  3)   3  m   2
Bài 93. TS LỚP 10 An Giang 2015 – 2016 Cho hàm số 2
y  x có đồ thị là Parabol P
a) Vẽ đồ thị hàm số đã cho trên mặt phẳng tọa độ Oxy .
b) Viết phương trình đường thẳng d đi qua điểm nằm trên Parabol P có hoành độ x  2 và
có hệ số góc k. Với giá trị k nào thì d tiếp xúc P? Lời giải: a) Bảng giá trị: x 2 1 0 1 2 2 y  x 4 1 0 1 4
Đồ thị hàm số là hình vẽ Trang 42 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10 y 4 1 -2 -1 2 0 1 x
b) Đường thẳng d có hệ số góc k nên có dạng y  kx  b
Điểm thuộc P có hoành độ x  2  y  4
d qua 2;4  4  k.2  b  b  2k  4
Suy ra d : y  kx  2k  4
Đường thẳng d tiếp xúc P khi đó phương trình sau có nghiệm kép 2 x  kx  2k  4 2
 x  kx  2k  4  0 2   k 8k 16
Phương trình có nghiệm kép khi 2
  0  k  8k 16  0  k  4 Vậy k  4 .
Bài 94. TS LỚP 10 Cần Thơ 2015 – 2016 1 
Trong mặt phẳng với hệ tọa độ Oxy , cho P : 2 y  x . 2
a) Vẽ đồ thị của P.
b) Gọi Ax , y và B x ; y là hoành độ giao điểm của P vàd : y  x  4 . Chứng minh: 2 2  1 1  y  y  5 x  x  0 1 2  1 2 Lời giải: y 1  a) P : 2 y  x -2 -1 0 1 2 2 x
Phương trình hoành độ giao điểm của P và d : 1 2 2
x  x  4  x  2x  8  0 2
Giải phương trình ta được: x  2; x  4 1 y=- x2 2
Tọa độ giao điểm là: 2;2 và 4;8
Khi đó: y  y  5 x  x  2  8  5 2  4  0 . 1 2  1 2     Trang 43 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10
Bài 95. TS LỚP 10 Bình Phước 2014– 2015 Cho parabol P 2
: y  x và đường thẳng d : y  3x  2 .
a) Vẽ parabol P và đường thẳng d trên cùng một hệ trục toạ độ.
b) Viết phương trình đường thẳng d vuông góc với đường thẳng d và tiếp xúc với P. Lời giải:
a) + Bảng một số giá trị của P : x 2 1 0 1 2 2 y  x 4 1 0 1 4
+ d đi qua 2 điểm 0;2 và 1;  1 . + Đồ thị: b) d có dạng : y  a x
  b ; d  d  . a a  1 1  1 với a  3  a   d : y  x  b 3 3 1  1
Phương trình hoành độ giao điểm của P và d : 2 2 x 
x  b  x  x  b  0(*) 3 3 1 PT (*) có    4b 9 1 1
d tiếp xúc với P khi    4b  0  b  9 36 1  1
Vậy d có phương trình: y  x  3 36
Bài 96. TS LỚP 10 Đà Nẵng 2014– 2015 Cho hàm số 2
y  x có đồ thị P và hàm số y  4x  m có đồ thị d m  a) Vẽ đồ thị P .
b) Tìm tất cả các giá trị của m sao cho d và P cắt nhau tại hai điểm phân biệt, trong đó m 
tung độ của một trong hai giao điểm đó bằng 1. Lời giải: Trang 44 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10 a) Vẽ đồ thị P . y 4 1 -2 -1 2 0 1 x
b) Phương trình hoành độ giao điểm của 2
y  x và đường thẳng y  4x  m là : 2 2
x  4x  m  x  4x  m  0  1 (1) có   4  m
Để d và P cắt nhau tại hai điểm phân biệt thì   0  4  m  0  m  4 m   m y  4x  m  1 1  x  4
Yêu cầu của bài toán tương đương với m  4  m  4 m  4      1 m   7  m hay  7  m 2  4  m  4  m   4  m   4  4     4  m  4 m  4    m  7  (L) hay m  7  7       m 4 4  m  7 4  m m  4 m  4   2 m  2m 15  0 m  4   m  3
  m  3 hay m  5  m  5
Bài 97. TS LỚP 10 Hà Nam 2014– 2015
Trong mặt phẳng tọa độ Oxy cho Parabol P có phương trình 2
y  x và đường thẳng d có phương trình: y  2
 x  m (với m là tham số).
a) Tìm giá trị của m để d cắt P tại điểm có hoành độ là 2. Trang 45 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10
b) Tìm giá trị của m để d cắt tại hai điểm phân biệt có hoành độ x ;x thỏa mãn hệ thức 1 2 2 2 2 2 x  x  6x x . 1 2 1 2 Lời giải:
a) Điểm thuộc Parabol P 2
: y  x có hoành độ x  2 nên tung độ 2 y  2  4
d cắt P tại điểm có hoành độ bằng 2  4  2.2  m  m  8
Vậy m  8 là giá trị cần tìm
b) Phương trình hoành độ giao điểm của d và P là: 2 2 x  2
 x  m  x  2x  m  0*
d cắt P tại hai điểm phân biệt   1 m  0  m  1
Với m  1 thì d cắt P tại hai điểm phân biệt có hoành độ x ;x . 1 2 x  x  2 Nên theo hệ thức Vi-ét: 1 2  x x    m 1 2 mà 2 2 2 2 2
x  x  (x  x )  2x x  6x x 1 1 1 2 1 2 1 2 2 2 2 2  ( 2
 )  2(m)  6(m)  3m  m  2  0  m 1;m  1 2 3 2  Vậy m  1; m 
là các giá trị cần tìm. 1 2 3
Bài 98. TS LỚP 10 Hà Nội 2014– 2015
Trên mặt phẳng tọa độ Oxy cho đường thẳng d : y  x  6 và parabol P 2 : y  x .
a) Tìm tọa độ các giao điểm của d và P. b) Gọi ,
A B là hai giao điểm của d và P. Tính diện tích tam giác OA . B Lời giải:
a) Phương trình hoành độ giao điểm của d và P là: 2 x  x  6  0
  25  0  phương trình có 2 nghiệm phân biệt x  2;x  3
Với x  2  y  4  A2;4
Với x  3  y  9 B 3;9
Vậy d cắt P tại 2 điểm phân biệt 2;4 và 3;9 .
b) Gọi A , B lần lượt là hình chiếu của A và B xuống trục hoành. Ta có S  S  S  S OAB A  A BB OA  A OBB Ta có :  A B |
 x  x  x  x  A  A  y  BB  y  B  | A B A 5, 9; 4 A B Diện tích hình thang : Trang 46 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10 A  A  BB 9  4 65 S   A B   dvdt A  A B . .5 ( ) B 2 2 2 1 27 S   A A  A O  dvdt OA  . ( ) A 2 2 1 S  BB BO  dvdt OBB . 4( ) 2 65 27 S  S  S  S     dvdt OAB A  A B OA  A OBB 4 15( ) B 2 2
Bài 99. TS LỚP 10 Kon Tum 2014– 2015
a) Vẽ đồ thị hai hàm số: 2
y  x và y  x  2 trên cùng hệ trục tọa độ Oxy .
b) Xác định đường thẳng y  ax  b biết rằng đường thẳng này song song với đường thẳng y  3  x  5 và cắt Parabol 2
y  2x tại điểm A có hoành độ bằng 1 . Lời giải:
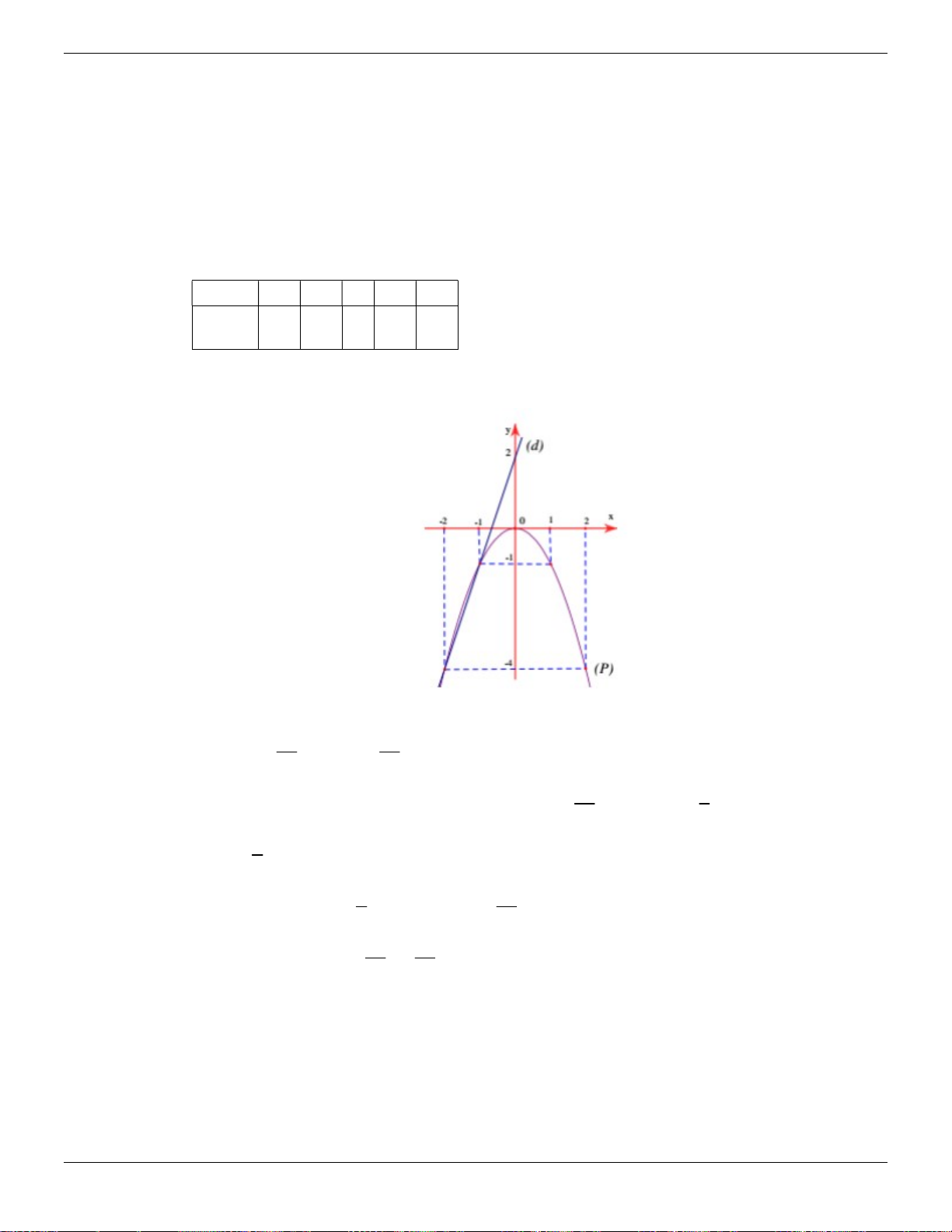
a) Gọi P và d là đồ thị của 2 hàm số : 2 y  x và y  x  2 2 y  x x -1 0 1 y 1 0 1 y  x  2 x 0 -2 y 2 0 y y=x2 y=x+2 4 1 -2 -1 2 0 1 x
b) Phương trình đường thẳng d có dạng y  ax  b
Vì d songsong với đường thẳng y  3
 x  5  a  3 và b  5  d ' : y  3x  b A thuộc Parabol: 2 y  2x  y   2 2 1  2 A
Suy ra tọa độ A1;2d  2   3  . 
1  b  b  1  d ' : y  3x – 1
Bài 100. TS LỚP 10 Long An 2014– 2015 Trang 47 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10
Trong mặt phẳng tọa độ Oxy cho Parabol P 2
: y  x và đường thẳng d : y  x  2.
a) Hãy vẽ P và d trên cùng một mặt phẳng tọa độ Ox . y
b) Tìm tọa độ giao điểm của P và d .
c) Viết phương trình đường thẳng d : y  ax  b . Biết rằng d song song với d và cắt P 1  1 
tại điểm A có hoành độ là 2 . Lời giải:
a) Hãy vẽ P và d
b) Tìm tọa độ giao điểm của P và d .
Dựa vào đồ thị hàm số ta có: hai giao điểm 1;  1 và 2;4 .
c) d song song với d  a  1  1 
Ta có A2;4 thuộc P  2a  b  4  b  6
Vậy d : y  x  6 . 1 
Bài 101. TS LỚP 10 Thái Bình 2014– 2015 Cho parabol P 2
: y  x và đường thẳng d : y  2m  3 x  2m  2 ( m là tham số).
a) Với m  5 , tìm tọa độ giao điểm của parabol P và đường thẳng d.
b) Chứng minh rằng: với mọi m parabol P và đường thẳng d cắt nhau tại hai điểm phân
biệt. Tìm m sao cho hai giao điểm đó có hoành độ dương.
c) Tìm điểm cố định mà đường thẳng d luôn đi qua với mọi . m Lời giải:
a) Với m  5, d có phương trình y  4  x 12
Hoành độ giao điểm của P và d là nghiệm phương trình: x  6 2 2
x  4x 12  x  4x 12  0  (x  6)(x  2)  0   x  2  x  6  y  36  x  2  y  4 Trang 48 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10
Vậy với m  5, thì P và d cắt nhau tại hai điểm 6;36,2;4.
b) Hoành độ giao điểm của P và d là nghiệm phương trình: 2 x  m   2 2
3 x  2m  2  x  2m  3 x  2m  2  0(1) 2 2 2
  (m  3)  (2m  2)  m  4m 11  (m  2)  6  0m
Do đó (1) có hai nghiệm phân biệt với mọi m suy ra P và d cắt nhau tại hai điểm phân biệt . m
x ; x là hai nghiệm của phương trình (1), áp dụng định lý Viet ta có: 1 2 x  x  2(m  3) 1 2 x x  2m2  1 2
Hai giao điểm đó có hoành độ dương khi và chỉ khi x  x  0 2 m  3  0 m  3 1 2         m  1 x x  0  2m  2  0 m  1 1 2
Vậy với m  1 thì P và d cắt nhau tại hai điểm phân biệt với hoành độ dương.
c) Gọi điểm cố định mà đường thẳng d đi qua với mọi m là  x ; y ta có: 0 0 
y  2 m  3 x  2m  2m 0   0
 m2x  2  6x  y  2  0m 0  0 0 2x  2  0 x  1 0 0     6x  y  2  0 y  8  0 0  0
Vậy với mọi m thì đường thẳng d luôn đi qua 1;8.
Bài 102. TS LỚP 10 Thanh HÓa 2014– 2015
Trong mặt phẳng tọa độ Oxy cho đường thẳng d : y  mx  3 tham số m và Parabol P 2 : y  x .
a) Tìm m để đường thẳng d đi qua điểm A1;0.
b) Tìm m để đường thẳng d cắt Parabol P tại hai điểm phân biệt có hoành độ lần lượt là
x ; x thỏa mãn x  x  2 . 1 2 1 2 Lời giải:
a) Đường thẳng d đi qua điểm A1;0 nên có 0  . m 1 3  m  3.
b) Xét phương trình hoành độ giao điểm giữa d và P : 2 x  mx  3  0 Có 2   m 12
d cắt P tại hai điểm phân biệt có hoành độ lần lượt là x ,x khi 1 2 m  2 3 2 2
  m 12  0  m 12   m  2  3 x  x  m
Áp dụng hệ thức Vi – Ét ta có: 1 2  x x  3  1 2 Theo bài ra ta có Trang 49 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10
x  x  2   x  x 2  4   x  x 2  4x x  4 1 2 1 2 1 2 1 2 2 2
 m  4.3  4  m 16  m  4
Vậy m  4 là giá trị cần tìm.
Bài 103. TS LỚP 10 Thừa Thiên Huế 2014– 2015 Cho hàm số 2
y  ax có đồ thị P và đường thẳng d : y  mx  m – 3
a) Tìm a để đồ thị P đi qua điểm B2;2 .
b) Chứng minh rằng đường thẳng d luôn cắt đồ thị P tại hai điểm phân biệt C và D với mọi giá trị của . m
c) Gọi x và x lần lượt là hoành độ của hai điểm C và .
D Tìm các giá trị của m sao cho C D 2 2 x  x  2x x  20  0 C D C D Lời giải: 1
a) P đi qua điểm B2;2 nên ta có: 2 2  . a 2  a  2 1  Vậy P : 2 y  x 2
b) Phương trình hoành độ giao điểm của P và d là: 1 2 2
x  mx  m  3  x  2mx  2m  6  0(*) 2
  m  2m  6  m  2m  6  m  2 2 2 1  5  0m
Do đó, đường thẳng d luôn cắt đồ thị P tại hai điểm phân biệt C và D với mọi giá trị của . m x  x  2m
c) Áp dụng định lí Vi-ét ta có: C D  x x  2m  6  C D Theo giả thiết
x  x  2x x  20  0  x x x x C D C D   C D 2 2 2  4  20  0 C D 2 2
 (2m)  4(2m  6)  20  0  4m  8m  4  0 2
 4(m 1)  0  m  1
Vậy với m  1 thỏa mãn yêu cầu bài toán.
Bài 104. TS LỚP 10 Tiền Giang 2014– 2015
Trong mặt phẳng tọa độ cho Paradol P 2
: y  x và đường thẳng d : y  x  2
a) Vẽ P và d trên cùng một hệ trục tọa độ.
b) Tìm tọa độ giao điểm A và B của P và d bằng phép tính.
c) Tính độ dài đoạn A . B Lời giải: a) Vẽ P và d
Lập bảng giá trị (có ít nhất 5 giá trị) x 2 1 0 1 2 y 4 1 0 1 4 Trang 50 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10 y y=x2 y=x+2 4 1 -2 -1 2 0 1 x
Phương trình hoành độ giao điểm của P và d là: 2 2
x  x  2  x  x  2  0
Ta có: a  b  c  1  
1  2  0 nên phương trình có nghiệm 2 nghiệm x  1  ; x  2 1 2
Từ đó tính được: y  1; y  4 1 2
Vậy tọa độ giao điểm giữa P và d là: A1;  1 ; B 2;4
Áp dụng công thức tính khoảng cách ta có: AB   x  x y y dvdt B A 2    B A 2 2 2  3  3  18  3 2( )
Bài 105. TS LỚP 10 Bà Rịa Vũng Tàu 2014– 2015 Cho parabol P 2
: y  2x và đường thẳng d : y  x  m 1 (với m là tham số) a) Vẽ Parabol P .
b) Tìm tất cả các giá trị của m để P cắt d có đúng một điểm chung.
c) Tìm tọa độ các điểm thuộc P có hoành độ bằng hai lần tung độ. Lời giải:
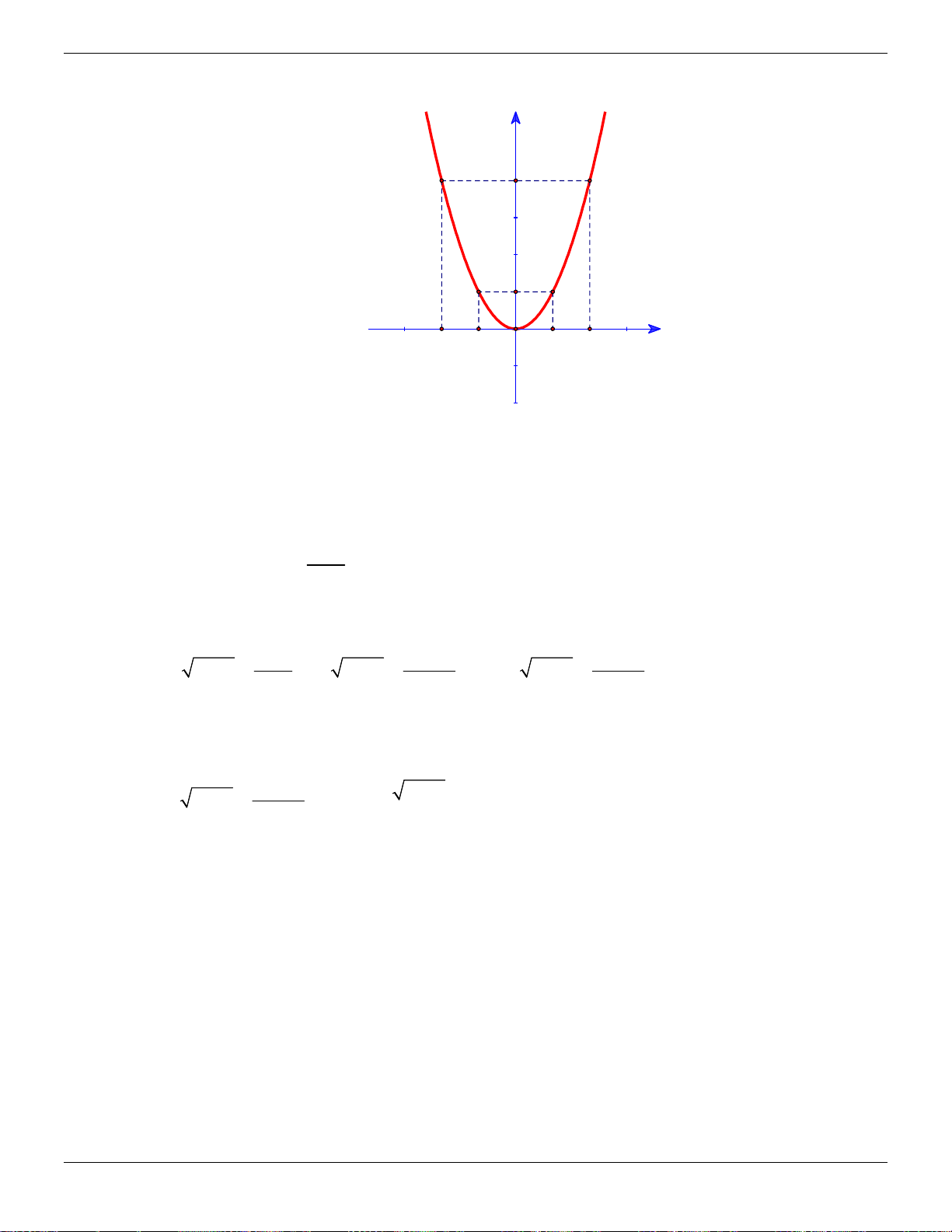
a) Vẽ đồ thị hàm số: x 2 1 0 1 2 2 y  2x 8 2 0 2 8 Trang 51 ThS.Nguyễn Đăng Tuấn
Chuyên đề luyện thi vào lớp 10
b) Xét phương trình hoành độ giao điểm cả P vàd : 2 2
2x  x  m 1  2x  x  m 1  0    2 1  4.2.m   1  9  8m 9
Để P vàd có một điểm chung thì :   0  9  8m  0  m  8 9
Vậy với m  thì P vàd có một điểm chung. 8
c) Điểm thuộc P mà hoành độ bằng hai lần tung độ nghĩa là x  2y nên ta có:  y  0  y  22y2 2  y  8y   1 y   8  
Vậy điểm thuộc P mà hoành độ bằng hai lần tung độ là 0;0 1 1 ; ;   .  4 8 
__________ THCS.TOANMATH.com __________ Trang 52

Chuyên đề hàm số và đồ thị ôn thi vào lớp 10 môn Toán – Nguyễn Đăng Tuấn

Thông tin :

Tài liệu liên quan:

Tổng hợp kiến thức Đại số THCS

Cấu trúc đề thi vào 10 năm 2023 tỉnh Tỉnh Bà Rịa - Vũng Tàu

Cấu trúc đề thi tuyển sinh lớp 10 tỉnh Thái Nguyên năm 2023 - 2024

Cấu trúc đề thi vào lớp 10 năm 2023 - 2024 tỉnh Thanh Hóa

Cấu trúc đề thi vào 10 tỉnh Quãng Ngãi năm 2023 - 2024