























Preview text:
TÀi LIỆU ÔN THI THPT QUỐC GIA 2016 1
PHẦN 1. KIẾN THỨC CƠ BẢN
A – KIẾN THỨC CƠ BẢN
1. Chứng minh đường thẳng d song song mp() (d ())
Cách 1. Chứng minh d //d ' và d ' ( )
Cách 2. Chứng minh d ( ) và ( ) / /( )
Cách 3. Chứng minh d và () cùng vuông góc với 1 đường thẳng hoặc cùng vuông góc với 1 mặt phẳng
2. Chứng minh mp() song song với mp()
Cách 1. Chứng minh mp() chứa hai đường thẳng cắt nhau cùng song song với () (Nghĩa là 2 đường
thẳng cắt nhau trong mặt này song song với 2 đường thẳng trong mặt phẳng kia)
Cách 2. Chứng minh () và () cùng song song với 1 mặt phẳng hoặc cùng vuông góc với 1 đường thẳng.
3. Chứng minh hai đường thẳng song song:
Cách 1. Hai mặt phẳng (), () có điểm chung S lần lượt chứa hai đường thẳng song song a và b thì
() () = Sx // a // b.
Cách 2. () // a, a () () () = b // a
Cách 3. Hai mặt phẳng cắt nhau cùng song song với một đường thẳng thì giao tuyến của chúng song
song với đường thẳng đó.
Cách 4. Một mặt phẳng cắt hai mặt phẳng song song cho 2 giao tuyến song song
Cách 5. Một mặt phẳng song song với giao tuyến của 2 mặt phẳng cắt nhau, ta được 3 giao tuyến song song.
Cách 6. Hai đường thẳng cùng song song với đường thẳng thứ 3 hoặc cùng vuông góc với một mặt
phẳng thì song song với nhau.
Cách 7. Sử dụng phương pháp hình học phẳng: đường trung bình, định lí Thales đảo, cạnh đối tứ giác đặc biệt, …
4. Chứng minh đường thẳng d vuông góc với mặt phẳng ()
Cách 1. Chứng minh đường thẳng d vuông góc với hai đường thẳng cắt nhau nằm trong ().
Cách 2. Chứng minh d nằm trong một trong hai mặt phẳng vuông góc và d vuông góc với giao tuyến
d vuông góc với mp còn lại.
Cách 3. Chứng minh d là giao tuyến của hai mặt phẳng cùng vuông góc với mặt thứ 3.
Cách 4. Chứng minh đường thẳng d song song với a mà a ().
Cách 5. Đường thẳng nào vuông góc với một trong hai mặt phẳng song song thì cũng vuông góc với mặt phẳng còn lại.
Cách 6. Chứng minh d là trục của tam giác ABC nằm trong ()
5. Chứng minh hai đường thẳng d và d vuông góc:
Cách 1. Chứng minh d () và () d.
Cách 2. Sử dụng định lí 3 đường vuông góc.
Cách 3. Chứng tỏ góc giữa d, d bằng 900.
6. Chứng minh hai mặt phẳng () và () vuông góc:
Cách 1. Chứng minh () d và d ().
Cách 2. Chứng tỏ góc giữa hai mặt phẳng () và () bằng 900.
Cách 3. Chứng minh a // () mà () a
Cách 4. Chứng minh () // (P) mà () (P)
GV. TRẦN QUỐC NGHĨA
TOÁN HỌC BẮC – TRUNG – NAM
Chuyên đê: HÌNH HỌC KHÔNG GIAN 2
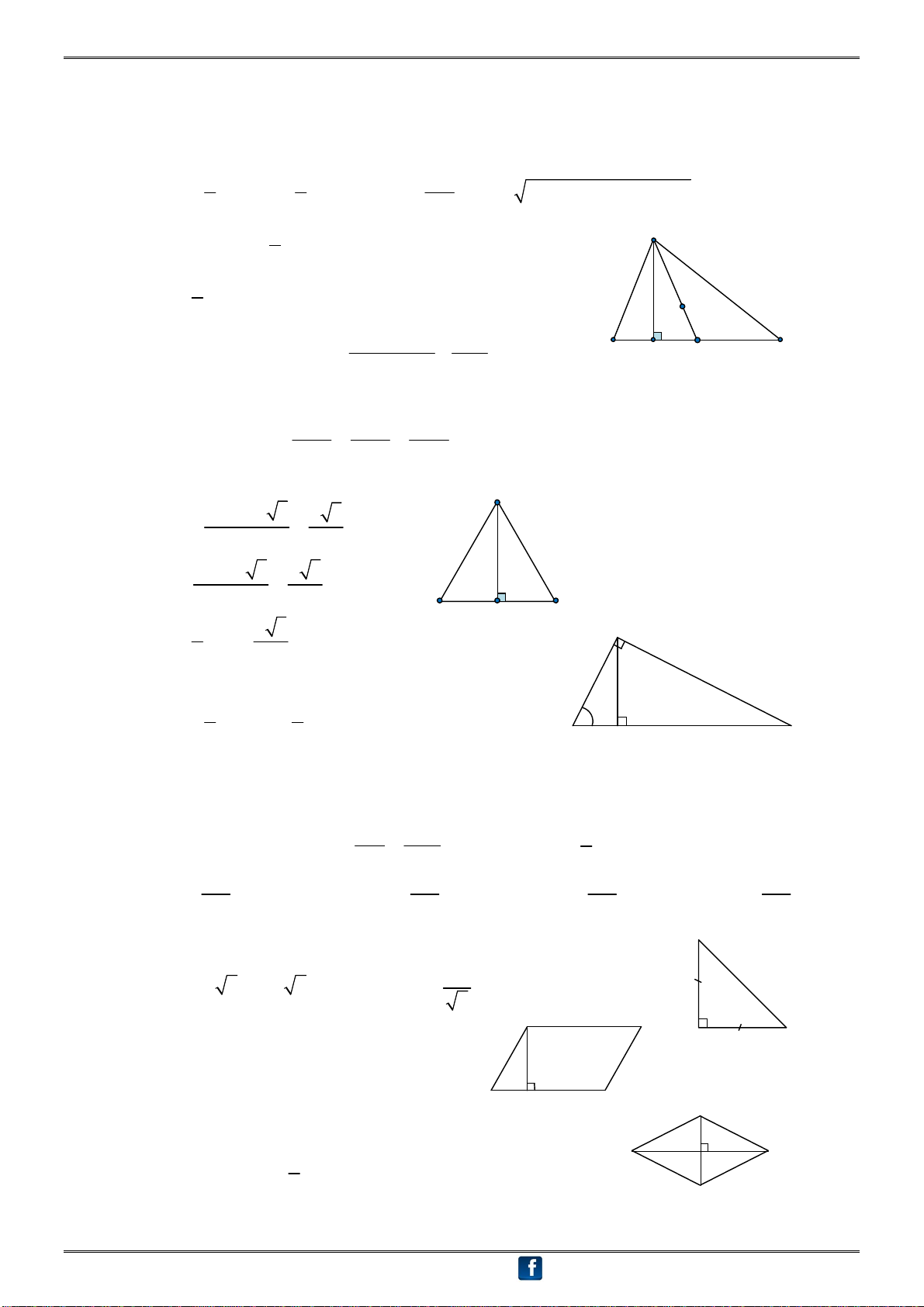
B – CÔNG THỨC CƠ BẢN I. TAM GIÁC 1. Tam giác thường: 1 1 abc ① S BC.AH A . B AC.sin A pr
p( p a)( p b)( p c) ABC 2 2 4R 1 A ② S S S ABM A CM 2 ABC 2 ③ AG
AM (G là trọng tâm) G 3 2 2 2 AB AC BC
④ Độ dài trung tuyến: 2 AM B H M C 2 4
⑤ Định lí hàm số cosin: 2 2 2
BC AB AC 2 A .
B AC.cos A a b c
⑥ Định lí hàm số sin: 2R sin A sin B sin C
2. Tam giác đều ABC cạnh a: A canh2 3 a 3 ① S ABC a 4 a canh 3 a 3 ② AH 3 2 B H C 2 a 3 A ③ AG AH 3 3
3. Tam giác ABC vuông tại a: 1 1 ① S A . B AC AH .BC ABC 2 2 B H C ② 2 2 2
BC AB AC ③ 2 2 2
BA BH BC ④ 2 2 2
CA CH CB ⑤ 2 HA H . B HC 2 HB AB 1
⑥ AH .BC A . B AC ⑦ ⑧ AM BC 2 HC AC 2 AC AC AC AB ⑨ sin B ⑩ sin B ⑪ tan B ⑫ cot B BC BC AB AC C
4. Tam giác ABC vuông cân tại A BC
① BC AB 2 AC 2 ② AB AC 2 A D II. TỨ GIÁC A B 1. Hình bình hành: Diện tích: S
BC.AH A . B A . D sin A B H C ABCD A 2. Hình thoi: B D 1 Diện tích: S
AC.BD A . B A . D sin A ABCD 2 C Đặc biệt: khi 0 ABC 60 hoặc 0
BAC 120 thì các tam giác ABC, ACD đều.
GV. TRẦN QUỐC NGHĨA
TOÁN HỌC BẮC – TRUNG – NAM
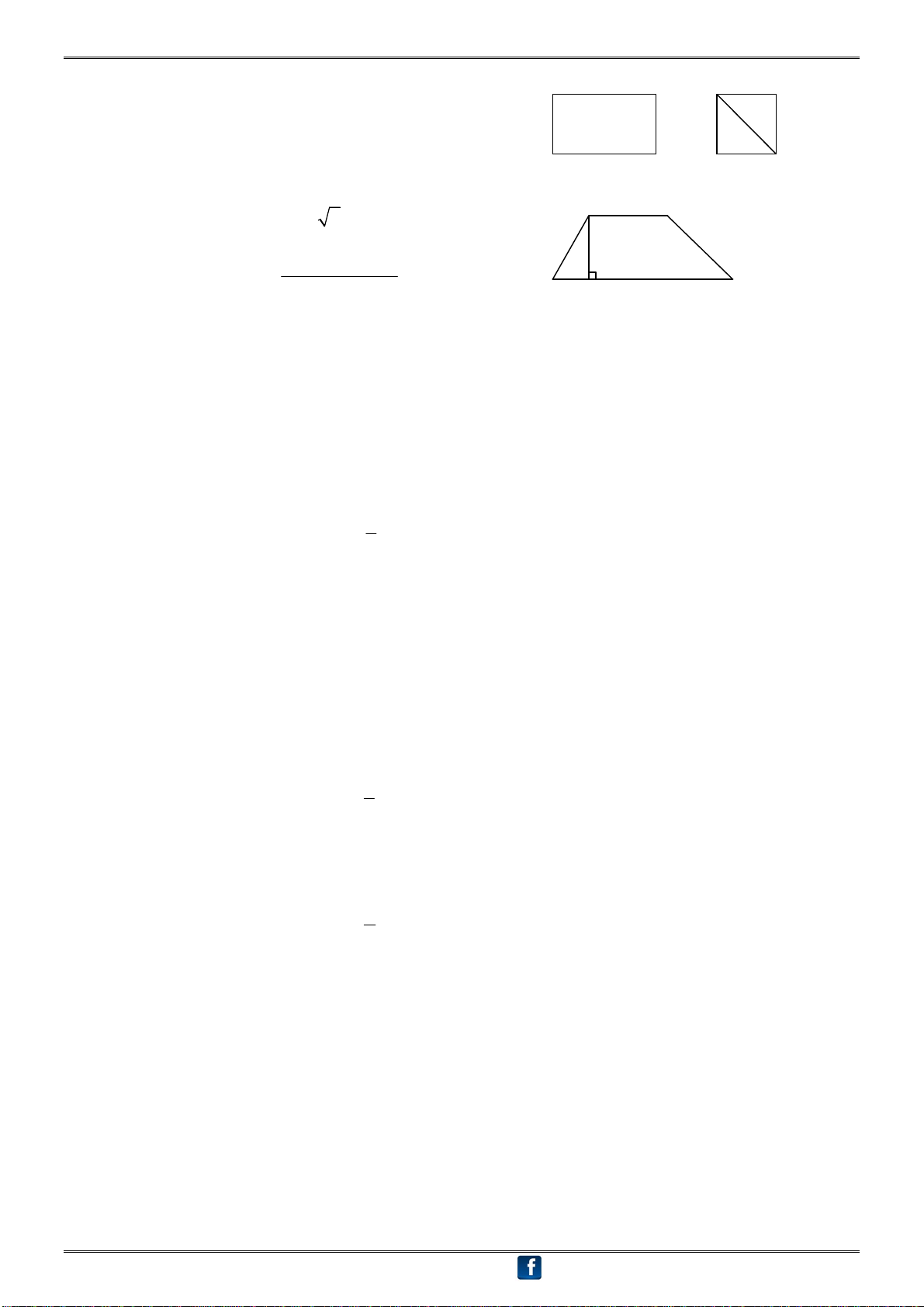
TÀi LIỆU ÔN THI THPT QUỐC GIA 2016 3 3. Hình chữ nhật: A D A D S A . B AD ABCD 4. Hình vuông: B C B C Diện tích: 2 S AB ABCD A D
Đường chéo: AC AB 2
( AD BC).AH 5. Hình thang: S ABCD 2 B H C
III. CÁC HÌNH TRONG KHÔNG GIAN 1. Hình lăng trụ:
① Thể tích khối lăng trụ: V = Sđáy.Chiều cao
② Diện tích xung quanh: Sxq = Tổng diện tích các mặt bên
③ Diện tích toàn phần: Stp = Sxq + S2đáy. 2. Hình chóp: 1
① Thể tích khối chóp: V = Sđáy.Chiều cao 3
② Diện tích xung quanh: Sxq = Tổng diện tích các mặt bên
③ Diện tích toàn phần:
Stp = Sxq + Sđáy. 3. Hình trụ:
① Thể tích khối trụ: 2 V R l
② Diện tích xung quanh: S 2 R l xq 4. Hình nón: 1
① Thể tích khối nón: 2 V R h 3
② Diện tích xung quanh: S R l xq 5. Hình cầu: 4
① Thể tích khối cầu: 3 V R 3
② Diện tích mặt cầu: 2 S 4 R
GV. TRẦN QUỐC NGHĨA
TOÁN HỌC BẮC – TRUNG – NAM
Chuyên đê: HÌNH HỌC KHÔNG GIAN 4
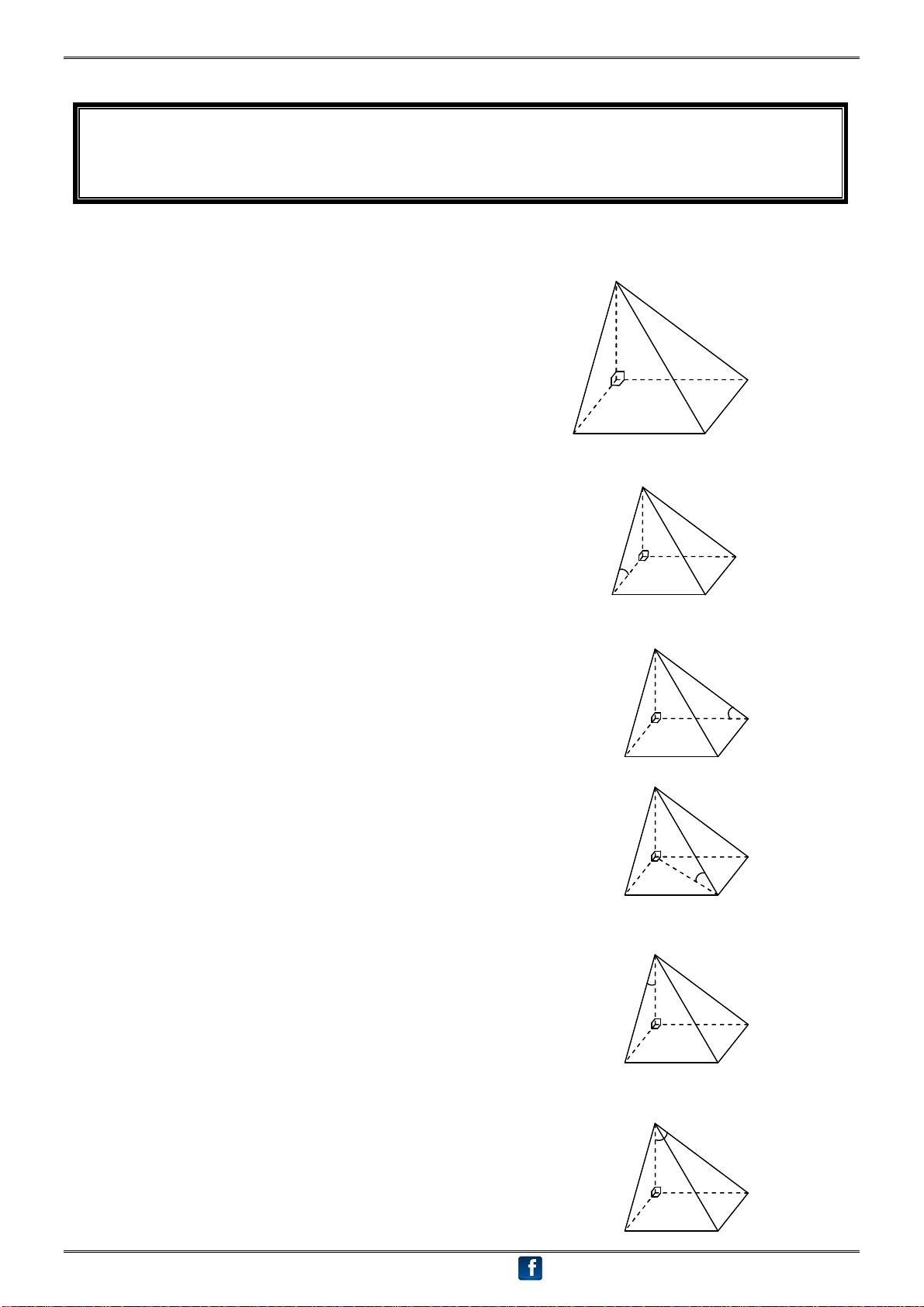
C - VÀI HÌNH THƯỜNG GẶP HÌNH 1
Hình chóp S.ABCD, có đáy ABCD là hình chữ nhật (hoặc hình vuông) và
SA vuông góc với đáy
H1.1 - Đáy, đường cao, cạnh đáy, cạnh bên, mặt bên của hình chóp
1. Đáy: ABCD là hình vuông hoặc hình chữ nhật S
2. Đường cao: SA
3. Cạnh bên: SA, SB, SC, SD
4. Cạnh đáy: AB, BC, CD, DA
5. Mặt bên: SAB là tam giác vuông tại A. D
SBC là tam giác vuông tại B. A
SCD là tam giác vuông tại D.
SAD là tam giác vuông tại A. B C S
H1.2 - Góc giữa cạnh bên và đáy
1. Góc giữa cạnh bên SB và mặt đáy (ABCD) bằng : Ta có: SA (ABCD) (gt) D
Hình chiếu của SB lên (ABCD) là AB A SB, (ABCD) SB, AB SBA B C S
2. Góc giữa cạnh bên SD và mặt đáy (ABCD) bằng : Ta có: SA (ABCD) (gt)
Hình chiếu của SD lên (ABCD) là AD D A SD, (ABCD) SD, AD SDA B C S
3. Góc giữa cạnh bên SC và mặt đáy (ABCD) bằng : Ta có: SA (ABCD) (gt)
Hình chiếu của SC lên (ABCD) là AC D SC, (ABCD) SC, AC SCA A B C
H1.3 - Góc giữa cạnh bên và mặt bên: S
1. Góc giữa cạnh bên SB và mặt bên (SAD) bằng : Ta có: AB (SAD) D
Hình chiếu của SB lên (SAD) là SA A SB, (SAD) SB, SA BSA B C
2. Góc giữa cạnh bên SD và mặt bên (SAB) bằng : S Ta có: AD (SAB)
Hình chiếu của SD lên (SAB) là SA D SD, (SAB) SD,SA DSA A B C
GV. TRẦN QUỐC NGHĨA
TOÁN HỌC BẮC – TRUNG – NAM
TÀi LIỆU ÔN THI THPT QUỐC GIA 2016 5
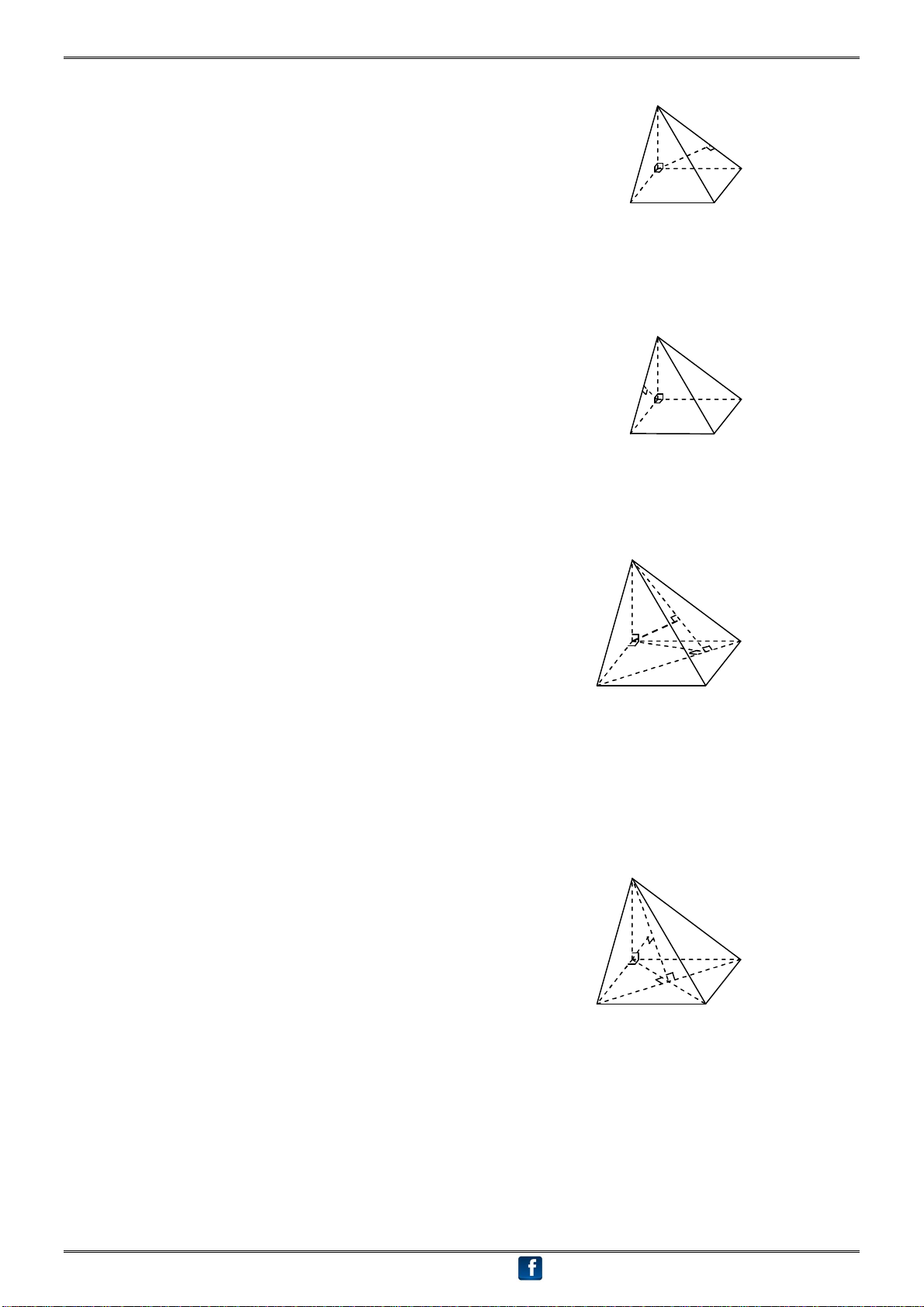
3. Góc giữa cạnh bên SC và mặt bên (SAB) bằng : Ta có: BC (SAB)
Hình chiếu của SC lên (SAB) là SB S SC, (SAB) SC, SB BSC D
4. Góc giữa cạnh bên SC và mặt bên (SAD) bằng : A Ta có: DC (SAD) B S C
Hình chiếu của SC lên (SAD) là SD SC, (SAD) SC,SD DSC D A
H1.4 - Góc giữa mặt bên và mặt đáy: B C
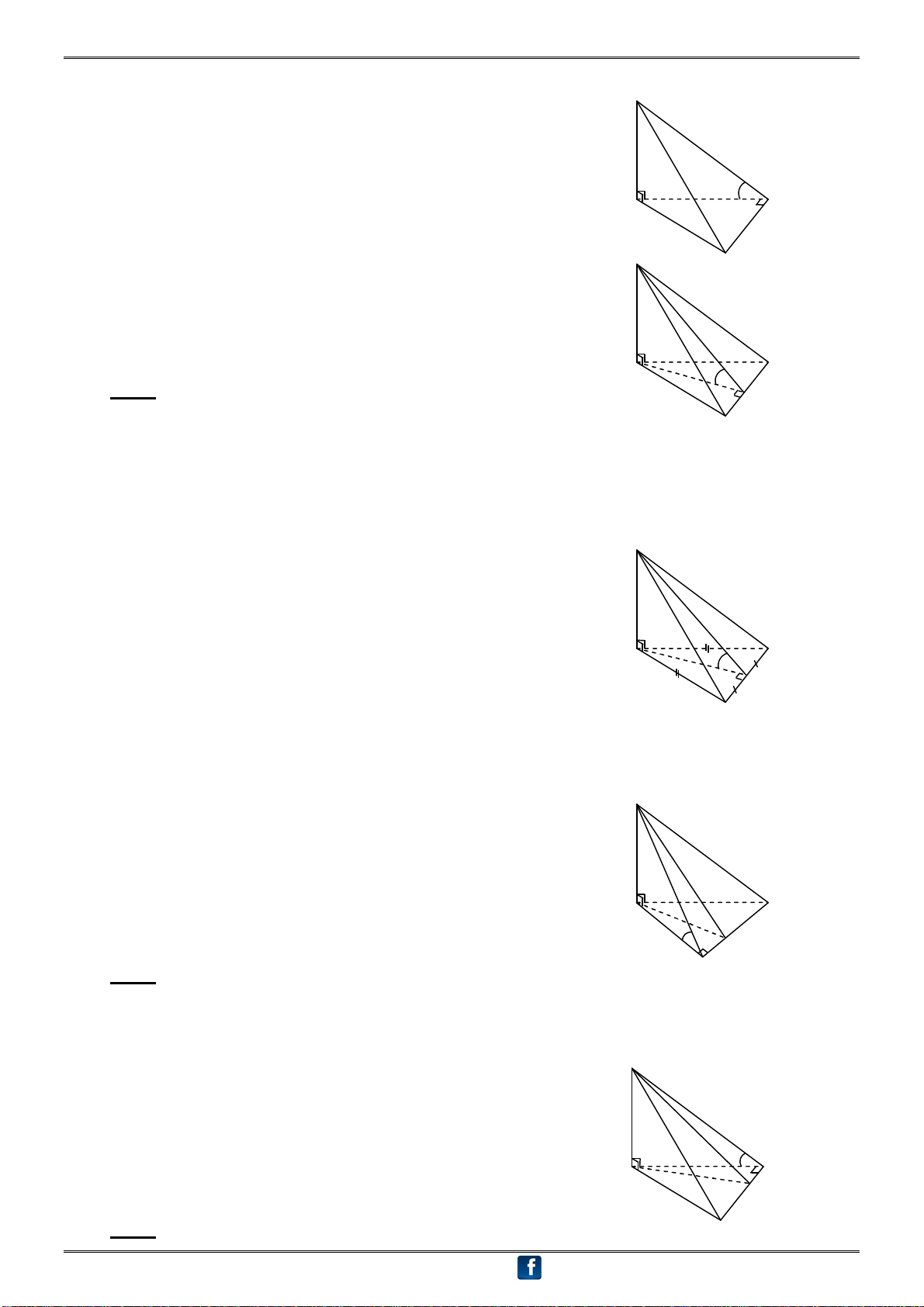
1. Góc giữa mặt bên (SBC) và mặt đáy (ABCD) bằng : S Ta có: BC AB tại B (?) BC SB tại B (?) D (SBC) (ABCD) = BC A (SBC), (ABCD) AB,SB SBA B C
2. Góc giữa mặt bên (SCD) và mặt đáy (ABCD) bằng : S
Ta có: CD AD tại D (?), CD SD tại D (?) D (SCD) (ABCD) = CD A (SCD), (ABCD) AD,SD SDA B C
3. Góc giữa mặt phẳng (SBD) và mặt đáy (ABCD) bằng : S
Đáy ABCD là hình chữ nhật:
Trong (ABCD), vẽ AH BD tại H BD SH (?) A D (SBD),(ABCD) H AH,SH SHA B C
Chú ý: Nếu AB < AD thì điểm H ở gần B hơn
Nếu AB > AD thì điểm H ở gần D hơn S
Đáy ABCD là hình vuông: Gọi O = AC BD AO BD (?) A D BD SO (?) O (SBD), (ABCD) SO, AO SOA B C
GV. TRẦN QUỐC NGHĨA
TOÁN HỌC BẮC – TRUNG – NAM
Chuyên đê: HÌNH HỌC KHÔNG GIAN 6
H1.5 – Khoảng cách “điểm – mặt” S
1. Khoảng cách từ A đến mặt phẳng (SCD) H
Trong mp(SAD), vẽ AH SD tại H D AH (SCD) (?) A d[A,(SCD)] = AH B C
2. Khoảng cách từ B đến mặt phẳng (SCD)
Vì AB // (SCD) (?) nên d[B,(SCD)] = d[A,(SCD)] (xem dạng 1) S
3. Khoảng cách từ A đến mặt phẳng (SBC)
Trong mp(SAB), vẽ AH SB tại H H AH (SBC) (?) D A d[A,(SBC)] = AH B C
4. Khoảng cách từ D đến mặt phẳng (SBC)
Vì AD // (SBC) (?) nên d[D,(SBC)] = d[A,(SBC)] (xem dạng 3)
5. Khoảng cách từ A đến mặt phẳng (SBD) S
Đáy ABCD là hình chữ nhật:
Trong (ABCD), vẽ AI BD tại I H A D BD (SAI) (?) I
Trong (SAI), vẽ AH SI tại H B C AH (SBD) (?) d[A, (SBD)] = AH
Chú ý: Nếu AB < AD thì điểm I ở gần B hơn
Nếu AB > AD thì điểm I ở gần D hơn
Đáy ABCD là hình vuông: S Gọi O = AC BD AO BD (?) H BD (SAO) (?) A D
Trong (SAO), vẽ AH SO tại H O AH (SBD) (?) B C d[A, (SBD)] = AH
6. Khoảng cách từ C đến mặt phẳng (SBD)
Vì O là trung điểm của AC nên d[C,(SBD)] = d[A,(SBD)]
GV. TRẦN QUỐC NGHĨA
TOÁN HỌC BẮC – TRUNG – NAM
TÀi LIỆU ÔN THI THPT QUỐC GIA 2016 7 HÌNH 2
Hình chóp S.ABCD, có đáy ABCD là hình thang vuông tại A và B và SA
vuông góc với đáy
H2.1 - Đáy, đường cao, cạnh đáy, cạnh bên, mặt bên của hình chóp S
1. Đáy: Hình thang ABCD vuông tại A và B
2. Đường cao: SA
3. Cạnh bên: SA, SB, SC, SD
4. Cạnh đáy: AB, BC, CD, DA A D
5. Mặt bên: SAB là tam giác vuông tại A.
SBC là tam giác vuông tại B. B C
SAD là tam giác vuông tại A.
Chú ý: Nếu AB = BC và AD = 2BC thì AC CD
CD (SAC) SCD vuông tại C A D
H2.2 - Góc giữa cạnh bên SB và đáy
1. Góc giữa cạnh bên SB và mặt đáy (ABCD): B C Ta có: SA ABCD (gt)
Hình chiếu của SB lên (ABCD) là AB SB, (ABCD) SB, AB SBA
2. Góc giữa cạnh bên SD và mặt đáy (ABCD): S Ta có: SA ABCD (gt)
Hình chiếu của SD lên (ABCD) là AD SD, (ABCD) SD, AD SDA A D
3. Góc giữa cạnh bên SC và mặt đáy (ABCD): Ta có: SA ABCD (gt) B C
Hình chiếu của SC lên (ABCD) là AC SC, (ABCD) SC, AC SCA S
H2.3 - Góc giữa mặt bên và mặt đáy:
1. Góc giữa mặt bên (SBC) và mặt đáy (ABCD): Ta có: BC AB tại B (?) A D BC SB tại B (?) (SBC) (ABCD) = BC B C (SBC), (ABCD) AB,SB SBA
GV. TRẦN QUỐC NGHĨA
TOÁN HỌC BẮC – TRUNG – NAM
Chuyên đê: HÌNH HỌC KHÔNG GIAN 8 S
2. Góc giữa mặt bên (SCD) và mặt đáy (ABCD):
Trong (ABCD), vẽ AM CD tại M SM CD tại M (?) Mà (SCD) (ABCD) = CD A D (SCD), (ABCD) AM, SM SMA M B C
Chú ý: Nếu AB = BC và AD = 2BC thì AC CD. Do đó M C. S
H2.4 – Khoảng cách “điểm – mặt” H
1. Khoảng cách từ A đến mặt phẳng (SBC) A D
Trong mp(SAB), vẽ AH SB tại H AH (SBC) (?) d[A,(SBC)] = AH B C
2. Khoảng cách từ D đến mặt phẳng (SBC) S
Vì AD // (SBC) (?) nên d[D,(SBC)] = d[A,(SBC)] (xem dạng 3)
3. Khoảng cách từ A đến mặt phẳng (SCD) H
Trong (ABCD), vẽ AM CD tại M A D CD (SAM) (?) M
Trong (SAM), vẽ AH SM tại H AH (SCD) (?) B C D[A,(SCD)] = AH
Chú ý: Nếu AB = BC và AD = 2BC thì AC CD. Do đó M C. HÌNH 3
Hình chóp tứ giác đều S.ABCD S
H3.1 - Đáy, đường cao, cạnh đáy, cạnh bên, mặt bên của hình chóp
1. Đáy: ABCD là hình vuông
2. Đường cao: SO
3. Cạnh bên: SA = SB = SC = SD A D
4. Cạnh đáy: AB = BC = CD = DA
5. Mặt bên: SAB, SBC, SCD, SAD O
là các tam giác cân tại S và bằng nhau. B C
Gọi O là tâm hình vuông ABCD SO (ABCD)
H3.2 - Góc giữa cạnh bên và đáy
1. Góc giữa cạnh bên SA và mặt đáy (ABCD): Ta có: SO (ABCD) (?)
Hình chiếu của SA lên (ABCD) là AO SA, (ABCD) SA, AO SAO
GV. TRẦN QUỐC NGHĨA
TOÁN HỌC BẮC – TRUNG – NAM
TÀi LIỆU ÔN THI THPT QUỐC GIA 2016 9
2. Góc giữa cạnh bên SB và mặt đáy (ABCD): S Tương tự SB, (ABCD) SB, BO SBO
3. Góc giữa cạnh bên SC và mặt đáy (ABCD): Tương tự SC, (ABCD) SC, CO SCO A D
4. Góc giữa cạnh bên SD và mặt đáy (ABCD): O Tương tự SD, (ABCD) SD, DO SDO B C
Chú ý: SAO SBO SCO SDO
“Góc giữa các cạnh bên với mặt đáy bằng nhau” S
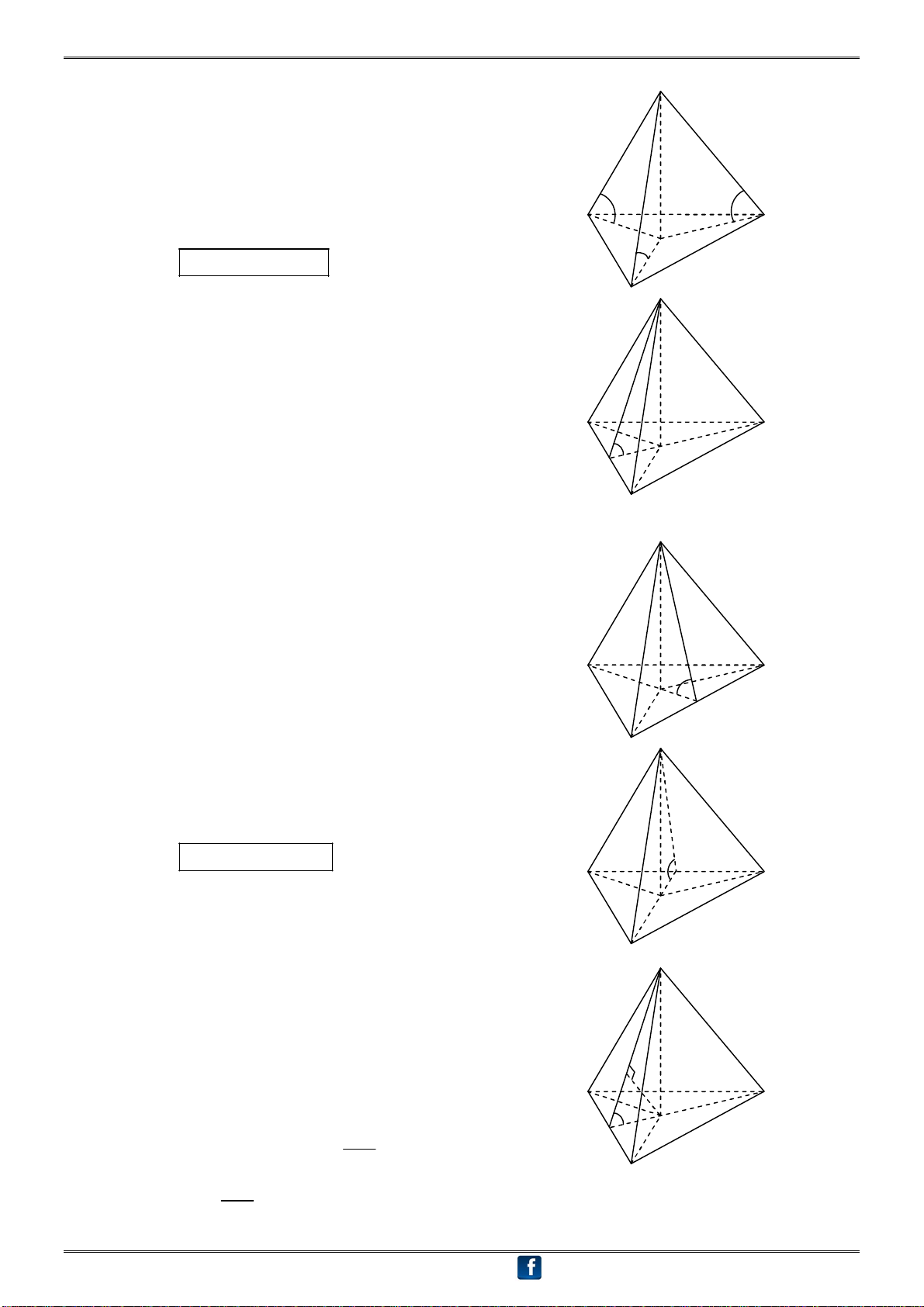
H3.3 - Góc giữa mặt bên và mặt đáy:
1. Góc giữa mặt bên (SAB) và mặt đáy (ABCD): Ta có: OM AB tại M (?) A D AB SM tại M (?) M Mà (SAB) (ABCD) = AB O B C (SAB), (ABCD) OM, SM SMO S
2. Góc giữa mặt bên (SBC) và mặt đáy (ABCD): Ta có: ON BC tại N (?) BC SN tại N (?) A D Mà (SBC) (ABCD) = BC (SBC), (ABCD) ON,SN SNO O B N C S
3. Góc giữa mặt bên (SCD) và mặt đáy (ABCD): Ta có: OP CD tại P (?) CD SP tại P (?) Mà (SCD) (ABCD) = CD A D (SCD), (ABCD) OP, SP SPO O P B C
4. Góc giữa mặt bên (SAD) và mặt đáy (ABCD): S Ta có: OQ AD tại Q (?) AD SQ tại Q (?) Mà (SAD) (ABCD) = AD (SAD), (ABCD) OQ,SQ SQO A Q D O
Chú ý: SMO SNO SPO SQO B C
“Góc giữa các mặt bên với mặt đáy bằng nhau”
GV. TRẦN QUỐC NGHĨA
TOÁN HỌC BẮC – TRUNG – NAM
Chuyên đê: HÌNH HỌC KHÔNG GIAN 10
H3.4 – Khoảng cách “điểm – mặt” S
1. Khoảng cách từ O đến mặt phẳng (SCD)
Trong mp(ABCD), vẽ OM CD tại M H CD (SOM) (?) A D
Trong mp(SOM), vẽ OH SM tại H d[O,(SCD)] = OH O M B C
2. Khoảng cách từ A đến mặt phẳng (SCD)
Vì O là trung điểm của AC nên d[A,(SCD)] = 2d[O,(SCD)]
3. Khoảng cách từ B đến mặt phẳng (SCD)
Vì O là trung điểm của BD nên d[B,(SCD)] = 2d[O,(SCD)] HÌNH 4
Hình chóp S.ABC, SA vuông góc với đáy
H4.1 - Đáy, đường cao, cạnh đáy, cạnh bên, mặt bên của hình chóp
1. Đáy: tam giác ABC S
2. Đường cao: SA
3. Cạnh bên: SA, SB, SC
4. Cạnh đáy: AB, BC, CA
5. Mặt bên: SAB là tam giác vuông tại A. A C
SAC là tam giác vuông tại A.
Chú ý: Nếu ABC vuông tại B thì SBC vuông tại B
Nếu ABC vuông tại C thì SBC vuông tại C B
H4.2 - Góc giữa cạnh bên và đáy
1. Góc giữa cạnh bên SB và mặt đáy (ABC): Ta có: SA (ABC) (gt) S
Hình chiếu của SB lên (ABC) là AB SB, (ABC) SB, AB SBA
2. Góc giữa cạnh bên SC và mặt đáy (ABC): A C Ta có: SA (ABC) (gt)
Hình chiếu của SC lên (ABC) là AC B SC, (ABC) SC, AC SCA
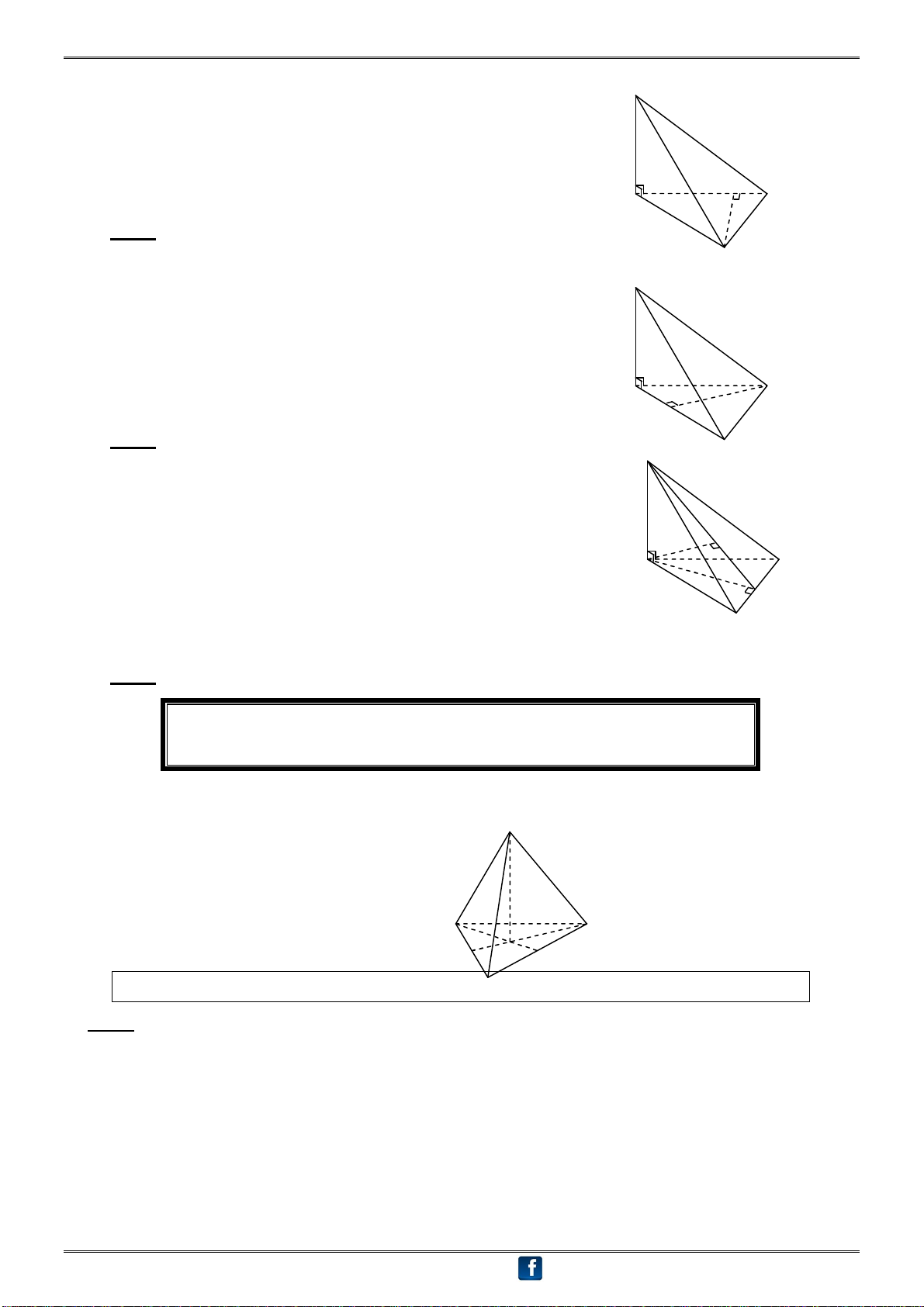
H4.3 - Góc giữa mặt bên (SBC) và mặt đáy (ABC): S
1. Tam giác ABC vuông tại B Ta có: BC AB tại B (?) BC SB tại B (?) (SBC) (ABC) = BC A C (SBC), (ABC) AB,SB SBA B
GV. TRẦN QUỐC NGHĨA
TOÁN HỌC BẮC – TRUNG – NAM
TÀi LIỆU ÔN THI THPT QUỐC GIA 2016 11
2. Tam giác ABC vuông tại C S Ta có: BC AC tại C (?) BC SC tại C (?) (SBC) (ABC) = BC (SBC), (ABC) AC, SC SCA A C
3. Tam giác ABC vuông tại A
Trong (ABC), vẽ AM BC tại M (?) S B BC SM tại M(?) (SBC) (ABC) = BC (SBC), (ABC) AM,SM SMA A C
Chú ý: M không là trung điểm BC M Nếu
ABC ACB thì M ở trên đoạn BC và gần B hơn B Nếu
ABC ACB thì M ở trên đoạn BC và gần C hơn
Nếu AB > AC thì M ở trên đoạn BC và gần C hơn
Nếu AB < AC thì M ở trên đoạn BC và gần B hơn
4. Tam giác ABC cân tại A (hoặc đều) S Gọi M là trung điểm BC BC AM tại M (?) BC SM tại M (?) A C Mà (SBC) (ABC) = SM M (SBC), (ABC) AM,SM SMA B
5. Tam giác ABC có 0 ABC 90 S
Trong (ABC), vẽ AM BC tại M (?) BC SM tại M(?) (SBC) (ABC) = BC A C (SBC), (ABC) AM,SM SMA B
Chú ý: M nằm ngoài đoạn BC và ở về phía B M
6. Tam giác ABC có 0 ACB 90 S
Trong (ABC), vẽ AM BC tại M (?) BC SM tại M(?) (SBC) (ABC) = BC A M (SBC), (ABC) AM,SM SMA C
Chú ý: M nằm ngoài đoạn BC và ở về phía C B
GV. TRẦN QUỐC NGHĨA
TOÁN HỌC BẮC – TRUNG – NAM
Chuyên đê: HÌNH HỌC KHÔNG GIAN 12
H4.4 – Khoảng cách “điểm – mặt” S
1. Khoảng cách từ B đến mặt phẳng (SAC)
Trong mp(ABC), vẽ BH AC tại H BH (SAC) (?) H A C d[B,(SAC)] = BH Chú ý:
Nếu ABC vuông tại A thì H A và khi đó AB = d[B,(SAC)] B
Nếu ABC vuông tại C thì H C và khi đó BC = d[B,(SAC)] S
2. Khoảng cách từ C đến mặt phẳng (SAB)
Trong mp(ABC), vẽ CH AB tại H CH (SAB) (?) A C d[C,(SAB)] = CH H Chú ý: S B
Nếu ABC vuông tại A thì H A và khi đó CA = d[C,(SAB)]
Nếu ABC vuông tại B thì H C và khi đó CB = d[B,(SAB)]
3. Khoảng cách từ A đến mặt phẳng (SBC) H C A
Trong (ABC), vẽ AM BC tại M (?) BC SM tại M (?) M
Trong mp(SAM), vẽ AH SM tại H B d[A,(SBC)] = AH
Chú ý: Tùy đặc điểm của ABC để các định đúng vị trí của điểm M trên đường thẳng BC. HÌNH 5
Hình chóp tam giác đều S.ABC
H5.1 - Đáy, đường cao, cạnh đáy, cạnh bên, mặt bên của hình chóp S
1. Đáy: Tam giác ABC đều
2. Đường cao: SO
3. Cạnh bên: SA = SB = SC = SD
4. Cạnh đáy: AB = BC = CA A C
5. Mặt bên: SAB, SBC, SCA
là các tam giác cân tại S và bằng nhau. O
Gọi O là trọng tâm của tam giác
B ABC SO (ABC)
Chú ý: Tứ diện đều S.ABC là hình chóp có đáy và các mặt bên là những tam giác đều bằng nhau.
H5.2 - Góc giữa cạnh bên và đáy
1. Góc giữa cạnh bên SA và mặt đáy (ABC): Ta có: SO (ABC) (?)
Hình chiếu của SA lên (ABC) là AO SA, (ABC) SA, AO SAO
GV. TRẦN QUỐC NGHĨA
TOÁN HỌC BẮC – TRUNG – NAM
TÀi LIỆU ÔN THI THPT QUỐC GIA 2016 13
2. Góc giữa cạnh bên SB và mặt đáy (ABC): S Tương tự SB,(ABC) SB, BO SBO
3. Góc giữa cạnh bên SC và mặt đáy (ABC): Tương tự SC, (ABC) SC, CO SCO A C O
Chú ý: SAO SBO SCO
“Góc giữa các cạnh bên với mặt đáy bằng nhau” S B
H5.3 - Góc giữa mặt bên và mặt đáy:
1. Góc giữa mặt bên (SAB) và mặt đáy (ABC): Ta có: OM AB tại M (?) A C AB SM tại M (?) O Mà (SAB) (ABC) = AB M (SAB), (ABC) OM,SM SMO B S
2. Góc giữa mặt bên (SBC) và mặt đáy (ABC): Ta có: ON BC tại N (?) BC SN tại N (?) Mà (SBC) (ABC) = BC (SBC), (ABCD) ON,SN SNO A C
3. Góc giữa mặt bên (SAC) và mặt đáy (ABC): O N Ta có: OP AC tại P (?) S B AC SP tại P (?) Mà (SAC) (ABC) = AC (SAC), (ABC) OP,SP SPO
Chú ý: SMO SNO SPO P A C
“Góc giữa các mặt bên với mặt đáy bằng nhau” O
H5.4 – Khoảng cách “điểm – mặt” B S
1. Khoảng cách từ O đến mặt phẳng (SAB)
Trong mp(ABC), vẽ OM AB tại M AB (SOM) (?)
Trong mp(SOM), vẽ OH SM tại H d[O,(SAB)] = OH H A C
2. Khoảng cách từ C đến mặt phẳng (SAB) O MC M
Vì O là trọng tâm của ABC nên 3 MO B MC d[C,(SAB)] =
d[O,(SAB)] = 3 d[O,(SAB)] MO
GV. TRẦN QUỐC NGHĨA
TOÁN HỌC BẮC – TRUNG – NAM
Chuyên đê: HÌNH HỌC KHÔNG GIAN 14 HÌNH 6a
Hình chóp S.ABC có một mặt bên (SAB) vuông góc với đáy (ABCD) S
“Luôn luôn vẽ SH vuông góc với giao tuyến”
H6a.1 - Góc giữa cạnh bên và mặt đáy Vẽ SH AB tại H
Vì (SAB) (ABC) nên SH (ABC) A C
Chú ý: Tùy đặc điểm của tam giác SAB để xác định đúng vị trí của điểm H H
trên đường thẳng AB. S B
1. Góc giữa cạnh bên SA và mặt đáy (ABC): Ta có: SH (ABC) (?)
Hình chiếu của SA lên (ABC) là AH SA, (ABC) SA, AH SAH A C
2. Góc giữa cạnh bên SB và mặt đáy (ABC): H Ta có: SH (ABC) (?) B
Hình chiếu của SB lên (ABC) là BH SB,(ABC) SB, BH SBH
3. Góc giữa cạnh bên SC và mặt đáy (ABC): Ta có: SH (ABC) (?)
Hình chiếu của SC lên (ABC) là CH SC, (ABC) SC, CH SCH S
H6a.2 - Góc giữa mặt bên và mặt đáy: Vẽ SH AB tại H
Vì (SAB) (ABC) nên SH (ABC) A C
Chú ý: Tùy đặc điểm của tam giác SAB để xác định đúng vị trí của điểm H
trên đường thẳng AB. H
1. Góc giữa mặt bên (SAB) và mặt đáy (ABC): B S Vì (SAB) (ABC) nên 0 (SAB), (ABC) 90
2. Góc giữa mặt bên (SAC) và mặt đáy (ABC): Vẽ HM AC tại M M A C HM AC Ta có: H SH AC B
AC (SHM) , mà SM (SHM) SM AC S (SBC), (ABC) HM, SM SMH
3. Góc giữa mặt bên (SBC) và mặt đáy (ABC): Vẽ HN BC tại N A C HN BC Ta có:
BC (SHN) , mà SN (SHN) SH BC H N SN AB B (SBC), (ABC) HN,SN SNH
GV. TRẦN QUỐC NGHĨA
TOÁN HỌC BẮC – TRUNG – NAM
TÀi LIỆU ÔN THI THPT QUỐC GIA 2016 15 HÌNH 6b
Hình chóp S.ABCD có một mặt bên (SAB) vuông góc với đáy (ABCD) và
ABCD là hình chữ nhật hoặc hình vuông
“Luôn luôn vẽ SH vuông góc với giao tuyến”
H6b.1 - Góc giữa cạnh bên và mặt đáy S Vẽ SH AB tại H
Vì (SAB) (ABCD) nên SH (ABCD)
Chú ý: Tùy đặc điểm của tam giác SAB để xác định đúng vị trí của điểm H
trên đường thẳng AB. A D
1. Góc giữa cạnh bên SA và mặt đáy (ABCD): H Ta có: SH (ABCD) (?) B C
Hình chiếu của SA lên (ABC) là AH SA, (ABCD) SA, AH SAH S
2. Góc giữa cạnh bên SB và mặt đáy (ABCD): Tương tự SB, (ABCD) SB, BH SBH A
3. Góc giữa cạnh bên SC và mặt đáy (ABCD): D Tương tự SC, (ABCD) SC, CH SCH H B C
4. Góc giữa cạnh bên SD và mặt đáy (ABCD): S Tương tự SC, (ABCD) SD, DH SDH
H6b.2 - Góc giữa mặt bên và mặt đáy: A D
1. Góc giữa mặt bên (SAD) và mặt đáy (ABCD): H Ta có: HA AD (?) SH AD (?) B C S
AD (SHA) AD SA
Mà (SAD) (ABCD) = AD (SAD), (ABCD) SA, AH SAH
2. Góc giữa mặt bên (SBC) và mặt đáy (ABCD): A D Ta có: BA BC (?) SH BC (?) H
BC (SHB) BC SB B C Mà (SBC) (ABCD) = BC (SBC), (ABCD) SB, AH SBH S
3. Góc giữa mặt bên (SCD) và mặt đáy (ABCD):
Trong (ABCD), vẽ HM CD tại M HM CD A Ta có: D
CD (SHM) CD SM SH CD H M Mà (SCD) (ABCD) = CD B C (SCD), (ABCD) HM, SM SMH
GV. TRẦN QUỐC NGHĨA
TOÁN HỌC BẮC – TRUNG – NAM
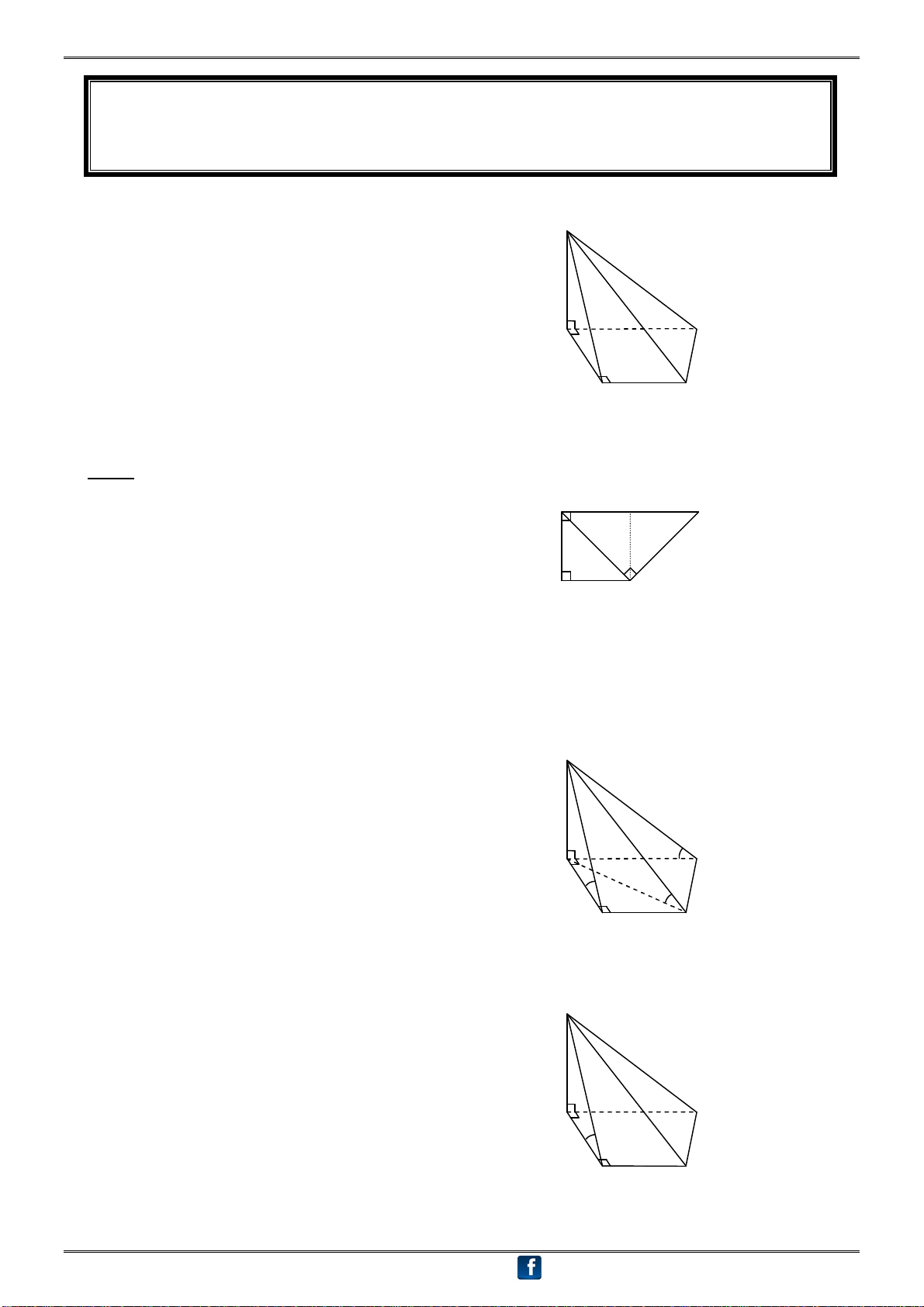
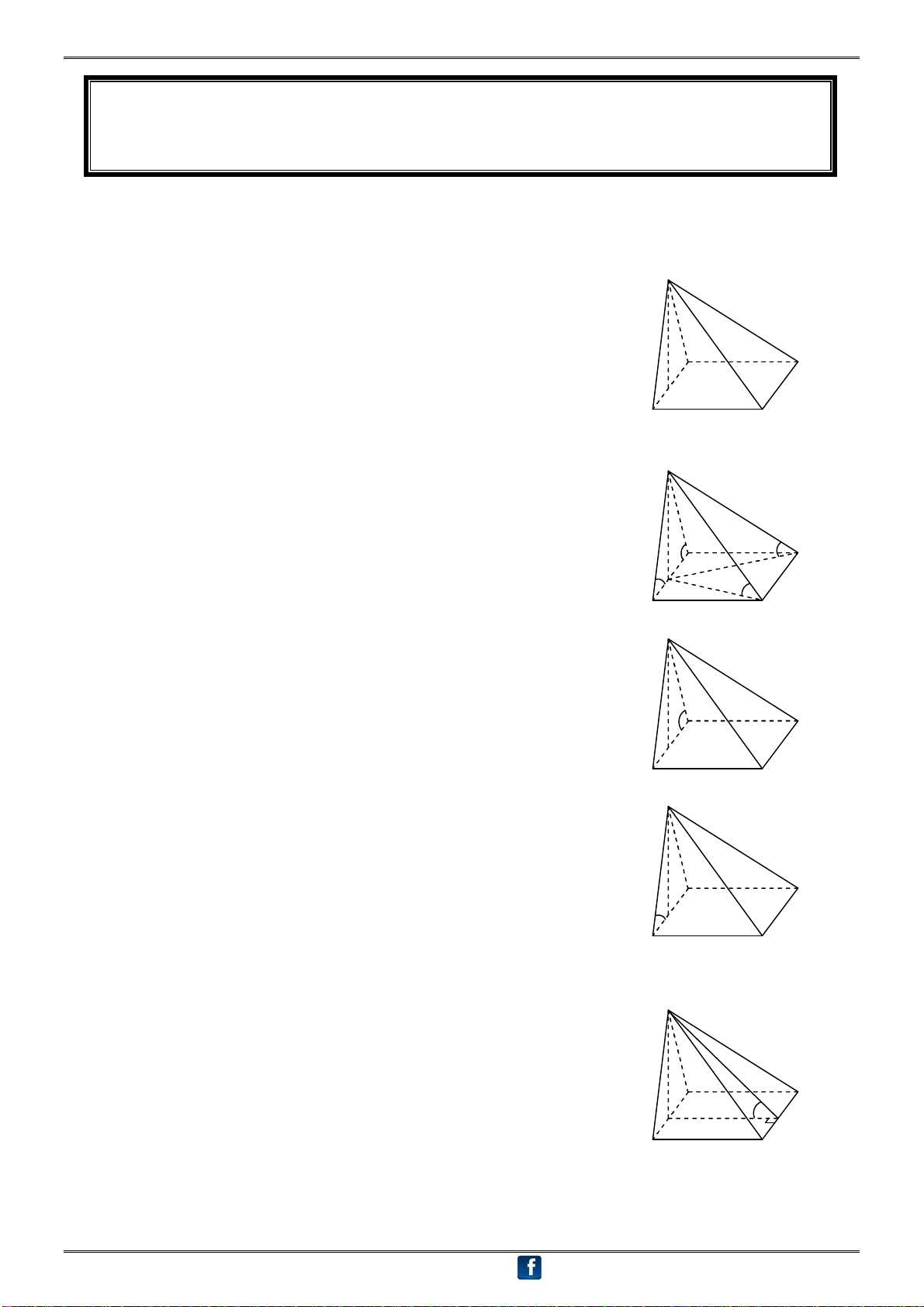
Chuyên đê: HÌNH HỌC KHÔNG GIAN 16 HÌNH 7 Hình lăng trụ ① Lăng trụ có:
Hai đáy song song và là 2 đa giác bằng nhau Lăng trụ xiên
Các cạnh bên song song và bằng nhau
Các mặt bên là các hình bình hành Cạnh bên vuông góc đáy
② Lăng trụ đứng là lăng trụ có các cạnh bên vuông góc với đáy
③ Lăng trụ tam giá đều là lăng trụ đứng, có đáy là tam giác đều Lăng trụ đứng
④ Lăng trụ có đáy là tam giác đều là lăng trụ xiên, có đáy là tam giác đều Đáy là
⑤ Lăng trụ tứ giác đều là lăng trụ đứng, có đáy là hình vuông đa giác đều
⑥ Lăng trụ có đáy là tứ giác đều là lăng trụ xiên, có đáy là hình vuông Lăng trụ đều
⑦ Hình hộp là hình lăng trụ xiên, có đáy là hình bình hành
⑧ Hình hộp đứng là lăng trụ đứng, có đáy là hình bình hành
⑨ Hình hộp chữ nhật là lăng trụ đứng, có đáy là hình chữ nhật
⑩ Hình lập phương là lăng trụ đứng, có đáy và các mặt bên là hình vuông. A ' C '
⑪ Lăng trụ đứng ABC.ABC. B '
Góc giữa mp(ABC) và mp(ABC): Vẽ AM BC tại M A C M AM BC (?) B (A'B C), (ABC) AMA '
Chú ý: Tùy đặc điểm của tam giác ABC để xác định đúng vị trí của điểm M trên đường thẳng BC.
⑫ Hình hộp chữ nhật ABCD.ABCD. A ' D '
Góc giữa mp(ABCD) và mp(ABCD): B ' C ' Ta có: BC CD CD BC (?) A D (A'B'CD), (ABCD) BCB ' B C
GV. TRẦN QUỐC NGHĨA
TOÁN HỌC BẮC – TRUNG – NAM
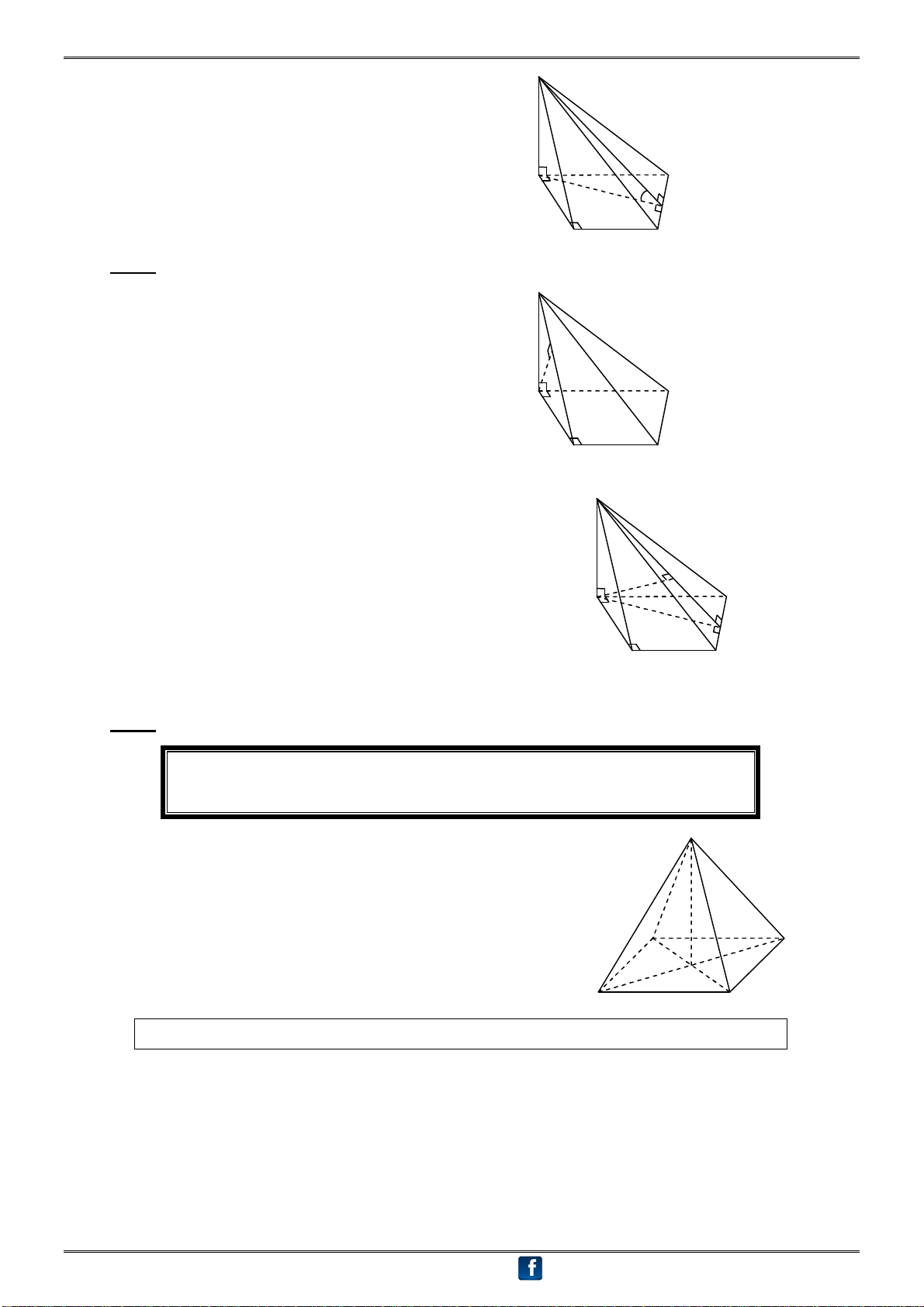
TÀi LIỆU ÔN THI THPT QUỐC GIA 2016 17 HÌNH 8
Mặt cầu ngoại tiếp hình chóp
1. Tâm mặt cầu ngoại tiếp hình chóp: Là điểm cách đều các đỉnh của đáy và đỉnh của hình chóp ấy.
2. Cách xác định tâm I: M
Cách 1 : Nếu A, B, C, … cùng nhìn đoạn MN theo 1 góc vuông thì A, B, C,
…, M, N cùng thuộc mặt cầu có đường kính MN. Tâm I là trung điểm MN. I
Cách 2 : (Tổng quát) Dựng tâm I theo các bước: N Bước 1: A
Dựng trục của đáy. (vuông góc đáy tại tâm ngoại) B Bước 2: C
o Nếu cạnh bên SA cắt hoặc song song với thì trong mặt phẳng (SA, ), đường trung trực
SA cắt tại I (hình a, b).
o Nếu cạnh bên SA không đồng phẳng với thì mặt phẳng trung trực của SA cắt tại I.
Cách 3 : I là giao của hai trục
Bước 1: Dựng trục 1 của đáy.
Bước 2: Dựng trục 2 của 1 mặt bên (chọn mặt bên là tam giác đặc biệt). Tâm I là giao của 1 và 2 (hình c). S S S 1 I I I 2 A A Hình a Hình b Hình c
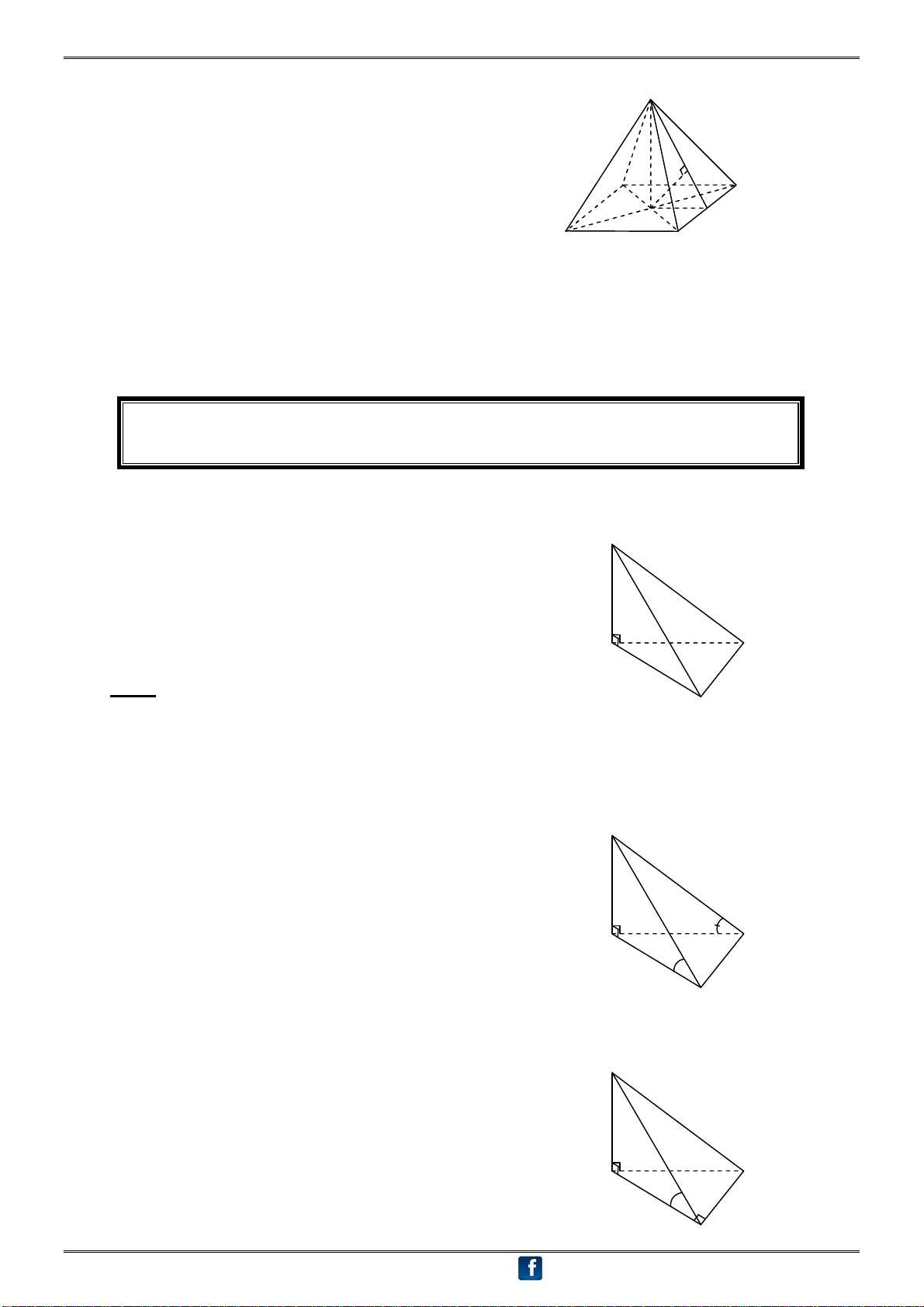
3. Tâm mặt cầu ngoại tiếp một số hình đặc biệt:
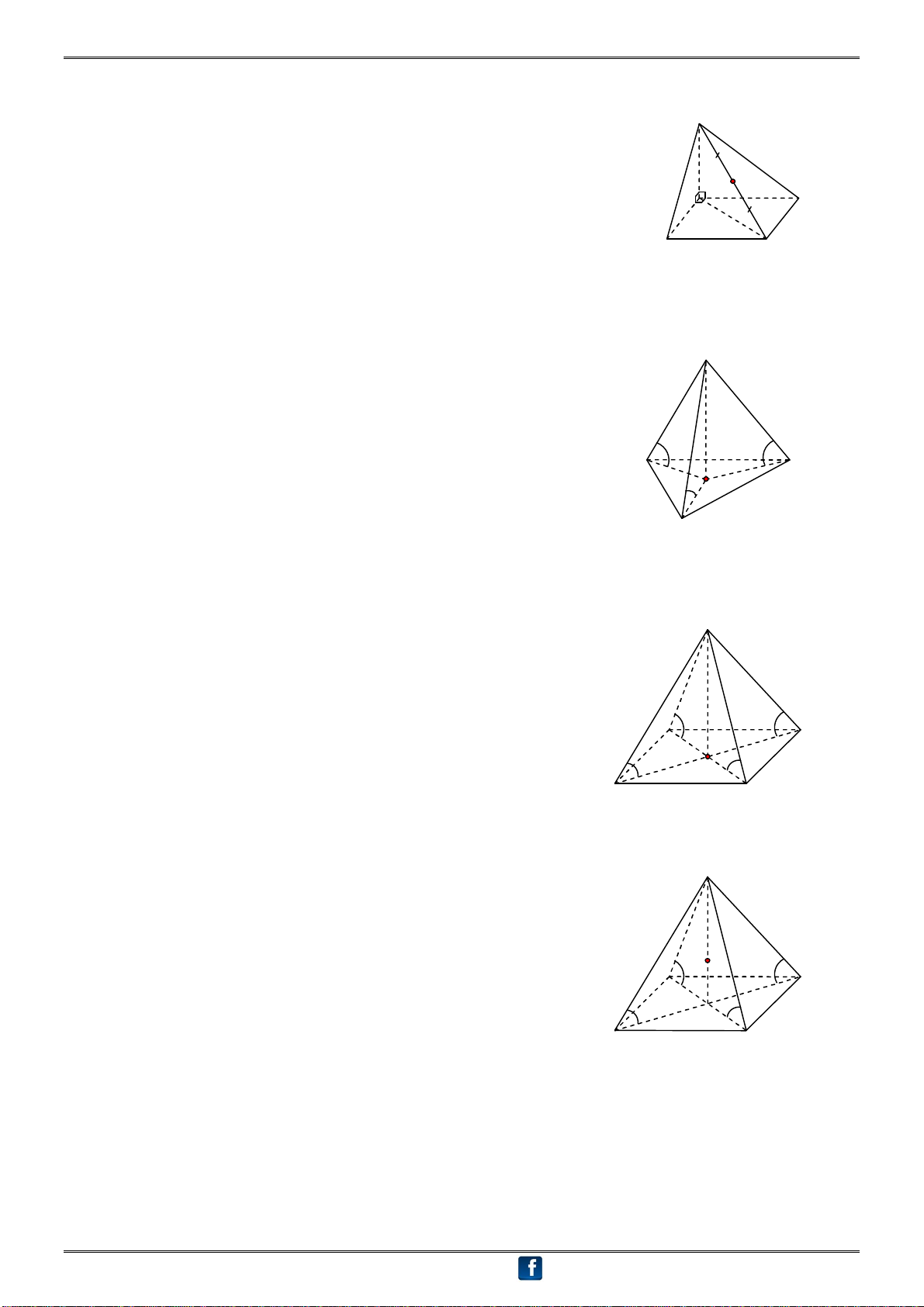
① Hình chóp S.ABC có SA vuông góc với mặt phẳng đáy và tam giác ABC vuông tại B: Ta có BC AB (?) S BC SB (?) 0 SBC 90 (1) I
Mặt khác ta có: SA AC 0 SAC 90 (2) A C
Từ (1) và (2) suy ra A, B, S, C cùng thuộc mặt cầu B
đường kính SC. Tâm I là trung điểm SC.
② Hình chóp S.ABC có SA vuông góc với mặt phẳng đáy và tam giác ABC vuông tại C: Ta có BC AC (?) S BC SC (?) 0 SCB 90 (1) I
Mặt khác ta có: SA AB 0 SAB 90 (2) A C
Từ (1) và (2) suy ra A, C, S, B cùng thuộc mặt cầu B
đường kính SB. Tâm I là trung điểm SB.
GV. TRẦN QUỐC NGHĨA
TOÁN HỌC BẮC – TRUNG – NAM
Chuyên đê: HÌNH HỌC KHÔNG GIAN 18
③ Hình chóp S.ABCD có SA vuông góc với mặt phẳng đáy và ABCD là hình chữ nhật: S Ta có 0 SAC 90 (?) 0 SBC 90 (?) I D 0 SDC 90 (?) A
A, B, D cùng thuộc mặt cầu đường kính B C
SC. Tâm I là trung điểm SC.
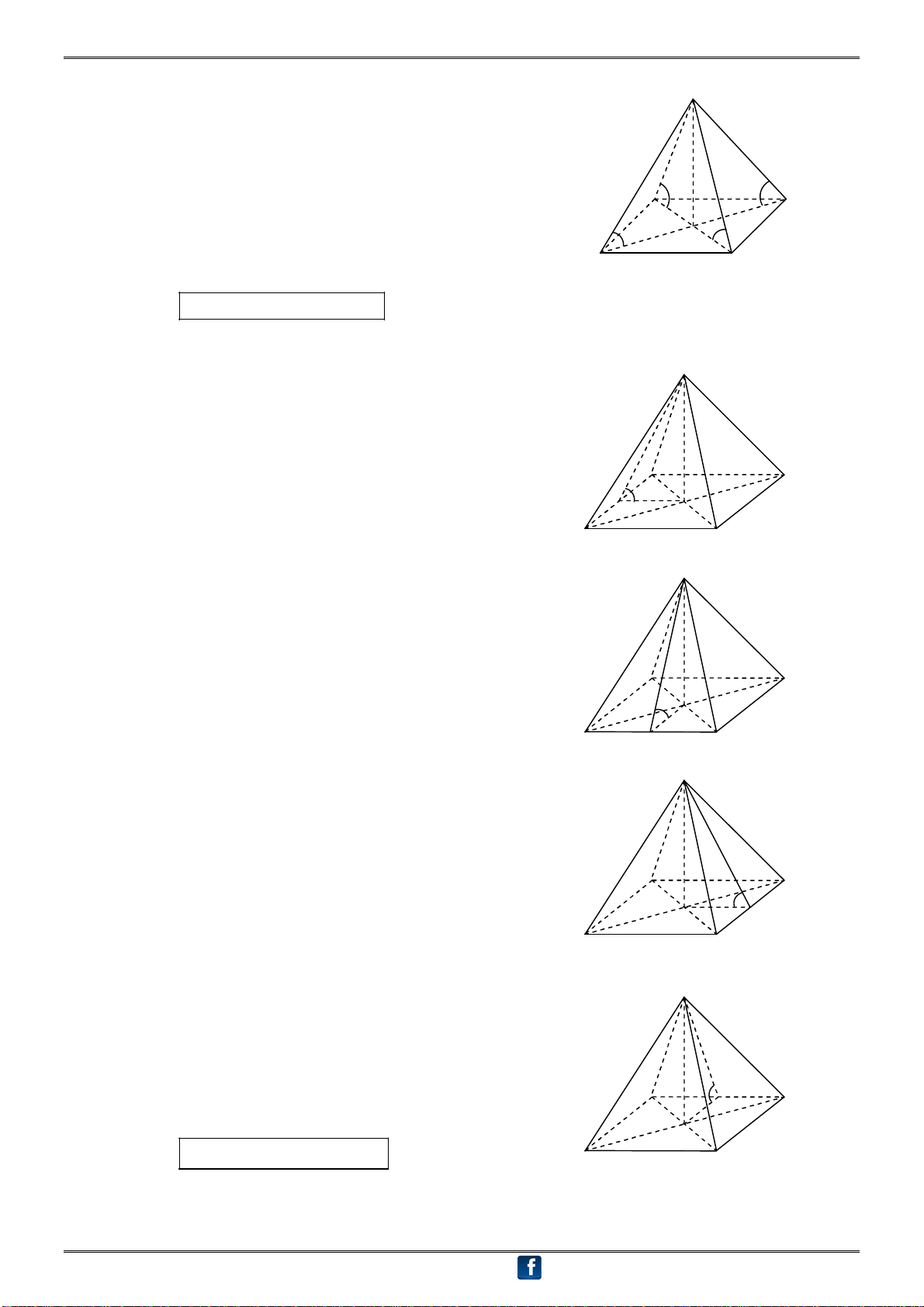
④ Hình chóp tam giác đều S.ABC có góc giữa cạnh bên và mặt đáy bằng 450: S
Ta có góc giữa cạnh bên và mặt đáy bằng 450 0 SAO SBO SCO 45
SOA, SOB, SOC là các tam giác vuông cân tại O A OS = OA = OB = OC C O
O là tâm mặt cầu ngoại tiếp hình chóp S.ABC. B
⑤ Hình chóp tứ giác đều S.ABCD có góc giữa cạnh bên và mặt đáy bằng 450:
Ta có góc giữa cạnh bên và mặt đáy bằng 450 S 0
SAO SBO SCO SDO 45
SOA, SOB, SOC, SOD là các tam giác vuông cân tại O OS = OA = OB = OC = OD A D
O là tâm mặt cầu ngoại tiếp hình chóp S.ABCD. O B C
⑥ Hình chóp tứ giác đều S.ABCD có góc giữa cạnh bên và mặt đáy bằng 600:
Ta có góc giữa cạnh bên và mặt đáy bằng 600 S 0
SAO SBO SCO SDO 60
SAC, SBD là các tam giác đều I A
Gọi I là trọng tâm SAC thì I cũng là trọng tâm SBD D IS = IA = IB = IC = ID O B C
I là tâm mặt cầu ngoại tiếp hình chóp S.ABCD
GV. TRẦN QUỐC NGHĨA
TOÁN HỌC BẮC – TRUNG – NAM
TÀi LIỆU ÔN THI THPT QUỐC GIA 2016 19
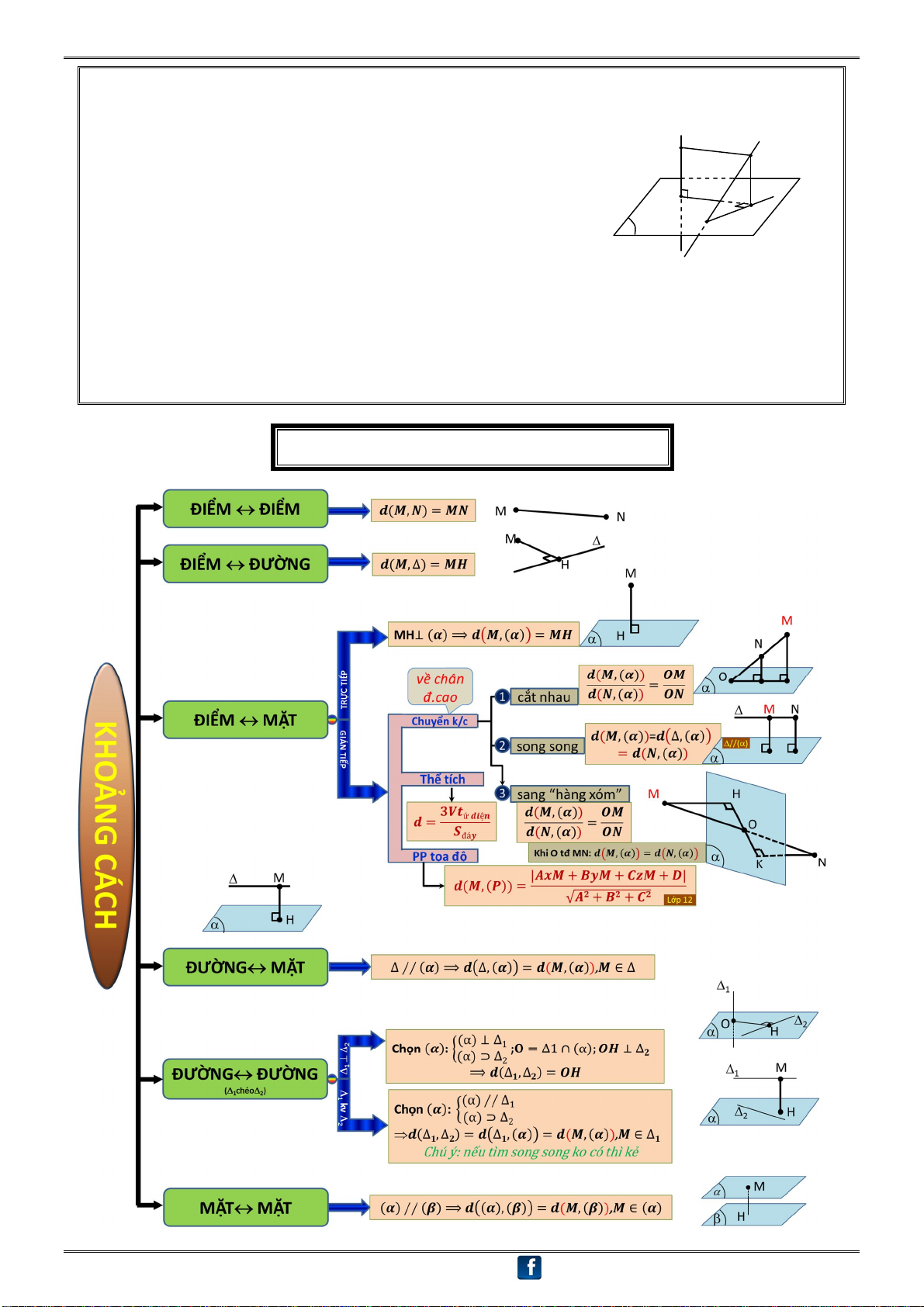
D – KHOẢNG CÁCH
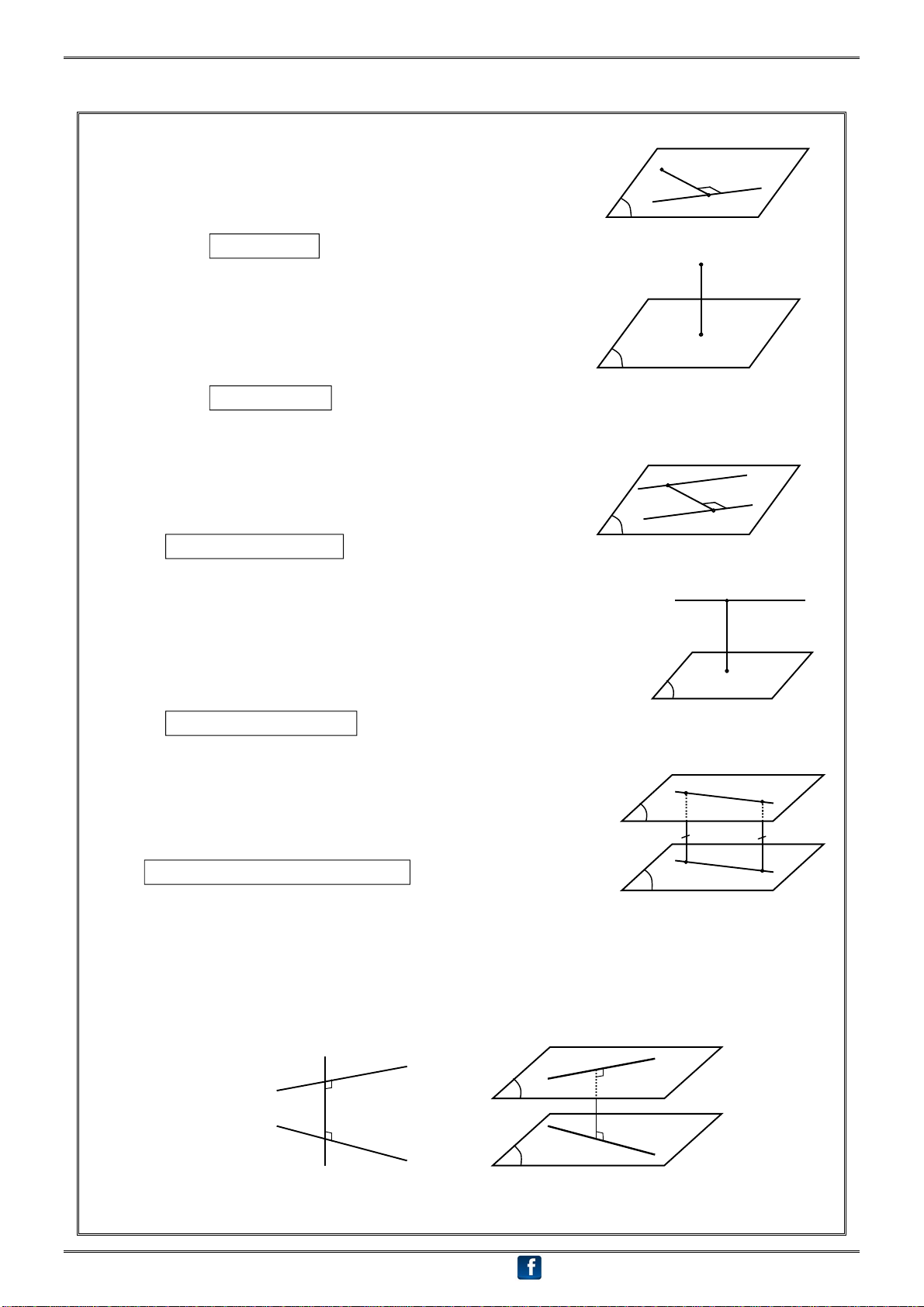
① Khoảng cách từ một điểm đến một đường thẳng M
Khoảng cách từ điểm M đến đường thẳng a là MH, với H a
là hình chiếu của M trên đường thẳng a. H Kí hiệu: d(M , a) MH . M
② Khoảng cách từ một điểm đến một mặt phẳng.
Khoảng cách từ điểm M đến mặt phẳng () là MH, với H H
là hình chiếu của M trên mặt phẳng ().
Kí hiệu: d[M , ()] MH .
③ Khoảng cách giữa hai đường thẳng song song.
Khoảng cách giữa hai đường thẳng song song là khoảng M b a
cách từ một điểm bất kì thuộc đường này đến đường kia. H
d(a , b) d(M , b) MH (M a)
④ Khoảng cách giữa đường thẳng và mặt phẳng song song. a M
Khoảng cách giữa đường thẳng a và mặt phẳng () song song với
nhau là khoảng cách từ một điểm M bất kì thuộc đường a đến mặt phẳng (). H
d[a , ()] d[M , ()] MH (Ma)
⑤ Khoảng cách giữa hai mặt phẳng song song. A B a
Khoảng cách giữa hai mặt phẳng song song là khoảng cách từ
một điểm bất kì của mặt phẳng này đến mặt phẳng kia. d[(),( )
] d[a , ()] d[A , ( ) ] AH H K (với a (); A a.)
⑥ Khoảng cách giữa hai đường thẳng chéo nhau.
- Đường thẳng c cắt hai đường thẳng a, b và cùng vuông góc với mỗi đường thẳng ấy gọi
là đường vuông góc chung của a và b. IJ gọi là đoạn vuông góc chung của a và b. c I a I a J b J b
- Khoảng cách giữa hai đường thẳng chéo nhau là độ dài đoạn vuông góc chung của hai đường thẳng đó.
GV. TRẦN QUỐC NGHĨA
TOÁN HỌC BẮC – TRUNG – NAM
Chuyên đê: HÌNH HỌC KHÔNG GIAN 20
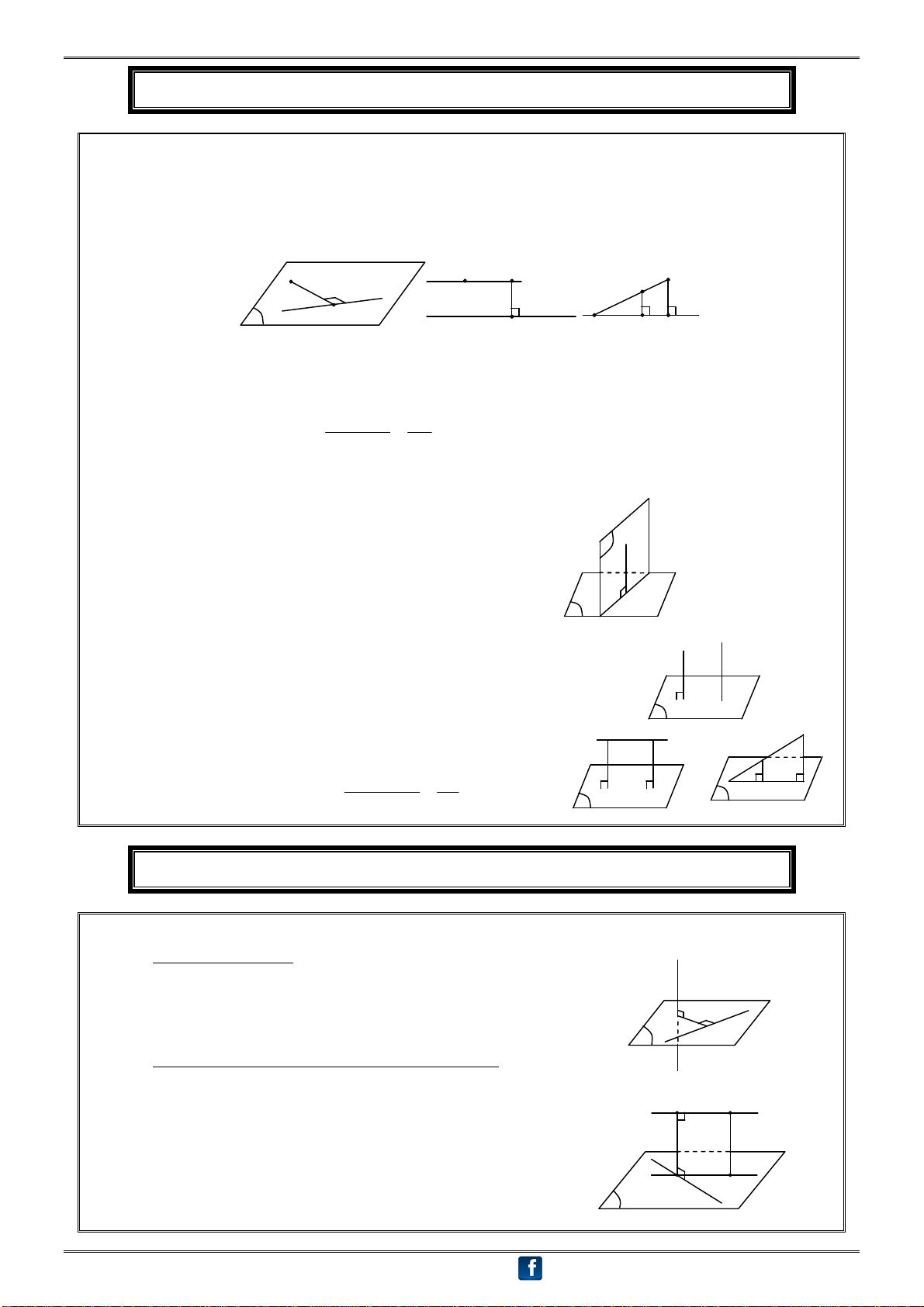
1. Khoảng cách từ một điểm đến đường thẳng, mặt phẳng
1. Khoảng cách từ điểm M đến đường thẳng d cho trước
Các bước thực hiện:
Bước 1. Trong mặt phẳng (M, d) hạ MH d với H d.
Bước 2. Thực hiện việc xác định độ dài MH dựa trên hệ thức lượng trong tam giác, tứ giác,
đường tròn, … M a M A A M a d d H K I H K Chú ý:
Nếu tồn tại đường thẳng a qua A và song song với d thì: d[M, d] = d[A, d] = AK với A d. d [ M ,d ] MI
Nếu MA d = I, thì: d [ A,d ] AI
2. Khoảng cách từ điểm O đến mặt phẳng ()
Các bước thực hiện:
Bước 1. Tìm hình chiếu H của O lên (). O
- Tìm mặt phẳng () qua O và vuông góc với ().
- Tìm = () ().
- Trong mặt phẳng (), kẻ OH tại H H
H là hình chiếu vuông góc của O lên (). O d
Bước 2. Khi đó OH là khoảng cách từ O đến (). Chú ý:
Chọn mặt phẳng () sao cho dễ tìm giao tuyến với (). H
Nếu đã có đường thẳng d () thì kẻ Ox // d cắt () tại H. A O A
Nếu OA // () thì: d[O,()] = d[A,()]. O d [ O,( )] OI I
Nếu OA cắt () tại I thì: K K H d [ A,( )] AI H
2. Khoảng cách giữa hai đường thẳng chéo nhau
Đoạn vuông góc chung của hai đường thẳng chéo nhau a và b
Trường hợp a b: b
- Dựng mặt phẳng () chứa a và vuông góc với b tại B.
- Trong () dựng BA a tại A. a B
AB là đoạn vuông góc chung. A
Trường hợp a và b không vuông góc với nhau.
Cách 1: (Hình a)
- Dựng mp () chứa a và song song với b. b B M
- Lấy điểm M tùy ý trên b dựng MM () tại M - a
Từ M dựng b// b cắt a tại A. b' - A M'
Từ A dựng AB // MM cắt b tại B.
AB là đoạn vuông góc chung. (Hình a)
GV. TRẦN QUỐC NGHĨA
TOÁN HỌC BẮC – TRUNG – NAM
TÀi LIỆU ÔN THI THPT QUỐC GIA 2016 21
Cách 2: (Hình b)
- Dựng mặt phẳng () a tại O, () cắt b tại I
- Dựng hình chiếu vuông góc b của b lên () a b
- Trong mp (), vẽ OH b tại H. A B
- Từ H dựng đường thẳng song song với a cắt b tại B
- Từ B dựng đường thẳng song song với OH cắt a tại A. b' O
AB là đoạn vuông góc chung. I H
Khoảng cách giữa hai đường thẳng chéo nhau a và b (Hình b)
Cách 1. Dùng đường vuông góc chung:
- Tìm đoạn vuông góc chung AB của a và b. - d[a , b] = AB.
Cách 2. Dựng mặt phẳng () chứa a và song song với b. Khi đó: d[a , b] = d[b , ()]
Cách 3. Dựng 2 mặt phẳng song song và lần lượt chứa a và b. Khi đó: d[a , b] = d[() , ()]
3. Tổng hợp khoảng cách
GV. TRẦN QUỐC NGHĨA
TOÁN HỌC BẮC – TRUNG – NAM
Chuyên đê: HÌNH HỌC KHÔNG GIAN 22
PHẦN 2. TRÍCH ĐỀ THI THỬ THPT QUỐC GIA 2016
ĐỀ SỐ 1 - THPT CHUYÊN VĨNH PHÚC - LẦN 1 - NĂM 2016
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, mặt bên SAB là tam giác đều và nằm
trong mặt phẳng vuông góc với mặt phẳng (ABC), gọi M là điểm thuộc cạnh SC sao cho
MC 2MS . Biết AB 3 , BC 3 3 . Tính thể tích của khối chóp S.ABC và khoảng cách giữa
hai đường thẳng AC và BM.
ĐỀ SỐ 2 - THPT HÀN THUYÊN, BẮC NINH (CLĐN)
Cho hình chóp đều S.ABCD, có đáy ABCD là hình vuông cạnh a. Góc giữa cạnh bên và mặt đáy
bằng 600. Tính diện tích tam giác SAC và khoảng cách giữa hai đường thẳng SA và CD.
ĐỀ SỐ 3 - THPT HÀN THUYÊN, BẮC NINH (L1)
Cho hình chóp S.ABCD, có đáy ABCD là hình chữ nhật với AD 2 AB 2a . Tam giác SAD là
tam giác vuông cân đỉnh S và nằm trên mặt phẳng vuông góc với mặt đáy (ABCD). Tính thể tích
khối chóp S.ABCD và khoảng cách giữa hai đường thẳng SA và BD.
ĐỀ SỐ 4 - THPT THẠCH THÀNH 1, THANH HÓA
Cho hình chóp S.ABC có đường cao SA bằng 2a, tam giác ABC vuông ở C có AB = 2a, 0
CAB 30 . Gọi H là hình chiếu vuông của A trên SC Tính theo a thể tích của khối chóp H.ABC.
Tính cô-sin của góc giữa hai mặt phẳng (SAB), (SBC).
ĐỀ SỐ 5 - THPT KHOÁI CHÂU, HƯNG YÊN a a 3
Cho hình chóp S.ABCD, đáy ABCD là hình thoi cạnh a, SA , SB , 0 BAD 60 và mặt 2 2
phẳng (SAB) vuông góc với đáy. Gọi H, K lần lượt là trung điểm của AB, BC. Tính thể tích tứ
diện KSDC và tính cosin của góc giữa đường thẳng SH và DK.
ĐỀ SỐ 6 - THPT YÊN MỸ, HƯNG YÊN 0
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm I và có cạnh bằng a, góc BAD 60 .Gọi a 13
H là trung điểm của IB và SH vuông góc với mặt phẳng (ABCD) biết SH 4
a) Hãy tính thể tích của khối chóp S.ABCD.
b) Gọi M là trung điểm của SB , N thuộc SC sao cho SC = 3SN . Tính tỉ số thể tích khối chóp
S.AMN và khối chóp S.ABCD.
c) Tính khoảng cách từ điểm A đến mặt phẳng (SCD).
ĐỀ SỐ 7 - THPT TAM ĐẢO, VĨNH PHÚC
Cho hình chóp S.ABCD có đáy là hình chữ nhật với cạnh AB = 2a, AD = a. Hình chiếu của S lên
mặt phẳng (ABCD) là trung điểm H của AB, SC tạo với đáy một góc bằng 450. Tính thể tích khối
chóp S.ABCD và khoảng cách từ điểm A tới mặt phẳng (SCD).
GV. TRẦN QUỐC NGHĨA
TOÁN HỌC BẮC – TRUNG – NAM
TÀi LIỆU ÔN THI THPT QUỐC GIA 2016 23
ĐỀ SỐ 8 - THPT TRẦN HƯNG ĐẠO, ĐĂK NÔNG (Lần 1)
Cho khối chóp S.ABC có SA vuông góc với mặt đáy (ABC), tam giác ABC vuông cân tại B, SA =
a, SB hợp với đáy một góc 300.Tính thể tích của khối chóp S.ABC và tính khoảng cách giữa AB và SC.
ĐỀ SỐ 9 - THPT TRẦN HƯNG ĐẠO, TP HCM
Cho hình vuông ABCD cạnh 4a. Lấy H, K lần lượt trên AB, AD sao cho BH = 3HA, AK = 3KD.
Trên đường thẳng vuông góc với mặt phẳng ABCD tại H lấy S sao cho góc 0
SBH 30 . Gọi E là
giao điểm của CH và BK. a) Tính VS.ABCD.
b) Tính VS.BHKC và d(D,(SBH)).
c) Tính cosin góc giữa SE và BC.
ĐỀ SỐ 10 - THPT LÝ THÁI TỔ, BẮC NINH (L1)
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B và AB = 2, AC = 4. Hình chiếu vuông
góc của đỉnh S trên mặt phẳng (ABC) là trung điểm H của đoạn thẳng AC. Cạnh bên SA tạo với
mặt đáy một góc 600. Tính thể tích khối chóp S.ABC và khoảng cách giữa hai đường thẳng AB và SC.
ĐỀ SỐ 11 - THPT NGÔ SỸ LIÊN, BẮC GIANG (L1)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB =a, BC = 2a. SA vuông góc với
mặt phẳng (ABCD), góc giữa đường thẳng SB và mặt phẳng (ABCD) bằng 450. Tính theo a thể
tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng SB, AC.
ĐỀ SỐ 12 - THPT NGÔ SỸ LIÊN, BẮC GIANG (L2)
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, BA = 3a, BC = 4a và AB vuông góc
với mặt phẳng (SBC). Biết SB = 2a 3 và 0
SBC 30 . Tính thể tích khối chóp S.ABC và khoảng
cách từ điểm B đến mặt phẳng (SAC) theo a.
ĐỀ SỐ 13 - THPT VIỆT YÊN II, BẮC GIANG
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng 600 .
Gọi M, N lần lượt là trung điểm AB, BC. Tính thể tích khối chóp S.ABC và khoảng cách từ C đến mặt phẳng (SMN).
ĐỀ SỐ 14 - THPT CHUYÊN VĨNH PHÚC (Lần 2)
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 4. Mặt bên (SAB) nằm trong mặt phẳng
vuông góc với đáy, hình chiếu vuong góc của S trên mặt đáy là điểm H thuộc đoạn AB sao cho
BH = 2AH. Góc giữa SC và mặt phẳng đáy là 600. Tính thể tích khối chóp S.ABCD và khoảng
cách từ điểm H đến mặt phẳng (SCD).
ĐỀ SỐ 15 – THPT ĐĂK MIL, ĐĂK NÔNG (Lần 1)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a, AD = 2a, cạnh bên SA
vuông góc với mặt đáy và cạnh bên SC tạo với mặt đáy một góc 600. Gọi M, N lần lượt là trung
GV. TRẦN QUỐC NGHĨA
TOÁN HỌC BẮC – TRUNG – NAM
Chuyên đê: HÌNH HỌC KHÔNG GIAN 24
điểm của các cạnh bên SA và SB. Tính theo a thể tích khối chóp S.ABCD và khoảng cách từ S
đến mặt phẳng (DMN).
ĐỀ SỐ 16 - THPT BỐ HẠ, BẮC GIANG (Lần 2)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB 2a , AD a 3 . Mặt bên (SAB)
là tam giác cân tại S và nằm trong mặt phẳng vuông góc với mặt đáy. Biết đường thẳng SD tạo
với mặt đáy một góc 450. Tính thể tích của khối chóp S.ABCD và khoảng cách giữa hai đường
thẳng SA và BD.
ĐỀ SỐ 17 - THPT ĐỨC THỌ, HÀ TĨNH
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB a , AD 2a , SA ( ABCD) và
SA a . Tính theo a thể tích của khối chóp S.ABCD và khoảng cách từ D đến mặt phẳng (SBM)
với M là trung điểm của CD.
ĐỀ SỐ 18 - THPT ĐỘI CẤN, BẮC NINH
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA a 3 và SA vuông góc với mặt
phẳng đáy. Biết tam giác SAB cân và góc giữa SD với mặt đáy bằng 300.
a) Tính thể tích khối chóp S.ABCD theo a.
b) Tính khoảng cách giữa hai đường thẳng BD và SC.
ĐỀ SỐ 19 - THPT VIỆT TRÌ, PHÚ THỌ (Lần 1)
Cho lăng trụ đứng AB . C '
A B'C' , có đáy ABC là tam giác vuông tại A, AB a, AC a 3 , mặt bên
BCC' B' là hình vuông; M, N lần lượt là trung điểm của CC ' và B'C' . Tính thể tích khối lăng trụ AB . C '
A B'C' và tính khoảng cách giữa hai đường thẳng ' A B' và MN .
ĐỀ SỐ 20 - THPT TRẦN HƯNG ĐẠO, ĐĂKNÔNG (Lần 2)
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), SA = 8a, tam giác ABC đều cạnh
bằng 4a; M, N lần lượt là trung điểm của cạnh SB và BC. Tính theo a thể tích hình chóp và
khoảng cách từ điểm đến mặt phẳng (AM).
ĐỀ SỐ 21 - THPT YÊN LẠC 2, VĨNH PHÚC (Lần 1)
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B. Các cạnh AB = BC = 2a,
AD = a, tam giác SBC đều, mặt phẳng (SBC) vuông góc với mặt phẳng (ABCD).
ĐỀ SỐ 22 - THPT LAM KINH, THANH HÓA (Lần 1)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Gọi I là trung điểm AB, H là giao
điểm của BD với IC. Các mặt phẳng (SBD) và (SIC) cùng vuông góc với đáy. Góc giữa (SAB) và (ABCD) bằng 0
60 . Tính thể tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng SA và IC.
ĐỀ SỐ 23 - THPT XUÂN TRƯỜNG, NAM ĐỊNH
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Tam giác SAB đều và nằm trong mặt
phẳng vuông góc với mặt phẳng đáy (ABCD). Biết SD 2a 3 và góc tạo bởi đường thẳng SC
GV. TRẦN QUỐC NGHĨA
TOÁN HỌC BẮC – TRUNG – NAM
TÀi LIỆU ÔN THI THPT QUỐC GIA 2016 25
với mặt phẳng (ABCD) bằng 0
30 . Tính theo a thể tích khối chóp S.ABCD và khoảng cách từ điểm
B đến mặt phẳng (SAC).
ĐỀ SỐ 24 - THPT NGUYỄN TRUNG THIÊN, HÀ TĨNH (Lần 1)
THPT NGUYỄN THI MINH KHAI, HÀ TĨNH (Lần 1)
Cho lăng trụ đứng ABC.ABC có AC = a, BC = 2a, 0
ACB 120 và đường thẳng AC tạo với
mp(ABBA) một góc 300. Gọi M là trung điểm BB. Tính thể tích khối lăng trụ đã cho và khoảng
cách từ đỉnh A đến mp(ACM) theo a
ĐỀ SỐ 25 - THPT HẬU LỘC 2, THANH HÓA (Lần 1)
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, mặt bên SAD là tam giác đều nằm a 6
trong mặt phẳng vuông góc với đáy, SC
. Tính thể tích khối chóp S.ABCD và khoảng cách 2
giữa hai đường thẳng AD, SB theo a.
ĐỀ SỐ 26 - THPT YÊN LẠC, VĨNH PHÚC
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, cạnh AB = 2a. Hình chiếu vuông góc của S
lên mặt phẳng (ABCD) trùng với trọng tâm G của tam giác ABC, góc giữa SA và mặt phẳng
( ABCD) bằng 300. Tính theo a thể tích khối chóp S.ABCD và cosin của góc giữa đường thẳng AC
và mặt phẳng (SAB).
ĐỀ SỐ 27 - THPT CHUYÊN NGUYỄN ĐÌNH CHIỂU, ĐỒNG THÁP
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật .Biết SA ( ABCD) , SC hợp với mặt 4
phẳng ( ABCD) một góc với tan , AB a
3 và BC 4a . Tính thể tích của khối chóp 5
S.ABCD và khoảng cách từ điểm D đến mặt phẳng (SBC) .
ĐỀ SỐ 28 - THPT TRIỆU SƠN, THANH HÓA
Cho hình chóp S.ABCD có SA vuông góc với mặt đáy (ABCD), đáy ABCD là hình chữ nhật có
AD = 3a, AC = 5a, góc giữa hai mặt phẳng (SCD) và (ABCD) bằng 450. Tính theo a thể tích khối
chóp S.ABCD và tính góc giữa đường thẳng SD và mặt phẳng (SBC).
ĐỀ SỐ 29 - SỞ GIÁO DỤC VÀ ĐÀO TẠO VĨNH PHÚC 3a
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SD
. Hình chiếu vuông góc H của đỉnh 2
S lên mặt phẳng (ABCD) là trung điểm của đoạn AB. Gọi K là trung điểm của đoạn AD. Tính theo
a thể tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng KH và SD.
ĐỀ SỐ 30 - THPT THUẬN THÀNH 1, BẮC NINH
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB a , AD 2a , SA ( ABCD) .
Tính theo a thể tích của khối chóp S.ABCD và khoảng cách từ D đến mặt phẳng (SBM) với M là 1
trung điểm của CD biết góc giữa SC và mặt phẳng chứa đáy là với tan 5
GV. TRẦN QUỐC NGHĨA
TOÁN HỌC BẮC – TRUNG – NAM
Chuyên đê: HÌNH HỌC KHÔNG GIAN 26
ĐỀ SỐ 31 - THPT LÝ THÁI TỔ, BẮC NINH (Lần 2)
Cho hình lăng trụ đứng ABCD.ABCD có đáy là hình thoi cạnh a, 0
BAD 120 và AC ' a 5
Tính thể tích khối lăng trụ ABCD.ABCD và khoảng cách giữa hai đường thẳng AB và BD theo a.
ĐỀ SỐ 32 - THPT NGUYỄN KHUYẾN, TPHCM (Lần 1)
Cho hình lập phương ABCD.A ' B 'C ' D ' có cạnh bằng 2. Gọi M là trung điểm của AD và N là tâm
của hình vuông CC ' D ' D . Tính thể tích của khối cầu đi qua bốn đỉnh M, N, B, C và khoảng cách
giữa hai đường thẳng AB với MN.
ĐỀ SỐ 33 - THPT PHÙ CỪ, HƯNG YÊN
Cho lăng trụ đứng ABCD.ABCD, đáy ABCD là hình chữ nhật có AB a , AD a 3 . Biết góc
giữa đường thẳng AC và mặt phẳng (ABCD) bằng 600. Tính thể tích khối lăng trụ
ABCD.ABCD và khoảng cách giữa hai đường thẳng chéo nhau BC và CD theo a.
ĐỀ SỐ 34 - THPT KIM LIÊN, HÀ NỘI
Cho hình lăng trụ tam giác ABC.ABC, có đáy ABC là tam giác vuông cân ở B và AB = a. Hình
chiếu vuông góc của A lên (ABC) trùng với trung điểm H của cạnh AB. Biết diện tích mặt bên
ABBA bằng 2 3a .
a) Tính thể tích khối lăng trụ đã cho.
b) Tính khoảng cách từ điểm B đến mp(ACB).
ĐỀ SỐ 35 - THPT THANH CHƯƠNG 1, NGHỆ AN (Lần 1)
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của S lên mặt
phẳng (ABC) là điểm H thuộc cạnh BC sao cho HC = 2HB, góc giữa SA với (ABC) bằng 450. Tính
theo a thể tích khối chóp S.ABC và khoảng cách giữa hai đường thẳng SC và AB.
ĐỀ SỐ 36 - THPT BÌNH MINH, NINH BÌNH
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm I và có cạnh bằng a, 0
BAD 60 .Gọi H là
trung điểm của IB, vẽ SH vuông góc với mặt phẳng (ABCD). Góc giữa SC với mặt phẳng (ABCD)
bằng 450. Tính thể tích của khối chóp S.ABCD và tính khoảng cách từ điểm A đến mặt phẳng (SCD).
ĐỀ SỐ 37 - THPT LƯƠNG NGỌC QUYẾN, THÁI NGUYÊN
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm I. Cạnh SA vuông góc với mặt phẳng a 3
(ABCD), SA a 3 . Bán kính đường tròn ngoại tiếp hình chữ nhật ABCD bằng , góc 3 30o ACB
. Tính theo a thể tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng AC và SB.
GV. TRẦN QUỐC NGHĨA
TOÁN HỌC BẮC – TRUNG – NAM
TÀi LIỆU ÔN THI THPT QUỐC GIA 2016 27
ĐỀ SỐ 38 - THPT CHUYÊN VĨNH PHÚC (Lần 3)
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Gọi I là trung điểm cạnh AB. Hình
chiếu vuông góc của S lên mặt đáy là trung điểm H của CI, góc giữa đường thẳng SA và mặt đáy
bằng 600. Tính theo a thể tích khối chóp S.ABC và khoảng cách từ điểm H đến mặt phẳng (SBC).
ĐỀ SỐ 39 - THPT NGUYỄN VĂN TRỖI, HÀ TĨNH (Lần 1)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA = a, AB = a, AC = 2a, SA vuông góc
với mặt phẳng (ABCD). Gọi G là trọng tâm tam giác SAC. Tính theo a thể tích khối chóp
S.ABCD và khoảng cách từ điểm A đến mặt phẳng (BGC).
ĐỀ SỐ 40 - THPT SỐ 3 BẢO THẮNG, LÀO CAI (Lần 1)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 4a , cạnh SA vuông góc với mặt
phẳng đáy. Góc giữa cạnh SC và mặt phẳng (ABCD) bằng 600, M là trung điểm của BC, N là điểm
thuộc cạnh AD sao cho DN = a . Tính theo a thể tích khối chóp S.ABCD và khoảng cách giữa hai
đường thẳng SB và MN .
ĐỀ SỐ 41 - THPT TRẦN PHÚ, HÀ TĨNH
Cho lăng trụ ABC.ABC có đáy ABC là tam giác vuông tại A, cạnh AB = 3a,
BC = 5a. Hình chiếu vuông góc của điểm B trên mặt phẳng (ABC) là tâm đường tròn ngoại tiếp tam
giác ABC. Góc giữa hai mặt phẳng (ABBA) và mặt phẳng (ABC) bằng 600. Tính thể tích khối lăng
trụ ABC.ABC và khoảng cách từ điểm B' đến mặt phẳng (ACCA).
ĐỀ SỐ 42 - THPT NGHÈN, HÀ TĨNH
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt đáy, góc tạo bởi
SB và mặt đáy bằng 600, I là trung điểm cạnh BC, là hình chiểu của lên S. Tính theo thể tích khối
chóp S.ABC và khoảng cách từ tâm đường tròn ngoại tiếp tam giác ABC đến mặt phẳng (ABH)
ĐỀ SỐ 43 - THPT NÚI THÀNH, QUẢNG NAM
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, Đường thẳng SA vuông góc với mặt
đáy. Góc giữa đường thẳng SB và mặt phẳng (ABC) bằng 600 .
1) Tính thể tích khối chóp S.ABC theo a
2) Tính khoảng cách giữa hai đường thẳng AC và SB theo a.
ĐỀ SỐ 44 – THPT PHAN THÚC TRỰC, NGHỆ AN (Lần 1)
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 3a, hình chiếu của S lên mặt phẳng
(ABC) là điểm H thuộc cạnh AB sao cho AB = 3AH. Góc tạo bởi SA và mặt phẳng (ABC) bằng
600. Tính theo a thể tích khối chóp S.ABC và khoảng cách giữa hai đường thẳng SA và BC.
ĐỀ SỐ 45 - THPT MARIE-CURIE, TPHCM
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B, AB = BC = a và IAD = 2a. Hình
chiếu vuông góc của S trên đáy là trung điểm H của đoạn AB. Cạnh bên SC tạo với mặt đáy một
góc bằng 600. Tính theo a thể tích khối chóp S.ABCD và khoảng cách từ điểm H đến mặt phẳng (SCD).
GV. TRẦN QUỐC NGHĨA
TOÁN HỌC BẮC – TRUNG – NAM
Chuyên đê: HÌNH HỌC KHÔNG GIAN 28
ĐỀ SỐ 46 - THPT HÙNG VƯƠNG, BÌNH PHƯỚC (Lần 1)
1) Cho hình chóp S.ABCD có đáy ABCD là hình vuông, cạnh AB = a, SA vuông góc với mặt
phẳng (ABCD), SD hợp với mặt phẳng (ABCD) góc bằng 450. Gọi M là trung điểm của cạnh
CD. Tính theο a thể tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng SB và AM.
2) Cho hình lăng trụ đứng ABC.A1B1C1 có đáy ABC là tam giác đều, cạnh AB = a, AA1 = 2a. Tính
theο a thể tích khối lăng trụ ABC.A1B1C1 và khoảng cách từ A đến (A1BC).
ĐỀ SỐ 47 - THPT HÙNG VƯƠNG, BÌNH PHƯỚC (Lần 2)
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại C, BC = a. Hình chiếu vuông góc
của S trên mặt phẳng (ABC) là trung điểm H của cạnh AB, biết rằng SH = a. Tính theο a thể tích
khối chóp S.ABC và khoảng cách từ điểm B đến mặt phẳng (MAC), trong đó M là trung điểm của cạnh SB.
ĐỀ SỐ 48 - THPT ĐA PHÚC, HÀ NỘI (Lần 1)
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và cạnh bên bằng a 3 . Tính thể tích khối
chóp S.ABC và diện tích của mặt cầu ngoại tiếp hình chóp S.ABC theo a.
ĐỀ SỐ 49 - THPT KẺ SẶT, HẢI DƯƠNG
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Tam giác SAB cân tại S và nằm
trong mặt phẳng vuông góc với đáy, góc giữa cạnh bên SC và đáy bằng 600. Tính theo a thể tích
khối chóp S.ABCD và khoảng cách giữa hai đường thẳng BD và SA.
ĐỀ SỐ 50 - THPT TRẦN NHÂN TÔNG, QUẢNG NINH
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Hai mặt phẳng (SAB) và (SAC) cùng
vuông góc với mặt phẳng (ABCD). Biết rằng AB = a, BC = a 3 và góc giữa SC với (ABCD)
bằng 600. Tính thể tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng CE và SB trong
đó E là trung điểm của SD.
ĐỀ SỐ 51 - THPT QUỲNH LƯU, THANH HÓA
Cho hình chóp S.ABC có đáy là tam giác vuông tại B, cạnh AC = 2a, 0
BAC 30 , SA vuông góc
với đáy và SA = a. Tính thể tích khối chóp S.ABC và tính khoảng cách giữa hai đường thẳng SB với AC.
ĐỀ SỐ 52 - THPT LÊ LỢI, THANH HÓA
Cho hình chóp S.ABC có tam giác ABC vuông tại A, BC = 2a, Góc 0
ACB 60 . Mặt phẳng
(SAB) vuông góc với mp(ABC), tam giác SAB cân tại S, tam giác SBC vuông tại S. Tính thể tích
khối chóp S.ABC và khoảng cách từ điểm A tới mp(SBC).
ĐỀ SỐ 53 - THPT NGUYỄN VIẾT XUÂN, PHÚ YÊN
Cho lăng trụ ABC.ABC có đáy là tam giác đều cạnh a, hình chiếu vuông góc của A trên (ABC)
là trung điểm cạnh AB, góc giữa đường thẳng AC và mặt đáy bằng 0
60 . Tính thể tích khối lăng
trụ ABC.ABC và tính khoảng cách từ B đến mặt phẳng (ACCA).
GV. TRẦN QUỐC NGHĨA
TOÁN HỌC BẮC – TRUNG – NAM
TÀi LIỆU ÔN THI THPT QUỐC GIA 2016 29
ĐỀ SỐ 54 - THPT ĐỒNG ĐẬU, VĨNH PHÚC (Lần 2)
Cho hình chóp S.ABCD có đáy là hình thoi, tam giác SAB đều và nằm trong mặt phẳng vuông góc
với mp(ABCD). Biết AC = 2a, BD = 4a. Tính theo a thể tích khối chóp S.ABCD và khoảng cách
giữa hai đường thẳng AD và SC.
ĐỀ SỐ 55 - THPT LÝ TỰ TRỌNG, NAM ĐỊNH
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, biết AB = a; AD = 2a, tam giác SAB là
tam giác đều nằm trong mặt phẳng vuông góc với đáy. Gọi I là trung điểm của SD. Tính thể tích
khối chóp S.ACD và khoảng cách giữa hai đường thẳng AI và SC.
ĐỀ SỐ 56 - THPT HỒNG LĨNH, HÀ TĨNH
Cho hình lăng trụ ABC.ABC có đáy là tam giác đều có cạnh bằng a, cạnh bên tạo với đáy góc
300. Biết hình chiếu vuông góc của A trên (ABC) trùng với trung điểm cạnh BC. Tính theo a thể
tích khối lăng trụ ABC.ABC và bán kính mặt cầu ngoại tiếp tứ diện AABC.
ĐỀ SỐ 57 - THPT LƯƠNG TÀI 2, BẮC NINH
Cho hình chóp S.ABCD có đáy ABCD là hình thoi, 0
ABC 60 , BC 2a, hình chiếu vuông góc
của S trên mặt phẳng (ABCD) trùng với giao điểm O của AC và BD, SO = a, G là trọng tâm của
tam giác SBO. Tính theo a thể tích của khối chóp S.ABCD và khoảng cách giữa hai đường thẳng AD và CG.
ĐỀ SỐ 58 - THPT NHƯ XUÂN, THANH HÓA
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, 0
ABC 60 . Cạnh bên SA vuông góc
với mặt đáy và cạnh bên SC tạo với mặt đáy một góc 600. Gọi I là trung điểm BC, H là hình chiếu
vuông góc của A lên SI.
a) Tính thể tích khối chóp S.ABCD.
b) Tính khoảng cách từ điểm H đến mặt phẳng (SCD) theo a.
ĐỀ SỐ 59 - THPT HỒNG QUANG, HẢI DƯƠNG
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Gọi M là trung điểm CD, SH vuông
góc với mặt phẳng (ABCD) với H là giao điểm của AC với BM. Góc giữa (SCD) và (ABCD) bằng
600. Tính thể tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng AB và SM theo a.
ĐỀ SỐ 60 - THPT TĨNH GIA 1, THANH HÓA
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và góc 0
BAD 60 ; các mặt phẳng
(SAD) và (SAB) cùng vuông góc với mặt phẳng đáy (ABCD); góc tạo bởi SC với (ABCD) bằng
600. Tính thể tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng NC và SD với N là
điểm nằm trên cạnh AD sao cho DN = 2AN.
ĐỀ SỐ 61 - THPT CHUYÊN NGUYỄN HUỆ, HÀ NỘI (Lần 1)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, hình chiếu của S lên (ABCD) là
trung điểm của AD, góc giữa đường thẳng SB và mặt đáy bằng 600.Gọi M là trung điểm của DC.
Tính thể tích khối chóp S.ABM và khoảng cách giữa hai đường thẳng SA và BM.
GV. TRẦN QUỐC NGHĨA
TOÁN HỌC BẮC – TRUNG – NAM
Chuyên đê: HÌNH HỌC KHÔNG GIAN 30
ĐỀ SỐ 62 - THPT NGÔ SĨ LIÊN, BẮC GIANG (Lần 3)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB a, AD a 2 . Hình chiếu vuông
góc của đỉnh S lên (ABCD) trùng với trọng tâm của tam giác ABC, đường thẳng SD tạo với mặt đáy ABCD một góc 0
45 . Tính thể tích của khối chóp S.ABCD và tính khoảng cách giữa hai
đường thẳng SC và BD theo a .
ĐỀ SỐ 63 - THPT CHUYÊN HẠ LONG, QUẢNG NINH
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, mặt bên SAC là tam giác cân tại S và
nằm trong mặt phẳng vuông góc với mặt (ABC), đường thẳng SB tạo với mặt phẳng (ABC) một
góc 600, M là trung điểm cạnh BC. Tính theo a thể tích khối S.ABC và khoảng cách giưa hai
đường thẳng SM, AC.
ĐỀ SỐ 64 - THPT CHUYÊN ĐH VINH (Lần 1)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O, SD vuông góc với mặt (ABCD), AD a , 0
AOB 120 , góc giữa hai mặt phẳng (SBC) và (ABCD) bằng 0 45 . Tính theo a thể tích
khối chóp S.ABCD và khoảng cách giữa hai đường thẳng AC, SB.
ĐỀ SỐ 65 - NHÓM GIA SƯ TRỰC TUYẾN
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O và SO ABCD . Biết khoảng
cách từ O đến SA là a 2 , góc tạo bởi giữa đáy và mặt bên SAD là 600 và độ dài đường chéo
AC của hình chữ nhật bằng 4 lần khoảng cách từ O đến mặt bên SAD . Tính thể tích khối chóp
S.ABCD và khoảng cách giữa hai đường thẳng SA và DC .
ĐỀ SỐ 66 - THPT HÀN THUYÊN, BẮC NINH (Lần 2)
Cho hình lăng trụ ABC.ABC có đáy ABC là tam giác vuông cân tại B với
AB = 2a. Hình chiếu vuông góc của B xuống mặt đáy (ABC) là trung điểm H của cạnh AB.
Tính theo a thể tích khối lăng trụ ABC.ABC và khoảng cách từ Cđến mặt phẳng (ABC) biết
góc giữa đường thẳng BC’ và mặt phẳng (ABC) bằng 0 45 .
ĐỀ SỐ 67 - THPT CHUYÊN HÙNG VƯƠNG, GIA LAI (Lần 1)
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A với AB=AC= a. Trên cạnh BC lấy 1
điểm H sao cho BH
BC , SH vuông góc với mp (ABC), góc giữa SA và mp (ABC) bằng 0 60 . 4
Tính theo a thể tích hình chóp S.ABC và khoảng cách giữa hai đường thẳng AB và SC.
ĐỀ SỐ 68 - THPT NGUYỄN KHUYẾN, TP HCM (Lần 3)
Cho hình chóp S.ABCD có đáy ABCD là hình thoi với SA = AB = a. góc 0
BAD 120 . Các mặt
phẳng (SAC), (SBD) cùng vương góc với đáy (ABCD). Tính theo a thể tích tứ diện S.ABC và góc
giữa SB và (SCD).
GV. TRẦN QUỐC NGHĨA
TOÁN HỌC BẮC – TRUNG – NAM
TÀi LIỆU ÔN THI THPT QUỐC GIA 2016 31
ĐỀ SỐ 69 - THPT HÀ HUY TẬP, NGHỆ AN
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a. H là trung điểm AB, SH vuông góc với
mp (ABCD), tam giác SAB vuông tại S. Tính thể tích khối chóp S.ABCD và khoảng cách giữa hai
đường BD, SC theo a.
ĐỀ SỐ 70 - THPT QUẢNG XƯƠNG 4, THANH HÓA
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B. AB = 2a, 0
BAC 60 , cạnh bên SA
vuông góc với đáy và SA a 3 . Gọi M là trung điểm của cạnh AB. Tính thể tích khối chóp
S.ABC và khoảng cách giữa hai đường thẳng SB và CM theo a.
ĐỀ SỐ 71 - THPT CHUYÊN LƯƠNG THẾ VINH, ĐỒNG NAI
Cho hình lăng trụ đứng ABC.ABC có tam giác ABC vuông tại A, AB = a, AC a 3 . Góc giữa
AC và mặt phẳng (ABC) là 300. Gọi N là trung điểm của BB. Tính thể tích khối lăng trụ
ABC.ABC và cosin của góc tạo bởi AB và CN.
ĐỀ SỐ 72 - THPT QUỐC OAI, HÀ NỘI
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB 2a, AD .
a Trên cạnh AB lấy điểm a M sao cho AM
. H là giao điểm của AC và MD. Biết SH vuông góc với mặt phẳng (ABCD) 2
và SH = a. Tính thể tích khối chóp S.ADCM và khoảng cách giữa hai đường thẳng SD và AC theo a.
ĐỀ SỐ 73 - THPT ANH SƠN 2, NGHỆ AN (Lần 1)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB a, AD 2 2a . Hình chiếu vuông
góc của điểm S trên mặt phẳng (ABCD) trùng với trọng tâm tam giác BCD. Đường thẳng SA tạo
với mặt phẳng (ABCD) một góc 450. Tính thể tích khối chóp S.ABCD và khoảng cách giữa hai
đường thẳng AC và SD theo a.
ĐỀ SỐ 74 - THPT TRẦN QUANG KHẢI (Lần 3)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, mặt phẳng (SAB) vuông góc với
đáy, tam giác SAB cân tại S và SC tạo với đáy một góc 600. Tính thể tích khối chóp S.ABCD và
khoảng cách giữa hai đường thẳng BD và SA theo a.
ĐỀ SỐ 75 - THPT PHÚ XUYÊN B, HÀ NỘI
Cho hình chóp đều S.ABC có SA=2a, AB=a. Gọi M là trung điểm của cạnh BC. Tính theo a thể
tích khối chóp S.ABC và khoảng cách từ M tới mặt phẳng (SAB).
ĐỀ SỐ 76 - THPT CHUYÊN KHTN HÀ NỘI (Lần 3)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a 2 , tam giác SAC vuông tại S và
nằm trong mặt phẳng vuông góc với đáy, SA = a. Tính theo a thể tích của khối chóp S.ABCD và
khoảng cách giữa hai đường thẳng SD và BC.
GV. TRẦN QUỐC NGHĨA
TOÁN HỌC BẮC – TRUNG – NAM
Chuyên đê: HÌNH HỌC KHÔNG GIAN 32
ĐỀ SỐ 77 - THPT CHUYÊN NG. QUANG DIỆU, ĐỒNG THÁP (Lần 1)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = 2a, AD = a, K là hình chiếu vuông
góc của B lên đường chéo AC, các điểm H, M lần lượt là trung điểm của AK và DC, SH vuông
góc với mặt phẳng (ABCD), góc giữa đường thẳng SB và mặt phẳng (ABCD) bằng 450. Tính theo
a thể tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng SB và MH.
ĐỀ SỐ 78 - THPT TRUNG GIÃ, HÀ NỘI (Lần 2)
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, AD 3BC 3 3a ,
AB 2 2a tam giác SAB đều trong mặt phẳng vuông góc với mặt phẳng (ABCD). Tính thể tích
khối chóp S.ABCD và góc tạo bởi đường thẳng SA với mặt phẳng (SCD).
ĐỀ SỐ 79 - THPT CHUYÊN THOẠI NGỌC HẦU, AN GIANG (Lần 1)
Cho lăng trụ đứng ABC.A' B 'C ' có đáy ABC là tam giác vuông tại A, AB a, AC a 3 và
mặt bên BB 'C 'C là hình vuông. Tính theo a thể tích khối lăng trụ AB .
C A' B 'C ' và khoảng cách
giữa 2 đường thẳng AA', BC ' .
ĐỀ SỐ 80 - THPT CHUYÊN LÀO CAI (Lần 2)
Cho khối chóp S.ABCD có ABCD là hình chữ nhật có các cạnh AB = 2a, a
AD = a. Trên cạnh AB lấy điểm M sao cho AM
, cạnh AC cắt MD tại H. Biết SH vuông góc 2
với mặt phẳng (ABCD) và SH = a. Tính thể tích khối chóp S.HCD và tính khoảng cách giữa hai
đường thẳng SD và AC theo a.
ĐỀ SỐ 81 - THPT CHUYÊN NGUYỄN HUỆ, HÀ NỘI (Lần 2)
Cho hình chóp S.ABC có mặt phẳng (SAC) vuông góc với mặt phẳng (ABC) , SA AB ,
a AC 2a và 0
ASC ABC 90 . Tính thể tích khối chóp S.ABC và cosin của góc
giữa hai mặt phẳng (SAB) và (SBC) .
ĐỀ SỐ 82 - THPT LƯƠNG TÀI 2, BẮC NINH (Lần 3)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Cạnh bên SA vuông góc với đáy.
Góc giữa SC và mặt đáy bằng 0
45 . Gọi E là trung điểm BC. Tính thể tích khối chóp S.ABCD và
khoảng cách giữa hai đường thẳng DE và SC theo a.
ĐỀ SỐ 83 - THPT LÊ LỢI, THANH HÓA (Lần 2)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a, SA ( ABCD) , SC tạo với
mp(ABCD) một góc 450 và SC 2a 2 . Tính thể tích khối chóp S.ABCD và khoảng cách từ
trọng tâm G của tam giác ABC đến mp(SCD) theo a.
ĐỀ SỐ 84 - THPT PHẠM VĂN ĐỒNG, PHÚ YÊN
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, hình chiếu vuông góc của S lên mặt
phẳng đáy là trung điểm của cạnh AB . Biết AB a; AC a 3 ; góc giữa SD với mặt phẳng đáy
bằng 600. Tích theo a thể tích khối chóp S.ABCD và khoảng cách từ điểm C đến mặt phẳng (SBD) .
GV. TRẦN QUỐC NGHĨA
TOÁN HỌC BẮC – TRUNG – NAM
TÀi LIỆU ÔN THI THPT QUỐC GIA 2016 33
ĐỀ SỐ 85 - THPT CÙ HUY CẬN, HÀ TĨNH (Lần 2)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với mặt phẳng
(ABCD), góc giữa SC và mặt phẳng (ABCD) bằng 600. Gọi M là trung điểm của CD, N là hình
chiếu vuông góc của D trên SM. Tính thể tích khối chóp S.ABCD và khoảng cách từ N đến mặt
phẳng (SBC) theo a .
ĐỀ SỐ 86 - THPT HÀ TRUNG, THANH HÓA (Lần 2)
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại A, AB = 2a,
AC = a, AA' = 3a. Tính thể tích khối lăng trụ và khoảng cách giữa hai đường thẳng AB' và BC.
ĐỀ SỐ 87 - THPT CHUYÊN BIÊN HÒA, HÀ NAM (Lần 1)
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Các mặt bên (SAB) và (SAD) cùng
vuông góc với mặt phẳng đáy. Cho AB 2a, AD a, SA BC a , CD 2a 5 . Gọi H là điểm
nằm trên đoạn AD sao cho AH a . Tính thể tích của khối chóp S.ABCD và khoảng cách giữa hai
đường thẳng BH và SC theo a.
ĐỀ SỐ 88 - THPT BẢO YÊN 1, LÀO CAI (ĐỀ 1)
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, 0
ABC 60 . Cạnh bên SA vuông góc
với mặt đáy và cạnh bên SC tạo với mặt đáy một góc 0
60 . Gọi I là trung điểm BC, H là hình
chiếu vuông góc của A lên SI. Tính thể tích khối chóp S.ABCD và khoảng cách từ điểm H đến
mặt phẳng (SCD) theo a.
ĐỀ SỐ 89 - THPT BẢO YÊN 1, LÀO CAI (ĐỀ 2)
Cho hình chóp đều A.BCD có AB a 3 , BC = a. Gọi M là trung điểm của CD. Tính thể tích
khối chóp A.BCD theo a và khoảng cách giữa hai đường thẳng BM, AD.
ĐỀ SỐ 90 - THPT YÊN PHONG 2, BẮC NINH (Lần 2)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Mặt bên SAB là tam giác đều và nằm
trong mặt phẳng vuông góc với đáy. Gọi M là trung điểm của cạnh AD. Tính theo a thể tích của
khối chóp S.ABCD và khoảng cách giữa hai đường thẳng SA ,CM.
ĐỀ SỐ 91 - SỞ GIÁO DỤC VÀ ĐÀO TẠO NAM ĐỊNH
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B;
AB = BC = 4a. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD).
Gọi H là trung điểm của AB, biết khoảng cách từ C đến mặt phẳng (SHD) bằng a 10 . Tính thể
tích khối chóp S.HBCD và cosin của góc giữa hai đường thẳng SC và HD.
ĐỀ SỐ 92 - THPT THỪA LƯU, HUẾ
Cho hình chóp S.ABCD có đáy ABCD là hình thang với đáy lớn là AD; các đường thẳng S , A AC
và CD đôi một vuông góc với nhau; SA AC CD a 2 , AD 2BC . Tính thể tích của khối
chóp S.ABCD và khoảng cách giữa hai đường thẳng SB và CD.
GV. TRẦN QUỐC NGHĨA
TOÁN HỌC BẮC – TRUNG – NAM
Chuyên đê: HÌNH HỌC KHÔNG GIAN 34
ĐỀ SỐ 93 - THPT THẠCH THÀNH 1, THANH HÓA (Lần 3)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a,
AD = 2a, SA (ABCD), SA = a. Tính theo a thể tích khối chóp S.ABCD và khoảng cách từ điểm
A đến mặt phẳng (SBM), với Mlà trung điểm của cạnh CD.
ĐỀ SỐ 94 - THPT CHUYÊN NGUYỄN TẤT THÀNH, YÊN BÁI
Cho hình chóp S.ABC có AB = AC = a , 0
ABC 30 , SA vuông góc với mặt phẳng (ABC), góc
giữa hai mặt phẳng (SBC) và (ABC) là 600. Tính thể tích khối chóp S.ABC và khoảng cách từ
trọng tâm G của tam giác ABC đến mặt phẳng (SBC) theo a .
ĐỀ SỐ 95 - THPT HỒNG QUANG, HẢI DƯƠNG (Lần 2)
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a , góc 0 ABC 60 . cạnh a 7 bên SC
. Hình chiếu vuông góc của S trên mặt phẳng ( ABCD) là trung điểm cạnh AB . 2
Gọi M là điểm thuộc cạnh CD sao cho MC 2MD . Tính theo a thể tích của khối chóp
S.ABCD và tính côsin của góc giữa hai đường thẳng AM và SB .
ĐỀ SỐ 96 - THCS-THPT ĐÔNG DU, ĐẮK LẮK (Lần 1)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, mặt bên SAD là tam giác vuông tại S, hình
chiếu vuông góc của S lên mặt phẳng (ABCD) là điểm H thuộc cạnh AD sao cho HA = 3HD. Gọi M
là trung điểm của AB. Biết rằng SA 2a 3 và đường thẳng SC tạo với đáy một góc 0 30 . Tính theo
a thể tích khối chóp S.ABCD và khoảng cách từ M đến mặt phẳng (SBC).
ĐỀ SỐ 97 - THPT THUẬN THÀNH 1, BẮC NINH (Lần 2)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = 2a, AD = a. Hình chiếu vuông
góc của S trên mặt phẳng (ABCD) là trung điểm H của AB. SC tạo với đáy một góc 450. Tính theo
a thể tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng SB, AC.
ĐỀ SỐ 98 - SỞ GD - ĐT TỈNH BẮC GIANG
Cho lăng trụ ABC.ABC, có đáy là một tam giác đều cạnh bằng 2a. Hình chiếu vuông góc của B
lên mặt phẳng (ABC) trùng với trung điểm H của cạnh BC, K là điểm trên cạnh AC sao cho
CK = 2AK và BA' 2a 3. Tính thể tích của khối lăng trụ ABC.ABC và khoảng cách giữa hai
đường thẳng CC và BK theo a.
ĐỀ SỐ 99 - SỞ GD - ĐT TỈNH QUẢNG NINH
Cho hình hộp đứng ABC .
D A' B 'C ' D ' có đáy là hình thoi cạnh a , góc 0
ACB 60 , mặt phẳng
( A' BD) tạo với đáy một góc 0
60 . Tính theo a thể tích khối hộp và khoảng cách giữa hai đường
thẳng CD ', BD .
ĐỀ SỐ 100 - THPT CHUYÊN LONG AN, LONG AN (Lần 1)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = 2a, BC = a. Hình chiếu vuông góc
H của đỉnh S trên mặt phẳng đáy là trung điểm của cạnh AB; Góc giữa đường thẳng SC và mặt
GV. TRẦN QUỐC NGHĨA
TOÁN HỌC BẮC – TRUNG – NAM
TÀi LIỆU ÔN THI THPT QUỐC GIA 2016 35
phẳng đáy bằng 600. Tính theo a thể tích khối chóp S.ABCD và góc giữa hai đường thẳng SB và AC.
ĐỀ SỐ 101 - THPT NGUYỄN TRÃI, KON TUM (Lần 1)
Cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật có AB a , BC a 3 . Cạnh bên SA vuông
góc với mặt phẳng (ABCD), góc giữa đường thẳng SC và mặt phẳng đáy (ABCD) bằng 600, M là
trung điểm của cạnh SD. Tính thể tích khối chóp S.ABCD và khoảng cách từ đỉnh S đến mp(BCM).
ĐỀ SỐ 102 - THPT CHUYÊN SƠN LA, SƠN LA (Lần 1)
Cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật có AB = a, BC = 2a. H là trung điểm cạnh a 5
AB, SH vuông góc với mặt phẳng đáy, cạnh bên SA
. Tính thể tích hình chóp S.ABCD và 2
khoảng cách giữa hai đường thẳng HC và SD.
ĐỀ SỐ 103 - THPT ĐA PHÚC, HÀ NỘI (Lần 2)
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB là tam giác đều,
SC SD a 3 . Tính thể tích khối chóp S.ABCD và cosin của góc giữa hai mặt phẳng (SAD) và (SBC).
ĐỀ SỐ 104 - THPT CHUYÊN. ĐH VINH (Lần 2)
Cho hình lăng trụ ABC.AB C
có đáy ABC là tam giác đều cạnh bằng. Góc giữa cạnh bên và
đáy là 450, hình chiếu vuông góc của lên A mặt phẳng là A B C
trung điểm cạnh A B . Gọi M là
trung điểm cạnh B C
. Tính thể tích khối lăng trụ ABC.AB C
theo a và cosin của góc giữa hại
đường thẳng AM , AB .
ĐỀ SỐ 105 - THPT THỐNG NHẤT, THANH HÓA (Lần 1)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB a , AD 2a , SA ( ABCD) .
Tính theo a thể tích của khối chóp S.ABCD và khoảng cách từ D đến mặt phẳng (SBM) với M là 1
trung điểm của CD biết góc giữa SC và mặt phẳng chứa đáy là với tan 5
ĐỀ SỐ 106 - THPT THANH CHƯƠNG 3, NGHỆ AN
Cho hình chóp S.ABC có tam giác ABC vuông tại A, AB AC a , I là trung điểm của SC, hình
chiếu vuông góc của S lên mặt phẳng (ABC) là trung điểm H của BC, mặt phẳng (SAB) tạo với
đáy 1 góc bằng 600. Tính thể tích khối chóp S.ABC và tính khoảng cách từ điểm I đến mặt phẳng
(SAB) theo a.
ĐỀ SỐ 107 - THPT LÝ THƯỜNG KIỆT, BÌNH THUẬN (Lần 2)
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng a, tam giác SAC cân tại S và nằm
trong mặt phẳng vuông góc với đáy, SB hợp với đáy một góc 300. Gọi M là trung điểm của đoạn
BC. Tính thể tích khối chóp S.ABM và khoảng cách giữa hai đường thẳng SB, AM theo a
GV. TRẦN QUỐC NGHĨA
TOÁN HỌC BẮC – TRUNG – NAM
Chuyên đê: HÌNH HỌC KHÔNG GIAN 36
ĐỀ SỐ 108 - THPT VIỆT TRÌ, PHÚ THỌ (Lần 2)
Cho hình chóp S.ABC có SA ABC , SA 2a tam giác ABC cân tại A, BC 2a 2 , 1 cos ACB
. Tính thể tích của khối chóp S.ABC , xác định tâm và tính diện tích mặt cầu ngoại 3
tiếp hình chóp S.ABC .
ĐỀ SỐ 109 - THPT THUẬN CHÂU, SƠN LA (Lần 2)
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a Mặt bên SAD là tam giác đều nằm a 6
trong mặt phẳng vuông góc với đáy, SC
. Tính thể tích khối chóp S.ABCD và khoảng cách 2
giữa hai đường thẳng AD, SB theo a.
ĐỀ SỐ 110 - THPT MINH CHÂU, HƯNG YÊN (Lần 2) 3a
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SD
. Hình chiếu vuông góc H của đỉnh 2
S lên mặt phẳng (ABCD) là trung điểm của đoạn AB . Gọi K là trung điểm của đoạn AD. Tính
theo a thể tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng HKvà SD.
ĐỀ SỐ 111 - THPT MINH CHÂU, HƯNG YÊN (Lần 3)
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân đỉnh A, AB a 2. Gọi I là trung điểm
của BC, hình chiếu vuông góc của S lên mặt đáy (ABC) là điểm H thỏa mãn IA 2IH , góc giữa
SC và mặt đáy (ABC) bằng 600. Tính thể tích khối chóp S.ABC và khoảng cách giữa hai đường
thẳng AC và SB.
ĐỀ SỐ 112 - THCS-THPT ĐÔNG DU, ĐẮK LẮK (Lần 2)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a. Cạnh bên SA vuông góc với
mặt phẳng đáy, SC tạo với mặt phẳng đáy một góc 0
45 và SC 2a 2 . Tính thể tích khối chóp
S.ABCD và khoảng cách từ điểm B đến mặt phẳng (SCD) theo a.
ĐỀ SỐ 113 - BÁO DÂN TRÍ
Cho hình chóp S.ACBD có đáy ABCD là hình chữ nhật, biết AB 2 ,
a AD a Trên cạnh AB lấy a
điểm M sao cho AM
cạnh AC cắt MD tại H. Biết SH vuông góc với mặt phẳng (ABCD) và 2
SH = a. Tính thể tích khối chóp S.MHCB và khoảng cách giữa hai đường thẳng SD và AC.
ĐỀ SỐ 114 - THPT HƯƠNG KHÊ, HÀ TĨNH (Lần 1)
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A với AB = a, AC 2a 2 . Hình chiếu
vuông góc của S lên mặt phẳng (ABC) là điểm A thuộc đoạn BC thỏa mãn HB = 2HC, góc giữa
SB và mặt phẳng đáy bằng 0
60 . Tính thể tích của khối chóp S.ABC và khoảng cách giữa hai
đường thẳng SB và AC theo a .
GV. TRẦN QUỐC NGHĨA
TOÁN HỌC BẮC – TRUNG – NAM
TÀi LIỆU ÔN THI THPT QUỐC GIA 2016 37
ĐỀ SỐ 115 - THPT HÀM NGHI, HÀ TĨNH (Lần 2)
Cho hình chóp S.ABCD đáy là hình chữ nhật có cạnh AB a, AD a 3 . Hình chiếu vuông góc
của S lên mặt phẳng (ABCD) là trọng tâm của tam giác ABC và SB tạo với mặt phẳng (ABCD) một góc 0
60 . Tính thể tích của khối chóp S.ABCD và khoảng cách giữa hai đường thẳng SA và CD .
ĐỀ SỐ 116 - SỞ GIÁO DỤC VÀ ĐÀO TẠO THANH HÓA
Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, AD là đáy lớn, AD = 2a, AB = BC = CD
= a. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) là điểm H thuộc đoạn thẳng AC sao cho
HC = 2HA. Góc giữa hai mặt phẳng (SCD) và (ABCD) bằng 600. Tính theo a thể tích của khối
chóp S.ABCD và khoảng cách giữa hai đường thẳng SA và CD.
ĐỀ SỐ 117 - SỞ GD & ĐT BÀ RỊA - VŨNG TÀU
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a ; tam giác SAB đều và nằm trong
mặt phẳng vuông góc với đáy. Gọi H là trung điểm của cạnh AB. Tính theo a thể tích khối chóp
S.ABCD và khoảng cách giữa hai đường thẳng DH và SC .
ĐỀ SỐ 118 - THPT ĐỒNG GIA, HẢI DƯƠNG
Cho hình chóp S.ABC có đáy là tam giác vuông tại B, AB = a và BC = a 3 . Gọi BH là đường cao
của tam giác ABC. Tính thể tích khối chóp S.ABC và khoảng cách giữa hai đường thẳng BH và
SC, biết SH (ABC) và góc giữa SB với mặt phẳng (ABC) bằng 600.
ĐỀ SỐ 119 - THPT KINH MÔN, HẢI DƯƠNG (Lần 1)
Cho hình chóp S.ABC có tam giác ABC vuông tại A, AB = AC = a, I là trung điểm của SC, hình
chiếu vuông góc của S lên mặt phẳng (ABC) là trung điểm H của BC, mặt phẳng (SAB) tạo với
đáy một góc bằng 600. Tính thể tích khối chóp S.ABC và tính khoảng cách từ điểm I đến mặt
phẳng (SAB) theo a.
ĐỀ SỐ 120 - THPT NAM DUYÊN HÀ, THÁI BÌNH (Lần 1)
Cho hình chóp S.ABC có
SA SB SC a , 0 0
ASB 90 , BSC 120 , 0
CSA 90 . Tính theo a thể
tích khối chóp S.ABC và khoảng cách từ C đến mp(SAB).
ĐỀ SỐ 121 - THPT GIA LỘC, HẢI DƯƠNG (Lần 1)
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a (a > 0), 0
ABC 60 . Cạnh bên SA
vuông góc với mặt đáy (ABCD) góc tạo bởi SC và mặt phẳng (ABCD) bằng 0 60 . Gọi M là trung
điểm của SB. Tính thể tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng AM, SD theo a.
ĐỀ SỐ 122 - SỞ GD & ĐT QUẢNG NAM
Cho hình lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy bằng a, góc giữa hai mặt phẳng (A’BC)
và (ABC) bằng 600. Gọi M là trung điểm cạnh BC, N là trung điểm cạnh CC’. Tính theo a thể tích
khối chóp A.BB’C’C và khoảng cách từ M đến mặt phẳng (AB’N).
GV. TRẦN QUỐC NGHĨA
TOÁN HỌC BẮC – TRUNG – NAM
Chuyên đê: HÌNH HỌC KHÔNG GIAN 38
ĐỀ SỐ 123 - THPT BẮC YÊN THÀNH, NGHỆ AN (12A4) a
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, với AC
, BC a . Hai mặt phẳng 2
(SAB) và (SAC) cùng tạo với mặt đáy (ABC) góc 600. Tính theo a thể tích khối chóp S.ABC và
khoảng cách từ điểm B tới mặt phẳng (SAC), biết rằng mặt phẳng (SBC) vuông góc với đáy (ABC).
ĐỀ SỐ 124 - THPT PHƯỚC BÌNH, BÌNH PHƯỚC (Lần 1)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Gọi I là trung điểm AB, H là giao
điểm của BD với IC. Các mặt phẳng (SBD) và (SIC) cùng vuông góc với đáy. Góc giữa (SAB) và (ABCD) bằng 0
60 . Tính thể tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng SA và IC.
ĐỀ SỐ 125 - THPT PHƯỚC BÌNH, BÌNH PHƯỚC (Lần 2)
Trong không gian Oxyz, cho hình lăng trụ tam giác ABC.A'B'C' có A(1; 1; 1), B(1; 2; 1), C(1; 1;
2) và A'(2; 2; 1). Tìm tọa độ các đỉnh B', C' và viết phương trình mặt cầu đi qua bốn điểm A, B, C, A'.
ĐỀ SỐ 126 - THPT QUỲNH LƯU 3, NGHỆ AN (Lần 1)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Hình chiếu đỉnh S lên mặt đáy là
trung điểm H của đoạn thẳng AB. Biết góc hợp bởi SC và mặt đáy là 450.
a) Tính thể tích khối chóp S.ABCD.
b) Tính khoảng cách giữa hai đường thẳng BD và SC.
ĐỀ SỐ 127 - THPT PHƯỚC BÌNH (Lần 3) (ĐỀ MINH HỌA)
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, 0
ABC 60 . Cạnh bên SA vuông góc
với mặt đáy và cạnh bên SC tạo với mặt đáy một góc 0
60 . Gọi I là trung điểm BC, H là hình chiếu
vuông góc của A lên SI. Tính thể tích khối chóp S.ABCD và khoảng cách từ điểm H đến mặt
phẳng (SCD) theo a.
ĐỀ SỐ 128 - THPT PHƯỚC BÌNH (Lần 4) (ĐỀ MINH HỌA)
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a mặt bên SAD là tam giác đều nằm trong a 6
mặt phẳng vuông góc với đáy, SC
. Tính thể tích khối chóp S.ABCD và khoảng cách giữa 2
hai đường thẳng AD, SB theo a
ĐỀ SỐ 129 - THPT PHƯỚC BÌNH (Lần 5) (ĐỀ MINH HỌA)
Trong mặt phẳng Oxy, cho hình chữ nhật ABCD có AB = 2BC. Gọi H là hình chiếu của A lên
đường thẳng BD; E, F lần lượt là trung điểm đoạn CD và BH. Biết A(1; 1), phương trình đường
thẳng EF là 3x – y – 10 = 0 và điểm E có tung độ âm. Tìm tọa độ các đỉnh B, C, D.
GV. TRẦN QUỐC NGHĨA
TOÁN HỌC BẮC – TRUNG – NAM
TÀi LIỆU ÔN THI THPT QUỐC GIA 2016 39
ĐỀ SỐ 130 - THPT ĐỒNG XOÀI (Lần 1) (ĐỀ MINH HỌA)
Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B, BA = a. Tam giác SAC đều và nằm
trong mặt phẳng vuông góc với mp(ABC). Gọi M, N lần lượt là trung điểm của SA, BC. Tính thể
tích khối chóp S.ABC và khoảng cách giữa hai đường thẳng chéo nhau AC, MN theo a.
ĐỀ SỐ 131 - THPT ĐỒNG XOÀI (Lần 2) (ĐỀ MINH HỌA)
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, mặt bên (SAB) nằm trong mặt phẳng
vuông góc với đáy (ABCD), tam giác SAB vuông tại S, SA = a. Hãy tính thể tích của khối chóp
S.ABCD và khoảng cách giữa hai đường thẳng AB, SC theo a.
ĐỀ SỐ 132 - THPT ĐỒNG XOÀI (Lần 3) (ĐỀ MINH HỌA)
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, SA vuông góc với đáy và SB tạo với đáy
một góc 600. M là trung điểm BC. Tính thể tích khối chóp S.ABC và khoảng cách giữa hai đường
thẳng SM, AC theo a.
ĐỀ SỐ 133 - THPT ĐỒNG XOÀI (Lần 4) (ĐỀ MINH HỌA)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a, AD = 2a, SA (ABCD) và SA
= a. Tính theo a thể tích của khối chóp S.ABCD và khoảng cách từ A đến mặt phẳng (SBM) với M
là trung điểm của CD.
ĐỀ SỐ 134 - THPT CHUYÊN QUANG TRUNG, BÌNH PHƯỚC (Lần 1)
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a. góc giữa mặt bên và mặt đáy bằng 600.
M, N lần lượt là trung điểm cạnh SD và DC. Tính theo a thể tích khối chóp M.ABC và khoảng
cách từ điểm N đến mặt phẳng (MAB).
ĐỀ SỐ 135 - THPT NGUYỄN HỮU CẢNH, BÌNH PHƯỚC (Lần 1)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Tam giác SAB cân tại S và nằm
trong mặt phẳng vuông góc với đáy, góc giữa cạnh bên SC và đáy bằng 0
60 . Tính theo a thể tích
khối chóp S.ABCD và khoảng cách giữa hai đường thẳng BD và SA.
ĐỀ SỐ 136 - THPT NGUYỄN HỮU CẢNH, BÌNH PHƯỚC (Lần 2)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 2a. E, F lần lượt là trung điểm
của AB và BC, H là giao điểm của AF và DE. Biết SH vuông góc với mặt phẳng (ABCD) và góc
giữa đường thẳng SA và mặt phẳng (ABCD) bằng 600. Tính thể tích khối chóp S.ABCD và khoảng
cách giữa hai đường thẳng SH, DF.
ĐỀ SỐ 137 - THPT CHUYÊN ĐHSP HÀ NỘI (Lần 2)
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, mặt bên SAC vuông góc với đáy và là
tam giác cân tại S, góc 0
SBC 60 . Tính thể tích khối chóp S.ABC theo a.
ĐỀ SỐ 138 - SỞ GIÁO DỤC & ĐÀO TẠO HÀ NỘI
Cho hình chóp S.ABCD có đáy ABC là tam giác vuông tại B, AB = 2a, 0
BAC 60 , cạnh bên SA
vuông góc với mặt phẳng đáy và SA a 3 . Gọi M là trung điểm của cạnh AB. Tính theo a thể
tích khối chóp S.ABC và khoảng cách giữa 2 đường thẳng SB, CM.
GV. TRẦN QUỐC NGHĨA
TOÁN HỌC BẮC – TRUNG – NAM
Chuyên đê: HÌNH HỌC KHÔNG GIAN 40
ĐỀ SỐ 139 - THPT THỰC HÀNH CAO NGUYÊN
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D; AB AD 2a, CD a ;
góc giữa hai mặt phẳng (SBC) và (ABCD) bằng 0
60 , SI là đường cao của khối chóp với I là điểm
trên cạnh AD sao cho AD = 3AI. Tính thể tích của khối chóp S.ABCD và khoảng cách từ A đến mặt phẳng (SBC).
ĐỀ SỐ 140 - SỞ GIÁO DỤC & ĐÀO TẠO QUẢNG NGÃI (ĐỀ 1)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a, SA vuông góc với đáy. Góc tạo
bởi SC và mặt phẳng (SAB) bằng 300. Gọi E là trung điểm của BC. Tính thể tích khối chóp
S.ABCD và khoảng cách giữa hai đường thẳng DE, SC theo a.
ĐỀ SỐ 141 - SỞ GIÁO DỤC & ĐÀO TẠO QUẢNG NGÃI (ĐỀ 2)
Câu 5 (1,0 điểm). Cho hình lăng trụ ABC.ABC, ABC đều có cạnh bằng a, AA = a và đỉnh A
cách đều A, B, C. Gọi M, N lần lượt là trung điểm của cạnh BC và AB . Tính theo a thể tích khối
lăng trụ ABC.ABC và khoảng cách từ C đến mặt phẳng (AMN).
ĐỀ SỐ 142 - SỞ GIÁO DỤC & ĐÀO TẠO NAM ĐỊNH
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng a , tam giác SAB vuông cân tại đỉnh
S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích của khối chóp S.ABC và
khoảng cách giữa hai đường thẳng SB và AC theo a .
ĐỀ SỐ 143 - THPT ĐOÀN THƯỢNG, HẢI DƯƠNG (Lần 1)
Cho hình chóp S.ABCD có đáy ABCD là hình thang với đáy lớn là AD và AD 2BC , SA vuông
góc với mặt phẳng (ABCD), tam giác ACD vuông tại C và SA AC a 3, CD a . Tính thể
tích của khối chóp S.ABCD và khoảng cách giữa hai đường thẳng SB và CD.
ĐỀ SỐ 144 - THPT ĐOÀN THƯỢNG, HẢI DƯƠNG (Lần 2)
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh 2a , 0
ABC 60 , SA vuông góc với mặt
phẳng (ABCD) , góc giữa mặt bên (SCD) và mặt đáy (ABCD) bằng 0
45 . Tính thể tích khối chóp
S.ABCD và góc giữa đường thẳng SB và mặt phẳng (SCD).
ĐỀ SỐ 145 - THPT ANH SƠN 2. NGHỆ AN (Lần 2)
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A. Cạnh AC = a, BC a 5 . Mặt phẳng
(SAB) vuông góc mặt phẳng đáy và tam giác SAB đều. Gọi K điểm thuộc cạnh SC sao cho SC =
3SK. Tính thể tích của khối chóp S.ABC và khoảng cách giữa hai đường thẳng AC và BK theo a.
ĐỀ SỐ 146 - THCS-THPT ĐÔNG DU, ĐẮK LẮK (L3)
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA (ABCD), SB = a 3 , gọi M là trung
điểm AD. Tính theo a thể tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng SM và AB.
GV. TRẦN QUỐC NGHĨA
TOÁN HỌC BẮC – TRUNG – NAM
TÀi LIỆU ÔN THI THPT QUỐC GIA 2016 41
ĐỀ SỐ 147 - SỞ GIÁO DỤC & ĐÀO TẠO LÀO CAI
Cho hình chóp S.ABCD có đáy ABCD là nửa lục giác đều và AB BC CD a . Hai mặt phẳng
(SAC) và (SBD) cùng vuông góc với mặt phẳng đáy (ABCD), góc giữa SC và (ABCD) bằng 600.
Tính theo a thể tích của khối chóp S.ABCD và góc giữa đường thẳng SC và mặt phẳng (SAD).
ĐỀ SỐ 148 - THPT GIA LỘC, HẢI DƯƠNG (Lần 1)
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a (a > 0), 0
ABC 60 . Cạnh bên SA
vuông góc với mặt đáy (ABCD) góc tạo bởi SC và mặt phẳng (ABCD) bằng 0 60 . Gọi M là trung
điểm của SB. Tính thể tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng AM, SD theo a.
ĐỀ SỐ 149 - THPT CHÍ LINH, HẢI DƯƠNG (Lần 1)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, AD = 2a. Gọi M là trung điểm
của cạnh BC, cạnh bên SA vuông góc với mặt phẳng (ABCD), góc giữa SM và mặt phẳng (ABCD)
bằng 600. Tính theo a thể tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng DM, SB.
ĐỀ SỐ 150 - SỞ GIÁO DỤC & ĐÀO TẠO HÀ TĨNH
Cho hình chóp S.ABCD đáy là hình chữ nhật có cạnh AB = a, AD = 2a. Gọi O là giao điểm của
hai đường thẳng AC và BD, G là trọng tâm của tam giác SAD. Biết SO vuông góc với mặt phẳng
(ABCD), góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng 600. Tính theo a thể tích khối
chóp S.ABCD và khoảng cách từ điểm G đến mặt phẳng (SCD).
GV. TRẦN QUỐC NGHĨA
TOÁN HỌC BẮC – TRUNG – NAM




