




























Preview text:
TÀI LIỆU ÔN TẬP KỲ THI THPT QUỐC GIA NĂM HỌC 2016 – 2017
(Dành cho đối tượng học sinh trung bình – mục tiêu đạt điểm 5, 6) CHUYÊN ĐỀ 7 HÌNH HỌC KHÔNG GIAN
Các thầy cô tham gia biên soạn tài liệu:
Thầy Lê Văn Định – TTGDNN-GDTX Thanh Oai – Hà Nội
Thầy Dương Phước Sang – Trường THPT Chu Văn An –
Huyện Phú Tân – An Giang
Thầy Phùng Hoàng Em – Trường THPT Trương Vĩnh Ký – Bến Tre.
Cô Trần Thị Thu Thảo – Sinh viên K40 Sư phạm Toán – Đại học Cần Thơ.
Việt Nam, 30 tháng 3 năm 2017 Lời nói đầu
Kỳ thi THPT Quốc Gia 2016 – 2017 đã cận kề, từ nhu cầu thực
tế ôn luyện của các học sinh trung bình và yếu, các thầy cô
giáo ở khắp mọi miền trong cả nước trên Diễn đàn toàn học
Bắc Trung Nam đã biên soạn bộ tài liệu ÔN TẬP KỲ THI
THPTQG dành cho đối tượng học sinh trung bình.
Chuyên đề 7: HÌNH HỌC KHÔNG GIAN
Được nhóm 04 thầy cô: Lê Văn Định, Dương Phước Sang,
Phùng Hoàng Em, Trần Thị Thu Thảo biên soạn nội dung. Hỗ
trợ hình học thầy Lê Quang Hòa. Nguồn tài liệu dùng để biên
soạn được lấy từ các nguồn tài liệu trên Toán học Bắc Trung
Nam, SGK, SBT … Chuyên đề bao gồm 04 nội dung chính:
Phần 1: Đa diện – Thể tích khối đa diện
Phần 2: Mặt nón – Khối nón
Phần 3: Mặt cầu – Khối cầu
Phần 4: Mặt trụ - Khối trụ
Với nội dung các câu hỏi thuộc các mức độ nhận biết và thông
hiểu, nhằm giúp học sinh quen với các hình không gian cơ bản
nhớ được công thức tính diện tích thể tích và các yếu tố liên quan đến các hình.
Tài liệu biên soạn không tránh khỏi các sai sót, mọi ý kiến
đóng góp các thầy cô và các em học sinh có thể phản hồi về
địa chỉ mail: levandinh.k46daihoctoan@gmail.com để nhóm
chúng tôi có thể hoàn thiện sản phẩm tốt hơn/
Chúc các em học sinh đạt kết quả cao trong kỳ thi sắp tới. Xin cảm ơn! Lê Văn Định
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu
CHUYÊN ĐỀ 7: HÌNH HỌC KHÔNG GIAN KIẾN THỨC CHUNG I. HÌNH HỌC PHẲNG
1. Các hệ thức lượng trong tam giác vuông:
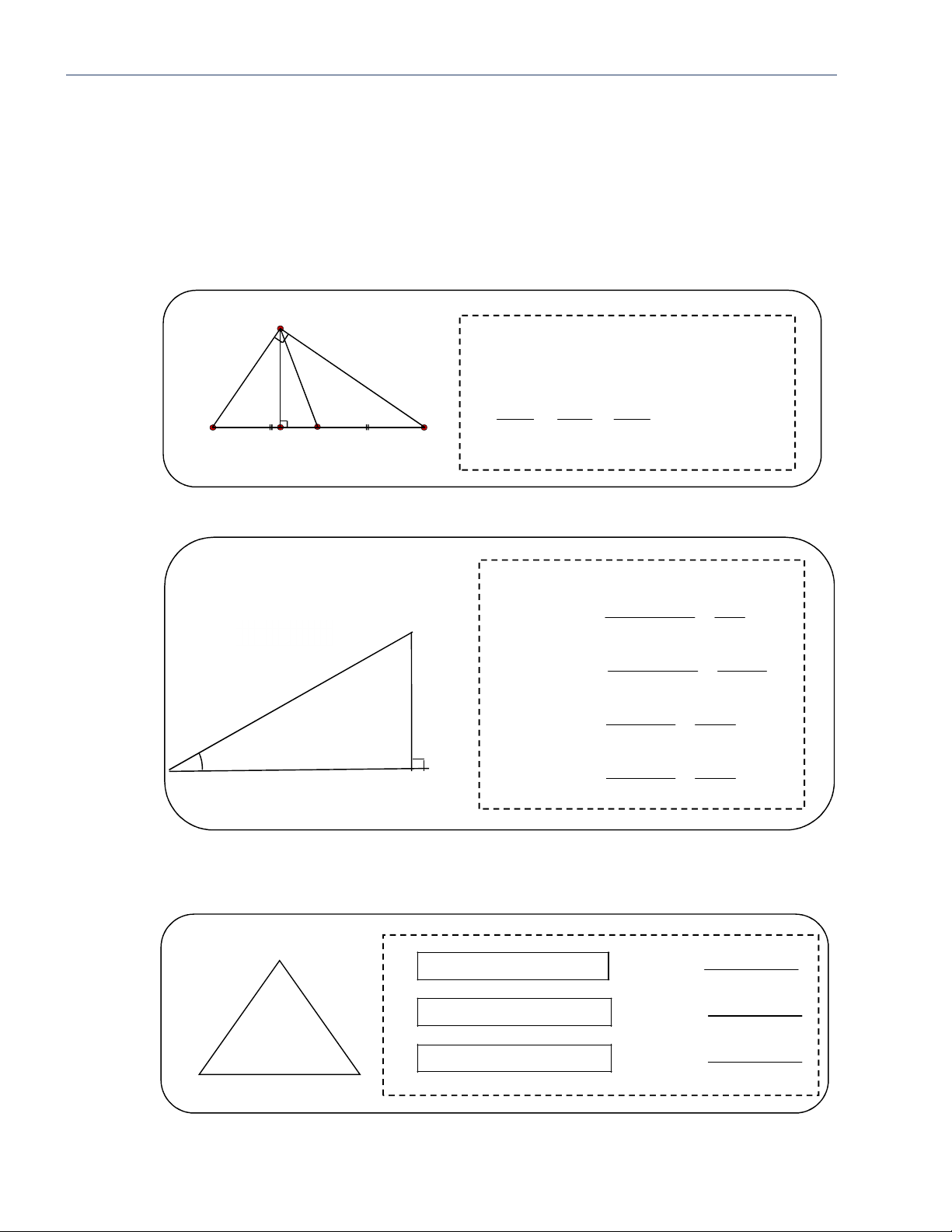
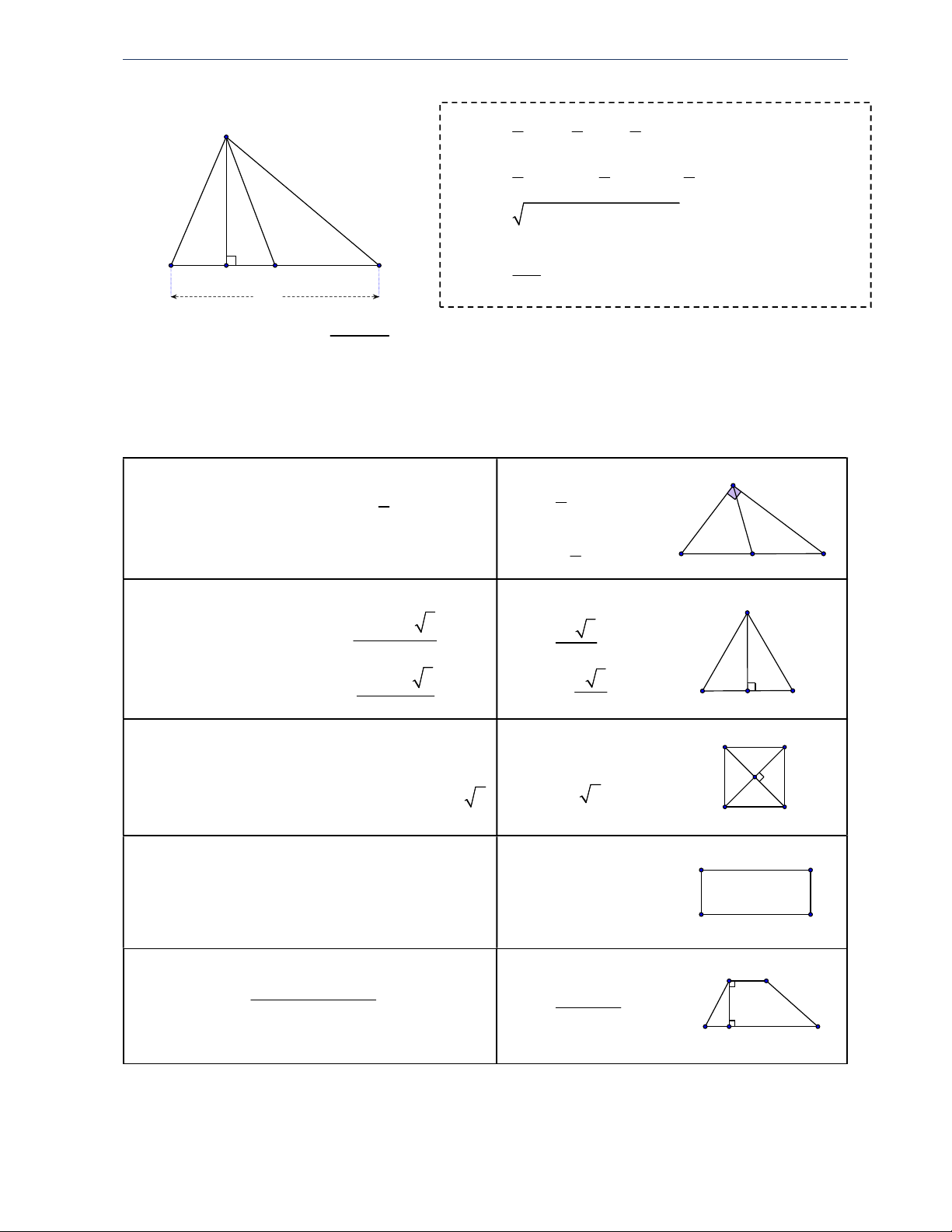
Cho tam giác ABC vuông tại A , AH là đường cao, AM là đường trung tuyến. Ta có: A 2 2 2 BC AB AC AH.BC AB.AC 2 AB BH BC 2 . , AC CH.CB 1 1 1 , 2 AH HB.HC B 2 2 2 C AH AB AC H M 2AM BC
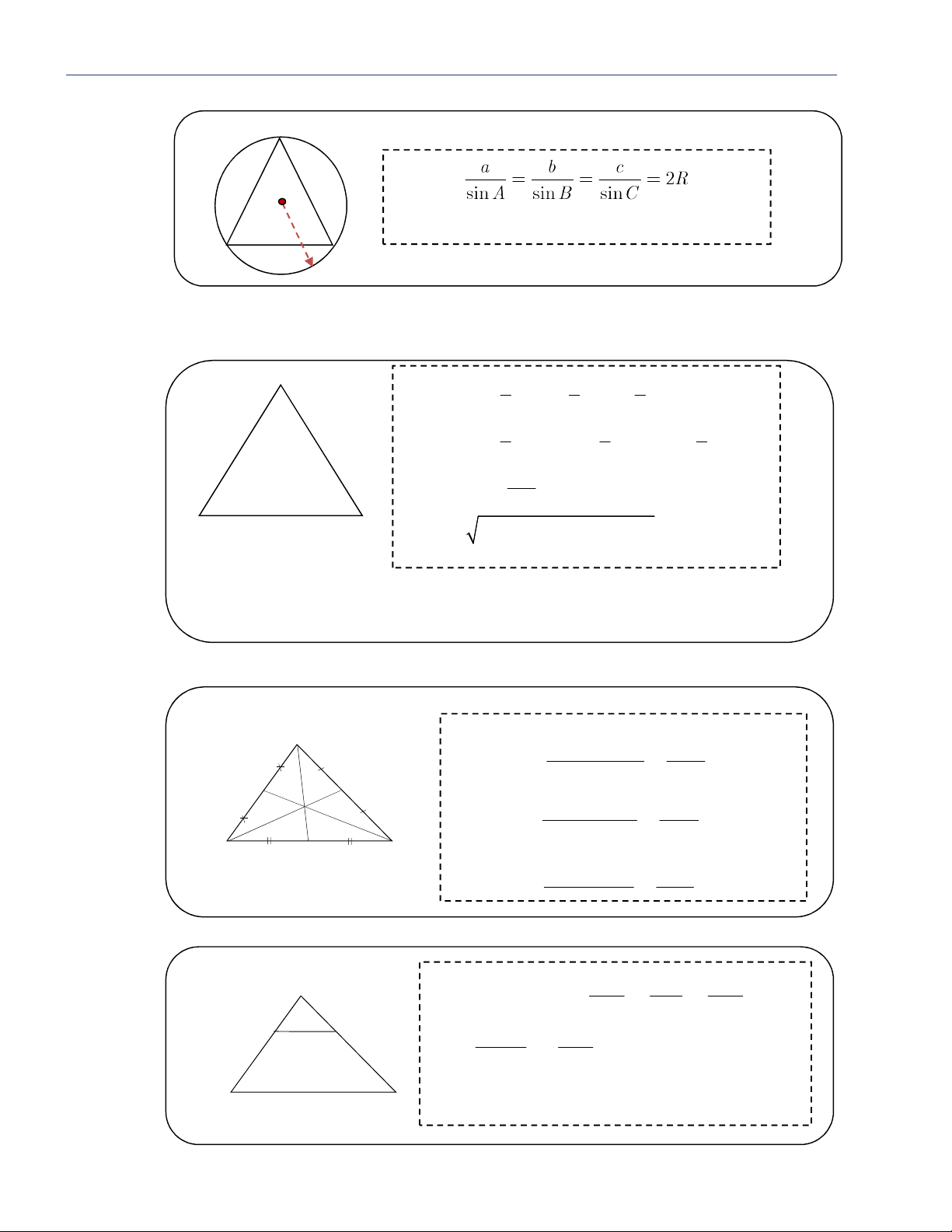
2. Các tỉ số lượng giác của góc nhọn trong tam giác vuông: Ch C ọ h n ọ n g ó g c ó c n h n ọn là caïnh ñoái ñi ñ sin ; Cạnh huyền caïnh hu h yeàn n hoïc caïnh keà khoâng cos ; Cạnh caïnh huyeàn n hö đối caïnh ño ñ ái ñ o ñ aøn tan ; c aïnh keà keát caïnh keà keát cot ; Cạnh kề caïnh ñoái i ñoaøn
3. Các hệ thức lượng trong tam giác thường: a. Định lý cosin: A 2 2 2 b c a 2 2 2
a b c 2bc cosA cosA 2bc c b 2 2 2 a c b 2 2 2
b a c 2ac cosB cosB 2ac 2 2 2 a b c a 2 2 2
c a b 2ab cosC cosC B C 2ab b. Định lý sin:
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 1
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu A c b R
(R là bán kı́nh đường tròn ngoa ̣i tiếp ABC) B a C
c. Công thức tính diện tích tam giác: A 1 1 1 S A BC a. a h . b bh .ch c 2 2 2 1 1 1 c b S A BC
ab sinC bc sinA ac sinB 2 2 2 abc S A BC , S A BC . p r 4R B C a
p p p a p b p c p - nửa chu vi
r - bán kính đường tròn nội tiếp
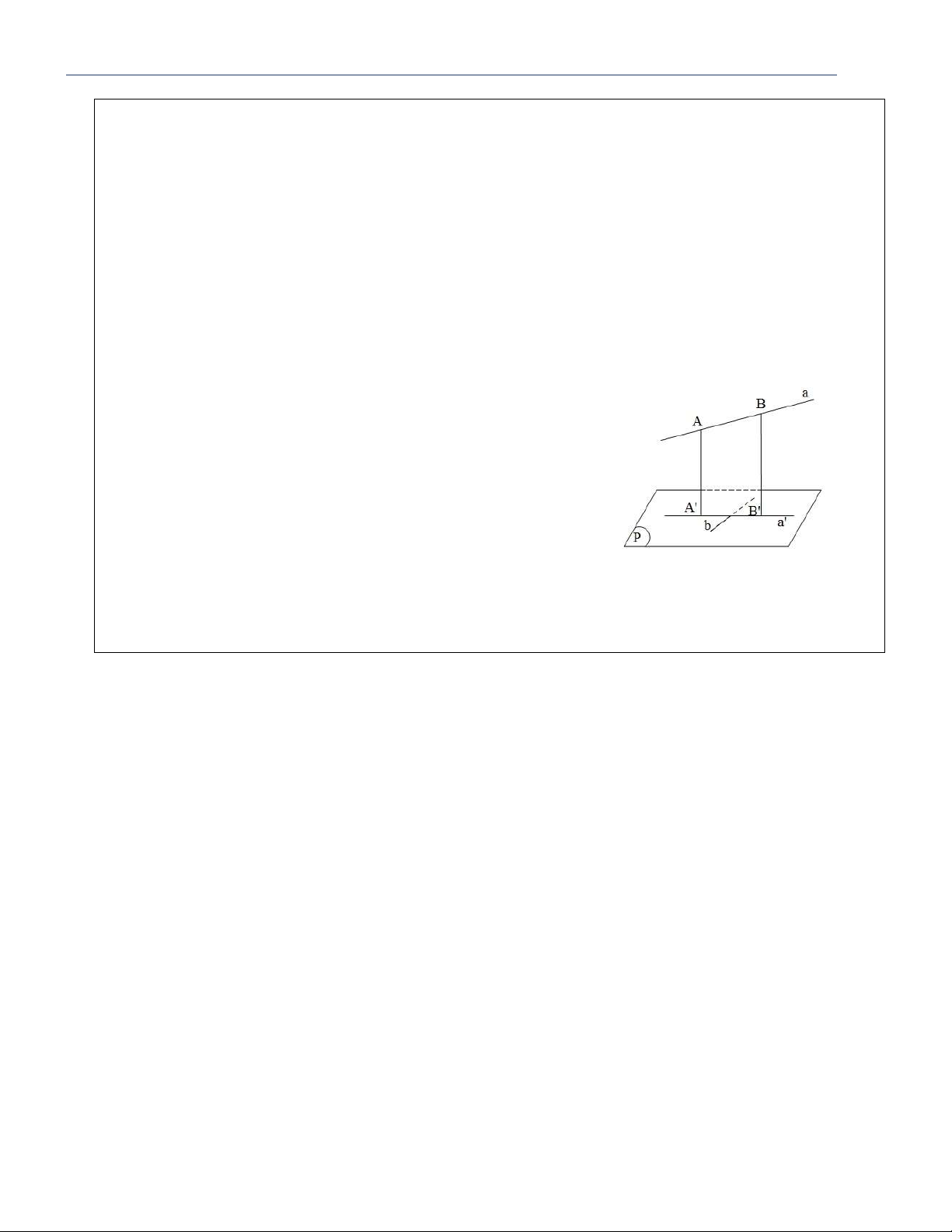
d. Công thức tính độ dài đường trung tuyến: 2 2 2 AB AC BC 2 AM 2 4 2 2 2 BA BC AC 2 BN 2 4 M 2 2 2 CA CB AB 2 CK 2 4 4. Định lý Thales: AM AN MN MN / /BC k AB AC BC 2 N S AMN AM 2 k S AB A BC
(Tı̉ diê ̣n tı́ch bằng tı̉ bı̀nh phương đồng da ̣ng)
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 2
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu 5. Diện tích đa giác: B
a. Diê ̣n tı́ch tam giác vuông:
Diê ̣n tı́ch tam giác vuông bằng ½ tı́ch 2 ca ̣nh góc A C vuông.
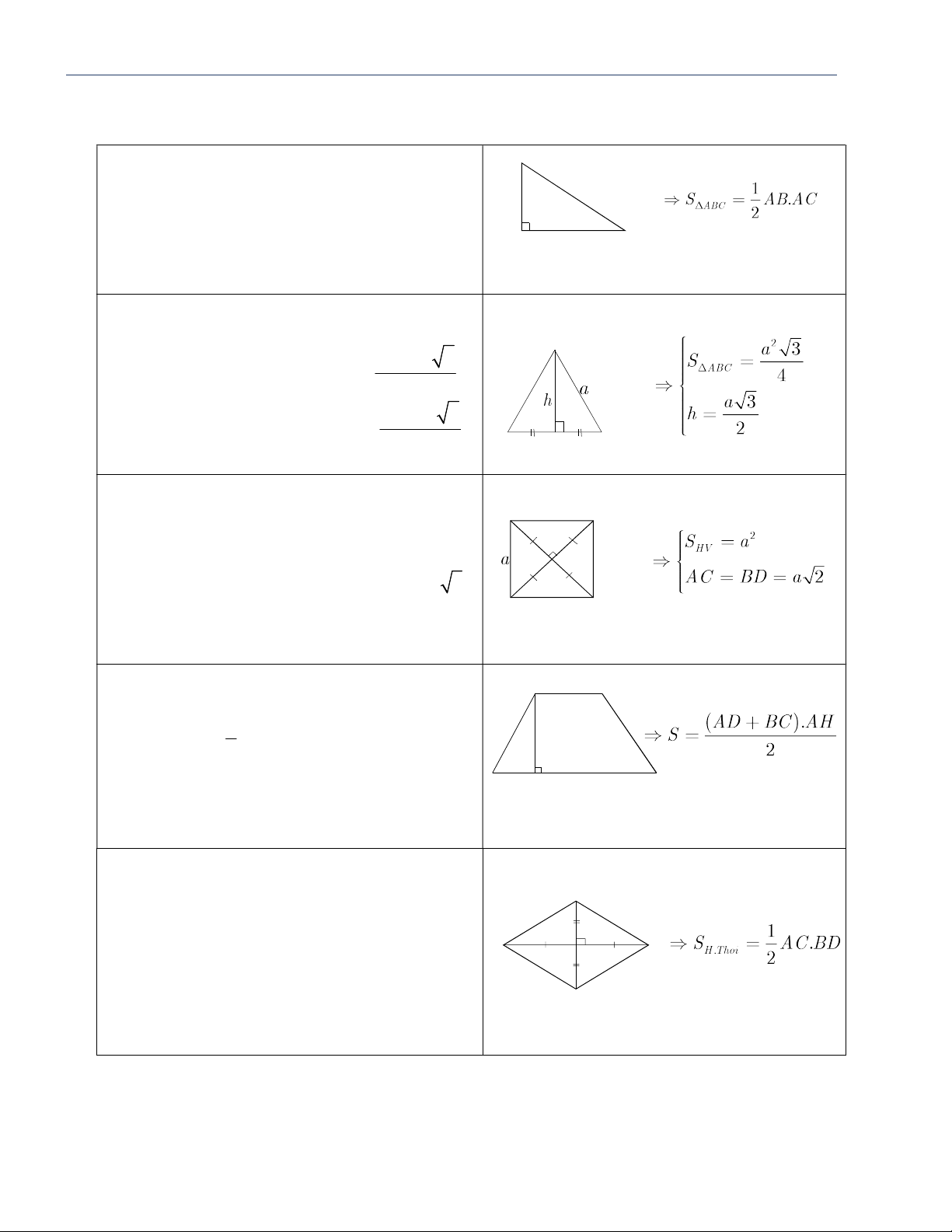
b. Diê ̣n tı́ch tam giác đều: B ( c a ̣ n h.)2 3
Diê ̣n tı́ch tam giác đều: S đều 4 ( c a ̣ n . h) 3
Chiều cao tam giác đều: h đều 2 A C
c. Diê ̣n tı́ch hı̀nh vuông và hı̀nh chữ nhật: A B
Diê ̣n tı́ch hı̀nh vuông bằng ca ̣nh bı̀nh phương. O
Đường chéo hı̀nh vuông bằng ca ̣nh nhân 2 . Diê ̣n tı D
́ch hı̀nh chữ nhâ ̣t bằng dài nhân rô ̣ng. C A D
d. Diê ̣n tı́ch hı̀nh thang: 1 SHı ̀nh Thang .(đa 2
́y lớn + đáy bé) x chiều cao B H C
e. Diê ̣n tı́ch tứ giác có hai đường chéo vuông góc: B
Diê ̣n tı́ch tứ giác có hai đường chéo vuông góc
nhau bằng ½ tı́ch hai đường chéo. A C
Hı̀nh thoi có hai đường chéo vuông góc nhau
ta ̣i trung điểm của mỗi đường. D
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 3
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu
II. CÁC PHƯƠNG PHÁP CHỨNG MINH HÌNH HỌC
1. Chứng minh đường thẳng song song với mặt phẳng : d ( ) d d d ( )
(Định lý 1, trang 61, SKG HH11) d ( ) ()
d () (Hệ quả 1, trang 66, SKG HH11) d () d d ' ( ) d ' d ()
(Tính chất 3b, trang 101, SKG HH11) d ( )
2. Chứng minh hai mặt phẳng song song: ( )
a,a () ( ) ,bb () ( ) ()
(Định lý 1, trang 64, SKG HH11) a b O () (Q) ( ) () () (Q)
(Hệ quả 2, trang 66, SKG HH11) () () () d ( ) ()
. (Tính chất 2b, trang 101, SKG HH11) () d
3. Chứng minh hai đường thẳng song song: Áp du ̣ng mô ̣t trong các đi ̣nh lı́ sau
Hai mặt phẳng (), có điểm chung S và lần lượt chứa 2 đường thẳng song song ,ab thı̀ giao
tuyến của chúng đi qua điểm S cùng song song với a,B.
S () () a, b
() Sx ( a b).
(Hệ quả trang 57, SKG HH11) a b
Cho đường thẳng a song song với mặt phẳng (). Nếu mặt phẳng () chứa a và cắt () theo
giao tuyến b thì b song song với a.
a (),a b a . (Định lý 2, trang 61, SKG HH11)
() b
Hai mă ̣t phẳng cùng song song với mô ̣t đường thẳng thı̀ giao tuyến của chúng song song với đường thẳng đó.
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 4
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu ( ) ()
( )() =d,d ( ) () P P d
d . (Định lý 3, trang 67, SKG HH11)
Hai đường thẳng phân biệt cùng vuông góc với mô ̣t mă ̣t phẳng thı̀ song song với nhau. d d d ( ) d d
(Tính chất 1b, trang 101, SKG HH11) d ( )
Sử du ̣ng phương pháp hı̀nh ho ̣c phẳng: Đường trung bı̀nh, đi ̣nh lı́ Talét đảo, …
4. Chứng minh đường thẳngvuông góc với mặt phẳng:
Định lý (Trang 99 SGK HH11). Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau
nằm trong một mặt phẳng thì nó vuông góc với mặt phẳng ấy. d a ( ) d b ( ) d . a b {O}
Tính chất 1a (Trang 101 SGK HH11). Cho hai đường thẳng song song. Mặt phẳng nào vuông
góc với đường thẳng này thì vuông góc với đường thẳng kia.
d d ( ) d d .
Tính chất 2a (Trang 101 SGK HH11). Cho hai mặt phẳng song song. Đường thẳng nào vuông
góc với mặt phẳng này thì cũng vuông góc với mặt phẳng kia.
. d d
Định lý 2 (Trang 109 SGK HH11). Nếu hai mă ̣t phẳng cắt nhau và cùng vuông góc với mă ̣t
phẳng thứ ba thı̀ giao tuyến của chúng vuông góc với mă ̣t phẳng thứ ba đó. P P d P .
d
Định lý 1 (Trang 108 SGK HH11). Nếu hai mă ̣t phẳng vuông góc thì bất cứ đường thẳng nào nào
nằm trong mă ̣t phẳng này và vuông góc với giao tuyến đều vuông góc với mă ̣t phẳng kiA.
P a P d P
d ,d a
5. Chứng minh hai đường thẳng vuông góc:
Cách 1: Dùng định nghĩa: a b a b 0 , 90 .
Hay a b a b a.b 0 a . b .cos a,b 0
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 5
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu
Cách 2: Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì phải
vuông góc với đường kia. b//c a b a c .
Cách 3: Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường
thẳng nằm trong mặt phẳng đó. a a . b b
Cách 4: (Sử dụng Đi ̣nh lý Ba đường vuông góc) Cho đường thẳng b nằm trong mặt phẳng P
và a là đường thẳng không thuộc P đồng thời không vuông góc với P. Gọi a’ là hình chiếu
vuông góc của a trên P. Khi đó b vuông góc với a khi và chỉ khi b vuông góc với a’. a ' hch (P) b P b a b a '.
Cách khác: Sử dụng hı̀nh học phẳng (nếu được).
6. Chứng minh mp mp:
Cách 1: Theo định nghĩa: 0 ,
90 . Chứng tỏ góc giữa hai mă ̣t phẳng bằng 90 .
Cách 2: Theo định lý 1 (Trang 108 SGK HH11):
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 6
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu
1. Các hệ thức lượng trong tam giác vuông:
Cho tam giác ABC vuông tại A , AH là đường cao, AM là đường trung tuyến. Ta có: A 2 2 2 BC AB AC 1 1 1 A . B AC AH 2 2 2 2 2 AH AB AC AB AC 2 2 AB BH.BC ; AC CH.CB B H M C A . B AC BC.AH BC 2AM
2. Các tỉ số lượng giác của góc nhọn trong tam giác vuông: ñoái keà sin cos huyeàn huyeàn kề đối α ñoái keà tan cot huyền keà ñoái
3. Các hệ thức lượng trong tam giác thường a) Định lý cosin: A 2 2 2 2 2 2 2 cos cos b c a a b c bc A A 2bc 2 2 2 c b 2 2 2 2 cos cos a c b b a c ac B B 2ac 2 2 2 2 2 2 B a C 2 cos cos a b c c a b ab C C 2ab b) Định lý sin A a c b b c 2R sin A sin B sin C R
( R là bán kính đường tròn ngoại tiếp tam giác ABC ) B a C
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 7
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu
c) Công thức tính diện tích tam giác: A 1 1 1 S . a h . b h . c h 2 a 2 b 2 c 1 1 1
S ab sin C bc sin A ac sin B 2 2 2 c b h m a a
S p( p a)( p b)( p c) S pr abc B C S H M 4R a
p là nửa chu vi, a b c p 2
r là bán kính đường tròn nội tiếp tam giác ABC.
R là bán kính đường tròn ngoại tiếp tam giác ABC
4. Các công thức diện tích thường gặp Tam giác vuông A 1 1
Diện tích tam giác vuông bằng tích hai cạnh S A . B AC 2 2 góc vuông. 1 AM BC. 2 B M C Tam giác đều A caïnh2 3 2 Diện tích tam giác S a 3 ñeàu . 4 S . a 4 caïnh. 3 a 3
Đường cao tam giác đều h AM . 2 2 B M C Hình vuông a A B 2
Diện tích hình vuông S caïnh 2 S a .
Độ dài đường chéo hình vuông bằng caïnh. 2 AC a 2 D C Hình chữ nhật A a B
Diện tích hình chữ nhật S daøi. roäng S A . B AD ab b D C Hình thang A B ñaùy lôùn + ñaùy beù Diện tích S . chieàu cao AB CD 2 S .AH 2 D H C
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 8
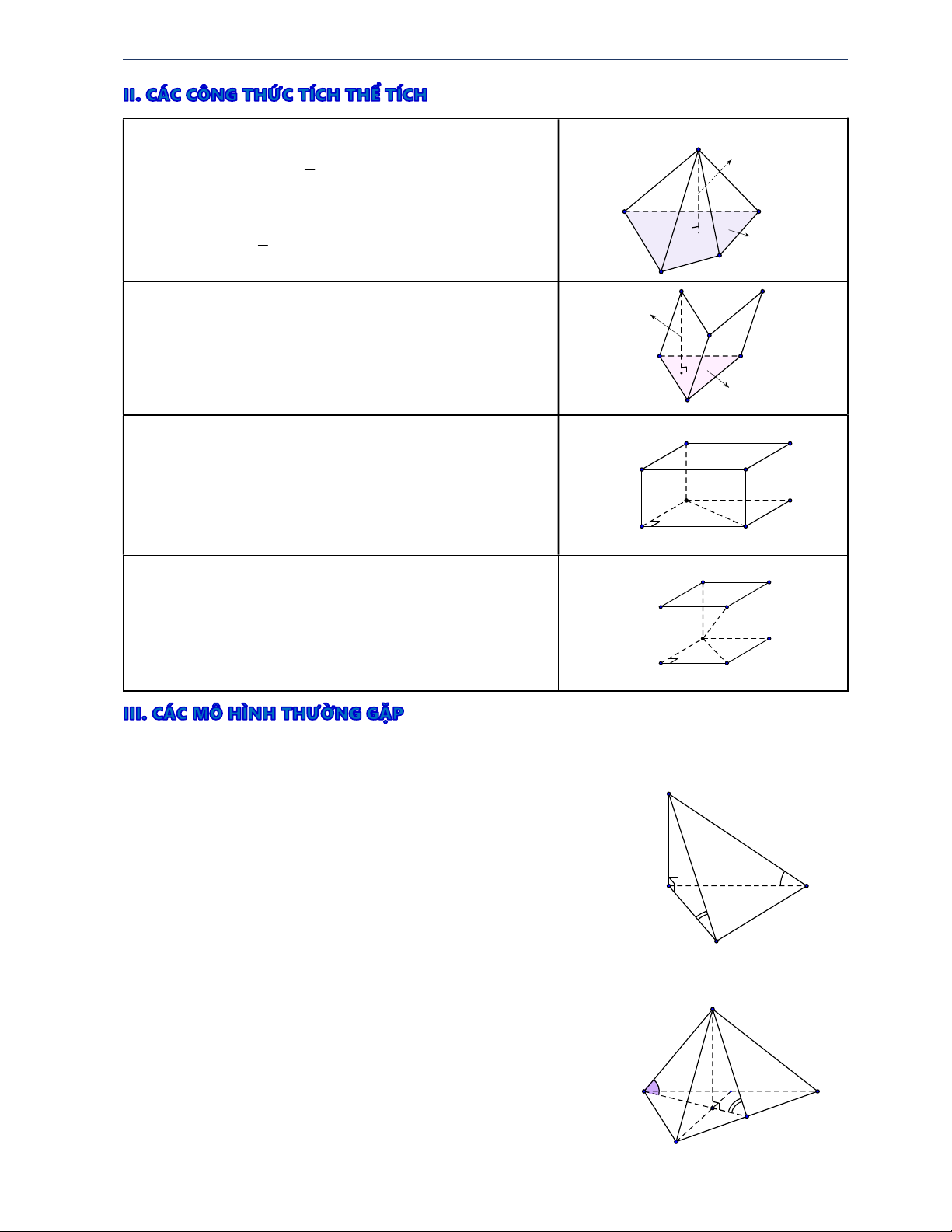
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu Thể tích khối chóp: S V 1 h S . ñ . öôøng cao choùp ñaùy 3
Gọi B là diện tích đáy; h là đường cao tương ứng. 1 Suy ra : V Bh B 3
Thể tích khối lăng trụ: V S ñ . öôøng c ao. h laêng truï ñaùy
Gọi B là diện tích đáy; h là đường cao tương ứng. Suy ra : V Bh B
Thể tích khối hộp chữ nhật: bằng tích của ba kích A' D' thước B' Gọi a, ,
b c lần lượt là ba kích thước tương ứng. c C' A b Suy ra: V abc a D B C
Thể tích khối lập phương: bằng độ dài cạnh lũy thừa 3 A' D' (mũ ba). B'
Gọi a là độ dài cạnh của hình lập phương. a C' A a Suy ra: 3 V a . a D B C HÌNH 1
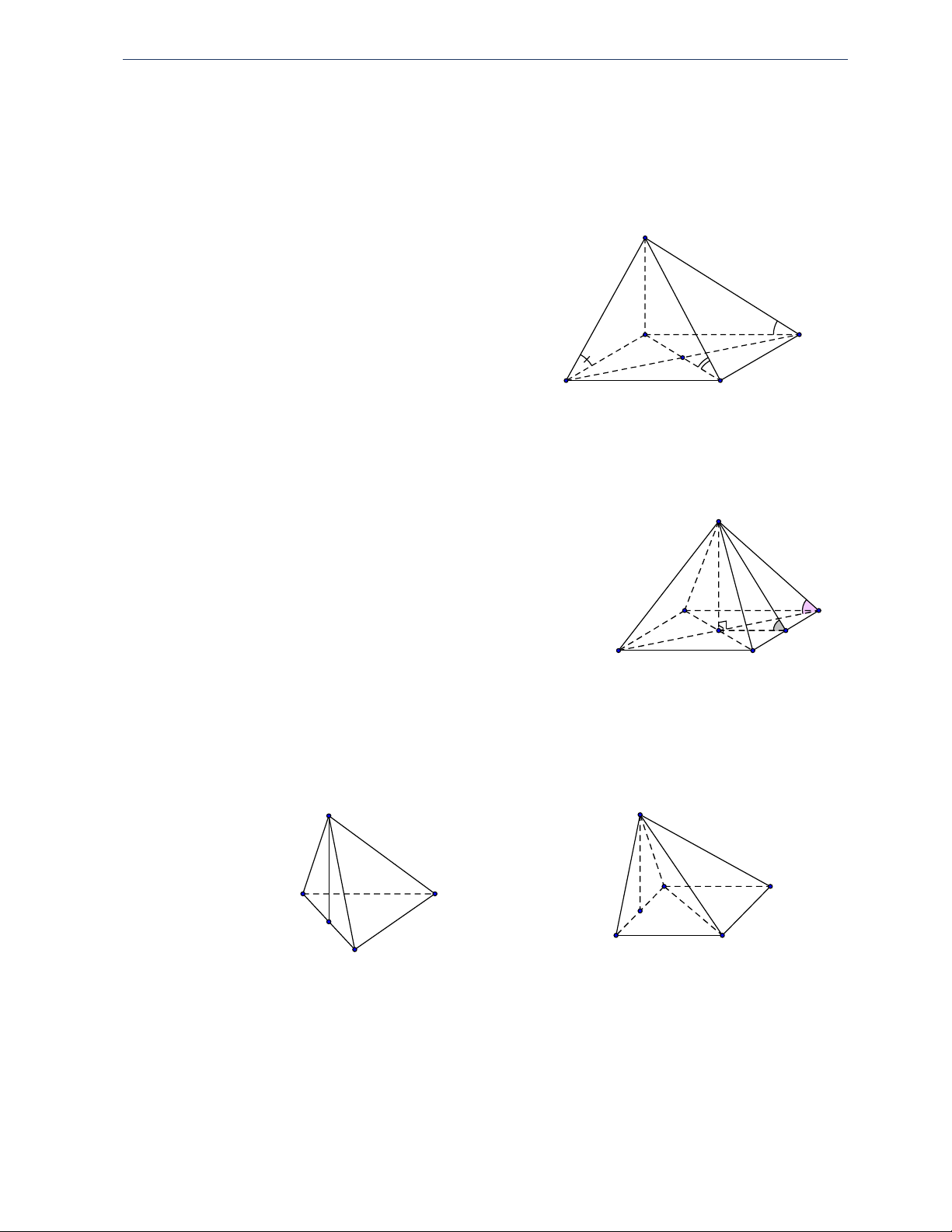
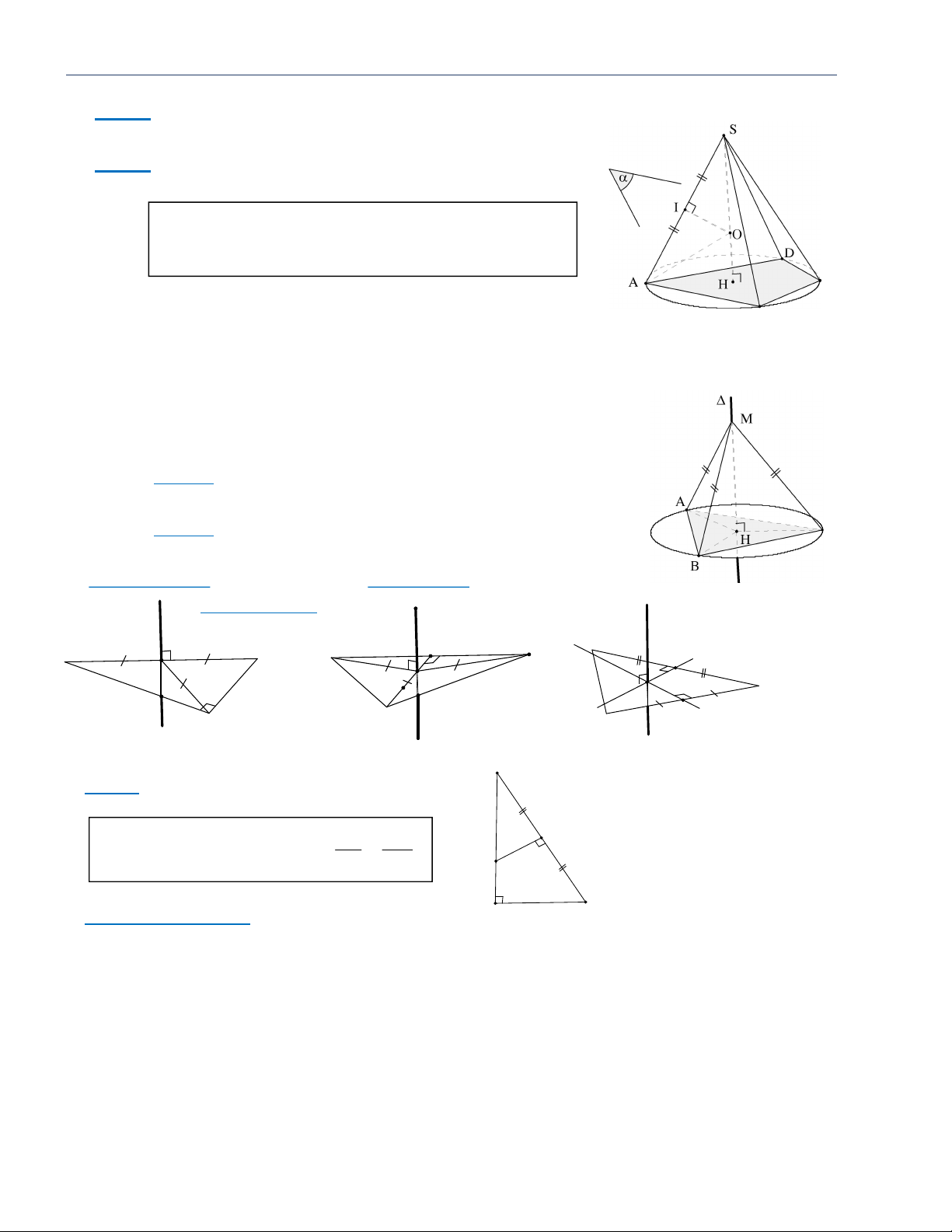
Hình chóp S.ABC, SA vuông góc với đáy S Đáy là tam giác ABC . Đường cao SA . Cạnh bên SB, SC, SA . SAB, S
AC là các tam giác vuông tại A . A C
Góc giữa cạnh SB với đáy ABC là góc SBA .
Góc giữa cạnh SC với đáy ABC là góc SCA . B HÌNH 2 S
Hình chóp tam giác đều S.ABC
Đáy là tam giác đều ABC .
Đường cao SG , với G là trọng tâm tam giác ABC . Cạnh bên S ,
A SB, SC hợp với đáy một góc bằng nhau. A C
Góc giữa cạnh bên với đáy bằng SAG (hoặc SCG, SBG ). G M
Mặt bên SAB, SBC, SCA hợp với đáy một góc bằng nhau. B
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 9
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu
Góc giữa mặt bên với đáy là góc SMG . HÌNH 3
Hình chóp S.ABCD, có đáy ABCD là hình chữ nhật (hoặc hình vuông) và SA vuông góc với đáy
Đáy là hình chữ nhật (hình vuông) ABCD . S Đường cao SA .
Cạnh bên SB, SC, SD, SA . S AB, S AC, S
AD là các tam giác vuông tại A . A
Góc giữa cạnh SB với đáy ABCD là góc SBA . B
Góc giữa cạnh SC với đáy ABCD là góc SCA . D
Góc giữa cạnh SD với đáy ABCD là góc SDA . C HÌNH 4
Hình chóp tứ giác đều S.ABCD
Đáy là hình vuông ABCD . S
Đường cao SO , với O là giao điểm của AC và BD . Cạnh bên S ,
A SB, SC, SD hợp với đáy một góc bằng nhau.
Góc giữa cạnh bên với đáy bằng SBO (hoặc SAO, SCO, SDO ) A B
Mặt bên SAB, SBC, SCA hợp với đáy một góc bằng nhau. M
Góc giữa mặt bên với đáy là góc SMG . O D C HÌNH 5
Hình chóp S.ABC (hoặc S.ABCD) có một mặt bên SAB là tam giác đều và
nằm trong mặt phẳng vuông góc với đáy. S S A D A C H H B C B
Đáy là tam giác ABC (hoặc ABCD )
Đường cao SH , với H là trung điểm của AB
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 10
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu HÌNH 6
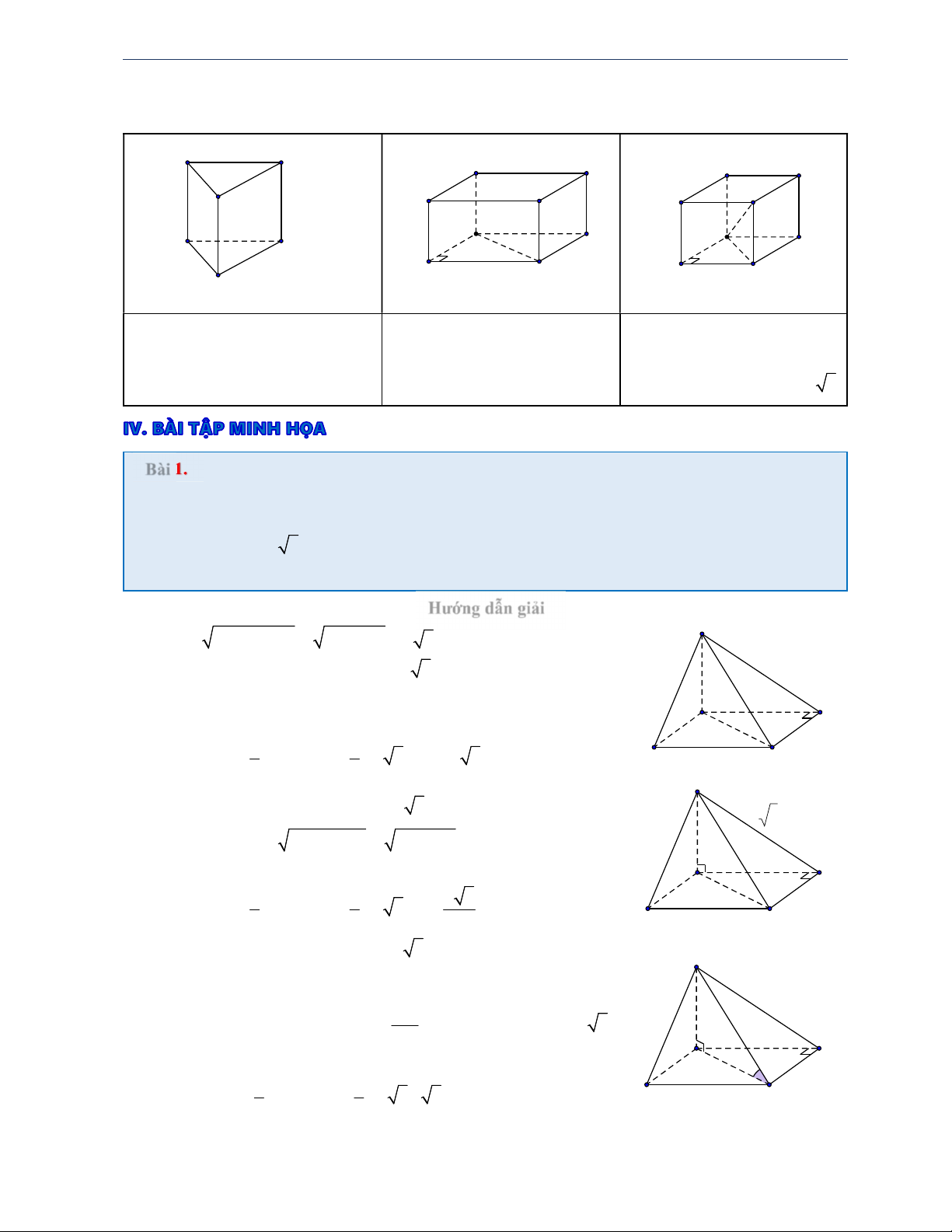
Hình lăng trụ đứng, hình hộp chữ nhật, hình lập phương A B A' D' A' D' C B' B' c C' a C' A b A' A a D B' a a D B C B C C'
Hình lăng trụ đứng tam giác Hình hộp chữ nhật Hình lập phương
Đường cao là cạnh bên AA Thể tích: V A . B A . D AA Thể tích: 3 3 V AB a hoặc BB , CC . abc .
Đường chéo: AC a 3
Bài 1. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB a, AC 2 . a Cạnh bên SA
vuông góc với ABCD . Tính thể tích khối chóp S.ABCD trong các trường hợp sau: a) Biết SA 3 . a b) Biết SB a 5 .
c) Biết góc giữa SC với mặt đáy bằng o 60 . Hướng dẫn giải S a) 2 2 2 2
BC AC AB 4a a a 3. Diện tích đáy: 2 S A . B BC a 3 ABCD 3a Đường cao: SA 3a a A
Thể tích khối chóp S.ABCD là: B 2a 1 1 2 3 D S V . .S .SA .a 3.3a a 3. ABCD C 3 ABCD 3 S b) Diện tích đáy 2 S A . B BC a 3 ABCD a 5 Đường cao 2 2 2 2
SA SB AB 5a a 2 . a
Thể tích khối chóp S.ABCD là: a A B 1 1 2a 2 2 3 3 S V . .S .SA .a 3.2a a . ABCD 3 ABCD 3 3 D C c) Diện tích đáy 2 S A . B BC a 3 ABCD S
Góc giữa SC với ABCD bằng góc o SCA 60 SA SAC vuông tại A o tan SCA SA AC.tan 60 2 3 . a AC a A B
Thể tích khối chóp S.ABCD là: 60o 2a 1 1 2 3 D S V . .S .SA .a 3.2 3a 2a . ABCD C 3 ABCD 3
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 11
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu
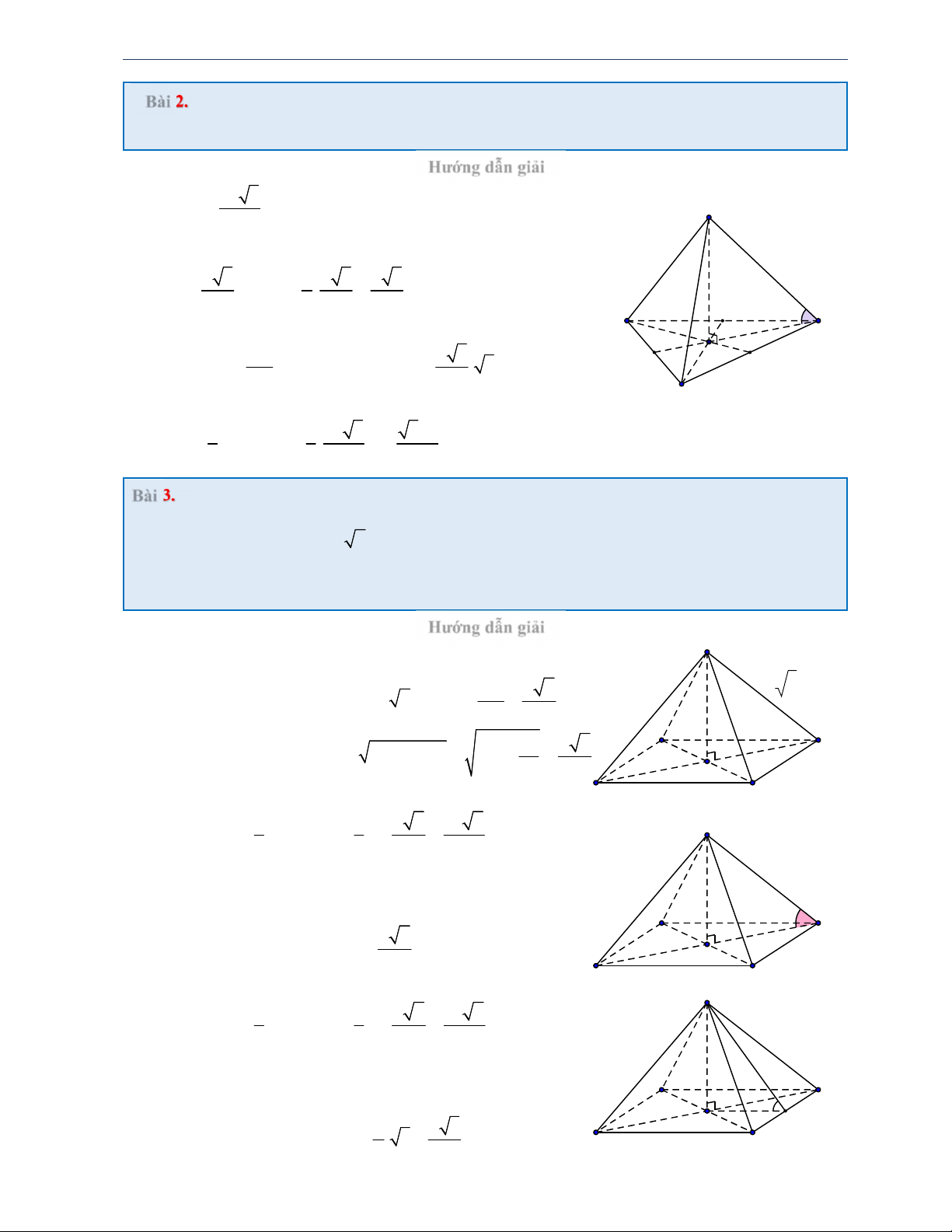
Bài 2. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và góc giữa SC với ABC bằng o
60 . Tính thể tích khối chóp S.ABC . Hướng dẫn giải 2 a 3 S . ABC S 4
Góc giữa SC với đáy bằng o SCG 60 a 3 2 a 3 a 3 CK CG . 2 3 2 3 60o
SGC vuông tại G , suy ra: A C o SG o a 3 tan 60 SG CG.tan 60 . 3 . a K G CG 3
Thể tích khối chóp S.ABC là: B 2 3 1 1 a 3 3a . V S .SG . .a 3 ABC 3 4 12
Bài 3. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng .
a Tính thể tích khối chóp S.ABCD
trong các trường hợp sau:
a) Biết cạnh bên SB a 2 .
b) Biết góc giữa cạnh bên SB với đáy bằng o 45 .
c) Biết góc giữa mặt bên SBC với đáy bằng o 60 . Hướng dẫn giải S
a) Diện tích đáy ABCD là 2 S a . ABCD BD a 2 a 2
ABCD là hình vuông BD a 2 BO 2 2 A a 2 a a B SBO vuông tại 2 2 2 6
O SO SB OB 2a . 2 2 O
Thể tích khối chóp S.ABCD là: D C 3 1 1 a 6 a 6 2 S S V . S .SO .a . . ABCD 3 ABCD 3 2 6
b) Diện tích đáy ABCD là 2 S a . ABCD
Góc giữa SB với đáy bằng góc o SBO 45 A 45o a B a Đường cao o 2 SO B . O tan 45 . 2 O D Thể tích khối chóp C S.ABCD là: S 3 1 1 a 2 a 2 2 S V . S .SO .a . . ABCD 3 ABCD 3 2 6
c) Diện tích đáy ABCD là 2 S a . ABCD a A Góc giữa mặt bên B
SBC với đáy bằng góc o SIO 60 600 a a O I Đường cao o 3 SO I . O tan 60 . 3 . D C 2 2
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 12
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu
Thể tích khối chóp S.ABCD là: 3 1 1 a 3 a 3 2 S V . S .SO .a . . ABCD 3 ABCD 3 2 6
Bài 4. Cho hình lăng trụ đứng ABC.AB C
có đáy là tam giác vuông cân tại A , cạnh AB a . Gọi I
là trung điểm của BC , AI a . Tính thể tích khối lăng trụ ABC.AB C . Hướng dẫn giải 1 1
ABC cân tại A AB AC a ; 2 S A . B AC a . ABC A' 2 2 C' BC a 2 2 2
BC AB AC a 2 AI B' 2 2 2 a a A AI vuông tại 2 2 2 A AA A I AI a . a 2 a A C
Thể tích khối lăng trụ ABC.AB C là: 3 a 1 2 a M V S .AA a .a . ABC 2 2 B
Câu 1. Cho khối chóp có diện tích đáy bằng S; chiều cao bằng h và thể tích bằng V. Trong các đẳng
thức dưới đây, hãy tìm đẳng thức đúng: 3V 1 V A. S B. S V .h C. S D. S V.h h 3 h
Câu 2. Cho hình chóp S.ABC có tam giác ABC vuông tại A , AB a 2 , AC a 3 , cạnh bên SA
vuông góc với mặt phẳng đáy và SA a . Thể tích của khối chóp S.ABC bằng 3 a 6 3 a 6 3 a 6 3 6a A. . B. . C. . D. . 3 6 2 12
Câu 3. Cho hình chóp S.ABC có tam giác ABC vuông tại A , AB a 2 , AC a , cạnh bên SA
vuông góc với mặt phẳng đáy, góc giữa SB với mặt phẳng đáy bằng o 60 . Thể tích của khối chóp S.ABC bằng 3 a 6 3 a 3 A. . B. . C. 3 a 6. D. 3 a 3. 3 3
Câu 4. Cho hình chóp S.ABC có tam giác ABC vuông tại B , AB a 2, AC a 3 , cạnh bên SA
vuông góc với mặt phẳng đáy và SB a 3 . Thể tích của khối chóp S.ABC bằng 3 3a 3 3a 3 2a 3 2a A. . B. . C. . D. . 6 8 6 12
Câu 5. Cho hình tứ diện OABC có O ,
A OB, OC vuông góc nhau đôi một. Gọi V là thể tích khối tứ
diện OABC . Khẳng định nào sau đây là khẳng định đúng ? 1 1 A. V O . A O . B OC. B. V O . A O . B OC. 2 6 1 C. V O . A O . B OC. D. V O . A O . B OC. 3
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 13
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu
Câu 6. Cho tứ diện OABC có O ,
A OB, OC đôi một vuông góc với nhau OA a , OB 2a ,
OC 3a . Thể tích tứ diện OABC là A. 3 2a . B. 3 3a . C. 3 a . D. 3 6a .
Câu 7. Khối chóp S.ABC có đáy ABC là tam giác đều cạnh 2a , SA vuông góc với mặt phẳng
ABC, SA 2a . Thể tích khối chóp S.ABC bằng 3 a 3 3 2a 3 3 a 3 3 a 3 A. . B. . C. . D. . 6 3 3 12
Câu 8. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA ABCD , SA 3a . Khi
đó, thể tích khối chóp S.ABCD bằng 3 a A. . B. 3 3a . C. 3 2a . D. 3 a . 2
Câu 9. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a 2 , cạnh bên SA vuông góc với
mặt phẳng đáy, SC a 5 . Thể tích khối chóp S.ABCD bằng 3 3a 3 2 5a 3 4a 3 2a A. . B. . C. . D. . 3 3 3 3
Câu 10. Cho hình chóp S.ABCD có SA ABCD , đáy là hình thang vuông tại A và D thỏa mãn
AB 2a, AD CD a, SA a 2 . Tính thể tích khối chóp S.BCD bằng 3 2a 2 3 2a 3 a 2 3 a 2 A. . B. . C. . D. . 3 3 2 6
Câu 11. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a , cạnh bên bằng 2a . Thể tích khối chóp S.ABC bằng 3 a 3 3 a 11 A. 3 a . B. . C. a 6. D. . 12 12
Câu 12. Cho hình chóp tam giác đều có cạnh đáy bằng a , góc giữa mặt bên và mặt phẳng đáy bằng o
45 . Thể tích khối chóp được tính theo a là 3 a 3 a 3 3 a A. 3 a . B. . C. . D. . 8 12 24
Câu 13. Cho hình chóp đều S.ABCD . Gọi O là tâm của hình vuông ABCD. Chiều cao hình chóp S.ABCD là A. S . A B. S . B C. SC. D. SO.
Câu 14. Cho hình chóp đều S.ABCD có AB 2a, SD 3a , AC và BD cắt nhau tại O . Chiều cao
hình chóp S.ABCD có độ dài tính theo a là A. 2a 2. B. a 6. C. a 7. D. a 5.
Câu 15. Cho lăng trụ đứng ABC.AB C
có tam giác ABC vuông tại B và a
AB a, AC a 5, AA . Thể tích của khối lăng trụ ABC.AB C bằng 2 3 a 3 a 3 a 5 3 a 5 A. V . B. V . C. V . D. V . 2 6 4 12
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 14
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu a
Câu 16. Cho lăng trụ đứng ABC.AB C
có đáy là tam giác ABC , AA , thể tích khối lăng trụ là 2 3 a
2 thì diện tích tam giác ABC bằng 3 2 2a 2 2 a 2 A. 2 2a 2. B. . C. 2 a 2. D. . 3 3
Câu 17. Cho hình lăng trụ đứng ABC.A B C
có đáy ABC là tam giác đều cạnh a , AA . a Thể tích
khối lăng trụ ABC.A' B 'C ' bằng 3 a 3 3 a 3 3 a A. . B. . C. 3 a . D. . 4 12 3 a
Câu 18. Cho hình lăng trụ đứng ABC.A B C
có đáy là tam giác ABC đều cạnh và CC 2A . B 2
Thể tích khối lăng trụ ABC.A B C bằng 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 4 8 16 48
Câu 19. Khối hộp chữ nhật ABC . D AB C D
có AB 2 , AD 3, AA 4 thì thể tích bằng A. 8 B. 10 C. 12 D. 24
Câu 20. Cho khối hộp chữ nhật ABC . D AB C D
có thể tích V. Tính theo V thể tích VABCD của khối tứ diện ABCD'. 1 1 1 1 A. V V B. V V C. V V D. V V ABCD 2 ABCD 3 ABCD 6 ABCD 4
Câu 1. Cho hình tứ diện OABC có O ,
A OB, OC vuông góc nhau đôi một. Gọi V là thể tích khối tứ
diện OABC . Khẳng định nào sau đây là khẳng định đúng ? 1 1 A. V O . A O . B OC. B. V O . A O . B OC. C. V O . A O . B OC. D. 1 V O . A O . B OC. 2 6 3
Câu 2. Khối chóp S.ABC có các cạnh S ,
A SB, SC đôi một vuông góc với nhau, SA 2 ,
a SB 3a, SC 4a . Thể tích khối chóp S.ABC bằng A. 3 32a . B. 3 4a . C. 3 12a . D. 3 8a .
Câu 3. Cho hình chóp S.ABC có tam giác ABC vuông tại A , AB a 2 , BC a 3 , cạnh bên SA
vuông góc với mặt phẳng đáy và SA a . Thể tích của khối chóp S.ABC bằng 3 a 2 3 a 6 3 2a 3 a 6 A. . B. . C. . D. . 6 6 3 3
Câu 4. Cho hình chóp S.ABC có tam giác ABC vuông tại A , AB a , AC a 3 , SB a 5 , cạnh
bên SA vuông góc với mặt phẳng đáy. Thể tích của khối chóp S.ABC bằng 3 a 3 3 a 3 3 a 3 A. . B. 3 2a 3. C. . D. . 6 3 12
Câu 5. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại C , AC a 2 , SA vuông góc
với mặt phẳng ABC , cạnh SC tạo với đáy một góc o
45 . Thể tích khối chóp S.ABC bằng 3 a 2 3 a 3 3 a 2 3 a 3 A. . B. . C. . D. . 3 6 6 3
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 15
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu
Câu 6. Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a , cạnh bên SA a 3
nằm trên đường thẳng vuông góc với mặt phẳng đáy. Thể tích khối chóp S.ABC bằng 3 a 3 3 a 3 3 a 3 a A. . B. . C. . D. . 3 6 4 3
Câu 7. Cho hình chóp S.ABC đáy là tam giác đều cạnh a , SA vuông góc đáy và góc SC và đáy bằng o
30 . Thể tích khối chóp S.ABC bằng 3 a 3 3a 3 a 3 3a A. . B. . C. . D. . 6 6 12 3
Câu 8. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a , SD 4a , SA vuông góc
với mặt phẳng ABCD . Chiều cao hình chóp S.ABCD bằng A. 3a 2. B. a 6. C. 2a 3. D. 2a.
Câu 9. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a , SA 2a , SA vuông góc với
mặt phẳng ABCD . Thể tích khối chóp S.ABCD bằng 3 6a 3 8a 3 4a 3 2a A. . B. . C. . D. . 3 3 3 3
Câu 10. Khối chóp S.ABCD có đáy là hình thoi cạnh 2a , AC 2a , SC vuông góc với mặt phẳng
ABCD , SA 4a . Thể tích khối chóp S.ABCD bằng A. . 3 4a . B. 3 12a . C. 3 3a . D. 3 6a .
Câu 11. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a , 0
ABC 60 , SA ABCD ,
SA 2a . Thể tích khối chóp S.ABCD bằng 3 a 3 3 a 3 3 a 3 3 2a 3 A. . B. . C. . D. . 6 12 3 3
Câu 12. Khối chóp đều S.ABC , AC 2a , các mặt bên đều tạo với mặt phẳng đáy ABC một góc o
60 . Thể tích khối chóp S.ABC tính theo a là 3 2a 3 3 a 3 A. 3 a 3. B. . C. 3 2a . D. . 3 3
Câu 13. Cho hình chóp tam giác đều có cạnh đáy bằng a , cạnh bên tạo với mặt phẳng đáy một góc o
60 . Thể tích tứ diện được tính theo a là 3 a 3 3 a 3 a 3 a 3 A. . B. . C. . D. . 6 12 6 12
Câu 14. Khối chóp tứ giác đều có cạnh bên và cạnh đáy đều bằng a có thể tích là 3 a 3 3 a 3 3 a 2 3 a 2 A. . B. . C. . D. . 6 3 6 3
Câu 15. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a , đường cao gấp đôi cạnh đáy của
hình chóp. Khi đó, khối chóp S.ABCD có thể tích là 3 3a 3 5a 3 2a 3 2a A. . B. . C. . D. . 2 2 3 5
Câu 16. Cho hình lăng trụ ABC.A B C
có đáy ABC là tam giác vuông tại B , AB a , AC a 3 , AA' .
a Thể tích của khối lăng trụ ABC.A B C bằng
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 16
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu 3 a 2 3 a 2 3 a 3 A. . B. . C. 3 a 3. D. . 2 6 3
Câu 17. Cho hình lăng trụ đứng ABC.A B C
có đáy là tam giác ABC vuông tại B, AA AB a, BC a 5, và 3 V a . Tỉ số giữa bằng AB 2 1 6 3 A. . B. . C. . D. 5 5 5 5.
Câu 18. Cho lăng trụ đứng ABC.A B C
có đáy là tam giác đều ABC , 3 CC a, V a 3. Độ ABC. A B C
dài chiều cao của tam giác ABC bằng a 3 a 6 A. a 3. B. . C. . D. a 6. 2 2
Câu 19. Cho lăng trụ ABC . D AB C D
có ABCD là hình chữ nhật, AA AB AD . Tính thể tích khối lăng trụ ABC . D AB C D
biết AB a , AD a 3 , AA' 2a . A. 3 3a . B. 3 a . C. 3 a 3 . D. 3 3a 3 .
Câu 20. Cho lăng trụ ABC . D AB C D
có ABCD là hình thoi. Hình chiếu của A lên ABCD là
trọng tâm của tam giác ABD . Tính thể tích khối lăng trụ ABC . D AB C D , biết AB a , o ABC 120 , AA a . 3 a 2 3 a 2 3 a 2 A. 3 a 2. B. . C. . D. . 6 3 2
Câu 1. Cho hình chóp S.ABC có tam giác ABC vuông tại B , AB a 2, AC a 3 , cạnh bên SA
vuông góc với mặt phẳng đáy và SA a . Thể tích của khối chóp S.ABC bằng 3 3a 3 3a 3 2a 3 2a A. . B. . C. . D. . 6 8 6 12
Câu 2. Cho tam giác ABC nằm trong mặt phẳng (P) có AB 3 cm, BC 4 cm và AC 5 cm. Trên
đường thẳng d vuông góc với (P) tại A lấy điểm S sao cho SA 6 cm. Thể tích khối tứ diện ABCD là A. 3 48 cm . B. 3 24 cm . C. 3 36 cm . D. 3 12 cm .
Câu 3. Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại B , SA AC 2a . Biết cạnh
bên SA nằm trên đường thẳng vuông góc với mặt phẳng đáy. Thể tích khối chóp S.ABC bằng 3 2a 3 2a 3 2a 3 3 a 3 A. . B. . C. . D. . 9 3 3 3
Câu 4. Cho tứ diện ABCD có các cạnh AB, AC và AD đôi một vuông góc với nhau; AB 3a ,
AC 5a và AD 8a . Tính thể tích V của tứ diện ABCD theo . a A. 3 V 40a . B. 3 V 120a . C. 3 V 60a . D. 3 V 20a .
Câu 5. Cho hình chóp S.ABC có SA vuông góc với mặt phẳng ABC , đáy ABC là tam giác vuông
tại B , AB a 3, BC a , góc giữa cạnh bên SB và mặt đáy ABC bằng o 30 . Thể tích khối chóp S.ABC bằng 3 a 3 3 3a 3 2a 3 a 2 A. . B. . C. . D. . 6 3 6 3
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 17
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu
Câu 6. Cho hình chóp S.ABC có tam giác ABC là tam giác đều cạnh bằng a , SA vuông góc với
đáy và SB a 6 . Thể tích của khối chóp S.ABC bằng 3 a 2 3 a 3 3 a 6 3 a 18 A. . B. . C. . D. . 4 8 6 4
Câu 7. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , hai mặt bên SAB và SAC
cùng vuông với mặt phẳng ABC . Biết cạnh bên SB tạo với mặt phẳng đáy một góc o 60 .
Thể tích khối chóp S.ABC bằng 3 a 3 a 3 a 3 a A. . B. . C. . D. . 3 2 4 6
Câu 8. Cho hình chóp S.ABCD đáy là hình vuông cạnh a , SA vuông góc đáy và góc giữa SC và đáy bằng o
45 . Thể tích khối chóp S.ABCD bằng 3 a 3 3a 3 a 3 2a A. . B. . C. . D. . 2 3 3 3
Câu 9. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , SA a 3 và SA (AB D C ) , H là
hình chiếu của A trên cạnh SB . Thể tích khối chóp S.AHC bằng 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 6 8 3 12
Câu 10. Cho hình chóp S.ABCD đáy là hình vuông cạnh a , SA vuông góc đáy và góc giữa SBD với ABCD bằng o
60 Thể tích khối chóp S.ABCD bằng 3 a 3 6a 3 3a 3 2a A. . B. . C. . D. . 9 6 3 9
Câu 11. Cho hình chóp S.ABCD có đáy ABCD là hình vuông có đường chéo bằng 10 2 cm , SA
vuông góc với mặt phẳng ABCD và SA 15 cm . Thể tích khối chóp S.ABCD bằng A. 3 V 150 2 cm . B. 3 V 250 2 cm . C. 3 V 500 2 cm . D. 3 V 500 cm .
Câu 12. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với đáy. Góc
giữa SB với mặt đáy bằng o
45 . Thể tích của khối chóp S.ABCD bằng 3 a 3 2a 3 2a 3 a A. . B. . C. . D. . 6 3 6 3
Câu 13. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB a , AD a 2 , o SCA 30 ,
SA vuông góc với mặt phẳng ABCD . Thể tích khối chóp S.ABCD bằng 3 a 2 3 4a 3 6a 3 2a A. . B. . C. . D. 3 3 3 3
Câu 14. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a , góc o ABC 60 , SA vuông góc
với mặt phẳng ABCD . SD tạo với mặt phẳng ABCD một góc o 60 . Thể tích khối chóp S.ABCD bằng 3 a 3 a 3 3a A. . B. . C. . D. 3 2a . 2 3 2
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 18
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu
Câu 15. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D với AD CD a ,
AB 3a . Cạnh bên SA vuông góc với mặt đáy và cạnh bên SC tạo với đáy một góc o 45 .
Tính thể tích khối chóp S.ABCD theo a . 3 2 2a 3 2 3a 3 2a 3 2 3a A. . B. . C. . D. . 3 5 6 3
Câu 16. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và cạnh bên bằng 2a . Thể tích khối chóp S.ABCD bằng 3 a 14 3 a 14 3 a 14 A. . B. . C. . D. 3 a 14. 2 6 18
Câu 17. Cho lăng trụ đứng ABC.A B C
có đáy là ABC đều cạnh 2a và AA a 2. Thể tích của khối lăng trụ bằng 3 a 6 3 a 6 3 a 6 A. 3 a 6. B. . C. . D. . 3 2 6
Câu 18. Cho hình lăng trụ đứng ABC.A B C
có đáy ABC là tam giác đều cạnh 3 2 , a V a 3. ABC.A'B'C '
Độ dài đường cao của khối chóp là A. 6 . a B. 2 . a C. 3 . a D. . a
Câu 19. Cho lăng trụ đứng ABC.AB C
. Tam giác ABC vuông tại A , AB a, AC 2a . Thể tích
của khối lăng trụ ABC.AB C bằng 3 a
2 . Khẳng định đúng là a 2 a 2 a 2 A. AA' a 2. B. AA' . C. AA' . D. AA' . 6 2 3
Câu 20. Cho hình lăng trụ đứng ABC.A B C
có đáy ABC là tam giác đều cạnh a, M trung điểm cạnh BC, 3 V
a 3. Độ dài đoạn thẳng A M bằng ABC.A B C a 67 a 13 a 19 a 61 A. . B. . C. . D. . 2 2 2 2
Câu 1. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , AB a , AC a 3 , hai mặt
bên (SAB) và (SAC) cùng vuông góc với mặt phẳng đáy và SA a 2 . Thể tích của khối chóp S.ABC bằng 3 a 3 a 3 3 a 3 a 2 A. . B. . C. . D. . 4 3 3 3
Câu 2. Cho hình chóp S.ABC có tam giác ABC vuông tại B , AB a , o ACB 30 , cạnh bên SA
vuông góc với mặt phẳng đáy và SB tạo với mặt đáy một góc bằng o 45 .Thể tích khối chóp S.ABC bằng 3 2a 3 a 3 3 a 2 3 a 3 A. . B. . C. . D. . 3 2 6 6
Câu 3. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại C , AC a , o ASB 30 , SA
vuông góc với mặt phẳng ABC . Thể tích khối chóp S.ABC bằng 3 a 6 3 a 3 3 a 2 3 a 6 A. . B. . C. . D. . 6 6 6 3
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 19
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu
Câu 4. Cho hình chóp S.ABC đáy là tam giác đều cạnh a , hình chiếu vuông góc S lên đáy trùng
với trung điểm BC và góc SA và đáy bằng o
60 . Thể tích khối chóp S.ABC bằng 3 a 3 3a 3 a 3 3a A. . B. . C. . D. . 3 4 4 8
Câu 5. Cho hình chóp S.ABC có tam giác ABC là tam giác đều cạnh bằng a , SB vuông góc với
đáy và SB a 6 . Thể tích của khối chóp S.ABC bằng 3 a 2 3 a 3 3 a 6 3 a 18 A. . B. . C. . D. . 4 8 6 4
Câu 6. Cho hình chóp S.ABC đáy là tam giác đều cạnh a , SA vuông góc đáy và góc giữa SBC và đáy bằng o
60 . Thể tích khối chóp S.ABC bằng 3 a 3 3a 3 a 3 3a A. . B. . C. . D. . 3 8 4 3
Câu 7. Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a . Hai mặt bênSAB và SAC
cùng vuông góc với đáy. Tính thể tích khối chóp S.ABC , biết SC a 3 . 3 2a 6 3 a 6 3 a 3 3 a 3 A. . B. . C. . D. . 9 12 4 2
Câu 8. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a , SD 4a , SA vuông góc
với mặt phẳng ABCD . Chiều cao hình chóp S.ABCD có độ dài tính theo a là A. 3a 2. B. a 6. C. 2a 3 . D. 2a.
Câu 9. Cho hình chóp S.ABCD có đáy ABCD là hình vuông có cạnh .
a Mặt bên SAB là tam giác
đều nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABC . D 3 a 3 3 a 3 3 a 3 A. . B. 3 a 3. C. . D. . 6 2 3
Câu 10. Cho hình chóp tứ giác S.ABCD có đáy là hình vuông cạnh a ; cạnh bên SA vuông góc với
mặt phẳng đáy, góc giữa hai mặt phẳng (SCD) và (ABCD) một góc bằng 60 . Tính thể tích
V của khối chóp S.ABCD theo . a 3 3a 3 a 3 3a A. V . B. 3 V 3a . C. V . D. V . 6 3 3
Câu 11. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB a , BC 2a , SA 2a , SA
vuông góc với mặt phẳng ABCD . Thể tích khối chóp S.ABCD bằng 3 8a 3 4a 3 6a 3 2a A. . B. . C. . D. 3 3 3 3
Câu 12. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB a , BC 2a , SB 3a , SA
vuông góc với mặt phẳng ABCD . Thể tích khối chóp S.ABCD bằng 3 4 2a 3 2a 5 3 4a 5 A. . B. . C. . D. 3 2a . 3 3 3
Câu 13. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB a , BC 2a , Mặt phẳng
SBC tạo với mặt phẳng ABCD một góc o
45 , SA vuông góc với mặt phẳng ABCD .
Thể tích khối chóp S.ABCD bằng
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 20
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu 3 4a 3 6a 3 2a A. 3 2a . B. . C. . D. . 3 3 3
Câu 14. Cho hình chóp tứ giác S.ABCD có đáy là hình thang vuông tại A và D , AB 2a ,
AD CD a , cạnh bên SA vuông góc với mặt phẳng đáy và SA 2a . Tính thể tích của khối chóp S.ABCD theo . a 3 3a 3 2a 3 2a A. V . B. V . C. V . D. 3 V 2a . 3 3 2
Câu 15. Cho hình chóp tam giác S.ABC có đáy là tam giác đều tâm O . Biết SO 3a và diện tích tam giác ABC là 2
a 3 . Thể tích khối chóp S.ABC là 3 a 3 3 a A. 3 a 3. B. . C. 3 a . D. . 3 3
Câu 16. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và cạnh bên bằng 2a . Tính thể tích khối chóp S.ABC. 3 a 11 3 a 11 3 a 33 3 a 33 A. . B. . C. . D. . 12 4 12 4
Câu 17. Cho hình chóp đều S.ABCD có cạnh bên bằng a 3 , góc giữa cạnh bên và mặt đáy bằng 45
. Thể tích khối chóp S.ABCD bằng 2 6 3 6 3 6 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 3 2 3 2
Câu 18. Cho hình chóp đều S.ABCD có cạnh đáy bằng 2a . Gọi là góc tạo bởi các mặt bên với đáy.
Tính thể tích khối chóp S.ABCD , biết tan 2 . 3 8a 3 4a A. . B. . C. 3 8a . D. 3 4a . 3 3
Câu 19. Cho lăng trụ đứng ABC.A B C
có đáy ABC là tam giác vuông tại A , AB a, AC 2a, 3 V
a 3. Độ dài đoạn AB bằng ABC.A B C a 7 A. 2 . a B. a 3. C. a 28. D. . 2
Câu 20. Cho hình lăng trụ đứng có đáy là tam giác ABC đều cạnh a , M trung điểm AB, AA' AM .
Thể tích của khối lăng trụ bằng 3 3 3 3 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 8 24 16 48
Câu 1. Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông cân tại B, AC a 2 , cạnh
bên SA vuông góc với mặt đáy và SB a 3 . Tính thể tích V của khối chóp S.ABC . 3 a 3 a 3 a 2 3 a 2 A. V . B. V . C. V . D. V . 6 3 6 3
Câu 2. Cho hình chóp S.ABCD có đáy ABCD là hình vuông với AB 1 m , SA vuông góc với đáy;
SC tạo với đáy một góc o
45 . Thể tích khối chóp S.ABCD là
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 21
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu 2 A. 3 cm . B. 3 1 cm . C. 3 2 cm . D. 3 3 cm . 3
Câu 3. Cho hình chóp S.ABC có đáy là tam giác đều cạnh bằng a , SA vuông góc với đáy, mặt phẳng
SBC tạo với đáy một góc o
45 . Thể tích khối chóp S.ABC bằng 3 a 3 a 2 3 a 3 2a A. . B. . C. . D. . 27 18 8 6
Câu 4. Cho hình chóp tứ giác S.ABCD có đáy là hình vuông, AC a 2 , cạnh bên SA vuông góc
với mặt phẳng đáy và SA a 3 . Tính thể tích V của khối chóp S.ABCD theo . a 3 2 3a 3 3a A. 3 V 2 3a . B. 3 V 3a . C. V . D. V . 3 3
Câu 5. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB a , BC a 3 , SA a 3 ,
SA vuông góc với mặt phẳng ABCD . Thể tích khối chóp S.ABCD bằng 3 a 3 3 a A. 3 a . B. 3 3a . C. . D. . 3 3
Câu 6. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB a, AC a 5 , góc giữa SC với mặt đáy bằng o
45 và SA vuông góc với ABCD . Thể tích khối chóp S.ABCD bằng 2 5 10 5 5 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 3 3 3 3
Câu 7. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B . Biết S
AB là tam giác đều và
thuộc mặt phẳng vuông góc với mặt phẳng ABC . Tính thể tích khối chóp S.ABC biết AB a , AC a 3 . 3 a 6 3 a 6 3 a 2 3 a A. B. C. D. 12 4 6 4
Câu 8. Cho hình chóp S.ABCD có đáy ABCD là hình thoi. Mặt bên SAB là tam giác vuông cân tại
S và thuộc mặt phẳng vuông góc với mặt phẳng ABCD . Tính thể tích khối chóp S.ABCD
biết BD a , AC a 3 . 3 a 3 3 a 3 3 a A. 3 a . B. C. D. 4 12 3
Câu 9. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A . Hình chiếu của S lên mặt phẳng
ABClà trung điểm H của BC . Tính thể tích khối chóp S.ABC biết AB a , AC a 3 , SB a 2 . 3 a 6 3 a 3 3 a 3 3 a 6 A. B. C. D. 6 2 6 2
Câu 10. Cho hình chóp S.ABCD có đáy ABCD hình vuông cạnh a . Hình chiếu của S lên mặt phẳng 3a
ABCD là trung điểm H của AD . Tính thể tích khối chóp S.ABCD biết SB . 2 3 a 3 a 3 3a A. B. 3 a . C. D. 3 2 2
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 22
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu a 13
Câu 11. Hình chóp S.ABCD đáy là hình vuông cạnh a, SD
. Hình chiếu của S lên ABCD 2
là trung điểm H của AB . Thể tích khối chóp là 3 a 2 3 a 2 3 a A. B. C. 3 a 12 . D. 3 3 3
Câu 12. Thể tích của khối chóp tam giác đều có tất cả các cạnh bằng 2a là 2 2 6 A. 3 a . B. 3 2 2a . C. 3 2a . D. 3 a . 3 3
Câu 13. Khối chóp đều S.ABCD có các cạnh đều bằng 3 m . Thể tích khối chóp S.ABCD bằng 9 2 9 2 A. 3 m . B. . 2 m . C. 3 9 2 m . D. 3 27 m . 2 2
Câu 14. Cho hình chóp đều S.ABCD có cạnh đáy bằng a , góc giữa cạnh bên và mặt đáy bằng 60 .
Thể tích khối chóp S.ABCD bằng 3 a 6 3 a 6 3 a 2 A. . B. . C. 3 a 6. D. . 6 2 6
Câu 15. Cho hình chóp đều S.ABCD có các mặt bên là các tam giác đều và đường cao SO a 2 .
Tính thể tích khối chóp S.ABCD . 4 2 4 4 3 2 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 3 3 3 3
Câu 16. Cho hình chóp tứ giác đều có cạnh đáy bằng 2a và cạnh bên bằng a 3 . Thể tích khối chóp đó bằng 3 2a 3 4 3a 3 4a 3 a 3 A. . B. . C. . D. . 3 3 3 3
Câu 17. Cho hình chóp đều S.ABCD có AB 2a , SD tạo với mặt phẳng ABCD một góc o 60 .
Thể tích khối chóp S.ABCD bằng 3 a 6 3 4a 6 3 8a 6 A. . B. . C. . D. 3 a 6. 3 3 3
Câu 18. Cho hình lăng trụ đứng có đáy là tam giác ABC đều, 3 V
a , BB a 3. Độ dài cạnh ABC.A'B'C ' của tam giác ABC bằng 2 6 A. . a B. 2 . a C. . a D. 2 . a 3 3
Câu 19. Cho lăng trụ ABC.A B C
có ABC là tam giác vuông tại A . Hình chiếu của A lên ABC
là trung điểm của BC . Tính thể tích khối lăng trụ ABC.A B C
biết AB a , AC a 3 , AA' 2a . 3 a 3 3a A. B. C. 3 a 3 . D. 3 3a 3 . 2 2
Câu 20. Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh đều bằng a là 3 a 3 3 a 3 3 a 2 3 a 2 A. B. C. D. 4 3 3 2
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 23
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu BẢNG ĐÁP ÁN ĐỀ 1 1 2 3 4 5 6 7 8 9 10 A B B C B A B D D C 11 12 13 14 15 16 17 18 19 20 D D D C A B A C D C ĐỀ 2 1 2 3 4 5 6 7 8 9 10 B B A C A C C C B A 11 12 13 14 15 16 17 18 19 20 C D D C C A A A A D ĐỀ 3 1 2 3 4 5 6 7 8 9 10 C D B D A A C D B B 11 12 13 14 15 16 17 18 19 20 D D A A A B A D A A ĐỀ 4 1 2 3 4 5 6 7 8 9 10 C B A D A C B C A D 11 12 13 14 15 16 17 18 19 20 AB D C A A D A A A ĐỀ 5 1 2 3 4 5 6 7 8 9 10 C A C D A A A C C A 11 12 13 14 15 16 17 18 19 20 A A A A A C B A B D
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 24
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu
CHUYÊN ĐỀ 7: HÌNH HỌC KHÔNG GIAN
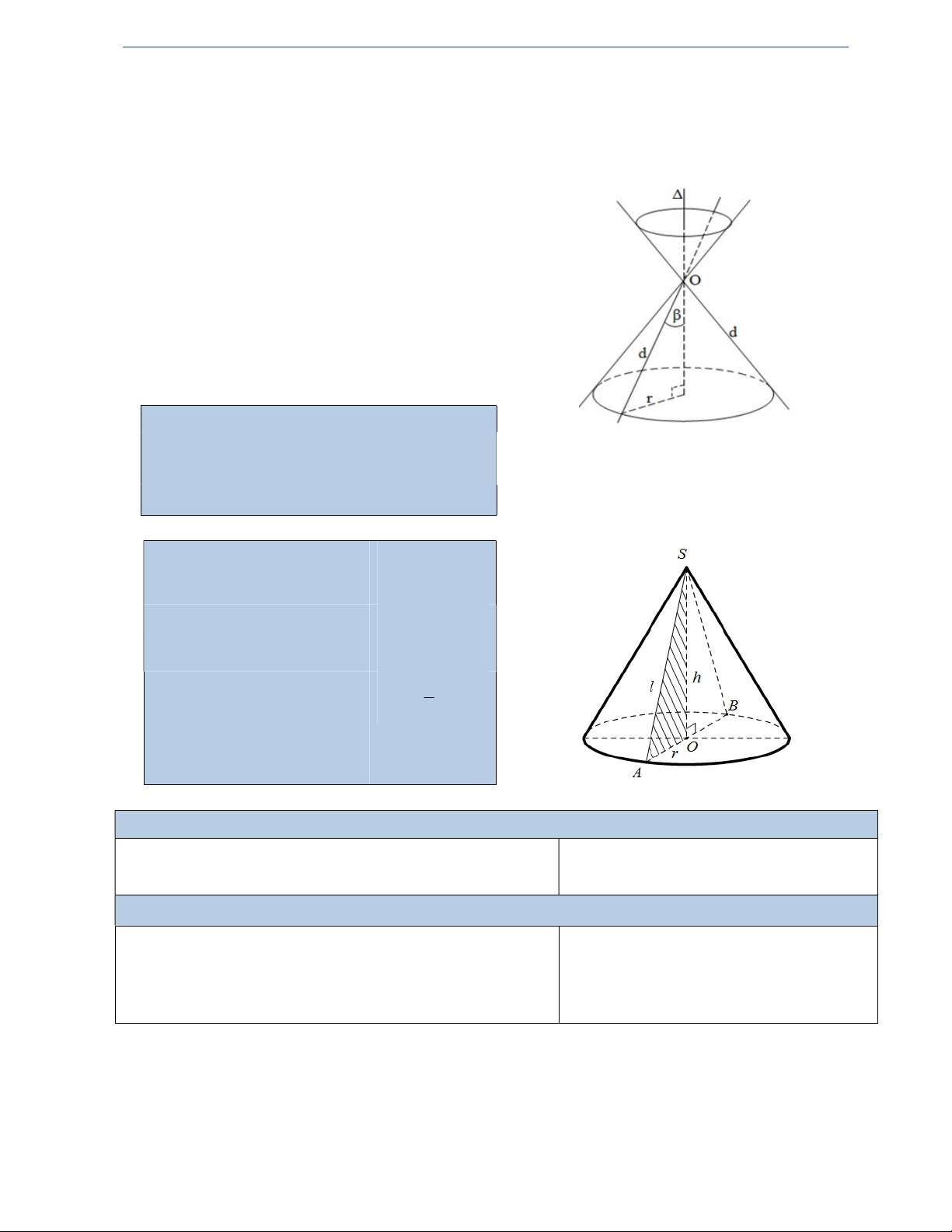
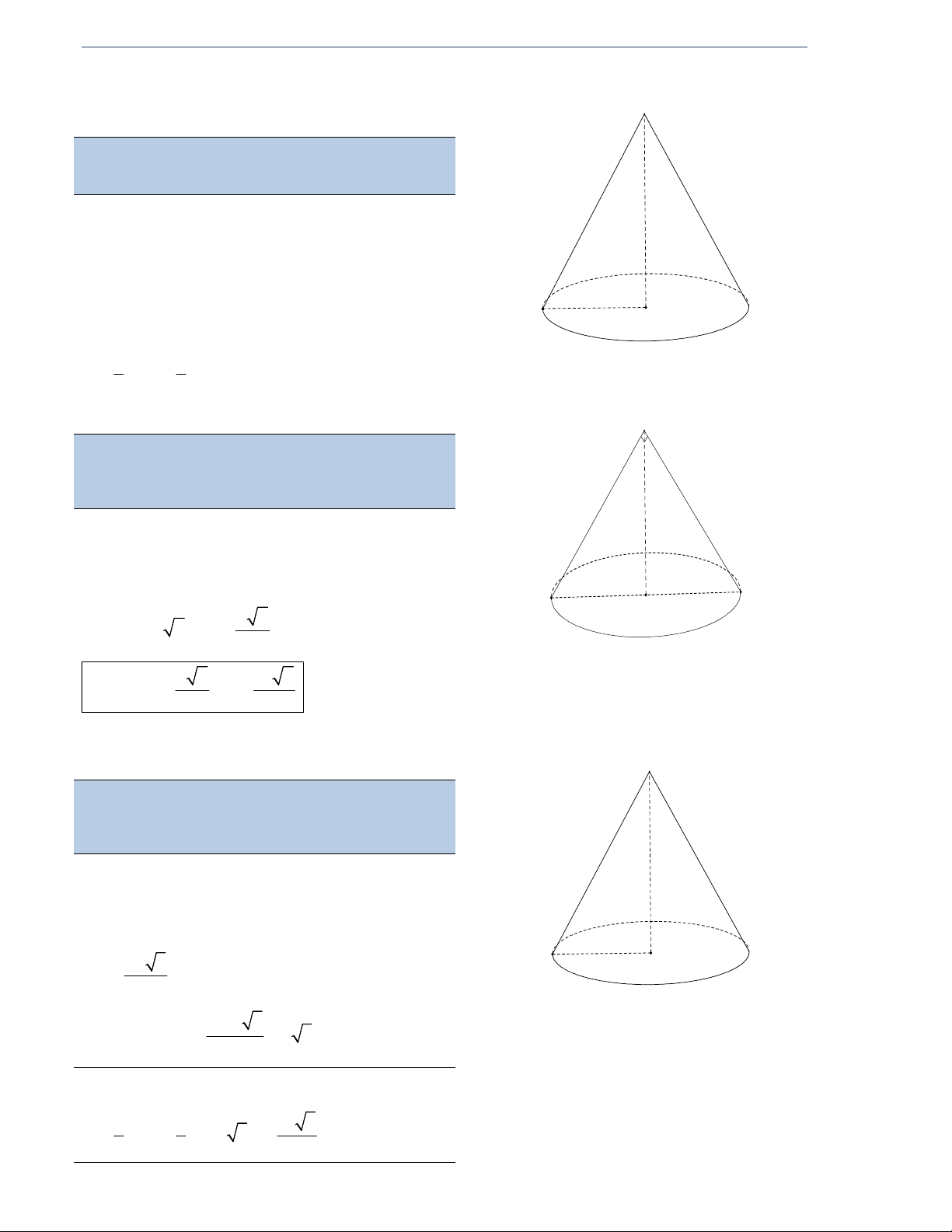
CHỦ ĐỀ: MẶT NÓN TRÒN XOAY VÀ KHỐI NÓN I. TÓM TẮT LÝ THUYẾT 1) Mặt nón tròn xoay.
Đường thẳng d , cắt nhau ta ̣i O và ta ̣o thành góc với 0 0
0 90 , mp P chứa d , .
P quay quanh trục với góc không đổi.
mặt nón tròn xoay đỉnh . O go ̣i là trục.
d đươ ̣c go ̣i là đường sinh.
Góc 2 go ̣i là góc ở đı̉nh.
Các thông số thường gặp r bán kính đáy
h chiều cao (khoảng cách từ đỉnh đến đáy) l đường sinh
β là góc hợp bởi l và h
2) Các công thức cần nhớ. Diện tích đáy S 2 r ñ Chu vi đáy CV 2πr đ Diện tích xung quanh S rl xq Diện tích toàn phần S S S tp xq ñ Thể tích khối nón 1 V 2 r h noùn 3
3) Thiết diện khi cắt bởi mặt phẳng
Cắt mă ̣t nón tròn xoay bởi mp (Q) đi qua đı̉nh của mặt nón.
mp(Q) cắt mă ̣t nón theo 2 đường sinh.
Thiết diê ̣n là tam giác cân.
mp(Q) tiếp xúc với mă ̣t nón theo mô ̣t đường sinh.
(Q) là mặt phẳng tiếp diện của hình nón.
Cắt mă ̣t nón tròn xoay bởi mp (Q) không đi qua đı̉nh của mặt nón.
mp(Q) vuông góc với tru ̣c hı̀nh nón.
Giao tuyến là 1 đường parabol.
mp(Q) song song với 2 đường sinh hı̀nh nón.
Giao tuyến là 2 nhánh của 1 hypebol. mp(Q) song song vơ Giao tuyến la
́ i 1 đường sinh hı̀nh nón. ̀ mô ̣t đường tròn.
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 25
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu
II. CÁC DẠNG TOÁN THƯỜNG GẶP
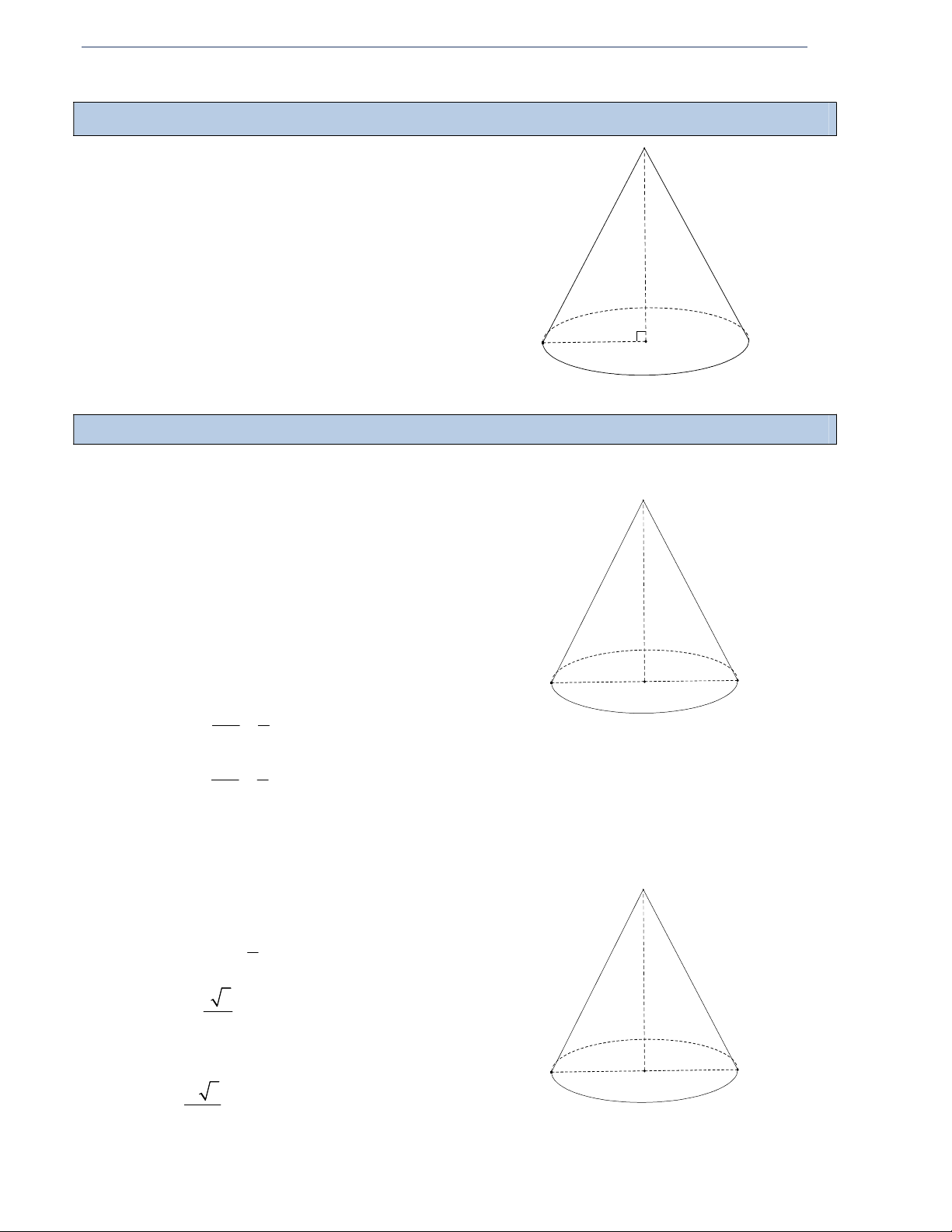
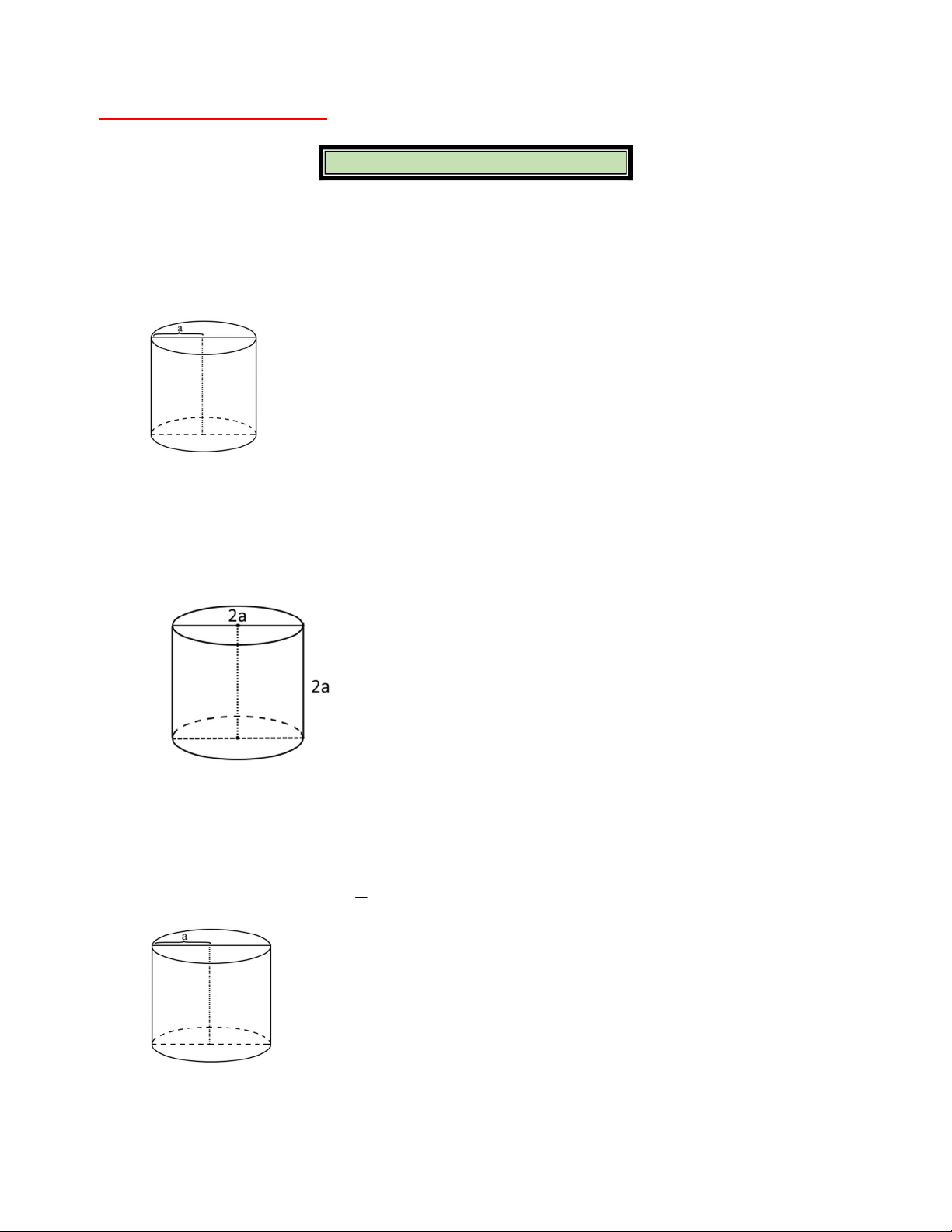
DẠNG 1: DẠNG CƠ BẢN (cho các thông số r, , h l ) r là bán kính. h là chiều cao. 2 2 2
l h r là đường sinh Góc giữa l và h l h Góc giữa l và r r
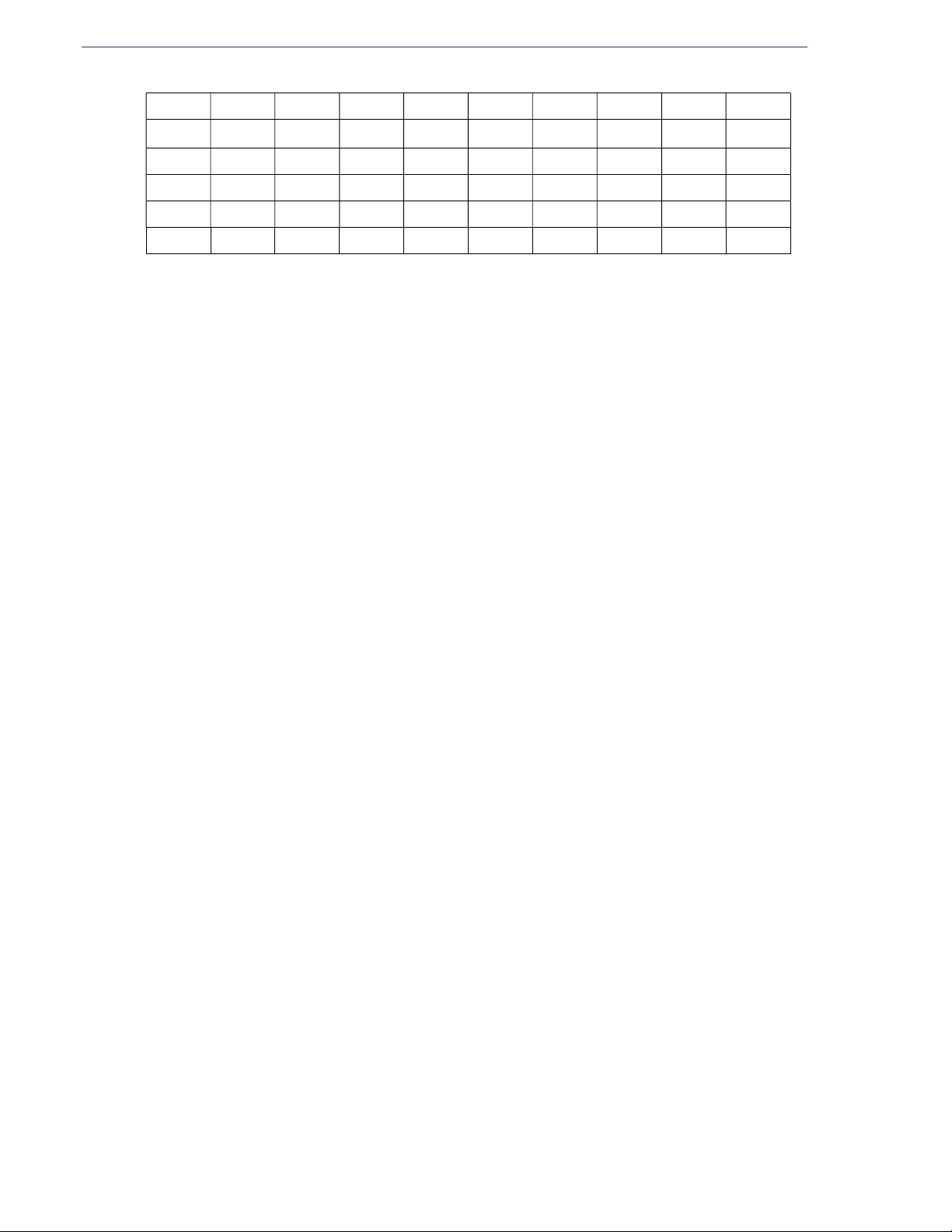
DẠNG 2: THIẾT DIỆN QUA TRỤC
Thiết diện qua trục là tam giác cân
Tam giác SAB cân tại S nên: S l SA SB r AO BO h SO Góc ở đỉnh là ASB 2 ASO SAO SBO
Hệ thức lượng trong SAO vuông tại O A O B SO h tan SAO AO r AO r tan ASB SO h
Thiết diện qua trục là tam giác đều Tam giác SAB đều nên: S l SA SB AB l r AO BO 2 l 3 h SO 2 ASB SAB 0
2ASO 60 là góc ở đỉnh. A O B 2 l 3 S SAB 4
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 26
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu
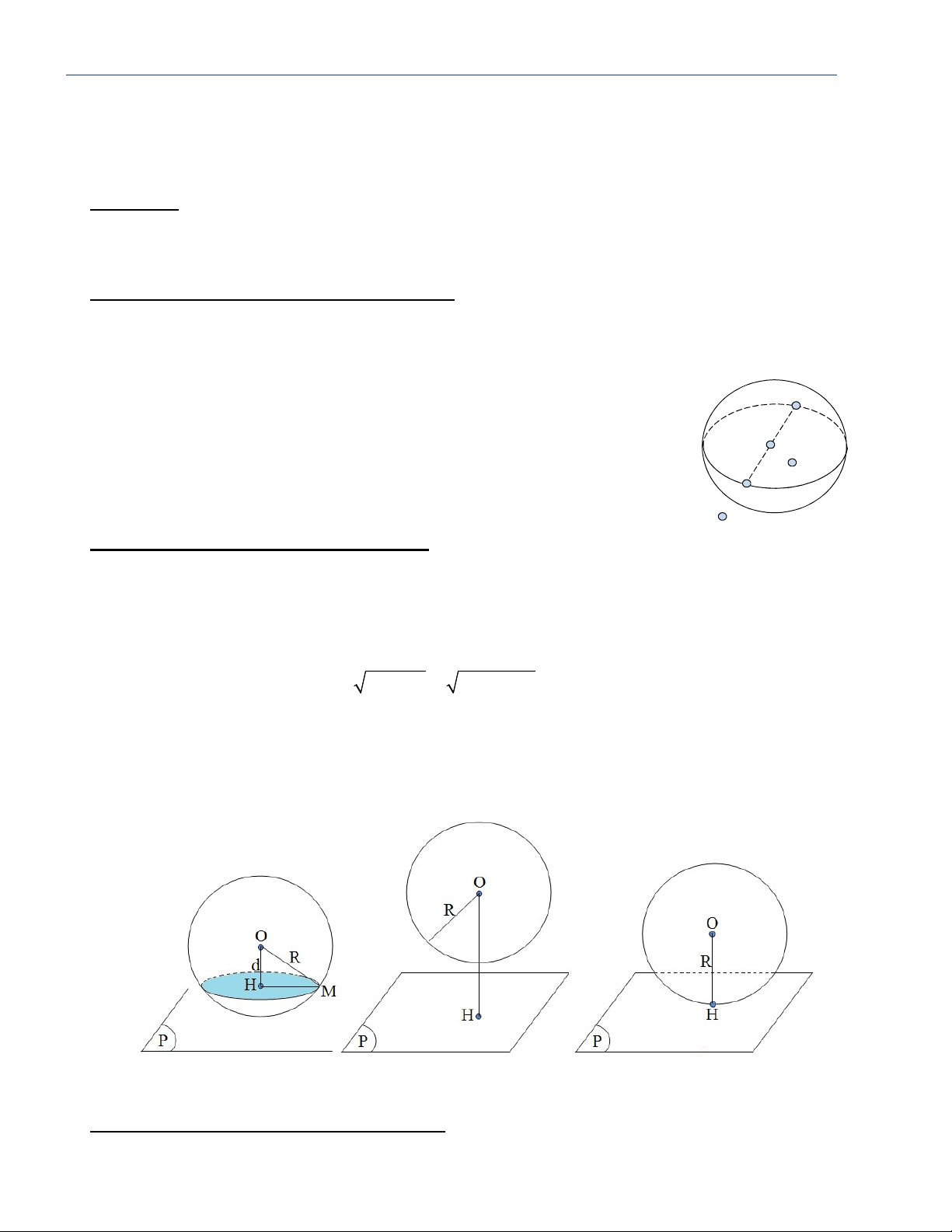
Thiết diện qua trục là tam giác vuông cân
Tam giác SAB vuông cân tại S nên: S l r 2
AB SA SB 2r2 2 2 2 2 2l d l 2
Với d 2r là đường kính đáy. SO AO r h
Góc ở đỉnh là góc vuông B A O 1 1 2 2 2 S l . h 2r . h r r h SAB 2 2
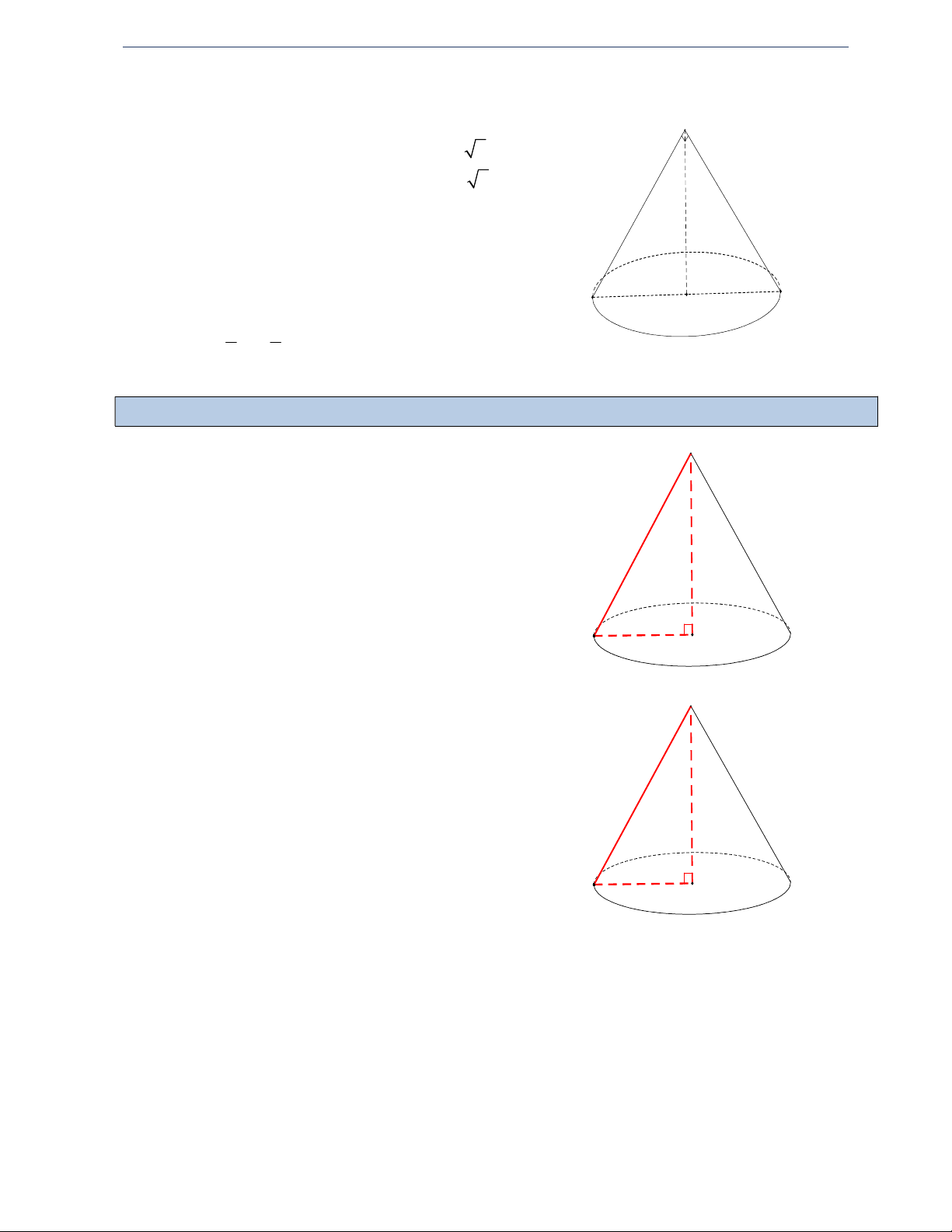
DẠNG 3: KHỐI NÓN SINH BỞI TAM GIÁC QUAY QUANH TRỤC
Quay tam giác SOA vuông tại O quanh trục SO S h SO r AO l SA A O
Quay tam giác SOA vuông tại O quanh trục AO A h AO r SO l SA S O
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 27
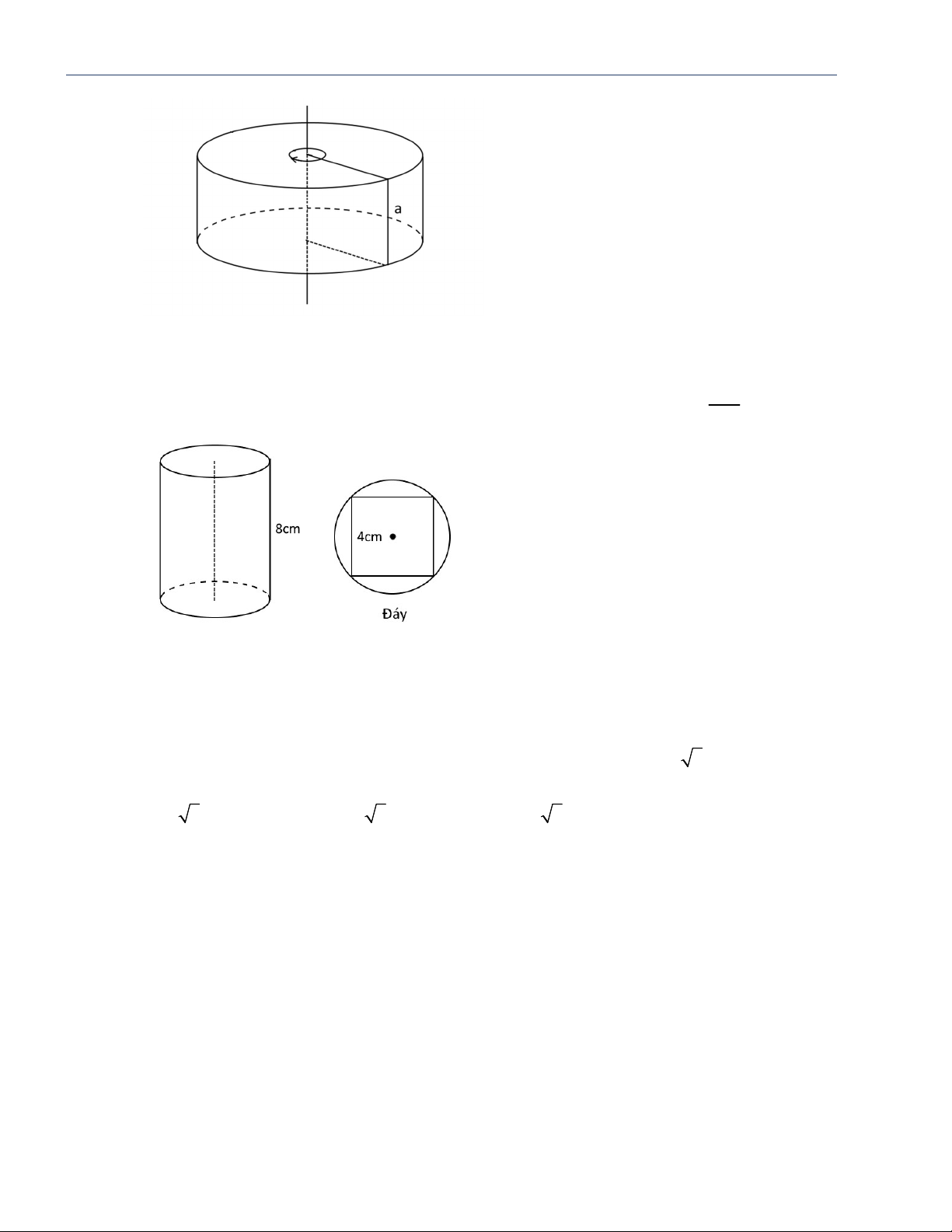
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu III. CÁC BÀI TẬP MẪU Câu 1.
Cho hình nón có bán kính đáy và đường cao lần lượt là r 3c , m h 4 c . m Tính l, S , S , V xq tp l=5 cm Giải: h = 4 cm 2 2 2 2 2
l h r 4 3 5cm S πrl π π 2 .3.5 15 cm xq 2 2 S πrl πr π π π 2 15 .3 24 cm r = 3 cm tp 1 2 1 2
V πr h π.3 .4 12π 3 cm 3 3 Câu 2. S
Thiết diện qua trục của một hình nón là một tam
giác vuông cân có cạnh góc vuông bằng . a Diện
tích xung quanh của hình nón bằng bao nhiêu? a Giải:
Xét tam giác ASB vuông cân tại S
Cạnh góc vuông l SA SB a B A O a 2 d AB a 2 r 2 2 a 2 a 2 S πrl π .a π . xq 2 2 Câu 3. S
Thiết diện qua trục của hình nón là tam giác đều cạnh 2 .
a Diện tích toàn phần và thể tích của hình nón bằng bao nhiêu? 2a Giải: 2a
Xét tam giác ASB đều cạnh 2a SA SB AB 2a SA 3 A a O SO
(đường cao trong tam giác đều) 2 2a 3 l 2a, r a, h a 3 2 2 2 2 S πrl πr π. . a 2a π.a π.3a tp 3 1 2 1 2 a 3
V πr h πa .a 3 π 3 3 3
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 28
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu
IV. BÀI TẬP TRẮC NGHIỆM
Câu 1. Gọi l, h, r lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình nón. Diện tích
xung quanh S của hình nón bằng: xq A. S rl. B. S r . h C. S 2 rl. D. 2 S r . h xq xq xq xq Câu 2. Gọi l, ,
h r lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình nón. Diện tích toàn
phần S của hình nón bằng: tp A. 2 S rh r . B. 2 S 2 rl 2 r . tp tp C. 2 S rl 2 r . D. 2 S rl r . tp tp
Câu 3. Gọi l, h, r lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình nón. Thể tích của khối nón bằng: 1 A. 2 V r . h B. 2 V r . h 3 1 C. 2 V r l. D. 2 V r l. 3
Câu 4. Một hình nón có đường sinh l gấp đôi bán kính r của mặt đáy. Diện tích xung quanh của hình nón là: 1 1 A. 2 S 2 r . B. S 2 rl. C. 2 S r . D. S rl. xq xq xq 2 xq 2
Câu 5. Một khối nón có đường cao a (cm) , bán kính r cm thì có thể tích bằng: 1 1 A. V r . a B. V 3 r . noùn 3 noùn 3 1 1 C. V 2 r . a D. V 2 a r. noùn 3 noùn 3
Câu 6. Một khối nón có thể tích bằng 4π và chiều cao bằng 3. Bán kính đường tròn đáy bằng: 2 3 4 A. 2. B. . C. . D. 1. 3 3 1
Câu 7. Một khối nón có diện tích xung quanh bằng 2
2 cm và bán kính đáy r c . m Khi đó độ dài 2
đường sinh của khối nón là: A. 3 B. 4 C. 2 D. 1
Câu 8. Thể tích của khối nón sẽ thay đổi như thế nào nếu tăng độ dài bán kính đáy lên hai lần mà vẫn
giữ nguyên chiều cao của khối nón ? A. Tăng 4 lần. B. Giảm 2 lần. C. Tăng 2 lần D. Không đổi.
Câu 9. Giao tuyến của mặt nón tròn xoay với một phẳng song song với trục của mặt nón là: A. một parabol. B. một hypebol. C. một elip. D. một đường tròn.
Câu 10. Quay tam giác ABC vuông tại A quanh cạnh AB thì được hình nón có
A. độ dài đường cao bằng độ dài cạnh A . B
B. bán kính đáy bằng độ dài cạnh A . B
C. bán kính đáy bằng độ dài cạnh AC.
D. độ dài đường cao bằng độ dài cạnh AC.
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 29
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu Câu 11. Gọi l, ,
h r lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình nón. Đẳng thức nào sau đây luôn đúng ? 1 1 1 A. 2 2 2 r h l . B. 2 2 2 l h r . C. . D. 2 l hr. 2 2 2 l h r
Câu 12. Hình nón có bán kính đáy là 4a, chiều cao là 3 .
a có diện tích xung quanh bằng: A. 2 20 a . B. 2 40 a . C. 2 24 a . D. 2 12 a .
Câu 13. Một khối nón có đường cao và đường kính mặt đáy cùng bằng a thì có thể tích bằng: 3 a 3 a 3 a A. 3 a . B. . C. . D. . 2 3 6
Câu 14. Thể tích của khối nón có chiều cao bằng a và độ dài đường sinh bằng a 5 bằng: 4 2 5 A. 3 V a . B. 3 V 4 a . C. 3 V a . D. 3 V a . 3 3 3
Câu 15. Hình nón có diện tích xung quanh bằng 24 và bán kính đường tròn đáy bằng 3. Chiều cao khối nón là: A. 8. B. 89. C. 3. D. 39.
Câu 16. Một hình nón có đường kính đáy là 2a 3 , góc ở đỉnh là 0
120 . Độ dài đường sinh bằng: 3 3 3 A. l . B. 3. C. . D. . 2 2 3 a 3
Câu 17. Một hình nón có đường cao bằng và góc ở đỉnh bằng 0
60 . Thể tích của khối nón bằng: 2 3 1 3 3 3 A. 3 πa . B. 3 πa . C. 3 πa . D. 3 πa . 4 8 24 8
Câu 18. Quay tam giác đều ABC lần lượt xung quanh các cạnh của nó tạo thành bao nhiêu hình nón? A. 0. B. 1. C. 2. D. 3.
Câu 19. Cho tam giác ABC vuông tại A và AB a, AC a 3. Quay tam giác ABC quanh trục AB
để tạo thành một hình nón tròn xoay. Khi đó độ dài đường sinh l của hình nón bằng bao nhiêu? A. a 3 B. 2a C. a D. a 2
Câu 20. Cho tam giác ABC vuông tại A có AB 6, AC 8. Quay tam giác ABC xung quanh cạnh AC
ta được hình nón có diện tích xung quanh và diện tích toàn phần lần lượt là S , S . Hãy chọn 1 2 kết quả đúng ? S 5 S 5 S 8 S 3 A. 1 B. 1 . C. 1 . D. 1 . S 8 S 9 S 9 S 5 2 2 2 2
Câu 21. Cho một hình nón có thiết diện qua trục là một tam giác vuông cân với cạnh góc vuông bằng
a 2. Thể tích của khối nón đó bằng: 3 a 3 a 3 a A. . B. . C. 3 a . D. . 3 2 6
Câu 22. Thiết diện qua trục của một hình nón là tam giác đều có cạnh bằng a 2, khi đó diện tích xung quanh của hình nón là: A. 2 a . B. 2 2a . C. 2 3a . D. 2 4a .
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 30
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu
Câu 23. Thiết diện qua trục của một hình nón là tam giác vuông có cạnh huyền là 2a 2. Thể tích khối
nón giới hạn bởi hình nón đó là: 3 2 a 2 3 2 a 3 3 4 a 3 A. . B. . C. . D. 3 2 a 2. 3 3 3
Câu 24. Cho hình nón có thiết diện qua trục là một tam giác vuông cân. Trong các khẳng định sau đây, khẳng định nào sai ?
A. Hai đường sinh tùy ý của hình nón đều vuông góc với nhau.
B. Đường sinh hợp với mặt đáy một góc 45 .
C. Đường cao và bán kính mặt đáy của hình nón bằng nhau.
D. Đường sinh và trục của hình nón hợp với nhau một góc 45 .
Câu 25. Một hình nón có diện tích mặt đáy bằng 2
4 cm , diện tích xung quanh bằng 2 8 cm . Khi đó
đường sinh của hình nón đó bằng bao nhiêu? A. 2. B. 4. C. 2. D. 2 2.
Câu 26. Cho khối nón có bán kính đường tròn đáy bằng 10 và diện tích xung quanh bằng 120 . Chiều cao h của khối nón là: 11 11 A. 2 11. B. . C. 11. D. . 3 2
Câu 27. Cho hı̀nh chóp tứ giác đều S.ABCD có ca ̣nh đáy bằng a, ca ̣nh bên SA 2 . a Diện tích xung
quanh của hình nón ngoại tiếp hình chóp là: 2 A. 2 2 2a . B. 2 a . C. 2 2 a . D. 2 a . 2
Câu 28. Cho hı̀nh chóp tam giác đều S.ABC có ca ̣nh đáy bằng a, ca ̣nh bên SA . a Chiều cao của hình
nón ngoại tiếp hình chóp bằng: 6 A. . a B. 2 . a C. 2 . a D. 3 . a 3
Câu 29. Cho hı̀nh chóp tam giác đều S.ABC có ca ̣nh đáy bằng a 3 và ca ̣nh bên SA a 5. Thể tích
của khối nón ngoại tiếp hình chóp bằng: 6 2 4 5 A. 3 πa . B. 3 πa . C. 3 πa . D. 3 a π. 3 3 3 3
Câu 30. Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh a, SO a 3 và
SO ABCD. Gọi N là hình nón đỉnh S ngoại tiếp hình chóp S.ABCD. Cho các khẳng định sau:
I. SO là chiều cao của N . a 2 II. r
là bán kính đáy của N . 2 2 III. 3 V
πa . là thể tích khối nón N . 3 IV. S π.O .
A SO là diện tích xung quanh của N . xq
Có bao nhiêu khẳng định sai? A. 2. B. 3. C. 4. D. 1.
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 31
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu ĐÁP ÁN 1 2 3 4 5 6 7 8 9 10 A D B A C A B A B A 11 12 13 14 15 16 17 18 19 20 B A C A D A C A B B 21 22 23 24 25 26 27 28 29 30 A A A A B A C A C A
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 32
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu
CHUYÊN ĐỀ 7: HÌNH HỌC KHÔNG GIAN CHỦ ĐỀ: MẶT CẦU A. – LÝ THUYẾT 1/ Đi ̣nh nghı ̃a
Tâ ̣p hơ ̣p các điểm M trong không gian cách điểm O cố đi ̣nh mô ̣t khoảng R go ̣i là mă ̣t cầu tâm O , bán kı́nh
R , kı́ hiê ̣u là: S O; R . Khi đó S O; R M | OM R
2/ Vi ̣trı́ tương đối của mô ̣t điểm đối với mă ̣t cầu
Cho mă ̣t cầu S O; R và mô ̣t điểm A bất kı̀, khi đó:
Nếu OA R A S O; R . Khi đó OA go ̣i là bán kı́nh mă ̣t cầu. Nếu OA và OB là hai bán kı́nh sao cho OA O
B thı̀ đoa ̣n thẳng AB gọi là một đường kı́nh của mă ̣t cầu.
Nếu OA R A nằm trong mă ̣t cầu.
Nếu OA R A nằm ngoài mă ̣t cầu.
Khối cầu S O; R là tâ ̣p hợp tất cả các điểm M sao cho OM R .
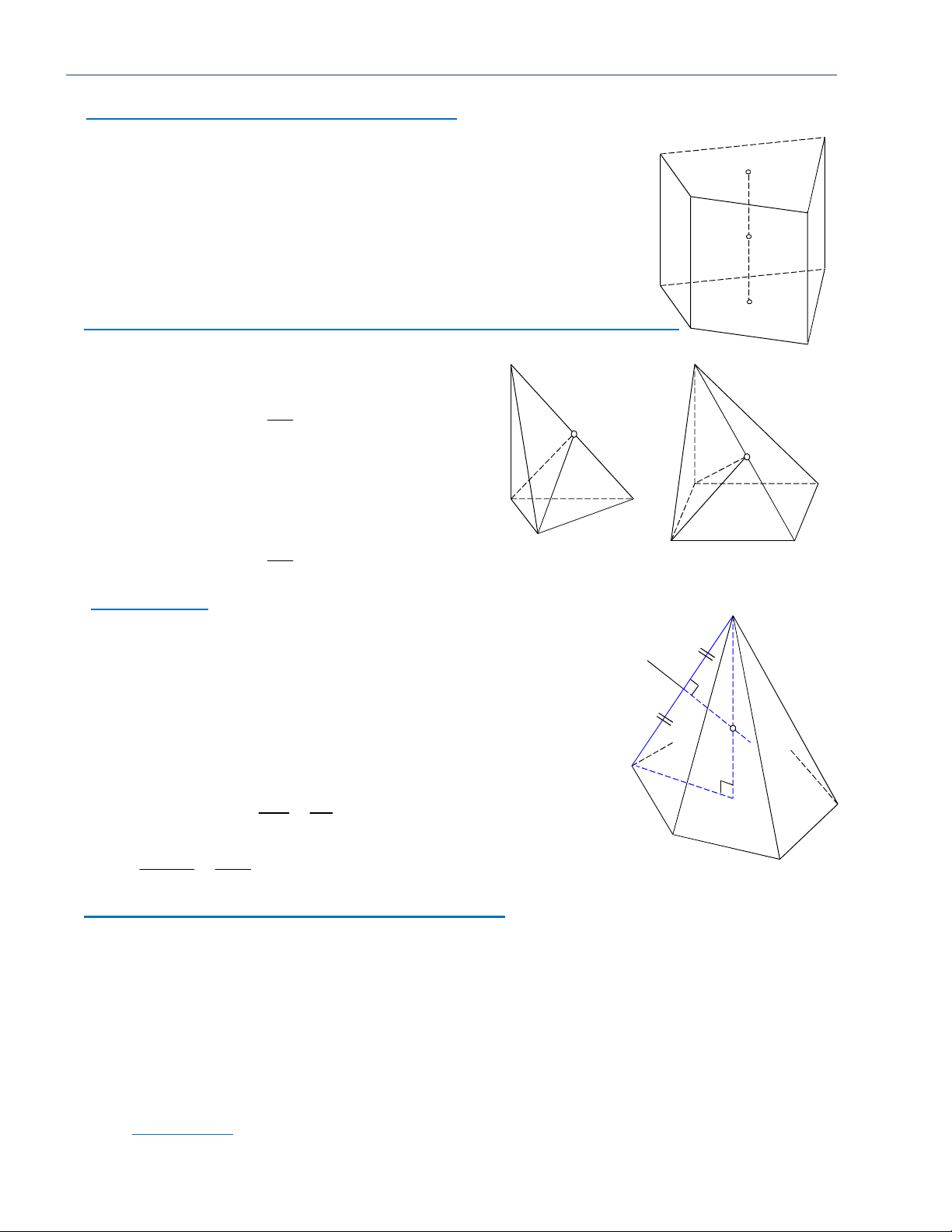
3/ Vi ̣trı́ tương đối của mă ̣t phẳng và mă ̣t cầu
Cho mă ̣t cầu S O; R và mô ̣t mp P . Go ̣i d là khoảng cách từ tâm O của mă ̣t cầu đến mp P và H là
hı̀nh chiếu của O trên mp P d OH .
Nếu d R mp P cắt mă ̣t cầu S O; R theo giao tuyến là đường tròn nằm trên mp P có tâm là H và bán kı 2 2 2 2
́nh r HM R d R OH (hı̀nh a).
Nếu d R mp P không cắt mă ̣t cầu S O; R (hı̀nh b).
Nếu d R mp P có mô ̣t điểm chung duy nhất. Ta nói mă ̣t cầu S O; R tiếp xúc mp P . Do
đó, điều kiê ̣n cần và đủ để mp P tiếp xúc với mă ̣t cầu S O; R là d O, P R (hı̀nh c). d d = Hı̀nh a Hı̀nh b Hı̀nh c
4/ Vi ̣trı́ tương đối của đường thẳng và mă ̣t cầu
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 33
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu
Cho mă ̣t cầu S O; R và mô ̣t đường thẳng . Go ̣i H là hı̀nh chiếu củaO trên đường thẳng và d OH là
khoảng cách từ tâmO của mă ̣t cầu đến đường thẳng . Khi đó:
Nếu d R không cắt mă ̣t cầu S O; R .
Nếu d R cắt mă ̣t cầu S O; R ta ̣i hai điểm phân biê ̣t.
Nếu d R và mă ̣t cầu tiếp xúc nhau (ta ̣i mô ̣t điểm duy nhất). Do đó: điều kiê ̣n cần và đủ để
đường thẳng tiếp xúc với mă ̣t cầu là d d O, R .
Đi ̣nh lı́: Nếu điểm A nằm ngoài mă ̣t cầu S O; R thı̀:
Qua A có vô số tiếp tuyến với mă ̣t cầu S O; R .
Đô ̣ dài đoa ̣n thẳng nối A với các tiếp điểm đều bằng nhau.
Tâ ̣p hợp các điểm này là mô ̣t đường tròn nằm trên mă ̣t cầu S O; R .
5/ Diê ̣n tı́ch và thể tı́ch mă ̣t cầu 4
• Diê ̣n tı́ch mă ̣t cầu: 2 S 4 R . • Thể tı 3 V R C ́ch mă ̣t cầu: C . 3
*MẶT CẦU NGOẠI TIẾP KHỐI ĐA DIỆN (Đọc thêm)
1/ Các khái niê ̣m cơ bản
Tru ̣c của đa giác đáy: là đường thẳng đi qua tâm đường tròn ngoa ̣i tiếp của đa giác đáy và vuông góc
với mă ̣t phẳng chứa đa giác đáy.
Bất kı̀ một điểm nào nằm trên trục của đa giác thı̀ cách đều các đı̉nh của đa giác đó.
Đường trung trực của đoa ̣n thẳng: là đường thẳng đi qua trung điểm của đoa ̣n thẳng và vuông góc
với đoa ̣n thẳng đó.
Bất kı̀ mô ̣t điểm nào nằm trên đường trung trực thı̀ cách đều hai đầu mút của đoa ̣n thẳng.
Mă ̣t trung trực của đoa ̣n thẳng: là mă ̣t phẳng đi qua trung điểm của đoa ̣n thẳng và vuông góc với đoa ̣n thẳng đó.
Bất kı̀ một điểm nào nằm trên mă ̣t trung trực thı̀ cách đều hai đầu mút của đoa ̣n thẳng.
2/ Tâm và bán kı́nh mă ̣t cầu ngoa ̣i tiếp hı̀nh chóp
Tâm mă ̣t cầu ngoa ̣i tiếp hı̀nh chóp: là điểm cách đều các đı̉nh của hı̀nh chóp. Hay nói cách khác, nó
chı́nh là giao điểm I của tru ̣c đường tròn ngoại tiếp mặt phẳng đáy và mặt phẳng trung trực của một cạnh bên hı̀nh chóp.
Bán kı́nh: là khoảng cách từ I đến các đı̉nh của hı̀nh chóp.
3/ Cách xác đi ̣nh tâm và bán kı́nh mă ̣t cầu của mô ̣t số hı̀nh đa diê ̣n cơ bản
a/ Hı̀nh hô ̣p chữ nhâ ̣t, hı̀nh lâ ̣p phương.
- Tâm: trùng với tâm đối xứng của hı̀nh hô ̣p chữ nhâ ̣t (hı̀nh lâ ̣p phương).
Tâm là I , là trung điểm của AC ' .
- Bán kı́nh: bằng nửa đô ̣ dài đường chéo hı̀nh hô ̣p chữ nhâ ̣t (hı̀nh lâ ̣p phương). AC ' Bán kı́nh: R . 2
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 34
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu
b/ Hı̀nh lăng tru ̣ đứng có đáy nô ̣i tiếp đường tròn.
Xét hı̀nh lăng tru ̣ đứng ' ' ' ' A A A ...A .A A A ...A 1 2 3 n 1 2 3 n , trong đó có 2 đáy A A A ...A va ' ' ' ' A A A ...A O O' 1 2 3 n ̀ 1 2 3
n nô ̣i tiếp đường tròn và . Lúc đó,
mă ̣t cầu nô ̣i tiếp hı̀nh lăng tru ̣ đứng có:
- Tâm: I với I là trung điểm của OO ' . - Bán kı́nh: ' R IA IA ... IA 1 2 n .
c/ Hı̀nh chóp có các đı̉nh nhı̀n đoa ̣n thẳng nối 2 đı̉nh còn la ̣i dưới 1 góc vuông. A’2
- Hı̀nh chóp S.ABC có SAC 0 SBC 90 .
+ Tâm: I là trung điểm của SC . SC + Bán kı́nh: R IA IB IC . 2 - Hı̀nh chóp S.ABCD có SAC SBC 0 SDC 90 .
+ Tâm: I là trung điểm của SC . SC + Bán kı́nh: R IA IB IC ID . 2 d/ Hı̀nh chóp đều.
Cho hı̀nh chóp đều S.ABC...
- Go ̣i O là tâm của đáy SO là tru ̣c của đáy.
- Trong mă ̣t phẳng xác đi ̣nh bởi SO và mô ̣t ca ̣nh bên,
chẳng ha ̣n như mp SAO , ta vẽ đường trung trực của ca ̣nh SA
là cắt SA ta ̣i M và cắt SO ta ̣i I I là tâm của mă ̣t cầu. - Bán kı́nh: SM SI Ta có: SMI SOA Bán kı́nh là: SO SA 2 SM .SA SA R IS IA IB IC ... SO 2SO
e/ Hı̀nh chóp có ca ̣nh bên vuông góc với mă ̣t phẳng đáy.
Cho hı̀nh chóp S.ABC... có ca ̣nh bên SA đáy ABC... và đáy ABC... nô ̣i tiếp được trong đường tròn
tâm O . Tâm và bán kı́nh mă ̣t cầu ngoa ̣i tiếp hı̀nh chóp S.ABC... được xác đi ̣nh như sau:
- Từ tâm O ngoa ̣i tiếp của đường tròn đáy, ta vẽ đường thẳng d vuông góc với mp ABC... ta ̣i O .
- Trong mp d, SA , ta dựng đường trung trực của ca ̣nh SA , cắt SA ta ̣i M , cắt d ta ̣i I .
I là tâm mă ̣t cầu ngoa ̣i tiếp hı̀nh chóp
và bán kı́nh R IA IB IC IS ... - Tı̀m bán kı́nh:
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 35
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu
Ta có: MIOB là hı̀nh chữ nhâ ̣t.
Xét MAI vuông ta ̣i M có: d 2 SA 2 2 2
R AI MI MA AO . 2 f/ Hı̀nh chóp khác.
- Dựng tru ̣c của đáy.
- Dựng mă ̣t phẳng trung trực của mô ̣t ca ̣nh bên bất kı̀.
- I I là tâm mă ̣t cầu ngoa ̣i tiếp hı̀nh chóp.
- Bán kı́nh: khoảng cách từ I đến các đı̉nh của hı̀nh chóp.
g/ Đường tròn ngoa ̣i tiếp mô ̣t số đa giác thường gă ̣p.
Khi xác đi ̣nh tâm mă ̣t cầu, ta cần xác đi ̣nh tru ̣c của mă ̣t phẳng đáy, đó chı́nh là đường thẳng vuông góc với
mă ̣t phẳng đáy ta ̣i tâm O của đường tròn ngoa ̣i tiếp đáy. Do đó, viê ̣c xác đi ̣nh tâm ngoa ̣i O là yếu tố rất quan tro ̣ng của bài toán. O O O Hı̀nh vuông: O là giao
Hı̀nh chữ nhâ ̣t: O là giao
∆ đều: O là giao điểm của 2 điểm 2 đường điểm của hai đường trung tuyến O O
∆ vuông: O là trung điểm
∆ thường: O là giao điểm của của ca ̣nh hai đường trung trực huyền.
KỸ THUẬT XÁC ĐỊNH MẶT CẦU NGOẠI TIẾP HÌNH CHÓP. (Đọc thêm)
Cho hình chóp S.A A ...A (thoả mãn điều kiện tồn tại mặt cầu ngoại tiếp). Thông thường, để xác định 1 2 n
mặt cầu ngoại tiếp hình chóp ta thực hiện theo hai bước:
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 36
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu
Bước 1: Xác định tâm của đường tròn ngoại tiếp đa giác đáy. Dựng : trục đường tròn ngoại tiếp đa giác đáy. S
Bước 2: Lập mặt phẳng trung trực ( ) của một cạnh bên. I
Lúc đó : - Tâm O của mặt cầu: mp() O O
- Bán kính: R SA SO . Tuỳ vào từng trường hợp. D A H C
Lưu ý: Kỹ năng xác định trục đường tròn ngoại tiếp đa giác đáy. B
1. Trục đường tròn ngoại tiếp đa giác đáy: là đường thẳng đi qua tâm đường tròn ngoại tiếp đáy và
vuông góc với mặt phẳng đáy. Tính chất: M
: MA MB MC
Suy ra: MA MB MC M M
2. Các bước xác định trục:
- Bước 1: Xác định tâm H của đường tròn ngoại tiếp đa giác đáy. A
- Bước 2: Qua H dựng vuông góc với mặt phẳng đáy. H C
VD: Một số trường hợp đặc biệt B A. Tam giác vuông B. Tam giác đều C. Tam giác bất kì B H B C B C H C H A A A S
3. Lưu ý: Kỹ năng tam giác đồng dạng M SO SM
SMO đồng dạng với SIA . SA SI O I A 4. Nhận xét quan trọng: MA MB MC M , S :
SM là trục đường tròn ngoại tiếp ABC . SA SB SC
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 37
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu
5. Ví dụ: Tìm tâm và bán kính mặt cầu ngoại tiếp hình chóp
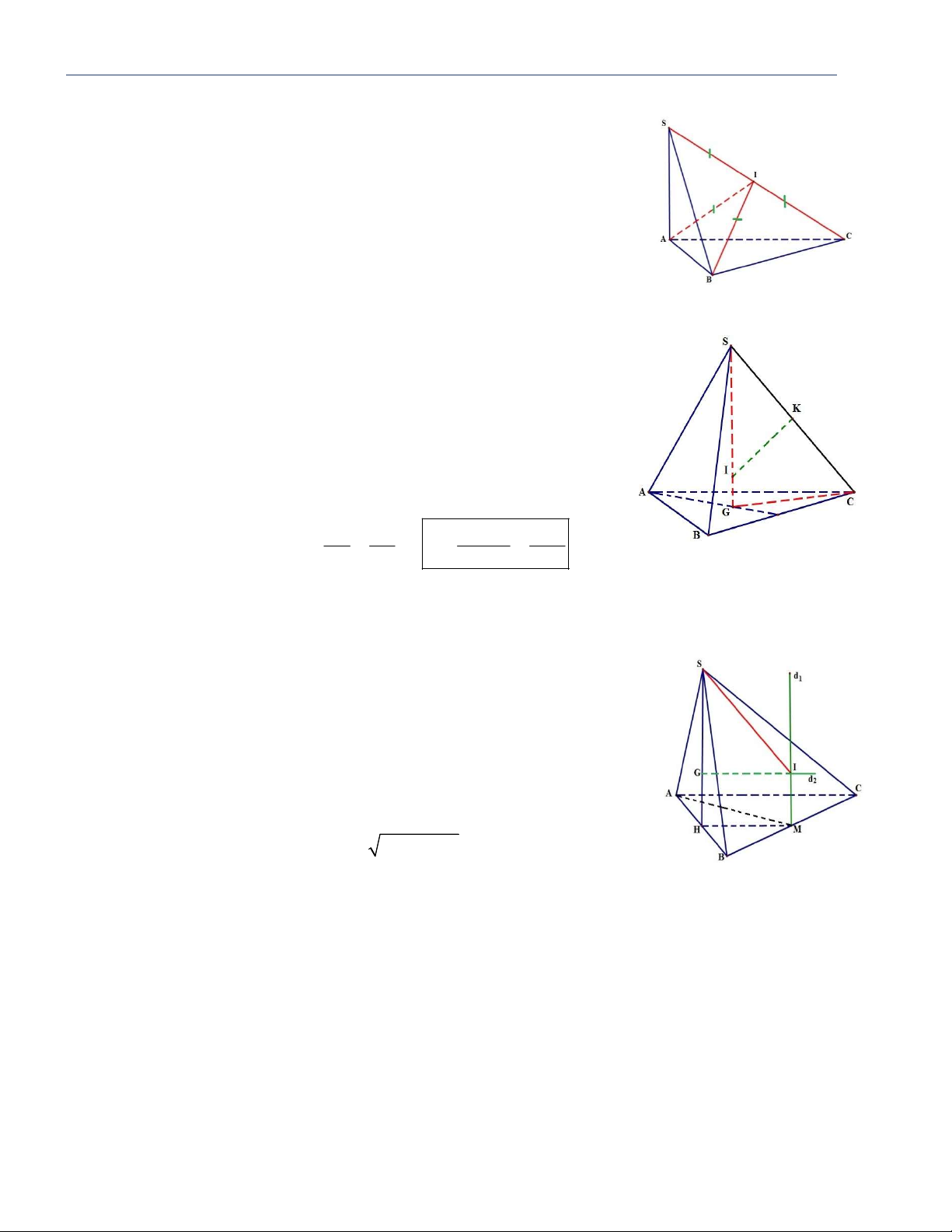
Dạng 1: Chóp có các điểm cùng nhìn một đoạn dưới một góc vuông. SA ABC BC AB gt Ví dụ: Cho S.ABC : . Theo đề bài: ABC B BC SA SA ABC
BC (SAB) BC SB
Ta có B và A nhìn SC dưới một góc vuông
nên B và A cùng nằm trên một mặt cầu có đường kính là SC.
Gọi I là trung điểm SC I là tâm MCNT khối chóp S.ABC và bán kính R SI .
Dạng 2: Chóp có các cạnh bên bằng nhau.
Ví dụ: Cho hình chóp tam giác đều S.ABC .
+ Vẽ SG ABC thì G là tâm đường tròn ngoại tiếp ABC .
+ Trên mặt phẳng SGC , vẽ đường trung trực của SC , đường này cắt
SG tại I thì I là tâm mặt cầu ngoại tiếp S.ABC và bán kính R IS . 2 SG SC SC.SK SC
+ Ta có SGC SKI g g R SK SI SG 2SG
Dạng 3: Chóp có một mặt bên vuông góc với đáy.
Ví dụ: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A. Mặt bên SAB ABC và S AB đều.
Gọi H , M lần lượt là trung điểm của AB, AC .
Ta có M là tâm đường tròn ngoại tiếp A
BC (do MA MB MC ). Dựng d A BC d M SH
1 là trục đường tròn ngoại tiếp ( 1 qua và song song ).
Gọi G là tâm đường tròn ngoại tiếp S
AB và d2 là trục đường tròn ngoại tiếp S AB , d d I I 2 cắt 1 tại
là tâm mặt cầu ngoại tiếp khối chóp S.ABC
Bán kính R SI . Xét 2 2 S GI SI GI SG .
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 38
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu B. BÀI TẬP TRẮC NGHIỆM ĐỀ ÔN TẬP SÔ 1
Câu 1. Cho một mặt cầu có diện tích là S , thể tích khối cầu đó là V . Tính bán kính R của mặt cầu. 3V S V A. R . B. R 4V . C. R . D. R . S 3V S 3S
Câu 2. Cho mặt cầu S(O; R) và điểm A cố định với OA d . Qua A , kẻ đường thẳng tiếp xúc với mặt
cầu S(O; R) tại M . Công thức nào sau đây được dùng để tính độ dài đoạn thẳng AM ? A. 2 2 2R d . B. 2 2 d R . C. 2 2 R 2d . D. 2 2 d R .
Câu 3. Một hình hộp chữ nhật có ba kích thước là a, ,
b c . Gọi (S) là mặt cầu đi qua 8 đỉnh của hình hộp
chữ nhật đó. Tính diện tích của hình cầu (S) theo a, , b c . A. 2 2 2 (a b c ) . B. 2 2 2 2 (a b c ) . C. 2 2 2 4 (a b c ) . D. 2 2 2 (a b c ) . 2
Câu 4. Một hình hộp chữ nhật có ba kích thước là a, ,
b c . Gọi (S) là mặt cầu đi qua 8 đỉnh của hình hộp
chữ nhật đó. Tâm của mặt cầu (S) là
A. một đỉnh bất kì của hình hộp chữ nhật.
B. tâm của một mặt bên của hình hộp chữ nhật.
C. trung điểm của một cạnh của hình hộp chữ nhật.
D. tâm của hình hộp chữ nhật.
Câu 5. Cho mặt cầu S(O; R) và đường thẳng . Biết khoảng cách từ O tới bằng d . Đường thẳng
tiếp xúc với S(O; R) khi thỏa mãn điều kiện nào trong các điều kiện sau ? A. d R . B. d R . C. d R . D. d R .
Câu 6. Cho đường tròn (C) và điểm A nằm ngoài mặt phẳng chứa (C) . Có tất cả bao nhiêu mặt cầu chứa
đường tròn (C) và đi qua A ? A. 2. B. 0. C. 1. D. vô số. Câu 7. Cho hai điểm ,
A B phân biệt. Tập hợp tâm những mặt cầu đi qua A và B là
A. mặt phẳng trung trực của đoạn thẳng AB . B. đường thẳng trung trực của AB .
C. mặt phẳng song song với đường thẳng AB . D. trung điểm của đoạn thẳng AB .
Câu 8. Cho mặt cầu S(O; R) và mặt phẳng ( ) . Biết khoảng cách từ O tới ( ) bằng d . Nếu d R thì
giao tuyến của mặt phẳng ( ) với mặt cầu S(O; R) là đường tròn có bán kính bằng bao nhiêu? A. Rd . B. 2 2 R d . C. 2 2 R d . D. 2 2 R 2d .
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 39
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu
Câu 9. Từ điểm M nằm ngoài mặt cầu S(O; R) có thể kẻ được bao nhiêu tiếp tuyến với mặt cầu ? A. Vô số. B. 0. C. 1. D. 2.
Câu 10. Một đường thẳng d thay đổi qua A và tiếp xúc với mặt cầu S(O; R) tại M . Gọi H là hình chiếu
của M lên đường thẳng OA . M thuộc mặt phẳng nào trong những mặt phẳng sau đây?
A. Mặt phẳng qua H và vuông góc với OA .
B. Mặt phẳng trung trực của OM .
C. Mặt phẳng qua O và vuông góc với AM . D. Mặt phẳng qua A và vuông góc với OM .
Câu 11. Một đường thẳng thay đổi d qua A và tiếp xúc với mặt cầu S(O; R) tại M . Gọi H là hình chiếu
của M lên đường thẳng OA . Độ dài đoạn thẳng MH tính theo R là: R R 3 2R 3 3R 3 A. . B. . C. . D. . 2 3 3 4 1 22
Câu 12. Thể tích của một khối cầu là 3
113 cm thì bán kính nó là bao nhiêu ? (lấy ) 7 7 A. 6 cm . B. 2 cm . C. 4 cm . D. 3cm .
Câu 13. Khinh khí cầu của nhà Mông–gôn–fie (Montgolfier) (người Pháp) phát minh ra khinh khí cầu dùng
khí nóng. Coi khinh khí cầu này là một mặt cầu có đường kính 11m thì diện tích của mặt khinh khí 22
cầu là bao nhiêu? (lấy
và làm tròn kết quả đến chữ số thập phân thứ hai). 7 A. 2 379, 94 (m ) . B. 2 697,19 (m ) . C. 190,14 cm . D. 2 95, 07 (m ) .
Câu 14. Cho hình lập phương ABC .
D A' B 'C ' D ' có độ dài mỗi cạnh là 10 cm . Gọi O là tâm mặt cầu đi qua
8 đỉnh của hình lập phương. Khi đó, diện tích S của mặt cầu và thể tích V của hình cầu là: A. 2 3
S 150 (cm );V 125 3 (cm ) . B. 2 3
S 100 3 (cm );V 500 (cm ) . C. 2 3
S 300 (cm );V 500 3 (cm ) . D. 2 3
S 250 (cm );V 500 6 (cm ) .
Câu 15. Cho đường tròn (C) ngoại tiếp một tam giác đều ABC có cạnh bằng a , chiều cao AH . Quay
đường tròn (C) xung quanh trục AH , ta được một mặt cầu. Thể tích của khối cầu tương ứng là: 3 a 3 3 4 a 3 4 a 3 3 4 a A. . B. . C. . D. . 54 9 27 3
Câu 16. Cho đường tròn (C) ngoại tiếp một tam giác đều ABC có cạnh bằng a , chiều cao AH . Quay
đường tròn (C) xung quanh trục AH , ta được một mặt cầu. Thể tích của khối cầu tương ứng là: 3 4 a 3 3 4 a 3 a 3 3 4 a A. . B. . C. . D. . 27 9 54 3
Câu 17. Cho hình chóp tứ giác đều S. ABCD có cạnh đáy và cạnh bên cùng bằng .
a Bán kính của mặt cầu
ngoại tiếp hình chóp này bằng
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 40
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu 2 3 A. a . B. a 2 . C. a 3 . D. a . 2 3
Câu 18. Mặt cầu có bán kính a 6 có thể tích là 4 6 A. 3 8 a . B. 3 4 6 a . C. 3 8 6 a . D. 3 a . 3
Câu 19. Gọi R là bán kính, S là diện tích và V là thể tích của một khối cầu. Công thức nào sai ? 4 A. 2 S 4 R . B. 3 V R . C. 2 S R . D. 3V SR . 3
Câu 20. Một mặt cầu có diện tích bằng cm2 100
thì đó bán kính bằng bao nhiêu ? 5 5 5 A. . B. . C. . D. . 5 5 ĐỀ ÔN TẬP SÔ 2 Câu 1.
Cho hình trụ có thiết diện qua trục là hình vuông cạnh a, khi đó thể tích khối cầu ngoại tiếp khối trụ là 3 4 a 3 4 a 2 3 a 3 a 2 A. . B. . C. . D. . 3 3 6 3
Câu 2. Cho tứ diện DABC có mặt đáy ABC là tam giác vuông tại B, DA vuông góc với mặt đáy. Biết
AB 3a, BC 4a, DA 5 .
a Mặt cầu ngoại tiếp hình chóp DABC có bán kính bằng 5a 2 5a 3 5a 2 5a 3 A. . B. . C. . D. . 2 2 3 3
Câu 3. Mặt cầu có bán kính a 3 có diện tích là A. 2 4 a . B. 2 12 a . C. 2 4 3a . D. 2 3 a .
Câu 4. Đường tròn lớn của một mặt cầu có chu vi bằng 4 . Thể tích của hình cầu là 16 8 4 32 A. . B. . C. . D. . 3 3 3 3
Câu 5. Một khối cầu có thể tích là 3
288 m . Diện tích của mặt cầu giới hạn khối cầu này bằng A. 2 72 m . B. 2 144 m . C. 2 36 m . D. 2 288 m .
Câu 6. Cho hình chóp S.ABCD có đáy là hình chữ nhật, SA ABCD . Tâm mặt cầu ngoại tiếp hình chóp S.ABCD là
A. Giao điểm của hai đường chéo AC và BD . B. Trọng tâm tam giác SAC . C. Trung điểm cạnh SD . D. Trung điểm cạnh SC .
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 41
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu
Câu 7. Thể tích của hình cầu có đường kính bằng 8 là 256 A. 64 64 . B. . C. . D. 256 . 3 3
Câu 8. Một khối cầu có bán kính 2R thì có thể tích bằng 3 4 R 3 24 R 3 32 R A. . B. 2 4 R . C. . D. . 3 3 3 2 8 a
Câu 9. Cho mặt cầu có diện tích bằng
. Khi đó, bán kính mặt cầu bằng 3 a 6 a 6 a 2 a 3 A. . B. . C. . D. . 2 3 3 3
Câu 10. Cho hình cầu có bán kính bằng 6 cm. Thể tích của hình cầu này là A. 72 cm3. B. 864 cm3. C. 48 cm3. D. 288 cm3.
Câu 11. Mặt cầu nội tiếp hình lập phương cạnh a (mặt cầu tiếp xúc với tất cả các mặt của hình lập phương) có thể tích bằng 3 4 a 3 8 a 3 a A. 3 2 a . B. . C. . D. . 3 3 6
Câu 12. Khối cầu có thể tích bằng 36 cm3 có bán kính là A. 3 cm. B. 3 3 cm. C. 2 cm. D. 27 cm.
Câu 13. Một mặt cầu có đường kính bằng 2a thì có diện tích bằng A. 2 2 a . B. 2 4 a . C. 2 8 a . D. 2 16 a .
Câu 14. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AC a 2, SA ABC, SC tạo với
đáy một góc 45 . Bán kính mặt cầu ngoại tiếp hình chóp bằng a 2 A. a 2 . B. a . C. . D. 2a 2 . 2
Câu 15. Mặt phẳng P cắt mặt cầu có tâm O theo đường tròn có bán kính bằng 4 cm và khoảng cách từ O
đến mặt phẳng P bằng 3 c .
m Bán kính của mặt cầu là A. 3 3 cm. B. 5 cm. C. 3 2 cm. D. 6 cm.
Câu 16. Thể tích của hình cầu ngoại tiếp hình lập phương cạnh bằng a là 3 4 a 3 3a A. 3 a . B. 3 4 3a . C. . D. . 3 2
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 42
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu
Câu 17. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, SA ABCD, SA AC. Bán kính
mặt cầu ngoại tiếp hình chóp bằng A. a . B. a 2 . C. 2a . D. 2a 2 .
Câu 18. Một mặt cầu có diện tích 2
36 m . Thể tích của khối cầu này bằng 4 A. 3 36 m . B. 3 m . C. 3 72 m . D. 3 108 m . 3
Câu 19. Cho mặt cầu S có đường kính 10cm và điểm A nằm ngoài S . Qua A dựng mặt phẳng (P) cắt
S theo một đường tròn có bán kính 4c .
m Số các mặt phẳng P là A. vô số. B. 0. C. 2. D. 1. 3 8 a 6
Câu 20. Cho khối cầu có thể tích bằng
. Khi đó, bán kính mặt cầu bằng 27 a 2 a 6 a 3 a 6 A. 3 . B. 3 . C. 3 . D. 2 . ĐỀ ÔN TẬP SÔ 3
Câu 1. Thể tích của khối cầu nội tiếp khối lập phương có cạnh bằng a là 2 3 1 2 3 a 3 a 3 a 3 a A. 3 . B. 6 . C. 6 . D. 9 .
Câu 2. Cho mặt cầu có bán kính bằng 5 cm. Diện tích của mặt cầu này là A. 100 cm. B. 50 cm2. C. 400 cm2. D. 500 cm2.
Câu 3. Bán kính của mặt cầu ngoại tiếp hình chóp tứ giác đều S.ABCD có cạnh đáy và cạnh bên cùng bằng a là 2 3 A. a 3 . B. a 2 . C. a . D. a . 2 3 Câu 4. Cho mặt cầu S R S R R 2R 2 1 có bán kính , mặt cầu có bán kính và
. Tỉ số diện tích của mặt 1 2 2 1 cầu S S1 2 và mặt cầu bằng 1 1 A. . B. . C. 2 . D. 4 . 4 2
Câu 5. Cho mặt cầu có bán kính R. Diện tích của mặt cầu đó bằng A. 2 R . B. 2 4 R . C. 2 6 R . D. 2 2 R .
Câu 6. Cho hình lập phương có cạnh bằng a, khi đó bán kính mặt cầu nội tiếp hình lập phương bằng
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 43
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu a 3 a 2 a a 2 A. . B. . C. . D. . 2 2 2 4
Câu 7. Mặt cầu có bán kính bằng 10 cm, khi đó diện tích mặt cầu bằng 100 400 A. 2 100 cm . B. 2 cm . C. 2 400 cm . D. 2 cm . 3 3
Câu 8. Cho hình tròn đường kính 4a quay quanh đường kính của nó. Khi đó thể tích khối tròn xoay sinh ra bằng 3 16 a 3 4 a 3 8 a 3 32 a A. . B. . C. . D. . 3 3 3 3
Câu 9. Mặt cầu đi qua các đỉnh của hình lập phương cạnh a có bán kính bằng a 3 A. a 3 . B. a . C. a 2 . D. . 2
Câu 10. Mặt cầu đi qua các đỉnh của hình hộp chữ nhật có ba kích thước 2, 3, 6 có bán kính bằng A. 5. B. 7. C. 49. D. 3,5.
Câu 11. Bán kính của mặt cầu có diện tích bằng 36 là: 1 1 A. . B. 3. C. . D. 9. 3 9
Câu 12. Gọi S là mặt cầu tâm O, bán kính R ; d là khoảng cách từ O đến mặt phẳng P, với d R .
Khi đó, số điểm chung giữa S và P là A. 2. B. vô số. C. 1. D. 0.
Câu 13. Một mặt cầu có bán kính R 3 thì có diện tích bằng A. 2 4 R 3 . B. 2 12 R . C. 2 8 R . D. 2 4 R
Câu 14. Cho hình chóp S.ABCD có đáy là hình chữ nhật, SA vuông góc với mặt đáy. Đường kính mặt cầu
ngoại tiếp hình chóp S.ABCD bằng A. Độ dài cạnh SC .
B. Độ dài đường chéo AC. C. Độ dài cạnh SB . D. Độ dài cạnh SA .
Câu 15. Nếu tăng diện tích hình tròn lớn của một hình cầu lên 4 lần thì thể tích của hình cầu đó tăng lên bao nhiêu lần A. 8. B. 4. C. 6. D. 16.
Câu 16. Cho hình cầu có bán kính R. Khi đó thể tích khối cầu giới hạn bởi hình cầu đó bằng 3 3 R 3 3 R 3 4 R 3 2 R A. . B. . C. . D. . 4 2 3 3
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 44
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu
Câu 17. Trong các hình đa diện sau, hình nào luôn nội tiếp được trong một mặt cầu ? A. Hình tứ diện. B. Hình lăng trụ. C. Hình chóp. D. Hình hộp.
Câu 18. Cho hình lập phương cạnh a nội tiếp trong một mặt cầu. Bán kính đường tròn lớn của mặt cầu đó bằng a 3 a 2 A. . B. a 2 . C. D. a 3 . 2 2
Câu 19. Biết hình tròn lớn của một mặt cầu có chu vi bằng 6 . Thể tích của hình cầu này là A. 36 . B. 12 . C. 18 . D. 108 .
Câu 20. Khối cầu có diện tích bằng 32a 2 có bán kính là A. 4a . B. 3a . C. 2a 2 . D. 2a .
----------------------------------------------- ----------- HẾT ---------- ĐÁP ÁN ĐỀ 1 1 2 3 4 5 6 7 8 9 10 A B B D A C A C A A 11 12 13 14 15 16 17 18 19 20 B D A C C A A C C C ĐỀ 2 1 2 3 4 5 6 7 8 9 10 D A B D B D C D B D 11 12 13 14 15 16 17 18 19 20 D A B B B D C A A B ĐỀ 3 1 2 3 4 5 6 7 8 9 10 C A C D B C C D D D 11 12 13 14 15 16 17 18 19 20 B B B A A C A A A C
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 45
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu
CHUYÊN ĐỀ 7: HÌNH HỌC KHÔNG GIAN CHỦ ĐỀ: MẶT TRỤ A. – LÝ THUYẾT 1/ Mă ̣t tru ̣ tròn xoay
Trong mp P cho hai đường thẳng và l song song nhau, cách nhau một
khoảng r . Khi quay mp P quanh trục cố đi ̣nh thı̀ đường thẳng l sinh ra
một mă ̣t tròn xoay được gọi là mă ̣t trụ tròn xoay hay gọi tắt là mă ̣t trụ.
Đường thẳng được go ̣i là tru ̣C.
Đường thẳng l được go ̣i là đường sinh.
Khoảng cách r được go ̣i là bán kı́nh của mă ̣t tru ̣. 2/ Hı̀nh tru ̣ tròn xoay
Khi quay hı̀nh chữ nhâ ̣t ABCD xung quanh đường thẳng chứa mô ̣t ca ̣nh,
chẳng ha ̣n ca ̣nh AB thı̀ đường gấp khúc ABCD ta ̣o thành mô ̣t hı̀nh, hı̀nh
đó được go ̣i là hı̀nh tru ̣ tròn xoay hay go ̣i tắt là hı̀nh tru ̣.
Đường thẳng AB được go ̣i là tru ̣C.
Đoa ̣n thẳng CD được go ̣i là đường sinh.
Đô ̣ dài đoa ̣n thẳng AB CD h được go ̣i là chiều cao của hı̀nh tru ̣.
Hı̀nh tròn tâm A , bán kı́nh r AD và hı̀nh tròn tâm B , bán kı́nh r BC được gọi là 2 đáy của hı̀nh trụ.
Khối trụ tròn xoay, gọi tắt là khối trụ, là phần không gian giới ha ̣n bởi hı̀nh trụ tròn xoay kể cả hı̀nh trụ.
3/ Công thức tı́nh diê ̣n tı́ch và thể tı́ch của hı̀nh tru ̣
Cho hı̀nh tru ̣ có chiều cao là h và bán kı́nh đáy bằng r , khi đó:
Diê ̣n tı́ch xung quanh của hı̀nh tru ̣: S 2 rh xq
Diê ̣n tı́ch toàn phần của hı̀nh tru ̣: 2 S S 2.S 2 rh 2 r tp xq Ðay
Thể tı́ch khối tru ̣: 2 V . B h r h 4/ Tı́nh chất:
Nếu cắt mă ̣t tru ̣ tròn xoay (có bán kı́nh là r ) bởi mô ̣t mp vuông góc với tru ̣c thı̀ ta được
đường tròn có tâm trên và có bán kı́nh bằng r với r cũng chı́nh là bán kı́nh của mă ̣t tru ̣ đó.
Nếu cắt mă ̣t tru ̣ tròn xoay (có bán kı́nh là r ) bởi mô ̣t mp không vuông góc với tru ̣c nhưng cắt
tất cả các đường sinh, ta được giao tuyến là mô ̣t đường elı́p có tru ̣ nhỏ bằng 2r và tru ̣c lớn bằng
2r , trong đó là góc giữa trục và mp với 0 0 0 90 . sin
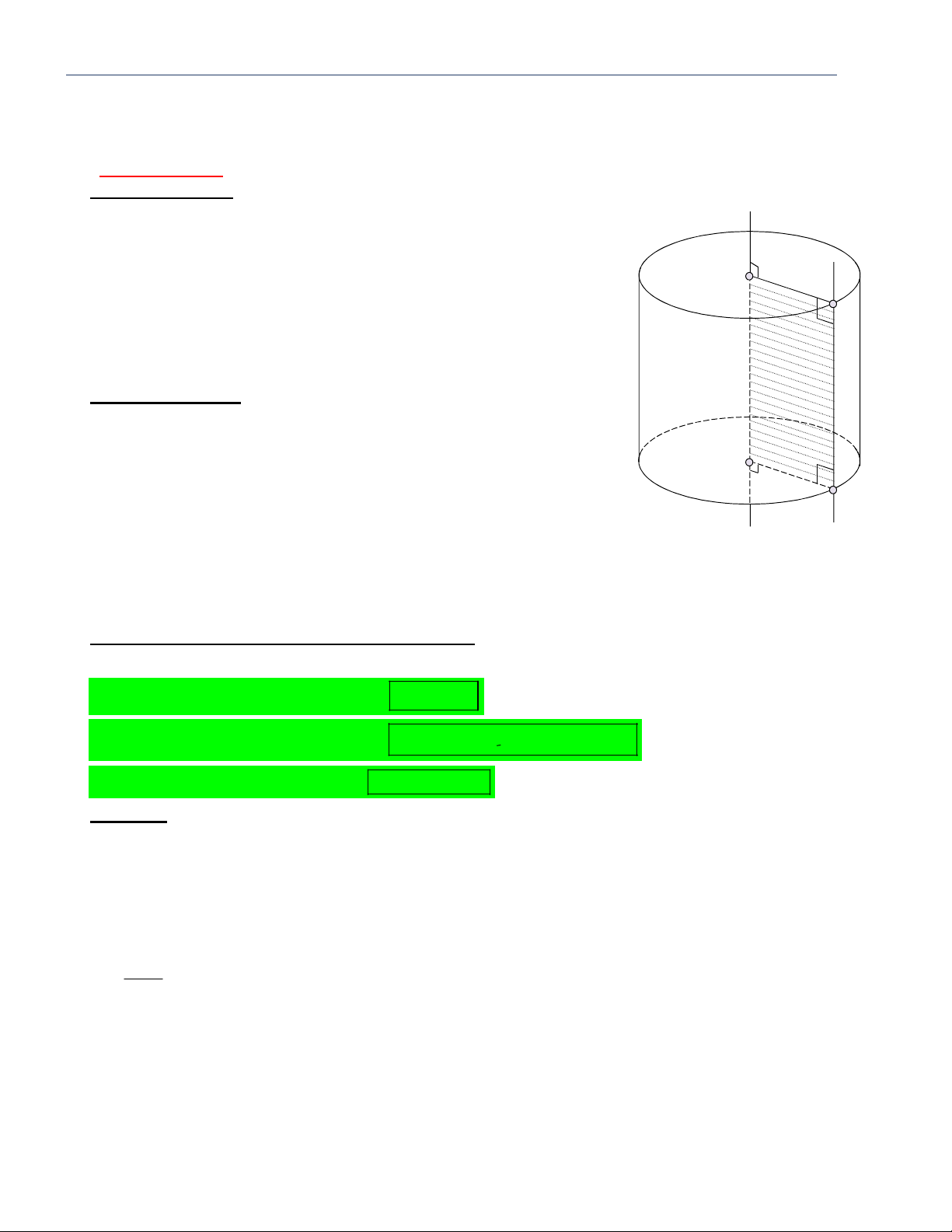
Cho mp song song với tru ̣c của mă ̣t tru ̣ tròn xoay và cách mô ̣t khoảng d .
+ Nếu d r thı̀ mp cắt mă ̣t tru ̣ theo hai đường sinh thiết diê ̣n là hı̀nh chữ nhâ ̣t.
+ Nếu d r thı̀ mp tiếp xúc với mă ̣t tru ̣ theo mô ̣t đường sinh.
+ Nếu d r thı̀ mp không cắt mă ̣t tru ̣.
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 46
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu
B. - BÀI TẬP TRẮC NGHIỆM
ĐỀ ÔN TẬP SỐ 1 (Có hình vẽ cụ thể)
Câu 1: Tính thể tích V của khối trụ có bán kính đáy R , chiều cao là h . A. 2 V R h . B. 2 V Rh . C. 2 V Rh . D. V 2 Rh .
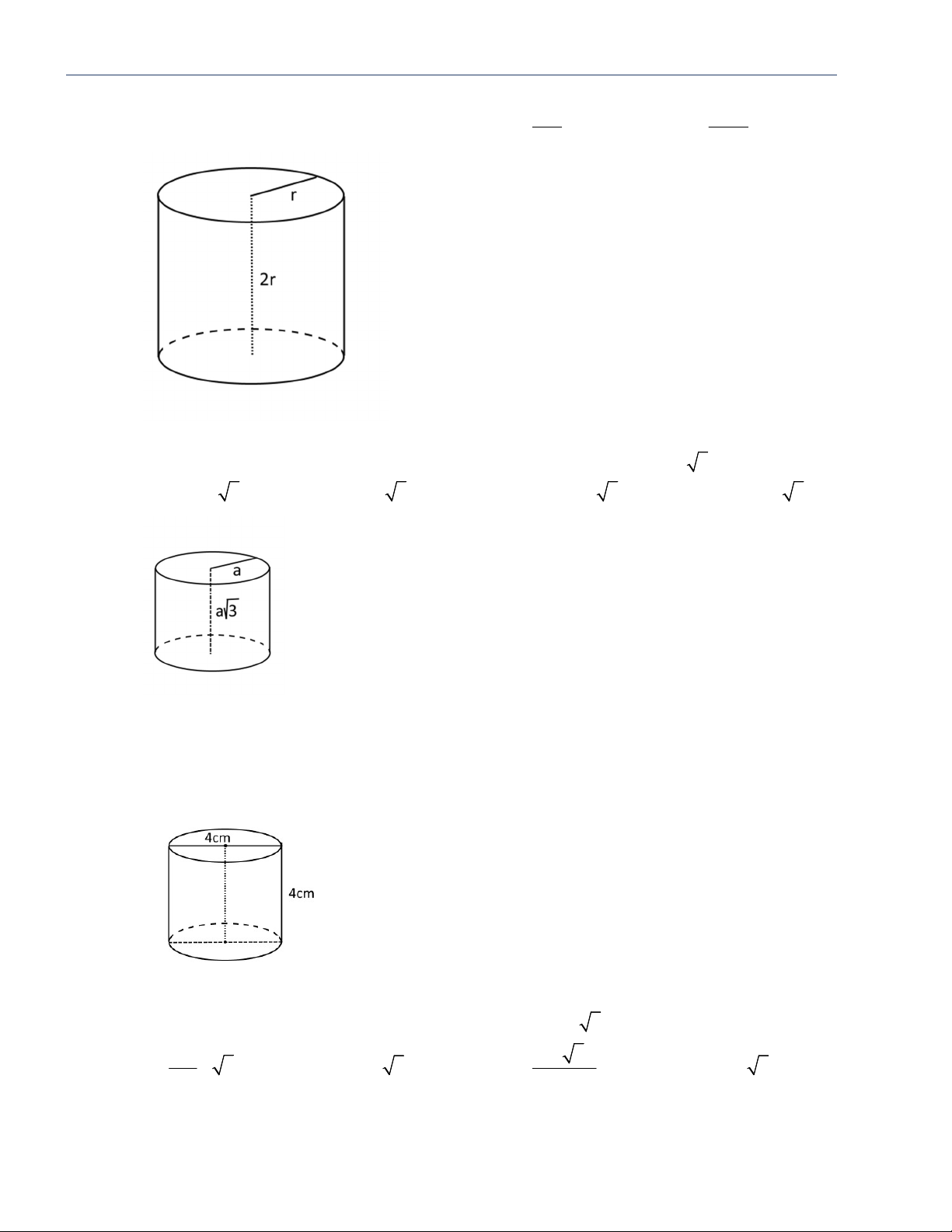
Câu 2: Một hình trụ có bán kính đáy a , có thiết diện qua trục là một hình vuông. Tính diện tích xung quanh của hình trụ. A. 2 a . B. 2 2 a . C. 2 3 a . D. 2 4 a .
Câu 3: Thiết diện qua trục của một hình trụ là hình vuông có cạnh 2 .
a Diện tích xung quanh của hình trụ này bằng A. 2 2 a . B. 2 4 a . C. 2 8 a . D. 2 6 a .
Câu 4: Tính thể tích của khối trụ biết bán kính đáy của hình trụ đó bằng a và thiết diện đi qua trục là một hình vuông. 2 A. 3 2 a . B. 3 a . C. 3 4 a . D. 3 a . 3
Câu 5: Một hình trụ có bán kính đường tròn đáy là r và chiều cao bằng 2r. Khi đó thể tích khối trụ giới
hạn bởi hình trụ đã cho là
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 47
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu 3 r 3 2 r A. 3 2 r . B. 3 r . C. . D. . 3 3
Câu 6: Tính diện tích toàn phần của hình trụ có bán kính đáy a và đường cao a 3 . A. 2 2 a 3 1 . B. 2 a 3 . C. 2 a 1 3 . D. 2 2 a 1 3 .
Câu 7: Thiết diện qua trục của một hình trụ là một hình vuông cạnh bằng 4 cm. Diện tích toàn phần của hình trụ là A. 20 cm2. B. 16 cm2. C. 48 cm2. D. 24 cm2.
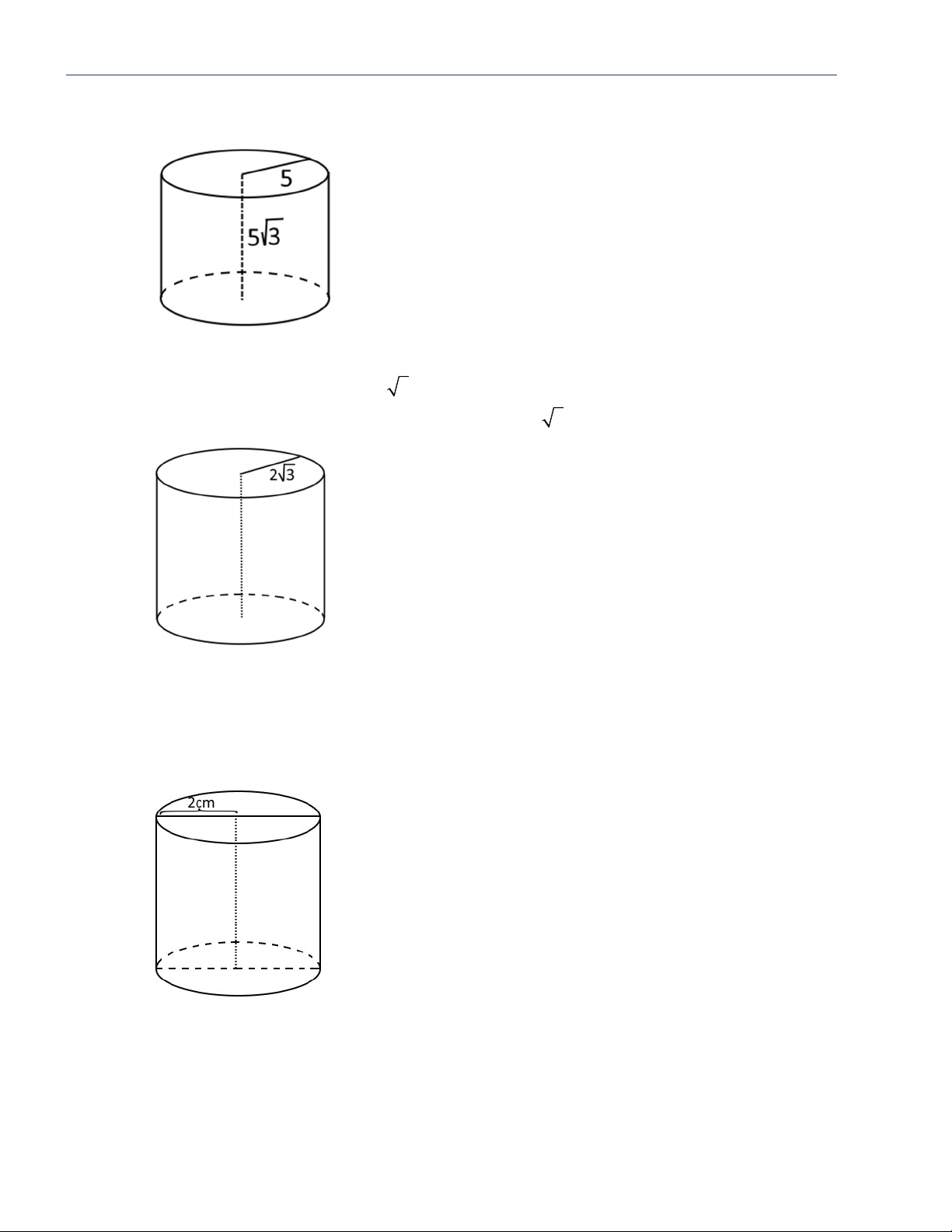
Câu 8: Thể tích của khối trụ có bán kính r 5 và chiều cao h 5 3 là 125 250 3 A. 3 3 cm . B. 3 500 3 cm . C. 3 cm . D. 3 125 3 cm . 3 3
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 48
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu
Câu 9: Hình trụ có bán kính đáy bằng 2 3 và thể tích bằng 24 . Chiều cao của hình trụ này bằng A. 6. B. 2. C. 2 3 . D. 1.
Câu 10: Một hình trụ có bán kính đáy bằng 2 cm, thiết diện qua trục là hình vuông. Thể tích của khối trụ tương ứng bằng: A. 3 24 cm . B. 3 12 cm . C. 3 20 3 cm 16 cm . D. .
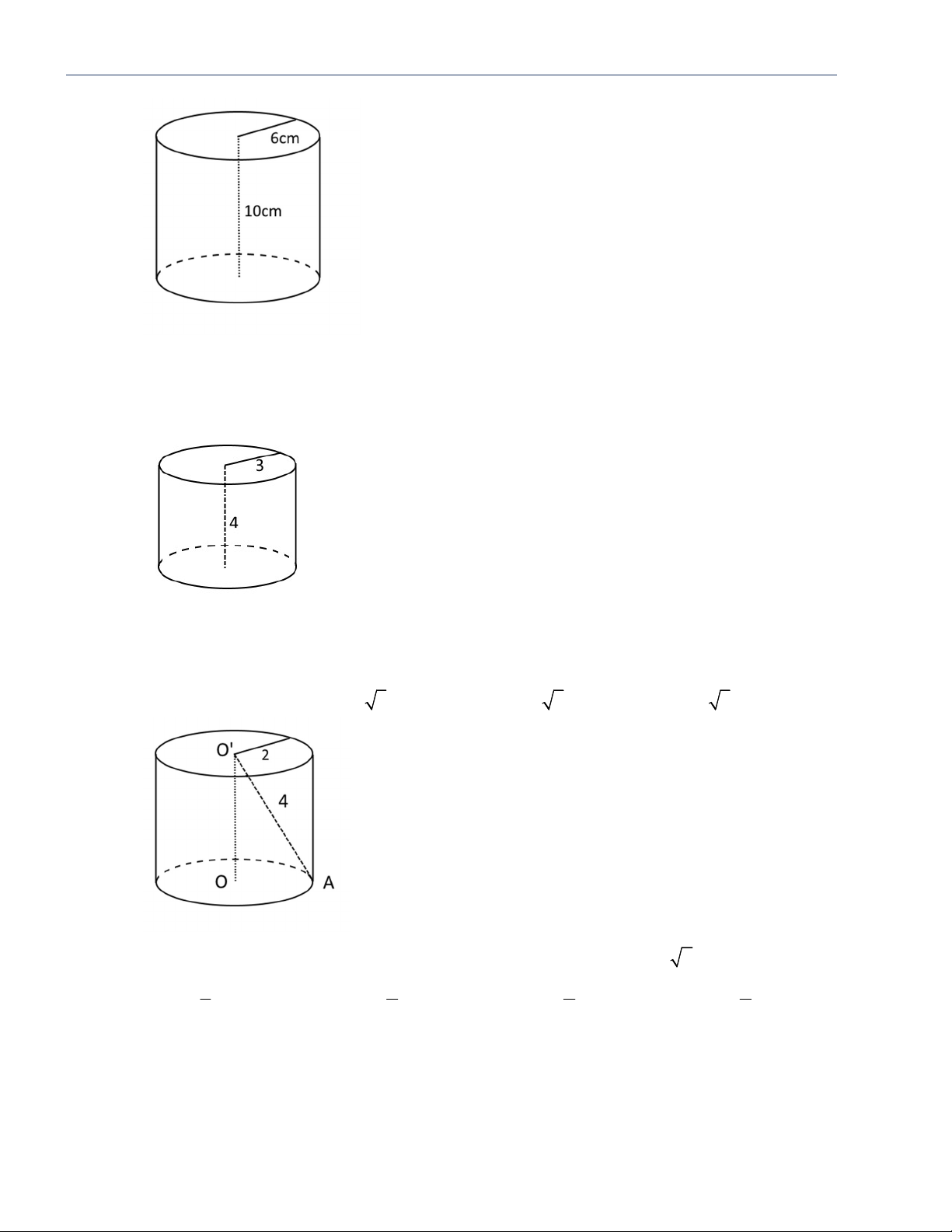
Câu 11: Một hình trụ có bán kính đáy 6 cm, chiều cao 10 cm. Thể tích của khối trụ này là A. 3 360 (cm ) . B. 3 300 (cm ) . C. 3 340 (cm ) . D. 3 320 (cm ) .
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 49
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu
Câu 12: Một hình trụ có bán kính bằng 3 và đường cao bằng 4 thì có diện tích xung quanh bằng A. 12 . B. 24 . C. 30 . D. 15 .
Câu 13: Cho hình trụ có các đáy là hai hình tròn tâm O và O , bán kính đáy bằng 2. Trên đường tròn đáy
tâm O lấy điểm A sao cho O A
4. Chiều cao của hình trụ đó là A. 3. B. 2 3 . C. 2 5 . D. 3 .
Câu 14: Thể tích V của khối trụ có chiều cao bằng a và đường kính đáy bằng a 2 là 1 1 2 1 A. 3 V a . B. 3 V a . C. 3 V a . D. 3 V a . 3 6 3 2
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 50
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu
Câu 15: Cho hình trụ có đường sinh l 2a , đáy là hình tròn ngoại tiếp hình vuông cạnh . a Thể tích khối
trụ giới hạn bởi hình trụ đó là 1 2 A. 3 a . B. 3 a . C. 3 a . D. 3 2a . 3 3
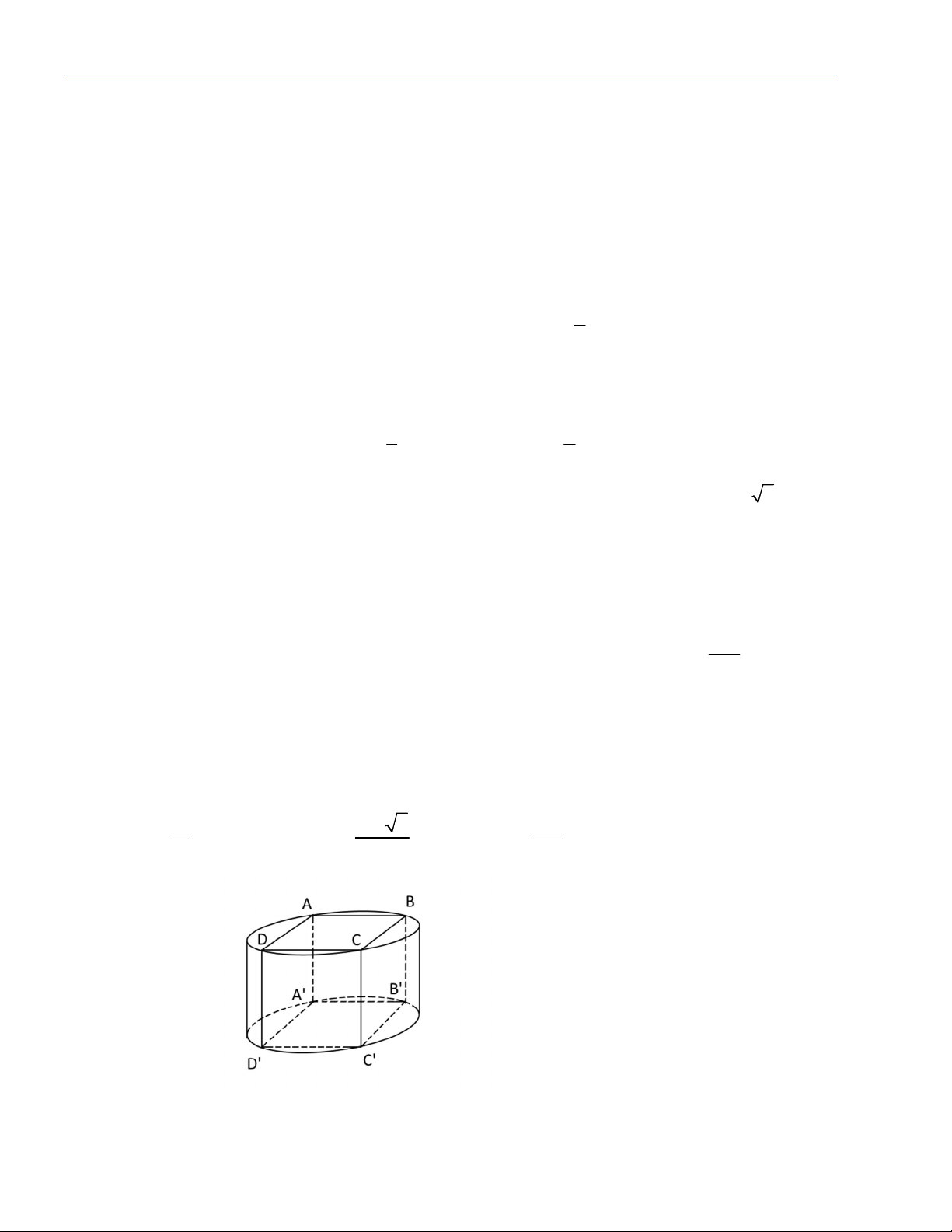
Câu 16: Trong không gian, cho hình chữ nhật ABCD có AB 1 và AD 2 . Gọi M, N lần lượt là trung
điểm của AD và BC . Quay hình chữ nhật đó xung quanh trục MN, ta được một hình trụ. Tính diện
tích toàn phần Stp của hình trụ đó. A. S 6 S 2 S 4 S 10 tp . B. tp . C. tp . D. tp .
Câu 17: Từ một tấm tôn hình chữ nhật kích thước 50cm x 240cm, người ta làm các thùng đựng nước hình
trụ có chiều cao bằng 50cm, theo hai cách sau (xem hình minh họa dưới đây):.
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 51
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu .
- Cách 1: Gò tấm tôn ban đầu thành mặt xung quanh của thùng.
- Cách 2: Cắt tấm tôn ban đầu thành hai tấm bằng nhau, rồi gò mỗi tấm đó thành mặt xung quanh của một thùng.
Kí hiệu V là thể tích của thùng gò được theo cách 1 và V là tổng thể tích của hai thùng gò được 1 2 V
theo cách 2. Tính tỉ số 1 . V2 V V V 1 V A. 1 1. B. 1 2 . C. 1 . D. 1 4 . V V V 2 V 2 2 2 2
Câu 18: Cho hình chữ nhật ABCD có AB = a, AD = a 3 quay quanh cạnh AB của nó. Diện tích xung quanh
của hình tròn xoay sinh ra bằng A. 2 12a . B. 2 12 a 3 . C. 2 6a . D. 2 2 a 3 .
Câu 19: Cho hình chữ nhật ABCD cạnh AB 4, AD 2. Gọi M , N là trung điểm các cạnh AB và C . D
Cho hình chữ nhật quay quanh MN , ta được hình trụ tròn xoay có thể tích bằng A. V 16 . B. V 4 . C. V 8 . D. V 32 .
Câu 20: Cho hình vuông ABCD cạnh .
a Gọi M, N lần lượt là trung điểm AB và C . D Quay hình vuông đó
quanh trục MN ta được hình trụ có thể tích là
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 52
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu 3 a 3 a 3 a 3 a A. . B. . C. . D. . 4 12 2 6
ĐỀ ÔN TẬP SỐ 2 ( Tự luyện)
Câu 1: Cho một hình trụ có bán kính đáy R , chiều cao h và thể tích V ; một hình nón có đáy trùng với một 1
đáy của hình trụ, có đỉnh trùng với tâm đáy còn lại của hình trụ (hình vẽ bên dưới) và có thể tích V2
. Khẳng định nào sau đây là khẳng định đúng ? h R A.V 3V . B. V 2V . C. V 3V . D. V V . 2 1 1 2 1 2 2 1
Câu 2: Tính thể tích của khối trụ biết chu vi đáy của hình trụ đó bằng 6 (cm) và thiết diện đi qua trục là
một hình chữ nhật có độ dài đường chéo bằng 10 (cm) . A. 3 48 (cm ) . B. 3 24 (cm ) . C. 3 72 (cm ) . D. 3 18 3472 (cm ) .
Câu 3: Một hình trụ có mặt đáy là hình tròn ngoại tiếp hình vuông có cạnh bằng 4 và độ dài đường sinh
bằng 8 thì có diện tích xung quanh bằng A. 32 2 . B. 32 . C. 32 . D. 32 2 .
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 53
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu
Câu 4: Cho hình chữ nhật ABCD có AB a, AD a 3 quay quanh cạnh AB của nó. Thể tích của khối tròn xoay sinh ra bằng: 1 A. 3 3a . B. 3 a 3 . C. 3 a 3 . D. 3 a . 3
Câu 5: Cho hình trụ (T ) có bán kính mặt đáy bằng 5cm, thiết diện qua trục của (T ) có diện tích bằng 2
20 cm . Khi đó hình trụ (T ) có diện tích xung quanh bằng bao nhiêu ? A. 2 30 cm . B. 2 20 cm . C. 2 45 cm . D. 2 15 cm .
Câu 6: Một hình vuông cạnh a quay xung quanh một cạnh của nó tạo thành một hình tròn xoay có diện tích bằng bao nhiêu ? A. 2 6a . B. 2 3a . C. 2 4a . D. 2 2a .
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 54
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu
Câu 7: Cho hình trụ có hai đáy là hình tròn nội tiếp của hình lập phương cạnh .
a Diện tích xung quanh của hình trụ đó bằng 2 a A. 3 a . B. 2 a . C. 2 2 a . D. . 2
Câu 8: Một hình trụ có đường kính đáy là 10cm , khoảng cách hai mặt đáy bằng 7cm . Khi đó diện tích xung
quanh của hình trụ đó bằng bao nhiêu ? A. 2 70 cm . B. 2 35 cm . C. 2 140 cm . D. 2 175 cm .
Câu 9: Một hình trụ có bán kính đường tròn đáy bằng 2 và chiều cao bằng 2 3 . Khi đó diện tích xung quanh của hình trụ là A. 2 3 . B. 4 3 . C. 8 3 . D. 16 .
Câu 10: Thiết diện qua trục của hình trụ là một hình vuông có cạnh bằng 2 .
a Khi đó thể tích khối trụ là A. 3 8a . B. 3 4a . C. 3 2a . D. 3 a .
Câu 11: Khối trụ có đường kính đáy và đường cao cùng bằng 2a thì có thể tích bằng A. 3 2 a . B. 3 a . C. 3 3 a . D. 3 4 a .
Câu 12: Gọi l, h, R lần lượt là độ dài đường sinh, chiều cao và bán kính mặt đáy của hình trụ (T ). Diện tích
toàn phần Stp của hình trụ (T) tính bởi công thức A. 2 S Rl R 2 S Rl 2 R 2 S 2 Rl 2 R 2 S Rh R tp . B. tp . C. tp . D. tp .
Câu 13: Gọi l, h, R lần lượt là độ dài đường sinh, chiều cao và bán kính mặt đáy của hình trụ (T ). Diện tích
xung quanh Sxq của hình trụ (T) tính bởi công thức
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 55
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu A. S Rl S 2 Rl 2 S R h S Rh xq . B. xq . C. xq . D. xq .
Câu 14: Gọi l, h, R lần lượt là độ dài đường sinh, chiều cao và bán kính mặt đáy của một hình trụ. Đẳng
thức nào sau đây luôn đúng ? A. R h . B. 2 2 2 l h R . C. l h . D. 2 2 2 R h l .
Câu 15: Thiết diện qua trục của hình trụ (T ) là một hình vuông có cạnh bằng . a Diện tích xung quanh Sxq của hình trụ (T ) là 1 A. 2 S 2 a 2 S a 2 S a 2 S a xq . B. xq . C. xq . D. xq . 2
Câu 16: Gọi l, h, R lần lượt là độ dài đường sinh, chiều cao và bán kính mặt đáy của khối trụ (T ). Thể tích
V của khối trụ (T ) tính bởi công thức 1 4 A. 3 V 4 R . B. 2 V R l . C. 2 V R h . D. 2 V R h . 3 3
Câu 17: Cho hình trụ có đường cao h a , đáy là hình tròn ngoại tiếp hình vuông cạnh a 2. Thể tích khối trụ là A. 2 6a . B. 2 2a . C. 2 a . D. 2 4a .
Câu 18: Quay hình vuông ABCD với cạnh a xung quanh trục là một đường trung bình của nó tạo thành một
hình trụ tròn xoay. Tính diện tích của hình trụ tròn xoay đó ? 2 a A. 2 a . B. 2 4 a . C. 2 2 a . D. . 2
Câu 19: Một hình trụ có chiều cao 5m và bán kính đường tròn đáy 3m . Diện tích xung quanh của hình trụ này là A. 2 45 (m ) . B. 2 30 (m ) . C. 2 15 (m ) . D. 2 48 (m ) .
Câu 20: Khối trụ ngoại tiếp hình lập phương ABC . D AB C D
cạnh a có thể tích bằng bao nhiêu ? 3 a 3 a 2 3 a A. . B. . C. . D. 3 a . 2 2 2
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 56
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu
Câu 21: Cho hình trụ có bán kı́nh đáy bằng 10, khoảng cách giữa hai đáy bằng 5. Diện tı́ch toàn phần của hình trụ đó bằng A. 400 . B. 200 . C. 250 . D. 300 .
Câu 22: Một hình trụ có chu vi của đường tròn đáy 4 a, chiều cao .
a Thể tích của khối trụ này bằng 4 A. 3 16 a . B. 3 2 a . C. 3 4 a . D. 3 a . 3
Câu 23: Cho hình chữ nhật ABCD có AB 4, AD 3. Quay hình chữ nhật đó quanh trục AB ta được một
hình trụ có thể tích là A. 36 . B. 36 . C. 48. D. 48 .
Câu 24: Cho hình trụ có bán kính đáy 5c , m chiều cao 4c .
m Diện tích toàn phần của hình trụ này là A. 2 92 cm . B. 2 94 cm . C. 2 90 cm . D. 2 96 cm .
Câu 25: Một hình trụ có bán kính đáy bằng 4cm, thiết diện qua trục là một hình vuông. Diện tích xung quanh của hình trụ bằng A. 2 64 cm . B. 2 16 cm . C. 2 32 cm . D. 2 24 cm .
Câu 26: Cho hình chữ nhật ABCD có AB 1, BC 2 . Quay hình chữ nhật ABCD đó xung quanh cạnh AD
tạo thành một hình trụ tròn xoay. Hình trụ đó có thể tích bằng bao nhiêu ? A. 8 . B. 4 . C. 2 . D. 2 .
Câu 27: Một hình trụ có bán kính mặt đáy bằng 5c ,
m đường cao bằng 7cm thì có thể tích bằng 175 A. 3 245 cm . B. 3 cm . C. 3 70 cm . D. 3 175 cm . 3
Câu 28: Một hình trụ có bán kính đáy và chiều cao không đổi. Hai điểm A và B lần lượt di động trên mỗi
đáy sao cho độ dài đoạn thẳng AB không đổi. Tập hợp các trung điểm của đoạn thẳng AB là A. đường tròn. B. mặt trụ. C. mặt cầu. D. đoạn thẳng. ----------- HẾT ----------
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 57
Tài liệu ôn tập THPT Quốc gia năm 2017 Dành cho học sinh TB – Yếu BẢNG ĐÁP ÁN ĐỀ 1 1 2 3 4 5 6 7 8 9 10 A D B A A D D D B D 11 12 13 14 15 16 17 18 19 20 A B B D B C B D C A ĐỀ 2 1 2 3 4 5 6 7 8 9 10 C C A A B C D A C C 11 12 13 14 15 16 17 18 19 20 A C B C D D B A B C 21 22 23 24 25 26 27 28 D C B C A C D A
SẢN PHẨM HỢP TÁC CÙNG TOÁN HỌC BẮC TRUNG NAM Trang 58
Document Outline
- 1.pdf (p.1-2)
- 2.pdf (p.3-8)
- 3.pdf (p.9-26)
- 4.pdf (p.27-34)
- 5.pdf (p.35-47)
- 6.pdf (p.48-60)




