TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
DẠNG TOÁN DÀNH CHO ĐỐI TƯỢNG HỌC SINH TRUNG BÌNH
Dạng 1. Tìm khoảng đơn điệu của hàm số thông qua bảng biến thiên, đồ thị
Định lí (thừa nhận): Giả sử hàm số
( )y f x
có đạo hàm trên khoảng
.K
Nếu
( ) 0, f x x K
thì hàm số đồng biến trên khoảng
.K
Nếu
( ) 0, f x x K
thì hàm số nghịch biến trên khoảng
.K
Nếu
( ) 0, f x x K
thì hàm số không đổi trên khoảng
.K
Hình dáng đồ thị
Nếu hàm số đồng biến trên
K
thì từ trái sang phải đồ thị đi lên.
Nếu hàm số nghịch biến trên
K
thì từ trái sang phải đồ thị đi xuống.
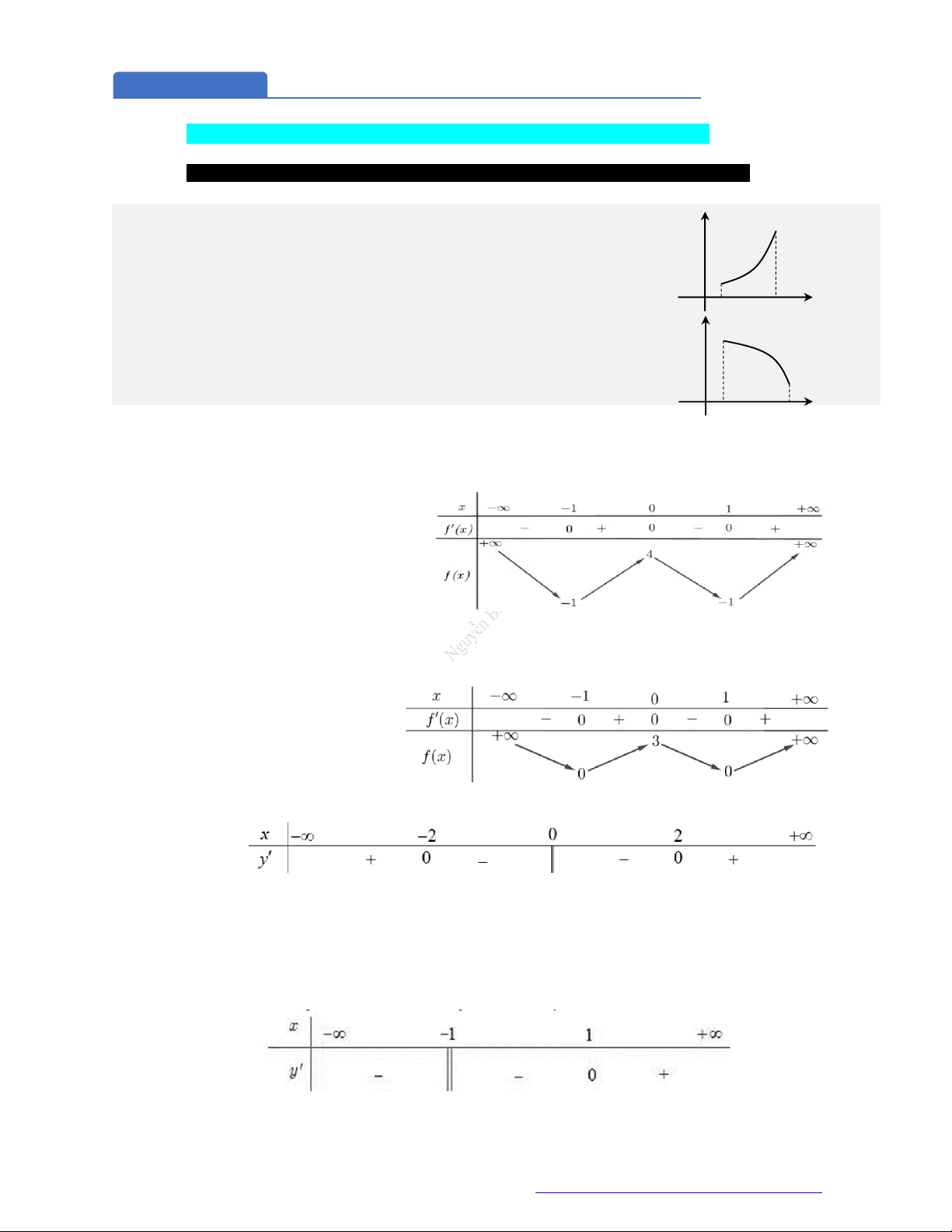
Câu 1. (Mã 101 – 2020 Lần 1) Cho hàm số
f x
có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
; 1
.
B.
0;1
.
C.
1;1
.
D.
1;0
Câu 2. (Mã 103 - 2019) Cho hàm số
f x
có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào sau đây?
A.
; 1 .
B.
0;1 .
C.
1;0 .
D.
1; .
Câu 3. (Mã 104 - 2017) Cho hàm số
y f x
có bảng xét dấu đạo hàm như sau
Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng
; 2
B. Hàm số đồng biến trên khoảng
2;0
C. Hàm số đồng biến trên khoảng
;0
D. Hàm số nghịch biến trên khoảng
0;2
Câu 4. (Kim Liên - Hà Nội - 2019) Cho hàm số
y f x
có bảng xét dấu của đạo hàm như hình vẽ.
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
1;
. B.
;1
. C.
1;
. D.
; 1
.
TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
Chuyên đề 1
x
y
a
b
Đồng biến
O
Nghịch biến
x
y
a
b
O

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 5. (Mã 101 - 2018) Cho hàm số
y f x
có bảng biến thiên như sau
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
1;0
B.
;0
C.
1;
D.
0;1
Câu 6. (Mã 102 - 2019) Cho hàm số
f x
có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây
A.
0;
.
B.
0;2
.
C.
2;0
.
D.
; 2
.
Câu 7. (Mã 103 - 2018) Cho hàm số
y f x
có bảng biến thiên như sau :
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
0;1
B.
1;
C.
;1
D.
1;0
Câu 8. (Mã 101 - 2019) Cho hàm số có bảng biến thiên như sau
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
0;2 .
B.
0; .
C.
2;0 .
D.
2; .
Câu 9. (Mã 102 - 2018) Cho hàm số
y f x
có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
1;
.
B.
1;
.
C.
1;1
.
D.
;1
.
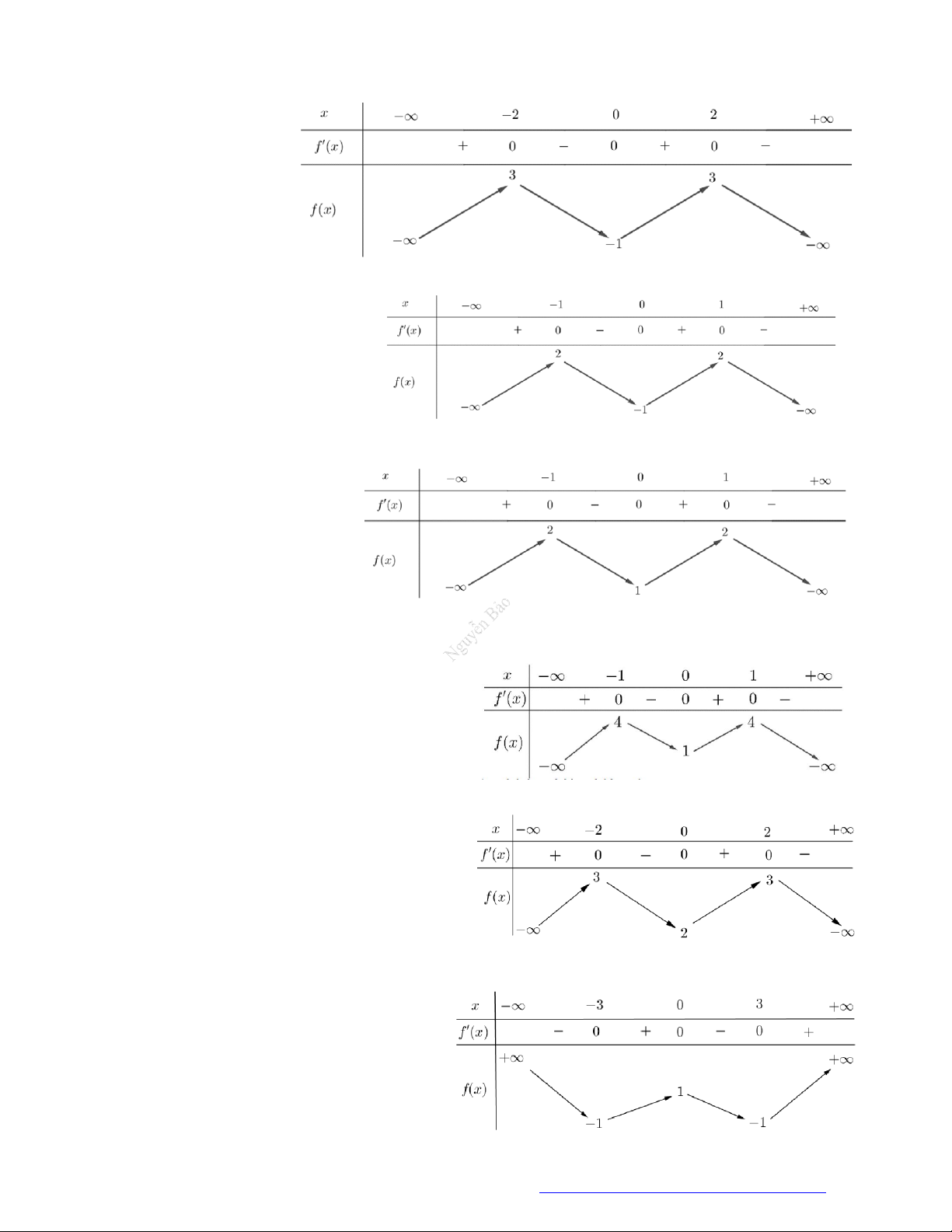
Câu 10. (Mã 104 -2018) Cho hàm số
y f x
có bảng biến thiên như sau
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
2;3
B.
3;
C.
; 2
D.
2;
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Câu 11. (Đề Tham Khảo 2018) Cho hàm số
y f x
có bảng biến thiên như sau:
Hàm số
y f x
nghịch biến trên khoảng nào dưới đây?
A.
0;
B.
; 2
C.
0;2
D.
2;0
Câu 12. (Đề Minh Họa 2020 – Lần 1) Cho hàm số
f x
có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
; 1
.
B.
0;1
.
C.
1;0
.
D.
;0
.
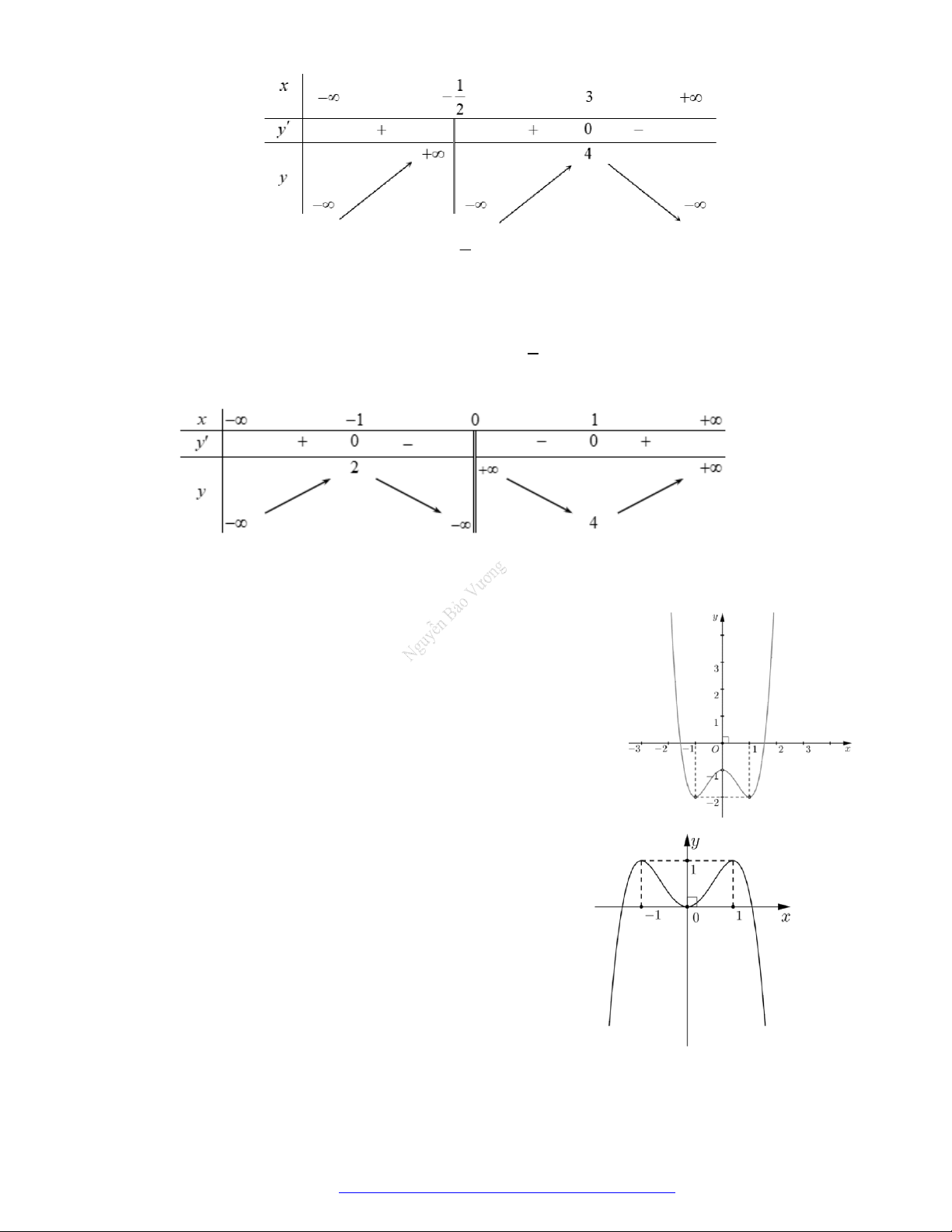
Câu 13. (Đề Minh Họa 2020 – Lần 2) Cho hàm số
y f x
có bảng biến thiên như sau
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
1;
.
B.
1;0
.
C.
1;1
.
D.
0;1
.
Câu 14. (Mã 102 – 2020 Lần 1) Cho hàm số có bảng biến thiên như sau.
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A. .
B. .
C. .
D. .
Câu 15. (Mã 103 – 2020 Lần 1) Cho hàm số
( )f x
có bảng biến thiên như sau:
Hàm số đã chođồng biến trên khoảng nào dưới đây
A.
( 2;2)
B.
(0;2)
C.
( 2;0)
D.
(2; )
.
Câu 16. (Mã 104 – 2020 Lần 1) Cho hàm số
f x
có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
3;0
.
B.
3;3
.
C.
0;3
.
D.
; 3
.
f x
1;
1;1
0;1
1;0
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 17. Cho hàm số
y f x
có bảng biến thiên như hình dưới đây. Mệnh đề nào sau đây là đúng?
A. Hàm số đã cho đồng biến trên khoảng
1
;
2
.
B. Hàm số đã cho đồng biến trên khoảng
;3
.
C. Hàm số đã cho nghịch biến trên khoảng
3;
.
D. Hàm số đã cho nghịch biến trên các khoảng
1
;
2
và
3;
.
Câu 18. Cho hàm số
y f x
có bảng biến thiên như sau:
Hàm số nghịch biến trong khoảng nào?
A.
1;1
. B.
0;1
. C.
4;
. D.
;2
.
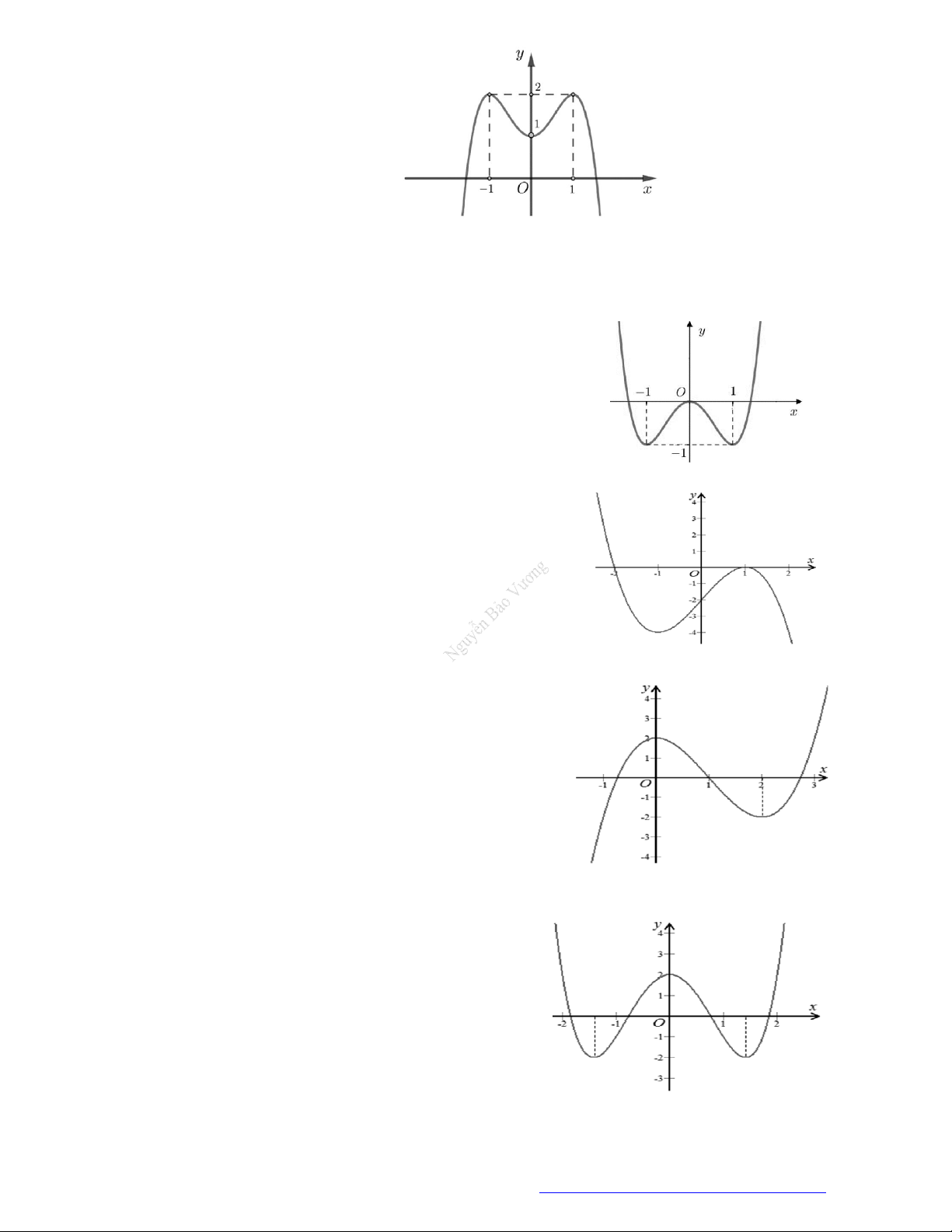
Câu 19. (Đề Tham Khảo 2019) Cho hàm số
y f x
có đồ thị như hình vẽ bên.
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
1
B.
1;1
C.
1;0
D.
0;1
Câu 20. (Mã 102 – 2020 – Lần 2) Cho hàm số
y f x
có đồ thị là đường cong trong hình bên.
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
1;0 .
B.
; 1
.
C.
0;1
.
D.
0;
.
Câu 21. (Mã 107 – 2020 Lần 2) Cho hàm số
y f x
có đồ thị là đường cong trong hình bên.
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
0;1
. B.
;0
. C.
1;
. D.
1;0
.
Câu 22. (Mã 103 – 2020 – Lần 2) Cho hàm số
y f x
có đồ thị là đường cong hình bên. Hàm số đã
cho đồng biến trên khoảng nào dưới đây?
A.
1;0
.
B.
; 1
.
C.
0;
.
D.
0;1
.
Câu 23. Cho hàm số
y f x
có đồ thị như hình vẽ bên. Hàm số đã cho đồng biến trên khoảng nào dưới
đây?
A.
; 1 .
B.
1;1 .
C.
0; .
D.
; .
Câu 24. Cho hàm số
y f x
có đồ thị như hình vẽ bên. Hàm số đã cho nghịch biến trên khoảng nào
dưới đây?
A.
1;1 .
B.
1; 2 .
C.
1;2 .
D.
2; .
Câu 25. Cho hàm số
y f x
có đồ thị như hình vẽ bên. Hàm số đã cho nghịch biến trên khoảng nào
dưới đây?
A.
; 1 .
B.
1;1 .
C.
1;2 .
D.
0;1 .
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
O
1
2
3
2
4
y
x
O
x
2
1
1
y
3
2
1
1
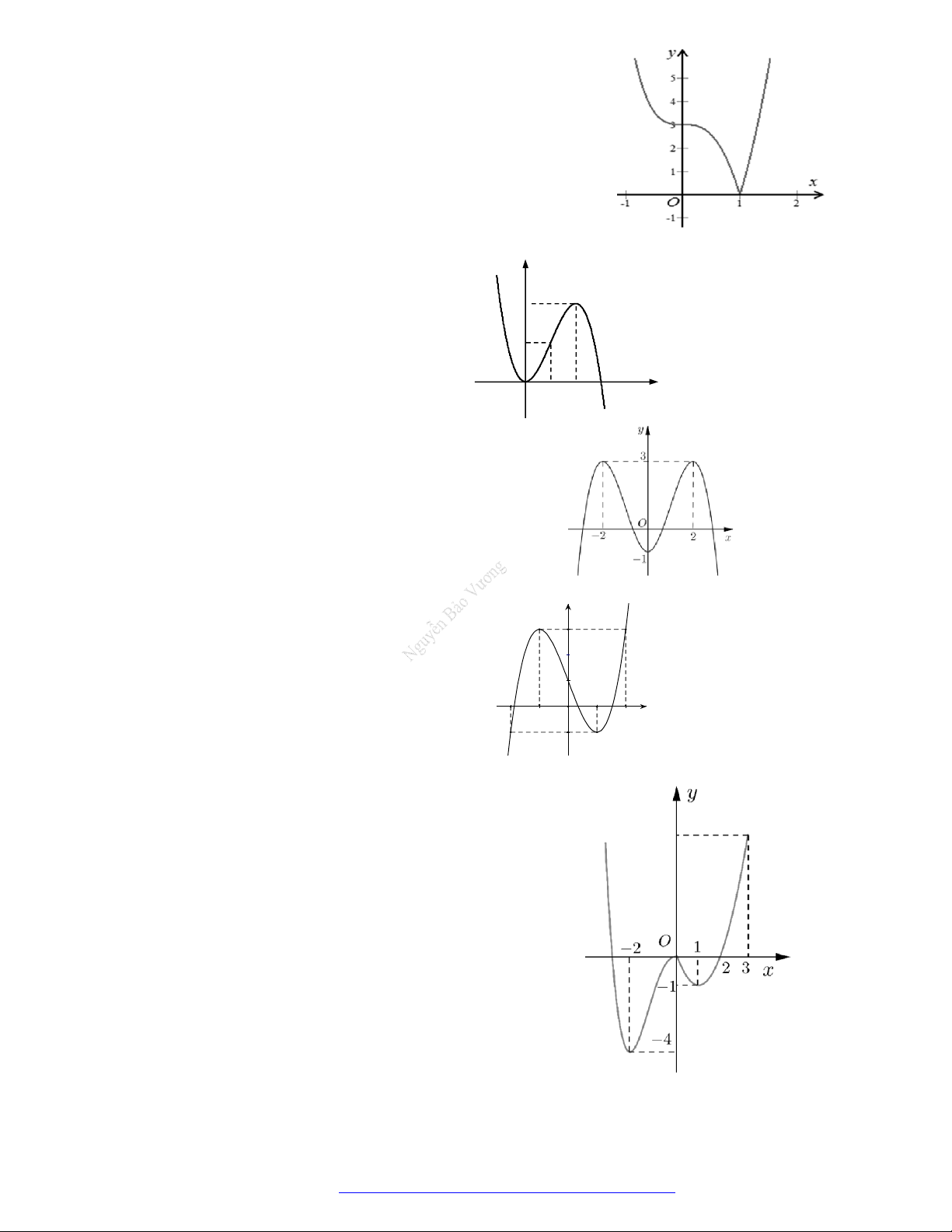
Câu 26. Cho hàm số
y f x
có đồ thị như hình vẽ bên.
Mệnh đề nào sau đây là đúng?
A. Hàm số đã cho đồng biến trên khoảng
0;2
.
B. Hàm số đã cho đồng biến trên khoảng
1;
.
C. Hàm số đã cho nghịch biến trên khoảng
1;2
.
D. Hàm số đã cho nghịch biến trên khoảng
;1
.
Câu 27. Cho hàm số
y f x
có đồ thị như hình vẽ. Hàm số đã cho đồng biến trên khoảng nào?
A.
;0
.
B.
1;3
.
C.
0;2
.
D.
0;
.
Câu 28. Cho hàm số
y f x
có đồ thị như hình vẽ. Hàm số đã cho nghịch biến trên khoảng nào?
A.
2;0
.
B.
;0
.
C.
2;2
.
D.
0;2
.
Câu 29. Cho hàm số
y f x
có đồ thị như hình vẽ. Hàm số đã cho nghịch biến trên khoảng nào?
A.
1;1
.
B.
2; 1
.
C.
1;2
.
D.
1;
.
Câu 30. (Chuyên ĐH Vinh - Nghệ An -2020) Cho hàm số
y f x
có đồ thị như hình vẽ bên.
Hàm số đã cho nghịch biến trên khoảng
A.
1;0
.
B.
2; 1
.
C.
0;1
.
D.
1;3
.
Câu 31. (Chuyên Hưng Yên - 2020) Cho hàm số
f x
liên tục trên
và có đồ thị như hình vẽ bên.
Khẳng định nào sau đây là đúng?

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
A. Hàm số đồng biến trên
;0
và
0;
.
B. Hàm số đồng biến trên
1;0
và
1;
.
C. Hàm số đồng biến trên
1;0 1;
.
D. Hàm số đồng biến trên
; 1 1;
.
Dạng 2. Tìm khoảng đơn điệu của hàm số cho trước
Bước 1. Tìm tập xác định
D
của hàm số.
Bước 2. Tính đạo hàm
( ).y f x
Tìm các điểm
, ( 1,2,3,..., )
i
x i n
mà tại đó đạo hàm bằng 0
hoặc không xác định.
Bước 3. Sắp xếp các điểm
i
x
theo thứ tự tăng dần và lập bảng biến thiên.
Bước 4. Nêu kết luận về các khoảng đồng biến và nghịch biến dưa vào bảng biến thiên.
Câu 1. (Mã 110 - 2017) Hàm số nào dưới đây đồng biến trên khoảng
;
?
A.
1
2
x
y
x
B.
3
y x x
C.
3
3y x x
D.
1
3
x
y
x
Câu 2. (Đề Tham Khảo - 2017) Cho hàm số
2
1
x
y
x
. Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng
;
B. Hàm số nghịch biến trên khoảng
1;
C. Hàm số nghịch biến trên khoảng
; 1
D. Hàm số đồng biến trên khoảng
; 1
Câu 3. (Đề Tham Khảo - 2017) Hàm số nào dưới đây đồng biến trên khoảng
;
?
A.
4 2
3y x x
. B.
2
1
x
y
x
. C.
3
3 3 2y x x
. D.
3
2 5 1y x x
.
Câu 4. (Mã 110 - 2017) Cho hàm số
3 2
3y x x
. Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng
0;2
B. Hàm số nghịch biến trên khoảng
0;2
C. Hàm số nghịch biến trên khoảng
;0
D. Hàm số nghịch biến trên khoảng
2;
Câu 5. (Dề Minh Họa - 2017) Hỏi hàm số
4
2 1y x
đồng biến trên khoảng nào?
A.
;0 .
B.
1
;
2
. C.
0;
. D.
1
;
2
.
Câu 6. (Mã 105 - 2017) Cho hàm số
y f x
có đạo hàm
2
1f x x
,
x
. Mệnh đề nào dưới
đây đúng?
A. Hàm số nghịch biến trên khoảng
1;
B. Hàm số nghịch biến trên khoảng
1;1
C. Hàm số đồng biến trên khoảng
;
D. Hàm số nghịch biến trên khoảng
; 0
Câu 7. (Mã 105 - 2017) Cho hàm số
3 2
2 1 y x x x . Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng
1;
B. Hàm số nghịch biến trên khoảng
1
;1
3
C. Hàm số nghịch biến trên khoảng
1
;
3
D. Hàm số đồng biến trên khoảng
1
;1
3
Câu 8. (Mã 105 - 2017) Cho hàm số
4 2
2y x x
. Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng
; 2
B. Hàm số đồng biến trên khoảng
1;1

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
C. Hàm số nghịch biến trên khoảng
1;1
D. Hàm số đồng biến trên khoảng
; 2
Câu 9. (Mã 123 - 2017) Hàm số
2
2
1
y
x
nghịch biến trên khoảng nào dưới đây?
A.
( ; )
B.
(0; )
C.
( ; 0)
D.
( 1;1)
Câu 10. (Mã 123 - 2017) Cho hàm số
3
3 2
y x x
. Mệnh đề nào dưới đây là đúng?
A. Hàm số nghịch biến trên khoảng
; 0
và đồng biến trên khoảng
0;
B. Hàm số đồng biến trên khoảng
; 0
và đồng biến trên khoảng
0;
C. Hàm số đồng biến trên khoảng
;
D. Hàm số nghịch biến trên khoảng
;
Câu 11. (Mã 104 - 2017) Cho hàm số
2
2 1
y x
. Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng
0;
B. Hàm số đồng biến trên khoảng
;0
C. Hàm số nghịch biến trên khoảng
0;
D. Hàm số nghịch biến trên khoảng
1;1
Câu 12. (Chuyên Lê Hồng Phong - Nam Định - 2019) Cho hàm số
3
2
2019
3
x
y x x
A. Hàm số đã cho đồng biến trên
.
B. Hàm số đã cho nghịch biến trên
;1
.
C. Hàm số đã cho đồng biến trên
;1
và nghịch biến trên
1;
.
D. Hàm số đã cho đồng biến trên
1;
và nghịch biến trên
;1
.
Câu 13. (Lê Quý Đôn - Đà Nẵng - 2019) Hàm số
5 2
3
x
y
x
nghịch biến trên
A.
R\ 3
. B.
R
. C.
; 3
. D.
3;
.
Câu 14. (Chuyên Hà Tĩnh - Lần 1 - 2019) Hàm số nào sau đây nghịch biến trên
?
A.
3
3 2y x x
. B.
4 2
2 2
y x x
.
C.
3 2
2 4 1y x x x
. D.
3 2
2 5 2y x x x
.
Câu 15. (Chuyên Nguyễn Trãi - Hải Dương - 2019) Hàm số
3 2
3 2
y x x
đồng biến trên khoảng
A.
0;2
. B.
;0
. C.
1;4
. D.
4;
.
Câu 16. (HSG - TP Đà Nẵng - 2019) Hàm số
4 3
4y x x
đồng biến trên khoảng
A.
;
. B.
3;
. C.
1;
. D.
;0
.
Câu 17. (Chuyên Nguyễn Tất Thành - Yên Bái - 2019) Cho hàm số
4 2
2 2
y x x
. Mệnh đề nào dưới
đây đúng?
A. Hàm số nghịch biến trên khoảng
;0
. B. Hàm số nghịch biến trên khoảng
2;
.
C. Hàm số đồng biến trên khoảng
;0
. D. Hàm số đồng biến trên khoảng
2;
.
Câu 18. (THPT Ngô Quyền - Hải Phòng - 2019) Cho hàm số
y f x
liên tục trên
và có đạo hàm
2 3
1 1 3
f x x x x
. Hàm số
y f x
đồng biến trên khoảng nào dưới đây?
A.
;1
. B.
; 1
. C.
1;3
. D.
3;
.
Câu 19. (HSG 12 - TP Nam Định - 2019) Hàm số
3 2
1
3 2019
3
y x x x
nghịch biến trên
A.
1;3
. B.
; 1
. C.
; 1
và
3;
. D.
3;
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Câu 20. (Ch
uyên Ngoại Ngữ - Hà Nội - 2019) Hàm số
2
2018
y x
x
nghịch bi
ến trên khoảng nào
trong các khoảng sau đây?
A.
1010;
2018
. B.
2018;
. C.
0;
1009
. D.
1;
2018
.
Câu 21. (Chuyên Lê Quý Đôn - Quảng Trị - 2019) Hàm số
3 2
3 4
y x x
đồng biến trên tập hợp nào
trong các tập hợp được cho dưới đây?
A.
2;
. B.
0;
2
. C.
;0
2;
. D.
;0
.
Câu 22. (SG
D&ĐT Hà Nội - 2018) Hàm số
y f x
có đạo h
àm
2
y x
. Mệnh đề nào s
au đây đúng?
A. Hàm số nghịch biến trên
.
B. Hàm s
ố nghịch biến trên
;0
và đồng biến trên
0;
.
C. Hàm
số đồng biến trên
.
D. Hàm
số đồng biến trên
;0
và nghịch biến trên
0;
.
Câu 23. (THPT
Lương Thế Vinh - HN - 2018) Hàm số
3
3y x
x
nghịch biến trê
n khoảng nào?
A.
; 1
. B.
;
. C.
1;
1
. D.
0;
.
Câu 24. (Ch
uyên Thái Bình - 2018) Cho hàm
2
6 5
y x x
.
Mệnh đề nào sau đây là đúng?
A. Hàm số đồng biến trên khoảng
5;
.
B. Hàm số đồng biến trên khoảng
3;
.
C. Hàm
số đồng biến trên khoảng
;1
.
D. Hàm
số nghịch biến trên khoảng
;3
.
Câu 25. (Thpt K
inh Môn - HD - 2018) Cho hàm số
3 2
3 1
y x
x
,
kết luận nào sau đây về tính đơn
điệu của hàm số là đúng nhất:
A. Hàm số đồng biến trên khoảng
0;
2
và nghịch biến trên các khoảng
;0
;
2;
;
B. Hàm số đồng biến trên khoảng
0;
2
;
C. Hàm
số nghịch biến trên khoảng
0;
2
và đồng biế
n trên các khoảng
;0
;
2;
;
D. Hàm
số nghịch biến trên các khoảng
;0
và
2;
.
Câu 26. (Ch
uyên ĐH Vinh - 2018) Cho hàm số
y f
x
có đạ
o hàm
3
2
f x x x
, với
mọi
x
. Hàm s
ố đã cho nghịch biến trên khoảng nào dưới đây?
A.
1; 3
. B.
1; 0
. C.
0; 1
. D.
2; 0
.
Câu 27. (THPT
Can Lộc - Hà Tĩnh - 2018) Cho hàm số
3 2
1 1
12
1
3 2
xy
x x
.
Mệnh đề nào sau đây
là đúng?
A. Hàm số đồng biến trên khoảng
3;
4
.
B. Hàm số đồng biến trên khoảng
4;
.
C. Hàm
số nghịch biến trên khoảng
;4
.
D. Hàm số nghịch biến trên khoảng
3;
.
-------------------- HẾT --------------------

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 1
TÀI LIỆU DÀNH CHO HỌC SINH MỤC TIÊU 7-8 ĐIỂM
Dạng 1. Tìm m để hàm số đơn điệu trên các khoảng xác định của nó
Xéthàmsốbậcba
3 2
( ) .y f x ax bx cx d
–Bước1.Tậpxácđịnh:
.D
–Bước2.Tínhđạohàm
2
( ) 3 2 .y f x ax bx c
+Để
( )f x
đồngbiếntrên
( )
2
( )
3 0
( ) 0, ?
4 12 0
f x
f x
a a
y f x x m
b ac
+Đề
( )f x
nghịchbiếntrên
( )
2
( )
3 0
( ) 0, ?
4 12 0
f x
f x
a a
y f x x m
b ac
Lưuý:Dấucủatamthứcbậchai
2
( ) .f x ax bx c
Để
0
( ) 0,
0
a
f x x
0
( ) 0,
0
a
f x x
Câu 1. (Đề Tham Khảo Lần 2 2020)Có bao nhiêu giá trị nguyên của tham số
m
sao cho hàm số
3 2
1
( ) 4 3
3
f x x mx x
đồngbiếntrên
.
A.
5
. B.
4
. C.
3
. D.
2
.
Câu 2. (Mã123-2017)Chohàmsố
3 2
4 9 5y x mx m x
,vớimlàthamsố.Hỏicóbaonhiêu
giátrịnguyêncủamđểhàmsốnghịchbiếntrênkhoảng
;
A.
5
B.
4
C.
6
D.
7
Câu 3. Chohàmsố
3 2
1
3 2 1
3
y x mx m x
.Tìmtấtcảgiátrịcủa
m
đểhàmsốnghịchbiếntrên
.
A.
1
2
m
m
. B.
2 1m
. C.
2 1m
. D.
1
2
m
m
.
Câu 4. Tìm
m
đểhàmsố
3 2
3 3 2 1 1y x mx m
đồngbiếntrên
.
A. Khôngcógiátrị
m
thỏamãn. B.
1m
.
C.
1m
. D. Luônthỏamãnvớimọi
m
.
Câu 5. Tìmđiềukiệncủathamsốthực
m
đểhàmsố
3 2
3 3 1 2y x x m x
đồngbiếntrên
.
A.
2m
. B.
2m
. C.
0m
. D.
0m
.
Câu 6. Tìmtậphợptấtcảcácgiátrịcủathamsốthực
m
đểhàmsố
3 2
1
4
3
y x mx x m
đồngbiến
trênkhoảng
;
.
A.
2;2
. B.
;2
. C.
; 2
. D.
2;
.
Câu 7. Giátrịcủa
m
đểhàmsố
3 2
1
– 2 3 – 5
3
y x mx m x m
đồngbiếntrên
là.
A.
3
1
4
m
. B.
3
4
m
. C.
3
1
4
m
. D.
1m
.
TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
Chuyên đề 1

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 8. (Chuyên KHTN - Hà Nội - 2020) Tập hợp tất cả các giá trị của tham số
m
để hàm số
3 2
1 3 2y x m x x
đồngbiếntrên
là
A.
4;2
. B.
4;2
. C.
; 4 2;
. D.
; 4 2;
.
Câu 9. (Đề Tham Khảo - 2017) Hỏi có bao nhiêu số nguyên
m
để hàm số
2 3 2
1 1 4y m x m x x
nghịchbiếntrênkhoảng
;
.
A.
0
B.
3
C.
2
D.
1
Câu 10. Hỏi có tất cả bao nhiêu giá trị nguyên của tham số
m
để hàm số hàm số
2 3 2
1
2 3 2
3
y m m x mx x
đồngbiếntrênkhoảng
;
?
A.
4
. B.
5
. C.
3
. D.
0
.
Câu 11. Tìmtấtcảcácgiátrịcủathamsốthực
m
đểhàmsố
3 2
1 2
y mx mx m m x
đồngbiến
trên
.
A.
4
3
m
và
0
m
. B.
0
m
hoặc
4
3
m
.
C.
4
3
m
. D.
4
3
m
.
Câu 12. Cótấtcảbaonhiêugiátrịnguyêncủathamsố
m
đểhàmsố
3 2
2 3 5
3
m
y x mx m x
đồng
biếntrên
.
A.
4
. B.
2
. C.
5
. D.
6
.
Câu 13. Tìmtấtcảcácgiátrịcủa
m
đểhàmsố
3 2
1 3 1 3 2
y m x m x x
đồngbiếnbiếntrên
?
A.
1 2
m
. B.
1 2
m
. C.
1 2
m
. D.
1 2
m
Câu 14. (THPT Hoàng Hoa Thám - Hưng Yên - 2018) Số giá trị nguyên của
m
để hàm số
2 3 2
(4 ) ( 2) 1
y m x m x x m
1
đồngbiếntrên
bằng.
A.
5
. B.
3
. C.
2
. D.
4
.
Câu 15. (ChuyênHoàngVănThụ-HòaBình-2018)Sốcácgiátrịnguyêncủathamsố
m
trongđoạn
100;100
đểhàmsố
3 2
1 3y mx mx m x
nghịchbiếntrên
là:
A.
200
. B.
99
. C.
100
. D.
201
.
Câu 16. (LiêntrườngNghệAn-2020)Tổngbìnhphươngcủatấtcảcácgiátrịnguyêncủathamsố
m
để
hàmsố
2 3 2
3 12 3 2 2
y m x m x x
nghịchbiếntrên
là?
A.
9
. B.
6
. C.
5
. D.
14
.
Câu 17. (Lý Nhân Tông - Bắc Ninh - 2020) Hỏi có bao nhiêu số nguyên
m
để hàm số
2 3 2
1 1 4y m x m x x
nghịchbiếntrênkhoảng
;
.
A.
2.
B.
1.
C.
0.
D.
3.
Xéthàmsốnhấtbiến
( )
ax b
y f x
cx d
–Bước1.Tậpxácđịnh:
\
d
D
c
–Bước2.Tínhđạohàm
2
. .
( )
( )
a d b c
y f x
cx d
+Để
( )f x
đồngbiếntrên
( ) 0, . . 0 ?D y f x x D a d b c m
+Để
( )f x
nghịchbiếntrên
( ) 0, . . 0 ?D y f x x D a d b c m
Lưuý:Đốivớihàmphânthứcthìkhôngcódấu
" "
xảyratạivịtrí
.y

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Câu 18. (Mã105-2017)Chohàmsố
2 3mx m
y
x m
với
m
làthamsố.Gọi
S
làtậphợptấtcảcácgiá
trịnguyêncủa
m
đểhàmsốđồngbiếntrêncáckhoảngxácđịnh.Tìmsốphầntửcủa
S
.
A. Vôsố B.
3
C.
5
D.
4
Câu 19. (Mã104-2017)Chohàmsố
4mx m
y
x m
với
m
làthamsố.Gọi
S
làtậphợptấtcảcácgiátrị
nguyêncủa
m
đểhàmsốnghịchbiếntrêncáckhoảngxácđịnh.Tìmsốphầntửcủa
S
.
A.
4
B. Vôsố C.
3
D.
5
Câu 20. (THPTHoaLưA-2018)Cótấtcảbaonhiêusốnguyên
m
đểhàmsố
1 2
m x
y
x m
đồng
biếntrêntừngkhoảngxácđịnhcủanó?
A. 1. B. 0. C. 2. D. 3.
Câu 21. (SGD&ĐT Bắc Giang - 2018) Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
2
4
x m
y
x
đồngbiếntrêntừngkhoảngxácđịnhcủanó?
A.
5
. B.
3
. C.
1
. D.
2
.
Câu 22. (THPTHàHuyTập-2018)Tìmtấtcảgiátrịthựccủathamsố
m
đểhàmsố
2
1
x m
y
x
nghịch
biếntrêncáckhoảngmànóxácđịnh?
A.
1
m
. B.
3
m
. C.
3
m
. D.
1
m
.
Câu 23. (SỞGD&ĐTYênBái-2018)Tìmtấtcảcácgiátrịthựccủathamsố
m
đểhàmsố
4
mx
y
x m
nghịchbiếntrêntừngkhoảngxácđịnhcủanó.
A.
2
2
m
m
. B.
2 2
m
. C.
2
2
m
m
. D.
2 2
m
.
Câu 24. (THCS&THPTNguyễnKhuyến-BìnhDương-2018)Tìmtấtcảcácgiátrịthựccủa
m
để
hàmsố
2
2
mx
y
x m
đồngbiếntrênmỗikhoảngxácđịnh
A.
2
2
m
m
. B.
2 2
m
. C.
2
2
m
m
. D.
2 2
m
.
Dạng 2. Tìm m để hàm số nhất biến đơn điệu trên khoảng cho trước
TìmTìmthamsố
m
đểhàmsố
ax b
y
cx d
đơnđiệutrênkhoảng
;
.
Tìmtậpxácđịnh,chẳnghạn
d
x
c
.Tínhđạohàm
y
.
Hàmsốđồngbiến
0
y
(hàmsốnghịchbiến
0
y
).Giảiratìmđược
m
1
.
Vì
d
x
c
vàcó
;
x
nên
;
d
c
.Giảiratìmđược
m
2
.
Lấygiaocủa
1
và
2
đượccácgiátrị
m
cầntìm.
Các trường hợp đặc biệt:
Hàmsố
0
ax b
y ad bc
cx d
đồngbiếntrêntừngkhoảngxácđịnhkhi:
0
ad bc
Hàmsố
0
ax b
y ad bc
cx d
nghịchbiếntrêntừngkhoảngxácđịnhkhi:
0
ad bc
Hàmsố
0
ax b
y ad bc
cx d
đồngbiếntrênkhoảng
;
khi:
0
ad bc
d
c

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Hàmsố
0
ax b
y ad bc
cx d
nghịchbiếntrênkhoảng
;
khi:
0
ad bc
d
c
Hàmsố
0
ax b
y ad bc
cx d
đồngbiếntrênkhoảng
;
khi:
0ad bc
d
c
d
c
Hàmsố
0
ax b
y ad bc
cx d
nghịchbiếntrênkhoảng
;
khi:
0ad bc
d
c
d
c
Câu 1. (ĐềThamKhảoLần12020)Chohàmsố
4mx
f x
x m
(
m
làthamsốthực).Cóbaonhiêu
giátrịnguyêncủa
m
đểhàmsốđãchođồngbiếntrênkhoảng
0;
?
A.
5
. B.
4
. C.
3
. D.
2
.
Câu 2. (Mã101–2020–Lần1)Tậphợptấtcảcácgiátrịthựccủathamsố
m
đểhàmsố
4x
y
x m
đồngbiếntrênkhoảng
; 7
là
A.
4;7
. B.
4;7
. C.
4;7
. D.
4;
.
Câu 3. (Mã102–2020–Lần1)Tậphợptấtcảcácgiátrịthựccủathamsố đểhàmsố
đồngbiếntrênkhoảng
là
A. . B. . C. . D. .
Câu 4. (Mã103–2020–Lần1)Tậphợptấtcảcácgiátrịthựccủathamsốmđểhàmsố
2x
y
x m
đồngbiếntrênkhoảng
( ; 5)
A.
(2;5]
. B.
[2;5)
. C.
(2; )
. D.
(2;5)
.
Câu 5. (Mã104-2020–Lần1)Tậphợptấtcảcácgiátrịthựccủathamsố
m
đểhàmsố
3x
y
x m
đồngbiếntrênkhoảng
; 6
là
A.
3;6
. B.
3;6
. C.
3;
. D.
3;6
.
Câu 6. (Mã104-2018)Cóbaonhiêugiátrịnguyêncủathamsố
m
đểhàmsố
2
3
x
y
x m
đồngbiếntrên
khoảng
; 6
.
A.
2
B.
6
C. Vôsố D.
1
Câu 7. (Mã103-2018)Cóbaonhiêugiátrịnguyêncủathamsố
m
đểhàmsố
1
3
x
y
x m
nghịchbiến
trênkhoảng
6;
?
A.
0
B.
6
C.
3
D. Vôsố
m
5
x
y
x m
; 8
5;
5;8
5;8
5;8

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Câu 8. (Mã101-2018)Cóbaonhiêugiátrịnguyêncủathamsố
m
đểhàmsố
2
5
x
y
x m
đồngbiến
trênkhoảng
; 10
?
A.
2
B. Vôsố C.
1
D.
3
Câu 9. (Mã102-2018)Cóbaonhiêugiátrịnguyêncủathamsố
m
đểhàmsố
6
5
x
y
x m
nghịchbiến
trênkhoảng
10;
?
A. Vôsố B.
4
C.
5
D.
3
Câu 10. (ChuyênKHTN-2020)Tậphợptấtcảcácgiátrịcủathamsố
m
đểhàmsố
4
mx
y
x m
đồng
biếntrênkhoảng
1;
là
A.
2;1
. B.
2;2
. C.
2; 1
. D.
2; 1
.
Câu 11. (ChuyênNguyễnBỉnhKhiêm-QuảngNam-2020)Tìmtấtcảcácgiátrịthựccủathamsố
m
đểhàmsố
1
4
mx
y
m x
nghịchbiếntrênkhoảng
1
;
4
.
A.
2
m
. B.
1 2
m
. C.
2 2
m
. D.
2 2
m
.
Câu 12. (ChuyênTháiNguyên-2020)Chohàmsố
2 3
mx m
y
x m
với
m
làthamsố.Gọi
S
làtậphợp
tấtcảcácgiátrịnguyêncủa
m
đểhàmsốnghịchbiếntrênkhoảng
2;
.Tìmsốphầntửcủa
S
.
A.
5
. B.
3
. C.
4
. D.
1
.
Câu 13. (ĐHQGHàNội - 2020) Có bao nhiêugiátrị nguyêncủathamsố
m
đểhàmsố
18
4
x
y
x m
nghịchbiếntrênkhoảng
2;
?
A. Vôsố. B.
0
. C.
3
. D.
5
.
Câu 14. (SởHàTĩnh-2020)Cóbaonhiêugiátrịnguyêncủathamsố
m
đểhàmsố
9
4
mx
y
x m
nghịch
biếntrênkhoảng
0;4
?
A.
5
. B.
11
. C.
6
. D.
7
.
Câu 15. (SởYênBái-2020)Tìmtấtcảcácgiátrịthựccủathamsố
m
saochohàmsố
3 4
mx m
y
x m
nghịchbiếntrênkhoảng
1;
A.
1 4
m
. B.
1 1
m
. C.
1
4
m
m
. D.
1 4
m
.
Câu 16. (Đặng Thúc Hứa - Nghệ An - 2020) Có bao nhiêu giá trị nguyên của tham số
2020;2020
m
saochohàmsố
3 18
x
y
x m
nghịchbiếntrênkhoảng
; 3
?
A.
2020
. B.
2026
. C.
2018
. D.
2023
.
Câu 17. (LươngThếVinh-HàNội-2020)Cóbaonhiêugiátrịnguyênâmcủathamsố
m
đểhàmsố
4
2
x
y
x m
nghịchbiếntrênkhoảng
3;4
.
A. Vôsố. B.
1
. C.
3
. D.
2
.
Câu 18. (Chuyên KHTN - Hà Nội - Lần 3) Có bao nhiêu giá trị nguyên của tham số
m
đểhàmsố
4
mx
y
x m
nghịchbiếntrênkhoảng
0;
?
A.
1
. B.
2
. C.
3
. D.
5
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Dạng 3. Tìm m để hàm số bậc 3 đơn điệu trên khoảng cho trước
Tìmthamsố
m
đểhàmsố
;y f x m
đơnđiệutrênkhoảng
;
.
Bước 1: Ghiđiềukiệnđể
;y f x m
đơnđiệutrên
;
.Chẳnghạn:
Đềyêucầu
;y f x m
đồngbiếntrên
;
; 0
y f x m
.
Đềyêucầu
;y f x m
nghịchbiếntrên
;
; 0
y f x m
.
Bước 2: Độclập
m
rakhỏibiếnsốvàđặtvếcònlạilà
g x
,cóhaitrườnghợpthườnggặp:
m g x
,
;
x
;
max
m g x
.
m g x
,
;
x
;
min
m g x
.
Bước 3: Khảosáttínhđơnđiệucủahàmsố
g x
trên
D
(hoặcsửdụngCauchy)đểtìmgiátrịlớnnhấtvà
giátrịnhỏnhất.Từđósuyra
m
.
Câu 1. (Mã 101 – 2020 -Lần 2) Tập hợp tất cả các giá trị thực của tham số
m
để hàm số
3 2
3 4
y x x m x
đồngbiếntrênkhoảng
2;
là
A.
;1
B.
;4
C.
;1
D.
;4
Câu 2. (Mã 102 – 2020 – Lần 2) Tập hợp tất cả các giá trị của tham số
m
để hàm số
3 2
3 5
y x x m x
đồngbiếntrênkhoảng
2;
là
A.
;2
. B.
;5
. C.
;5
. D.
;2
.
Câu 3. (Mã 103 – 2020 – Lần 2) Tập hợp tất cả các giá trị thực của tham số
m
để hàm số
3 2
3 2
y x x m x
đồngbiếntrênkhoảng
2;
là
A.
; 1
. B.
;2
. C.
; 1
. D.
;2
.
Câu 4. (Mã 104 – 2020 – Lần 2) Tập hợp tất cả các giá trị thực của tham số
m
để hàm số
3 2
3 1
y x x m x
đồngbiếntrênkhoảng
2;
là
A.
; 2
. B.
;1
. C.
; 2
. D.
;1
.
Câu 5. (Đề Tham Khảo 2019) Tập hợp tất cả các giá trị thực của tham số
m
để hàm số
3 2
6 4 9 4
y x x m x
nghịchbiếntrênkhoảng
; 1
là
A.
3
;
4
B.
0;
C.
;0
D.
3
;
4
Câu 6. Chohàmsố
3 2
3 4y x x mx
.Tậphợptấtcảcácgiátrịcủathamsố
m
đểhàmsốđồngbiến
trênkhoảng
;0
là
A.
1;5
. B.
; 3
. C.
; 4
. D.
1;
.
Câu 7. Tìmtấtcảcácgiátrịthựccủathamsố
m
saochohàmsố
3
2
( ) 7 14 2
3
mx
y f x mx x m
giảmtrênnửakhoảng
[1; )
?
A.
14
;
15
. B.
14
2;
15
. C.
14
;
15
. D.
14
;
15
.
Câu 8. Xácđịnhcácgiátrịcủathamsốmđểhàmsố
3 2
3
y x mx m
nghịchbiếntrênkhoảng
0;1 ?
A.
0m
. B.
1
2
m
. C.
0m
. D.
1
2
m
.
Câu 9. Tìm tất cả các giá trị của tham số
m
để hàm số
3 2
3 1y x x mx
đồng biến trên khoảng
;0
.
A.
0
m
. B.
2
m
. C.
3
m
. D.
1
m
.
Câu 10. Tìm tất cả các giá trị thực của tham số
m
để hàm số
3 2 2
3 9
y x mx m x
nghịch biến trên

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
khoảng
0;1
.
A.
1
1
3
m
. B.
1
3
m
.
C.
1
m
. D.
1
3
m
hoặc
1
m
.
Câu 11. Tìm các giá trị của tham số
m
để hàm số
3 2
1
2 1 2
3
y x mx m x m
nghịch biến trên
khoảng
2;0 .
.
A.
0
m
. B.
1
m
. C.
1
2
m
. D.
1
2
m
.
Câu 12. Tìmtấtcảcácgiátrị
m
đểhàmsố
3 2
3 2y x x mx
tăngtrênkhoảng
1;
.
A.
3
m
. B.
3
m
. C.
3
m
. D.
3
m
.
Câu 13. Tậphợptất cảcácgiá trị củathamsố
m
đểhàmsố
3 2
6 1y x mx m x
đồng biến trên
khoảng
0;4
là:
A.
;3
. B.
;3
. C.
3;6
. D.
;6
.
Câu 14. Tìmtấtcảcácgiáthựccủathamsố
m
saochohàmsố
3 2
2 3 6
y x x mx m
nghịchbiếntrên
khoảng
1;1
.
A.
1
4
m
. B.
1
4
m
. C.
2
m
. D.
0
m
.
Câu 15. Tìmtấtcảcácgiátrịthựccủathamsố
m
saochohàmsố
3 2
6 1y x x mx
đồngbiếntrên
khoảng
0;
?
A.
12
m
. B.
12
m
. C.
0
m
. D.
0
m
.
Câu 16. Tìm
m
đểhàmsố
3 2
3 3 1
y x x mx m
nghịchbiếntrên
0;
.
A.
1
m
. B.
1
m
. C.
1
m
. D.
1
m
.
Câu 17. (THPTChuyênHạLong-2018)Gọi
S
làtậphợpcácgiátrịnguyêndươngcủa
m
đểhàmsố
3 2
3 2 1 12 5 2
y x m x m x
đồngbiếntrênkhoảng
2;
.Sốphầntửcủa
S
bằng
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 18. (Chuyên KHTN - 2018). Tập hợp tất cả các giá trị của tham số
m
để hàm số
3 2
6 1y x mx m x
đồngbiếntrênkhoảng
0;4
là:
A.
;6
. B.
;3
. C.
;3
. D.
3;6
.
Câu 19. (Chuyên ĐH Vinh - Nghệ An -2020) Có bao nhiêu số nguyên
m
để hàm số
3 2
1 2
6
3 3
f x x mx m x
đồngbiếntrênkhoảng
0;
?
A. 9. B. 10. C. 6. D. 5.
Câu 20. (Chuyên Sơn La - 2020) Tìm tất cả các giá trị thực của tham số
m
để hàm số
3 2
6 4 9 4
y x x m x
nghịchbiếntrênkhoảng
; 1
là
A.
3
;
4
. B.
3
;
4
. C.
0;
. D.
;0
.
Câu 21. (SởBắcNinh-2020)Chohàmsố
3
2
1 3 1 1
3
x
y m x m x
.Sốcácgiátrịnguyêncủa
m
đểhàmsốđồngbiếntrên
1;
là
A. 7. B. 4. C. 5. D. 6.
Câu 22. (KimLiên-HàNội-2020)Sốgiátrịnguyênthuộckhoảng
2020;2020
củathamsố
m
để
hàmsố
3 2
3 2019
y x x mx
đồngbiếntrên
0;
là
A.
2018
. B.
2019
. C.
2020
. D.
2017
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 23. (LêLai-ThanhHóa-2020)Cóbaonhiêugiátrịnguyêncủa thuộc đểhàmsố
đồngbiếntrên .
A. . B. . C. . D. .
Câu 24. (NguyễnHuệ-PhúYên-2020)Chohàmsố
3 2 2
1 2 3 2 2f x x m x m m x
.Cóbao
nhiêugiátrịnguyêncủathamsố
m
saochohàmsốđãchođồngbiếntrênkhoảng
2;
?
A.
2
. B.
3
. C.
4
. D.
5
.
Câu 25. (TiênDu-BắcNinh-2020)Gọi
S
làtậphợptấtcảcácgiátrịnguyêncủathamsố
m
thuộc
2020;2020
saochohàmsố
3 2
2 2y x mx x
đồngbiếntrênkhoảng
2;0
.Tínhsốphần
tửcủatậphợp
S
.
A.
2025
. B.
2016
. C.
2024
. D.
2023
.
Câu 26. (Tiên Lãng - Hải Phòng - 2020) Với mọi giá trị m a b ,
,a b
thì hàm số
3 2
2 2 5y x mx x đồngbiếntrênkhoảng
2;0
.Khiđó
a b
bằng
A.
1
. B.
2
. C.
3
. D.
5
.
Dạng 4. Tìm m để hàm số khác đơn điệu trên khoảng cho trước
Câu 1. (ĐềMinhHọa2017)Tìmtấtcảcácgiátrịthựccủathamsố
m
saochohàmsố
tan 2
tan
x
y
x m
đồngbiếntrênkhoảng
0; .
4
A.
0m
hoặc
1 2m
B.
0m
C.
1 2m
D.
2m
Câu 2. (Đề Tham Khảo 2018) Có bao nhiêu giá trị nguyên âm của tham số
m
để hàm số
3
5
1
5
y x mx
x
đồngbiếntrênkhoảng
0;
A.
0
B.
4
C.
5
D.
3
Câu 3. (THPTBạchĐằngQuảngNinh2019)Gọi
S
làtậphợptấtcảcácgiátrịcủathamsố
m
để
hàmsố
2 5 3 2 2
1 1
10 20
5 3
f x m x mx x m m x
đồngbiếntrên
.Tổnggiátrịcủatấtcả
cácphầntửthuộc
S
bằng
A.
5
2
. B.
2
. C.
1
2
. D.
3
2
.
Câu 4. (THPT Lê Quý Đôn Đà Nẵng 2019) Tập hợp các giá trị thực của tham số m để hàm số
1
2
m
y x
x
đồngbiếntrênmỗikhoảngxácđịnhcủanólà
A.
0;1
. B.
;0
. C.
0; \ 1
. D.
;0
.
Câu 5. (THPT Minh Khai Hà Tĩnh 2019) Tìm tất cả các giá trị thực của tham số để hàm số
cos 3
cos
x
y
x m
nghịchbiếntrênkhoảng
;
2
A.
0 3
1
m
m
. B.
0 3
1
m
m
. C.
3m
. D.
3m
.
Câu 6. (HoàngHoaThám2019)Chohàmsố
(4 ) 6 3
6
m x
y
x m
.Cóbaonhiêugiátrịnguyêncủam
trongkhoảng
10;10
saochohàmsốđồngbiếntrên
8;5
?
A.
14
. B.
13
. C.
12
. D.
15
.
Câu 7. (THPTLươngThếVinhHàNội2019)Cóbaonhiêugiátrịnguyênâmcủathamsố
m
đểhàm
số
4
1 3
4 2
y x mx
x
đồngbiếntrênkhoảng
0;
.
A.
2
. B.
1
. C.
3
. D.
0
.
m
2020;2020
3 2
6 1y x x mx
0;
2004
2017
2020
2009
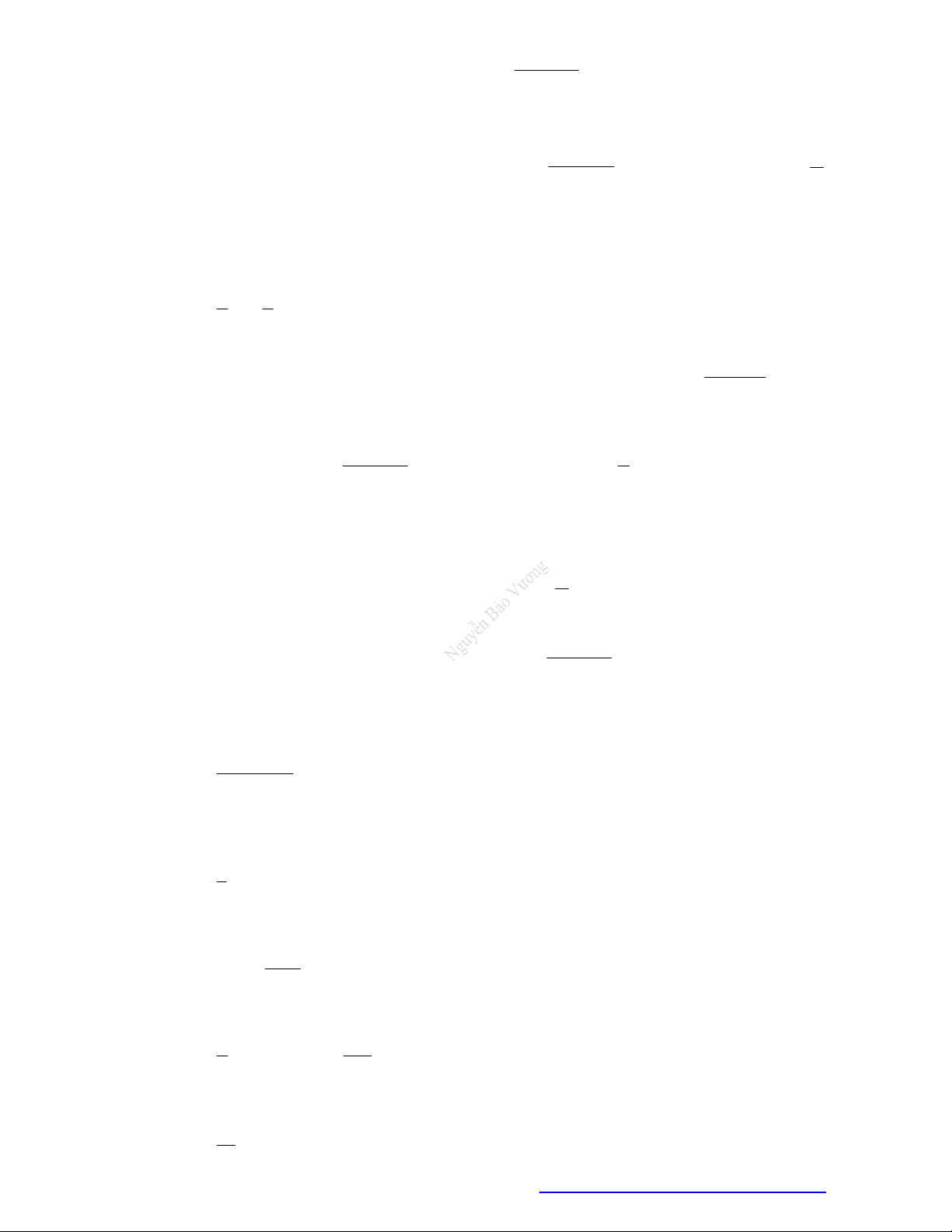
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Câu 8. (ChuyênBắcGiang2019)Chohàmsố
ln 4
ln 2
x
y
x m
với
m
làthamsố.Gọi
S
làtậphợpcác
giátrịnguyêndươngcủa
m
đểhàmsốđồngbiếntrênkhoảng
1;e
.Tìmsốphầntửcủa
S
.
A.
3
B.
2
C.
1
D.
4
Câu 9. (ChuyênVĩnhPhúc2019)Tìm
m
đểhàmsố
cos 2
cos
x
y
x m
đồngbiếntrênkhoảng
0;
2
A.
2
2
m
m
B.
2
m
C.
0
1 2
m
m
D.
1 1
m
Câu 10. (ChuyênLươngThếVinhĐồngNai2019)Cóbaonhiêugiátrịnguyênâmcủathamsố
m
để
hàmsố
4 2
3 9
2 15 3 1
4 2
y x x m x m
đồngbiếntrênkhoảng
0;
?
A.
2.
B.
3.
C.
5.
D.
4.
Câu 11. Cótấtcảbaonhiêugiátrịnguyêncủathamsố
m
đểhàmsố
2
3
3
1
m m
y x
x
đồngbiếntrên
từngkhoảngxácđịnhcủanó?
A.
4
. B.
2
. C.
1
. D.
3
.
Câu 12. Tìmmđểhàmsố
cos 2
cos
x
y
x m
nghịchbiếntrênkhoảng
0 ;
2
A.
2m
. B.
0
1 2
m
m
. C.
2m
. D.
2m
.
Câu 13. (Toán Học Tuổi Trẻ Số 5 2018) Tìm tất cả các giá trị của
m
để hàm số
cot cot
8 3 .2 3 2
x x
y m m
(1)đồngbiếntrên
;
4
.
A.
9 3
m
. B.
3
m
. C.
9
m
. D.
9
m
.
Câu 14. (ToánHọcTuổiTrẻSố6 2018)Chohàmsố
ln 4
ln 2
x
y
x m
với
m
làthamsố.Gọi
S
làtậphợp
cácgiátrịnguyêndươngcủa
m
đểhàmsốđồngbiếntrênkhoảng
1;e
.Tìmsốphầntửcủa
S
.
A.
2
. B.
4
. C.
3
. D.
1
.
Câu 15. (THPTChuyênLêHồngPhong2018)Tìmtấtcảcácgiátrịthựccủathamsố
m
đểhàmsố
ln 2
ln 1
m x
y
x m
nghịchbiếntrên
2
;e
.
A.
2
m
hoặc
1
m
. B.
2
m
hoặc
1
m
.
C.
2.
m
D.
2
m
hoặc
1
m
.
Câu 16. (Chuyên Lương Thế Vinh - 2018) Có bao nhiêu số nguyên âm
m
để hàm số
3
1
cos 4cot 1 cos
3
y x x m x
đồngbiếntrênkhoảng
0;
?
A.
5
. B.
2
. C. vôsố. D.
3
.
Câu 17. (Chuyên Ngữ - Hà Nội - 2018) Có bao nhiêu giá trị nguyên âm của
m
để hàm số
1
5
2
m
y x
x
đồngbiếntrên
5;
?
A.
10
. B.
8
. C.
9
. D.
11
.
Câu 18. (Chuyên Vĩnh Phúc - 2018) Có bao nhiêu giá trị nguyên dương của tham số
m
để hàm số
4 2
4
3 1
1
4 4
y x m x
x
đồngbiếntrênkhoảng
0; .
A.
1.
B.
2.
C.
3.
D.
4.
Câu 19. (Kim Liên - Hà Nội - 2018) Có bao nhiêu giá trị nguyên dương củatham số
m
đểhàm số
2
ln 1
2
x
y mx x
đồngbiếntrênkhoảng
1;
?
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
3
. B.
4
. C.
2
. D.
1
.
Câu 20. (Chuyên Vinh - 2018) Có bao nhiêu giá trị nguyên
10;10
m
để hàm số
2 4 2
2 4 1 1
y m x m x
đồngbiếntrênkhoảng
1;
?
A.
15
. B.
6
. C.
7
. D.
16
.
Câu 21. (ChuyênTháiBình-2018)Cóbaonhiêugiátrịnguyêncủathamsố
2018;2018
m
đểhàm
số
2
1 1y x mx
đồngbiếntrên
;
.
A.
2017
. B.
2019
. C.
2020
. D.
2018
.
Câu 22. (LêQuýĐôn-QuảngTrị-2018)Tìmtấtcảcácgiátrịcủa
m
đểhàmsố
1
2
mx
x m
y
nghịchbiến
trên
1
;
2
.
A.
1;1
m
. B.
1
;1
2
m
. C.
1
;1
2
m
. D.
1
;1
2
m
.
Câu 23. (Chuyên Hưng Yên - 2020) Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
2
2
1
x x m
y
x
nghịchbiếntrênkhoảng
(1;3)
vàđồngbiếntrênkhoảng
(4;6)
.
A.
6
. B.
7
. C.
5
. D.
4
.
Câu 24. (Chuyên Hưng Yên - 2020)Cho hàm số
1 ln 1
1 ln
x
y
x m
.Có bao nhiêu giá trị nguyên của
thamsố
m
thuộc
5;5
đểhàmsốđãchođồngbiếntrênkhoảng
3
1
;1
e
.
A.
7
. B.
6
. C.
5
. D.
4
.
Câu 25. (ChuyênHùngVương-PhúThọ-2020)Cóbaonhiêugiátrịnguyêndươngcủa
m
đểhàmsố
ln 6
ln 2
x
y
x m
đồngbiếntrênkhoảng
1;e
?
A.
2
. B.
1
. C.
4
. D.
3
.
Câu 26. (Chuyên Lê Hồng Phong - Nam Định - 2020) Có bao nhiêu số nguyên m để hàm số
2020 2 sin
f x m x co s x x x
nghịchbiếntrên
?
A. Vôsố. B. 2. C. 1. D. 0.
Câu 27. (Chuyên Quang Trung - 2020) Tập hợp tất cả các giá trị thực của tham số m để hàm số
2
ln( 4) 12
y x mx
đồngbiếntrên
là
A.
1
;
2
. B.
1 1
;
2 2
C.
1
( ;
2
. D.
1
;
2
Câu 28. (Chuyên Thái Bình - 2020) Có tất cả bao nhiêu giá trị nguyên của
m
để hàm số
3 2
12 2y x mx x m
luônđồngbiếntrênkhoảng
1;
?
A.
18
. B.
19
. C.
21
. D.
20
.
Câu 29. (ĐHQGHàNội-2020)Cóbaonhiêugiátrịnguyêncủathamsố
m
thuộckhoảng
8;8
sao
chohàmsố
3
2 3 2
y x mx
đồngbiếntrênkhoảng
1;
?
A.
10.
B.
9.
C.
8.
D.
11.
Câu 30. (SởNinhBình)Gọi
T
làtập hợp tấtcả cácgiá trịnguyêndương củathamsố
m
đểhàm số
4 2
2 1
y x mx
đồngbiếntrênkhoảng
3;
.Tổnggiátrịcácphầntửcủa
T
bằng
A.
9
. B.
45
. C.
55
. D.
36
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Câu 31. (Đ
ôLương4-NghệAn-2020)Tìmtậphợptấtcảcácgiátrịcủa
m
đểhà
msố
2
si
n
cos
m x
y
x
nghịchbiếntrê
n
0
;
6
.
A.
1
m
. B.
2
m
. C.
5
4
m
. D.
0
m
.
Câu 32. (Y
ên Lạc 2 - Vĩnh Phúc - 2020) Cho hàm số
y
f x
có đạo hàm
2
3 6 4,f x x x x
.
Cótấtcảbaonhiêugiátrịnguyênthuộc
2020;2020
của
thamsố
m
đểhà
msố
2
4 5g x f x m x
nghịc
hbiếntrên
0
;2
?
A.
2
008
. B.
2
007
. C.
2
018
. D.
2
019
.
Câu 33. (ThanhChương1-NghệAn-2020)Cóbaonhiêugiátrịnguyêncủathamsố
m
thuộcđoạn
10;10
saochohàmsố
4 3 2
2020
4 3 2
x
mx x
y mx
nghịchbiếntrênkhoảng
0;1
?
A. 12. B. 11. C. 9. D. 10.
Câu 34. (Chuyên Lê Hồng Phong - Nam Định - 2020) Có bao nhiêu số nguyên
m
để hàm số
2020 2cos sin
f x m x x x x
nghịc
hbiếntrên
?
A. V
ôsố. B.
2
. C.
1
. D.
0
.
Câu 35. (ChuyênQuangTrung-BìnhPhước-Lần2-2020)Tậphợptấtcảcácgiátrịthựccủatham
sốthực
m
đểhà
msố
2
l
n 4 12
y
x mx
đồngbiến
trên
là
A.
1
;
2
. B.
1
1
;
2 2
. C.
1
;
2
. D.
1
;
.
2
Câu 36. (ChuyênTháiBình-Lần3-2020)Tìmtấtcảcácgiátrịthựccủa
m
đểhàmsố
3
2
1
2
x
x mx
y
đồngbiếntrên
1;2
.
A.
8
m
. B.
1
m
. C.
8
m
. D.
1
m
.
-------------------- HẾT --------------------
T
ÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
DẠNG TOÁN DÀNH CHO ĐỐI TƯỢNG HỌC SINH 9 – 10 ĐIỂM
Dạng 1. Tìm khoảng
đơn điệu của hàm số g(x)=f[u(x)] khi biết đồ thị hàm số f’(x)
Các
h 1:
Bướ
c 1: Tính đạo hàm của hàm số
g
x
,
.g x u x f u x
.
Bước 2: Sử dụng đồ thị của
f
x
, lập bảng xét dấu của
g
x
.
Bướ
c 3: Dựa vào bảng dấu kết luận khoảng đồng biến, nghịch biến của hàm số.
Các
h 2:
Bướ
c 1: Tính đạo hàm của hàm số
g
x
,
.g
x u x f u x
.
Bướ
c 2: Hàm số
g
x
đồng biến
0g
x
; (Hà
m số
g
x
nghịc
h biến
0g
x
) (*)
Bướ
c 3: Giải bất phương trình
*
(dự
a vào đồ thị hàm số
y f x
)
từ đó kết luận khoảng đồng
biến, nghịch biến của hàm số.
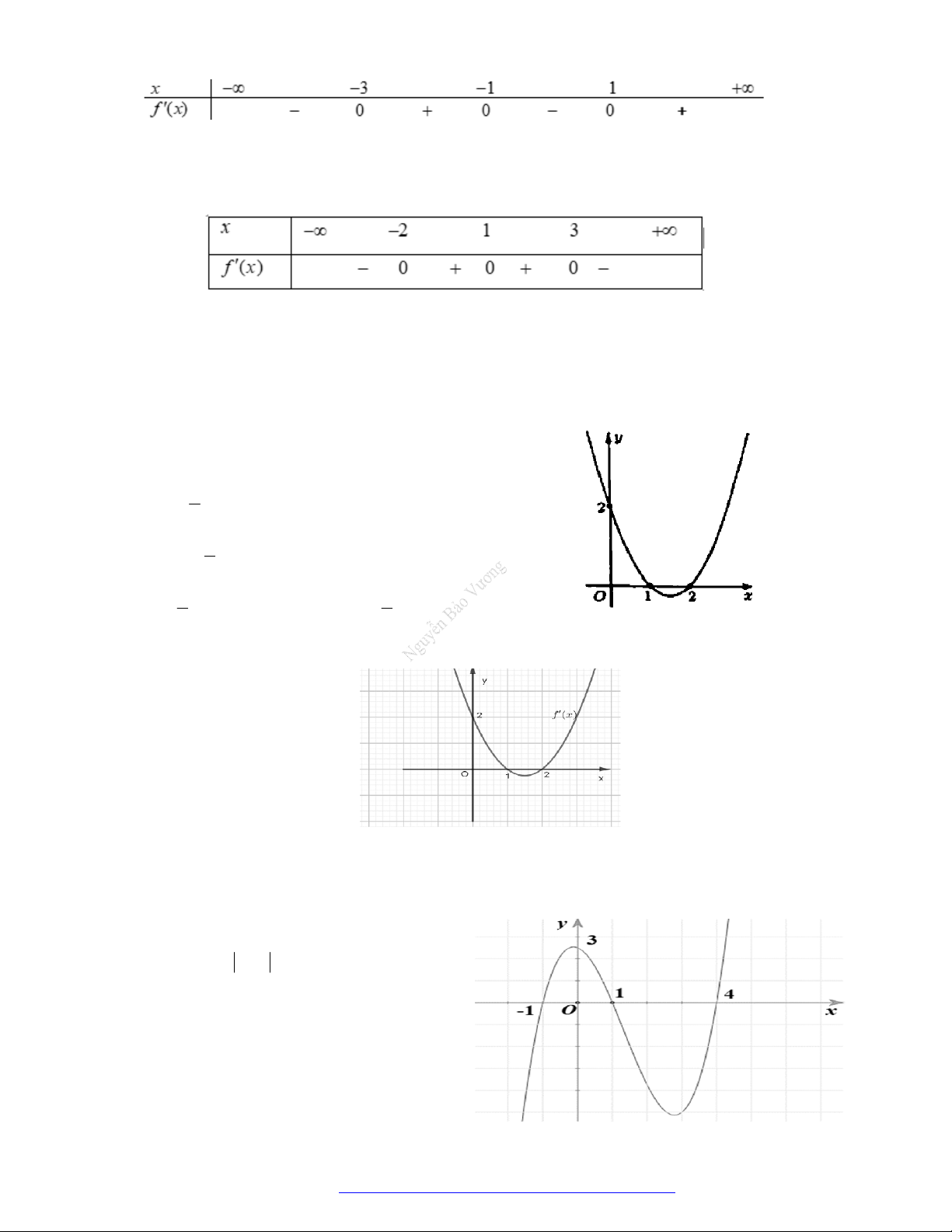
Câu 1. (Đề Tham Khảo 2018) Cho hàm số
(
)y f x
.
Hàm số
'
( )y f x
có đồ t
hị như hình bên. Hàm số
(
2 ) y f x
đồng biến trê
n khoảng
A.
2
;
B.
2
;1
C.
;
2
D.
1
;3
Câu 2.
(Mã đề 104 - 2019) Cho hàm số
f
x
, bảng xét dấu của
f
x
như sau:
Hàm số
5 2 y f x
đồng biến trên khoảng nào dưới đây?
A.
3
;4
.
B.
1
;3
.
C.
;
3
.
D.
4
;5
.
Câu 3. (Mã 103 - 2019) Cho hàm số
(
)f x
, bảng xét dấu của
(
)f x
như sau:
Hàm số
3
2y f x
đồng biến trên khoảng nào dưới đây?
A.
0;2
. B.
2;3
. C.
; 3
. D.
3;4
.
Câu 4. (Mã 102 - 2019) Cho hàm số
(
)f x
có bảng dấu
(
)f x
như sau:
Hàm số
(
5 2 )y f x
nghịc
h biến trên khoảng nào dưới đây?
A.
3
;5
. B.
5
;
. C.
2
;3
. D.
0
;2
.
T
ÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
Ch
uyên đề 1
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 5. (Mã đề 101 - 2019) Cho hàm số
f x
, bảng xét dấu của
'f x
như sau:
Hàm số
3 2y f x
nghịch biến trên khoảng nào dưới đây?
A.
2;1 .
B.
2;4 .
C.
1;2 .
D.
4; .
Câu 6. (Đề Thi Công Bằng KHTN 2019) Cho hàm số
( )f x
có bảng xét dấu như sau:
Hàm số
2
2y f x x
nghịch biến trên khoảng nào dưới đây?
A.
2;1
. B.
4; 3
. C.
0;1
. D.
2; 1
.
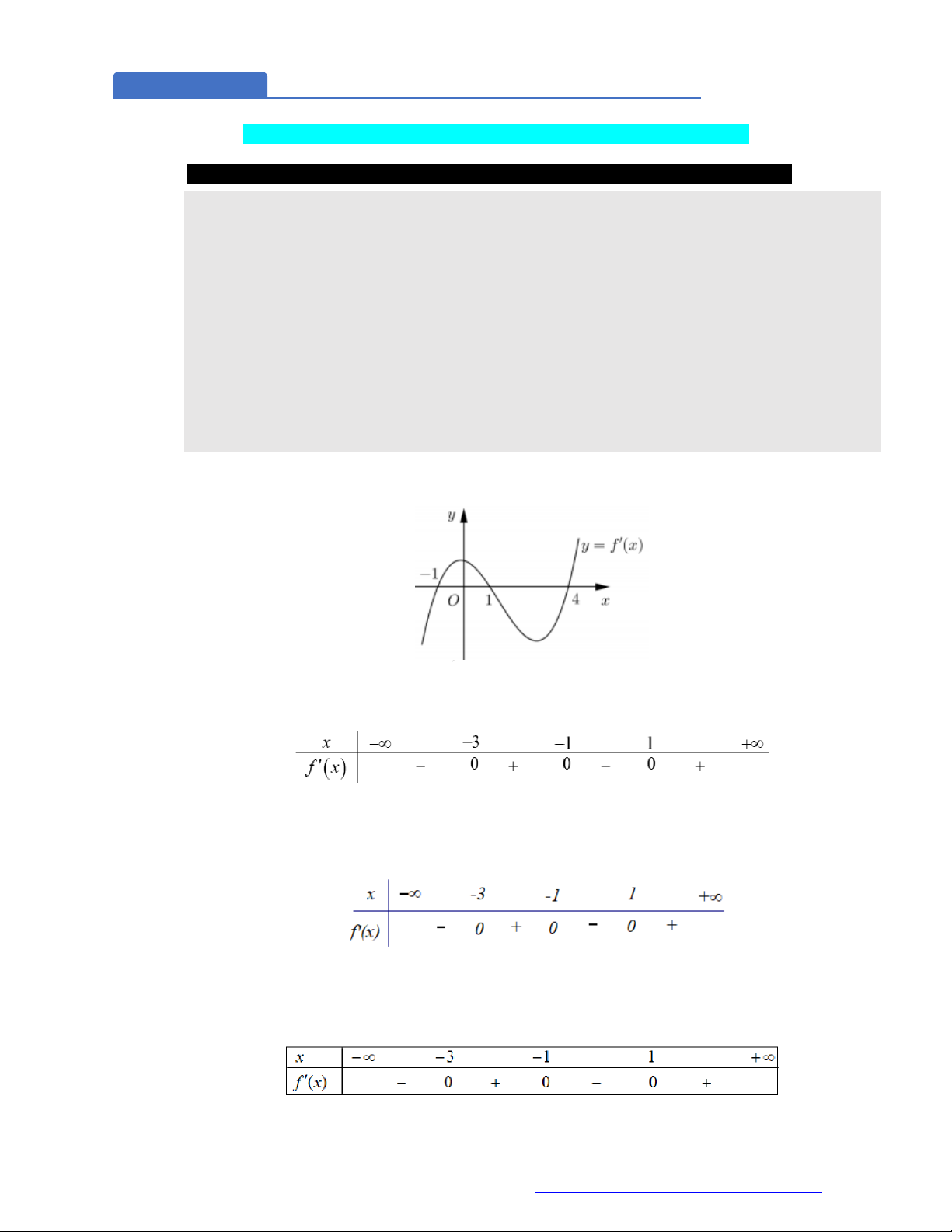
Câu 7. (Chuyên Thái Nguyên -2019) Cho hàm số
y f x
có đạo hàm
'f x
trên
. Hình vẽ bên
là đồ thị của hàm số
'y f x
. Hàm số
2
g x f x x
nghịch biến trên khoảng nào trong
các khoảng dưới đây?
A.
3
;
2
.
B.
3
;
2
.
C.
1
;
2
. D.
1
;
2
.
Câu 8. (Chuyên Lê Hồng Phong Nam Định 2019) Cho hàm số
'y f x
có đồ thị như hình vẽ
Hàm số
2
2y f x
đồng biến trên khoảng nào dưới đây
A.
;0
. B.
0;1
. C.
1;2
. D.
0;
.
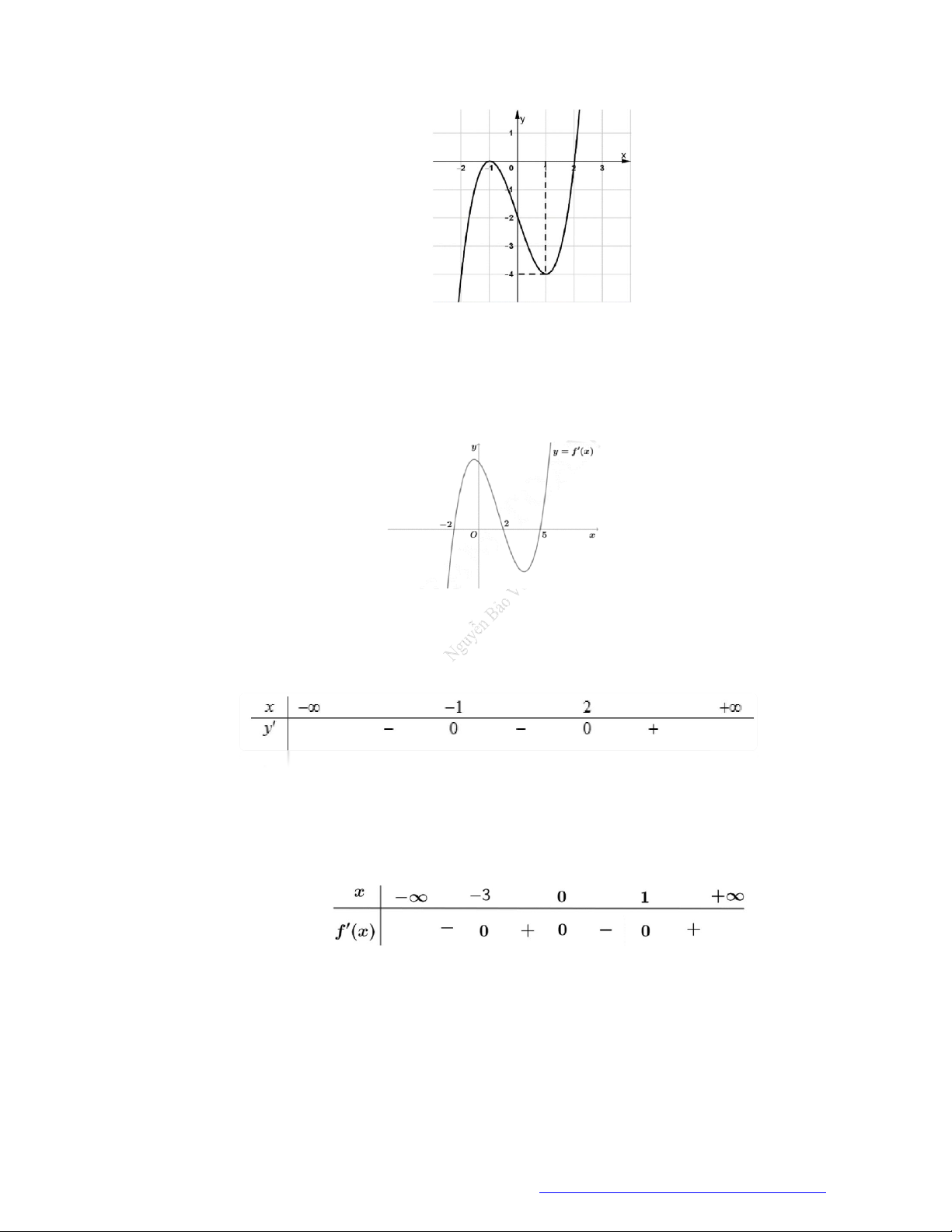
Câu 9. (THPT Gia Lộc Hải Dương 2019) Cho hàm số
( )f x
, đồ thị hàm số
( )y f x
như hình vẽ dưới
đây.
Hàm số
3y f x
đồng biến trên khoảng nào dưới đây?
A.
4;6
.
B.
1;2
.
C.
; 1 .
D.
2;3
.
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Câu 10. (THPT Minh Châu Hưng Yên 2019) Cho hàm số
y f x
. Hàm số
'y f x
có đồ thị như
hình vẽ. Hàm số
2
( ) ( 2).g x f x Mệnhvđề nào sai?
A. Hàm số
g x
nghịch biến trên
; 2
B. Hàm số
g x
đồng biến trên
2;
C. Hàm số
g x
nghịch biến trên
1;0
D. Hàm số
g x
nghịch biến trên
0;2
Câu 11. (THPT Việt Đức Hà Nội 2019) Cho hàm số
y f x
có đạo hàm liên tục trên
và đồ thị hàm
số
'y f x
như hình bên.
Hỏi hàm số
3 2g x f x
nghịch biến trên khoảng nào trong các khoảng sau?
A.
1;
B.
; 1
C.
1;3
D.
0;2
Câu 12. (Chuyên Lê Quý Đôn Điện Biên 2019) Cho hàm số
y f x
có bảng xét dấu đạo hàm như sau:
Hàm số
2
2y f x
nghịch biến trên khoảng nào dưới đây?
A.
2; 1
. B.
2;
. C.
0;2
. D.
1;0
.
Câu 13. (Chuyên KHTN - 2020) Cho hàm số
y f x
có bảng xét dấu đạo hàm như sau.
Hàm số
2 3 y f x
đồng biến trên khoảng nào sau đây?
A.
2;3
. B.
1;2
. C.
0;1
. D.
1;3
.
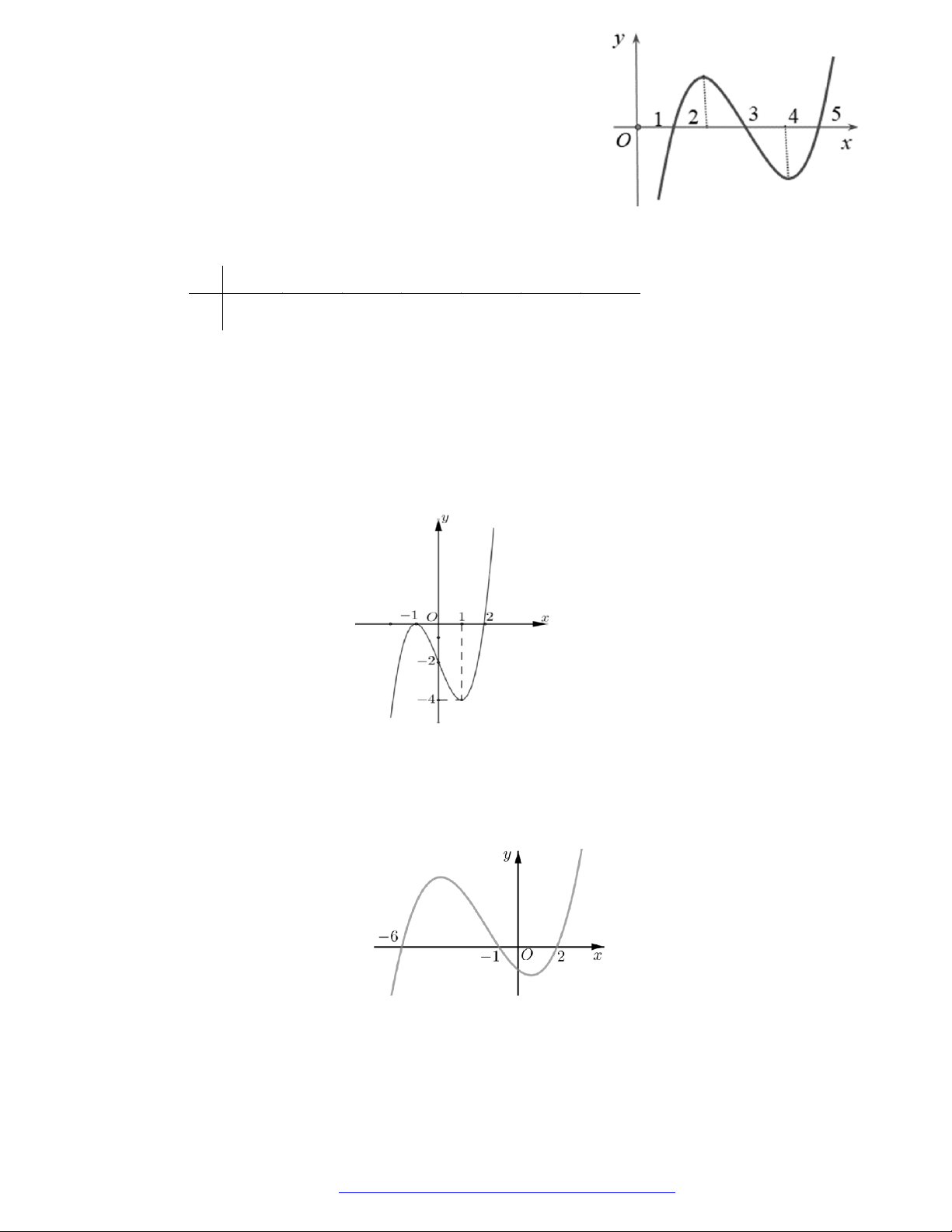
Câu 14. (Chuyên Bến Tre - 2020) Cho hàm số
y f x
biết hàm số
f x
có đạo hàm
f x
và hàm
số
y f x
có đồ thị như hình vẽ. Đặt
1g x f x
. Kết luận nào sau đây đúng?
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A. Hàm số
g x
đồng biến trên khoảng
3;4
.
B. Hàm số
g x
đồng biến trên khoảng
0;1
.
C. Hàm số
g x
nghịch biến trên khoảng
2;
.
D. Hàm số
g x
nghịch biến trên khoảng
4;6
.
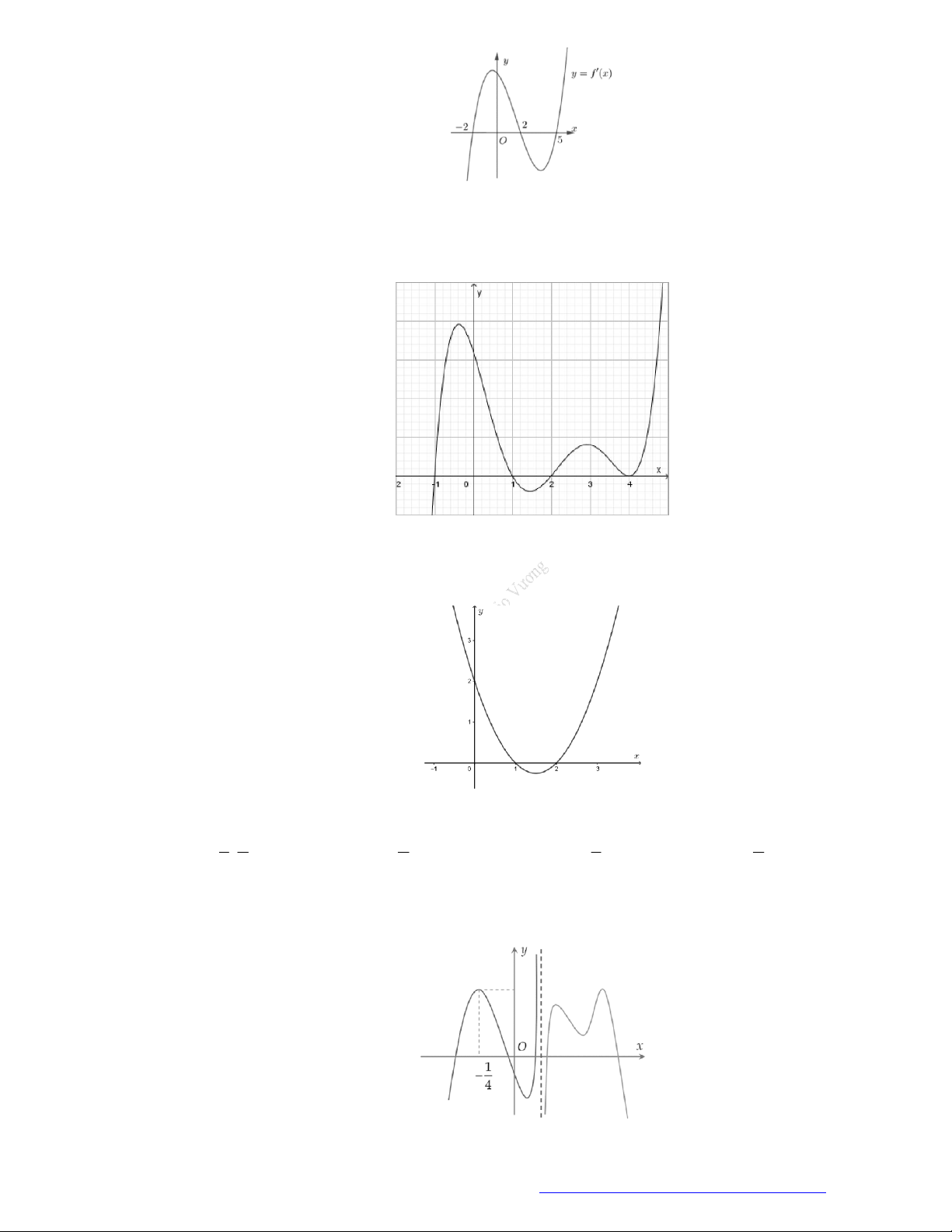
Câu 15. (Chuyên Phan Bội Châu - Nghệ An - 2020) Cho hàm số
y f x
có bảng xét dấu đạo hàm
như sau:
Hàm số
3 2
x
g x f
đồng biến trên khoảng nào sau đây
A.
3;
. B.
; 5
. C.
1;2
. D.
2;7
.
Câu 16. (Chuyên Vĩnh Phúc - 2020) Cho hàm số
f x
có đạo hàm liên tục trên
và có đồ thị của hàm
số
y f x
như hình vẽ. Xét hàm số
2
2 g x f x
. Mệnh đề nào dưới đây sai?
A. Hàm số
g x
nghịch biến trên
0;2
. B. Hàm số
g x
đồng biến trên
2;
.
C. Hàm số
g x
nghịch biến trên
1;0
. D. Hàm số
g x
nghịch biến trên
; 2
.
Câu 17. (Đại Học Hà Tĩnh - 2020) Cho hàm số
y f x
. Biết rằng hàm số
y f x
có đồ thị như
hình vẽ bên dưới.
Hàm số
2
3y f x
đồng biến trên khoảng
A.
0;1
. B.
1;0
. C.
2;3
. D.
2; 1
.
Câu 18. (Sở Ninh Bình) Cho hàm số bậc bốn
y f x
có đạo hàm trên
. Đồ thị hàm số
'y f x
như hình vẽ. Hàm số
2
2y f x
nghịch biến trên khoảng nào dưới đây?
x
5
2
y
0
0
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
A.
2;3
. B.
3; 2
. C.
1;1
. D.
1;0
.
Câu 19. (Hậu Lộc 2 - Thanh Hóa - 2020) Cho hàm số
y f x
có đồ thị hàm đạo hàm
y f x
như
hình vẽ. Hàm số
2019 2020g x f x
đồng biến trên khoảng nào trong các khoảng sau?
A.
1;0
. B.
; 1
. C.
0;1
. D.
1;
.
Câu 20. (Trường VINSCHOOL - 2020) Cho hàm số
y f x
. Biết đồ thị hàm số
y f x
có đồ thị
như hình vẽ bên
Hàm số
2
2 3g x f x x
đồng biến trên khoảng nào dưới đây?
A.
1 1
;
3 2
. B.
1
;
2
. C.
1
;
3
. D.
1
2;
2
.
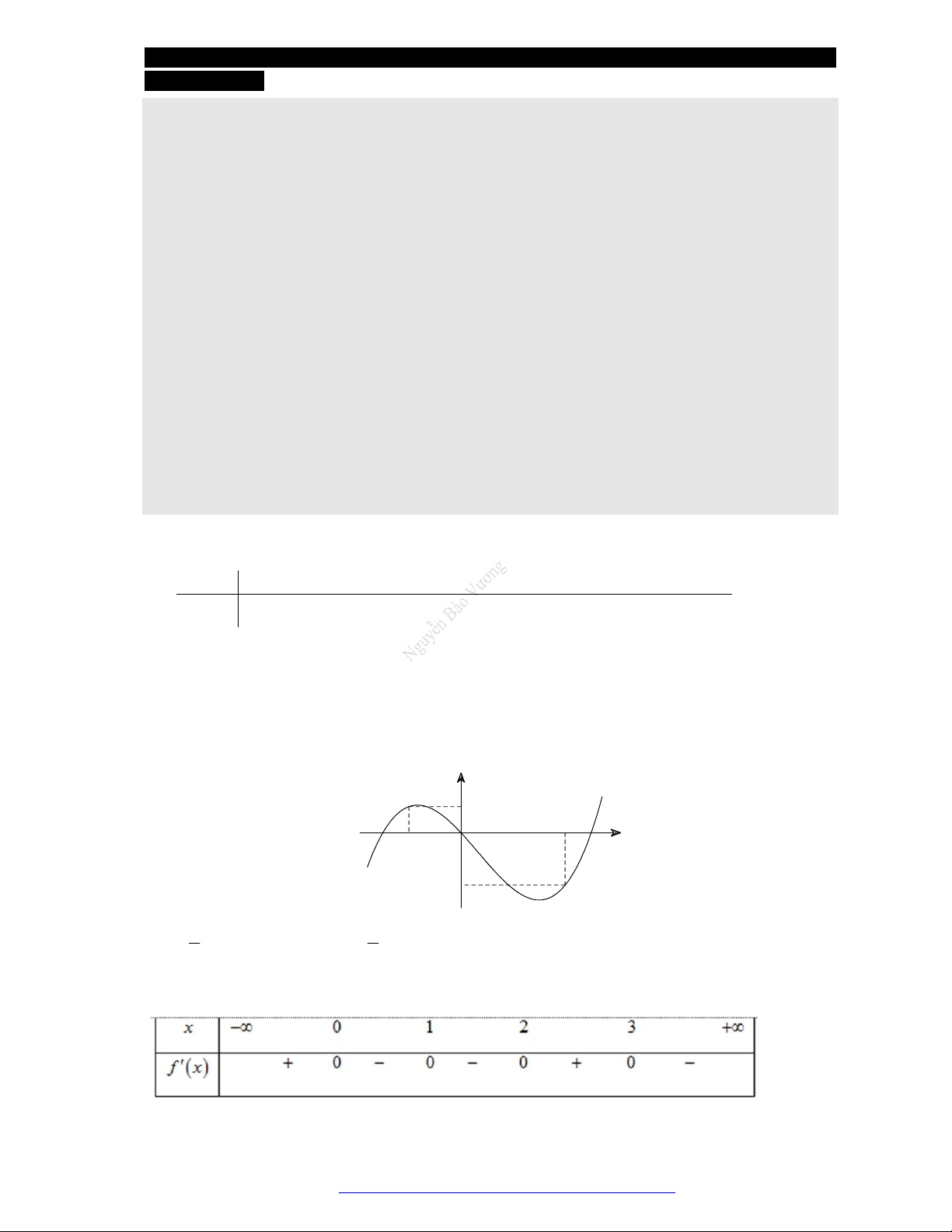
Câu 21. Cho hàm số
( )f x
liên tục trên R và có đồ thị
'( )f x
như hình vẽ. Tìm số điểm cực trị của hàm số
2
( )y f x x
?
A.
10
. B.
11
. C.
12
. D.
13
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Dạng 2. Tìm khoảng đơn điệu của hàm số g(x)=f[u(x)]+v(x) khi biết đồ thị, bảng biến thiên
của hàm số f’(x)
Cách 1:
Bước 1: Tính đạo hàm của hàm số
g x
,
.g x u x f u x v x
.
Bước 2: Sử dụng đồ thị của
f x
, lập bảng xét dấu của
g x
.
Bước 3: Dựa vào bảng dấu kết luận khoảng đồng biến, nghịch biến của hàm số.
Cách 2:
Bước 1: Tính đạo hàm của hàm số
g x
,
.g x u x f u x v x
.
Bước 2: Hàm số
g x
đồng biến
0g x
; (Hàm số
g x
nghịch biến
0g x
) (*)
Bước 3: Giải bất phương trình
*
(dựa vào đồ thị hàm số
y f x
) từ đó kết luận khoảng đồng
biến, nghịch biến của hàm số.
Cách 3: (Trắc nghiệm)
Bước 1: Tính đạo hàm của hàm số
g x
,
.g x u x f u x v x
.
Bước 3: Hàm số
g x
đồng biến trên
K
0,g x x K
; (Hàm số
g x
nghịch biến trên
K
0,g x x K
) (*)
Bước 3: Lần lượt chọn thay giá trị từ các phương án vào
g x
để loại các phương án sai.
Câu 1. (Đề Tham Khảo 2019) Cho hàm số
f x
có bảng xét dấu của đạo hàm như sau
x
1 2 3 4
f x
0
0
0
0
Hàm số
3
3 2 3y f x x x
đồng biến trên khoảng nào dưới đây?
A.
; 1 .
B.
1;0 .
C.
0;2 .
D.
1; .
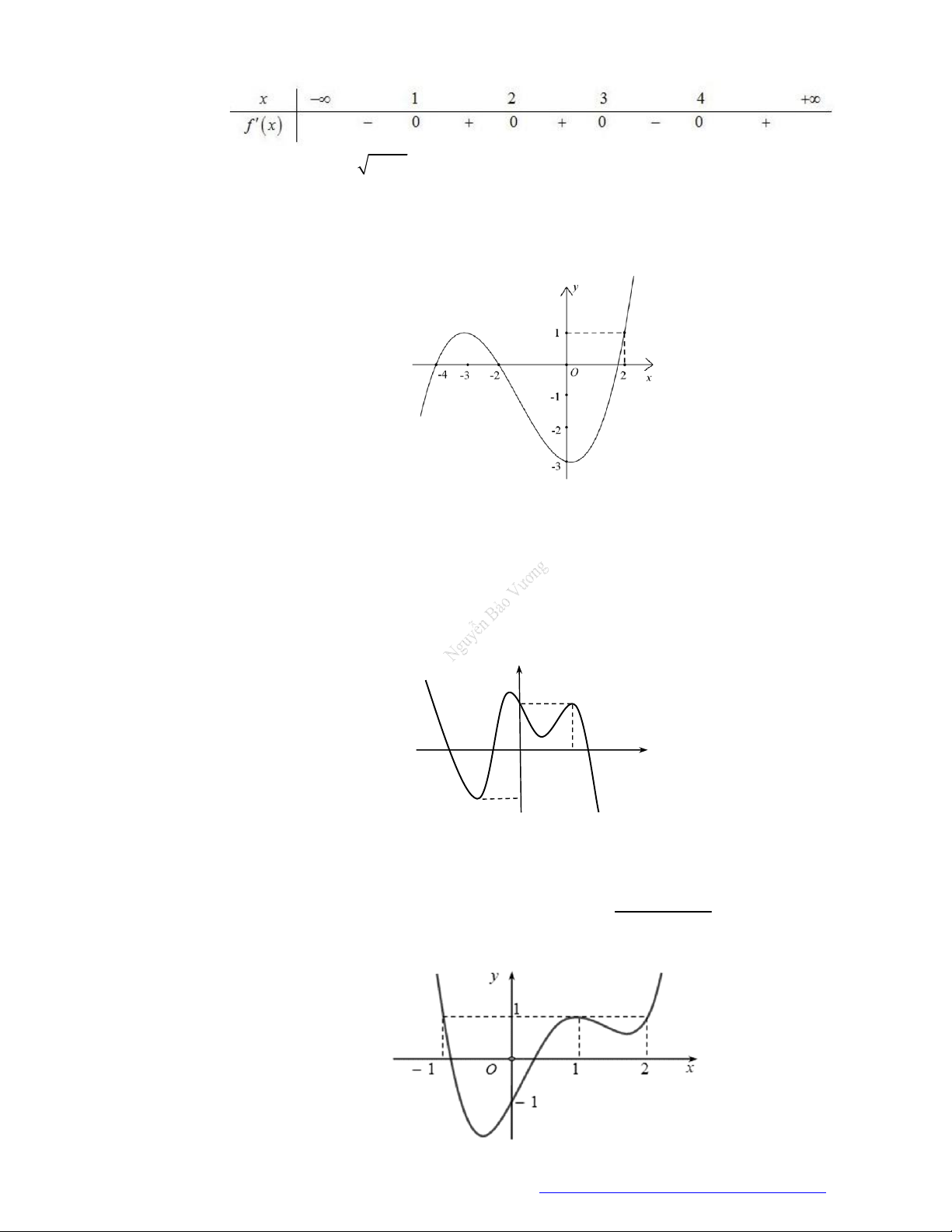
Câu 2. (Đề Tham Khảo 2020 – Lần 1) Cho hàm số
f x
. Hàm số
'y f x
có đồ thị như hình bên.
Hàm số
2
1 2 g x f x x x
nghịch biến trên khoảng nào dưới đây ?
A.
3
1;
2
. B.
1
0;
2
. C.
2; 1
. D.
2;3
.
Câu 3. (Chuyên Lê Quý Đôn Điện Biên 2019) Cho hàm số
f x
có bảng xét dấu của đạo hàm như sau
Hàm số
3
1 12 2019y f x x x
nghịch biến trên khoảng nào dưới đây?
A.
1;
. B.
1;2
. C.
;1
. D.
3;4
.
x
y
– 2
4
1
– 2
O
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Câu 4. (Chuyên Phan Bội Châu Nghệ An 2019) Cho hàm số
f x
có bảng xét dấu đạo hàm như sau:
Hàm số
2
2 1 1y f x x x
nghịch biến trên những khoảng nào dưới đây
A.
; 2
. B.
;1
. C.
2;0
. D.
3; 2
.
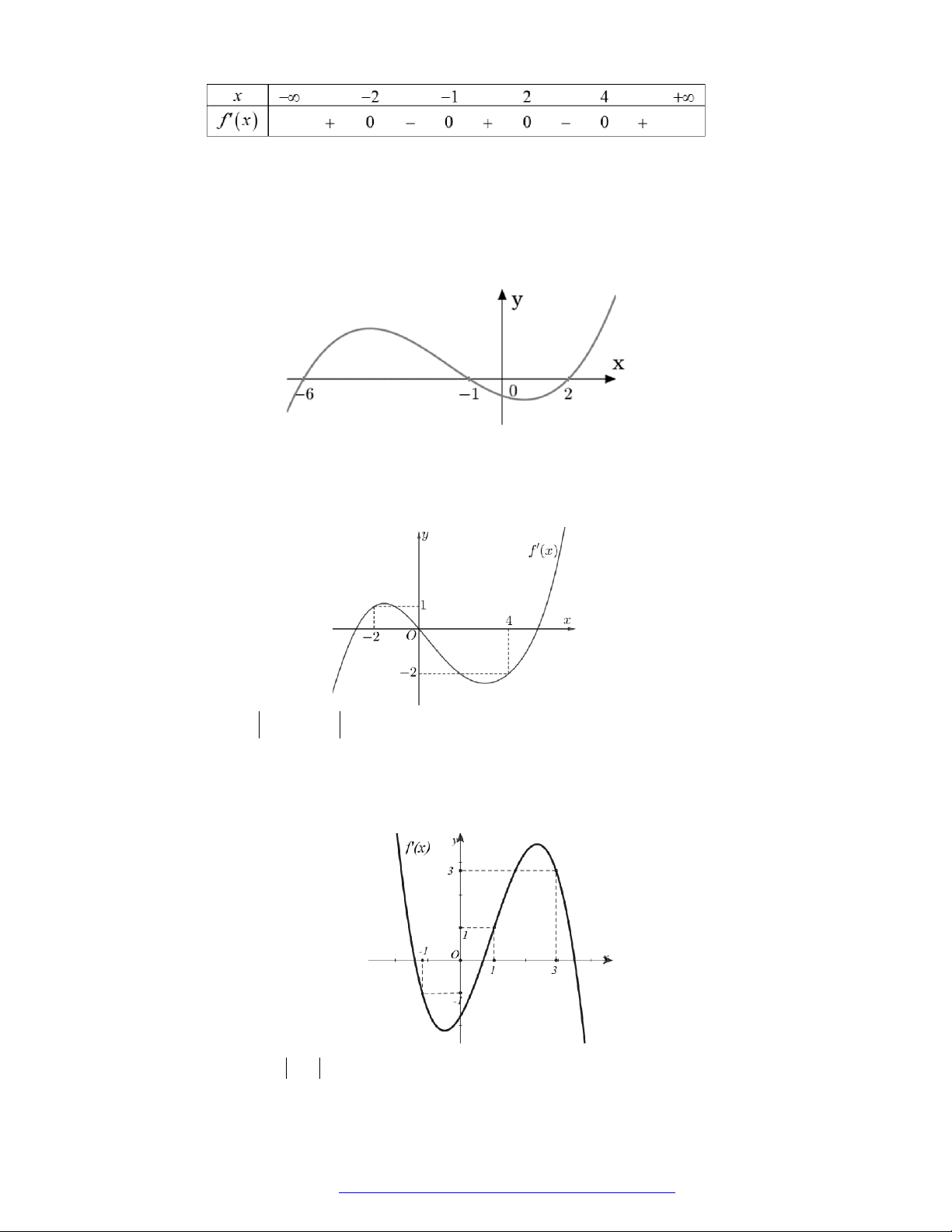
Câu 5. (Sở Vĩnh Phúc 2019) Cho hàm số bậc bốn
( )y f x
có đồ thị của hàm số
( )y f x
như hình vẽ
bên.
Hàm số
3 2
3 ( ) 6 9y f x x x x
đồng biến trên khoảng nào trong các khoảng sau đây?
A.
0;2
. B.
1;1
. C.
1;
. D.
2;0
.
Câu 6. (Học Mãi 2019) Cho hàm số
y f x
có đạo hàm trên
. Đồ thị hàm số
y f x
như hình
bên. Hỏi đồ thị hàm số
2y f x x
có bao nhiêu điểm cực trị?
A.
4
. B.
3
. C.
2
. D.
1
.
Câu 7. (THPT Hoàng Hoa Thám Hưng Yên 2019) Cho hàm số
y f x
liên tục trên
. Hàm số
y f x
có đồ thị như hình vẽ. Hàm số
2019 2018
1
2018
x
g x f x
đồng biến trên khoảng
nào dưới đây?
A.
2 ; 3
. B.
0 ; 1
. C.
-1 ; 0
. D.
1 ; 2
.
y
x
2
2
2
O
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 8. (Sở Ninh Bình 2019) Cho hàm số
y f x
có bảng xét dấu của đạo hàm như sau
Hàm số
2 2019y f x
nghịch biến trên khoảng nào trong các khoảng dưới đây?
A.
4;2
. B.
1;2
. C.
2; 1
. D.
2;4
.
Câu 9. (THPT Lương Thế Vinh Hà Nội 2019) Cho hàm số
y f x
. Biết đồ thị hàm số
y f x
có đồ thị như hình vẽ bên. Hàm số
2
3 2018y f x
đồng biến trên khoảng nào dưới đây?
A.
1; 0
B.
2; 3
C.
2; 1
D.
0; 1
Câu 10. (Chuyên Biên Hòa - Hà Nam - 2020) Cho hàm số đa thức
f x
có đạo hàm trên
. Biết
0 0f
và đồ thị hàm số
y f x
như hình sau.
Hàm số
2
4g x f x x
đồng biến trên khoảng nào dưới đây?
A.
4; .
B.
0;4 .
C.
; 2 .
D.
2 0; .
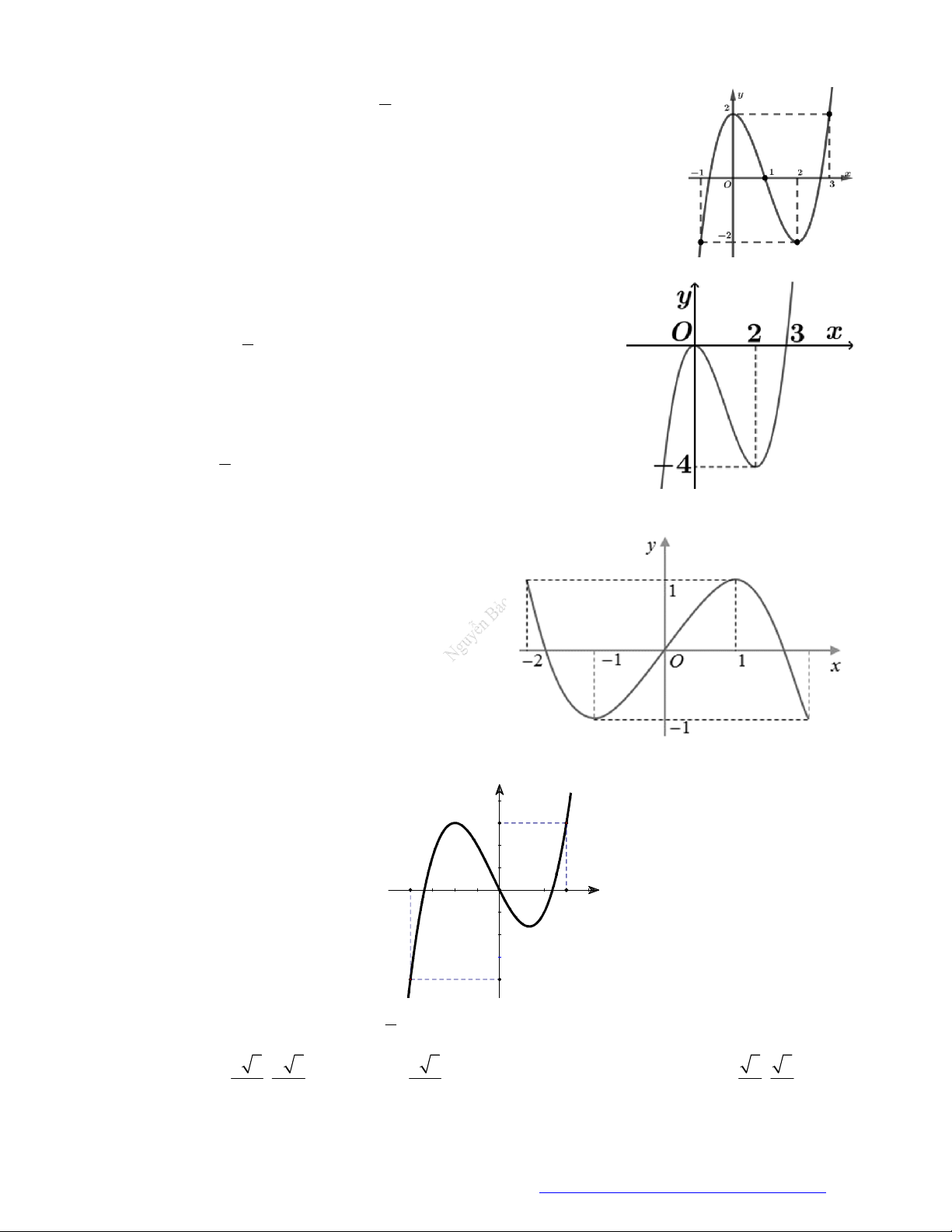
Câu 11. (Chuyên Thái Bình - 2020) Cho hàm số
( )f x
liên tục trên
có đồ thị hàm số
( )y f x
cho
như hình vẽ
Hàm số
2
( ) 2 1 2 2020g x f x x x
đồng biến trên khoảng nào?
A.
(0;1)
. B.
( 3;1)
. C.
(1;3)
. D.
( 2;0)
.
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Câu 12. (Chuyên Lào Cai - 2020) Cho hàm số
f x
có đồ thị như hình bên. Hàm số
3 2
9
3 1 9
2
g x f x x x
đồng biến trên khoảng nào dưới đây?
A.
1;1
.
B.
2;0
.
C.
;0
. D.
1;
.
Câu 13. (Sở Phú Thọ - 2020) Cho hàm số
y f x
có đồ thị hàm số
y f x
như hình vẽ
Hàm số
e 2 2020
x
g x f
nghịch biến trên khoảng nào dưới đây?
A.
3
1;
2
.
B.
1;2
.
C.
0;
.
D.
3
;2
2
.
Câu 14. (Lý Nhân Tông - Bắc Ninh - 2020) Cho hàm số
f x
có đồ thị hàm số
f x
như hình vẽ.
Hàm số
2
cosy f x x x
đồng biến trên khoảng
A.
2;1
.
B.
0;1
.
C.
1;2
.
D.
1;0
.
Câu 15. (THPT Nguyễn Viết Xuân - 2020) Cho hàm số
f x
. Hàm số
y f x
có đồ thị như hình
vẽ.
Hàm số
2 4 2
9
( ) 3 1 3
2
g x f x x x
đồng biến trên khoảng nào dưới đây.
A.
2 3 3
;
3 3
. B.
2 3
0;
3
. C.
1;2
. D.
3 3
;
3 3
.
Câu 16. (Trần Phú - Quảng Ninh - 2020) Cho hàm số
f x
có bảng xét dấu của đạo hàm như sau
x
y
O
-4
3
3
-4
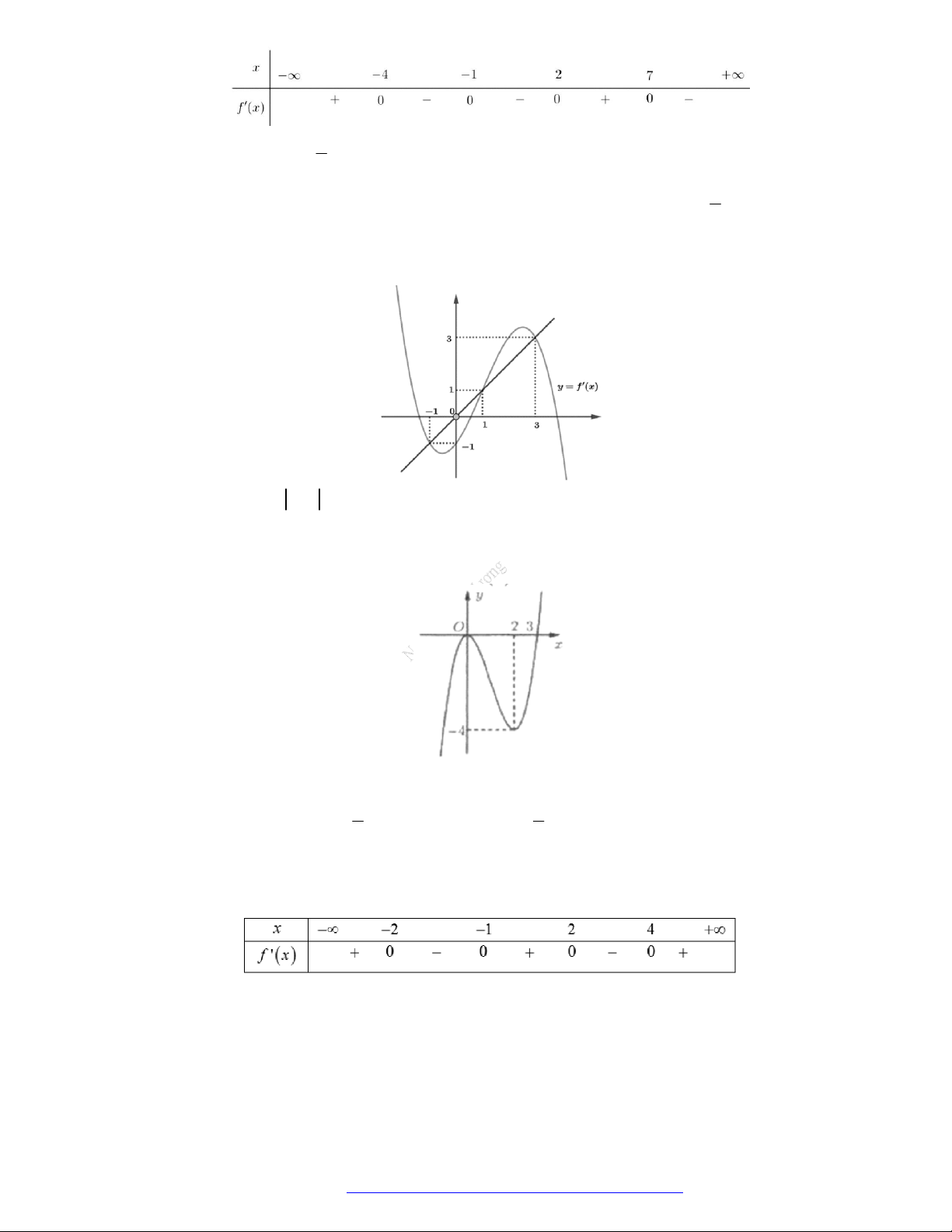
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Hàm số
3
2
2 1 8 5
3
y f x x x
nghịch biến trên khoảng nào dưới đây?
A.
; 2
. B.
1;
. C.
1;7
. D.
1
1;
2
.
Câu 17. (Chuyên Thái Bình - Lần 3 - 2020) Cho hàm số
( )y f x
liên tục trên
có đồ thị hàm số
( )y f x
cho như hình vẽ.
Hàm số
2
( ) 2 1 2 2020g x f x x x
đồng biến trên khoảng nào?
A.
0;1
. B.
13;
. C.
1; 3
. D.
02;
.
Câu 18. (Sở Phú Thọ - 2020) Cho hàm số
y f x
có đồ thị hàm số
f x
như hình vẽ
Hàm số
1 2020
x
g x f e
nghịch biến trên khoảng nào dưới đây?
A.
0;
. B.
1
;1
2
. C.
1
0;
2
. D.
1;1
.
Câu 19. (THPT Anh Sơn - Nghệ An - 2020) Cho hàm số
y f x
có bảng xét dấu của đạo hàm như
sau.
Hàm số
2 2019y f x
nghịch biến trên khoảng nào trong các khoảng dưới đây?
A.
2;4
. B.
4;2
. C.
2; 1
. D.
1;2
.
Câu 20. (THPT Anh Sơn - Nghệ An - 2020) Cho hàm số
f x
xác định và liên tục trên
và có đạo
hàm
f x
thỏa mãn
1 2 2019f x x x g x
với
0g x
,
x
. Hàm số
1 2019 2020y f x x
nghịch biến trên khoảng nào?
A.
1;
. B.
0;3
. C.
;3
. D.
3;
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Câu 21. Cho hàm số
y f x
xác định trên
và có bảng xét dấu đạo hàm như sau:
Biết
2,f x x
. Xét hàm số
3 2
3 2 3 2020g x f f x x x
. Khẳng định nào sau
đây đúng?
A. Hàm số
g x
đồng biến trên khoảng
2; 1
.
B. Hàm số
g x
nghịch biến trên khoảng
0;1
.
C. Hàm số
g x
đồng biến trên khoảng
3;4
.
D. Hàm số
g x
nghịch biến trên khoảng
2;3
.
Câu 22. Cho hàm số
f x
có bảng biến thiên như sau:
Hàm số
3 2
3.y f x f x
nghịch biến trên khoảng nào dưới đây?
A.
1; 2
. B.
3 ; 4
. C.
; 1
. D.
2 ; 3
.
Câu 23. Cho hàm số
y f x
có đồ thị nằm trên trục hoành và có đạo hàm trên
, bảng xét dấu của biểu
thức
f x
như bảng dưới đây.
Hàm số
2
2
2
2 1
f x x
y g x
f x x
nghịch biến trên khoảng nào dưới đây?
A.
;1
. B.
5
2;
2
. C.
1;3
. D.
2;
.
Dạng 3. Bài toán hàm ẩn, hàm hợp liên quan đến tham số và một số bài toán khác
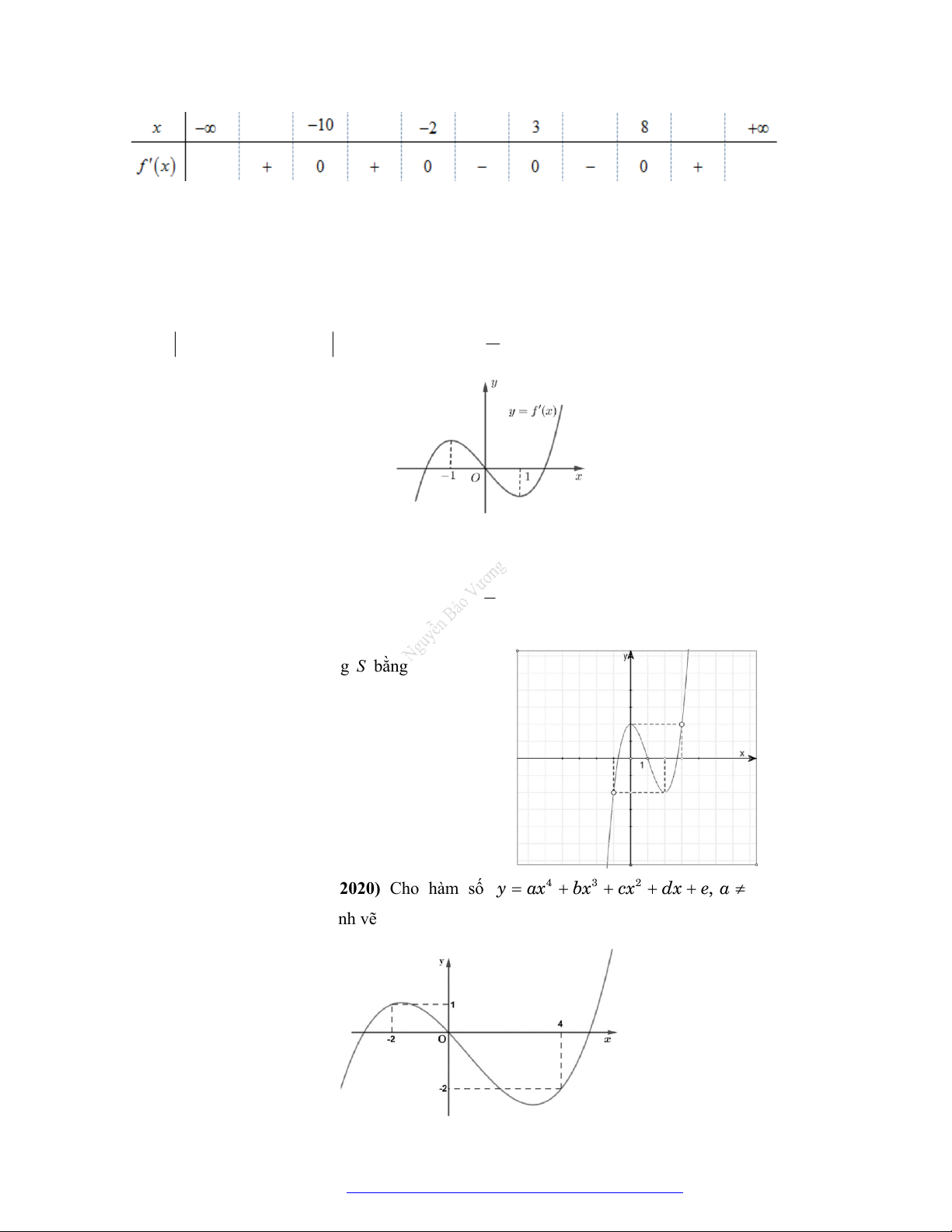
Câu 1. (Chuyên Lê Hồng Phong Nam Định 2019) Cho hàm số
y f x
có đạo hàm liên tục trên
.
Biết hàm số
y f x
có đồ thị như hình vẽ. Gọi
S
là tập hợp các giá trị nguyên
5;5m
để
hàm số
g x f x m
nghịch biến trên khoảng
1;2
. Hỏi
S
có bao nhiêu phần tử?
A.
4
. B.
3
. C.
6
. D.
5
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 2. (Chuyên Nguyễn Bỉnh Khiêm - Quảng Nam - 2020) Cho hàm số
y f x
có đạo hàm trên
và bảnng xét dấu đạo hàm như hình vẽ sau:
Có bao nhiêu số nguyên
m
để hàm số
3
4y f x x m
nghịch biến trên khoảng
1;1
?
A.
3
. B.
0
. C.
1
. D.
2
.
Câu 3. (Chuyên ĐH Vinh - Nghệ An -2020) Cho hàm số
f x
có đạo hàm trên
và
1 1f
. Đồ thị
hàm số
y f x
như hình bên. Có bao nhiêu số nguyên dương
a
để hàm số
4 sin cos 2y f x x a
nghịch biến trên
0;
2
?
A.
2
. B.
3
. C. Vô số. D.
5
.
Câu 4. (Chuyên Quang Trung - 2020) Cho hàm số
y f x
có đạo hàm liên tục trên
và có đồ thị
y f x
như hình vẽ. Đặt
2
1
1 2019
2
g x f x m x m
, với
m
là tham số thực. Gọi
S
là tập hợp các giá trị nguyên dương của
m
để hàm số
y g x
đồng biến trên khoảng
5;6
.
Tổng tất cả các phần tử trong
S
bằng
A.
4
.
B.
11
.
C.
14
.
D.
20
.
Câu 5. (Sở Hà Nội - Lần 2 - 2020) Cho hàm số
4 3 2
, 0y ax bx cx dx e a
. Hàm số
'y f x
có đồ thị như hình vẽ
Gọi S là tập hợp tất cả các giá trị nguyên thuộc khoảng
6;6
của tham số
m
để hàm số
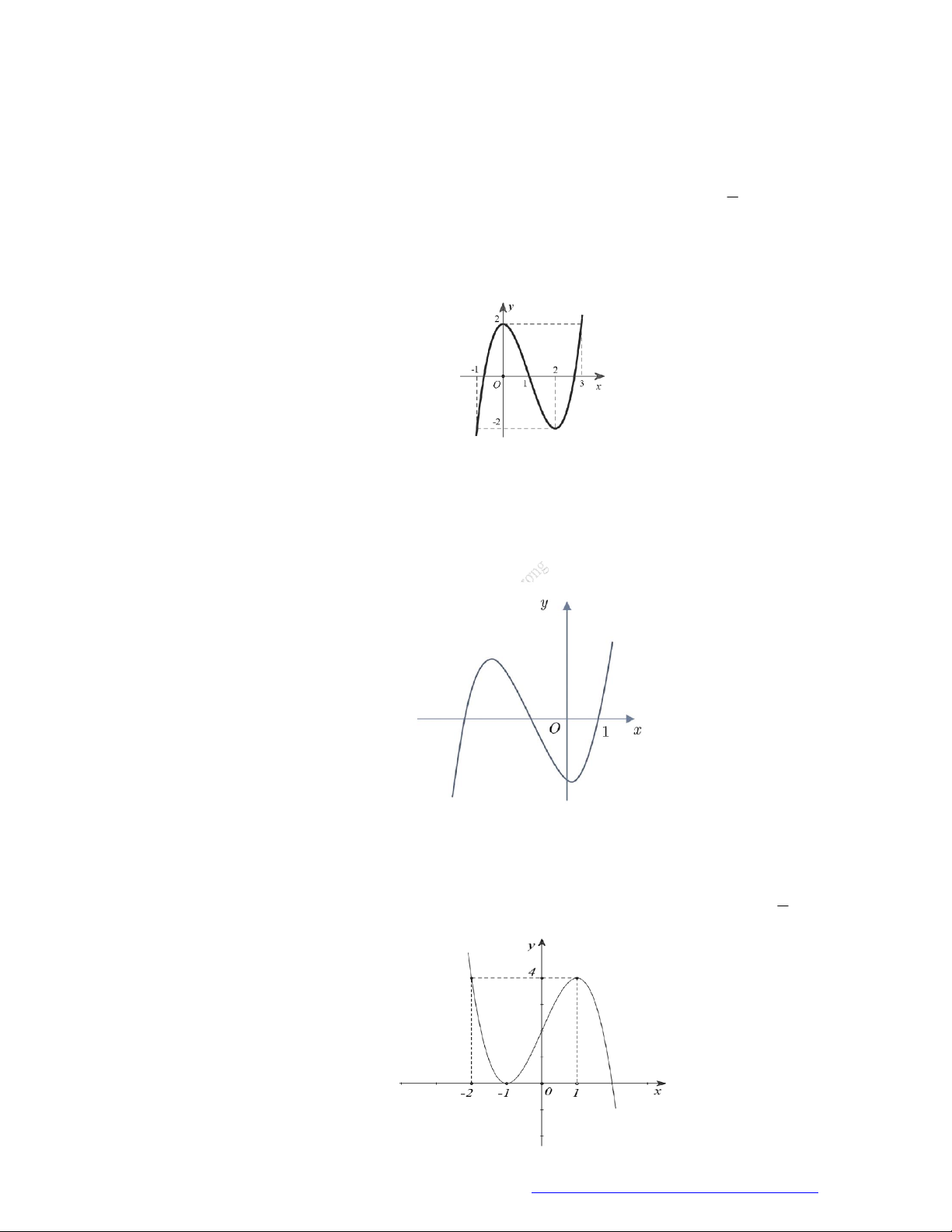
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
2 2
3 2 3 2g x f x m x m x m
nghịch biến trên
0;1
. Khi đó, tổng giá trị các
phần tử của S là
A. 12. B. 9. C. 6. D. 15.
Câu 6. (Chuyên Quang Trung - Bình Phước - Lần 2 - 2020) Cho hàm số
y f x
có đạo hàm liên
tục trên
và có đồ thị
y f x
như hình vẽ bên. Đặt
2
1
1 2019
2
g x f x m x m
,
với
m
là tham số thực. Gọi
S
là tập hợp các giá trị nguyên dương của
m
để hàm số
y g x
đồng biến trên khoảng
5 6;
. Tổng tất cả các phần tử trong
S
bằng:
A.
4
. B.
11
. C.
14
. D.
20
.
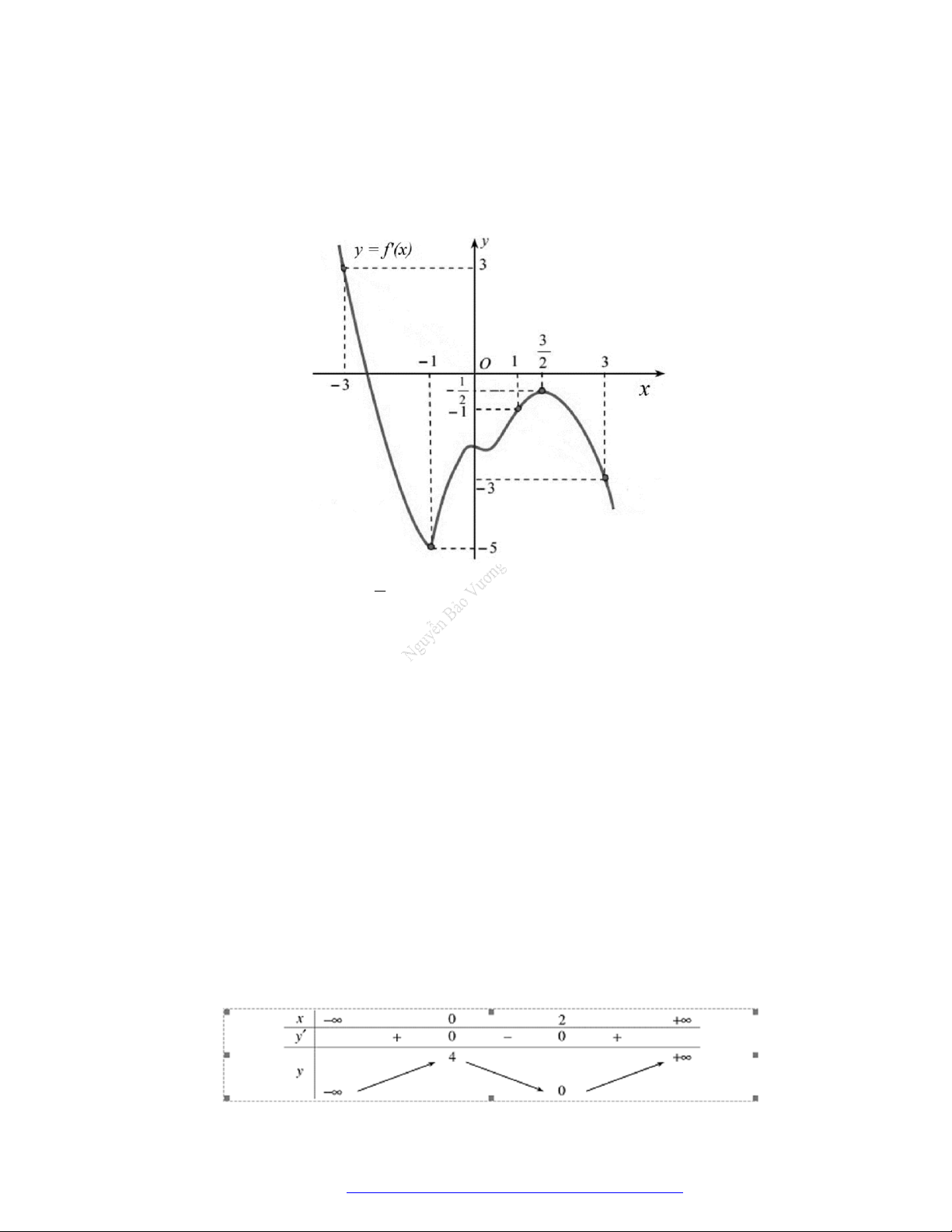
Câu 7. Cho hàm số
y f x
liên tục có đạo hàm trên
. Biết hàm số
'f x
có đồ thị cho như hình vẽ.
Có bao nhiêu giá trị nguyên của
m
thuộc
2019;2019
để hàm só
2019 2
x
g x f mx
đồng biến trên
0;1
A.
2028
. B.
2019
. C.
2011
. D.
2020
Câu 8. Cho hàm số
( )y f x
có đồ thị
( )f x
như hình vẽ. Có bao nhiêu giá trị nguyên
2020;2020m
để hàm số
2
2 3 ln 1 2g x f x x mx
đồng biến trên
1
;2
2
?
A.
2020
. B.
2019
. C.
2021
. D.
2018
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 9. Cho hàm số
f x
liên tục trên
và có đạo hàm
2 2
2 6f x x x x x m
với mọi
x
.
Có bao nhiêu số nguyên
m
thuộc đoạn
2020;2020
để hàm số
1g x f x
nghịch biến
trên khoảng
; 1
?
A.
2016
. B.
2014
. C.
2012
. D.
2010
.
Câu 10. Cho hàm số
f x
xác định và liên tục trên
R
. Hàm số
y f x
liên tục trên
và có đồ thị
như hình vẽ.
Xét hàm số
2
1
2 2 2020
2
g x f x m m x
, với
m
là tham số thực. Gọi
S
là tập hợp các
giá trị nguyên dương của
m
để hàm số
y g x
nghịch biến trên khoảng
3;4
. Hỏi số phần tử
của
S
bằng bao nhiêu?
A.
4
. B.
2
. C.
3
. D. Vô số.
Câu 11. Cho hàm số
f x
có đạo hàm trên
là
1 3f x x x
. Có bao nhiêu giá trị nguyên của
tham số
m
thuộc đoạn
10;20
để hàm số
2
3y f x x m
đồng biến trên khoảng
0;2
?
A.
18
. B.
17
. C.
16
. D.
20
.
Câu 12. Cho các hàm số
3
4f x x x m
và
2 3
2 2 2
2018 2019 2020g x x x x
. Có bao
nhiêu giá trị nguyên của tham số
2020;2020m
để hàm số
g f x
đồng biến trên
2;
?
A.
2005
. B.
2037
. C.
4016
. D.
4041
.
Câu 13. Cho hàm số có đạo hàm
2
2
1 2 1f x x x x mx
với mọi Có bao nhiêu số
nguyên âm
m
để hàm số
2 1g x f x
đồng biến trên khoảng
3;5
?
A.
3
B.
2
C.
4
D.
6
Câu 14. Cho hàm số
y f x
có bảng biến thiên như sau
Có bao nhiêu số nguyên
2019m
để hàm số
2
2g x f x x m
đồng biến trên khoảng
1;
?
y f x
.
x
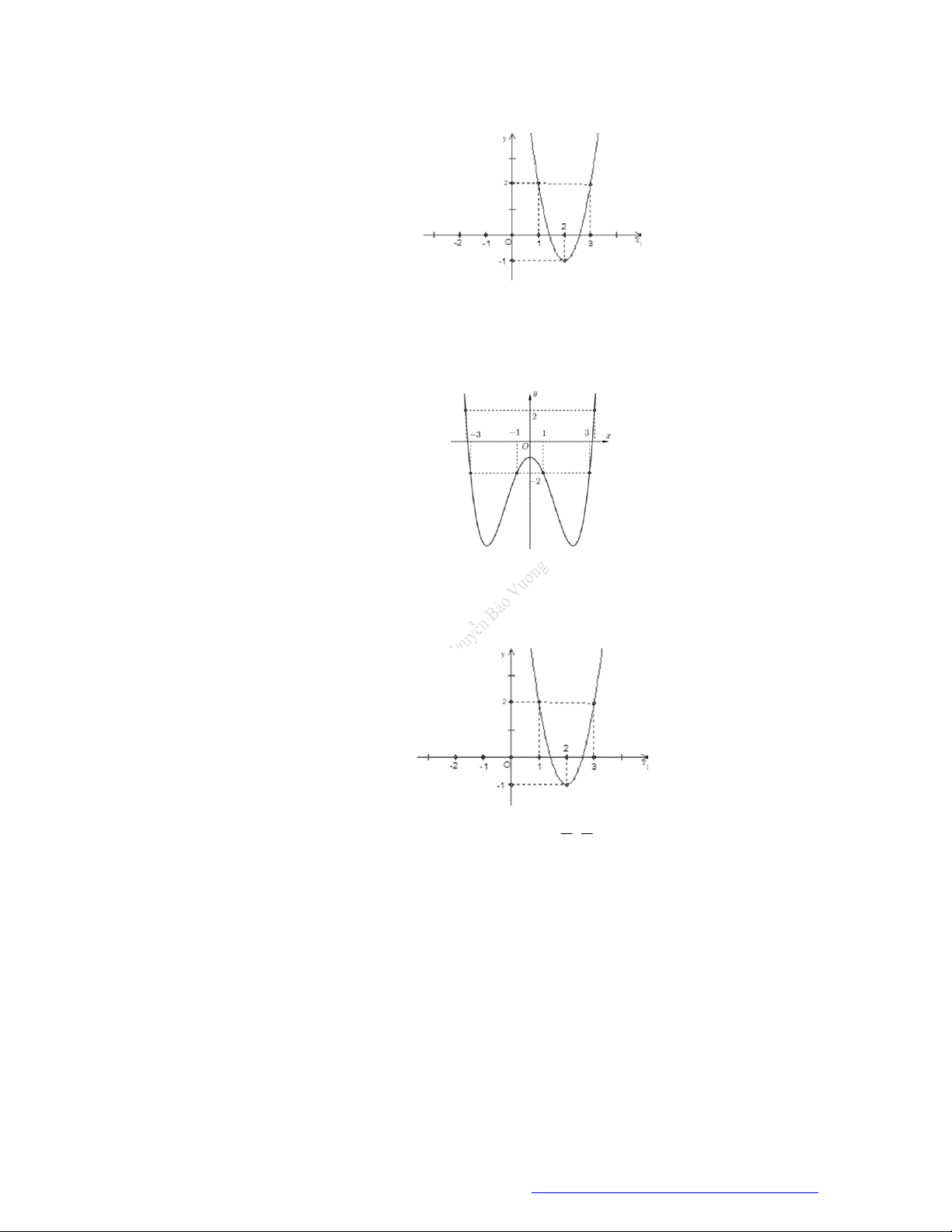
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
A. 2016. B. 2015. C. 2017. D. 2018.
Câu 15. Cho hàm số
y f x
có đạo hàm là hàm số
f x
trên
. Biết rằng hàm số
2 2y f x
có đồ thị như hình vẽ bên dưới. Hàm số
f x
đồng biến trên khoảng nào?
A.
;3 , 5;
. B.
; 1 , 1;
. C.
1;1
. D.
3;5
.
Câu 16. Cho hàm số
y f x
có đạo hàm là hàm số
f x
trên
. Biết rằng hàm số
2 2y f x
có đồ thị như hình vẽ bên dưới. Hàm số
f x
nghịch biến trên khoảng nào?
A.
3; 1 , 1;3
. B.
1;1 , 3;5
. C.
; 2 , 0;2
. D.
5; 3 , 1;1
.
Câu 17. Cho hàm số
y f x
có đạo hàm là hàm số
f x
trên
. Biết rằng hàm số
2 2y f x
có đồ thị như hình vẽ bên dưới. Hàm số
f x
nghịch biến trên khoảng nào?
A.
;2
. B.
1;1
. C.
3 5
;
2 2
. D.
2;
.
Câu 18. Cho hàm số
y f x
có đạo hàm cấp
3
liên tục trên
và thỏa mãn
2 3
. 1 4f x f x x x x
với mọi
x
và
2
2 .g x f x f x f x
. Hàm số
2
2h x g x x
đồng biến trên khoảng nào dưới đây?
A.
;1
. B.
2;
. C.
0;1
. D.
1;2
.
Câu 19. Cho hàm số
( )y f x
xác định trên
. Hàm số
( ) ' 2 3 2y g x f x
có đồ thị là một
parabol với tọa độ đỉnh
2; 1I
và đi qua điểm
1;2A
. Hỏi hàm số
( )y f x
nghịch biến trên
khoảng nào dưới đây?
A.
5;9
. B.
1;2
. C.
;9
. D.
1;3
.
Câu 20. Cho hàm số
y f x
, hàm số
3 2
, ,f x x ax bx c a b c
có đồ thị như hình vẽ
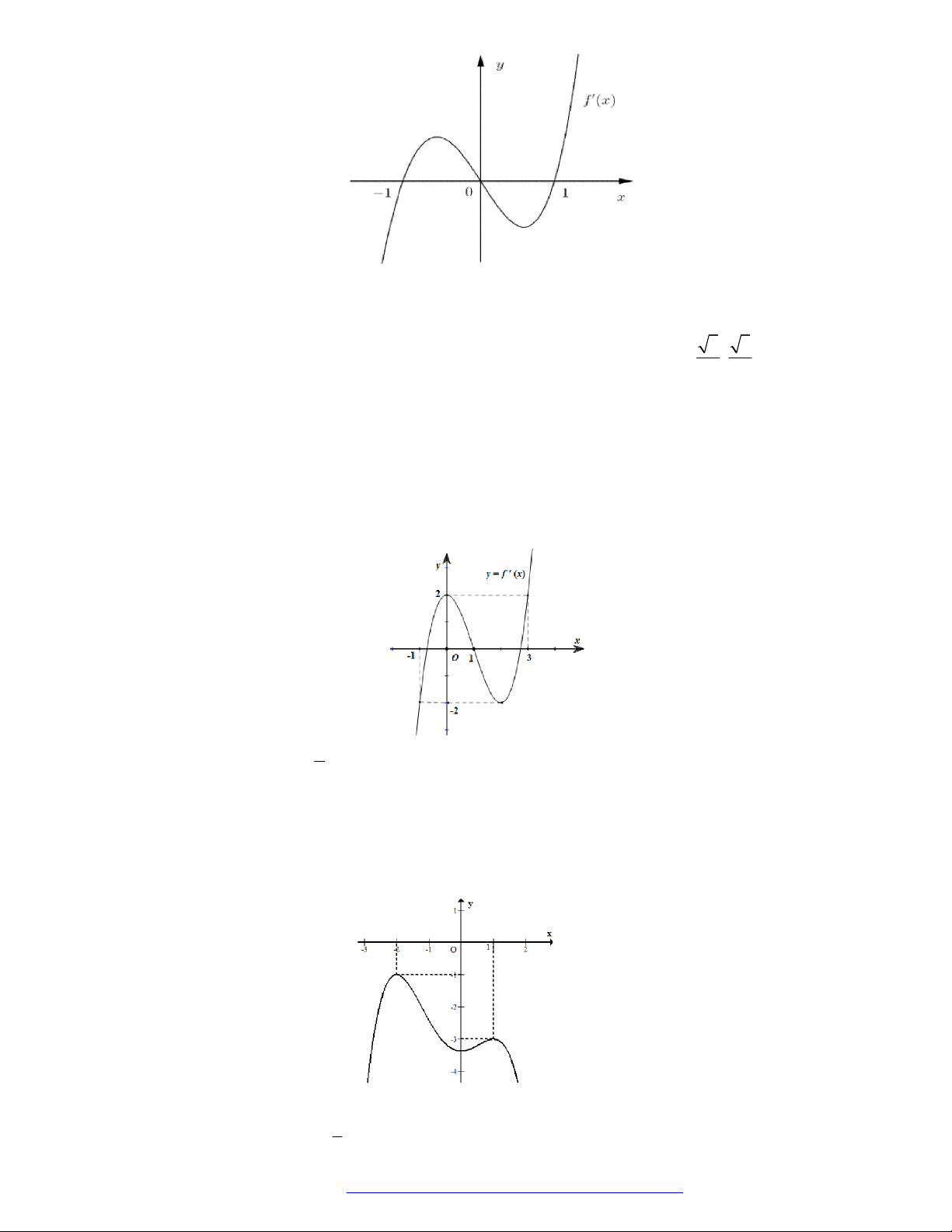
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Hàm số
g x f f x
nghịch biến trên khoảng nào dưới đây?
A.
1;
. B.
; 2
. C.
1;0
. D.
3 3
;
3 3
.
Câu 21. Cho hàm số
y f x
có đạo hàm
2
' 2 3, .f x x x x
Có bao nhiêu giá trị nguyên
của tham số m thuộc đoạn
10;20
để hàm số
2 2
3 1g x f x x m m
đồng biến trên
0;2 ?
A. 16. B. 17. C. 18. D. 19.
Câu 22. Cho hàm số
y f x
có đạo hàm liên tục trên
và đồ thị của hàm số
'y f x
như hình vẽ.
Đặt
2
1
1 2019
2
g x f x m x m
với
m
là tham số thực. Gọi
S
là tập các giá trị
nguyên dương của
m
để hàm số
y g x
đồng biến trên khoản
5;6
.Tổng các phần tử của
S
bằng:
A.
4
. B. 11. C.
14
. D. 20.
Câu 23. Cho hàm số
y f x
là hàm đa thức có đồ thị hàm số
y f x
như hình vẽ.
Có bao nhiêu giá trị nguyên của tham số
m
,
, 2020 2020m Z m
để hàm số
2 2 2
8
6
3
g x f x mx x x
đồng biến trên khoảng
3;0

T
ÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
A. 2021
. B. 2020. C. 2019. D. 2022.
Câu 24. Cho hàm số
f
x
.
Hàm số
y
f x
c
ó đồ thị như hình sau.
Có tất cả bao nhiêu giá trị nguyên dương của tham số
m
đề hàm số
20202)(4)(
2
mxxmxfxg
đồng
biến trên khoảng
).2;1(
A.
2
. B.
3
. C.
0
. D.
1
.
Câu
25. Cho hàm số
f
x
có đạo hàm
1
1 4 ;f x x x x x
.Có bao nhiêu số nguyên
2
020m
để hà
m số
2
1
x
g x f m
x
đồng biến trên
2
;
.
A.
2
018
. B.
2
019
. C.
2
020
. D.
2
021
Câu
26. Cho hàm số
y
f x
c
ó đạo hàm
'
1
x
f
x x e
,
có bao nhiêu giá trị nguyên của tham số
m
t
rong đoạn
2
019;2019
để hàm số
2
l
n 2y g x f x mx mx
nghịc
h biến trên
2
1;e
.
A. 2018
. B. 2019. C. 2020. D. 2021.
-------------------- HẾT --------------------
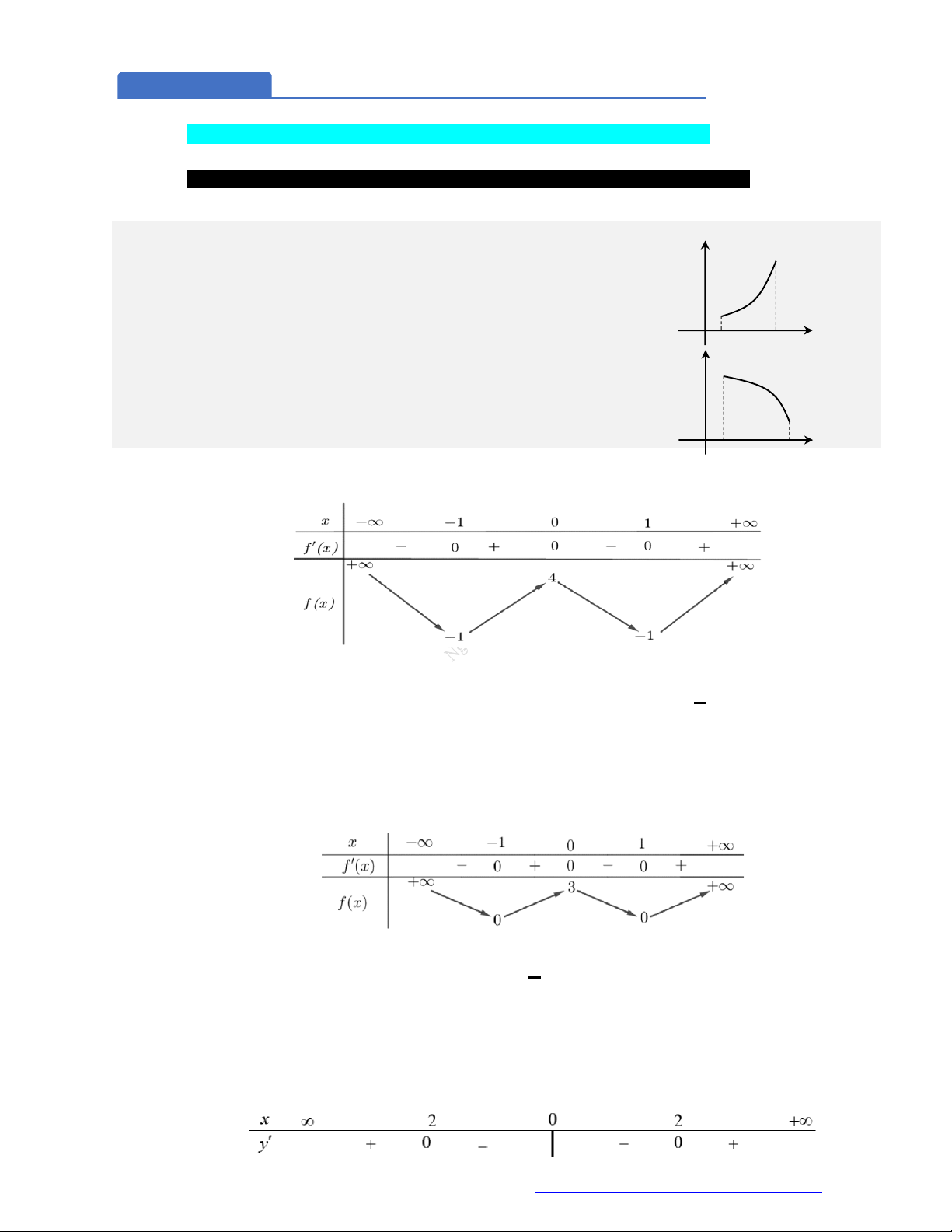
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
DẠNG TOÁN DÀNH CHO ĐỐI TƯỢNG HỌC SINH TRUNG BÌNH
Dạng 1. Tìm khoảng đơn điệu của hàm số thông qua bảng biến thiên, đồ thị
Định lí (thừa nhận): Giả sử hàm số
( )y f x
có đạo hàm trên khoảng
.K
Nếu
( ) 0, f x x K
thì hàm số đồng biến trên khoảng
.K
Nếu
( ) 0, f x x K
thì hàm số nghịch biến trên khoảng
.K
Nếu
( ) 0, f x x K
thì hàm số không đổi trên khoảng
.K
Hình dáng đồ thị
Nếu hàm số đồng biến trên
K
thì từ trái sang phải đồ thị đi lên.
Nếu hàm số nghịch biến trên
K
thì từ trái sang phải đồ thị đi xuống.
Câu 1. (Mã 101 – 2020 Lần 1) Cho hàm số
f x
có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
; 1
. B.
0;1
. C.
1;1
. D.
1;0
Lời giải
Chọn D.
Hàm số đã cho đồng biến trên khoảng
1;0
và
1;
Câu 2. (Mã 103 - 2019) Cho hàm số
f x
có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào sau đây?
A.
; 1 .
B.
0;1 .
C.
1;0 .
D.
1; .
Lời giải
Chọn C
Hàm số đã cho đồng biến trên khoảng
1;0 .
Câu 3. (Mã 104 - 2017) Cho hàm số
y f x
có bảng xét dấu đạo hàm như sau
TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
Chuyên đề 1
x
y
a
b
Đồng biến
O
Nghịch biến
x
y
a
b
O
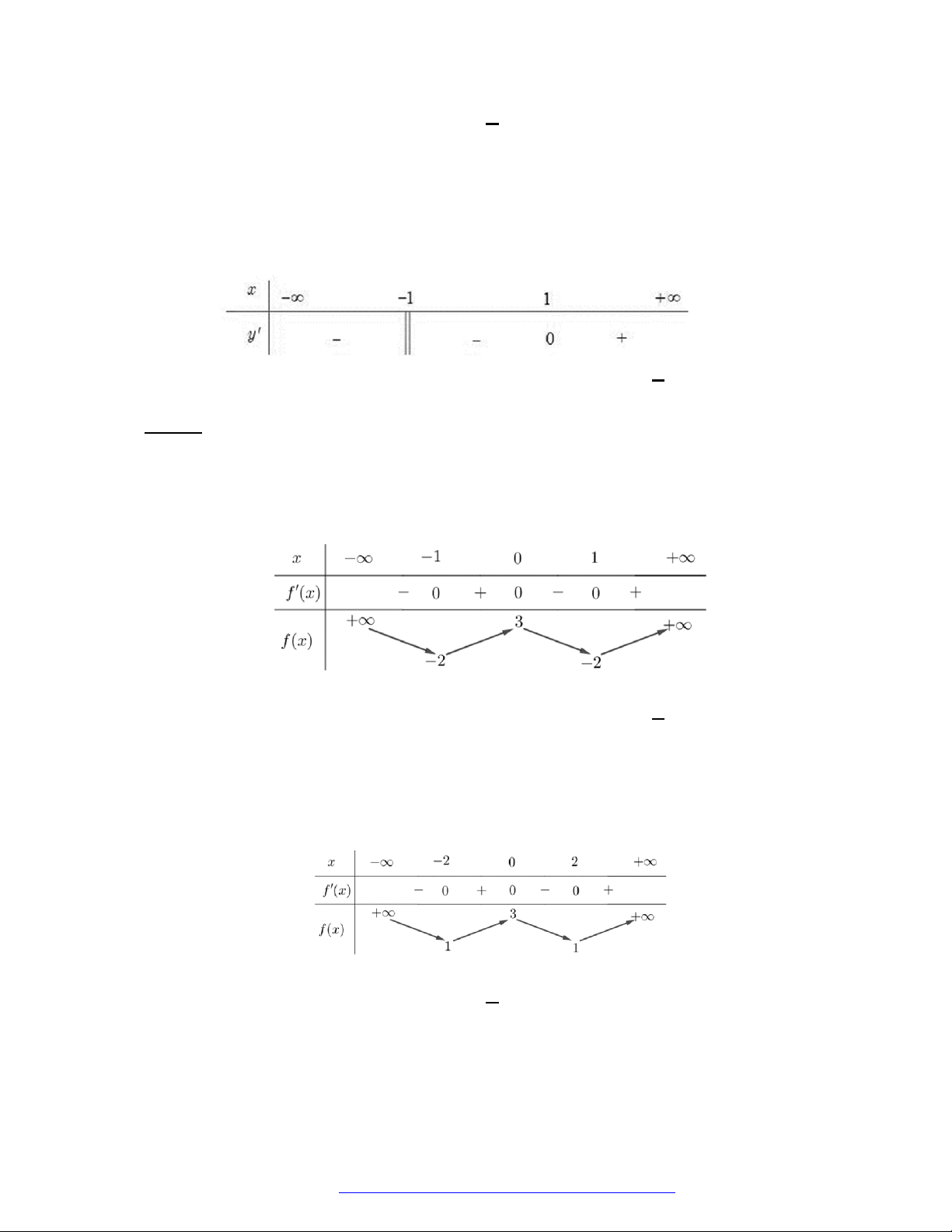
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng
; 2
B. Hàm số đồng biến trên khoảng
2;0
C. Hàm số đồng biến trên khoảng
;0
D. Hàm số nghịch biến trên khoảng
0;2
Lời giải
Chọn D
Theo bảng xét dấu thì
' 0y
khi
(0;2)x
nên hàm số nghịch biến trên khoảng
(0;2)
.
Câu 4. (Kim Liên - Hà Nội - 2019) Cho hàm số
y f x
có bảng xét dấu của đạo hàm như hình vẽ.
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
1;
. B.
;1
. C.
1;
. D.
; 1
.
Lời giải
Chọn D
Từ bảng xét dấu ta thấy hàm số đã cho nghịch biến trên khoảng
; 1
và
1;1
.
Vậy hàm số đã cho nghịch biến trên khoảng
; 1
.
Câu 5. (Mã 101 - 2018) Cho hàm số
y f x
có bảng biến thiên như sau
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
1;0
B.
;0
C.
1;
D.
0;1
Lời giải
Chọn D
Dựa vào bảng biến thiên ta có hàm số đã cho nghịch biến trên các khoảng
0;1
và
; 1
.
Câu 6. (Mã 102 - 2019) Cho hàm số
f x
có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây
A.
0;
. B.
0;2
. C.
2;0
. D.
; 2
.
Lời giải
Chọn C
Từ bảng biến thiên, suy ra trên khoảng
2;0
hàm số đồng biến.
Câu 7. (Mã 103 - 2018) Cho hàm số
y f x
có bảng biến thiên như sau :
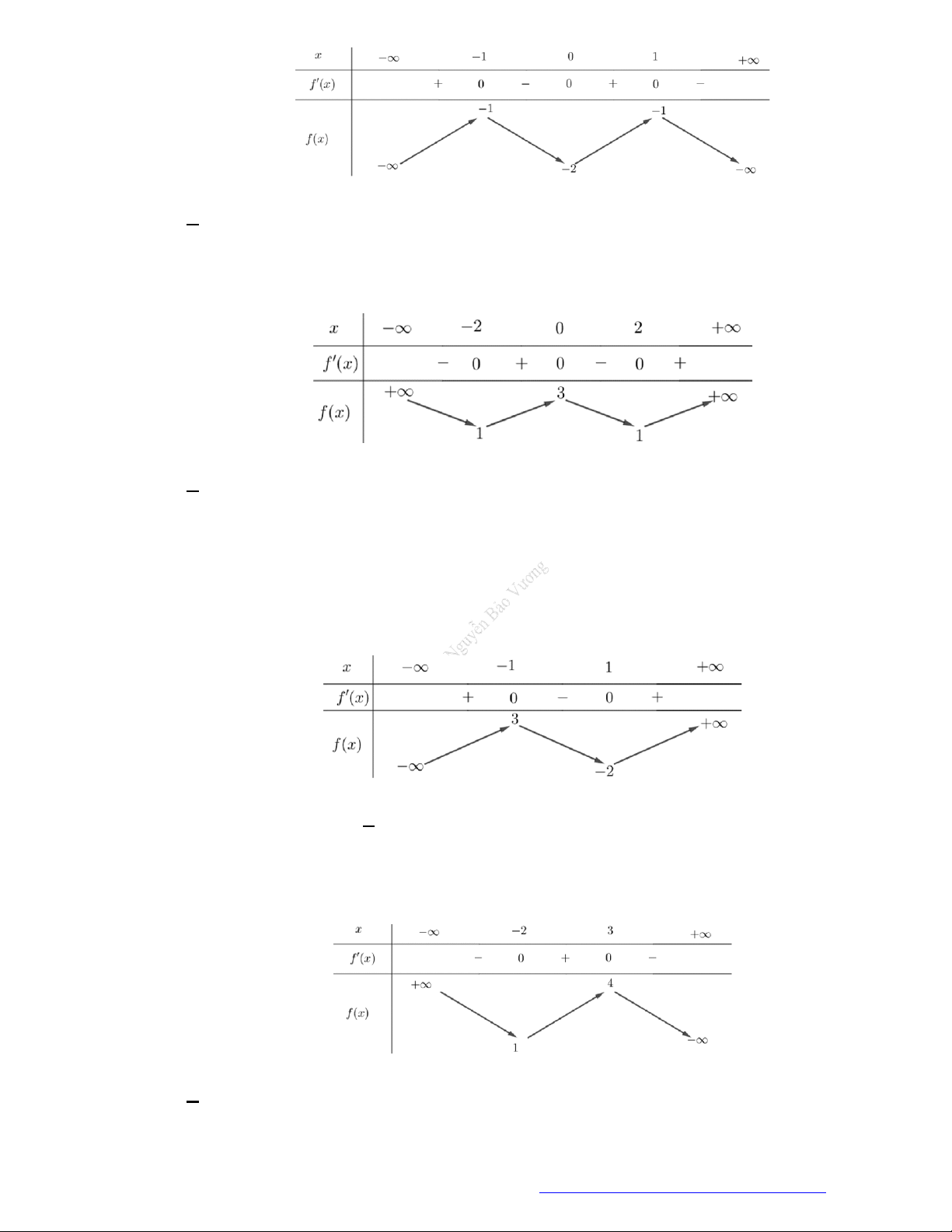
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
0;1
B.
1;
C.
;1
D.
1;0
Lời giải
Chọn A
Câu 8. (Mã 101 - 2019) Cho hàm số có bảng biến thiên như sau
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
0;2 .
B.
0; .
C.
2;0 .
D.
2; .
Lời giải
Chọn A
Dựa vào bảng biến thiên ta thấy trên khoảng
0;2
thì
' 0f x
.
Vậy hàm số nghịch biến trên khoảng
0;2
.
Câu 9. (Mã 102 - 2018) Cho hàm số
y f x
có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
1;
. B.
1;
. C.
1;1
. D.
;1
.
Lời giải
Chọn B
Câu 10. (Mã 104 -2018) Cho hàm số
y f x
có bảng biến thiên như sau
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
2;3
B.
3;
C.
; 2
D.
2;
Lời giải
Chọn A
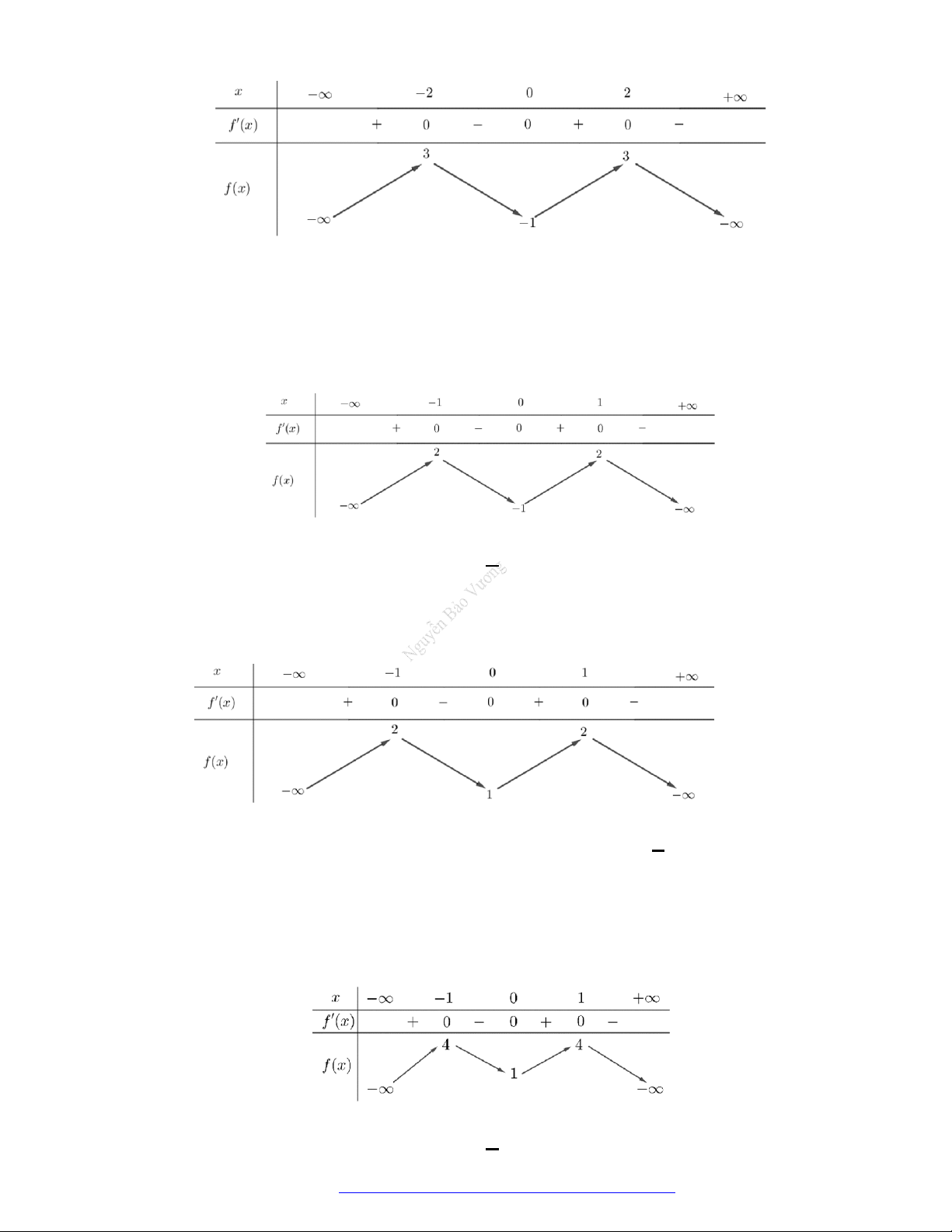
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 11. (Đề Tham Khảo 2018) Cho hàm số
y f x
có bảng biến thiên như sau:
Hàm số
y f x
nghịch biến trên khoảng nào dưới đây?
A.
0;
B.
; 2
C.
0;2
D.
2;0
Lời giải
Chọn D
Câu 12. (Đề Minh Họa 2020 – Lần 1) Cho hàm số
f x
có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
; 1
. B.
0;1
. C.
1;0
. D.
;0
.
Lời giải
Chọn C
Câu 13. (Đề Minh Họa 2020 – Lần 2) Cho hàm số
y f x
có bảng biến thiên như sau
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
1;
. B.
1;0
. C.
1;1
. D.
0;1
.
Lời giải
Chọn D
Dựa vào bảng biến thiên ta thấy: Hàm số đã cho đồng biến trên các khoảng
; 1
và
0;1
.
Câu 14. (Mã 102 – 2020 Lần 1) Cho hàm số có bảng biến thiên như sau.
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A. . B. . C. . D. .
f x
1;
1;1
0;1
1;0
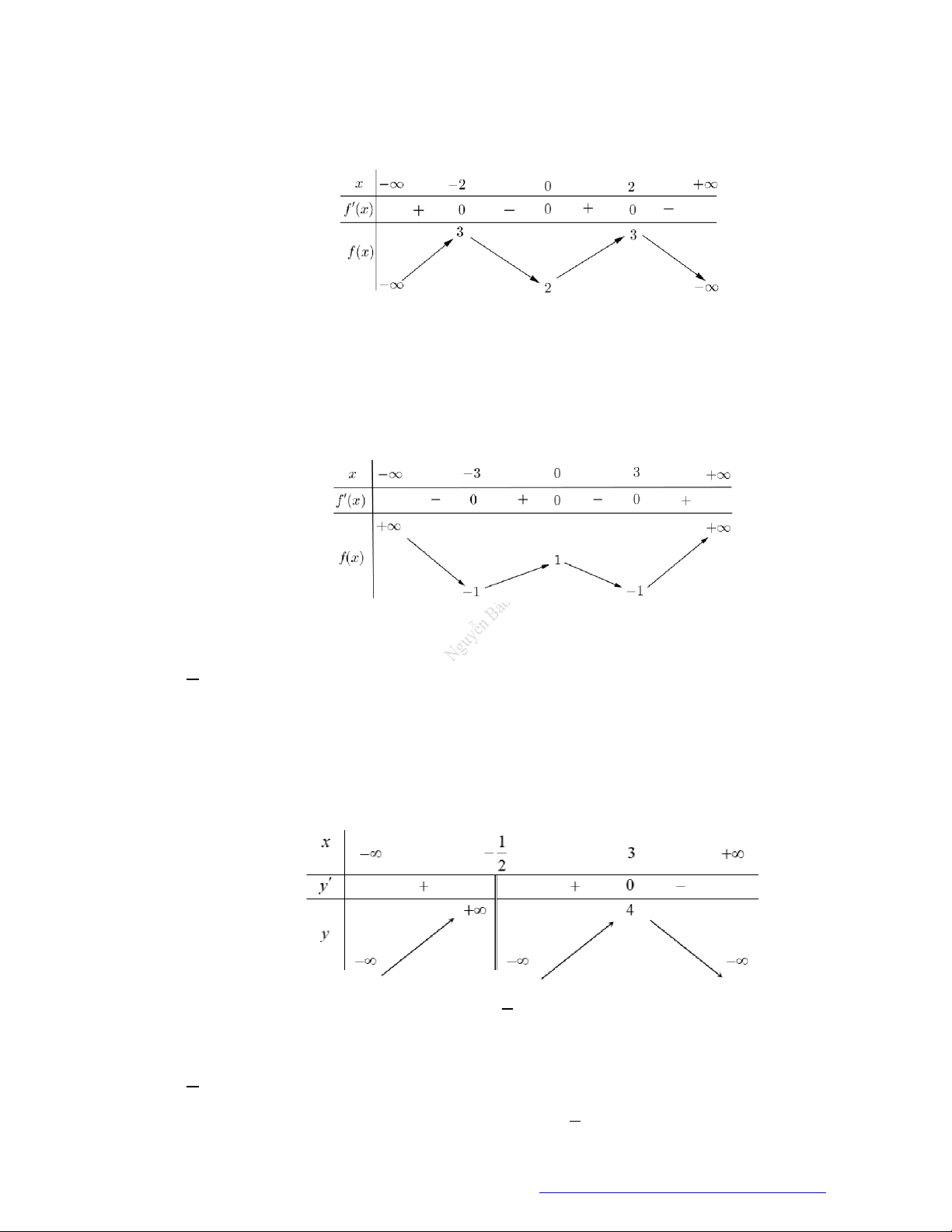
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Lời giải
Chọn C
Dựa vào bảng biến thiên, ta thấy hàm số đã cho đồng biến trên các khoảng và .
Câu 15. (Mã 103 – 2020 Lần 1) Cho hàm số
( )f x
có bảng biến thiên như sau:
Hàm số đã chođồng biến trên khoảng nào dưới đây
A.
( 2;2)
B.
(0;2)
C.
( 2;0)
D.
(2; )
.
Lời giải
Chọn B
Câu 16. (Mã 104 – 2020 Lần 1) Cho hàm số
f x
có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
3;0
. B.
3;3
. C.
0;3
. D.
; 3
.
Lời giải
Chọn A
Hàm số đã cho đồng biến trên khoảng
3;0
và
3;
.
Câu 17. Cho hàm số
y f x
có bảng biến thiên như hình dưới đây. Mệnh đề nào sau đây là đúng?
A. Hàm số đã cho đồng biến trên khoảng
1
;
2
.
B. Hàm số đã cho đồng biến trên khoảng
;3
.
C. Hàm số đã cho nghịch biến trên khoảng
3;
.
D. Hàm số đã cho nghịch biến trên các khoảng
1
;
2
và
3;
.
Lời giải
; 1
0;1
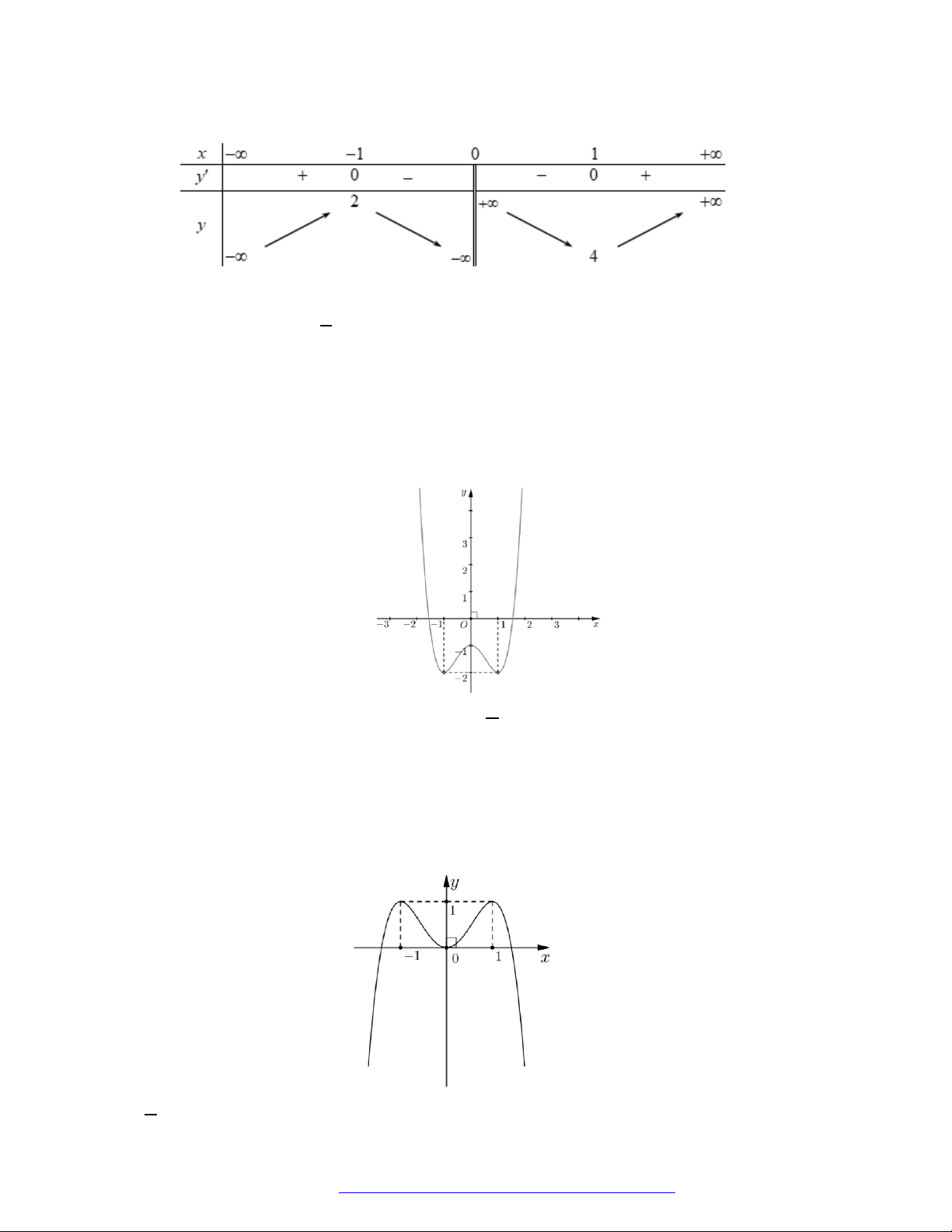
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Chọn C
Từ bảng biến thiên ta thấy hàm số đã cho nghịch biến trên khoảng
3;
.
Câu 18. Cho hàm số
y f x
có bảng biến thiên như sau:
Hàm số nghịch biến trong khoảng nào?
A.
1;1
. B.
0;1
. C.
4;
. D.
;2
.
Lời giải
Chọn B
Từ bảng biến thiên ta thấy hàm số đã cho nghịch biến trên khoảng
0;1
.
Câu 19. (Đề Tham Khảo 2019) Cho hàm số
y f x
có đồ thị như hình vẽ bên. Hàm số đã cho đồng
biến trên khoảng nào dưới đây?
A.
1
B.
1;1
C.
1;0
D.
0;1
Lời giải
Chọn C
Từ đồ thị, ta thấy hàm số đồng biến trên các khoảng
1;0
và
1;
. Chọn
Câu 20. (Mã 102 – 2020 – Lần 2) Cho hàm số
y f x
có đồ thị là đường cong trong hình bên. Hàm số
đã cho nghịch biến trên khoảng nào dưới đây?
A.
1;0 .
B.
; 1
. C.
0;1
. D.
0;
.
Lời giải
Chọn A
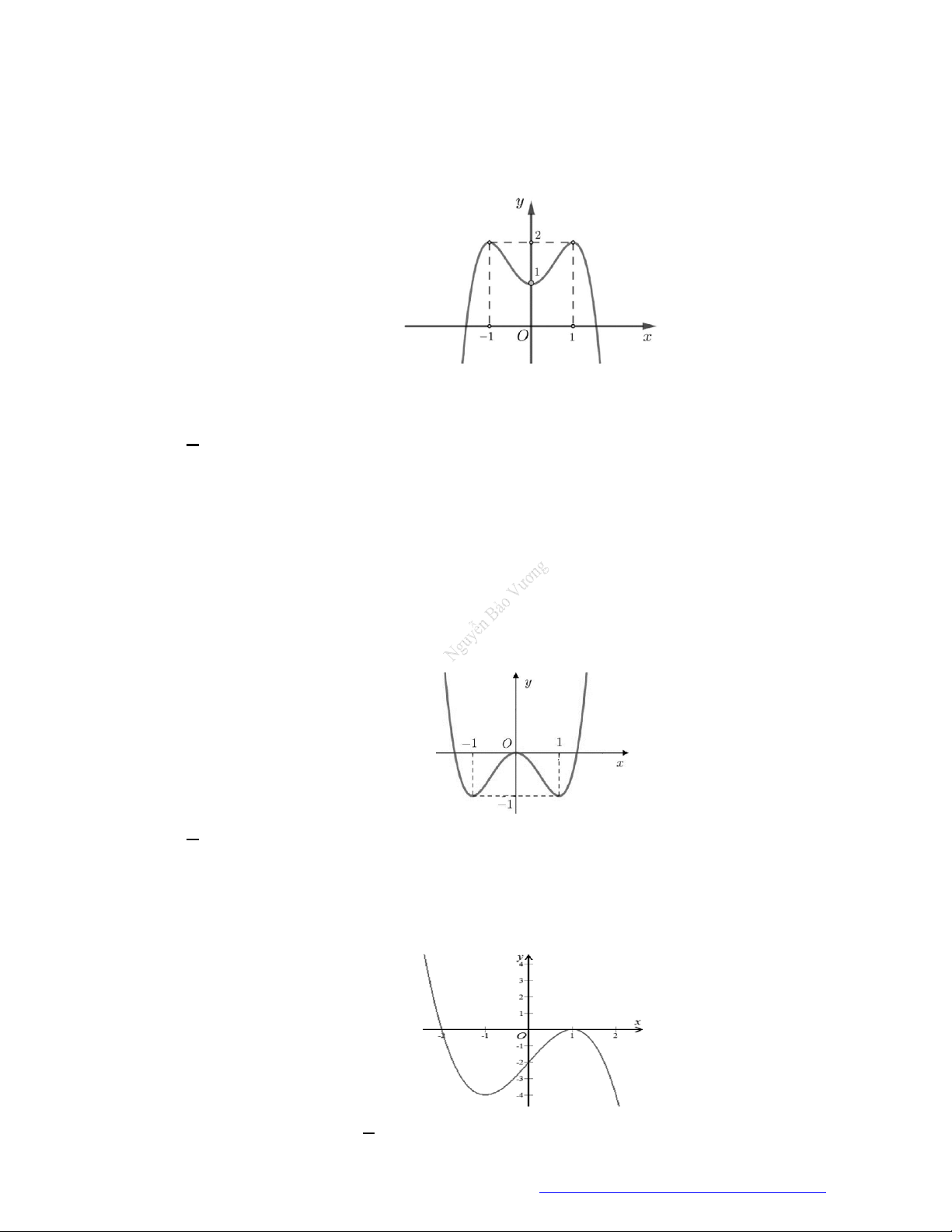
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Dựa vào đồ thị của hàm số
y f x
ta có:
Hàm số
y f x
nghịch biến trên các khoảng
1;0
và
1;
, đồng biến trên các khoảng
; 1
và
0;1 .
Câu 21. (Mã 107 – 2020 Lần 2) Cho hàm số
y f x
có đồ thị là đường cong trong hình bên.
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
0;1
. B.
;0
. C.
1;
. D.
1;0
.
Lời giải
Chọn A
Từ đồ thị hàm số
y f x
ta có hàm số đồng biến trên hai khoảng
; 1
và
0;1
chọn đáp án A.
Câu 22. (Mã 103 – 2020 – Lần 2) Cho hàm số
y f x
có đồ thị là đường cong hình bên. Hàm số đã
cho đồng biến trên khoảng nào dưới đây?
A.
1;0
. B.
; 1
. C.
0;
. D.
0;1
.
Lời giải
Chọn A
Câu 23. Cho hàm số
y f x
có đồ thị như hình vẽ bên. Hàm số đã cho đồng biến trên khoảng nào dưới
đây?
A.
; 1 .
B.
1;1 .
C.
0; .
D.
; .
Lời giải
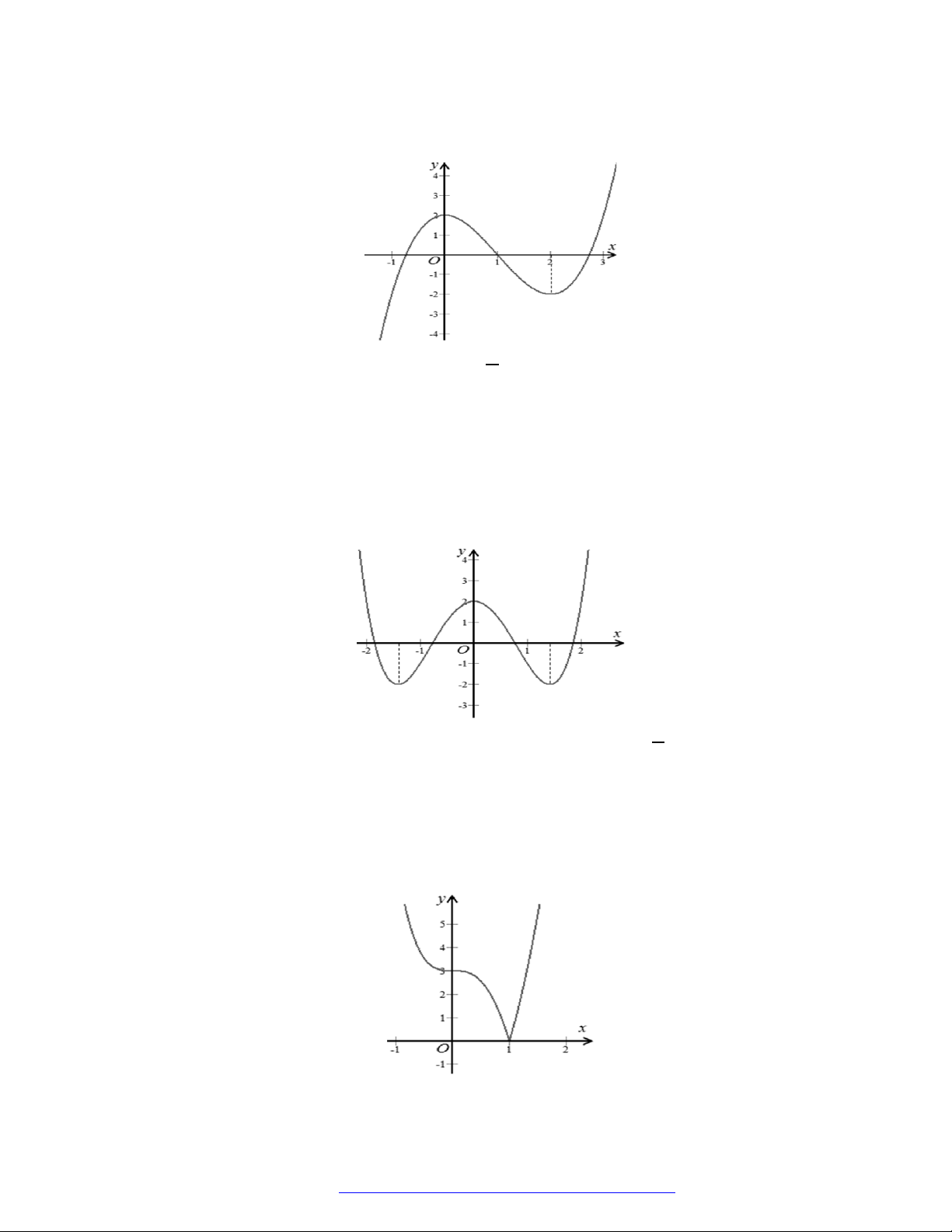
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Chọn B
Nhìn vào đồ thị đã cho, ta có hàm số đồng biến trên khoảng
1;1
.
Câu 24. Cho hàm số
y f x
có đồ thị như hình vẽ bên. Hàm số đã cho nghịch biến trên khoảng nào
dưới đây?
A.
1;1 .
B.
1; 2 .
C.
1; 2 .
D.
2; .
Lời giải
Chọn C
Nhìn vào đồ thị đã cho, ta có hàm số nghịch biến trên khoảng
0;2
nên nghịch biến trên khoảng
1; 2 .
Câu 25. Cho hàm số
y f x
có đồ thị như hình vẽ bên. Hàm số đã cho nghịch biến trên khoảng nào
dưới đây?
A.
; 1 .
B.
1;1 .
C.
1; 2 .
D.
0;1 .
Lời giải
Chọn D
Nhìn vào đồ thị đã cho, ta có trên khoảng
0;1
đồ thị hàm số đi xuống (theo chiều từ trái qua
phải) nên nghịch biến trên khoảng
0;1 .
Câu 26. Cho hàm số
y f x
có đồ thị như hình vẽ bên.
Mệnh đề nào sau đây là đúng?
A. Hàm số đã cho đồng biến trên khoảng
0;2
.
B. Hàm số đã cho đồng biến trên khoảng
1;
.
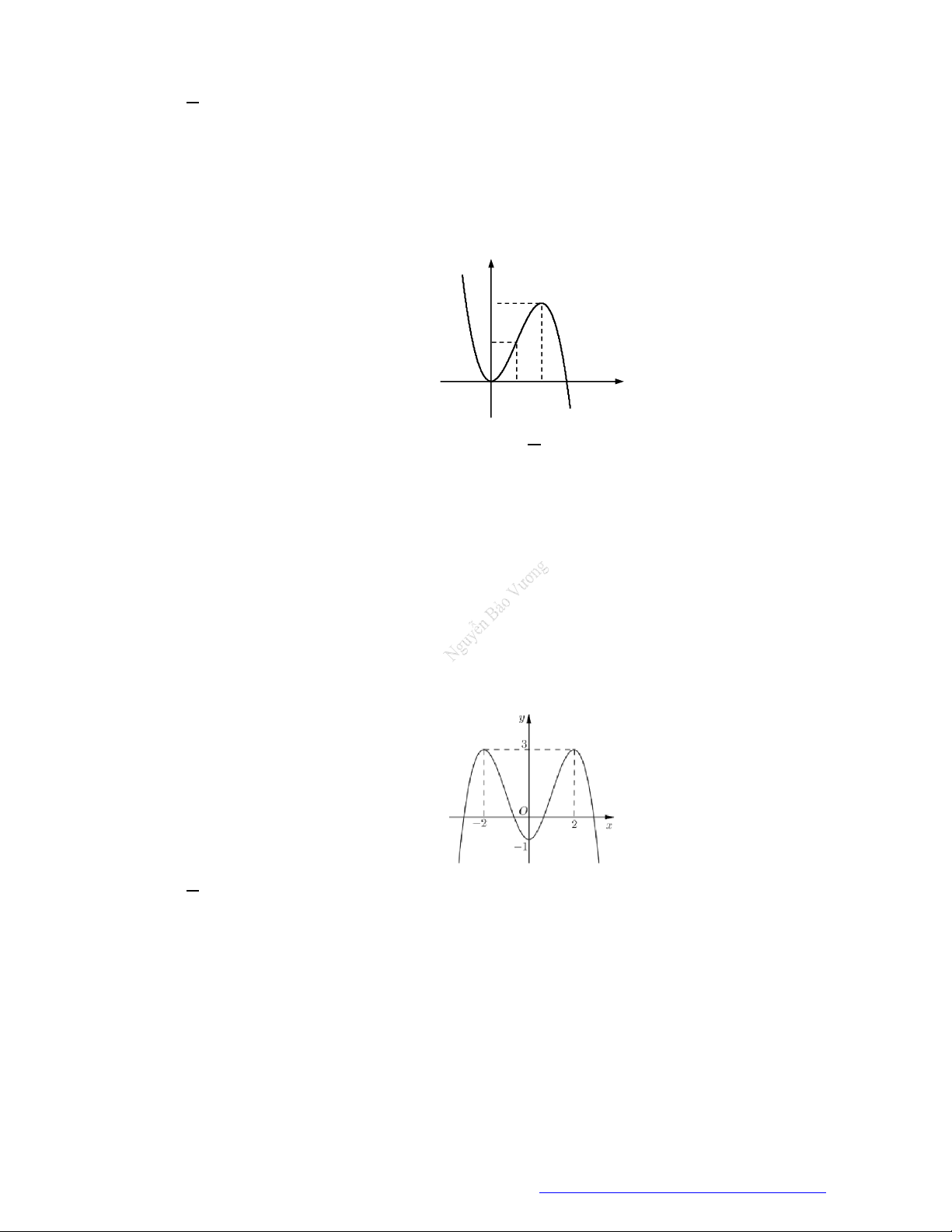
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
C. Hàm số đã cho nghịch biến trên khoảng
1;2
.
D. Hàm số đã cho nghịch biến trên khoảng
;1
.
Lời giải
Chọn D
Nhìn vào đồ thị đã cho, ta có trên khoảng
;1
đồ thị hàm số đi xuống (theo chiều từ trái qua
phải) nên nghịch biến trên khoảng
;1
.
Câu 27. Cho hàm số
y f x
có đồ thị như hình vẽ. Hàm số đã cho đồng biến trên khoảng nào?
A.
;0
. B.
1;3
. C.
0;2
. D.
0;
.
Lời giải
Chọn C
Xét đáp án A, trên khoảng
;0
đồ thị có hướng đi xuống là hàm số nghịch biến nên loại.
Xét đáp án B, trên khoảng
1;3
đồ thị có đoạn hướng đi lên là hàm số đồng biến và có đoạn
hướng đi xuống là hàm số nghịch biến nên loại.
Xét đáp án C, trên khoảng
0;2
đồ thị có hướng đi lên là hàm số đồng biến nên chọn.
Xét đáp án D, trên khoảng
0;
đồ thị có đoạn hướng đi lên là hàm số đồng biến và có đoạn
hướng đi xuống là hàm số nghịch biến nên loại.
Câu 28. Cho hàm số
y f x
có đồ thị như hình vẽ. Hàm số đã cho nghịch biến trên khoảng nào?
A.
2;0
. B.
;0
. C.
2;2
. D.
0;2
.
Lời giải
Chọn A
Xét đáp án A, trên khoảng
2;0
đồ thị hướng đi xuống là hàm số nghịch biến nên chọn.
Xét đáp án B, trên khoảng
;0
đồ thị có đoạn hướng đi lên là hàm số đồng biến và có đoạn
hướng xuống là hàm số đồng nghịch biến nên loại.
xét đáp án C, trên khoảng
2;2
đồ thị có hướng đi xuống là hàm số nghịch biến và có đoạn
hướng đi lên là hàm số đồng biến nên loại.
Xét đáp án D, trên khoảng
0;2
đồ thị có hướng đi lên là hàm số đồng biến nên loại.
Câu 29. Cho hàm số
y f x
có đồ thị như hình vẽ. Hàm số đã cho nghịch biến trên khoảng nào?
O
1
2
3
2
4
y
x
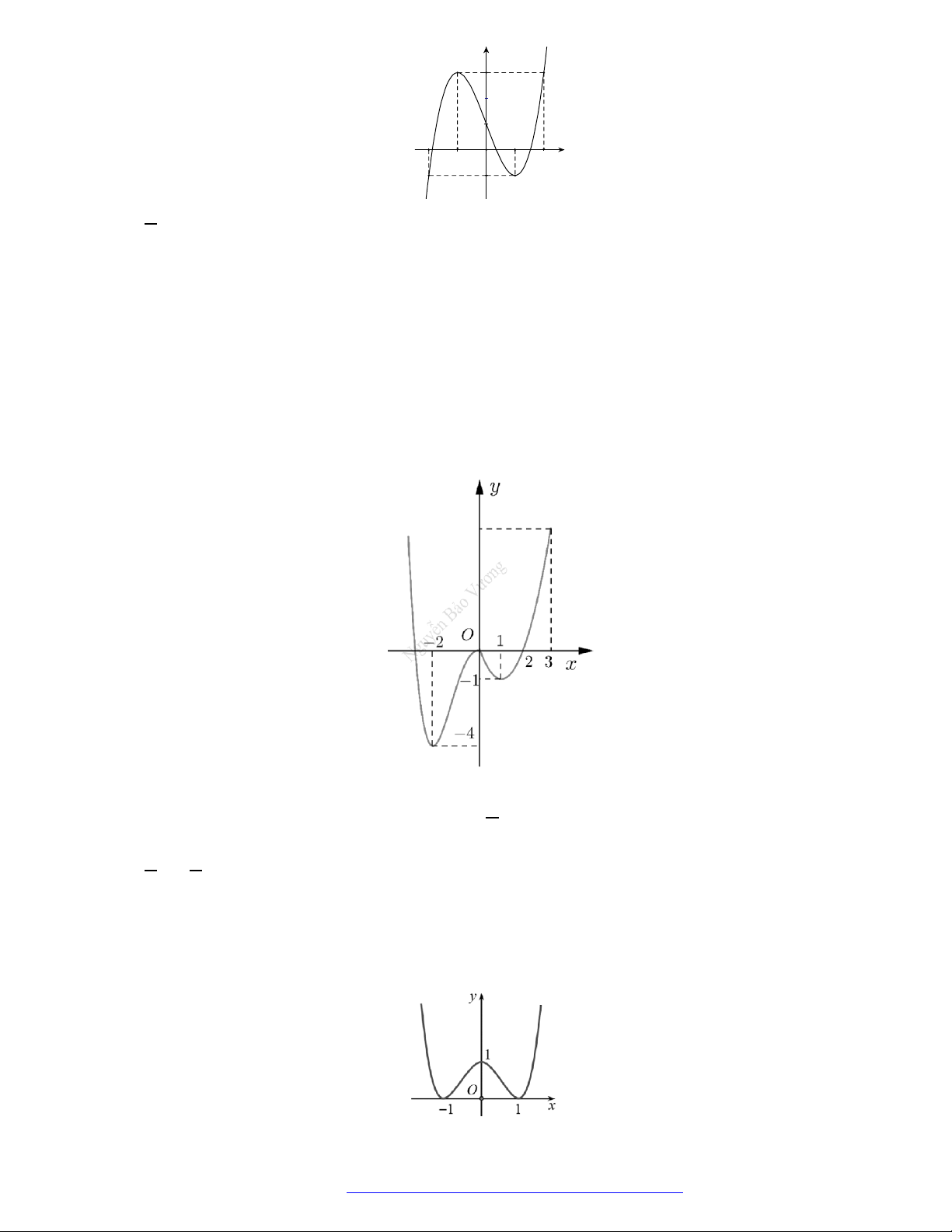
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
1;1
. B.
2; 1
. C.
1;2
. D.
1;
.
Lời giải
Chọn A
Xét đáp án A, trên khoảng
1;1
đồ thị có hướng đi xuống là hàm số nghịch biến nên chọn.
Xét đáp án B, trên khoảng
2; 1
đồ thị có hướng đi lên là hàm số đồng biến nên loại.
Xét đáp án C, trên khoảng
1;2
đồ thị có đoạn hướng đi xuống là hàm số nghịch biến và có
đoạn hướng đi lên là hàm số đồng biến nên loại.
Xét đáp án D, trên khoảng
1;
đồ thị có hướng đi lên là hàm số đồng biến nên loại.
Câu 30. (Chuyên ĐH Vinh - Nghệ An -2020) Cho hàm số
y f x
có đồ thị như hình vẽ bên.
Hàm số đã cho nghịch biến trên khoảng
A.
1;0
. B.
2; 1
. C.
0;1
. D.
1;3
.
Lời giải
Chọn C
Từ đồ thị hàm số ta có hàm số nghịch biến trên các khoảng
; 2
và
0;1
.
Câu 31. (Chuyên Hưng Yên - 2020) Cho hàm số
f x
liên tục trên
và có đồ thị như hình vẽ bên.
Khẳng định nào sau đây là đúng?
A. Hàm số đồng biến trên
;0
và
0;
.
O
x
2
1
1
y
3
2
1
1

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
B. Hàm số đồng biến trên
1;0
và
1;
.
C. Hàm số đồng biến trên
1;0 1;
.
D. Hàm số đồng biến trên
; 1 1;
.
Lời giải
Chọn B
Hàm số đồng biến trên
1;0
và
1;
.
Dạng 2. Tìm khoảng đơn điệu của hàm số cho trước
Bước 1. Tìm tập xác định
D
của hàm số.
Bước 2. Tính đạo hàm
( ).y f x
Tìm các điểm
, ( 1,2,3,..., )
i
x i n
mà tại đó đạo hàm bằng 0
hoặc không xác định.
Bước 3. Sắp xếp các điểm
i
x
theo thứ tự tăng dần và lập bảng biến thiên.
Bước 4. Nêu kết luận về các khoảng đồng biến và nghịch biến dưa vào bảng biến thiên.
Câu 1. (Mã 110 - 2017) Hàm số nào dưới đây đồng biến trên khoảng
;
?
A.
1
2
x
y
x
B.
3
y x x
C.
3
3y x x
D.
1
3
x
y
x
Lời giải
Chọn B
Vì
3
y x x
2
3 1 0,y x x
.
Câu 2. (Đề Tham Khảo - 2017) Cho hàm số
2
1
x
y
x
. Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng
;
B. Hàm số nghịch biến trên khoảng
1;
C. Hàm số nghịch biến trên khoảng
; 1
D. Hàm số đồng biến trên khoảng
; 1
Lời giải
Chọn D
Tập xác định:
1
\
.
Ta có
2
3
' 0
1
y
x
,
1
\x
.
Câu 3. (Đề Tham Khảo - 2017) Hàm số nào dưới đây đồng biến trên khoảng
;
?
A.
4 2
3y x x
. B.
2
1
x
y
x
. C.
3
3 3 2
y x x
. D.
3
2 5 1y x x
.
Lời giải
Chọn C
Hàm số
3
3 3 2
y x x
có TXĐ:
D
.
2
9 3 0,y x x
, suy ra hàm số đồng biến trên khoảng
;
.
Câu 4. (Mã 110 - 2017) Cho hàm số
3 2
3y x x
. Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng
0;2
B. Hàm số nghịch biến trên khoảng
0;2
C. Hàm số nghịch biến trên khoảng
;0
D. Hàm số nghịch biến trên khoảng
2;
Lời giải
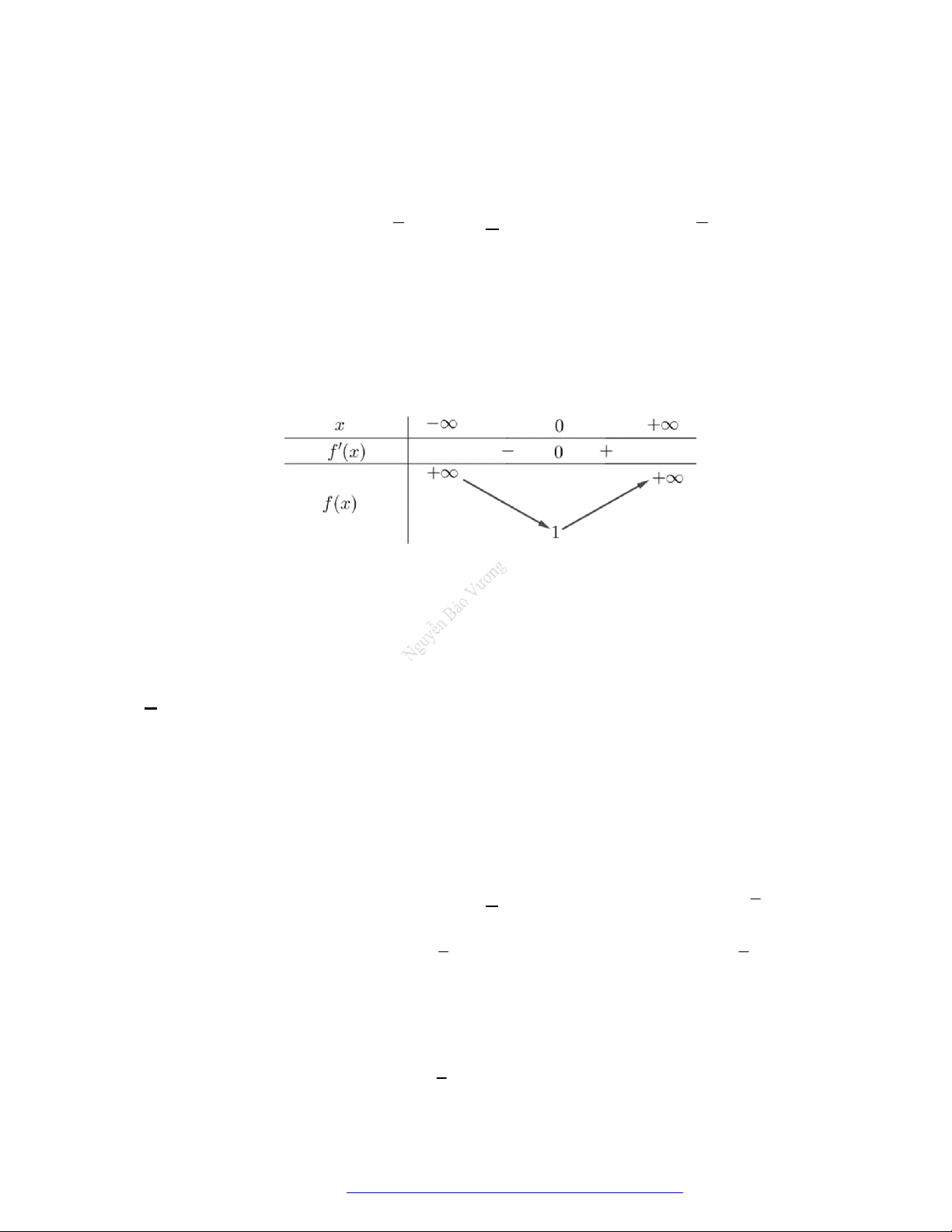
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Chọn B
Ta có
2
3 6y x x
;
0
0
2
x
y
x
.
Lập bảng biến thiên rồi suy ra hàm số nghịch biến trên khoảng
0;2
Câu 5. (Dề Minh Họa - 2017) Hỏi hàm số
4
2 1y x đồng biến trên khoảng nào?
A.
;0 .
B.
1
;
2
. C.
0;
. D.
1
;
2
.
Lời giải
Chọn C
4
2 1y x . Tập xác định:
D
Ta có:
3
8y x
;
3
0 8 0 0y x x
suy ra
0 1y
Giới hạn:
lim
x
y
;
lim
x
y
Bảng biến thiên:
Vậy hàm số đồng biến trên khoảng
0; .
Câu 6. (Mã 105 - 2017) Cho hàm số
y f x
có đạo hàm
2
1f x x
,
x
. Mệnh đề nào dưới
đây đúng?
A. Hàm số nghịch biến trên khoảng
1;
B. Hàm số nghịch biến trên khoảng
1;1
C. Hàm số đồng biến trên khoảng
;
D. Hàm số nghịch biến trên khoảng
; 0
Lời giải
Chọn C
Do hàm số
y f x
có đạo hàm
2
1 0f x x
x
nên hàm số đồng biến trên khoảng
;
.
Câu 7. (Mã 105 - 2017) Cho hàm số
3 2
2 1 y x x x . Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng
1;
B. Hàm số nghịch biến trên khoảng
1
;1
3
C. Hàm số nghịch biến trên khoảng
1
;
3
D. Hàm số đồng biến trên khoảng
1
;1
3
Lời giải
Chọn B
Ta có
2
1
3 4 1 0
1
3
x
y x x y
x
Bảng biến thiên:
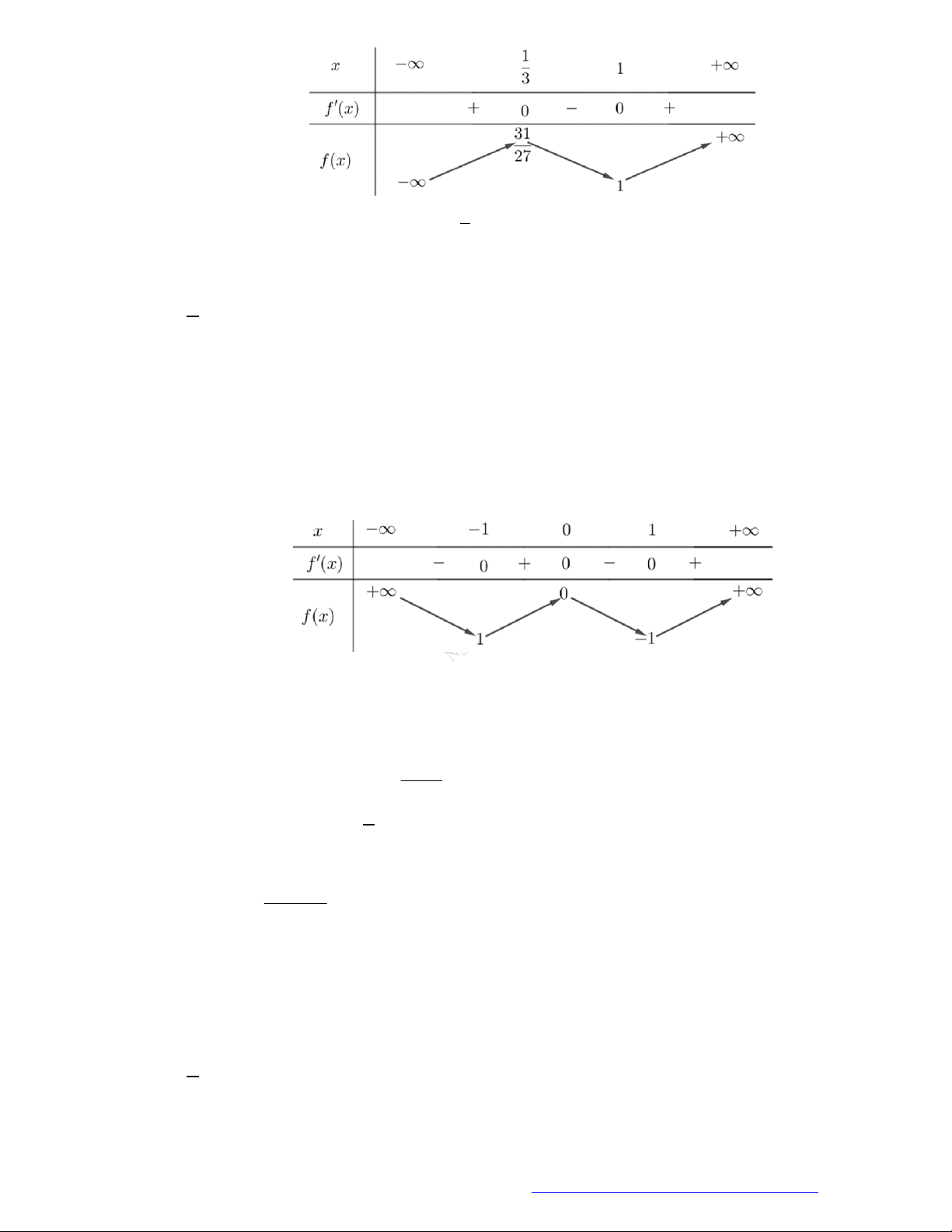
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Vậy hàm số nghịch biến trên khoảng
1
;1
3
.
Câu 8. (Mã 105 - 2017) Cho hàm số
4 2
2y x x
. Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng
; 2
B. Hàm số đồng biến trên khoảng
1;1
C. Hàm số nghịch biến trên khoảng
1;1
D. Hàm số đồng biến trên khoảng
; 2
Lời giải
Chọn A
TXĐ:
.D
3 3
0
4 4 ; 0 4 4 0 1
1
x
y x x y x x x
x
Suy ra hàm số đồng biến trên các khoảng
1; 0
,
1;
; hàm số nghịch biến trên các khoảng
; 1
,
0;1
. Vậy hàm số nghịch biến trên khoảng
; 2
.
Cách 2: Dùng chức năng mode 7 trên máy tính kiểm tra từng đáp án.
Câu 9. (Mã 123 - 2017) Hàm số
2
2
1
y
x
nghịch biến trên khoảng nào dưới đây?
A.
( ; )
B.
(0; )
C.
( ; 0)
D.
( 1;1)
Lời giải
Chọn B
Ta có
2
2
4
0 0
1
x
y x
x
Câu 10. (Mã 123 - 2017) Cho hàm số
3
3 2y x x
. Mệnh đề nào dưới đây là đúng?
A. Hàm số nghịch biến trên khoảng
; 0
và đồng biến trên khoảng
0;
B. Hàm số đồng biến trên khoảng
; 0
và đồng biến trên khoảng
0;
C. Hàm số đồng biến trên khoảng
;
D. Hàm số nghịch biến trên khoảng
;
Lời giải
Chọn C

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta có:
+) TXĐ:
D
.
+)
2
' 3 3 0,y x x
, do đó hàm số đồng biến trên
.
Câu 11. (Mã 104 - 2017) Cho hàm số
2
2 1
y x
. Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng
0;
B. Hàm số đồng biến trên khoảng
;0
C. Hàm số nghịch biến trên khoảng
0;
D. Hàm số nghịch biến trên khoảng
1;1
Lời giải
Chọn A
Ta có
D
,
2
2
2 1
x
y
x
;
0 0
y x
.
Vậy hàm số nghịch biến trên khoảng
;0
và đồng biến trên khoảng
0;
.
Câu 12. (Chuyên Lê Hồng Phong - Nam Định - 2019) Cho hàm số
3
2
2019
3
x
y x x
A. Hàm số đã cho đồng biến trên
.
B. Hàm số đã cho nghịch biến trên
;1
.
C. Hàm số đã cho đồng biến trên
;1
và nghịch biến trên
1;
.
D. Hàm số đã cho đồng biến trên
1;
và nghịch biến trên
;1
.
Lời giải
Chọn A
Ta có
2
2
2 1 1 0,y x x x x
và
0 1y x
(tại hữu hạn điểm)
Do đó hàm số đã cho đồng biến trên
Câu 13. (Lê Quý Đôn - Đà Nẵng - 2019) Hàm số
5 2
3
x
y
x
nghịch biến trên
A.
R\ 3
. B.
R
. C.
; 3
. D.
3;
.
Lời giải
Chọn C
Hàm số
5 2
3
x
y
x
có tập xác định là
\ 3
D
.
2
11
' 0,
3
y
x
với
x D
.
Vậy hàm số đã cho nghịch biến trên các khoảng
; 3
và
3;
.
Câu 14. (Chuyên Hà Tĩnh - Lần 1 - 2019) Hàm số nào sau đây nghịch biến trên
?
A.
3
3 2y x x
. B.
4 2
2 2
y x x
.
C.
3 2
2 4 1y x x x
. D.
3 2
2 5 2y x x x
.
Lời giải
Chọn C
3 2 2 2 2
2 4 1 3 4 4 2 2 0
' ( ) ,
y x x x y x x x x x
Do đó hàm số nghịch biến trên
.
Câu 15. (Chuyên Nguyễn Trãi - Hải Dương - 2019) Hàm số
3 2
3 2
y x x
đồng biến trên khoảng
A.
0;2
. B.
;0
. C.
1;4
. D.
4;
.
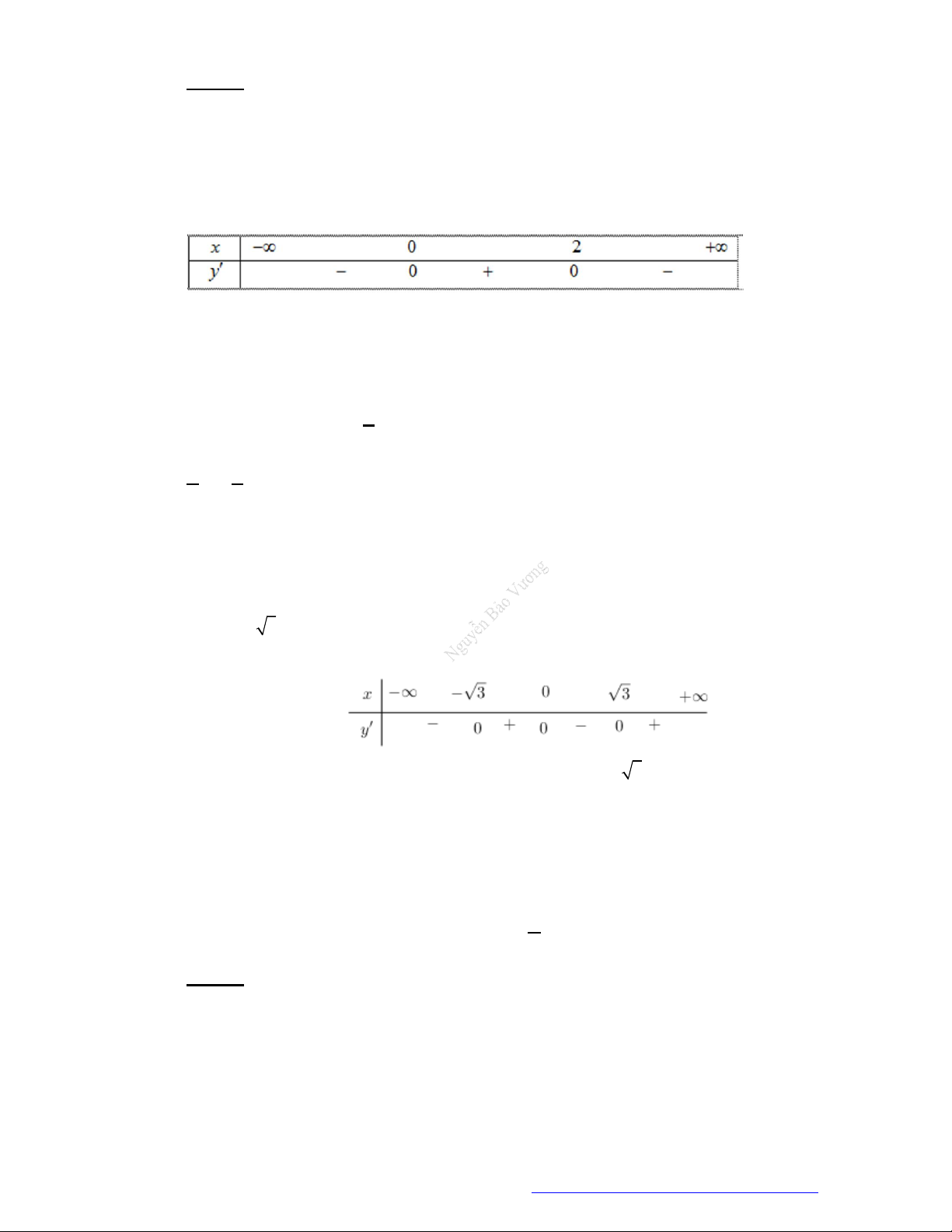
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Lời giải
Chọn A
Tập xác định
D
.
Ta có:
2
3 6y x x
.
0
0
2
x
y
x
.
Bảng xét dấu của
y
như sau:
Nhìn vào bảng xét dấu của
y
ta thấy hàm số
3 2
3 2y x x đồng biến trên khoảng
0;2
.
Vậy hàm số
3 2
3 2y x x đồng biến trên khoảng
0;2
.
Câu 16. (HSG - TP Đà Nẵng - 2019) Hàm số
4 3
4y x x
đồng biến trên khoảng
A.
;
. B.
3;
. C.
1;
. D.
;0
.
Lời giải
Chọn B
Tập xác định
D
.
Ta có
3 2
4 12y x x
Cho
3 2
0 4 12 0y x x
0
3
x
x
.
Bảng xét dấu
Dựa vào bảng xét dấu ta thấy hàm số đồng biến trên khoảng
3; nên cũng đồng biến trên
khoảng
3;
.
Câu 17. (Chuyên Nguyễn Tất Thành - Yên Bái - 2019) Cho hàm số
4 2
2 2y x x
. Mệnh đề nào dưới
đây đúng?
A. Hàm số nghịch biến trên khoảng
;0
. B. Hàm số nghịch biến trên khoảng
2;
.
C. Hàm số đồng biến trên khoảng
;0
. D. Hàm số đồng biến trên khoảng
2;
.
Lời giải
Chọn D
Tập xác định:
D
.
Đạo hàm:
3
4 4y x x
.
Xét
0y
3
4 4 0x x
1 1
0 2
1 1
x y
x y
x y
.
Bảng biến thiên:
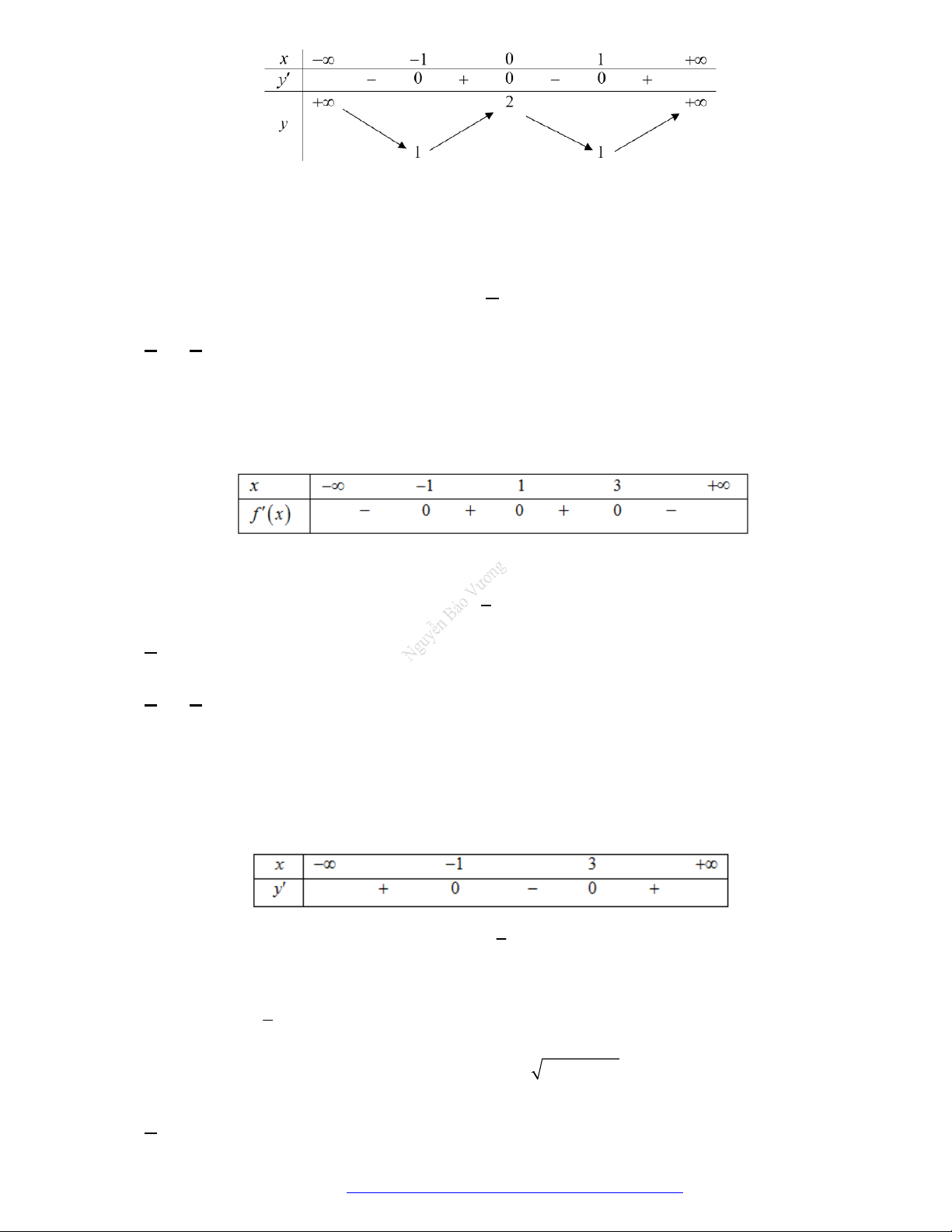
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Dựa vào bảng biến thiên ta thấy, hàm số đồng biến trên khoảng
2;
.
Câu 18. (THPT Ngô Quyền - Hải Phòng - 2019) Cho hàm số
y f x
liên tục trên
và có đạo hàm
2 3
1 1 3f x x x x
. Hàm số
y f x
đồng biến trên khoảng nào dưới đây?
A.
;1
. B.
; 1
. C.
1;3
. D.
3;
.
Lời giải
Chọn C
Ta có:
2 3
1
0 1 1 3 0 1
3
x
f x x x x x
x
.
Bảng xét dấu:
Hàm số đồng biến trên các khoảng
1;3
.
Câu 19. (HSG 12 - TP Nam Định - 2019) Hàm số
3 2
1
3 2019
3
y x x x
nghịch biến trên
A.
1;3
. B.
; 1
. C.
; 1
và
3;
. D.
3;
.
Lời giải
Chọn A
Tập xác định
D
.
2
2 3y x x
.
Cho
1
0
3
x
y
x
.
Ta có bảng xét dấu của
y
như sau:
Nhìn vào bảng xét dấu của
y
ta thấy hàm số
3 2
1
3 2019
3
y x x x
nghịch biến trên khoảng
1;3
.
Vậy hàm số
3 2
1
3 2019
3
y x x x
nghịch biến trên khoảng
1;3
.
Câu 20. (Chuyên Ngoại Ngữ - Hà Nội - 2019) Hàm số
2
2018y x x nghịch biến trên khoảng nào
trong các khoảng sau đây?
A.
1010;2018
. B.
2018;
. C.
0;1009
. D.
1;2018
.
Lời giải
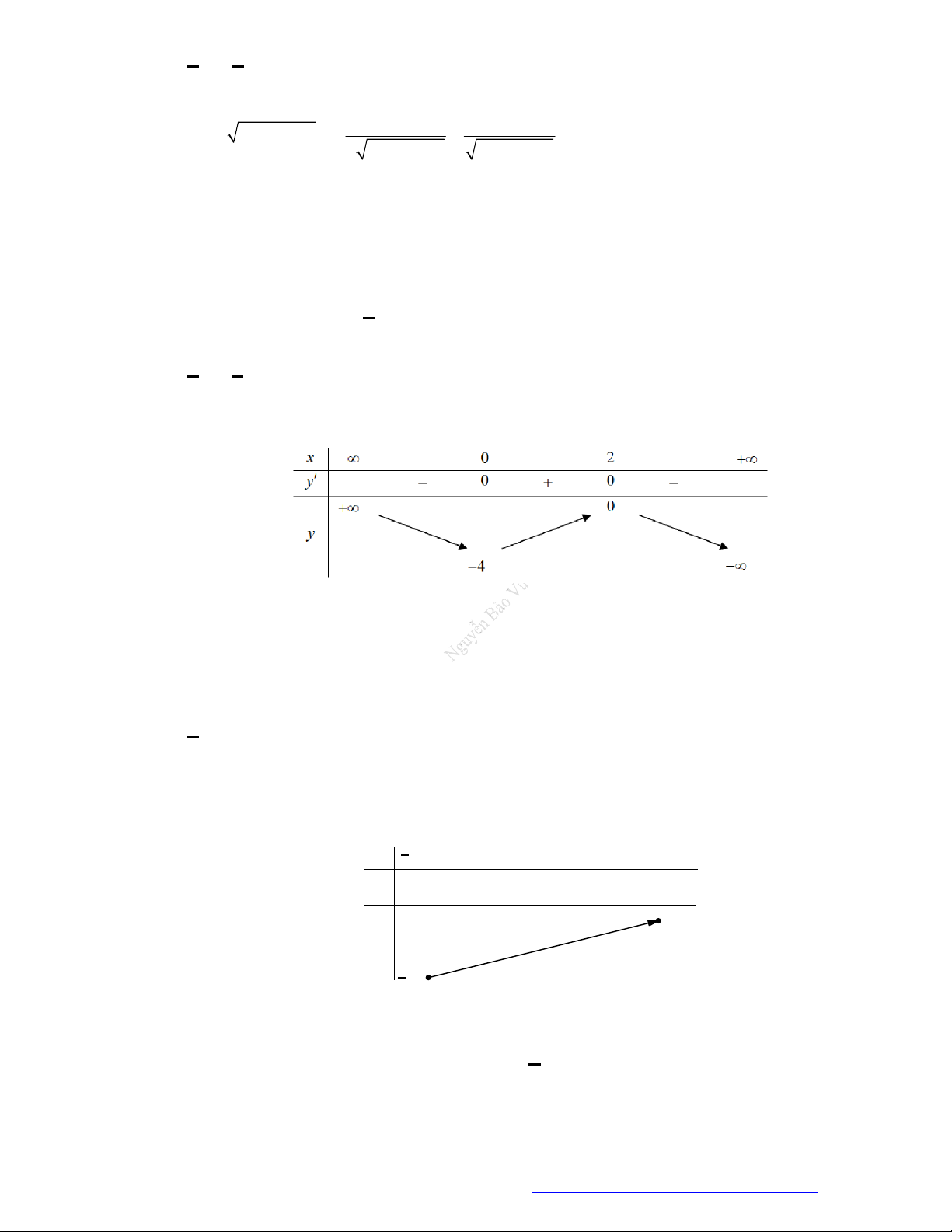
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
Chọn A
TXĐ:
0;2018D
2
2 2
2018 2 1009
2018 ; 0 1009
2 2018 2018
x x
y x x y x
x x x x
' 0 1009;2018y x
, suy ra hàm số nghịch biến trên khoảng
1009;2018
, suy ra hàm số
nghịch biến trên khoảng
1010;2018
, chọn A.
Câu 21. (Chuyên Lê Quý Đôn - Quảng Trị - 2019) Hàm số
3 2
3 4y x x đồng biến trên tập hợp nào
trong các tập hợp được cho dưới đây?
A.
2;
. B.
0;2
. C.
;0 2;
. D.
;0
.
Lời giải
Chọn B
Ta có:
2
3 6y x x
;
0
0
2
x
y
x
.
Dựa vào bảng biến thiên thì hàm số đã cho đồng biến trên khoảng
0;2
.
Câu 22. (SGD&ĐT Hà Nội - 2018) Hàm số
y f x
có đạo hàm
2
y x
. Mệnh đề nào sau đây đúng?
A. Hàm số nghịch biến trên
.
B. Hàm số nghịch biến trên
;0
và đồng biến trên
0;
.
C. Hàm số đồng biến trên
.
D. Hàm số đồng biến trên
;0
và nghịch biến trên
0;
.
Lời giải
2
0 0 0y x x
Câu 23. (THPT Lương Thế Vinh - HN - 2018) Hàm số
3
3y x x nghịch biến trên khoảng nào?
A.
; 1
. B.
;
. C.
1;1
. D.
0;
.
Lời giải
Tập xác định
D
.
0
0
+
+
∞
∞
∞
∞
+
+
y
y'
x
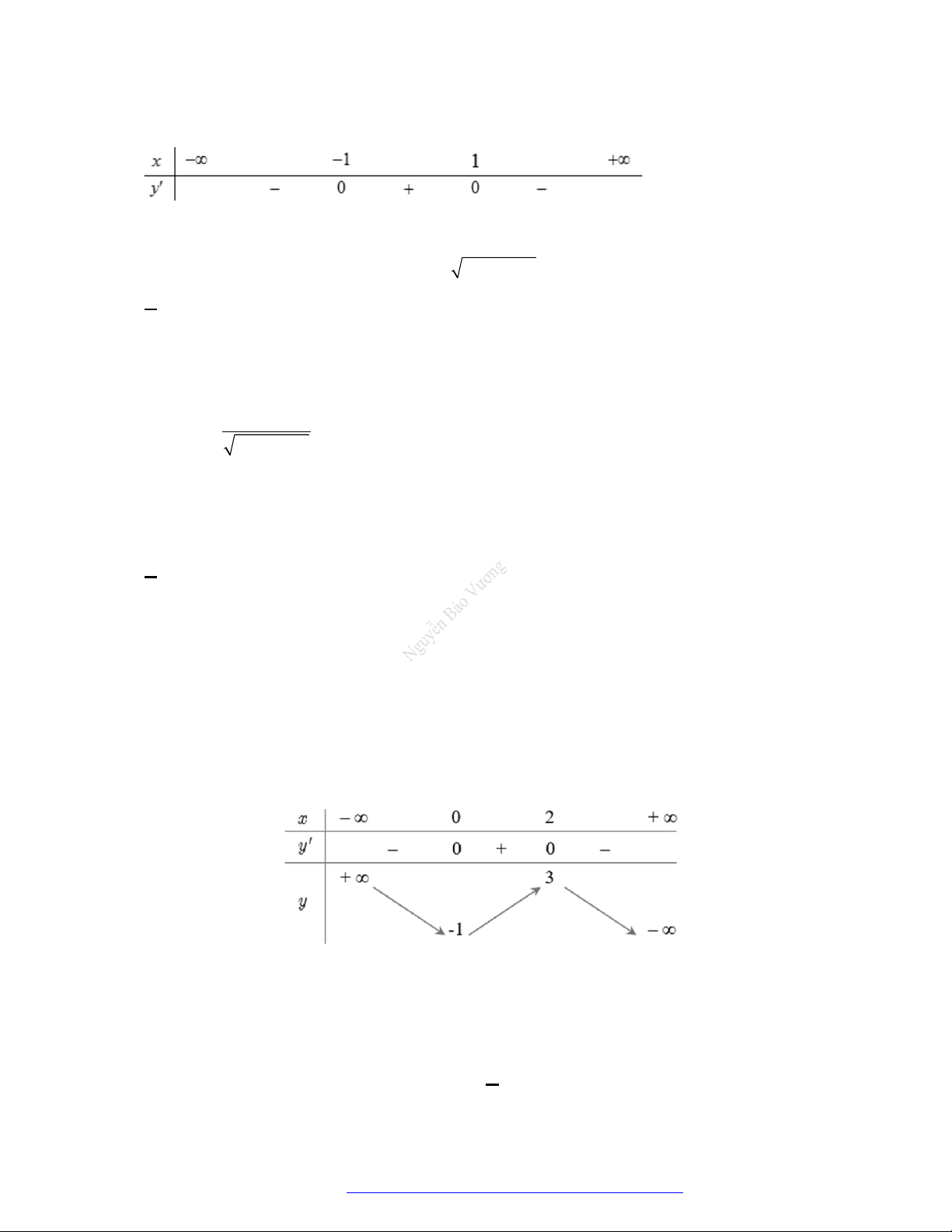
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta có
2
3 3;y x
1
0
1
x
y
x
.
Ta có bảng xét dấu
y
:
Từ bảng xét dấu ta thấy hàm số nghịch biến trên khoảng
1;1
.
Câu 24. (Chuyên Thái Bình - 2018) Cho hàm
2
6 5y x x . Mệnh đề nào sau đây là đúng?
A. Hàm số đồng biến trên khoảng
5; .
B. Hàm số đồng biến trên khoảng
3; .
C. Hàm số đồng biến trên khoảng
;1 .
D. Hàm số nghịch biến trên khoảng
;3 .
Lời giải
Tập xác định:
;1 5;D
.
Ta có
2
3
0
6 5
x
y
x x
,
5;x
.
Vậy hàm số đồng biến trên khoảng
5; .
Câu 25. (Thpt Kinh Môn - HD - 2018) Cho hàm số
3 2
3 1y x x , kết luận nào sau đây về tính đơn
điệu của hàm số là đúng nhất:
A. Hàm số đồng biến trên khoảng
0;2
và nghịch biến trên các khoảng
;0
;
2;
;
B. Hàm số đồng biến trên khoảng
0;2
;
C. Hàm số nghịch biến trên khoảng
0;2
và đồng biến trên các khoảng
;0
;
2;
;
D. Hàm số nghịch biến trên các khoảng
;0
và
2;
.
Lời giải
Ta có hàm số xác định trên
.
3 2
3 1y x x
2
3 6 0y x x
0
2
x
x
.
Bảng biến thiên
Vậy đáp án A là đúng nhất.
Câu 26. (Chuyên ĐH Vinh - 2018) Cho hàm số
y f x
có đạo hàm
3
2f x x x
, với mọi
x
. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
1; 3
. B.
1; 0
. C.
0; 1
. D.
2; 0
.
Lời giải
Ta có:
0f x
0
2
x
x
.
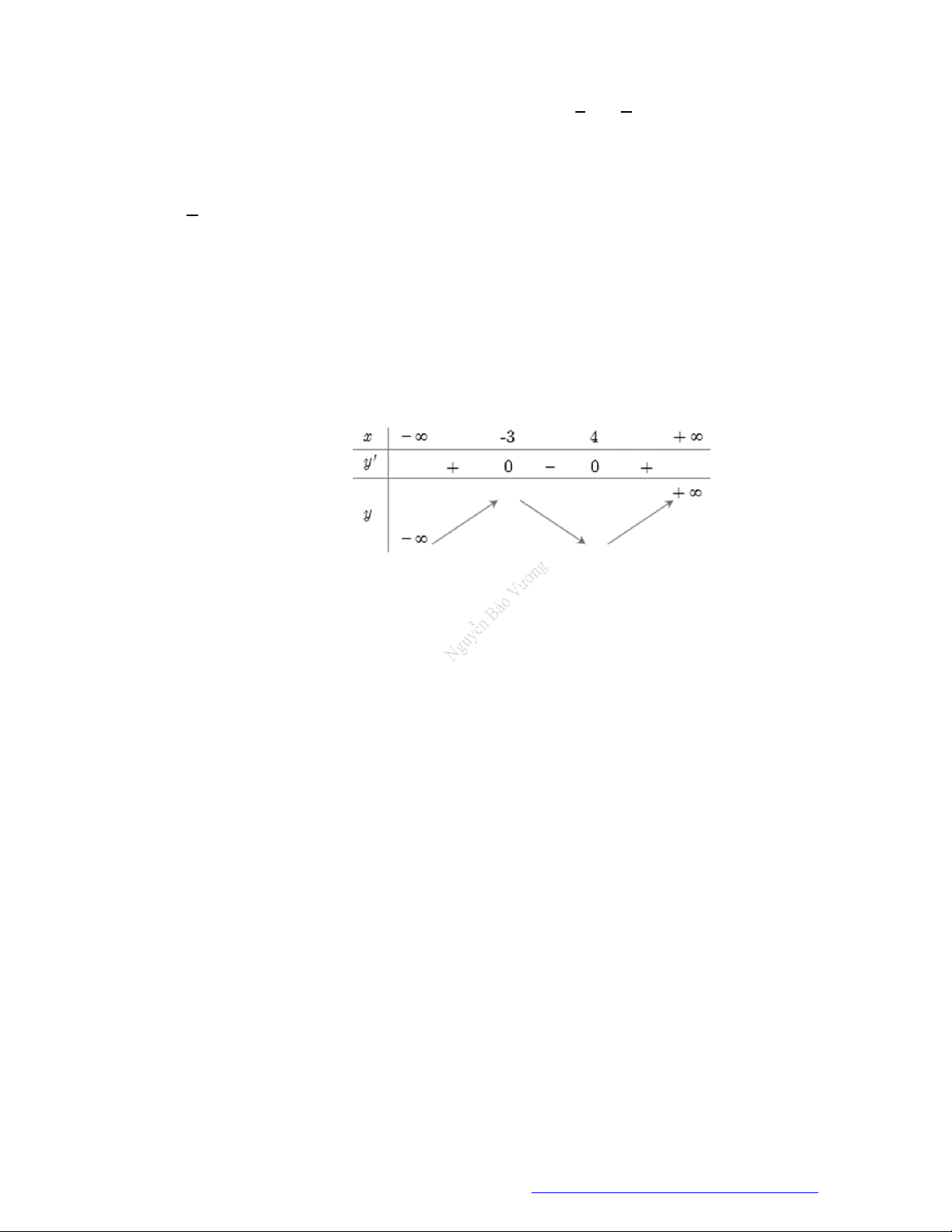
T
ÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
Đồng
thời
0f
x
0
;2x
nê
n ta chọn đáp án theo đề bài là
0
; 1
.
Câu
27. (THPT Can Lộc - Hà Tĩnh - 2018) Cho hàm số
3
2
1
1
12 1
3 2
xy x x
.
Mệnh đề nào sau đây
là đúng?
A. Hàm số đồng biến trên khoảng
3
;4
.
B
. Hà
m số đồng biến trên khoảng
4
;
.
C. Hà
m số nghịch biến trên khoảng
;
4
.
D. Hà
m số nghịch biến trên khoảng
3;
.
Lời
giải
2
12xy
x
0
4
3
x
x
y
Bảng biến thiên
Hàm số đồng biến trên khoảng
4
;
.
-------------------- HẾT --------------------

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 1
TÀI LIỆU DÀNH CHO HỌC SINH MỤC TIÊU 7-8 ĐIỂM
Dạng 1. Tìm m để hàm số đơn điệu trên các khoảng xác định của nó
Xéthàmsốbậcba
3 2
( ) .y f x ax bx cx d
–Bước1.Tậpxácđịnh:
.D
–Bước2.Tínhđạohàm
2
( ) 3 2 .y f x ax bx c
+Để
( )f x
đồngbiếntrên
( )
2
( )
3 0
( ) 0, ?
4 12 0
f x
f x
a a
y f x x m
b ac
+Đề
( )f x
nghịchbiếntrên
( )
2
( )
3 0
( ) 0, ?
4 12 0
f x
f x
a a
y f x x m
b ac
Lưuý:Dấucủatamthứcbậchai
2
( ) .f x ax bx c
Để
0
( ) 0,
0
a
f x x
0
( ) 0,
0
a
f x x
Câu 1. (Đề Tham Khảo Lần 2 2020)Có bao nhiêu giá trị nguyên của tham số
m
sao cho hàm số
3 2
1
( ) 4 3
3
f x x mx x
đồngbiếntrên
.
A.
5
. B.
4
. C.
3
. D.
2
.
Lờigiải
ChọnA
Tacó
2
( ) 2 4f x x mx
.
Hàmsốđãchođồngbiếntrên
khivàchỉkhi
( ) 0,f x x
(Dấu‘=’xảyratạihữuhạn
điểm).
Tacó
( ) 0, ' 0f x x
2
' 4 0m
2 2m
.
Vì
m
nên
2; 1;0;1;2m
,vậycó
5
giátrịnguyêncủa
m
thỏamãn.
Câu 2. (Mã123-2017)Chohàmsố
3 2
4 9 5y x mx m x
,vớimlàthamsố.Hỏicóbaonhiêu
giátrịnguyêncủamđểhàmsốnghịchbiếntrênkhoảng
;
A.
5
B.
4
C.
6
D.
7
Lờigiải
ChọnD
Tacó:
+)TXĐ:
D
+)
2
' 3 2 4 9y x mx m
.
Hàmsốnghịchbiếntrên
;
khi
' 0, ;y x
2
3 0
' 3 4 9 0
a
m m
9; 3m
có7giátrịnguyêncủamthỏamãn.
TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
Chuyên đề 1

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 3. Chohàmsố
3 2
1
3 2 1
3
y x mx m x
.Tìmtấtcảgiátrịcủa
m
đểhàmsốnghịchbiếntrên
.
A.
1
2
m
m
. B.
2 1
m
. C.
2 1
m
. D.
1
2
m
m
.
Lờigiải
ChọnB
TXĐ:
D
,
2
2 3 2
y x mx m
.
Hàmsốnghịchbiếntrên
khivàchỉkhi
0
y
,
x
2
1 0
3 2 0
a
m m
2 1
m
.
Câu 4. Tìm
m
đểhàmsố
3 2
3 3 2 1 1
y x mx m
đồngbiếntrên
.
A.Khôngcógiátrị
m
thỏamãn. B.
1
m
.
C.
1
m
. D.Luônthỏamãnvớimọi
m
.
Lờigiải
ChọnC
2
3 6 3 2 1
y x mx m
Tacó:
2
3 3.3. 2 1
m m
.Đểhàmsốluônđồngbiếntrên
thì
0
2
2 2
9 18 9 0 9 2 1 0 9 1 0
m m m m m
1
m
.
Câu 5. Tìmđiềukiệncủathamsốthực
m
đểhàmsố
3 2
3 3 1 2
y x x m x
đồngbiếntrên
.
A.
2
m
. B.
2
m
. C.
0
m
. D.
0
m
.
Lờigiải
ChọnD
Tậpxácđịnh:
D
.
Tacó:
2
3 6 3 1
y x x m
0, 9 0 0
YCBT y x m m
.
Câu 6. Tìmtậphợptấtcảcácgiátrịcủathamsốthực
m
đểhàmsố
3 2
1
4
3
y x mx x m
đồngbiến
trênkhoảng
;
.
A.
2;2
. B.
;2
. C.
; 2
. D.
2;
.
Lờigiải
ChọnA
Tacó:
2
2 4y x mx
.
Hàmsốđồngbiếntrênkhoảng
;
khivàchỉkhi
0, ;y x
.
2
4 0 2 2
m m
.
Câu 7. Giátrịcủa
m
đểhàmsố
3 2
1
– 2 3 – 5
3
y x mx m x m
đồngbiếntrên
là.
A.
3
1
4
m
. B.
3
4
m
. C.
3
1
4
m
. D.
1
m
.
Lờigiải
ChọnA

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Tacótậpxácđịnh
D
.
2
– 4 3
y x mx m
.
2
0 – 4 3 0
y x mx m
.
Hàmsốđãchođồngbiếntrên
khivàchỉkhi
0,y x
,đẳngthứcchỉxảyratạihữuhạn
điểm
2
2
3
0 2 1. 3 0 4 3 0 1
4
m m m m m
.
Vậy
3
1
4
m
.
Câu 8. (Chuyên KHTN - Hà Nội - 2020) Tập hợp tất cả các giá trị của tham số
m
để hàm số
3 2
1 3 2y x m x x
đồngbiếntrên
là
A.
4;2
. B.
4;2
. C.
; 4 2;
. D.
; 4 2;
.
Lờigiải
ChọnA
Tậpxácđịnh:
D
.
Tacó:
2
3 2 1 3y x m x
.
Hàmsố
3 2
1 3 2y x m x x
đồngbiếntrên
khivàchỉkhi
0,y x
.
2
2
1 9 0 2 8 0 4 2.
m m m m
Vậy
4;2
m
.
Nếu hệ số
a
chứa tham số thì phải xét trường hợp
0
a
và
0
a
Câu 9. (Đề Tham Khảo - 2017) Hỏi có bao nhiêu số nguyên
m
để hàm số
2 3 2
1 1 4y m x m x x
nghịchbiếntrênkhoảng
;
.
A.
0
B.
3
C.
2
D.
1
Lờigiải
ChọnC
TH1:
1
m
.Tacó:
4y x
làphươngtrìnhcủamộtđườngthẳngcóhệsốgócâmnênhàmsố
luônnghịchbiếntrên
.Dođónhận
1
m
.
TH2:
1
m
.Tacó:
2
2 4
y x x
làphươngtrìnhcủamộtđườngParabolnênhàmsốkhông
thểnghịchbiếntrên
.Dođóloại
1
m
.
TH3:
1
m
.Khiđóhàmsốnghịchbiếntrênkhoảng
;
0y x
,dấu“=”chỉ
xảyraởhữuhạnđiểmtrên
.
2 2
3 1 2 1 1 0
m x m x
,
x
2
2
2
2
1 1
1 0
1 0
0
1
1
1
0
2
11 4 2 0
1 3 1 0
2
m
m
m
a
m
mm m
m m
. Vì
m
nên
0
m
.
Vậycó
2
giátrị
m
nguyêncầntìmlà
0
m
hoặc
1
m
.
Câu 10. Hỏi có tất cả bao nhiêu giá trị nguyên của tham số
m
để hàm số hàm số
2 3 2
1
2 3 2
3
y m m x mx x
đồngbiếntrênkhoảng
;
?
A.
4
. B.
5
. C.
3
. D.
0
.
Lờigiải

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
ChọnA
2 2
4 3y m m x mx
Hàmsốđãchođồngbiếntrênkhoảng
;
0
y
với
x
.
+Với
0
m
tacó
3 0
y
với
x
Hàmsốđồngbiếntrênkhoảng
;
.
+Với
1
m
tacó
3
4 3 0
4
y x x
1
m
khôngthảomãn.
+Với
1
0
m
m
tacó
0
y
với
x
2
2
0
3 0
m m
m m
1
0
3 0
m
m
m
3 0
m
.
Tổnghợpcáctrườnghợptađược
3 0
m
.
3; 2; 1;0
m m
.
Vậycó
4
giátrịnguyêncủa
m
thỏamãnbàira.
Câu 11. Tìmtấtcảcácgiátrịcủathamsốthực
m
đểhàmsố
3 2
1 2
y mx mx m m x
đồngbiến
trên
.
A.
4
3
m
và
0
m
. B.
0
m
hoặc
4
3
m
.
C.
4
3
m
. D.
4
3
m
.
Lờigiải
ChọnC
TH1:
0 2
m y
làhàmhằngnênloại
0
m
.
TH2:
0
m
.Tacó:
2
3 2 1
y mx mx m m
.
Hàmsốđồngbiếntrên
'( ) 0f x x
2 2
3 1 0
3 0
m m m
m
2
4 3 0
0
m m
m
4
4
3
3
0
m
m
m
Câu 12. Cótấtcảbaonhiêugiátrịnguyêncủathamsố
m
đểhàmsố
3 2
2 3 5
3
m
y x mx m x
đồng
biếntrên
.
A.
4
. B.
2
. C.
5
. D.
6
.
Lờigiải
ChọnD
Tacó
2
4 3 5
y mx mx m
.
Với
0 0
a m
5 0
y
.Vậyhàmsốđồngbiếntrên
.
Với
0 0
a m
.Hàmsốđãchođồngbiếntrên
khivàchỉkhi
0
0,
0
a
y x
2
0
2 3 5 0
m
m m m
2
0
0
0 5
0 5
5 0
m
m
m
m
m m
.
Vì
0;1;2;3;4;5
m m
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Câu 13. Tìmtấtcảcácgiátrịcủa
m
đểhàmsố
3 2
1 3 1 3 2
y m x m x x
đồngbiếnbiếntrên
?
A.
1 2
m
. B.
1 2
m
. C.
1 2
m
. D.
1 2
m
Lờigiải
ChọnC
Tacó
2
3 1 6 1 3y m x m x
.
Hàmsốđãchođồngbiếntrên
khivàchỉkhi
0,y x
1 0
1 0
0
m
m
2
1
1
9 1 9 1 0
m
m
m m
1
1
1 2
m
m
m
1 2
m
.
Câu 14. (THPT Hoàng Hoa Thám - Hưng Yên - 2018) Số giá trị nguyên của
m
để hàm số
2 3 2
(4 ) ( 2) 1
y m x m x x m
1
đồngbiếntrên
bằng.
A.
5
. B.
3
. C.
2
. D.
4
.
Lờigiải
TH1:
2
4 0 2
m m
.
2
m
:
1 1y x
hàmsốluôntăngtrên
2
m
(nhận).
2
m
:
2
1 4 3y x x
làhàmsốbậchainêntăngtrênkhoảng
1
;
8
,giảmtrên
khoảng
1
;
8
2
m
(loại).
TH2:
2
4 0
m
.
2 2
3 4 2 2 1y m x m x
.
2
2
2 3 4
m m
2
4 4 8
m m
.
hàmsốđồngbiếntrên
0y x
.
0
0
a
2
2
4 0
4 4 8 0
m
m m
2;2
1;2
m
m
1;2
m
.
m
1
m
;
0
m
;
1
m
.
Vậycó
4
giátrịnguyêncủa
m
thỏayêucầubàitoán.
Câu 15. (ChuyênHoàngVănThụ-HòaBình-2018)Sốcácgiátrịnguyêncủathamsố
m
trongđoạn
100;100
đểhàmsố
3 2
1 3y mx mx m x
nghịchbiếntrên
là:
A.
200
. B.
99
. C.
100
. D.
201
.
Lờigiải
Trườnghợp1:
0
m
.Tacó:
3y x
có
1 0
y
vớimọi
x
nênhàmsốluônđồngbiếntrêntrên
.
Dođóloại
0
m
.
Trườnghợp2:
0
m
.Tacó:
2
3 2 1
y mx mx m
,
2
2 3 2 3
m m m m
Hàmsốnghịchbiếntrên
khivàchỉkhi
0
y
vớimọi
x
0
0
m
0
2 3 0
m
m m
0
2 3 0
m
m
3
2
m
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Vì
m
làsốnguyênthuộcđoạn
100;100
nên
2; 3;...; 99; 100
m
.
Vậycó
99
giátrị
m
.
Câu 16. (LiêntrườngNghệAn-2020)Tổngbìnhphươngcủatấtcảcácgiátrịnguyêncủathamsố
m
để
hàmsố
2 3 2
3 12 3 2 2
y m x m x x
nghịchbiếntrên
là?
A.
9
. B.
6
. C.
5
. D.
14
.
Lờigiải
ChọnC
Tậpxácđịnh:
D
.
Tacó:
2 2
9 4 6 2 1y m x m x
.
Hàmsốnghịchbiếntrên
' 0y x
(dấu
" "
xãyratạihữuhạn
x
)
TH1:
2
4 0 2
m m
.
+Với
2
m
tacó
' 1 0
y
x
nên
2
m
thỏamãn.
+Với
2
m
tacó
1
' 24 1 0
24
y x x
(khôngthỏavớimọi
x
)nênloại
2
m
.
TH2:
2
4 0 2
m m
.Tacó
2
2
' 2
9 4 0
2 2
' 0, 0 2 0;1
0 2
9 2 9 4 0
m
a m
m
y x m m
m
m m
V
ậy
2 2 2
0;1;2 0 1 2 5
m
.
Câu 17. (Lý Nhân Tông - Bắc Ninh - 2020) Hỏi có bao nhiêu số nguyên
m
để hàm số
2 3 2
1 1 4y m x m x x
nghịchbiếntrênkhoảng
;
.
A.
2.
B.
1.
C.
0.
D.
3.
Lờigiải
ChọnA
Tacó
2 2
3 1 2 1 1y m x m x
Hàmsốđãchonghịchbiếntrênkhoảng
; 0,y x
2 2
3 1 2 1 1 0,m x m x x
.
*Trườnghợp1:
2
1 0 1
m m
.
+Với
1
m
,tađược
1 0, x
(luônđúng),suyra
1
m
(nhận).
+Với
1
m
,tađược
1
4 1 0
4
x x
,suyra
1
m
(loại).
*Trườnghợp2:
2
1 0 1
m m
.
Tacó
2
2 2 2 2
1 3 1 2 1 3 3 4 2 2
m m m m m m m
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Để
2
2
1 1
1 0
1
0, 1
1
2
1
4 2 2 0
2
m
m
y x m
m
m m
.
Tổnghợplại,tacótấtcảgiátrị
m
cầntìmlà
1
1
2
m
.
Vì
m
,suyra
0;1
m
,nêncó2giátrịnguyêncủathamsố
m
.
Xéthàmsốnhấtbiến
( )
ax b
y f x
cx d
–Bước1.Tậpxácđịnh:
\
d
D
c
–Bước2.Tínhđạohàm
2
. .
( )
( )
a d b c
y f x
cx d
+Để
( )f x
đồngbiếntrên
( ) 0, . . 0 ?D y f x x D a d b c m
+Để
( )f x
nghịchbiếntrên
( ) 0, . . 0 ?D y f x x D a d b c m
Lưuý:Đốivớihàmphânthứcthìkhôngcódấu
" "
xảyratạivịtrí
.y
Câu 18. (Mã105-2017)Chohàmsố
2 3mx m
y
x m
với
m
làthamsố.Gọi
S
làtậphợptấtcảcácgiá
trịnguyêncủa
m
đểhàmsốđồngbiếntrêncáckhoảngxácđịnh.Tìmsốphầntửcủa
S
.
A.Vôsố B.
3
C.
5
D.
4
Lờigiải
ChọnB
2
2
2 3
'
m m
y
x m
hàmsốđồngbiếntrênkhoảngxácđịnhkhi
1 3m
nêncó3giátrịcủam
nguyên
Câu 19. (Mã104-2017)Chohàmsố
4mx m
y
x m
với
m
làthamsố.Gọi
S
làtậphợptấtcảcácgiátrị
nguyêncủa
m
đểhàmsốnghịchbiếntrêncáckhoảngxácđịnh.Tìmsốphầntửcủa
S
.
A.
4
B.Vôsố C.
3
D.
5
Lờigiải
ChọnD
\
D m
;
2
2
4m m
y
x m
.
Hàmsốnghịchbiếntrêncáckhoảngxácđịnhkhi
0,
y x D
2
4 0
m m
0 4
m
.
Mà
m
nêncó
3
giátrịthỏamãn.
Câu 20. (THPTHoaLưA-2018)Cótấtcảbaonhiêusốnguyên
m
đểhàmsố
1 2
m x
y
x m
đồng
biếntrêntừngkhoảngxácđịnhcủanó?
A.1. B.0. C.2. D.3.
Lờigiải
TXĐ:
\
D m
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
2
2
m m
y
x m
.
Đểhàmsốđồngbiếntrêntừngkhoảngxácđịnhcủatacầntìm
m
để
0
y
trên
;m
và
;m
vàdấu
" "
chỉxảyratạihữuhạnđiểmtrêncáckhoảngđó
ĐK:
2
2 0m m
2 1.
m
Vì
m
nên
1,
m
0
.
Câu 21. (SGD&ĐT Bắc Giang - 2018) Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
2
4
x m
y
x
đồngbiếntrêntừngkhoảngxácđịnhcủanó?
A.
5
. B.
3
. C.
1
. D.
2
.
Lờigiải
TXĐ:
\ 4
D
,
2
2
4
4
m
y
x
.
Đểhàmsốđồngbiếntrêntừngkhoảngxácđịnhcủanóthì
2
4 0 2 2
m m
.
Dođócó
3
giátrịnguyêncủathamsố
m
thỏamãn.
Câu 22. (THPTHàHuyTập-2018)Tìmtấtcảgiátrịthựccủathamsố
m
đểhàmsố
2
1
x m
y
x
nghịch
biếntrêncáckhoảngmànóxácđịnh?
A.
1
m
. B.
3
m
. C.
3
m
. D.
1
m
.
Lờigiải
Với
1
m
thìhàmsốlàhàmhằng
1
x
nênkhôngnghịchbiến.
Tacó
2
1
,
1
m
y
x
1
x
.
Hàmsốnghịchbiếntrêntừngkhoảngcủatậpxácđịnhkhivàchỉkhi
0,
y
1
x
1
m
.
Câu 23. (SỞGD&ĐTYênBái-2018)Tìmtấtcảcácgiátrịthựccủathamsố
m
đểhàmsố
4
mx
y
x m
nghịchbiếntrêntừngkhoảngxácđịnhcủanó.
A.
2
2
m
m
. B.
2 2
m
. C.
2
2
m
m
. D.
2 2
m
.
Lời giải
Tậpxácđịnh
; ;D m m
.
Tacó
2
2
4 4
'
mx m
y y
x m
x m
.Vìhàmsốnghịchbiếntrêntừngkhoảngxácđịnhcủanónên
2
2
4 0
2
m
m
m
.
Câu 24. (THCS&THPTNguyễnKhuyến-BìnhDương-2018)Tìmtấtcảcácgiátrịthựccủa
m
để
hàmsố
2
2
mx
y
x m
đồngbiếntrênmỗikhoảngxácđịnh
A.
2
2
m
m
. B.
2 2
m
. C.
2
2
m
m
. D.
2 2
m
.
Lờigiải

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Tacó:
2
2
2
4m
y
x m
,
2
m
x
Hàmsốđồngbiếntrêntừngkhoảngxácđịnhkhi
2
20 24m m
.
Dạng 2. Tìm m để hàm số nhất biến đơn điệu trên khoảng cho trước
Câu 1. (ĐềThamKhảoLần12020)Chohàmsố
4mx
f x
x m
(
m
làthamsốthực).Cóbaonhiêu
giátrịnguyêncủa
m
đểhàmsốđãchođồngbiếntrênkhoảng
0;
?
A.
5
. B.
4
. C.
3
. D.
2
.
Lờigiải
ChọnD
Tậpxácđịnh
\D m
.
Đạohàm
2
2
4m
f x
x m
.
Hàmsốđồngbiếntrên
0;
khivàchỉkhi
2
4 0
2 2
0 0; 2 0
0
0;
m
m
f x x m
m
m
.
Do
1;0m m
.Vậycóhaigiátrịnguyêncủa
m
thỏamãnđềbài.
Câu 2. (Mã101–2020–Lần1)Tậphợptấtcảcácgiátrịthựccủathamsố
m
đểhàmsố
4x
y
x m
đồngbiếntrênkhoảng
; 7
là
A.
4;7
. B.
4;7
. C.
4;7
. D.
4;
.
Lờigiải
ChọnB
Tậpxácđịnh:
\D m
.
Tacó:
2
4m
y
x m
.
Hàmsốđãchođồngbiếntrênkhoảng
; 7
0y
,
; 7x
4 0
; 7
m
m
4 4
4 7
7 7
m m
m
m m
.
Câu 3. (Mã102–2020–Lần1)Tậphợptấtcảcácgiátrịthựccủathamsố đểhàmsố
đồngbiếntrênkhoảng
là
A. . B. . C. . D. .
Lờigiải
m
5
x
y
x m
; 8
5;
5;8
5;8
5;8
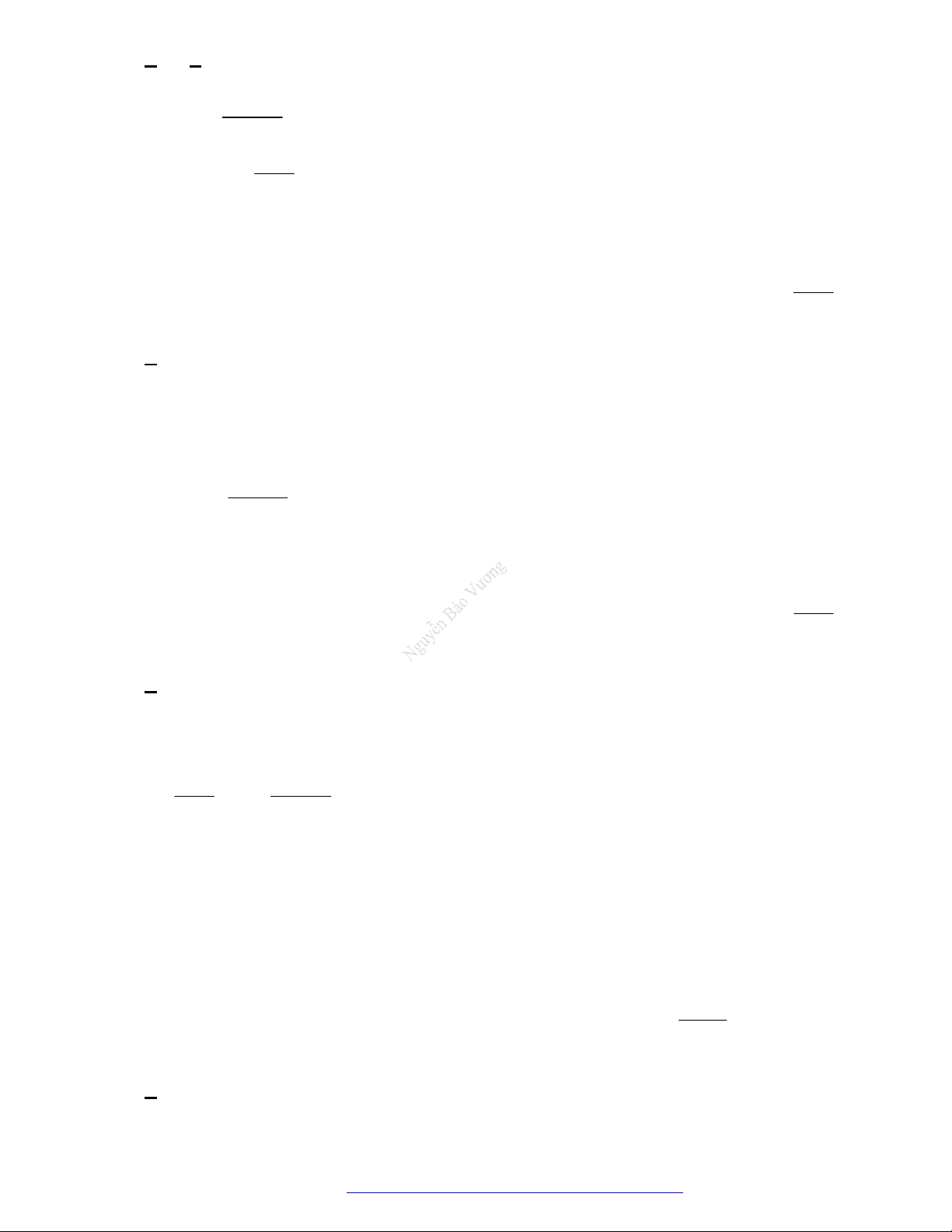
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
ChọnB
Điềukiện .
Tacó
Đểhàmsố đồngbiếntrênkhoảng
thì
.
Câu 4. (Mã103–2020–Lần1)Tậphợptấtcảcácgiátrịthựccủathamsốmđểhàmsố
2x
y
x m
đồngbiếntrênkhoảng
( ; 5)
A.
(2;5]
. B.
[2;5)
. C.
(2; )
. D.
(2;5)
.
Lờigiải
ChọnA
Tậpxácđịnh:
\ .D m
Tacó:
2
2
'
( )
m
y
x m
Hàmsốđồngbiếntrênkhoảng
' 0 ( ; 5)
( ; 5)
( ; 5)
y x
m
2 0
2 5
5
m
m
m
.
Câu 5. (Mã104-2020–Lần1)Tậphợptấtcảcácgiátrịthựccủathamsố
m
đểhàmsố
3x
y
x m
đồngbiếntrênkhoảng
; 6
là
A.
3;6
. B.
3;6
. C.
3;
. D.
3;6
.
Lờigiải
ChọnA
Hàmsốxácđịnhkhi:
0x m x m
.
2
3 3x m
y y
x m
x m
Hàmsốđồngbiếntrênkhoảng
; 6
khivàchỉkhi:
0, ; 6
; 6
y x
m
3 0
3 3
3 6
6;
6 6
m
m m
m
m
m m
.
Vậy:
3;6m
.
Câu 6. (Mã104-2018)Cóbaonhiêugiátrịnguyêncủathamsố
m
đểhàmsố
2
3
x
y
x m
đồngbiếntrên
khoảng
; 6
.
A.
2
B.
6
C.Vôsố D.
1
Lờigiải
ChọnA
x m
2
5
m
y
x m
5
x
y
x m
; 8
0
5 0
5 8
; 8
8
y
m
m
m
m

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Tậpxácđịnh:
; 3 3 ;D m m
.
Tacó
2
3 2
3
m
y
x m
Hàmsốđổngbiếntrênkhoảng
; 6
2
3 2 0
3
6 3
2
m
m
m
m
2
2
3
m
.
Mà
m
nguyênnên
1;2
m
.
Câu 7. (Mã103-2018)Cóbaonhiêugiátrịnguyêncủathamsố
m
đểhàmsố
1
3
x
y
x m
nghịchbiến
trênkhoảng
6;
?
A.
0
B.
6
C.
3
D.Vôsố
Lờigiải
ChọnC
Tậpxácđịnh
\
3D m
;
2
3 1
3
m
y
x m
.
Hàmsố
1
3
x
y
x m
nghịchbiếntrênkhoảng
6;
khivàchỉkhi:
0
6;
y
D
3 1 0
3 6
m
m
1
3
2
m
m
1
2
3
m
.
Vì
m
2; 1;0
m
.
Câu 8. (Mã101-2018)Cóbaonhiêugiátrịnguyêncủathamsố
m
đểhàmsố
2
5
x
y
x m
đồngbiến
trênkhoảng
; 10
?
A.
2
B.Vôsố C.
1
D.
3
Lờigiải
ChọnA
TXĐ:
\ 5D m
.
2
5 2
'
5
m
y
x m
.
Hàmsốđồngbiếntrênkhoảng
; 10
khivàchỉkhi
5 2 0
5 10;
m
m
2
5
5 10
m
m
2
2
5
m
.
Vì
m
nguyênnên
1;2
m
.Vậycó
2
giátrịcủathamsố
m
.
Câu 9. (Mã102-2018)Cóbaonhiêugiátrịnguyêncủathamsố
m
đểhàmsố
6
5
x
y
x m
nghịchbiến
trênkhoảng
10;
?
A.Vôsố B.
4
C.
5
D.
3
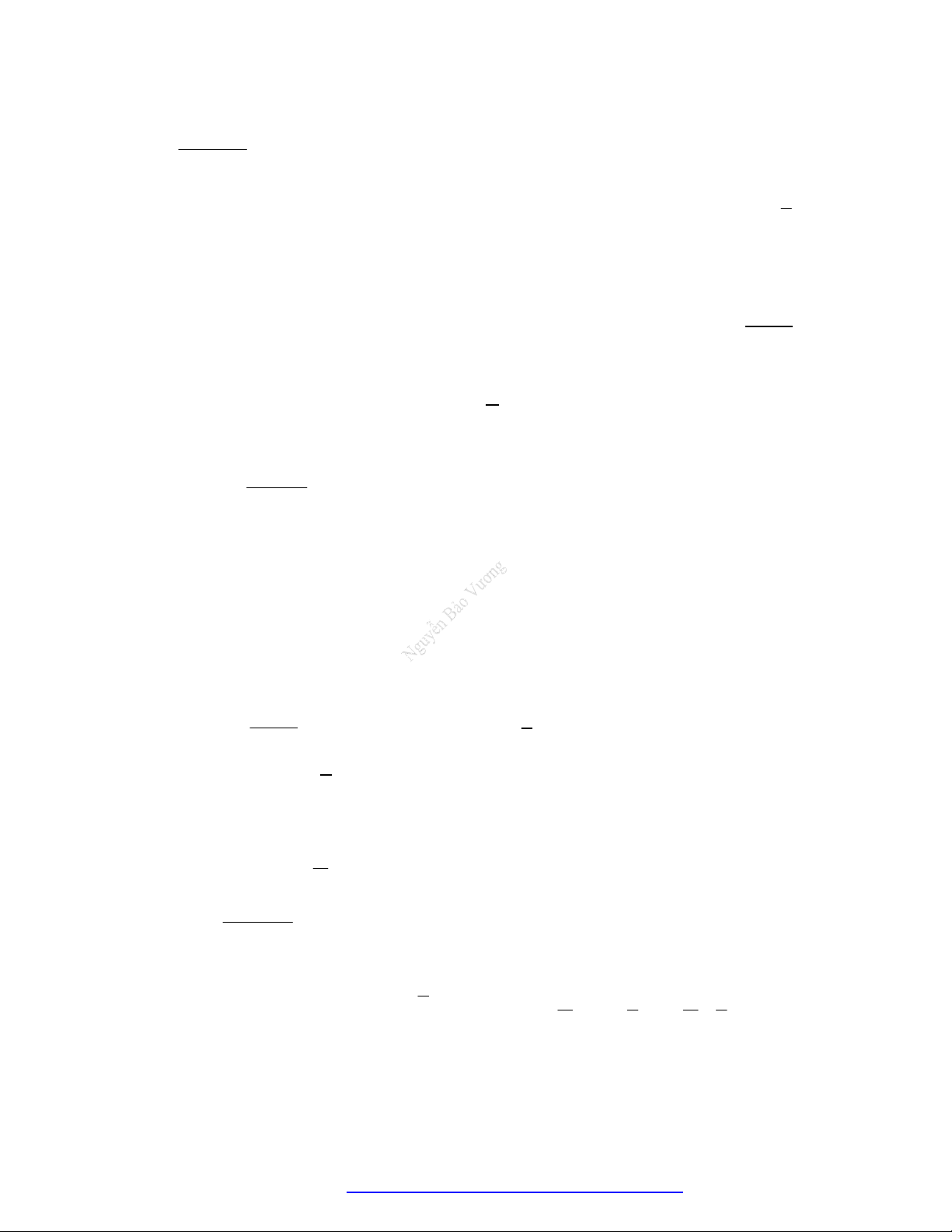
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Lờigiải
ChọnB
Tậpxácđịnh
\ 5D m
.
2
5 6
5
m
y
x m
Hàmsốnghịchbiếntrên
10;
khivàchỉkhi
0,
5 10;
y x D
m
5 6 0
5 10
m
m
6
5
2
m
m
.
Mà
m
nên
2; 1;0;1
m
.
Câu 10. (ChuyênKHTN-2020)Tậphợptấtcảcácgiátrịcủathamsố
m
đểhàmsố
4
mx
y
x m
đồng
biếntrênkhoảng
1;
là
A.
2;1
. B.
2;2
. C.
2; 1
. D.
2; 1
.
Lờigiải
ChọnC
Đạohàm
2
2
4
0,
m
y x m
x m
.
Do đó hàm số đồng biến trên
1;
khi
2 2
4 0 4 0
0, 1;
0, 1; , 1;
m m
y x
x m x x m x
2 2
2 1
1
m
m
m
.
Câu 11. (ChuyênNguyễnBỉnhKhiêm-QuảngNam-2020)Tìmtấtcảcácgiátrịthựccủathamsố
m
đểhàmsố
1
4
mx
y
m x
nghịchbiếntrênkhoảng
1
;
4
.
A.
2
m
. B.
1 2
m
. C.
2 2
m
. D.
2 2
m
.
Lờigiải
ChọnB
Tậpxácđịnh:
\
4
m
D
.
Tacó
2
2
4
4
m
y
m x
.
Hàmsốnghịchbiếntrênkhoảng
1
;
4
khivàchỉkhi
2
4 0
2 2
11
;
4 4
4 4
m
m
mm
2 2
1 2
1
m
m
m
.
Vậy
1 2
m
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Câu 12. (ChuyênTháiNguyên-2020)Chohàmsố
2 3
mx m
y
x m
với
m
làthamsố.Gọi
S
làtậphợp
tấtcảcácgiátrịnguyêncủa
m
đểhàmsốnghịchbiếntrênkhoảng
2;
.Tìmsốphầntửcủa
S
.
A.
5
. B.
3
. C.
4
. D.
1
.
Lờigiải
ChọnC
Điềukiệnxácđịnh:
x m
.
Tacó:
2
2
2 3
m m
y
x m
.
Đểhàmsốnghịchbiếntrênkhoảng
2;
thì:
0; 2;y x
x m
2
2 3 0
2
m m
m
3 1
2
m
m
2 1
m
.
Vậygiátrịnguyêncủa
m
là
2; 1;0
S
.
Câu 13. (ĐHQG HàNội-2020)Cóbaonhiêu giá trị nguyêncủatham số
m
đểhàmsố
18
4
x
y
x m
nghịchbiếntrênkhoảng
2;
?
A.Vôsố. B.
0
. C.
3
. D.
5
.
Lờigiải
ChọnD
Điềukiện
4x m
.
Tacó
18
4
x
y
x m
2
4 18
4
m
y
x m
.
Hàmsốđãchonghịchbiếntrênkhoảng
2;
9
0
4 18 0
1 9
2
4 2;
4 2 1
2 2
2
m
y
m
m
m
m
m
.
Vì
m
nên
0;1;2;3;4
m
.Vậycó5giátrịnguyêncủathamsố
m
đểhàmsố
18
4
x
y
x m
nghịchbiếntrênkhoảng
2;
.
Câu 14. (SởHàTĩnh-2020)Cóbaonhiêugiátrịnguyêncủathamsố
m
đểhàmsố
9
4
mx
y
x m
nghịch
biếntrênkhoảng
0;4
?
A.
5
. B.
11
. C.
6
. D.
7
.
Lờigiải
ChọnC
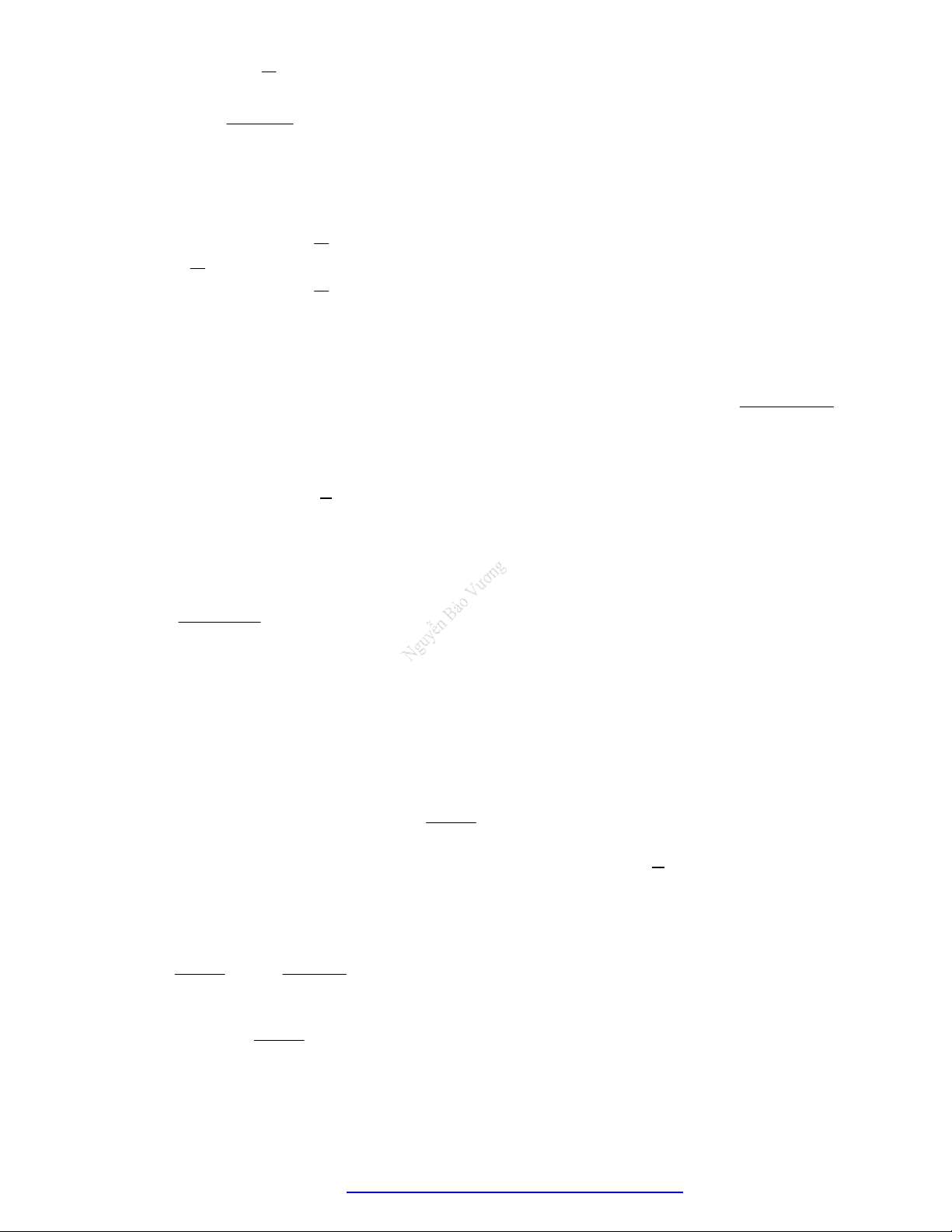
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Điềukiện:
4
m
x
.
Tacó:
2
2
36
'
4
m
y
x m
.
Hàmsốđãchonghịchbiếntrênkhoảng
0;4
' 0, 0;4
y x
2
36 0
0;4
4
m
m
6 6
0
4
4
4
m
m
m
6 6
0 6
0
16
m
m
m
m
.
Vì
m
nên
0,1,2,3,4,5
m
.
Vậycó
6
giátrị
m
thỏamãnyêucầubàitoán.
Câu 15. (SởYênBái-2020)Tìmtấtcảcácgiátrịthựccủathamsố
m
saochohàmsố
3 4
mx m
y
x m
nghịchbiếntrênkhoảng
1;
A.
1 4
m
. B.
1 1
m
. C.
1
4
m
m
. D.
1 4
m
.
Lờigiải
ChọnB
2
2
3 4
m m
y
x m
Đểhàmsốnghịchbiếntrênkhoảng
1;
thì
0, 1;y x
.
2
3 4 0
1;4
1 1
1;
1
m m
m
m
m
m
.
Câu 16. (Đặng Thúc Hứa - Nghệ An - 2020) Có bao nhiêu giá trị nguyên của tham số
2020;2020
m
saochohàmsố
3 18
x
y
x m
nghịchbiếntrênkhoảng
; 3
?
A.
2020
. B.
2026
. C.
2018
. D.
2023
.
Lờigiải
ChọnD
Điềukiện:
x m
nên
; 3
m
2
3 18 3 18
'
x m
y y
x m
x m
Đểhàmsố
3 18
x
y
x m
nghịchbiếntrênkhoảng
; 3
thì
3 18 0 6
m m
Vì
2020;2020
m
và
; 3
m
nên
2;2020
m
Vậycó2023giátrị
m
nguyênthoảmãn.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Câu 17. (LươngThếVinh-HàNội-2020)Cóbaonhiêugiátrịnguyênâmcủathamsố
m
đểhàmsố
4
2
x
y
x m
nghịchbiếntrênkhoảng
3;4
.
A.Vôsố. B.
1
. C.
3
. D.
2
.
Lờigiải
ChọnD
Tậpxácđịnh
\
2
m
D
.
Có
2
8
2
m
y
x m
Hàmsốnghịchbiếntrên
3;4
2
8
0 3;4 0 3;4
2
m
y x x
x m
8
8 0
8 6
3
2
8
3;4
2
4
2
m
m
m
m
m
m
m
.
Do
m
nguyênâmnên
7; 6
m
,gồm
2
giátrịthỏamãn.
Câu 18. (Chuyên KHTN-HàNội-Lần 3) Có bao nhiêu giá trị nguyên của tham số
m
đểhàmsố
4
mx
y
x m
nghịchbiếntrênkhoảng
0;
?
A.
1
. B.
2
. C.
3
. D.
5
.
Lờigiải
ChọnB
TXĐ:
D
m
Tacó
2
2
4
m
y
x m
.
Hàmsốnghịchbiếntrênkhoảng
0;
khivàchỉkhi
0, 0
0;
y x
m
2
2 2
4 0
0 2
0
0
m
m
m
m
m
.
Vậysốgiátrịnguyêncủathamsố
m
là
2
.
Dạng 3. Tìm m để hàm số bậc 3 đơn điệu trên khoảng cho trước
Câu 1. (Mã 101 – 2020 -Lần 2) Tập hợp tất cả các giá trị thực của tham số
m
để hàm số
3 2
3 4
y x x m x
đồngbiếntrênkhoảng
2;
là
A.
;1
B.
;4
C.
;1
D.
;4
Lờigiải
ChọnB
Tacó.
' 2
3 6 4
y x x m
.
'
0, 2;ycbt y x
2
3 6 4 0, 2;x x m x
2
3 6 4, 2;m x x x
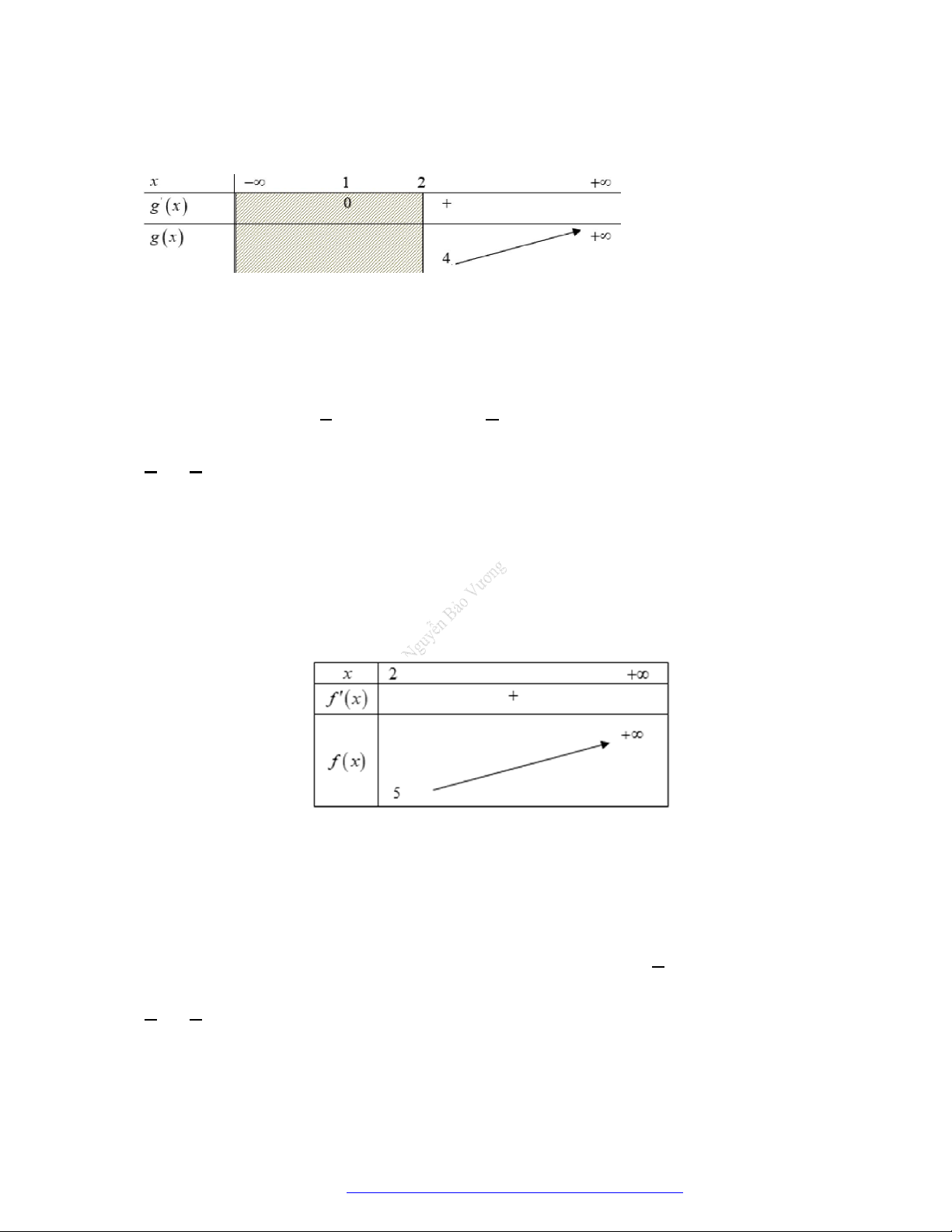
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2;
minm g x
với
2
3 6 4g x x x
Tacó.
'
6 6g x x
'
0 6 6 0 1g x x x
Dựavàobảngbiếnthiên,suyra:
4m
thỏayêucầubàitoán.
Vậy:
;4m
thìhàmsốđồngbiếntrênkhoảng
2;
.
Câu 2. (Mã 102 – 2020 – Lần 2) Tập hợp tất cả các giá trị của tham số
m
để hàm số
3 2
3 5y x x m x
đồngbiếntrênkhoảng
2;
là
A.
;2
. B.
;5
. C.
;5
. D.
;2
.
Lờigiải
ChọnC
Tacó
2
3 6 5y x x m
.
Hàmsốđãchođồngbiếntrên
2;
khivàchỉkhi
0, 2;y x
2 2
3 6 5 0, 2 3 6 5, 2x x m x m x x x .
Xéthàmsố
2
3 6 5f x x x
trênkhoảng
2;
.
Có
6 6f x x
,
0 6 6 0 1(lo i)f x x x
¹
.
Bảngbiếnthiên
Từbàngbiếnthiêntacó
2
3 6 5, 2m x x x
5m
.
Vậy
;5m
.
Câu 3. (Mã 103 – 2020 – Lần 2) Tập hợp tất cả các giá trị thực của tham số
m
để hàm số
3 2
3 2y x x m x
đồngbiếntrênkhoảng
2;
là
A.
; 1
. B.
;2
. C.
; 1
. D.
;2
.
Lờigiải
ChọnD
Tacó
2
' 3 6 2y x x m
.
Đểhàmsốđồngbiếntrênkhoảng
2;
khivàchỉkhi
' 0, 2;y x
2
3 6 2 0, 2;x x m x
2
3 6 2, 2;m x x x
.
Xéthàmsố
2
3 6 2, 2;f x x x x
.
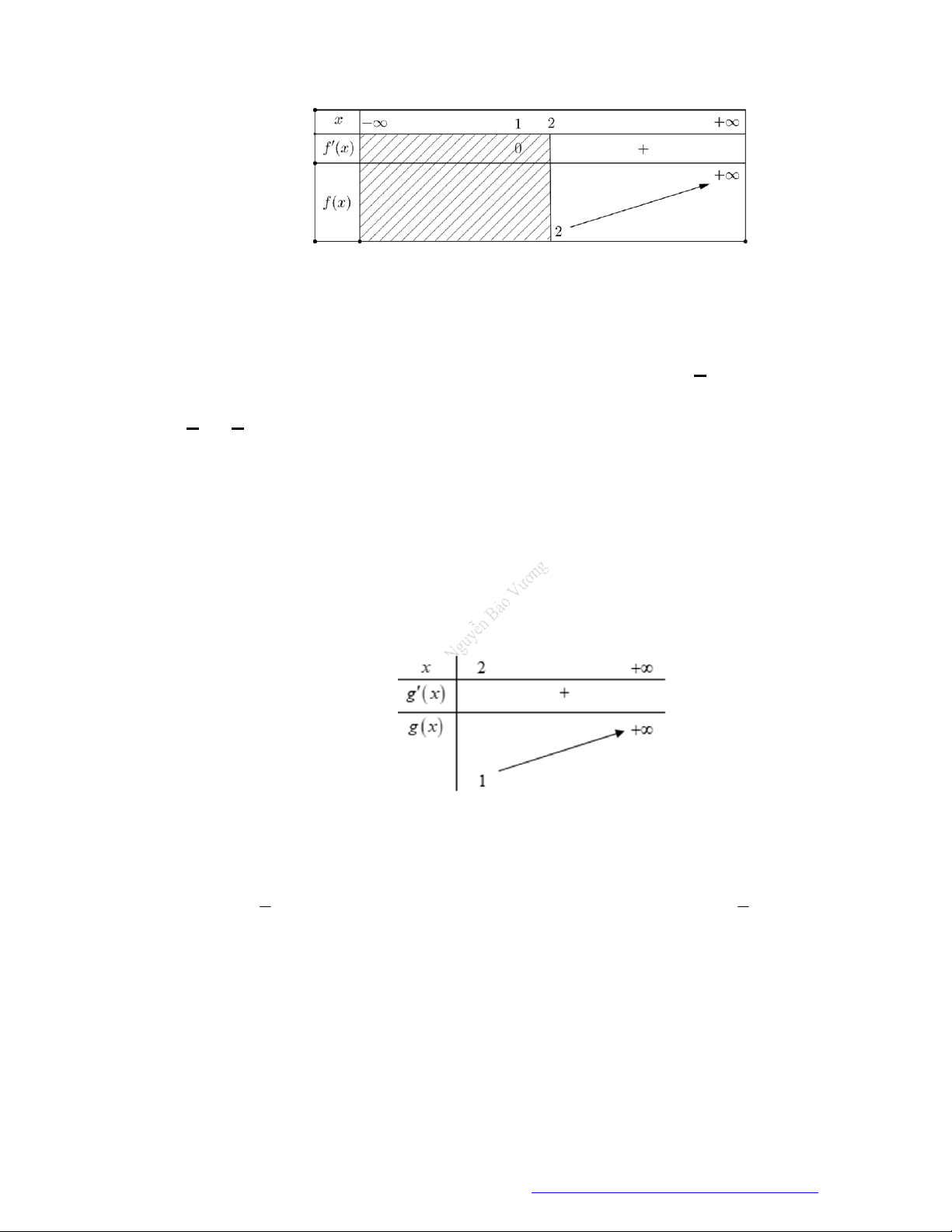
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
' 6 6f x x
;
' 0 6 6 0 1f x x x
.
Bảngbiếnthiên:
Từbảngbiếnthiêntathấy
2m
.Vậy
;2m
.
Câu 4. (Mã 104 – 2020 – Lần 2) Tập hợp tất cả các giá trị thực của tham số
m
để hàm số
3 2
3 1y x x m x
đồngbiếntrênkhoảng
2;
là
A.
; 2
. B.
;1
. C.
; 2
. D.
;1
.
Lờigiải
ChọnD
Tacó
2
3 6 1y x x m
.
Hàmsốđồngbiếntrênkhoảng
2;
0y
,
2;x
2
3 6 1 0x x m
,
2;x
2
3 6 1x x m
,
2;x
.
Xéthàmsố
2
3 6 1g x x x
với
2;x
.
6 6g x x
;
0g x
,
2;x
.
Bảngbiếnthiên
g x
:
Vậy
1m
.
Câu 5. (Đề Tham Khảo 2019) Tập hợp tất cả các giá trị thực của tham số
m
để hàm số
3 2
6 4 9 4y x x m x
nghịchbiếntrênkhoảng
; 1
là
A.
3
;
4
B.
0;
C.
;0
D.
3
;
4
Lờigiải
ChọnA
Tacó
2
3 12 4 9y x x m
Đểhàmsốnghịchbiếntrênkhoảng
; 1
thì
2
3 6 4 9 0 ; 1y x x m x
2
4 3 12 9 ; 1m x x x
; 1
4 min ,m f x
2
3 12 9f x x x
Tacó
' 6 12;f x x
' 0 2f x x
.
Khiđó,tacóbảngbiếnthiên
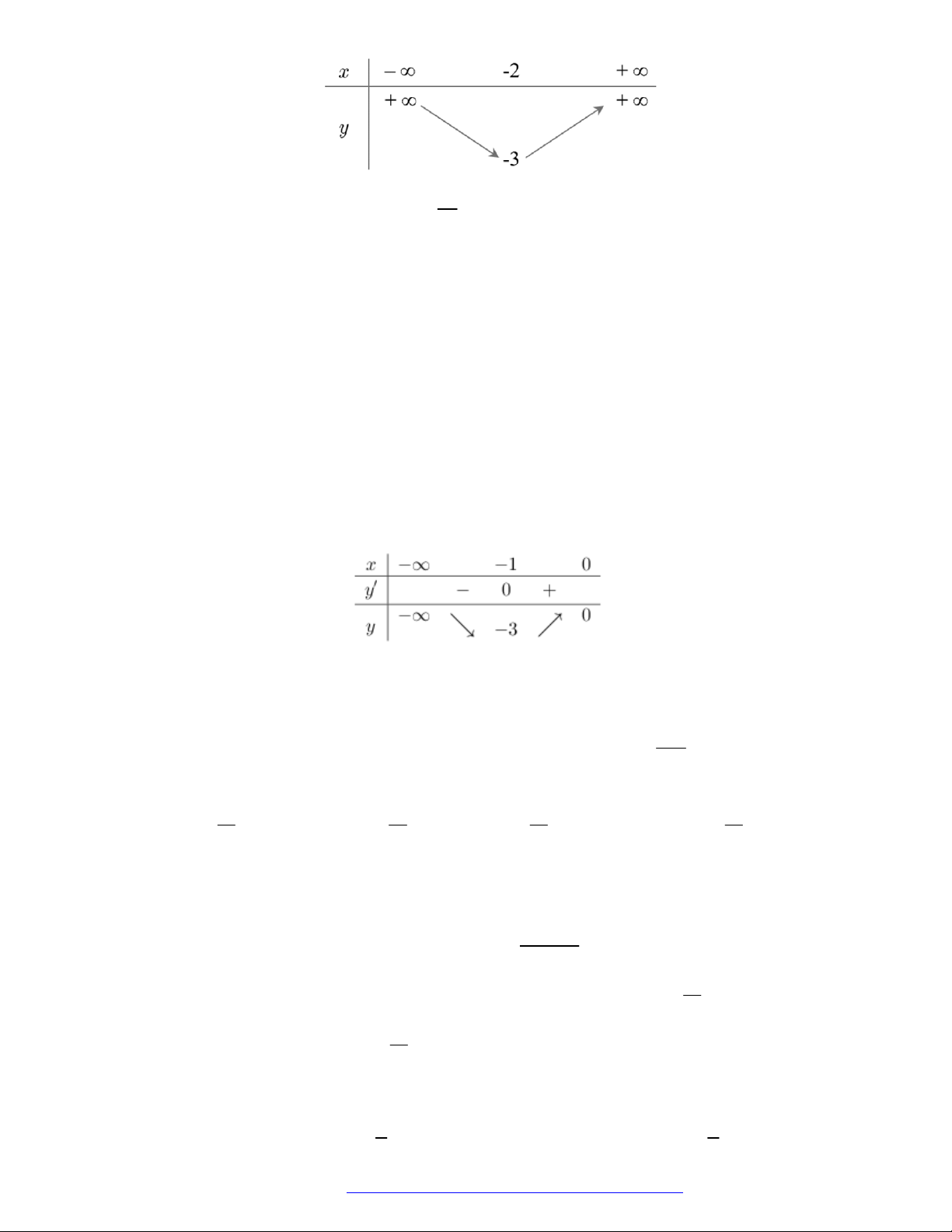
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Suyra
;0
3
min 3 4 3
4
f x m m
.
Câu 6. Chohàmsố
3 2
3 4y x x mx .Tậphợptấtcảcácgiátrịcủathamsố
m
đểhàmsốđồngbiến
trênkhoảng
;0
là
A.
1;5
. B.
; 3
. C.
; 4
. D.
1;
.
Lờigiải
ChọnB
Tacó
2
3 6y x x m
.
Đểhàmsốđồngbiếntrênkhoảng
;0
thì
0, ;0y x
2
3 6 0, ;0x x m x
2
3 6 , ;0m x x x
.
Đặt
2
3 6g x x x
,hàmsố
g x
cóbảngbiếnthiên
Dựavàobảngbiếnthiêntacó
2
3 6 , ;0m x x x
3m
.
Câu 7. Tìmtấtcảcácgiátrịthựccủathamsố
m
saochohàmsố
3
2
( ) 7 14 2
3
mx
y f x mx x m
giảmtrênnửakhoảng
[1; )
?
A.
14
;
15
. B.
14
2;
15
. C.
14
;
15
. D.
14
;
15
.
Lờigiải
ChọnA
Tậpxácđịnh
D
,yêucầucủabàitoánđưađếngiảibấtphươngtrình
2
14 14 0, 1mx mx x
,tươngđươngvới
2
14
( )
14
g x m
x x
(1)
Dễdàngcóđược
( )g x
làhàmtăng
1;x
,suyra
1
14
min ( ) (1)
15
x
g x g
Kếtluận:(1)
1
14
min ( )
15
x
g x m m
Câu 8. Xácđịnhcácgiátrịcủathamsốmđểhàmsố
3 2
3y x mx m
nghịchbiếntrênkhoảng
0;1 ?
A.
0m
. B.
1
2
m
. C.
0m
. D.
1
2
m
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
Lờigiải
ChọnD
2
2
' 3 6 0
0
x m
y x mx
x
Hàmsố
3 2
3y x mx m
nghịchbiếntrênkhoảng
1
0;1 2 1
2
m m
Câu 9. Tìm tất cả các giá trị của tham số
m
để hàm số
3 2
3 1y x x mx đồng biến trên khoảng
;0
.
A.
0m
. B.
2m
. C.
3m
. D.
1m
.
Lờigiải
ChọnC
Tậpxácđịnh:
D
.
Đạohàm:
2
3 6y x x m
.
Hàmsốđồngbiếntrênkhoảng
;0
khivàchỉkhi
0y
,
0x
2
3 6 0x x m
,
0x
.
Cách1:
2
3 6 0x x m
,
0x
2
3 6x x m
,
0x
.
Xéthàmsố
2
3 6f x x x
trênkhoảng
;0
,tacó:
6 6f x x
.Xét
0f x
6 6 0x 1x
.Tacó
1 3f
.
Bảngbiếnthiên:
Dựavàobảngbiếnthiên,tacó:
3m
.
Cách2:
Tacó
9 3m
.
Nếu
0 3m
thì
0y
x
0y
0x
.
Nếu
0
thì
y
cóhainghiệmphânbiệt
1 2
,x x .Khiđóđể
0y
0x
thìtaphảicó
1 2
0 x x .Điềunàykhôngthểxảyravì
1 2
2 0S x x .
Vậy
3m
.
Cách3:
PhươngánB:Với
3m
tacó
3
3 2
3 3 1 1y x x x x
.Khiđó
2
3 1 0y x
x
.
Suyrahàmsốđồngbiếntrênkhoảng
;0
.VậyBlàđápánđúng.
Câu 10. Tìm tất cả các giá trị thực của tham số
m
để hàm số
3 2 2
3 9 y x mx m x
nghịch biến trên
khoảng
0;1
.
A.
1
1
3
m
. B.
1
3
m
.
C.
1 m
. D.
1
3
m
hoặc
1 m
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Lờigiải
ChọnD
Tậpxácđịnh
D
.
2 2
3 6 9
y x mx m
;
2 2 2 2
0 3 6 9 0 2 3 0
3
x m
y x mx m x mx m
x m
.
Nếu
3 0 m m m
thì
0;
y x
nênhàmsốkhôngcókhoảngnghịchbiến.
Nếu
3 0 m m m
thìhàmsốnghịchbiếntrênkhoảng
;3m m
.
Dođóhàmsốnghịchbiếntrênkhoảng
0;1
0
1
3 1
3
m
m
m
.
Kếthợpvớiđiềukiệntađược
1
3
m
.
Nếu
3 0 m m m
thìhàmsốnghịchbiếntrênkhoảng
3 ; m m
.
Dođóhàmsốnghịchbiếntrênkhoảng
0;1
3 0
1
1
m
m
m
.
Kếthợpvớiđiềukiệntađược
1 m
.
Vậyhàmsốnghịchbiếntrênkhoảng
0;1
khi
1 m
hoặc
1
3
m
.
Câu 11. Tìm các giá trị của tham số
m
để hàm số
3 2
1
2 1 2
3
y x mx m x m
nghịch biến trên
khoảng
2;0 .
.
A.
0m
. B.
1m
. C.
1
2
m
. D.
1
2
m
.
Lờigiải
ChọnC
Tacó:
2
2 2 1.y x mx m
Cho
2
1
0 2 2 1 0 .
2 1
x
y x mx m
x m
.
Nếu
1 2 1m
thìtacóbiếnđổi
0 1 2 1y x m
.
(trườnghợpnàyhàmsốkhôngthểnghịchbiếntrênkhoảng
2;0
).
Xét
2 1 1m
tacóbiếnđổi
0 2 1;1y x m
.
.
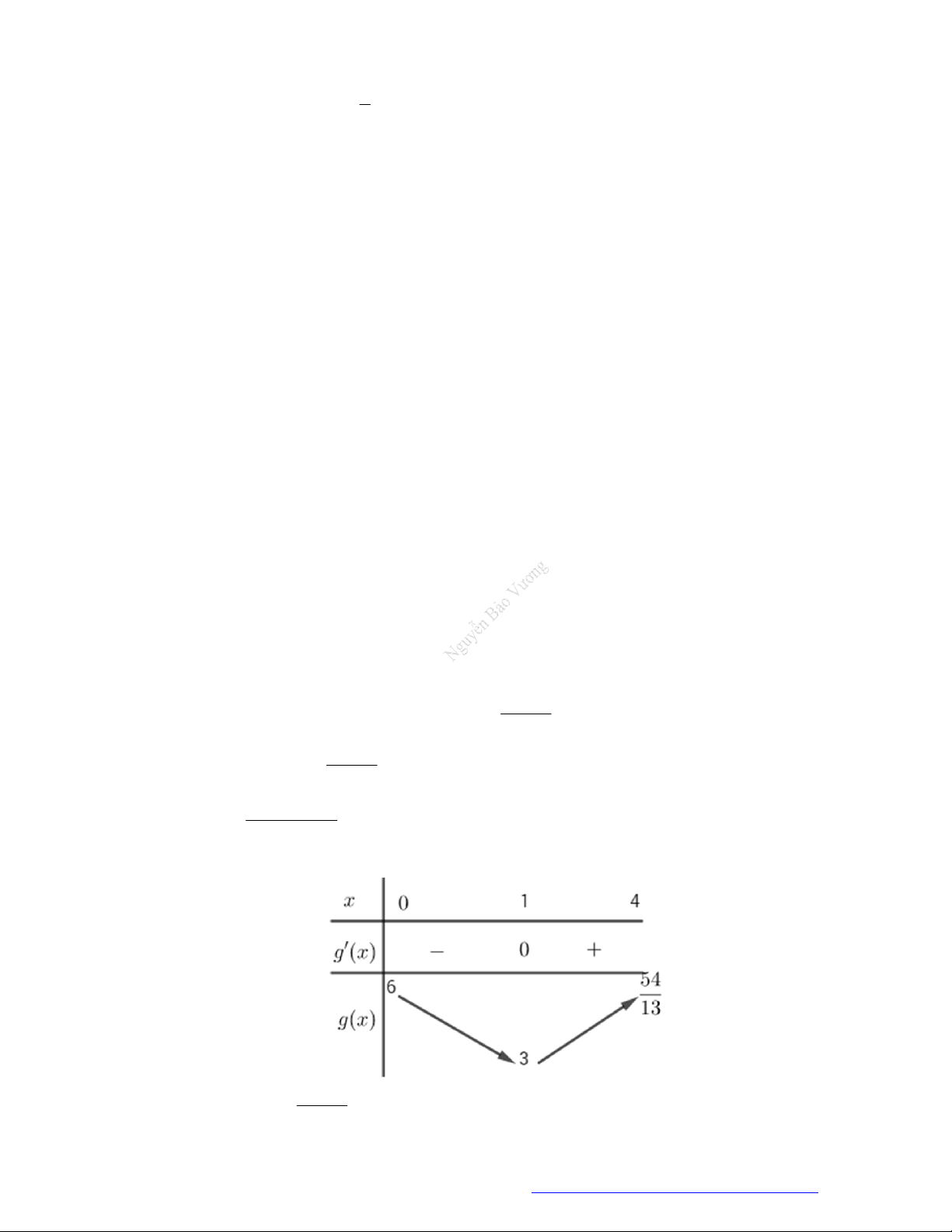
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
Vậy,hàmsốnghịchbiếntrênkhoảng
2;0
thì
2;0 2 1;1m
.
1
2 1 2 .
2
m m
.
Câu 12. Tìmtấtcảcácgiátrị
m
đểhàmsố
3 2
3 2y x x mx
tăngtrênkhoảng
1;
.
A.
3m
. B.
3m
. C.
3m
. D.
3m
.
Lờigiải
ChọnB
Đạohàm:
2
3 6y x x m
YCBT
0, 1;y x
.
2 2
3 6 0, 1; 3 6 , 1;x x m x m x x x
Xéthàmsố:
2
3 6 , 1; 6 6 0 1f x x x x f x x f x x
.
lim
x
f x
,
1 3f
.Dođó:
, 1; 3m f x x m
.
Câu 13. Tậphợp tấtcảcácgiátrịcủathamsố
m
đểhàmsố
3 2
6 1y x mx m x
đồngbiếntrên
khoảng
0;4
là:
A.
;3
. B.
;3
. C.
3;6
. D.
;6
.
Lờigiải
ChọnB
2
3 2 6y x mx m
.Đểhàmsốđồngbiếntrênkhoảng
0;4
thì:
0y
,
0;4x
.
tứclà
2
3 2 6 0 0;4x mx m x
2
3 6
0;4
2 1
x
m x
x
Xéthàmsố
2
3 6
2 1
x
g x
x
trên
0;4
.
2
2
6 6 12
2 1
x x
g x
x
,
1 0;4
0
2 0;4
x
g x
x
Tacóbảngbiếnthiên:
Vậyđể
2
3 6
0;4
2 1
x
g x m x
x
thì
3m
.
Câu 14. Tìmtấtcảcácgiáthựccủathamsố
m
saochohàmsố
3 2
2 3 6y x x mx m
nghịchbiếntrên
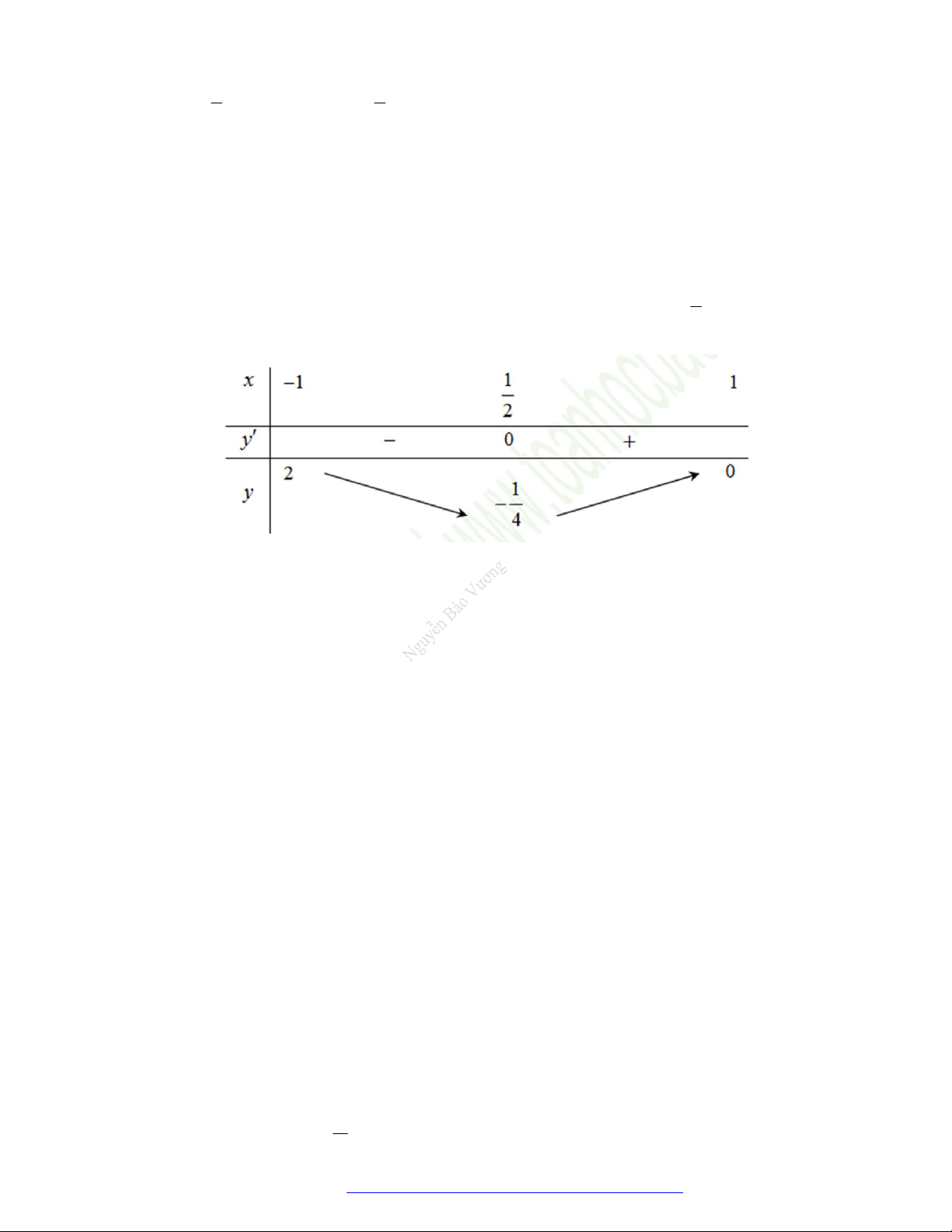
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 22 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
khoảng
1;1
.
A.
1
4
m
. B.
1
4
m
. C.
2m
. D.
0m
.
Lờigiải
ChọnC
Tacó
2
6 6 6y x x m
.
Hàmsốnghịchbiếntrênkhoảng
1;1
khivàchỉkhi
0y
với
1;1x
hay
2
m x x
với
1;1x
.
Xét
2
f x x x
trênkhoảng
1;1
tacó
2 1f x x
;
1
0
2
f x x
.
Bảngbiếnthiên
Dựavàobảngbiếnthiêntacó
m f x
với
1;1x
2m
.
*Cóthểsửdụng
0y
với
1;1x
1 0
1 0
y
y
6 0
12 6 0
m
m
0
2
m
m
2m
.
Câu 15. Tìmtấtcảcácgiátrịthựccủathamsố
m
saochohàmsố
3 2
6 1y x x mx
đồngbiếntrên
khoảng
0;
?
A.
12m
. B.
12m
. C.
0m
. D.
0m
.
Lờigiải
ChọnA
Cách 1:Tậpxácđịnh:
D
.Tacó
2
3 12y x x m
Trườnghợp1:
Hàmsốđồngbiếntrên
0,y x
3 0 ( )
12
36 3 0
hn
m
m
Trườnghợp2:Hàmsốđồngbiếntrên
0;
0y
cóhainghiệm
1 2
,x x thỏa
1 2
0x x
(*)
Trườnghợp2.1:
0y
cónghiệm
0x
suyra
0m
.Nghiệmcònlạicủa
0y
là
4x
(khôngthỏa(*))
Trườnghợp2.2:
0y
cóhainghiệm
1 2
,x x thỏa
1 2
0
0 0
0
x x S
P
36 3 0
4 0( )
0
3
m
vl
m
khôngcó
m
.Vậy
12m
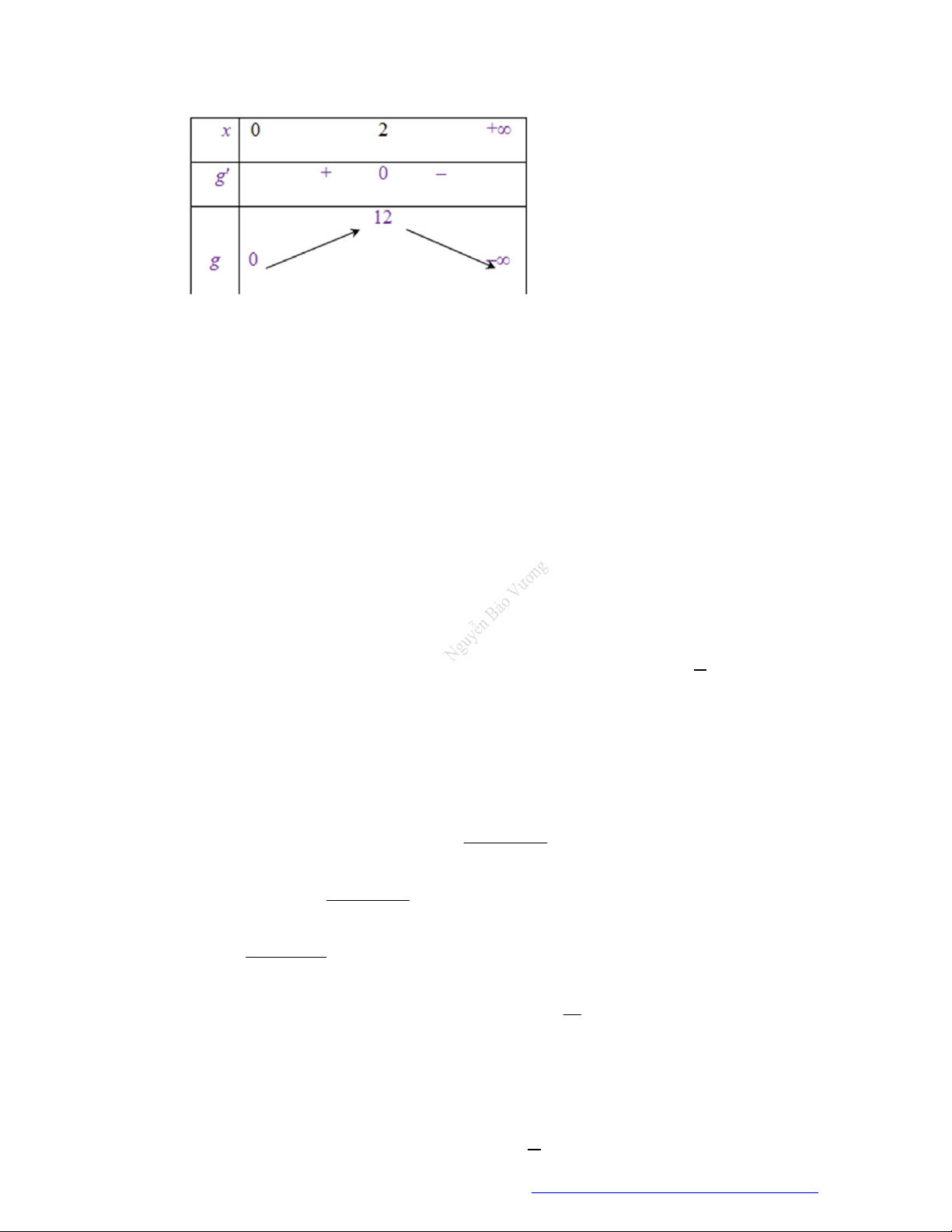
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
Cách 2:Hàmsốđồngbiếntrên
0;
2
12 3 ( ), (0; )m x x g x x .
Lậpbảngbiếnthiêncủa
( )g x
trên
0;
.
Câu 16. Tìm
m
đểhàmsố
3 2
3 3 1y x x mx m
nghịchbiếntrên
0;
.
A.
1m
. B.
1m
. C.
1m
. D.
1m
.
Lờigiải
ChọnA
Tacó
2 2
3 6 3 3 2y x x m x x m
.
Vìhàmsốliêntụctrênnửakhoảng
0;
nênhàmsốnghịchbiếntrên
0;
cũngtương
đươnghàmsốnghịchtrên
0;
khichỉkhi
0, 0,y x
.
2 2
0;
2 0 0; 2 0;
min 1 1
x x m x m x x f x x
m f x f
.
Câu 17. (THPTChuyênHạLong-2018)Gọi
S
làtậphợpcácgiátrịnguyêndươngcủa
m
đểhàmsố
3 2
3 2 1 12 5 2y x m x m x
đồngbiếntrênkhoảng
2;
.Sốphầntửcủa
S
bằng
A.
1
. B.
2
. C.
3
. D.
0
.
Lờigiải
Tậpxácđịnh
D
.
2
3 6 2 1 12 5y x m x m
.
Hàmsốđồngbiếntrongkhoảng
2;
khi
0y
,
2;x
2
3 6 2 1 12 5 0x m x m
,
2;x
.
2
3 6 2 1 12 5 0x m x m
2
3 6 5
12 1
x x
m
x
Xéthàmsố
2
3 6 5
12 1
x x
g x
x
với
2;x
.
2
2
3 6 1
0
12 1
x x
g x
x
với
2;x
hàmsố
g x
đồngbiếntrênkhoảng
2;
.
Dođó
m g x
,
2;x
2m g
5
12
m
.
Vậykhôngcógiátrịnguyêndươngnàocủa
m
thỏamãnbàitoán.
Câu 18. (Chuyên KHTN - 2018). Tập hợp tất cả các giá trị của tham số
m
để hàm số
3 2
6 1y x mx m x
đồngbiếntrênkhoảng
0;4
là:
A.
;6
. B.
;3
. C.
;3
. D.
3;6
.
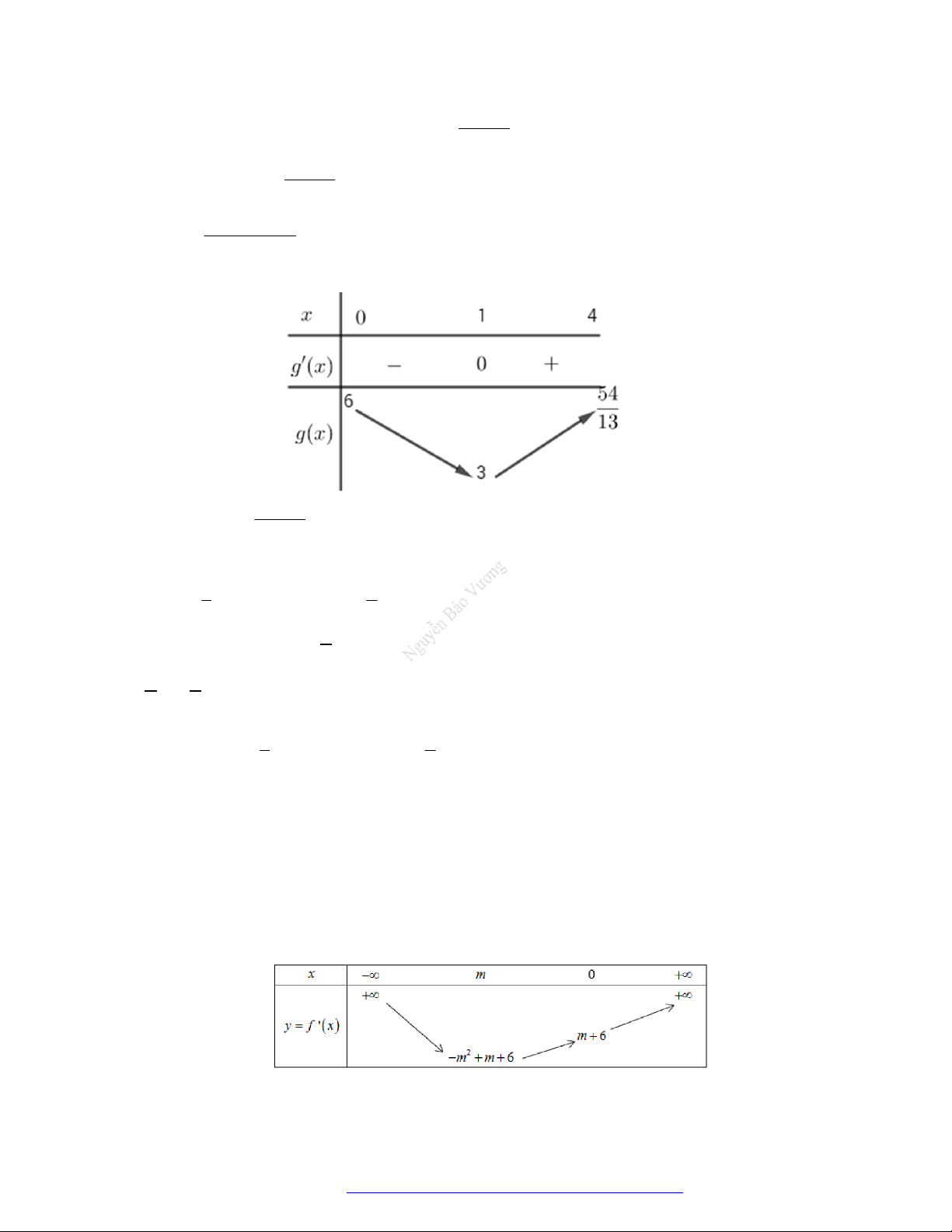
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 24 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Lờigiải
2
3 2 6y x mx m
.Đểhàmsốđồngbiếntrênkhoảng
0;4
thì:
0y
,
0;4x
.
tứclà
2
3 2 6 0 0;4x mx m x
2
3 6
0;4
2 1
x
m x
x
Xéthàmsố
2
3 6
2 1
x
g x
x
trên
0;4
.
2
2
6 6 12
2 1
x x
g x
x
,
1 0;4
0
2 0;4
x
g x
x
Tacóbảngbiếnthiên:
Vậyđể
2
3 6
0;4
2 1
x
g x m x
x
thì
3m
.
Câu 19. (Chuyên ĐH Vinh - Nghệ An -2020) Có bao nhiêu số nguyên
m
để hàm số
3 2
1 2
6
3 3
f x x mx m x
đồngbiếntrênkhoảng
0;
?
A.9. B.10. C.6. D.5.
Lờigiải.
ChọnB
Tacó
2
' 2 6f x x mx m
Hàmsố
3 2
1 2
6
3 3
f x x mx m x
đồngbiếntrênkhoảng
0;
khivàchỉkhi
' 0, 0;f x x
.
Xéthàmsố
2
' 2 6y f x x mx m
trong3trườnghợp:
Trường hợp 1:
0m
2
' 6 0,y f x x x
.Lúcnàyhàmsố
f x
đồngbiếntrên
nêncũngđồngbiếntrên
0; 1
.
Trường hợp 2:
0m
,tacóbảngbiếnthiêncủahàmsố
2
' 2 6y f x x mx m
nhưsau:
6 0
' 0, 0; 6 0
0
m
f x x m
m
2
.
Trường hợp 3:
0m
,tacóbảngbiếnthiêncủahàmsố
2
' 2 6y f x x mx m
nhưsau:

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25
2
6 0
' 0, 0; 0 3
0
m m
f x x m
m
3
.
Từ
1 , 2
và
3
suyracó10giátrịnguyêncủa
m
đểhàmsố
3 2
1 2
6
3 3
f x x mx m x
đồngbiếntrênkhoảng
0;
.
Câu 20. (Chuyên Sơn La - 2020) Tìm tất cả các giá trị thực của tham số
m
để hàm số
3 2
6 4 9 4y x x m x
nghịchbiếntrênkhoảng
; 1
là
A.
3
;
4
. B.
3
;
4
. C.
0;
. D.
;0
.
Lờigiải
ChọnA
Tacó:
2
3 12 4 9y x x m
.
Ycbt
2
3 12 4 9 0, ; 1x x m x
2
3
4 3 , ; 1
4
m x x x
2
3
2 1 , ; 1
4
m x x
2
; 1
3 3
min 2 1
4 4
x
m x
.
Câu 21. (SởBắcNinh-2020)Chohàmsố
3
2
1 3 1 1
3
x
y m x m x .Sốcácgiátrịnguyêncủa
m
đểhàmsốđồngbiếntrên
1;
là
A.7. B.4. C.5. D.6.
Lờigiải
ChọnC
Tacó:
2
2 1 3 1y x m x m
.
Ycbt
2
2 1 3 1 0, 1;x m x m x
2
2
1 3 1 5 4m m m m
.
Trườnghợp1:
2
0 5 4 0 1;4m m m
.Tađược4giátrịnguyêncủa
m
.
Trườnghợp2:
2
1
0 5 4 0
4
m
m m
m
. Khi đó phương trình
2
2 1 3 1 0x m x m
có hai
nghiệmphânbiệt
1 2
1x x
1 2
1 2
1 1 0
1 1 0
x x
x x
1 2
1 2 1 2
2 0
1 0
x x
x x x x
2 1 2 0
3 1 2 1 1 0
m
m m
0 2m
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 26 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Kếthợpvớiđiềukiệntađược
0 1m
.Khiđócó1giátrịnguyêncủa
m
.
Vậycó5giátrịnguyêncủa
m
.
Câu 22. (KimLiên-HàNội-2020)Sốgiátrịnguyênthuộckhoảng
2020;2020
củathamsố
m
để
hàmsố
3 2
3 2019y x x mx
đồngbiếntrên
0;
là
A.
2018
. B.
2019
. C.
2020
. D.
2017
.
Lờigiải
ChọnD
Tacó
2
3 6y x x m
.
Hàmsốđồngbiếntrênkhi
2
0, 0; 3 6 0, 0;y x x x m x
2
3 6 , 0; 1x x m x
Xéthàmsố
2
3 6f x x x
trên
0;
Tacó
6 6, 0 1.f x x f x x
Dođó
0;
min 1 3f x f
1 3.m
Kếthợpvớigiảthiếttađược
2020; 3m
.Nêncó2017sốnguyênthỏamãn
Vậychọn D.
Câu 23. (LêLai-ThanhHóa-2020)Cóbaonhiêugiátrịnguyêncủa thuộc đểhàmsố
đồngbiếntrên .
A. . B. . C. . D. .
Lờigiải
ChọnD
Tacó:
2
3 12y x x m
.
Hàmsốđồngbiếntrên
0;
khivàchỉkhi
2
0, 0; 3 12 0, 0;y x x x m x
.
Dođó
2
0;
3 12 , 0; maxm x x x m g x
với
2
3 12g x x x
.
Tacó:
2
3 2 12 12, 0;g x x x
nên
0;
max 12 2g x g
.
Vậy
12m
.
Sốcácsốnguyên
m
cầntìmlà:
2020 12 1 2009
.
Câu 24. (NguyễnHuệ-PhúYên-2020)Chohàmsố
3 2 2
1 2 3 2 2f x x m x m m x
.Cóbao
nhiêugiátrịnguyêncủathamsố
m
saochohàmsốđãchođồngbiếntrênkhoảng
2;
?
A.
2
. B.
3
. C.
4
. D.
5
.
Lờigiải
ChọnC
3 2 2 2 2
1 2 3 2 2 3 2 1 2 3 2f x x m x m m x f x x m x m m
Nhậnxét
2
2 3 2 0m m m
nên
2 2
3 2 1 2 3 2 0f x x m x m m
m
2020;2020
3 2
6 1y x x mx
0;
2004
2017
2020
2009
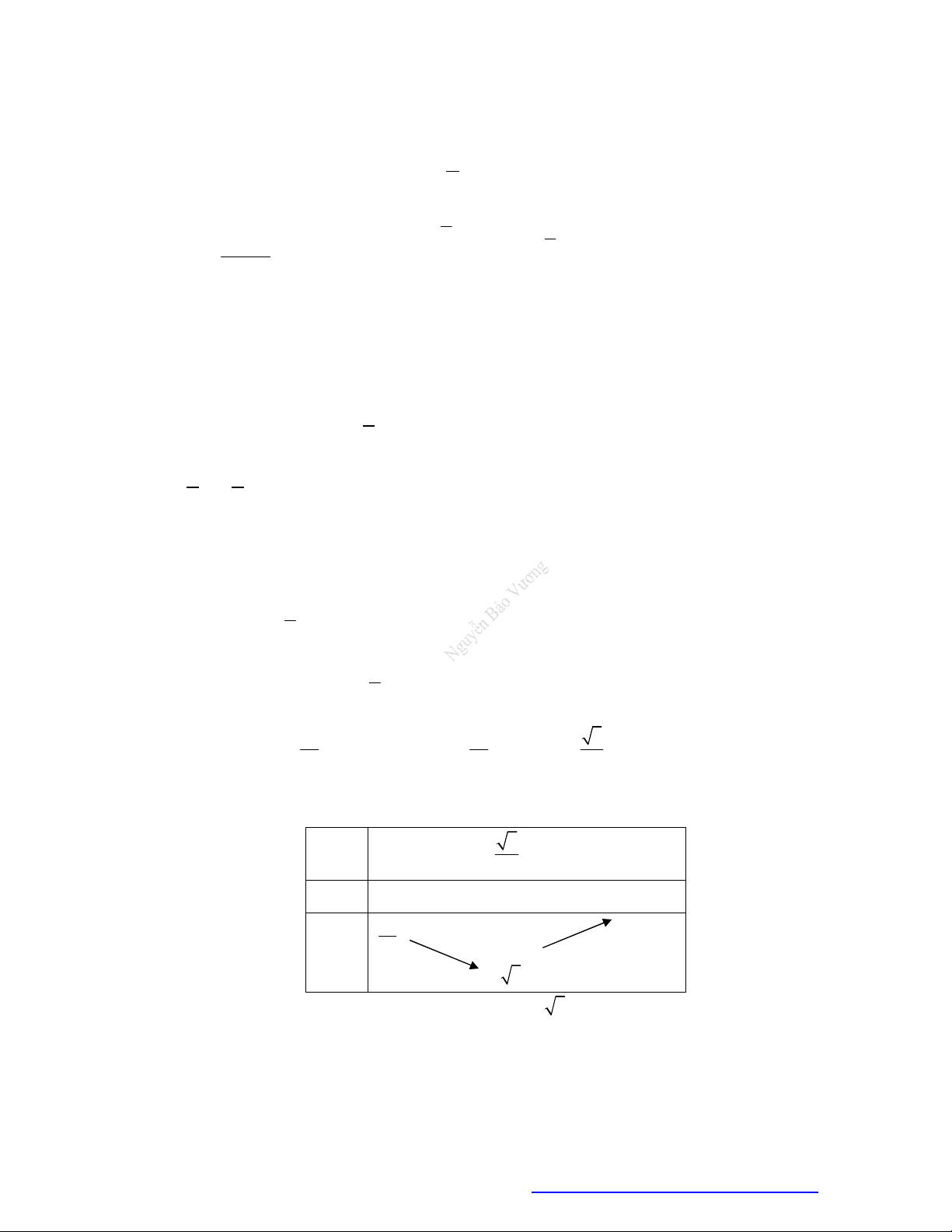
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27
luôncóhainghiệmphânbiệtvớimọi
m
Dođóhàmsốđãchođồngbiếntrênkhoảng
2;
khivàchỉkhi
0
f x
vớimọi
2;x
Điềunàyxảyrakhi
2
1 2
3. 3.4 4 1 2 3 2 0
3. 2 0
2
2
2
m m m
f
S
x x
2
3
2 6 0
2
3
2
2
1
2
2
5
3
m m
m
m
m
m
Do
m
nguyênnên
2; 1;0;1
m
.
Câu 25. (TiênDu-BắcNinh-2020)Gọi
S
làtậphợptấtcảcácgiátrịnguyêncủathamsố
m
thuộc
2020;2020
saochohàmsố
3 2
2 2y x mx x
đồngbiếntrênkhoảng
2;0
.Tínhsốphần
tửcủatậphợp
S
.
A.
2025
. B.
2016
. C.
2024
. D.
2023
.
Lờigiải
ChọnC
Tacó
3 2 2
2 2 6 2 2y x mx x y x mx
.
Hàmsốđãchođồngbiêntrênkhoảng
2
2;0 6 2 2 0, 2;0
y x mx x
1
3 , 2;0
m x x
x
.
Xéthàmsố
1
3 , 2;0
g x x x
x
2 2
1 1 3
3 0 3 0
3
g x g x x
x x
.
Bảngbiếnthiên
x
2
3
3
0
g x
0
0
g x
13
2
2 3
Từ bảng biến thiên suy ra
2 3
m
. Mà
, 2020;2020
m m
nên
2019; 2018;...; 4
m
.
Vậy có 2016 giá trị nguyên của tham số
m
thuộc
2020;2020
sao cho hàm số
3 2
2 2y x mx x
đồngbiếntrênkhoảng
2;0
.
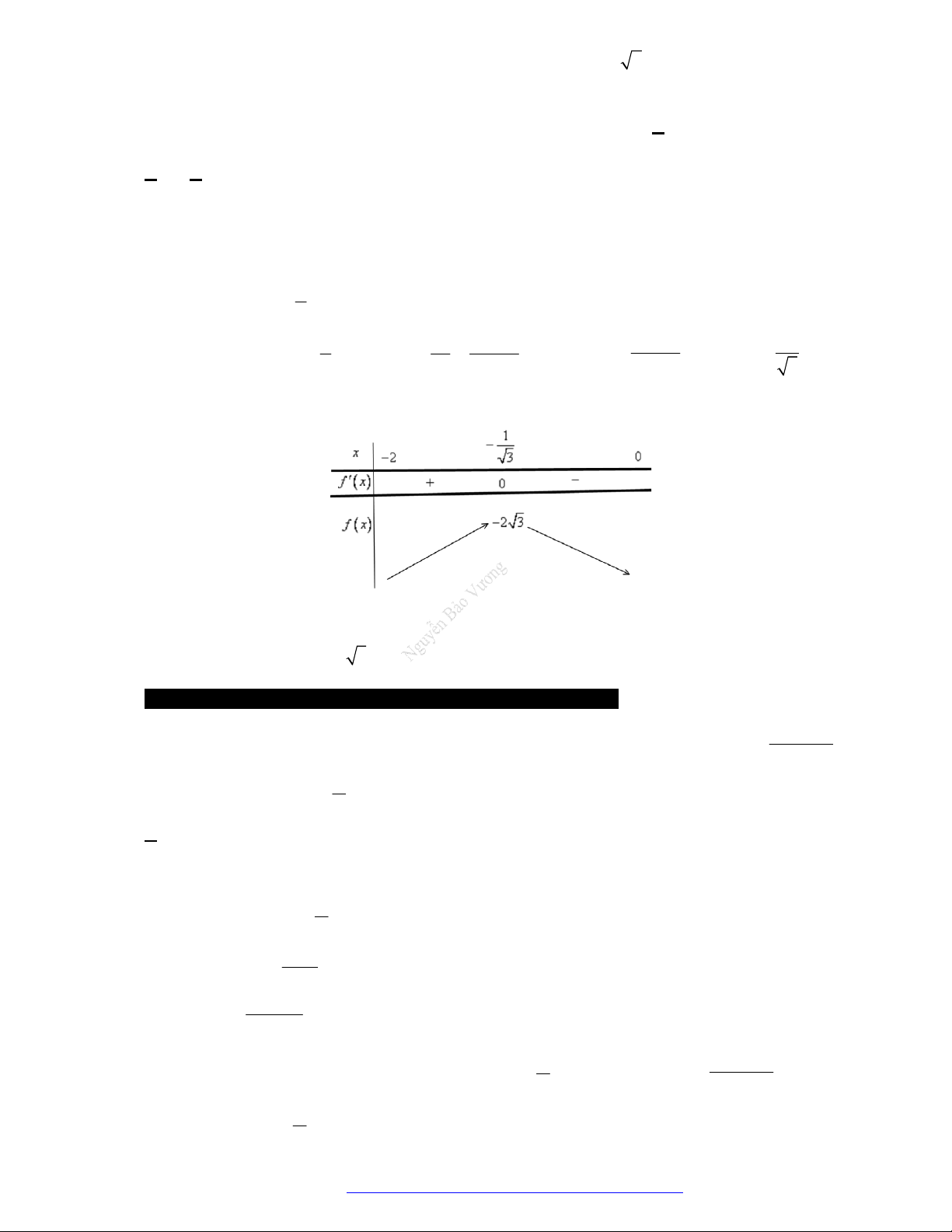
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 28 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 26. (Tiên Lãng - Hải Phòng - 2020) Với mọi giá trị
m a b
,
,a b
thì hàm số
3 2
2 2 5y x mx x
đồngbiếntrênkhoảng
2;0
.Khiđó
a b
bằng
A.
1
. B.
2
. C.
3
. D.
5
.
Lờigiải
ChọnD
Tacó:
2
6 2 2y x mx
.
Hàmsốđồngbiếntrênkhoảng
2;0
khi
0, 2;0y x
2
3 1 0, 2;0x mx x
2
1
3 1 3x mx x m
x
.
Xéthàmsố
1
3f x x
x
;
2
2 2
1 3 1
3
x
f x
x x
;
2
2
3 1 1
0 0
3
x
f x x
x
Bảngbiếnthiêncủahàmsố
f x
.
Từbảngbiếnthiênđể
f x m
,
2;0x
thì
2;0
max 2 3f x m m
2
5
3
a
a b
b
.
Dạng 4. Tìm m để hàm số khác đơn điệu trên khoảng cho trước
Câu 1. (ĐềMinhHọa2017)Tìmtấtcảcácgiátrịthựccủathamsố
m
saochohàmsố
tan 2
tan
x
y
x m
đồngbiếntrênkhoảng
0; .
4
A.
0m
hoặc
1 2m
B.
0m
C.
1 2m
D.
2m
Lờigiải
ChọnA
Đặt
tant x
,vì
0; 0;1
4
x t
Xéthàmsố
2
0;1
t
f t t
t m
.Tậpxácđịnh:
\D m
Tacó
2
2 m
f t
t m
.
Tathấyhàmsố
tant x x
đồngbiếntrênkhoảng
0;
4
.Nênđểhàmsố
tan 2
tan
x
y
x m
đồng
biếntrênkhoảng
0;
4
khivàchỉkhi:
0 0;1f t t
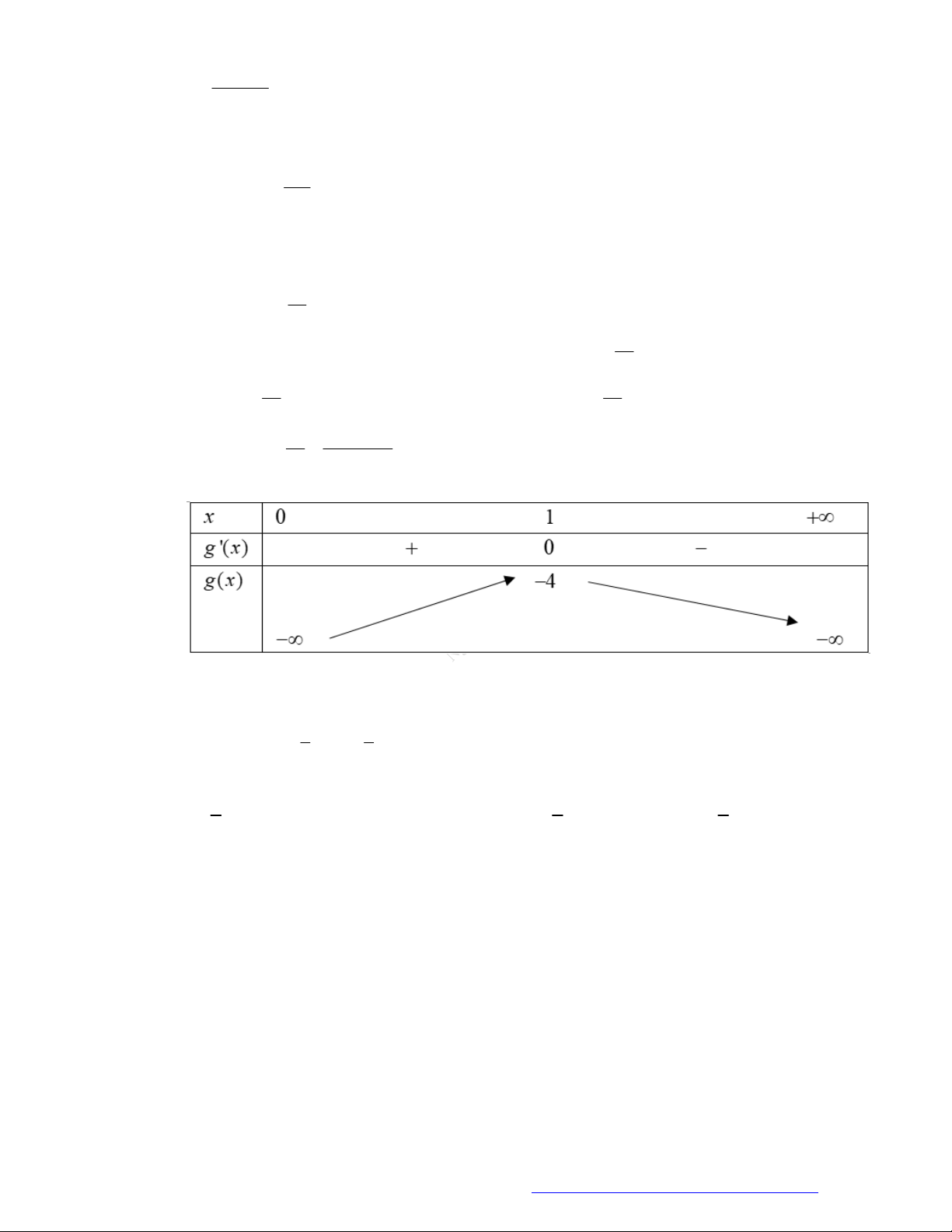
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 29
2
2
2 0
2
0 0;1 ;0 1;2
0
0;1
1
m
m
m
t m
m
m
t m
m
Câu 2. (Đề Tham Khảo 2018) Có bao nhiêu giá trị nguyên âm của tham số
m
để hàm số
3
5
1
5
y x mx
x
đồngbiếntrênkhoảng
0;
A.
0
B.
4
C.
5
D.
3
Lờigiải
ChọnB
2
6
1
3y x m
x
Hàmsốđồngbiếntrên
0;
khivàchỉkhi
2
6
1
3 0, 0;y x m x
x
2
6
1
3 , 0;x m x
x
.Xéthàmsố
2
6
1
( ) 3g x x m
x
,
0;x
8
7 7
6( 1)
( ) 6
6
x
g x x
x x
,
1
( ) 0
1(loai)
x
g x
x
Bảngbiếnthiên:
DựavàoBBTtacó
4m
,suyracácgiátrịnguyênâmcủathamsố
m
là
4; 3; 2; 1
Câu 3. (THPTBạchĐằngQuảngNinh2019)Gọi
S
làtậphợptấtcảcácgiátrịcủathamsố
m
để
hàmsố
2 5 3 2 2
1 1
10 20
5 3
f x m x mx x m m x
đồngbiếntrên
.Tổnggiátrịcủatấtcả
cácphầntửthuộc
S
bằng
A.
5
2
. B.
2
. C.
1
2
. D.
3
2
.
Lờigiải
Tacó
2 4 2 2 2 4 2
20 20 1 1 20 1f x m x mx x m m m x m x x
2 2
1 1 1 1 1 20 1m x x x m x x x
2 2
1 1 1 1 20x m x x m x
2 2
1
0
1 1 1 20 0 *
x
f x
m x x m x
Tacó
0f x
cómộtnghiệmđơnlà
1x
,dođónếu
*
khôngnhận
1x
lànghiệmthì
f x
đổidấuqua
1x
.Dođóđể
f x
đồngbiếntrên
thì
0,f x x
hay
*
nhận
1x
làmnghiệm(bậclẻ).
Suyra
2 2
1 1 1 1 1 1 20 0 4 2 20 0m m m m
.
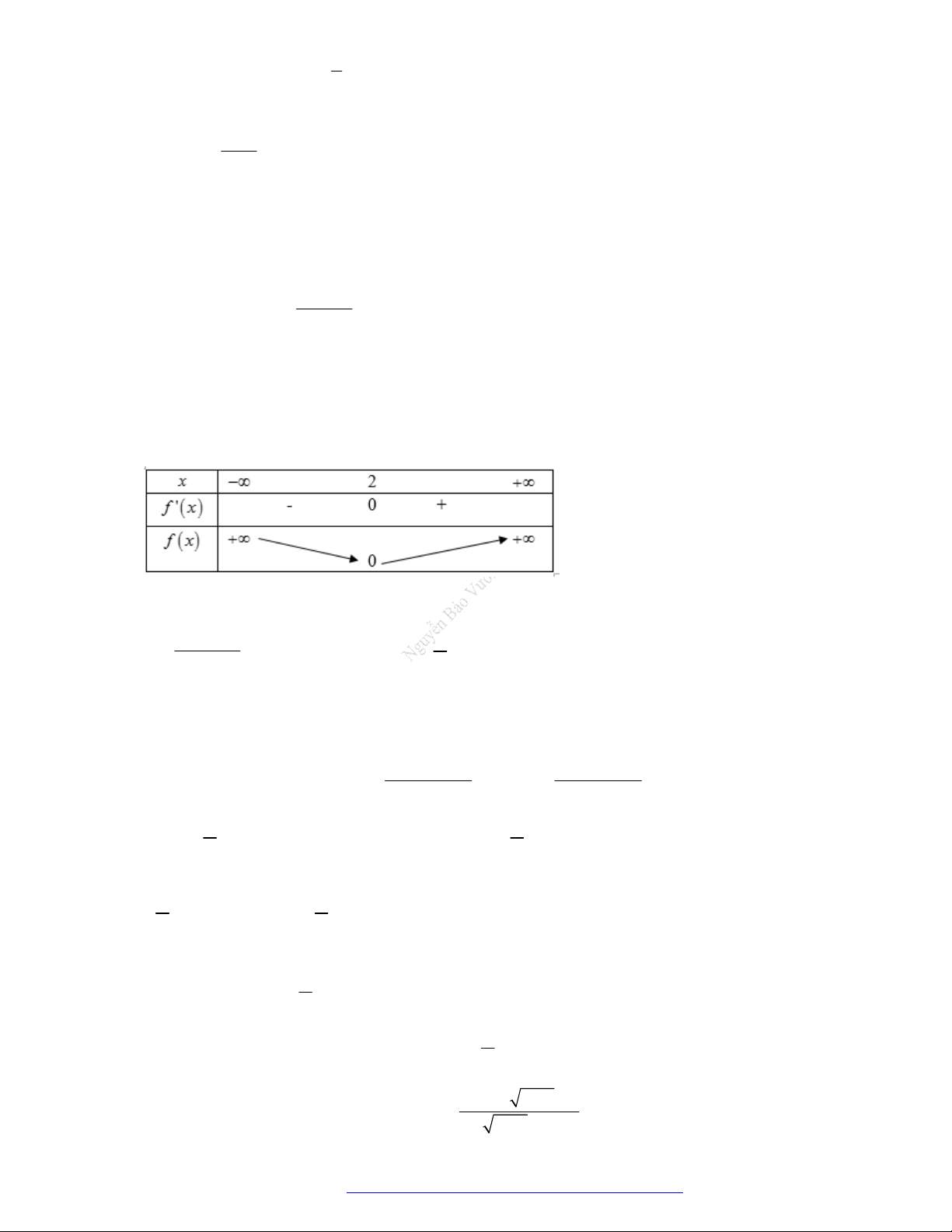
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 30 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Tổngcácgiátrịcủa
m
là
1
2
.
Câu 4. (THPT Lê Quý Đôn Đà Nẵng 2019) Tập hợp các giá trị thực của tham số m để hàm số
1
2
m
y x
x
đồngbiếntrênmỗikhoảngxácđịnhcủanólà
A.
0;1
. B.
;0
. C.
0; \ 1
. D.
;0
.
Lờigiải
•Tậpxácđịnh:
\ 2D
.
Hàmsốđãchođồngbiếntrênmỗikhoảngxácđịnhcủanókhivàchỉkhi:
' 0,y x D
2
1 0,
2
m
x D
x
2
2 ,m x x D
Xéthàmsố
2
2f x x
tacó:
' 2 4 ' 0 2f x x f x x
Bảngbiếnthiên:
Vậy,đểhàmsốđãchođồngbiếntrênmỗikhoảngxácđịnhcủanóthì
0m
.
Câu 5. (THPT Minh Khai Hà Tĩnh 2019) Tìm tất cả các giá trị thực của tham số để hàm số
cos 3
cos
x
y
x m
nghịchbiếntrênkhoảng
;
2
A.
0 3
1
m
m
. B.
0 3
1
m
m
. C.
3m
. D.
3m
.
Lờigiải
Điềukiện:cosx m .Tacó:
2 2
( 3) ( 3)
.( sin ) .sin
cos cos
m m
y x x
x m x m
Vì
; sin 0
2
x x
,
2
cos 0, ; : cos
2
x m x x m
.
Đểhàmsốnghịchbiếntrênkhoảng
;
2
0 ;
2
y x
3
3 0
3 0
0 3
1
cos ; 1;0
1
0
2
m
m
m
m
m
x m x m
m
m
.
Chúý:Tậpgiátrịcủahàmsố
cos , ;
2
y x x
là
1;0
.
Câu 6. (HoàngHoaThám2019)Chohàmsố
(4 ) 6 3
6
m x
y
x m
.Cóbaonhiêugiátrịnguyêncủam
trongkhoảng
10;10
saochohàmsốđồngbiếntrên
8;5
?

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 31
A.
14
. B.
13
. C.
12
. D.
15
.
Lờigiải
Đặt 6
t x
vì
8;5
x
14; 1
t
và 6
t x
đồngbiếntrên
8;5
.
Hàmsốtrởthành
(4 ) 3m t
y
t m
tậpxácđịnh
\
D m
2
2
4 3
'
( )
m m
y
t m
.
Đểhàmsốđồngbiếntrênkhoảng
14; 1
2
4 3 0
14
1
m m
m
m
14
1 1
3
m
m
m
.
9, 8, 7, 6, 5, 4, 1,0,4,5,6,7,8,9
m
có14giátrị.
Câu 7. (THPTLươngThếVinhHàNội2019)Cóbaonhiêugiátrịnguyênâmcủathamsố
m
đểhàm
số
4
1 3
4 2
y x mx
x
đồngbiếntrênkhoảng
0;
.
A.
2
. B.
1
. C.
3
. D.
0
.
Lờigiải
Tậpxácđịnh:
.
D
3
2
3
2
y x m
x
.
Tacó:hàmsốđãchođồngbiếntrênkhoảng
0;
khivàchỉkhi
0
y
với
0;x
3
2
3
0, 0;
2
x m x
x
3
2
3
, 0;
2
x m x
x
0;
Min
m f x
,với
3
2
3
1
2
f x x
x
.
Cách1:
TheobấtđẳngthứcCauchytacó
3 3
3
5
2 2 2 2 5
3 1 1 1 1 5
5
2 2 2 2 2 2 2 2
x x
f x x
x x x x
.
Dấubằngxảyrakhivàchỉkhi
1x
.Dođó
0;
5
Min 2
2
f x
.
Từ
1
và
2
tacó
5 5
2 2
m m
.Do
m
nguyênâmnên
1
m
hoặc
2
m
.
Vậycóhaigiátrịnguyênâmcủathamsố
m
thỏamãnđiềukiệnbàira.
Cách2:
Xéthàmsố
3
2
3
, 0;
2
f x x x
x
.
Tacó
2
3
3
3 , 0 1f x x f x x
x
.
Bảngbiếnthiên
Từbảngbiếnthiêntacó
5 5
2 2
m m
.Do
m
nguyênâmnên
1
m
hoặc
2
m
.
x
0
2
f x
–
0
f x
5
2
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 32 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Vậycóhaigiátrịnguyênâmcủathamsố
m
thỏamãnđiềukiệnbàira.
Câu 8. (ChuyênBắcGiang2019)Chohàmsố
ln 4
ln 2
x
y
x m
với
m
làthamsố.Gọi
S
làtậphợpcác
giátrịnguyêndươngcủa
m
đểhàmsốđồngbiếntrênkhoảng
1;e
.Tìmsốphầntửcủa
S
.
A.
3
B.
2
C.
1
D.
4
Lờigiải
ChọnC
ln 4
ln 2
x
y f x
x m
Đặt
lnt x
,điềukiện
0;1
t
4
2
t
g t
t m
;
2
2 4
2
m
g t
t m
Đểhàmsố
f x
đồngbiếntrên
1;e
thìhàmsố
g t
đồngbiếntrên
0;1
0, t 0;1
g t
2
2 4
0, 0;1
2
m
t
t m
1
2 4 0
2
2
2 0;1
0
m
m
m
m
S
làtậphợpcácgiátrịnguyêndương
1
S
.
Vậysốphầntửcủatập
S
là
1
.
Câu 9. (ChuyênVĩnhPhúc2019)Tìm
m
đểhàmsố
cos 2
cos
x
y
x m
đồngbiếntrênkhoảng
0;
2
A.
2
2
m
m
B.
2
m
C.
0
1 2
m
m
D.
1 1
m
Lờigiải
ChọnC
Tacó
2
2
' . sin ,sin 0 0;
2
cos
m
y x x x
x m
.
Dođó:Hàmsốnghịchbiếntrênkhoảng
0;
2
khivàchỉkhi
2 0
2
cos 0 0; 0;1
2
m
m
x m x m
0
1 2
m
m
.
Câu 10. (ChuyênLươngThếVinhĐồngNai2019)Cóbaonhiêugiátrịnguyênâmcủathamsố
m
để
hàmsố
4 2
3 9
2 15 3 1
4 2
y x x m x m
đồngbiếntrênkhoảng
0;
?
A.
2.
B.
3.
C.
5.
D.
4.
Lờigiải
Yêucầubàitoán
3
3 9 2 15 0 0;y x x m x
vàdấubằngxảyratạihữuhạnđiểm
thuộc
0;
3
3 9 15 2 0;x x m x
.
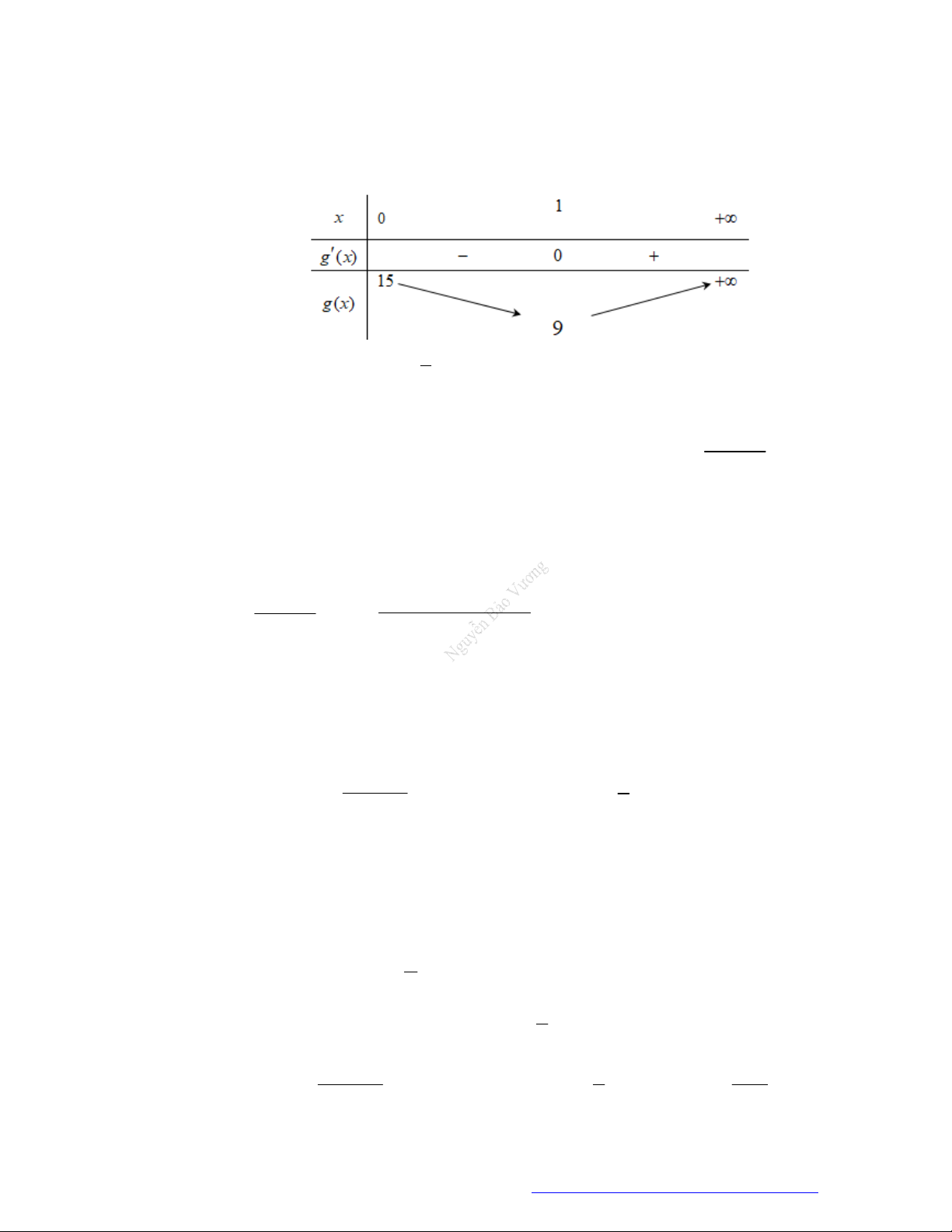
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 33
Xéthàmsố:
3
( ) 3 9 15g x x x
trên
0;
.
Tacó:
2
( ) 9 9g x x
0g x
1
1 ( )
x
x l
.
Bảngbiếnthiên:
TừBBTtacó:
9
2 9
2
m m
Vậy
{ 4; 3; 2; 1}m
.
Câu 11. Cótấtcảbaonhiêugiátrịnguyêncủathamsố
m
đểhàmsố
2
3
3
1
m m
y x
x
đồngbiếntrên
từngkhoảngxácđịnhcủanó?
A.
4
. B.
2
. C.
1
. D.
3
.
Lờigiải
Tậpxácđịnh
\ 1D
.
2
3
3
1
m m
y x
x
2
2
2
3 1 3
1
x m m
y
x
.
Hàmsốđồngbiếntrêntừngkhoảngxácđịnhkhi
0y
,
1x
2
3 0m m
3 0m .
Do
m
3; 2; 1;0m
.
Vậycó
4
giátrịnguyêncủa
m
thỏayêucầubàitoán.
Câu 12. Tìmmđểhàmsố
cos 2
cos
x
y
x m
nghịchbiếntrênkhoảng
0;
2
A.
2m
. B.
0
1 2
m
m
. C.
2m
. D.
2m
.
Lờigiải
Đặt cost x .
Tacó:
sin 0, 0;
2
t x x
.
hàmsố cost x nghịchbiếntrênkhoảng
0;
2
.
Dođóhàmsố
cos 2
cos
x
y
x m
nghịchbiếntrênkhoảng
0;
2
hàmsố
2t
y
t m
đồngbiếntrên
khoảng
0;1
.
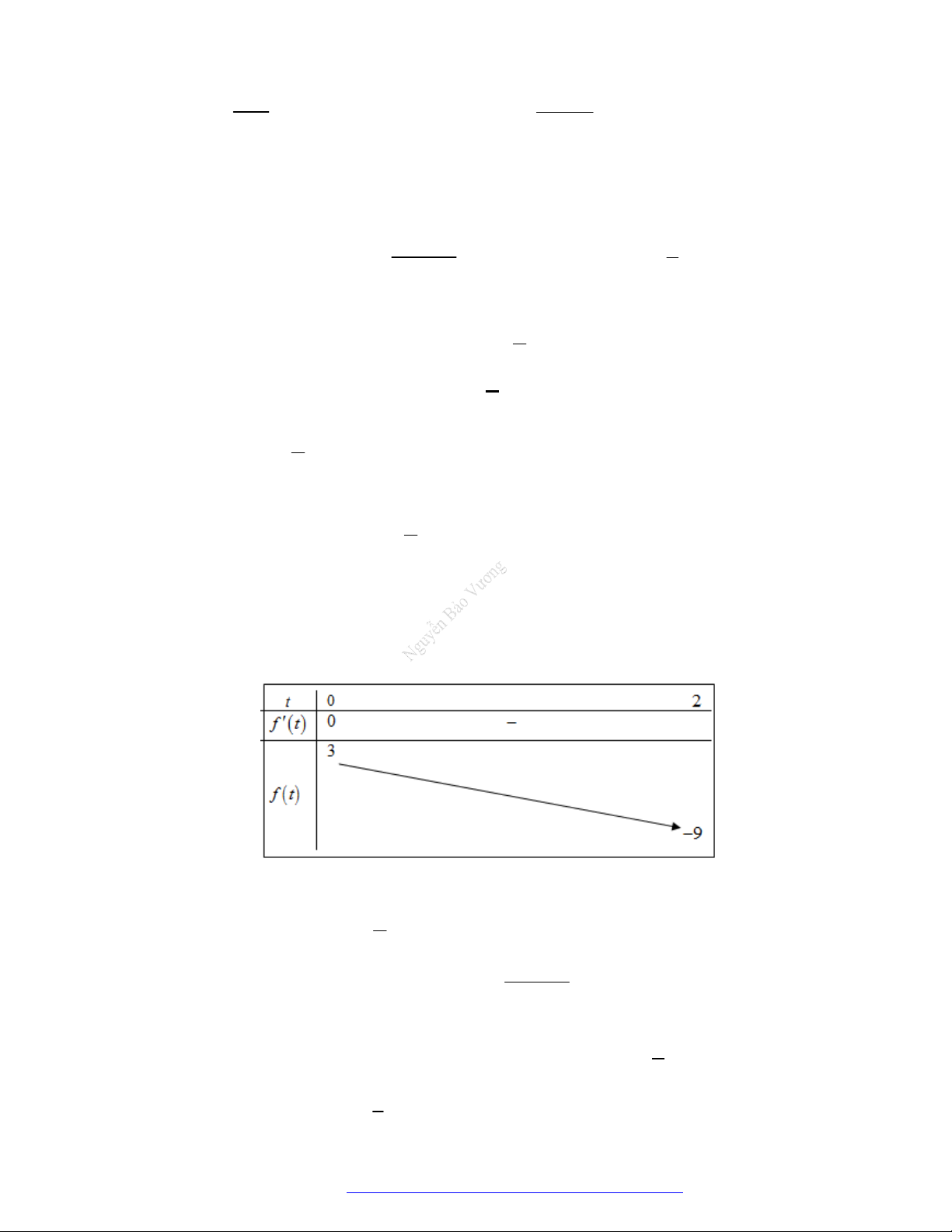
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 34 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Tậpxácđịnh
\D m
.
Hàmsố
2t
y
t m
đồngbiếntrênkhoảng
0;1
2
2
0, 0;1
m
y t
t m
.
2 0 2
1 2
1 1
0
0 0
m m
m
m m
m
m m
.
Vậyvới
0
1 2
m
m
thìhàmsố
cos 2
cos
x
y
x m
nghịchbiếntrênkhoảng
0;
2
.
Câu 13. (Toán Học Tuổi Trẻ Số 5 2018) Tìm tất cả các giá trị của
m
để hàm số
cot cot
8 3 .2 3 2
x x
y m m
(1)đồngbiếntrên
;
4
.
A.
9 3m
. B.
3m
. C.
9m
. D.
9m
.
Lờigiải
Đặt
cot
2
x
t
vì
;
4
x
nên
0 2t
.Khiđótacóhàmsố:
3
3 3 2y t m t m
(2).
2
3 3y t m
.
Để hàm số (1) đồng biến trên
;
4
thì hàm số (2) phải nghịch biến trên
0;2
hay
2
3 3 0, 0;2t m t
2
3 3 , 0;2m t t
.
Xéthàmsố:
2
3 3 , 0;2f t t t
6f t t
.
0f t
0t
.
Tacóbảngbiếnthiên:
Dựavàobảngbiếnthiêntathấy
9 3, 0;2f t t
.
Vậyhàmsố(1)đồngbiếntrên
;
4
khi
9m
.
Câu 14. (ToánHọcTuổiTrẻSố6 2018)Chohàmsố
ln 4
ln 2
x
y
x m
với
m
làthamsố.Gọi
S
làtậphợp
cácgiátrịnguyêndươngcủa
m
đểhàmsốđồngbiếntrênkhoảng
1;e
.Tìmsốphầntửcủa
S
.
A.
2
. B.
4
. C.
3
. D.
1
.
Lờigiải
Điềukiện
ln 2 0x m
1
ln
2
m x
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 35
Do
1;e
x
nên
ln 0;1
x
1
;0 ;
2
m
.
Tacó
2
1
4 2
ln 2
m
x
y
x m
.
Đểhàmsốđồngbiếntrênkhoảng
0;1
thì
0
y
vớimọi
0;1
x
2
1
4 2
0
ln 2
m
x
x m
4 2 0
m
2
m
.
Do
m
làsốnguyêndươngnên
1
m
.
Câu 15. (THPTChuyênLêHồngPhong2018)Tìmtấtcảcácgiátrịthựccủathamsố
m
đểhàmsố
ln 2
ln 1
m x
y
x m
nghịchbiếntrên
2
;e
.
A.
2
m
hoặc
1
m
. B.
2
m
hoặc
1
m
.
C.
2.
m
D.
2
m
hoặc
1
m
.
Lờigiải
Tậpxácđịnh
1
0; \
m
D e
.
Cách1:
2
2
2
ln 1
y
mm
x x m
Vậyyêucầubàitoántươngđương
1 2
2
2
1
0
2
2
;
1 2
m
m
m
e
m
m
m
e
m
Cách2:Đặt
lnt x
,tabiếtrằnghàmsố
lnf x x
đồngbiếntrên
2
;e
.
Xéthàmsố
2
1
mt
g t
t m
với
2;t
,tacó
2
2
2
1
m m
g t
t m
.
Vậyhàmsốbanđầunghịchbiếntrên
2
;e
hàmsố
g
nghịchbiếntrên
2;
0
1 2;
g t
m
2
1 1
2 0
2 2
1
1 2
2
1
m m
m m
m m
m
m m
2
m
Câu 16. (Chuyên Lương Thế Vinh - 2018) Có bao nhiêu số nguyên âm
m
để hàm số
3
1
cos 4cot 1 cos
3
y x x m x
đồngbiếntrênkhoảng
0;
?
A.
5
. B.
2
. C.vôsố. D.
3
.
Lờigiải
-Tacó:
2
2
4
cos .sin 1 .sin
sin
y x x m x
x
3
2
4
sin .sin
sin
x m x
x
.
-Hàmsốđồngbiếntrên
0;
khivàchỉkhi
0
y
,
0;
x
3
2
4
sin .sin 0
sin
x m x
x
,
0;
x
2
3
4
sin
sin
x m
x
,
0;
x
1
.
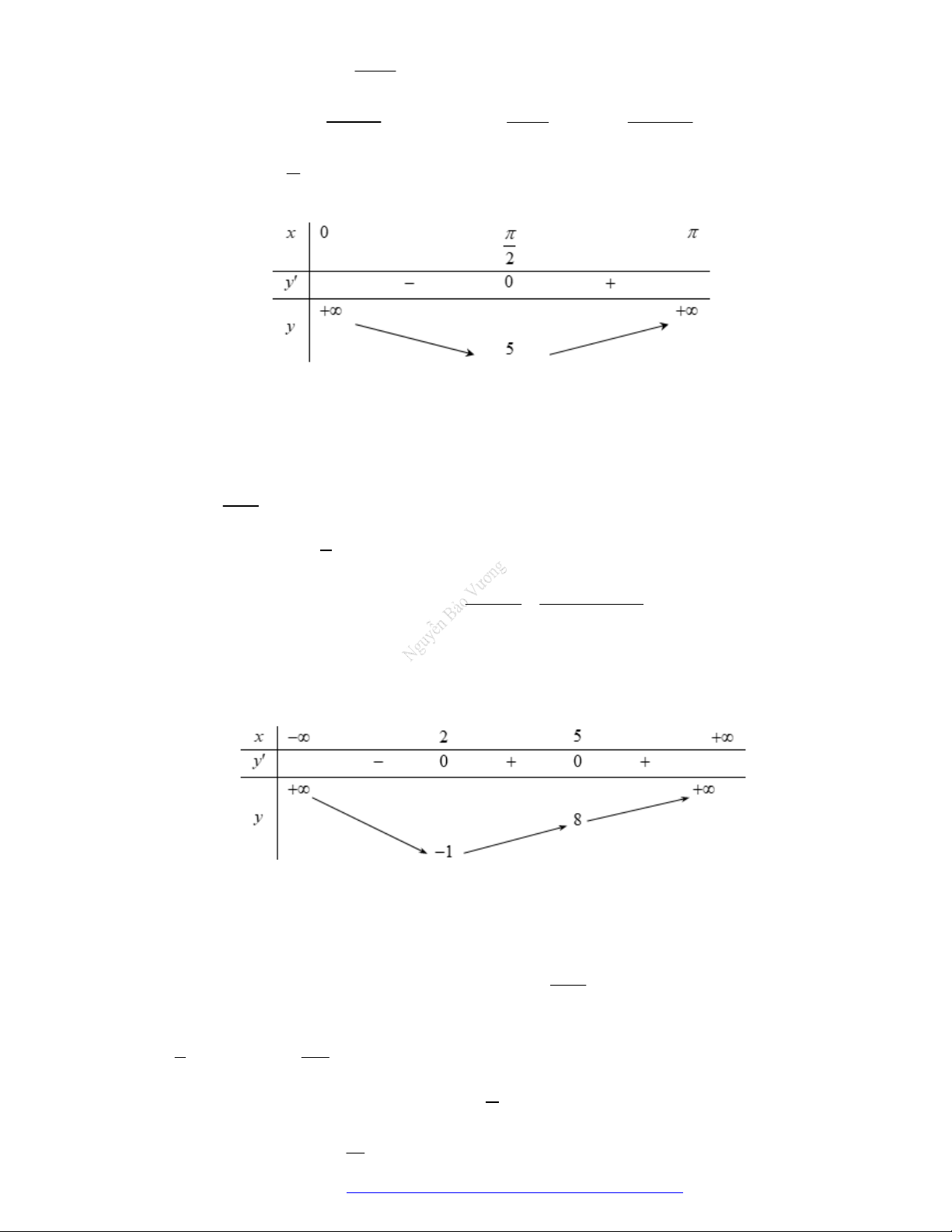
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 36 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
-Xéthàmsố:
2
3
4
sin
sin
g x x
x
,trên
0;
.
Có
4
12cos
2sin .cos
sin
x
g x x x
x
4
6
2cos . sin
sin
x x
x
5
4
sin 6
2cos .
sin
x
x
x
0
2
g x x
0;
.
Bảngbiếnthiên:
-Dođó:
0;
1 min
x
m g x
5m 5m
.
Lạido
m
nguyênâmnên
5; 4; 3; 2; 1m
.Vậycó5sốnguyênâm.
Câu 17. (Chuyên Ngữ - Hà Nội - 2018) Có bao nhiêu giá trị nguyên âm của
m
để hàm số
1
5
2
m
y x
x
đồngbiếntrên
5;
?
A.
10
. B.
8
. C.
9
. D.
11
.
Lờigiải
Tậpxácđịnh:
\ 2D
.Đạohàm:
2
2 2
1 4 3
1
2 2
m x x m
y
x x
.
Xéthàmsố
2
4 3f x x x
trên
5;
.
Đạohàm:
2 4f x x
.Xét
0 2 1f x x y
.Tacó:
5 8f
.
Bảngbiếnthiên:
Do
2
2 0x
với mọi
5;x
nên
0y
,
5;x
khi và chỉ khi
f x m
,
5;x
.Dựavàobảngbiếnthiêntacó:
8 8m m
.
Mà
m
nguyênâmnêntacó:
8; 7; 6; 5; 4; 3; 2; 1m
.
Vậycó
8
giátrịnguyênâmcủa
m
đểhàmsố
1
5
2
m
y x
x
đồngbiếntrên
5;
.
Câu 18. (Chuyên Vĩnh Phúc - 2018) Có bao nhiêu giá trị nguyên dương của tham số
m
để hàm số
4 2
4
3 1
1
4 4
y x m x
x
đồngbiếntrênkhoảng
0; .
A.
1.
B.
2.
C.
3.
D.
4.
Lờigiải
Tacó
3
5
1
3 2 1y x m x
x
.
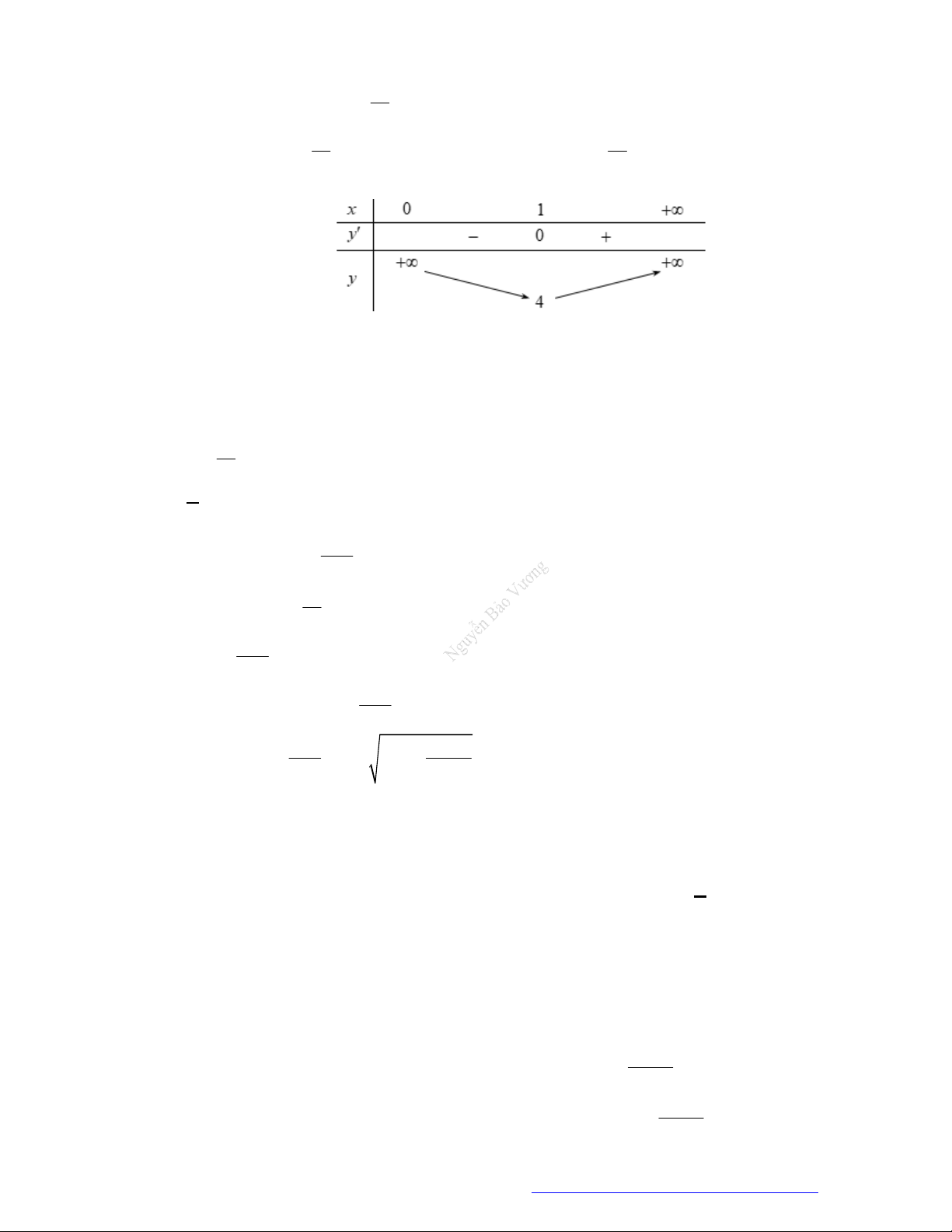
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 37
Hàmsốđồngbiếntrongkhoảng
0;
khivàchỉkhi
0y
với
0;x
.
2
6
1
0 2 1 3y m x
x
.
Xét
2
6
1
3g x x
x
với
0;x
.Tacó
7
6
6g x x
x
;
0 1g x x
Bảngbiếnthiên:
2 1 2 1 4 3m g x m m
.
Vìmnguyêndươngnên
1, 2,3m
.
Vậycó
3
giátrị
m
nguyêndươngthỏamãnbàitoán.
Câu 19. (Kim Liên - Hà Nội- 2018)Có bao nhiêugiá trị nguyên dương của tham số
m
đểhàm số
2
ln 1
2
x
y mx x đồngbiếntrênkhoảng
1;
?
A.
3
. B.
4
. C.
2
. D.
1
.
Lờigiải
Tacó
1
1
y x m
x
.
Đểhàmsố
2
ln 1
2
x
y mx x đồngbiếntrênkhoảng
1;
thì
0y
với
1;x
1
1
x m
x
với
1;x
1;
minm f x
.
Xéthàmsố
1
1
f x x
x
trênkhoảng
1;
tacó
1 1
1 1 2 1 1 3
1 1
f x x x
x x
1;
min 3f x
.Do
m
nên
1;2;3m
.
Câu 20. (Chuyên Vinh - 2018) Có bao nhiêu giá trị nguyên
10;10m
để hàm số
2 4 2
2 4 1 1y m x m x
đồngbiếntrênkhoảng
1;
?
A.
15
. B.
6
. C.
7
. D.
16
.
Lờigiải
+Với
0m
,hàmsốtrởthành
2
2 1y x đồngbiếntrên
0;
nênhàmsốcũngđồngbiến
trênkhoảng
1;
,dođó
0m
thỏamãn.
+Với
0m
,hàmsốđãcholàmhàmsốtrùngphươngvớihệsố
2
0a m
.
2 3
4 4 4 1y m x m x
2 2
4 4 1x m x m
,
2
2
0
0
4 1
x
y
m
x
m
.
Đểhàmsốđồngbiếntrênkhoảng
1;
thìphươngtrình
2
2
4 1m
x
m
vônghiệmhoặccóhai
nghiệmphânbiệt
1
x ,
2
x saocho
1 2
1 1x x

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 38 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
4 1 0
4 1 0
4 1
1
m
m
m
m
2
1
4
1
4
4 1 0
m
m
m m
1
4
1
2 3
4
2 3
m
m
m
.
Vậyđiềukiệnđểhàmsốđồngbiếntrên
1;
là
;2 3 2 3;m .
Vì
m
nguyên,
10;10m
nên
9; 8;...;0;4;5;...;9m
,có
16
giátrị.
Câu 21. (ChuyênTháiBình-2018)Cóbaonhiêugiátrịnguyêncủathamsố
2018;2018m
đểhàm
số
2
1 1y x mx đồngbiếntrên
;
.
A.
2017
. B.
2019
. C.
2020
. D.
2018
.
Lờigiải
TXĐ
:
D
.
2
1
x
y m
x
.
Hàmsốđồngbiếntrên
0y
,
x
2
1
x
m
x
,
x
1
.
Xét
2
1
x
f x
x
trên
.
lim 1
x
f x
;
lim 1
x
f x
.
2 2
1
1 1
f x
x x
0
,
x
nênhàmsốđồngbiếntrên
.
Tacó:
2
1
x
m
x
,
x 1m
.
Mặtkhác
2018;2018m
2018; 1m
.
Vậycó
2018
sốnguyên
m
thoảđiềukiện.
Câu 22. (LêQuýĐôn-QuảngTrị-2018)Tìmtấtcảcácgiátrịcủa
m
đểhàmsố
1
2
mx
x m
y
nghịchbiến
trên
1
;
2
.
A.
1;1m
. B.
1
;1
2
m
. C.
1
;1
2
m
. D.
1
;1
2
m
.
Lờigiải
Hàmsố
1
2
mx
x m
y
nghịchbiếntrên
1
;
2
khivàchỉkhihàmsố
1mx
y
x m
nghịchbiếntrên
1
;
2
.
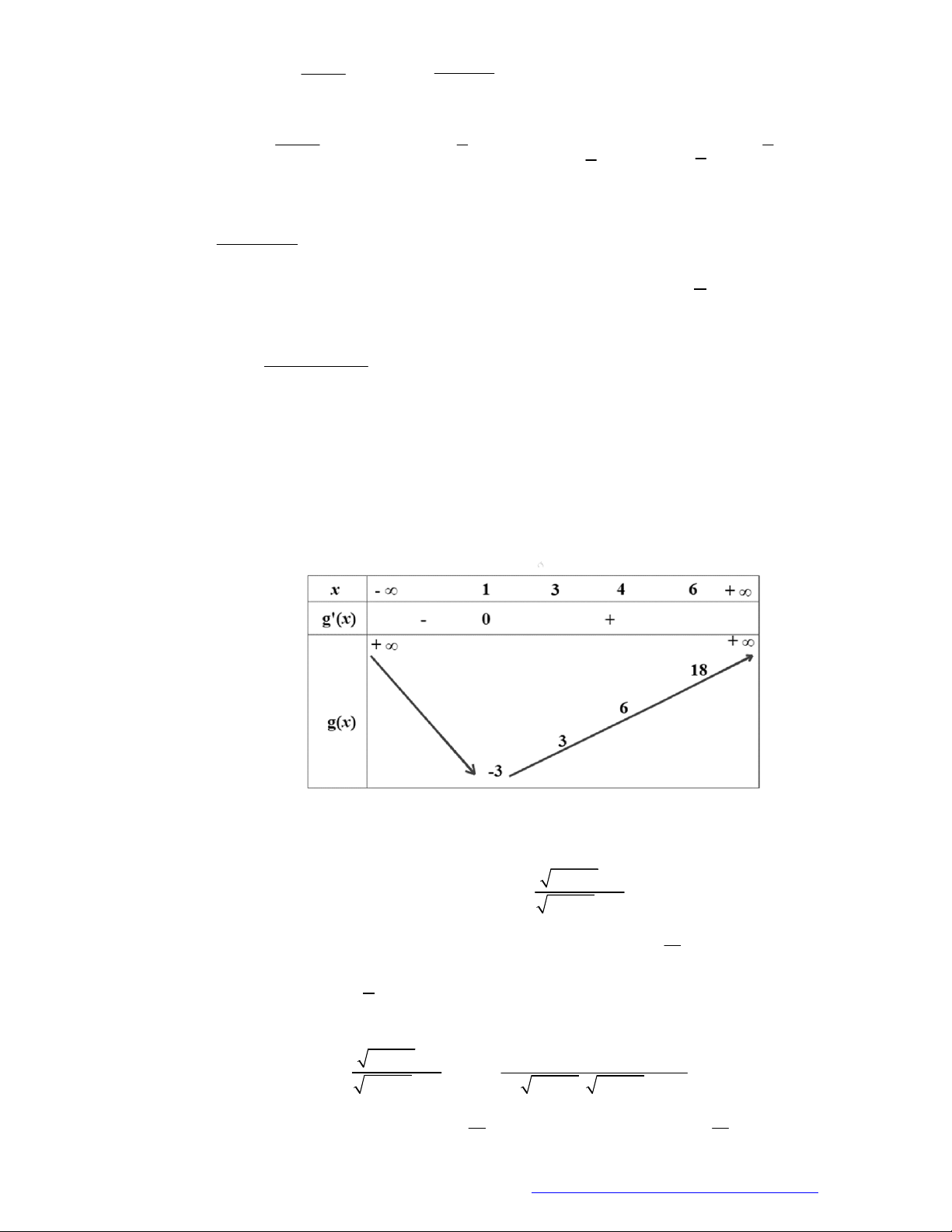
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 39
Xéthàmsố
1mx
y
x m
,tacó:
2
2
1m
y
x m
.
Hàmsố
1mx
y
x m
nghịchbiếntrên
1
;
2
2
1 0
1
2
m
m
1 1
1
2
m
m
1
1
2
m
.
Câu 23. (Chuyên Hưng Yên - 2020) Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
2
2
1
x x m
y
x
nghịchbiếntrênkhoảng
(1;3)
vàđồngbiếntrênkhoảng
(4;6)
.
A.
6
. B.
7
. C.
5
. D.
4
.
Lờigiải
ChọnD
Tacó
2
2
2 2
( 1)
x x m
y
x
.
Hàmsốnghịchbiếntrênkhoảng
(1;3)
vàđồngbiếntrênkhoảng
(4;6)
khivàchỉkhi
0, (1;3)
0, (4;6)
y x
y x
2 2
2 2
2 2 0, (1;3) 2 2, (1;3)
2 2 0, (4;6) 2 2, (4;6)
x x m x m x x x
x x m x m x x x
(*)
Xéthàmsố
2
( ) 2 2, ( ) 2 2g x x x g x x
tacóbảngbiếnthiêncủa
( )g x
nhưsau
Từbảngbiếnthiêncủa
( )g x
tacó
(*) 3 6m
,vàvì
m
làsốnguyênnênchọn
3;4;5;6m
.Vậycó4giátrịnguyêncủa
m
thỏamãnbàitoán.
Câu 24. (ChuyênHưngYên-2020)Chohàmsố
1 ln 1
1 ln
x
y
x m
.Có baonhiêugiátrị nguyêncủa
thamsố
m
thuộc
5;5
đểhàmsốđãchođồngbiếntrênkhoảng
3
1
;1
e
.
A.
7
. B.
6
. C.
5
. D.
4
.
Lờigiải
ChọnB
Tacóđạohàmcủa
1 ln 1
1 ln
x
y
x m
là
2
1
2 1 ln ( 1 ln )
m
y
x x x m
.
Hàmsốđãchođồngbiếntrênkhoảng
3
1
;1
e
khivàchỉkhi
3
1
0, ;1y x
e
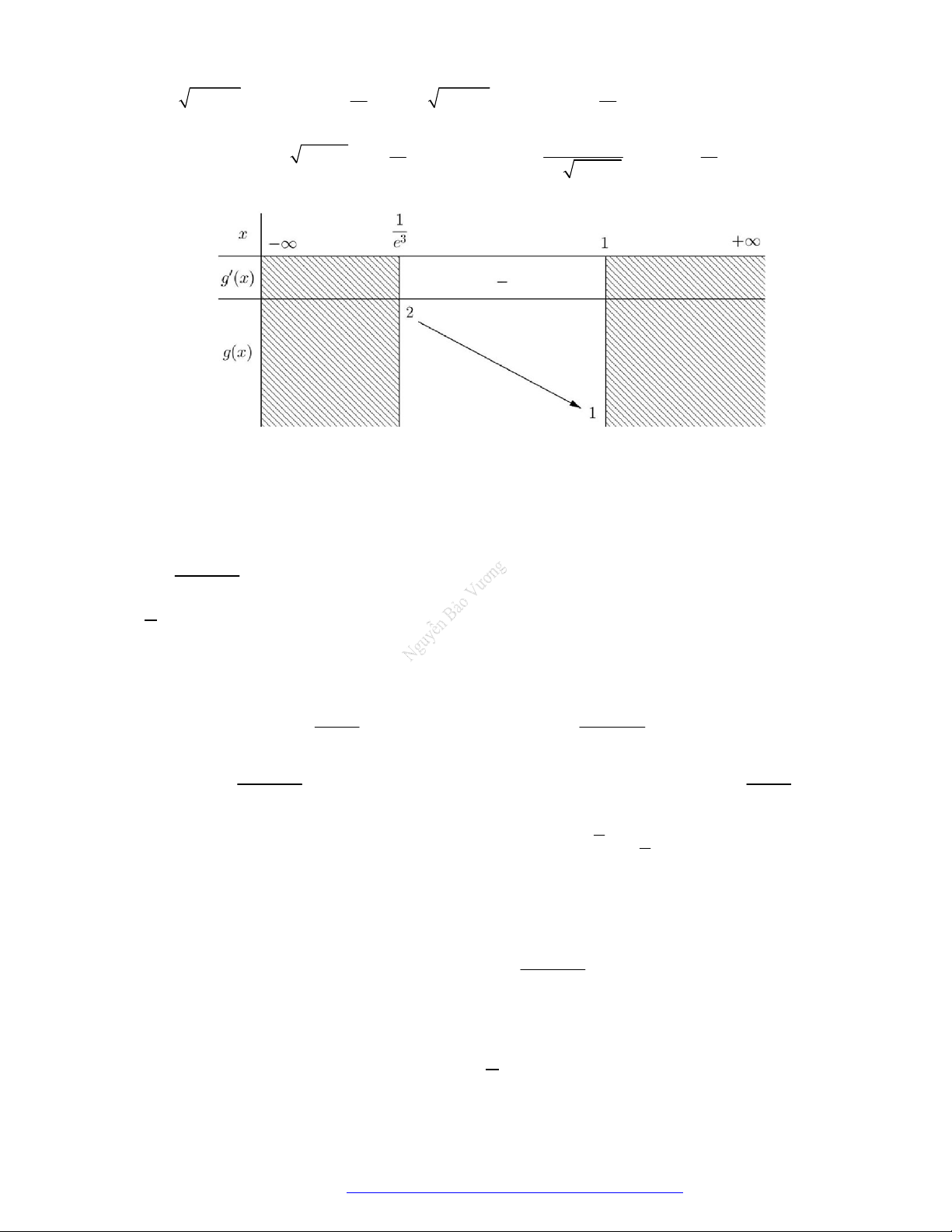
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 40 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
3 3
1 0 1
1 1
1 ln 0, ;1 1 ln 0, ;1
m m
x m x x m x
e e
(*)
Xét hàm số
3
1
( ) 1 ln , ;1g x x x
e
, ta có
3
1 1
( ) 0, ;1
2 1 ln
g x x
e
x x
do đó ta có
bảngbiếnthiêncủahàmsố
( )g x
nhưsau
Quabảngbiếnthiêntacó
1
(*)
( 2; 1)
m
m
,kếthợpvới
5;5m
tacó6giátrịnguyêncủa
m
là
5; 4; 3; 2; 1;0m
.
Câu 25. (ChuyênHùngVương-PhúThọ-2020)Cóbaonhiêugiátrịnguyêndươngcủa
m
đểhàmsố
ln 6
ln 2
x
y
x m
đồngbiếntrênkhoảng
1;e
?
A.
2
. B.
1
. C.
4
. D.
3
.
Lờigiải
ChọnA
Đặt
lnt x
thì
lnt x
đồngbiếntrênkhoảng
1;e
và
0;1t
Tađượchàmsố
6
2
t
f t
t m
.Điềukiện
2t m
và
2
6 2
2
m
f t
t m
.
Hàmsố
ln 6
ln 2
x
y
x m
đồngbiếntrênkhoảng
1;e
khivàchỉ khihàmsố
6
2
t
f t
t m
đồng
biếntrênkhoảng
0;1
1
2 1
1
2 0;1
3
2
2 0
2
0
0
0
6 2 0
3
m
m
m
m
m
m
f t
m
m
m
.
Vì
m
nguyêndươngnên
1;2m
.
Vậycó2giátrịnguyêndươngcủa
m
đểhàmsố
ln 6
ln 2
x
y
x m
đồngbiếntrênkhoảng
1;e
.
Câu 26. (Chuyên Lê Hồng Phong - Nam Định - 2020) Có bao nhiêu số nguyên m để hàm số
2020 2 sinf x m x co s x x x
nghịchbiếntrên
?
A.Vôsố. B.2. C.1. D.0.
Lờigiải
ChọnC
Tacó:
Hàmsố
2020 2 sinf x m x cosx x x
nghịchbiếntrên
khivàchỉkhi
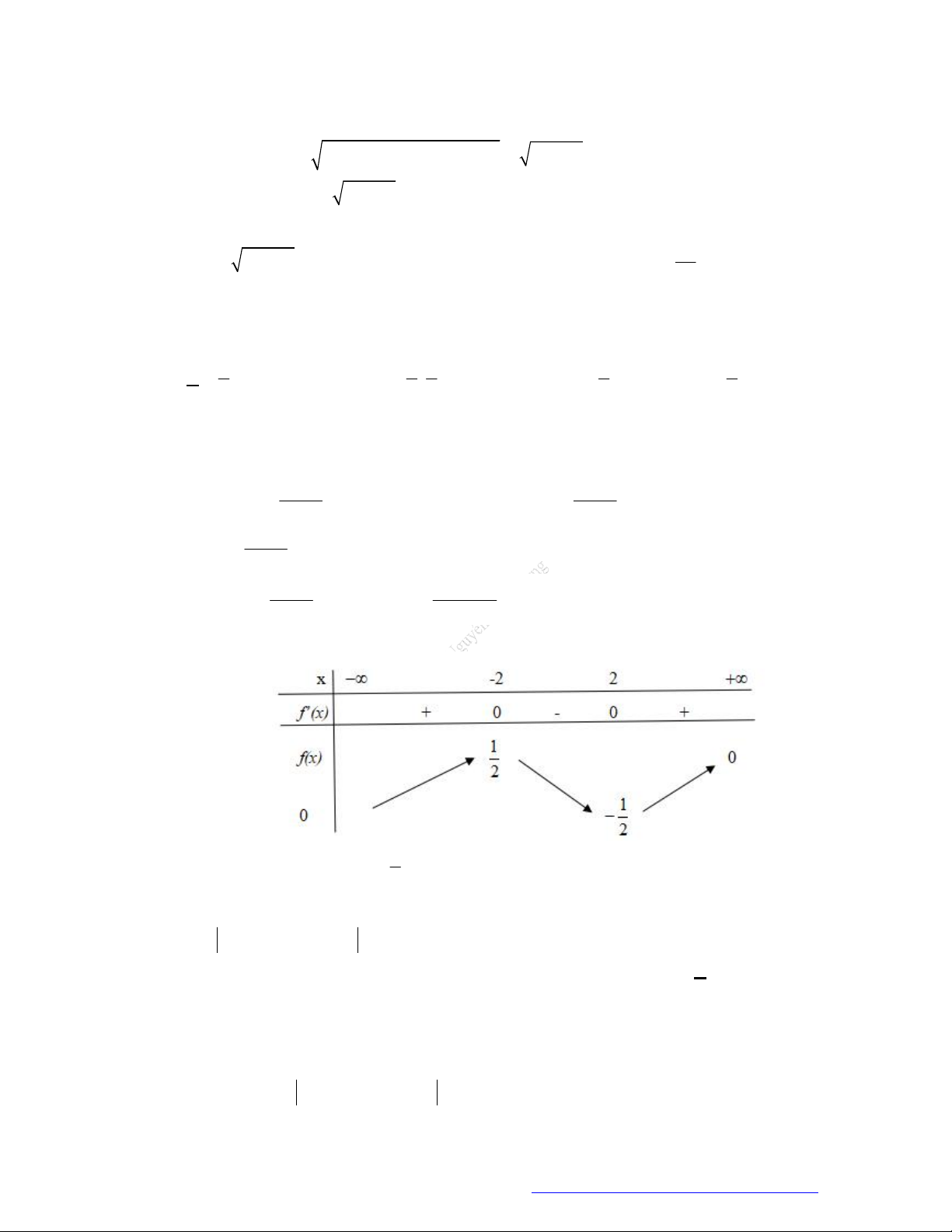
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 41
0 2sin 1 1 0f x x m x cosx x
2 sin 1 1 ;m x cosx m x
Talạicó:
2 2 2 2
2 sin 4 1 sin 4 1m x co s x m x co s x m
2
2 sin 4 1m x co s x m
.Dấubằngxảyrakhi
2 sinmcosx x
Dođó
2
2 2 2
1 0 1
2
1 4 1 1 0
3
4 1 1 2 3 2 0
m m
m m m
m m m m m
Câu 27. (Chuyên Quang Trung - 2020) Tập hợp tất cả các giá trị thực của tham số m để hàm số
2
ln( 4) 12y x mx đồngbiếntrên
là
A.
1
;
2
. B.
1 1
;
2 2
C.
1
( ;
2
. D.
1
;
2
Lờigiải
Chọn A
+TXĐ:
+Tacó
,
2
2
4
x
y m
x
.Hàmsốđồngbiếntrên
2
2
0,
4
x
m x
x
2
2
,
4
x
m x
x
Xét
2
2
( )
4
x
f x
x
.Tacó:
2
,
2
2( 4)
( ) 0 2
( 4)
x
f x x
x
Bảngbiếnthiên
Vậygiátrịmcầntìmlà
1
2
m
Câu 28. (Chuyên Thái Bình - 2020) Có tất cả bao nhiêu giá trị nguyên của
m
để hàm số
3 2
12 2y x mx x m
luônđồngbiếntrênkhoảng
1;
?
A.
18
. B.
19
. C.
21
. D.
20
.
Lờigiải
ChọnD
Xét
3 2
12 2f x x mx x m
.Tacó
2
3 2 12f x x mx
và
1 13f m
.
Đểhàmsố
3 2
12 2y x mx x m
đồngbiếntrênkhoảng
1;
thìcóhaitrườnghợpsau
Trườnghợp1:Hàmsố
f x
nghịchbiếntrên
1;
và
1 0f
.
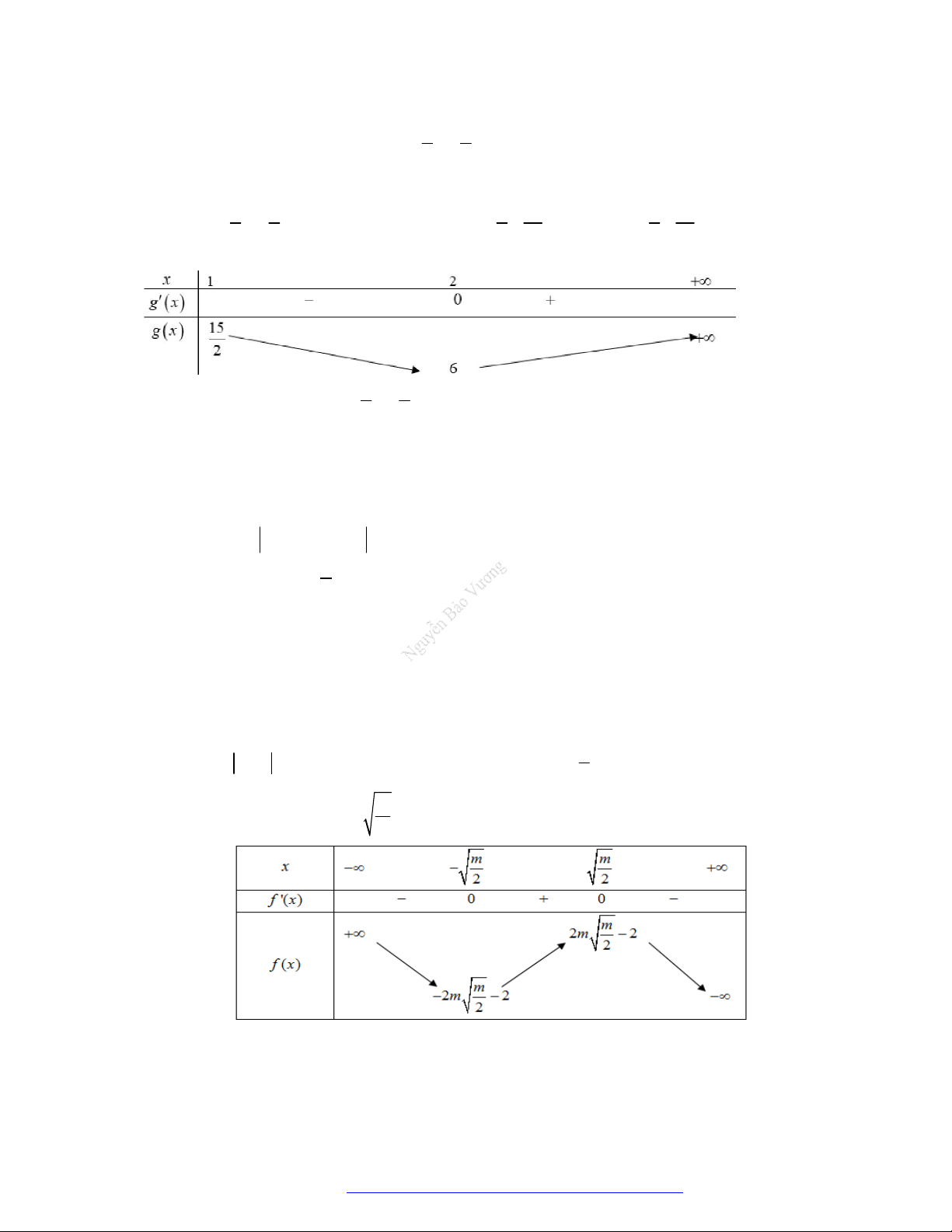
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 42 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Điềunàykhôngxảyravì
3 2
lim 12 2
x
x mx x m
.
Trườnghợp2:Hàmsố
f x
đồngbiếntrên
1;
và
1 0f
.
2
3 6
, 1
3 2 12 0, 1
2
13 0
13 *
m x x
x mx x
x
m
m
.
Xét
3 6
2
g x x
x
trênkhoảng
1;
:
2
3 6
2
g x
x
;
2
3 6
0 0 2
2
g x x
x
.
Bảngbiếnthiên:
Từbảngbiếnthiênsuyra
3 6
, 1
2
m x x
x
6m
.
Kếthợp
*
suyra
13 6m
.Vì
m
nguyênnên
13; 12; 11;...;5;6m
.Vậycó
20
giátrị
nguyêncủa
m
.
Câu 29. (ĐHQGHàNội-2020)Cóbaonhiêugiátrịnguyêncủathamsố
m
thuộckhoảng
8;8
sao
chohàmsố
3
2 3 2y x mx
đồngbiếntrênkhoảng
1;
?
A.
10.
B.
9.
C.
8.
D.
11.
Lờigiải
ChọnB
3
( ) 2 3 2f x x mx
2
'( ) 6 3f x x m
Nếu
0 : '( ) 0,m f x x
hàmsố
( )f x
nghịchbiếntrênℝ.
Hàmsố
( )y f x
đồngbiếntrên
4
1; 1 0 0.
3
f m m
Nếu
0: '( ) 0
2
m
m f x x

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 43
Hàmsố
( )y f x
đồngbiếntrên
3
1
2
1
0
2
2
2( )
1
2( )
2
4
1; 0 .
3
2 2 0
0
2
2
2
4
1
2
3
(1) 0
m
m
m
f
m L
m
m L
m
m
m
m
f
m
m
m
f
m
ℤ,
8;8 7; 6;...; 1;0;1 .m m
Câu 30. (SởNinh Bình) Gọi
T
làtậphợptấtcả cácgiátrịnguyêndươngcủathamsố
m
đểhàm số
4 2
2 1y x mx
đồngbiếntrênkhoảng
3;
.Tổnggiátrịcácphầntửcủa
T
bằng
A.
9
. B.
45
. C.
55
. D.
36
.
Lờigiải
ChọnB
+Tậpxácđịnh:
D
.
+Tacó
3 2
4 4 4y x mx x x m
Theođề
0m
nên
0y
có3nghiệmphânbiệt
, 0,x m x x m
.
Đểhàmsốđồngbiếntrênkhoảng
3;
thì
0, 3; 3 9y x m m
Vì
m
nguyêndươngnên
1, 2,3,4,5, 6, 7,8,9m
(làcấpsốcộng)
VậyTổnggiátrịcácphầntửcủa
T
bằng
9
1 9 45
2
.
Câu 31. (ĐôLương4-NghệAn-2020)Tìmtậphợptấtcảcácgiátrịcủa
m
đểhàmsố
2
sin
cos
m x
y
x
nghịchbiếntrên
0;
6
.
A.
1m
. B.
2m
. C.
5
4
m
. D.
0m
.
Lờigiải
ChọnC
Tacó
2 2 2
3 3
cos 2 sin 2sin 1 2 sin sin
cos cos
x m x x m x x
y
x x
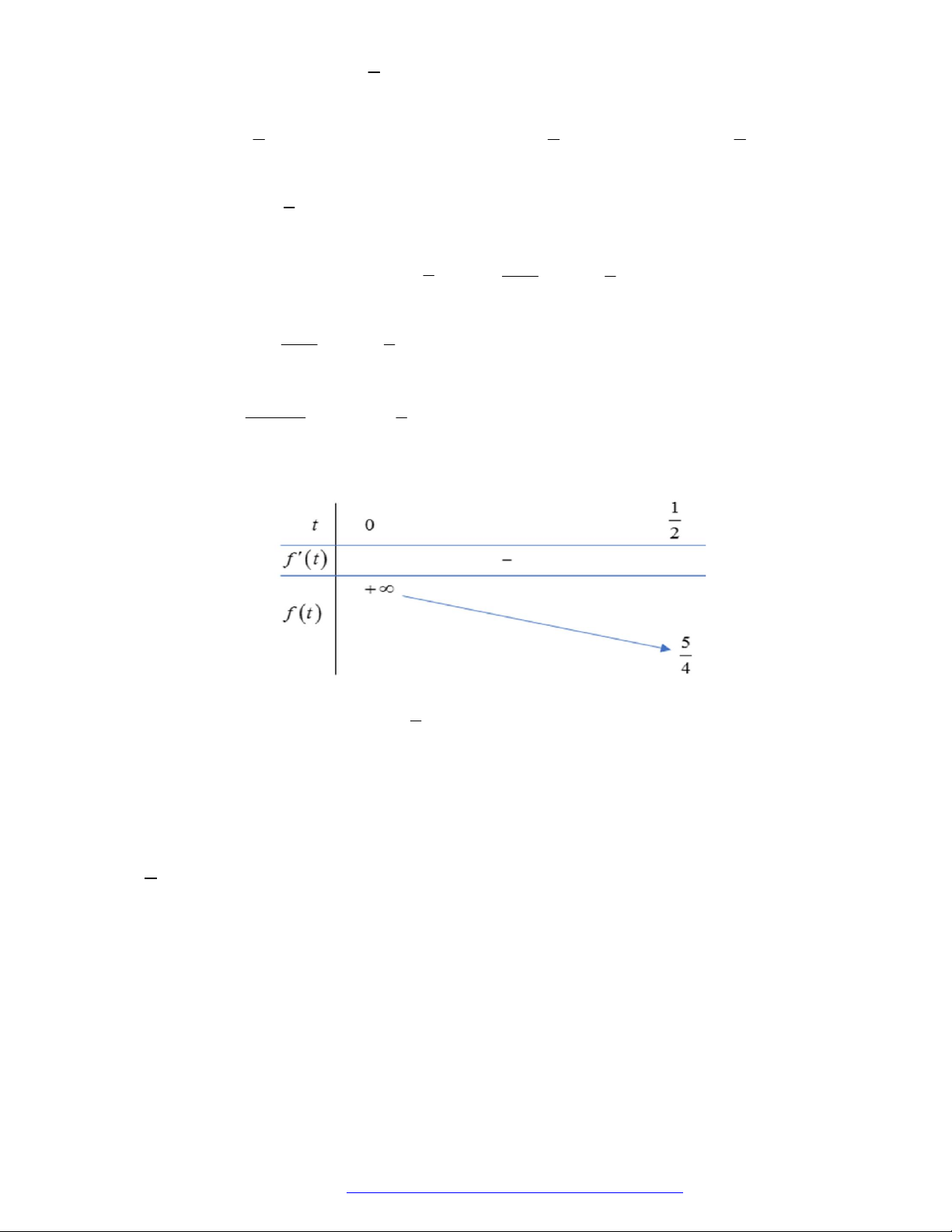
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 44 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Đểhàmsốnghịchbiếntrên
0;
6
thì
0, 0;
6
y x
2
sin 2 sin 1 0x m x
,
0;
6
x
,vì
3
cos 0, 0;
6
x x
1
Đặt
1
sin , 0;
2
x t t
.
Khiđó
1
2
1
2 1 0, 0;
2
t mt t
2
1 1
, 0;
2 2
t
m t
t
2
Taxéthàm
2
1 1
, 0;
2 2
t
f t t
t
Tacó
2
2
2 1
1
0, 0;
4 2
t
f t t
t
.
Bảngbiếnthiên
Từbảngbiếnthiênsuyra
5
2
4
m
.
Câu 32. (Yên Lạc 2 - Vĩnh Phúc - 2020) Cho hàm số
y f x
có đạo hàm
2
3 6 4,f x x x x
.Cótấtcảbaonhiêugiátrịnguyênthuộc
2020;2020
củathamsố
m
đểhàmsố
2 4 5g x f x m x
nghịchbiếntrên
0;2
?
A.
2008
. B.
2007
. C.
2018
. D.
2019
.
Lờigiải
ChọnA
Tacó
2 4g x f x m
.
Hàmsố
2 4 5g x f x m x
nghịchbiếntrên
0;2
khi
0, 0;2g x x
2
2 4 0, 0;2 3 6 4 2 4, 0;2f x m x x x m x
.
Xéthàmsố
2
3 6 4 6 6h x x x h x x
.TacóBBT:
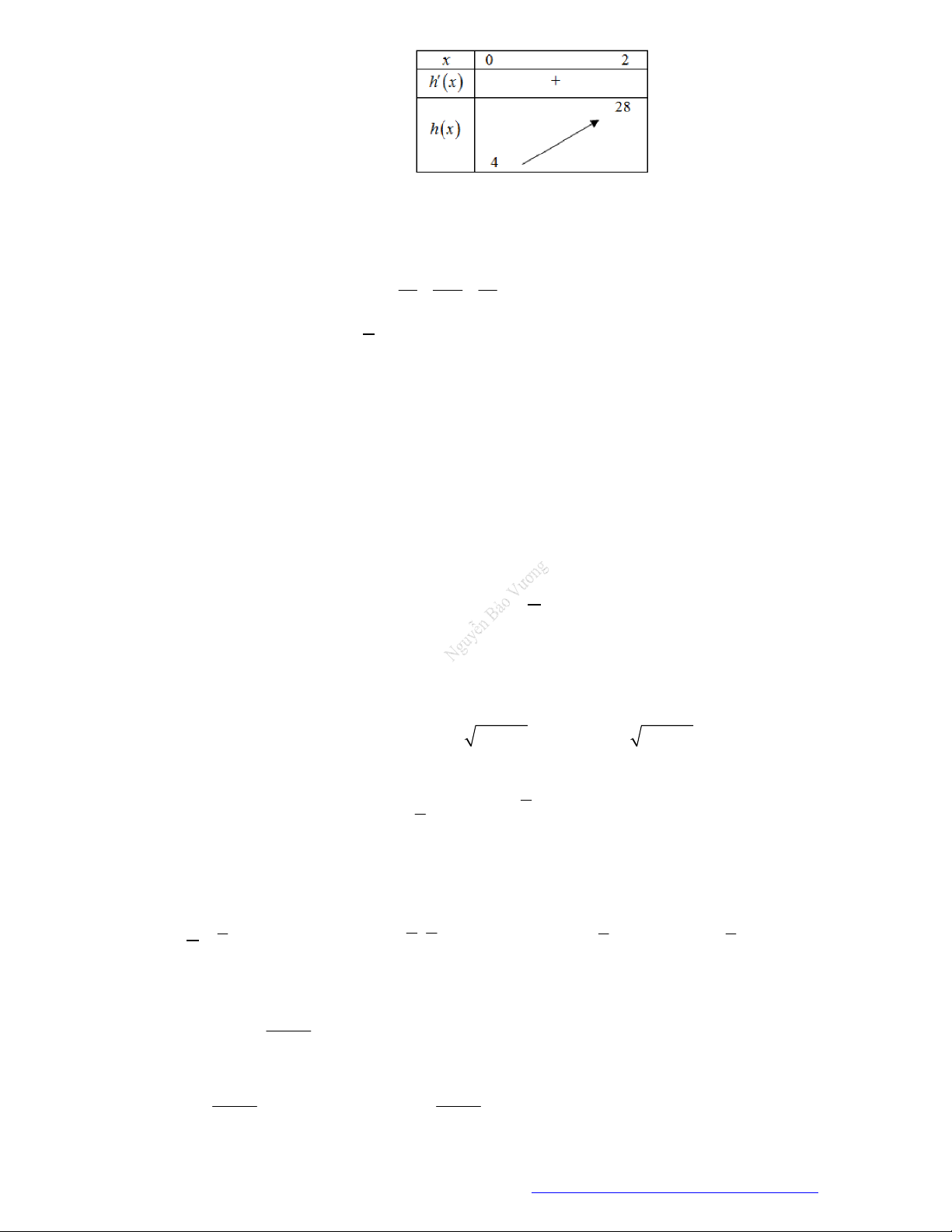
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 45
Vậy
2 4 28 12m m
.Vìm nguyênthuộc
2020;2020
nêncó2008giátrịthỏamãn.
Câu 33. (ThanhChương1-NghệAn-2020)Cóbaonhiêugiátrịnguyêncủathamsố
m
thuộcđoạn
10;10
saochohàmsố
4 3 2
2020
4 3 2
x mx x
y mx nghịchbiếntrênkhoảng
0;1
?
A.12. B.11. C.9. D.10.
Lờigiải.
ChọnB
Tacó
3 2
y x mx x m
.Hàmsốđãchonghịchbiếntrênkhoảng
0;1
khivàchỉkhi
0, 0;1y x
hay
3 2
1 , 0;1x x m x x
.
Vì
2
0;1 : 1 0x x
nên
3 2
1 , 0;1 , 0;1x x m x x m x x
0m
.
Mặtkhác
10;10m
nêncó
0 10 11
giátrịcủa
m
thỏamãnyêucầubàitoán.
Câu 34. (Chuyên Lê Hồng Phong - Nam Định - 2020) Có bao nhiêu số nguyên
m
để hàm số
2020 2cos sinf x m x x x x
nghịchbiếntrên
?
A.Vôsố. B.
2
. C.
1
. D.
0
.
Lờigiải
ChọnC
Tacó
sin 2 cos 1 2020f x x m x m x m
cóđạohàmliêntụctrên
.
Cầntìm
m
nguyênđể
/
cos 2 sin 1 0,f x x m x m x
2 2
max cos 2 sin 1 0 1 4 1 0 1 4 1
x
x m x m m m m m
2 2
1
1 0
2
0
2
3
0
1 4 1 2
3
m
m
m
m
m m m
.Kếthợpmnguyêncó
0m
.
Câu 35. (ChuyênQuangTrung-BìnhPhước-Lần2-2020)Tậphợptấtcảcácgiátrịthựccủatham
sốthực
m
đểhàmsố
2
ln 4 12y x mx
đồngbiếntrên
là
A.
1
;
2
. B.
1 1
;
2 2
. C.
1
;
2
. D.
1
; .
2
Lờigiải
ChọnA
Tacó
2
2
' ,
4
x
y m x
x
.
Hàmsốđãchođồngbiếntrên
' 0y x
(vì
' 0y
chỉcóhữuhạnnghiệm)
2 2
2 2
0
4 4
x x
m x m x
x x
.

NGUYỄN B
ẢO VƯƠNG - 0946798489
Tacó
2
2 2 2
1 2 (
2) 2 1
0
2 2
4 2( 4) 4
x x x
x x
x x x
trên
.
Dođó,
2
2
4
x
m x
x
1
2
m
.
Câu 36. (ChuyênTháiBình-Lần3-2020)Tìmtấtcảcácgiátrịthựccủa
m
đểhàm
số
3 2
1
2
x x m
x
y
đồngbiế
ntrên
1;2
.
A.
8m
. B.
1m
. C.
8m
. D.
1m
.
Lờigiải
ChọnB
Tacó:
3 2
2 1
3 2 .2 .ln 2
x x m
x
y x x m
Hàmsốđồngbiếntrên
1;2
0y
,
1;2x
3 2
2 1
3 2 .
2 .ln 2 0
x x mx
x x m
,
1;2x
2
3 2 0x
x m
,
1;2x
2
3 2m x
x
,
1;2x
2
1;2
3 2m ma
x x x
.
Xéthàms
ố
2
3 2f x
x x
,với
1;2x
.
Tacó
:
6 2f x
x
.
Cho
0f x
6 2 0x
1
3
x
.
Bảngbiếnthi
ên:
Vậy
1m
thỏayê
ucầubàitoán.
-------------------- HẾT --------------------
Trang 46 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
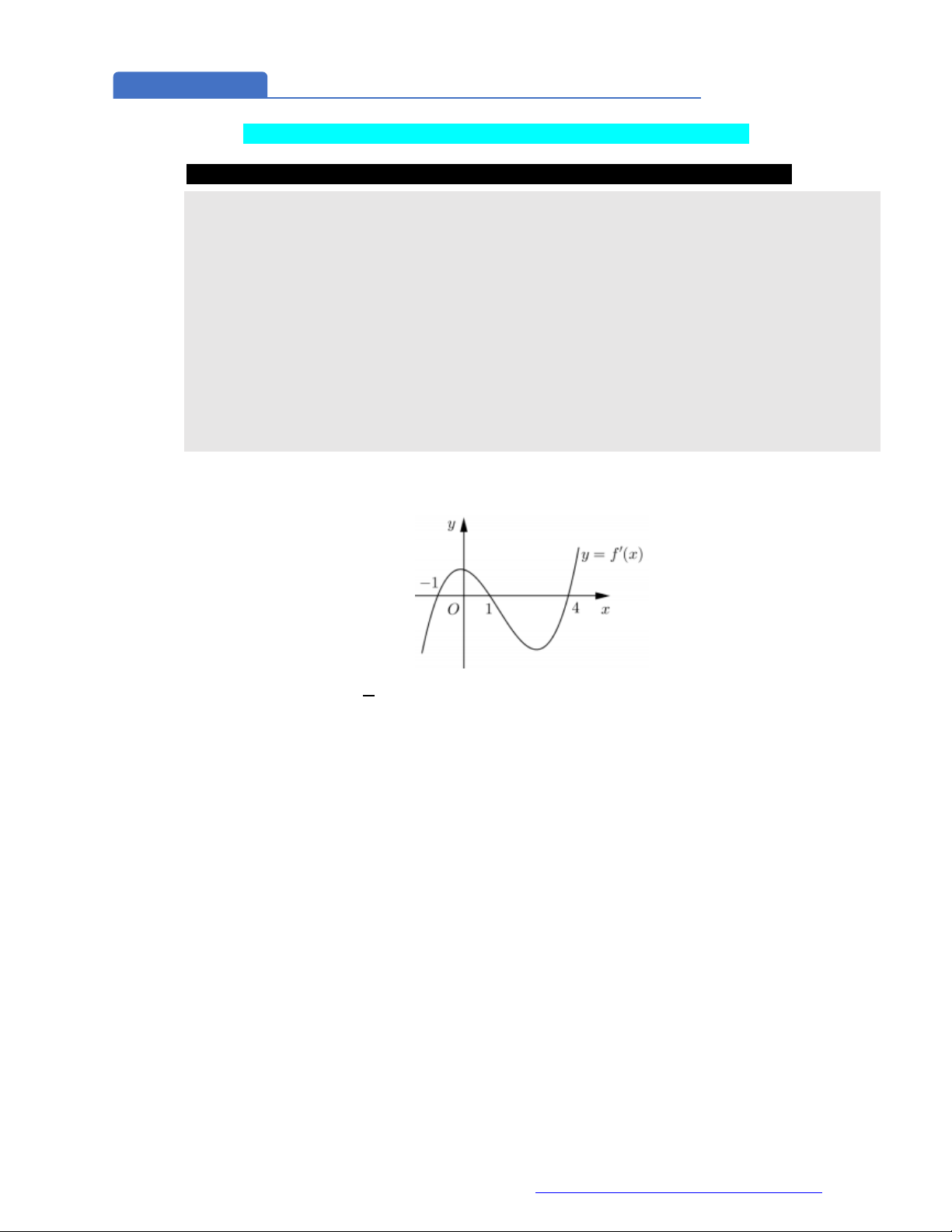
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
DẠNG TOÁN DÀNH CHO ĐỐI TƯỢNG HỌC SINH 9 – 10 ĐIỂM
Dạng 1. Tìm khoảng đơn điệu của hàm số g(x)=f[u(x)] khi biết đồ thị hàm số f’(x)
Cách 1:
Bước 1: Tính đạo hàm của hàm số
g x
,
.g x u x f u x
.
Bước 2: Sử dụng đồ thị của
f x
, lập bảng xét dấu của
g x
.
Bước 3: Dựa vào bảng dấu kết luận khoảng đồng biến, nghịch biến của hàm số.
Cách 2:
Bước 1: Tính đạo hàm của hàm số
g x
,
.g x u x f u x
.
Bước 2: Hàm số
g x
đồng biến
0g x
; (Hàm số
g x
nghịch biến
0g x
) (*)
Bước 3: Giải bất phương trình
*
(dựa vào đồ thị hàm số
y f x
) từ đó kết luận khoảng đồng
biến, nghịch biến của hàm số.
Câu 1. (Đề Tham Khảo 2018) Cho hàm số
( )y f x
. Hàm số
'( )y f x
có đồ thị như hình bên. Hàm số
(2 ) y f x
đồng biến trên khoảng
A.
2;
B.
2;1
C.
; 2
D.
1;3
Lời giải
Chọn B
Cách 1:
Ta thấy
'( ) 0f x
với
(1; 4)
1
x
x
nên
( )f x
nghịch biến trên
1;4
và
; 1
suy ra
( ) ( )g x f x
đồng biến trên
( 4; 1)
và
1;
. Khi đó
(2 )f x
đồng biến biến trên khoảng
( 2;1)
và
3;
Cách 2:
Dựa vào đồ thị của hàm số
y f x
ta có
1
0
1 4
x
f x
x
.
Ta có
2 2 . 2 2f x x f x f x
.
Để hàm số
2y f x
đồng biến thì
2 0 2 0f x f x
2 1 3
1 2 4 2 1
x x
x x
.
Câu 2.
(Mã đề 104 - 2019) Cho hàm số
f x
, bảng xét dấu của
f x
như sau:
TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
Chuyên đề 1
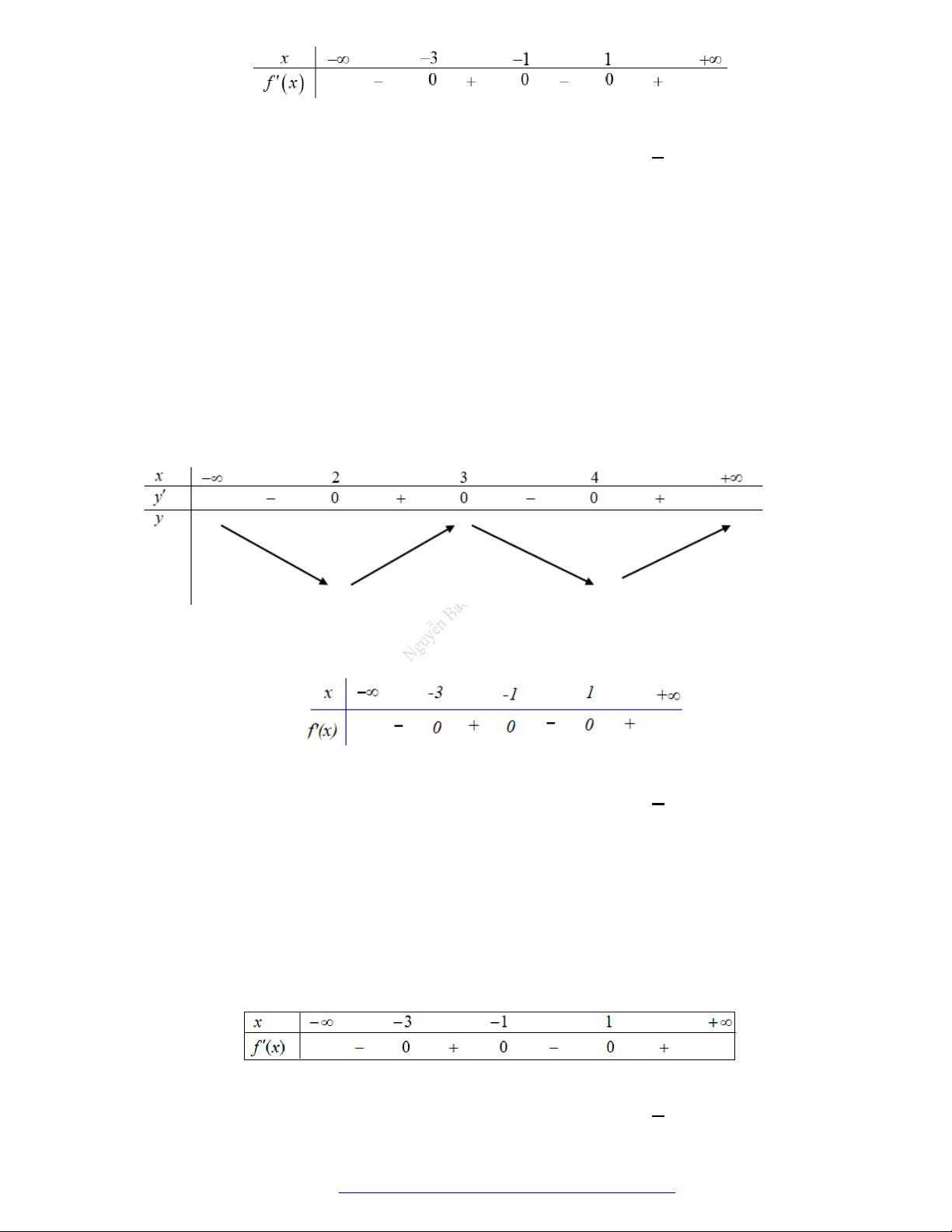
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Hàm số
5 2 y f x
đồng biến trên khoảng nào dưới đây?
A.
3;4
.
B.
1;3
.
C.
; 3
.
D.
4;5
.
Lời giải
Chọn D
Ta có
5 2
y f x
2 5 2
f x
.
0
y
2 5 2 0
f x
5 2 3
5 2 1
5 2 1
x
x
x
4
3
2
x
x
x
.
5 2 0
f x
5 2 3
1 5 2 1
x
x
4
2 3
x
x
;
5 2 0
f x
5 2 1
3 5 2 1
x
x
2
3 4
x
x
.
Bảng biến thiên
Dựa vào bảng biến thiên hàm số
5 2 y f x
đồng biến trên khoảng
4;5
.
Câu 3. (Mã 103 - 2019) Cho hàm số
( )f x
, bảng xét dấu của
( )f x
như sau:
Hàm số
3 2y f x
đồng biến trên khoảng nào dưới đây?
A.
0;2
. B.
2;3
. C.
; 3
. D.
3;4
.
Lời giải
Chọn D
Ta có
2. 3 2 0 3 2 0y f x f x
3 2 3 3
1 3 2 1 1 2.
x x
x x
Vậy chọn A.
Câu 4. (Mã 102 - 2019) Cho hàm số
( )f x
có bảng dấu
( )f x
như sau:
Hàm số
(5 2 )y f x
nghịch biến trên khoảng nào dưới đây?
A.
3;5
. B.
5;
. C.
2;3
. D.
0;2
.
Lời giải
Chọn D
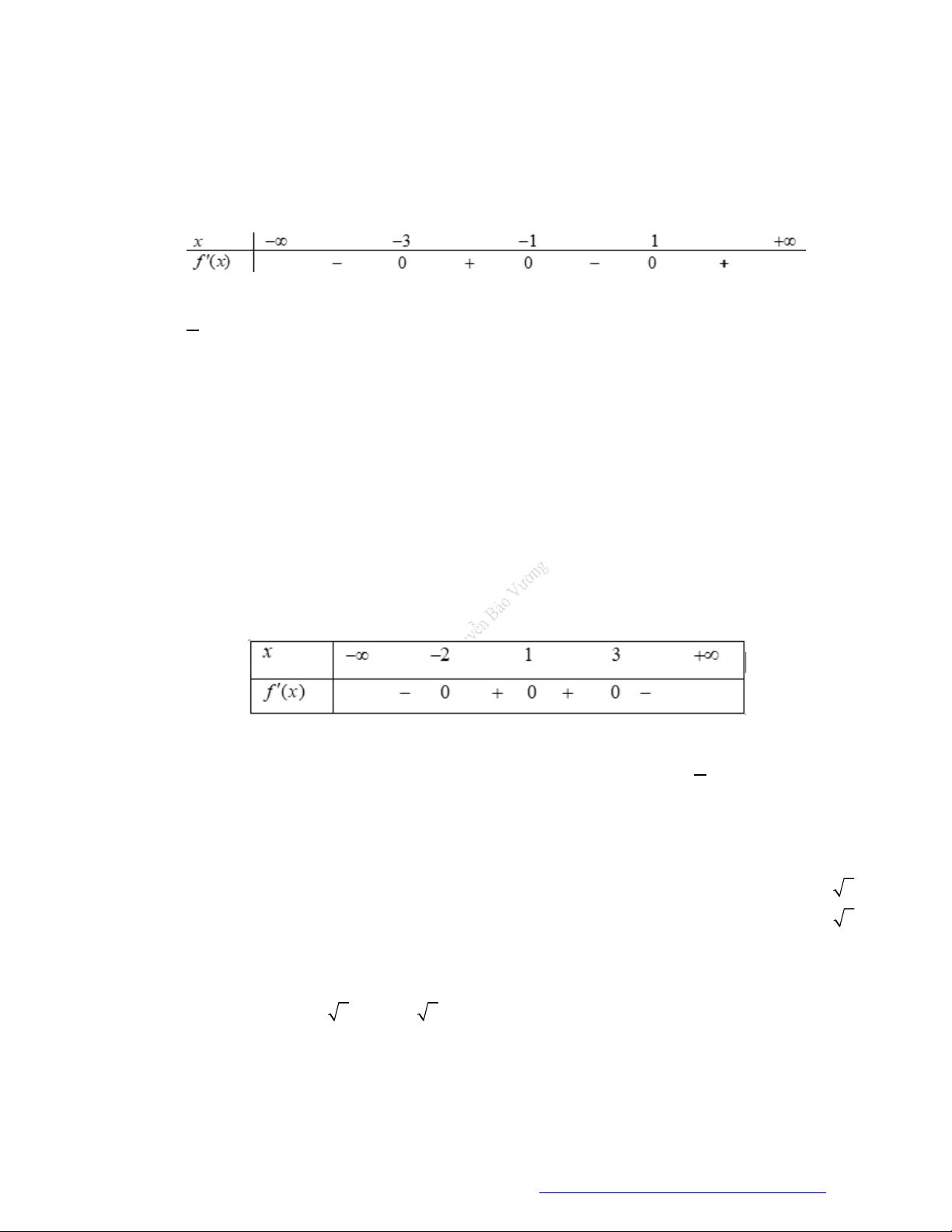
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Hàm số
( )y f x
có tập xác định là
suy ra hàm số
(5 2 )y f x
có tập xác định là
.
Hàm số
(5 2 )y f x
có
y 2. (5 2 ), xf x
.
3 5 2 1 3 4
y 0 (5 2 ) 0
5 2 1 2
x x
f x
x x
.
Vậy hàm số nghịch biến trên các khoảng
;2
;
3;4
. Do đó B phương án chọn.
Câu 5. (Mã đề 101 - 2019) Cho hàm số
f x
, bảng xét dấu của
'f x
như sau:
Hàm số
3 2y f x
nghịch biến trên khoảng nào dưới đây?
A.
2;1 .
B.
2;4 .
C.
1;2 .
D.
4; .
Lời giải
Chọn A
2. 3 2y f x
.
Hàm số nghịch biến khi
0 2. 3 2 0 3 2 0y f x f x
3 3 2x 1
3 2x 1
2 3
1
x
x
.
Vậy chọn đáp án B.
Câu 6. (Đề Thi Công Bằng KHTN 2019) Cho hàm số
( )f x
có bảng xét dấu như sau:
Hàm số
2
2y f x x
nghịch biến trên khoảng nào dưới đây?
A.
2;1
. B.
4; 3
. C.
0;1
. D.
2; 1
.
Lời giải
Ta có: Đặt:
2
( ) 2y g x f x x
;
2 2
( ) ( 2 ) 2 2 . ( 2 )g x f x x x f x x
2
( ) 0 2 2 . ( 2 ) 0g x x f x x
2
2 2
2
1
1
1 2
2 2 0 2 2( )
1 2
( 2 ) 0 2 1
1
2 3
3
x
x
x
x x x VN
x
f x x x x
x
x x
x
(Trong đó:
1 2 ; 1 2x x
là các nghiệm bội chẵn của PT:
2
2 1x x )
+ Ta có bảng biến thiên
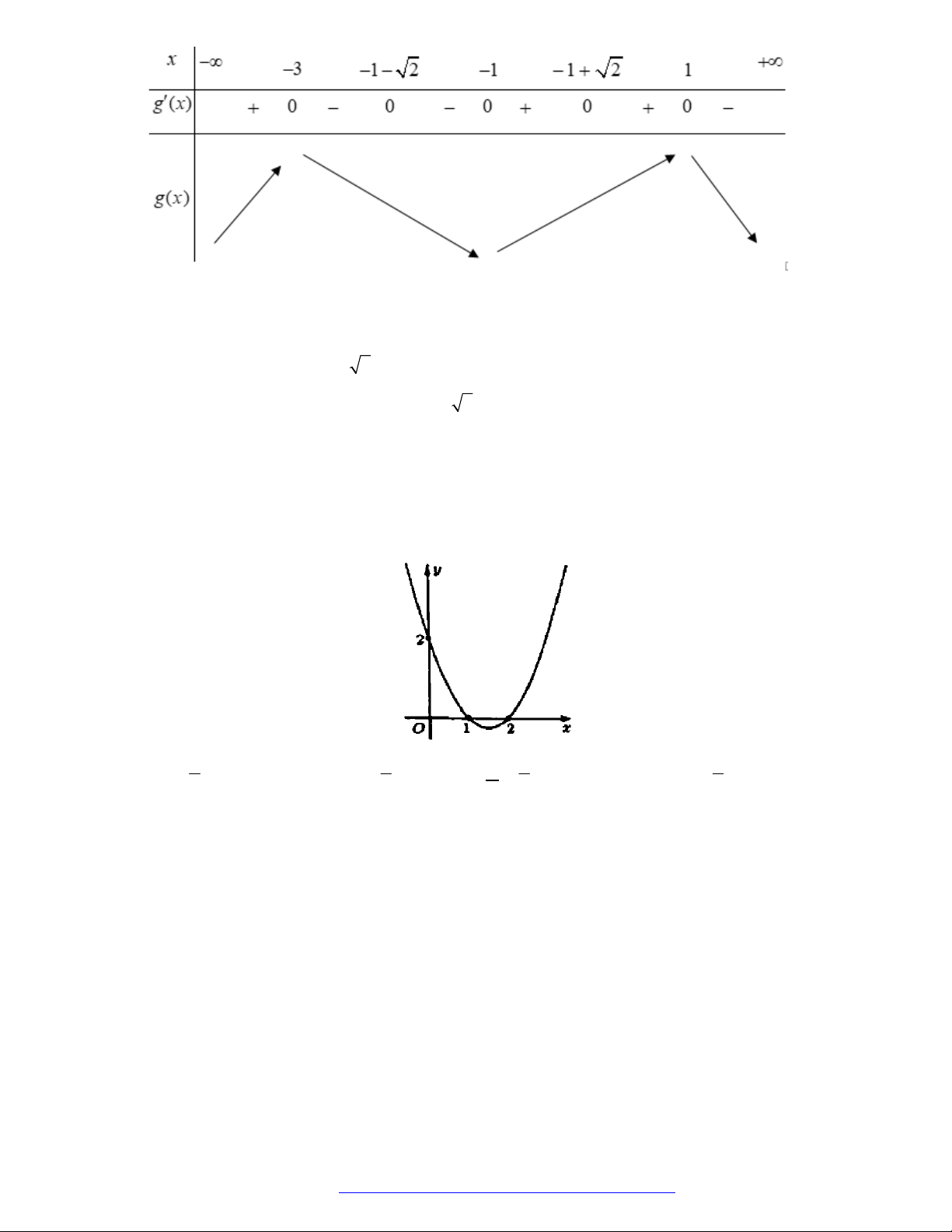
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Dựa vào bảng biến thiên, suy ra hàm số
2
2y f x x
nghịch biến trên khoảng
2; 1
.
Chú ý: Cách xét dấu
( )g x
:
Chọn giá trị
2
0 1; 1 2 2 0 (0) (0) 0x x x g f
( dựa theo bảng xét dấu của
hàm
( )f x
). Suy ra
( ) 0 1; 1 2g x x
, sử dụng quy tắc xét dấu đa thức “ lẻ đổi, chẵn
không” suy ra dấu của
( )g x
trên các khoảng còn lại
Câu 7. (Chuyên Thái Nguyên -2019) Cho hàm số
y f x
có đạo hàm
'f x
trên
. Hình vẽ bên
là đồ thị của hàm số
'y f x
. Hàm số
2
g x f x x
nghịch biến trên khoảng nào trong
các khoảng dưới đây?
A.
3
;
2
. B.
3
;
2
. C.
1
;
2
. D.
1
;
2
.
Lời giải
Phương pháp
Hàm số
y g x
nghịch biến trên
; ' 0 ; a b g x x a b
và bằng 0 tại hữu hạn điểm.
Cách giải
Ta có:
2
' 1 2 'g x x f x x
.
Hàm số
y g x
nghịch biến trên
; ' 0 ; a b g x x a b
và bằng 0 tại hữu hạn điểm.
Ta có
' 1 3 ' 2 0g f
Loại đáp án A, B và D
Câu 8. (Chuyên Lê Hồng Phong Nam Định 2019) Cho hàm số
'y f x
có đồ thị như hình vẽ

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Hàm số
2
2y f x
đồng biến trên khoảng nào dưới đây
A.
;0
. B.
0;1
. C.
1;2
. D.
0;
.
Lời giải
Chọn B
Hàm số
2
2y f x
có
2
' 2 . ' 2y x f x
2
2
2
2
0
0
1 2 2
1 1
0 1
0
' 2 . ' 2 0
0
1
1
2 1
1
2 2
x
x
x
x
x
x
y x f x
x
x
x
x
x
x
Do đó hàm số đồng biến trên
0;1
.
Câu 9. (THPT Gia Lộc Hải Dương 2019) Cho hàm số
( )f x
, đồ thị hàm số
( )y f x
như hình vẽ dưới
đây.
Hàm số
3y f x
đồng biến trên khoảng nào dưới đây?
A.
4;6
. B.
1;2
. C.
; 1 .
D.
2;3
.
Lời giải
Ta có:
3
3 3 3 ( 3)
3
3 0
3
3 0 3 0
3
3 0
x
y f x f x f x x
x
f x
x
f x f x
x
x
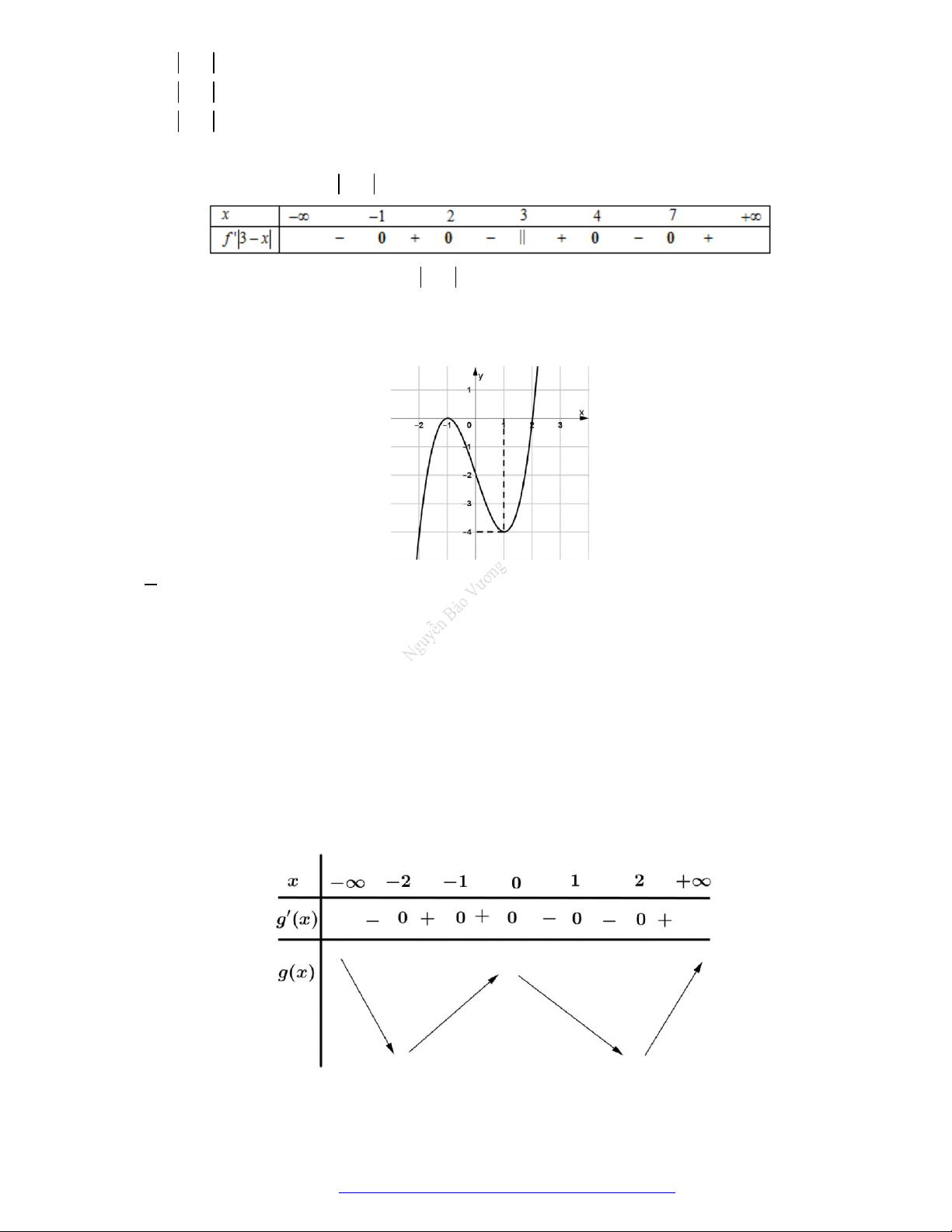
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
3 1
1
3 1
7
2
3 4
4
3
x L
x
x N
x
x
x N
x
x L
Ta có bảng xét dấu của
3 :f x
Từ bảng xét dấu ta thây hàm số
3y f x
đồng biến trên khoảng
1;2 .
Câu 10. (THPT Minh Châu Hưng Yên 2019) Cho hàm số
y f x
. Hàm số
'y f x
có đồ thị như
hình vẽ. Hàm số
2
( ) ( 2).g x f x Mệnhvđề nào sai?
A. Hàm số
g x
nghịch biến trên
; 2
B. Hàm số
g x
đồng biến trên
2;
C. Hàm số
g x
nghịch biến trên
1;0
D. Hàm số
g x
nghịch biến trên
0;2
Lờigiải
ChọnA
Ta có
2 2
2
2
0
0
0
'( ) 2 . '( 2) 0 2 1 1
( 2) 0
2
2 2
x
x
x
g x x f x x x
f x
x
x
Từ đồ thị
'( )f x
ta có
2 2
2
'( 2) 0 2 0
2
x
f x x
x
BBT
Từ BBT ta thấy đáp án C sai
Câu 11. (THPT Việt Đức Hà Nội 2019) Cho hàm số
y f x
có đạo hàm liên tục trên
và đồ thị hàm
số
'y f x
như hình bên.
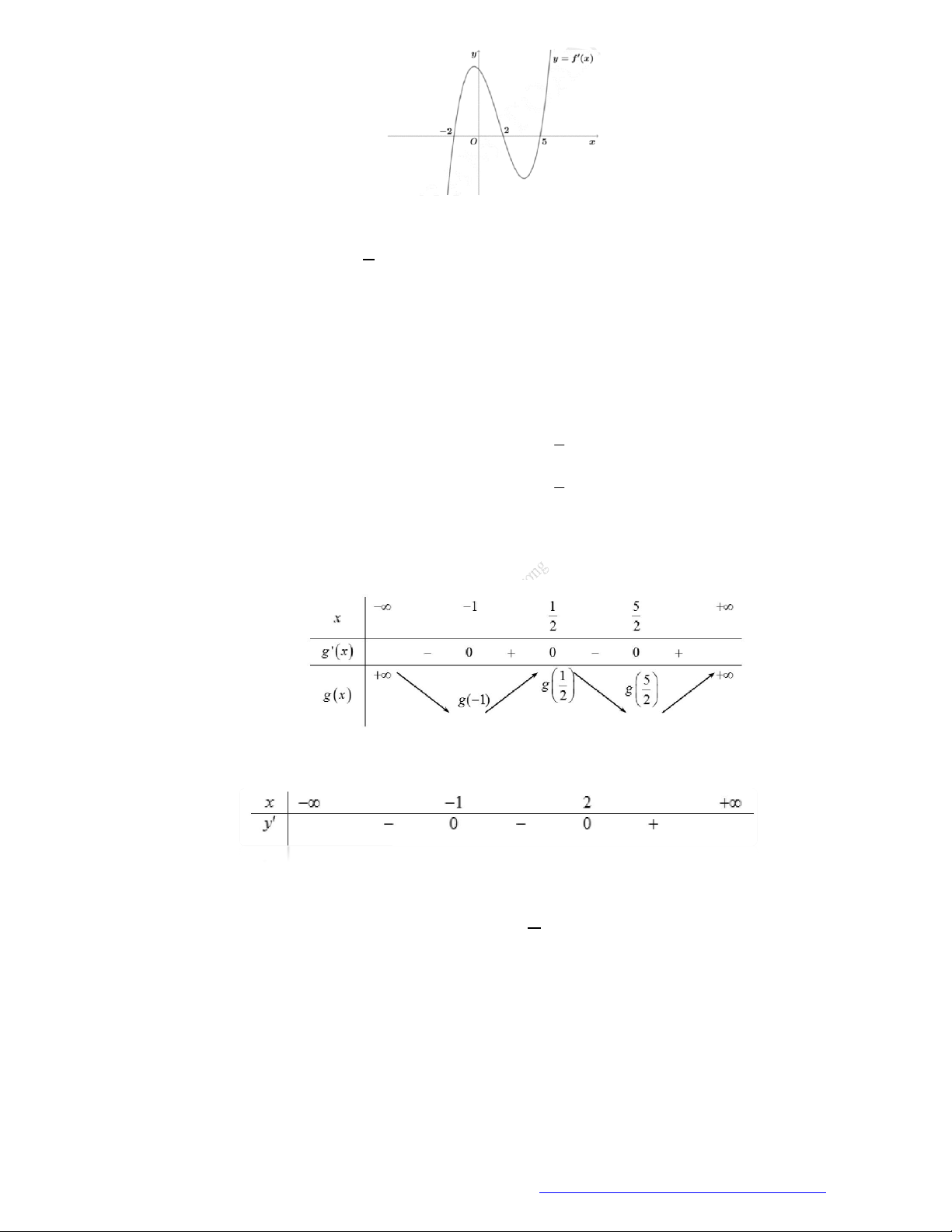
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Hỏi hàm số
3 2g x f x
nghịch biến trên khoảng nào trong các khoảng sau?
A.
1;
B.
; 1
C.
1;3
D.
0;2
Lời giải
Chọn B
Ta có
2
' 0 2
5
x
f x x
x
Khi đó
' 2 ' 3 2g x f x
Với
5
2
3 2 2
1
' 0 ' 3 2 0 3 2 2
2
3 2 5
1
x
x
g x f x x x
x
x
Bảng biến thiên:
Câu 12. (Chuyên Lê Quý Đôn Điện Biên 2019) Cho hàm số
y f x
có bảng xét dấu đạo hàm như sau:
Hàm số
2
2y f x
nghịch biến trên khoảng nào dưới đây?
A.
2; 1
. B.
2;
. C.
0;2
. D.
1;0
.
Lời giải
Xét hàm số
2
2g x f x
. Ta có:
2
' 2 . ' 2g x x f x
.
2
0
' 0
' 2 0
x
g x
f x
2 2
2 2
0
0 0
1
2 1 1 1
2
2 2 4
2
x
x x
x
x x x
x
x x
x
.
Ta có bảng xét dấu
'g x
:
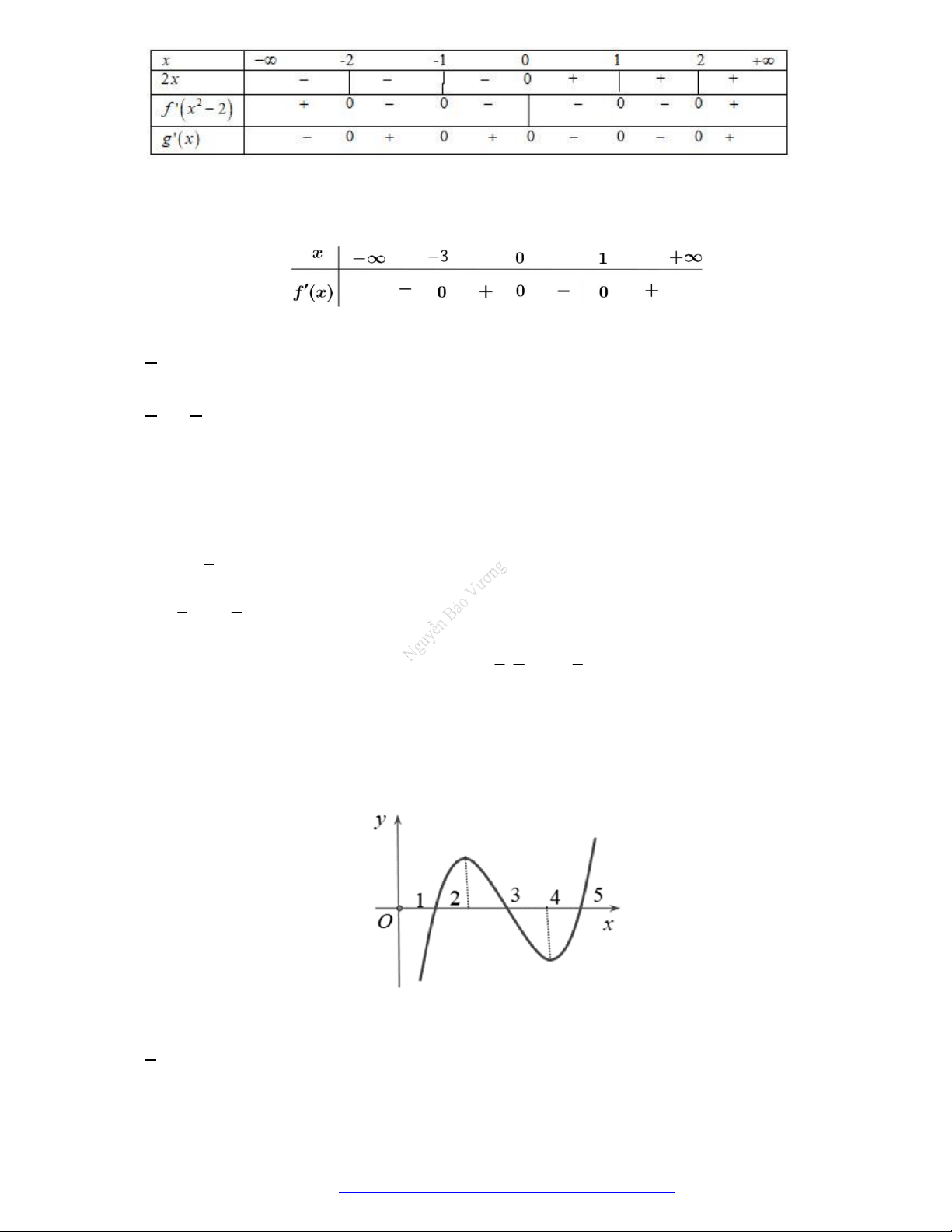
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Dựa vào bảng xét dấu
'g x
ta thấy hàm số
2
2y f x
nghịch biến trên khoảng
0;2
Câu 13. (Chuyên KHTN - 2020) Cho hàm số
y f x
có bảng xét dấu đạo hàm như sau.
Hàm số
2 3 y f x
đồng biến trên khoảng nào sau đây?
A.
2;3
. B.
1;2
. C.
0;1
. D.
1;3
.
Lời giải
Chọn A
Đặt
2 3 3. 2 3
g x f x g x f x
Ta có
0 2 3 0
g x f x
2 3 3
0 2 3 1
x
x
5
3
1 2
3 3
x
x
.
Suy ra hàm số
g x
đồng biến trên các khoảng
1 2
;
3 3
và
5
;
3
, do đó hàm số đồng biến trên
khoảng
2;3
.
Câu 14. (Chuyên Bến Tre - 2020) Cho hàm số
y f x
biết hàm số
f x
có đạo hàm
f x
và hàm
số
y f x
có đồ thị như hình vẽ. Đặt
1g x f x
. Kết luận nào sau đây đúng?
A. Hàm số
g x
đồng biến trên khoảng
3;4
.
B. Hàm số
g x
đồng biến trên khoảng
0;1
.
C. Hàm số
g x
nghịch biến trên khoảng
2;
.
D. Hàm số
g x
nghịch biến trên khoảng
4;6
.
Lời giải

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Chọn B
1g x f x
.
Ta có:
1g x f x
Hàm số
g x
đồng biến
1 5 4
0 1 0
1 1 3 0 2
x x
g x f x
x x
.
Hàm số
g x
nghịch biến
3 1 5 2 4
0 1 0
1 1 0
x x
g x f x
x x
.
Vậy hàm số
g x
đồng biến trên khoảng
0;2
;
4;
và nghịch biến trên khoảng
2;4
;
;0
.
Câu 15. (Chuyên Phan Bội Châu - Nghệ An - 2020) Cho hàm số
y f x
có bảng xét dấu đạo hàm
như sau:
Hàm số
3 2
x
g x f
đồng biến trên khoảng nào sau đây
A.
3;
. B.
; 5
. C.
1;2
. D.
2;7
.
Lời giải
Chọn C
Ta có
' 2 ln 2. ' 3 2
x x
g x f
.
Để
( ) 3 2
x
g x f
đồng biến thì
' 2 ln 2. ' 3 2 0
x x
g x f
' 3 2 0 5 3 2 2 0 3
x x
f x
.
Vậy hàm số đồng biến trên
1;2
.
Câu 16. (Chuyên Vĩnh Phúc - 2020) Cho hàm số
f x
có đạo hàm liên tục trên
và có đồ thị của hàm
số
y f x
như hình vẽ. Xét hàm số
2
2 g x f x
. Mệnh đề nào dưới đây sai?
A. Hàm số
g x
nghịch biến trên
0;2
. B. Hàm số
g x
đồng biến trên
2;
.
C. Hàm số
g x
nghịch biến trên
1;0
. D. Hàm số
g x
nghịch biến trên
; 2
.
x
5
2
y
0
0

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Lời giải
Chọn C
Ta có
2 2 2
2 . 2 2 . 2
g x x f x x f x
.
Hàm số nghịch biến khi
0g x
2
. 2 0x f x
2
2
0
2 0
0
2 0
x
f x
x
f x
Từ đồ thị hình của hàm số
y f x
như hình vẽ, ta thấy
0 2f x x
và
0f x
2x
.
+ Với
2
0
2 0
x
f x
2
0
2 2
x
x
2
0
4
x
x
0
2
2
x
x
x
2x
.
+ Với
2
0
2 0
x
f x
2
0
2 2
x
x
2
0
4
x
x
0 2x
.
Như vậy hàm số nghịch biến trên mỗi khoảng
; 2
,
0;2
; suy ra hàm số đồng biến trên
2;0
và
2;
.
Do
1;0 2;0
nên hàm số đồng biến trên
1;0
. Vậy C sai.
Câu 17. (Đại Học Hà Tĩnh - 2020) Cho hàm số
y f x
. Biết rằng hàm số
y f x
có đồ thị như
hình vẽ bên dưới.
Hàm số
2
3y f x
đồng biến trên khoảng
A.
0;1
. B.
1;0
. C.
2;3
. D.
2; 1
.
Lời giải
Chọn B
Cách 1:
Đặt
2
3y g x f x
.
Ta có:
2
2 . 3g x x f x
.
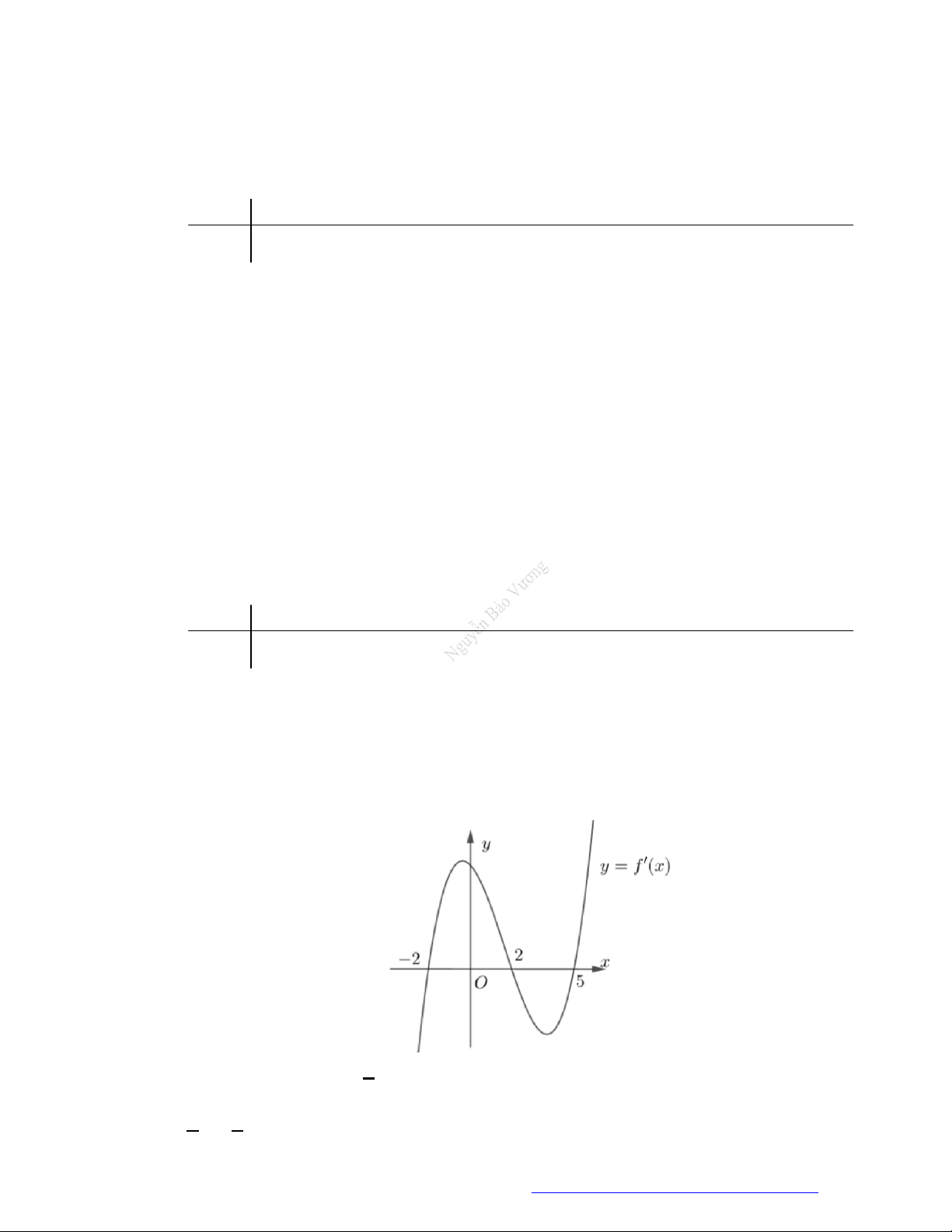
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
2
0 2 . 3 0g x x f x
2
0
3 0
x
f x
2
2
2
0
3 6
3 1
3 2
x
x
x
x
0
3
2
1
x
x
x
x
.
Bảng xét dấu của
g x
:
x
g x
3
0
0
2
0
1
0
0
0
1
2
3
0
0
Suy ra hàm số
2
3y f x
đồng biến trên mỗi khoảng:
3; 2 , 1;0 , 1;2 , 3;
.
Vậy hàm số
2
3y f x
đồng biến trên khoảng
1;0
.
Cách 2:
Dựa vào đồ thị của
y f x
ta chọn
6 1 2y f x x x x
.
Đặt
2
3y g x f x
.
Ta có:
2 2 2 2
2 . 3 2 9 4 1g x x f x x x x x
.
0g x
0
3
2
1
x
x
x
x
.
Bảng xét dấu của
g x
:
x
g x
3
0
0
2
0
1
0
0
0
1
2
3
0
0
Suy ra hàm số
2
3y f x
đồng biến trên mỗi khoảng:
3; 2 , 1;0 , 1;2 , 3;
.
Vậy hàm số
2
3y f x
đồng biến trên khoảng
1;0
.
Câu 18. (Sở Ninh Bình) Cho hàm số bậc bốn
y f x
có đạo hàm trên
. Đồ thị hàm số
'y f x
như hình vẽ. Hàm số
2
2y f x
nghịch biến trên khoảng nào dưới đây?
A.
2;3
. B.
3; 2
. C.
1;1
. D.
1;0
.
Lời giải
Chọn B
Đặt
2
2g x f x
, hàm số có đạo hàm trên
.
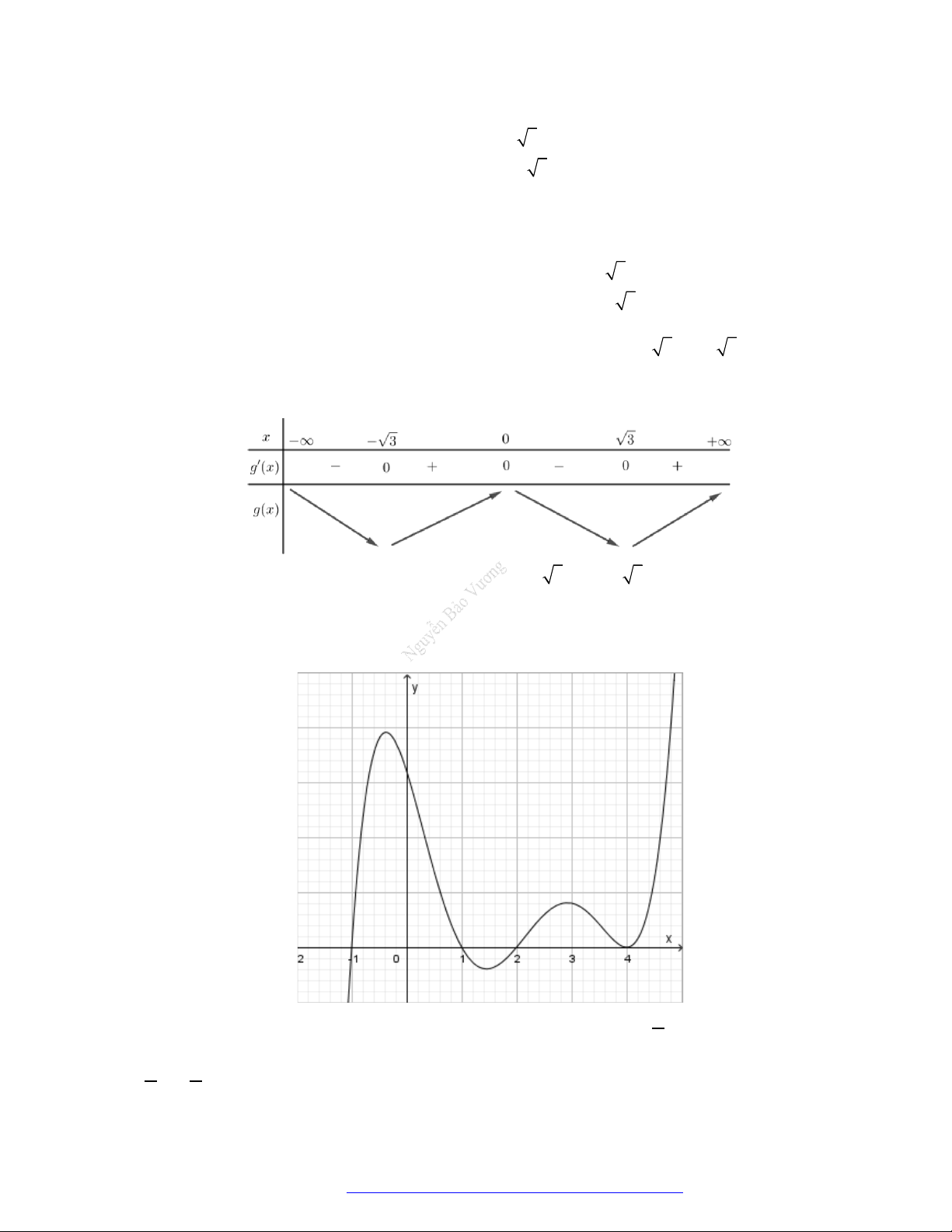
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
2 2g x xf x
, kết hợp với đồ thị hàm số
y f x
ta được:
2
2
2
2
0
0
0
2 2
0 3
2 0
2 2
3
2 5
x
x
x
x
g x x
f x
x
x
x
.
Từ đồ thị đã cho ta có
2 2
0
5
x
f x
x
Suy ra
2 2
2
2 2
2 2 2 4 0 3
2 0
2 5 3
3
x x x
f x
x x
x
.
Và lập luận tương tự
2
2 2
2
2 2 5
2 0 0 3 3 3
2 2
x
f x x x
x
.
Bảng biến thiên ( Dấu của
g x
phụ thuộc vào dấu của
2x
và
2
2f x
trên từng khoảng)
Dựa vào bảng biến thiên hàm số nghịch biền trên
; 3
và
0; 3
chọn đáp án.
Câu 19. (Hậu Lộc 2 - Thanh Hóa - 2020) Cho hàm số
y f x
có đồ thị hàm đạo hàm
y f x
như
hình vẽ. Hàm số
2019 2020g x f x
đồng biến trên khoảng nào trong các khoảng sau?
A.
1;0
. B.
; 1
. C.
0;1
. D.
1;
.
Lời giải
Chọn D
Ta có
2019 2020 2019 2020 2020 2019 2020g x x f x f x
,
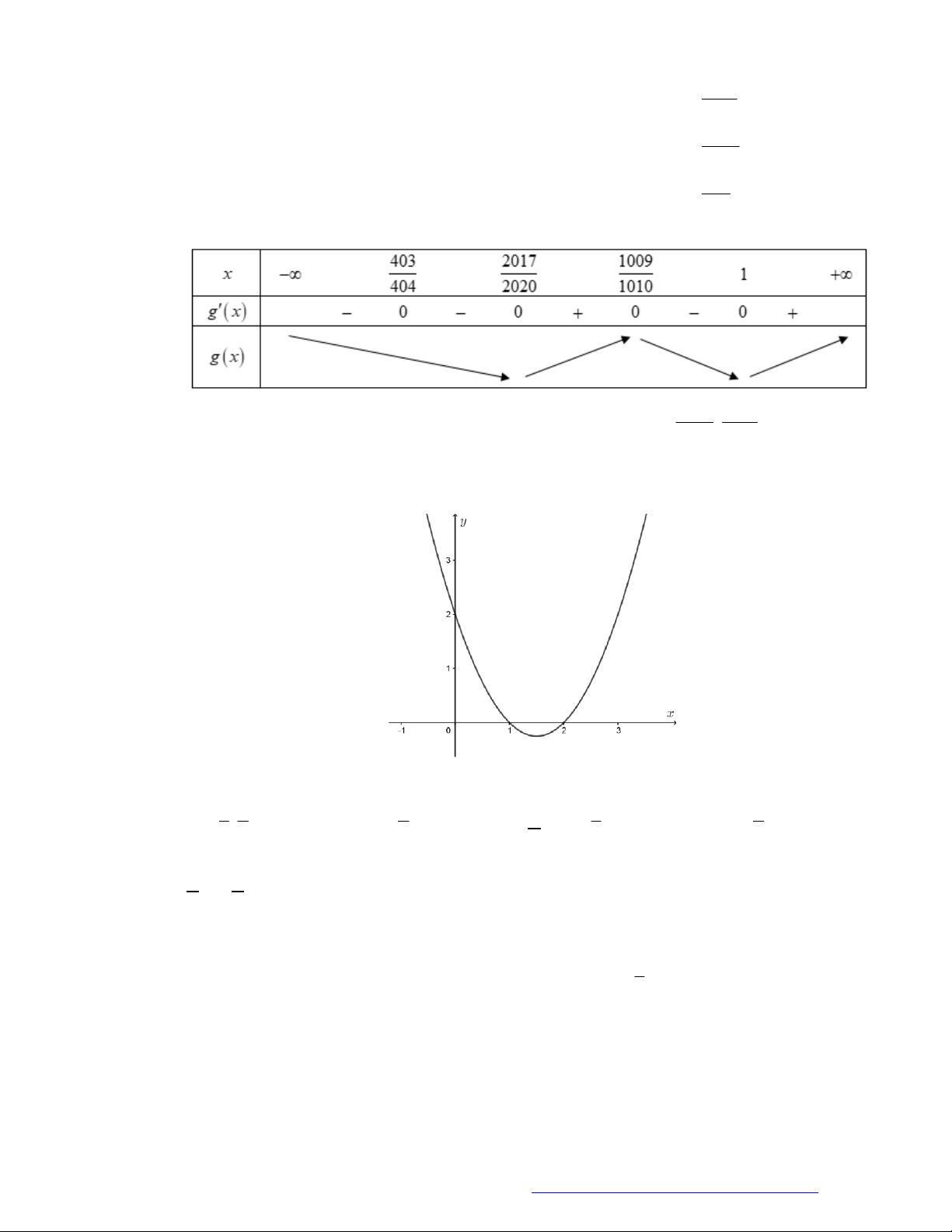
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
1
1009
2019 2020 1
1010
2019 2020 1
2019 2020 0
2017
2019 2020 2
2020
2019 2020 4
403
404
x
x
x
x
f x
x
x
x
x
Bảng biến thiên
Dựa vào bảng biến thiên, hàm số
g x
đồng biến trên từng khoảng
2017 1009
;
2020 1010
,
1;
.
Câu 20. (Trường VINSCHOOL - 2020) Cho hàm số
y f x
. Biết đồ thị hàm số
y f x
có đồ thị
như hình vẽ bên
Hàm số
2
2 3g x f x x
đồng biến trên khoảng nào dưới đây?
A.
1 1
;
3 2
. B.
1
;
2
. C.
1
;
3
. D.
1
2;
2
.
Lời giải
Chọn C
Cách 1. Ta có
2
2 6 . 2 3g x x f x x
2 2
2
2 6 0
1
0 2 6 . 2 3 0 2 3 1
3
2 3 2
x
g x x f x x x x x
x x
Bảng xét dấu của
g x
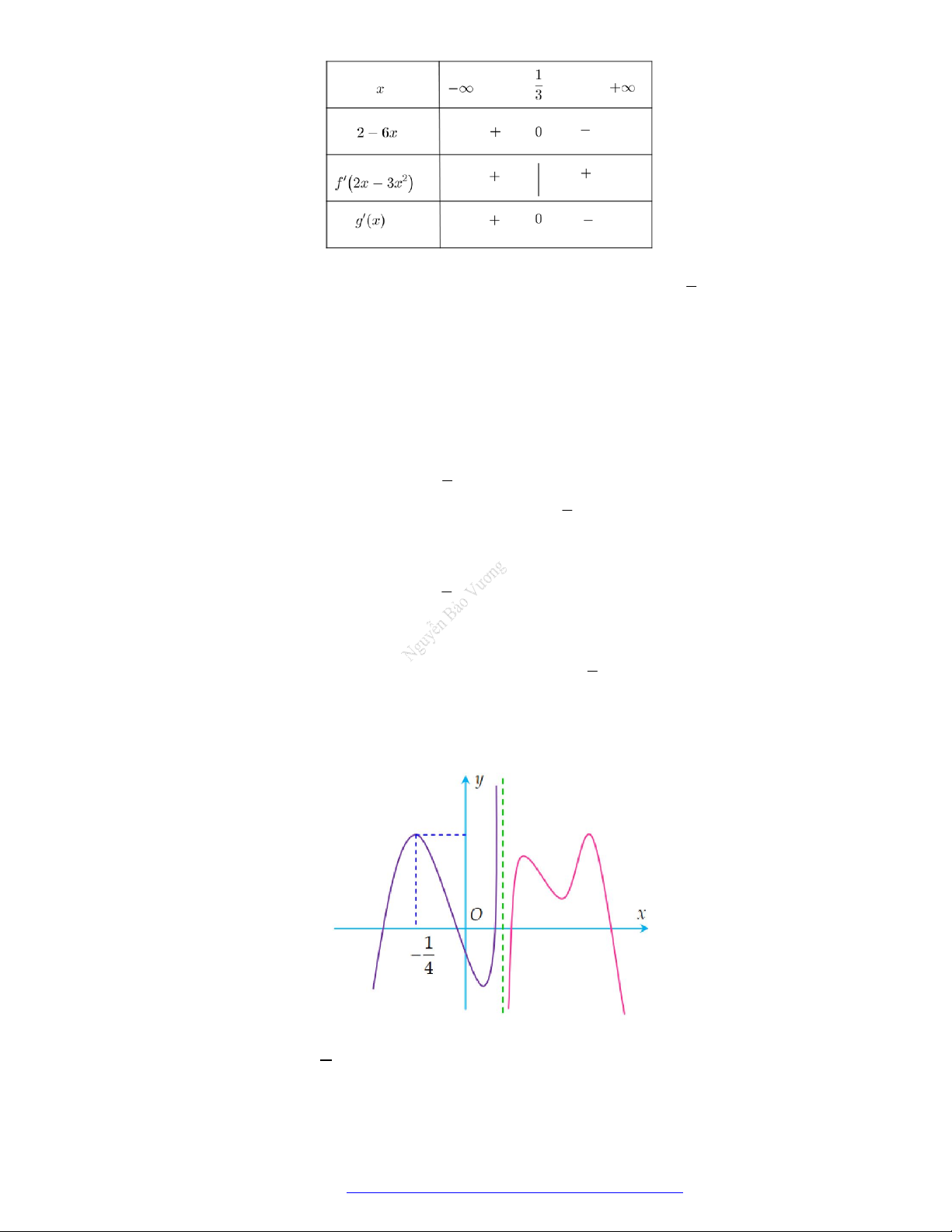
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Từ bảng trên ta có hàm số
2
2 3g x f x x
đồng biến trên khoảng
1
;
3
Cách 2:
2
2 6 . 2 3g x x f x x
Để hàm số
2
2 3g x f x x
đồng biến thì
2
2 2
2 6 0 2 6 0
0 2 6 . 2 3 0
2 3 0 2 3 0
x x
g x x f x x
f x x f x x
Trường hợp 1.
2
2
2
1
2 6 0
3
1
2 3 1
3
2 3 0
2 3 2
x
x
x
x x
f x x
x x
Trường hợp 2.
2
2
1
2 6 0
3
2 3 0
1 2 3 2
x
x
f x x
x x
hệ vô nghiệm
Vậy hàm số
2
2 3g x f x x
đồng biến trên khoảng
1
;
3
Câu 21. 1: Cho hàm số
( )f x
liên tục trên R và có đồ thị
'( )f x
như hình vẽ. Tìm số điểm cực trị của hàm
số
2
( )y f x x ?
A.
10
. B.
11
. C.
12
. D.
13
.
Lời giải
Chọn B

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Ta có
2
' (2 1) '( )y x f x x
;
2
x x m
có nghiệm khi và chỉ khi
1
4
m
.
Dựa vào đồ thị ta thấy đồ thị hàm
'( )f x
cắt trục hoành tại 5 điểm trong đó 1 điểm có hoành độ
nhỏ hơn
1
4
và có một tiệm cận.
Khi đó ứng với mỗi giao điểm có hoành độ lớn hơn
1
4
và 1 điểm không xác định thì
' 0
y
có
hai nghiệm. Từ đây dễ dàng suy ra hàm
2
( )y f x x
có 11 cực trị.
Dạng 2. Tìm khoảng đơn điệu của hàm số g(x)=f[u(x)]+v(x) khi biết đồ thị, bảng biến thiên
của hàm số f’(x)
Cách 1:
Bước 1: Tính đạo hàm của hàm số
g x
,
.
g x u x f u x v x
.
Bước 2: Sử dụng đồ thị của
f x
, lập bảng xét dấu của
g x
.
Bước 3: Dựa vào bảng dấu kết luận khoảng đồng biến, nghịch biến của hàm số.
Cách 2:
Bước 1: Tính đạo hàm của hàm số
g x
,
.
g x u x f u x v x
.
Bước 2: Hàm số
g x
đồng biến
0
g x
; (Hàm số
g x
nghịch biến
0
g x
) (*)
Bước 3: Giải bất phương trình
*
(dựa vào đồ thị hàm số
y f x
) từ đó kết luận khoảng đồng
biến, nghịch biến của hàm số.
Cách 3: (Trắc nghiệm)
Bước 1: Tính đạo hàm của hàm số
g x
,
.
g x u x f u x v x
.
Bước 3: Hàm số
g x
đồng biến trên
K
0,
g x x K
; (Hàm số
g x
nghịch biến trên
K
0,
g x x K
) (*)
Bước 3: Lần lượt chọn thay giá trị từ các phương án vào
g x
để loại các phương án sai.
Câu 1. (Đề Tham Khảo 2019) Cho hàm số
f x
có bảng xét dấu của đạo hàm như sau
x
1 2 3 4
f x
0
0
0
0
Hàm số
3
3 2 3y f x x x
đồng biến trên khoảng nào dưới đây?
A.
; 1 .
B.
1;0 .
C.
0;2 .
D.
1; .
Lời giải
Chọn B
Ta có:
2
3 2 3
y f x x
Với
1;0 2 1;2 2 0
x x f x
, lại có
2
3 0 0; 1;0
x y x
Vậy hàm số
3
3 2 3y f x x x
đồng biến trên khoảng
1;0 .
Chú ý:
+) Ta xét
2
1;2 1; 2 3;4 2 0; 3 0
x x f x x
Suy ra hàm số nghịch biến trên khoảng
1;2
nên loại hai phương án
A,D.
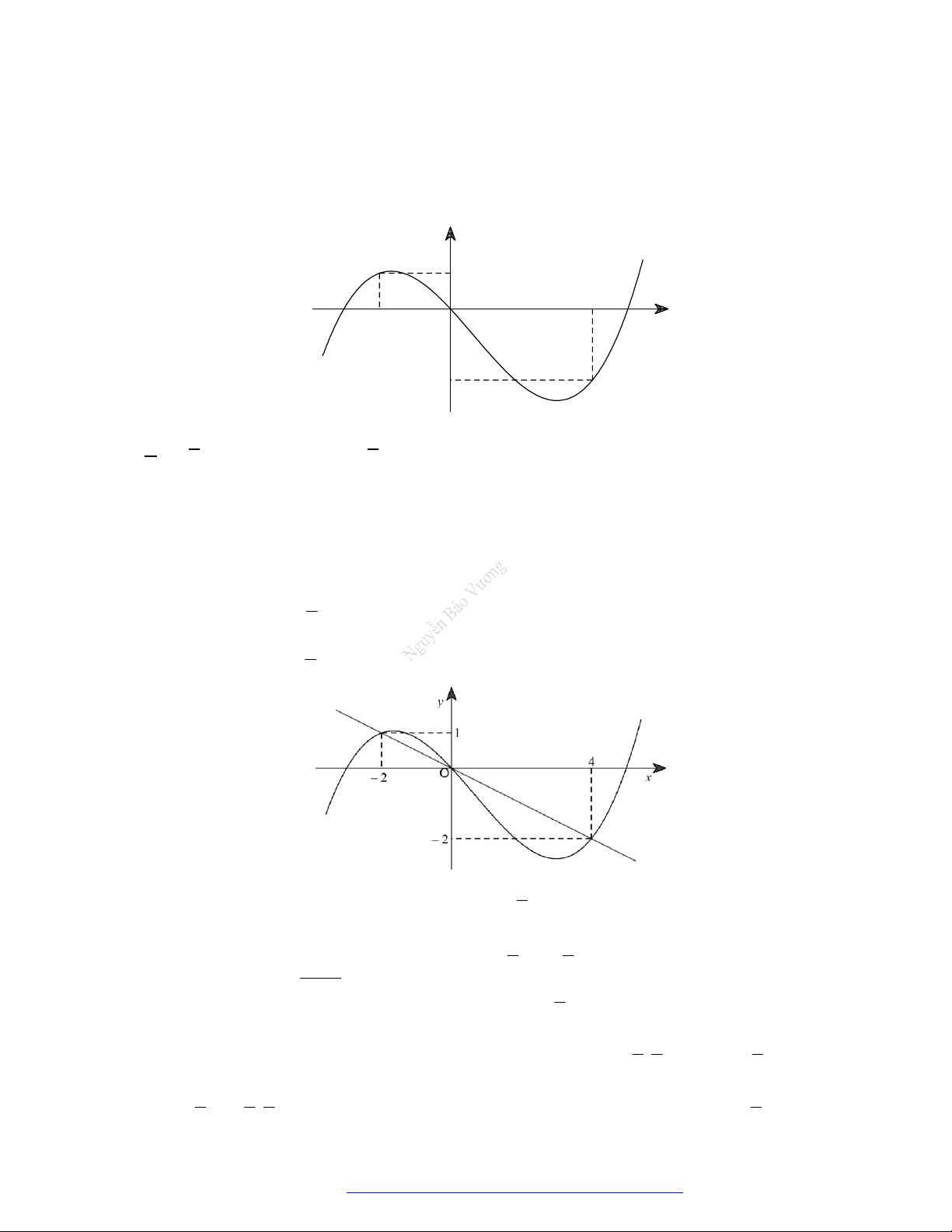
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
+) Tương tự ta xét
2
; 2 2 ;0 2 0; 3 0 0; ; 2x x f x x y x
Suy ra hàm số nghịch biến trên khoảng
; 2
nên loại hai phương án
B.
Câu 2. (Đề Tham Khảo 2020 – Lần 1) Cho hàm số
f x
. Hàm số
'y f x
có đồ thị như hình bên.
Hàm số
2
1 2 g x f x x x
nghịch biến trên khoảng nào dưới đây ?
A.
3
1;
2
. B.
1
0;
2
. C.
2; 1
. D.
2;3
.
Lời giải
Chọn A
Ta có :
2
1 2 g x f x x x
' 2 ' 1 2 2 1 g x f x x
Đặt
1 2 2t x g x f t t
' 0 '
2
t
g x f t
Vẽ đường thẳng
2
x
y
và đồ thị hàm số
'f x
trên cùng một hệ trục
Hàm số
g x
nghịch biến
2 0
' 0 '
4
2
t
t
g x f t
t
Như vậy
1 3
2 1 2 0
1 2
2 2
1 2
4 1 2 3
2
2
x
x
x
f x
x
x
.
Vậy hàm số
2
1 2g x f x x x
nghịch biến trên các khoảng
1 3
;
2 2
và
3
;
2
.
Mà
3 1 3
1; ;
2 2 2
nên hàm số
2
1 2g x f x x x
nghịch biến trên khoảng
3
1;
2
Câu 3. (Chuyên Lê Quý Đôn Điện Biên 2019) Cho hàm số
f x
có bảng xét dấu của đạo hàm như sau
x
y
– 2
4
1
– 2
O
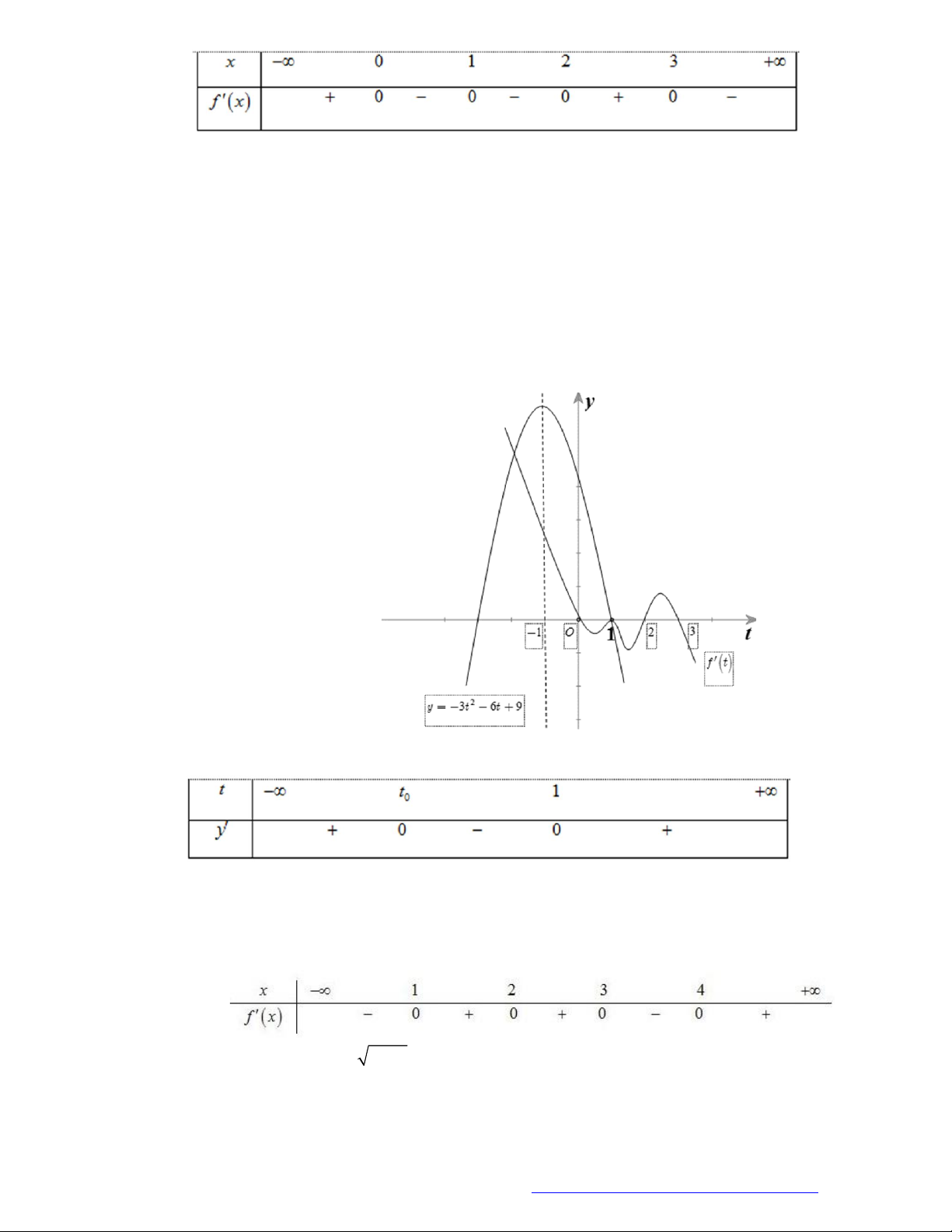
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
Hàm số
3
1 12 2019y f x x x
nghịch biến trên khoảng nào dưới đây?
A.
1;
. B.
1;2
. C.
;1
. D.
3;4
.
Lời giải
Ta có
2 2 2
1 3 12 3 6 9 3 6 9y f x x f t t t f t t t
, với
1t x
Nghiệm của phương trình
0y
là hoành độ giao điểm của các đồ thị hàm số
2
; 3 6 9y f t y t t
.
Vẽ đồ thị của các hàm số
2
; 3 6 9y f t y t t
trên cùng một hệ trục tọa độ như hình vẽ
sau:
Dựa vào đồ thị trên, ta có BXD của hàm số
2
3 6 9y f t t t
như sau:
0
1t
Vậy hàm số nghịch biến trên khoảng
0
;1t t
. Do đó hàm số nghịch biến trên khoảng
0
1;2 1;1x t
.
Câu 4. (Chuyên Phan Bội Châu Nghệ An 2019) Cho hàm số
f x
có bảng xét dấu đạo hàm như sau:
Hàm số
2
2 1 1y f x x x
nghịch biến trên những khoảng nào dưới đây
A.
; 2
. B.
;1
. C.
2;0
. D.
3; 2
.
Lời giải.
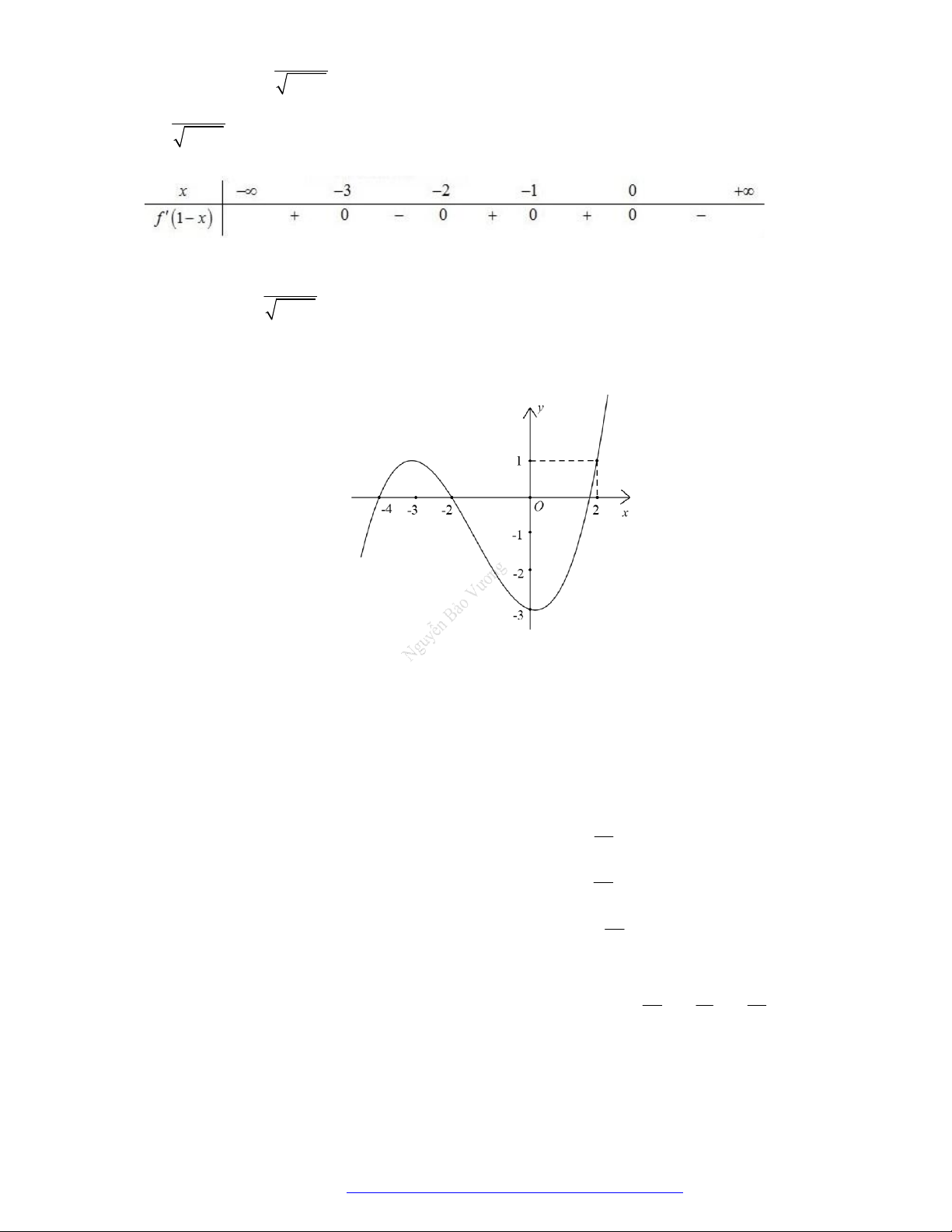
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
2 1 1
1
x
y f x
x
.
Có
2
1 0
1
x
x
,
2;0x
.
Bảng xét dấu:
2 1 0, 2;0f x x
2
2 1 1 0, 2;0
1
x
f x x
x
.
Câu 5. (Sở Vĩnh Phúc 2019) Cho hàm số bậc bốn
( )y f x
có đồ thị của hàm số
( )y f x
như hình vẽ
bên.
Hàm số
3 2
3 ( ) 6 9y f x x x x đồng biến trên khoảng nào trong các khoảng sau đây?
A.
0;2
. B.
1;1
. C.
1;
. D.
2;0
.
Lời giải
Hàm số
4 3 2
( ) ,( 0)f x ax bx cx dx e a ;
3 2
( ) 4 3 2f x ax bx cx d
.
Đồ thị hàm số
( )y f x
đi qua các điểm
( 4;0),( 2;0),(0; 3),(2;1)
nên ta có:
5
96
256 48 8 0
7
32 12 4 0
24
3
7
32 12 4 1
24
3
a
a b c d
a b c d
b
d
c
a b c d
d
Do đó hàm số
3 2 2 3 2
5 15 55
3 ( ) 6 9 ; 3 ( ) 4 3 3
24 8 12
y f x x x x y f x x x x x x
11
0 0
2
x
y x
x
. Hàm số đồng biến trên các khoảng
( 11;0)
và
2;
.
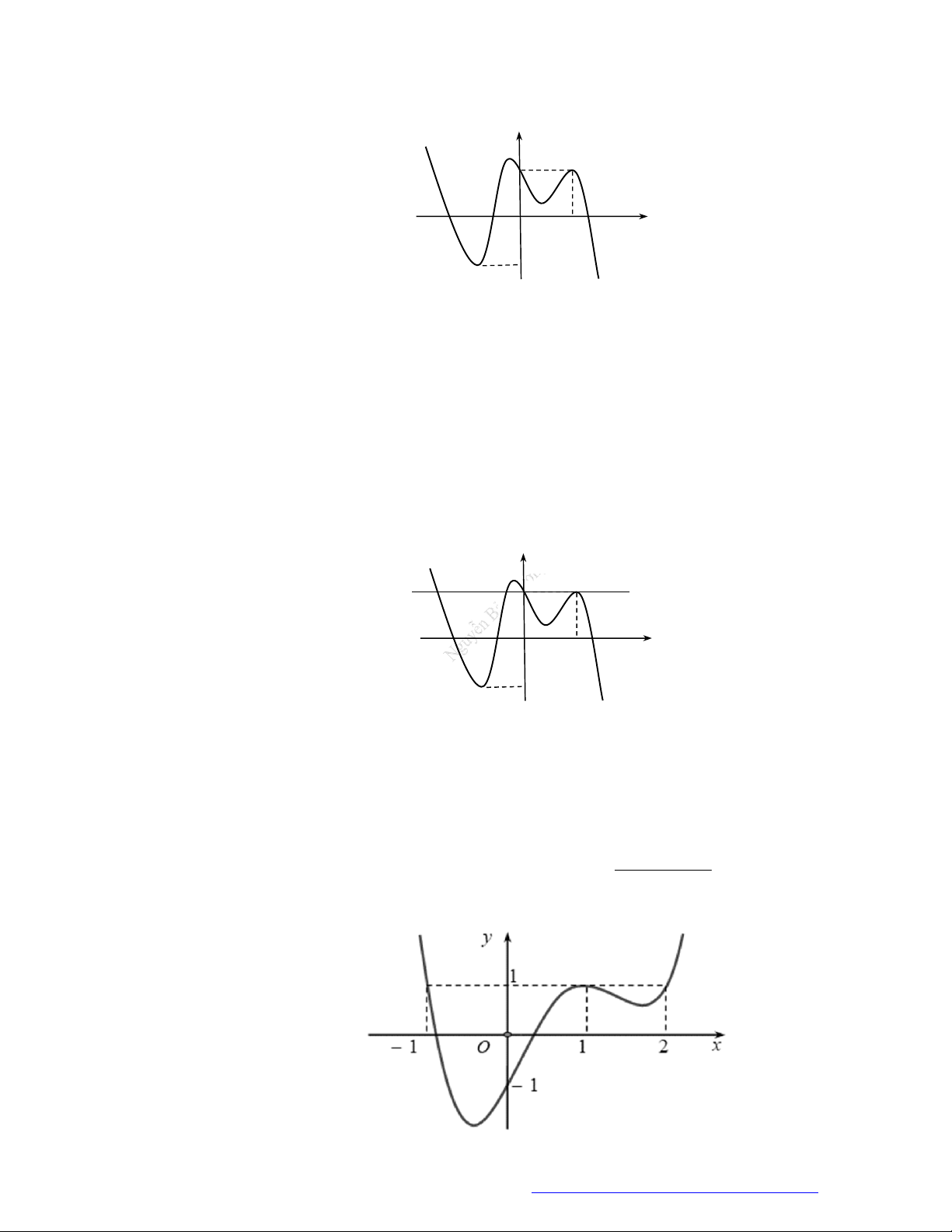
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
Câu 6. (Học Mãi 2019) Cho hàm số
y f x
có đạo hàm trên
. Đồ thị hàm số
y f x
như hình
bên. Hỏi đồ thị hàm số
2y f x x
có bao nhiêu điểm cực trị?
A.
4
. B.
3
. C.
2
. D.
1
.
Lời giải
Chọn B
Đặt
2g x f x x
.
2g x f x
.
Vẽ đường thẳng
2y
.
phương trình
0g x
có 3 nghiệm bội lẻ.
đồ thị hàm số
2y f x x
có 3 điểm cực trị.
Câu 7. (THPT Hoàng Hoa Thám Hưng Yên 2019) Cho hàm số
y f x
liên tục trên
. Hàm số
y f x
có đồ thị như hình vẽ. Hàm số
2019 2018
1
2018
x
g x f x
đồng biến trên khoảng
nào dưới đây?
A.
2 ; 3
. B.
0 ; 1
. C.
-1 ; 0
. D.
1 ; 2
.
y
x
2
2
2
O
2
y
y
x
2
2
2
O
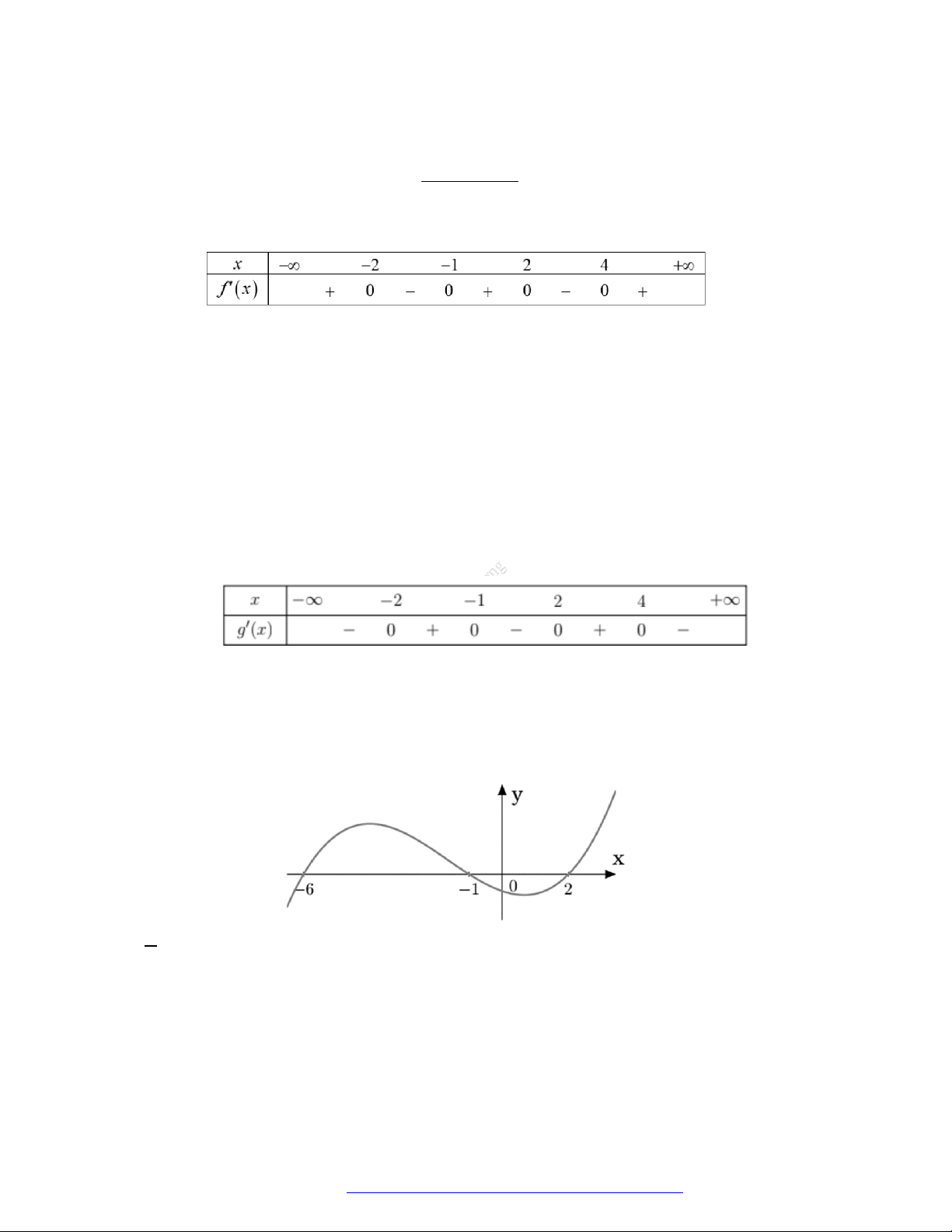
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Lời giải
Ta có
1 1g x f x
.
0 1 1 0 1 1g x f x f x
1 1 0
.
1 2 3
x x
x x
Từ đó suy ra hàm số
2019 2018
1
2018
x
g x f x
đồng biến trên khoảng
-1 ; 0
.
Câu 8. (Sở Ninh Bình 2019) Cho hàm số
y f x
có bảng xét dấu của đạo hàm như sau
Hàm số
2 2019y f x
nghịch biến trên khoảng nào trong các khoảng dưới đây?
A.
4;2
. B.
1;2
. C.
2; 1
. D.
2;4
.
Lời giải
Xét
2 2019y g x f x
.
Ta có
2 2019 2g x f x f x
,
2
1
0
2
4
x
x
g x
x
x
.
Dựa vào bảng xét dấu của
f x
, ta có bảng xét dấu của
g x
:
Dựa vào bảng xét dấu, ta thấy hàm số
y g x
nghịch biến trên khoảng
1;2
.
Câu 9. (THPT Lương Thế Vinh Hà Nội 2019) Cho hàm số
y f x
. Biết đồ thị hàm số
y f x
có đồ thị như hình vẽ bên. Hàm số
2
3 2018y f x
đồng biến trên khoảng nào dưới đây?
A.
1; 0
B.
2; 3
C.
2; 1
D.
0; 1
Lời giải
Chọn A
Ta có
2 2
3 2018 2 . 3f x x f x
.
2
2
2
2
0
0
3 6
3
2 . 3 0
2
3 1
1
3 2
x
x
x
x
x f x
x
x
x
x
.
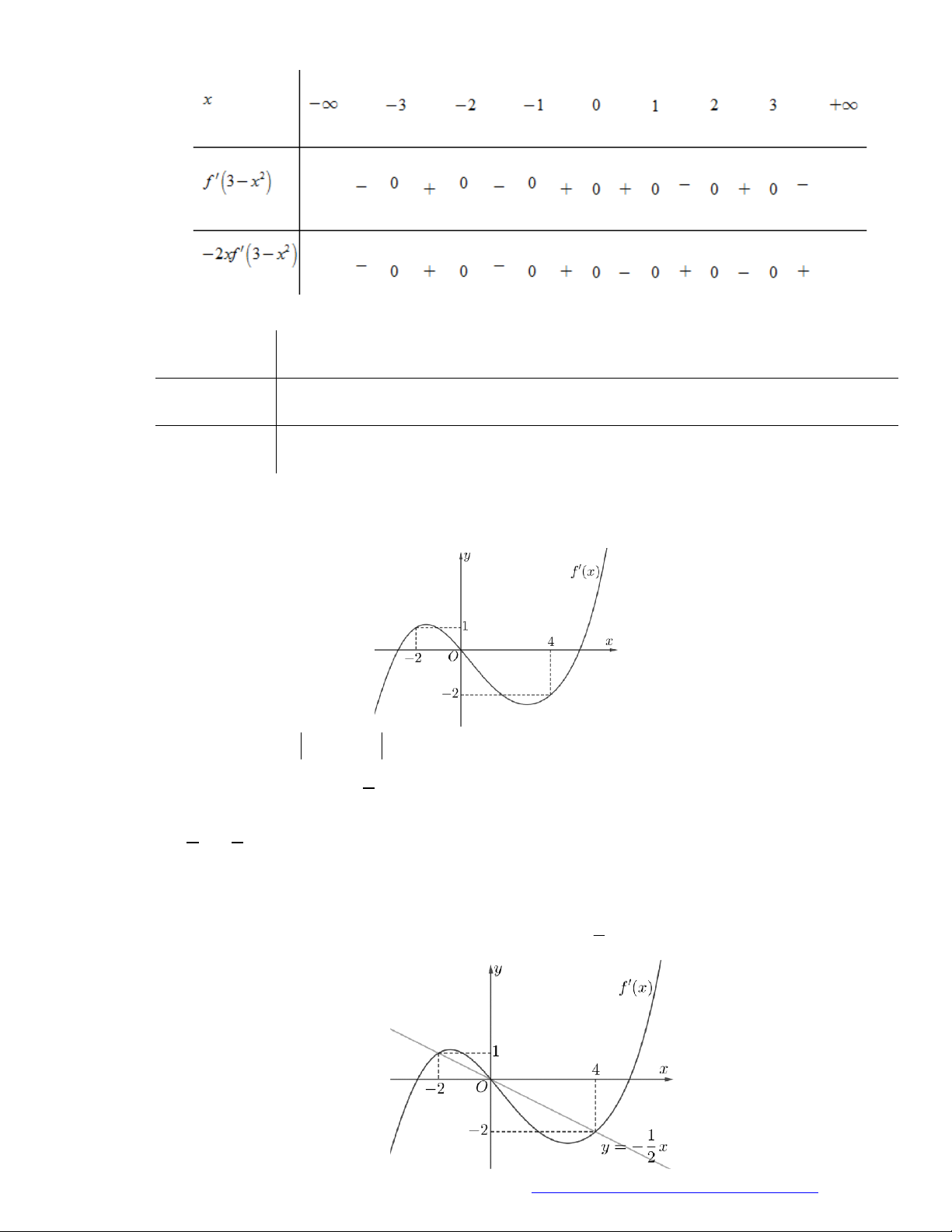
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
Bảng xét dấu của đạo hàm hàm số đã cho
Từ bảng xét dấu suy ra hàm số đồng biến trên
1; 0
.
x
3
2
1
0
1
2
3
2
3f x
0
0
0
0
0
0
0
2
2 3
xf x
0
0
0
0
0
0
0
Câu 10. (Chuyên Biên Hòa - Hà Nam - 2020) Cho hàm số đa thức
f x
có đạo hàm trên
. Biết
0 0f
và đồ thị hàm số
y f x
như hình sau.
Hàm số
2
4g x f x x
đồng biến trên khoảng nào dưới đây?
A.
4; .
B.
0;4 .
C.
; 2 .
D.
2 0; .
Lời giải
Chọn B
Xét hàm số
2
4h x f x x
trên
.
Vì
f x
là hàm số đa thức nên
h x
cũng là hàm số đa thức và
0 4 0 0h f
.
Ta có
4 2h x f x x
. Do đó
1
0
2
h x f x x
.
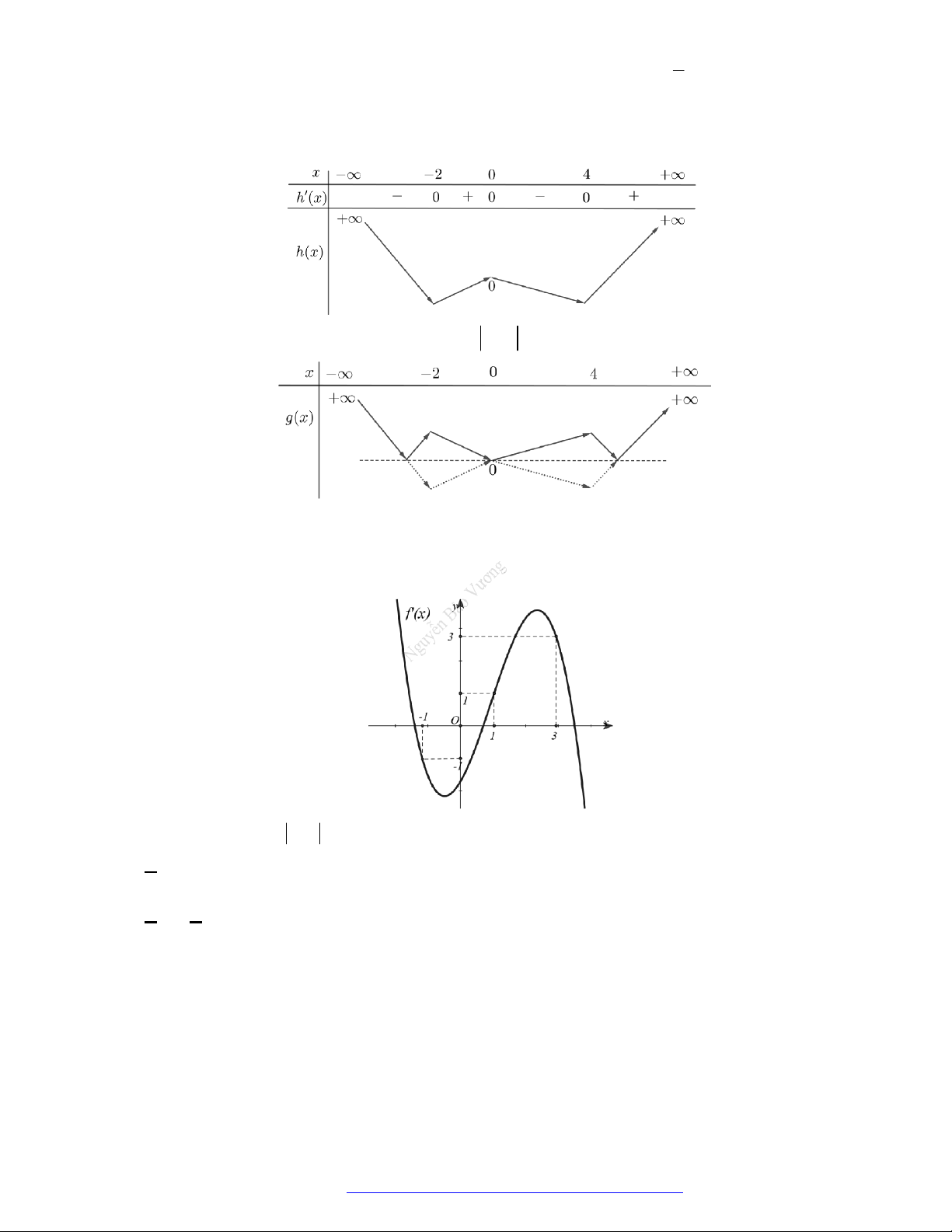
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 22 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Dựa vào sự tương giao của đồ thị hàm số
y f x
và đường thẳng
1
2
y x
, ta có
0 2;0;4h x x
Suy ra bảng biến thiên của hàm số
h x
như sau:
Từ đó ta có bảng biến thiên của hàm số
g x h x
như sau:
Dựa vào bảng biến thiên trên, ta thấy hàm số
g x
đồng biến trên khoảng
0;4
.
Câu 11. (Chuyên Thái Bình - 2020) Cho hàm số
( )f x
liên tục trên
có đồ thị hàm số
( )y f x
cho
như hình vẽ
Hàm số
2
( ) 2 1 2 2020g x f x x x
đồng biến trên khoảng nào?
A.
(0;1)
. B.
( 3;1)
. C.
(1;3)
. D.
( 2;0)
.
Lời giải
Chọn A
Ta có đường thẳng
y x
cắt đồ thị hàm số
( )y f x
tại các điểm
1; 1; 3x x x
như hình vẽ
sau:
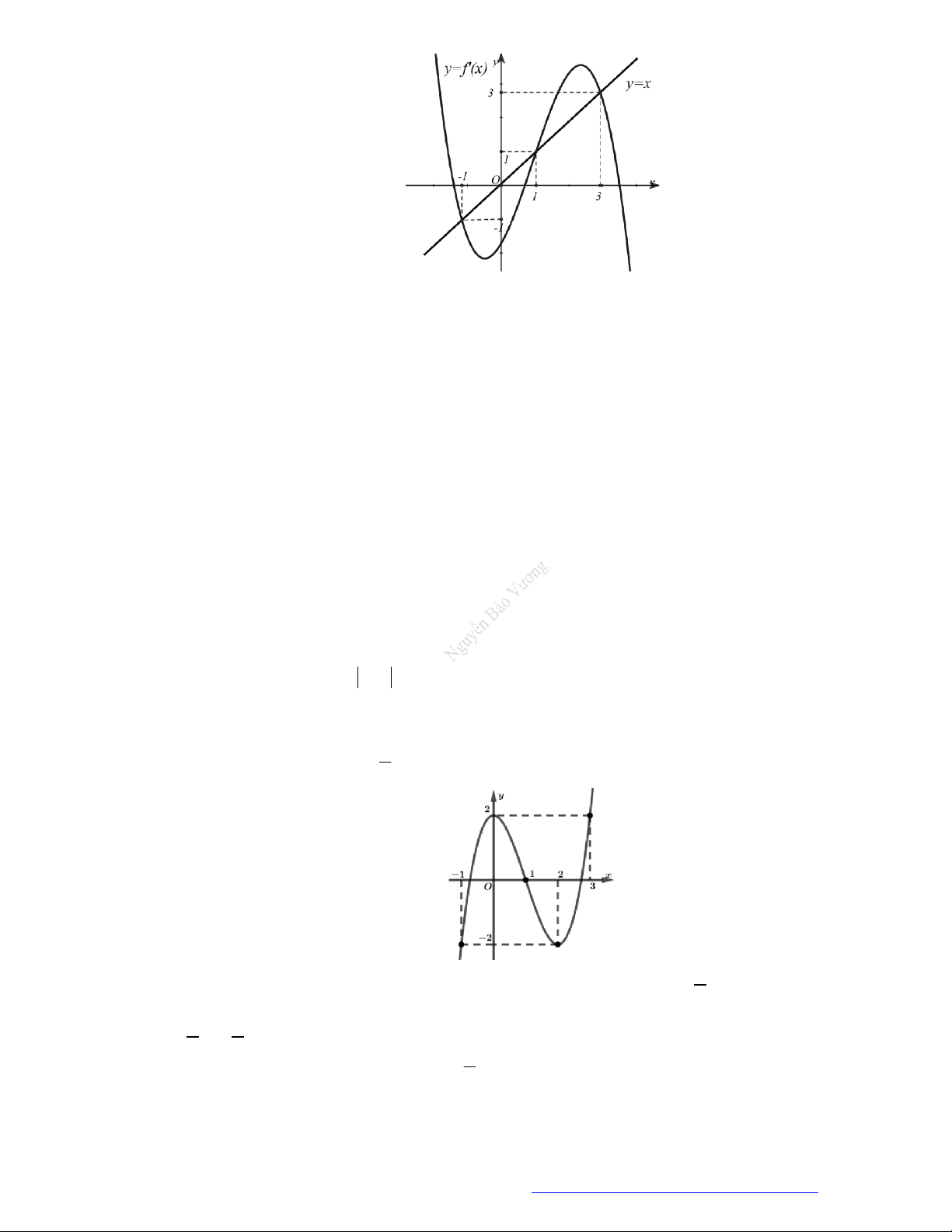
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
Dựa vào đồ thị của hai hàm số trên ta có
1
( )
1 3
x
f x x
x
và
1 1
( )
3
x
f x x
x
.
+ Trường hợp 1:
1 0 1x x
, khi đó ta có
2
( ) 2 1 2 2020g x f x x x
.
Ta có
( ) 2 1 2(1 )g x f x x
.
1 1 1 0 2
( ) 0 2 1 2(1 ) 0 1 1
1 3 2
x x
g x f x x f x x
x x
.
Kết hợp điều kiện ta có
0 1
( ) 0
2
x
g x
x
.
+ Trường hợp 2:
1 0 1x x
, khi đó ta có
2
( ) 2 1 2 2020g x f x x x
.
( ) 2 1 2( 1)g x f x x
1 1 0
( ) 0 2 1 2( 1) 0 1 1
1 1 3 2 4
x x
g x f x x f x x
x x
.
Kết hợp điều kiện ta có
( ) 0g x
2 4x
.
Vậy hàm số
2
( ) 2 1 2 2020g x f x x x
đồng biến trên khoảng
(0;1)
.
Câu 12. (Chuyên Lào Cai - 2020) Cho hàm số
f x
có đồ thị như hình bên. Hàm số
3 2
9
3 1 9
2
g x f x x x
đồng biến trên khoảng nào dưới đây?
A.
1;1
. B.
2;0
. C.
;0
. D.
1;
.
Lời giải
Chọn D
Xét hàm số
3 2 2
9
3 1 9 3 3 1 27 9
2
g x f x x x g x f x x x
Hàm số đồng biến tương đương
2
0 3 3 1 27 9 0g x f x x x
3 1 3 3 1 0 *f x x x
.
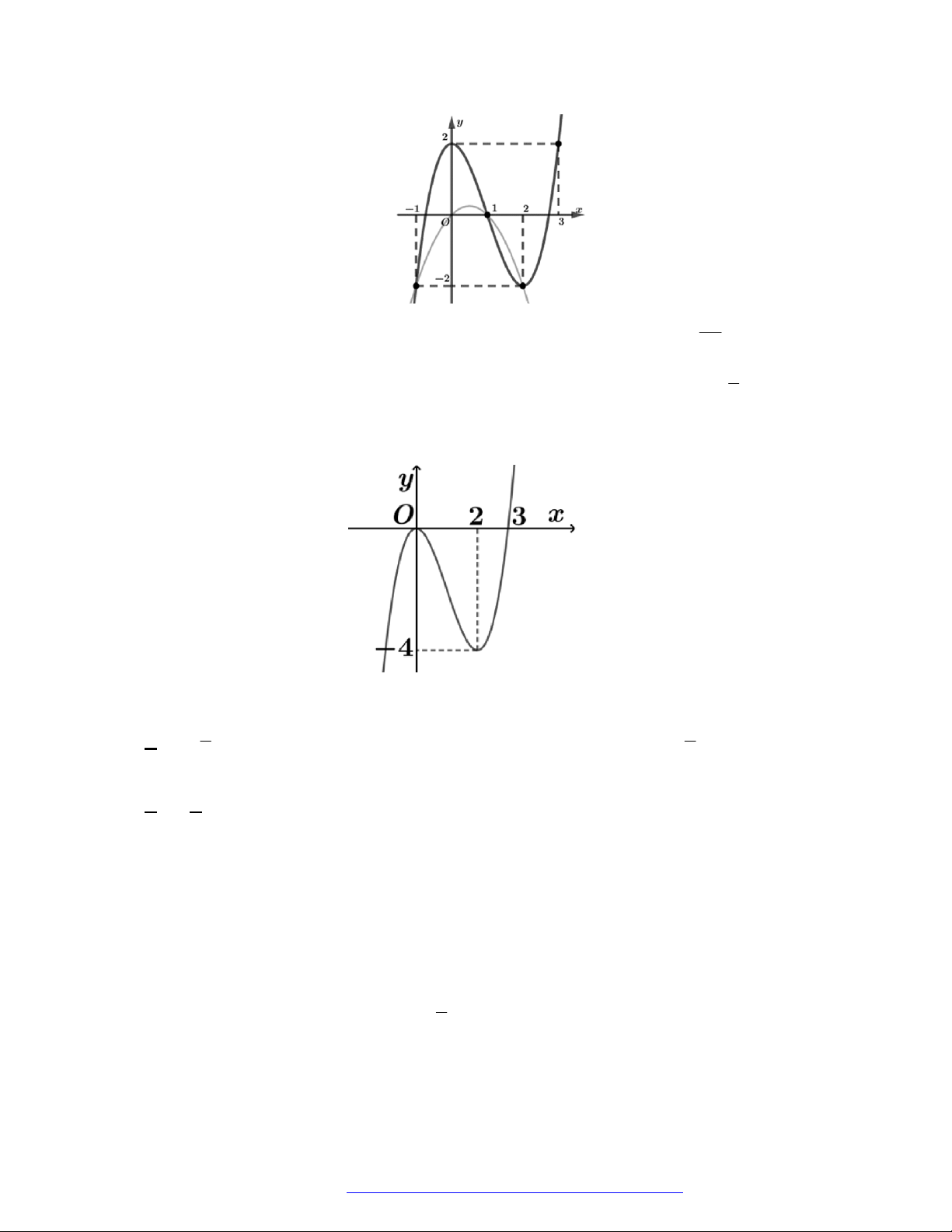
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 24 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Đặt
2
3 1 * 1 0t x f t t t f t t t
Vẽ parabol
2
y x x
và đồ thị hàm số
f x
trên cùng một hệ trục
Dựa vào đồ thị ta thấy
2
2
0
1 1 1 3 1 1
3
2 3 1 2
3
x
t x
f t t t
t x
x
.
Câu 13. (Sở Phú Thọ - 2020) Cho hàm số
y f x
có đồ thị hàm số
y f x
như hình vẽ
Hàm số
e 2 2020
x
g x f
nghịch biến trên khoảng nào dưới đây?
A.
3
1;
2
. B.
1;2
. C.
0;
. D.
3
;2
2
.
Lời giải
Chọn A
Dựa vào đồ thị hàm số
y f x
suy ra
0 3f x x
và
0 3f x x
.
e e 2
x x
g x f
.
Hàm số
e 2 2020
x
g x f
nghịch biến nếu
0g x
e e 2 0
x x
f
e 2 0
x
f
e 2 3 e 5 ln5
x x
x
.
Vậy hàm số đã cho nghịch biến trên
3
1;
2
.
Câu 14. (Lý Nhân Tông - Bắc Ninh - 2020) Cho hàm số
f x
có đồ thị hàm số
f x
như hình vẽ.
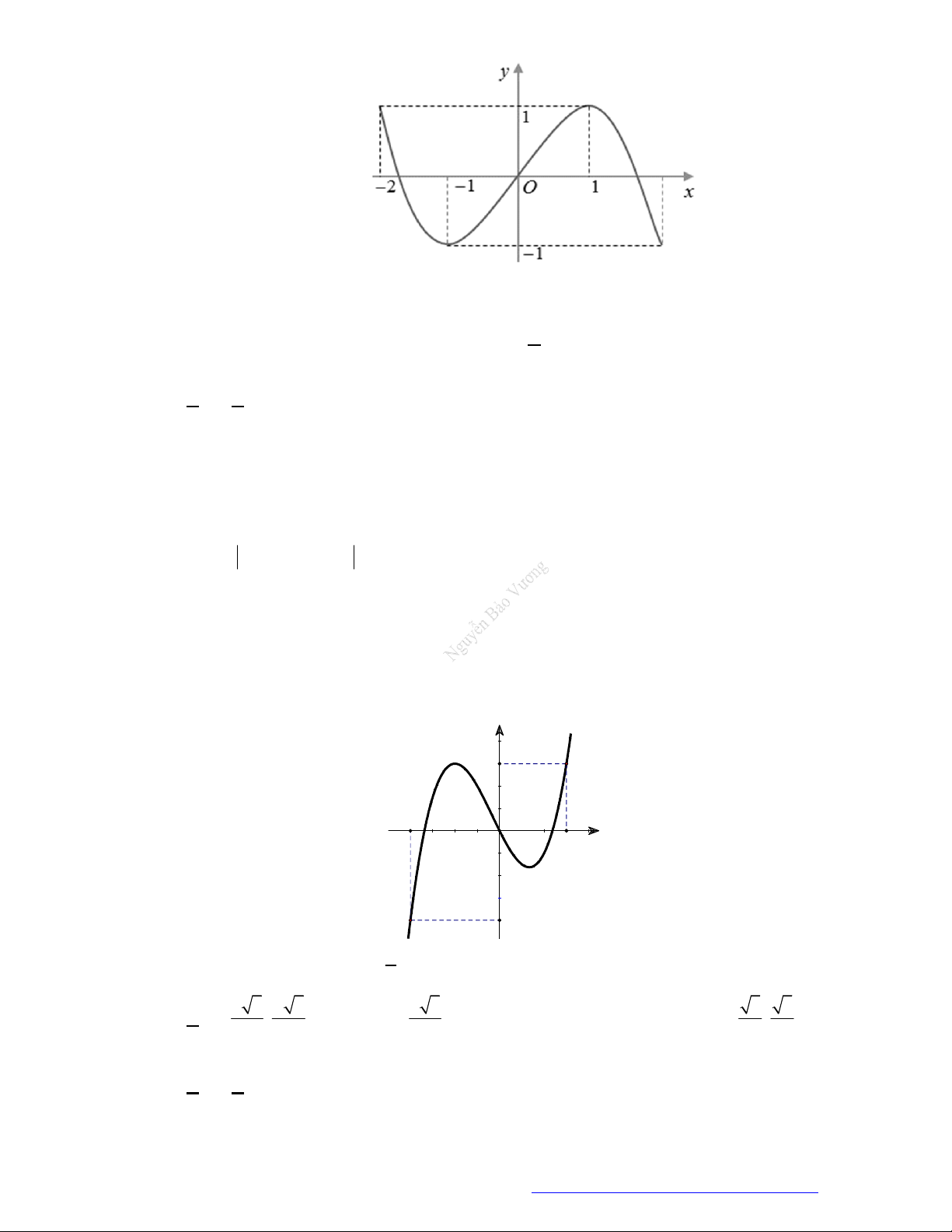
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25
Hàm số
2
cosy f x x x
đồng biến trên khoảng
A.
2;1
. B.
0;1
. C.
1;2
. D.
1;0
.
Lời giải
Chọn C
Đặt hàm
2
cosg x f x x x
.
Ta có:
sin . cos 2 1g x x f x x
.
Vì
cos 1;1x
nên từ đồ thị
f x
ta suy ra
cos 1;1f x
.
Do đó
sin . cos 1x f x
,
x
.
Ta suy ra
sin . cos 2 1 1 2 1 2 2g x x f x x x x
0, 1g x x
. Vậy hàm số đồng biến trên
1;2
.
Câu 15. (THPT Nguyễn Viết Xuân - 2020) Cho hàm số
f x
. Hàm số
y f x
có đồ thị như hình
vẽ.
Hàm số
2 4 2
9
( ) 3 1 3
2
g x f x x x
đồng biến trên khoảng nào dưới đây.
A.
2 3 3
;
3 3
. B.
2 3
0;
3
. C.
1;2
. D.
3 3
;
3 3
.
Lời giải
Chọn A
TXĐ:
D
Ta có:
2 3
6 3 1 18 6g x xf x x x
2 2
6 3 1 3 1x f x x
x
y
O
-4
3
3
-4
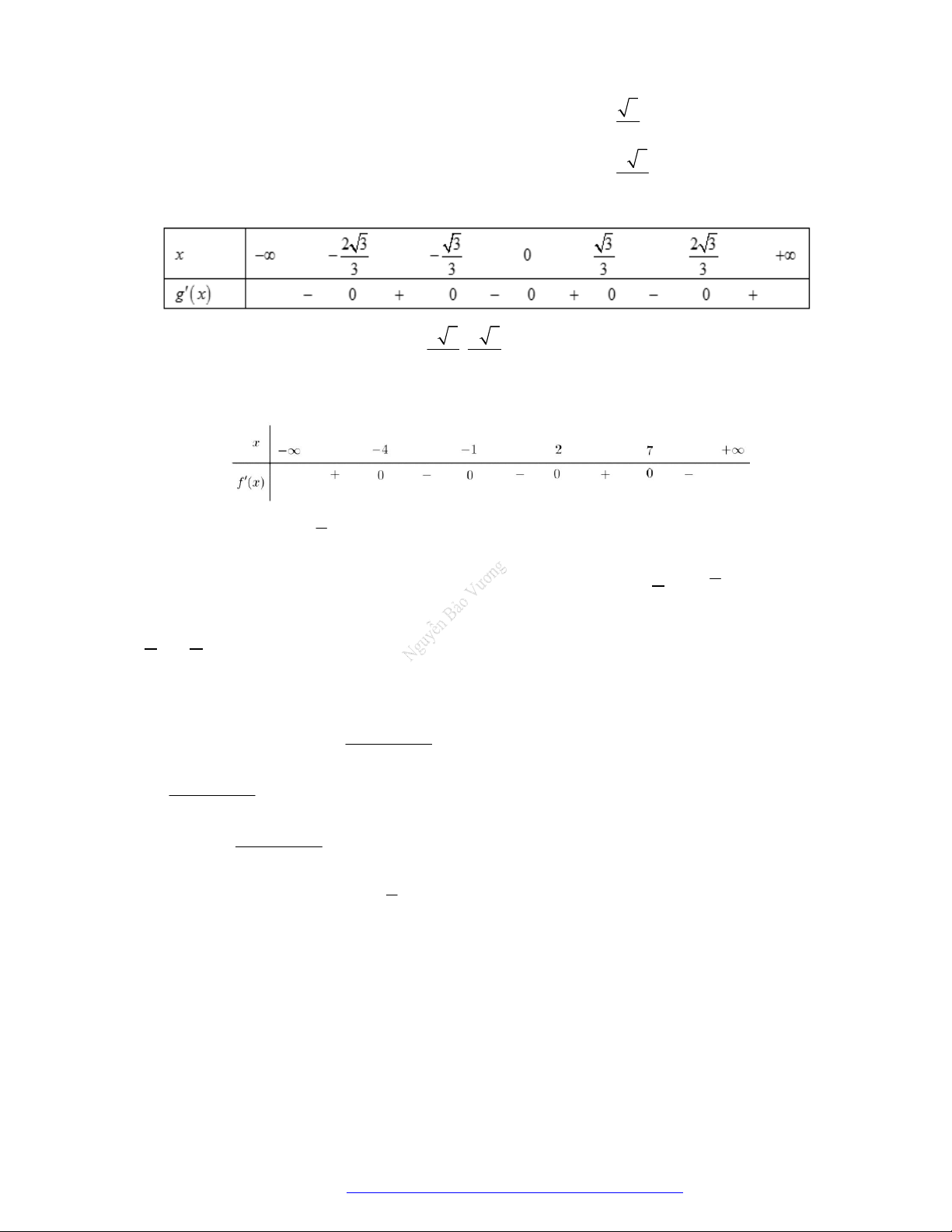
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 26 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
0g x
2 2
0
3 1 3 1
x
f x x
2
2
2
0
3 1 4( )
3 1 0
3 1 3
x
x VN
x
x
0
3
3
2 3
3
x
x
x
Bảng xét dấu:
Vậy hàm số đồng biến trong khoảng
2 3 3
;
3 3
.
Câu 16. (Trần Phú - Quảng Ninh - 2020) Cho hàm số
f x
có bảng xét dấu của đạo hàm như sau
Hàm số
3
2
2 1 8 5
3
y f x x x
nghịch biến trên khoảng nào dưới đây?
A.
; 2
. B.
1;
. C.
1;7
. D.
1
1;
2
.
Lời giải
Chọn D
Ta có
2
2 2 1 2 8y f x x
.
Xét
22
2 2 1 2 8 00 2 1 4f x xy f x x
Đặt
2 1t x
, ta có
2
2 15
4
t t
f t
Vì
2
2 15
0, 3;5
4
t t
t
. Mà
( ) 0, 3;2f t t
.
Nên
2
2 15
4
3;2
t t
f t t
.
Suy ra
1
3 2 1 2 2
2
x x
. Vậy chọn phương án D.
Câu 17. (Chuyên Thái Bình - Lần 3 - 2020) Cho hàm số
( )y f x
liên tục trên
có đồ thị hàm số
( )y f x
cho như hình vẽ.
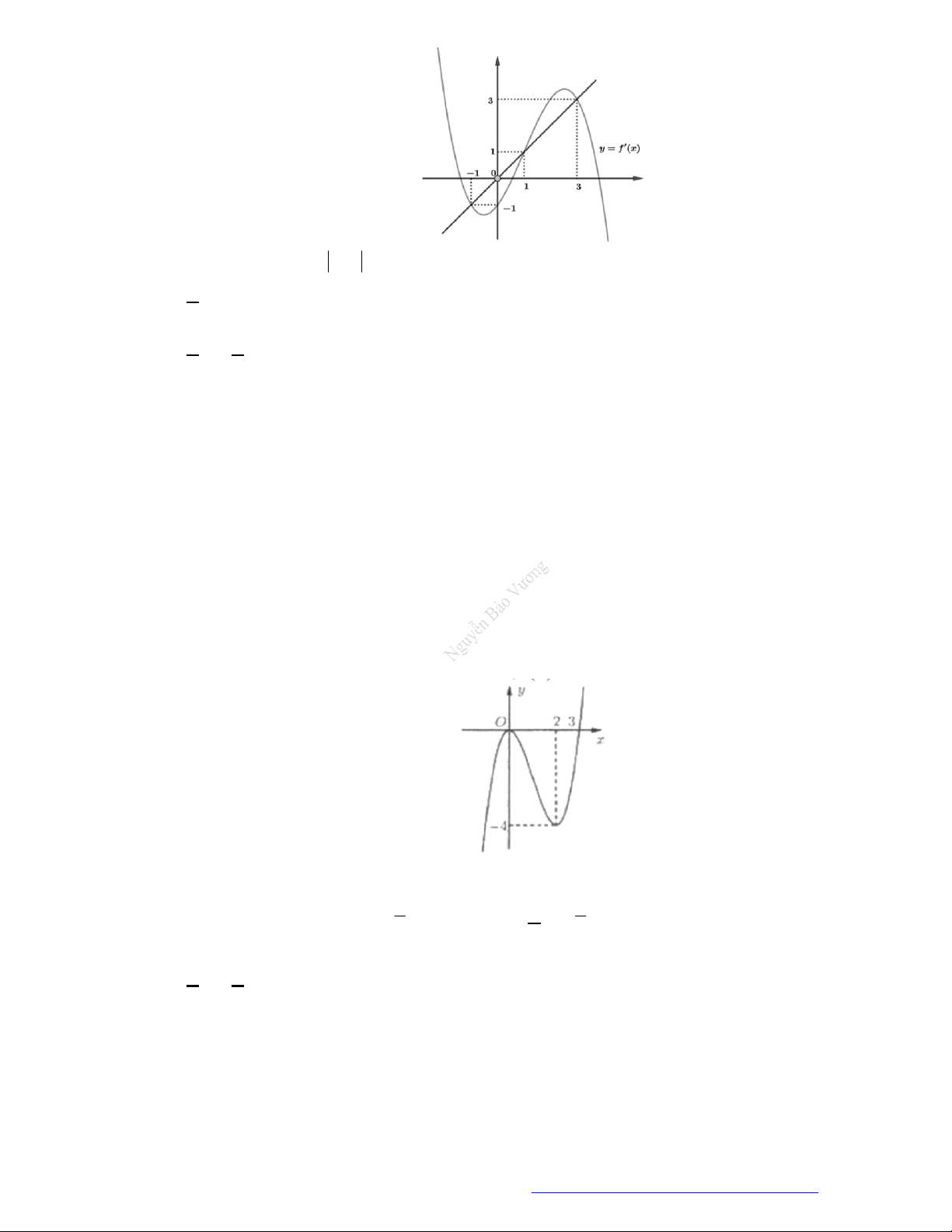
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27
Hàm số
2
( ) 2 1 2 2020g x f x x x
đồng biến trên khoảng nào?
A.
0;1
. B.
13;
. C.
1; 3
. D.
02;
.
Lời giải
Chọn A
+Với
1x
, ta có
2
2 1 1 2021g x f x x
2 1 2 1g x f x x
.
Hàm số đồng biến
2 1 2 1 0 1 1 *f x x f x x
.
Đặt
1t x
, khi đó
1 3 2 4
*
1 0 ( )
t x
f t t
t x loai
.
+Với
1,x
ta có
2
2 1 1 2021g x f x x
2 1 2 1g x f x x
Hàm số đồng biến
2 1 2 1 0 1 1 **f x x f x x
.
Đặt
1t x
, khi đó
1 1 0 2 0 1
**
3 2 2
t x x
f t t
t x x
.
Vậy hàm số
g x
đồng biến trên các khoảng
; 2
,
0;1
,
2;4
.
Câu 18. (Sở Phú Thọ - 2020) Cho hàm số
y f x
có đồ thị hàm số
f x
như hình vẽ
Hàm số
1 2020
x
g x f e
nghịch biến trên khoảng nào dưới đây?
A.
0;
. B.
1
;1
2
. C.
1
0;
2
. D.
1;1
.
Lời giải
Chọn C
1
x x
g x e f e
Do 0,
x
e x nên
0 1 0
x
g x f e
1 3
x
e
ln2x
, dấu bằng xảy ra tại hữu
hạn điểm.
Nên
g x
nghịch biến trên
;ln2
.
So với các đáp án thì chỉ có C thỏa mãn.
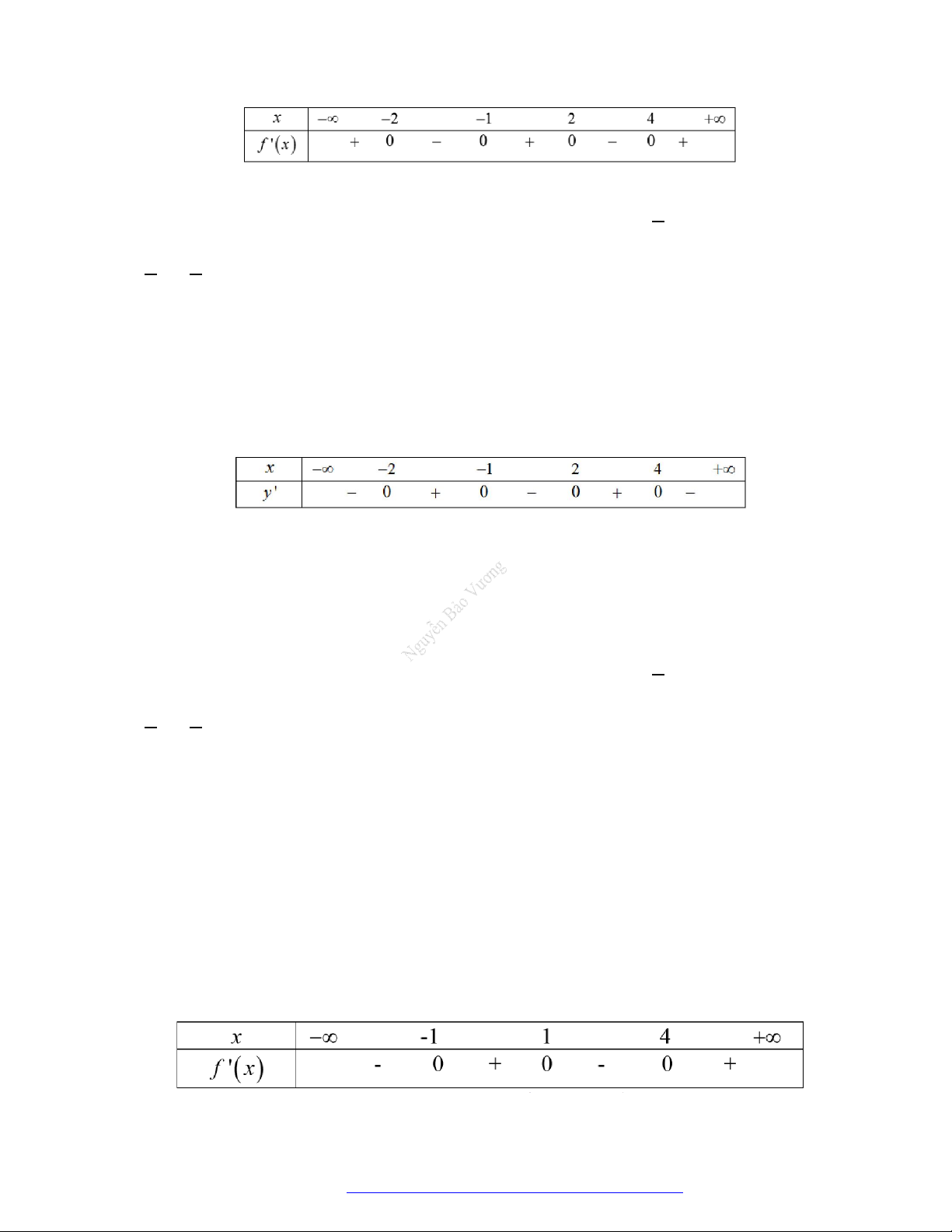
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 28 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 19. (THPT Anh Sơn - Nghệ An - 2020) Cho hàm số
y f x
có bảng xét dấu của đạo hàm như
sau.
Hàm số
2 2019y f x
nghịch biến trên khoảng nào trong các khoảng dưới đây?
A.
2;4
. B.
4;2
. C.
2; 1
. D.
1;2
.
Lời giải
Chọn D
Ta có
' 2 'y f x
2
1
' 0 2 ' 0
2
4
x
x
y f x
x
x
Từ bảng xét dấu của
'f x
ta có
Từ bảng xét dấu ta có hàm số nghịch biến trên khoảng
; 2
,
1;2
và
4;
Câu 20. (THPT Anh Sơn - Nghệ An - 2020) Cho hàm số
f x
xác định và liên tục trên
và có đạo
hàm
f x
thỏa mãn
1 2 2019f x x x g x
với
0g x
,
x
. Hàm số
1 2019 2020y f x x
nghịch biến trên khoảng nào?
A.
1;
. B.
0;3
. C.
;3
. D.
3;
.
Lời giải
Chọn D
Đặt
1 2019 2020h x f x x
.
Vì hàm số
f x
xác định trên
nên hàm số cũng xác định trên
.
Ta có
1 2019h x f x
.
Do
0h x
tại hữu hạn điểm nên để tìm khoảng nghịch biến của hàm số
h x
, ta tìm các giá trị
của
x
sao cho
0h x
1 2019 0f x
1 2019 0f x
3 0x x
(Do
0g x
,
x
)
0
3
x
x
.
Vậy hàm số
1 2019 2020y f x x
nghịch biến trên các khoảng
;0
và
3;
.
Câu 21. Cho hàm số
y f x
xác định trên
và có bảng xét dấu đạo hàm như sau:
Biết
2,f x x
. Xét hàm số
3 2
3 2 3 2020g x f f x x x
. Khẳng định nào sau
đây đúng?
h x
3 1 0
x x g x

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 29
A. Hàm số
g x
đồng biến trên khoảng
2; 1
.
B. Hàm số
g x
nghịch biến trên khoảng
0;1
.
C. Hàm số
g x
đồng biến trên khoảng
3;4
.
D. Hàm số
g x
nghịch biến trên khoảng
2;3
.
Lời giải
Chọn D
Ta có:
2
' 2 ' ' 3 2 3 6g x f x f f x x x
.
Vì
2,f x x
nên
3 2 1f x
x
Từ bảng xét dấu
'f x
suy ra
' 3 2 0,f f x x
Từ đó ta có bảng xét dấu sau:
Từ bảng xét dấu trên, loại trừ đáp án suy ra hàm số
g x
nghịch biến trên khoảng
2;3
.
Câu 22. Cho hàm số
f x
có bảng biến thiên như sau:
Hàm số
3 2
3.y f x f x
nghịch biến trên khoảng nào dưới đây?
A.
1; 2
. B.
3 ; 4
. C.
; 1
. D.
2 ; 3
.
Lời giải
Chọn D
Ta có
2
3. . 6. .y f x f x f x f x
= 3 . . 2f x f x f x
1 1
2 3 4 1 2 3 4
0 ,4 | 1
0 2 , ,3, | 1 2;4
' 0 1, 2,3,4
f x x x x
y f x x x x x x x x x
f x x
Lập bảng xét dấu ta có
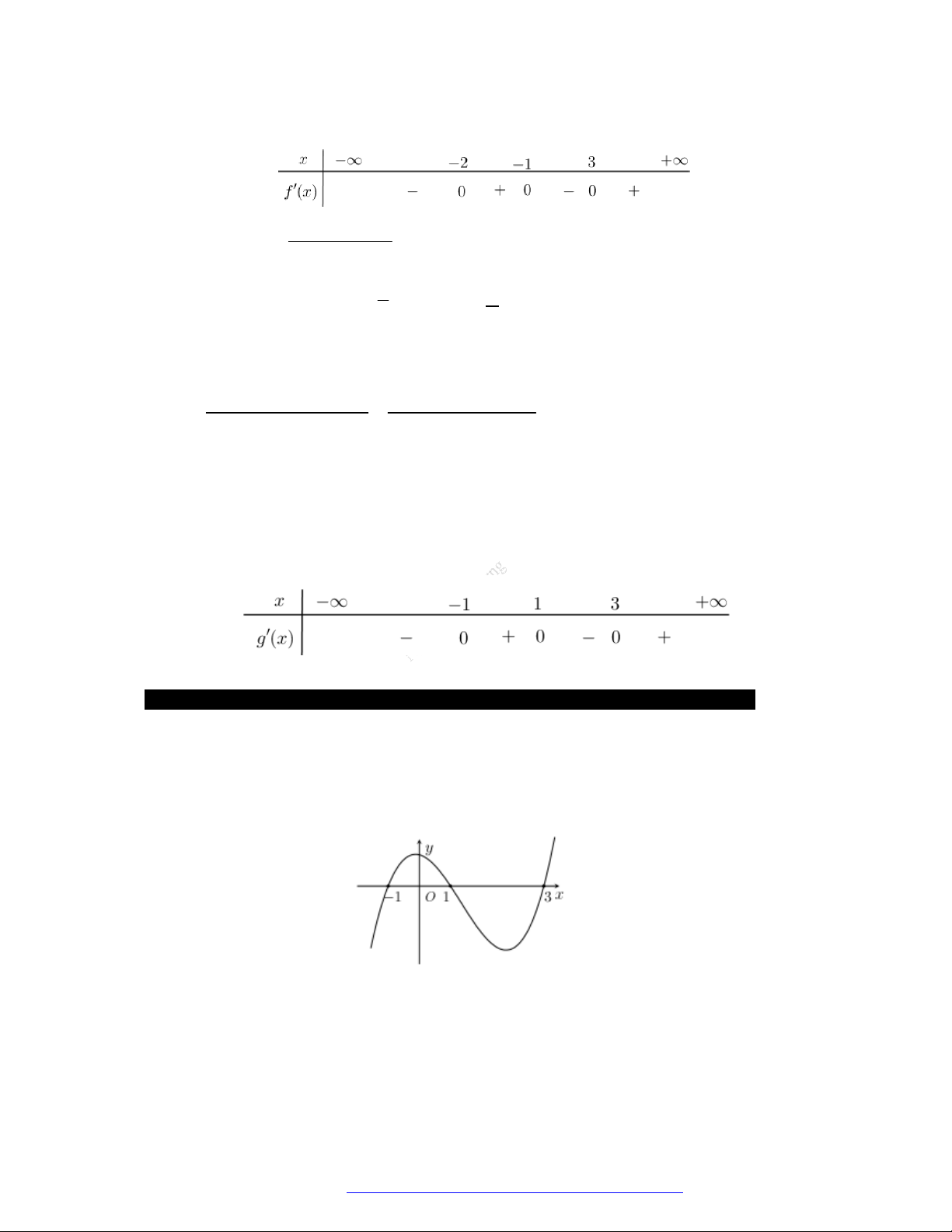
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 30 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Do đó ta có hàm số nghịch biến trên khoảng
2 ; 3
.
Câu 23. Cho hàm số
y f x
có đồ thị nằm trên trục hoành và có đạo hàm trên
, bảng xét dấu của biểu
thức
f x
như bảng dưới đây.
Hàm số
2
2
2
2 1
f x x
y g x
f x x
nghịch biến trên khoảng nào dưới đây?
A.
;1
. B.
5
2;
2
. C.
1;3
. D.
2;
.
Lời giải
Chọn C
2 2 2
2 2
2 2
2 . 2 2 2 . 2
2 1 2 1
x x f x x x f x x
g x
f x x f x x
.
2
2
2
2
1
1
2 2 0
2 2
0 1
2 0
2 1
3
2 3
x
x
x
x x
g x x
f x x
x x
x
x x
Ta có bảng xét dấu của
g x
:
Dựa vào bảng xét dấu ta có hàm số
y g x
nghịch biến trên các khoảng
; 1
và
1;3
.
Dạng 3. Bài toán hàm ẩn, hàm hợp liên quan đến tham số và một số bài toán khác
Câu 1. (Chuyên Lê Hồng Phong Nam Định 2019) Cho hàm số
y f x
có đạo hàm liên tục trên
.
Biết hàm số
y f x
có đồ thị như hình vẽ. Gọi
S
là tập hợp các giá trị nguyên
5;5m
để
hàm số
g x f x m
nghịch biến trên khoảng
1;2
. Hỏi
S
có bao nhiêu phần tử?
A.
4
. B.
3
. C.
6
. D.
5
.
Lời giải
Ta có
g x f x m
. Vì
y f x
liên tục trên
nên
g x f x m
cũng liên tục trên
. Căn cứ vào đồ thị hàm số
y f x
ta thấy
0 0g x f x m
1 1
1 3 1 3
x m x m
x m m x m
.
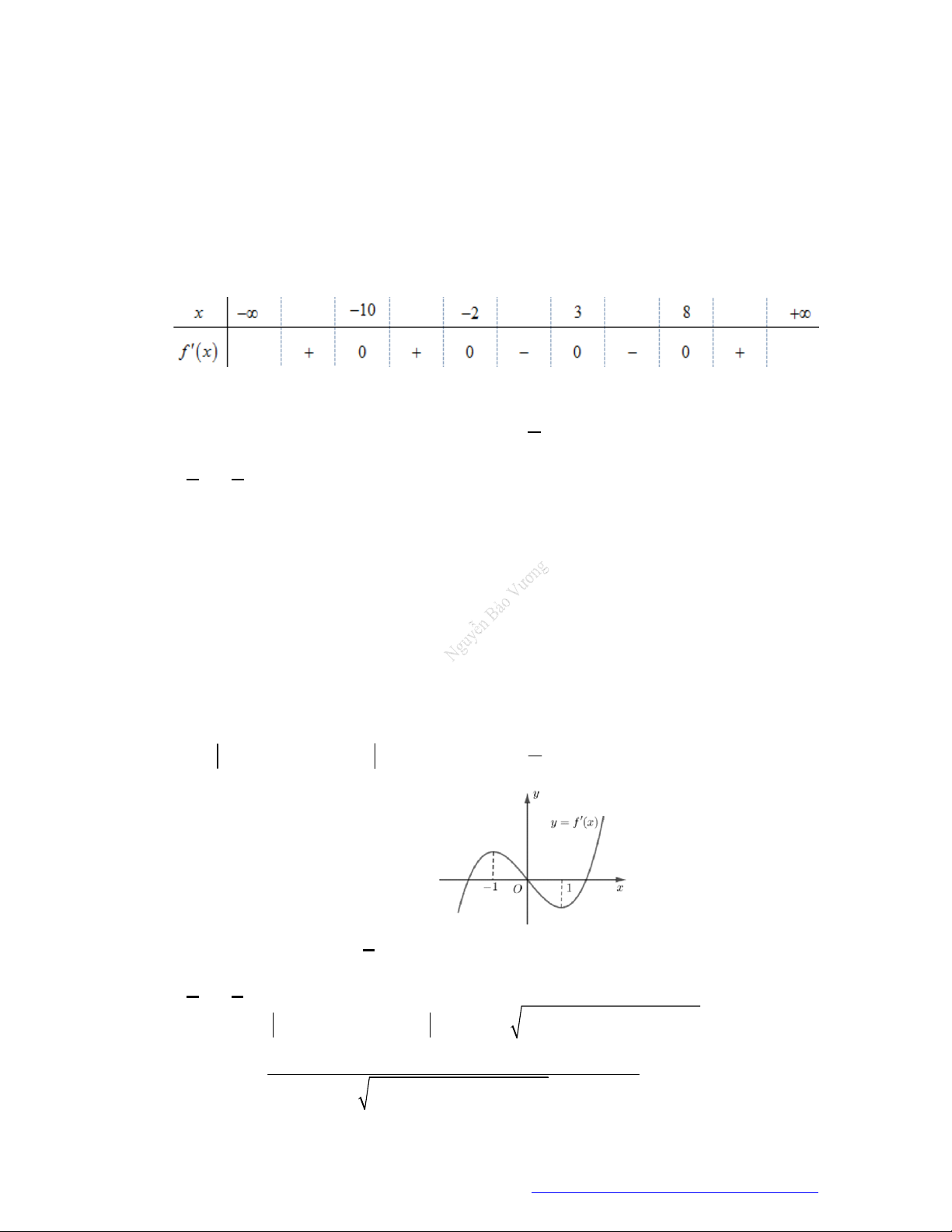
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 31
Hàm số
g x f x m
nghịch biến trên khoảng
1;2
2 1
3 2
1 1
m
m
m
3
0 1
m
m
.
Mà
m
là số nguyên thuộc đoạn
5;5
nên ta có
5; 4; 3;0;1S
.
Vậy
S
có 5 phần tử.
Câu 2. (Chuyên Nguyễn Bỉnh Khiêm - Quảng Nam - 2020) Cho hàm số
y f x
có đạo hàm trên
và bảnng xét dấu đạo hàm như hình vẽ sau:
Có bao nhiêu số nguyên
m
để hàm số
3
4y f x x m
nghịch biến trên khoảng
1;1
?
A.
3
. B.
0
. C.
1
. D.
2
.
Lời giải
Chọn C
Đặt
3 2
4 3 4t x x m t x
nên t đồng biến trên
1;1
và
5; 5t m m
Yêu cầu bài toán trở thành tìm
m
để hàm số
f t
nghịch biến trên khoảng
5; 5m m
.
Dựa vào bảng biến thiên ta được
5 2 3
3
5 8 3
m m
m
m m
Câu 3. (Chuyên ĐH Vinh - Nghệ An -2020) Cho hàm số
f x
có đạo hàm trên
và
1 1f
. Đồ thị
hàm số
y f x
như hình bên. Có bao nhiêu số nguyên dương
a
để hàm số
4 sin cos2y f x x a
nghịch biến trên
0;
2
?
A.
2
. B.
3
. C. Vô số. D.
5
.
Lời giải
Chọn B
Đặt
2
4 sin cos2 4 sin cos 2g x f x x a g x f x x a
.
2
4cos . sin 2sin 2 4 sin cos 2
4 sin cos2
x f x x f x x a
g x
f x x a
.
Ta có
4cos . sin 2sin 2 4cos sin sinx f x x x f x x
.
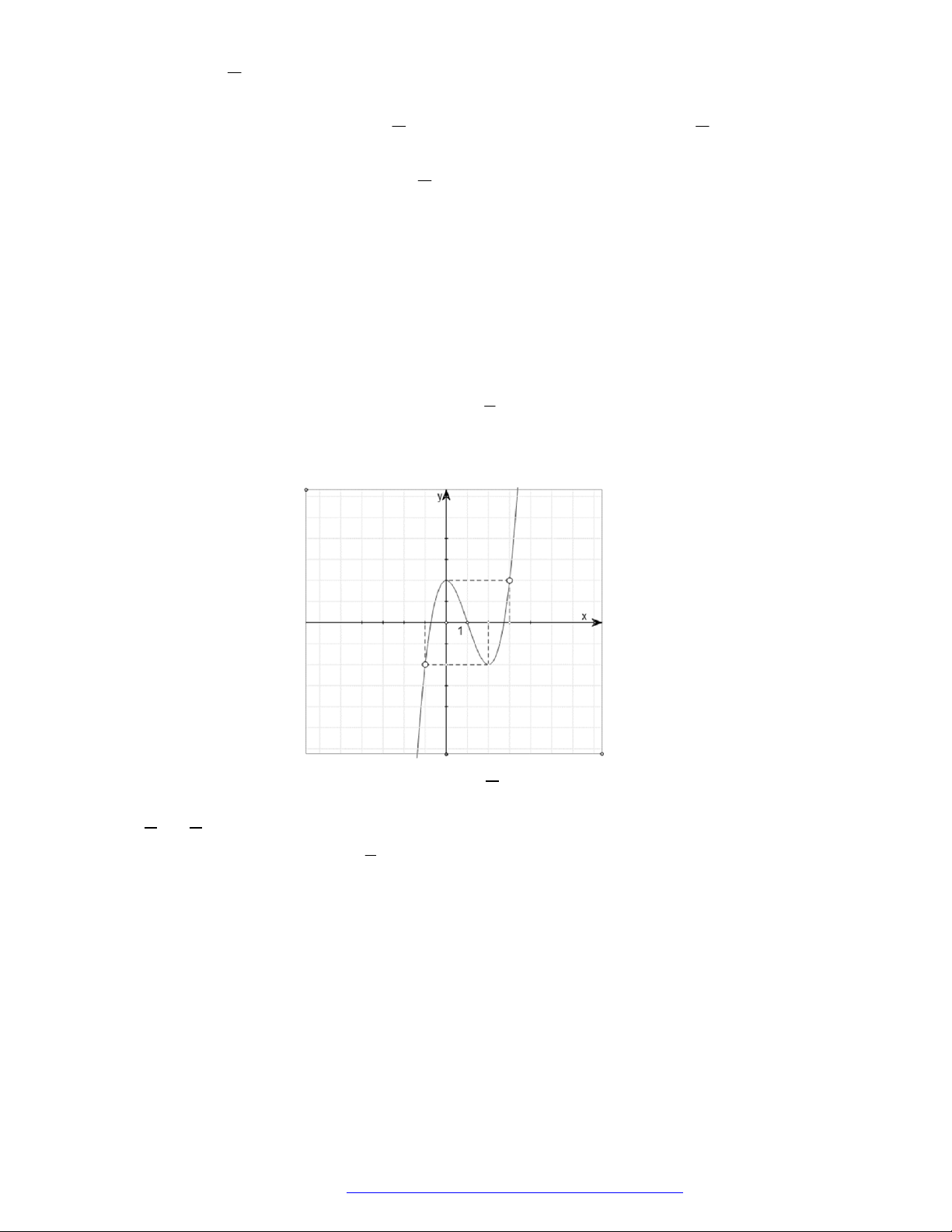
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 32 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Với
0;
2
x
thì
cos 0,sin 0;1 sin sin 0x x f x x
.
Hàm số
g x
nghịch biến trên
0;
2
khi
4 sin cos2 0, 0;
2
f x x a x
2
4 sin 1 2sin , 0;
2
f x x a x
.
Đặt
sint x
được
2
4 1 2 , 0;1f t t a t
(*).
Xét
2
4 1 2 4 4 4 1h t f t t h t f t t f t
.
Với
0;1t
thì
0h t h t
nghịch biến trên
0;1
.
Do đó (*)
2
1 4 1 1 2.1 3a h f
. Vậy có 3 giá trị nguyên dương của a thỏa mãn.
Câu 4. (Chuyên Quang Trung - 2020) Cho hàm số
y f x
có đạo hàm liên tục trên
và có đồ thị
y f x
như hình vẽ. Đặt
2
1
1 2019
2
g x f x m x m
, với
m
là tham số thực. Gọi
S
là tập hợp các giá trị nguyên dương của
m
để hàm số
y g x
đồng biến trên khoảng
5;6
.
Tổng tất cả các phần tử trong
S
bằng
A.
4
. B.
11
. C.
14
. D.
20
.
Lời giải
Chọn C
Xét hàm số
2
1
1 2019
2
g x f x m x m
1g x f x m x m
Xét phương trình
0 1g x
Đặt x m t , phương trình
1
trở thành
1 0 1 2f t t f t t
Nghiệm của phương trình
2
là hoành độ giao điểm của hai đồ thị hàm số
y f t
và
1y t
Ta có đồ thị các hàm số
y f t
và
1y t
như sau:
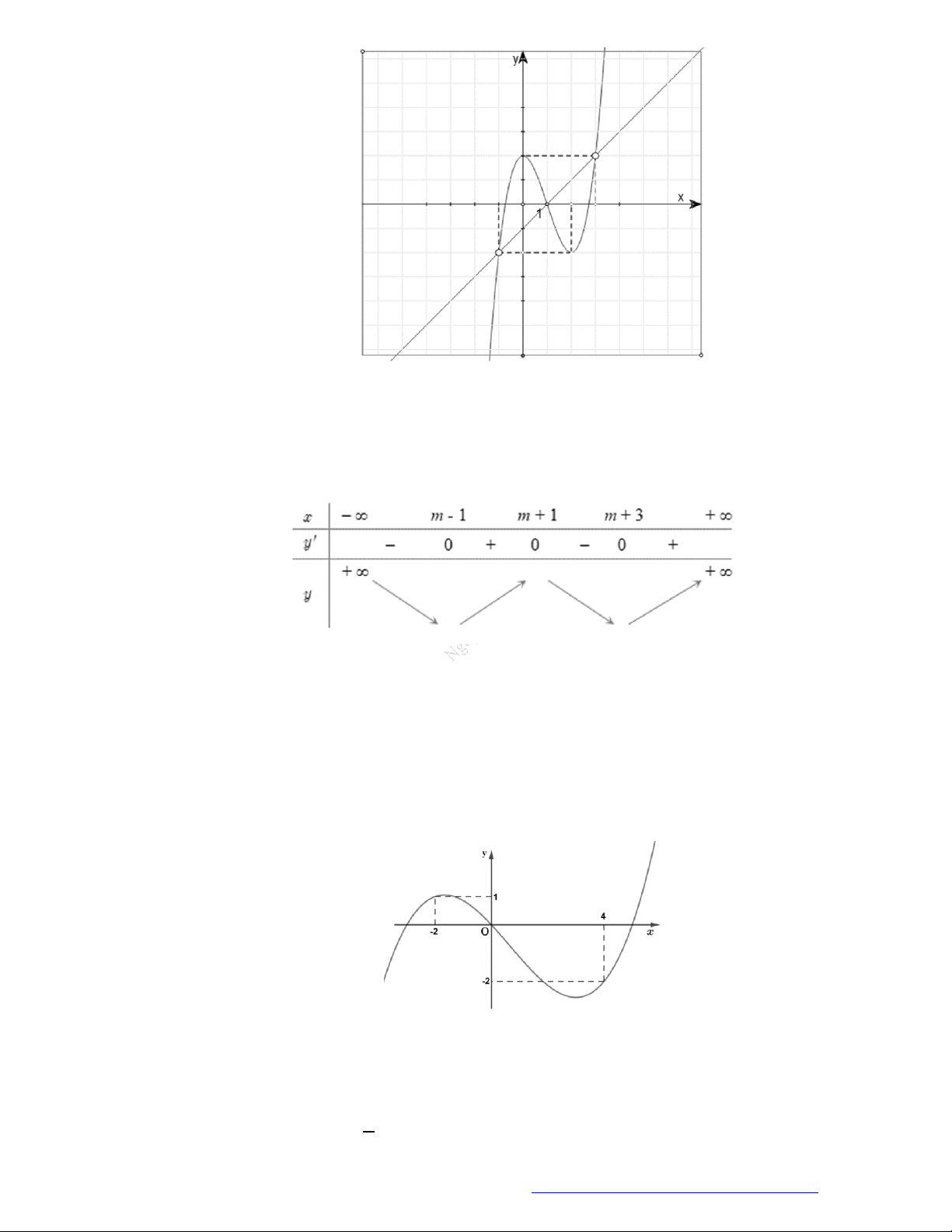
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 33
Căn cứ đồ thị các hàm số ta có phương trình
2
có nghiệm là:
1 1
1 1
3 3
t x m
t x m
t x m
Ta có bảng biến thiên của
y g x
Để hàm số
y g x
đồng biến trên khoảng
5;6
cần
1 5
5 6
1 6
2
3 5
m
m
m
m
m
Vì
*m m
nhận các giá trị
1;2;5;6 14S
.
Câu 5. (Sở Hà Nội - Lần 2 - 2020) Cho hàm số
4 3 2
, 0y ax bx cx dx e a
. Hàm số
'y f x
có đồ thị như hình vẽ
Gọi S là tập hợp tất cả các giá trị nguyên thuộc khoảng
6; 6
của tham số
m
để hàm số
2 2
3 2 3 2g x f x m x m x m
nghịch biến trên
0;1
. Khi đó, tổng giá trị các
phần tử của S là
A. 12. B. 9. C. 6. D. 15.
Lời giải

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 34 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Chọn B
Xét
' 2 ' 3 2 2 3g x f x m x m
. Xét phương trình
' 0g x
, đặt
3 2t x m
thì phương trình trở thành
2
2. ' 0 4
2
0
t
t
f t t
t
.
Từ đó,
1 2 3
5 3 1
' 0 , ,
2 2 2
m m m
g x x x x
. Lập bảng xét dấu, đồng thời lưu ý
nếu
1
x x
thì
1
t t
nên
0f x
. Và các dấu đan xen nhau do các nghiệm đều làm đổi dấu
đạo hàm nên suy ra
2 1 3
' 0 ; ;g x x x x x
.
Vì hàm số nghịch biến trên
0;1
nên
' 0, 0;1g x x
từ đó suy ra
3 5
0 1
2 2
1
1
2
m m
m
và giải ra các giá trị nguyên thuộc
6;6
của
m
là -3; 3; 4; 5. Từ đó
chọn câu B
Câu 6. (Chuyên Quang Trung - Bình Phước - Lần 2 - 2020) Cho hàm số
y f x
có đạo hàm liên
tục trên
và có đồ thị
y f x
như hình vẽ bên. Đặt
2
1
1 2019
2
g x f x m x m
,
với
m
là tham số thực. Gọi
S
là tập hợp các giá trị nguyên dương của
m
để hàm số
y g x
đồng biến trên khoảng
5 6;
. Tổng tất cả các phần tử trong
S
bằng:
A.
4
. B.
11
. C.
14
. D.
20
.
Lời giải
Chọn C
Ta có
1
g x f x m x m
Cho
0 1
g x f x m x m
Đặt
1 'x m t f t t
Khi đó nghiệm của phương trình là hoành độ giao điểm của đồ thị hàm số
y f t
và và đường
thẳng
1 y t
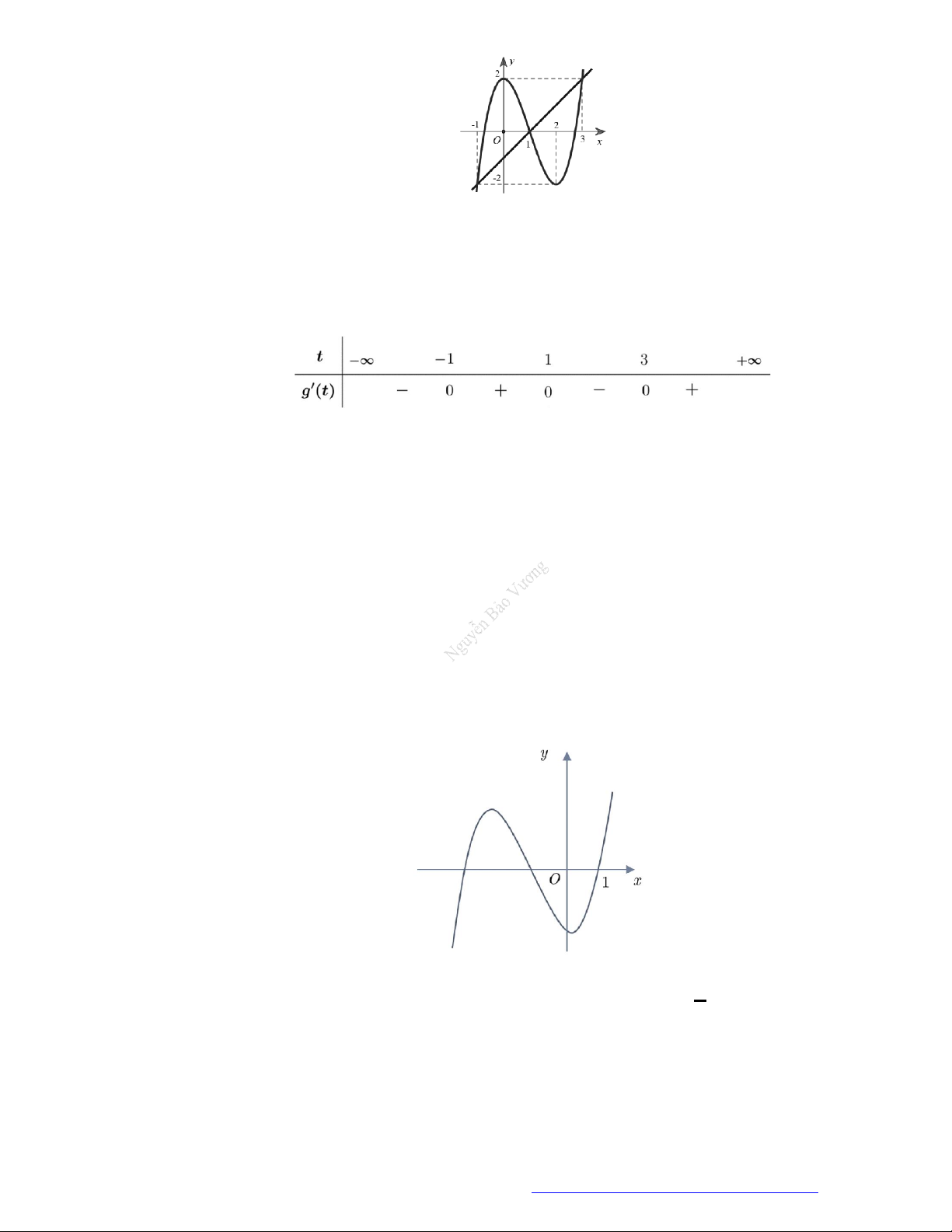
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 35
Dựa vào đồ thị hàm số ta có được
1
1 1
3
t
f t t t
t
Bảng xét dấu của
g t
Từ bảng xét dấu ta thấy hàm số
g t
đồng biến trên khoảng
1 1 ;
và
3 ;
Hay
1 1 1 1 1 1
3 3 3
t x m m x m
t x m x m
Để hàm số
g x
đồng biến trên khoảng
5 6;
thì
1 5 6 1 5 6
3 5 6 2
m m m
m m
Vì
m
là các số nguyên dương nên
1 2 5 6 ; ; ;S
Vậy tổng tất cả các phần tử của
S
là:
1 2 5 6 14
.
Câu 7. Cho hàm số
y f x
liên tục có đạo hàm trên
. Biết hàm số
'f x
có đồ thị cho như hình vẽ.
Có bao nhiêu giá trị nguyên của
m
thuộc
2019;2019
để hàm só
2019 2
x
g x f mx
đồng biến trên
0;1
A.
2028
. B.
2019
. C.
2011
. D.
2020
Lời giải
Chọn D
Ta có
' 2019 ln 2019. ' 2019
x x
g x f m
.
Ta lại có hàm số 2019
x
y đồng biến trên
0;1
.
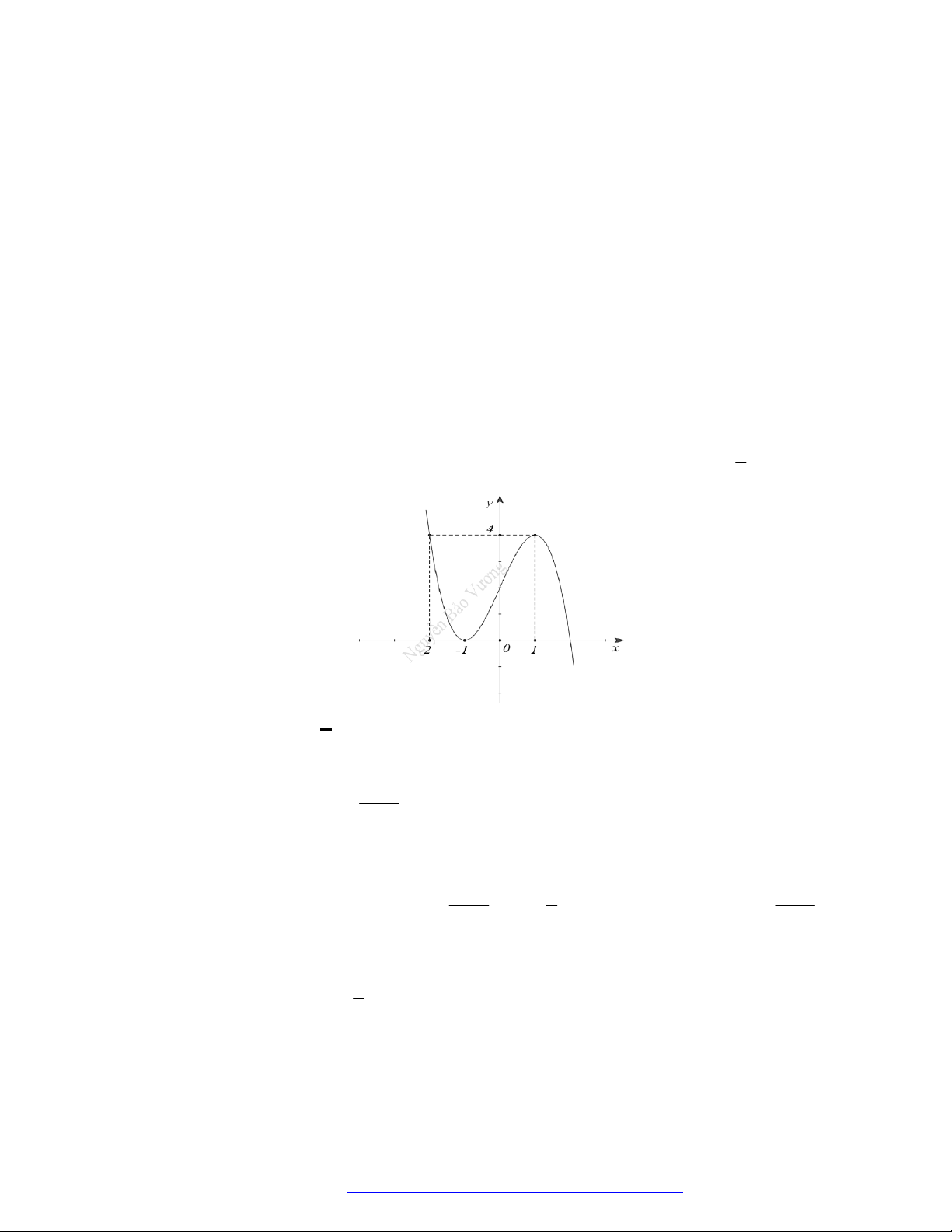
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 36 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Với
0;1x
thì
2019 1;2019
x
mà hàm
'y f x
đồng biến trên
1;
nên hàm
' 2019
x
y f
đồng biến trên
0;1
Mà
2019 1; ' 2019 0 0;1
x x
f x
nên hàm
2019 ln 2019. ' 2019
x x
h x f
đồng biến trên
0;1
Hay
0 0, 0;1h x h x
Do vậy hàm số
g x
đồng biến trên đoạn
0;1
' 0, 0;1g x x
2019 ln 2019. ' 2019 , 0;1
x x
m f x
0;1
min 0 0
x
m h x h
Vì
m
nguyên và
2019;2019m
có
2020
giá trị
m
thỏa mãn yêu cầu bài toán.
Câu 8. Cho hàm số
( )y f x
có đồ thị
( )f x
như hình vẽ. Có bao nhiêu giá trị nguyên
2020;2020m
để hàm số
2
2 3 ln 1 2g x f x x mx
đồng biến trên
1
;2
2
?
A.
2020
. B.
2019
. C.
2021
. D.
2018
.
Lời giải
Chọn B
+ Ta có
2
2
2 2 3 2
1
x
g x f x m
x
.
Hàm số
g x
đồng biến trên
1
;2
2
khi và chỉ khi
2
1
0, 1;2 2 3 , ;2
1 2
x
g x x m f x x
x
2
1
;2
2
min 2 3
1
x
x
m f x
x
1
+ Đặt
2 3t x
, khi đó
1
;2 2;1
2
x t
.
Từ đồ thị hàm
f x
suy ra
0, 2;1f t t
và
0f t
khi
1t
.
Tức là
1
2 3 0, ;2
2
f x x
1
;2
2
min 2 3 0
x
f x
khi
1x
.
2
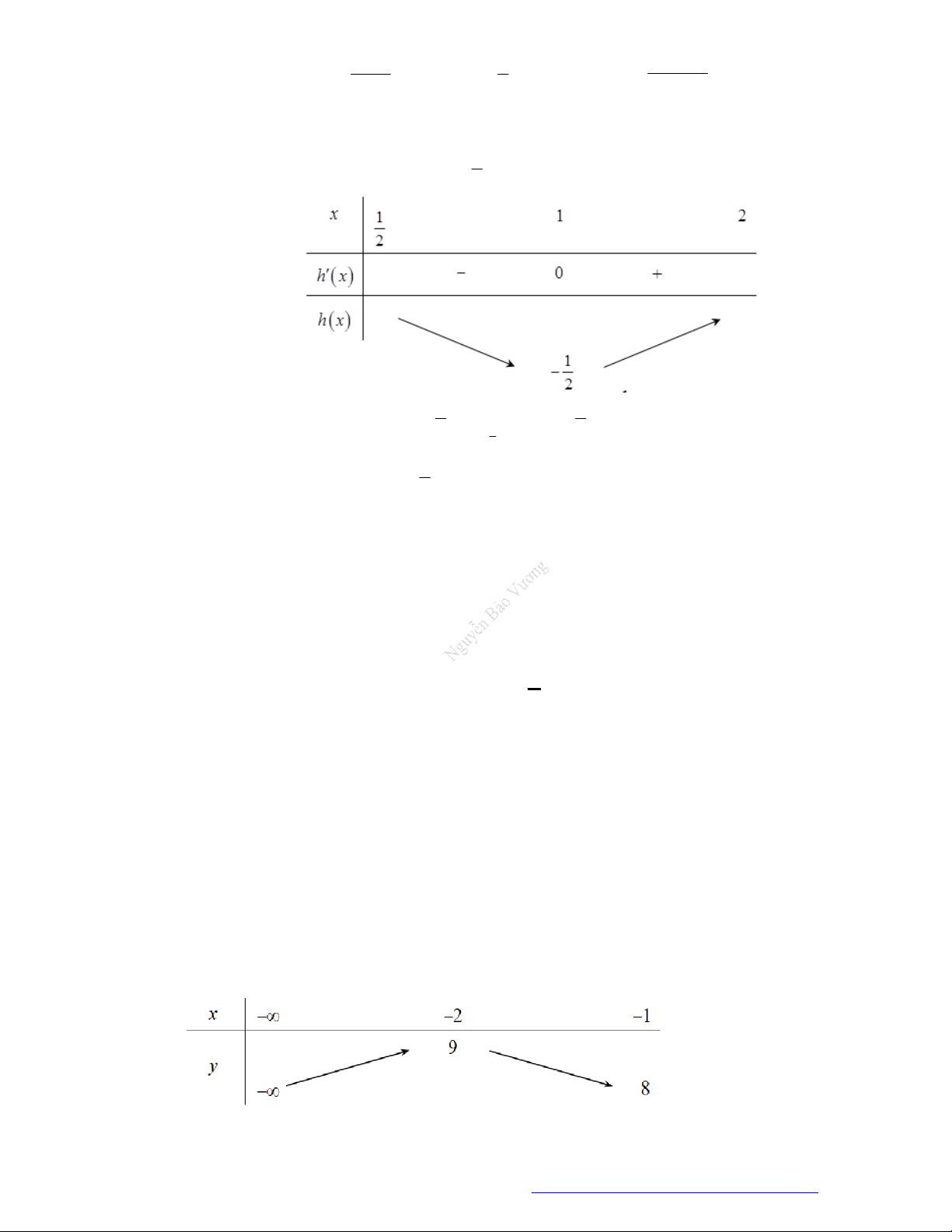
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 37
+ Xét hàm số
2
1
x
h x
x
trên khoảng
1
;2
2
. Ta có
2
2
2
1
1
x
h x
x
và
2
0 1 0 1h x x x
.
Bảng biến thiên của hàm số
h x
trên
1
;2
2
như sau:
Từ bảng biến thiên suy ra
1
2
h x
1
;2
2
1
min
2
x
h x
khi
1x
.
3
Từ
1
,
2
và
3
suy ra
1
2
m
.
Kết hợp với
m
,
2020;2020m
thì
2019; 2018;....; 2; 1m
.
Vậy có tất cả
2019
giá trị
m
cần tìm.
Câu 9. Cho hàm số
f x
liên tục trên
và có đạo hàm
2 2
2 6f x x x x x m
với mọi
x
.
Có bao nhiêu số nguyên
m
thuộc đoạn
2020;2020
để hàm số
1g x f x
nghịch biến
trên khoảng
; 1
?
A.
2016
. B.
2014
. C.
2012
. D.
2010
.
Lời giải
Chọn C
Ta có:
2 2
1 1 1 1 6 1g x f x x x x x m
2
2
1 1 4 5x x x x m
Hàm số
g x
nghịch biến trên khoảng
; 1
0, 1g x x
*
, (dấu
" "
xảy ra tại hữu hạn điểm).
Với
1x
thì
2
1 0x
và
1 0x
nên
*
2
4 5 0, 1x x m x
2
4 5, 1m x x x .
Xét hàm số
2
4 5y x x trên khoảng
; 1
, ta có bảng biến thiên:
Từ bảng biến thiên suy ra
9m
.
Kết hợp với
m
thuộc đoạn
2020;2020
và
m
nguyên nên
9;10;11;...;2020m
.
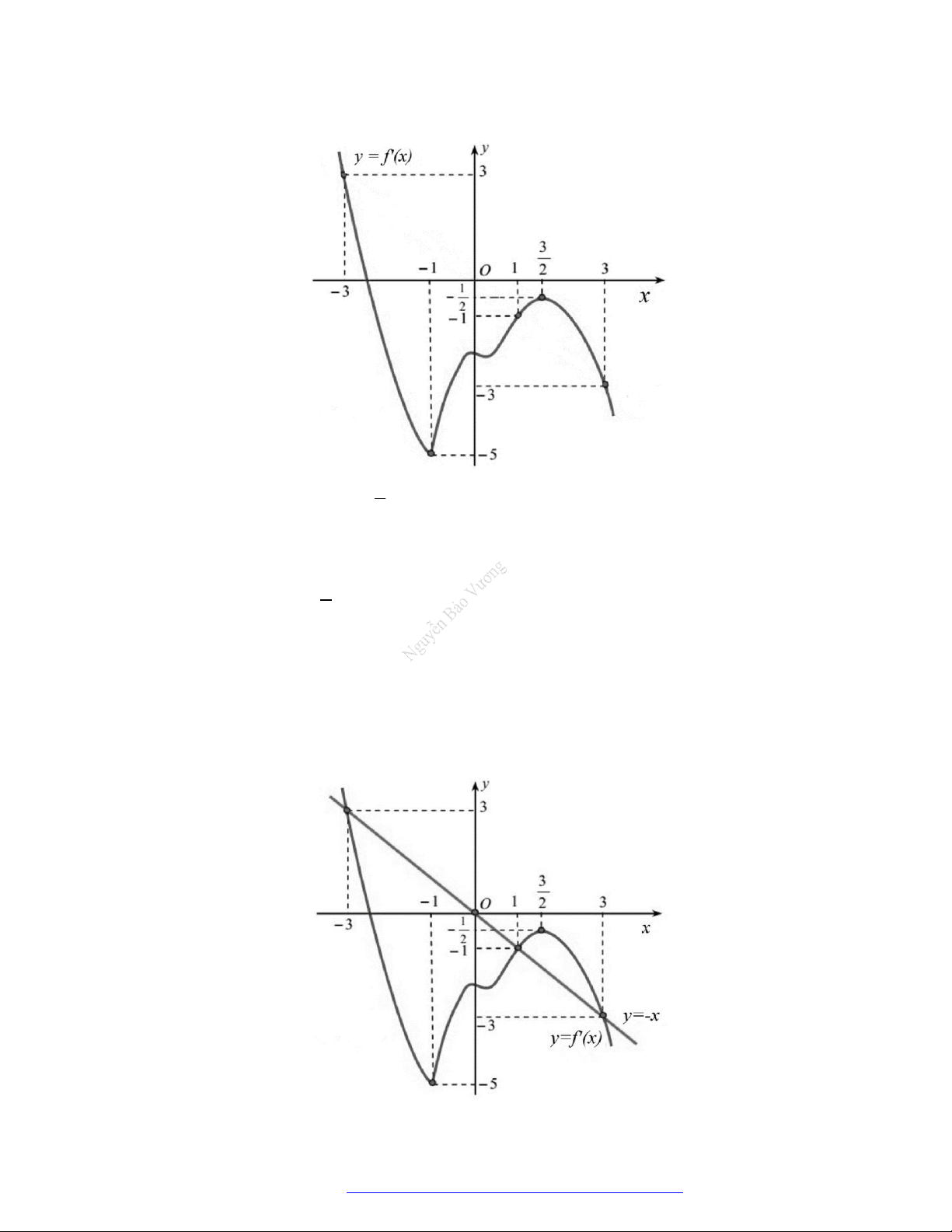
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 38 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Vậy có
2012
số nguyên
m
thỏa mãn đề bài.
Câu 10. Cho hàm số
f x
xác định và liên tục trên
R
. Hàm số
y f x
liên tục trên
và có đồ thị
như hình vẽ.
Xét hàm số
2
1
2 2 2020
2
g x f x m m x
, với
m
là tham số thực. Gọi
S
là tập hợp các
giá trị nguyên dương của
m
để hàm số
y g x
nghịch biến trên khoảng
3;4
. Hỏi số phần tử
của
S
bằng bao nhiêu?
A.
4
. B.
2
. C.
3
. D. Vô số.
Lời giải
Chọn B
Ta có
' ' 2 2g x f x m m x
.
Đặt
'h x f x x
. Từ đồ thị hàm số
'y f x
và đồ thị hàm số
y x
trên hình vẽ suy
ra:
3 1
0 '
3
x
h x f x x
x
.
Ta có
3 2 1 2 3 2 1
' 2 0
2 3 2 3
x m m x m
g x h x m
x m x m
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 39
Suy ra hàm số
y g x
nghịch biến trên các khoảng
2 3;2 1
m m
và
2 3;m
.
Do đó hàm số
y g x
nghịch biến trên khoảng
3;4
2 3 3
3
3
2 1 4
2
0
2 3 3
m
m
m
m
m
.
Mặt khác, do
m
nguyên dương nên
2;3 2;3
m S
. Vậy số phần tử của
S
bằng 2.
Từ đó chọn đáp án B.
Câu 11. Cho hàm số
f x
có đạo hàm trên
là
1 3
f x x x
. Có bao nhiêu giá trị nguyên của
tham số
m
thuộc đoạn
10;20
để hàm số
2
3
y f x x m
đồng biến trên khoảng
0;2
?
A.
18
. B.
17
. C.
16
. D.
20
.
Lời giải
Chọn A
Ta có
2 2
3 2 3 3
y f x x m x f x x m
.
Theo đề bài ta có:
1 3
f x x x
suy ra
3
0
1
x
f x
x
và
0 3 1f x x
.
Hàm số đồng biến trên khoảng
0;2
khi
0, 0;2
y x
2
2 3 3 0, 0;2
x f x x m x
.
Do
0;2
x
nên
2 3 0, 0;2
x x
. Do đó, ta có:
2 2
2
2 2
3 3 3 3
0, 0;2 3 0
3 1 3 1
x x m m x x
y x f x x m
x x m m x x
2
0;2
2
0;2
max 3 3
13
1
min 3 1
m x x
m
m
m x x
.
Do
10;20
m
,
m
nên có
18
giá trị nguyên của
m
thỏa yêu cầu đề bài.
Câu 12. Cho các hàm số
3
4
f x x x m
và
2 3
2 2 2
2018 2019 2020
g x x x x . Có bao
nhiêu giá trị nguyên của tham số
2020;2020
m
để hàm số
g f x
đồng biến trên
2;
?
A.
2005
. B.
2037
. C.
4016
. D.
4041
.
Lời giải
Chọn B
Ta có
3
4
f x x x m
,
2 3
2 2 2 12 10 2
12 10 2 0
2018 2019 2020 ...
g x x x x a x a x a x a
.
Suy ra
2
3 4
f x x
,
11 9
12 10 2
12 10 ... 2
g x a x a x a x
.
Và
11 9
12 10 2
12 10 ... 2
g f x f x a f x a f x a f x
10 8
12 10 2
12 10 ... 2f x f x a f x a f x a
.
Dễ thấy
12 10 2 0
; ;...; ; 0
a a a a
và
2
3 4 0
f x x
,
2
x
.
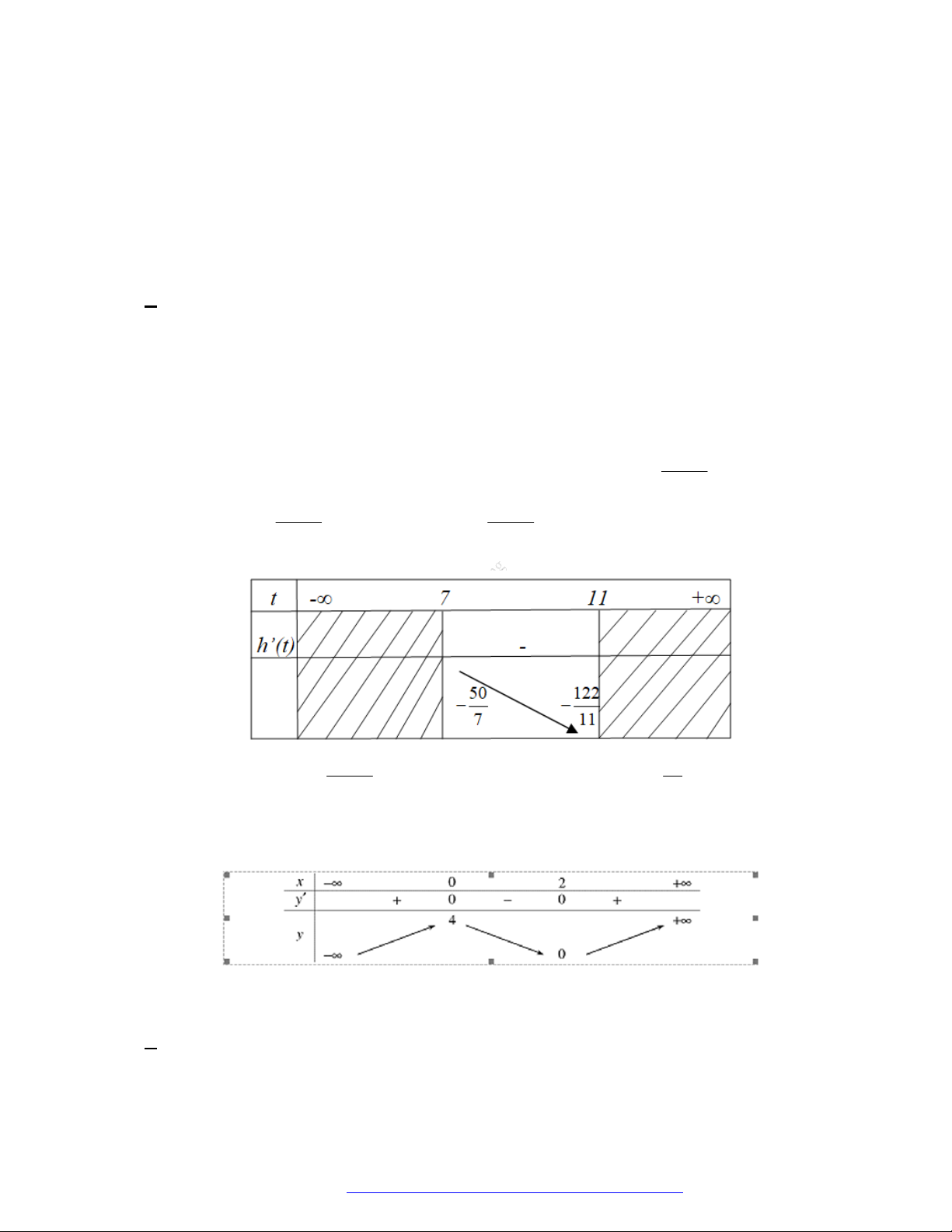
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 40 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Do đó
10 8
12 10 2
12 10 ... 2 0f x a f x a f x a
,
2x
.
Hàm số
g f x
đồng biến trên
2;
khi
0g f x
,
2x
0f x
,
2x
.
3
4 0x x m
,
3x
3
4m x x
,
2x
3
2;
max 4 16m x x
.
Vì
2020;2020m
và
m
nên có 2037 giá trị thỏa mãn
m
.
Câu 13. Cho hàm số có đạo hàm
2
2
1 2 1f x x x x mx
với mọi Có bao nhiêu số
nguyên âm
m
để hàm số
2 1g x f x
đồng biến trên khoảng
3;5
?
A.
3
B.
2
C.
4
D.
6
Lời giải
Chọn A
Ta có:
2 2
2 '(2 1) 2(2 1)(2 2) [(2 1) 2 (2 1) 1]g x f x x x x m x
Đặt
2 1t x
Để hàm số đồng biến trên khoảng
3;5
khi và chỉ khi
0, 3;5g x x
2
2 2
1
( 2 1) 0, 7;11 2 1 0, 7;11 2 , 7;11
t
t t mt t t mt t m t
t
Xét hàm số
2
1
( )
t
h t
t
trên
7;11
, có
2
2
1
'( )
t
h t
t
BBT:
Dựa vào BBT ta có
2
7;11
1 50
2 , 7;11 2 max
14
t
m t m h t m
t
Vì { 3; 2; 1}m m
.
Câu 14. Cho hàm số
y f x
có bảng biến thiên như sau
Có bao nhiêu số nguyên
2019m
để hàm số
2
2g x f x x m
đồng biến trên khoảng
1;
?
A. 2016. B. 2015. C. 2017. D. 2018.
Lời giải
Chọn A
Ta có
2 2 2
2 2 2 1 2g x x x m f x x m x f x x m
.
y f x
.
x
g x
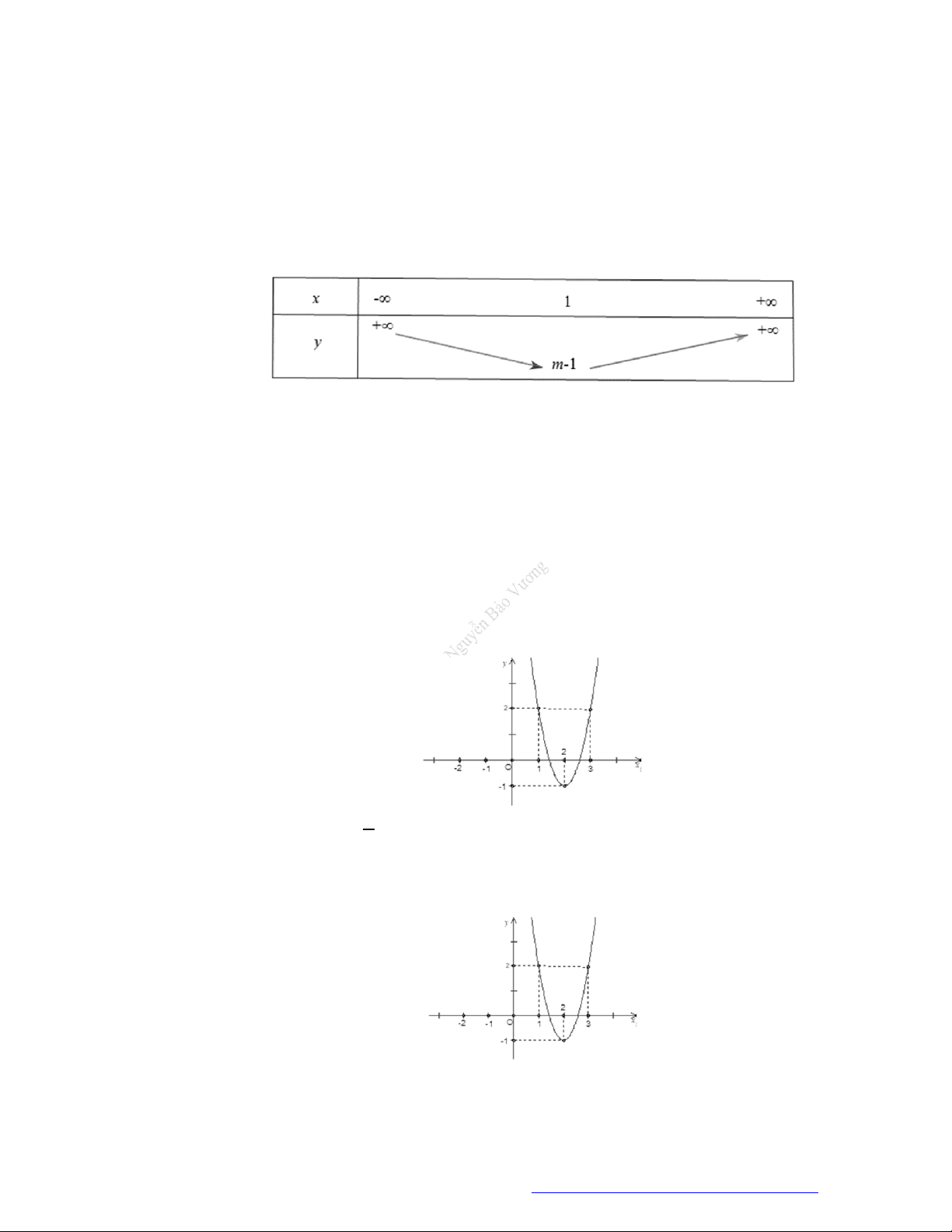
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 41
Hàm số
y g x
đồng biến trên khoảng
1;
khi và chỉ khi
0, 1;g x x
và
0g x
tại hữu hạn điểm
2
2 1 2 0, 1;x f x x m x
2
2 0, 1;f x x m x
2
2
2 2, 1;
2 0, 1;
x x m x
x x m x
Xét hàm số
2
2y x x m
, ta có bảng biến thiên
Dựa vào bảng biến thiên ta có
TH1:
2
2 2, 1; 1 2 3x x m x m m
.
TH2:
2
2 0, 1;x x m x
: Không có giá trị
m
thỏa mãn.
Vậy có 2016 số nguyên
2019m
thỏa mãn yêu cầu bài toán.
Câu 15. Cho hàm số
y f x
có đạo hàm là hàm số
f x
trên
. Biết rằng hàm số
2 2y f x
có đồ thị như hình vẽ bên dưới. Hàm số
f x
đồng biến trên khoảng nào?
A.
;3 , 5;
. B.
; 1 , 1;
. C.
1;1
. D.
3;5
.
Lời giải.
Chọn B
Hàm số
2 2y f x
có đồ thị
C
như sau:
Dựa vào đồ thị
C
ta có:
2 2 2, ;1 3; 2 0, ;1 3;f x x f x x
.
Đặt
* 2x x
suy ra:
* 0, * ; 1 1;f x x
.
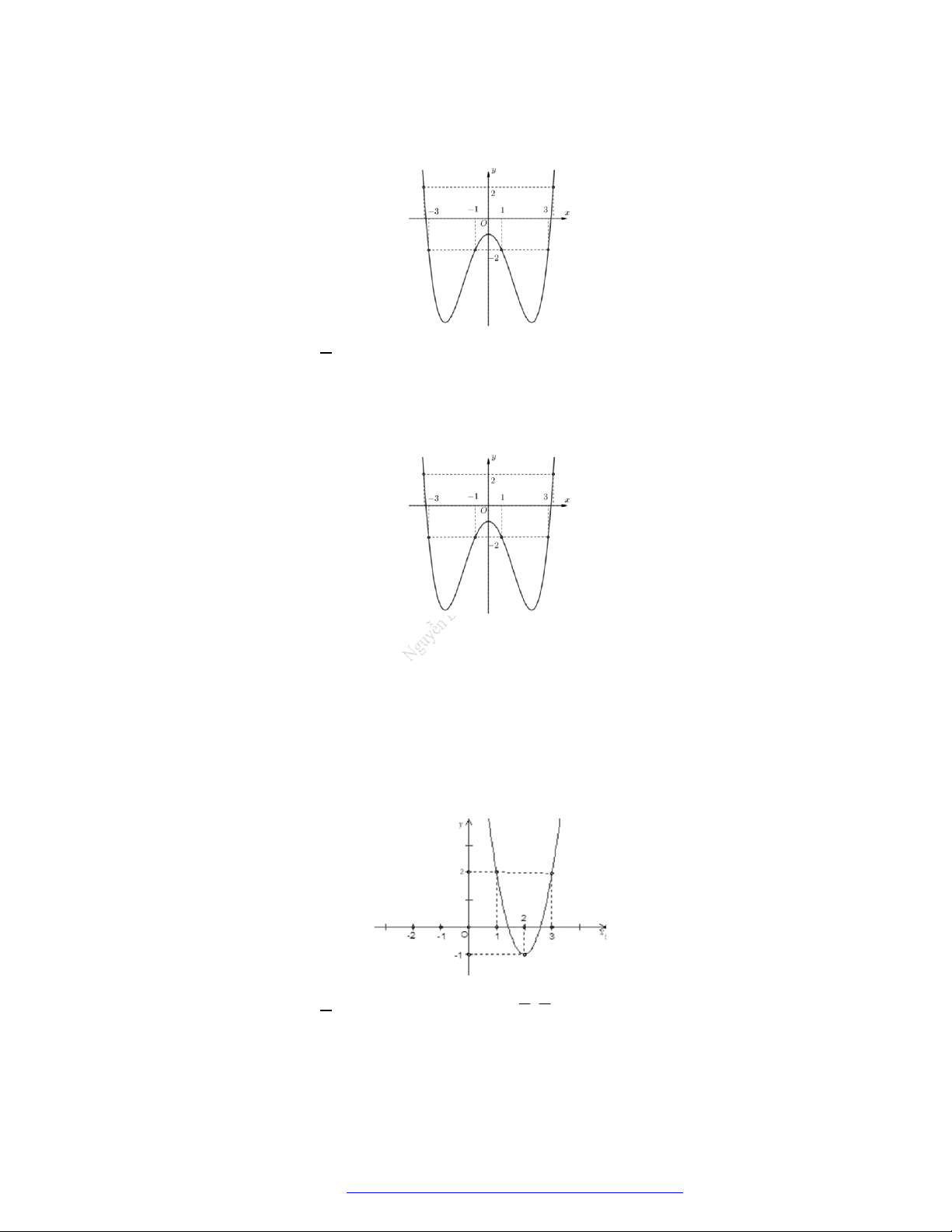
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 42 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Vậy: Hàm số
f x
đồng biến trên khoảng
; 1 , 1;
.
Câu 16. Cho hàm số
y f x
có đạo hàm là hàm số
f x
trên
. Biết rằng hàm số
2 2y f x
có đồ thị như hình vẽ bên dưới. Hàm số
f x
nghịch biến trên khoảng nào?
A.
3; 1 , 1;3
. B.
1;1 , 3;5
. C.
; 2 , 0;2
. D.
5; 3 , 1;1
.
Lời giải
Chọn B
Hàm số
2 2y f x
có đồ thị
C
như sau:
Dựa vào đồ thị
C
ta có:
2 2 2, 3; 1 1;3 2 0, 3; 1 1;3f x x f x x
.
Đặt
* 2x x
suy ra:
* 0, * 1;1 3;5f x x
.
Vậy: Hàm số
f x
đồng biến trên khoảng
1;1 , 3;5
.
Câu 17. Cho hàm số
y f x
có đạo hàm là hàm số
f x
trên
. Biết rằng hàm số
2 2y f x
có đồ thị như hình vẽ bên dưới. Hàm số
f x
nghịch biến trên khoảng nào?
A.
;2
. B.
1;1
. C.
3 5
;
2 2
. D.
2;
.
Lời giải.
Chọn B
Hàm số
2 2y f x
có đồ thị
C
như sau:
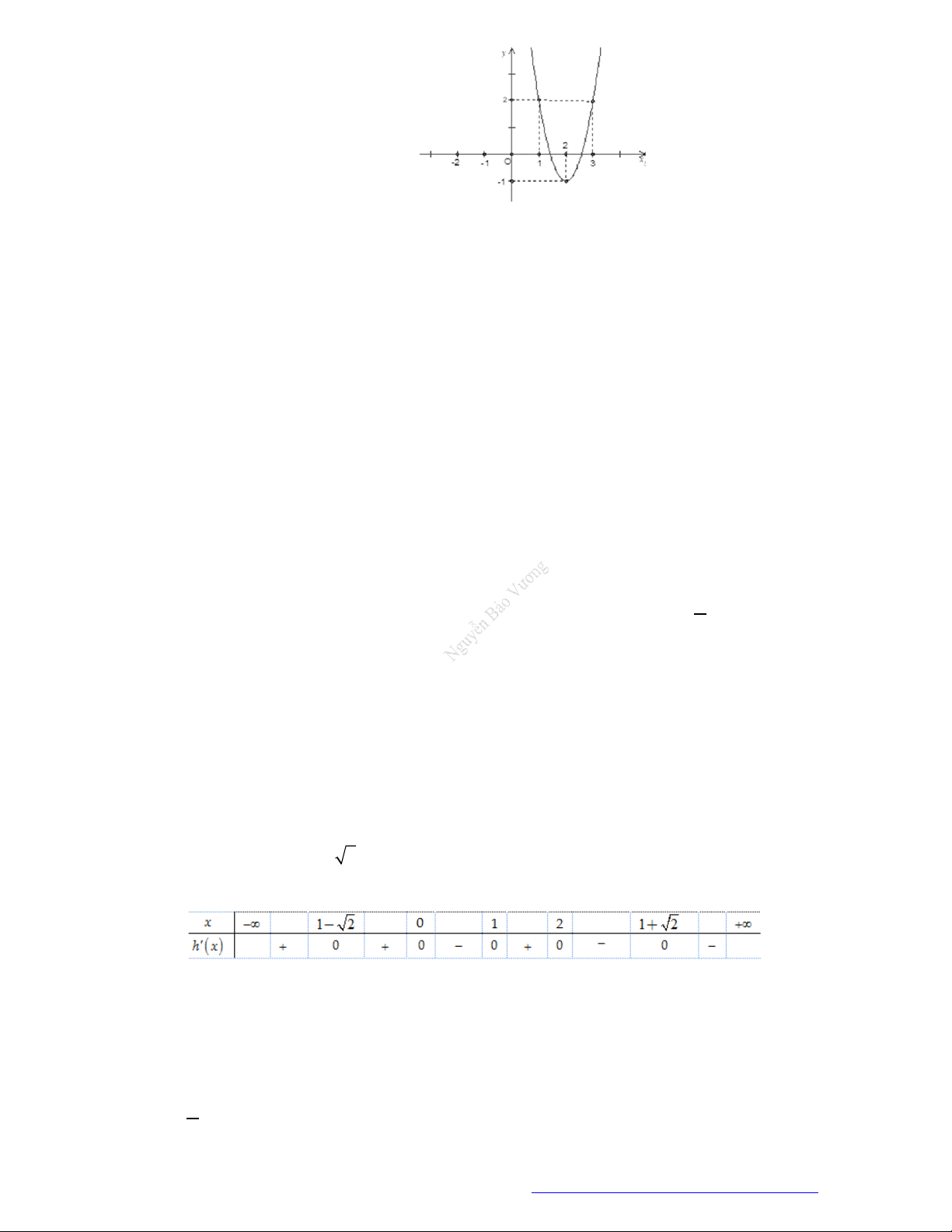
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 43
Dựa vào đồ thị
C
ta có:
2 2 2, 1;3 2 0, 1;3f x x f x x
.
Đặt
* 2x x
thì
* 0, * 1;1
f x x
.
Vậy: Hàm số
f x
nghịch biến trên khoảng
1;1
.
Cách khác:
Tịnh tiến sang trái hai đơn vị và xuống dưới 2 đơn vị thì từ đồ thị
C
sẽ thành đồ thị của
hàm
y f x
. Khi đó:
0, 1;1f x x
.
Vậy: Hàm số
f x
nghịch biến trên khoảng
1;1
.
Phân tích: Cho biết đồ thị của hàm số
f x
sau khi đã tịnh tiến và dựa vào đó để xét sự đồng
biến của hàm số
f x
.
Câu 18. Cho hàm số
y f x
có đạo hàm cấp
3
liên tục trên
và thỏa mãn
2 3
. 1 4f x f x x x x
với mọi
x
và
2
2 .g x f x f x f x
. Hàm số
2
2h x g x x
đồng biến trên khoảng nào dưới đây?
A.
;1
. B.
2;
. C.
0;1
. D.
1;2
.
Lời giải
Chọn D
Ta có
2 2 . 2 . 2 . ;g x f x f x f x f x f x f x f x f x
Khi đó
2 3
2 2 2 2
2 2 2 2 2 2 2 2 1 2 4h x x g x x x x x x x x x
0
1
0
2
1 2
x
x
h x
x
x
Ta có bảng xét dấu của
h x
Suy ra hàm số
2
2h x g x x
đồng biến trên khoảng
1;2
.
Câu 19. Cho hàm số
( )y f x
xác định trên
. Hàm số
( ) ' 2 3 2y g x f x
có đồ thị là một
parabol với tọa độ đỉnh
2; 1I
và đi qua điểm
1;2A
. Hỏi hàm số
( )y f x
nghịch biến trên
khoảng nào dưới đây?
A.
5;9
. B.
1;2
. C.
;9
. D.
1;3
.
Lời giải
Chọn A
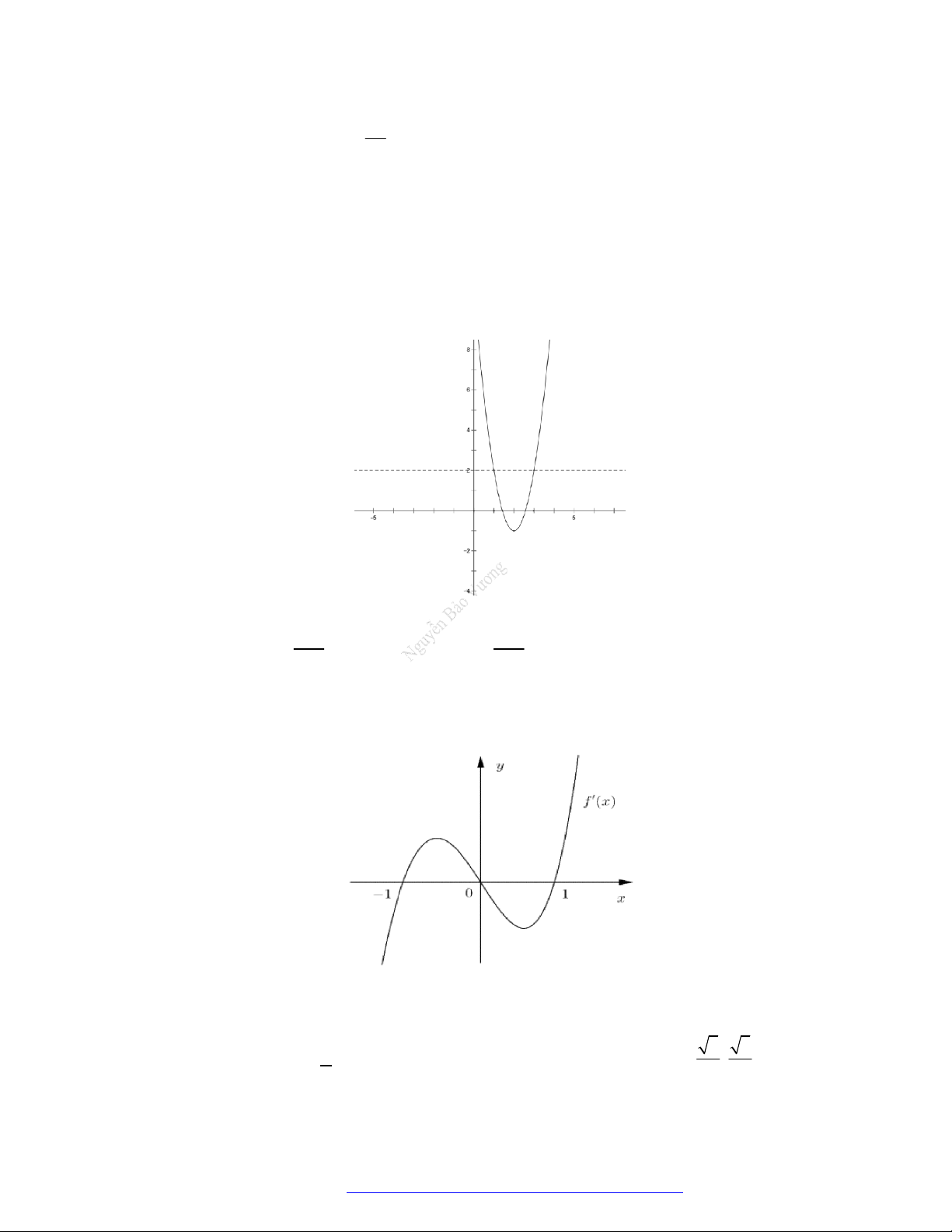
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 44 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Xét hàm số
( ) ' 2 3 2g x f x
có đồ thị là một Parabol nên có phương trình dạng:
2
( )y g x ax bx c P
Vì
P
có đỉnh
2; 1I
nên
2
4 4 0
2
4 2 1 4 2 1
2 1
b
b a a b
a
a b c a b c
g
.
P
đi qua điểm
1;2A
nên
1 2 2g a b c
Ta có hệ phương trình
4 0 3
4 2 1 12
2 11
a b a
a b c b
a b c c
nên
2
3 12 11g x x x
.
Đồ thị của hàm
( )y g x
là
Theo đồ thị ta thấy
'(2 3) 0 '(2 3) 2 2 1 3f x f x x
.
Đặt
3
2 3
2
t
t x x
khi đó
3
'( ) 0 1 3 5 9
2
t
f t t
.
Vậy
( )y f x
nghịch biến trên khoảng
5;9
.
Câu 20. Cho hàm số
y f x
, hàm số
3 2
, ,f x x ax bx c a b c
có đồ thị như hình vẽ
Hàm số
g x f f x
nghịch biến trên khoảng nào dưới đây?
A.
1;
. B.
; 2
. C.
1;0
. D.
3 3
;
3 3
.
Lời giải
Chọn B
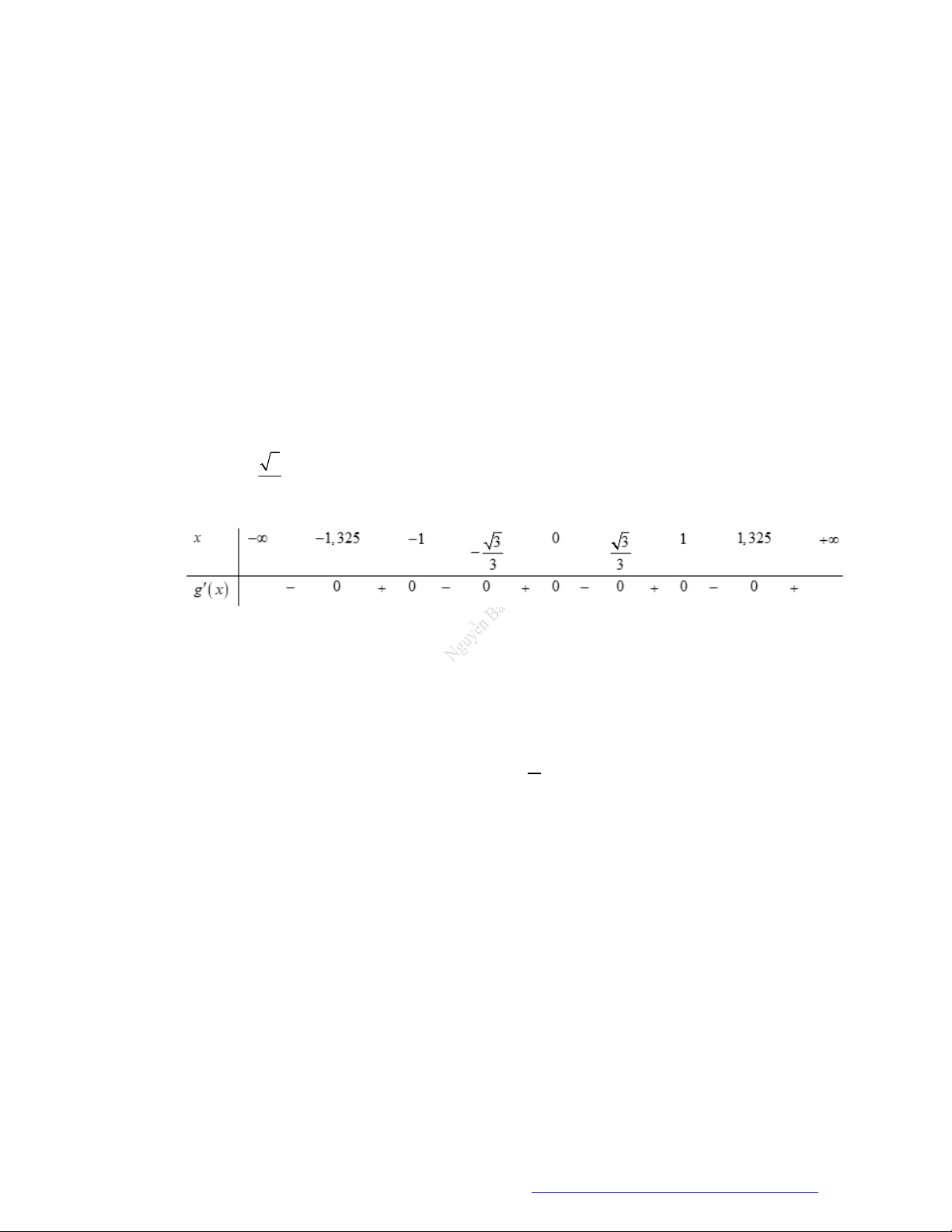
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 45
Vì các điểm
1;0 , 0;0 , 1;0
thuộc đồ thị hàm số
y f x
nên ta có hệ:
3 2
1 0 0
0 1 '' 3 1
1 0 0
a b c a
c b f x x x f x x
a b c c
Ta có:
. ''g x f f x g x f f x f x
Xét
3
3
3 2
3
2
0
1
0 ' . 0 3 1 0
1
3 1 0
x x
x x
g x g x f f x f x f x x x
x x
x
1 1
2 2
1
0
( 1,325 )
( 1,325)
3
3
x
x
x x x
x x x
x
Bảng biến thiên
Dựa vào bảng biến thiên ta có
g x
nghịch biến trên
; 2
Câu 21. Cho hàm số
y f x
có đạo hàm
2
' 2 3, .f x x x x
Có bao nhiêu giá trị nguyên
của tham số m thuộc đoạn
10;20
để hàm số
2 2
3 1g x f x x m m
đồng biến trên
0;2 ?
A. 16. B. 17. C. 18. D. 19.
Lời giải
Chọn C
Ta có
2
3
' 2 3 0 * .
1
t
f t t t
t
Có
2
' 2 3 ' 3g x x f x x m
Vì
2 3 0, 0;2x x
nên
g x
đồng biến trên
0;2 ' 0, 0;2g x x
2
' 3 0, 0;2f x x m x
2 2
2 2
3 3, 0;2 3 3, 0;2
3 1, 0;2 3 1, 0;2
x x m x x x m x
x x m x x x m x
(**)
Có
2
3h x x x
luôn đồng biến trên
0;2
nên từ (**)
3 10 13
1 0 1
m m
m m
Vì
10;20m
m
Có 18 giá trị của tham số m.
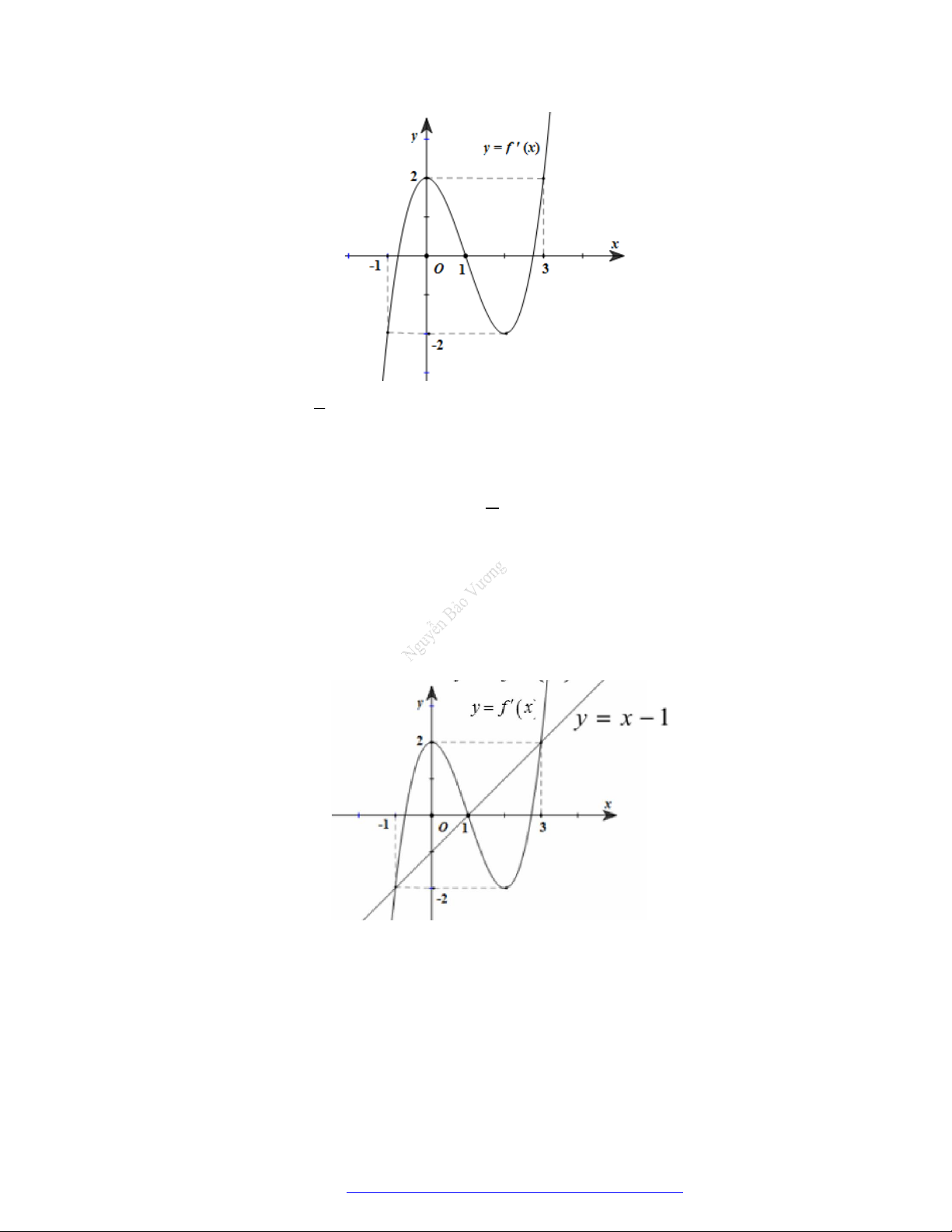
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 46 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Vậy có 18 giá trị của tham số m cần tìm.
Câu 22. Cho hàm số
y f x
có đạo hàm liên tục trên
và đồ thị của hàm số
'y f x
như hình vẽ.
Đặt
2
1
1 2019
2
g x f x m x m
với
m
là tham số thực. Gọi
S
là tập các giá trị
nguyên dương của
m
để hàm số
y g x
đồng biến trên khoản
5;6
.Tổng các phần tử của
S
bằng:
A.
4
. B. 11. C.
14
. D. 20.
Lời giải
Chọn C
Ta có
' ' 1g x f x m x m
Đặt
' 1h x f x x
. Từ đồ thị
'y f x
và đồ thị
1y x
trên hình vẽ ta suy ra
1 1
0
3
x
h x
x
Ta có
1 1 1 1
' 0
3 3
x m m x m
g x h x m
x m x m
Do đó hàm số
y g x
đồng biến trên các khoảng
1; 1m m
và
3;m
Do vậy, hàm số
y g x
đồng biến trên khoảng
5;6
1 5
5 6
1 6
2
3 5
m
m
m
m
m
Do
m
nguyên dương nên
1;2;5;6m
, tức
1;2;5;6S
Tổng các phần tử của
S
bằng 14.
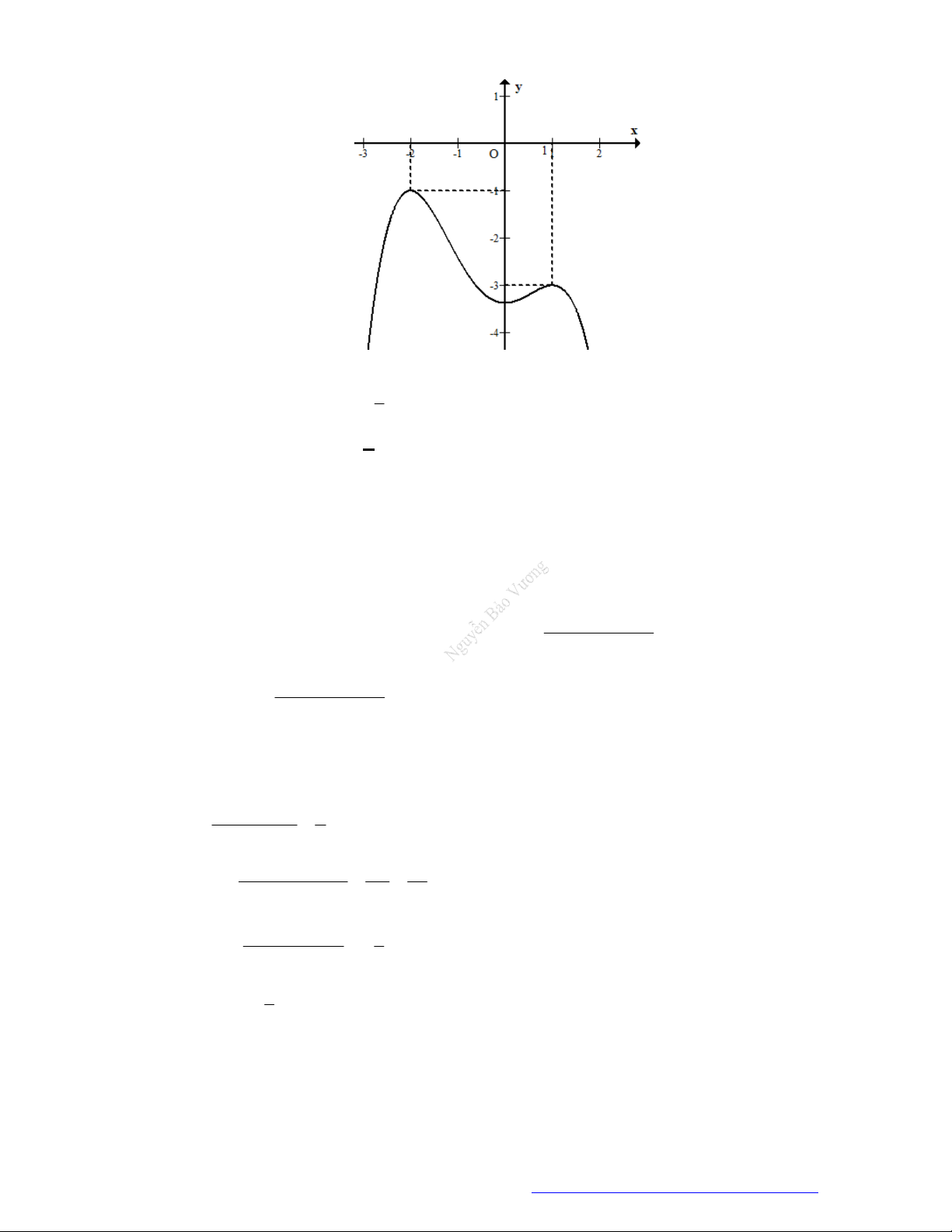
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 47
Câu 23. Cho hàm số
y f x
là hàm đa thức có đồ thị hàm số
y f x
như hình vẽ.
Có bao nhiêu giá trị nguyên của tham số
m
,
, 2020 2020m Z m
để hàm số
2 2 2
8
6
3
g x f x mx x x
đồng biến trên khoảng
3;0
A. 2021. B. 2020. C. 2019. D. 2022.
Lời giải
Chọn B
Ta có
2 2
2 4 2 3g x xf x mx x x
.
Hàm số
g x
đồng biến trên khoảng
3;0
suy ra
0, 3;0g x x
.
2 2 2 2
2 4 2 3 0, 3;0 2 2 3 0, 3;0xf x mx x x x f x m x x x
2
2 2
2
2 2 3 , 3;0 , 3;0
2 2 3
f x
f x m x x x m x
x x
2
2
3;0
max
2 2 3
f x
m
x x
.
Ta có
2 2
3 0 0 9 3x x f x
dấu “ ” khi
2
1 1x x
.
2
2 2
2 3 1 4 0 2 3 4, 3;0x x x x x x
2
1 1
,
2 3 4x x
dấu “
” khi
1x
.
Suy ra
2
2
3 3
2.4 8
2 2 3
f x
x x
,
3;0x
, dấu “
” khi
1x
.
2
2
3;0
3
max
8
2 2 3
f x
x x
.
Vậy
3
8
m
, mà
m
,
2020 2020m
nên có 2020 giá trị của tham số
m
thỏa mãn bài
toán.
Câu 24. Cho hàm số
f x
. Hàm số
y f x
có đồ thị như hình sau.
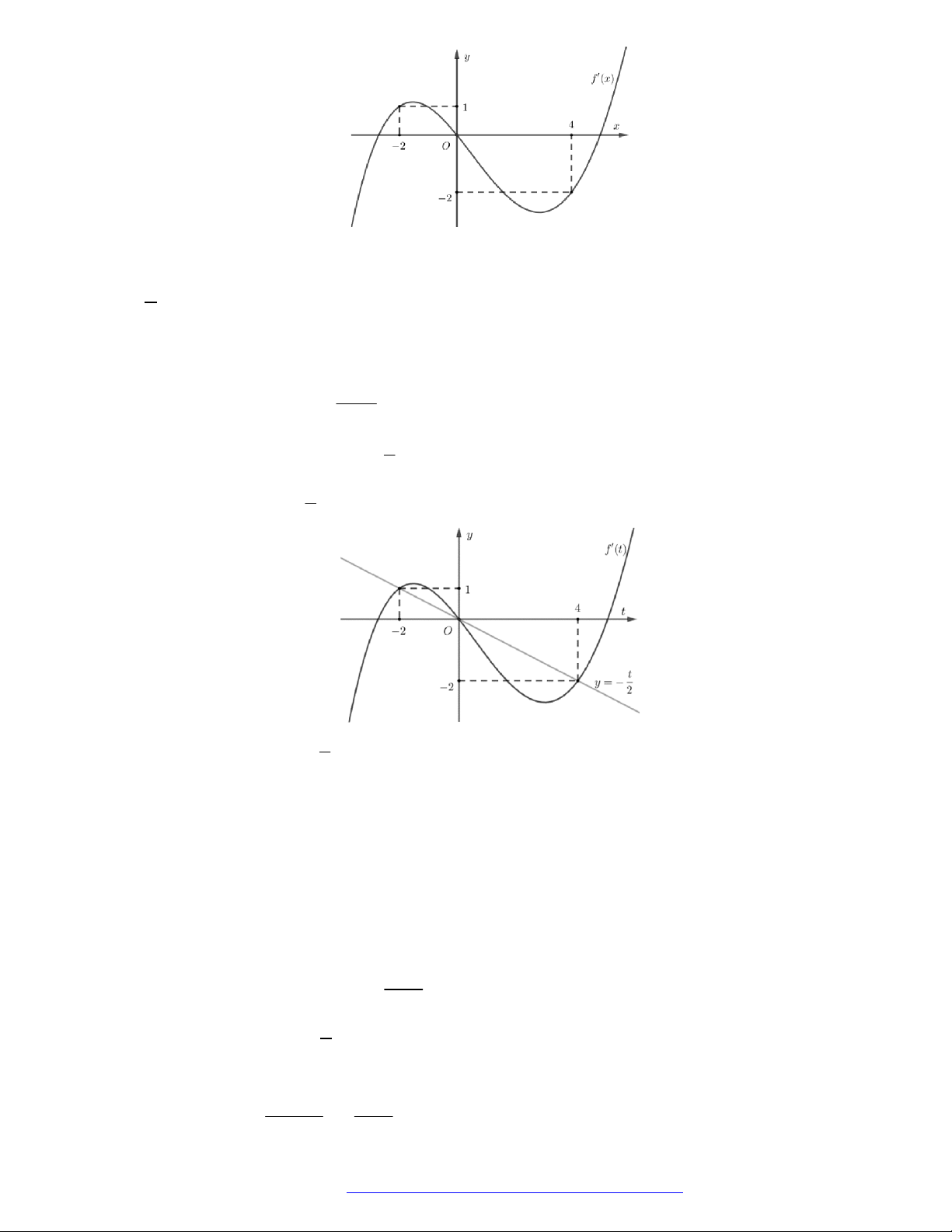
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 48 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Có tất cả bao nhiêu giá trị nguyên dương của tham số
m
đề hàm số
20202)(4)(
2
mxxmxfxg
đồng biến trên khoảng
).2;1(
A.
2
. B.
3
. C.
0
. D.
1
.
Lời giải
Chọn A
Ta có
mxmxfxg 22)('4)('
(*)
2
)('0)('
mx
mxfxg
Đặt mxt thì
2
)('(*)
t
tf
Vẽ đường thẳng
2
x
y
trên cùng hệ trục
Oxy
với đồ thị
y f x
như hình vẽ sau
Từ đồ thị ta có
4
2
4
02
2
)('
mx
mxm
t
t
t
tf
Hàm số
)(xg
đồng biến trên khoảng
)2;1(
2;10)(' xxg
3
32
14
212
m
m
m
mm
Vì
m
nguyên dương nên
.3;2m
Vậy có hai giá trị nguyên dương của
m
đề hàm số
)(xg
đồng biến trên khoảng
).2;1(
Câu 25. Cho hàm số
f x
có đạo hàm
1 1 4 ;f x x x x x
.Có bao nhiêu số nguyên
2020m
để hàm số
2
1
x
g x f m
x
đồng biến trên
2;
.
A.
2018
. B.
2019
. C.
2020
. D.
2021
Lời giải
Chọn B
Ta có:
2
3 2
1
1
x
g x f m
x
x
.
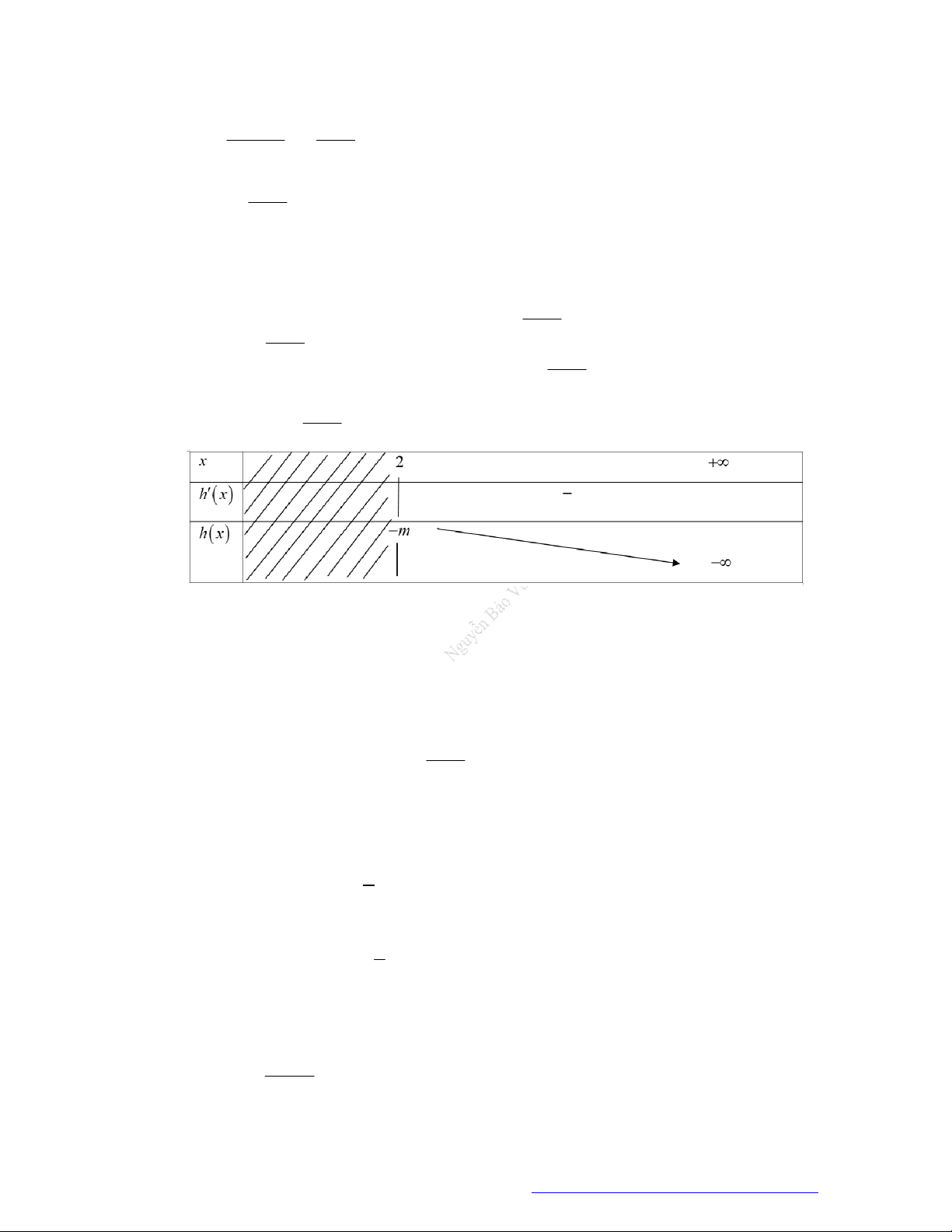
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 49
Hàm số
g x
đồng biến trên
2;
0; 2;g x x
2
3 2
0; 2;
1
1
x
f m x
x
x
2
0; 2;
1
x
f m x
x
Ta có:
0f x
1 1 4 0x x x
1
1 4
x
x
Do đó:
2
0; 2;
1
x
f m x
x
2
1; 2; 1
1
2
1 4; 2; 2
1
x
m x
x
x
m x
x
Hàm số
2
1
x
h x m
x
;
2;x
có bảng biến thiên:
Căn cứ bảng biến thiên suy ra: Điều kiện
2
không có nghiệm
m
thỏa mãn.
Điều kiện
1
1m
1m
,kết hợp điều kiện
2020m
suy ra có
2019
giá trị
m
thỏa mãn yêu cầu bài toán.
Nhận xét: Có thể mở rộng bài toán đã nêu như sau:
Cho hàm số
f x
có đạo hàm
1 1 4 ;f x x x x x
.Có bao nhiêu số nguyên
2020m
để hàm số
2
1
x
g x f h m
x
đồng biến trên
2;
.
Câu 26. Cho hàm số
y f x
có đạo hàm
' 1
x
f x x e
, có bao nhiêu giá trị nguyên của tham số
m
trong đoạn
2019;2019
để hàm số
2
ln 2y g x f x mx mx
nghịch biến trên
2
1;e
.
A. 2018. B. 2019. C. 2020. D. 2021.
Lời giải
Chọn B
Trên
2
1;e
ta có
1
' . ' ln 2 ln 1 2 1g x f x mx m x x m
x
Để hàm số
y g x
nghịch biến trên
2
1;e
thì
2
' ln 1 2 1 0, 1;g x x x m x e
2
2
ln 1 2 1 0, 1;
ln 1
, 1;
2 1
x x m x e
x
m x e
x

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 50 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Xét hàm số
l
n 1
2 1
x
h
x
x
trên
2
1
;e
,
ta có
2
2
1
2
ln
'
0, 1;
2
1
x
x
h
x x e
x
,
từ đây suy ra
1
m
. Vậy có 2019 giá
trị nguyên của
m
thỏa bài
toán.
-------------------- HẾT --------------------
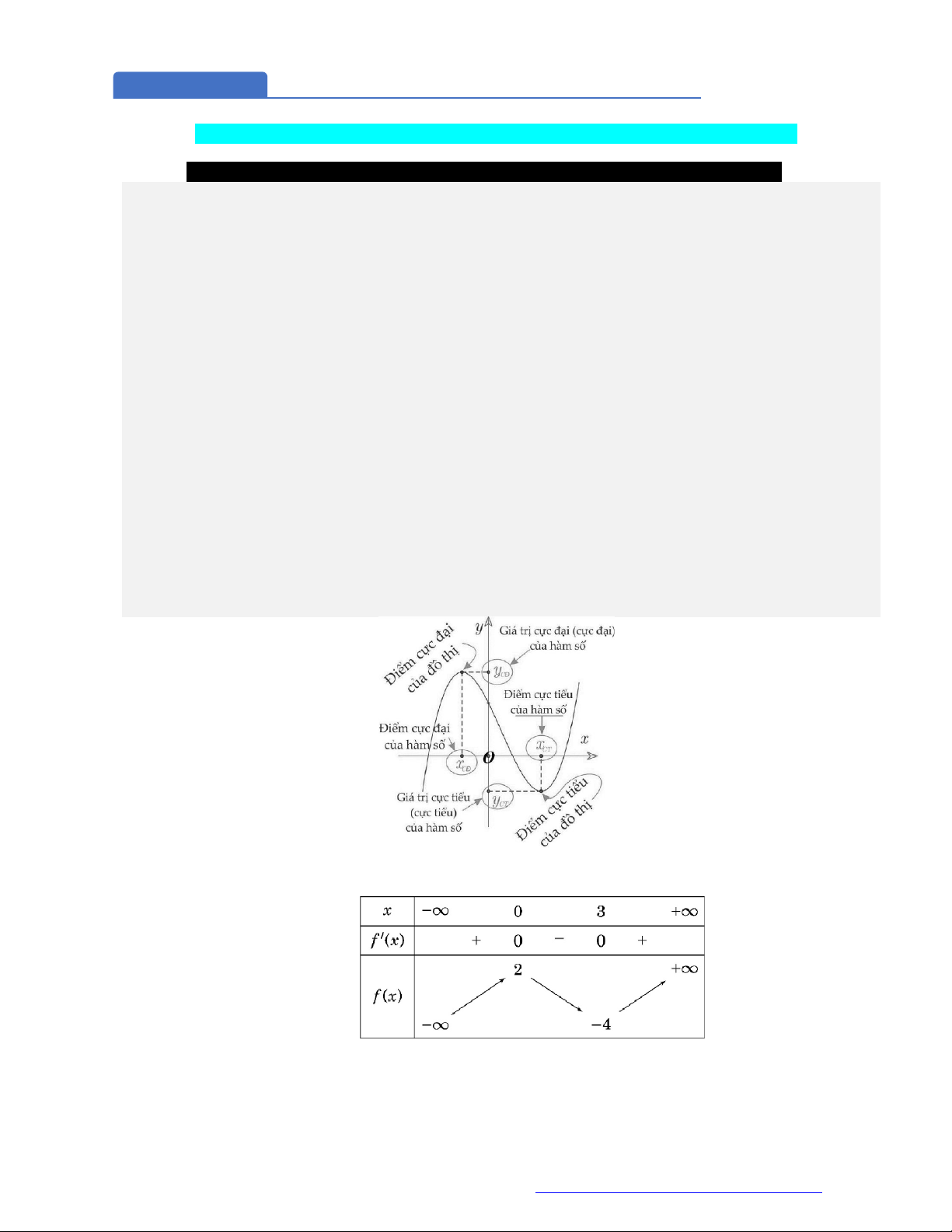
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
DẠNG TOÁN DÀNH CHO ĐỐI TƯỢNG HỌC SINH TRUNG BÌNH 5-6 ĐIỂM
Dạng 1. Tìm cực trị của hàm số dựa vào bảng biến thiên, đồ thị của hàm số y, y’
-Định lí cực trị
Điều kiện cần (định lí 1): Nếu hàm số
( )y f x
có đạo hàm trên khoảng
( ; )a b
và đạt cực đại
(hoặc cực tiểu) tại
x
thì
( ) 0.f x
Điều kiện đủ (định lí 2):
Nếu
( )f x
đổi dấu từ âm sang dương khi
x
đi qua điểm
x
(theo chiều tăng) thì hàm số
( )y f x
đạt cực tiểu tại điểm
.x
Nếu
( )f x
đổi dấu từ dương sang âm khi
x
đi qua điểm
x
(theo chiều tăng) thì hàm số
( )y f x
đạt cực đại tại điểm
.x
Định lí 3: Giả sử
( )y f x
có đạo hàm cấp
2
trong khoảng
( ; ),x h x h
với
0.h
Khi đó:
Nếu
( ) 0, ( ) 0y x y x
thì
x
là điểm cực tiểu.
Nếu
( ) 0, ( ) 0
o o
y x y x
thì
x
là điểm cực đại.
- Các THUẬT NGỮ cần nhớ
Điểm cực đại (cực tiểu) của hàm số là
,x
giá trị cực đại (cực tiểu) của hàm số là
( )f x
(hay
y
CĐ
hoặc
CT
).y
Điểm cực đại của đồ thị hàm số là
( ; ( )).M x f x
Nếu
( ; )M x y
là điểm cực trị của đồ thị hàm số
( ) 0
( )
( ; ) ( )
y x
y f x
M x y y f x
Câu 1. (Đề Tham Khảo 2020 – Lần 1) Cho hàm số
y f x
có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng
A.
2
. B.
3
. C.
0
. D.
4
.
Câu 2. (Đề Tham Khảo 2020 – Lần 2) Cho hàm số
f x
có bảng biến thiên như sau:
CỰC TRỊ CỦA HÀM SỐ
Chuyên đề 2
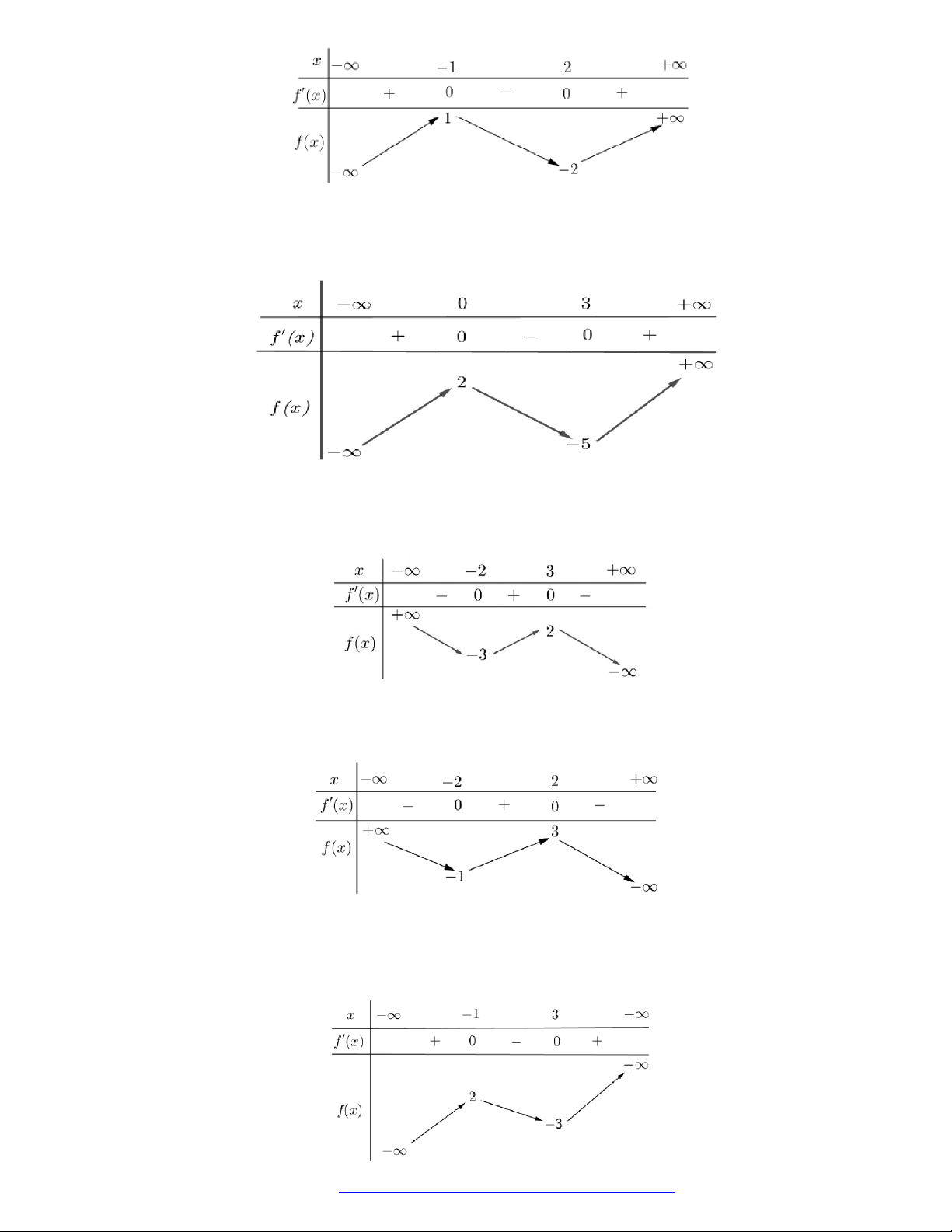
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Hàm số đã cho đạt cực đại tại
A.
2 x
. B.
2x
. C.
1x
. D.
1 x
.
Câu 3. (Mã 101 – 2020 Lần 1) Cho hàm
f x
có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng
A.
3
. B.
5
. C.
0
. D.
2
.
Câu 4. (Mã 102 - 2020 Lần 1) Cho hàm số có bảng biến thiên như sau.
Giá trị cực đại của hàm số đã cho bằng
A. . B. . C. . D. .
Câu 5. (Mã 103 - 2020 Lần 1) Cho hàm số
f x
có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng
A.
2
. B.
2
. C.
3
. D.
1
.
Câu 6. (Mã 104 - 2020 Lần 1) Cho hàm số
f x
có bảng biến thiên như sau:
f x
3
2
2
3
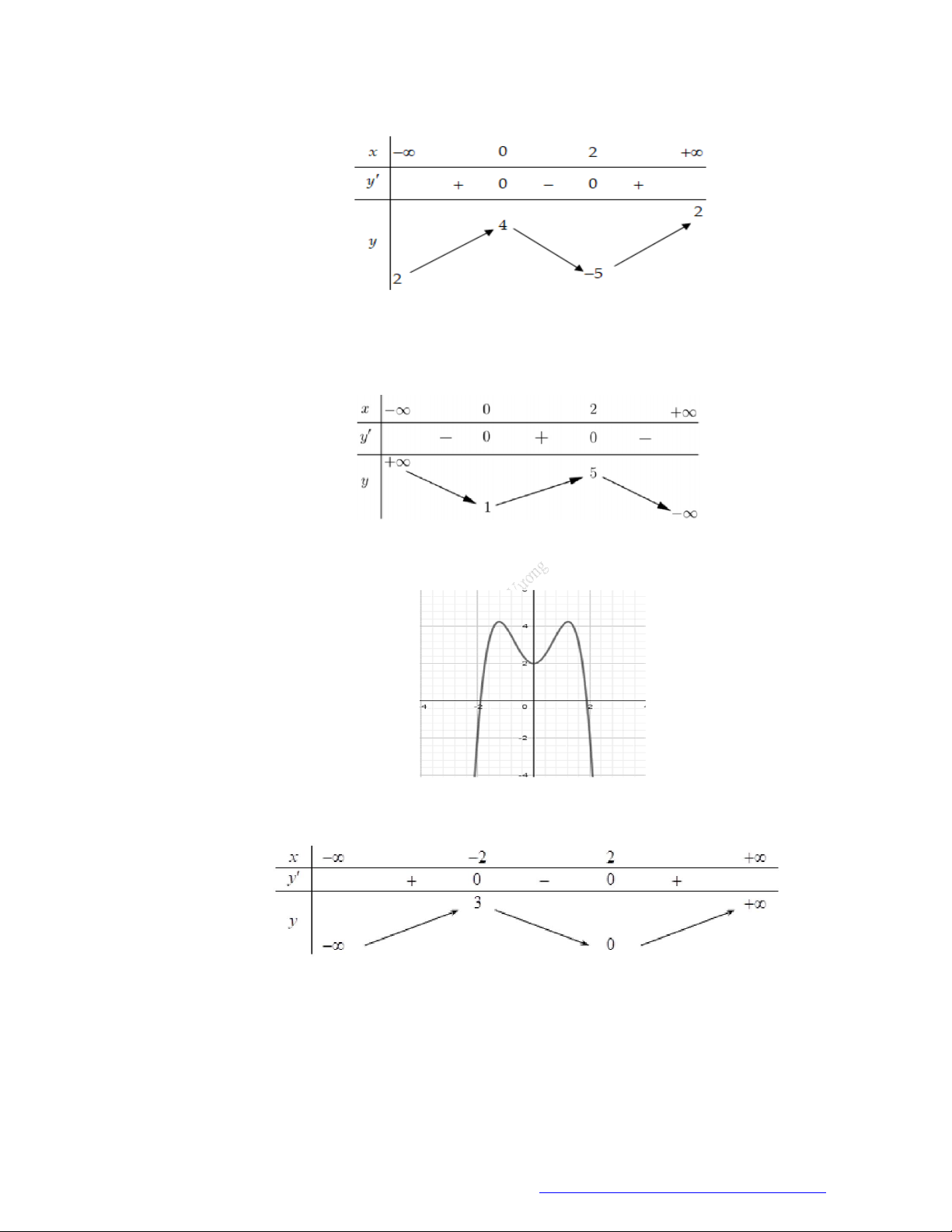
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Giá trị cực đại của hàm số đã cho bằng
A.
3
. B.
3
. C.
1
. D.
2
.
Câu 7. (Mã 105 - 2017) Cho hàm số
y f x
có bảng biến thiên như sau
Mệnh đề nào dưới đây đúng?
A. Hàm số đạt cực tiểu tại
5x
B. Hàm số có bốn điểm cực trị
C. Hàm số đạt cực tiểu tại
2x
D. Hàm số không có cực đại
Câu 8. (Đề Tham Khảo 2019) Cho hàm số
y f x
có bảng biến thiên như sau
Giá trị cực đại của hàm số đã cho bằng
A.
5
B.
2
C.
0
D.
1
Câu 9. (Mã 104 - 2018) Cho hàm số có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số đã cho là:
A.
3
B.
1
C.
2
D.
0
Câu 10. (Mã 110 - 2017) Cho hàm số
y f x
có bảng biến thiên như sau
Tìm giá trị cực đại
CĐ
y
và giá trị cực tiểu
CT
y
của hàm số đã cho.
A.
2
CĐ
y
và
0
CT
y
B.
3
CĐ
y
và
0
CT
y
C.
3
CĐ
y
và
2
CT
y
D.
2
CĐ
y
và
2
CT
y
Câu 11. (Mã 103 - 2019) Cho hàm số
( )f x
có bảng biến thiên như sau:
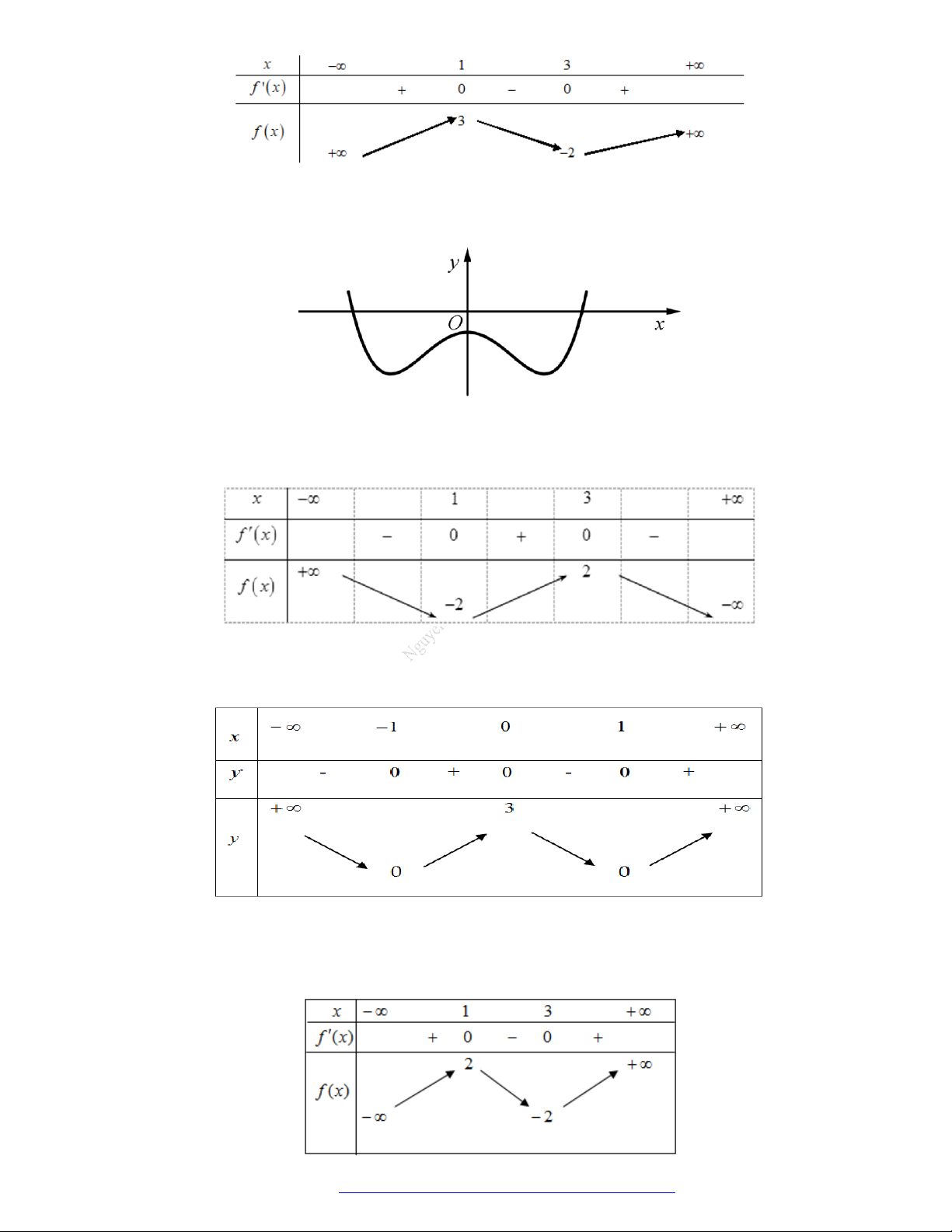
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Hàm số đạt cực đại tại:
A.
2x
. B.
3x
. C.
1x
. D.
2x
.
Câu 12. (Mã 103 - 2018) Cho hàm số
4 2
y ax bx c (
a
,
b
,
c
) có đồ thị như hình vẽ bên.
Số điểm cực trị của hàm số đã cho là
A.
3
B.
0
C.
1
D.
2
Câu 13. (Mã 102 - 2019) Cho hàm số
f x
có bảng biến thiên như sau:
Hàm số đạt cực đại tại
A.
2x
. B.
3x
. C.
1x
. D.
2x
.
Câu 14. (Mã 123 - 2017) Cho hàm số
( )y f x
có bảng biến thiên như sau
Mệnh đề nào dưới đây sai
A. Hàm số có giá trị cực đại bằng
3
B. Hàm số có hai điểm cực tiểu
C. Hàm số có giá trị cực đại bằng
0
D. Hàm số có ba điểm cực trị
Câu 15. (Mã 104 - 2019) Cho hàm số
( )f x
có bảng biến thiên như sau:
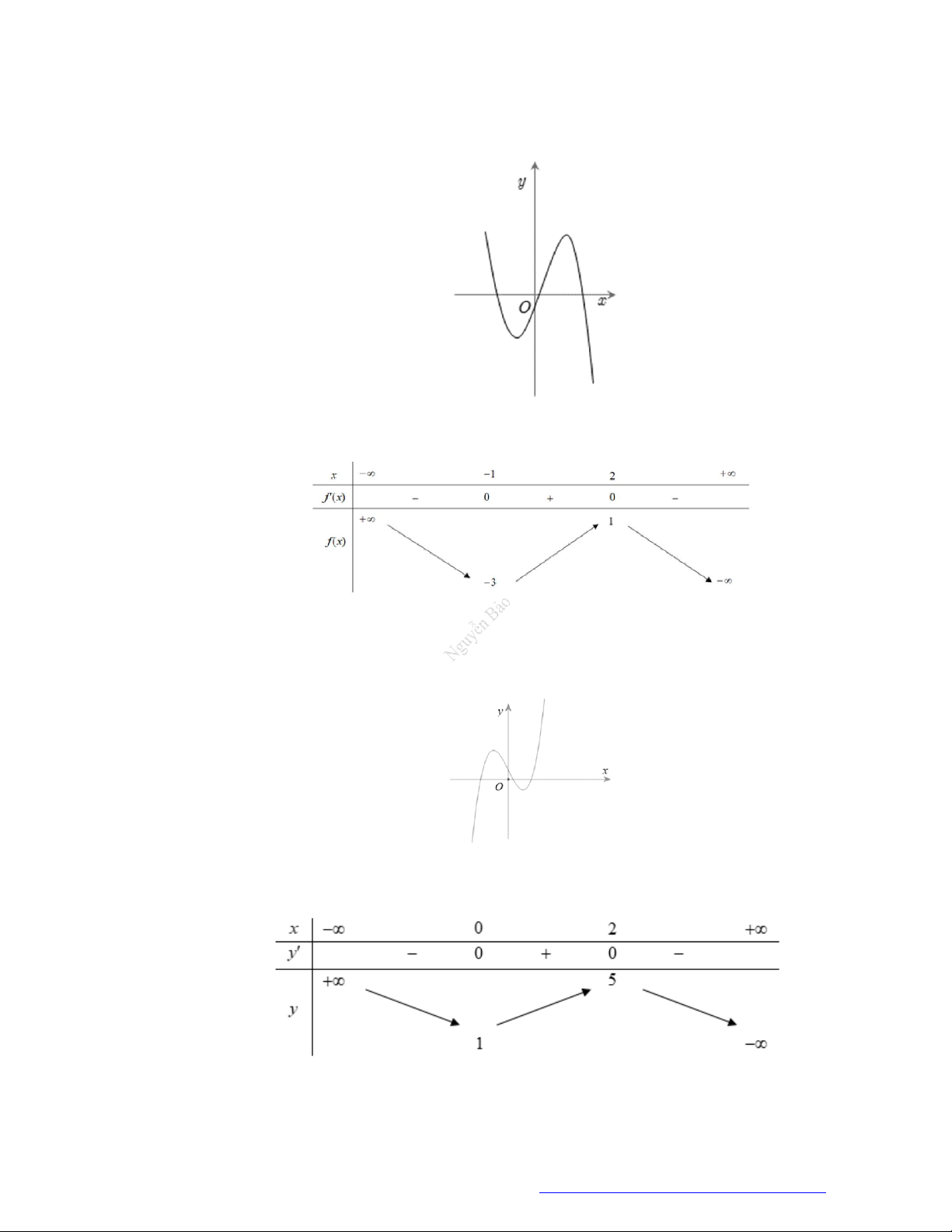
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Hàm số đã cho đạt cực tiểu tại
A.
2x
. B.
2 x
. C.
1x
. D.
3x
.
Câu 16. (Mã 102 - 2018) Cho hàm số
3 2
y ax bx cx d
, , ,a b c d
có đồ thị như hình vẽ bên. Số
điểm cực trị của hàm số này là
A.
3
B.
2
C.
0
D.
1
Câu 17. (Mã 101 - 2019) Cho hàm số
( )f x
có bảng biến thiên như sau:
Hàm số đã cho đạt cực tiểu tại
A.
1x
. B.
3x
. C.
2x
. D.
1x
.
Câu 18. (Mã 101 - 2018) Cho hàm số
3 2
, , ,y ax bx cx d a b c d
có đồ thị như hình vẽ bên. Số
điểm cực trị của hàm số đã cho là
A.
2
B.
0
C.
3
D.
1
Câu 19. (Đề Tham Khảo 2018) Cho hàm số
y f x
có bảng biến thiên như sau
Hàm số đạt cực đại tại điểm
A.
1x
B.
0x
C.
5x
D.
2x
Câu 20. (Mã 101 – 2020 Lần 2) Cho hàm số
f x
có bảng biến thiên như sau:
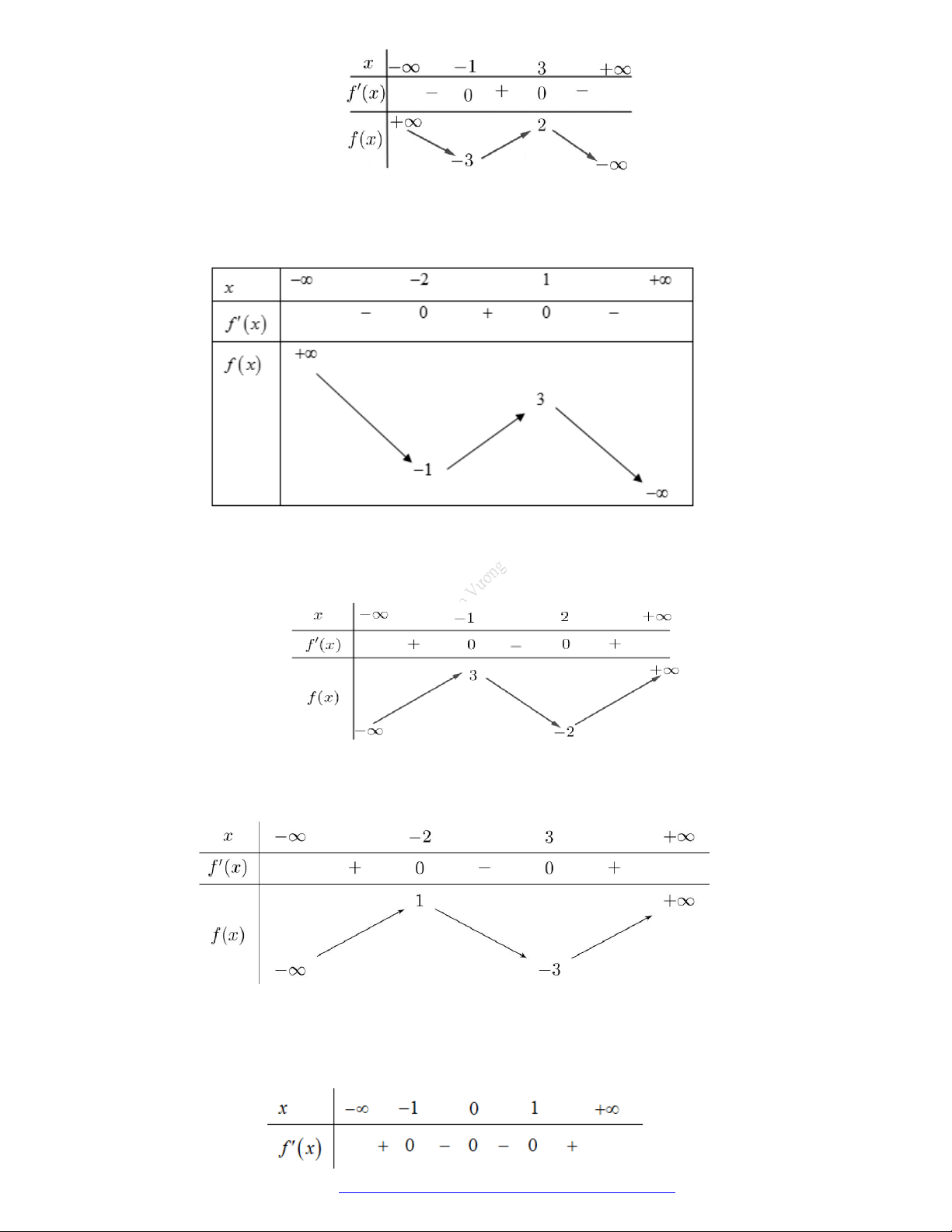
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Điểm cực đại của hàm số đã cho là
A.
3
x
. B.
1
x
. C.
2
x
. D.
3
x
.
Câu 21. (Mã 102 - 2020 Lần 2) Cho hàm số
f x
có bảng biến thiên như sau:
Điểm cực đại của hàm số đã cho là
A.
3x
. B.
1x
. C.
1x
. D.
2x
.
Câu 22. (Mã 103 - 2020 Lần 2) Cho hàm số
f x
có bảng biến thiên như sau :
Điểm cực đại của hàm số đã cho là
A.
3.x
B.
2.x
C.
2.x
D.
1.x
Câu 23. (Mã 104 - 2020 Lần 2) Cho hàm số
f x
có bảng biến thiên như sau:
Điểm cực đại của hàm số đã cho là
A.
2x
. B.
3x
. C.
1x
. D.
3x
.
Câu 24. (Đề Tham Khảo 2020 – Lần 1) Cho hàm số
f x
, bảng xét dấu của
f x
như sau:

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Số điểm cực trị của hàm số đã cho là
A.
0
. B.
2
. C.
1
. D.
3
.
Câu 25. (Đề Tham Khảo 2020 – Lần 2) Cho hàm số
f x
có bảng xét dấu của
f x
như sau:
Số điểm cực trị của hàm số đã cho là
A.
3
. B.
0
. C.
2
. D.
1
.
Câu 26. (Mã 101 - 2020 Lần 1) Cho hàm số
f x
liên tục trên
và có bảng xét dấu của
f x
như
sau:
Số điểm cực đại của hàm số đã cho là
A.
4
. B.
1
. C.
2
. D.
3
.
Câu 27. (Mã 102 - 2020 Lần 1) Cho hàm
f x
liên tục trên và có bảng xét dấu
f x
như sau:
Số điểm cực tiểu của hàm số là
A. . B. . C. . D. .
Câu 28. (Mã 103 - 2020 Lần 1) Cho hàm số
( )f x
liên tục trên
và có bảng xét dấu của
( )f x
như sau:
Số điểm cực tiểu của hàm số đã cho là
A.
2.
B.
4.
C.
3.
D.
1.
Câu 29. (Mã 104 - 2020 Lần 1) Cho hàm số
f x
liên tục trên R có bảng xét dấu
'f x
Số điểm cực đại của hàm số đã cho là:
A. 3. B. 1. C. 2. D. 4.
Dạng 2. Tìm cực trị của hàm số khi biết y, y’
Bài toán: Tìm các điểm cực đại, cực tiểu (nếu có) của hàm số
( ).y f x
Phương pháp: Sự dụng 2 qui tắc tìm cực trị sau:
Quy tắc I: sử dụng nội dụng định lý 1
Bước 1. Tìm tập xác định
D
của hàm số.
Bước 2. Tính đạo hàm
( ).y f x
Tìm các điểm
, ( 1,2, 3,..., )
i
x i n
mà tại đó đạo hàm bằng 0 hoặc không
xác định.
Bước 3. Sắp xếp các điểm
i
x
theo thứ tự tăng dần và lập bảng biến thiên.
Bước 4. Từ bảng biến thiên, suy ra các điểm cực trị (dựa vào nội dung định lý 1).
Quy tắc II: sử dụng nội dụng định lý 2
1
2
3
4

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Bước 1. Tìm tập xác định
D
của hàm số.
Bước 2. Tính đạo hàm
( ).y f x
Giải phương trình
( ) 0f x
và kí hiệu
, ( 1,2,3,..., )
i
x i n
là các nghiệm
của nó.
Bước 3. Tính
( )f x
và
( ).
i
f x
Bước 4. Dựa vào dấu của
( )
i
y x
suy ra tính chất cực trị của điểm
:
i
x
+ Nếu
( ) 0
i
f x
thì hàm số đạt cực đại tại điểm
.
i
x
+ Nếu
( ) 0
i
f x
thì hàm số đạt cực tiểu tại điểm
.
i
x
Câu 1. (Mã 101 – 2020 Lần 2) Cho hàm số
f x
có đạo hàm
3
1 4 ,f x x x x x
. Số
điểm cực đại của hàm số đã cho là
A.
3
. B.
4
. C.
2
. D.
1
.
Câu 2. (Mã 103 - 2020 Lần 2) Cho hàm số
f x
có đạo hàm
3
1 4 ,f x x x x x
. Số
điểm cực đại của hàm số đã cho là
A.
2
. B.
3
. C.
4
. D.
1
.
Câu 3. (Mã 104 - 2020 Lần 2) Cho hàm số
f x
có
3
1 4
f x x x x
,
x
. Số điểm cực tiểu
của hàm số đã cho là
A.
4
. B.
3
. C.
1
. D.
2
.
Câu 4. (Mã 102 - 2020 Lần 2) Cho hàm số
f x
có đạo hàm
3
' 1 4 ,f x x x x x
. Số điểm
cực tiểu của hàm số đã cho là
A.
2
B.
3
C.
4
D.
1
Câu 5. (Đề Tham Khảo 2019) Cho hàm số
( )f x
có đạo hàm
3
( ) ( 1)( 2)
f x x x x
,
x R
. Số điểm
cực trị của hàm số đã cho là
A.
1
B.
3
C.
2
D.
5
Câu 6. (Mã 101 - 2019) Cho hàm số
( )f x
có đạo hàm
2
( ) 2 , xf x x x
.
Số điểm cực trị của
hàm số đã cho là
A.
2
. B.
1
. C.
0
. D.
3
.
Câu 7. (Mã 103 - 2019) Cho hàm số
f x
có đạo hàm
2
1 , .f x x x x R
Số điểm cực trị của
hàm số đã cho là
A.
2
. B.
0
. C.
1
. D.
3
.
Câu 8. (Mã 104 - 2019) Cho hàm số
f x
có đạo hàm
2
1 , f x x x x
. Số điểm cực trị của
hàm số đã cho là
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 9. (Mã 102 - 2019) Cho hàm số
( )y f x
có đạo hàm
2
( ) ( 2)
f x x x
,
x
. Số điểm cực trị
của hàm số đã cho là
A.
0
. B.
3
. C.
2
. D.
1
.
Câu 10. (THPT Lê Quý Dôn Dà Nẵng 2019) Cho hàm số
f x
có đạo hàm
2 3 4
' 1 3 2
f x x x x x
với mọi
x
. Điểm cực tiểu của hàm số đã cho là
A.
2
x
. B.
3
x
. C.
0
x
. D.
1x
.
Câu 11. (Chuyên Sơn La 2019) Cho hàm số
f x
có đạo hàm
3
1 2 ,f x x x x x
. Số
điểm cực trị của hàm số đã cho là
A.
1
. B.
3
. C.
5
. D.
2
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Câu 12. (VTED 2019) Hàm số
y f x
có đạo hàm
1 2 ... 2019
f x x x x
,
x R
. Hàm
số
y f x
có tất cả bao nhiêu điểm cực tiểu?
A.
1008
B.
1010
C.
1009
D.
1011
Câu 13. (THPT Yên Phong 1 Bắc Ninh 2019) Hàm số
f x
có đạo hàm
3
2
1 2
f x x x x
,
x
. Hỏi
f x
có bao nhiêu điểm cực đại?
A.
2
. B.
0
. C.
1
. D.
3
.
Câu 14. (THPT Cù Huy Cận 2019) Cho hàm số
f x
có đạo hàm là
2
1 2f x x x x x
. Số
điểm cực trị của hàm số là?
A.
5
. B.
2
. C.
1
. D.
3
.
Câu 15. (Sở Bình Phước 2019) Cho hàm số
f x
có đạo hàm
2 3 4
1 2 3 4 , x .
f x x x x x
Số điểm cực trị của hàm số đã cho là
A.
3
B.
5
C.
2
D.
4
Câu 16. (THPT Gia Lộc Hải Dương 2019) Cho hàm số
f x
có đạo hàm
2
1 2 ,f x x x x x
. Số điểm cực trị của hàm số đã cho là
A.
5
. B.
2
. C.
1
. D.
3
.
Câu 17. (THPT Ba Đình 2019) Cho hàm số
y f x
có đạo hàm
2 4
2 3 9
f x x x x
. Số
điểm cực trị của hàm số
y f x
là
A.
3
. B.
4
. C.
2
. D.
1
.
Câu 18. (THCS - THPT Nguyễn Khuyến 2019) Nếu hàm số
f x
có đạo hàm là
4
2 2
' 2 2 1
f x x x x x x
thì tổng các điểm cực trị của hàm số
f x
bằng
A.
1
. B.
2
. C.
1
. D.
0
.
Câu 19. (Chuyên Quang Trung Bình Phước 2019) Cho hàm số
y f x
có đạo hàm
3
2 2
' 2 2
f x x x x x x
. Số điểm cực trị của hàm số là
A.
4
B.
1
C.
2
D.
3
Câu 20. (Chuyên Lam Sơn Thanh Hóa 2019) Cho hàm số
y f x
có đạo hàm trên
và
2
1 2 3
f x x x x
. Số điểm cực trị của hàm số đã cho là:
A.
3
B.
1
C.
0
D.
2
Câu 21. (Đề Minh Họa 2017) Tìm giá trị cực đại
C§
y
của hàm số
3
3 2y x x
.
A.
C§
1
y
B.
C§
4
y
C.
C§
1
y
D.
C§
0
y
Câu 22. (Mã 104 - 2017) Hàm số
2 3
1
x
y
x
có bao nhiêu điểm cực trị?
A.
1
B.
3
C.
0
D.
2
Câu 23. Cho hàm số
2
3
1
x
y
x
. Mệnh đề nào dưới đây đúng?
A. Cực tiểu của hàm số bằng
3
B. Cực tiểu của hàm số bằng
1
C. Cực tiểu của hàm số bằng
6
D. Cực tiểu của hàm số bằng
2
Câu 24. (Chuyên Hùng Vương Gia Lai 2019) Điểm cực đại của đồ thị hàm số
3 2
6 9y x x x
có tổng
hoành độ và tung độ bằng
A.
5
. B.
1
. C.
3
. D.
1
.

NGUYỄN BẢO VƯƠNG - 0946798489
Câu 25. (Chuyên
Vĩnh Phúc 2019) Tìm giá trị cực tiểu
CT
y
của hàm s
ố
3
3 4
y x x
.
A.
6
CT
y
B.
1
CT
y
C.
2
CT
y
D.
1
CT
y
Câu 26.
(THPT Cù Huy Cận 2019) Giá trị cực tiểu
CT
y
của hàm s
ố
3 2
3 4
y x x
là:
A.
0
CT
y
. B.
3
CT
y
. C.
2
CT
y
. D.
4
CT
y
.
Câu 27.
(Liên Trường Thpt Tp Vinh Nghệ An 2019) Đồ thị hàm số
4 2
1
y x x
có
bao nhiêu điểm
cực trị có tung độ là số dương?
A.
3
. B.
1
. C.
2
. D.
0
.
Câu 28. (Hsg Bắc Ninh 2019) Hàm số nào dưới đây không có cực trị?
A.
2
1
x
y
x
B.
2 2
1
x
y
x
C.
2
2 1y
x x
D.
3
1y x
x
Câu 29.
(THPT Ba Đình 2019) Cho hàm số
4 2
2 1
y x
x
. Xét
các mệnh đề sau đây
1) Hàm số có 3 điểm cực trị.
2) Hàm số đồng biến trên các khoảng
1;
0
;
1;
.
3) Hàm
số có 1 điểm cực trị.
4) Hàm số nghịch biến trên các khoảng
; 1
;
0;1
.
Có bao nhiêu mệnh đề đúng trong bốn mệnh đề trên?
A. 2. B. 1. C. 4. D. 3.
Câu 30. (THPT Ba Đình 2019) Tìm giá trị cực đại của hàm số
3 2
3 2
y x
x
.
A.
2
. B.
0
. C.
2
. D.
1
.
Câu 31. (THCS - THPT Nguyễn Khuyến 2019) Hàm số
4 3
2
1 1
5
3 201
9
4 3 2
y x x x x m
m
đạt
c
ực tiểu tại điểm:
A.
3
x
. B.
3
x
. C.
1x
. D.
1
x
.
Câu 32. (THCS - THPT Nguyễn Khuyến 2019) Điểm cực đại của đồ thị hàm số
3
3 1y x x
là:
A.
1;
1
M
. B.
0;1
N
. C.
2;
1
P
. D.
1;
3
Q
.
Câu 33.
(Sở Ninh Bình 2019) Hàm số
3 2
1
3 1
3
y
x x x
đạt cực tiểu tại điểm
A.
1
x
. B.
1x
. C.
3
x
. D.
3
x
.
Câu 34. (THPT
Sơn Tây Hà Nội 2019) Tìm số điểm cực trị của hàm số
4 2
2y x
x
.
A. 2. B. 4. C. 3. D. 1.
Câu 35. (Chuyên Quang Trung Bình Phước 2019) Điểm cực tiểu của đồ thị hàm số
3 2
5 5 y x x x
là
A.
1;
8
B.
0;
5
C.
5 4
0
;
3 27
D.
1;
0
Câu 36. Hàm s
ố nào trong bốn hàm số được liệt kê dưới đây không có cực trị?
A.
2 3
2
x
y
x
. B.
4
y x
. C.
3
y x x
. D.
2
y x
.
-------------------- HẾT --------------------
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
DẠNG TOÁN DÀNH CHO ĐỐI TƯỢNG HỌC SINH 7-8 ĐIỂM
Dạng 1. Tìm m để hàm số đạt cực trị tại x = x0
Bước 1. Tính
0 0
' , ''y x y x
Bước 2. Giải phương trình
0
' 0 ?y x m
Bước 3. Thế
m
vào
0
''y x
nếu giá trị
0
0
'' 0
'' 0
y x CT
y x CD
Dạng 1.1 Hàm số bậc 3
Câu 1. (Mã 110 - 2017) Tìm giá trị thực của tham số
m
để hàm số
3 2 2
1
4 3
3
y x mx m x
đạt
cực đại tại
3x
.
A.
1m
B.
7m
C.
5m
D.
1m
Câu 2. (Chuyên Hạ Long 2019) Tìm
m
để hàm số
3 2
2 1y x mx mx đạt cực tiểu tại
1x
A. không tồn tại
m
. B.
1m
. C.
1m
. D.
1;2m
.
Câu 3. Tìm tất cả các giá trị của tham số
m
để hàm số
3 2
3 1y x x mx đạt cực tiểu tại
2x
.
A.
0m
. B.
4m
. C.
0 4m
. D.
0 4m
.
Câu 4. (THPT Đoàn Thượng - Hải Dương 2019) Tìm các giá trị thực của tham số m để hàm số
3 2 2
1
4 3
3
y x mx m x
đạt cực đại tại
3x
.
A.
1, 5 m m
. B.
5m
. C.
1m
. D.
1m
.
Câu 5. (THPT An Lão Hải Phòng 2019) Có bao nhiêu số thực
m
để hàm số
3 2 2
1
1 1
3
y x mx m m x
đạt cực đại tại
1x
.
A.
0
B.
2
C.
1
D.
3
Câu 6. (THPT Đoàn Thượng – Hải Dương) Tìm các giá trị thực của tham số m để hàm số
3 2 2
1
4 3
3
y x mx m x
đạt cực đại tại
3x
.
A.
1, 5 m m
. B.
5m
. C.
1m
. D.
1m
.
Câu 7. (THPT Thăng Long - Hà Nội - Lần 2 - 2019) Tìm tập hợp tất cả các giá trị của
m
để hàm số
3 2 2
3 1 3y x m x m x
đạt cực tiểu tại
1x
.
A.
5;1
. B.
5
. C.
. D.
1
.
Câu 8. (THPT Kinh Môn - 2019) Tìm tất cả các giá trị thực của tham số
m
để hàm số
3 2
1
1 1
3
y x mx m x
đạt cực đại tại
2x
?
A.
2m
. B.
3m
. C. Không tồn tại
m
. D.
1m
.
Câu 9. (Chuyên ĐHSPHN - Lần 3 - 2019) Tập hợp các số thực
m
để hàm số
3 2
3 ( 2)y x mx m x m đạt cực tiểu tại
1x
là.
A.
1
. B.
1
. C.
. D.
R
.
CỰC TRỊ CỦA HÀM SỐ
Chuyên đề 2

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Dạng 1.2 Hàm số đa thức bậc cao, hàm căn thức …
Câu 10. (Chuyên QH Huế - Lần 2 - 2019) Xác định tham số m sao cho hàm số
y x m x
đạt cực trị
tại
1x
.
A.
2
m
. B.
2
m
. C.
6
m
. D.
6
m
.
Câu 11. (Trường THPT Hoàng Hoa Thám - Hưng Yên 2019) Tìm tất cả tham số thực
m
để hàm số
4 2 2
1 2 2019
y m x m x
đạt cực tiểu tại
1
x
.
A.
0
m
. B.
2
m
. C.
1
m
. D.
2
m
.
Câu 12. (Chuyên Trần Phú Hải Phòng 2019) Cho hàm số
y f x
xác định trên tập số thực
và có
đạo hàm
3
2
' sin 3 9f x x x x m x m x
(
m
là tham số). Có bao nhiêu giá trị
nguyên của
m
để hàm số
y f x
đạt cực tiểu tại
0
x
?
A.
6
B.
7
C.
5
D.
4
Câu 13. (Mã 101 - 2018) Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
8 5 2 4
2 4 1
y x m x m x
đạt cực tiểu tại
0
x
?
A. Vô số B.
3
C.
5
D.
4
Câu 14. (Chuyên Quang Trung- Bình Phước 2019) Tất cả các giá trị thực của tham số
m
để hàm số
5 4
2
5 4
x mx
y
đạt cực đại tại
0
x
là:
A.
m
. B.
0
m
. C. Không tồn tại
m
. D.
0
m
.
Câu 15. Có bao nhiêu giá trị nguyên của
m
thuộc khoảng
2019;2019
để hàm số
5 4
1 2
5
5 4
m m
y x x m
đạt cực đại tại
0
x
?
A.
101
. B.
2016
. C.
100
. D.
10
.
Câu 16. (Mã 104 - 2018) Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
8 5 2 4
3 9 1
y x m x m x
đạt cực tiểu tại
0
x
?
A.
6
B. Vô số C.
4
D.
7
Câu 17. (Mã 103 - 2018) Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
8 5 2 4
4 16 1
y x m x m x
đạt cực tiểu tại
0
x
.
A.
8
B. Vô số C.
7
D.
9
Câu 18. Có bao nhiêu giá trị nguyên của tham số m để hàm số
12 7 2 6
( 5) ( 25) 1
y x m x m x
đạt cực
đại tại
0
x
?
A.
8
B.
9
C. Vô số D.
10
Câu 19. (Mã 102 - 2018) Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
8 5 2 4
( 1) ( 1) 1
y x m x m x
đạt cực tiểu tại
0?
x
A.
3
B.
2
C. Vô số D.
1
Dạng 2. Tìm m để hàm số có n cực trị
Hàm số có
n
cực trị
0y
có
n
nghiệm phân biệt.
Xét hàm số bậc ba
3 2
:y ax bx cx d
Hàm số có hai điểm cực trị khi
2
0
.
3 0
a
b ac
Hàm số không có cực trị khi
0y
vô nghiệm hoặc có nghiệm kép.
Xét hàm số bậc bốn trùng phương
4 2
.y ax bx c

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Hàm số có ba cực trị khi
0.ab
Hàm số có
1
cực trị khi 0.ab
Câu 1. Biết rằng hàm số
3 3
3
y x a x b x
có hai điểm cực trị. Mệnh đề nào sau đây là đúng?
A.
0ab
. B.
0ab
. C.
0ab
. D.
0ab
.
Câu 2. (THPT Hai Bà Trưng - Huế - 2019) Tìm tất cả các giá trị của tham số thực
m
để hàm số
3 2
2 ( 2) 1y mx mx m x
không có cực trị
A.
( ;6) (0; )m
. B.
6;0m
. C.
6;0m
. D.
6;0m
.
Câu 3. (Đề Tham Khảo 2017) Tìm tất cả các giá trị thực của tham số
m
để hàm số
4 2
1 2 3 1y m x m x
không có cực đại?
A.
1 3m
B.
1m
C.
1m
D.
1 3m
Câu 4. (Chuyên Sơn La - Lần 2 - 2019) Để đồ thị hàm số
4 2
3 1y x m x m
có điểm cực đại
mà không có điểm cực tiểu thì tất cả các giá trị thực của tham số
m
là
A.
3m
. B.
3m
. C.
3.m
D.
3m
.
Câu 5. (Quang Trung - Bình Phước - Lần 5 - 2019) Cho hàm số
4 2
2y x mx m . Tìm tất cả các giá
trị thực của
m
để hàm số có
3
cực trị
A.
0m
. B.
0m
. C.
0m
. D.
0m
.
Câu 6. (Chuyên Hà Tĩnh - Lần 1 - 2019) Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
2 4 2 2
2019 1 y m x m m x
có đúng một cực trị?
A.
2019
. B.
2020
. C.
2018
. D.
2017
.
Câu 7. (THPT Yên Khánh A - Ninh Bình - 2019) Cho hàm số
3 2
3 1 3 7 3y x m x m x
. Gọi
S
là tập các giá trị nguyên của tham số m để hàm số không có cực trị. Số phần tử của
S
là
A.
2
. B.
4
. C.
0
. D. Vô số.
Câu 8. (HSG - TP Đà Nẵng - 2019) Tìm tất cả các giá trị của tham số
m
để hàm số
4 3 2
4 3 1 1y x mx m x
có cực tiểu mà không có cực đại.
A.
1 7
; .
3
m
B.
1 7
;1 1 .
3
m
C.
1 7
; .
3
m
D.
1 7 1 7
; 1 .
3 3
m
Câu 9. (HSG 12 - Bắc Ninh - 2019) Cho hàm số
f x
có đạo hàm
2 2
1 2 5f x x x x mx
. Có
tất cả bao nhiêu giá trị nguyên của
m
để hàm số có đúng một điểm cực trị?
A.
0
. B.
5
. C.
6
. D.
7
.
Câu 10. (THPT Hùng Vương Bình Phước 2019) Tìm tất cả các giá trị của tham số
m
để hàm số
3
2
2 1
3
x
y mx mx
có hai điểm cực trị.
A.
0 2m
. B.
2m
. C.
0m
. D.
2
0
m
m
.
Câu 11. (THPT Ba Đình 2019) Tìm tất cả các giá trị của tham số để hàm số
có cực đại và cực tiểu?
A. . B. C. . D. .
Câu 12. (Chuyên Bắc Giang 2019) Tập hợp các giá trị của
m
để hàm số
3 2
1
2 1
3
y x mx m x
có
hai cực trị là:
m
3 2
3 2
y x x mx m
3
2
m
3
.
2
m
3
2
m
3
2
m

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
; 1 2;
B.
; 1 2;
C.
1;2
D.
1;2
Câu 13. (THPT Quỳnh Lưu 3 Nghệ An 2019) Cho hàm số
4 2
1
y mx x
. Tập hợp các số thực
m
để
hàm số đã cho có đúng một điểm cực trị là
A.
0;
. B.
;0
. C.
0;
. D.
;0
.
Câu 14. (THPT Yên Định Thanh Hóa 2019) Cho hàm số
4 2
(2 1) 1
y mx m x
. Tìm tất cả các giá trị
thực của tham số
m
để hàm số có đúng một điểm cực tiểu.
A. Không tồn tại
m
. B.
0.
m
C.
1
.
2
m
D.
1
0.
2
m
Câu 15. (Cụm Liên Trường Hải Phòng 2019) Tìm số các giá trị nguyên của tham số
m
để hàm số
4 2 2
2 6 1
y x m m x m
có ba điểm cực trị.
A.
6
. B.
5
. C.
4
. D.
3
.
Câu 16. (THCS - THPT Nguyễn Khuyến 2019) Hàm số
4 2
1 1 2y mx m x m
có một điểm cực
trị khi
A.
0 1
m
. B.
0 1
m m
. C.
0
m
. D.
0 1
m m
.
Câu 17. (Chuyên Lam Sơn Thanh Hóa 2019) Có tất cả bao nhiêu giá trị nguyên của
m
trên miền
10;10
để hàm số
4 2
2 2 1 7
y x m x
có ba điểm cực trị?
A.
20
B.
10
C. Vô số D.
11
Câu 18. (THPT An Lão Hải Phòng 2019) Cho hàm số
4 2 2
6 4
y mx m x
. Có bao nhiêu số
nguyên
m
để hàm số có ba điểm cực trị trong đó có đúng hai điểm cực tiểu và một điểm cực đại ?
A.
4
B.
3
C.
2
D.
5
Câu 19. (THPT Nguyễn Khuyến 2019) Tìm tất cả các giá trị thực của tham số
m
để hàm số
4 2
1 1 2y mx m x m
có một cực trị.
A.
1
m
B.
0
m
C.
0 1
m
D.
0 1
m m
Câu 20. (Chuyên Lào Cai - 2020) Cho hàm số
f x
có đạo hàm
4 3
2 2
2 4 2 3 6 18 .
f x x x x x m x m
Có tất cả bao nhiêu giá trị nguyên của
m
để hàm số
f x
có đúng một điểm cực trị?
B.
7
. B.
5
. C.
8
. D.
6
.
Câu 21. (Chuyên Sơn La - 2020) Gọi
S
là tập hợp những giá trị của tham số
m
để hàm số sau không có
cực trị trên
.
2 4 3 2 2
1 1 1
( ) . . ( 1)
4 3 2
x x x x
f x m e m e e m m e
. Tổng tất cả các phần tử của tập
S
bằng
A.
2
3
B.
2
.
3
C.
1
.
3
D.
1.
Dạng 3. Đường thẳng đi qua 2 điểm cực trị
Phương trình hai đường thẳng đi qua 2 điểm cực trị của hàm số bậc ba là phần dư của phép chia
của
y
cho
'y
Phân tích (bằng cách chia đa thức
y
cho
)y
:
1 1
2 2
( )
( ) ( )
( )
y h x
y y q x h x
y h x
Đường thẳng qua 2 điểm cực trị là
( ).y h x

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Câu 1. (Mã 123 - 2017) Đồ thị hàm số
3 2
3 9 1y x x x
có hai cực trị
A
và
B
. Điểm nào dưới đây
thuộc đường thẳng
AB
?
A.
0; 1
M
B.
1; 10
N
C.
1; 0
P
D.
1;10
Q
Câu 2. (Mã 104 - 2017) Tìm giá trị thực của tham số
m
để đường thẳng
: 2 1 3
d y m x m
vuông
góc với đường thẳng đi qua hai điểm cực trị của đồ thị hàm số
3 2
3 1
y x x
.
A.
3
2
m
B.
3
4
m
C.
1
2
m
D.
1
4
m
Câu 3. Tìm giá trị thực của tham số
m
để đường thẳng
2 1 3
y m x m
song song với đường thẳng
đi qua các điểm cực trị của đồ thị hàm số
3 2
3 1
y x x
A.
3
4
m
. B.
1
2
m
. C.
3
4
m
. D.
1
2
m
.
Câu 4. Đồ thị của hàm số
3 2
3 9 1y x x x
có hai điểm cực trị
A
và
B
. Điểm nào dưới đây thuộc
đường thẳng
AB
.
A.
1;0
P
. B.
0; 1
M
. C.
1; 10
N
. D.
1;10
Q
.
Câu 5. (Lương Văn Chánh - Phú Yên – 2018) Tìm giá trị thực của tham số
m
để đường thẳng
: 3 1 3
d y m x m
vuông góc với đường thẳng đi qua hai điểm cực trị của đồ thị hàm số
3 2
3 1
y x x
.
A.
1
3
. B.
1
6
. C.
1
6
m
. D.
1
3
.
Câu 6. (TT Tân Hồng Phong - 2018) Tìm tổng tất cả các giá trị thực của tham số
m
sao cho đường
thẳng đi qua hai điểm cực trị của đồ thị hàm số
3 2
2 3 1 6 1 2
y x m x m m x
song song
đường thẳng
4y x
.
A.
1
3
m
. B.
2
3
m
. C.
2
3
m
. D.
1
m
.
Câu 7. (THPT Xuân Hòa-Vĩnh Phúc- 2018) Biết đồ thị hàm số
3
3 1y x x
có hai điểm cực trị
A
,
B
. Khi đó phương trình đường thẳng
AB
là
A.
2 1y x
. B.
2 1.
y x
C.
2.
y x
D.
2y x
.
Câu 8. (Chuyên Vĩnh Phúc - 2018) Tìm tất cả các giá trị của tham số
m
để đồ thị hàm số
3 2
2 3
y x x m x m
có hai điểm cực trị và điểm
9; 5
M
nằm trên đường thẳng đi qua
hai điểm cực trị của đồ thị.
A.
1.
m
B.
5.
m
C.
3.
m
D.
2.
m
Câu 9. (Nguyễn Khuyến 2019)
Đường thẳng nối hai điểm cực đại và cực tiểu của đồ thị hàm số
3
2
y x x m
đi qua điểm
3;7
M
khi
m
bằng bao nhiêu?
A. 1. B.
1
. C. 3. D. 0.
Câu 10. (Chuyên Lương Văn Chánh - Phú Yên - 2018) Tìm giá trị thực của tham số
m
để đường thẳng
: 3 1 3
d y m x m
vuông góc với đường thẳng đi qua hai điểm cực trị của đồ thị hàm số
3 2
3 1
y x x
.
A.
1
6
m
. B.
1
3
. C.
1
3
. D.
1
6
.
Câu 11. (TT Diệu Hiền - Cần Thơ - 2018) Giả sử
A
,
B
là hai điểm cực trị của đồ thị hàm số
3 2
f x x ax bx c
và đường thẳng
AB
đi qua gốc tọa độ. Tìm giá trị nhỏ nhất của
P abc ab c
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
16
25
. B.
9
. C.
25
9
. D.
1
.
Câu 12. (Chuyên Hạ Long - 2018) Tìm tất cả giá trị thực của tham số
m
để đồ thị hàm số
3 2
3 2
y x mx
có hai điểm cực trị
A
và
B
sao cho các điểm
A
,
B
và
1; 2
M
thẳng hàng.
A.
2
m
. B.
2
m
. C.
2
m
. D.
2
m
;
2
m
.
Dạng 4. Tìm m để hàm số bậc 3 có cực trị thỏa mãn điều kiện cho trước
Bài toán tổng quát: Cho hàm số
3 2
( ; ) .y f x m ax bx cx d
Tìm tham số m để đồ thị
hàm số có 2 điểm cực trị
1 2
, x x
thỏa mãn điều kiện K cho trước?
Phương pháp:
— Bước 1. Tập xác định
.
D
Tính đạo hàm:
2
3 2 .y ax bx c
— Bước 2. Để hàm số có 2 cực trị
0
y
có 2 nghiệm phân biệt
2
3 0
(2 ) 4.3 0
y
y
a a
b ac
và giải hệ này sẽ tìm được
1
.m D
— Bước 3. Gọi
1 2
, x x
là 2 nghiệm của phương trình
0.
y
Theo Viét, ta có:
1 2
1 2
b
S x x
a
c
P x x
a
— Bước 4. Biến đổi điều kiện
K
về dạng tổng S và tích P. Từ đó giải ra tìm được
2
.m D
— Bước 5. Kết luận các giá trị m thỏa mãn:
1 2
.m D D
Lưu ý:
— Hàm số bậc 3 không có cực trị
0
y
không có 2 nghiệm phân biệt
0.
y
— Trong trường hợp điều kiện K liên quan đến hình học phẳng, tức là cần xác định tọa độ 2 điểm
cực trị
1 1 2 2
( ; ), ( ; )A x y B x y
với
1 2
, x x
là 2 nghiệm của
0.
y
Khi đó có 2 tình huống thường gặp
sau:
Nếu giải được nghiệm của phương trình
0,
y
tức tìm được
1 2
, x x
cụ thể, khi đó ta sẽ thế vào
hàm số đầu đề
( ; )y f x m
để tìm tung độ
1 2
, y y
tương ứng của A và B.
Nếu tìm không được nghiệm
0,
y
khi đó gọi 2 nghiệm là
1 2
, x x
và tìm tung độ
1 2
, y y
bằng
cách thế vào phương trình đường thẳng nối 2 điểm cực trị.
Để viết phương trình đường thẳng nối hai điểm cực trị, ta thường dùng phương pháp tách đạo hàm
(phần dư bậc nhất trong phép chia
y
cho
)y
, nghĩa là:
Phân tích (bằng cách chia đa thức
y
cho
)y
:
1 1
2 2
( )
( ) ( )
( )
y h x
y y q x h x
y h x
Đường thẳng qua 2 điểm cực trị là
( ).y h x
Dạng toán: Tìm tham số m để các hàm số sau có cực trị thỏa điều kiện cho trước (cùng phía,
khác phía d):
Vị trí tương đối giữa 2 điểm với đường thẳng:
Cho 2 điểm
( ; ), ( ; )
A A B B
A x y B x y
và đường thẳng
: 0.
d ax by c
Khi đó:
Nếu
( ) ( ) 0
A A B B
ax by c ax by c
thì
, A B
nằm về 2 phía so với đường
thẳng
.d
Nếu
( ) ( ) 0
A A B B
ax by c ax by c
thì
, A B
nằm cùng phía so với đường
.d
Trường hợp đặc biệt:
Để hàm số bậc ba
( )y f x
có 2 điểm cực trị nằm cùng phía so với trục tung

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Oy
phương trình
0
y
có 2 nghiệm trái dấu và ngược lại.
Để hàm số bậc ba
( )y f x
có 2 điểm cực trị nằm cùng phía so với trục hoành
Ox
đồ thị hàm số
( )y f x
cắt trục
Ox
tại 3 điểm phân biệt
phương trình
hoành độ giao điểm
( ) 0
f x
có 3 nghiệm phân biệt (áp dụng khi nhẩm được
nghiệm).
Dạng toán: Tìm m để các hàm số sau có cực trị thỏa điều kiện cho trước (đối xứng và cách đều):
Bài toán 1. Tìm m để đồ thị hàm số có 2 điểm cực trị
, A B
đối xứng nhau qua
đường
:d
— Bước 1. Tìm điều kiện để hàm số có cực đại, cực tiểu
1
.m D
— Bước 2. Tìm tọa độ 2 điểm cực trị
, .A B
Có 2 tình huống thường gặp:
+ Một là
0
y
có nghiệm đẹp
1 2
, ,x x
tức có
1 1 2 2
( ; ), ( ; ).A x y B x y
+ Hai là
0
y
không giải ra tìm được nghiệm. Khi đó ta cần viết phương trình đường
thẳng nối 2 điểm cực trị là
và lấy
1 1 2 2
( ; ), ( ; ) .
A x y B x y
— Bước 3. Gọi
1 2 1 2
;
2 2
x x y y
I
là trung điểm của đoạn thẳng
.AB
Do
, A B
đối xứng qua
d
nên thỏa hệ
2
0
.
d
d
AB u
m D
I d
I d
— Bước 4. Kết luận
1 2
.m D D
Bài toán 2. Tìm m để đồ thị hàm số có 2 điểm cực trị
, A B
cách đều đường thẳng
:d
— Bước 1. Tìm điều kiện để hàm số có cực đại, cực tiểu
1
.m D
— Bước 2. Tìm tọa độ 2 điểm cực trị
, .A B
Có 2 tình huống thường gặp:
+ Một là
0
y
có nghiệm đẹp
1 2
, ,x x
tức có
1 1 2 2
( ; ), ( ; ).A x y B x y
+ Hai là
0
y
không giải ra tìm được nghiệm. Khi đó ta cần viết phương trình đường
thẳng nối 2 điểm cực trị là
và lấy
1 1 2 2
( ; ), ( ; ) .
A x y B x y
— Bước 3. Do
, A B
cách đều đường thẳng
d
nên
2
( ; ) ( ; ) .d A d d B d m D
— Bước 4. Kết luận
1 2
.m D D
Lưu ý: Để 2 điểm
, A B
đối xứng nhau qua điểm
I I
là trung điểm
.AB
Câu 1. Với giá trị nào của tham số
m
để đồ thị hàm số
3 2
3
y x x m
có hai điểm cực trị
A
,
B
thỏa
mãn
OA OB
(
O
là gốc tọa độ)?
A.
3
2
m
. B.
3
m
. C.
1
2
m
. D.
5
2
m
.
Câu 2. (Đề Tham Khảo 2017) Gọi
S
là tập hợp tất cả các giá trị thực của tham số
m
để đồ thị của hàm
số
3 2 2
1
1
3
y x mx m x
có hai điểm cực trị
A
và
B
sao cho
,A B
nằm khác phía và cách
đều đường thẳng
: 5 9
d y x
. Tính tổng tất cả các phần tử của
S
.
A.
3
B.
6
C.
6
D.
0
Câu 3. (Chuyên Biên Hòa - Hà Nam - 2020) Có tất cả bao nhiêu giá trị thực của tham số
m
để đồ thị
hàm số
3 2 2
2 2
2 3 1
3 3
y x mx m x
có hai điểm cực trị có hoành độ
1
x
,
2
x
sao cho
1 2 1 2
2 1
x x x x
.
A.
1
. B.
0
. C.
3
. D.
2
.
Câu 4. (Chuyên KHTN - 2020) Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số
3 2
(2 1) 2 1
y mx m x mx m
có hai điểm cực trị nằm về hai phía của trục hoành?

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A. 4. B. 2. C. 1. D. 3.
Câu 5. (Chuyên Hạ Long - Quảng Ninh - 2020) Cho hàm số
3 2
6 2 9 2.
y x m x m x
Tìm
m
để đồ thị hàm số có hai điểm cực trị nằm về hai phía của trục hoành.
A.
2
.
6
m
m
B.
2.
m
C.
6.
m
D.
2
6
.
3
2
m
m
m
Câu 6. (THPT Lê Quy Đôn Điện Biên 2019) Cho hàm số
3 2
1
1 3 2 2018
3
y mx m x m x
với
m
là tham số. Tổng bình phương tất cả các giá trị của
m
để hàm số có hai điểm cực trị
1 2
;x x
thỏa mãn
1 2
2 1
x x bằng
A.
40
9
B.
22
9
C.
25
4
D.
8
3
Câu 7. (Chuyên Lê Quý Đôn Điện Biên 2019) Cho hàm số
3 2
3 3 1
y x mx m
với
m
là một tham
số thực. Giá trị của
m
thuộc tập hợp nào sau đây để đồ thị hàm số đã cho có hai điểm cực trị đối
xứng nhau qua đường thẳng
: 8 74 0
d x y
.
A.
1;1
m
. B.
3; 1
m
. C.
3;5
m
. D.
1;3
m
.
Câu 8. Có bao nhiêu giá trị nguyên của tham số
m
để đồ thị hàm số
3 2 2 2
8 11 2 2
y x x m x m
có hai điểm cực trị nằm về hai phía của trục
Ox
.
A.
4.
B.
5.
C.
6.
D.
7.
Câu 9. (Chuyên Hạ Long 2019) Cho hàm số
3 2
2 1 1 1
y x m x m x m
. Có bao nhiêu giá
trị của số tự nhiên
20
m
để đồ thị hàm số có hai điểm cực trị nằm về hai phía trục hoành?
A.
18
. B.
19
. C.
21
. D.
20
.
Câu 10. (Chuyên KHTN 2019) Có bao nhiêu giá trị nguyên của tham số
m
để đồ thị của hàm số
3 2 2 2
1 2 3
y x m x m x m
có hai điểm cực trị và hai điểm cực trị đó nằm về hai phía
khác nhau đối với trục hoành?
A.
2
. B.
1
.
C.
3
. D.
4
.
Câu 11. (THPT Lương Thế Vinh Hà Nội 2019) Tìm tất cả cả các giá trị của tham số m để
3 2
y x 3x mx 1
đạt cực trị tại
1 2
,x x
thỏa mãn
2 2
1 2
6
x x
A.
3
m
B.
3
m
C.
1
m
D.
1
m
Câu 12. Có bao nhiêu giá trị nguyên của
m
để hàm số
3 2
2 6 1
f x x x m
có các giá trị cực trị trái
dấu?
A.
7
. B.
9
. C.
2
. D.
3
.
Câu 13. (Thi thử SGD Hưng Yên) Cho hàm số
3 2
2 3 1 6 2 1y x m x m x
với
m
là tham số
thực. Tìm tất cả các giá trị của
m
để hàm số có điểm cực đại và điểm cực tiểu nằm trong khoảng
2;3
.
A.
1;4 \ 3
m
. B.
3;4
m
. C.
1;3
m
. D.
1;4
m
.
Câu 14. (THPT Cẩm Bình Hà Tỉnh 2019) Cho hàm số
3 2 2
3 4 2
y x mx m
có đồ thị
C
và điểm
1;4
C
. Tính tổng các giá trị nguyên dương của
m
để
C
có hai điểm cực trị
,A B
sao cho tam
giác
ABC
có diện tích bằng 4.
A.
6
. B.
5
. C.
3
. D.
4

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Câu 15. (THPT Lê Quy Đôn Điện Biên 2019) Cho hàm số
3 2
2 3 1 6 2 1
y x m x m x
với
m
là tham số thực. Tìm tất cả các giá trị của
m
để hàm số có điểm cực đại và điểm cực tiểu nằm
trong khoảng
2; 3
.
A.
1; 3 3; 4
m
. B.
1; 3
m
. C.
3; 4
m
. D.
1; 4
m
.
Câu 16. (Chuyên Lam Sơn Thanh Hóa 2019) Tổng tất cả các giá trị thực của tham số m để hàm số:
3 2
3 2 1 3 5
y x m x mx m
có hai điểm cực trị
1 2
;x x
đồng thời
1 2
. 0
y x y x
là:
A.
21
B.
39
C.
8
D.
3 11 13
Câu 17. (Chuyên Bắc Ninh 2019) Gọi S là tập các giá trị dương của tham số
m
sao cho hàm
số
3 2
3 27 3 2
y x mx x m
đạt cực trị tại
1 2
,x x
thỏa mãn
1 2
5
x x
. Biết
;S a b
. Tính
2
T b a
.
A.
51 6
T
B.
61 3
T
C.
61 3
T
D.
51 6
T
Câu 18. (Sở Bắc Giang 2019) Gọi
S
là tập hợp các giá trị nguyên của tham số
m
để hàm số
3
2
2 3
3
x
y x mx
có hai điểm cực trị
1 2
, 4
x x
. Số phần tử của
S
bằng
A.
5
. B.
3
. C.
2
. D.
4
.
Câu 19. (Toán Học Tuổi Trẻ 2019) Tìm giá trị thực của tham số
m
để hàm số
3 2
4 2 7 1y x m x x
có hai điểm cực trị
1 2
;x x
1 2
x x
thỏa mãn
1 2
4
x x
A.
5
m
. B.
1
2
m
. C.
3
m
. D.
7
2
m
.
Câu 20. Có bao nhiêu giá trị nguyên của tham số
m
để điểm
3
(2 ; )M m m
tạo với hai điểm cực đại, cực
tiểu của đồ thị hàm số
3 2
2 3(2 1) 6 ( 1) 1 ( )y x m x m m x C
một tam giác có diện tích nhỏ
nhất?
A.
0
B.
1
C.
2
D. không tồn tại
Câu 21. (HSG Bắc Ninh 2019) Tìm tất cả các giá trị thực của tham số thực m để đường thẳng đi qua hai
điểm cực đại, cực tiểu của đồ thị hàm số
3
3 2 y x mx
cắt đường tròn
C
có tâm
1;1
I
, bán
kính bằng 1 tại hai điểm phân biệt A,B sao cho diện tích tam giác IAB đạt giá trị lớn nhất.
A.
2 3
3
m
B.
2 3
2
m
C.
1 3
2
m
D.
2 5
2
m
Câu 22. (VTED 2019) Biết đồ thị hàm số
3 2
y x ax bx c
có hai điểm cưc trị
1 1 2 2
; , ;M x y N x y
thỏa mãn
1 1 2 1 1 2
x y y y x x
. Giá trị nhỏ nhất của biểu thức
2 3P abc ab c
bằng
A.
49
4
B.
25
4
C.
841
36
D.
7
6
Câu 23. Cho hàm số
3 2 2 3
3 3 1
y x mx m x m m
(
m
là tham số). Gọi
A
,
B
là hai điểm cực trị
của đồ thị hàm số và
2; 2
I
. Tổng tất cả các giá trị của
m
để ba điểm
I
,
A
,
B
tạo thành tam
giác nội tiếp đường tròn có bán kính bằng
5
là
A.
4
17
B.
14
17
C.
2
17
D.
20
17
Câu 24. Cho hàm số
3
6 4
y x mx
có đồ thị
m
C
. Gọi
0
m
là giá trị của
m
để đường thẳng đi qua
điểm cực đại, điểm cực tiểu của
m
C
cắt đường tròn tâm
1;0
I
, bán kính
2
tại hai điểm phân
biệt
,A B
sao cho tam giác
IAB
có diện tích lớn nhất. Chọn khẳng định đúng
A.
0
3;4
m
. B.
0
1;2
m
. C.
0
0;1
m
. D.
0
2;3
m
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 25. (Chuyên Lương Văn Chánh - Phú Yên - 2018) Cho hàm số
3 2
1 1
4 10
3 2
y x mx x
, với
m
là tham số; gọi
1
x
,
2
x
là các điểm cực trị của hàm số đã cho. Giá trị lớn nhất của biểu thức
2 2
1 2
1 1
P x x
bằng
A.
4
. B.
1
. C.
0
. D.
9
.
Câu 26. (Chuyên Lương Văn Chánh - Phú Yên - 2018) Cho hàm số
3 2 2 3
3 3 1
y x mx m x m
,
với
m
là tham số; gọi
C
là đồ thị của hàm số đã cho. Biết rằng khi
m
thay đổi, điểm cực đại
của đồ thị
C
luôn nằm trên một đường thẳng
d
cố định. Xác định hệ số góc
k
của đường thẳng
d
.
A.
1
3
k
. B.
1
3
k
. C.
3
k
. D.
3
k
.
Câu 27. (Chuyên Hùng Vương - Phú Thọ - 2018) Biết
0
m
là giá trị của tham số
m
để hàm số
3 2
3 1y x x mx
có hai điểm cực trị
1 2
,x x
sao cho
2 2
1 2 1 2
13
x x x x
. Mệnh đề nào dưới đây
đúng?
A.
0
1;7
m
. B.
0
7;10
m
. C.
0
15; 7
m
. D.
0
7; 1
m
.
Câu 28. (THPT Thanh Miện I - Hải Dương 2018) Biết rằng đồ thị hàm số
3 2
1 1
2
3 2
f x x mx x
có giá trị tuyệt đối của hoành độ hai điểm cực trị là độ dài hai cạnh của tam giác vuông có cạnh
huyền là
7
. Hỏi có mấy giá trị của
m
?
A.
3
. B.
1
. C. Không có
m
. D.
2
.
Câu 29. (Phan Đăng Lưu - Huế - 2018) Gọi
A
,
B
là hai điểm cực trị của đồ thị hàm số
3
3 4
f x x x
và
0
;0
M x
là điểm trên trục hoành sao cho tam giác
MAB
có chu vi nhỏ
nhất, đặt
0
4 2015
T x
. Trong các khẳng định dưới đây, khẳng định nào đúng?
A.
2017
T
. B.
2019
T
. C.
2016
T
. D.
2018
T
.
Câu 30. (Chuyên Hà Tĩnh - 2018) Tổng tất cả các giá trị của tham số thực
m
sao cho đồ thị hàm số
3 2 3
3 4y x mx m
có điểm cực đại và cực tiểu đối xứng với nhau qua đường phân giác của góc
phần tư thứ nhất là
A.
2
2
. B.
1
2
. C.
0
. D.
1
4
.
Câu 31. (THPT Triệu Thị Trinh - 2018) Tìm tất cả các giá trị của tham số thực
m
sao cho đồ thị hàm số
3 2
5 4
y x x m x m
có hai điểm cực trị nằm về hai phía đối với trục hoành.
A.
. B.
;3 3;4
. C.
;3 3;4
. D.
;4
.
Câu 32. (CTN - LẦN 1 - 2018) Biết
a
b
(trong đó
a
b
là phân số tối giản và
a
,
*
b
) là giá trị của tham
số
m
để hàm số
3 2 2
2 2
2 3 1
3 3
y x mx m x
có 2 điểm cực trị
1
x
,
2
x
sao cho
1 2 1 2
2 1
x x x x
. Tính giá trị biểu thức
2 2
S a b
.
A.
13
S
. B.
25
S
. C.
10
S
. D.
34
S
.
Câu 33. Gọi
S
là tập hợp tất cả các giá trị nguyên của tham số
m
để điểm cực tiểu của đồ thị hàm số
3 2
1y x x mx
nằm bên phải trục tung. Tìm số phần tử của tập hợp
5;6
S
.
A.
2
. B.
5
. C.
3
. D.
4
.
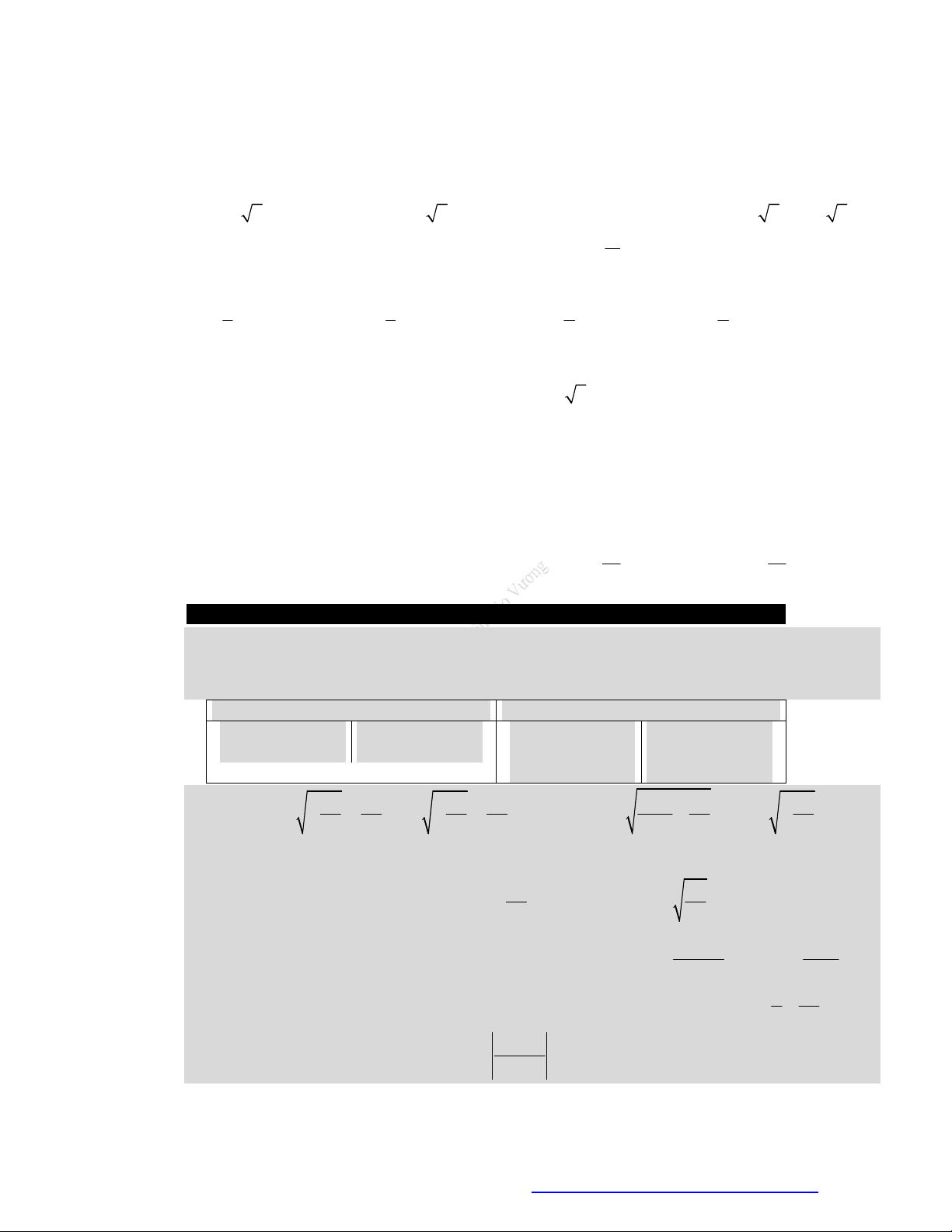
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Câu 34. (THPT Nghen - Hà Tĩnh - 2018) Cho hàm số
3 2 2 2
3 3 1 3 1
y x x m x m
. Có bao
nhiêu giá trị nguyên của
m
để đồ thị hàm số có điểm cực đại, cực tiểu nằm bên trái đường thẳng
2
x
?
A.
3
. B.
1
. C.
2
. D.
0
.
Câu 35. (Chuyên Hạ Long - 2018) Tìm tất cả giá trị thực của tham số
m
để đồ thị hàm số
3 2
3 2
y x mx
có hai điểm cực trị
A
và
B
sao cho các điểm
A
,
B
và
1; 2
M
thẳng hàng.
A.
2
m
. B.
2
m
. C.
2
m
. D.
2
m
;
2
m
.
Câu 36. (THPT Nam Trực - Nam Định - 2018) Cho hàm số
3 2
1 3 2 2
3
m
y x m x m x
. Hàm
số đạt cực trị tại
1 2
,x x
thỏa mãn
1 2
2 1
x x
khi
m a
và
m b
. Hãy tính tổng
a b
.
A.
8
3
. B.
8
3
. C.
5
2
. D.
5
2
.
Câu 37. (THPT Cao Bá Quát - 2018) Cho hàm số
3 2 3
2 3 1 6
y x m x mx m
. Tìm
m
để đồ thị
hàm số có hai điểm cực trị
,A B
sao cho độ dài
2
AB
.
A.
0
m
. B.
0
m
hoặc
2
m
. C.
1
m
. D.
2
m
.
Câu 38. (THPT Phú Lương - Thái Nguyên - 2018) Tìm tất cả các giá trị của tham số
m
để đồ thị hàm
số
3 2
3 3 3
y mx mx m
có hai điểm cực trị
,A B
sao cho
2 2 2
2 20
AB OA OB
(trong đó
O
là gốc tọa độ)
A.
1
m
. B.
1
m
. C.
1
17
11
m
m
. D.
1
17
11
m
m
.
Dạng 5. Tìm m để hàm số trùng phương có cực trị thỏa mãn điều kiện cho trước
Một số công thức tính nhanh “thường gặp“
liên quan cực trị hàm số
4 2
y ax bx c
1
cực trị:
0
ab
3
cực trị:
0
ab
0
a
:
1
cực
tiểu
0
a
:
1
cực đại
0
a
:
1
cực
đại,
2
cực tiểu
0
a
:
2
cực
đại,
1
cực tiểu
4
2
(0; ), ; , ; , 2
2 4 2 4 16 2 2
b b b b b
A c B C AB AC BC
a a a a a a a
với
2
4b ac
Phương trình qua điểm cực trị:
:
4
BC y
a
và
3
, :
2
b
AB AC y x c
a
Gọi
BAC
, luôn có:
3
3
3
8
8 (1 ) (1 ) 0
8
b a
a cos b cos cos
b a
và
5
2
3
32
b
S
a
Phương trình đường tròn đi qua
2 2
, , : . 0,
A B C x y c n x c n
với
2
4
n
b a
và bán
kính đường tròn ngoại tiếp tam giác là
3
8
8
b a
R
ab
Câu 1. (THPT Lương Thế Vinh - 2018) Cho hàm số
4 2
2 2
y x x
. Diện tích
S
của tam giác có ba
đỉnh là ba điểm cực trị của đồ thị hàm số đã cho có giá trị là

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
3
S
. B.
1
2
S
. C.
1
S
. D.
2
S
.
Câu 2. (Chuyên Lê Hồng Phong - 2018) Tìm
m
đề đồ thị hàm số
4 2
2 1
y x mx
có ba điểm cực trị
0; 1 , , A B C
thỏa mãn
4?
BC
A.
2
m
. B.
4
m
. C.
4
m
. D.
2
m
.
Câu 3. (Đề Minh Họa 2017) Tìm tất cả các giá trị thực của tham số
m
sao cho đồ thị của hàm số
4 2
2 1
y x mx
có ba điểm cực trị tạo thành một tam giác vuông cân
A.
3
1
9
m
. B.
1
m
. C.
3
1
9
m
. D.
1
m
.
Câu 4. (Mã 105 -2017) Tìm tất cả các giá trị thực của tham số
m
để đồ thị của hàm số
4 2
2
y x mx
có
ba điểm cực trị tạo thành một tam giác có diện tích nhỏ hơn
1
.
A.
0 1m
B.
0m
C.
3
0 4m
D.
1m
Câu 5. (Chuyên Nguyễn Trãi - Hải Dương - Lần 2 - 2020) Cho hàm số
4 2 2 4
2 2
y x mx m m
có
đồ thị (C). Biết đồ thị (C) có ba điểm cực trị A, B, C thỏa mãn ABCD là hình thoi với
0; 3
D
.
Số
m
thuộc khoảng nào sau đây?
A.
1 9
;
2 5
m
. B.
9
;2
5
m
. C.
1
1;
2
m
. D.
2;3
m
.
Câu 6. (THPT Lê Quý Đôn Đà Nẵng 2019) Gọi S là tập hợp tất cả các giá trị của tham số m để đồ thị
hàm số
4 2 2
2 1
y x m x m
có ba điểm cực trị tạo thành ba đỉnh của một tam giác vuông. Số
phần tử của tập hợp S là
A.
2
. B.
0
. C.
4
. D.
1
.
Câu 7. (THPT Đoàn Thượng - Hải Phòng 2019) Cho hàm số
4 2
2 1 1
y x mx
. Tổng lập phương
các giá trị của tham số
m
để đồ thị hàm số
1
có ba điểm cực trị và đường tròn đi qua
3
điểm
này có bán kính
1R
bằng
A.
5 5
2
. B.
1 5
2
. C.
2 5
. D.
1 5
.
Câu 8. (THPT Minh Châu Hưng Yên 2019) Tìm tất cả các giá trị thực của tham số m để đồ thị hàm
số
4 2 2
2 4
y x m x m
có ba điểm cực trị tạo thành ba đỉnh của một tam giác đều?
A.
0; 3; 3
m
B.
6 6
0; 3; 3
m
C.
6 6
3; 3
m
D.
3; 3
m
Câu 9. (THPT Quang Trung Đống Đa Hà Nội 2019) Tìm
m
để đồ thị hàm số
4 2 2
2 1
y x m x
có 3
điểm cực trị lập thành một tam giác vuông cân.
A.
1
m
. B.
1;1
m
. C.
1;0;1
m
. D.
m
.
Câu 10. (Toán Học Tuổi Trẻ Số 5) Tìm tất cả các giá trị
m
sao cho đồ thị hàm số
4 2
1 2 1
y x m x m
có ba điểm cực trị là ba đỉnh của một tam giác có một góc bằng
120
.
A.
3
2
1
3
m
. B.
3
2
1
3
m
,
1
m
.
C.
3
1
3
m
. D.
1
m
.
Câu 11. (Chuyên Lương Văn Chánh - Phú Yên - 2018) Gọi
S
là tập hợp tất cả các giá trị thực của
tham số
m
để đồ thị
C
của hàm số
4 2 2 4
2 5
y x m x m
có ba điểm cực trị, đồng thời ba
điểm cực trị đó cùng với gốc tọa độ
O
tạo thành một tứ giác nội tiếp. Tìm số phần tử của
S
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
A.
1
. B.
0
. C.
2
. D.
3
.
Câu 12. (Chuyên Quang Trung - 2018) Cho hàm số
4 2 2 4
2 2
y x mx m m
có đồ thị
C
. Biết đồ thị
C
có ba điểm cực trị
A
,
B
,
C
và
ABDC
là hình thoi trong đó
0; 3
D
,
A
thuộc trục tung.
Khi đó
m
thuộc khoảng nào?
A.
9
;2
5
m
. B.
1
1;
2
m
. C.
2;3
m
. D.
1 9
;
2 5
m
.
Câu 13. (THPT Nguyễn Huệ - Ninh Bình - 2018) Cho hàm số
4 2
2 2
y x mx
có đồ thị
m
C
. Tìm
m
để đồ thị hàm số có ba điểm cực trị tạo thành một tam giác vuông.
A.
3
3
m . B.
3
3
m . C.
1
m
. D.
1
m
.
Câu 14.
(CHUYÊN ĐHSPHN - 2018) Gọi
A
,
B
,
C
là các điểm cực trị của đồ thị hàm số
4 2
2 4
y x x
. Bán kính đường tròn nội tiếp tam giác
ABC
bằng
A.
1
. B.
2 1
. C.
2 1
. D.
2
.
Câu 15. (Hồng Bàng - Hải Phòng - 2018) Cho hàm số
4 2
2 4 5
y x m x m
có đồ thị
m
C
. Tìm
m
để
m
C
có ba điểm cực trị tạo thành một tam giác nhận gốc tọa độ
O
làm trọng tâm.
A.
1
m
hoặc
17
2
m
. B.
1
m
. C.
4
m
. D.
17
2
m
.
Câu 16. (Chuyên Vĩnh Phúc 2018) Tìm tất cả các giá trị thực của tham số
m
để đồ thị của hàm số
4 2
2
y x mx
có ba điểm cực trị tạo thành một tam giác có diện tích nhỏ hơn
1
.
A.
1
m
. B.
0 1
m
. C.
3
0 4
m
. D.
0
m
.
Câu 17. (Liên Trường - Nghệ An -2018) Gọi
0
m
là giá trị của tham số
m
để đồ thị hàm số
4 2
2 1
y x mx
có ba điểm cực trị tạo thành một tam giác có diện tích bằng
4 2
. Mệnh đề nào
sau đây đúng
A.
0
1;0
m
. B.
0
2; 1
m
. C.
0
; 2
m
. D.
0
1;0
m
.
Câu 18. (Chuyên Bắc Ninh - 2018) Tìm tất cả các giá trị thực của tham số
m
sao cho đồ thị của hàm số
4 2 2
2 1
y x m x m
có ba điểm cực trị tạo thành một tam giác vuông cân.
A.
0
m
.
B.
1; 0
m m
. C.
1
m
. D.
1; 0
m m
.
Câu 19. (THPT Triệu Thị Trinh - 2018) Cho hàm số:
4 2 2
2
y x mx m m
. Tìm
m
để đồ thị hàm số
có 3 điểm cực trị lập thành tam giác có một góc bằng
120
.
A.
1
3
m
. B.
3
1
3
m
. C.
3
1
3
m
. D.
1
3
m
.
Câu 20. (THPT Thái Phiên - Hải Phòng - 2018) Đồ thị hàm số
4 2
2
y x mx m
có ba điểm cực trị và
đường tròn đi qua ba điểm cực trị này có bán kính bằng
1
thì giá trị của
m
là:
A.
1 5
1;
2
m m
. B.
1 5
1;
2
m m
.
C.
1 5
1;
2
m m
. D.
1 5
1;
2
m m
.
Dạng 6. Tìm m để hàm số bậc 2 trên bậc 1 có cực trị thỏa mãn yêu cầu bài toán
Câu 1. (Toán Học Tuổi Trẻ Số 5) Viết phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm
số
2
2 3
2 1
x x
y
x
.
A.
2 2
y x
. B.
1y x
. C.
2 1y x
. D.
1y x
.
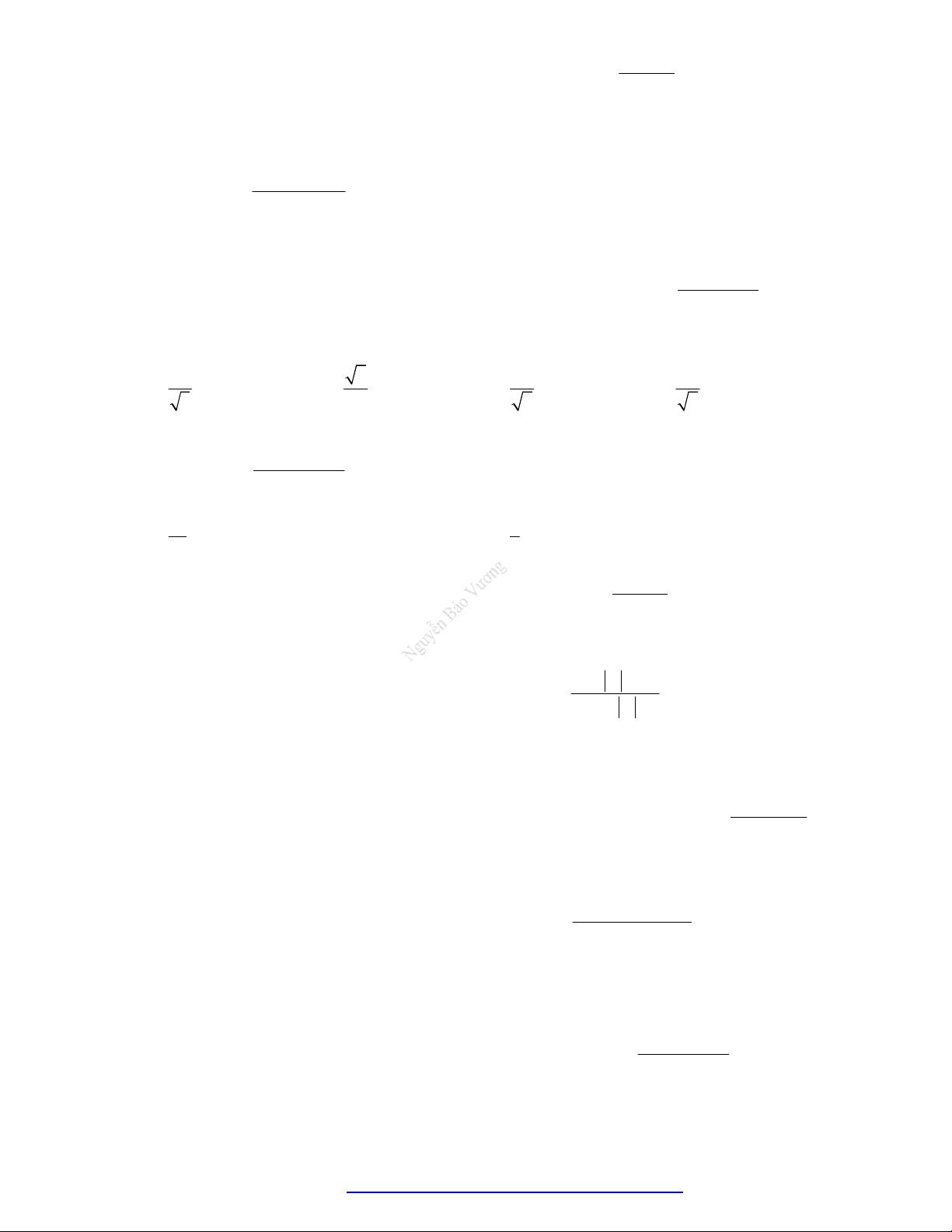
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 2. (ĐHQG Hà Nội - 2020) Điều kiện của tham số
m
để hàm số
2
1
x mx
y
x
có cực đại và cực tiểu
là
A.
0
m
. B.
1
m
. C.
2
m
. D.
2
m
.
Câu 3. (Chuyên KHTN - Hà Nội - Lần 3) Gọi
S
là tập hợp tất cả các giá trị thực của tham số
m
để đồ
thị hàm số
2
2
1
x mx m
y
x
có
hai điểm cực trị
A
,
B
và tam giác
OAB
vuông tại
O
. Tổng tất cả các phần tử của
S
bằng
A.
9
. B.
1
. C.
4
. D.
5
.
Câu 4. (Chuyên Lê Hồng Phong - Nam Định - 2020) Biết rằng đồ thị
2
2
:
2
x x m
H y
x
(với
m
là
tham số thực) có hai điểm cực trị là
,A B
. Hãy tính khoảng cách từ gốc tọa độ
0;0
O
đến đường
thẳng
AB
.
A.
2
5
. B.
5
5
. C.
3
5
. D.
1
5
.
Câu 5. (Chuyên Hùng Vương - Phú Thọ - 2018) Gọi
S
là tập hợp các giá trị thực của tham số
m
để đồ
thị hàm số
2 2
1
x mx m
y
x
có hai điểm cực trị
,A B
. Khi
90
AOB
thì tổng bình phương tất
cả các phần tử của
S
bằng:
A.
1
16
. B.
8
. C.
1
8
. D.
16
.
Câu 6. (Chuyên KHTN - 2018) Với tham số
m
, đồ thị của hàm số
2
1
x mx
y
x
có hai điểm cực trị
A
,
B
và
5
AB
. Mệnh đề nào dưới đây đúng?
A.
2
m
. B.
0 1
m
. C.
1 2
m
. D.
0
m
.
Câu 7. (Cụm 5 Trường Chuyên - ĐBSH - 2018) Cho hàm số
2
4
x m x
y
x m
. Biết rằng đồ thị hàm số
có hai điểm cực trị phân biệt là
A
,
B
. Tìm số giá trị
m
sao cho ba điểm
A
,
B
,
4;2
C
phân
biệt và thẳng hàng.
A.
0
. B.
2
. C.
1
. D.
3
.
Câu 8. (THCS - THPT Nguyễn Khuyến - 2018) Giá trị của tham số
m
để hàm số
2
1x mx
y
x m
đạt
cực đại tại điểm
0
2
x
là:
A.
1
m
. B.
3
m
. C.
1
m
. D.
3
m
.
Câu 9. (THPT Nam Trực - Nam Định - 2018) Cho hàm số
2
2 2
2 2
x mx m
y
x m
. Để hàm số có cực
đại và cực tiểu, điều kiện của tham số
m
là:
A.
1
2
m
m
B.
1 2
m
. C.
2 1
m
. D.
2
1
m
m
.
Câu 10. (Chuyên Nguyễn Dình Triểu - Dồng Tháp - 2018) Để hàm số
2
1
x mx
y
x m
đạt cực đại tại
2x
thì
m
thuộc khoảng nảo?
A.
0;2
. B.
4; 2
. C.
2; 0
. D.
2; 4
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Câu 11. (C
huyên Quốc Học Huế 2019) Cho hàm số
1
q
y
x p
x
đạt
cực đại tại điểm
2
; 2
A
.
Tính
p
q
.
A.
2
p
q
. B.
1
2
pq
. C.
3
p
q
. D.
1p
q
.
Câu 12. Cho
hàm số
2
1x
mx
y
x
m
(
với
m
là
tham số). Tìm tất cả các giá trị của tham số
m
để
hàm số
có giá trị cực đại là 7.
A.
7
m
. B.
5
m
. C.
9
m
. D.
5
m
.
-------------------- HẾT --------------------
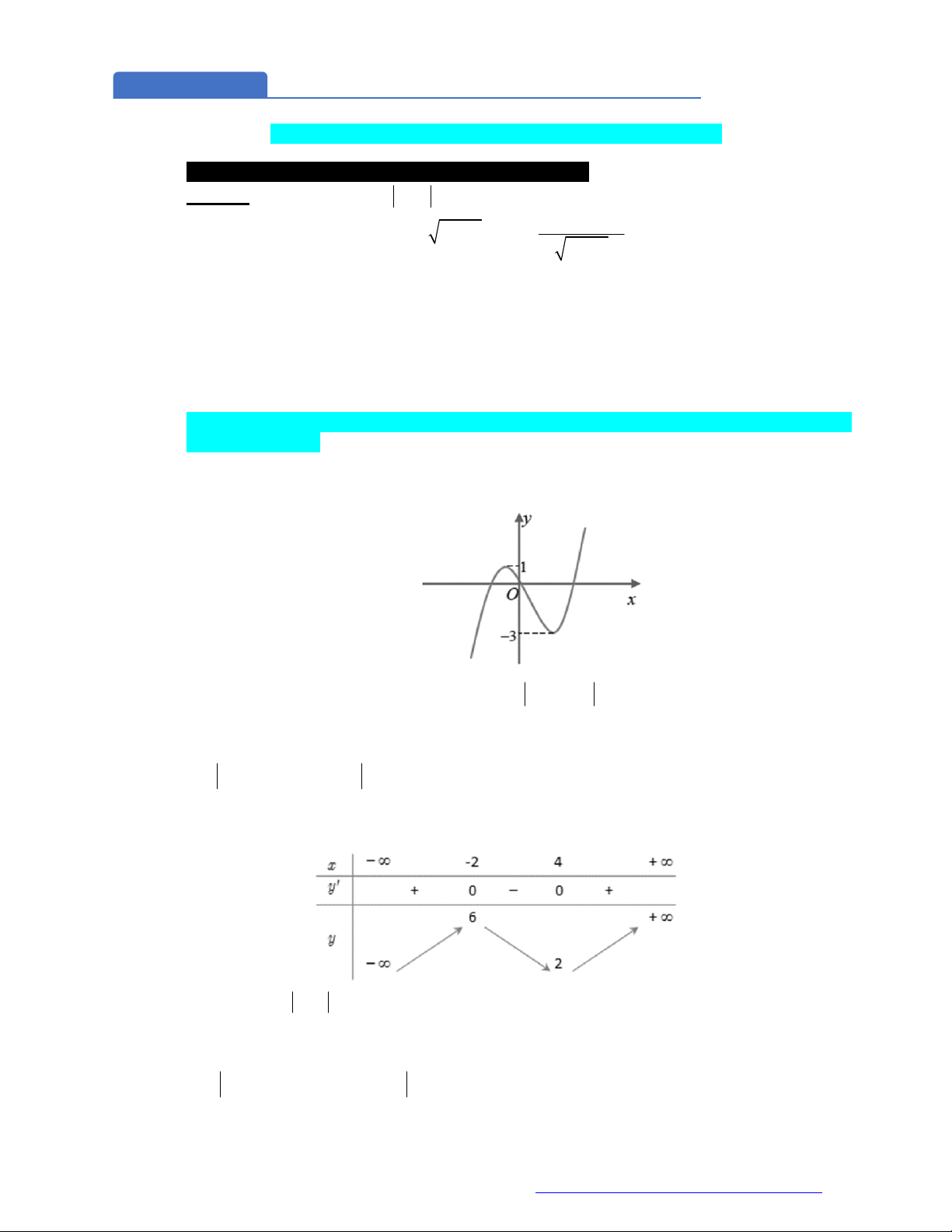
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
DẠNG TOÁN DÀNH CHO ĐỐI TƯỢNG HỌC SINH 9 - 10
Dạng 1. Bài toán cực trị hàm số chứa dấu trị tuyệt đối
Bài toán: Đồ thị hàm số
( )y f x
có bao nhiêu điểm cực trị
(Áp dụng định nghĩa).
2
2
2 ( ). ( )
( ) ( )
( )
f x f x
y f x f x y
f x
( ) 0 1
0
( ) 0 2
f x
y
f x
Số nghiệm của
1
chính là số giao điểm của đồ thị
( )y f x
và trục hoành
0y
. Còn số nghiệm
của
2
là số cực trị của hàm số
( )y f x
, dựa vào đồ thị suy ra
2
. Vậy tổng số nghiệm bội lẻ
của
1
và
2
chính là số cực trị cần tìm.
Dạng toán này mình làm tựa theo đề tham khảo 2018, vẫn xuất hiện ở dạng toán hàm hợp, các
bạn học chú ý nhé!
Câu 1. (Chuyên Vinh – Lần 2). Đồ thị
C
có hình vẽ bên.
Tất cả các giá trị của tham số
m
để hàm số
y f x m
có ba điểm cực trị là:
A.
1m
hoặc
3m
. B.
3m
hoặc
1.m
C.
1m
hoặc
3m
. D.
1 3.m
Câu 2. (Đề Tham Khảo 2018) Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
4 3 2
3 4 12y x x x m
có
7
điểm cực trị?
A.
5
B.
6
C.
4
D.
3
Câu 3. (Gia Bình 2019) Cho hàm số
( )y f x
có bảng biến thiên như sau.
Hàm số
3 y f x
có bao nhiêu điểm cực trị
A.
5
B.
6
C.
3
D.
1
Câu 4. (Cụm Liên Trường Hải Phòng 2019) Tìm số các giá trị nguyên của tham số
m
để đồ thị hàm số
4 2 2
2 2 12y x mx m m
có bảy điểm cực trị
A.
1
. B.
4
. C.
0
. D.
2
.
CỰC TRỊ CỦA HÀM SỐ
Chuyên đề 2
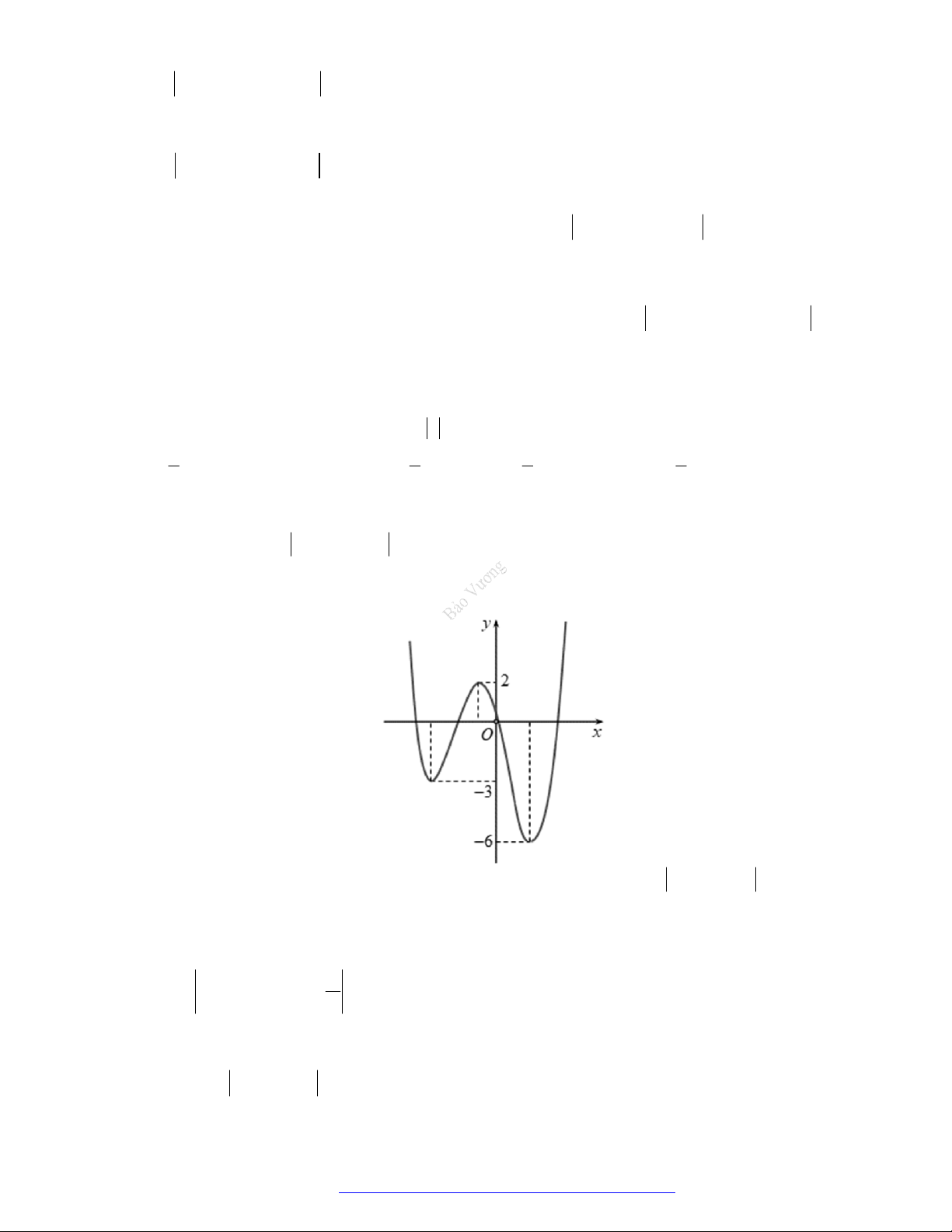
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 5. (Sở Vĩnh Phúc 2019) Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
4 3 2 2
3 4 12y x x x m
có đúng 5 điểm cực trị?
A.
5
. B.
7
. C.
6
. D.
4
.
Câu 6. (Chuyên Vĩnh Phúc 2019) Có bao nhiêu giá trị nguyên dương của tham số
m
để hàm số
4 3 2
3 4 12y x x x m
có
5
điểm cực trị.
A.
16
B.
44
C.
26
D.
27
Câu 7. (THPT Lương Thế Vinh Hà Nội 2019) Cho hàm số
4 2
2 2 1y x mx m
với
m
là tham số
thực. Số giá trị nguyên trong khoảng
2;2
của
m
để hàm số đã cho có
3
điểm cực trị là
A.
2
B.
4
C.
3
D.
1
Câu 8. (Chuyên Bắc Ninh 2019) Tập hợp các giá trị của
m
để hàm số
4 3 2
3 4 12 1y x x x m
có
7
điểm cực trị là:
A.
(0;6)
B.
(6;33)
C.
(1;33)
D.
(1;6)
Câu 9. (THPT Kinh Môn - 2018) Cho hàm số
3 2
( ) (2 1) (2 ) 2y f x x m x m x . Tìm tất cả các
giá trị của tham số
m
để hàm số
( )y f x
có 5 điểm cực trị.
A.
5
2
4
m
. B.
5
2
4
m
. C.
5
2
4
m
. D.
5
2
4
m
.
Câu 10. (Chuyên Đh Vinh - 2018) Cho hàm số
y f x
có đạo hàm
3 2 3
2 2f x x x x x
với
mọi
x
. Hàm số
1 2018f x
có nhiều nhất bao nhiêu điểm cực trị?
A.
9
. B.
2018
. C.
2022
. D.
11
.
Câu 11. (THPT Thạch Thanh 2 - Thanh Hóa - 2018) Hình vẽ bên là đồ thị của hàm số
y f x
.
Gọi
S
là tập hợp các giá trị nguyên dương của tham số
m
để hàm số
1y f x m
có
5
điểm cực trị. Tổng giá trị tất cả các phần tử của
S
bằng
A.
9
. B.
12
. C.
18
. D.
15
.
Câu 12. (THPT Quảng Yên - Quảng Ninh - 2018) Có bao nhiêu giá trị nguyên của tham số
m
để hàm
số
4 3 2
3 4 12
2
m
y x x x
có
7
điểm cực trị?
A.
3
. B.
9
. C.
6
. D.
4
.
Câu 13. (THPT Nguyễn Tất Thành - Yên Bái - 2018) Có bao nhiêu giá trị nguyên của tham số
m
để
hàm số
3 2
3y x x m
có
5
điểm cực trị?
A.
5
. B.
3
. C.
6
. D.
4
.
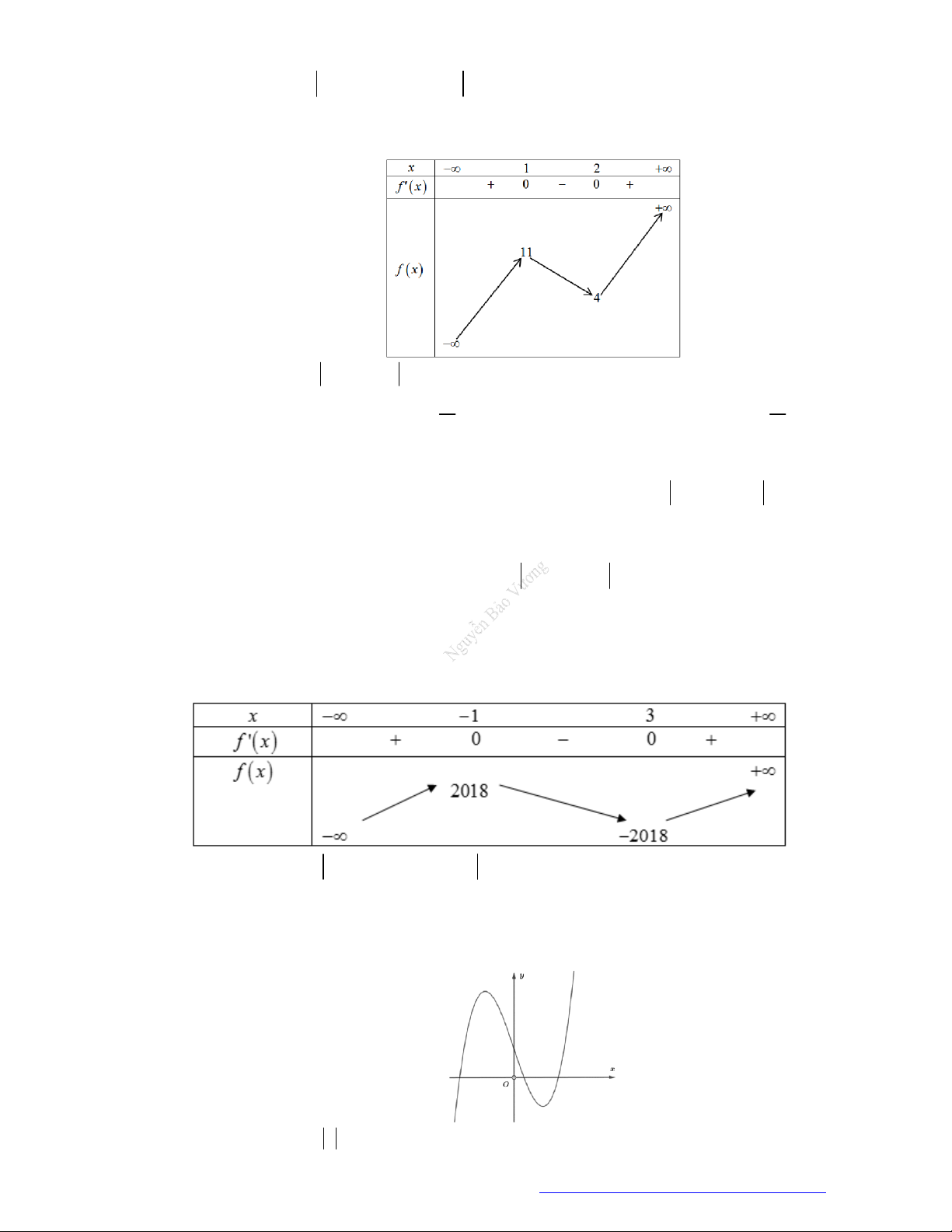
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Câu 14. (Chuyên Nguyễn Thị Minh Khai - Sóc Trăng - 2018) Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
5 3
3 25 60y x x x m
có 7 điểm cực trị?
A.
42
. B.
21
. C.
40
. D.
20
.
Câu 15. (Sở Nam Định - 2018) Cho hàm số
y f x
có bảng biến thiên như hình vẽ
Đồ thị hàm số
2 y f x m
có
5
điểm cực trị khi và chỉ khi
A.
4;11m
. B.
11
2;
2
m
. C.
3m
. D.
11
2;
2
m
.
Câu 16. (THPT Nguyễn Huệ - Tt Huế - 2018) Hình vẽ bên là đồ thị của hàm số
y f x
. Gọi
S
là tập
hợp các giá trị nguyên dương của tham số
m
để đồ thị hàm số
2y f x m
có
5
điểm cực
trị. Tổng giá trị tất cả các phần tử của
S
bằng
A.
15
. B.
18
. C.
9
. D.
12
.
Câu 17. (Sở Hưng Yên - 2018) Cho hàm số
3 2
( ) 3f x x x m
với
5;5m
là tham số. Có bao
nhiêu giá trị nguyên của
m
để hàm số
( )f x
có đúng ba điểm cực trị.
A.
3
. B.
0
. C.
8
. D.
6
.
Câu 18. (Chuyên Hùng Vương - Bình Dương - 2018)
Cho hàm số
y f x
có bảng biến thiên như
sau.
Đồ thị hàm số
2017 2018y f x
có bao nhiêu điểm cực trị?
A.
2
.
B.
3
.
C.
5
.
D.
4
.
Câu 19. (Chuyên Ngữ - Hà Nội - 2018) Hàm số
f x
có đạo hàm
f x
trên
. Hình vẽ bên là đồ thị
của hàm số
f x
trên
.
Hỏi hàm số
2018y f x
có bao nhiêu điểm cực trị?
A.
5
. B.
3
. C.
2
. D.
4
.
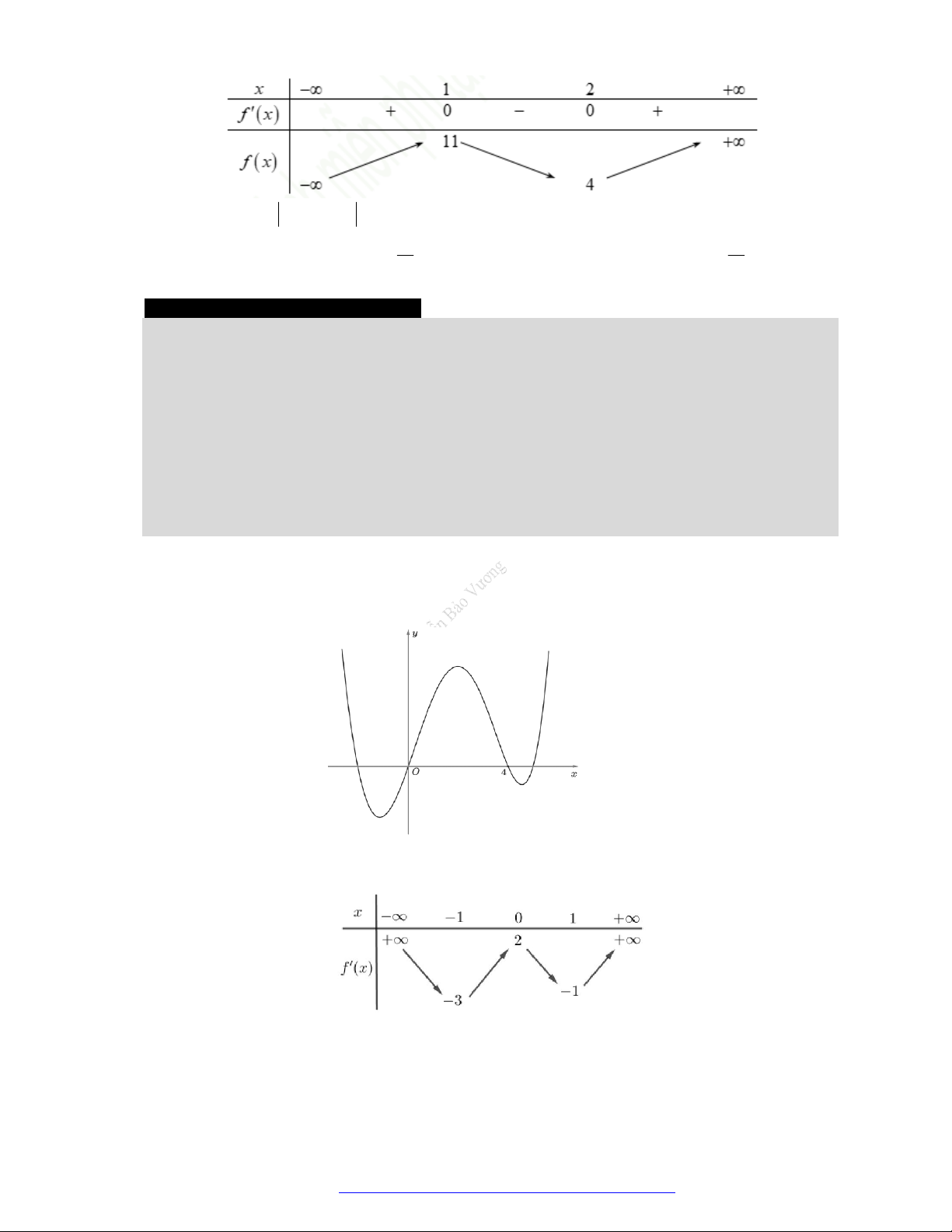
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 20. (Sở- Nam Định - 2018) Cho hàm số
y f x
có bảng biến thiên như hình vẽ
Đồ thị hàm số
2y f x m
có
5
điểm cực trị khi và chỉ khi
A.
4;11m
. B.
11
2;
2
m
. C.
3m
. D.
11
2;
2
m
.
Dạng 2. Số điểm cực trị của hàm hợp
Bài toán: Cho hàm số
y f x
(Đề có thể cho bằng hàm, đồ thị, bảng biến thiên của
, 'f x f x
). Tìm số điểm cực trị của hàm số
y f u
trong đó
u
là một hàm số đối với
x
Ta thực hiện phương pháp tương tự xét số điểm cực trị của hàm số
y f x
Bước 1. Tính đạo hàm
' '. 'y u f u
Bước 2. Giải phương trình
' 0
' 0
' 0
u
y
f u
Bước 3.Tìm số nghiệm đơn và bội lẻ hoặc các điểm mà
'y
không xác định.
Kết luận
Câu 1. (Đề Tham Khảo 2020 Lần 1) Cho hàm số bậc bốn
y f x
có đồ thị như hình bên. Số điểm
cực trị của hàm số
3 2
3g x f x x
là
A.
5
. B.
3
. C.
7
. D.
11
.
Câu 2. (Mã 101 - 2019) Cho hàm số
y f x
, bảng biến thiên của hàm số
'f x
như sau:
Số điểm cực trị của hàm số
2
2y f x x
là
A.
9.
B.
3.
C.
7.
D.
5.
Câu 3. (Mã 104 - 2019) Cho hàm số
f x
, bảng biến thiên của hàm số
f x
như sau:
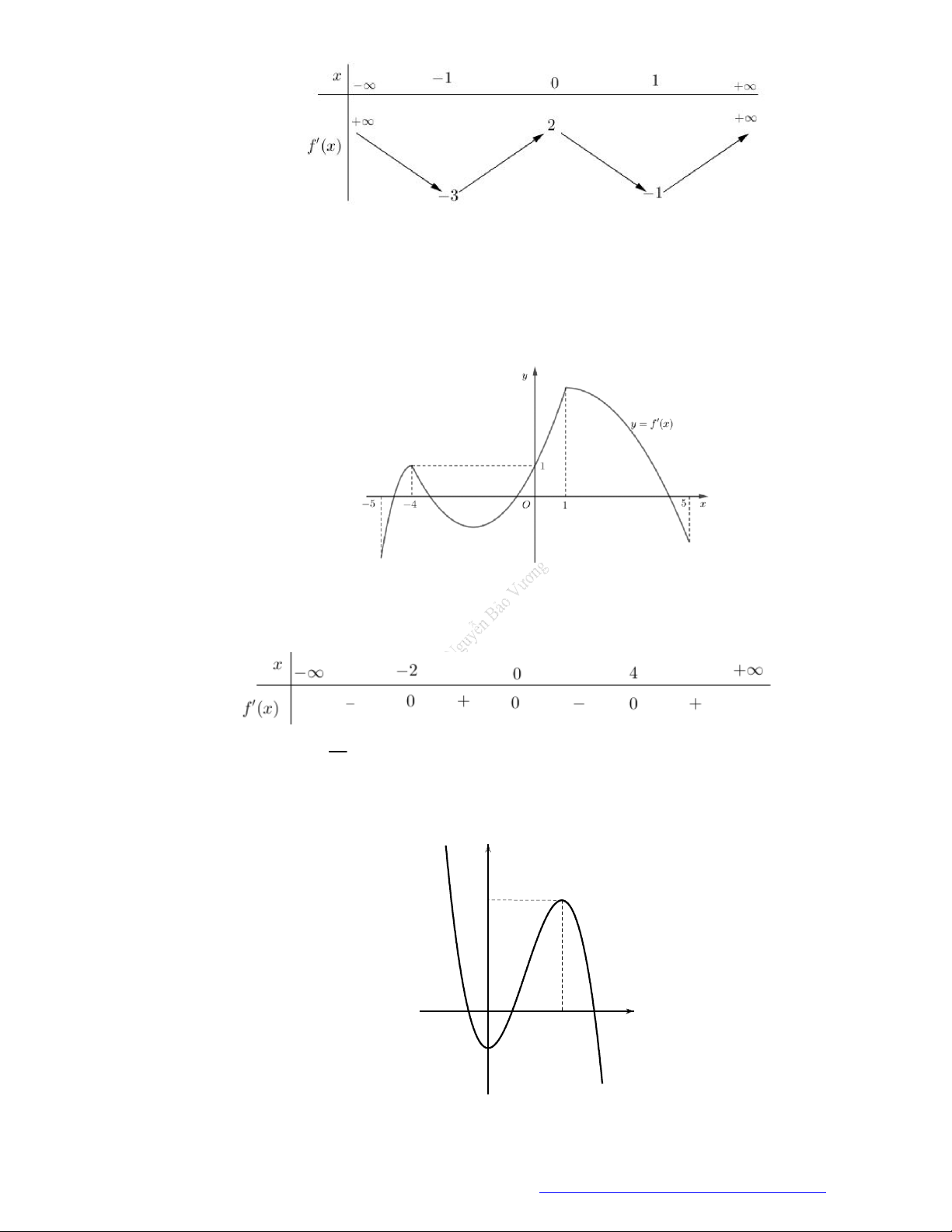
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Số điểm cực trị của hàm số
2
4 4y f x x
là
A. 5. B. 9. C. 7. D. 3.
Câu 4. (Chuyên ĐH Vinh - Nghệ An -2020) Cho hàm số
f x
có đạo hàm liên tục trên
. Đồ thị
hàm số
y f x
như hình vẽ bên. Hàm số
2 2
4 4y f x x x x
có bao nhiêu điểm cực trị
thuộc khoảng
5;1
?
A.
5
. B.
4
. C.
6
. D.
3
.
Câu 5. (Chuyên Hưng Yên - 2020) Cho hàm số
y f x
có đạo hàm đến cấp hai trên
và có bảng
xét dấu của hàm số
'y f x
như hình sau:
Hỏi hàm số
3
2
1 2 3
3
x
g x f x x x
đạt cực tiểu tại điểm nào trong các điểm sau?
A.
3x
. B.
0x
. C.
3x
. D.
1x
.
Câu 6. (Chuyên KHTN - 2020) Cho hàm số
y f x
xác định trên
, có đồ thị
f x
như hình vẽ.
Hàm số
3
g x f x x
đạt cực tiểu tại điểm
0
x . Giá trị
0
x thuộc khoảng nào sau đây
A.
1;3
. B.
1;1
. C.
0;2
. D.
3;
.
O
-1
3
2
y=f(x)
x
y
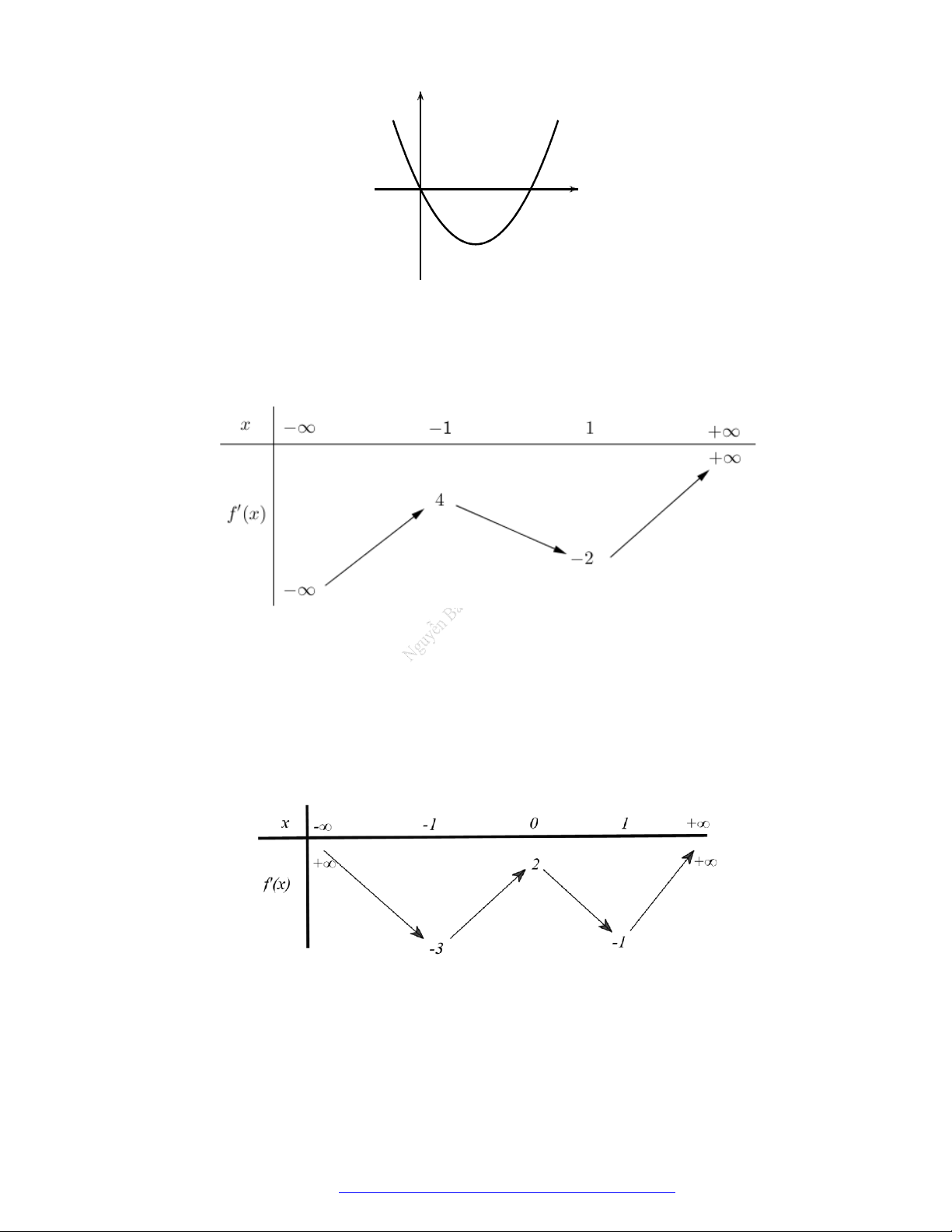
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 7. (Chuyên KHTN - 2020) Cho hàm số
y f x
liên tục trên
, có đồ thị
f x
như hình vẽ.
Số điểm cực tiểu của hàm số
2
g x f x x
là
A.
1
. B.
4
. C.
3
. D.
2
.
Câu 8. (Chuyên Lam Sơn - 2020) Cho hàm số
y f x
có đạo hàm liên tục trên
, bảng biến thiên
của hàm số
'f x
như sau:
Số điểm cực trị của hàm số
2
2y f x x
là
A. 4. B. 5. C. 1. D. 7.
Câu 9. (Sở Bắc Giang - 2018) Cho hàm số
y f x
có đúng ba điểm cực trị là
2; 1;0
và có đạo hàm
liên tục trên
. Khi đó hàm số
2
2y f x x
có bao nhiêu điểm cực trị?
A.
3
. B.
8
. C.
10
. D.
7
.
Câu 10. (Mã 102 - 2019) Cho hàm số
f x
, bảng biến thiên của hàm số
'f x
như sau
Số điểm cực trị của hàm số
2
2y f x x
là
A.
9
. B.
5
. C.
7
. D.
3
.
Câu 11. (Mã 103 - 2019) Cho hàm số
f x
, bảng biến thiên của hàm số
f x
như sau:
y=f'(x)
O
2 x
y
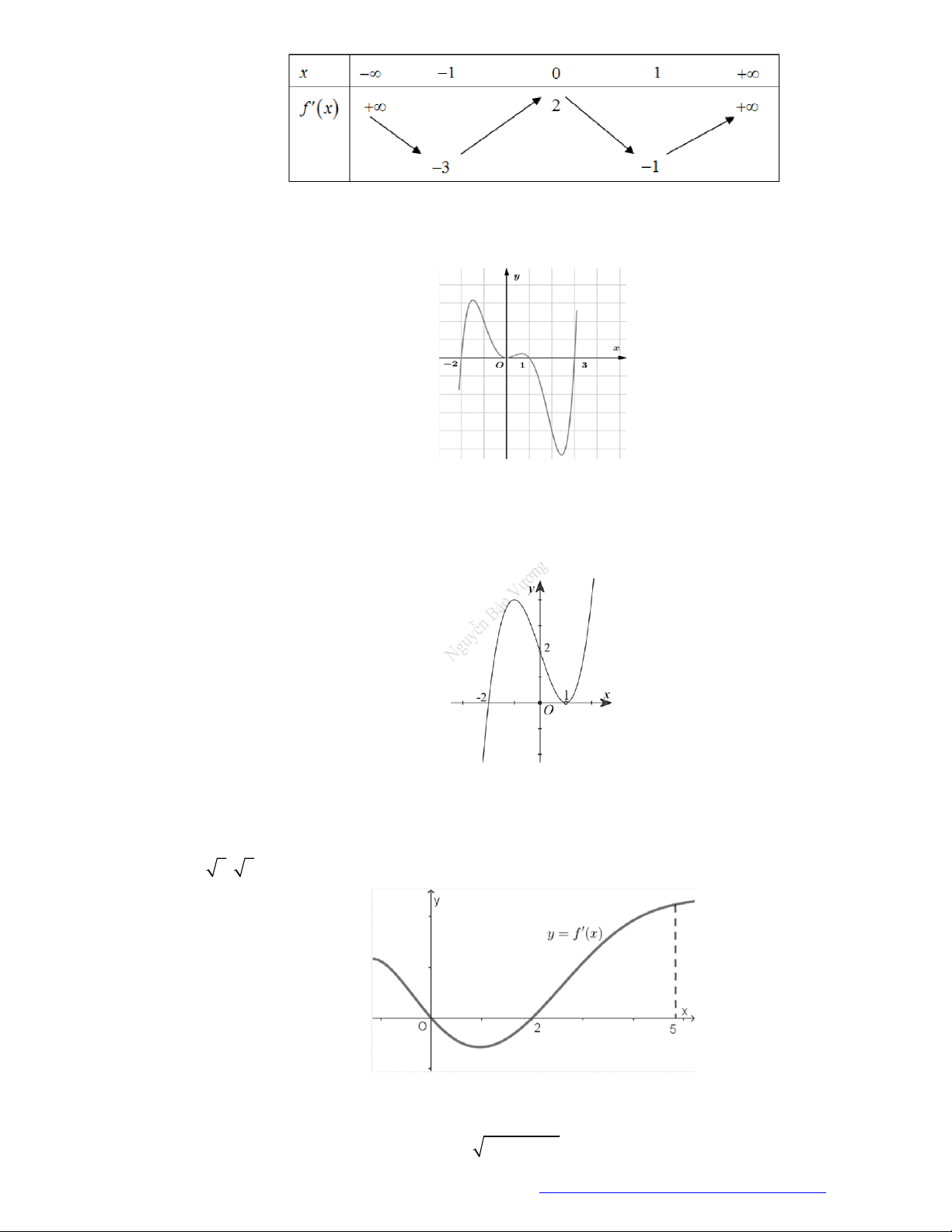
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Số cực trị của hàm số
2
4 4y f x x
là
A.
3
. B.
9
. C.
5
. D.
7
.
Câu 12. (Chuyên An Giang - 2018) Cho hàm số
y f x
. Đồ thị của hàm số
y f x
như hình bên.
Hàm số
2
g x f x
có bao nhiêu điểm cực trị?
A.
4
. B.
3
. C.
5
. D.
2
.
Câu 13. (THPT Lê Văn Thịnh Bắc Ninh 2019) Cho hàm số
y f x
xác định trên
và hàm số
y f x
có đồ thị như hình vẽ. Tìm số điểm cực trị của hàm số
2
3y f x
.
A.
4
B.
2
C.
5
D.
3
Câu 14. (Chuyên Lê Quý Đôn Quảng Trị 2019) Cho hàm số
f x
có đạo hàm là
f x
. Đồ thị của
hàm số
y f x
như hình vẽ bên. Tính số điểm cực trị của hàm số
2
y f x
trên khoảng
5; 5 .
A.
2
. B.
4
. C.
3
. D.
5
.
Câu 15. (Chuyên Vinh - 2018) Cho hàm số bậc bốn
y f x
. Hàm số
y f x
có đồ thị như hình vẽ
bên. Số điểm cực đại của hàm số
2
2 2y f x x
là
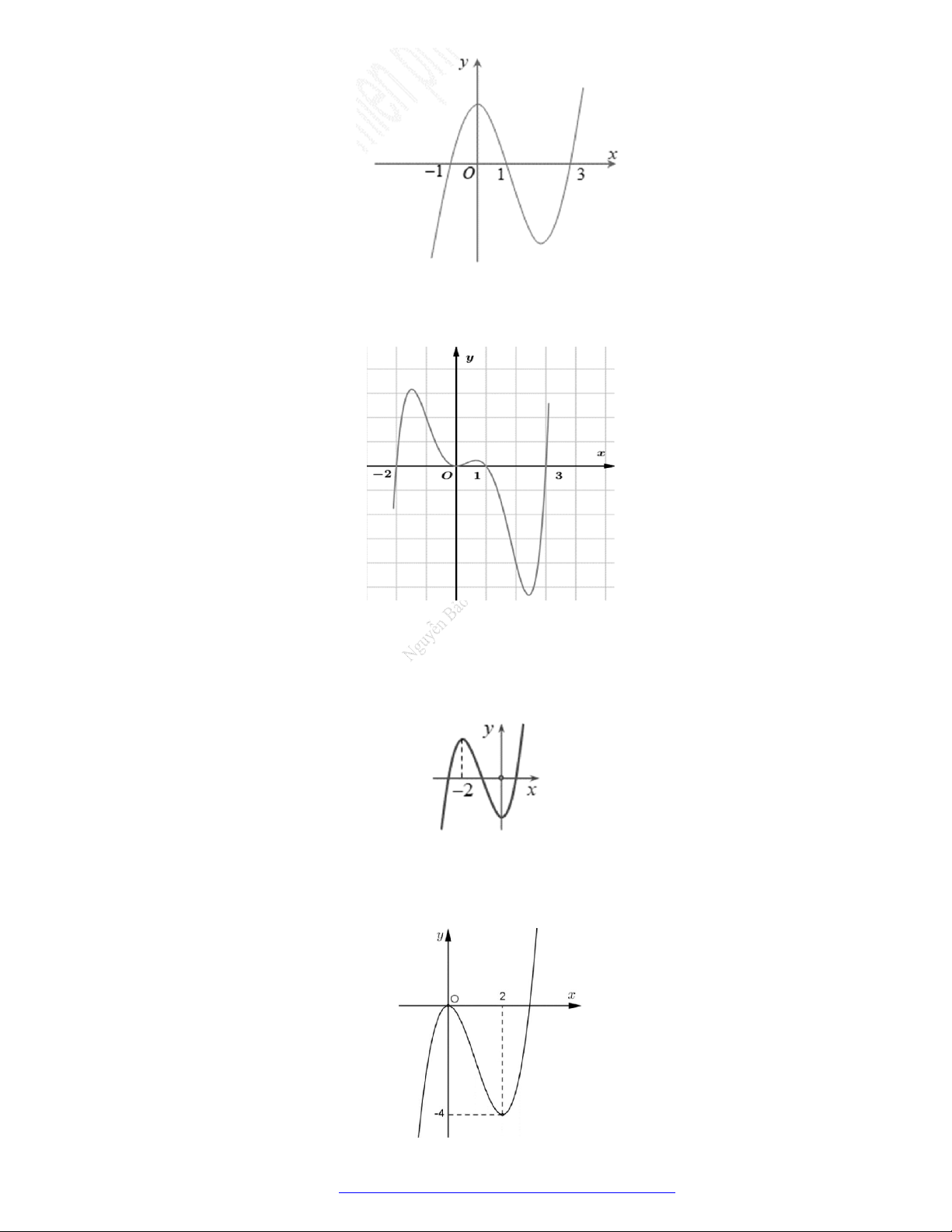
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
1
. B.
2
. C.
4
. D.
3
.
Câu 16. (Chuyên Thoại Ngọc Hầu 2018) Cho hàm số
y f x
. Đồ thị hàm số
y f x
như hình vẽ
sau.
Hàm số
2
g x f x
có bao nhiêu điểm cực trị?
A.
4
. B.
3
. C.
5
. D.
2
.
Câu 17. Cho hàm số
y f x
xác định và liên tục trên
có đồ thị như hình vẽ. Hàm số
2
2 4g x f x x
có bao nhiêu điểm cực tiểu?
A.
1
. B.
3
. C.
2
. D.
4
.
Câu 18. (Đặng Thúc Hứa - Nghệ An -2018) Biết rằng hàm số
f x
có đồ thị được cho như hình vẽ bên.
Tìm số điểm cực trị của hàm số
y f f x
.
A.
5
. B.
3
. C.
4
. D.
6
.
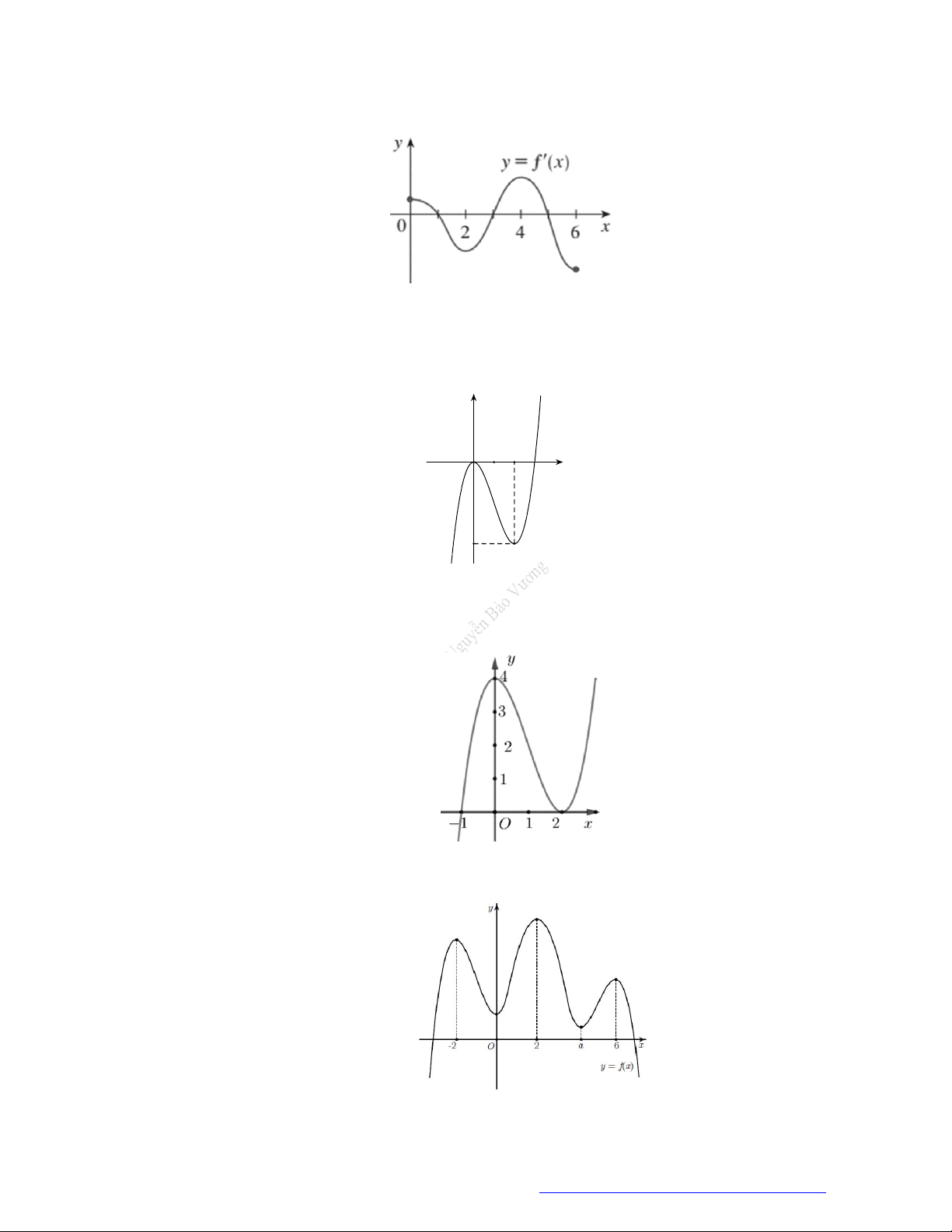
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Câu 19. (Sở Bình Phước - 2018) Cho hàm số
y f x
liên tục và có đạo hàm trên
0;6
. Đồ thị của
hàm số
y f x
trên đoạn
0;6
được cho bởi hình bên dưới. Hỏi hàm số
2
y f x
có tối đa
bao nhiêu cực trị.
A.
3
. B.
7
. C.
6
. D.
4
.
Câu 20. Biết rằng hàm số
f x
có đồ thị được cho như hình vẽ bên. Tìm số điểm cực trị của hàm số
y f f x
?
A. 5. B. 4. C. 3. D. 6.
Câu 21. (THPT Đô Lương 3 - Nghệ An - 2019) Cho hàm số
f x
có đồ thị như hình vẽ bên dưới. Số
điểm cực trị của hàm số
g x f f x
là.
A.
3.
B.
7.
C.
6.
D.
5.
Câu 22. (Sở GD Bắc Ninh - 2019) Cho hàm số
y f x
có đồ thị như hình vẽ.
Biết tất cả các điểm cực trị của hàm số
y f x
là
2
;
0
;
2
;
a
;
6
với
4 6a
. Số điểm cực
trị của hàm số
6 2
3y f x x
là
A. 8. B. 11. C. 9. D. 7.
x
y
-4
2
O
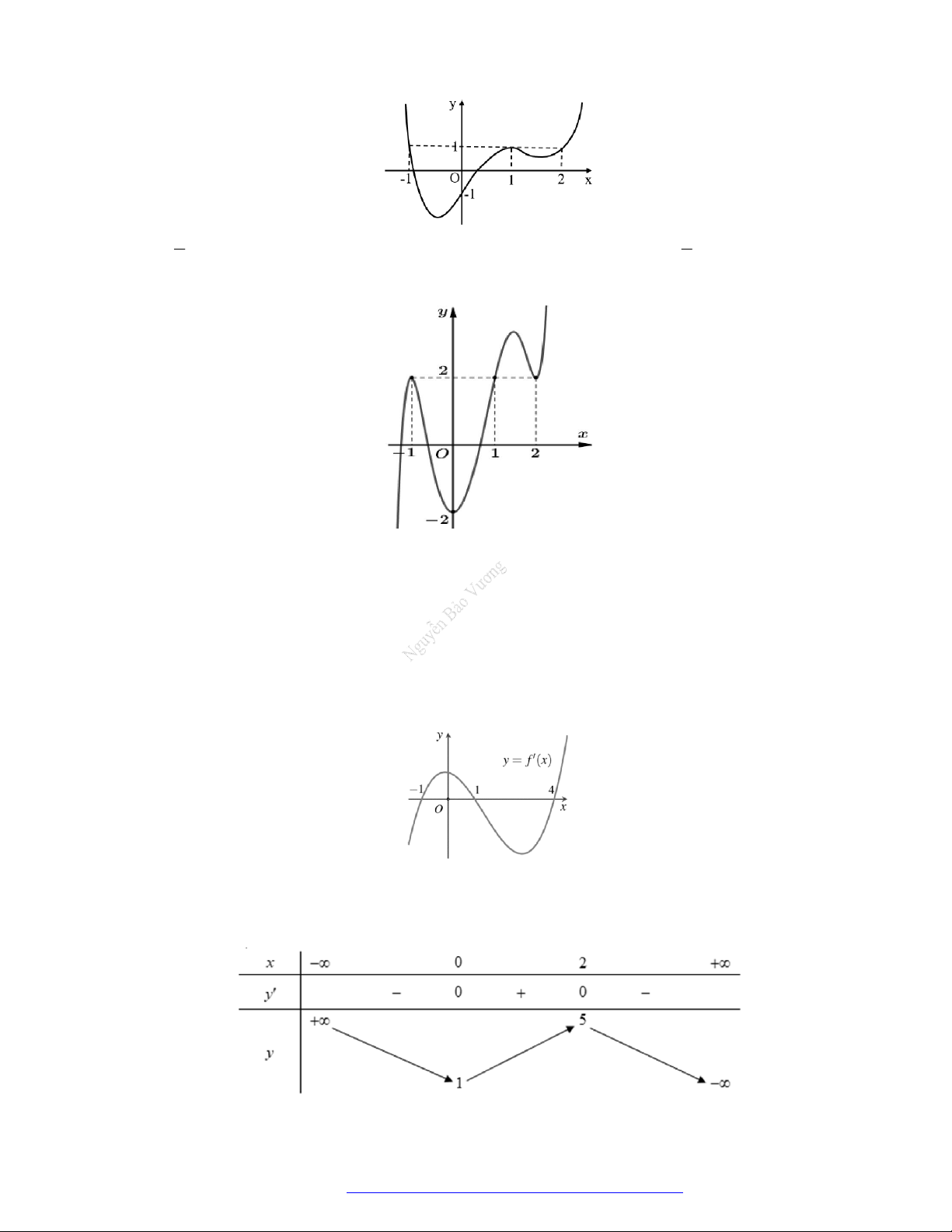
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 23. (Toán Học Tuổi Trẻ 2019) Cho hàm số
(x)f
xác định trên
và có đồ thị
( )f x
như hình vẽ
bên. Đặt
( ) ( )g x f x x
. Hàm số đạt cực đại tại điểm thuộc khoảng nào dưới đây?
A.
3
;3
2
B.
2;0
C.
0;1
D.
1
;2
2
Câu 24. (Thpt Hoàng Hoa Thám Hưng Yên 2019) Cho hàm số
( 1)y f x
có đồ thị như hình vẽ.
Hàm số
2 4f x x
y
đạt cực tiểu tại điểm nào?
A.
1x
. B.
0x
. C.
2x
. D.
1x
.
Câu 25. (THPT Minh Châu Hưng Yên 2019) Cho hàm số
y f x
có đạo hàm liên tục trên
và đồ thị
hàm số
y f ' x
như hình vẽ bên.
Số điểm cực trị của hàm số
y f x 2017 2018x 2019
là.
A.
3
B.
4
C.
1
D.
2
Câu 26. (Chuyên Thái Bình - 2018) Cho hàm số
'( )y f x
có đồ thị như hình vẽ dưới đây:
Tìm số điểm cực trị của hàm số
2 ( ) 1 ( )
e 5
f x f x
y
.
A.
1
. B.
2
. C.
4
. D.
3
.
Câu 27. (THPT Quỳnh Lưu - Nghệ An - 2018) Cho hàm số
y f x
có bảng biến thiên như sau
Hàm số
2 1y f x
đạt cực tiểu tại điểm
A.
2x
. B.
0x
. C.
1x
. D.
5x
.
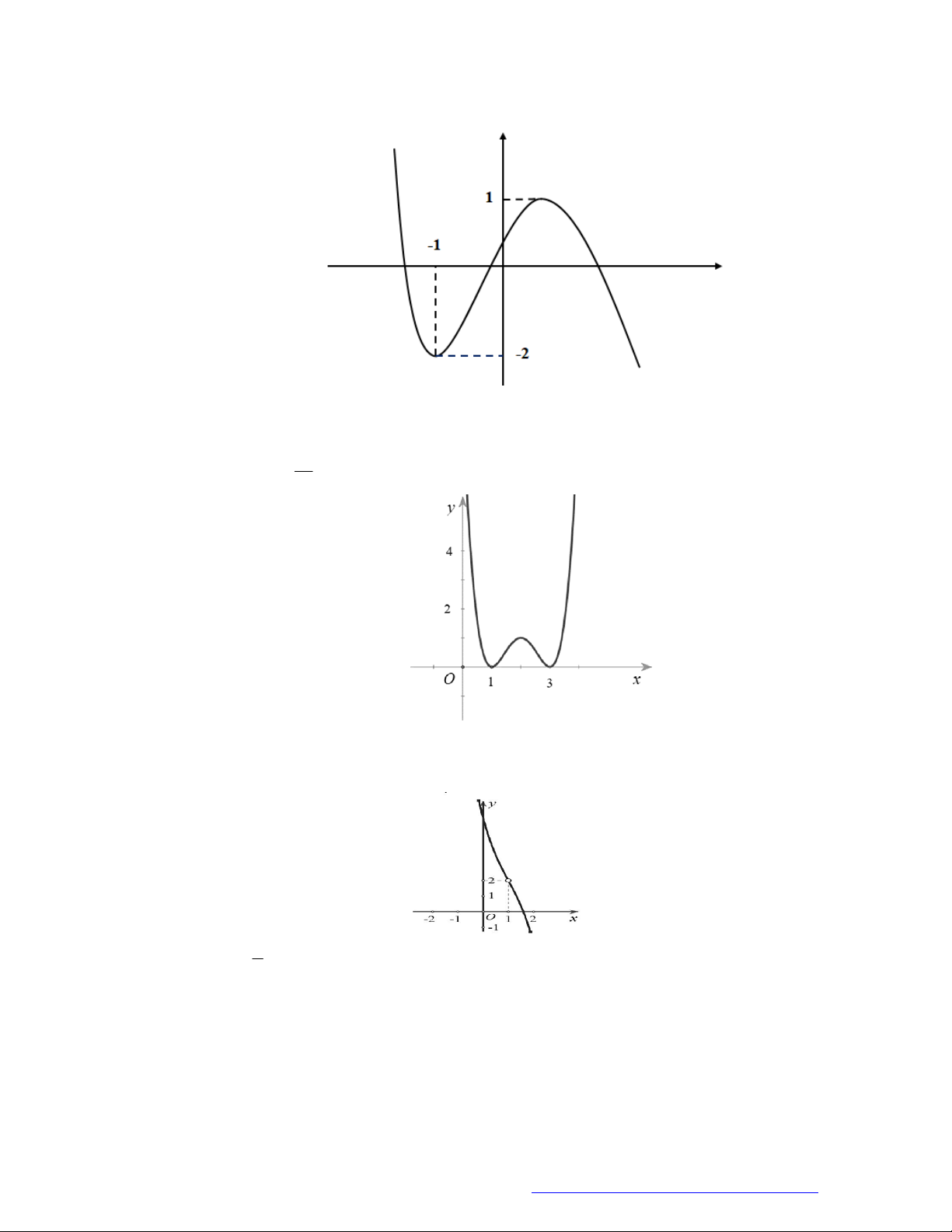
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Câu 28. (Liên Trường - Nghệ An - 2018) Cho hàm số
y f x
có đạo hàm liên tục trên
. Đồ thị hàm
số
y f x
như hình vẽ sau. Số điểm cực trị của hàm số
2y f x x
là:
A.
4
. B.
1
. C.
3
. D.
2
.
Câu 29. Cho hàm số
f x
có đồ thị
f x
như hình vẽ dưới. Hàm số
3
2
2 5 2001
3
x
g x f x x x
có bao nhiêu điểm cực trị?
A.
3
. B.
1
. C.
2
. D.
0
.
Câu 30. Cho hàm số
y f x
có đạo hàm trên
và không có cực trị, đồ thị của hàm số
y f x
là
đường cong của như hình vẽ dưới đây.
Xét hàm số
2
2
1
2 . 2
2
h x f x x f x x
. Mệnh đề nào sau đây đúng?
A. Đồ thị của hàm số
y h x
có điểm cực tiểu là
1;0M
.
B. Hàm số
y h x
không có cực trị.
C. Đồ thị hàm số
y h x
có điểm cực đại là
1;2N
.
D. Đồ thị hàm số
y h x
có điểm cực đại là
1;0M
.
Câu 31. Cho hàm số
4
f x x
. Hàm số
2
' 3 6 1g x f x x x
đạt cực tiểu, cực đại lần lượt tại
1 2
,x x . Tính
1 2
m g x g x
.
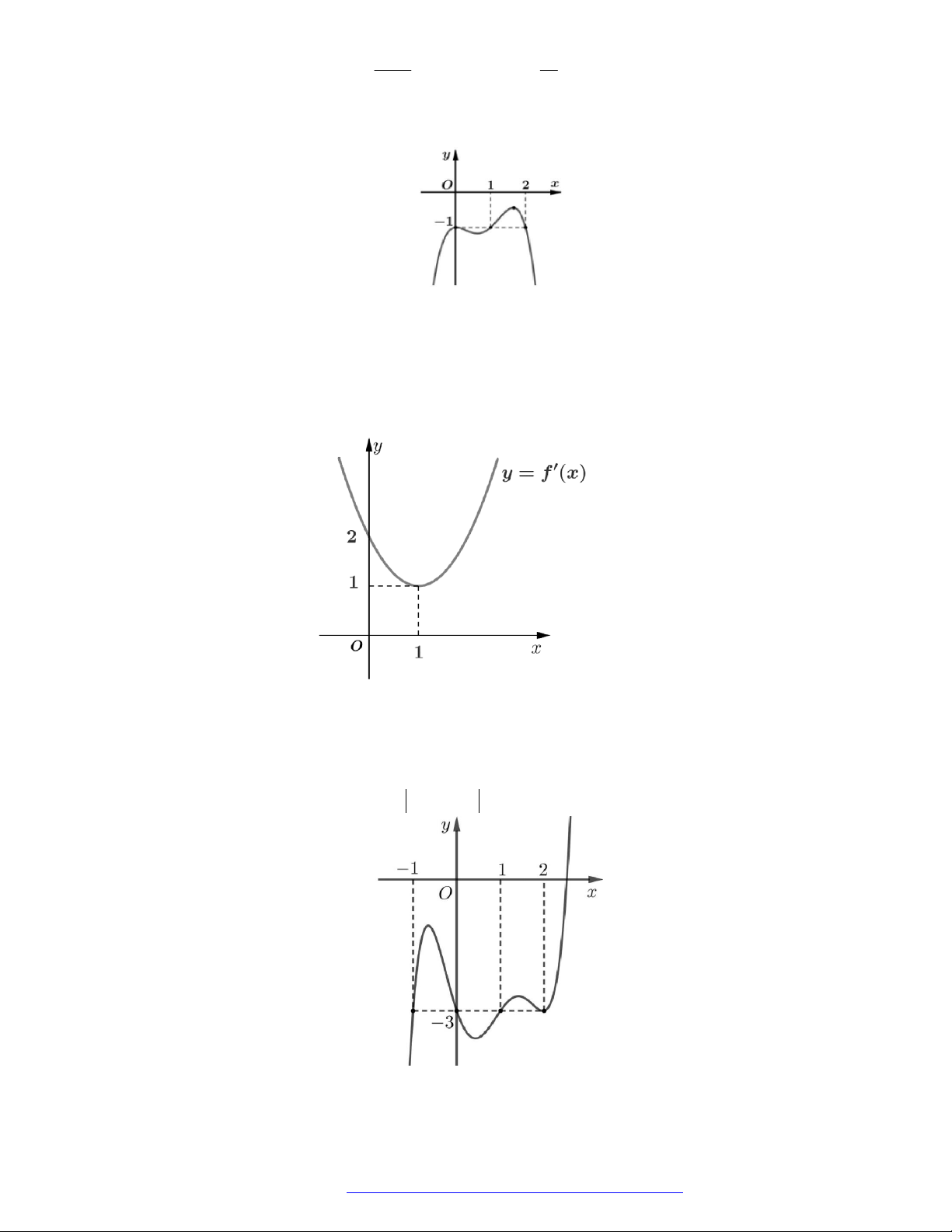
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
0m
. B.
371
16
m
. C.
1
16
m
. D.
11m
.
Câu 33. (Kim Liên - Hà Nội 2019) Cho hàm số
y f x có đạo hàm trên
. Biết hàm số
y f x có
đồ thị như hình vẽ.
Hàm số
g x f x x
đạt cực tiểu tại điểm
A.
1x
. B.
2x
.
C. Không có điểm cực tiểu. D.
0x
.
Câu 34. Cho hàm số
y f x
có đạo hàm liên tục trên
và đồ thị hàm số
y f x
là parabol như
hình bên dưới.
Hàm số
2y f x x
có bao nhiêu cực trị?
A.
3
. B.
2
. C.
0
. D.
1
.
Câu 35. Cho hàm số đa thức
y f x
có đạo hàm trên
,
0 0f
và đồ thị hình bên dưới là đồ thị của
đạo hàm
f x
. Hỏi hàm số
3g x f x x
cóbao nhiêu cực trị?
A.
4.
B.
5.
C.
3.
D.
6.
Câu 36. Cho hàm số
( )y f x
có đồ thị đạo hàm
'( )y f x
như hình bên.
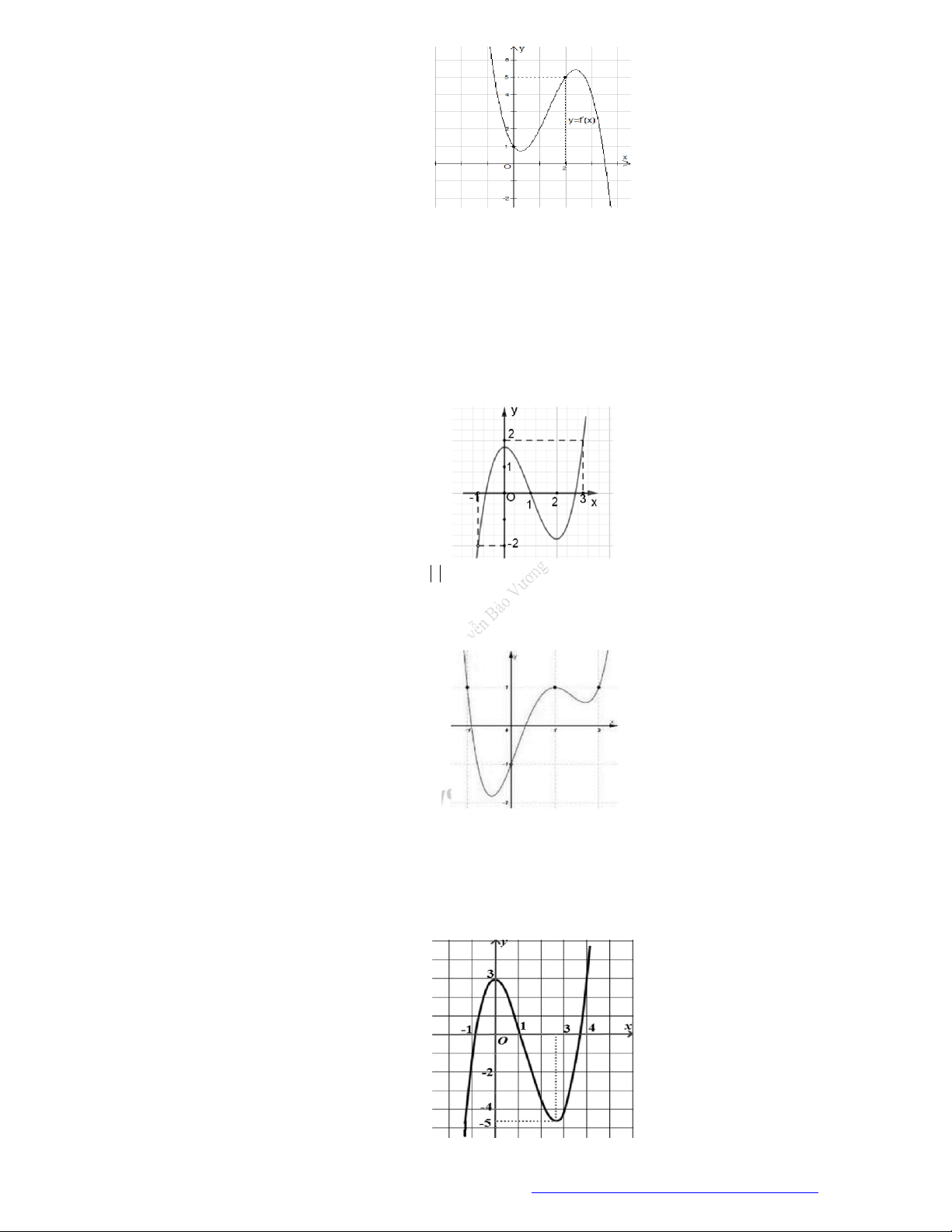
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Khẳng định nào sau đây là đúng?
A. Hàm số
2
( )y f x x x
đạt cực đại tại
0x
.
B. Hàm số
2
( )y f x x x
đạt cực tiểu tại
0x
.
C. Hàm số
2
( )y f x x x
không đạt cực trị tại
0x
.
D. Hàm số
2
( )y f x x x
không có cực trị.
Câu 37. (THPT Minh Khai) Cho hàm số Cho hàm số
y f x
liên tục trên
và hàm số
2
2 2 2019g x f x x x
. Biết đồ thị hàm số
y f x
như hình vẽ.
Số điểm cực trị của hàm số
x
y g
là
A.
5
. B.
3
. C.
2
. D.
4
.
Câu 38. Cho hàm số
f x
xác định trên
và có đồ thị
'f x
như hình vẽ.
Đặt
g x f x x
. Hàm số
g x
đạt cực đại tại điểm nào sau đây?
A.
1.x
B.
2.x
C.
0x
.
D.
1.x
Câu 39. (THPT Hoàng Hoa Thám - Hưng Yên 2019) Cho hàm số
( )y f x
có đạo hàm trên
và có
đồ thị là đường cong như hình vẽ.
Đặt
( ) 3 ( ) 4g x f f x
. Tìm số cực trị của hàm số
( )g x
A.
2.
B.
8.
C.
10.
D.
6.
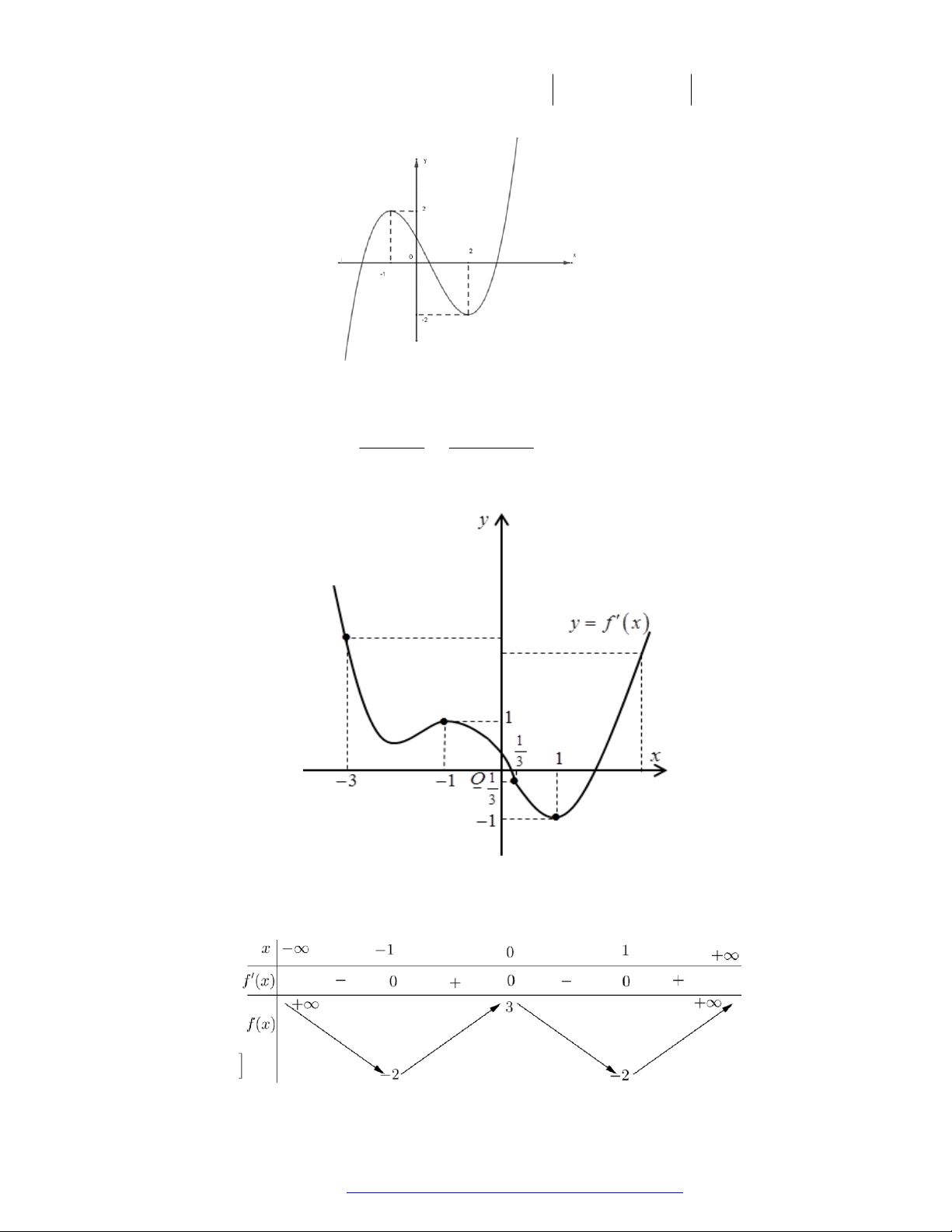
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 40. (HSG 12 - Sở Quảng Nam - 2019) Cho hàm số
(x)y f
có đạo hàm trên
, đồ thị hàm số
( )y f x
là đường cong ở hình vẽ. Hỏi hàm số
2
( ) 4 1h x f x f x
có bao nhiêu điểm
cực trị?
A.
2
. B.
3
. C.
5
. D.
7
.
Câu 41. (THPT Thăng Long - Hà Nội - 2019) Cho hàm số
y f x
, hàm số
y f x
có đồ thị như
hình bên. Hàm số
2
5sin 1 (5sin 1)
( ) 2 3
2 4
x x
g x f
có bao nhiêu điểm cực trị trên khoảng
(0;2 )
.
A.
9
. B.
7
. C.
6
. D.
8
.
Câu 42. (Mã 101 - 2020 Lần 1) Cho hàm số bậc bốn
f x
có bảng biến thiên như sau:
Số điểm cực trị của hàm số
2
4
1g x x f x
là
A.
11
. B.
9
. C.
7
. D.
5
.
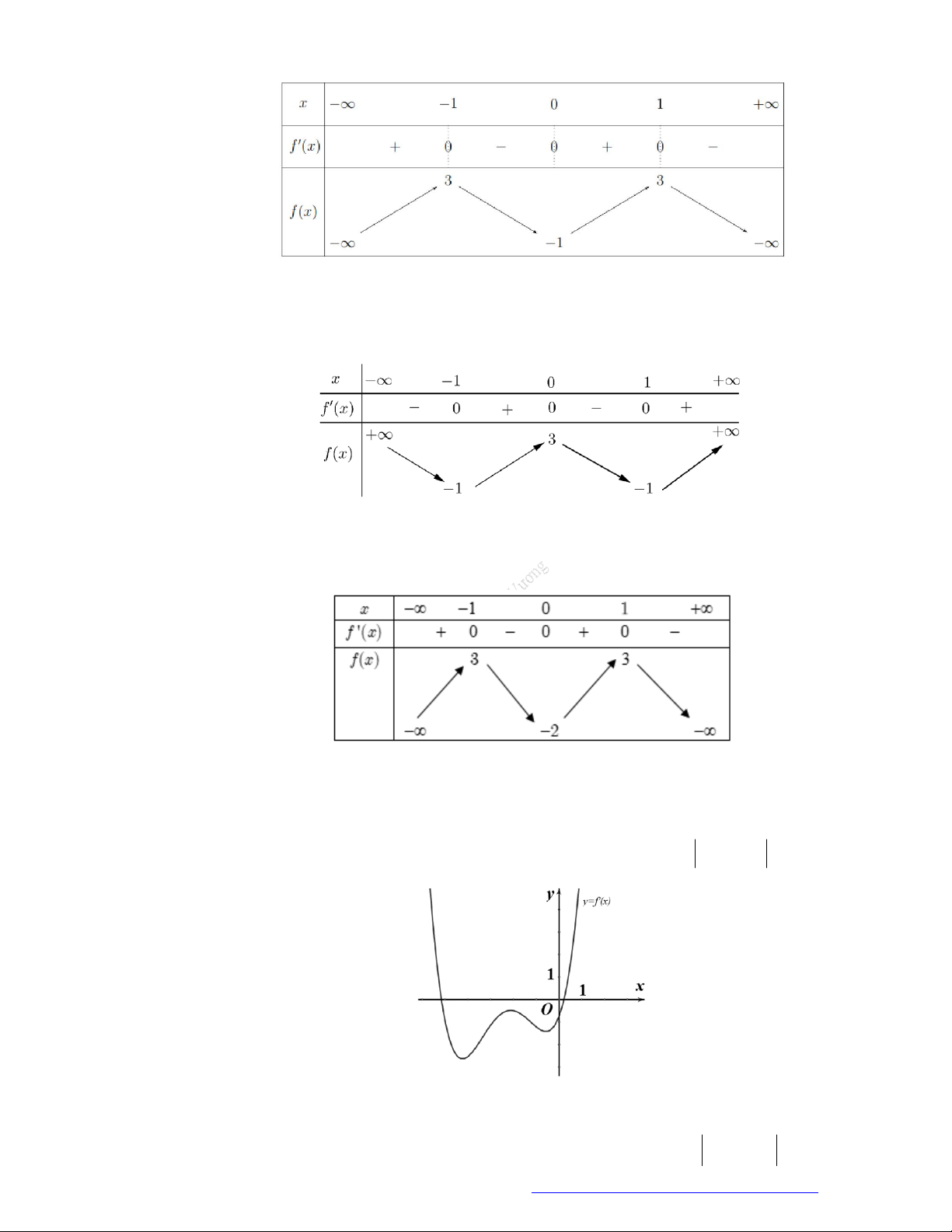
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Câu 43. (Mã 102 - 2020 Lần 1) Cho hàm số bậc bốn
f x
có bảng biến thiên như sau:
Số điểm cực trị của hàm số
g x x f x
4
2
1 là
A.
7
. B.
8
. C.
5
. D.
9
.
Câu 44. (Mã 103 - 2020 Lần 1) Cho hàm số bậc bốn
( )f x
có bảng biên thiên như sau:
Số điểm cực trị của hàm số
4 2
( ) [ ( 1)]g x x f x
là
A.
7
. B.
5
. C.
9
. D.
11
.
Câu 45. (Mã 104 - 2020 Lần 1) Cho hàm số bậc bốn
( )f x
có bảng biến thiên như sau
Số điểm cực trị của hàm số
4
2
( ) ( 1)g x x f x
A.
7
. B.
8
. C.
9
. D. 5 .
Câu 46. (Mã 101 – 2020 Lần 2) Cho hàm số
f x
có
0 0.f
Biết
y f x
là hàm số bậc bốn và có
đồ thị là đường cong trong hình bên. Số điểm cực trị của hàm số
3
( )g x f x x là
A.
5.
B.
4.
C.
6.
D.
3.
Câu 47. (Mã 102 - 2020 Lần 2) Cho hàm số
f x
có
0 0f
. Biết
y f x
là hàm số bậc bốn và có
đồ thị là đường cong trong hình bên. Số điểm cực trị của hàm số
3
g x f x x
là
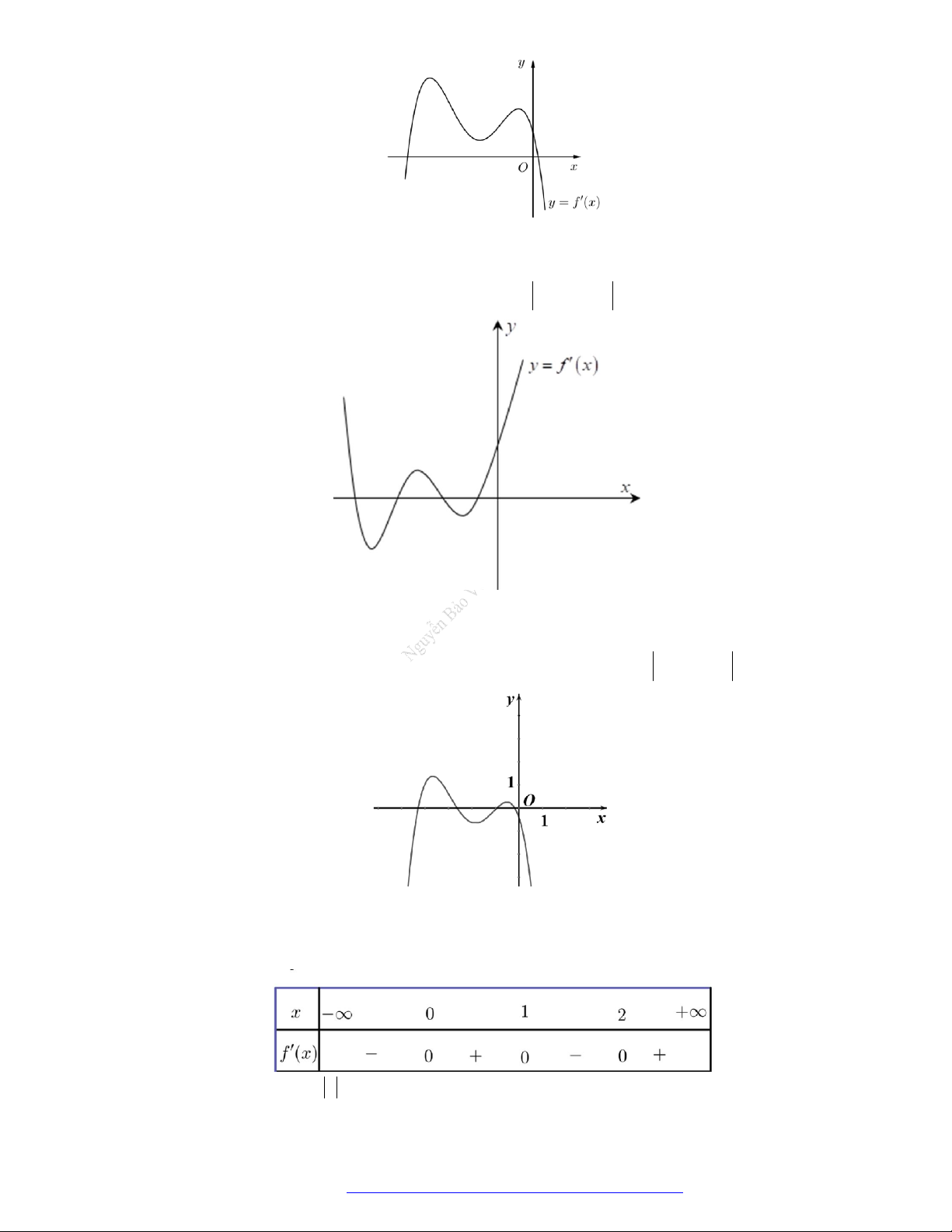
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A. 4. B. 5. C. 3. D. 6.
Câu 48. (Mã 103 - 2020 Lần 2) Cho hàm số
f x
có
0 0f
. Biết
y f x
là hàm số bậc bốn và có
đồ thị như hình vẽ. Số điểm cực trị của hàm số
4 2
g x f x x là
A. 4. B. 3. C. 6. D. 5.
Câu 49. (Mã 104 - 2020 Lần 2) Cho hàm số
( )f x
có
0 0.f
Biết
( )y f x
là hàm số bậc bốn và có
đồ thị là đường cong trong hình bên. Số điểm cực trị của hàm số
4 2
( )g x f x x
là
A.
3.
B.
6.
C.
5.
D.
4.
Câu 50. (Chuyên Quang Trung - 2020) Cho hàm số
y f x
liên tục trên
có đạo hàm
f x
liên
tục trên
và có bảng xét dấu như hình vẽ bên
Hỏi hàm số
2
2y f x x
có tất cả bao nhiêu điểm cực trị?
A.
4
B.
7
C.
9
D.
11
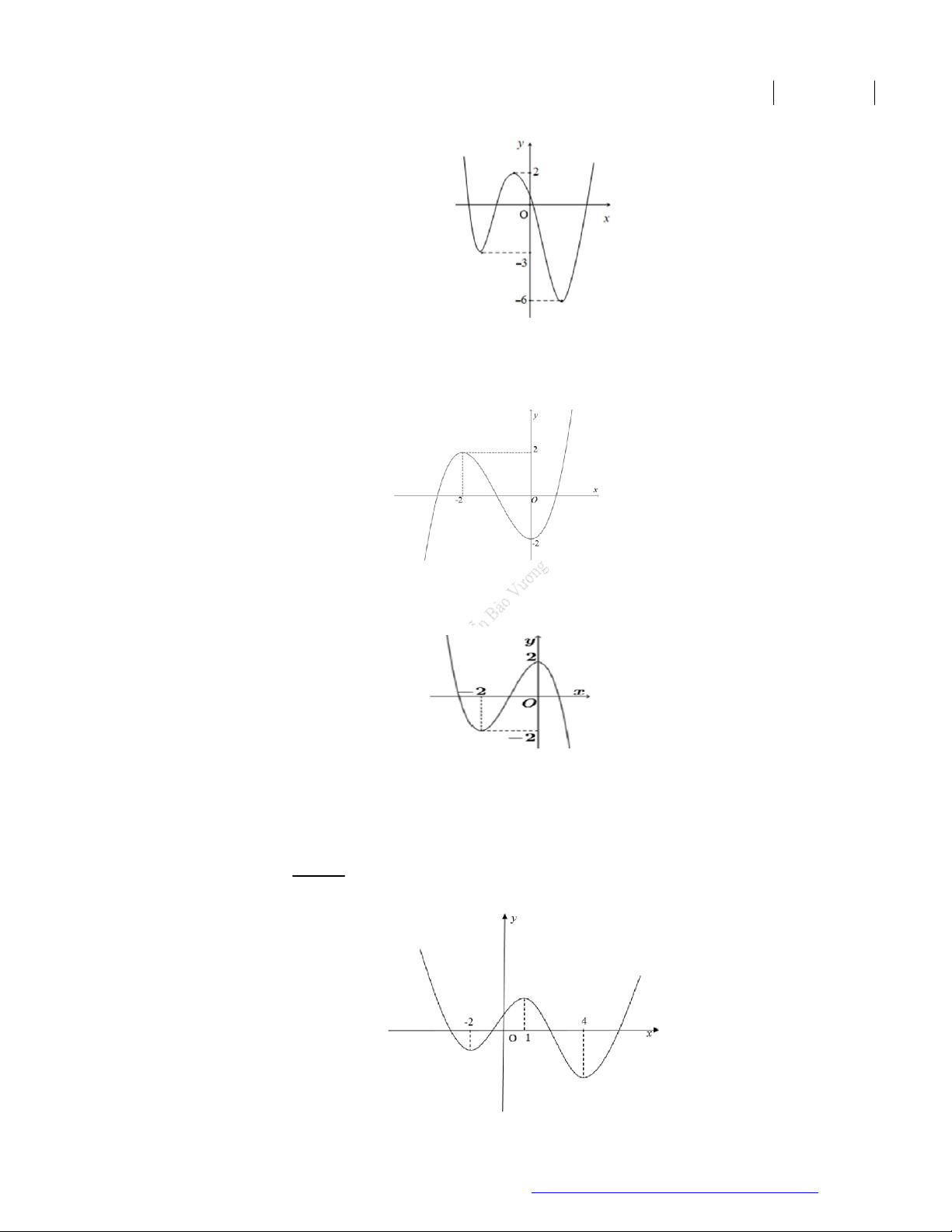
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
Câu 51. (Chuyên Thái Bình - 2020) Cho
y f x
là hàm đa thức bậc
4
và có đồ thị như hình vẽ. Có
bao nhiêu giá trị nguyên của tham số
m
thuộc đoạn
12;12
để hàm số
2 1 g x f x m
có
5
điểm cực trị?
A.
13
. B.
14
. C.
15
. D.
12
.
Câu 52. (Chuyên Vĩnh Phúc - 2020) Cho hàm số
3 2
f x ax bx cx d
(với
, , ,a b c d
và
0a
)
có đồ thị như hình vẽ. Số điểm cực trị của hàm số
2
2 4g x f x x
A. 2. B. 5. C. 4. D. 3.
Câu 53. (Sở Phú Thọ - 2020) Cho hàm số bậc ba
y f x
có đồ thị như hình vẽ
Số điểm cực tiểu của hàm số
2
g x f x x
bằng
A.
1
. B.
5
. C.
2
. D.
3
.
Câu 54. (Sở Bắc Ninh - 2020) Cho hàm số
( )f x
liên tục trên
và có đồ thị như hình vẽ. Hàm số
2
2
( )
2
x
x x
g x f e
có bao nhiêu điểm cực trị?
A.
3
. B.
7
. C.
6
. D.
4
.
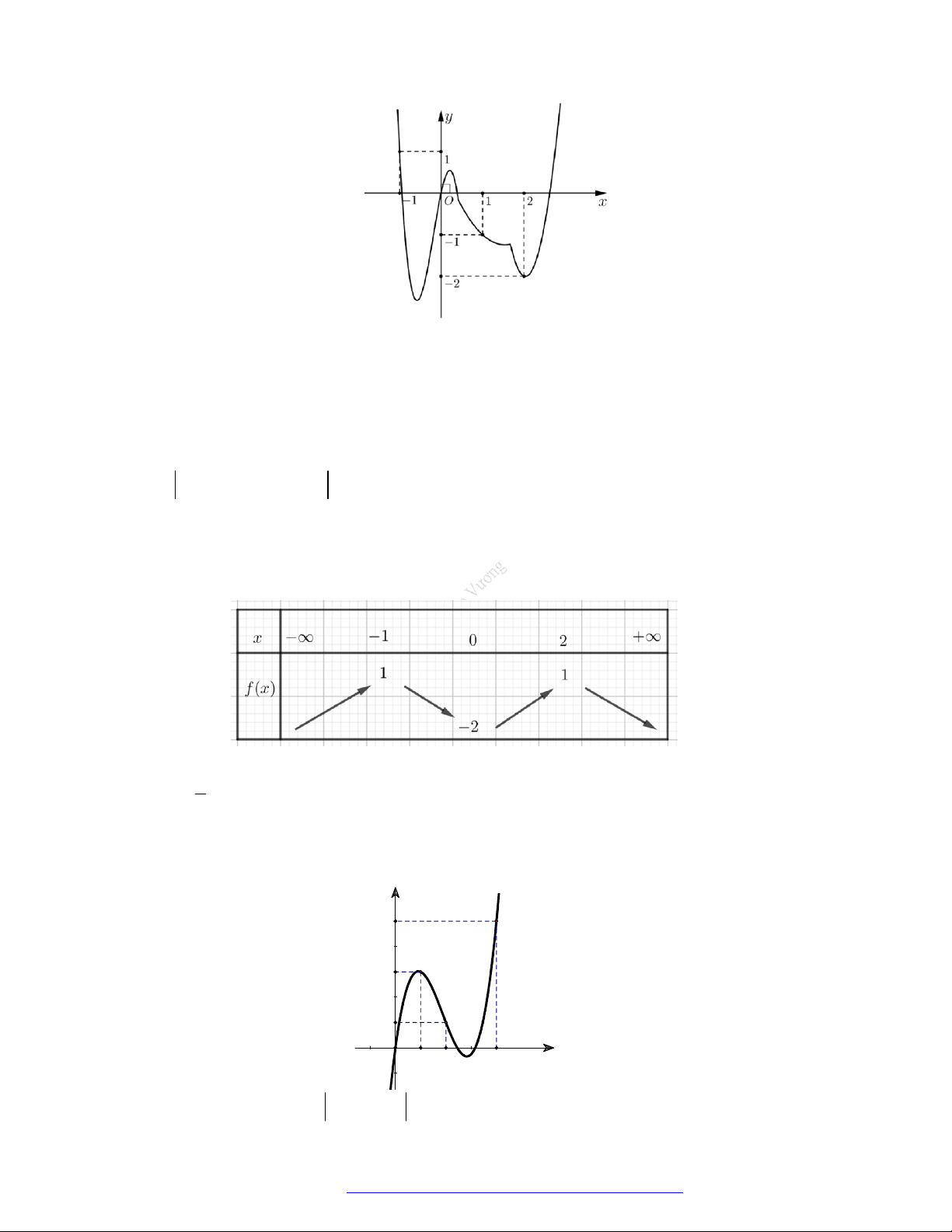
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 55. (Sở Yên Bái - 2020) Cho hàm số
y f x
có đạo hàm trên
. Đồ thị hàm số
y f x
như
hình bên. Đặt
2
2 1 g x f x x
. Khẳng định nào sau đây đúng?
A. Hàm số
y g x
nghịch biến trên khoảng
1;
.
B. Hàm số
y g x
đồng biến trên khoảng
1;0
.
C. Hàm số
y g x
đạt cực tiểu tại
0x
.
D. Hàm số
y g x
đạt cực đại tại
1x
.
Câu 56. (Kim Liên - Hà Nội - 2020) Có tất cả bao nhiêu giá trị nguyên dương của tham số
m
để hàm số
4 3 2
3 4 12y x x x m
có 5 điểm cực trị?
A.
16
. B.
28
. C.
26
. D.
27
.
Câu 57. (Lý Nhân Tông - Bắc Ninh - 2020) Cho hàm số
( )y f x
có bảng biến thiên như hình vẽ dưới
đây:
Hàm số
(2 )y f x
đạt cực đại tại
A.
1
2
x
. B.
1x
. C.
1x
. D.
2x
.
Câu 58. (THPT Nguyễn Viết Xuân - 2020) Cho hàm số
y f x
có đạo hàm liên tục trên
và
0 0; 4 4f f
. Biết hàm
y f x
có đồ thị như hình vẽ.
Số điểm cực trị của hàm số
2
2g x f x x là
A.
2
. B.
1
. C.
4
. D.
3
.
x
y
2
5
3
1
4
O
1
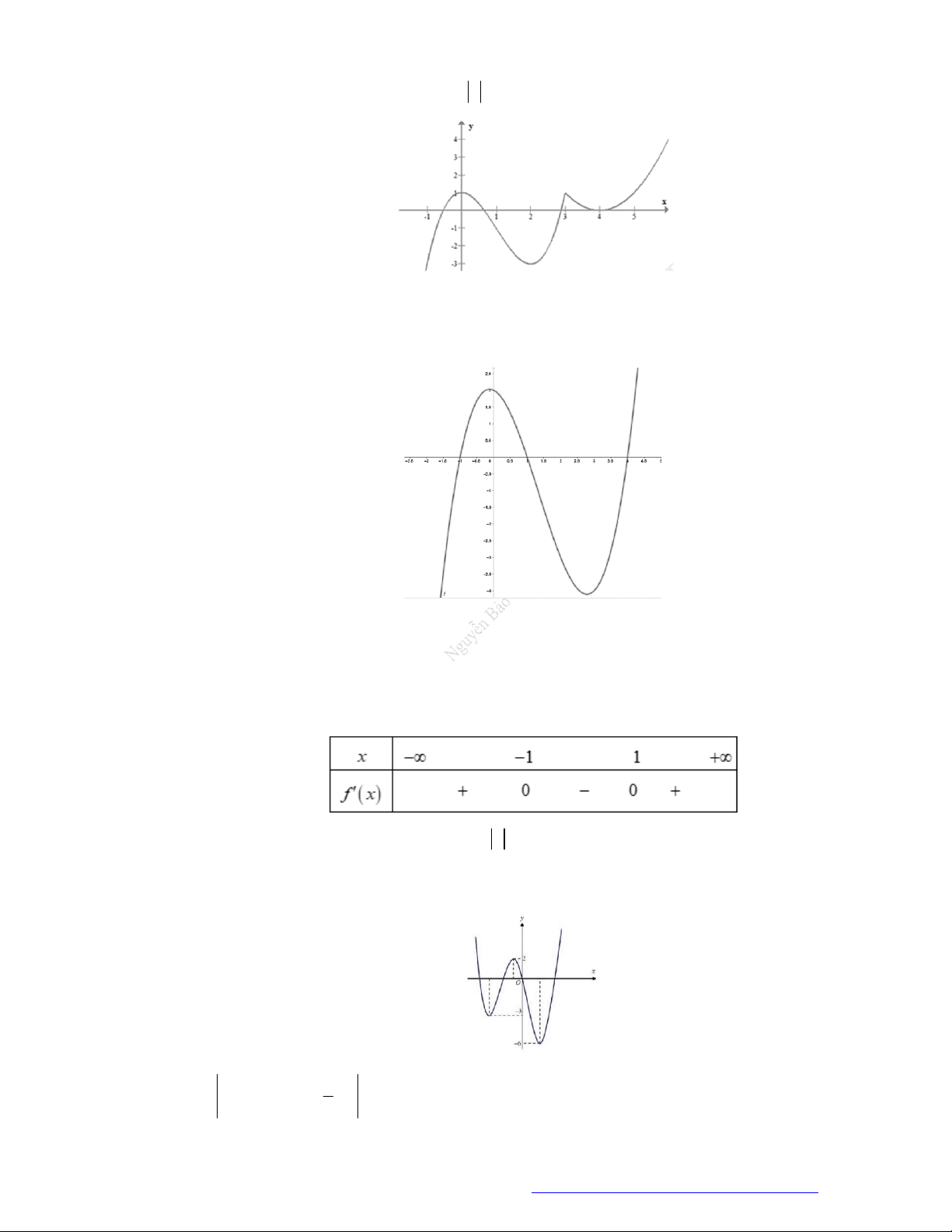
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
Câu 59. (Hải Hậu - Nam Định - 2020) Cho hàm số
( )y f x
đồng biến trên
4;
có đồ thị như hình
vẽ. Số điểm cực trị của hàm số
(2 2)y f x
bằng
A.
7
. B. 5. C.
4
. D.
9
.
Câu 60. (Hải Hậu - Nam Định - 2020) Cho hàm số
y f x
liên tục trên
và có đồ thị hàm số
y f x
như hình vẽ dưới đây:
Tìm điểm cực đại của hàm số
2019 2020 .
f x f x
y
A.
2
. B.
3
. C.
0
. D.
1
.
Câu 61. (Kìm Thành - Hải Dương - 2020) Cho hàm số
y f x
là một hàm đa thức có bảng xét dấu
f x
như sau
Số điểm cực trị của hàm số
2
g x f x x
A.
5
. B.
3
. C.
1
. D.
7
.
Câu 62. (Trần Phú - Quảng Ninh - 2020) Cho đồ thị
y f x
như hình vẽ dưới đây:
Gọi
S
là tập hợp tất cả các giá trị nguyên dương của tham số
m
để hàm số
2
1
2018
3
y f x m
có
5
điểm cực trị. Tổng tất cả các giá trị của các phần tử trong tập
S
bằng
A.
6
. B.
5
. C.
7
. D.
9
.
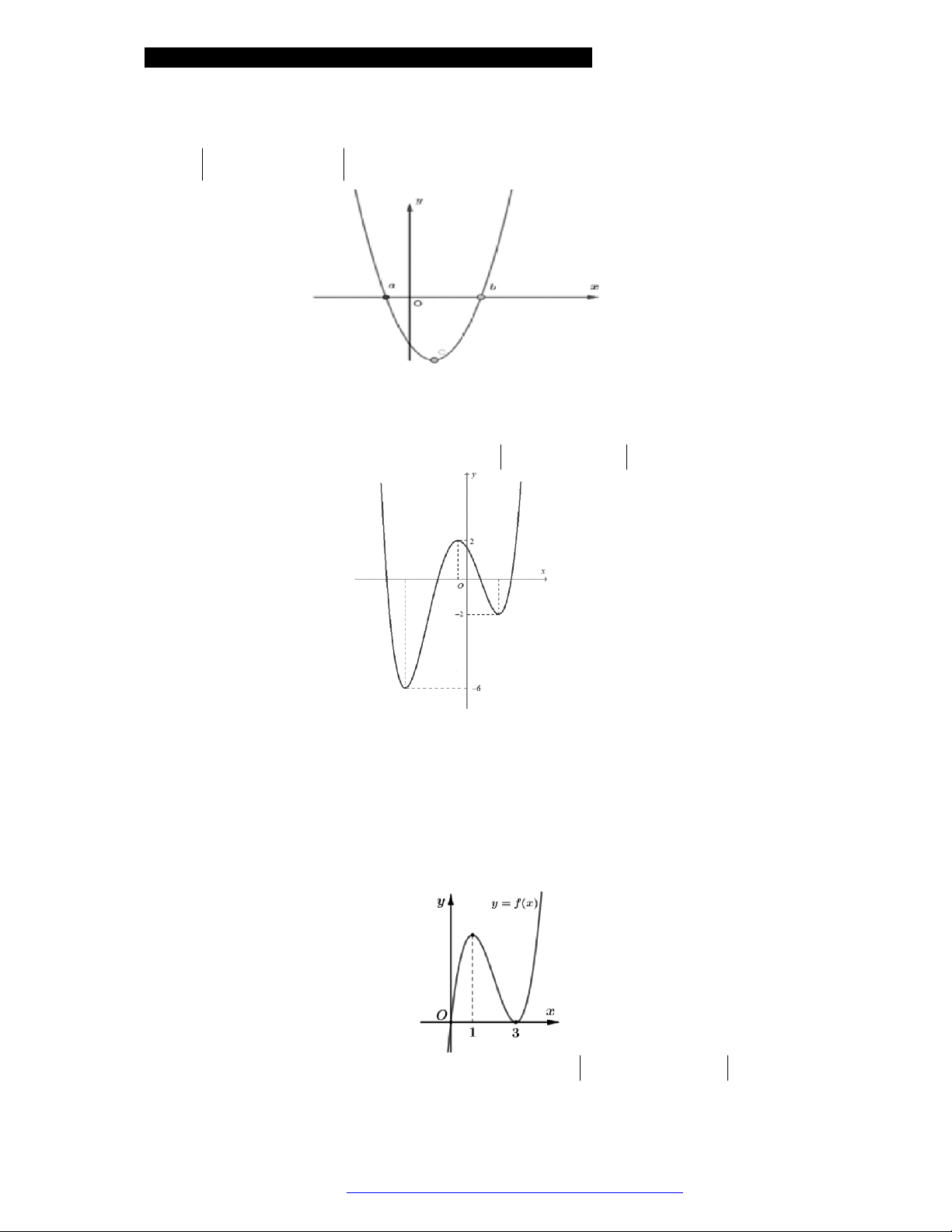
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Dạng 3. Tìm m để hàm số f(u) thỏa mãn điều kiện cho trước
Câu 1. (Hậu Lộc 2 - Thanh Hóa - 2020) Cho hàm số bậc ba
y f x
có đồ thị của hàm đạo hàm
'
f x
như hình vẽ và
1f b
.Số giá trị nguyên của
5;5m
để hàm số
2
4g x f x f x m
có đúng 5 điểm cực trị là
A.
8
. B.
10
. C.
9
. D.
7
.
Câu 2. (Sở Bình Phước - 2020) Cho hàm số
y f x
có đồ thị như hình vẽ bên dưới. Có bao nhiêu giá
trị nguyên của tham số thực
m
để hàm số
2
2020g x f x m
có 5 điểm cực trị?
A. 1. B. 2. C. 4. D. 5.
Câu 3. (Chuyên Lào Cai - 2020) Cho hàm số
f x
có đạo hàm
4 3
2 2
2 4 2 3 6 18 .f x x x x x m x m
Có tất cả bao nhiêu giá trị nguyên của
m
để hàm số
f x
có đúng một điểm cực trị?
B.
7
. B.
5
. C.
8
. D.
6
.
Câu 4. (THPT Thiệu Hóa – Thanh Hóa 2019) Cho hàm số
y f x
có đồ thị như hình vẽ bên dưới
Tìm tất cả các giá trị của tham số
m
để đồ thị hàm số
2
2 2h x f x f x m
có đúng
3
điểm cực trị.
A.
1m
B.
1m
C.
2m
D.
2m
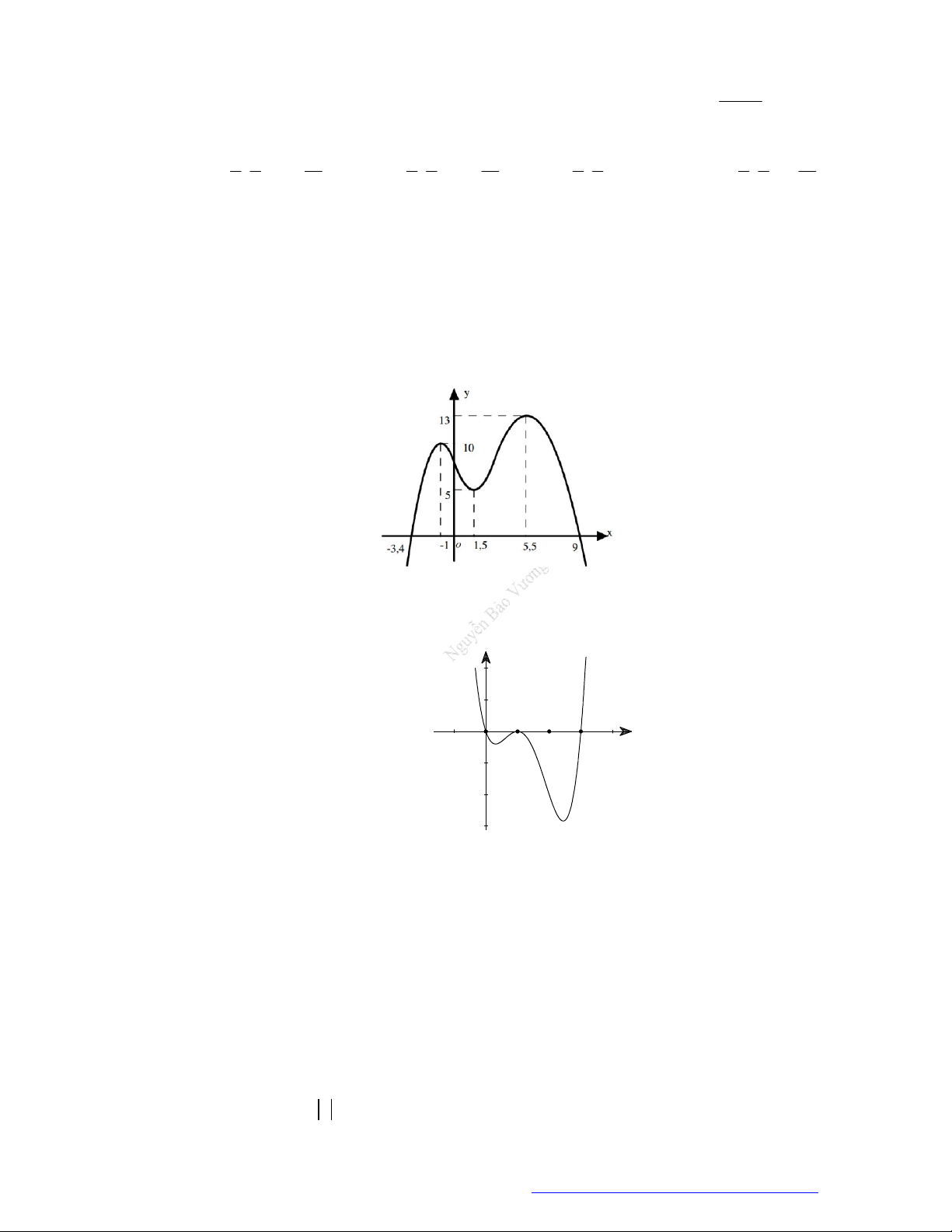
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
Câu 5. (THPT Hàm Rồng - Thanh Hóa - 2018) Cho hàm số
f x
có đạo hàm
3
2
13 15f x x x a x
. Tập hợp các giá trị của
a
để hàm số
2
5
4
x
y f
x
có 6 điểm cực
trị là
A.
5 5 15
; \ 0;
4 4 13
. B.
5 5 15
; \ 0;
4 4 13
. C.
5 5
; \ 0
4 4
. D.
5 5 15
; \
4 4 13
.
Câu 6. (Chuyên Vinh - 2018) Cho hàm số
y f x
có đạo hàm
2
2
1 2f x x x x
với
x
.
Có bao nhiêu giá trị nguyên dương của tham số
m
để hàm số
2
8f x x m
có
5
điểm cực trị?
A.
15
. B.
17
. C.
16
D.
18
Câu 7. Cho hàm số
( )y f x
xác định trên
và hàm số
'( )y f x
có đồ thị như hình bên. Biết rằng
'( ) 0f x
với mọi
; 3,4 9; .x
Có bao nhiêu giá trị nguyên dương của tham số
m
để hàm số
( ) ( ) 5g x f x mx
có đúng hai điểm cực trị.
A.
7.
B.
8.
C.
6.
D.
5.
Câu 8. (Chuyên Vĩnh Phúc 2019) Cho hàm số
( )y f x
. Hàm số
( )y f x
có đồ thị như hình vẽ
dưới đây.
Tìm
m
để hàm số
2
( )y f x m
có
3
điểm cực trị.
A.
3;m
. B.
0;3m
. C.
0;3m
. D.
;0m
.
Câu 9. (THPT Hàm Rồng - Thanh Hóa - 2019) Cho hàm số
2
2
2 4 3f x x x x
với mọi
x
. Có bao nhiêu giá trị nguyên
dương của
m
để hàm số
2
10 9y f x x m
có
5
điểm cực trị?
A.
18
. B.
16
. C.
17
. D.
15
.
Câu 10. (Chuyên Bắc Giang - Lần 4 - 2019) Cho hàm số
y f x
có đạo hàm
2
2 2
2 1 2 1 1f x x x x m x m
, x
. Có bao nhiêu giá trị nguyên của
m
để
hàm số
g x f x
có 5 điểm cực trị?
A. 3. B. 5. C. 2. D. 4.
x
y
3
2
0
1
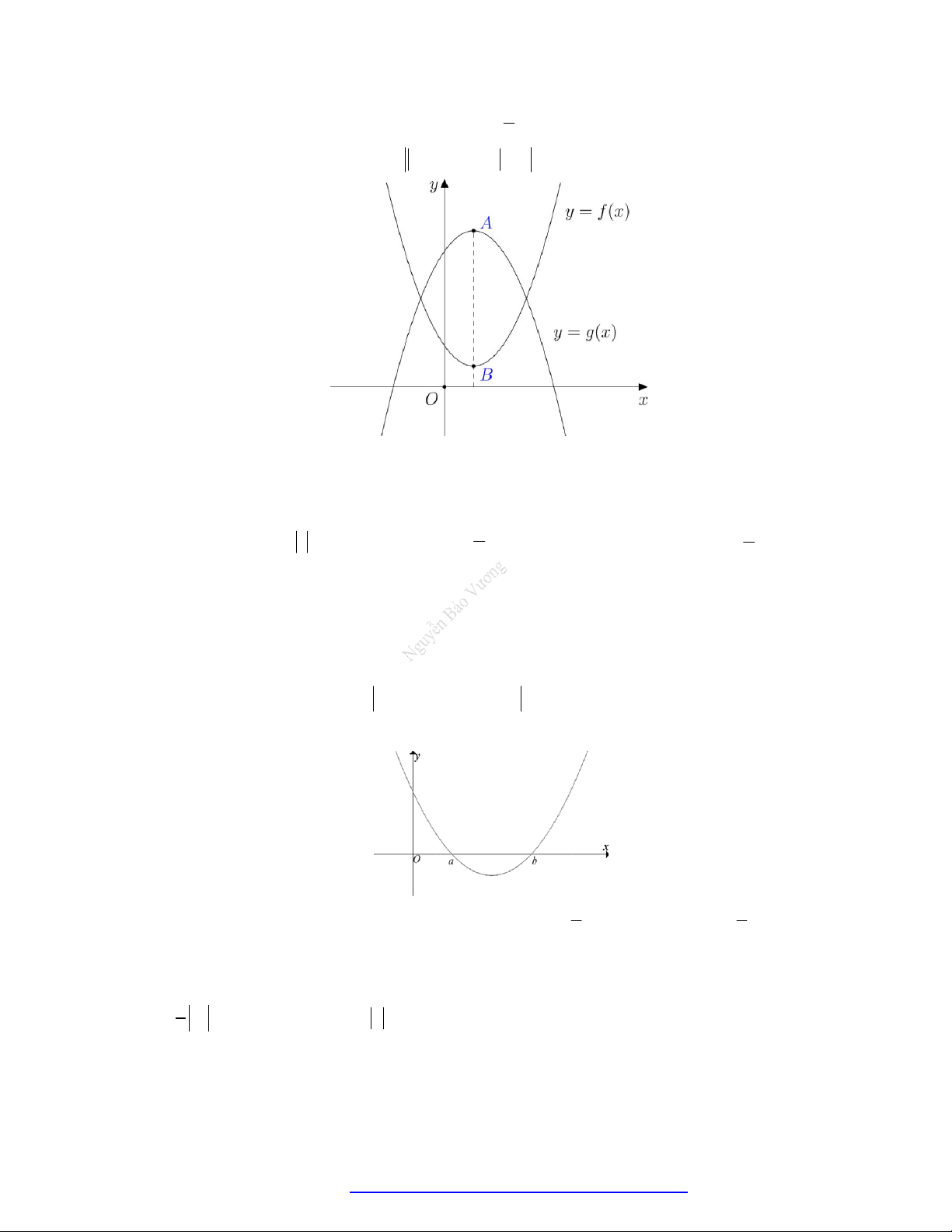
NGUYỄN
BẢO VƯƠNG - 0946798489
Câu 11. (Sở GD Qu
ảng Nam - 2019) Cho hai hàm đa thức
y f
x ,
y g
x có đồ thị là hai đường
cong ở hình vẽ. Biết rằng đồ thị hàm số
y f
x có đúng một điểm cực trị là
A
, đ
ồ thị hàm số
y g
x
có đúng một điểm cực trị là
B
và
7
4
AB
. Có
bao nhiêu giá trị nguyên của tham số
m
thuộc khoả
ng
5;5
để hàm số
y f
x g x m có đúng
5
điểm cực tr
ị?
A.
1
. B.
3
. C.
4
. D.
6
.
Câu 12. (Sở
GD Bạc Liêu - 2019) Cho hàm số
3 2
2 1 2 2y f x x m x m x
.
Tập hợp tất cả
các giá trị của tham số
m
để
hàm số
y f
x
có 5 đ
iểm cực trị là
;
a
c
b
, (v
ới
,
, a b c
là
các số nguyên,
a
b
là phâ
n số
tối giản). Giá trị của biểu thức
2 2
2
M a
b c
là
A.
40M
. B.
11M
. C.
31M
. D.
45M
.
Câu 13. (Chuyên Lam Sơn - Thanh Hóa - Lần 3 - 2019) Cho hàm số
y f
x
có
đạo hàm liên tục
trên
. Hà
m số
'y f x
có
đồ thị như hình vẽ bên. Tìm tập hợp
S
tất cả
các giá trị thực của
tham số
m
để
hàm số
2
2 3g
x f x f x m
có
đúng 7 điểm cực trị, biết phương trình
'(
) 0f x
có đúng
2 nghiệm phân biệt,
1,
0f a f b
,
lim
x
f x
và
li
m
x
f x
.
A.
5;0 .S
B.
8;0 .S
C.
1
8;
.
6
S
D.
9
5;
.
8
S
Câu 14. (THPT
Thanh Chương - Nghệ An - 2018) Có bao nhiêu giá trị nguyên của tham số
m
để hàm
số
3 2
1
(3 ) (3 7) 1
3
y x m x m x
có
5
điểm cực tr
ị?
A.
3
. B.
5
. C.
2
. D.
4
.
-------------------- HẾT --------------------
Trang 22 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
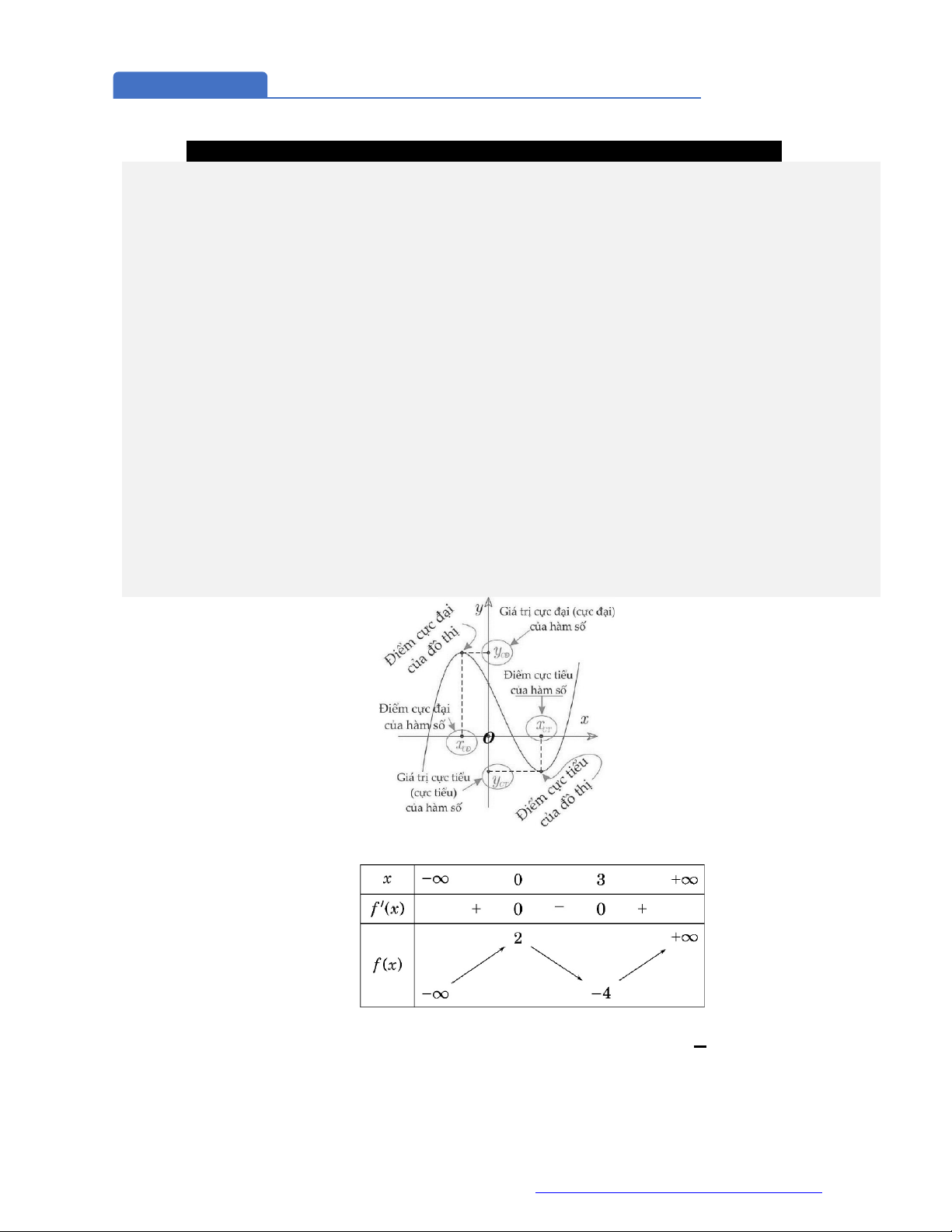
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
Dạng 1. Tìm cực trị của hàm số dựa vào bảng biến thiên, đồ thị của hàm số y, y’
-Định lí cực trị
Điều kiện cần (định lí 1): Nếu hàm số
( )y f x
có đạo hàm trên khoảng
( ; )a b
và đạt cực đại
(hoặc cực tiểu) tại
x
thì
( ) 0.f x
Điều kiện đủ (định lí 2):
Nếu
( )f x
đổi dấu từ âm sang dương khi
x
đi qua điểm
x
(theo chiều tăng) thì hàm số
( )y f x
đạt cực tiểu tại điểm
.x
Nếu
( )f x
đổi dấu từ dương sang âm khi
x
đi qua điểm
x
(theo chiều tăng) thì hàm số
( )y f x
đạt cực đại tại điểm
.x
Định lí 3: Giả sử
( )y f x
có đạo hàm cấp
2
trong khoảng
( ; ),x h x h
với
0.h
Khi đó:
Nếu
( ) 0, ( ) 0y x y x
thì
x
là điểm cực tiểu.
Nếu
( ) 0, ( ) 0
o o
y x y x
thì
x
là điểm cực đại.
- Các THUẬT NGỮ cần nhớ
Điểm cực đại (cực tiểu) của hàm số là
,x
giá trị cực đại (cực tiểu) của hàm số là
( )f x
(hay
y
CĐ
hoặc
CT
).y
Điểm cực đại của đồ thị hàm số là
( ; ( )).M x f x
Nếu
( ; )M x y
là điểm cực trị của đồ thị hàm số
( ) 0
( )
( ; ) ( )
y x
y f x
M x y y f x
Câu 1. (Đề Tham Khảo 2020 – Lần 1) Cho hàm số
y f x
có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng
A.
2
. B.
3
. C.
0
. D.
4
.
Lời giải
Chọn D
Từ bảng biến thiên, ta thấy giá trị cực tiểu của hàm số đã cho bằng
4
.
Câu 2. (Đề Tham Khảo 2020 – Lần 2) Cho hàm số
f x
có bảng biến thiên như sau:
CỰC TRỊ CỦA HÀM SỐ
Chuyên đề 2
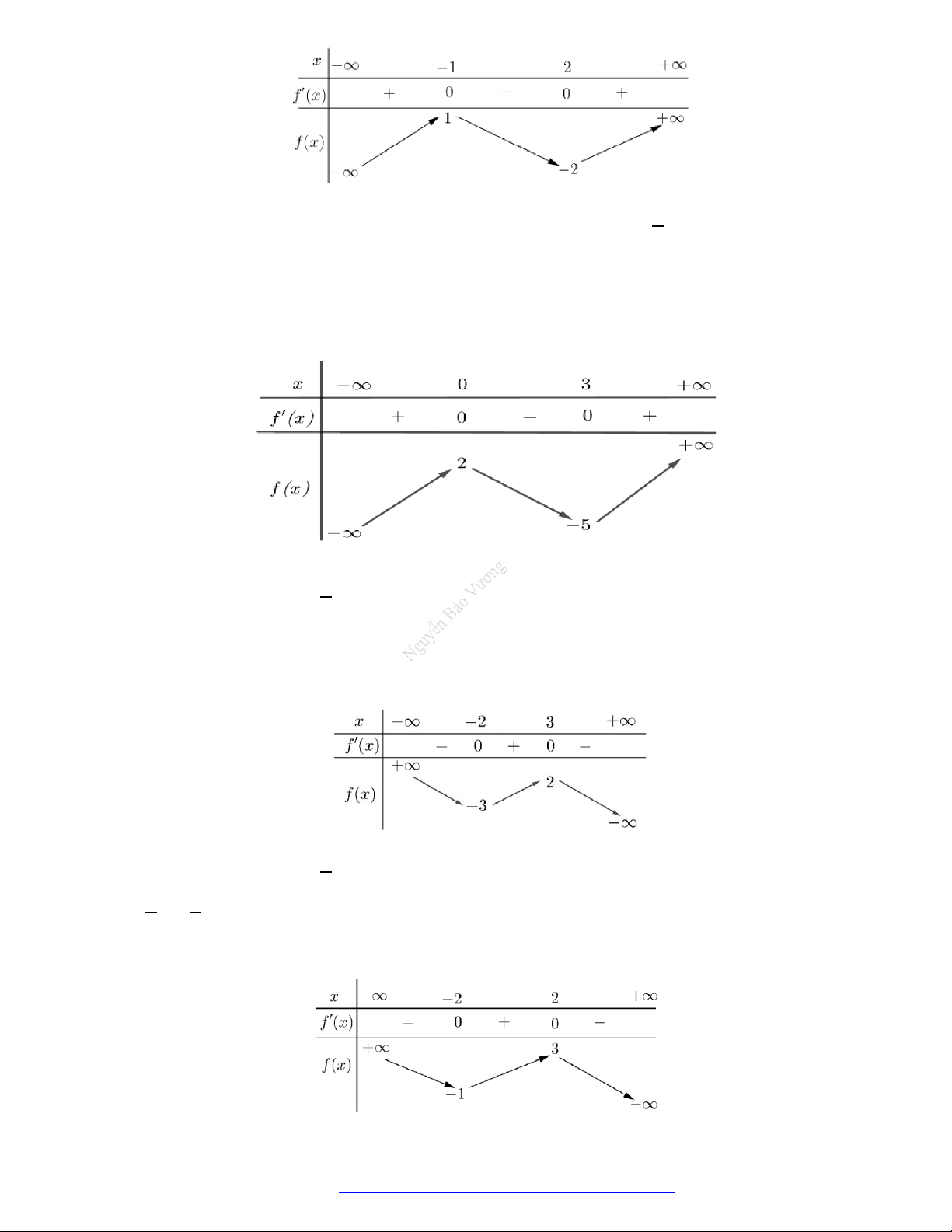
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Hàm số đã cho đạt cực đại tại
A.
2 x
. B.
2x
. C.
1x
. D.
1 x
.
Lời giải
Chọn D
Hàm số đạt cực đại tại điểm mà đạo hàm đổi dấu từ dương sang âm.
Từ bảng biến thiên hàm số đạt cực đại tại
1x
.
Câu 3. (Mã 101 – 2020 Lần 1) Cho hàm
f x
có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng
A.
3
. B.
5
. C.
0
. D.
2
.
Lời giải
Chọn B.
Từ BBT ta có hàm số đạt giá trị cực tiểu
3 5f
tại
3x
Câu 4. (Mã 102 - 2020 Lần 1) Cho hàm số có bảng biến thiên như sau.
Giá trị cực đại của hàm số đã cho bằng
A.
3
. B.
2
. C.
2
. D.
3
.
Lời giải
Chọn B
Dựa vào bảng biến thiên, ta thấy giá trị cực đại của hàm số đã cho là 2
CĐ
y .
Câu 5. (Mã 103 - 2020 Lần 1) Cho hàm số
f x
có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng
A.
2
. B.
2
. C.
3
. D.
1
.
f x
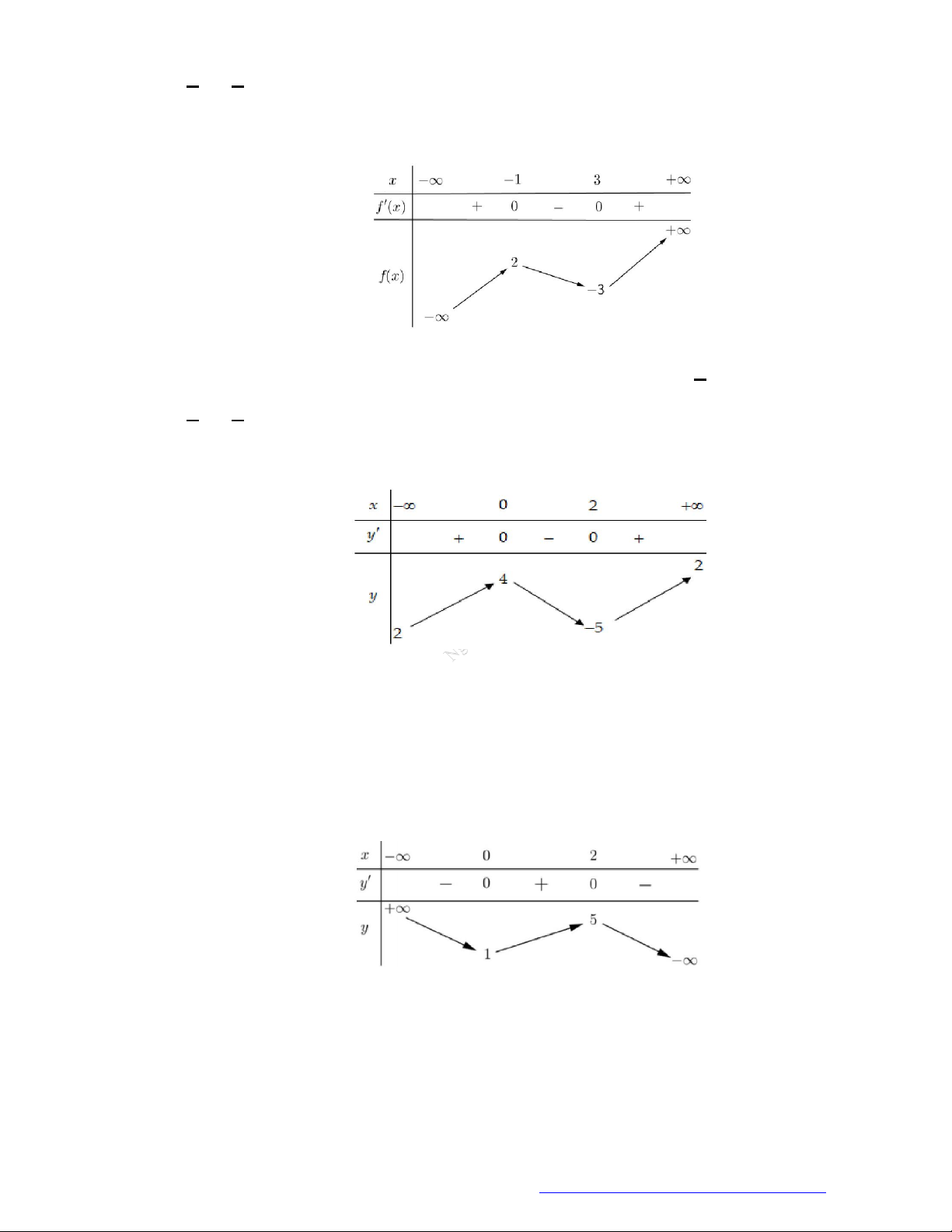
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Lời giải
Chọn D
Gía trị cực tiểu của hàm số đã cho bằng
1
.
Câu 6. (Mã 104 - 2020 Lần 1) Cho hàm số
f x
có bảng biến thiên như sau:
Giá trị cực đại của hàm số đã cho bằng
A.
3
. B.
3
. C.
1
. D.
2
.
Lời giải
Chọn D
Giá trị cực đại của hàm số đã cho bằng 2.
Câu 7. (Mã 105 - 2017) Cho hàm số
y f x
có bảng biến thiên như sau
Mệnh đề nào dưới đây đúng?
A. Hàm số đạt cực tiểu tại
5x
B. Hàm số có bốn điểm cực trị
C. Hàm số đạt cực tiểu tại
2x
D. Hàm số không có cực đại
Lời giải
Chọn.C
Dựa vào bảng biến thiên. Hàm số có đạo hàm trên
và
2 0;y y
đổi dấu từ âm sang dương
khi đi qua
2x
nên hàm số đạt cực tiểu tại
2x
.
Câu 8. (Đề Tham Khảo 2019) Cho hàm số
y f x
có bảng biến thiên như sau
Giá trị cực đại của hàm số đã cho bằng
A.
5
B.
2
C.
0
D.
1
Lời giải
Chọn A
Dựa bào BBT ta có: Giá trị cực đại của hàm số là 5
CD
y
Câu 9. (Mã 104 - 2018) Cho hàm số có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số đã cho là:
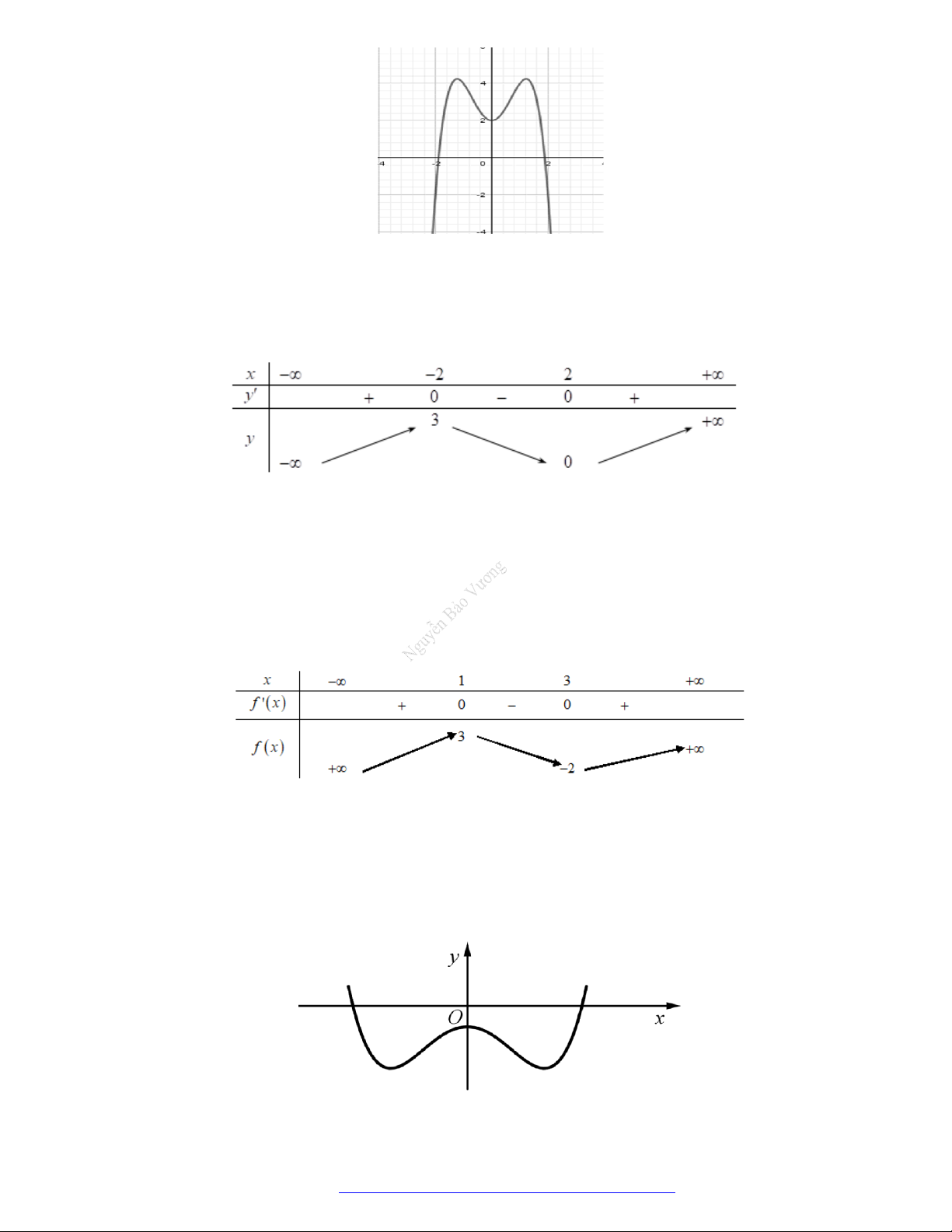
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
3
B.
1
C.
2
D.
0
Lời giải
Chọn A
Hàm số có ba điểm cực trị.
Câu 10. (Mã 110 - 2017) Cho hàm số
y f x
có bảng biến thiên như sau
Tìm giá trị cực đại
CĐ
y
và giá trị cực tiểu
CT
y
của hàm số đã cho.
A.
2
CĐ
y
và
0
CT
y
B.
3
CĐ
y
và
0
CT
y
C.
3
CĐ
y
và
2
CT
y
D.
2
CĐ
y
và
2
CT
y
Lời giải
Chọn B
Dựa vào bảng biến thiên của hàm số ta có
3
CĐ
y
và
0
CT
y
.
Câu 11. (Mã 103 - 2019) Cho hàm số
( )f x
có bảng biến thiên như sau:
Hàm số đạt cực đại tại:
A.
2x
. B.
3x
. C.
1x
. D.
2x
.
Lời giải
Chọn C
Hàm số
f x
xác định tại
1x
,
'(1) 0f
và đạo hàm đổi dấu từ
( )
sang
( )
Câu 12. (Mã 103 - 2018) Cho hàm số
4 2
y ax bx c (
a
,
b
,
c
) có đồ thị như hình vẽ bên.
Số điểm cực trị của hàm số đã cho là
A.
3
B.
0
C.
1
D.
2
Lời giải
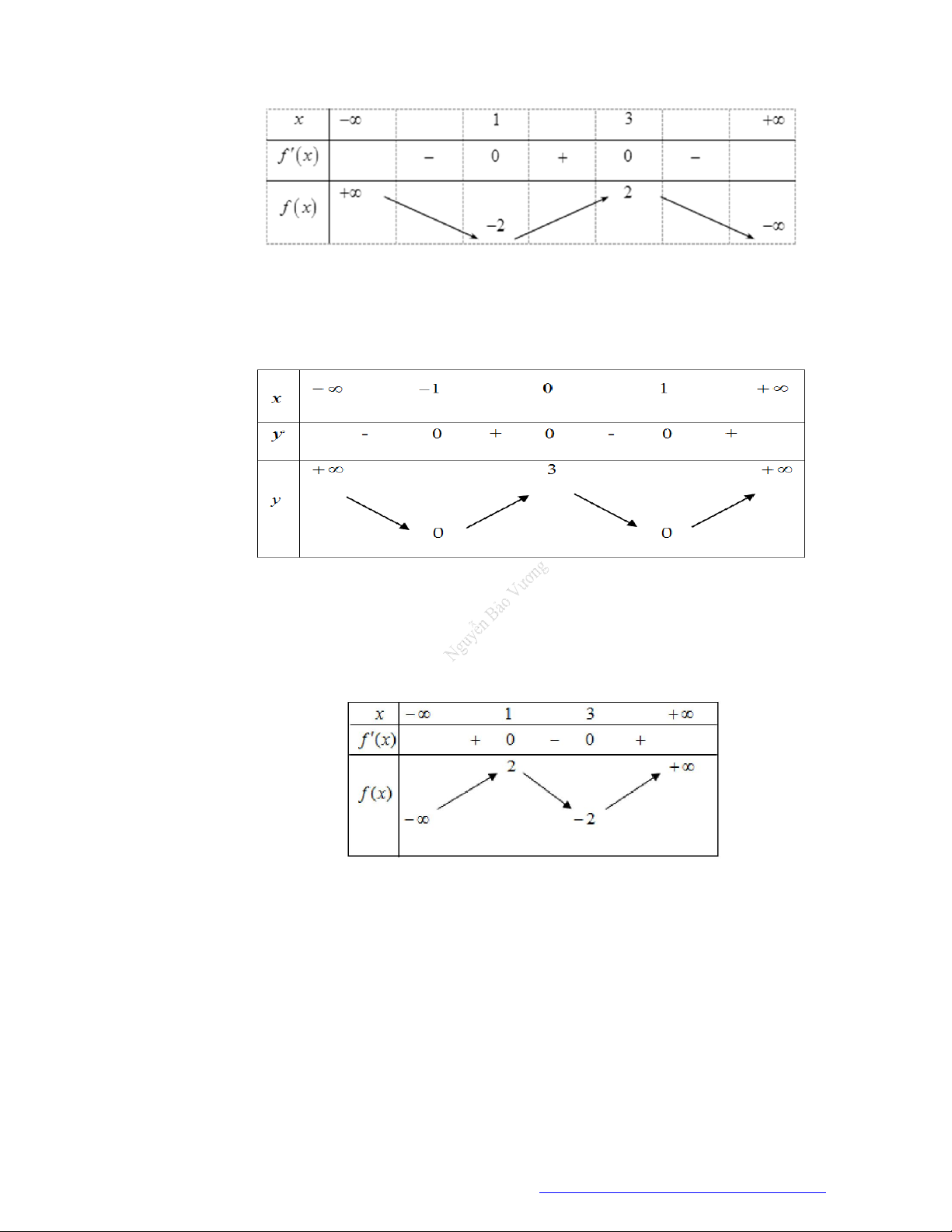
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Chọn A
Câu 13. (Mã 102 - 2019) Cho hàm số
f x
có bảng biến thiên như sau:
Hàm số đạt cực đại tại
A.
2x
. B.
3x
. C.
1x
. D.
2x
.
Lời giải
Chọn B
Câu 14. (Mã 123 - 2017) Cho hàm số
( )y f x
có bảng biến thiên như sau
Mệnh đề nào dưới đây sai
A. Hàm số có giá trị cực đại bằng
3
B. Hàm số có hai điểm cực tiểu
C. Hàm số có giá trị cực đại bằng
0
D. Hàm số có ba điểm cực trị
Lời giải
Chọn C
Câu 15. (Mã 104 - 2019) Cho hàm số
( )f x
có bảng biến thiên như sau:
Hàm số đã cho đạt cực tiểu tại
A.
2x
. B.
2 x
. C.
1x
. D.
3x
.
Lời giải
Chọn D
Từ bảng biến thiên ta có điểm cực tiểu của hàm số là
3x
.
Câu 16. (Mã 102 - 2018) Cho hàm số
3 2
y ax bx cx d
, , ,a b c d
có đồ thị như hình vẽ bên. Số
điểm cực trị của hàm số này là
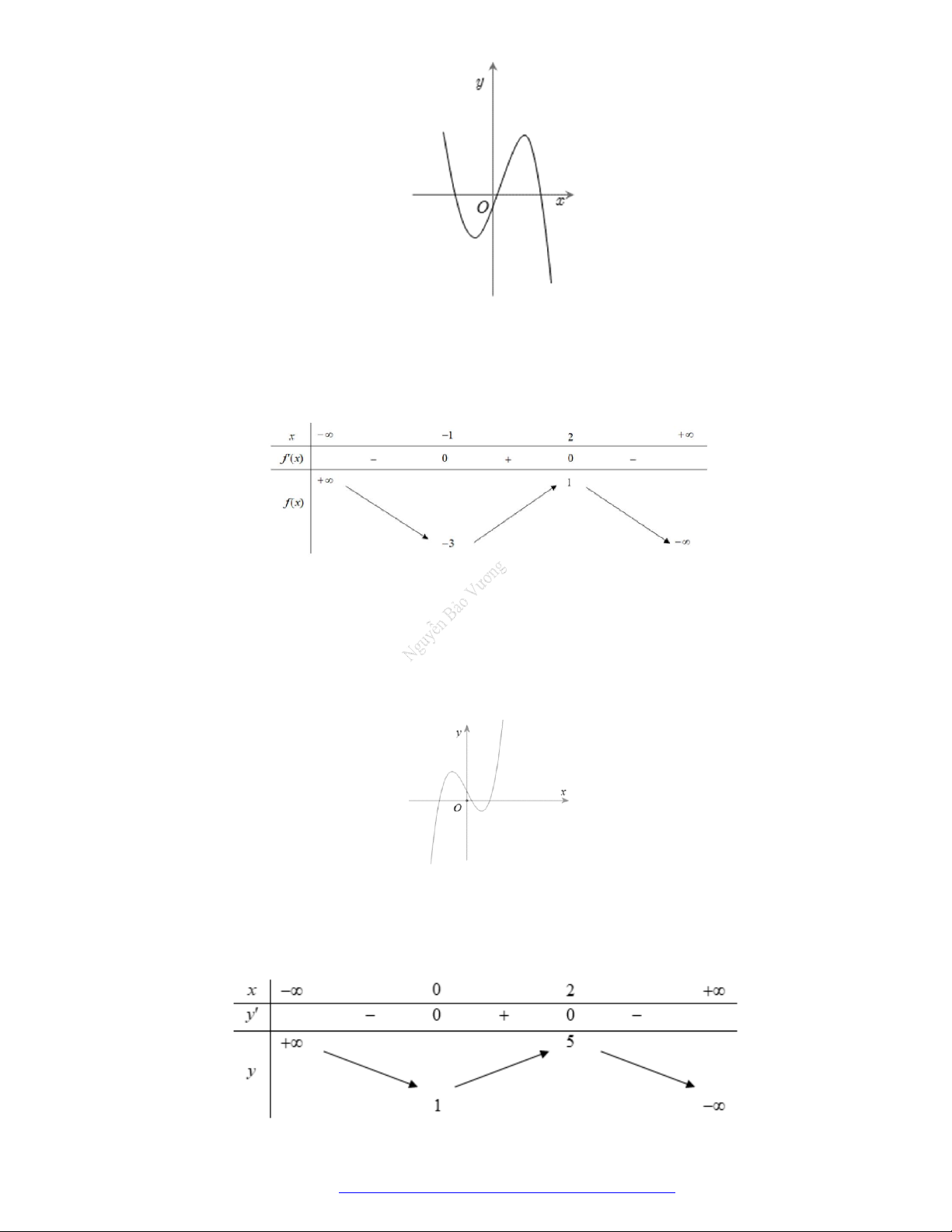
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
3
B.
2
C.
0
D.
1
Lời giải
Chọn B
Dựa vào hình dạng đồ thị hàm số có hai điểm cực trị.
Câu 17. (Mã 101 - 2019) Cho hàm số
( )f x
có bảng biến thiên như sau:
Hàm số đã cho đạt cực tiểu tại
A.
1x
. B.
3x
. C.
2x
. D.
1x
.
Lời giải
Chọn A
Theo bảng biến thiên thì hàm số đạt cực tiểu tại điểm
1x
Câu 18. (Mã 101 - 2018) Cho hàm số
3 2
, , ,y ax bx cx d a b c d
có đồ thị như hình vẽ bên. Số
điểm cực trị của hàm số đã cho là
A.
2
B.
0
C.
3
D.
1
Lời giải
Chọn A
Câu 19. (Đề Tham Khảo 2018) Cho hàm số
y f x
có bảng biến thiên như sau
Hàm số đạt cực đại tại điểm
A.
1x
B.
0x
C.
5x
D.
2x
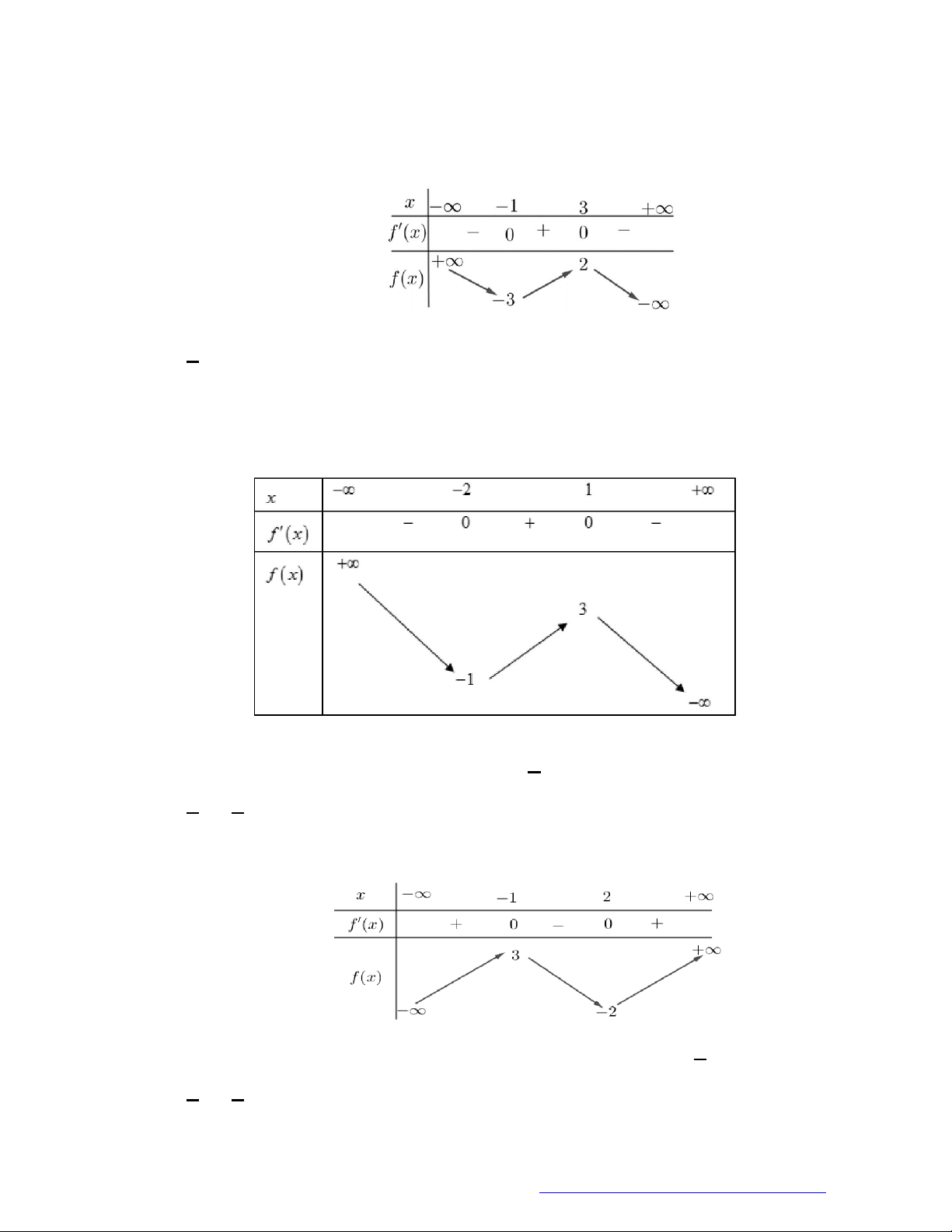
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Lời giải
Chọn D
Dựa vào bảng biến thiên ta thấy
y
đối dấu từ
sang
tại
2x
.
Nên hàm số đạt cực đại tại điểm
2x
.
Câu 20. (Mã 101 – 2020 Lần 2) Cho hàm số
f x
có bảng biến thiên như sau:
Điểm cực đại của hàm số đã cho là
A.
3x
. B.
1x
. C.
2x
. D.
3x
.
Lời giải
Chọn A
Dựa vào bảng biến thiên ta có: hàm số đạt cực đại tại điểm
3x
.
Câu 21. (Mã 102 - 2020 Lần 2) Cho hàm số
f x
có bảng biến thiên như sau:
Điểm cực đại của hàm số đã cho là
A.
3x
. B.
1x
. C.
1x
. D.
2x
.
Lời giải
Chọn C
Từ BBT của hàm số
f x
suy ra điểm cực đại của hàm số
f x
là
1x
.
Câu 22. (Mã 103 - 2020 Lần 2) Cho hàm số
f x
có bảng biến thiên như sau :
Điểm cực đại của hàm số đã cho là
A.
3.x
B.
2.x
C.
2.x
D.
1.x
Lời giải
Chọn D
Câu 23. (Mã 104 - 2020 Lần 2) Cho hàm số
f x
có bảng biến thiên như sau:
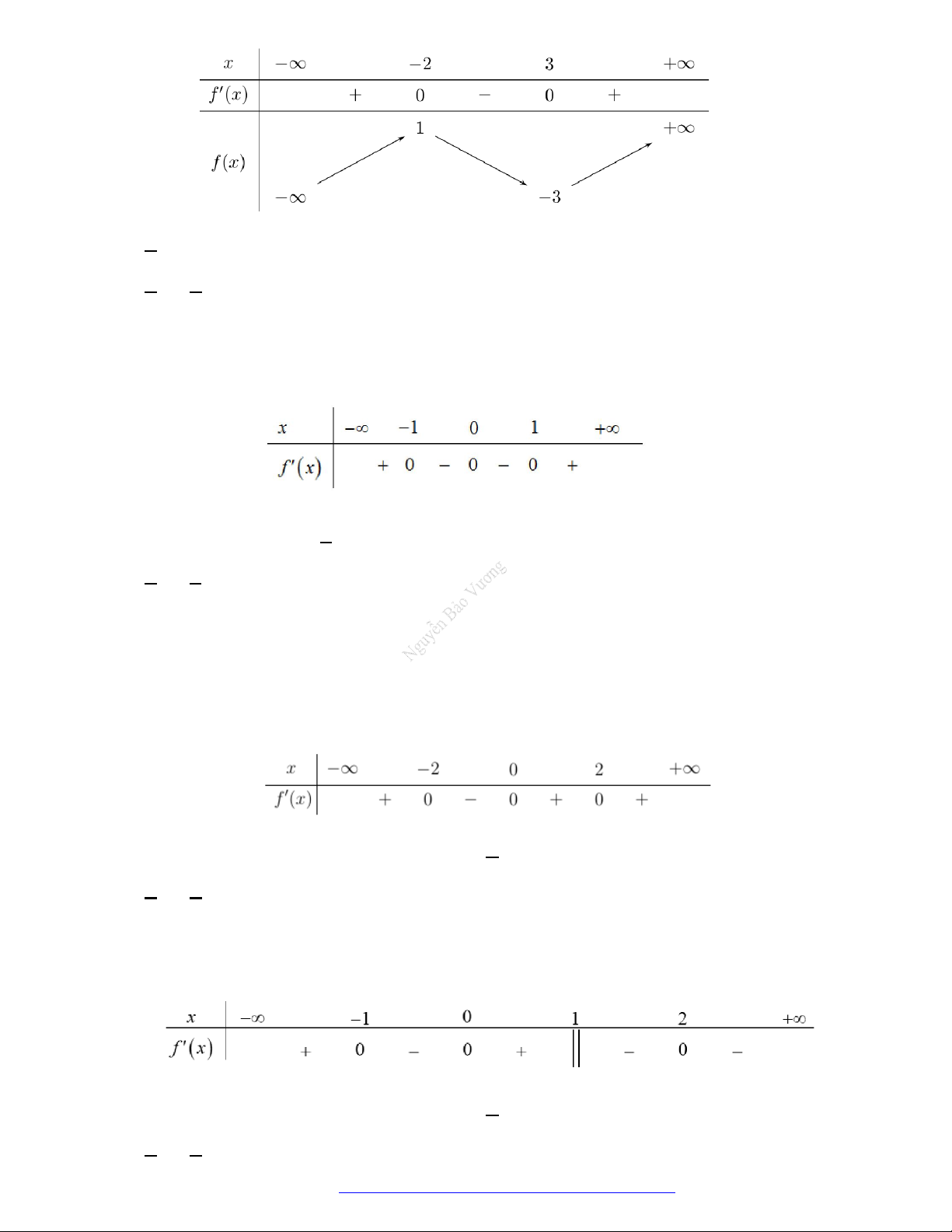
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Điểm cực đại của hàm số đã cho là
A.
2x
. B.
3x
. C.
1x
. D.
3x
.
Lời giải
Chọn A
Hàm số đã cho xác định trên
.
Qua
2x
, đạo hàm
f x
đổi dấu từ dương sang âm nên hàm số đạt cực đại tại
2x
.
Câu 24. (Đề Tham Khảo 2020 – Lần 1) Cho hàm số
f x
, bảng xét dấu của
f x
như sau:
Số điểm cực trị của hàm số đã cho là
A.
0
. B.
2
. C.
1
. D.
3
.
Lời giải
Chọn B
Ta có
1
0 0
1
x
f x x
x
Từ bảng biến thiên ta thấy
f x
đổi dấu khi
x
qua nghiệm
1
và nghiệm
1
; không đổi dấu khi
x
qua nghiệm
0
nên hàm số có hai điểm cực trị.
Câu 25. (Đề Tham Khảo 2020 – Lần 2) Cho hàm số
f x
có bảng xét dấu của
f x
như sau:
Số điểm cực trị của hàm số đã cho là
A.
3
. B.
0
. C.
2
. D.
1
.
Lời giải
Chọn C
Dựa vào bảng xét dấu của
f x
hàm số đã cho có
2
điểm cực trị.
Câu 26. (Mã 101 - 2020 Lần 1) Cho hàm số
f x
liên tục trên
và có bảng xét dấu của
f x
như
sau:
Số điểm cực đại của hàm số đã cho là
A.
4
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn C

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Do hàm số
f x
liên tục trên
,
1 0
f
,
1f
không xác định nhưng do hàm số liên tục trên
nên tồn tại
1f
và
f x
đổi dấu từ
" "
sang
" "
khi đi qua các điểm
1x
,
1x
nên hàm số đã cho đạt cực
đại tại 2 điểm này.
Vậy số điểm cực đại của hàm số đã cho là 2.
Câu 27. (Mã 102 - 2020 Lần 1) Cho hàm
f x
liên tục trên
và có bảng xét dấu
f x
như sau:
Số điểm cực tiểu của hàm số là
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn B
Ta thấy
f x
đổi dấu 2 lần từ
sang
khi qua các điểm
1; 1x x
nên hàm số có 2
điểm cực tiểu.
Câu 28. (Mã 103 - 2020 Lần 1) Cho hàm số
( )f x
liên tục trên
và có bảng xét dấu của
( )f x
như sau:
Số điểm cực tiểu của hàm số đã cho là
A.
2.
B.
4.
C.
3.
D.
1.
Lời giải
Chọn A
Câu 29. (Mã 104 - 2020 Lần 1) Cho hàm số
f x
liên tục trên R có bảng xét dấu
'f x
Số điểm cực đại của hàm số đã cho là:
A. 3. B. 1. C. 2. D. 4.
Lời giải
Chọn C
Ta có:
' 0f x
,
'f x
không xác định tại
2; 1; 2, 3x x x x
. Nhưng có 2 giá trị
2; 2x x
mà qua đó
'f x
đổi dấu từ dương sang âm nên hàm số đã cho có 2 điểm cực đại.
Dạng 2. Tìm cực trị của hàm số khi biết y, y’
Bài toán: Tìm các điểm cực đại, cực tiểu (nếu có) của hàm số
( ).y f x
Phương pháp: Sự dụng 2 qui tắc tìm cực trị sau:
Quy tắc I: sử dụng nội dụng định lý 1
Bước 1. Tìm tập xác định
D
của hàm số.
Bước 2. Tính đạo hàm
( ).y f x
Tìm các điểm
, ( 1,2, 3,..., )
i
x i n
mà tại đó đạo hàm bằng 0 hoặc không
xác định.
Bước 3. Sắp xếp các điểm
i
x
theo thứ tự tăng dần và lập bảng biến thiên.
Bước 4. Từ bảng biến thiên, suy ra các điểm cực trị (dựa vào nội dung định lý 1).
Quy tắc II: sử dụng nội dụng định lý 2

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Bước 1. Tìm tập xác định
D
của hàm số.
Bước 2. Tính đạo hàm
( ).y f x
Giải phương trình
( ) 0f x
và kí hiệu
, ( 1,2, 3,..., )
i
x i n
là các nghiệm
của nó.
Bước 3. Tính
( )f x
và
( ).
i
f x
Bước 4. Dựa vào dấu của
( )
i
y x
suy ra tính chất cực trị của điểm
:
i
x
+ Nếu
( ) 0
i
f x
thì hàm số đạt cực đại tại điểm
.
i
x
+ Nếu
( ) 0
i
f x
thì hàm số đạt cực tiểu tại điểm
.
i
x
Câu 1. (Mã 101 – 2020 Lần 2) Cho hàm số
f x
có đạo hàm
3
1 4 ,f x x x x x
. Số
điểm cực đại của hàm số đã cho là
A.
3
. B.
4
. C.
2
. D.
1
.
Lời giải
Chọn D
Ta có
0
0 1
4
x
f x x
x
Bảng xét dấu
f x
:
Từ bảng xét dấu suy ra hàm số có đúng
1
điểm cực đại.
Câu 2. (Mã 103 - 2020 Lần 2) Cho hàm số
f x
có đạo hàm
3
1 4 ,f x x x x x
. Số
điểm cực đại của hàm số đã cho là
A.
2
. B.
3
. C.
4
. D.
1
.
Lời giải
Chọn D
3
0
0 1 4 0 1
4
x
f x x x x x
x
.
Lập bảng biến thiên của hàm số
f x
Vậy hàm số đã cho có một điểm cực đại.
Câu 3. (Mã 104 - 2020 Lần 2) Cho hàm số
f x
có
3
1 4f x x x x
,
x
. Số điểm cực tiểu
của hàm số đã cho là
A.
4
. B.
3
. C.
1
. D.
2
.
Lời giải
Chọn D
3
0
1 4 0 1
4
x
f x x x x x
x
.
Bảng xét dấu của
f x
x
1
0
4
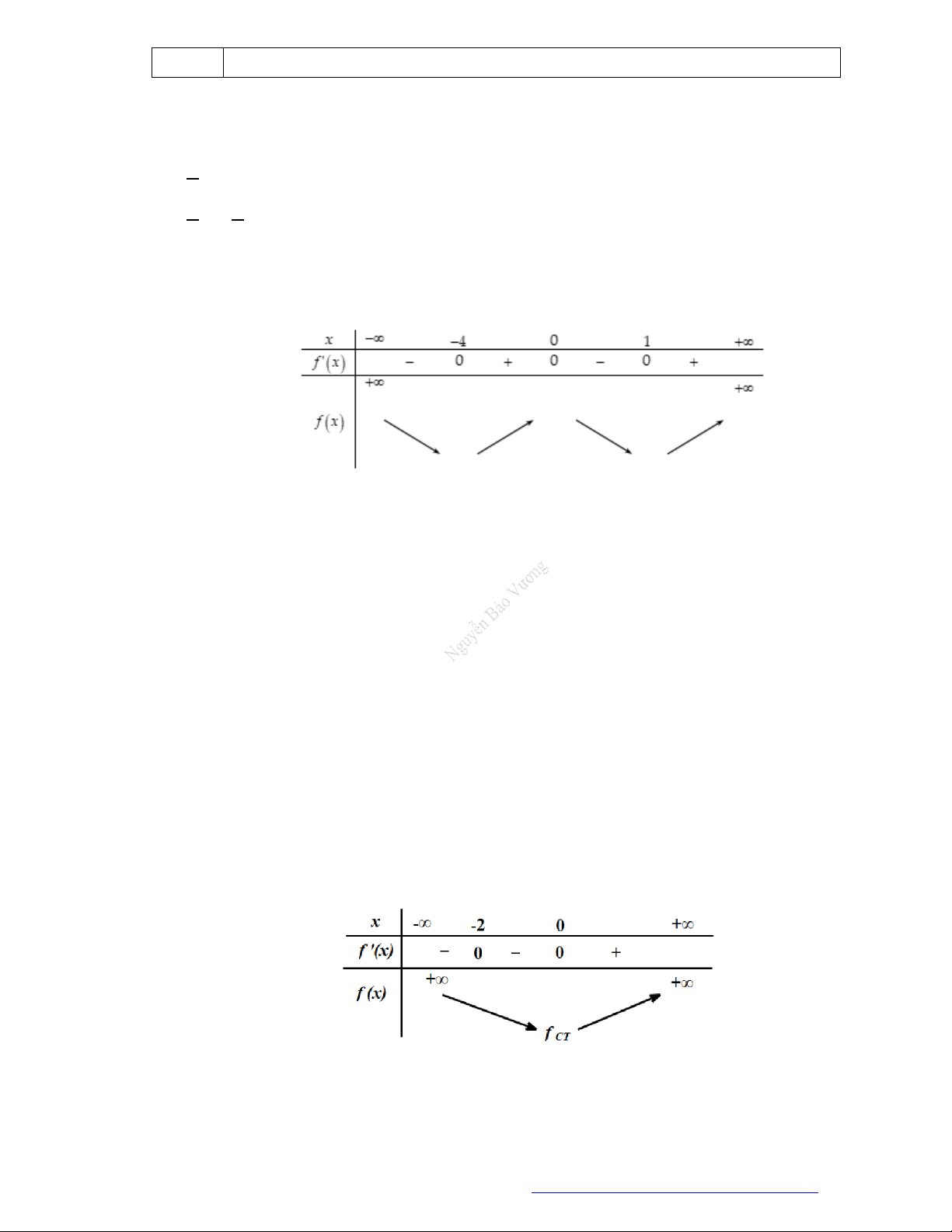
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
f x
0
0
0
Vậy hàm số đã cho có hai điểm cực tiểu là
1x
và
4x
.
Câu 4. (Mã 102 - 2020 Lần 2) Cho hàm số
f x
có đạo hàm
3
' 1 4 ,f x x x x x
. Số điểm
cực tiểu của hàm số đã cho là
A.
2
B.
3
C.
4
D.
1
Lời giải
Chọn A
Ta có:
3
0
' 0 1 4 0 1
4
x
f x x x x x
x
.
Bảng biến thiên:
Dựa vào bảng biến thiên ta thấy hàm số đã cho có
2
điểm cực tiểu.
Câu 5. (Đề Tham Khảo 2019) Cho hàm số
( )f x
có đạo hàm
3
( ) ( 1)( 2)f x x x x
,
x R
. Số điểm
cực trị của hàm số đã cho là
A.
1
B.
3
C.
2
D.
5
Lời giải
Chọn B
Phương trình
3
( ) 0 ( 1)( 2) 0f x x x x
0
1
2
x
x
x
Do
( ) 0f x
có ba nghiệm phân biệt và
( )f x
đổi dấu qua ba nghiệm này nên hàm số có ba điểm
cực trị.
Câu 6. (Mã 101 - 2019) Cho hàm số
( )f x
có đạo hàm
2
( ) 2 , xf x x x
.
Số điểm cực trị của
hàm số đã cho là
A.
2
. B.
1
. C.
0
. D.
3
.
Lời giải
Chọn B
Bảng biến thiên
Từ bảng biến thiên ta thấy hàm số đã cho có đúng một điểm cực trị đó là điểm cực tiểu
0x
.
Câu 7. (Mã 103 - 2019) Cho hàm số
f x
có đạo hàm
2
1 , .f x x x x R
Số điểm cực trị của
hàm số đã cho là
A.
2
. B.
0
. C.
1
. D.
3
.
Lời giải
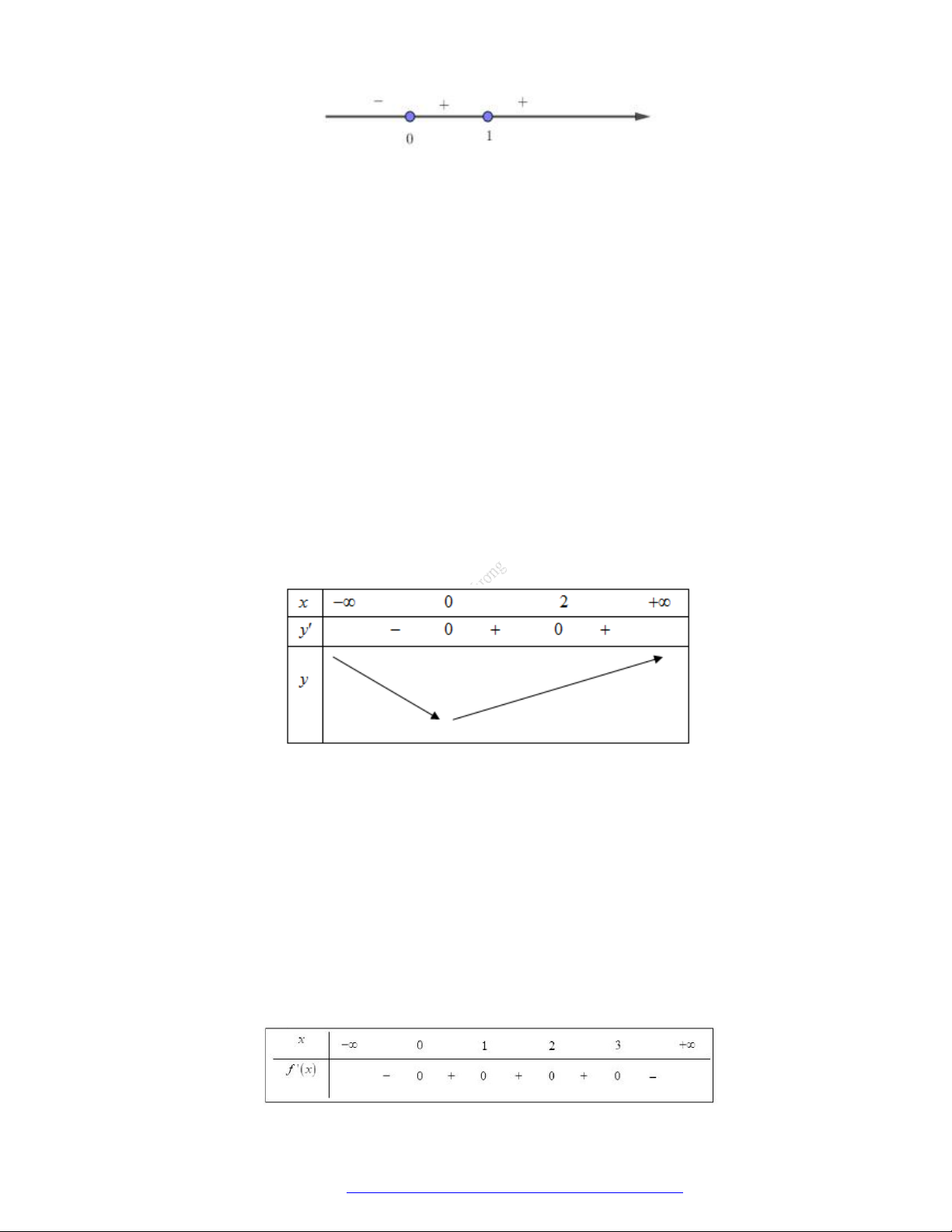
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Chọn C
Xét dấu của đạo hàm:
Ta thấy đạo hàm đổi dấu đúng 1 lần nên hàm số đã cho có đúng 1 điểm cực trị
Câu 8. (Mã 104 - 2019) Cho hàm số
f x
có đạo hàm
2
1 , f x x x x
. Số điểm cực trị của
hàm số đã cho là
A.
1
. B.
2
. C.
3
. D.
0
.
Lời giải
Chọn A
Ta có
2
2
0
0
0 1 0
1
1 0
x
x
f x x x
x
x
.
Vì nghiệm
0x
là nghiệm bội lẻ và
1x
là nghiệm bội chẵn nên số điểm cực trị của hàm số là
1.
Câu 9. (Mã 102 - 2019) Cho hàm số
( )y f x
có đạo hàm
2
( ) ( 2)f x x x
,
x
. Số điểm cực trị
của hàm số đã cho là
A.
0
. B.
3
. C.
2
. D.
1
.
Lời giải
Chọn D
Ta có:
2
0 0
( ) 0 ( 2) 0
2 0 2
x x
f x x x
x x
Bảng biến thiên:
Dựa vào bảng biến thiên, ta thấy hàm số có 1 điểm cực trị
0x
.
Câu 10. (THPT Lê Quý Dôn Dà Nẵng 2019) Cho hàm số
f x
có đạo hàm
2 3 4
' 1 3 2f x x x x x
với mọi
x
. Điểm cực tiểu của hàm số đã cho là
A.
2x
. B.
3x
. C.
0x
. D.
1x
.
Lời giải
Ta có
2 3 4
0
1
' 1 3 2 ' 0
2
3
x
x
f x x x x x f x
x
x
.
Bảng xét dấu đạo hàm.
Suy ra hàm số
f x
đạt cực tiểu tại
0x
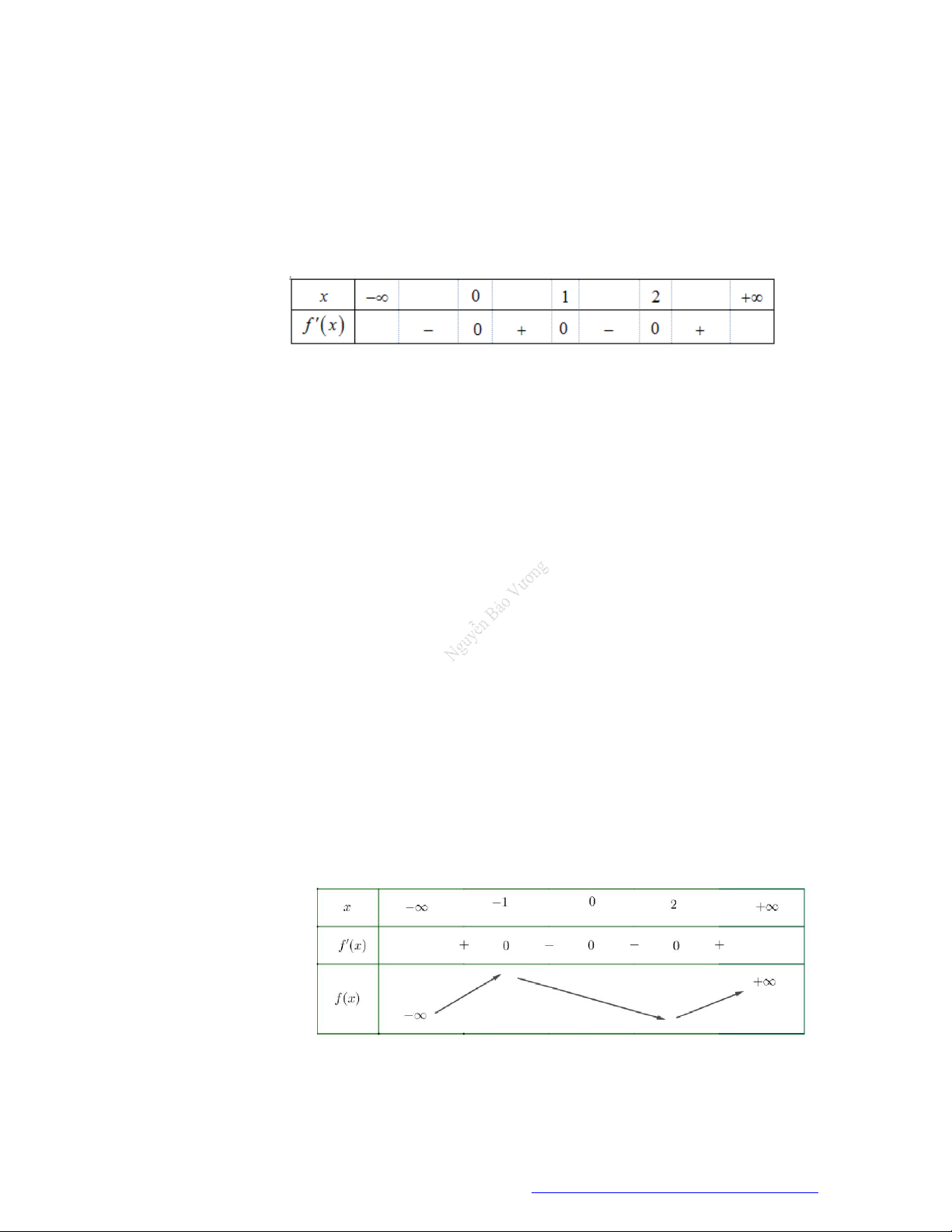
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Câu 11. (Chuyên Sơn La 2019) Cho hàm số
f x
có đạo hàm
3
1 2 ,f x x x x x
. Số
điểm cực trị của hàm số đã cho là
A.
1
. B.
3
. C.
5
. D.
2
.
Lời giải
Ta có:
3
0
0 1 2 0 1
2
x
f x x x x x
x
.
Bảng xét dấu:
Dựa vào bảng xét dấu nhận thấy hàm số
f x
có
3
điểm cực trị.
Câu 12. (VTED 2019) Hàm số
y f x
có đạo hàm
1 2 ... 2019f x x x x
,
x R
. Hàm
số
y f x
có tất cả bao nhiêu điểm cực tiểu?
A.
1008
B.
1010
C.
1009
D.
1011
Lời giải
Chọn B
Ta có:
1
2
1 2 ... 2019 0
......
2019
x
x
f x x x x
x
0
f x
có
2019
nghiệm bội lẻ và hệ số
a
dương nên có
1010
cực tiểu
Câu 13. (THPT Yên Phong 1 Bắc Ninh 2019) Hàm số
f x
có đạo hàm
3
2
1 2f x x x x
,
x
. Hỏi
f x
có bao nhiêu điểm cực đại?
A.
2
. B.
0
. C.
1
. D.
3
.
Lời giải
Ta có
2
3
0 0
0 1 0 1
2
2 0
x x
f x x x
x
x
.
Bảng biến thiên
Dựa vào bảng biến thiên suy ra hàm số có
1
điểm cực đại.
Câu 14. (THPT Cù Huy Cận 2019) Cho hàm số
f x
có đạo hàm là
2
1 2f x x x x x
. Số
điểm cực trị của hàm số là?
A.
5
. B.
2
. C.
1
. D.
3
.
Lời giải
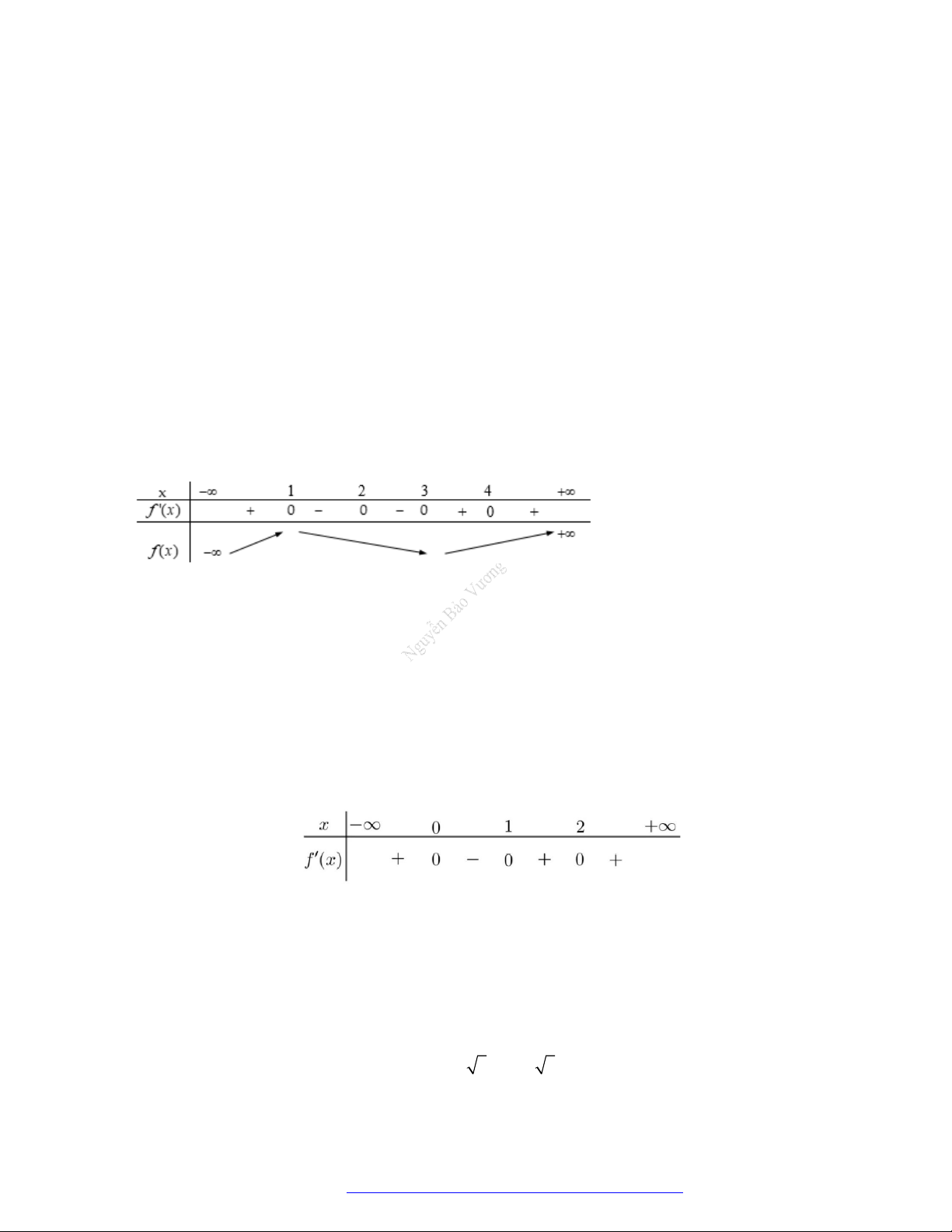
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta có
0
0 1
2
x
f x x
x
. Do
0, 1x x
là nghiệm đơn, còn các nghiệm và
2x
là nghiệm
bội chẵn nên
f x
chỉ đổi khi đi qua
0, 1x x
.
Hàm số
2
0
1 4 0 2 2
0
a
m m m
có
2
điểm cực trị.
Câu 15. (Sở Bình Phước 2019) Cho hàm số
f x
có đạo hàm
2 3 4
1 2 3 4 , x .f x x x x x
Số điểm cực trị của hàm số đã cho là
A.
3
B.
5
C.
2
D.
4
Lời giải
Chọn C
1
2
0
3
4
x
x
f x
x
x
Bảng biến thiên:
Dựa vào bảng biến thiên: Số điểm cực trị của hàm số đã cho là 2.
Câu 16. (THPT Gia Lộc Hải Dương 2019) Cho hàm số
f x
có đạo hàm
2
1 2 ,f x x x x x
. Số điểm cực trị của hàm số đã cho là
A.
5
. B.
2
. C.
1
. D.
3
.
Lời giải
Ta có
2
0
0 1 2 0 1
2
x
f x x x x x
x
.
Lập bảng xét dấu của
f x
như sau:
Ta thấy
f x
đổi dấu khi đi qua các điểm
0x
và
1x
, do đó hàm số
y f x
có hai điểm
cực trị.
Câu 17. (THPT Ba Đình 2019) Cho hàm số
y f x
có đạo hàm
2 4
2 3 9f x x x x
. Số
điểm cực trị của hàm số
y f x
là
A.
3
. B.
4
. C.
2
. D.
1
.
Lời giải
2 2
2
2 2 2
2 3 3 2 3 3 3f x x x x x x x x
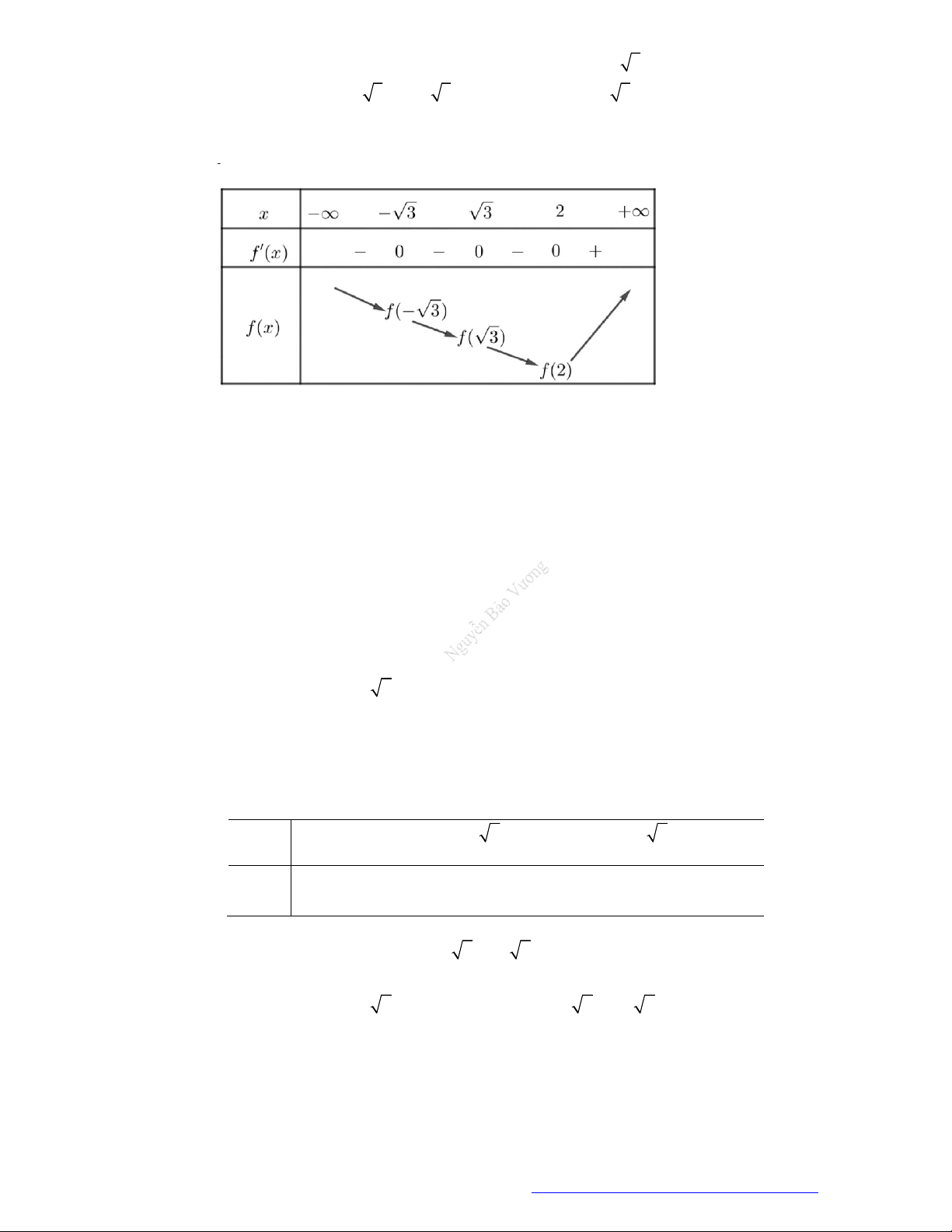
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
2 2
2
0 2 3 3 3 0f x x x x x
3
3
2
x
x
x
.
Bảng biến thiên
Từ bảng biến thiên của hàm số
y f x
, ta thấy hàm số
y f x
có đúng 1 điểm cực trị.
Câu 18. (THCS - THPT Nguyễn Khuyến 2019) Nếu hàm số
f x
có đạo hàm là
4
2 2
' 2 2 1f x x x x x x
thì tổng các điểm cực trị của hàm số
f x
bằng
A.
1
. B.
2
. C.
1
. D.
0
.
Lời giải
Có
2 5
2
' 2 1f x x x x
. Ta thấy
'f x
chỉ đổi dấu qua nghiệm
1x
nên hàm số
f x
có đúng một điểm cực trị là
1x
.
Vậy tổng các điểm cực trị của hàm số
f x
bằng
1
.
Câu 19. (Chuyên Quang Trung Bình Phước 2019) Cho hàm số
y f x
có đạo hàm
3
2 2
' 2 2 f x x x x x x
. Số điểm cực trị của hàm số là
A.
4
B.
1
C.
2
D.
3
Lời giải
Chọn D
Cách 1: Sử dụng MTCT chọn một số nằm giữa các khoảng suy ra bảng xét dấu
x
2
4
2
0
4
2
'
f x
0
0
0
0
'f x
đổi dấu 3 lần qua
2 x
,
4
2 x
,
4
2x
. suy ra hàm số có 3 cực trị.
Cách 2: Sử dụng nghiệm bội chẵn lẻ, nghiệm đơn.
3
2
2 2 4
4 4
' 2 2 2 2 2 2 f x x x x x x x x x x
'f x
đổi dấu qua 3 nghiệm đơn. 2 nghiệm bội chẵn không đổi dấu nên có 3 cực trị.
Câu 20. (Chuyên Lam Sơn Thanh Hóa 2019) Cho hàm số
y f x
có đạo hàm trên
và
2
1 2 3f x x x x
. Số điểm cực trị của hàm số đã cho là:
A.
3
B.
1
C.
0
D.
2
Lời giải
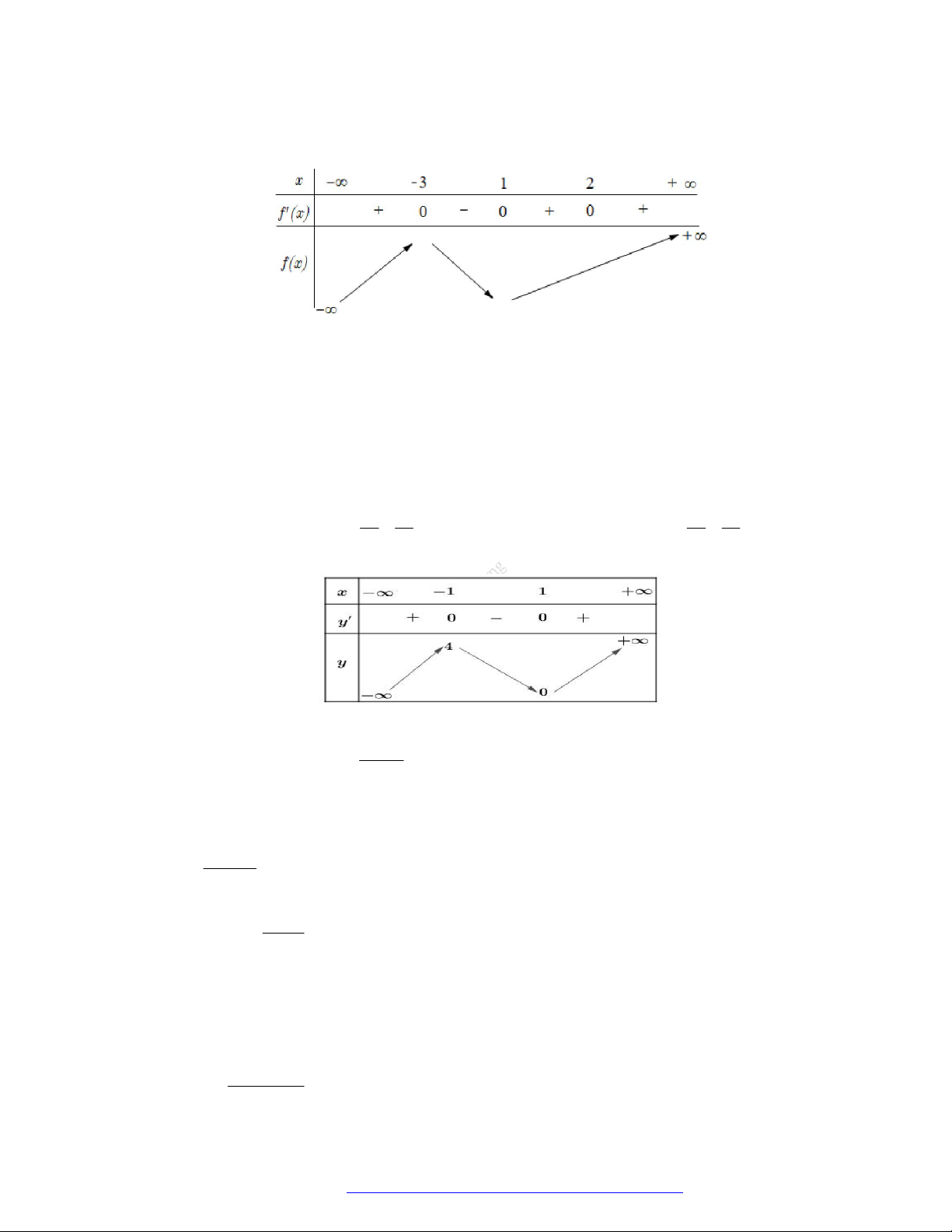
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Chọn D
Ta có
1
0 2
3
x
f x x
x
Bảng biến thiên
Từ bảng biến thiên ta thấy hàm số đã cho có
2
điểm cực trị.
Câu 21. (Đề Minh Họa 2017) Tìm giá trị cực đại
C§
y của hàm số
3
3 2y x x
.
A.
C§
1y B.
C§
4y C.
C§
1y D.
C§
0y
Lời giải
Chọn B
Ta có
2
3 3y x
0y
2
3 3 0x
1 1 0
1 1 4
x y
x y
3
lim 3 2
x
x x
3
2 3
3 2
lim 1 ,
x
x
x x
3
lim 3 2
x
x x
3
2 3
3 2
lim 1
x
x
x x
Bảng biến thiên
Từ bảng biến thiên, ta thấy giá trị cực đại của hàm số bằng
4
Câu 22. (Mã 104 - 2017) Hàm số
2 3
1
x
y
x
có bao nhiêu điểm cực trị?
A.
1
B.
3
C.
0
D.
2
Lời giải
Chọn C
Có
2
1
0, 1
1
y x
x
nên hàm số không có cực trị.
Câu 23. Cho hàm số
2
3
1
x
y
x
. Mệnh đề nào dưới đây đúng?
A. Cực tiểu của hàm số bằng
3
B. Cực tiểu của hàm số bằng
1
C. Cực tiểu của hàm số bằng
6
D. Cực tiểu của hàm số bằng
2
Lời giải
Chọn D
Cách 1.
Ta có:
2
2
2 3
1
x x
y
x
;
2
0 2 3 0y x x
3
1
x
x
Lập bảng biến thiên. Vậy hàm số đạt cực tiểu tại
1x
và giá trị cực tiểu bằng
2
.
Cách 2.
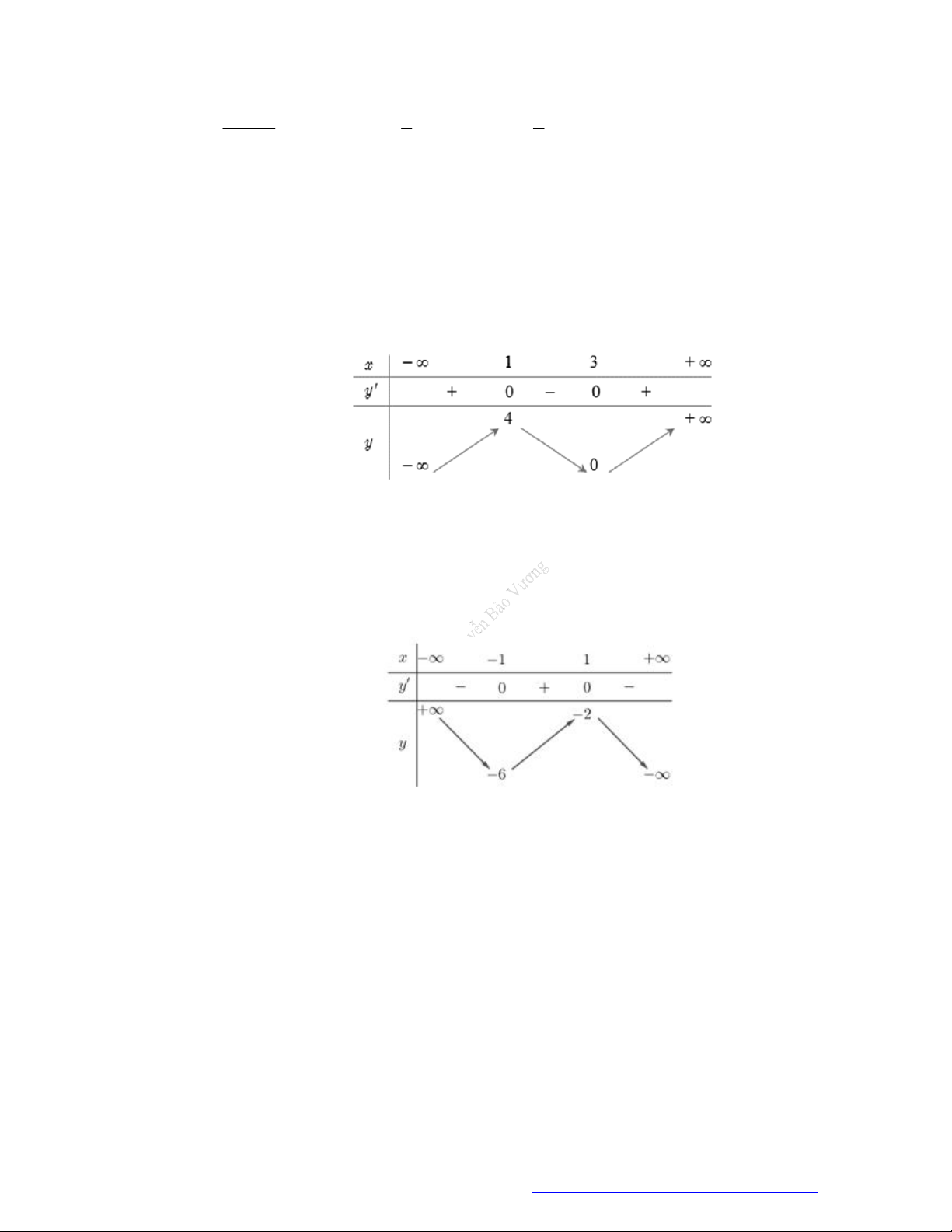
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
Ta có
2
2
2 3
1
x x
y
x
;
2
0 2 3 0y x x
3
1
x
x
3
8
1
y
x
. Khi đó:
1
1 0
2
y
;
1
3 0
2
y
.
Nên hàm số đạt cực tiểu tại
1x
và giá trị cực tiểu bằng
2
.
Câu 24. (Chuyên Hùng Vương Gia Lai 2019) Điểm cực đại của đồ thị hàm số
3 2
6 9y x x x
có tổng
hoành độ và tung độ bằng
A.
5
. B.
1
. C.
3
. D.
1
.
Lời giải
Ta có:
2
1
' 3 12 9 0
3
x
y x x
x
Bảng biến thiên
Khi đó: 1 4 5.
CD CD CD CD
x y x y
Câu 25. (Chuyên Vĩnh Phúc 2019) Tìm giá trị cực tiểu
CT
y
của hàm số
3
3 4y x x
.
A.
6
CT
y
B.
1
CT
y
C.
2
CT
y
D.
1
CT
y
Lời giải
Tập xác định:
D
;
2
3 3y x
;
0y
1x
.
Bảng biến thiên
Vậy
1 2
CD
y y
;
1 6
CT
y y
.
Câu 26. (THPT Cù Huy Cận 2019) Giá trị cực tiểu
CT
y của hàm số
3 2
3 4y x x là:
A. 0
CT
y . B. 3
CT
y . C. 2
CT
y . D. 4
CT
y .
Lời giải
Ta có
2
3 6 , 6 6y x x y x
0
0
2
0 6, 2 6
x
y
x
y y
Do đó hàm số đạt cực tiểu tại
2x
2 0
CT
y y
.
Câu 27. (Liên Trường Thpt Tp Vinh Nghệ An 2019) Đồ thị hàm số
4 2
1y x x
có bao nhiêu điểm
cực trị có tung độ là số dương?
A.
3
. B.
1
. C.
2
. D.
0
.
Lời giải
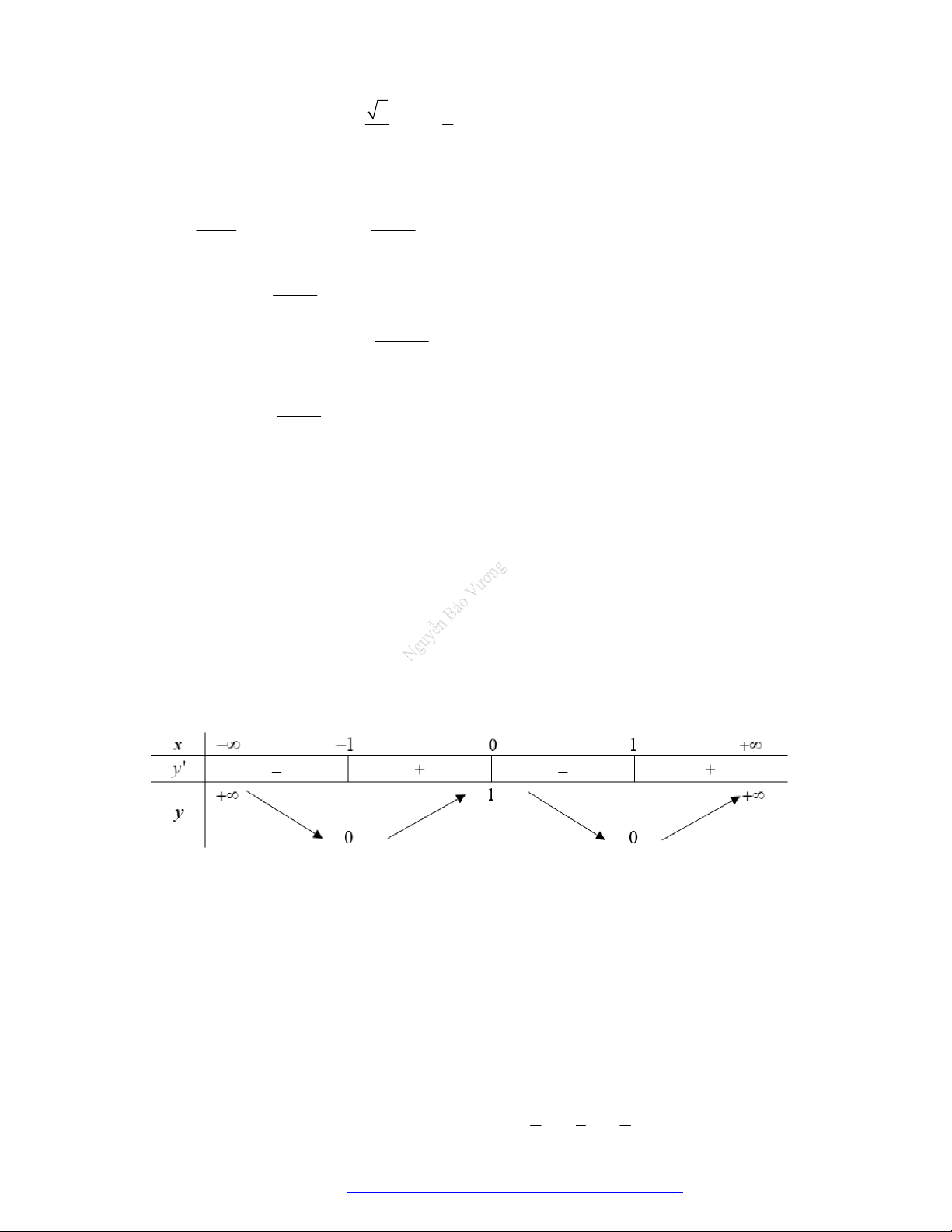
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Tập xác định
D
.
3
4 2y x x
;
0 1
0
2 3
2 4
x y
y
x y
.
Suy ra đồ thị có hàm số
4 2
1y x x
có
3
điểm cực trị có tung độ là số dương.
Câu 28. (Hsg Bắc Ninh 2019) Hàm số nào dưới đây không có cực trị?
A.
2
1x
y
x
B.
2 2
1
x
y
x
C.
2
2 1y x x
D.
3
1y x x
Lời giải
+ Xét hàm số
2 2
1
x
y
x
.
Tập xác định
\ 1D
,
2
4
0,
1
y x D
x
.
Nên hàm số luôn đồng biến trên từng khoảng xác định.
Do đó hàm số
2 2
1
x
y
x
không có cực trị.
Câu 29. (THPT Ba Đình 2019) Cho hàm số
4 2
2 1y x x
. Xét các mệnh đề sau đây
1) Hàm số có 3 điểm cực trị.
2) Hàm số đồng biến trên các khoảng
1;0
;
1;
.
3) Hàm số có 1 điểm cực trị.
4) Hàm số nghịch biến trên các khoảng
; 1
;
0;1
.
Có bao nhiêu mệnh đề đúng trong bốn mệnh đề trên?
A. 2. B. 1. C. 4. D. 3.
Lời giải
3
0 1
' 4 4 ' 0 1 0
1 0
x y
y x x y x y
x y
Bảng xét dấu:
Hàm số có
3
điểm cực trị, đồng biến trên khoảng
1;0
;
1;
và nghịch biến trên khoảng
; 1
;
0;1
. Vậy mệnh đề
1
,
2
,
4
đúng.
Câu 30. (THPT Ba Đình 2019) Tìm giá trị cực đại của hàm số
3 2
3 2y x x
.
A.
2
. B.
0
. C.
2
. D.
1
.
Lời giải
Tập xác định của hàm số là
D
.
Ta có:
2
0
3 6 0
2
x
y x x y
x
.
6 6 0 6 0y x y
Giá trị cực đại của hàm số là:
0 2y
.
Câu 31. (THCS - THPT Nguyễn Khuyến 2019) Hàm số
4 3 2
1 1 5
3 2019
4 3 2
y x x x x m
m
đạt
cực tiểu tại điểm:
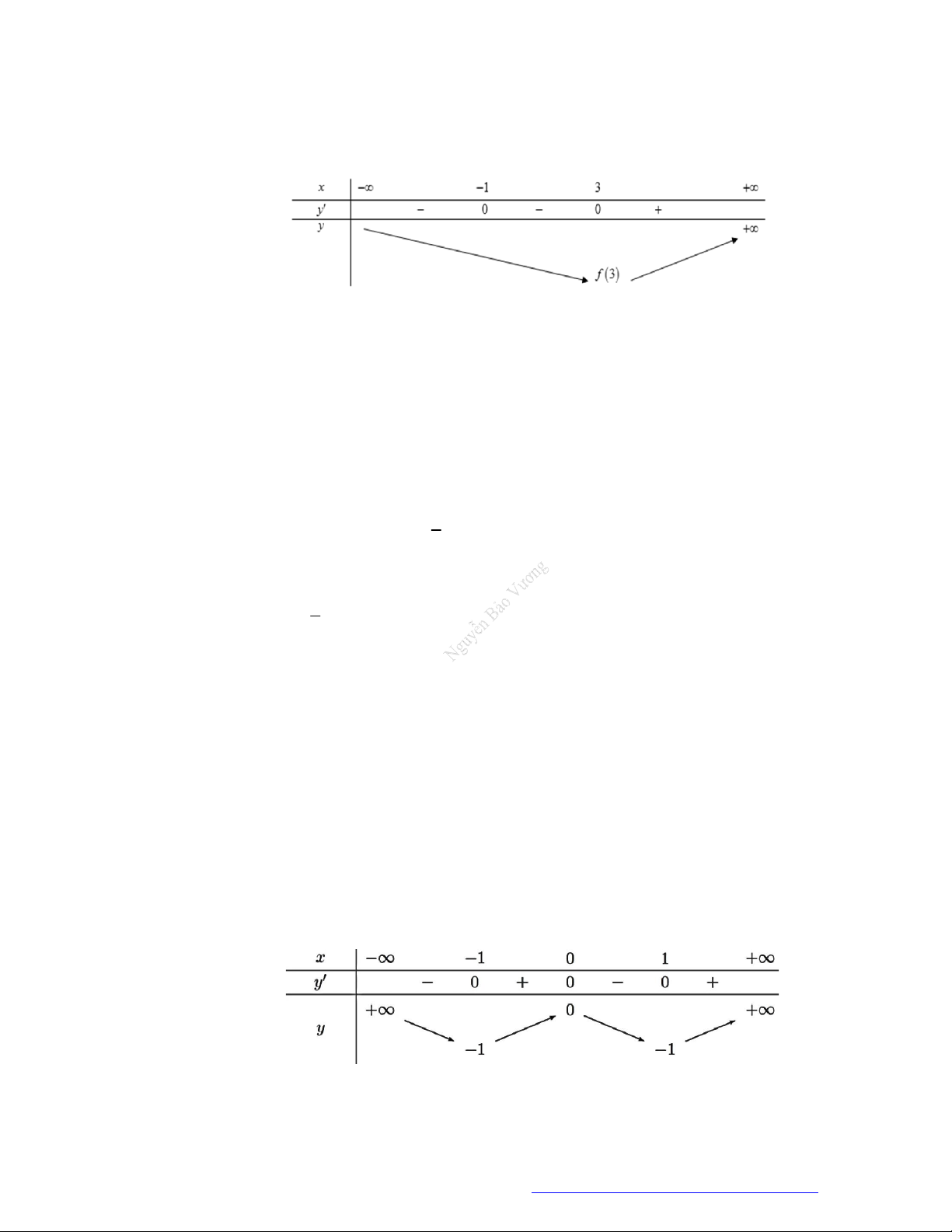
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
A.
3x
. B.
3
x
. C.
1x
. D.
1
x
.
Lời giải
TXĐ:
D
.
3 2
5 3y x x x
;
3 2
3
0 5 3 0
1
x
y x x x
x
.
Hàm số đạt cực tiểu tại
3x
.
Câu 32. (THCS - THPT Nguyễn Khuyến 2019) Điểm cực đại của đồ thị hàm số
3
3 1y x x
là:
A.
1; 1M
. B.
0;1N
. C.
2; 1P
. D.
1;3Q
.
Lời giải
2
' 3 3; ' 0 1
'' 6 ; '' 1 6 0; '' 1 6 0
y x y x
y x y y
Do đó hàm số đạt cực đại tại
1; 1 3x y
. Vậy chọn đáp án
1;3Q
.
Câu 33. (Sở Ninh Bình 2019) Hàm số
3 2
1
3 1
3
y x x x
đạt cực tiểu tại điểm
A.
1x
. B.
1x
. C.
3x
. D.
3x
.
Lời giải
Ta có hàm số
3 2
1
3 1
3
y x x x
có tập xác định
D
.
2
2 3y x x
;
1
0
3
x
y
x
.
2 2y x
;
3 4 0y
;
1 4 0y
.
Suy ra hàm số đạt cực tiểu tại điểm
1x
.
Câu 34. (THPT Sơn Tây Hà Nội 2019) Tìm số điểm cực trị của hàm số
4 2
2y x x .
A. 2. B. 4. C. 3. D. 1.
Lời giải
Chọn C
Tự luận
Tập xác định:
D
.
3
0
4 4 0
1
x
y x x
x
.
Bảng biến thiên:
Dựa vào bảng biến thiên suy ra hàm số có 3 điểm cực trị.
Trắc nghiệm
Hàm số bậc 4 trùng phương
4 2
y ax bx c
có hệ số
. 0a b
thì sẽ có 3 điểm cực trị.
Vậy chọn ngay đáp án C.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu
35. (Chuyên Quang Trung Bình Phước 2019) Điểm cực tiểu của đồ thị hàm số
3
2
5
5 y x x x
là
A.
1
; 8
B.
0
; 5
C.
5 40
;
3
27
D.
1
;0
Lời
giải
Chọn A
2
1
3 2 5 0
5
3
x
y
x x
x
.
6
2
y
x
.
T
a có:
1
8 0
y
Hàm số đạt cực tiểu tại
1
x
;
1
8
CT
y
y
.
Vậy điểm cực tiểu của đồ thị hàm số là
1
; 8
.
Câu
36. Hàm số nào trong bốn hàm số được liệt kê dưới đây không có cực trị?
A.
2 3
2
x
y
x
. B.
4
y
x
. C
.
3
y
x x
. D
.
2
y
x
.
Lời
giải
Chọn A.
+ Hàm số
2
3
2
x
y
x
Tậ
p xác định:
; 2 2;D
.
Có
2
7
'
0
2
y x D
x
hà
m số luôn đồng biến trên từng khoảng xác định
hà
m số
không có cực trị.
Các hàm số khác dễ dàng chứng minh được y’ có nghiệm và đổi dấu qua các nghiệm. Riêng hàm
số cuối y’ không xác định tại -2 nhưng hàm số xác định trên R và y’ đổi dấu qua -2 do đó có hàm
số có điểm cực trị x = -2.
-------------------- HẾT --------------------

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
Dạng 1. Tìm m để hàm số đạt cực trị tại x = x0
Bước 1. Tính
0 0
' , ''y x y x
Bước 2. Giải phương trình
0
' 0 ?y x m
Bước 3. Thế
m
vào
0
''y x
nếu giá trị
0
0
'' 0
'' 0
y x CT
y x CD
Dạng 1.1 Hàm số bậc 3
Câu 1. (Mã 110 - 2017) Tìm giá trị thực của tham số
m
để hàm số
3 2 2
1
4 3
3
y x mx m x
đạt
cực đại tại
3x
.
A.
1m
B.
7m
C.
5m
D.
1m
Lời giải
Chọn C
Ta có
2 2
2 4y x mx m
;
2 2y x m
.
Hàm số
3 2 2
1
4 3
3
y x mx m x
đạt cực đại tại
3x
khi và chỉ khi:
3 0
3 0
y
y
2 2
1
9 6 4 0 6 5 0
5
6 2 0 3
3
m L
m m m m
m TM
m m
m
.
Vậy
5m
là giá trị cần tìm.
Câu 2. (Chuyên Hạ Long 2019) Tìm
m
để hàm số
3 2
2 1y x mx mx đạt cực tiểu tại
1x
A. không tồn tại
m
. B.
1m
. C.
1m
. D.
1;2m
.
Lời giải
Để
1x
là điểm cực tiểu của hàm số
1 0
1 0
y
y
1
3 4 0
1.
3
6 4 0
2
m
m m
m
m
m
Thử lại với 1,m ta có
3 2
2 1y x x x ;
2
3 4 1y x x
.
2
1
0 3 4 1 0 .
1
3
x
y x x
x
Bảng biến thiên:
Quan sát bảng biến thiên ta thấy
1m
thỏa yêu cầu bài toán.
Câu 3. Tìm tất cả các giá trị của tham số
m
để hàm số
3 2
3 1y x x mx đạt cực tiểu tại
2x
.
A.
0
m
. B.
4
m
. C.
0 4
m
. D.
0 4
m
.
Lời giải
Chọn A
CỰC TRỊ CỦA HÀM SỐ
Chuyên đề 2

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
3 6
y x x m
;
6 6y x
.
Hàm số đạt cực tiểu tại
2 0
0
2 0
6 0
2 0
y
m
x m
y
.
Câu 4. (THPT Đoàn Thượng - Hải Dương 2019) Tìm các giá trị thực của tham số m để hàm số
3 2 2
1
4 3
3
y x mx m x
đạt cực đại tại
3
x
.
A.
1, 5
m m
. B.
5
m
. C.
1
m
. D.
1
m
.
Lời giải
Tập xác định
.
Ta có
2 2
2 4,
y x mx m
2 2 .y x m
Để hàm số
3 2 2
1
4 3
3
y x mx m x
đạt cực đại tại
3
x
thì
2
5
3 0
6 5 0
5.
1
6 2 0
3 0
3
m
y
m m
m
m
m
y
m
.
Câu 5. (THPT An Lão Hải Phòng 2019) Có bao nhiêu số thực
m
để hàm số
3 2 2
1
1 1
3
y x mx m m x
đạt cực đại tại
1x
.
A.
0
B.
2
C.
1
D.
3
Lời giải
Chọn C
2 2
' 2 1
y x mx m m
'' 2 2y x m
Hàm số đạt cực đại tại
1x
nên ta có
2
' 1 0
1 2
3 2 0
2
1
2 2 0
'' 1 0
y
m m
m m
m
m
m
y
Thử lại với
2
m
ta có
'' 2 4 '' 1 2 0
y x y
Do đó Hàm số đạt cực đại tại
1x
Câu 6. (THPT Đoàn Thượng – Hải Dương) Tìm các giá trị thực của tham số m để hàm số
3 2 2
1
4 3
3
y x mx m x
đạt cực đại tại
3
x
.
A.
1, 5
m m
. B.
5
m
. C.
1
m
. D.
1
m
.
Lời giải
Chọn B
Tập xác định
.
Ta có
2 2
2 4,
y x mx m
2 2 .y x m
Để hàm số
3 2 2
1
4 3
3
y x mx m x
đạt cực đại tại
3
x
thì
2
5
3 0
6 5 0
5.
1
6 2 0
3 0
3
m
y
m m
m
m
m
y
m
Câu 7. (THPT Thăng Long - Hà Nội - Lần 2 - 2019) Tìm tập hợp tất cả các giá trị của
m
để hàm số
3 2 2
3 1 3y x m x m x
đạt cực tiểu tại
1
x
.
A.
5;1
. B.
5
. C.
. D.
1
.
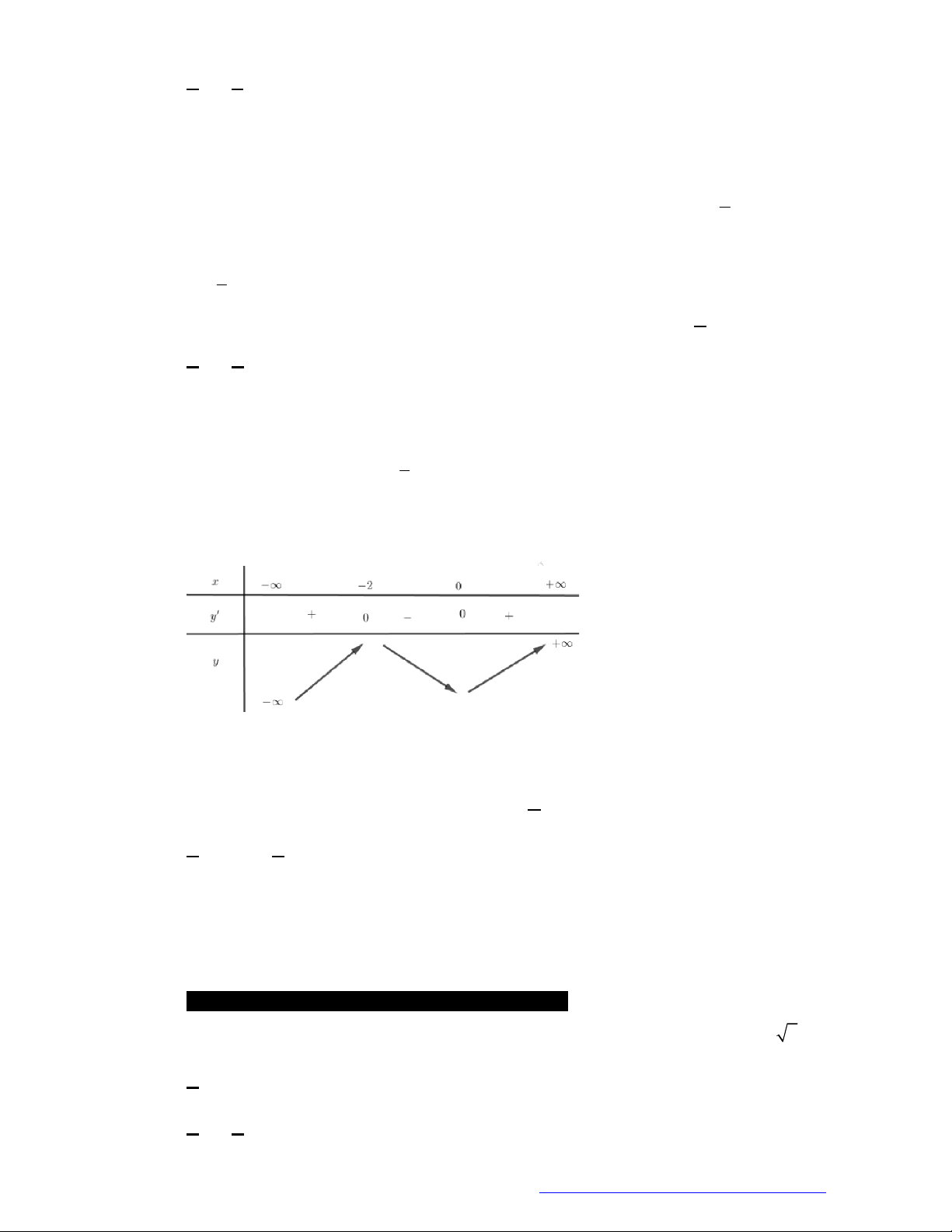
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Lời giải
Chọn B
Ta có
2 2
3 2 3 1 6 6 2y x m x m y x m
.
Hàm số đạt cực tiểu tại
2
1
1 0
6 5 0
5
1 5
6 8 0
1 0
4
3
m
f
m m
m
x m
m
f
m
.
Câu 8. (THPT Kinh Môn - 2019) Tìm tất cả các giá trị thực của tham số
m
để hàm số
3 2
1
1 1
3
y x mx m x
đạt cực đại tại
2x
?
A.
2m
. B.
3m
. C. Không tồn tại
m
. D.
1m
.
Lời giải
Chọn D
Ta có
2
2 1y x mx m
.
Giả sử
2x
là điểm cực đại của hàm số đã cho, khi đó
2
2 0 2 2 2 1 0 5 5 0 1y m m m m
.
Với
1m
, ta có
3 2
1
1
3
y x x
.
2
2y x x
;
2
2
0 2 0
0
x
y x x
x
.
Ta có bảng biến thiên:
Dựa vào bảng biến thiên, ta kết luận
1m
là giá trị cần tìm.
Câu 9. (Chuyên ĐHSPHN - Lần 3 - 2019) Tập hợp các số thực
m
để hàm số
3 2
3 ( 2)y x mx m x m
đạt cực tiểu tại
1x
là.
A.
1
. B.
1
. C.
. D.
R
.
Lời giải
Chọn C.
2
3 6 2y x mx m
6 6y x m
Hàm số đạt cực tiểu tại
1x
khi
(1) 0
(1) 0
y
y
5 5 0
6 6 0
m
m
1
1
m
m
không có giá trị của
m
.
Dạng 1.2 Hàm số đa thức bậc cao, hàm căn thức …
Câu 10. (Chuyên QH Huế - Lần 2 - 2019) Xác định tham số m sao cho hàm số
y x m x
đạt cực trị
tại
1x
.
A.
2m
. B.
2m
. C.
6m
. D.
6m
.
Lời giải
Chọn A
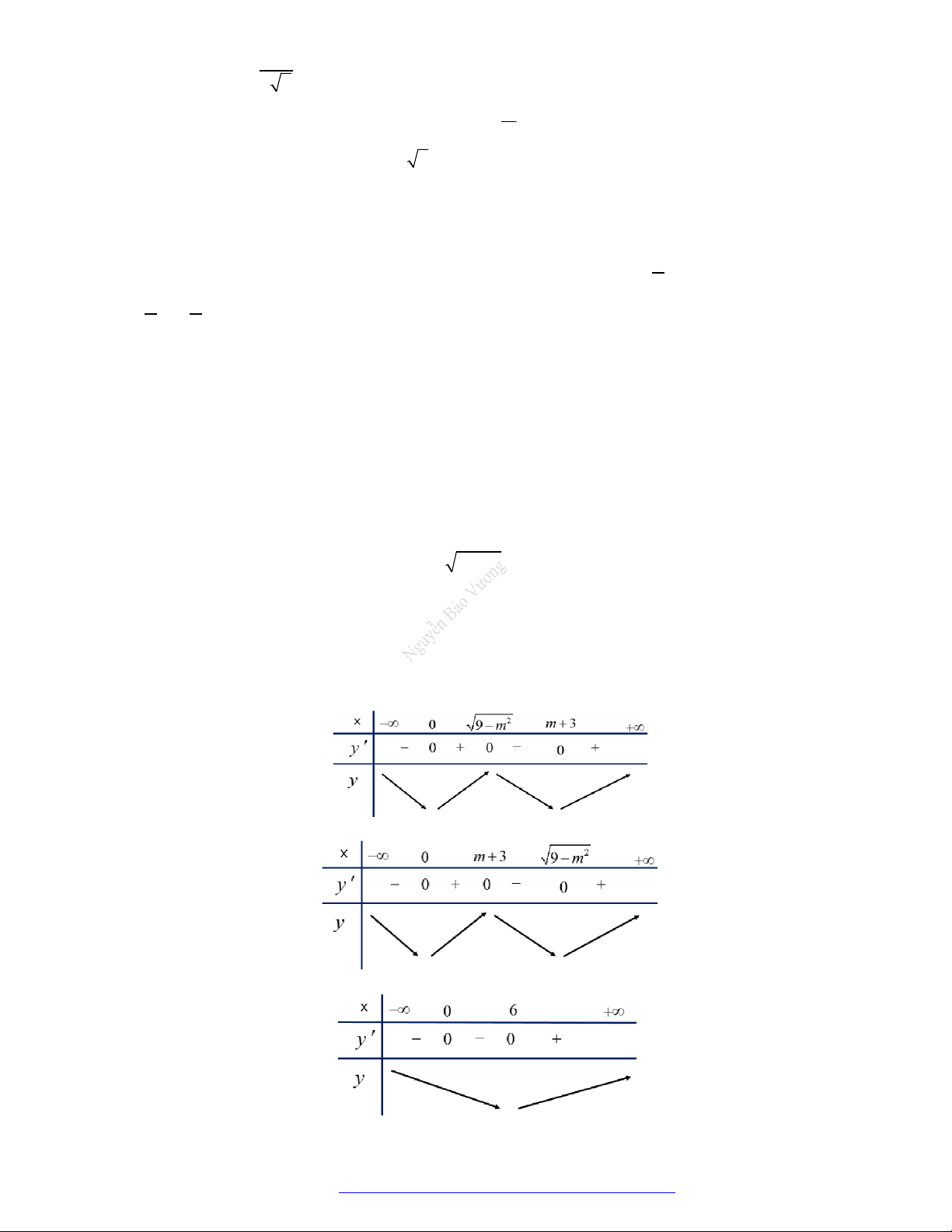
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
1 , 0
2
m
y f x x
x
Để hàm số đạt cực trị tại
1x
thì
1 0 1 0 2
2
m
f m
.
Thử lại với
2m
, hàm số
2y x x
có cực tiểu tại
1x
, do đó
2m
thỏa mãn yêu cầu đề
bài.
Câu 11. (Trường THPT Hoàng Hoa Thám - Hưng Yên 2019) Tìm tất cả tham số thực
m
để hàm số
4 2 2
1 2 2019y m x m x
đạt cực tiểu tại
1x
.
A.
0m
. B.
2m
. C.
1m
. D.
2m
.
Lời giải
Chọn D
Tập xác định:
D
.
Đạo hàm:
3 2
4 1 2 2
y m x m x
.
Hàm số đạt cực tiểu tại
1 x
1 0
y
2
4 1 2 2 0 m m
0
2
m
m
.
Với
0m
, hàm số trở thành
4 2
2 2019 y x x
. Dễ thấy hàm số đạt cực đại tại
1 x
.
Với
2m
, hàm số trở thành
4 2
2 2019 y x x
. Dễ thấy hàm số đạt cực tiểu tại
1 x
.
Vậy
2m
thì hàm số
4 2 2
1 2 2019y m x m x
đạt cực tiểu tại
1x
.
Câu 12. (Chuyên Trần Phú Hải Phòng 2019) Cho hàm số
y f x
xác định trên tập số thực
và có
đạo hàm
3
2
' sin 3 9f x x x x m x m x
(
m
là tham số). Có bao nhiêu giá trị
nguyên của
m
để hàm số
y f x
đạt cực tiểu tại
0x
?
A.
6
B.
7
C.
5
D.
4
Lời giải
Điều kiện
2
9 0 3 3m m
TH 1:
0 3m
ta có BTT
TH 2:
3 0m
ta có BTT
TH 2:
3m
ta có BTT
Từ đó suy ra
3 3m
có 6 giá trị nguyên của
m
thỏa mãn.
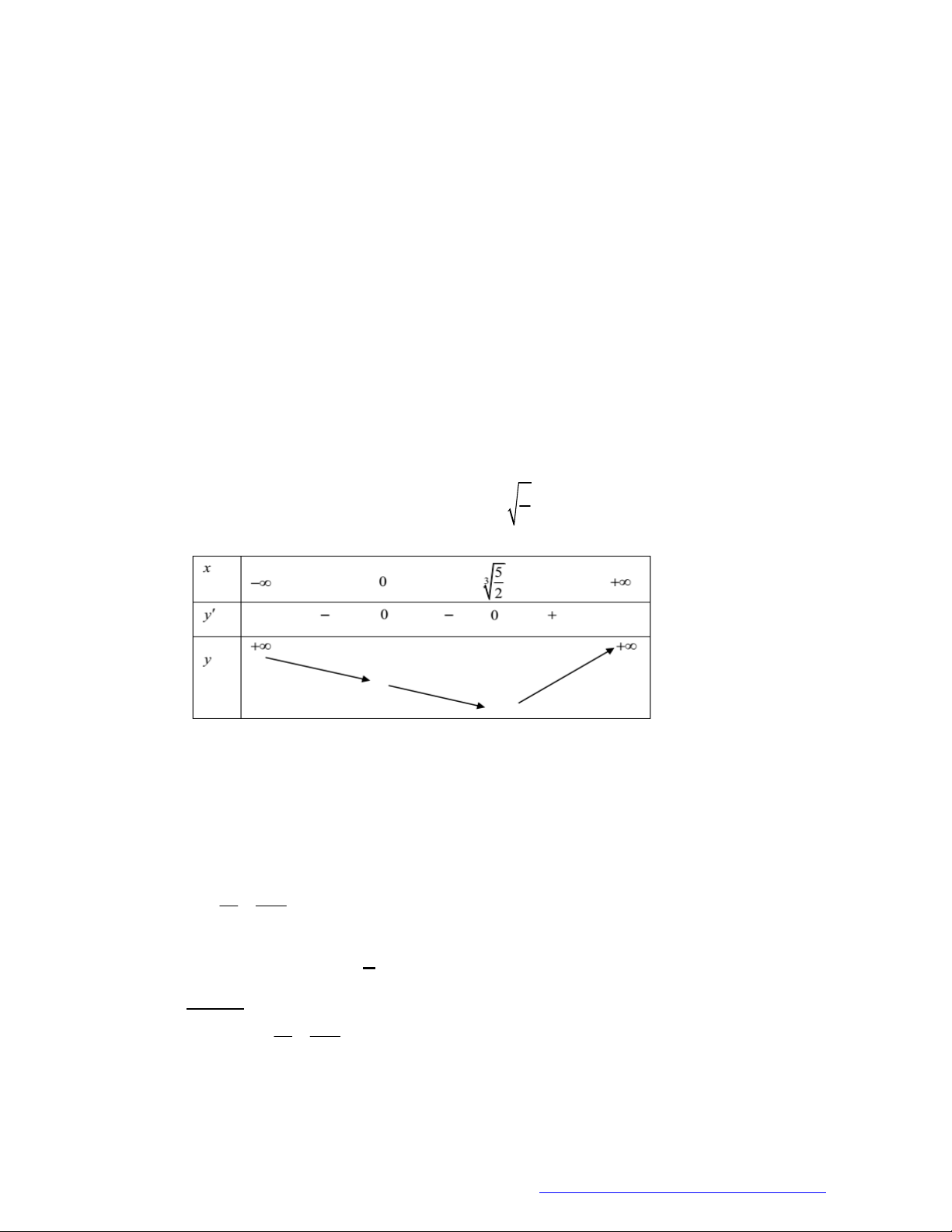
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Câu 13. (Mã 101 - 2018) Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
8 5 2 4
2 4 1y x m x m x
đạt cực tiểu tại
0x
?
A. Vô số B.
3
C.
5
D.
4
Lời giải
Chọn D
Ta có
8 5 2 4
2 4 1y x m x m x
7 4 2 3
8 5 2 4 4y x m x m x
.
0y
3 4 2
8 5 2 4 4 0x x m x m
4 2
0
8 5 2 4 4 0
x
g x x m x m
Xét hàm số
4 2
8 5 2 4 4g x x m x m
có
3
32 5 2g x x m
.
Ta thấy
0g x
có một nghiệm nên
0g x
có tối đa hai nghiệm
+ TH1: Nếu
0g x
có nghiệm
0x
2m
hoặc
2m
Với
2m
thì
0x
là nghiệm bội
4
của
g x
. Khi đó
0x
là nghiệm bội 7 của
y
và
y
đổi
dấu từ âm sang dương khi đi qua điểm
0x
nên
0x
là điểm cực tiểu của hàm số. Vậy
2m
thỏa ycbt.
Với
2m
thì
4
3
0
8 20 0
5
2
x
g x x x
x
.
Bảng biến thiên
Dựa vào BBT
0x
không là điểm cực tiểu của hàm số. Vậy
2m
không thỏa ycbt.
+ TH2:
0 0g
2m
. Để hàm số đạt cực tiểu tại
0x
0 0g
2
4 0 2 2m m
.
Do
m
nên
1;0;1m
.
Vậy cả hai trường hợp ta được 4 giá trị nguyên của
m
thỏa ycbt.
Câu 14. (Chuyên Quang Trung- Bình Phước 2019) Tất cả các giá trị thực của tham số
m
để hàm số
5 4
2
5 4
x mx
y đạt cực đại tại
0x
là:
A.
m
. B.
0m
.
C. Không tồn tại
m
. D.
0m
.
Lời giải
Chọn D
Đặt
5 4
2
5 4
x mx
f x .
Ta có:
4 3
f x x mx
.
Khi
0m
thì
4
0f x x
,
x
nên hàm số không có cực trị.
Khi
0m
, xét
4 3
0 0f x x mx
3
0x x m
0x
x m
.
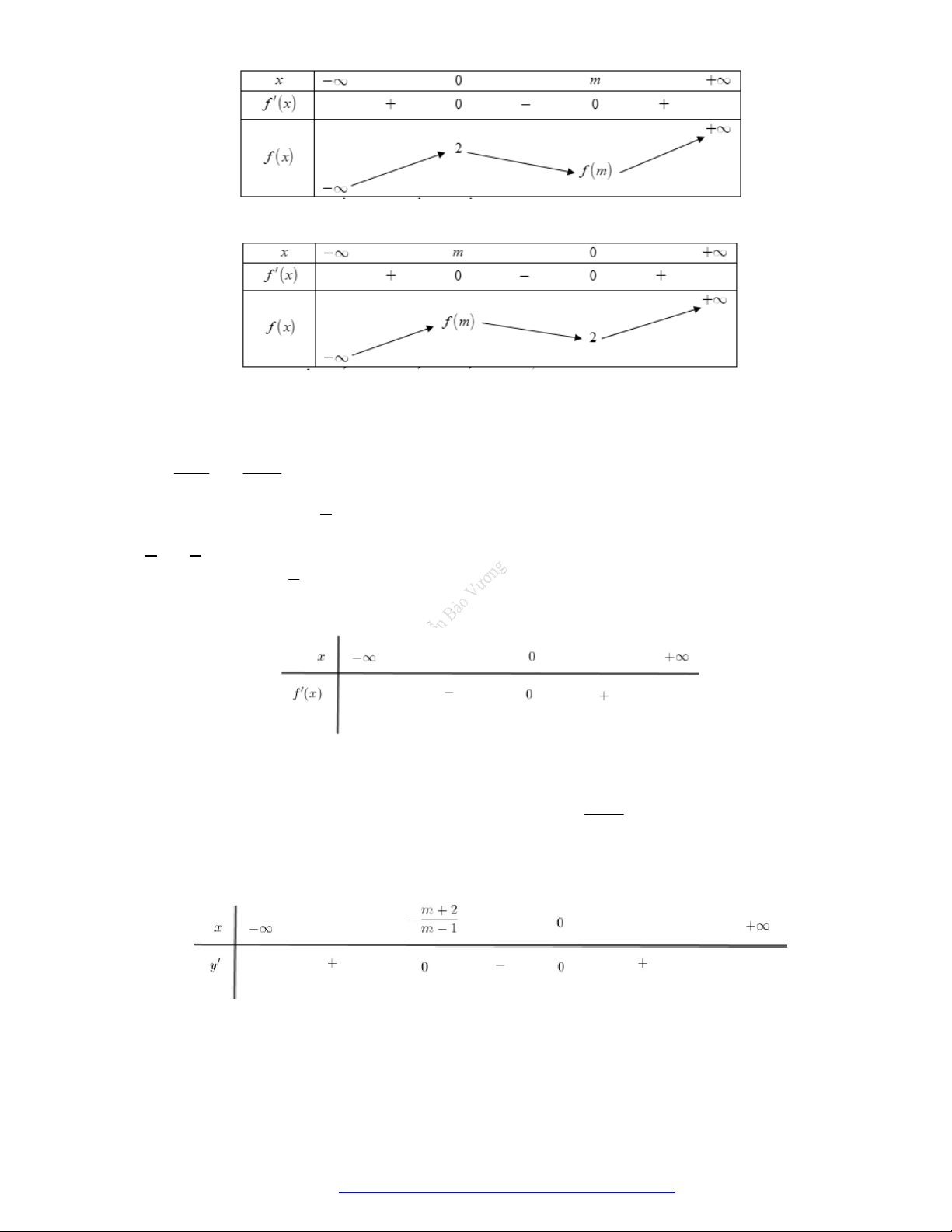
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
+ Trường hợp
0m
ta có bảng biến thiên:
Dựa vào bảng biến thiên ta thấy hàm số đạt cực đại tại
0x
.
+ Trường hợp
0m
ta có bảng biến thiên:
Dựa vào bảng biến thiên ta thấy hàm số đạt cực tiểu tại
0x
.
Như vậy, để hàm số đạt cực đại tại
0x
thì
0m
.
Câu 15. Có bao nhiêu giá trị nguyên của
m
thuộc khoảng
2019;2019
để hàm số
5 4
1 2
5
5 4
m m
y x x m
đạt cực đại tại
0x
?
A.
101
. B.
2016
. C.
100
. D.
10
.
Lời giải
Chọn B
Ta xét:
4 3
3
1 6 3 0 0
4
m y x y x y x
.
Ta có, bảng xét dấu
3
2y x
Dựa, vào bảng xét dấu ta thấy
0x
là điểm cực tiểu. Suy ra
1m
(loại).
Ta xét:
1
4 3
2
0
1 1 2 ' 0
2
1
x
m y m x m x y
m
x
m
.
Trường hợp 1: xét
1m
, suy ra
2 1
x x
.
Ta có, bảng xét dấu
4 3
1 2y m x m x
Dựa, vào bảng xét dấu ta thấy
0x
là điểm cực tiểu. Suy ra
1m
(loại).
Trường hợp 2:
2 1m
, suy ra
2 1
x x
.
Ta có, bảng xét dấu
4 3
1 2y m x m x
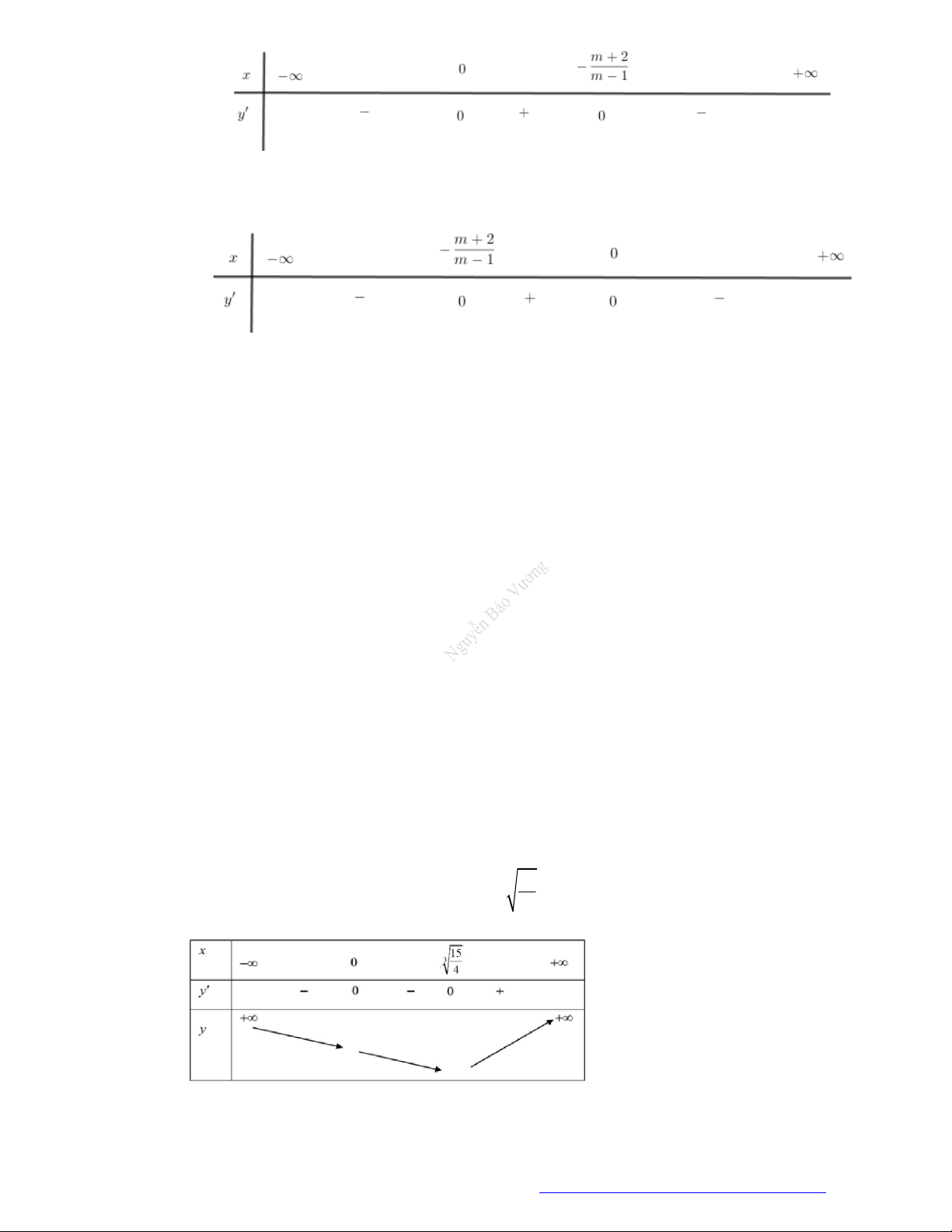
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Dựa, vào bảng xét dấu ta thấy
0x
là điểm cực tiểu. Suy ra
2 1m
(loại).
Trường hợp 3:
2m
, suy ra
2 1
x x
.
Ta có, bảng xét dấu
4 3
1 2y m x m x
Dựa, vào bảng xét dấu ta thấy
0x
là điểm cực đại. Suy ra
2m
(nhận).
Vậy, tập hợp tất cả các giá trị của tham số
m
thỏa mãn đề bài là
2m
mà
m
thuộc khoảng
2019;2019
.
Suy ra, số giá trị nguyên của
m
là 2016.
Câu 16. (Mã 104 - 2018) Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
8 5 2 4
3 9 1y x m x m x
đạt cực tiểu tại
0x
?
A.
6
B. Vô số C.
4
D.
7
Lời giải
Chọn A
Ta có
8 5 2 4
3 9 1y x m x m x
7 4 2 3
8 5 3 4 9y x m x m x
.
0y
3 4 2
8 5 3 4 9 0x x m x m
4 2
0
8 5 3 4 9 0
x
g x x m x m
Xét hàm số
4 2
8 5 3 4 9g x x m x m
có
3
32 5 3g x x m
.
Ta thấy
0g x
có một nghiệm nên
0g x
có tối đa hai nghiệm
+) TH1: Nếu
0g x
có nghiệm
0x
3m
hoặc
3m
Với
3m
thì
0x
là nghiệm bội
4
của
g x
. Khi đó
0x
là nghiệm bội 7 của
y
và
y
đổi
dấu từ âm sang dương khi đi qua điểm
0x
nên
0x
là điểm cực tiểu của hàm số. Vậy
3m
thỏa ycbt.
Với
3m
thì
4
3
0
8 30 0
15
4
x
g x x x
x
.
Bảng biến thiên
Dựa vào BBT
0x
không là điểm cực tiểu của hàm số. Vậy
3m
không thỏa ycbt.
+) TH2:
0 0g
3m
. Để hàm số đạt cực tiểu tại
0x
0 0g
2
9 0 3 3m m
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Do
m
nên
2; 1;0;1;2
m
.
Vậy cả hai trường hợp ta được
6
giá trị nguyên của
m
thỏa ycbt.
Câu 17. (Mã 103 - 2018) Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
8 5 2 4
4 16 1
y x m x m x
đạt cực tiểu tại
0
x
.
A.
8
B. Vô số C.
7
D.
9
Lời giải
Chọn A
Ta có
7 4 2 3
' 8 5 5 4 16y x m x m x
3 4 2
8 5 4 4 16
x x m x m
3
.
x g x
Với
4 2
8 5 5 4 16
g x x m x m
.
● Trường hợp
1
:
0 0 4
g m
.
Với
7
4 ' 8m y x
. Suy ra
0
x
là điểm cực tiểu của hàm số.
Với
4 3
4 ' 8 5
m y x x
. Suy ra
0
x
không là điểm cực trị của hàm số.
● Trường hợp
2
:
0 0 4
g m
.
Để hàm số đạt cực tiểu tại
0
x
thì qua giá trị
0
x
dấu của
'y
phải chuyển từ âm sang dương do
đó
0 0 4 4
g m
.
Kết hợp hai trường hợp ta được
4 4
m
.
Do
3; 2; 1;0;1;2;3;4
m m
.
Vậy có
8
giá trị nguyên của tham số
m
thỏa mãn.
Câu 18. Có bao nhiêu giá trị nguyên của tham số m để hàm số
12 7 2 6
( 5) ( 25) 1
y x m x m x
đạt cực
đại tại
0
x
?
A.
8
B.
9
C. Vô số D.
10
Lời giải
Chọn B
Ta có
11 6 2 5
' 12 7( 5) 6( 25)y x m x m x
TH1:
11
5 ' 12m y x
. Khi đó
' 0 0
y x
là nghiệm bội lẻ, đồng thời dấu của
’y
đổi từ
âm sang dương, nên
0
x
là điểm cực tiểu của hàm số,do đó không thỏa mãn,
5
m
loại.
TH2:
6 5
5 ' (12 70) 0 0
m y x x x
là nghiệm bội chẵn, do đó
’y
không đổi dấu khi
đi qua
0
x
,
5
m
loại.
TH3:
5 6 2 5
5 ' 12 7( 5) 6( 25) . ( )m y x x m x m x g x
Với
6 2
( ) 12 7( 5) 6( 25)
g x x m x m , ta thấy
0
x
không là nghiệm của
g x
.
Để hàm số đạt cực đại tại
0
x
thì y’ phải đổi dấu từ dương sang âm khi đi qua
0
x
, xảy ra khi
và chỉ khi
0
2
0
lim ( ) 0
6( 25) 0 5 5
lim ( ) 0
x
x
g x
m m
g x
Vì
m
nguyên nên
4; 3;...;3;4
m
, vậy có
9
giá trị của
m
thỏa mãn bài toán.
Câu49. Cho hàm số
6 5 2 4
4 16 2
y x m x m x
. Gọi
S
là tập hợp các gia trị
m
nguyên dương để
hàm số đã cho đạt cực tiểu tại
0
x
. Tổng các phần tử của
S
bằng
A. 10. B. 9. C. 6. D. 3.
Lời giải.
Chọn C
Ta có
5 4 2 3 3 2 2
6 5 4 4 16 6 5 4 16
y x m x m x x x m x m
.
3
2 2
0
0
6 5 4 16 0 *
x
y
x m x m
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
*
có
4 49 4m m
.
Với mọi
m
nguyên dương thì
0
5 4
0
6
m
do đó ta xét các trường hợp sau:
Trường hợp 1:
2
16 0 0 4m m
:
*
có hai nghiệm âm phân biệt
1 2 1 2
,x x x x
, ta có
bảng xét dấu
y
như sau:
Lúc này
0x
là điểm cực tiểu.
Trường hợp 2:
2
16 0 4m m
:
*
có hai nghiệm trái dấu
1 2 1 2
, 0x x x x
, ta có bảng
xét dấu
y
như sau:
Từ đây suy ra
0x
là điểm cực đại (không thỏa mãn).
Trường hợp 3:
*
có một nghiệm bằng 0 và một nghiệm âm, lúc này
0x
là nghiệm bội 4 của
đạo hàm nên không phải là điểm cực trị.
Vậy có ba giá trị nguyên dương của
m
thỏa mãn yêu cầu bài toán là 1, 2, 3. Tổng các phần tử của
S
bằng 6.
Câu 19. (Mã 102 - 2018) Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
8 5 2 4
( 1) ( 1) 1y x m x m x
đạt cực tiểu tại
0?x
A.
3
B.
2
C. Vô số D.
1
Lời giải
Chọn B
Ta có:
7 4 2 3
' 8 5( 1) 4( 1) 1y x m x m x
3 4 2
8 5 1 4 1x x m x m
4 2
0
' 0
8 5 1 4 1 0 (1)
x
y
x m x m
*Nếu
1m
thì
7
' 8y x
, suy ra hàm số đạt cực tiểu tại
0x
.
*Nếu
1m
thì
4
0
' 0
8 10 0
x
y
x x
3
0
5
4
x
x
, nhưng
0x
là nghiệm bội chẵn nên
không phải cực trị.
*Nếu
1m
: khi đó
0x
là nghiệm bội lẻ. Xét
4 2
( ) 8 5 1 4 1g x x m x m
. Để
0x
là điểm cực tiểu thì
2
0
lim ( ) 4( 1) 0
x
g x m
2
1 0 1 1m m
. Vì
m
nguyên nên chỉ
có giá trị
0m
.
Vậy chỉ có hai tham số
m
nguyên để hàm số đạt cực tiểu tại
0x
là
0m
và
1m
.
Dạng 2. Tìm m để hàm số có n cực trị
Hàm số có
n
cực trị
0y
có
n
nghiệm phân biệt.
Xét hàm số bậc ba
3 2
:y ax bx cx d
Hàm số có hai điểm cực trị khi
2
0
.
3 0
a
b ac
Hàm số không có cực trị khi
0y
vô nghiệm hoặc có nghiệm kép.
Xét hàm số bậc bốn trùng phương
4 2
.y ax bx c

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Hàm số có ba cực trị khi
0.ab
Hàm số có
1
cực trị khi
0.ab
Câu 1. Biết rằng hàm số
3 3
3
y x a x b x
có hai điểm cực trị. Mệnh đề nào sau đây là đúng?
A.
0
ab
. B.
0
ab
. C.
0
ab
. D.
0
ab
.
Lời giải
Chọn C
Ta có
3 2 2 2 3 3
3 3
y x a b x a b x a b
.
2 2 2
3 6 3
y x a b x a b
.
Hàm số có hai điểm cực trị khi và chỉ khi
y
có hai nghiệm phân biệt
18 0
ab
0
ab
.
Câu 2. (THPT Hai Bà Trưng - Huế - 2019) Tìm tất cả các giá trị của tham số thực
m
để hàm số
3 2
2 ( 2) 1y mx mx m x
không có cực trị
A.
( ;6) (0; )
m
. B.
6;0
m
. C.
6;0
m
. D.
6;0
m
.
Lời giải
Chọn D
Ta có
2
' 3 4 ( 2)
y mx mx m
.
+ Nếu
0
m
.
' 2 0 ( )
y x
. Nên hàm số không có cực trị.
Do đó
0
m
(chọn) (1).
+ Nếu
0
m
.
Hàm số không có cực trị
'y
không đổi dấu
2 2
' 0 4 3 ( 2) 0 6 0 6 0
m m m m m m
(do
0
m
) (2).
Kết hợp (1) và (2) ta được
6 0
m
.
Câu 3. (Đề Tham Khảo 2017) Tìm tất cả các giá trị thực của tham số
m
để hàm số
4 2
1 2 3 1
y m x m x
không có cực đại?
A.
1 3
m
B.
1
m
C.
1
m
D.
1 3
m
Lời giải
Chọn D
TH1: Nếu
2
1 4 1
m y x
. Suy ra hàm số không có cực đại.
TH2: Nếu
1
m
.
Để hàm số không có cực đại thì
2 3 0 3
m m
. Suy ra
1 3
m
.
Vậy
1 3
m
.
Câu 4. (Chuyên Sơn La - Lần 2 - 2019) Để đồ thị hàm số
4 2
3 1
y x m x m
có điểm cực đại
mà không có điểm cực tiểu thì tất cả các giá trị thực của tham số
m
là
A.
3
m
. B.
3
m
. C.
3.
m
D.
3
m
.
Lời giải
Chọn A
3 2
' 4 2 3 2 2 3
y x m x x x m
.
2
0
' 0
3
2
x
y
m
x
.
Vì hàm số đã cho là hàm trùng phương với
1 0
a
nên hàm số có điểm cực đại mà không có
điểm cực tiểu
' 0
y
có đúng 1 nghiệm bằng
0
3
0
2
m
3.
m

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Câu 5. (Quang Trung - Bình Phước - Lần 5 - 2019) Cho hàm số
4 2
2
y x mx m
. Tìm tất cả các giá
trị thực của
m
để hàm số có
3
cực trị
A.
0
m
. B.
0
m
. C.
0
m
. D.
0
m
.
Lời giải
Chọn A
Tập xác định
D
.
3 2
' 4 4 4
y x mx x x m
.
2
2
0
' 0 4 0
x
y x x m
x m
Hàm số có
3
cực trị
' 0
y
có
3
nghiệm phân biệt
phương trình
có
2
nghiệm phân biệt
0
x
0
m
.
Câu 6. (Chuyên Hà Tĩnh - Lần 1 - 2019) Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
2 4 2 2
2019 1
y m x m m x
có đúng một cực trị?
A.
2019
. B.
2020
. C.
2018
. D.
2017
.
Lời giải
Chọn A
Trường hợp 1:
0
m
1
y
nên hàm số không có cực trị.
0
m
(loại).
Trường hợp 2:
2
0 0
m m
.
Hàm số
2 4 2 2
2019 1
y m x m m x
có đúng một cực trị
2 2 2
. 2019 0 2019 0 0 2019
m m m m m m
.
Vì
0
m
0 2019
m
.
Do
m
nên có
2019
giá trị nguyên của tham số
m
thỏa đề.
Câu 7. (THPT Yên Khánh A - Ninh Bình - 2019) Cho hàm số
3 2
3 1 3 7 3y x m x m x
. Gọi
S
là tập các giá trị nguyên của tham số m để hàm số không có cực trị. Số phần tử của
S
là
A.
2
. B.
4
. C.
0
. D. Vô số.
Lời giải
Chọn B
Ta có:
2
3 6 1 3 7 3
y x m x m
.
2
0 2 1 7 3 0
y x m x m
.
Để hàm số không có cực trị thì
2
0 1 7 3 0
m m
2
5 4 0
m m
1 4
m
.
Do
1;2;3;4
m S
. Vậy
S
có 4 phần tử.
Câu 8. (HSG - TP Đà Nẵng - 2019) Tìm tất cả các giá trị của tham số
m
để hàm số
4 3 2
4 3 1 1
y x mx m x
có cực tiểu mà không có cực đại.
A.
1 7
; .
3
m
B.
1 7
;1 1 .
3
m
C.
1 7
; .
3
m
D.
1 7 1 7
; 1 .
3 3
m
Lời giải
Chọn D
Ta có:
3 2
4 12 6 1y x mx m x
.
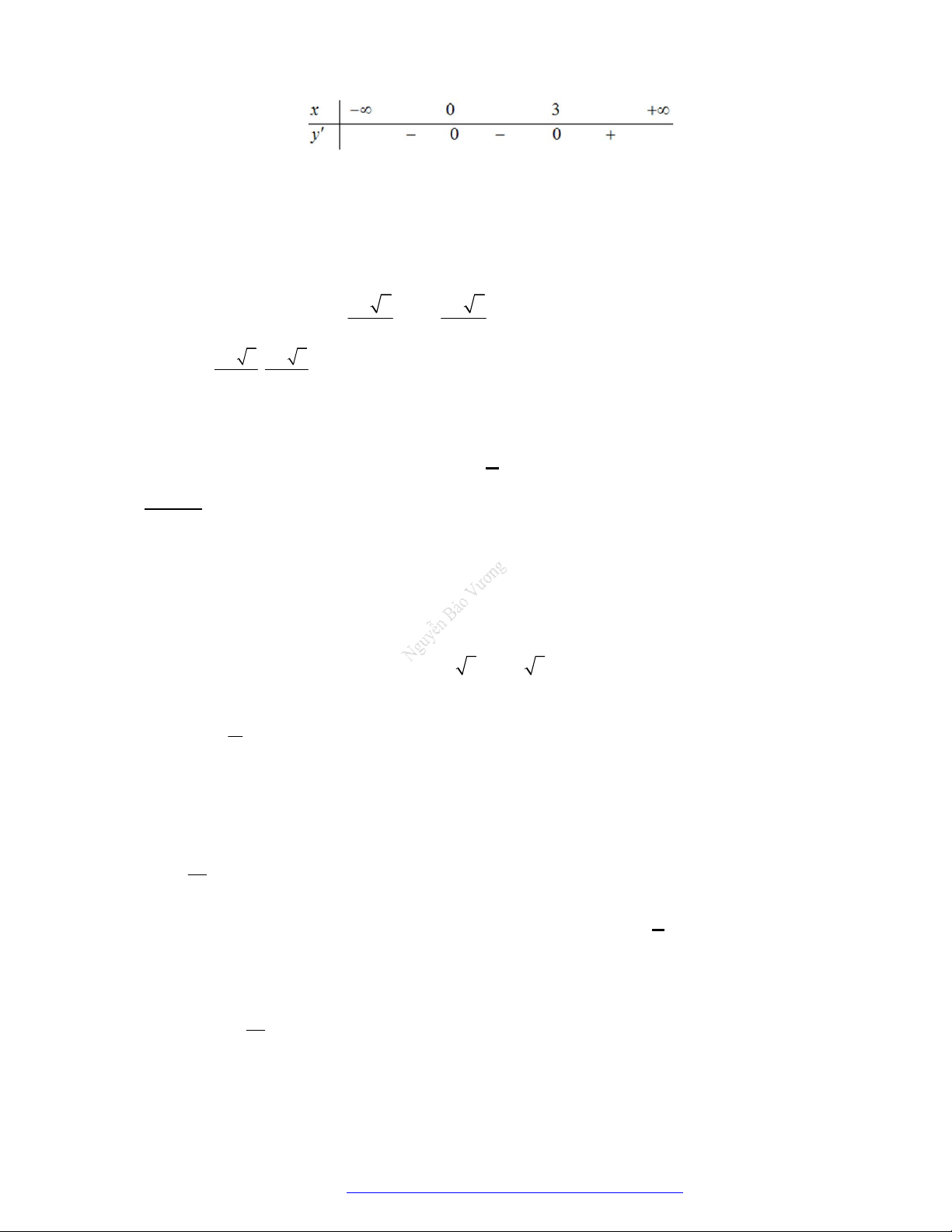
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
+ TH1:
1m
, ta có:
3 2 2
4 12 4 ( 3)y x x x x
.
Bảng xét dấu
Hàm số có 1 cực tiểu duy nhất.
Ta có:
2
0
0
2 6 3 3 0(*)
x
y
x mx m
+ TH2:
1m
Để hàm số đã cho chỉ có một cực tiểu thì phương trình
*
không có hai nghiệm phân biệt
2
1 7 1 7
3 2 3 3 0
2 2
m m m
.
Vậy
1 7 1 7
; 1 .
3 3
m
Câu 9. (HSG 12 - Bắc Ninh - 2019) Cho hàm số
f x
có đạo hàm
2 2
1 2 5f x x x x mx
. Có
tất cả bao nhiêu giá trị nguyên của
m
để hàm số có đúng một điểm cực trị?
A.
0
. B.
5
. C.
6
. D.
7
.
Lời giải
Chọn C
Hàm số
f x
có đúng một điểm cực trị khi và chỉ khi tam thức
2
2 5g x x mx
vô nghiệm
hoặc có hai nghiệm phân biệt trong đó một nghiệm là
1x
, hoặc
g x
có nghiệm kép
1x
Tức là
2
2
0
5 0
1 0
2 6 0
5 5
0
5 0
3
1
1
0
0
g
g
g
g
m
g
m
m
m
m
m
b
a
. Do đó tập các giá trị nguyên thỏa mãn
yêu cầu bài toán là
2, 1, 0, 1, 2, 3S
.
Câu 10. (THPT Hùng Vương Bình Phước 2019) Tìm tất cả các giá trị của tham số
m
để hàm số
3
2
2 1
3
x
y mx mx
có hai điểm cực trị.
A.
0 2m
. B.
2m
. C.
0m
. D.
2
0
m
m
.
Lời giải
Ta có:
2
2 2y x mx m
Hàm số
3
2
2 1
3
x
y mx mx
có hai điểm cực trị
0y
có hai nghiệm phân biệt
2
2
2 0
0
m
m m
m
.
Câu 11. (THPT Ba Đình 2019) Tìm tất cả các giá trị của tham số để hàm số
có cực đại và cực tiểu?
m
3 2
3 2
y x x mx m

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
A. . B. C. . D. .
Lời giải
+ TXĐ:
+
+ Hàm số có cực đại và cực tiểu có 2 nghiệm phân biệt.
Câu 12. (Chuyên Bắc Giang 2019) Tập hợp các giá trị của
m
để hàm số
3 2
1
2 1
3
y x mx m x
có
hai cực trị là:
A.
; 1 2;
B.
; 1 2;
C.
1;2
D.
1;2
Lời giải
Chọn B
Ta có
2
2 2y x mx m
. Để hàm số có hai cực trị thì
0y
có hai nghiệm phân biệt nên
2
1
0 0 2 0
2
m
y m m
m
Câu 13. (THPT Quỳnh Lưu 3 Nghệ An 2019) Cho hàm số
4 2
1y mx x . Tập hợp các số thực
m
để
hàm số đã cho có đúng một điểm cực trị là
A.
0;
. B.
;0
. C.
0;
. D.
;0
.
Lời giải
Tập xác định
D
.
TH1:
0m
hàm số đã cho trở thành
2
1y x là một hàm bậc hai nên luôn có một cực trị.
TH2:
0m
, ta có
3
4 2y mx x
.
0y
3
4 2 0mx x
2
2 2 1 0x mx
2
0
2 1 0
x
mx
.
Để hàm số có đúng một cực trị thì phương trình
0y
có đúng 1 nghiệm.
Ycbt Phương trình
có một nghiệm
0x
hoặc vô nghiệm suy ra
0m
.
Vậy
0m
.
Câu 14. (THPT Yên Định Thanh Hóa 2019) Cho hàm số
4 2
(2 1) 1y mx m x
. Tìm tất cả các giá trị
thực của tham số
m
để hàm số có đúng một điểm cực tiểu.
A. Không tồn tại
m
. B.
0.m
C.
1
.
2
m
D.
1
0.
2
m
Lời giải
Với
0m
, ta có
2
1y x
' 2y x
. Khi đó hàm số có 1 cực trị và cực trị đó là cực tiểu. Suy ra
0m
thỏa mãn yêu cầu bài toán. (1)
Với
0m
, ta có
3 2
' 4 2(2 1) 2 (2 2 1)y mx m x x mx m
Hàm số có một cực trị là cực tiểu
2
0
2 2 1 0 vô nghiêm
m
mx m
0
2 1
0
2
m
m
m
0
1
0
2
0
m
m
m
m
(2)
Từ (1) và (2) suy ra hàm số có một cực trị là cực tiểu khi
0.m
3
2
m
3
.
2
m
3
2
m
3
2
m
D
2
3 6 2y x x m
0
y
3
36 24 0 .
2
m m

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 15. (Cụm Liên Trường Hải Phòng 2019) Tìm số các giá trị nguyên của tham số
m
để hàm số
4 2 2
2 6 1
y x m m x m
có ba điểm cực trị.
A.
6
. B.
5
. C.
4
. D.
3
.
Lời giải
Ta có
3 2 2 2
4 4 6 4 6
y x m m x x x m m
.
2 2
0
0
6 0(1)
x
y
x m m
Hàm số có ba điểm cực trị
(1) có hai nghiệm phân biệt khác 0
2
6 0 2 3
m m m
.
Ta có:
, 2 3 1;0;1;2
m m m
.
Vậy có
4
giá trị nguyên của tham số
m
để hàm số có ba điểm cực trị.
Câu 16. (THCS - THPT Nguyễn Khuyến 2019) Hàm số
4 2
1 1 2y mx m x m
có một điểm cực
trị khi
A.
0 1
m
. B.
0 1
m m
. C.
0
m
. D.
0 1
m m
.
Lời giải
Trường hợp 1:
0
m
thì hàm số đã cho trở thành
2
1
y x
. Hàm số này có 1 cực trị là cực đại
0
m
thỏa mãn.
Trường hợp 2:
0
m
thì hàm số đã cho trở thành
4 2
1 1 2y mx m x m
Ta có
3 2
4 2 1 2 2 1
y mx m x x mx m
;
2
2
0
2 0
0
1
*
2 1 0
2
x
x
y
m
x
mx m
m
YCBT
y
đổi dấu một lần
Phương trình
*
vô nghiệm hoặc có nghiệm
0
x
.
1
1
0
0
2
m
m
m
m
Kết hợp hai trường hợp ta được
0 1
m m
.
Giải nhanh: Với
a
khác
0
thì hàm số đã cho có 1 cực trị
1
0 1 0
0
m
ab m m
m
.
Câu 17. (Chuyên Lam Sơn Thanh Hóa 2019) Có tất cả bao nhiêu giá trị nguyên của
m
trên miền
10;10
để hàm số
4 2
2 2 1 7
y x m x
có ba điểm cực trị?
A.
20
B.
10
C. Vô số D.
11
Lời giải
Chọn D
Ta có
2
' 4 2 1 y x x m x
.
2
0
0
2 1 *
x
y
x m
Hàm số đã cho có ba cực trị khi và chỉ khi
0
y
có ba nghiệm phân biệt, hay (*) có hai nghiệm
phân biệt khác
0
1
2 1 0
2
m m
.
Do
10;10
m
nên có
11
giá trị thỏa mãn.
Câu 18. (THPT An Lão Hải Phòng 2019) Cho hàm số
4 2 2
6 4
y mx m x
. Có bao nhiêu số
nguyên
m
để hàm số có ba điểm cực trị trong đó có đúng hai điểm cực tiểu và một điểm cực đại ?
A.
4
B.
3
C.
2
D.
5
Lời giải

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Chọn C
Tập xác định
D
.
Ta có
3 2
4 2 6y mx m x
.
Hàm số đã cho có ba điểm cực trị trong đó có đúng hai điểm cực tiểu và một điểm cực đại khi và
chỉ khi
2
4 0
0 6
6 0
m
m
m m
.
Do đó có hai giá trị nguyên của tham số
m
.
Câu 19. (THPT Nguyễn Khuyến 2019) Tìm tất cả các giá trị thực của tham số
m
để hàm số
4 2
1 1 2y mx m x m
có một cực trị.
A.
1
m
B.
0
m
C.
0 1
m
D.
0 1
m m
Lời giải
Chọn D
Ta có:
3
4 2 1y mx m x
Trường hợp 1: Xét
0 2m y x
. Ta thấy phương trình
0
y
đổi dấu một lần nên hàm số
có một điểm cực trị. Suy ra
0
m
(thoả YCBT) (1)
Trường hợp 2: Xét
3
1 4m y x
.Ta thấy phương trình
0
y
đổi dấu một lần nên hàm số
có một điểm cực trị. Suy ra
1
m
(thoả YCBT) (2)
Trường hợp 3: Xét
0
m
,
2
0
0
1
2
x
y
m
x
m
Để hàm số có một điểm cực trị thì
0
1
0
1
2
m
m
m
m
(3)
Từ (1), (2) và (3) suy ra
0
1
m
m
Ghi chú: Dùng công thức tính nhanh
Hàm số có một điểm cực trị khi và chỉ khi
0
1 0 .
1
m
m m
m
Câu 20. (Chuyên Lào Cai - 2020) Cho hàm số
f x
có đạo hàm
4 3
2 2
2 4 2 3 6 18 .
f x x x x x m x m
Có tất cả bao nhiêu giá trị nguyên của
m
để hàm số
f x
có đúng một điểm cực trị?
B.
7
. B.
5
. C.
8
. D.
6
.
Lời giải
Chọn C
Ta có
2
4
3
2
2
0
0
2 0
2
0
4
4 0
2 3 6 18 0 *
2 3 6 18 0
x
x
x
x
f x
x
x
x m x m
x m x m
Để hàm số
f x
có đúng một điểm cực trị
Phương trình
*
vô nghiệm, có nghiệm kép
hoặc có hai nghiệm phân biệt trong đó có nghiệm là
4.
Trường hợp 1. Phương trình
*
vô nghiệm
2 2
4 24 36 24 72 4 36 0m m m m
3 3m
2 ; 1 ; 0 ; 1 ; 2
m

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Trường hợp 2. Phương trình
*
có nghiệm kép
2
3
4 36 0
3
m
m
m
.
Trường hợp 3. Phương trình
*
có hai nghiệm phân biệt
1
x
,
2
x
. Trong đó
1
4.
x
Phương trình có hai nghiệm phân biệt
2
1 2
3
, 4 36 0
3
m
x x m
m
.
Theo định lí Viète ta có
1 2 2
1 2 2
4 2 6
. 4. 6 18
S x x x m
P x x x m
2
2
2 2
3 9
2 2 5
3 9
2 2
2 2
x m
m m m
x m
.
Vậy
3 ; 2 ; 1 ; 0 ; 1 ; 2 ; 3 ; 5
m
thỏa mãn yêu cầu đề bài.
Câu 21. (Chuyên Sơn La - 2020) Gọi
S
là tập hợp những giá trị của tham số
m
để hàm số sau không có
cực trị trên
.
2 4 3 2 2
1 1 1
( ) . . ( 1)
4 3 2
x x x x
f x m e m e e m m e
. Tổng tất cả các phần tử của tập
S
bằng
A.
2
3
B.
2
.
3
C.
1
.
3
D.
1.
Lời giải
Chọn A
2 4 3 2 2 2 3 2 2
'( ) . . ( 1) ( . . 1) 0
x x x x x x x x
f x m e m e e m m e e m e m e e m m
2 3 2 2
. . 1 0
x x x
m e m e e m m
.
Đặt
0
x
t e
ta có
Ta có:
2 3 2 2
1 0m t mt t m m
2 3 2 2 2
2 2 2 2
( 1) ( 1) 1 0 ( 1)[ ( 1) ( 1) 1) 0
( 1)[ ( ) 1] 0
m t m t t t m t t m t
t m t m m t m m
Điều kiện cần để hàm số không có cực trị thì phương trình
2 2 2 2
( ) 1m t m m t m m
có
nghiệm
2
1
1 3 2 1 0 1,
3
t m m m m
.
Thử lại ta thấy với hai giá trị
m
trên ta đều có nghiệm đơn
1t
.
Vậy hai giá trị
1
1,
3
m m
thỏa mãn.
Dạng 3. Đường thẳng đi qua 2 điểm cực trị
Phương trình hai đường thẳng đi qua 2 điểm cực trị của hàm số bậc ba là phần dư của phép chia
của
y
cho
'y
Phân tích (bằng cách chia đa thức
y
cho
)y
:
1 1
2 2
( )
( ) ( )
( )
y h x
y y q x h x
y h x
Đường thẳng qua 2 điểm cực trị là
( ).y h x
Câu 1. (Mã 123 - 2017) Đồ thị hàm số
3 2
3 9 1y x x x
có hai cực trị
A
và
B
. Điểm nào dưới đây
thuộc đường thẳng
AB
?
A.
0; 1
M
B.
1; 10
N
C.
1; 0
P
D.
1;10
Q
Lời giải
Chọn B

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
Ta có:
2
3 6 9
y x x
thực hiện phép chia
y
cho
y
ta được số dư là
8 2y x
.
Như thế điểm
1; 10
N
thuộc đường thẳng
AB
.
Câu 2. (Mã 104 - 2017) Tìm giá trị thực của tham số
m
để đường thẳng
: 2 1 3
d y m x m
vuông
góc với đường thẳng đi qua hai điểm cực trị của đồ thị hàm số
3 2
3 1
y x x
.
A.
3
2
m
B.
3
4
m
C.
1
2
m
D.
1
4
m
Lời giải
Chọn B
Ta có
2
3 6y x x
. Từ đó ta có tọa độ hai điểm cực trị
0;1
A
,
2; 3
B
. Đường thẳng qua hai
điểm cực trị có phương trình
2 1y x
. Đường thẳng này vuông góc với đường thẳng
2 1 3
y m x m
khi và chỉ khi
3
2 1 2 1
4
m m
.
Câu 3. Tìm giá trị thực của tham số
m
để đường thẳng
2 1 3
y m x m
song song với đường thẳng
đi qua các điểm cực trị của đồ thị hàm số
3 2
3 1
y x x
A.
3
4
m
. B.
1
2
m
. C.
3
4
m
. D.
1
2
m
.
Lời giải
Chọn D
Hàm số
3 2
3 1
y x x
có TXĐ:
;
2
3 6y x x
;
0
' 0
2
x
y
x
Suy ra đồ thị hàm số có hai điểm cực trị là
0;1
A
,
2; 3 2; 4
B AB
.
Đường thẳng
d
đi qua hai điểm
A
,
B
có phương trình:
1
2 1
2 4
x y
y x
.
Đường thẳng
2 1 3
y m x m
song song với đường thẳng
2 1 2
1
3 1
2
m
d m
m
.
Câu 4. Đồ thị của hàm số
3 2
3 9 1y x x x
có hai điểm cực trị
A
và
B
. Điểm nào dưới đây thuộc
đường thẳng
AB
.
A.
1;0
P
. B.
0; 1
M
. C.
1; 10
N
. D.
1;10
Q
.
Lời giải
TXĐ:
D
.
2
' 3 6 9y x x
.
2
1 6
' 0 3 6 9 0
3 26
x y
y x x
x y
Ta có
1;6 , 3; 26
A B
4; 32
AB
nên ) Chọn
8;1
AB
n
.
Phương trình đường thẳng
AB
là:
8 1 1 6 0 8 2 0
x y x y
.
Thay tọa độ các điểm
, , ,P M N Q
vào phương trình đường thẳng
AB
ta có điểm
1; 10
N
thuộc
đường thẳng.
Câu 5. (Lương Văn Chánh - Phú Yên – 2018) Tìm giá trị thực của tham số
m
để đường thẳng
: 3 1 3
d y m x m
vuông góc với đường thẳng đi qua hai điểm cực trị của đồ thị hàm số
3 2
3 1
y x x
.
A.
1
3
. B.
1
6
. C.
1
6
m
. D.
1
3
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Lời giải
Chọn B
Xét hàm số
3 2
3 1
y x x
Có :
2
3 6y x x
,
1 1
2 1
3 3
y x y x
.
Do đó, đường thẳng
qua hai điểm cực trị của đồ thị hàm số này có phương trình là
2 1y x
.
Để
d
vuông góc với
thì
3 1 . 2 1
m
1
6
m
.
Vậy giá trị cần tìm của
m
là
1
6
m
.
Câu 6. (TT Tân Hồng Phong - 2018) Tìm tổng tất cả các giá trị thực của tham số
m
sao cho đường
thẳng đi qua hai điểm cực trị của đồ thị hàm số
3 2
2 3 1 6 1 2
y x m x m m x
song song
đường thẳng
4y x
.
A.
1
3
m
. B.
2
3
m
. C.
2
3
m
. D.
1
m
.
Lời giải
Chọn A
Ta có
2
6 6 1 6 1 2y x m x m m
, 0
1 2
x m
y
x m
.
Để hàm số có hai cực trị thì
1 2m m
1
3
m
.
Hai điểm cực trị của đồ thị hàm số là
3 2
; 7 3
A m m m
,
3 2
1 2 ;20 24 9 1
B m m m m
. Do
đó
3
1 3 ; 3 1
AB m m
. Do đó
AB
có vectơ pháp tuyến là
2
3 1 ;1
n m
.
Do đó
2
3 2
: 3 1 2 3 0
AB m x y m m m
2
3 2
3 1 2 3
y m x m m m
.
Để đường thẳng
AB
song song với đường thẳng
4y x
thì:
2
3 2
3 1 4
2 3 0
m
m m m
1
1
3
0
1
2
1
m
m
m
m
m
1
3
m
.
Câu 7. (THPT Xuân Hòa-Vĩnh Phúc- 2018) Biết đồ thị hàm số
3
3 1y x x
có hai điểm cực trị
A
,
B
. Khi đó phương trình đường thẳng
AB
là
A.
2 1y x
. B.
2 1.
y x
C.
2.
y x
D.
2y x
.
Lời giải
Chọn B
Thực hiện phép chia
y
cho
y
ta được:
1
. 2 1
3
y y x x
.
Giả sử hai điểm cực trị của đồ thị hàm số lần lượt là:
1 1
;A x y
và
2 2
;B x y
.
Ta có:
1 1 1 1 1 1
2 2 2 2 2 2
1
. 2 1 2 1
3
1
. 2 1 2 1
3
y y x y x x x x
y y x y x x x x
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
Ta thấy, toạ độ hai điểm cực trị
A
và
B
thoả mãn phương trình
2 1y x
.
Vậy phương trình đường thẳng qua hai điểm cực trị là:
2 1y x
.
Câu 8. (Chuyên Vĩnh Phúc - 2018) Tìm tất cả các giá trị của tham số
m
để đồ thị hàm số
3 2
2 3
y x x m x m
có hai điểm cực trị và điểm
9; 5
M
nằm trên đường thẳng đi qua
hai điểm cực trị của đồ thị.
A.
1.
m
B.
5.
m
C.
3.
m
D.
2.
m
Lời giải
Chọn C
Ta có
2
3 4 3
y x x m
, để hàm số có hai điểm cực trị thì phương trình
0
y
có hai nghiệm
phân biệt
0
13
*
3
m
Ta có
1 2 2 26 7 2
.
3 9 3 9 9 3
m m
y y x x
nên phương trình đường thẳng đi qua hai điểm
cực trị là
2 26 7 2
.
3 9 9 3
m m
y x
Theo giả thiết, đường thẳng này đi qua
9; 5
M
nên
3
m
(thỏa mãn điều kiện
*
).
Câu 9. (Nguyễn Khuyến 2019)
Đường thẳng nối hai điểm cực đại và cực tiểu của đồ thị hàm số
3
2
y x x m
đi qua điểm
3;7
M
khi
m
bằng bao nhiêu?
A. 1. B.
1
. C. 3. D. 0.
Lời giải
Chọn C
Tập xác định:
D
.
2
3 2
y x
.
3
1 4
2 .
3 3
y x x m x y x m
Suy ra đường thẳng đi qua các điểm cực trị của đồ thị hàm số có phương trình là
4
3
y x m
đường thẳng này đi qua điểm
3;7
M
khi và chỉ khi
4
7 . 3 3
3
m m
.
Câu 10. (Chuyên Lương Văn Chánh - Phú Yên - 2018) Tìm giá trị thực của tham số
m
để đường thẳng
: 3 1 3
d y m x m
vuông góc với đường thẳng đi qua hai điểm cực trị của đồ thị hàm số
3 2
3 1
y x x
.
A.
1
6
m
. B.
1
3
. C.
1
3
. D.
1
6
.
Lời giải
Xét hàm số
3 2
3 1
y x x
Có :
2
3 6y x x
,
1 1
2 1
3 3
y x y x
.
Do đó, đường thẳng
qua hai điểm cực trị của đồ thị hàm số này có phương trình là
2 1y x
.
Để
d
vuông góc với
thì
3 1 . 2 1
m
1
6
m
.
Vậy giá trị cần tìm của
m
là
1
6
m
.
Câu 11. (TT Diệu Hiền - Cần Thơ - 2018) Giả sử
A
,
B
là hai điểm cực trị của đồ thị hàm số
3 2
f x x ax bx c
và đường thẳng
AB
đi qua gốc tọa độ. Tìm giá trị nhỏ nhất của
P abc ab c
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
16
25
. B.
9
. C.
25
9
. D.
1
.
Lời giải
TXĐ
D
.
2
3 2
f x x ax b
. Điều kiện để hàm số có hai điểm cực trị là
0
f x
có hai nghiệm phân
biệt
2
3 0
a b
.
Lấy
f x
chia cho
f x
.
Ta có
1 1 2 2 1
.
3 9 3 9 9
f x f x x a b x c ab
.
Suy ra đường thẳng đi qua
A
,
B
là:
2 2 1
3 9 9
y b x c ab d
.
Theo đầu bài
d
đi qua gốc tọa độ
1
0
9
c ab
9ab c
.
Khi đó
P abc ab c
2
9 10P c c
2
5 25
3
3 9
P c
.
Suy ra
25
min
9
P
.
Câu 12. (Chuyên Hạ Long - 2018) Tìm tất cả giá trị thực của tham số
m
để đồ thị hàm số
3 2
3 2
y x mx
có hai điểm cực trị
A
và
B
sao cho các điểm
A
,
B
và
1; 2
M
thẳng hàng.
A.
2
m
. B.
2
m
. C.
2
m
. D.
2
m
;
2
m
.
Lời giải
Ta có:
2
3 6y x mx
;
0
y
2
3 6 0
x mx
0
x
,
2x m
.
Đồ thị hàm số có hai điểm cực trị khi và chỉ khi phương trình
0
y
có hai nghiệm phân biệt
2 0
m
0
m
.
Khi đó hai điểm cực trị là
0;2
A
,
3
2 ;2 4
B m m
.
Ta có
1;4
MA
,
3
2 1;4 4
MB m m
.
Ba điểm
A
,
B
và
1; 2
M
thẳng hàng
MA
,
MB
cùng phương
3
2 1 4 4
1 4
m m
3
2 1 1
1 1
m m
3
2 1 1
m m
3
2m m
2
2
m
2
m
(do
0
m
).
Dạng 4. Tìm m để hàm số bậc 3 có cực trị thỏa mãn điều kiện cho trước
Bài toán tổng quát: Cho hàm số
3 2
( ; ) .y f x m ax bx cx d
Tìm tham số m để đồ thị
hàm số có 2 điểm cực trị
1 2
, x x
thỏa mãn điều kiện K cho trước?
Phương pháp:
— Bước 1. Tập xác định
.
D
Tính đạo hàm:
2
3 2 .y ax bx c
— Bước 2. Để hàm số có 2 cực trị
0
y
có 2 nghiệm phân biệt
2
3 0
(2 ) 4.3 0
y
y
a a
b ac
và giải hệ này sẽ tìm được
1
.m D
— Bước 3. Gọi
1 2
, x x
là 2 nghiệm của phương trình
0.
y
Theo Viét, ta có:
1 2
1 2
b
S x x
a
c
P x x
a
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
— Bước 4. Biến đổi điều kiện
K
về dạng tổng S và tích P. Từ đó giải ra tìm được
2
.m D
— Bước 5. Kết luận các giá trị m thỏa mãn:
1 2
.m D D
Lưu ý:
— Hàm số bậc 3 không có cực trị
0
y
không có 2 nghiệm phân biệt
0.
y
— Trong trường hợp điều kiện K liên quan đến hình học phẳng, tức là cần xác định tọa độ 2 điểm
cực trị
1 1 2 2
( ; ), ( ; )A x y B x y
với
1 2
, x x
là 2 nghiệm của
0.
y
Khi đó có 2 tình huống thường gặp
sau:
Nếu giải được nghiệm của phương trình
0,
y
tức tìm được
1 2
, x x
cụ thể, khi đó ta sẽ thế vào
hàm số đầu đề
( ; )y f x m
để tìm tung độ
1 2
, y y
tương ứng của A và B.
Nếu tìm không được nghiệm
0,
y
khi đó gọi 2 nghiệm là
1 2
, x x
và tìm tung độ
1 2
, y y
bằng
cách thế vào phương trình đường thẳng nối 2 điểm cực trị.
Để viết phương trình đường thẳng nối hai điểm cực trị, ta thường dùng phương pháp tách đạo hàm
(phần dư bậc nhất trong phép chia
y
cho
)y
, nghĩa là:
Phân tích (bằng cách chia đa thức
y
cho
)y
:
1 1
2 2
( )
( ) ( )
( )
y h x
y y q x h x
y h x
Đường thẳng qua 2 điểm cực trị là
( ).y h x
Dạng toán: Tìm tham số m để các hàm số sau có cực trị thỏa điều kiện cho trước (cùng phía,
khác phía d):
Vị trí tương đối giữa 2 điểm với đường thẳng:
Cho 2 điểm
( ; ), ( ; )
A A B B
A x y B x y
và đường thẳng
: 0.
d ax by c
Khi đó:
Nếu
( ) ( ) 0
A A B B
ax by c ax by c
thì
, A B
nằm về 2 phía so với đường
thẳng
.d
Nếu
( ) ( ) 0
A A B B
ax by c ax by c
thì
, A B
nằm cùng phía so với đường
.d
Trường hợp đặc biệt:
Để hàm số bậc ba
( )y f x
có 2 điểm cực trị nằm cùng phía so với trục tung
Oy
phương trình
0
y
có 2 nghiệm trái dấu và ngược lại.
Để hàm số bậc ba
( )y f x
có 2 điểm cực trị nằm cùng phía so với trục hoành
Ox
đồ thị hàm số
( )y f x
cắt trục
Ox
tại 3 điểm phân biệt
phương trình
hoành độ giao điểm
( ) 0
f x
có 3 nghiệm phân biệt (áp dụng khi nhẩm được
nghiệm).
Dạng toán: Tìm m để các hàm số sau có cực trị thỏa điều kiện cho trước (đối xứng và cách đều):
Bài toán 1. Tìm m để đồ thị hàm số có 2 điểm cực trị
, A B
đối xứng nhau qua
đường
:d
— Bước 1. Tìm điều kiện để hàm số có cực đại, cực tiểu
1
.m D
— Bước 2. Tìm tọa độ 2 điểm cực trị
, .A B
Có 2 tình huống thường gặp:
+ Một là
0
y
có nghiệm đẹp
1 2
, ,x x
tức có
1 1 2 2
( ; ), ( ; ).A x y B x y
+ Hai là
0
y
không giải ra tìm được nghiệm. Khi đó ta cần viết phương trình đường
thẳng nối 2 điểm cực trị là
và lấy
1 1 2 2
( ; ), ( ; ) .
A x y B x y
— Bước 3. Gọi
1 2 1 2
;
2 2
x x y y
I
là trung điểm của đoạn thẳng
.AB
Do
, A B
đối xứng qua
d
nên thỏa hệ
2
0
.
d
d
AB u
m D
I d
I d
— Bước 4. Kết luận
1 2
.m D D
Bài toán 2. Tìm m để đồ thị hàm số có 2 điểm cực trị
, A B
cách đều đường thẳng

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 22 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
:d
— Bước 1. Tìm điều kiện để hàm số có cực đại, cực tiểu
1
.m D
— Bước 2. Tìm tọa độ 2 điểm cực trị
, .A B
Có 2 tình huống thường gặp:
+ Một là
0
y
có nghiệm đẹp
1 2
, ,x x
tức có
1 1 2 2
( ; ), ( ; ).A x y B x y
+ Hai là
0
y
không giải ra tìm được nghiệm. Khi đó ta cần viết phương trình đường
thẳng nối 2 điểm cực trị là
và lấy
1 1 2 2
( ; ), ( ; ) .
A x y B x y
— Bước 3. Do
, A B
cách đều đường thẳng
d
nên
2
( ; ) ( ; ) .d A d d B d m D
— Bước 4. Kết luận
1 2
.m D D
Lưu ý: Để 2 điểm
, A B
đối xứng nhau qua điểm
I I
là trung điểm
.AB
Câu 1. Với giá trị nào của tham số
m
để đồ thị hàm số
3 2
3
y x x m
có hai điểm cực trị
A
,
B
thỏa
mãn
OA OB
(
O
là gốc tọa độ)?
A.
3
2
m
. B.
3
m
. C.
1
2
m
. D.
5
2
m
.
Lời giải
Chọn D
Tập xác định:
D
.
2
3 6y x x
,
2
0
0 3 6 0
2
x
y x x
x
.
Do đó đồ thị hàm số đã cho luôn có hai điểm cực trị lần lượt có tọa độ là
0;A m
và
2; 4
B m
.
Ta có
2 2
2 2 2 2
0 2 4 4 4
OA OB m m m m
5
20 8 0
2
m m
.
Câu 2. (Đề Tham Khảo 2017) Gọi
S
là tập hợp tất cả các giá trị thực của tham số
m
để đồ thị của hàm
số
3 2 2
1
1
3
y x mx m x
có hai điểm cực trị
A
và
B
sao cho
,A B
nằm khác phía và cách
đều đường thẳng
: 5 9
d y x
. Tính tổng tất cả các phần tử của
S
.
A.
3
B.
6
C.
6
D.
0
Lời giải
Chọn D
Cách 1: Ta có
2 2
' 2 1
y x mx m
3
1
3 2
' 0 1;
1
3
x m
m m
y A m
x m
và
3
3 2
1;
3
m m
B m
Dễ thấy phương trình đường thẳng
2
1
2
:
3 3
m m
AB y x
nên
AB
không thể song song hoặc
trùng với
d
,A B
cách đều đường thẳng
: 5 9
d y x
nếu trung điểm
I
của
AB
nằm trên
d
3 3
3
3 3
; 5 9 18 27 0
3 3
m m m m
I m d m m m
3
3 3 5
2
m
m
Với
3 ,m A B
thỏa điều kiện nằm khác phía so với
d
.
Với
3 3 5
,
2
m A B
thỏa điều kiện nằm khác phía so với
d
.
Tổng các phần tử của
S
bằng 0.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
Câu 3. (Chuyên Biên Hòa - Hà Nam - 2020) Có tất cả bao nhiêu giá trị thực của tham số
m
để đồ thị
hàm số
3 2 2
2 2
2 3 1
3 3
y x mx m x
có hai điểm cực trị có hoành độ
1
x
,
2
x
sao cho
1 2 1 2
2 1
x x x x
.
A.
1
. B.
0
. C.
3
. D.
2
.
Lời giải
Chọn A
Ta có:
2 2 2 2
' 2 2 2 3 1 2 3 1
y x mx m x mx m
,
2 2
3 1
g x x mx m
;
2
13 4
m
.
Đồ thị hàm số có hai điểm cực trị khi và chỉ khi
'y
có hai nghiệm phân biệt
g x
có hai nghiệm phân biệt
0
2 13
13
2 13
13
m
m
. (*)
1
x
,
2
x
là các nghiệm của
g x
nên theo định lý Vi-ét, ta có
1 2
2
1 2
3 1
x x m
x x m
.
Do đó
1 2 1 2
2 1
x x x x
2
3 2 1 1
m m
2
3 2 0
m m
0
2
3
m
m
.
Đối chiếu với điều kiện (*), ta thấy chỉ
2
3
m
thỏa mãn yêu cầu bài toán.
Câu 4. (Chuyên KHTN - 2020) Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số
3 2
(2 1) 2 1
y mx m x mx m có hai điểm cực trị nằm về hai phía của trục hoành?
A. 4. B. 2. C. 1. D. 3.
Lời giải
Chọn C
Đồ thị hàm số có hai điểm cực trị nằm về hai phía đối với trục hoành khi và chỉ khi phương
trình
3 2
(2 1) 2 1 0
mx m x mx m
(1) có 3 nghiệm phân biệt.
Ta có (1)
2
( 1) ( 1) 1 0
x mx m x m
Phương trình (1) có 3 nghiệm phân biệt khi và chỉ khi pt
2
( 1) 1 0
mx m x m
có 2 nghiệm
phân biệt khác 1
2
0
( 1) 1 0
( 1) 4 ( 1) 0
m
m m m
m m m
2
0
2 0
3 6 1 0
m
m
m m
0
2
3 2 3 3 2 3
3 3
m
m
m
Do
1
m m
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 24 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 5. (Chuyên Hạ Long - Quảng Ninh - 2020) Cho hàm số
3 2
6 2 9 2.
y x m x m x
Tìm
m
để đồ thị hàm số có hai điểm cực trị nằm về hai phía của trục hoành.
A.
2
.
6
m
m
B.
2.
m
C.
6.
m
D.
2
6
.
3
2
m
m
m
Lời giải
Chọn D
2
2
' 3 2 6 2 9.
1
' 3 2 6 2 9 0 .
2 9
3
y x m x m
x
y x m x m
m
x
Hàm số có 2 cực trị
2 9
1 3.
3
m
m
1
(1) 2.
y m
2
2 9
2 9
2.
3 27
m
m
y m
Ycbt
2 9
(1). 0
3
m
y y
2
3 2
6
2 9
2
2 . 2 0 2 . 4 36 81 54 0 .
27
3
2
m
m
m
m m m m m m
m
2
Từ
1
,
2
ta có ycbt
2
6
.
3
2
m
m
m
Câu 6. (THPT Lê Quy Đôn Điện Biên 2019) Cho hàm số
3 2
1
1 3 2 2018
3
y mx m x m x
với
m
là tham số. Tổng bình phương tất cả các giá trị của
m
để hàm số có hai điểm cực trị
1 2
;x x
thỏa mãn
1 2
2 1
x x bằng
A.
40
9
B.
22
9
C.
25
4
D.
8
3
Lời giải
Chọn A
Ta có
2
' x 2 1 3 2
y m m x m
Để hàm số có hai điểm cực trị thì phương trình
2
x 2 1 3 2 0
m m x m
phải có hai
nghiệm phân biệt.
2
2
0
0
2 4 1 0
1 3 2 0
m
m
m m
m m m
Theo định lý Vi-ét ta có
1 2
1 2
2 1
.
3 2
.
m
x x
m
m
x x
m

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25
Theo bài ta có hệ phương trình
1
1
2
1 2
2
2 1
1
3 4
2 1
.
2 1
2
m
x
m
x x m
m
m
m
m m
x x
x
2 /
3 2
3 4 2
. 3 2 3 4 2 0
2
/
3
m t m
m
m m
m m m m
m m m
m t m
Vậy
2 2
1 2
40
9
m m
.
Câu 7. (Chuyên Lê Quý Đôn Điện Biên 2019) Cho hàm số
3 2
3 3 1
y x mx m
với
m
là một tham
số thực. Giá trị của
m
thuộc tập hợp nào sau đây để đồ thị hàm số đã cho có hai điểm cực trị đối
xứng nhau qua đường thẳng
: 8 74 0
d x y
.
A.
1;1
m
. B.
3; 1
m
. C.
3;5
m
. D.
1;3
m
.
Lời giải
Chọn D
2
3 6y x mx
0
0
2
x
y
x m
Đồ thị có hai cực trị khi:
0
m
Khi đó hai điểm cực trị là:
3
0; 3 1 , 2 ;4 3 1
A m B m m m
Tọa độ trung điểm
AB
là:
3
;2 3 1
I m m m
A
và
B
đối xứng qua
d
khi và chỉ khi:
. 0
d
I d
AB u
3
2 ; 4 , 8; 1
d
AB m m u
+
3
0
. 0 16 4 0 2
2
d
m
AB u m m m
m
.
Với
0
m
loại
Với
2
m
, ta có
2;9
I I d
Với
2
m
, ta có
2; 11
I I d
Do đó
2
m
thỏa mãn yêu cầu.
Câu 8. Có bao nhiêu giá trị nguyên của tham số
m
để đồ thị hàm số
3 2 2 2
8 11 2 2
y x x m x m
có hai điểm cực trị nằm về hai phía của trục
Ox
.
A.
4.
B.
5.
C.
6.
D.
7.
Lời giải
Chọn D
Yêu cầu bài toán
đồ thị hàm số cắt trục hoành tại ba điểm phân biệt
3 2 2 2
8 11 2 2 0
x x m x m
có ba nghiệm phân biệt
3 2 2 2
8 11 2 2 0
x x m x m
2 2
2 6 1 0
x x x m
2 2
2
6 1 0(*)
x
x x m
Suy ra phương trình (*) có hai nghiệm phân biệt khác
2

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 26 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
2
' 10 0
8 0
m
m
2 2
10 10
m
m
Vậy có
7
giá trị nguyên của tham số thỏa mãn đề bài.
Câu 9. (Chuyên Hạ Long 2019) Cho hàm số
3 2
2 1 1 1
y x m x m x m
. Có bao nhiêu giá
trị của số tự nhiên
20
m
để đồ thị hàm số có hai điểm cực trị nằm về hai phía trục hoành?
A.
18
. B.
19
. C.
21
. D.
20
.
Lời giải
+ Ta có:
2
1 2 1
y x x mx m
.
+ Hàm số có hai điểm cực trị nằm về hai phía trục hoành khi và chỉ khi đồ thị
y
cắt trục hoành tại
ba điểm phân biệt.
2
1 2 1 0
y x x mx m
có ba nghiệm phân biệt.
2
2 1 0
x mx m
có hai nghiệm phân biệt khác 1.
2
1 5
2
1 0
1 5
2 3 0
2
2
3
m
m m
m
m
m
.
+ Do
, 20
m N m
nên
1 20
m
. Vậy có 19 số tự nhiên thỏa mãn bài toán.
Câu 10. (Chuyên KHTN 2019) Có bao nhiêu giá trị nguyên của tham số
m
để đồ thị của hàm số
3 2 2 2
1 2 3
y x m x m x m
có hai điểm cực trị và hai điểm cực trị đó nằm về hai phía
khác nhau đối với trục hoành?
A.
2
. B.
1
.
C.
3
. D.
4
.
Lời giải
Ta có
2 2
0 3 2 1 2 0
y x m x m
.
Để hàm số có hai điểm cực trị
2
1 15 1 15
0 2 2 7 0 *
2 2
m m m
.
Ta lần lượt thử bốn giá trị nguyên của
m
thỏa mãn
*
là
1;0;1;2
.
Ta được bốn hàm số
3 3 2 3 2 3 2
2; 2 3; 2 2; 3 1y x x y x x x y x x x y x x x
.
Khi đó ta nhận thấy chỉ có
1
m
thỏa mãn yêu cầu bài toán.
Câu 11. (THPT Lương Thế Vinh Hà Nội 2019) Tìm tất cả cả các giá trị của tham số m để
3 2
y x 3x mx 1
đạt cực trị tại
1 2
,x x
thỏa mãn
2 2
1 2
6
x x
A.
3
m
B.
3
m
C.
1
m
D.
1
m
Lời giải
Chọn A
2
y' 3x 6x m
. Hàm số đạt cực trị tại
1 2
,x x
.Vậy
1 2
,x x
là nghiệm của phương trình
y' 0
Theo viet ta có
1 2
1 2
2
.
3
x x
m
x x
2 2 2
1 2 1 2 1 2
( ) 2
x x x x x x
2
4
3
m
2
4 6
3
m
3
m

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27
Câu 12. Có bao nhiêu giá trị nguyên của
m
để hàm số
3 2
2 6 1
f x x x m
có các giá trị cực trị trái
dấu?
A.
7
. B.
9
. C.
2
. D.
3
.
Lời giải
Chọn A
Có
2
' 6 12
f x x x
.
0
' 0
2
x
f x
x
0 0 1
x f m
2 2 7
x f m
Hàm số có các giá trị cực trị trái dấu
1 7 0
m m
1 7 0 7 1
m m m
.
Vậy có
7
giá trị nguyên của
m
thỏa mãn.
Câu 13. (Thi thử SGD Hưng Yên) Cho hàm số
3 2
2 3 1 6 2 1y x m x m x
với
m
là tham số
thực. Tìm tất cả các giá trị của
m
để hàm số có điểm cực đại và điểm cực tiểu nằm trong khoảng
2;3
.
A.
1;4 \ 3
m
. B.
3;4
m
. C.
1;3
m
. D.
1;4
m
.
Lời giải
Chọn A
Ta có
2
6 6 1 6 2
y x m x m
.
2
1
0 1 2 0
2
x
y x m x m
x m
.
Để hàm số có điểm cực đại cực tiểu nằm trong khoảng
2;3
thì
0
y
có hai nghiệm phân biệt
nằm trong khoảng
2;3
2 1 3
2 2 3 1 4
m m
m m
.
Câu 14. (THPT Cẩm Bình Hà Tỉnh 2019) Cho hàm số
3 2 2
3 4 2
y x mx m
có đồ thị
C
và điểm
1;4
C
. Tính tổng các giá trị nguyên dương của
m
để
C
có hai điểm cực trị
,A B
sao cho tam
giác
ABC
có diện tích bằng 4.
A.
6
. B.
5
. C.
3
. D.
4
Lời giải
Chọn C
Ta có
2
0
' 3 6 0
2
x
y x mx
x m
Đồ thị
C
có hai điểm cực trị
2 0 0
m m
.
Khi đó
2 3 2
0;4 2 , 2 ; 4 4 2
A m B m m m
2 6 4
4 16 2 4 1
AB m m m m
Phương trình đường thẳng
AB
là:
2
2 2
3
4 2
0
2 4 2 0
2 0 4
y m
x
m x y m
m m
2 2 2
4 4
2 4 4 2 2 3
,
4 1 4 1
m m m
d C AB
m m
Diện tích tam giác
ABC
là

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 28 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
4
4
2 3
1 1
. . , 4 .2 . 4 1. 4
2 2
4 1
m
S AB d C AB m m
m
2
2 6 4 2 2 2
1
3 2 6 9 4 0 1 4 0
2
m
m m m m m m m
m
Do
m
nguyên dương nên ta được
1, 2
m m
, tổng thu được là
3
.
Câu 15. (THPT Lê Quy Đôn Điện Biên 2019) Cho hàm số
3 2
2 3 1 6 2 1
y x m x m x
với
m
là tham số thực. Tìm tất cả các giá trị của
m
để hàm số có điểm cực đại và điểm cực tiểu nằm
trong khoảng
2; 3
.
A.
1; 3 3; 4
m
. B.
1; 3
m
. C.
3; 4
m
. D.
1; 4
m
.
Lời giải
Chọn A
Ta có:
2
' 6 6 1 6 2
y x m x m
Để hàm số có điểm cực đại và điểm cực tiểu nằm trong khoảng
2; 3
pt
' 0y
có 2 nghiệm
thuộc khoảng
2; 3
2
1 2 0
x m x m
có 2 nghiệm thuộc khoảng
2; 3
1 2 0
x x m
1 2; 3
2
x
x m
2 1 3
2 2 3 1 4
m m
YCBT
m m
Câu 16. (Chuyên Lam Sơn Thanh Hóa 2019) Tổng tất cả các giá trị thực của tham số m để hàm số:
3 2
3 2 1 3 5
y x m x mx m
có hai điểm cực trị
1 2
;x x
đồng thời
1 2
. 0
y x y x
là:
A.
21
B.
39
C.
8
D.
3 11 13
Lời giải
Chọn A
+) Để hàm số có hai cực trị thì phương trình
0
y
phải có hai nghiệm phân biệt:
2
9 4 1 3y x m x m
có hai nghiệm phân biệt
2
4 1 27 0
m m
+) Xét
1 2
. 0
y x y x
nên ta có
3 2
3 2 1 3 5
y x m x mx m
phải tiếp xúc với trục hoành
3 2
3 2 1 3 5 0
x m x mx m
phải có nghiệm kép
2
1 3 2 5 5 0 1
x x m x m
phải có nghiệm kép
+) TH1: Phương trình
2
3 2 5 5 0
x m x m
có một nghiệm
1
1 13
x m
+) TH2: Phương trình
2
3 2 5 5 0
x m x m
có nghiệm kép khác
1
2
2
2 3
2 5 12 5 0 4 32 35 0 8
m m m m m m
1 2 3
21
m m m
Câu 17. (Chuyên Bắc Ninh 2019) Gọi S là tập các giá trị dương của tham số
m
sao cho hàm
số
3 2
3 27 3 2
y x mx x m
đạt cực trị tại
1 2
,x x
thỏa mãn
1 2
5
x x
. Biết
;S a b
. Tính
2
T b a
.
A.
51 6
T
B.
61 3
T
C.
61 3
T
D.
51 6
T
Lời giải
Chọn C
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 29
+) Ta có
2
3 6 27
y x mx
,
2
0 2 9 0
y x mx
(1)
+) Theo giả thiết hàm số đạt cực trị tại
1 2
,x x
phương trình
(1)
có
2
nghiệm phân biệt
0
2
3
9 0
3
m
m
m
(*)
+) Với điều kiện (*) thì phương trình
(1)
có
2
nghiệm
1 2
,x x
, theo Vi-ét ta có:
1 2
1 2
2
9
x x m
x x
+) Ta lại có
1 2
5
x x
2 2
1 2 1 2 1 2
25 4 25 0
x x x x x x
2
61 61
4 61 0
2 2
m m
(**)
+) Kết hợp (*), (**) và điều kiện
m
dương ta được:
61
3
2
m
3
2 61 3
61
2
a
T b a
b
.
Câu 18. (Sở Bắc Giang 2019) Gọi
S
là tập hợp các giá trị nguyên của tham số
m
để hàm số
3
2
2 3
3
x
y x mx
có hai điểm cực trị
1 2
, 4
x x
. Số phần tử của
S
bằng
A.
5
. B.
3
. C.
2
. D.
4
.
Lời giải
Ta có:
3
2 2
2 3 ' 4
3
x
y x mx y x x m
.
Hàm số có hai điểm cực trị
1 2
,x x
thì phương trình
' 0
y
có hai nghiệm phân biệt
' 0 4 0 4
m m
.
Khi đó giả sử
1 2
x x
,
1
2
2 4
' 0
2 4
x m
y
x m
Yêu cầu bài toán trở thành
2
4 2 4 4 0 4
x m m
.
Kết hợp với
4
m
ta được
0 4
m
. Do
m
nguyên nên
0;1;2;3
m
. Vậy có 4 giá trị của
m
thỏa mãn yêu cầu bài toán.
Câu 19. (Toán Học Tuổi Trẻ 2019) Tìm giá trị thực của tham số
m
để hàm số
3 2
4 2 7 1y x m x x
có hai điểm cực trị
1 2
;x x
1 2
x x
thỏa mãn
1 2
4
x x
A.
5
m
. B.
1
2
m
. C.
3
m
. D.
7
2
m
.
Lời giải
Ta có
3 2
4 2 7 1y x m x x
(1)
2
' 3 8 2 7
y x m x
. Xét phương trình
2
3 8 2 7 0
x m x
(2)
2
' 4 2 21 0
m
, với mọi m
hàm số (1) luôn có hai điểm cực trị
1 2
;x x
với mọi
m
.
*Ta thấy
21 0
ac
phương trình (2) có 2 nghiệm trái dấu
1 2
0; 0
x x
1 1 2 2
;
x x x x
*Ta có
1 2
4
x x
1 2
4
x x
1 2
8 2
4 4
3
m
x x
1
2
m
Câu 20. Có bao nhiêu giá trị nguyên của tham số
m
để điểm
3
(2 ; )M m m
tạo với hai điểm cực đại, cực
tiểu của đồ thị hàm số
3 2
2 3(2 1) 6 ( 1) 1 ( )y x m x m m x C
một tam giác có diện tích nhỏ
nhất?

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 30 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
0
B.
1
C.
2
D. không tồn tại
Lời giải
Chọn B
Ta có
2
' 6 6(2 1) 6 ( 1)
y x m x m m
' 0
1
x m
y m R
x m
, hàm số luôn có CĐ, CT
Tọa độ các điểm CĐ, CT của đồ thị là
3 2 3 2
( ;2 3 1), ( 1;2 3 )A m m m B m m m
Suy ra
2
AB
và phương trình đường thẳng
3 2
: 2 3 1 0
AB x y m m m
Do đó, tam giác
MAB
có diện tích nhỏ nhất khi và chỉ khi khoảng cách từ
M
tới
AB
nhỏ nhất
Ta có
2
3 1 1
( , )
2 2
m
d M AB
, dấu "=" khi
0
m
Câu 21. (HSG Bắc Ninh 2019) Tìm tất cả các giá trị thực của tham số thực m để đường thẳng đi qua hai
điểm cực đại, cực tiểu của đồ thị hàm số
3
3 2 y x mx
cắt đường tròn
C
có tâm
1;1
I
, bán
kính bằng 1 tại hai điểm phân biệt A,B sao cho diện tích tam giác IAB đạt giá trị lớn nhất.
A.
2 3
3
m
B.
2 3
2
m
C.
1 3
2
m
D.
2 5
2
m
Lời giải
Ta có:
2
3 3
y x m
suy ra đồ thị hàm số có điểm cực đại và cực tiểu khi
0
m
. Các điểm cực
đại, cực tiểu của đồ thị hàm số là
;2 2 ; ;2 2 .
C m m m D m m m
Đường thẳng
đi qua các điểm CĐ, CT của đồ thị hàm số có phương trình là:
2 2 y mx
. Do
2
2 1
, 1
4 1
m
d I R
m
(vì m > 0)
luôn cắt đường tròn tâm
1;1
I
, bán kính
1R
tại 2
điểm
,A B
phân biệt. Dễ thấy
1
2
m
không thõa mãn do
, ,A I B
thẳng hàng.
Với
1
2
m
:
không đi qua I, ta có:
2
1 1 1
. .sin
2 2 2
ABI
S IA IB AIB R
.
Do đó
IAB
S
lớn nhất bằng
1
2
khi
sin 1
AIB hay
AIB
vuông cân tại
I
1
2 2
R
IH
2
2 1
1 2 3
2
2
4 1
m
m
m
(
H
là trung điểm của
AB
)
Câu 22. (VTED 2019) Biết đồ thị hàm số
3 2
y x ax bx c
có hai điểm cưc trị
1 1 2 2
; , ;M x y N x y
thỏa mãn
1 1 2 1 1 2
x y y y x x
. Giá trị nhỏ nhất của biểu thức
2 3P abc ab c
bằng
A.
49
4
B.
25
4
C.
841
36
D.
7
6
Lời giải
Chọn A
Ta có
2
3 2
y x ax b
Chia
y
cho
y
ta được
2
1 1 2
3 9 9 3 9
a b ab
y y x a x c
.
Do
1 1 2 2
; , ;M x y N x y
là hai điểm cực trị nên
1 2
0, 0
y x y x
Do đó
2 2
1 1 2 2
2 2
;
9 3 9 9 3 9
a b ab a b ab
y x c y x c
Theo giả thiết
1 1 2 1 1 2 1 2 2 1
x y y y x x x y x y

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 31
2 2
1 2 2 1
2 2
9 3 9 9 3 9
a b ab a b ab
x x c x x c
1 2 1 2
0( ) 9
9 9 9
ab ab ab
x c x c c x x ab c
Ta có:
2
2
7 49 49
2 3 9 21 3
2 4 4
P abc ab c c c c
Vậy giá trị nhỏ nhất của biểu thức
2 3P abc ab c
bằng
49
4
Câu 23. Cho hàm số
3 2 2 3
3 3 1
y x mx m x m m
(
m
là tham số). Gọi
A
,
B
là hai điểm cực trị
của đồ thị hàm số và
2; 2
I
. Tổng tất cả các giá trị của
m
để ba điểm
I
,
A
,
B
tạo thành tam
giác nội tiếp đường tròn có bán kính bằng
5
là
A.
4
17
B.
14
17
C.
2
17
D.
20
17
Lời giải
Chọn D
Tập xác định
D
.
2 2
3 6 3 1
y x mx m
.
Cho
0
y
2 2
2 1 0
x mx m
.
Vì
1 0
m
nên phương trình
0
y
luôn có hai nghiệm phân biệt
1
x m
.
Gọi
1; 4 2
A m m
,
1; 4 2
B m m
.
Suy ra
2;4 2 1; 2
AB
,
1; 4IA m m
,
3; 4 4
IB m m
.
Phương trình đường thẳng
AB
qua
1; 4 2
A m m
và có vectơ pháp tuyến
2;1
n
là
: 2 2 0
AB x y m
.
Suy ra
2 2
,
5
m
d I AB
Khi đó
1
. ,
2
IAB
S AB d I AB
2 2
1
2 5
2
5
m
2 2m
.
Mặt khác
. .
4
IAB
AB IA IB
S
R
. . 4 5 2 2AB IA IB m
.
2 2
20 17 2 1 17 38 25 4 5 2 2m m m m m
2 2 2
17 2 1 17 38 25 4 4 8 4
m m m m m m
4 3 2
289 680 502 120 9 0
m m m m
1
3
17
m
m
.
Vậy
1 2
20
17
m m
Câu 24. Cho hàm số
3
6 4
y x mx
có đồ thị
m
C
. Gọi
0
m
là giá trị của
m
để đường thẳng đi qua
điểm cực đại, điểm cực tiểu của
m
C
cắt đường tròn tâm
1;0
I
, bán kính
2
tại hai điểm phân
biệt
,A B
sao cho tam giác
IAB
có diện tích lớn nhất. Chọn khẳng định đúng
A.
0
3;4
m
. B.
0
1;2
m
. C.
0
0;1
m
. D.
0
2;3
m
.
Lời giải
Chọn C
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 32 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta có:
2
3 6y x m
2
0 2y x m
Hàm số có cực đại, cực tiểu
0y
có hai nghiệm phân biệt
0m
Gọi
2 ;4 4 2A m m m và
2 ;4 4 2B m m m
Phương trình đường thẳng
: 4 4 0AB mx y
Đặt
,a d I AB
0 2a
2
2HB a
Suy ra
2 2 2
1
2 2 1
2
IAB
S a a a a
Dấu “ ” xảy ra
2
2 1a a a
Khi đó
2
2
4 0 4
; 1 16 1 4 1
16 1
m
d I AB m m
m
2 2
15
16 1 16 32 16
32
m m m m
Câu 25. (Chuyên Lương Văn Chánh - Phú Yên - 2018) Cho hàm số
3 2
1 1
4 10
3 2
y x mx x
, với
m
là tham số; gọi
1
x ,
2
x là các điểm cực trị của hàm số đã cho. Giá trị lớn nhất của biểu thức
2 2
1 2
1 1P x x
bằng
A.
4
. B.
1
. C.
0
. D.
9
.
Lời giải
Tập xác định
D
.
Đạo hàm
2
4y x mx
.
Khi đó
2
0 4 0y x mx
.
Ta có
2
16 0m
,
m
0y
luôn có hai nghiệm phân biệt
m
hay hàm số luôn
có hai điểm cực trị
1
x ,
2
x
m
.
Do
1
x ,
2
x
là hai nghiệm phân biệt của
0y
nên theo định lý Viet ta có
1 2
1 2
. 4
x x m
x x
.
2 2
1 2
1 1P x x
2
2 2
1 2 1 2
1x x x x
2 2
1 2 1 2 1 2
2 1x x x x x x
2
16 8 1m
2
9m
9
,
m
.
Do đó giá trị lớn nhất của biểu thức
P
bằng
9 0m
.
Câu 26. (Chuyên Lương Văn Chánh - Phú Yên - 2018) Cho hàm số
3 2 2 3
3 3 1y x mx m x m
,
với
m
là tham số; gọi
C
là đồ thị của hàm số đã cho. Biết rằng khi
m
thay đổi, điểm cực đại
của đồ thị
C
luôn nằm trên một đường thẳng
d
cố định. Xác định hệ số góc
k
của đường thẳng
d
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 33
A.
1
3
k
. B.
1
3
k
. C.
3
k
. D.
3
k
.
Lời giải
Tập xác định
D
.
Ta có
2 2
3 6 3 1
y x mx m
và
6 6y x m
.
Khi đó
2 2
0 3 6 3 1 0
y x mx m
.
2 2
9 9 1 9
m m
nên hàm số luôn có hai điểm cực trị
3 3
1
3
m
x m
và
3 3
1
3
m
x m
.
1 6 1 6y m m m
6 0
1
x m
là điểm cực đại của hàm số
1; 3 2
A m m
là điểm cực đại của đồ thị
C
.
Ta có
1
3 2
A
A
x m
y m
3 1
A A
y x
A
luôn thuộc đường thẳng
d
có phương trình
3 1y x
.
Do đó hệ số góc
k
của đường thẳng
d
là
3
.
Câu 27. (Chuyên Hùng Vương - Phú Thọ - 2018) Biết
0
m
là giá trị của tham số
m
để hàm số
3 2
3 1y x x mx
có hai điểm cực trị
1 2
,x x
sao cho
2 2
1 2 1 2
13
x x x x
. Mệnh đề nào dưới đây
đúng?
A.
0
1;7
m
. B.
0
7;10
m
. C.
0
15; 7
m
. D.
0
7; 1
m
.
Lời giải
TXĐ:
D
2
3 6
y x x m
.
Xét
2
0 3 6 0
y x x m
;
9 3m
.
Hàm số có hai điểm cực trị
0 3
m
.
Hai điểm cực trị
1 2
;x x
là nghiệm của
0
y
nên:
1 2 1 2
2; .
3
m
x x x x
.
Để
2
2 2
1 2 1 2 1 2 1 1
13 3 . 13
x x x x x x x x
4 13 9
m m
. Vậy
0
9 15; 7
m
.
Câu 28. (THPT Thanh Miện I - Hải Dương 2018) Biết rằng đồ thị hàm số
3 2
1 1
2
3 2
f x x mx x
có giá trị tuyệt đối của hoành độ hai điểm cực trị là độ dài hai cạnh của tam giác vuông có cạnh
huyền là
7
. Hỏi có mấy giá trị của
m
?
A.
3
. B.
1
. C. Không có
m
. D.
2
.
Lời giải
Có
2
1y x x mx
,
2
0 1 0
y x mx
1
.
Để hàm số có cực trị thì
1
phải có hai nghiệm phân biệt.
Điều này tương đương với
0
2
4 0
m
2
2
m
m
.
Gọi hai nghiệm của
1
là
1
x
,
2
x
. Khi đó, ta có
1 2
1 2
. 1
x x m
x x
.
Độ dài hai cạnh của tam giác vuông đó là
1
x
,
2
x
. Theo bài ra ta có phương trình:
2 2
1 2
7
x x
2
1 2 1 2
2 7
x x x x
2
2 7
m
2
9
m
3
m
(thỏa mãn).
Vậy có hai giá trị của
m
thỏa mãn yêu cầu bài toán.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 34 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 29. (Phan Đăng Lưu - Huế - 2018) Gọi
A
,
B
là hai điểm cực trị của đồ thị hàm số
3
3 4
f x x x
và
0
;0
M x
là điểm trên trục hoành sao cho tam giác
MAB
có chu vi nhỏ
nhất, đặt
0
4 2015
T x
. Trong các khẳng định dưới đây, khẳng định nào đúng?
A.
2017
T
. B.
2019
T
. C.
2016
T
. D.
2018
T
.
Lời giải
Tập xác định:
D
. Đạo hàm:
2
3 3
f x x
.
Xét
2
0 3 3 0
f x x
1 2
1 6
x y
x y
. Đặt
1; 2
A
và
1; 6
B
.
Ta thấy hai điểm
A
và
B
nằm cùng phía với trục hoành.
Gọi
1;2
A
là điểm đối xứng với điểm
A
qua trục hoành. Chu vi tam giác
MAB
đạt giá trị nhỏ
nhất khi và chỉ khi ba điểm
B
,
M
và
A
thẳng hàng.
Ta có:
0
1; 2
A M x
và
2; 8
A B
0
1
2
2 8
x
0
1
2
x
1
;0
2
M
.
Vậy
1
4. 2015 2017
2
T
.
Câu 30. (Chuyên Hà Tĩnh - 2018) Tổng tất cả các giá trị của tham số thực
m
sao cho đồ thị hàm số
3 2 3
3 4y x mx m
có điểm cực đại và cực tiểu đối xứng với nhau qua đường phân giác của góc
phần tư thứ nhất là
A.
2
2
. B.
1
2
. C.
0
. D.
1
4
.
Lời giải
Ta có:
2
3 6y x mx
,
0
0
2
x
y
x m
.
Để hàm số có cực đại cực tiểu thì
0
m
.
Khi đó các điểm cực trị của đồ thị hàm số là:
3
0;4
A m
,
2 ;0
B m
.
Ta có
3
;2
I m m
là trung điểm của đoạn thẳng
AB
.
Đường phân giác của góc phần tư thứ nhất là
: 0
d x y
.
Do đó để điểm cực đại và cực tiểu đối xứng với nhau qua
d
thì:
3
2
3
2 4 0
2
1 2 0
2
2 0
m m
m m
m m
.
Vậy tổng tất cả các giá trị của tham số thực
m
là
0
.
Câu 31. (THPT Triệu Thị Trinh - 2018) Tìm tất cả các giá trị của tham số thực
m
sao cho đồ thị hàm số
3 2
5 4
y x x m x m
có hai điểm cực trị nằm về hai phía đối với trục hoành.
A.
. B.
;3 3;4
. C.
;3 3;4
. D.
;4
.
Lời giải
Ta có
3 2 2
5 4 1 4
y x x m x m x x x m
Đồ thị hàm số đã cho có hai điểm cực trị nằm về hai phía trục hoành khi và chỉ khi phương trình
0
y
có ba nghiệm phân biệt
2
4 0
x x m
có hai nghiệm phân biệt khác
1
4 0 4
1 4 0 3
m m
m m
.
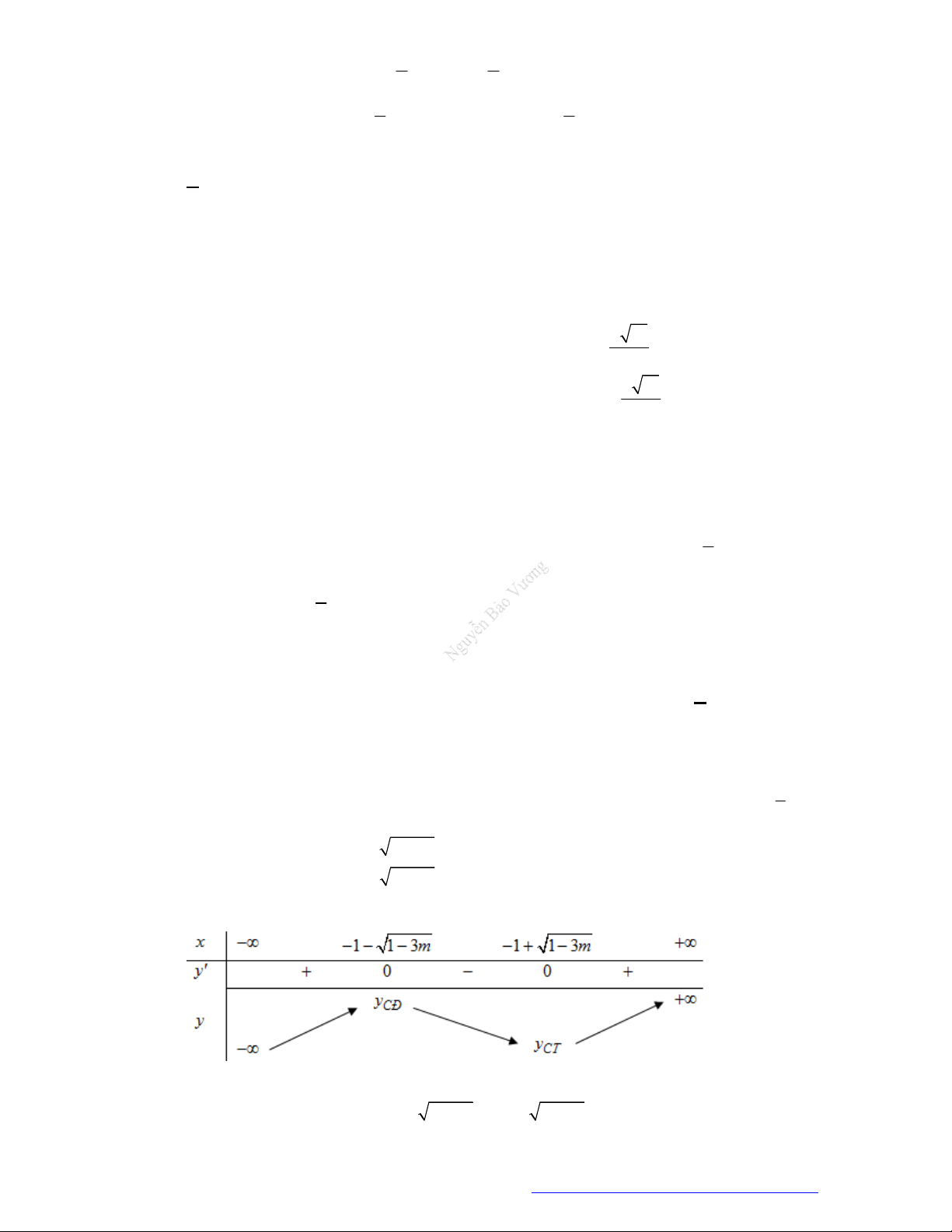
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 35
Câu 32. (CTN - LẦN 1 - 2018) Biết
a
b
(trong đó
a
b
là phân số tối giản và
a
,
*b
) là giá trị của tham
số
m
để hàm số
3 2 2
2 2
2 3 1
3 3
y x mx m x
có 2 điểm cực trị
1
x ,
2
x sao cho
1 2 1 2
2 1x x x x
. Tính giá trị biểu thức
2 2
S a b
.
A.
13S
. B.
25S
. C.
10S
. D.
34S
.
Lời giải
Tập xác định:
D
.
Đạo hàm
2 2
2 2 6 2y x mx m
.
Hàm số có hai điểm cực trị
0
2 2
2 6 2 0m m
2
13 4 0m
2 13
13
2 13
13
m
m
Theo định lý Viet thì
1 2
2
1 2
3 1
x x m
x x m
Ta có
1 2 1 2
2 1x x x x
2
3 1 2 1m m
2
3 2 0m m
0
2
3
m
m
Chỉ có giá trị
2
3
m
thỏa điều kiện, khi đó
2 2 2 2
2 3 13S a b
.
Câu 33. Gọi
S
là tập hợp tất cả các giá trị nguyên của tham số
m
để điểm cực tiểu của đồ thị hàm số
3 2
1y x x mx nằm bên phải trục tung. Tìm số phần tử của tập hợp
5;6 S
.
A.
2
. B.
5
. C.
3
. D.
4
.
Lời giải
Tập xác định:
D
;
2
3 2y x x m
.
Hàm bậc ba có cực trị khi
0y
có
2
nghiệm phân biệt
1 3 0m
1
1
3
m
.
Khi đó
0y
1 1 3
1 1 3
x m
x m
Bảng biến thiên:
Điểm cực tiểu của đồ thị hàm số nằm về phía bên phải trục tung khi
1 1 3 0m
1 3 1m
0m
.
Kết hợp với
1
ta có
0m
thì điểm cực tiểu của đồ thị hàm số đã cho nằm bên phải trục tung.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 36 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Khi đó
S
là tập hợp tất cả các giá trị nguyên âm.
Vậy
5;6 4; 3; 2; 1
S
5;6
S
có
4
phần tử.
Vậy giá trị
m
cần tìm là
1
m
hoặc
3
m
.
Câu 34. (THPT Nghen - Hà Tĩnh - 2018) Cho hàm số
3 2 2 2
3 3 1 3 1
y x x m x m
. Có bao
nhiêu giá trị nguyên của
m
để đồ thị hàm số có điểm cực đại, cực tiểu nằm bên trái đường thẳng
2
x
?
A.
3
. B.
1
. C.
2
. D.
0
.
Lời giải
3 2 2 2
3 3 1 3 1
y x x m x m
2 2
3 6 3 1
y x x m
.
1
0
1
x m
y
x m
.
Để đồ thị hàm số có điểm cực đại, cực tiểu nằm bên trái đường thẳng
2
x
thì
0 0
1 2 1
1 2 1
m m
m m
m m
.
Vậy không có giá trị nguyên nào của
m
thỏa yêu cầu bài toán.
Câu 35. (Chuyên Hạ Long - 2018) Tìm tất cả giá trị thực của tham số
m
để đồ thị hàm số
3 2
3 2
y x mx
có hai điểm cực trị
A
và
B
sao cho các điểm
A
,
B
và
1; 2
M
thẳng hàng.
A.
2
m
. B.
2
m
. C.
2
m
. D.
2
m
;
2
m
.
Lời giải
Ta có:
2
3 6y x mx
;
0
y
2
3 6 0
x mx
0
x
,
2x m
.
Đồ thị hàm số có hai điểm cực trị khi và chỉ khi phương trình
0
y
có hai nghiệm phân biệt
2 0
m
0
m
.
Khi đó hai điểm cực trị là
0;2
A ,
3
2 ;2 4
B m m
.
Ta có
1;4
MA
,
3
2 1;4 4
MB m m
.
Ba điểm
A
,
B
và
1; 2
M
thẳng hàng
MA
,
MB
cùng phương
3
2 1 4 4
1 4
m m
3
2 1 1
1 1
m m
3
2 1 1
m m
3
2m m
2
2
m
2
m
(do
0
m
).
Câu 36. (THPT Nam Trực - Nam Định - 2018) Cho hàm số
3 2
1 3 2 2
3
m
y x m x m x
. Hàm
số đạt cực trị tại
1 2
,x x
thỏa mãn
1 2
2 1
x x
khi
m a
và
m b
. Hãy tính tổng
a b
.
A.
8
3
. B.
8
3
. C.
5
2
. D.
5
2
.
Lời giải
Có
2
2 1 3 2
y mx m x m
.
Hàm số đạt cực trị tại
1 2
,x x
thỏa mãn
1 2
2 1
x x
suy ra
2
2
m
x
m
.
Do
2
2
m
x
m
là nghiệm của phương trình
2
2 1 3 2 0
mx m x m
nên
2
2 2
2 1 3 2 0
m m
m m m
m m
2
2
3
m
m
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 37
Thử lại thấy
2
2
3
m
m
đều thỏa mãn yêu cầu bài toán.
Vậy
8
3
a b
.
Câu 37. (THPT Cao Bá Quát - 2018) Cho hàm số
3 2 3
2 3 1 6
y x m x mx m
. Tìm
m
để đồ thị
hàm số có hai điểm cực trị
,A B
sao cho độ dài
2
AB
.
A.
0
m
. B.
0
m
hoặc
2
m
. C.
1
m
. D.
2
m
.
Lời giải
Ta có
2
' 6 6 1 6y x m x m
.
2
1
' 0 1 0
x
y x m x m
x m
.
Để đồ thị hàm số có hai điểm cực trị thì
1
m
.
Khi đó ta có
3 2
1; 3 1 , ;3
A m m B m m
.
Có
2
2 2 6
3 2
2 1 3 3 1 2 1 1 2
AB m m m m m m
.
2
0
1 1
2
m
m
m
(thỏa mãn yêu cầu bài toán).
Câu 38. (THPT Phú Lương - Thái Nguyên - 2018) Tìm tất cả các giá trị của tham số
m
để đồ thị hàm
số
3 2
3 3 3
y mx mx m
có hai điểm cực trị
,A B
sao cho
2 2 2
2 20
AB OA OB
(trong đó
O
là gốc tọa độ)
A.
1
m
. B.
1
m
. C.
1
17
11
m
m
. D.
1
17
11
m
m
.
Lời giải
Tập xác định
D R
Ta có:
2
' 3 6y mx mx
Hàm số có hai điểm cực trị
0
m
Khi đó
0
' 0
2
x
y
x
Tọa độ điểm cực trị:
0;3 3 , 2; 3
A m B m
Theo giả thiết
2 2 2
2 20
AB OA OB
2
1
22 12 34 0 .
17
11
m
m m
m
Dạng 5. Tìm m để hàm số trùng phương có cực trị thỏa mãn điều kiện cho trước
Một số công thức tính nhanh “thường gặp“
liên quan cực trị hàm số
4 2
y ax bx c
1
cực trị:
0
ab
3
cực trị:
0
ab
0
a
:
1
cực
tiểu
0
a
:
1
cực đại
0
a
:
1
cực
đại,
2
cực tiểu
0
a
:
2
cực
đại,
1
cực tiểu
4
2
(0; ), ; , ; , 2
2 4 2 4 16 2 2
b b b b b
A c B C AB AC BC
a a a a a a a
với
2
4b ac
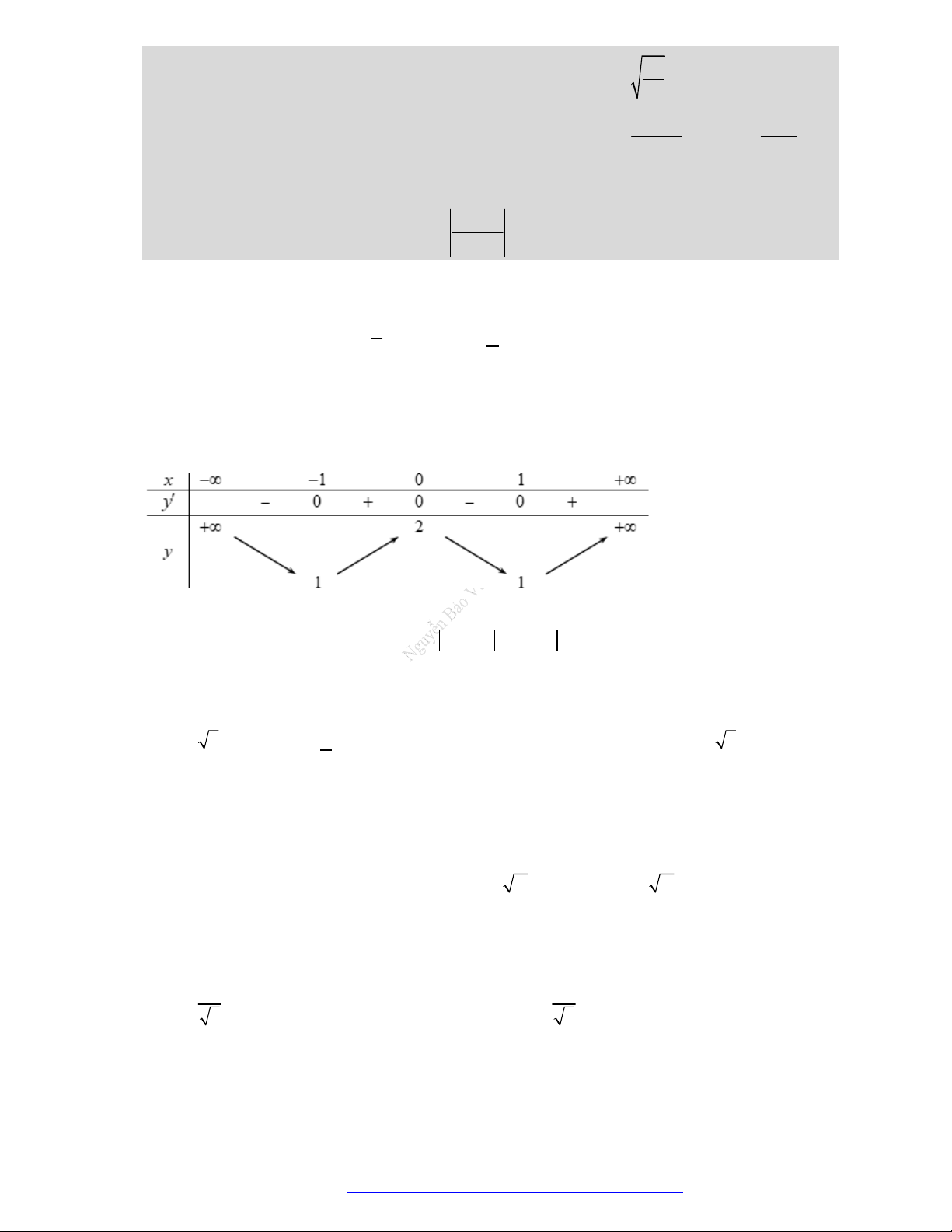
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 38 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Phương trình qua điểm cực trị:
:
4
BC y
a
và
3
, :
2
b
AB AC y x c
a
Gọi
BAC
, luôn có:
3
3
3
8
8 (1 ) (1 ) 0
8
b a
a cos b cos cos
b a
và
5
2
3
32
b
S
a
Phương trình đường tròn đi qua
2 2
, , : . 0,A B C x y c n x c n
với
2
4
n
b a
và bán
kính đường tròn ngoại tiếp tam giác là
3
8
8
b a
R
ab
Câu 1. (THPT Lương Thế Vinh - 2018) Cho hàm số
4 2
2 2y x x . Diện tích
S
của tam giác có ba
đỉnh là ba điểm cực trị của đồ thị hàm số đã cho có giá trị là
A.
3S
. B.
1
2
S
. C.
1S
. D.
2S
.
Lời giải
Tập xác định
D
.
Ta có
3
0 2
4 4 0
1 1
x y
y x x
x y
Bảng biến thiên
Đồ thị hàm số có ba điểm cực trị
0;2A
,
1;1B
,
1;1C
.
Nhận xét
ABC
cân tại
A
. Vì vậy
1 1
. .1.2 1
2 2
A B C B
S y y x x
.
Câu 2. (Chuyên Lê Hồng Phong - 2018) Tìm
m
đề đồ thị hàm số
4 2
2 1y x mx có ba điểm cực trị
0; 1 , , A B C
thỏa mãn
4?BC
A.
2m
. B.
4m
. C.
4m
. D.
2m
.
Lời giải
Tập xác định:
D
.
3
2
0
' 4 4 0
x
y x mx
x m
.
Hàm số đã cho có ba điểm cực trị
0m
.
Tọa độ điểm cực trị của đồ thị hàm số:
2 2
0;1 , ; 1 , ; 1 .A B m m C m m
4 4 16 4.BC m m
Câu 3. (Đề Minh Họa 2017) Tìm tất cả các giá trị thực của tham số
m
sao cho đồ thị của hàm số
4 2
2 1 y x mx
có ba điểm cực trị tạo thành một tam giác vuông cân
A.
3
1
9
m
. B.
1m
. C.
3
1
9
m
. D.
1m
.
Lời giải
Chọn D
Hàm số
4 2
2 1y x mx có tập xác định:
D
Ta có:
3 3 2
2
0
' 4 4 ; ' 0 4 4 0 4 0
x
y x mx y x mx x x m
x m

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 39
Hàm số có 3 cực trị khi và chỉ khi phương trình
có 2 nghiệm phân biệt khác
0
0 0
m m
.
Vậy tọa độ 3 điểm lần lượt là:
2 2
0;1 ; ;1 ; ;1
A B m m C m m
Ta có
2 2
; ; ;
AB m m AC m m
Vì
ABC
vuông cân tại
2 2 2 4 4
. 0 . 0 0 0
A AB AC m m m m m m m
1
m
( vì
0
m
)
Vậy với
1
m
thì hàm số có 3 cực trị tạo thành một tam giác vuông cân.
Câu 4. (Mã 105 -2017) Tìm tất cả các giá trị thực của tham số
m
để đồ thị của hàm số
4 2
2
y x mx
có
ba điểm cực trị tạo thành một tam giác có diện tích nhỏ hơn
1
.
A.
0 1m
B.
0m
C.
3
0 4m
D.
1m
Lời giải
Chọn A
Tập xác định
D
Ta có
3
4 4y x mx
.
3
2
0
0 4 4 0
x
y x mx
x m
.
Hàm số có ba điểm cực trị khi và chỉ khi
0m
. Khi đó đồ thị hàm số có ba điểm cực trị là
0; 0
O
,
2
;
A m m
,
2
;
B m m
.
Do đó
2 2
1 1
. .2 1 0 1.
2 2
OAB
S OH AB m m m m m
Câu 5. (Chuyên Nguyễn Trãi - Hải Dương - Lần 2 - 2020) Cho hàm số
4 2 2 4
2 2
y x mx m m
có
đồ thị (C). Biết đồ thị (C) có ba điểm cực trị A, B, C thỏa mãn ABCD là hình thoi với
0; 3
D
.
Số
m
thuộc khoảng nào sau đây?
A.
1 9
;
2 5
m
. B.
9
;2
5
m
. C.
1
1;
2
m
. D.
2;3
m
.
Lời giải
Chọn A
Tập xác định:
D
.
Ta có
3
2
0
' 4 4 ' 0
x
y x mx y
x m
.
Hàm số đã cho có ba điểm cực trị
0
m
.
Khi đó ba điểm cực trị của đồ thị hàm số là:
2 4
0; 2
A m m
;
4 2
; 3 ;
B m m m
4 2
; 3
C m m m
.
Gọi I trung điểm của BC
4 2
0; 3
I m m
Vì
,
A D Oy
, B và C đối xứng nhau qua Oy nên tứ giác ABCD là hình thoi
I là trung điểm
của AD
x
y
A
O
H
B
m
m
2
m
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 40 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
4 2 2 4 4 2
2
0
2
2 3 2 3 4 3 0
1 1
1
3 3
3
m
m m m m m m
m m
m
m m
m
.
Câu 6. (THPT Lê Quý Đôn Đà Nẵng 2019) Gọi S là tập hợp tất cả các giá trị của tham số m để đồ thị
hàm số
4 2 2
2 1
y x m x m
có ba điểm cực trị tạo thành ba đỉnh của một tam giác vuông. Số
phần tử của tập hợp S là
A.
2
. B.
0
. C.
4
. D.
1
.
Lời giải
•
4 2 2 3 2
2 1 ' 4 4 1 4 1
y x m x m y x m x x x m
.
• Hàm số có 3 điểm cực trị
' 0
y
có 3 nghiệm phân biệt.
2
1 0
x m
có 2 nghiệm phân biệt khác 0.
1 0
m
.
1
m
.
Khi đó:
1
' 0 0
1
x m
y x
x m
.
• Giả sử
, ,A B C
là ba điểm cực trị của đồ thị hàm số.
2
1; 2 1 , 0; , 1; 2 1
A m m B m C m m
2 2
1; 1 , 1; 1
AB m m CB m m
ABC
vuông tại
B
. 0
AB CB
4
1
1 1 0 0
0
m
m m m
m
.
Câu 7. (THPT Đoàn Thượng - Hải Phòng 2019) Cho hàm số
4 2
2 1 1
y x mx
. Tổng lập phương
các giá trị của tham số
m
để đồ thị hàm số
1
có ba điểm cực trị và đường tròn đi qua
3
điểm
này có bán kính
1R
bằng
A.
5 5
2
. B.
1 5
2
. C.
2 5
. D.
1 5
.
Lời giải
TXĐ:
.
D
3 2
' 4 4 4 ( ).y x mx x x m
Để đồ thị hs (1) có 3 điểm cực trị
0.
m
Gọi
2 2
(0;1), ( ; 1), ( ; 1)
A B m m C m m
là các điểm cực trị của đồ thị hs (1),
2
(0; 1)
I m
là trung điểm
.BC
Ta có
2 4
, .AI m AB AC m m
Suy ra
1 . . 2
.
2 4 .
AB AC BC AI
AI BC R
R AB AC
2
4 2
4
0 ( )
1 ( )
2
1 5
1 2 0
( )
2
1 5
( )
2
m l
m n
m
m m m
m l
m m
m n
Câu 8. (THPT Minh Châu Hưng Yên 2019) Tìm tất cả các giá trị thực của tham số m để đồ thị hàm
số
4 2 2
2 4
y x m x m
có ba điểm cực trị tạo thành ba đỉnh của một tam giác đều?

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 41
A.
0; 3; 3
m
B.
6 6
0; 3; 3
m
C.
6 6
3; 3
m
D.
3; 3
m
Lời giải
Chọn C
Đồ thị hàm số có
3
điểm cực trị
0
m
.
Khi đó,
3
điểm cực trị của đồ thị hàm số là
0; 4
A m
,
4
; 4
B m m m
,
4
; 4
C m m m
.
Tam giác
ABC
có
AB AC
nên tam giác
ABC
cân tại
A
, suy ra tam giác
ABC
đều
AB BC
2 8 8 2 2
6
0
2 4
3
m
m m m m m m
m
.
Kết hợp điều kiện ta được
6 6
3; 3
m
.
Câu 9. (THPT Quang Trung Đống Đa Hà Nội 2019) Tìm
m
để đồ thị hàm số
4 2 2
2 1
y x m x
có 3
điểm cực trị lập thành một tam giác vuông cân.
A.
1
m
. B.
1;1
m
. C.
1;0;1
m
. D.
m
.
Lời giải
4 2 2
2 1
y x m x
.
+ Cách 1:
Hàm số có 3 cực trị
2
0 2 0 0
ab m m
.
3 2
4 4
y x m x
3 2
2 2
1
1
4
2 2
4
3
3
0 4 4 0
4 0
1
0
1
1
y x m x
x x m
y
x
x m y m
x m
y m
Giả sử
0;1
A
,
4
; 1
B m m
,
4
; 1
C m m
là 3 điểm cực trị của đồ thị hàm số.
4
;
AB m m
2 8
AB m m
.
4
;
AC m m
2 8
AC m m
.
Yêu cầu bài toán
ABC
vuông cân tại
A
. 0
AB AC
AB AC
2 8
0
m
m m
2 6
1 0
m m
0 ( )
1 ( )
1( )
m l
m n
m n
.
Vậy
1;1
m
.
+ Cách 2: (Áp dụng công thức tính nhanh cực trị hàm trùng phương)
Yêu cầu bài toán
2
6
3
2
3
2 0
0
0
0
8
1 ( )
8
1
1
1
1( )
2
m
m
ab
m
m n
a
m
m n
m
b
.
Vậy
1;1
m
.
Câu 10. (Toán Học Tuổi Trẻ Số 5) Tìm tất cả các giá trị
m
sao cho đồ thị hàm số
4 2
1 2 1
y x m x m
có ba điểm cực trị là ba đỉnh của một tam giác có một góc bằng
120
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 42 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
3
2
1
3
m
. B.
3
2
1
3
m
,
1
m
.
C.
3
1
3
m
. D.
1
m
.
Lời giải
Ta có
3 2
4 2 1 2 2 1
y x m x x x m
.
2
0
0
2 1
x
y
x m
Hàm số có ba điểm cực trị khi và chỉ khi
0
y
có ba nghiệm phân biệt
1 0 1
m m
.
Khi đó
0; 2 1
A m
,
2
1
1
; 2 1
2 4
m
m
B m
,
2
1
1
; 2 1
2 4
m
m
C m
, là các điểm
cực trị của đồ thị.
Ta thấy
4
1
1
2 16
m
m
AB AC
nên tam giác
ABC
cân tại
A
.
Từ giả thiết suy ra
120
A
.
Gọi
H
là trung điểm
BC
, ta có
2
1
0; 2 1
4
m
H m
2
1
1
tan 60 . 3
4 2
m
m
BH AH
4
3
3
3 1
1 2
3 1 8 1
16 2
3
m
m
m m
.
Câu 11. (Chuyên Lương Văn Chánh - Phú Yên - 2018) Gọi
S
là tập hợp tất cả các giá trị thực của
tham số
m
để đồ thị
C
của hàm số
4 2 2 4
2 5
y x m x m
có ba điểm cực trị, đồng thời ba
điểm cực trị đó cùng với gốc tọa độ
O
tạo thành một tứ giác nội tiếp. Tìm số phần tử của
S
.
A.
1
. B.
0
. C.
2
. D.
3
.
Lời giải
Ta có
3 2
4 4
y x m x
.
Hàm số có cực đại cực tiểu
phương trình
0
y
có ba nghiệm phân biệt
0
m
.
Gọi
4
0; 5
A m
,
;5
B m
,
;5
C m
lần lượt là ba điểm cực trị của đồ thị hàm số.
Gọi
I
là tâm đường tròn ngoại tiếp tứ giác
ABOC
khi đó ta có ba điểm
A
,
I
,
O
thẳng hàng.
Mặt khác do hai điểm
B
và
C
đối xứng nhau qua
AO
nên
AO
là đường kính của đường tròn
ngoại tiếp tứ giác
ABOC
AB OB
. 0
AB OB
.
Trong đó
4
;
AB m m
,
;5
OB m
. Ta có phương trình
2 4
5 0
m m
5
5
m
Câu 12. (Chuyên Quang Trung - 2018) Cho hàm số
4 2 2 4
2 2
y x mx m m
có đồ thị
C
. Biết đồ thị
C
có ba điểm cực trị
A
,
B
,
C
và
ABDC
là hình thoi trong đó
0; 3
D
,
A
thuộc trục tung.
Khi đó
m
thuộc khoảng nào?
A.
9
;2
5
m
. B.
1
1;
2
m
. C.
2;3
m
. D.
1 9
;
2 5
m
.
Lời giải

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 43
Ta có
2
4
y x x m
2
0
0
x
y
x m
;
Với điều kiện
0
m
đồ thị hàm số có ba điểm cực trị là
4 2
0; 2
A m m
;
4 2
; 3
B m m m
;
4 2
; 3
C m m m
. Để
ABDC
là hình thoi điều kiện là
BC AD
và trung điểm
I
của
BC
trùng
với trung điểm
J
của
AD
. Do tính đối xứng ta luôn có
BC AD
nên chỉ cần
I J
với
4 2
0; 3 ,
I m m
4 2
2 3
0;
2
m m
J
.
ĐK:
4 2 4 2
2 3 2 6m m m m
4 2
4 3 0
m m
1
3
m
m
1 9
;
2 5
m
.
Câu 13. (THPT Nguyễn Huệ - Ninh Bình - 2018) Cho hàm số
4 2
2 2
y x mx
có đồ thị
m
C
. Tìm
m
để đồ thị hàm số có ba điểm cực trị tạo thành một tam giác vuông.
A.
3
3
m . B.
3
3
m . C.
1
m
. D.
1
m
.
Lời giải
Cách 1:
Ta có
3 2
4 4 4
y x mx x x m
.
Để hàm số có ba cực trị thì phương trình
0
y
có ba nghiệm phân biệt
2
4 0
x x m
có ba
nghiệm phân biệt
0
m
.
Gọi
0;2
A
,
2
, 2
B m m
,
2
, 2
C m m
là ba điểm cực trị của đồ thị hàm số.
Vì
ABC
cân tại
A
nên
ABC
chỉ có thể vuông tại
A
0
AB AC
.
Với
2
;
AB m m
,
2
;
AC m m
4 3
0 1 0 1
m m m m m
.
Cách 2: Áp dụng công thức tính nhanh: Ba điểm cực trị của đồ thị hàm số
4 2
y ax bx c
tạo
thành một tam giác vuông khi
3 3
8 0 8 8 0 1
a b m m
.
Câu 14.
(CHUYÊN ĐHSPHN - 2018) Gọi
A
,
B
,
C
là các điểm cực trị của đồ thị hàm số
4 2
2 4
y x x
. Bán kính đường tròn nội tiếp tam giác
ABC
bằng
A.
1
. B.
2 1
. C.
2 1
. D.
2
.
Lời giải
3
0 0;4
4 4 0 1 1;3
1 1;3
x A
y x x x B
x C
.
1; 1 2
AB AB
;
1; 1 2
AC AC
;
2;0 2
BC BC
.
Ta có
ABC
vuông cân tại
A
có
2
1
2 1
2
S
,
2 1
2
AB AC BC
p
.
Vậy
1
2 1
2 1
S
r
p
.
Câu 15. (Hồng Bàng - Hải Phòng - 2018) Cho hàm số
4 2
2 4 5
y x m x m
có đồ thị
m
C
. Tìm
m
để
m
C
có ba điểm cực trị tạo thành một tam giác nhận gốc tọa độ
O
làm trọng tâm.
A.
1
m
hoặc
17
2
m
. B.
1
m
. C.
4
m
. D.
17
2
m
.
Lời giải
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 44 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta có
3
4 4 4y x m x
;
2
0
0
4
x
y
x m
.
Để hàm số có ba điểm cực trị
4
m
. Khi đó các điểm cực trị của
m
C
là
0; 5
A m
,
2
4 ; 5 4
B m m m
,
2
4 ; 5 4
C m m m
.
Do
O
là trọng tâm tam giác
ABC
nên
2
3 5 2 4
m m
1
17
2
m
m
.
Do
4
m
nên
1
m
.
Câu 16. (Chuyên Vĩnh Phúc 2018) Tìm tất cả các giá trị thực của tham số
m
để đồ thị của hàm số
4 2
2
y x mx
có ba điểm cực trị tạo thành một tam giác có diện tích nhỏ hơn
1
.
A.
1
m
. B.
0 1
m
. C.
3
0 4
m
. D.
0
m
.
Lời giải
Hàm số
4 2
2
y x mx
có
TXĐ: D
. Ta có
3
4 4y x mx
;
2
0
0
x
y
x m
.
Để đồ thị hàm số có ba điểm cực trị thì
0
m
. Khi đó ba điểm cực trị là
0;0
O
,
2
;
B m m
,
2
;
C m m
. Ta giác
OBC
cân tại
O
, với
2
0;
I m
trung điểm của
BC
Theo yêu cầu bài toán, ta có:
2
1 1
. .2 1 0 1
2 2
ABC
S OI BC m m m
.
Câu 17. (Liên Trường - Nghệ An -2018) Gọi
0
m
là giá trị của tham số
m
để đồ thị hàm số
4 2
2 1
y x mx
có ba điểm cực trị tạo thành một tam giác có diện tích bằng
4 2
. Mệnh đề nào
sau đây đúng
A.
0
1;0
m
. B.
0
2; 1
m
. C.
0
; 2
m
. D.
0
1;0
m
.
Lời giải
Ta có:
4 2
2 1
y x mx
3
4 4y x mx
.
0
y
2
0
x
x m
(1).
Để đồ thị hàm số
4 2
2 1
y x mx
có ba điểm cực trị thì
0
y
phải có ba nghiệm phân biệt tức
là
0
m
.
Khi đó
0
1
x
x m
nên ta gọi
0; 1
A
,
2
; 1
B m m
,
2
; 1
C m m
Tam giác
ABC
cân tại
A
nên
1
.
2
ABC
S AH BC
với
H
là trung điểm của
BC
nên
2
0; 1
H m
. Nên:
2
2 2
AH m m
và
2
2 2
BC m m
.
Ta có:
2
1
. .2
2
ABC
S m m
theo giả thiết
4 2
ABC
S
nên
2
4 2 2
m m m
.
Câu 18. (Chuyên Bắc Ninh - 2018) Tìm tất cả các giá trị thực của tham số
m
sao cho đồ thị của hàm số
4 2 2
2 1
y x m x m
có ba điểm cực trị tạo thành một tam giác vuông cân.
A.
0
m
.
B.
1; 0
m m
. C.
1
m
. D.
1; 0
m m
.
Lời giải
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 45
Cách 1: Điều kiện để đồ thị hàm trùng phương
4 2
y ax bx c
có ba điểm cực trị là
0 1ab m
loại B
Khi đó ba điểm cực trị lập thành tam giác vuông cân khi
3
3
8 0 8 1 8 0 0b a m m
.
Cách 2: Ta có
2
4 1y x x m
Xét
2
0
0
1
x
y
x m
. Để đồ thị số có ba điểm cực trị thì
1m
*
Tọa độ ba điểm cực trị là
2
0; ,A m
1; 2 1 ,B m m
1; 2 1C m m
Gọi
H
là trung điểm của đoạn thẳng
BC
thì
0; 2 1H m
Khi đó ba điểm cực trị lập thành tam giác vuông cân khi
AH BH
4
1 1m m
0 : / *m T m
.
Câu 19. (THPT Triệu Thị Trinh - 2018) Cho hàm số:
4 2 2
2y x mx m m . Tìm
m
để đồ thị hàm số
có 3 điểm cực trị lập thành tam giác có một góc bằng
120
.
A.
1
3
m
. B.
3
1
3
m . C.
3
1
3
m
. D.
1
3
m .
Lời giải
3 2
4 4 4y x mx x x m
.
Hàm số có ba điểm cực trị
0y
có ba nghiệm phân biệt
0m
.
Khi đó
0y
0x
x m
.
Ba điểm cực trị của đồ thị hàm số là
2
0;A m m
,
;B m m ,
;C m m .
Do
ABC
cân tại
A
nên gọi
0;H m
là trung điểm của
BC
thì
AHC
vuông tại
H
.
ABC
có một góc bằng
120
khi và chỉ khi
60HAB HAC
.tanHB AH HAB
2
3m m
3
1
3
m . Bỏ cặp ngoặc.
Câu 20. (THPT Thái Phiên - Hải Phòng - 2018) Đồ thị hàm số
4 2
2y x mx m
có ba điểm cực trị và
đường tròn đi qua ba điểm cực trị này có bán kính bằng
1
thì giá trị của
m
là:
A.
1 5
1;
2
m m
. B.
1 5
1;
2
m m
.
C.
1 5
1;
2
m m
. D.
1 5
1;
2
m m
.
Lời giải
4 2 3
2 4 4y x mx m y x mx
.
Với
0m
ta có ba cực trị
2 2
0; ; ; ; ;A m B m m m C m m m .

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 46 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
4R
ABC
abc
S
2
2
1
2 2
2 4
mAB
m m
2 4 4 2
2 2 0
m m m m m m
.
0
1
1 5
2
1 5
2
m l
m n
m n
m l
Dạng 6. Tìm m để hàm số bậc 2 trên bậc 1 có cực trị thỏa mãn yêu cầu bài toán
Câu 1. (Toán Học Tuổi Trẻ Số 5) Viết phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm
số
2
2 3
2 1
x x
y
x
.
A.
2 2
y x
. B.
1y x
. C.
2 1y x
. D.
1y x
.
Lời giải
Tập xác định
1
\
2
D
.
2
2
2 2 4
2 1
x x
y
x
,
2
0 2 2 4 0
y x x
1 2
2 1
x y
x y
.
Đồ thị hàm số có hai điểm cực trị là
1;2
M
và
2; 1
N
.
Vậy phương trình đường thẳng qua hai điểm cực trị
,M N
của đồ thị hàm số đã cho là:
1y x
.
Cách khác:
Áp dụng tính chất: Nếu
0
x
là điểm cực trị của hàm số hữu tỷ
u x
y
v x
thì giá trị cực trị tương
ứng của hàm số là
0 0
0
0 0
u x u x
y
v x v x
. Suy ra với bài toán trên ta có phương trình đường thẳng
qua hai điểm cực trị của đồ thị hàm số là
2
2 3
1
2 1
x x
y x
x
.
Câu 2. (ĐHQG Hà Nội - 2020) Điều kiện của tham số
m
để hàm số
2
1
x mx
y
x
có cực đại và cực tiểu
là
A.
0
m
. B.
1
m
. C.
2
m
. D.
2
m
.
Lời giải
Chọn A
Điều kiện
1x
.
Ta có
2
1
x mx
y
x
2
2
2
1
x x m
y
x
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 47
Hàm số
2
1
x mx
y
x
có cực đại và cực tiểu
0
y
có hai nghiệm phân biệt và đổi dấu khi đi
qua hai điểm đó
2
2 0
x x m
có hai nghiệm phân biệt khác
1
0 1 0
1
1 2 0 1
m
m
m m
.
Vậy
1
m
thì hàm số đã cho có cực đại và cực tiểu.
Không có đáp án hoặc chọn A.
Câu 3. (Chuyên KHTN - Hà Nội - Lần 3) Gọi
S
là tập hợp tất cả các giá trị thực của tham số
m
để đồ
thị hàm số
2
2
1
x mx m
y
x
có
hai điểm cực trị
A
,
B
và tam giác
OAB
vuông tại
O
. Tổng tất cả các phần tử của
S
bằng
A.
9
. B.
1
. C.
4
. D.
5
.
Lời giải
Chọn A
2
2
2
, 1
1
x x m
x
x
y
. Đặt
2
2
m
f x xx
,
2
2m
h xx mx
,
1
g x
x
.
Đồ thị hàm số đã cho có hai điểm cực trị
A
,
B
khi
f x
có hai nghiệm phân biệt
1
x
,
2
x
khác
1
1 0
1 1 0
m
f m
1 1
m
. Khi đó
1
1 1
1
2
2 2
2
( )
( )
2
2
h x
y x x m
g x
h x
y x x m
g x
.
Suy ra
1 1
;2
A x x m
,
2 2
;2
B x x m
. Suy ra
1 1
;2
OA x x m
,
2 2
;2
OB x x m
.
OAB
vuông tại
O
khi
1 2 1 2
2 2
, 0 2
. . 0 3
OA OB
OA OB x x x m x m
.
2 1 2
2
1
5 . 2 0
3 m x x m x x
. Kết hợp với định lí Vi-et cho phương trình
0
f x
ta
được
2
5 4 0m mm
0 « · 2
9 · 1 , 2
m kh ng tháa m n
m tháa m n
9
S
.
Vậy tổng tất cả các phần tử của
S
bằng 9.
Câu 4. (Chuyên Lê Hồng Phong - Nam Định - 2020) Biết rằng đồ thị
2
2
:
2
x x m
H y
x
(với
m
là
tham số thực) có hai điểm cực trị là
,A B
. Hãy tính khoảng cách từ gốc tọa độ
0;0
O
đến đường
thẳng
AB
.
A.
2
5
. B.
5
5
. C.
3
5
. D.
1
5
.
Lời giải
Chọn A
+ Phương trình của đường thẳng AB là
/
2
/
2
2 2 2 2 0
2
x x m
y y x x y
x
.
+ Khoảng cách
2
2
2.0 0 2
2
;
5
2 1
d O AB
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 48 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 5. (Chuyên Hùng Vương - Phú Thọ - 2018) Gọi
S
là tập hợp các giá trị thực của tham số
m
để đồ
thị hàm số
2 2
1
x mx m
y
x
có hai điểm cực trị
,A B
. Khi
90
AOB
thì tổng bình phương tất
cả các phần tử của
S
bằng:
A.
1
16
. B.
8
. C.
1
8
. D.
16
.
Lời giải
2 2
2
2 1
1
x m x x mx m
y
x
2 2
2
2
1
x x m m
x
Để đồ thị hàm số có hai điểm cực trị
,A B
thì
0
y
phải có hai nghiệm phân biệt khác
1
2
2
1 0
1 0
m m
m m
m
.
Phương trình đường thẳng đi qua 2 điểm cực đại, cực tiểu là 2
A
y x m
.
Gọi
;
A
x
B
x
là hoành độ của
A
,
B
khi đó
;
A
x
B
x
là nghiệm của
2 2
2
x x m m
.
Theo định lí Viet ta có
2
A B
x x
;
2
.
A B
x x m m
.
2
A A
y x m
; 2
B B
y x m
.
90
AOB
. . 0
A B A B
x x y y
2
4 2 0
A B A B A B
x x x x m x x m
2 2
5 4 0
m m m m
2
4 0
m m
1
0;
4
m m
.
Tổng bình phương tất cả các phần tử của
S
bằng:
2
2
1 1
0
4 16
.
Câu 6. (Chuyên KHTN - 2018) Với tham số
m
, đồ thị của hàm số
2
1
x mx
y
x
có hai điểm cực trị
A
,
B
và
5
AB
. Mệnh đề nào dưới đây đúng?
A.
2
m
. B.
0 1
m
. C.
1 2
m
. D.
0
m
.
Lời giải
Ta có
\ 1
D
và có đạo hàm là
2
2
2
1
x x m
y
x
.
Để hàm số có hai điểm cực trị ta phải có
1 0
1 2 0
m
m
1
m
.
Gọi hai hoành độ cực trị là
1
x
và
2
x
ta có
1 2
1 2
2
x x
x x m
.
Khi đó điểm
1 1
,2
A x x m
và
2 2
,2
B x x m
.
4 4 . 5 5
AB m
1
4 4 5
4
m m
.
Câu 7. (Cụm 5 Trường Chuyên - ĐBSH - 2018) Cho hàm số
2
4
x m x
y
x m
. Biết rằng đồ thị hàm số
có hai điểm cực trị phân biệt là
A
,
B
. Tìm số giá trị
m
sao cho ba điểm
A
,
B
,
4;2
C
phân
biệt và thẳng hàng.
A.
0
. B.
2
. C.
1
. D.
3
.
Lời giải
Tập xác định
\
D m
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 49
Ta có
2
4
4
x m x
y x
x m x m
.
2
4
1y
x m
,
x D
,
0
y
2
2
x m
x m
.
Tọa độ hai điểm cực trị là
2 ;4
B m m
,
2 ; 4
A m m
.
4;8
AB
,
6 ;6
AC m m
.
Ba điểm
A
,
B
,
4;2
C
phân biệt và thẳng hàng
6 0
AC k AB
m
6 4
6 8
6 0
m k
m k
m
(vô nghiệm).
Vậy không có giá trị
m
nào thỏa mãn.
Câu 8. (THCS - THPT Nguyễn Khuyến - 2018) Giá trị của tham số
m
để hàm số
2
1x mx
y
x m
đạt
cực đại tại điểm
0
2
x
là:
A.
1
m
. B.
3
m
. C.
1
m
. D.
3
m
.
Lời giải
2 3
1 2
' 1 ; ''y y
x m x m
.
Hàm số
2
1x mx
y
x m
đạt cực đại tại điểm
0
2
x
khi
' 2 0
'' 2 0
y
y
2
3
1
1 0
2
2
0
2
m
m
1
3
3
2
m
m
m
m
. Thử lại thấy thỏa mãn.
Câu 9. (THPT Nam Trực - Nam Định - 2018) Cho hàm số
2
2 2
2 2
x mx m
y
x m
. Để hàm số có cực
đại và cực tiểu, điều kiện của tham số
m
là:
A.
1
2
m
m
B.
1 2
m
. C.
2 1
m
. D.
2
1
m
m
.
Lời giải
Điều kiện:
x m
.
Đạo hàm
2 2
2
2 2 2
2
x mx m m
y
x m
.
Để hàm số có cực đại và cực tiểu, thì
0
y
2 2
2 2 2 0
x mx m m
có hai nghiệm phân
biệt khác
m
.
Ta có:
2
2 2
2 0
2 . 2 2 0
m m
m m m m m
2
1 2
2 0
m
m m
1 2
m
.
Câu 10. (Chuyên Nguyễn Dình Triểu - Dồng Tháp - 2018) Để hàm số
2
1
x mx
y
x m
đạt cực đại tại
2x
thì
m
thuộc khoảng nảo?
A.
0;2
. B.
4; 2
. C.
2; 0
. D.
2;4
.
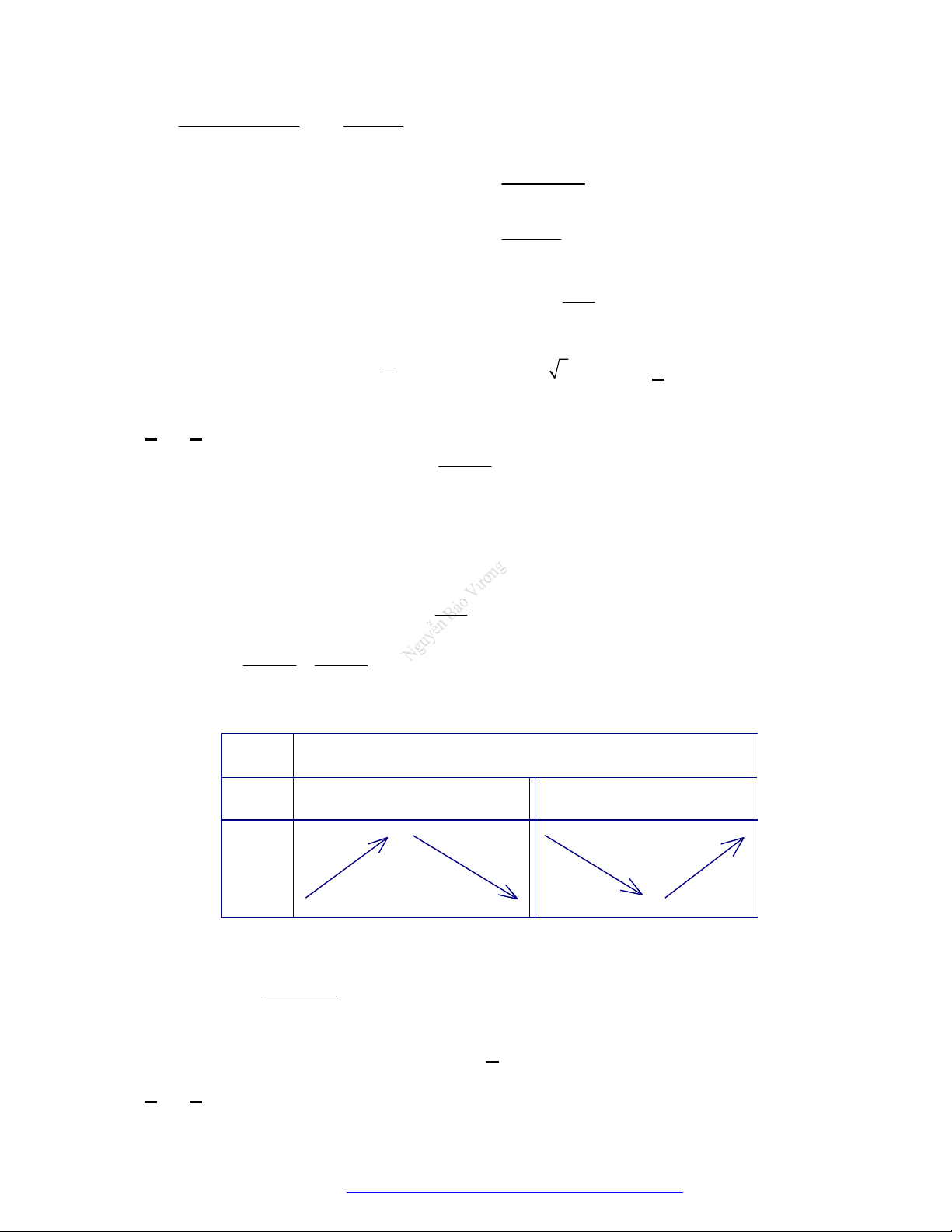
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 50 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Lời giải
TXĐ:
\D m
2 2
2 3
2 1 2
,
x mx m
y y
x m x m
Hàm số đạt cực đại tại
2x
nên
2
2
3
4 3
0
2 0
2
3
2
2 0
0
2
m m
y
m
m
y
m
thuộc
4; 2
.
Câu 11. (Chuyên Quốc Học Huế 2019) Cho hàm số
1
q
y x p
x
đạt cực đại tại điểm
2; 2A
.
Tính
pq
.
A.
2pq
. B.
1
2
pq
. C.
3pq
. D.
1pq
.
Lời giải
Chọn D
Tập xác định
\ 1D
. Ta có
2
1
1
q
y
x
.
Hàm số đạt cực đại tại
2x
, suy ra
2 0 0 1 1y q q
.
Lại có đồ thị hàm số đi qua điểm
2; 2A
nên
2 2 0p q p q
.
Do đó
1p q
.
Thử lại: với
1p q
ta được
1
1
1
y x
x
.
Ta có
2
2
2 2
0
1 2
1 0 2 0
2
1 1
x
x x
y x x
x
x x
.
Từ đó có bảng biến thiên của hàm số:
Rõ ràng đồ thị hàm số đạt cực đại tại điểm
2; 2A
. Vậy
1 1p q pq
.
Câu 12. Cho hàm số
2
1x mx
y
x m
( với
m
là tham số). Tìm tất cả các giá trị của tham số
m
để hàm số
có giá trị cực đại là 7.
A.
7m
. B.
5m
. C.
9m
. D.
5m
.
Lời giải
Chọn C
Tập xác định của hàm số là:
\D m
2
-2
+∞ +∞
-∞
-∞
0
-1
-2
x
0
0
y'
y
-
-
++
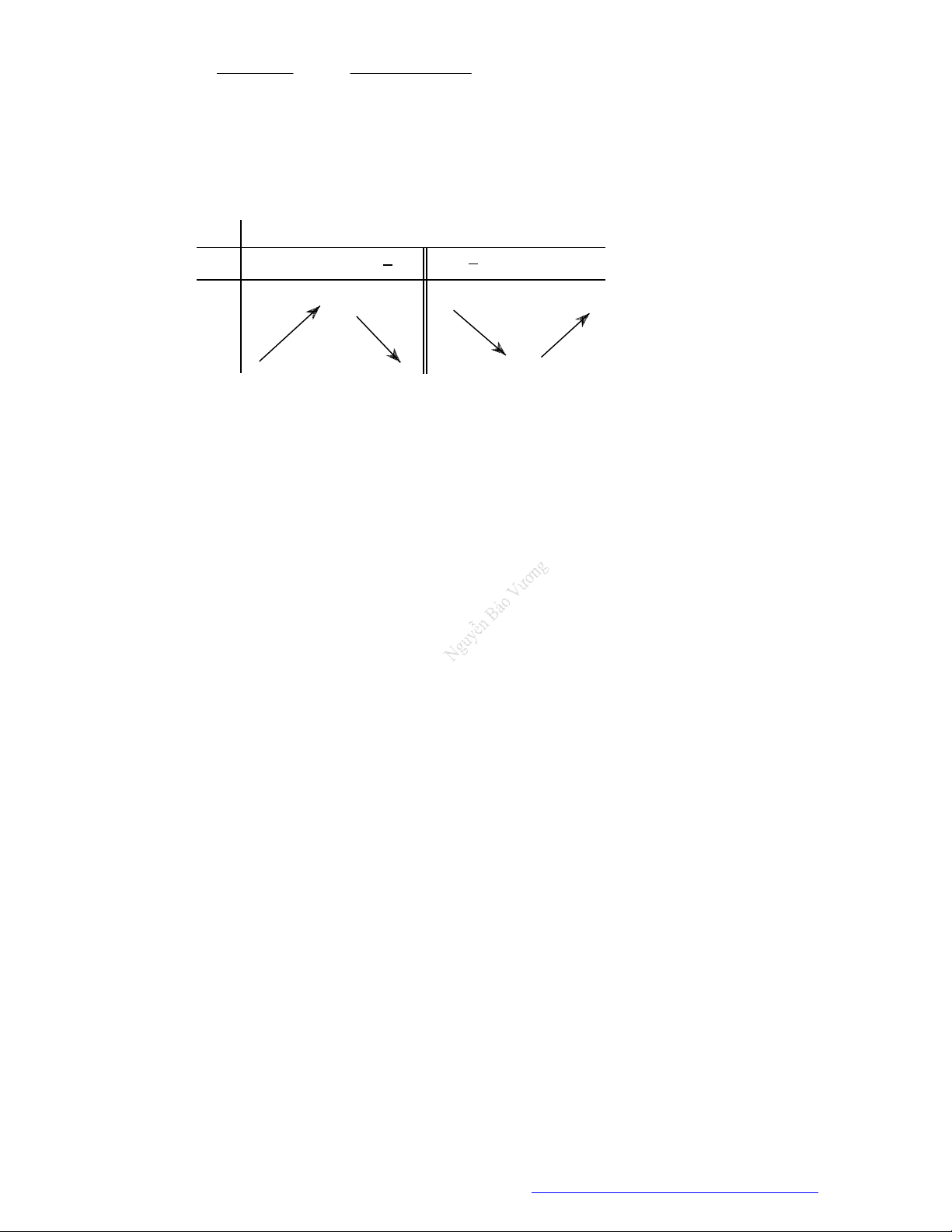
T
ÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 51
2 2 2
2
1
2 1x mx x mx m
y y
x m
x m
2
2
1
0
1
1
2 1 0
1
x m
x m
x m
y
x m
x m
x mx m
x m
Bảng
biến thiên
Từ bảng biến thiên ta thấy hàm số đạt cực đại tại
1x
m
.
Vậy
1
7 2 7 9y m m m
.
-------------------- HẾT --------------------
-∞
-∞
+∞
+∞
y
-∞ -
m
+
+
y'
x -m-1
-m+1 +∞
0
0
y
C
T
y
CĐ

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
Dạng 1. Bài toán cực trị hàm số chứa dấu trị tuyệt đối
Bài toán: Đồ thị hàm số
( )y f x
có bao nhiêu điểm cực trị
(Áp dụng định nghĩa).
2
2
2 ( ). ( )
( ) ( )
( )
f x f x
y f x f x y
f x
( ) 0 1
0
( ) 0 2
f x
y
f x
Số nghiệm của
1
chính là số giao điểm của đồ thị
( )y f x
và trục hoành
0y
. Còn số nghiệm
của
2
là số cực trị của hàm số
( )y f x
, dựa vào đồ thị suy ra
2
. Vậy tổng số nghiệm bội lẻ
của
1
và
2
chính là số cực trị cần tìm.
Dạng toán này mình làm tựa theo đề tham khảo 2018, vẫn xuất hiện ở dạng toán hàm hợp, các
bạn học chú ý nhé!
Câu 1. (Chuyên Vinh – Lần 2). Đồ thị
C
có hình vẽ bên.
Tất cả các giá trị của tham số
m
để hàm số
y f x m
có ba điểm cực trị là:
A.
1m
hoặc
3m
. B.
3m
hoặc
1.m
C.
1m
hoặc
3m
. D.
1 3.m
Giải
Cách 1:
Do
y f x m
là hàm số bậc ba
Khi đó, hàm số
y f x m
có ba điểm cực trị
hàm số
y f x m
có
D
. 0
C CT
y y
(hình minh họa)
CỰC TRỊ CỦA HÀM SỐ
Chuyên đề 2
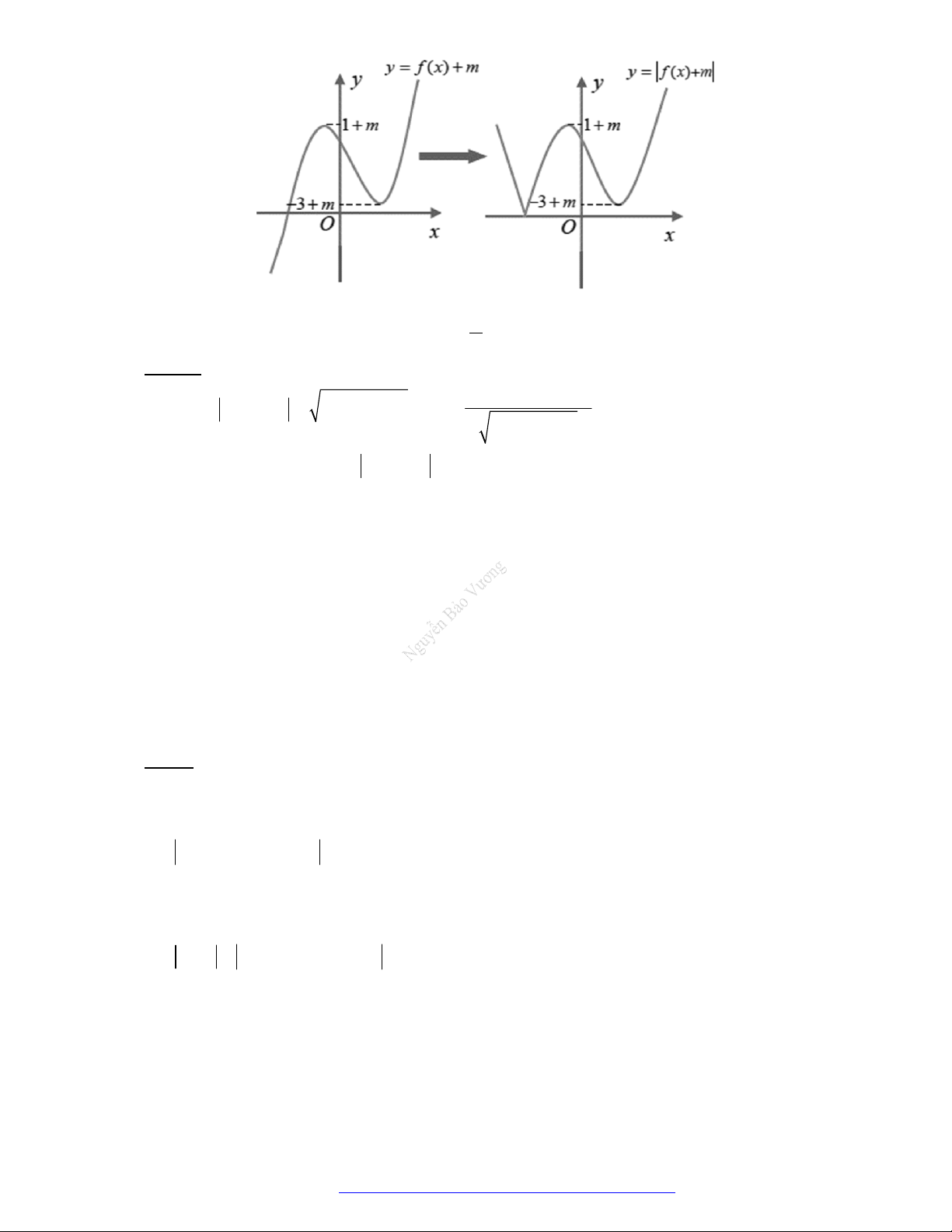
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
1
1 3 0
3
m
m m
m
Đáp án A
Cách 2:
Ta có
y f x m
=
2
2
.
.
f x m f x
f x m y
f x m
Để tìm cực trị của hàm số
y f x m
, ta tìm
x
thỏa mãn
'
0y hoặc
'
y không xác định.
1
2
0
f x
f x m
Dựa vào đồ thị, suy ra hàm số có 2 điểm cực trị
1 2
,x x trái dấu.
Suy ra (1) có hai nghiệm
1 2
,x x trái dấu.
Vậy để đồ thị hàm số có 3 cực trị thì (2) có một nghiệm khác
1 2
,x x .
Số nghiệm của (2) chính là số giao điểm của đồ thị
C
và đường thẳng
y m
.
Do đó để (2) có một nghiệm thì dựa vào đồ thị ta có điều kiện:
1 1
3 3
m m
m m
Đáp án. A.
Chú ý:
Nếu
0
x x là cực trị của hàm số
y f x
thì
'
0
0f x
hoặc không tồn tại
0
f x
.
Câu 2. (Đề Tham Khảo 2018) Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
4 3 2
3 4 12y x x x m
có
7
điểm cực trị?
A.
5
B.
6
C.
4
D.
3
Lời giải.
Chọn C
4 3 2
3 4 12y f x x x x m
Ta có:
3 2
12 12 24f x x x x
.;
0 0f x x
hoặc
1x
hoặc
2x
.
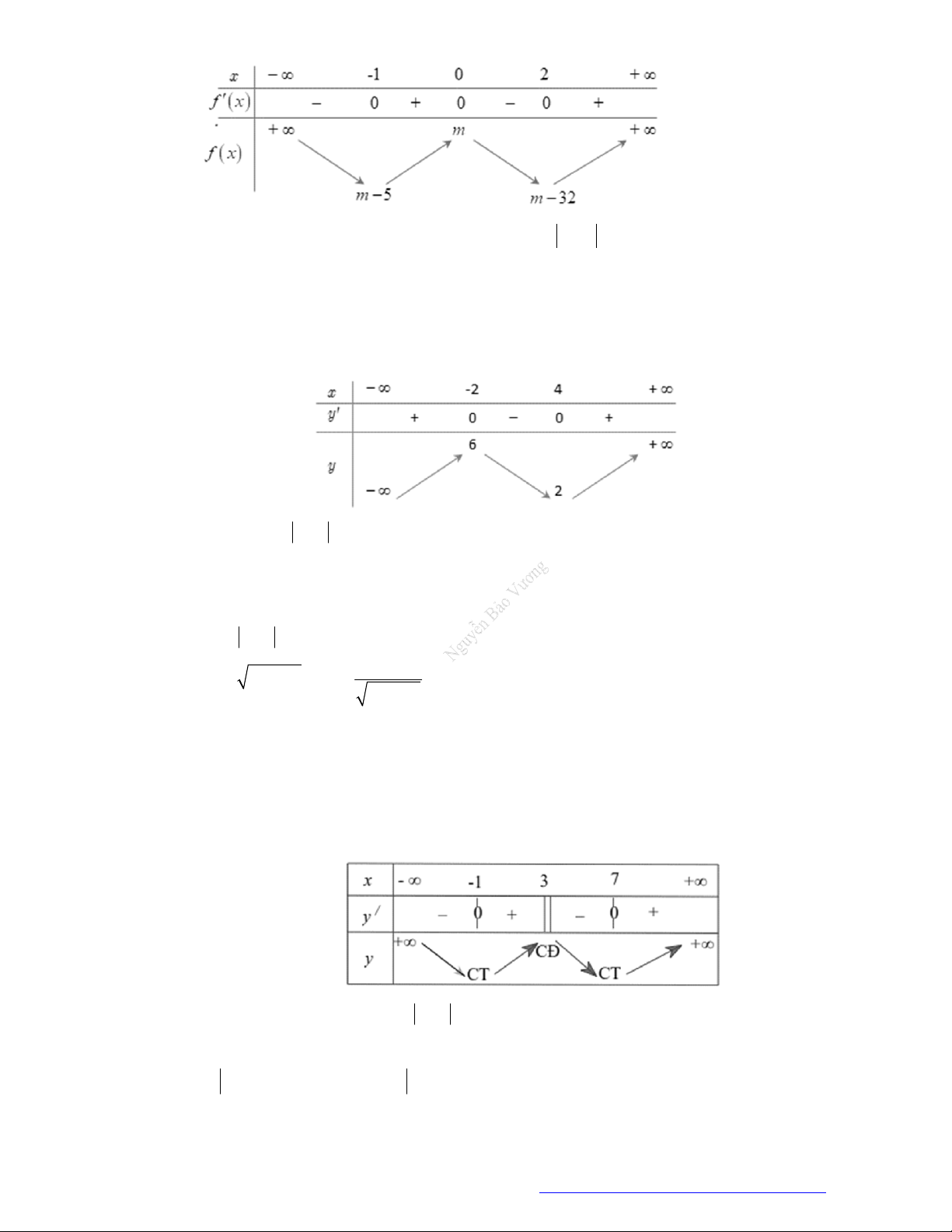
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Do hàm số
f x
có ba điểm cực trị nên hàm số
y f x
có
7
điểm cực trị khi
Phương trình
0f x
có 4 nghiệm
0
0 5
5 0
m
m
m
.
Vậy có
4
giá trị nguyên thỏa đề bài là
1; 2; 3; 4m m m m
.
Câu 3. (Gia Bình 2019) Cho hàm số
( )y f x
có bảng biến thiên như sau.
Hàm số
3 y f x
có bao nhiêu điểm cực trị
A.
5
B.
6
C.
3
D.
1
Lời giải
Chọn C
3 1 y f x
, Đặt
| 3 |, 0 t x t
Thì (1) trở thành:
( )( 0) y f t t
Có
2
2
3
( 3) '
( 3)
x
t x t
x
Có
( )
x x
y t f t
3 3
0
0 ( ) 0 2( ) 7
( ) 0
4 1
x
x x
x x
t
y t f t t L x
f t
t x
Lấy x=8 có
'(8) '(5) 0t f
, đạo hàm đổi dấu qua các nghiệm đơn nên ta có bảng biến thiên:
Dựa vào BBT thì hàm số
3 y f x
có 3 cực trị.
Câu 4. (Cụm Liên Trường Hải Phòng 2019) Tìm số các giá trị nguyên của tham số
m
để đồ thị hàm số
4 2 2
2 2 12y x mx m m
có bảy điểm cực trị
A.
1
. B.
4
. C.
0
. D.
2
.
Lời giải
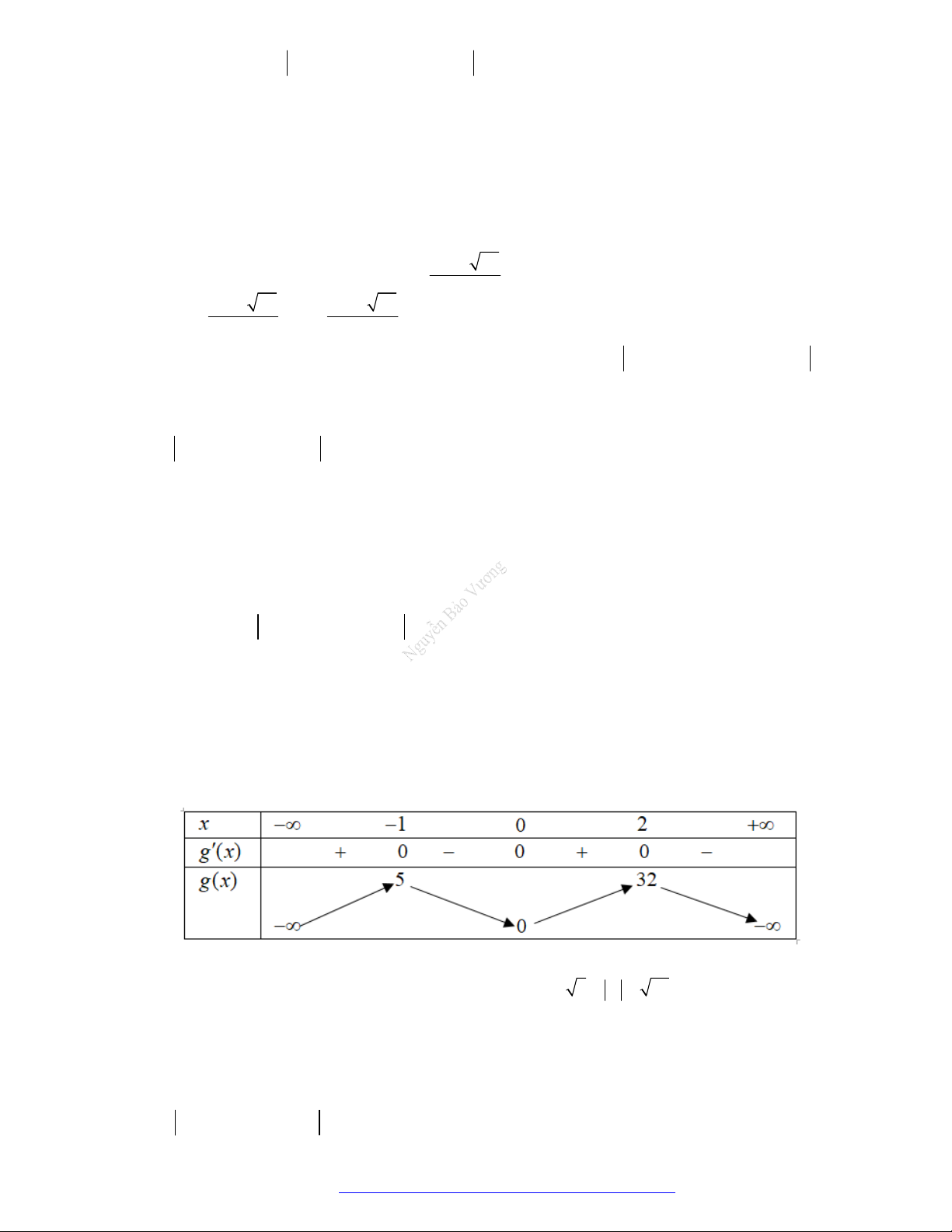
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Đồ thị hàm số
4 2 2
2 2 12y x mx m m
có bảy điểm cực trị khi và chỉ khi đồ thị hàm số
4 2 2
2 2 12y x mx m m
cắt trục hoành tại bốn điểm phân biệt
4 2 2
2 2 12 0x mx m m
có bốn nghiệm phân biệt khi và chỉ khi
2 2
2
2 12 0
2 0
2 12 0
m m m
m
m m
4 3
0
1 97 1 97
4 4
m
m
m m
1 97
3
4
m
Vậy không có giá trị nguyên của tham số
m
để đồ thị hàm số
4 2 2
2 2 12y x mx m m
có
bảy điểm cực trị.
Câu 5. (Sở Vĩnh Phúc 2019) Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
4 3 2 2
3 4 12y x x x m
có đúng 5 điểm cực trị?
A.
5
. B.
7
. C.
6
. D.
4
.
Lời giải
Xét hàm số
4 3 2 2
( ) 3 4 12f x x x x m ;
3 2
( ) 12 12 24f x x x x
1 2 3
( ) 0 0; 1; 2f x x x x
. Suy ra, hàm số
( )y f x
có 3 điểm cực trị.
Hàm số
4 3 2 2
3 4 12y x x x m
có 5 điểm cực trị khi đồ thị hàm số
( )y f x
cắt trục hoành
tại 2 điểm phân biệt
4 3 2 2
3 4 12 0x x x m
có 2 nghiệm phân biệt.
Phương trình
4 3 2 2 4 3 2 2
3 4 12 0 3 4 12x x x m x x x m
(1).
Xét hàm số
4 3 2
g( ) 3 4 12x x x x ;
3 2
g ( ) 12 12 24x x x x
.
Bảng biến thiên:
Phương trình (1) cớ 2 nghiệm phân biệt
2
2
0
5 32
5 32
m
m
m
.
Vậy
3;4;5; 3; 4; 5m
.
Câu 6. (Chuyên Vĩnh Phúc 2019) Có bao nhiêu giá trị nguyên dương của tham số
m
để hàm số
4 3 2
3 4 12y x x x m
có
5
điểm cực trị.
A.
16
B.
44
C.
26
D.
27
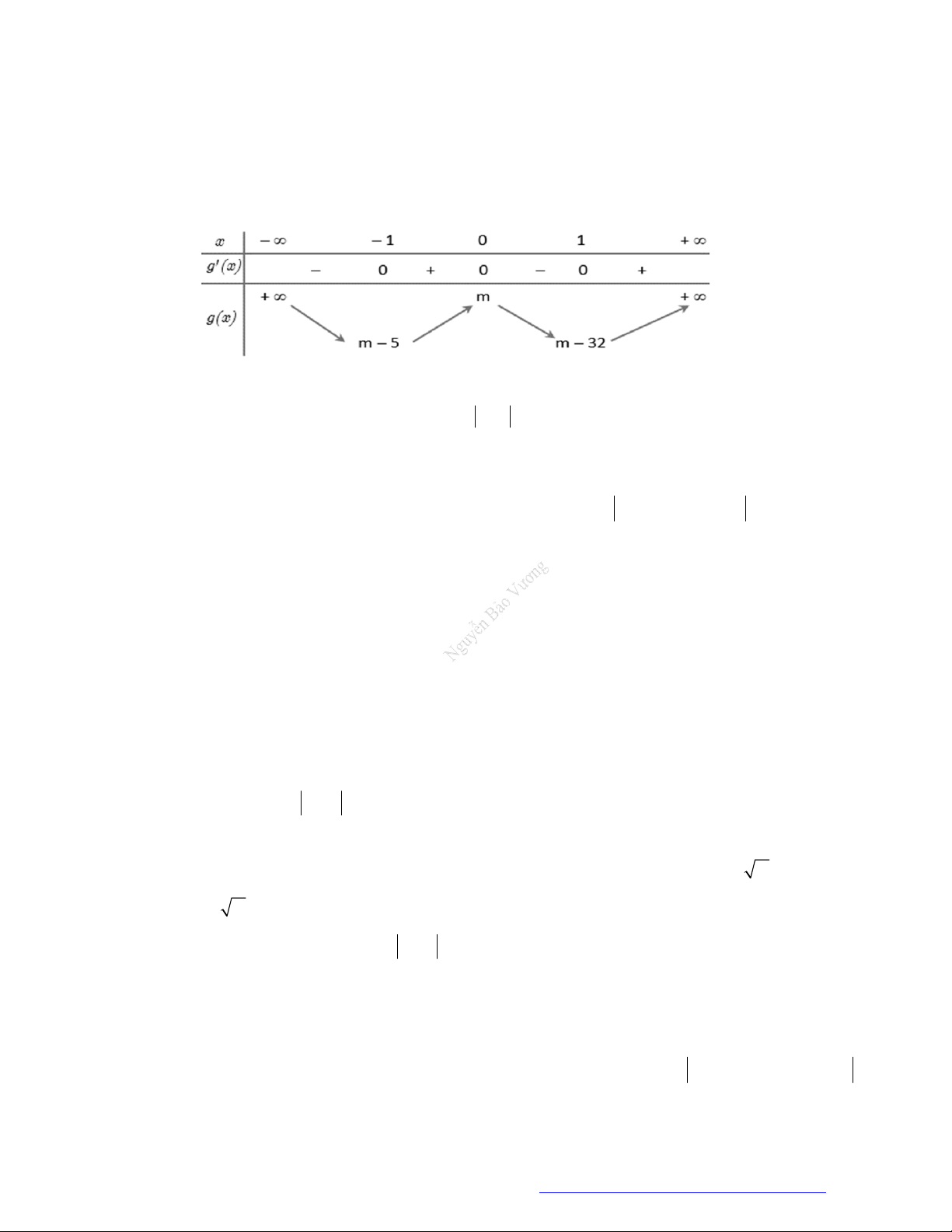
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Lời giải
Chọn C
Đặt:
4 3 2
( ) 3 4 12g x x x x m
Ta có:
3 2
2 32
'( ) 12 12 24 0 1 5
0
x y m
g x x x x x y m
x y m
Dựa vào bảng biến thiên, hàm số có
( )y g x
có
5
điểm cực trị khi
0
0
5 0
5 32
32 0
m
m
m
m
m
.
Vì m là số nguyên dương cho nên có 26 số m thỏa đề bài
Câu 7. (THPT Lương Thế Vinh Hà Nội 2019) Cho hàm số
4 2
2 2 1y x mx m
với
m
là tham số
thực. Số giá trị nguyên trong khoảng
2;2
của
m
để hàm số đã cho có
3
điểm cực trị là
A.
2
B.
4
C.
3
D.
1
Lời giải
Chọn B
Đặt
4 2
2 2 1f x x mx m
,
3
4 4f x x mx
,
2
0
0
x
f x
x m
+ Trường hợp 1: hàm số có một cực trị
2;0m
.
Đồ thị hàm số
y f x
có một điểm cực trị là
0;2 1A m
.
Do
2;0m
2 1 0
A
y m
nên đồ thị hàm số
y f x
cắt trục hoành tại
2
điểm phân biệt
nên hàm số
y f x
có
3
cực trị có
3
giá trị nguyên của
m
thỏa ycbt.
+ Trường hợp 2: hàm số có ba cực trị
0;2m
.
Khi đó đồ thị hàm số có
3
điểm cực trị là
0;2 1A m
,
2
; 2 1B m m m ,
2
; 2 1C m m m .
Do
1 0a
nên hàm số
y f x
có
3
điểm cực trị khi hàm số
y f x
có
0
B C
y y
2
2 1 0m m
1m
.
Nếu
0
B C
y y
(trong bài toán này không xảy ra) thì hàm số có ít nhất
5
điểm cực trị.
Vậy có
4
giá trị của
m
thỏa ycbt.
Câu 8. (Chuyên Bắc Ninh 2019) Tập hợp các giá trị của
m
để hàm số
4 3 2
3 4 12 1y x x x m
có
7
điểm cực trị là:
A.
(0;6)
B.
(6;33)
C.
(1;33)
D.
(1;6)
Lời giải
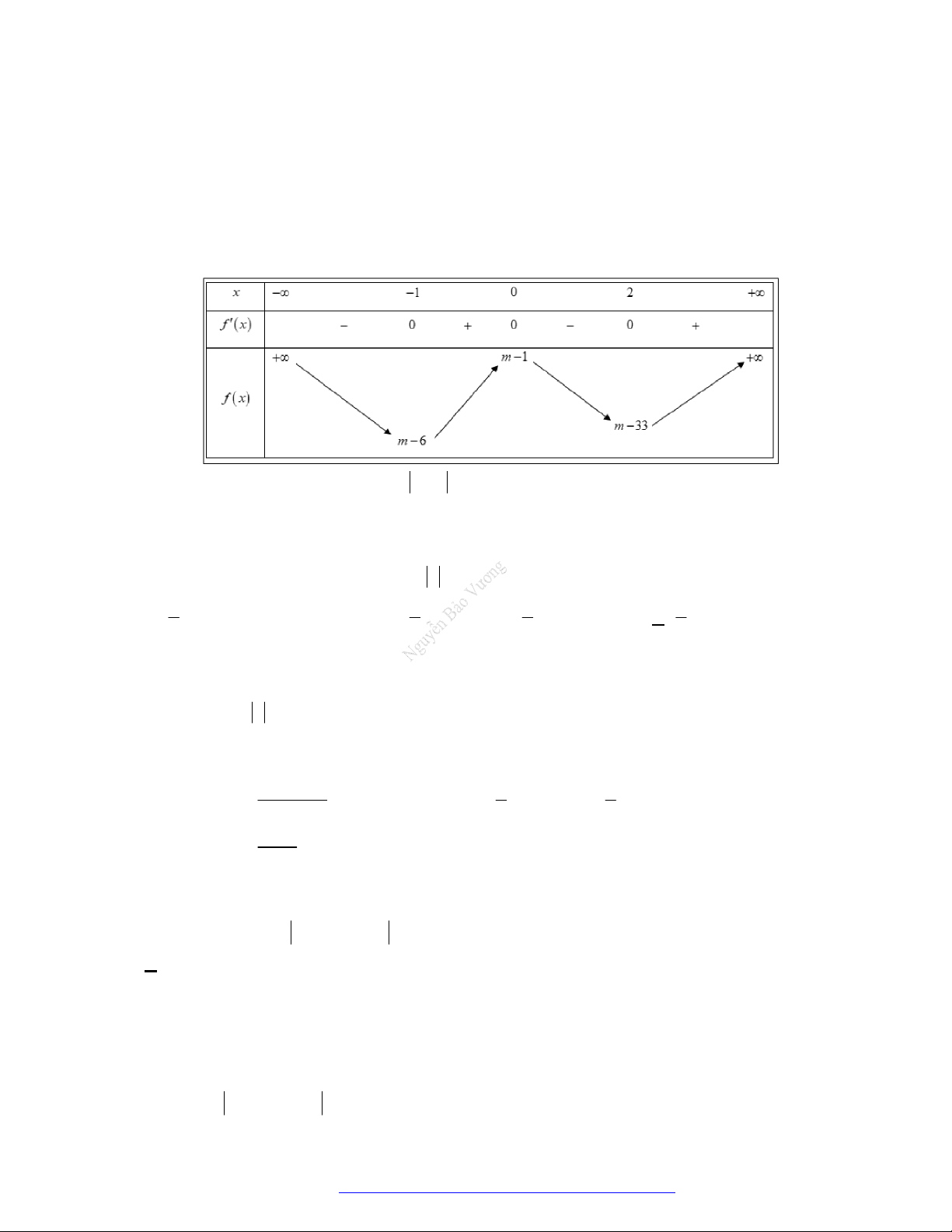
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Chọn D
Xét hàm số
4 3 2
( ) 3 4 12 1f x x x x m
,
Có
xf
x
lim
,
xf
x
lim
3 2 2
( ) 12 12 24 12 2f x x x x x x x
0
( ) 0 1
2
x
f x x
x
.
Bảng biến thiên:
Từ bảng biến thiên, ta có hàm số
( )y f x
có
7
điểm cực trị đồ thị hàm số
( )y f x
cắt
Ox
tại
4
điểm phân biệt
6 0 1 1 6m m m
.
Câu 9. (THPT Kinh Môn - 2018) Cho hàm số
3 2
( ) (2 1) (2 ) 2y f x x m x m x . Tìm tất cả các
giá trị của tham số
m
để hàm số
( )y f x
có 5 điểm cực trị.
A.
5
2
4
m
. B.
5
2
4
m
. C.
5
2
4
m
. D.
5
2
4
m
.
Lời giải
Ta có:
2
' 3 2 2 1 2y x m x m
Hàm số
( )y f x
có 5 điểm cực trị khi chi khi hàm số
f x
có hai cực trị dương.
0
0
0
S
P
2
2 1 3 2 0
2 2 1
0
3
2
0
3
m m
m
m
2
4 5 0
1
2
2
m m
m
m
5
2
4
m
Câu 10. (Chuyên Đh Vinh - 2018) Cho hàm số
y f x
có đạo hàm
3 2 3
2 2f x x x x x
với
mọi
x
. Hàm số
1 2018f x
có nhiều nhất bao nhiêu điểm cực trị?
A.
9
. B.
2018
. C.
2022
. D.
11
.
Lời giải
Ta có
3 2
2 2 0f x x x x
có
4
nghiệm và đổi dấu
4
lần nên hàm số
y f x
có
4
cực trị. Suy ra
0f x
có tối đa
5
nghiệm phân biệt.
Do đó
1 2018y f x
có tối đa
9
cực trị.
Câu 11. (THPT Thạch Thanh 2 - Thanh Hóa - 2018) Hình vẽ bên là đồ thị của hàm số
y f x
.
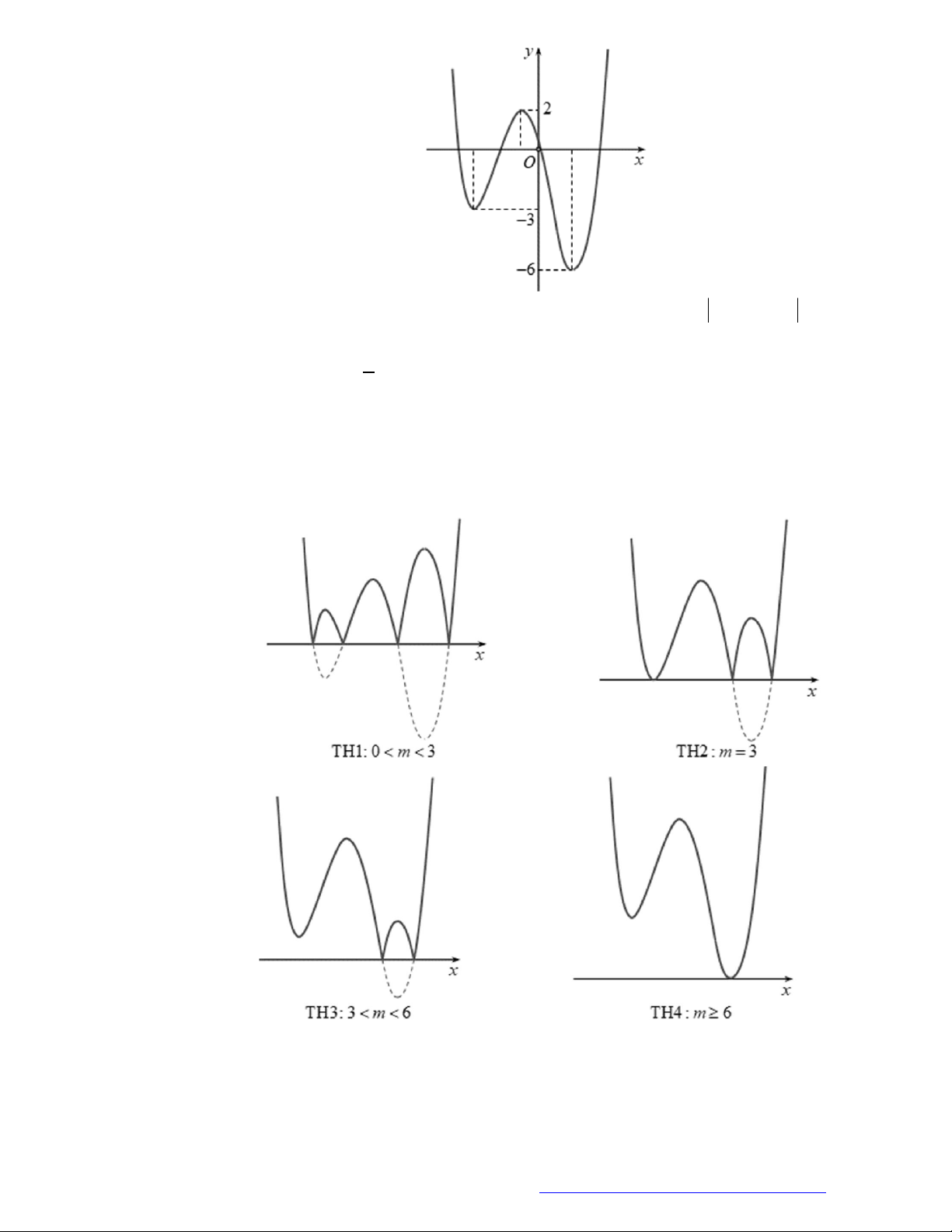
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Gọi
S
là tập hợp các giá trị nguyên dương của tham số
m
để hàm số
1y f x m
có
5
điểm cực trị. Tổng giá trị tất cả các phần tử của
S
bằng
A.
9
. B.
12
. C.
18
. D.
15
.
Lời giải
Nhận xét: Số giao điểm của
:C y f x
với
Ox
bằng số giao điểm của
: 1C y f x
với
Ox
.
Vì
0m
nên
: 1C y f x m
có được bằng cách tịnh tiến
: 1C y f x
lên trên
m
đơn vị.
TH1:
0 3m
. Đồ thị hàm số có
7
điểm cực trị. Loại.
TH2:
3m
. Đồ thị hàm số có
5
điểm cực trị. Nhận.
TH3:
3 6m
. Đồ thị hàm số có
5
điểm cực trị. Nhận.
TH4:
6m
. Đồ thị hàm số có
3
điểm cực trị. Loại.
Vậy
3 6m
. Do
*
m
nên
3;4;5m
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Vậy tổng giá trị tất cả các phần tử của
S
bằng
12
.
Câu 12. (THPT Quảng Yên - Quảng Ninh - 2018) Có bao nhiêu giá trị nguyên của tham số
m
để hàm
số
4 3 2
3 4 12
2
m
y x x x
có
7
điểm cực trị?
A.
3
. B.
9
. C.
6
. D.
4
.
Lời giải
Ta có
2
4 3 2 4 3 2
3 4 12 3 4 12
2 2
m m
y x x x x x x
3 2 4 3 2
2
4 3 2
12 12 24 3 4 12
2
3 4 12
2
m
x x x x x x
y
m
x x x
3 2
4 3 2
12 12 24 0 1
0
3 4 12 0 2
2
x x x
y
m
x x x
.
Từ
0
1 1
2
x
x
x
.
Vậy để hàm số có
7
điểm cực trị thì (2) phải có bốn nghiệm phân biệt khác
0;1; 2
.
Xét hàm số
4 3 2 3 2
0
3 4 12 ' 12 12 24 ' 0 1
2
2
x
m
f x x x x f x x x x f x x
x
Để (2) có
4
nghiệm phân biệt thì
f x
cắt trục hoành tại 4 điểm phân biệt
5 0
10
2
0 10
0
0
2
m
m
m
m m
.
Vậy có
9
giá trị nguyên của tham số
m
để hàm số
4 3 2
3 4 12
2
m
y x x x
có
7
điểm cực trị.
Câu 13. (THPT Nguyễn Tất Thành - Yên Bái - 2018) Có bao nhiêu giá trị nguyên của tham số
m
để
hàm số
3 2
3
y x x m
có
5
điểm cực trị?
A.
5
. B.
3
. C.
6
. D.
4
.
Lời giải
x
2
0
1
f x
0
0
0
f x
32
2
m
2
m
5
2
m
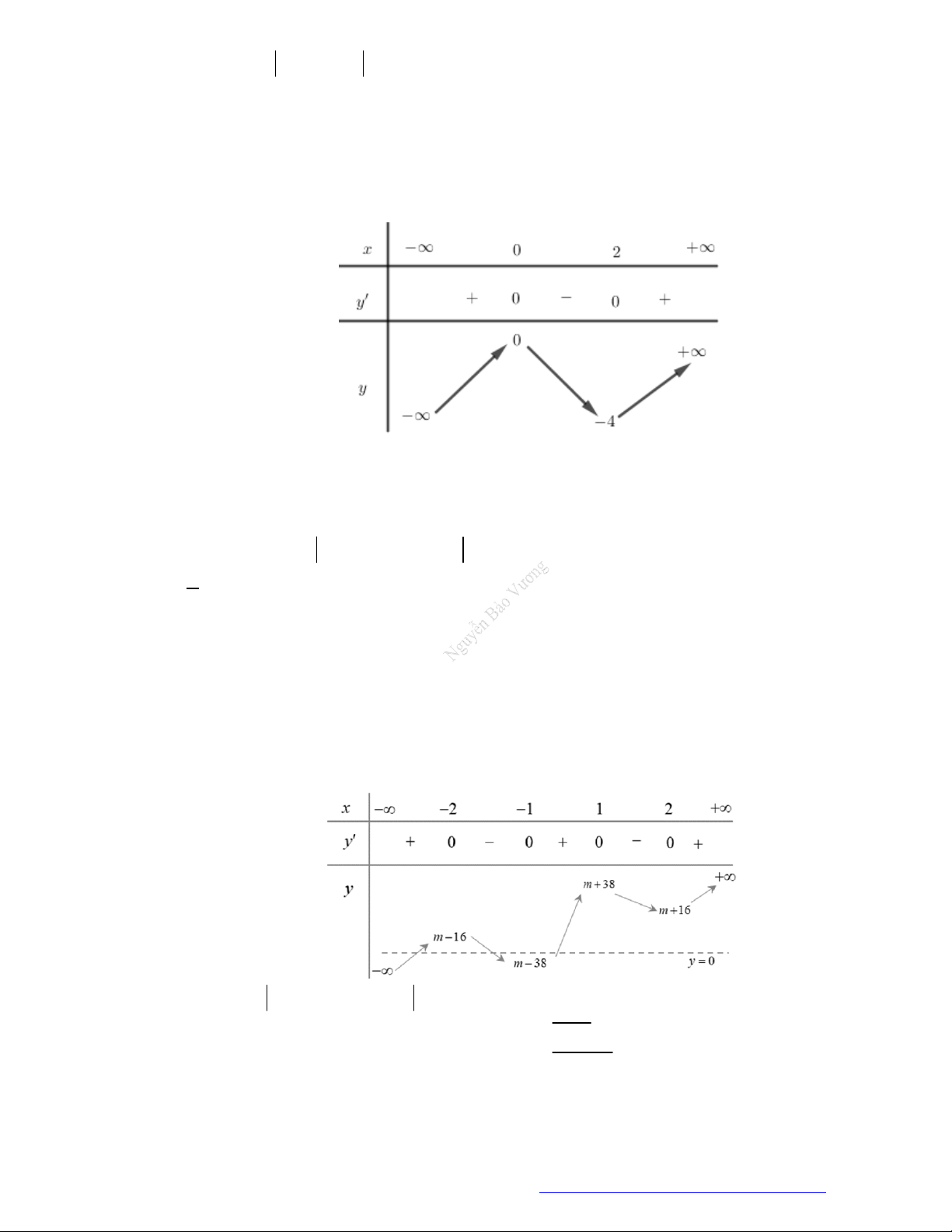
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Hàm số
3 2
3y x x m
có
5
điểm cực trị đồ thị hàm số
3 2
3y x x m có hai điểm cực
trị và nằm về hai phía của trục hoành phương trình
3 2
3 0 1x x m
có ba nghiệm phân
biệt.
Xét bbt của hàm số
3 2
3y x x
2
0
3 6 0
2
x
y x x
x
Từ đó ta được
1
có ba nghiệm phân biệt
4 0 0 4m m
. Vậy có
3
giá trị nguyên
của
m
thỏa mãn.
Câu 14. (Chuyên Nguyễn Thị Minh Khai - Sóc Trăng - 2018) Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
5 3
3 25 60y x x x m
có 7 điểm cực trị?
A.
42
. B.
21
. C.
40
. D.
20
.
Lời giải
5 3
4 2
2
2
3 25 60
15 75 60
2 16
1 1 38
0
1 38
4
2 16
y x x x m
y x x
x y m
x x y m
y
x y m
x
x y m
Suy ra
5 3
3 25 60y x x x m
có 7 điểm cực trị
38 0 16 16 38 17,37
16 0 38 38 16
37, 17
m m m m
m m m
m
Có tất cả 42 giá trị nguyên của
.m
Câu 15. (Sở Nam Định - 2018) Cho hàm số
y f x
có bảng biến thiên như hình vẽ
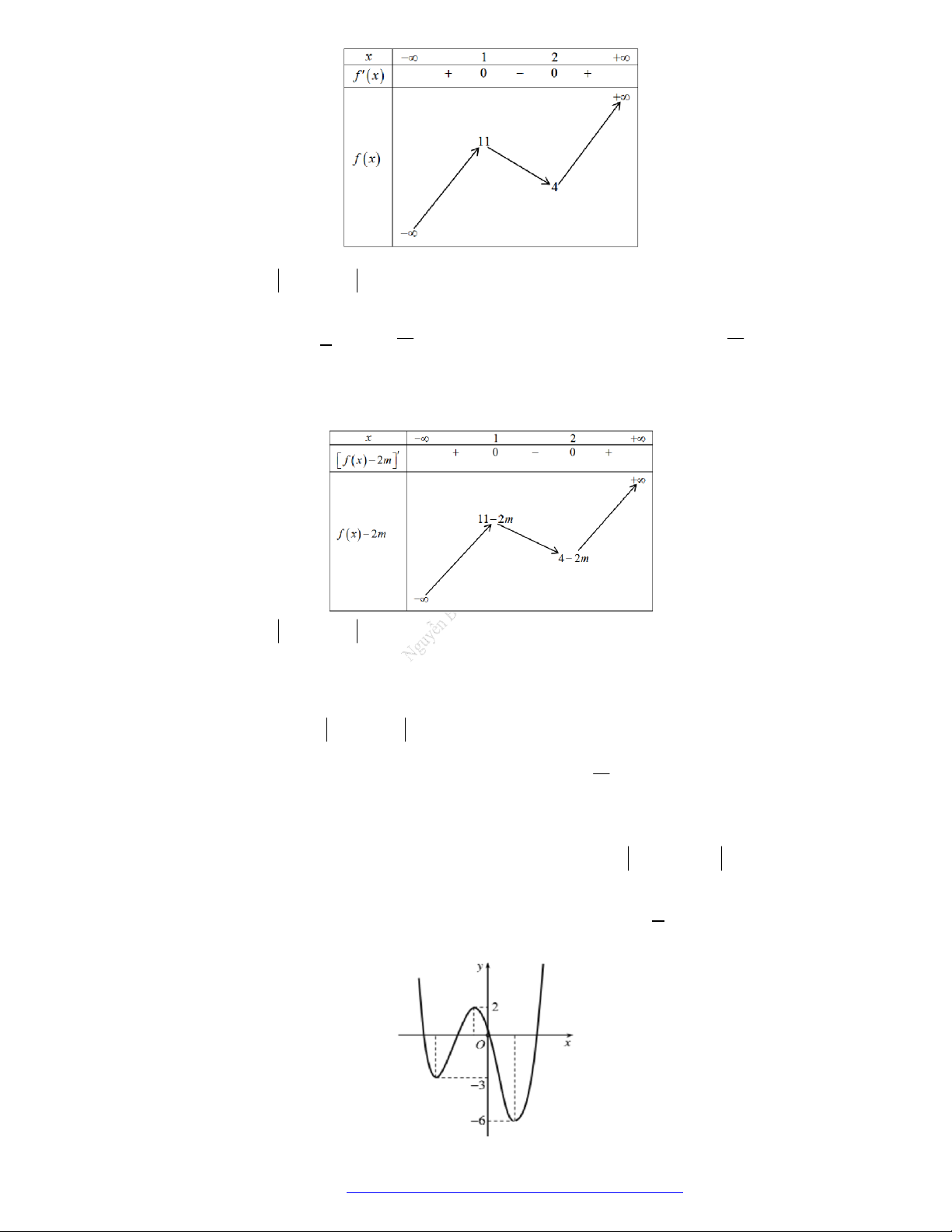
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Đồ thị hàm số
2 y f x m
có
5
điểm cực trị khi và chỉ khi
A.
4;11m
. B.
11
2;
2
m
. C.
3m
. D.
11
2;
2
m
.
Lời giải
Từ BBT của hàm số
y f x
ta có bảng biến thiên của hàm số
2 y f x m
như sau
Đồ thị hàm số
2 y f x m
gồm hai phần:
+ Phần đồ thị của hàm số
2 y f x m
nằm phía trên trục hoành.
+ Phần đối xứng với đồ thị của hàm số
2 y f x m
nằm phía dưới trục hoành qua trục
Ox
.
Do đó, đồ thị hàm số
2 y f x m
có
5
điểm cực trị khi và chỉ khi
4 2 11 2 0m m
11
2;
2
m
.
Câu 16. (THPT Nguyễn Huệ - Tt Huế - 2018) Hình vẽ bên là đồ thị của hàm số
y f x
. Gọi
S
là tập
hợp các giá trị nguyên dương của tham số
m
để đồ thị hàm số
2y f x m
có
5
điểm cực
trị. Tổng giá trị tất cả các phần tử của
S
bằng
A.
15
. B.
18
. C.
9
. D.
12
.
Lời giải
Cách 1: dùng đồ thị.
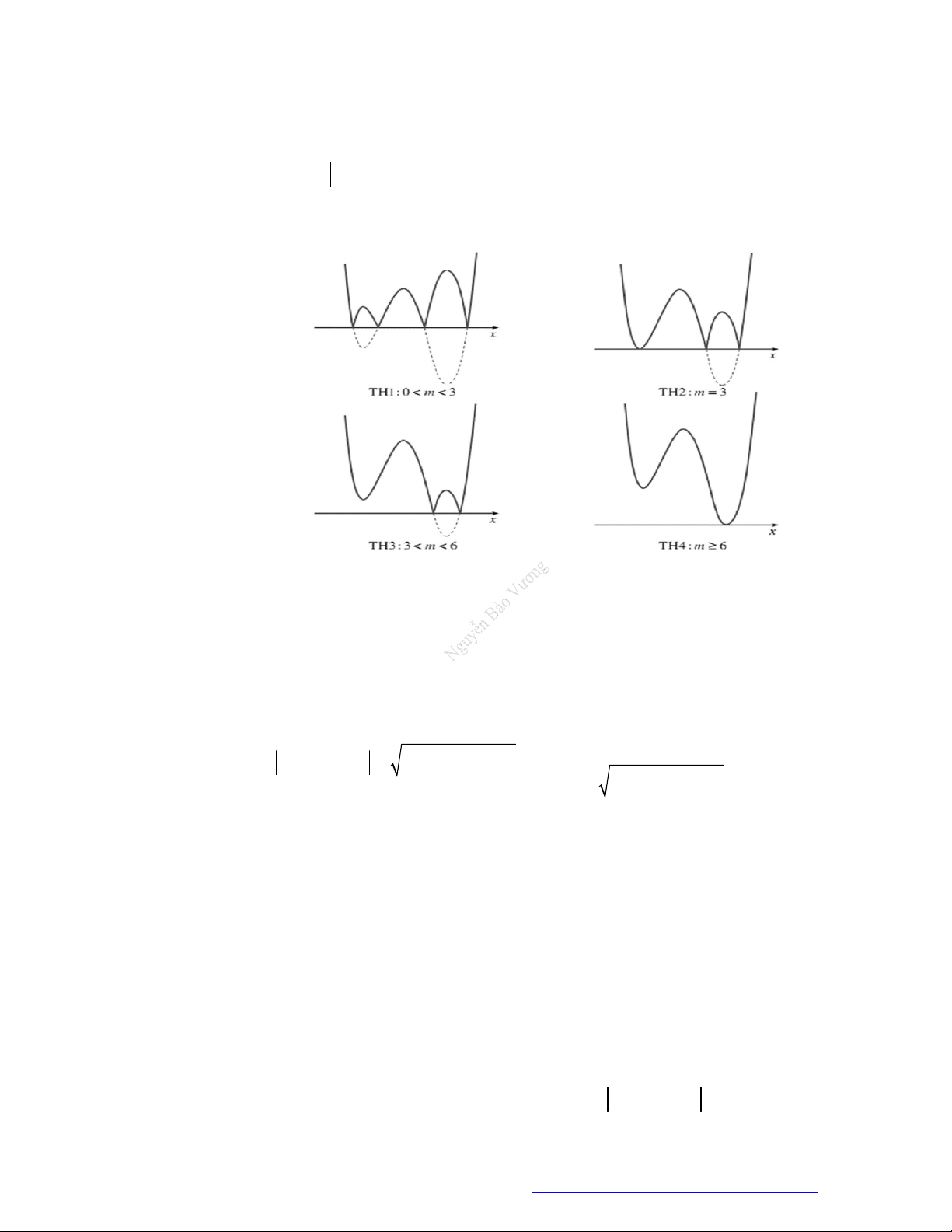
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
- Nhận thấy: số giao điểm của
:C y f x
với
Ox
bằng số giao điểm của
1
: 2C y f x
với
Ox
.
Vì
0m
nên
2
: 2C y f x m
có được bằng cách tịnh tiến
1
: 2C y f x
lên trên
m
đơn vị.
- Đồ thị hàm số
2y f x m
có được bằng cách lấy đối xứng qua trục hoành
Ox
phần đồ
thị
2
C
nằm phía dưới trục
Ox
và giữ nguyên phần phía trên trục
Ox
.
- Ta xét các trường hợp sau:
+ Trường hợp 1:
0 3m
: đồ thị hàm số có 7 điểm cực trị (loại).
+ Trường hợp 2:
3m
: đồ thị hàm số có 5 điểm cực trị (thỏa mãn).
+ Trường hợp 3:
3 6m
: đồ thị hàm số có 5 điểm cực trị (thỏa mãn).
+ Trường hợp 4:
6m
: đồ thị hàm số có 3 điểm cực trị (loại).
Vậy
3 6m
Do
m
nên
3;4;5m
hay
3;4;5S
.
Vậy tổng giá trị tất cả các phần tử của
S
bằng
12
.
* Cách 2: đạo hàm hàm số hợp.
- Ta có:
2y f x m
2
2f x m
2
2 . 2
2
f x m f x
y
f x m
- Xét
2 0f x
1
+ Do phương trình
0f x
có
3
nghiệm phân biệt nên phương trình
2 0f x
cũng có
3
nghiệm phân biệt.
- Xét
2 0f x m
2f x m
2
+ Nếu
6 3m 3 6m
thì phương trình
2
có
2
nghiệm phân biệt khác
3
nghiệm của
1
.
+ Nếu
3m 3m
thì
2
có
3
nghiệm phân biệt (trong đó có
2
nghiệm đơn khác
3
nghiệm của
1
và
1
nghiệm kép trùng với
1
nghiệm của
1
)
Tóm lại : với
3 6m
thì hai phương trình
1
và
2
có tất cả
5
nghiệm bội lẻ phân biệt và
y
đổi dấu khi
x
đi qua các nghiệm đó, hay đồ thị hàm số
2y f x m
có
5
điểm cực trị.
- Lại do
m
nên
3;4;5m
hay
3;4;5S
.
Vậy tổng giá trị tất cả các phần tử của
S
bằng
12
.
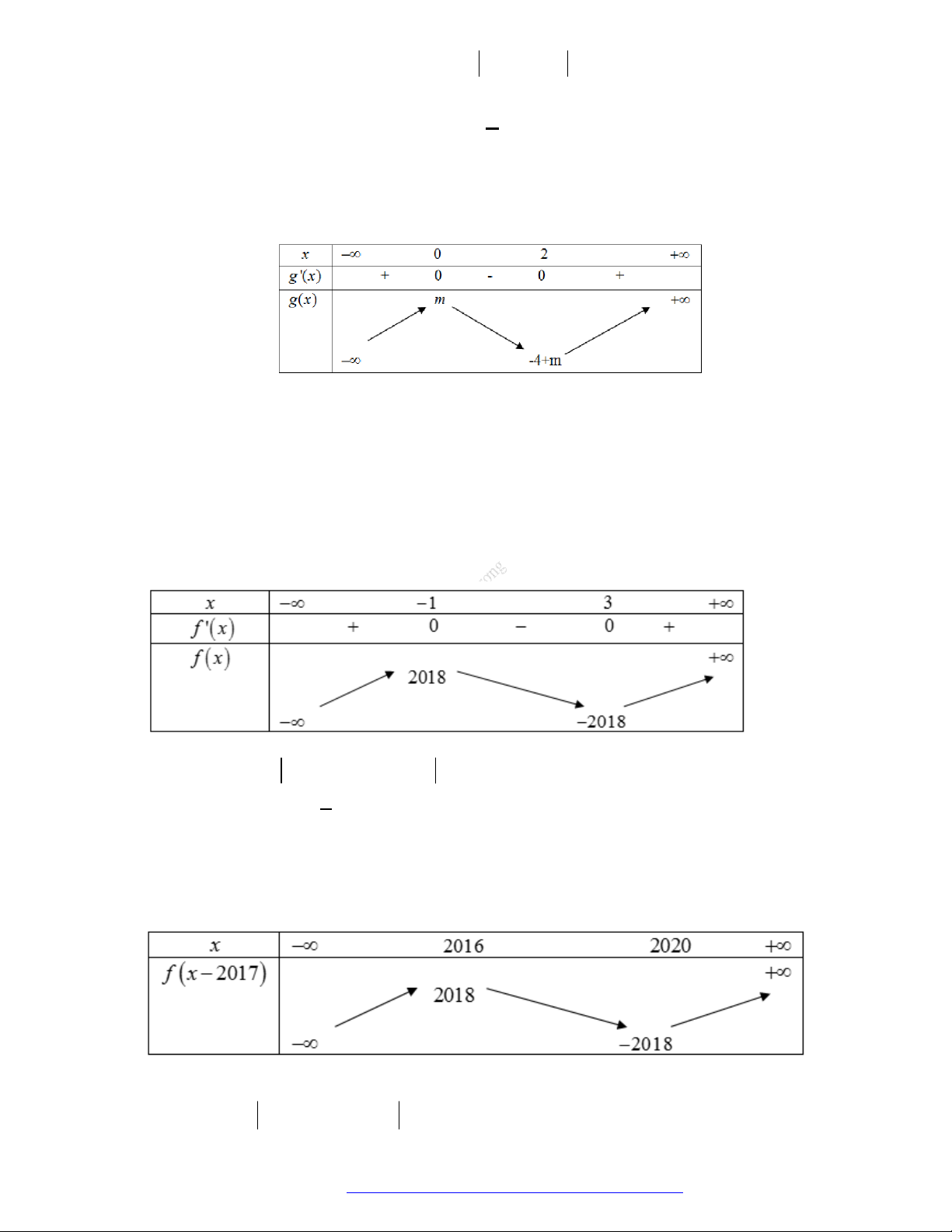
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 17. (Sở Hưng Yên - 2018) Cho hàm số
3 2
( ) 3f x x x m
với
5;5m
là tham số. Có bao
nhiêu giá trị nguyên của
m
để hàm số
( )f x
có đúng ba điểm cực trị.
A.
3
. B.
0
. C.
8
. D.
6
.
Lời giải
Xét hàm số
3 2
( ) 3g x x x m
có
2
0
'( ) 0 3 6 0
2
x
g x x x
x
.
Bảng biến thiên
Từ bảng biến thiên ta thấy để hàm số
( )f x
có đúng ba điểm cực trị thì đồ thị hàm số
( )g x
phải
có đúng một giao điểm hoặc tiếp xúc với
Ox
.
Điều kiện này tương đương với
0 0
4 0 4
m m
m m
. Kết hợp điều kiện
5;5m
ta có
5; 4; 3; 2; 1;0;4;5m
. Vậy có 8 giá trị thoả mãn.
Câu 18.
(Chuyên Hùng Vương - Bình Dương - 2018)
Cho hàm số
y f x
có bảng biến thiên như
sau.
Đồ thị hàm số
2017 2018y f x
có bao nhiêu điểm cực trị?
A.
2
.
B.
3
.
C.
5
.
D.
4
.
Lời giải
Có
2017 y f x
bằng cách tịnh tiến sang bên phải
2017
đơn vị ta có
bảng biến thiên của hàm số
2017y f x
Tịnh tiến đồ thị hàm số
2017f x
lên trên 2018 đơn vị và lấy trị tuyệt đối ta có bảng biến thiên
của hàm số
2017 2018y f x
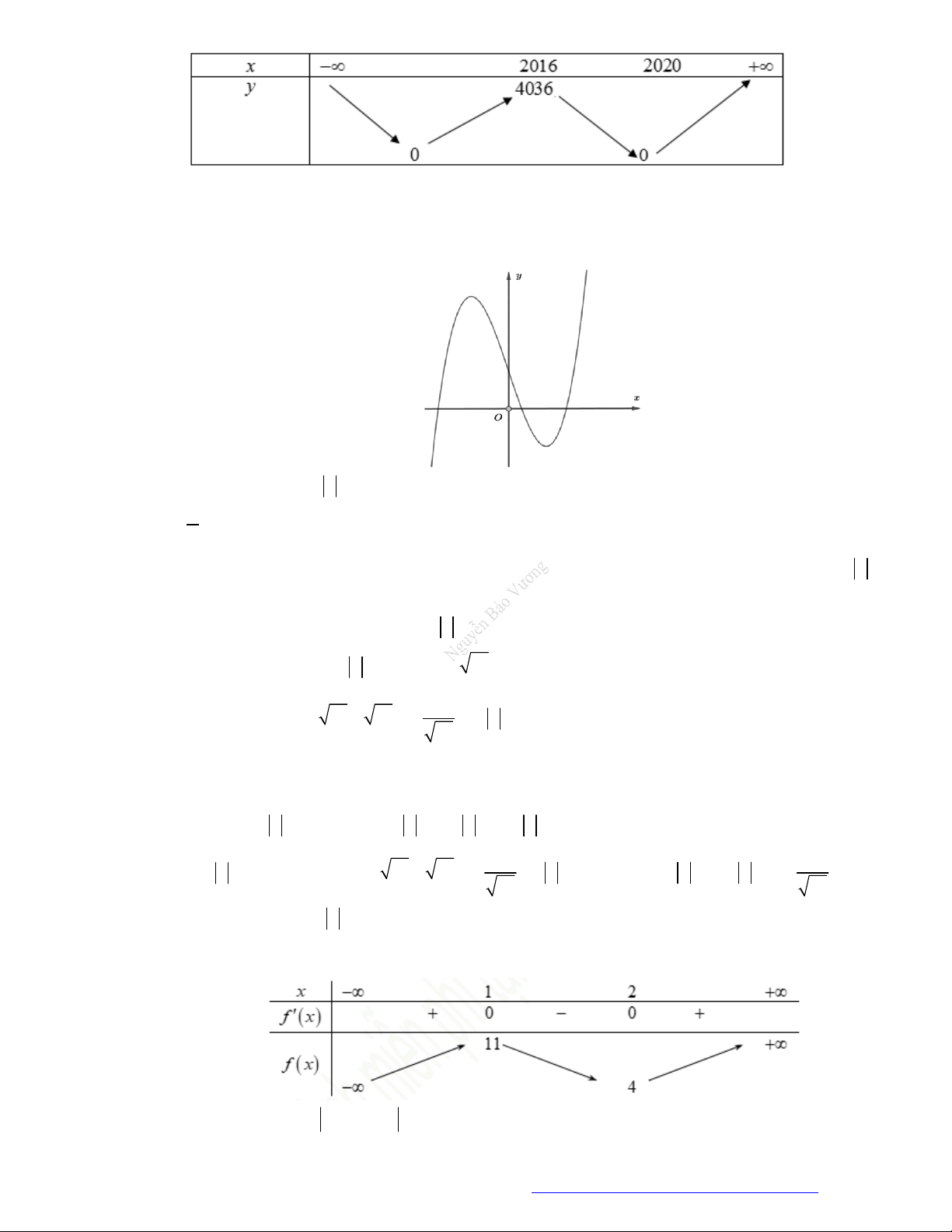
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Từ bảng biến thiên, suy ra hàm số có 3 cực trị.
Câu 19. (Chuyên Ngữ - Hà Nội - 2018) Hàm số
f x
có đạo hàm
f x
trên
. Hình vẽ bên là đồ thị
của hàm số
f x
trên
.
Hỏi hàm số
2018y f x
có bao nhiêu điểm cực trị?
A.
5
. B.
3
. C.
2
. D.
4
.
Lời giải
Cách 1: Từ đồ thị hàm số của
f x
ta thấy
f x
có hai cực trị dương nên hàm số
y f x
lấy đối xứng phần đồ thị hàm số bên phải trục tung qua trục tung ta được bốn cực trị, cộng thêm
giao điểm của đồ thị hàm số
2018y f x
với trục tung nữa ta được tổng cộng là
5
cực trị.
Cách 2: Ta có:
2
2018 2018y f x f x
.
Đạo hàm:
2 2
2
.
x
y f x x f x
x
.
Từ đồ thị hàm số của
f x
suy ra
f x
cùng dấu với
1 2 3
x x x x x x
với
1
0x ,
2 3
0 x x .
Suy ra:
f x
cùng dấu với
1 2 3
x x x x x x
.
Do
1
0x x
nên
2 2
2
x
y f x x f x
x
cùng dấu với
2 3
2
.
x
x x x x
x
.
Vậy hàm số
2018y f x
có
5
cực trị.
Câu 20. (Sở- Nam Định - 2018) Cho hàm số
y f x
có bảng biến thiên như hình vẽ
Đồ thị hàm số
2y f x m
có
5
điểm cực trị khi và chỉ khi
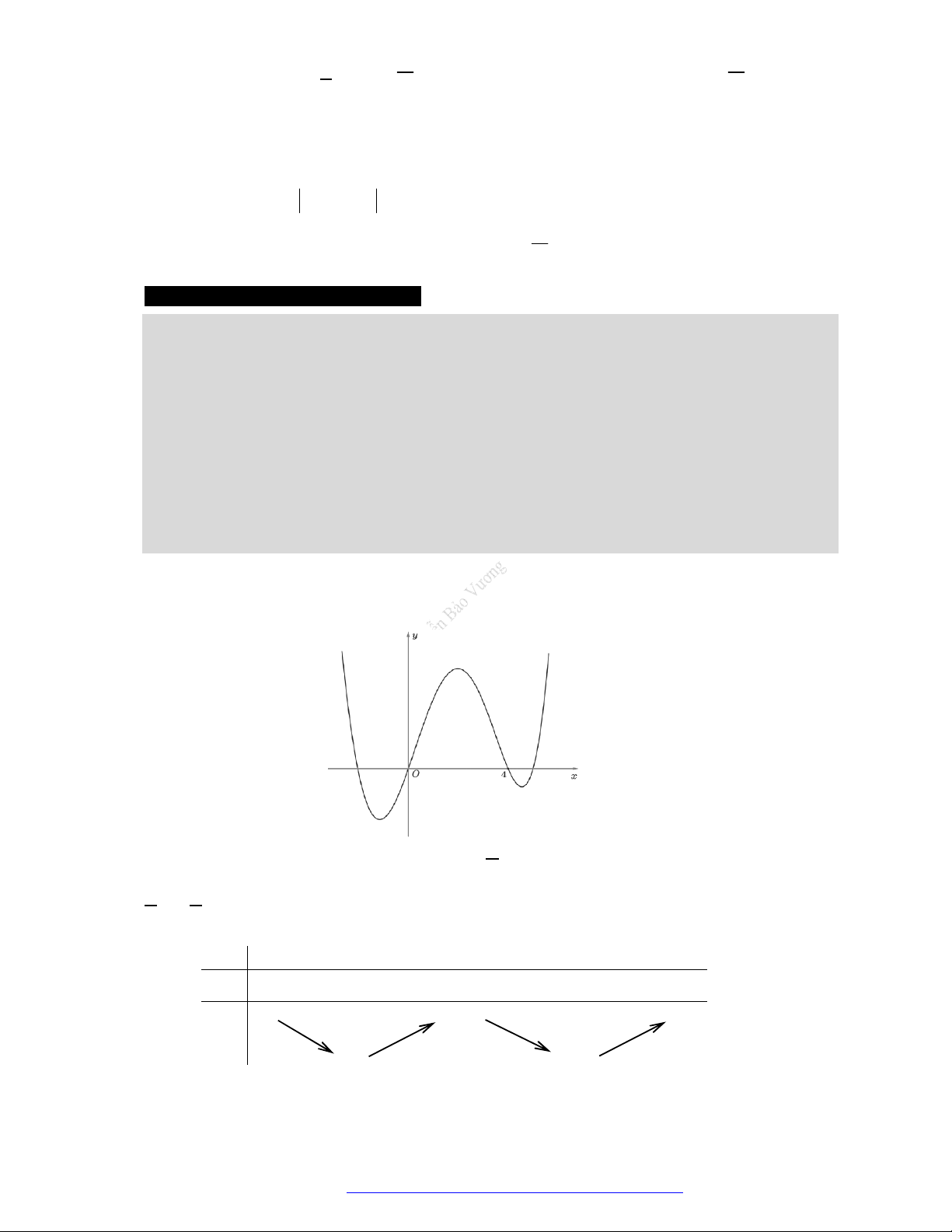
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
4;11m
. B.
11
2;
2
m
. C.
3m
. D.
11
2;
2
m
.
Lời giải
Từ bảng biến thiên ta có đồ thị hàm số
y f x
có hai điểm cực trị.
Để đồ thị hàm số
2y f x m
có
5
điểm cực trị thì đồ thị
y f x
cắt đường thẳng
2y m
tại
5 2 3
điểm phân biệt
4 2 11m
11
2
2
m
.
Dạng 2. Số điểm cực trị của hàm hợp
Bài toán: Cho hàm số
y f x
(Đề có thể cho bằng hàm, đồ thị, bảng biến thiên của
, 'f x f x
). Tìm số điểm cực trị của hàm số
y f u
trong đó
u
là một hàm số đối với
x
Ta thực hiện phương pháp tương tự xét số điểm cực trị của hàm số
y f x
Bước 1. Tính đạo hàm
' '. 'y u f u
Bước 2. Giải phương trình
' 0
' 0
' 0
u
y
f u
Bước 3.Tìm số nghiệm đơn và bội lẻ hoặc các điểm mà
'y
không xác định.
Kết luận
Câu 1. (Đề Tham Khảo 2020 Lần 1) Cho hàm số bậc bốn
y f x
có đồ thị như hình bên. Số điểm
cực trị của hàm số
3 2
3g x f x x
là
A.
5
. B.
3
. C.
7
. D.
11
.
Lời giải
Chọn C
Từ đồ thị ta có bảng biến thiên của hàm số
y f x
như sau
x
a
b
c
f x
0
0
0
f x
Ta có
3 2
3g x f x x
2 3 2
3 6 . 3g x x x f x x
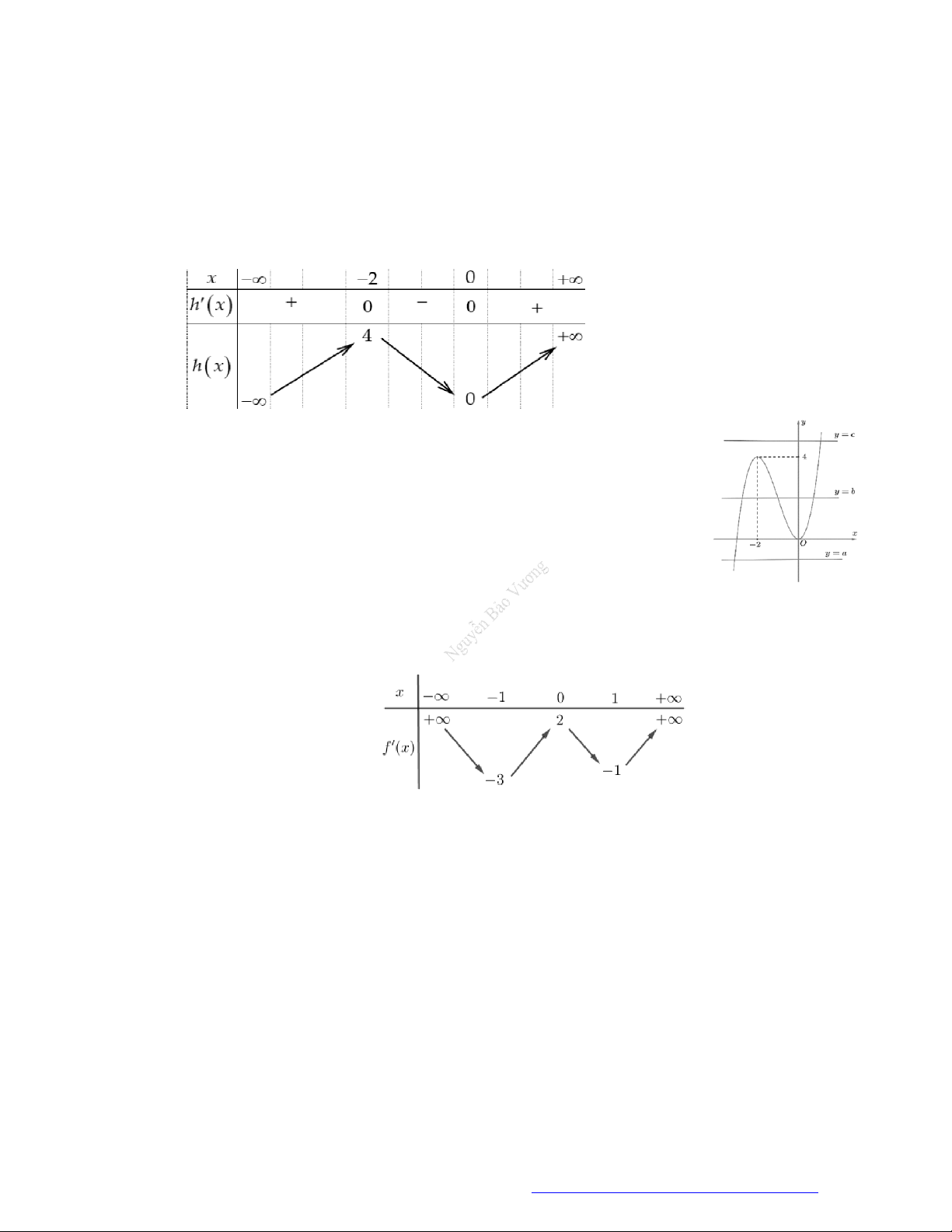
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Cho
0g x
2
3 2
3 6 0
3 0
x x
f x x
3 2
3 2
3 2
0
2
3 ; 0
3 ; 0 4
3 ; 4
x
x
x x a a
x x b b
x x c c
Xét hàm số
3 2
3h x x x
2
3 6h x x x
. Cho
0h x
0
2
x
x
Bảng biến thiên
Ta có đồ thị của hàm
3 2
3h x x x
như sau
Từ đồ thị ta thấy:
Đường thẳng
y a
cắt đồ thị hàm số
y h x
tại 1 điểm.
Đường thẳng
y b
cắt đồ thị hàm số
y h x
tại 3 điểm.
Đường thẳng
y c
cắt đồ thị hàm số
y h x
tại 1 điểm.
Như vậy phương trình
0g x
có tất cả 7 nghiệm đơn phân biệt.
Vậy hàm số
3 2
3g x f x x
có 7 cực trị.
Câu 2. (Mã 101 - 2019) Cho hàm số
y f x
, bảng biến thiên của hàm số
'f x
như sau:
Số điểm cực trị của hàm số
2
2y f x x
là
A.
9.
B.
3.
C.
7.
D.
5.
Lời giải
Chọn C
Ta có
2
2 1 . 2y x f x x
.
2
1
0
2 0
x
y
f x x
2 2
2 2
2 2
2 2
1 1
2 ; 1 2 0, ; 1 (1)
2 1;0 2 0, 1;0 (2)
2 0;1 2 0, 0;1 (3)
2 1; 2 0, 1; (4)
x x
x x a x x a a
x x b x x b b
x x c x x c c
x x d x x d d
.
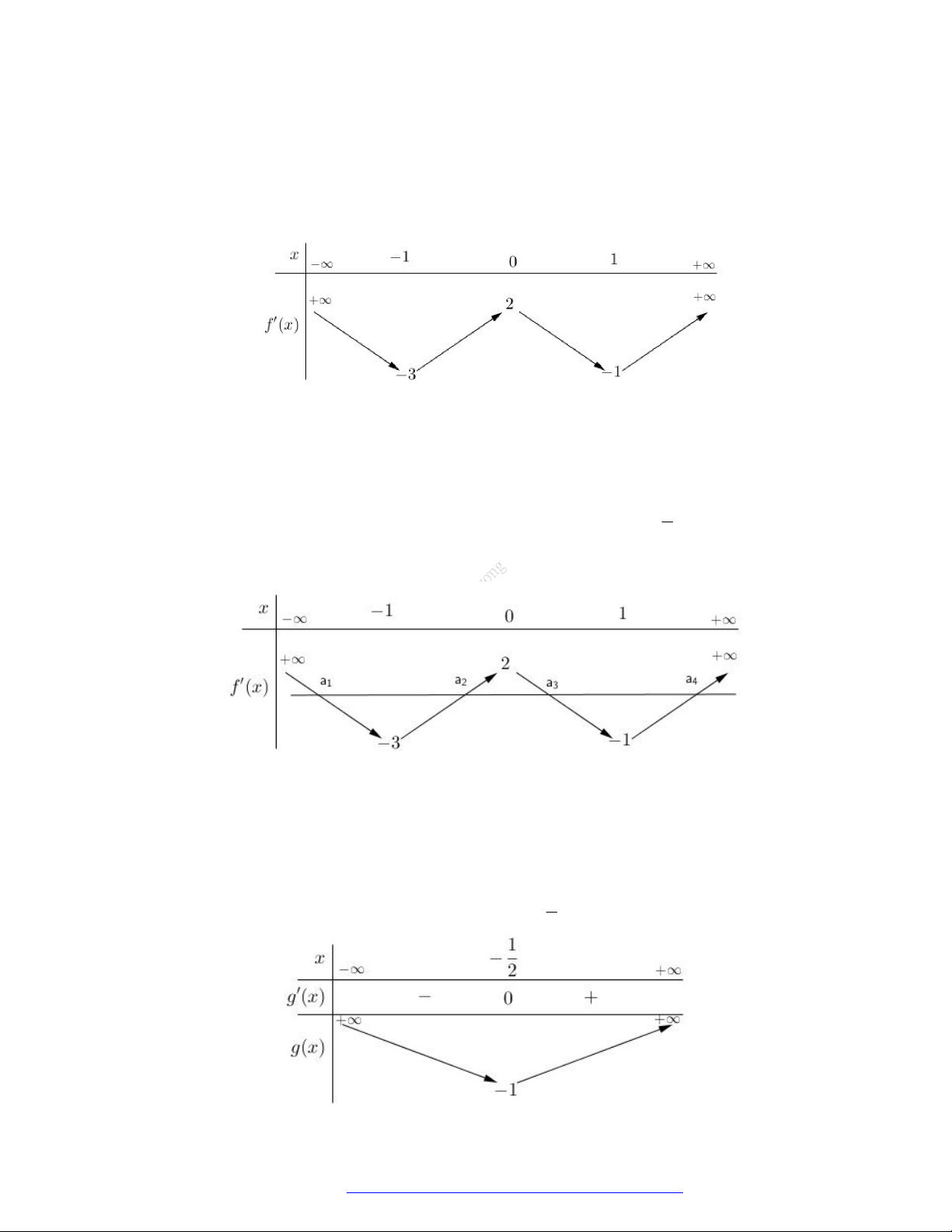
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Phương trình
(1)
vô nghiệm, các phương trình
(2),(3),(4)
đều có hai nghiệm phân biệt khác 1 và
do
, ,b c d
đôi một khác nhau nên các nghiệm của phương trình
(2),(3),(4)
cũng đôi một khác
nhau. Do đó
2
2 0f x x
có 6 nghiệm phân biệt.
Vậy
0y
có 7 nghiệm phân biệt, do đó số điểm cực trị của hàm số
2
2y f x x
là 7.
Câu 3. (Mã 104 - 2019) Cho hàm số
f x
, bảng biến thiên của hàm số
f x
như sau:
Số điểm cực trị của hàm số
2
4 4y f x x
là
A. 5. B. 9. C. 7. D. 3.
Lời giải
Chọn C
Có
2 2
4 4 8 4 4 4f x x x f x x
,
2
2
1
2
4 4 0
4 4 0
x
f x x
f x x
.
Từ bảng biến thiên trên ta có
2
1
2
2
2
2
3
2
4
4 4 ; 1
4 4 1;0
4 4 0
4 4 0;1
4 4 1;
x x a
x x a
f x x
x x a
x x a
. (1)
Xét
2
4 4g x x x
,
8 4g x x
,
1
0
2
g x x
ta có bảng biến thiên
Kết hợp bảng biến thiên của
g x
và hệ (1) ta thấy:
Phương trình
2
1
4 4 ; 1x x a
vô nghiệm.
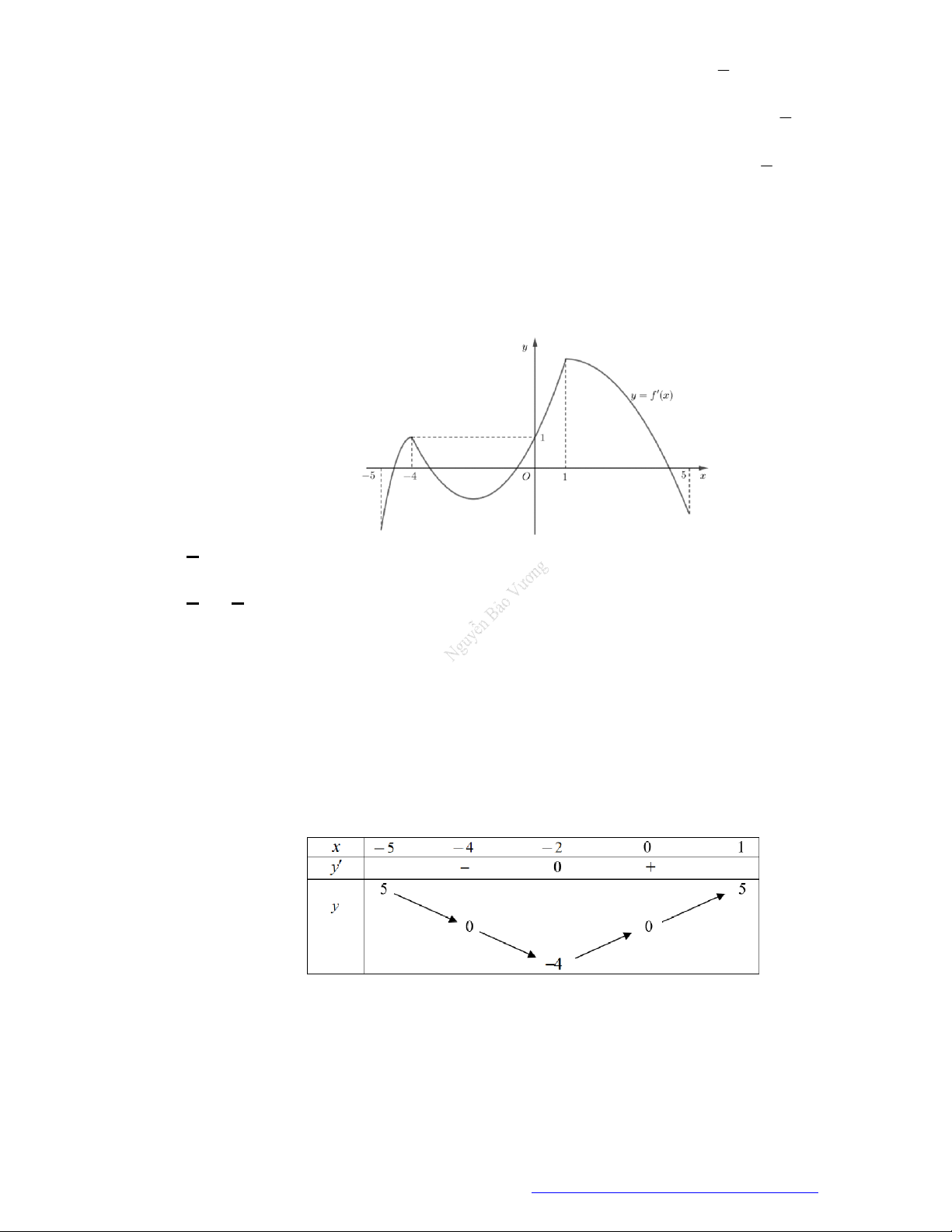
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
Phương trình
2
2
4 4 1;0x x a
tìm được hai nghiệm phân biệt khác
1
2
.
Phương trình
2
2
4 4 0;1x x a
tìm được thêm hai nghiệm mới phân biệt khác
1
2
.
Phương trình
2
2
4 4 1;x x a
tìm được thêm hai nghiệm phân biệt khác
1
2
.
Vậy hàm số
2
4 4y f x x
có tất cả 7 điểm cực trị.
Câu 4. (Chuyên ĐH Vinh - Nghệ An -2020) Cho hàm số
f x
có đạo hàm liên tục trên
. Đồ thị
hàm số
y f x
như hình vẽ bên. Hàm số
2 2
4 4y f x x x x
có bao nhiêu điểm cực trị
thuộc khoảng
5;1
?
A.
5
. B.
4
. C.
6
. D.
3
.
Lời giải
Chọn A
Đặt
2 2
4 4g x f x x x x
2 2
2 4 4 2 4 2 4 4 1g x x f x x x x f x x
.
Ta có
2
2
2
2 4 0
4 4 (1)
0
4 0 (2)
4 1;5 (3)
x
x x
g x
x x
x x a
.
Xét phương trình
2
4 1;5x x a
, ta có BBT của hàm số
2
4y x x
trên
5;1
như sau:
Suy ra (1) có nghiệm kép
2x
, (2) có 2 nghiệm phân biệt
4; 0x x
, (3) có 2 nghiệm phân
biệt
1 2
;x x x x
khác
2; 0; 4
. Do đó phương trình
0g x
có 5 nghiệm trong đó có
2x
là nghiệm bội ba, các nghiệm
4; 0x x
;
1 2
;x x x x
là các nghiệm đơn.
Vậy
g x
có 5 điểm cực trị.
Câu 5. (Chuyên Hưng Yên - 2020) Cho hàm số
y f x
có đạo hàm đến cấp hai trên
và có bảng
xét dấu của hàm số
'y f x
như hình sau:
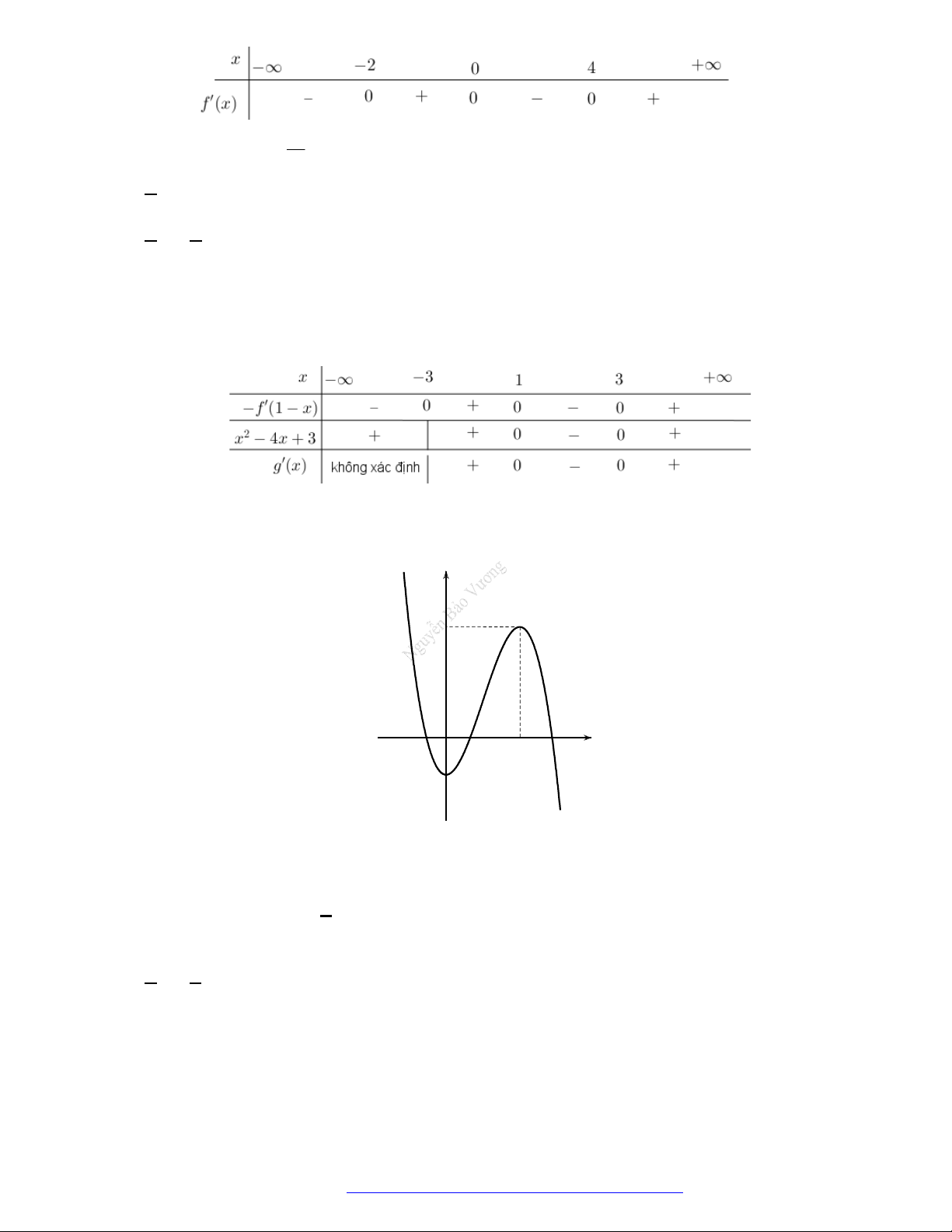
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Hỏi hàm số
3
2
1 2 3
3
x
g x f x x x
đạt cực tiểu tại điểm nào trong các điểm sau?
A.
3x
. B.
0x
. C.
3x
. D.
1x
.
Lời giải
Chọn A
2
1 4 3g x f x x x
.
1 2
1 0 1 0
0 1 4
x
f x f x
x
3
3 1
x
x
Bảng xét dấu
g x
:
Từ bảng xét dấu
g x
ta suy ra hàm số đạt cực tiểu tại
3x
.
Câu 6. (Chuyên KHTN - 2020) Cho hàm số
y f x
xác định trên
, có đồ thị
f x
như hình vẽ.
Hàm số
3
g x f x x
đạt cực tiểu tại điểm
0
x . Giá trị
0
x thuộc khoảng nào sau đây
A.
1;3
. B.
1;1
. C.
0;2
. D.
3;
.
Lời giải
Chọn B
Ta có
3 2 3
3 1
g x f x x g x x f x x
.
3
2 3 3
3
0 0
0 3 1 0 0
1
2
x x x
g x x f x x f x x
x
x x
.
Do đó
2 3 3 3
0 3 1 0 0 0 2 0 1
g x x f x x f x x x x x
.
O
-1
3
2
y=f(x)
x
y
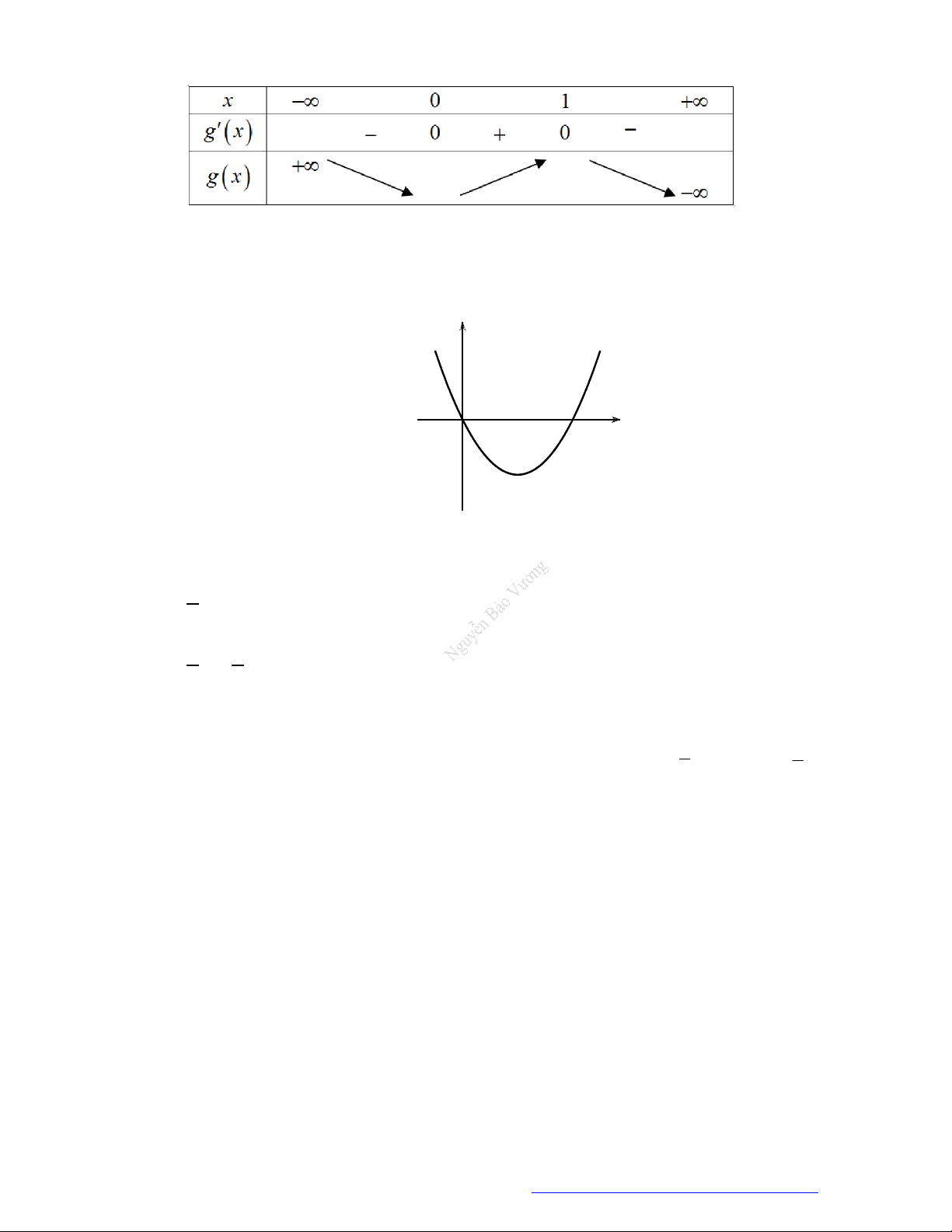
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
Bảng biến thiên
Vây hàm số
3
g x f x x
đạt cực tiểu tại điểm
0
0x . Suy ra
0
1;1 x
.
Câu 7. (Chuyên KHTN - 2020) Cho hàm số
y f x
liên tục trên
, có đồ thị
f x
như hình vẽ.
Số điểm cực tiểu của hàm số
2
g x f x x
là
A.
1
. B.
4
. C.
3
. D.
2
.
Lời giải
Chọn A
Ta có
2 2
2 1
g x f x x g x x f x x
.
2 2
2
2
1
2
2 1 0
0 2 1 0 0
0
2
x
x
g x x f x x x x
f x x
x x
1
2
1
0
x
x
x
.
Do đó
2
2
2
2 1 0
0
0 2 1 0
2 1 0
0
x
f x x
g x x f x x
x
f x x
y=f'(x)
O
2 x
y
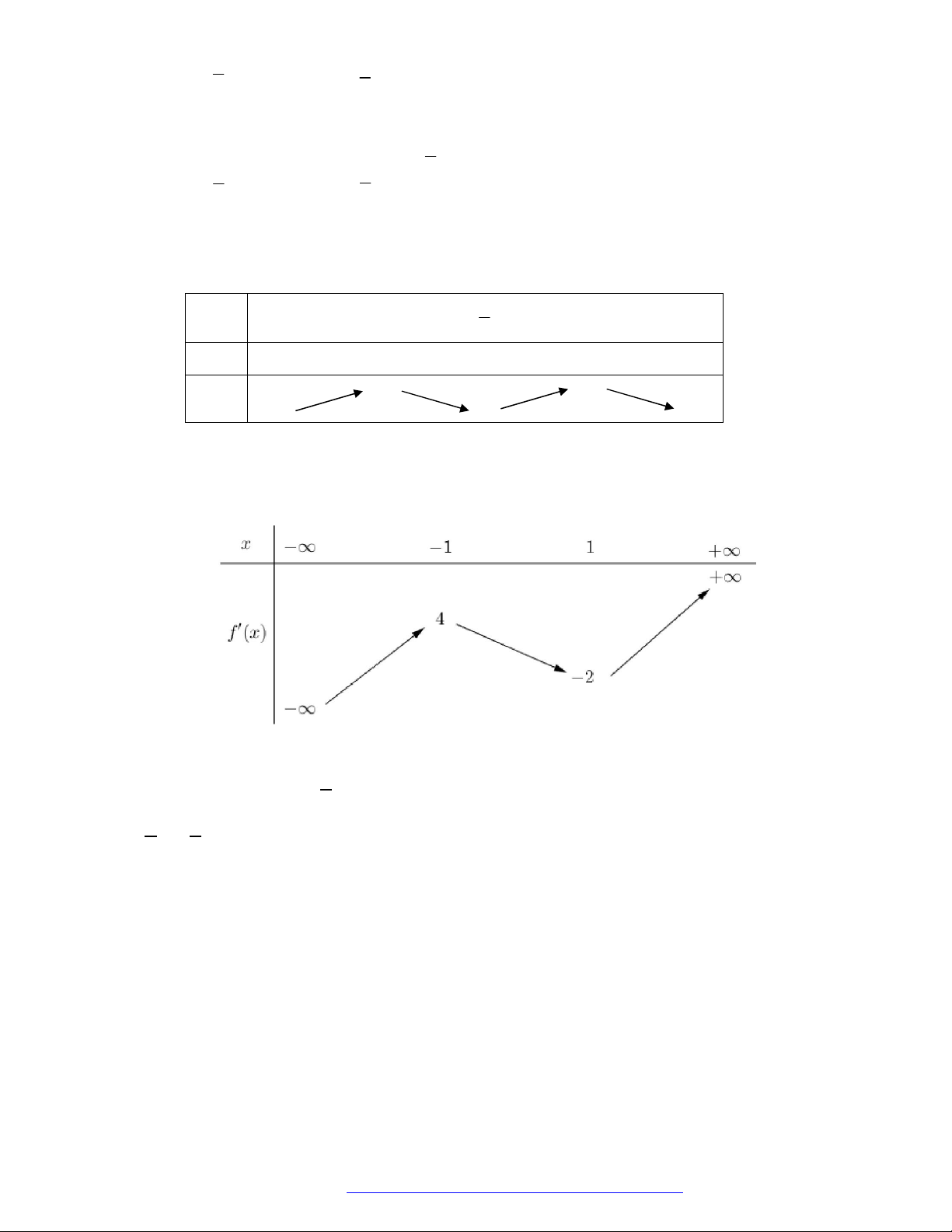
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
2
2
1
1
2
2
2
1
0
0
0
1
1
2
1
1
2
2
0 1
0 2
x
x
x x
x
x
x
x x
x
x
x
x
x x
.
Bảng biến thiên
x
0
1
2
1
g x
0
0
0
g x
Vậy hàm số có 1 điểm cực tiểu.
Câu 8. (Chuyên Lam Sơn - 2020) Cho hàm số
y f x
có đạo hàm liên tục trên
, bảng biến thiên
của hàm số
'f x
như sau:
Số điểm cực trị của hàm số
2
2y f x x
là
A. 4. B. 5. C. 1. D. 7.
Lời giải
Chọn B
Ta có
2
2
1
' 2 2 ' 2 0
' 2 0 1
x
y x f x x
f x x
.
Từ BBT ta thấy phương trình
2
2
2
2 1 2
1 2 1;1 3
2 1 4
x x a
x x b
x x c
.
Đồ thị hàm số
2
2y x x
có dạng
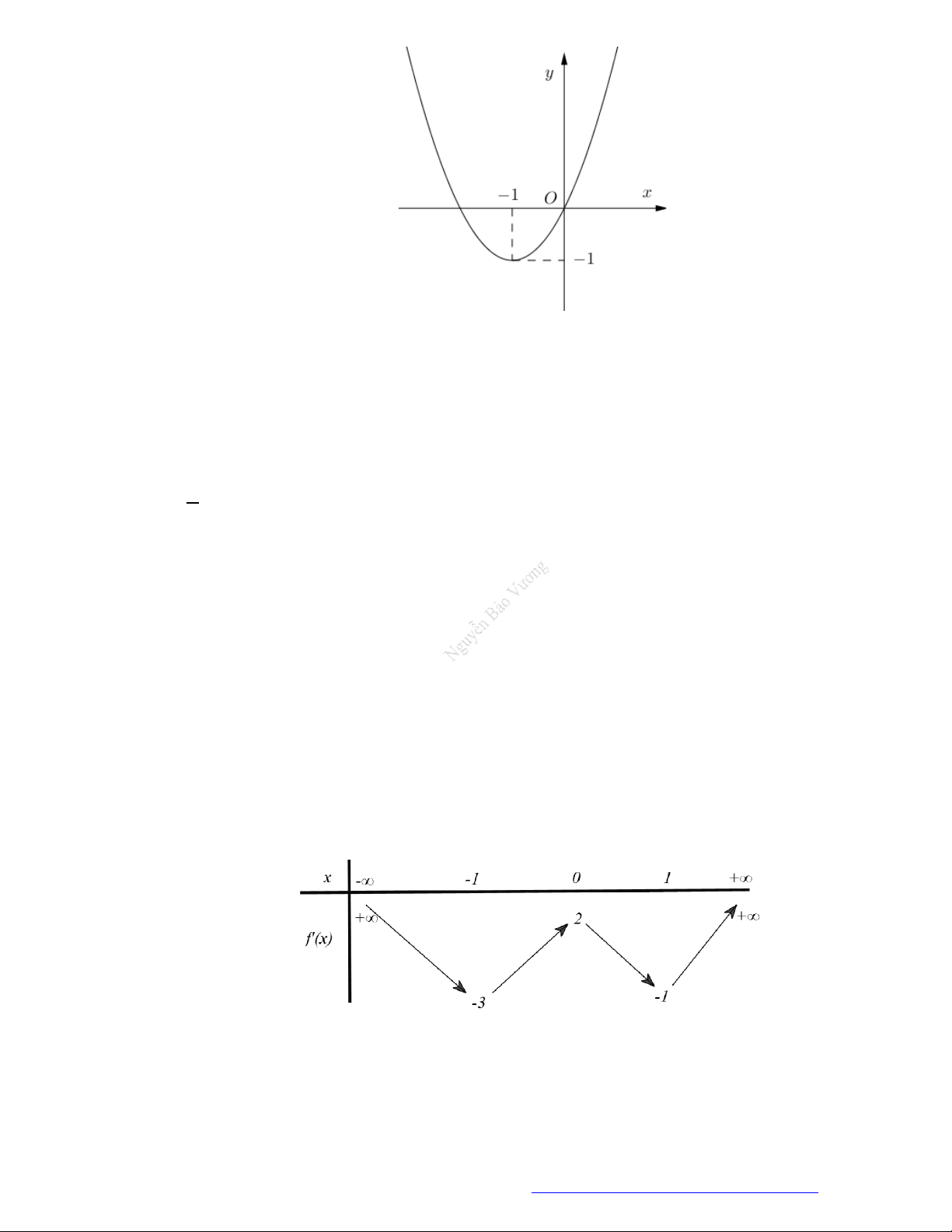
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
Từ đồ thị hàm số
2
2y x x
ta thấy phương trình (2) vô nghiệm; phương trình (3) ; phương trình
(4) đều có 2 nghiệm phân biệt.
Do đó
' 0y
có 5 nghiệm đơn phân biệt. Vậy hàm số
2
2y f x x
có 5 điểm cực trị.
Câu 9. (Sở Bắc Giang - 2018) Cho hàm số
y f x
có đúng ba điểm cực trị là
2; 1;0
và có đạo hàm
liên tục trên
. Khi đó hàm số
2
2y f x x
có bao nhiêu điểm cực trị?
A.
3
. B.
8
. C.
10
. D.
7
.
Lời giải
Vì hàm số
y f x
có đúng ba điểm cực trị là
2; 1;0
và có đạo hàm liên tục trên
nên
0f x
có ba nghiệm là
2; 1;0
(ba nghiệm bội lẻ).
Xét hàm số
2
2y f x x
có
2
2 2 . 2y x f x x
;
2
0 2 2 . 2 0y x f x x
2
2
2
1
2 2
2 1
2 0
x
x x
x x
x x
1
0
2
x
x
x
.
Do
0y
có một nghiệm bội lẻ (
1x
) và hai nghiệm đơn (
0x
;
2x
) nên hàm số
2
2y f x x
chỉ có ba điểm cực trị.
Câu 10. (Mã 102 - 2019) Cho hàm số
f x
, bảng biến thiên của hàm số
'f x
như sau
Số điểm cực trị của hàm số
2
2y f x x
là
A.
9
. B.
5
. C.
7
. D.
3
.
Lời giải
Chọn C
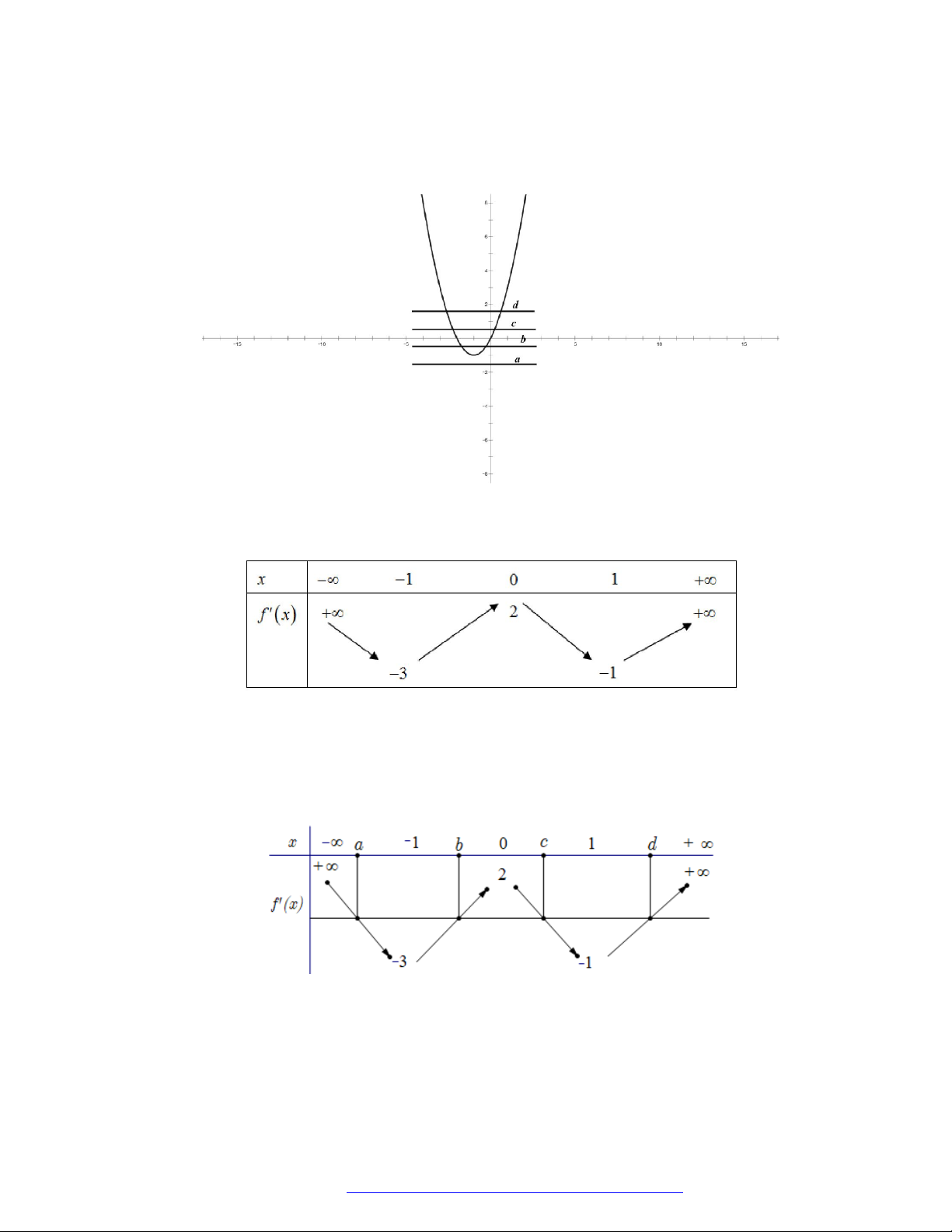
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 22 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta có
2
2 2
2
2
2 2 0
2 , 1
' 2 2 ' 2 0 2 , 1 0
2 ,0 1
2 , 1
x
x x a a
y x f x x x x b b
x x c c
x x d d
Dựa vào đồ thị ta được
' 0y
có 7 nghiệm đơn nên nó có 7 cực trị
Câu 11. (Mã 103 - 2019) Cho hàm số
f x
, bảng biến thiên của hàm số
f x
như sau:
Số cực trị của hàm số
2
4 4y f x x
là
A.
3
. B.
9
. C.
5
. D.
7
.
Lời giải
Chọn D
Từ bảng biến thiên
Ta thấy
; 1
1;0
0
0;1
1;
x a
x b
f x
x c
x d
Với
2
4 4y f x x
, ta có
2
8 4 4 4y x f x x
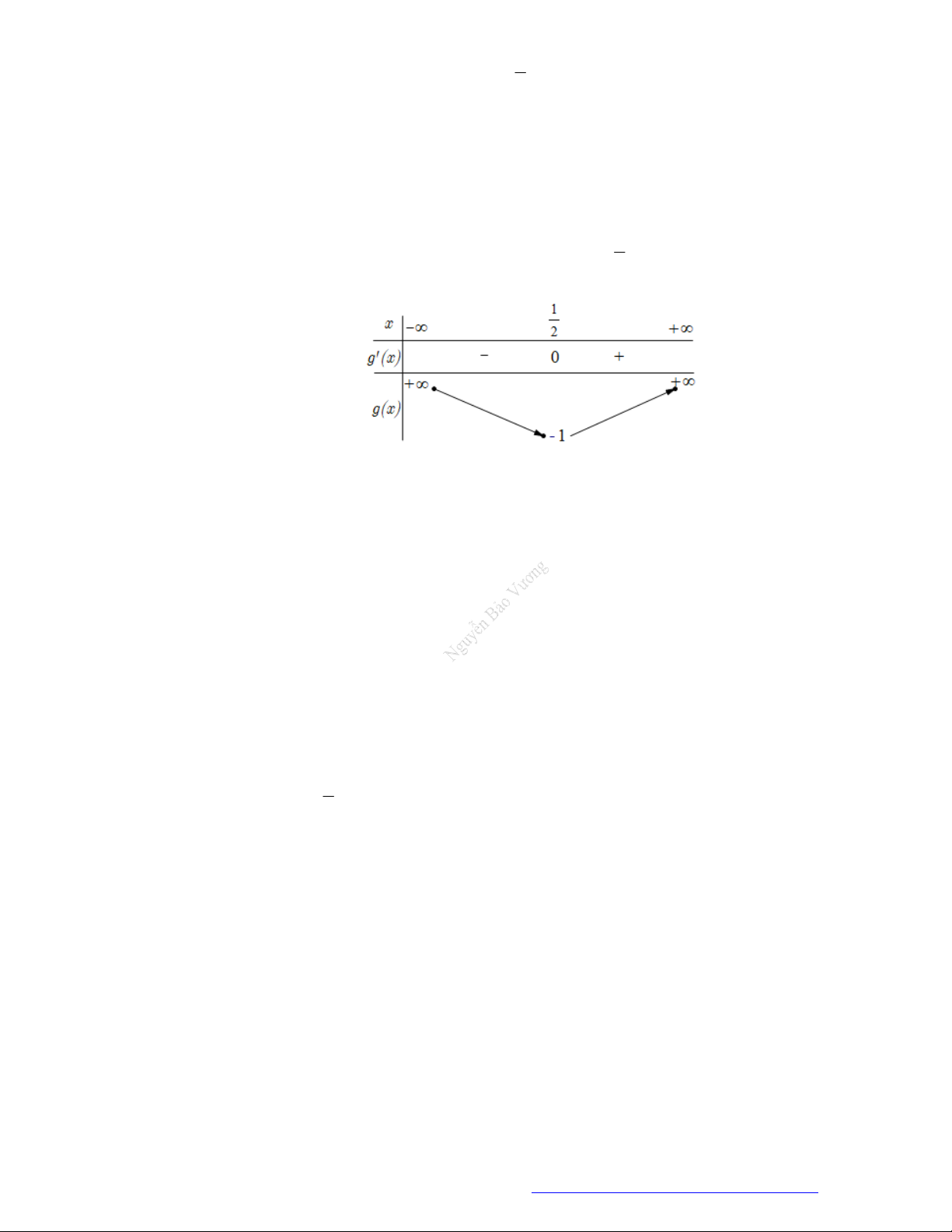
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
2
2
2
2
2
1
2
4 4 ; 1 1
8 4 0
0 4 4 1;0 2
4 4 0
4 4 0;1 3
4 4 1; 4
x
x x a
x
y x x b
f x x
x x c
x x d
Xét hàm số
2
4 4g x x x
, ta có
1
8 4 0
2
g x x x
Bảng biến thiên
Từ bảng biến thiên của
g x
ta có:
Vì
; 1a
nên
1
vô nghiệm.
Vì
1;0b
nên
2
có
2
nghiệm phân biệt.
Vì
0;1c
nên
3
có
2
nghiệm phân biệt.
Vì
1;d
nên
4
có
2
nghiệm phân biệt.
Vậy hàm số
2
4 4y f x x
có
7
điểm cực trị
Cách khác:
Ta có:
2
8 4 . 4 4y x f x x
.
2
2
8 4 0
0 8 4 . 4 4 0
4 4 0
x
y x f x x
f x x
+
1
8 4 0
2
x x
.
+
2
2
2
2
2
4 4 1 1
4 4 1 0 2
4 4 0
4 4 0 1 3
4 4 1 4
x x a a
x x b b
f x x
x x c c
x x d d
+ Phương trình
2 2
4 4 4 4 0x x m x x m
có nghiệm khi
4 4 0m
hay
1m
.
Từ đó, ta có phương trình
1
;
2
;
3
luôn có hai nghiệm phân biệt.
Phương trình
4
vô nghiệm.
Do đó, hàm số đã cho có
7
cực trị.
Câu 12. (Chuyên An Giang - 2018) Cho hàm số
y f x
. Đồ thị của hàm số
y f x
như hình bên.
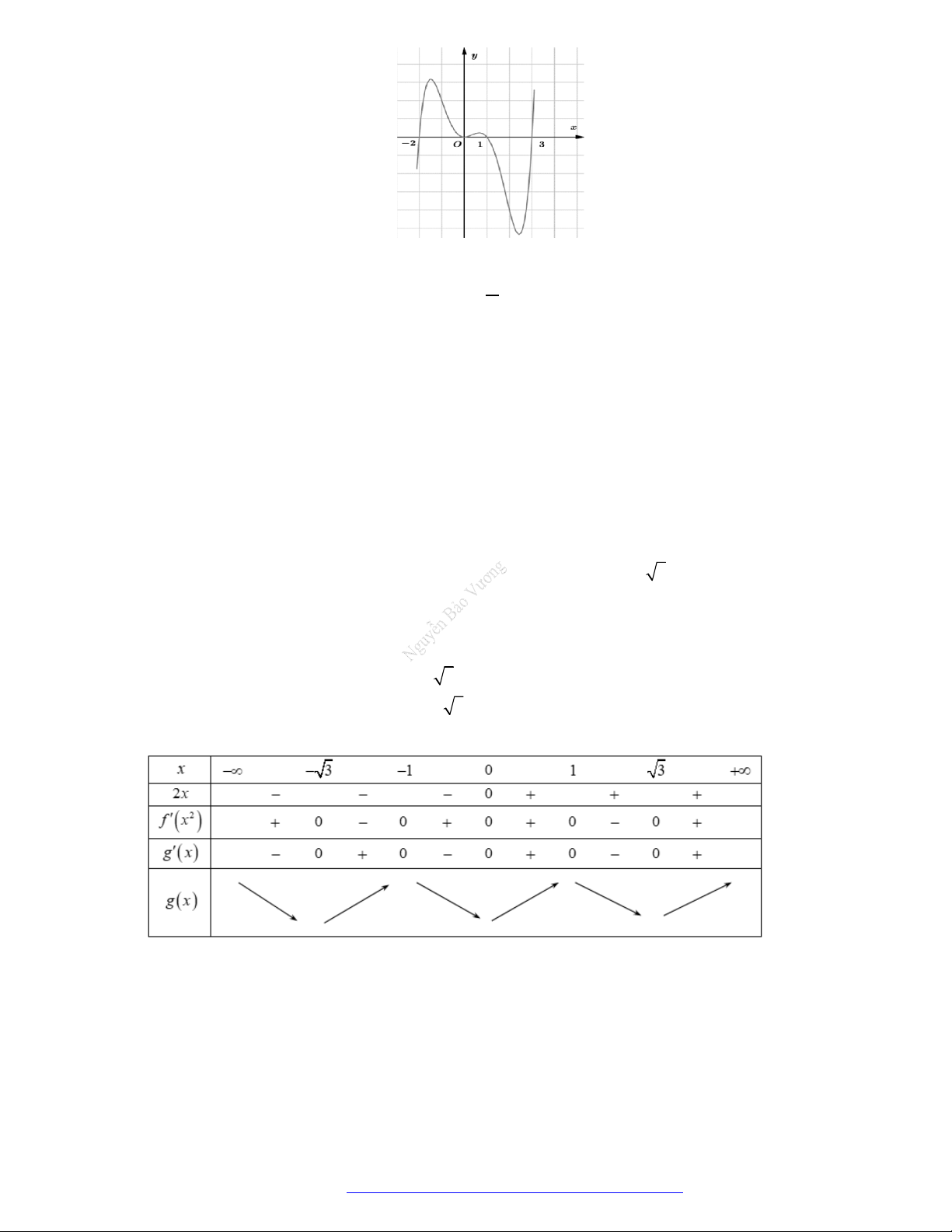
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 24 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Hàm số
2
g x f x
có bao nhiêu điểm cực trị?
A.
4
. B.
3
. C.
5
. D.
2
.
Lời giải
Từ đồ thị
y f x
ta có
2
0
0
1
3
x
x
f x
x
x
;
3
0
2 1
x
f x
x
;
2
0
1 3
x
f x
x
.
Ta có
2
2g x xf x
;
2
2
2
2
0
0
0
1
0 1
0
3
3
0
x
x
x
x
g x x
f x
x
x
x
.
Ta có
2
2
2
1 1
0
0 1
0
3
3
3
x
x
x
f x
x
x
x
.
Ta có bảng biến thiên
Từ bảng biến thiên ta có hàm số
2
g x f x
có
5
điểm cực trị.
Câu 13. (THPT Lê Văn Thịnh Bắc Ninh 2019) Cho hàm số
y f x
xác định trên
và hàm số
y f x
có đồ thị như hình vẽ. Tìm số điểm cực trị của hàm số
2
3y f x
.
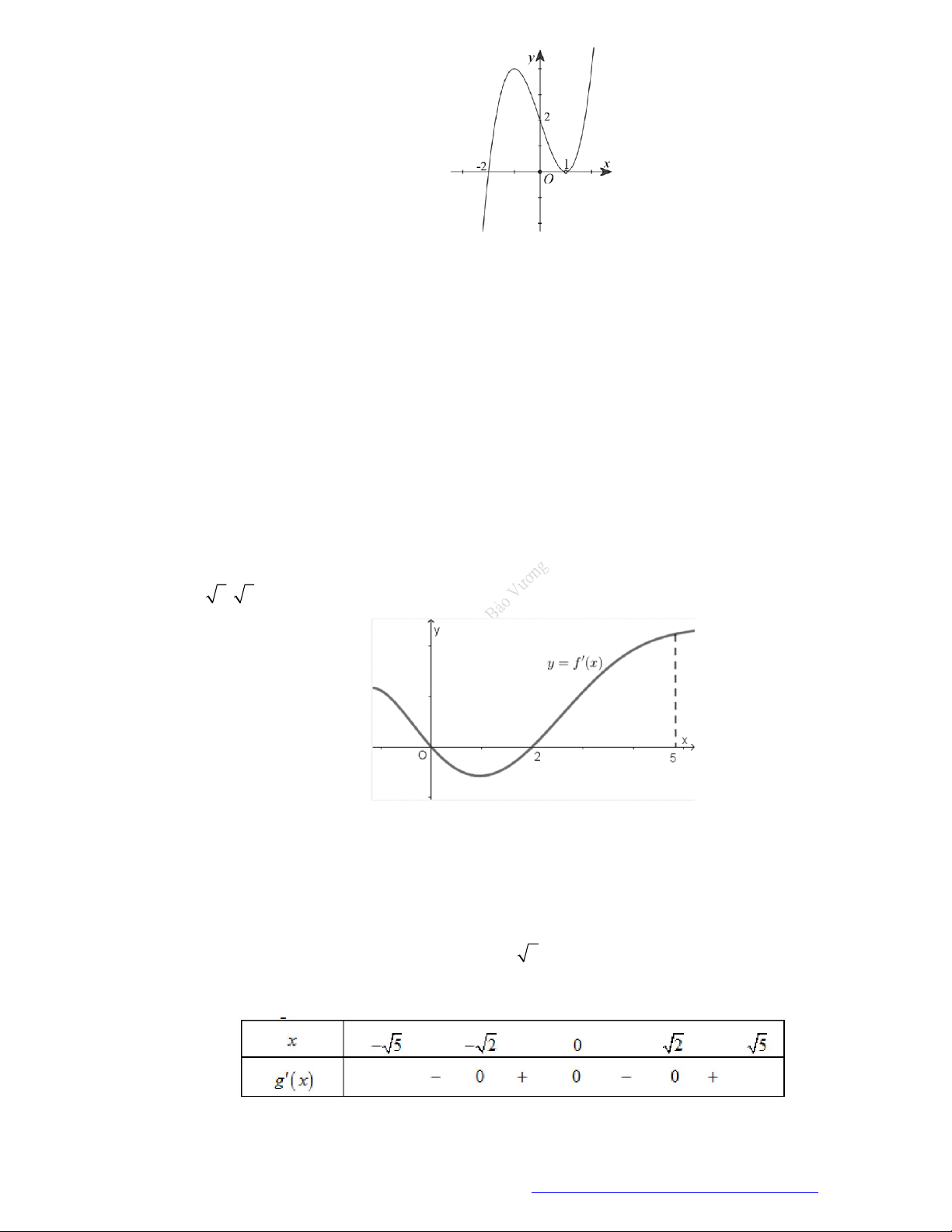
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25
A.
4
B.
2
C.
5
D.
3
Lời giải
Chọn D
Quan sát đồ thị ta có đổi dấu từ âm sang dương qua nên hàm số có
một điểm cực trị là
2x
.
Ta có
2 2
3 2 . 3y f x x f x
2
2
0
0
0 3 2 1
2
3 1
x
x
x x
x
x
.
Mà
2x
là nghiệp kép, còn các nghiệm còn lại là nghiệm đơn nên hàm số
2
3y f x
có ba
cực trị.
Câu 14. (Chuyên Lê Quý Đôn Quảng Trị 2019) Cho hàm số
f x
có đạo hàm là
f x
. Đồ thị của
hàm số
y f x
như hình vẽ bên. Tính số điểm cực trị của hàm số
2
y f x
trên khoảng
5; 5 .
A.
2
. B.
4
. C.
3
. D.
5
.
Lời giải
Xét hàm số
2 2
2g x f x g x xf x
.
2
0
0
0
x
g x
f x
2
2
0
0
0
2
2
x
x
x
x
x
.
Ta có bảng xét dấu:
Từ đó suy ra hàm số
2
y f x
có 3 điểm cực trị.
y f x
2x
y f x
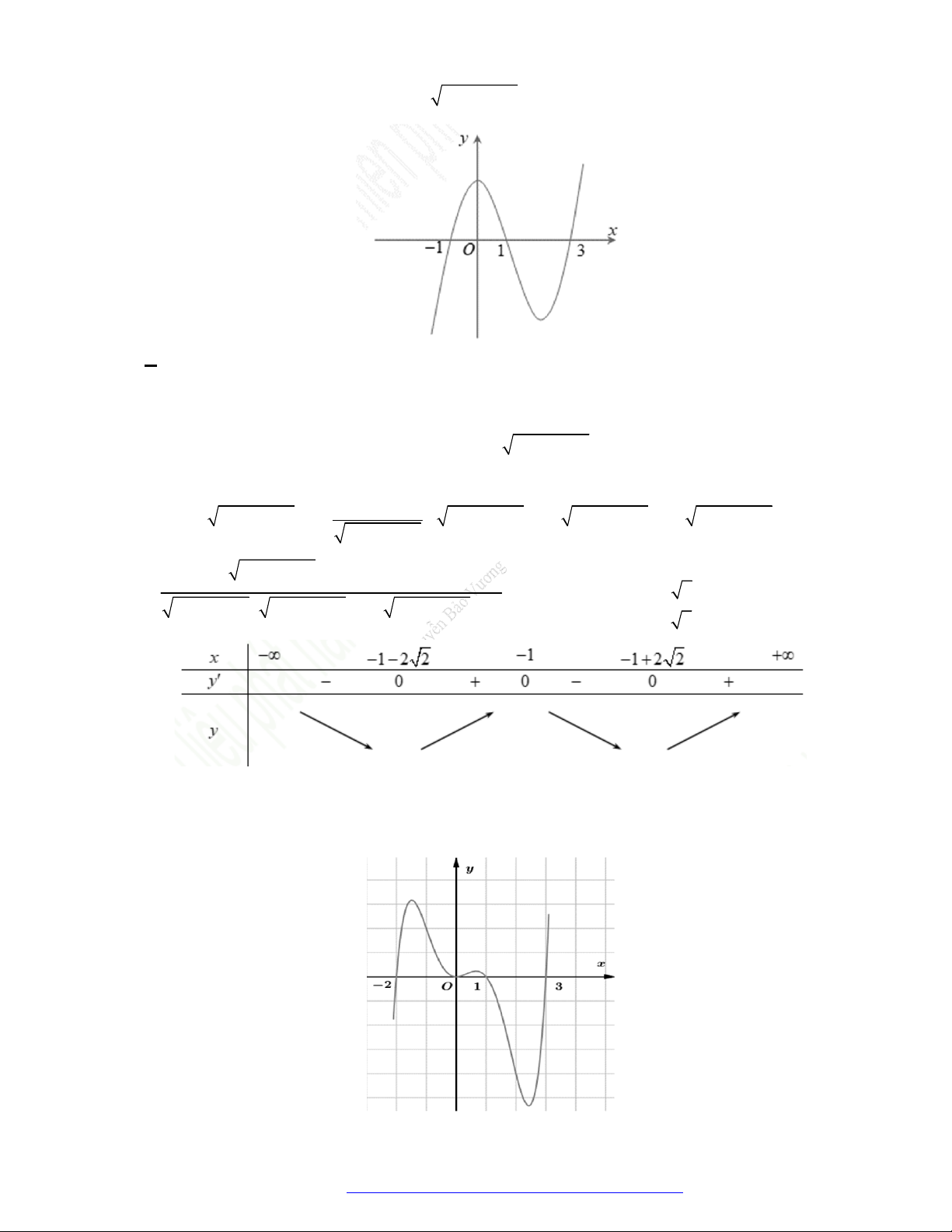
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 26 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 15. (Chuyên Vinh - 2018) Cho hàm số bậc bốn
y f x
. Hàm số
y f x
có đồ thị như hình vẽ
bên. Số điểm cực đại của hàm số
2
2 2y f x x
là
A.
1
. B.
2
. C.
4
. D.
3
.
Lời giải
Từ đồ thị của
y f x
ta chọn
1 1 3f x x x x
.
Áp dụng công thức
y f u u f u
với
2
2 2u x x
Ta có
2 2 2 2
2
1
2 2 . 2 2 1 2 2 1 2 2 3
2 2
x
y f x x x x x x x x
x x
2
2 2
2 2 2
1 2 2 1 1 2 7
2 2 2 2 1 2 2 3
x x x x x x
x x x x x x
1
0 1 2 2
1 2 2
x
y x
x
Từ bảng biến thiên ta thấy hàm số có một điểm cực đại.
Câu 16. (Chuyên Thoại Ngọc Hầu 2018) Cho hàm số
y f x
. Đồ thị hàm số
y f x
như hình vẽ
sau.
Hàm số
2
g x f x
có bao nhiêu điểm cực trị?
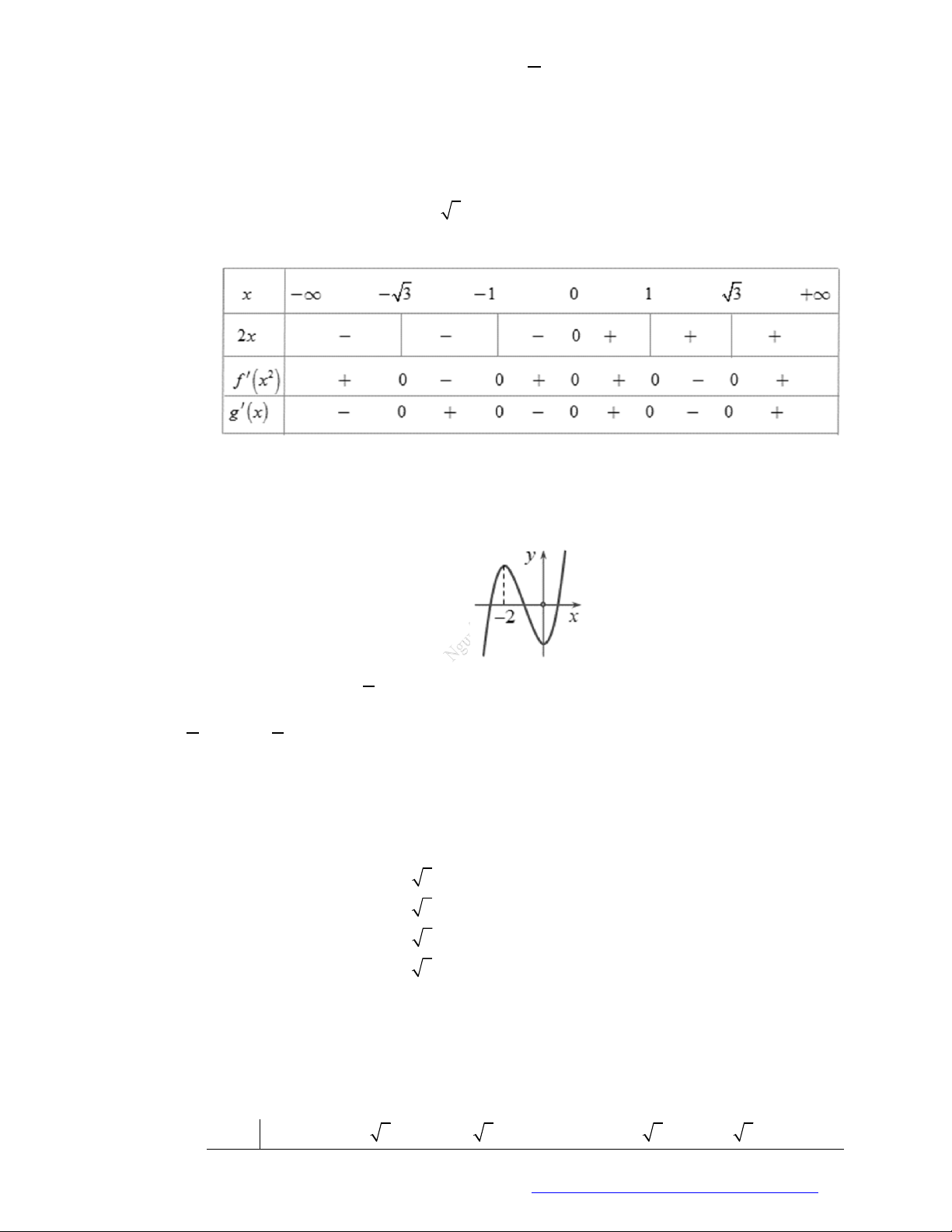
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27
A.
4
. B.
3
. C.
5
. D.
2
.
Lời giải
Có
2 2
2g x f x xf x
2
0
0
0
x
g x
f x
0
1
3
x
x
x
Bảng xét dấu
g x
Từ bảng xét dấu của
g x
suy ra hàm số có
5
điểm cực trị.
Câu 17. Cho hàm số
y f x
xác định và liên tục trên
có đồ thị như hình vẽ. Hàm số
2
2 4g x f x x
có bao nhiêu điểm cực tiểu?
A.
1
. B.
3
. C.
2
. D.
4
.
Lời giải
Chọn B.
Ta có:
2
2 1 2 4g x x f x x
.
2
2
1
0 1 2 4 0
2 4 0
x
g x x f x x
f x x
2
2
1
1 3
1
2 4 2 1 3
2 4 0
1 5
1 5
x
x
x
x x x
x x
x
x
(Tất cả đều là nghiệm bội lẻ).
Ta chọn
2x
để xét dấu của
g x
:
2 2. 3 . 4g f
.
Vì hàm số
y f x
đồng biến trên khoảng
0;
do đó:
4 0f
.
Suy ra:
2 0g
.
Theo tính chất qua nghiệm bội lẻ
g x
đổi dấu, ta có bảng xét dấy
g x
như sau:
x
1 5
1 3
1
1 3
1 5
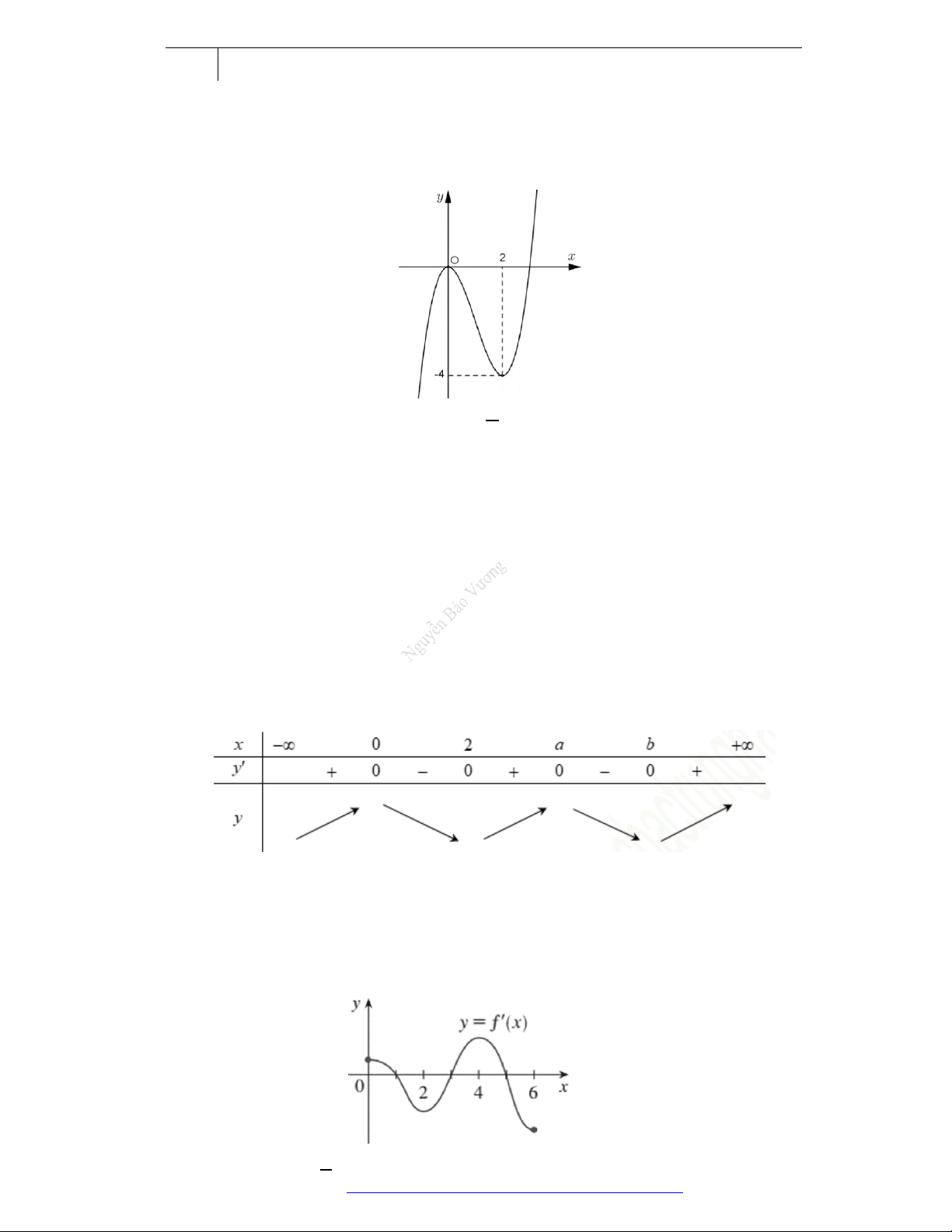
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 28 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
g x
0
0
0
0
0
Từ bảng xét dấu, suy ra hàm số
y g x
có 3 điểm cực tiểu.
Câu 18. (Đặng Thúc Hứa - Nghệ An -2018) Biết rằng hàm số
f x
có đồ thị được cho như hình vẽ bên.
Tìm số điểm cực trị của hàm số
y f f x
.
A.
5
. B.
3
. C.
4
. D.
6
.
Lời giải
Xét hàm số
y f f x
,
.y f x f f x
;
0 0
0 2 2
0
0 2;
0
2 ;
x x
f x x x
y
f x x a
f f x
f x x b a
.
Với
x b
, ta có
2f x
0f f x
Với
a x b
, ta có
0 2f x
0f f x
Với
0 x a
hoặc
0x
, ta có
0f x
0f f x
BBT:
Dựa vào BBT suy ra hàm số
y f f x
có bốn điểm cực trị.
Câu 19. (Sở Bình Phước - 2018) Cho hàm số
y f x
liên tục và có đạo hàm trên
0;6
. Đồ thị của
hàm số
y f x
trên đoạn
0;6
được cho bởi hình bên dưới. Hỏi hàm số
2
y f x
có tối đa
bao nhiêu cực trị.
A.
3
. B.
7
. C.
6
. D.
4
.
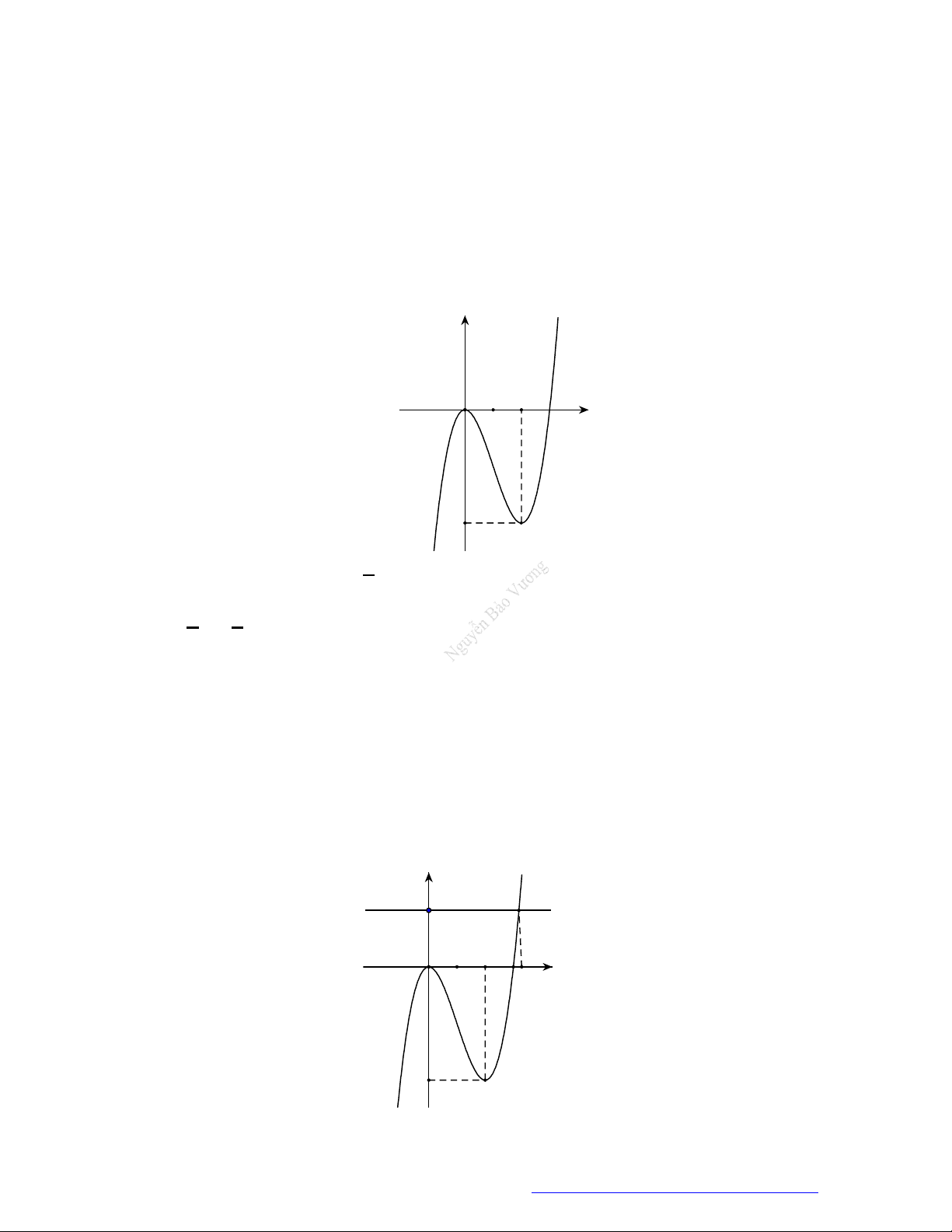
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 29
Lời giải
Ta có
2y f x f x
nên
0
0
0
f x
y
f x
.
Từ đồ thị ta suy ra
0f x
có tối đa
4
nghiệm,
0f x
có tối đa
3
nghiệm.
Do đó, hàm số
2
y f x
có tối đa
7
điểm cực trị nên có tối đa
7
cực trị.
Câu 20. Biết rằng hàm số
f x
có đồ thị được cho như hình vẽ bên. Tìm số điểm cực trị của hàm số
y f f x
?
A. 5. B. 4. C. 3. D. 6.
Lời giải
Chọn B
Ta có:
' .y f f x f x f f x
;
0
' 0
0
f x
y
f f x
+
0
0
2
x
f x
x
vì hàm số
f x
có hai điểm cực trị
0; 2x x
+
0
0
2
f x
f f x
f x
Quan sát đồ thị ta thấy phương trình
0f x
có một nghiệm bội chẵn
0x
và
một
x
y
-4
2
O
x
y
y=2
a
-4
2
2
O
b
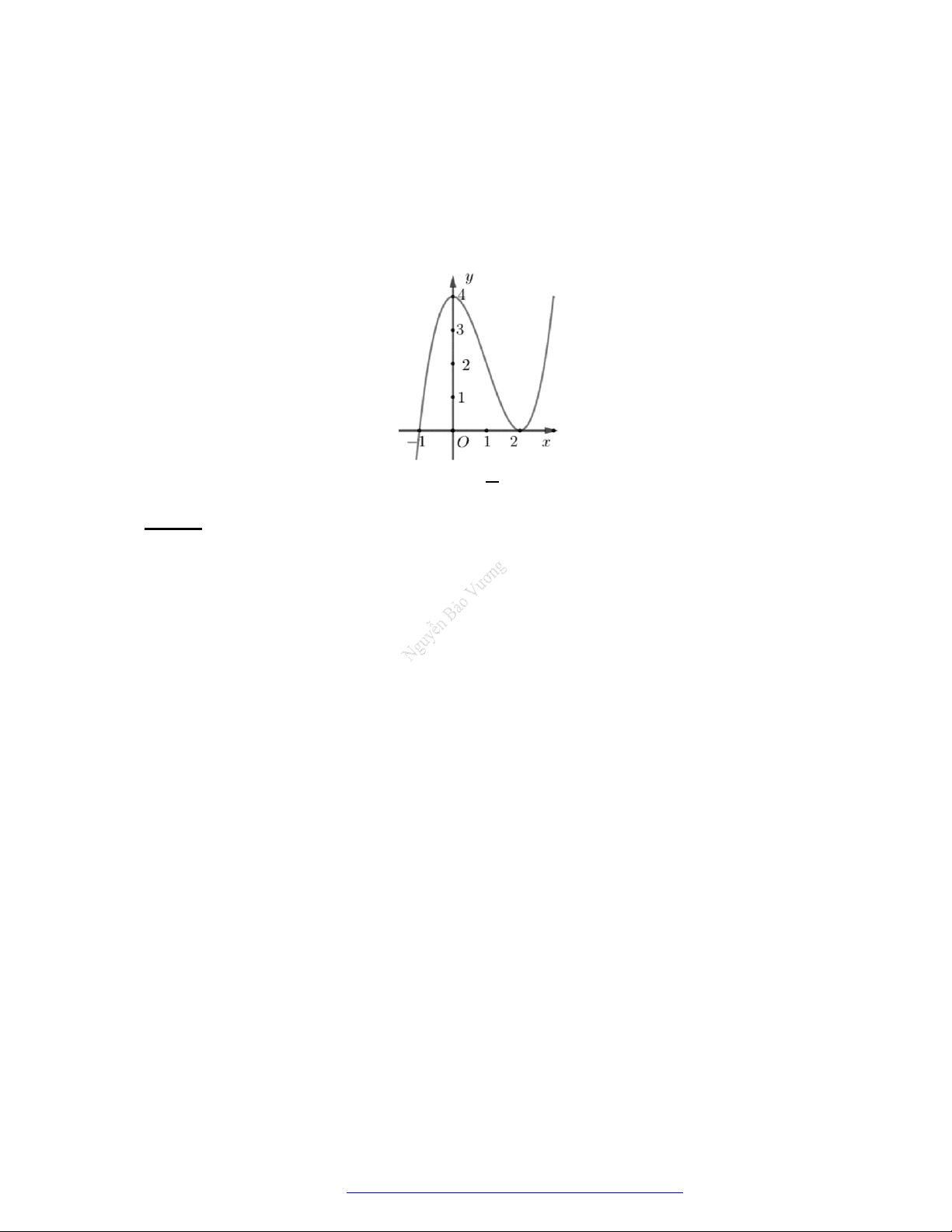
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 30 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
nghiệm đơn hoặc bội lẻ
2x a
.
Kẻ đường thẳng
2y
nhận thấy phương trình
2f x
có một nghiệm đơn hoặc
bội lẻ
x b a
Do đó
y
có các điểm đổi dấu là
0; 2, ,x x x a x b
.
Vậy hàm số có 4 điểm cực trị.
Câu 21. (THPT Đô Lương 3 - Nghệ An - 2019) Cho hàm số
f x
có đồ thị như hình vẽ bên dưới. Số
điểm cực trị của hàm số
g x f f x
là.
A.
3.
B.
7.
C.
6.
D.
5.
Lời giải
Chọn C
Ta có
' ' . 'g x f x f f x
.
' 0
' 0
' 0
f x
g x
f f x
.
0
' 0
2
x
f x
x
.
0 *
' 0
2 **
f x
f f x
f x
Dựa vào đồ thị suy ra:
Phương trình (*) có hai nghiệm
1
2
x
x
.
Phương trình ( **) có ba nghiệm
1 0
0 1
2
x m n
x n n
x p p
' 0g x
có nghiệm
1
0
2
x
x m
x
x n
x
x p
.
Bảng biến thiên
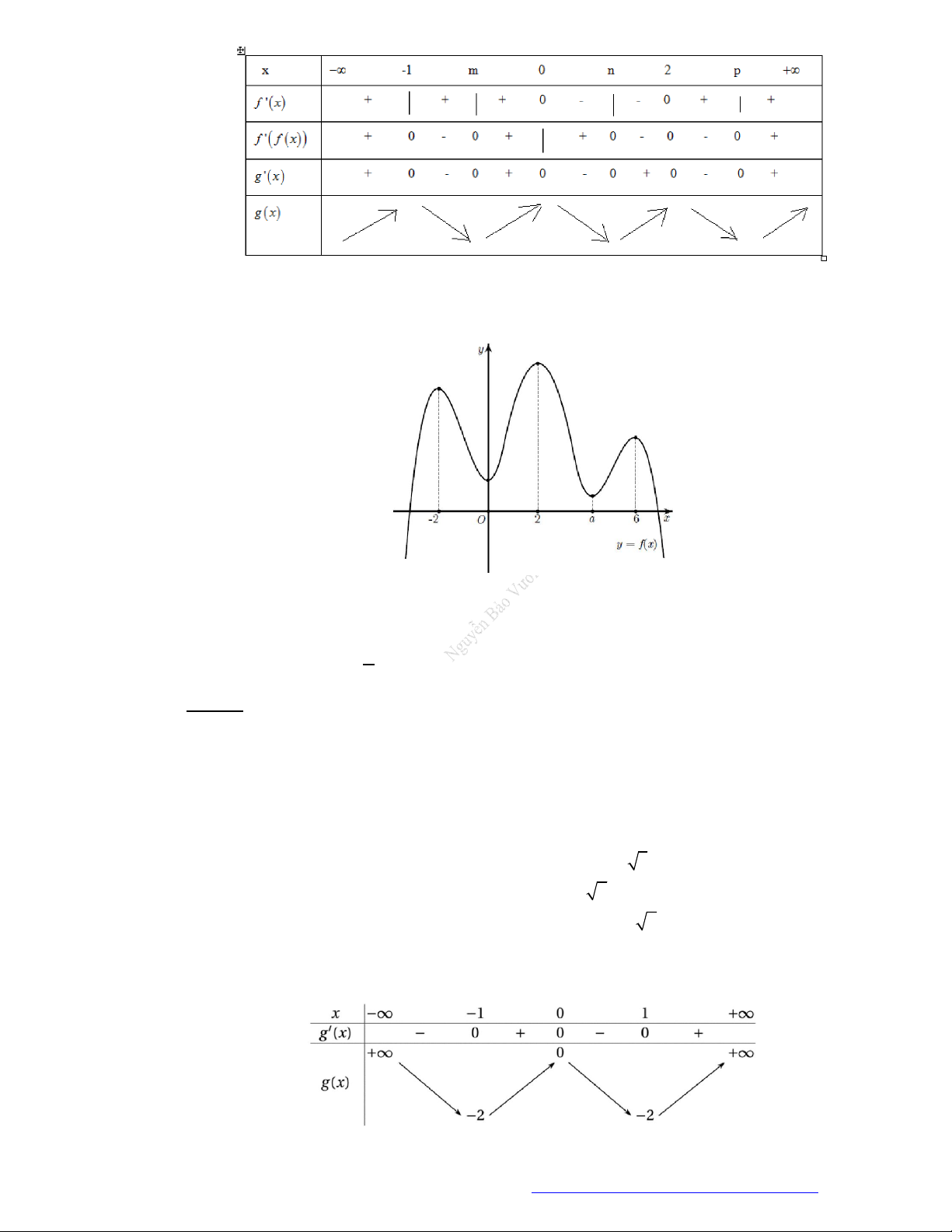
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 31
Nhìn bảng biến thiên ta thấy hàm số
g x f f x
có 6 cực trị.
Câu 22. (Sở GD Bắc Ninh - 2019) Cho hàm số
y f x
có đồ thị như hình vẽ.
Biết tất cả các điểm cực trị của hàm số
y f x
là
2
;
0
;
2
;
a
;
6
với
4 6a
. Số điểm cực
trị của hàm số
6 2
3y f x x
là
A. 8. B. 11. C. 9. D. 7.
Lời giải
Chọn B
Từ đồ thị ta có -2; 0; 2;
a
; 6 là tất cả các nghiệm của
f x
.
Ta có:
6 2 5 6 2
3 6 6 3y f x x x x f x x
5
6 2
6 6 0
' 0
3 0
x x
y
f x x
6 2
6 2
6 2
6 2
6 2
0, 1
3 2
3 0
3 2
3
3 6
x x
x x
x x
x x
x x a
x x
4
0, 1
1
0, 3
2
, 2
,
x x
x
x x
x
x m m
x n n m
Ta có bảng biến thiên của hàm số
6 2
3g x x x
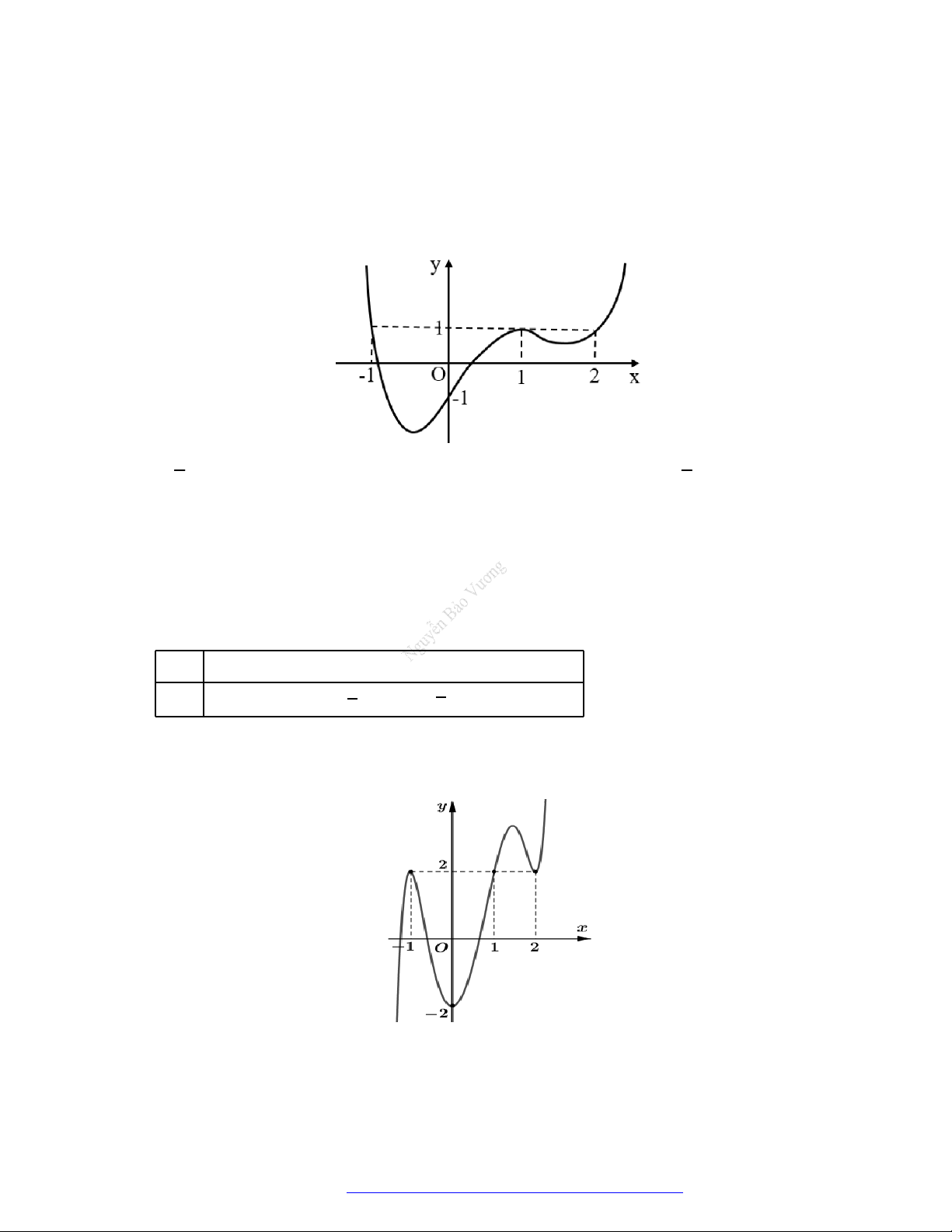
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 32 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Dựa vào bảng biến thiên của hàm số
6 2
3g x x x
, ta suy ra
1
là nghiệm kép của phương
trình
6 2
3 2x x
và
0
là nghiệm kép của phương trình
6 2
3 0x x
. Do đó
1
và
0
là nghiệm
kép của
6 2
3f x x
. Do vậy
1
và
0
là nghiệm bội ba của
y
.
Các nghiệm khác
1
và
0
của
y
đều là nghiệm đơn.
Vậy hàm số đã cho có 11 cực trị.
Câu 23. (Toán Học Tuổi Trẻ 2019) Cho hàm số
(x)f
xác định trên
và có đồ thị
( )f x
như hình vẽ
bên. Đặt
( ) ( )g x f x x
. Hàm số đạt cực đại tại điểm thuộc khoảng nào dưới đây?
A.
3
;3
2
B.
2;0
C.
0;1
D.
1
;2
2
Lời giải
Ta có
1
1; 0 1 1
2
x
g x f x g x f x x
x
Bảng xét dấu của
g x
:
Từ bảng xét dấu nhận thấy
g x
đạt cực đại tại
1 2;0x
.
Câu 24. (Thpt Hoàng Hoa Thám Hưng Yên 2019) Cho hàm số
( 1)y f x
có đồ thị như hình vẽ.
Hàm số
2 4f x x
y
đạt cực tiểu tại điểm nào?
A.
1x
. B.
0x
. C.
2x
. D.
1x
.
Lời giải:
Ta có:
2 4
2 4 ln
f x x
y f x
.
0 2 4 0 2y f x f x
.
+
0
2
0
-1
1
+
x
g'(x) 0
-∞ +∞
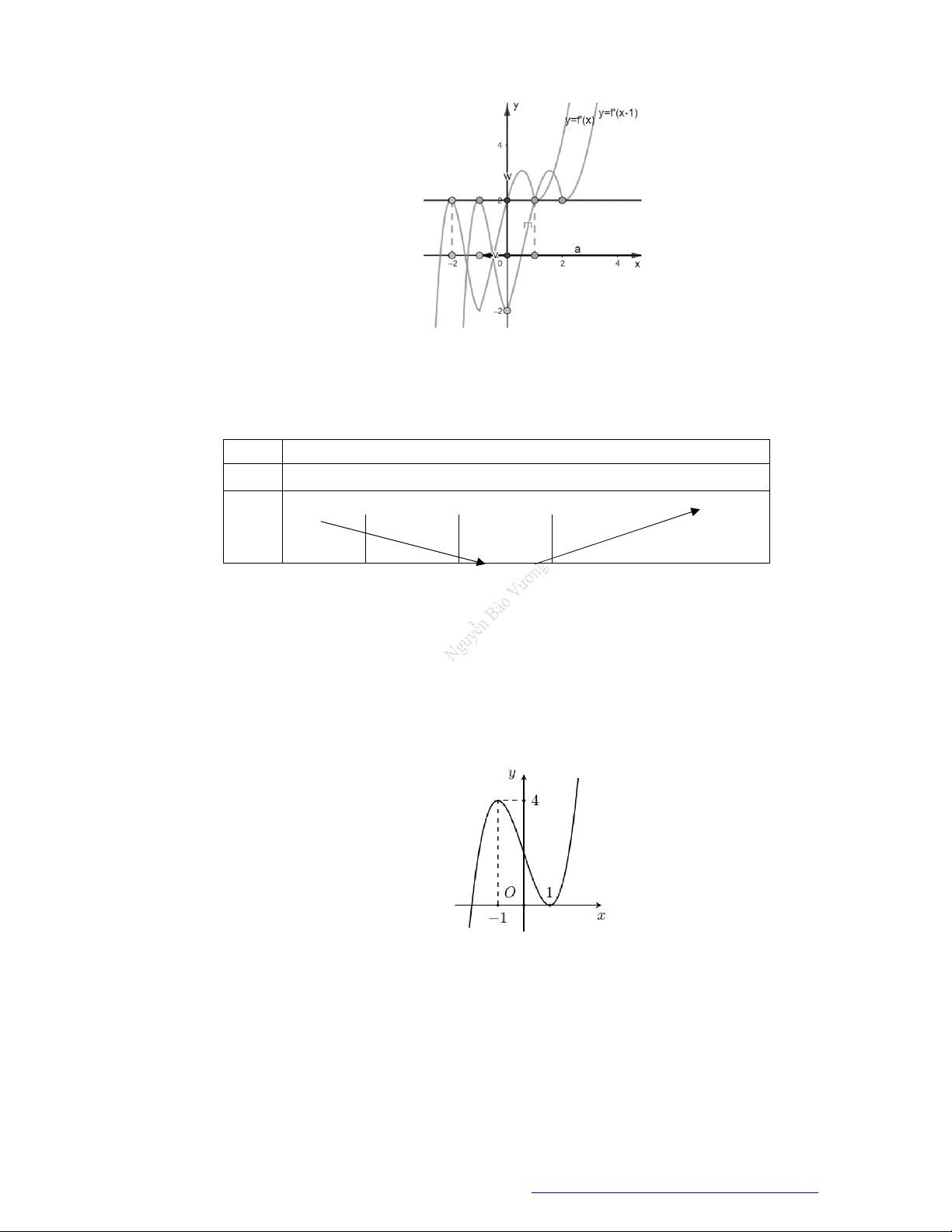
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 33
Đồ thị hàm số
y f x
nhận được từ việc tịnh tiến đồ thị hàm số
1y f x
sang trái 1 đơn
vị
nên
2f x
2
0
1
x
x
x
.
Do
2x
và
1x
là nghiệm bội chẵn nên ta có bảng biến thiên sau:
x
2
0
1
y
0
0
0
y
Từ bảng biến thiên ta có hàm số đạt cực tiểu tại
0x
.
Câu 25. (THPT Minh Châu Hưng Yên 2019) Cho hàm số
y f x
có đạo hàm liên tục trên
và đồ thị
hàm số
y f ' x
như hình vẽ bên.
Số điểm cực trị của hàm số
y f x 2017 2018x 2019
là.
A.
3
B.
4
C.
1
D.
2
Lời giải
Chọn C
Ta có:
f x 2017 2018x 2019 0 f x 2017 2018 0 f x 2017 2018
Dựa vào đồ thị hàm số
y f ' x
suy ra phương trình
f x 2017 2018
có 1 nghiệm đơn duy
nhất. Suy ra hàm số
y f x 2017 2018x 2019
có 1 điểm cực trị.
Câu 26. (Chuyên Thái Bình - 2018) Cho hàm số
'( )y f x
có đồ thị như hình vẽ dưới đây:
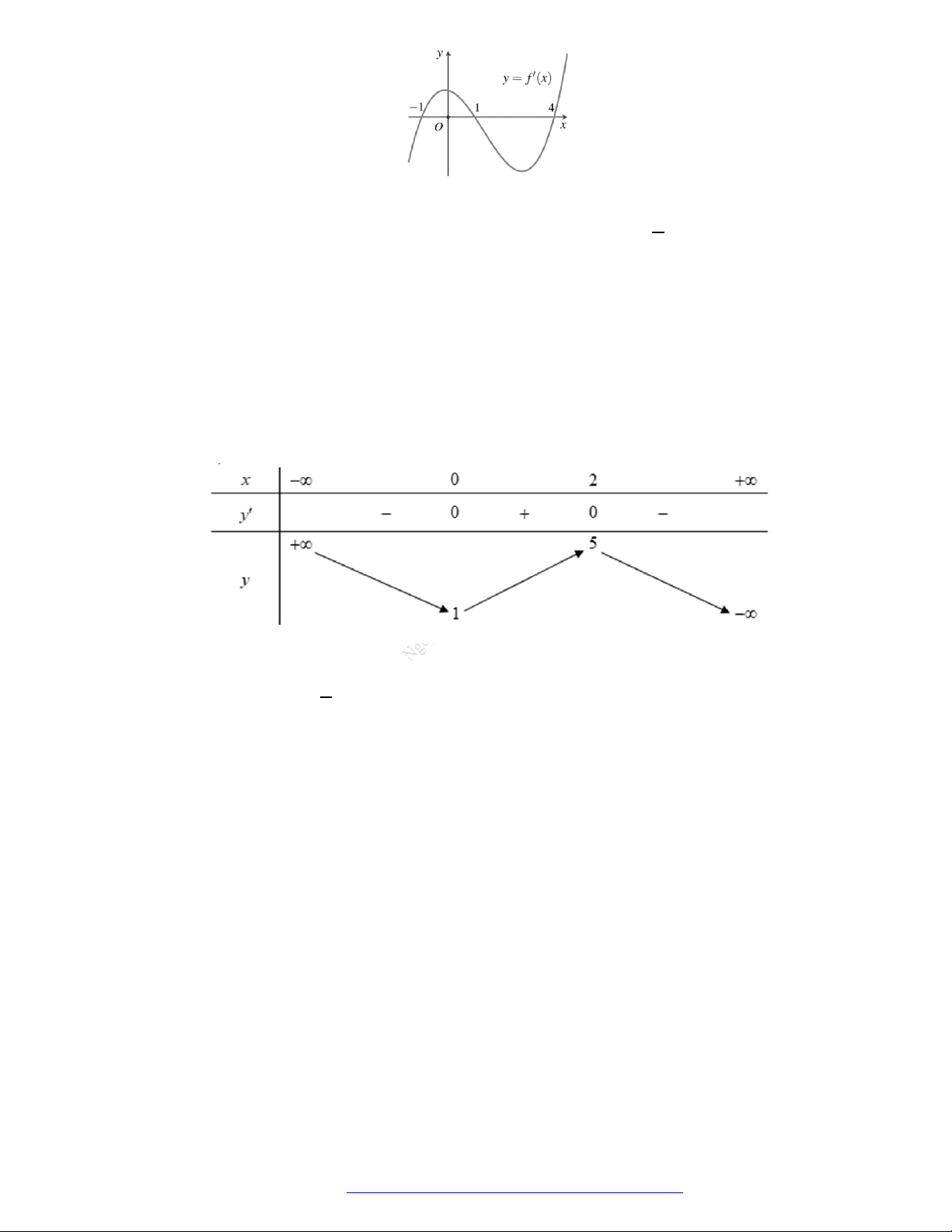
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 34 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Tìm số điểm cực trị của hàm số
2 ( ) 1 ( )
e 5
f x f x
y
.
A.
1
. B.
2
. C.
4
. D.
3
.
Lời giải
Ta có
2 ( ) 1 ( )
e 5
f x f x
y
2 ( ) 1 ( )
2 .e .5 ln5
f x f x
y f x f x
2 ( ) 1 ( )
2e 5 ln 5
f x f x
f x
.
Nhận xét
2 ( ) 1 ( )
2e 5 ln5 0,
f x f x
x
làm cho
f x
xác định nên dấu của
y
phụ thuộc hoàn toàn
vào
f x
.
Vì vậy do
f x
đổi dấu
3
lần nên số điểm cực trị của hàm số
2 ( ) 1 ( )
e 5
f x f x
y
là
3
.
Câu 27. (THPT Quỳnh Lưu - Nghệ An - 2018) Cho hàm số
y f x
có bảng biến thiên như sau
Hàm số
2 1y f x
đạt cực tiểu tại điểm
A.
2x
. B.
0x
. C.
1x
. D.
5x
.
Lời giải
Ta có:
2 1y f x
2y f x
.
Suy ra: Điểm cực tiểu của hàm số
y f x
cũng chính là điểm cực tiểu của hàm số
2 1y f x
.
Vậy: Hàm số
2 1y f x
đạt cực tiểu tại điểm
0x
.
Câu 28. (Liên Trường - Nghệ An - 2018) Cho hàm số
y f x
có đạo hàm liên tục trên
. Đồ thị hàm
số
y f x
như hình vẽ sau. Số điểm cực trị của hàm số
2y f x x
là:
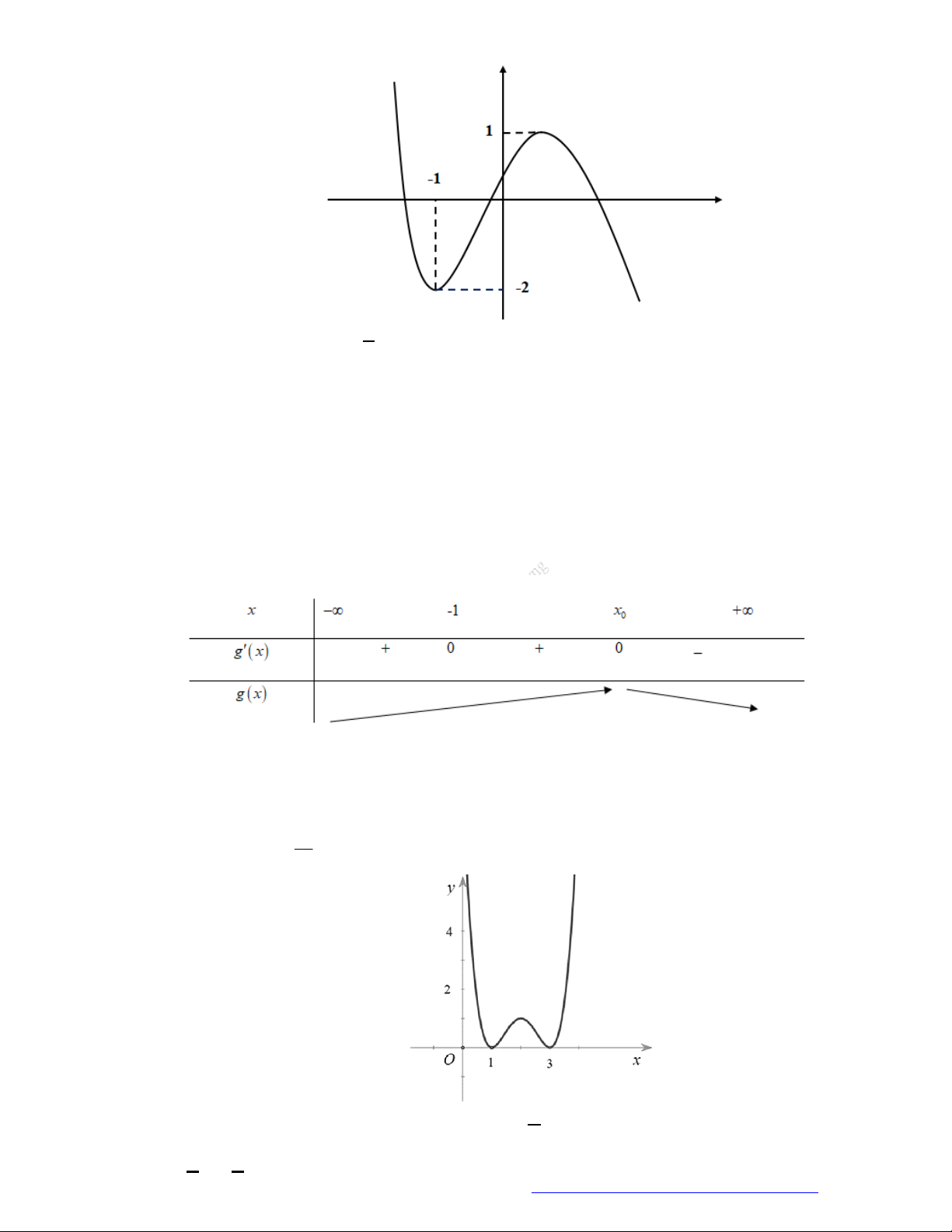
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 35
A.
4
. B.
1
. C.
3
. D.
2
.
Lời giải
Đặt
2g x f x x
suy ra
0
1
0 2 0 2
1
x
g x f x f x
x x
.
Dựa vào đồ thị ta có: Trên
; 1
thì
2 2 0f x f x
.
Trên
0
1; x
thì
2 2 0f x f x
.
Trên
0
;x
thì
2 2 0f x f x
.
Vậy hàm số
2g x f x x
có
1
cực trị.
Câu 29. Cho hàm số
f x
có đồ thị
f x
như hình vẽ dưới. Hàm số
3
2
2 5 2001
3
x
g x f x x x
có bao nhiêu điểm cực trị?
A.
3
. B.
1
. C.
2
. D.
0
.
Lời giải
Chọn C
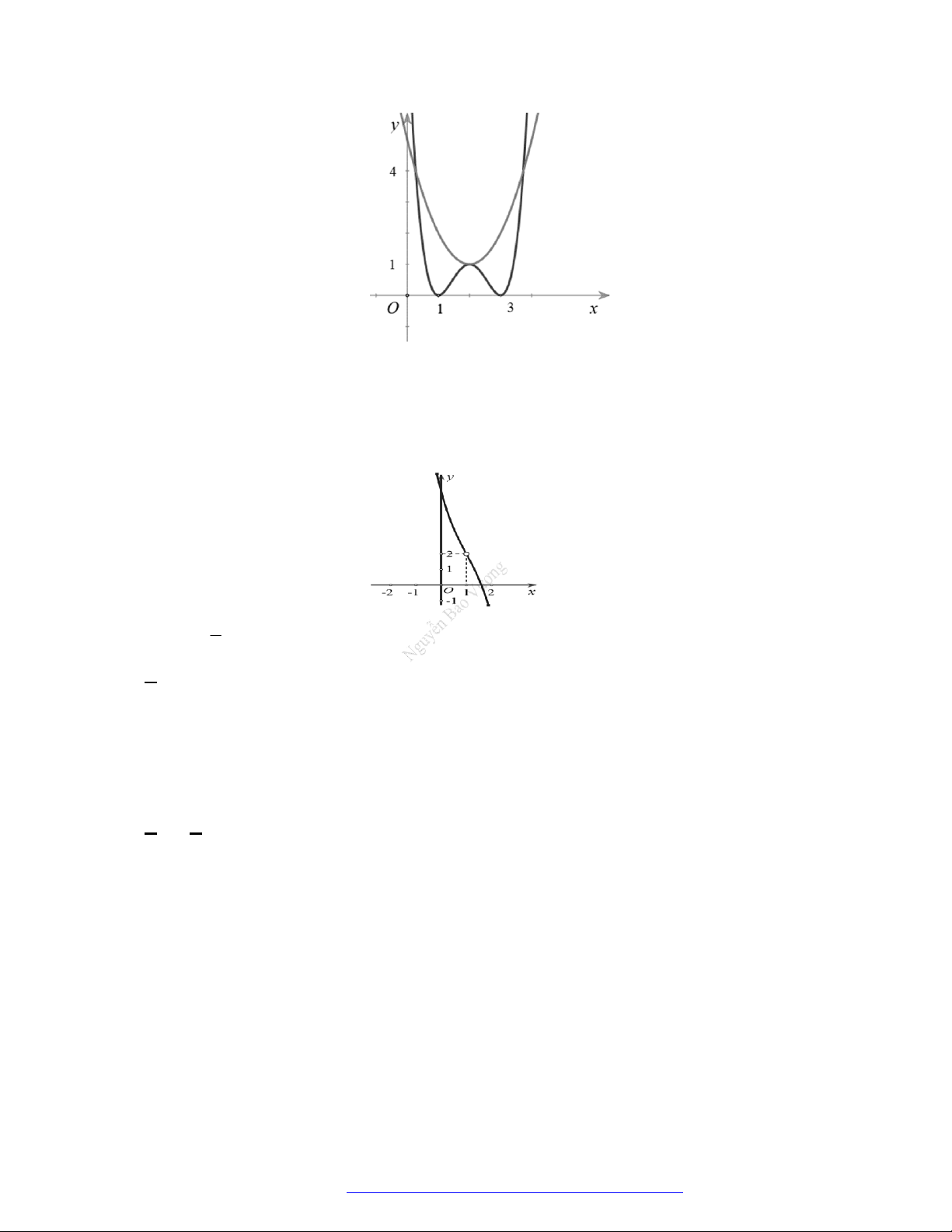
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 36 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Có
2
4 5g x f x x x
2
0 4 5f xg x x x
Ta có đồ thị hàm số
2
4 5y x x và đồ thị hàm
y f x
như hình vẽ dưới
Quan sát hình vẽ ta thấy
0g x
có 3 nghiệm phân biệt trong đó chỉ có 1 nghiệm bội chẵn
Vậy hàm số
g x
có 2 điểm cực trị.
Câu 30. Cho hàm số
y f x
có đạo hàm trên
và không có cực trị, đồ thị của hàm số
y f x
là
đường cong của như hình vẽ dưới đây.
Xét hàm số
2
2
1
2 . 2
2
h x f x x f x x
. Mệnh đề nào sau đây đúng?
A. Đồ thị của hàm số
y h x
có điểm cực tiểu là
1;0M
.
B. Hàm số
y h x
không có cực trị.
C. Đồ thị hàm số
y h x
có điểm cực đại là
1;2N
.
D. Đồ thị hàm số
y h x
có điểm cực đại là
1;0M
.
Lời giải
Chọn A
Theo bài ra ta có
' . 2 2 . 4h x f x f x f x x f x x
2 2 2f x f x x f x x
2 2f x f x x
Từ đồ thị ta thấy
y f x
nghịch biến nên
' 0f x
suy ra
2 0f x
.
Suy ra
0 2 0h x f x x
.
Từ đồ thị dưới ta thấy
2 0 1f x x x
.
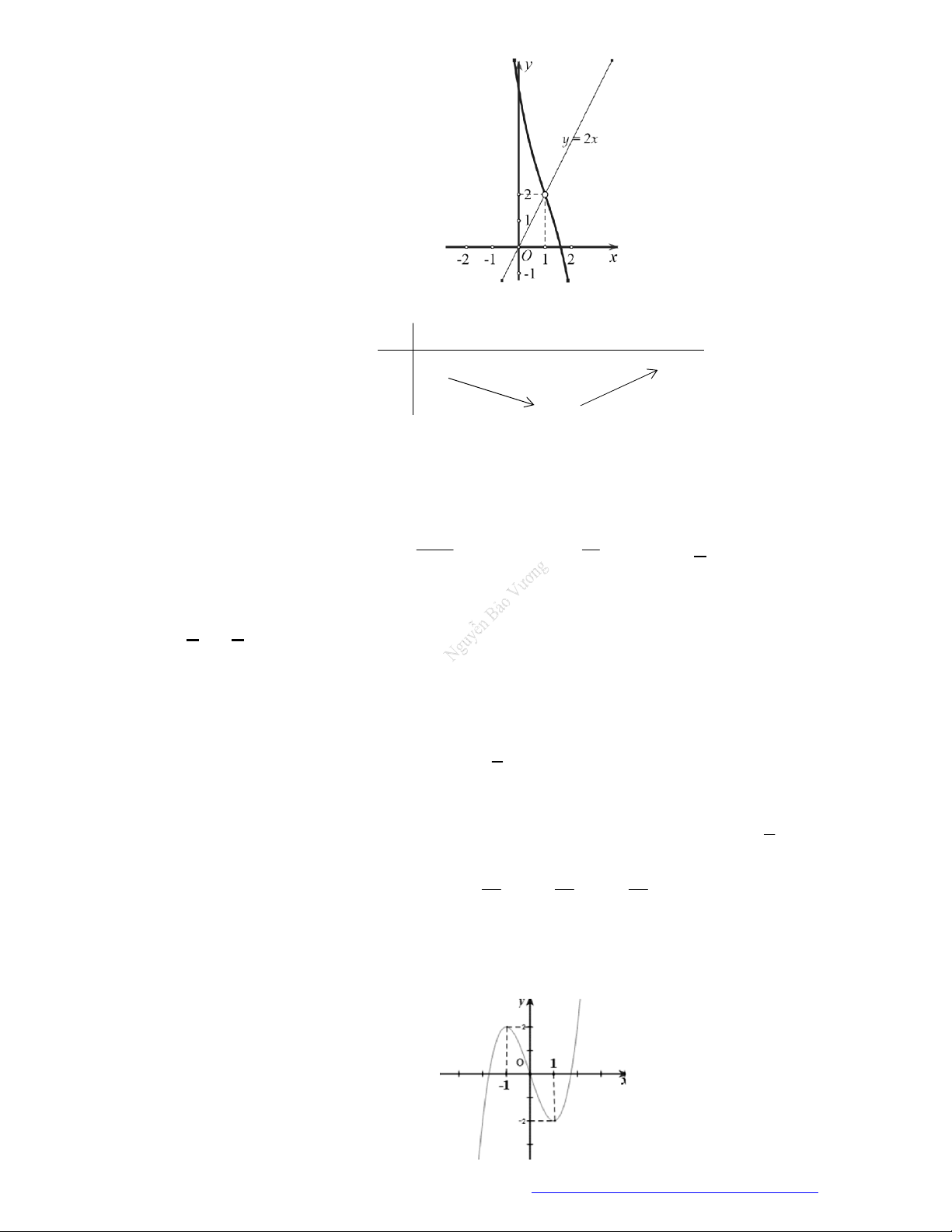
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 37
Ta có bảng biến thiên:
Suy ra đồ thị của hàm số
y h x
có điểm cực tiểu là
1;0M
.
Câu 31. Cho hàm số
4
f x x
. Hàm số
2
' 3 6 1g x f x x x
đạt cực tiểu, cực đại lần lượt tại
1 2
,x x . Tính
1 2
m g x g x
.
A.
0m
. B.
371
16
m
. C.
1
16
m
. D.
11m
.
Lời giải
Chọn D
Theo bài ra ta có
3
' 4f x x
.
Suy ra
3 2
4 3 6 1g x x x x
.
Suy ra
1
2
2
1
' 12 6 6 0
1
2
x
g x x x
x
Đồ thị hàm số lên - xuống – lên.
Hàm số
2
' 3 6 1g x f x x x
đạt cực tiểu, cực đại lần lượt tại
1 2
1
1,
2
x x
.
Suy ra
3 2
1 1 1
1 . 2 4 3 6 1 4. 3. 6. 1 11
2 2 2
m g g
.
Câu 32. (Chuyên Lê Quý Đôn Điện Biên 2019) Biết đạo hàm của hàm số
y f x
có đồ thị như hình
vẽ. Hàm số
2y f x x
có bao nhiêu điểm cực trị?
x
1
h x
0
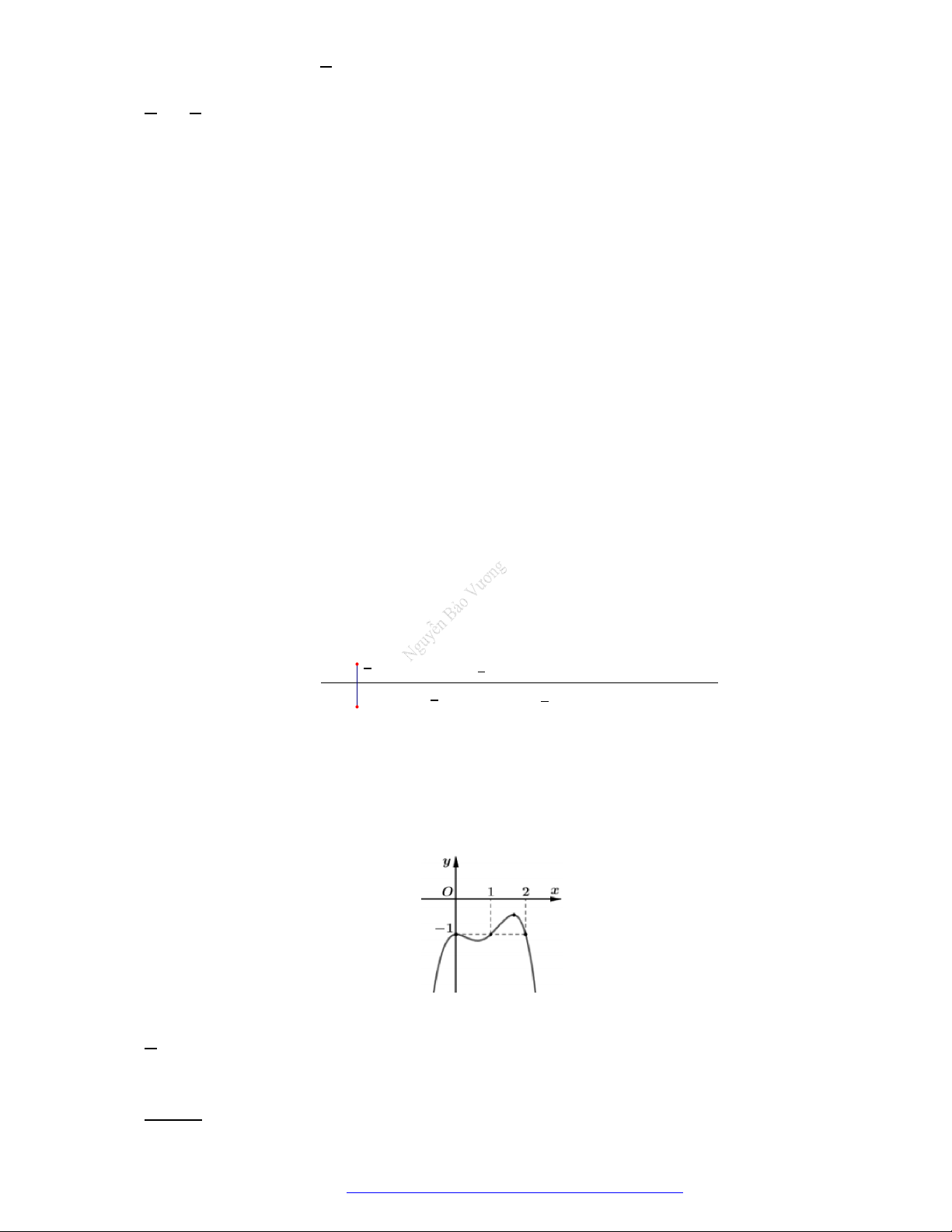
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 38 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
2
. B.
1
. C.
0
. D.
3
.
Lời giải
Chọn B
Đặt
g x f x
3 2
g x ax bx cx d
Đồ thị hàm số
g x
đi qua các điểm
0;0O
,
1;2
,
1; 2
nên ta có:
0 0
2 0
2 2
d d
a b c d b
a b c d a c
Do đó:
3 2
3g x ax cx g x ax c
Hàm số đạt cực trị tại
1x
nên
1 0 3 0g a c
Từ đó có:
3
1; 3 ( ) 3a c g x f x x x
Xét hàm số:
2y f x x
2
3
2 3 2 1 2y f x x x x x
1
0
2
x
y
x
Dấu của
y
Do đó hàm số có 1 điểm cực trị.
Câu 33. (Kim Liên - Hà Nội 2019) Cho hàm số
y f x có đạo hàm trên
. Biết hàm số
y f x có
đồ thị như hình vẽ.
Hàm số
g x f x x
đạt cực tiểu tại điểm
A.
1x
. B.
2x
.
C. Không có điểm cực tiểu. D.
0x
.
Lời giải
Chọn A
Xét hàm số
g x f x x
có
1g x f x
+
0
0
2
x
y'
1
+
∞
∞
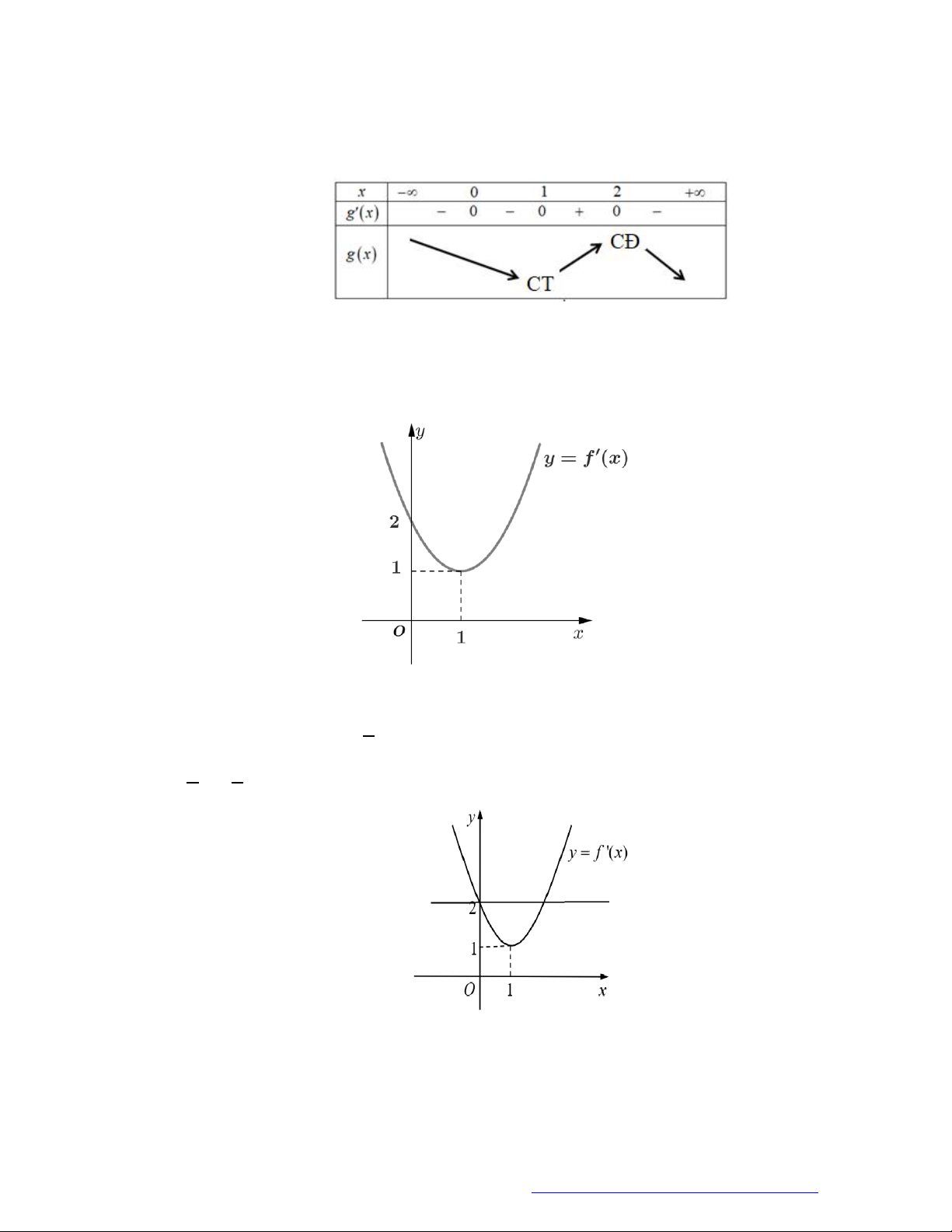
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 39
Dựa vào đồ thị hàm số
y f x có:
0g x
1f x
0
1
2
x
x
x
Bảng biến thiên
Từ đó suy ra hàm số
y g x đạt cực tiểu tại điểm
1x
.
Câu 34. Cho hàm số
y f x
có đạo hàm liên tục trên
và đồ thị hàm số
y f x
là parabol như
hình bên dưới.
Hàm số
2y f x x
có bao nhiêu cực trị?
A.
3
. B.
2
. C.
0
. D.
1
.
Lời giải
Chọn B
Ta có
2y f x
.
0 2 0y f x
2f x
1
0
1
x
x x
.
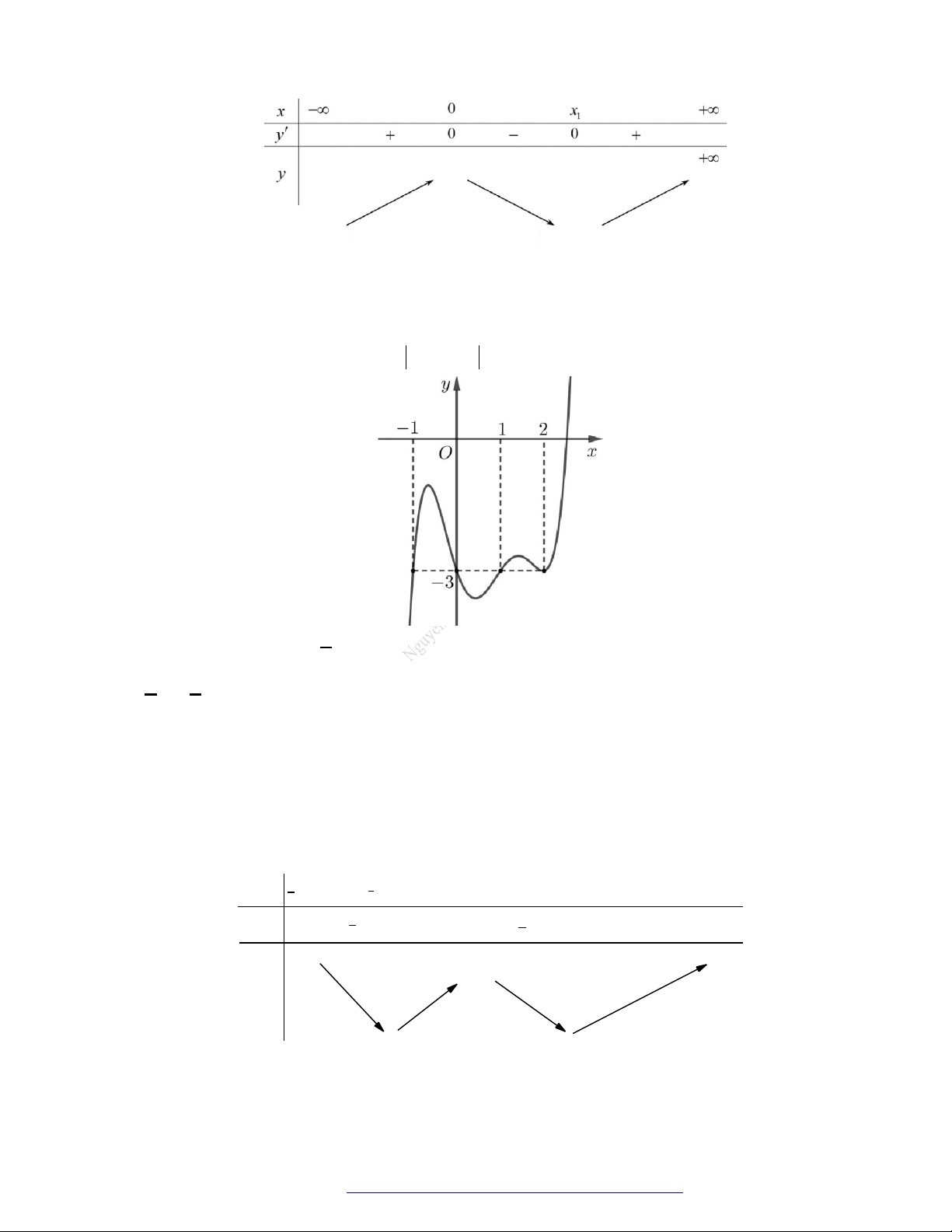
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 40 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Dựa vào đồ thị
y f x
và đường thẳng
2y
, ta có bảng biến thiên sau
Vậy hàm số
2y f x x
có hai điểm cực trị.
Câu 35. Cho hàm số đa thức
y f x
có đạo hàm trên
,
0 0f
và đồ thị hình bên dưới là đồ thị của
đạo hàm
f x
. Hỏi hàm số
3g x f x x
cóbao nhiêu cực trị?
A.
4.
B.
5.
C.
3.
D.
6.
Lời giải
Chọn B
Đặt
3h x f x x
3h x f x
0 3 0 3h x f x f x
Theo đồ thị của hàm số
f x
thì phương trình
3f x
có
4
nghiệm
1;0;1;2
Ta có bảng biết thiên
Theo bảng biến thiên ta có phương trình
0h x
có hai nghiệm
1
1;x và
2
1x (do có
0 0f
)
Khi đó ta có
+
+
∞ +
∞
2
0
f
0( )
+
00
0
x
h' x( )
h x( )
1
1
+
+
0
∞
∞
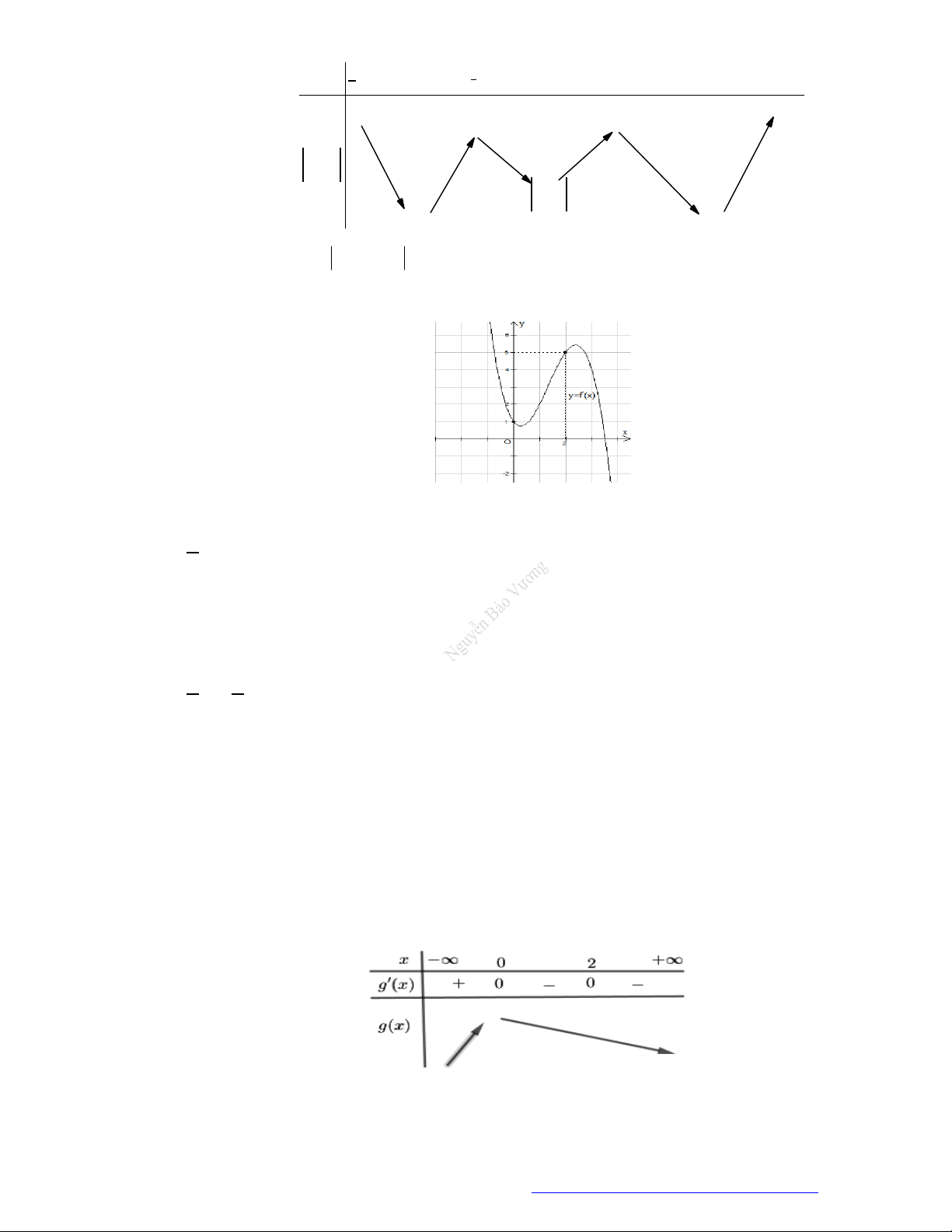
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 41
Vậy hàm số
3g x f x x
có
5
cực trị.
Câu 36. Cho hàm số
( )y f x
có đồ thị đạo hàm
'( )y f x
như hình bên.
Khẳng định nào sau đây là đúng?
A. Hàm số
2
( )y f x x x
đạt cực đại tại
0x
.
B. Hàm số
2
( )y f x x x
đạt cực tiểu tại
0x
.
C. Hàm số
2
( )y f x x x
không đạt cực trị tại
0x
.
D. Hàm số
2
( )y f x x x
không có cực trị.
Lời giải
Chọn A
Xét hàm số
2
( )g x f x x x
.
Tập xác định:
D
.
Ta có
2 1g x f x x
.
Cho
0
0 2 1
2
x
g x f x x
x
.
Dựa vào đồ thị ta có:
1 1 3 0g f
,
3 3 7 0g f
nên
0x
là nghiệm đơn và
2x
là nghiệm kép.
Bảng biến thiên
Từ bảng biến thiên ta có
0x
là điểm cực đại.
x
2
+
∞
+
∞
x
1
0
0
f
0( )
0
x
g x( )= h x( )
1
1
+
∞
∞
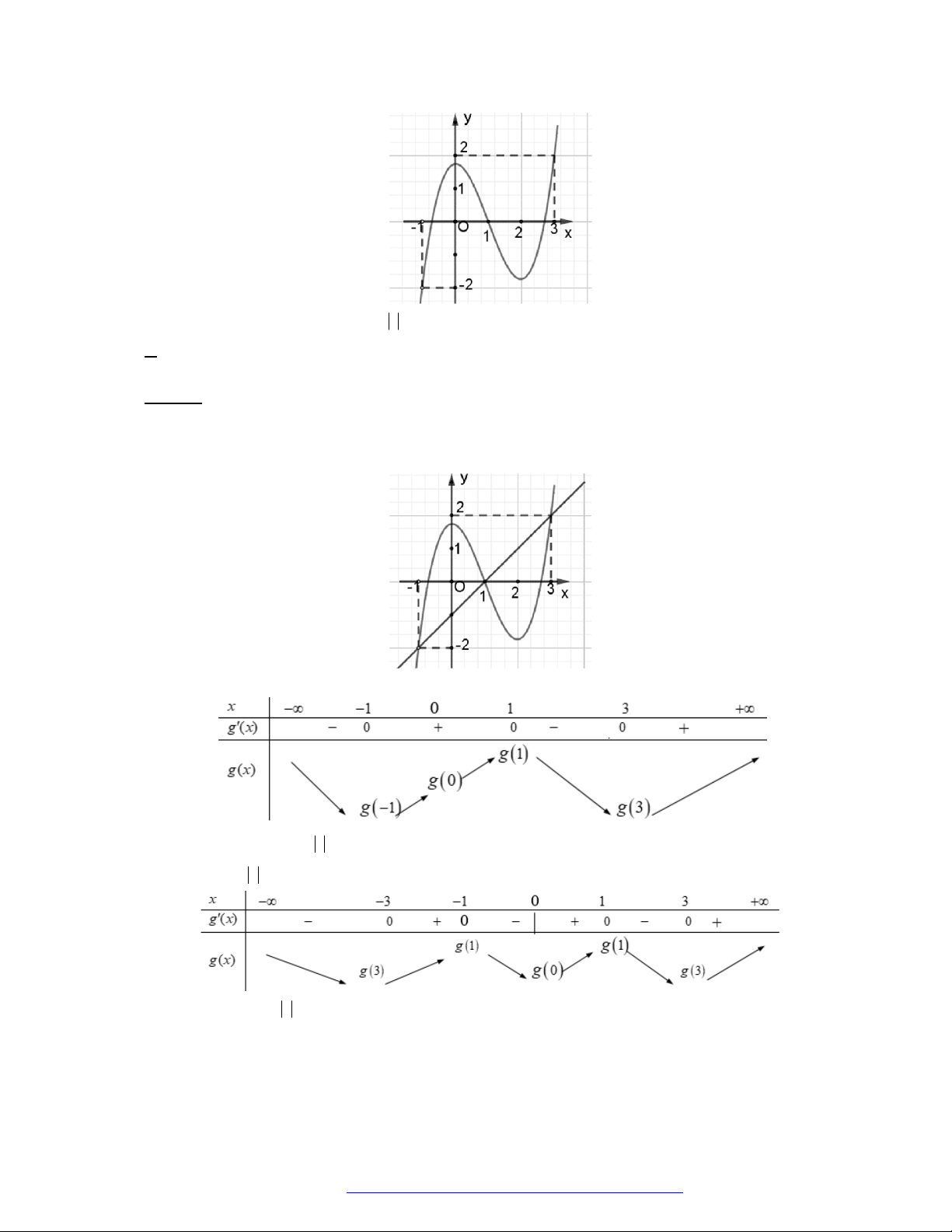
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 42 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 37. (THPT Minh Khai) Cho hàm số Cho hàm số
y f x
liên tục trên
và hàm số
2
2 2 2019g x f x x x
. Biết đồ thị hàm số
y f x
như hình vẽ.
Số điểm cực trị của hàm số
x
y g
là
A.
5
. B.
3
. C.
2
. D.
4
.
Lời giải
Chọn A
2 2 2g x f x x
,
0 1g x f x x
Đường thẳng
1y x
đi qua các điểm
1 ; 2
,
1 ; 0
,
3 ; 2
Quan sát vào vị trí tương đối của hai đồ thị trên hình vẽ, ta có BBT của hàm số
x
y g
như sau
Đồ thị hàm số
x
y g
nhận trục
Oy
làm trục đối xứng nên từ BBT trên ta suy ra BBT của
hàm số
x
y g
như sau
Vậy hàm số
x
y g
có 5 điểm cực trị.
Câu 38. Cho hàm số
f x
xác định trên
và có đồ thị
'f x
như hình vẽ.
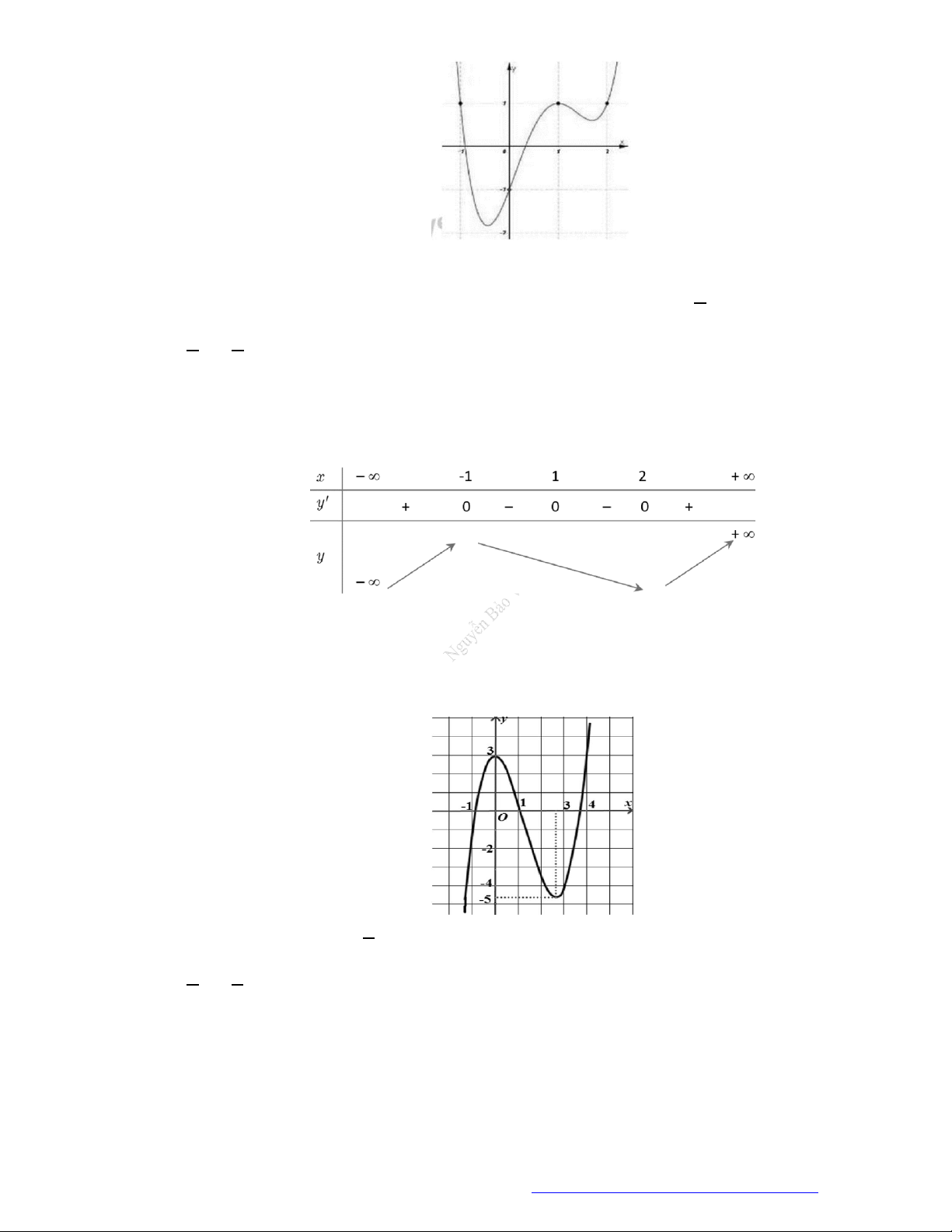
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 43
Đặt
g x f x x
. Hàm số
g x
đạt cực đại tại điểm nào sau đây?
A.
1.x
B.
2.x
C.
0x
.
D.
1.x
Lời giải
Chọn D
Ta có
' ' 1 0 ' 1g x f x f x
.
Từ đồ thị ta thấy đường thẳng
1y
cắt đồ thị
'f x
tại ba điểm có hoành độ là
1, 1x x
và
2x
Bảng biến thiên
Từ bảng biến thiên ta suy ra 1
CD
x .
Câu 39. (THPT Hoàng Hoa Thám - Hưng Yên 2019) Cho hàm số
( )y f x
có đạo hàm trên
và có
đồ thị là đường cong như hình vẽ.
Đặt
( ) 3 ( ) 4g x f f x
. Tìm số cực trị của hàm số
( )g x
A.
2.
B.
8.
C.
10.
D.
6.
Lời giải
Chọn B
Ta có:
' 0
' 3 ' . ' , ' 0 3 ' . '
' 0
f x
g x f x f f x g x f x f f x
f f x
.
Từ đồ thị hàm số trên ta thấy:
+ Phương trình
' 0f x
có 2 nghiệm phân biệt là
0;x x
với
1;3
.
+ Phương trình
0
' 0
f x
f f x
f x
.
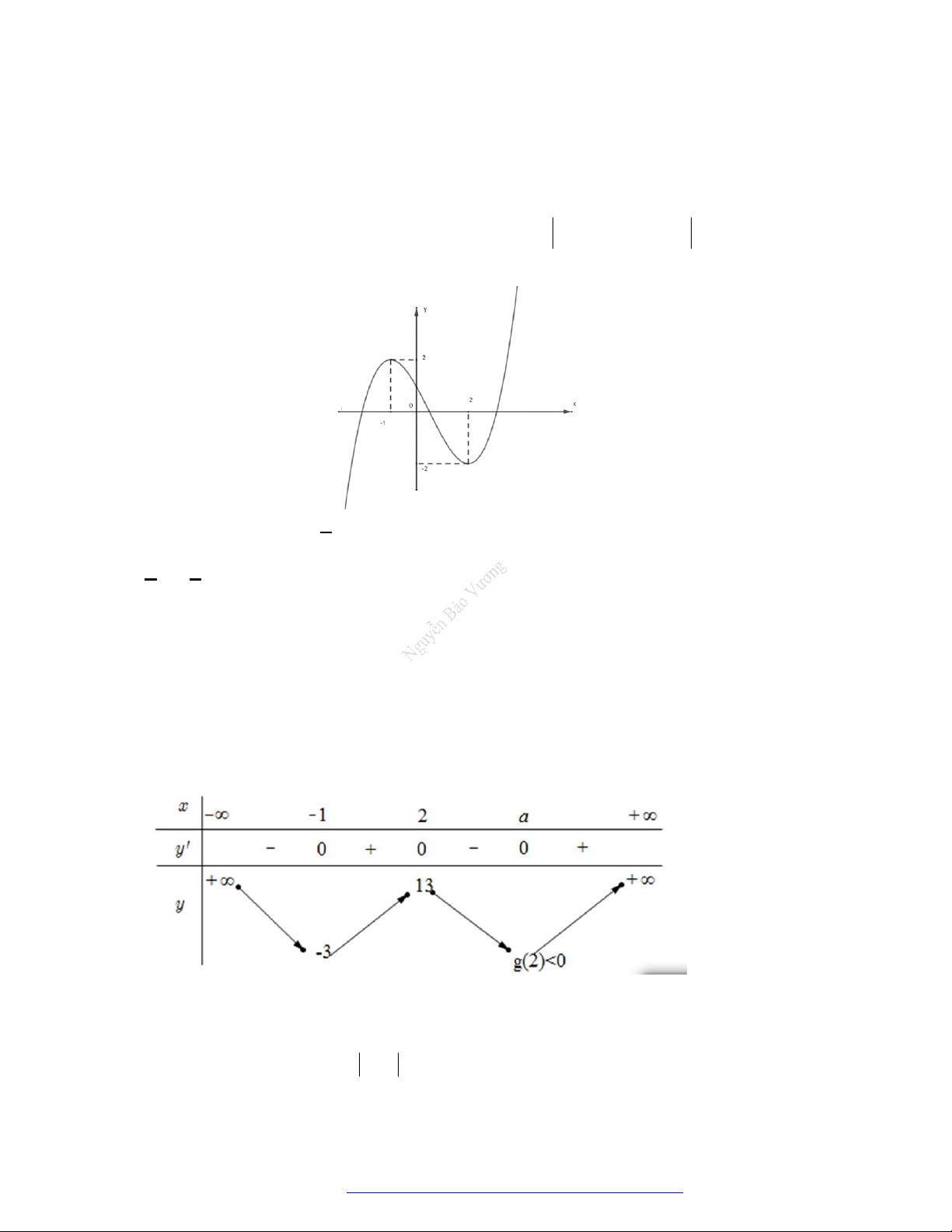
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 44 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
+ Phương trình
0f x
có 3 nghiệm phân biệt khác 2 nghiệm trên.
+ Phương trình
f x
với
1;3
có 3 nghiệm phân biệt khác các nghiệm trên.
Vậy phương trình
' 0g x
có 8 nghiệm phân biệt và
'g x
đổi dấu qua các nghiệm.
Do đó hàm số
g x
có 8 điểm cực trị.
Câu 40. (HSG 12 - Sở Quảng Nam - 2019) Cho hàm số
(x)y f
có đạo hàm trên
, đồ thị hàm số
( )y f x
là đường cong ở hình vẽ. Hỏi hàm số
2
( ) 4 1h x f x f x
có bao nhiêu điểm
cực trị?
A.
2
. B.
3
. C.
5
. D.
7
.
Lời giải
Chọn B
Đặt
2
( ) 4 1g x f x f x
.
Khi đó,
2
( ) 2
2 ( ). ( ) 4 0 1
0
2
x a a
f x
g x f x f x f x x
f x
x
Do đó, ta có bảng biến thiên:
Suy ra đồ thị hàm số
y g x
có ba điểm cực không nằm trên trục hoành và bốn giao điểm với
Ox
.
Vậy đồ thị hàm số
y h x g x
có số cực trị là
3 4 7
.
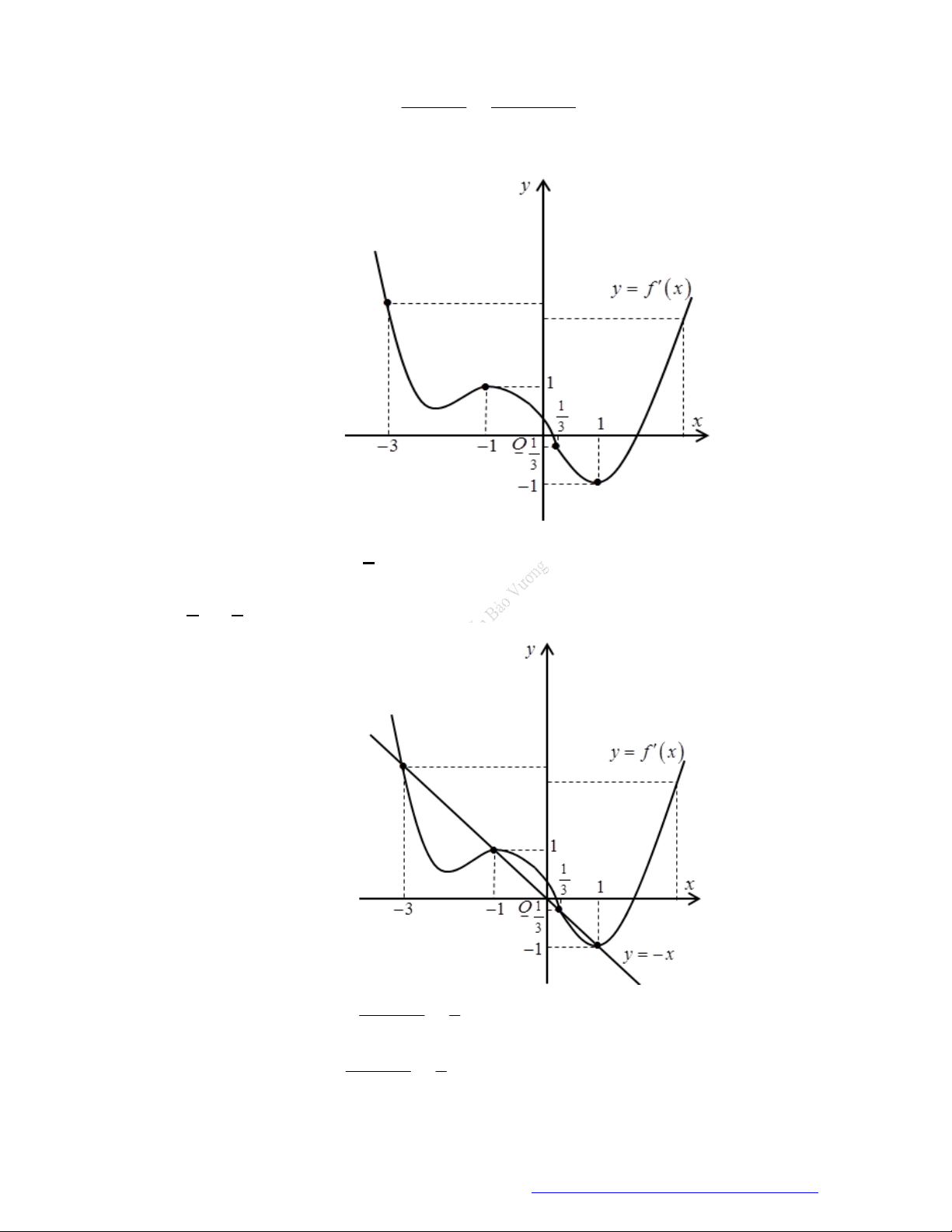
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 45
Câu 41. (THPT Thăng Long - Hà Nội - 2019) Cho hàm số
y f x
, hàm số
y f x
có đồ thị như
hình bên. Hàm số
2
5sin 1 (5sin 1)
( ) 2 3
2 4
x x
g x f
có bao nhiêu điểm cực trị trên khoảng
(0;2 )
.
A.
9
. B.
7
. C.
6
. D.
8
.
Lời giải
Chọn B
Ta có:
5sin 1 5
( ) 5cos cos 5sin 1
2 2
x
g x xf x x
.
5sin 1 5
( ) 0 5cos cos 5sin 1 0
2 2
x
g x xf x x
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 46 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
cos 0
5sin 1 5sin 1
2 2
x
x x
f
cos 0
cos 0
5sin 1
cos 0
3
sin 1
2
5sin 1 6
5sin 1 1
1 5sin 1 2 sin
2 5
2
5sin 1 1
1
5sin 1
sin
3
2 3
3
5sin 1 2
5sin 1
3
1
sin
2
5
x
x
x
x
x
x
x
x x
x
x
x
x
x
x
3
2 2
cos 0
3
sin 1
2
1 1 1
sin sin 2 sin
5 5 5
1
1 1
sin
sin sin
3
3 3
3
3 3
sin
sin sin
5
5 5
x x
x
x
x
x x arc x arc
x
x arc x arc
x
x arc x arc
, ( Vì
0 2x
).
Suy phương trình
0g x
có
9
nghiệm, trong đó có nghiệm
3
2
x
là nghiệm kép.
Vậy hàm số
y g x
có
7
cực trị.
Câu 42. (Mã 101 - 2020 Lần 1) Cho hàm số bậc bốn
f x
có bảng biến thiên như sau:
Số điểm cực trị của hàm số
2
4
1g x x f x
là
A.
11
. B.
9
. C.
7
. D.
5
.
Lời giải
Chọn B.
Ta chọn hàm
4 2
5 10 3f x x x
.
Đạo hàm
2
3 4 3
4 1 2 1 1 2 1 2 1 1g x x f x x f x f x x f x f x xf x
.
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 47
Ta có
3
0
2 1 0
0 1 0
2 1 1 0
2 1 1 0
x
x f x
g x f x
f x xf x
f x xf x
.
+)
1 0f x
*
4
5 1 10 1 3 0x x
1 1,278
1 0,606
1 0,606
1 1, 278
x
x
x
x
Phương trình có bốn nghiệm phân biệt khác
0
.
+)
1
4 2 3
2 1 1 0 2 5 10 3 1 20 20 0
t x
f x xf x t t t t t
4 3 2
30 20 40 20 6 0t t t t
1,199
0,731
0,218
1,045
t
t
t
t
Phương trình có bốn nghiệm phân biệt khác
0
và khác các nghiệm của phương trình
*
.
Vậy số điểm cực trị của hàm số
g x
là
9
.
Câu 43. (Mã 102 - 2020 Lần 1) Cho hàm số bậc bốn
f x
có bảng biến thiên như sau:
Số điểm cực trị của hàm số
g x x f x
4
2
1 là
A.
7
. B.
8
. C.
5
. D.
9
.
Lời giải
Chọn C
Ta có
4 3 3
2
2 . 1 4 1 1 2 . 1 1 2 1g x x f x x f x f x x f x f x xf x
Vậy
0
0 1 0 1
1 2 1 0 2
x
g x f x
f x xf x
Phương trình
1
có
4
nghiệm phân biệt
Phương trình
2
có
1 2 1 2 1f x xf x f x x f x
Từ bảng biến thiên suy ra hàm
f x
là bậc bốn trùng phương nên ta có
f x x x
4 2
3 6 1
thay vào
2 1f x x f x
vô nghiệm
Vậy hàm
g x
có 5 điểm cực trị.
Câu 44. (Mã 103 - 2020 Lần 1) Cho hàm số bậc bốn
( )f x
có bảng biên thiên như sau:
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 48 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Số điểm cực trị của hàm số
4 2
( ) [ ( 1)]g x x f x
là
A.
7
. B.
5
. C.
9
. D.
11
.
Lời giải
Chọn C
Ta có :
4 2 2
( ) 4 8 3 ( ) 16 ( 1)f x x x f x x x
Ta có
3
( ) 2 . ( 1).[2 ( 1) . ( 1)]g x x f x f x x f x
3
0
( ) 0 ( 1) 0
2 ( 1) . ( 1) 0
x
g x f x
f x x f x
(1)
(2)
(3)
Phương trình
(1)
có
0x
(nghiệm bội ba).
Phương trình
(2)
có cùng số nghiệm với phương trình
( ) 0f x
nên
(2)
có 4 nghiệm đơn.
Phương trình
(3)
có cùng số nghiệm với phương trình :
4 2 2
2 ( ) ( 1). ( ) 0 2(4 8 3) 16 ( 1)( 1) 0f x x f x x x x x x
4 3 2
24 16 32 16 6 0x x x x
có 4 nghiệm phân biệt.
Dễ thấy 9 nghiệm trên phân biệt nên hàm số
( ) 0g x
có tất cả 9 điểm cực trị.
Câu 45. (Mã 104 - 2020 Lần 1) Cho hàm số bậc bốn
( )f x
có bảng biến thiên như sau
Số điểm cực trị của hàm số
4
2
( ) ( 1)g x x f x
A.
7
. B.
8
. C.
9
. D.
5
.
Lời giải
Chọn C
4 3 3
2
'( ) 2 ( 1) 4 ( 1) . '( 1) 2 ( 1) . ( 1) 2 . '( 1)g x x f x x f x f x x f x f x x f x
'( ) 0g x
ta được
+ TH1:
0x
+ TH2:
2
( 2; 1)
( 1) 0
( 1;0)
0
x a
x b
f x
x c
x d
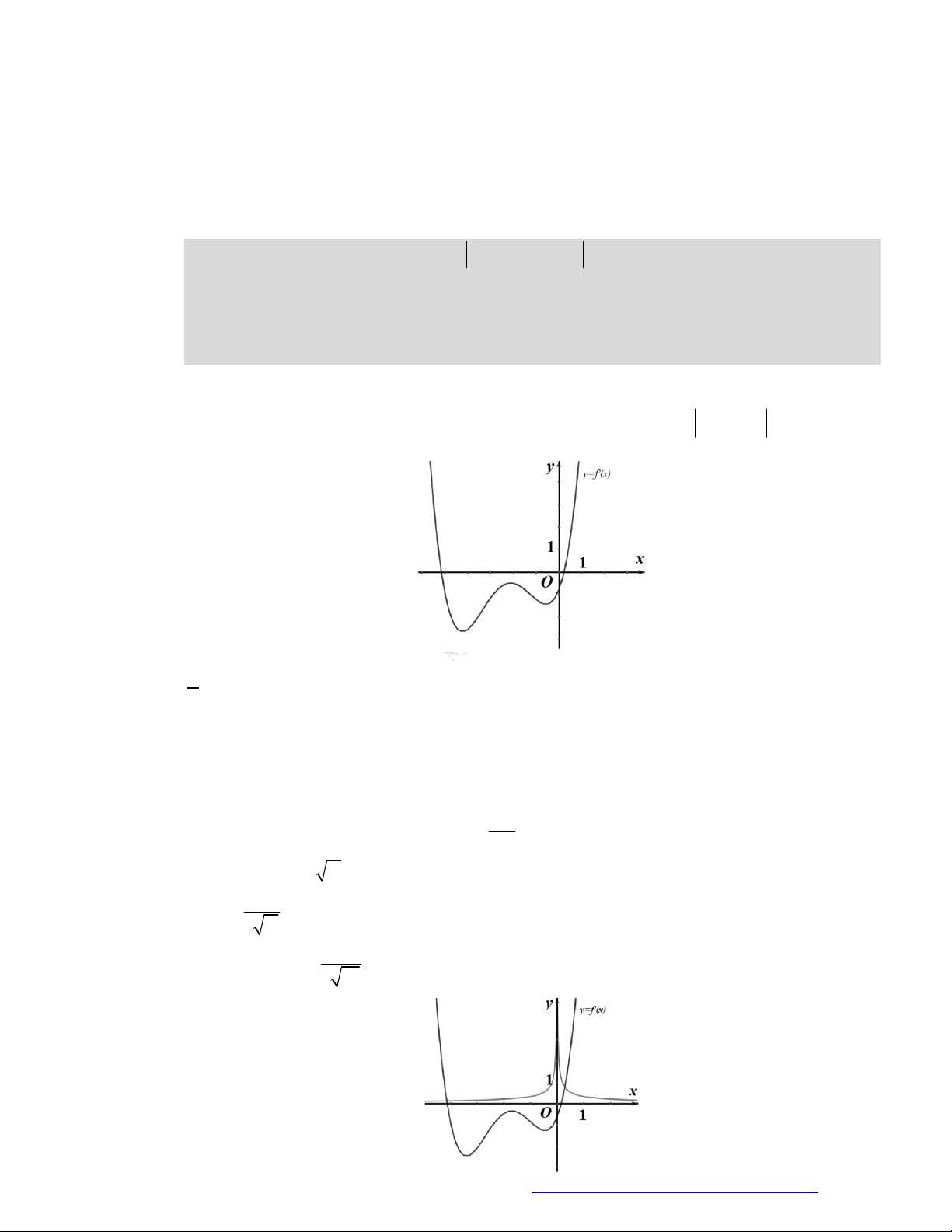
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 49
+ TH3:
( 1) 2 . '( 1) 0f x x f x
.
Từ bảng biến thiên ta có hàm số thỏa mãn là
4 2
( ) 5 10 2f x x x
( 1) 2 . '( 1) 0 ( 1) 2( 1). '( 1) 2 '( 1) 0f x x f x h x f x x f x f x
Với
1t x
ta có:
4 2 3 3
( ) 5 10 2 2 ( 20 20 ) 2( 20 20 ) 0h t t t t t t t t
4 3 2
45 40 50 40 2 0t t t t
Lập bảng biến thiên ta suy ra có
4
nghiệm
4t
nghiệm
x
Vậy có
9
cực trị.
Bài toán tìm cực trị của hàm số
g x f u x h x
Bước 1. Tìm cực trị của hàm số
v x f u x h x
Bước 2. Sử dụng phương pháp biến đổi đồ thị hàm số trị tuyệt đối để tìm số cực trị của hàm số
g x
Câu 46. (Mã 101 – 2020 Lần 2) Cho hàm số
f x
có
0 0.f
Biết
y f x
là hàm số bậc bốn và có
đồ thị là đường cong trong hình bên. Số điểm cực trị của hàm số
3
( )g x f x x
là
A.
5.
B.
4.
C.
6.
D.
3.
Lời giải
Chọn A
Xét
3
( )h x f x x
Có
2 3
' 3 ' 1h x x f x
2 3 3
2
1
0 3 1 0 0 1
3
h x x f x f x x
x
Đặt
3
3 2 2
x t x t
phương trình (1) trở thành:
3 2
1
0 2
3
f t t
t
Vẽ đồ thị hàm
3 2
1
3
y
x
trên cùng hệ trục tọa độ với hàm
y f x
.
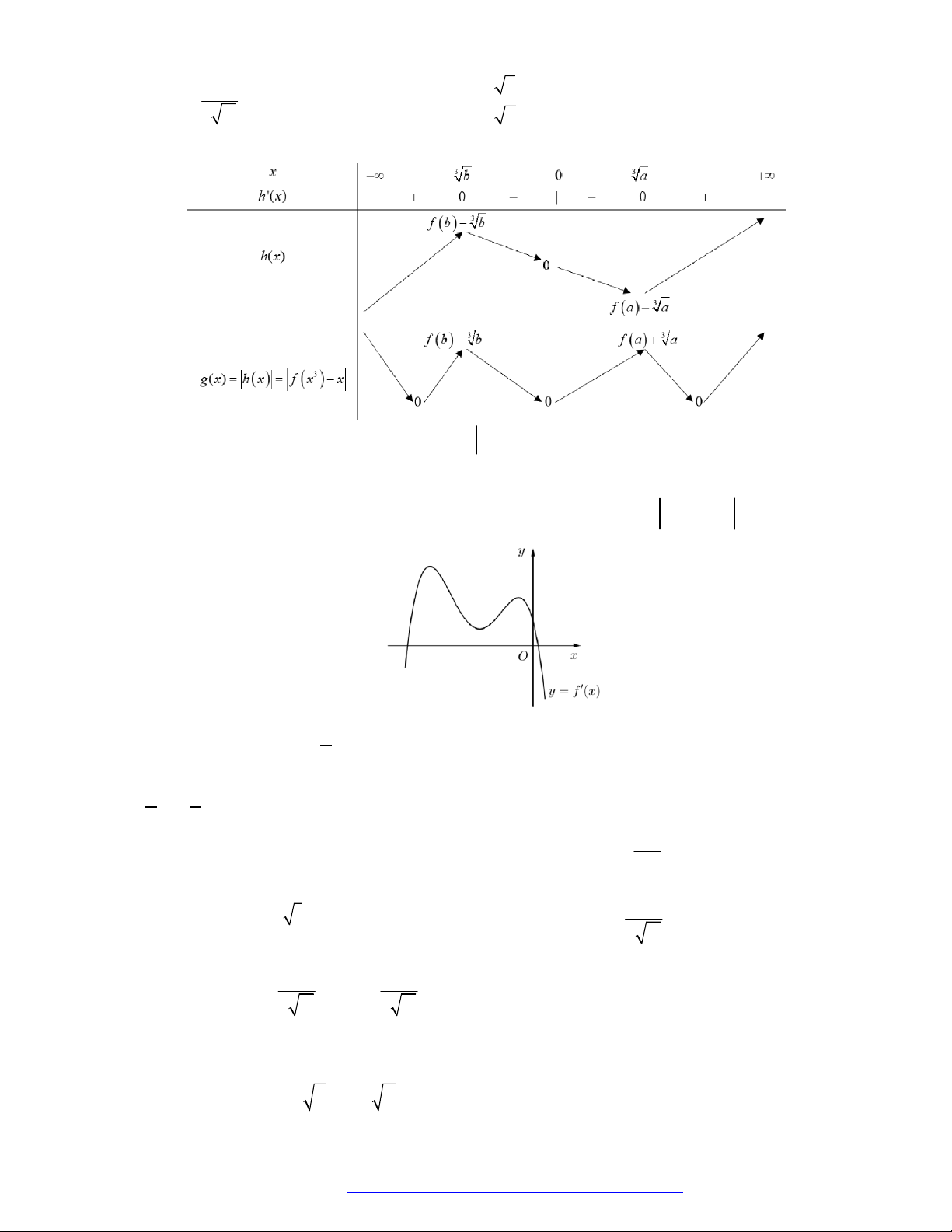
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 50 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Dựa vào đồ thị ta có:
3
3
3
3 2
3
0 0 0
1
0
0
3 0
t b x b x b
f t
t a
x a
t x a
Bảng biến thiên
Dựa vào BBT ta thầy hàm số
3
( )g x f x x có 5 điểm cực trị.
Câu 47. (Mã 102 - 2020 Lần 2) Cho hàm số
f x
có
0 0f
. Biết
y f x
là hàm số bậc bốn và có
đồ thị là đường cong trong hình bên. Số điểm cực trị của hàm số
3
g x f x x
là
A. 4. B. 5. C. 3. D. 6.
Lời giải
Chọn B
Đặt
3 2 3 3
2
1
3 1 0
3
h x f x x h x x f x f x
x
Đặt
3
3
t x x t
thế vào phương trình trên ta được
3
2
1
3
f t
t
Xét hàm số
3 3
2 5
1 2
3 9
y y
t t
đổi dấu khi qua 0 và đồ thị hàm số có tiệm cận ngang
0y
. Khi vẽ đồ thị trên cùng một mặt phẳng tọa độ với đồ thị hàm số
y f t
ta thấy hai đồ
thị cắt nhau tại 2 điểm phân biệt thuộc góc phần từ thứ 3 và 4, gọi 2 giao điểm lần lượt là
3 3
1 2 1 1 2 2
0, 0 ,t t x t x t . Như vậy ta có bảng biến thiên của hàm số
h x
như sau
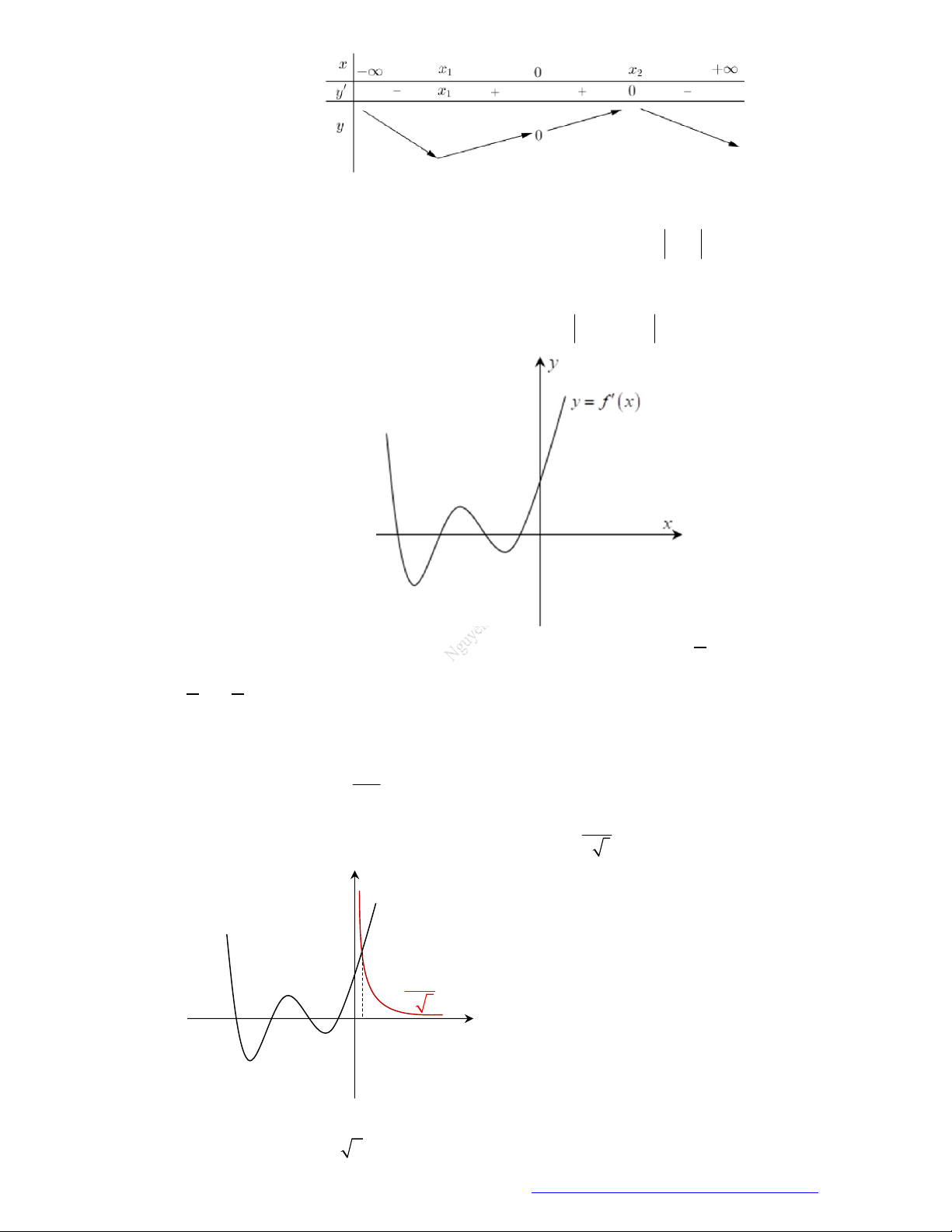
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 51
Dựa vào bảng biến thiên ta thấy phương trình
0h x
có 3 nghiệm phân biệt và hàm số
h x
có 2 điểm cực trị không nằm trên trục hoành, do đó hàm số
g x h x có 5 điểm cực trị.
Câu 48. (Mã 103 - 2020 Lần 2) Cho hàm số
f x
có
0 0f
. Biết
y f x
là hàm số bậc bốn và có
đồ thị như hình vẽ. Số điểm cực trị của hàm số
4 2
g x f x x là
A. 4. B. 3. C. 6. D. 5.
Lời giải
Chọn D
Xét hàm số
4 2
h x f x x
có
3 4
4 2h x x f x x
.
4
2
0
0
1
*
2
x
h x
f x
x
Xét phương trình
*
: Đặt
4
t x
thì
*
thành
1
2
f t
t
với
0t
.
Dựa vào đồ thị, phương trình
*
có duy nhất một nghiệm
0a
.
Khi đó, ta được
4
x a
.
a
y f t
y
t
1
2
y
t
O
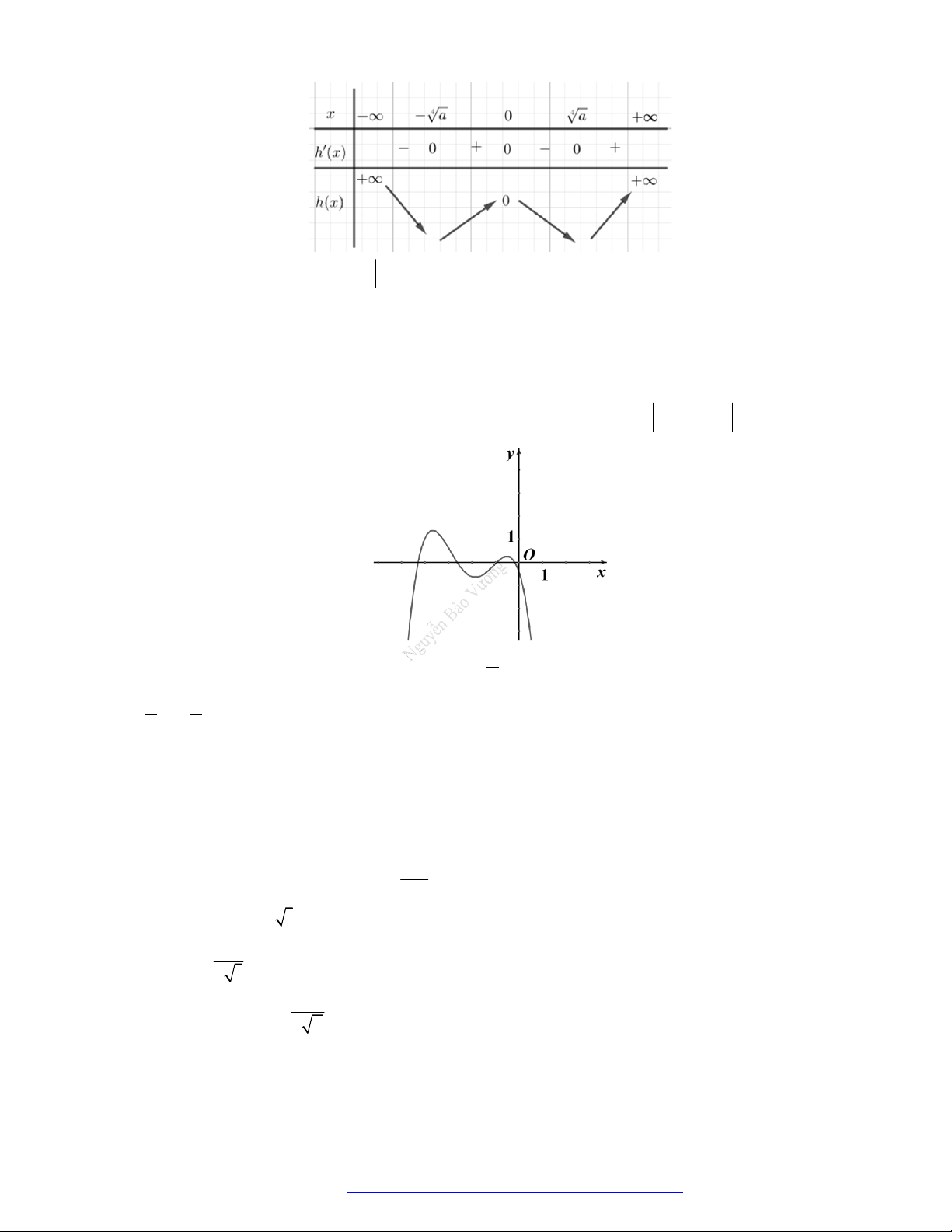
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 52 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Bảng biến thiên của hàm số
4 2
h x f x x
Số cực trị của hàm số
4 2
g x f x x bằng số cực trị của hàm
4 2
h x f x x
và số
nghiệm đơn hoặc bội lẻ của phương trình
0h x
.
Dựa vào bảng biến thiên của hàm
f x
thì số cực trị của
g x
là 5.
Câu 49. (Mã 104 - 2020 Lần 2) Cho hàm số
( )f x
có
0 0.f
Biết
( )y f x
là hàm số bậc bốn và có
đồ thị là đường cong trong hình bên. Số điểm cực trị của hàm số
4 2
( )g x f x x
là
A.
3.
B.
6.
C.
5.
D.
4.
Lời giải
Chọn C
Xét
4 2
( )h x f x x
Có
3 4 2 4
( ) 4 2 2 2 1h x x f x x x x f x
2 4
2 4
0
( ) 0 2 2 1 0
2 1 0 1
x
h x x x f x
x f x
2 4 4
2
1
1 : 2 1 0 0 2
2
x f x f x x
x
Đặt
4 2
0x t x t t phương trình (2) trở thành:
1
0 3
2
f t t
t
Vẽ đồ thị hàm
1
2
y
x
trên cùng hệ trục tọa độ với hàm
y f x
.
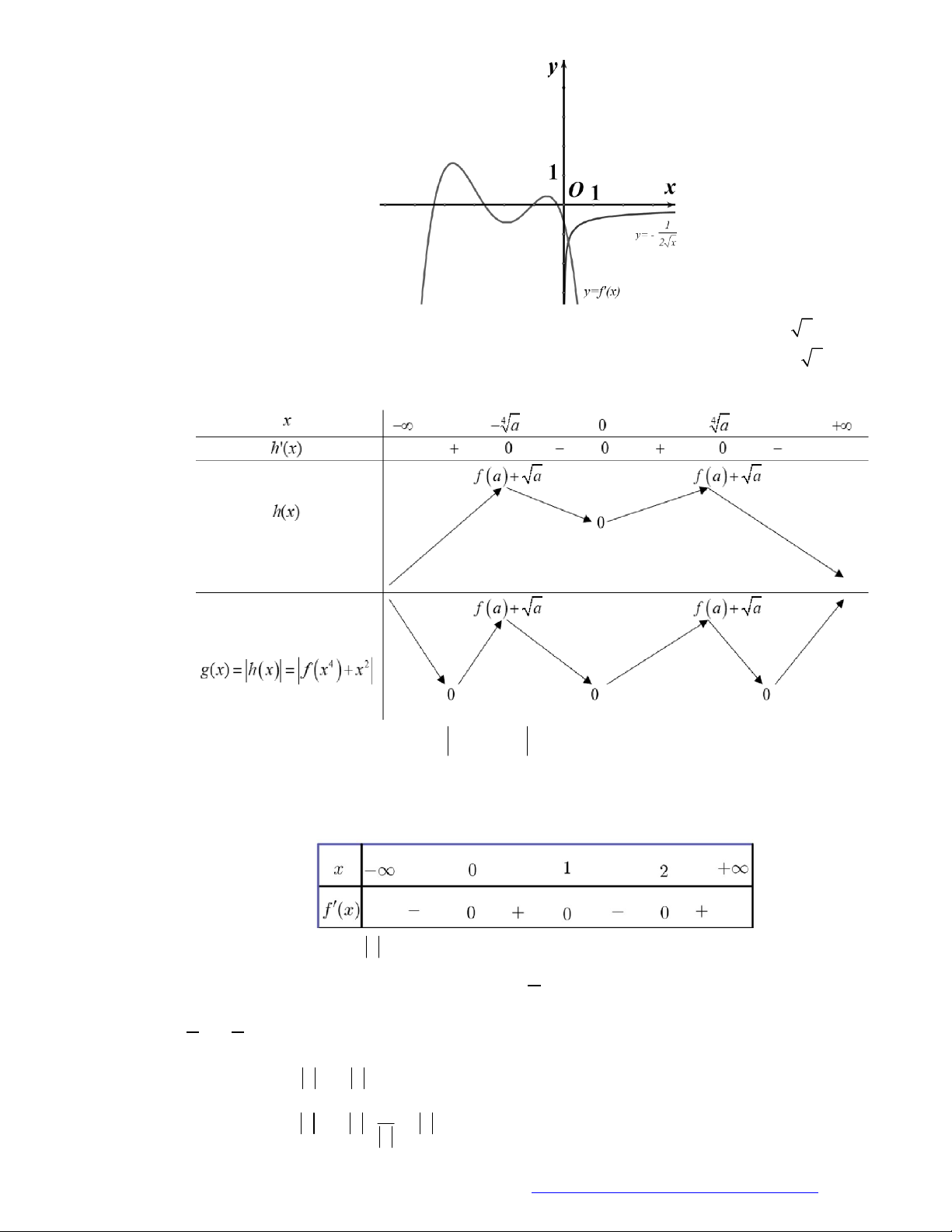
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 53
Dựa vào đồ thị ta có: phương trình (3) có nghiệm duy nhất
4
4
4
0
x a
t a x a
x a
Bảng biến thiên:
Dựa vào BBT ta thầy hàm số
4 2
( )g x f x x
có 5 điểm cực trị.
Câu 50. (Chuyên Quang Trung - 2020) Cho hàm số
y f x
liên tục trên
có đạo hàm
f x
liên
tục trên
và có bảng xét dấu như hình vẽ bên
Hỏi hàm số
2
2y f x x
có tất cả bao nhiêu điểm cực trị?
A.
4
B.
7
C.
9
D.
11
Lời giải
Chọn C
Tập xác định của hàm số:
D
.
*
2
2y h x f x x
2
2 . . 2 2 .
x
y h x f x x x
x
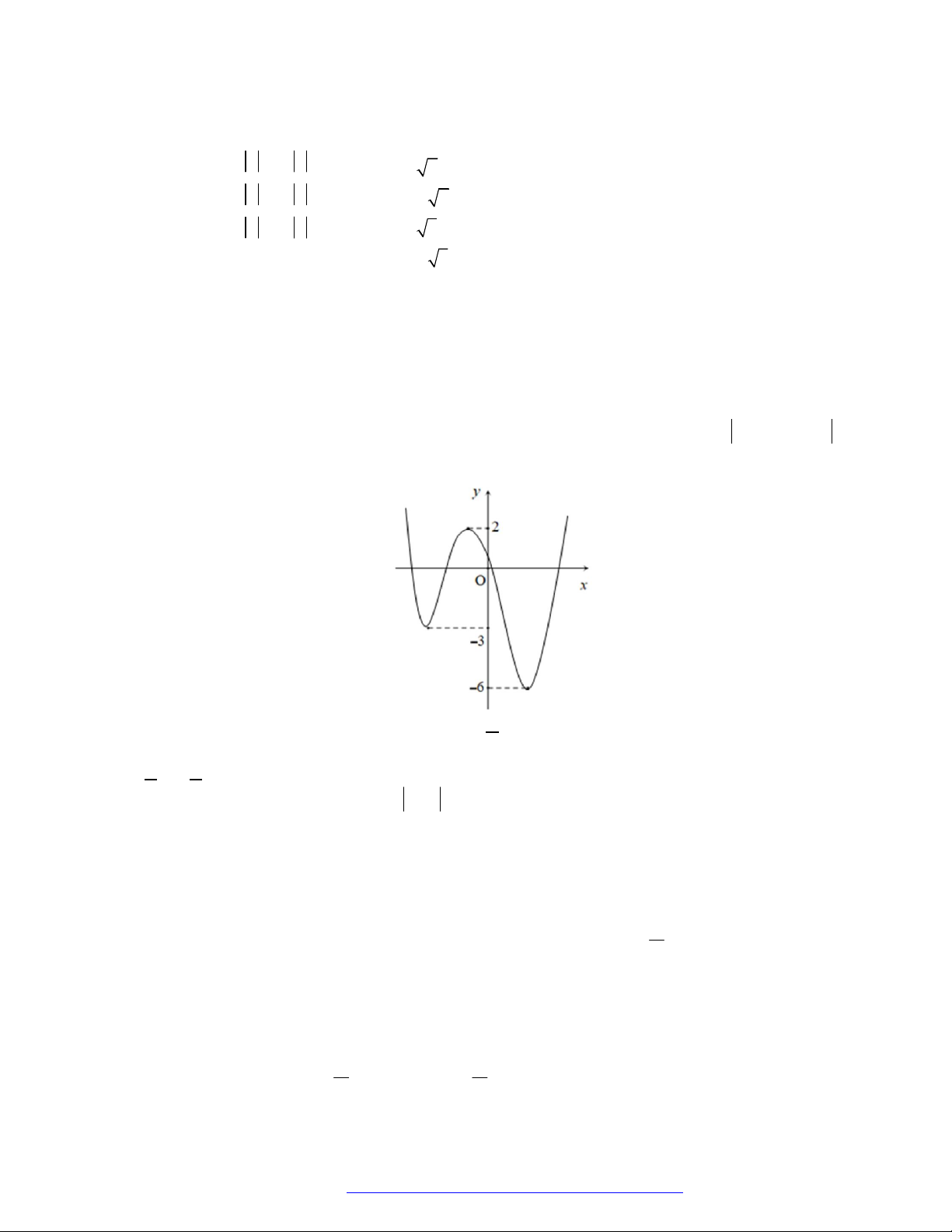
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 54 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
2
2
1
1
1
2
1
2
0 2 0
1 2
2 1
1 2
2 2
1 3
1 3
x
x
x
x
x
x
h x x x
x
x x
x
x x
x
x
.
Ta thấy phương trình
0h x
có 8 nghiệm đơn
1
.
h x
không tồn tại tại
0x
mà
0x
thuộc tập xác định đồng thời qua đó
h x
đổi dấu
2
.
Từ
1
và
2
suy ra hàm số đã cho có
9
điểm cực trị.
Câu 51. (Chuyên Thái Bình - 2020) Cho
y f x
là hàm đa thức bậc
4
và có đồ thị như hình vẽ. Có
bao nhiêu giá trị nguyên của tham số
m
thuộc đoạn
12;12
để hàm số
2 1 g x f x m
có
5
điểm cực trị?
A.
13
. B.
14
. C.
15
. D.
12
.
Lời giải
Chọn C
Đặt
2 1 h x f x m g x h x
.
Số điểm cực trị của
g x
= số điểm cực trị của
y h x
+ số giao điểm của
y h x
với trục
Ox
khác với điểm cực trị của
y h x
.
Hàm số
y f x
có
3
điểm cực trị. Suy ra hàm số
y h x
cũng có
3
điểm cực trị.
Hàm số
g x
có 5 điểm cực trị khi và chỉ khi
0 1
2
m
h x f x
có
2
nghiệm phân biệt
khác điểm cực trị của
h x
.
Đồ thị hàm số
1 y f x
có được bằng cách tịnh tiến đồ thị hàm số
y f x
sang bên phải
1
đơn vị.
Dựa vào đồ thị, ta được:
2
2
m
hoặc
6 3
2
m
.
; 12;12
4
6 12
m m
m
m
có
15
giá trị
m
nguyên thỏa mãn yêu cầu bài toán.
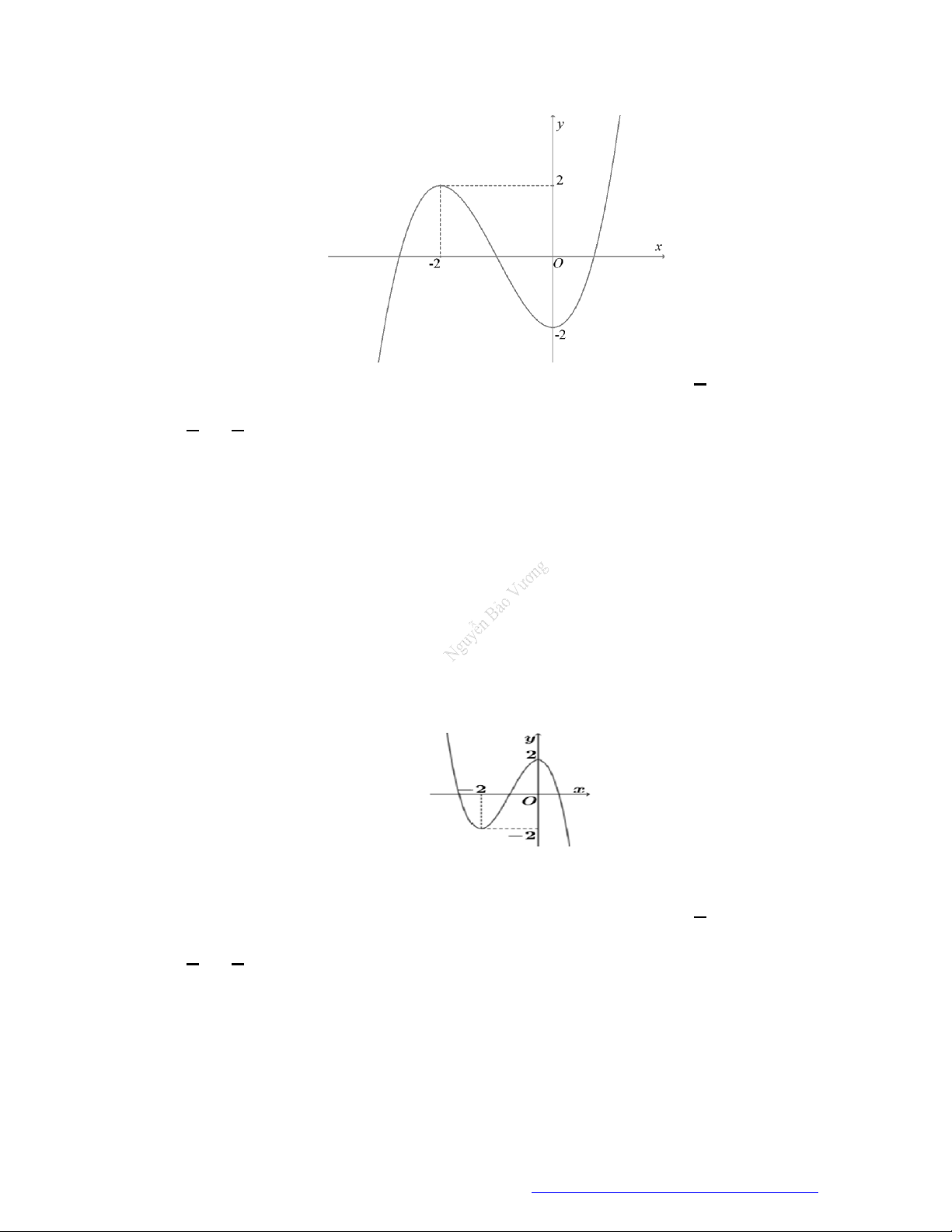
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 55
Câu 52. (Chuyên Vĩnh Phúc - 2020) Cho hàm số
3 2
f x ax bx cx d
(với
, , ,a b c d
và
0a
)
có đồ thị như hình vẽ. Số điểm cực trị của hàm số
2
2 4g x f x x
A. 2. B. 5. C. 4. D. 3.
Lời giải.
Chọn D
Dựa vào đồ thị hàm số
y f x
có hai điểm cực trị là
2; 0x x
.
2
2 4g x f x x
liên tục trên
.
2
' 4 4 ' 2 4g x x f x x
.
2
2
4 4 0
' 0 2 4 0
2 4 2
x
g x x x
x x
2
1
0
2
1 0
x
x
x
x
Như vậy
'g x
có 3 nghiệm, trong đó 1 là nghiệm bội 3, 0 và 2 là nghiệm đơn nên
g x
có 3
điểm cực trị.
Câu 53. (Sở Phú Thọ - 2020) Cho hàm số bậc ba
y f x
có đồ thị như hình vẽ
Số điểm cực tiểu của hàm số
2
g x f x x
bằng
A.
1
. B.
5
. C.
2
. D.
3
.
Lời giải
Chọn D
Đặt
3 2
f x ax bx cx d
. Khi đó
2
3 2f x ax bx c
.
Theo đồ thị hàm số
y f x
, ta có
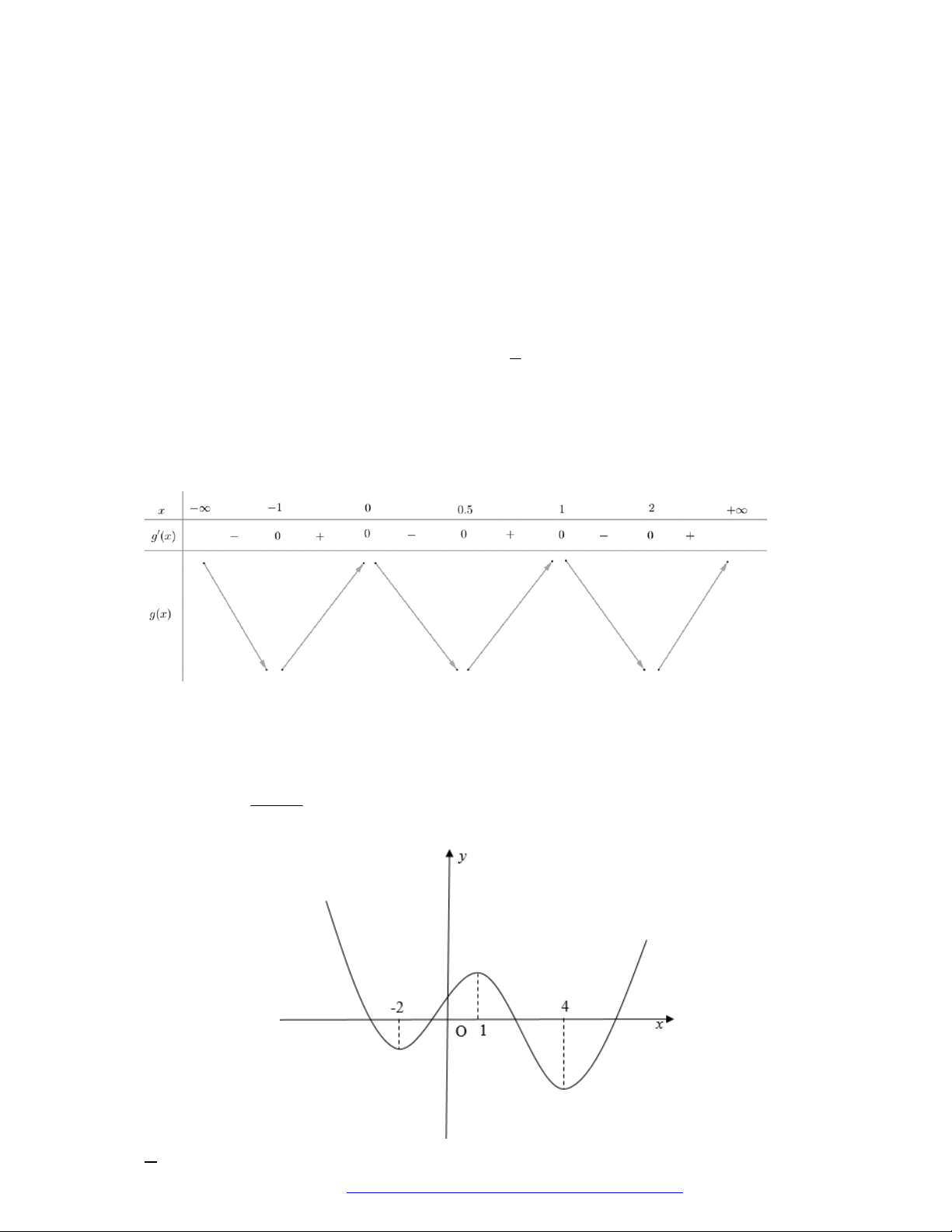
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 56 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2 0
12 4 0 12 4 0 1
0 0
0 8 4 4 3
8 4 2 2 0 0
2 2
2 2 2
0 2
f
a b c a b a
f
c a b b
a b c d c c
f
d d d
f
.
Vậy
3 2
3 2f x x x
.
Khi đó, ta có
2 6 5 3 2
3 5 3 2g x f x x x x x x
.
4 3
1
0
1
3 2 5 5 2 0
2
1
2
x
x
g x x x x x g x x
x
x
.
Bảng biến thiên
Suy ra, hàm số
2
g x f x x
có ba điểm cực tiểu.
Câu 54. (Sở Bắc Ninh - 2020) Cho hàm số
( )f x
liên tục trên
và có đồ thị như hình vẽ. Hàm số
2
2
( )
2
x
x x
g x f e
có bao nhiêu điểm cực trị?
A.
3
. B.
7
. C.
6
. D.
4
.
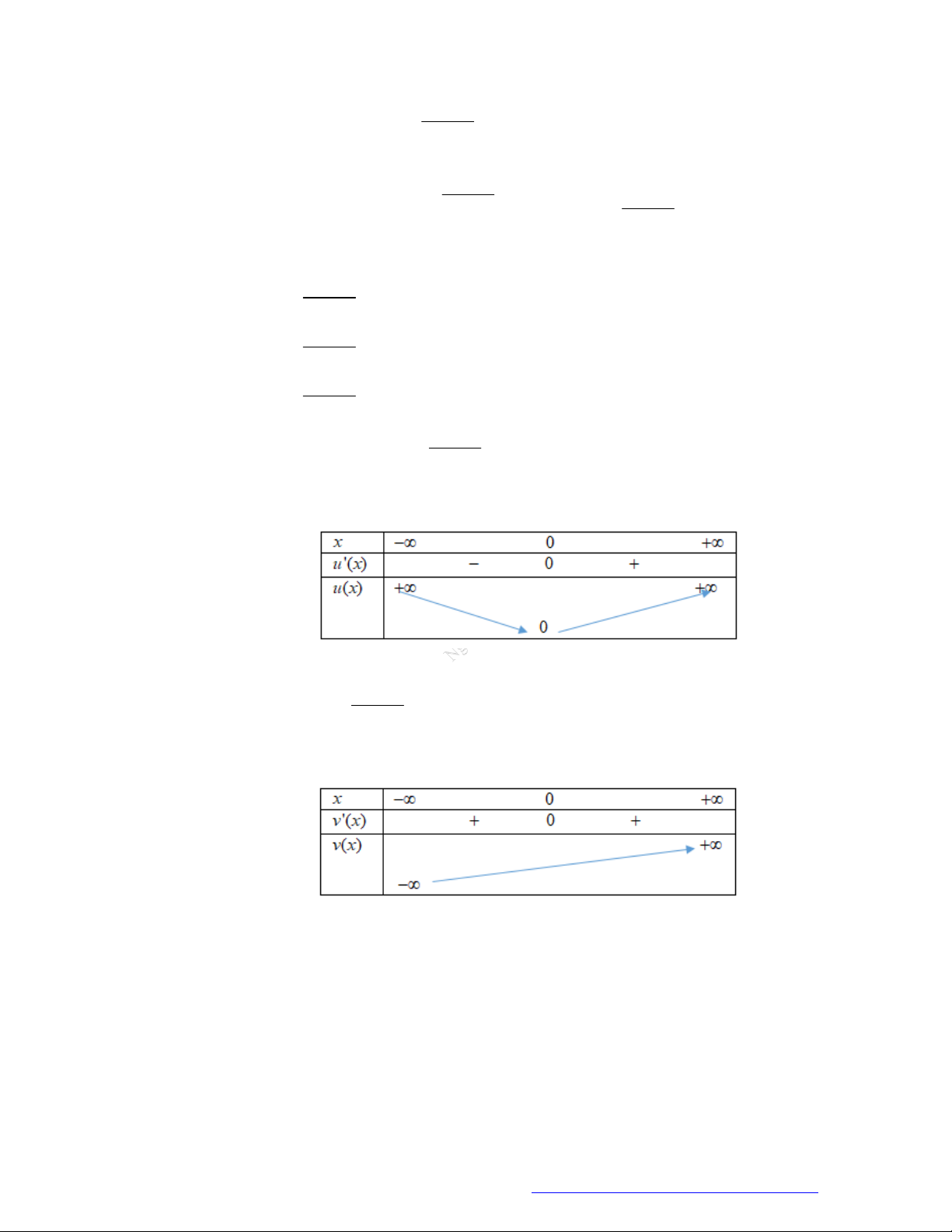
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 57
Lời giải
Chọn A
Ta có
2
2
'( ) 1 '
2
x x
x x
g x e x f e
Xét
2
2
1 0
2
'( ) 0 1 ' 0
2
2
' 0
2
x
x x
x
e x
x x
g x e x f e
x x
f e
2
2
2
1 0 1
2
2 2
2
2
1 3
2
2
4 4
2
x
x
x
x
e x
x x
e
x x
e
x x
e
Ta xét
2
2
( ) 1; ( )
2
x x
x x
u x e x v x e
Ta có
'( ) 1; '( ) 0 0
x
u x e u x x '( ) 1; '( ) 1
x x
u x e v x e x
Bảng biến thiên:
Vậy
( ) 0 u x x
Xét hàm số
2
2
( )
2
x
x x
v x e
Ta có
'( ) 1 0
x
v x e x x
hàm số đồng biến trên
Bảng biến thiên:
Khi đó các phương trình
(2),(3),(4)
có nghiệm duy nhất và
'( )g x
đổi dấu qua các nghiệm đó.
Vậy hàm số
( )g x
có 3 điểm cực trị.
Câu 55. (Sở Yên Bái - 2020) Cho hàm số
y f x
có đạo hàm trên
. Đồ thị hàm số
y f x
như
hình bên. Đặt
2
2 1 g x f x x
. Khẳng định nào sau đây đúng?
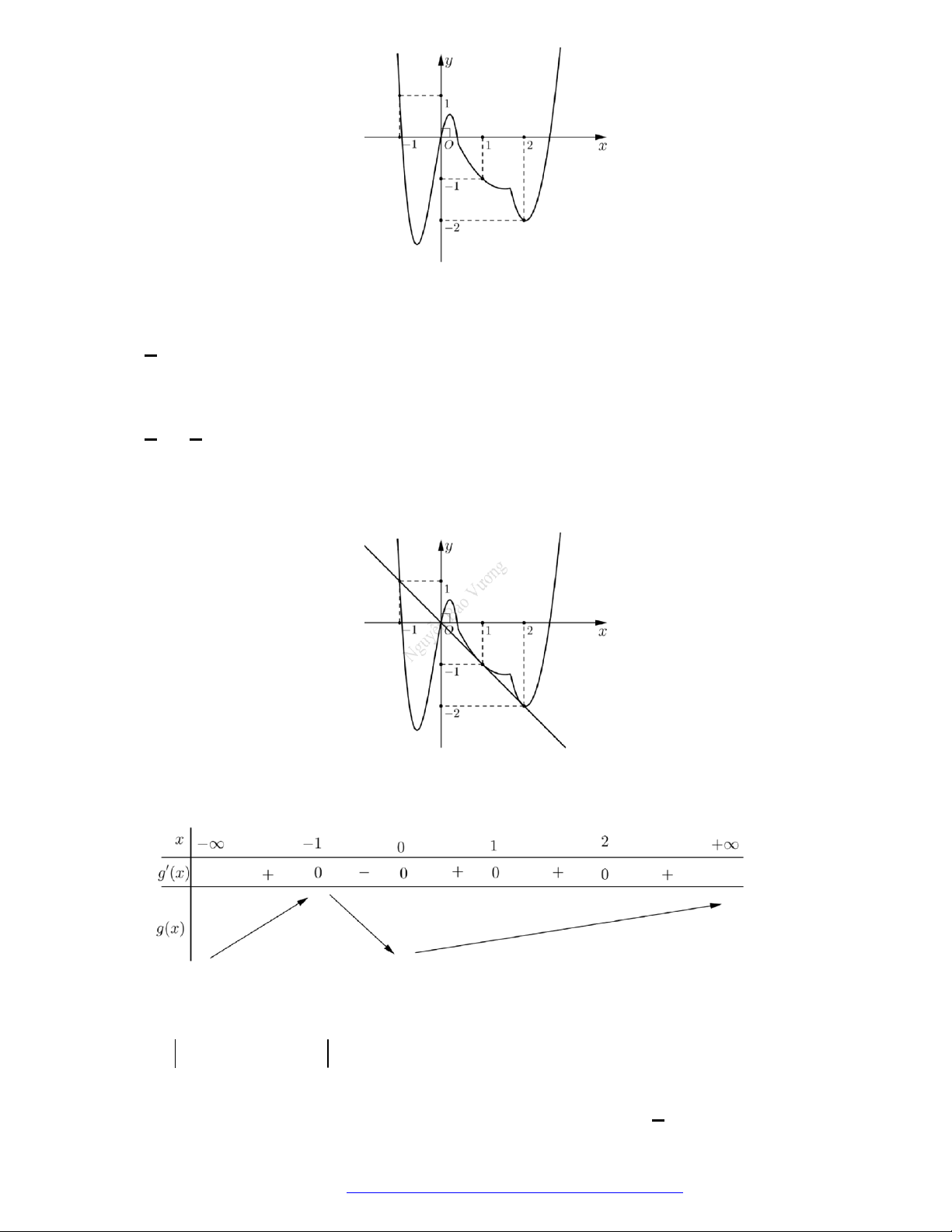
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 58 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A. Hàm số
y g x
nghịch biến trên khoảng
1;
.
B. Hàm số
y g x
đồng biến trên khoảng
1;0
.
C. Hàm số
y g x
đạt cực tiểu tại
0x
.
D. Hàm số
y g x
đạt cực đại tại
1x
.
Lời giải
Chọn C
2 2
g x f x x
.
0
g x f x x
.
Ta vẽ thêm đường thẳng
y x
và đồ thị.
Khi đó phương trình
0
g x
có các nghiệm
1 x
,
1x
,
2x
.
Ta có bảng biến thiên
Dựa vào bảng biến thiên, hàm số đạt cực tiểu tại
0x
.
Câu 56. (Kim Liên - Hà Nội - 2020) Có tất cả bao nhiêu giá trị nguyên dương của tham số
m
để hàm số
4 3 2
3 4 12y x x x m
có 5 điểm cực trị?
A.
16
. B.
28
. C.
26
. D.
27
.
Lời giải
Chọn D
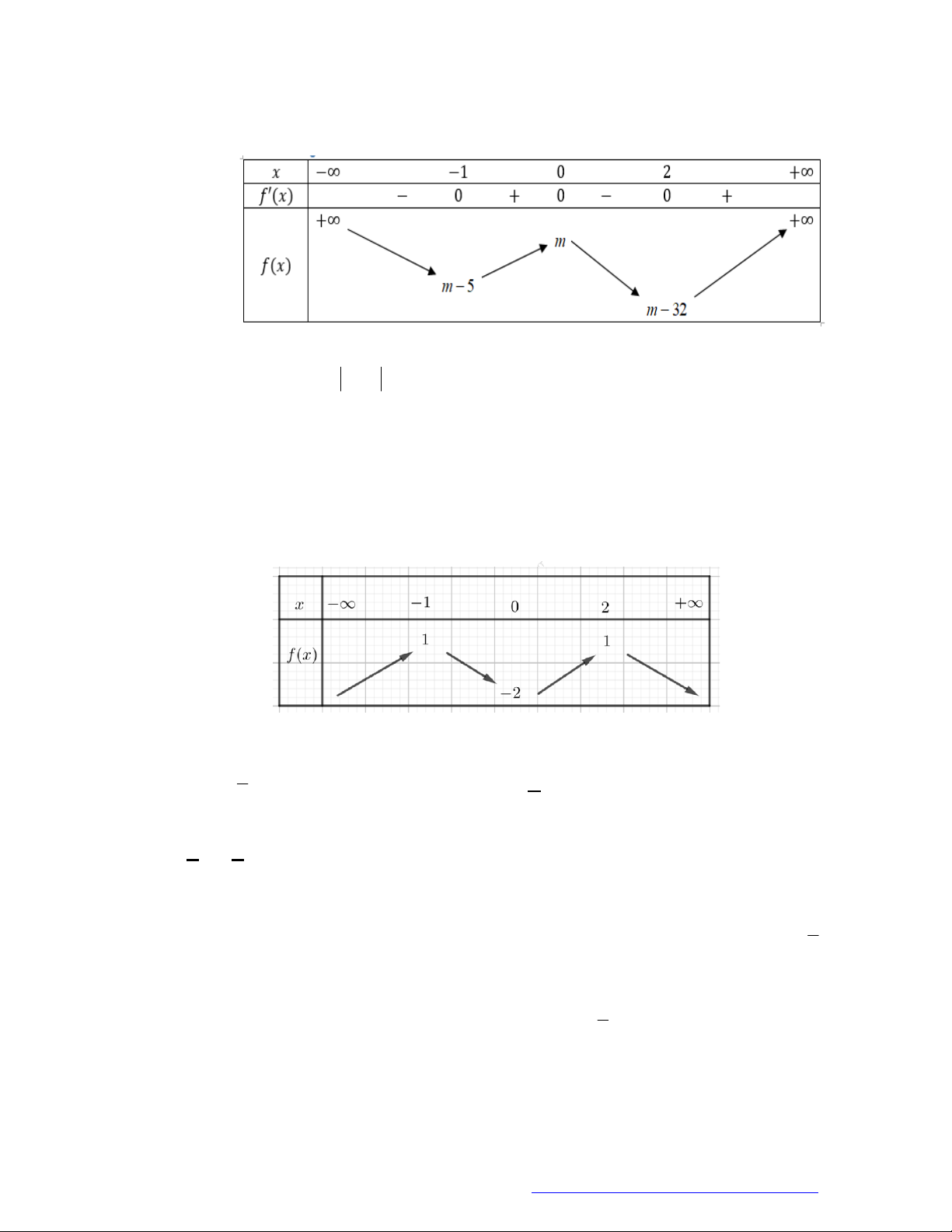
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 59
Xét hàm số
4 3 2
3 4 12f x x x x m
. Ta có
3 2
12 12 24 0f x x x x
0
1
2
x
x
x
.
Bảng biến thiên:
Vậy với mọi
m
hàm số
f x
luôn có ba điểm cực trị.
Do đó để hàm số
y f x
có 5 điểm cực trị khi và chỉ khi phương trình
0f x
có đúng hai
nghiệm đơn hoặc nghiệm bội lẻ
0
5 0
32 0
m
m
m
0
5 32
m
m
.
Vì
m
là số nguyên dương cho nên có
27
số
m
thỏa đề bài.
Câu 57. (Lý Nhân Tông - Bắc Ninh - 2020) Cho hàm số
( )y f x
có bảng biến thiên như hình vẽ dưới
đây:
Hàm số
(2 )y f x
đạt cực đại tại
A.
1
2
x
. B.
1x
. C.
1x
. D.
2x
.
Lời giải
Chọn C
Đặt
2 ( )t x y f t
.
Từ bảng biến thiên ta thấy hàm số
( )y f t
đạt cực đại tại
1
1 2 1
2
2 2 2
1
t x
x
t x
x
.
Vậy hàm số
(2 )y f x
đạt cực đại tại điểm
1x
và
1
2
x
.
Câu 58. (THPT Nguyễn Viết Xuân - 2020) Cho hàm số
y f x
có đạo hàm liên tục trên
và
0 0; 4 4f f
. Biết hàm
y f x
có đồ thị như hình vẽ.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 60 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Số điểm cực trị của hàm số
2
2g x f x x là
A.
2
. B.
1
. C.
4
. D.
3
.
Lời giải
Chọn D
Xét hàm số
2
2h x f x x
.
Ta có:
2
2 2h x xf x
;
2
1
0h x f x
x
(vô nghiệm
0x
).
Đặt
2
, 0t x x t t
.
Khi đó:
1
f t
t
(*). Nhận thấy trên khoảng
0;1
thì
1
w t
t
nghịch biến và
f t
đồng
biến, do đó (*) nếu có nghiệm là duy nhất.
Mặt khác:
0 . 1 2 2 1 2 8 0h h f
và
h x
liên tục trên
0;1
nên
0 0
0;1 : 0x h x
.
Vậy
0h x
có nghiệm duy nhất
0
0;1x
và
h x
có một điểm cực tiểu (vẽ bảng biến thiên).
(1)
Xét phương trình:
2
0 2 0h x f x x
(**).
Ta có:
0 0 0 0h f x
là một nghiệm của (**).
Mặt khác:
0 0 0 1 0 1
. 2 2 4 4 0 ;2 : 0h x h f x x f x x h x .
Nên (**) có nghiệm
1 0
;2x x .
Vì
h x
có một điểm cực trị, nên (**) có không quá
2
nghiệm.
Vậy
2
2 0h x f x x
có hai nghiệm phân biệt. (2)
Từ (1) và (2) ta được: hàm số
2
2g x f x x có 3 điểm cực trị.
Câu 59. (Hải Hậu - Nam Định - 2020) Cho hàm số
( )y f x
đồng biến trên
4;
có đồ thị như hình
vẽ. Số điểm cực trị của hàm số
(2 2)y f x
bằng
x
y
2
5
3
1
4
O
1
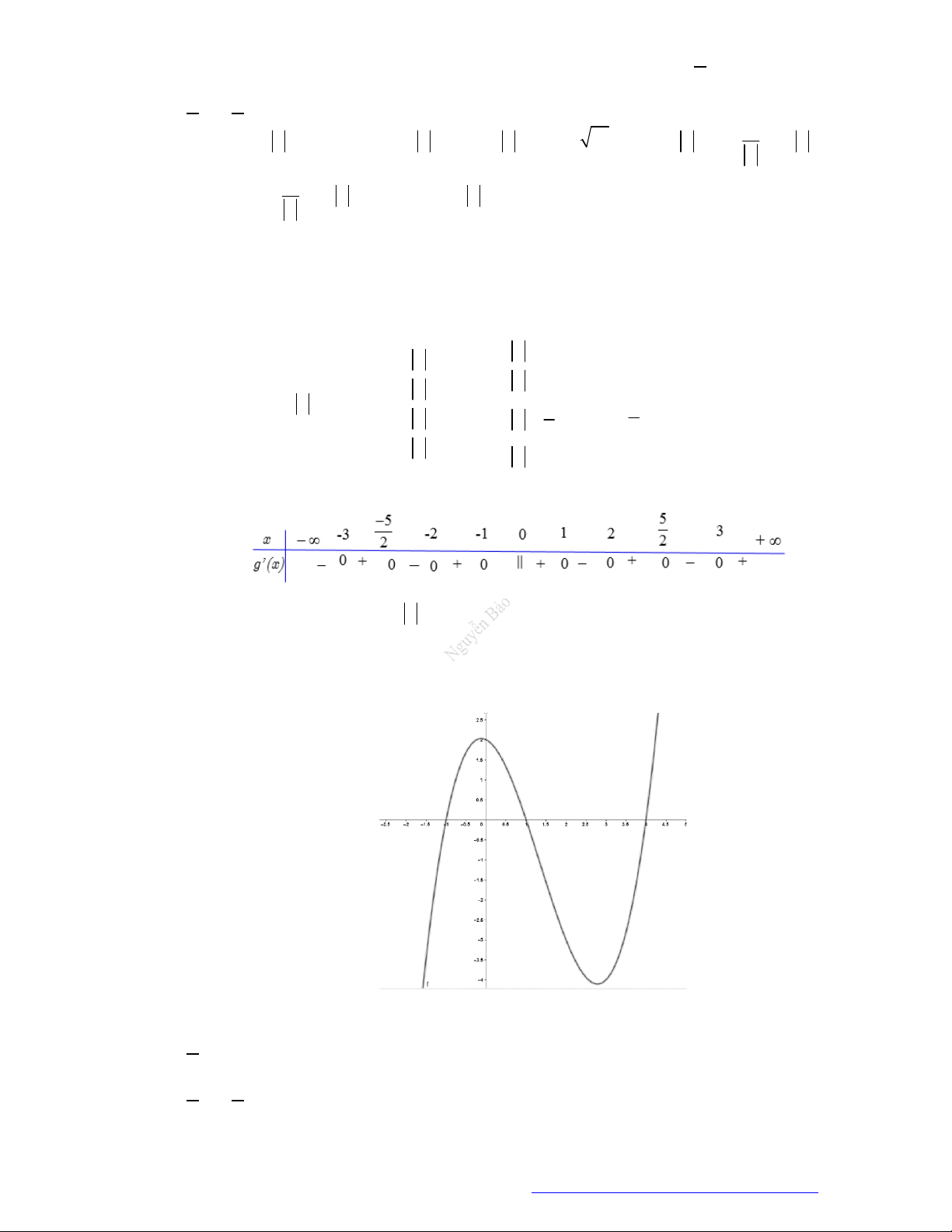
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 61
A.
7
. B. 5. C.
4
. D.
9
.
Lời giải
Chọn D
'
'
' 2 ' '
(2 2) ' 2 2 (2 2) 2 2 (2 2) (2 2)
x
g x f x g x x f x x f x f x
x
' '
' 0 (2 2) 0 (2 2) 0 0
x
g x f x f x x
x
Dựa vào đồ thị ta có
'
0
2
( ) 0
3
4
x
x
f x
x
x
'
1
1
2 2 0
2
2
2 2 2
(2 2) 0
5
5
2 2 3
2
2
2 2 4
3
3
x
x
x
x
x
x
f x
x
x
x
x
x
x
Ta có bảng xét dấu
'g x
Suy ra hàm số
(2 2)y f x
có 9 điểm cực trị
Câu 60. (Hải Hậu - Nam Định - 2020) Cho hàm số
y f x
liên tục trên
và có đồ thị hàm số
y f x
như hình vẽ dưới đây:
Tìm điểm cực đại của hàm số
2019 2020 .
f x f x
y
A.
2
. B.
3
. C.
0
. D.
1
.
Lời giải
Chọn A
Từ đồ thị hàm số
y f x
ta có bảng xét dấu của
y f x
như sau:
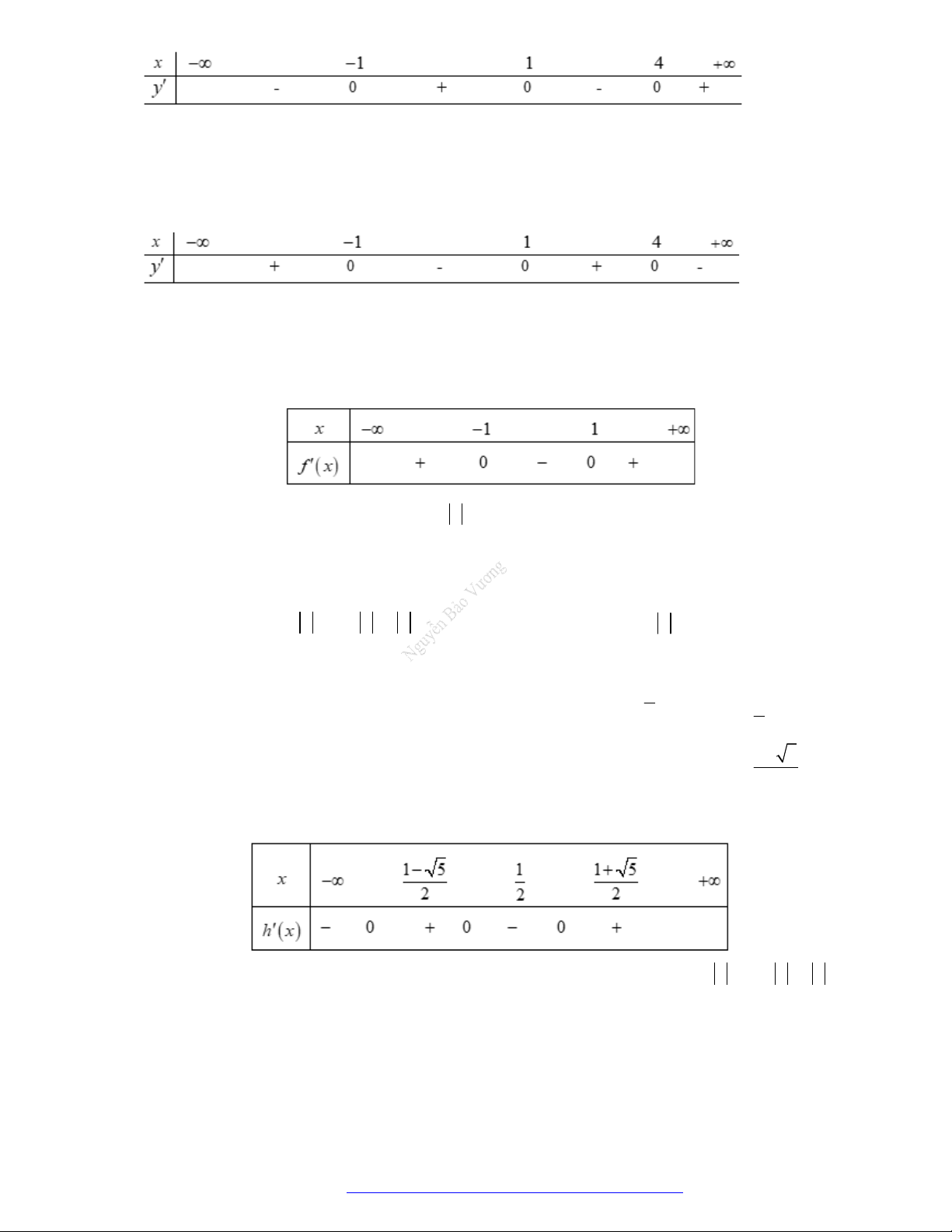
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 62 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Xét hàm số
2019 2020 2019 ln2019 2020 ln 2020
f x f x f x f x
y y f x
Vì
2019 ln 2019 2020 ln 2020 0
f x f x
Nên
2019 ln 2019 2020 ln2020
f x f x
y f x
có bảng xét dấu như sau:
Vậy hàm số
2019 2020
f x f x
y
có hai điểm cực đại.
Câu 61. (Kìm Thành - Hải Dương - 2020) Cho hàm số
y f x
là một hàm đa thức có bảng xét dấu
f x
như sau
Số điểm cực trị của hàm số
2
g x f x x
A.
5
. B.
3
. C.
1
. D.
7
.
Lời giải
Chọn A
Ta có
2
2
g x f x x f x x
. Số điểm cực trị của hàm số
f x
bằng hai lần số điểm
cực trị dương của hàm số
f x
cộng thêm 1.
Xét hàm số
2 2 2
2
1
1
2
2
2 1 0 1
1 5
1
2
x
x
h x f x x h x x f x x x x
x
x x
.
Bảng xét dấu hàm số
2
h x f x x
Hàm số
2
h x f x x
có 2 điểm cực trị dương, vậy hàm số
2
2
g x f x x f x x
có 5 điểm cực trị.
Câu 62. (Trần Phú - Quảng Ninh - 2020) Cho đồ thị
y f x
như hình vẽ dưới đây:
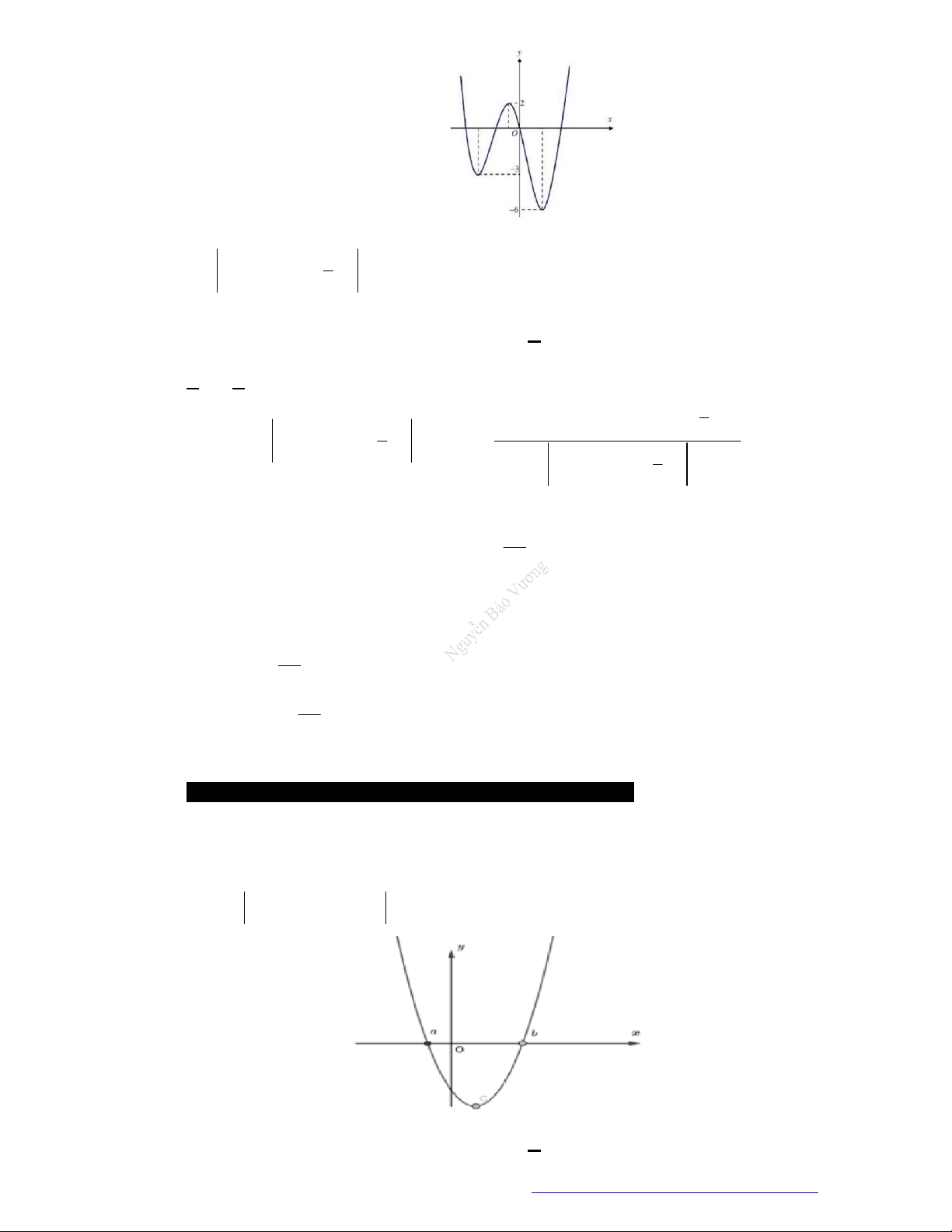
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 63
Gọi
S
là tập hợp tất cả các giá trị nguyên dương của tham số
m
để hàm số
2
1
2018
3
y f x m
có
5
điểm cực trị. Tổng tất cả các giá trị của các phần tử trong tập
S
bằng
A.
6
. B.
5
. C.
7
. D.
9
.
Lời giải
Chọn C
Đặt
2
2
2
1
2018 2018
1
3
2018
1
3
2018
3
f x f x m
g x f x m g x
f x m
Phương trình
2
2018 0 1
0
2018 2
3
f x
g x
m
f x
Dựa vào đồ thị ta thấy phương trình
1
luôn có 3 nghiệm phân biệt.
Vậy để đồ thị hàm số
y g x
có 5 điểm cực trị thì phương trình
2
phải có 2 nghiệm đơn phân
biệt
2
*
2
2
3
3;4
6 3
3
m
m m
m
.
Vậy tổng các phần tử là 7.
Dạng 3. Tìm m để hàm số f(u) thỏa mãn điều kiện cho trước
Câu 1. (Hậu Lộc 2 - Thanh Hóa - 2020) Cho hàm số bậc ba
y f x
có đồ thị của hàm đạo hàm
'
f x
như hình vẽ và
1f b
.Số giá trị nguyên của
5;5m
để hàm số
2
4g x f x f x m
có đúng 5 điểm cực trị là
A.
8
. B.
10
. C.
9
. D.
7
.
Lời giải
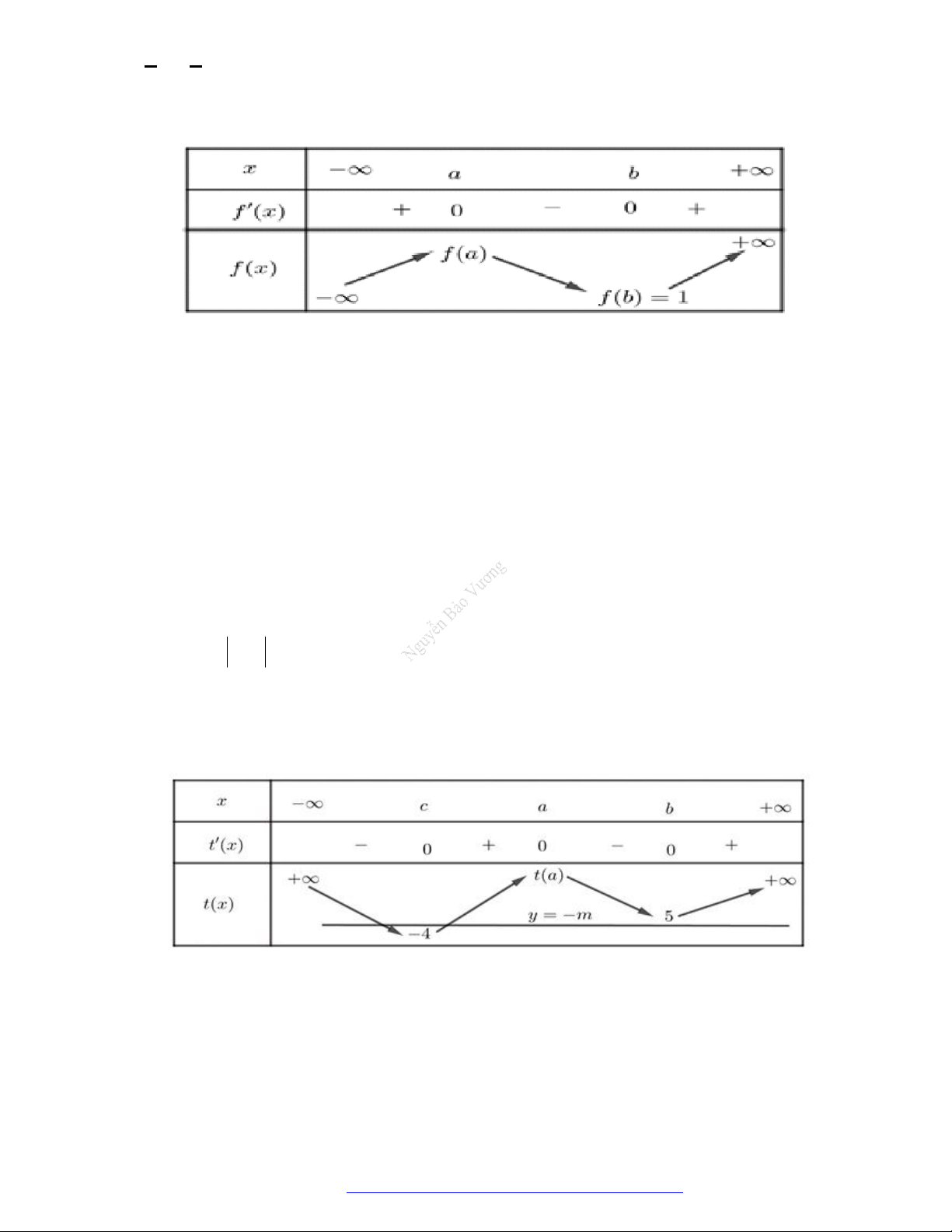
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 64 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Chọn C
Cách 1:
Ta có bảng biến thiên của
f x
:
Xét hàm số
2
4h x f x f x m
' ' '
' '
' '
'
2 4
2 2
0 2 2 0
;
0
2
h x f x f x f x
h x f x f x
h x f x f x
x a x b
f x
x c c a
f x
Pt có
3
nghiệm phân biệt
có
3
điểm cực trị
Xét
0h x
2
4 2f x f x m
Để
g x h x
có 5 điểm cực trị khi và chỉ khi PT
2
có 2 nghiệm đơn hoặc nghiệm bội lẻ
phân biệt
Xét hàm số
2
4t x f x f x
Ta có Bảng biến thiên của
t x
:
Từ YCBT
t x m
có hai nghiệm đơn hoặc nghiệm bội lẻ pb
5 5
5 4
4 5 4 5
5 5; 5 5
m t a m t a
m
m m
m
m m m
5; 4; 3; 2; 1;0;1;2;3 .m
Cách 2:
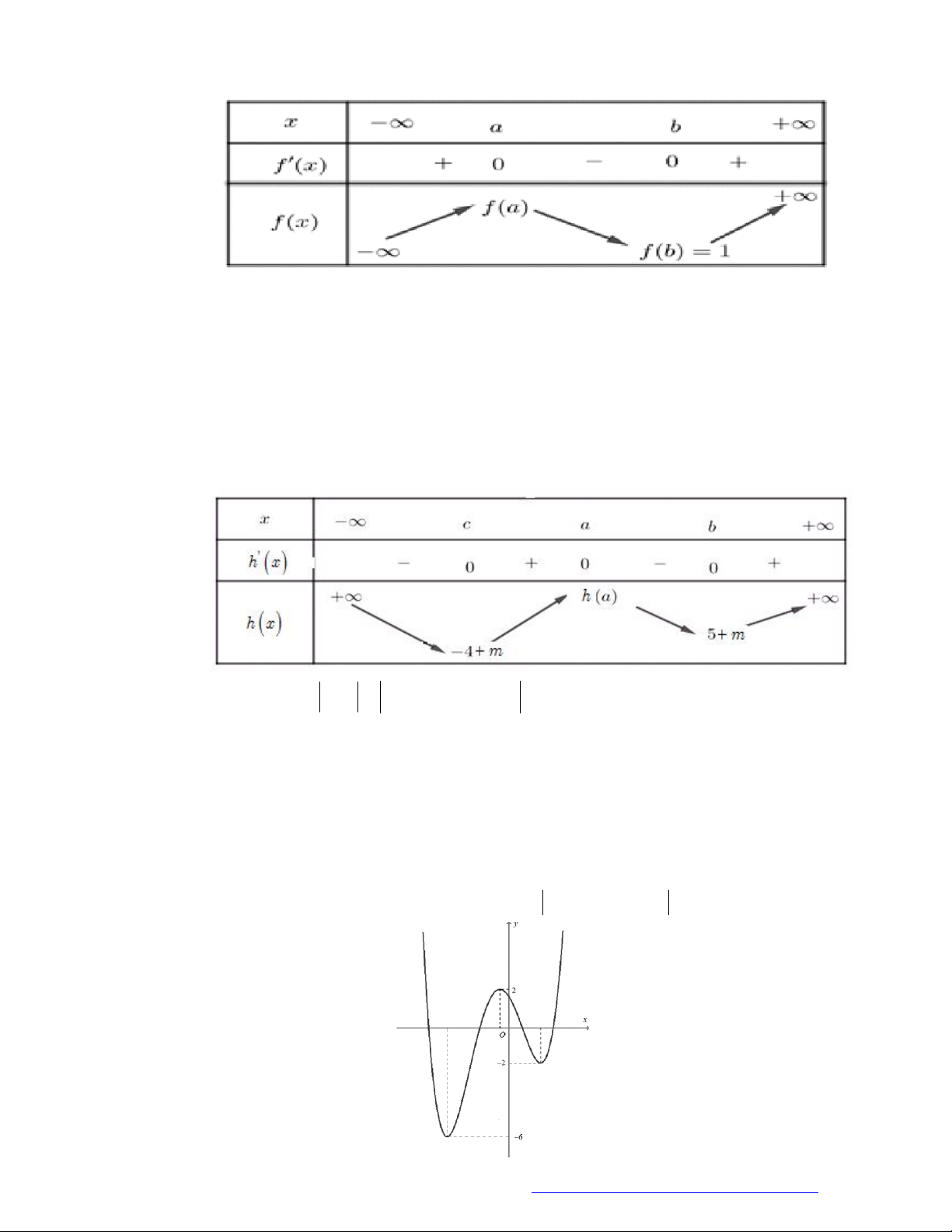
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 65
Ta có bảng biến thiên của hàm số
y f x
:
Xét hàm số
2
4h x f x f x m
' ' '
' '
' '
'
2 4
2 2
0 2 2 0
;
0
2
h x f x f x f x
h x f x f x
h x f x f x
x a x b
f x
x c c a
f x
Từ YCBT
2
4g x h x f x f x m
có 5 điểm cực trị khi:
2
0
4 (a) 5
4 0 5
5 4
; 5;5
; 5;5
5; 4; 3; 2; 1;0;1;2; 3
h a
m f a f
m m
m
m m
m m
m
Câu 2. (Sở Bình Phước - 2020) Cho hàm số
y f x
có đồ thị như hình vẽ bên dưới. Có bao nhiêu giá
trị nguyên của tham số thực
m
để hàm số
2
2020g x f x m
có 5 điểm cực trị?
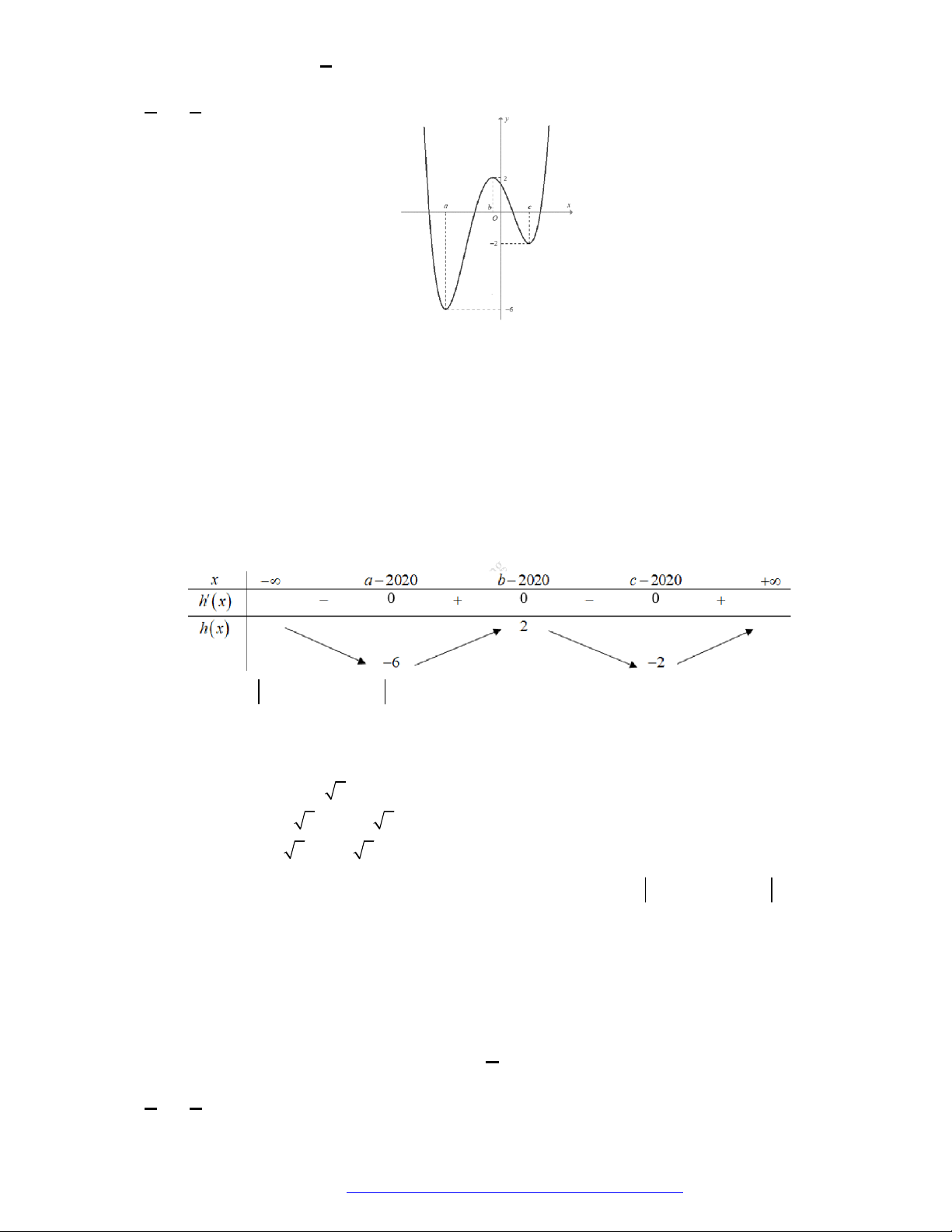
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 66 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A. 1. B. 2. C. 4. D. 5.
Lời giải
Chọn B
Gọi
, ,a b c
a b c
là ba điểm cực trị của hàm số
y f x
.
Khi đó:
6; 2; 2f a f b f c
.
Xét hàm
2020h x f x
với
x
.
Khi đó:
2020 . 2020 2020h x f x x f x
.
2020
0 2020
2020
x a
h x x b
x c
.
Bảng biến thiên của hàm
h x
Hàm số
2
2020g x f x m
có 5 điểm cực trị
Phương trình
2
2020 0f x m
có đúng 2 nghiệm không thuộc
2020; 2020; 2020a b c
2
2
2
2
2
2 6 2
2 6
2 6
m
m
m m
m
m
.
Vậy có 2 giá trị nguyên của
m
là
2m
và
2m
thì hàm số
2
2020g x f x m
có 5
điểm cực trị.
Câu 3. (Chuyên Lào Cai - 2020) Cho hàm số
f x
có đạo hàm
4 3
2 2
2 4 2 3 6 18 .f x x x x x m x m
Có tất cả bao nhiêu giá trị nguyên của
m
để hàm số
f x
có đúng một điểm cực trị?
B.
7
. B.
5
. C.
8
. D.
6
.
Lời giải
Chọn C
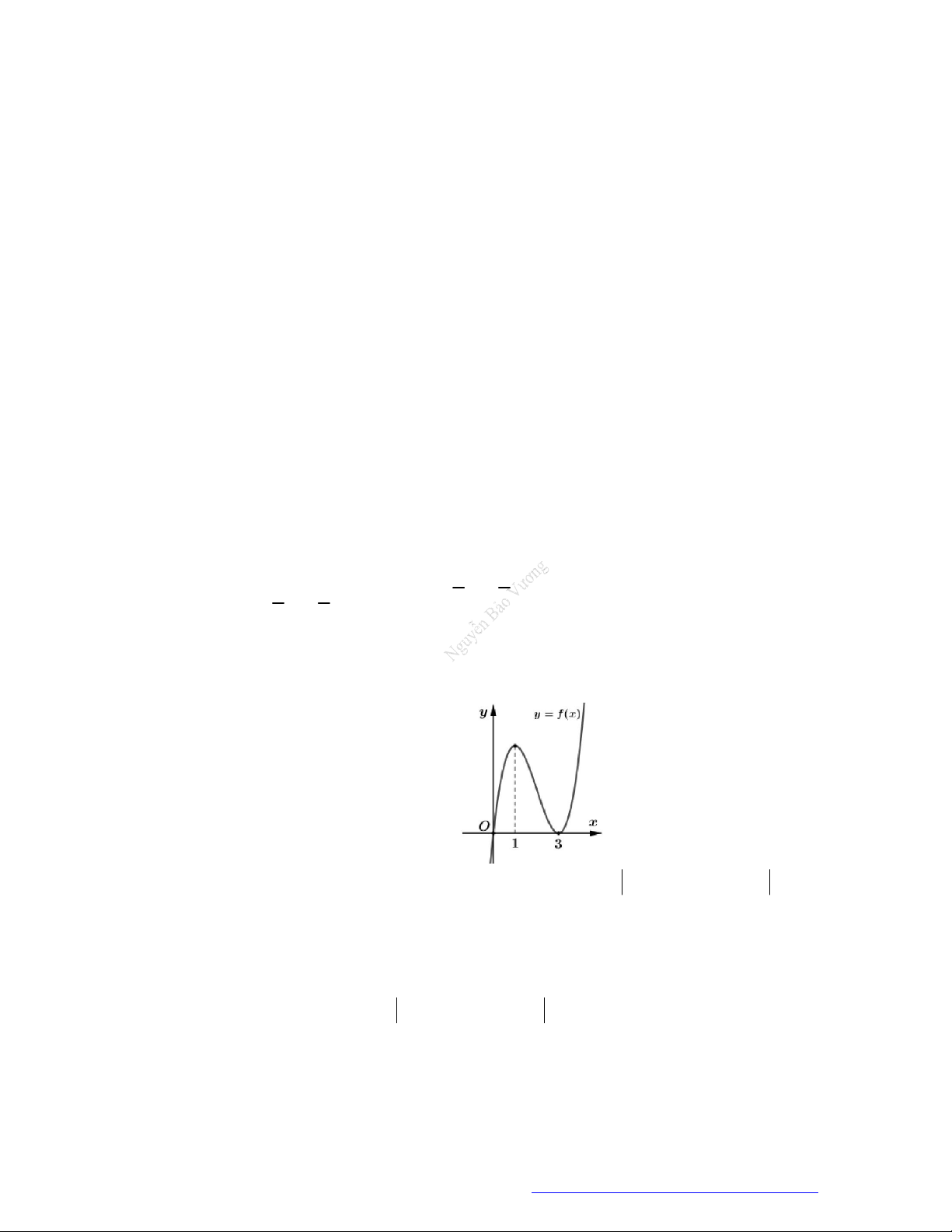
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 67
Ta có
2
4
3
2
2
0
0
2 0
2
0
4
4 0
2 3 6 18 0 *
2 3 6 18 0
x
x
x
x
f x
x
x
x m x m
x m x m
Để hàm số
f x
có đúng một điểm cực trị
Phương trình
*
vô nghiệm, có nghiệm kép
hoặc có hai nghiệm phân biệt trong đó có nghiệm là
4.
Trường hợp 1. Phương trình
*
vô nghiệm
2 2
4 24 36 24 72 4 36 0m m m m
3 3m
2 ; 1 ; 0 ; 1 ; 2m
Trường hợp 2. Phương trình
*
có nghiệm kép
2
3
4 36 0
3
m
m
m
.
Trường hợp 3. Phương trình
*
có hai nghiệm phân biệt
1
x
,
2
x
. Trong đó
1
4.x
Phương trình có hai nghiệm phân biệt
2
1 2
3
, 4 36 0
3
m
x x m
m
.
Theo định lí Viète ta có
1 2 2
1 2 2
4 2 6
. 4. 6 18
S x x x m
P x x x m
2
2
2 2
3 9
2 2 5
3 9
2 2
2 2
x m
m m m
x m
.
Vậy
3 ; 2 ; 1 ; 0 ; 1 ; 2 ; 3 ; 5m
thỏa mãn yêu cầu đề bài.
Câu 4. (THPT Thiệu Hóa – Thanh Hóa 2019) Cho hàm số
y f x
có đồ thị như hình vẽ bên dưới
Tìm tất cả các giá trị của tham số
m
để đồ thị hàm số
2
2 2h x f x f x m
có đúng
3
điểm cực trị.
A.
1m
B.
1m
C.
2m
D.
2m
Lời giải
Chọn B
Số cực trị của hàm số
2
2 2h x f x f x m
bằng số cực trị của hàm
số
2
2 2 y x f x f x m
cộng với số giao điểm (khác điểm cực trị) của đồ thị hàm số
2
2 2 y x f x f x m
và
0y
.
Xét hàm số
2
2 2g x f x f x m
2 2 2 1g x f x f x f x f x f x.
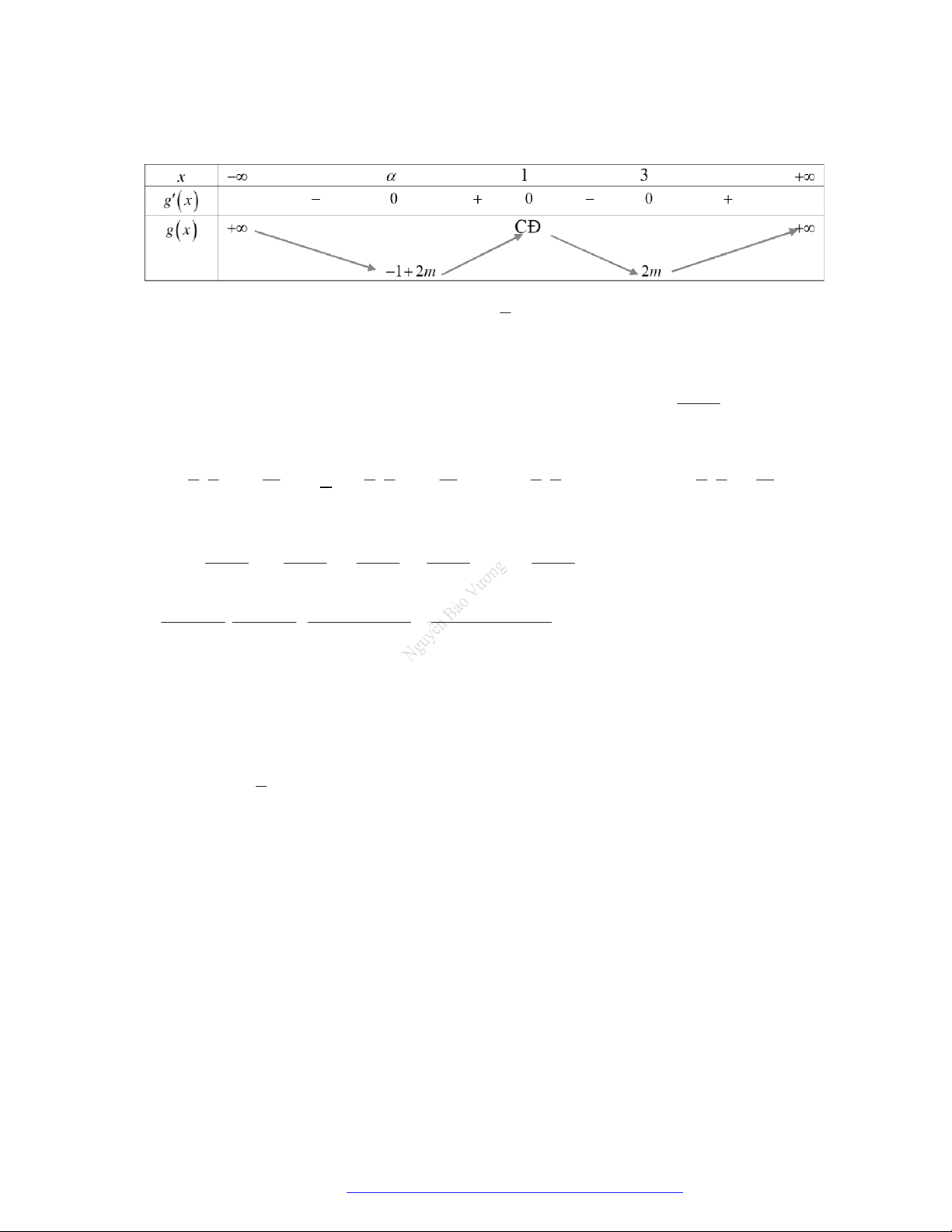
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 68 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
1
0
0 3
1
0
x
f x
g x x
f x
x
BBT
Hàm số
h x
có 3 điểm cực trị
1
2 0
2
m m
. Đáp án B là gần kết quả nhất
Câu 5. (THPT Hàm Rồng - Thanh Hóa - 2018) Cho hàm số
f x
có đạo hàm
3
2
13 15f x x x a x
. Tập hợp các giá trị của
a
để hàm số
2
5
4
x
y f
x
có 6 điểm cực
trị là
A.
5 5 15
; \ 0;
4 4 13
. B.
5 5 15
; \ 0;
4 4 13
. C.
5 5
; \ 0
4 4
. D.
5 5 15
; \
4 4 13
.
Lời giải
2 3
2 2 2 2 2
5 5 5 5 5
. 13 15
4 4 4 4 4
x x x x x
y f a
x x x x x
=
3
2 2 2 2
2 2
2 2
2 2
20 5 25 5 4 15 65 60
.
4 4
4 4
x x ax x a x x
x x
x x
.
0y
2
2
0
3
4
3
5 4 0 (1)
x
x
x
x
ax x a
(
0x
là nghiệm kép ).
đặt
2
5 4g x ax x a
Ycbt thỏa mãn khi phương trình
0y
có
6
nghiệm bội lẻ phương trình
1
có hai nghiệm
phân biệt khác
2;0;1;4
. (Nếu
0 0g
thì
0y
chỉ có 5 nghiệm bội lẻ).

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 69
Điều kiện:
2
0
5 4 .4 0
2 0
2 0
0 0
3 0
4
0
3
a
a a
g
g
g
g
g
0
5 5
4 4
5
4
0
15
13
a
a
a
a
a
5 5
4 4
0
15
13
a
a
a
.
Câu 6. (Chuyên Vinh - 2018) Cho hàm số
y f x
có đạo hàm
2
2
1 2f x x x x
với
x
.
Có bao nhiêu giá trị nguyên dương của tham số
m
để hàm số
2
8f x x m
có
5
điểm cực trị?
A.
15
. B.
17
. C.
16
D.
18
Lời giải
Đặt
2
8g x f x x m
2
2
1 2f x x x x
2
2 2 2
2 8 8 1 8 8 2g x x x x m x x m x x m
0g x
2
2
2
4
8 1 0 1
8 0 2
8 2 0 3
x
x x m
x x m
x x m
Các phương trình
1
,
2
,
3
không có nghiệm chung từng đôi một và
2
2
8 1 0x x m
với
x
Suy ra
g x
có
5
điểm cực trị khi và chỉ khi
2
và
3
có hai nghiệm phân biệt khác
4
16 0
16 2 0
16 32 0
16 32 2 0
m
m
m
m
16
18
16
18
m
m
m
m
16m
.
m
nguyên dương và
16m
nên có
15
giá trị
m
cần tìm.
Câu 7. Cho hàm số
( )y f x
xác định trên
và hàm số
'( )y f x
có đồ thị như hình bên. Biết rằng
'( ) 0f x
với mọi
; 3,4 9; .x
Có bao nhiêu giá trị nguyên dương của tham số
m
để hàm số
( ) ( ) 5g x f x mx
có đúng hai điểm cực trị.
A.
7.
B.
8.
C.
6.
D.
5.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 70 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Lời giải
Chọn B
'( ) '( )g x f x m
Số điểm cực trị của hàm số
( )g x
bằng số nghiệm đơn (bội lẻ) của phương trình
'( ) .f x m
Dựa và đồ thị ta có điều kiện
0 5
10 13
m
m
.
Vậy có 8 giá trị nguyên dương của
m
thỏa mãn.
Câu 8. (Chuyên Vĩnh Phúc 2019) Cho hàm số
( )y f x
. Hàm số
( )y f x
có đồ thị như hình vẽ
dưới đây.
Tìm
m
để hàm số
2
( )y f x m
có
3
điểm cực trị.
A.
3;m
. B.
0;3m
. C.
0;3m
. D.
;0m
.
Lời giải
Chọn C
Do hàm số
2
( )y f x m
là hàm chẵn nên hàm số có
3
cực trị khi và chỉ khi hàm số này có
đúng
1
điểm cực trị dương.
2 2
( ) 2y f x m y xf x m
2 2
2
2 2
2 2
0 0
0
0
0
0
1 1
3 3
x x
x
x m x m
y
f x m
x m x m
x m x m
Đồ thị hàm số
y f x
tiếp xúc trục hoành tại điểm có hoành độ là
1x
nên các nghiệm của
pt
2
1x m
(nếu có) không làm
2
f x m
đổi dấu khi
x
đi qua, do đó các điểm cực trị của
hàm số
2
( )y f x m
là các điểm nghiệm của hệ
2
2
0
3
x
x m
x m
Hệ trên có duy nhất nghiệm dương khi và chỉ khi
0
0 3
3 0
m
m
m
.
Câu 9. (THPT Hàm Rồng - Thanh Hóa - 2019) Cho hàm số
2
2
2 4 3f x x x x
với mọi
x
. Có bao nhiêu giá trị nguyên
x
y
3
2
0
1

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 71
dương của
m
để hàm số
2
10 9
y f x x m
có
5
điểm cực trị?
A.
18
. B.
16
. C.
17
. D.
15
.
Lời giải
Chọn B
Ta có
2
0 1
3
x
f x x
x
,
2
x
là nghiệm kép nên khi qua giá trị
2
x
thì
f x
không bị đổi dấu.
Đặt
2
10 9
g x f x x m
khi đó
' . 2 10
g x f u x
với
2
10 9
u x x m
.
Nên
2
2
2
2
2 10 0
10 9 2 0
0
10 9 1
10 9 3
x
x x m
g x
x x m
x x m
2
2
2
2
5
10 9 2 0
10 8 0 1
10 6 0 2
x
x x m
x x m
x x m
Hàm số
2
10 9
y f x x m
có
5
điểm cực trị khi và chỉ khi
g x
đổi dấu
5
lần
Hay phương trình
1
và phương trình
2
phải có hai nghiệm phân biệt khác
5
'
1
'
2
0
0
5 0
5 0
h
p
, (Với
2
10 8
h x x x m
và
2
10 6
p x x x m
).
17 0
19 0
17
17 0
19 0
m
m
m
m
m
.
Vậy có
16
giá trị nguyên dương
m
thỏa mãn.
Câu 10. (Chuyên Bắc Giang - Lần 4 - 2019) Cho hàm số
y f x
có đạo hàm
2
2 2
2 1 2 1 1
f x x x x m x m
, x
. Có bao nhiêu giá trị nguyên của
m
để
hàm số
g x f x
có 5 điểm cực trị?
A. 3. B. 5. C. 2. D. 4.
Lời giải
Chọn C
Dựa vào cách vẽ đồ thị hàm số
g x f x
, số điểm cực trị của đồ thị hàm số
g x f x
bằng số điểm cực trị dương của đồ thị hàm số
y f x
cộng thêm 1.
Để hàm số
g x f x
có 5 điểm cực trị thì đồ thị hàm số
y f x
có 2 cực trị dương.
Ta có
2 2
1
0 2.
2 1 1 0 *
x
f x x
x m x m
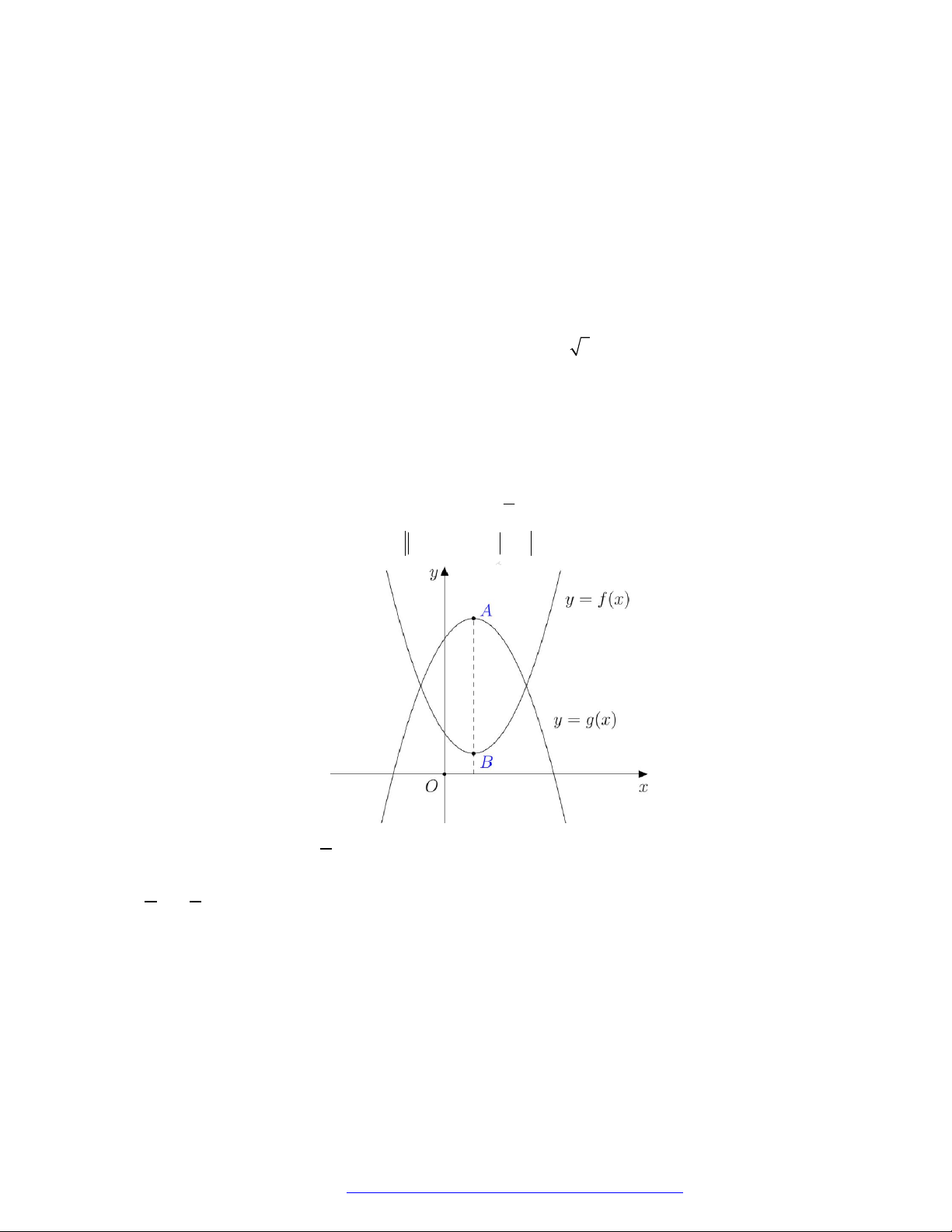
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 72 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Có
2x
là nghiệm bội 2,
1x
là nghiệm đơn.
Vậy
2 2
2 1 1 0x m x m
có hai nghiệm phân biệt, có một nghiệm dương
1x
, có một
nghiệm
0x
Trường hợp 1: Có nghiệm
0x
khi đó
2 2 2
2 1 1 0 1 0 1x m x m m m
Với
1m
, có
2 2 2
0
2 1 1 0 4 0 TM
4
x
x m x m x x
x
Với
1m
, có
2 2 2
2 1 1 0 0 0x m x m x x
(Loại)
Trường hợp 2:
2 2
2 1 1 0x m x m
có hai nghiệm phân biệt, có một nghiệm dương
1x
,
có một nghiệm âm
Điều kiện tương đương
2
2 2
1;1
1 0
1 2 1 .1 1 0
1 3
m
m
m m
m
Vì
0m m
Vậy có hai giá trị nguyên của
m
thỏa mãn.
Câu 11. (Sở GD Quảng Nam - 2019) Cho hai hàm đa thức
y f x ,
y g x có đồ thị là hai đường
cong ở hình vẽ. Biết rằng đồ thị hàm số
y f x có đúng một điểm cực trị là
A
, đồ thị hàm số
y g x có đúng một điểm cực trị là
B
và
7
4
AB
. Có bao nhiêu giá trị nguyên của tham số
m
thuộc khoảng
5;5 để hàm số
y f x g x m có đúng
5
điểm cực trị?
A.
1
. B.
3
. C.
4
. D.
6
.
Lời giải
Chọn B
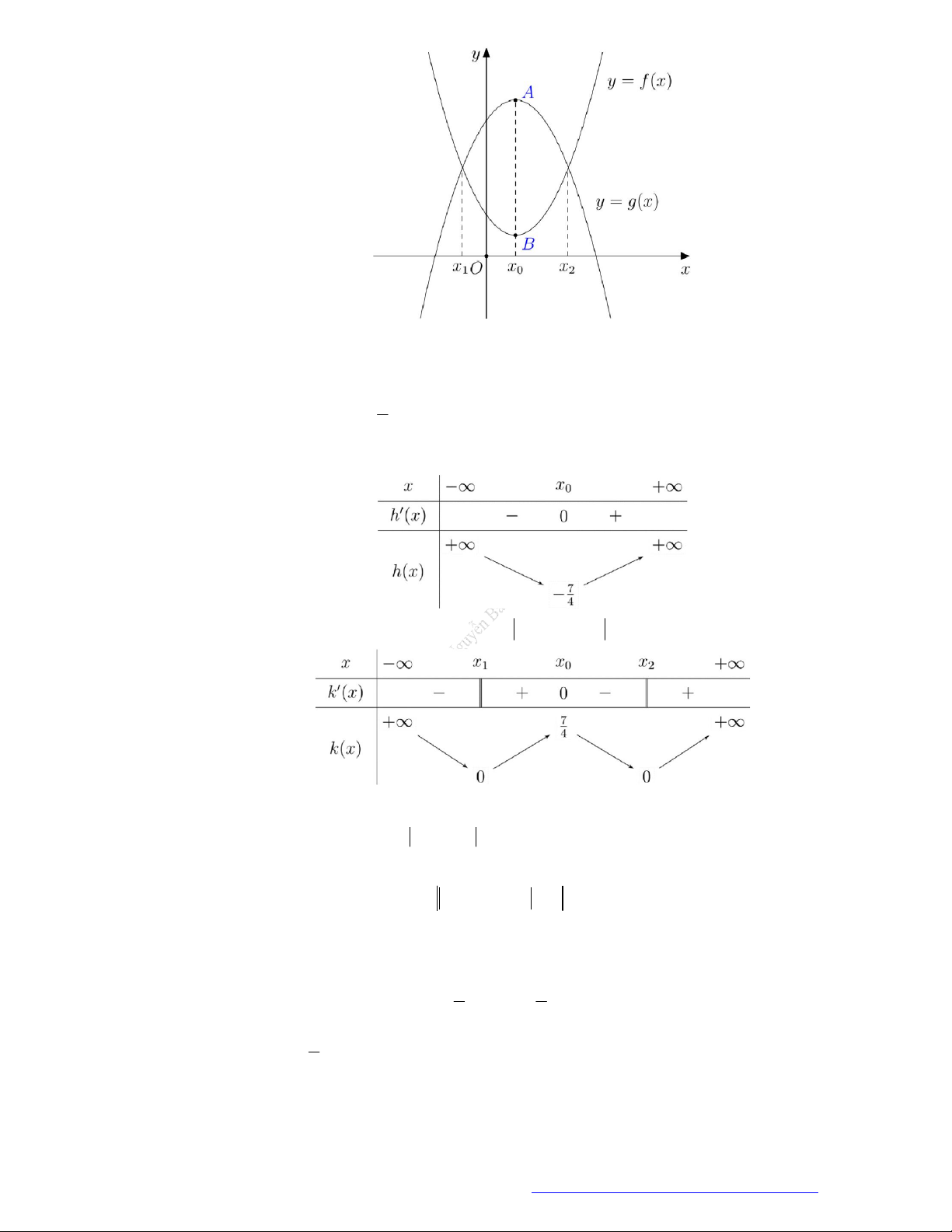
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 73
Đặt
h x f x g x , ta có:
h x f x g x
;
0
0h x x x
;
1
0h x x x
hoặc
2
x x (
1 0 2
x x x );
0 0 0
7
4
h x f x g x
.
Bảng biến thiên của hàm số
y h x là:
Suy ra bảng biến thiên của hàm số
y k x f x g x
là:
Do đó, hàm số
y k x m
cũng có ba điểm cực trị.
Vì số điểm cực trị hàm số
y k x m
bằng tổng số điểm cực trị của hàm số
y k x m và
số nghiệm đơn và số nghiệm bội lẻ của phương trình
0k x m
, mà hàm số
y k x m cũng
có ba điểm cực trị nên hàm số
y f x g x m có đúng năm điểm cực trị khi phương trình
0k x m
có đúng hai nghiệm đơn (hoặc bội lẻ).
Dựa vào bảng biến thiên của hàm số
y k x
, phương trình
0k x m
có đúng hai nghiệm
đơn (hoặc bội lẻ) khi và chỉ khi
7
4
m
7
4
m
.
Vì
m
,
7
4
m
và
5;5m nên
4; 3; 2m .
Câu 12. (Sở GD Bạc Liêu - 2019) Cho hàm số
3 2
2 1 2 2y f x x m x m x
. Tập hợp tất cả
các giá trị của tham số
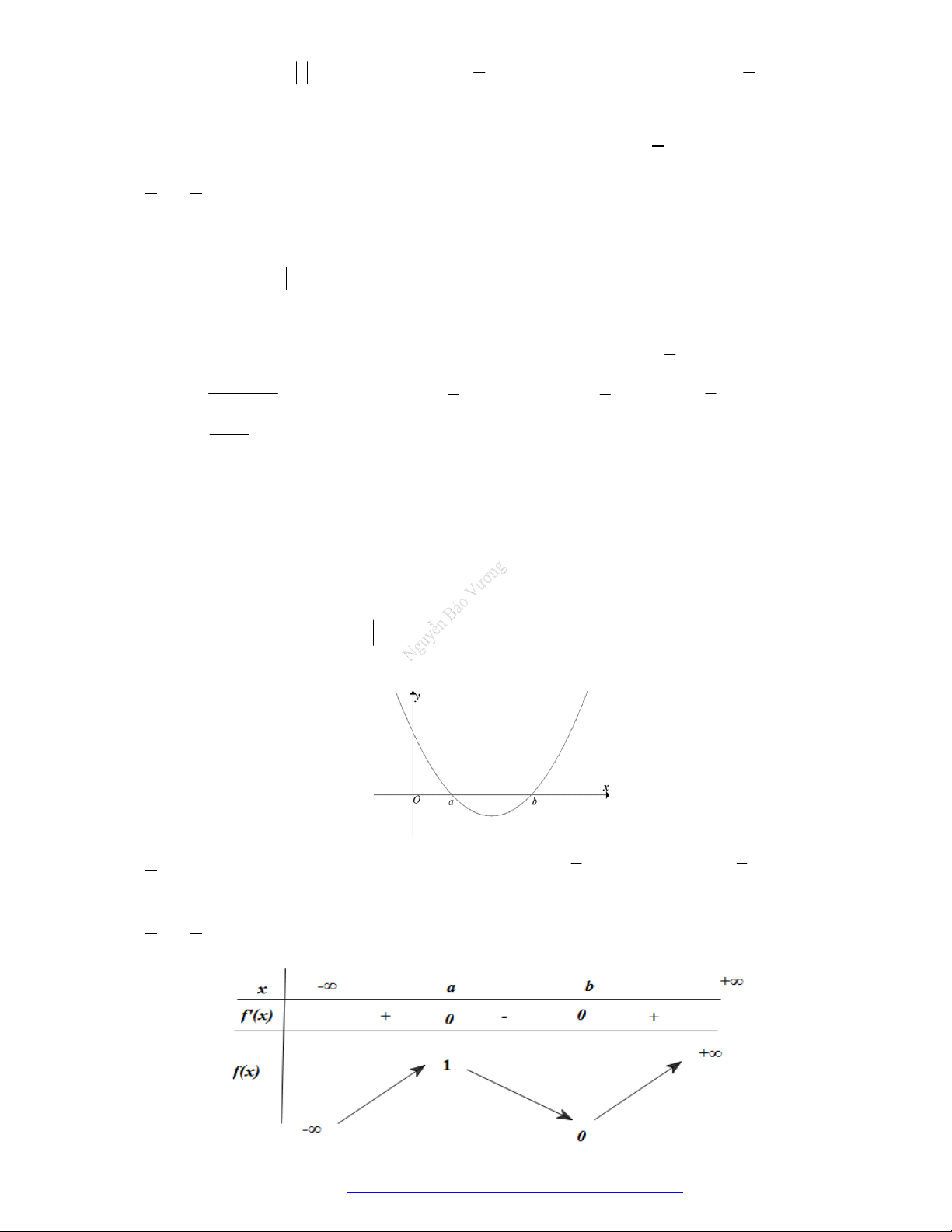
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 74 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
m
để hàm số
y f x
có 5 điểm cực trị là
;
a
c
b
, (với
, , a b c
là các số nguyên,
a
b
là phân số
tối giản). Giá trị của biểu thức
2 2 2
M a b c
là
A.
40M
. B.
11M
. C.
31M
. D.
45M
.
Lời giải
Chọn D
Hàm số
3 2
2 1 2 2y f x x m x m x
có đạo hàm là
2
3 2 2 1 2y f x x m x m
- Để hàm số
y f x
có 5 điểm cực trị thì hàm số
y f x
có hai điểm cực trị
1 2
, x x
dương.
Tương đương với phương trình
0f x
có 2 nghiệm dương phân biệt.
2
2 1 3 2 0
2 2 1
0
3
2
0
3
m m
m
S
m
P
2
4 5 0
1
2
2
m m
m
m
5
1
4
1
2
2
m m
m
m
5
2
4
m
.
Suy ra
5
4
2
a
b
c
2 2 2
45M a b c
.
Câu 13. (Chuyên Lam Sơn - Thanh Hóa - Lần 3 - 2019) Cho hàm số
y f x
có đạo hàm liên tục
trên
. Hàm số
'y f x
có đồ thị như hình vẽ bên. Tìm tập hợp
S
tất cả các giá trị thực của
tham số
m
để hàm số
2
2 3g x f x f x m
có đúng 7 điểm cực trị, biết phương trình
'( ) 0f x
có đúng 2 nghiệm phân biệt,
1, 0f a f b
,
lim
x
f x
và
lim
x
f x
.
A.
5;0 .S
B.
8;0 .S
C.
1
8; .
6
S
D.
9
5; .
8
S
Lời giải
Chọn A
Từ gt ta có BBT của
( )f x
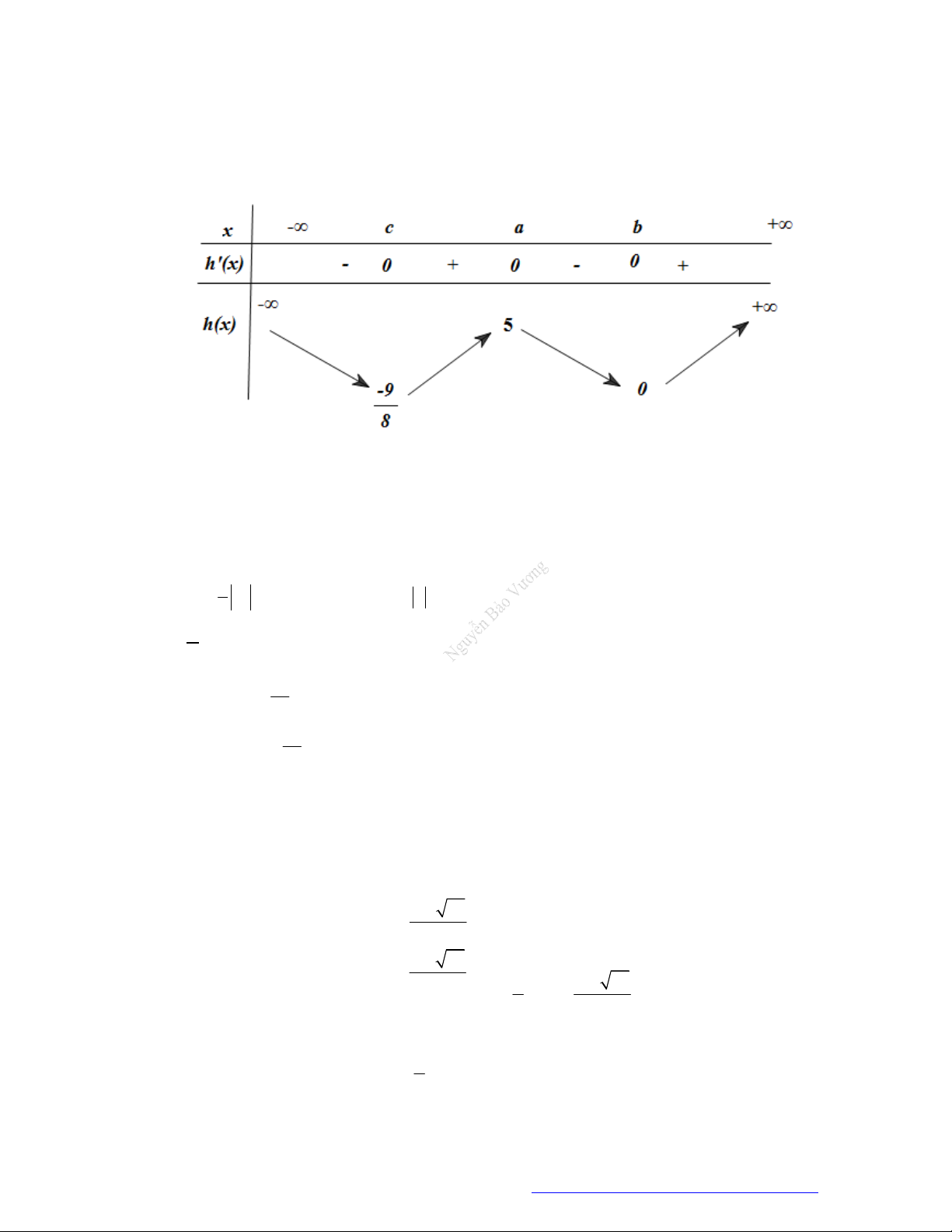
T
ÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 75
Xé
t hàm số
2
2
3h x f x f x
, c
ó
'
4 . '( ) 3 'h x f x f x f x
'
0 4 . '( ) 3 ' 0 ' 0 4 ( ) 3 0h x f x f x f x f x f x
(
) 3 / 4x a x b f x
( ) 3 / 4f x x c a
(t
heo BBT)
BBT của
(
)h x
Để hà
m số
2
(
) | 2 3 | | |g x f x f x m h x m
c
ó đúng 7 điểm cực trị thì phương tr
ình
h
x m
phải
có 4 nghiệm phân biệt, hay
0
5 5 0m m
Câu
14. (THPT Thanh Chương - Nghệ An - 2018) Có bao nhiêu giá trị nguyên của tham số
m
để hà
m
số
3
2
1
(
3 ) (3 7) 1
3
y x m x m x
c
ó
5
điểm
cực trị?
A.
3
. B.
5
. C.
2
. D.
4
.
Lời
giải
Ta có
3
2
3
2
3
3 7 1, 0
3
3 3 7 1, 0
3
x
m x m x khi x
y
x
m x m x khi x
2
2
2
3 3 7 , 0
2 3 3 7 , 0
x m x m khi x
y
x m x m khi x
.
Dễ thấy tại
0x
đạo hà
m không tồn tại
0x
l
à một điểm cực trị
Để hàm số có
5
điểm
cực trị thì phương trình
2
2
3 3 7 0 x m x m
c
ó 2 nghiệm dương
phân biệt
9 73
2
9 73
' 0
2
0
0
3
7
3
m
m
P
S
m
m
7
9 73
3 2
m
.
Do
m
nguy
ên nên
2
; 1;0 m
.
-------------------- HẾT --------------------
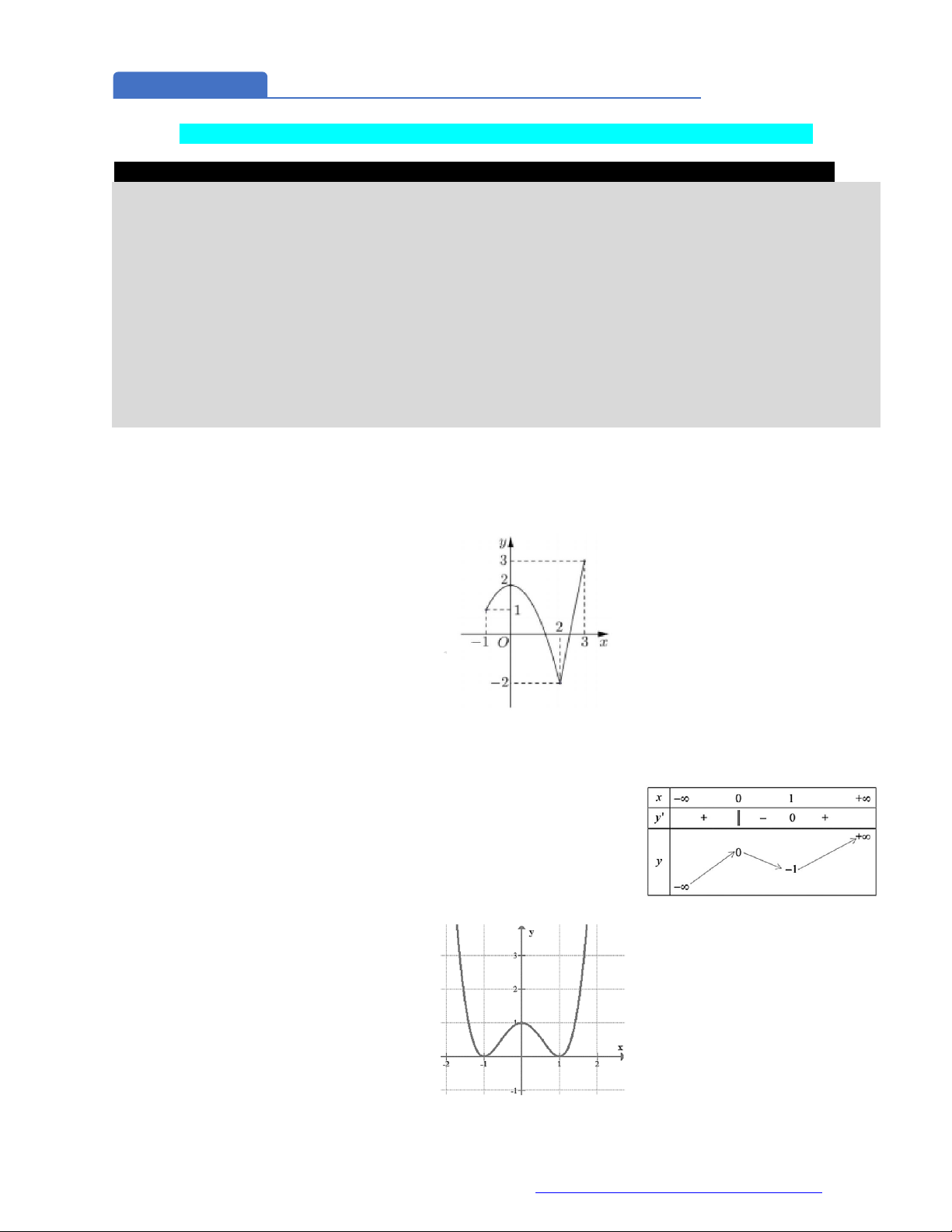
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH TRUNG BÌNH (MỨC 5-6 ĐIỂM)
Dạng 1. Xác định giá trị lớn nhất – giá trị nhỏ nhất của hàm số thông qua đồ thị, bảng biến thiên
Giá trị lớn nhất của hàm số
f x
trên đoạn
;a b
Hàm số
f x
liên tục trên đoạn
;a b
và
0, ;
i i
f x x a b
. Khi đó giá trị lớn nhất của hàm số
f x
là
max , ,
i
M f a f b f x
Giá trị nhỏ nhất của hàm số
f x
trên đoạn
;a b
Hàm số
f x
liên tục trên đoạn
;a b
và
0, ;
i i
f x x a b
. Khi đó giá trị nhỏ nhất của hàm số
f x
là
, ,
i
m Min f a f b f x
Hàm số
y f x
đồng biến trên đoạn
;a b
thì
; ;
;
a b a b
Max f x f b Min f x f a
Hàm số
y f x
nghịch biến trên đoạn
;a b
thì
; ;
;
a b a b
Max f x f a Min f x f b
Câu 1. (Đề Tham Khảo 2019) Cho hàm số
y f x
liên tục trên đoạn
1;3
và có đồ thị như hình vẽ
bên. Gọi
M
và
m
lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn
1;3
.
Giá trị của
M m
bằng
A.
1
B.
4
C.
5
D.
0
Câu 2. (Đề Minh Họa 2017) Cho hàm số
y f x
xác định, liên tục trên
và có bảng biến thiên:
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có giá trị cực tiểu bằng
1
.
B. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng
1
.
C. Hàm số đạt cực đại tại
x 0
và đạt cực tiểu tại
x 1
.
D. Hàm số có đúng một cực trị.
Câu 3. Cho hàm số
y f x
liên tục trên đoạn
1;1
và có đồ thị như hình vẽ.
Gọi
M
và
m
lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn
1;1
. Giá trị
của
M m
bằng
A.
0
. B.
1
. C.
2
. D.
3
.
GIÁ TRỊ LỚN NHẤT - GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ
Chuyên đề 5
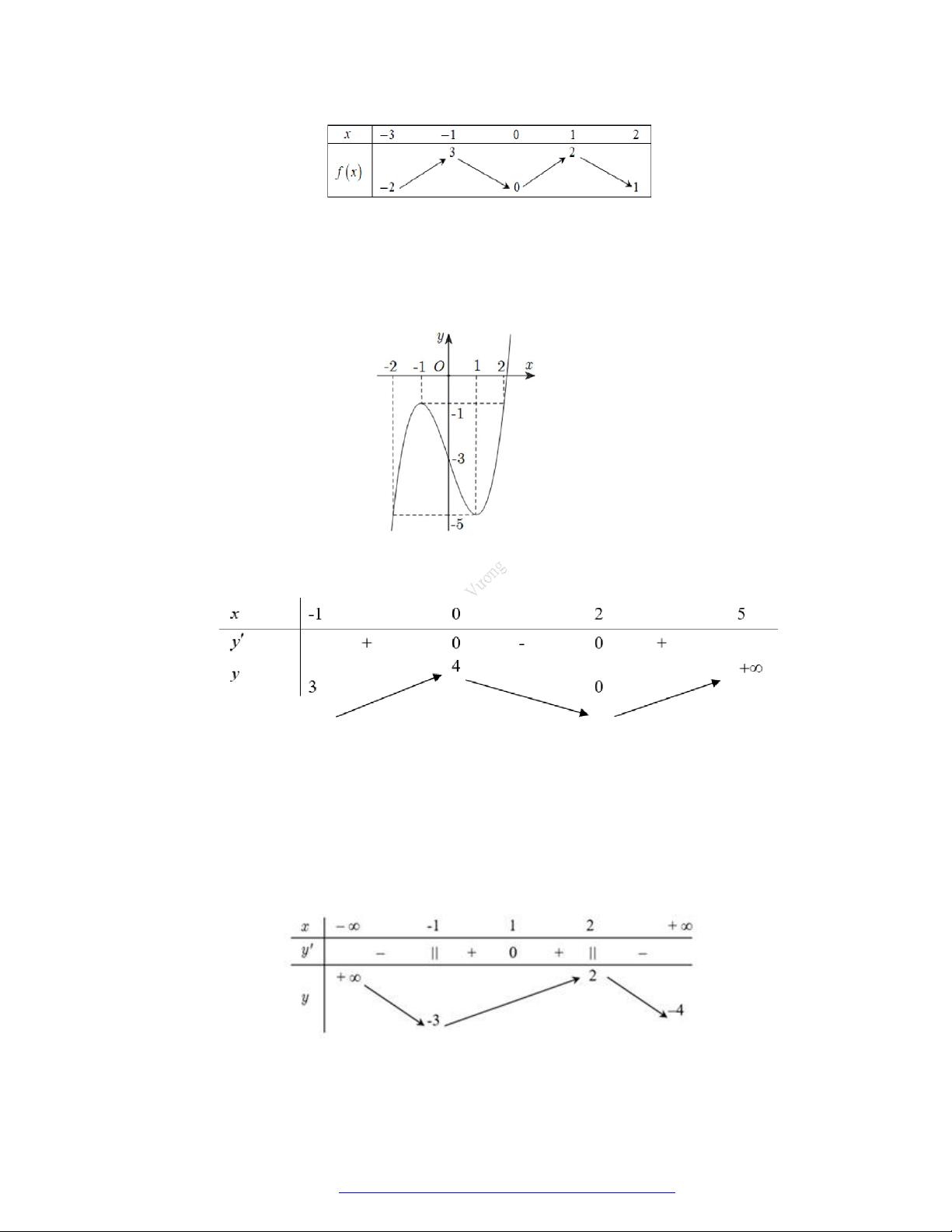
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 4. Cho hàm số
y f x
liên tục trên
3;2
và có bảng biến thiên như sau. Gọi
,M m
lần lượt là
giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y f x
trên đoạn
1; 2
. Tính
M m
.
A.
3
. B.
2
. C.
1
. D.
4
.
Câu 5. (Chuyên Lương Thế Vinh Đồng Nai 2019) Cho hàm số
y f x
xác định và liên tục trên
có đồ thị như hình vẽ bên. Tìm giá trị nhỏ nhất
m
và giá trị lớn nhất
M
của hàm số
y f x
trên đoạn
2;2
.
A.
5; 1m M
. B.
2; 2m M
. C.
1; 0m M
. D.
5; 0m M
.
Câu 6. (THPT Ba Đình 2019) Xét hàm số với có bảng biến thiên như sau:
Khẳng định nào sau đây là đúng
A. Hàm số đã cho không tồn taị GTLN trên đoạn
B. Hàm số đã cho đạt GTNN tại và trên đoạn
C. Hàm số đã cho đạt GTNN tại và đạt GTLN tại trên đoạn
D. Hàm số đã cho đạt GTNN tại trên đoạn
Câu 7. (Chuyên Lê Thánh Tông 2019) Cho hàm số
y f x
liên tục trên
, có bảng biến thiên như
hình sau:
Trong các mệnh đề sau, mệnh đề nào sai?
A. Hàm số có hai điểm cực trị.
B. Hàm số có giá trị lớn nhất bằng
2
và giá trị nhỏ nhất bằng
3
.
C. Đồ thị hàm số có đúng một đường tiệm cận.
D. Hàm số nghịch biến trên mỗi khoảng
; 1 , 2;
.
( )y f x
1;5
x
1;5
1
x
2
x
1;5
1
x
5
x
1;5
0
x
1;5
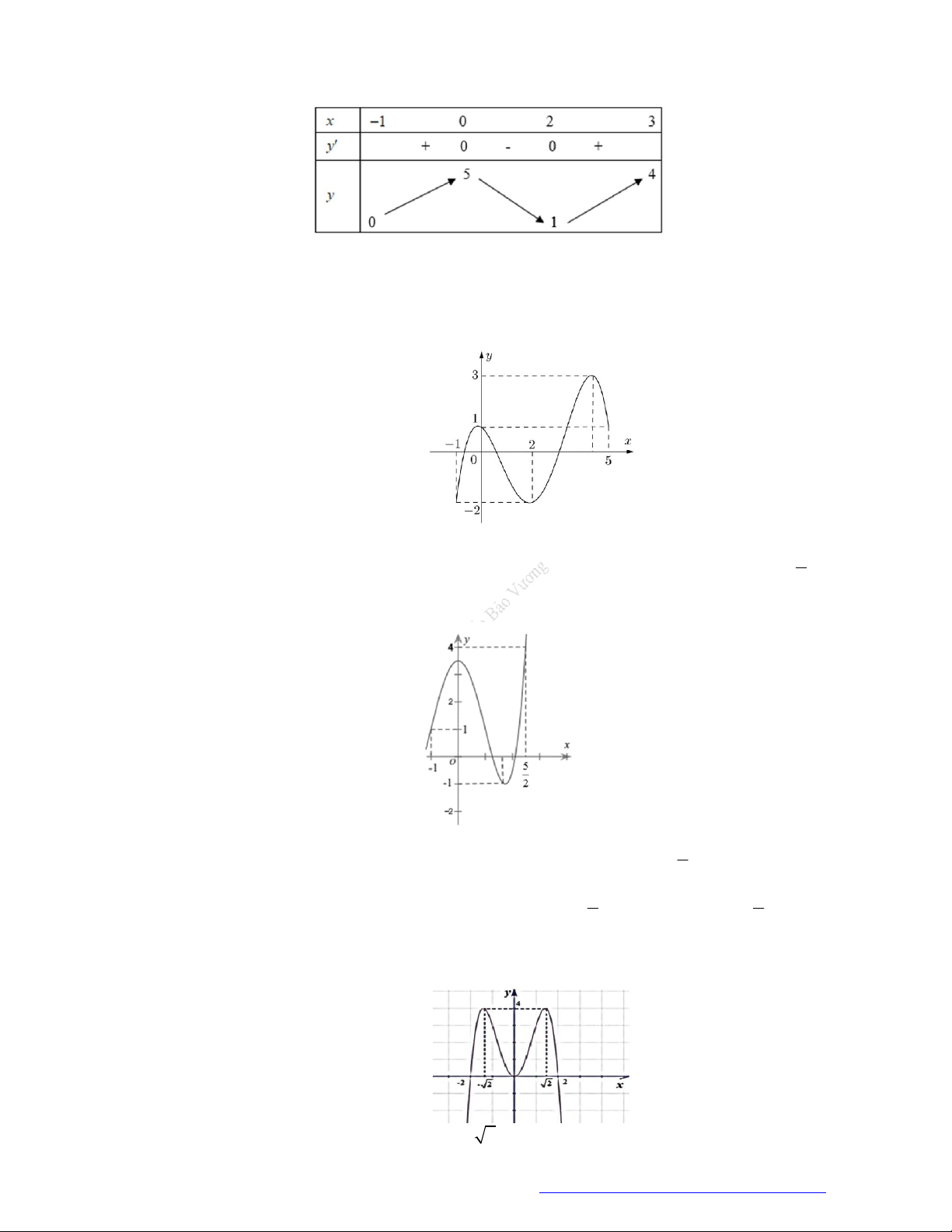
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Câu 8. (Chuyên Nguyễn Tất Thành Yên Bái 2019) Cho hàm số
( )y f x
liên tục và có bảng biến thiên
trên đoạn
1;3
như hình vẽ bên. Khẳng định nào sau đây đúng?
A.
1;3
max ( ) (0)f x f
. B.
1;3
max 3
f x f
. C.
1;3
max 2
f x f
. D.
1;3
max 1
f x f
.
Câu 9. (VTED 2019) Cho hàm số
f x
liên tục trên
1;5
và có đồ thị trên đoạn
1;5
như hình vẽ
bên dưới. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
f x
trên đoạn
1;5
bằng
A.
1
B.
4
C.
1
D.
2
Câu 10. (THPT Yên Mỹ Hưng Yên 2019) Cho hàm số
y f x
xác định, liên tục trên
5
1,
2
và có đồ
thị là đường cong như hình vẽ.
Giá trị lớn nhất
M
và giá trị nhỏ nhất
m
của hàm số
f x
trên
5
1,
2
là:
A.
4, 1M m
B.
4, 1M m
C.
7
, 1
2
M m
D.
7
, 1
2
M m
Câu 11. (THPT Nghĩa Hưng Nam Định 2019) Cho hàm số
y f x
có đồ thị như hình vẽ. Giá trị lớn
nhất của hàm số
f x
trên đoạn
0;2
là:
A.
0;2
2Max f x
. B.
0;2
2Max f x
. C.
0;2
4Max f x
. D.
0;2
0Max f x
.
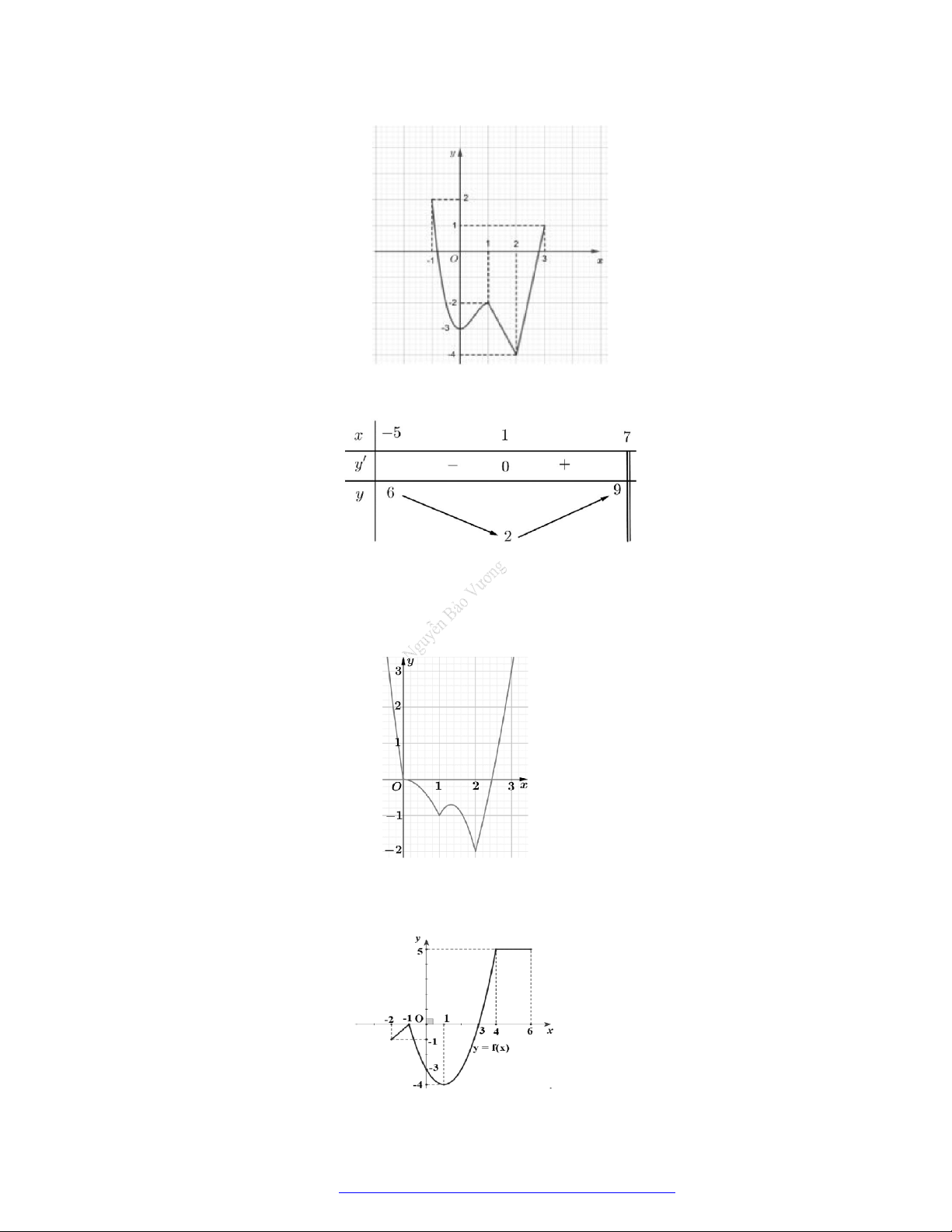
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 12. (Sở Bắc Giang 2019) Cho hàm số
( )y f x
liên tục trên đoạn
1;3
và có đồ thị như hình vẽ
bên. Gọi
,M m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn
1;3
.
Giá trị của
M m
là
A.
2
B.
6
C.
5
D.
2
Câu 13. (Sở Hà Nội 2019) Cho hàm số
y f x
có bảng biến thiên trên
5;7
như sau
Mệnh đề nào dưới đây đúng?
A.
5;7
Min 6f x
. B.
5;7
Min 2f x
. C.
-5;7
Max 9f x
. D.
5;7
Max 6f x
.
Câu 14. Cho hàm số
f x
liên tục trên đoạn
0;3
và có đồ thị như hình vẽ bên. Gọi
M
và
m
lần lượt là
giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên
0;3
. Giá trị của
M m
bằng?
A.
5
. B.
3
. C.
2
. D.
1
.
Câu 15. (Chuyên Lê Quý Đôn Điện Biên 2019) Cho hàm số
y f x
liên tục trên đoạn
2; 6
và có
đồ thị như hình vẽ bên dưới.
Gọi
M
và
m
lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn
2;6
. Giá trị
của
M m
bằng
A.
9
. B.
8
. C.
9
. D.
8
.
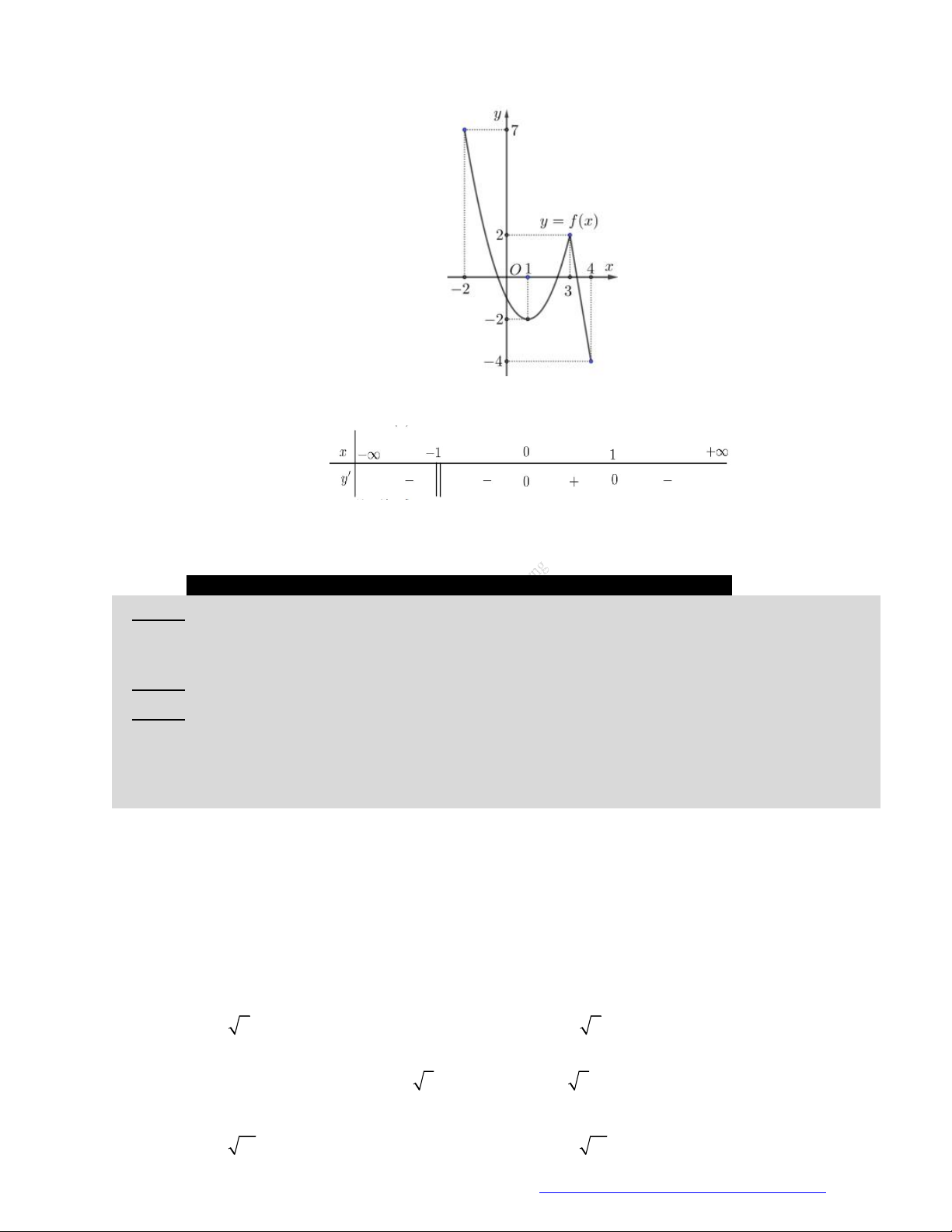
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Câu 16. (VTED 2019) Cho hàm số
y f x
liên tục và có đồ thị trên đoạn
2;4
như hình vẽ bên.
Tổng giá trị lớn nhất và nhỏ nhất của hàm số
y f x
trên đoạn
2;4
bằng
A.
5
B.
3
C.
0
D.
2
Câu 17. (THPT Ngô Sĩ Liên Bắc Giang 2019) Cho hàm số
y f x
có bảng xét dấu đạo hàm như sau:
Mệnh đề nào sau đây đúng
A.
1;1
max 0f x f
B.
0;
max 1f x f
C.
; 1
min 1f x f
D.
1;
min 0f x f
Dạng 2. Xác định giá trị lớn nhất – giá trị nhỏ nhất của hàm số trên đoạn
Bước 1: Hàm số đã cho
y f x xác định và liên tục trên đoạn
a b; .
Tìm các điểm
n
x x x
1 2
, ,...,
trên khoảng
a b; , tại đó
f x 0 hoặc
f x không xác định.
Bước 2: Tính
n
f a f x f x f x f b
1 2
, , ,..., , .
Bước 3: Khi đó:
n
a b
max f x max f x f x f x f a f b
1 2
,
, ,..., , , .
n
a b
min f x min f x f x f x f a f b
1 2
,
, ,..., , , .
Câu 1. (Đề Minh Họa 2020 Lần 1) Giá trị lớn nhất của hàm số
4 2
( ) 12 1f x x x
trên đoạn
1; 2
bằng:
A.
1
. B.
37
. C.
33
. D.
12
.
Câu 2. (Đề Tham Khảo 2020 Lần 2) Giá trị nhỏ nhất của hàm số
4 2
10 2f x x x
trên đoạn
1;2
bằng
A.
2
. B.
23
. C.
22
. D.
7
.
Câu 3. (Mã 101 - 2020 Lần 1) Giá trị nhỏ nhất của hàm số
3
24f x x x
trên đoạn
2;19
bằng
A.
32 2
. B.
40
. C.
32 2
. D.
45
.
Câu 4. (Mã 102 - 2020 Lần 1) Giá trị nhỏ nhất của hàm số
3
21f x x x
trên đoạn
2;19
bằng
A.
36
. B.
14 7
. C.
14 7
. D.
34
.
Câu 5. (Mã 103 - 2020 Lần 1) Giá trị nhỏ nhất của hàm số
3
( ) 30f x x x
trên đoạn
2;19
bằng
A. 20 10. B.
63.
C. 20 10. D.
52.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 6. (Mã 104 - 2020 Lần 1) Giá trị nhỏ nhất của hàm số
3
33f x x x
trên đoạn
2;19
bằng
A.
72
. B.
22 11
. C.
58
. D.
22 11
.
Câu 7. (Mã 101 – 2020 Lần 2) Giá trị nhỏ nhất của hàm số
4 2
10 4
f x x x
trên
0;9
bằng
A.
28
. B.
4
. C.
13
. D.
29
.
Câu 8. (Mã 102 - 2020 Lần 2) Giá trị nhỏ nhất của hàm số
4 2
12 4
f x x x
trên đoạn
0;9
bằng
A.
39
. B.
40
. C.
36
. D.
4
.
Câu 9. (Mã 103 - 2020 Lần 2) Giá trị nhỏ nhất của hàm số
4 2
10 2
f x x x
trên đoạn
0;9
bằng
A.
2
. B.
11
. C.
26
. D.
27
.
Câu 10. (Mã 104 - 2020 Lần 2) Giá trị nhỏ nhất của hàm số
4 2
12 1
f x x x
trên đoạn
0;9
bằng
A.
28
. B.
1
. C.
36
. D.
37
.
Câu 11. (Mã 102 - 2019) Giá trị nhỏ nhất của hàm số
3
3 2
f x x x
trên đoạn
3;3
bằng
A.
0
. B.
16
. C.
20
. D.
4
.
Câu 12. (Mã 110 2017) Tìm giá trị lớn nhất
M
của hàm số
4 2
2 3
y x x
trên đoạn
0; 3
.
A.
6
M
B.
1M
C.
9
M
D.
8 3
M
Câu 13. (Đề Minh Họa 2017) Tìm giá trị nhỏ nhất của hàm số
2
3
1
x
y
x
trên đoạn
2;4
.
A.
2;4
min 3
y B.
2;4
19
min
3
y
C.
2;4
min 6
y D.
2;4
min 2
y
Câu 14. (Mã 103 - 2019) Giá trị lớn nhất của hàm số
3
3f x x x
trên đoạn
[ 3;3]
bằng
A.
2
. B.
18
. C.
2
. D.
18
.
Câu 15. (Mã 104 2018) Giá trị lớn nhất của hàm số
4 2
13
y x x
trên đoạn
[ 1;2]
bằng
A.
85
B.
51
4
C.
13
D.
25
Câu 16. (Mã 104 2017) Tìm giá trị nhỏ nhất
m
của hàm số
2
2
y x
x
trên đoạn
1
;2
2
.
A.
5
m
B.
3
m
C.
17
4
m
D.
10
m
Câu 17. (Chuyên Bắc Ninh 2018) Tìm tập giá trị của hàm số
1 9
y x x
A.
1; 9
T
. B.
2 2; 4
T
. C.
1; 9
T
. D.
0; 2 2
T
.
Câu 18. (Mã 123 2017) Tìm giá trị nhỏ nhất
m
của hàm số
3 2
7 11 2
y x x x
trên đoạn
[0; 2]
.
A.
3m
B.
0m
C.
2m
D.
11m
Câu 19. (Mã 101 2018) Giá trị lớn nhất của hàm số
4 2
4 9
y x x
trên đoạn
2;3
bằng
A.
201
B.
2
C.
9
D.
54
Câu 20. (Đề Tham Khảo 2018) Giá trị lớn nhất của hàm số
4 2
4 5
f x x x
trêm đoạn
2;3
bằng
A.
122
B.
50
C.
5
D.
1
Câu 21. (Mã 105 2017) Tìm giá trị nhỏ nhất
m
của hàm số
4 2
13
y x x
trên đoạn
2;3
.
A.
13m
B.
51
4
m
C.
51
2
m
D.
49
4
m
Câu 22. (Mã 104 2019) Giá trị nhỏ nhất của hàm số
3
3 f x x x
trên đoạn
3;3
bằng
A.
18.
B.
2.
C.
2.
D.
18.
Câu 23. (Mã 103 2018) Giá trị nhỏ nhất của hàm số
3 2
3y x x
trên đoạn
4; 1
bằng
A.
16
B.
0
C.
4
D.
4

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Câu 24. (Mã 102 2018) Giá trị nhỏ nhất của hàm số
3 2
2 7y x x x
trên đoạn
0;4
bằng
A.
259
B.
68
C.
0
D.
4
Câu 25. (Mã 101 - 2019) Giá trị lớn nhất của hàm số
3
3 2
f x x x
trên đoạn
3;3
là
A.
4
. B.
16
. C.
20
. D.
0
.
Câu 26. (SGD Nam Định) Giá trị nhỏ nhất của hàm số
2
2
y x
x
trên đoạn
2;3
bằng
A.
15
2
. B.
5
. C.
29
3
. D.
3
.
Câu 27. (Sở Quảng Trị 2019) Tìm giá trị lớn nhất
M
của hàm số
3 1
3
x
y
x
trên đoạn
0;2
A.
1
3
M
. B.
1
3
M
. C.
5
M
. D.
5
M
Câu 28. (Sở Nam Định-2019) Giá trị lớn nhất của hàm số
2
4
y x
là
A. 2. B. 0. C. 4. D. 1.
Câu 29. (Chuyên Bắc Ninh 2018) Tìm giá trị nhỏ nhất của hàm số
2
sin 4sin 5y x x
.
A.
20
. B.
8
. C.
9
. D.
0
.
Câu 30. (THPT Hoa Lư A 2018) Gọi
m
,
M
lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số
1
1
2
f x x x
trên đoạn
0;3
. Tính tổng
2 3S m M
.
A.
7
2
S
. B.
3
2
S
. C.
3
. D.
4
S
.
Câu 31. (Chuyên ĐHSPHN - 2018) Tìm giá trị lớn nhất của hàm số
sin cosf x x x
2
trên
;
0
là
A.
9
8
. B.
5
4
. C.
2
. D.
1
.
Câu 32. (THPT Hà Huy Tập - 2018) Giá trị lớn nhất của hàm số
3
4
2cos os
3
y x c x
trên
0;
.
A.
0;
2
ax
3
m y
. B.
0;
10
ax
3
m y
. C.
0;
2 2
ax
3
m y
. D.
0;
ax 0
m y
.
Câu 33. Gọi
,M m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3sin 2
sin 1
x
y
x
trên đoạn
0;
2
. Khi đó giá trị của
2 2
M m
là
A.
31
2
. B.
11
2
. C.
41
4
. D.
61
4
.
Câu 34. (THPT Can Lộc - Hà Tĩnh - 2018) Cho hàm số
2
sin 1
sin sin 1
x
y
x x
. Gọi
M
là giá trị lớn nhất
và
m
là giá trị nhỏ nhất của hàm số đã cho. Chọn mệnh đề đúng.
A.
3
2
M m
. B.
3
2
M m
. C.
1
M m
. D.
2
3
M m
.
Dạng 3. Xác định giá trị lớn nhất – giá trị nhỏ nhất của hàm số trên khoảng (a;b)
Bước 1: Tính đạo hàm
f x( )
.
Bước 2: Tìm tất cả các nghiệm
i
x a b( ; )
của phương trình
f x( ) 0
và tất cả các điểm
i
a b( ; )
làm
cho
f x( )
không xác định.
Bước 3. Tính
x a
A f xlim ( )
,
x b
B f xlim ( )
,
i
f x( )
,
i
f ( )
.
Bước 4. So sánh các giá trị tính được và kết luận
a b
M f x
( ; )
max ( )
,
a b
m f x
( ; )
min ( )
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Nếu giá trị
lớn nhất (nhỏ nhất) là A hoặc B thì ta kết luận không có giá trị lớn nhất (nhỏ nhất).
Câu 1. (Đề Tham Khảo 2017) Tính giá trị nhỏ nhất của hàm số
2
4
3y
x
x
trê
n khoảng
0
;
.
A.
0
;
33
min
5
y
B.
3
0;
m
in 2 9
y
C
.
3
0
;
m
in 3 9
y
D
.
0;
m
in 7
y
Câu
2. Gọi
m
là giá trị nhỏ nhất
của hàm số
4
1
1
y x
x
t
rên khoảng
1
;
.
Tìm
m
?
A.
5
m
. B.
4
m
. C
.
2
m
. D
.
3
m
.
Câu
3. (THPT Minh Châu Hưng Yên 2019) Giá trị nhỏ nhất của hàm số
1
5y
x
x
trên khoảng
0
;
bằng b
ao nhiêu?
A.
0
B.
1
C.
3
D.
2
Câu
4. (Chuyên Lương Thế Vinh Đồng Nai 2019) Gọi
m
là gi
á trị nhở nhất của hàm số
4
y
x
x
trên
khoảng
0
;
. T
ìm
m
A.
4
m
. B.
2
m
. C
.
1
m
. D
.
3
m
.
Câu
5. (Chuyên Bắc Giang 2019) Giá trị nhỏ nhất của hàm số
1
(
)f x x
x
t
rên nửa khoảng
2
;
là
:
A.
2
B.
5
2
C
.
0
D
.
7
2
Câu
6. Gọi
m
l
à giá trị nhỏ nhất của hàm số
4
y
x
x
t
rên khoảng
0
;
.
Tìm
m
.
A.
3
m
. B.
4
m
. C
.
2
m
. D
.
1
m
.
Câu
7. Giá trị nhỏ nhất của hàm số
4
3
y
x
t
rên tập xác định của nó là
A.
2 3.
B.
2 3.
C
.
0
.
D
.
3.
Câu
8. Với giá trị nào của
x
thì hàm số
2
1
y
x
x
đạt
giá trị nhỏ nhất trên khoảng
0
;
?
A.
3
3
4
. B.
1
2
. C
.
1
. D
.
3
1
2
.
Câu
9. Giá trị nhỏ nhất của hàm số
2
2
1 2
y x
x
trên khoảng
0
;
A. không tồn tại. B.
3
. C
.
1 2
. D
.
0
.
Câu
10. Cho hàm số
2
1
2
x
f x
x
với
x
thuộc
3
;
1 1;
2
D
. Mệnh đề nà
o dưới đây đúng?
A.
m
ax 0;min 5
D
D
f
x f x
. B.
m
ax 0
D
f
x
; không tồn
tại
mi
n
D
f
x
.
C.
m
ax 0;min 1
D
D
f
x f x
. D
.
mi
n 0
D
f
x
;
không tồn tại
m
ax
D
f
x
.
Câu
11. (Cụm liên trường Hải Phòng 2019) Mệnh đề nào sau đây là đúng về hàm số
2
1
5
x
y
x
trên
tập xác
định của nó.
A. Hàm số không có giá trị lớn nhất và không có giá trị nhỏ nhất.
B. Hàm số không có giá trị lớn nhất và có giá trị nhỏ nhất.
C. Hàm số có giá trị lớn nhất và giá trị nhỏ nhất.
D. Hàm số có giá trị lớn nhất và không có giá trị nhỏ nhất.
-------------------- HẾT --------------------

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH KHÁ 7-8 ĐIỂM
Dạng. Định m để GTLN-GTNN của hàm số thỏa mãn điều kiện cho trước
Bước 1. Tìm nghiệm ( 1, 2,...)
i
x i của
0y
thuộc
;a b
Bước 2. Tính các giá trị
; ;
i
f x f a f b
theo tham số
Bước 3. So sánh các giá trị, suy ra giá trị lớn nhất, giá trị nhỏ nhất.
Bước 4. Biện luận m theo giả thuyết đề để kết luận
Lưu ý:
Hàm số
y f x
đồng biến trên đoạn
;a b
thì
; ;
;
a b a b
Max f x f b Min f x f a
Hàm số
y f x
nghịch biến trên đoạn
;a b
thì
; ;
;
a b a b
Max f x f a Min f x f b
Câu 1. (Mã 123 2017) Cho hàm số
1
x m
y
x
(
m
là tham số thực) thỏa mãn
[2 ;4]
min 3.y
Mệnh đề nào
dưới đây đúng?
A.
4m
B.
3 4m
C.
1m
D.
1 3m
Câu 2. (Mã 110 2017) Cho hàm số
1
x m
y
x
(
m
là tham số thực) thoả mãn
1;2
1;2
16
min max
3
y y
. Mệnh
đề nào dưới đây đúng?
A.
4m
B.
2 4m
C.
0m
D.
0 2m
Câu 3. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
1
x m
y
x
trên đoạn
1;2
bằng
8
(
m
là tham
số thực). Khẳng định nào sau đây là đúng?
A.
10m
.
B.
8 10m
.
C.
0 4m
.
D.
4 8m
.
Câu 4. Có bao nhiêu giá trị của tham số
m
để giá trị lớn nhất của hàm số
2
2x m
y
x m
trên đoạn
0;4
bằng
1.
A.
3
. B.
2
. C.
1
. D.
0
.
Câu 5. Cho hàm số
2
1x
y
x m
(m là tham số thực) thỏa mãn
3; 2
1
min
2
y
. Mệnh đề nào dưới đây đúng?
A.
3 4m
. B.
2 3m
. C.
4m
. D.
2m
.
Câu 6. Tìm giá trị dương của tham số
m
để giá trị nhỏ nhất của hàm số
2
1
2
m x
y
x
trên đoạn
1;3
bằng
1
.
A.
2m
. B. 3m . C.
4m
. D.
2m
.
Câu 7. Cho hàm số
2
8
x m
y
x
với
m
là tham số thực. Giả sử
0
m là giá trị dương của tham số
m
để
hàm số có giá trị nhỏ nhất trên đoạn
0;3
bằng 3. Giá trị
0
m thuộc khoảng nào trong các khoảng
cho dưới đây?
A.
2;5
. B.
1;4
. C.
6;9
. D.
20;25
.
Câu 8. (THPT Hai Bà Trưng - Huế 2019) Tìm giá trị của tham số thực
m
để giá trị nhỏ nhất của hàm
số
2
1
x m
y
x
trên đoạn
0;4
bằng
3
.
A.
3m
. B.
1m
. C.
7m
. D.
5m
Câu 9. (Thpt Vĩnh Lộc - Thanh Hóa 2019) Tìm các giá trị của tham số
m
để giá trị nhỏ nhất của hàm
số
2
1
x m m
y
x
trên đoạn
0;1
bằng
2
.
GIÁ TRỊ LỚN NHẤT - GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ
Chuyên đề 5

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
1
2
m
m
. B.
1
2
m
m
. C.
1
2
m
m
. D.
1
2
m
m
.
Câu 10. (THPT Lê Văn Thịnh Bắc Ninh 2019) Cho hàm số
1
x m
y
x
(
m
là tham số thực) thỏa mãn
0;1
min 3y
. Mệnh đề nào dưới đây đúng?
A.
1 3m
B.
6m
C.
1m
D.
3 6m
Câu 11. (Chuyên KHTN 2019) Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
1
x m
y
x
trên
1; 2
bằng
8
(
m
là tham số thực). Khẳng định nào sau đây đúng?
A.
10
m
. B.
8 10
m
. C.
0 4
m
. D.
4 8
m
.
Câu 12. (Chuyên Bắc Ninh 2019) Gọi
,A B
lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của hàm số
2
1
x m m
y
x
trên đoạn
2;3
. Tìm tất cả các giá trị thực của tham số
m
để
13
2
A B
.
A.
1; 2
m m
. B.
2
m
. C.
2
m
. D.
1; 2
m m
.
Câu 13. (Sở Hưng Yên) Cho hàm số
2
8
x m
f x
x
với
m
là tham số thực. Giả sử
0
m
là giá trị dương
của tham số
m
để hàm số có giá trị nhỏ nhất trên đoạn
0;3
bằng
3
. Giá trị
0
m
thuộc khoảng
nào trong các khoảng cho dưới đây?
A.
20;25
. B.
5;6
. C.
6;9
. D.
2;5
.
Câu 14. (Chuyên - Vĩnh Phúc 2019) Tìm tất cả các giá trị của tham số
m
để giá trị nhỏ nhất của hàm số
3 2
3
y x x m
trên đoạn
1;1
bằng
0
.
A.
2.
m
B.
6.
m
C.
0.
m
D.
4.
m
Câu 15. (Sở Quảng Trị 2019) Tìm tất cả các giá trị thực của tham số m để hàm số
3 2
3
y x x m
có giá
trị nhỏ nhất trên đoạn
1;1
bằng
2
A.
2
m
. B.
2 2
m
. C.
4 2
m
. D.
2 2
4 2
m
m
.
Câu 16. (Cụm Liên Trường Hải Phòng 2019) Có một giá trị
0
m
của tham số
m
để hàm số
3 2
1 1
y x m x m
đạt giá trị nhỏ nhất bằng
5
trên đoạn
0;1
. Mệnh đề nào sau đây là
đúng?
A.
2
0 0
2018 0
m m
. B.
0
2 1 0
m
. C.
2
0 0
6 0
m m
. D.
0
2 1 0
m
.
Câu 17. (THCS - THPT Nguyễn Khuyến 2019) Nếu hàm số
2
1
y x m x
có giá trị lớn nhất bằng
2 2
thì giá trị của
m
là
A.
2
2
. B.
2
. C.
2
. D.
2
2
.
Câu 18. (THPT Ngô Gia Tự Vĩnh Phúc 2019) Cho hàm số
3 2
2 3
y x x m
. Trên
1;1
hàm số có giá
trị nhỏ nhất là
1
. Tính
m
?
A.
6
m
. B.
3
m
. C.
4
m
. D.
5
m
.
Câu 19. Biết
S
là tập giá trị của
m
để tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
4 2 3 2
2
y x m x x m
trên đoạn
0;1
bằng
16
. Tính tích các phần tử của
S
.
A.
2
. B.
2
. C.
15
. D.
17
.
Câu 20. (THPT An Lão Hải Phòng 2019) Tìm tất cả giá trị thực của tham số
m
để hàm số
2
1x mx
y
x m
liên tục và đạt giá trị nhỏ nhất trên đoạn
0;2
tại một điểm
0
0; 2
x
.
A.
0 1
m
B.
1
m
C.
2
m
D.
1 1
m

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Câu 21. (THPT Bạch Đằng Quảng Ninh 2019) Cho hàm số
1 sin
cos 2
m x
y
x
. Có bao nhiêu giá trị nguyên
của tham số
m
thuộc đoạn
0;10
để giá trị nhỏ nhất của hàm số nhỏ hơn
2
?
A.
1
. B.
9
. C.
3
. D.
6
.
Câu 22. (HSG Bắc Ninh 2019) Cho hàm số
3
, 0y ax cx d a có
;0
min 2
x
f x f
. Giá trị lớn
nhất của hàm số
y f x
trên đoạn
1;3
bằng
A.
11d a
. B.
16d a
. C.
2d a
. D.
8d a
.
Câu 23. (THPT Nghĩa Hưng Nam Định 2019) Tìm tất cả các giá trị của tham số m để hàm số
2
1
x m
y
x x
có giá trị lớn nhất trên
nhỏ hơn hoặc bằng 1.
A.
1m
. B.
1m
. C.
1m
. D.
1m
.
Câu 24. (Chuyên Nguyễn Trãi Hải Dương 2019) Giá trị lớn nhất của hàm số
3 2
1
x x m
y
x
trên
0;2
bằng
5
. Tham số
m
nhận giá trị là
A.
5
. B.
1
. C.
3
. D.
8
.
Câu 25. Cho hàm số
2
3
3y x x m . Tổng tất cả các giá trị của tham số
m
sao cho giá trị nhỏ nhất của
hàm số trên đoạn
1;1
bằng
1
là
A.
1
. B.
4
. C.
0
. D.
4
.
Câu 26. (Chuyên Vĩnh Phúc 2018) Tìm tất cả các giá trị của
0m
để giá trị nhỏ nhất của hàm số
3
3 1y x x trên đoạn
1; 2m m
luôn bé hơn
3
.
A.
0;2m
. B.
0;1m
. C.
1;m
. D.
0;m
.
Câu 27. (Chuyên Đh Vinh 2018) Biết rằng giá trị nhỏ nhất của hàm số
36
1
y mx
x
trên
0;3
bằng
20
. Mệnh đề nào sau đây đúng?
A.
0 2m
. B.
4 8m
. C.
2 4m
. D.
8m
.
Câu 28. (Chuyên Thái Bình - 2020) Cho hàm số
3 2 2
3 3 1 2020y x mx m x
. Có tất cả bao nhiêu
giá trị nguyên của
m
sao cho hàm số có giá trị nhỏ nhất trên khoảng
0;
?
A.
2
. B.
1
. C. Vô số. D.
3
.
Câu 29. (Sở Bình Phước - 2020) Cho hàm số
1f x m x (
m
là tham số thực khác 0). Gọi
1 2
,m m là
hai giá trị của
m
thoả mãn
2
2;5
2;5
min ax 10f x m f x m
. Giá trị của
1 2
m m bằng
A. 3. B. 5. C. 10. D. 2.
Câu 30. (Bỉm Sơn - Thanh Hóa - 2020) Cho hàm số có bao nhiêu giá trị nguyên của tham
số thuộc đoạn
để giá trị nhỏ nhất của nhỏ hơn .
A. . B. . C. . D. .
Câu 31. (Lê Lai - Thanh Hóa - 2020) Gọi là tập hợp tất cả các giá trị thực của tham số sao cho giá
trị nhỏ nhất của hàm số trên đoạn bằng 2. Tổng tất cả các phần
tử của bằng
A. . B. . C. . D. .
sin 1
cos 2
m x
y
x
m
5;5
y
1
4
2
6
8
S
m
2
3
34
3 2 1
f x
x x m
0;3
S
8
8
6
1

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu
32. (THPT Nguyễn Viết Xuân - 2020) Cho hàm số
2
3
3
1
y
x x m
.
Tổng tất cả các giá trị của
tham số
m
sao c
ho giá trị nhỏ nhất của hàm số trên đoạn
1
;1
bằ
ng
1
là
A.
2
. B.
4
. C
.
4
. D
.
0
.
Câu
33. (Chuyên Hạ Long - Quảng Ninh - 202
0) Cho
hàm số
2
2
2
2 4 4 1
y
f x m x x x m
.
Tính tổng tất cả các giá trị của
m
để hà
m số
y f x
c
ó giá trị nhỏ nhất bằng
4
.
A.
7
2
. B.
5
2
. C
.
1
2
. D
.
1
2
.
Câu
34. (Chuyên Nguyễn Trãi - Hải Dương - Lần 2 - 2020) Cho hàm số
2
1
x
m
f
x
x
với
2
m
.
Mệnh đề nào dưới đây sai?
A.
1
;3
2 6
max max ;
2 4
m m
f
x
. B.
1;3
6
max
4
m
f
x
khi
2
m
.
C.
1;3
2
6
min min ;
2 4
m
m
f x
. D
.
1
;3
2
m
in
2
m
f
x
khi
2
m
.
Câu
35. (Chuyên Sư Phạm Hà Nội - 2020) Có bao nhiêu số nguyên
m
t
huộc đoạn
2
0 ; 20
để giá
trị
lớn nhất của hàm số
6
x
m
y
x
m
trên
đoạn
1
; 3
là số dương?
A. 9. B. 8. C
. 11. D. 10.
-------------------- HẾT --------------------

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH GIỎI – MỨC ĐỘ 9-10 ĐIỂM
Dạng 1. Định m để GTLN-GTNN của hàm số chứa dấu giá trị tuyệt đối thỏa mãn điều kiện cho trước
Dạng 1: Tìm
m
để
;
max 0 .y f x m a a
Phương pháp:
Cách 1:Trước tiên tìm
;
;
max ; min .f x K f x k K k
Kiểm tra
max , .
2 2 2
m K m k m K m k K k
m K m k
TH1: .
2
K k
a
Để
;
max ;
m k a m a k
y a m a k a K
m K a m a K
.
TH2:
2
K k
a
m
.
Cách 2: Xét trường hợp
TH1:
m K a
Max m K
m K m k
TH2:
m k a
Max m k
m k m K
Dạng 2: Tìm
m
để
;
min 0 .y f x m a a
Phương pháp:
Trước tiên tìm
;
;
max ; min .f x K f x k K k
Để
;
min .
0 0
m k a m K a m a k m a K
y a
m k m K m k m K
Vậy
1 2
.m S S
Dạng 3: Tìm
m
để
;
max y f x m
không vượt quá giá trị
M
cho trước.
Phương pháp: Trước tiên tìm
;
;
max ; min .f x K f x k K k
Để
;
max .
m k M
y M M k m M K
m K M
Dạng 4: Tìm
m
để
;
min y f x m
không vượt quá giá trị
a
cho trước.
Phương pháp: Trước tiên tìm
;
;
max ; min .f x K f x k K k
Để
;
min 0 .
0 0
m k a m K a m a k m a K
y a m K m k K m k
m k m K m k m K
Dang 5: Tìm
m
để
;
max
a b
y f x m
đạt min.
GIÁ TRỊ LỚN NHẤT - GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ
Chuyên đề 5

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Phương pháp:
Trước tiên tìm
;
;
max ; min .
a b
a b
f x K f x k K k
Đề hỏi tìm
.
2
K k
m m
Đề hỏi tìm min của
;
max
a b
y
giá trị này là
.
2
K k
Dạng 6: Tìm
m
để
;
min
a b
y f x m
đạt min.
Phương pháp: Trước tiên tìm
;
;
max ; min .
a b
a b
f x K f x k K k
Đề hỏi tìm
0
m m K m k K m k
. Đề hỏi tìm min của
;
min
a b
y
giá trị này là
0.
Dạng 7: Cho hàm số
y f x m
.Tìm
m
để
;
;
max .min 0
a b
a b
y h y h
hoặc
max
Min
Phương pháp: Trước tiên tìm
;
;
max ; min .
a b
a b
f x K f x k K k
TH1:
1
cung dau
.
K m k m
K m k m
K m h k m m S
TH2:
2
cung dau
.
k m K m
K m k m
k m h K m m S
Vậy
1 2
.m S S
Dạng 8: Cho hàm số
y f x m
.
Phương pháp: Trước tiên tìm
;
;
max ; min .
a b
a b
f x K f x k K k
BT1: Tìm
m
để
;
;
min max
a b
a b
y y m K m k
.
BT2: Tìm
m
để
;
;
min *max *
a b
a b
y y m K m k
.
Câu 1. (Đề Tham Khảo 2018) Gọi S là tập hợp tất cả các giá trị của tham số thực m sao cho giá trị lớn
nhất của hàm số
3
3
y x x m
trên đoạn
0;2
bằng 3. Số phần tử của S là
A. 0 B. 6 C. 1 D. 2
Câu 2. (Đề Minh Họa 2020 Lần 1) Gọi
S
là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị
lớn nhất của hàm số
3
3
f x x x m
trên đoạn
0;3
bằng 16. Tổng tất cả các phần tử của
S
là:
A.
16
. B.
16
. C.
12
.
D.
2
.
Câu 3. (Đề Tham Khảo 2020 Lần 2) Cho hàm số
1
x m
f x
x
(
m
là tham số thực). Gọi
S
là tập hợp
tất cả các giá trị của
m
sao cho
0;1
0;1
max min 2
f x f x
. Số phần tử của
S
là
A.
6
. B.
2
. C.
1
. D.
4
.
Câu 4. (THPT Đông Sơn 1 - Thanh Hóa 2019) Tìm
m
để giá trị lớn nhất của hàm số
3
3 2 1
y x x m
trên đoạn
0;2
là nhỏ nhất. Giá trị của
m
thuộc khoảng nào?
A.
3
; 1
2
. B.
2
;2
3
. C.
1;0
. D.
0;1
.
Câu 5. (Sở Vĩnh Phúc 2019) Tính tổng tất cả các giá trị của tham số
m
sao cho giá trị lớn nhất của hàm
số
2
2
y x x m
trên đoạn
1;2
bằng
5
.
A.
1
. B.
2
. C.
2
. D.
1
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Câu 6. (THPT Nguyễn Huệ 2018) Cho hàm số
2
2 4
y x x a
(
a
là tham số ). Tìm
a
để giá trị
lớn nhất của hàm số trên đoạn
2;1
đạt giá trị nhỏ nhất
A.
1
a
. B.
3
a
. C.
2
a
. D.
5
a
.
Câu 7. (Chuyên Vĩnh Phúc 2019) Gọi
S
là tập hợp tất cả các giá trị thực của tham số
m
sao cho giá trị
lớn nhất của hàm số
2
1
x mx m
y
x
trên
1;2
bằng
2
. Số phần tử của tập
S
A.
3
. B.
1
. C.
4
. D.
2
.
Câu 8. (HSG Bắc Ninh 2019) Xét hàm số
2
f x x ax b
, với
a
,
b
là tham số. Gọi
M
là giá trị
lớn nhất của hàm số trên
1;3
. Khi
M
nhận giá trị nhỏ nhất có thể được, tính
2a b
.
A.
2
. B.
4
. C.
4
. D.
3
.
Câu 9. Cho hàm số
3 2 2
1 27
y x x m x . Giá trị lớn nhất của hàm số trên đoạn
3; 1
có giá trị
nhỏ nhất bằng
A.
26
. B.
18
. C.
28
. D.
16
.
Câu 10. (Sở Quảng Nam - 2018) Có bao nhiêu giá trị thực của tham số
m
để giá trị lớn nhất của hàm số
2
2 4
y x x m
trên đoạn
2;1
bằng
4
?
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 11. (Chuyên Nguyễn Thị Minh Khai - Sóc Trăng - 2018) Gọi
S
là tập hợp tất cả các giá trị của
tham số
m
sao cho giá trị lớn nhất của hàm số
3 2
3 9
y x x x m
trên đoạn
2;4
bằng
16
.
Số phần tử của
S
là
A.
0
. B.
2
. C.
4
. D.
1
.
Câu 12. (Chuyên Hạ Long 2018) Gọi
S
là tập tất cả các giá trị nguyên của tham số
m
sao cho giá trị lớn
nhất của hàm số
4 2
1 19
30 20
4 2
y x x x m
trên đoạn
0;2
không vượt quá
20
. Tổng các
phần tử của
S
bằng
A.
210
. B.
195
. C.
105
. D.
300
.
Câu 13. Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số
2
sin 2sin
y x x m
bằng
1
. Số phần tử của S là
A. 0 B. 1 B. 4 D. 3
Câu 14. (Chuyên Hưng Yên - 2020) Cho hàm số
4
1
x ax a
y
x
, với
a
là tham số thực. Gọi
,M m
lần
lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn
1;2
. Có bao nhiêu giá trị nguyên của
tham số
a
để
2M m
?
A.
10
. B.
14
. C.
5
. D.
20
.
Câu 15. (Chuyên Lương Văn Chánh - Phú Yên - 2020) Gọi
S
là tập hợp tất cả các giá trị nguyên của
tham số thực
m
sao cho giá trị lớn nhất của hàm số
4 2
1
14 48 30
4
y x x x m
trên đoạn
0;2
không vượt quá
30
. Tổng giá trị các phần tử của tập hợp
S
bằng bao nhiêu?
A.
120
. B.
210
. C.
108
. D.
136
.
Câu 16. (Chuyên Lương Văn Tỵ - Ninh Bình - 2020) Cho hàm số
4 3 2
3 4 24 48
x x x x
f x e e e e m
. Gọi
A
,
B
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
của hàm số đã cho trên
0;ln 2
.Gọi S là tập hợp tất cả các giá trị nguyên của tham số
m
thuộc
23;10
thỏa mãn
3A B
. Tổng các phần tử của tập S bằng
A.
33
. B.
0
. C.
111
. D.
74
.
Câu 17. (Chuyên Bến Tre - 2020) Cho hàm số
4 3 2
2
y x x x a
. Có bao nhiêu số thực
a
để
1;2 1;2
min max 10
y y
?
A. 3. B. 5. C. 2. D. 1.
Câu 18. (Chuyên Hùng Vương - Gia Lai - 2020) Cho hàm số
3 2
3
f x x x m
. Có bao nhiêu số
nguyên
m
để giá trị nhỏ nhất của hàm số
f x
trên đoạn
1;3
không lớn hơn 2020?
A.
4045
. B.
4046
. C.
4044
. D.
4042
.
Câu 19. (Chuyên Lê Hồng Phong - Nam Định - 2020) Xét hàm số
2 4
2 4
mx x
f x
x
, với
m
là
tham số thực. Có bao nhiêu số nguyên
m
thỏa mãn điều kiện
1;1
0 min 1
f x
?
A.
4
. B.
8
. C.
2
. D.
1
.
Câu 20. (Chuyên Sơn La - 2020) Gọi
S
là tập hợp những giá trị của tham số
m
để giá trị lớn nhất của
hàm số
3
( ) 12
f x x x m
trên đoạn
[1; 3]
bằng
12
.Tổng tất cả các phần tử của tập
S
bằng
A.
25.
B.
4.
C.
15.
D.
21.
Câu 21. (Chuyên Thái Nguyên - 2020) Gọi
0
S
là tập tất cả các giá trị nguyên của tham số thực
m
sao
cho giá trị lớn nhất của hàm số
4 2
1
14 48
4
y x x x m
trên đoạn
2; 4
không vượt quá
30
. Số
phần tử của
S
là
A.
50
. B.
49
. C.
66
. D.
73
.
Câu 22. (Đại Học Hà Tĩnh - 2020) Có bao nhiêu giá trị của tham số
m
để giá trị nhỏ nhất của ham số
2
e 4e
x x
f x m
trên đoạn
0;ln 4
bằng 6?
A.
3
. B.
4
. C.
2
. D.
1
.
Câu 23. (Đặng Thúc Hứa - Nghệ An - 2020) Gọi
S
là tập tất cả các giá trị nguyên của tham số
m
sao
cho giá trị lớn nhất của hàm số
3
1
9 10
3
y x x m
trên đoạn
0;3
không vượt quá
12
. Tổng
giá trị các phần tử của
S
bằng bao nhiêu?
A.
7
. B.
0
. C.
3
. D.
12
.
Câu 24. (Đô Lương 4 - Nghệ An - 2020) Gọi
S
là tập tất cả các giá trị nguyên của tham số thực
m
sao
cho giá trị lớn nhất của hàm số
4 2
1
14 48 30
4
y x x x m
trên đoạn
0;2
không vượt quá
30
. Tổng tất cả các giá trị của
S
là
A.
180
. B.
136
. C.
120
.
D.
210
.
Câu 25. (Liên trường Nghệ An - 2020) Biết giá trị lớn nhất của hàm số
3
2 15 5 9y f x x x m x
trên
0;3
bằng
60
. Tính tổng tất cả các giá trị của tham số
thực
m
.
A.
48
. B.
5
. C.
6
. D.
62
.
Câu 26. (Lý Nhân Tông - Bắc Ninh - 2020) Gọi S là tập hợp tất cả các giá trị của tham số thực
m
sao
cho giá trị lớn nhất của hàm số
3
3
y x x m
trên đoạn
0;2
bằng
3
. Số phần tử của S là
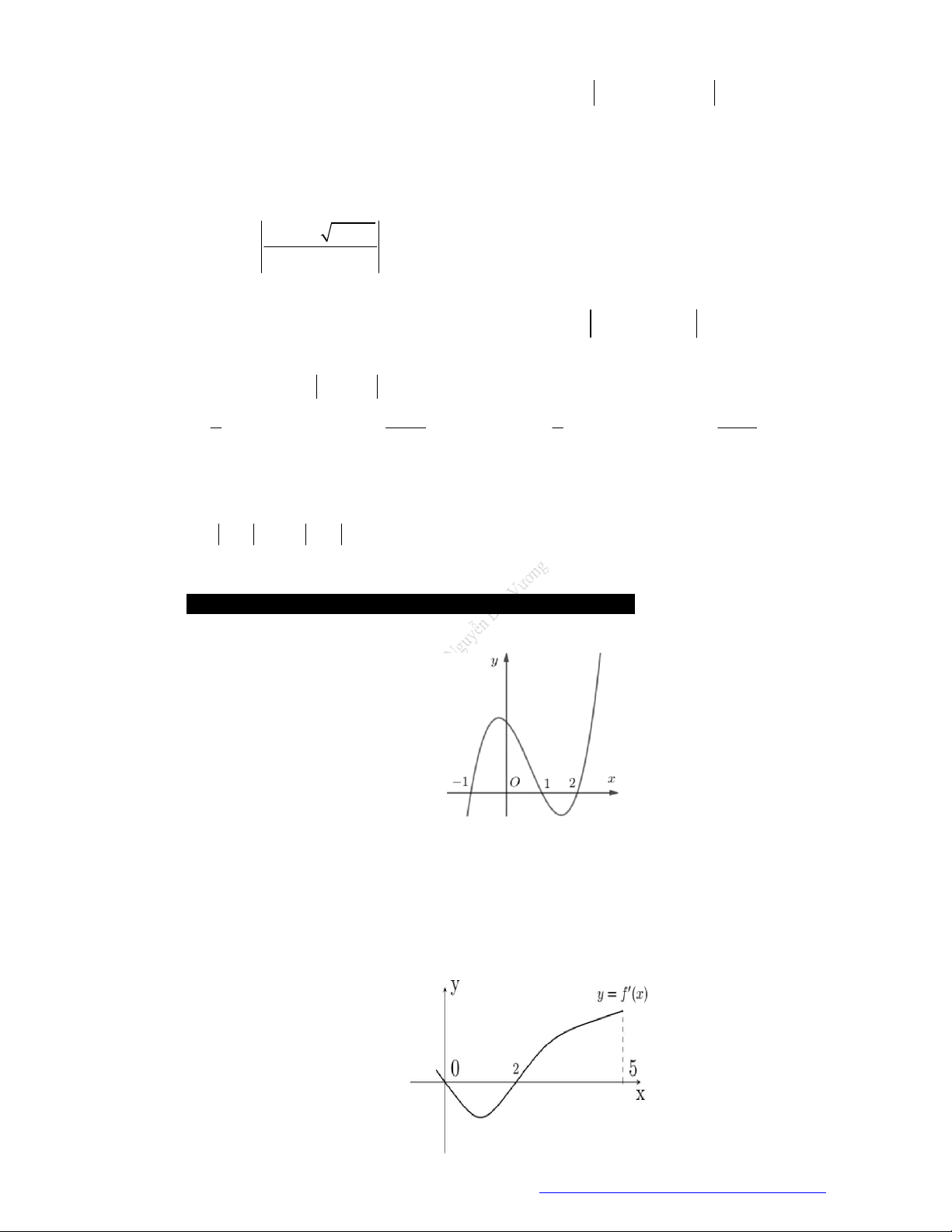
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
A.
2.
B.
6.
C.
1.
D.
0.
Câu 27. (Nguyễn Huệ - Phú Yên - 2020) Cho hàm số
4 3 2
2 f x x x x m
(
m
là tham số thực).
Gọi
S
là tập hợp tất cả các giá trị của
m
sao cho
1;2
1;2
min max 10
f x f x
. Số phần tử của
S
là?
A.
2
. B.
3
. C.
5
. D.
1
.
Câu 28. (Hải Hậu - Nam Định - 2020) Có tất cả bao nhiêu giá trị nguyên dương của tham số
m
để hàm
số
2 2 4 8
( )
2
mx x
f x
x
có giá trị nhỏ nhất trên đoạn
1;1
là
a
thỏa mãn
0 1.a
A.
3.
B.
4.
C.
5.
D.
2.
Câu 29. (Lương Thế Vinh - Hà Nội - 2020) Cho hàm số
4 2
2 3y x x m
với
m
là tham số. Biết
rằng có đúng hai giá trị
1 2
,m m
của
m
để giá trị nhỏ nhất của hàm số đã cho trên
1;2
bằng
2021. Tính giá trị
1 2
m m
.
A.
1
3
. B.
4052
3
. C.
8
3
. D.
4051
3
.
Câu 30. (Thanh Chương 1 - Nghệ An - 2020) Cho hàm số
3 2
3 1f x x x m
(
m
là tham số thực).
Gọi
S
là tập hợp tất cả các giá trị nguyên của
m
thuộc đoạn
2020;2020
sao cho
1;4
1;4
max 3minf x f x
. Số phần tử của
S
là
A.
4003
. B.
4002
. C.
4004
. D.
4001
.
Dạng 2. Giá trị lớn nhất – giá trị nhỏ nhất hàm ẩn, hàm hợp
Câu 1. Cho hàm số
y f x
xác định và liên tục trên
, đồ thị của hàm số
y f x
như hình vẽ.
Giá trị lớn nhất của hàm số
y f x
trên đoạn
1;2
là
A.
1f
. B.
1f
. C.
2f
. D.
0f
.
Câu 2. Cho hàm số
y f x
có đạo hàm là hàm
f x
. Đồ thị của hàm số
y f x
được cho như
hình vẽ. Biết rằng
0 3 2 5f f f f
. Giá trị nhỏ nhất, giá trị lớn nhất của
y f x
trên đoạn
0;5
lần lượt là:
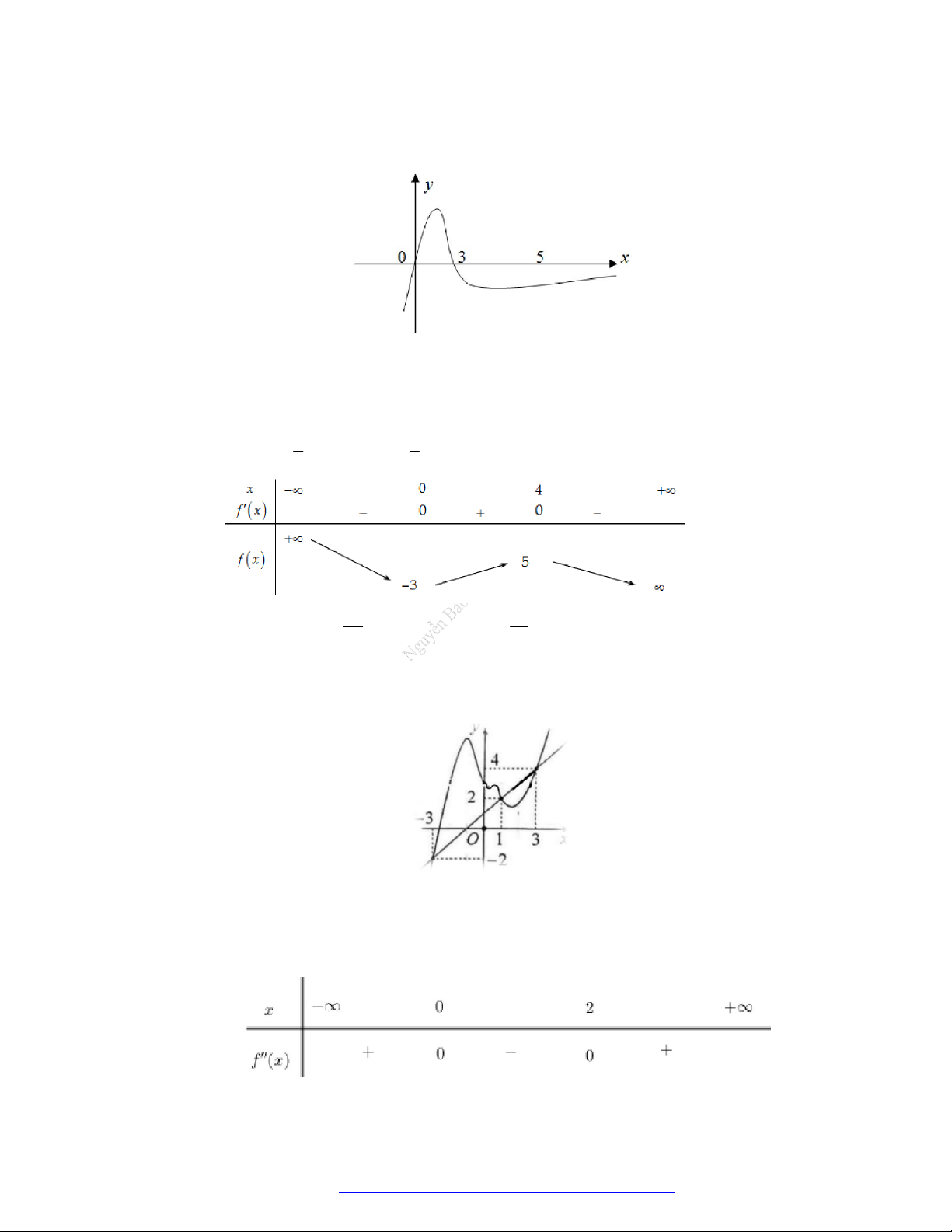
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
2f
;
5f
. B.
0f
;
5f
. C.
2f
;
0f
. D.
1f
;
5f
.
Câu 3. Cho hàm số
f x
có đạo hàm là
f x
. Đồ thị của hàm số
y f x
được cho như hình vẽ bên.
Biết rằng
0 1 2 3 5 4f f f f f
. Tìm giá trị nhỏ nhất
m
và giá trị lớn nhất
M
của
f x
trên đoạn
0;5
.
A.
5 , 3m f M f
B.
5 , 1m f M f
C.
0 , 3m f M f
D.
1 , 3m f M f
Câu 4. Cho hàm số
y f x
có bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất của hàm số
2 3 2
1 1
4 3 8
3 3
g x f x x x x x
trên đoạn
1;3
.
A. 15. B.
25
3
. C.
19
3
. D. 12.
Câu 5. Cho hàm số
y f x
liên tục trên
.
Đồ thị của hàm số
y f x
như hình bên. Đặt
2
2 1 .g x f x x
Mệnh đề dưới đây đúng.
A.
3;3
max 3 .g x g
B.
3;3
min 1 .g x g
C.
3;3
max 0 .g x g
D.
3;3
max 1 .g x g
Câu 6. Cho hàm số có đạo hàm cấp hai trên . Biết , và bảng xét
dấu của như sau:
Hàm số đạt giá trị nhỏ nhất tại điểm thuộc khoảng nào sau đây?
A.
; 2017
B.
2017;
C.
0;2
D.
2017;0
y f x
0 3
f
2 2018
f
f x
2017 2018y f x x
0
x
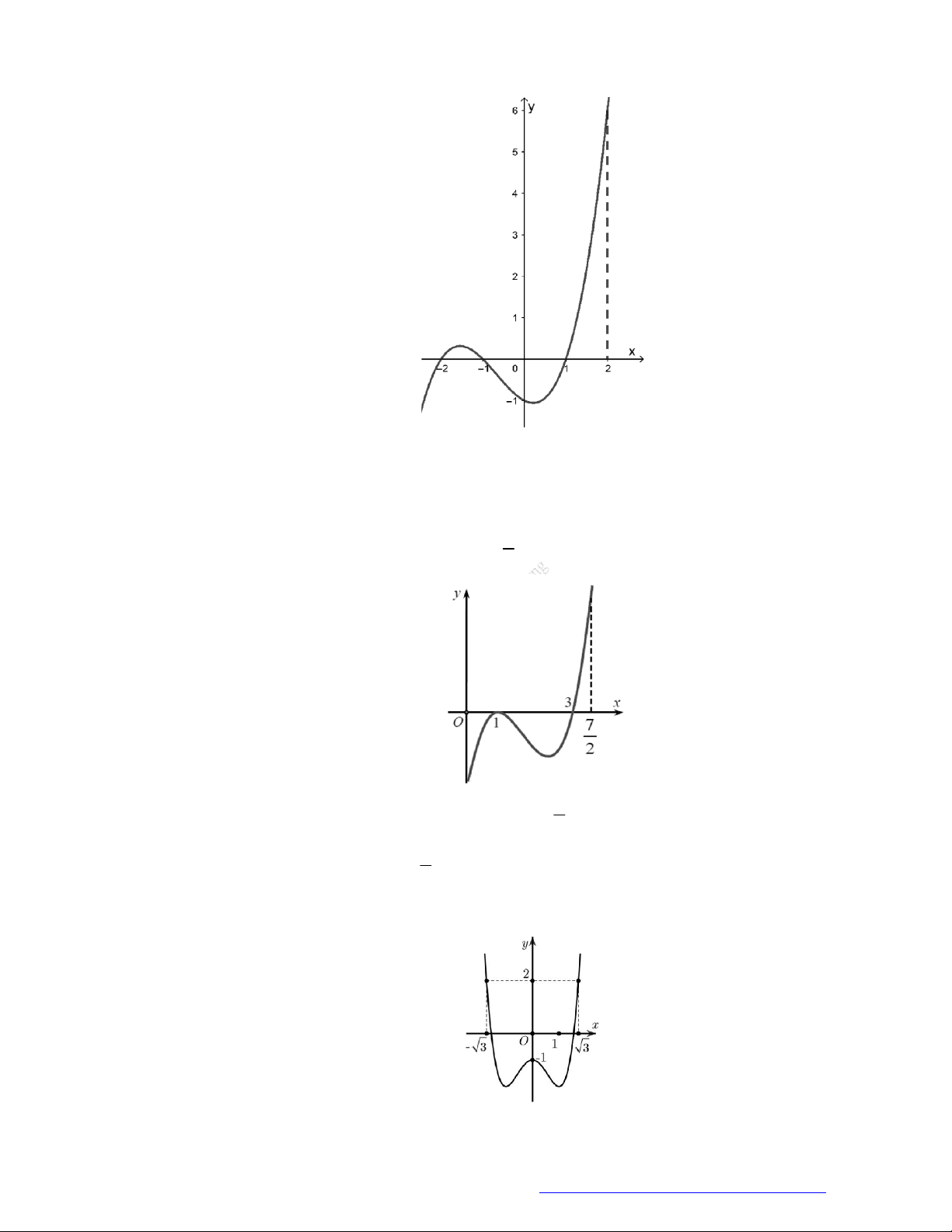
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Câu 7. Cho hàm số
f x
có đạo hàm là
f x
. Đồ thị của hàm số
y f x
được cho như hình vẽ
dưới đây:
Biết rằng
1 0 1 2f f f f
. Giá trị nhỏ nhất và giá trị lớn nhất của hàm số
y f x
trên đoạn
1;2
lần lượt là:
A.
1f
;
2f
. B.
2f
;
0f
. C.
0f
;
2f
. D.
1f
;
1f
.
Câu 8. Cho hàm số
y f x
liên tục trên đoạn
7
0;
2
có đồ thị hàm số
'y f x
như hình vẽ.
Hàm số
y f x
đạt giá trị nhỏ nhất trên đoạn
7
0;
2
tại điểm
0
x
nào dưới đây?
A.
0
0x
. B.
0
7
2
x
. C.
0
1x
. D.
0
3x
.
Câu 9. Cho hàm số
y f x
. Đồ thị hàm
y f x
như hình vẽ
Đặt
3
3 3h x f x x x
. Tìm mệnh đề đúng trong các mệnh đề sau:
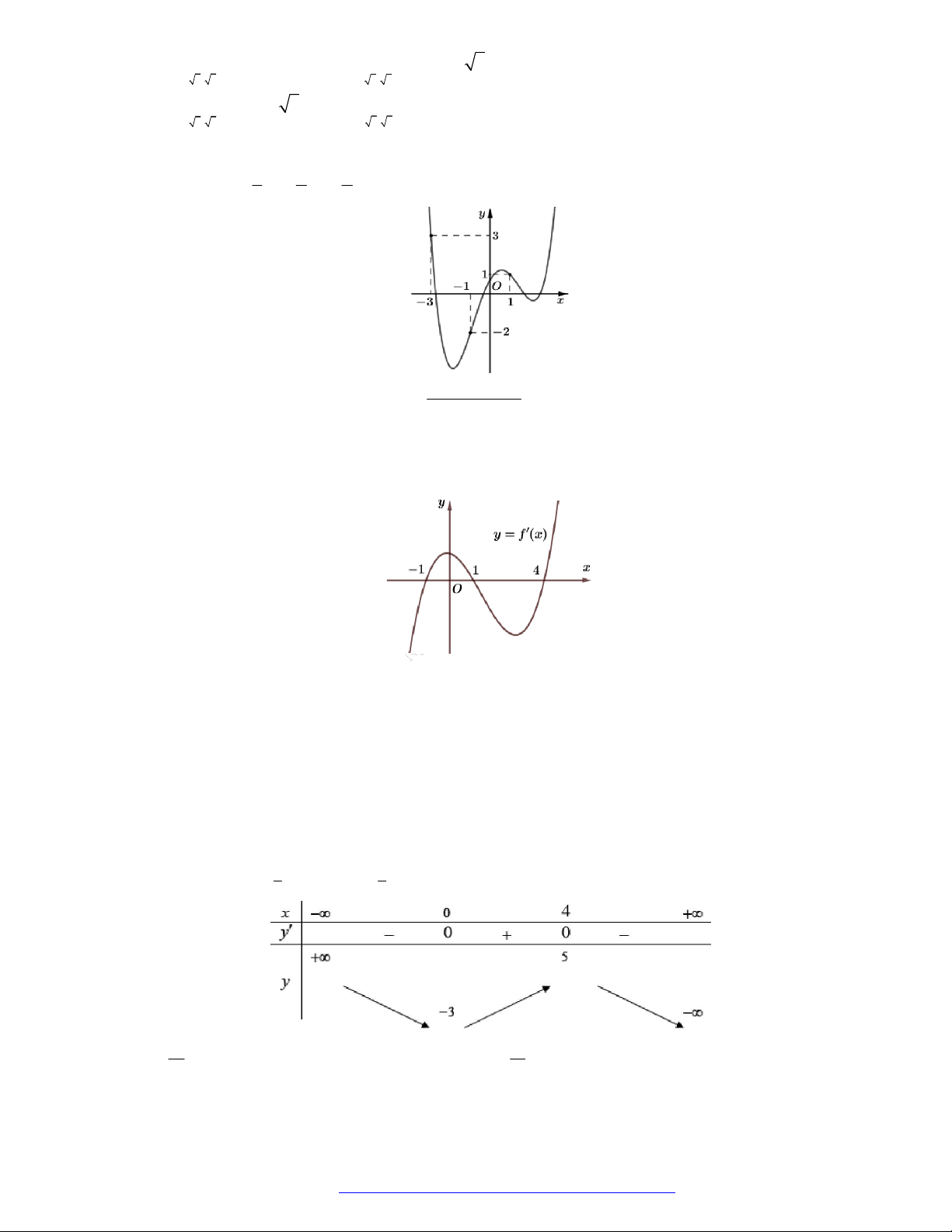
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
[ 3; 3]
max ( ) 3 1h x f
. B.
[ 3; 3 ]
max ( ) 3 3h x f
.
C.
[ 3; 3 ]
max ( ) 3 3h x f
. D.
[ 3; 3]
max ( ) 3 0h x f
.
Câu 10. Cho hàm số
y f x
có đồ thị
y f x
ở hình vẽ bên. Xét hàm số
3 2
1 3 3
2018,
3 4 2
g x f x x x x
mệnh đề nào dưới đây đúng?
A.
3;1
min 1g x g
. B.
3;1
3 1
min
2
g g
g x
.
C.
3;1
min 3g x g
. D.
3;1
min 1g x g
.
Câu 11. Cho hàm số
y f x
có đạo hàm liên tục trên
R
. Hàm số
'y f x
có đồ thị như hình sau:
Cho bốn mệnh đề sau:
1) Hàm số
y f x
có hai cực trị
2) Hàm số
y f x
đồng biến trên khoảng
1;
3)
1 2 4 .f f f
4) Trên đoạn
1;4
, giá trị lớn nhất của hàm số
y f x
là
1 .
f
Số mệnh đề đúng trong bốn mệnh đề trên là:
A.
3.
B.
1.
C.
4.
D.
2.
Câu 12. Cho hàm số
y f x
có bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất của hàm số
2 3 2
1 1
4 3 8
3 3
g x f x x x x x
trên đoạn
1;3 .
A.
25
.
3
B.
15.
C.
19
.
3
D.
12.
Câu 13. Cho hàm số
y f x
. Hàm số
y f x
có bảng biến thiên như hình vẽ bên. Giá trị lớn nhất
của hàm số
2
2 sing x f x x
trên đoạn
1;1
là
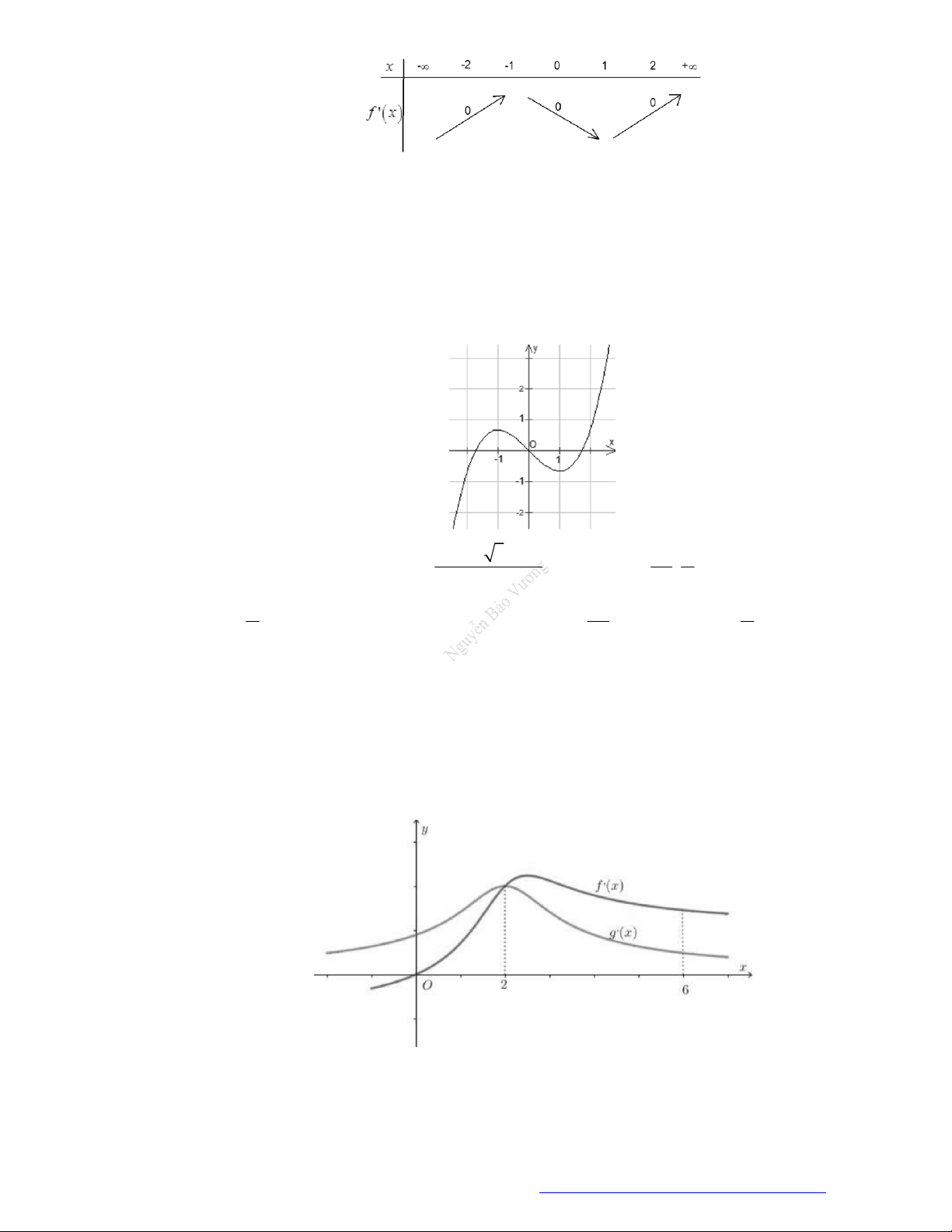
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
A.
1f
. B.
0f
. C.
2f
. D.
1f
.
Câu 14. Cho hàm số
y f x
liên tục trên
sao cho
1;2
max 3f x
. Xét hàm số
3 1g x f x m
.
Tìm tất cả các giá trị của tham số
m
để
0;1
max 10g x
.
A.
13
. B.
7
. C.
13
. D.
1
.
Câu 15. Cho hàm số
y f x
có đạo hàm cấp 2 trên
, hàm số
y f x
có đồ thị như hình vẽ bên.
Giá trị lớn nhất của hàm số
sin 3 cos
2
x x
y f
trên đoạn
5
;
6 6
bằng
A.
3
f
. B.
0f
. C.
5
6
f
. D.
6
f
.
Câu 16. Cho hàm số
y f x
liên tục trên
sao cho
0;10
max 2 4
x
f x f
. Xét hàm số
3 2
2g x f x x x x m
. Giá trị của tham số
m
để
0;2
max 8
x
g x
là
A.
5
. B.
4
. C.
1
. D.
3
.
Câu 17. Cho hai hàm số
y f x
,
y g x
có đạo hàm là
f x
,
g x
. Đồ thị hàm số
y f x
và
g x
được cho như hình vẽ bên dưới.
Biết rằng
0 6 0 6f f g g
. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
h x f x g x
trên đoạn
0;6
lần lượt là:
A.
6h
,
2h
. B.
2h
,
6h
. C.
0h
,
2h
. D.
2h
,
0h
.
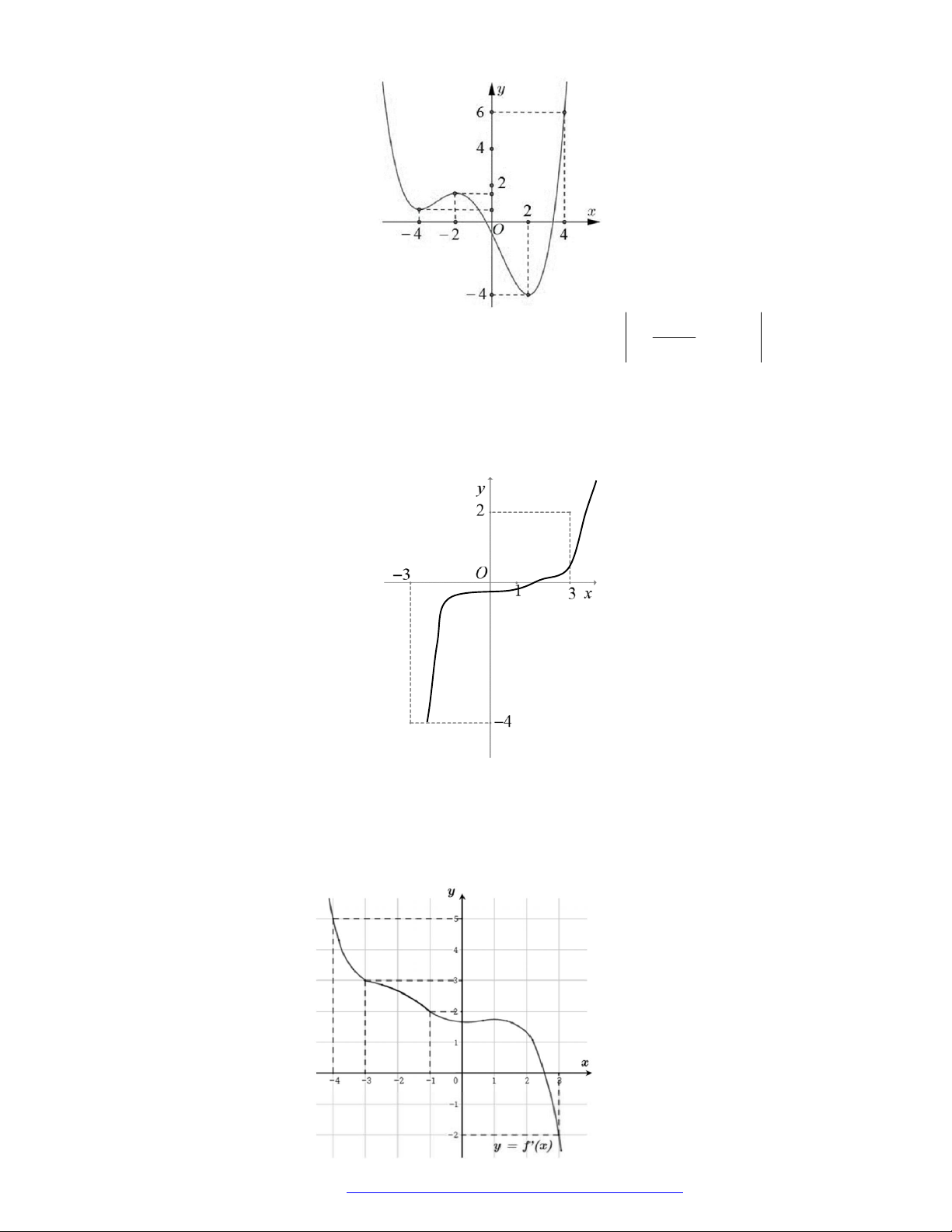
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 18. (Chuyên Lào Cai - 2020) Cho hàm số
f x
liên tục trên
, có đồ thị như hình vẽ
Có tất cả bao nhiêu giá trị nguyên của tham số
m
để hàm số
2
8
1
1
x
y f m
x
có giá trị
lớn nhất không vượt quá
2020
?
A.
4029
. B.
4035
. C.
4031
. D.
4041
.
Câu 19. (Sở Hưng Yên - 2020) Cho hàm số
y f x
liên tục trên
có đồ thị
y f x
như hình bên.
Đặt
2
2 1g x f x x
.
Khi đó
y g x
đạt giá trị nhỏ nhất trên đoạn
3;3
tại
A.
3x
. B.
3x
. C.
0x
. D.
1x
.
Câu 20. (Kim Liên - Hà Nội - 2020) Cho hàm số
f x
. Biết hàm số
f x
có đồ thị như hình dưới đây.
Trên
4;3
, hàm số
2
2 1g x f x x
đạt giá trị nhỏ nhất tại điểm

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
A.
3x
. B.
4x
. C.
3x
. D.
1x
.
Câu 21. (Yên Lạc 2 - Vĩnh Phúc - 2020) Cho hàm số
y f x
có đạo hàm cấp hai trên
. Biết
0 3, 2 2018 0f f f
, và bảng xét dấu của
f x
như sau
Hàm số
1 2018y f x
đạt giá trị nhỏ nhất tại
0
x thuộc khoảng nào sau đây?
A.
; 2015
. B.
1;3
. C.
1009;2
. D.
2015;1
.
Câu 22. (THPT Anh Sơn - Nghệ An - 2020) Cho hàm số
y f x
có đạo hàm cấp hai trên
. Biết
0 3f
,
2 2020f
,
lim
x
f x
và bảng xét dấu của
f x
như hình sau:
Hàm số
2019 2020y f x x
đạt giá trị nhỏ nhất tại điểm
0
x thuộc khoảng nào sau đây?
A.
; 2019
. B.
0;2
. C.
2019;0
. D.
2019;
.
Dạng 3. Ứng dụng gtln-gtnn giải bài toán thực tế
Câu 1. (Chuyên Quang Trung - Bình Phước - Lần 2 - 2020) Cho số
0a
. Trong số các tam giác
vuông có tổng một cạnh góc vuông và cạnh huyền bằng
a
, tam giác có diện tích lớn nhất bằng
A.
2
3
3
a
. B.
2
3
6
a
. C.
2
3
9
a
. D.
2
3
18
a
.
Câu 2. (Mã 101 2018) Ông
A
dự định dùng hết
2
6,5m kính để làm một bể cá có dạng hình hộp chữ
nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có không đáng kể). Bể cá có dung
tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm).
A.
3
2,26 m B.
3
1,61m C.
3
1,33 m D.
3
1,50 m
Câu 3. (Mã 104 2017) Một vật chuyển động theo quy luật
3 2
1
6
3
s t t
với
t
(giây) là khoảng thời
gian tính từ khi vật bắt đầu chuyển động và
s
(mét) là quãng đường vật di chuyển được trong
khoảng thời gian đó. Hỏi trong khoảng thời gian
9
giây kể từ khi bắt đầu chuyển động, vận tốc
lớn nhất của vật đạt được bằng bao nhiêu?
A.
243
(m/s) B.
27
(m/s) C.
144
(m/s) D.
36
(m/s)
Câu 4. (Mã 103 2018) Ông A dự định sử dụng hết
2
5 m kính để làm một bể cá bằng kính có dạng hình
hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng
kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?
A.
3
1,01 m B.
3
0,96 m C.
3
1,33 m D.
3
1,51m
Câu 5. Một loại thuốc được dùng cho một bệnh nhân và nồng độ thuốc trong máu của bệnh nhân được
giám sát bởi bác sĩ. Biết rằng nồng độ thuốc trong máu của bệnh nhân sau khi tiêm vào cơ thể
trong t giờ được cho bởi công thức
2
1
t
c t
t
/mg L
. Sau khi tiêm thuốc bao lâu thì nồng độ
thuốc trong máu của bệnh nhân cao nhất?
A. 4 giờ. B. 1 giờ. C. 3 giờ. D. 2 giờ.
Câu 6. (Dề Minh Họa 2017) Cho một tấm nhôm hình vuông cạnh
12
cm. Người ta cắt ở bốn góc của
tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng
x
(cm), rồi gập tấm nhôm
lại như hình vẽ dưới đây để được một cái hộp không nắp. Tìm
x
để hộp nhận được có thể tích lớn
nhất.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
3x
B.
2x
C.
4x
D.
6x
Câu 7. (Chuyên Lê Quý Đôn Điện Biên 2019) Một sợi dây có chiều dài
28m
được cắt thành hai đoạn
để làm thành một hình vuông và một hình tròn. Tính chiều dài (theo đơn vị mét) của đoạn dây làm
thành hình vuông được cắt ra sao cho tổng diện tích của hình vuông và hình tròn là nhỏ nhất?
A.
56
4
. B.
112
4
. C.
84
4
. D.
92
4
.
Câu 8. (THPT Minh Châu Hưng Yên 2019) Cho một tấm nhôm hình chữ nhật có chiều dài bằng
10cm
và chiều rộng bằng
8cm
. Người ta cắt bỏ ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau,
mỗi hình vuông có cạnh bằng
x cm
, rồi gập tấm nhôm lại (như hình vẽ) để được một cái hộp
không nắp. Tìm
x
để hộp nhận được có thể tích lớn nhất.
A.
8 2 21
3
x
B.
10 2 7
3
x
C.
9 21
9
x
. D.
9 21
3
x
Câu 9. (Mã 103 2018) Ông A dự định sử dụng hết
2
5 m
kính để làm một bể cá bằng kính có dạng hình
hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng
kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?
A.
3
1,01m
. B.
3
0,96 m
. C.
3
1,33 m
. D.
3
1,51m
.
Câu 10. Một người nông dân có 15.000.000 đồng muốn làm một cái hàng rào hình chữ E dọc theo một con
sông (như hình vẽ) để làm một khu đất có hai phần chữ nhật để trồng rau. Đối với mặt hàng rào
song song với bờ sông thì chi phí nguyên vật liệu là 60.000 đồng một mét, còn đối với ba mặt
hàng rào song song nhau thì chi phí nguyên vật liệu là 50.000 đồng một mét. Tìm diện tích lớn
nhất của đất rào thu được
A.
2
3125m . B.
2
50m . C.
2
1250m . D.
2
6250m .
Câu 11. (Chuyên Long An-2019) Ông Khoa muốn xây một cái bể chứa nước lớn dạng một khối hộp chữ
nhật không nắp có thể tích bằng
3
288m
. Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng,
giá thuê nhân công để xây bể là
500000
đồng/
2
m
. Nếu ông Khoa biết xác định các kích thước
của bể hợp lí thì chi phí thuê nhân công sẽ thấp nhất. Hỏi ông Khoa trả chi phí thấp nhất để xây
dựng bể đó là bao nhiêu (Biết độ dày thành bể và đáy bể không đáng kể)?
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
A.
90
triệu đồng. B.
168
triệu đồng. C.
54
triệu đồng. D.
108
triệu đồng.
Câu 12. (Kinh Môn - Hải Dương L2 2019) Một người nông dân có 3 tấm lưới thép B40, mỗi tấm dài
12 m
và muốn rào một mảnh vườn dọc bờ sông có dạng hình thang cân
ABCD
như hình vẽ (bờ
sông là đường thẳng
DC
không phải rào, mỗi tấm là một cạnh của hình thang). Hỏi ông ta có thể
rào được mảnh vườn có diện tích lớn nhất là bao nhiêu
2
m
?
A. 100 3 . B. 106 3 . C. 108 3 . D. 120 3 .
Câu 13. (Sở GD Quảng Nam - 2019) Cho nửa đường tròn đường kính
2AB
và hai điểm
C
,
D
thay
đổi trên nửa đường tròn đó sao cho
ABCD
là hình thang. Diện tích lớn nhất của hình thang
ABCD
bằng
A.
1
2
. B.
3 3
4
. C.
1
. D.
3 3
2
.
Câu 14. (THPT Lương Văn Tụy - Ninh Bình 2018) Một người đàn ông muốn chèo thuyền ở vị trí
A
tới
điểm
B
về phía hạ lưu bờ đối diện, càng nhanh càng tốt, trên một bờ sông thẳng rộng
3 km
(như
hình vẽ). Anh có thể chèo thuyền của mình trực tiếp qua sông để đến
C
và sau đó chạy đến
B
,
hay có thể chèo trực tiếp đến
B
, hoặc anh ta có thể chèo thuyền đến một điểm
D
giữa
C
và
B
và sau đó chạy đến
B
. Biết anh ấy có thể chèo thuyền
6 km/ h
, chạy
8 km/ h
và quãng đường
8 kmBC
. Biết tốc độ của dòng nước là không đáng kể so với tốc độ chèo thuyền của người đàn
ông. Tính khoảng thời gian ngắn nhất (đơn vị: giờ) để người đàn ông đến
B
.
A.
3
2
. B.
9
7
. C.
73
6
. D.
7
1
8
.
Dạng 4. Dùng phương pháp hàm số để tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức
Câu 1. (HSG 12 - Sở Quảng Nam - 2019) Cho ba số thực
, ,x y z
thỏa mãn
0, 0, 1x y z
,
2x y z
.Biết giá trị lớn nhất của biểu thức
P xyz
bằng
a
b
với
*
,a b và
a
b
là phân số tối
giản. Giá trị của
2a b
bằng
A.
5
. B.
43
. C.
9
. D.
6
.
Câu 2. (Chuyên Bắc Giang Nam 2019) Cho
2 2
2x xy y . Giá trị nhỏ nhất của
2 2
P x xy y
bằng:
A.
2
3
B.
1
6
C.
1
2
D.
2
Câu 3. (Chuyên Bắc Giang 2019) Cho
x
,
y
là các số thực thỏa mãn
1 2 2x y x y
. Gọi
M
,
m
lần lượt là giá trị lớn nhất và nhỏ nhất của
2 2
2 1 1 8 4P x y x y x y
. Tính giá
trị
M m
C
D
B
A
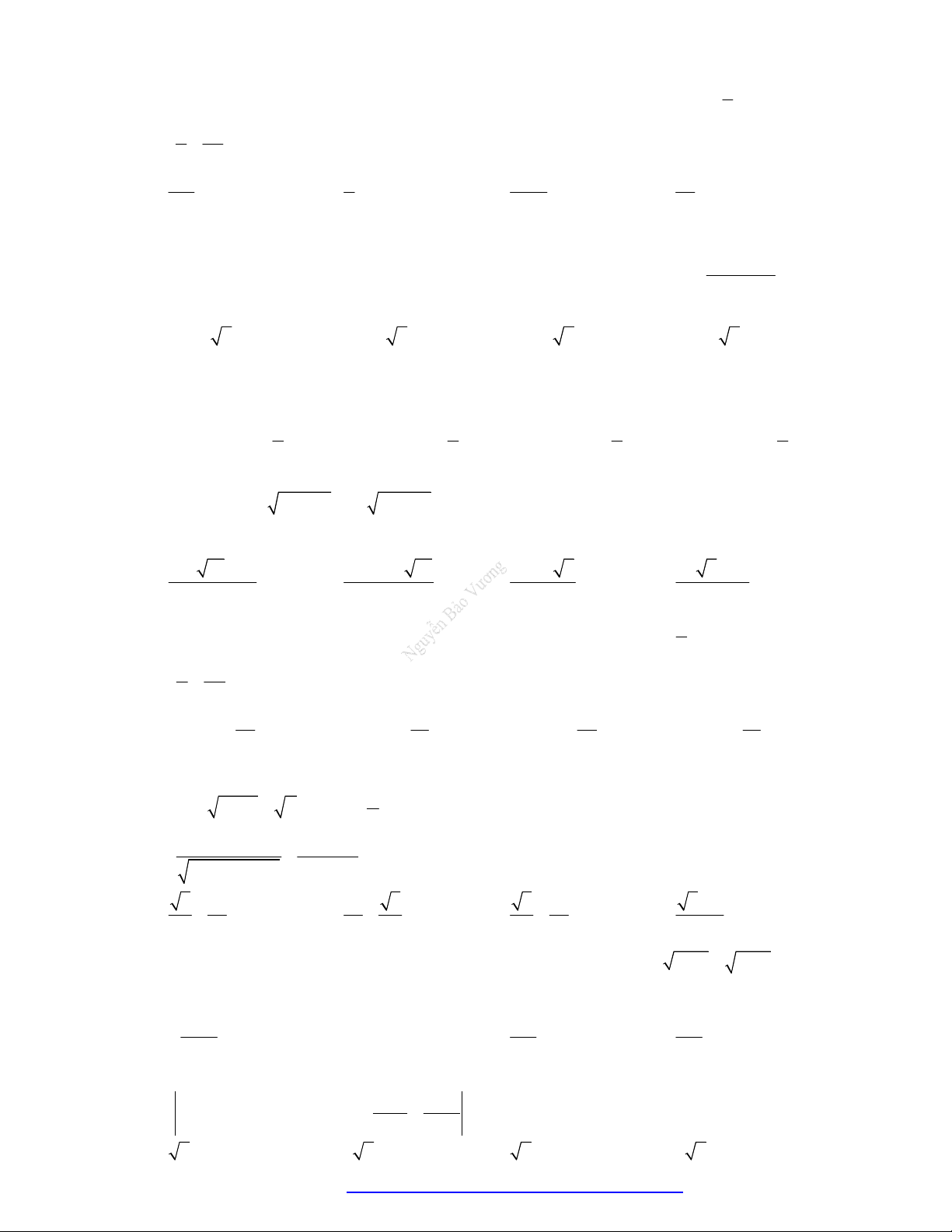
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
42
B.
41
C.
43
D.
44
Câu 4. (Chuyên Lê Quý Đôn - Quảng Trị -2019) Cho
x
,
0y
thỏa mãn
3
2
x y
và biểu thức
4 1
4
P
x y
đạt giá trị nhỏ nhất. Tính
2 2
x y
.
A.
153
100
. B.
5
4
. C.
2313
1156
. D.
25
16
.
Câu 5. (Chuyên Hà Tĩnh - 2019) Cho các số thực
x
,
y
thay đổi thỏa mãn
2 2
1x y xy
và hàm số
3 2
2 3 1
f t t t
. Gọi
M
,
m
tương ứng là GTLN và GTNN của
5 2
4
x y
Q f
x y
. Tổng
M m
bằng:
A.
4 3 2
. B.
4 5 2
. C.
4 4 2
. D.
4 2 2
.
Câu 6. (Sở Lào Cai - 2019) Cho hàm số
4 3 2
1
f x x ax bx cx
. Biết rằng đồ thị hàm số
y f x
có ít nhất một giao điểm với trục hoành. Bất đẳng thức nào sau đây là đúng?
A.
2 2 2
4
3
a b c
. B.
2 2 2
4
3
a b c
. C.
2 2 2
4
3
a b c
. D.
2 2 2
4
3
a b c
.
Câu 7. (THPT Trần Nhân Tông 2018) Cho hai số thực
,x y
thỏa
mãn:
3
9 2 3 5 3 5 0
x y xy x xy
Tìm giá trị nhỏ nhất của
3 3 2
6 3 3 1 2
xy x x y
P x y
A.
296 15 18
9
. B.
36 296 15
9
. C.
36 4 6
9
. D.
4 6 18
9
.
Câu 8. (THPT Nguyễn Huệ - Ninh Bình - 2018) Cho
, 0
x y
và
5
4
x y
sao cho biểu thức
4 1
4
P
x y
đạt giá trị nhỏ nhất. Khi đó
A.
2 2
25
32
x y
. B.
2 2
17
16
x y
. C.
2 2
25
16
x y
. D.
2 2
13
16
x y
.
Câu 9. (Xuân Trường - Nam Định -2018) Cho
,x y
là hai số thực dương thay đổi thỏa mãn điều kiện
1
1 1 1xy xy y x
y
. Tìm giá trị lớn nhất của biểu thức
2 2
2
6
3
x y x y
P
x y
x xy y
?
A.
5 7
3 30
. B.
7 5
30 3
. C.
5 7
3 30
. D.
5 7
30
.
Câu 10. (THPT Lê Xoay - 2018) Cho các số thực
x
,
y
thỏa mãn
1 2 2 3
x y x y
. Giá trị
lớn nhất của biểu thức
4 7 2 2
3 1 .2 3
x y x y
M x y x y
bằng
A.
9476
243
. B.
76
. C.
193
3
. D.
148
3
.
Câu 11. (Cụm 5 Trường Chuyên - Đbsh - 2018) Tìm giá trị nhỏ nhất của hàm số
1 1
sin cos tan cot
sin cos
y x x x x
x x
A.
2 1
. B.
2 2 1
. C.
2 1
. D.
2 2 1
.
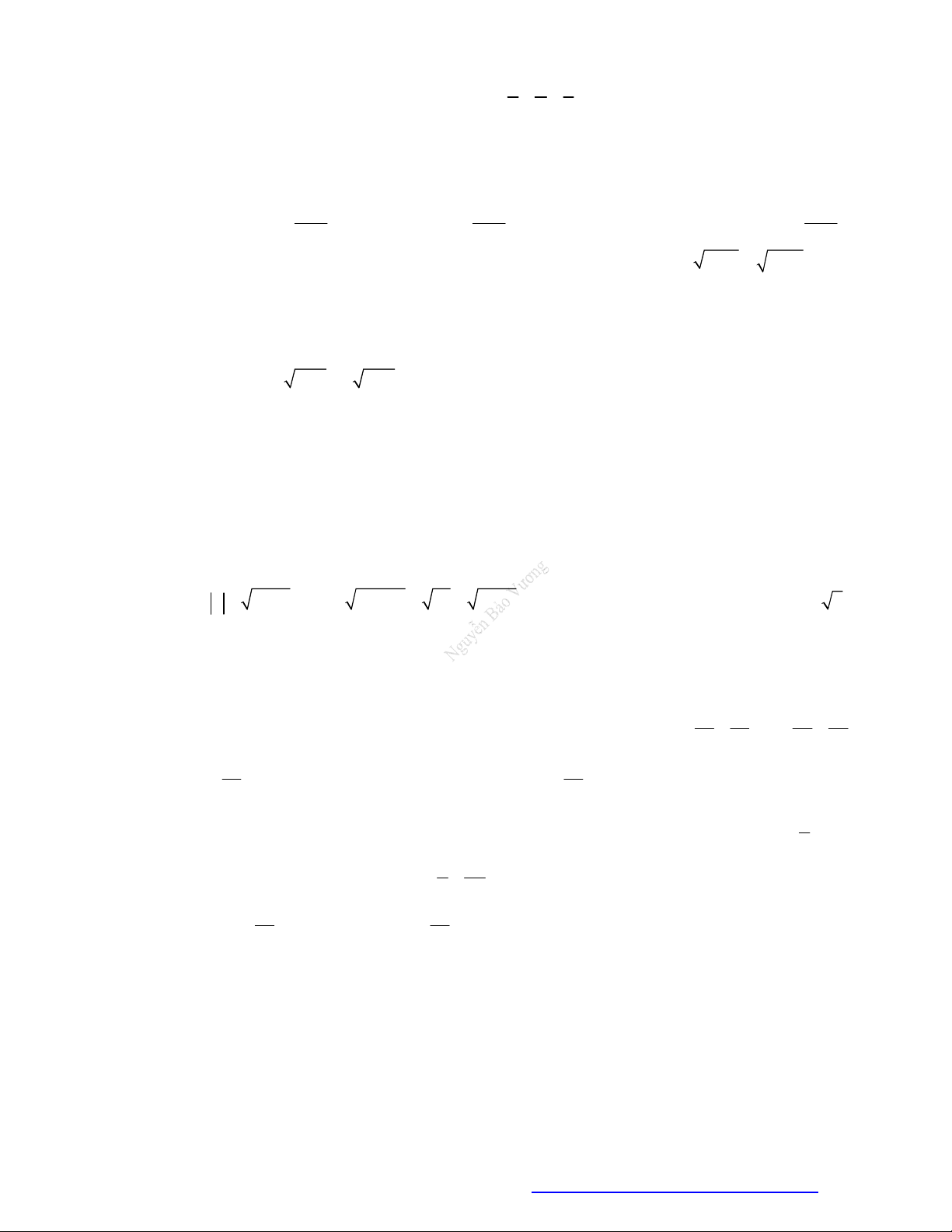
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Câu 12. (Sở Phú
Thọ - 2018) Xét các số thực dương
,
, x y z
thỏa
mãn
4
x
y z
và
5
x
y yz zx
.
Giá
trị nhỏ nhất của biểu thức
3
3 3
1
1 1
x y z
x
y z
bằng:
A.
20
. B.
25
. C.
1
5
. D.
35
.
Câu 13. (Sở Bắc Nin
h - 2018) Gọi
M
,
m
lần
lượt là giá lớn nhất, giá trị nhỏ nhất của hàm số
201
8 2018
s
in cos
y
x x
trên
. Khi đó:
A.
2M
,
1
008
1
2
m
. B.
1M
,
1
009
1
2
m
. C.
1M
,
0
m
. D.
1M
,
1
008
1
2
m
.
Câu 14. (Chuyên Long An - 2018) Cho các số thực
x
,
y
thỏa
mãn
2
3 3
x
y x y
.
Tìm giá
trị nhỏ nhất của biểu thức
2
2
4
15P x y xy
.
A.
mi
n 80
P
. B.
min
91
P
. C.
mi
n 83
P
. D.
mi
n 63
P
.
Câu 15. (THP
T Trần Phú - Đà Nẵng - 2018) Cho hai số thực
x
,
y
t
hỏa mãn:
3
2
2 7 2 1 3 1 3 2 1
y y x x x y
.
Tìm giá trị lớn nhất của biểu thức
2P
x y
.
A.
1
0
P
B.
4P
. C.
6
P
. D.
8
P
.
Câu 16. (Chuyên Trần Phú - Hải Phòng 2018) Cho
x
,
y
l
à các số thực dương thỏa mãn điều kiện:
2
3
0
2 3 14 0
x
xy
x y
.
Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
2
2 3
3
2 2P x y xy x x
A.
8
. B.
0
. C.
1
2
. D.
4
.
Câu 17. (Sở N
am Định -
2018) Biết
rằng bấ
t
phương trình
2
2 4 2 2
1
1 2 1 2
m
x x x x x x
có
nghiệm khi và chỉ khi
;
2
m
a b
với
,a
b
. Tí
nh giá trị của
T a b
.
A.
3
T
. B.
2T
. C.
0
T
. D.
1T
.
Câu 18. (THPT Nguyễn Huệ 2018) Cho
,x y
là các số thực dương thỏa mãn
2
2
2
2
x
y xy x y xy
. G
iá trị nhỏ nhất của biểu thức
3
3 2 2
3 3 2 2
4
9
x y x y
P
y
x y x
.
A.
2
5
4
. B.
5
. C.
23
4
. D.
13
.
Câu 19. (THP
T Kim Liên - Hà Nội - 2018) Cho các số thực dương
x
,
y
t
hỏa mãn
5
2
4
x
y
.
Tìm giá
trị nhỏ nhất
m
in
P
của biểu thức
2
1
4
P
x
y
.
A.
min
3
4
5
P
. B.
min
6
5
4
P
. C.
min
P
không
tồn tại. D.
min
5
P
.
-------------------- HẾT --------------------
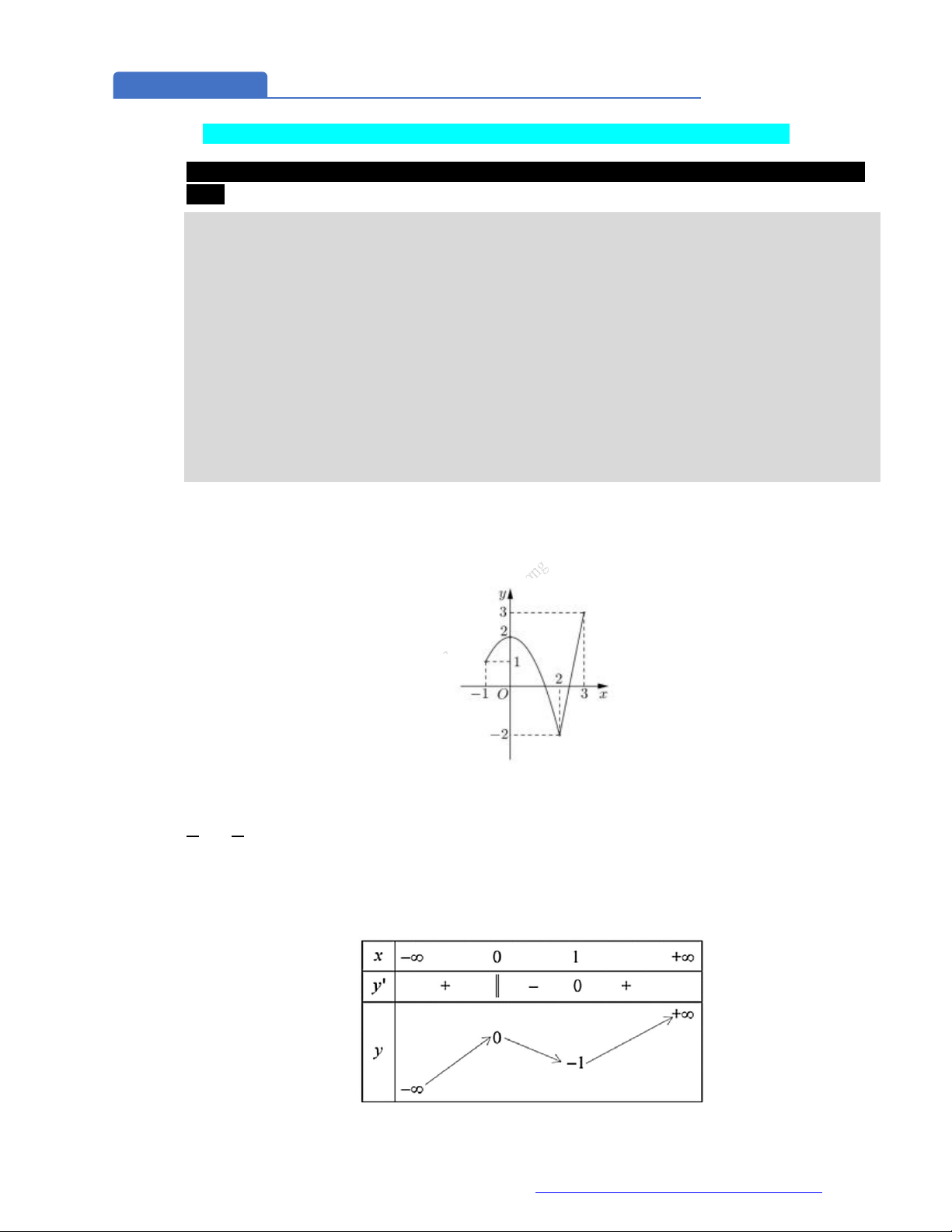
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH TRUNG BÌNH (5-6 ĐIỂM)
Dạng 1. Xác định giá trị lớn nhất – giá trị nhỏ nhất của hàm số thông qua đồ thị, bảng biến
thiên
Giá trị lớn nhất của hàm số
f x
trên đoạn
;a b
Hàm số
f x
liên tục trên đoạn
;a b
và
0, ;
i i
f x x a b
. Khi đó giá trị lớn nhất của hàm
số
f x
là
max , ,
i
M f a f b f x
Giá trị nhỏ nhất của hàm số
f x
trên đoạn
;a b
Hàm số
f x
liên tục trên đoạn
;a b
và
0, ;
i i
f x x a b
. Khi đó giá trị nhỏ nhất của hàm
số
f x
là
, ,
i
m Min f a f b f x
Hàm số
y f x
đồng biến trên đoạn
;a b
thì
; ;
;
a b a b
Max f x f b Min f x f a
Hàm số
y f x
nghịch biến trên đoạn
;a b
thì
; ;
;
a b a b
Max f x f a Min f x f b
Câu 1. (Đề Tham Khảo 2019) Cho hàm số
y f x
liên tục trên đoạn
1;3
và có đồ thị như hình vẽ
bên. Gọi
M
và
m
lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn
1;3
.
Giá trị của
M m
bằng
A.
1
B.
4
C.
5
D.
0
Lời giải
Chọn C
Dựa và đồ thị suy ra
3 3; 2 2M f m f
Vậy
5M m
Câu 2. (Đề Minh Họa 2017) Cho hàm số
y f x
xác định, liên tục trên
và có bảng biến thiên:
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có giá trị cực tiểu bằng
1
.
B. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng
1
.
GIÁ TRỊ LỚN NHẤT - GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ
Chuyên đề 5
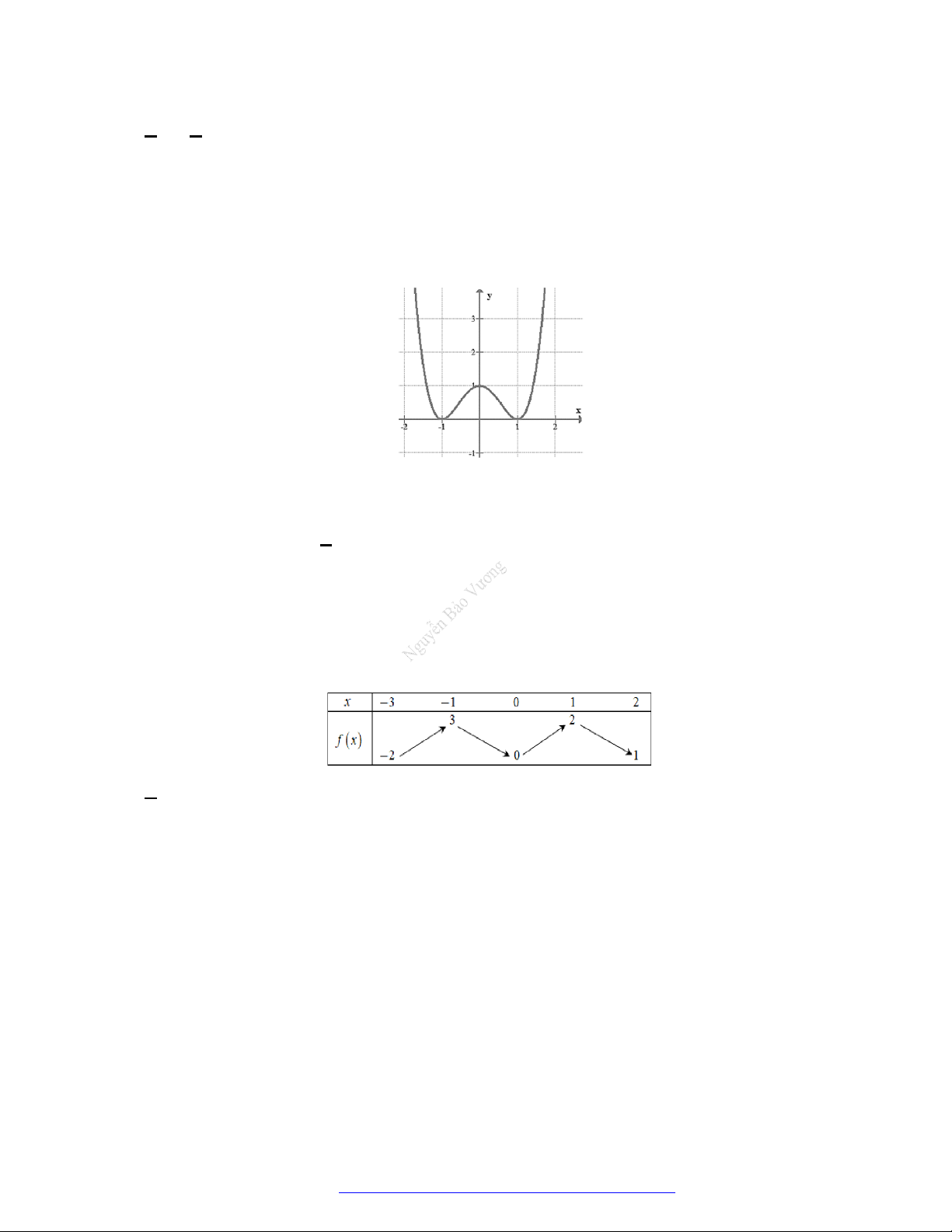
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
C. Hàm số đạt cực đại tại
x 0
và đạt cực tiểu tại
x 1
.
D. Hàm số có đúng một cực trị.
Lời giải
Chọn C
Đáp án A sai vì hàm số có
2
điểm cực trị.
Đáp án B sai vì hàm số có giá trị cực tiểu
y 1
khi
x 0
.
Đáp án C sai vì hàm số không có GTLN và GTNN trên
.
Đáp án D đúng vì hàm số đạt cực đại tại
x 0
và đạt cực tiểu tại
x 1
.
Câu 3. Cho hàm số
y f x
liên tục trên đoạn
1;1
và có đồ thị như hình vẽ.
Gọi
M
và
m
lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn
1;1
. Giá trị
của
M m
bằng
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Từ đồ thị ta thấy
1, 0M m
nên
1M m
.
Câu 4. Cho hàm số
y f x
liên tục trên
3;2
và có bảng biến thiên như sau. Gọi
,M m
lần lượt là
giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y f x
trên đoạn
1; 2
. Tính
M m
.
A.
3
. B.
2
. C.
1
. D.
4
.
Lời giải
Trên đoạn
1; 2
ta có giá trị lớn nhất
3M
khi
1x
và giá trị nhỏ nhất
0m
khi
0x
.
Khi đó
3 0 3M m
.
Câu 5. (Chuyên Lương Thế Vinh Đồng Nai 2019) Cho hàm số
y f x
xác định và liên tục trên
có đồ thị như hình vẽ bên. Tìm giá trị nhỏ nhất
m
và giá trị lớn nhất
M
của hàm số
y f x
trên đoạn
2;2
.
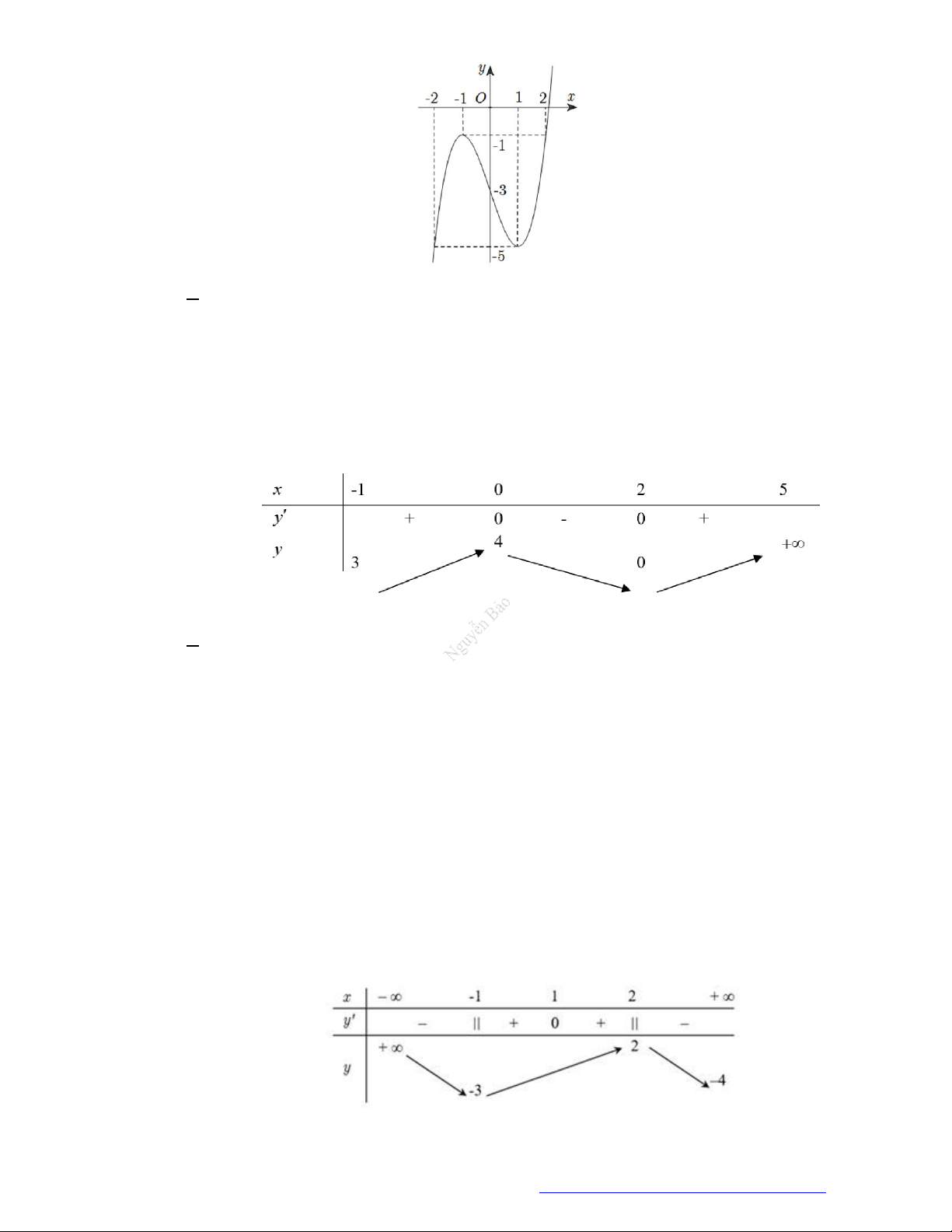
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
A.
5; 1m M
. B.
2; 2m M
. C.
1; 0m M
. D.
5; 0m M
.
Lời giải
Nhìn vào đồ thị ta thấy:
2;2
max 1M f x
khi
1x
hoặc
2x
.
2;2
min 5m f x
khi
2x
hoặc
1x
.
Câu 6. (THPT Ba Đình 2019) Xét hàm số với có bảng biến thiên như sau:
Khẳng định nào sau đây là đúng
A. Hàm số đã cho không tồn taị GTLN trên đoạn
B. Hàm số đã cho đạt GTNN tại và trên đoạn
C. Hàm số đã cho đạt GTNN tại và đạt GTLN tại trên đoạn
D. Hàm số đã cho đạt GTNN tại trên đoạn
Lời giải
A. Đúng. Vì
5
lim
x
y
nên hàm số không có GTLN trên đoạn .
B. Sai. Hàm số đã cho chỉ đạt GTNN tại trên đoạn .
C. Sai. Hàm số đã cho chỉ đạt GTNN tại trên đoạn và .
D. Sai. Hàm số đã cho chỉ đạt GTNN tại trên đoạn .
Câu 7. (Chuyên Lê Thánh Tông 2019) Cho hàm số
y f x
liên tục trên
, có bảng biến thiên như
hình sau:
Trong các mệnh đề sau, mệnh đề nào sai?
A. Hàm số có hai điểm cực trị.
( )y f x
1;5
x
1;5
1
x
2
x
1;5
1
x
5
x
1;5
0
x
1;5
1;5
2
x
1;5
2
x
1;5
5
lim
x
y
2
x
1;5
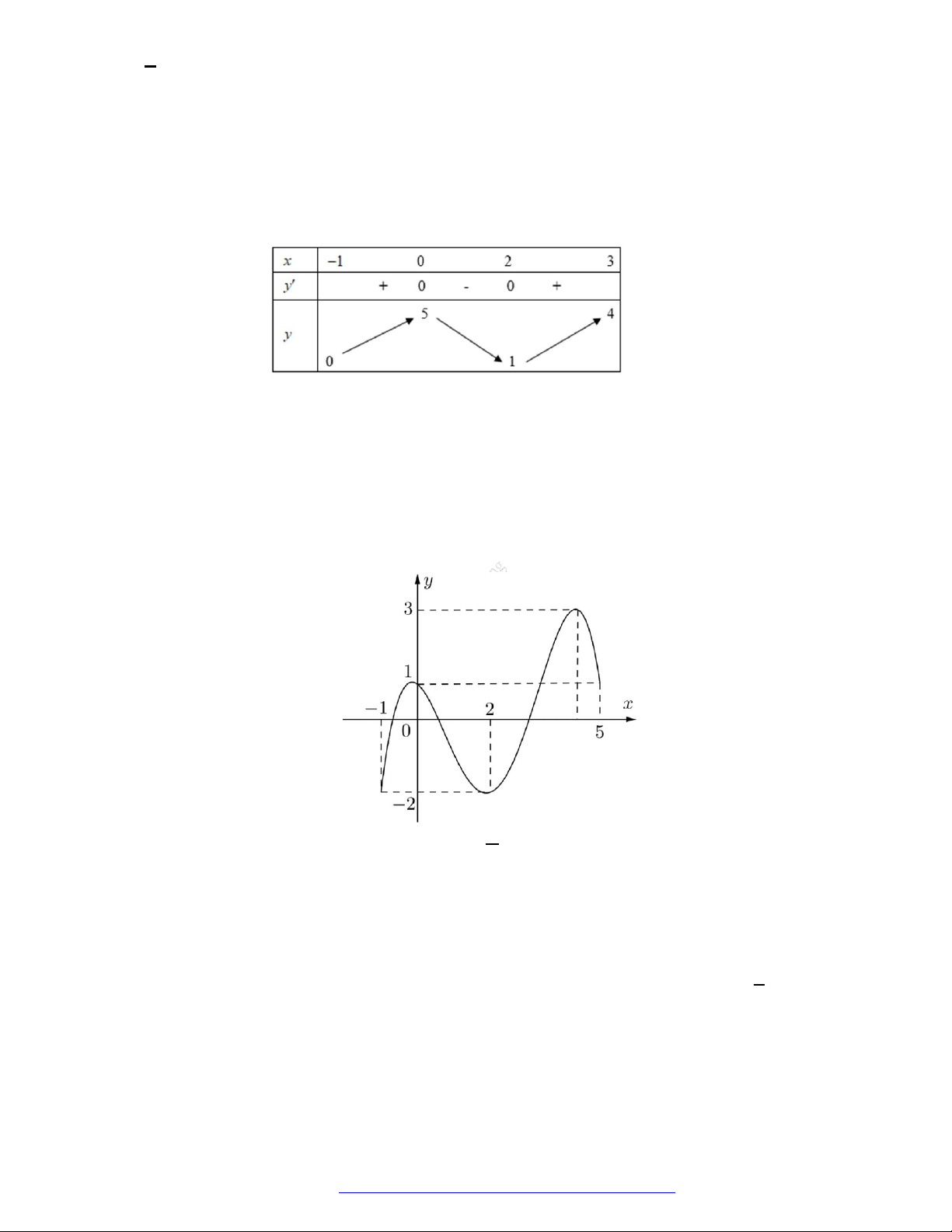
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
B. Hàm số có giá trị lớn nhất bằng
2
và giá trị nhỏ nhất bằng
3
.
C. Đồ thị hàm số có đúng một đường tiệm cận.
D. Hàm số nghịch biến trên mỗi khoảng
; 1 , 2;
.
Lời giải
Dựa vào BBT ta thấy hàm số không có GTLN, GTNN.
Câu 8. (Chuyên Nguyễn Tất Thành Yên Bái 2019) Cho hàm số
( )y f x
liên tục và có bảng biến thiên
trên đoạn
1;3
như hình vẽ bên. Khẳng định nào sau đây đúng?
A.
1;3
max ( ) (0)f x f
. B.
1;3
max 3
f x f
. C.
1;3
max 2
f x f
. D.
1;3
max 1
f x f
.
Lời giải
Nhìn vào bảng biến thiên ta thấy
1;3
max 0 .f x f
Câu 9. (VTED 2019) Cho hàm số
f x
liên tục trên
1;5
và có đồ thị trên đoạn
1;5
như hình vẽ
bên dưới. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
f x
trên đoạn
1;5
bằng
A.
1
B.
4
C.
1
D.
2
Lời giải
Từ đồ thị ta thấy:
1;5
1;5
max 3
1.
min 2
M f x
M n
n f x
Câu 10. (THPT Yên Mỹ Hưng Yên 2019) Cho hàm số
y f x
xác định, liên tục trên
5
1,
2
và có đồ
thị là đường cong như hình vẽ.
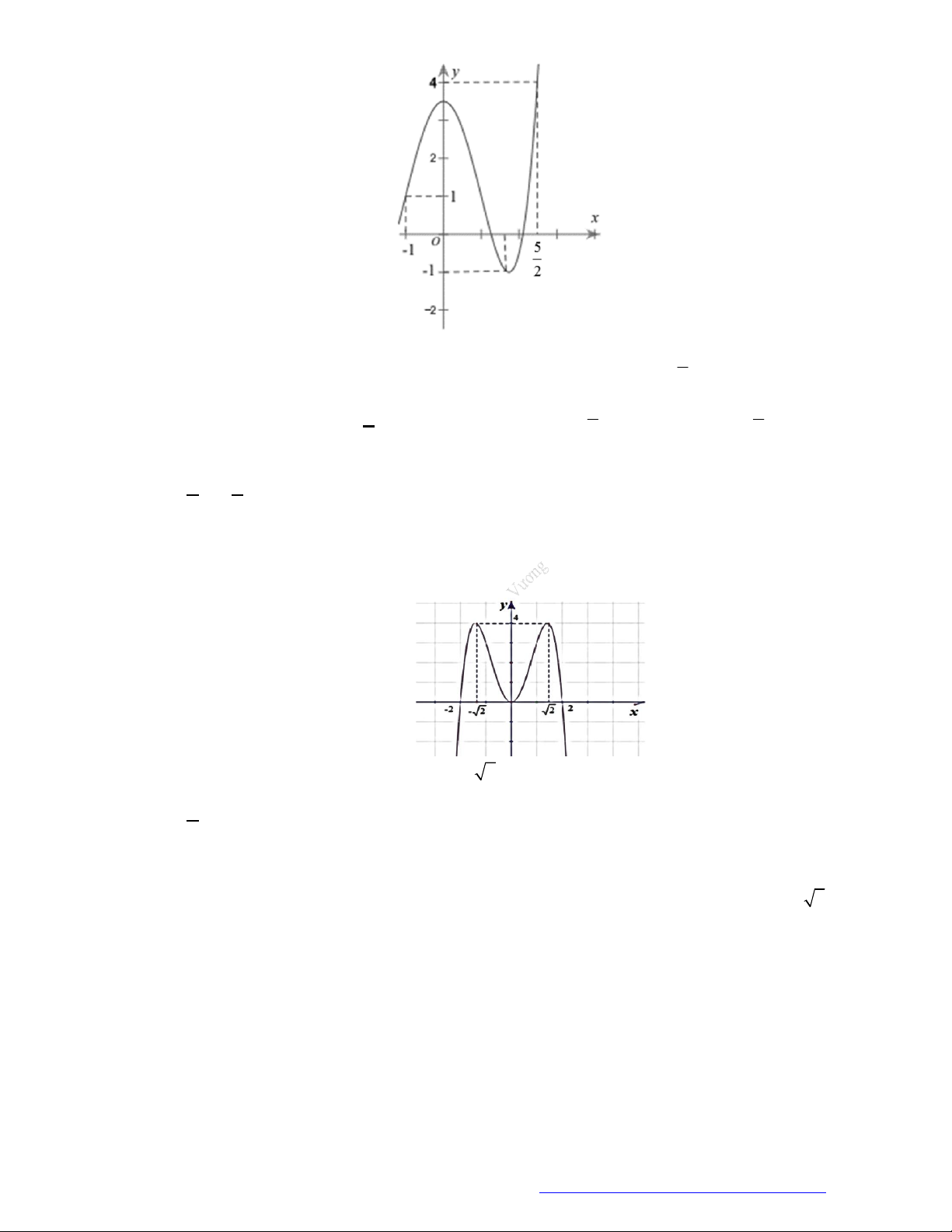
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Giá trị lớn nhất
M
và giá trị nhỏ nhất
m
của hàm số
f x
trên
5
1,
2
là:
A.
4, 1M m
B.
4, 1M m
C.
7
, 1
2
M m
D.
7
, 1
2
M m
Lời giải
Chọn B
Dựa vào đồ thị
4, 1M m
.
Câu 11. (THPT Nghĩa Hưng Nam Định 2019) Cho hàm số
y f x
có đồ thị như hình vẽ. Giá trị lớn
nhất của hàm số
f x
trên đoạn
0;2
là:
A.
0;2
2Max f x
. B.
0;2
2Max f x
.
C.
0;2
4Max f x
. D.
0;2
0Max f x
.
Lời giải
Chọn C
Dựa vào đồ thị ta thấy trên đoạn
0;2
hàm số
f x
có giá trị lớn nhất bằng
4
khi
2x
Suy ra
0;2
4Max f x
Câu 12. (Sở Bắc Giang 2019) Cho hàm số
( )y f x
liên tục trên đoạn
1;3
và có đồ thị như hình vẽ
bên. Gọi
,M m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn
1;3
.
Giá trị của
M m
là
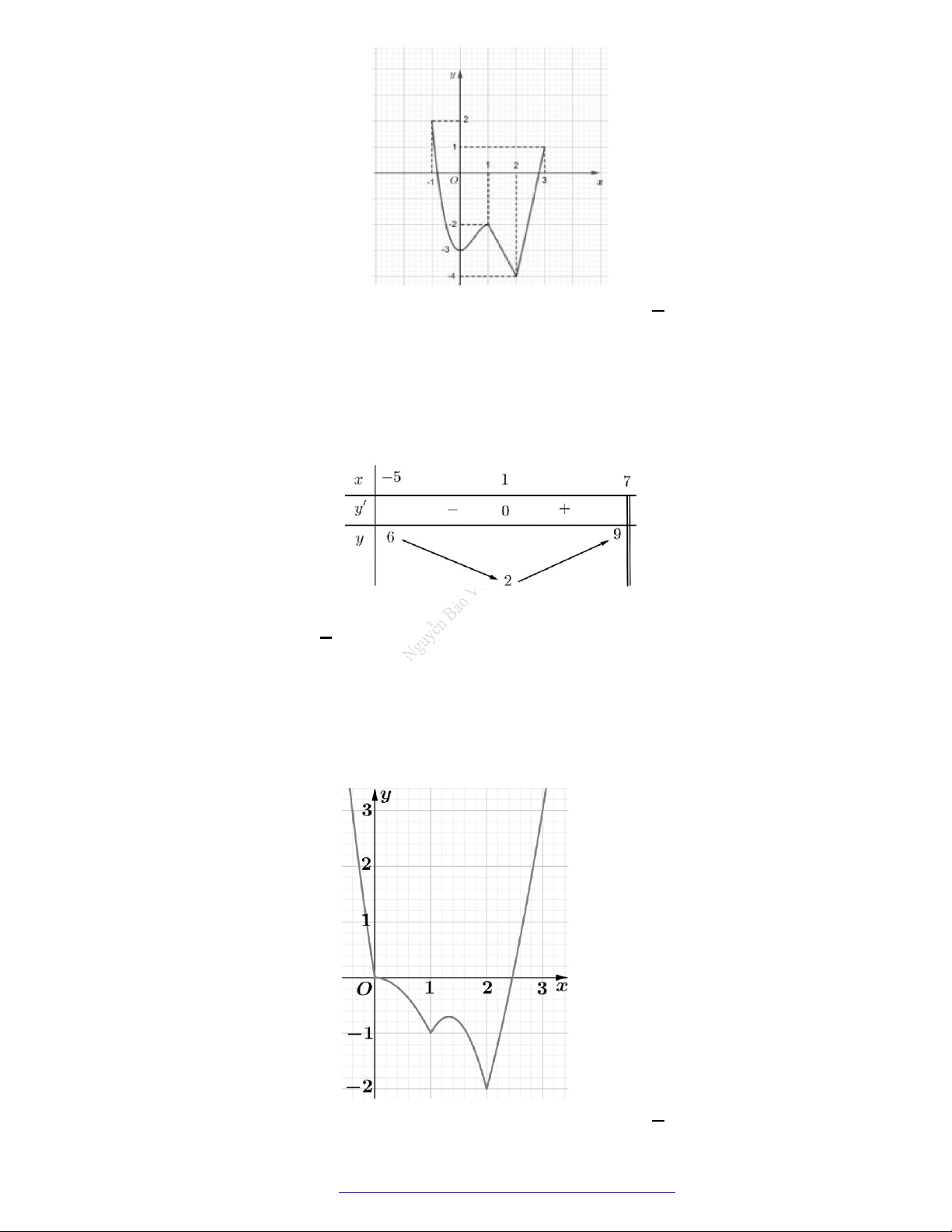
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
2
B.
6
C.
5
D.
2
Lời giải
Dựa vào đồ thị ta thấy GTLN của hàm số trên đoạn
1;3
là
2M
đạt được tại
1x
và
GTNN của hàm số số trên đoạn
1;3
là
4m
đạt được tại
2x
2 ( 4) 2M m
Câu 13. (Sở Hà Nội 2019) Cho hàm số
y f x
có bảng biến thiên trên
5;7
như sau
Mệnh đề nào dưới đây đúng?
A.
5;7
Min 6f x
. B.
5;7
Min 2f x
. C.
-5;7
Max 9f x
. D.
5;7
Max 6f x
.
Lời giải
Dựa vào bảng biến thiên trên
5;7
, ta có:
5;7
Min 1 2f x f
.
Câu 14. Cho hàm số
f x
liên tục trên đoạn
0;3
và có đồ thị như hình vẽ bên. Gọi
M
và
m
lần lượt là
giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên
0;3
. Giá trị của
M m
bằng?
A.
5
. B.
3
. C.
2
. D.
1
.
Lời giải
Dựa vào hình vẽ ta có:
3M
,
2m
nên
1M m
.
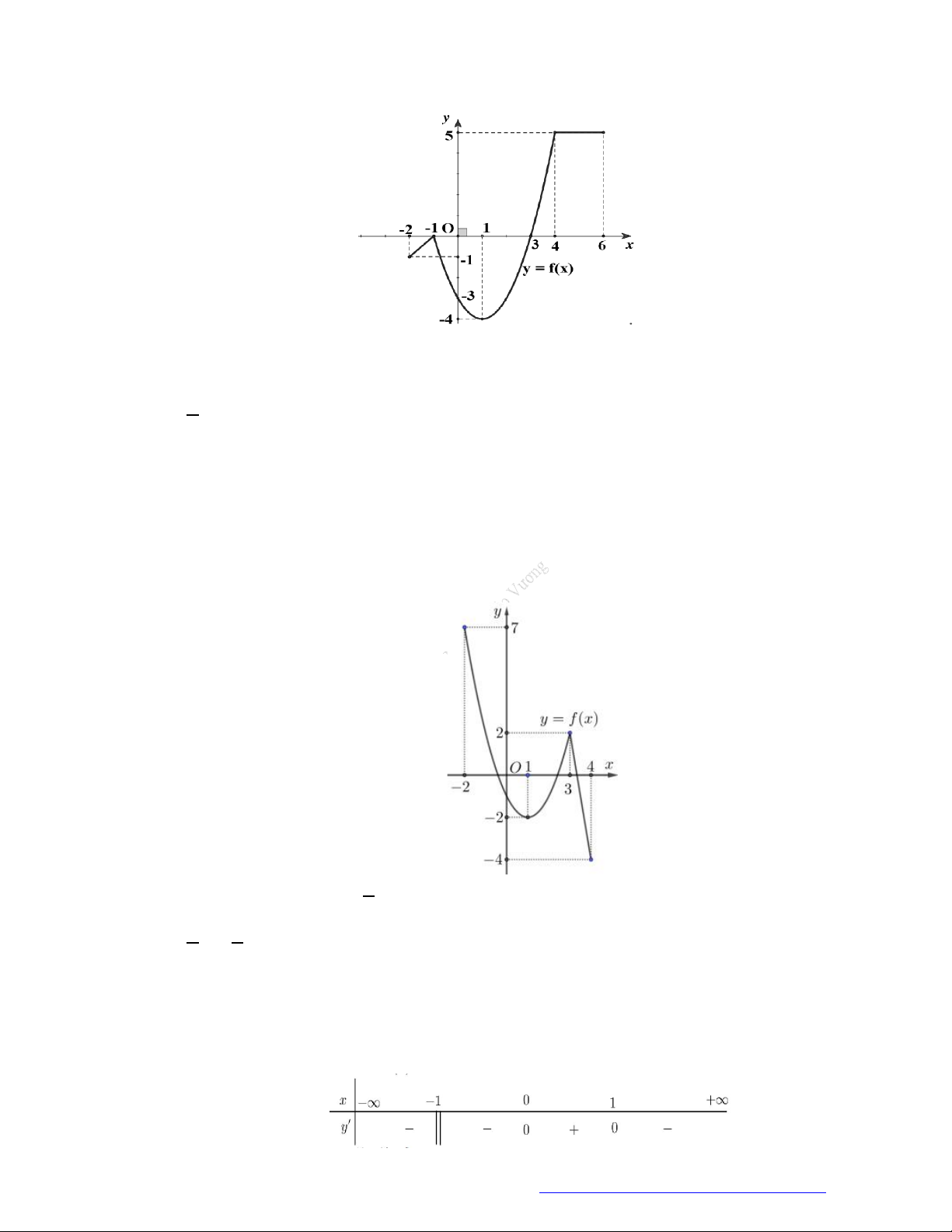
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Câu 15. (Chuyên Lê Quý Đôn Điện Biên 2019) Cho hàm số
y f x
liên tục trên đoạn
2; 6
và có
đồ thị như hình vẽ bên dưới.
Gọi
M
và
m
lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn
2; 6
. Giá trị
của
M m
bằng
A.
9
. B.
8
. C.
9
. D.
8
.
Lời giải
Từ đồ thị suy ra
4 5f x
2;6 ;x
1 4; 4 5f f
5
4
M
m
9M m
.
Câu 16. (VTED 2019) Cho hàm số
y f x
liên tục và có đồ thị trên đoạn
2;4
như hình vẽ bên.
Tổng giá trị lớn nhất và nhỏ nhất của hàm số
y f x
trên đoạn
2;4
bằng
A.
5
B.
3
C.
0
D.
2
Lời giải
Chọn B
Dựa vào đồ thị hàm số ta có
2;4
4
x
m Min f x
,
2;4
7
x
M Max f x
Khi đó
3M m
Câu 17. (THPT Ngô Sĩ Liên Bắc Giang 2019) Cho hàm số
y f x
có bảng xét dấu đạo hàm như sau:
Mệnh đề nào sau đây đúng

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
1;1
max 0f x f
B.
0;
max 1f x f
C.
; 1
min 1f x f
D.
1;
min 0f x f
Lời giải
Chọn B
Dạng 2. Xác định giá trị lớn nhất – giá trị nhỏ nhất của hàm số trên đoạn
Bước 1: Hàm số đã cho
y f x xác định và liên tục trên đoạn
a b; .
Tìm các điểm
n
x x x
1 2
, ,...,
trên khoảng
a b; , tại đó
f x 0 hoặc
f x không xác định.
Bước 2: Tính
n
f a f x f x f x f b
1 2
, , ,..., , .
Bước 3: Khi đó:
n
a b
max f x max f x f x f x f a f b
1 2
,
, ,..., , , .
n
a b
min f x min f x f x f x f a f b
1 2
,
, ,..., , , .
Câu 1. (Đề Minh Họa 2020 Lần 1) Giá trị lớn nhất của hàm số
4 2
( ) 12 1f x x x
trên đoạn
1; 2
bằng:
A.
1
. B.
37
. C.
33
. D.
12
.
Lời giải
Chọn C
4 2
( ) 12 1f x x x
liên tục trên
1; 2
và
3 2
0
'( ) 4 24 0 6 ( )
6 ( )
x
f x x x x L
x L
Ta có:
( 1) 12; (2) 33; (0) 1f f f
Vậy, giá trị lớn nhất của hàm số
4 2
( ) 12 1f x x x
trên đoạn
1; 2
bằng 33 tại
2x
Câu 2. (Đề Tham Khảo 2020 Lần 2) Giá trị nhỏ nhất của hàm số
4 2
10 2f x x x
trên đoạn
1;2
bằng
A.
2
. B.
23
. C.
22
. D.
7
.
Lời giải
Chọn C
Hàm số đã cho liên tục trên đoạn
1;2
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Ta có:
3
0
4 20 , 0
5
x
f x x x f x
x
.
Xét hàm số trên đoạn
1;2
có:
1 7; 0 2; 2 22
f f f
.
Vậy
1;2
min 22
x
f x
.
Câu 3. (Mã 101 - 2020 Lần 1) Giá trị nhỏ nhất của hàm số
3
24f x x x
trên đoạn
2;19
bằng
A.
32 2
. B.
40
. C.
32 2
. D.
45
.
Lời giải
Chọn C.
Ta có
2
2 2 2;19
3 24 0 .
2 2 2;19
x
f x x
x
3
2 2 24.2 40
f
;
3
2 2 2 2 24.2 2 32 2
f
;
3
19 19 24.19 6403
f
.
Vậy giá trị nhỏ nhất của hàm số
3
24f x x x
trên đoạn
2;19
bằng
32 2
.
Câu 4. (Mã 102 - 2020 Lần 1) Giá trị nhỏ nhất của hàm số
3
21f x x x
trên đoạn
2;19
bằng
A.
36
. B.
14 7
. C.
14 7
. D.
34
.
Lời giải
Chọn B
Trên đoạn
2;19
, ta có:
2
7 2;19
3 21 0
7 2;19
x
y x y
x
.
Ta có:
2 34; 7 14 7; 19 6460
y y y
. Vậy
14 7
m
.
Câu 5. (Mã 103 - 2020 Lần 1) Giá trị nhỏ nhất của hàm số
3
( ) 30f x x x
trên đoạn
2;19
bằng
A.
20 10.
B.
63.
C.
20 10.
D.
52.
Lời giải
Chọn C
Ta có
2 2
10
3 30 0 3 30 0
10
x n
f x x f x x
x l
.
Khi đó
2 52
f
;
10 20 10
f và
19 6289
f
.
Vậy
2;19
min 10 20 10
x
f x f
.
Câu 6. (Mã 104 - 2020 Lần 1) Giá trị nhỏ nhất của hàm số
3
33f x x x
trên đoạn
2;19
bằng
A.
72
. B.
22 11
. C.
58
. D.
22 11
.
Lời giải
Chọn B
Ta có
2
11 2;19
3 33 0
11 2;19
x
f x x
x
.
Khi đó ta có
2 58
f
,
11 22 11
f
,
19 6232
f
. Vậy
min
11 22 11
f f
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 7. (Mã 101 – 2020 Lần 2) Giá trị nhỏ nhất của hàm số
4 2
10 4
f x x x
trên
0;9
bằng
A.
28
. B.
4
. C.
13
. D.
29
.
Lời giải
Chọn D
Hàm số
y f x
liên tục trên
0;9
.
Có
3
4 20f x x x
,
0
0 5
5 0;9
x
f x x
x
Ta có
0 4
f
,
5 29
f
,
9 5747
f
Do đó
0;9
min 5 29
f x f
.
Câu 8. (Mã 102 - 2020 Lần 2) Giá trị nhỏ nhất của hàm số
4 2
12 4
f x x x
trên đoạn
0;9
bằng
A.
39
. B.
40
. C.
36
. D.
4
.
Lời giải
Chọn B
Ta có:
3
4 24f x x x
;
0
0
6
x
f x
x
Tính được:
0 4
f
;
9 5585
f
và
6 40
f
.
Suy ra
0;9
min 40
f x
.
Câu 9. (Mã 103 - 2020 Lần 2) Giá trị nhỏ nhất của hàm số
4 2
10 2
f x x x
trên đoạn
0;9
bằng
A.
2
. B.
11
. C.
26
. D.
27
.
Lời giải
Chọn D
Ta có
3
' 4 20f x x x
' 0
f x
3
4 20 0
x x
0 0;9
5 0;9
5 0;9
x
x
x
0 2
f
;
5 27
f
;
9 5749
f
.
Vậy
0;9
min 27
f x
.
Câu 10. (Mã 104 - 2020 Lần 2) Giá trị nhỏ nhất của hàm số
4 2
12 1
f x x x
trên đoạn
0;9
bằng
A.
28
. B.
1
. C.
36
. D.
37
.
Lời giải
Chọn D
Ta có
3
4 24f x x x
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
3
0 0;9
0 4 24 0 6 0;9
6 0;9
x
f x x x x
x
.
0 1
f
,
6 37
f
,
9 5588
f
Câu 11. (Mã 102 - 2019) Giá trị nhỏ nhất của hàm số
3
3 2
f x x x
trên đoạn
3;3
bằng
A.
0
. B.
16
. C.
20
. D.
4
.
Lời giải
Chọn B
Cách 1:Mode 7
3
3 2
f x x x
.
Start -3
end3step 1
Chọn B
Cách 2:
2
3 3
f x x
.
0 1 3;3
f x x
.
3 16
f
;
1 4
f
;
1 0
f
;
3 20
f
.
Giá trị nhỏ nhất là
16
.
Câu 12. (Mã 110 2017) Tìm giá trị lớn nhất
M
của hàm số
4 2
2 3
y x x
trên đoạn
0; 3
.
A.
6
M
B.
1M
C.
9
M
D.
8 3
M
Lời giải
Chọn A
Ta có:
3 2
4 4 4 1
y x x x x
0
y
2
4 1 0
x x
0
1
1( )
x
x
x l
Ta có :
0 3
y
;
1 2
y
;
3 6
y
Vậy giá trị lớn nhất của hàm số
4 2
2 3
y x x
trên đoạn
0; 3
là
3 6
M y
Câu 13. (Đề Minh Họa 2017) Tìm giá trị nhỏ nhất của hàm số
2
3
1
x
y
x
trên đoạn
2;4
.
A.
2;4
min 3
y B.
2;4
19
min
3
y
C.
2;4
min 6
y D.
2;4
min 2
y
Lời giải
Chọn C
Tập xác định:
\ 1
D
Hàm số
2
3
1
x
y
x
xác định và liên tục trên đoạn
2;4
Ta có
2
2
2
2 3
; 0 2 3 0 3
1
x x
y y x x x
x
hoặc
1
x
(loại)
Suy ra
19
2 7; 3 6; 4
3
y y y
. Vậy
2;4
min 6y
tại
3
x
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 14. (Mã 103 - 2019) Giá trị lớn nhất của hàm số
3
3f x x x
trên đoạn
[ 3;3]
bằng
A.
2
. B.
18
. C.
2
. D.
18
.
Lời giải
Chọn B
Ta có
2
3 3 0 1
y x x
3 18; 1 2; 1 2; 3 18
f f f f
.
Câu 15. (Mã 104 2018) Giá trị lớn nhất của hàm số
4 2
13
y x x
trên đoạn
[ 1;2]
bằng
A.
85
B.
51
4
C.
13
D.
25
Lời giải
Chọn D
4 2
13
y f x x x
3
' 4 2y x x
3
0 [ 1;2]
1
4 2 0 [ 1;2]
2
1
[ 1;2]
2
x
x x x
x
1 51 1 51
( 1) 13; (2) 25; (0) 13; ;
4 4
2 2
f f f f f
Giá trị lớn nhất của hàm số
4 2
13
y x x
trên đoạn
[ 1;2]
bằng
25.
Câu 16. (Mã 104 2017) Tìm giá trị nhỏ nhất
m
của hàm số
2
2
y x
x
trên đoạn
1
;2
2
.
A.
5
m
B.
3
m
C.
17
4
m
D.
10
m
Lời giải
Chọn B
Đặt
2
2
y f x x
x
.
Ta có
3
2 2
2 2 2
2
x
y x
x x
,
1
0 1 ;2
2
y x
.
Khi đó
1 17
1 3, , 2 5
2 4
f f f
.
Vậy
1
;2
2
min 1 3
m f x f
.
Câu 17. (Chuyên Bắc Ninh 2018) Tìm tập giá trị của hàm số
1 9
y x x
A.
1; 9
T
. B.
2 2; 4
T
. C.
1; 9
T
. D.
0; 2 2
T
.
Lời giải
Tập xác định:
1; 9
D

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
1 1
0 9 1
2 1 2 9
y x x
x x
1
5
9 1
x
x
x x
.
1 9 2 2
f f
;
5 4
f
Vậy tập giá trị là
2 2; 4
T
.
Câu 18. (Mã 123 2017) Tìm giá trị nhỏ nhất
m
của hàm số
3 2
7 11 2
y x x x
trên đoạn
[0; 2]
.
A.
3m
B.
0m
C.
2m
D.
11m
Lời giải
Chọn C
Xét hàm số trên đoạn
[0; 2]
. Ta có
2
3 14 11
y x x
suy ra
0 1y x
Tính
0 2; 1 3, 2 0
f f f
. Suy ra
0;2
min 0 2
f x f m
.
Câu 19. (Mã 101 2018) Giá trị lớn nhất của hàm số
4 2
4 9
y x x
trên đoạn
2;3
bằng
A.
201
B.
2
C.
9
D.
54
Lời giải
Chọn D
3
4 8
y x x
;
0
0
2
x
y
x
.
Ta có
2 9
y
;
3 54
y
;
0 9
y
;
2 5
y
.
Vậy
2;3
max 54
y
.
Câu 20. (Đề Tham Khảo 2018) Giá trị lớn nhất của hàm số
4 2
4 5
f x x x
trêm đoạn
2;3
bằng
A.
122
B.
50
C.
5
D.
1
Lời giải
Chọn B
3
0
'( ) 4 8 0 2;3
2
x
f x x x
x
;
0 5; 2 1; 2 5; 3 50
f f f f
Vậy
2;3
50
Max y
Câu 21. (Mã 105 2017) Tìm giá trị nhỏ nhất
m
của hàm số
4 2
13
y x x
trên đoạn
2;3
.
A.
13m
B.
51
4
m
C.
51
2
m
D.
49
4
m
Lời giải
Chọn B
3
4 2y x x
;
0 2;3
0
1
2;3
2
x
y
x
;
Tính
2 25
y
,
3 85
y
,
0 13
y
,
1 51
12,75
4
2
y
;

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Kết luận: giá trị nhỏ nhất
m
của hàm số là
51
4
m
.
Câu 22. (Mã 104 2019) Giá trị nhỏ nhất của hàm số
3
3 f x x x
trên đoạn
3;3
bằng
A.
18.
B.
2.
C.
2.
D.
18.
Lời giải
Chọn A
Ta có
2
1
3 3 0 .
1
x
f x x
x
Mà
3 18; 1 2; 1 2; 3 18.
f f f f
Vậy giá trị nhỏ nhất của hàm số
3
3 f x x x
trên đoạn
3;3
bằng
18.
Câu 23. (Mã 103 2018) Giá trị nhỏ nhất của hàm số
3 2
3y x x
trên đoạn
4; 1
bằng
A.
16
B.
0
C.
4
D.
4
Lời giải
Chọn A
Ta có
2
3 6y x x
;
2
4; 1
0
0 3 6 0
4; 1
2
x
y x x
x
.
Khi đó
4 16
y
;
2 4
y
;
1 2
y
.
Nên
4; 1
min 16
y
.
Câu 24. (Mã 102 2018) Giá trị nhỏ nhất của hàm số
3 2
2 7y x x x
trên đoạn
0;4
bằng
A.
259
B.
68
C.
0
D.
4
Lời giải
Chọn D
TXĐ
D .
Hàm số liên tục trên đoạn
0;4
.
Ta có
2
3 4 7
y x x
0
y
1 0 4
7
0 4
3
x ;
x ;
0 0; 1 4; 4 68
y y y
.
Vậy
0;4
min 4
y
.
Câu 25. (Mã 101 - 2019) Giá trị lớn nhất của hàm số
3
3 2
f x x x
trên đoạn
3;3
là
A.
4
. B.
16
. C.
20
. D.
0
.
Lời giải
Chọn C
3
3 2
f x x x
tập xác định
.
2
' 0 3 3 0 1 3;3
f x x x
.
1 0; 1 4; 3 20; 3 16
f f f f
.
Từ đó suy ra
3;3
max (3) 20
f x f
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Câu 26. (SGD Nam Định) Giá trị nhỏ nhất của hàm số
2
2
y x
x
trên đoạn
2;3
bằng
A.
15
2
. B.
5
. C.
29
3
. D.
3
.
Lời giải
Chọn B
+ Ta có hàm số
2
2
( )y f x x
x
xác định và liên tục trên
2;3
.
+
2
2
' '( ) 2y f x x
x
;
'( ) 0 1 2;3
f x x
mà
(2) 5
f
,
29
(3)
3
f
.
+ Vậy
2;3
min 5
y
tại
2
x
.
Câu 27. (Sở Quảng Trị 2019) Tìm giá trị lớn nhất
M
của hàm số
3 1
3
x
y
x
trên đoạn
0;2
A.
1
3
M
. B.
1
3
M
. C.
5
M
. D.
5
M
Lời giải
Chọn A
Trên đoạn
0;2
ta luôn có
2
8
0 0;2
3
y x
x
( đạo hàm vô nghiệm trên (0; 2))
Vì
1
0 , 2 5
3
y y
nên
0;2
1
max
3
M y
.
Câu 28. (Sở Nam Định-2019) Giá trị lớn nhất của hàm số
2
4
y x
là
A. 2. B. 0. C. 4. D. 1.
Lời giải
Chọn A
• Tập xác định:
2;2
D
• Ta có:
2
'
4
x
y
x
0 0 2;2
y x
• Ta có:
2;2
2 2 0
max 2
0 2
y y
y
y
.
Câu 29. (Chuyên Bắc Ninh 2018) Tìm giá trị nhỏ nhất của hàm số
2
sin 4sin 5y x x
.
A.
20
. B.
8
. C.
9
. D.
0
.
Lời giải
Đặt
sin , 1;1
t x t
. Xét
2
( ) 4 5f t t t
,
1;1
t
.
( ) 2 4 0 2 1;1
f t t t
.
1 8, 1 0
f f
.
Ta thấy
1;1
min 1 8
f t f
. Vậy giá trị nhỏ nhất của hàm số là
8
.
Câu 30. (THPT Hoa Lư A 2018) Gọi
m
,
M
lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số
1
1
2
f x x x
trên đoạn
0;3
. Tính tổng
2 3S m M
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
7
2
S
. B.
3
2
S
. C.
3
. D.
4
S
.
Lời giải
Ta có:
1 1 1 1
2
2 1 2 1
x
f x
x x
, cho
0 1 1 0 0;3
f x x x
.
Khi đó:
0 1
f
,
1
3
2
f
nên
1
m
và
1
2
M
.
Vậy
7
2 3
2
S m M
.
Câu 31. (Chuyên ĐHSPHN - 2018) Tìm giá trị lớn nhất của hàm số
sin cosf x x x
2
trên
;
0
là
A.
9
8
. B.
5
4
. C.
2
. D.
1
.
Lời giải
sin cosf x x x
2
sin sinx x
2
1 2
Đặt
sin
x t
t
0 1
f t t t
2
2 1
,
f t t
4 1
f t
0
t
1
4
f
0 1
,
f
1 0
,
f
1 9
4 8
Vậy
;
max f x
0 1
9
8
.
Câu 32. (THPT Hà Huy Tập - 2018) Giá trị lớn nhất của hàm số
3
4
2cos os
3
y x c x
trên
0;
.
A.
0;
2
ax
3
m y
. B.
0;
10
ax
3
m y
. C.
0;
2 2
ax
3
m y
. D.
0;
ax 0
m y
.
Lời giải
Đặt:
cost x
1;1
t
3
4
2
3
y t t
.
2
' 2 4y t
' 0
y
1
1;1
2
1
1;1
2
x
x
.
Tính:
2
1
3
y
,
1 2 2
3
2
y
,
1 2 2
3
2
y
,
2
1
3
y
.
Vậy:
0;
2 2
ax
3
m y
.
Câu 33. Gọi
,M m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3sin 2
sin 1
x
y
x
trên đoạn
0;
2
. Khi đó giá trị của
2 2
M m
là

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
A.
31
2
. B.
11
2
. C.
41
4
. D.
61
4
.
Lời giải
Chọn C
Đặt
sint x
,
0;1
t
.
Xét hàm
3 2
1
t
f t
t
liên tục trên đoạn
0;1
có
2
1
0, 0;1
1
f t t
t
.
Suy ra hàm số đồng biến trên
0;1
.
0;1
5
Max ( ) (1)
2
M f t f
và
0;1
Min ( ) (0) 2
m f t f
.
Khi đó
2
2 2 2
5 41
2
2 4
M m
.
Câu 34. (THPT Can Lộc - Hà Tĩnh - 2018) Cho hàm số
2
sin 1
sin sin 1
x
y
x x
. Gọi
M
là giá trị lớn nhất
và
m
là giá trị nhỏ nhất của hàm số đã cho. Chọn mệnh đề đúng.
A.
3
2
M m
. B.
3
2
M m
. C.
1
M m
. D.
2
3
M m
.
Lời giải
Đặt
sin
x t
,
1 1
t
ta được
2
1
1
t
y
t t
.
Xét hàm số
2
1
1
t
y
t t
trên đoạn
1;1
ta có
2
2
2
2
1
t t
y
t t
.
Giải phương trình
0
y
2
2 0t t
0 ( / )
2 ( )
t t m
t loai
.
Vì
1 0
y
;
0 1
y
;
2
1
3
y
nên
1;1
max 0 1
y y
1
M
;
1;1
min 1 0
y y
0
m
.
Vậy
1
M m
.
Dạng 3. Xác định giá trị lớn nhất – giá trị nhỏ nhất của hàm số trên khoảng (a;b)
Bước 1: Tính đạo hàm
f x( )
.
Bước 2: Tìm tất cả các nghiệm
i
x a b( ; )
của phương trình
f x( ) 0
và tất cả các điểm
i
a b( ; )
làm
cho
f x( )
không xác định.
Bước 3. Tính
x a
A f xlim ( )
,
x b
B f xlim ( )
,
i
f x( )
,
i
f ( )
.
Bước 4. So sánh các giá trị tính được và kết luận
a b
M f x
( ; )
max ( )
,
a b
m f x
( ; )
min ( )
.
Nếu giá trị lớn nhất (nhỏ nhất) là A hoặc B thì ta kết luận không có giá trị lớn nhất (nhỏ nhất).
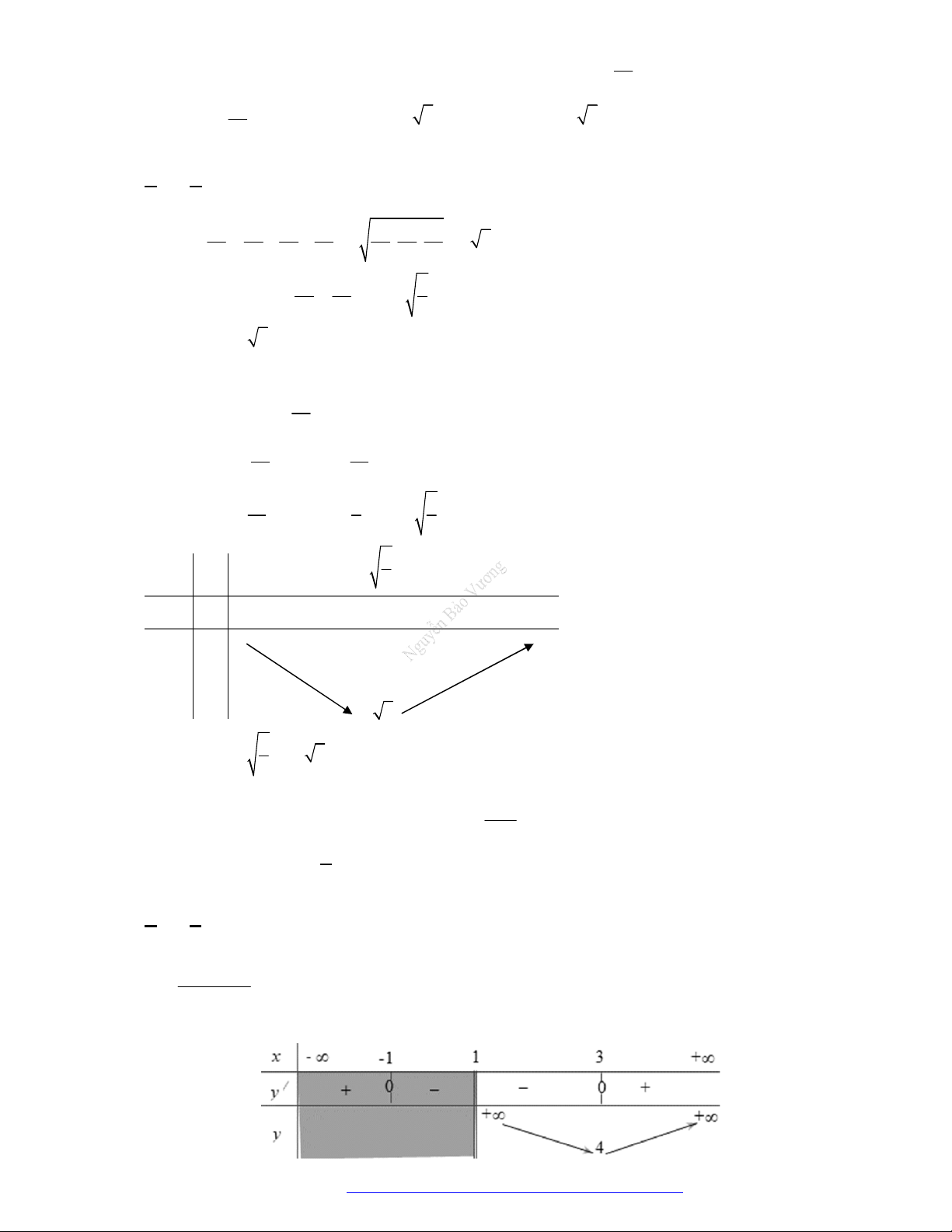
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 1. (Đề Tham Khảo 2017) Tính giá trị nhỏ nhất của hàm số
2
4
3y x
x
trên khoảng
0;
.
A.
0;
33
min
5
y
B.
3
0;
min 2 9y
C.
3
0;
min 3 9y
D.
0;
min 7y
Lời giải
Chọn C
Cách 1:
3
3
2 2 2
4 3 3 4 3 3 4
3 3 . . 3 9
2 2 2 2
x x x x
y x
x x x
Dấu
" "
xảy ra khi
3
2
3 4 8
2 3
x
x
x
.
Vậy
3
0;
min 3 9y
Cách 2:
Xét hàm số
2
4
3y x
x
trên khoảng
0;
Ta có
2 3
4 8
3 ' 3y x y
x x
Cho
3
3
3
8 8 8
' 0 3
3 3
y x x
x
3
3
0;
8
min 3 9
3
y y
Câu 2. Gọi
m
là giá trị nhỏ nhất của hàm số
4
1
1
y x
x
trên khoảng
1;
. Tìm
m
?
A.
5m
. B.
4m
. C.
2m
. D.
3m
.
Lời giải
Chọn B
Tập xác định
\ 1D R
.
2
2
1
2 3
, 0
3
1
x
x x
y y
x
x
.
Bảng biến thiên:
x
0
3
8
3
'y
y
3
3 9
0
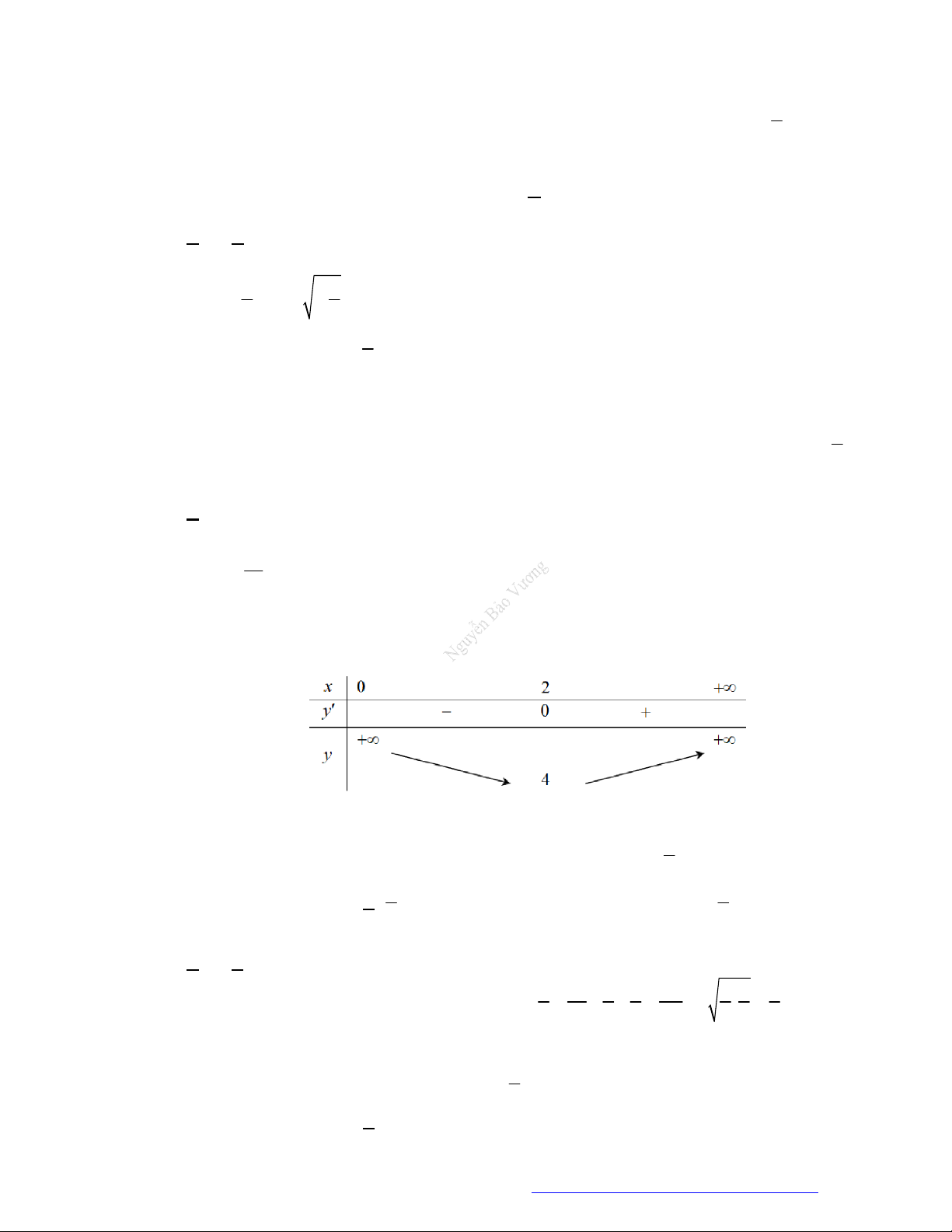
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
1;
min 4m y
khi
3x
Câu 3. (THPT Minh Châu Hưng Yên 2019) Giá trị nhỏ nhất của hàm số
1
5y x
x
trên khoảng
0;
bằng bao nhiêu?
A.
0
B.
1
C.
3
D.
2
Lời giải
Chọn C
Áp dụng bất đẳng thức Cô – si ta có:
1 1
5 2 . 5 3y x x
x x
Dấu bằng xảy ra khi
2
1
1 1x x x
x
(vì
0x
).
Vậy
0;
min 3y
Câu 4. (Chuyên Lương Thế Vinh Đồng Nai 2019) Gọi
m
là giá trị nhở nhất của hàm số
4
y x
x
trên
khoảng
0;
. Tìm
m
A.
4m
. B.
2m
. C.
1m
. D.
3m
.
Lời giải
2
4
' 1
' 0 2; 2 0; .
y
x
y x x
Bảng biến thiên:
Suy ra giá trị nhỏ nhất của hàm số bằng
2) 4( 4.y m
Câu 5. (Chuyên Bắc Giang 2019) Giá trị nhỏ nhất của hàm số
1
( )f x x
x
trên nửa khoảng
2;
là:
A.
2
B.
5
2
C.
0
D.
7
2
Lời giải
Chọn B
Áp dụng bất đẳng thức Cô-si, ta được:
1 3 1 3.2 1 5
( ) 2 .
4 4 4 4 2
x x x
f x x
x x x
.
Dấu bằng xảy ra khi
2x
.
Câu 6. Gọi
m
là giá trị nhỏ nhất của hàm số
4
y x
x
trên khoảng
0;
. Tìm
m
.
A.
3m
. B.
4m
. C.
2m
. D.
1m
.
Lời giải
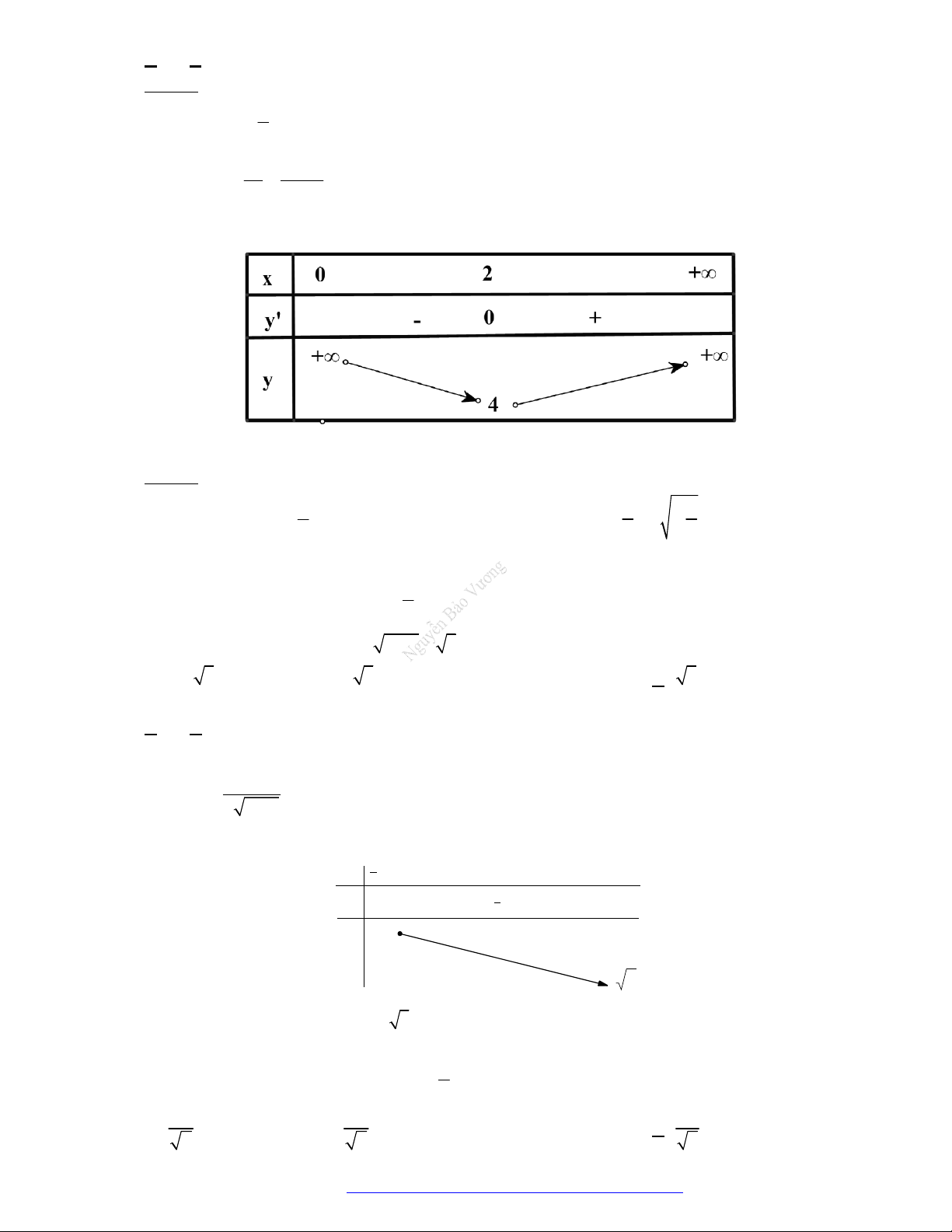
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Chọn B
Cách 1:
Hàm số
4
y x
x
liên tục và xác định trên
0;
.
Ta có
2
2 2
2 0;
4 4
' 1 ' 0
2 0;
x
x
y y
x x
x
.
Bảng biến thiên
Vậy giá trị nhỏ nhất là
4m
khi
2.x
Cách 2:
Với
4
0; ; 0.x x
x
Áp dụng bất đẳng thức Cô si ta có:
4 4
2 . 4.x x
x x
Dấu bằng xảy ra khi và chỉ khi
0
2.
4
x
x
x
x
Vậy
4m
khi
2.x
Câu 7. Giá trị nhỏ nhất của hàm số
4 3y x
trên tập xác định của nó là
A.
2 3.
B.
2 3.
C.
0.
D.
3.
Lời giải
Chọn D
Tập xác định của hàm số là:
;4 .D
Ta có
1
' 0,
2 4
y x D
x
Bảng biến thiên
Từ bảng biến thiên suy ra
;4
min 3y
khi
4x
.Vậy chọn
D
.
Câu 8. Với giá trị nào của
x
thì hàm số
2
1
y x
x
đạt giá trị nhỏ nhất trên khoảng
0;
?
A.
3
3
4
. B.
1
2
. C.
1
. D.
3
1
2
.
3
+
∞
x
y'
y
∞
4
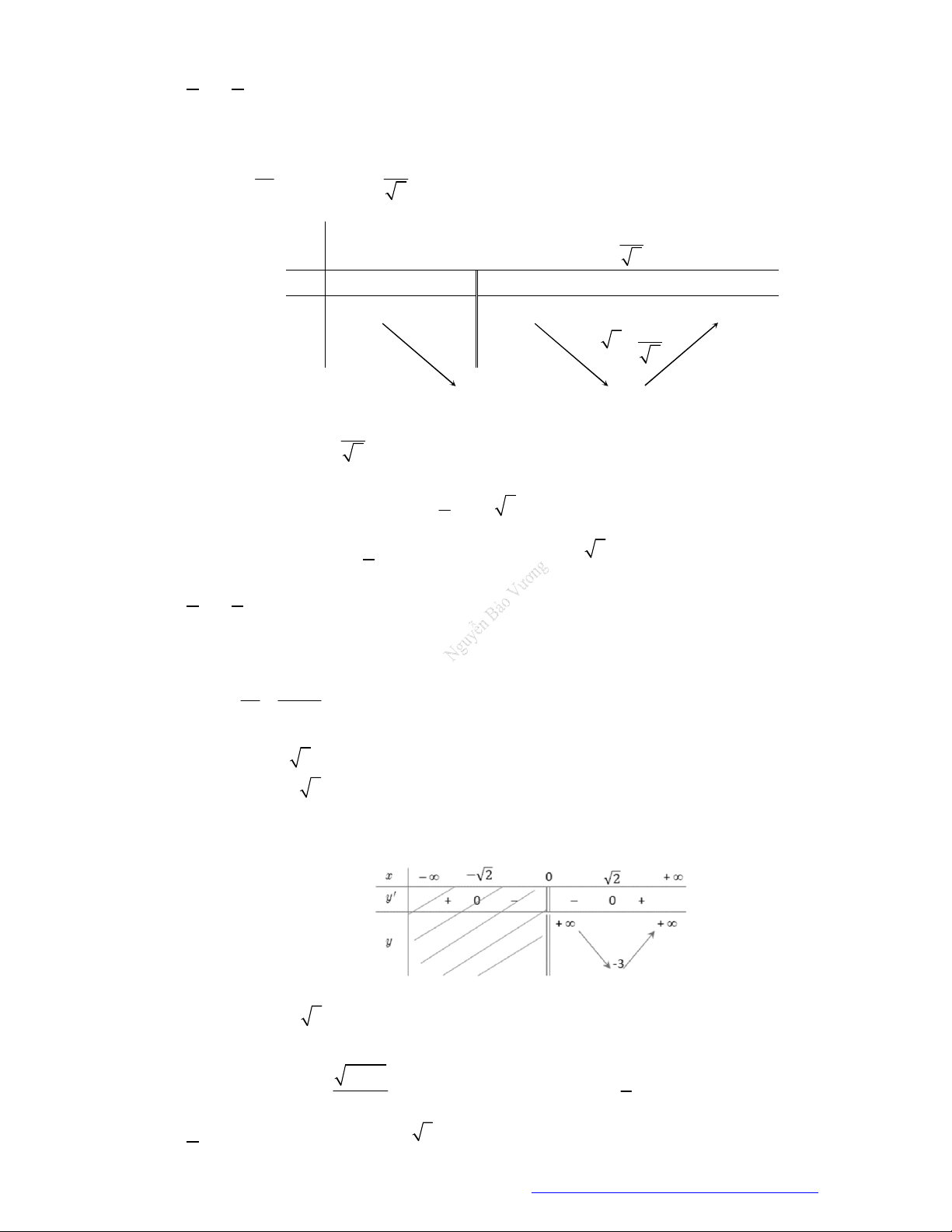
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
Lời giải
Chọn D
TXD:
\ 0D
.
2
1
' 2y x
x
,
3
1
' 0 .
2
y x
Dựa vào BBT thì
3
1
2
x
hàm số đạt giá trị nhỏ nhất trên
0;
.
Câu 9. Giá trị nhỏ nhất của hàm số
2
2
1 2y x
x
trên khoảng
0;
A. không tồn tại. B.
3
. C.
1 2
. D.
0
.
Lời giải
Chọn B
Hàm số xác định và liên tục trên khoảng
0; .
2
2 2
2 2
1 .
x
y
x x
2
0 .
2
x
y
x
Bảng biến thiên:
Vậy
0;
min 2 3.y f
Câu 10. Cho hàm số
2
1
2
x
f x
x
với
x
thuộc
3
; 1 1;
2
D
. Mệnh đề nào dưới đây đúng?
A.
max 0;min 5
D
D
f x f x
. B.
max 0
D
f x
; không tồn tại
min
D
f x
.
x
0
3
1
2
y
0
y
3
3
1
2
4
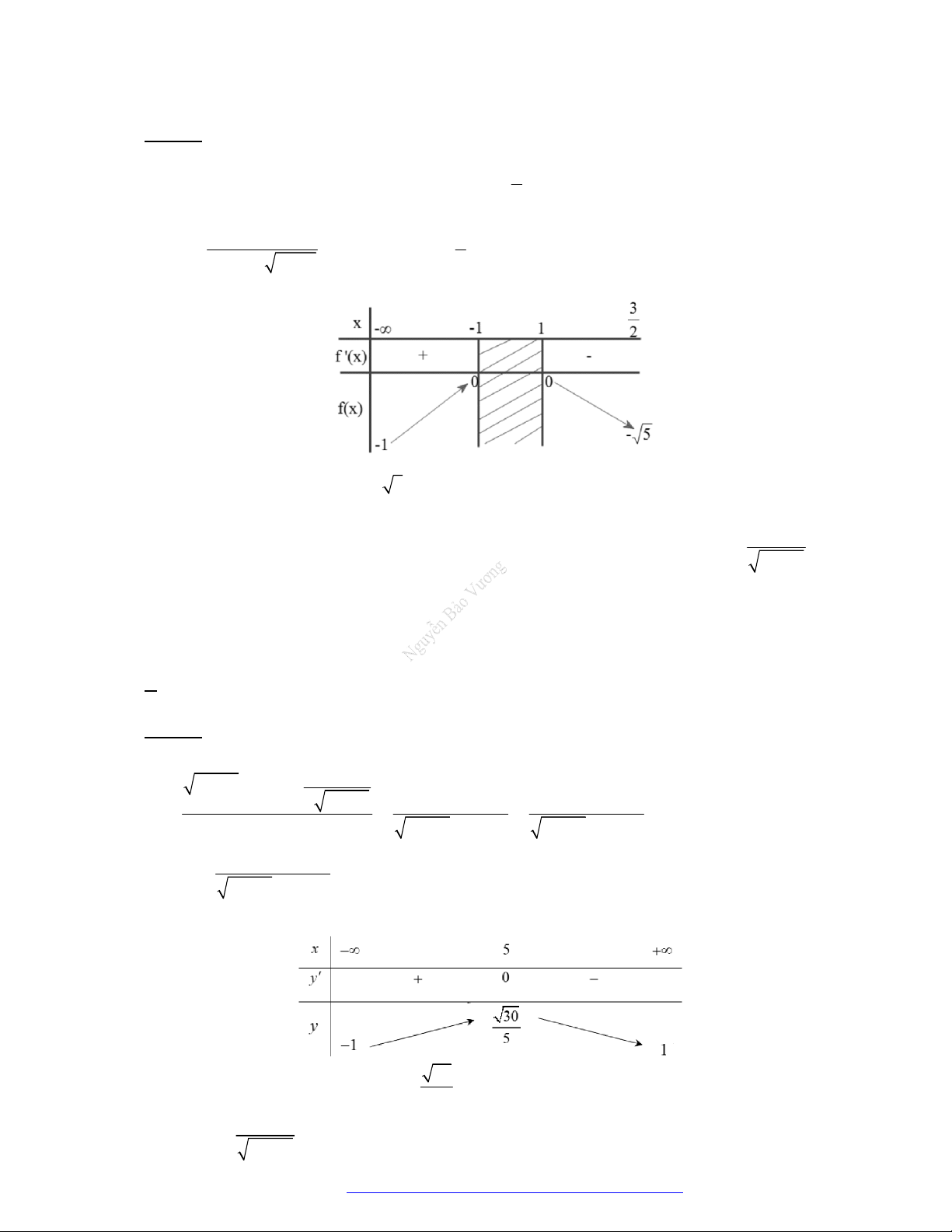
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 22 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
C.
max 0;min 1
D
D
f x f x
. D.
min 0
D
f x
; không tồn tại
max
D
f x
.
Lời giải
Chọn A
Hàm số xác định và liên tục trên
3
; 1 1;
2
D
.
2
2
2 1
'
2 1
x
f x
x x
;
1
' 0
2
f x x D
Vậy
max 0;min 5
D
D
f x f x .
Câu 11. (Cụm liên trường Hải Phòng 2019) Mệnh đề nào sau đây là đúng về hàm số
2
1
5
x
y
x
trên
tập xác định của nó.
A. Hàm số không có giá trị lớn nhất và không có giá trị nhỏ nhất.
B. Hàm số không có giá trị lớn nhất và có giá trị nhỏ nhất.
C. Hàm số có giá trị lớn nhất và giá trị nhỏ nhất.
D. Hàm số có giá trị lớn nhất và không có giá trị nhỏ nhất.
Lời giải
Chọn D
Tập xác định:
D
.
2
2 2
2
2
2 2 2 2
2
5 1
5 5
2 5
'
5
5 5 5 5
x
x x
x x x x
x
y
x
x x x x
.
2 2
5
' 0 0 5 0 5
5 5
x
y x x
x x
.
Bảng biến thiên:
Từ bảng biến thiên có
30
max 5
5
y y
khi
5x
.
Hàm số
2
1
5
x
y
x
không có giá trị nhỏ nhất.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
Vậ
y hàm số có giá trị lớn nhất và không có giá trị nhỏ nhất.
-------------------- HẾT --------------------

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG KHÁ – MỨC ĐỘ 7-8 ĐIỂM
Dạng. Định m để GTLN-GTNN của hàm số thỏa mãn điều kiện cho trước
Bước 1. Tìm nghiệm ( 1, 2,...)
i
x i của
0y
thuộc
;a b
Bước 2. Tính các giá trị
; ;
i
f x f a f b
theo tham số
Bước 3. So sánh các giá trị, suy ra giá trị lớn nhất, giá trị nhỏ nhất.
Bước 4. Biện luận m theo giả thuyết đề để kết luận
Lưu ý:
Hàm số
y f x
đồng biến trên đoạn
;a b
thì
; ;
;
a b a b
Max f x f b Min f x f a
Hàm số
y f x
nghịch biến trên đoạn
;a b
thì
; ;
;
a b a b
Max f x f a Min f x f b
Câu 1. (Mã 123 2017) Cho hàm số
1
x m
y
x
(
m
là tham số thực) thỏa mãn
[2 ;4]
min 3.y
Mệnh đề nào
dưới đây đúng?
A.
4m
B.
3 4m
C.
1m
D.
1 3m
Lời giải
Chọn A
Ta có
2
1
'
1
m
y
x
* TH 1.
1 0 1m m
suy ra
y
đồng biến trên
2; 4
suy ra
2;4
2
min 2 3 1
1
m
f x f m
(loại)
* TH 2.
1 0 1m m
suy ra
y
nghịch biến trên
2; 4
suy ra
2;4
4
min 4 3 5
3
m
f x f m
suy ra
4m
.
Câu 2. (Mã 110 2017) Cho hàm số
1
x m
y
x
(
m
là tham số thực) thoả mãn
1;2
1;2
16
min max
3
y y
. Mệnh
đề nào dưới đây đúng?
A.
4m
B.
2 4m
C.
0m
D.
0 2m
Lời giải
Chọn A
Ta có
2
1
1
m
y
x
.
Nếu
1 1, 1m y x
. Không thỏa mãn yêu cầu đề bài.
Nếu
1m
Hàm số đồng biến trên đoạn
1;2
.
Khi đó:
1;2
1;2
16
min max
3
y y
16 1 2 16
1 2 5
3 2 3 3
m m
y y m
(loại).
Nếu
1m
Hàm số nghịch biến trên đoạn
1;2
.
GIÁ TRỊ LỚN NHẤT - GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ
Chuyên đề 5
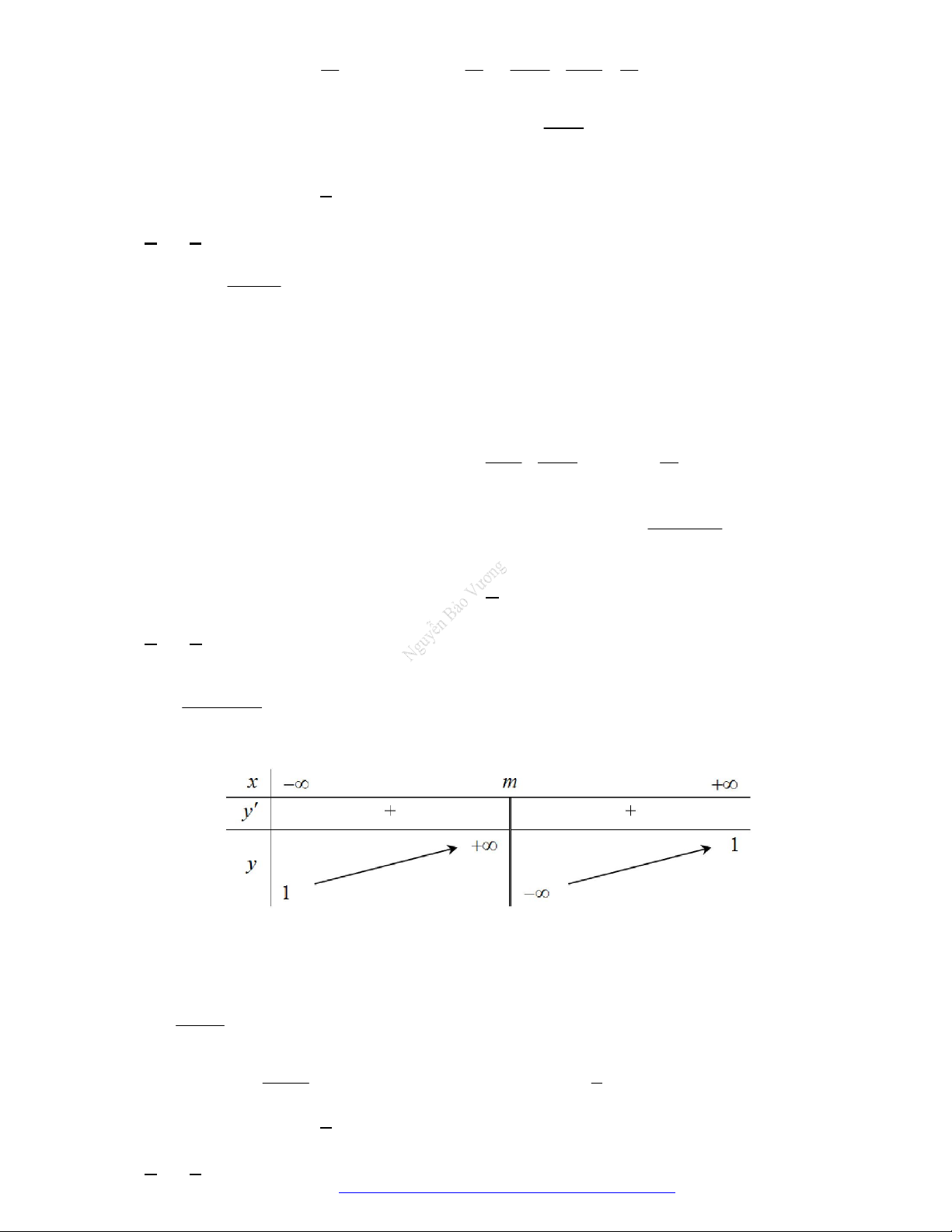
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Khi đó:
1;2
1;2
16 16 2 1 16
min max 2 1 5
3 3 3 2 3
m m
y y y y m
( t/m)
Câu 3. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
1
x m
y
x
trên đoạn
1;2
bằng
8
(
m
là tham
số thực). Khẳng định nào sau đây là đúng?
A.
10m
.
B.
8 10m
.
C.
0 4m
.
D.
4 8m
.
Lời giải
Chọn B
Ta có:
2
1
1
m
y
x
.
- Nếu
1 1m y
(loại).
- Nếu
1m
khi đó
0, 1;2y x
hoặc
0, 1;2y x
nên hàm số đạt giá trị lớn nhất và
nhỏ nhất tại
1, 2x x
.
Theo bài ra:
1;2
1;2
1 2 41
max min 8 1 2 8 8;10
2 3 5
m m
y y y y m
.
Câu 4. Có bao nhiêu giá trị của tham số
m
để giá trị lớn nhất của hàm số
2
2x m
y
x m
trên đoạn
0;4
bằng
1.
A.
3
. B.
2
. C.
1
. D.
0
.
Lời giải
Chọn C
Tập xác định:
\D m
.
2
2
2
0,
m m
y x m
x m
. Do đó hàm số đồng biến trên mỗi khoảng
;m
và
;m
.
Bảng biến thiên của hàm số:
Từ bảng biến thiên suy ra, hàm số đạt giá trị lớn nhất trên đoạn
0;4
bằng
1
khi
0
4 1
m
f
2
0
2
1
4
m
m
m
2
0
6 0
m
m m
0
2, 3
m
m m
3m
.
Câu 5. Cho hàm số
2
1x
y
x m
(m là tham số thực) thỏa mãn
3; 2
1
min
2
y
. Mệnh đề nào dưới đây đúng?
A.
3 4m
. B.
2 3m
. C.
4m
. D.
2m
.
Lời giải
Chọn B
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
+TXĐ:
2
\ , 3; 2
D m D
.
+ Ta có
2
2
2
1
' 0,
m
y x D
x m
. Nên hàm số nghịch biến trên từng khoảng xác định.
Nên
2
2
3; 2
1 2 1
min 2 2 2 0 2 3
2 2
y y m m m
m
.
Câu 6. Tìm giá trị dương của tham số
m
để giá trị nhỏ nhất của hàm số
2
1
2
m x
y
x
trên đoạn
1;3
bằng
1
.
A.
2
m
. B.
3
m . C.
4
m
. D.
2
m
.
Lời giải
Chọn A
Tập xác định:
\ 2
D
.
Ta có:
2
2
2 1
0, 2
2
m
y x
x
.
Hàm số đồng biến trên đoạn
1;3
nên
1;3
max 3y y
2
3 1
1
5
m
2
m
(vì
0
m
).
Câu 7. Cho hàm số
2
8
x m
y
x
với
m
là tham số thực. Giả sử
0
m
là giá trị dương của tham số
m
để
hàm số có giá trị nhỏ nhất trên đoạn
0;3
bằng 3. Giá trị
0
m
thuộc khoảng nào trong các khoảng
cho dưới đây?
A.
2;5
. B.
1;4
. C.
6;9
. D.
20;25
.
Lời giải
Chọn A
+ TXĐ:
\ 8
D
.
+
2
'
2
8
0,
8
m
y x D
x
Vậy hàm số
2
8
x m
y
x
đồng biến trên
0;3
.
2
0;3
min (0)
8
m
y y
Để
2
0;3
min 3 3 2 6.
8
m
y m
0
2 6 2;5
m
. Vậy chọnA.
Câu 8. (THPT Hai Bà Trưng - Huế 2019) Tìm giá trị của tham số thực
m
để giá trị nhỏ nhất của hàm
số
2
1
x m
y
x
trên đoạn
0;4
bằng
3
.
A.
3
m
. B.
1
m
. C.
7
m
. D.
5
m
Lời giải
Chọn C

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta có:
2
2
'
1
m
y
x
.
+ Xét
2
m
.
Hàm số trở thành:
2
y
là hàm số hằng nên không đạt giá trị nhỏ nhất bằng
3
2
m
(loại)
+ Xét
2
m
.
2
2
' 0 ( 1)
1
m
y x
x
0;4
8
min (4)
5
m
y y
.
8
3 7
5
m
m
(thoả mãn).
+ Xét
2
m
.
2
2
' 0 ( 1)
1
m
y x
x
0;4
min (0)
y y m
.
3
m
(loại).
Vậy
7
m
.
Câu 9. (Thpt Vĩnh Lộc - Thanh Hóa 2019) Tìm các giá trị của tham số
m
để giá trị nhỏ nhất của hàm
số
2
1
x m m
y
x
trên đoạn
0;1
bằng
2
.
A.
1
2
m
m
. B.
1
2
m
m
. C.
1
2
m
m
. D.
1
2
m
m
.
Lời giải
Chọn D
Tập xác định:
\ 1
D
.
Hàm số đã cho liên tục trên
0;1
.
Ta có:
2
2
2 2
1
1
0
1 1
m m
m m
y
x x
;
x D
.
Hàm số đồng biến trên đoạn
0;1
.
Trên
0;1
hàm số đạt giá trị nhỏ nhất tại
0
x
.
Ta có:
2 2
1
0 2 2 2 0
2
m
y m m m m
m
.
Câu 10. (THPT Lê Văn Thịnh Bắc Ninh 2019) Cho hàm số
1
x m
y
x
(
m
là tham số thực) thỏa mãn
0;1
min 3y
. Mệnh đề nào dưới đây đúng?
A.
1 3m
B.
6m
C.
1m
D.
3 6m
Lời giải
Chọn D
Tập xác định:
\ 1
D
.
Với
1m
1y
,
0;1
x
thì
0;1
min 3y
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Suy ra
1m
. Khi đó
2
1
1
m
y
x
không đổi dấu trên từng khoảng xác định.
TH 1:
0 1y m
thì
0;1
min 0 3
y y m
(loại).
TH 2:
0 1y m
thì
0;1
min 1 5
y y m
( thỏa mãn).
Câu 11. (Chuyên KHTN 2019) Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
1
x m
y
x
trên
1; 2
bằng
8
(
m
là tham số thực). Khẳng định nào sau đây đúng?
A.
10
m
. B.
8 10
m
. C.
0 4
m
. D.
4 8
m
.
Lời giải
Nếu
1
m
thì
1
y
(không thỏa mãn tổng của giá trị lớn nhất và nhỏ nhất bằng 8)
Nếu
1
m
thì hàm số đã cho liên tục trên
1; 2
và
2
1
'
1
m
y
x
.
Khi đó đạo hàm của hàm số không đổi dấu trên đoạn
1;2
.
Do vậy
1;2 1;2
1 2 41
1 2 8
2 3 5
x x
m m
Min y Max y y y m
.
Câu 12. (Chuyên Bắc Ninh 2019) Gọi
,A B
lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của hàm số
2
1
x m m
y
x
trên đoạn
2;3
. Tìm tất cả các giá trị thực của tham số
m
để
13
2
A B
.
A.
1; 2
m m
. B.
2
m
. C.
2
m
. D.
1; 2
m m
.
Lời giải
Xét hàm số
2
1
x m m
y
x
trên đoạn
2;3
.
2 2 2
2
1 3 2
' 0 2;3 3 , 2
2 1
1
m m m m m m
y x A f B f
x
.
2 2
1
13 3 2 13
2
2 2 1 2
m
m m m m
A B
m
.
Câu 13. (Sở Hưng Yên) Cho hàm số
2
8
x m
f x
x
với
m
là tham số thực. Giả sử
0
m
là giá trị dương
của tham số
m
để hàm số có giá trị nhỏ nhất trên đoạn
0;3
bằng
3
. Giá trị
0
m
thuộc khoảng
nào trong các khoảng cho dưới đây?
A.
20;25
. B.
5;6
. C.
6;9
. D.
2;5
.
Lời giải
Chọn D
Xét hàm số
2
8
x m
f x
x
trên đoạn
0;3
.
Ta có:
2
2
8
0, 0;3
8
m
y x
x
hàm số
2
8
x m
f x
x
đồng biến trên đoạn
0;3

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
0;3
min 0 .
8
m
f x f
Theo giả thiết, ta có:
2
2
0;3
2 6
min 3 3 24 .
8
2 6
m
m
f x m
m
Mà
0, 2 6 4,9 2;5
m m m
.
Câu 14. (Chuyên - Vĩnh Phúc 2019) Tìm tất cả các giá trị của tham số
m
để giá trị nhỏ nhất của hàm số
3 2
3
y x x m
trên đoạn
1;1
bằng
0
.
A.
2.
m
B.
6.
m
C.
0.
m
D.
4.
m
Lời giải
Chọn D
Xét hàm số
3 2
3
y x x m
trên đoạn
1;1
, ta có
2
0 1;1
3 6 ; 0
2 1;1
x
y x x y
x
Mà
( 1) m 2
(0) m
(1) m 4
y
y
y
Do đó
1;1
min 4 0 4.
y m m
Vậy
4
m
thỏa yêu cầu bài toán.
Câu 15. (Sở Quảng Trị 2019) Tìm tất cả các giá trị thực của tham số m để hàm số
3 2
3
y x x m
có giá
trị nhỏ nhất trên đoạn
1;1
bằng
2
A.
2
m
. B.
2 2
m
. C.
4 2
m
. D.
2 2
4 2
m
m
.
Lời giải
Chọn C
2
' 3 6y x x
0
' 0
2
x
y
x
Trên
1;1
thì
1 0 1
' 4; ' ; ' 2
y m y m y m
nên
1;1
2 4 2 4 2
Miny m m
Câu 16. (Cụm Liên Trường Hải Phòng 2019) Có một giá trị
0
m
của tham số
m
để hàm số
3 2
1 1
y x m x m
đạt giá trị nhỏ nhất bằng
5
trên đoạn
0;1
. Mệnh đề nào sau đây là
đúng?
A.
2
0 0
2018 0
m m
. B.
0
2 1 0
m
. C.
2
0 0
6 0
m m
. D.
0
2 1 0
m
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Lời giải
+ Đặt
3 2
1 1
f x x m x m
.
+ Ta có:
2 2
3 1
y x m
. Dễ thấy rằng
0
y
với mọi
x
,
m
thuộc
nên hàm số đồng biến
trên
, suy ra hàm số đồng biến trên
0;1
. Vì thế
0;1
min y
0;1
min
f x
0f
1
m
.
+ Theo bài ra ta có:
1 5
m
, suy ra
4
m
.
+ Như vậy
0
4
m
và mệnh đề đúng là
2
0 0
2018 0
m m
.
Câu 17. (THCS - THPT Nguyễn Khuyến 2019) Nếu hàm số
2
1
y x m x
có giá trị lớn nhất bằng
2 2
thì giá trị của
m
là
A.
2
2
. B.
2
. C.
2
. D.
2
2
.
Lời giải
Xét hàm số
2
1
y x m x
Tập xác định:
1;1
D
.
Ta có:
2
1
1
x
y
x
2
2
1
0
1 0
x x
y
x
2
1 0
1
x
x x
2
1 0
1
1 0
1
2
2 1
2
1
2
x
x
x
x
x
x
.
Ta có:
1
1 1 , 1 1 , 2
2
y m y m y m
.
Do hàm số
2
1
y x m x
liên tục trên
1;1
nên
1;1
Max 2
y m
.
Theo bài ra thì
1;1
Max 2 2
y
, suy ra
2 2 2 2
m m
.
Câu 18. (THPT Ngô Gia Tự Vĩnh Phúc 2019) Cho hàm số
3 2
2 3
y x x m
. Trên
1;1
hàm số có giá
trị nhỏ nhất là
1
. Tính
m
?
A.
6
m
. B.
3
m
. C.
4
m
. D.
5
m
.
Lời giải
Chọn C
Xét
1;1
có
2
6 6y x x
.
0
y
2
6 6 0
x x
0 1;1
1 1;1
x
x
.
Khi đó
1 5
y m
;
0
y m
;
1 1
y m
Ta thấy
5 1
m m m
nên
1;1
min 5
y m
.
Theo bài ra ta có
1;1
min 1
y
nên
5 1
m
4
m
.
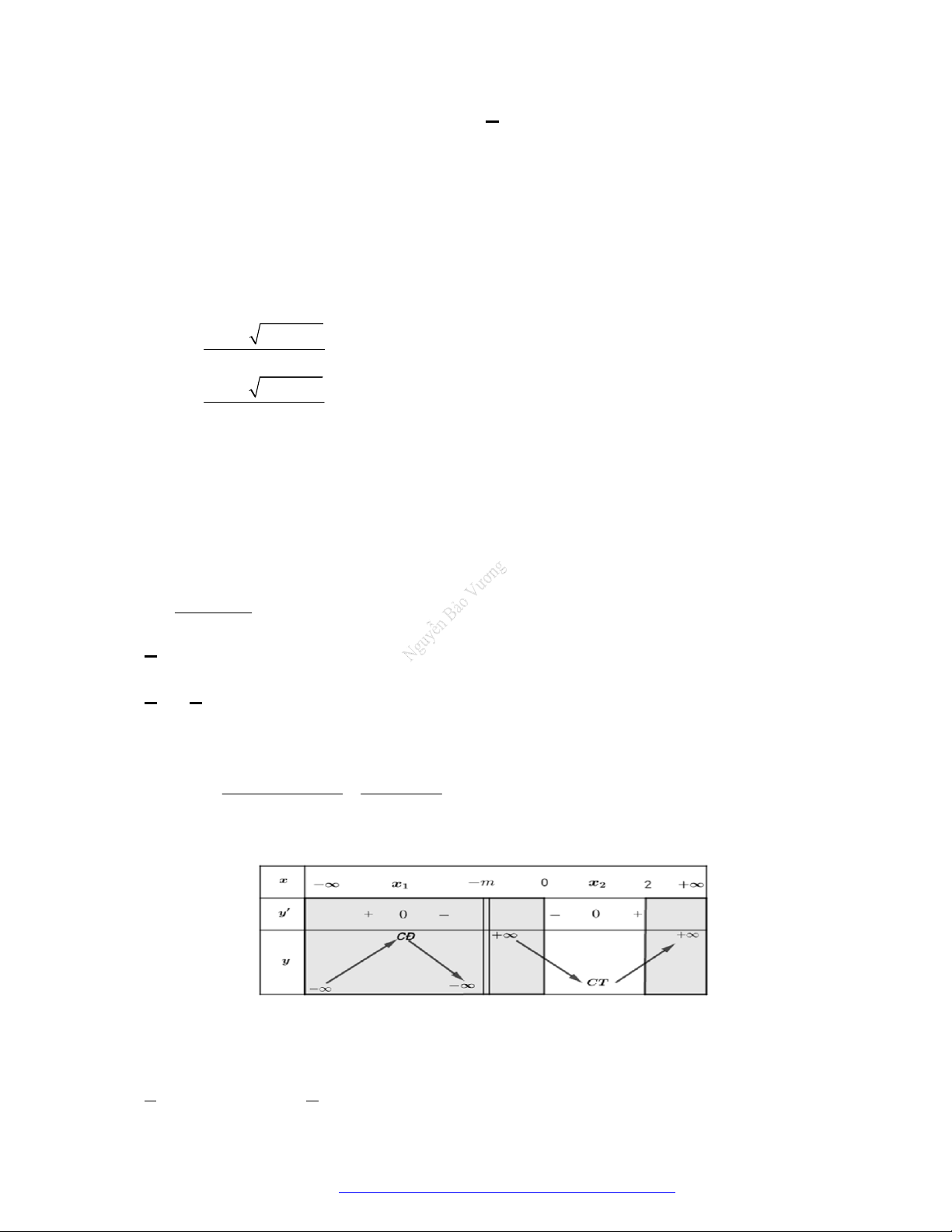
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 19. Biết
S
là tập giá trị của
m
để tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
4 2 3 2
2y x m x x m
trên đoạn
0;1
bằng
16
. Tính tích các phần tử của
S
.
A.
2
. B.
2
. C.
15
. D.
17
.
Lời giải
TXĐ:
D
.
Ta có:
3 2 2
4 3 4y x m x x
3 2 2
2 2 2
0
0 4 3 4 0
4 3 4 0 9 64
x
y x m x x
x m x m
2 4
2 4
0
3 9 64
1
8
3 9 64
0
8
x
m m
x
m m
x
Nên hàm số đơn điệu trên
0;1
.
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn
0;1
bằng
16
nên
2 2
0 1 16 1 16 2 15 0y y m m m m m
.
Vậy
1 2
. 15m m
.
Câu 20. (THPT An Lão Hải Phòng 2019) Tìm tất cả giá trị thực của tham số
m
để hàm số
2
1x mx
y
x m
liên tục và đạt giá trị nhỏ nhất trên đoạn
0;2
tại một điểm
0
0;2x
.
A.
0 1m
B.
1m
C.
2m
D.
1 1m
Lời giải
Chọn A
Tập xác định:
\ D m
. Hàm số liên tục trên
0;2
0 0
2 2
m m
m m
Ta có
2
2 2
2 2
1
2 1
x m
x mx m
y
x m x m
. Cho
1
2
1
0
1
x m
y
x m
.
Ta có bảng biến thiên
Hàm số đạt giá trị nhỏ nhất tại
0
0;2x
nên
0 1 2 1 1m m
So với điều kiện hàm số liên tục trên đoạn
0;2
. Ta có
0 1m
.
CÓ THỂ GIẢI NHƯ SAU:
Điều kiện xác định x m
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Hàm số liên tục trên đoạn
0;2
nên
0 0
0;2 *
2 2
m m
m
m m
2
2 2
2 2
1
2 1
'
x m
x mx m
y
x m x m
' 0
y
có hai nghiệm là
1
2
1
1
x m
x m
,
1 2
2
x x
nên chỉ có nhiều nhất một nghiệm thuộc
0;2
Ta thấy
1 1,m m m
và do đó để hàm số liên tục và đạt giá trị nhỏ nhất trên
0;2
tại một
điểm
0
0; 2
x
thì
0 1 2 1 1 **
m m
Từ
* , **
ta có
0 1
m
Câu 21. (THPT Bạch Đằng Quảng Ninh 2019) Cho hàm số
1 sin
cos 2
m x
y
x
. Có bao nhiêu giá trị nguyên
của tham số
m
thuộc đoạn
0;10
để giá trị nhỏ nhất của hàm số nhỏ hơn
2
?
A.
1
. B.
9
. C.
3
. D.
6
.
Lời giải
Tập xác định:
D
.
Ta có:
1 sin
cos 2
m x
y
x
cos sin 1 2y x m x y
.
Phương trình có nghiệm khi và chỉ khi:
2 2 2
1 4 4y m y y
2 2
3 4 1 0
y y m
2 2
2 1 3 2 1 3
3 3
m m
y
.
Theo đề bài, ta có:
2
2 1 3
min 2
3
0;10
x
m
y
m
m
2
1 3 8
0;10
m
m
m
2
3 63
0;10
m
m
m
2
21
0;10
m
m
m
5,6,7,8,9,10
m
.
Vậy có
6
giá trị nguyên của tham số
m
thỏa yêu cầu bài toán.
Câu 22. (HSG Bắc Ninh 2019) Cho hàm số
3
, 0
y ax cx d a
có
;0
min 2
x
f x f
. Giá trị lớn
nhất của hàm số
y f x
trên đoạn
1;3
bằng
A.
11d a
. B.
16d a
. C.
2d a
. D.
8d a
.
Lời giải
Vì
3
, 0
y ax cx d a
là hàm số bậc ba và có
;0
min 2
x
f x f
nên
0
a
và
' 0
y
có hai
nghiệm phân biệt.
Ta có
2
' 3 0
y ax c
có hai nghiệm phân biệt
0
ac
.
Vậy với
0, 0
a c
thì
' 0
y
có hai nghiệm đối nhau
3
c
x
a
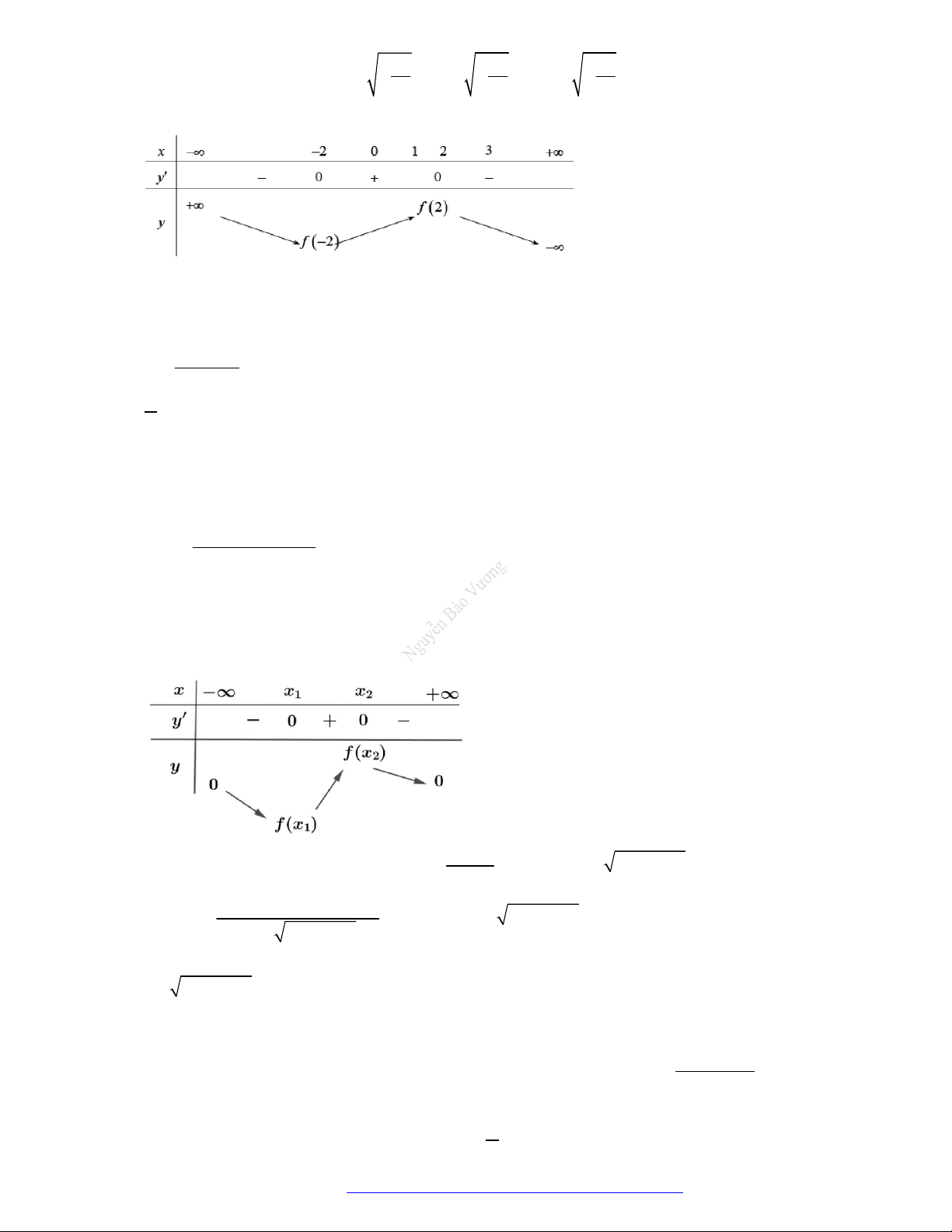
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Từ đó suy ra
;0
min
3
x
c
f x f
a
2 2 12
3 3
c c
c a
a a
Ta có bảng biến thiên
Ta suy ra
1;3
max 2 8 2 16
x
f x f a c d a d
.
Câu 23. (THPT Nghĩa Hưng Nam Định 2019) Tìm tất cả các giá trị của tham số m để hàm số
2
1
x m
y
x x
có giá trị lớn nhất trên
nhỏ hơn hoặc bằng 1.
A.
1m
. B.
1m
. C.
1m
. D.
1m
.
Lời giải
Chọn A
+ TXĐ:
D
.
+
lim 0
x
y
+
2
2
2
2 1
1
x mx m
y
x x
.
2
0 2 1 0 (*)y x mx m
2
(*)
1 0,m m m
nên (*) có 2 nghiệm phân biệt
1 2
,x x m
+ BBT:
Vậy hàm số đạt giá trị lón nhất là
2
2
1
2 1
f x
x
với
2
2
1x m m m
2
2
1
1 1 2 2 1 1
2 2 1 1
YCBT m m m
m m m
( vì
2 2
0 2 1 0f x x
)
2
2 2
0
0
1 1
1
m
m
m m m m
m m m
Câu 24. (Chuyên Nguyễn Trãi Hải Dương 2019) Giá trị lớn nhất của hàm số
3 2
1
x x m
y
x
trên
0;2
bằng
5
. Tham số
m
nhận giá trị là
A.
5
. B.
1
. C.
3
. D.
8
.
Lời giải
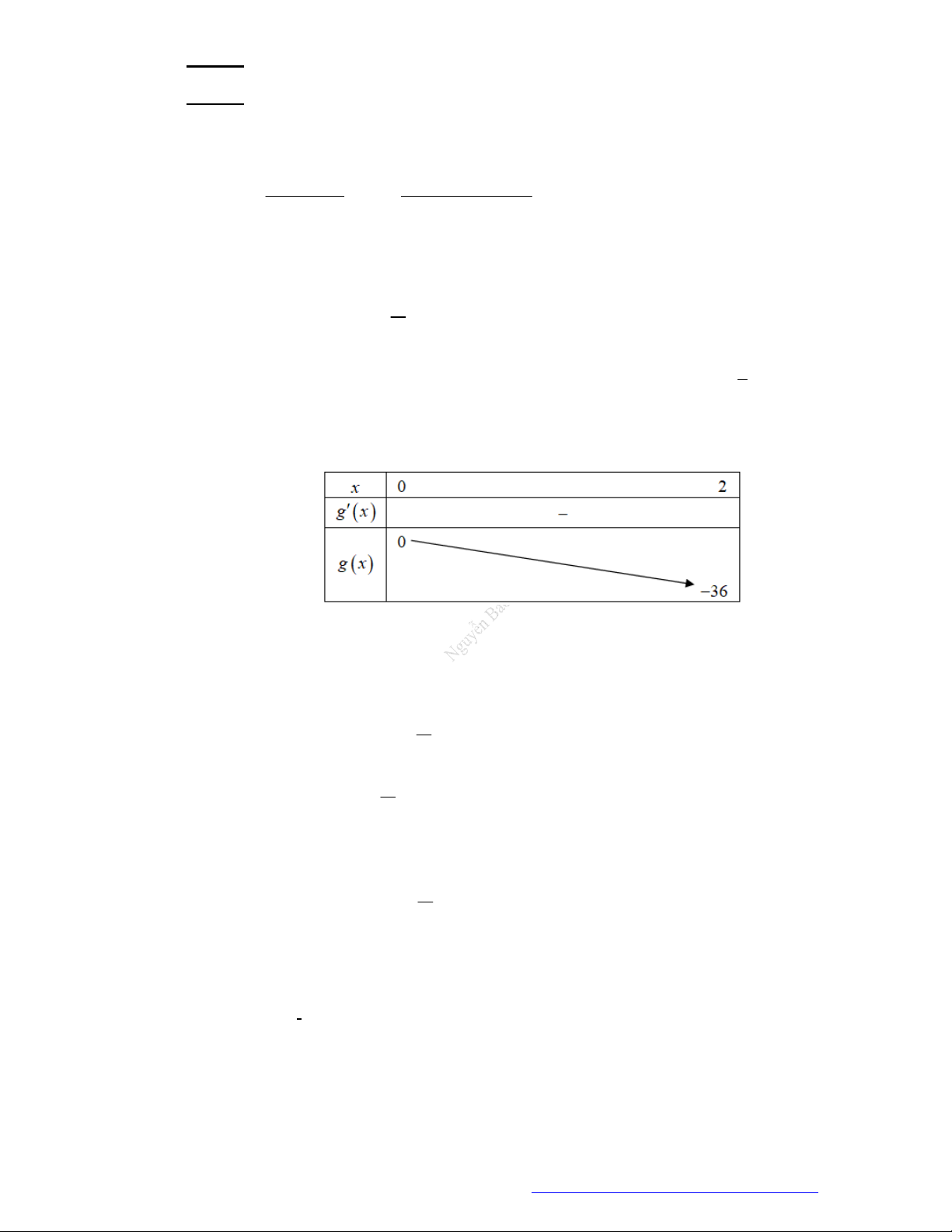
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Chọn C
Cách 1:
Tập xác định của hàm số:
\ 1 0;2D D
.
Ta có:
3 2 3 2
2
2 4 2
1
1
x x m x x x m
y y
x
x
.
3 2 3 2
0 2 4 2 0 2 4 2y x x x m x x x m
(1).
Ta có
0 ; 2 4
3
m
y m y
Đặt
3 2 2
1
2 4 2 6 8 2 0 1
3
g x x x x g x x x x x
.
Trên
0;2
ta có bảng biến thiên:
Từ bảng biến thiên ta có
36;0 , 0;2g x x
.
Trường hợp 1:
0m
phương trình (1) vô nghiệm phương trình
0y
vô nghiệm.
Dễ thấy
0 2 4 0
3
m
y m y khi m
.
Khi đó
0;2
Max 2 4 5 3
3
m
y y m
loại do
0m
.
Trường hợp 2:
36m
phương trình (1) vô nghiệm phương trình
0y
vô nghiệm.
Dễ thấy
0 2 4 36
3
m
y m y khi m
.
Khi đó
0;2
Max 0 5 5y y m m
loại do
36m
.
Trường hợp 3:
36;0m
phương trình
0y
có nghiệm duy nhất (giả sử
0
x x ).
Trên
0;2
ta có bảng biến thiên:
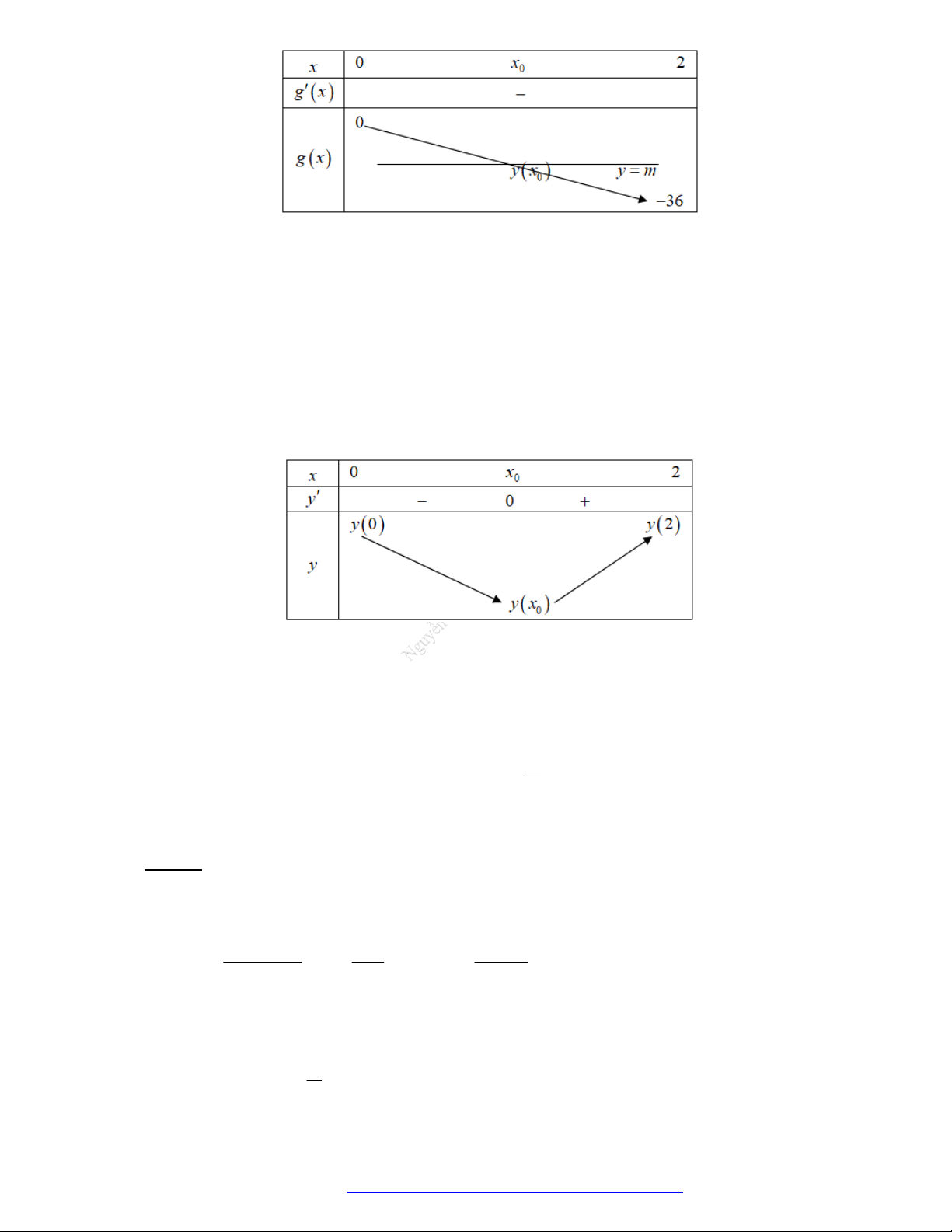
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Nhìn vào bảng biến thiên ta có:
+
3 2 3 2
0
: 2 4 2 2 4 2 0 0x x g x m x x x m x x x m y
.
+
3 2 3 2
0
0; : 2 4 2 2 4 2 0 0x x g x m x x x m x x x m y
.
+
3 2 3 2
0
;0 : 2 4 2 2 4 2 0 0x x g x m x x x m x x x m y
.
Ta có bảng biến thiên sau:
Từ bảng biến thiên ta thấy
0;2
Max 2 ; 0y y y
.
Nếu m
0;2
36; 6 0 2 Max 0 5 5y y y y m m l
.
Nếu m
0;2
6;0 0 2 Max 2 4 5 3( )
3
m
y y y y m n
.
Vậy
3m
thỏa đề.
Cách 2:
Tập xác định của hàm số:
\ 1 0;2D D
.
Ta có:
3 2
2
2
2
1 1
1
x x m m m
y x y x
x x
x
.
Trường hợp 1:
0 0, 0;2m y x
Hàm số đồng biến trên
0;2
.
0;2
Max 2 4 5 3
3
m
y y m
loại do
0m
.
Trường hợp 2:
0m
, giả sử
0
0;2
Max y y x
với
0
0;2x
. Do hàm số liên tục trên
0;2
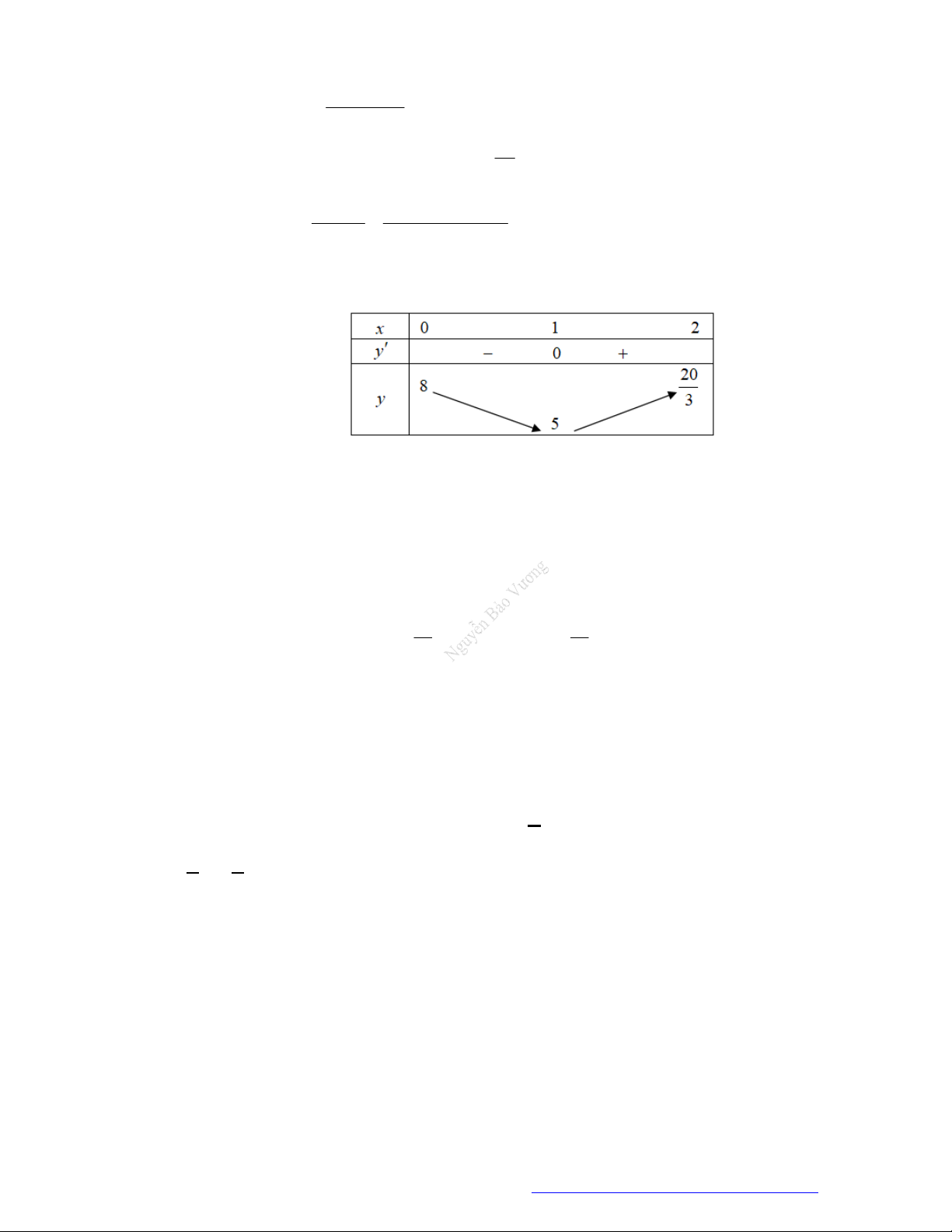
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
2
0 0
0
3 2
0 0
0
0
2 1
0
5
5
1
m x x
y x
x x m
y x
x
2
3 2
0 0 0 0 0 0
5
2 1 5 1 1( ) 8
3
x x x x x x x n m
.
Khi đó:
3 2
2 2
8 2 4 2 8
2 0 1
1 1
x x x
y x y x
x x
.
Ta có bảng biên thiên:
8m
không thỏa yêu cầu đề.
Nên không tồn tại
0
0;2x
để
0
0;2
Max y y x
.
0; 2
0; 2
Max 2 5
Max 0 3
y y m
y y m
.
Nếu
0;2
17 17
5 0 5; 2 Max 2 5 5
3 3
m y y y y m l
.
Nếu
0;2
3 0 3; 2 5 Max 2 5 3m y y y y m n
.
Vậy
3m
thỏa đề.
Câu 25. Cho hàm số
2
3
3y x x m . Tổng tất cả các giá trị của tham số
m
sao cho giá trị nhỏ nhất của
hàm số trên đoạn
1;1
bằng
1
là
A.
1
. B.
4
. C.
0
. D.
4
.
Lời giải
Chọn C
.D
Đặt
3
3 , 1;1 2;2 .t x x x t
Khi đó ta có hàm số
2
.f t t m
2 ; 0 .f t t m f t t m
Trường hợp 1:
2 2 2 2.m m
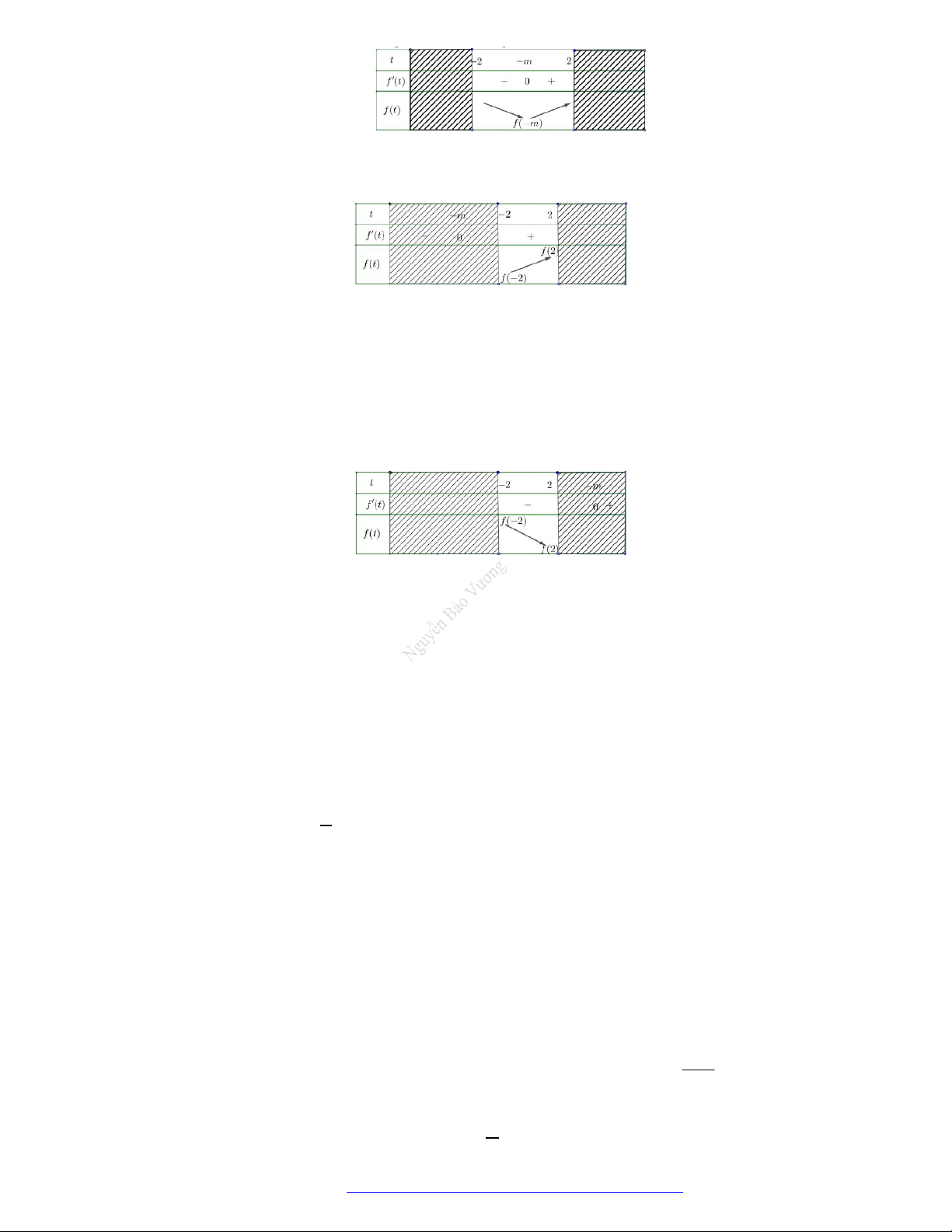
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Từ bảng biến thiên ta thấy:
2;2
min 0f t f m
không thỏa mãn yêu cầu.
Trường hợp 2:
2 2m m
Từ bảng biến thiên ta thấy:
2
2;2
min 2 2f t f m
.
Theo yêu cầu bài toán:
2
2
3
2 1 3.
1
m
m
m m
m
Trường hợp 3:
2 2m m
Từ bảng biến thiên ta thấy:
2
2;2
min 2 2 .f t f m
Theo yêu cầu bài toán:
2
2
3
2 1 3.
1
m
m
m m
m
Vậy tổng các giá trị của tham số
m
thỏa mãn yêu cầu là:
3 3 0.
Câu 26. (Chuyên Vĩnh Phúc 2018) Tìm tất cả các giá trị của
0m
để giá trị nhỏ nhất của hàm số
3
3 1y x x trên đoạn
1; 2m m
luôn bé hơn
3
.
A.
0;2m
. B.
0;1m
. C.
1;m
. D.
0;m
.
Lời giải
Ta có
2
3 3y x
,
0 1y x
do đó
1 1
CT
y y
và
C
1 3
Đ
y y
.
Thấy ngay với
0m
thì trên đoạn
1; 2m m
hàm số luôn đồng biến.
Vậy GTNN của hàm số đã cho trên đoạn
1; 2m m
là
3
1 1 3 1 1y m m m
.
GTNN luôn bé hơn
3
3
1 3 1 2 0m m
1 2
1 1
m
m
1
2
m
m
.
Kết hợp điều kiện
0m
ta được
0;1m
.
Câu 27. (Chuyên Đh Vinh 2018) Biết rằng giá trị nhỏ nhất của hàm số
36
1
y mx
x
trên
0;3
bằng
20
. Mệnh đề nào sau đây đúng?
A.
0 2m
. B.
4 8m
. C.
2 4m
. D.
8m
.
Lời giải
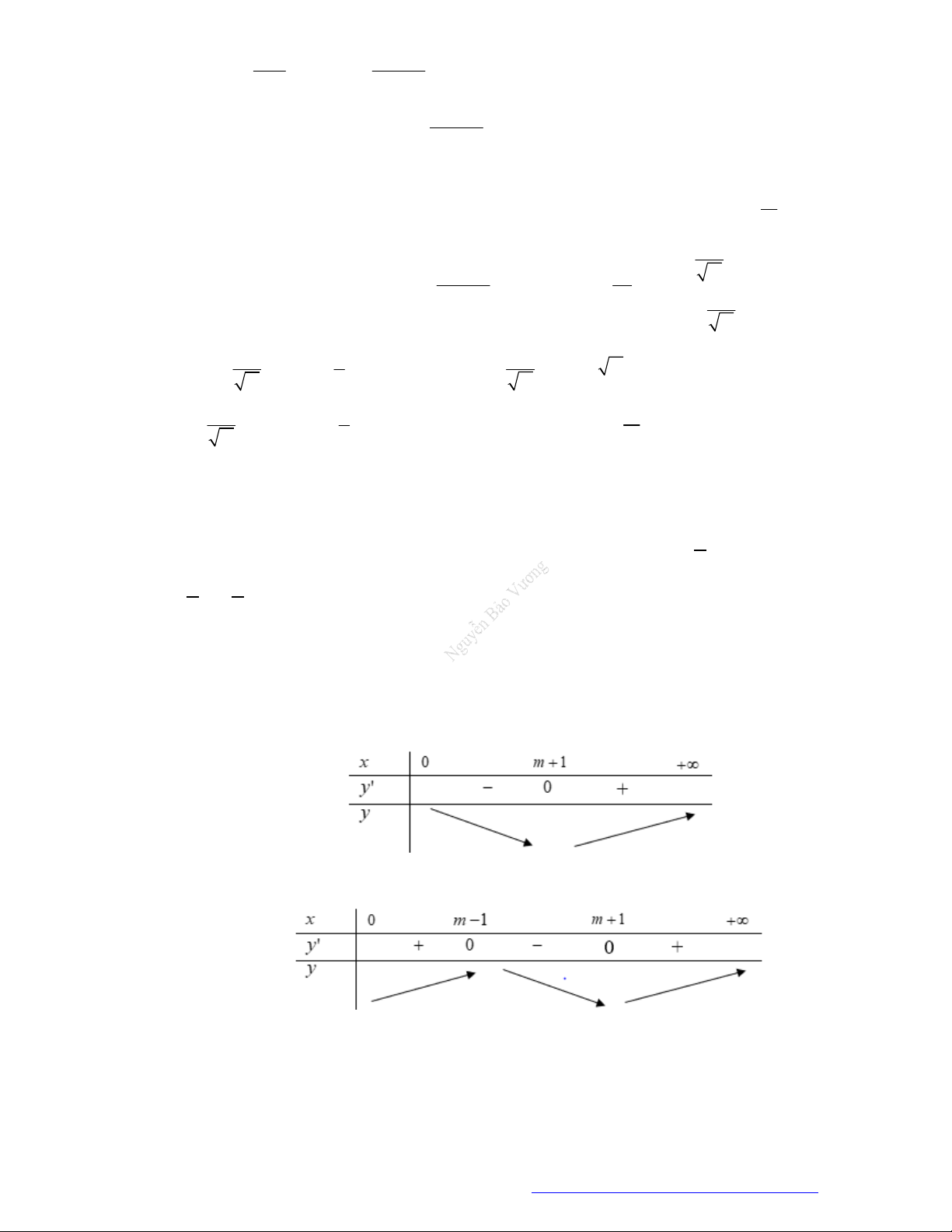
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
36
1
y mx
x
2
36
1
y m
x
Trường hợp 1:
0m
, ta có
2
36
0, 1
1
y x
x
.Khi đó
0;3
min 3 9
x
y y
(loại).
Trường hợp 2:
0m
Nếu
0m
, ta có
0y
,
1x
Khi đó
0;3
min 3
x
y y
11
20 3 9
3
m m
(loại).
Nếu
0m
, khi đó
2
36
0 0
1
y m
x
2
36
1x
m
6
1
6
1
x
m
x l
m
.
6 4
0 1 3 36
9
m
m
,
0;3
4
6
min 1 12 20
100
x
m
y y m m
m l
m
.
6 9
1 3
4
m
m
,
0;3
min 3
x
y y
11
20 3 9
3
m m l
.
Câu 28. (Chuyên Thái Bình - 2020) Cho hàm số
3 2 2
3 3 1 2020y x mx m x
. Có tất cả bao nhiêu
giá trị nguyên của
m
sao cho hàm số có giá trị nhỏ nhất trên khoảng
0;
?
A.
2
. B.
1
. C. Vô số. D.
3
.
Lời giải
Chọn D
Ta có:
1
2 2
2
1
' 3 6 3 1 0
1
x m
y x mx m
x m
.
Để hàm số có giá trị nhỏ nhất trên khoảng
0;
thì
1 2
0x x hoặc
1 2
0 x x .
TH1:
1 2
0x x
1 0 1m m 1 1m
. Do
m
0;1m
.
BBT của hàm số:
TH2:
1 2
0 x x .
BBT của hàm số
Hàm số có giá trị nhỏ nhất trên khoảng
0;
khi và chỉ khi
1 0
1 0
m
y m y
.
3 2
2
1
1 3 1 3 1 1 2020 2020
m
m m m m m

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
1
1 2 0
m
m m
1
2
1
m
m
m
1 2m
.
Do
m 2m
.
Vậy
0;1;2m
.
Câu 29. (Sở Bình Phước - 2020) Cho hàm số
1f x m x (
m
là tham số thực khác 0). Gọi
1 2
,m m là
hai giá trị của
m
thoả mãn
2
2;5
2;5
min ax 10f x m f x m
. Giá trị của
1 2
m m bằng
A. 3. B. 5. C. 10. D. 2.
Lời giải
Chọn A
Ta có
'
1
.
2 1
f x m
x
;
Do
0m
nên
'
f x
khác 0 và có dấu không thay đổi với
1; .x
Nếu
0m
thì
'
0, 2;5f x x
. Do đó
2;5
2;5
min 2 ; ax 5 2 .f x f m m f x f m
2
2;5
2;5
2
1
2
2
min ax 10
2 10
2
3 10 0
5
f x m f x m
m m m
m
m m
m
Do
0m
nên nhận
2
5.m
Nếu
0m
thì
'
0, 2;5f x x
. Do đó
2;5
2;5
min 5 2 ; ax 2 .f x f m m f x f m
2
2;5
2;5
2
1
2
2
min ax 10
2 10
2
3 10 0
5
f x m f x m
m m m
m
m m
m
Do
0m
nên nhận
1
2.m
Vậy
1 2
3.m m
Câu 30. (Bỉm Sơn - Thanh Hóa - 2020) Cho hàm số có bao nhiêu giá trị nguyên của tham
số thuộc đoạn
để giá trị nhỏ nhất của nhỏ hơn .
A. . B. . C. . D. .
Lời giải
Chọn C
Điều kiện: luôn đúng .
(do luôn đúng )
sin 1
cos 2
m x
y
x
m
5;5
y
1
4
2
6
8
cos 2 0
x
x
sin 1
cos 2 sin 1
cos 2
m x
y y x m x
x
cos 2 0
x
x

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
(*).
Phương trình (*) có nghiệm
.
Vậy .
.
Mà nên .
Câu 31. (Lê Lai - Thanh Hóa - 2020) Gọi là tập hợp tất cả các giá trị thực của tham số sao cho giá
trị nhỏ nhất của hàm số trên đoạn bằng 2. Tổng tất cả các phần
tử của bằng
A. . B. . C. . D. .
Lời giải
Chọn B
Ta có
Nhận thấy .
Xét hàm số trên , ta có:
+ ,
+
Do đó , tức .
Từ đây ta có
. Suy ra . Vậy, tổng các phần tử của là .
Câu 32. (THPT Nguyễn Viết Xuân - 2020) Cho hàm số
2
3
3 1y x x m
. Tổng tất cả các giá trị của
tham số
m
sao cho giá trị nhỏ nhất của hàm số trên đoạn
1;1
bằng
1
là
A.
2
. B.
4
. C.
4
. D.
0
.
Lời giải
Chọn A
Đặt
2
3
( ) 3 1y f x x x m là hàm số xác định và liên tục trên đoạn
1;1
.
Ta có
3 2
( ) 2 3 1 3 3y f x x x m x
.
sin cos 2 1m x y x y
2 2
2
2 2 2 2
2 1 3 2 1 3
2 1 3 4 1 0
3 3
m m
m y y y y m y
2
2 1 3
3
m
Min y
2
2 2
2 2 2,82
2 1 3
1 1 1 3 5 8 0
3
2 2 2,82
m
m
Min y m m
m
, 5;5
m m
5; 4; 3;3;4;5
m
S
m
2
3
34
3 2 1
f x
x x m
0;3
S
8
8
6
1
2
3 3
3 2 3 2x x m x x m
0;3
min 2
f x
3
0;3
max 3 2 16 1
x x m
3
3 2g x x x m
0;3
2
' 3 3
g x x
2
' 3 3 0
g x x
1 0;3
1 0;3
x
x
0 2 , 1 2 2, 3 2 18
g m g m g m
2 2 2 18, 0;3
m g x m x
3
0;3 0;3
max 3 2 max 2 2 ; 2 18
x x m m m
0;3
1 max 2 2 ; 2 18 16
m m
2 18 2 2
2 18 16
1
7
2 18 2 2
2 2 16
m m
m
m
m
m m
m
7; 1
S
S
8

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
3
1
( ) 0
3 1 ( )
x
f x
m x x g x
.
Ta khảo sát hàm số
( )g x
trên đoạn
1;1
.
Bảng biến thiên của
( )g x
Nếu
3;1m
thì luôn tồn tại
0
1;1x
sao cho
0
( )m g x hay
0
( ) 0f x . Suy ra
1;1
min 0y
, tức là không tồn tại
m
thỏa mãn yêu cầu bài toán.
Nếu
3;1m
thì
( ) 0 1 1;1f x x
.
Ta có:
2 2
1;1
min ( ) min (1); ( 1) min ( 1) ;( 3)f x f f m m
Trường hợp 1:
1m
tức là
3 1 0m m
suy ra
2
1;1
2 ( )
min ( ) ( 1) 1
0 ( )
m TM
f x m
m KTM
Trường hợp 2:
3m
tức là
1 3 0m m
suy ra
2
1;1
4 ( )
min ( ) ( 3) 1
2 ( )
m TM
f x m
m KTM
Vậy có hai giá trị của
m
thỏa mãn yêu cầu bài toán:
2; 4m m
, từ đó tổng tất cả các giá trị
của
m
là
2
.
Câu 33. (Chuyên Hạ Long - Quảng Ninh - 2020) Cho hàm số
2 2
2 2 4 4 1y f x m x x x m
. Tính tổng tất cả các giá trị của
m
để hàm số
y f x
có giá trị nhỏ nhất bằng
4
.
A.
7
2
. B.
5
2
. C.
1
2
. D.
1
2
.
Lời giải
Chọn C
TXĐ:
2;2D
.
Đặt
2 2t x x
; 2;2 2t
.
2 2
4 2 4t x
2 2
2 4 4x t
.
2 2
2 4 1y g t m t t m
2 2
2 7t m t m
với 2;2 2t
.
Ta có:
2
4g t t m
.
2
0
4
m
g t t
0; m
g t
đồng biến trên 2;2 2
2;2 2
min 2g t g
4
.
Mà
2
2 2 1g m m
2
2 1 4m m
1
3
2
m
m
.
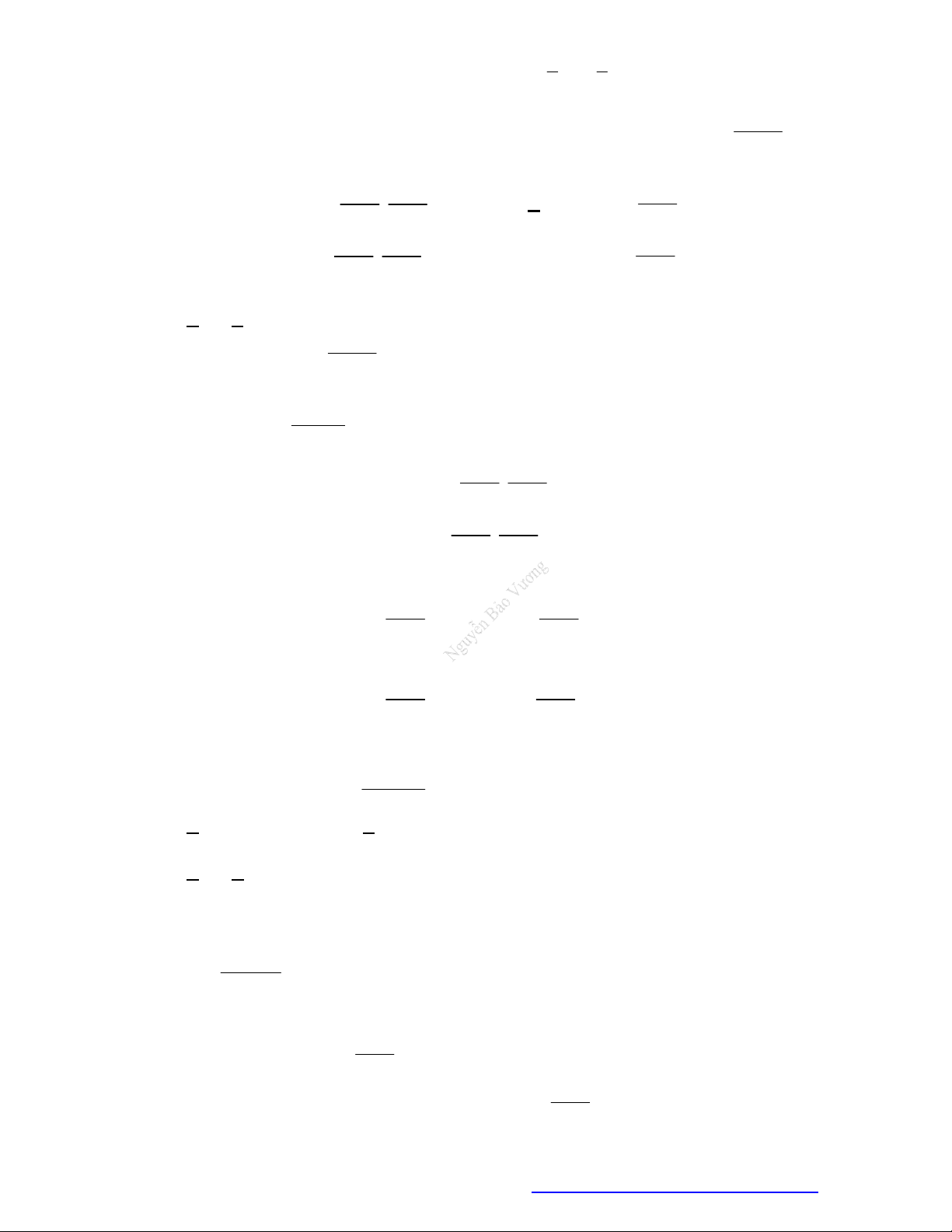
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
Tổng các giá trị của
m
thỏa mãn ycbt là
3 1
1
2 2
S
.
Câu 34. (Chuyên Nguyễn Trãi - Hải Dương - Lần 2 - 2020) Cho hàm số
2
1
x m
f x
x
với
2
m
.
Mệnh đề nào dưới đây sai?
A.
1;3
2 6
max max ;
2 4
m m
f x
. B.
1;3
6
max
4
m
f x
khi
2
m
.
C.
1;3
2 6
min min ;
2 4
m m
f x
. D.
1;3
2
min
2
m
f x
khi
2
m
.
Lời giải
Chọn B
Xét hàm số
2
1
x m
f x
x
với
2
m
.
Tập xác định
1
x
.
Ta có
2
2
1
m
f x
x
suy đạo hàm không đổi dấu
1;3
x
suy ra
1;3
2 6
max max 1 ; 3 max ;
2 4
m m
f x f f
;
1;3
2 6
min min 1 ; 3 min ;
2 4
m m
f x f f
.
Xét với
2
m
0
f x
1;3
x
. Vậy
2
1;3 1
2
m
x f x f
1;3
2
max
2
m
f x
.
Xét với
2
m
0
f x
1;3
x
. Vậy
2
1;3 1
2
m
x f x f
1;3
2
min
2
m
f x
.
Câu 35. (Chuyên Sư Phạm Hà Nội - 2020) Có bao nhiêu số nguyên
m
thuộc đoạn
20 ; 20
để giá trị
lớn nhất của hàm số
6
x m
y
x m
trên đoạn
1 ; 3
là số dương?
A. 9. B. 8. C. 11. D. 10.
Lời giải
Chọn A
Tập xác định
\ .D m
Để hàm số có giá trị lớn nhất trên
1 ; 3
thì
1 ; 3 .
m
2
2 6
.
m
y
x m
Trường hợp 1:
2 6 0 3.
m m
Khi đó
1 ; 3
9
max 3 .
3
x
m
y y
m
Để giá trị lớn nhất trên đoạn
1 ; 3
là số dương thì
9
0 9 0 9.
3
m
m m
m
Vậy các số nguyên
m
thỏa là
8,
7,
6,
5,
4.
Trường hợp 2:
2 6 0 3.
m m

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Khi đó
1;
3
7
ma
x 1 .
1
x
m
y y
m
Để giá t
rị lớn nhất trên đoạn
1 ;
3
là số dương thì
7
0 1 0 1.
1
m
m m
m
Vậy cá
c số nguyên
m
thỏa
mãn là
2,
1,
0.
Trư
ờng hợp 3:
2 6
0 3.
m m
Khi đó
1.
y
Nên
1;
3
max 1.
x
y
Vậy
3
m
thỏa.
Kết luận: có
9 số nguyên
m
thỏa mãn yêu cầu bài toán.
-------------------- HẾT --------------------

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH GIỎI – MỨC ĐỘ 9-10 ĐIỂM
Dạng 1. Định m để GTLN-GTNN của hàm số chứa dấu giá trị tuyệt đối thỏa mãn điều kiện cho trước
Dạng 1: Tìm
m
để
( ) ( )
;
max 0 .y f x m a a
Phương pháp:
Cách 1:Trước tiên tìm
( )
( ) ( )
;
;
max ; min .f x K f x k K k
Kiểm tra
max , .
2 2 2
m K m k m K m k K k
m K m k
TH1: .
2
K k
a
Để
;
max ;
m k a m a k
y a m a k a K
m K a m a K
.
TH2:
2
K k
a
m
.
Cách 2: Xét trường hợp
TH1:
m K a
Max m K
m K m k
TH2:
m k a
Max m k
m k m K
Dạng 2: Tìm
m
để
( ) ( )
;
min 0 .y f x m a a
Phương pháp:
Trước tiên tìm
( )
( ) ( )
;
;
max ; min .f x K f x k K k
Để
;
min .
0 0
m k a m K a m a k m a K
y a
m k m K m k m K
Vậy
1 2
.m S S
Dạng 3: Tìm
m
để
( )
;
max y f x m
không vượt quá giá trị
M
cho trước.
Phương pháp: Trước tiên tìm
( )
( ) ( )
;
;
max ; min .f x K f x k K k
Để
;
max .
m k M
y M M k m M K
m K M
Dạng 4: Tìm
m
để
( )
;
min y f x m
không vượt quá giá trị
a
cho trước.
Phương pháp: Trước tiên tìm
( )
( ) ( )
;
;
max ; min .f x K f x k K k
Để
( )( )
;
min 0 .
0 0
m k a m K a m a k m a K
y a m K m k K m k
m k m K m k m K
Dang 5: Tìm
m
để
( )
;
max
a b
y f x m
đạt min.
GIÁ TRỊ LỚN NHẤT - GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ
Chuyên đề 5

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Phương pháp:
Trước tiên tìm
( )
( ) ( )
;
;
max ; min .
a b
a b
f x K f x k K k
Đề hỏi tìm
.
2
K k
m m
Đề hỏi tìm min của
;
max
a b
y
giá trị này là
.
2
K k
Dạng 6: Tìm
m
để
( )
;
min
a b
y f x m
đạt min.
Phương pháp: Trước tiên tìm
( )
( ) ( )
;
;
max ; min .
a b
a b
f x K f x k K k
Đề hỏi tìm
( )( )
0m m K m k K m k
. Đề hỏi tìm min của
;
min
a b
y
giá trị này là
0.
Dạng 7: Cho hàm số
( )
y f x m
.Tìm
m
để
( )
;
;
max .min 0
a b
a b
y h y h
hoặc
maxMin
Phương pháp: Trước tiên tìm
( )
( ) ( )
;
;
max ; min .
a b
a b
f x K f x k K k
TH1:
1
cung dau
.
K m k m
K m k m
K m h k m m S
TH2:
2
cungdau
.
k m K m
K m k m
k m h K m m S
Vậy
1 2
.m S S
Dạng 8: Cho hàm số
( )
y f x m
.
Phương pháp: Trước tiên tìm
( )
( ) ( )
;
;
max ; min .
a b
a b
f x K f x k K k
BT1: Tìm
m
để
;
;
min max
a b
a b
y y m K m k
.
BT2: Tìm
m
để
;
;
min *max *
a b
a b
y y m K m k
.
Câu 1. (Đề Tham Khảo 2018) Gọi S là tập hợp tất cả các giá trị của tham số thực m sao cho giá trị lớn
nhất của hàm số
3
3y x x m
trên đoạn
0;2
bằng 3. Số phần tử của S là
A. 0 B. 6 C. 1 D. 2
Lời giải
Chọn D
Xét hàm số
( )
3
3f x x x m
, ta có
( )
2
3 3f x x
. Ta có bảng biến thiên của
( )
f x
:
TH 1 :
2 0 2m m
. Khi đó
( ) ( )
0;2
2 2
max f x m m
2 3 1m m
(loại).
TH 2 :
2 0
2 0
0
m
m
m
. Khi đó :
2 2 2 2m m m
( ) ( )
0;2
2 2
max f x m m
2 3 1m m
(thỏa mãn).
TH 3 :
0
0 2
2 0
m
m
m
. Khi đó :
2 2 2 2m m m
( )
0;2
2max f x m

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
2 3 1
m m
(thỏa mãn).
TH 4:
2 0 2
m m
. Khi đó
( )
0;2
2
max f x m
2 3 1
m m
(loại).
Câu 2. (Đề Minh Họa 2020 Lần 1) Gọi
S
là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị
lớn nhất của hàm số
( )
3
3
f x x x m
trên đoạn
0;3
bằng 16. Tổng tất cả các phần tử của
S
là:
A.
16
. B.
16
. C.
12
.
D.
2
.
Lời giải
Chọn A
Xét
3
3
u x x m
trên đoạn
0;3
có
2
0 3 3 0 1 0;3
u x x
.
Khi đó
0;3
0;3
max u max 0 , 1 , 3 max m,m 2,m 18 18
min u min 0 , 1 , 3 min m,m 2,m 18 2
u u u m
u u u m
.
Suy ra
0;3
18 16
18 2
2
ax max 2 , 18 16
14
2 16
2 18
m
m m
m
M f x m m
m
m
m m
.
Do đó tổng tất cả các phần tử của
S
bằng
16
.
Câu 3. (Đề Tham Khảo 2020 Lần 2) Cho hàm số
( )
1
x m
f x
x
(
m
là tham số thực). Gọi
S
là tập hợp
tất cả các giá trị của
m
sao cho
( )
( )
0;1
0;1
max min 2
f x f x
. Số phần tử của
S
là
A.
6
. B.
2
. C.
1
. D.
4
.
Lời giải
Chọn B
Do hàm số
( )
1
x m
f x
x
liên tục trên
0;1
.
Khi
1
m
hàm số là hàm hằng nên
( )
( )
0;1
0;1
max min 1
f x f x
Khi
1
m
hàm số đơn điệu trên đoạn
0;1
nên
+ Khi
( ) ( )
0 ; 1f f
cùng dấu thì
( )
( ) ( ) ( )
0;1
0;1
1
max min 0 1
2
m
f x f x f f m
.
+ Khi
( ) ( )
0 ; 1f f
trái dấu thì
( )
0;1
min 0
f x
,
( ) ( ) ( )
0;1
1
max max 0 ; 1 max ;
2
m
f x f f m
.
TH1:
( ) ( )
1
0 . 1 0 ( 1) 0
0
m
f f m m
m
.
( )
( )
0;1
0;1
1
1
max min 2 2
5
2
3
m
m
f x f x m
m
(thoả mãn).

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TH2:
( ) ( )
0 . 1 0 ( 1) 0 1 0
f f m m m
( )
( )
0;1
0;1
2
2
max min 2 5
1
2
3
2
m
m
f x f x m
m
m
(không thoả mãn).
Số phần tử của
S
là
2
.
Câu 4. (THPT Đông Sơn 1 - Thanh Hóa 2019) Tìm
m
để giá trị lớn nhất của hàm số
3
3 2 1
y x x m
trên đoạn
0;2
là nhỏ nhất. Giá trị của
m
thuộc khoảng nào?
A.
3
; 1
2
. B.
2
;2
3
. C.
1;0
. D.
( )
0;1
.
Lời giải
Chọn D
Xét hàm số
( )
3
3 2 1
y f x x x m
trên đoạn
0;2
.
Ta có
( )
2
1 0;2
' 3 3 0
1
x
f x x
x
.
Ta có
( )
0 2 1
f m
,
( )
1 2 3
f m
và
( )
2 2 1
f m
Suy ra
( )
0;2
2 1 ; 2 3 ; 2 1 2 3 ; 2 1
max f x max m m m max m m P
.
Trường hợp 1: Xét
( )
1
2 3 2 1 4 4 2 0
2
m m m m
.
Khi đó
2 3 2
P m
,
1
2
m
. Suy ra
min
1
2
2
P m
.
Trường hợp 2: Xét
( )
1
2 3 2 1 4 4 2 0
2
m m m m
.
Khi đó
2 1 2
P m
,
1
2
m
. Suy ra
min
P
không tồn tại.
Vậy
1
2
m
.
Câu 5. (Sở Vĩnh Phúc 2019) Tính tổng tất cả các giá trị của tham số
m
sao cho giá trị lớn nhất của hàm
số
2
2
y x x m
trên đoạn
1;2
bằng
5
.
A.
1
. B.
2
. C.
2
. D.
1
.
Lời giải
Ta có
2
2 2
2
x
y
x x m
,
0 1y x
.
Do đó yêu cầu bài toán tương đương
( ) ( ) ( )
max 1 , 2 , 1 5
y y y
.
max 3 , , 1 5
m m m
.
+ Trường hợp
1
m
, ta có
max 3 , , 1 5 3 5 2
m m m m m
.
+ Trường hợp
1
m
ta có
max 3 , , 1 5 1 5 4
m m m m m
.
Vậy tổng các giá trị
m
bằng
2
.
Câu 6. (THPT Nguyễn Huệ 2018) Cho hàm số
2
2 4
y x x a
(
a
là tham số ). Tìm
a
để giá trị
lớn nhất của hàm số trên đoạn
2;1
đạt giá trị nhỏ nhất
A.
1
a
. B.
3
a
. C.
2
a
. D.
5
a
.
Lời giải

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Hàm số đã cho xác định và liên tục trên đoạn
2;1
.
Ta có:
( ) ( )
2
2
2 4 1 5
y x x a x a
Đặt
( )
2
1 , 2;1 0;4
t x x a
.
Lúc đó hàm số trở thành:
( )
5
f t t a
với
0;4
t
.
Nên
( )
0;4 0;4
2;1
0;4
max max max (0); (4) max 5 ; 1
t t
x
t
y f t f f a a
1 5 1 5
2
2 2
a a a a
Đẳng thức xảy ra khi
1 5 2 3
a a a
.
Do đó giá trị nhỏ nhất của
( )
0;4
max
t
f t
là
2
khi
3
a
.
Câu 7. (Chuyên Vĩnh Phúc 2019) Gọi
S
là tập hợp tất cả các giá trị thực của tham số
m
sao cho giá trị
lớn nhất của hàm số
2
1
x mx m
y
x
trên
1;2
bằng
2
. Số phần tử của tập
S
A.
3
. B.
1
. C.
4
. D.
2
.
Lời giải
Chọn D
Xét
2
1
x mx m
y
x
. Ta có:
( )
( )
2
2
2
1
x x
f x
x
,
( )
0 1;2
0
2 1;2
x
f x
x
.
Mà
( ) ( )
1;2
2 1 3 4 2 1 3 4
1 ,f 2 max ;
2 3 2 3
x
m m m m
f y
.
Trường hợp 1:
1;2
3
2 1
2
max 2
5
2
2
x
m
m
y
m
.
• Với
3 3 4 17
2
2 3 6
m
m
(loại)
• Với
5 3 4 7
2
2 3 6
m
m
(thỏa mãn)
Trường hợp 2:
1;2
2
3 4 6
3 4
3
max 2
3 4 6 10
3
3
x
m
m
m
y
m
m
.
• Với
2 2 1 7
2
3 2 6
m
m
(thỏa mãn)
• Với
10 2 1 17
2
3 2 6
m
m
(loại)
Vậy có
2
giá trị của
m
thỏa mãn.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 8. (HSG Bắc Ninh 2019) Xét hàm số
( )
2
f x x ax b
, với
a
,
b
là tham số. Gọi
M
là giá trị
lớn nhất của hàm số trên
1;3
. Khi
M
nhận giá trị nhỏ nhất có thể được, tính
2a b
.
A.
2
. B.
4
. C.
4
. D.
3
.
Lời giải
Xét hàm số
( )
2
f x x ax b
. Theo đề bài,
M
là giá trị lớn nhất của hàm số trên
1;3
.
Suy ra
( )
( )
( )
1
3
1
M f
M f
M f
1
9 3
1
M a b
M a b
M a b
4 1 9 3 2 1
M a b a b a b
1 9 3 2( 1 )a b a b a b
4 8
M
2
M
.
Nếu
2M
thì điều kiện cần là
1 9 3 1 2
a b a b a b
và
1
a b
,
9 3
a b
,
1
a b
cùng dấu
1 9 3 1 2
1 9 3 1 2
a b a b a b
a b a b a b
2
1
a
b
.
Ngược lại, khi
2
1
a
b
ta có, hàm số
( )
2
2 1f x x x
trên
1;3
.
Xét hàm số
( )
2
2 1g x x x
xác định và liên tục trên
1;3
.
( )
2 2
g x x
;
( )
0 1 1;3
g x x
M
là giá trị lớn nhất của hàm số
( )
f x
trên
1;3
( ) ( ) ( )
max 1 ; 3 ; 1
M g g g
=2
.
Vậy
2
1
a
b
. Ta có:
2 4
a b
.
Câu 9. Cho hàm số
( )
3 2 2
1 27
y x x m x
. Giá trị lớn nhất của hàm số trên đoạn
3; 1
có giá trị
nhỏ nhất bằng
A.
26
. B.
18
. C.
28
. D.
16
.
Lời giải
Chọn B
Xét
( )
3 2 2
1 27
u x x m x
trên đoạn
3; 1
ta có:
2 2
3 2 1 0,u x x m x
.
Do đó
( )
2
3; 1
max 1 26
A u u m
;
( )
2
3; 1
min 3 6 3a u u m
.
Do
2 2
3; 1
M max max 26 , 6 3
y m m
và
2 2
4 3 26 6 3 72
M m m
.
Vậy
18
M
.
Dấu bằng xảy ra khi
2 2
26 6 3 18 2 2
m m m
.
Câu 10. (Sở Quảng Nam - 2018) Có bao nhiêu giá trị thực của tham số
m
để giá trị lớn nhất của hàm số
2
2 4
y x x m
trên đoạn
2;1
bằng
4
?
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
( )
2
2 4
f x x x m
có
( )
2 2
f x x
,
( )
0 1
f x x
. Do đó
2
2;1
max 2 4 max 1 ; 4 ; 5
x x m m m m
.
Ta thấy
5 4 1
m m m
với mọi
m
, suy ra
2;1
max y
chỉ có thể là
5
m
hoặc
1
m
.
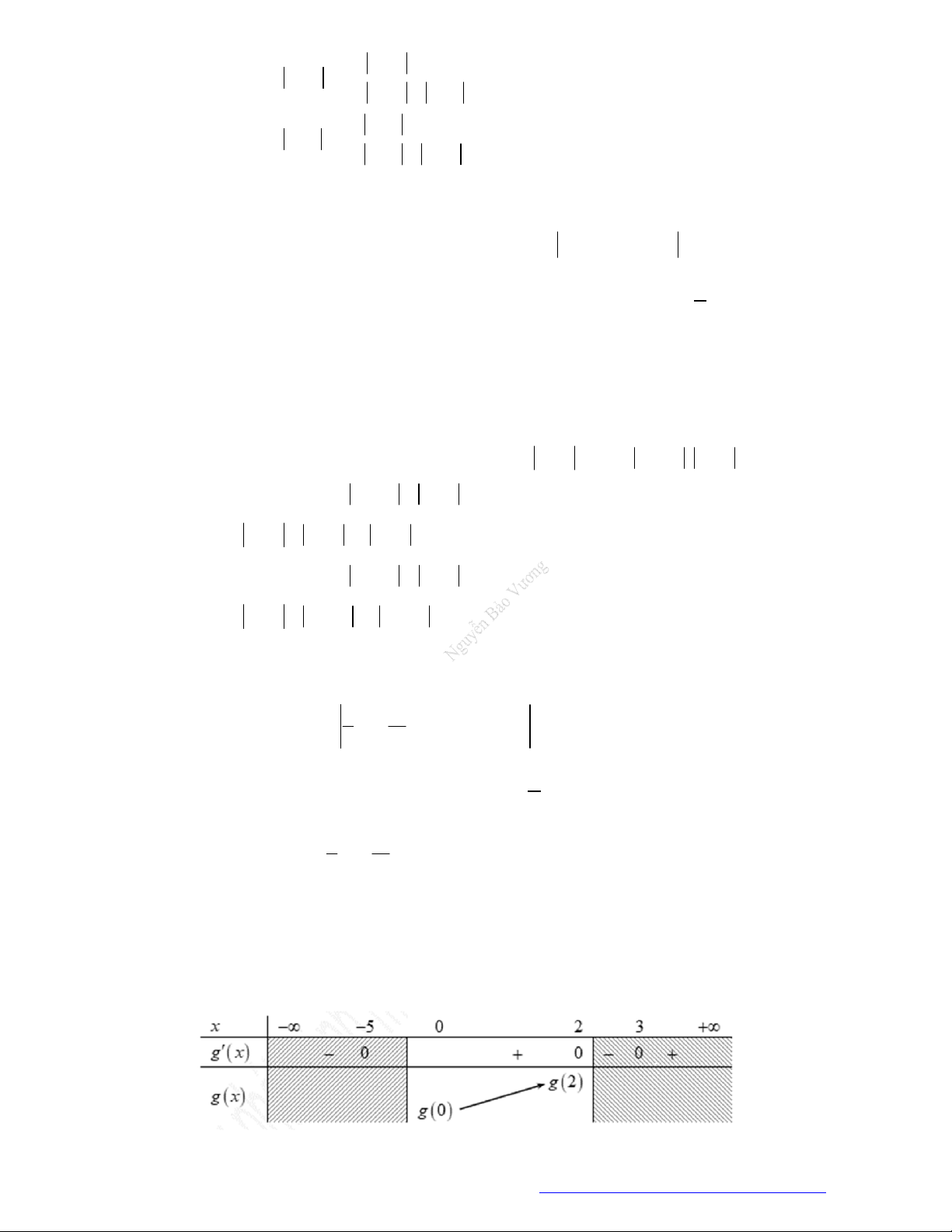
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Nếu
2;1
max 5y m
thì
5 4
5 1
m
m m
1m
.
Nếu
2;1
max 1y m
thì
1 4
1 5
m
m m
5m
.
Vậy
1; 5m
.
Câu 11. (Chuyên Nguyễn Thị Minh Khai - Sóc Trăng - 2018) Gọi
S
là tập hợp tất cả các giá trị của
tham số
m
sao cho giá trị lớn nhất của hàm số
3 2
3 9y x x x m
trên đoạn
2;4
bằng
16
.
Số phần tử của
S
là
A.
0
. B.
2
. C.
4
. D.
1
.
Lời giải
Xét hàm số
( )
3 2
3 9f x x x x m
trên đoạn
2;4
.
2
3 6 9f x x
;
( )
1
0
3
x
f x
x
(thỏa mãn).
( ) ( ) ( ) ( )
2 2 ; 1 5 ; 3 27 ; 4 20f m f m f m f m
( )
( )
2;4
2;4
min 27;max 5f x m f x m
( )
2;4
max max 27 ; 5f x m m
.
+) Trường hợp 1: Nếu
( )
27 5 *m m
( )
2;4
11
max 5 5 16
21
m
f x m m
m
. Đối chiếu điều kiện
( )
* 11m
.
+) Trường hợp 1: Nếu
( )
27 5 **m m
( )
2;4
43
max 27 27 16
11
m
f x m m
m
(Không thỏa mãn điều kiện
( )
**
).
Vậy
11S
S
có
1
phần tử.
Câu 12. (Chuyên Hạ Long 2018) Gọi
S
là tập tất cả các giá trị nguyên của tham số
m
sao cho giá trị lớn
nhất của hàm số
4 2
1 19
30 20
4 2
y x x x m
trên đoạn
0;2
không vượt quá
20
. Tổng các
phần tử của
S
bằng
A.
210
. B.
195
. C.
105
. D.
300
.
Lời giải
Xét hàm số
( )
4 2
1 19
30 20
4 2
g x x x x m
trên đoạn
0;2
Ta có
( )
3
19 30g x x x
;
( )
5 0;2
0 2
3 0;2
x
g x x
x
Bảng biến thiên
( )
0 20g m
;
( )
2 6g m
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Để
( )
0;2
max 20g x
thì
( )
( )
0 20
2 20
g
g
20 20
6 20
m
m
0 14m
.
Mà
m
nên
0;1;2;...;14m
.
Vậy tổng các phần tử của
S
là
105
.
Câu 13. Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số
2
sin 2siny x x m
bằng
1
. Số phần tử của S là
A. 0 B. 1 B. 4 D. 3
Lời giải
Chọn A
Đặt
( )
2
sin 1;1 2x t t y t t m
Xét hàm số
( )
2
2f t t t m
có
( )
' 2 2 0 1 1;1f t t t
Có
( ) ( )
1 3, 1 1f m f m
. Khi đó
( )
( )
1;1
1;1
max max 3; 1 3
min min 3; 1 1
f x m m m
f x m m m
TH1:
3 1 1m m m
( )
( )
( )
2
max 3 1
4
m l
f x m
m l
TH1:
3 1 1m m m
( )
( )
( )
2
max 1 1
0
m l
f x m
m l
Không tồn tại m thỏa mãn
Câu 14. (Chuyên Hưng Yên - 2020) Cho hàm số
4
1
x ax a
y
x
, với
a
là tham số thực. Gọi
,M m
lần
lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn
1;2
. Có bao nhiêu giá trị
nguyên của tham số
a
để
2M m
?
A.
10
. B.
14
. C.
5
. D.
20
.
Lời giải
Chọn B
Xét hàm số
4 4
1 1
x ax a x
y a
x x
.
Ta có
( )
4 3
2
4
3 4
0
3
1
0
x
x x
y y
x
x
.
Bảng biến thiên
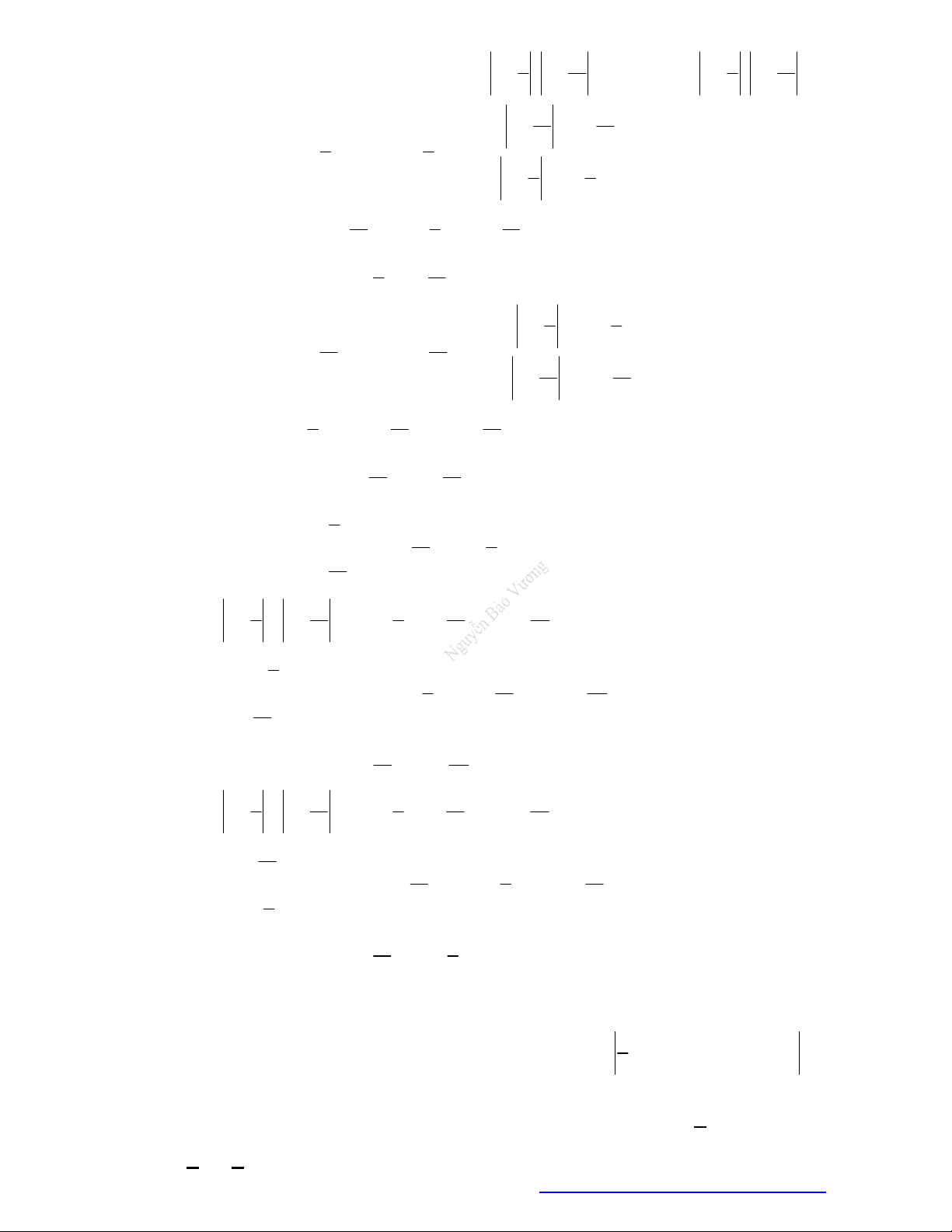
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Dựa vào bảng biến thiên suy ra
1 16
max ;
2 3
M a a
và
1 16
min ;
2 3
m a a
.
Trường hợp 1.
1 1
0
2 2
a a
16 16
3 3
1 1
2 2
M a a
m a a
.
Khi đó
16 1 13
2 2
3 2 3
M m a a a
.
Kết hợp điều kiện, ta có
1 13
2 3
a
có
5
giá trị nguyên thỏa mãn điều kiện.
Trường hợp 2.
1 1
2 2
16 16
0
3 3
16 16
3 3
M a a
a a
m a a
.
1 16 61
2 2
2 3 6
M m a a a
.
Kết hợp điều kiện ta có
61 16
6 3
a
. Suy ra có
5
giá trị nguyên của
a
thỏa mãn.
Trường hợp 3.
1
0
16 1
2
16
3 2
0
3
a
a
a
.
Nếu
1 16 1 16 35
2 3 2 3 12
a a a a a
thì
1
1 16 67
2
2 2
16
2 3 18
3
M a
M m a a a
m a
.
Kết hợp điều kiện, ta có
16 67
3 18
a
. Suy ra có
2
giá trị nguyên của
a
thỏa mãn điều kiện.
Nếu
1 16 1 16 35
2 3 2 3 12
a a a a a
thì
16
16 1 19
3
2 2
1
3 2 9
2
M a
M m a a a
m a
.
Kết hợp điều kiện, ta có
19 1
9 2
a
. Suy ra có
2
giá trị nguyên của
a
thỏa mãn điều kiện.
Vậy có
14
giá trị nguyên của
a
thỏa mãn điều kiện.
Câu 15. (Chuyên Lương Văn Chánh - Phú Yên - 2020) Gọi
S
là tập hợp tất cả các giá trị nguyên của
tham số thực
m
sao cho giá trị lớn nhất của hàm số
4 2
1
14 48 30
4
y x x x m
trên đoạn
0;2
không vượt quá
30
. Tổng giá trị các phần tử của tập hợp
S
bằng bao nhiêu?
A.
120
. B.
210
. C.
108
. D.
136
.
Lời giải
Chọn D

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Đặt
4 2
1
( ) 14 48 30
4
f x x x x m
là hàm số xác định và liên tục trên
0;2
.
Với mọi
0;2
x
ta có
3
'( ) 0 28 48 0 2
f x x x x
.
Suy ra
0;2
max ( ) max (0) ; (2)
f x f f
.
Theo đề
0;2
30 30
14 30
30 30
max ( ) 30
14 30
14 30
30 14
m
m m
m
f x
m
m
m m
30 30 30 0 60
0 16
30 14 30 44 16
m m
m
m m
.
Do
0;1;2;...;16 .
m m S
Vậy tổng tất cả 17 giá trị trong tập
S
là
136
.
Câu 16. (Chuyên Lương Văn Tỵ - Ninh Bình - 2020) Cho hàm số
( )
4 3 2
3 4 24 48
x x x x
f x e e e e m
. Gọi
A
,
B
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất
của hàm số đã cho trên
0;ln 2
.Gọi S là tập hợp tất cả các giá trị nguyên của tham số
m
thuộc
)
23;10
thỏa mãn
3A B
. Tổng các phần tử của tập S bằng
A.
33
. B.
0
. C.
111
. D.
74
.
Lời giải
Chọn A
Đặt
, 0;ln 2 1;2
x
t e x t
Xét hàm số
( )
4 3 2
|3 4 24 48 |h t t t t t m
trên
1;2
.
Đặt
( )
4 3 2
3 4 24 48
g t t t t t m
( )
3 2
12 12 48 48
g t t t t
;
( )
0
g t
2 [1;2]
2
1
t
t
t
;
( )
1 23
g m
,
( )
2 16
g m
.
TH1:
16 10
m
23 16 0
m m
( )
1;2
max
A h t
23
m
;
( )
1;2
min
B h t
16
m
.
Suy ra::
16 10
16 10
25
23 3 48
2
m
m
m m
m
25
10
2
m
.
Do đó: có
22
giá trị
TH2:
23 16
m
23 23, | 16| 16
m m m m
.
Dễ thấy
0
B
. Suy ra
23 16
16 0
16 19.5
( )
19.5 23
23 16
23 0
m m
m
m
VL
m
m m
m
Vậy
12; 11;...;0;1;...9
S
và tổng các phần tử của tập S bằng
( ) ( )
12 11 10 33
.
Câu 17. (Chuyên Bến Tre - 2020) Cho hàm số
4 3 2
2
y x x x a
. Có bao nhiêu số thực
a
để
1;2 1;2
min max 10
y y
?
A. 3. B. 5. C. 2. D. 1.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Lời giải.
Chọn C.
Đặt
4 3 2
2 ( )y x x x a f x
.
Xét hàm số
( )
4 3 2
2
f x x x x a
Khi đó
3 2 2
1
( ) 4 6 2 2 (2 3 1) 0 0; ;1
2
f x x x x x x x x
.
( )
0, 1;2
f x x
và
(1) ; (2) 4
f a f a
Ta có
1;2
x
thì
max , 4
min ,0, 4
y a a
y a a
.
Xét các trường hợp
+
0 max 4;min 2 4 10 3
a y a y a a a
, nhận.
+
4 max ;min 4 4 10 7
a y a y a a a a
, nhận.
+
0
4 0 min 0;max 4;
4 0
a
a y y a a
a
4 10 6
10 10
a a
a a
(Loại).
Vậy tồn tại hai giá trị
a
thỏa mãn.
Câu 18. (Chuyên Hùng Vương - Gia Lai - 2020) Cho hàm số
( )
3 2
3
f x x x m
. Có bao nhiêu số
nguyên
m
để giá trị nhỏ nhất của hàm số
( )
f x
trên đoạn
1;3
không lớn hơn 2020?
A.
4045
. B.
4046
. C.
4044
. D.
4042
.
Lời giải
Chọn A
Với
3 2
3
u x x m
có
2
3 6 ; 0 0; 2
u x x u x x
Do đó
( ) ( ) ( )
( ) ( ) ( )
1;3
1;3
min min 1 ; 3 ; 2 min 2; ; 4 4
max max 1 ; 3 ; 2 max 2; ; 4
u u u u m m m m
u u u u m m m m
* Nếu
( )
1;3
4 0 4 min 4 2020 2024 4,..., 2024 .
m m f x m m m
* Nếu
( )
1;3
0 min 2020 2020 2020;...;0 .
m f x m m m
* Nếu
0 m 4
khi đó
( )
1;3 1;3
1;3
min 0; max 0 min 0
u u f x
(thỏa mãn).
Vậy
2020,...,2024
m
có tất cả 4045 số nguyên thỏa mãn.
Câu 19. (Chuyên Lê Hồng Phong - Nam Định - 2020) Xét hàm số
( )
2 4
2 4
mx x
f x
x
, với
m
là
tham số thực. Có bao nhiêu số nguyên
m
thỏa mãn điều kiện
( )
1;1
0 min 1
f x
?
A.
4
. B.
8
. C.
2
. D.
1
.
Lời giải
Chọn B
Cách 1:
Xét hàm số
( )
2 4
2 4
mx x
g x
x
liên tục trên
1;1
và
( ) ( )
f x g x
.
Ta có
( ) ( ) ( )
2 5 2 3
0 1; 1 ; 1
6 2
m m
g g g
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
- Nếu
( )
( )
1 0
2 5
1 0
2 3
g
m
g
m
thì
( )
1;1
min 0
f x
, không thỏa mãn bài toán.
- Nếu
( )
( )
1 0
2 3 2 5
1 0
g
m
g
Mà
m
nguyên nên
3; 2; 1;0;1;2;3;4
m
.
Ta có
( )
( )
2
2 12
4
4
2 4
x
m
x
g x
x
.
TH1:
0
m
.
Khi đó
( )
0 1;1
g x x
. Do đó hàm số
( )
g x
đồng biến trên
1;1
.
Mà
( ) ( )
0 1 1 1
g g
. Do đó
( )
1 1 0
g
. Vậy
( )
1;1
0 min 1
f x
hay
0;1;2;3;4
m
thỏa mãn bài toán.
TH2:
0
m
.
Xét hàm số
( )
2 12
4
x
h x
x
trên
1;1
. Ta có
( )
( )
2
0 1;1
4 4
x
h x x
x x
.
Khi đó dễ thấy
( )
10 14
;
3 5
h x
.
* Khi
( )
( )
1 4 0 1;1 0 1;1
m m h x x g x x
hay hàm số
( )
g x
đồng
biến trên
1;1
. Khi đó
( )
1 1 0
g
nên
( )
1;1
0 min 1
f x
. Vậy
1
m
thỏa mãn.
* Khi
3; 2
m
( )
( )
4 0 1;1 0 1;1
m h x x g x x
hay hàm số
( )
g x
nghịch biến trên
1;1
. Khi đó
( ) ( ) ( )
1 0 1 1 0
g g g
nên
( )
1;1
0 min 1
f x
. Vậy
3; 2
m
thỏa mãn.
Do đó
3; 2; 1;0;1;2;3;4
m
hay có
8
giá trị nguyên của
m
.
Cách 2
Nhận thấy
( )
f x
liên tục trên
1;1
nên tồn tại giá trị nhỏ nhất của
( )
f x
trên đoạn
1;1
.
Ta có
( )
( )
0, 1;1
0 1
f x x
f
nên suy ra
( )
1;1
0 min 1
x
f x
.
Vậy điều kiện
( )
( )
( )
1;1
1;1
1;1
min 0 (1)
0 min 1
min 1 (2)
x
x
x
f x
f x
f x
.
Ta có
( )
1
Phương trình
2 4 0
mx x
vô nghiệm trên
1;1
Phương trình
2 4
x
m
x
vô nghiệm trên
1;1 \ 0
Xét hàm số
( )
2 4
, 1;1 \ 0
x
g x x
x
( )
/
2
8
0, 1;1 \ 0
4
x
g x x
x x
Bảng biến thiên

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Từ bảng biến thiên suy ra điều kiện phương trình
2 4x
m
x
vô nghiệm trên
1;1 \ 0
2 3 2 5m
.
Do
m
nguyên nên
3; 2; 1;0;1;2;3;4m
.
Để giải
( )
2
trước hết ta đi tìm điều kiện để
( )
1;1
min 1
x
f x
.
Do
( )
0 1f
nên
( ) ( )
1;1
min 0
x
f x f
, mà
( )
0 1;1
, suy ra x = 0 là điểm cực trị của hàm số
( )
f x
.
Đặt
( ) ( )
/
2 4
0 0
2 4
mx x
h x h
x
3
2
m
. Do đó với m nguyên thì (2) chắc chắn xảy ra.
Vậy
3; 2; 1;0;1; 2;3; 4m
thỏa mãn điều kiện
( )
2
Kết luận: Có 8 giá trị nguyên của m thỏa mãn yêu cầu.
Câu 20. (Chuyên Sơn La - 2020) Gọi
S
là tập hợp những giá trị của tham số
m
để giá trị lớn nhất của
hàm số
3
( ) 12f x x x m trên đoạn
[1; 3]
bằng
12
.Tổng tất cả các phần tử của tập
S
bằng
A.
25.
B.
4.
C.
15.
D.
21.
Lời giải
Chọn A
Xét hàm số
3 2
( ) 12 (1 3) '( ) 3 12 0 2, 2g x x x m x g x x x x
.
(1) 11, (2) 16, (3) 9g m g m g m
.
Suy ra
[1;3]
max ( ) { 16 ; 9 }f x m m
.
Giả sử
16 12 28, 4m m m
thử lại ta thấy
4m
nhận.
Giả sử
9 12 21, 3m m m
thử lại ta thấy
21m
nhận.
Vậy
4m
và
21m
.
Câu 21. (Chuyên Thái Nguyên - 2020) Gọi
0
S
là tập tất cả các giá trị nguyên của tham số thực
m
sao
cho giá trị lớn nhất của hàm số
4 2
1
14 48
4
y x x x m
trên đoạn
2;4
không vượt quá
30
. Số
phần tử của
S
là
A.
50
. B.
49
. C.
66
. D.
73
.
Lời giải
Chọn B
Xét hàm số
( )
4 2
1
14 48
4
f x x x x m
.
( )
3
28 48f x x x

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
( )
( )
( )
( )
6
0 4
2
x ktm
f x x tm
x tm
.
( ) ( )
2 44; 4 32
f m f m
.
( )
( )
2;4
2;4
min 32; max 4
f x m f x m
.
2;4
max max 44 ; 32
y m m
.
Để giá trị lớn nhất của hàm số
4 2
1
14 48
4
y x x x m
trên đoạn
2;4
không vượt quá
30
thì
44 30
74 14
62 14
62 2
32 30
m
m
m
m
m
.
Câu 22. (Đại Học Hà Tĩnh - 2020) Có bao nhiêu giá trị của tham số
m
để giá trị nhỏ nhất của ham số
( )
2
e 4e
x x
f x m
trên đoạn
0;ln 4
bằng 6?
A.
3
. B.
4
. C.
2
. D.
1
.
Lời giải
Chọn C
Đặt
e
x
t
, vì
0;ln 4
x
1;4
t
.
Khi đó yêu cầu bài toán trở thành tìm
m
để giá trị nhỏ nhất của hàm số
( )
2
4
f t t t m
trên
đoạn
1;4
bằng 6.
Đặt
2
4s t t
, vì
1;4
t
4;0
s
.
Xét hàm số
( )
g s s m
với
4;0
s
suy ra hàm số
( )
g s
đồng biến trên đoạn
4;0
.
Khi đó giá trị nhỏ nhất của
( )
f s s m
,
4;0
s
chỉ đạt tại các đầu mút.
TH1:
( )
4;0
min 4 6
4
f s m
m m
10
2
10
4
m
m
m
m m
thỏa mãn.
TH2:
( )
4;0
min 6
4
f s m
m m
6
6
6
4
m
m
m
m m
thỏa mãn.
Vậy có 2 giá trị của tham số
m
thỏa mãn yêu cầu bài toán.
Câu 23. (Đặng Thúc Hứa - Nghệ An - 2020) Gọi
S
là tập tất cả các giá trị nguyên của tham số
m
sao
cho giá trị lớn nhất của hàm số
3
1
9 10
3
y x x m
trên đoạn
0;3
không vượt quá
12
. Tổng
giá trị các phần tử của
S
bằng bao nhiêu?
A.
7
. B.
0
. C.
3
. D.
12
.
Lời giải
Chọn A
Xét hàm số
( )
3
1
9 10
3
g x x x m
. Dễ thấy hàm số
( )g x
liên tục trên đoạn
0;3
.
Ta có
( )
2
9
g x x
;
( )
3
0
3 0;3
x
g x
x
Ta có
( )
0 10
g m
;
( )
3 8
g m
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Theo yêu cầu bài toán,
( )
0;3 0;3
max max 12
y g x
( )
( )
0 12
3 12
g
g
10 12
8 12
m
m
4 2
m
Mà
m
nên
4; 3; 2; 1;0;1;2
m
.
Vậy tổng các phần tử của
S
là
7
.
Câu 24. (Đô Lương 4 - Nghệ An - 2020) Gọi
S
là tập tất cả các giá trị nguyên của tham số thực
m
sao
cho giá trị lớn nhất của hàm số
4 2
1
14 48 30
4
y x x x m
trên đoạn
0;2
không vượt quá
30
. Tổng tất cả các giá trị của
S
là
A.
180
. B.
136
. C.
120
.
D.
210
.
Lời giải
Chọn B
Xét
4 2
1
14 48 30
4
u x x x m
trên đoạn
0;2
.
3
6 0;2
0 28 48 0 2 0;2
4 0;2
x
u x x x
x
.
Khi đó
( )
0;2
max u max (0), 2 max 30, 14 14
u u m m m
.
Suy ra
0;2
max - 30 , 14
Max y m m
.
Trường hợp 1:
0;2
14
Max y m
2 2
14 30
14 30
14 30
30 14 30
m m
m m
m
m
88 704
44 16
m
m
8
44 16
m
m
8 16
m
, mà
m
.
8;9;10;...;16
m
.
Trường hợp 2:
0;2
-30
Max y m
2 2
30 14
14 30
30 30
30 30 30
m m
m m
m
m
88 704
0 60
m
m
8
0 60
m
m
0 8
m
, mà
m
.
0;1;2;...;8
m
.
Vậy tổng các giá trị
m
thỏa mãn là:
0 1 2 ... 16 136
.
Câu 25. (Liên trường Nghệ An - 2020) Biết giá trị lớn nhất của hàm số
( )
3
2 15 5 9y f x x x m x
trên
0;3
bằng
60
. Tính tổng tất cả các giá trị của tham số
thực
m
.
A.
48
. B.
5
. C.
6
. D.
62
.
Lời giải
Chọn C
Có
( ) ( )
0;3
max 60 60, 0;3
f x f x x
và
0
0;3
x
sao cho
( )
0
60.
f x

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Có
( )
3 3
60 2 15 5 9 60 2 15 5 60 9f x x x m x x x m x
3 3 3
9 60 2 15 5 60 9 2 24 55 2 6 65, 0;3 .
x x x m x x x m x x x
Có
3
2 6 65 29, 0;3
x x x
nên
3
2 6 65, 0;3 29.
m x x x m
Tương tự
3
2 24 55 23
x x
nên
3
2 24 55 , 0;3 23.
x x m x m
Vậy
23 29
m
thì
( )
60, 0;3 .
f x x
Để
0
0;3
x
sao cho
( )
0
60
f x
thì
3
3
2 24 55
2 6 65
x x m
x x m
có nghiệm trên
0;3 .
Hay
29
.
23
m
m
Vậy
29
23
m
m
thì
( )
0;3
max 60.
f x
Khi đó tổng các giá trị của
m
là
29 23 6.
Câu 26. (Lý Nhân Tông - Bắc Ninh - 2020) Gọi S là tập hợp tất cả các giá trị của tham số thực
m
sao
cho giá trị lớn nhất của hàm số
3
3
y x x m
trên đoạn
0;2
bằng
3
. Số phần tử của S là
A.
2.
B.
6.
C.
1.
D.
0.
Lời giải
Chọn A
Xét hàm số
3
( ) 3
g x x x m
, ta có
2
1 0;2
'( ) 3 3 0
1 0;2
x
g x x
x
.
( )
0
g m
,
( )
1 2
g m
,
( )
2 2
g m
.
Vậy giá trị lớn nhất của hàm số
( )
3
3
f x x x m
bằng max của
; 2 ; 2
F m m m
TH1:
3
3 .
3
m
m
m
Với
3 3;1;5
m F
loại vì max bằng 5.
Với
3 3;5;1
m F
loại vì max bằng 5.
TH2:
5
2 3 .
1
m
m
m
Với
5 5;3;7
m F
loại vì max bằng 7.
Với
1 1;3;1
m F
có max bẳng 3. Chọn
1.
m
TH3:
1
2 3 .
5
m
m
m
Với
1 1;1;3
m F
có max bằng 3. Chọn
1.
m
Với
5 5;7;3
m F
loại vì max bẳng 7.
Vậy
1;1S
có 2 giá trị
m
thoả mãn yêu cầu đề bài.
Câu 27. (Nguyễn Huệ - Phú Yên - 2020) Cho hàm số
( )
4 3 2
2
f x x x x m
(
m
là tham số thực).
Gọi
S
là tập hợp tất cả các giá trị của
m
sao cho
( )
( )
1;2
1;2
min max 10
f x f x
. Số phần tử của
S
là?
A.
2
. B.
3
. C.
5
. D.
1
.
Lời giải
Chọn A
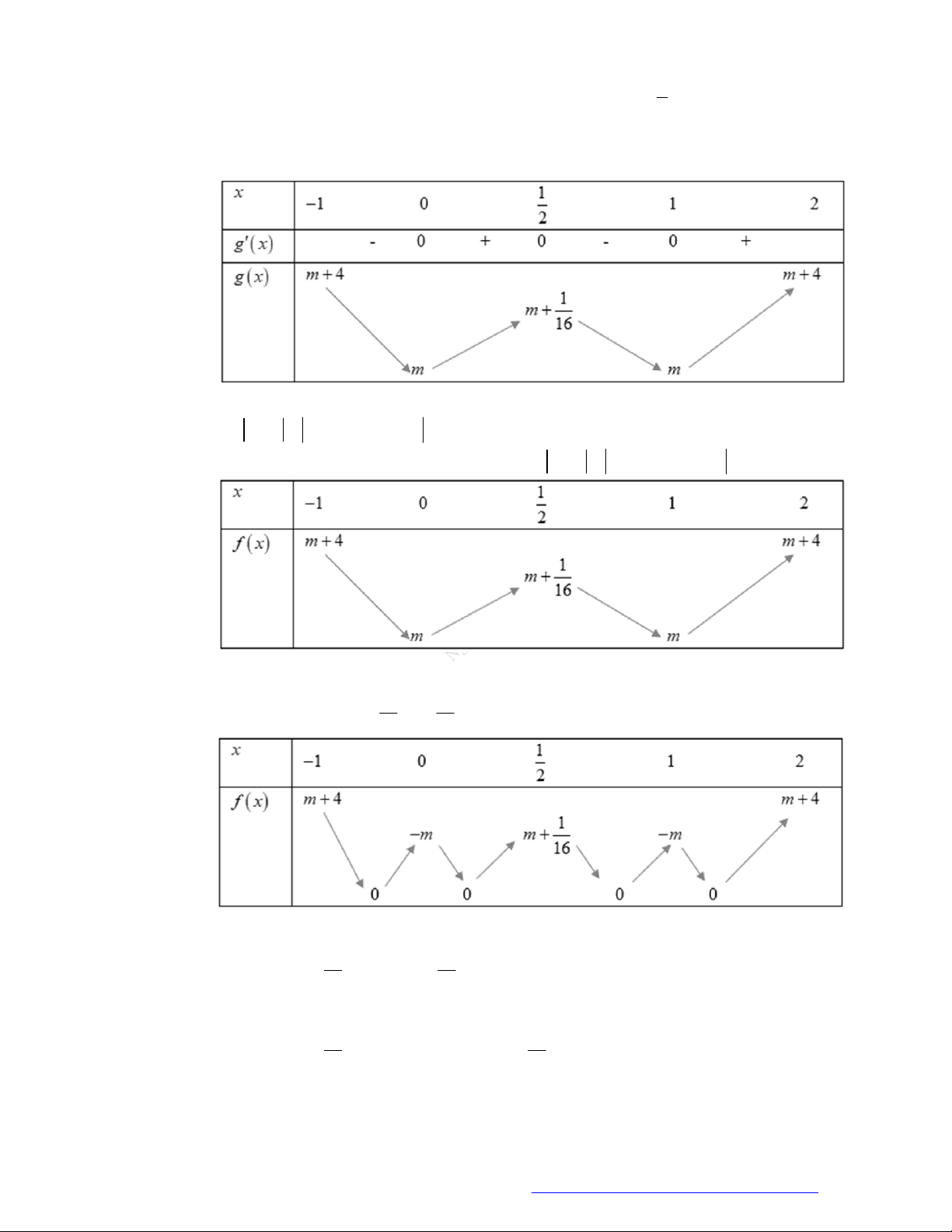
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
Đặt
( ) ( )
4 3 2 3 2
0
1
2 4 6 2 0
2
1
x
g x x x x m g x x x x x
x
Bảng biến thiên của hàm
( )
g x
Dựa vào bảng biến thiên của
( )
g x
ta suy ra bảng biến thiên của
( ) ( )
4 3 2
2 f x g x x x x m
. Ta có các trường hợp sau:
Trường hợp 1:
0m
. Bảng biến thiên của
( ) ( )
4 3 2
2 f x g x x x x m
Dựa vào bảng biến thiên ta có
( )
( )
1;2
1;2
min max 10 4 10 3
f x f x m m m
(TM)
Trường hợp 2:
1 1
0 0
16 16
m m m
. Bảng biến thiên:
Dựa vào bảng biến thiên ta có
( )
( )
1;2
1;2
min max 10 0 4 10 6
f x f x m m
(Loại)
Trường hợp 3:
1 1
0
16 16
m m
. Tương tự ta có:
( )
( )
1;2
1;2
min max 10 0 4 10 6
f x f x m m
(Loại)
Trường hợp 4:
1 1
0 4 4
16 16
m m m
. Bảng biến thiên:
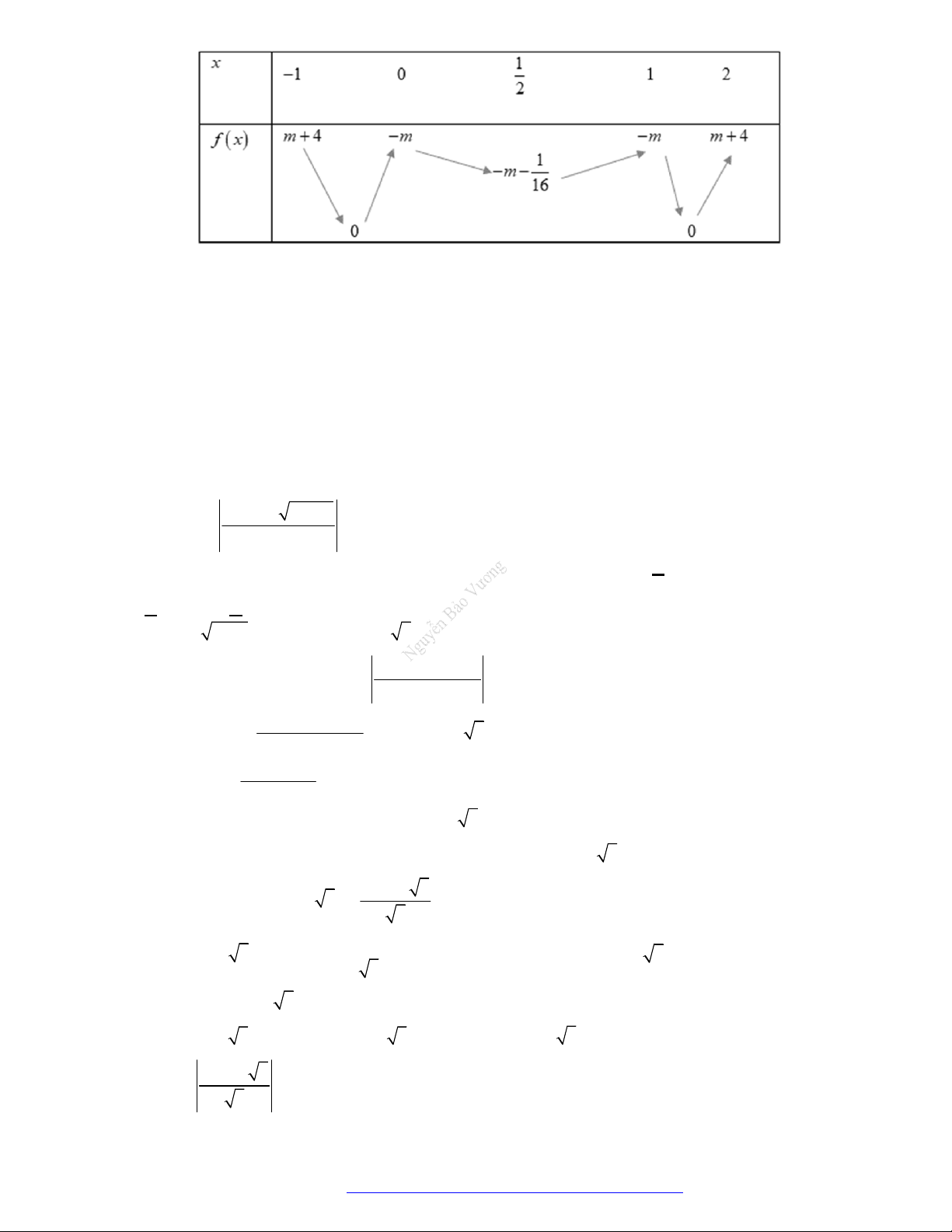
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Dụa vào bảng biến thiên ta có
( )
( )
( )
( )
( )
1;2
1;2
1;2
1;2
min max 10
0 4 10
6
0 10
10
min max 10
f x f x
m
m
m
m
f x f x
(Loại)
Trường hợp 5:
4 0 4 m m
. Ta có:
( )
( )
1;2
1;2
min max 10 0 10 10
f x f x m m
(Loại)
Trường hợp 6:
4 0 4 m m
. Ta có:
( )
( )
1;2
1;2
min max 10 4 10 7f x f x m m m
(Thỏa mãn)
Vậy
7;3m
.
Câu 28. (Hải Hậu - Nam Định - 2020) Có tất cả bao nhiêu giá trị nguyên dương của tham số
m
để hàm
số
2 2 4 8
( )
2
mx x
f x
x
có giá trị nhỏ nhất trên đoạn
1;1
là
a
thỏa mãn
0 1.a
A.
3.
B.
4.
C.
5.
D.
2.
Lời giải
Chọn D.
Đặt
2, 1;1 1; 3t x x t
;
2
2.x t
Hàm số đã cho trở thành
2
2 4 t 4
( )
mt m
g t
t
.
Xét hàm
2
2 4 t 4
( )
mt m
h t
t
trên đoạn 1; 3
.
Ta có
2
2
2 ( 2)
'( )
m t
h t
t
Th1:
0m
thì ( ) 4 ( ) 4 1; 3 4h t g t t a
(loại).
Th2:
0m
thì hàm số
( )h t
đồng biến hoặc nghịch biến trên 1; 3
Ta có
2 4 3
(1) 2 4; ( 3)
3
m
h m h
.
Nếu
2
(1).h( 3) 0
2 3
m
h
m
và hàm số
( )h t
liên tục trên đoạn 1; 3
suy ra đồ thị hàm số
( )h t
trên đoạn 1; 3
cắt trục hoành
0a
(loại).
Nếu
(1).h( 3) 0 2 2 3h m
. Khi đó,
( )
(1) 0; 3 0h h
2 4 3
3
m
a
. Suy ra
3
4
m
m
là các giá trị nguyên dương để
0 1a
.
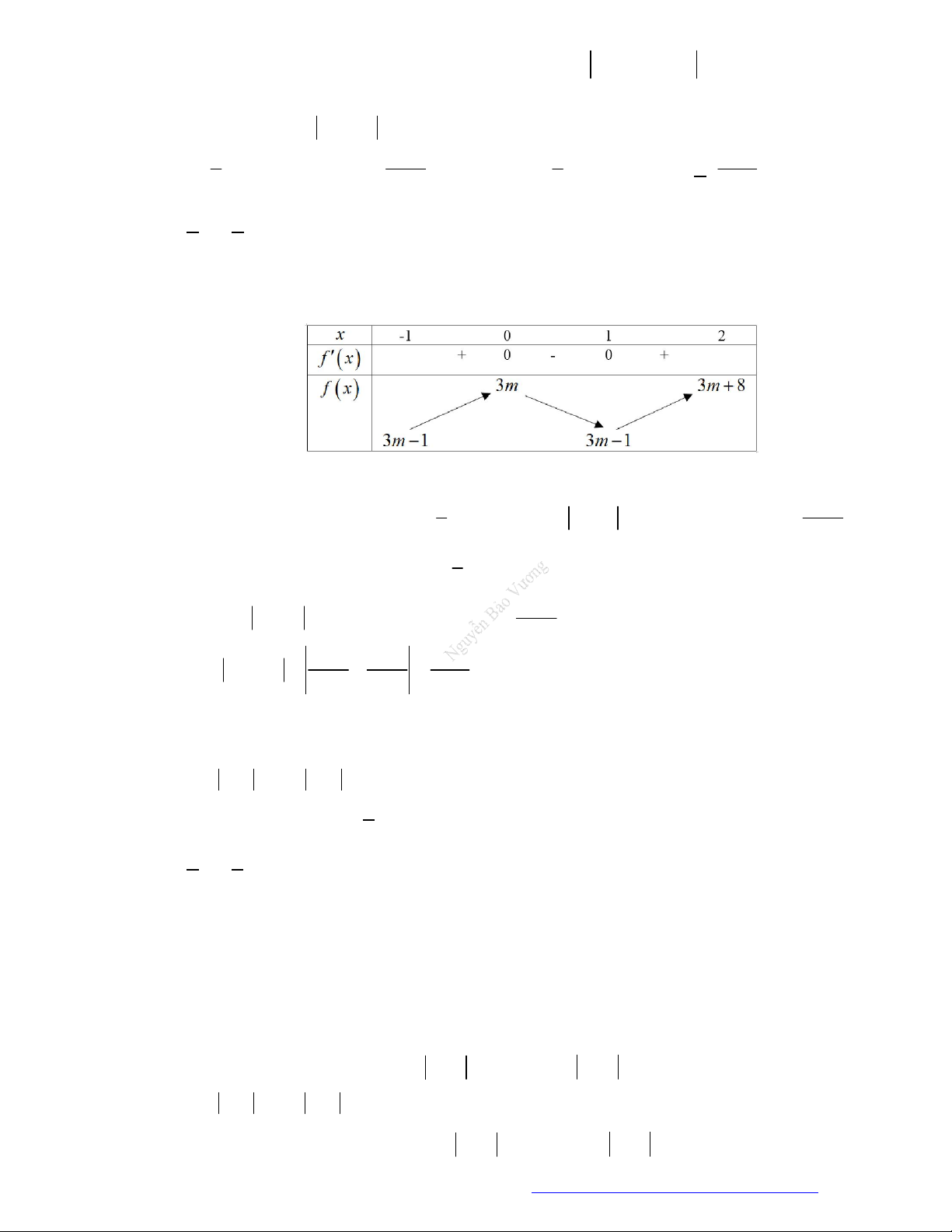
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
Câu 29. (Lương Thế Vinh - Hà Nội - 2020) Cho hàm số
4 2
2 3y x x m
với
m
là tham số. Biết
rằng có đúng hai giá trị
1 2
,m m
của
m
để giá trị nhỏ nhất của hàm số đã cho trên
1;2
bằng
2021. Tính giá trị
1 2
m m
.
A.
1
3
. B.
4052
3
. C.
8
3
. D.
4051
3
.
Lời giải
Chọn D
Xét hàm số
( )
4 2
2 3f x x x m
, ta có
( )
( )
3 2
4 4 4 1f x x x x x
( )
0
0
1
x
f x
x
Bảng biến thiên của hàm số trên
1;2
:
Vì
1;2
min 2021y
phương trình
( )
0f x
không có nghiệm thuộc
1;2
.
Trường hợp 1 :
1
3 1 0
3
m m
. Ta có
1;2
min 3 1 3 1 2021y m m
2022
3
m
Trường hợp 2 :
8
3 8 0
3
m m
. Ta có
1;2
min 3 8 3 8 2021y m m
2029
3
m
.
Vậy
1 2
2022 2029 4051
3 3 3
m m
.
Câu 30. (Thanh Chương 1 - Nghệ An - 2020) Cho hàm số
( )
3 2
3 1f x x x m
(
m
là tham số thực).
Gọi
S
là tập hợp tất cả các giá trị nguyên của
m
thuộc đoạn
2020;2020
sao cho
( )
( )
1;4
1;4
max 3minf x f x
. Số phần tử của
S
là
A.
4003
. B.
4002
. C.
4004
. D.
4001
.
Lời giải
Chọn B
Xét hàm số
( ) ( )
3 2 2
3 1 3 6y f x x x m y f x x x
.
( )
( )
2
0
0 3 6 0
2
x l
f x x x
x
.
( ) ( ) ( )
1 1; 2 3; 4 17f m f m f m
.
( )
( )
1;4
1;4
max 17; min 3f x m f x m
.
+Nếu
3 0 3m m
thì
( )
1;4
max 17f x m
,
( )
1;4
min 3f x m
. Khi đó:
( )
( ) ( )
1;4
1;4
max 3min 17 3 3 13f x f x m m m
.
+Nếu
17 0 17m m
thì
( )
1;4
max 3f x m
,
( )
1;4
min 17f x m
.
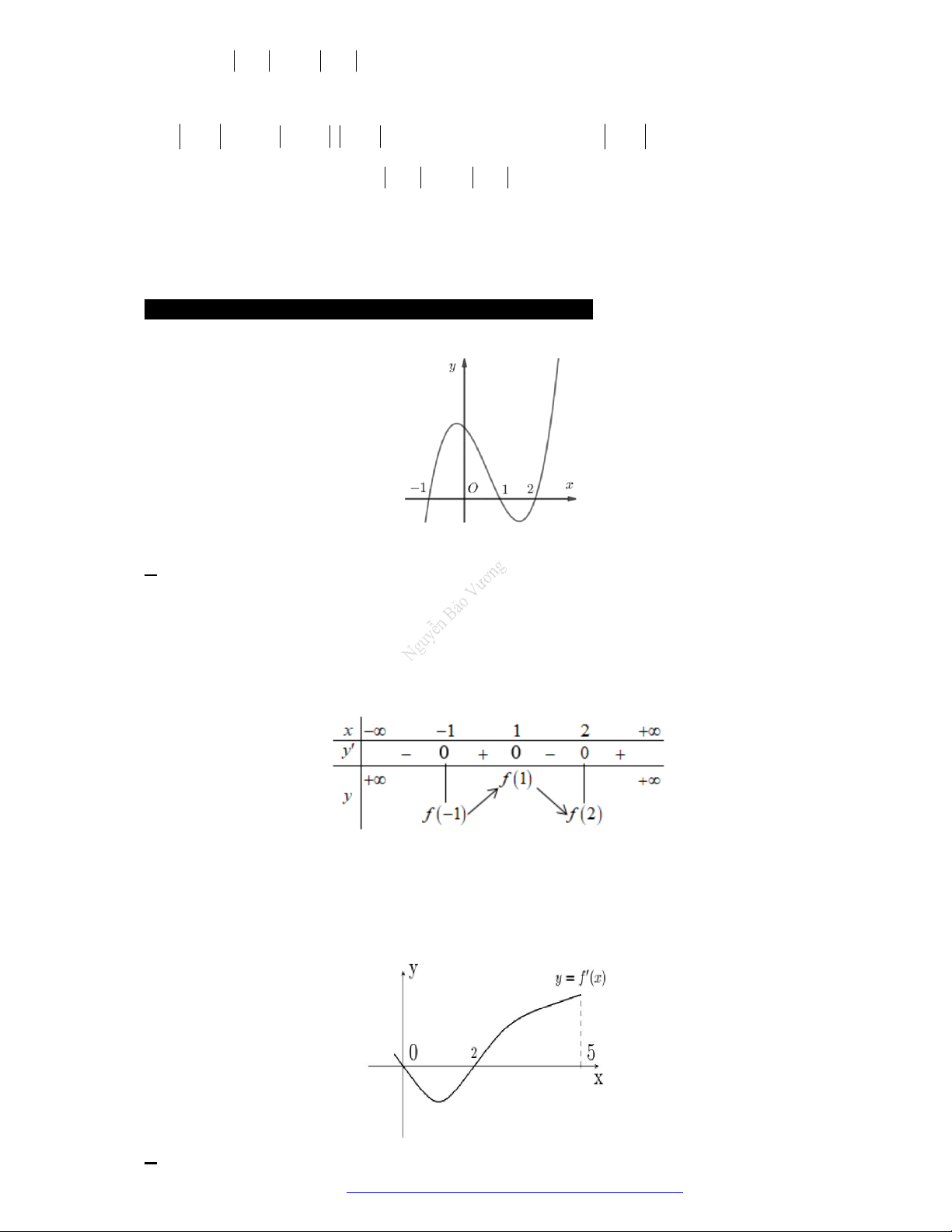
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Khi đó:
( )
( ) ( )
1;4
1;4
max 3min 3 3 17 27f x f x m m m
.
+Nếu
( )( )
3 17 0 17 3m m m
thì
( )
( )
1;4
1;4
max max 17 , 3 max 17,3 0;min 0f x m m m m f x
.
Khi đó, không thỏa điều kiện
( )
( )
1;4
1;4
max 3minf x f x
.
Do đó:
27
13
m
m
kết hợp với
2020;2020m
ta có
2020; 27 13;2020m
Vậy
4002
giá trị nguyên của
m
cần tìm.
Dạng 2. Giá trị lớn nhất – giá trị nhỏ nhất hàm ẩn, hàm hợp
Câu 1. Cho hàm số
( )
y f x
xác định và liên tục trên
, đồ thị của hàm số
( )
y f x
như hình vẽ.
Giá trị lớn nhất của hàm số
( )
y f x
trên đoạn
1;2
là
A.
( )
1f
. B.
( )
1f
. C.
( )
2f
. D.
( )
0f
.
Lời giải
( )
1
0 1
2
x
f x x
x
.
Từ đồ thị hàm
y f x
ta có bảng biến thiên
Từ đó suy ra giá trị lớn nhất của hàm số trên
1;2
là
1f
.
Câu 2. Cho hàm số
( )
y f x
có đạo hàm là hàm
( )
f x
. Đồ thị của hàm số
( )
y f x
được cho như
hình vẽ. Biết rằng
( ) ( ) ( ) ( )
0 3 2 5f f f f
. Giá trị nhỏ nhất, giá trị lớn nhất của
( )
y f x
trên đoạn
0;5
lần lượt là:
A.
( )
2f
;
( )
5f
. B.
( )
0f
;
( )
5f
. C.
( )
2f
;
( )
0f
. D.
( )
1f
;
( )
5f
.
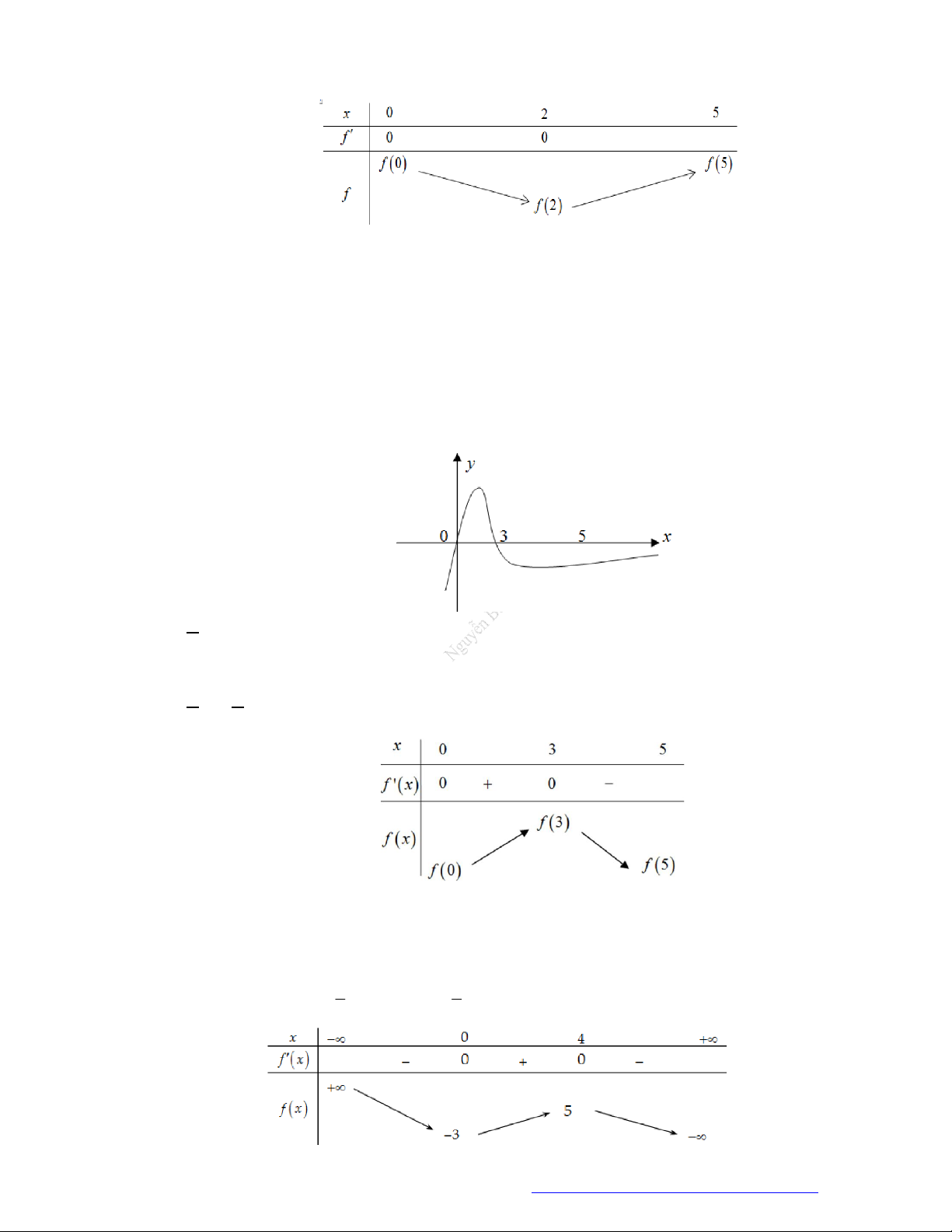
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
Lời giải
Dựa vào đồ thị hàm số
( )
f x
ta có bảng biến thiên.
Khi đó:
( )
( )
( ) ( )
0;5
min 2
3 2
f x f
f f
,
mà
( ) ( ) ( ) ( )
0 3 2 5f f f f
( ) ( ) ( ) ( )
0 2 2 5f f f f
( ) ( )
0 5f f
.
Vậy giá trị nhỏ nhất, giá trị lớn nhất của
( )
y f x
trên đoạn
0;5
lần lượt là:
( )
2f
;
( )
5f
.
Câu 3. Cho hàm số
( )
f x
có đạo hàm là
( )
f x
. Đồ thị của hàm số
( )
y f x
được cho như hình vẽ bên.
Biết rằng
( ) ( ) ( ) ( ) ( )
0 1 2 3 5 4f f f f f
. Tìm giá trị nhỏ nhất
m
và giá trị lớn nhất
M
của
( )
f x
trên đoạn
0;5
.
A.
( ) ( )
5 , 3m f M f
B.
( ) ( )
5 , 1m f M f
C.
( ) ( )
0 , 3m f M f
D.
( ) ( )
1 , 3m f M f
Lời giải
Chọn A
Từ đồ thị ta có bảng biến thiên của
( )
f x
trên đoạn
0;5
( )
3
M f
và
( ) ( ) ( ) ( )
1 3 , 4 3
f f f f
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
5 0 1 3 4 3 0 5 0 5f f f f f f f f m f
.
Câu 4. Cho hàm số
( )
y f x
có bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất của hàm số
( )
( )
2 3 2
1 1
4 3 8
3 3
g x f x x x x x
trên đoạn
1;3
.
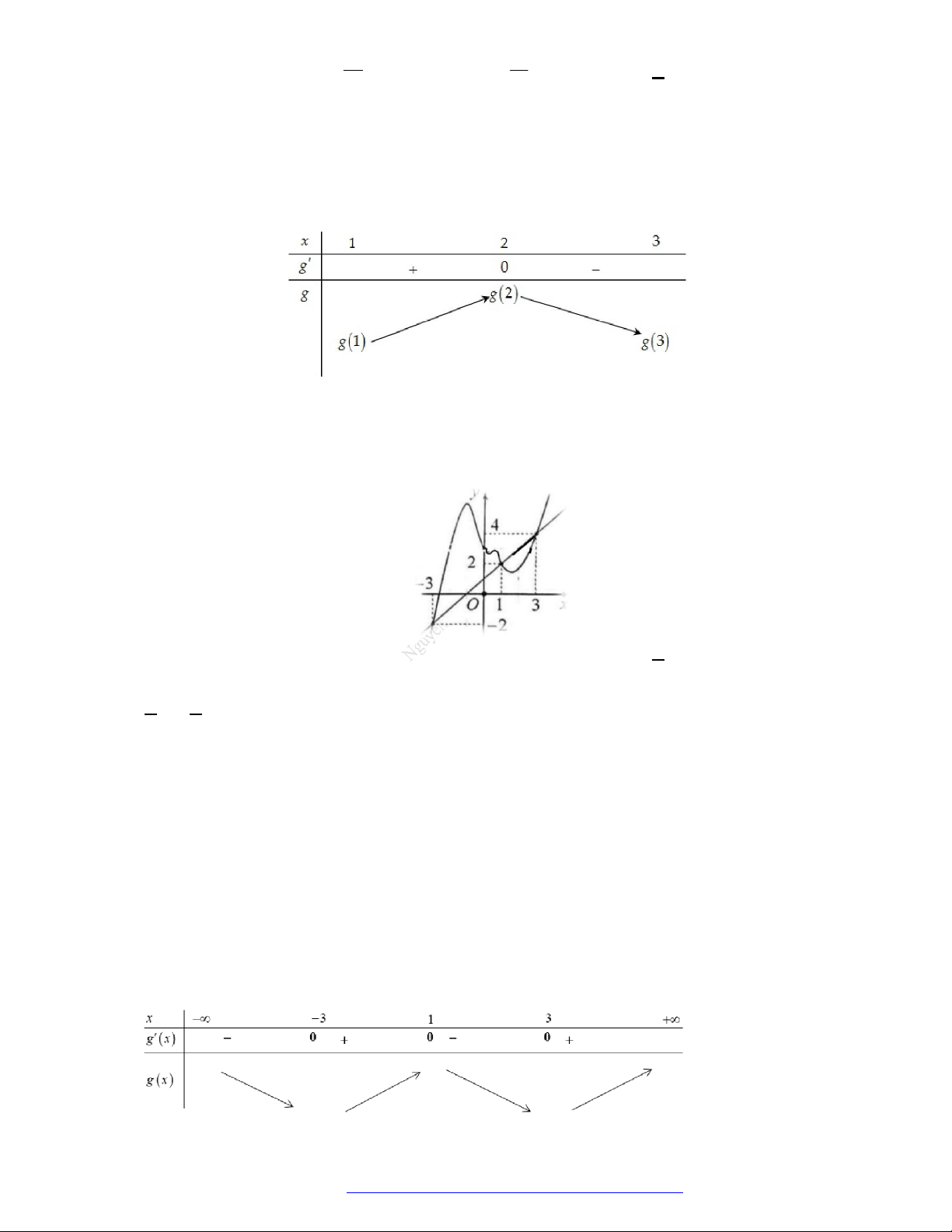
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 22 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A. 15. B.
25
3
. C.
19
3
. D. 12.
Lời giải
( ) ( )
( )
2 2
4 2 4 6 8g x x f x x x x
( )
( )
2
2 2 4 4x f x x x
.
Với
1;3x
thì
4 0x
;
2
3 4 4x x
nên
( )
2
4 0f x x
.
Suy ra
( )
2
2 4 4 0f x x x
,
1;3x
.
Bảng biến thiên
Suy ra
( ) ( )
1;3
max 2g x g
( )
4 7 12f
.
Câu 5. Cho hàm số
( )
y f x
liên tục trên
.
Đồ thị của hàm số
( )
y f x
như hình bên. Đặt
( ) ( ) ( )
2
2 1 .g x f x x
Mệnh đề dưới đây đúng.
A.
( ) ( )
3;3
max 3 .g x g
B.
( ) ( )
3;3
min 1 .g x g
C.
( ) ( )
3;3
max 0 .g x g
D.
( ) ( )
3;3
max 1 .g x g
Lời giải
Chọn D
( ) ( ) ( ) ( ) ( ) ( )
2
2 1 2 2 1g x f x x g x f x x
Dựa vào đồ thị ta thấy
( ) ( )
3
0 1 1
3
x
g x f x x x
x
Và
với
( ) ( ) ( )
; 3 : 1 0x f x x g x
với
( ) ( ) ( )
3;1 : 1 0x f x x g x
,
với
( ) ( ) ( )
1;3 : 1 0x f x x g x
với
( ) ( ) ( )
3; : 1 0x f x x g x
Bảng biến thiên
Dựa vào bảng biến thiên suy ra
( ) ( )
3;3
max 1 .g x g
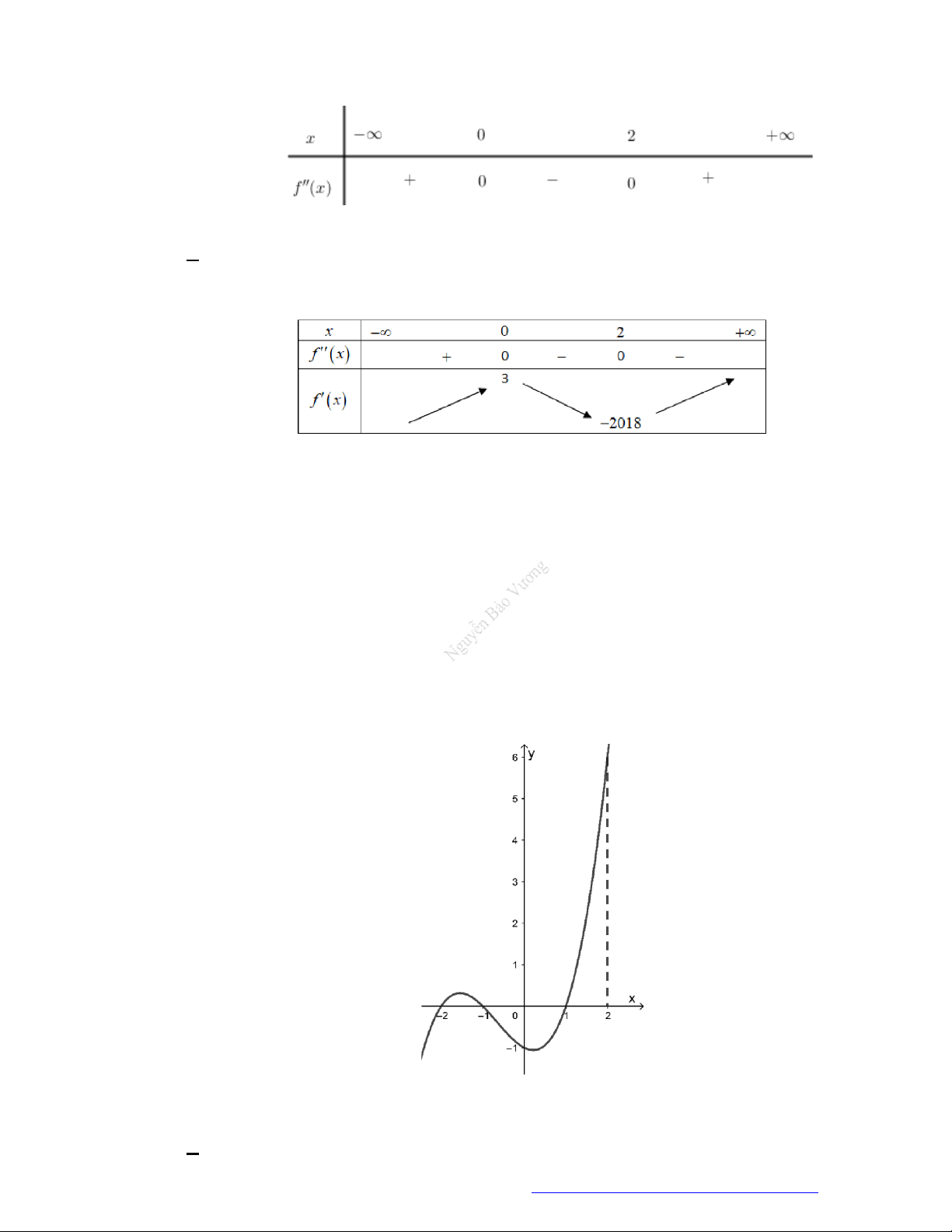
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
Câu 6. Cho hàm số có đạo hàm cấp hai trên . Biết , và bảng xét
dấu của như sau:
Hàm số đạt giá trị nhỏ nhất tại điểm thuộc khoảng nào sau đây?
A.
( )
; 2017
B.
( )
2017;
C.
( )
0;2
D.
( )
2017;0
Lời giải
Dựa vào bảng xét dấu của
( )
f x
ta có bảng biến thiên của hàm sồ
( )
f x
Đặt
2017t x
.
Ta có
( ) ( ) ( )
2017 2018 2018 2017.2018y f x x f t t g t
.
( ) ( )
2018g t f t
.
Dựa vào bảng biến thiên của hàm số
( )
f x
suy ra phương trình
( )
g t
có một nghiệm đơn
( )
;0
và một nghiệm kép
2t
.
Ta có bảng biến thiên
( )
g t
Hàm số
( )
g t
đạt giá trị nhỏ nhất tại
( )
0
;0t
.
Suy ra hàm số đạt giá trị nhỏ nhất tại
0
x mà
( ) ( )
0 0
2017 ;0 ; 2017x x
.
Câu 7. Cho hàm số
( )
f x
có đạo hàm là
( )
f x
. Đồ thị của hàm số
( )
y f x
được cho như hình vẽ
dưới đây:
Biết rằng
( ) ( ) ( ) ( )
1 0 1 2f f f f
. Giá trị nhỏ nhất và giá trị lớn nhất của hàm số
( )
y f x
trên đoạn
1;2
lần lượt là:
A.
( )
1f
;
( )
2f
. B.
( )
2f
;
( )
0f
. C.
( )
0f
;
( )
2f
. D.
( )
1f
;
( )
1f
.
( )
y f x
( )
0 3
f
( )
2 2018
f
( )
f x
( )
2017 2018y f x x
0
x
( )
2017 2018y f x x
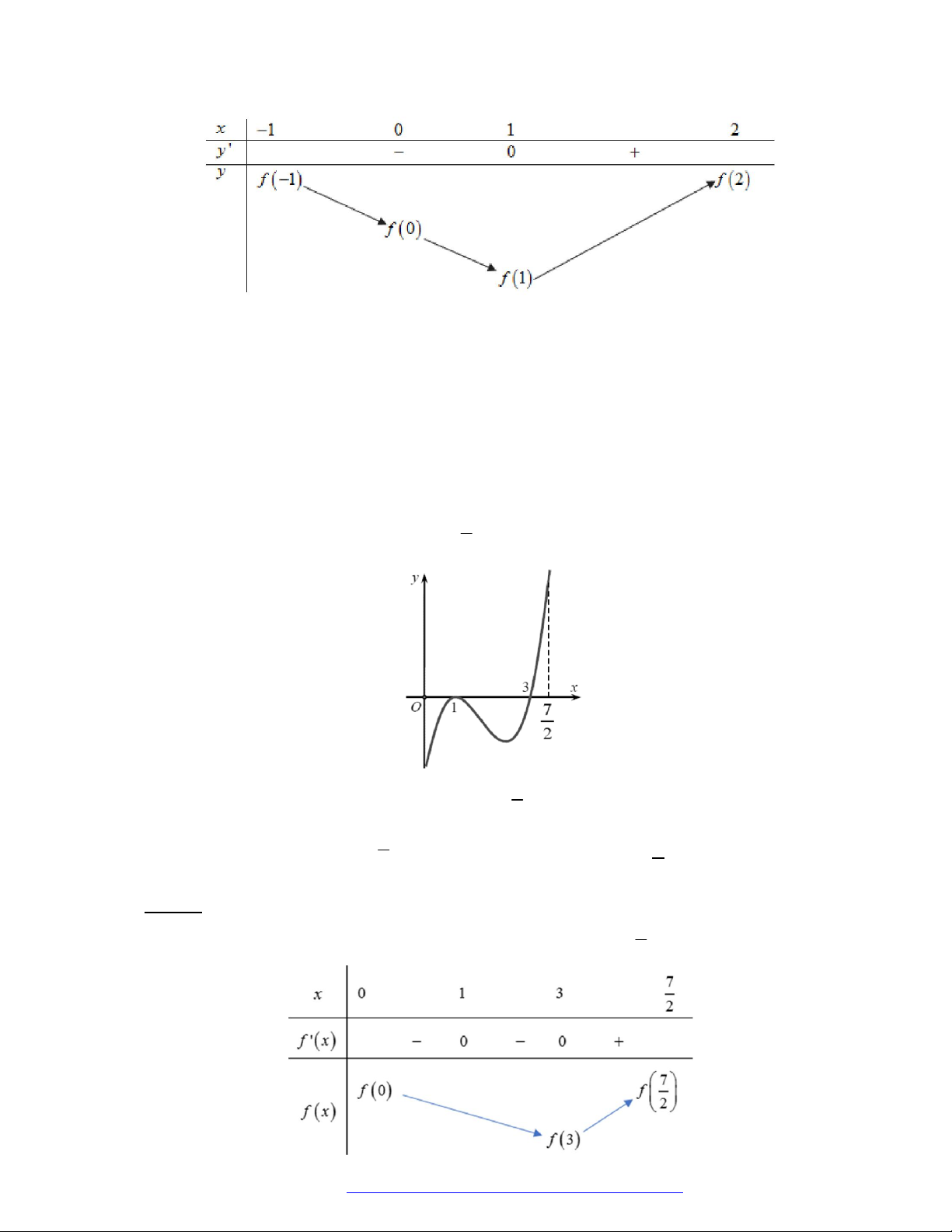
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 24 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Lời giải
Từ đồ thị của hàm số
( )
y f x
ta có bảng biến thiên của hàm số
( )
y f x
trên đoạn
1;2
như sau
Nhận thấy
( ) ( )
1;2
min 1f x f
.
Để tìm
( )
1;2
max f x
ta so sánh
( )
1f
và
( )
2f
.
Theo giả thiết,
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
1 0 1 2 2 1 0 1f f f f f f f f
.
Từ bảng biến thiên, ta có
( ) ( )
0 1 0f f
. Do đó
( ) ( ) ( ) ( )
2 1 0 2 1f f f f
.
Hay
( ) ( )
1;2
max 2f x f
.
Câu 8. Cho hàm số
( )
y f x
liên tục trên đoạn
7
0;
2
có đồ thị hàm số
( )
'y f x
như hình vẽ.
Hàm số
( )
y f x
đạt giá trị nhỏ nhất trên đoạn
7
0;
2
tại điểm
0
x
nào dưới đây?
A.
0
0x
. B.
0
7
2
x
. C.
0
1x
. D.
0
3x
.
Lời giải
Chọn D
Dựa vào đồ thị hàm số
( )
'y f x
ta có bảng biến thiên trên đoạn
7
0;
2
như sau:
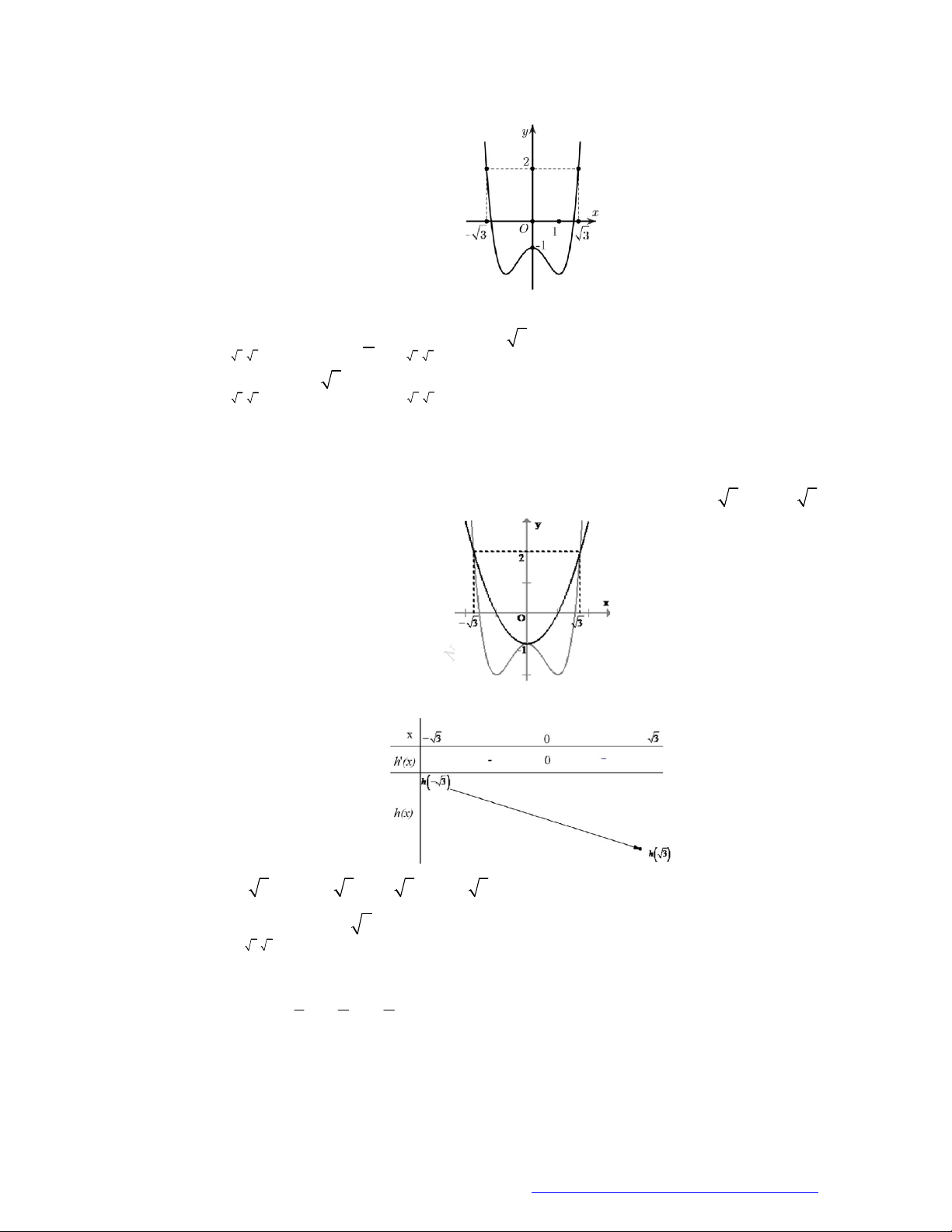
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25
Do đó hàm số đạt giá trị nhỏ nhất tại
0
3
x
.
Câu 9. Cho hàm số
( )
y f x
. Đồ thị hàm
( )
y f x
như hình vẽ
Đặt
( ) ( )
3
3 3h x f x x x
. Tìm mệnh đề đúng trong các mệnh đề sau:
A.
( )
[ 3; 3]
max ( ) 3 1h x f
. B.
( )
[ 3; 3]
max ( ) 3 3h x f
.
C.
( )
[ 3; 3 ]
max ( ) 3 3h x f
. D.
( )
[ 3; 3]
max ( ) 3 0h x f
.
Lời giải
Chọn B
Ta có:
( ) ( )
2
3 3 3h x f x x
( ) ( )
( )
2
3 1h x f x x
.
Đồ thị hàm số
2
1y x
là một parabol có toạ độ đỉnh
( )
0; 1C
, đi qua
( )
3;2A ,
( )
3;2B .
Từ đồ thị hai hàm số
y f x
và
2
1y x
ta có bảng biến thiên của hàm số
( )
y h x
.
Với
( ) ( )
3 3 3h f ,
( ) ( )
3 3 3h f .
Vậy
[ 3; 3 ]
max ( ) 3 3h x f
.
Câu 10. Cho hàm số
( )
y f x
có đồ thị
( )
y f x
ở hình vẽ bên. Xét hàm số
( ) ( )
3 2
1 3 3
2018,
3 4 2
g x f x x x x
mệnh đề nào dưới đây đúng?
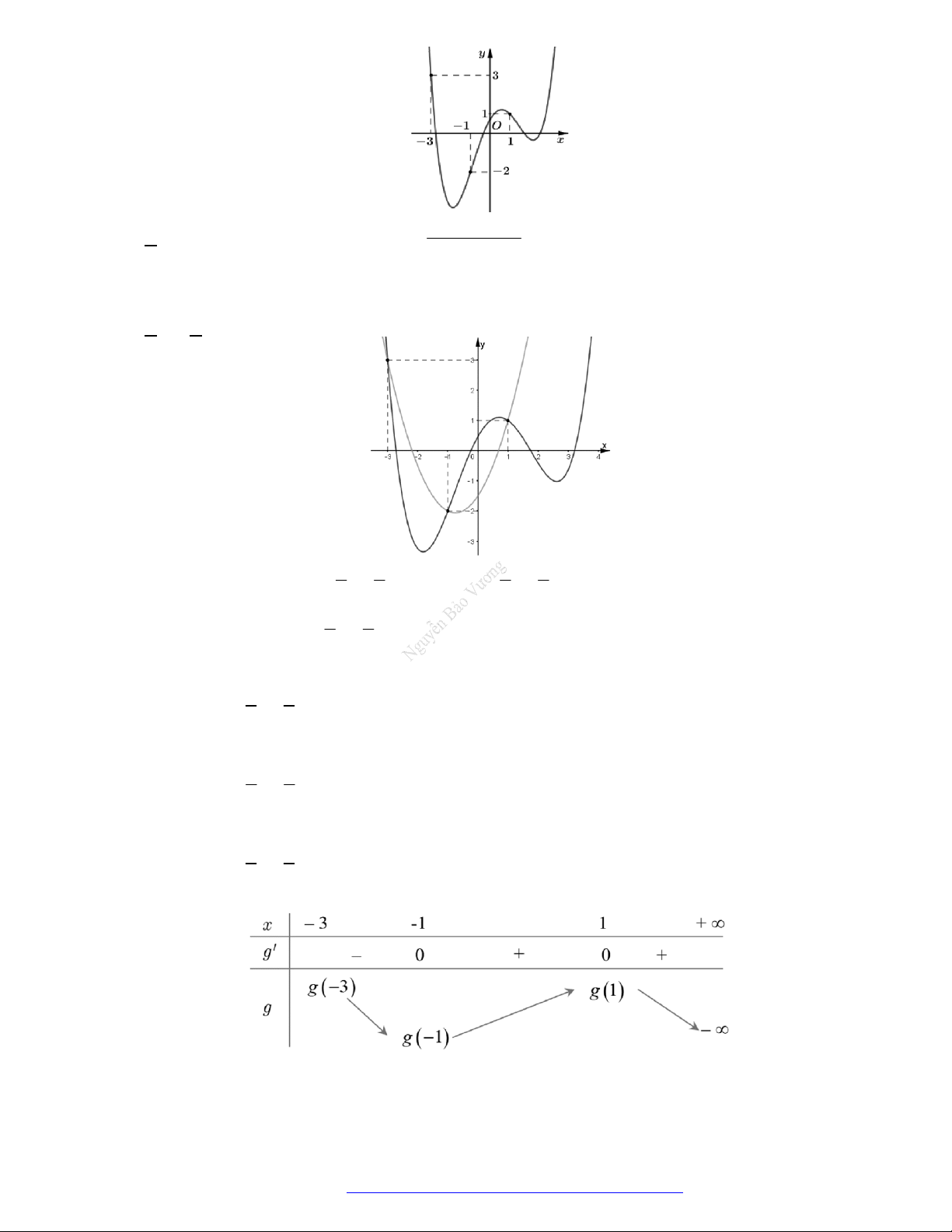
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 26 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
( ) ( )
3;1
min 1g x g
. B.
( )
( ) ( )
3;1
3 1
min
2
g g
g x
.
C.
( ) ( )
3;1
min 3g x g
. D.
( ) ( )
3;1
min 1g x g
.
Lời giải
Chọn A
Ta có
( ) ( ) ( )
2 2
3 3 3 3
2 2 2 2
g x f x x x f x x x
.
Vẽ parabol
( )
2
3 3
:
2 2
P y x x
. Ta thấy
( )
P
đi qua các điểm có toạ độ
( )
3;3
,
( )
1;2
,
( )
1;1
.
Trên khoảng
( )
3; 1
đồ thị hàm số
( )
f x
nằm phía dưới
( )
P
nên
( ) ( )
2
3 3
0
2 2
f x x x g x
.
Trên khoảng
( )
1;1
đồ thị hàm số
( )
f x
nằm phía trên
( )
P
nên
( ) ( )
2
3 3
0
2 2
f x x x g x
.
Trên khoảng
( )
1;
đồ thị hàm số
( )
f x
nằm phía dưới
( )
P
nên
( ) ( )
2
3 3
0
2 2
f x x x g x
.
Bảng biến thiên
Từ bảng biến thiên, ta có
( ) ( )
3;1
min 1g x g
.
Câu 11. Cho hàm số
( )
y f x
có đạo hàm liên tục trên
R
. Hàm số
( )
'y f x
có đồ thị như hình sau:
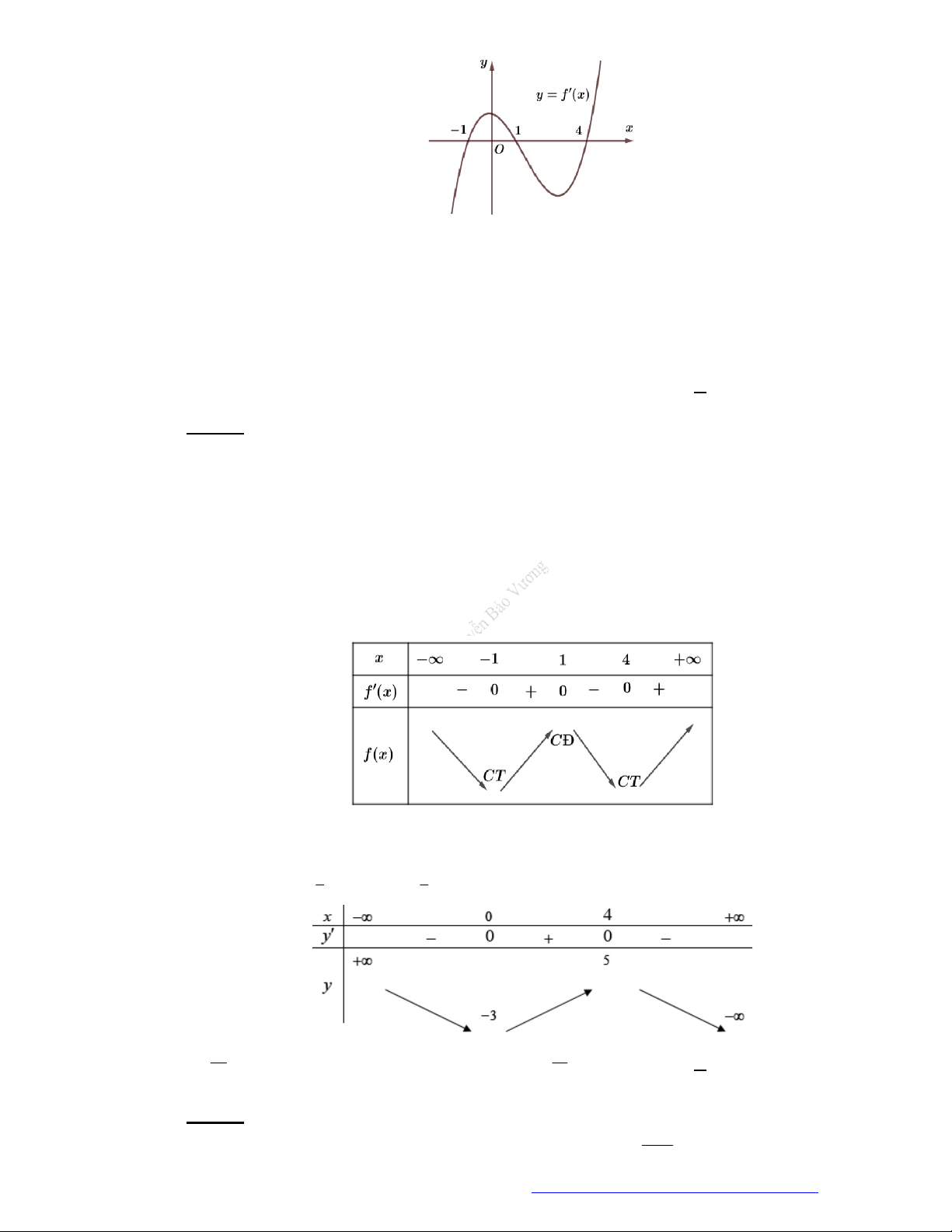
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27
Cho bốn mệnh đề sau:
1) Hàm số
( )
y f x
có hai cực trị
2) Hàm số
( )
y f x
đồng biến trên khoảng
( )
1;
3)
( ) ( ) ( )
1 2 4 .f f f
4) Trên đoạn
1;4
, giá trị lớn nhất của hàm số
( )
y f x
là
( )
1 .f
Số mệnh đề đúng trong bốn mệnh đề trên là:
A.
3.
B.
1.
C.
4.
D.
2.
Lời giải
Chọn D
Dựa vào đồ thị của hàm số
( )
'y f x
ta thấy:
( )
1
' 0 1
4
x
f x x
x
( ) ( ) ( )
' 0 ; 1 1;4f x x
( ) ( ) ( )
' 0 1;1 4;f x x
Ta có bảng biến thiên của hàm số
( )
y f x
Dựa vào bảng biến thiên đáp án đúng là mệnh đề số
3
và
4
Câu 12. Cho hàm số
y f x
có bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất của hàm số
2 3 2
1 1
4 3 8
3 3
g x f x x x x x
trên đoạn
1;3 .
A.
25
.
3
B.
15.
C.
19
.
3
D.
12.
Lời giải
Chọn D
Ta có
2 2 2
4
4 .(4 2 x) x 6 8 2 2 (4 )
2
x
g x f x x x x f x x
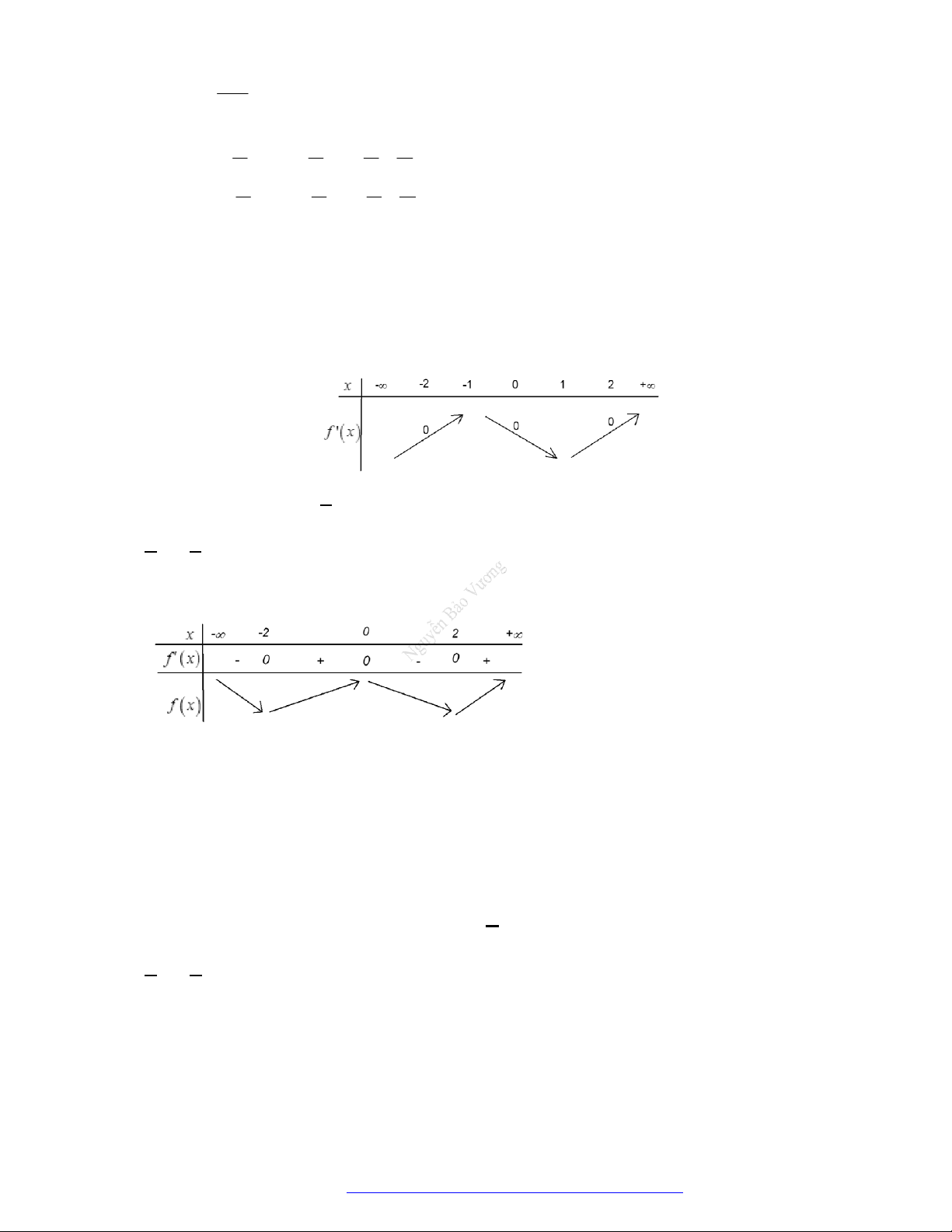
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 28 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Xét thấy
2 2
1;3 3 4 4 (4 ) 0x x x f x x
Mặt khác
4
0
2
x
1;3x
Suy ra
0 2g x x
19 17 17 32
1 (3) (4) 5
3 3 3 3
19 19 19 34
(3) (3) (4) 5
3 3 3 3
(2) 5 7 12.
g f f
g f f
g
1 3 2g g g
Vậy
1;3
max 12g x
tại
2.x
Câu 13. Cho hàm số
( )
y f x
. Hàm số
( )
y f x
có bảng biến thiên như hình vẽ bên. Giá trị lớn nhất
của hàm số
( ) ( )
2
2 sing x f x x
trên đoạn
1;1
là
A.
( )
1f
. B.
( )
0f
. C.
( )
2f
. D.
( )
1f
.
Lời giải
Chọn B
Ta có
1;1 2 2;2x x
.
Từ bảng biến thiên của
( )
'y f x
thì bảng biến thiên
( )
y f x
như sau:
Ta thấy
1;1x
ta có
( ) ( )
( )
2
2 0
sin 0 sin 0
f x f
x
, do đó
( ) ( ) ( )
0 0g x g f
.
Dấu “=” xảy ra khi
0x
.
Câu 14. Cho hàm số
( )
y f x
liên tục trên
sao cho
( )
1;2
max 3f x
. Xét hàm số
( ) ( )
3 1g x f x m
.
Tìm tất cả các giá trị của tham số
m
để
( )
0;1
max 10g x
.
A.
13
. B.
7
. C.
13
. D.
1
.
Lời giải
Chọn C
Đặt
3 1u x
( ) ( )
g x f u m
.
0;1 1;2x u
.
Do
( )
f x
liên tục trên
nên
( )
( )
( )
( )
0;1 1;2 1;2
max max max 3g x f u m f u m m
.
Để
( )
0;1
max 10 13g x m
.
Câu 15. Cho hàm số
( )
y f x
có đạo hàm cấp 2 trên
, hàm số
( )
y f x
có đồ thị như hình vẽ bên.
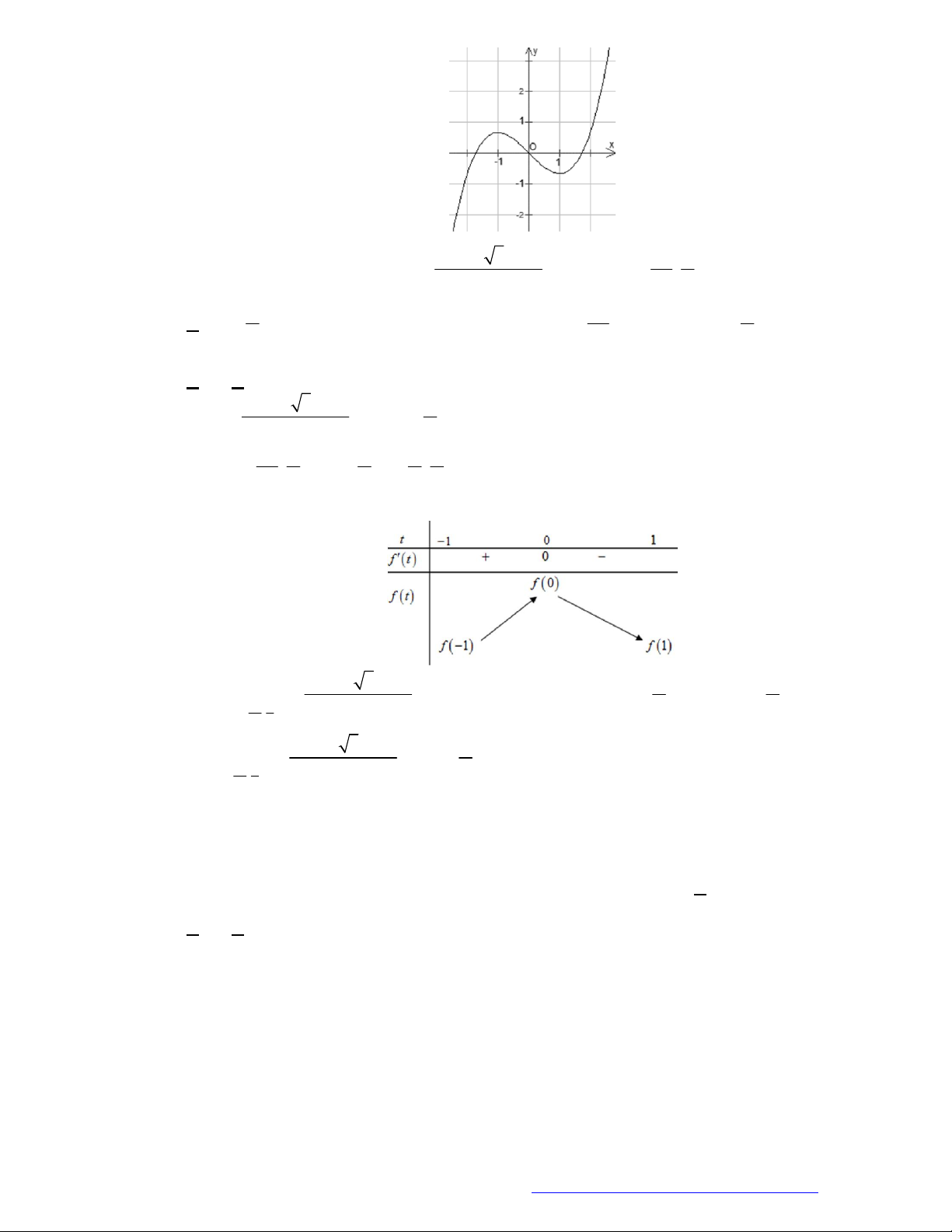
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 29
Giá trị lớn nhất của hàm số
sin 3 cos
2
x x
y f
trên đoạn
5
;
6 6
bằng
A.
3
f
. B.
( )
0f
. C.
5
6
f
. D.
6
f
.
Lời giải
Chọn A
Đặt
sin 3 cos
sin
2 3
x x
t x
.
Vì
5
; ; 1;1
6 6 3 2 2
x x t
.
Dựa vào đồ thị của hàm số
( )
f x
, ta có bảng biến thiên
Ta có:
( )
5
1;1
;
6 6
sin 3 cos
max max
2
x x
f f t
0 sin 0
3 3
t x x
.
Vậy
5
;
6 6
sin 3 cos
max
2 3
x x
f f
.
Câu 16. Cho hàm số
( )
y f x
liên tục trên
sao cho
( ) ( )
0;10
max 2 4
x
f x f
. Xét hàm số
( )
( )
3 2
2g x f x x x x m
. Giá trị của tham số
m
để
( )
0;2
max 8
x
g x
là
A.
5
. B.
4
. C.
1
. D.
3
.
Lời giải
Chọn D
Đặt
3
t x x
. Vì
0;2 0;10x t
.
Ta có:
( )
( )
( )
3 2 3 2
0;2 0;2 0;2 0;2
max max 2 max max 2
x x x x
g x f x x x x m f x x x x m
( )
0;10
max 1
t
f t m
(với
3
t x x
và
2
0;2
max 2 1
x
x x m m
).
( )
0;10
max 1 4 1 5
x
f x m m m
.
Suy ra:
( )
0;2
1
max 5 1
2
x
x
g x m x
t
.
Theo giả thiết, ta có:
( )
0;2
max 8 5 8 3
x
g x m m
.
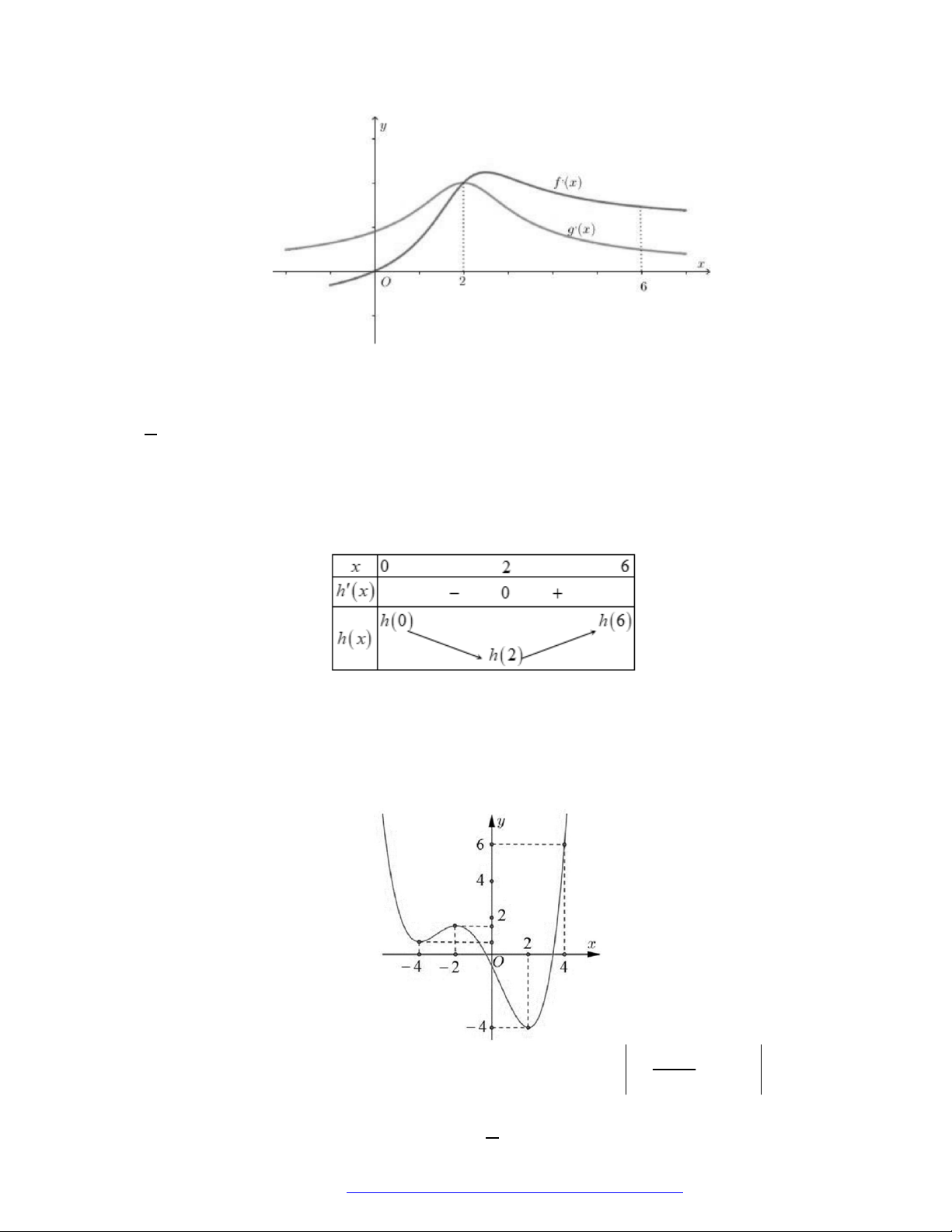
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 30 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 17. Cho hai hàm số
( )
y f x
,
( )
y g x
có đạo hàm là
( )
f x
,
( )
g x
. Đồ thị hàm số
( )
y f x
và
( )
g x
được cho như hình vẽ bên dưới.
Biết rằng
( ) ( ) ( ) ( )
0 6 0 6f f g g
. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
( ) ( ) ( )
h x f x g x
trên đoạn
0;6
lần lượt là:
A.
( )
6h
,
( )
2h
. B.
( )
2h
,
( )
6h
. C.
( )
0h
,
( )
2h
. D.
( )
2h
,
( )
0h
.
Lời giải
Ta có
( ) ( ) ( )
h x f x g x
.
( )
0 2h x x
Từ đồ thị ta có bảng biến thiên:
Và
( ) ( ) ( ) ( )
0 6 0 6f f g g
( ) ( ) ( ) ( )
0 0 6 6f g f g
.
Hay
( ) ( )
0 6h h
.
Vậy
( ) ( )
0;6
max 6h x h
;
( ) ( )
0;6
min 2h x h
.
Câu 18. (Chuyên Lào Cai - 2020) Cho hàm số
( )
f x
liên tục trên
, có đồ thị như hình vẽ
Có tất cả bao nhiêu giá trị nguyên của tham số
m
để hàm số
2
8
1
1
x
y f m
x
có giá trị
lớn nhất không vượt quá
2020
?
A.
4029
. B.
4035
. C.
4031
. D.
4041
.
Lời giải
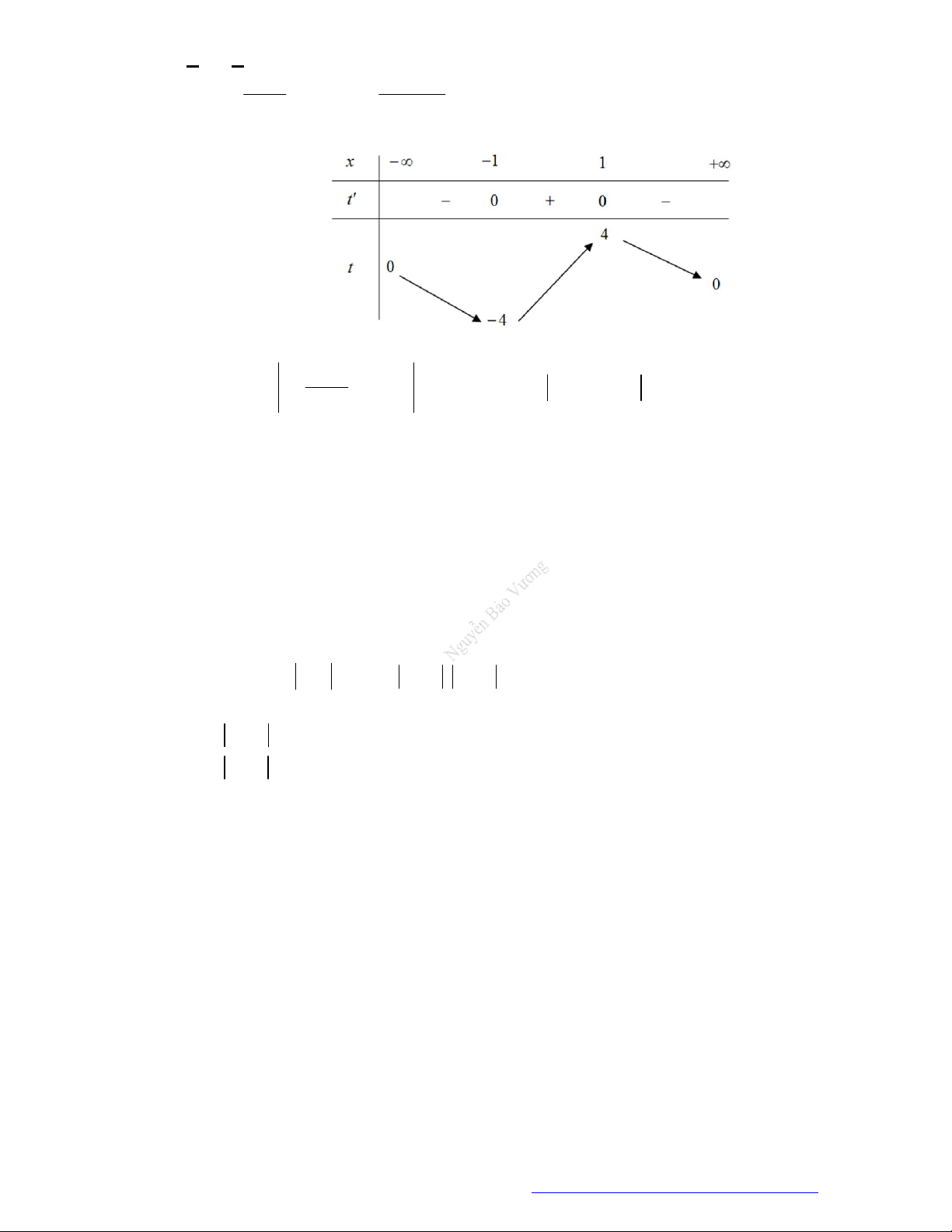
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 31
Chọn C
Đặt
2
8
1
x
t
x
. Ta có:
( )
2
2
2
8 8
1
x
t
x
;
0 1t x
.
BBT:
4;4t
.
Hàm số
2
8
1
1
x
y f m
x
trở thành
( ) ( )
1 , 4;4g t f t m t
.
Đặt
( ) ( )
1, 4;4h t f t m t
, ta có:
( ) ( )
h t f t
.
( ) ( )
0 0h t f t
4 4;4
2 4;4
2 4;4
t
t
t
.
Ta có:
( )
4 0,8 1 0,2h m m
;
( )
4 6 1 5h m m
;
( )
2 1,6 1 0,6h m m
;
( )
2 4 1 5h m m
.
( )
4;4
Max Maxy h t
Max 5 ; 5m m
.
Yêu cầu bài toán
5 2020
5 2020
m
m
2020 5 2020
2020 5 2020
m
m
2025 2015
2015 2025
m
m
2015 2015m
.
Vậy có tất cả
4031
giá trị nguyên của tham số
m
thỏa mãn yêu cầu bài toán.
Câu 19. (Sở Hưng Yên - 2020) Cho hàm số
( )
y f x
liên tục trên
có đồ thị
( )
y f x
như hình bên.
Đặt
( ) ( ) ( )
2
2 1g x f x x
.
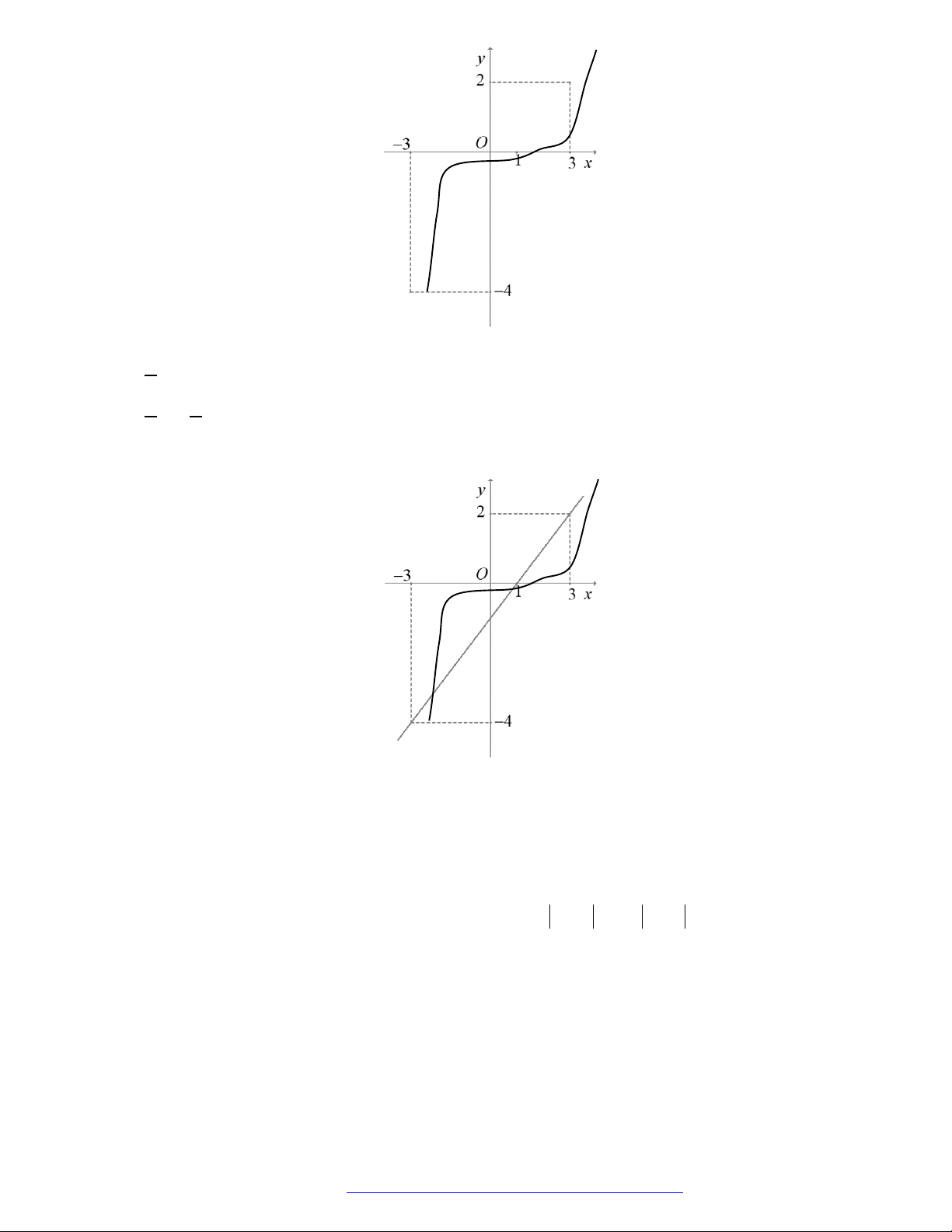
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 32 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Khi đó
( )
y g x
đạt giá trị nhỏ nhất trên đoạn
3;3
tại
A.
3x
. B.
3x
. C.
0x
. D.
1x
.
Lời giải.
Chọn A
Ta có
( ) ( ) ( ) ( ) ( ) ( )
( )
2
2 1 2 1g x f x x g x f x x
. Vẽ đồ thị hàm số
1y x
trên cùng
hệ trục tọa độ với đồ thị hàm số
( )
y f x
.
Dựa vào đồ thị ta thấy
+
( ) ( ) ( ) ( ) ( ) ( )
1 3
3 1
0 1 3 ; 0 1 3d dg x x g g g x x g g
. Do đó
( )
y g x
đạt giá trị nhỏ
nhất trên đoạn
3;3
tại
3x
hoặc
3x
.
+ Phần hình phẳng giới hạn bởi
( )
; 1; 3; 1y f x y x x x
có diện tích lớn hơn phần hình
phẳng giới hạn bởi
( )
; 1; 1; 3y f x y x x x
nên
( ) ( ) ( ) ( )
1 3
3 1
3 3d dg x x g x x g g
.
Vậy
( )
y g x
đạt giá trị nhỏ nhất trên đoạn
3;3
tại
3x
.
Câu 20. (Kim Liên - Hà Nội - 2020) Cho hàm số
( )
f x
. Biết hàm số
( )
f x
có đồ thị như hình dưới đây.
Trên
4;3
, hàm số
( ) ( ) ( )
2
2 1g x f x x
đạt giá trị nhỏ nhất tại điểm
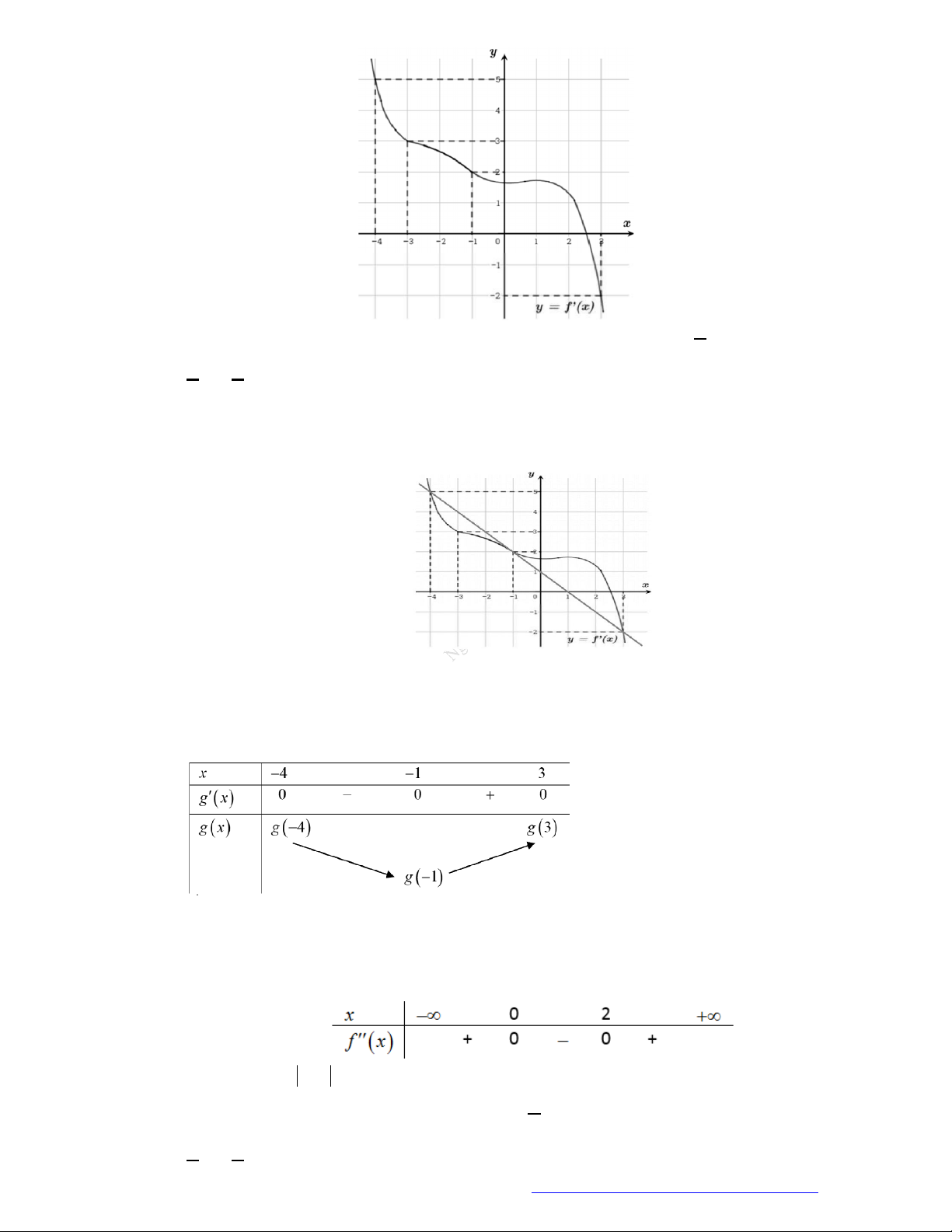
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 33
A.
3x
. B.
4x
. C.
3x
. D.
1x
.
Lời giải
Chọn D
Xét hàm số
( ) ( ) ( )
2
2 1g x f x x
trên
4;3
.
Ta có:
( ) ( ) ( )
2 2 1g x f x x
.
( ) ( )
0 1g x f x x
. Trên đồ thị hàm số
( )
f x
ta vẽ thêm đường thẳng
1y x
.
Từ đồ thị ta thấy
( )
4
1 1
3
x
f x x x
x
.
Bảng biến thiên của hàm số
( )
g x
như sau:
Vậy
( ) ( )
4;3
min 1 1g x g x
.
Câu 21. (Yên Lạc 2 - Vĩnh Phúc - 2020) Cho hàm số
( )
y f x
có đạo hàm cấp hai trên
. Biết
( ) ( ) ( )
0 3, 2 2018 0f f f
, và bảng xét dấu của
( )
f x
như sau
Hàm số
( )
1 2018y f x
đạt giá trị nhỏ nhất tại
0
x thuộc khoảng nào sau đây?
A.
( )
; 2015
. B.
( )
1;3
. C.
( )
1009;2
. D.
( )
2015;1
.
Lời giải.
Chọn C
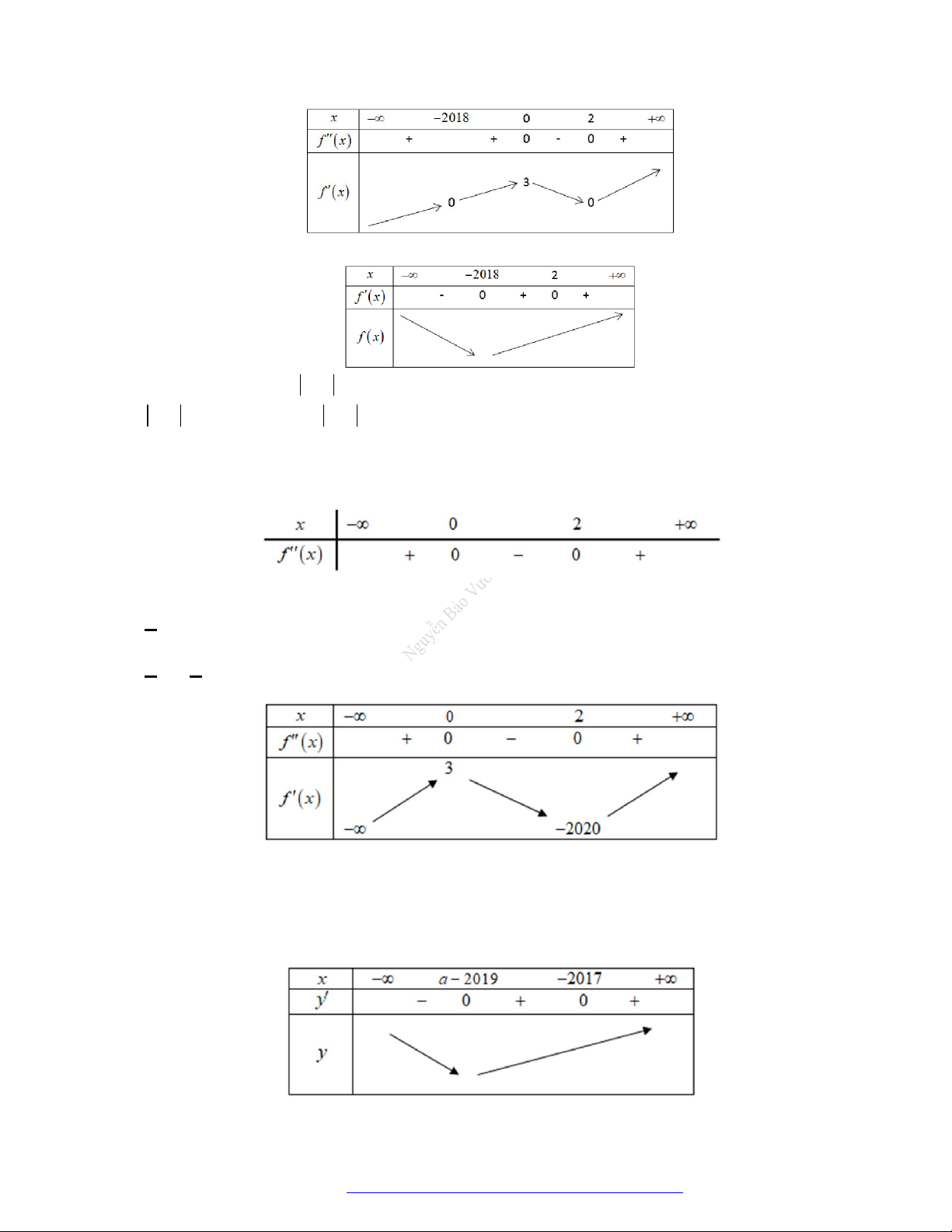
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 34 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Từ bảng xét dấu của
( )
f x
và giả thiết
( ) ( ) ( )
0 3, 2 2018 0f f f
suy ra bảng biến thiên
của hàm số
( )
y f x
như sau
Từ đó suy ra bảng biến thiên của hàm số
( )
y f x
:
Hàm số
( )
1 2018y f x
đạt giá trị nhỏ nhất khi và chỉ khi
1 2018 2018x
( )
1 0 1 1009;2x x
.
Câu 22. (THPT Anh Sơn - Nghệ An - 2020) Cho hàm số
( )
y f x
có đạo hàm cấp hai trên
. Biết
( )
0 3f
,
( )
2 2020f
,
( )
lim
x
f x
và bảng xét dấu của
( )
f x
như hình sau:
Hàm số
( )
2019 2020y f x x
đạt giá trị nhỏ nhất tại điểm
0
x thuộc khoảng nào sau đây?
A.
( )
; 2019
. B.
( )
0;2
. C.
( )
2019;0
. D.
( )
2019;
.
Lời giải
Chọn A
Theo giả thiết ta có
Ta có
( )
2019 2020y f x
( )
0 2019 2020y f x
.
Từ bảng biến thiên trên ta có
2019 2019
0
2019 2 2017
x a x a
y
x x
, với
0a
.
Từ đó ta có bảng biến thiên của hàm số
( )
2019 2020y f x x
Từ bảng biến thiên có hàm số
( )
2019 2020y f x x
đạt giá trị nhỏ nhất tại
0
2019x a .
Vì
0a
nên
( )
0
; 2019x
.
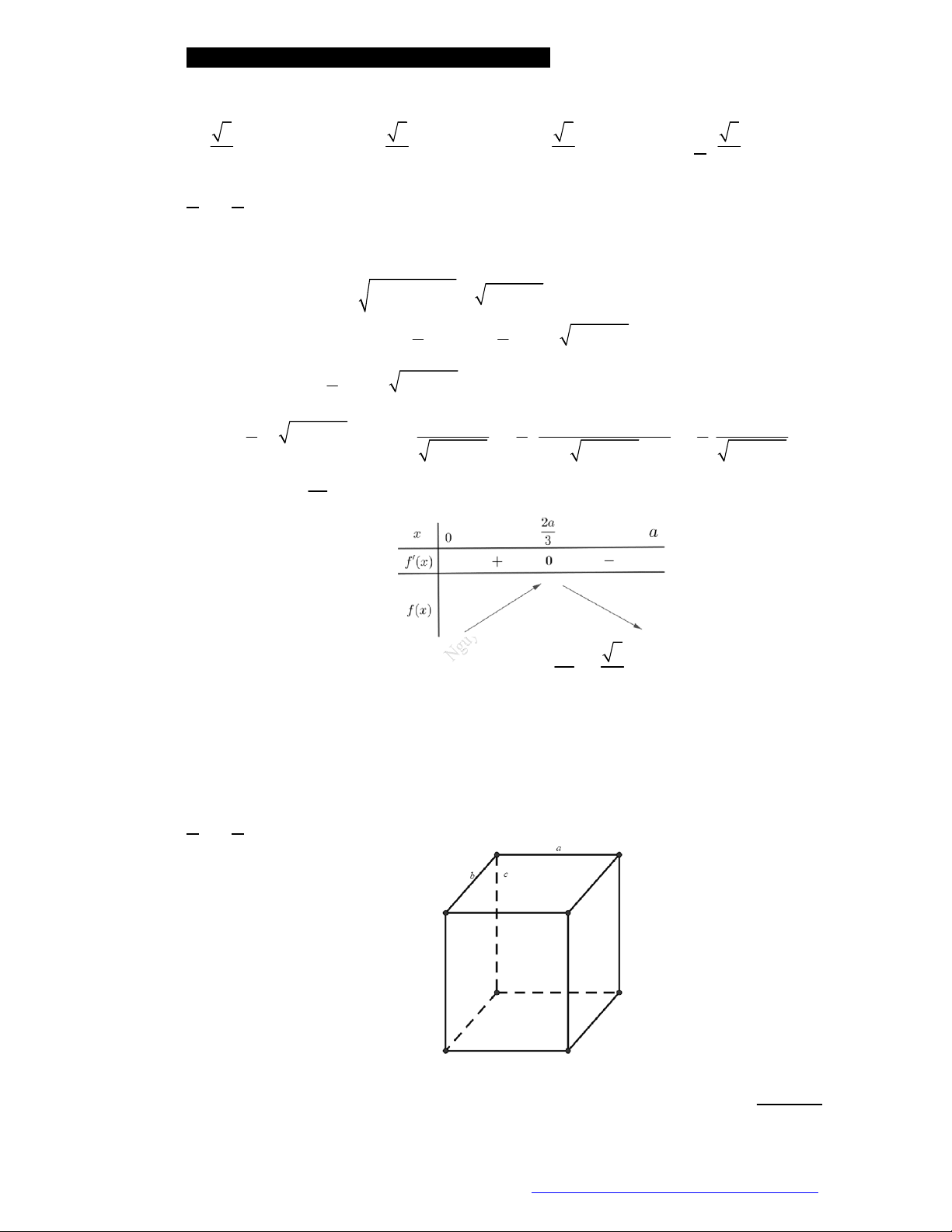
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 35
Dạng 3. Ứng dụng gtln-gtnn giải bài toán thực tế
Câu 1. (Chuyên Quang Trung - Bình Phước - Lần 2 - 2020) Cho số
0a
. Trong số các tam giác
vuông có tổng một cạnh góc vuông và cạnh huyền bằng
a
, tam giác có diện tích lớn nhất bằng
A.
2
3
3
a
. B.
2
3
6
a
. C.
2
3
9
a
. D.
2
3
18
a
.
Lời giải
Chọn D
Giả sử tam giác
ABC
vuông ở
A
thỏa mãn yêu cầu đề bài.
Giả sử
AB BC a AB a BC
Đặt
0 ;BC x x a
.
AB a x
và
( )
2
2 2
2 AC x a x ax a
Diện tích tam giác
ABC
là
( )
2
1 1
2
2 2
.S AB AC a x ax a
Xét hàm số
( ) ( )
2
1
2
2
f x a x ax a
( ) ( )
2
2
1
2
2
2
.
a
f x ax a a x
ax a
2 2 2
2 2 2 2
1 2 1 2 3
2 2
2 2
.
ax a a ax a ax
x a x a
( )
2
0
3
a
f x x
.
Vậy diện tích lớn nhất của tam giác
ABC
là
2
2a 3
3 18
S f a
.
Câu 2. (Mã 101 2018) Ông
A
dự định dùng hết
2
6,5m kính để làm một bể cá có dạng hình hộp chữ
nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có không đáng kể). Bể cá có dung
tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm).
A.
3
2,26 m B.
3
1,61m C.
3
1,33 m D.
3
1,50 m
Lời giải
Chọn D
Giả sử hình hộp chữ nhật có kích thước như hình vẽ. Ta có dung tích của bể cá:
V abc
Mặt khác theo giả thiết ta có:
2 2 6,5
2
ab bc ac
a b
2
2 6 6,5
2
b bc
a b
2
6,5 2
6
2
b
c
b
a b
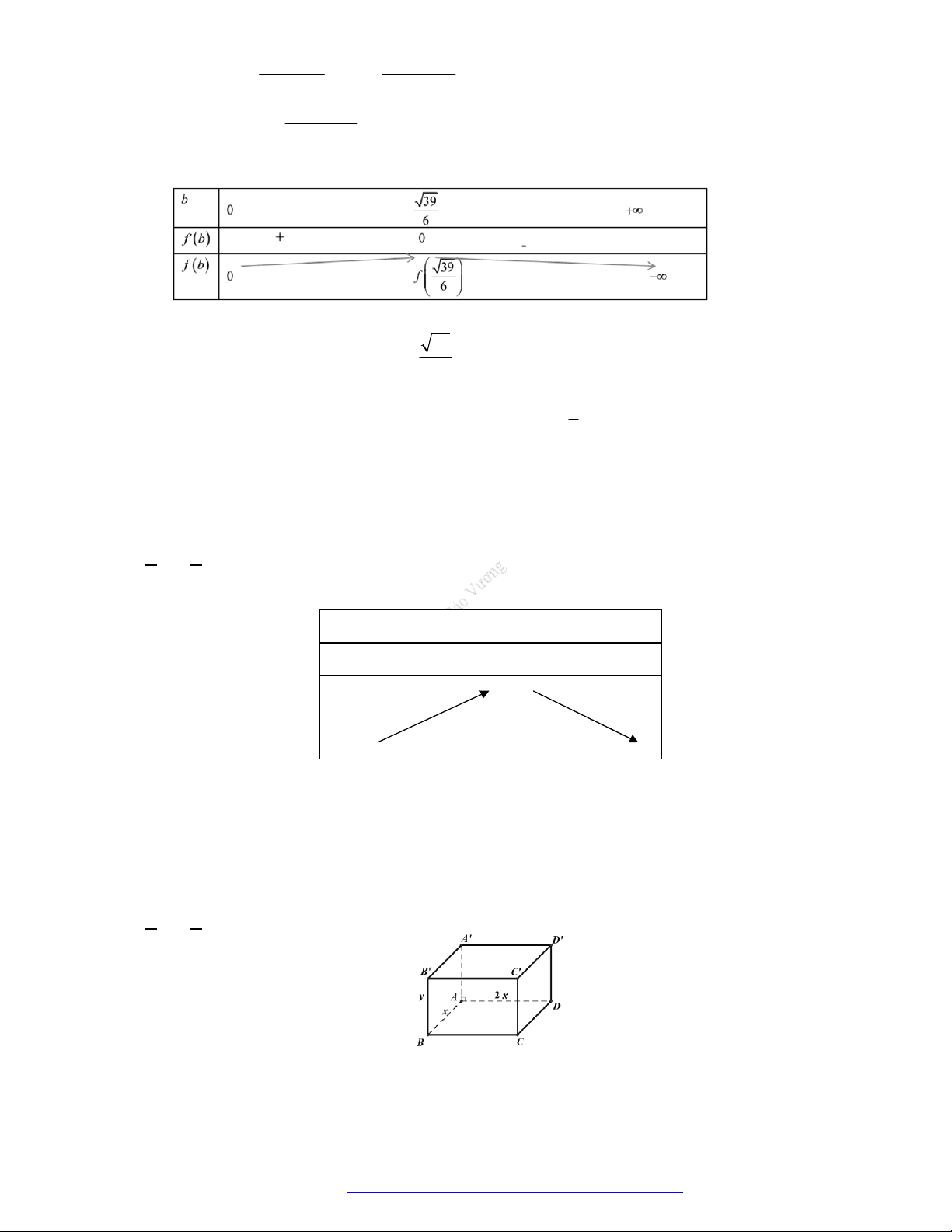
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 36 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Khi đó
2
2
6,5 2
2 .
6
b
V b
b
3
6,5 2
3
b b
V
.
Xét hàm số:
( )
3
6,5 2
3
b b
f b
. Có BBT
Vậy bể cá có dung tích lớn nhất là:
3
39
1,50
6
f m
.
Câu 3. (Mã 104 2017) Một vật chuyển động theo quy luật
3 2
1
6
3
s t t
với
t
(giây) là khoảng thời
gian tính từ khi vật bắt đầu chuyển động và
s
(mét) là quãng đường vật di chuyển được trong
khoảng thời gian đó. Hỏi trong khoảng thời gian
9
giây kể từ khi bắt đầu chuyển động, vận tốc
lớn nhất của vật đạt được bằng bao nhiêu?
A.
243
(m/s) B.
27
(m/s) C.
144
(m/s) D.
36
(m/s)
Lời giải
Chọn D
Ta có:
2
12v s t t
;
2 12v t
;
0 6v t
.
BBT
Nhìn bbt ta thấy vận tốc đạt giá trị lớn nhất khi
6t
. Giá trị lớn nhất là
( )
6 36m/sv
.
Câu 4. (Mã 103 2018) Ông A dự định sử dụng hết
2
5 m kính để làm một bể cá bằng kính có dạng hình
hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng
kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?
A.
3
1,01 m B.
3
0,96 m C.
3
1,33 m D.
3
1,51m
Lời giải
Chọn A
Gọi
,x y
lần lượt là chiều rộng và chiều cao của bể cá (điều kiện
, 0x y
).
Ta có thể tích bể cá
2
2V x y .
Theo đề bài ta có:
2
2 2.2 2 5xy xy x
2
6 2 5xy x
t
v
v
0
9
6
0
36
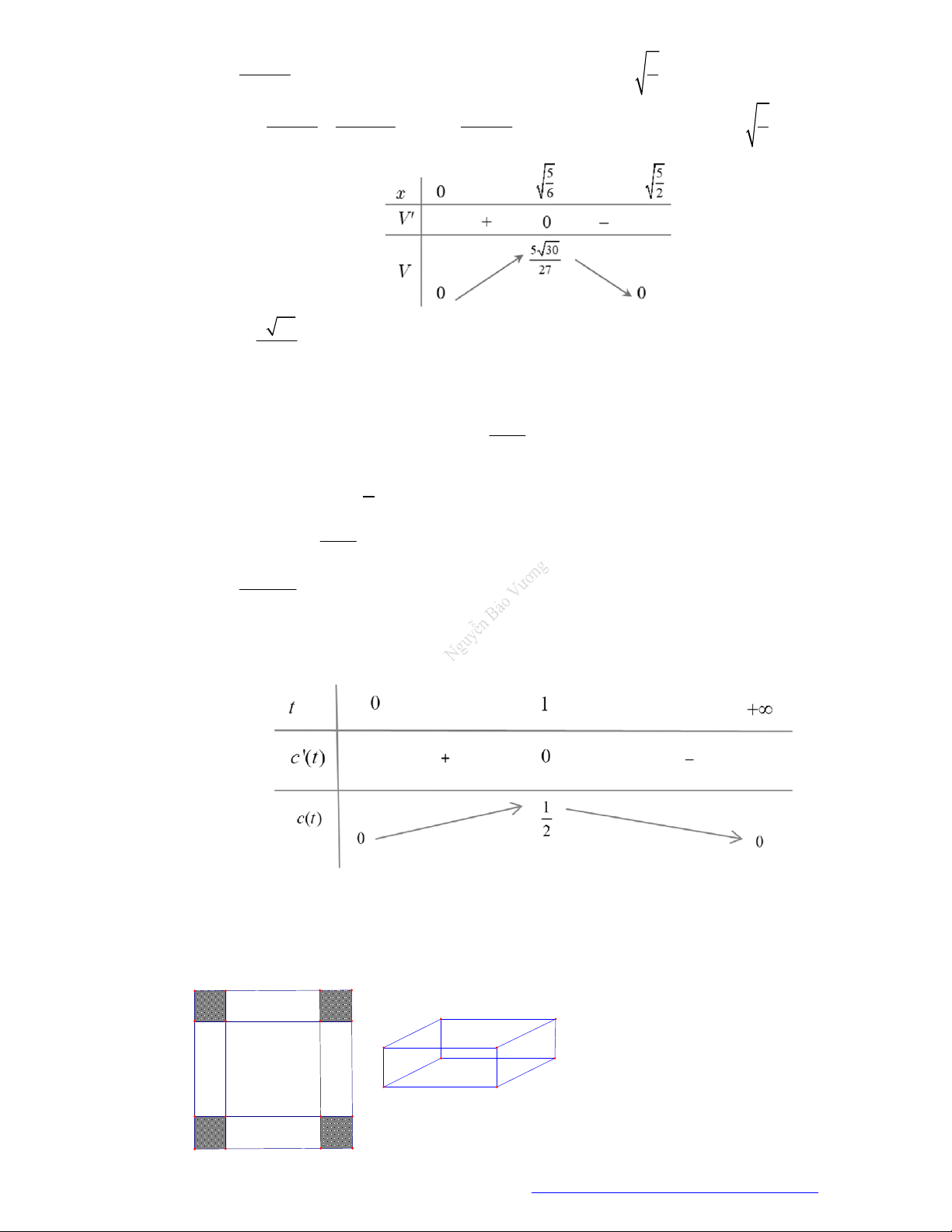
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 37
2
5 2
6
x
y
x
(Điều kiện kiện
2
0 5 2 0y x
5
0
2
x
)
2 3
2
5 2 5 2
2
6 3
x x x
V x
x
2
5 6
3
x
V
2
0 5 6 0V x
5
6
x
3
max
5 30
1,01
27
V m
.
Câu 5. Một loại thuốc được dùng cho một bệnh nhân và nồng độ thuốc trong máu của bệnh nhân được
giám sát bởi bác sĩ. Biết rằng nồng độ thuốc trong máu của bệnh nhân sau khi tiêm vào cơ thể
trong t giờ được cho bởi công thức
( )
2
1
t
c t
t
( )
/mg L
. Sau khi tiêm thuốc bao lâu thì nồng độ
thuốc trong máu của bệnh nhân cao nhất?
A. 4 giờ. B. 1 giờ. C. 3 giờ. D. 2 giờ.
Lời giải
Xét hàm số
( )
2
1
t
c t
t
,
( 0)t
.
( )
( )
2
2
2
1
1
t
c t
t
.
( )
1
0
1
t
c t
t
.
Với
1t
giờ thì nồng độ thuốc trong máu của bênh nhân cao nhất.
Câu 6. (Dề Minh Họa 2017) Cho một tấm nhôm hình vuông cạnh
12
cm. Người ta cắt ở bốn góc của
tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng
x
(cm), rồi gập tấm nhôm
lại như hình vẽ dưới đây để được một cái hộp không nắp. Tìm
x
để hộp nhận được có thể tích lớn
nhất.
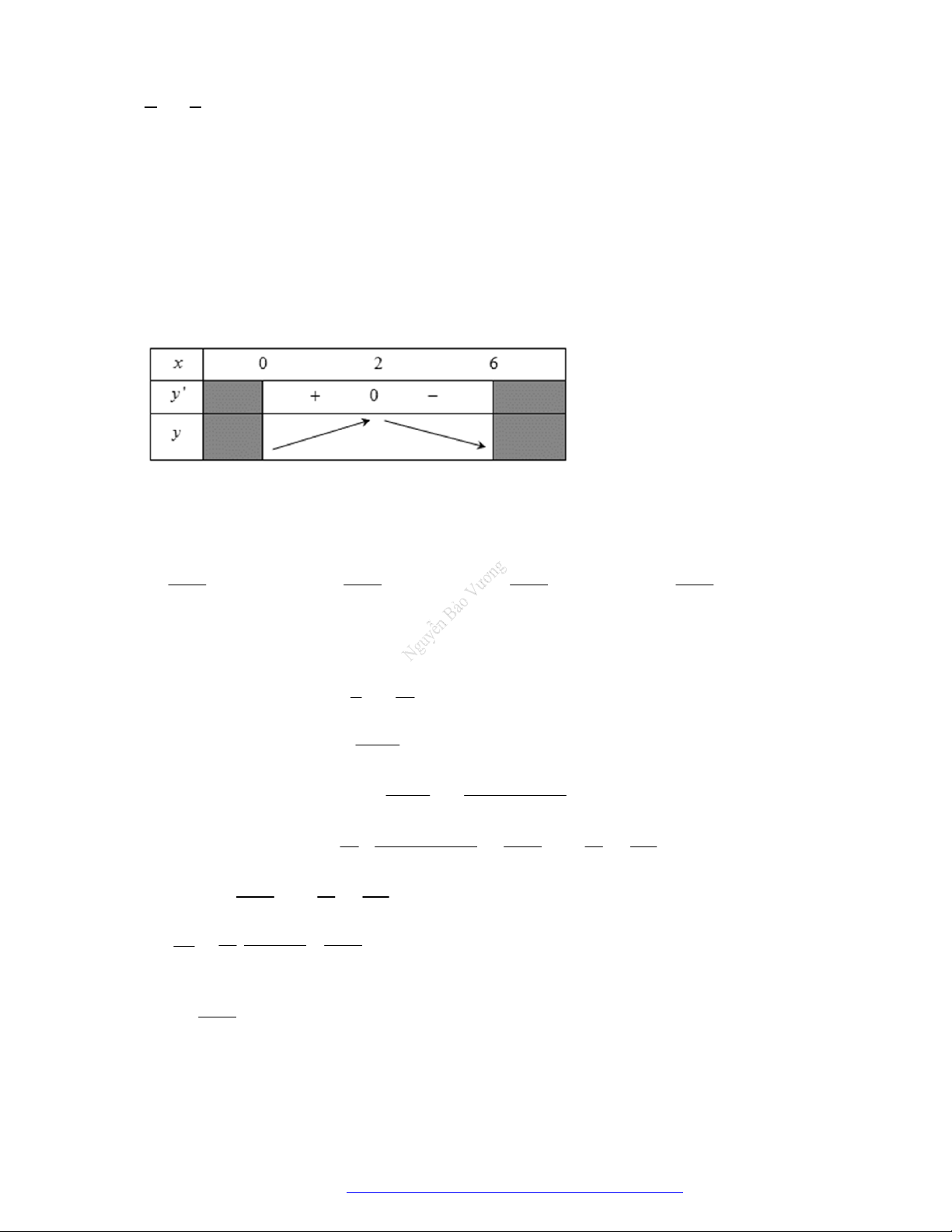
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 38 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
3x
B.
2x
C.
4x
D.
6x
Lời giải
Chọn B
Ta có :
( )
h x cm
là đường cao hình hộp
Vì tấm nhôm được gấp lại tạo thành hình hộp nên cạnh đáy của hình hộp là:
( )
12 2x cm
Vậy diện tích đáy hình hộp
( )
( )
2
2
12 2S x cm
. Ta có:
( )
0 0
0;6
12 2 0 6
x x
x
x x
Thể tích của hình hộp là:
( )
2
. 1. 2 2V S xh x
Xét hàm số:
( ) ( )
2
. 12 2 0;6y x x x
Ta có :
( ) ( ) ( )( )
2
' 12 2 4 12 2 12 2 12 6y x x x x x
;
( ) ( )
' 0 12 2 . 12 6 0 2y x x x
hoặc
6x
(loại).
Suy ra với
2x
thì thể tích hộp là lớn nhất và giá trị lớn nhất đó là
( )
2 128y
.
Câu 7. (Chuyên Lê Quý Đôn Điện Biên 2019) Một sợi dây có chiều dài
28m
được cắt thành hai đoạn
để làm thành một hình vuông và một hình tròn. Tính chiều dài (theo đơn vị mét) của đoạn dây làm
thành hình vuông được cắt ra sao cho tổng diện tích của hình vuông và hình tròn là nhỏ nhất?
A.
56
4
. B.
112
4
. C.
84
4
. D.
92
4
.
Lời giải
Gọi chiều dài của đoạn dây làm thành hình vuông là
x
(
m
) (
0 28x
)
=> chiều dài của đoạn dây làm thành hình tròn là
28 x
(
m
)
+) Diện tích hình vuông là:
2
2
4 16
x x
+) Bán kính hình tròn là: R =
28
2
x
=> Diện tích hình tròn:
2
2
2
28 784 56
.
2 4
x x x
R
+) Tổng diện tích hai hình:
2 2
2
784 56 4 14 196
16 4 16
x x x
x x
Xét
2
4 14 196
( )
16
f x x x
. Nhận thấy
( )f x
đạt giá trị nhỏ nhất tại
2
b
x
a
( )
14 16 112
.
2 4 4
Vậy chiều dài của đoạn dây làm thành hình vuông để tổng diện tích của hai hình đạt giá trị nhỏ
nhất là
112
4
m
Câu 8. (THPT Minh Châu Hưng Yên 2019) Cho một tấm nhôm hình chữ nhật có chiều dài bằng
10cm
và chiều rộng bằng
8cm
. Người ta cắt bỏ ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau,
mỗi hình vuông có cạnh bằng
( )
x cm
, rồi gập tấm nhôm lại (như hình vẽ) để được một cái hộp
không nắp. Tìm
x
để hộp nhận được có thể tích lớn nhất.
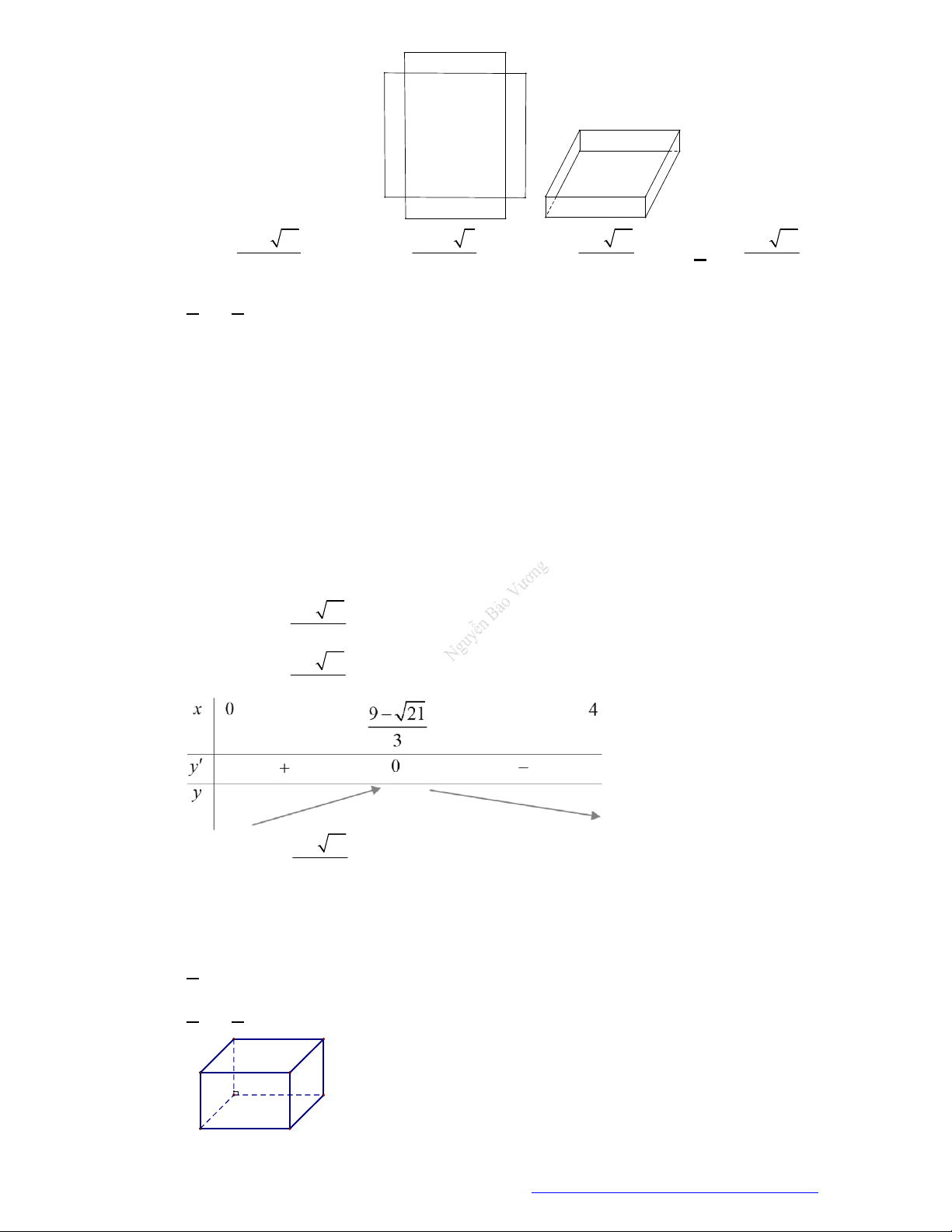
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 39
A.
8 2 21
3
x
B.
10 2 7
3
x
C.
9 21
9
x
. D.
9 21
3
x
Lời giải
Chọn D
Ta có :
( )
h x cm
là đường cao hình hộp
Vì tấm nhôm được gấp lại tạo thành hình hộp nên cạnh đáy của hình hộp là:
( )
10 2x cm
và
( )
8 2x cm
Vậy diện tích đáy hình hộp
( )( )
( )
2
10 2 8 2S x x cm
. Ta có:
( )
0
0
10 2 0 0;4
4
8 2 0
x
x
x x
x
x
Thể tích của hình hộp là:
( ) ( )
. 10 2 . 8 2.S xV x xh
Xét hàm số:
( ) ( ) ( )
. 10 2 . 8 2 0;4y x x x x
Ta có :
2
' 12 72 80y x x
;
( )
( )
9 21
4
3
' 0
9 21
3
x l
y
x n
.
Suy ra với
9 21
3
x
thì thể tích hộp là lớn nhất và giá trị lớn nhất.
Câu 9. (Mã 103 2018) Ông A dự định sử dụng hết
2
5 m
kính để làm một bể cá bằng kính có dạng hình
hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng
kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?
A.
3
1,01m
. B.
3
0,96 m
. C.
3
1,33 m
. D.
3
1,51m
.
Lời giải
Chọn A
Gọi
,x y
lần lượt là chiều rộng và chiều cao của bể cá (điều kiện
, 0x y
).
y
x
2
x
C
D
A
D'
B
C'
B'
A'
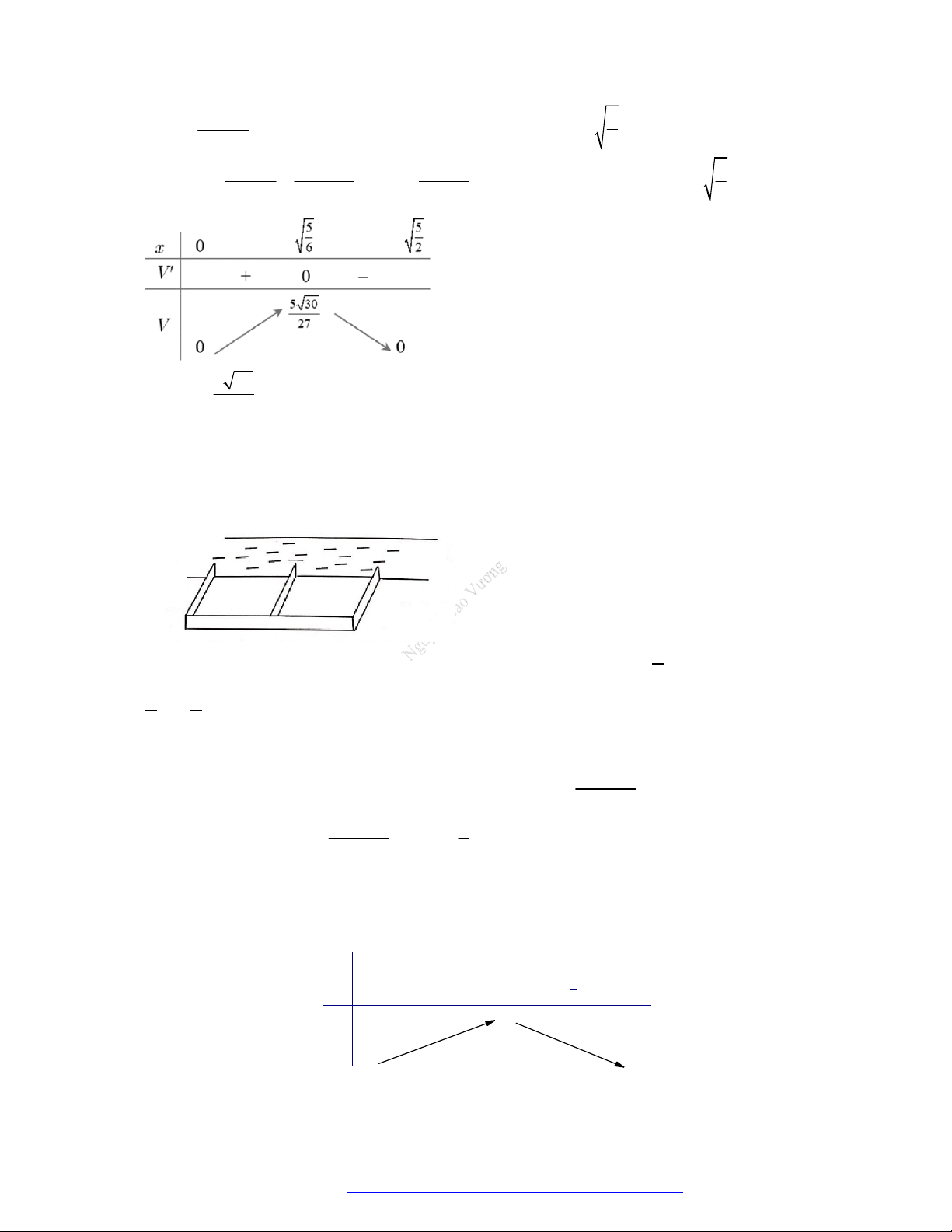
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 40 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta có thể tích bể cá
2
2V x y
.
Theo đề bài ta có:
2
2 2.2 2 5 xy xy x
2
6 2 5 xy x
2
5 2
6
x
y
x
(Điều kiện kiện
2
0 5 2 0 y x
5
0
2
x
)
2 3
2
5 2 5 2
2
6 3
x x x
V x
x
2
5 6
3
x
V
2
0 5 6 0
V x
5
6
x
x
3
ma
5 30
1,01
27
mV
.
Câu 10. Một người nông dân có 15.000.000 đồng muốn làm một cái hàng rào hình chữ E dọc theo một con
sông (như hình vẽ) để làm một khu đất có hai phần chữ nhật để trồng rau. Đối với mặt hàng rào
song song với bờ sông thì chi phí nguyên vật liệu là 60.000 đồng một mét, còn đối với ba mặt
hàng rào song song nhau thì chi phí nguyên vật liệu là 50.000 đồng một mét. Tìm diện tích lớn
nhất của đất rào thu được
A.
2
3125m . B.
2
50m . C.
2
1250m . D.
2
6250m .
Lời giải
Chọn D
Gọi
x
là chiều dài 1 mặt hàng rào hình chữ E ( trong ba mặt song song,
0x
).
Gọi
y
là chiều dài mặt hàng rào hình chữ E song song với bờ sông (
0y
).
Số tiền phải làm là:
500 5
.3.50000 .60000 15.000.000
2
x
x y y
.
Diện tích đất:
2
500 5 5
. . 250
2 2
x
S x y x x x
Ta có:
' 250 5S x
.
' 0 250 5 50.S x x
Bảng biến thiên:
Vậy:
( )
2
0;
max 6250 ( )S m
khi
50.x
-
∞
50
0
S'
S
0
x
+
+
∞
0
6250
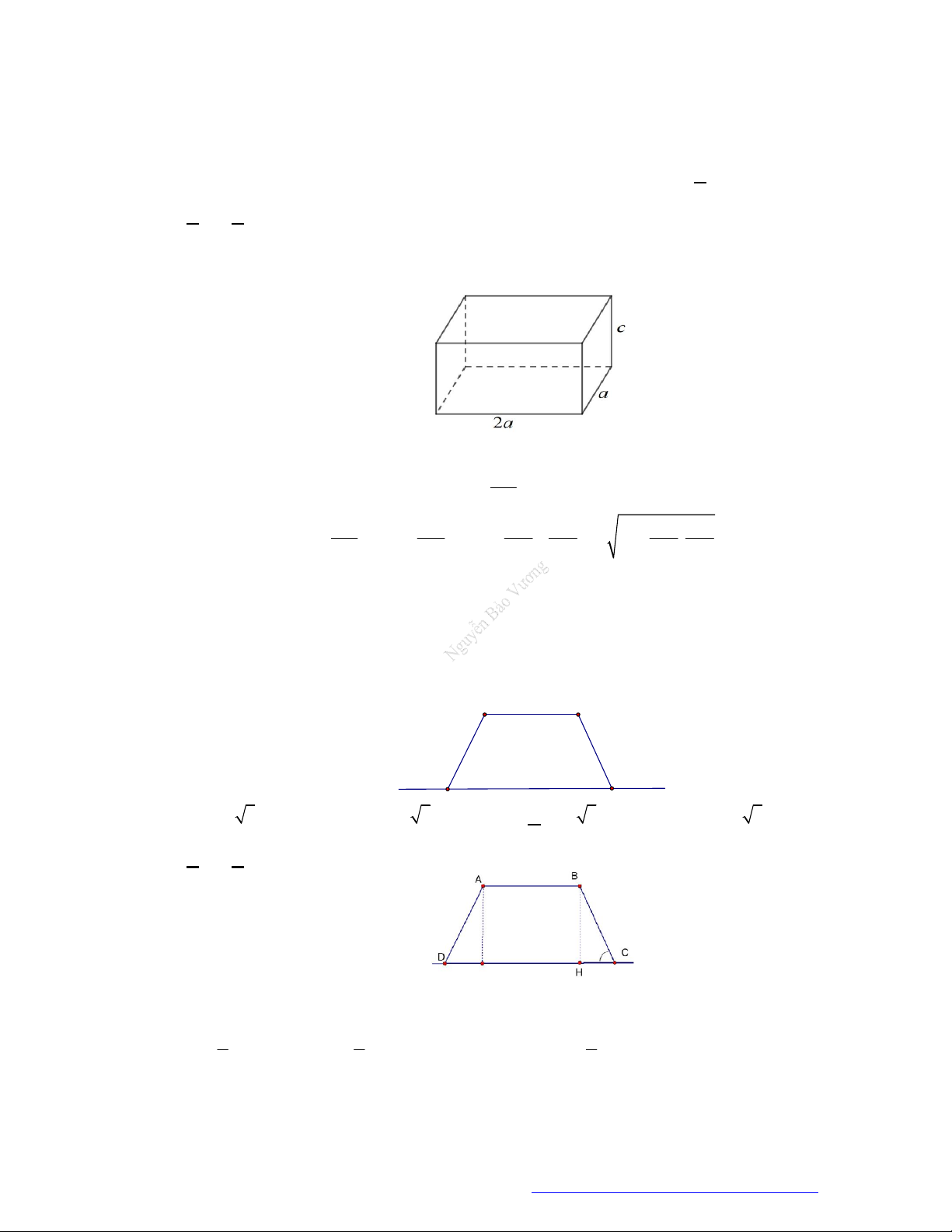
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 41
Câu 11. (Chuyên Long An-2019) Ông Khoa muốn xây một cái bể chứa nước lớn dạng một khối hộp chữ
nhật không nắp có thể tích bằng
3
288m
. Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng,
giá thuê nhân công để xây bể là
500000
đồng/
2
m
. Nếu ông Khoa biết xác định các kích thước
của bể hợp lí thì chi phí thuê nhân công sẽ thấp nhất. Hỏi ông Khoa trả chi phí thấp nhất để xây
dựng bể đó là bao nhiêu (Biết độ dày thành bể và đáy bể không đáng kể)?
A.
90
triệu đồng. B.
168
triệu đồng. C.
54
triệu đồng. D.
108
triệu đồng.
Lời giải
Chọn D
Theo bài ra ta có để chi phí thuê nhân công là thấp nhất thì ta phải xây dựng bể sao cho tổng diện
tích xung quanh và diện tích đáy là nhỏ nhất.
Gọi ba kích thước của bể là
a
,
2a
,
c
( ) ( )
( )
0, 0a m c m
.
Ta có diện tích cách mặt cần xây là
2 2
2 4 2 2 6S a ac ac a ac
.
Thể tích bể
2
.2 . 2 288V a a c a c
2
144
c
a
.
Suy ra
2 2 2 2
3
2
144 864 432 432 432 432
2 6 . 2 2 3. 2 . . 216S a a a a a
a a a a a a
.
Vậy
2
min
216 mS
, khi đó chi phí thấp nhất là
216.500000 108
triệu đồng.
Câu 12. (Kinh Môn - Hải Dương L2 2019) Một người nông dân có 3 tấm lưới thép B40, mỗi tấm dài
( )
12 m
và muốn rào một mảnh vườn dọc bờ sông có dạng hình thang cân
ABCD
như hình vẽ (bờ
sông là đường thẳng
DC
không phải rào, mỗi tấm là một cạnh của hình thang). Hỏi ông ta có thể
rào được mảnh vườn có diện tích lớn nhất là bao nhiêu
2
m
?
A. 100 3 . B. 106 3 . C. 108 3 . D. 120 3 .
Lời giải
Chọn C
Kẻ đường cao
BH
, gọi số đo 2 góc ở đáy
CD
của hình thang là
( )
, 0 ;90x x
.
Diện tích mảnh vườn là:
( ) ( ) ( )
2
1 1 1
.sin 2. 2 .cos 2sin sin 2
2 2 2
S BH AB CD BC x AB BC x AB x x
Xét hàm số
( )
2sin sin 2f x x x
với
( )
0 0
0 ;90x
có
( )
2cos 2cos 2f x x x
.
C
D
B
A
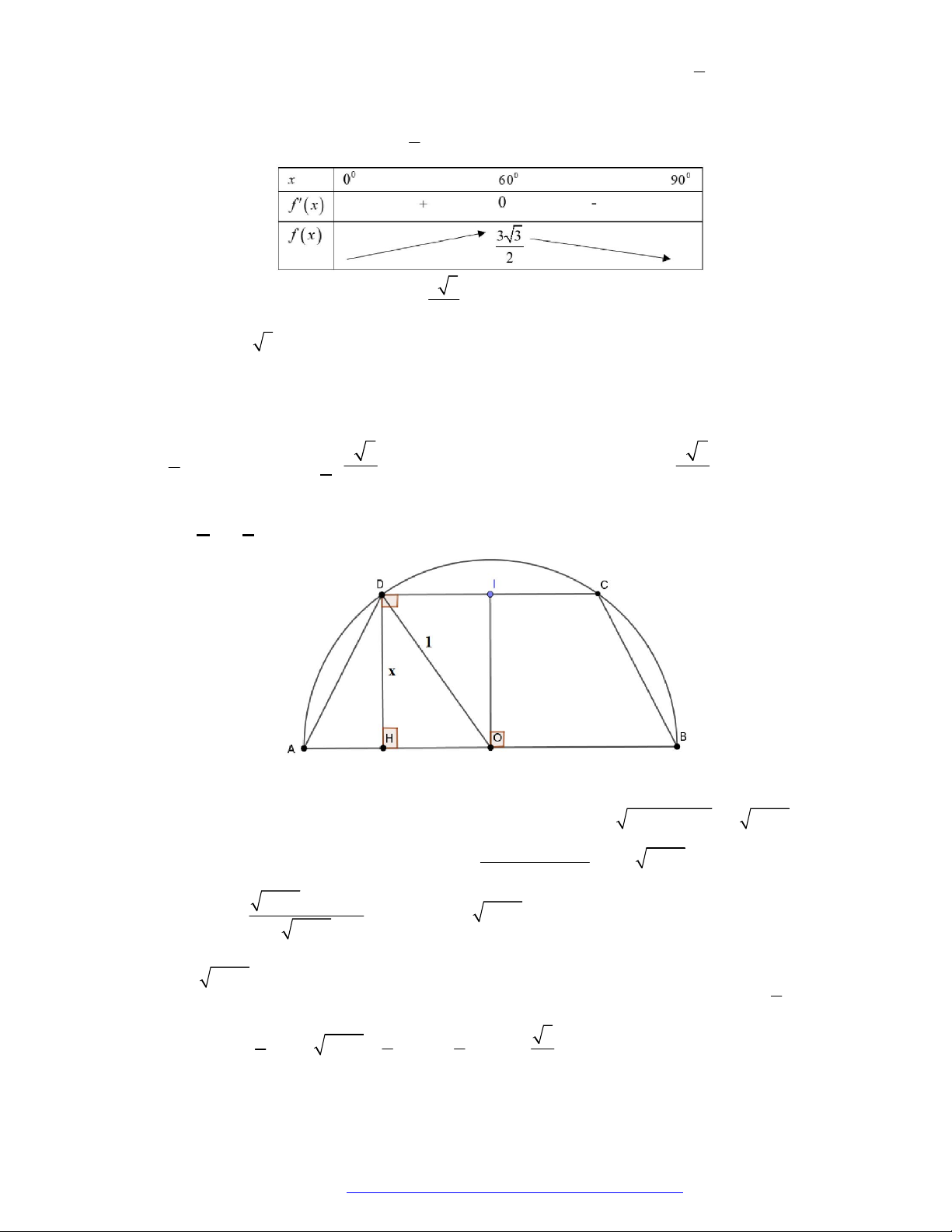
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 42 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta có:
( )
2
1
cos
0 2cos 2cos 2 0 2cos cos 1 0
2
cos 1
x
f x x x x x
x
Do
( )
0 0
0 ;90x
nên ta nhận
0
1
cos 60
2
x x
. Ta có bảng biến thiên:
Từ bảng biến thiên ta thấy:
( )
( )
0 0
0 ;90
3 3
max
2
f x
đạt được tại
0
60x
.
( )
2
max 108 3S m
khi góc ở đáy
CD
của hình thang bằng
0
60
( )
0
60C D
.
Câu 13. (Sở GD Quảng Nam - 2019) Cho nửa đường tròn đường kính
2AB
và hai điểm
C
,
D
thay
đổi trên nửa đường tròn đó sao cho
ABCD
là hình thang. Diện tích lớn nhất của hình thang
ABCD
bằng
A.
1
2
. B.
3 3
4
. C.
1
. D.
3 3
2
.
Lời giải
Chọn B
Gọi
H
là hình chiếu vuông góc của
D
lên
AB
,
I
là trung điểm của đoạn
CD
và
O
là trung
điểm của
AB
. Đặt
DH x
,
0 1x
. Ta có
2 2 2
2 2 2 2 1DC DI OH OD DH x
.
Diện tích của hình thang
ABCD
là
( )
( )
( )
2
1 1
2
AB CD DH
S f x x x
.
Ta có
( )
2 2
2
1 1 2
1
x x
f x
x
.
( )
2 2
0 1 1 2 0f x x x
(*)
Đặt
2
1t x
, (điều kiện
0t
) khi đó phương trình (*) trở thành
2
1
2 1 0
1
2
t
t t
t
.
1t
loại.
1
2
t
ta có
2 2
1 3 3
1
2 4 2
x x x
.
Bảng biến thiên
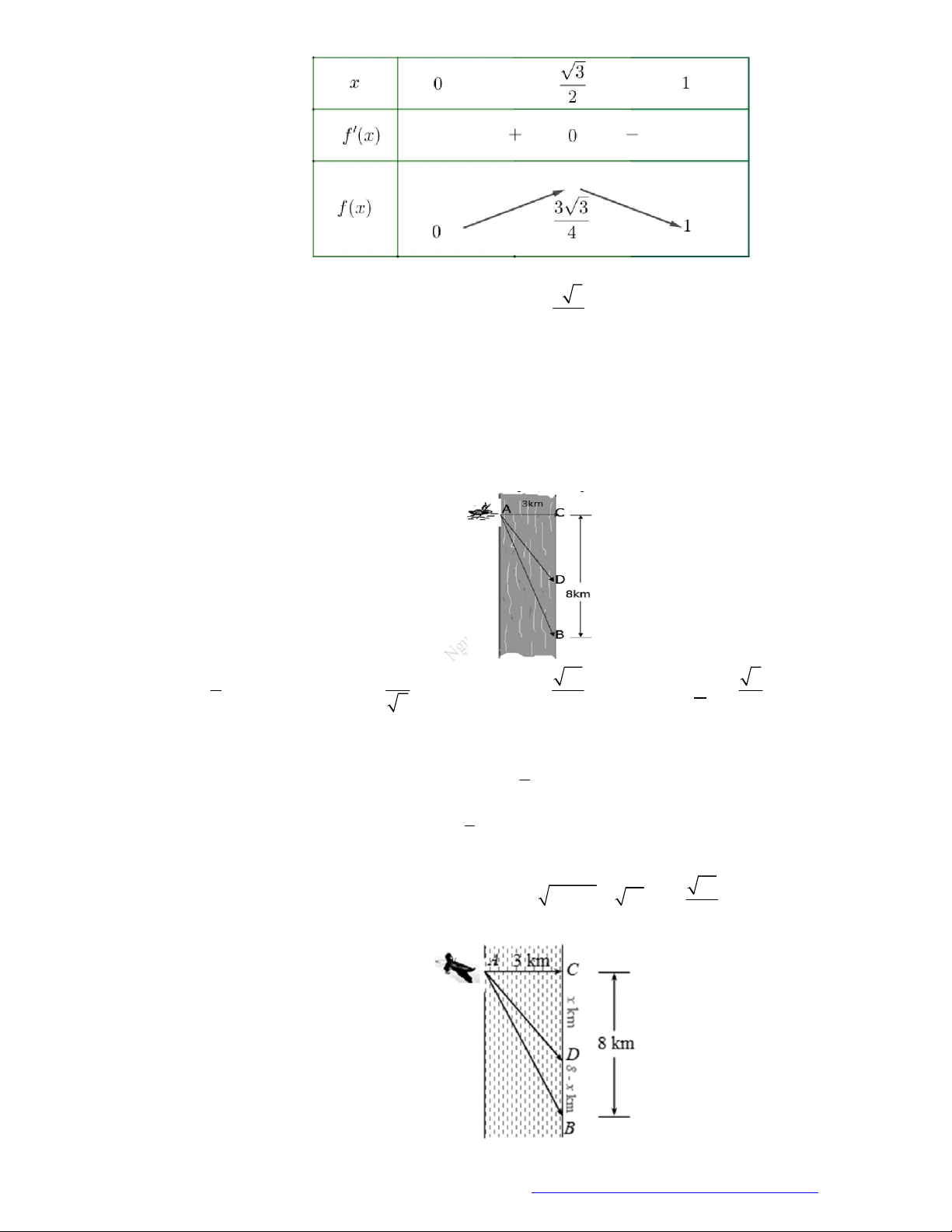
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 43
Vậy diện tích lớn nhất của hình thang
ABCD
bằng
3 3
4
.
Câu 14. (THPT Lương Văn Tụy - Ninh Bình 2018) Một người đàn ông muốn chèo thuyền ở vị trí
A
tới
điểm
B
về phía hạ lưu bờ đối diện, càng nhanh càng tốt, trên một bờ sông thẳng rộng
3 km
(như
hình vẽ). Anh có thể chèo thuyền của mình trực tiếp qua sông để đến
C
và sau đó chạy đến
B
,
hay có thể chèo trực tiếp đến
B
, hoặc anh ta có thể chèo thuyền đến một điểm
D
giữa
C
và
B
và sau đó chạy đến
B
. Biết anh ấy có thể chèo thuyền
6 km/ h
, chạy
8 km/ h
và quãng đường
8 kmBC
. Biết tốc độ của dòng nước là không đáng kể so với tốc độ chèo thuyền của người đàn
ông. Tính khoảng thời gian ngắn nhất (đơn vị: giờ) để người đàn ông đến
B
.
A.
3
2
. B.
9
7
. C.
73
6
. D.
7
1
8
.
Lời giải
Cách 1: Anh chèo thuyền của mình trực tiếp qua sông để đến
C
và sau đó chạy đến
B
Thời gian chèo thuyền trên quãng đường
AC
:
3
0,5
6
(giờ)
Thời gian chạy trên quãng đường
CB
:
8
1
8
(giờ)
Tổng thời gian di chuyển từ
A
đến
B
là
1,5
(giờ).
Cách 2: chèo trực tiếp trên quãng đường
2 2
3 8 73AB
mất
h
73
1 26
6
.
Cách 3:
Gọi
( )
kmx
là độ dài quãng đường
BD
;
( )
8 kmx
là độ dài quãng đường
CD
.
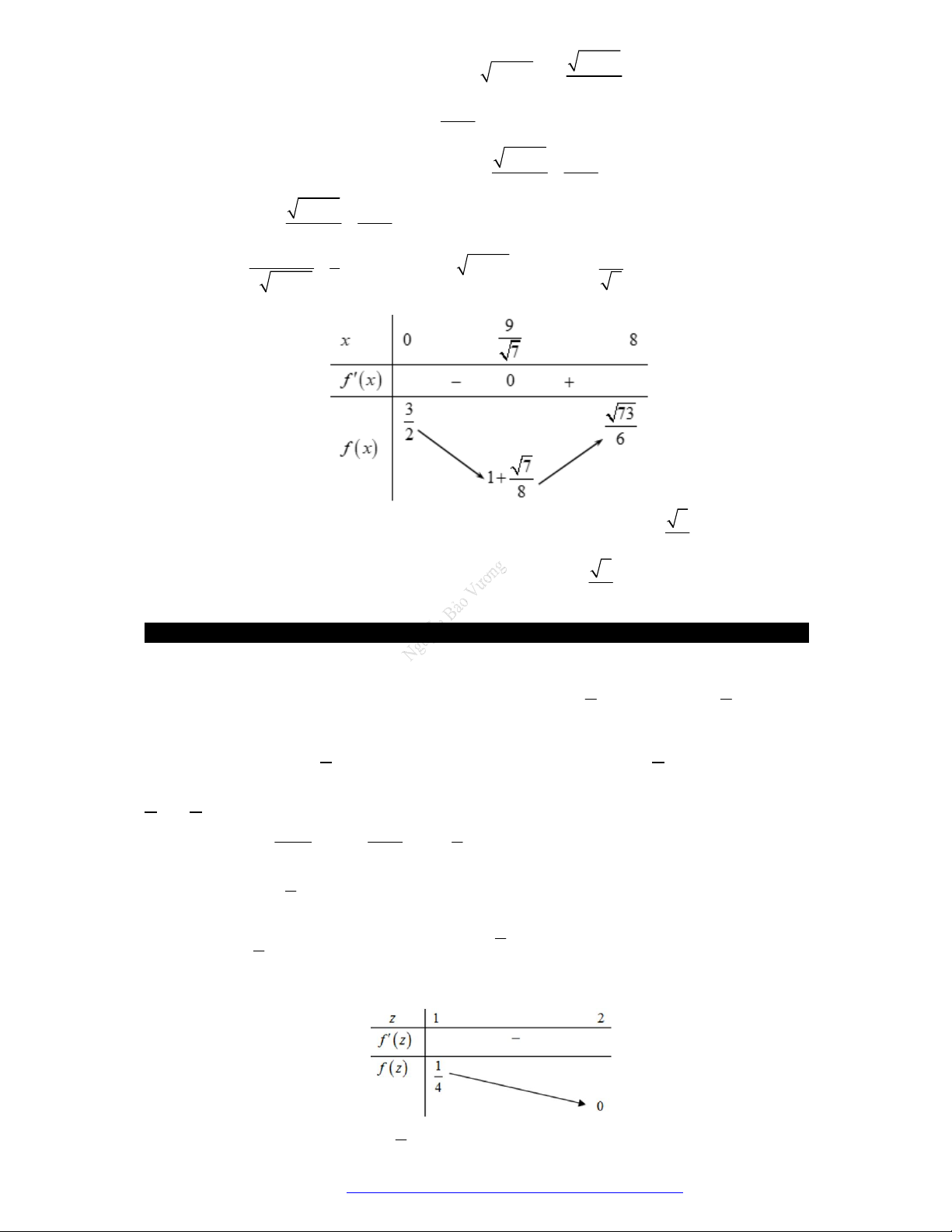
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 44 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Thời gian chèo thuyền trên quãng đường
2
9AD x
là:
2
9
6
x
(giờ)
Thời gian chạy trên quãng đường
DB
là:
8
8
x
(giờ)
Tổng thời gian di chuyển từ
A
đến
B
là
( )
2
9 8
6 8
x x
f x
Xét hàm số
( )
2
9 8
6 8
x x
f x
trên khoảng
( )
0; 8
Ta có
( )
2
1
8
6 9
x
f x
x
;
( )
2
9
0 3 9 4
7
f x x x x
Bảng biến thiên
Dựa vào BBT ta thấy thời gian ngắn nhất để di chuyển từ
A
đến
B
là
h
7
1 1 20
8
.
Vậy khoảng thời gian ngắn nhất để người đàn ông đến
B
là
h
7
1 1 20
8
.
Dạng 4. Dùng phương pháp hàm số để tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức
Câu 1. (HSG 12 - Sở Quảng Nam - 2019) Cho ba số thực
, ,x y z
thỏa mãn
0, 0, 1x y z
,
2x y z
.Biết giá trị lớn nhất của biểu thức
P xyz
bằng
a
b
với
*
,a b và
a
b
là phân số tối
giản. Giá trị của
2a b
bằng
A.
5
. B.
43
. C.
9
. D.
6
.
Lời giải
Chọn D
Ta có:
( )
2 2
2 3
2 1
. .z 4 4
2 2 4
x y z
P xyz z z z z
.
Xét hàm số
( )
( )
2 3
1
4 4
4
f z z z z
trên
1;2
.
Ta có:
( )
( )
( )
2
2
( )
1
4 8 3 ; 0
3
4
2
z loai
f z z z f z
z
Bảng biến thiên:
Dựa vào bảng biến thiên, ta có:
1
4
P
.
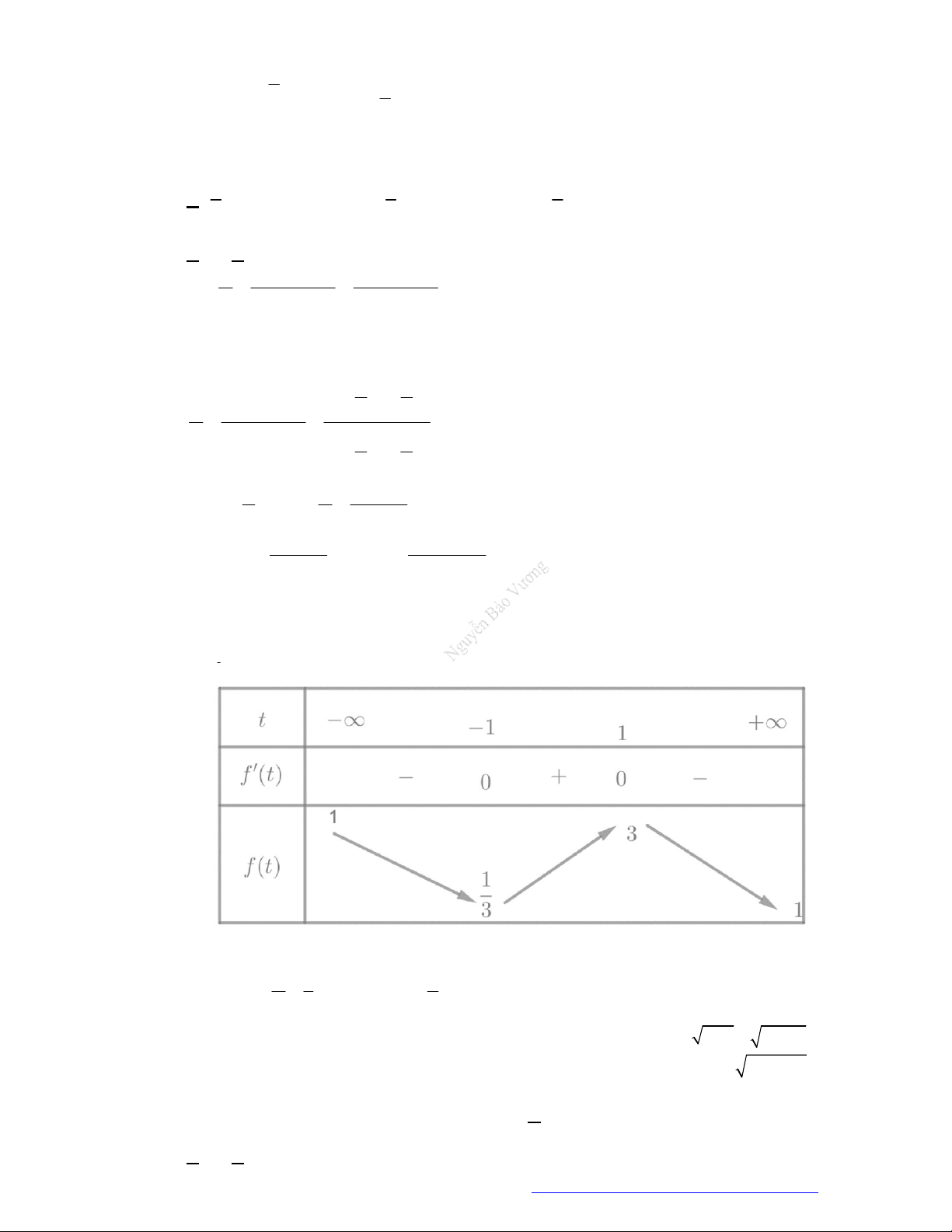
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 45
Vậy
max
1
4
P
khi
1
1
2
z
x y
1; 4 2 6a b a b
.
Câu 2. (Chuyên Bắc Giang Nam 2019) Cho
2 2
2x xy y . Giá trị nhỏ nhất của
2 2
P x xy y
bằng:
A.
2
3
B.
1
6
C.
1
2
D.
2
Lời giải
Chọn A
Xét
2 2 2 2
2 2
2 2
P x xy y x xy y
x xy y
+nếu
0y
thì
2
2x
. Do đó
2
2P x
suy ra
min 2P
+nếu
0y
ta chia tử mẫu cho
2
y ta được
2
2 2
2
2 2
1
2
1
x x
y y
P x xy y
x xy y
x x
y y
Đặt
x
t
y
, khi đó
2
2
1
2 1
P t t
t t
Xét
( ) ( )
( )
2 2
2
2
2
1 2 2
'
1
1
t t t
f t f t
t t
t t
( )
1
' 0
1
t
f t
t
Bảng biến thiên
Khi đó
1
min
2 3
P
do đó
2
min
3
P
.
Câu 3. (Chuyên Bắc Giang 2019) Cho
x
,
y
là các số thực thỏa mãn
1 2 2x y x y
. Gọi
M
,
m
lần lượt là giá trị lớn nhất và nhỏ nhất của
( )( )
2 2
2 1 1 8 4P x y x y x y
. Tính giá
trị
M m
A.
42
B.
41
C.
43
D.
44
Lời giải
Chọn C
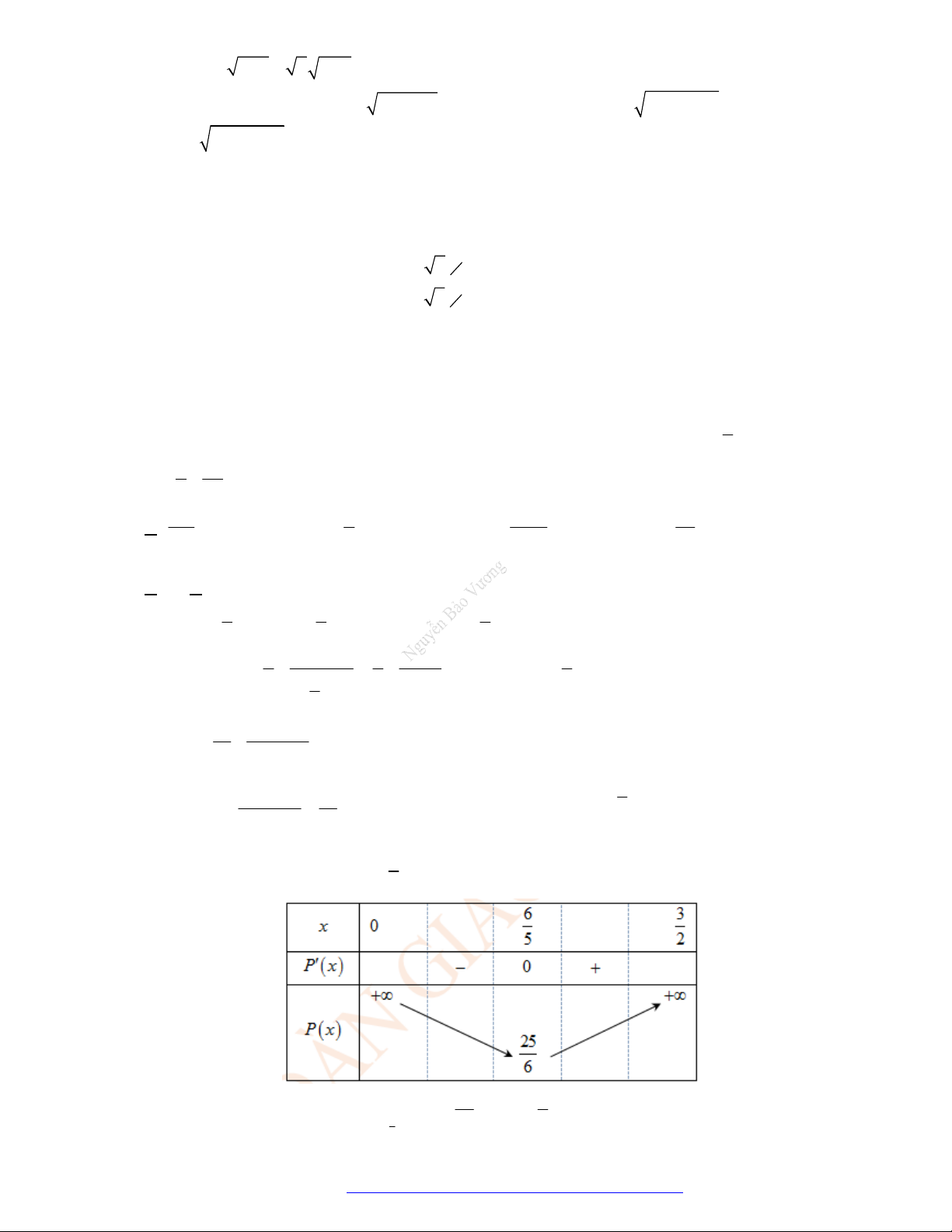
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 46 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
( )
( )
( )
2
2
1 2 1 3 0 3
x y x y x y x y
( )( ) ( ) ( ) ( )
2
2 2
2 1 1 8 4 2 2 8 4P x y x y x y x y x y x y
Đặt
( )
4 , 1;2t x y t
.
Ta có:
( )
( ) ( )
2
2 2 4 2
4 2 4 2 8 10 8 26f t t t t t t t
.
( )
3
4 20 8f t t t
( )
2
2 1;2
2
0 1 2 1;2
2 1 0
1 2 1;2
t
t
f t t
t t
t
( ) ( )
1 25; 2 18f f
.
Suy ra
( ) ( )
( ) ( )
1;2
1;2
min 2 18; max 1 25m f t f M f t f
.
Vậy
43M m
.
Câu 4. (Chuyên Lê Quý Đôn - Quảng Trị -2019) Cho
x
,
0y
thỏa mãn
3
2
x y
và biểu thức
4 1
4
P
x y
đạt giá trị nhỏ nhất. Tính
2 2
x y
.
A.
153
100
. B.
5
4
. C.
2313
1156
. D.
25
16
.
Lời giải
Chọn A
Từ
3
2
x y
suy ra
3
2
y x
. Ta có:
3
0 ,
2
x y
.
Xét hàm
( )
4 1
3
4
2
P x
x
x
4 1
6 4x x
trên khoảng
3
0;
2
, ta có:
( )
( )
2
2
4 4
6 4
P x
x
x
.
( )
0P x
( )
2
2
4 4
6 4
x
x
( )
2
2
6 4x x
6 4
4 6
x x
x x
6
5
2
x
x
.
Bảng biến thiên của
( )
P x
trên
3
0;
2
:
Dựa vào bảng biến thiên ta thấy
( )
3
0;
2
25
min
6
P x
khi
6
5
x
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 47
Với
6
5
x
thì
3
10
y
.
Như vậy
25
min
6
P
khi
6
5
x
,
3
10
y
.
Khi đó,
2 2
153
100
x y
.
Câu 5. (Chuyên Hà Tĩnh - 2019) Cho các số thực
x
,
y
thay đổi thỏa mãn
2 2
1x y xy
và hàm số
( )
3 2
2 3 1
f t t t
. Gọi
M
,
m
tương ứng là GTLN và GTNN của
5 2
4
x y
Q f
x y
. Tổng
M m
bằng:
A.
4 3 2
. B.
4 5 2
. C.
4 4 2
. D.
4 2 2
.
Lời giải
Chọn C
Đặt
5 2
4
x y
t
x y
. Theo giả thiết,
( ) ( )
2 2
2 2
3 1
1 1
4 4
x xy y x y x y
nên ta đặt
( )
( )
( )
1
3
cos sin
2
cos
cos
3
2
0 2
3
1
1
cos sin
2sin
sin
3
2
x
x y
x y
y
x y
x y
.
Khi đó,
( ) ( )
2 3 cos 4sin 2
2 .sin 3.cos 1 2 1
2sin 4
t t t
.
Phương trình
( )
1
có nghiệm
( )
( )
( )
2
2 2
2
2 3 1 2 3 6 0 2 2
t t t t
.
Xét hàm số
( )
3 2
2 3 1, 2 ; 2
Q f t t t t
.
( )
2
6 6f t t t
. Cho
( )
0 2 ; 2
0
1 2 ; 2
t
f t
t
.
( )
2 5 4 2
f
;
( )
0 1
f
;
( )
1 0
f
;
( )
2 5 4 2
f
.
( ) ( )
( )
( )
2 ; 2
2; 2
max max 0 1
min min 2 5 4 2
M Q f t f
m Q f t f
.
Vậy
4 4 2
M m
.
Câu 6. (Sở Lào Cai - 2019) Cho hàm số
( )
4 3 2
1
f x x ax bx cx
. Biết rằng đồ thị hàm số
( )
y f x
có ít nhất một giao điểm với trục hoành. Bất đẳng thức nào sau đây là đúng?
A.
2 2 2
4
3
a b c
. B.
2 2 2
4
3
a b c
. C.
2 2 2
4
3
a b c
. D.
2 2 2
4
3
a b c
.
Lời giải
Chọn C
Phương trình hoành độ giao điểm
( )
4 3 2
1 0 1
x ax bx cx
Nhận xét
0
x
không phải là nghiệm. Với
0
x
phương trình trở thành
( ) ( )
2 3
1
1 0
ax bx c x x
x
( ) ( )( )
2
2
3 2 2 2 2 4 2
1
1
x ax bx c a b c x x
x

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 48 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2 2
3 2
2
2 2 2
4 2
2
2
1 1
1
1
1
x x
x x
a b c
x x
x
x
( ) ( )
( )
2 2
2
2
2
1 2
2 , 2 ' 0, 2
1
1
t t t
t x t f t t f t t
x t
t
Bảng biến thiên
Vậy để đồ thị hàm số
( )
y f x
có ít nhất một giao điểm với trục hoành thì
2 2 2
4
3
a b c
Câu 7. (THPT Trần Nhân Tông 2018) Cho hai số thực
,x y
thỏa
mãn:
( )
3
9 2 3 5 3 5 0
x y xy x xy
Tìm giá trị nhỏ nhất của
( )
( )
3 3 2
6 3 3 1 2
xy x x y
P x y
A.
296 15 18
9
. B.
36 296 15
9
. C.
36 4 6
9
. D.
4 6 18
9
.
Lời giải
Ta có
( )
3
9 2 3 5 3 5 0
x y xy x xy
( )
3
27 6 3 5 3 5 2 3 5
x x xy xy xy
.
Xét hàm
( )
3
2f t t t
với
( )
0;t
có
( ) ( )
2
' 3 2 0 0;f t t t
nên hàm số liên tục và đồng biến trên
( )
0;
.
Khi đó ta có
3 3 5
x xy
0
x
và
2
9 3 5x xy
.
Với
0
x
thì
( )
0 5 l
.
với
0
x
thì
( )
( )
3 3 2
6 3 3 1 2
xy x x y
P x y
( )
( )
3 3 2
6 9 3 2
xy x x y
x y
( )( )
3 3
6 3 2 2
xy xy x y
x y
( )
3 3 2 2
3 3 2 4
x y xy x y
x y
( ) ( )
3
2 4
x y x y
Mà
2
9 5 5 5 4 5
4 2 4 .
3 3 3
3
x
x y x x x
x x x
. Đặt
t x y
thì
4 5
3
t .
Xét
( )
3
2 4f t t t
với
4 5
3
t . Khi đó
( )
2
3 2 0
f t t
với
4 5
3
t .
Do đó
( )
4 5 36 296 15
9
3
f t f
Suy ra
36 296 15
9
P
. Vậy GTNN của
P
là
36 296 15
9
.
Câu 8. (THPT Nguyễn Huệ - Ninh Bình - 2018) Cho
, 0
x y
và
5
4
x y
sao cho biểu thức
4 1
4
P
x y
đạt giá trị nhỏ nhất. Khi đó
A.
2 2
25
32
x y
. B.
2 2
17
16
x y
. C.
2 2
25
16
x y
. D.
2 2
13
16
x y
.
Lời giải
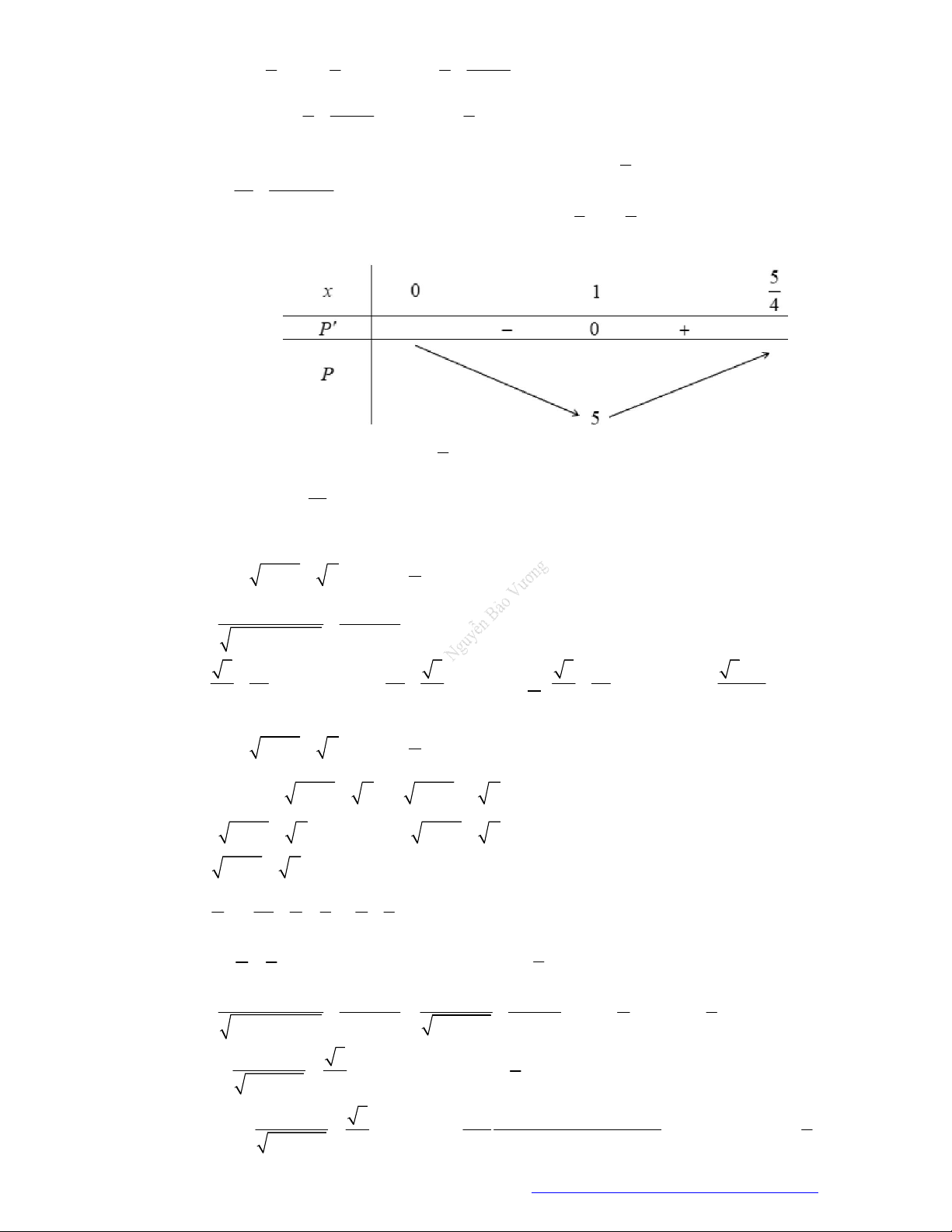
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 49
Từ
5 5
4 4
x y y x
, nên
4 1
5 4
P
x x
.
Xét hàm số
4 1
5 4
P
x x
với
5
0
4
x
.
( )
2
2
4 4
5 4
P
x
x
;
( )
2
2
0 5 4P x x
5
1 0;
4
5 5
0;
3 4
x
x
.
Bảng biến thiên
Như vậy:
min 5P
khi
1x
;
1
4
y
.
Khi đó
2 2
17
16
x y
.
Câu 9. (Xuân Trường - Nam Định -2018) Cho
,x y
là hai số thực dương thay đổi thỏa mãn điều kiện
( )
( )
1
1 1 1xy xy y x
y
. Tìm giá trị lớn nhất của biểu thức
( )
2 2
2
6
3
x y x y
P
x y
x xy y
?
A.
5 7
3 30
. B.
7 5
30 3
. C.
5 7
3 30
. D.
5 7
30
.
Lời giải
( )
( )
1
1 1 1xy xy y x
y
( )
( )
(
)
2 2
1 1 1 0y xy xy y xy y
( )
( )
( )
1 1 1 0xy y y xy xy y
1 0 1xy y xy y
2
2
1 1 1 1 1
4 2
x
y y y y
1
0
4
x
y
. Dấu bằng đạt được khi
2y
,
1
2
x
.
( )
2 2
2
6
3
x y x y
P
x y
x xy y
( )
2
1 2
6 1
3
t t
t
t t
với
x
t
y
và
1
0;
4
t
.
Ta có
( )
2
1 5
8 7
27
3
t
t
t t
với mọi
1
0;
4
t
Thật vậy
( )
2
1 5
8 7
27
3
t
t
t t
( )
( )
2
2
2
4 1 20 25 6
1
0
729 3
t t t
t t
với mọi
1
0;
4
t
.
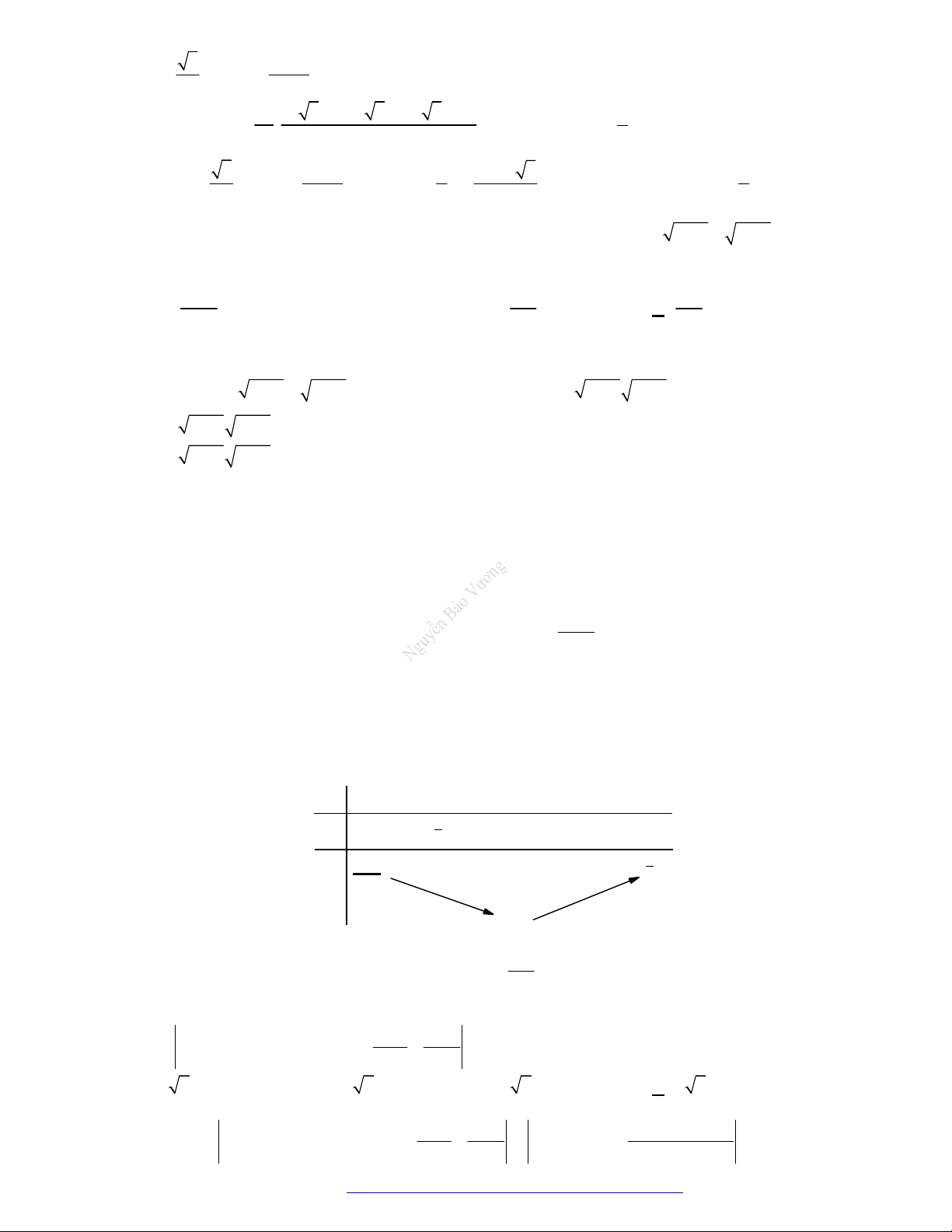
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 50 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
( ) ( )
5 2
8 7
27 6 6
t
P t f t
t
.
Khi đó
( )
( )
2
2
1 16 5 32 5 16 5 27
. 0
54
1
t t
f t
t
với mọi
1
0;
4
t
.
Vậy
( ) ( )
5 2
8 7
27 6 6
t
P t f t
t
1 7 10 5
4 30
f
, dấu bằng đạt được khi
1
2
x
,
2y
.
Câu 10. (THPT Lê Xoay - 2018) Cho các số thực
x
,
y
thỏa mãn
( )
1 2 2 3x y x y . Giá trị
lớn nhất của biểu thức
( )
( )
4 7 2 2
3 1 .2 3
x y x y
M x y x y
bằng
A.
9476
243
. B.
76
. C.
193
3
. D.
148
3
.
Lời giải
Điều kiện
2; 3x y
.
( )
1 2 2 3x y x y
( )
( )
2
1 4 1 2 2 3x y x y x y .(*)
Vì
2 2 3 1x y x y
nên từ (*) suy ra
( ) ( )
2
1 8 1x y x y
7x y
.
Vì
2 2 3 0x y
nên từ (*) suy ra
( ) ( )
2
1 4 1x y x y
1 0
1 4
x y
x y
1 0
1 4
x y
x y
1
3
x y
x y
.
Do
2x
nên
2
2x x
,
2
1 2y y , suy ra
( )
2 2
1 2x y x y
. Từ đó ta có
( )
( )
( ) ( )
4 7 2 2 4 7
3 1 .2 3 3 1 .2 6 3
x y x y x y x y
M x y x y x y x y
.
Đặt
t x y
với
1t
hoặc
3 7t
.
Xét hàm số
( ) ( )
4 7
3 1 2 6 3
t t
f t t t
, ta có
( )
2188
1
243
f
.
( ) ( )
4 7 7
3 ln3 2 1 .2 ln 2 6
t t t
f t t
.
( ) ( )
4 2 7
3 ln 3 1 ln 2 2 2 .ln 2 0
t t
f t t
,
3;7t
.
Suy ra
( )
f t
đồng biến trên
( )
3;7
, mà
( )
f t
liên tục trên
3;7
và
( ) ( )
3 . 7 0f f
nên phương
trình
( )
0f t
có nghiệm duy nhất
( )
0
3;7t
.
Suy ra
( )
( )
4 7 2 2
148
3 1 .2 3
3
x y x y
M x y x y
. Đẳng thức xảy ra khi
2x
,
1y
.
Câu 11. (Cụm 5 Trường Chuyên - Đbsh - 2018) Tìm giá trị nhỏ nhất của hàm số
1 1
sin cos tan cot
sin cos
y x x x x
x x
A.
2 1
. B.
2 2 1
. C.
2 1
. D.
2 2 1
.
Lời giải
Ta có
1 1
sin cos tan cot
sin cos
y x x x x
x x
1 sin cos
sin cos
sin .cos
x x
x x
x x
.
4
148
3
f
(t
o
)
f
(t)
0
t
f'
(t)
t
o
+
3
7
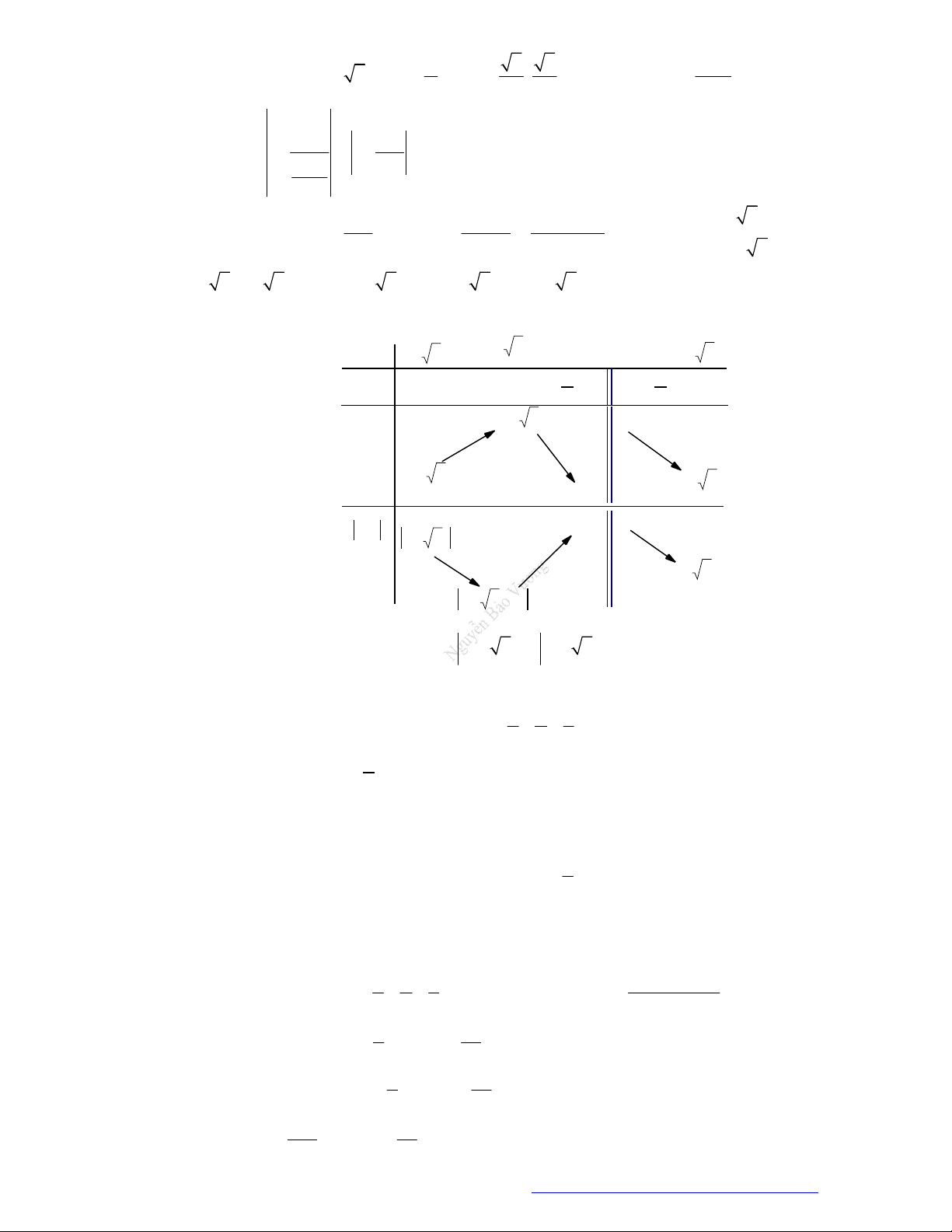
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 51
Đặt
sin cost x x
2 sin
4
x
,
2 2
; \ 1
2 2
t
,
2
1
sin .cos
2
t
x x
.
Suy ra
2
1
1
2
t
y t
t
2
1
t
t
.
Xét hàm số
( )
2
1
g t t
t
,
( )
( )
2
2
1
1
g t
t
( )
( )
2
2
1 2
1
t
t
,
( )
0g t
( )
( )
2 1
2 1 t/m
t l
t
.
( )
2 3 2 2 0,g
( )
2 0,g
( )
2 1 2 2 1 0g
Ta có bảng biến thiên
Dựa vào bảng biến thiên suy ra
( )
min
2 1y y
2 2 1
.
Câu 12. (Sở Phú Thọ - 2018) Xét các số thực dương
, , x y z
thỏa mãn
4x y z
và
5xy yz zx
.
Giá trị nhỏ nhất của biểu thức
( )
3 3 3
1 1 1
x y z
x y z
bằng:
A.
20
. B.
25
. C.
15
. D.
35
.
Lời giải
Ta có:
( )
2
4
4
5
5 5 4
x y z
x y z
xy yz zx
xy z x y z z
.
Lại có:
( )
2
4x y xy
( )
( )
2
2
2
4 4 5 4 2
3
z z z z
. Dấu
" "
xảy ra khi
x y
.
Và
( ) ( )( ) ( )
3
3 3 3
3 3x y z x y z x y z x y z xy x y
( ) ( )
3 3 3 3
4 12 3x y z x y z xy x y
( )
( )
2
64 3 4 5z z .
Ta có:
( )
3 3 3
1 1 1
P x y z
x y z
( )
3 2
3 2
5
3 12 15 4
4 5
z z z
z z z
.
Đặt
3 2
4 5t z z z
, với
2 50
2 2
3 27
z t
.
Do đó xét hàm số
( )
4
5 3f t
t
, với
50
2
27
t
.
Ta có
( )
2
20 50
0, ;2
27
f t t
t
nên hàm số
( )
f t
liên tục và nghịch biến.
g
-
2
( )
g
-
2+1
( )
g
2
( )
+∞+∞
-∞
y=
g
(t)
+∞
g
2
( )
g
-
2+1
( )
g
-
2
( )
- 2+1
2
g
(t)
0
t
g'
(t)
1
+
-
2
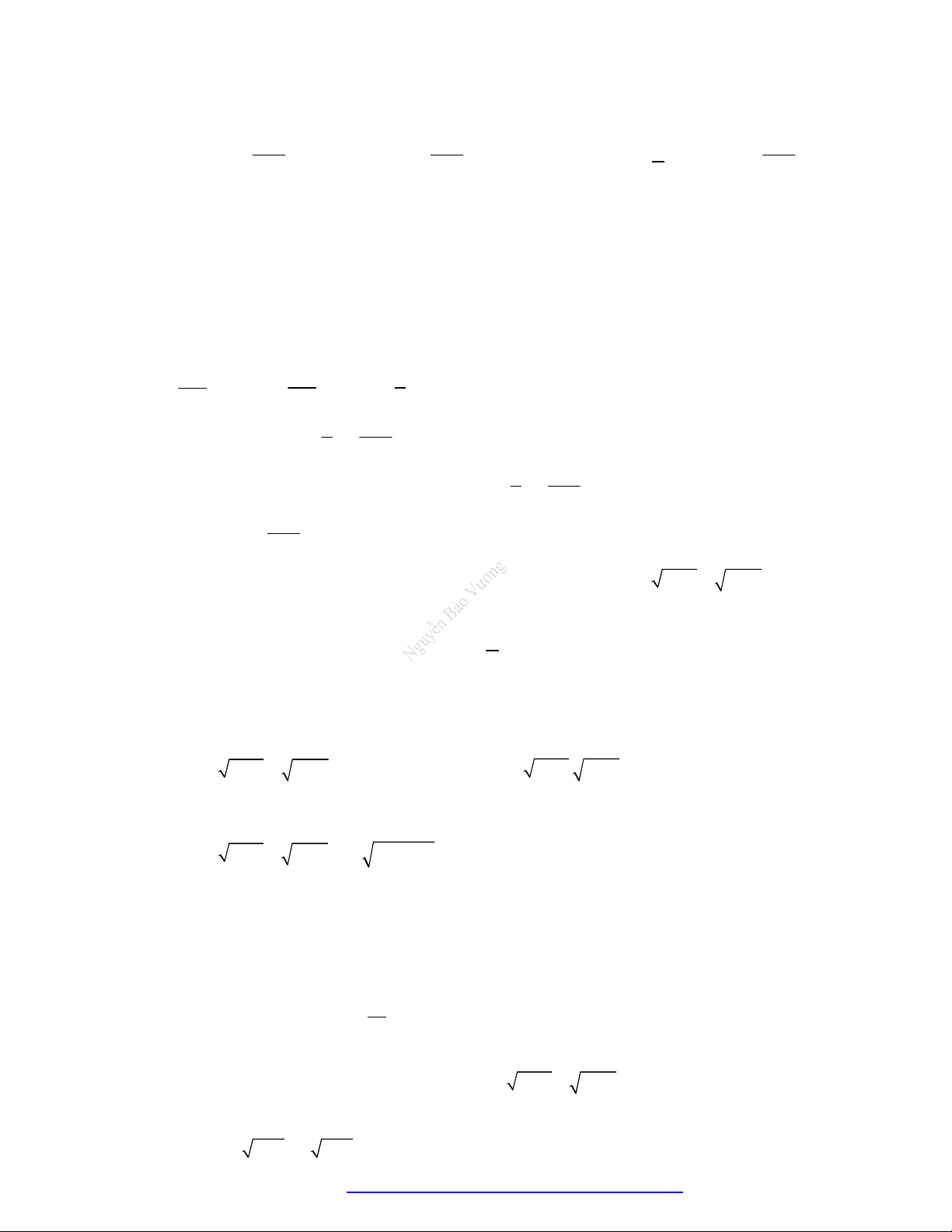
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 52 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Do đó
( )
min
2 25
P f
đạt tại
1x y
,
2z
.
Câu 13. (Sở Bắc Ninh - 2018) Gọi
M
,
m
lần lượt là giá lớn nhất, giá trị nhỏ nhất của hàm số
2018 2018
sin cos
y x x
trên
. Khi đó:
A.
2M
,
1008
1
2
m
. B.
1M
,
1009
1
2
m
. C.
1M
,
0
m
. D.
1M
,
1008
1
2
m
.
Lời giải
Ta có:
2018 2018
y sin cos
x x
( ) ( )
1009 1009
2 2
sin 1 sinx x .
Đặt
2
sint x
,
0 1t
thì hàm số đã cho trở thành
( )
1009
1009
1y t t
.
Xét hàm số
( ) ( )
1009
1009
1f t t t
trên đoạn
0;1
.
Ta có:
( ) ( )
1008
1008
1009. 1009. 1f t t t
( )
0
f t
( )
1008
1008
1009 1009 1 0
t t
1008
1
1
t
t
1
1
t
t
1
2
t
Mà
( ) ( )
1 0 1
f f
,
1008
1 1
2 2
f
.
Suy ra
( ) ( ) ( )
0;1
max 0 1 1
f t f f
,
( )
1008
0;1
1 1
min
2 2
f t f
Vậy
1M
,
1008
1
2
m
.
Câu 14. (Chuyên Long An - 2018) Cho các số thực
x
,
y
thỏa mãn
( )
2 3 3
x y x y
. Tìm giá
trị nhỏ nhất của biểu thức
( )
2 2
4 15P x y xy
.
A.
min 80
P
. B.
min 91
P
. C.
min 83
P
. D.
min 63
P
.
Lời giải
Điều kiện:
3
3
x
y
.
Ta có
( )
2 3 3
x y x y
( ) ( ) ( )
2
4 8 3. 3 4
x y x y x y x y
( )
4
1
0
x y
x y
.
Mặt khác áp dụng bất đẳng thức Bunhiacopski ta được:
( )
( ) ( )
2 3 3 2 2 8 2
x y x y x y x y .
Từ
( )
1
và
( )
2
ta có
4;8
x y
Ta lại có
( )( ) ( )
3 3 0 3 9
x y xy x y
.
Đặt
t x y
suy ra
( )
( )
2
2 2 2
4 15 4 7 4 21 63
P x y xy x y xy t t
.
Xét hàm số
( )
2
4 21 63
f t t t
, với
4;8
t
Ta có
( )
21
8 21 0 4;8
8
f t t t
. Do đó
( ) ( )
4;8
min 4 83
f t f
.
Do đó
83
P
suy ra
min 83
P
khi
( )
4
7
2 3 3
3
x y
x
x y x y
y
.
Câu 15. (THPT Trần Phú - Đà Nẵng - 2018) Cho hai số thực
x
,
y
thỏa mãn:
( )
3 2
2 7 2 1 3 1 3 2 1
y y x x x y
. Tìm giá trị lớn nhất của biểu thức
2P x y
.
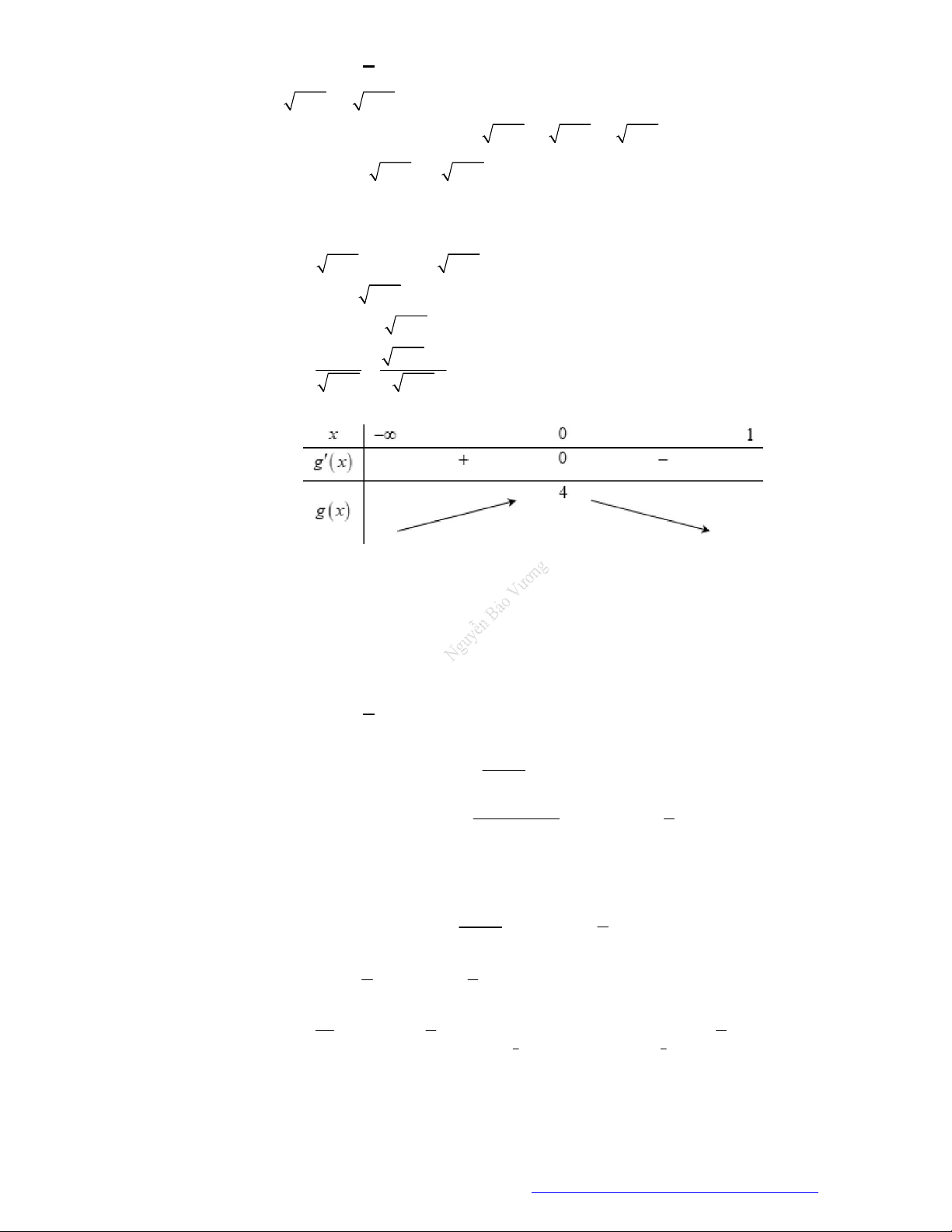
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 53
A.
10P
B.
4P
. C.
6P
. D.
8P
.
Lời giải
( )
3 2
2 7 2 1 3 1 3 2 1y y x x x y
.
( )
( ) ( )
3 2
2 3 3 1 1 2 1 1 3 1 2 1y y y y x x x x
.
( ) ( )
( )
( )
3
3
2 1 1 2 1 1 1y y x x .
Xét hàm số
( )
3
2f t t t
trên
)
0;
.
Ta có:
( )
2
6 1f t t
0
với
0t
( )
f t
luôn đồng biến trên
)
0;
.
Vậy
( )
1 1 1y x
1 1y x
.
2 2 2 1P x y x x
với
( )
1x
.
Xét hàm số
( )
2 2 1g x x x trên
(
;1
.
Ta có:
( )
1
1
1
g x
x
1 1
1
x
x
.
( )
0 0g x x
.
Bảng biến thiên
( )
g x
:
Từ bảng biến thiên của hàm số
( )
g x
suy ra giá trị lớn nhất của
P
là:
(
( )
;1
max 4g x
.
Câu 16. (Chuyên Trần Phú - Hải Phòng 2018) Cho
x
,
y
là các số thực dương thỏa mãn điều kiện:
2
3 0
2 3 14 0
x xy
x y
. Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
2 2 3
3 2 2P x y xy x x
A.
8
. B.
0
. C.
12
. D.
4
.
Lời giải
Theo giả thiết ta có
2
2
3
3 0
x
x xy y
x
Từ bất phương trình
2
5 4 9
2 3 14 0 0
x x
x y
x
9
1
5
x
.
Mặt khác ta có
2 3 2
2 2 2
3 3
3 3
x xy x x y x
xy x xy x y y
Thay vào ta được
3 8P y x
2
3
3 8
x
x
x
9
5x
x
.
Xét hàm số
( )
9
5f x x
x
trên đoạn
9
1;
5
.
Ta có
( )
2
9 9
5 0, 1;
5
f x x
x
do đó
( )
9
1;
5
min 1 4f
và
9
1;
5
9
max 4
5
f
.
Suy ra tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
P
bằng
0
.
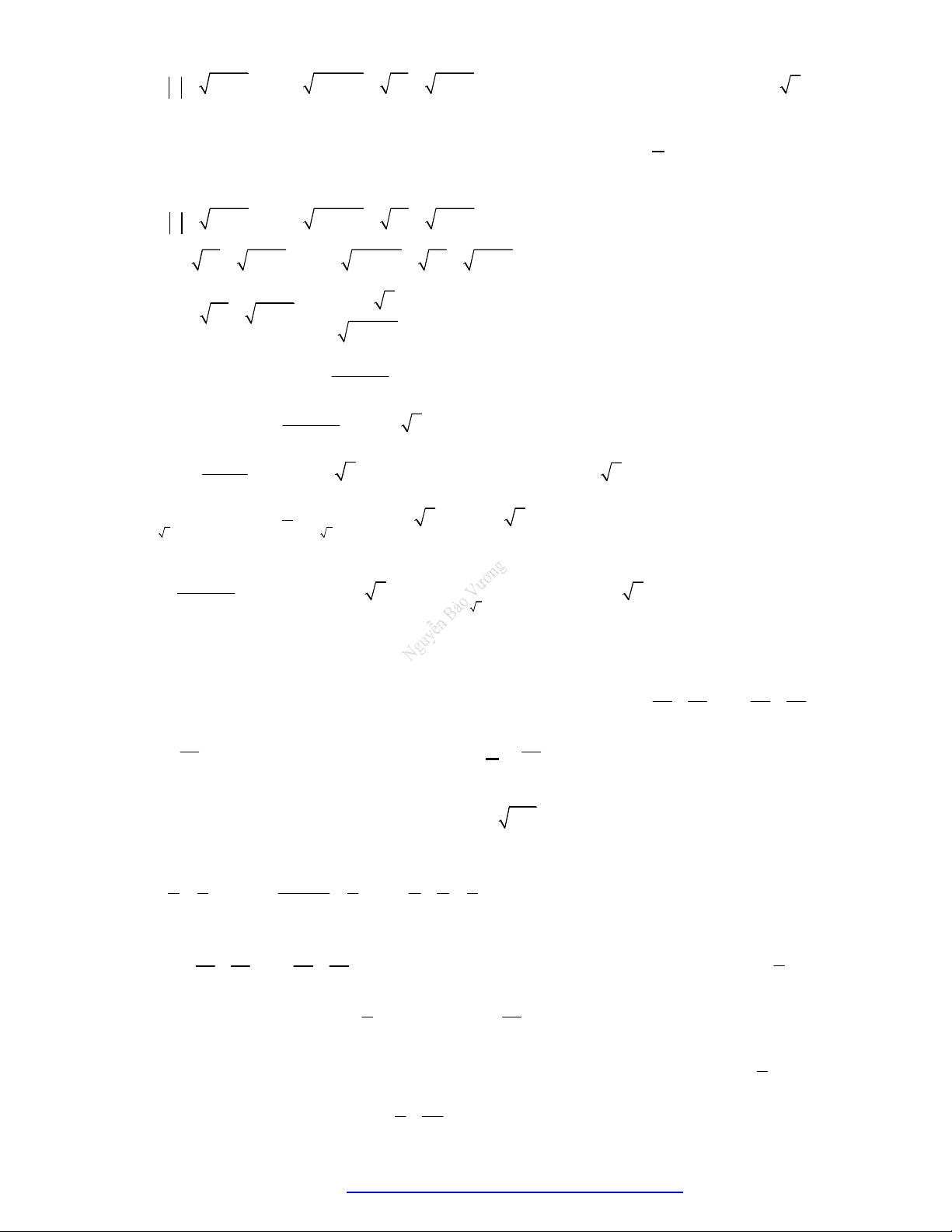
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 54 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 17. (Sở Nam Định - 2018) Biết rằng bất phương trình
(
)
2 2 4 2 2
1 1 2 1 2
m x x x x x x
có nghiệm khi và chỉ khi
(
; 2
m a b
với
,a b
. Tính giá trị của
T a b
.
A.
3
T
. B.
2T
. C.
0
T
. D.
1T
.
Lời giải
Điều kiện:
1 1x
.
(
)
2 2 4 2 2
1 1 2 1 2
m x x x x x x
(
)
2 2 2 4 2 2
1 1 2 1 2
m x x x x x x
Đặt
2 2
2 4 2
1 2
1
2 1
t
t x x
x x t
. Khi đó, bất phương trình trở thành:
( )
2
2
1
1 1
1
t t
m t t t m
t
(vì
1;2
t
nên
1 0
t
).
Xét hàm số
( )
2
1
1
t t
f t
t
trên
1; 2
.
( )
2
2
0, 1; 2
1
t t
f t t
t
suy ra hàm số đồng biến trên
1; 2
.
( ) ( )
1; 2
3
min 1
2
f t f
;
( )
( )
1; 2
max 2 1 2 2
f t f
.
Bất phương trình đã cho có nghiệm khi và chỉ khi bất phương trình
2
1
1
t t
m
t
có nghiệm
1; 2
t
( )
1; 2
max 1 2 2
m f t m
2
a
,
1
b
1
a b
.
Câu 18. (THPT Nguyễn Huệ 2018) Cho
,x y
là các số thực dương thỏa mãn
( )
( )( )
2 2
2 2
x y xy x y xy
. Giá trị nhỏ nhất của biểu thức
3 3 2 2
3 3 2 2
4 9
x y x y
P
y x y x
.
A.
25
4
. B.
5
. C.
23
4
. D.
13
.
Lời giải
Ta có
( )
( )( )
2 2
2 2
x y xy x y xy
( )
2 2x y xy
.
Đặt
2 2
;
a x y b xy
ta được:
( ) ( )
2
2 2
2 8 2 4 4 15 0
a b b a b a ab b
5
2
a
b
. Suy ra:
2 2
5 5
2 2
x y x y
t
xy y x
.
Ta có:
3 3 2 2
3 3 2 2
4 9
x y x y
P
y x y x
( ) ( )
( )
3 2 3 2
4 3 9 2 4 9 12 18
t t t t t t f t
với
5
2
t
.
Khảo sát hàm số
( )
f t
với
5
2
t
ta được
( )
23
4
f t
. Vậy chọn C
Câu 19. (THPT Kim Liên - Hà Nội - 2018) Cho các số thực dương
x
,
y
thỏa mãn
5
2
4
x y
. Tìm giá
trị nhỏ nhất
min
P
của biểu thức
2 1
4
P
x y
.
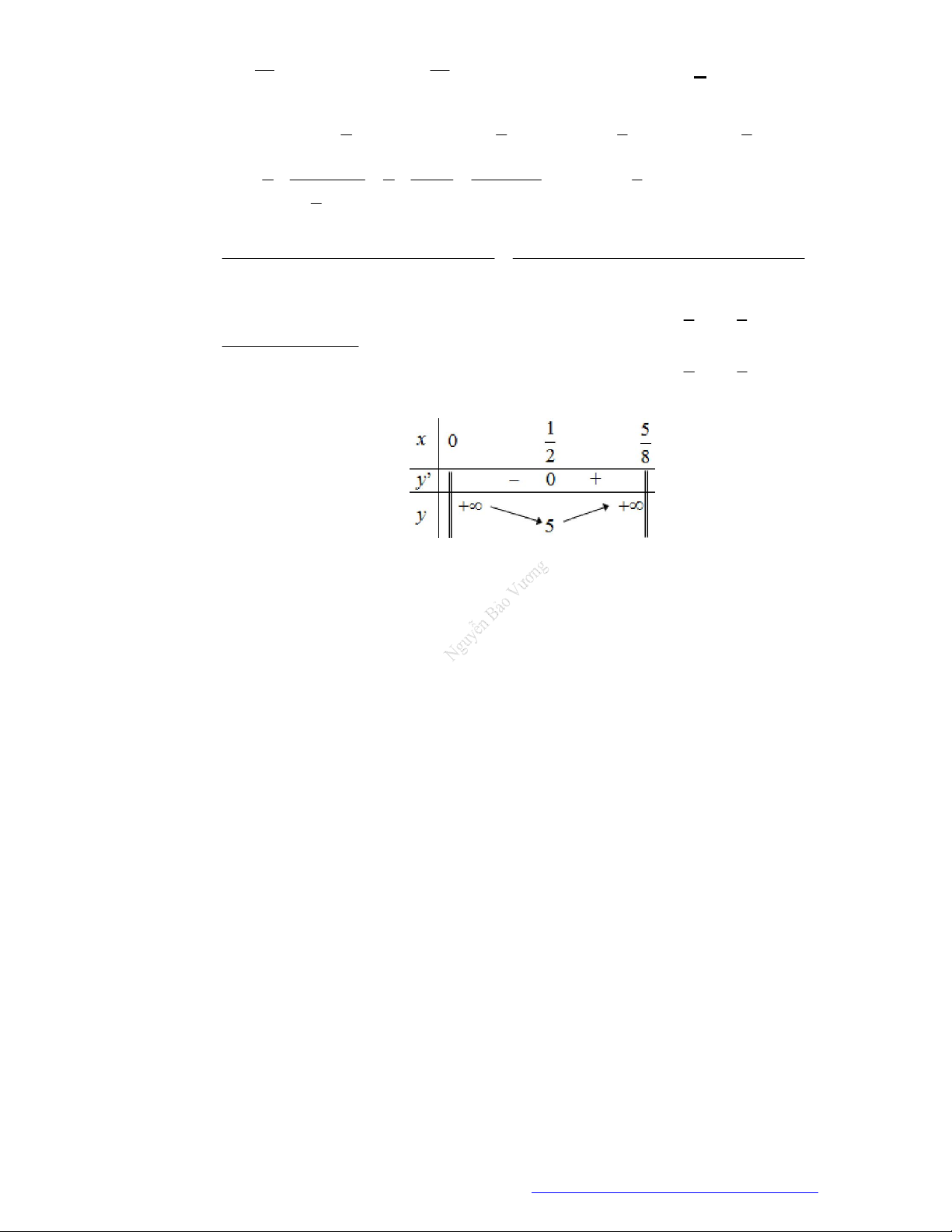
T
ÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 55
A.
min
3
4
5
P
. B.
min
65
4
P
. C.
m
in
P khôn
g tồn tại. D.
m
in
5P .
Lờ
i giải
Từ giả thiết ta có
5
2
4
y x
. Vì
0y
nên
5 5
2 0
4 8
x x
. Do
đó
5
0
8
x
.
Ta
có
2
2 1 2 1 10 15
5
5 8 8 5
4 2
4
x
P
x x x x x
x
với
5
0
8
x
.
( )
( )( )
( )
( )
( )
2
2 2
2 2
2 2
15 8 5 16 5 10 15 120 75 160 240 50 75
8 5 8 5
x x x x x x x x x
P
x x x x
( )
2
2
2
120
160 50
8 5
x x
P
x x
. Có
2
5 5
0;
6 8
0 120 160 50 0
1 5
0;
2 8
x
P x x
x
.
Bảng biến thiên
Dựa vào bảng biến thiên ta có
m
in
5P .
-------------------- HẾT --------------------

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
DẠNG TOÁN DÀNH CHO ĐỐI TƯỢNG HỌC SINH TRUNG BÌNH – MỨC 5-6 ĐIỂM
Dạng. Xác định đường tiệm cận thông qua bảng biến thiên, đồ thị
1.1.1 Đường tiệm cận ngang
Cho hàm số
y f x( )
xác định trên một khoảng vô hạn (là khoảng dạng
a b; , ; hoặc
;
).
Đường thẳng
y y
0
là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số
y f x( )
nếu ít nhất một trong các điều kiện sau được thỏa mãn:
x x
f x y f x y
0 0
lim ( ) , lim ( )
1.1.2 Đường tiệm cận đứng
Đường thẳng
x x
0
được gọi là đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số
( )y f x
nếu
ít nhất một trong các điều kiện sau được thỏa mãn:
x x x x
f x f x
0 0
lim ( ) , lim ( ) ,
0 0
lim ( ) , lim ( )
x x x x
f x f x
Lưu ý: Với đồ thị hàm phân thức dạng
ax b
y c ad bc
cx d
0; 0 luôn có tiệm cận ngang là
a
y
c
và tiệm cận đứng
d
x
c
.
Câu 1. (Đề Minh Họa 2017) Cho hàm số
( )y f x
có
lim ( ) 1
x
f x
và
lim ( ) 1
x
f x
. Khẳng định nào
sau đây là khẳng định đúng?
A. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng
1x
và
1x
.
B. Đồ thị hàm số đã cho không có tiệm cận ngang.
C. Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
D. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng
1y
và
1y
.
Câu 2. (Đề Tham Khảo 2020 Lần 2) Tiệm cận ngang của đồ thị hàm số
2
1
x
y
x
là
A.
2y
. B.
1y
. C.
1x
. D.
2x
.
Câu 3. (Mã 101 - 2020 Lần 1) Tiệm cận ngang của đồ thị hàm số
4 1
1
x
y
x
là
A.
1
4
y
. B.
4y
. C.
1y
. D.
1y
.
Câu 4. (Mã 102 - 2020 Lần 1) Tiệm cận ngang của đồ thị hàm số là
A. . B. . C. . D. .
Câu 5. (Mã 103 - 2020 Lần 1) Tiệm cận ngang của đồ thị hàm số
2 1
1
x
y
x
là:
A.
1
2
y
. B.
1y
. C.
1y
. D.
2y
.
Câu 6. (Mã 104 - 2020 Lần 1) Tiệm cận ngang của đồ thị hàm số
3 1
1
x
y
x
là:
TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
Chuyên đề 6
5 1
1
x
y
x
1y
1
5
y
1
y
5
y
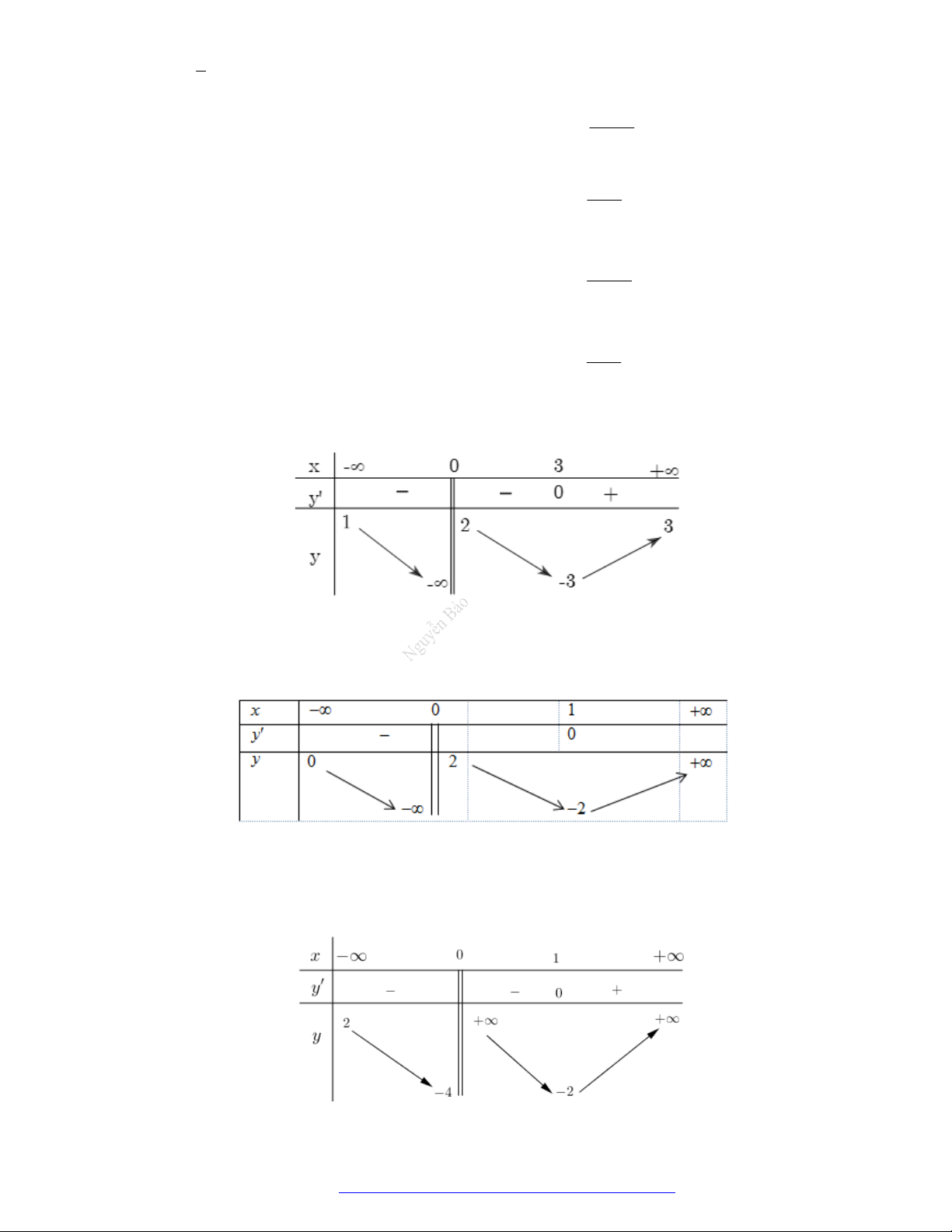
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
1
3
y
. B.
3y
. C.
1y
. D.
1y
.
Câu 7. (Mã 101 – 2020 Lần 2) Tiệm cận đứng của đồ thị hàm số
2 2
1
x
y
x
là
A.
2x
. B.
2 x
. C.
1.x
D.
1x
.
Câu 8. (Mã 102 - 2020 Lần 2) Tiệm cận đứng của đồ thị hàm số
1
3
x
y
x
là
A.
3x
. B.
1x
. C.
1x
. D.
3x
.
Câu 9. (Mã 103 - 2020 Lần 2) Tiệm cận đứng của đồ thị hàm số
2 2
1
x
y
x
là
A.
2x
. B.
1x
. C.
1x
. D.
2x
.
Câu 10. (Mã 104 - 2020 Lần 2) Tiệm cận đứng của đồ thị hàm số
1
3
x
y
x
là
A.
1x
. B.
1x
. C.
3x
. D.
3x
.
Câu 11. (Mã 103 - 2019) Cho hàm số
y f x
có báng biến thiên như sau:
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là:
A. 2. B. 3. C. 4. D. 1.
Câu 12. (Mã 102 - 2019) Cho hàm số
f x
có bảng biến thiên như sau
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
A.
1
. B.
2
. C.
4
. D.
3
.
Câu 13. (Mã 101 - 2019) Cho hàm số
y f x
có bảng biến thiên như sau:
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là:
A.
4
. B.
1
. C.
3
. D.
2
.
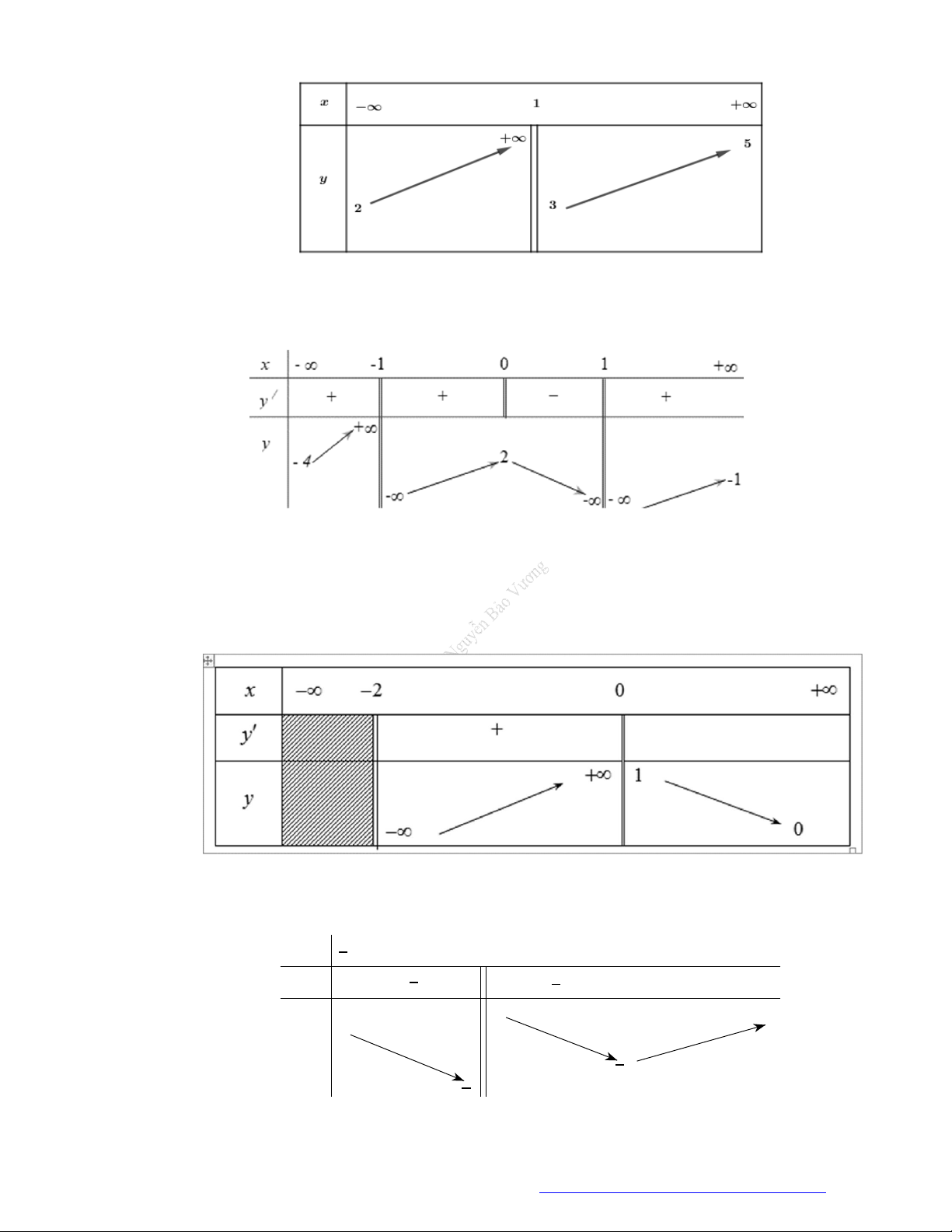
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Câu 14. (Đề Tham Khảo 2019) Cho hàm số
y f x
có bảng biến thiên như sau
Tổng số đường tiệm cận ngang và đường tiệm cận đứng của đồ thị hàm số đã cho là
A.
3
B.
2
C.
4
D.
1
Câu 15. (THPT - Yên Dịnh Thanh Hóa 2019) Cho hàm số có bảng biến thiên như hình sau
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
y f x
là
A.
3
. B.
2
. C.
4
. D.
1
.
Câu 16. (Đề Tham Khảo 2017) Cho hàm số
y f x
có bảng biến thiên như hình vẽ dưới đây. Hỏi đồ
thị của hàm số đã cho có bao nhiêu đường tiệm cận?
A.
3
B.
2
C.
4
D.
1
Câu 17. (Mã 104 2019) Cho hàm số
y f x
có bảng biến thiên như sau:
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
A. 1. B. 3. C. 4. D. 2.
y'
+
∞
0
3
4
3
0
+
3
0
+
∞
∞
y
x
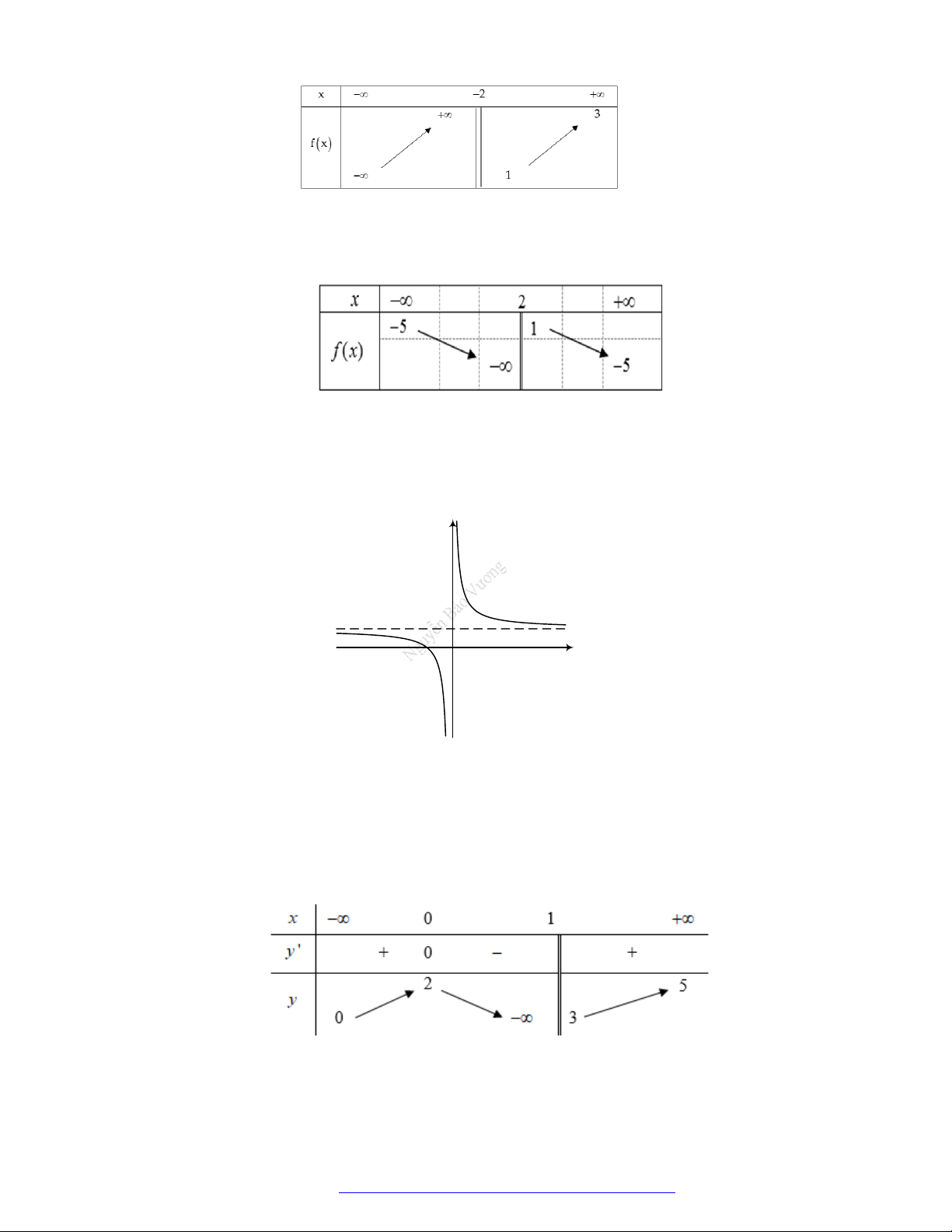
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 18. (Chuyên Lê Quý Đôn Điện Biên 2019) Cho hàm số
f x
có bảng biến thiên như sau:
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là:
A.
4
. B.
3
. C.
1
. D.
2
.
Câu 19. (Liên Trường Thpt Tp Vinh Nghệ An 2019) Cho hàm số
( )y f x
có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A.
4
B.
2
C.
3
D.
1
Câu 20. (THPT Hùng Vương Bình Phước 2019) Cho đồ thị hàm số
y f x
như hình bên. Khẳng
định nào sau đây là đúng?
x
y
O
1
1
A. Đồ thị hàm số có tiệm cận đứng
0x
, tiệm cận ngang
1y
.
B. Hàm số có hai cực trị.
C. Đồ thị hàm số chỉ có một đường tiệm cận.
D. Hàm số đồng biến trong khoảng
;0
và
0;
.
Câu 21. Cho hàmsố
( )f x
có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A.
4
. B.
1
. C.
3
. D.
2
.
Câu 22. Cho hàm số
( )y f x
có bảng biến thiên như sau
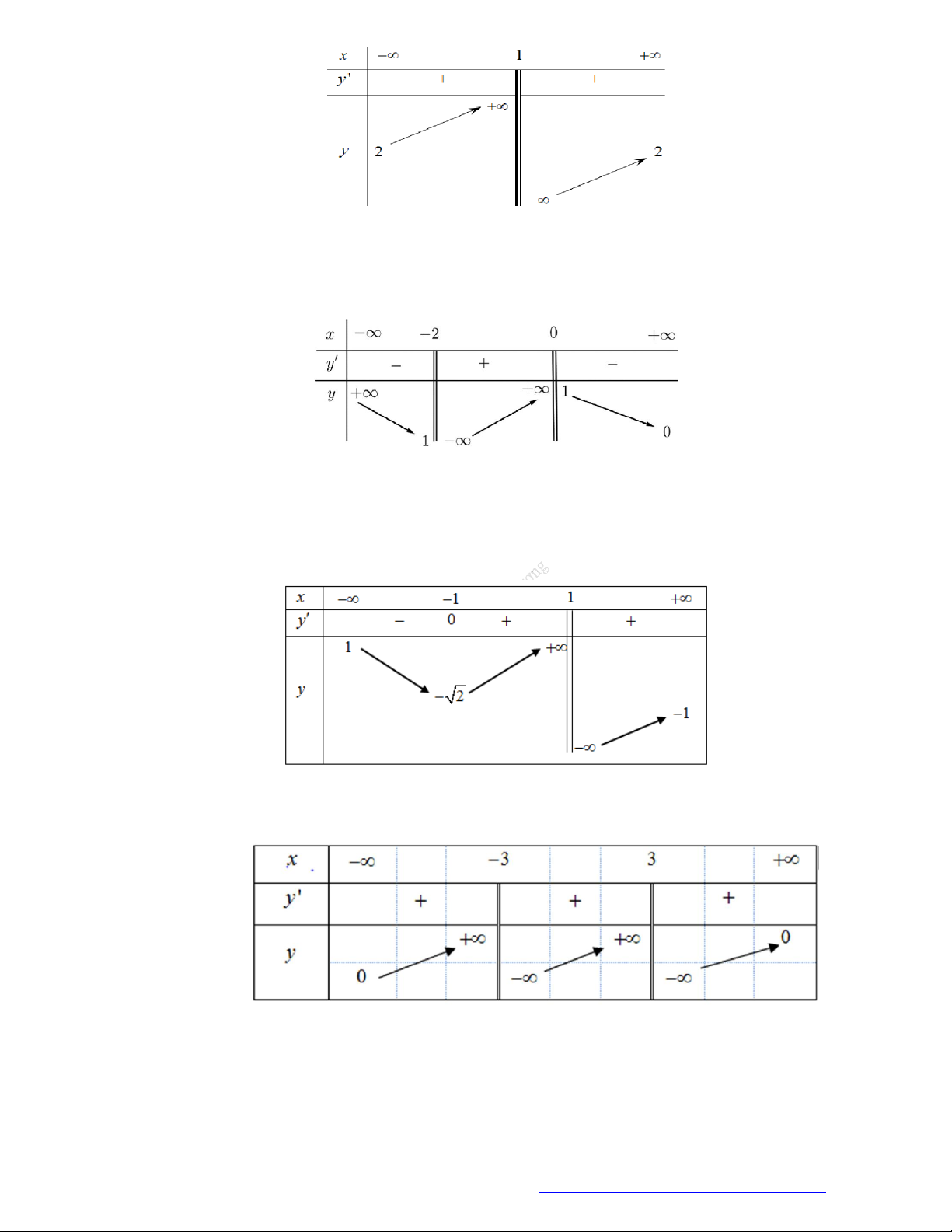
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A.
4
. B.
1
. C.
3
. D.
2
.
Câu 23. (Sở Hà Nội 2019) Cho hàm số
y f x
có bảng biến thiên như sau
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho bằng
A.
2
. B.
1
. C.
0
. D.
3
.
Câu 24. Cho hàm số
y f x
liên tục trên
\ 1
có bảng biến thiên như hình vẽ. Tổng số đường tiệm
cận đứng và đường tiệm cận ngang của đồ thị hàm số
y f x
A.
1
. B.
4
. C.
2
. D.
3.
Câu 25. (Cụm liên trường Hải Phòng 2019) Cho hàm số
y f x
có bảng biến như sau:
Số đường tiệm cận của đồ thị hàm số là:
A. 3 B. 1. C. 4. D. 2.
Câu 26. (Thi thử cụm Vũng Tàu 2019) Cho hàm số
y f x
có bảng biến thiên như sau

NGUYỄ
N BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Tổng số tiệm c
ận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
A.
4
. B.
2
. C
.
3
. D.
1
.
-------------------- HẾT --------------------
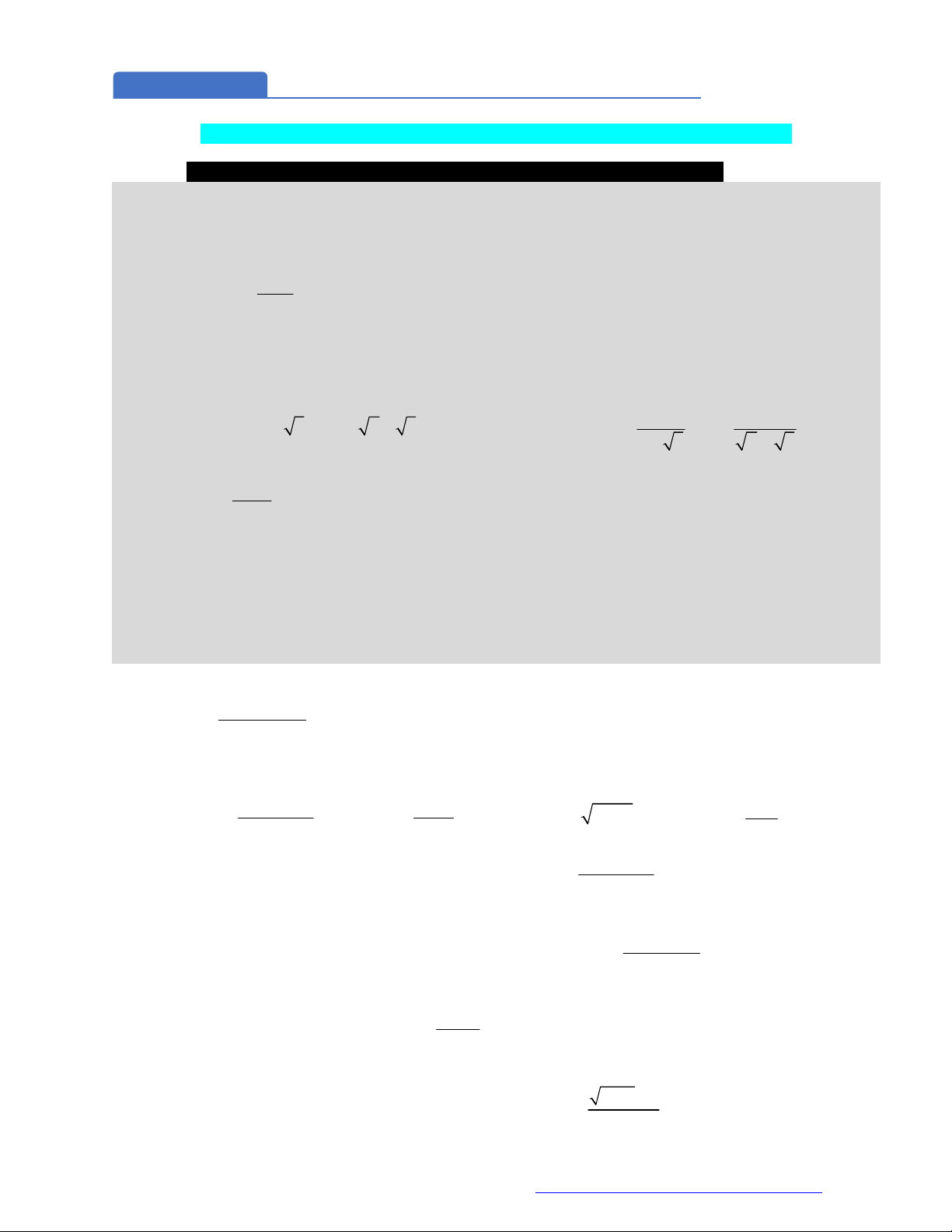
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
DẠNG TOÁN DÀNH CHO ĐỐI TƯỢNG HỌC SINH KHÁ – MỨC 7-8 ĐIỂM
Dạng 1. Xác định đường tiệm cận đồ thị hàm số thông hàm số cho trước
1 Đường tiệm cận ngang
Cho hàm số
y f x
có TXD:
D
Điều kiện cần:
D
phải chứa
hoặc
Điều kiện đủ:
Dạng 1.
( )
( )
( )
P x
y f x
Q x
.
Nếu
:degP x degQ x
thì không có tiệm cận ngang
Nếu
:degP x degQ x
TCN
0y
Nếu
:degP x degQ x
y k
(k là tỉ số hệ số bậc cao nhất của tử và mẫu)
Dạng 2:
( )y f x u v
(hoặc u v ): Nhân liên hợp
2
( )
u v
y f x
u v
(hoặc
u v
u v
)
2 Đường tiệm cận đứng
Cho hàm số
P x
y
Q x
có TXD:
D
Đkiện cần: giải
0
0Q x x x
là TCĐ khi thỏa mãn đk đủ
Đkiện đủ:
Đkiện 1:
0
x làm cho
( )P x
và
( )Q x
xác định.
Đkiện 2: -
0
x không phải nghiêm
0
( )P x x x là TCĐ
-
0
x là nghiêm
0
( )P x x x là TCĐ nếu
0
lim ( )
x x
f x
Câu 1. (Đề Minh Họa 2020 Lần 1) Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
2
5 4 1
1
x x
y
x
là
A.
0.
B.
1.
C.
2.
D.
3.
Câu 2. (Đề Tham Khảo 2018) Đồ thị của hàm số nào dưới đây có tiệm cận đứng?
A.
2
3 2
1
x x
y
x
B.
2
2
1
x
y
x
C.
2
1 y x D.
1
x
y
x
Câu 3. (Mã 110 2017) Tìm số tiệm cận của đồ thị hàm số
2
2
5 4
1
x x
y
x
.
A.
2
B.
3
C.
0
D.
1
Câu 4. (Mã 123 2017) Tìm số tiệm cận đứng của đồ thị hàm số:
2
2
3 4
16
x x
y
x
A.
2
B.
3
C.
1
D.
0
Câu 5. (Mã 104 2017) Đồ thị hàm số
2
2
4
x
y
x
có mấy tiệm cận.
A.
3
B.
1
C.
2
D.
0
Câu 6. (Mã 101 2018) Số tiệm cận đứng của đồ thị hàm số
2
9 3x
y
x x
là
A.
1
B.
2
C.
0
D.
3
TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
Chuyên đề 6

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 7. (Mã 102 2018) Số tiệm cận đứng của đồ thị hàm số
2
4 2
x
y
x x
là
A.
2
B.
1
C.
3
D.
0
Câu 8. (THPT Lê Văn Thịnh Bắc Ninh 2019) Đồ thị hàm số
2
5 1 1
2
x x
y
x x
có tất cả bao nhiêu
đường tiệm cận?
A.
3
B.
0
C.
2
D.
1
Câu 9. Tìm tất cả các tiệm cận đứng của đồ thị hàm số
2
2
2 1 3
5 6
x x x
y
x x
.
A.
3
x
và
2
x
. B.
3
x
. C.
3
x
và
2
x
. D.
3
x
.
Câu 10. (Mã 103 2018) Số tiệm cận đứng của đồ thị hàm số
2
25 5
x
y
x x
là
A.
3
B.
2
C.
0
D.
1
Câu 11. (Mã 104 2018) Số tiệm cận đứng của đồ thị hàm số
2
16 4
x
y
x x
là
A.
3
B.
2
C.
1
D.
0
Câu 12. (Chuyên Sơn La 2019) Số tiệm cận đứng của đồ thị hàm số
2
4 2
x
y
x x
là
A.
3
. B.
0
. C.
1
. D.
2
.
Câu 13. (THPT Gang Thép Thái Nguyên 2019) Đồ thị hàm số
2
1
1
x
f x
x
có tất cả bao nhiêu tiệm
cận đứng và tiệm cận ngang?
A.
4
. B.
3
. C.
1
. D.
2
.
Câu 14. Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
4 6 2
2
x x
y
x
là?
A.
1
B.
3
C.
2
D.
4
Câu 15. (THPT Bạch Đằng Quảng Ninh 2019) Cho hàm số
2
4 2
2 3
3 2
x x
y
x x
. Đồ thị hàm số đã cho có
bao nhiêu đường tiệm cận?
A.
4
. B.
5
. C.
3
. D.
6
.
Câu 16. (THPT Lê Quy Đôn Điện Biên 2019) Hàm số
2
3
1x x x
y
x x
có bao nhiêu đường tiệm cận?
A.
1
B.
3
C.
2
D.
4
Câu 17. (Chuyên Lam Sơn Thanh Hóa 2019) Số đường tiệm cận đứng và tiệm cận ngang của đồ thị
hàm số
2
2 1
3 2
x
y
x x
là
A.
4
B.
1
C.
3
D.
2
Câu 18. (THPT Thiệu Hóa – Thanh Hóa 2019) Cho hàm số
2
3
5 6 12
4 3 1
x x
y
x x
có đồ thị
C
. Mệnh
đề nào sau đây là đúng?
A. Đồ thị
C
của hàm số không có tiệm cận.
B. Đồ thị
C
của hàm số chỉ có một tiệm cận ngang
0
y
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
C. Đồ thị
C
của hàm số có một tiệm cận ngang
0
y
và hai tiệm cận đứng
1
1;
2
x x
.
D. Đồ thị
C
của hàm số chỉ có một tiệm cận ngang
0
y
và một tiện cận đứng
1x
Câu 19. (Chuyên Lê Quý Đôn Quảng Trị 2019) Đồ thị hàm số
2
2
3 1
x x x
y
x
có tất cả bao nhiêu
đường tiệm cận?
A.
2
. B.
3
. C.
0
. D.
1
.
Câu 20. Đồ thị hàm số
2
2
1 4
2 3
x
y
x x
có số đường tiệm cận đứng là
m
và số đường tiệm cận ngang là
n
. Giá trị của
m n
là
A.
1
B.
2
C.
3
D.
0
Câu 21. Gọi
,n d
lần lượt là số đường tiệm cận ngang và số tiệm cận đứng của đồ thị hàm số
1
1
x
y
x x
. Khẳng định nào sau đây là đúng?
A.
0, 2
n d
. B.
1
n d
. C.
1, 2
n d
. D.
0, 1
n d
.
Câu 22. (Chuyên Long An-2019) Đồ thị hàm số
2
5 1 1
2
x x
y
x x
có tất cả bao nhiêu đường tiệm cận?
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 23. (Chuyên Vĩnh Phúc 2019) Tìm số đường tiệm cận của đồ thị hàm số
1
4 3 1 3 5
x
y
x x
.
A.
2
. B.
3
. C.
1
. D.
0
.
Câu 24. Cho hàm số
2
4 2
2 3
3 2
x x
y
x x
. Đồ thị hàm số đã cho có bao nhiêu đường tiệm cận?
A.
4
. B.
5
. C.
3
. D.
6
.
Câu 25. (Chuyên Lê Quý Đôn Điện Biên 2019) Đồ thị hàm số
2
5 8
3
x
y
x x
có bao nhiêu đường tiệm
cận?
A. 2. B. 4. C. 1. D. 3.
Câu 26. Đồ thị hàm số
2
4 2 1
1
x x x
y
x
có bao nhiêu đường tiệm cận?
A.
1
. B.
0
. C.
2
. D.
3
.
Dạng 2. Định m để đồ thị hàm số có đường tiệm cận thỏa mãn điều kiện cho trước
1 Đường tiệm cận ngang
Cho hàm số
y f x
có TXD:
D
Điều kiện cần:
D
phải chứa
hoặc
Điều kiện đủ:
Dạng 1.
( )
( )
( )
P x
y f x
Q x
.
Nếu
:degP x degQ x
thì không có tiệm cận ngang
Nếu
:degP x degQ x
TCN
0
y
Nếu
:degP x degQ x
y k
(k là tỉ số hệ số bậc cao nhất của tử và mẫu)
Dạng 2:
( )
y f x u v
(hoặc
u v
): Nhân liên hợp
2
( )
u v
y f x
u v
(hoặc
u v
u v
)

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2 Đường tiệm cận đứng
Cho hàm số
P x
y
Q x
có TXD:
D
Đkiện cần: giải
0
0
Q x x x
là TCĐ khi thỏa mãn đk đủ
Đkiện đủ:
Đkiện 1:
0
x
làm cho
( )P x
và
( )Q x
xác định.
Đkiện 2: -
0
x
không phải nghiêm
0
( )
P x x x
là TCĐ
-
0
x
là nghiêm
0
( )
P x x x
là TCĐ nếu
0
lim ( )
x x
f x
Câu 1. (Đề Minh Họa 2017) Tìm tất cả các giá trị thực của tham số
m
sao cho đồ thị của hàm số
2
1
1
x
y
mx
có hai tiệm cận ngang
A.
0
m
B.
0
m
C.
0
m
D. Không có giá trị thực nào của
m
thỏa mãn yêu cầu đề bài
Câu 2. (Chuyên KHTN - 2020) Gọi
S
là tập hợp các giá trị nguyên
m
để đồ thị hàm số
2
2
6 2
x
y
x x m
có hai đường tiệm cận đứng. Số phần tử của
S
là
A. vô số. B.
12
. C.
14
. D.
13
.
Câu 3. (Chuyên Phan Bội Châu - Nghệ An - 2020) Có bao nhiêu giá trị nguyên dương của tham số
m
để đồ thị hàm số
2
1
8
x
y
x x m
có 3 đường tiệm cận?
A.
14
. B.
8
. C.
15
. D.
16
.
Câu 4. (THPT Nguyễn Viết Xuân - 2020) Cho hàm số
3 2 2
3
3 2 1
x
y
x mx m x m
. Có bao nhiêu
giá trị nguyên của tham số
m
thuộc đoạn
2020;2020
để đồ thị hàm số có 4 đường tiệm cận?
A. 4039. B. 4040. C. 4038. D. 4037.
Câu 5. (Chuyên Sư Phạm Hà Nội - 2020) Có bao nhiêu số nguyên của
m
thuộc đoạn
100;100
để đồ
thị hàm số
2
1
2
y
x m x x
có đúng hai đường tiệm cân?
A.
200.
B.
2.
C.
199.
D.
0.
Câu 6. (HSG Bắc Ninh 2019) Tìm tất cả các giá trị của tham số thực
m
để đồ thị hàm số
2
2
3 2
x m
y
x x
có đúng hai đường tiệm cận.
A.
1
m
B.
{1;4}
m
C.
4
m
D.
{ 1; 4}
m
Câu 7. (THPT Hoàng Hoa Thám Hưng Yên 2019) Có bao nhiêu giá trị nguyên của
m
để đồ thị hàm
số
2 2
6 3
6 3 9 6 1
x
y
mx x x mx
có đúng một đường tiệm cận?
A.
0
. B.
2
. C.
1
. D. Vô số.
Câu 8. (THPT Lương Thế Vinh Hà Nội 2019) Cho hàm số
2
1
2 4
x
x
y f
m
x
x
. Tìm tất cả các giá
trị của tham số
m
để đồ thị có ba đường tiệm cận

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
A.
2
m
B.
2
5
2
m
m
C.
2
2
5
2
m
m
m
D.
2
2
m
m
Câu 9. (Chuyên Vĩnh Phúc 2019) Biết rằng đồ thị của hàm số
3 2017
3
n x n
y
x m
(
,m n
là các số
thực) nhận trục hoành làm tiệm cận ngang và trục tung là tiệm cận đứng. Tính tổng
m n
.
A.
0
B.
3
C.
3
D.
6
Câu 10. (Sở Vĩnh Phúc 2019) Có bao nhiêu giá trị nguyên của tham số
m
để đồ thị hàm số
2
1
8 2
x
y
mx x
có đúng bốn đường tiệm cận?
A.
8
B.
6
C.
7
D. Vô số
Câu 11. (THPT Việt Đức Hà Nội 2019) Với giá trị nào của hàm số
m
để đồ thị hàm số
2
3 7
y x mx x
có tiệm cạn ngang.
A.
1
m
B.
1
m
C.
1
m
D. Không có
m
Câu 12. Cho hàm số
1
.
2
ax
y
bx
Tìm
,a b
để đồ thị hàm số có
1x
là tiệm cận đứng và
1
2
y
là tiệm
cận ngang.
A.
1; 2
a b
. B.
4; 4
a b
. C.
1; 2
a b
. D.
1; 2
a b
.
Câu 13. Có bao nhiêu giá trị nguyên
10;10
m
sao cho đồ thị hàm số
2
1
2 6 3
x
y
x x m
có hai
đường tiệm cận đứng?
A.
19
. B.
15
. C.
17
. D.
18
.
Câu 14. Có bao nhiêu giá trị nguyên của
m
để tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
2
3 4
2
mx mx
y
x
bằng 3?
A.
4
. B.
2
. C. Vô số. D.
3
.
Câu 15. (Thi thử Lômônôxốp - Hà Nội 2019) Tổng các giá trị của tham số
m
để đồ thị của hàm số
2 2
1
2 1 2
x
y
x m x m
có đúng một tiệm cận đứng.
A.
1
2
. B.
2
. C.
3
. D.
3
2
.
Câu 16. Cho hàm số
3 2 2
3
3 2 1
x
y
x mx m x m
. Có bao nhiêu giá trị nguyên thuộc đoạn
6;6
của
tham số
m
để đồ thị hàm số có bốn đường tiệm cận?
A.
12
. B.
9
. C.
8
. D.
11
.
Câu 17. (THPT Yên Dũng 2-Bắc Giang) Tìm tất cả các giá trị thực của tham số m sao cho đồ thị hàm số
2
2 3
x x m
y
x m
không có tiệm cận đứng.
A.
1
m
. B.
1
m
. C.
1
m
và
0
m
. D.
0
m
.
Câu 18. (Cụm liên trường Hải Phòng 2019) Có bao nhiêu giá trị nguyên của tham số thực
m
thuộc đoạn
2017;2017
để đồ thị hàm số
2
2
4
x
y
x x m
có hai tiệm cận đứng.
A.
2019
. B.
2021
. C.
2018
. D.
2020
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 19. (THPT Quỳnh Lưu- Nghệ An- 2019) Cho hàm số
( )y f x
thỏa mãn
lim ( ) 2019
x
f x m
,
4
lim ( ) 2020
x
f x m
(với
m
là tham số thực). Hỏi có tất cả bao nhiêu giá trị
của
m
để đồ thị của hàm số
( )y f x
có duy nhất một tiệm cận ngang?
A. 4. B. 2. C. 3. D. 1.
Câu 20. (THPT Hai Bà Trưng - Huế - Lần 1- 2019) Cho hàm số
2
1
2 1 2
y
x m x m x m
.
Tìm tất cả các giá trị thực của tham số
m
để đồ thị hàm số có 4 đường tiệm cận.
A.
0 1
1
2
m
m
. B.
1
1
2
m
m
. C.
1
m
. D.
0 1
1
2
m
m
.
Câu 21. (THPT Hoàng Hoa Thám - Hưng Yên 2019) Có bao nhiêu giá trị nguyên của
m
để đồ thị hàm
số
2 2
6 3
6 3 9 6 1
x
y
mx x x mx
có đúng 1 đường tiệm cận?
A.
0.
B. 2. C.
1.
D. Vô số.
Câu 22. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số:
2
1
y x mx
có tiệm cận ngang.
A.
0 1.
m
B.
1.
m
C.
1.
m
D.
1.
m
Câu 23. (Chuyên Lê Hồng Phong Nam Định 2019) Cho hàm số
2
2
2 4
x
y
mx x
. Có tất cả bao nhiêu
giá trị của tham số
m
để đồ thị hàm số có đúng hai đường tiệm cận ( tiệm cận đứng và tiệm cận
ngang)?
A.
0
. B.
2
. C.
3
. D.
1
.
Câu 24. (HSG Sở Nam Định-2019) Gọi S là tập các giá trị nguyên của
m
sao cho đồ thị hàm số
2
2019
17 1
x
y
x m x
có bốn đường tiệm cận (bao gồm tiệm cận đứng và tiệm cận ngang). Tính số
phần tử của tập S.
A. Vô số B. 3 C. 5 D. 4
Câu 25. Gọi
S
là tập hợp tất cả các giá trị của tham số thực
m
sao cho đồ thị hàm số
3
3 4 2
( )
1 1
x
f x
x mx x x m x
nhận trục tung làm tiệm cận đứng. Khi đó tổng các phần
tử của
S
bằng
A.
1
2
. B.
1
2
. C.
1
3
. D.
1
3
.
Câu 26. (Trường THPT Thăng Long Lần 2019) Có bao nhiêu giá trị
m
nguyên thuộc khoảng
10;10
để đồ thị hàm số
( ) 1
2
x x m
y
x
có đúng ba đường tiệm cận?
A.
12
. B.
11
. C.
0
. D.
10
.
Câu 27. Tìm số giá trị nguyên thuộc đoạn
2019;2019
của tham số
m
để đồ thị hàm số
2
3
x
y
x x m
có đúng hai đường tiệm cận.
A.
2007
. B.
2010
. C.
2009
. D.
2008
.
Câu 28. (Chuyên Bắc Ninh 2019) Cho hàm số
2
1
2 3
x
y
mx x
. Có tất cả bao nhiêu giá trị
m
để đồ thị
hàm số có đúng hai đường tiệm cận.
A. 2 B. 3 C. 0 D. 1

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Câu 29. Cho
hàm số
3
2
1
3 1
y
x
x m
vớ
i
m
là
tham số. Tìm tất cả các giá trị của
m
để
đồ thị hàm
số đã cho có
4
đường t
hẳng tiệm cận.
A.
1
5
m
. B.
1
2
m
. C.
1
m
hoặc
5
m
. D.
2
m
hoặc
1
m
.
Câu 30. Hà
m số
2
3
1
1
x
ax b
y
x
không
có tiệm cận đứng. Khi đó hiệu
a b
bằ
ng:
A.
1
2
.
B.
3
4
. C.
5
4
. D.
1
2
.
Câu 31. Có
bao nhiêu giá trị nguyên của tham để
m
đồ
thị hàm số
2
2
016 2017 24 7
x
x
y
x
m
c
ó
tiệm cận đứng?
A. vô số. B.
2
. C.
2
017
D.
2
019
.
Câu 32. Gọi
S
là tập hợp tất cả các giá trị của tham số thực
m
sao cho đồ thị hàm số
3
3
4 2
(
)
1 1
x
f x
x mx x x m x
nhận trục tung làm tiệm cận đứng. Khi đó tổng các phần
tử của
S
bằng
A.
1
2
. B.
1
2
. C.
1
3
. D.
1
3
.
Câu 33. (THPT Thăng Long 2019) Có bao nhiêu giá trị
m
nguyê
n thuộc khoảng
1
0;10
để
đồ thị
hàm số
( ) 1
2
x
x m
y
x
có đúng ba đường tiệm cận?
A.
12
. B.
11
. C.
0
. D.
10
.
Câu 34. (THPT
Mai Anh Tuấn_Thanh Hóa 2019) Tìm tất cả các giá trị thực của
m
sao
cho đồ thị hàm
số
1
1
2
x
mx
y
có đúng một đường tiệm cận.
A.
01
m
. B.
01
m
. C.
1
m
. D.
0
m
.
-------------------- HẾT --------------------

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
DẠNG TOÁN DÀNH CHO ĐỐI TƯỢNG HỌC SINH GIỎI – MỨC 9-10 ĐIỂM
Dạng. Xác định tiệm cận của đồ thị hàm số g khi biết bảng biến thiên hàm số f(x)
Câu 1. (THPT Lương Văn Can - 2018) Cho đồ thị hàm số
3 1
1
x
y f x
x
. Khi đó đường thẳng nào
sau đây là đường tiệm cận đứng của đồ thị hàm số
1
2
y
f x
?
A.
1x
. B.
2x
. C.
1x
. D.
2x
.
Câu 2. Cho hàm số
y f x
có đồ thị như hình vẽ
Số tiệm cận đứng của đồ thị hàm số
2019
1
y
f x
là
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 3. (Chuyên Thái Bình - 2020) Cho hàm số
f x
xác định và liên tục trên
\ 1
có bảng biến
thiên như sau:
Hỏi đồ thị hàm số
1
y
f x
có tất cả bao nhiêu đường tiệm cận đứng và tiệm cận
ngang?
A.
4
. B.
3
. C.
2
. D.
1
.
Câu 4. (Chuyên Vĩnh Phúc - 2020) Cho hàm số
y f x
thỏa mãn
lim 1
x
f x
và
lim
x
f x m
.
Có bao nhiêu giá trị thực của tham số
m
để hàm số
1
2
y
f x
có duy nhất một tiệm cận
ngang.
A.
1
. B.
0
. C.
2
. D. Vô số.
TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
Chuyên đề 6
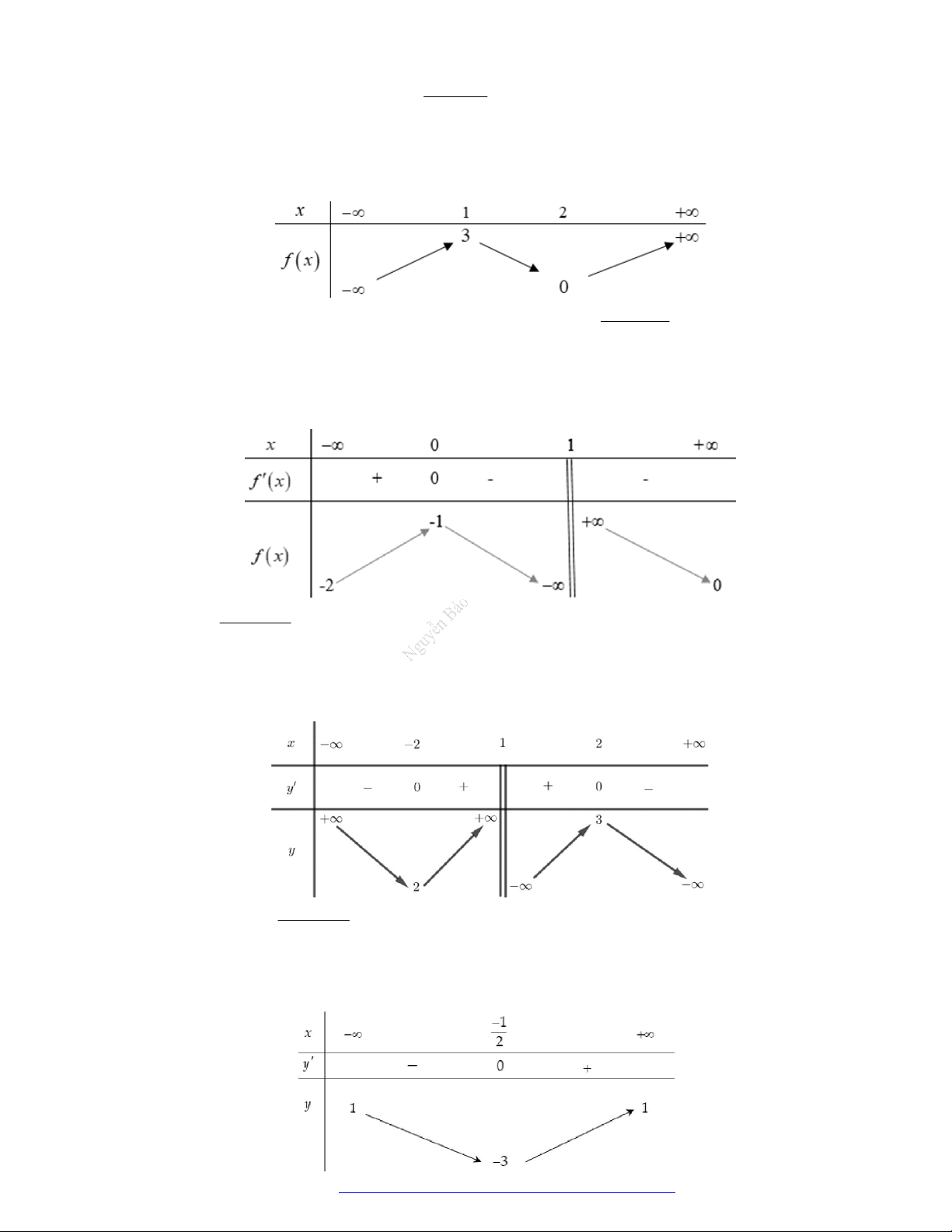
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 5. (Kim Liên - Hà Nội 2019) Cho hàm số
( )y f x
thỏa mãn
4
(tan ) cosf x x . Tìm tất cả các giá
trị thực của
m
để đồ thị hàm số
2019
( )
( )
g x
f x m
có hai tiệm cận đứng.
A.
0m
. B.
0 1m
. C.
0m
. D.
1m
.
Câu 6. (THPT Quỳnh Lưu 3 Nghệ An 2019) Cho hàm số
y f x
xác định, liên tục trên
và có
bảng biến thiên như hình bên dưới:
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
1
2 1
y
f x
là:
A.
4
. B.
3
. C.
1
. D.
2
.
Câu 7. (Bình Giang-Hải Dương -2019) Cho hàm số
( )y f x
liên tục trên
\ 1
và có bảng biến thiên
như sau:
Đồ thị
1
2 3
y
f x
có bao nhiêu đường tiệm cận đứng?
A. 2. B. 0. C. 1. D. 3.
Câu 8. (Chuyên Thoại Ngọc Hầu 2018) Cho hàm số
y f x
liên tục trên
\ 1
và có bảng biến
thiên như sau:
Đồ thị hàm số
1
2 5
y
f x
có bao nhiêu đường tiệm cận đứng?
A.
0
. B.
4
. C.
2
. D.
1
.
Câu 9. (Chuyên Hưng Yên 2019) Cho hàm số
y f x
có bảng biến thiên như hình dưới đây.
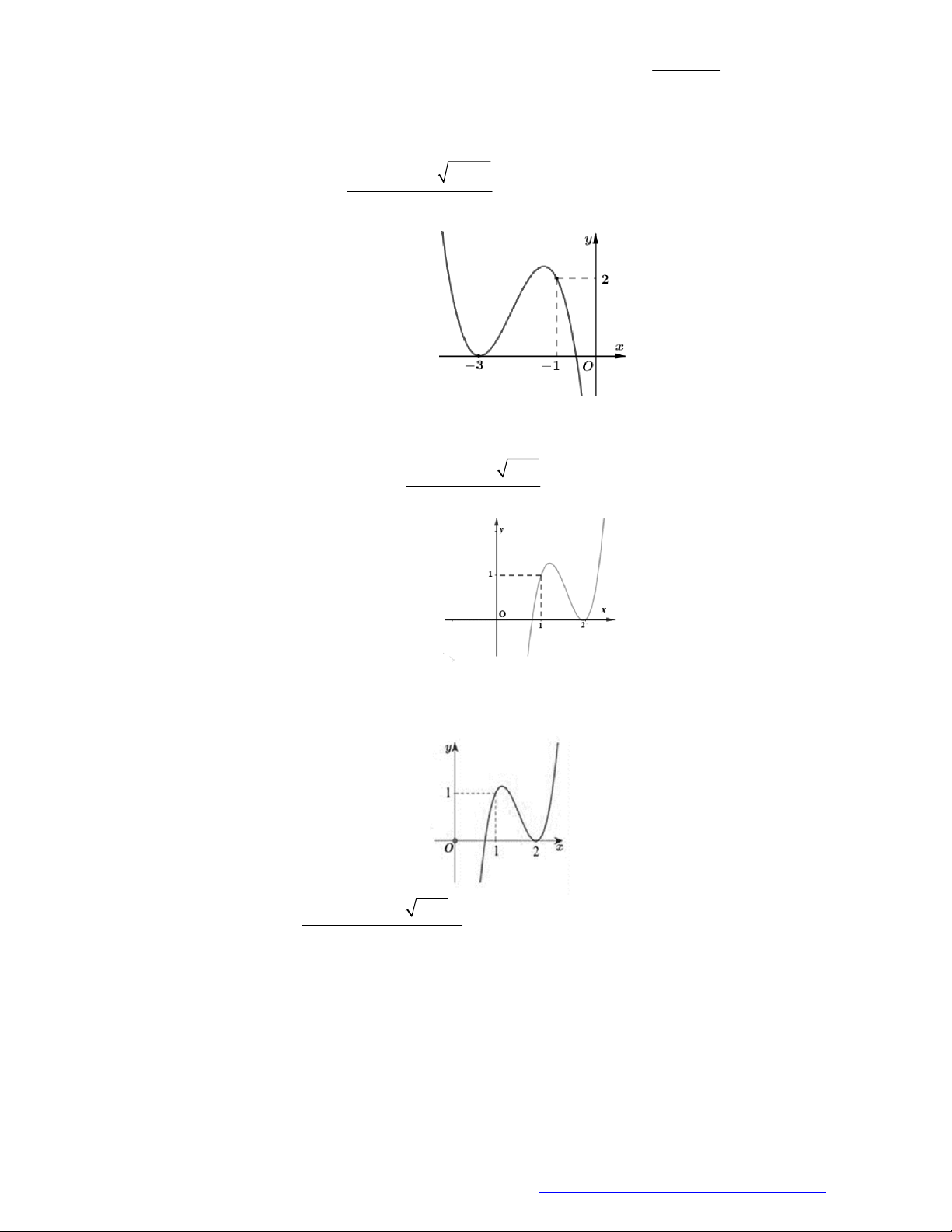
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
1
2 1
y
f x
là
A.
0.
B.
1.
C.
2.
D.
3.
Câu 10. (THPT Bạch Dằng Quảng Ninh 2019) Cho hàm bậc ba
y f x
có đồ thị như hình vẽ bên.
Hỏi đồ thị hàm số
2 2
2
4 3
2
x x x x
y
x f x f x
có bao nhiêu đường tiệm cận đứng?
A.
2
. B.
3
. C.
4
. D.
6
.
Câu 11. (Lý Nhân Tông - Bắc Ninh 2019) Cho hàm số
3 2
f x ax bx cx d
có đồ thị như hình vẽ
bên. Hỏi đồ thị hàm số
2
2
3 2 1x x x
g x
x f x f x
có bao nhiêu tiệm cận đứng?
A.
2
. B.
4
. C.
3
. D.
5
.
Câu 12. (THPT Quỳnh Lưu- Nghệ An- 2019) Cho hàm số bậc ba
3 2
f x ax bx cx d
có đồ thị
như hình vẽ sau.
Hỏi đồ thị hàm số
2
2
3 2 1
1
x x x
g x
x f x f x
có bao nhiêu tiệm cận đứng?
A.
5
. B.
4
. C.
6
. D.
3
.
Câu 13. (THPT Thuận Thành 3 - Bắc Ninh 2019) Cho hàm số
( )y f x
là hàm số đa thức có đồ thì
như hình vẽ dưới đây, đặt
2
2
2
x x
g x
f x f x
. Hỏi đồ thị hàm số
y g x
có bao nhiêu tiệm
cận đứng?
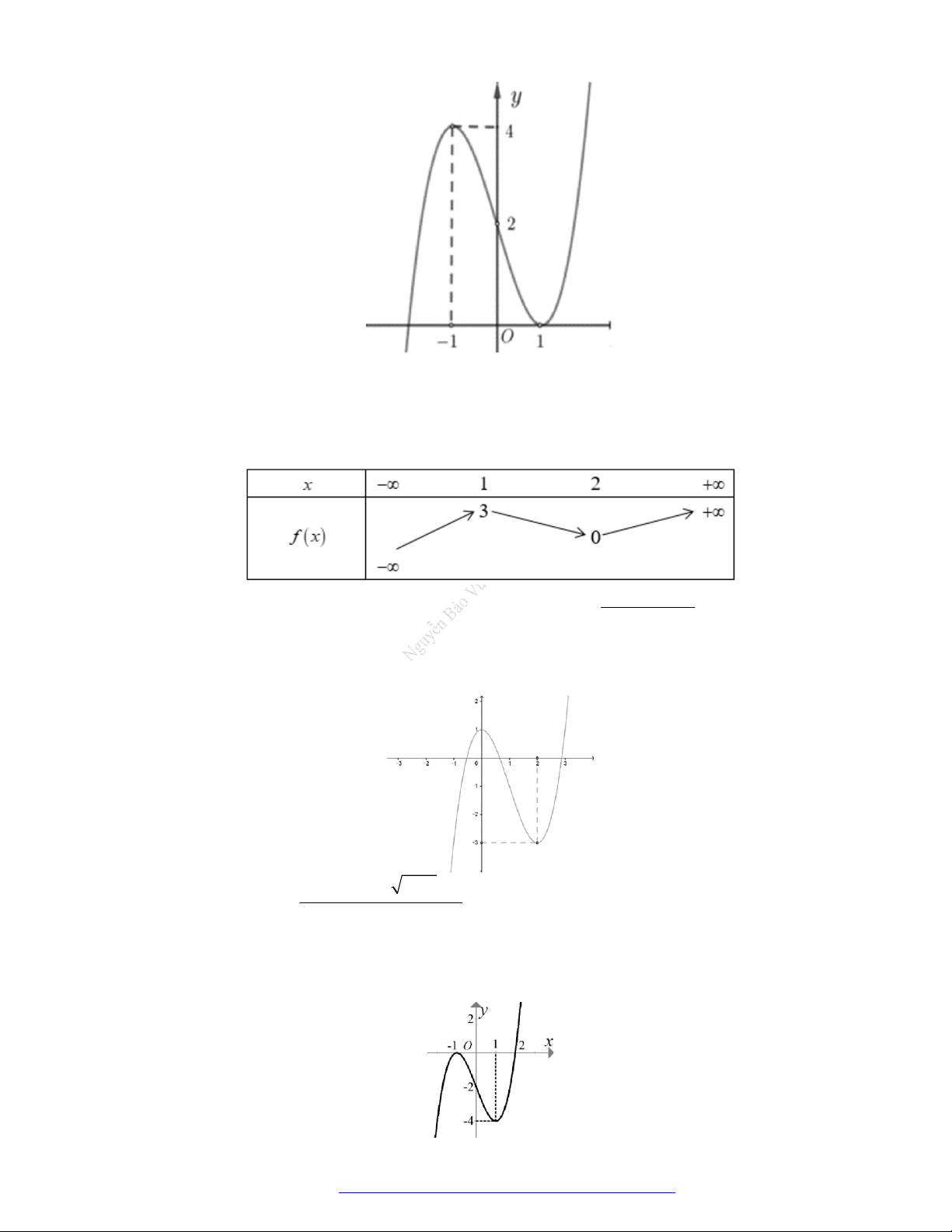
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
5
. B.
3
. C.
4
. D.
2
.
Câu 14. (Chuyên Bắc Giang 2019) Cho hàm số
y f x
xác định, liên tục trên
và có bảng biến
thiên như hình bên dưới.
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
3
1
3
y
f x x
là
A. 2. B. 4. C. 3. D. 1.
Câu 15. (THPT Minh Khai 2020) Cho hàm số
3 2
y f x ax bx cx d
có đồ thị như bên dưới.
Hỏi đồ thị hàm số
2
2
2 2
3
x x x
y
x f x f x
có bao nhiêu đường tiệm cận đứng
A.
4
. B.
6
. C.
3
. D.
5
.
Câu 16. (Yên Phong 1 - 2018) Cho hàm số
3 2
y ax bx cx d
,
0a
có đồ thị như hình dưới đây.
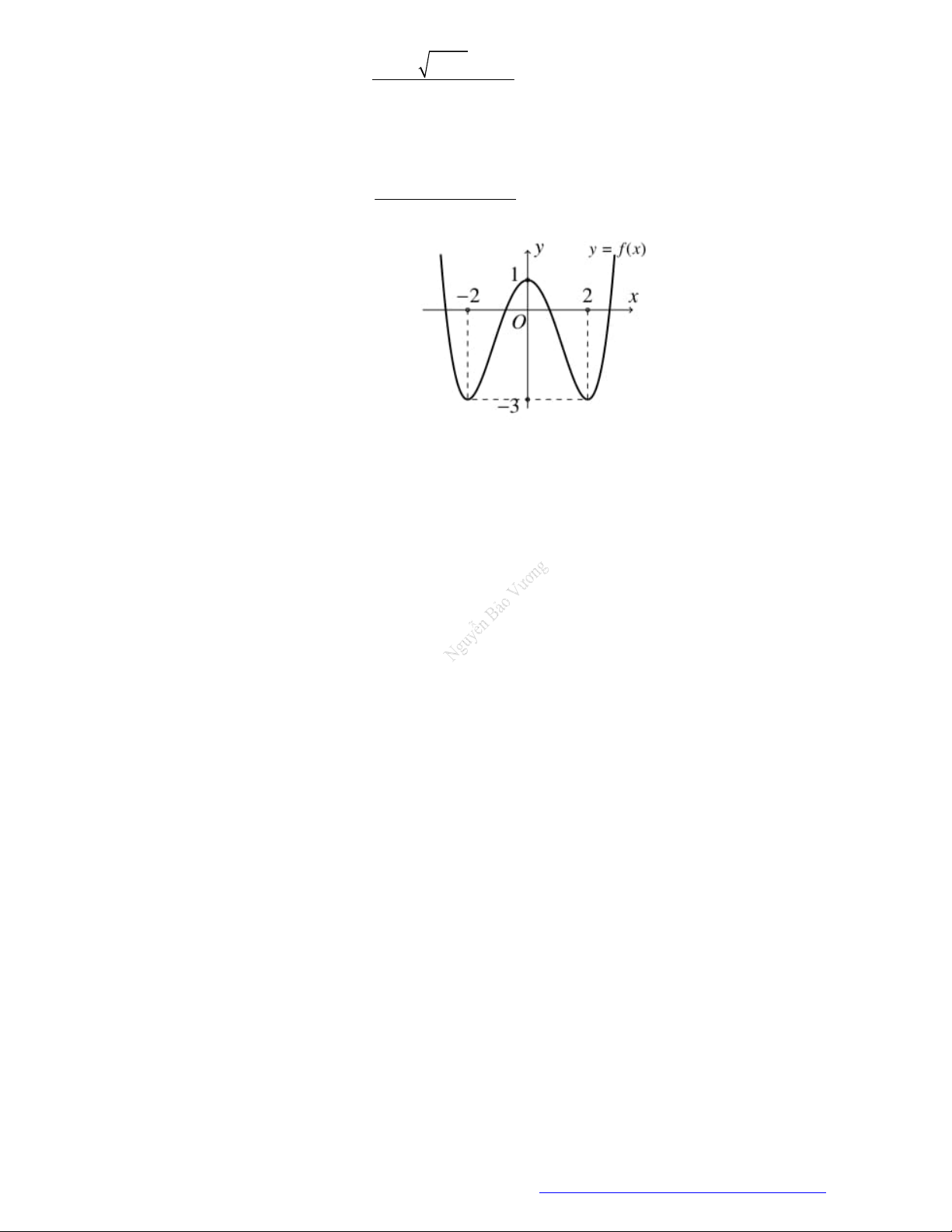
T
ÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Hỏi đồ t
hị hàm số
2
2
1
4 3
f x
g x
x x x
có
bao nhiêu đường tiệm cận đứng?
A.
2
. B.
1
. C.
3
. D.
4
.
Câu
17. (Chuyên Quang Trung - 2020) Cho hàm số trùng phương
4
2
y
ax bx c có đồ thị như hình
vẽ. Hỏi đồ thị hàm số
2
2
2
4 2
2 3
x x x
y
f x f x
c
ó tổng cộng bao nhiêu tiệm cận đứng?
A. 5. B. 2. C. 3. D. 4.
-------------------- HẾT --------------------

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
DẠNG TOÁN DÀNH CHO ĐỐI TƯỢNG HỌC SINH TRUNG BÌNH – MỨC 5-6 ĐIỂM
Dạng. Xác định đường tiệm cận thông qua bảng biến thiên, đồ thị
1.1.1 Đường tiệm cận ngang
Cho hàm số
y f x( )
xác định trên một khoảng vô hạn (là khoảng dạng
a b; , ; hoặc
;
). Đường thẳng
y y
0
là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm
số
y f x( )
nếu ít nhất một trong các điều kiện sau được thỏa mãn:
x x
f x y f x y
0 0
lim ( ) , lim ( )
1.1.2 Đường tiệm cận đứng
Đường thẳng
x x
0
được gọi là đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số
( )y f x
nếu ít nhất một trong các điều kiện sau được thỏa mãn:
x x x x
f x f x
0 0
lim ( ) , lim ( ) ,
0 0
lim ( ) , lim ( )
x x x x
f x f x
Lưu ý: Với đồ thị hàm phân thức dạng
ax b
y c ad bc
cx d
0; 0 luôn có tiệm cận ngang
là
a
y
c
và tiệm cận đứng
d
x
c
.
Câu 1. (Đề Minh Họa 2017) Cho hàm số
( )y f x
có
lim ( ) 1
x
f x
và
lim ( ) 1
x
f x
. Khẳng định nào
sau đây là khẳng định đúng?
A. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng
1x
và
1x
.
B. Đồ thị hàm số đã cho không có tiệm cận ngang.
C. Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
D. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng
1y
và
1y
.
Lời giải
Chọn D
Dựa vào định nghĩa đường tiệm cận ngang của đồ thị hàm số ta chọn đáp án D.
Câu 2. (Đề Tham Khảo 2020 Lần 2) Tiệm cận ngang của đồ thị hàm số
2
1
x
y
x
là
A.
2y
. B.
1y
. C.
1x
. D.
2x
.
Lời giải
Chọn B
Ta có
2
lim 1
1
x
x
x
và
2
lim 1
1
x
x
x
Suy ra
1y
là tiệm cận ngang của đồ thị hàm số.
Câu 3. (Mã 101 - 2020 Lần 1) Tiệm cận ngang của đồ thị hàm số
4 1
1
x
y
x
là
A.
1
4
y
. B.
4y
. C.
1y
. D.
1y
.
Lời giải
Chọn B.
Tiệm cận ngang
4
lim lim 4
1
x x
y y
TIỆM CẬN ĐỒ THỊ CỦA HÀM SỐ
Chuyên đề 6
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 4. (Mã 102 - 2020 Lần 1) Tiệm cận ngang của đồ thị hàm số
5 1
1
x
y
x
là
A.
1y
. B.
1
5
y
. C.
1
y
. D.
5
y
.
Lời giải
Chọn D
Ta có
5 1
lim lim 5
1
5 1
lim lim 5
1
x x
x x
x
y
x
x
y
x
5
y
là tiệm cận ngang của đồ thị hàm số.
Câu 5. (Mã 103 - 2020 Lần 1) Tiệm cận ngang của đồ thị hàm số
2 1
1
x
y
x
là:
A.
1
2
y
. B.
1
y
. C.
1y
. D.
2
y
.
Lời giải
Chọn D
Ta có
1
2
2 1
lim lim 2
1
1
1
x x
x
x
x
x
. Suy ra đồ thị hàm số có tiệmcận ngang là
2
y
.
Câu 6. (Mã 104 - 2020 Lần 1) Tiệm cận ngang của đồ thị hàm số
3 1
1
x
y
x
là:
A.
1
3
y
. B.
3
y
. C.
1
y
. D.
1y
.
Lời giải
Chọn B
Ta có :
3 1
lim lim 3
1
x x
x
y
x
và
3 1
lim lim 3
1
x x
x
y
x
nên
3
y
là tiệm cận ngang của đồ thị
hàm số.
Câu 7. (Mã 101 – 2020 Lần 2) Tiệm cận đứng của đồ thị hàm số
2 2
1
x
y
x
là
A.
2
x
. B.
2
x
. C.
1.
x
D.
1
x
.
Lời giải
Chọn C
Tập xác định
\ 1
D
.
Ta có
1 1
lim ; lim
x x
y y
, suy ra đồ thị có tiệm cận đứng là
1x
.
Câu 8. (Mã 102 - 2020 Lần 2) Tiệm cận đứng của đồ thị hàm số
1
3
x
y
x
là
A.
3
x
. B.
1
x
. C.
1x
. D.
3
x
.
Lời giải.
Chọn D
3
1
lim
3
x
x
x
. Suy ta tiệm cận đứng là đường thẳng
3
x
.
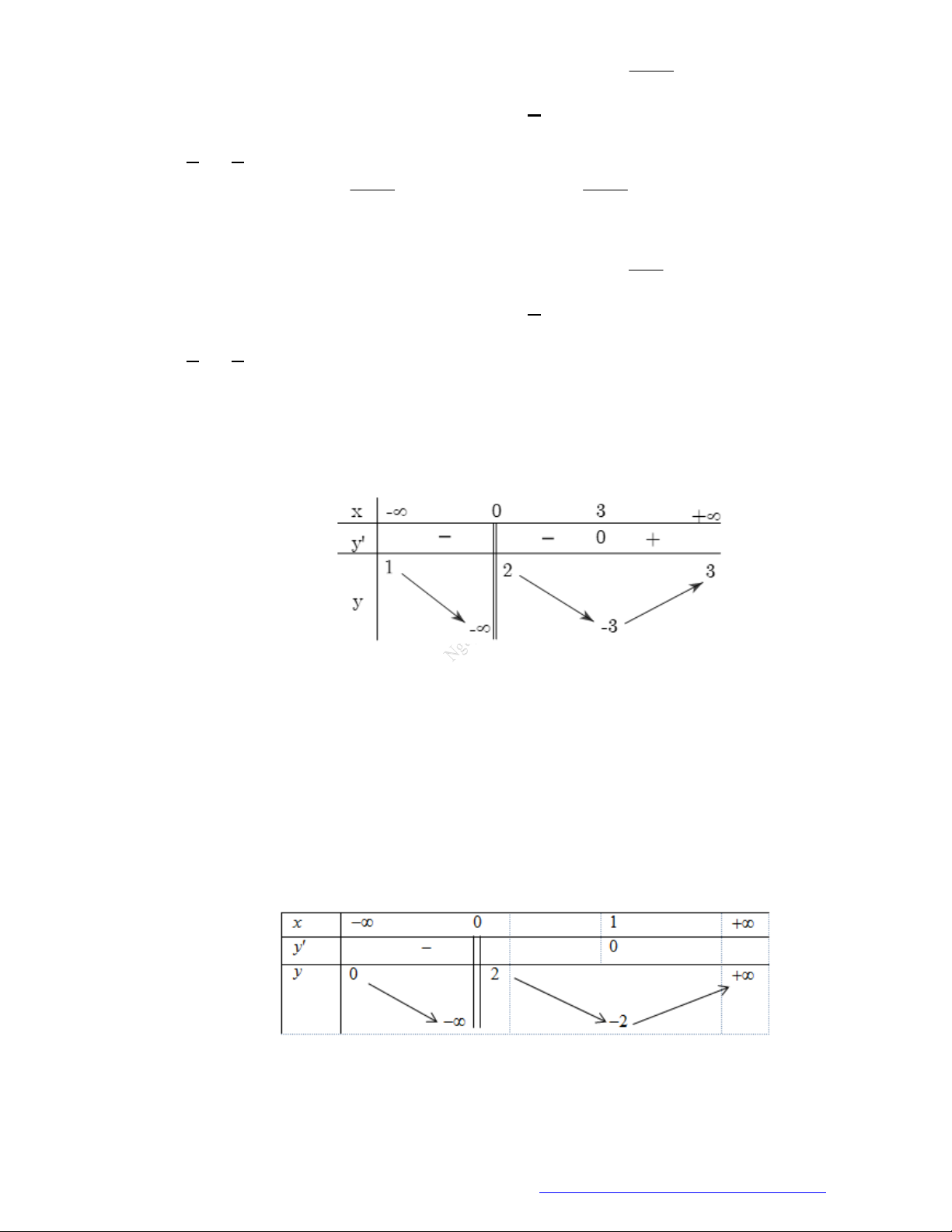
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Câu 9. (Mã 103 - 2020 Lần 2) Tiệm cận đứng của đồ thị hàm số
2 2
1
x
y
x
là
A.
2x
. B.
1x
. C.
1x
. D.
2x
.
Lời giải
Chọn C
Ta có
1 1
2 2
lim lim
1
x x
x
y
x
và
1 1
2 2
lim lim
1
x x
x
y
x
nên đường thẳng
1x
là
tiệm cận đứng của đồ thị hàm số.
Câu 10. (Mã 104 - 2020 Lần 2) Tiệm cận đứng của đồ thị hàm số
1
3
x
y
x
là
A.
1x
. B.
1x
. C.
3x
. D.
3x
.
Lời giải
Chọn C
Ta có
3
lim
x
y
và
3
lim
x
y
nên đồ thị hàm số nhận đường thẳng
3x
làm tiệm cận
đứng.
Câu 11. (Mã 103 - 2019) Cho hàm số
y f x
có báng biến thiên như sau:
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là:
A. 2. B. 3. C. 4. D. 1.
Lời giải
Chọn B
Nhìn bảng biến thiên ta thấy x=0 hàm số không xác định nên x=0 là TCĐ của đồ thị hàm số
lim 3 3
x
f x y
là TCN của đồ thị hàm số
lim 1 1
x
f x y
là TCN của đồ thị hàm số
Vậy hàm số có 3 tiệm cận
Câu 12. (Mã 102 - 2019) Cho hàm số
f x
có bảng biến thiên như sau
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
A.
1
. B.
2
. C.
4
. D.
3
.
Lời giải
Chọn B
Từ bảng biến thiên đã cho ta có :
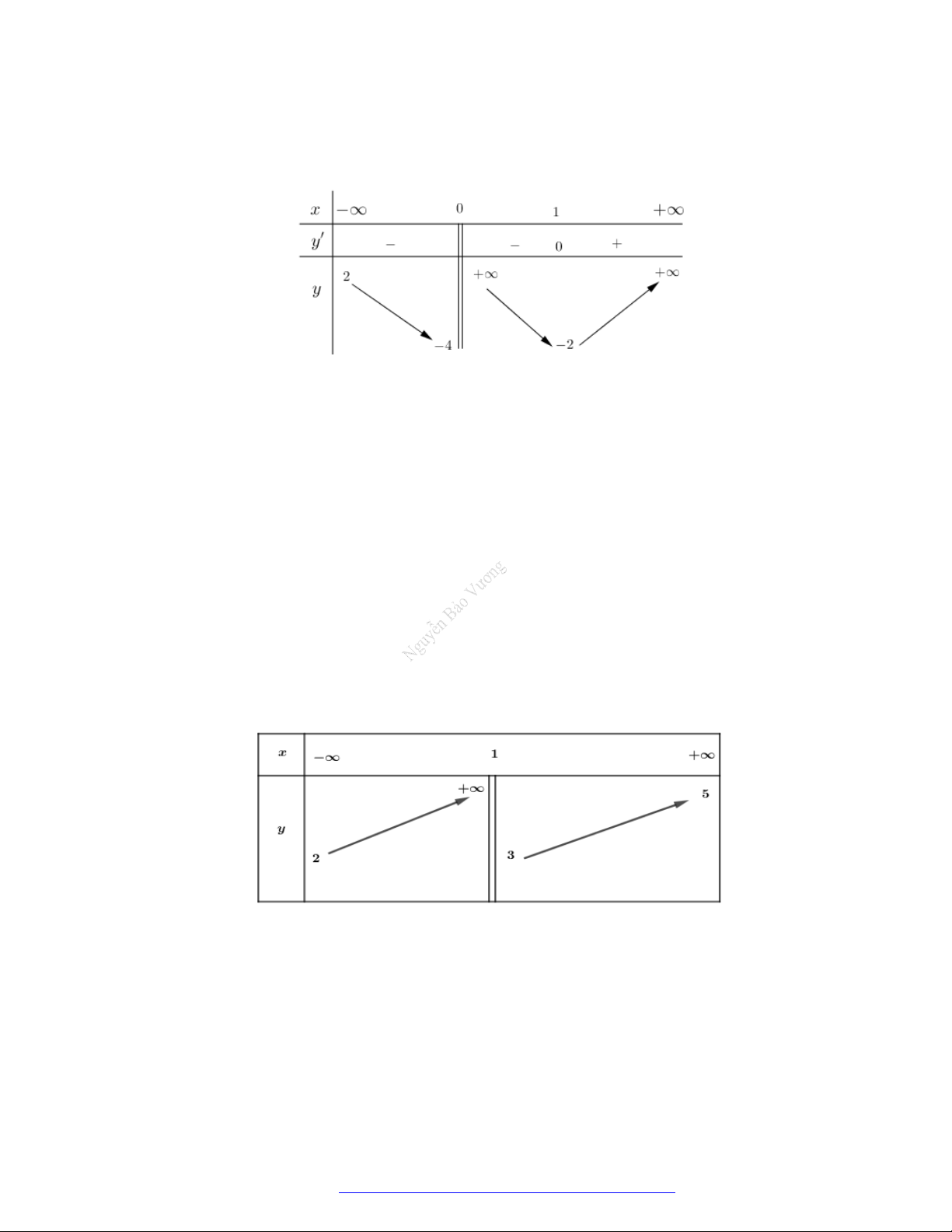
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
lim 0
x
f x
nên đường thẳng
0y
là một tiệm cận ngang của đồ thị hàm số.
0
lim
x
f x
nên đường thẳng
0x
là một tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số đã cho có hai đường tiệm cận.
Câu 13. (Mã 101 - 2019) Cho hàm số
y f x
có bảng biến thiên như sau:
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là:
A.
4
. B.
1
. C.
3
. D.
2
.
Lời giải
Chọn D
Hàm số
y f x
có tập xác định:
\ 0 .D
Ta có:
lim
x
f x
Không tồn tại tiệm cận ngang khi .x
lim 2
x
f x
vậy hàm số
y f x
có tiệm cận ngang
2.y
0
lim
x
f x
;
0
lim 4.
x
f x
Đồ thị hàm số
y f x
có tiệm cận đứng
0.x
Vậy tổng số tiệm cận đứng và ngang là 2.
Câu 14. (Đề Tham Khảo 2019) Cho hàm số
y f x
có bảng biến thiên như sau
Tổng số đường tiệm cận ngang và đường tiệm cận đứng của đồ thị hàm số đã cho là
A.
3
B.
2
C.
4
D.
1
Lời giải
Chọn A
Từ bảng biến thiên ta có:
1
lim
x
y
nên đường thẳng
1x
là đường tiệm cận đứng của đồ thị hàm số
lim 2, lim 5
x x
y y
nên đường thẳng
2y
và
5y
là các đường tiệm cận ngang của đồ thị
hàm số
Tổng số đường tiệm cận ngang và đường tiệm cận đứng của đồ thị hàm số đã cho là 3
Câu 15. (THPT - Yên Dịnh Thanh Hóa 2019) Cho hàm số có bảng biến thiên như hình sau
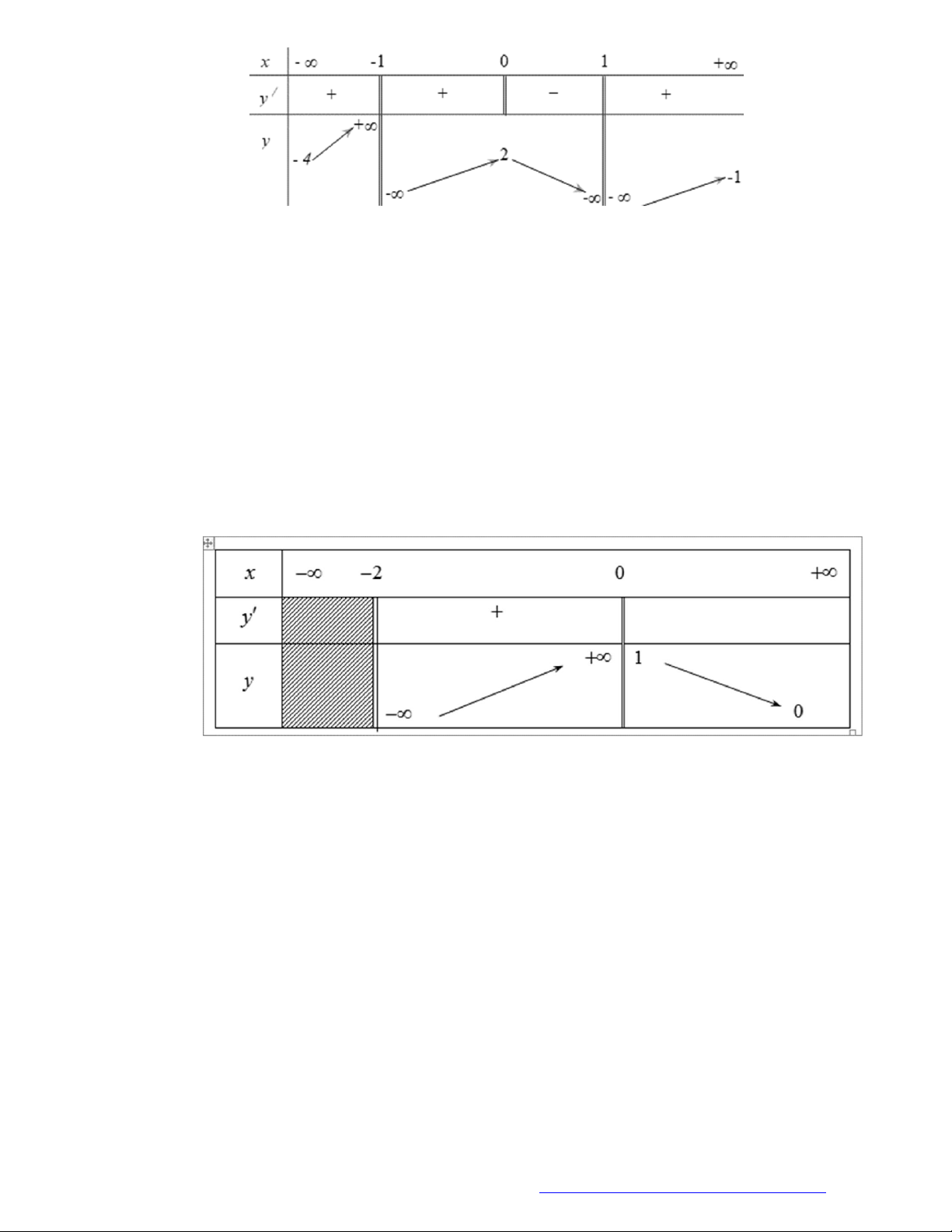
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
y f x
là
A.
3
. B.
2
. C.
4
. D.
1
.
Lời giải
Vì
lim 4, lim 1
x x
y y
Đồ thị hàm số có hai tiệm cận ngang là
1y
và
4y
.
1 1
lim , lim
x x
y y
Đồ thị hàm số có tiệm cận đứng
1x
.
1 1
lim , lim
x x
y y
Đồ thị hàm số có tiệm cận đứng
1x
.
Nên đồ thị hàm số có 4 đường tiệm cận.
Câu 16. (Đề Tham Khảo 2017) Cho hàm số
y f x
có bảng biến thiên như hình vẽ dưới đây. Hỏi đồ
thị của hàm số đã cho có bao nhiêu đường tiệm cận?
A.
3
B.
2
C.
4
D.
1
Lời giải
Chọn A
Dựa vào bảng biến thiên ta có :
2
lim
x
f x
, suy ra đường thẳng
2x
là tiệm cận đứng của đồ thị hàm số.
0
lim
x
f x
, suy ra đường thẳng
0x
là tiệm cận đứng của đồ thị hàm số.
lim 0
x
f x
, suy ra đường thẳng
0y
là tiệm cận ngang của đồ thị hàm số.
Vậy đồ thị hàm số có 3 đường tiệm cận.
Câu 17. (Mã 104 2019) Cho hàm số
y f x
có bảng biến thiên như sau:
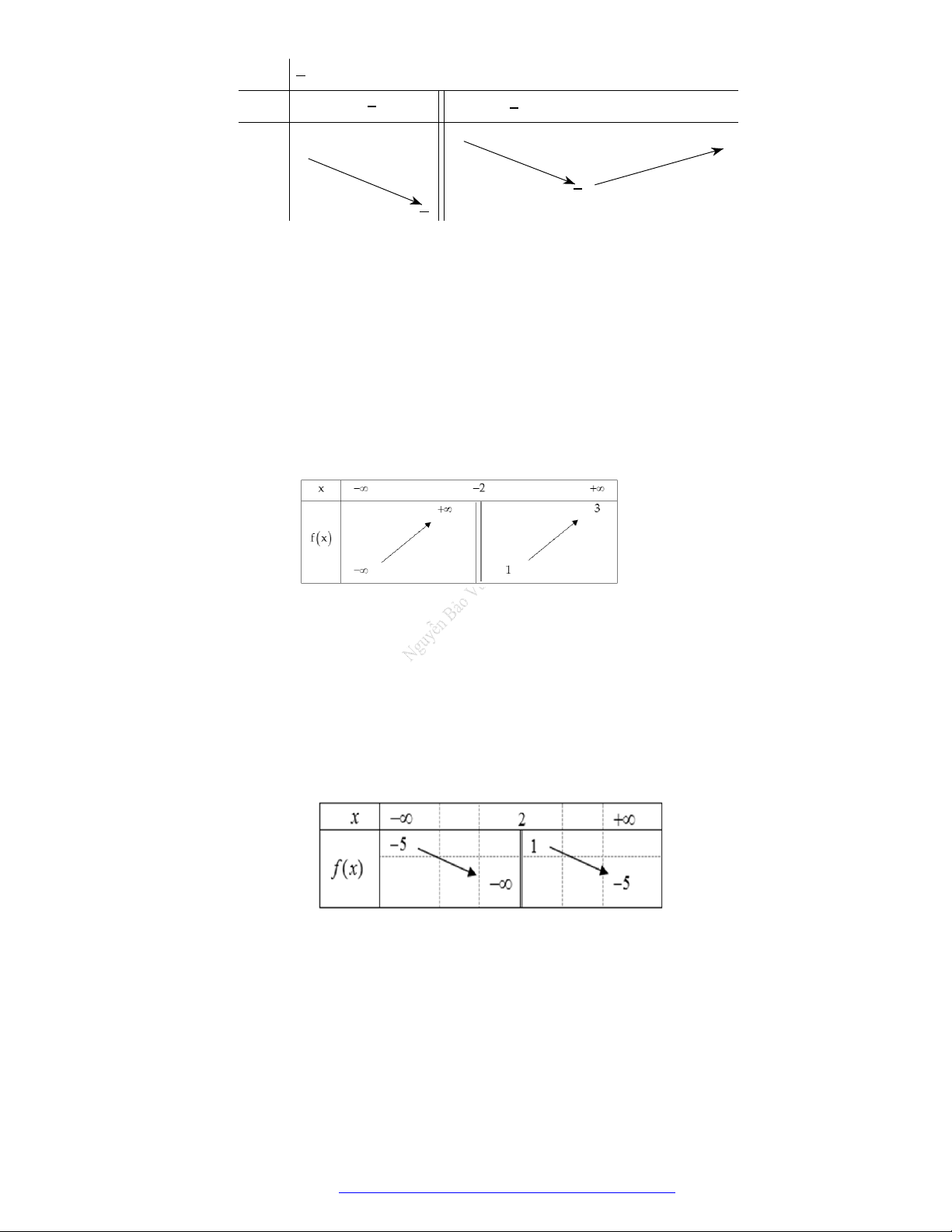
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
A. 1. B. 3. C. 4. D. 2.
Lời giải
Chọn B
Ta có
lim 3
x
f x
và
lim 0
x
f x
nên đồ thị hàm số có 2 tiệm cận ngang là các đường thẳng
có phương trình
3y
và
0.y
Và
0
lim
x
f x
nên hàm số có 1 tiệm cận đứng là đường thẳng có phương trình
0.x
Câu 18. (Chuyên Lê Quý Đôn Điện Biên 2019) Cho hàm số
f x
có bảng biến thiên như sau:
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là:
A.
4
. B.
3
. C.
1
. D.
2
.
Lời giải
lim 3
x
f x
ta được tiệm cận ngang
3y
2
lim
x
f x
ta được tiệm cận đứng
2 x
Câu 19. (Liên Trường Thpt Tp Vinh Nghệ An 2019) Cho hàm số
( )y f x
có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A.
4
B.
2
C.
3
D.
1
Lời giải
Từ bảng biến thiên ta có:
+ Tiệm cận ngang
5y
+ Tiệm cận đứng
2.x
Câu 20. (THPT Hùng Vương Bình Phước 2019) Cho đồ thị hàm số
y f x
như hình bên. Khẳng
định nào sau đây là đúng?
y'
+
∞
0
3
4
3
0
+
3
0
+
∞
∞
y
x
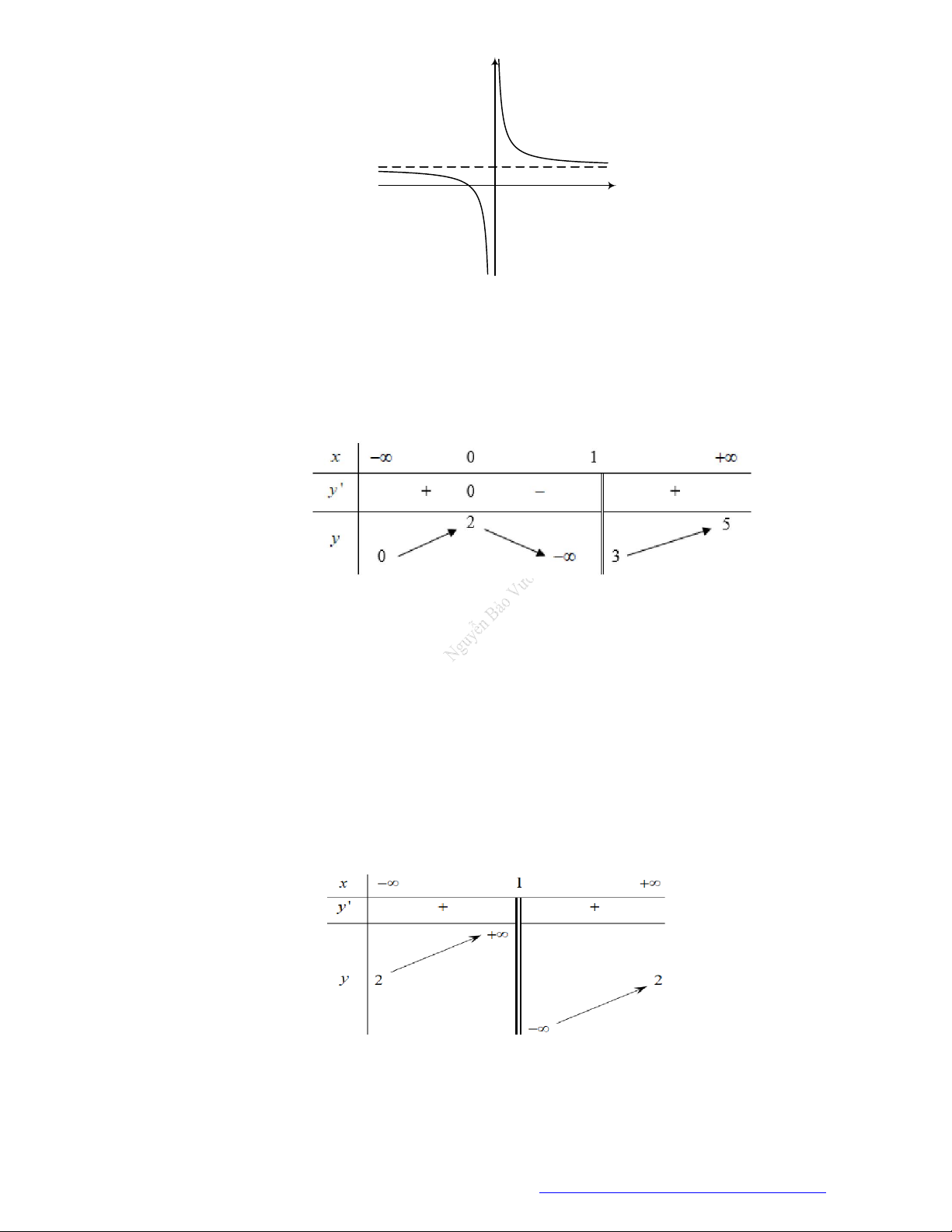
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
x
y
O
1
1
A. Đồ thị hàm số có tiệm cận đứng
0x
, tiệm cận ngang
1y
.
B. Hàm số có hai cực trị.
C. Đồ thị hàm số chỉ có một đường tiệm cận.
D. Hàm số đồng biến trong khoảng
;0
và
0;
.
Câu 21. Cho hàmsố
( )f x
có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A.
4
. B.
1
. C.
3
. D.
2
.
Lời giải
Dựa vào bảng biến thiên của hàm số ta có:
lim ( ) 0 0
x
f x y
là một tiệm cận ngang
lim ( ) 5 5
x
f x y
là một tiệm cận ngang
1
lim ( ) 1
x
f x x
là một tiệm cận đứng
Vậy đồ thị hàm số có tổng số đường tiệm cận là 3.
Câu 22. Cho hàm số
( )y f x
có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A.
4
. B.
1
. C.
3
. D.
2
.
Lời giải
Dựa vào bảng biến thiên của hàm số ta có:
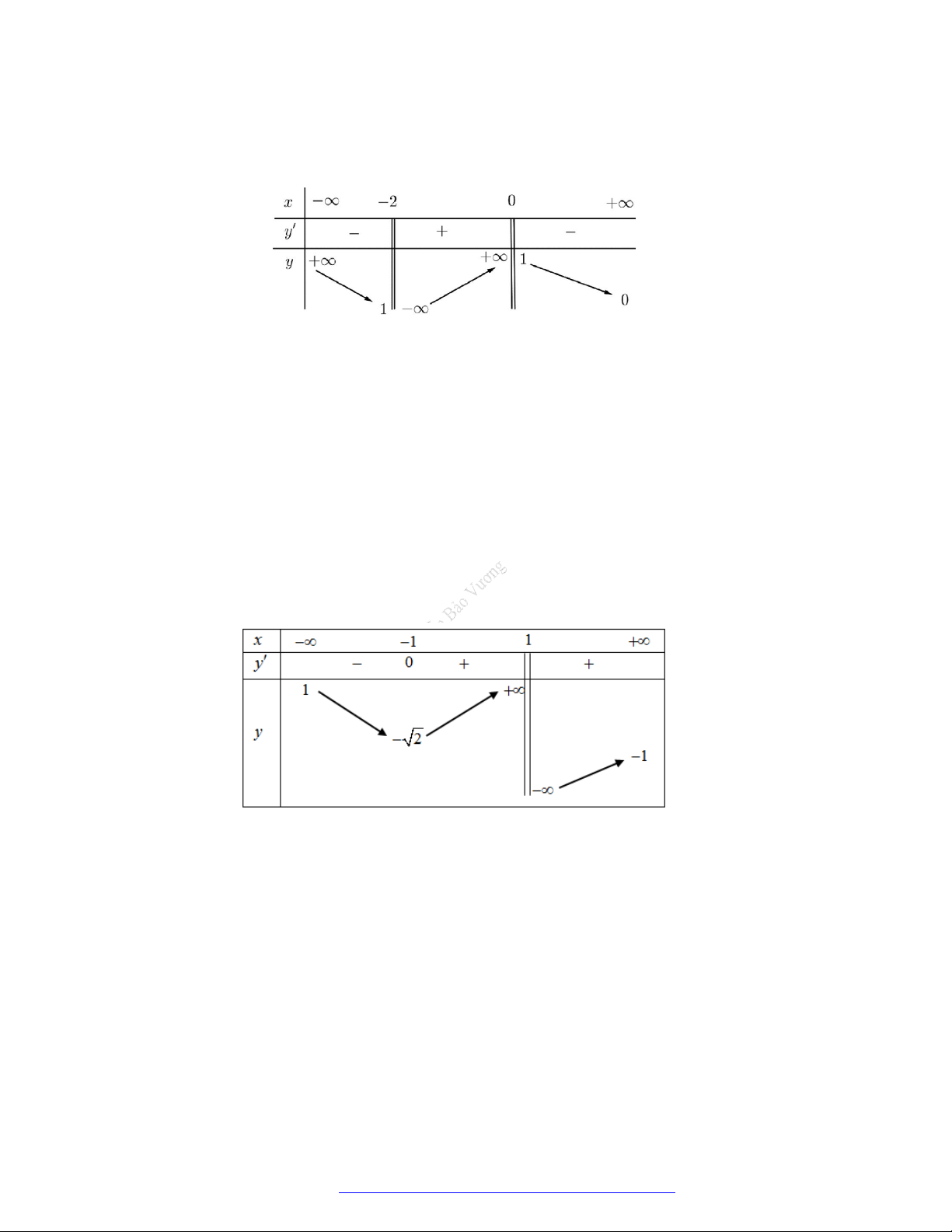
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
lim ( ) 2 2
x
f x y
là một tiệm cận ngang
1
lim ( ) 1
x
f x x
là một tiệm cận đứng
Vậy đồ thị hàm số có tổng số đường tiệm cận là
2
.
Câu 23. (Sở Hà Nội 2019) Cho hàm số
y f x
có bảng biến thiên như sau
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho bằng
A.
2
. B.
1
. C.
0
. D.
3
.
Lời giải
Ta có
2
lim 2
x
y x
là tiệm cận đứng của đồ thị hàm số đã cho.
0
lim 0
x
y x
là tiệm cận đứng của đồ thị hàm số đã cho.
lim 0 0
x
y y
là tiệm cận ngang của đồ thị hàm số đã cho.
Vậy đồ thị hàm số đã cho có tổng đường tiệm cận đứng và tiệm cận ngang là
3
.
Câu 24. Cho hàm số
y f x
liên tục trên
\ 1
có bảng biến thiên như hình vẽ. Tổng số đường tiệm
cận đứng và đường tiệm cận ngang của đồ thị hàm số
y f x
A.
1
. B.
4
. C.
2
. D.
3.
Lời giải
Chọn D
Do
1 1
lim ; lim
x x
y
TCĐ:
1.x
lim 1; lim 1
x x
y y
đồ thị có 2 tiệm cận ngang là
1y
Vậy, đồ thị hàm số đã cho có tổng số TCĐ và TCN là 3.
Câu 25. (Cụm liên trường Hải Phòng 2019) Cho hàm số
y f x
có bảng biến như sau:
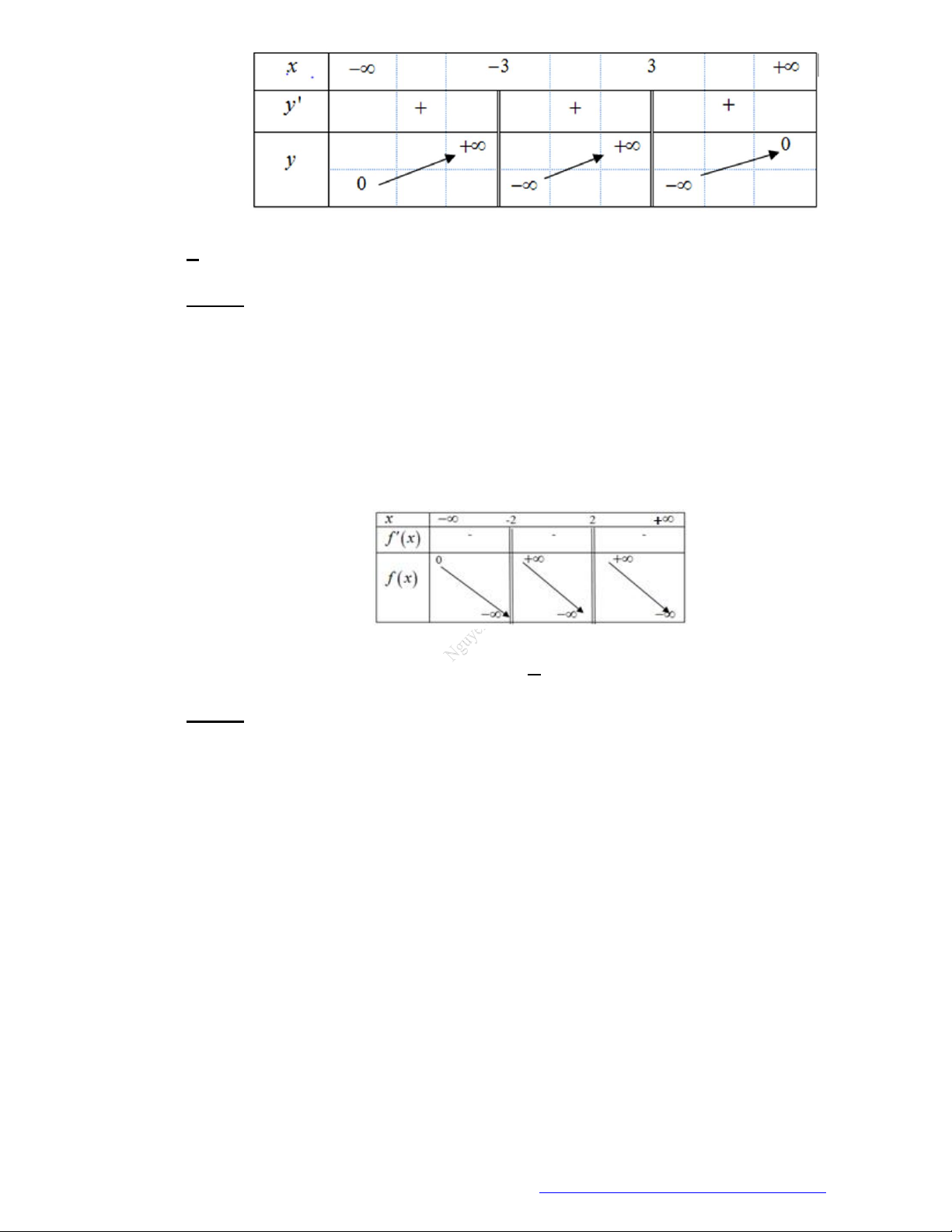
T
ÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Số
đường tiệm cận của đồ thị hàm số là:
A. 3
B. 1. C. 4. D. 2.
Lờ
i giải
Chọn A
Từ bảng biến thi
ên của hàm số ta có:
+
lim 0; lim 0
x
x
y y
đồ t
hị hàm số nhận đường thẳng
0y
l
à tiệm cận ngang.
+
3
3
l
im ; lim
x
x
y
đồ thị hàm số nhận đường thẳng
3x
là tiệm cận đứng.
+
3
3
l
im ; lim
x
x
y
đồ thị hà
m số nhận đường thẳng
3x
l
à tiệm cận đứng.
Vậy số đường tiệm cận của đồ thị hàm số là 3.
Câu 26. (Thi thử cụm Vũng Tàu 2019) Cho hàm số
y
f x
có
bảng biến thiên như sau
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
A.
4
. B.
2
. C.
3
. D.
1
.
Lờ
i giải
Chọn C
Ta có:
l
im ( ) 0
x
f
x
nên đường thẳng
0y
là đường tiệm cận ngang của đồ thị hàm số
y
f x
.
li
m ( )
x
f
x
nên
đồ thị hàm số
y
f x
khôn
g có tiệm cận ngang khi
x
.
2
lim ( )
x
f x
,
2
lim ( )
x
f x
nê
n đường thẳng
2x
là
đường tiệm cận đứng của đồ
thị hàm số
y
f x
.
2
li
m ( )
x
f
x
,
2
li
m ( )
x
f
x
nê
n đường thẳng
2x
l
à đường tiệm cận đứng của đồ
thị
hàm
số
y
f x
.
Vậ
y tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là 3 tiệm cận.
-------------------- HẾT --------------------

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 1
DẠNG TOÁN DÀNH CHO ĐỐI TƯỢNG HỌC SINH KHÁ – MỨC 7-8 ĐIỂM
Dạng 1. Xác định đường tiệm cận đồ thị hàm số thông hàm số cho trước
1 Đường tiệm cận ngang
Chohàmsố
y f x
cóTXD:
D
Điều kiện cần:
D
phảichứa
hoặc
Điều kiện đủ:
Dạng 1.
( )
( )
( )
P x
y f x
Q x
.
Nếu
:degP x degQ x
thìkhôngcótiệmcậnngang
Nếu
:degP x degQ x
TCN
0y
Nếu
:degP x degQ x
y k
(klàtỉsốhệsốbậccaonhấtcủatửvàmẫu)
Dạng 2:
( )y f x u v
(hoặc u v ):Nhânliênhợp
2
( )
u v
y f x
u v
(hoặc
u v
u v
)
2 Đường tiệm cận đứng
Chohàmsố
P x
y
Q x
cóTXD:
D
Đkiện cần:giải
0
0Q x x x
làTCĐkhithỏamãnđkđủ
Đkiện đủ:
Đkiện 1:
0
x làmcho
( )P x
và
( )Q x
xácđịnh.
Đkiện 2:-
0
x khôngphảinghiêm
0
( )P x x x làTCĐ
-
0
x lànghiêm
0
( )P x x x làTCĐnếu
0
lim ( )
x x
f x
Câu 1. (Đề Minh Họa 2020 Lần 1) Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
2
5 4 1
1
x x
y
x
là
A.
0.
B.
1.
C.
2.
D.
3.
Lời giải
Chọn C
Tiệm cận ngang:
Tacó:
2
2
2
2
2
2
2
2
4 1
4 1
5
5
5 4 1
lim lim lim lim 5
1
1
1
1
1
x x x x
x
x x
x
x
x
x
y
x
x
x
x
nênđồthịhàm
sốcómộttiệmcậnngang
5y
.
Tiệm cận đứng:
Cho
2
1
1
1
x
x
x
TIỆM CẬN ĐỒ THỊ CỦA HÀM SỐ
Chuyên đề 6

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Tacó:
2
2
1 1 1 1
5 1 1
5 4 1 5 1 6
lim lim lim lim 3
1 1 1 2
1
x x x x
x x
x x x
y
x x x
x
nên
1x
khônglàtiệm
cậnđứng.
2 2 2
2
1 1 1 1
5 4 1 5 4 1 1 5 4 1
lim lim lim lim .
1 1 1 1
1
x x x x
x x x x x x
y
x x x x
x
vì
1
2
1
1
lim
1
5 4 1
lim 4 0
1
x
x
x
x x
x
.
Khiđó,đồthịhàmsốcómộttiệmcậnđứng
1
x
.
Tổngcộngđồthịhàmsốcó2tiệmcận.
Câu 2. (ĐềThamKhảo2018)Đồthịcủahàmsốnàodướiđâycótiệmcậnđứng?
A.
2
3 2
1
x x
y
x
B.
2
2
1
x
y
x
C.
2
1
y x
D.
1
x
y
x
Lờigiải
ChọnD
Tacó
1 1
lim , lim
1 1
x x
x x
x x
nênđườngthẳng
1
x
làtiệmcậnđứngcủađồthịhàm
số.
Câu 3. (Mã 110 2017) Tìmsốtiệmcậncủađồthịhàmsố
2
2
5 4
1
x x
y
x
.
A.
2
B.
3
C.
0
D.
1
Lời giải
Chọn A
Tậpxácđịnh:
\ 1
D
Tacó:
2
2
2
2
5 4
1
5 4
lim lim lim 1
1
1
1
x x x
x x
x x
y
x
x
1y
làđườngtiệmcậnngang.
Mặckhác:
2
2
1 1
1 1
1 4 4
5 4 3
lim lim lim lim
1 1 1 1 2
x x
x x
x x x
x x
y
x x x x
1x
khônglàđườngtiệmcậnđứng.
2
2
1
1 1 1
1 4 4
5 4
lim lim lim lim
1 1 1 1
x
x x x
x x x
x x
y
x x x x
2
2
1 1 1 1
1 4 4
5 4
lim lim lim lim
1 1 1 1
x x x x
x x x
x x
y
x x x x
1
x
làđườngtiệmcậnđứng.
Vậyđồthịhàmsốcó2đườngtiệmcận
Câu 4. (Mã 123 2017) Tìmsốtiệmcậnđứngcủađồthịhàmsố:
2
2
3 4
16
x x
y
x
A.
2
B.
3
C.
1
D.
0
Lờigiải

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Chọn C
Tacó
2
2
3 4 1
4
16
x x x
y
x
x
(vớiđiềukiệnxácđịnh),dođóđồthịhàmcó1tiệmcậnđứng.
Câu 5. (Mã 104 2017) Đồthịhàmsố
2
2
4
x
y
x
cómấytiệmcận.
A.
3
B.
1
C.
2
D.
0
Lờigiải
Chọn C
Tacó
2
4 0 2
x x
2
2
2 1
lim
4 4
x
x
x
nênđườngthẳng
2
x
khôngphảilàtiệmcânđứngcủađồthịhàmsố.
2
2 2
2 1
lim lim ,
4 2
x x
x
x x
2
2 2
2 1
lim lim ,
4 2
x x
x
x x
nênđườngthẳng
2
x
là
tiệmcânđứngcủađồthịhàmsố.
2
2
lim 0
4
x
x
x
nênđườngthẳng
0
y
làtiệmcậnngangcủađồthịhàmsố.
Vậycóđồthịcóhaiđườngtiệmcận.
Câu 6. (Mã1012018)Sốtiệmcậnđứngcủađồthịhàmsố
2
9 3
x
y
x x
là
A.
1
B.
2
C.
0
D.
3
Lờigiải
Chọn A
Tậpxácđịnhcủahàmsố:
9; \ 0; 1
D
Tacó:
1
lim
x
y
2
1
9 3
lim
x
x
x x
và
1
lim
x
y
2
1
9 3
lim
x
x
x x
.
TCĐ:
1
x
.
0
lim
x
y
2
0
9 3
lim
x
x
x x
2
0
lim
9 3
x
x
x x x
0
1
lim
1 9 3
x
x x
1
6
.
0
lim
x
y
2
0
9 3
lim
x
x
x x
2
0
lim
9 3
x
x
x x x
0
1
lim
1 9 3
x
x x
1
6
.
0
x
khônglàđườngtiệmcậnđứngcủađồthịhàmsố.
Vậyđồthịhàmsốcó
1
tiệmcậnđứng.
Câu 7. (Mã 102 2018) Sốtiệmcậnđứngcủađồthịhàmsố
2
4 2
x
y
x x
là
A.
2
B.
1
C.
3
D.
0
Lời giải
Chọn B
Tậpxácđịnhcủahàmsố:
4; \ 0; 1
D
Tacó:
0
1
lim
4
x
y
.
2
1 1
4 2
lim lim
x x
x
y
x x
và
2
1 1
4 2
lim lim
x x
x
y
x x

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
TCĐ:
1
x
.
Vậyđồthịhàmsốcó
1
tiệmcậnđứng.
Câu 8. (THPT Lê Văn Thịnh Bắc Ninh 2019) Đồthịhàmsố
2
5 1 1
2
x x
y
x x
cótấtcảbaonhiêu
đườngtiệmcận?
A.
3
B.
0
C.
2
D.
1
Lời giải
Chọn D
Tậpxácđịnh:
1; \ 0
D
.
lim
x
y
2
5 1 1
lim
2
x
x x
x x
2 3 4
5 1 1 1
lim
2
1
x
x
x x x
x
0
0
y
là đường tiệm cận ngang
củađồthịhàmsố.
0
lim
x
y
2
0
5 1 1
lim
2
x
x x
x x
2
2
0
5 1 1
lim
2 5 1 1
x
x x
x x x x
2
2
0
25 9
lim
2 5 1 1
x
x x
x x x x
0
25 9
lim
2 5 1 1
x
x
x x x
9
4
0
x
không làđườngtiệmcậnđứngcủađồthịhàmsố.
Vậyđồthịhàmsốcótấtcả
1
đườngtiệmcận.
Câu 9. Tìmtấtcảcáctiệmcậnđứngcủađồthịhàmsố
2
2
2 1 3
5 6
x x x
y
x x
.
A.
3
x
và
2
x
. B.
3
x
. C.
3
x
và
2
x
. D.
3
x
.
Lời giải
Chọn B
Tậpxácđịnh
2;3
\
D
2
2
2
2
2 2
2 2
2
2
2 2
2
2 1 3
2 1 3
lim lim
5 6
5 6 2 1 3
2 1 3
lim
5 6 2 1 3
x x
x
x x x
x x x
x x
x x x x x
x x x
x x x x x
2
2
(3 1) 7
lim
6
3 2 1 3
x
x
x x x x
Tươngtự
2
2
2
2 1 3 7
lim
5 6 6
x
x x x
x x
.Suyrađườngthẳng
2
x
khônglàtiệmcậnđứngcủa
đồthịhàmsốđãcho.
2 2
2 2
3 3
2 1 3 2 1 3
lim ; lim
5 6 5 6
x x
x x x x x x
x x x x
.Suyrađườngthẳng
3
x
làtiệmcận
đứngcủađồthịhàmsốđãcho.
Câu 10. (Mã 103 2018) Sốtiệmcậnđứngcủađồthịhàmsố
2
25 5
x
y
x x
là

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
A.
3
B.
2
C.
0
D.
1
Lời giải
Chọn D
Tậpxácđịnh
25; \ 1;0
D
.Biếnđổi
1
( ) .
1 25 5
f x
x x
Vì
1 1
1
lim lim
1 25 5
x x
y
x x
nênđồthịhàmsốđãchocó1tiệmcậnđứng
1
x
.
Câu 11. (Mã 104 2018) Sốtiệmcậnđứngcủađồthịhàmsố
2
16 4
x
y
x x
là
A.
3
B.
2
C.
1
D.
0
Lời giải
Chọn C
Tậpxácđịnhhàmsố
16; \ 1;0
D
.
Tacó
0 0 0 0
16 4 1 1
lim lim lim lim
1 8
1 16 4 1 16 4
x x x x
x x
y
x x
x x x x x
.
1 1 1
16 4 1
lim lim lim
1
1 16 4
x x x
x
y
x x
x x
.
vì
1
lim 16 4 15 4 0
x
x
,
1
lim 1 0
x
x
và
1
x
thì
1 1 0
x x
.
Tươngtự
1 1
1
lim lim
1 16 4
x x
y
x x
.
Vậyđồthịhàmsốđãchocótiệmcậnđứnglà
1
x
.
Câu 12. (Chuyên Sơn La 2019) Sốtiệmcậnđứngcủađồthịhàmsố
2
4 2
x
y
x x
là
A.
3
. B.
0
. C.
1
. D.
2
.
Lời giải
TXĐ:
4; \ 1;0
D
.
Tacó:
2
1 1
4 2
lim lim
x x
x
y
x x
Nênđườngthẳng
1
x
làmộtđườngtiệmcậnđứngcủađồthịhàmsốđãcho.
2
0 0 0 0
4 2 4 2
4 2 1 1
lim lim lim lim
4
1 4 2 1 4 2
x x x x
x x
x
y
x x
x x x x x
Nênđườngthẳng
0
x
khônglàtiệmcậnđứngcủađồthịhàmsốđãcho.
Vậyđồthịhàmsốđãchocómộttiệmcậnđứng
1
x
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 13. (THPT Gang Thép Thái Nguyên 2019) Đồthịhàmsố
2
1
1
x
f x
x
cótấtcảbaonhiêutiệm
cậnđứngvàtiệmcậnngang?
A.
4
. B.
3
. C.
1
. D.
2
.
Lờigiải
Tậpxácđịnhcủahàmsố
; 1 1;D
TH1:
1 1 0
x x
.Khiđó
2
2
1
1 1
1
1 1
1
x
x x
f x
x
x x
x
.
SuyrahàmsốTCN
1
y
,khôngcóTCĐ.
TH2:
1 1 0
x x
.Khiđó
2
2
1
1 1
1
1 1
1
x
x x
f x
x
x x
x
.
SuyrahàmsốTCN
1y
,TCĐ
1
x
.
Vậyhàmsốcó2TCNvà1TCN
Câu 14. Tổngsốtiệmcậnđứngvàtiệmcậnngangcủađồthịhàmsố
4 6 2
2
x x
y
x
là?
A.
1
B.
3
C.
2
D.
4
Lời giải
Chọn C
6 2
4
4 6 2
lim lim 2
2
2
1
x x
x x
x x
x
x
6 2
4
4 6 2
lim lim 2
2
2
1
x x
x x
x x
x
x
2 2 2
4 6 2
2 4 2
4 2 5
lim lim lim
2 2
4 6 2
2 4 6 2
x x x
x x
x x
x
x
x x
x x x
Vậyhàmsốcóhaitiệmcậnngang
2
y
.
Câu 15. (THPT Bạch Đằng Quảng Ninh 2019) Chohàmsố
2
4 2
2 3
3 2
x x
y
x x
.Đồthịhàmsốđãchocó
baonhiêuđườngtiệmcận?
A.
4
. B.
5
. C.
3
. D.
6
.
Lời giải
Điềukiện:
; 2 1;1 2;x
.
Do
lim lim
x x
y y
2
4 2
2 3
lim
3 2
x
x x
x x
2
2 4
2 3
1
lim 1
3 2
1
x
x x
x x
1y
làđườngtiệmcậnngang
củađồthịhàmsố.
Có
1
lim
x
y
nênđườngthẳng
1x
làđườngtiệmcậnđứng.
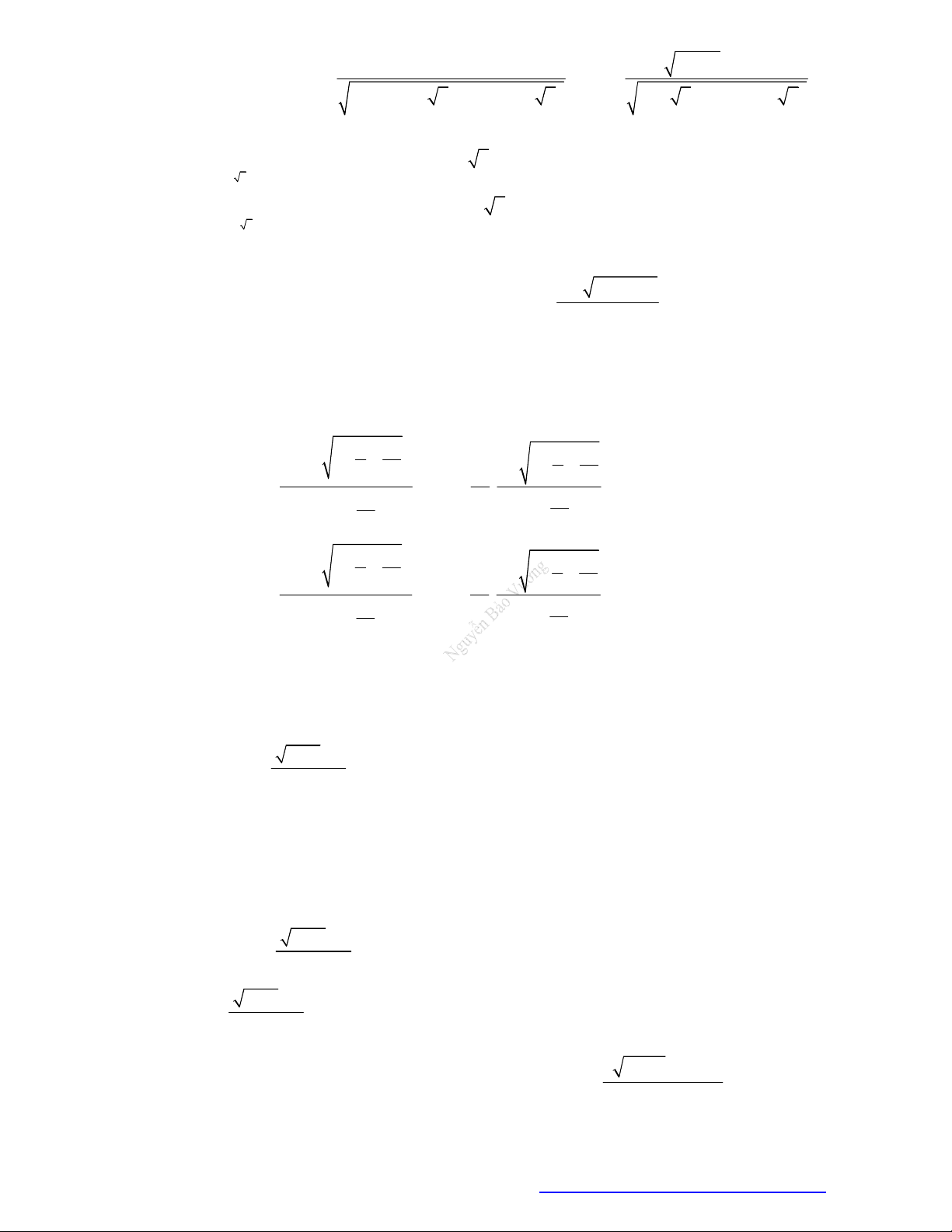
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Có
1 1 1
1 2
1 2
lim lim lim 0
1 2 1 2 2 1 2
x x x
x x
x x
y
x x x x x x x
nên
đườngthẳng
1
x
khônglàđườngtiệmcậnđứng.
Có
2
lim
x
y
nênđườngthẳng
2
x
làđườngtiệmcậnđứng.
Có
2
lim
x
y
nênđườngthẳng
2
x
làđườngtiệmcậnđứng.
Vậyđồthịhàmsốcó
4
đườngtiệmcận(
1
tiệmcậnngang,
3
tiệmcậnđứng).
Câu 16. (THPT Lê Quy Đôn Điện Biên 2019) Hàmsố
2
3
1x x x
y
x x
cóbaonhiêuđườngtiệmcận?
A.
1
B.
3
C.
2
D.
4
Lời giải
Chọn C
TXĐ:
\ 0
D
2
2
2
3
2
2
1 1
1 1
1 1
1 1
1
lim lim lim . 0
1
1
1
1
x x x
x
x x
x x
y
x
x
x
x
2
2
2
3
2
2
1 1
1 1
1 1
1 1
1
lim lim lim . 0
1
1
1
1
x x x
x
x x
x x
y
x
x
x
x
TCN:
0
y
0
lim
x
y
TCĐ:
0
x
.
Câu 17. (Chuyên Lam Sơn Thanh Hóa 2019) Sốđườngtiệmcậnđứngvàtiệmcậnngangcủađồthị
hàmsố
2
2 1
3 2
x
y
x x
là
A.
4
B.
1
C.
3
D.
2
Lời giải
Chọn D
Đkxđ:
2
2 0
2
2
2, 1
3 2 0
x
x
x
x x
x x
Tacó:
2
2
2 1
lim
3 2
x
x
x x
nênđườngthẳng
2
x
làtiệmcậnđứngcủađồthịhàmsố.
2
2 1
lim 0
3 2
x
x
x x
nênđườngthẳng
0
y
làtiệmcậnngangcủađồthịhàmsố.
Câu 18. (THPT Thiệu Hóa – Thanh Hóa 2019) Chohàmsố
2
3
5 6 12
4 3 1
x x
y
x x
cóđồthị
C
.Mệnh
đềnàosauđâylàđúng?
A. Đồthị
C
củahàmsốkhôngcótiệmcận.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
B. Đồthị
C
củahàmsốchỉcómộttiệmcậnngang
0
y
.
C. Đồthị
C
củahàmsốcómộttiệmcậnngang
0
y
vàhaitiệmcậnđứng
1
1;
2
x x
.
D. Đồthị
C
củahàmsốchỉcómộttiệmcậnngang
0
y
vàmộttiệncậnđứng
1x
Lời giải
Chọn D
TXĐ:
1
\ 1;
2
D R
Tacó:
1 1
lim ; lim
x x
y y
ĐồthịhàmsốcómộtTCĐlà
1x
lim 0
x
y
ĐồthịhàmsốcómộtTCNlà
0y
Câu 19. (Chuyên Lê Quý Đôn Quảng Trị 2019) Đồthịhàmsố
2
2
3 1
x x x
y
x
cótấtcảbaonhiêu
đườngtiệmcận?
A.
2
. B.
3
. C.
0
. D.
1
.
Lời giải
Chọn A
Xéthàmsố
2
2
3 1
x x x
y
x
cótậpxácđịnh
1
;0 1; \
3
D
.
Tacó
2
1
3
2
lim
3 1
x
x x x
x
2
1
2
3
3
lim
3 1 2
x
x x
x x x x
1
2
3
lim
2
x
x
x x x
1
4
;
2
0
2
lim 0
3 1
x
x x x
x
và
2
1
2 1
lim
3 1 2
x
x x x
x
nênđồthịkhôngcótiệmcậnđứng.
2
1 1
3 3
1 1
2 1 2 1
2 1
lim lim lim
1
3 1 3 1 3
3
x
x x
x x
x x x
x x
x x
x
,
và
2
1 1
3 3
1 1
2 1 2 1
2
lim lim lim 1
1
3 1 3 1
3
x
x x
x x
x x x
x x
x x
x
nênđồthịcóhaitiệmcậnnganglà
1
3
y
và
1y
.
Vậyđồthịhàmsốcótấtcảhaiđườngtiệmcận.
Câu 20. Đồthịhàmsố
2
2
1 4
2 3
x
y
x x
cósốđườngtiệmcậnđứnglà
m
vàsốđườngtiệmcậnnganglà
n
.Giátrịcủa
m n
là
A.
1
B.
2
C.
3
D.
0
Lời giải
Chọn A
2;2 \ 1
D
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
2
2
1 1
1 4
lim lim ;
2 3
x x
x
y
x x
2
2
1 1
1 4
lim lim
2 3
x x
x
y
x x
1
x
làtiệmcậnđứng.
Đồthịhàmsốkhôngcóđườngtiệmcậnngang.
Vậy
1
m n
.
Câu 21. Gọi
,n d
lần lượt là số đường tiệm cận ngang và số tiệm cận đứng của đồ thị hàm số
1
1
x
y
x x
.Khẳngđịnhnàosauđâylàđúng?
A.
0, 2
n d
. B.
1
n d
. C.
1, 2
n d
. D.
0, 1
n d
.
Lời giải
Chọn A
Tậpxácđịnh:
0;1
D
.
Từtậpxácđịnhsuyrađồthịhàmsốkhôngcótiệmcậnngang.
0
n
.
+)
0 0 0
1 1
lim lim lim
1 1
x x x
x
y
x x x x
+)
1 1 1
1 1
lim lim lim
1 1
x x x
x
y
x x x x
Suyrađồthịhàmsốcóhaitiệmcậnđứng,
2
d
.
Câu 22. (Chuyên Long An-2019) Đồthịhàmsố
2
5 1 1
2
x x
y
x x
cótấtcảbaonhiêuđườngtiệmcận?
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn C
Tậpxácđịnhcủahàmsốlà
1;0 2;D
.Tacó
2
2
0 0 0
25 9 25 9 9
lim lim lim
4
2 5 1 1 2 5 1 1
x x x
x x x
y
x x x x x x x
.
2
lim
x
y
.
2 3 4
5 1 1 1
lim lim 0
2
1
x x
x x x x
y
x
.
Vậyđồthịcủahàmsốcóhaiđườngtiệmcậncóphươngtrình
2
x
và
0
y
.
Câu 23. (Chuyên Vĩnh Phúc 2019) Tìmsốđườngtiệmcậncủađồthịhàmsố
1
4 3 1 3 5
x
y
x x
.
A.
2
. B.
3
. C.
1
. D.
0
.
Lời giải
Chọn A

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Tậpxácđịnh:
1
; \ 1
3
D
+Tacó:
2
1 1 1
1 4 3 1 3 5
1 4 3 1 3 5
lim lim lim
9 1
4 3 1 3 5
9 1
x x x
x x x
x x x
x
x x
x
dođóđườngthẳng
1x
làđườngtiệmcậnđứngcủađồthịhàmsố.
+
2
1
1
1 1
lim lim
3
4 3 1 3 5 3 1 5
4 3
x x
x
x
x x
x x x
dođóđườngthẳng
1
3
y
làđường
tiệmcậnngangcủađồthịhàmsố.Vậyđồthịhàmsốcó2đườngtiệmcận.
Câu 24. Chohàmsố
2
4 2
2 3
3 2
x x
y
x x
.Đồthịhàmsốđãchocóbaonhiêuđườngtiệmcận?
A.
4
. B.
5
. C.
3
. D.
6
.
Lời giải
Chọn B
□Tậpxácđịnh
; 2 1;1 2;D
.
□
1 1
2 2
lim lim lim lim
x x
x x
y y y y
.
Cácđườngtiệmcậnđứngcủađồthịlà
2
x
,
1
x
.
□
lim lim 1
x x
y y
đồthịcómộttiệmcậnngang
1y
.
Câu 25. (Chuyên Lê Quý Đôn Điện Biên 2019) Đồthịhàmsố
2
5 8
3
x
y
x x
cóbaonhiêuđườngtiệm
cận?
A. 2. B. 4. C. 1. D. 3.
Lời giải
Chọn B
Tậpxácđịnh
;0 3;D
2
8
5
5 8 5 8
lim lim lim lim 5
3 3
3
1 1
x x x x
x x
x
y
x x
x
x x
Đườngthẳng
5
y
làtiệmcậnngangcủađồthịhàmsố.
2
8
5
5 8 5 8
lim lim lim lim 5
3 3
3
1 1
x x x x
x x
x
y
x x
x
x x
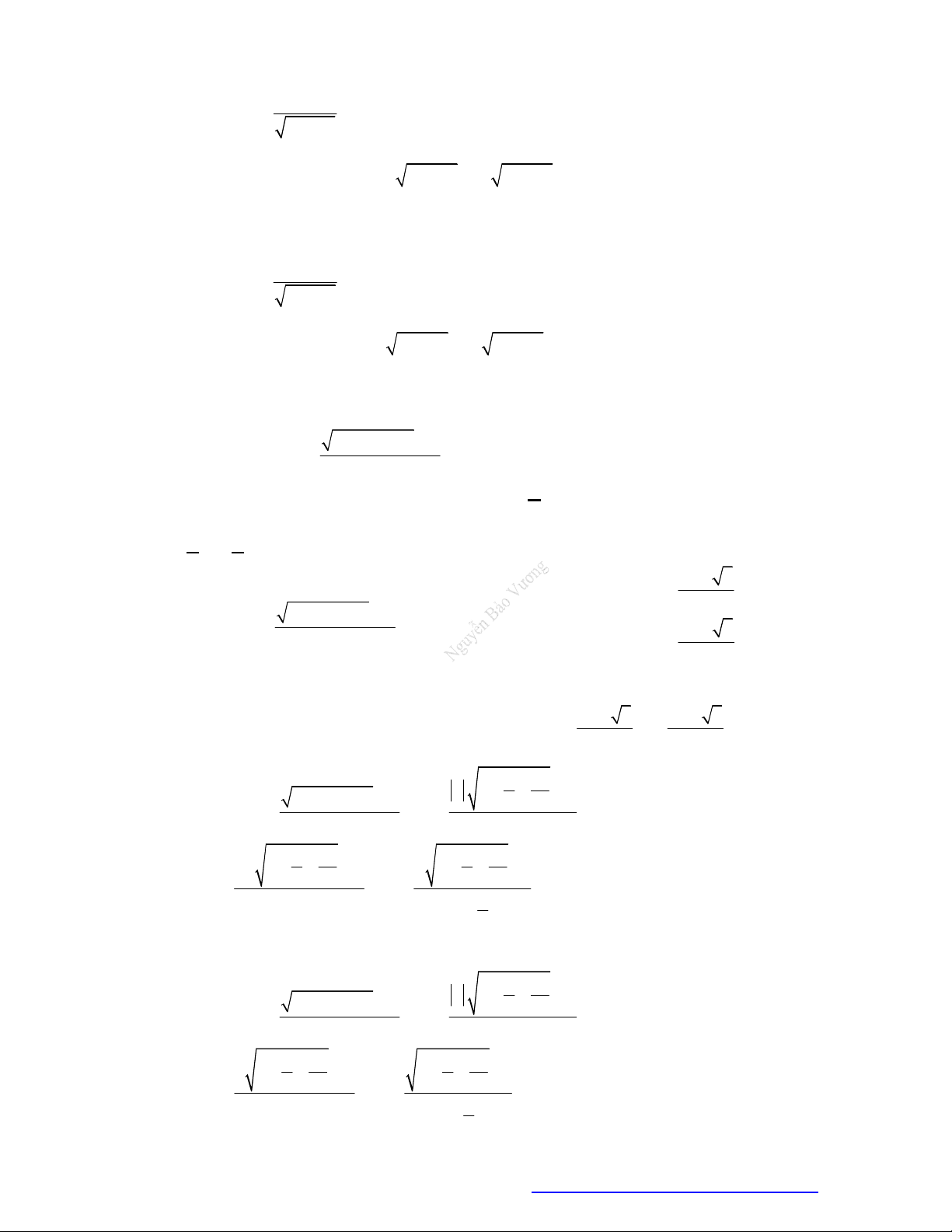
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Đườngthẳng
5
y
làtiệmcậnngangcủađồthịhàmsố.
2
0 0
5 8
lim lim
3
x x
x
y
x x
(vì
2 2
0 0
lim(5 8) 8 0; lim 3 0; 3 0 0 )
x x
x x x x x x
Suyra:đườngthẳng
0
x
làtiệmcậnđứngcủađồthịhàmsố.
2
3 3
5 8
lim lim
3
x x
x
y
x x
(vì
2 2
3 3
lim(5 8) 7 0; lim 3 0; 3 0 3 )
x x
x x x x x x
Suyra:đườngthẳng
3
x
làtiệmcậnđứngcủađồthịhàmsố.
Câu 26. Đồthịhàmsố
2
4 2 1
1
x x x
y
x
cóbaonhiêuđườngtiệmcận?
A.
1
. B.
0
. C.
2
. D.
3
.
Lời giải
Chọn C
Hàmsố
2
4 2 1
1
x x x
y
x
xácđịnh
2
1 5
4
4 2 1 0
1 5
1 0
4
1
x
x x
x
x
x
.
Tậpxácđịnhcủahàmsốđãcholà
1 5 1 5
; 1 1; ;
4 4
D
.
2
2
2 1
4
4 2 1
lim lim lim
1 1
x x x
x x
x x x
x x
y
x x
2 2
2 1 2 1
4 4 1
lim lim 1
1
1
1
x x
x x
x x x x
x
x
.
1
y
làđườngtiệmcậnngangcủađồthịhàmsốkhi
x
.
2
2
2 1
4
4 2 1
lim lim lim
1 1
x x x
x x
x x x
x x
y
x x
2 2
2 1 2 1
4 4 1
lim lim 3
1
1
1
x x
x x
x x x x
x
x
.
3
y
làđườngtiệmcậnngangcủađồthịhàmsốkhi
x
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2 2 2
1 1 1 1
2 2
1 3 1
4 2 1 4 2 1
lim lim lim lim 2.
1
1 4 2 1 1 4 2 1
x x x x
x x
x x x x x x
y
x
x x x x x x x x
Vậyđồthịhàmsố
2
4 2 1
1
x x x
y
x
có
2
đườngtiệmcận.
Dạng 2. Định m để đồ thị hàm số có đường tiệm cận thỏa mãn điều kiện cho trước
1 Đường tiệm cận ngang
Chohàmsố
y f x
cóTXD:
D
Điều kiện cần:
D
phảichứa
hoặc
Điều kiện đủ:
Dạng 1.
( )
( )
( )
P x
y f x
Q x
.
Nếu
:degP x degQ x
thìkhôngcótiệmcậnngang
Nếu
:degP x degQ x
TCN
0
y
Nếu
:degP x degQ x
y k
(klàtỉsốhệsốbậccaonhấtcủatửvàmẫu)
Dạng 2:
( )
y f x u v
(hoặc
u v
):Nhânliênhợp
2
( )
u v
y f x
u v
(hoặc
u v
u v
)
2 Đường tiệm cận đứng
Chohàmsố
P x
y
Q x
cóTXD:
D
Đkiện cần:giải
0
0
Q x x x
làTCĐkhithỏamãnđkđủ
Đkiện đủ:
Đkiện 1:
0
x
làmcho
( )P x
và
( )Q x
xácđịnh.
Đkiện 2:-
0
x
khôngphảinghiêm
0
( )
P x x x
làTCĐ
-
0
x
lànghiêm
0
( )
P x x x
làTCĐnếu
0
lim ( )
x x
f x
Câu 1. (Đề Minh Họa 2017) Tìm tất cả các giá trị thực của tham số
m
sao cho đồ thị của hàm số
2
1
1
x
y
mx
cóhaitiệmcậnngang
A.
0
m
B.
0
m
C.
0
m
D. Khôngcógiátrịthựcnàocủa
m
thỏamãnyêucầuđềbài
Lời giải
Chọn C
Xétcáctrườnghơpsau:
Với
0
m
:hàmsốtrởthành
1y x
nênkhôngcótiệmcậnngang.
Với
0
m
:

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
hàmsố
2 2
1 1
1 1
x x
y
mx m x
cótậpxácđịnhlà
1 1
;D
m m
suyrakhôngtồntại
giớihạn
lim
x
y
hayhàmsốkhôngcótiệmcậnngang.
Với
0
m
:
Tacó:
2
2 2 2
1
1
1 1 1 1
lim lim lim lim lim .
1 1 1
1
x x x x x
x x x
x
y
m
mx
x m x m m
x x x
và
2
2 2 2
1
1
1 1 1 1
lim lim lim lim lim .
1 1 1
1
x x x x x
x x x
x
y
m
mx
x m x m m
x x x
Vậyhàmsốcóhaitiệmcậnnganglà:
1 1
;y y
m m
khi
0
m
.
Câu 2. (Chuyên KHTN - 2020) Gọi
S
là tập hợp các giá trị nguyên
m
để đồ thị hàm số
2
2
6 2
x
y
x x m
cóhaiđườngtiệmcậnđứng.Sốphầntửcủa
S
là
A. vôsố. B.
12
. C.
14
. D.
13
.
Lời giải
Chọn B
Điềukiệnxácđịnh
2
2 0
6 2 0
x
x x m
.
Đểđồthịhàmsốcóhaiđườngtiệmcậnđứngthìphươngtrình
2
6 2 0
x x m
cóhainghiệm
phânbiệt
1 2
,x x
lớnhơn
2
1 2
2
9
9 2 0
9
2
2 3 2
2
8
4 12 2 0
2 6 2 2 0
m
m
m
x x
m
m
m
.
Dođótập
7; 6; 5;...;4
S
có
12
giátrị.
Câu 3. (Chuyên Phan Bội Châu - Nghệ An - 2020) Cóbaonhiêugiátrịnguyêndươngcủathamsố
m
đểđồthịhàmsố
2
1
8
x
y
x x m
có3đườngtiệmcận?
A.
14
. B.
8
. C.
15
. D.
16
.
Lời giải
Chọn A
Tacó
2 2
1 1
lim lim 0
8 8
x x
x x
x x m x x m
nênhàmsốcómộttiệncậnngang
0
y
.
Hàmsốcó3đườngtiệmcậnkhivàchỉkhihàmsốcóhaiđườngtiệmcậnđứng
phươngtrình
2
8 0
x x m
cóhainghiệmphânbiệtkhác
1
Δ 16 0 16
7 0 7
m m
m m
.
Kếthợpvớiđiềukiện
m
nguyêndươngtacó
1;2;3;...;6;8;...;15
m
.Vậycó
14
giátrịcủa
m
thỏamãnđềbài.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 4. (THPT Nguyễn Viết Xuân - 2020) Chohàmsố
3 2 2
3
3 2 1
x
y
x mx m x m
.Cóbaonhiêu
giátrịnguyêncủathamsố
m
thuộcđoạn
2020;2020
đểđồthịhàmsốcó4đườngtiệmcận?
A. 4039. B. 4040. C. 4038. D. 4037.
Lời giải
Chọn D
Tacó
lim 0, lim 0
x x
y y
đồthịhàmsốđãchocó1tiệmcậnngang.
Dođóđồthịhàmsốđãchocó4đườngtiệmcậnkhivàchỉkhinócó3tiệmcậnđứng
*
.
Có
3 2 2 2
3 2 1 2 1
x mx m x m x m x mx
3 2 2
2
3 2 1 0
2 1 0 2
x m
x mx m x m
x mx
*
3 2 2
3 2 1 0
x mx m x m
có3nghiệmphânbiệtkhác
3
.
3
m
và
2
có2nghiệmphânbiệtkhác
m
vàkhác3.
2
2
2
2
3
5
3,
2 . 1 0
3
1
3 2 .3 1 0
1
1 0
m
m m
m m m
m
m
m
m
Dođótậptấtcảgiátrịnguyêncủa
m
thỏaycbtlà
2020; 2019;...; 2;2;4;5;...;2020
.
Vậycó4037giátrị
m
thỏaycbt.
Câu 5. (Chuyên Sư Phạm Hà Nội - 2020) Cóbaonhiêusốnguyêncủa
m
thuộcđoạn
100;100
đểđồ
thịhàmsố
2
1
2
y
x m x x
cóđúnghaiđườngtiệmcân?
A.
200.
B.
2.
C.
199.
D.
0.
Lời giải
Chọn A
Tacóđiềukiệnxácđịnhlà
0;2
x m
x
,khiđóđồthịhàmsốsẽkhôngcótiệmcậnngang.
Tacó
0 2
lim , lim
x x
y y
Suyra
0, 2
x x
làhaiđườngtiệmcậnđứng
Vậyđểđồthịhàmsốcóđúnghaiđườngtiệmcậnthì
0
2
m
m
,theobài
m
thuộcđoạn
100;100
.
Vậycó200sốnguyêncủa
m
thỏamãnđầubài.
Câu 6. (HSG Bắc Ninh 2019) Tìm tất cả các giá trị của tham số thực
m
để đồ thị hàm số
2
2
3 2
x m
y
x x
cóđúnghaiđườngtiệmcận.
A.
1
m
B.
{1;4}
m
C.
4
m
D.
{ 1; 4}
m
Lờigiải
2 2
2
3 2 1 2
x m x m
y
x x x x
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
lim 1
x
y
1y
làđườngtiệmcậnngang.
Đồthịhàmsố
2
2
3 2
x m
y
x x
cóđúnghaiđườngtiệmcận
đồthịhàmsốcóđúngmộttiệm
cậnđứng
pt
2
0
x m
nhậnnghiệm
1x
hoặc
2
x
.
Khiđó:
1
4
m
m
.
Với
1
m
cómộttiệmcậnđứng
2
x
.
Với
4
m
cómộttiệmcậnđứng
1x
.
Vậy
{ 1; 4}
m
.
Câu 7. (THPT Hoàng Hoa Thám Hưng Yên 2019) Cóbaonhiêugiátrịnguyêncủa
m
đểđồthịhàm
số
2 2
6 3
6 3 9 6 1
x
y
mx x x mx
cóđúngmộtđườngtiệmcận?
A.
0
. B.
2
. C.
1
. D. Vôsố.
Lời giải
Kíhiệu
C
làđồthịhàmsố
2 2
6 3
6 3 9 6 1
x
y
mx x x mx
.
*Trườnghợp1:
0
m
.
Khiđó
2
6 3
6 3 9 1
x
y
x x
.Đồthịhàmsốcóđúngmộtđườngtiệmcậnngang
0
y
.
Dođóchọn
0
m
.
*Trườnghợp2:
0
m
.
Xétphươngtrình
2 2
6 3 9 6 1 0 1
mx x x mx
Nhậnthấy:
C
luôncómộtđườngtiệmcậnngang
0
y
vàphươngtrình
1
khôngthểcóduy
nhấtmộtnghiệmđơnvớimọi
m
.
Dođó
C
cóđúngmộtđườngtiệmcậnkhivàchỉkhi
C
khôngcótiệmcậnđứng
1
vô
nghiệm
2
9 3 0
9 9 0
m
m
3
1 1
m
m
,(khôngtồntại
m
).
Kếthợpcáctrườnghợptađược
0
m
.
Câu 8. (THPT Lương Thế Vinh Hà Nội 2019) Chohàmsố
2
1
2 4
x
x
y f
m
x
x
.Tìmtấtcảcácgiá
trịcủathamsố
m
đểđồthịcóbađườngtiệmcận
A.
2
m
B.
2
5
2
m
m
C.
2
2
5
2
m
m
m
D.
2
2
m
m
Lời giải
Chọn C
Đểđồthịcóbađườngtiệmcậnthì
2
2 4 0
x mx
cóhainghiệmphânbiệt
1

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
2
0
2
1 2 1 4 0
5
2
m
m
m
m
Câu 9. (Chuyên Vĩnh Phúc 2019) Biếtrằngđồthịcủahàmsố
3 2017
3
n x n
y
x m
(
,m n
làcácsố
thực)nhậntrụchoànhlàmtiệmcậnngangvàtrụctunglàtiệmcậnđứng.Tínhtổng
m n
.
A.
0
B.
3
C.
3
D.
6
Lờigiải
Chọn A
Theocôngthứctìmnhanhtiệmcậncủađồthịhàmsố
ax b
y
cx d
tacó
Đồthịhàmsốnhận
3 0
d
x m
c
làmTCĐ
3
m
Đồthịhàmsốnhận
3 0
a
y n
c
làmTCN
3
n
.
Vậy
0
m n
.
Câu 10. (Sở Vĩnh Phúc 2019) Có bao nhiêu giá trị nguyên của tham số
m
để đồ thị hàm số
2
1
8 2
x
y
mx x
cóđúngbốnđườngtiệmcận?
A.
8
B.
6
C.
7
D. Vôsố
Lờigiải
TH1:
0
m
suyratậpxácđịnhcủahàmsốlà
1 2
;
D x x
,(
1 2
;x x
lànghiệmcủaphươngtrình
2
8 2 0
mx x
).Dođó
0
m
khôngthỏayêucầucủabàitoán.
TH2:
1
0
8 2
x
m y
x
suyratậpxácđịnhcủahàmsốlà
;4
D
.
4
lim ; lim
x
x
y y
.Khiđótacó
4
x
làđườngtiệmcậnđứngcủađồthịhàmsố.
Dođó
0
m
khôngthỏayêucầucủabàitoán
TH3:
0
m
suyratậpxácđịnhcủahàmsốlà
1 2
; ;
D x x
(
1 2
;x x
lànghiệmcủa
phươngtrình
2
8 2 0
mx x
).Dođóđồthịhàmsốcóbốnđườngtiệmcậnkhiphươngtrình
2
8 2 0
mx x
cóhainghiệmphânbiệtkhác
16 2 0 8
1 0; 0; 1;2;3;4;5;7
8 2 0 6
m m
m m m m m
m m
.Suyracótấtcả
6
giátrịnguyêncủa
thamsố
m
thỏamãnyêucầucủabàitoán.
Câu 11. (THPT Việt Đức Hà Nội 2019) Với giá trị nào của hàm số
m
để đồ thị hàm số
2
3 7
y x mx x
cótiệmcạnngang.
A.
1
m
B.
1
m
C.
1
m
D. Khôngcó
m
Lờigiải
ChọnA
Đồthịhàmsốcótiệmcậnngang
Hàmsốxácđịnhtrênmộttrongcácmiền
; , ; , ,
a a a
hoặc
;
a

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
0
m
TH1: 0 3 7, lim
x
m y x x y đồthịkhôngcótiệmcậnngang
TH2:
2
0, 3 7
m y x mx x
Khi
2
3 7 3
lim lim
2
x
x
y x x m
x x
đồthịhàmsốcótiệmcậnngangkhivàchỉkhi
1
m
.
Vậy
1
m
Cáchtrắcnghiệm:
Thay
1
m
2 2
3
3 7 lim 3 7
2
x
y x x x x x x
đồthịhàmsốcótiệmcậnngang
2
lim 3 7
x
x x x
khôngcótiệmcậnngang.
Thay
1
m
2 2
3 7 lim 3 7
x
y x x x x x x
khôngxácđịnh.
2
lim 3 7
x
x x x
khôngxácđịnh.
Vậy
1
m
Câu 12. Chohàmsố
1
.
2
ax
y
bx
Tìm
,a b
đểđồthịhàmsốcó
1x
làtiệmcậnđứngvà
1
2
y
làtiệm
cậnngang.
A.
1; 2
a b
. B.
4; 4
a b
. C.
1; 2
a b
. D.
1; 2
a b
.
Lời giải
Chọn C
+
0
b
đồthịhàmsố
1
2
ax
y
khôngcótiệmcận.
+
0
b
,tậpxácđịnhcủahàmsố
1
2
ax
y
bx
là
2
\
D R
b
.
1
1
lim lim lim
2
2
x x x
a
ax a
x
y
bx b
b
x
.
đồthịhàmsố
1
2
ax
y
bx
cótiệmcậnnganglàđườngthẳng
1
2
2
a a
y b a
b b
.
2 2
1
lim lim
2
x x
b b
ax
y
bx
.
đồthịhàmsố
1
2
ax
y
bx
cótiệmcậnđứnglàđườngthẳng
2 2
1 2 1 x b a
b b
.
Vậy
1; 2
a b
.
Câu 13. Có bao nhiêu giá trị nguyên
10;10
m
sao cho đồ thị hàm số
2
1
2 6 3
x
y
x x m
có hai
đườngtiệmcậnđứng?
A.
19
. B.
15
. C.
17
. D.
18
.
Lời giải
Chọn C

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Tacóđồthịhàmsố
2
1
2 6 3
x
y
x x m
cóhaiđườngtiệmcậnđứngkhiphươngtrình
2
2 6 3 0
x x m
cóhainghiệmphânbiệtkhác
1
2
2
3 2 3 0
2.1 6.1 3 0
m
m
15
2
5
m
m
Từđótasuyratậpcácgiátrịnguyêncủa
m
thỏamãnlà
7, 6, 5, 4, 3, 2, 1,0,1,2,3,4,6,7,8,9,10
.Vậycó
17
giátrịnguyêncủa
m
thỏamãn.
Câu 14. Cóbaonhiêugiátrịnguyêncủa
m
đểtổngsốtiệmcậnngangvàtiệmcậnđứngcủađồthịhàmsố
2
3 4
2
mx mx
y
x
bằng3?
A.
4
. B.
2
. C. Vôsố. D.
3
.
Lời giải
Chọn B
Đồthịhàmsố
2
3 4
2
mx mx
y
x
cónhiềunhấtmộttiệmcậnđứngvàhaitiệmcậnngang.
Điềukiệnđểđồthịhàmsố
2
3 4
2
mx mx
y
x
có3tiệmcậnlànócóđúng1tiệmcậnđứngvà2
tiệmcậnngang.
*Xétđiềukiệntồntại
lim
x
y
và
lim
x
y
Trườnghợp1:
2
3 4 0
g x mx mx
với
x
2
0
16
0
0
9
9 16 0
m
m
m
m m
Trườnghợp2:
2
3 4 0
g x mx mx
với
1 2
; ;x x x
với
1
x
;
2
x
lànghiệmcủa
g x
2
0
16
9
9 16 0
m
m
m m
Vậy
0
m
thìtồntại
lim
x
y
và
lim
x
y
Khiđó:
2
2
3 4
3 4
lim lim lim
2
2
1
x x x
m
m
mx mx
x x
y m
x
x
2
2
3 4
3 4
lim lim lim
2
2
1
x x x
m
m
mx mx
x x
y m
x
x
Vậyđiềukiệnđểđồthịhàmsốcóhaiđườngtiệmcậnnganglà
0
m
*Xéttrườnghợp
2
x
lànghiệmcủatửsố
2
x
lànghiệmcủa
2
3 4
g x mx mx
2 0 2
g m
Khiđó
2
2 6 4
2
x x
y
x
2 2
2 1 2
2 1
lim lim
2 2
x x
x x
x
y
x x

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
Đồthịhàmsốcómộttiệmcậnđứng
2
x
.
2
m
thỏamãn
*Xéttrườnghợp
2
x
khônglànghiệmcủatửsố,để
2
x
làtiệmcậnđứngcủađồthịhàm
sốthì
2 0
2 0 4 2 0 2
2 0
g
g m m
g
đồthịhàmsốcómộtđườngtiệmcậnđứng
2
x
với
0;2
m
Vậyđiềukiệnđểđồthịhàmsố
2
3 4
2
mx mx
y
x
có3tiệmcậnlà
0;2
m
Vậycóhaigiátrịnguyêncủa
m
thỏamãnđềbàilà
1
m
;
2
m
.
Câu 15. (Thi thử Lômônôxốp - Hà Nội 2019) Tổngcácgiátrịcủathamsố
m
đểđồthịcủahàmsố
2 2
1
2 1 2
x
y
x m x m
cóđúngmộttiệmcậnđứng.
A.
1
2
. B.
2
. C.
3
. D.
3
2
.
Lời giải
Chọn A
Đặt
2 2
2 1 2
x m mf x x
Đồthịhàmsốcóđúngmộttiệmcậnđứngkhivàchỉkhi
0
f x
có2nghiệmphânbiệttrong
đócó1nghiệm
1x
hoặc
0
f x
cónghiệmkép
2
2
2
3
1 2 0
0
1
2
1 2 1 2 0
1 0 3
1; 3
3
3
3
0
2
2
2
m m
m
m
m m
f m
m m
m
m
m
.
Vậytổngcácgiátrị
m
thỏamãnlà:
1
2
.
Câu 16. Chohàmsố
3 2 2
3
3 2 1
x
y
x mx m x m
.Cóbaonhiêugiátrịnguyênthuộcđoạn
6;6
của
thamsố
m
đểđồthịhàmsốcóbốnđườngtiệmcận?
A.
12
. B.
9
. C.
8
. D.
11
.
Lời giải
Chọn B
lim lim 0
x x
y y
nênđồthịhàmsốcótiệmcậnnganglàđườngthẳng
0
y
.
Dođó,đồthịhàmsốcóbốnđườngtiệmcậnkhiphươngtrình
3 2 2
3 2 1 0
x mx m x m
có
3nghiệmphânbiệt
3
x
.
Xétphươngtrình
3 2 2
3 2 1 0
x mx m x m
(*)tacó
3 2 2
3 2 1 0
x mx m x m
2
2 1 0
x m x mx
2
2 1 0
x m
x mx
.
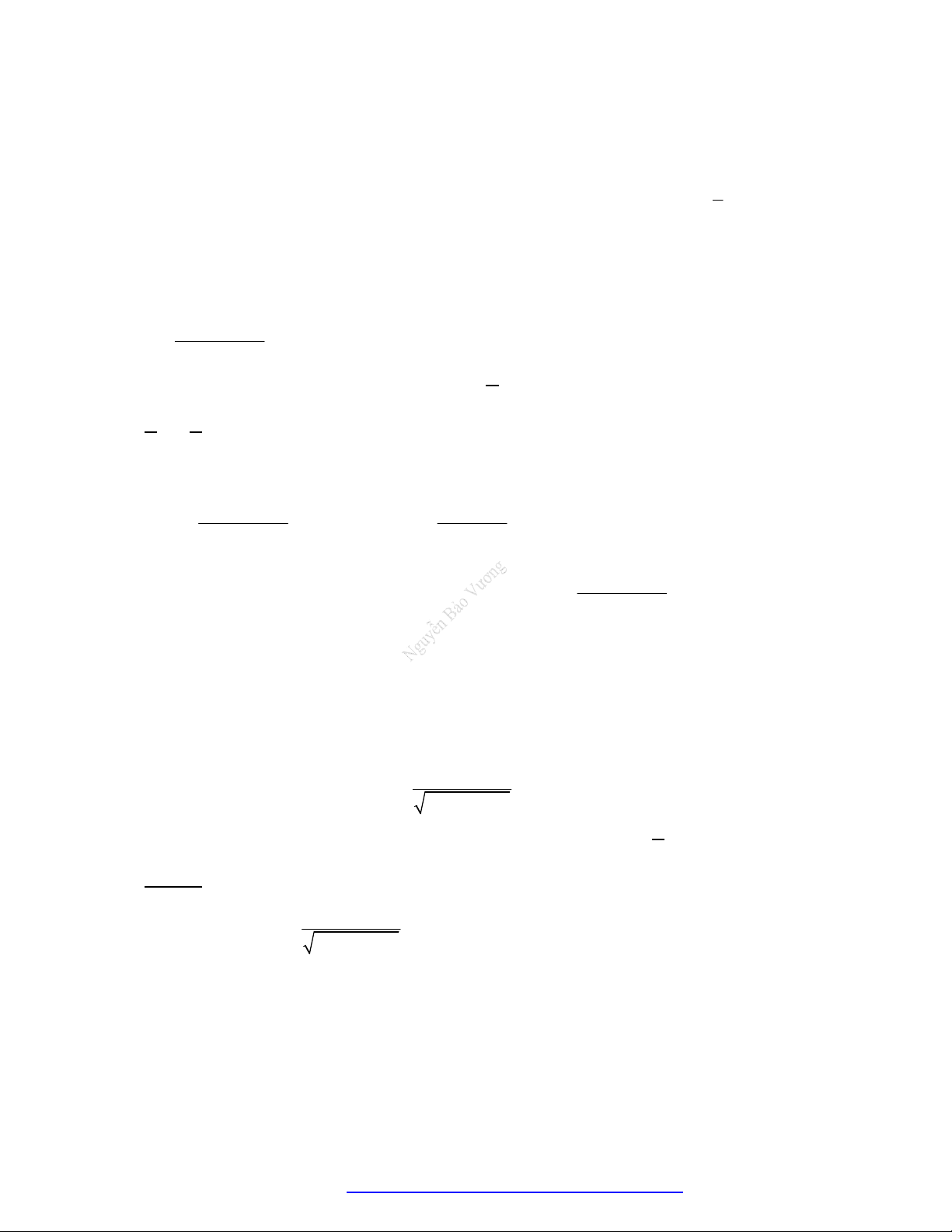
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Phương trình (*) có ba nghiệm phân biệt
3
x
khi và chỉ khi
3
m
và phương trình
2
2 1 0
x mx
cóhainghiệmphânbiệt
3
x
2
2
3
3
1
1 0
1
3 2.3. 1 0
5
3
m
m
m
m
m
m
m
.
Do
m
nguyênvà
6;6
m
nên
6; 5; 4; 3; 2;2;4;5;6
m
.
Vậycó
9
giátrịnguyêncủa
m
thỏamãnđềbài.
Câu 17. (THPT Yên Dũng 2-Bắc Giang) Tìmtấtcảcácgiátrịthựccủathamsốmsaochođồthịhàmsố
2
2 3
x x m
y
x m
khôngcótiệmcậnđứng.
A.
1
m
. B.
1
m
. C.
1
m
và
0
m
. D.
0
m
.
Lời giải
Chọn C
TXĐ
\
m
.
Có
2 2
2 3 2 2
lim lim 2 2 3
x m x m
x x m m m
x m
x m x m
.
Đểđồthịhàmsốkhôngcótiệmcậnđứngthìphảitồntại
2
2 3
lim
x m
x x m
x m
,
2
0
2 2 0
1
m
m m
m
VậyđápánC.
Câu 18. (Cụm liên trường Hải Phòng 2019) Cóbaonhiêugiátrịnguyêncủathamsốthực
m
thuộcđoạn
2017;2017
đểđồthịhàmsố
2
2
4
x
y
x x m
cóhaitiệmcậnđứng.
A.
2019
. B.
2021
. C.
2018
. D.
2020
.
Lời giải
Chọn D
Đểđồthịhàmsố
2
2
4
x
y
x x m
cóhaitiệmcậnđứngthìphươngtrình
2
4 0
x x m
có
hainghiệmphânbiệtkhác
2
2017 4
4 0
12 2017; 2016;..;3 \ 12
12 0
m
m
m m
m
m
.
Dođósốgiátrịnguyêncủathamsố
m
thỏađềbàilà:
3 ( 2017) 1 1 2020
giátrị.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
Câu 19. (THPT Quỳnh Lưu- Nghệ An- 2019) Cho hàm số
( )y f x
thỏa mãn
lim ( ) 2019
x
f x m
,
4
lim ( ) 2020
x
f x m
(với
m
làthamsốthực).Hỏicótấtcảbaonhiêugiátrị
của
m
đểđồthịcủahàmsố
( )y f x
códuynhấtmộttiệmcậnngang?
A. 4. B. 2. C. 3. D. 1.
Lời giải
Chọn B
Đồthịhàmsố
y f x
códuynhấtmộttiệmcậnngang
4
3
0
2019 2020
2019
2020
m
m m
m
.
Vậycó2giátrịcủa
m
thỏabàitoán
Câu 20. (THPT Hai Bà Trưng - Huế - Lần 1- 2019) Cho hàm số
2
1
2 1 2
y
x m x m x m
.
Tìmtấtcảcácgiátrịthựccủathamsố
m
đểđồthịhàmsốcó4đườngtiệmcận.
A.
0 1
1
2
m
m
. B.
1
1
2
m
m
. C.
1
m
. D.
0 1
1
2
m
m
.
Lời giải
Chọn A
Điềukiện
.x m
Tacó
lim 0 0
x
y y
làtiệmcậnngangcủađồthịhàmsố.
Xétphươngtrình
2
2
2 1 2 0
2 1 2 0(*)
x m
x m x m x m
x m x m
Đểhàmsốcó4đườngtiệmcậnthìphươngtrình
(*)
có2nghiệmphânbiệt
1 2
m x x
.
2
2 2
1 2 1 2 1 2
1 2
1 1
2 1 0
2 2
1
0 0 0
2
0 1
1 0
2 2 1 2
m m
m
m
x m x m x x m x x m m m
m
x x m m m
.
Câu 21. (THPT Hoàng Hoa Thám - Hưng Yên 2019) Cóbaonhiêugiátrịnguyêncủa
m
đểđồthịhàm
số
2 2
6 3
6 3 9 6 1
x
y
mx x x mx
cóđúng1đườngtiệmcận?
A.
0.
B. 2. C.
1.
D. Vôsố.
Lời giải
Chọn C
Đặt
2
6 3f x mx x
và
2
9 6 1g x x mx
.Taxétcáctrườnghợp:
+Trườnghợp1:
0
m
khiđótacó
2
6 3
6 3 9 1
x
y
x x
đồthịhàmsốcó1đườngtiệmcận
nganglàđườngthẳng
0
y
dođó
0
m
thỏamãnyêucầubàitoán.
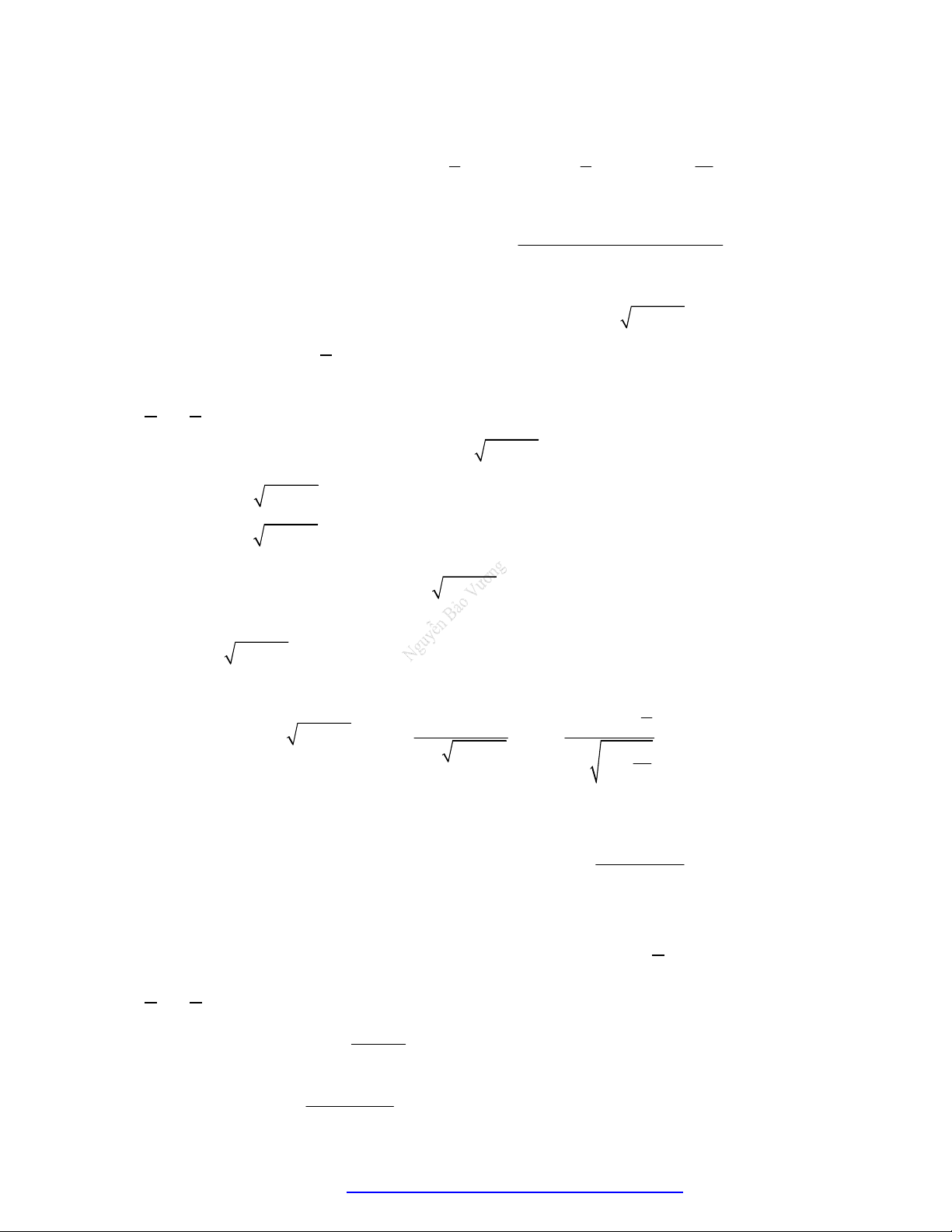
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 22 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
+Trườnghợp2:
0
m
vàcảhaitamthức
f x
và
g x
đềuvô
nghiệm
2
' 0
9 3 0
3
' 0 1 1
9 9 0
f
g
m
m
m
m
m
.
+Trườnghợp3:Tamthức
g x
nhận
1
2
x
làmnghiệm
1 13
0
2 12
g m
khiđó
f x
luôncó2nghiệmphânbiệtnênđồthịhàmsốđãchocónhiềuhơn1đườngtiệmcận.
Vậycó1giátrịnguyêncủa
m
đểđồthịhàmsố
2 2
6 3
6 3 9 6 1
x
y
mx x x mx
cóđúng1
đườngtiệmcận
Câu 22. Tìmtấtcảcácgiátrịthựccủathamsốmđểđồthịhàmsố:
2
1
y x mx
cótiệmcậnngang.
A.
0 1.
m
B.
1.
m
C.
1.
m
D.
1.
m
Lời giải
Chọn B
Điềukiệncầnvàđủđểđồthịhàmsố:
2
1
y x mx
cótiệmcậnnganglàtồntạisốthựcksao
cho:
2
2
lim ( 1) k
lim ( 1) k
x
x
x
x mx
x mx
Hiểnnhiênnếu
0
m
thìgiới
2
lim ( 1)
x
x mx
khônghữuhạn
Nếu
0
m
tacó
+
2
lim ( 1) .
x
x mx
+
2
2
2
2
1
x(1 )
(1 ) 1
lim y lim ( 1) lim lim
1
1
1
x x x x
m
x m
x
x mx
x mx
m
x
Đểgiớihạntrênhữuhạnkhivàchỉkhim=1.
Câu 23. (Chuyên Lê Hồng Phong Nam Định 2019) Chohàmsố
2
2
2 4
x
y
mx x
.Cótấtcảbaonhiêu
giátrịcủathamsố
m
đểđồthịhàmsốcóđúnghaiđườngtiệmcận(tiệmcậnđứngvàtiệmcận
ngang)?
A.
0
. B.
2
. C.
3
. D.
1
.
Lời giải
Chọn D
Với
0
m
;tacóhàmsố
2
2
2 4
x
y
x
Khôngthỏamãnyêucầubàitoán.
Với
0
m
,tacó:
2
2
lim 0
2 4
x
x
mx x
0
y
làtiệmcậnngangcủađồthịhàmsố.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
Đồthịhàmsốcóđúnghaiđườngtiệmcận
đồthịhàmsốcóđúng1tiệmcậnđứng
2
2 4 0
mx x
cónghiệmduynhấthoặc
2
2 4 0
mx x
cóhainghiệmphânbiệttrongđócó
mộtnghiệm
2
x
.
2
2 4 0
mx x
cónghiệmduynhất
1
0 1 4 0
4
m m
.
2
2 4 0
mx x
cóhainghiệmphânbiệttrongđócómộtnghiệm
2
x
.
1
0
4
4 0
0
m
m
m
0
m
khôngthỏamãnđiềukiện.
Vậychỉcómộtgiátrịcủa
m
thỏamãnyêucầubàitoán.
Câu 24. (HSG Sở Nam Định-2019) Gọi S là tập các giá trị nguyên của
m
sao cho đồ thị hàm số
2
2019
17 1
x
y
x m x
cóbốnđườngtiệmcận(baogồmtiệmcậnđứngvàtiệmcậnngang).Tínhsố
phầntửcủatậpS.
A. Vôsố B. 3 C. 5 D. 4
Lời giải
Chọn C
2019 2019
lim , lim
17 17
x x
y y
m m
.
Với
17
m thìđồthịhàmsốcóhaiđườngtiệmcậnnganglà
2019 2019
,
17 17
y y
m m
.
Khiđóđồthịhàmsốđãchocó4đườngtiệmcậnkhivàchỉkhiphươngtrình
2
17 1 0 1
x m x
cóhainghiệmphânbiệtkhác0.
Tacó:
2
2 2
2 2 2
0
0
1 17 1
17 1 2
17 1
m
m
x m x
m x
x m x
Phươngtrình(1)có2nghiệmphânbiệtkhác0khivàchỉkhiphươngtrình(2)cóhainghiệmphân
biệtkhác0
2
0
0 17
17 0
m
m
m
.
Suyra
0,1,2,3,4
S
.
Câu 25. Gọi
S
là tập hợp tất cả các giá trị của tham số thực
m
sao cho đồ thị hàm số
3
3 4 2
( )
1 1
x
f x
x mx x x m x
nhậntrụctunglàmtiệmcậnđứng.Khiđótổngcácphần
tửcủa
S
bằng
A.
1
2
. B.
1
2
. C.
1
3
. D.
1
3
.
Lời giải
Chọn B
Tacó:
33 4 2
0 0
1
lim ( ) lim
1 1
x x
f x
x mx x x m x
x
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 24 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Mà
3
3 4 2
0
1 1
lim
x
x mx x x m x
x
33 4 2
0
3 4
2
33 4 2 4
0
3
1 1 1 1
lim
lim .
( 1 1) ( ( 1) 1 1)
x
x
x mx x x m x
x x x
x mx x x
m
x x mx x x x x x
Đồthịhàmsố
( )f x
nhậntrụctunglàmtiệmcậnđứng
2 3
2 2
33 4 2 4
0
3
( ) ( 1) 1
lim( ) 0 0
2 3
( 1 1) ( 1) 1 1
x
x m x m
m m
x mx x x x x
.
2
6 3 2 0
m m
Vậy
1 2
1
.
2
m m
Câu 26. (Trường THPT Thăng Long Lần 2019) Có bao nhiêu giá trị
m
nguyên thuộc khoảng
10;10
đểđồthịhàmsố
( ) 1
2
x x m
y
x
cóđúngbađườngtiệmcận?
A.
12
. B.
11
. C.
0
. D.
10
.
Lời giải
Chọn A
Xét
1
g x x x m
.
Tacó
( ) 1
lim 1
2
x
x x m
x
và
( ) 1
lim 1
2
x
x x m
x
.Nênđồthịhàmsốluôncóhaiđường
tiệmcậnngang
1
y
và
1
y
.
Trường hợp 1:
0
m
khiđóhàmsốlà
1
2
x
y
x
.Đồthịhàmsốcótiệmcậnđứnglà
2
x
.
Vậy
0
m
thỏamãnyêucầuđềbài.
Trường hợp 2:
0
m
.Hàmsố
g x
cótậpxácđịnhlà
;0 ;D m
.
2
x D
.
( 2) 2 2 1 0
g m
nên
2
x
làtiệmcậnđứngcủađồthịhàmsố
Vậy
1
m
,
2
m
,.
9
m
thỏamãn.Nêncó
9
giátrị
m
.
Trường hợp 3:
0
m
.Hàmsố
g x
cótậpxácđịnhlà
; 0;D m
.
Để
2
x
làtiệmcậnđứngcủađồthịhàmsốthìtrướchết
2
x D
hay
2
m
.Nênchỉcó
2
m
,
1
m
thỏamãn
Với
1
m
tacó
( ) 1 1
g x x x
,
( 2) 2 1 0
g
nên
2
x
làtiệmcậnđứngcủa
đồthịhàmsố.
Với
2
m
tacó
( ) 2 1
g x x x
,
( 2) 2 1 1 0
g x x
nên
2
x
làtiệm
cậnđứngcủađồthịhàmsố.
Vậy
12
giátrị
m
nguyênthỏamãnyêucầu.
Câu 27. Tìmsốgiátrịnguyênthuộcđoạn
2019;2019
củathamsố
m
đểđồthịhàmsố
2
3
x
y
x x m
cóđúnghaiđườngtiệmcận.
A.
2007
. B.
2010
. C.
2009
. D.
2008
.
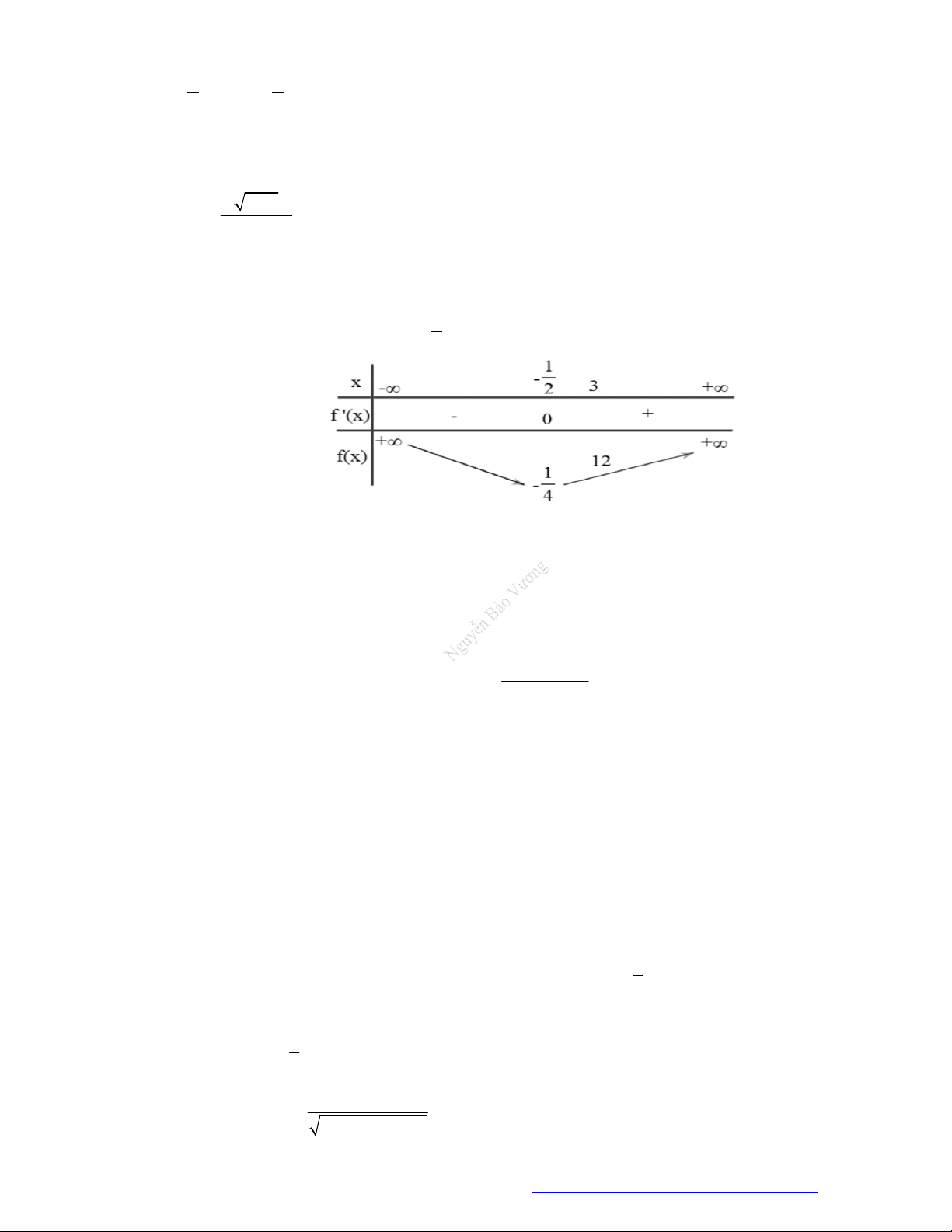
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25
Lời giải
Chọn D.
Điềukiệnxácđịnh:
2
3 0x
x x m
.
Dựavàođiềukiệnxácđịnhtasuyrahàmsốđãchokhôngcógiớihạnkhi
x
.
2
3
lim 0,
x
x
m
x x m
.
0y
làptđườngtiệmcậnngang.
Xéthàmsố
2
f x x x
.
1
' 2 1; ' 0
2
f x x f x x
Dựavàobảngbiếnthiêntathấy:
Khi
12m
thìđồthịhàmsốkhôngcótiệmcậnđứng.
Khi
12m
thìđồthịhàmsốcó1tiệmcậnđứng.
Dođóđểhàmsốcóđúng2đườngtiệmcậnthì
12;2019m
.
Vậycó
2008
giátrịnguyêncủa
m
.
Câu 28. (ChuyênBắcNinh2019)Chohàmsố
2
1
2 3
x
y
mx x
.Cótấtcảbaonhiêugiátrị
m
đểđồthị
hàmsốcóđúnghaiđườngtiệmcận.
A. 2 B. 3 C. 0 D. 1
Lờigiải
ChọnB
Nhận xét:
+
2
( ) 2 3f x mx x có bậc
1
nên đồ thị hàm số luôn có
1
tiệm cận ngang.
+ Do đó: Yêu cầu bài toán
9
đồ thị hàm số có đúng
1
tiệm cận đứng.
+
0m
,đồthịhàmsốcó1tiệmcậnđứnglàđườngthẳng
3
0
2
x m
thỏabàitoán.
+
0m
,đồthịhàmsốcóđúng1tiệmcậnđứngkhivàchỉkhiphươngtrình
2
2 3 0mx x
có
nghiệmképhoặcnhận
1x
làmnghiệm
1
0
3
(1) 0
1
f
m
f
m
+KL:
1
0; ; 1
3
m
.
Câu 29. Chohàmsố
3 2
1
3 1
y
x x m
với
m
làthamsố.Tìmtấtcảcácgiátrịcủa
m
đểđồthịhàm
sốđãchocó
4
đườngthẳngtiệmcận.
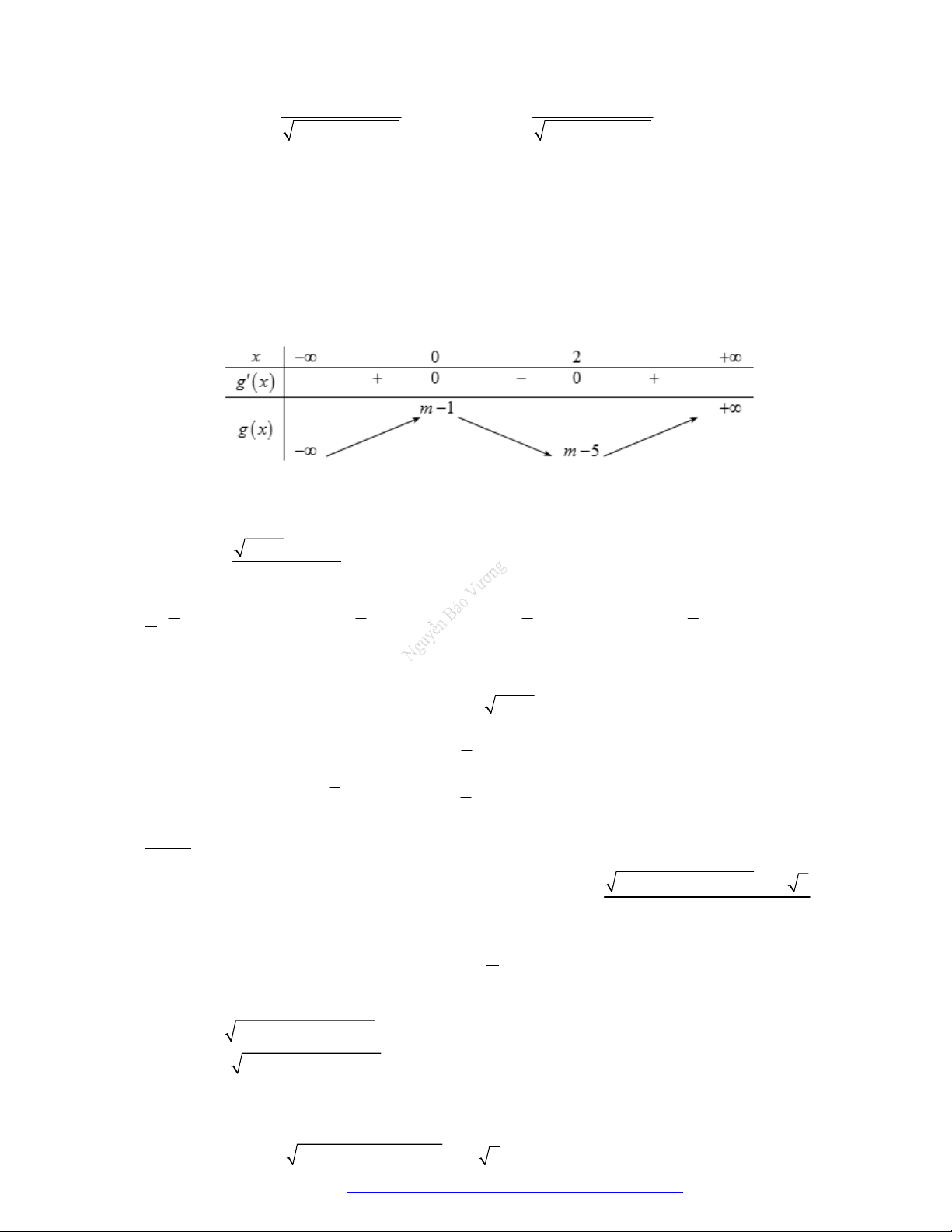
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 26 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
1 5m
. B.
1 2m
. C.
1m
hoặc
5m
. D.
2m
hoặc
1m
.
Lời giải
Tacó
3 2
1
lim lim 0
3 1
x x
y
x x m
,
3 2
1
lim lim
3 1
x x
y
x x m
khôngtồntại.Suyra
0y
làđườngtiệmcậnngangcủađồthịhàmsố.
Dođó,đểđồthịhàmsốđãchocó
4
đườngthẳngtiệmcậnthìphươngtrình
3 2
3 1 0x x m
có
3
nghiệmphânbiệt.
Xéthàmsố
3 2
3 1g x x x m
.Tậpxácđịnh
D
.
2
3 6g x x x
;
0
0
2
x
g x
x
.
Bảngbiếnthiên:
Từbảngbiếnthiên,tathấyphươngtrình
3 2
3 1 0x x m
có
3
nghiệmphânbiệtkhivàchỉkhi
5 0 1 1 5m m m
.
Câu 30. Hàmsố
2
3 1
1
x ax b
y
x
khôngcótiệmcậnđứng.Khiđóhiệu
a b
bằng:
A.
1
2
.
B.
3
4
. C.
5
4
.
D.
1
2
.
Lời giải
Chọn A
Dohàmsốkhôngcótiệmcậnđứngnên
2
3 1 1f x x ax b x g x
.
Suyra
3
2 0
1 0
1
4
3
5
2
0
' 1 0
4
4
a b
a
f
a b
a
f
b
đápán A.
Chú ý:Với
0
n
f x x x g x
thìtaluôncó
1
0 0 0 0
' '' ... 0
n
f x f x f x f x
.
Câu 31. Cóbaonhiêugiátrịnguyêncủathamđể
m
đồthịhàmsố
2
2016 2017 24 7x x
y
x m
có
tiệmcậnđứng?
A. vôsố.
B.
2
. C.
2017
D.
2019
.
Lời giải
Chọn C
Biểuthức:
2
2016 2017x x
cónghĩakhi
2
2016 2017 0 1 2017x x x
.
Đặt
2
2016 2017f x x x
.
Xét
0x m x m
.Vậyđồthịnếucótiệmcậnđứngchỉcóthểlà
x m
,khiđóđiềukiệnlà:
2
1;2017 1
1 2017
0
2016 2017
24 7 *
m
x
f m
m m

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27
Tacó
2
1
* 2016 2015 0 2
2015
m
m m
m
Từ
1 , 2 1;2017 \ 1;2015
m
m
có
2019 2 2017
sốnguyên
m
thỏamãnbài
toán
đápán C.
Câu 32. Gọi
S
là tập hợp tất cả các giá trị của tham số thực
m
sao cho đồ thị hàm số
3
3 4 2
( )
1 1
x
f x
x mx x x m x
nhậntrụctunglàmtiệmcậnđứng.Khiđótổngcácphần
tửcủa
S
bằng
A.
1
2
. B.
1
2
. C.
1
3
. D.
1
3
.
Lời giải
Chọn B
Tacó:
33 4 2
0 0
1
lim ( ) lim
1 1
x x
f x
x mx x x m x
x
.
Mà
3
3 4 2
0
1 1
lim
x
x mx x x m x
x
33 4 2
0
3 4
2
3
3 4 2 4
0
3
1 1 1 1
lim
lim .
( 1 1) ( ( 1) 1 1)
x
x
x mx x x m x
x x x
x mx x x
m
x x mx x x x x x
Đồthịhàmsố
( )f x
nhậntrụctunglàmtiệmcậnđứng
2 3
2 2
33 4 2 4
0
3
( ) ( 1) 1
lim( ) 0 0
2 3
( 1 1) ( 1) 1 1
x
x m x m
m m
x mx x x x x
.
2
6 3 2 0
m m
Vậy
1 2
1
.
2
m m
Câu 33. (THPT Thăng Long 2019) Cóbaonhiêugiátrị
m
nguyênthuộckhoảng
10;10
đểđồthị
hàmsố
( ) 1
2
x x m
y
x
cóđúngbađườngtiệmcận?
A.
12
. B.
11
. C.
0
. D.
10
.
Lời giải
Chọn A
Xét
1
g x x x m
.
Tacó
( ) 1
lim 1
2
x
x x m
x
và
( ) 1
lim 1
2
x
x x m
x
.Nênđồthịhàmsốluôncóhaiđường
tiệmcậnngang
1
y
và
1
y
.
Trường hợp 1:
0
m
khiđóhàmsốlà
1
2
x
y
x
.Đồthịhàmsốcótiệmcậnđứnglà
2
x
.
Vậy
0
m
thỏamãnyêucầuđềbài.
Trường hợp 2:
0
m
.Hàmsố
g x
cótậpxácđịnhlà
;0 ;D m
.
NGUYỄN BẢO VƯƠNG - 0946798489
2
x D
.
( 2)
2 2 1 0
g m
nên
2
x
làtiệmc
ậnđứngcủađồthịhàmsố
Vậy
1
m
,
2
m
,.
9
m
thỏam
ãn.Nêncó
9
giátrị
m
.
Trườn
g hợp 3:
0
m
.Hàms
ố
g x
cótậpxácđị
nhlà
; 0;D
m
.
Để
2
x
làtiệm
cậnđứngcủađồthịhàmsốthìtrướchết
2
x D
hay
2
m
.N
ênchỉcó
2
m
,
1
m
thỏamãn
Với
1
m
tacó
( ) 1 1
g x x x
,
( 2)
2 1 0
g
nên
2
x
làti
ệmcậnđứngcủa
đồthịhàmsố.
Với
2
m
tacó
( ) 2
1
g x x
x
,
( 2)
2 1 1 0
g x x
nên
2
x
làtiệ
m
cậnđứngcủađồthịhàmsố.
Vậy
12
giátrị
m
nguyênthỏamãnyêucầu.
Câu 34. (THPT Mai Anh Tuấn_Thanh Hóa 2019) Tìmtấtcảcácgiátrịthựccủa
m
saoc
hođồthịhàm
số
1
1
2
x
mx
y
cóđúng
mộtđườngtiệmcận.
A.
01
m
. B.
01
m
. C.
1
m
. D.
0
m
.
Lời giải
Chọn A
Nếu
0
m
thì
1
1
y
x
.Hàms
ốnàycótậpxácđịnh
\ 1
D
.
Tacó
1
lim 0
1
x
x
nênđồthịhàmsốcótiệmcậnnganglà
0
y
.
1
1
lim
1
x
x
nênđồthịhàms
ốcótiệmcậnđứng
1
x
.
Vậyvới
0
m
thìđồthị
hàmsốcóhaiđườngtiệmcận(loại).
Nếu
0
m
thì
2
1 0
mx
vớimọi
x
vàtậpxácđịnhcủahàmsốlà
\ 1
D
.
2
1
lim
1
x
mx
x
2
1
lim
1
1
x
m
x
m
x
,
2
1
lim
1
x
mx
x
2
1
lim
1
1
x
m
x
m
x
. Suy
ra đồ thị hàm
sốcóhaitiệmcậnnganglà
y m
và
y m
.
2
1
1
lim
1
x
mx
x
nên
1
x
làđ
ườngtiệmcậnđứngcủađồthịhàmsố.
Vậy
0
m
khôngthỏam
ãn.
Nếu
0
m
thìtậpxácđịnhcủahàmsốlà
1 1
; \ 1
D
m m
.
Trườnghợpnàyđồthịhàmsốkhôngcótiệmcậnngang.Đểđồthịhàmsốcóđúngmộtđường
tiệmcậnthìđồthịhàmsốphảicómộttiệmcậnđứng.Điềunàyxảyrakhi
1
1
m
1
1
m
1
1
m
1
m
.
Vậyvới
1 0
m
thìđồthị
hàmsốcóđúngmộtđườngtiệmcận.
-------------------- HẾT --------------------
Trang 28 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
DẠNG TOÁN DÀNH CHO ĐỐI TƯỢNG HỌC SINH GIỎI – MỨC 9-10 ĐIỂM
Dạng. Xác định tiệm cận của đồ thị hàm số g khi biết bảng biến thiên hàm số f(x)
Câu 1. (THPT Lương Văn Can - 2018) Cho đồ thị hàm số
3 1
1
x
y f x
x
. Khi đó đường thẳng nào
sau đây là đường tiệm cận đứng của đồ thị hàm số
1
2
y
f x
?
A.
1x
. B.
2x
. C.
1x
. D.
2x
.
Lời giải
3 1
2 2
1
x
f x
x
3 1 2 2 1x x x
.
Với
1
2
y
f x
ta có
1 1
lim ; lim
x x
y y
Vậy đồ thị hàm số
1
2
y
f x
có đường tiệm cận đứng
1x
.
Câu 2. Cho hàm số
y f x
có đồ thị như hình vẽ
Số tiệm cận đứng của đồ thị hàm số
2019
1
y
f x
là
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn C
Từ đồ thị của hàm số
y f x
suy ra tập xác định của hàm số
y f x
là
D
Do đó số đường tiệm cận đứng của đồ thị hàm số
2019
1
y
f x
chính là số nghiệm của phương
trình
1f x
.
TIỆM CẬN ĐỒ THỊ HÀM SỐ
Chuyên đề 6

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Qua đồ thị ta có: Đường thẳng
1y
cắt đồ thị hàm số
y f x
tại 3 điểm phân biệt nên phương
trình
1f x
có 3 nghiệm phân biệt.
Vậy đồ thị hàm số
2019
1
y
f x
có 3 đường tiệm cận đứng.
Câu 3. (Chuyên Thái Bình - 2020) Cho hàm số
f x
xác định và liên tục trên
\ 1
có bảng biến
thiên như sau:
Hỏi đồ thị hàm số
1
y
f x
có tất cả bao nhiêu đường tiệm cận đứng và tiệm cận
ngang?
A.
4
. B.
3
. C.
2
. D.
1
.
Lời giải
Chọn A
Ta có:
1 1
lim 2 lim
2
x x
f x
f x
;
1 1
lim 2 lim
2
x x
f x
f x
.
Suy ra đồ thị hàm số
1
y
f x
có hai đường tiệm cận ngang là
1
2
y
và
1
2
y
.
Dựa vào bảng biến thiên của hàm số
y f x
ta thấy: phương trình
0f x
có hai nghiệm
phân biệt
1 2
1x x .
Khi đó:
1 2
0f x f x
.
Ta có:
1
1
1
lim 0
1
lim
0
x x
x x
f x
f x
f x khi x x
và
2
2
2
lim 0
1
lim
0
x x
x x
f x
f x
f x khi x x
.
Vậy đồ thị hàm số
1
y
f x
có hai tiệm cận đứng là đường thẳng
1
x x
và
2
x x
.
Do đó chọn A.
Câu 4. (Chuyên Vĩnh Phúc - 2020) Cho hàm số
y f x
thỏa mãn
lim 1
x
f x
và
lim
x
f x m
.
Có bao nhiêu giá trị thực của tham số
m
để hàm số
1
2
y
f x
có duy nhất một tiệm cận
ngang.
A.
1
. B.
0
. C.
2
. D. Vô số.
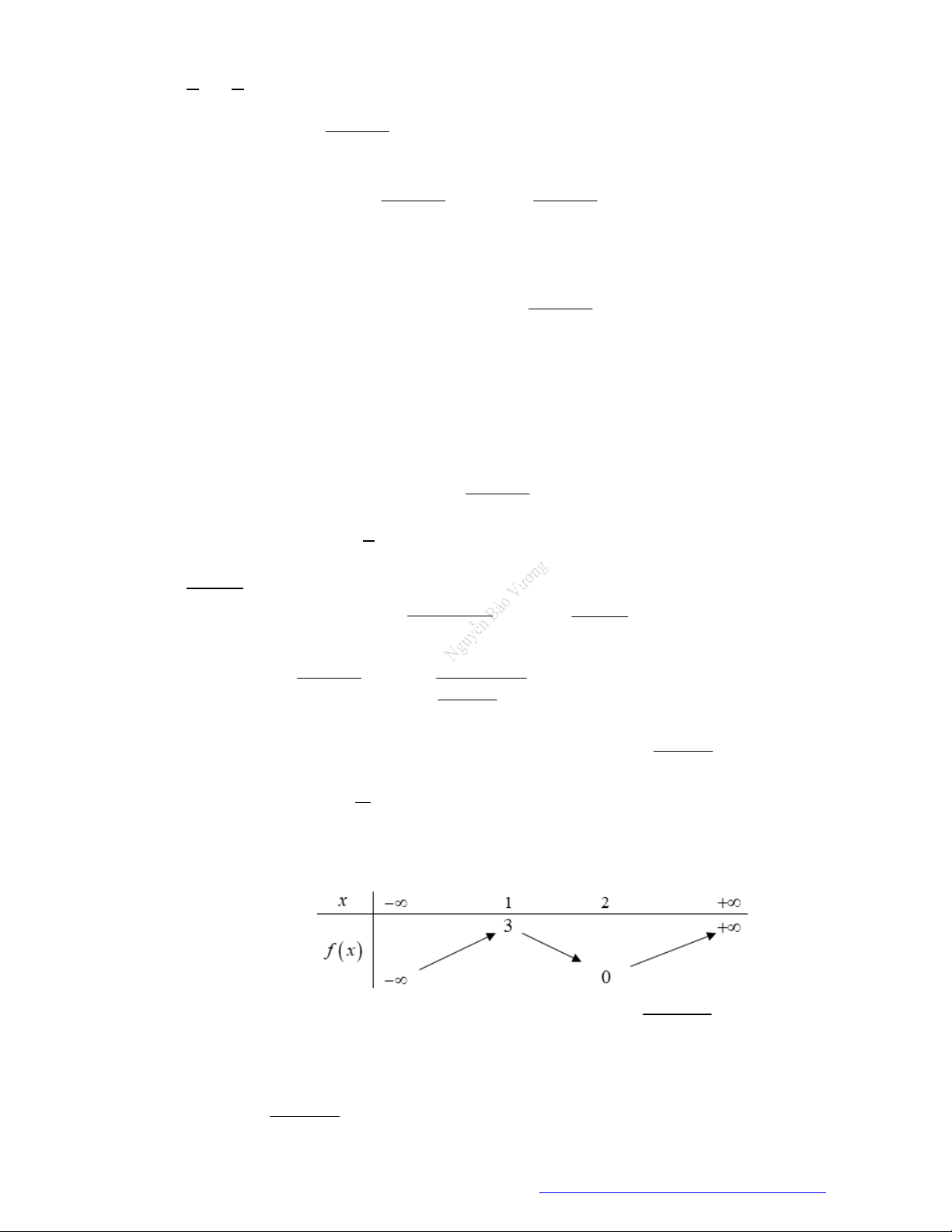
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Lời giải
Chọn C
Ta có
1
lim lim 1
2
x x
y
f x
Đồ thị hàm số có tiệm cận ngang
1y
.
TH 1: Nếu
1m
thì
1
lim 1
2
x
f x
và
1
lim 1
2
x
f x
thì đồ thị hàm số có một tiệm cận.
TH 2: Nếu
1m
Để đồ thị hàm số có một tiệm cận ngang
1
lim
2
x
f x
không có giá trị hữu hạn
2 0 2m m
.
Vậy khi
2; 1m
thì đồ thị hàm số có duy nhất một tiệm cận ngang.
Câu 5. (Kim Liên - Hà Nội 2019) Cho hàm số
( )y f x
thỏa mãn
4
(tan ) cosf x x
. Tìm tất cả các giá
trị thực của
m
để đồ thị hàm số
2019
( )
( )
g x
f x m
có hai tiệm cận đứng.
A.
0m
. B.
0 1m
. C.
0m
. D.
1m
.
Lời giải
Chọn B
4
2
2
1
(tan ) cos (tan )
1 tan
f x x f x
x
2 2
1
( )
(1 )
f t
t
Hàm số
2 2
2019 2019
( ) ( )
1
( )
(1 )
g x g x
f x m
m
x
Hàm số
( )g x
có hai tiện cận đứng khi và chỉ khi phương trình
2 2
1
0
(1 )
m
x
có hai nghiệm
phân biệt
2 2
1
(1 ) 1 0 1x m
m
.
Câu 6. (THPT Quỳnh Lưu 3 Nghệ An 2019) Cho hàm số
y f x
xác định, liên tục trên
và có
bảng biến thiên như hình bên dưới:
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
1
2 1
y
f x
là:
A.
4
. B.
3
. C.
1
. D.
2
.
Lời giải
Đặt
1
2 1
h x
f x
.
*) Tiệm cận ngang:
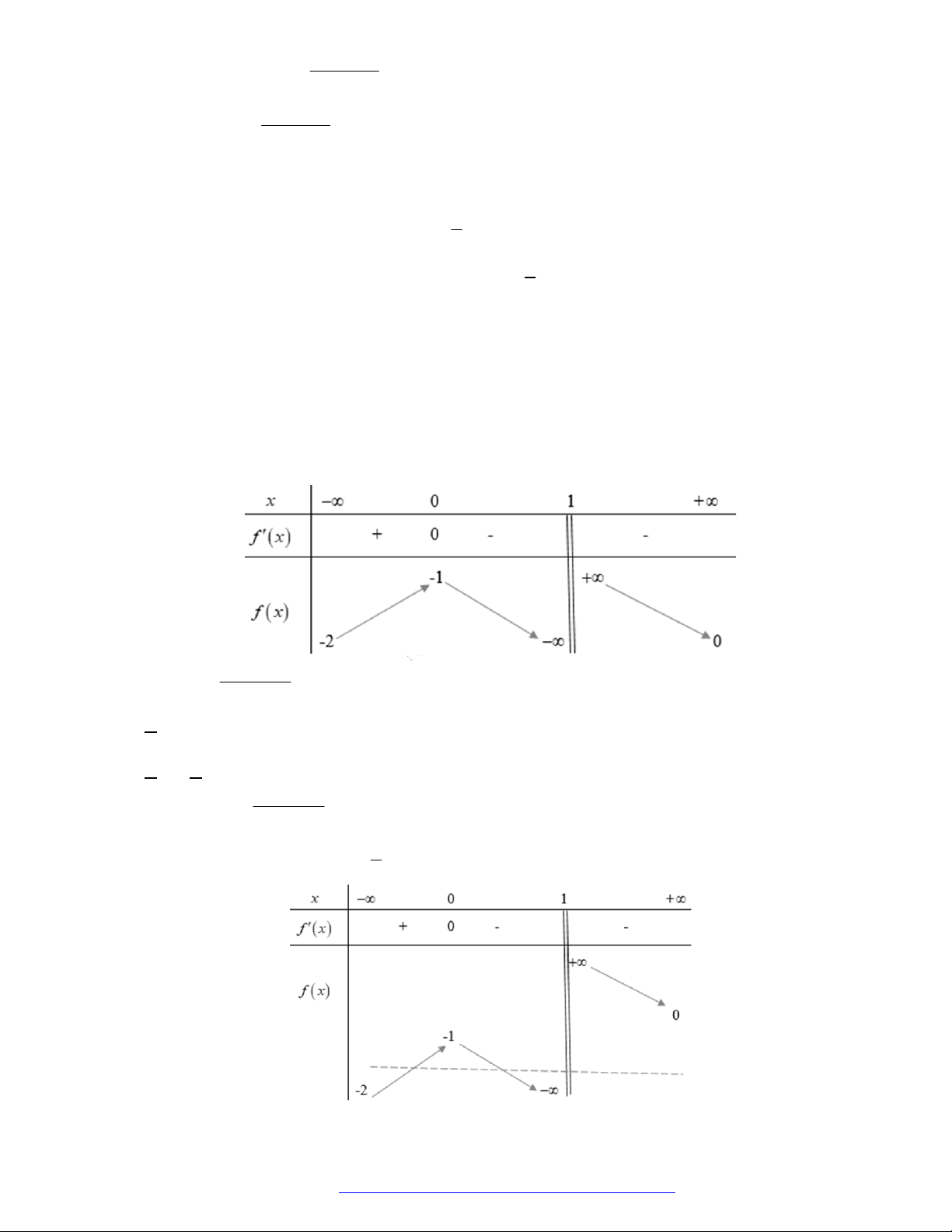
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta có:
1
lim lim 0
2 1
x x
h x
f x
.
1
lim lim 0
2 1
x x
h x
f x
.
Suy ra đồ thị hàm số có một đường tiệm cận ngang
0y
.
*) Tiệm cận đứng:
Xét phương trình:
2 1 0f x
1
2
f x
.
Dựa vào bảng biến thiên ta thấy phương trình
1
2
f x
có ba nghiệm phân biệt
, ,a b c
thỏa mãn
1 2a b c
.
Đồng thời
lim lim lim
x a x b x c
h x h x h x
nên đồ thị hàm số
y h x
có ba đường tiệm
cận đứng là
x a
,
x b
và
x c
.
Vậy tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
y h x
là 4.
Câu 7. (Bình Giang-Hải Dương -2019) Cho hàm số
( )y f x
liên tục trên
\ 1
và có bảng biến thiên
như sau:
Đồ thị
1
2 3
y
f x
có bao nhiêu đường tiệm cận đứng?
A. 2. B. 0. C. 1. D. 3.
Lời giải
Chọn A
Đặt
1
2 3
y g x
f x
có tử số là
1 0, x
Ta có
3
2 3 0
2
f x f x
(1).
Từ bảng biến thiên có phương trình (1) có 2 nghiệm phân biệt:
1 2
( ;0), (0;1)x x .
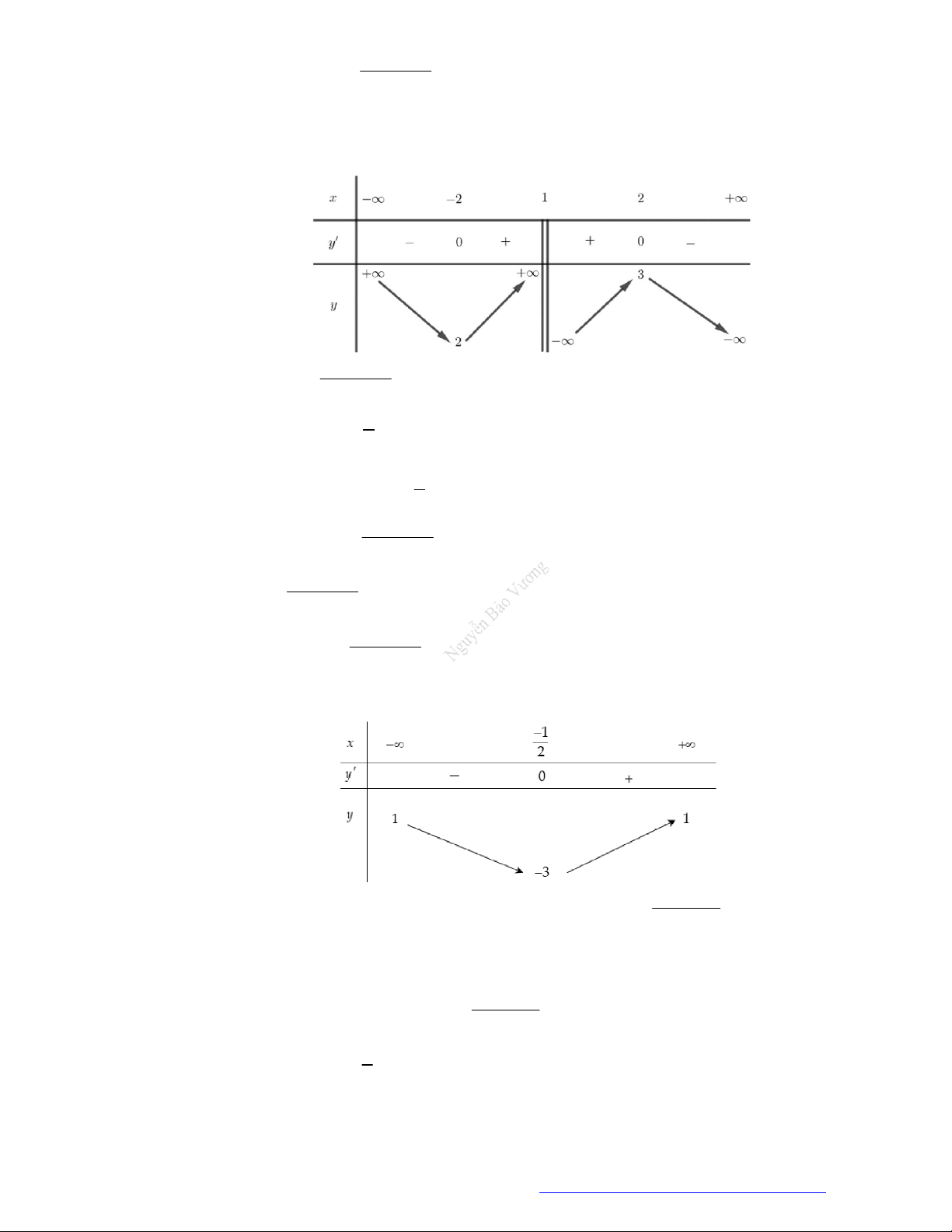
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Do đó đồ thị hàm số
1
2 3
y
f x
có 2 đường tiệm cận đứng.
Câu 8. (Chuyên Thoại Ngọc Hầu 2018) Cho hàm số
y f x
liên tục trên
\ 1
và có bảng biến
thiên như sau:
Đồ thị hàm số
1
2 5
y
f x
có bao nhiêu đường tiệm cận đứng?
A.
0
. B.
4
. C.
2
. D.
1
.
Lời giải
Ta có:
5
2 5 0 1
2
f x f x
. Phương trình
1
có
4
nghiệm phân biệt
1 2 3 4
, , , 1x x x x
và
giới hạn của hàm số
1
2 5
y
f x
tại các điểm
1 2 3 4
, , ,x x x x
đều bằng .
Mặt khác
1
1
lim 0
2 5
x
f x
nên
1x
không phải tiệm cận đứng.
Vậy đồ thị hàm số
1
2 5
y
f x
có
4
đường tiệm cận đứng.
Câu 9. (Chuyên Hưng Yên 2019) Cho hàm số
y f x
có bảng biến thiên như hình dưới đây.
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
1
2 1
y
f x
là
A.
0.
B.
1.
C.
2.
D.
3.
Lời giải
Số tiệm cận đứng của đồ thị hàm số
1
2 1
y
f x
đúng bằng số nghiệm thực của phương trình
1
2 1 0
2
f x f x
.
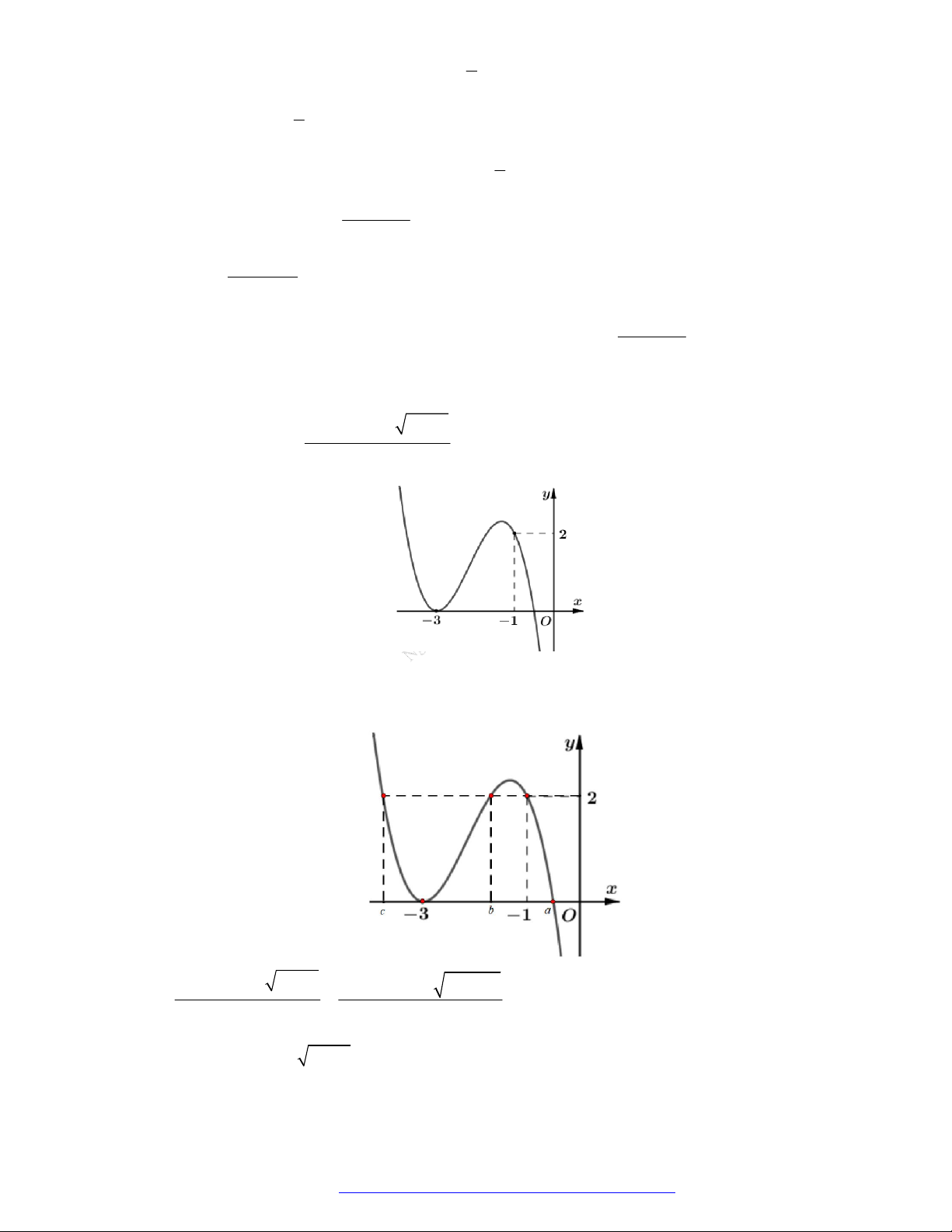
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Mà số nghiệm thực của phương trình
1
2
f x
bằng số giao điểm của đồ thị hàm số
y f x
với đường thẳng
1
2
y
.
Dựa vào bảng biến thiên ta thấy đường thẳng
1
2
y
cắt đồ thị hàm số
( )y f x
tại 2 điểm phân
biệt. Vậy đồ thị hàm số
1
2 1
y
f x
có 2 tiệm cận đứng.
Lại có
1
lim 1
2 1
x
f x
đồ thị hàm số có một tiệm cận ngang là
1y
.
Vậy tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
1
2 1
y
f x
là
3
.
Câu 10. (THPT Bạch Dằng Quảng Ninh 2019) Cho hàm bậc ba
y f x
có đồ thị như hình vẽ bên.
Hỏi đồ thị hàm số
2 2
2
4 3
2
x x x x
y
x f x f x
có bao nhiêu đường tiệm cận đứng?
A.
2
. B.
3
. C.
4
. D.
6
.
Lời giải
2 2
2
4 3
1 3 1
. . 2
2
x x x x
x x x x
y
x f x f x
x f x f x
Điều kiện tồn tại căn
2
x x
:
0
1
x
x
.
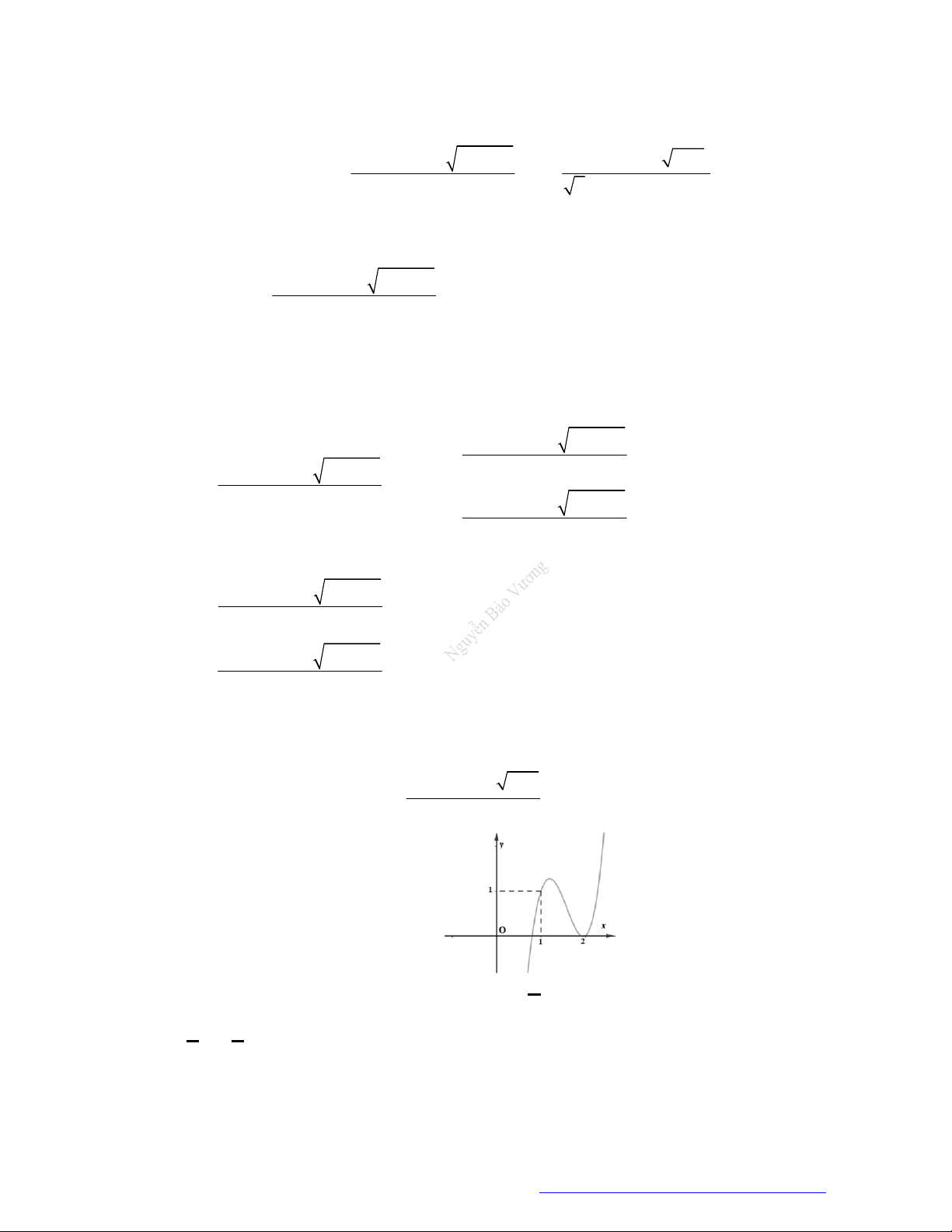
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Xét phương trình
2
0
2 0 0
2
x
x f x f x f x
f x
.
Với
0x
ta có
0 0
1 3 1
1 3 1
lim lim
. . 2
. . 2
x x
x x x x
x x x
x f x f x
x f x f x
. Suy ra
0x
là
tiệm cận đứng.
Với
0f x
3x
(nghiệm bội 2) hoặc
x a
(loại vì
1 0a
).
Ta có:
3
1 3 1
lim
. . 2
x
x x x x
x f x f x
nên
3x
là tiệm cận đứng.
Với
2f x
1
3 1
3
x
x b b
x c c
(nghiệm bội 1). Ta có:
1 3 1
lim 0
. . 2
x b
x x x x
x f x f x
1
1
1 3 1
lim 0
. . 2
1 3 1
lim 0
. . 2
x
x
x x x x
x f x f x
x x x x
x f x f x
nên
1x
không là tiệm cận
đứng.
1 3 1
lim
. . 2
x b
x x x x
x f x f x
(do
x b
thì
2f x
) nên
x b
là tiệm cận đứng.
1 3 1
lim
. . 2
x c
x x x x
x f x f x
(do
x c
thì
2f x
) nên
x c
là tiệm cận đứng.
Vậy đồ thị hàm số có 4 tiệm cận đứng.
Câu 11. (Lý Nhân Tông - Bắc Ninh 2019) Cho hàm số
3 2
f x ax bx cx d
có đồ thị như hình vẽ
bên. Hỏi đồ thị hàm số
2
2
3 2 1x x x
g x
x f x f x
có bao nhiêu tiệm cận đứng?
A.
2
. B.
4
. C.
3
. D.
5
.
Lời giải
Chọn C
Nhận xét 1: Với
0
1x
và
0
lim
x x
g x
hoặc
0
lim
x x
g x
có kết quả là
hoặc
thì
0
x x
là tiệm
cận đứng của của đồ thị hàm số
g x
.
Nhận xét 2: Dựa vào đồ thị hàm số
f x
ta có:
2
1
2f x a x x x
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta có
2
0
0 0
1
x
x f x f x f x
f x
.
1 1
,0 1
0
2
x x x
f x
x
.
2 2
3 3
1
1 ,1 2
, 2
x
f x x x x
x x x
suy ra
2 3
1 1f x a x x x x x
.
Khi đó ta có
2
2
3 2 1
1 2 1
. 1
x x x
x x x
g x
x f x f x
x f x f x
.
2
2
1 2 3
1 2 3
1 2 1
1
2
. 2 . 1
x x x
x
g x
a x x x x x x x x
x a x x x a x x x x x
.
1
0,x x x
không phải tiệm cận đứng của đồ thị hàm số
y g x
không thỏa mãn điều kiện
0
1x
. Đồ thị hàm số
g x
có
3
đường tiệm cận đứng là:
2 3
2, ,x x x x x
.
Câu 12. (THPT Quỳnh Lưu- Nghệ An- 2019) Cho hàm số bậc ba
3 2
f x ax bx cx d
có đồ thị
như hình vẽ sau.
Hỏi đồ thị hàm số
2
2
3 2 1
1
x x x
g x
x f x f x
có bao nhiêu tiệm cận đứng?
A.
5
. B.
4
. C.
6
. D.
3
.
Lời giải
Chọn D
Ta có
1 2 1
1 1
x x x
g x
x f x f x
Đkxđ:
1
0
1
x
f x
f x
Dựa vào đồ thị hàm số
y f x
, ta có:
1
2
0
x
f x
x x
với
2x
là nghiệm kép,
1
0;1x
.
2
3
1
1
x
f x x x
x x
với
2 3
1;2 ; 2x x
.
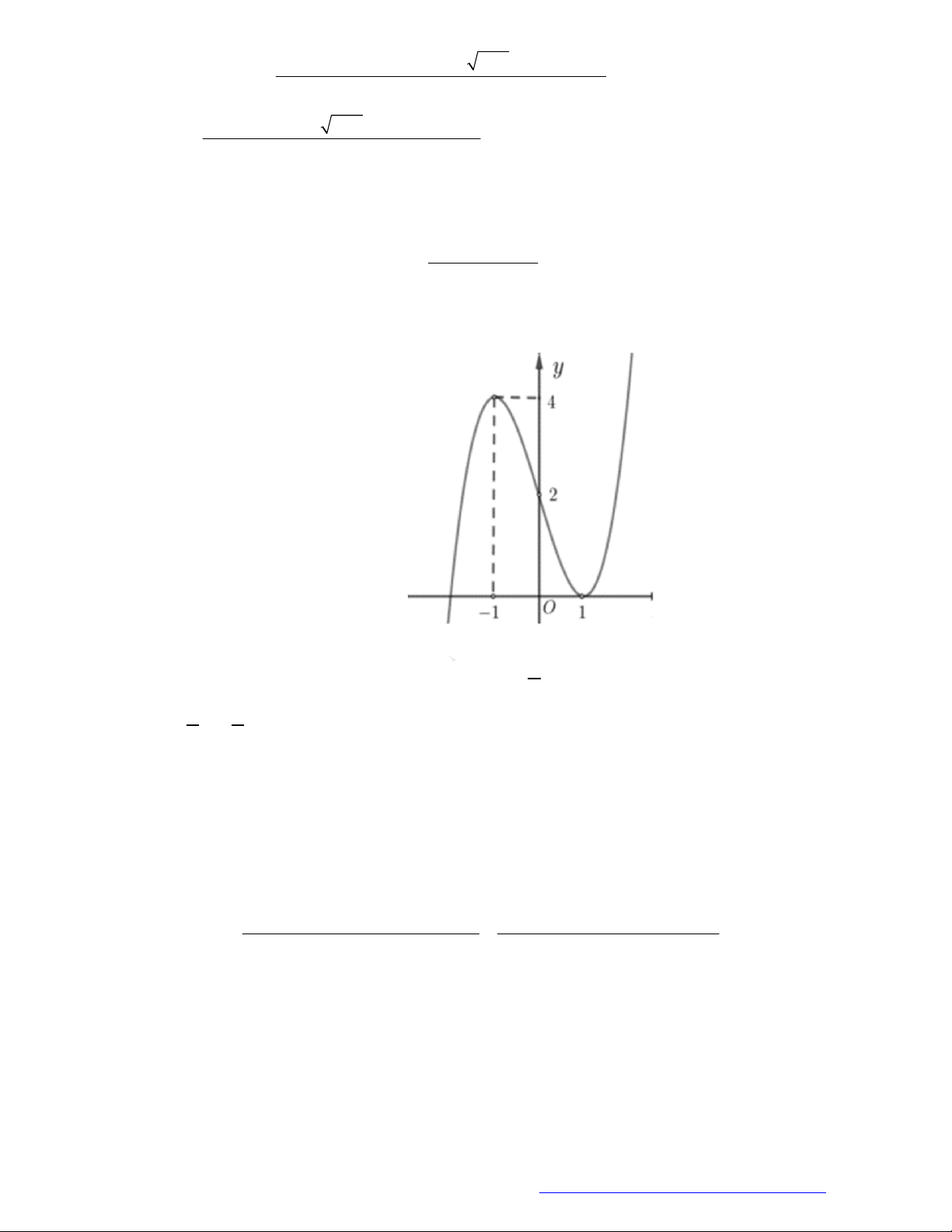
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Vậy
2
2
1 2 3
1 2 1
1 2 1
x x x
g x
a x x x x x x x x x
2
1 2 3
1
1 2
x
a x x x x x x x x
Vậy đồ thị hàm số có 3 TCĐ
2 3
2; ;x x x x x (do
1x
nên ta loại
1
1;x x x ).
Câu 13. (THPT Thuận Thành 3 - Bắc Ninh 2019) Cho hàm số
( )y f x
là hàm số đa thức có đồ thì
như hình vẽ dưới đây, đặt
2
2
2
x x
g x
f x f x
. Hỏi đồ thị hàm số
y g x
có bao nhiêu tiệm
cận đứng?
A.
5
. B.
3
. C.
4
. D.
2
.
Lời giải
Chọn C
Ta xét phương trình
1
2
2
3 3 1
1
1
0
2 0
0
2
1
1,
x
x x
f x
f x f x
x
f x
x x
x x x x
. Khi đó
2
2
1 2 3
1 2 3
1
; 0
1
1
x x
g x a
a x x x x x x x
ax x x x x x x x
.
Vậy đồ thị hàm số
y g x
có
4
đường tiệm cận đứng.
Câu 14. (Chuyên Bắc Giang 2019) Cho hàm số
y f x
xác định, liên tục trên
và có bảng biến
thiên như hình bên dưới.
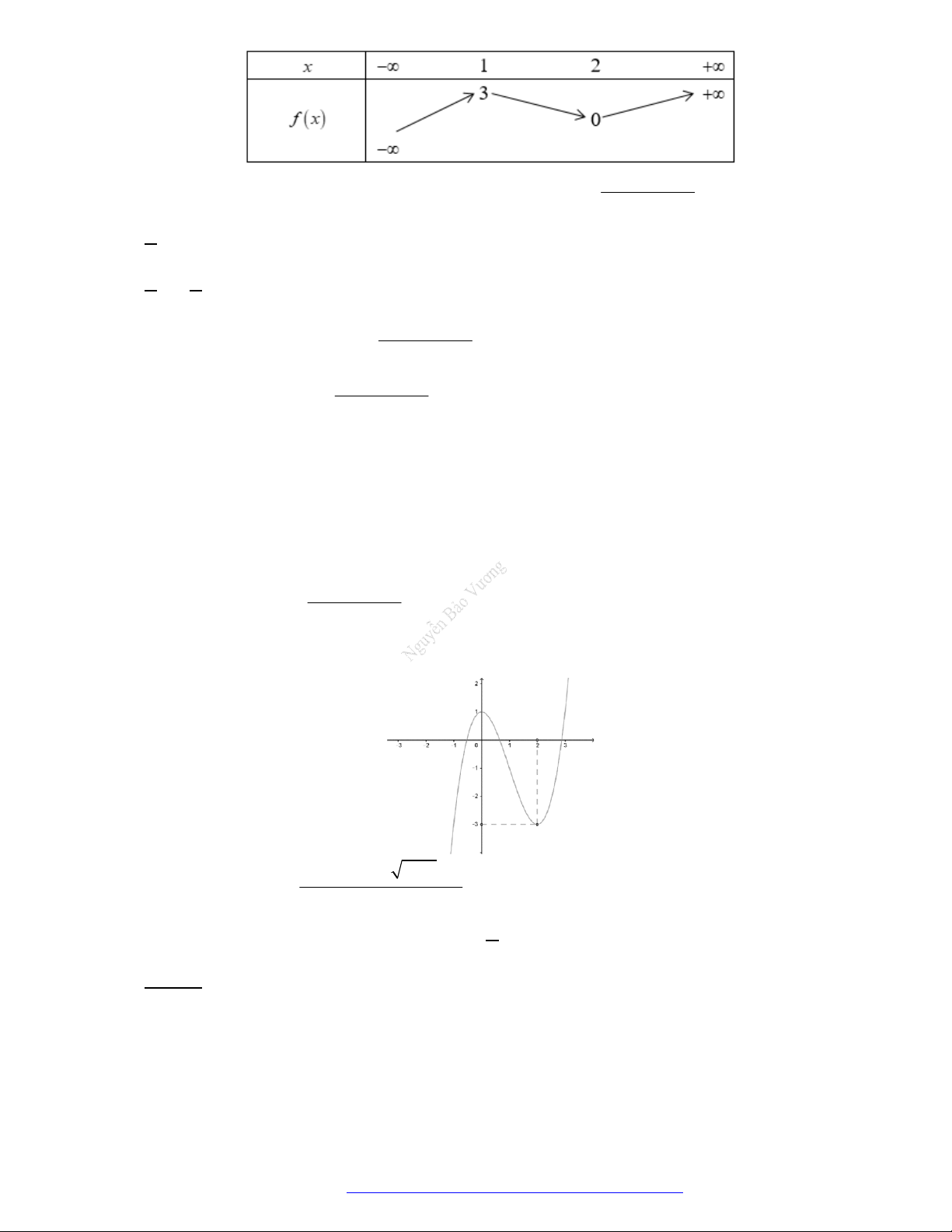
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
3
1
3
y
f x x
là
A. 2. B. 4. C. 3. D. 1.
Lời giải
Chọn A
Tính tiệm cận ngang.
Ta có
3
3
1
lim 0
3
x
x
x x
f x x
3
3
1
lim 0
3
x
x
x x
f x x
Vậy đồ thị hàm số có 1 tiệm cận ngang
0y
.
Tính tiệm cận đứng.
Số đường tiệm cận đứng của đồ thị hàm số là số nghiệm của phương trình
3
3 0f x x
.
Dựa vào bảng biến thiên ta có
3 3 3
0 0
3 0 3 ; ;1f x x f x x x x x x
Vì hàm số
3
y x x
đồng biến trên
do đó
3
0 0
; ;1x x x x
có một nghiệm duy nhất.
Vậy đồ thị hàm số
3
1
3
y
f x x
có 1 tiệm cần đứng.
Câu 15. (THPT Minh Khai 2020) Cho hàm số
3 2
y f x ax bx cx d
có đồ thị như bên dưới.
Hỏi đồ thị hàm số
2
2
2 2
3
x x x
y
x f x f x
có bao nhiêu đường tiệm cận đứng
A.
4
. B.
6
. C.
3
. D.
5
.
Lời giải
Chọn C
Ta có
2
3 2y x ax bx c
.
Dựa vào đồ thị hàm số, ta thấy hàm số đạt cực trị tại
0x
,
2x
. Do đó, ta có hệ
0 1
2 3
0 0
2 0
y
y
y
y
1
0
12 4 0
8 4 4
d
c
a b
a b
1
3
0
1
a
b
c
d
.
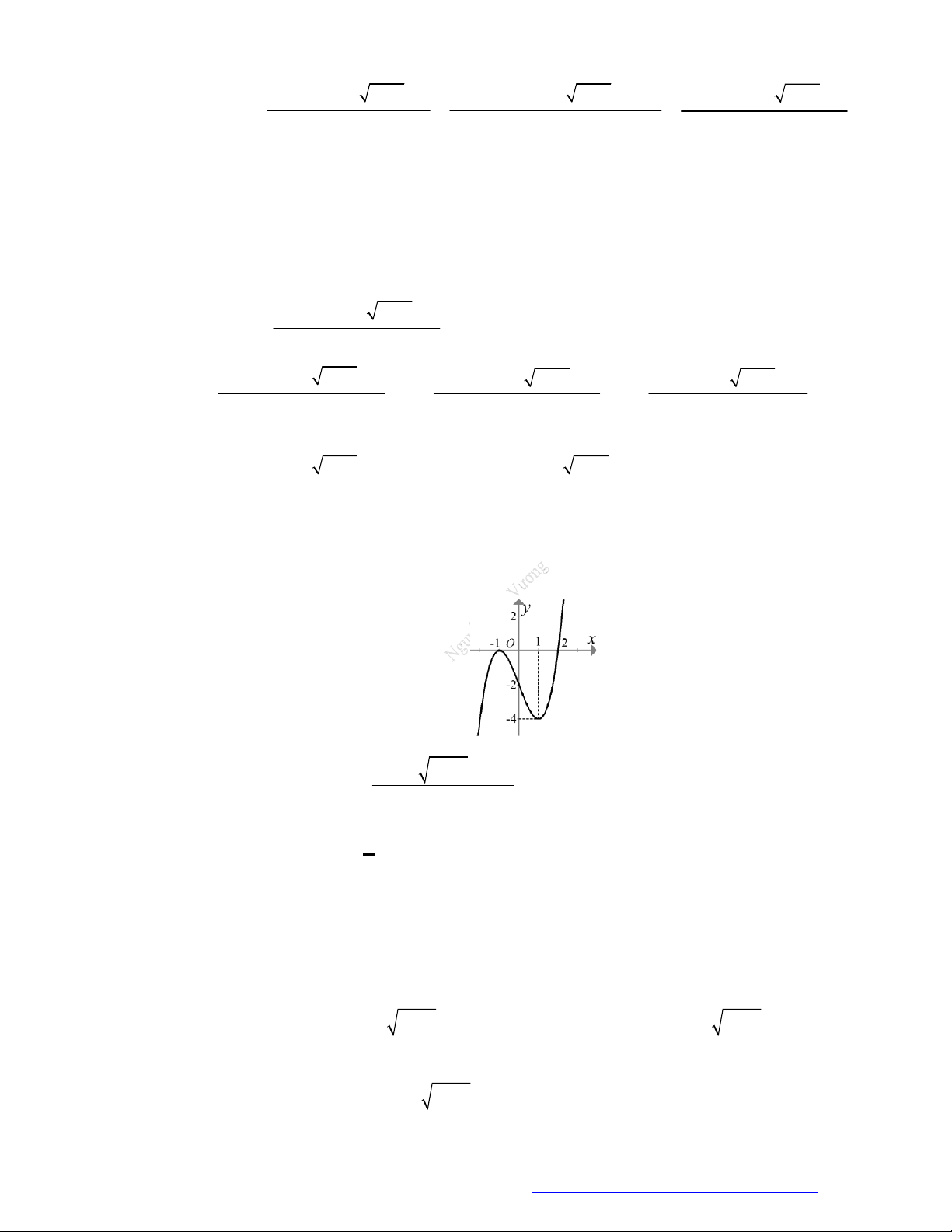
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Vậy
3 2
3 1y f x x x
.
Khi đó
2
2
2 2
3
x x x
y
x f x f x
2
3 2 3 2
2 2
3 3 1 3
x x x
x x x x x
2
2
2 3 2
2 2
3 3 1
x x x
x x x x
.
Ta có
2
2 3 2
3 3 1 0x x x x
1
2
3
0
3
1;0
0;1
2;3
x
x
x x
x x
x x
.
Hàm số
2
2
2 3 2
2 2
3 3 1
x x x
y
x x x x
có tập xác định
1 2
;2 \ 0; ;D x x
.
2
2
2 3 2
0
2 2
lim
3 3 1
x
x x x
x x x x
2
2 3 2
0
2 2
lim
3 3 1
x
x x x
x x x x
2
3 2
0
2 2
lim
3 3 1
x
x x
x x x x
.
Suy ra
0x
là đường tiệm cận đứng.
1
2
2
2 3 2
2 2
lim
3 3 1
x x
x x x
x x x x
,
2
2
2
2 3 2
2 2
lim
3 3 1
x x
x x x
x x x x
.
Suy ra
1
x x
và
2
x x
cũng là các đường tiệm cận đứng của đồ thị hàm số.
Câu 16. (Yên Phong 1 - 2018) Cho hàm số
3 2
y ax bx cx d ,
0a
có đồ thị như hình dưới đây.
Hỏi đồ thị hàm số
2
2
1 4 3
f x
g x
x x x
có bao nhiêu đường tiệm cận đứng?
A.
2
. B.
1
. C.
3
. D.
4
.
Lời giải
Điều kiện xác định:
2
0
1
4 3 0
f x
x
x x
2
1
1
3
x
x
x
x
2
3
x
x
.
Ta có
3
lim
x
g x
2
2
3
lim
1 4 3
x
f x
x x x
và
3
lim
x
g x
2
2
3
lim
1 4 3
x
f x
x x x
.
Vậy đồ thị hàm số
2
2
1 4 3
f x
g x
x x x
có một đường tiệm cận đứng là:
3x
.

NGUYỄ
N BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 17. (Ch
uyên Quang Trung - 2020) Cho hàm số trùng phương
4
2
y
ax bx c có đồ thị như hình
vẽ. Hỏi đồ thị hàm số
2
2
2
4
2
2 3
x x x
y
f x f x
có tổng cộng bao nhiêu tiệm cận đứng?
A
. 5. B. 2. C. 3. D. 4.
Lời giải
Chọn D
2
2
2
4
2
2 3
x x x
y
f x f x
2
2
2
2
2 3
x x x
f x f x
T
a có:
2
2
3 0
f x f x
1
3
f x
f x
2
0
2
2
2
x m m
x
x n n
x
x
Dựa vào đồ thị ta thấy các nghiệm
0
; 2x x
là các nghiệm kép (nghiệm bội 2) và đa thức
2
2
3f x f x
có bậc là 8 nên
2
2
2
2 2
2
2
2 2
x x x
y
a x x x x m x n
Vậy hàm số có các tiệm cận đứng là
0
; 2; ; x x x m x n
.
-------------------- HẾT --------------------
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
DẠNG TOÁN DÀNH CHO ĐỐI TƯỢNG HỌC SINH TRUNG BÌNH 5-6 ĐIỂM
Dạng. Nhận dạng hàm số thường gặp thông qua đồ thị
A. Hàm số bậc ba
y ax bx cx d a
3 2
0
TRƯỜNG HỢP
a 0
0a
Phương trình
y
/
0
có
2 nghiệm phân biệt
Phương trình
y
/
0
có
nghiệm kép
Phương trình
/
0y
vô
nghiệm
B. Hàm số trùng phương
y ax bx c a
4 2
0
TRƯỜNG HỢP
a 0
0a
Phương trình
y
/
0
có
3 nghiệm phân biệt
(ab<0)
Phương trình
y
/
0
có
1 nghiệm.
C. Hàm số nhất biến
0, 0
ax b
y c ad bc
cx d
ĐỌC ĐỒ THỊ CỦA HÀM SỐ
Chuyên đề 7
x
y
1
O
1
x
y
1
O
1
x
y
1
O
1
x
y
1
O
1
x
y
1
O
1
x
y
1
O
1
x
y
O
1
1
x
y
1
O
1
x
y
1
O
1
x
y
O
1
1
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
D ad bc 0
D ad bc 0
Câu 1. (Đề Minh Họa 2020 Lần 1) Đồ thị của hàm số nào dưới đây có dạng như đường cong trong dưới
đây?
A.
4 2
2y x x
. B.
4 2
2y x x
. C.
3 2
3y x x
. D.
3 2
3y x x .
Câu 2. (Đề Tham Khảo 2020 Lần 2) Đồ thị của hàm số nào dưới đây có dạng như đường cong trong
hình bên?
A.
3
3 y x x
. B.
3
3 y x x
. C.
4 2
2 y x x
. D.
4 2
2 y x x
.
Câu 3. (Mã 101 - 2020 Lần 1) Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên?
A.
3 2
3 1y x x
. B.
3 2
3 1y x x
. C.
4 2
2 1y x x
. D.
4 2
2 1y x x
.
Câu 4. (Mã 102 - 2020 Lần 1) Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên?
A. . B. . C. . D. .
4 2
2y x x
3
3y x x
4 2
2y x x
3
3y x x
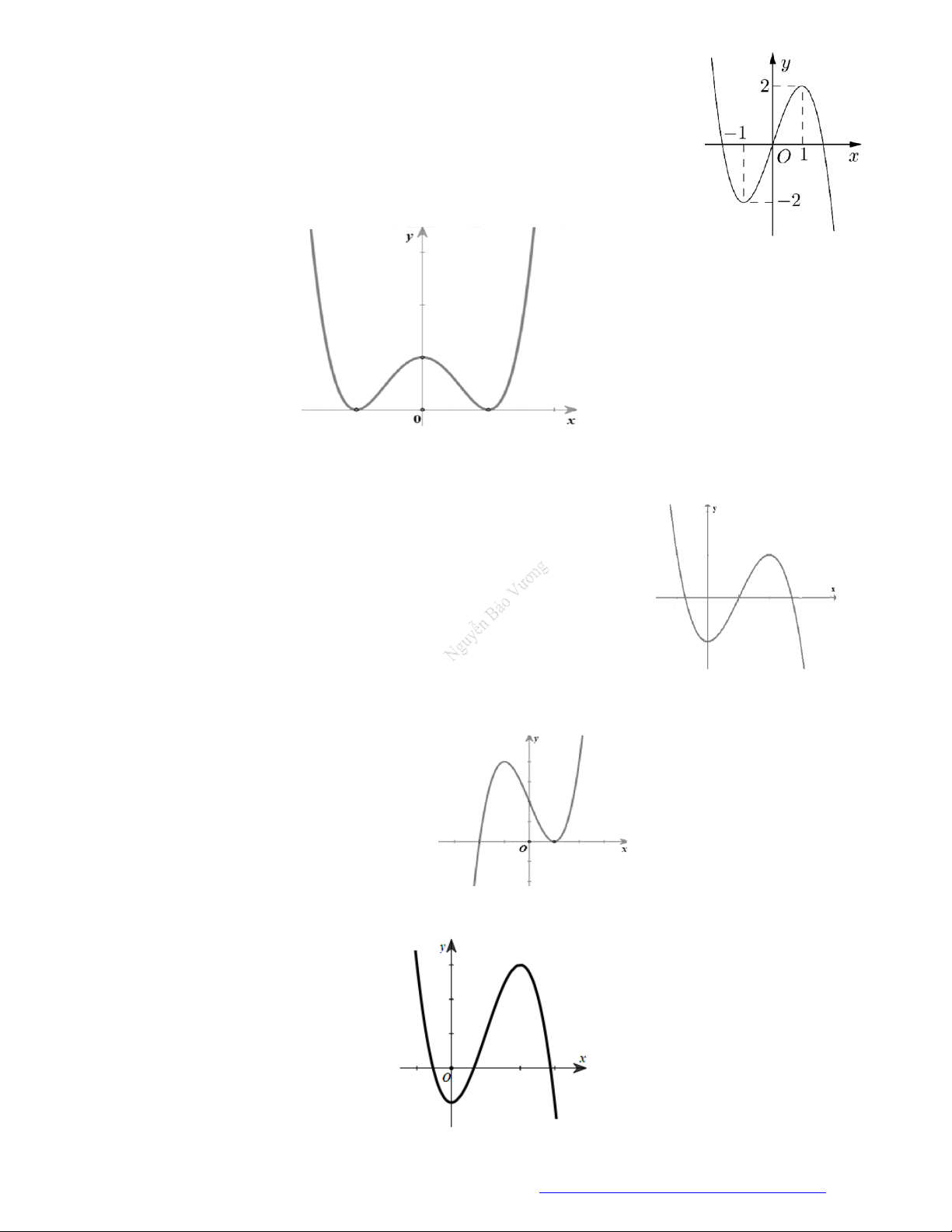
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Câu 5. (Mã 103 - 2020 Lần 1) Cho hàm số bậc ba
y f x
có đồ thị là
đường cong trong hình bên. Số nghiệm thực của phương trình
1f x
là
A.
1
. B.
0
.
C.
2
. D.
3
.
Câu 6. (Mã 104 - 2020 Lần 1) Đồ thị hàm số nào dưới đây có dạng như
đường cong trong hình bên?
A.
4 2
2 1y x x
. B.
3 2
3 1y x x
. C.
3 2
3 1y x x
. D.
4 2
2 1y x x
.
Câu 7. (Mã 101 - 2020 Lần 2) Đồ thị hàm số nào dưới đây có dạng như đường cong hình bên
A.
4 2
y x 2x 2
B.
3 2
y x 2x 2
C.
3 2
y x 3x 2
D.
4 2
y x 2x 2
Câu 8. (Mã 104 2017) Đường cong hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là
hàm số nào?
A.
3
3 2y x x B.
4 2
1y x x C.
4 2
1y x x D.
3
3 2y x x
Câu 9. (Mã 102 - 2020 Lần 2) Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
A.
4 2
2 1y x x
. B.
4 2
2 1y x x
. C.
3 2
3 1y x x
. D.
3 2
3 1y x x
.
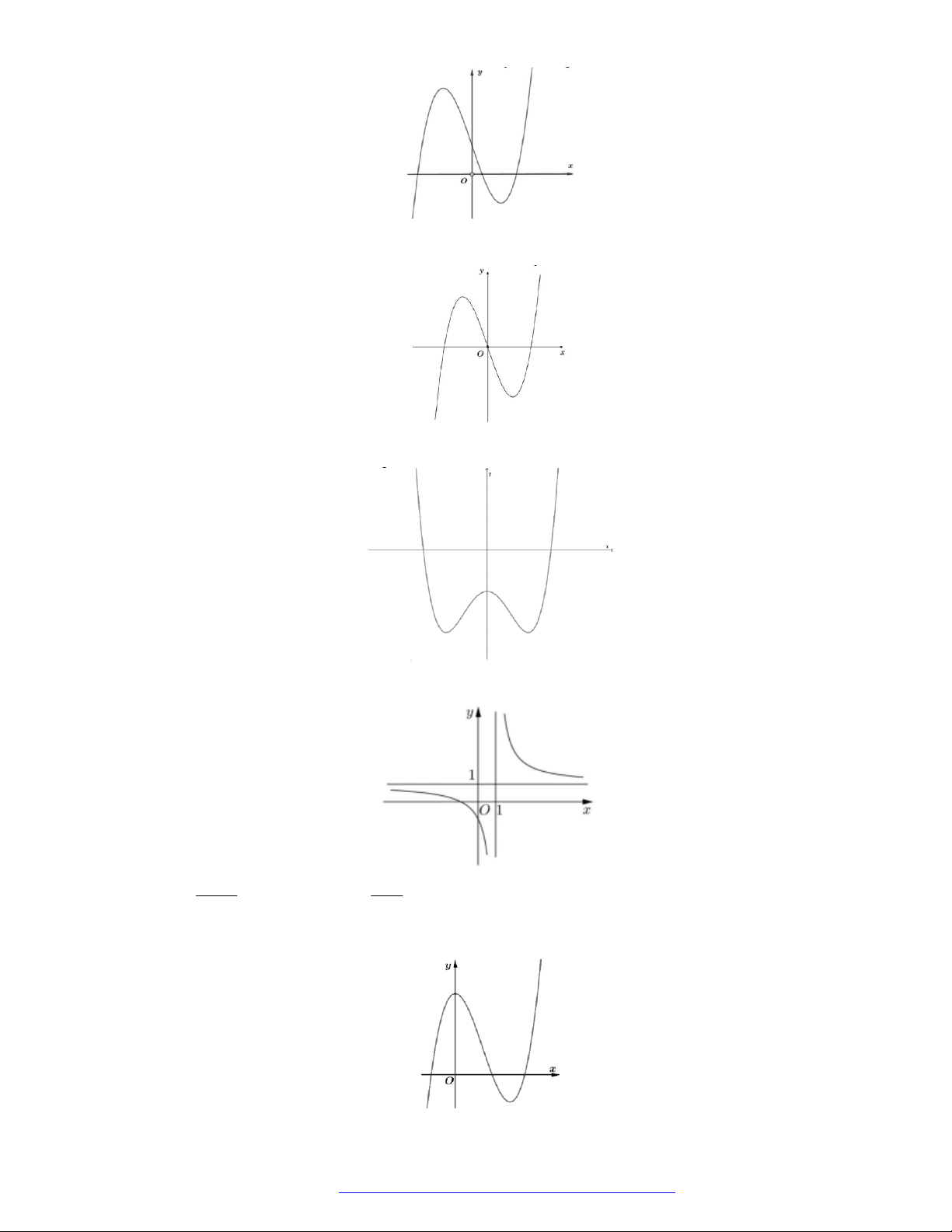
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 10. (Mã 103 - 2020 Lần 2) Đồ thị của hàm số dưới đây có dạng như đường cong bên?
A.
3
3 1y x x
. B.
4 2
2 1
y x x
. C.
4 2
2 1
y x x
. D.
3
3 1y x x
.
Câu 11. (Mã 104 - 2020 Lần 2) Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
A.
4 2
2y x x . B.
3
3y x x . C.
3
3y x x . D.
4 2
2y x x .
Câu 12. (Mã 102 2018) Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
A.
3 2
1y x x B.
4 2
2 1y x x C.
3 2
1y x x D.
4 2
2 1y x x
Câu 13. (Đề Tham Khảo 2019) Đường con trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
A.
2 1
1
x
y
x
B.
1
1
x
y
x
C.
4 2
1y x x
D.
3
3 1y x x
Câu 14. (Mã 110 2017) Đường cong ở hình bên dưới là đồ thị của một trong bốn hàm số dưới đây. Hàm
số đó là hàm số nào?
A.
3 2
3 1y x x
B.
3 2
3 3y x x
C.
4 2
2 1y x x
D.
4 2
2 1y x x
.
Câu 15. (Mã 103 2019) Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên?
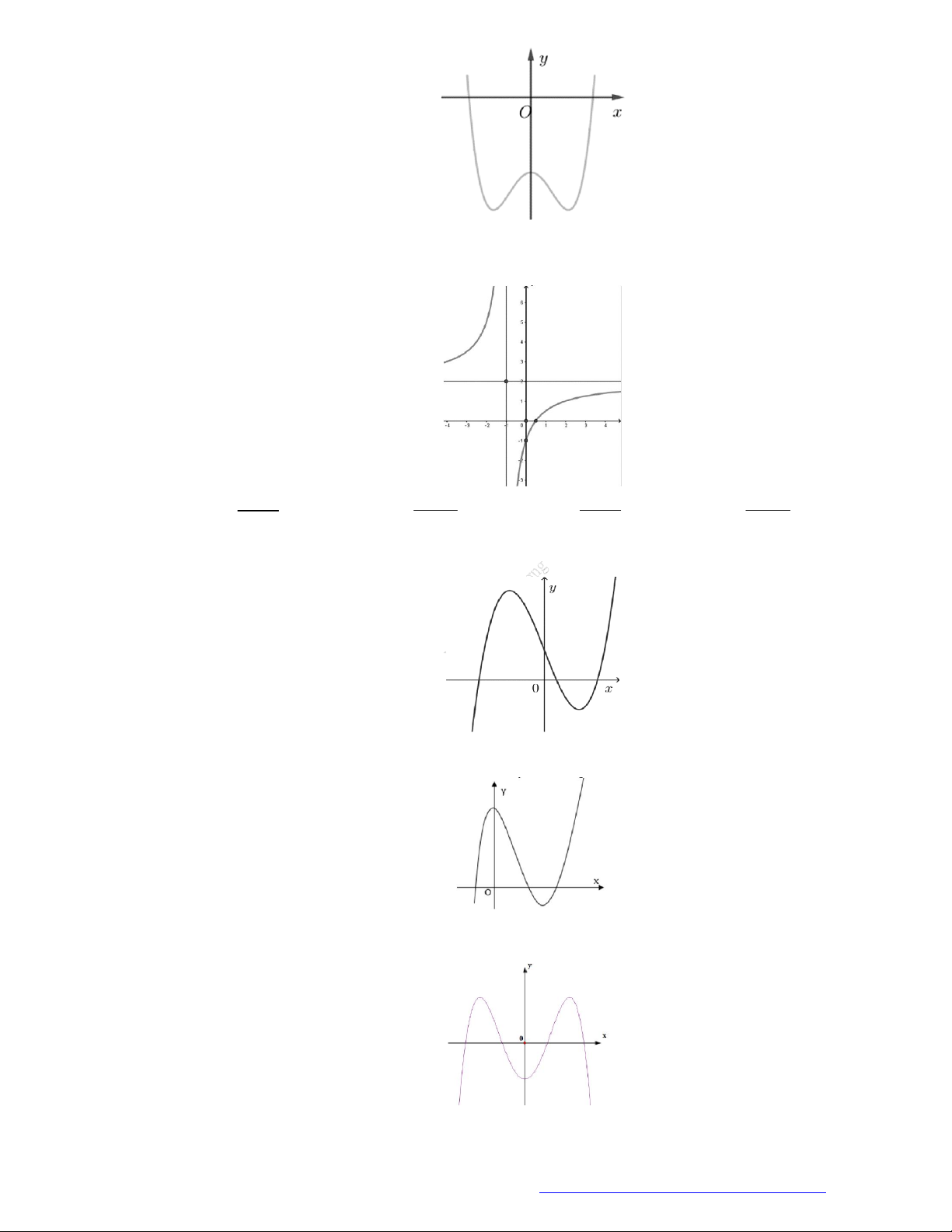
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
A.
3 2
3 2y x x
. B.
4 2
2 2y x x
. C.
3 2
3 2y x x
. D.
4 2
2 2y x x
.
Câu 16. (Đề Tham Khảo 2017) Cho đường cong hình vẽ bên là đồ thị của một hàm số trong bốn hàm số
được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi đó là hàm số nào?
A.
2 1
y
1
x
x
B.
2 3
1
x
y
x
C.
2 1
1
x
y
x
D.
2 2
1
x
y
x
Câu 17. (Đề Minh Họa 2017) Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số
được liệt kê ở bốn phương án
, , ,A B C D
dưới đây. Hỏi hàm số đó là hàm số nào?
A.
3
3 1y x x B.
3
3 1y x x C.
4 2
1y x x D.
2
1y x x
Câu 18. (Mã 101 2019) Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên?
A.
3 2
3 3y x x
. B. 33
23
xxy . C. 32
24
xxy . D. 32
24
xxy .
Câu 19. (Mã 101 2018) Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
A.
3 2
3 1y x x B.
3 2
3 1y x x C.
4 2
3 1y x x D.
4 2
3 1y x x
Câu 20. (Mã 104 2019) Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên?
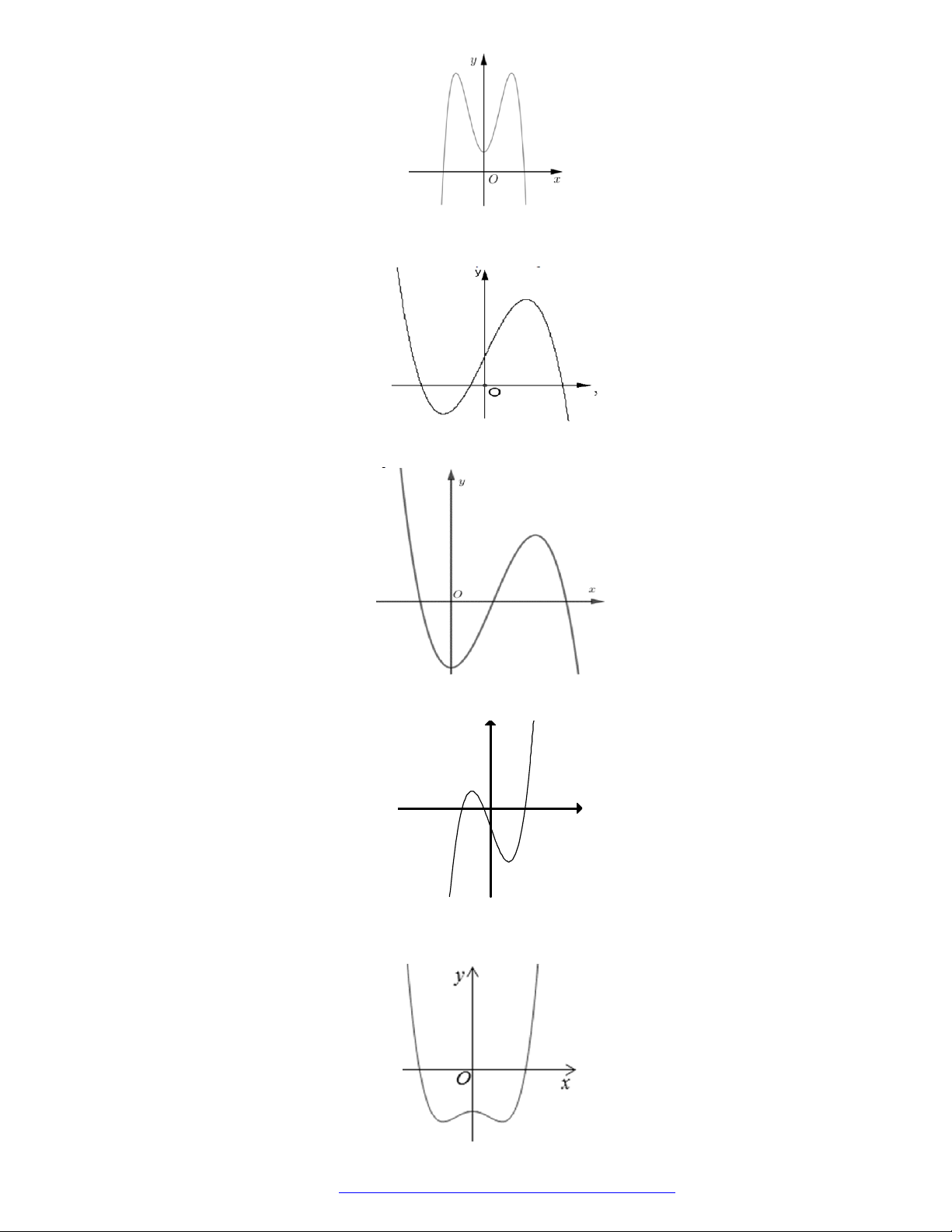
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
4 2
2 4 1y x x B.
3
2 3 1y x x C.
3
2 3 1y x x D.
4 2
2 4 1y x x
Câu 21. (Mã 102 2019) Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên
A.
3
3 1y x x
. B.
3
3 1y x x
. C.
4 2
2 1y x x
. D.
4 2
2 1y x x
.
Câu 22. (Mã 104 2018) Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
A.
4 2
2y x x
B.
4 2
2y x x
C.
3 2
3 2y x x
D.
3 2
3 2y x x
Câu 23. (Mã 103 2018) Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
A.
3
3 1y x x B.
4 2
3 1y x x C.
3
3 1y x x D.
4 2
1y x x
Câu 24. (Mã 123 2017) Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó
là hàm số nào?
A.
4 2
1y x x
B.
4 2
1y x x
C.
3 2
1y x x
D.
3 2
1y x x
x
y
O
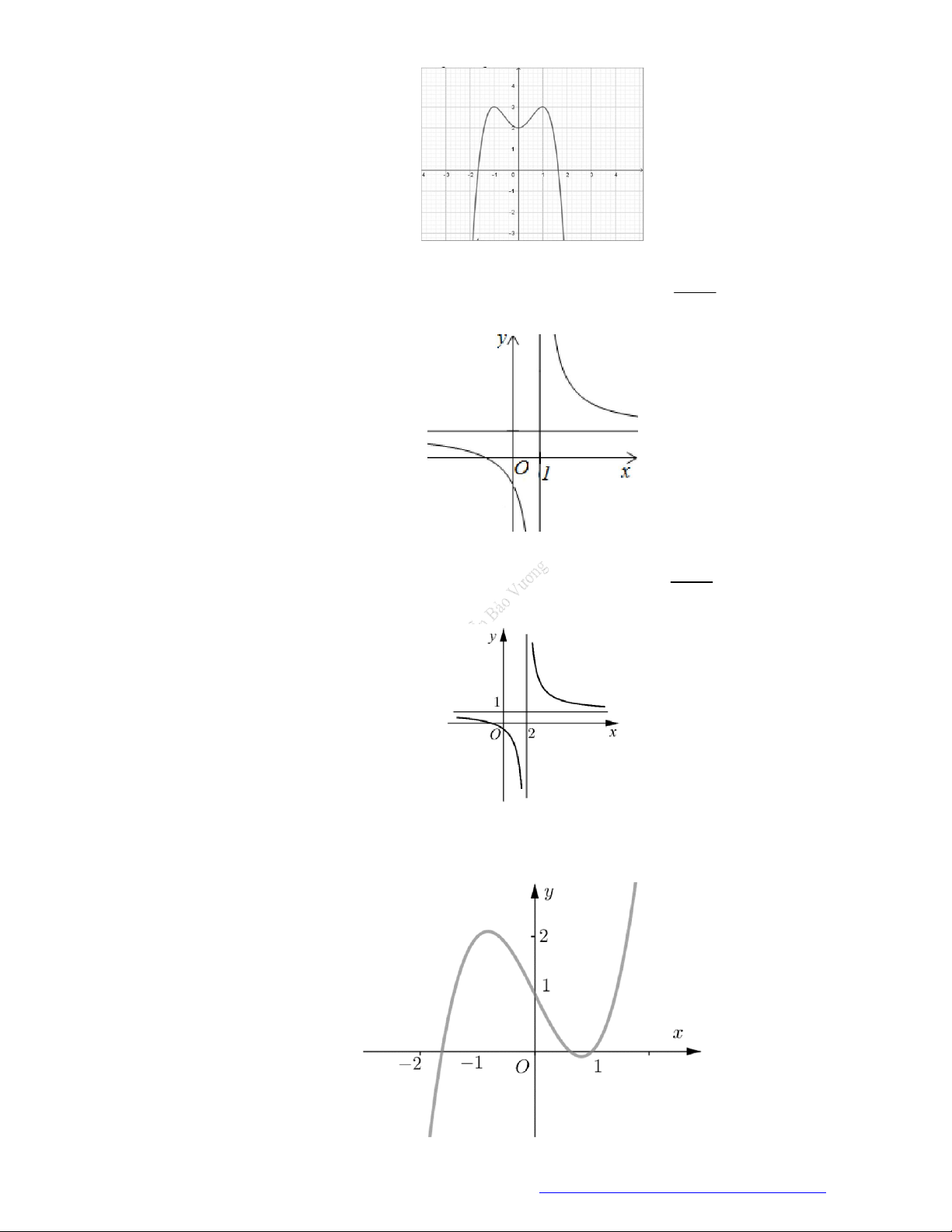
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Câu 25. (Đề Tham Khảo 2018) Đường cong trong hình bên là của đồ thị hàm số nào dưới đây?
A.
3 2
3 2 y x x
B.
3 2
3 2 y x x
C.
4 2
2 2 y x x
D.
4 2
2 2 y x x
Câu 26. (Mã 123 2017) Đường cong ở hình bên là đồ thị của hàm số
ax b
y
cx d
với , , ,a b c d là các số
thực. Mệnh đề nào dưới đây đúng?
A.
0,y x
B.
0, 1y x
C.
0, 1y x
D.
0,y x
Câu 27. (Mã 105 2017) Đường cong ở hình bên là đồ thị của hàm số
ax b
y
cx d
với , , ,a b c d là các số
thực. Mệnh đề nào dưới đây đúng?
A.
y 0, 1x
B.
y 0, x 1
C.
y 0, x 2
D.
y 0, 2
Câu 28. (THPT Yên Phong 1 Bắc Ninh 2019) Hình vẽ sau đây là đồ thị của một trong bốn hàm số cho ở
các đáp án
, , ,A B C D
. Hỏi đó là hàm số nào?
A.
3
2 1y x x . B.
3 2
2 1y x x . C.
3
2 1y x x
. D.
3
2 1y x x
.
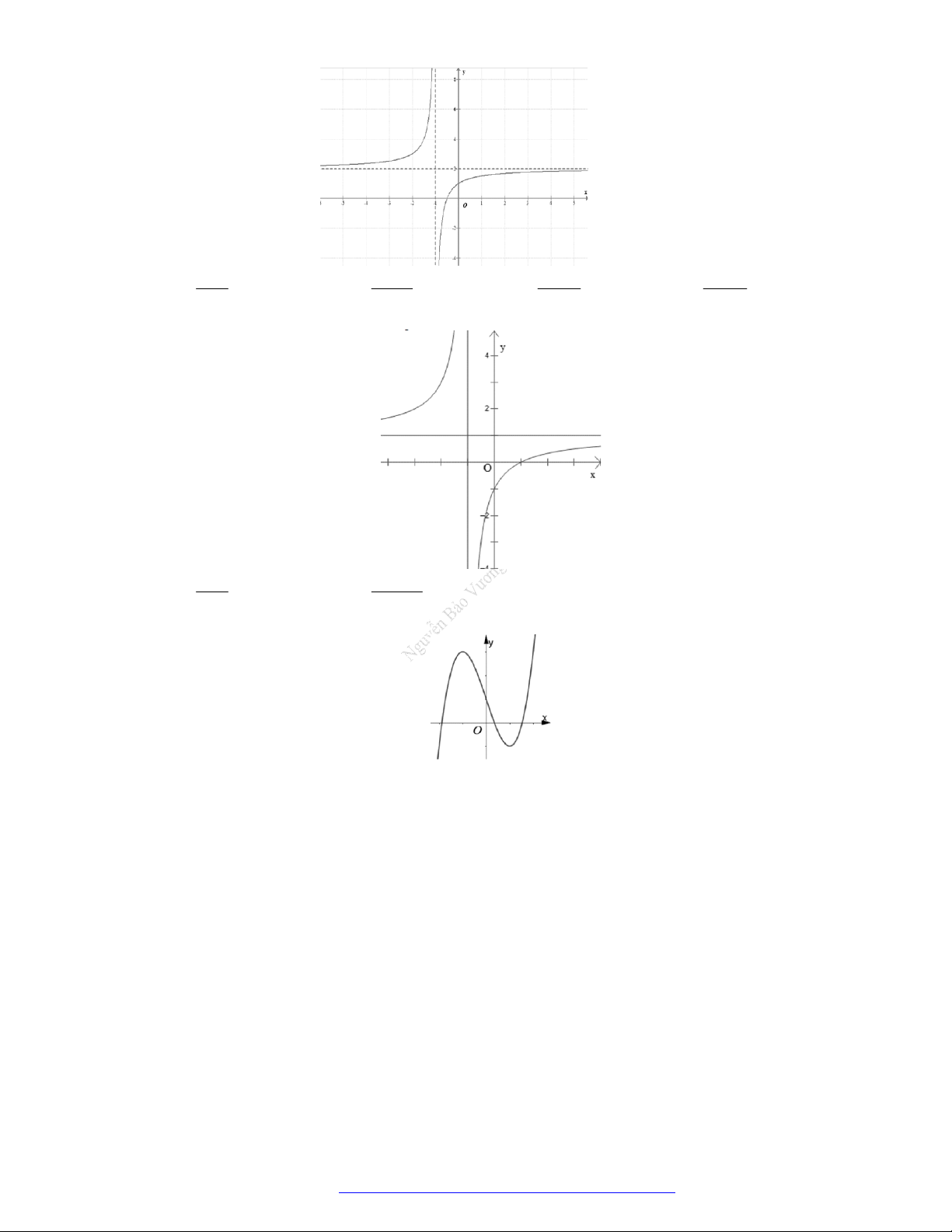
NGUYỄ
N BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 29. (Sở Cần Thơ - 2019
) Hình vẽ bên dưới là đồ thị của hàm số nào
A.
1
1
x
y
x
. B.
2
1
1
x
y
x
. C.
2
3
1
x
y
x
. D.
2
5
1
x
y
x
.
Câu 30. (SGD Nam Định) Đường cong trong hình là đồ thị của hàm số nào dưới đây?
A.
1
1
x
y
x
. B.
2 1
2 2
x
y
x
. C
.
4
2
3y
x x
. D.
3
2
3y
x x
.
Câu 31. (Sở Gia Lai 2019) Đường cong trong hình vẽ bên là đồ thị của hàm số nào sau đây?
A.
3
3
1y x x
. B.
4
2
1y
x x
. C
.
2
1y
x x
. D.
3
3
1y x x
.
-------------------- HẾT --------------------
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
DẠNG TOÁN DÀNH CHO ĐỐI TƯỢNG HỌC SINH KHÁ MỨC 7-8 ĐIỂM
Dạng 1. Xét dấu của các hệ số hàm số thông qua đồ thị
Câu 1. (Đề Minh Họa 2020 Lần 1) Cho hàm số
3
3 ;y ax x d a d
có đồ thị như hình bên.
Mệnh đề nào dưới đây đúng?
A.
0, 0a d
. B.
0, 0a d
. C.
0, 0a d
. D.
0, 0a d
.
Câu 2. (Đề Tham Khảo 2020 Lần 2) Cho hàm số
1ax
f x
bx c
, ,a b c
có bảng biến thiên như
sau:
ĐỌC ĐỒ THỊ CỦA HÀM SỐ
Chuyên đề 7
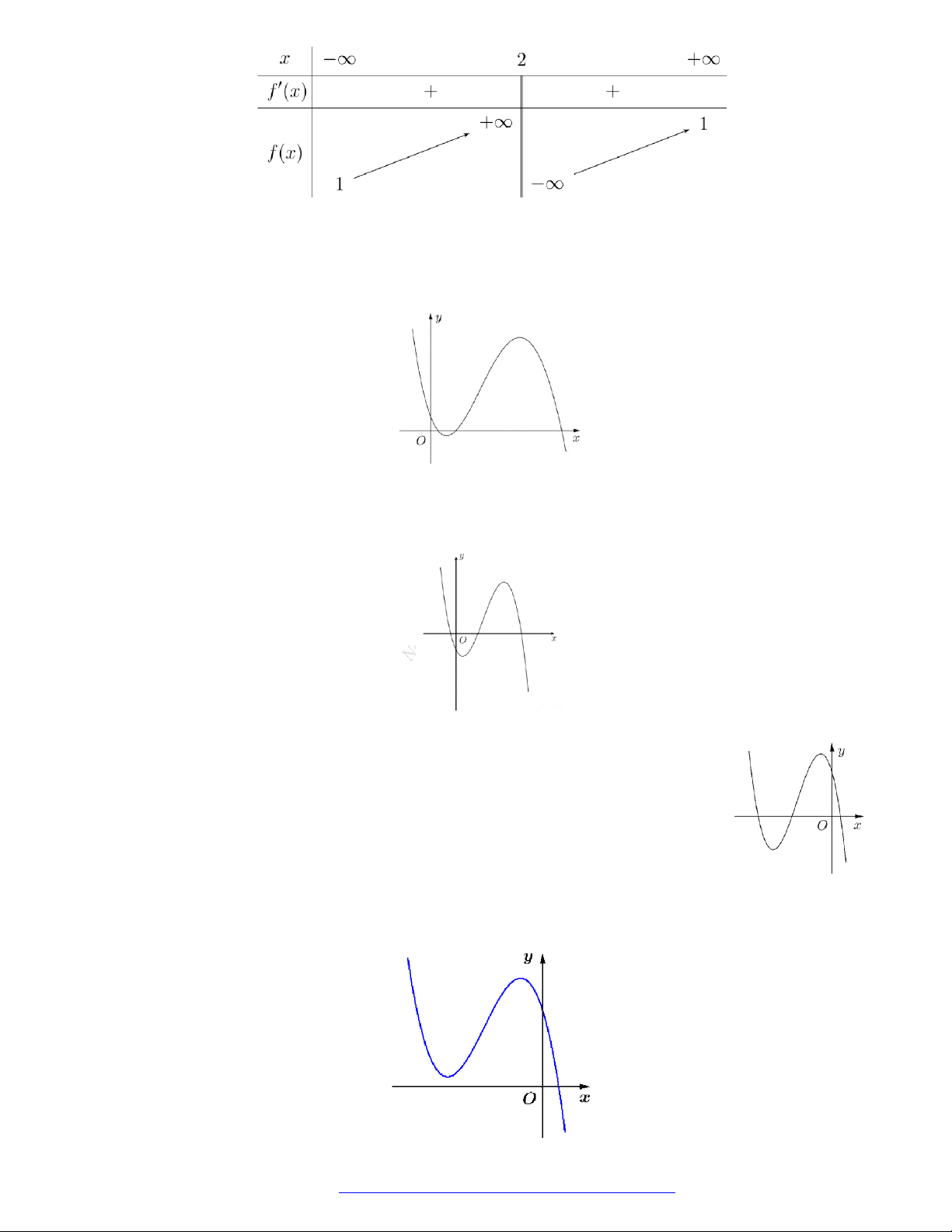
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Trong các số
,a b
và
c
có bao nhiêu số dương?
A. 2. B. 3. C. 1. D. 0.
Câu 3. (Mã 101 - 2020 Lần 1) Cho hàm số
3 2
y ax bx cx d
, , ,a b c d
có đồ thị là đường cong
trong hình bên. Có bao nhiêu số dương trong các số
a
,
b
,
c
,
d
?
A.
4
. B.
1
. C.
2
. D.
3
.
Câu 4. (Mã 102 - 2020 Lần 1) Cho hàm số y ax bx cx d
3 2
, , ,a b c d
có đồ thị là đường
cong trong hình bên. Có bao nhiêu số dương trong các hệ số
, , ,a b c d
?
A.
4
. B.
3
. C.
1
. D.
2
.
Câu 5. (Mã 103 - 2020 Lần 1) Cho hàm số
3 2
, , ,y ax bx cx d a b c d
có đồ
thị là đường cong trong hình bên. Có bao nhiêu số dương trong các số
, , ,a b c d
?
A.
4
. B.
2
.
C.
1
. D.
3
.
Câu 6. (Mã 104 - 2020 Lần 1) Cho hàm số
3 2
, , , y ax bx cx d a b c d
có đồ thị là đường cong
trong hình bên. Có bao nhiêu số dương trong các số
, , ,a b c d
?
A.
4
. B.
2
. C.
1
. D.
3
.
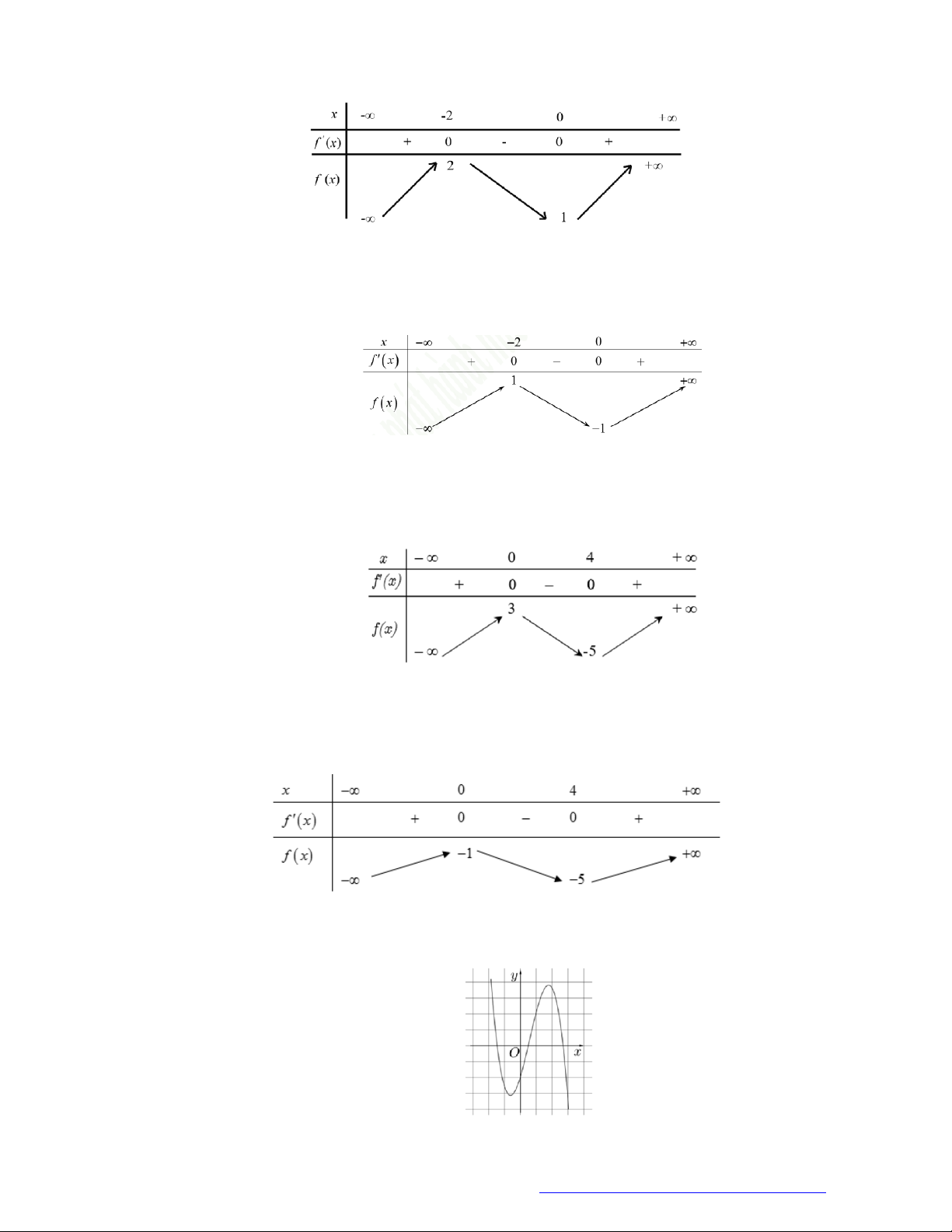
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Câu 7. (Mã 102 - 2020 Lần 2) Cho hàm số
3 2
, , , f x ax bx cx d a b c d
có bảng biến thiên
như sau
Có bao nhiêu số dương trong các số
, , , a b c d
?
A.
2
. B.
4
. C.
1
. D.
3
.
Câu 8. (Mã 103 - 2020 Lần 2) Cho hàm số
3 2
, , ,f x ax bx cx d a b c d
có bảng biến thiên
như sau:
Có bao nhiêu số dương trong các số
, , , ?a b c d
A.
3.
B.
4.
C.
2.
D.
1.
Câu 9. (Mã 101 – 2020 Lần 2) Cho hàm số
3 2
, , ,f x ax bx cx d a b c d
có bảng biến thiên
như sau:
Có bao nhiêu số dương trong các số
, , ,a b c d
?
A.
2
. B.
4
. C.
1
. D.
3
.
Câu 10. (Mã 104 - 2020 Lần 2) Cho hàm số
3 2
, , ,f x ax bx cx d a b c d
có bảng biến thiên
như sau:
Có bao nhiêu số dương trong các số
, , ,a b c d
?
A.
4
. B.
2
. C.
3
. D.
1
.
Câu 11. Cho hàm số
3 2
y ax bx cx d có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?
A.
0, 0, 0, 0 a b c d
B.
0, 0, 0, 0 a b c d
.
C.
0, 0, 0, 0 a b c d
D.
0, 0, 0, 0 a b c d
.
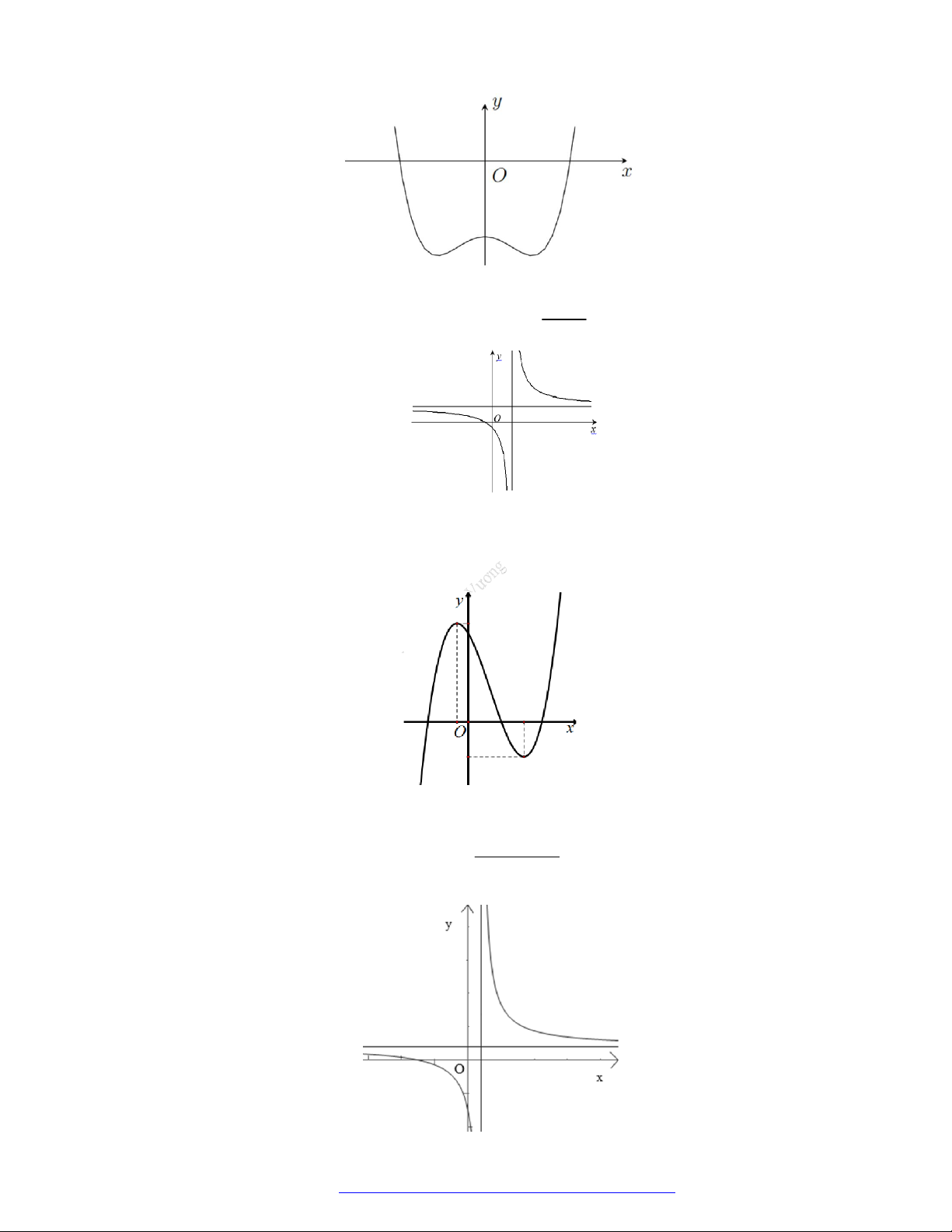
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 12. (THPT Nguyễn Khuyến 2019) Cho hàm số
4 2
y ax bx c có đồ thị như hình bên. Mệnh đề
nào dưới đây là đúng?
A.
0, 0, 0a b c
B.
0, 0, 0a b c
C.
0, 0, 0a b c
D.
0, 0, 0a b c
Câu 13. (Chuyên Trần Phú Hải Phòng 2019) Cho hàm số
ax b
y
cx d
có đồ thị như sau.
Mệnh đề nào sau đây đúng?
A.
0; 0ac bd
B.
0; 0ab cd
C.
0; 0bc ad
D.
0; 0ad bd
Câu 14. (THPT Thiệu Hóa – Thanh Hóa 2019) Cho hàm số
3 2
0y ax bx cx d a
có đồ thị như
hình vẽ dưới đây. Chọn khẳng định đúng về dấu của
a
,
b
,
c
,
d
?
A.
0a
,
0b
,
0d
,
0c
B.
0a
,
0c b
,
0d
C.
0, 0, 0, 0.a b c d
D.
0a
,
0b
,
0c
,
0d
Câu 15. (Toán Học Tuổi Trẻ 2019) Cho hàm số
1
, 0
1
a x b
y d
c x d
có đồ thị như hình trên. Khẳng
định nào dưới đây là đúng?
A.
1, 0, 1.a b c
B.
1, 0, 1.a b c
C.
1, 0, 1.a b c
D.
1, 0, 1.a b c
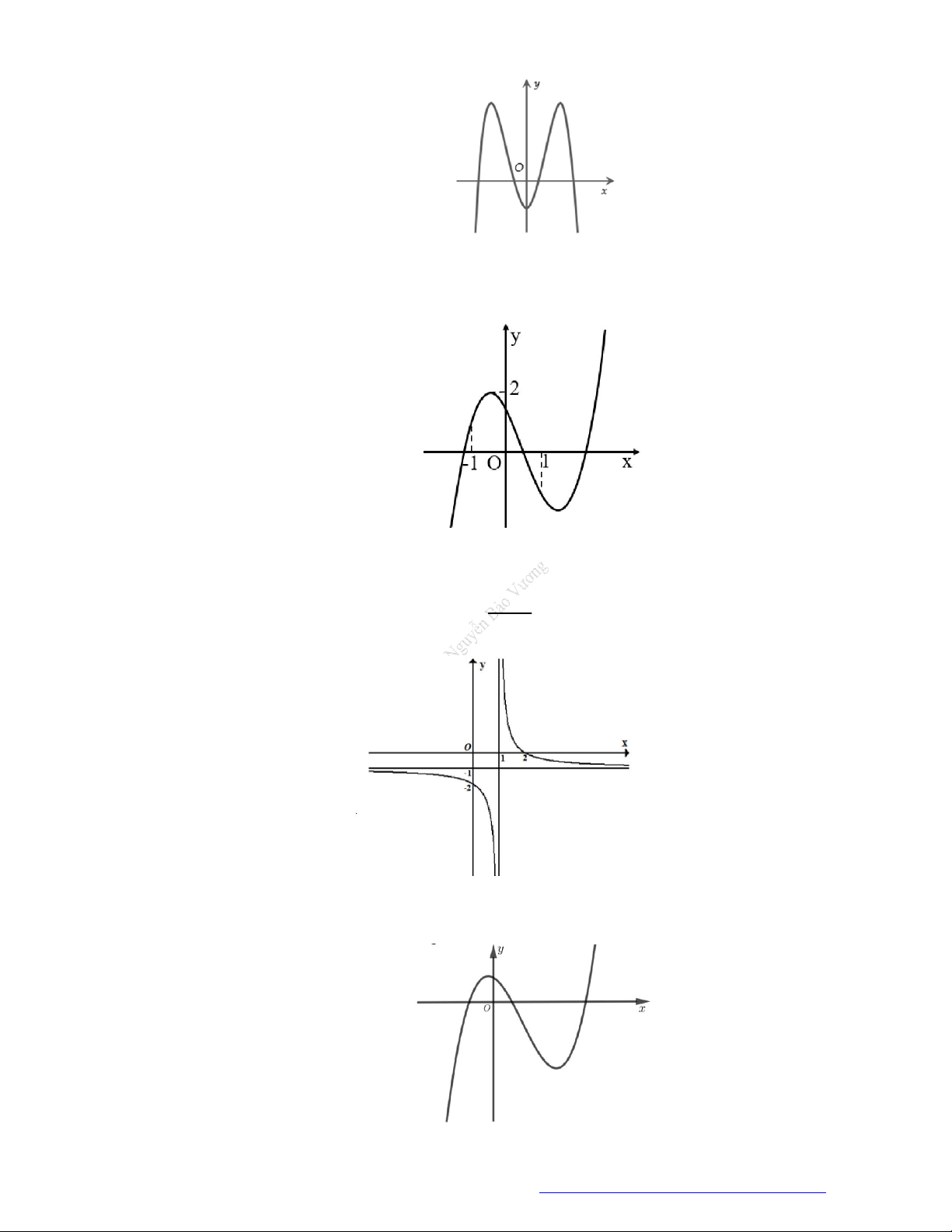
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Câu 16. (Sở Ninh Bình 2019) Cho hàm số
4 2
y ax bx c
(
0a
) có đồ thị như hình vẽ dưới đây.
Mệnh đề nào dưới đây đúng?
A.
0a
,
0b
,
0c
. B.
0a
,
0b
,
0c
. C.
0a
,
0b
,
0c
. D.
0a
,
0b
,
0c
.
Câu 17. (Cụm Liên Trường Hải Phòng 2019) Hàm số
3 2
y ax bx cx d
có đồ thị như hình vẽ bên
dưới:
Khẳng định nào là đúng?
A.
0a
,
0b
,
0c
,
0d
. B.
0a
,
0b
,
0c
,
0d
.
C.
0a
,
0b
,
0c
,
0d
. D.
0a
,
0b
,
0c
,
0d
.
Câu 18. (THPT Ba Đình 2019) Cho hàm số
ax b
y
x c
có đồ thị như hình bên dưới, với
a
,
b
,
c
.
Tính giá trị của biểu thức
2 3T a b c
?
A.
8T
. B.
2T
. C.
6T
. D.
0T
.
Câu 19. (THPT Việt Đức Hà Nội 2019) Cho hàm số
3 2
y ax bx cx d
có đồ thị như hình bên. Trong
các mệnh đề sau mệnh đề nào đúng?
A.
0, 0, 0ab bc cd
B.
0, 0, 0ab bc cd
C.
0, 0, 0ab bc cd
D.
0, 0, 0ab bc cd
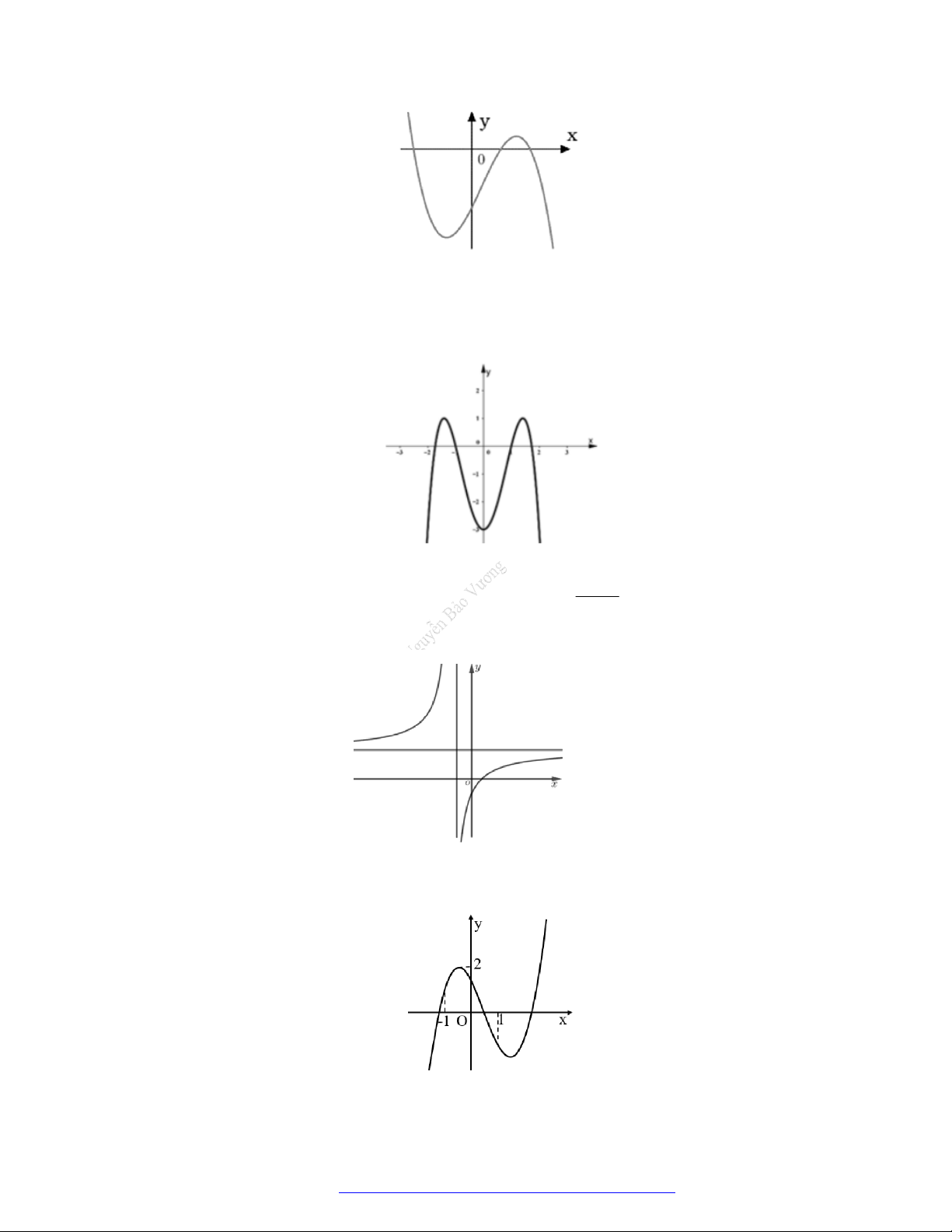
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 20. (THPT Lương Thế Vinh Hà Nội 2019) Cho hàm số
3 2
y ax bx cx d
có đồ thị như hình
dưới. Khẳng định nào sau đây đúng ?
A.
0, 0, 0, 0a b c d
B.
0, 0, 0, 0a b c d
C.
0, 0, 0, 0a b c d
D.
0, 0, 0, 0a b c d
Câu 21. (THPT Chuyên Bắc Ninh 2019) Cho hàm số có đồ thị như hình vẽ. Mệnh đề
nào dưới đây đúng?
A.
0, 0, 0a b c
. B.
0, 0, 0a b c
. C.
0, 0, 0a b c
. D.
0, 0, 0a b c
Câu 22. (Chuyên Lê Quý Đôn Quảng Trị 2019) Cho hàm số
ax b
y
cx d
có đồ thị như trong hình bên
dưới. Biết rằng
a
là số thực dương, hỏi trong các số
, ,b c d
có tất cả bao nhiêu số dương?
A.
1
. B.
2
. C.
0
. D.
3
.
Câu 23. (Cụm liên trường Hải Phòng 2019) Hàm số
3 2
y ax bx cx d
có đồ thị như hình vẽ bên
dưới:
Khẳng định nào là đúng?
A.
0a
,
0b
,
0c
,
0d
. B.
0a
,
0b
,
0c
,
0d
.
C.
0a
,
0b
,
0c
,
0d
. D.
0a
,
0b
,
0c
,
0d
.
4 2
y ax bx c

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Câu 24. (Chuyên Nguyễn Huệ 2019) Cho hàm số
ax b
y
cx d
có đồ thị như hình vẽ bên. Khẳng định nào
sau đây là khẳng định đúng?
A.
0
0
ad
bc
. B.
0
0
ad
bc
. C.
0
0
ad
bc
. D.
0
0
ad
bc
.
Câu 25. Tìm đồ thị hàm số
y f x
được cho bởi một trong các phương án dưới đây, biết
2
f x a x b x
với
a b
.
A. . B. .
C. . D. .
Câu 26. Cho đường cong
3 2
:C y ax bx cx d
có đồ thị như hình bên.
Khẳng định nào sau đây là đúng?
A.
0, 0, 0, 0a b c d
. B.
0, 0, 0, 0a b c d
.
C.
0, 0, 0, 0a b c d
. D.
0, 0, 0, 0a b c d
.
Câu 27. (Gia Lai 2019) Hàm số
4 2
y ax bx c
có đồ thị như hình vẽ bên. Mệnh đề nào sau đây
đúng?
A.
0a
,
0b
,
0c
. B.
0a
,
0b
,
0c
.
C.
0a
,
0b
,
0c
. D.
0a
,
0b
,
0c
.
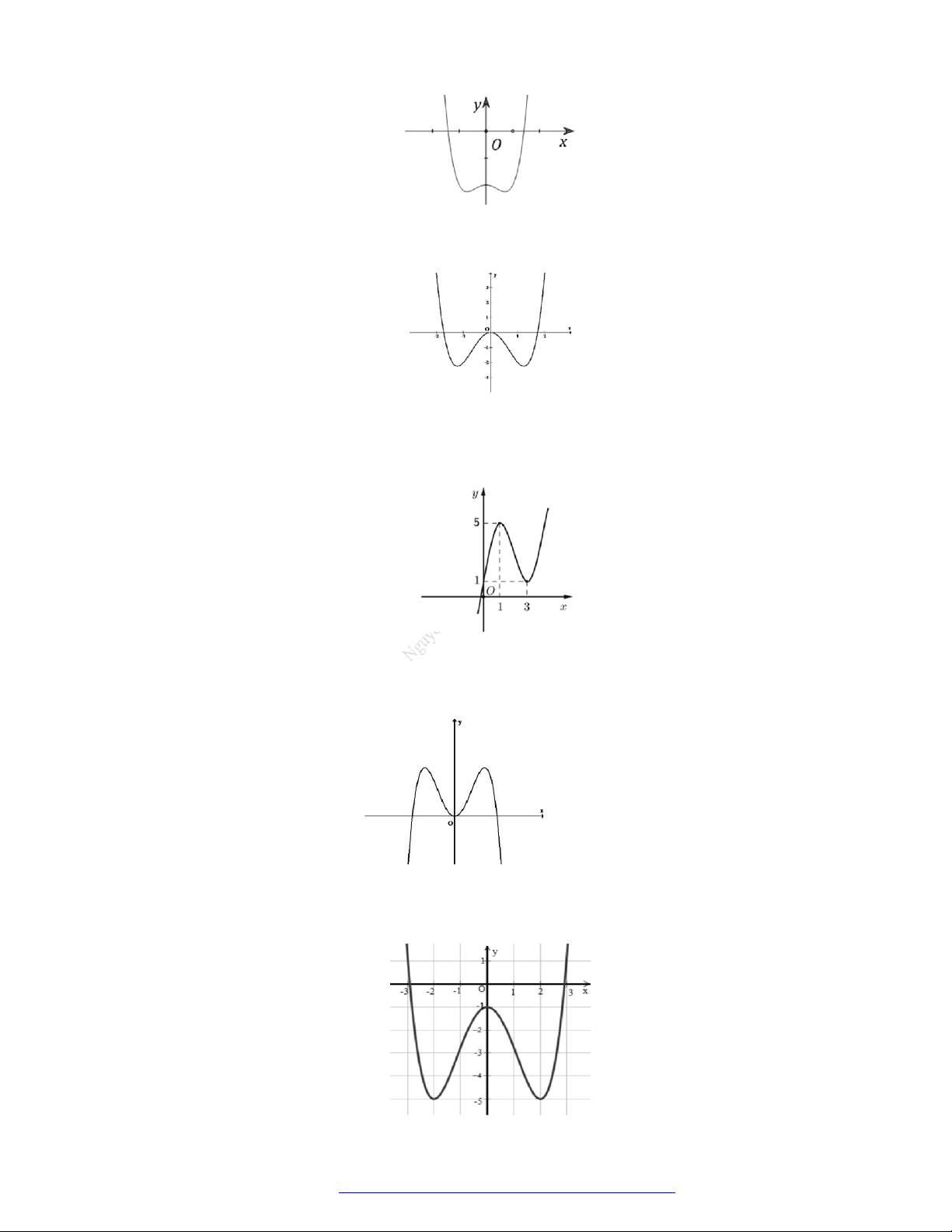
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 28. (THPT Thăng Long 2019) Cho hàm số
4 2
y ax bx c
có đồ thị như hình vẽ. Tìm kết luận
đúng
A.
0a b
. B.
0bc
. C.
0ab
. D.
0ac
.
Câu 29. (THPT Cẩm Bình Hà Tỉnh 2019) Cho hàm số
4 2
( 0)y ax bx c a
có đồ thị như hình bên.
Hãy chọn mệnh đề đúng.
A.
0, 0, 0a b c
. B.
0, 0, 0a b c
. C.
0, 0, 0a b c
. D.
0, 0, 0a b c
.
Câu 30. (Chuyên Long An 2019) Cho hàm số
3 2
( )y f x ax bx cx d có đồ thị như hình vẽ ở bên.
Mệnh đề nào
sau đây đúng?
A.
0a
,
0b
,
0c
,
0d
. B.
0a
,
0b
,
0c
,
0d
.
C.
0a
,
0b
,
0c
,
0d
. D.
0a
,
0b
,
0c
,
0d
.
Câu 31. (THPT Trần Phú 2019) Cho hàm số bậc bốn trùng phương
4 2
y ax bx c có đồ thị như
hình vẽ bên. Mệnh đề nào dưới đây là đúng?
A.
0, 0, 0a b c
. B.
0, 0, 0a b c
. C.
0, 0, 0a b c
. D.
0, 0, 0a b c
.
Câu 32. (THPT Cộng Hiền 2019) Cho hàm số
4 2
y ax bx c
có đồ thị như hình vẽ bên. Hỏi khẳng
định nào sau đây đúng?
A.
0, 0, 0a b c
. B.
0, 0, 0a b c
. C.
0, 0, 0a b c
. D.
0, 0, 0a b c
.
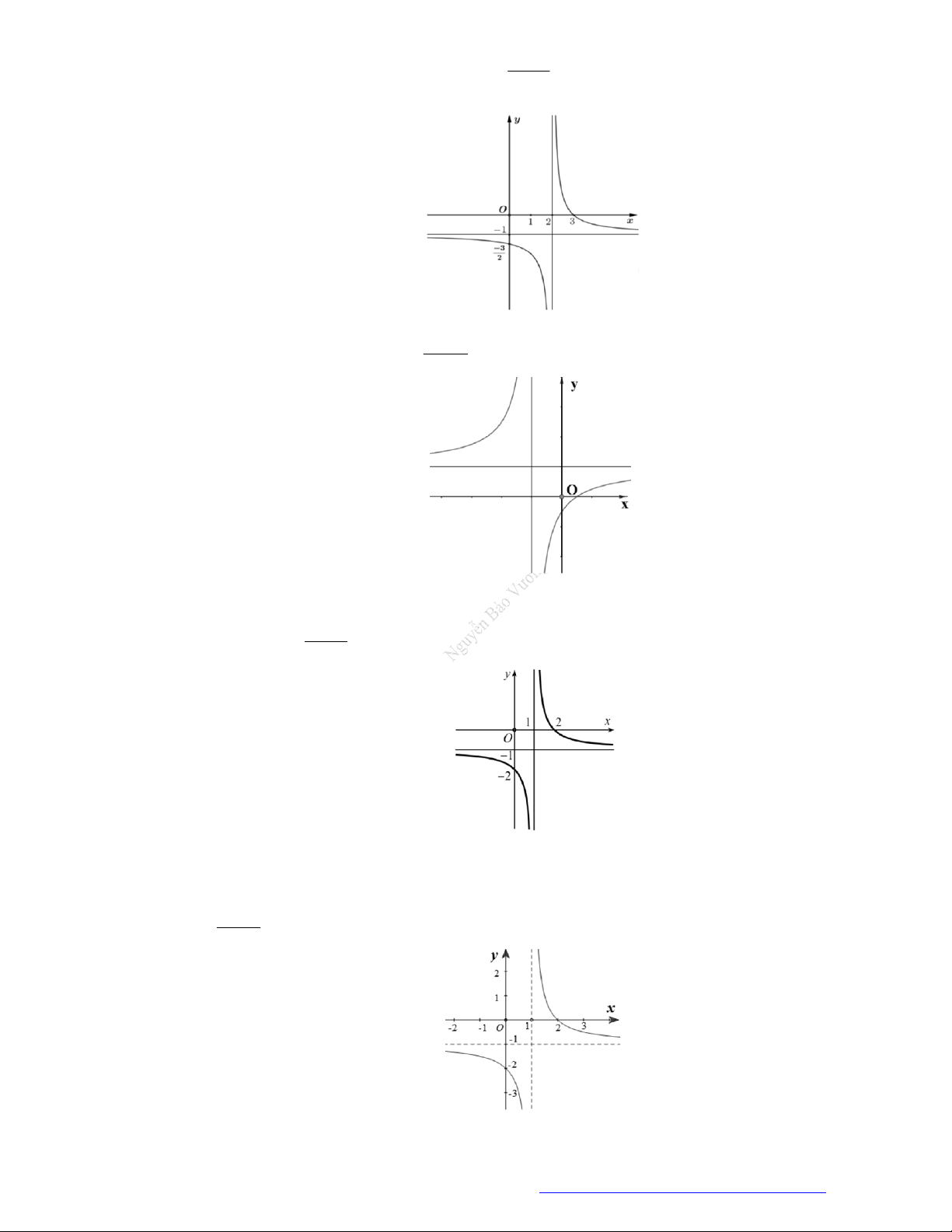
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Câu 33. (SGD Điện Biên - 2019) Cho hàm số
3ax
y
x c
có đồ thị như hình vẽ bên. Tính giá trị của
2 .a c
A.
2 3.a c
B.
2 3.a c
C.
2 1.a c
D.
2 2.a c
Câu 34. Hình vẽ bên là đồ thị hàm số
ax b
y
cx d
.
.
Mệnh đề nào dưới đây đúng?
A.
0ad
và
0bd
. B.
0ad
và
0ab
. C.
0bd
và
0ab
. D.
0ad
và
0ab
.
Câu 35. Cho hàm số
1
ax b
y
x
có đồ thị như hình vẽ dưới đây:
Khẳng định nào sau đây đúng?
A.
0b a
. B.
0a b
. C.
b a
và
0a
. D.
0a b
.
Câu 36. (Chuyên Lương Văn Chánh - Phú Yên - 2020) Đồ thị trong hình bên dưới là của hàm số
ax b
y
x c
(với
, ,a b c
).
Khi đó tổng
a b c
bằng
A.
1
. B.
1
. C.
2
. D.
0
.
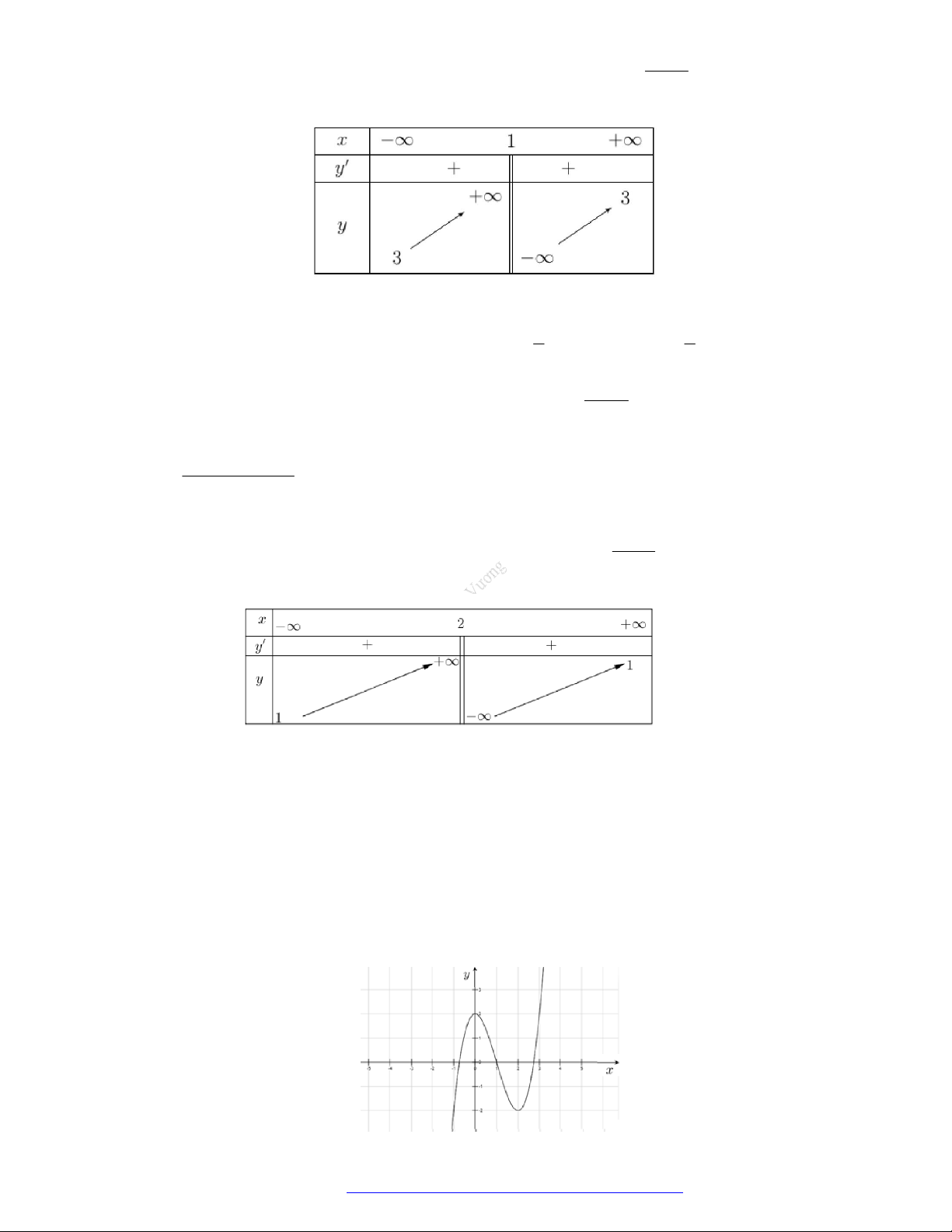
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 37. (Chuyên Lương Văn Tỵ - Ninh Bình - 2020) Cho hàm số
2
( )
ax
f x
bx c
, , , 0a b c b
có
bảng biến thiên như sau:
Tổng các số
2
a b c
thuộc khoảng nào sau đây
A.
1;2
. B.
2;3
. C.
4
0;
9
. D.
4
;1
9
.
Câu 38. (Chuyên Hùng Vương - Gia Lai - 2020) Cho hàm số
( )
ax b
f x
cx d
( , , ,a b c d
và
0c
). Biết
rằng đồ thị hàm số đã cho đi qua điểm
1;7
và giao điểm hai tiệm cận là
2;3
. Giá trị biểu
thức
2 3 4
7
a b c d
c
bằng
A.
7
. B.
4
. C.
6
. D.
5
.
Câu 39. (Chuyên Lê Hồng Phong - Nam Định - 2020) Cho hàm số
1ax
y
bx c
(
, ,a b c
là các tham số) có
bảng biến thiên như hình vẽ
Xét các phát biểu sau:
1 : 1; 2 : 0; 3 : 0; 4 : 0c a b a b c a
. Số phát biểu đúng
là?
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 40. (Đô Lương 4 - Nghệ An - 2020) Ta xác định được các số
, ,a b c
để đồ thị hàm số
3 2
y x ax bx c đi qua điểm
1;0
và có điểm cực trị
2;0
. Tính giá trị biểu thức
2 2 2
T a b c
.
A.
25.
B.
1.
C.
7.
D.
14.
Câu 41. (Lê Lai - Thanh Hóa - 2020) Cho hàm số có đồ thị như hình vẽ. Tính
?
A. . B. . C. . D. .
3 2
y ax bx cx d
S a b
2
S
0
S
1
S
1
S
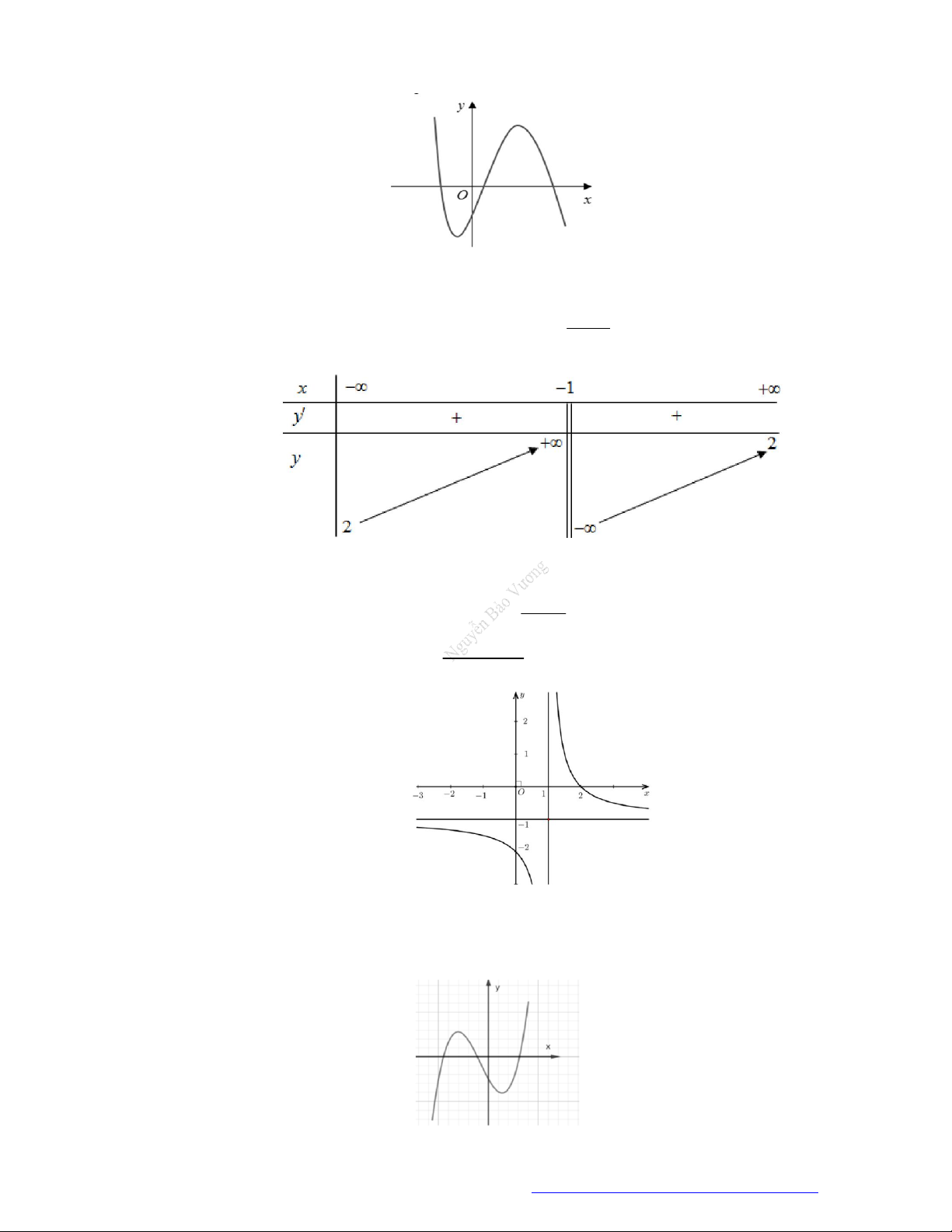
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Câu 42. (Lý Nhân Tông - Bắc Ninh - 2020) Cho hàm số
3 2
y ax bx cx d
có đồ thị như hình vẽ
bên. Mệnh đề nào dưới đây đúng?
A.
0, 0, 0, 0a b c d
. B.
0, 0, 0, 0a b c d
.
C.
0, 0, 0, 0a b c d
. D.
0, 0, 0, 0a b c d
.
Câu 43. (Nguyễn Huệ - Phú Yên - 2020) Cho hàm số
, ,
1
ax b
y a b c
cx
có bảng biến thiên như
sau:
Tập các giá trị
b
là tập nghiệm của bất phương trình nào dưới đây?
A.
3
8 0.b
B.
2
4 0.b
C.
2
3 2 0.b b
D.
3
8 0.b
Câu 44. (Tiên Du - Bắc Ninh - 2020) Cho hàm số
ax b
y
cx d
(với
, , ,a b c d
là số thực) có đồ thị như hình
dưới đây. Tính giá trị biểu thức
2 3a b d
T
c
.
A.
6T
. B.
0T
. C.
8 T
. D.
2T
.
Câu 45. (Thanh Chương 1 - Nghệ An - 2020) Cho hàm số
3 2
y ax bx cx d
có đồ thị như hình vẽ.
Trong các số
, ,a b c
và
d
có bao nhiêu số dương?
A.
1
. B.
4
. C.
3
. D.
2
.
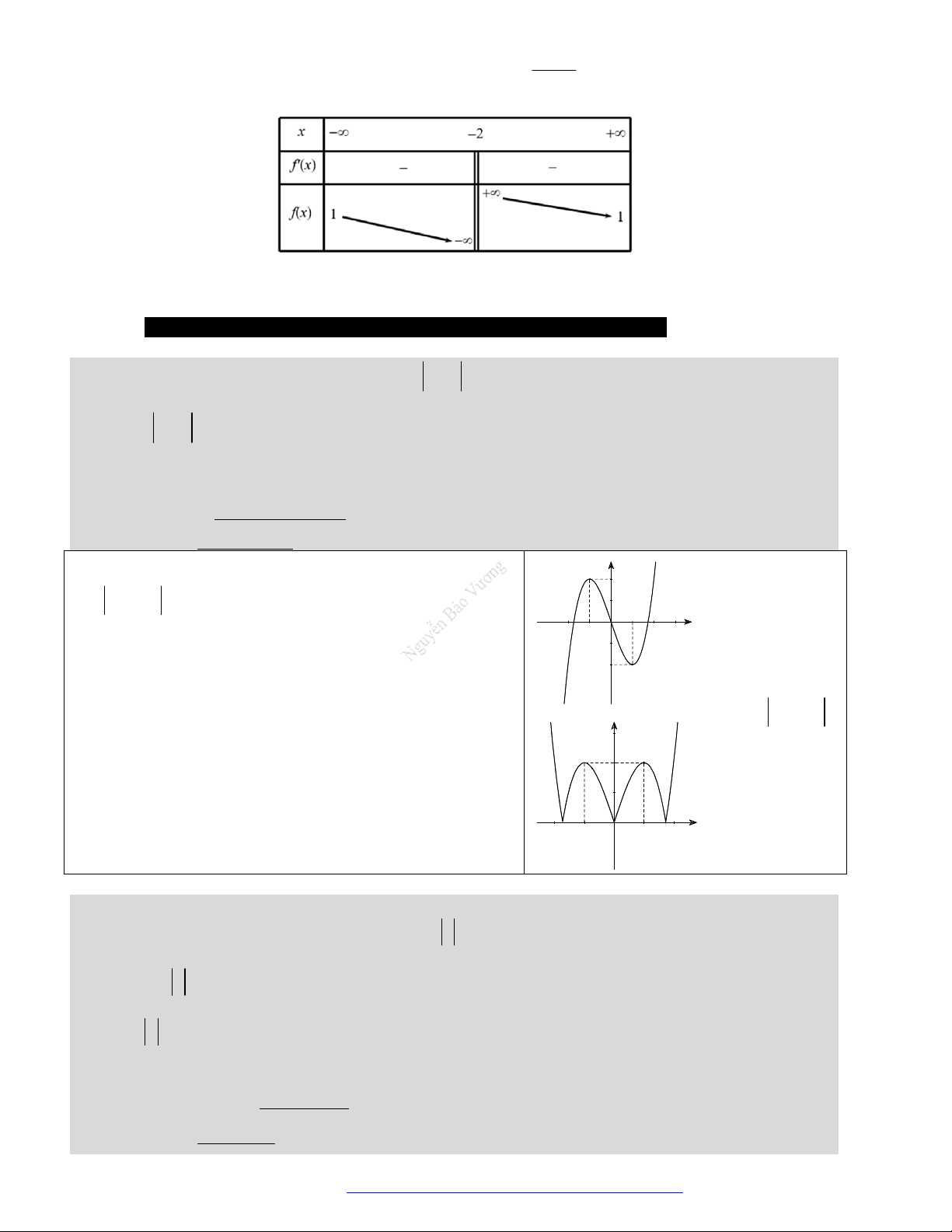
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 46. (Tiên Lãng - Hải Phòng - 2020) Cho hàm số
6
ax
f x
bx c
, , a b c
có bảng biến thiên như
sau:
Trong các số
, ,a b c
có bao nhiêu số âm?
A.
0
. B.
3
. C.
1
. D.
2
.
Dạng 2. Đồ thị hàm số chứa dấu giá trị tuyệt đối (BIẾN ĐỔI ĐỒ THỊ)
Dạng 1
Từ đồ thị
C y f x:
suy ra đồ thị
C y f x:
.
Ta có:
f x khi f x
y f x
f x khi f x
0
0
* Cách vẽ
C từ
C
:
Giữ nguyên phần đồ thị phía trên Ox của đồ thị (C):
y f x .
Bỏ phần đồ thị phía dưới Ox của (C), lấy đối xứng phần đồ thị bị bỏ qua Ox.
Ví dụ: Từ đồ thị
3
: 3C y f x x x
suy ra đồ thị
y x x
3
3 .
Biến đổi
C
:
Bỏ phần đồ thị của
C dưới ,Ox giữ nguyên
C phía trên
.Ox
L
ấy đối xứng phần đồ thị bị bỏ qua
Ox
.
Dạng 2
Từ đồ thị
C y f x: suy ra đồ thị
C y f x: .
Ta có:
f x khi x
y f x
f x khi x
0
0
và
y f x là hàm chẵn nên đồ thị
C
nhận Oy làm trục đối xứng.
* Cách vẽ
C từ
C :
Giữ nguyên phần đồ thị bên phải Oy của đồ thị
C y f x: .
Bỏ phần đồ thị bên trái Oy của
C , lấy đối xứng phần đồ thị được giữ qua Oy.
x
y
O
-2
2
-1
1
x
y
2
-1
O
1
3
: 3C y x x
C y x x
3
: 3
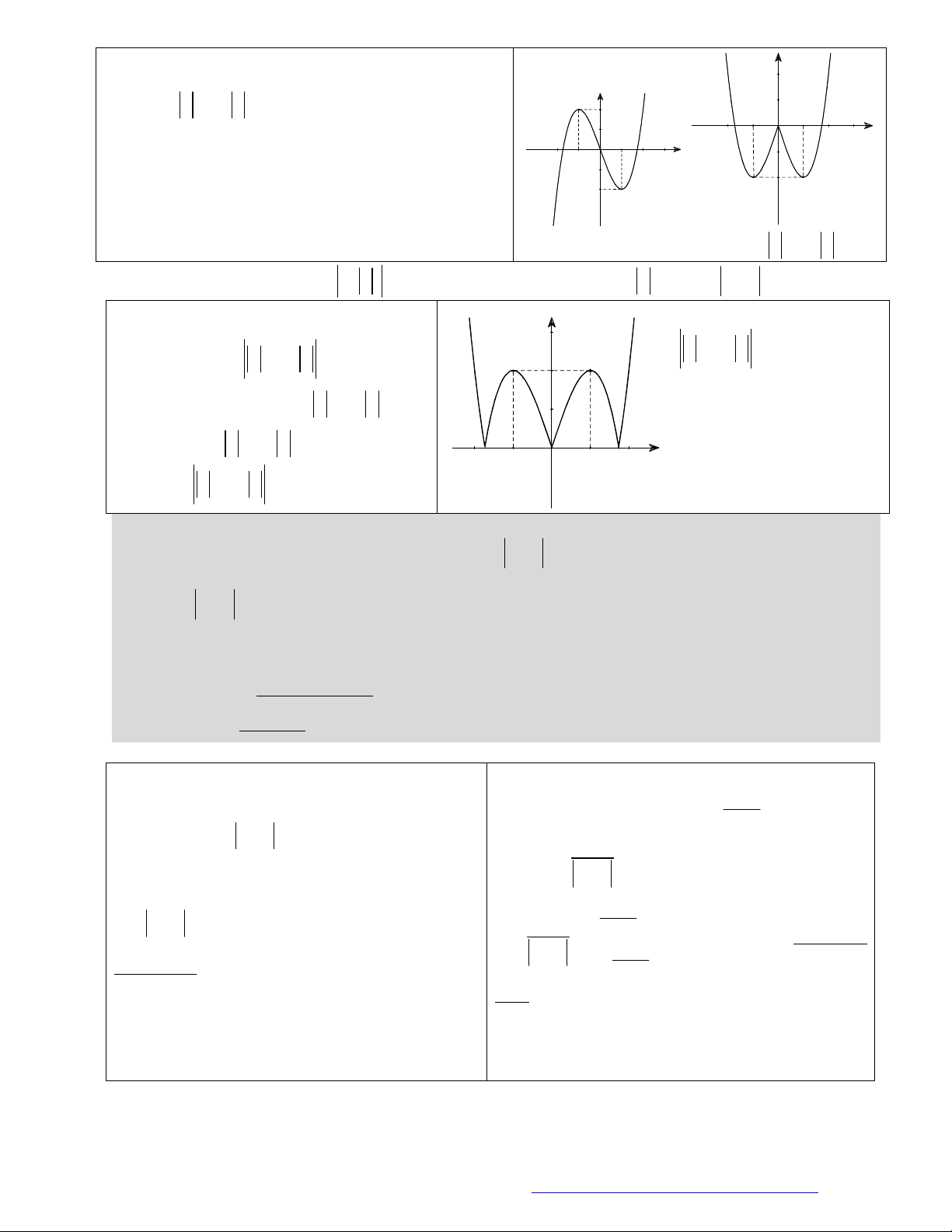
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Ví dụ: Từ đồ thị
C y f x x x
3
: 3 suy ra đồ thị
C y x x
3
: 3 .
Biến đổi
C :
Bỏ phần đồ thị của
C bên trái
Oy,
giữ nguyên
C
bên phải
.Oy
Lấy đối xứng phần đồ thị được giữ qua
Oy
.
Chú ý với dạng:
y f x
ta lần lượt biến đổi 2 đồ thị
y f x và
y f x
Ví dụ: Từ đồ thị
C y f x x x
3
: 3
suy ra đồ thị
y x x
3
3
. Biến đổi
C
để được đồ thị
C y x x
3
: 3 . Biến
đổi
C y x x
3
: 3 ta được đồ thị
C y x x
3
: 3
.
Dạng 3
Từ đồ thị
C y u x v x: . suy ra đồ thị
C y u x v x: .
.
Ta có:
u x v x f x khi u x
y u x v x
u x v x f x khi u x
. 0
.
. 0
* Cách vẽ
C từ
C
:
Giữ nguyên phần đồ thị trên miền
u x 0 của đồ thị
C y f x: .
Bỏ phần đồ thị trên miền
u x 0 của
C , lấy đối xứng phần đồ thị bị bỏ qua Ox.
Ví dụ
a) Từ đồ thị
C y f x x x
3 2
: 2 3 1 suy ra
đồ thị
C y x x x
2
: 1 2 1
Ví dụ
b) Từ đồ thị
x
C y f x
x
:
1
suy ra đồ thị
x
C y
x
:
1
f x khi x
y x x x
f x khi x
2
1
1 2 1
1
Đồ thị (C’):
Giữ nguyên (C) với
1x
.
Bỏ (C) với
x 1
. Lấy đối xứng phần đồ thị bị bỏ
qua Ox.
x
khi x
x
x
y
x
x
khi x
x
1;
1
.
1
;1
1
Đồ thị
(C’):
Bỏ phần đồ thị của
C
với
x ,1
giữ nguyên
C
với
1.x
Lấy đối xứng phần đồ thị bị bỏ qua
Ox.
x
y
O
-2
2
-1
1
x
y
O
-2
-1
1
x
y
2
-1
O
1
C y x x
3
: 3
C y x x
3
: 3
C y x x
3
: 3
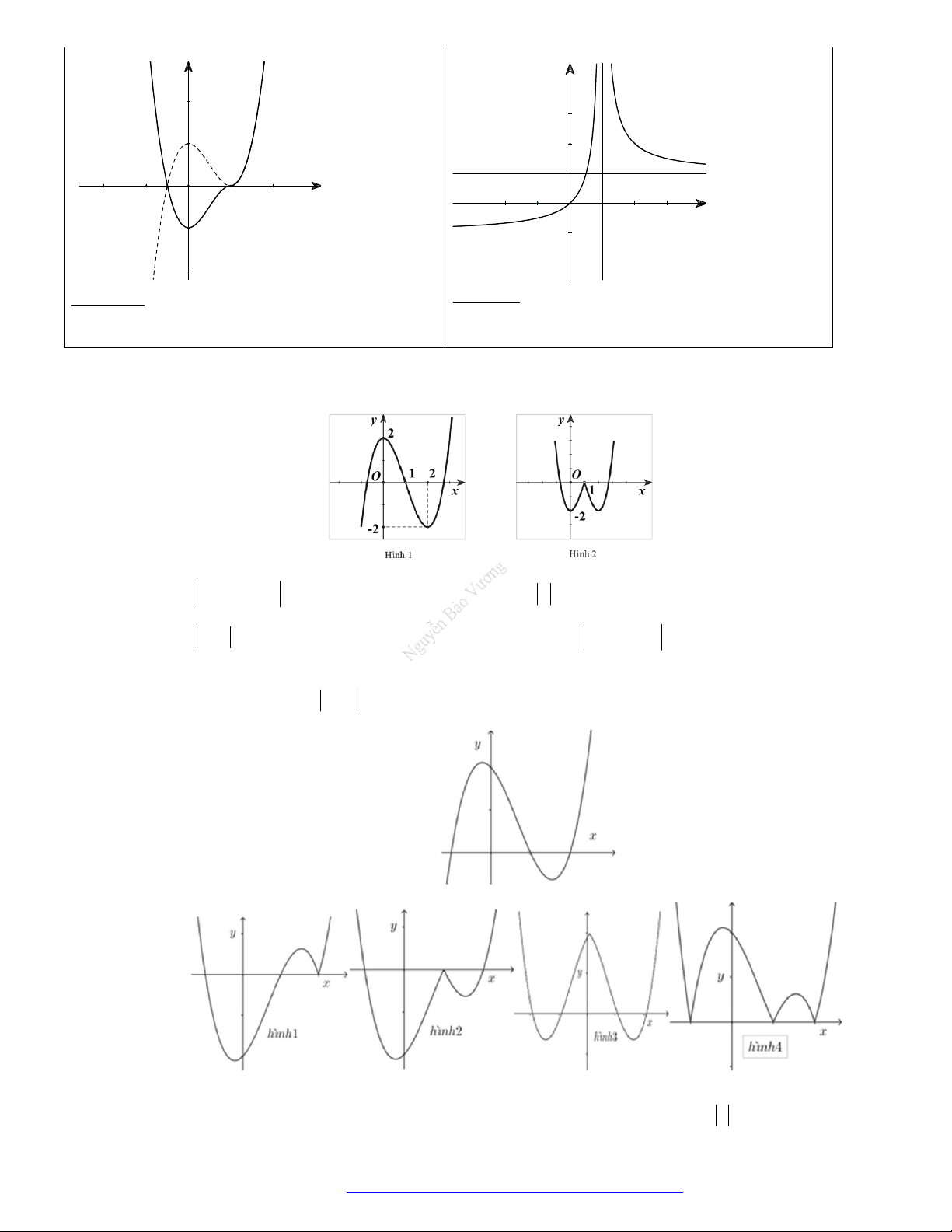
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Nhận xét: Trong quá trình thực hiện phép suy đồ thị
nên lấy đối xứng các điểm đặc biệt của (C): giao
điểm với Ox, Oy, CĐ, CT…
Nhận xét: Đối với hàm phân thức thì nên lấy đối
xứng các đường tiệm cận để thực hiện phép suy đồ
thị một cách tương đối chính xác.
Câu 1. Cho hàm số
3 2
3 2y x x
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?
A.
3 2
3 2 .y x x
B.
3
2
3 2y x x
C.
2
1 2 2 .y x x x
D.
2
1 2 2 .y x x x
Câu 2. (Đề Tham Khảo 2017) Hàm số
2
2 1y x x
có đồ thị như hình vẽ bên. Hình nào dưới đây
là đồ thị của hàm số
2
2 1y x x
?
A. Hình 1 B. Hình 2 C. Hình 3 D. Hình 4
Câu 3. (THPT Việt Đức Hà Nội 2019) Cho hàm số
y f x
có đồ thị hàm số
y f x
như hình vẽ.
x
y
(C)
(C')
1
O
1
x
y
1
O
1
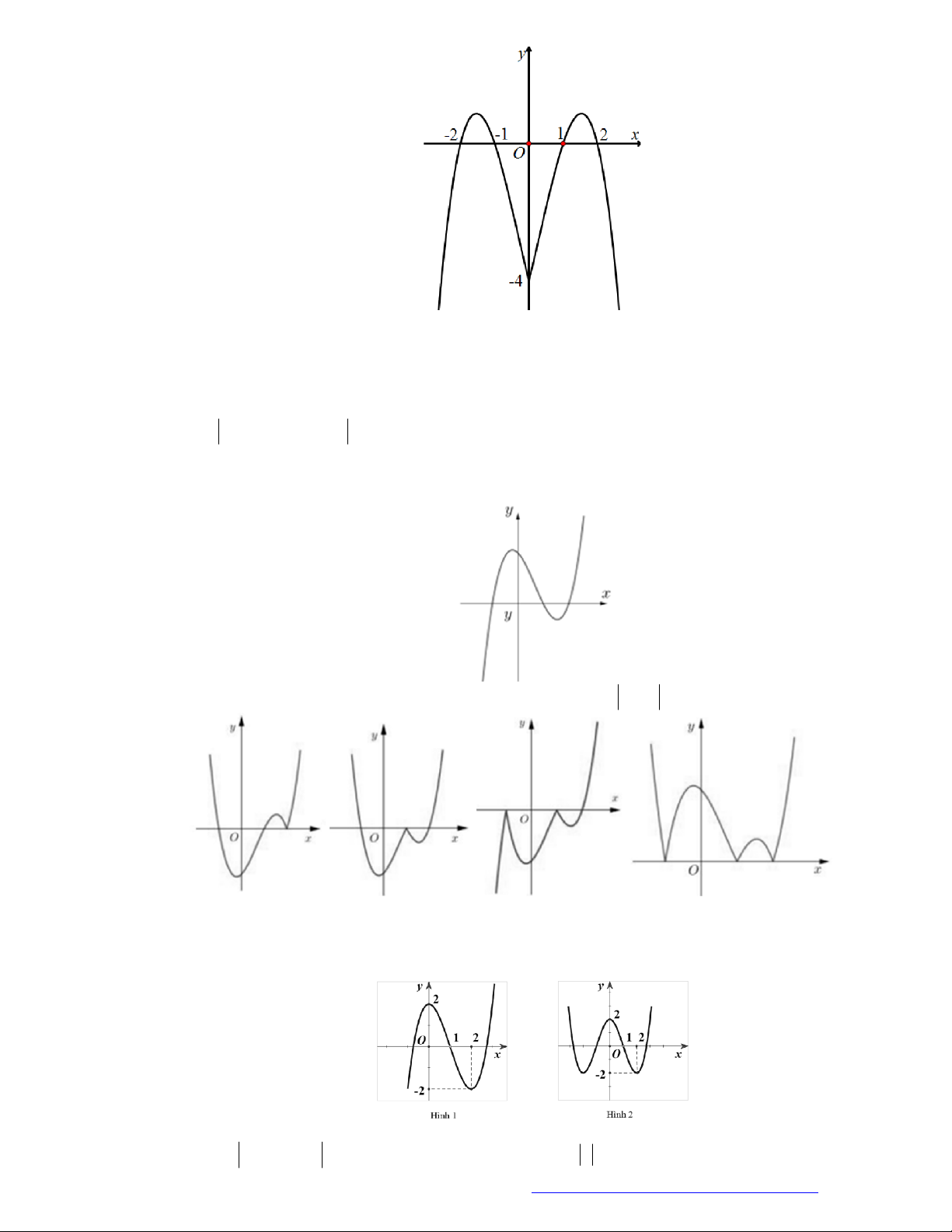
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Chọn kết luận đúng trong các kết luận sau:
A.
3 2
4 4f x x x x
B.
3 2
4 4f x x x x
C.
3 2
4 4f x x x x
D.
3 2
4 4.f x x x x
Câu 4. Biết phương trình
3 2
0ax bx cx d
( 0)a
có đúng hai nghiệm thực. Hỏi đồ thị hàm số
3 2
y ax bx cx d
có bao nhiêu điểm cực trị?
A. 4. B. 5. C. 2. D. 3.
Câu 5. (Chu Văn An - Hà Nội - 2019) Cho hàm số
2
2 1y x x
có đồ thị như hình vẽ
Một trong bốn hình dưới đây là đồ thị của hàm số
2
2 1y x x
. Hỏi đó là hình nào?
Hình 1 Hình 2 Hình 3 Hình 4
A. Hình 2. B. Hình 4. C. Hình 3. D. Hình 1.
Câu 6. Cho hàm số
3 2
3 2y x x
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?
A.
3 2
3 2 .y x x
B.
3
2
3 2y x x
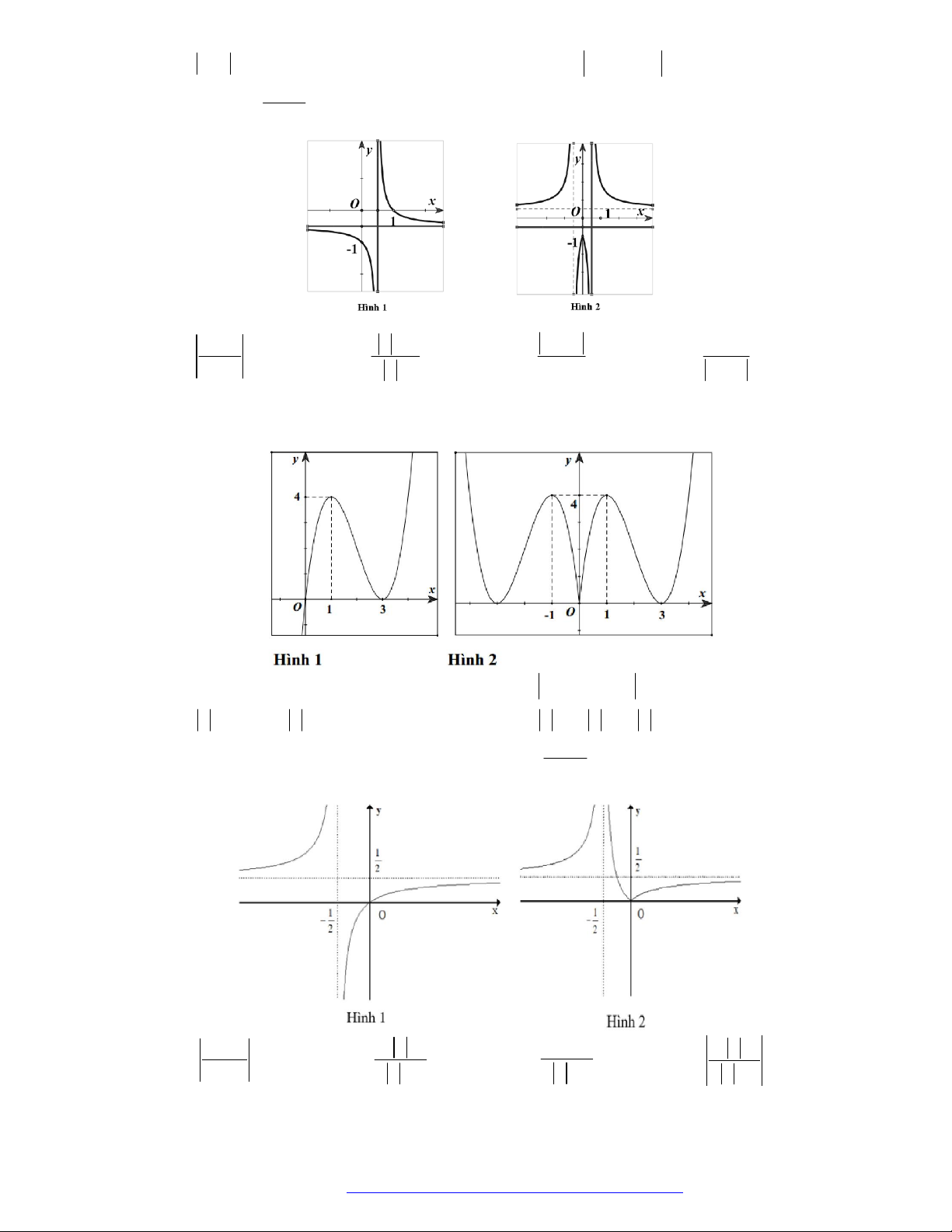
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
C.
2
1 2 2 .y x x x
D.
2
1 2 2 .y x x x
Câu 7. Cho hàm số
1
2 1
x
y
x
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?
A.
1
2 1
x
y
x
B.
1
2 1
x
y
x
C.
1
2 1
x
y
x
D.
1
2 1
x
y
x
Câu 8. Cho hàm số
3 2
6 9y x x x có đồ thị như Hình 1. Khi đó đồ thị Hình 2 là của hàm số nào dưới
đây?
A.
3 2
6 9 y x x x
. B.
3 2
6 9 y x x x
.
C.
3
2
6 9 y x x x
. D.
3 2
6 9 y x x x
.
Câu 9. (Cụm liên trường Hải Phòng -2019) Cho hàm số
2 1
x
y
x
có đồ thị như Hình 1. Đồ thị Hình
2 là của hàm số nào trong các đáp án A, B, C, D dưới đây?
A.
2 1
x
y
x
. B.
2 1
x
y
x
C.
2 1
x
y
x
D.
2 1
x
y
x
Câu 10. Cho hàm số
3 2
3 2y x x
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?
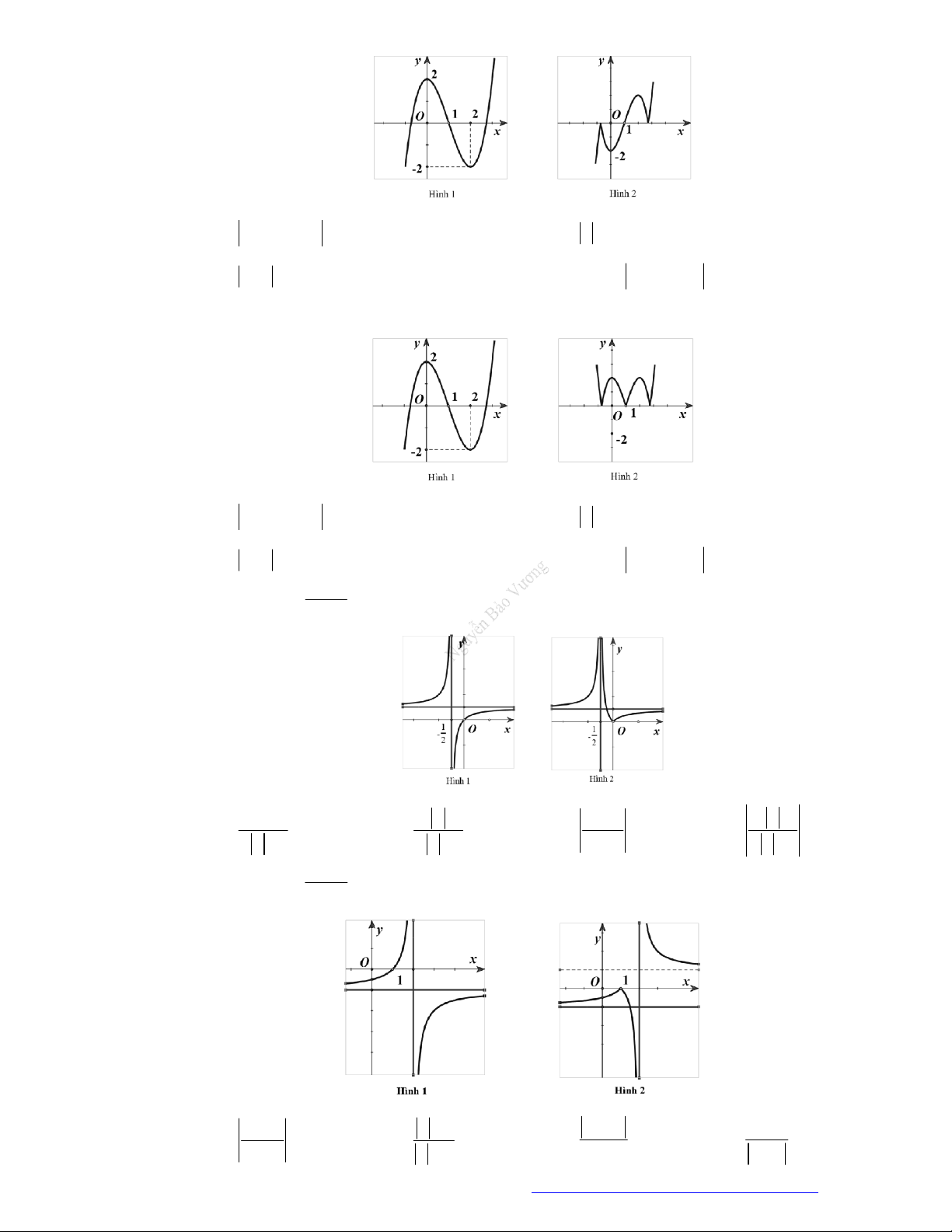
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
A.
3 2
3 2 .y x x
B.
3
2
3 2y x x
C.
2
1 2 2 .y x x x
D.
2
1 2 2 .y x x x
Câu 11. Cho hàm số
3 2
3 2y x x
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?
A.
3 2
3 2 .y x x
B.
3
2
3 2y x x
C.
2
1 2 2 .y x x x
D.
2
1 2 2 .y x x x
Câu 12. Cho hàm số
2 1
x
y
x
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?
A.
2 1
x
y
x
B.
2 1
x
y
x
C.
2 1
x
y
x
D.
2 1
x
y
x
Câu 13. Cho hàm số
1
2
x
y
x
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?
A.
1
.
2
x
y
x
B.
1
.
2
x
y
x
C.
1
2
x
y
x
D.
1
2
x
y
x
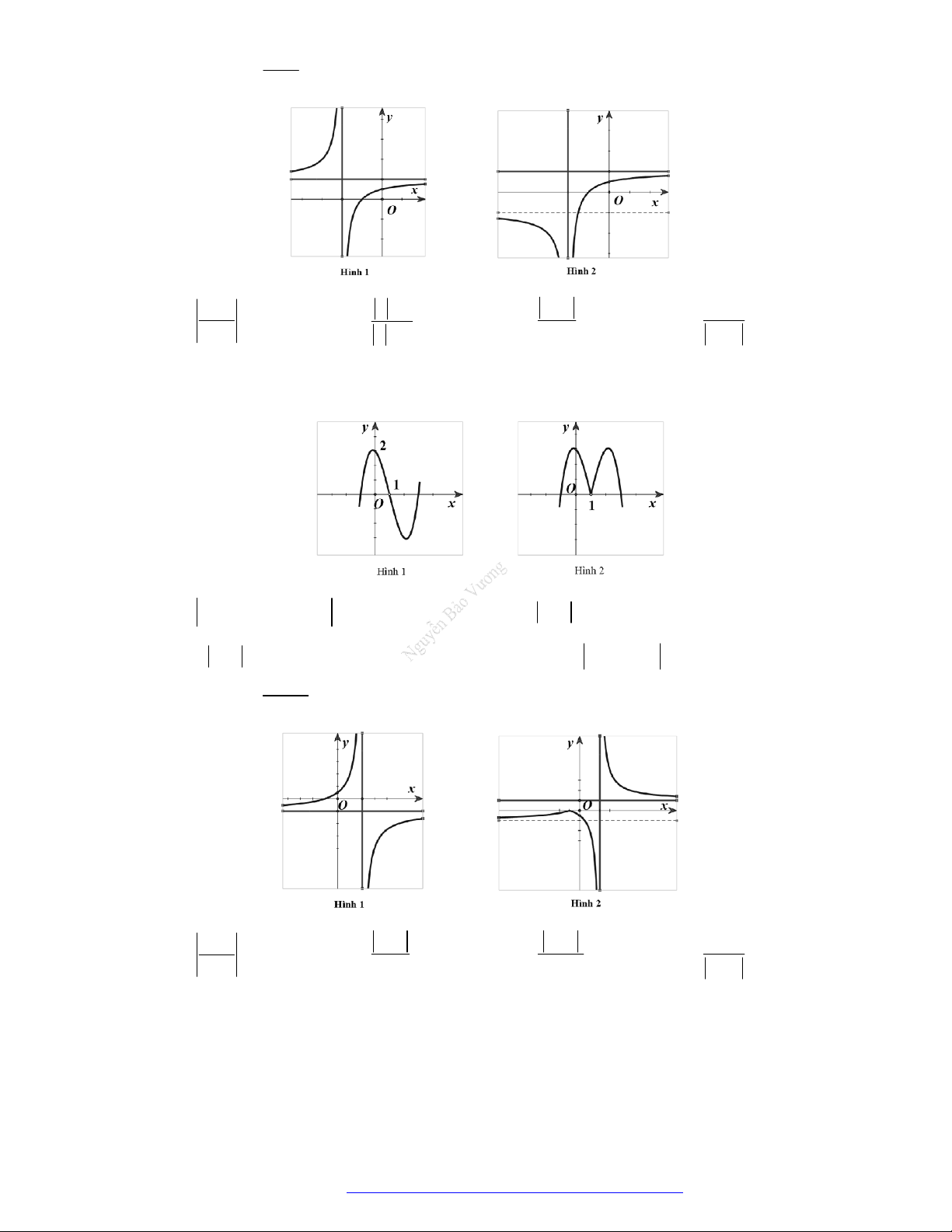
NGUYỄ
N BẢO VƯƠNG - 0946798489
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 14. Cho
hàm số
1
2
x
y
x
có
đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?
A.
1
.
2
x
y
x
B.
1
.
2
x
y
x
C.
1
.
2
x
y
x
D.
1
.
2
x
y
x
Câu 15. Cho hàm số
2
1
2 3y x x x
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới
đây?
A.
2
1
2 3 .y x x x B.
2
1 2 3 .y x x x
C
.
2
1
2 3y x x x
D
.
2
1
2 3y x x x
Câu 16. Cho hàm số
1
2
x
y
x
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?
A.
1
.
2
x
y
x
B.
1
.
2
x
y
x
C
.
1
.
2
x
y
x
D.
1
.
2
x
y
x
-------------------- HẾT --------------------
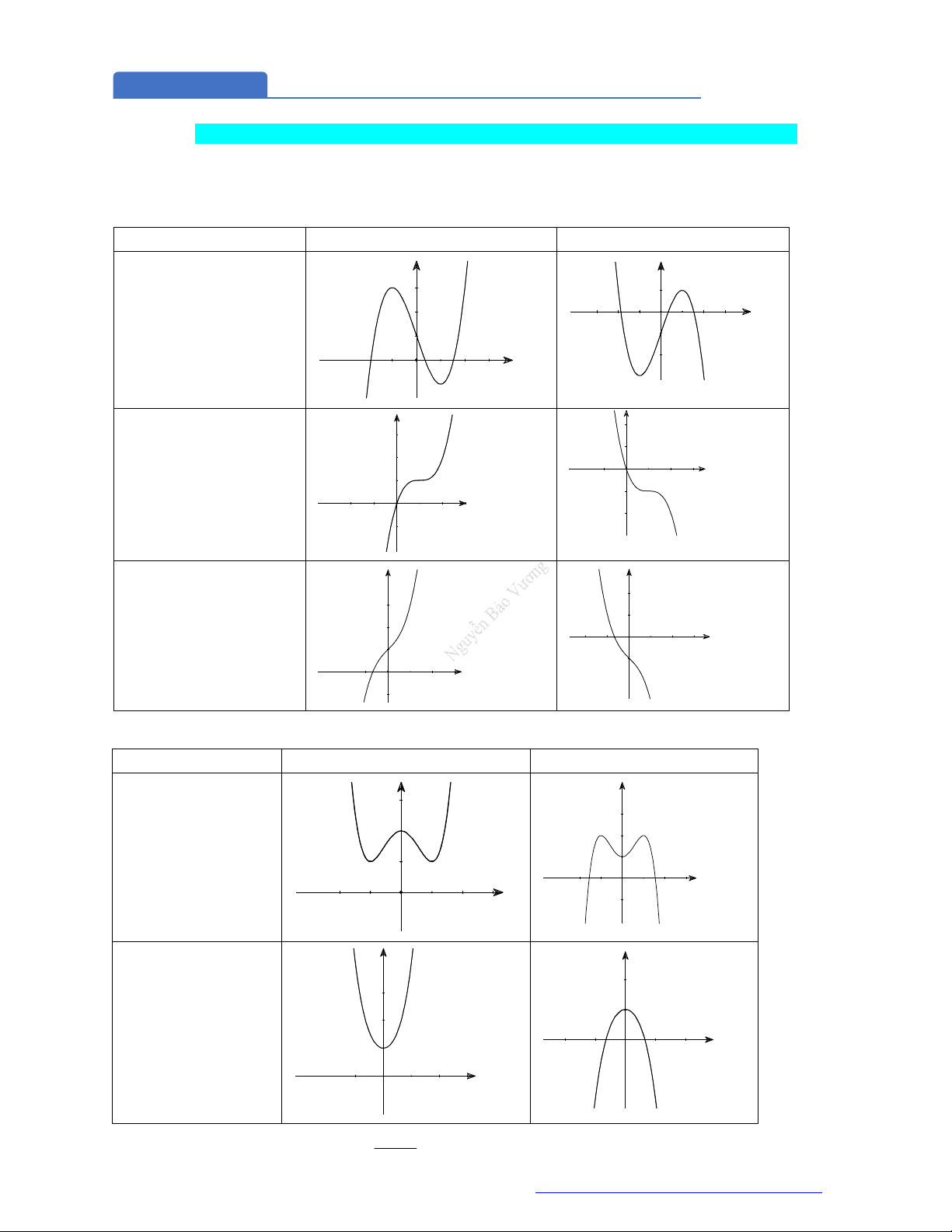
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
DẠNG TOÁN DÀNH CHO ĐỐI TƯỢNG HỌC SINH TRUNG BÌNH 5-6 ĐIỂM
Dạng. Nhận dạng hàm số thường gặp thông qua đồ thị
A. Hàm số bậc ba
y ax bx cx d a
3 2
0
TRƯỜNG HỢP
a 0
0a
Phương trình
y
/
0
có
2 nghiệm phân biệt
Phương trình
y
/
0
có
nghiệm kép
Phương trình
/
0y
vô
nghiệm
B. Hàm số trùng phương
y ax bx c a
4 2
0
TRƯỜNG HỢP
a 0
0a
Phương trình
y
/
0
có
3 nghiệm phân biệt
(ab<0)
Phương trình
y
/
0
có
1 nghiệm.
C. Hàm số nhất biến
0, 0
ax b
y c ad bc
cx d
ĐỌC ĐỒ THỊ CỦA HÀM SỐ
Chuyên đề 7
x
y
1
O
1
x
y
1
O
1
x
y
1
O
1
x
y
1
O
1
x
y
1
O
1
x
y
1
O
1
x
y
O
1
1
x
y
1
O
1
x
y
1
O
1
x
y
O
1
1
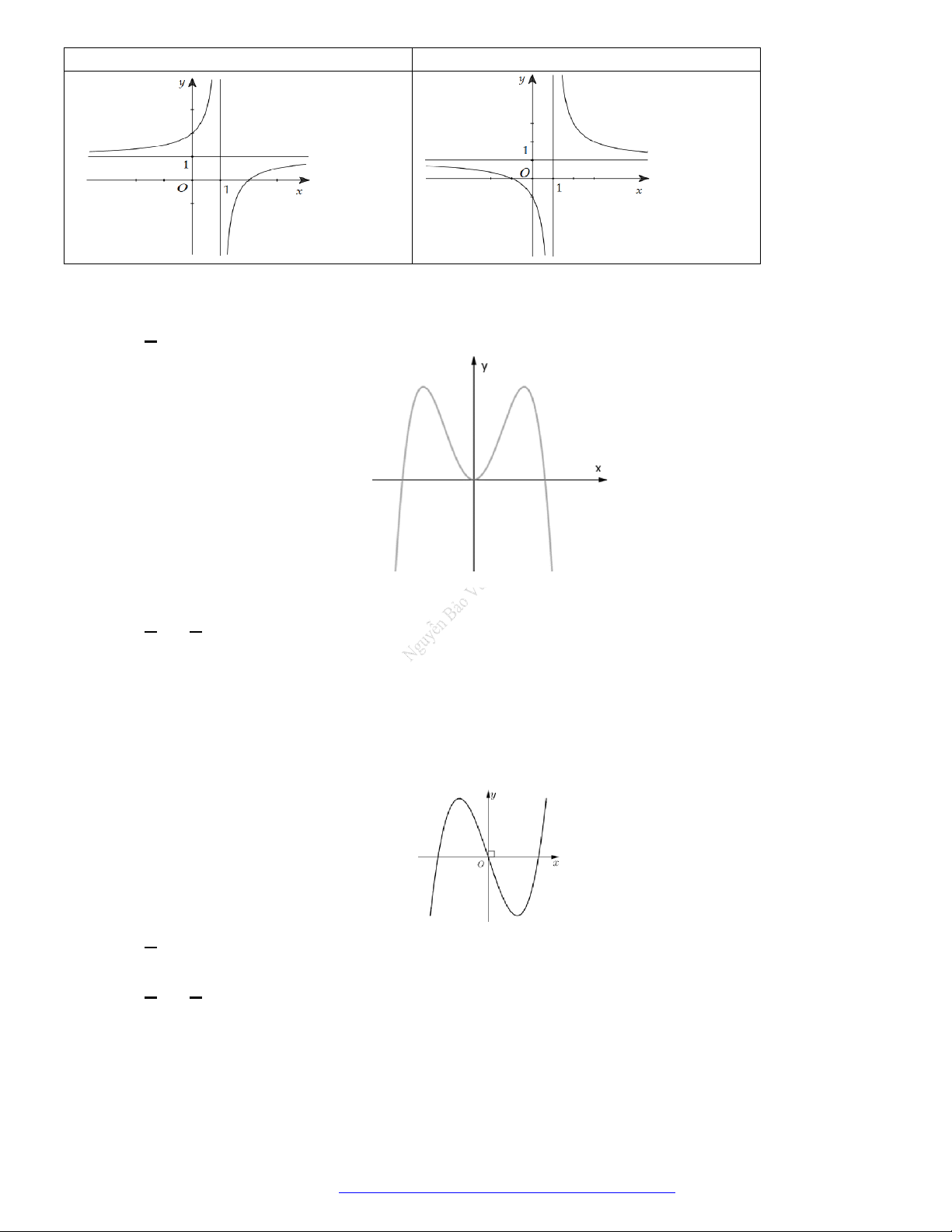
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
D ad bc 0
D ad bc 0
Câu 1. (Đề Minh Họa 2020 Lần 1) Đồ thị của hàm số nào dưới đây có dạng như đường cong trong dưới
đây?
A.
4 2
2y x x
. B.
4 2
2y x x
. C.
3 2
3y x x
. D.
3 2
3y x x .
Lời giải
Chọn A
Từ hình dạng của đồ thị ta loại phương án C và D.
Nhận thấy
lim ( )
x
f x
suy ra hệ số của
4
x
âm nên chọn phương án A.
Câu 2. (Đề Tham Khảo 2020 Lần 2) Đồ thị của hàm số nào dưới đây có dạng như đường cong trong
hình bên?
A.
3
3 y x x
. B.
3
3 y x x
. C.
4 2
2 y x x
. D.
4 2
2 y x x
.
Lời giải
Chọn A
Đường cong có dạng của đồ thị hàm số bậc
3
với hệ số
0a
nên chỉ có hàm số
3
3y x x
thỏa
yêu cầu bài toán.
Câu 3. (Mã 101 - 2020 Lần 1) Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên?
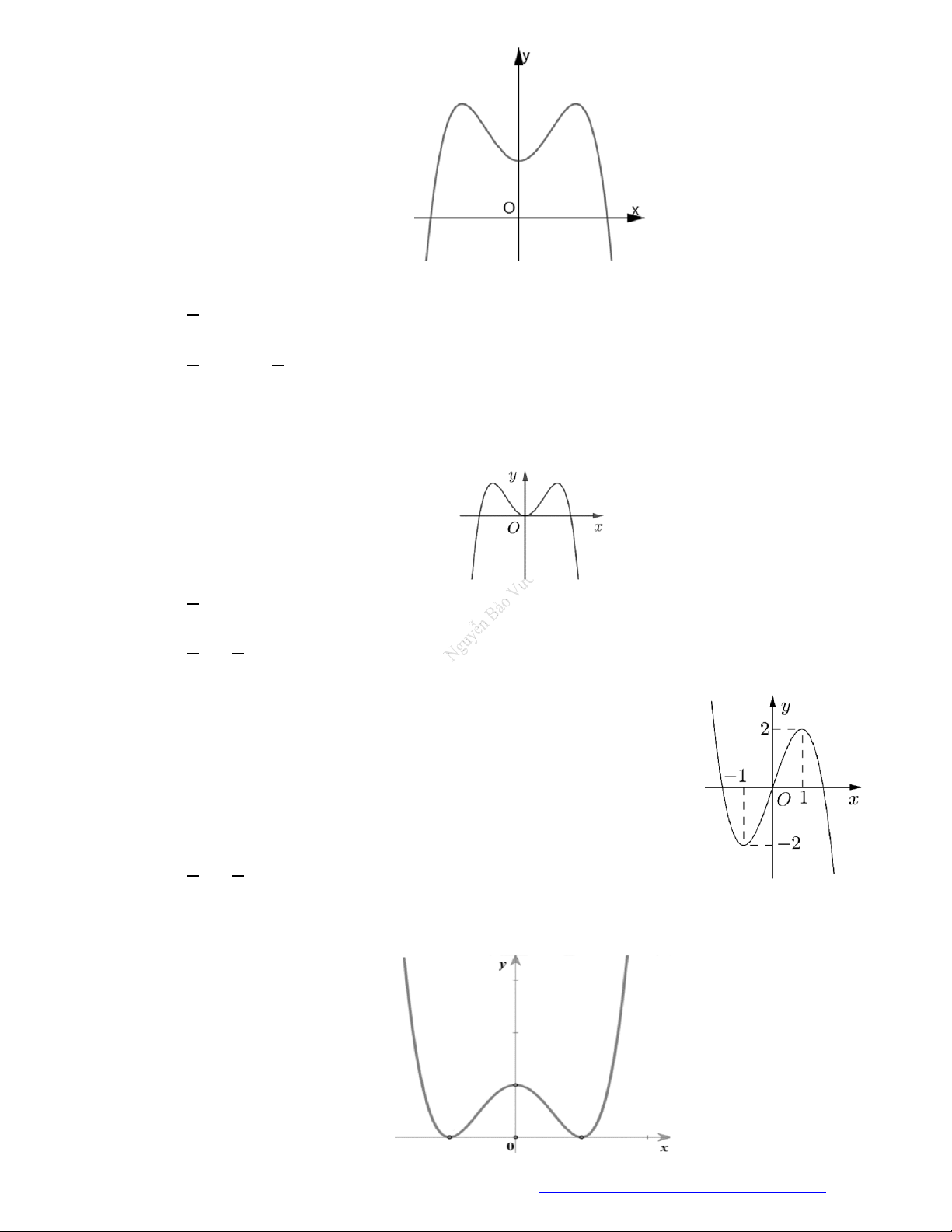
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
A.
3 2
3 1y x x . B.
3 2
3 1y x x .
C.
4 2
2 1y x x . D.
4 2
2 1y x x .
Lời giải
Chọn C.
Từ hình có đây là hình dạng của đồ thị hàm bậc 4.
lim lim 0
x x
f x f x a
Câu 4. (Mã 102 - 2020 Lần 1) Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên?
A.
4 2
2y x x . B.
3
3y x x . C.
4 2
2y x x . D.
3
3y x x .
Lời giải
Chọn A
Đường cong trong hình là đồ thị hàm trùng phương
4 2
y ax bx c
0a
có hệ số
0a
.
Câu 5. (Mã 103 - 2020 Lần 1) Cho hàm số bậc ba
y f x
có đồ thị là
đường cong trong hình bên. Số nghiệm thực của phương trình
1f x
là
A.
1
. B.
0
.
C.
2
. D.
3
.
Lời giải
Chọn D
Từ đồ thị hàm số ta có số nghiệm thực của phương trình
1f x
là
3
.
Câu 6. (Mã 104 - 2020 Lần 1) Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên?
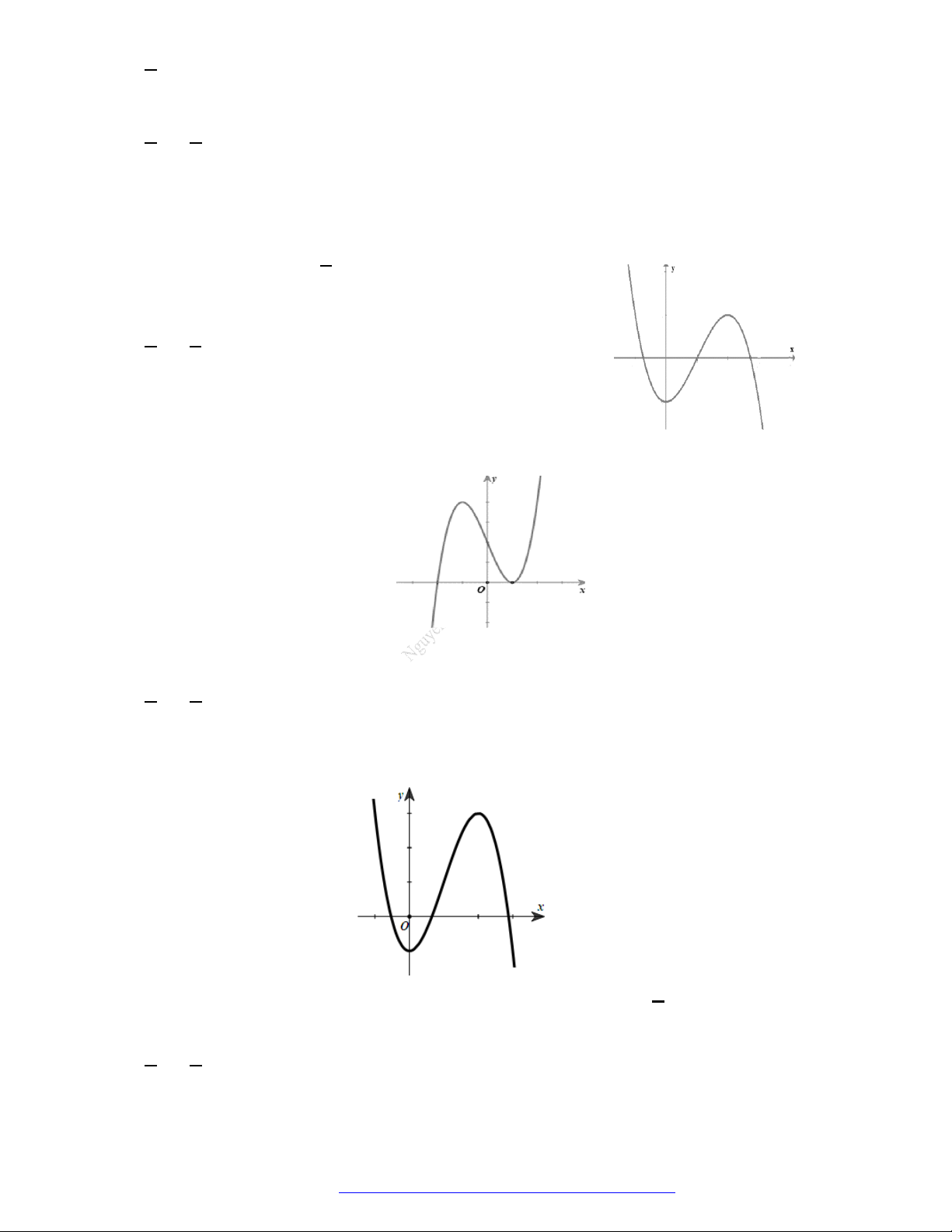
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
4 2
2 1y x x . B.
3 2
3 1y x x . C.
3 2
3 1y x x . D.
4 2
2 1y x x
.
Lời giải
Chọn A
Dựa vào hình vẽ, ta thấy đồ thị hàm số có ba điểm cực trị nên loại các đáp án B và C.
Mặt khác, ta thấy
4 2
lim 2 1
x
x x
nên chọn đáp án A.
Câu 7. (Mã 101 - 2020 Lần 2)Đồ thị hàm số nào dưới đây có dạng như đường cong hình bên
A.
4 2
y x 2x 2
B.
3 2
y x 2x 2
C.
3 2
y x 3x 2
D.
4 2
y x 2x 2
Lời giải
Chọn B
Qua đồ thị là hàm bậc 3 nên loại A, D.
Bên phải ngoài cùng của đồ thị đi xuống nên hệ số a < 0
loại đáp án C
Câu 8. (Mã 104 2017) Đường cong hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là
hàm số nào?
A.
3
3 2y x x
B.
4 2
1y x x
C.
4 2
1y x x
D.
3
3 2y x x
Lời giải
Chọn D
Đồ thị hình vẽ là đồ thị hàm số bậc ba có hệ số
0a
nên chỉ có hàm số
3
3 2y x x thỏa mãn
điều kiện trên.
Câu 9. (Mã 102 - 2020 Lần 2) Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
A.
4 2
2 1y x x
. B.
4 2
2 1y x x
. C.
3 2
3 1y x x
. D.
3 2
3 1y x x
.
Lời giải
Chọn D
Dựa vào đồ thị có dạng đồ thị của hàm số bậc 3 có hệ số
0a
nên đáp án D đúng.
Câu 10. (Mã 103 - 2020 Lần 2) Đồ thị của hàm số dưới đây có dạng như đường cong bên?
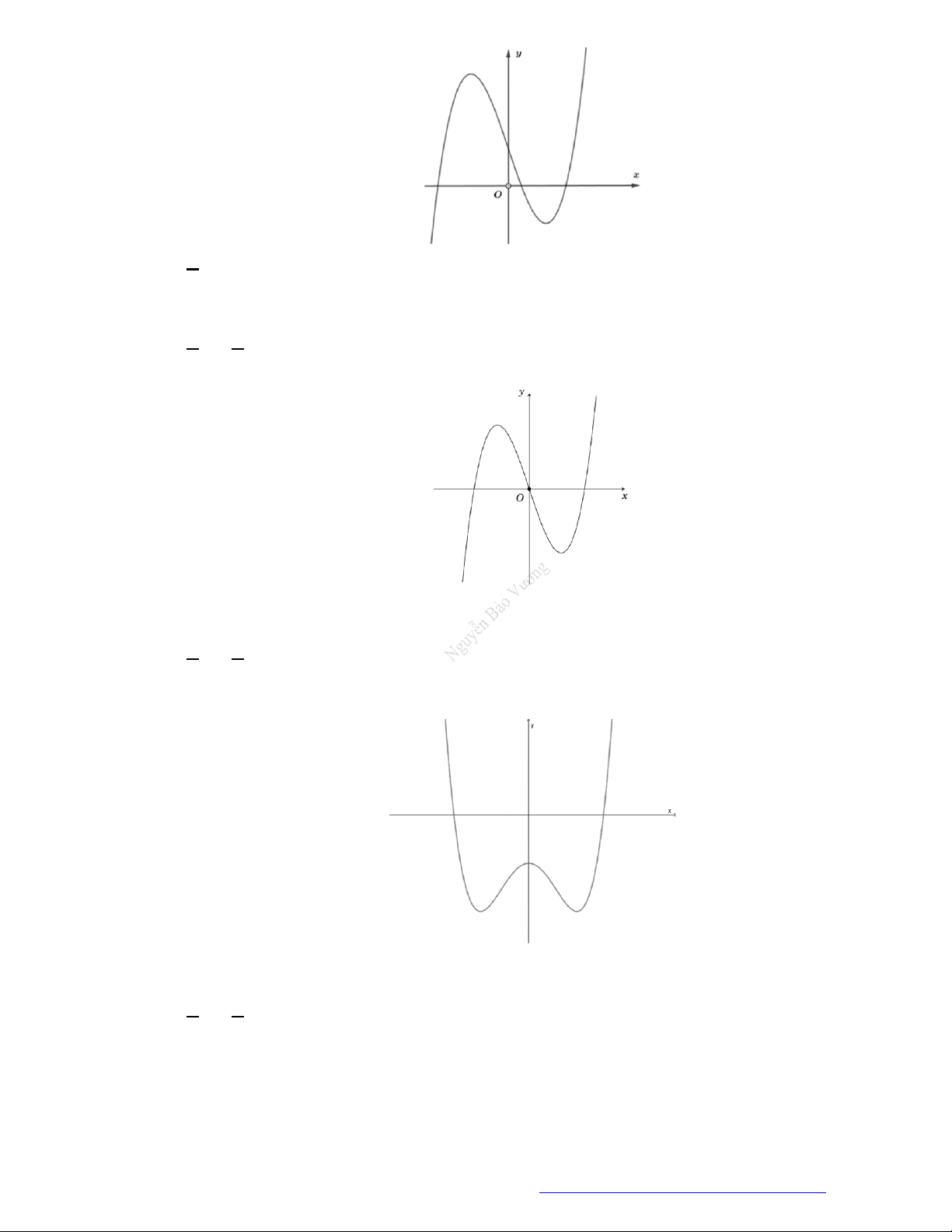
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
A.
3
3 1y x x
. B.
4 2
2 1y x x
.
C.
4 2
2 1y x x
. D.
3
3 1y x x
.
Lời giải
Chọn A
Câu 11. (Mã 104 - 2020 Lần 2) Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
A.
4 2
2y x x
. B.
3
3y x x
. C.
3
3y x x
. D.
4 2
2y x x
.
Lời giải
Chọn C
Đây là đồ thị của hàm số bậc ba với hệ số
0a
nên chọn C.
Câu 12. (Mã 102 2018) Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
A.
3 2
1y x x B.
4 2
2 1y x x C.
3 2
1y x x D.
4 2
2 1y x x
Lời giải
Chọn D
Dựa vào hình vẽ suy ra hàm số đã cho có
3
cực trị
loại C,
D.
Mặt khác nhánh bên tay phải của đồ thị hàm số đi lên suy ra hệ số
0a
Chọn D
Câu 13. (Đề Tham Khảo 2019) Đường con trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
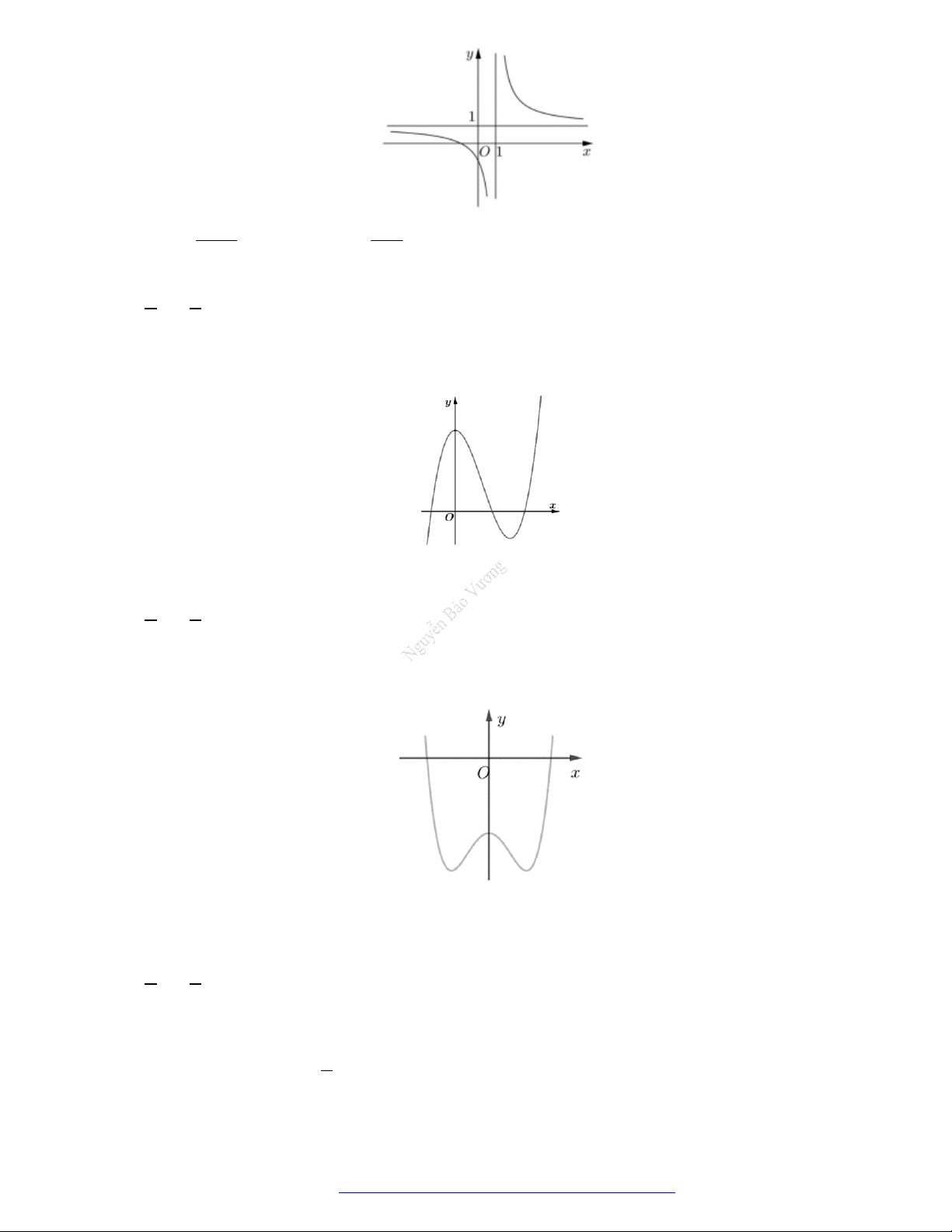
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
2 1
1
x
y
x
B.
1
1
x
y
x
C.
4 2
1y x x D.
3
3 1y x x
Lời giải
Chọn B
Vì từ đồ thị ta suy ra đồ thị của hàm phân thức có tiệm cận đứng và ngang
1; 1x y
Câu 14. (Mã 110 2017) Đường cong ở hình bên dưới là đồ thị của một trong bốn hàm số dưới đây. Hàm
số đó là hàm số nào?
A.
3 2
3 1y x x
B.
3 2
3 3y x x
C.
4 2
2 1y x x
D.
4 2
2 1y x x
.
Lời giải
Chọn B
Dựa vào đồ thị ta thấy đây là hình ảnh đồ thị của hàm số bậc ba nên loại đáp án B và C; Mặt khác
dựa vào đồ thị ta có
lim
x
y
nên hệ số của
3
x
dương nên ta chọn đáp án
3 2
3 3y x x
Câu 15. (Mã 103 2019) Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên?
A.
3 2
3 2y x x . B.
4 2
2 2y x x .
C.
3 2
3 2y x x . D.
4 2
2 2y x x .
Lời giải
Chọn B
Quan sát đò thị ta thấy đây là đồ thị của hàm số
4 2
0y ax bx c a
. Vậy chọn
B.
Câu 16. (Đề Tham Khảo 2017) Cho đường cong hình vẽ bên là đồ thị của một hàm số trong bốn hàm số
được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi đó là hàm số nào?

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
A.
2 1
y
1
x
x
B.
2 3
1
x
y
x
C.
2 1
1
x
y
x
D.
2 2
1
x
y
x
Lời giải
Chọn C
Dựa vào đồ thị suy ra tiệm cận đứng
1x
loại C, D
Đồ thị hàm số giao với trục hoành có hoành độ dương suy ra chọn B
Câu 17. (Đề Minh Họa 2017) Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số
được liệt kê ở bốn phương án
, , ,A B C D
dưới đây. Hỏi hàm số đó là hàm số nào?
A.
3
3 1y x x
B.
3
3 1y x x
C.
4 2
1y x x
D.
2
1y x x
Lời giải
Chọn A
Từ đồ thị :
lim
x
y
và đây là đồ thị hàm bậc ba nên ta chọn phương án
3
3 1.y x x
Câu 18. (Mã 101 2019) Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên?
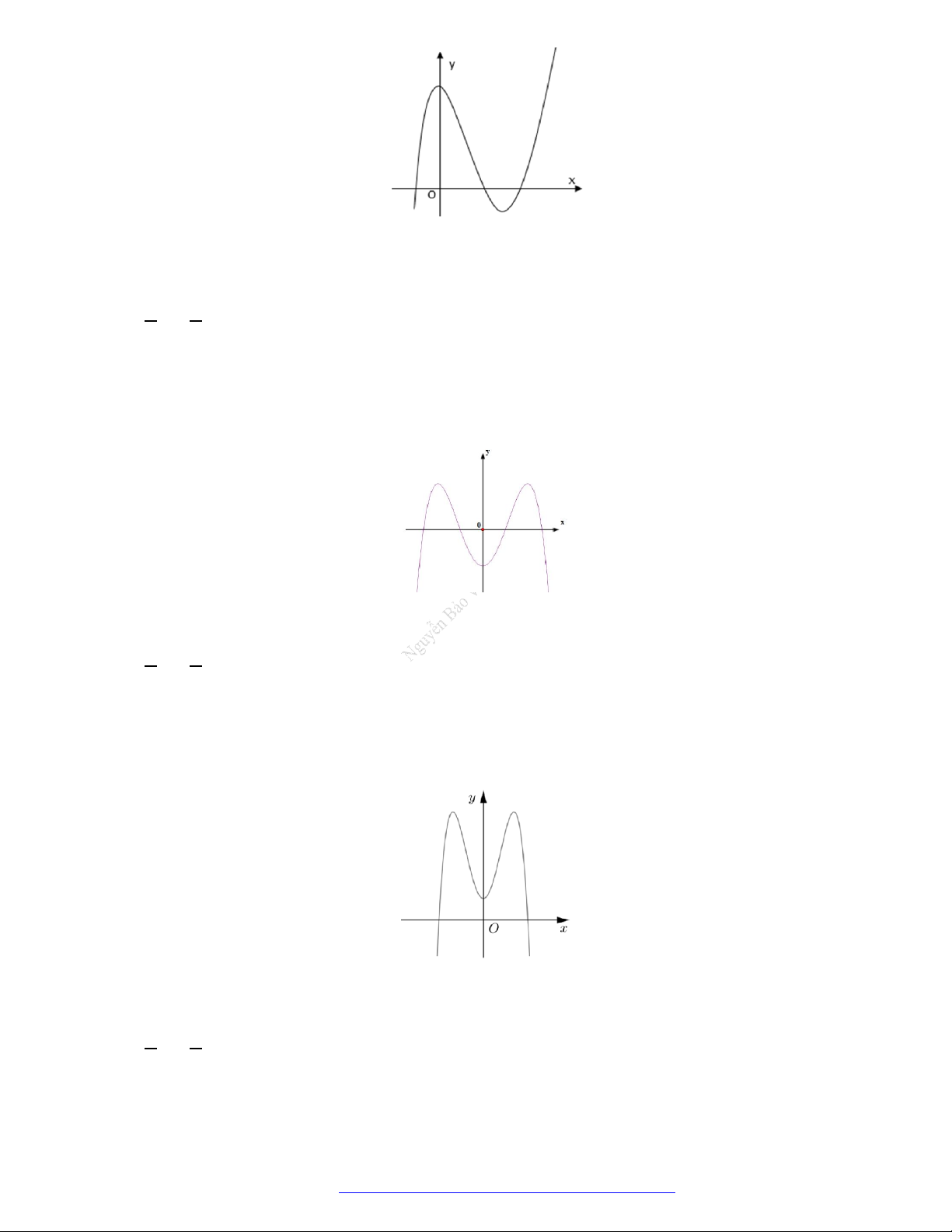
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
3 2
3 3y x x
. B. 33
23
xxy .
C. 32
24
xxy .s D. 32
24
xxy .
Lời giải
Chọn A
Dạng hàm bậc ba nên loại C
Từ đồ thị ta có
0a
. Do đó loại B,
D.
Câu 19. (Mã 101 2018) Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
A.
3 2
3 1y x x B.
3 2
3 1y x x C.
4 2
3 1y x x D.
4 2
3 1y x x
Lời giải
Chọn C
+ Nhìn đồ thị khẳng định đồ thị hàm trùng phương loại B, C
+
lim
x
y
nên chọn
D.
Câu 20. (Mã 104 2019) Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên?
A.
4 2
2 4 1y x x B.
3
2 3 1y x x C.
3
2 3 1y x x D.
4 2
2 4 1y x x
Lời giải
Chọn D
Dạng đồ thị hình bên là đồ thị hàm số trùng phương
4 2
y ax bx c có hệ số
0a
.
Do đó, chỉ có đồ thị ở đáp án
B
là thỏa mãn.
Câu 21. (Mã 102 2019) Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên
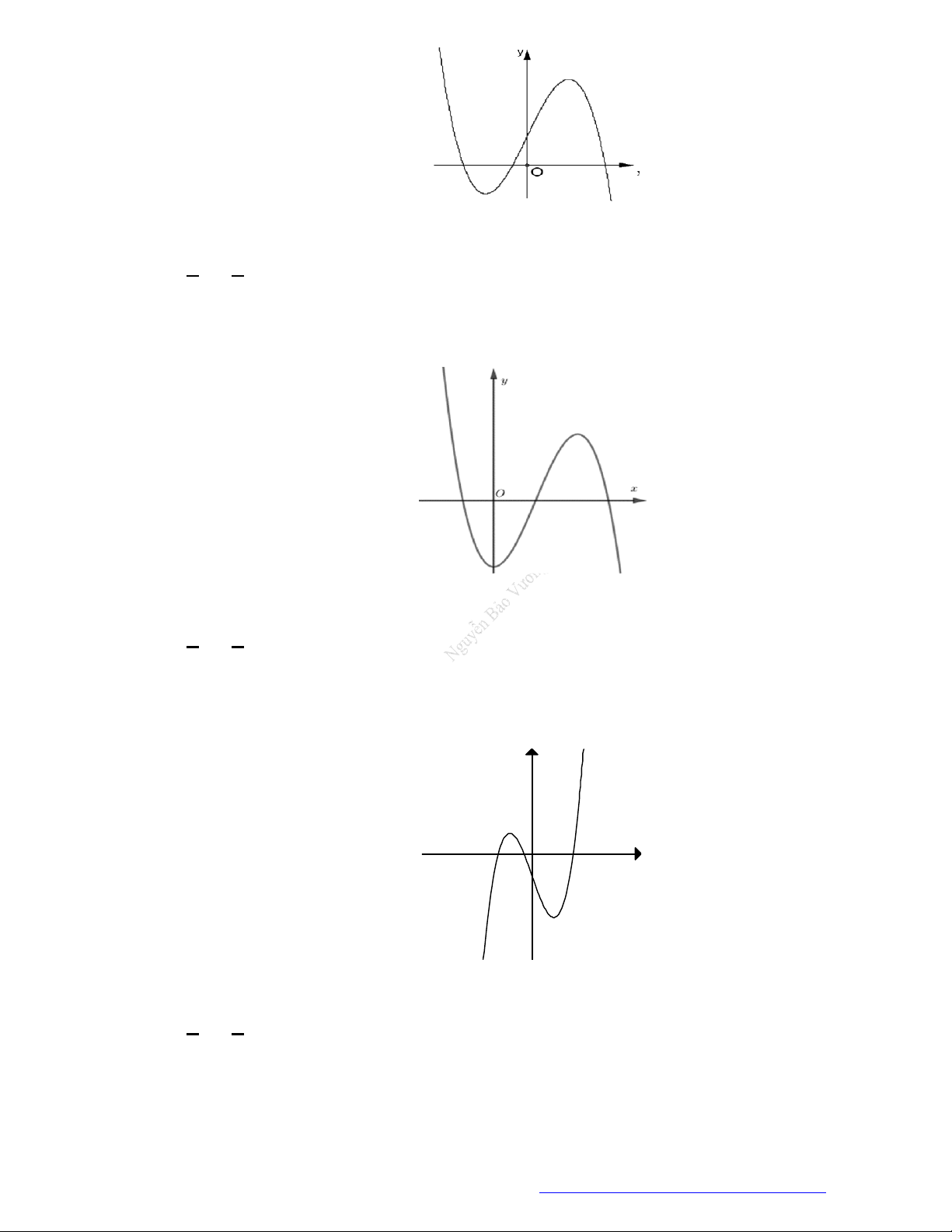
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
A.
3
3 1y x x
. B.
3
3 1y x x
. C.
4 2
2 1y x x
. D.
4 2
2 1y x x
.
Lời giải
Chọn A
Trong bốn hàm số đã cho thì chỉ có hàm số
3
3 1y x x
(hàm số đa thức bậc ba với hệ số
0a
) có dạng đồ thị như đường cong trong hình.
Câu 22. (Mã 104 2018) Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
A.
4 2
2y x x
B.
4 2
2y x x
C.
3 2
3 2y x x
D.
3 2
3 2y x x
Lời giải
Chọn C
Dựa trên hình dáng đồ thị, ta loại
3 2
3 2y x x
và
4 2
2y x x
Mặt khác từ đồ thị, ta thấy
lim
x
y
nên loại
4 2
2y x x
Câu 23. (Mã 103 2018) Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
A.
3
3 1y x x B.
4 2
3 1y x x C.
3
3 1y x x D.
4 2
1y x x
Lời giải
Chọn A
Đồ thị hàm số là đồ thị của hàm số bậc ba nên loại A và
B.
Đồ thi hàm số bậc ba có hệ số
0a
nên D đúng.
Câu 24. (Mã 123 2017) Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó
là hàm số nào?
x
y
O
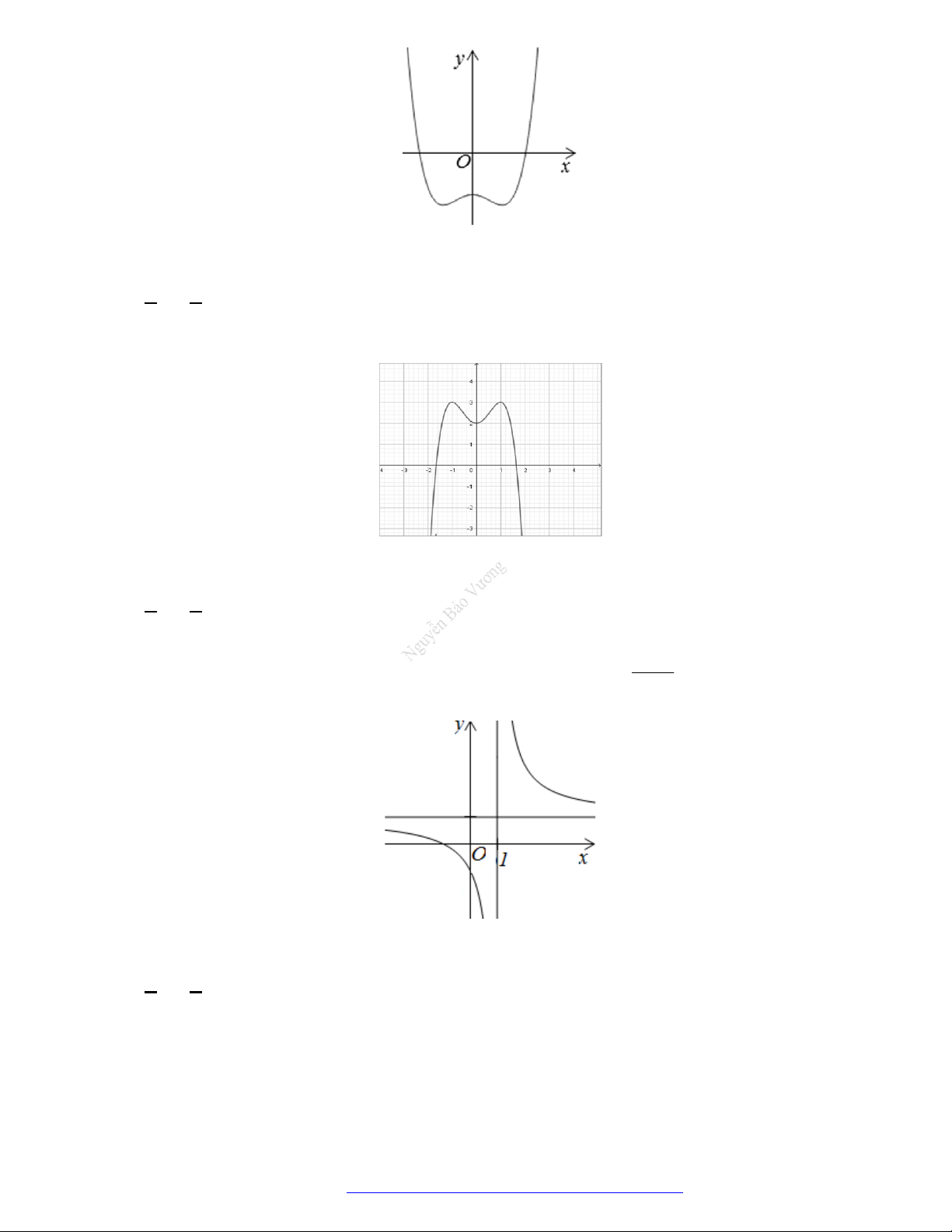
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
4 2
1y x x
B.
4 2
1y x x
C.
3 2
1y x x
D.
3 2
1y x x
Lời giải
Chọn A
Đây là hình dáng của đồ thị hàm bậc bốn trùng phương có hệ số
0a
Câu 25. (Đề Tham Khảo 2018) Đường cong trong hình bên là của đồ thị hàm số nào dưới đây?
A.
3 2
3 2 y x x
B.
3 2
3 2 y x x
C.
4 2
2 2 y x x
D.
4 2
2 2 y x x
Lời giải
Chọn C
Đồ thị hàm số trên là đồ thị hàm trùng phương có 3 cực trị và có
0a
Câu 26. (Mã 123 2017) Đường cong ở hình bên là đồ thị của hàm số
ax b
y
cx d
với , , ,a b c d là các số
thực. Mệnh đề nào dưới đây đúng?
A.
0,y x
B.
0, 1y x
C.
0, 1y x
D.
0,y x
Lời giải
Chọn C
Ta có :
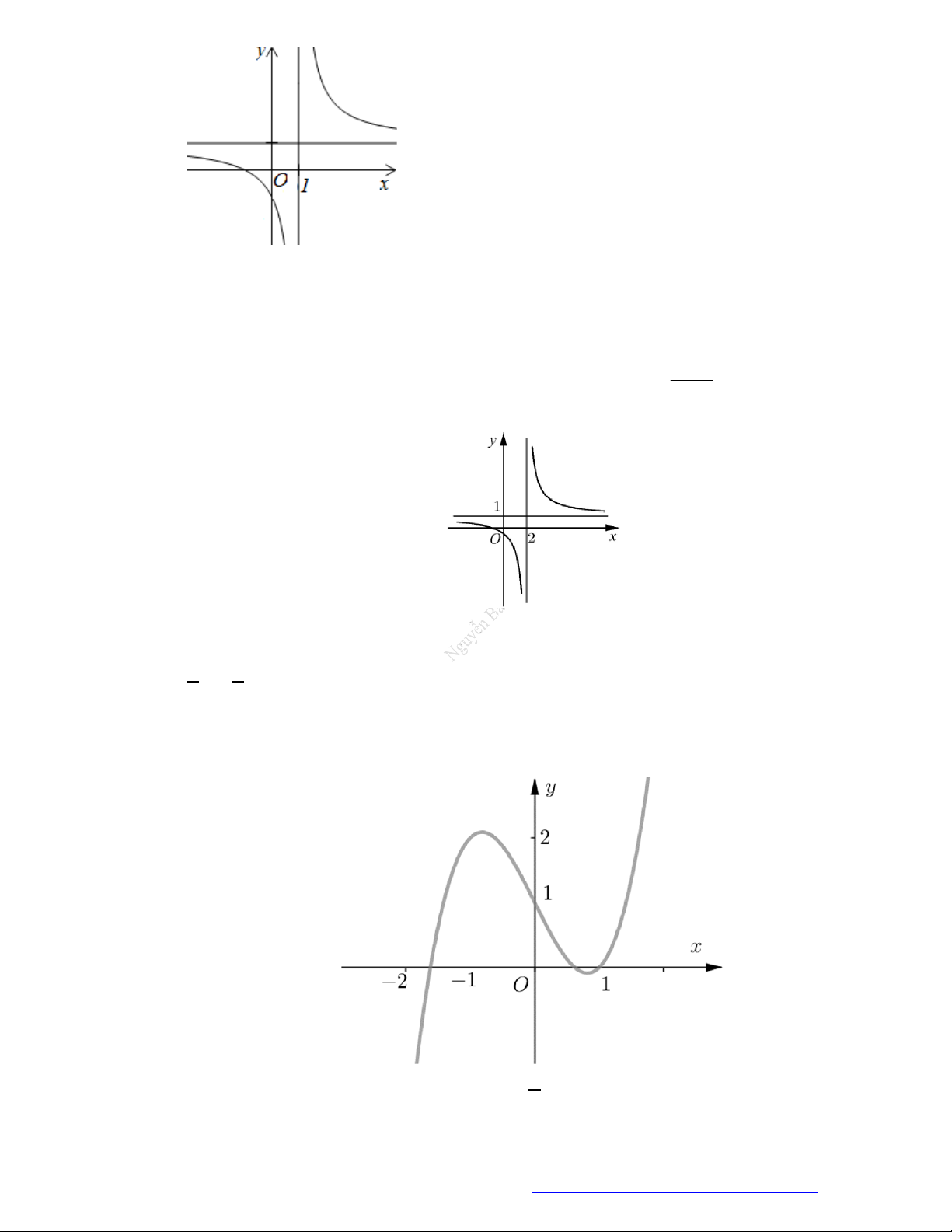
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Dựa vào hình dáng của đồ thị ta được:
+ Điều kiện
1x
+ Đây là đồ thị của hàm nghịch biến
Từ đó ta được
0, 1.y x
Câu 27. (Mã 105 2017) Đường cong ở hình bên là đồ thị của hàm số
ax b
y
cx d
với , , ,a b c d là các số
thực. Mệnh đề nào dưới đây đúng?
A.
y 0, 1x
B.
y 0, x 1
C.
y 0, x 2
D.
y 0, 2
Lời giải
Chọn C
Dựa vào đồ thị ta nhận thấy tiệm cận đứng bằng 2, Hàm số nghịch biến vậy chọn B
Câu 28. (THPT Yên Phong 1 Bắc Ninh 2019) Hình vẽ sau đây là đồ thị của một trong bốn hàm số cho ở
các đáp án
, , ,A B C D
. Hỏi đó là hàm số nào?
A.
3
2 1y x x . B.
3 2
2 1y x x . C.
3
2 1y x x
. D.
3
2 1y x x
.
Lời giải
Dựa vào đồ thị, ta có
lim
x
y
, loại phương án
D
.
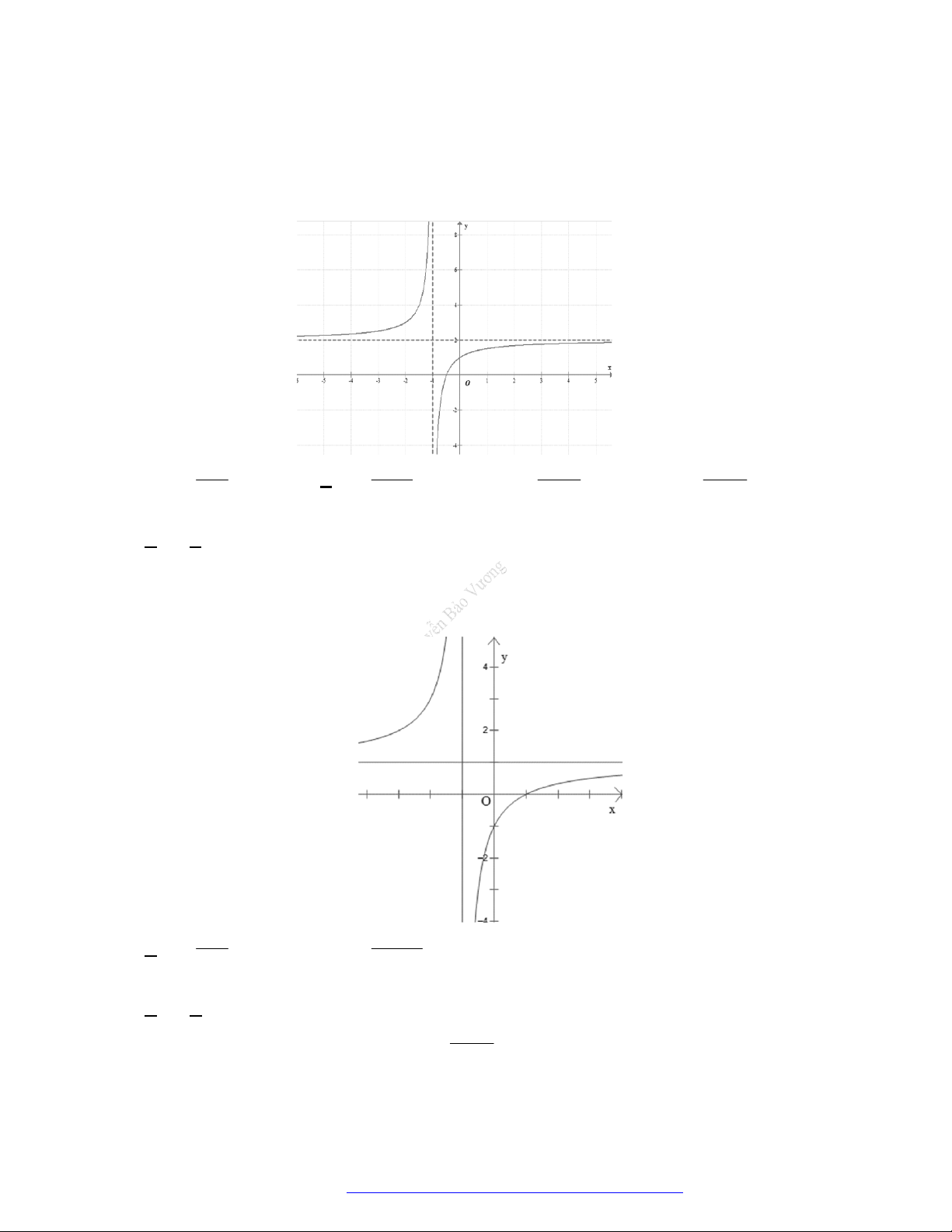
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Xét phương án
A
có
2
3 2 0,y x x
, hàm số không có cực tri, loại phương án
A
.
Xét phương án
B
có
2
3 6y x x
và
y
đổi dấu khi đi qua các điểm
0, 2x x
nên hàm số
đạt cực tri tại
0x
và
2x
, loại phương án
B
.
Vậy phương án đúng là
C
.
Câu 29. (Sở Cần Thơ - 2019) Hình vẽ bên dưới là đồ thị của hàm số nào
A.
1
1
x
y
x
. B.
2 1
1
x
y
x
. C.
2 3
1
x
y
x
. D.
2 5
1
x
y
x
.
Lời giải
Chọn B
Đồ thị hàm số cắt trục Oy tai điểm có tọa độ
0;1
nên chọn phương án B.
Câu 30. (SGD Nam Định) Đường cong trong hình là đồ thị của hàm số nào dưới đây?
A.
1
1
x
y
x
. B.
2 1
2 2
x
y
x
. C.
4 2
3y x x
. D.
3 2
3y x x
.
Lời giải
Chọn A
Hình vẽ trên là đồ thị của hàm số dạng
0; 0
ax b
y c ad bc
cx d
Loại phương án C, D
Ta thấy: Đồ thị có đường tiệm cận đứng là
1x
và đường tiệm cận ngang là
1y
Phương án B: Đồ thị có đường tiệm cận đứng là
2x
loại B
A đúng.
Câu 31. (Sở Gia Lai 2019) Đường cong trong hình vẽ bên là đồ thị của hàm số nào sau đây?

T
ÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
A.
3
3
1y x x
. B.
4
2
1y
x x
. C.
2
1y
x x
. D.
3
3
1y x x
.
Lờ
i giải
Chọn D
Đồ t
hị đã cho có hình dạng của đồ thị hàm số bậc ba
3
2
y
ax bx cx d
nê
n loại phương án
B và C
Dựa vào đồ thị, ta có
l
im 0
x
y
a
nên loại phương án A
-------------------- HẾT --------------------
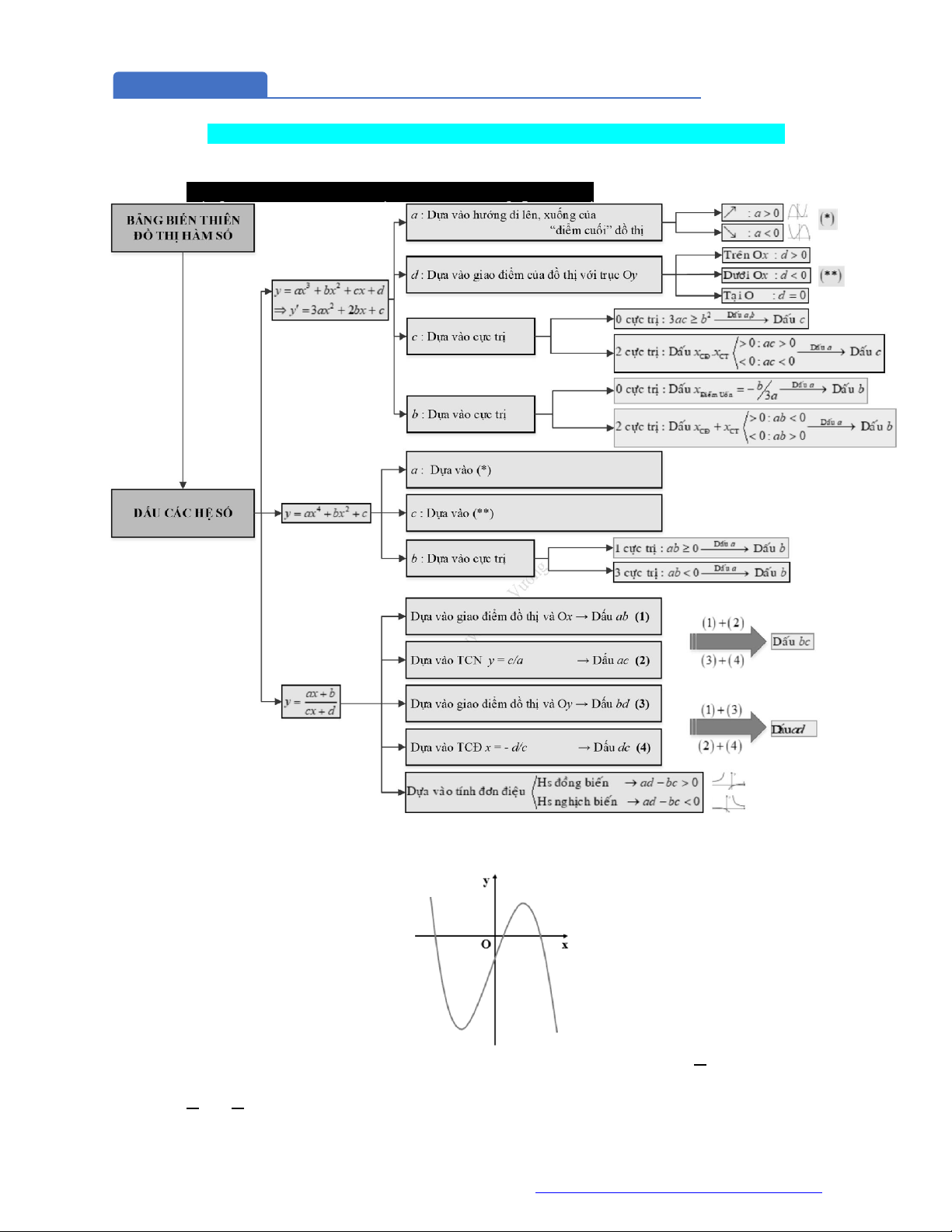
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
DẠNG TOÁN DÀNH CHO ĐỐI TƯỢNG HỌC SINH KHÁ MỨC 7-8 ĐIỂM
Dạng 1. Xét dấu của các hệ số hàm số thông qua đồ thị
Câu 1. (Đề Minh Họa 2020 Lần 1) Cho hàm số
3
3 ;y ax x d a d
có đồ thị như hình bên.
Mệnh đề nào dưới đây đúng?
A.
0, 0a d
. B.
0, 0a d
. C.
0, 0a d
. D.
0, 0a d
.
Lời giải
Chọn D
Ta có:
lim
x
đồ thị nhánh ngoài cùng của hàm số hướng đi xuống nên hệ số
0a
.
ĐỌC ĐỒ THỊ CỦA HÀM SỐ
Chuyên đề 7
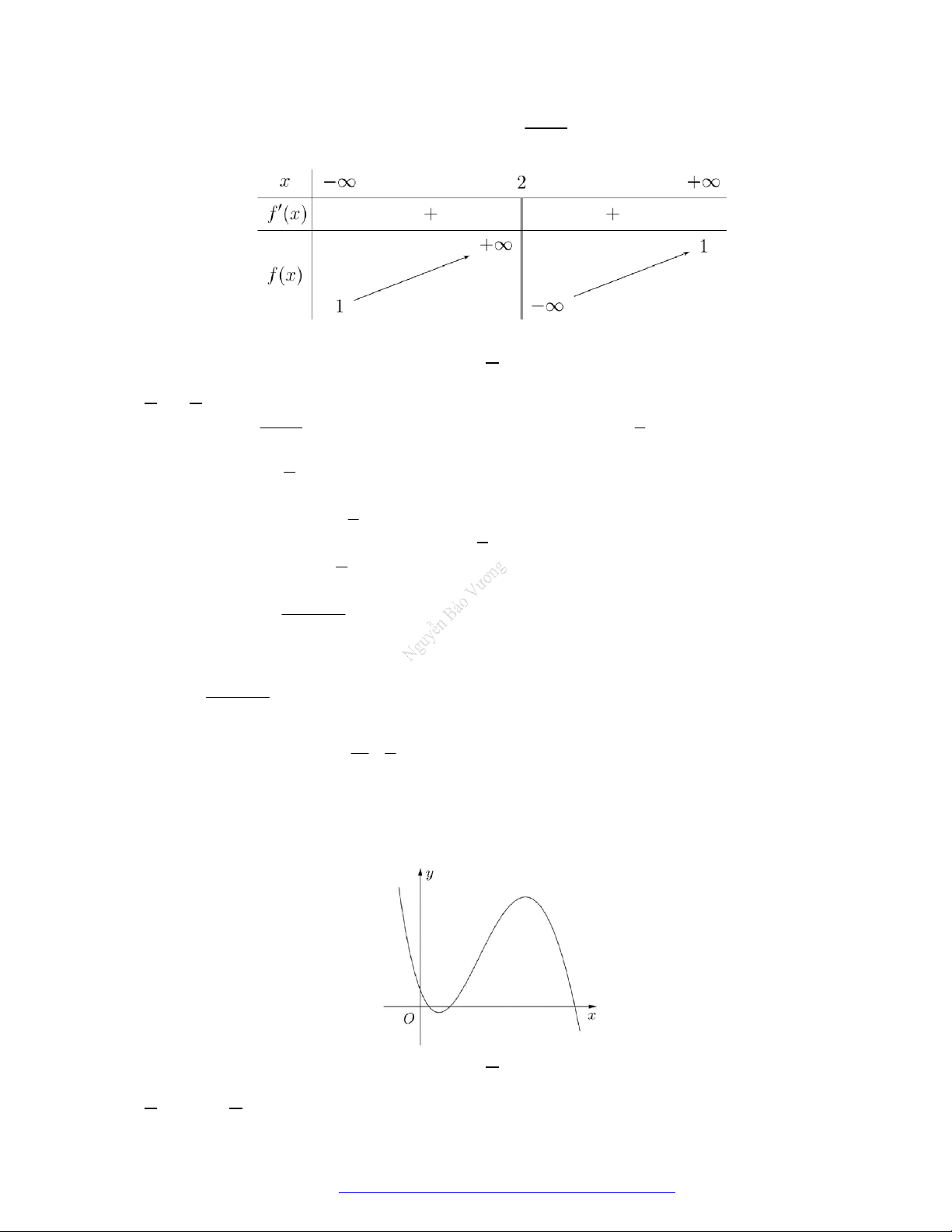
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Giao điểm của đồ thị hàm số với trục tung
: 0Oy x
là điểm nằm bên dưới trục hoành nên khi
0 0x y d
.
Câu 2. (Đề Tham Khảo 2020 Lần 2) Cho hàm số
1ax
f x
bx c
, ,a b c
có bảng biến thiên như
sau:
Trong các số
,a b
và
c
có bao nhiêu số dương?
A. 2. B. 3. C. 1. D. 0.
Lời giải
Chọn C
Hàm số
1ax
f x
bx c
có đường tiệm cận đứng là đường thẳng
c
x
b
và đường tiệm cận ngang
là đường thẳng
a
y
b
.
Từ bảng biến thiên ta có:
2
2
1
c
c
b
a b
a
b
1
Mặt khác:
2
'
ac b
f x
bx c
.
Vì hàm số đã cho đồng biến trên các khoảng
;2
và
2;
nên
2
' 0 0
ac b
f x ac b
bx c
2
Thay
1
vào
2
, ta được:
2
2
0 0 0 1
2 2
c c
c c c
.
Suy ra c là số dương và a, b là số âm.
Câu 3. (Mã 101 - 2020 Lần 1) Cho hàm số
3 2
y ax bx cx d
, , ,a b c d
có đồ thị là đường cong
trong hình bên. Có bao nhiêu số dương trong các số
a
,
b
,
c
,
d
?
A.
4
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn C.
Ta có
lim
x
y
0a
.
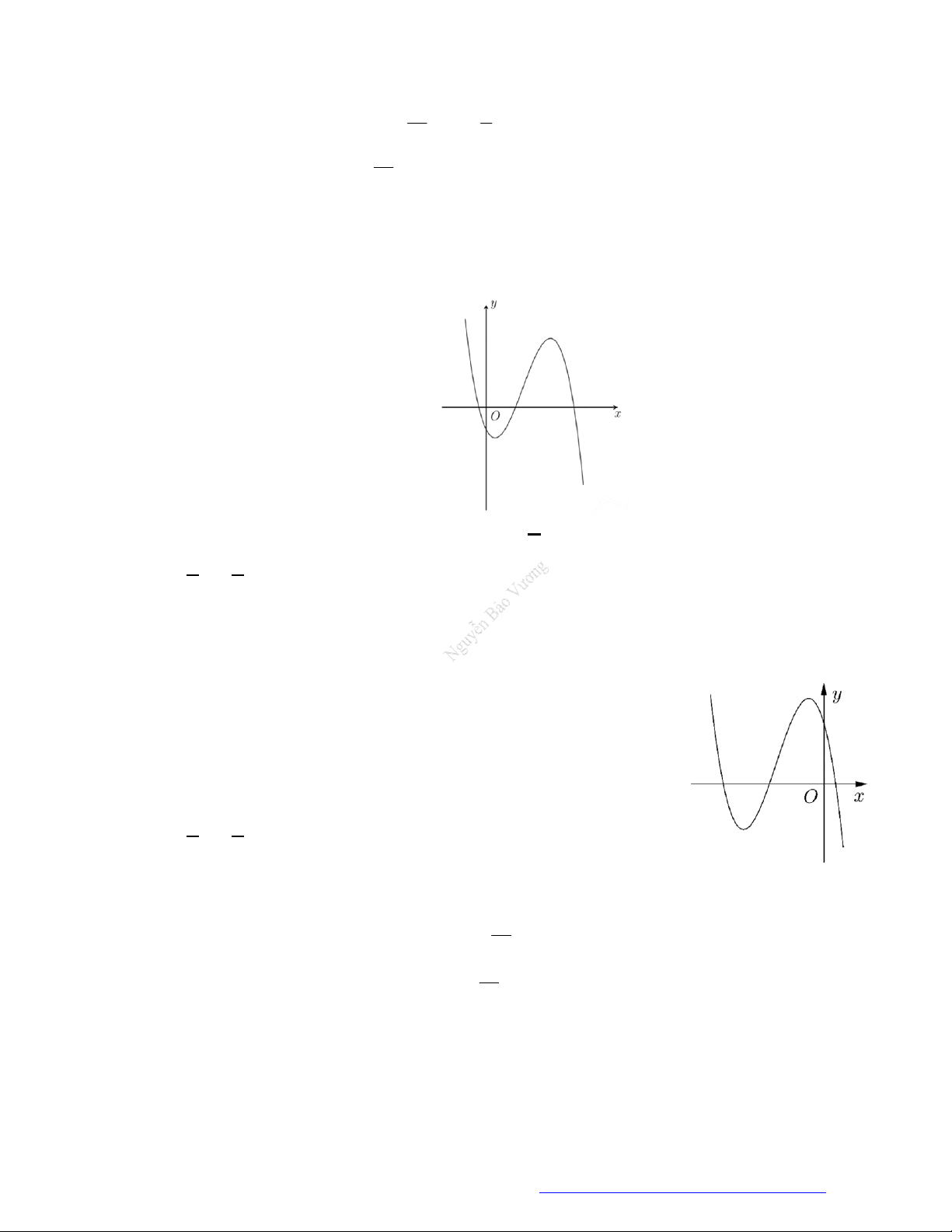
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Gọi
1
x ,
2
x là hoành độ hai điểm cực trị của hàm số suy ra
1
x ,
2
x nghiệm phương trình
2
3 2 0y ax bx c
nên theo định lý Viet:
+) Tổng hai nghiệm
1 2
2
0
3
b
x x
a
0
b
a
0b
.
+) Tích hai nghiệm
1 2
0
3
c
x x
a
0c
.
Lại có đồ thị hàm số cắt trục tung tại điểm có tung độ dương nên
0d
.
Vậy có
2
số dương trong các số
a
,
b
,
c
,
d
.
Câu 4. (Mã 102 - 2020 Lần 1) Cho hàm số y ax bx cx d
3 2
, , ,a b c d
có đồ thị là đường
cong trong hình bên. Có bao nhiêu số dương trong các hệ số
, , ,a b c d
?
A.
4
. B.
3
. C.
1
. D.
2
.
Lời giải
Chọn C
Ta có
lim
x
f x a
0
Đồ thị hàm số có hai điểm cực trị nằm cùng phía của trục tung nên
ac c 0 0
Đồ thị hàm số có điểm uốn nằm bên phải trục tung nên
ab b 0 0
Đồ thị hàm số cắt trục tung ở dưới trục hoành
d 0
Câu 5. (Mã 103 - 2020 Lần 1) Cho hàm số
3 2
, , ,y ax bx cx d a b c d
có đồ thị là đường cong trong
hình bên. Có bao nhiêu số dương trong các số
, , ,a b c d
?
A.
4
. B.
2
.
C.
1
. D.
3
.
Lời giải
Chọn C
Ta có
2
3 2y ax bx c
. Dựa vào đồ thị ta thấy
0a
Hàm số có 2 cực trị âm nên
2
9 0
0
0
2
0 0
0
3
0
0
3
y
b ac
b
b
S
c
a
P
c
a
Đồ thị cắt trục
Oy
tại điểm
0;d
nên
0d
.
Vậy có đúng một số dương trong các số
, , ,a b c d
Câu 6. (Mã 104 - 2020 Lần 1) Cho hàm số
3 2
, , , y ax bx cx d a b c d
có đồ thị là đường cong
trong hình bên. Có bao nhiêu số dương trong các số
, , ,a b c d
?
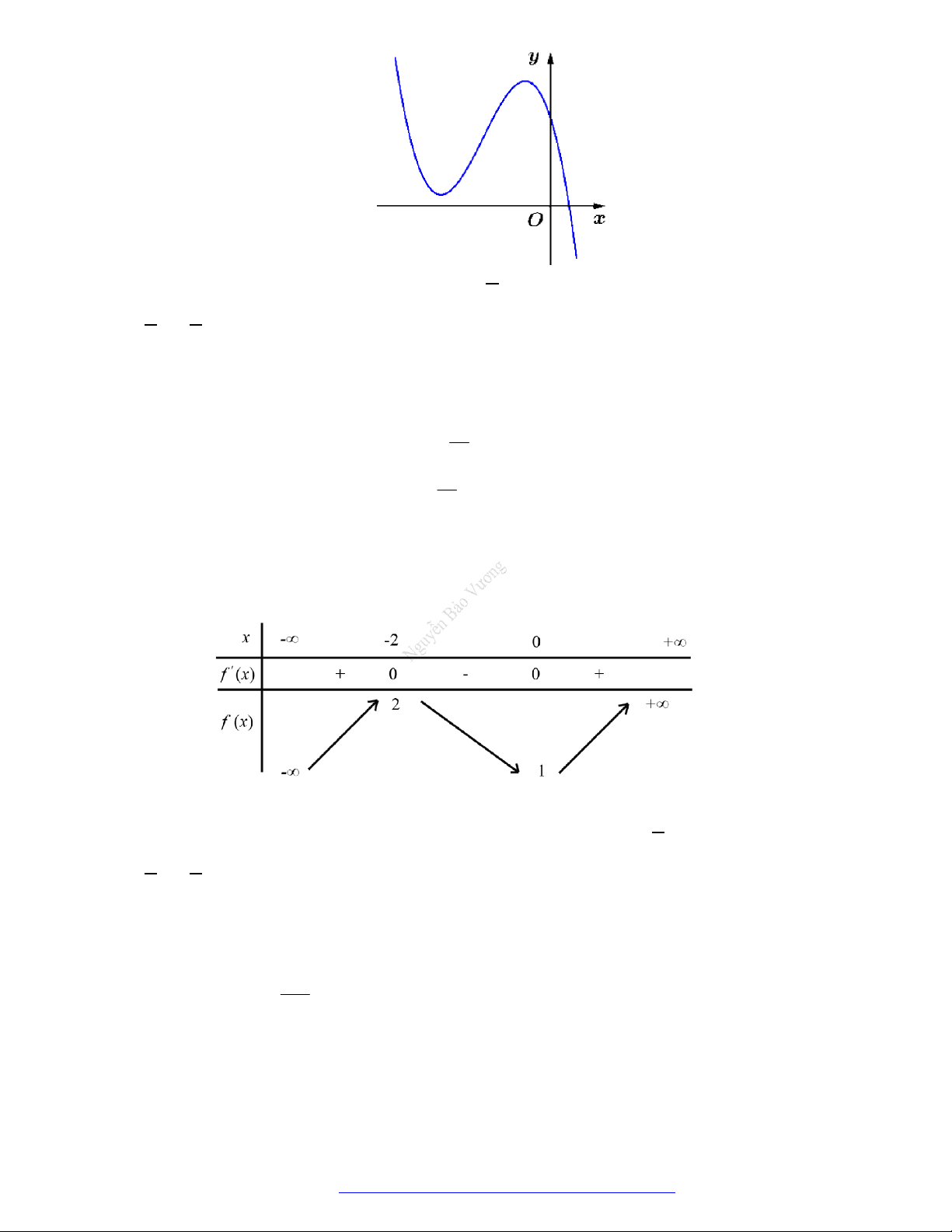
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
4
. B.
2
. C.
1
. D.
3
.
Lời giải
Chọn C
Ta có:
2
3 2
y ax bx c
Dựa vào đồ thị ta thấy
0a
Hàm số có 2 cực trị âm nên
2
9 0
0
0
2
0 0
0
3
0
0
3
y
b ac
b
b
S
c
a
P
c
a
Đồ thị cắt trục
Oy
tại điểm
0;d
nên
0d
Vậy có đúng 1 số dương trong các số
, , ,a b c d
.
Câu 7. (Mã 102 - 2020 Lần 2) Cho hàm số
3 2
, , , f x ax bx cx d a b c d
có bảng biến thiên
như sau
Có bao nhiêu số dương trong các số
, , , a b c d
?
A.
2
. B.
4
. C.
1
. D.
3
.
Lời giải
Chọn D
Từ dáng điệu sự biến thiên hàm số ta có
0.a
Khi
0x
thì
1 0y d
.
Mặt khác
2
3 2f x ax bx c
. Từ bảng biến thiên ta có
2
0
0
x
f x
x
.
Từ đó suy ra
2
0; 2 3 0
3
b
c b a
a
.
Vậy có 3 số dương là
, , a b d
.
Câu 8. (Mã 103 - 2020 Lần 2) Cho hàm số
3 2
, , ,f x ax bx cx d a b c d
có bảng biến thiên
như sau:
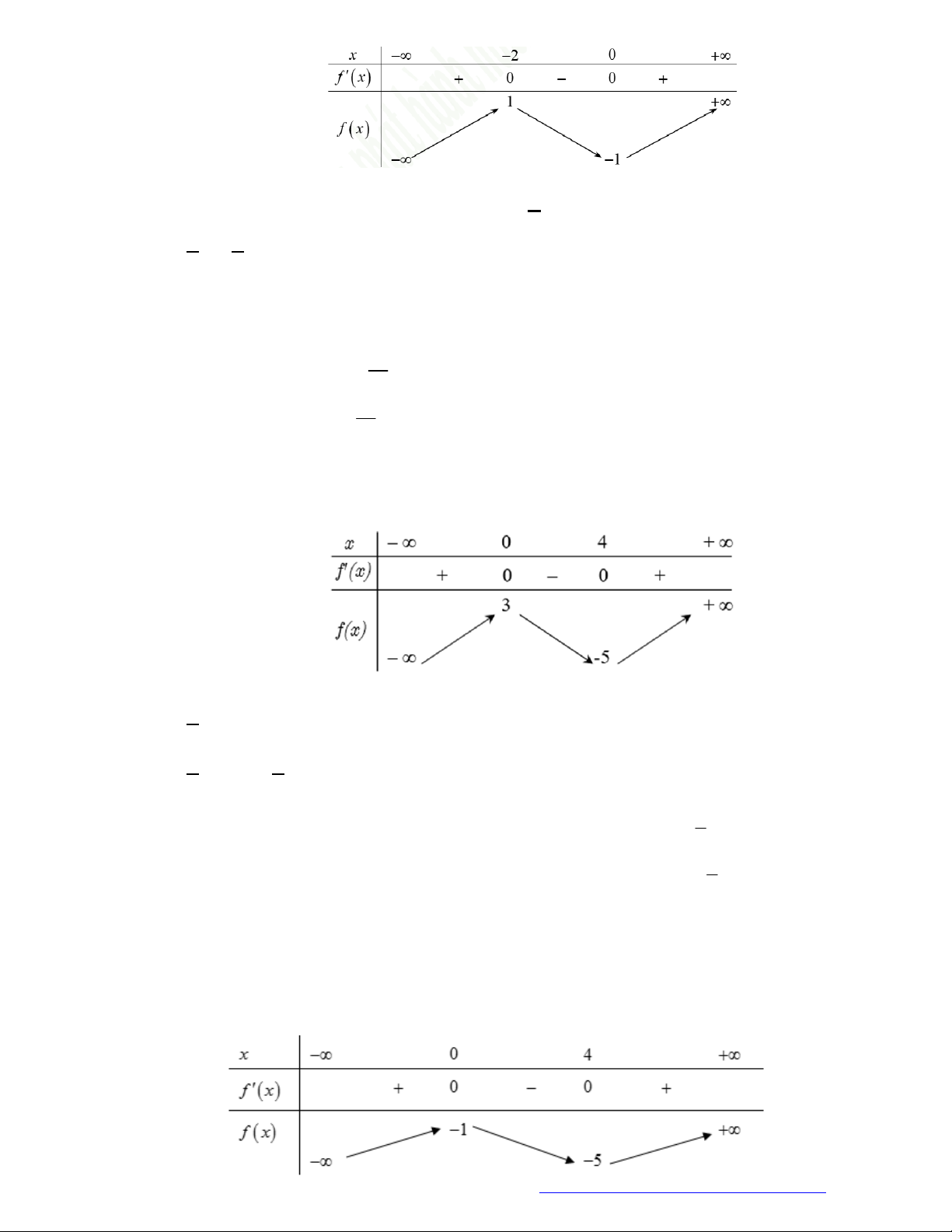
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Có bao nhiêu số dương trong các số
, , , ?a b c d
A.
3.
B.
4.
C.
2.
D.
1.
Lời giải
Chọn C
lim 0.
x
f x a
0 1 1 0.f d
2
3 2 .f x ax bx c
Ta có
1 2
1 2
2
2
2
3 0
3
.
0 0
0
3
b
x x
b a
a
x x c c
a
Có 2 số dương là a, b
Câu 9. (Mã 101 – 2020 Lần 2) Cho hàm số
3 2
, , ,f x ax bx cx d a b c d
có bảng biến thiên
như sau:
Có bao nhiêu số dương trong các số
, , ,a b c d
?
A.
2
. B.
4
. C.
1
. D.
3
.
Lời giải
Chọn A.
Từ bảng biến thiên, ta có
1
(0) 3 3
4
(4) 5 64 16 4 5 3
2
(0) 0 0
0
(4) 0 48 8 0
3
a
f d
f a b c d
b
f c
c
f a b c
d
Vậy trong các số
, , ,a b c d
có 2 số dương.
Câu 10. (Mã 104 - 2020 Lần 2) Cho hàm số
3 2
, , ,f x ax bx cx d a b c d
có bảng biến thiên
như sau:
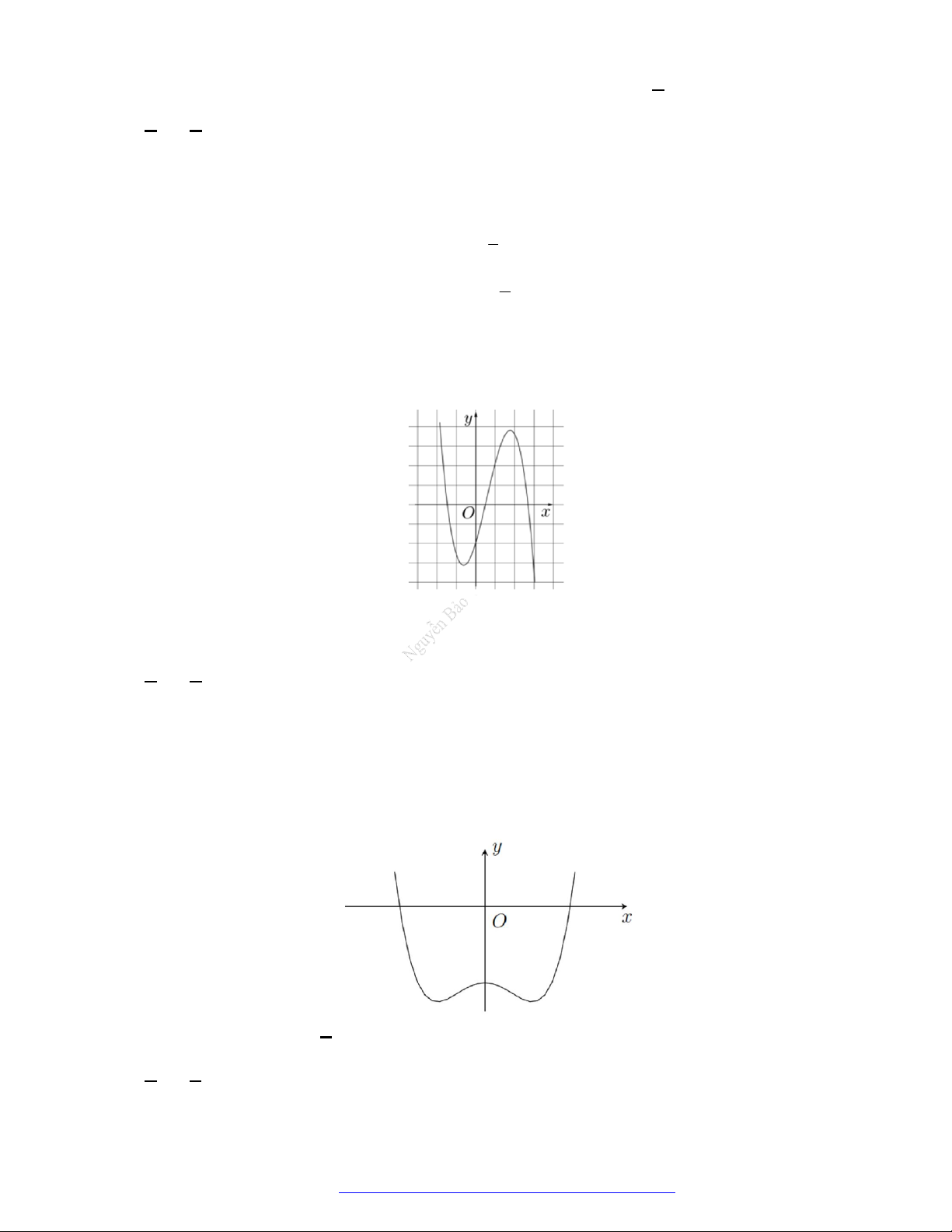
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Có bao nhiêu số dương trong các số
, , ,a b c d
?
A.
4
. B.
2
. C.
3
. D.
1
.
Lời giải
Chọn D
Ta có:
3 2
, , ,f x ax bx cx d a b c d
2
3 2f x ax bx c
Đồ thị hàm số
f x
có hai điểm cực trị
0; 1 , 4; 5A B
nên ta có hệ:
1
0 1
1
8
4 5
64 16 4 5
3
4
0
0 0
0
48 8 0
4 0
1
a
f
d
f
a b c d
b
c
f
c
a b c
f
d
. Trong các số
, , ,a b c d
có
1
số dương.
Câu 11. Cho hàm số
3 2
y ax bx cx d
có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?
A.
0, 0, 0, 0 a b c d
B.
0, 0, 0, 0 a b c d
.
C.
0, 0, 0, 0 a b c d
D.
0, 0, 0, 0 a b c d
.
Lời giải
Chọn A
Dựa vào đồ thị suy ra hệ số
0a
loại phương án C
2
3 2 0
y ax bx c có 2 nghiệm
1 2
,x x trái dấu (do hai điểm cực trị của đồ thị hàm số nằm hai
phía với
Oy
)
3 . 0 0 a c c
loại phương án D. Do
0; 0. C Oy D d d
Câu 12. (THPT Nguyễn Khuyến 2019) Cho hàm số
4 2
y ax bx c có đồ thị như hình bên. Mệnh đề
nào dưới đây là đúng?
A.
0, 0, 0a b c
B.
0, 0, 0a b c
C.
0, 0, 0a b c
D.
0, 0, 0a b c
Lời giải
Chọn B
Ta có đồ thị có hình dạng như trên với hàm bậc bốn trùng phương có hai điểm cực tiểu và một
điểm cực đại nên
0, 0a b
. Giá trị cực đại nhỏ hơn
0
nên
0c
.
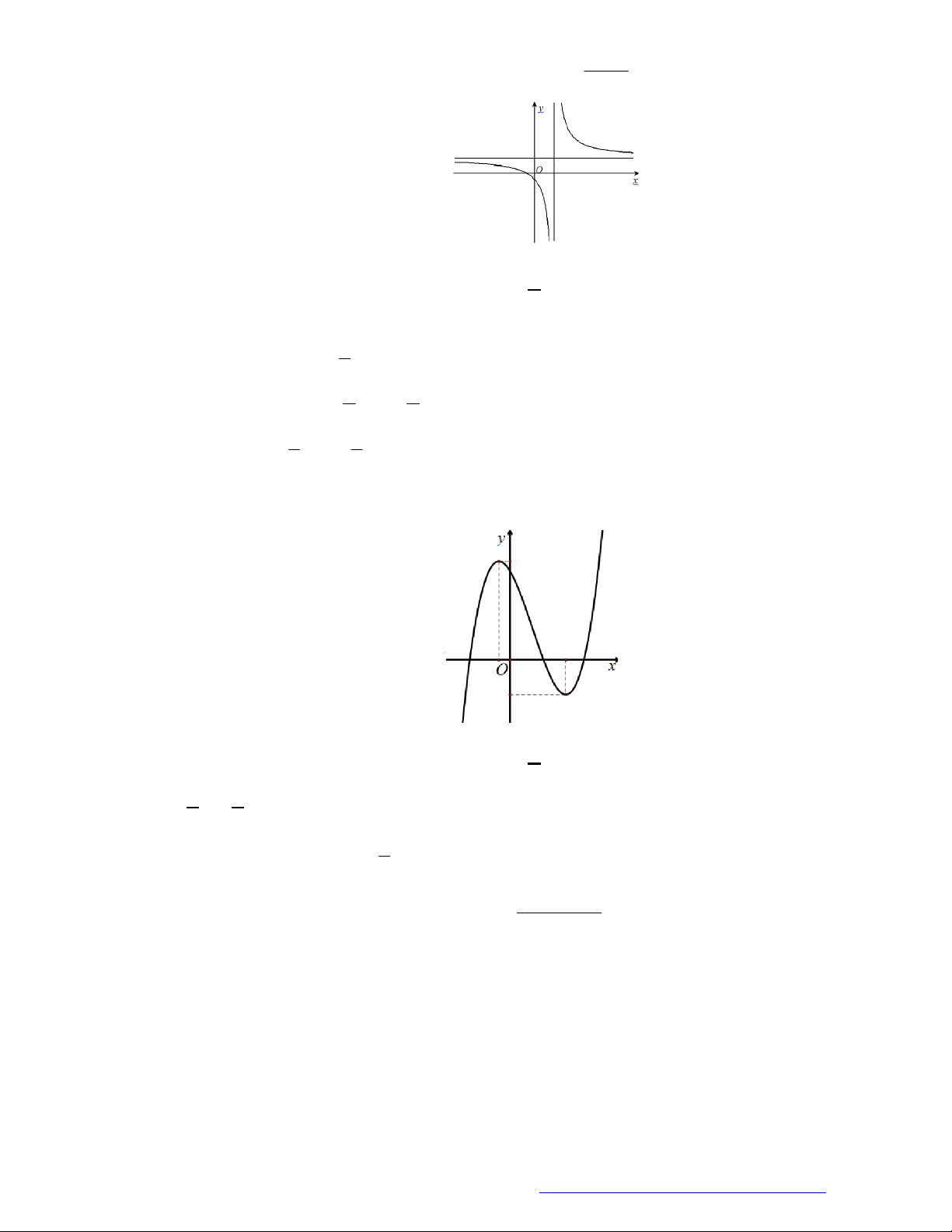
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Câu 13. (Chuyên Trần Phú Hải Phòng 2019) Cho hàm số
ax b
y
cx d
có đồ thị như sau.
Mệnh đề nào sau đây đúng?
A.
0; 0ac bd
B.
0; 0ab cd
C.
0; 0bc ad
D.
0; 0ad bd
Lời giải
Theo đồ thị:
Tiệm cận ngang:
0
a
y
c
1
Tiệm cận đứng:
0 0
d d
x
c c
2
0 0 0
b b
y x
a a
3
Câu 14. (THPT Thiệu Hóa – Thanh Hóa 2019) Cho hàm số
3 2
0y ax bx cx d a
có đồ thị như
hình vẽ dưới đây. Chọn khẳng định đúng về dấu của
a
,
b
,
c
,
d
?
A.
0a
,
0b
,
0d
,
0c
B.
0a
,
0c b
,
0d
C.
0, 0, 0, 0.a b c d
D.
0a
,
0b
,
0c
,
0d
lời giải
Chọn D
Dựa vào đồ thị ta có
0a
, đồ thị cắt
Oy
tại
1
điểm có tung độ dương nên
0d
, đồ thị có
2
cực
trị trái dấu nên
1 2
. 0 0 0
c
x x c
a
. Vậy đáp án D
Câu 15. (Toán Học Tuổi Trẻ 2019) Cho hàm số
1
, 0
1
a x b
y d
c x d
có đồ thị như hình trên. Khẳng
định nào dưới đây là đúng?

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
1, 0, 1.a b c
B.
1, 0, 1.a b c
C.
1, 0, 1.a b c
D.
1, 0, 1.a b c
Lời giải
Theo bài ra, đường tiệm cận đứng của đồ thị hàm số là
.
1
d
x
c
Đường tiệm cận ngang của đồ thị hàm số là:
1
.
1
a
y
c
Nhìn đồ thị ta thấy:
0
1
d
x
c
mà
0 1 0 1d c c
.
1
0 1 0 1
1
a
y a a
c
.
Đồ thị cắt trục tung tại điểm có tung độ bằng
0 0
b
b
d
.
Câu 16. (Sở Ninh Bình 2019) Cho hàm số
4 2
y ax bx c
(
0a
) có đồ thị như hình vẽ dưới đây.
Mệnh đề nào dưới đây đúng?
A.
0a
,
0b
,
0c
. B.
0a
,
0b
,
0c
.
C.
0a
,
0b
,
0c
. D.
0a
,
0b
,
0c
.
Lời giải
Đồ thị cắt trục tung tại điểm
0;c
, từ đồ thị suy ra
0c
Mặt khác đồ thị hàm số có ba điểm cực trị nên
0y
có ba nghiệm phân biệt, hay
3 2
4 2 2 2 0y ax bx x ax b
có ba nghiệm phân biệt. Suy ra
,a b
trái dấu.
Mà
0 0a b
Câu 17. (Cụm Liên Trường Hải Phòng 2019) Hàm số
3 2
y ax bx cx d
có đồ thị như hình vẽ bên
dưới:
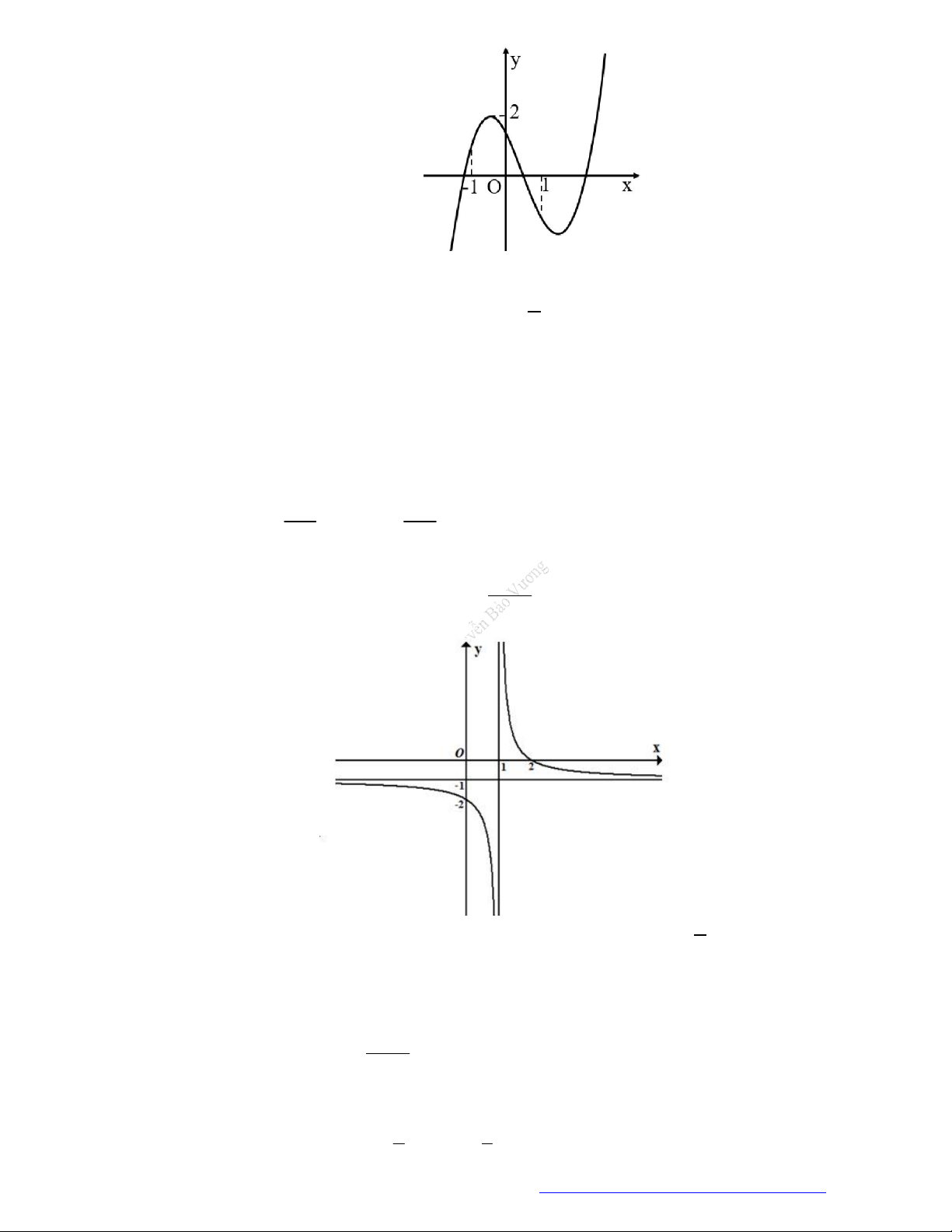
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Khẳng định nào là đúng?
A.
0a
,
0b
,
0c
,
0d
. B.
0a
,
0b
,
0c
,
0d
.
C.
0a
,
0b
,
0c
,
0d
. D.
0a
,
0b
,
0c
,
0d
.
Lời giải
+ Dựa vào hình dạng đồ thị ta khẳng định được
0a
.
+ Đồ thị cắt trục
Oy
tại điểm có tọa độ
0;d
. Dựa vào đồ thị suy ra
0d
.
+ Ta có:
2
3 2y ax bx c
. Hàm số có hai điểm cực trị
1
x
,
2
x
1 2
x x
trái dấu nên phương
trình
0y
có hai nghiệm phân biệt
1
x
,
2
x
trái dấu. Vì thế
3 . 0a c
, nên suy ra
0c
.
+ Mặt khác từ đồ thị ta thấy
1
2
1
1
x
x
nên
1 2
0x x
.
Mà
1 2
2
3
b
x x
a
nên suy ra
2
0
3
b
a
0b
.
Vậy
0a
,
0b
,
0c
,
0d
.
Câu 18. (THPT Ba Đình 2019) Cho hàm số
ax b
y
x c
có đồ thị như hình bên dưới, với
a
,
b
,
c
.
Tính giá trị của biểu thức
2 3T a b c
?
A.
8T
. B.
2T
. C.
6T
. D.
0T
.
Lời giải
Từ đồ thị hàm số, ta suy ra
Đồ thị hàm số có tiệm cận đứng là đường thẳng
1x
, tiệm cận ngang là đường thẳng
1y
.
Đồ thị hàm số đi qua các điểm
2;0A
,
0; 2B
.
Từ biểu thức hàm số
ax b
y
x c
(vì đồ thị hàm số là đồ thị hàm nhất biến nên
0ac b
), ta suy
ra
Đồ thị hàm số có tiệm cận đứng là đường thẳng
x c
, tiệm cận ngang là đường thẳng
y a
.
Đồ thị hàm số đi qua
;0
b
A
a
,
0;
b
B
c
.
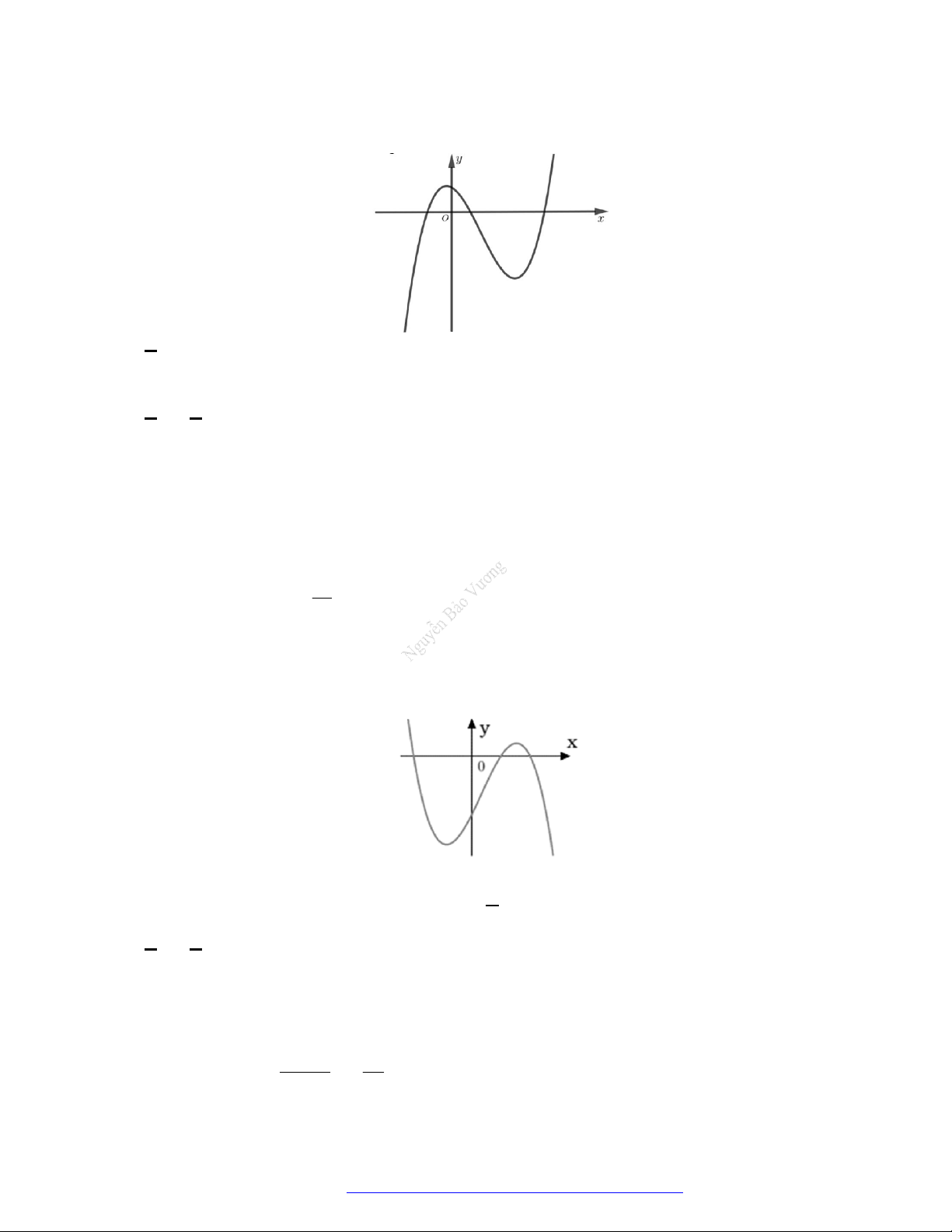
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Đối chiếu lại, ta suy ra
1c
,
1a
,
2b
.
Vậy
2 3 1 2.2 3 1 0T a b c
.
Câu 19. (THPT Việt Đức Hà Nội 2019) Cho hàm số
3 2
y ax bx cx d
có đồ thị như hình bên. Trong
các mệnh đề sau mệnh đề nào đúng?
A.
0, 0, 0ab bc cd
B.
0, 0, 0ab bc cd
C.
0, 0, 0ab bc cd
D.
0, 0, 0ab bc cd
Lời giải
Chọn A
Từ dáng điệu của đồ thị ta có ngay được:
lim ; lim 0
x x
y y a
.
Đồ thị hàm số cắt trục tung tại một điểm có tung độ dương nên
0d
.
Ta có:
2
' 3 2y ax bx c
Mặt khác dựa vào đồ thị ta thấy phương trình
' 0y
có hai nghiệm trái dấu và tổng hai nghiệm
này luôn dương nên
0
0
2
0
3
ac
c
b
b
a
(do
0a
)
Do đó:
0, , 0ab bc cd
.
Câu 20. (THPT Lương Thế Vinh Hà Nội 2019) Cho hàm số
3 2
y ax bx cx d
có đồ thị như hình
dưới. Khẳng định nào sau đây đúng ?
A.
0, 0, 0, 0a b c d
B.
0, 0, 0, 0a b c d
C.
0, 0, 0, 0a b c d
D.
0, 0, 0, 0a b c d
Lời giải
Chọn D
- Dựa vào hình dáng của đồ thị suy ra hệ số
0a
.
- Đồ thị cắt trục
Oy
tại điểm có tung độ âm nên
0d
.
- Ta thấy đồ thị như hình vẽ có hai điểm cực trị, hoành độ các điểm cực trị trái dấu suy ra phương
trình
2
3 2 0y ax bx c
có 2 nghiệm
1 2
,x x
trái dấu kéo theo
3 . 0 0a c c
.
- Mặt khác
1 2
0 0
2 3
x x b
b
a
.
Câu 21. (THPT Chuyên Bắc Ninh 2019) Cho hàm số có đồ thị như hình vẽ. Mệnh đề
nào dưới đây đúng ?
4 2
y ax bx c
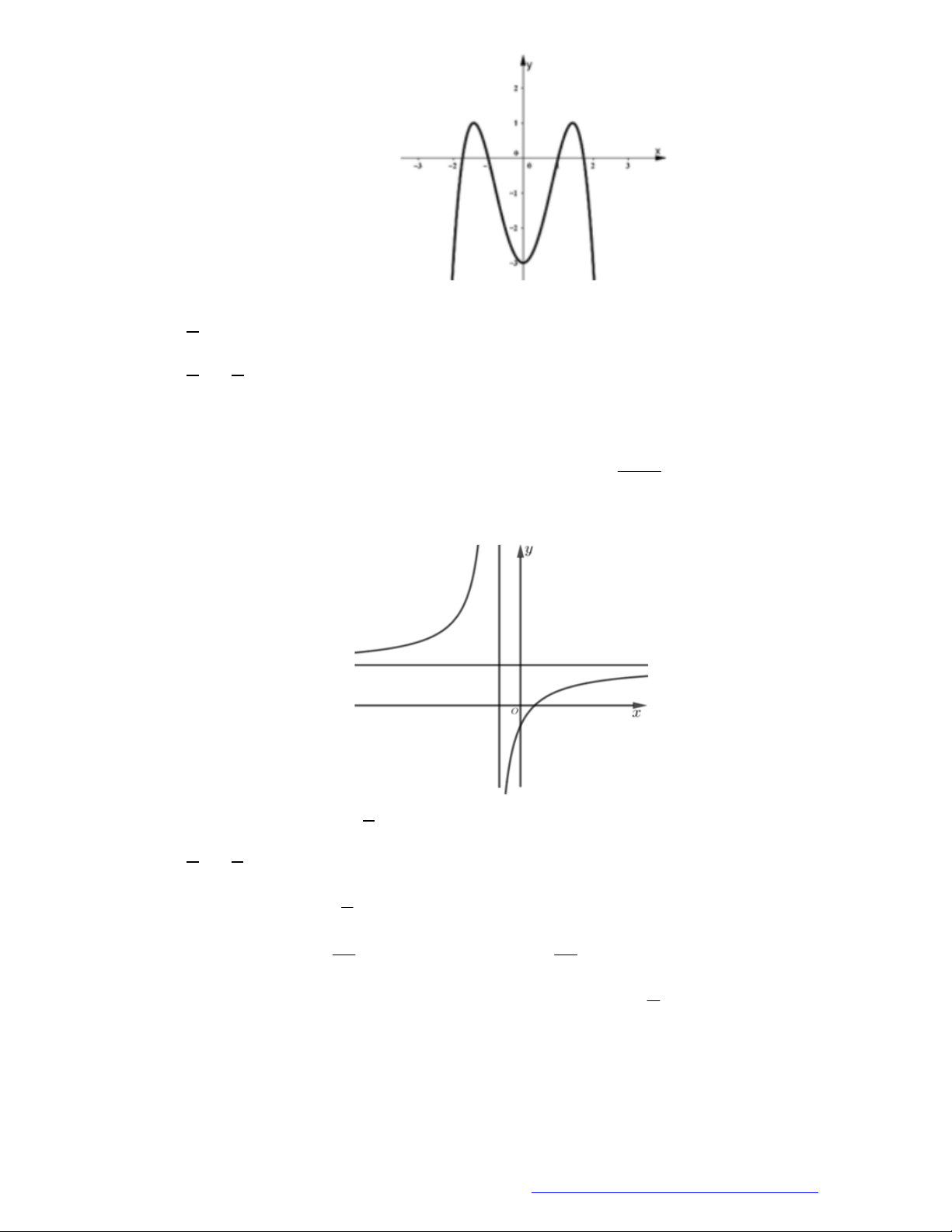
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
A.
0, 0, 0a b c
. B.
0, 0, 0a b c
.
C.
0, 0, 0a b c
. D.
0, 0, 0a b c
Lời giải
Chọn C
- Dựa vào hình dạng đồ thị suy ra
0a
- Hàm số có 3 điểm cực trị nên
0 0ab b
- Giao điểm với trục tung nằm dưới trục hoành nên
0c
.
Câu 22. (Chuyên Lê Quý Đôn Quảng Trị 2019) Cho hàm số
ax b
y
cx d
có đồ thị như trong hình bên
dưới. Biết rằng
a
là số thực dương, hỏi trong các số
, ,b c d
có tất cả bao nhiêu số dương?
A.
1
. B.
2
. C.
0
. D.
3
.
Lời giải
Chọn B
Nhìn vào đồ thị ta thấy
tiệm cận ngang
a
y
c
nằm trên trục hoành nên
0c
(vì
0a
)
tiệm cận đứng
d
x
c
nằm bên trái trục tung nên
0.
d
c
Suy ra
0d
(vì
0c
)
giao điểm của đồ thị và trục tung nằm bên dưới trục hoành nên
0.
b
d
Suy ra
0b
(vì
0d
)
Vậy
0, 0c d
Câu 23. (Cụm liên trường Hải Phòng 2019) Hàm số
3 2
y ax bx cx d
có đồ thị như hình vẽ bên
dưới:

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Khẳng định nào là đúng?
A.
0a
,
0b
,
0c
,
0d
. B.
0a
,
0b
,
0c
,
0d
.
C.
0a
,
0b
,
0c
,
0d
. D.
0a
,
0b
,
0c
,
0d
.
Lời giải
Chọn D
+ Dựa vào hình dạng đồ thị ta khẳng định được
0a
.
+ Đồ thị cắt trục
Oy
tại điểm có tọa độ
0;d
. Dựa vào đồ thị suy ra
0d
.
+ Ta có:
2
3 2y ax bx c
. Hàm số có hai điểm cực trị
1
x
,
2
x
1 2
x x
trái dấu nên phương
trình
0y
có hai nghiệm phân biệt
1
x
,
2
x
trái dấu. Vì thế
3 . 0a c
, nên suy ra
0c
.
+ Mặt khác từ đồ thị ta thấy
1
2
1
1
x
x
nên
1 2
0x x
.
Mà
1 2
2
3
b
x x
a
nên suy ra
2
0
3
b
a
0b
.
Vậy
0a
,
0b
,
0c
,
0d
.
Câu 24. (Chuyên Nguyễn Huệ 2019) Cho hàm số
ax b
y
cx d
có đồ thị như hình vẽ bên. Khẳng định nào
sau đây là khẳng định đúng?
A.
0
0
ad
bc
. B.
0
0
ad
bc
. C.
0
0
ad
bc
. D.
0
0
ad
bc
.
Lời giải
Chọn C
Nhận xét từ đồ thị:
+ Giao với trục hoành tại
0
o
b
x
a
a
và
b
trái dấu (1).
+ Giao với trục tung tại
0
o
b
y b
d
và
d
trái dấu (2).
+ Tiệm cận đứng:
0
d
x d
c
và
c
cùng dấu (3).
Từ (1) và (2) suy ra:
a
và
d
cùng dấu hay
0ad
.
Từ (2) và (3) suy ra:
b
và
c
trái dấu hay
0bc
.
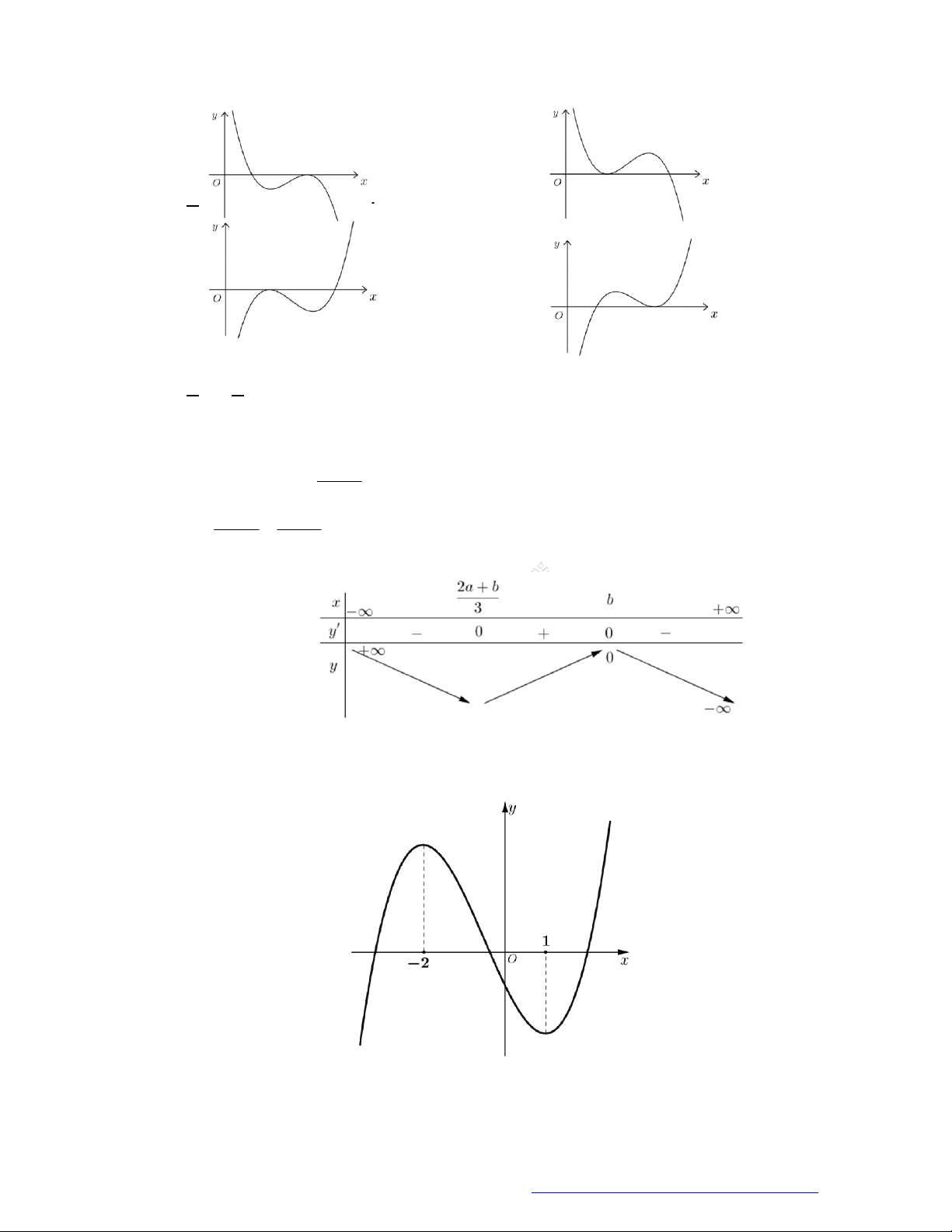
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Câu 25. Tìm đồ thị hàm số
y f x
được cho bởi một trong các phương án dưới đây, biết
2
f x a x b x
với
a b
.
A. . B. .
C. . D. .
Lời giải
Chọn A
Có
2
. 2 2 2 2 3f x b x a x b x b x b x a x b x b a x
0
2
3
x b
f x
a b
x
.
Có
2 2
3 3
a b b b
b
.
Ta có bảng biến thiên
Từ đó chọn đáp án A
Câu 26. Cho đường cong
3 2
:C y ax bx cx d
có đồ thị như hình bên.
Khẳng định nào sau đây là đúng?
A.
0, 0, 0, 0a b c d
.
B.
0, 0, 0, 0a b c d
.
C.
0, 0, 0, 0
a b c d
.
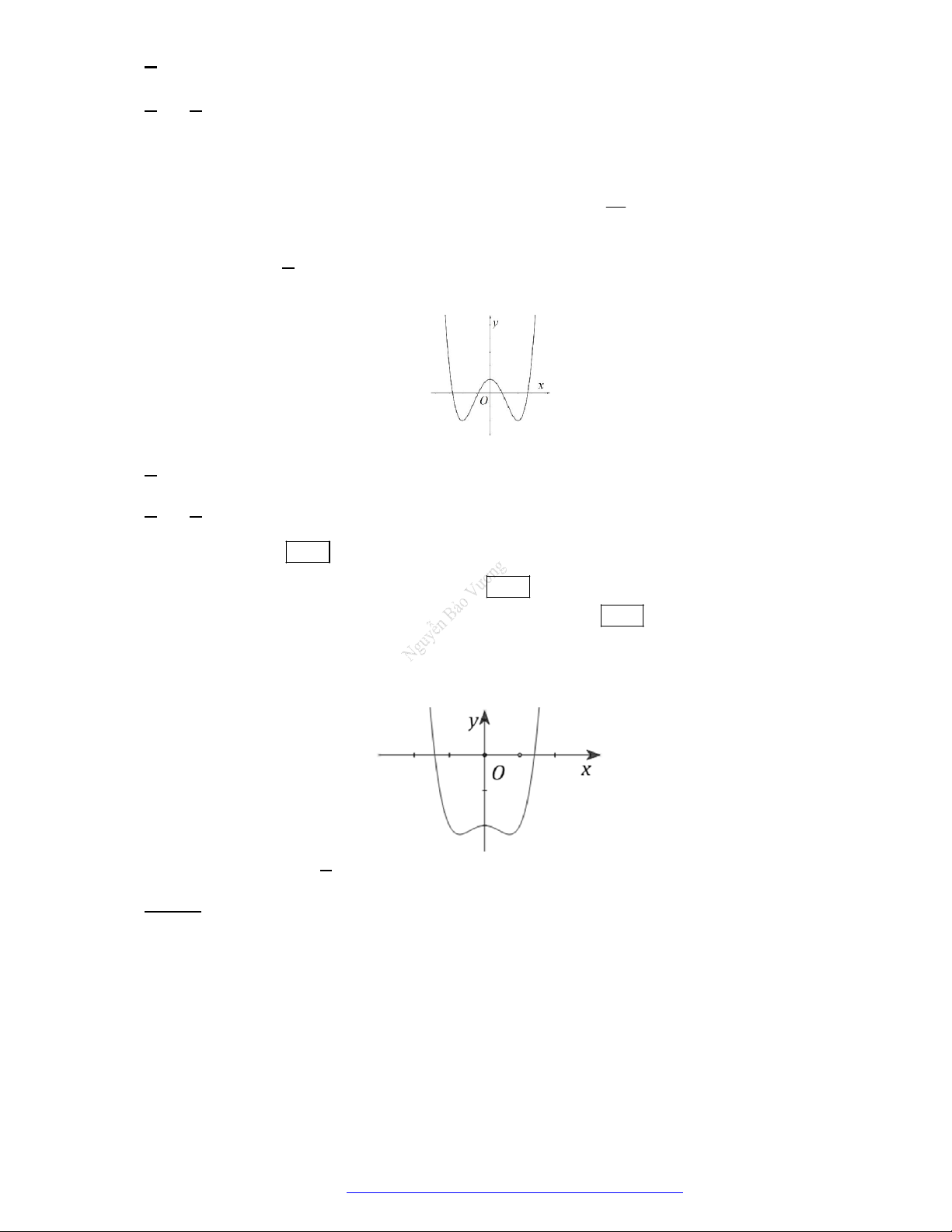
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
D.
0, 0, 0, 0a b c d
.
Lời giải
Chọn D
Từ đồ thị ta có
0 0x y d
, từ dạng đồ thị suy ra
0a
.
Mặt khác
2
' 3 2y ax bx c từ đồ thị ta có phương trình
' 0y
có hai nghiệm trái dấu suy ra
0ac
mà
0a
suy ra
0c
.
Hơn nữa phương trình
' 0y
có hai nghiệm phân biệt
1 2
2
1
3
b
x x
a
suy ra
3 2 0a b b
.
Vậy chọn đáp án D.
Câu 27. (Gia Lai 2019) Hàm số
4 2
y ax bx c
có đồ thị như hình vẽ bên. Mệnh đề nào sau đây
đúng?
A.
0a
,
0b
,
0c
. B.
0a
,
0b
,
0c
.
C.
0a
,
0b
,
0c
. D.
0a
,
0b
,
0c
.
Lời giải
Chọn C
Dựa vào đồ thị:
+
lim
x
y
0a
.
+ Đồ thị hàm số có ba điểm cực trị
0ab
0b
.
+ Giao điểm của đồ thị hàm số và trục tung có tung độ dương
0c
.
Vậy
0a
,
0b
,
0c
.
Câu 28. (THPT Thăng Long 2019) Cho hàm số
4 2
y ax bx c
có đồ thị như hình vẽ. Tìm kết luận
đúng
A.
0a b
. B.
0bc
. C.
0ab
. D.
0ac
.
Lời giải
Chọn B
Từ hình vẽ ta thấy:
Đồ thị hàm số có bề lõm hướng lên
0a
.
Đồ thị hàm số cắt trục tung tại điểm có tung độ âm
0c
.
Đồ thị hàm số có 3 điểm cực trị
0 0ab b
.
Vậy chỉ có
0bc
.
Câu 29. (THPT Cẩm Bình Hà Tỉnh 2019) Cho hàm số
4 2
( 0)y ax bx c a
có đồ thị như hình bên.
Hãy chọn mệnh đề đúng.
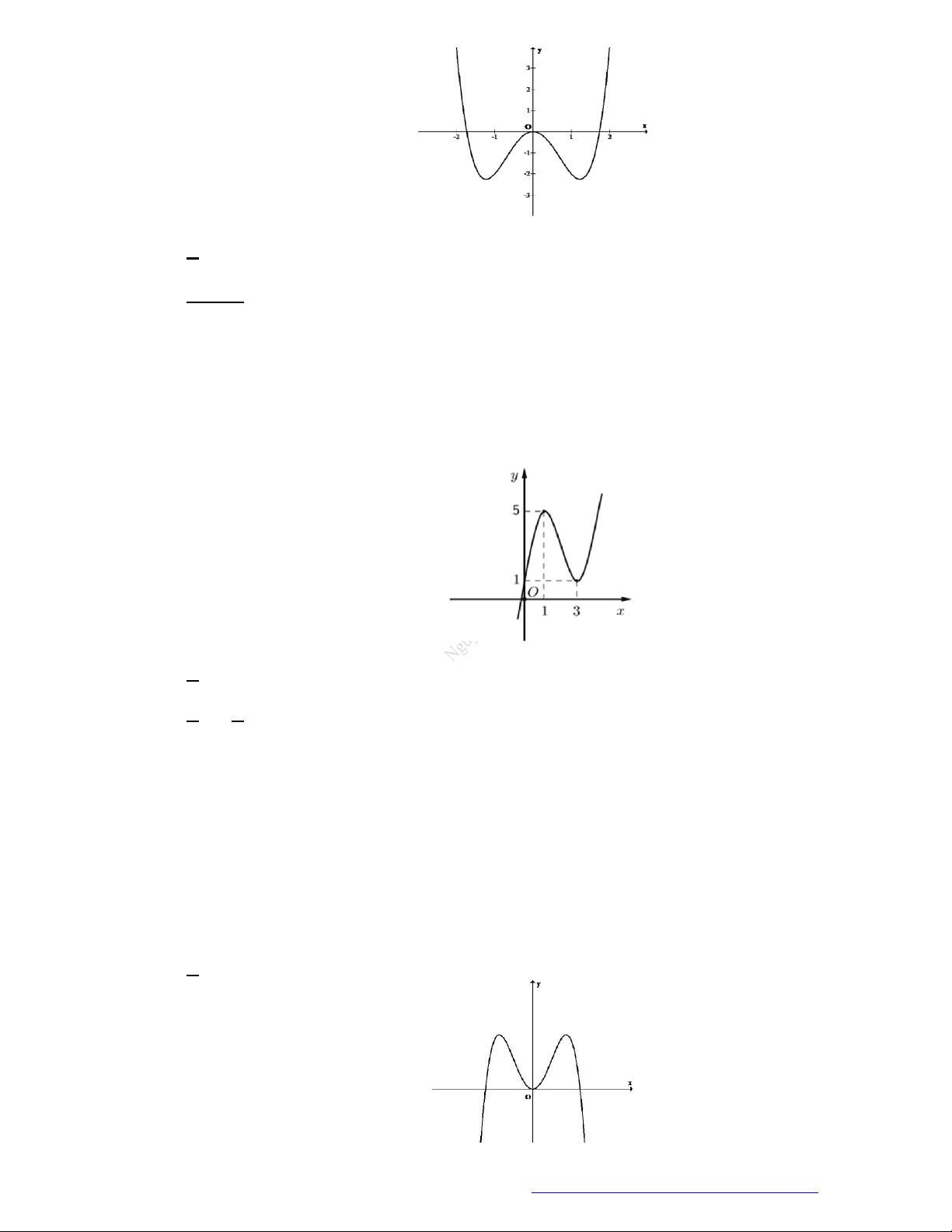
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
A.
0, 0, 0a b c
. B.
0, 0, 0a b c
.
C.
0, 0, 0a b c
. D.
0, 0, 0a b c
.
Lời giải
Chọn C
Dựa vào hình dạng đồ thị hàm số ta nhận thấy :
Hệ số
0a
Đồ thị hàm số đi qua gốc tọa tọa
0c
Hàm số có 3 điểm cực trị
. 0 0a b b
Câu 30. (Chuyên Long An 2019) Cho hàm số
3 2
( )y f x ax bx cx d có đồ thị như hình vẽ ở bên.
Mệnh đề nào
sau đây đúng?
A.
0a
,
0b
,
0c
,
0d
. B.
0a
,
0b
,
0c
,
0d
.
C.
0a
,
0b
,
0c
,
0d
. D.
0a
,
0b
,
0c
,
0d
.
Lời giải
Chọn C
Đồ thị hàm số đi qua các điểm
(0;1)A
,
(1;5)B
và
(3;1)C
và đạt cực trị tại các điểm
B
và
C
.
2
( ) 3 2f x ax bx c
. Ta có
(0) 1 1 1
(1) 5 5 6
(1) 0 3 2 0 9
(3) 0 27 6 0 1
f d a
f a b c d b
f a b c c
f a b c d
.
Câu 31. (THPT Trần Phú 2019) Cho hàm số bậc bốn trùng phương
4 2
y ax bx c có đồ thị như
hình vẽ bên. Mệnh đề nào dưới đây là đúng?
A.
0, 0, 0a b c
. B.
0, 0, 0a b c
.
C.
0, 0, 0a b c
. D.
0, 0, 0a b c
.
Lời giải
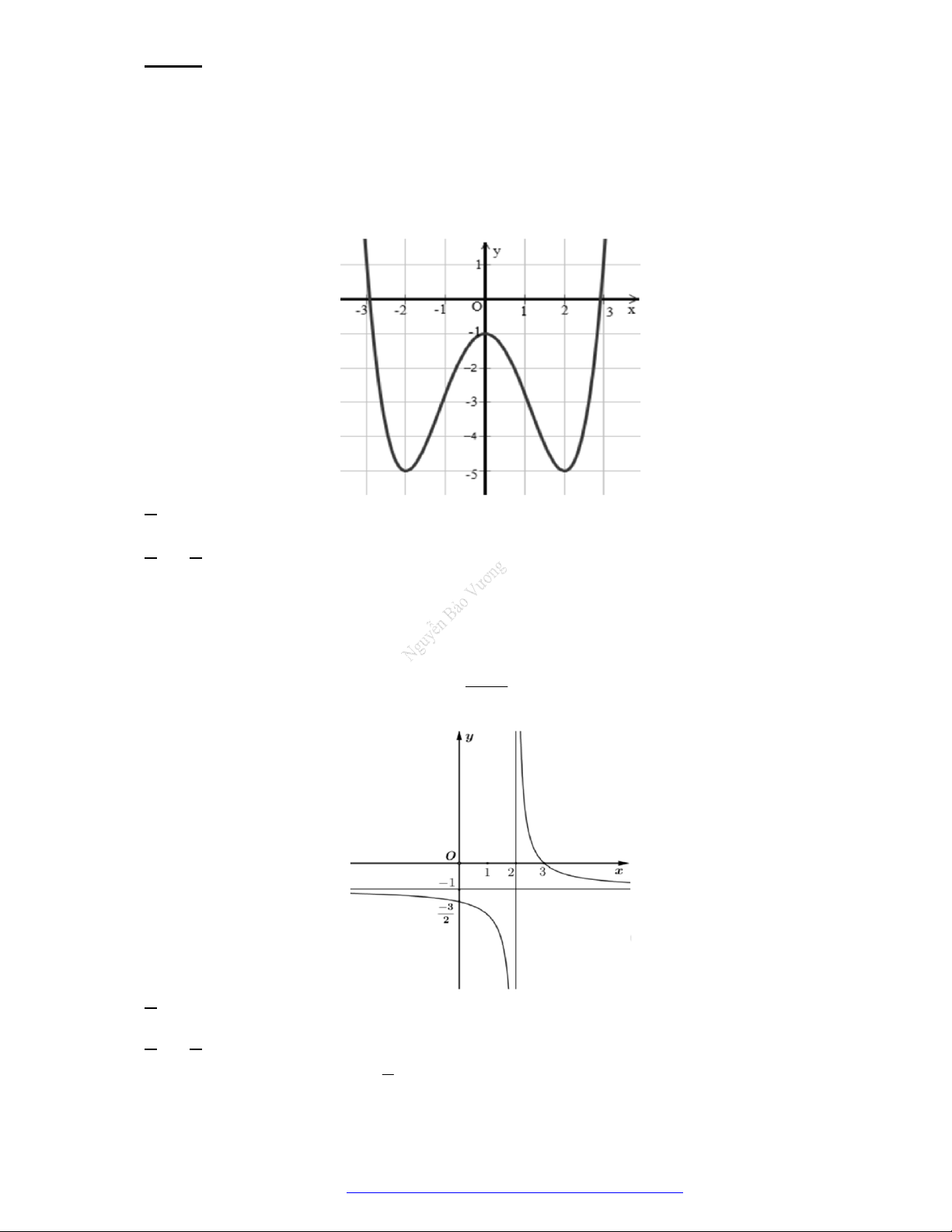
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Chọn C
Dựa vào hình dạng đồ thị hàm số ta nhận thấy :
Hệ số
0a
.
Hàm số có 3 điểm cực trị
. 0 0a b b
.
Đồ thị hàm số đi qua gốc tọa tọa
0c
.
Vậy
0, 0, 0a b c
.
Câu 32. (THPT Cộng Hiền 2019) Cho hàm số
4 2
y ax bx c có đồ thị như hình vẽ bên. Hỏi khẳng
định nào sau đây đúng?
A.
0, 0, 0a b c
. B.
0, 0, 0a b c
. C.
0, 0, 0a b c
. D.
0, 0, 0a b c
.
Lời giải
Chọn A
Nhìn vào đồ thị ta có:
Khi
x
2;
hàm số đồng biến
0a
.
Hàm số có
3
điểm cực trị nên
0a.b
mà
0 0a b
.
0 1 0y c c
.
Câu 33. (SGD Điện Biên - 2019) Cho hàm số
3ax
y
x c
có đồ thị như hình vẽ bên. Tính giá trị của
2 .a c
A.
2 3.a c
B.
2 3.a c
C.
2 1.a c
D.
2 2.a c
Lời giải
Chọn A
Đồ thị hàm số có TCN
1 1 1.
1
a
y a
Mặt khác Đồ thị hàm số có TCĐ
2x
nên
2 0 2.c c
2 1 2. 2 3.a c

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
Dựa vào đồ thị ta thấy các điểm
3;0
và
3
0;
2
thuộc vào đồ thị hàm số đã cho nên ta được hệ
phương trình
.3 3
0
3
3 .0 3
2 0
a
c
a
c
3 3 0
3 6
a
c
1
2
a
c
2 1 2. 2 3.a c
Câu 34. Hình vẽ bên là đồ thị hàm số
ax b
y
cx d
.
.
Mệnh đề nào dưới đây đúng?
A.
0ad
và
0bd
. B.
0ad
và
0ab
. C.
0bd
và
0ab
. D.
0ad
và
0ab
.
Lời giải
Chọn B
Đồ thị hàm số giao với trục
Ox
tại điểm có hoành độ
b
x
a
, giao với
Oy
tại điểm có tung độ
b
y
d
.
Dựa vào hình vẽ ta có
0 0
0
0
0
0 0
b b
ab
a a
ad
b b bd
d d
.
Trong các phương án chỉ có phương án B thỏa mãn.
Câu 35. Cho hàm số
1
ax b
y
x
có đồ thị như hình vẽ dưới đây:
Khẳng định nào sau đây đúng?
A.
0b a
. B.
0a b
. C.
b a
và
0a
. D.
0a b
.
Lời giải
Chọn A
Ta thấy đồ thị hàm số có tiệm cận ngang
1y
suy ra
1a
.
Do đồ thị hàm số đi qua điểm
2;0
nên
2 0 2 0 2a b b b
.
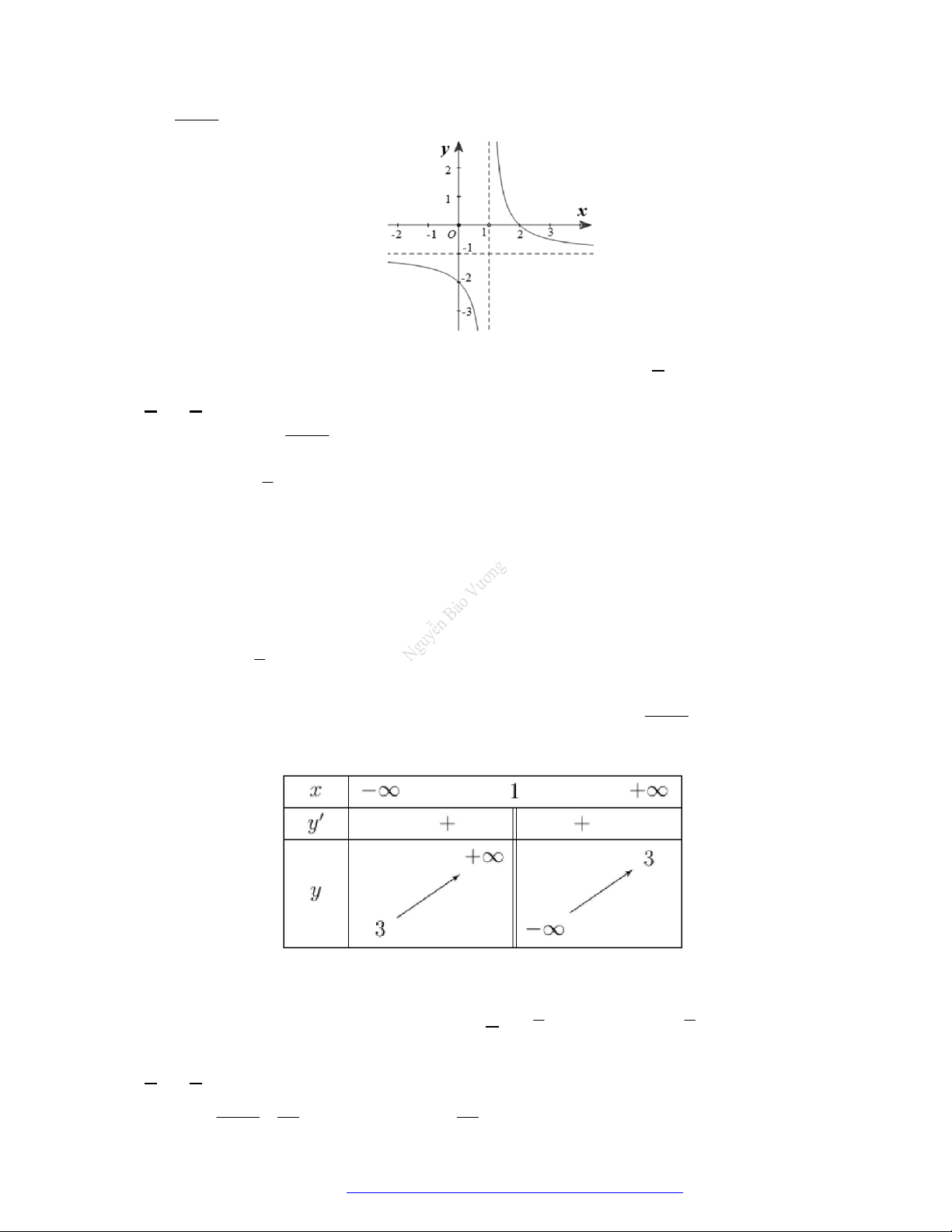
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Vậy
0b a
.
Câu 36. (Chuyên Lương Văn Chánh - Phú Yên - 2020) Đồ thị trong hình bên dưới là của hàm số
ax b
y
x c
(với
, ,a b c
).
Khi đó tổng
a b c
bằng
A.
1
. B.
1
. C.
2
. D.
0
.
Lời giải
Chọn D
Đồ thị hàm số
ax b
y
x c
có đường tiệm cận ngang
y a
, đường tiệm cận đứng
x c
và cắt
Oy
tại điểm
0;
b
c
.
Từ đồ thị hàm số ta có đường tiệm cận ngang
1y
, đường tiệm cận đứng
1x
và cắt
Oy
tại
điểm
0; 2
.
Từ đó suy ra:
1 1 1
1 1 1
2 2
2
a a a
c c c
b b c b
c
. Vậy
1 1 2 0a b c
.
Câu 37. (Chuyên Lương Văn Tỵ - Ninh Bình - 2020) Cho hàm số
2
( )
ax
f x
bx c
, , , 0a b c b
có
bảng biến thiên như sau:
Tổng các số
2
a b c
thuộc khoảng nào sau đây
A.
1;2
. B.
2;3
. C.
4
0;
9
. D.
4
;1
9
.
Lời giải
Chọn C
Ta có
2
lim
x
ax a
bx c b
, theo giả thiết suy ra
3 3
a
a b
b
Hàm số không xác định tại
1 0x b c b c
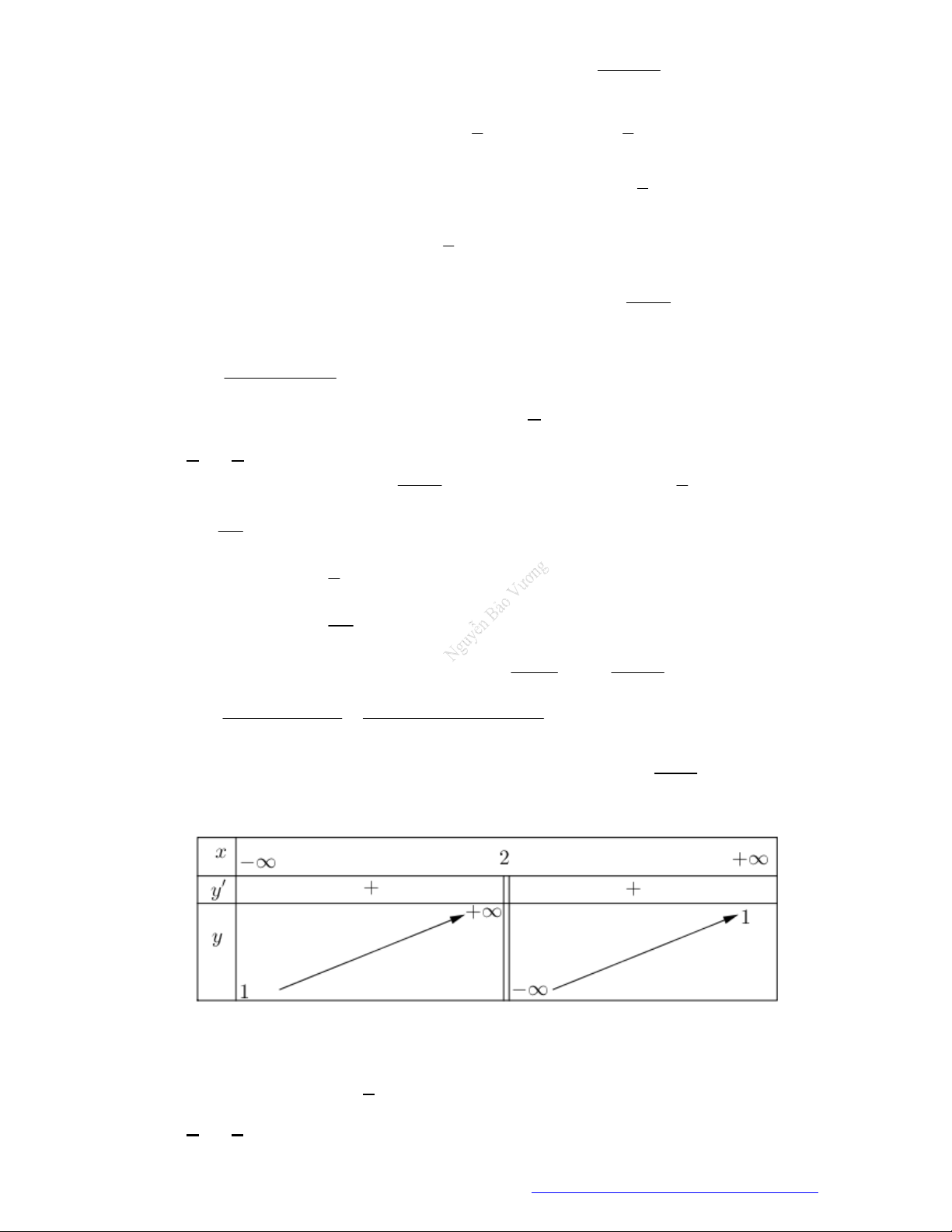
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
Hàm số đồng biến trên từng khoảng xác định nên
2
2
0
ac b
f x
bx c
với mọi
x
khác 1
Suy ra
2
2 2
2 0 3 2 0 0 0
3 3
ac b b b b b
Lại có
3a b c b b b b
. Suy ra
2
2
4
0;
9
a b c b
Vậy tổng
a b c
thuộc khoảng
4
0;
9
.
Câu 38. (Chuyên Hùng Vương - Gia Lai - 2020) Cho hàm số
( )
ax b
f x
cx d
( , , ,a b c d
và
0c
). Biết
rằng đồ thị hàm số đã cho đi qua điểm
1;7
và giao điểm hai tiệm cận là
2;3
. Giá trị biểu
thức
2 3 4
7
a b c d
c
bằng
A.
7
. B.
4
. C.
6
. D.
5
.
Lời giải
Chọn C
+ Ta có đồ thị hàm số
( )
ax b
f x
cx d
có đường tiệm cận ngang là
a
y
c
, đường tiệm cận đứng là
d
x
c
.
Theo bài ra, ta có:
3
3
2
2
a
a c
c
d d c
c
.
+ Điểm
1;7
thuộc đồ thị hàm số
( )f x
nên
3
7 7 10
2
a b c b
b c
c d c c
.
Vậy
2 3 4 2.(3 ) 3.(10 ) 4 2
6
7 7
a b c d c c c c
c c
.
Câu 39. (Chuyên Lê Hồng Phong - Nam Định - 2020) Cho hàm số
1ax
y
bx c
(
, ,a b c
là các tham số) có
bảng biến thiên như hình vẽ
Xét các phát biểu sau:
1 : 1; 2 : 0; 3 : 0; 4 : 0c a b a b c a
. Số phát biểu đúng
là?
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn B
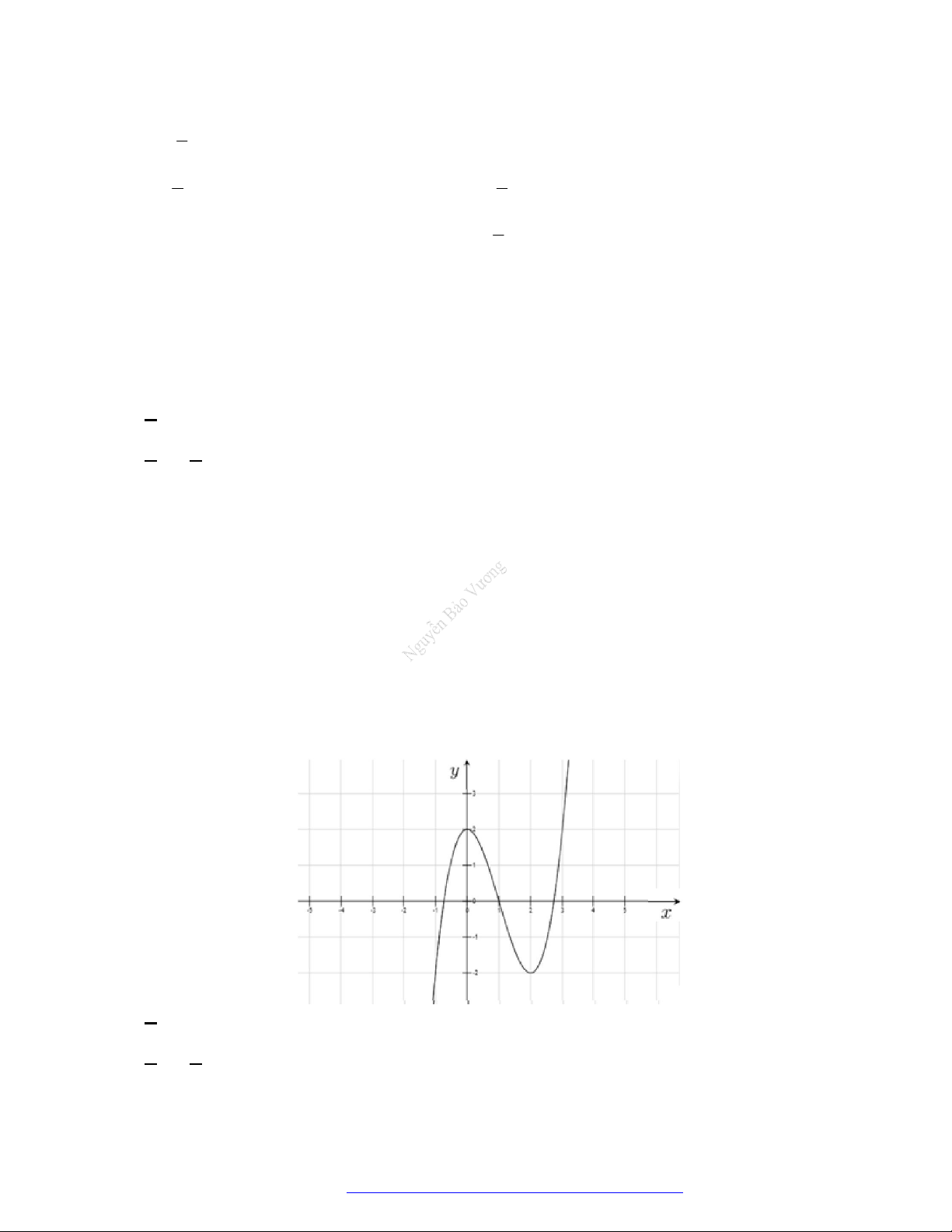
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Dựa vào bảng biến thiên ta có hàm số luôn đồng biến trên từng khoảng xác định, đồ thị hàm số có
tiệm cận đứng là đường thẳng
2x
và tiệm cận ngang là đường thẳng
1y
nên ta có hệ
2
2
0 1
2 2
1
1 0
2
0 2 0
1
0
0
2
0
c
c
b
c b c b
a
a b a b a
b
ac b b b
ac b
b
a b c
Dựa vào hệ trên ta có các phát biểu
1 , 4
là sai,
2 , 3
đúng.
Câu 40. (Đô Lương 4 - Nghệ An - 2020) Ta xác định được các số
, ,a b c
để đồ thị hàm số
3 2
y x ax bx c đi qua điểm
1;0
và có điểm cực trị
2;0
. Tính giá trị biểu thức
2 2 2
T a b c
.
A.
25.
B.
1.
C.
7.
D.
14.
Lời giải
Chọn A
Ta có
3 2 2
3 2y x ax bx c y x ax b
.
Theo đề, ta có hệ phương trình
3 2
3 2
2
0 1 .1 .1
1 0
2 0 0 2 . 2 . 2
2 0
0 3. 2 2 . 2
a b c
y
y a b c
y
a b
1 3
4 2 8 0
4 12 4
a b c a
a b c b
a b c
.
Vậy
2
2 2 2 2 2
3 0 4 25.T a b c
Câu 41. (Lê Lai - Thanh Hóa - 2020) Cho hàm số có đồ thị như hình vẽ. Tính
?
A. . B. . C. . D. .
Lời giải
Chọn A
Vì đồ thị hàm số cắt trục tung tại điểm
2y
nên
2d
.
2
3 2y ax bx c
.
Hàm số đạt cực trị tại
0x
và
2x
nên
3 2
y ax bx cx d
S a b
2
S
0
S
1
S
1
S
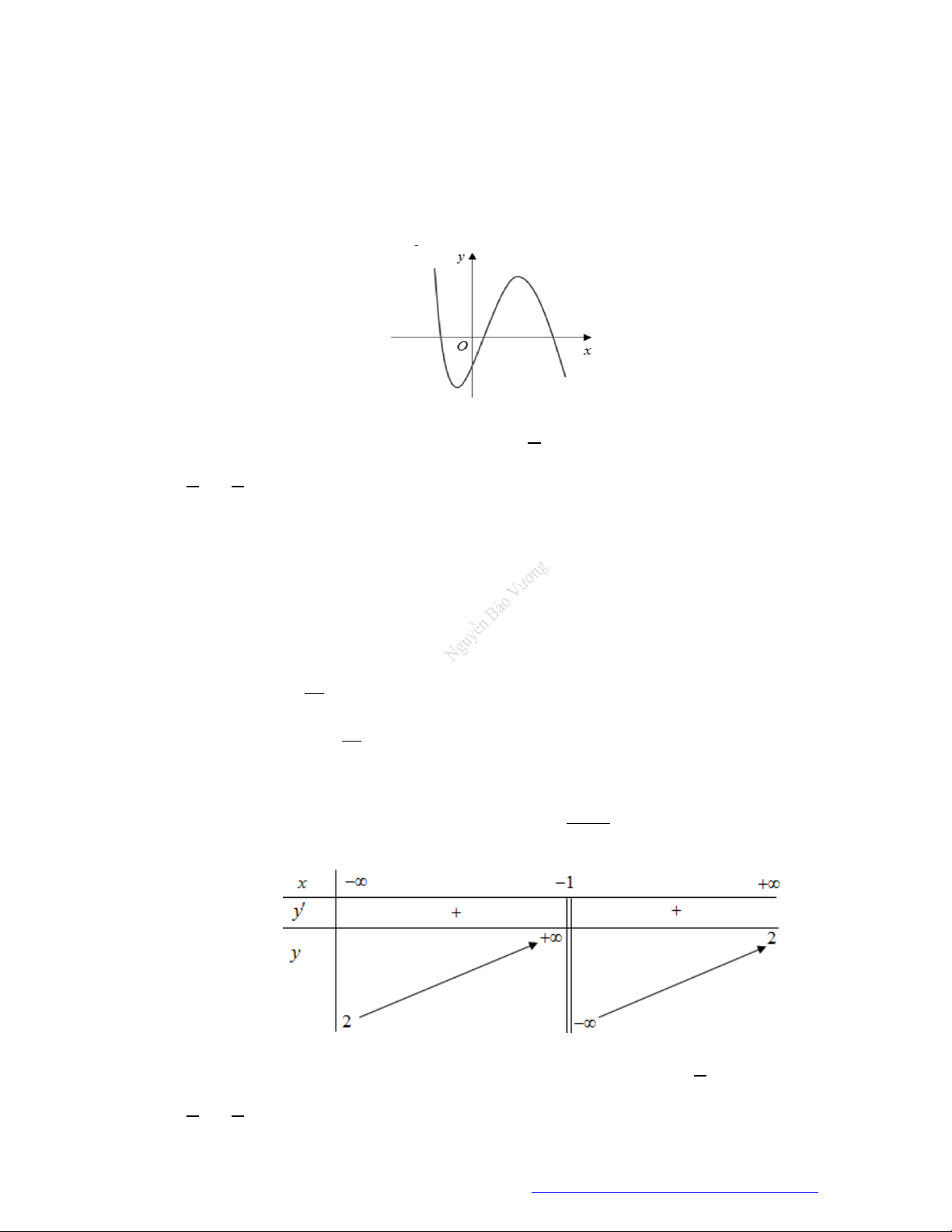
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
0 0
0
0
3 1
12 4 0
2 0
y
c
c
b a
a b c
y
Từ đồ thị ta nhận thấy
2 2 8 4 2 8 4 4 2 1 2y a b d a b a b
Thay
1
vào
2
ta tìm được
1, 3a b
.
Vậy
2S
.
Câu 42. (Lý Nhân Tông - Bắc Ninh - 2020) Cho hàm số
3 2
y ax bx cx d
có đồ thị như hình vẽ
bên. Mệnh đề nào dưới đây đúng?
A.
0, 0, 0, 0a b c d
. B.
0, 0, 0, 0a b c d
.
C.
0, 0, 0, 0a b c d
. D.
0, 0, 0, 0a b c d
.
Lời giải
Chọn D
Ta có:
2
3 2y ax bx c
,
6 2y ax b
Từ đồ thị ta thấy:
lim
x
y
. Ta suy ra
0a
.
0 0 0y d
loại C.
Đồ thị hàm số có hai điểm cực trị với hoành độ
1
x
,
2
x
trái dấu và
1 2
0x x
. Ta suy ra phương
trình
' 0y
có hai nghiệm trái dấu và
1 2
0x x
.
Ta suy ra
1 2
0
3
c
x x
a
,
0c
loại B.
Hơn nữa,
1 2
0
0
3
0
b
x x
b
a
a
. Lọai A.
Câu 43. (Nguyễn Huệ - Phú Yên - 2020) Cho hàm số
, ,
1
ax b
y a b c
cx
có bảng biến thiên như
sau:
Tập các giá trị
b
là tập nghiệm của bất phương trình nào dưới đây?
A.
3
8 0.b
B.
2
4 0.b
C.
2
3 2 0.b b
D.
3
8 0.b
Lời giải
Chọn D
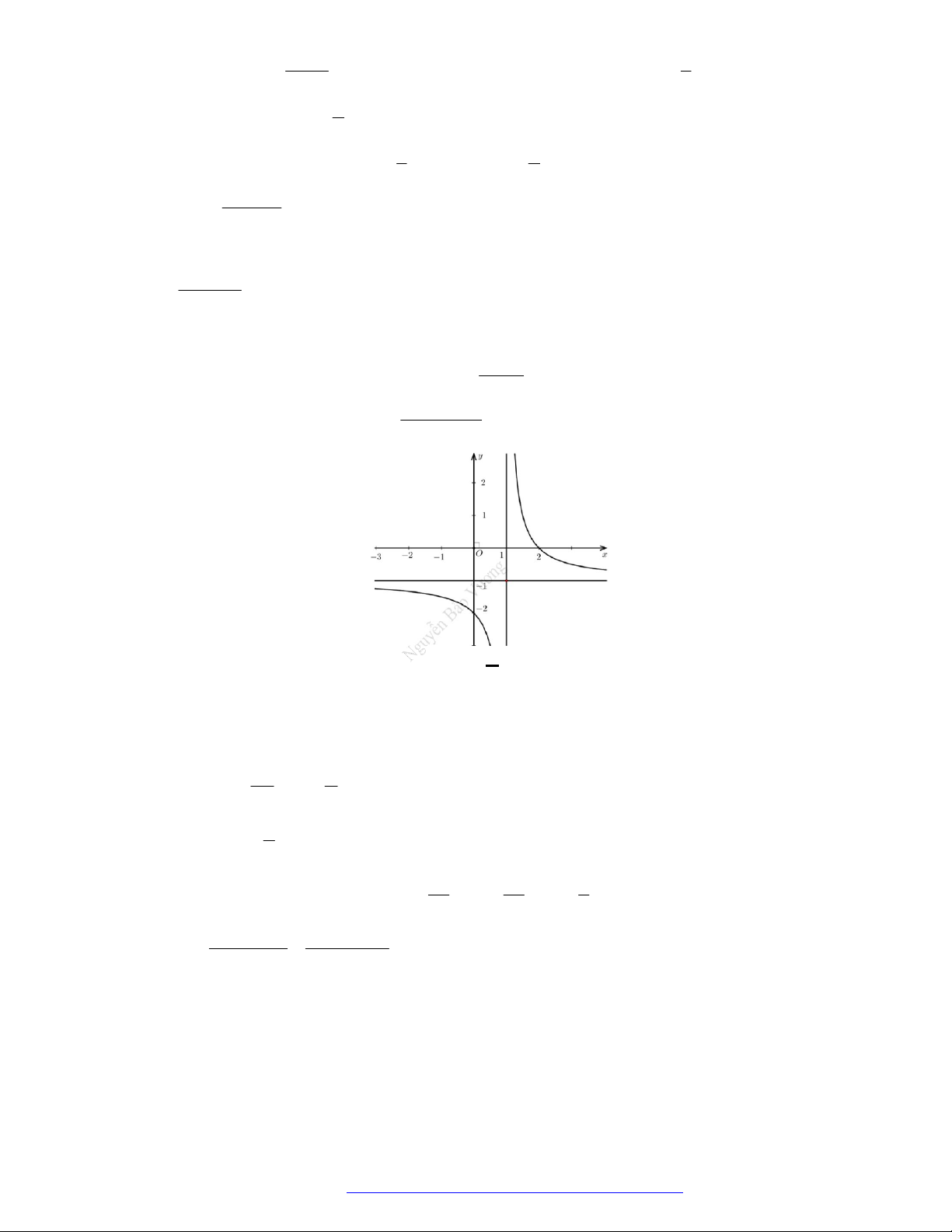
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 22 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Đồ thị hàm số
1
ax b
y
cx
có đường tiệm cận đứng là đường thẳng
1
x
c
và đường tiệm cận
ngang là đường thẳng
a
y
c
.
Nhìn vào bảng biến thiên, ta thấy
1
1 1c
c
và
2 2
a
a
c
(vì
1c
).
Ta có
2
1
a bc
y
cx
.
Vì hàm số đã cho đồng biến trên các khoảng
; 1
và
1;
nên
3 3
2
0 0 2 0 2 8 8 0
a bc
y a bc b b b b
bx c
.
Vậy tập các giá trị
b
là tập nghiệm của bất phương trình
3
8 0.b
Câu 44. (Tiên Du - Bắc Ninh - 2020) Cho hàm số
ax b
y
cx d
(với
, , ,a b c d
là số thực) có đồ thị như hình
dưới đây. Tính giá trị biểu thức
2 3a b d
T
c
.
A.
6T
. B.
0T
. C.
8 T
. D.
2T
.
Lời giải
Chọn C
Từ đồ thị ta có
TCĐ:
1 1 1
d d
x
c c
d c
TCN:
1 1
a
y a c
c
Đồ thị cắt trục hoành tại điểm:
2 2 2 2
b b b
x
a c c
2b c
Vậy
2 3 4 3
8
a b d c c c
T
c c
Câu 45. (Thanh Chương 1 - Nghệ An - 2020) Cho hàm số
3 2
y ax bx cx d có đồ thị như hình vẽ.
Trong các số
, ,a b c
và
d
có bao nhiêu số dương?
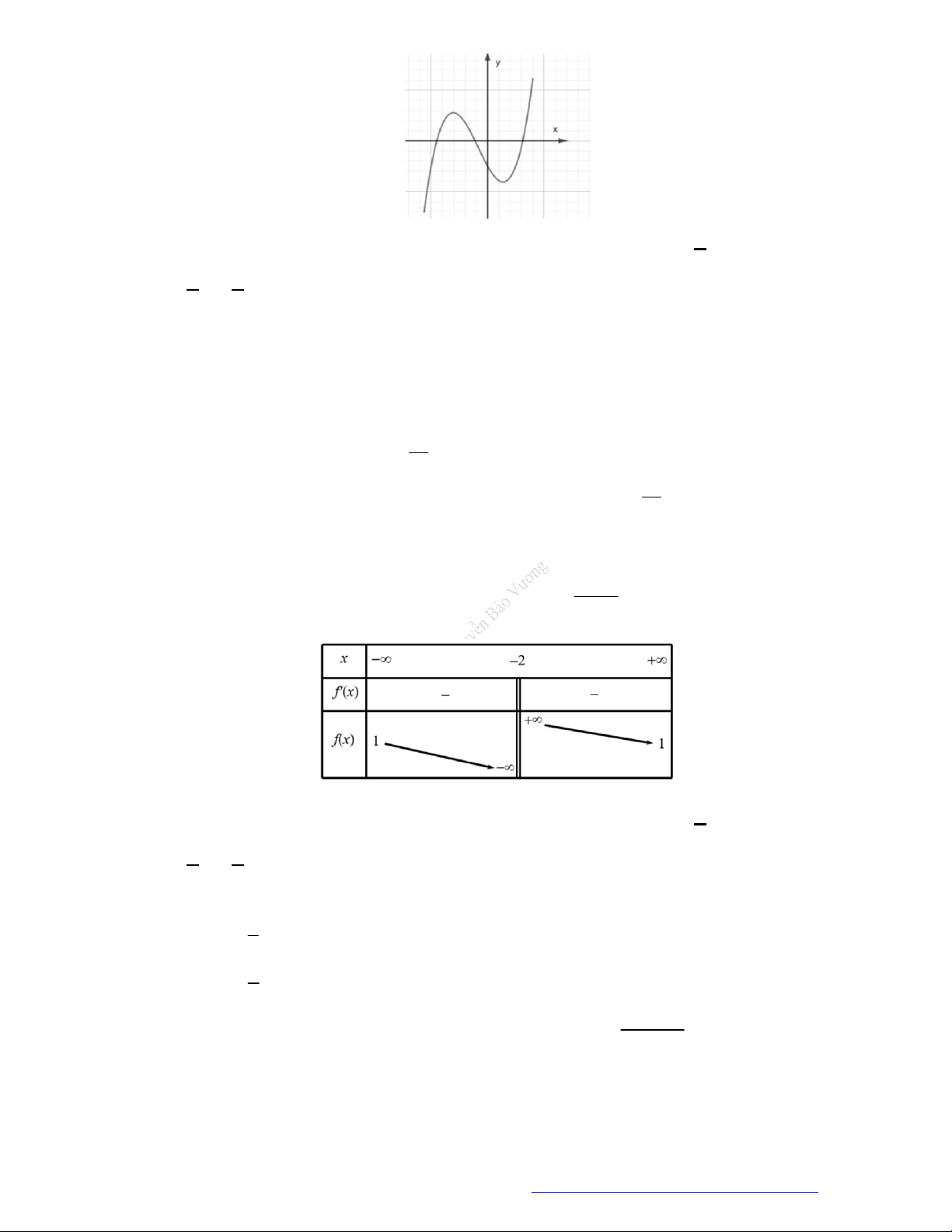
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
A.
1
. B.
4
. C.
3
. D.
2
.
Lời giải
Chọn D
Từ hình dạng đồ thị hàm số ta có
0a
Đồ thị hàm số cắt trục tung tại điểm có tung độ âm
0d
Ta có:
2
' 3 2y ax bx c
Hàm số có hai điểm cực trị trái dấu
' 0y
có hai nghiệm trái dấu
0ca
Mà
0a
nên
0c
Ta lại có:
'' 6 2y ax b
'' 0 6 2 0
3
b
y ax b x
a
Từ đồ thị hàm số ta thấy tâm đối xứng có hoành độ âm. Do đó
0
3
b
a
Mà
0a
nên
0b
Vậy trong các số
, ,a b c
và
d
có 2 số dương là
a
và
b
Câu 46. (Tiên Lãng - Hải Phòng - 2020) Cho hàm số
6
ax
f x
bx c
, , a b c
có bảng biến thiên như
sau:
Trong các số
, ,a b c
có bao nhiêu số âm?
A.
0
. B.
3
. C.
1
. D.
2
.
Lời giải
Chọn D
Từ bảng biến thiên của hàm số, ta thấy đồ thị có hai đường tiệm cận, trong đó tiệm cận đứng là
đường thẳng
2x
và tiệm cận ngang là đường thẳng
1y
.
Suy ra
2
1
c
b
a
b
0
0
bc
ab
1
0, 0, 0
2
0, 0, 0
b c a
b c a
Lại có hàm số nghịch biến trên mỗi khoảng xác định
2
6
0
ac b
f x
bx c
6ac b
.
Ta thấy
1
không thể xảy ra do nếu
0b
thì
6 0ac b
; và
2
có thể xảy ra do nếu
0, 0c a
thì
6 0b ac
.
Vậy trong các số
, ,a b c
có hai số âm.
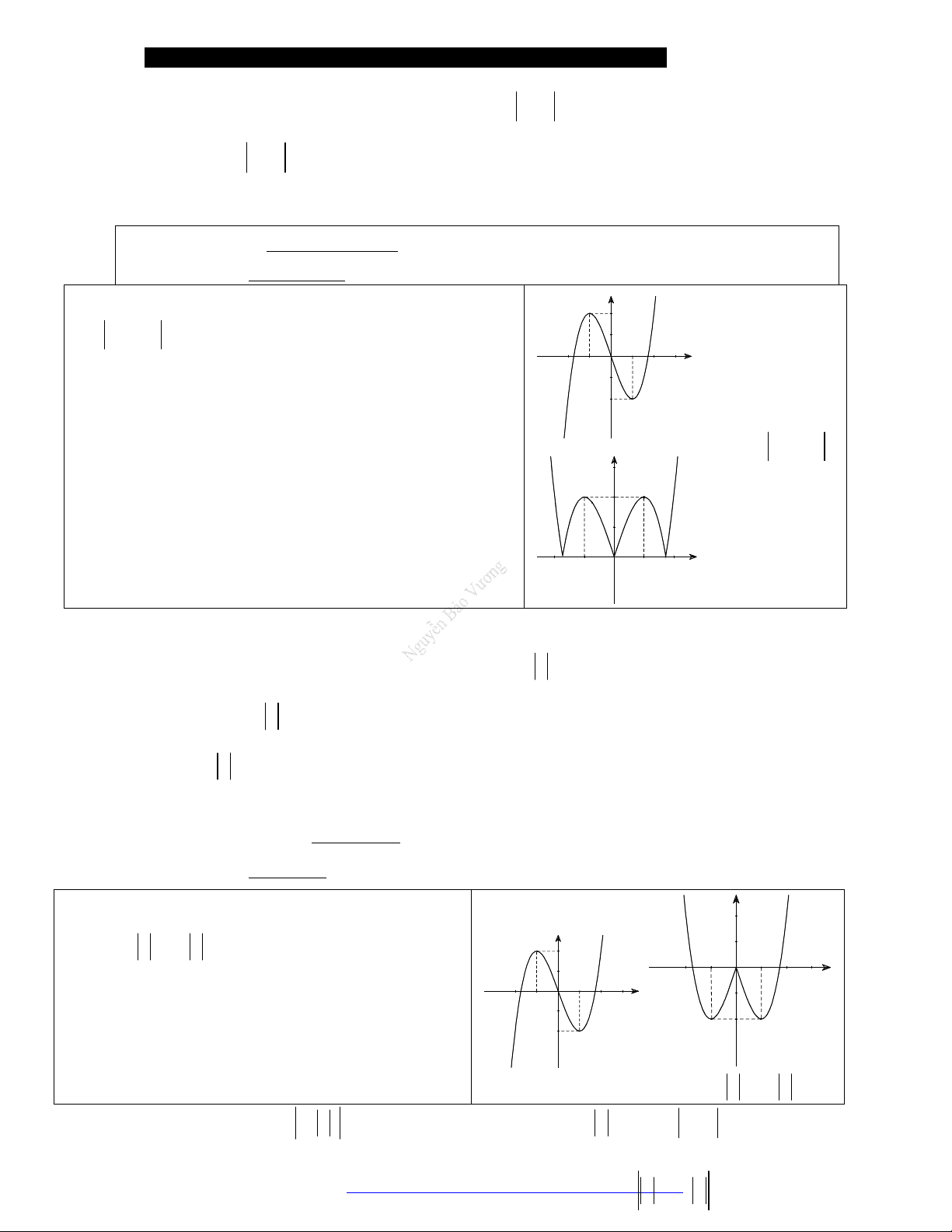
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 24 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Dạng 2. Đồ thị hàm số chứa dấu giá trị tuyệt đối (BIẾN ĐỔI ĐỒ THỊ)
Dạng 1
Từ đồ thị
C y f x: suy ra đồ thị
C y f x
:
.
Ta có:
f x khi f x
y f x
f x khi f x
0
0
* Cách vẽ
C từ
C
:
Giữ nguyên phần đồ thị phía trên Ox của đồ thị (C):
y f x .
Bỏ phần đồ thị phía dưới Ox của (C), lấy đối xứng phần đồ thị bị bỏ qua Ox.
Ví dụ: Từ đồ thị
3
: 3C y f x x x
suy ra đồ thị
y x x
3
3 .
Biến đổi
C
:
Bỏ phần đồ thị của
C dưới ,Ox giữ nguyên
C phía trên
.Ox
L
ấy đối xứng phần đồ thị bị bỏ qua
Ox
.
Dạng 2
Từ đồ thị
C y f x: suy ra đồ thị
C y f x: .
Ta có:
f x khi x
y f x
f x khi x
0
0
và
y f x là hàm chẵn nên đồ thị
C
nhận Oy làm trục đối xứng.
* Cách vẽ
C từ
C :
Giữ nguyên phần đồ thị bên phải Oy của đồ thị
C y f x: .
Bỏ phần đồ thị bên trái Oy của
C , lấy đối xứng phần đồ thị được giữ qua Oy.
Ví dụ: Từ đồ thị
C y f x x x
3
: 3 suy ra đồ thị
C y x x
3
: 3 .
Biến đổi
C :
Bỏ phần đồ thị của
C bên trái
Oy,
giữ nguyên
C
bên phải
.Oy
Lấy đối xứng phần đồ thị được giữ qua
Oy
.
Chú ý với dạng:
y f x
ta lần lượt biến đổi 2 đồ thị
y f x và
y f x
x
y
O
-2
2
-1
1
x
y
2
-1
O
1
x
y
O
-2
2
-1
1
x
y
O
-2
-1
1
C y x x
3
: 3
C y x x
3
: 3
3
: 3C y x x
C y x x
3
: 3
C y x x
3
: 3
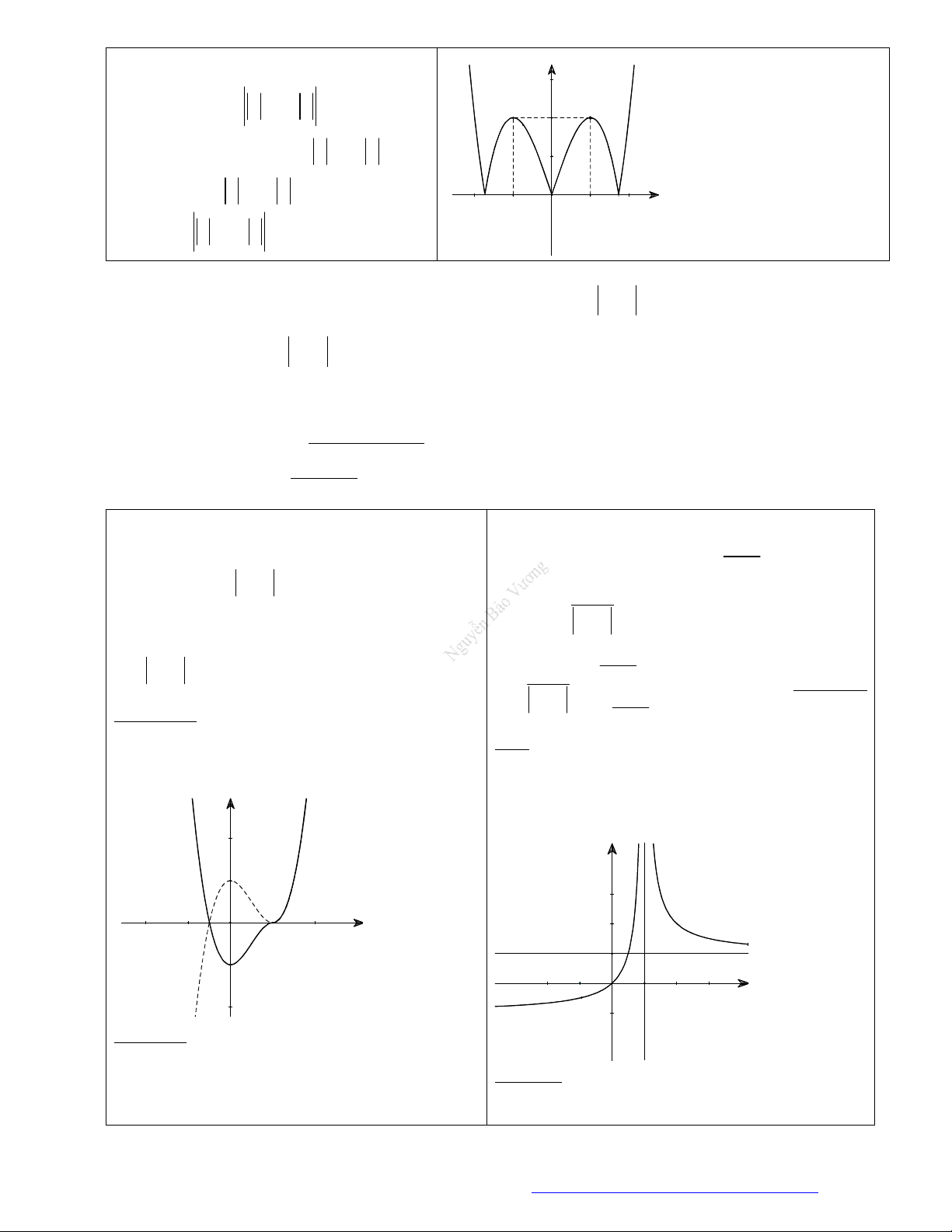
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25
Ví dụ: Từ đồ thị
C y f x x x
3
: 3
suy ra đồ thị
y x x
3
3
. Biến đổi
C
để được đồ thị
C y x x
3
: 3 . Biến
đổi
C y x x
3
: 3 ta được đồ thị
C y x x
3
: 3
.
Dạng 3
Từ đồ thị
C y u x v x: . suy ra đồ thị
C y u x v x: .
.
Ta có:
u x v x f x khi u x
y u x v x
u x v x f x khi u x
. 0
.
. 0
* Cách vẽ
C từ
C
:
Giữ nguyên phần đồ thị trên miền
u x 0 của đồ thị
C y f x: .
Bỏ phần đồ thị trên miền
u x 0 của
C , lấy đối xứng phần đồ thị bị bỏ qua Ox.
Ví dụ
a) Từ đồ thị
C y f x x x
3 2
: 2 3 1 suy ra
đồ thị
C y x x x
2
: 1 2 1
Ví dụ
b) Từ đồ thị
x
C y f x
x
:
1
suy ra đồ thị
x
C y
x
:
1
f x khi x
y x x x
f x khi x
2
1
1 2 1
1
Đồ thị (C’):
Giữ nguyên (C) với
1x
.
Bỏ (C) với
x 1
. Lấy đối xứng phần đồ thị bị bỏ
qua Ox.
Nhận xét: Trong quá trình thực hiện phép suy đồ thị
nên lấy đối xứng các điểm đặc biệt của (C): giao
điểm với Ox, Oy, CĐ, CT…
x
khi x
x
x
y
x
x
khi x
x
1;
1
.
1
;1
1
Đồ thị
(C’):
Bỏ phần đồ thị của
C với
x ,1
giữ nguyên
C
với
1.x
L
ấy đối xứng phần đồ thị bị bỏ qua
Ox.
Nhận xét: Đối với hàm phân thức thì nên lấy đối
xứng các đường tiệm cận để thực hiện phép suy đồ
thị một cách tương đối chính xác.
Câu 1. Cho hàm số
3 2
3 2y x x
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?
x
y
2
-1
O
1
x
y
(C)
(C')
1
O
1
x
y
1
O
1
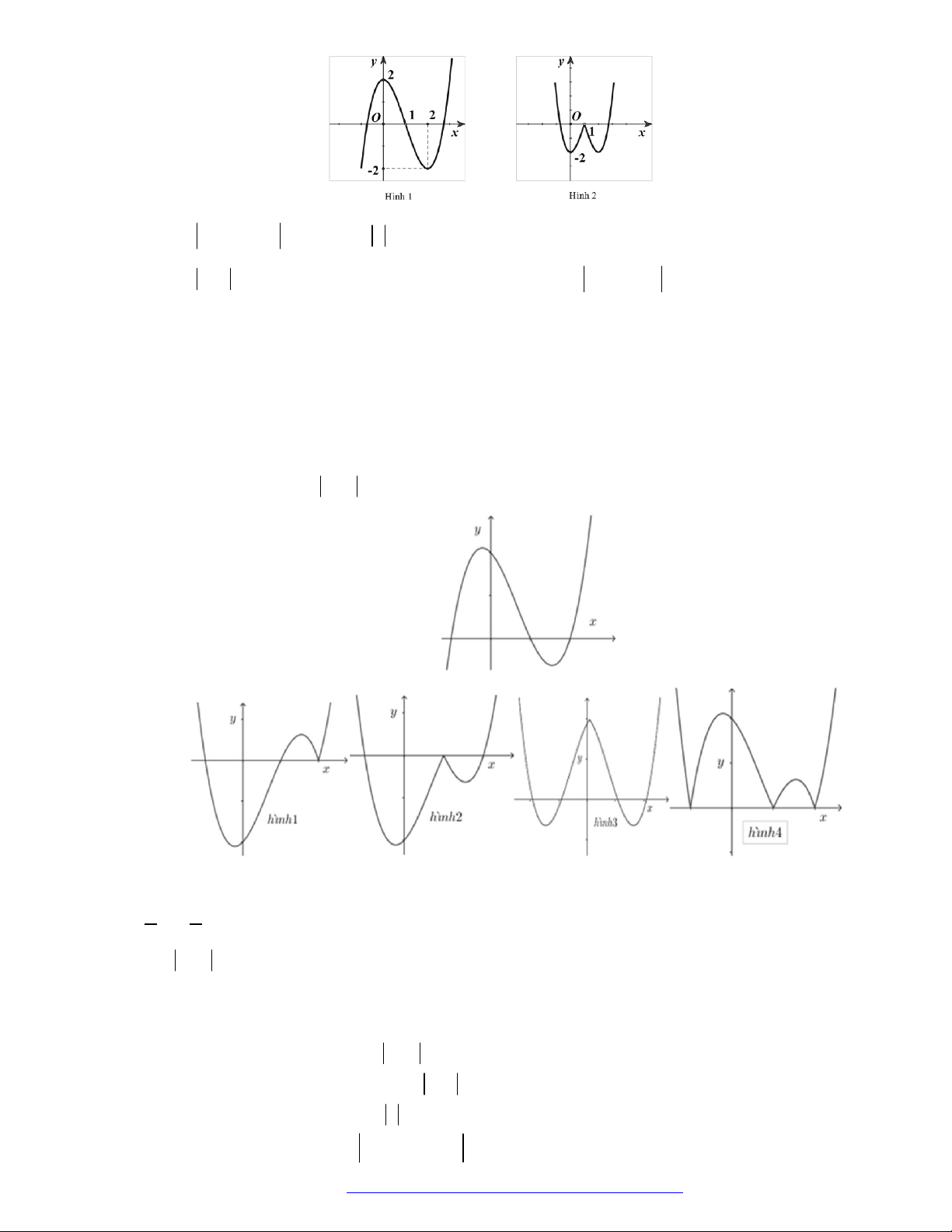
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 26 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
3 2
3 2 .y x x
B.
3
2
3 2y x x
C.
2
1 2 2 .y x x x
D.
2
1 2 2 .y x x x
Hướng dẫn
Ta có:
3 2 2
3 2 1 2 2y x x x x x
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy
Toàn bộ đồ thị ứng với
1x
được giữ nguyên.
Phần đồ thị ứng với
1x
lấy đối xứng qua trục hoành.
Chọn đáp án C.
Câu 2. (Đề Tham Khảo 2017) Hàm số
2
2 1y x x
có đồ thị như hình vẽ bên. Hình nào dưới đây
là đồ thị của hàm số
2
2 1y x x
?
A. Hình 1 B. Hình 2 C. Hình 3 D. Hình 4
Lời giải
Chọn A
2
2
2
2 1 , 2
2 1
2 1 , 2
x x x
y x x
x x x
Đồ thị gồm 2 phần:
+) Giữ nguyên phần đồ thị đã cho ứng với
2x
.
+) Lấy đối xứng phần đồ thị đã cho ứng với
2x
qua trục
Ox
Hình 1 nhận vì đồ thị là hàm
2
2 1y x x
Hình 2 loại vì đồ thị là hàm
2 1 1y x x x
Hình 3 loại vì đồ thị hàm số
2
2 1y x x
Hình 4 loại vì đồ thị hàm
2
2 1y x x
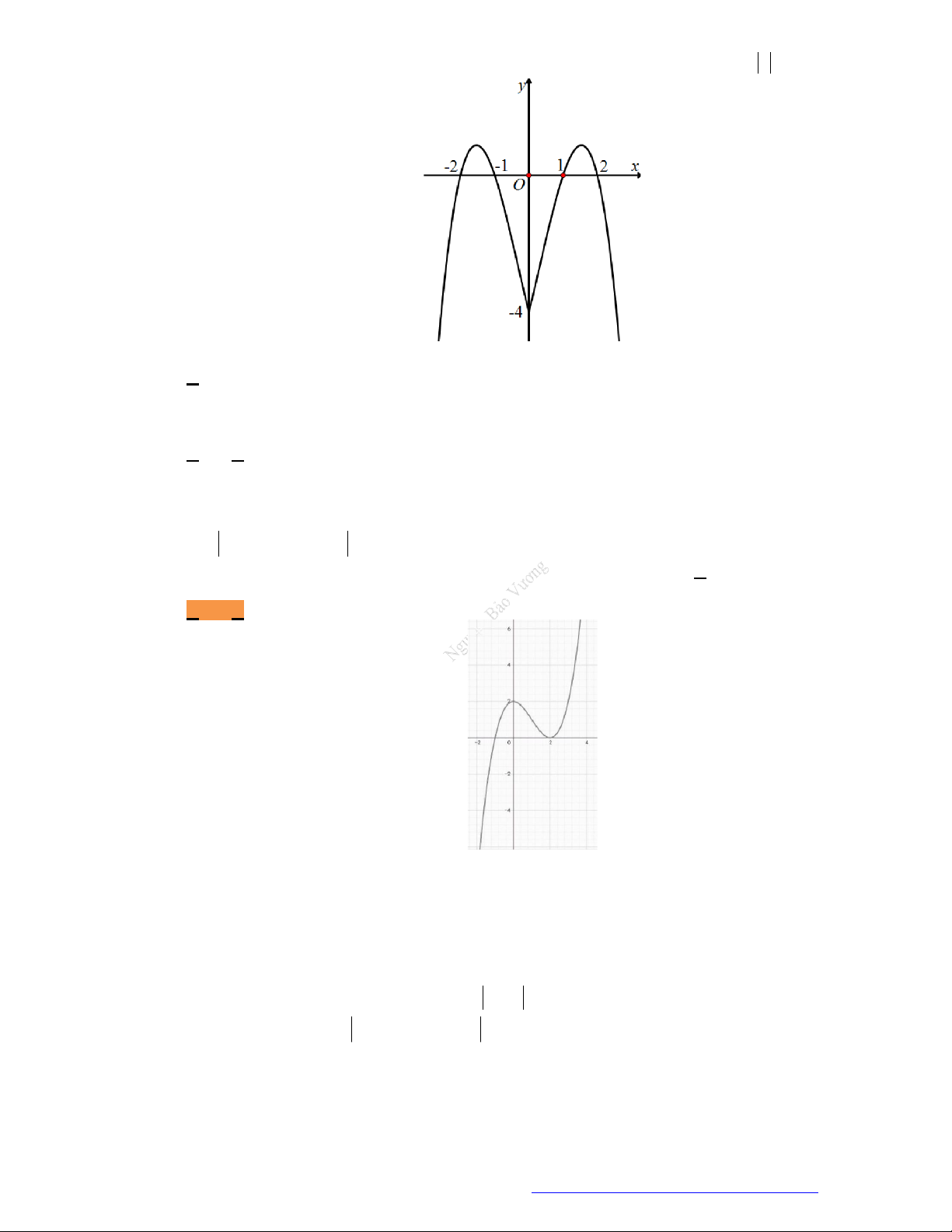
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27
Câu 3. (THPT Việt Đức Hà Nội 2019) Cho hàm số
y f x
có đồ thị hàm số
y f x
như hình vẽ.
Chọn kết luận đúng trong các kết luận sau:
A.
3 2
4 4f x x x x
B.
3 2
4 4f x x x x
C.
3 2
4 4f x x x x
D.
3 2
4 4.f x x x x
Lời giải
Chọn A
Do đồ thị giao với trục
Oy
tại điểm có tung độ bằng
4
và
lim
x
y
.
Câu 4. Biết phương trình
3 2
0ax bx cx d
( 0)a
có đúng hai nghiệm thực. Hỏi đồ thị hàm số
3 2
y ax bx cx d
có bao nhiêu điểm cực trị?
A. 4. B. 5. C. 2. D. 3.
Lời giải
Chọn D
Ta có:
Phương trình
3 2
0ax bx cx d
( 0)a
có đúng hai nghiệm thực
Nên đồ thị hàm số
3 2
y ax bx cx d
được minh họa như hình vẽ.
Gọi m là số điểm cực trị của hàm số
y f x
và k là nghiệm bội lẻ
của phương trình
0f x
.
Số điểm cực trị của đồ thị hàm số
y f x
là
m k
.
Vậy đồ thị hàm số
3 2
y ax bx cx d
có số điểm cực trị là
2 1
.
Câu 5. (Chu Văn An - Hà Nội - 2019) Cho hàm số
2
2 1y x x
có đồ thị như hình vẽ
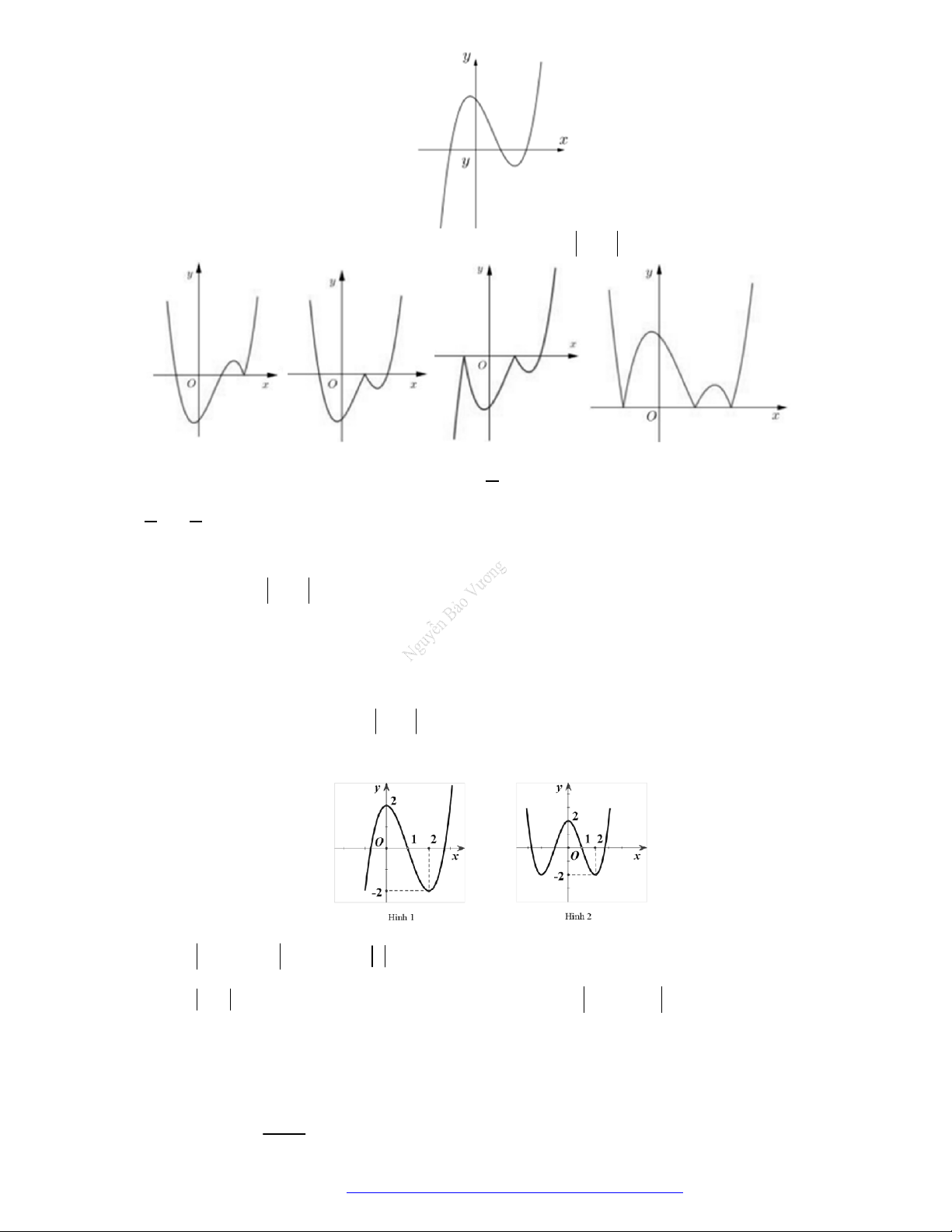
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 28 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Một trong bốn hình dưới đây là đồ thị của hàm số
2
2 1y x x
. Hỏi đó là hình nào?
Hình 1 Hình 2 Hình 3 Hình 4
A. Hình 2. B. Hình 4. C. Hình 3. D. Hình 1.
Lời giải
Chọn C
Gọi
C
là đồ thị hàm số
2
2 1y x x
.
Ta có
2
2
2
2 1 1 1
2 1
2 1 1 1
x x khi x hay x
y x x
x x khi x
.
Cách vẽ đồ thi như sau:
+ Giữ nguyên phần đồ
C
ứng với
; 1 1;x
ta được
1
C
.
+ Lấy đối xứng phần
C
ứng với
1;1x
qua trục hoành ta được
2
C
.
Khi đó đồ thị hàm số
2
2 1y x x
gồm
1
C
và
2
C
.
Câu 6. Cho hàm số
3 2
3 2y x x
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?
A.
3 2
3 2 .y x x
B.
3
2
3 2y x x
C.
2
1 2 2 .y x x x
D.
2
1 2 2 .y x x x
Hướng dẫn
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy
Toàn bộ đồ thị phía “phải”
Oy
sau đó lấy đối xứng sang trái.
Chọn đáp án B.
Câu 7. Cho hàm số
1
2 1
x
y
x
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?
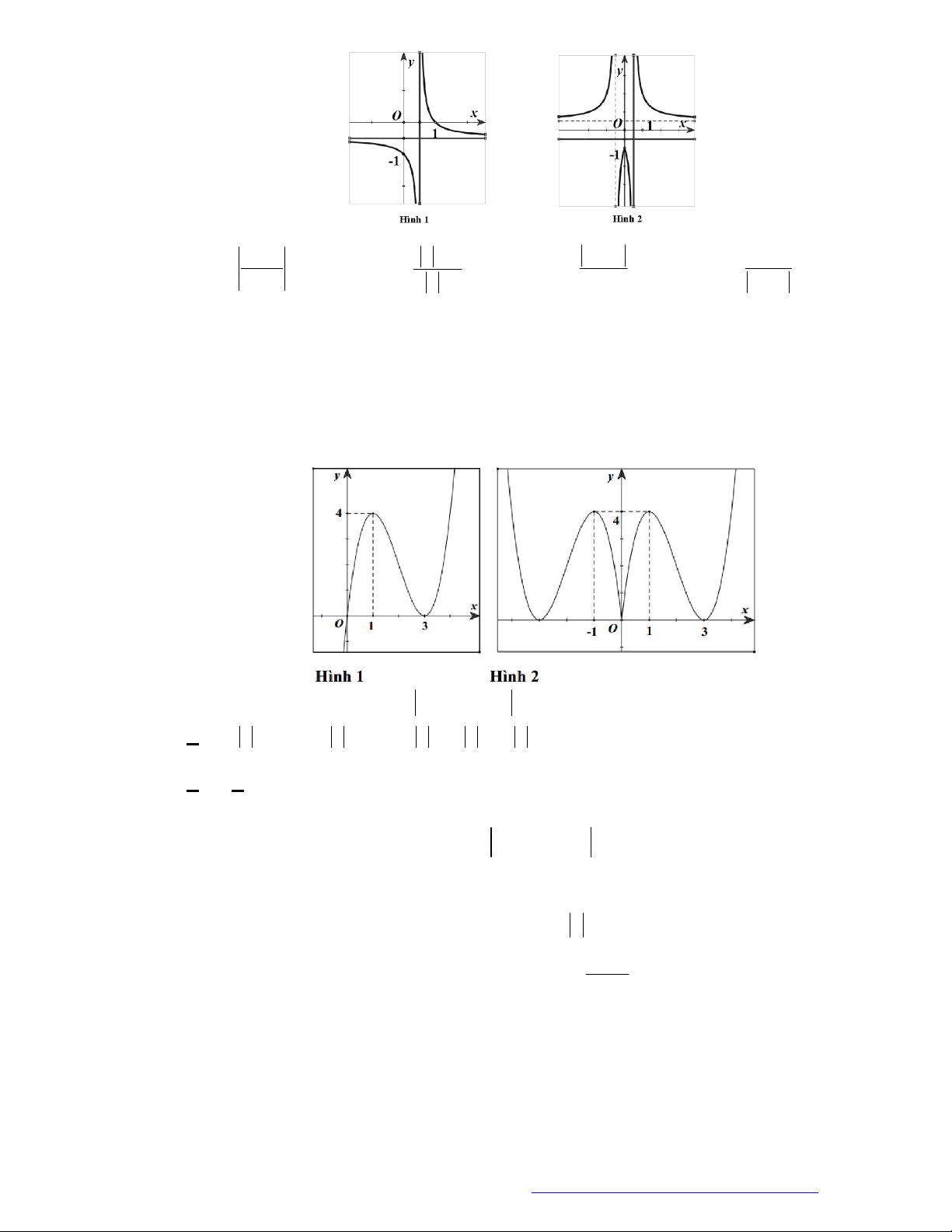
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 29
A.
1
2 1
x
y
x
B.
1
2 1
x
y
x
C.
1
2 1
x
y
x
D.
1
2 1
x
y
x
Hướng dẫn
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy
Toàn bộ đồ thị phía bên phải
Oy
được giữ nguyên
Sau đó, được lấy đối xứng sang trái.
Chọn đáp án B.
Câu 8. Cho hàm số
3 2
6 9y x x x có đồ thị như Hình 1. Khi đó đồ thị Hình 2 là của hàm số nào dưới
đây?
A.
3 2
6 9 y x x x . B.
3 2
6 9 y x x x
.
C.
3
2
6 9 y x x x
. D.
3 2
6 9 y x x x
.
Lời giải
Chọn C
+/ Loại đáp án A vì:
3 2 3 2
6 9 6 9 y x x x x x x
+/ Loại đáp án B, vì đồ thị của hàm số
3 2
6 9y x x x
giữ lại phần đồ thị phía trên trục hoành
và chỉ lấy đối xứng phần dưới trục hoành của đồ thị Hình 1.
+/ Loại đáp án D vì hệ số của
2
x khác -6.
+/ Đồ thị ở đáp án C là đồ thị của hàm số dạng
y f x . Chọn đáp án C
Câu 9. (Cụm liên trường Hải Phòng -2019) Cho hàm số
2 1
x
y
x
có đồ thị như Hình 1. Đồ thị Hình
2 là của hàm số nào trong các đáp án A, B, C, D dưới đây?
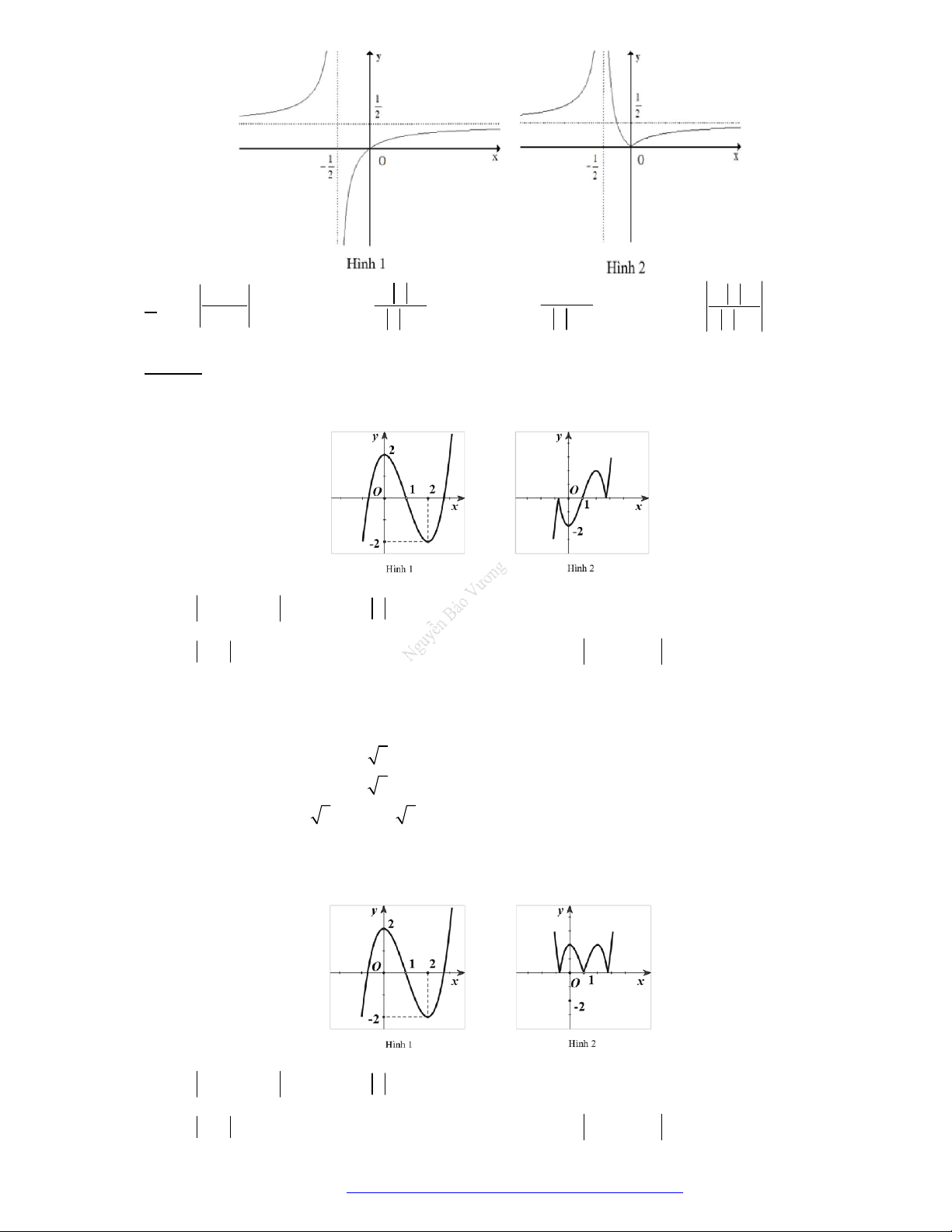
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 30 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
2 1
x
y
x
. B.
2 1
x
y
x
C.
2 1
x
y
x
D.
2 1
x
y
x
Lời giải
Chọn A
Câu 10. Cho hàm số
3 2
3 2y x x
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?
A.
3 2
3 2 .y x x
B.
3
2
3 2y x x
C.
2
1 2 2 .y x x x
D.
2
1 2 2 .y x x x
Hướng dẫn
Ta có:
3 2 2
3 2 1 2 2y x x x x x
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy
Toàn bộ đồ thị ứng với
1 3
1 3
x
x
được giữ nguyên.
Phần đồ thị ứng với 1 3 1 3x lấy đối xứng qua trục hoành.
Chọn đáp án D.
Câu 11. Cho hàm số
3 2
3 2y x x
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?
A.
3 2
3 2 .y x x
B.
3
2
3 2y x x
C.
2
1 2 2 .y x x x
D.
2
1 2 2 .y x x x
Hướng dẫn
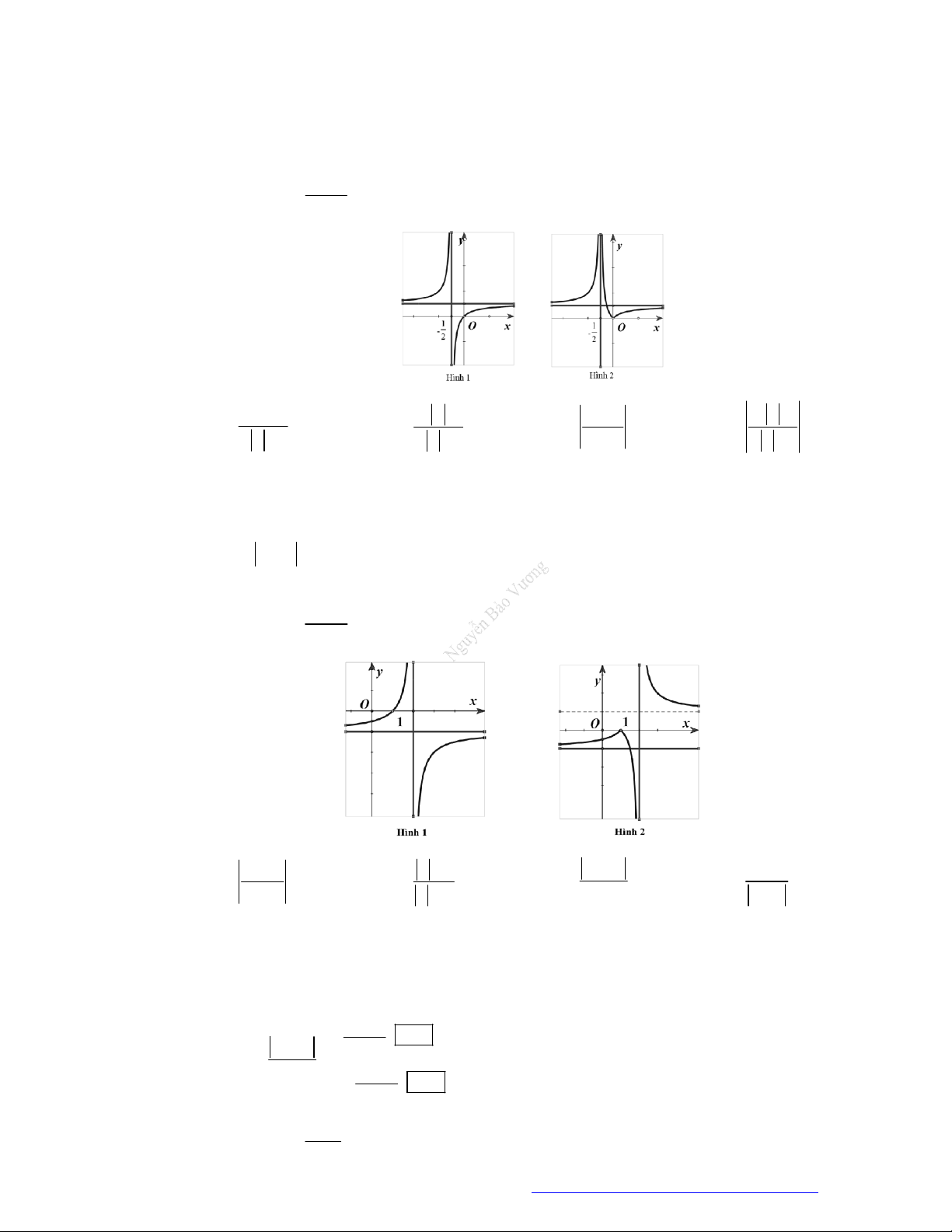
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 31
Ta có:
3 2 2
3 2 1 2 2y x x x x x
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy
Toàn bộ đồ thị nằm phía trên
Ox
được giữ nguyên.
Phần đồ thị phía dưới
Ox
được lấy đối xứng qua
Ox
.
Chọn đáp án A.
Câu 12. Cho hàm số
2 1
x
y
x
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?
A.
2 1
x
y
x
B.
2 1
x
y
x
C.
2 1
x
y
x
D.
2 1
x
y
x
Hướng dẫn
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy
Toàn bộ đồ thị phía trên
Ox
giữ nguyên
Toàn bộ phần phía dưới
Ox
được lấy đối xứng lên trên
dạng
f x
.
Chọn đáp án C.
Câu 13. Cho hàm số
1
2
x
y
x
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?
A.
1
.
2
x
y
x
B.
1
.
2
x
y
x
C.
1
2
x
y
x
D.
1
2
x
y
x
Hướng dẫn
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy
Toàn bộ đồ thị phía bên trái đường thẳng
1x
được giữ nguyên
Toàn bộ đồ thị phía bên phải đường thẳng
1x
lấy đối xứng qua
Ox
Chọn đáp án C.
Chú ý:
1
, 1
1
2
1
2
, 1
2
x
x
x
x
y
x
x
x
x
Câu 14. Cho hàm số
1
2
x
y
x
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?
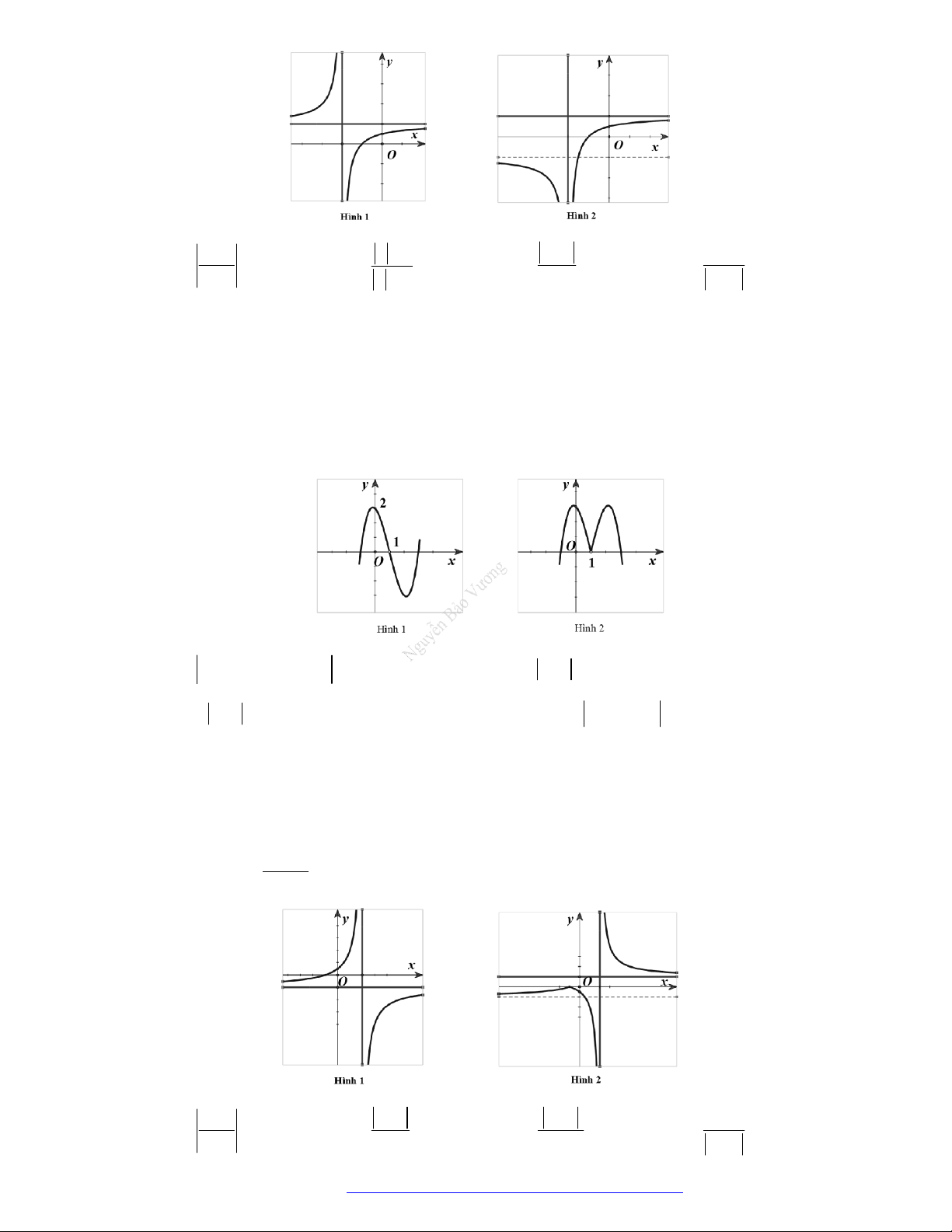
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 32 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
1
.
2
x
y
x
B.
1
.
2
x
y
x
C.
1
.
2
x
y
x
D.
1
.
2
x
y
x
Hướng dẫn
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy
Toàn bộ đồ thị phía bên phải đường thẳng
2x
được giữ nguyên
Toàn bộ đồ thị phía bên trái đường thẳng
2x
lấy đối xứng qua
Ox
Chọn đáp án D.
Câu 15. Cho hàm số
2
1 2 3y x x x
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới
đây?
A.
2
1 2 3 .y x x x B.
2
1 2 3 .y x x x
C.
2
1 2 3y x x x
D.
2
1 2 3y x x x
Hướng dẫn
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy
Toàn bộ đồ thị nằm bên trái (ứng với
1)x
đường thẳng
1x
được giữ nguyên
Toàn bộ đồ thị nằm bên phải (ứng với
1)x
đường thẳng
1x
được lấy đối xứng qua
.Ox
Chọn đáp án C.
Câu 16. Cho hàm số
1
2
x
y
x
có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?
A.
1
.
2
x
y
x
B.
1
.
2
x
y
x
C.
1
.
2
x
y
x
D.
1
.
2
x
y
x

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 33
H
ướng dẫn
Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy
Toàn bộ đồ thị phía bên trái đường thẳng
1
x
(ứ
ng với
1
)
x
được
giữ nguyên
Toàn bộ đồ thị phía bên phải đường thẳng
1
x
(ứng v
ới
1
)
x
được lấ
y đối xứng qua trục
.O
x
Chọn
đáp án B.
-------------------- HẾT --------------------
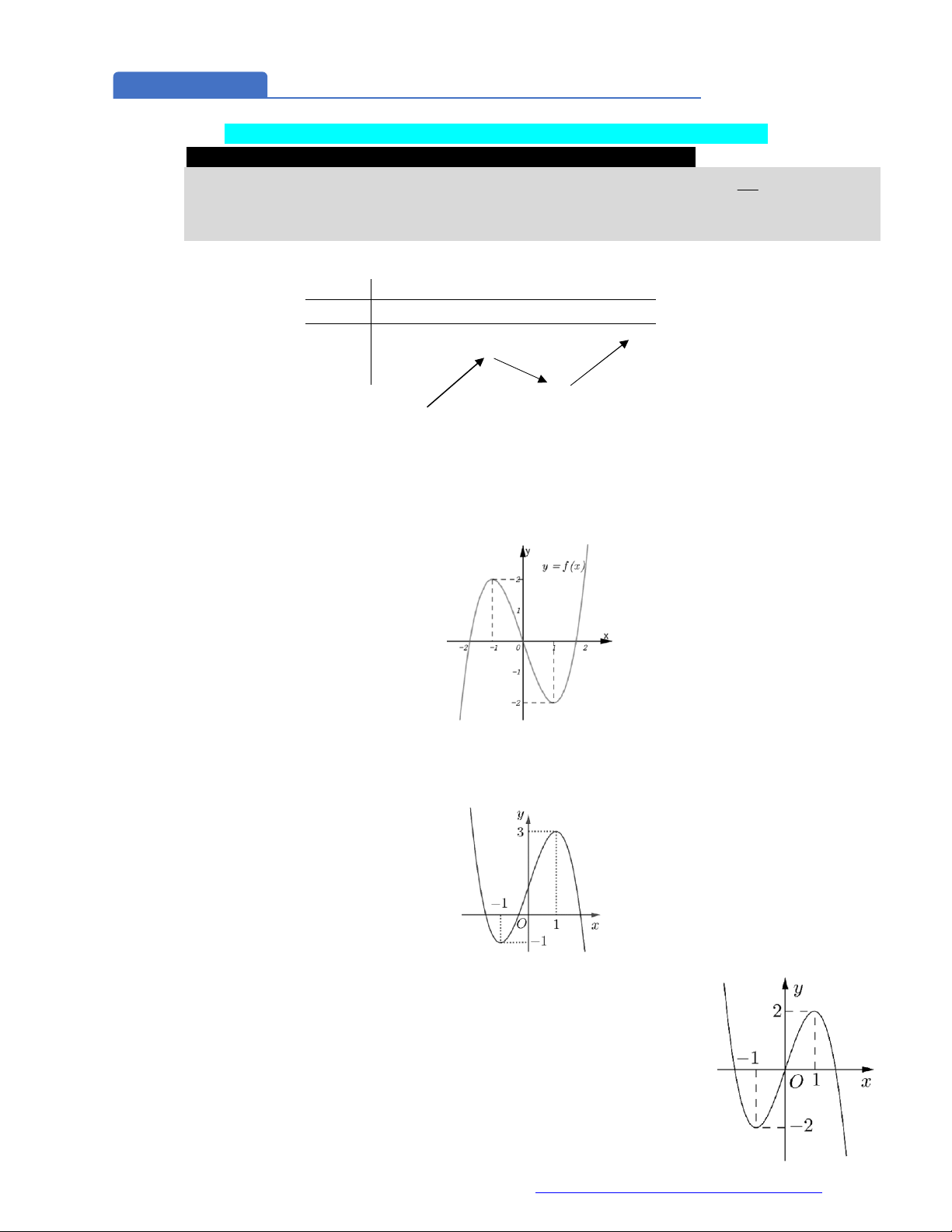
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
DẠNG TOÁN DÀNH CHO HỌC SINH TRUNG BÌNH MỨC 5-6 ĐIỂM
Dạng 1. Bài toán tương giao đồ thị thông qua đồ thị, bảng biến thiên
Nghiệm của phương trình là số giao điểm của đường thẳng với đồ thị hàm
số
Câu 1. (Đề Minh Họa 2020 Lần 1) Cho hàm số
f x
có bảng biến thiên như sau
x
2
3
( )f x
0
0
( )f x
1
0
Số nghiệm của phương trình
3 ( ) 2 0f x
là
A.
2.
B.
0.
C.
3.
D.
1.
Câu 2. (Mã 101 - 2020 Lần 1) Cho hàm số bậc ba
y f x
có đồ thị là đường cong trong hình bên. Số
nghiệm thực của phương trình
1f x
là:
A.
3
. B.
1
. C.
0
. D.
2
.
Câu 3. (Mã 102 - 2020 Lần 1) Cho hàm số bậc ba có đồ thị là đường cong trong hình bên. Số
nghiệm thực của phương trình là
A. . B. . C. . D. .
Câu 4. (Mã 103 - 2020 Lần 1) Cho hàm số bậc ba
y f x
có đồ thị là đường
cong trong hình bên. Số nghiệm thực của phương trình
1f x
là
A.
1
. B.
0
.
C.
2
. D.
3
.
TƯƠNG GIAO ĐỒ THỊ HÀM SỐ
Chuyên đề 8
0
af x b
b
y
a
y f x
y f x
1
f x
0
3
1
2
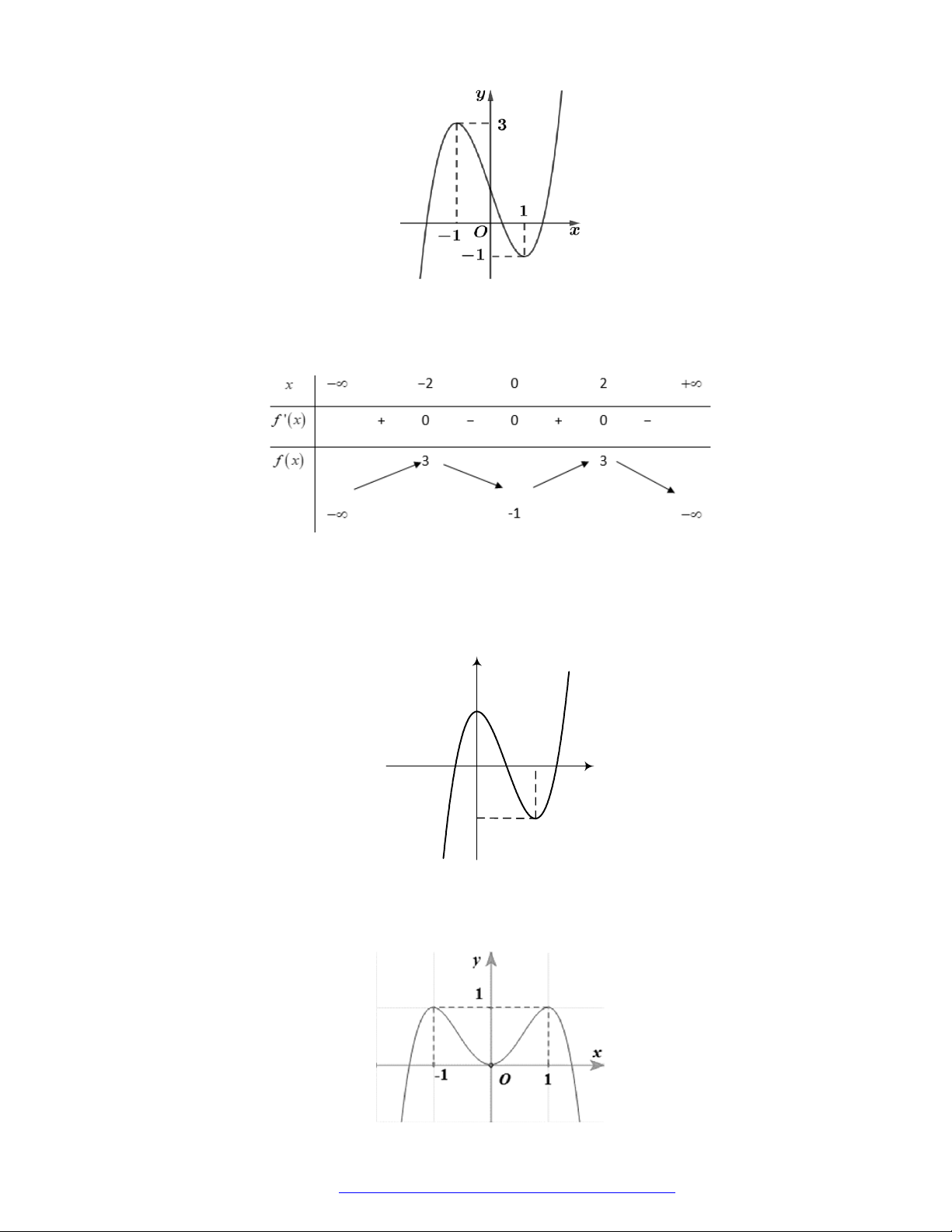
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 5. (Mã 104 - 2020 Lần 1) Cho hàm số bậc ba
y f x
có đồ thị là đường cong trong hình vẽ bên.
Số nghiệm thực của phương trình
2f x
là:
A.
0
. B.
3
. C.
1
. D.
2
.
Câu 6. (Mã 101 2019) Cho hàm số có bảng biến thiên như sau:
Số nghiệm thực của phương trình là
A. . B. . C. . D. .
Câu 7. (Mã 101 2018) Cho hàm số . Đồ thị của hàm số
như hình vẽ bên. Số nghiệm thực của phương trình là
A. B. C. D.
Câu 8. (Mã 102 2018) Cho hàm số . Đồ thị của hàm số như
hình vẽ bên.
Số nghiệm của phương trình là
A. B. C. D.
f x
2 3 0
f x
2
1
4
3
3 2
, , ,f x ax bx cx d a b c d
y f x
3 4 0
f x
x
y
O
2
2
2
2
0
1
3
4 2
, ,f x ax bx c a b c
y f x
4 3 0
f x
2
0
4
3
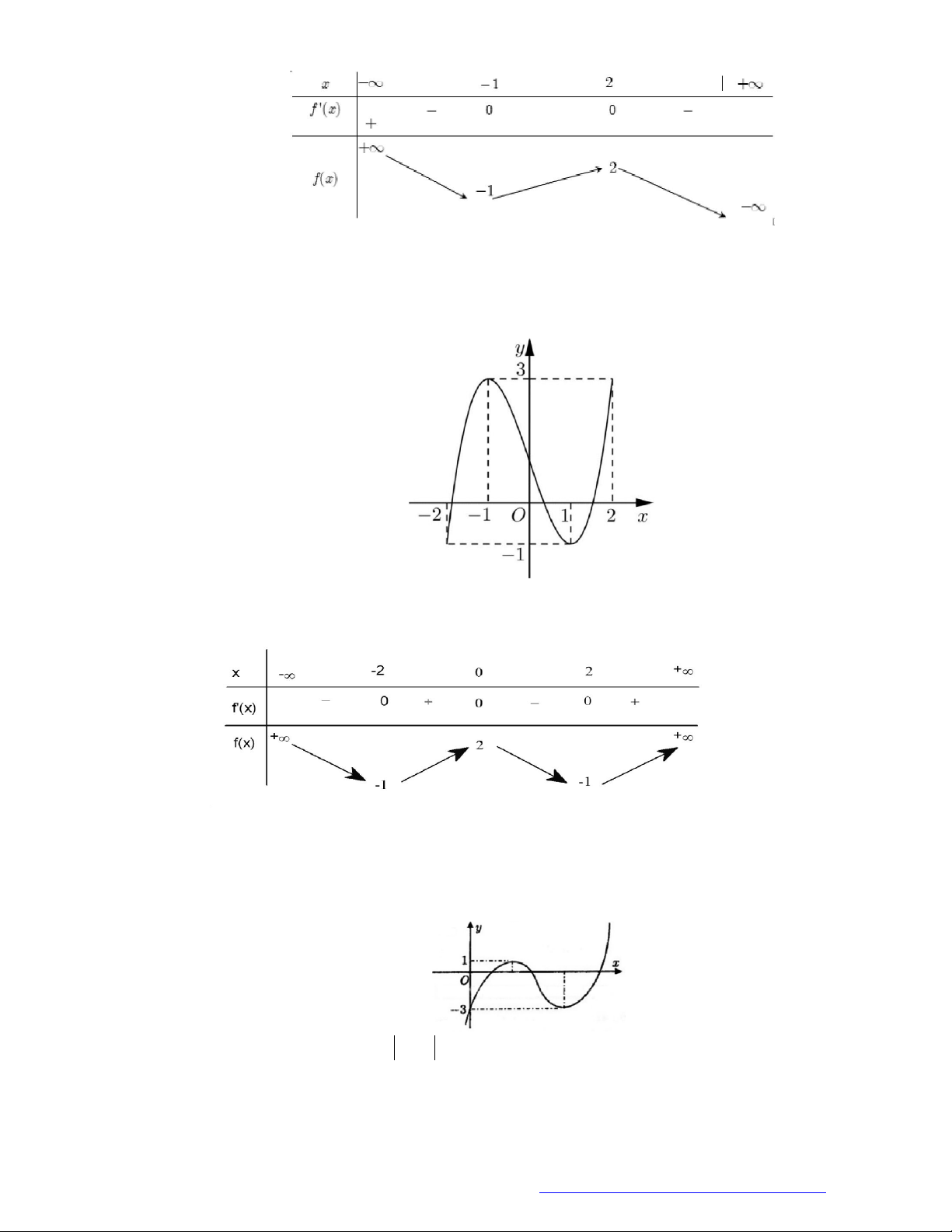
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Câu 9. (Mã 103 2019) Cho hàm số bảng biến thiên như sau:
Số nghiệm thực của phương trình là
A. . B. . C. . D. .
Câu 10. (Mã 103 2018) Cho hàm số liên tục trên và có đồ thị như hình vẽ bên. Số
nghiệm thực của phương trình trên đoạn là
A. . B. . C. . D. .
Câu 11. (Mã 102 2019) Cho hàm số có bảng biến thiên như
sau
Số nghiệm thực của phương trình là
A.
3
. B. . C. . D. .
Câu 12. (THCS - THPT Nguyễn Khuyến 2019) Cho hàm số liên tục trên và có đồ thị như
hình vẽ.
Số nghiệm của phương trình là
A. . B. . C. . D. .
Câu 13. (Mã 104 2019) Cho hàm số có bảng biến thiên như sau:
( )f x
2 ( ) 3 0
f x
3
0
1
2
y f x
2;2
3 4 0
f x
2;2
4
3
1
2
f x
3 5 0
f x
4
0
2
y f x
2
f x
3
2
4
6
f x
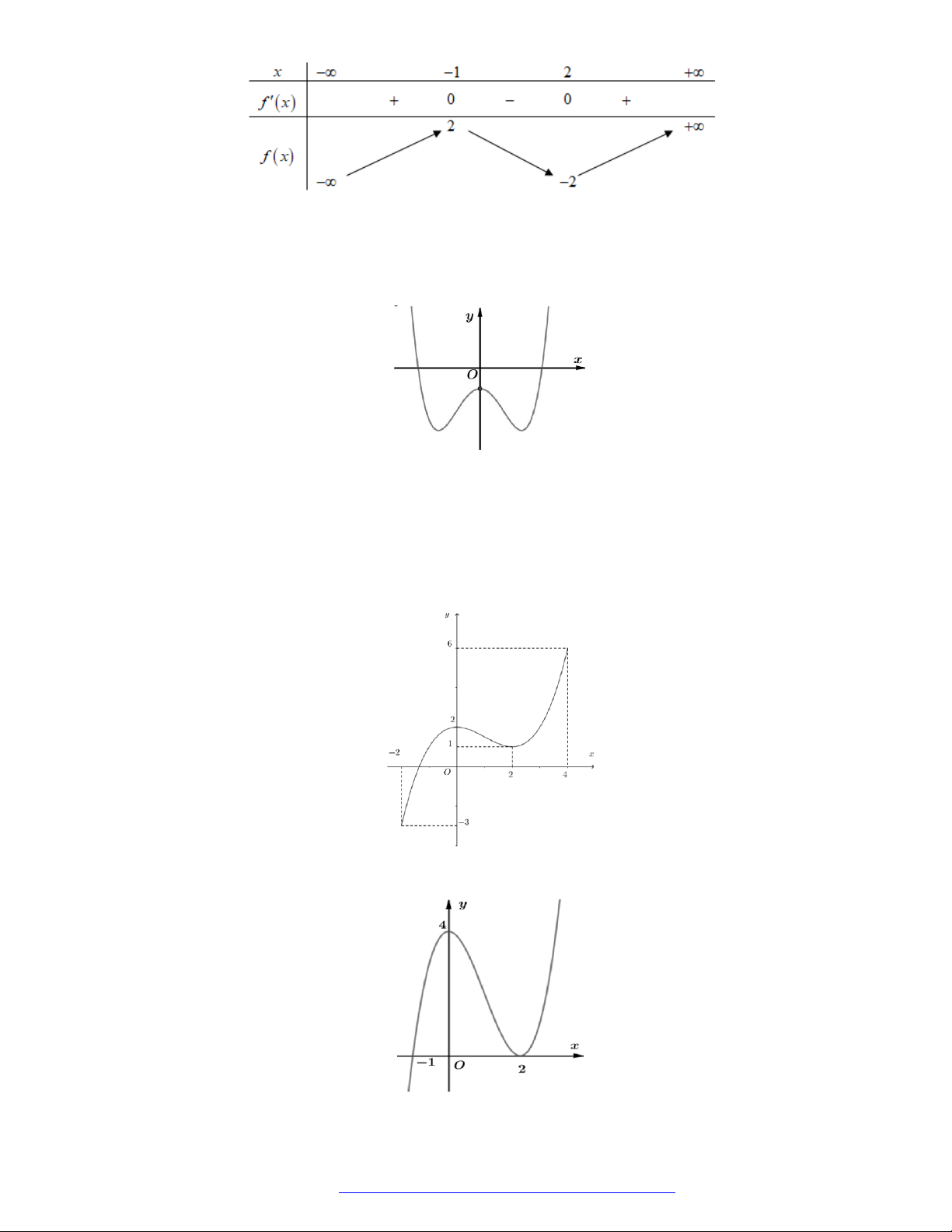
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Số nghiệm thực của phương trình là
A. . B. . C. . D. .
Câu 14. (Mã 110 2017) Đường cong ở hình bên là đồ thị của hàm số , với là các
số thực. Mệnh đề nào dưới đây đúng?
A. Phương trình vô nghiệm trên tập số thực
B. Phương trình có đúng một nghiệm thực
C. Phương trình có đúng hai nghiệm thực phân biệt
D. Phương trình có đúng ba nghiệm thực phân biệt
Câu 15. (Mã 104 2018) Cho hàm số liên tục trên đoạn và có đồ thị như hình vẽ bên. Số
nghiệm thực của phương trình trên đoạn là
A. B. C. D.
Câu 16. (THPT Cù Huy Cận 2019) Cho hàm số có đồ thị như hình vẽ.
Số nghiệm thực của phương trình
A. . B. . C. . D. .
2 3 0
f x
0
1
2
3
4 2
y ax bx c
, ,a b c
0
y
0
y
0
y
0
y
( )y f x
2;4
3 ( ) 5 0
f x
2;4
2
1
0
3
( )y f x
4 ( ) 7 0
f x
2
4
3
1
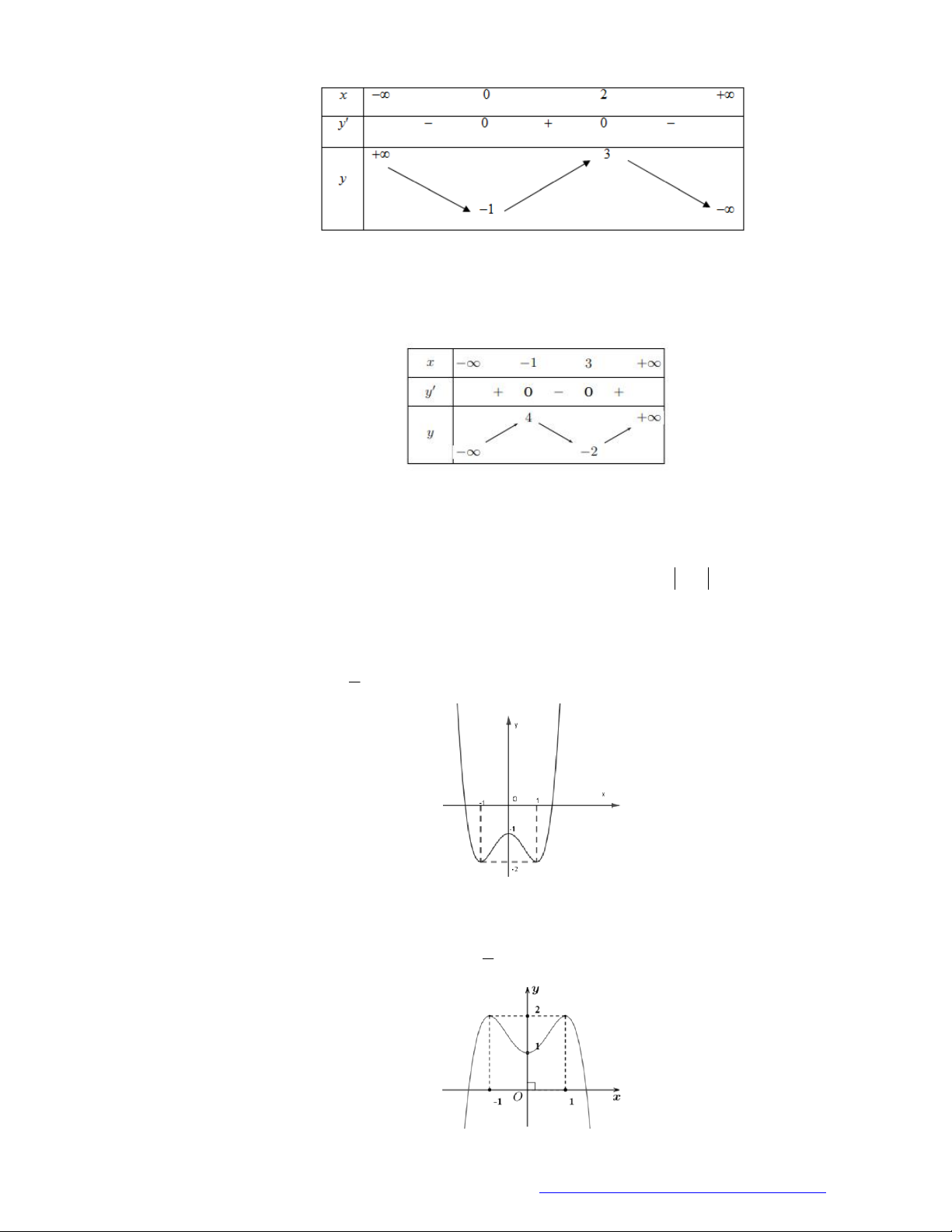
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Câu 18. (THPT Yên Phong 1 Bắc Ninh 2019) Cho hàm số có bảng biến thiên sau đây.
Hỏi phương trình có bao nhiêu nghiệm thực?
A. . B. . C. . D. .
Câu 19. (THPT Lương Thế Vinh Hà Nội 2019) Cho hàm số có bảng biến thiên như hình bên.
Số nghiệm của phương trình là
A. B. C. D.
Câu 20. (THPT - Yên Định Thanh Hóa 2019) Cho hàm số liên tục trên đoạn và có đồ
thị là đường cong như hình vẽ bên. Tìm số nghiệm của phương trình trên đoạn .
A. 3. B. 5. C. 6. D. 4.
Câu 21. (Mã 102 - 2020 Lần 2) Cho hàm số bậc bốn
( )y f x
có đồ thị là đường cong trong hình vẽ bên.
Số nghiệm thực của
phương trình
3
( )
2
f x
là
A.
4
B.
1
C.
3
D.
2
Câu 22. (Mã 103 - 2020 Lần 2) Cho hàm số bậc bốn
y f x
có đồ thị là đường cong trong hình bên.
Số nghiệm thực của phương trình
1
2
f x
là
A.
2
. B.
4
. C.
1
. D.
3
.
y f x
2. 5 0
f x
0
1
3
2
y f x
3 0
f x
3
2
1
0
y f (x)
2;2
f(x) 1
2;2
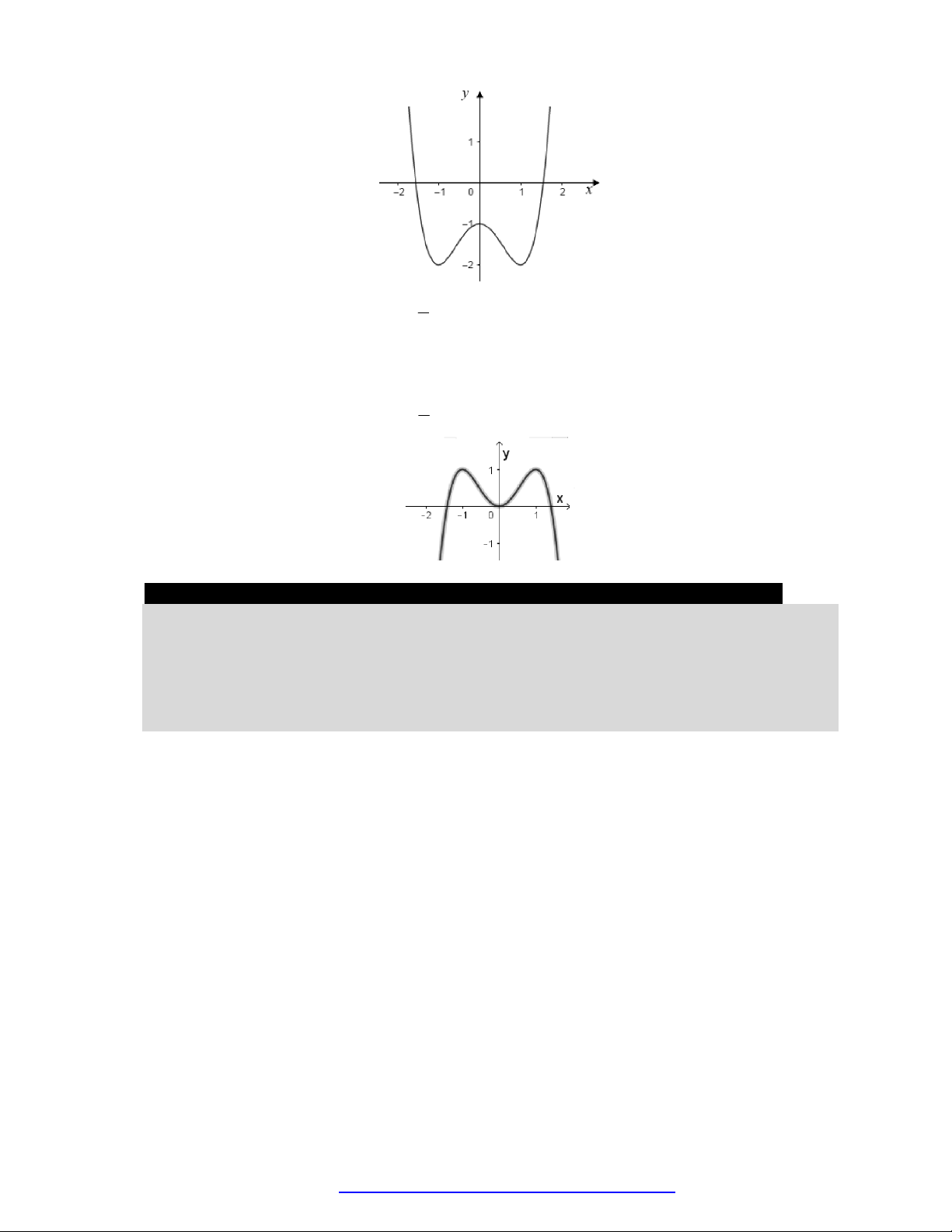
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 23. (Mã 101 – 2020 Lần 2) Cho hàm số bậc bốn
y f x
có đồ thị là đường cong trong hình bên.
Số nghiệm của phương trình
1
2
f x
là
A.
3
. B.
4
. C.
2
. D.
1x
.
Câu 24. (Mã 104 - 2020 Lần 2) Cho hàm số
y f x
có đồ thị là đường cong trong hình bên. Số
nghiệm thực của phương trình
1
2
f x
là
A.
4
. B.
2
. C.
1
. D.
3
.
Dạng 2. Bài toán tương giao đồ thị thông qua hàm số cho trước (không chứa tham số)
Cho hai đồ thị
( )y f x
và
( )y g x
.
Bước 1. Giải phương trình
( ) ( )f x g x
.
Bước 2. Tìm
Số giao điểm?
Hoành độ giao điểm?
Tung độ giao điểm?
Câu 25. (Đề Tham Khảo 2020 Lần 2) Số giao điểm của đồ thị hàm số
3
3 1y x x
và trục hoành là
A.
3
. B.
0
. C.
2
. D.
1
.
Câu 26. (Mã 101 - 2020 Lần 1) Số giao điểm của đồ thị hàm số
3 2
3y x x
và đồ thị hàm số
2
3 3y x x
là
A.
3
. B.
1
. C.
2
. D.
0
.
Câu 27. (Mã 102 - 2020 Lần 1) Số giao điểm của đồ thị hàm số
3 2
y x x
và đồ thị hàm số
2
5y x x
là
A.
2
. B.
3
. C.
1
. D.
0
.
Câu 28. (Mã 103 - 2020 Lần 1) Số giao điểm của đồ thị hàm số
3 2
y x x
và đồ thị hàm số
2
5y x x
A.
3.
B.
0
. C.
1.
D.
2.
Câu 29. (Mã 104 - 2020 Lần 1) Số giao điểm của đồ thị hàm số
2
3y x x
và đồ thị hàm số
3 2
y x x
là
A.
1
. B.
0
. C.
2
. D.
3
Câu 30. (Mã 102 - 2020 Lần 2) Số giao điểm của đồ thị hàm số
3
7y x x
với trục hoành là
A.
0
. B.
3
. C.
2
. D.
1
.
Câu 31. (Mã 103 - 2020 Lần 2) Số giao điểm của đồ thị hàm số
3
3 y x x
với trục hoành là

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
A.
2
. B.
0
. C.
3
. D.
1
.
Câu 32. (Mã 101 – 2020 Lần 2) Số giao điểm của đồ thị hàm số
3
6y x x
với trục hoành là
A.
2
. B.
3
. C.
1
. D.
0
.
Câu 33. (Mã 104 - 2020 Lần 2) Số giao điểm của đồ thị hàm số
3
5y x x
với trục hoành là:
A.
3
B.
2
C.
0
D.
1
Câu 34. (Mã 105 2017) Cho hàm số
2
2 1
y x x
có đồ thị
C
. Mệnh đề nào dưới đây đúng?
A.
C
cắt trục hoành tại một điểm. B.
C
cắt trục hoành tại ba điểm.
C.
C
cắt trục hoành tại hai điểm. D.
C
không cắt trục hoành.
Câu 35. (Đề Minh Họa 2017) Biết rằng đường thẳng
2 2y x
cắt đồ thị hàm số
3
2
y x x
tại
điểm duy nhất; kí hiệu
0 0
;x y
là tọa độ của điểm đó. Tìm
0
y
A.
0
4
y
B.
0
0
y
C.
0
2
y
D.
0
1
y
Câu 36. (THPT - Yên Định Thanh Hóa 2019) Gọi
P
là số giao điểm của hai đồ thị
3 2
1
y x x
và
2
1
y x
. Tìm
P
.
A.
0
P
. B.
2P
. C.
1P
. D.
3
P
.
Câu 37. (Đề Tham Khảo 2017) Cho hàm số
3
3 y x x
có đồ thị
C
. Tìm số giao điểm của
C
và
trục hoành.
A.
2
B.
3
C.
1
D.
0
Câu 38. (THPT Yên Khánh - Ninh Bình 2019) Cho hàm số
4 2
3y x x
có đồ thị
C
. Số giao điểm
của đồ thị
C
và đường thẳng
2
y
là
A.
2
. B.
1
. C.
0
. D.
4
.
Câu 39. (Chuyên Trần Phú Hải Phòng 2019) Biết rằng đường thẳng
4 5y x
cắt đồ thị hàm số
3
2 1y x x
tại điểm duy nhất; kí hiệu là tọa độ của điểm đó. Tìm .
A.
0
10
y
. B.
0
13
y
. C.
0
11
y
. D.
0
12
y
.
Câu 40. (THPT Yên Phong 1 Bắc Ninh 2019) Đồ thị của hàm số
4 2
3 1y x x
cắt trục tung tại
điểm có tung độ bao nhiêu
A. -3. B. 0. C. 1. D. -1.
Câu 41. (THPT Việt Đức Hà Nội 2019) Số giao điểm của đường cong
3 2
2 2 1y x x x
và đường
thẳng
1y x
là
A.
1
B.
2
C.
3
D.
0
Câu 42. đồ thị hàm số
4 2
3 1
y x x
và đồ thị hàm số
2
2 7
y x
có bao nhiêu điểm chung?
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 43. Cho hàm số
3
2 5y x x
có đồ thị
C
Tìm số giao điểm của
C
và trục hoành.
A.
2
. B.
3
. C.
1
. D.
0
.
Câu 44. Cho hàm số
2
3 2
y x x
có đồ thị
C
. Mệnh đề nào dưới đây đúng?
A.
C
cắt trục hoành tại hai điểm. B.
C
cắt trục hoành tại một điểm.
C.
C
không cắt trục hoành. D.
C
cắt trục hoành tại ba điểm.
Câu 45. Biết rằng đường thẳng
2
y x
cắt đồ thị hàm số
3 2
4
y x x x
tại điểm duy nhất, kí hiệu
0 0
;x y
là tọa độ của điểm đó. Tìm
0
y
.
0 0
;x y
0
y

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
0
1
y
. B.
0
3
y
. C
.
0
2
y
. D
.
0
4
y
.
Câu
46. đồ thị hàm số nào sau đây cắt trục tung tại điểm có tung độ âm?
A.
1
3
x
y
x
. B.
1
4
x
y
x
. C.
1
2
x
y
x
. D.
2
1
5
x
y
x
.
Câu 47. Gọi
,M
N
là
giao điểm của đường thẳng
1y
x
và
đường cong
2 4
1
x
y
x
.
Khi đó hoành độ
I
x
của
trung điểm
I
của đoạn
M
N
bằ
ng bao nhiêu?
A.
2
I
x
. B.
1
I
x
. C
.
5
I
x
. D
.
5
2
I
x
.
Câu
48. Cho hàm số
1
3
x
y
x
có
đồ thị
C
và
các đường thẳng
1
:
2d y x
,
2
:
2 2
d
y x
,
3
:
3 3d y x
,
4
:
3d y x
.
Hỏi có bao nhiêu đường thẳng trong bốn đường thẳng
1
2 3 4
,
, ,d d d d
đi
qua giao điểm của
C
và
trục hoành.
A.
1
. B.
2
. C
.
3
. D
.
4
.
Câu
49. (THPT Quang Trung Đống Đa Hà Nội 2019) Tìm số giao điểm của đồ thị hàm số
4
4
5
y
x
và đường thẳng
y
x
A.
3
. B.
0
. C
.
2
. D
.
1
.
-------------------- HẾT --------------------

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 1
DẠNG TOÁN DÀNH CHO ĐỐI TƯỢNG HỌC SINH KHÁ MỨC 7+8+9 ĐIỂM
Dạng 1. Bài toán tương giao đường thẳng với đồ thị hàm số bậc 3 (CHỨA THAM SỐ)
Bài toán tổng quát: Tìmcácgiátrịcủathamsố
m
đểđểđườngthẳng
:d y px q
cắtđồthịhàmsố
3 2
( ) :C y ax bx cx d tại3điểmphânbiệtthỏađiềukiện
K
?(dạng có điều kiện)
Phương pháp giải:
Bước 1. Lậpphươngtrìnhhoànhđộgiaođiểmcủa
d
và
( )C
là:
3 2
ax bx cx d px q
Đưavềphươngtrìnhbậcbavànhẩmnghiệmđặcbiệt
o
x x đểchiaHoocnerđược:
2
2
( ) ( ) 0
( ) 0
o
o
x x
x x ax b x c
g x ax b x c
Bước 2. Để
d
cắt
( )C
tại ba điểm phân biệt phương trình
( ) 0g x
có 2 nghiệm phân biệt khác
( )
0
( ) 0
g x
o
o
x
g x
Giảihệnày,tìmđượcgiátrị
1
.m D
Bước 3.Gọi
1 1 2 2
( ; ), ( ; ), ( ; )
o o
A x px q B x px q C x px q với
1 2
, x x làhainghiệmcủa
( ) 0.g x
TheoViét,tacó:
1 2
b
x x
a
và
1 2
c
x x
a
(1)
Bước 4.BiếnđổiđiềukiệnKvềdạngtổngvàtíchcủa
1 2
,x x (2)
Thế(1)vào(2)sẽthuđượcphươngtrìnhhoặcbấtphươngtrìnhvớibiếnlà
.m
Giảichúngsẽtìmđượcgiátrị
2
.m D
Kếtluận:
1 2
.m D D
Một số công thức tính nhanh “ thường gặp “ liên quan đến cấp số
Tìm điều kiện để đồ thị hàm số
3 2
y ax bx cx d cắt trục hoành tại
3
điểm phân biệt có hoành
độ lập thành cấp số cộng.
Điều kiện cần:
Giả sử
1 2 3
, ,x x x là nghiệm của phương trình
3 2
0ax bx cx d
Khi đó:
3 2
1 2 3
( )( )( )ax bx cx d a x x x x x x
, đồng nhất hệ số ta được
2
3
b
x
a
Thế
2
3
b
x
a
vào phương trình
3 2
0ax bx cx d
ta được điều kiện ràng buộc về tham số hoặc giá trị của
tham số.
Điều kiện đủ:
Thử các điều kiện ràng buộc về tham số hoặc giá trị của tham số để phương trình
3 2
0ax bx cx d
có
3
nghiệm phân biệt.
Tìm điều kiện để đồ thị hàm số
3 2
y ax bx cx d
cắt trục hoành tại
3
điểm phân biệt có hoành
độ lập thành cấp số nhân.
Điều kiện cần:
Giả sử
1 2 3
, ,x x x là nghiệm của phương trình
3 2
0ax bx cx d
Khi đó:
3 2
1 2 3
( )( )( )ax bx cx d a x x x x x x
, đồng nhất hệ số ta được
3
2
d
x
a
Thế
3
2
d
x
a
vào phương trình
3 2
0ax bx cx d
ta được điều kiện ràng buộc về tham số hoặc giá trị
TƯƠNG GIAO ĐỒ THỊ HÀM SỐ
Chuyên đề 8

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
của tham số.
Điều kiện đủ:
Thử các điều kiện ràng buộc về tham số hoặc giá trị của tham số để phương trình
3 2
0
ax bx cx d
có
3
nghiệm phân biệt.
Câu 1. (Sở Ninh Bình 2020) Chohàmsố
3 2
3 2y x mx m
.Cóbaonhiêugiátrịcủathamsốthực
m
đểđồthịhàmsốcắttrụchoànhtạibađiểmphânbiệtcóhoànhđộlậpthànhcấpsốcộng?
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 2. (Cụm Liên Trường Hải Phòng 2019) Tìmtấtcảcácgiátrịthựccủathamsố
m
đểđồthịhàmsố
3 2
3 2
y x x C
cắtđường
thẳng
: ( 1)
d y m x
tạibađiểmphânbiệt
1 2 3
, ,x x x
.
A.
2
m
. B.
2
m
. C.
3
m
. D.
3
m
.
Câu 3. (Chuyên Vĩnh Phúc 2019) Đườngthẳng
cóphươngtrình
2 1y x
cắtđồthịcủahàmsố
3
3
y x x
tạihaiđiểm
A
và
B
vớitọađộđượckíhiệulầnlượtlà
;
A A
A x y
và
;
B B
B x y
trongđó
B A
x x
.Tìm
B B
x y
?
A.
5
B B
x y
B.
2
B B
x y
C.
4
B B
x y
D.
7
B B
x y
Câu 4. (THPT Ba Đình 2019) Cho hàm số
3 2 3
3
y x mx m
có đồ thị
m
C
và đường thẳng
2 3
: 2d y m x m
.Biếtrằng
1 2 1 2
,
m m m m
làhaigiátrịthựccủa
m
đểđườngthẳng
d
cắtđồ
thị
m
C
tại
3
điểmphânbiệtcóhoànhđộ
1 2 3
, ,x x x
thỏamãn
4 4 4
1 2 3
83
x x x
.Phátbiểunào
sauđâylàđúng vềquanhệgiữahaigiátrị
1 2
,m m
?
A.
1 2
0
m m
. B.
2
1 2
2 4
m m
. C.
2
2 1
2 4
m m
. D.
1 2
0
m m
.
Câu 5. (THPT Bạch Đằng Quảng Ninh 2019) Tìmtấtcảcácgiátrịthựccủathamsố
m
đểđồthịhàm
số
3 2
3y x x
cắtđườngthẳng
y m
tạibađiểmphânbiệt.
A.
; 4
m
. B.
4;0
m
.
C.
0;m
. D.
; 4 0;m
.
Câu 6. (Mã 123 2017) Tìmtấtcảcácgiátrịthựccủathamsố
m
đểđườngthẳng
1y mx m
cắtđồthị
hàmsố
3 2
3 2
y x x x
tạibađiểm
, ,A B C
phânbiệtsao
AB BC
A.
5
;
4
m
B.
2;m
C.
m
D.
; 0 4;m
Câu 7. (Sở Cần Thơ - 2019) Tấtcảgiátrịcủathamsố
m
đểđồthịhàmsố
3 2 2
2 2 4
y x m x m
cắtcáctrụctọađộ
,Ox
Oy
lầnlượttại
,A
B
saochodiệntíchtamgiác
OAB
bằng8là
A.
2
m
. B.
1
m
. C.
3
m
. D.
2
m
.
Câu 8. (Mã 110 2017) Tìmtấtcảcácgiátrịthựccủathamsố
m
đểđườngthẳng
y mx
cắtđồthịcủa
hàmsố
3 2
3 2
y x x m
tạibađiểmphânbiệt
, ,A B C
saocho
AB BC
.
A.
; 1
m
B.
:m
C.
1:m
D.
;3
m
Câu 9. (Chuyên Bắc Ninh 2019) Tìmtấtcảcácgiátrịcủathamsố
m
đểphươngtrình
3 2
3 2
x x m
cóbanghiệmphânbiệt.
A.
2;m
. B.
; 2
m
. C.
2;2
m
. D.
2;2
m
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Câu 10. (Chuyên Vĩnh Phúc 2019) Đườngthẳng
cóphươngtrình
2 1y x
cắtđồthịcủahàmsố
3
3y x x
tạihaiđiểm
A
và
B
vớitọađộđượckíhiệulầnlượtlà
;
A A
A x y
và
;
B B
B x y
trongđó
B A
x x
.Tìm
B B
x y
?
A.
5
B B
x y
B.
2
B B
x y
C.
4
B B
x y
D.
7
B B
x y
Câu 11. (ChuyênLêQuýĐônĐiệnBiên2019)Gọi
S
làtậptấtcảcácgiátrịthựccủathamsố
m
để
phươngtrình
3 2
2 3 2 1
x x m
cóđúnghainghiệmphânbiệt.Tổngcácphầntửcủa
S
bằng
A.
1
2
. B.
3
2
. C.
5
2
. D.
1
2
.
Câu 12. (THPTMinhKhaiHàTĩnh2019)Tìmtấtcảcácgiátrịthựccủathamsố
m
đểđườngthẳng
5y x
cắtđồthịhàmsố
3 2
2 x 3( 1) 5
y x m m x
tại3điểmphânbiệt.
A.
1
2
m
m
. B.
2
3
1
2
m
m
m
. C.
2
3
1
2
m
m
m
. D.
1
2
m
m
.
Câu 13. (THPTLươngThếVinhHàNội2019)Chohàmsốbậcba
y f x
cóđồthị
C
nhưhình
vẽ, đường thẳng
d
có phương trình
1y x
. Biết phương trình
0
f x
có ba nghiệm
1 2 3
x x x
.Giátrịcủa
1 3
x x
bằng
A.
3
. B.
7
3
. C.
2
. D.
5
2
.
Câu 14. (ChuyênLêThánhTông2019)Cóbaonhiêugiátrịnguyêncủathamsố
2018;2019
m
để
đồthịhàmsố
3
3 3y x mx
vàđườngthẳng
3 1y x
códuynhấtmộtđiểmchung?
A.
1
. B.
2019
. C.
4038
. D.
2018
.
Câu 15. (THCS-THPTNguyễnKhuyến2019)Phươngtrình
3 2
6 5 5x mx m
có3nghiệmphânbiệt
lậpthànhcấpsốcộngkhi
A.
0
m
. B.
1 1
m m
. C.
1
m
. D.
m
.
Câu 16. Tínhtổngtấtcảcácgiátrịcủa
m
biếtđồthịhàmsố
3 2
2 3 4
y x mx m x
vàđườngthẳng
4
y x
cắtnhautạibađiểmphânbiệt
0;4
A
,
B
,
C
saochodiệntíchtamgiác
IBC
bằng
8 2
với
1;3
I
.
A.
3
. B.
8
. C.
1
. D.
5
.
Câu 17. Cóbaonhiêugiátrịnguyêncủathamsố
2018;2019
m
đểđồthịhàmsố
3
3 3y x mx
và
đườngthẳng
3 1y x
códuynhấtmộtđiểmchung?
A.
1
. B.
2019
. C.
4038
. D.
2018
.
Câu 18. Đường thẳngd cóphương trình
4
y x
cắt đồthị hàm số
3 2
2 ( 3) 4y x mx m x
tại3
điểmphânbiệt
(0;4)
A
,BvàCsaochodiệntíchcủatamgiácMBCbằng4,với
(1;3)
M
.Tìmtất
cảcácgiátrịcủa
m
thỏamãnyêucầubàitoán.
A.
3
m
. B.
2
m
hoặc
3
m
.
C.
2
m
hoặc
3
m
.D.
2
m
hoặc
3
m
Câu 19. (THPT Minh Khai - lần 1) Tìmtấtcảcácgiátrịthựccủathamsố
m
đểđườngthẳng
5y x
cắtđồthịhàmsố
3 2
2 3 1 5y x mx m x
tạibađiểmphânbiệt.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
1
2
m
m
. B.
2
3
1
2
m
m
m
. C.
2
3
1
2
m
m
m
. D.
1
2
m
m
.
Câu 20. (Chuyên Lê Quý Đôn Điện Biên 2019) Gọi
S
làtậptấtcảcácgiátrịthựccủathamsố
m
để
phươngtrình
3 2
2 3 2 1
x x m
cóđúnghainghiệmphânbiệt.Tổngcácphầntửcủa
S
bằng
A.
1
2
. B.
3
2
. C.
5
2
. D.
1
2
.
Câu 21. (Kiểm tra năng lực - ĐH - Quốc Tế - 2019) Giá trị lớn nhất của
m
để đường thẳng
: 1
d y x m
cắtđồthịhàmsố
3 2
2 2 8 5 5
y x m x m x m
tại3điểmphânbiệt
cóhoànhđộ
1 2 3
, ,x x x
thỏamãnđiềukiện
2 2 2
1 2 3
20
x x x
là
A.
3
. B.
1
. C.
0
. D.
3
2
.
Câu 22. Cóbaonhiêugiátrịcủa
m
đểđồthịhàmsố
3 2 2 3
2 3 2 2
y x m x m m x
cắttrụchoànhtại
bađiểmphânbiệtcóhoànhđộlàbasốhạngliêntiếpcủamộtcấpsốnhân?
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 23. (Kinh Môn - Hải Dương 2019) Tìm
m
để đồ thị
C
của
3 2
3 4
y x x
và đường thẳng
y mx m
cắtnhautại3điểmphânbiệt
1;0
A
,
B
,
C
saocho
OBC
códiệntíchbằng
64
.
A.
14
m
. B.
15
m
. C.
16
m
. D.
17
m
.
Câu 24. (Sở Bắc Ninh 2019) Chohàmsố
3 2
8 8y x x x
cóđồthị
C
vàhàmsố
2
(8 )
y x a x b
(với
,a b
)cóđồthị
P
.Biếtđồthịhàmsố
C
cắt
P
tạibađiểmcóhoànhđộnằmtrong
1;5
.Khi
a
đạtgiátrịnhỏnhấtthìtích
ab
bằng
A.
729
. B.
375
. C.
225
. D.
384
.
Câu 25. (Sở Quảng Trị 2019) Cóbaonhiêugiátrịnguyêncủathamsố
m
đểđườngthẳng
y mx m
cắt đồ thị hàm số
3 2
y x mx m
tại
3
điểm phân biêt có hoành độ
1 2 3
, ,x x x
thỏa mãn
1 2 3
1 3
x x x
?.
A.
6
. B.
5
. C.
2
. D.
3
.
Câu 26. (Chuyên Nguyễn Huệ 2019) Chohàmsố
3 2
2 3 4
y x mx m x
m
C
.Tấtcảcácgiátrị
củathamsố
m
đểđườngthẳng
: 4
d y x
cắt
m
C
tạibađiểmphânbiệt
0;4
A
,
B
,
C
sao
chotamgiác
KBC
códiệntíchbằng
8 2
vớiđiểm
1;3
K
là:
A.
1 137
2
m
. B.
1 137
2
m
. C.
1 137
2
m
. D.
1 137
2
m
.
Câu 27. (Chuyên Thái Nguyên - 2020) Gọi
T
làtậphợptấtcảcácgiátrịnguyêncủathamsố
m
để
phươngtrình
3 2 3 2
3 3 0
x x m m
cóbanghiệm phânbiệt.Tổng tất cảcácphần tử của
T
bằng
A.
1
. B.
5
. C.
0
. D.
3
.
Câu 28. (Đại Học Hà Tĩnh - 2020) Chođồthịhàmsố
3 2
f x x bx cx d
cắttrụchoànhtại3điểm
phânbiệtcóhoànhđộ
1 2 3
, ,x x x
.Tínhgiátrịcủabiểuthức
1 2 3
1 1 1
.
P
f x f x f x
A.
3 2
P b c
. B.
0
P
. C.
P b c d
. D.
1 1
2
P
b c
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Câu 29. (Sở Bắc Ninh - 2020) Cho hàm số bậc ba
y f x
có đồ thị đi qua điểm
1;1 , 2;4 , 3;9
A B C
. Các đường thẳng
, ,AB AC BC
lại cắt đồ thị lần lượt tại các điểm
, ,M N P
(
M
khác
A
và
B
,
N
khác
A
và
C
,
P
khác
B
và
C
.Biếtrằngtổngcáchoànhđộ
của
, ,M N P
bằng5,giátrịcủa
0
f
là
A.
6
. B.
18
. C. 18. D. 6.
Câu 30. (Đô Lương 4 - Nghệ An - 2020) Tìm giá trị thực của tham số
m
để đồ thị hàm số
3 2
3 2
y x x
cắtđườngthẳng
: 1
d y m x
tạibađiểmphânbiệtcóhoànhđộ
1
x
,
2
x
,
3
x
thỏamãn
2 2 2
1 2 2
5
x x x
.
A.
3
m
. B.
2
m
C.
3
m
. D.
2
m
.
Câu 31. (Yên Lạc 2 - Vĩnh Phúc - 2020) Gọi
S
làtậptấtcảcácgiátrịcủathamsố
m
đểđồthịhàmsố
3 2
3 9 2 1
y x x x m
vàtrục
Ox
cóđúnghaiđiểmchungphânbiệt.Tínhtổng
T
củacácphầntửthuộctập
S
A.
10
T
. B.
10
T
. C.
12T
. D.
12T
.
Dạng 2. Bài toán tương giao của đường thẳng với đồ thị hàm số nhất biến (CHỨA THAM SỐ)
Bài toán tổng quát
Chohàmsố
ax b
y
cx d
cóđồthị
C
.Tìmthamsốmđểđườngthẳng
:d y x
cắt
C
tạihaiđiểm
phânbiệt
, A B
thỏamãnđiềukiệnK?
Phương pháp giải
Bước 1.(Bướcnàygiốngnhauởcácbàitoántươnggiaocủahàmnhấtbiến)
Lậpphươngtrìnhhoànhđộgiaođiểmgiữadvà
:C
ax b
x
cx d
2
0,
d
g x cx c d a x d b x
c
.
-Đểdcắt
C
tạihaiđiểmphânbiệt
0
g x
cónghiệmnghiệmphânbiệt
d
c
0; 0
0
c
d
g
c
.
Giảihệnày,tasẽtìmđược
1
m D
i
-Gọi
1 1 2 2
; , ;A x x B x y
với
1 2
,x x
là
2
nghiệmcủa
0
g x
TheoViét:
1 2
;
c d a
S x x
c
1 2
d b
P x x
c
ii
Bước 2.
-BiếnđổiđiềukiệnKchotrướcvềdạngcóchứatổngvàtíchcủa
1 2
,x x
iii
-Thế
ii
vào
iii
sẽthuđượcphươngtrìnhhoặcbấtphươngtrìnhvớibiếnsốlàm.Giảinósẽtìmđược
2
m D
-Từ
1 2
,
i m D D
vàkếtluậngiátrịmcầntìm.
Một số công thức tính nhanh “ thường gặp “ liên quan đến tương giao giữa đường thẳng
y kx p
và
đồ thị hàm số
ax b
y
cx d
Giả sử
:
d y kx p
cắt đồ thị hàm số
ax b
y
cx d
tại
2
điểm phân biệt
,M N
.
Với
ax b
kx p
cx d
cho ta phương trình có dạng:
2
0
Ax Bx C
thỏa điều kiện
0
cx d
, có
2
4
B AC
. Khi đó:

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
1).
2
1 1 2 2 2 1 2 1
2
( ; ), ( ; ) ( ; ( )) ( 1)
M x kx p N x kx p MN x x k x x MN k
A
Chú ý: khi
min
MN
thì tồn tại
min ,
k const
2).
2 2 2 2 2 2
1 2 1 2
( 1)( ) ( )2 2OM ON k x x x x kp p
3).
2 2
1 2 1 2
. ( . )(1 ) ( )
OM ON x x k x x kp p
4).
2
1 2
( )(1 ) 2 0
OM ON x x k kp
Câu 1. (Sở Ninh Bình 2020) Cótấtcảbaonhiêugiátrịnguyênthuộcđoạn
2020;2020
củathamsố
m
đểđườngthẳng
y x m
cắtđồthịhàmsố
2 3
1
x
y
x
tạihaiđiểmphânbiệt?
A.
4036.
B.
4040.
C.
4038.
D.
4034.
Câu 2. (ĐHQG TPHCM 2019) Đườngthẳng
2y x m
cắtđồthịhàmsố
3
1
x
y
x
tạihaiđiểmphân
biệtkhivàchỉkhi
A.
1
3
m
m
. B.
1
3
m
m
. C.
3
1
m
m
. D.
3 1
m
.
Câu 3. (Gia Lai 2019) Tìmtấtcảcácgiátrịthựccủathamsố
m
đểđườngthẳng
2
y x m
cắtđồthị
củahàmsố
3
1
x
y
x
tạihaiđiểmphânbiệt.
A.
;m
. B.
1;m
. C.
2;4
m
. D.
; 2
m
.
Câu 4. Gọi
A
và
B
làhaiđiểmthuộchainhánhkhácnhaucủađồthịhàmsố
2
x
y
x
.Khiđóđộdài
đoạn
AB
ngắnnhấtbằng
A.
4 2
. B.
4
. C.
2 2
. D.
2 2
.
Câu 5. (Chuyên Nguyễn Du ĐăkLăk 2019) Chohàmsố
1
x
y C
x
vàđườngthẳng
: xd
y m
.
Gọi
S
làtậpcácsốthực
m
đểđườngthẳng
d
cắtđồthị
C
tạihaiđiểmphânbiệt
,A B
saocho
tamgiác
OAB
(
O
làgốctọađộ)cóbánkínhđườngtrònngoạitiếpbằng
2 2
.Tổngcácphầntử
của
S
bằng
A.
4
. B.
3
. C.
0
. D.
8
.
Câu 6. Đồthịhàmsố
2 1
1
x
y C
x
vàđườngthẳng
:
d y x m
.Tìmtấtcảcácgiátrịcủathamsố
m
đểđườngthẳng
d
cắtđồthị
C
tại
2
điểmphânbiệt
A.
1
m
. B.
5 1
m
. C.
5
m
. D.
5
m
hoặc
1
m
.
Câu 7. (Sở Cần Thơ 2019) Chohàmsố
3
1
x
y
x
cóđồthị
C
vàđườngthẳng
:
d y x m
,với
m
là
thamsốthực.Biếtrằngđườngthẳng
d
cắt
C
tạihaiđiểmphânbiệt
A
và
B
saochođiểm
2; 2
G
làtrọngtâmcủatamgiác
OAB
(
O
làgốctoạđộ).Giátrịcủa
m
bằng
A.
6
. B.
3
. C.
9
. D.
5
.
Câu 8. (Sở Nam Định 2019) Chohàmsố
3 2
1
x m
y
mx
với
m
làthamsố.Biếtrằngvớimọi
0,
m
đồ
thịhàmsốluôncắtđườngthẳng
: 3 3d y x m
tạihaiđiểmphânbiệt
A
,
.B
Tíchtấtcảcácgiá
trịcủa
m
tìmđượcđểđườngthẳng
d
cắtcáctrục
,Ox
Oy
lầnlượttại
,C
D
saochodiệntích
OAB
bằng2lầndiệntích
OCD
bằng
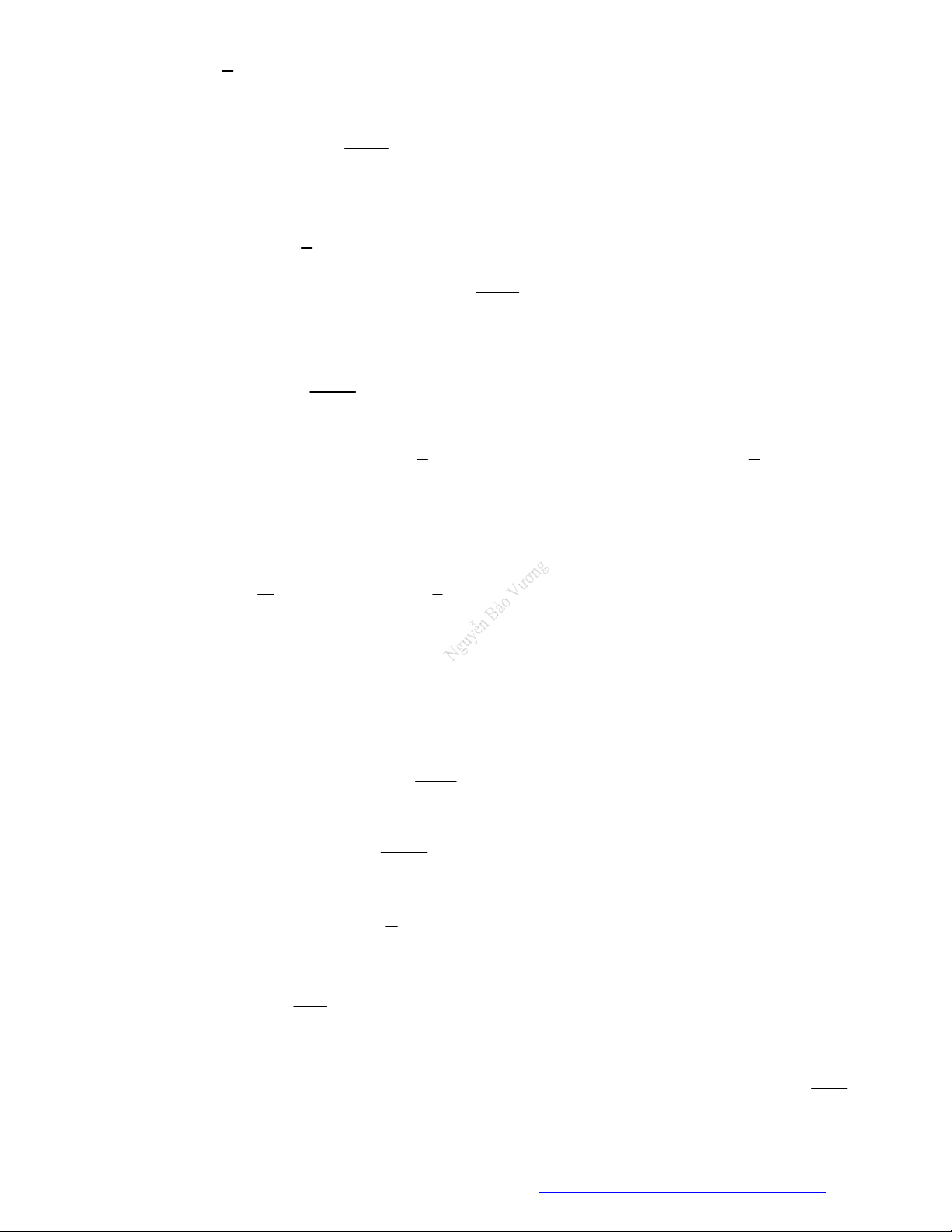
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
A.
4
9
. B.
4
. C.
1
. D.
0
.
Câu 9. (Gia Lai 2019) Cóbaonhiêugiátrịnguyêndươngcủathamsố
m
đểđườngthẳng
3
y x m
cắtđồthịhàmsố
2 1
1
x
y
x
tạihaiđiểmphânbiệt
A
và
B
saochotrọngtâmtamgiác
OAB
(
O
làgốctọađộ)thuộcđườngthẳng
2 2 0
x y
?
A.
2
. B.
1
. C.
0
. D.
3
.
Câu 10. Giả sử
b
m
a
,
,a b
,
, 1
a b
là giá trị thực của tham số
m
để đường thẳng
: 3
d y x m
cắtđồthịhàmsố
2 1
1
x
y
x
C
tạihaiđiểmphânbiệt
A
,
B
saochotrọng
tâmtamgiác
OAB
thuộcđườngthẳng
2 2 0
x y
,với
O
làgốctoạđộ.Tính
2a b
.
A.
2
. B.
5
. C.
11
. D.
21
.
Câu 11. Chohàmsố
3 2
,(C)
2
x
y
x
vàđườngthẳng
: 2 4
d y ax b
.Đườngthẳngdcắt(C)tạiA,
BđốixứngnhauquagốctọađộO,khiđó
T a b
bằng
A.
2T
. B.
5
2
T
. C.
4T
. D.
7
2
T
.
Câu 12. Tìmgiátrịthựccủathamsố
m
đểđườngthẳng
d
:
3
y x m
cắtđồthịhàmsố
2 1
1
x
y
x
tạihaiđiểmphânbiệt
A
,
B
saochotrọngtâm
OAB
thuộcđườngthẳng
:
2 2 0
x y
,
với
O
làgốctọađộ.
A.
11
5
m
. B.
1
5
m
. C.
0
m
. D.
2
m
.
Câu 13. Chohàmsố
2
1
x
y
x
cóđồthịlà
C
.Tìmtậphợptấtcảcácgiátrị
a
đểquađiểm
0;M a
cóthểkẻđượcđườngthẳngcắt
C
tạihaiđiểmphânbiệtđốixứngnhauquađiểm
M
.
A.
;0 2;
. B.
3;
. C.
;0
. D.
; 1 3;
.
Câu 14. (Đại học Hồng Đức –Thanh Hóa 2019) Cóbaonhiêusốnguyêndương
m
saochođườngthẳng
y x m
cắtđồthịhàmsố
2 1
1
x
y
x
tạihaiđiểmphânbiệt
M
,
N
saocho
10
MN
.
A.
2
. B.
3
. C.
1
. D.
4
.
Câu 15. Cholàđồthịhàmsố
x
y
x
2 1
1
.Tìm
k
đểđườngthẳng
d : y kx k 2 1
cắttạihaiđiểm
phânbiệt
A,B
saochokhoảngcáchtừ
A
đếntrụchoànhbằngkhoảngcáchtừ
B
đếntrụchoành.
A. 1. B.
2
5
C.
3
. D.
2
.
Câu 16. (THPT Lương Thế Vinh Hà Nội 2019) Tìmđiềukiệncủa
m
đểđườngthẳng
1y mx
cắtđồ
thịhàmsố
3
1
x
y
x
tạihaiđiểmphânbiệt.
A.
;0 16;
B.
16;
C.
;0
D.
;0 16;
Câu 17. (Chuyên Lê Quý Đôn Quảng Trị 2019) Gọi
;M a b
làđiểmtrênđồthịhàmsố
2
x
y
x
sao
chokhoảngcáchtừ
M
đếnđườngthẳng
: 2 6
d y x
nhỏnhất.Tính
2 2
4 5 2 7
a b
.
A.
162
. B.
2
. C.
18
. D.
0
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 18. (Toán Học TuổiTrẻ2019)Cóbaonhiêugiátrị của
m
để đồ thị củahàm số
1
x
y
x
cắt
đườngthẳng
y x m
tạihaiđiểmphânbiệt
,A B
saochogócgiữahaiđườngthẳng
OA
và
OB
bằng
0
60
(với
O
làgốctọađộ)?
A.
2
B.
1
C.
3
D.
0
Câu 19. (THPT Lê Quy Đôn Điện Biên 2019) Để đường thẳng
: 2
d y x m
cắt đồ thị hàm số
2
1
x
y
x
C
tạihaiđiểmphânbiệt
A
và
B
saochođộdài
AB
ngắnnhấtthìgiátrịcủa
m
thuộckhoảngnào?
A.
4; 2
m
B.
2;4
m
C.
2;0
m
D.
0;2
m
Câu 20. (THPT Lương Tài Số 2 2019) Biết rằng đường thẳng
2 2y x m
luôn cắt đồ thị hàm số
2
3
1
x
y
x
tạihaiđiểmphânbiệtA, Bvớimọigiátrịcủathamsốm.Tìmhoànhđộtrungđiểm
củaAB?
A.
1
m
B.
1
m
C.
2 2
m
D.
2 1
m
Câu 21. (THPTGia LộcHải Dương2019)Gọi
H
làđồ thị hàmsố
2 3
1
x
y
x
.Điểm
0 0
;M x y
thuộc
H
cótổngkhoảngcáchđếnhaiđườngtiệmcậnlànhỏnhất,với
0
0
x
khiđó
0 0
x y
bằng
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 22. (Chuyên Bến Tre - 2020) Gọi
S
làtậphợptấtcảcácgiátrịnguyêncủathamsố
m
đểđường
thẳng
:
d y x m
cắt đồ thị hàm số
2 1
1
x
y
x
tại hai điểm phân biệt
,A B
sao cho
2 2
AB
.Tổnggiátrịcácphầntửcủa
S
bằng
A.
6
. B.
27
. C.
9
. D.
0
.
Câu 23. (Lương Thế Vinh - Hà Nội - 2020) Chohàmsố
2
2
1
x m
y
x
cóđồthị
,
m
C
trongđó
m
là
thamsốthực.Đườngthẳng
:
d y m x
cắt
m
C
tạihaiđiểm
; , ;
A A B B
A x y B x y
với
;
A B
x x
đườngthẳng
': 2
d y m x
cắt
m
C
tạihaiđiểm
; , ;
C C D D
C x y D x y
với
.
C D
x x
Gọi
S
làtậphợptấtcảcácgiátrịcủathamsố
m
để
. 3.
A D
x x
Sốphầntửcủatập
S
là
A.
1.
B.
2.
C.
0.
D.
3.
Dạng 3. Bài toán tương giao của đường thẳng với hàm số trùng phương (CHỨA THAM SỐ)
. Bài toán tổng quát: Tìmmđểđườngthẳng
:d y
cắtđồthị
4 2
( ) : ( ; )
C y f x m ax bx c
tạinđiểm
phânbiệtthỏamãnđiềukiệnKchotrước?
Phương pháp giải:
Bước 1. Lậpphươngtrìnhhoànhđộgiaođiểmcủa
d
và
( )C
là:
4 2
0
ax bx c
(1)
Đặt
2
0
t x
thì
2
(1) 0
at bt c
(2)
Tùyvàosốgiaođiểmnmàtabiệnluậnđểtìmgiátrị
1
.m D
Cụthể:
Để
( ) 4
d C n
điểmphânbiệt
(1)
có4nghiệmphânbiệt
(2)
có2nghiệm
1 2
, t t
thỏađiềukiện:
1 2 1
0
0 0 .
0
t t S m D
P
Để
( ) 3
d C n
điểmphânbiệt
(1)
có3nghiệmphânbiệt

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
(2)
cónghiệm
1 2
, t t
thỏađiềukiện:
1 2 1
0
0 .
0
c
t t m D
b
a
Để
( ) 2
d C n
điểmphânbiệt
(1)
có2nghiệmphânbiệt
(2)
có2nghiệmtráidấuhoặccónghiệmképdương
1
0
.
0
0
ac
m D
S
Để
( ) 1d C n
điểmphânbiệt
(1)
cóđúng1nghiệm
(2)
cónghiệmkép
0
hoặc
1
1
2
0
0
0
.
0 0
0
c
t
m D
b
t c
a
Bước 2.BiếnđổiđiềukiệnKvềdạngcóchứatổngvàtíchcủa
1 2
, t t
(3)
Thếbiểuthứctổng,tíchvào(3)sẽthuđượcphươngtrình hoặcbấtphương trìnhvới biếnsốlà
.m
Giải
chúngtasẽtìmđược
2
.m D
Kếtluận:
1 2
.m D D
Tìm điều kiện để đồ thị hàm số
4 2
y ax bx c
cắt trục hoành tại
4
điểm phân biệt có hoành độ
lập thành cấp số cộng.
Ta có:
4 2
0 (1)
ax bx c
, đặt
2
0
t x
, thì có:
2
0
at bt c
(2)
Để
(1)
có
4
nghiệm phân biệt thì
(2)
có hai nghiệm phân biệt dương, tức là:
1 2
1 2
0
0
. 0
t t
t t
Khi đó
(1)
có
4
nghiệm phân biệt lần lượt là
2 1 1 2
; ; ;t t t t
lập thành cấp số cộng khi và chỉ khi:
2 1 1 1 2 1 2 1
( ) 3 9t t t t t t t t
. Theo định lý Vi – et
1 2
b
t t
a
suy ra
1 2
9
;
10 10
b b
t t
a a
, kết hợp
1 2
.
c
t t
a
nên có:
2 2
9 100
ab a c
Tóm lại: Hàm số
4 2
y ax bx c
cắt trục hoành tại
3
điểm phân biệt có hoành độ lập thành cấp số cộng,
thì điều kiện cần và đủ là:
2
2 2
4 0
0
0
9 100
b ac
b
a
c
a
ab a c
Câu 1. Tậptấtcảcácgiátrịcủathamsố
m
đểphươngtrình
4 2
4 3 0
x x m
có4nghiệmphânbiệt
là
A.
1;3
. B.
3;1
. C.
2;4
. D.
3;0
.
Câu 2. Tậptấtcảcácgiátrịcủathamsố
m
đểphươngtrình
4 2
2 (2 1) 0
x mx m
có4nghiệmthực
phânbiệtlà
A.
1
; \ 1 .
2
B.
(1; )
. C.
1
;
2
. D.
.
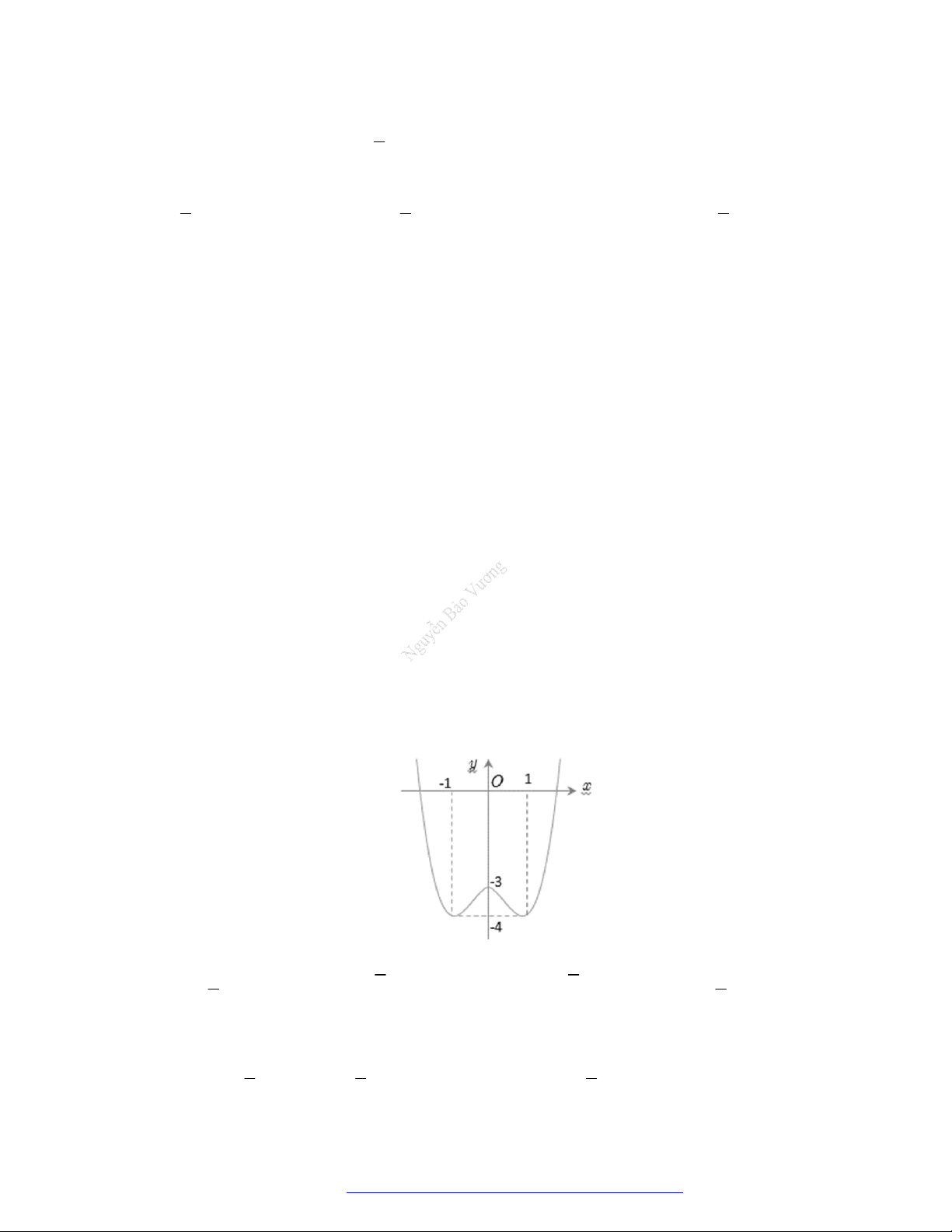
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 3. (THPT Lương Thế Vinh - Hn - 2018)Chohàmsố
4 2
3 2y x x .Tìmsốthựcdương
m
để
đườngthẳng
y m
cắtđồthịhàmsốtại
2
điểmphânbiệt
A
,
B
saochotamgiác
OAB
vuông
tại
O
,trongđó
O
làgốctọađộ.
A.
2m
. B.
3
2
m
. C.
3m
. D.
1m
.
Câu 4. Đườngthẳng
y m
cắtđồthịhàmsố
4 2
y x x
tại
4
điểmphânbiệtkhivàchỉkhi
A.
1
0
4
m
. B.
1
0
4
m
. C.
0m
. D.
1
4
m
Câu 5. (THPT Quỳnh Lưu- Nghệ An- 2019) Mộtđườngthẳngcắt đồthịhàm số
4 2
2y x x
tại4
điểmphânbiệtcóhoànhđộlà
0, 1,
,m
n
.Tính
2 2
.S m n
A.
1S
. B.
0S
. C.
3S
. D.
2S
.
Câu 6. Cóbaonhiêugiátrị nguyêncủa
m
để đồthịhàmsố
4 3 2
4 2 8 4y x x m x x
cắttrục
hoànhtạiđúnghaiđiểmcóhoànhđộlớnhơn
1
.
A.
8
. B.
7
. C.
5
. D.
3
.
Câu 7. (Sở Hà Nam - 2019) Chohàmsố
4 2
4 8 1f x x x
.Cóbaonhiêugiátrịnguyêndươngcủa
m
đểphươngtrình
f x m
cóđúnghainghiệmphânbiệt?
A. 0. B. 2. C. 3. D. 1.
Câu 8. (Sở Thanh Hóa 2018) Chohàmsố
4 2
2y x mx m (với
m
làthamsốthực).Tậptấtcảcácgiá
trịcủathamsố
m
đểđồthịhàmsốđãchocắtđườngthẳng
3y
tạibốnđiểmphânbiệt,trong
đócómộtđiểmcóhoànhđộlớnhơn
2
cònbađiểmkiacóhoànhđộnhỏhơn
1
,làkhoảng
;a b
(với
,a b
,
a
,
b
làphânsốtốigiản).Khiđó,
15ab
nhậngiátrịnàosauđây?
A.
63
. B.
63
. C.
95
. D.
95
.
Câu 9. (Chuyên Hà Tĩnh 2018)Đườngthẳng
2
y m cắtđồthịhàmsố
4 2
10y x x tạihaiđiểm
phânbiệt
A
,
B
saochotamgiác
OAB
vuông(
O
làgốctọađộ).Mệnhđềnàosauđâyđúng?
A.
2
5;7m
. B.
2
3;5m
. C.
2
1;3m
. D.
2
0;1m
.
Câu 10. (Sở Bình Phước 2018) Chohàmsố
4 2
2 3y x x cóđồthịnhưhìnhvẽbêndưới.Vớigiátrị
nàocủa
m
thìphươngtrình
4 2
2 3 2 4x x m
có
2
nghiệmphânbiệt.
A.
0
1
2
m
m
. B.
1
2
m
. C.
1
0
2
m
. D.
0
1
2
m
m
.
Câu 11. (THPT Bình Giang - Hải Dương - 2018) Tìmtấtcảcácgiátrịcủathamsố
m
đểphươngtrình
4 2
2 3 2 0x x m
có
4
nghiệmphânbiệt.
A.
3
2
2
m
. B.
3
2
2
m
. C.
3
2
2
m
. D.
3 4m
.
Câu 12. (THPT Vân Nội - Hà Nội - 2018) Tất cảcácgiátrịthựccủatham số
m
,đểđồthị hàmsố
4 2 2
2 2 2 2y x m x m m
khôngcắttrụchoành.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
A.
3
1.
m
B.
3.
m
C.
3
1.
m
D.
3
.
m
Câu 13. (Sở
Nam Định - 2018) Tìm tất cả các giá trị của tham số
m
để
đồ thị hàm
số
4
2
1
2 2 3 6 5
y
m x m x m
cắ
t trục hoành tại 4 điểm phân biệt có các hoành độ
1
2 3 4
,
, ,x x x x
thỏamãn
1
2 3 4
1
. x x x x
A.
5
1
;
6
m
. B.
3; 1
m
. C.
3;1
m
. D.
4; 1
m
.
Câu 14. (C
huyênVĩnhPhúc2019)Chohàmsố
4 2
3
2 3y x m x m
có
đồthịlà
(
)
m
C
.
Tìm
m
để
đườngthẳng
:
1
d
y
cắ
tđồthị
(
)
m
C
tạ
i4điểmphânbiệtđềucóhoànhđộnhỏhơn2.
A.
1
1
3
m
và
0
m
B.
1
1
2
m
và
0
m
C.
1
1
2 2
m
và
0
m
D.
1
1
3 2
m
và
0
m
-------------------- HẾT --------------------

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
DẠNG TOÁN DÀNH CHO ĐỐI TƯỢNG HỌC SINH GIỎI MỨC 9-10 ĐIỂM
Dạng 1. Biện luận m để phương trình có nghiệm thỏa mãn điều kiện k (hàm số khác)
Câu 1. (Mã 101 2019) (Mã đề 001) Cho hai hàm số
3 2 1
2 1 1
x x x x
y
x x x x
và
2y x x m
(
m
là tham số thực) có đồ thị lần lượt là
1
C
và
2
C
. Tập hợp tất cả các giá trị của
m
để
1
C
và
2
C
cắt nhau tại đúng bốn điểm phân biệt là
A.
2;
. B.
;2
. C.
2;
. D.
;2
.
Câu 2. (Mã 103 2019) Cho hai hàm số
1 1 2
1 2 3
x x x x
y
x x x x
và
2y x x m
(
m
là tham
số thực) có đồ thị lần lượt là
1 2
,C C
. Tập hợp tất cả các giá trị của
m
để
1
C
và
2
C
cắt
nhau tại đúng bốn điểm phân biệt là
A.
2;
. B.
; 2
. C.
2;
. D.
; 2
.
Câu 3. (Mã 102 2019) Cho hai hàm số
1 2 3
1 2 3 4
x x x x
y
x x x x
và
1y x x m
(
m
là tham
số thực) có đồ thị lần lượt là
1
C
và
2
C
. Tập hợp tất cả các giá trị của
m
để
1
C
và
2
C
cắt
nhau tại đúng 4 điểm phân biệt là
A.
;3
. B.
;3
. C.
3;
. D.
3;
.
Câu 4. (Mã 104 2019) Cho hai hàm số
2 1 1
1 1 2
x x x x
y
x x x x
và
1y x x m
(
m
là tham
số thực) có đồ thị lần lượt là
1
C
và
2
C
. Tập hợp tất cả các giá trị của
m
để
1
C
và
2
C
cắt
nhau tại đúng bốn điểm phân biệt là
A.
; 3
. B.
3;
. C.
; 3
. D.
3;
.
Câu 5. Cho hai hàm số
2 2 2 2
1 2 4 3 6 8
1 2 3
x x x x x x x
y
x x x x
và
2y x x m
( là tham số
thực) có đồ thị lần lượt là
1
( )C
và
2
( )C . Tính tổng tất cả các giá trị nguyên thuộc khoảng
( 15; 20)
của tham số
m
để
1
( )C
và
2
( )C cắt nhau tại nhiều hơn hai điểm phân biệt.
A.
210
. B.
85
. C.
119
. D.
105
.
Câu 6. Cho hai hàm số
1 2
1 1
x x x
y
x x x
và
2020 3
x
y e m
(
m
là tham số thực) có đồ thị lần
lượt là
1
( )C và
2
( )C . Có bao nhiêu số nguyên
m
thuộc
( 2019; 2020)
để
1
( )C và
2
( )C cắt nhau
tại 3 điểm phân biệt?
A.
2692
. B.
2691
. C.
2690
. D.
2693
.
Câu 7. Tìm tập hợp tất cả các giá trị của tham số
m
để đồ thị hai hàm số
2
2 1 1y x x
và
11 1
11
3 4 2
y m
x x
cắt nhau tại
2
điểm phân biệt?
A.
;0
. B.
;1
. C.
;1
. D.
;2
.
Câu 8. Cho hai hàm số
1 1 2
1 2 3
x x x x
y
x x x x
và
1
2 2
x
y m
( là tham số thực) có đồ thị lần
lượt là
1
( )C
và
2
( )C
. Tập hợp tất cả các giá trị của để
1
( )C
và
2
( )C
cắt nhau tại đúng năm
điểm phân biệt là
A.
2;
. B.
;2
. C.
;2
. D.
;4
.
TƯƠNG GIAO ĐỒ THỊ HÀM SỐ
Chuyên đề 8
m
m
m

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 9. Cho hai hàm số
2 2 2
1 2
1 2 4 3
x x x
y
x x x x x
và
1y x x m
( là tham số thực) có đồ
thị lần lượt là
1
( )C và
2
( )C . Số các giá trị
m
nguyên thuộc khoảng
20;20
để
1
( )C và
2
( )C cắt
nhau tại năm điểm phân biệt là
A.
22
. B.
39
. C.
21
. D.
20
.
Câu 10. Gọi
S
là tập hợp tất cả các giá trị của tham số
m
để bất phương trình
2 4 3 2 2
2 1 0m x m x x m x
nghiệm đúng với mọi
x
. Số phần tử của tập
S
là
A.
3
. B.
2
. C.
0
. D.
1
.
Câu 11. Có bao nhiêu cặp số thực
( ; )a b
để bất phương trình
2
1 2 2 0x x ax bx
nghiệm
đúng với mọi
x
A.
3
. B.
2
. C.
0
. D.
1
.
Câu 12. Trong số các cặp số thực
;a b
để bất phương trình
2
1 0x x a x x b
nghiệm đúng
với mọi
x
, tích
ab
nhỏ nhất bằng
A.
1
4
. B.
1
. C.
1
4
. D.
1
.
Câu 13. Cho 2 hàm số
7 5 3
3 1y x x x m
và
2 2y x x m
(
m
là tham số thực) có đồ thị lần
lượt là
1
C
,
2
C
. Tập hợp tất cả các giá trị của
m
để
1
C
cắt
2
C
là
A.
m
. B.
2;m
. C.
;2m
. D.
2;m
.
Câu 14. Có bao nhiêu giá trị nguyên của tham số thực
m
thuộc đoạn
2019;2019
để phương trình
2
3 2 3 1 5 1 2 4 2 3x x m x x m x x
có nghiệm thực?
A.
2019
. B.
4032
. C.
4039
. D.
4033
.
Câu 15. (Chuyên Nguyễn Bỉnh Khiêm - Quảng Nam - 2020) Tập hợp tất cả các số thực của tham số m
để phương trình
6 4 3 3 2 2
6 15 3 6 10 0x x m x m x mx
có đúng hai nghiệm phân biệt
thuộc đoạn
1
;2
2
là:
A.
5
2
2
m
. B.
7
3
5
m
. C.
11
4
5
m
. D.
9
0
4
m
.
Câu 16. (Chuyên Hùng Vương - Phú Thọ - 2020) Có bao nhiêu
m
nguyên dương để hai đường cong
1
2
: 2
10
C y
x
và
2
: 4C y x m cắt nhau tại ba điểm phân biệt có hoành độ dương?
A. 35. B. 37. C. 36. D. 34.
Câu 17. (Chuyên Phan Bội Châu - Nghệ An - 2020) Cho hàm số
( ) ( 1).( 2)...( 2020).f x x x x
Có
bao nhiêu giá trị nguyên của
m
thuộc đoạn
2020;2020
để phương trình
( ) . ( )f x m f x
có 2020 nghiệm phân biệt?
A. 2020. B. 4040. C. 4041. D. 2020.
Câu 18. (ĐHQG Hà Nội - 2020) Cho phương trình
3
3 2 2
4cos 12 cos 33cos 4 3 3cos 9cosx x x m x x m
. Có bao nhiêu giá trị nguyên của
tham số m để phương trình có nghiệm duy nhất thuộc
2
0;
3
.
A.
15.
B.
16.
C.
17.
D.
18.
m
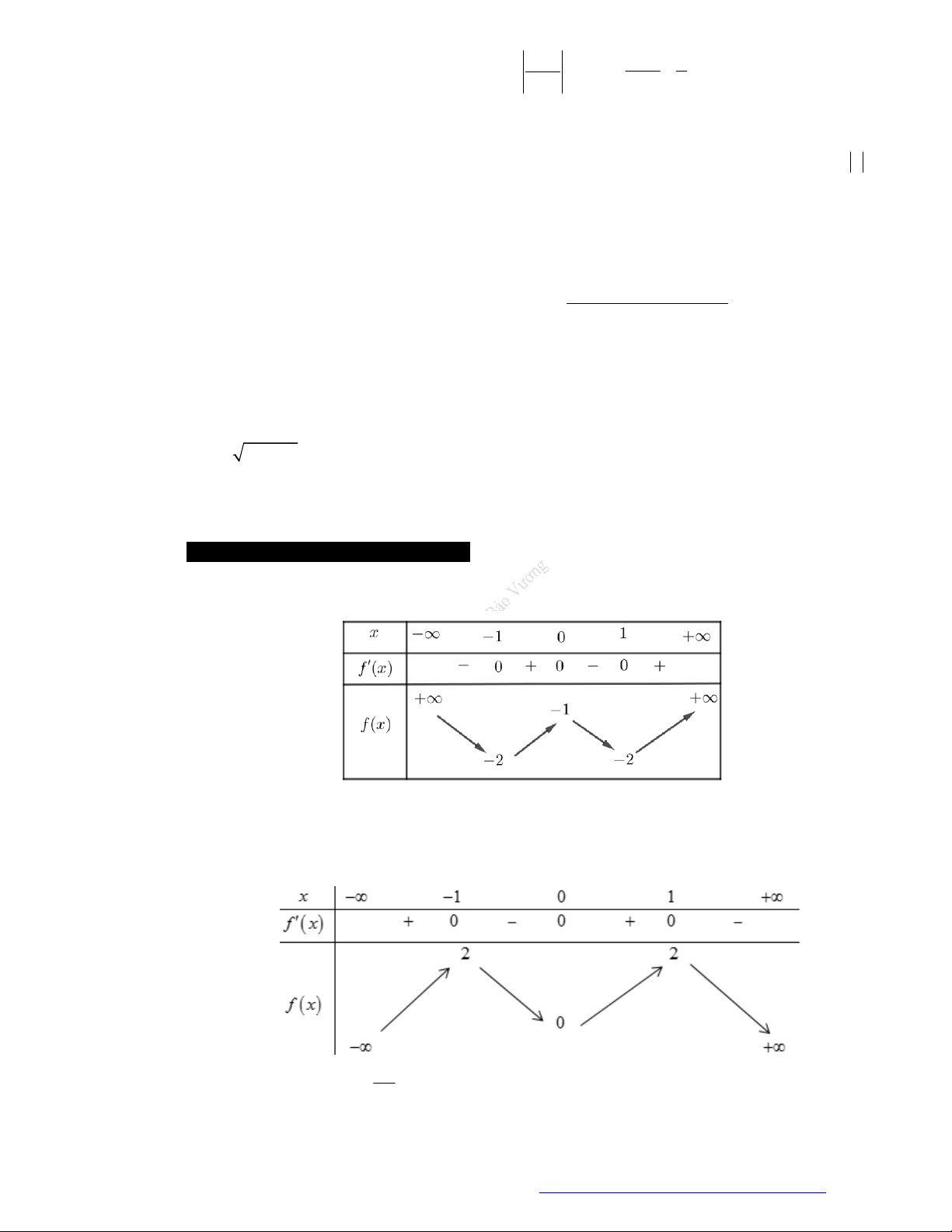
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Câu 19. (Sở Ninh Bình 2020) Cho hai hàm số
2
ln
x
y
x
và
3 1
4 2020
2
y m
x x
, Tổng tất các
các giá trị nguyên của tham số
m
để đồ thị hai hàm số cắt nhau tại một điểm duy nhất là
A.
506
. B.
1011
. C.
2020
. D.
1010
.
Câu 20. (Đặng Thúc Hứa - Nghệ An - 2020) Cho hai hàm số
1 2 1 3 1 2y x x x m x
;
4 3 2
12 22 10 3y x x x x có đồ thị lần lượt là
1
C
,
2
C
. Có bao nhiêu giá trị nguyên của
tham số
m
trên đoạn
2020;2020
để
1
C
cắt
2
C
tại 3 điểm phân biệt?
A.
4040
. B.
2020
. C.
2021
. D.
4041
.
Câu 21. (Hậu Lộc 2 - Thanh Hóa - 2020) Cho hàm số
2
2
2 3
( )
3
x x m x m
y C
x
và đường thẳng
( ) : 2d y x
( là tham số thực).
Số giá trị nguyên của
15;15m
để đường thẳng
( )d
cắt đồ thị
( )C
tại bốn điểm phân biệt là
A.
15
. B.
30
. C.
16
. D.
17
.
Câu 22. (Thanh Chương 1 - Nghệ An - 2020) Cho hai hàm số
6 4 2
6 6 1y x x x và
3
15 3 15y x m x m x có đồ thị lần lượt là
1
C
và
2
C
. Gọi
S
là tập hợp tất cả các giá
trị nguyên của tham số
m
thuộc đoạn
2019;2019
để
1
C
và
2
C
cắt nhau tại hai điểm phân
biệt. Số phần tử của tập hợp
S
bằng
A.
2006
. B.
2005
. C.
2007
. D.
2008
.
Dạng 2. Tương giao hàm hợp, hàm ẩn
Câu 1. (Đề Minh Họa 2020 Lần 1) Cho hàm số
f x
có bảng biến thiên như sau:
Số nghiệm thuộc đoạn
;2
của phương trình
2 sin 3 0f x
là
A.
4
. B.
6
. C.
3
. D.
8
.
Câu 2. (Đề Tham Khảo 2020 Lần 2) Cho hàm số
f x
có bảng biến thiên như sau
Số nghiệm thuộc đoạn
5
0;
2
của phương trình
sin 1f x
là
A.
7
. B.
4
. C.
5
. D.
6
.
m
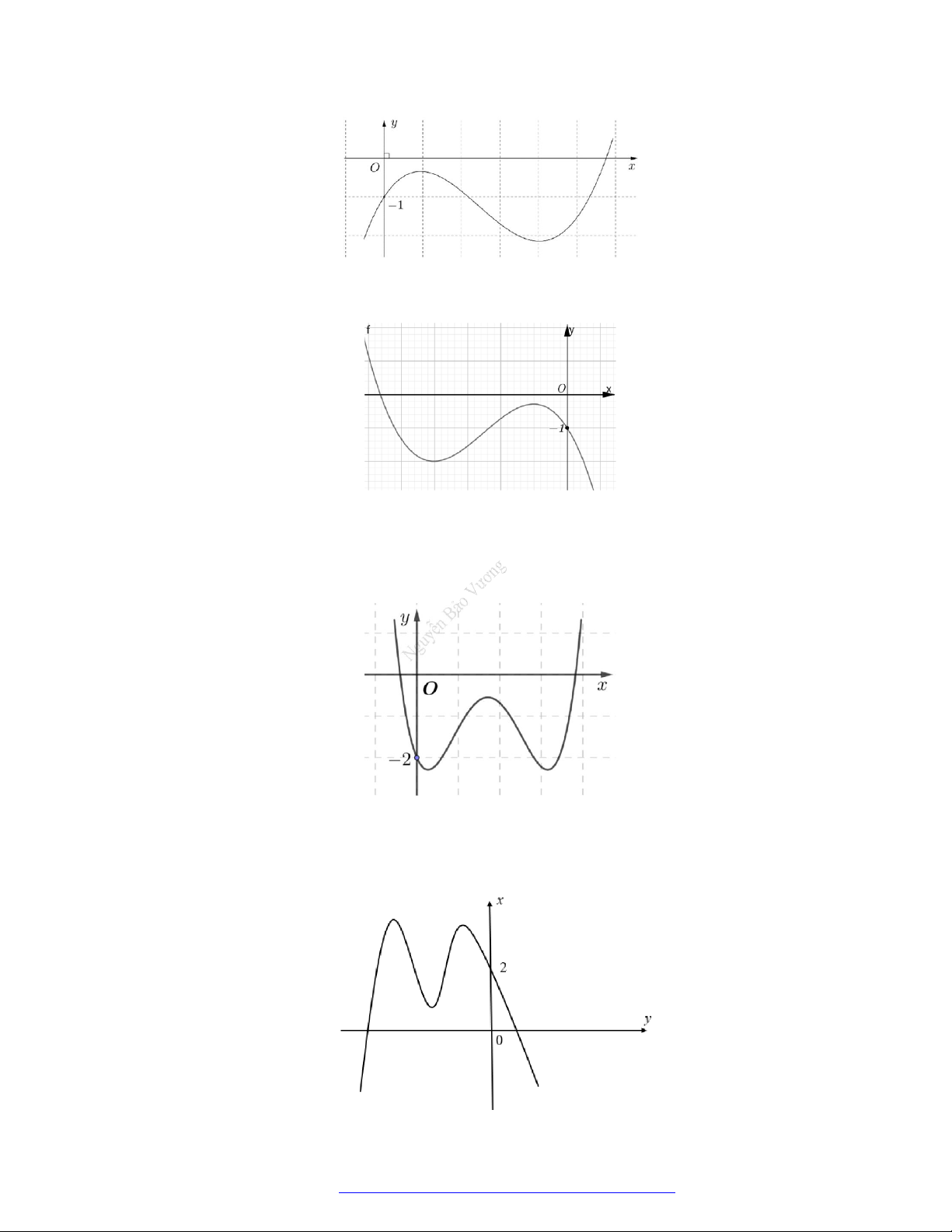
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 3. (Mã 101 - 2020 Lần 1) Cho hàm số bậc ba
( )y f x
có đồ thị là đường cong trong hình bên. Số
nghiệm thực phân biệt của phương trình
3
( ) 1 0
f x f x
là
A.
8
. B.
5
. C.
6
. D.
4
.
Câu 4. (Mã 102 - 2020 Lần 1) Cho hàm số
f x
có đồ thị là đường cong như hình vẽ bên dưới.
Số nghiệm thực phân biệt của phương trình
3
1 0f x f x
là
A.
6
. B.
4
. C.
5
. D.
8
.
Câu 5. (Mã 103 - 2020 Lần 1) Cho hàm số bậc bốn
y f x
có đồ thị là đường cong trong hình vẽ
bên.
Số nghiệm thực phân biệt của phương trình
2
( ) 2 0f x f x
là
A.
8
. B.
12
. C.
6
. D.
9
.
Câu 6. (Mã 104 - 2020 Lần 1) Cho hàm số
y f x
có đồ thị là đường cong trong hình vẽ bên.
Số nghiệm thực của phương trình
2
2f x f x
là:
A. 6. B. 12. C. 8. D. 9.
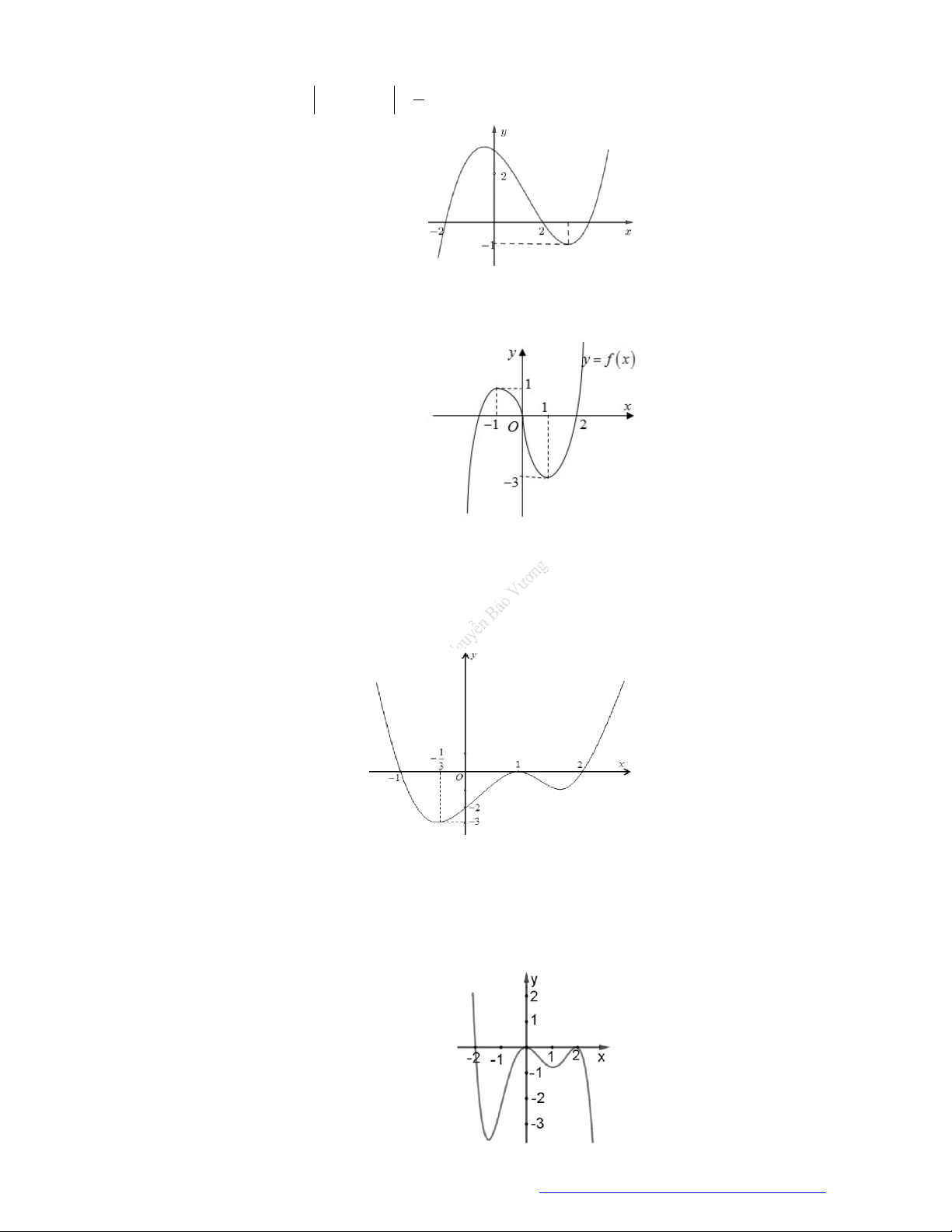
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Câu 7. (Mã 103 2019) Cho hàm số bậc ba
y f x
có đồ thị như hình vẽ dưới đây. Số nghiệm thực
của phương trình
3
3
3
2
f x x
là
A.
7
. B.
3
. C.
8
. D.
4
.
Câu 8. Cho hàm số
y f x
liên tục trên
và có đồ thị như hình vẽ sau
Số nghiệm của phương trình
2 e 1
x
f f là
A.
4
. B.
2
. C.
1
. D.
3
.
Câu 9. Cho hàm số
y f x
có đạo hàm cấp 2 trên
và có đồ thị
f x
là đường cong trong hình vẽ
bên.
Đặt
1 .g x f f x
Gọi
S
là tập nghiệm của phương trình
0.g x
Số phần tử của tập
S
là
A.
8
. B.
10
. C.
9
. D.
6
.
Câu 10. (THPT Cẩm Bình Hà Tỉnh 2019) Cho hàm số
f x
liên tục trên
và có đồ thị như hình vẽ.
Đặt
g x f f x
. Hỏi phương trình
0g x
có mấy nghiệm thực phân biệt?
A.
14
. B.
10
. C.
8
. D.
12
.
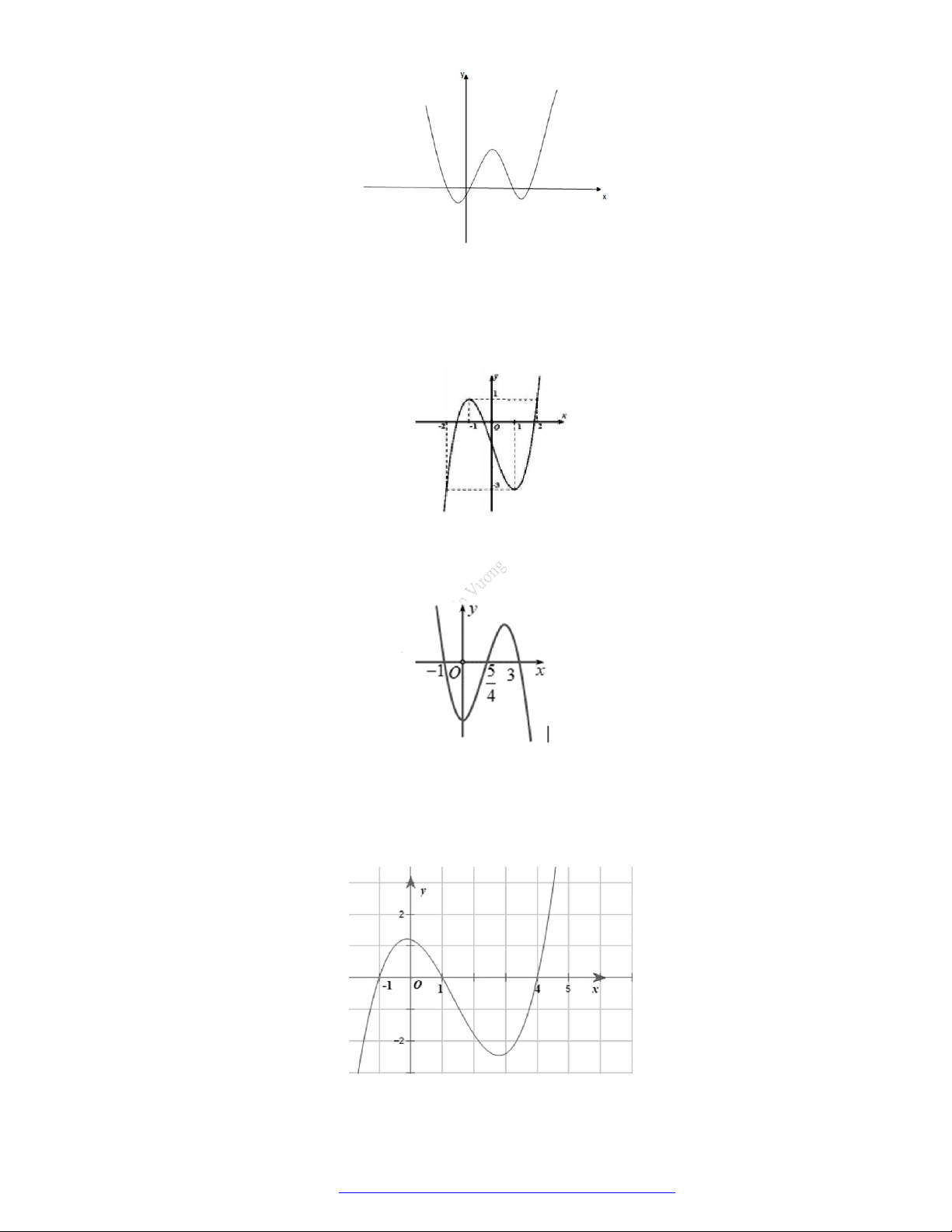
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 11. Biết rằng đồ thị hàm số
( )y f x
được cho như hình vẽ sau
Số giao điểm của đồ thị hàm số
2
.y f x f x f x
và trục
Ox
là:
A.
4
. B.
6
. C.
2
. D.
0
.
Câu 12. (Chuyên Lam Sơn 2019) Cho hàm số
y f x
liên tục trên
và có đồ thị như hình vẽ bên.
Phương trình
1 0
f f x
có tất cả bao nhiêu nghiệm thực phân biệt?
A.
6
. B.
5
. C.
7
. D.
4
.
Câu 13. (Đề tham khảo 2019) Cho hàm số
4 3 2
f x mx nx px qx r
,. Hàm số
y f x
có đồ thị
như hình vẽ bên dưới:
Tập nghiệm của phương trình
f x r
có số phần tử là
A.
4
. B.
3
. C.
1
. D.
2
.
Câu 14. (Chuyên Bắc Giang 2019) Cho hàm số
4 3 2
y f x mx nx px qx r
, trong đó
, , , ,m n p q r
. Biết rằng hàm số
'y f x
có đồ như hình vẽ dưới.
Tập nghiệm của phương trình
16 8 4 2f x m n p q r
có tất cả bao nhiêu phần tử.
A.
4
. B.
3
. C.
5
. D.
6
.
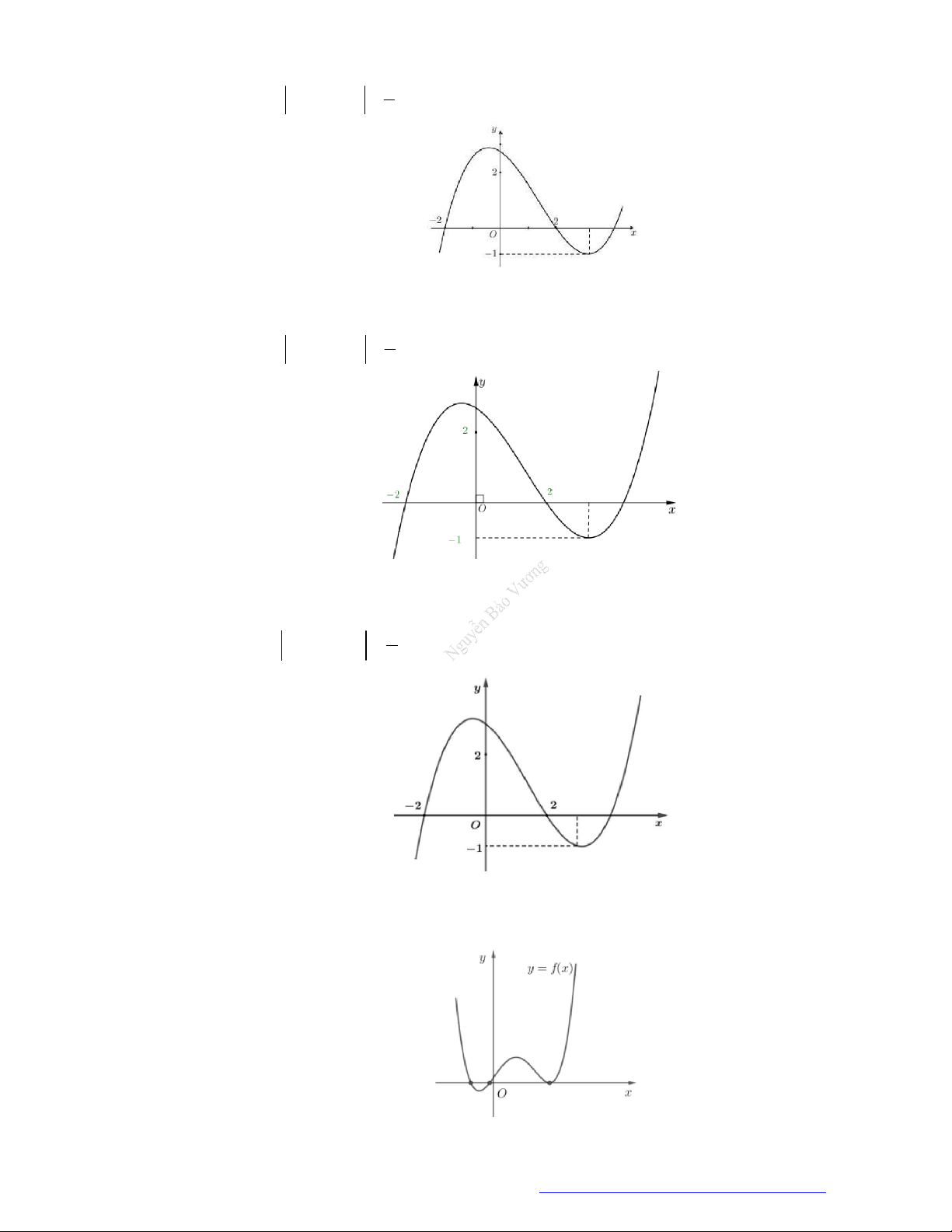
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Câu 15. (Mã 104 2019) Cho hàm số bậc ba
y f x
có đồ thị như hình vẽ bên. Số nghiệm thực của
phương trình
3
2
3
3
f x x
là
A.
10
B.
3
C.
9
D.
6
Câu 16. (Mã 101 2019) Cho hàm số bậc ba
y f x
có đồ thị như hình vẽ bên. Số nghiệm thực của
phương trình
3
4
3
3
f x x
là
A.
7
. B.
4
. C.
3
. D.
8
.
Câu 17. (Mã 102 2019) Cho hàm số bậc ba
y f x
có đồ thị như hình vẽ bên. Số nghiệm thực của
phương trình
3
1
3
2
f x x
A.
6
. B.
10
. C.
12
. D.
3
.
Câu 18. Cho
f x
là một hàm đa thức bậc bốn có đồ thị như hình dưới đây.
Tập nghiệm của phương trình
2
.f x f x f x
có số phần tử là
A.
1.
B.
2.
C.
6.
D.
0.
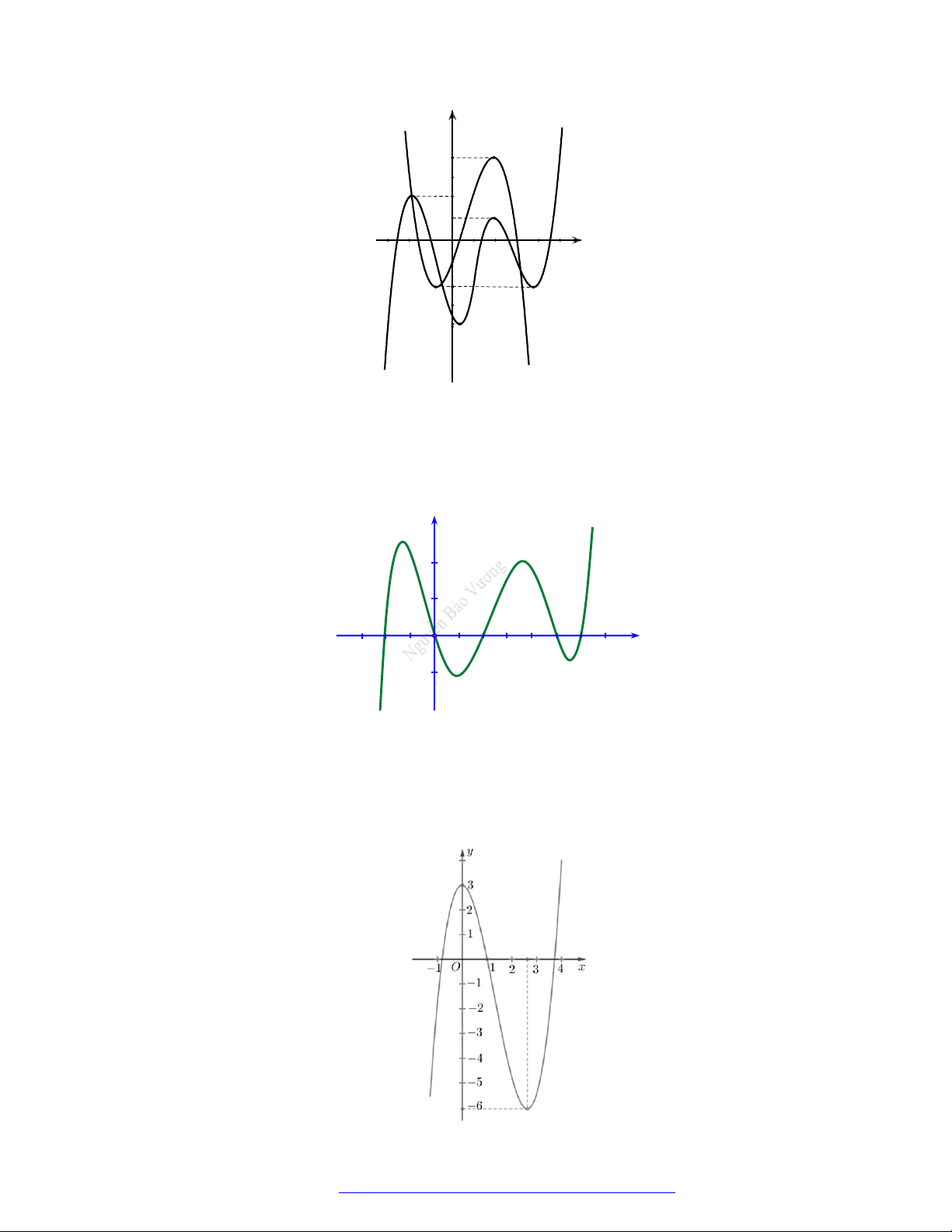
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 19. (KTNL GV Thuận Thành 2 Bắc Ninh 2019) Cho hai hàm số
,y f x y g x
có đồ thị như
hình sau:
Khi đó tổng số nghiệm của hai phương trình
0f g x
và
0g f x
là
A.
25
. B.
22
. C.
21
. D.
26
.
Câu 20. (THPT Nghĩa Hưng 2019) Cho hàm số
y f x
có đạo hàm liên tục trên
. Hàm số
y f x
có đồ thị như hình vẽ bên dưới:
Số nghiệm thuộc đoạn
2;6
của phương trình
0f x f
là
A. 5 B. 2 C. 3 D. 4
Câu 21. (Chuyên Vĩnh Phúc 2019) Cho hàm số
y f x
có đạo hàm trên
và có đồ thị là đường cong
trong hình vẽ dưới. Đặt
g x f f x
. Tìm số nghiệm của phương trình
0g x
.
.
A.
2
B.
8
C.
4
D.
6
5
y=g(x)
y=f(x)
y
x
-4
-3
-2
-1
4
3
2
1
43
2
1
O
-1
-2-3
O
1
2
3
1
2
3
4
5
6
7
x
y
4
2
2
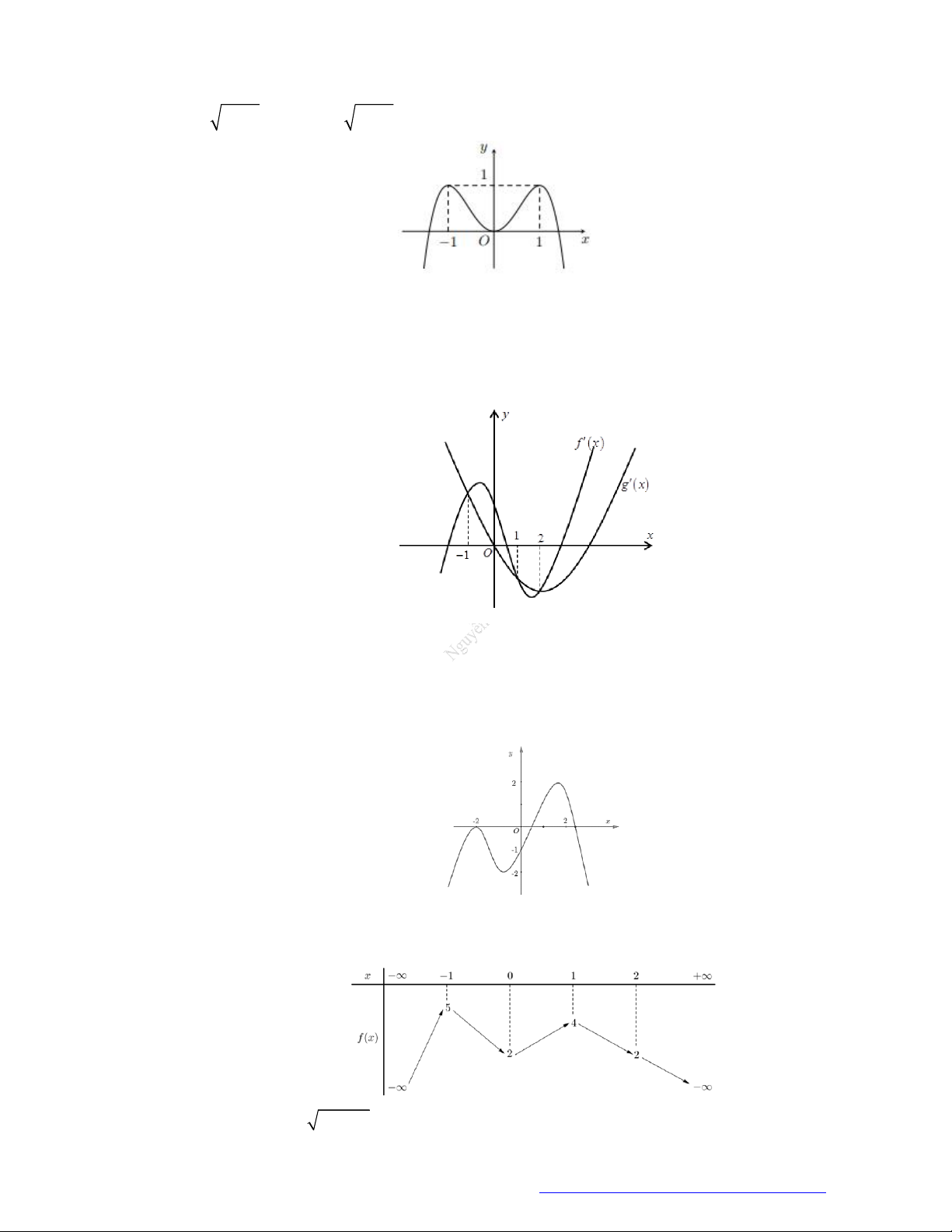
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Câu 22. (THPT Hậu Lộc 2 - Thanh Hóa - 2019) Cho hàm số
4 3 2
y f x =ax bx cx dx e
có đồ thị
như hình vẽ bên đây, trong đó a,b,c,d ,e là các hệ số thực. Số nghiệm của phương trình
2 1 0f f x f x f x
là
A. 3. B. 4. C. 2. D. 0.
Câu 23. (Sở Hưng Yên - 2019) Cho các hàm số
4 3 2
f x mx nx px qx r
và
3 2
g x ax bx cx d
,
, , , , , , , ,n n p q r a b c d
thỏa mãn
0 0f g
. Các hàm số
,f x g x
có đồ thị như hình vẽ dưới đây
Tập nghiệm của phương trình
f x g x
có số phần tử là
A.
4
. B.
2
. C.
1
. D.
3
.
Câu 24. (Sở Hà Tĩnh - 2019) Cho hàm số
y f x
liên tục trên
và có đồ thị như hình vẽ. Tập hợp
nghiệm của phương trình
1 0f f x
có bao nhiêu phần tử?
A.
4
. B.
7
. C.
6
. D.
9
.
Câu 25. (THPT Nguyễn Đức Cảnh - 2019) Cho hàm số
f x
có bảng biến thiên
Phương trình
2
2 3f x x
có bao nhiêu nghiệm?
A. 1. B. 2. C. 3. D. 4.
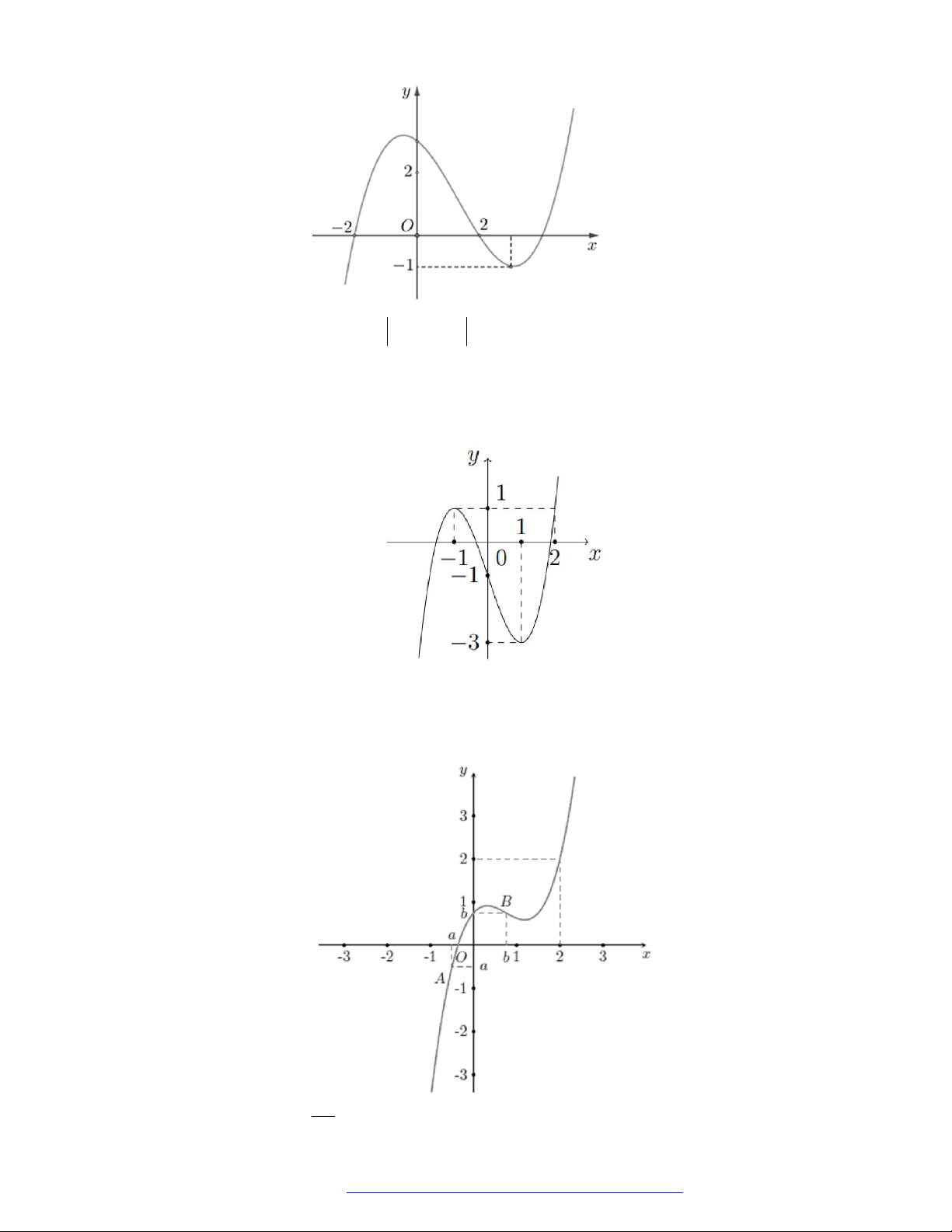
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 26. (Chuyên Lam Sơn - 2020) Cho hàm số bậc ba
y f x
có đồ thị như hình vẽ bên.
Số nghiệm thực của phương trình
3
3 1f x x là
A.
10
. B.
8
. C.
9
. D.
7
.
Câu 27. (Chuyên Lương Văn Chánh - Phú Yên - 2020) Cho hàm số
f x
có đồ thị như hình bên.
Phương trình
cos 1 0f f x
có bao nhiêu nghiệm thuộc đoạn
0;2
?
A.
2
. B.
5
. C.
4
. D.
6
.
Câu 28. (Chuyên Lương Văn Tỵ - Ninh Bình - 2020) Cho hàm số
3 2
f x ax bx bx c
có đồ thị
như hình vẽ:
Số nghiệm nằm trong
;3
2
của phương trình
cos 1 cos 1f x x
là
A.
2
. B.
3
. C. 5. D. 4.
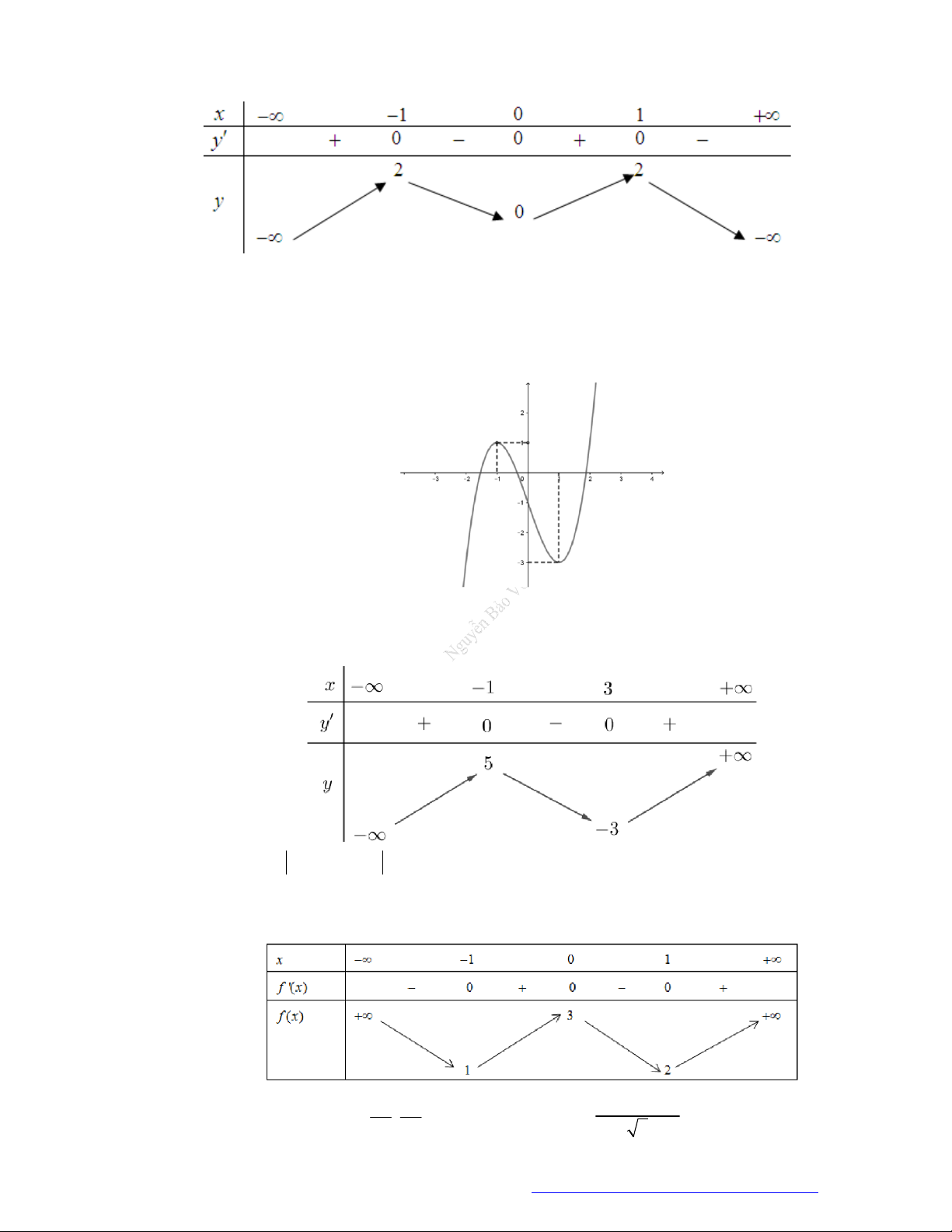
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Câu 29. (Chuyên Lê Hồng Phong - Nam Định - 2020) Cho hàm số
f x
liên tục trên
và có bảng
biến thiên như sau:
Số nghiệm thuộc khoảng
;ln 2
của phương trình
2019 1 2021 0
x
f e
là
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 30. (Chuyên Thái Bình - 2020) Cho
y f x
là hàm số đa thức bậc 3 và có đồ thị như hình vẽ bên.
Hỏi phương trình
cos 1 0f f x
có bao nhiêu nghiệm thuộc đoạn
0;3
?
A.
2
. B.
4
. C.
5
. D.
6
.
Câu 31. (Chuyên Thái Nguyên - 2020) Cho hàm số
y f x
liên tục trên
và có bảng biến thiên như
hình vẽ
Phương trình
3 1 2 5f x
có bao nhiêu nghiệm?
A.
3
. B.
5
. C.
6
. D.
4
.
Câu 32. (Sở Bắc Ninh - 2020) Cho hàm số
( )f x
có bảng biến thiên như sau:
Số nghiệm thuộc đoạn
5 5
;
4 4
của phương trình
sin cos
3 7 0
2
x x
f
là:
A.
6.
B.
3.
C.
5.
D.
4.
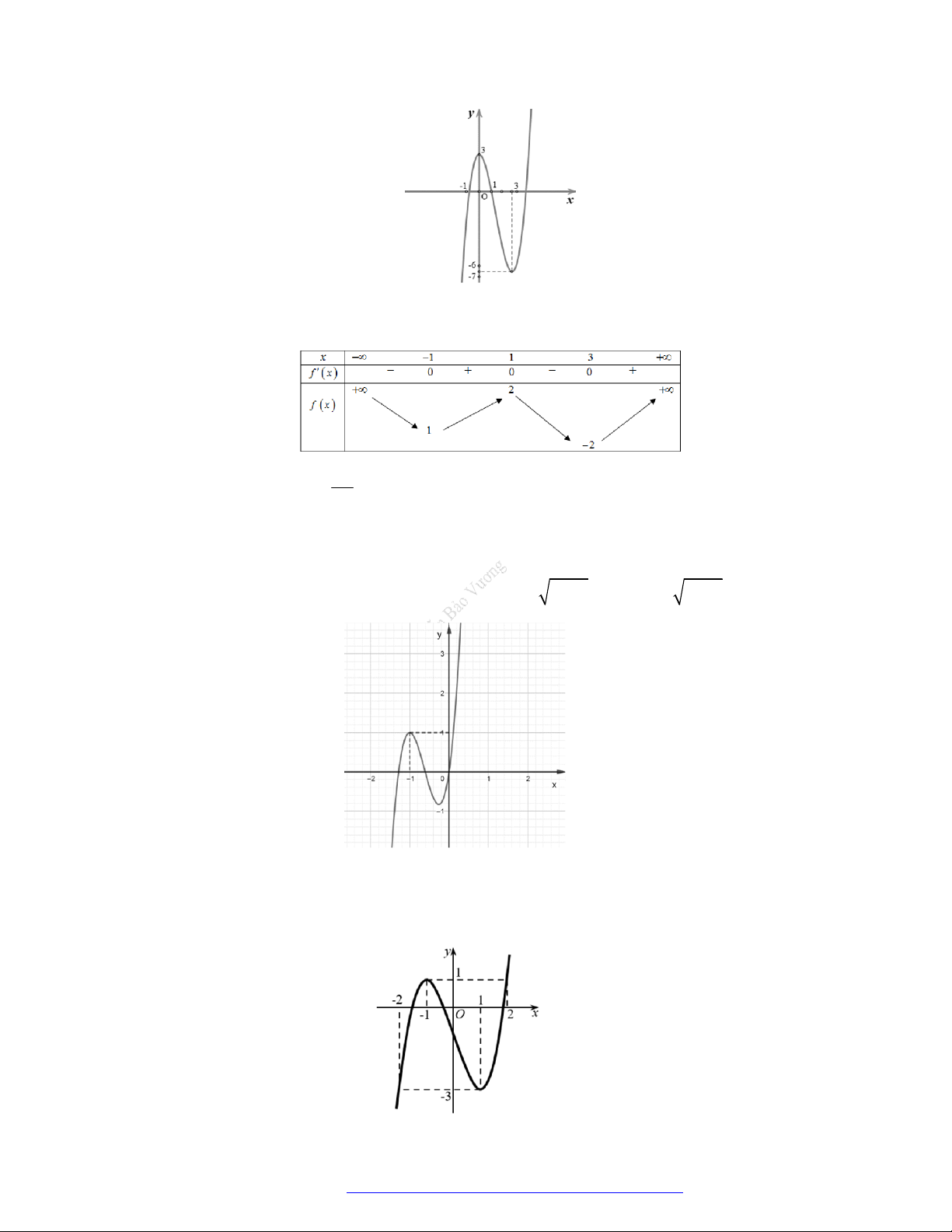
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 33. (Bỉm Sơn - Thanh Hóa - 2020) Cho hàm số có đạo hàm trên và có đồ thị là đường
cong trong hình vẽ bên dưới. Đặt . Tìm số nghiệm của phương trình .
A. . B. . C. . D. .
Câu 34. (Đặng Thúc Hứa - Nghệ An - 2020) Cho hàm số
f x
có bẳng biến thiên như hình vẽ.
Số nghiệm thuộc đoạn
9
0;
2
của phương trình
2sin 1 1f x
là
A.
7
. B.
5
. C.
4
. D.
6
.
Câu 35. (Hậu Lộc 2 - Thanh Hóa - 2020) Cho hàm số
3 2
, , ,y f x ax bx cx d a b c d
có đồ
thị như hình vẽ bên. Số nghiệm của phương trình
2 1 0f f f x f x f x f
là
A. 2. B. 3. C. 1. D. 0.
Câu 36. (Lý Nhân Tông - Bắc Ninh - 2020) Cho hàm số
y f x
liên tục trên
và có đồ thị như hình
vẽ. Phương trình
1 0 f f x
có tất cả bao nhiêu nghiệm thực phân biệt?
A.
6
. B.
5
. C.
7
. D.
4
.
y f x
g x f f x
0
g x
8
2
4
6
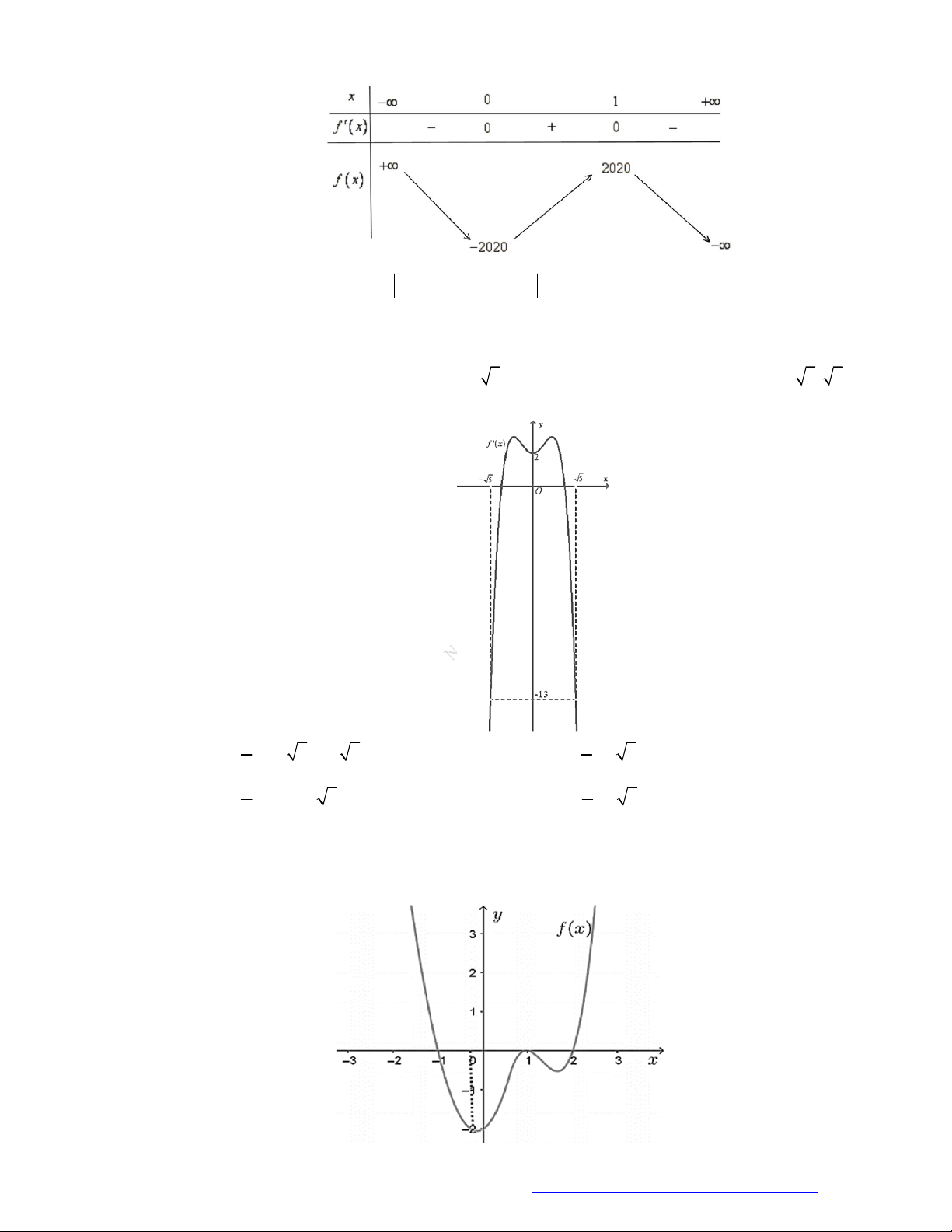
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Câu 37. (Nguyễn Huệ - Phú Yên - 2020) Cho hàm số
y f x
có bảng biến thiên như sau:
Số nghiệm của phương trình
2019 2020 2021f x
là
A.
4
. B.
6
. C.
2
. D.
3
.
Câu 38. (Nguyễn Trãi - Thái Bình - 2020) Cho hàm số
y f x
có đồ thị
'y f x
như hình vẽ. Xét
hàm số
3
2 2 4 3 6 5g x f x x x m với
m
là số thực. Để
0, 5; 5g x x
thì
điều kiện của
m
là
A.
2
5 4 5
3
m f
. B.
2
5
3
m f
.
C.
2
0 2 5
3
m f
. D.
2
5
3
m f
.
Câu 39. (THPT Nguyễn Viết Xuân - 2020) Cho hàm số
f x
có đồ thị như hình vẽ. Đặt
1g x f f x
. Số nghiệm của phương trình
0g x
là
A.
6
. B.
10
. C.
9
. D.
8
.
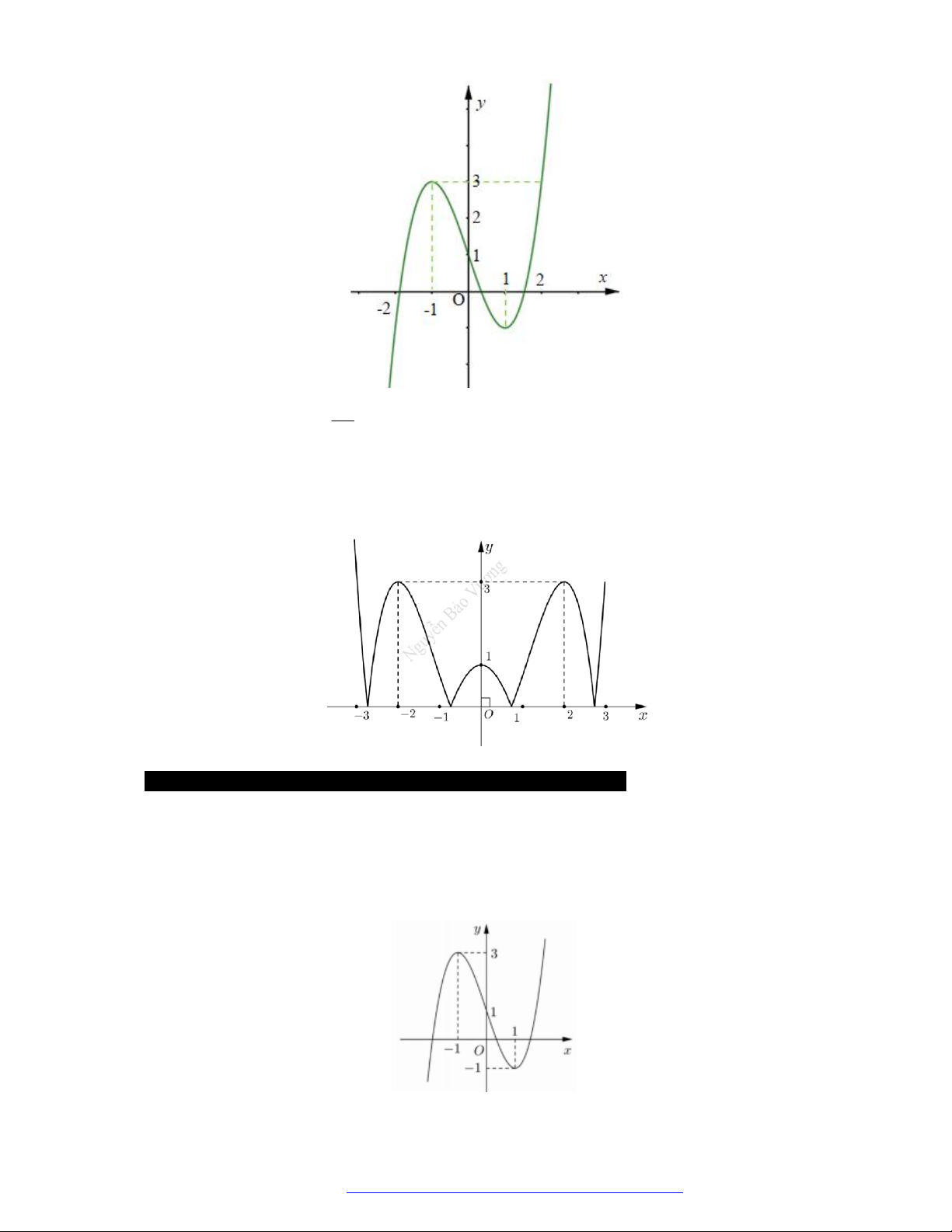
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 40. (Tiên Du - Bắc Ninh - 2020) Cho hàm số
( )y f x
liên tục trên
và có đồ thị như hình vẽ bên
Số nghiệm thuộc đoạn
7
0;
2
của phương trình
( (cos )) 0f f x
là
A.
7
. B.
5
. C.
8
. D.
6
.
Câu 41. (Lương Thế Vinh - Hà Nội - 2020) Cho hàm số
y f x
có đồ thị nhưu hình vẽ bên. Tìm số
nghiệm thuộc đoạn
2017 ;2020
của phương trình
3 2cos 8f x
.
A.
8
. B.
3
. C.
4
. D.
6
.
Dạng 3. Biện luận tương giao hàm hợp, hàm ẩn chứa THAM SỐ
Câu 1. (Đề Tham Khảo 2019) Cho hàm số
y f x
liên tục trên
và có đồ thị như hình vẽ bên. Tập
hợp tất cả các giá trị thực của tham số
m
để phương trình
sinf x m
có nghiệm thuộc khoảng
0;
là
A.
1;3
B.
1;1
C.
1;3
D.
1;1
Câu 2. (Mã 102 - 2020 Lần 2) Cho hàm số
y f x
có bảng biến thiên như hình vẽ:
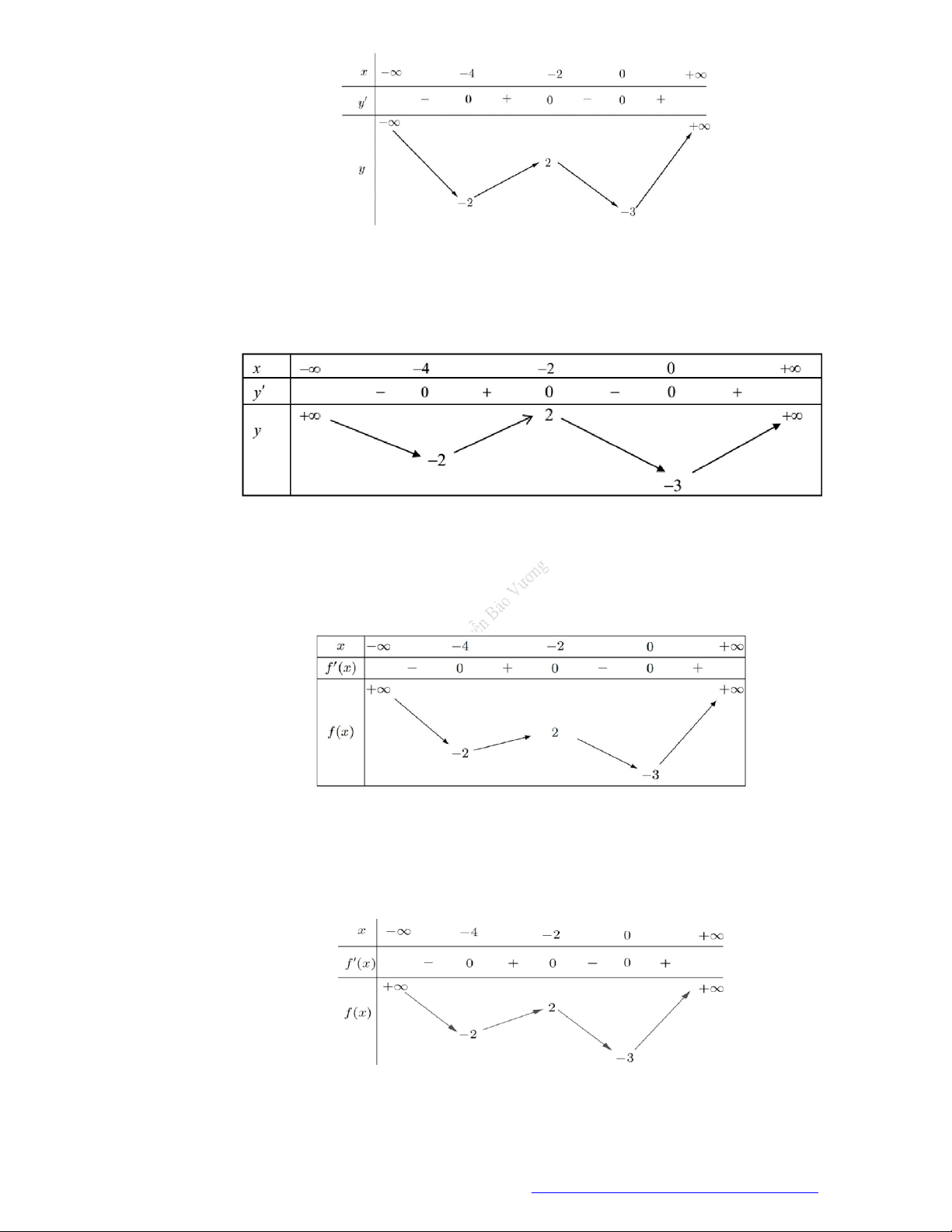
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
2
6 4f x x m
có ít nhất ba
nghiệm thực phân biệt thuộc khoảng
0;
?
A. 25. B. 30. C. 29. D. 24.
Câu 3. (Mã 103 - 2020 Lần 2) Cho hàm số
f x
có bảng biến thiên như sau
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
2
3 4f x x m
có ít nhất ba
nghiệm thực phân biệt thuộc khoảng
0;
?
A.
15
. B.
12
. C.
14
. D.
13
.
Câu 4. (Mã 101 – 2020 Lần 2) Cho hàm số
f x
có bảng biến thiên như sau:
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
2
5 4f x x m
có ít nhất 3 nghiệm
phân biệt thuộc khoảng
0;
A.
24
. B.
21
. C.
25
. D.
20
.
Câu 5. (Mã 104 - 2020 Lần 2) Cho hàm số
f x
có bảng biến thiên như sau:
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
2
4 4f x x m
có ít nhất 3 nghiệm
thực phân biệt thuộc khoảng
0;
?
A.
16
. B.
19
. C.
20
. D.
17
.
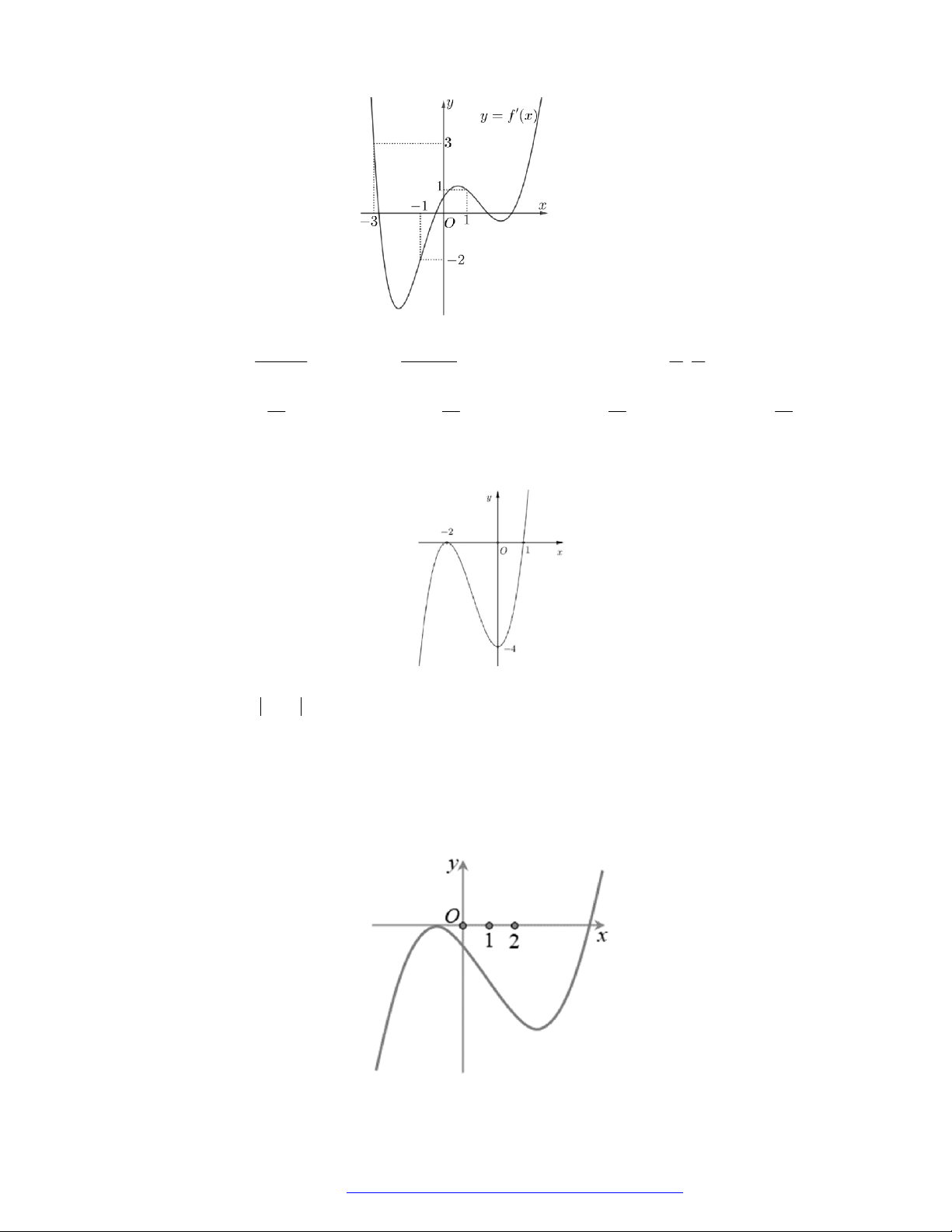
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 6. (Chuyên Biên Hòa - Hà Nam - 2020) Cho hàm số
f x
. Hàm số
y f x
có đồ thị như hình
sau.
Tìm tất cả các giá trị thực của tham số
m
để bất phương trình
3
2sin 5cos2
2 sin 2 sin
3 4
x x
f x x m nghiệm đúng với mọi
;
2 2
x
.
A.
11
2 3 .
12
m f
B.
19
2 1 .
12
m f
C.
19
2 1 .
12
m f
D.
11
2 3 .
12
m f
Câu 7. (Chuyên Biên Hòa - Hà Nam - 2020) Cho hàm số
3 2
( )y f x ax bx cx d
có đồ thị như
hình dưới đây
Có tất cả bao nhiêu giá trị nguyên của tham số
5;5m để phương trình
2
( ) ( 4) ( ) 2 4 0f x m f x m
có
6
nghiệm phân biệt
A.
2
. B.
4
. C.
3
. D.
5
.
Câu 8. (Chuyên Lam Sơn - 2020) Cho hàm số
y f x
, hàm số
y f x
liên tục trên
và có đồ
thị như hình vẽ bên. Bất phương trình
2
2f x x x m
(m là tham số thực) nghiệm đúng với
mọi
1;2x
khi và chỉ khi
A.
2 2m f
. B.
1 1m f
. C.
1 1m f
. D.
2m f
.
Câu 9. (Chuyên Thái Bình - 2020) Cho hàm số
y f x
liên tục trên đoạn
1; 4
và có đồ thị như
hình vẽ.
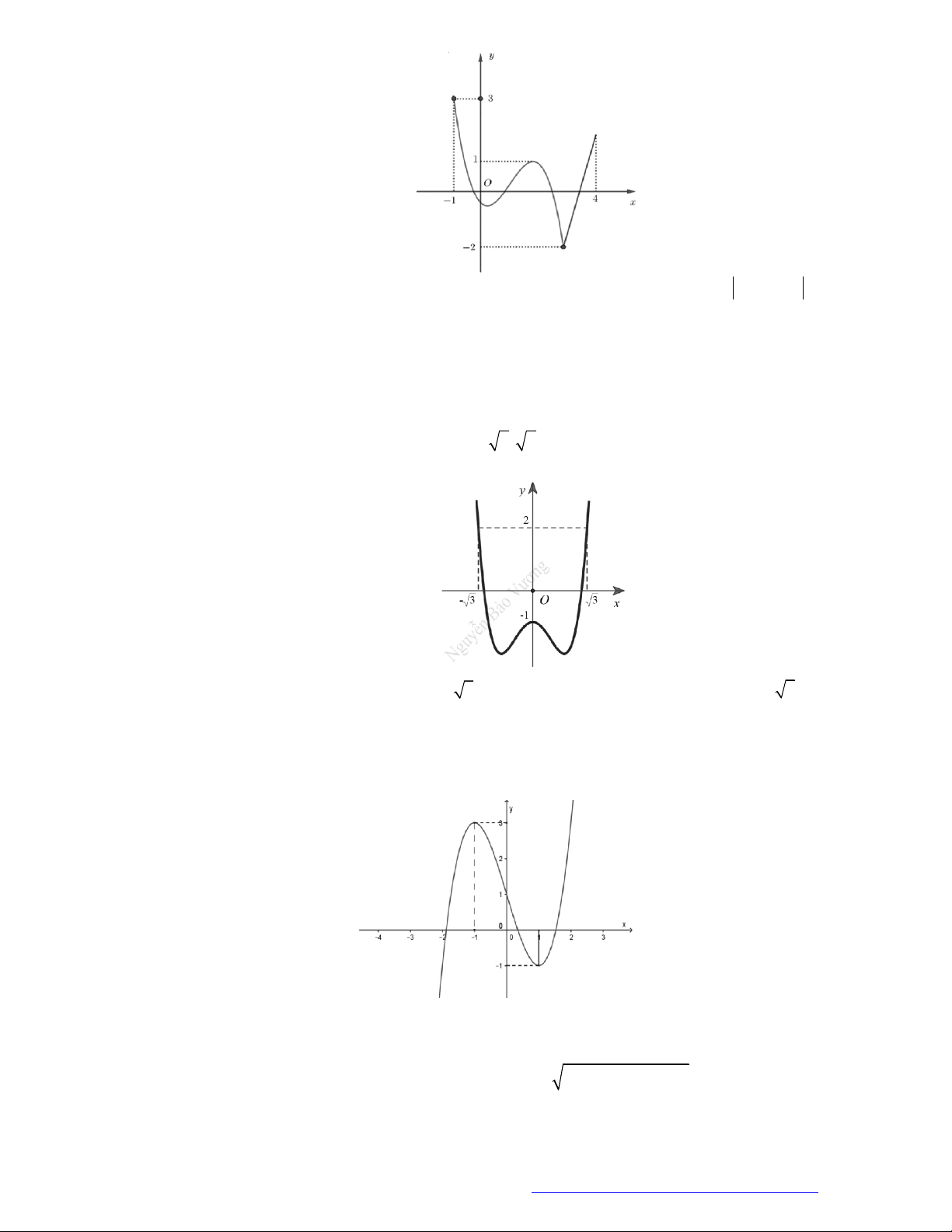
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
Có bao nhiêu giá trị
nguyên của
m
thuộc đoạn
10;10
để bất phương trình
2f x m m
đúng với mọi
x
thuộc đoạn
1;4
.
A.
6
. B.
5
. C.
7
. D.
8
.
Câu 10. (Chuyên Bến Tre - 2020) Cho hàm số
y f x
. Đồ thị hàm số
'y f x
như hình vẽ. Cho bất
phương trình
3
3 3f x x x m
(
m
là tham số thực). Điều kiện cần và đủ để bất phương trình
3
3 3f x x x m
đúng với mọi
3; 3x
là
A.
3 1m f
. B.
3 3 m f
. C.
3 0m f
. D.
3 3m f
.
Câu 11. (Chuyên Hùng Vương - Gia Lai - 2020) Cho hàm số
y f x
liên tục trên
và có đồ thị như
hình vẽ bên dưới. Gọi
S
là tập hợp tất cả giá trị nguyên của tham số
m
để phương trình
sin 2 2sinf x m x
có nghiệm thuộc khoảng
0;
. Tổng các phần tử của
S
bằng
A.
4
. B.
1
. C.
3
. D.
2
.
Câu 12. (Chuyên Hùng Vương - Gia Lai - 2020) Cho hàm số
3
2f x x x
. Có tất cả bao nhiêu giá
trị nguyên của tham số
m
để phương trình
3 3
3
2f f x f x m x x
có nghiệm
1;2x
?
A.
1750
. B.
1748
. C.
1747
. D.
1746
.
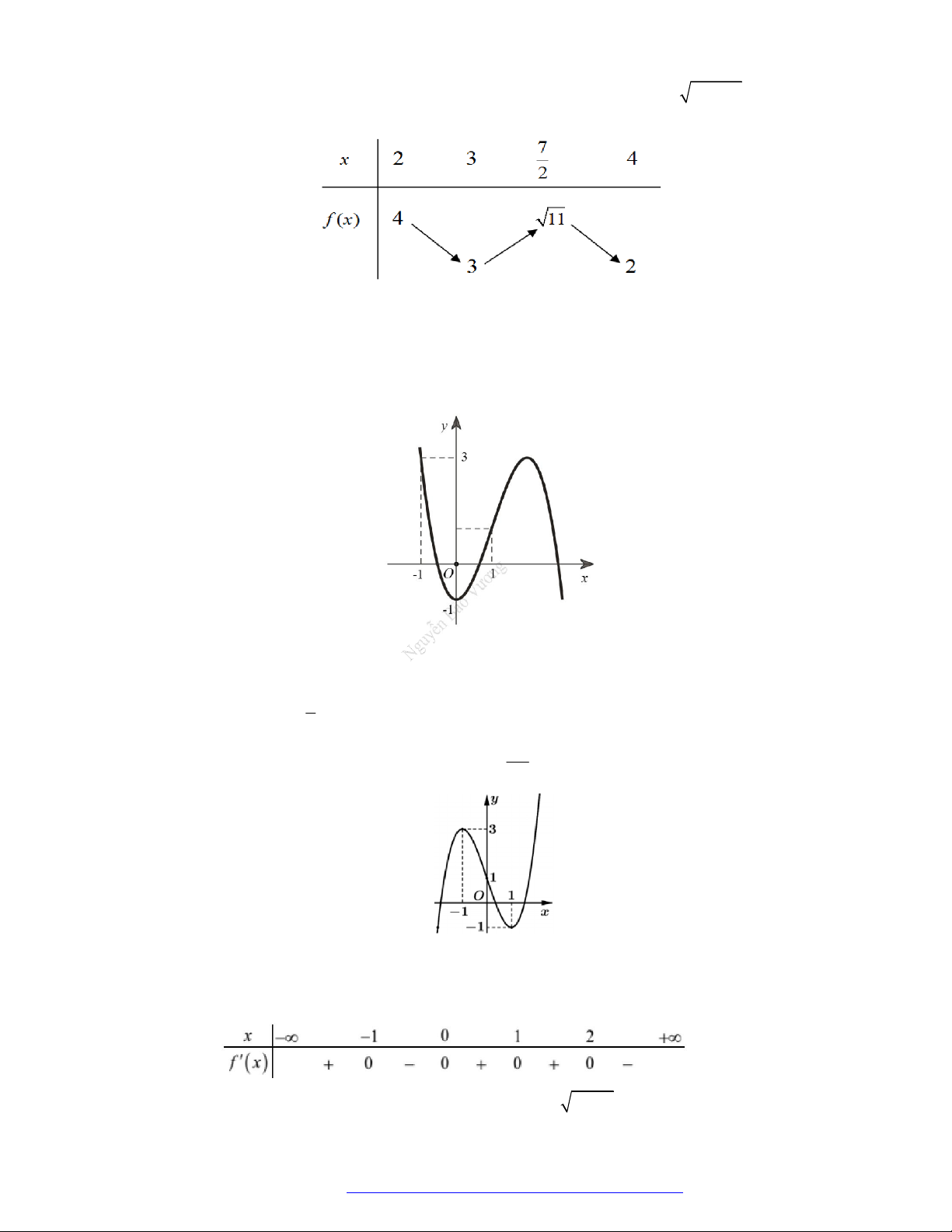
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 13. (Chuyên Quang Trung - 2020) Cho hàm số
( )f x
liên tục trên
2;4
và có bảng biến thiên như
hình vẽ bên. Có bao nhiêu giá trị nguyên của
m
để phương trình
2
2 2 . ( )x x x m f x
có
nghiệm thuộc đoạn
2;4
?
A.
6
. B.
5
. C.
4
. D.
3
.
Câu 14. (Chuyên Sơn La - 2020) Cho hàm số
f x
liên tục trên
và có đồ thị như hình vẽ. Số giá trị
nguyên của tham số
m
để phương trình
2
cos 2019 cos 2020 0f x m f x m
có đúng
6 nghiệm phân biệt thuộc đoạn
0;2
là
A.
1
. B.
3
. C.
2
. D.
5
.
Câu 15. (Chuyên Vĩnh Phúc - 2020) Cho hàm số
( )y f x
. Hàm số
( )y f x
có đồ thị như hình bên.
Biết
f f
e
1
1 1; 2
. Tìm tất cả các giá trị của
m
để bất phương trình
f x x mln
nghiệm đúng với mọi
1
1;x
e
.
A.
2m
. B.
3m
. C.
2m
. D.
3m
.
Câu 16. (Sở Phú Thọ - 2020) Cho hàm số
y f x
liên tục trên
thỏa mãn
1 5, 3 0f f
và
có bảng xét dấu đạo hàm như sau:
Số giá trị nguyên dương của tham số
m
để phương trình
2
3 2 4f x x x m
có nghiệm trong
khoảng
3;5
là
A.
16
. B.
17
. C.
0
. D.
15
.
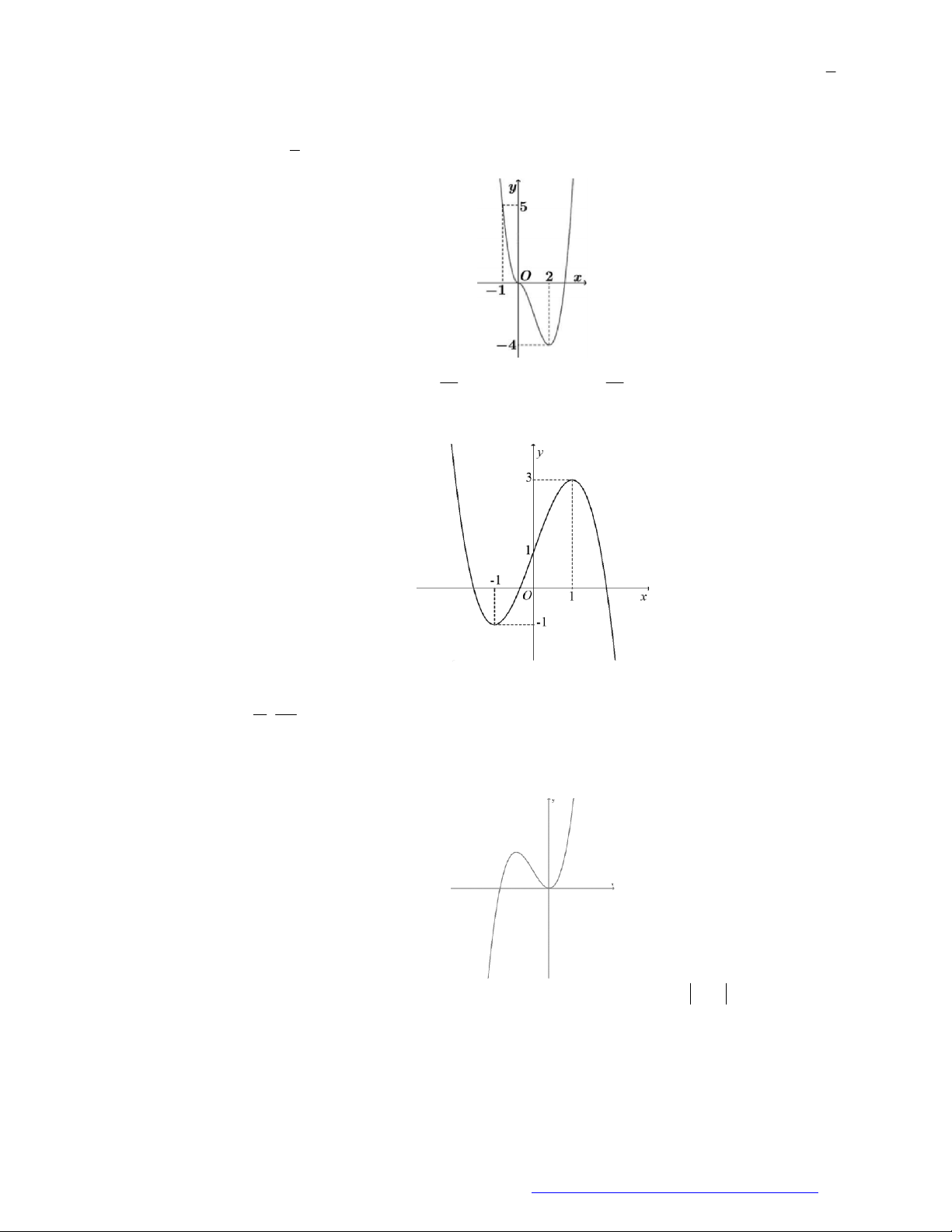
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
Câu 17. (Sở Phú Thọ - 2020) Cho hàm số
y f x
liên tục trên
và thỏa mãn
1
1 1, 2
e
f f
.
Hàm số
f x
có đồ thị như hình vẽ. Bất phương trình
2
lnf x x x m
nghiệm đúng với
mọi
1
1;
e
x
khi và chỉ khi
A.
0m
. B.
2
1
3
e
m
. C.
2
1
3
e
m
. D.
0m
.
Câu 18. (Sở Hà Tĩnh - 2020) Cho hàm số
y f x
liên tục trên
và có đồ thị như hình vẽ.
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
cosf f x m
có nghiệm thuộc
khoảng
3
;
2 2
?
A. 2. B. 4. C. 5. D. 3.
Câu 19. (Sở Ninh Bình) Cho hàm số bậc ba
y f x
có đồ thị như hình vẽ.
Có tất cả bao nhiêu giá trị nguyên của tham số
m
để phương trình
2
2 sin 6 10f x f m m
có nghiệm?
A. 2. B. 3. C. 4. D. 1.
Câu 20. (Sở Yên Bái - 2020) Cho hàm số bậc ba
y f x
có đồ thị như hình vẽ bên. Có tất cả bao nhiêu
giá trị nguyên của tham số
m
để phương trình
3 2
3 3 0 f x x m
có nghiệm thuộc đoạn
1;2
.
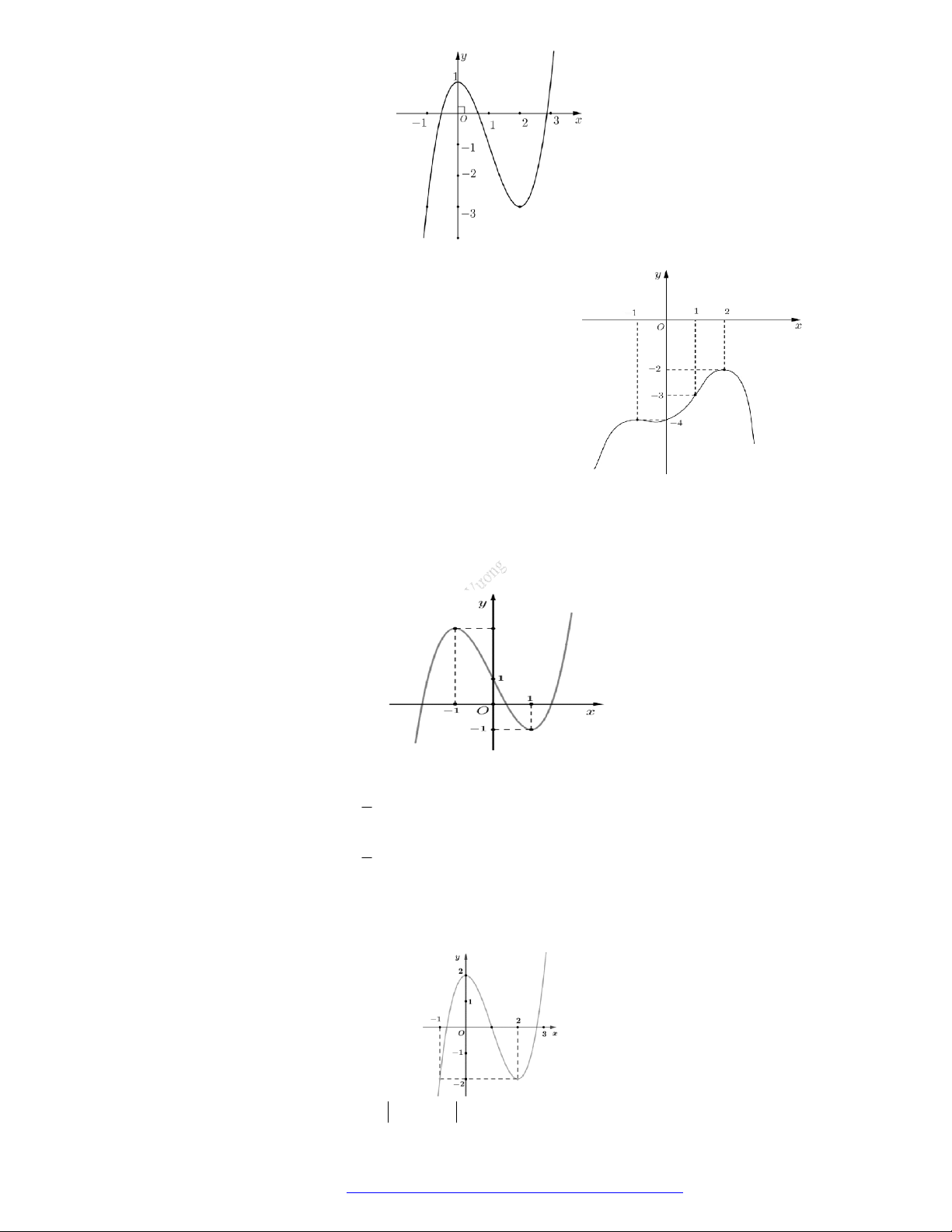
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
7
. B.
8
. C.
10
. D.
5
.
Câu 21. (Sở Yên Bái - 2020) Cho hàm số
( )y f x
liên tục trên
và có đồ thị như hình vẽ bên. Số các giá trị nguyên của
tham số
m
để bất phương trình
( ) 2 ( ) 2 ( )
16.8 ( 5 ).4 ((4 ( )).16
f x f x f x
m m f x
nghiệm
đúng với mọi số thực
x
là
A.
3.
B.
5.
C.
1.
D.
4.
Câu 22. (Hậu Lộc 2 - Thanh Hóa - 2020) Cho hàm số
y f x
, hàm số
y f x
liên tục trên
và
có đồ thị như hình vẽ bên. Bất phương trình
x
m e f x
có nghiệm với mọi
1;1x
khi và
chỉ khi.
A.
1
min 1 ; 1m f e f
e
. B.
0 1m f
.
C.
1
min 1 ; 1m f e f
e
. D.
0 1m f
.
Câu 23. (Liên trường Nghệ An - 2020) Cho hàm số
f x
là hàm số đa thức bậc bốn. Biết
0 0f
và
đồ thị hàm số
y f x
có hình vẽ bên dưới.
Tập nghiệm của phương trình
2sin 1 1f x m
(với
m
là tham số) trên đoạn
0;3
có tất
cả bao nhiêu phần tử?
A.
8
. B.
20
. C.
12
. D.
16
.
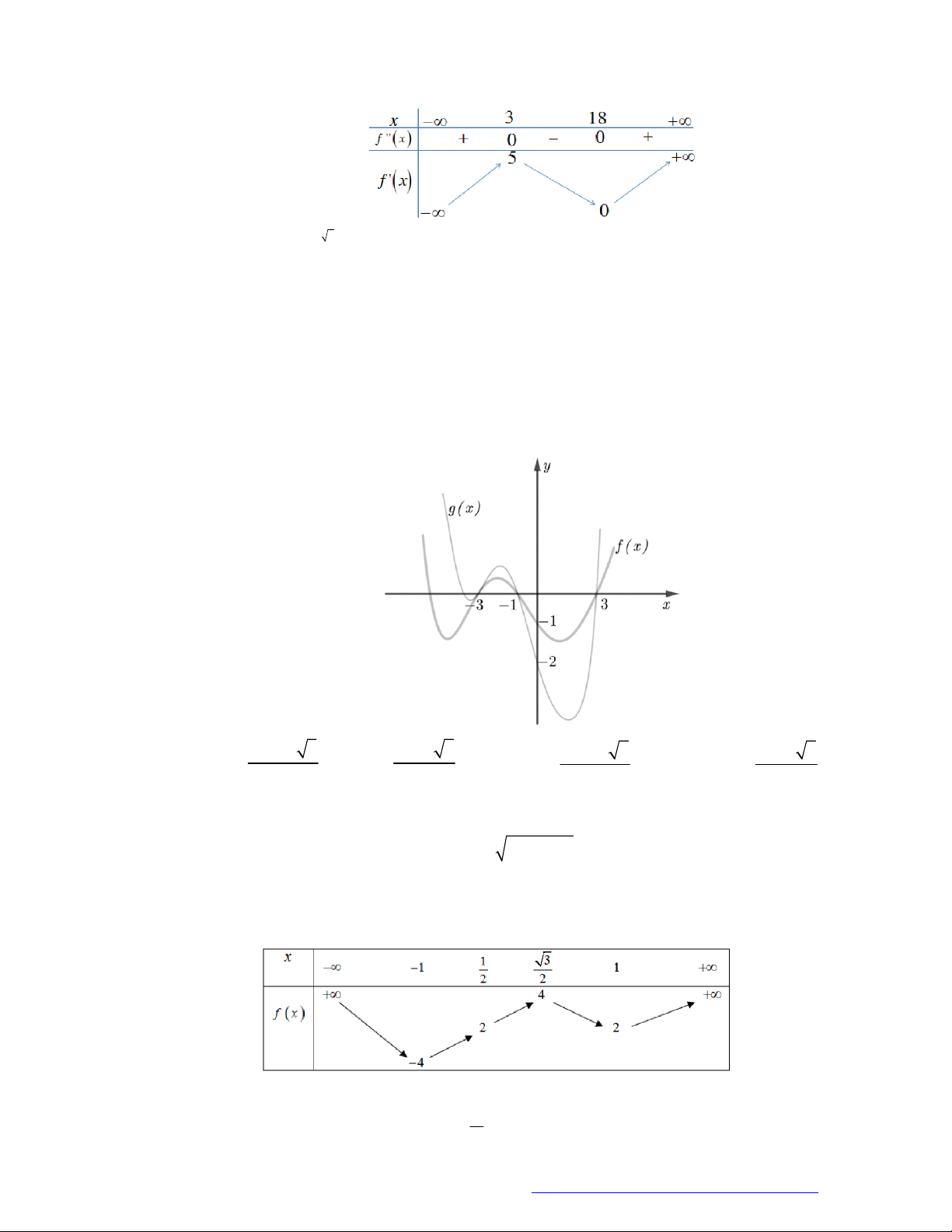
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
Câu 24. (Kìm Thành - Hải Dương - 2020) Cho hàm số
y f x
. Hàm số
'y f x
có bảng biến thiên
như hình vẽ:
Bất phương trình
x
e m f x
có nghiệm
4;16x
khi và chỉ khi:
A.
2
4m f e
. B.
2
4m f e
. C.
2
16m f e
. D.
2
16m f e
.
Câu 25. (Kìm Thành - Hải Dương - 2020) Cho hàm số đa thức bậc bốn
y f x
và
y g x
có đồ thị
như hình vẽ dưới đây đường đậm hơn là đồ thị hàm số
y f x
. Biết rằng hai đồ thị tiếp xúc với
nhau tại điểm có hoành độ là
3
và cắt nhau tại hai điểm nữa có hoành độ lần lượt là
1
và
3
.
Tìm tập hợp tất các giá trị thực của tham số
m
để bất phương trình
f x g x m
nghiệm
đúng với mọi
3;3x
.
A.
12 10 3
;
9
. B.
12 8 3
;
9
. C.
12 10 3
;
9
. D.
12 8 3
;
9
.
Câu 26. (Kìm Thành - Hải Dương - 2020) Cho hàm số
5 3
3 4f x x x m
. Có bao nhiêu giá trị
nguyên của tham số
m
để phương trình
3
3
f f x m x m
có nghiệm thuộc đoạn
1; 2
?
A.
18
. B.
17
. C.
15
. D.
16
.
Câu 27. (Tiên Lãng - Hải Phòng - 2020) Cho hàm số
f x
liên tục trên
và có bảng biến thiên như
hình vẽ.
Số giá trị nguyên của tham số
m
để phương trình
2
cos 3 cos 2 10 0f x m f x m
có
đúng 4 nghiệm phân biệt thuộc đoạn
;
3
là
A.
5
. B.
6
. C.
7
. D.
4
.
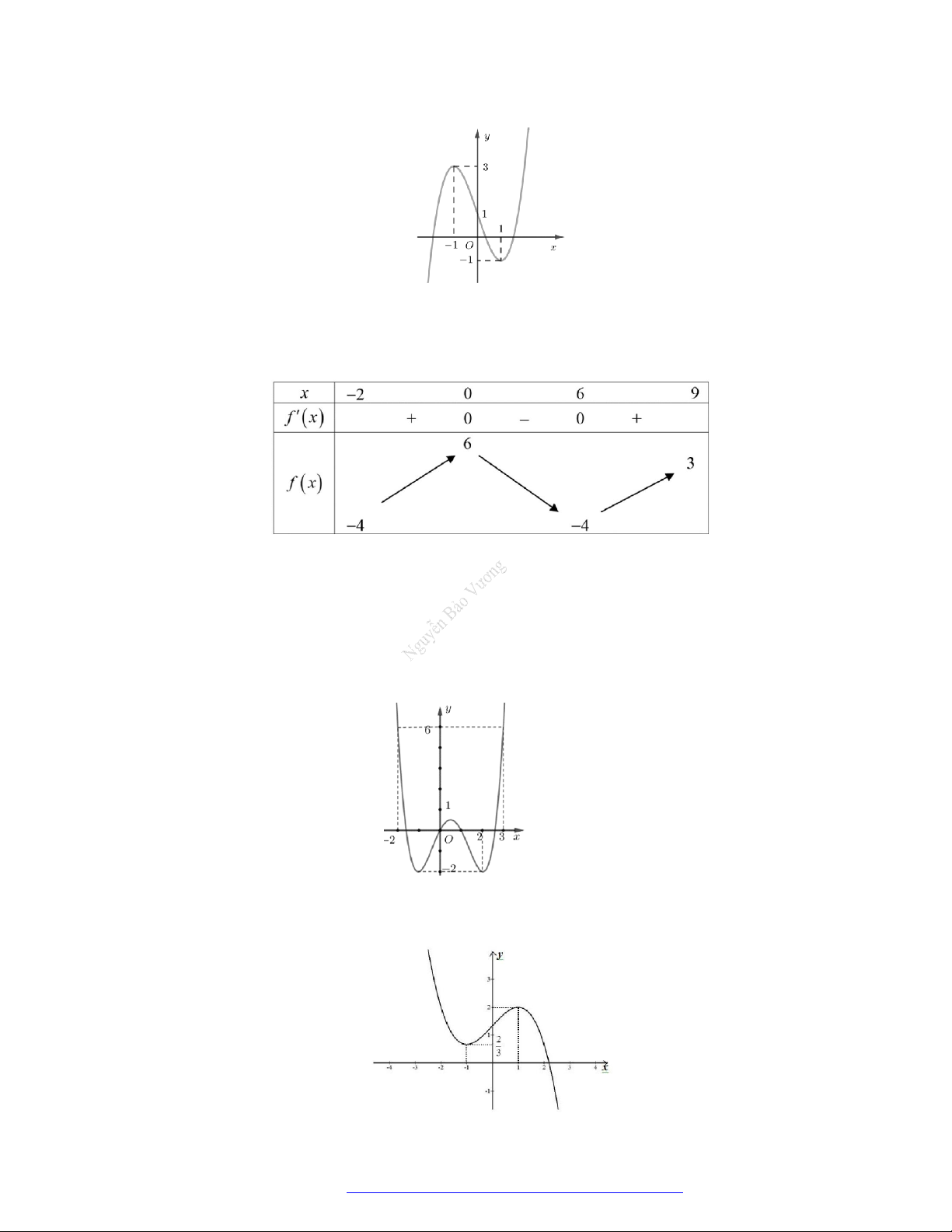
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 22 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 28. (Trần Phú - Quảng Ninh - 2020) Cho hàm số
y f x
liên tục trên
và có đồ thị như hình
vẽ. Gọi
S
là tập hợp tất cả các giá trị nguyên của tham số
m
để phương trình
sin 3siny f x x m
có nghiệm thuộc khoảng
0;
. Tổng các phần tử của
S
bằng
A.
5
. B.
8
. C.
6
. D.
10
.
Câu 29. (NK HCM-2019) Cho
f x
là một hàm số liên tục trên đoạn
2;9 ,
biết
1 2 9 3f f f
và
f x
có bảng biến thiên như sau:
Tìm
m
để phương trình
f x f m
có ba nghiệm phân biệt thuộc đoạn
2;9 .
A.
2;9 \ 1;2 6 .m
B.
2;9 \ 1;2 6 .m
C.
2;9 \ 6 .m
D.
2;9 \ 2;6 .m
Câu 30. (Chuyên Đại học Vinh 2019) Cho hàm số
y f x
có đồ thị như hình vẽ. Có bao nhiêu số
nguyên
m
để phương trình
3
3f x x m
có 6 nghiệm phân biệt thuộc đoạn
1;2
?
A.
3
. B.
2
. C.
6
. D.
7
.
Câu 31. (Hội 8 trường chuyên ĐBSH 2019) Cho hàm số
y f x
có đồ thị như hình vẽ bên dưới.
Số giá trị nguyên dương của
m
để phương trình
2
4 5 1f x x m
có nghiệm là
A. Vô số. B.
4
. C.
0
. D.
3
.
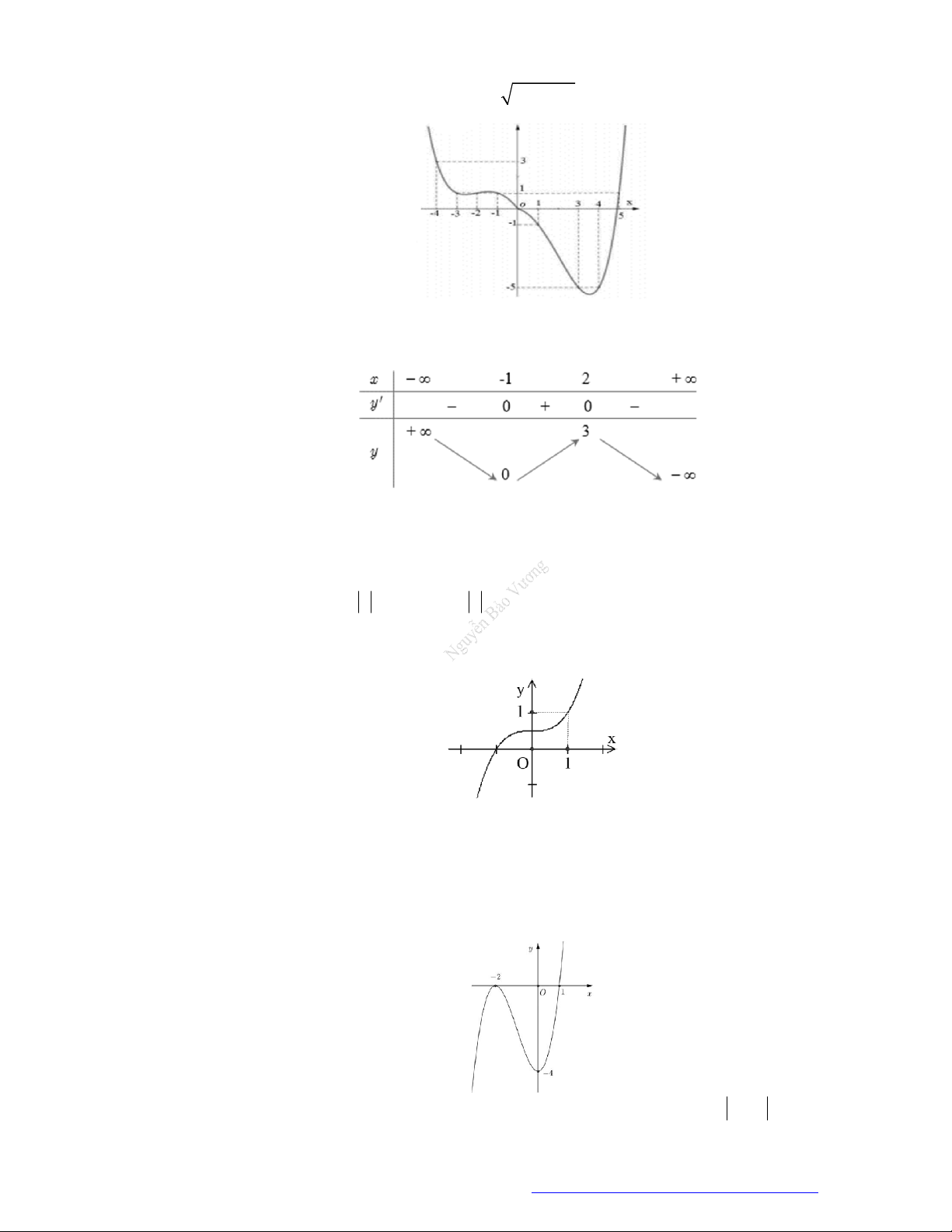
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
Câu 32. Cho hàm số
y f x
xác định, liên tục trên
và có đồ thị như hình vẽ dưới. Có bao nhiêu giá
trị nguyên của
m
để phương trình
2
2 3 4 6 9 3f x x m
có nghiệm
A.
13
. B.
12
. C.
8
. D.
10
.
Câu 33. (Chuyên Bắc Giang 2019) hàm số
y f x
có bảng biến thiên
Tìm
m
để phương trình
2
2 2 2 1 0f x f x m
có nghiệm trên
;1
A.
1;
. B.
2;
. C.
2;
. D.
1;
.
Câu 34. (Sở Hà Nam - 2019) Cho hàm số
2
4 3f x x x
. Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
2
6 5 0f x m f x m
có
6
nghiệm thực phân biệt?
A.
1
. B.
2
. C.
4
.
D.
3
.
Câu 35. Cho hàm số
3 2
f x ax bx cx d
có đồ thị như hình vẽ
Gọi
S
là tập hợp các giá trị của
m m
sao cho
3
1 2 1 1 0, .x m f x mf x f x x
Số phần tử của tập
S
là
A.
0.
B.
3.
C.
2
D.
1.
Câu 36. Cho hàm số
3 2
y f x ax bx cx d
có đồ thị như hình bên dưới
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
2
5 4 4 0f x m f x m
có
7
nghiệm phân biệt?
A.
1
. B.
2
. C.
3
. D.
4
.
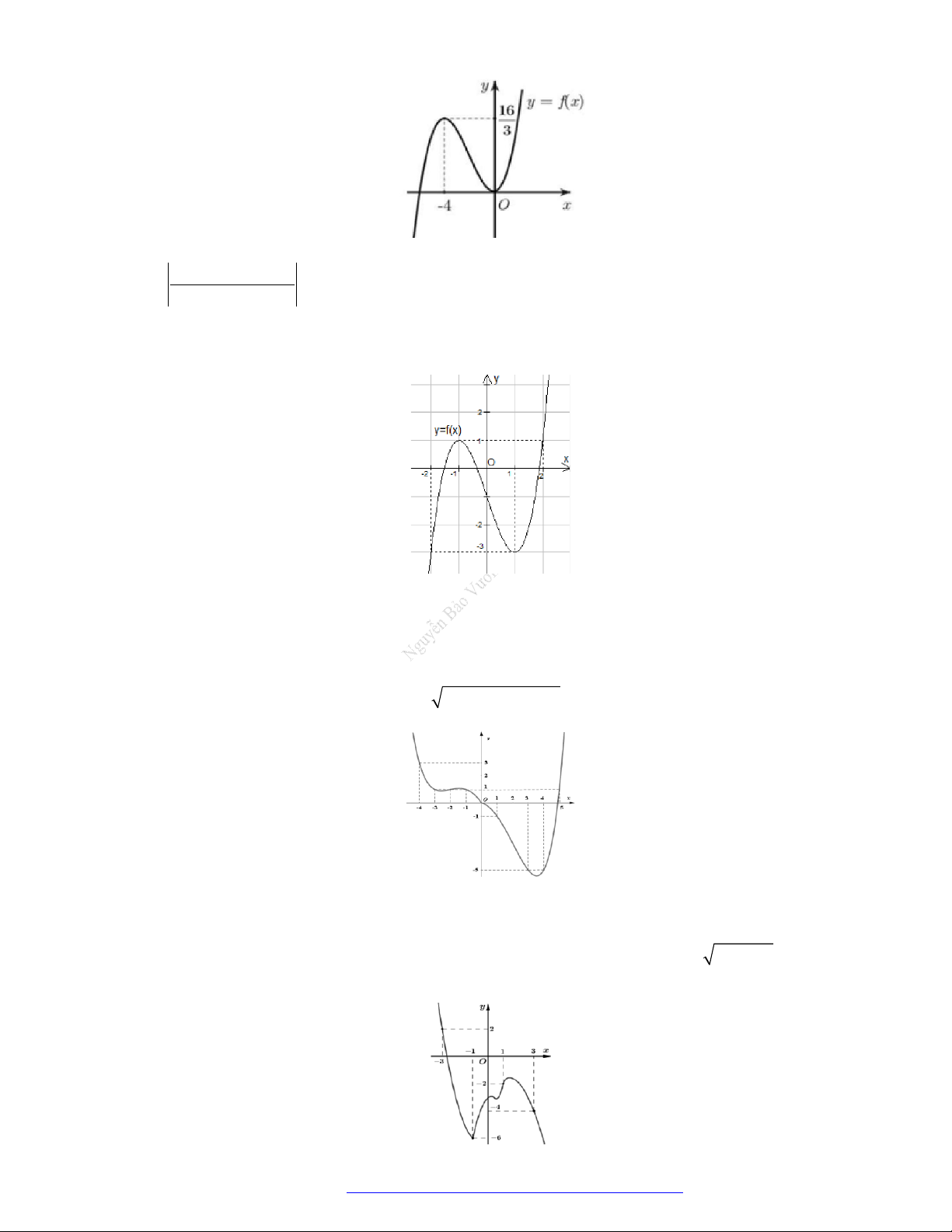
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 24 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 37. Cho hàm số
y f x
liên tục trên
và có đồ thị như hình vẽ
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
2
3sin cos 1
4 4
2cos sin 4
x x
f f m m
x x
có nghiệm.
A.
4
. B.
5
. C. Vô số. D.
3
.
Câu 38. Cho hàm số
( )y f x
liên tục trên R và có đồ thị như hình bên.
Phương trình
(2sin )f x m
có đúng ba nghiệm phân biệt thuộc đoạn
;
khi và chỉ khi
A.
3;1 .m
. B.
3;1 .m
. C.
3;1 .m
. D.
3;1 .m
Câu 39. Cho hàm số
y f x
xác định và liên tục trên
và có đồ thị như hình vẽ. Có bao nhiêu giá trị
nguyên của m để phương trình
2
302. 3 3 9 2021 19xf x m
có nghiệm.
A.
15
. B.
14
. C.
10
. D.
13
.
Câu 40. (Thi thử cụm Vũng Tàu - 2019) Cho hàm số
y f x
xác định, liên tục trên
và có đồ thị
như hình vẽ bên. Có bao nhiêu giá trị nguyên của
m
để phương trình
2
2 3 4 6 9 3f x x m
có nghiệm.
A.
9
. B.
17
. C.
6
. D.
5
.
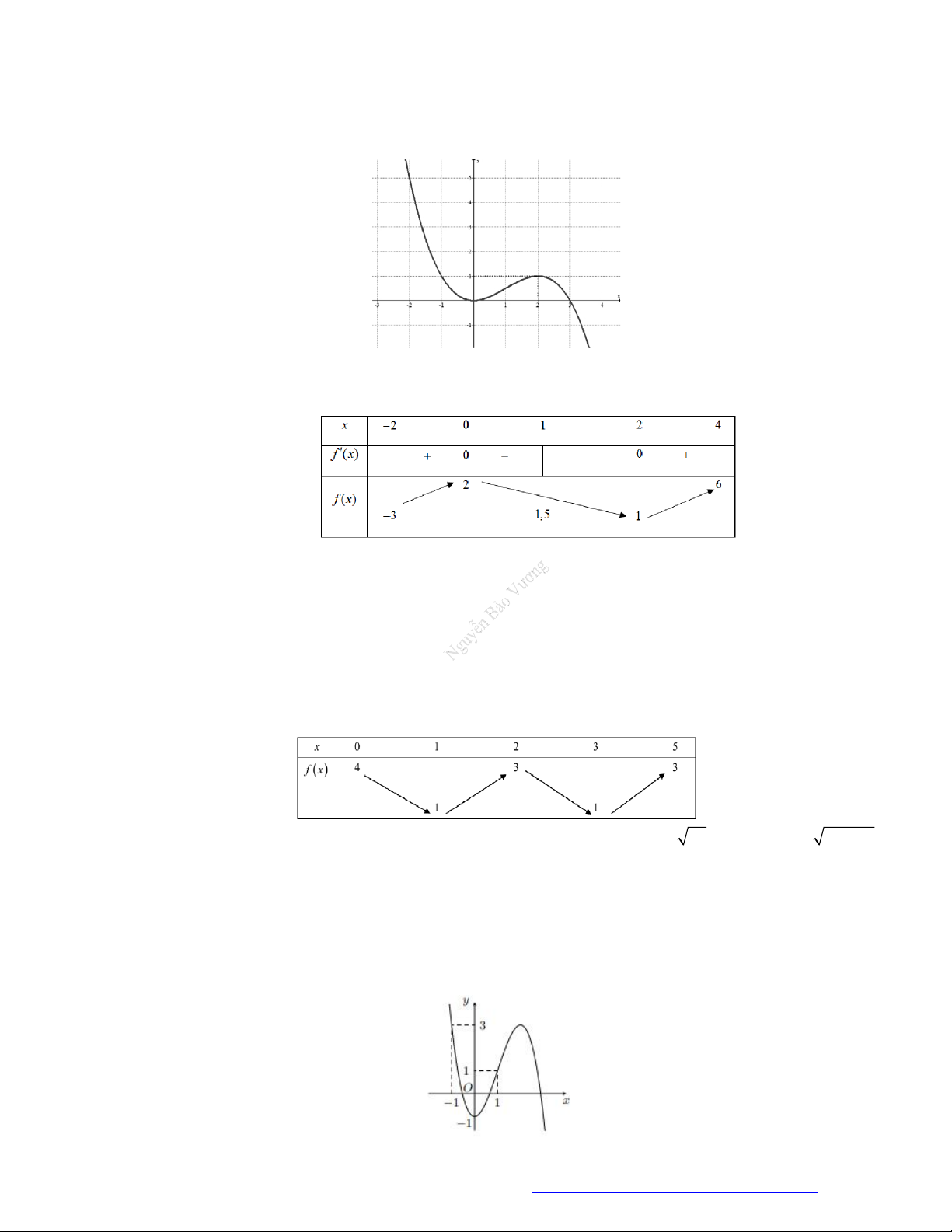
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25
Câu 41. (SGD Điện Biên - 2019) Cho hàm số
4 3 2
y f x ax bx cx dx e
với
, , , ,a b c d e
.
Biết hàm số
y f x
có đồ thị như hình vẽ, đạt cực trị tại điểm
0;0O
và cắt trục hoành tại
3;0A
. Có bao nhiêu giá trị nguyên của
m
trên
5;5
để phương trình
2
2f x x m e
có
bốn nghiệm phân biệt.
A.
0
. B.
2
. C.
5
. D.
7
.
Câu 42. Cho hàm số
y f x
liên tục và có đạo hàm trên đoạn
2; 4
và có bảng biến thiên như sau
Có bao nhiêu giá trị nguyên của tham số
m
để hệ phương trình
2
3
9
4 0
6 2 1 8 6 0
x
f x x x m
có ba
nghiệm phân biệt?
A.
9
. B.
11
. C.
10
. D.
8
.
Câu 43. (Hậu Lộc 2-Thanh Hóa 2019) Cho hàm số
y f x
liên tục trên đoạn
0 5;
và có bảng biến
thiên như hình sau:
Có bao nhiêu giá trị nguyên dương của tham số
m
để bất phương trình
3 2019 10 2mf x x f x x
nghiệm đúng với mọi
0 5x ; .
A. 2014. B. 2015. C. 2019. D. Vô số.
Câu 44. (Hậu Lộc 2-Thanh Hóa -2019) Cho hàm số
y f x
liên tục trên
và có đồ thị như hình vẽ
bên. Số giá trị nguyên của tham số
m
để phương trình
2
2018 2019 0
f cosx m f cosx m
có đúng 6 nghiệm phân biệt thuộc đoạn
0 2
;
là
A. 5. B. 3. C. 2. D. 1.
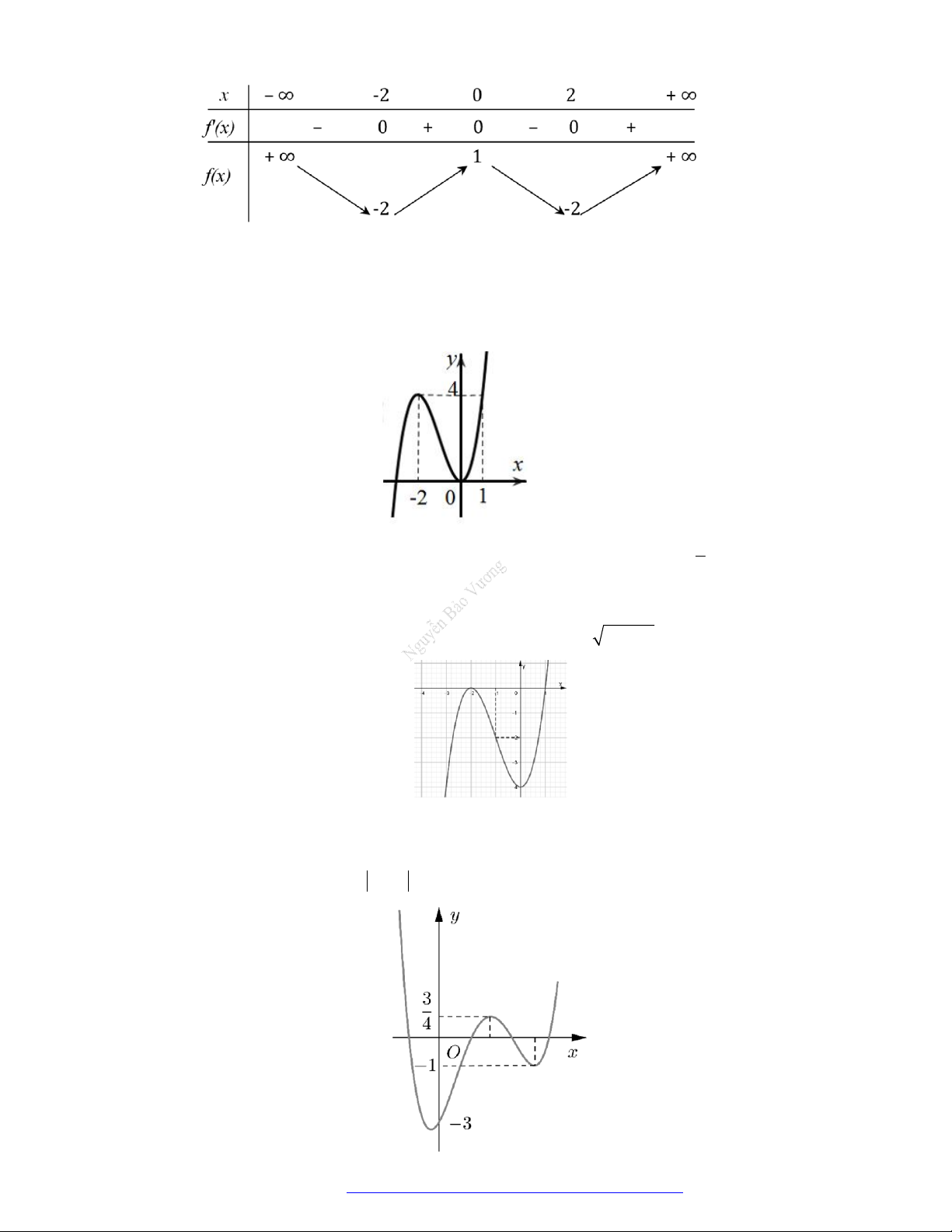
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 26 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 45. (THPT Gia Lộc Hải Dương 2019) Cho hàm số
y f x
có bảng biến thiên như sau
Tìm
m
để phương trình
2 2019 0 f x m
có
4
nghiệm phân biệt.
A.
0;2m
. B.
2;2 m
. C.
4;2 m
. D.
2;1 m
.
Câu 46. Cho hàm số
y f x
liên tục trên
R
và có đồ thị như hình vẽ dưới đây. Tập hợp tất cả các giá trị
thực của tham số
m
để phương trình
2
2 2 3 1f x x m
có nghiệm thuộc khoảng
0;1 .
.
A.
0;4
. B.
1;0
. C.
0;1
. D.
1
;1
3
Câu 47. (THPT Lê Quý Đôn Đà Nẵng 2019) Cho hàm số
y f x
liên tục trên
và có đồ thị như hình
vẽ. Tập hợp các giá trị thực của tham số
m
để phương trình
2
4 1f x x m
có nghiệm là
A.
2;0
. B.
4; 2
. C.
4;0
. D.
1;1
.
Câu 48. (Sở Hà Nội 2019) Cho hàm số bậc bốn
y f x
có đồ thị như hình vẽ. Số giá trị nguyên của
tham số
m
để phương trình
f x m m
có
4
nghiệm phân biệt là
A.
2.
B. Vô số. C.
1.
D.
0.
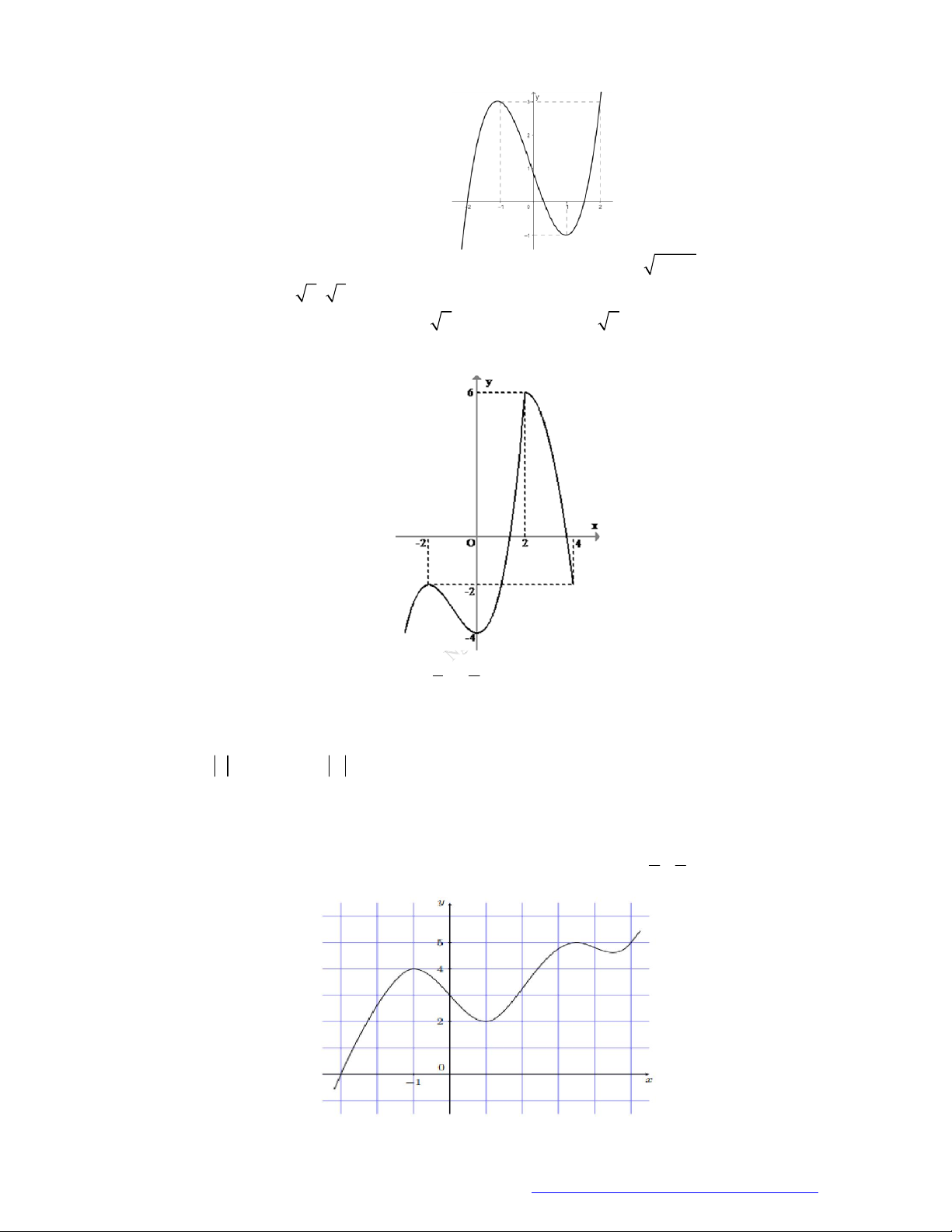
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27
Câu 49. (Chuyen Phan Bội Châu 2019) Cho hàm số
( )y f x
liên tục trên
và có đồ thị như hình vẽ
dưới đây.
Tập hợp tất cả các giá trị thực của tham số m để phương trình
2
( 4 )f x m
có nghiệm thuộc
nửa khoảng
[ 2 ; 3)
là:
A.
[-1;3]
. B.
[-1; ( 2)]f
. C.
(-1; ( 2)]f
. D.
(-1;3]
.
Câu 50. (Chuyên Dại Học Vinh 2019) Cho hàm số
y f x
có đồ thị như hình vẽ.
Có bao nhiêu số nguyên
m
để phương trình
1
1
3 2
x
f x m
có nghiệm thuộc đoạn
2;2
?
A.
11
B.
9
C.
8
D.
10
Câu 51. (THPT Thiệu Hóa – Thanh Hóa 2019) Có bao nhiêu số nguyên
m
để phương trình
2 2
3 2 3 0x x m m
có
4
nghiệm phân biệt.
A.
3
B.
12
C.
7T
D.
5
Câu 52. Cho hàm số
y f x
có đồ thị như hình vẽ. Tìm số giá trị nguyên của
m
để phương trình
2
2f x x m
có đúng
4
nghiệm thực phân biệt thuộc đoạn
3 7
;
2 2
.
A.
1
. B.
2
. C.
3
. D.
4
.
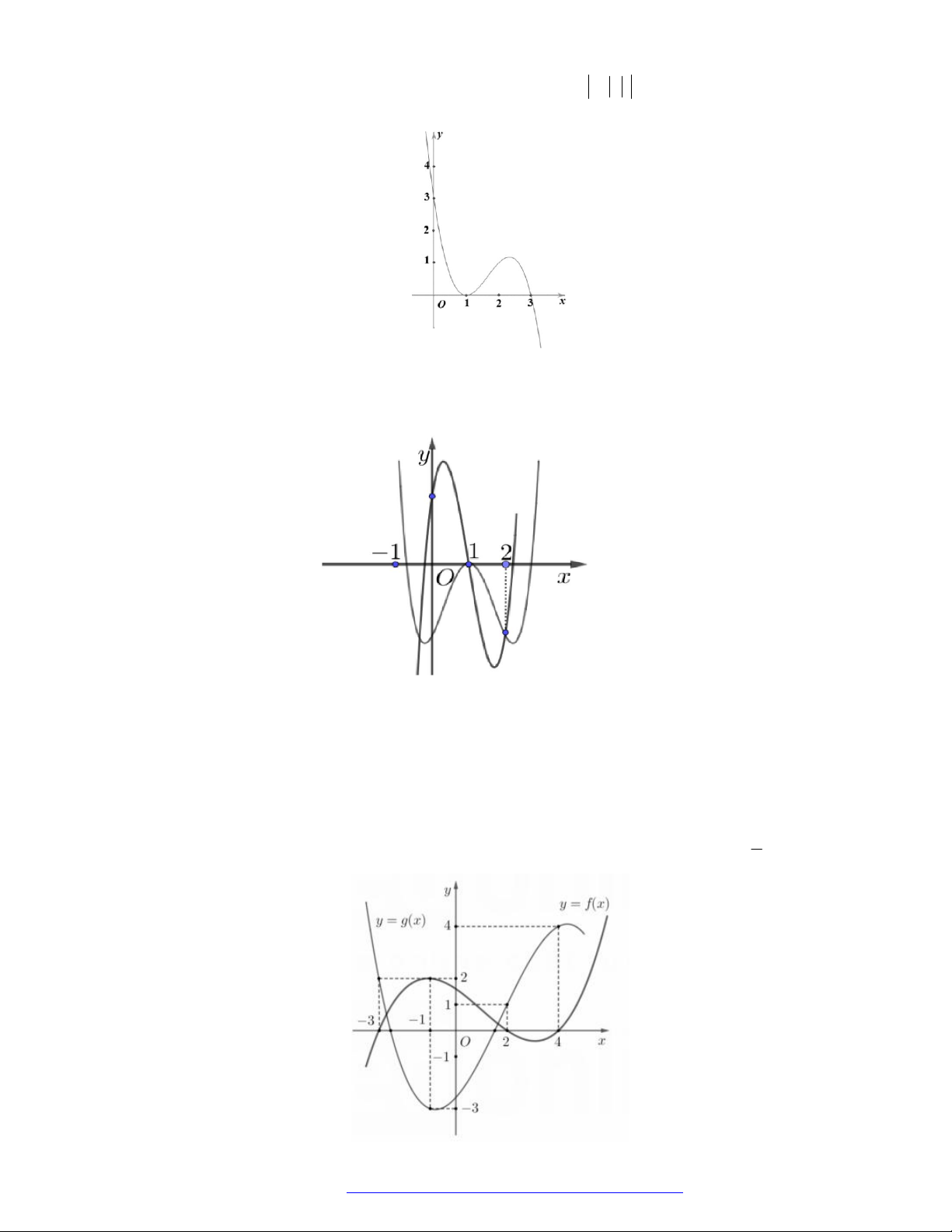
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 28 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 53. (Chuyên Lam Sơn Thanh Hóa 2019) Cho hàm số
( )y f x
có đạo hàm liên tục trên
. Biết
(0) 0f
và
f x
được cho như hình vẽ bên. Phương trình
( )f x m
( với
m
là tham số) có
nhiều nhất bao nhiêu nghiệm?
A.
8
B.
6
C.
2
D.
4
Câu 54. (Thanh Tường Nghệ An 2019) Cho hàm số
y f x
là hàm đa thức với hệ số thực. Hình vẽ
bên dưới là một phần đồ thị của hai hàm số:
y f x
và
y f x
.
Tập các giá trị của tham số
m
để phương trình
x
f x me
có hai nghiệm phân biệt trên
0;2
là
nửa khoảng
;a b
. Tổng
a b
gần nhất với giá trị nào sau đây?
A.
0.81
. B.
0.54
. C.
0.27
. D.
0.27
.
Câu 55. (VTED 2019) Cho hai hàm số
y f x
và
y g x
là các hàm xác định và liên tục trên
và
có đồ thị như hình vẽ bên (trong đó đường cong đậm hơn là đồ thị của hàm số
y f x
). Có bao
nhiêu số nguyên
m
để phương trình
1 2 1f g x m
có nghiệm thuộc đoạn
5
1;
2
.
A.
8
B.
3
C.
6
D.
4
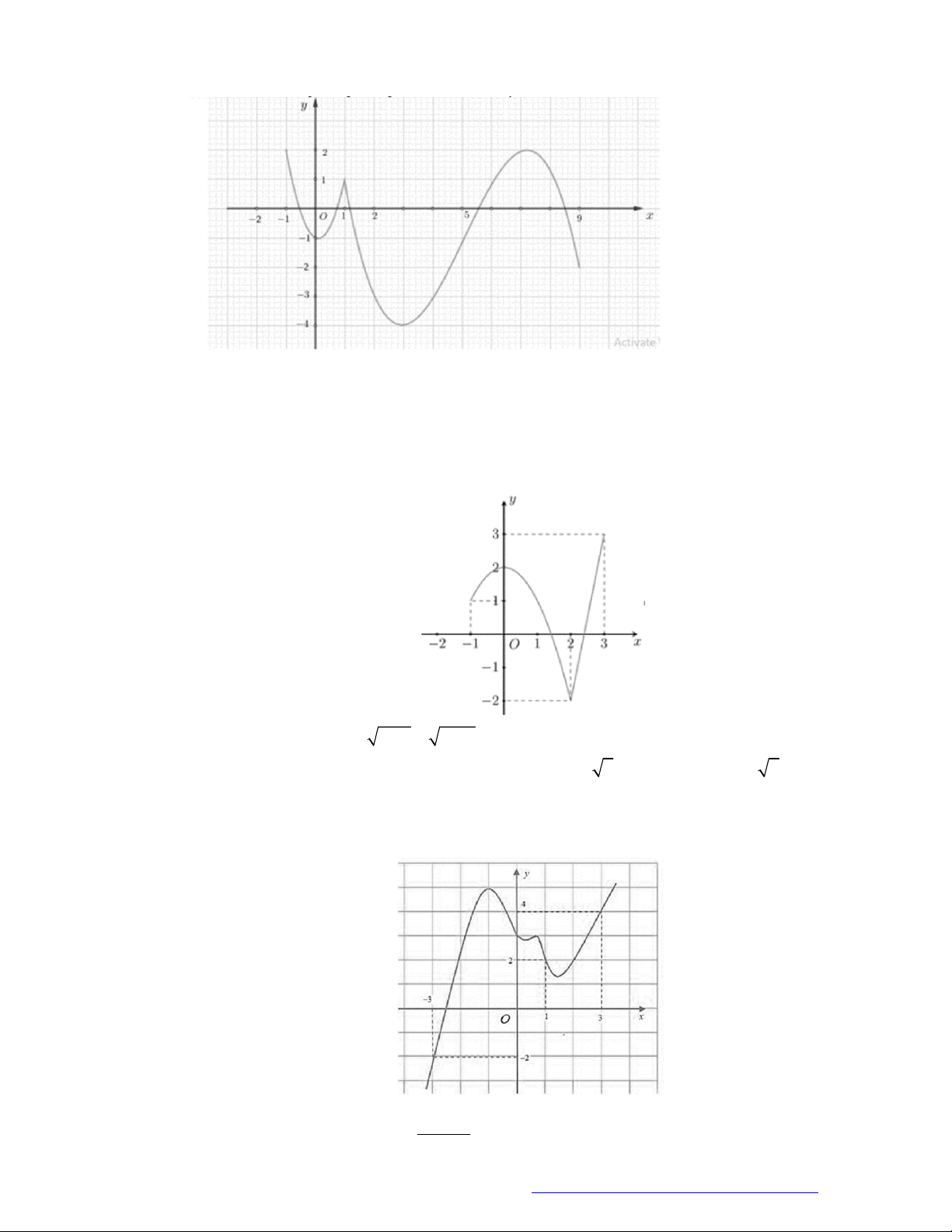
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 29
Câu 56. (THPT Yên Khánh A - Ninh Bình - 2019) Cho hàm số
y f x
liên tục trên đoạn
1;9
và
có đồ thị là đường cong trong hình vẽ dưới đây
Có bao nhiêu giá trị nguyên của tham số
m
để bất phương trình
2 2
16.3 2 8 .4 3 .6
f x f x f x
f x f x m m
nghiệm đúng với mọi giá trị thuộc
1;9
?
A.
32
. B.
31
. C.
5.
D.
6
.
Câu 57. (THPT Yên Khánh A - Ninh Bình - 2019) Cho hàm số
y f x
liên tục trên
1;3
và có đồ
thị như hình vẽ.
Bất phương trình
1 7f x x x m
có nghiệm thuộc
1;3
khi và chỉ khi
A.
7m
. B.
7m
. C.
2 2 2m
. D.
2 2 2m
.
Câu 58. (THPT Yên Khánh A - Ninh Bình - 2019) Cho hàm số
y f x
có đạo hàm liên tục trên đoạn
3;3
và đồ thị hàm số
y f x
như hình vẽ dưới đây
Biết
1 6f
và
2
1
2
x
g x f x . Mệnh đề nào sau đây là đúng?
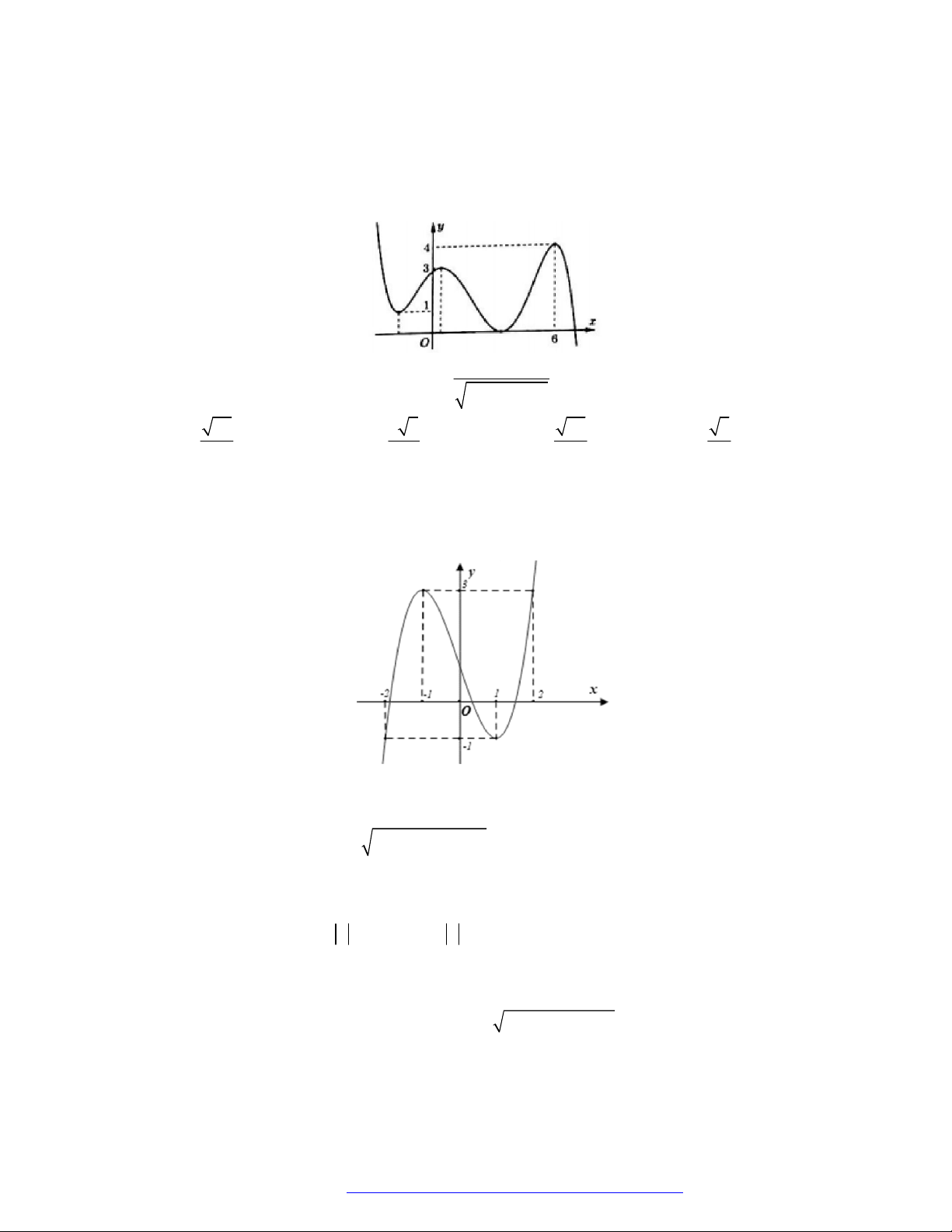
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 30 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A. Phương trình
0g x
có đúng hai nghiệm thuộc đoạn
3;3
.
B. Phương trình
0g x
không có nghiệm thuộc đoạn
3;3
.
C. Phương trình
0g x
có đúng một nghiệm thuộc đoạn
3;3
.
D. Phương trình
0g x
có đúng ba nghiệm thuộc đoạn
3;3
.
Câu 59. (Chuyên Sơn La - Lần 2 - 2019) Cho hàm số
y f x
liên tục trên
và có đồ thị như hình
vẽ.
Các giá trị của tham số
m
để phương trình
3
2
2
4
3
2 5
m m
f x
f x
có ba nghiệm phân biệt là
A.
37
2
m
. B.
3 3
2
m
. C.
37
2
m
. D.
3
2
m
.
Câu 60. (THPT Ngô Quyền - Ba Vì - 2019) Cho hàm số
3 2
f x ax bx cx d
có đồ thị như hình vẽ
sau đây. Hỏi có bao nhiêu giá trị nguyên của tham số thực
m
để phương trình
f f x m
có 4
nghiệm phân biệt thuộc đoạn
1;2
?
A.
5
. B.
4
. C.
0
. D.
3
.
Câu 61. (THPT Nguyễn Đức Cảnh - Thái Bình - 2019) Cho hàm số
3 2
2 8g x x x x
. Có bao nhiêu
số nguyên
m
để phương trình
3 2 7g g x m g x
có đúng 6 nghiệm thực phân biệt
A.
7
. B.
8
. C.
24
. D.
25
.
Câu 62. (THPT Hà Nam - 2019) Cho hàm số
2
4 3f x x x
. Có bao nhiêu giá trị nguyên của tham
số
m
để phương trình
2
6 5 0f x m f x m
có
6
nghiệm thực phân biệt?
A.
1
. B.
2
. C.
4
.
D.
3
.
Câu 63. (Sở GD Bạc Liêu - 2019) Cho hàm số
3 2
( ) 2 8 7 f x x x x
. Gọi
S
là tập hợp tất cả các giá trị
nguyên dương của tham số
m
để phương trình
( ( ) 3) 2 ( ) 5 f f x m f x
có 6 nghiệm thực
phân biệt. Tổng các phần tử của
S
bằng
A.
25
. B.
66
. C.
105
. D.
91
.
Câu 64. (Quang Trung - Bình Phước - 2019) Cho hàm số
f x
liên tục trên
. Hàm số
f x
có đồ
thị như hình vẽ:

T
ÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 31
Bất phương trình
2
2sin 2sinf x x m
đúng với mọi
0;x
khi và chỉ khi
A.
1
0
2
m
f
. B.
1
1
2
m
f
. C.
1
1
2
m
f
. D.
1
0
2
m
f
.
Câu 65. (Lương Thế Vinh - Hà Nội - 2019) Cho hàm số
5 3
3
4f x x x m
. Có bao nhiêu giá trị
nguyên của tham số
m
để phương
trình
3
3
f
f x m x m
c
ó nghiệm thuộc
1
;2
?
A.
15
. B.
16
. C.
17
. D.
18
.
-------------------- HẾT --------------------
2
2
1
1
y
x
O
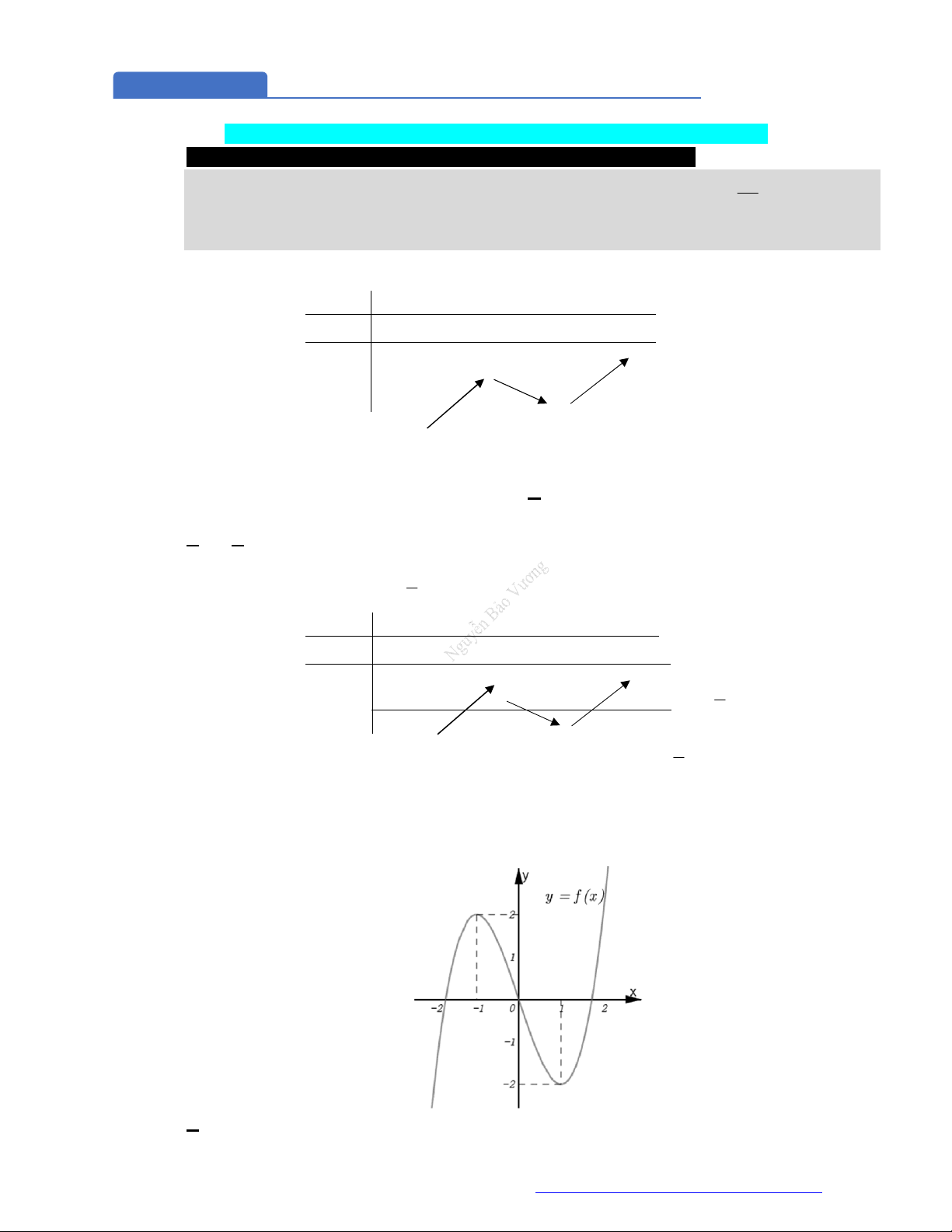
T
ÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
DẠNG TOÁN DÀNH CHO HỌC SINH TRUNG BÌNH MỨC 5-6 ĐIỂM
Dạng 1. Bài toán
tương giao đồ thị thông qua đồ thị, bảng biến thiên
Nghiệm
của phương trình là số giao điểm của đường thẳng với đồ thị hàm
số
Câu
1. (Đề Minh Họa 2020 Lần 1) Cho hàm số
f
x
có
bảng biến thiên như sau
x
2
3
(
)f x
0
0
(
)f x
1
0
Số nghiệm của phương trình
3
( ) 2 0f x
là
A.
2
.
B.
0
.
C.
3
.
D.
1
.
Lờ
i giải
Chọn C
Ta có
2
3
( ) 2 0 ( )
3
f x f x
x
2
3
(
)f x
0
0
( )f x
1
0
Căn cứ và
o bảng biến thiên thì phương trinh
2
3
( ) 2 0 ( )
3
f x f x
có
3 nghiệm phân biệt.
Câu 2. (Mã 101 - 2020 Lần 1) Cho hàm số bậc ba
y
f x
có đồ thị là đường cong trong hình bên. Số
nghiệm thực của phương trình
1f
x
là:
A.
3
. B.
1
. C.
0
. D.
2
.
Lờ
i giải
T
ƯƠNG GIAO ĐỒ THỊ HÀM SỐ
Ch
uyên đề 8
0
af
x b
b
y
a
y
f x
2
3
y
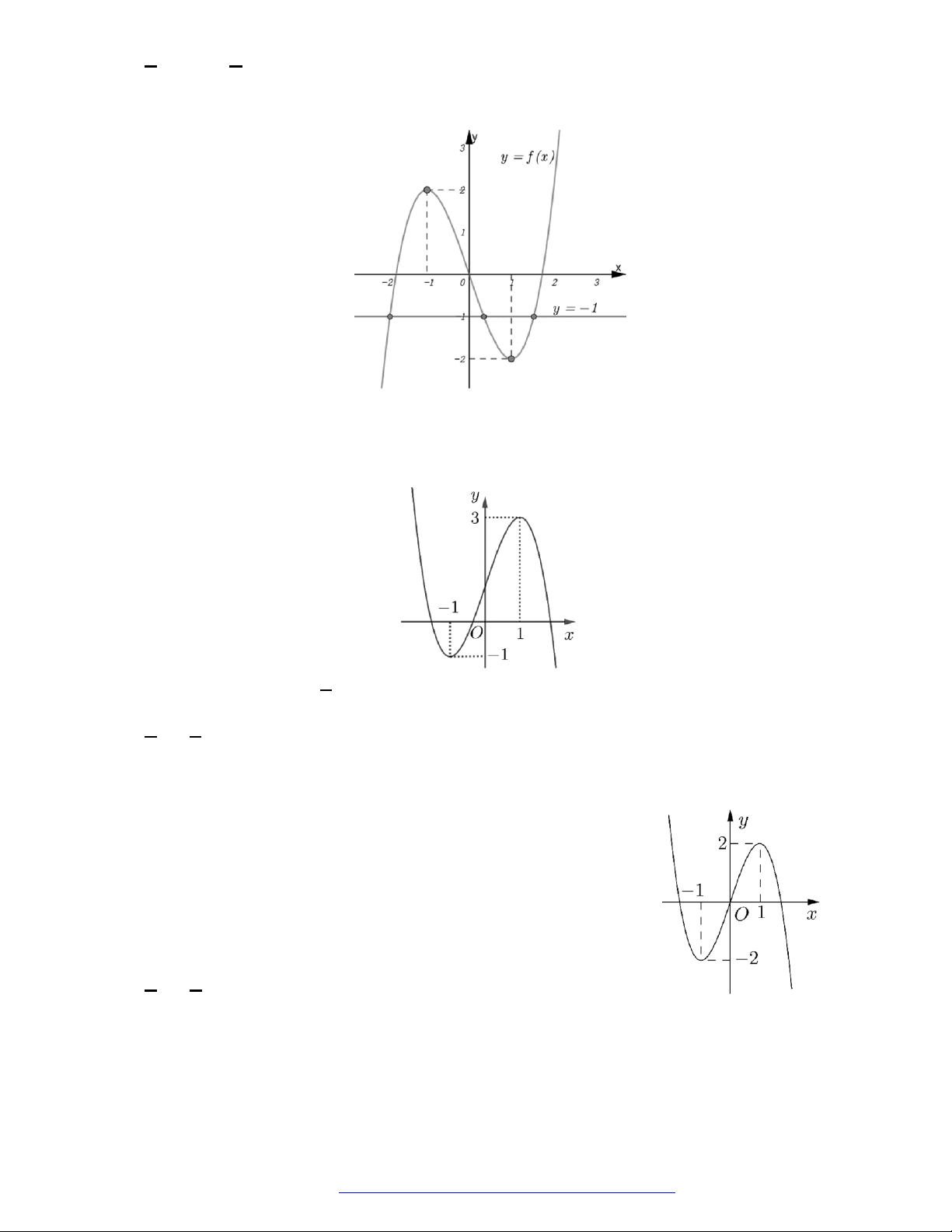
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Chọn A.
Số nghiệm thực của phương trình
1f x
chính là số giao điểm của đồ thị hàm số
y f x
và đường thẳng
1y
.
Từ hình vẽ suy ra
3
nghiệm.
Câu 3. (Mã 102 - 2020 Lần 1) Cho hàm số bậc ba
y f x
có đồ thị là đường cong trong hình bên. Số
nghiệm thực của phương trình
1f x
là
A.
0
. B.
3
. C.
1
. D.
2
.
Lời giải
Chọn B
Ta thấy đường thẳng
1y
cắt đồ thị hàm số
y f x
tại
3
điểm phân biệt nên phương trình
1f x
có
3
nghiệm.
Câu 4. (Mã 103 - 2020 Lần 1) Cho hàm số bậc ba
y f x
có đồ thị là
đường cong trong hình bên. Số nghiệm thực của phương trình
1f x
là
A.
1
. B.
0
.
C.
2
. D.
3
.
Lời giải
Chọn D
Từ đồ thị hàm số ta có số nghiệm thực của phương trình
1f x
là
3
.
Câu 5. (Mã 104 - 2020 Lần 1) Cho hàm số bậc ba
y f x
có đồ thị là đường cong trong hình vẽ bên.
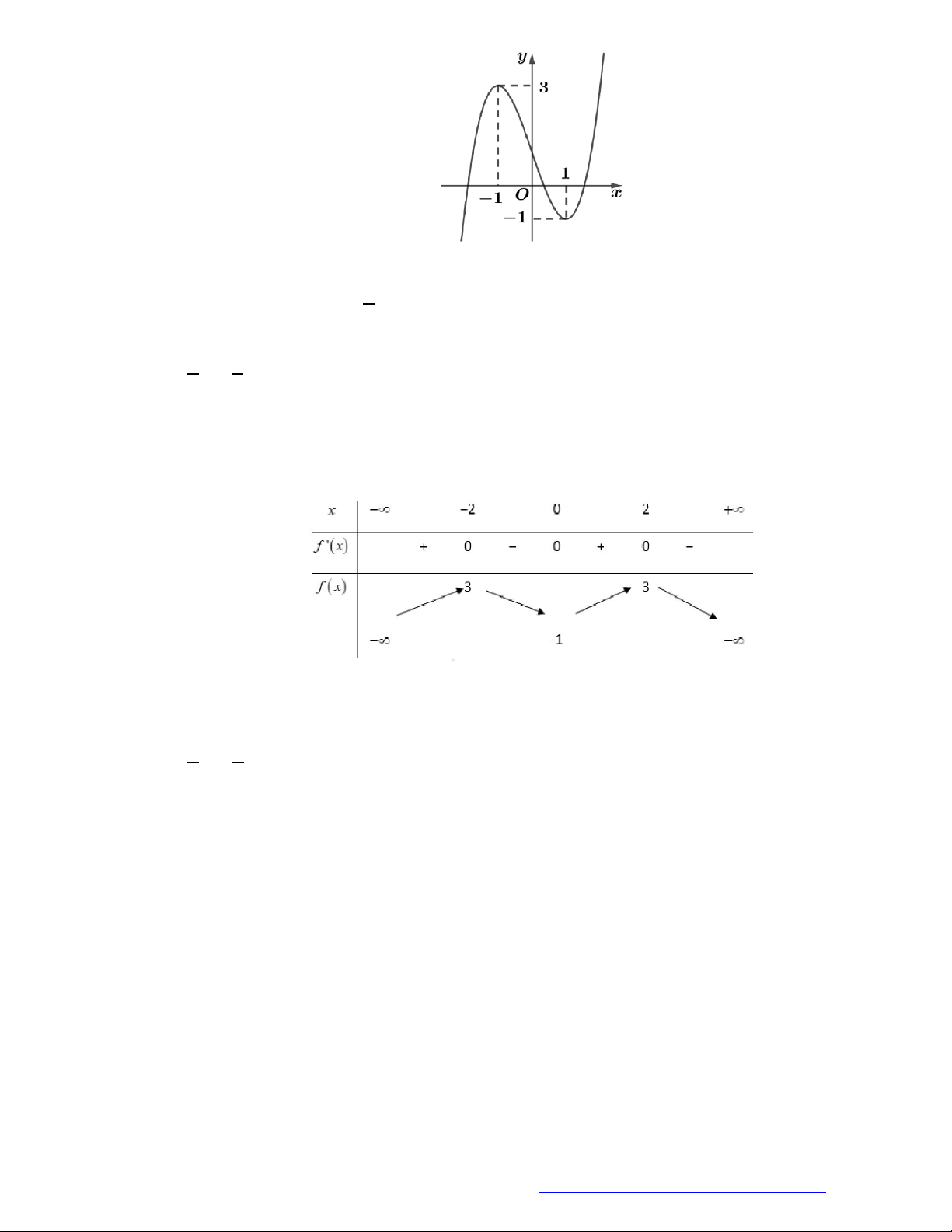
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Số nghiệm thực của phương trình
2f x
là:
A.
0
. B.
3
. C.
1
. D.
2
.
Lời giải
Chọn B
Ta có số nghiệm của phương trình là số giao điểm của đồ thị hàm số
y f x
với đường thẳng
2.y
Dựa vào đồ thị ta có phương trình có ba nghiệm phân biệt.
Câu 6. (Mã 101 2019) Cho hàm số có bảng biến thiên như sau:
Số nghiệm thực của phương trình là
A. . B. . C. . D. .
Lời giải
Chọn C
Ta có .
Số nghiệm của phương trình bằng số giao điểm của đồ thị hàm số và đường thẳng
.
Dựa vào bảng biến thiên của ta có số giao điểm của đồ thị
Câu 7. (Mã 101 2018) Cho hàm số . Đồ thị của hàm số
như hình vẽ bên. Số nghiệm thực của phương trình là
f x
2 3 0
f x
2
1
4
3
3
2 3 0
2
f x f x
y f x
3
2
y
f x
3 2
, , ,f x ax bx cx d a b c d
y f x
3 4 0
f x
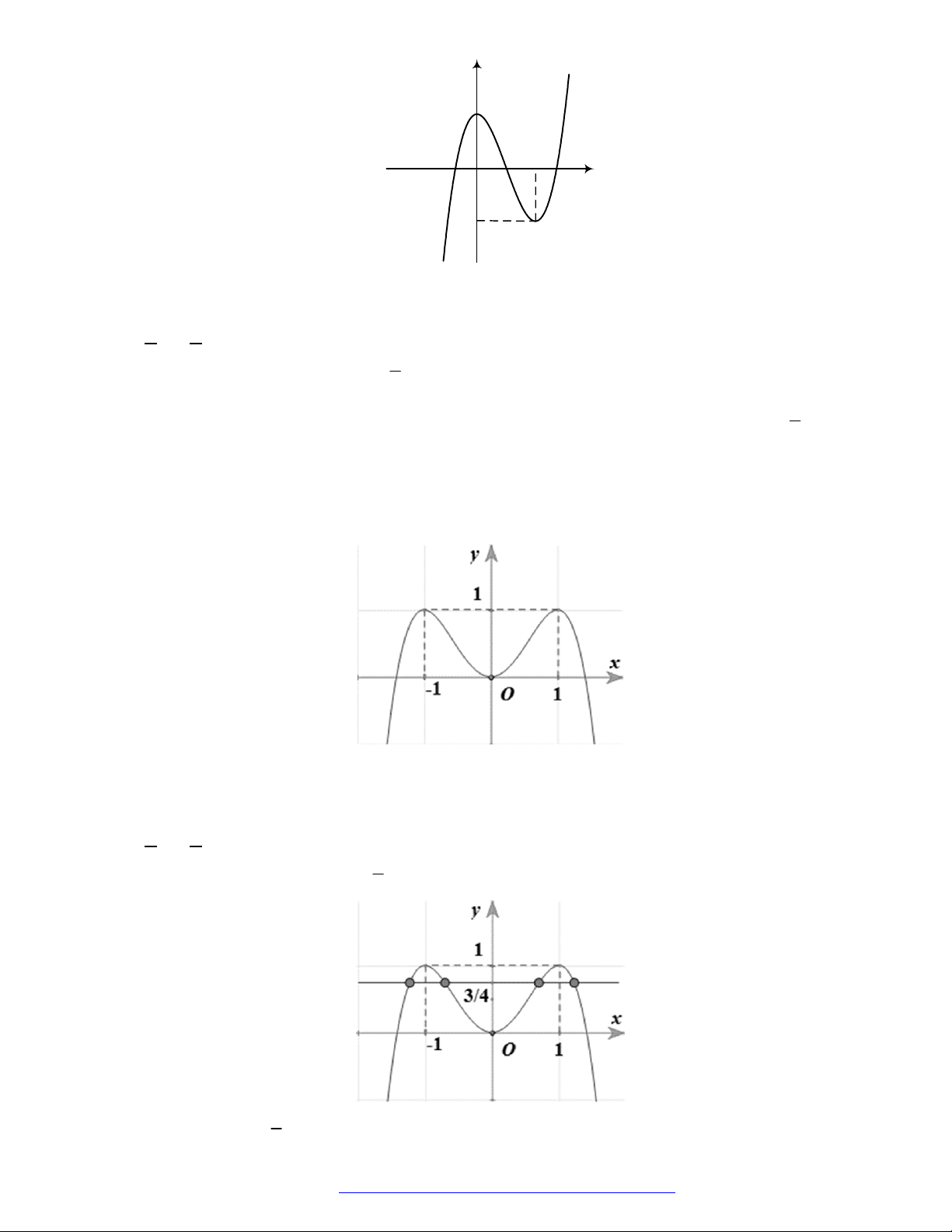
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A. B. C. D.
Lời giải
Chọn D
Ta có:
là phương trình hoành độ giao điểm của đồ thị hàm số và đường thẳng .
Dựa vào đồ thị hàm số, ta thấy có nghiệm.
Câu 8. (Mã 102 2018) Cho hàm số . Đồ thị của hàm số như
hình vẽ bên.
Số nghiệm của phương trình là
A. B. C. D.
Lời giải
Chọn C
Ta có
Đường thẳng cắt đồ thị hàm số
tại điểm phân biệt nên phương trình đã cho có
nghiệm phân biệt.
x
y
O
2
2
2
2
0
1
3
3 4 0
f x
4
3
f x
*
*
y f x
4
3
y
*
3
4 2
, ,f x ax bx c a b c
y f x
4 3 0
f x
2
0
4
3
4 3 0
f x
3
4
f x
3
4
y
y
f x
4
4
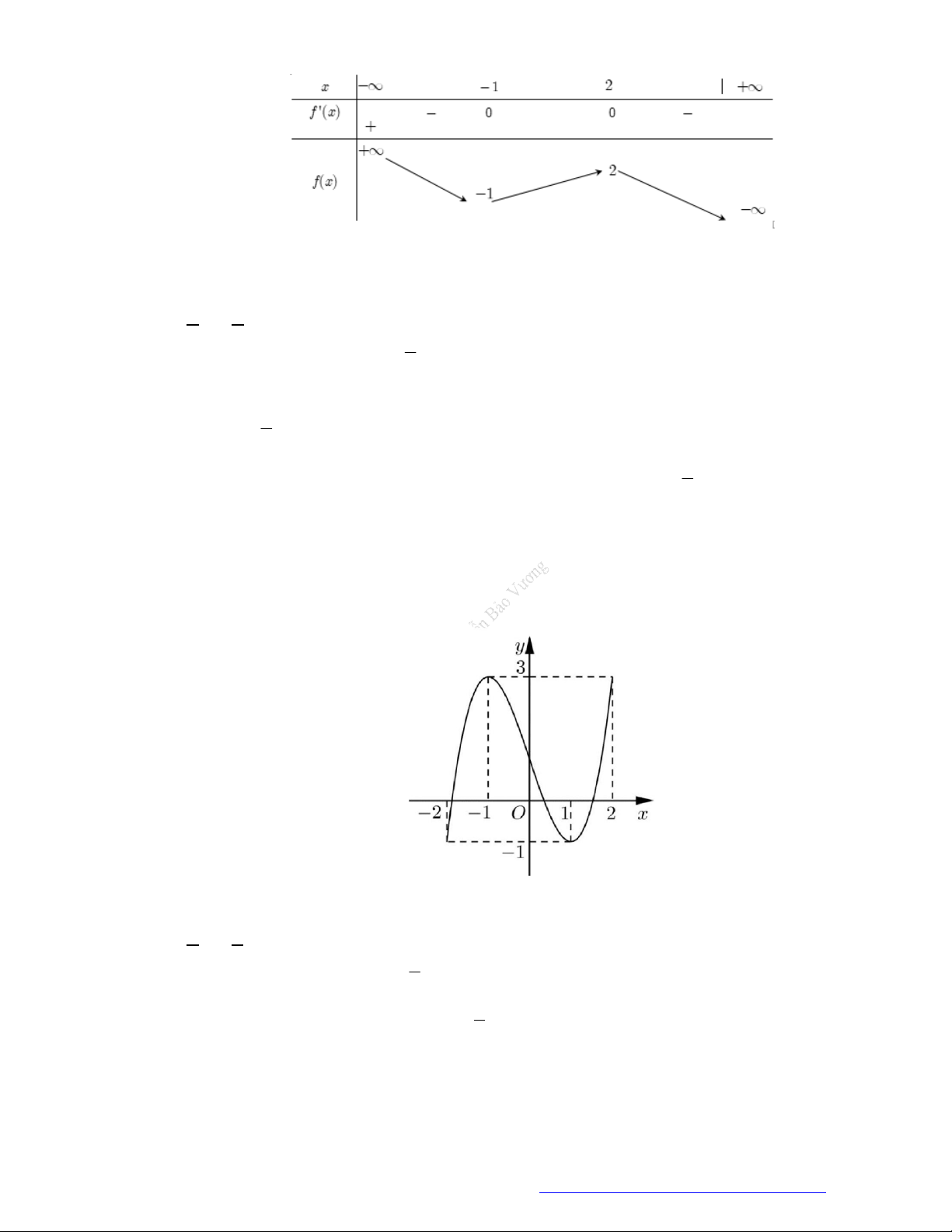
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Câu 9. (Mã 103 2019) Cho hàm số bảng biến thiên như sau:
Số nghiệm thực của phương trình là
A. . B. . C. . D. .
Lời giải
Chọn A
Ta có .
Số nghiệm thực của phương trình (1) bằng số giao điểm của đồ thị hàm số với đường
thẳng .
Từ bảng biến thiên đã cho của hàm số , ta thấy đường thẳng cắt đồ thị hàm số
tại ba điểm phân biệt.
Do đó phương trình (1) có ba nghiệm thực phân biệt.
Câu 10. (Mã 103 2018) Cho hàm số liên tục trên và có đồ thị như hình vẽ bên. Số
nghiệm thực của phương trình trên đoạn là
A. . B. . C. . D. .
Lời giải
Chọn B
Ta có .
Dựa vào đồ thị, ta thấy đường thẳng cắt tại 3 điểm phân biệt nên phương trình đã
cho có 3 nghiệm phân biệt.
( )f x
2 ( ) 3 0
f x
3
0
1
2
3
2 ( ) 3 0 ( ) (1)
2
f x f x
( )y f x
3
2
y
( )f x
3
2
y
( )y f x
y f x
2;2
3 4 0
f x
2;2
4
3
1
2
4
3 4 0
3
f x f x
4
3
y
y f x
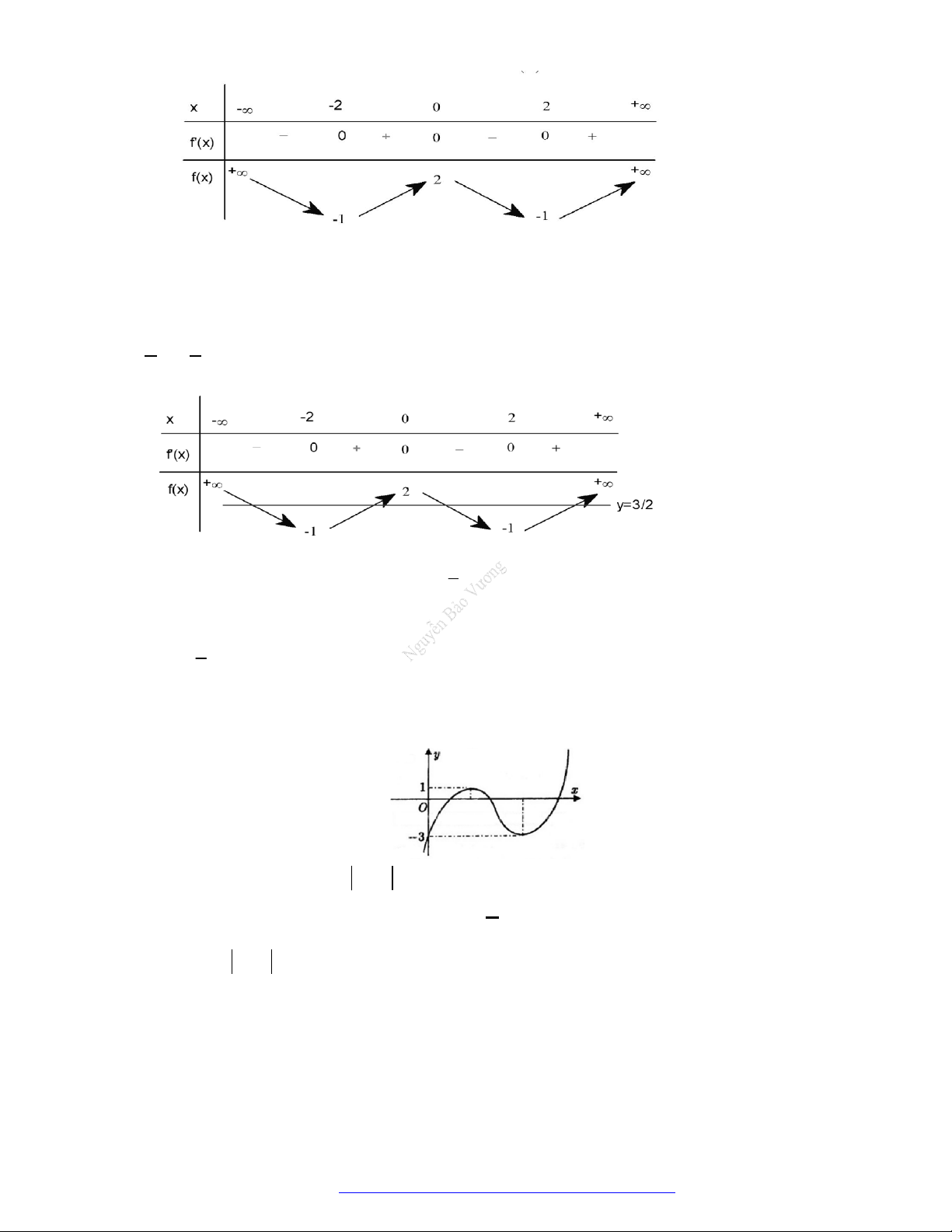
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 11. (Mã 102 2019) Cho hàm số có bảng biến thiên như
sau
Số nghiệm thực của phương trình là
A.
3
. B. . C. . D. .
Lời giải
Chọn B
Bảng biến thiên
Xét phương trình .
Số nghiệm của phương trình bằng số giao điểm của đồ thị hàm số và đường thẳng
. Dựa vào bảng biến thiên ta thấy đường thẳng cắt đồ thị tại bốn điểm phân biệt.
Câu 12. (THCS - THPT Nguyễn Khuyến 2019) Cho hàm số liên tục trên và có đồ thị như
hình vẽ.
Số nghiệm của phương trình là
A. . B. . C. . D. .
Lời giải
*Đồ thị
- Bước 1: Giữ nguyên phần đồ thị của nằm phía trên Ox
- Bước 2: Lấy đối xứng phần đồ thị của nằm phía dưới Ox qua trục hoàn.
- Bước 3: Xóa phần đồ thị của nằm phía dưới trục hoành
f x
3 5 0
f x
4
0
2
5
3 5 0
3
f x f x
:
C y f x
3
:
2
d y
d
C
y f x
2
f x
3
2
4
6
y f x
y f x
y f x
y f x
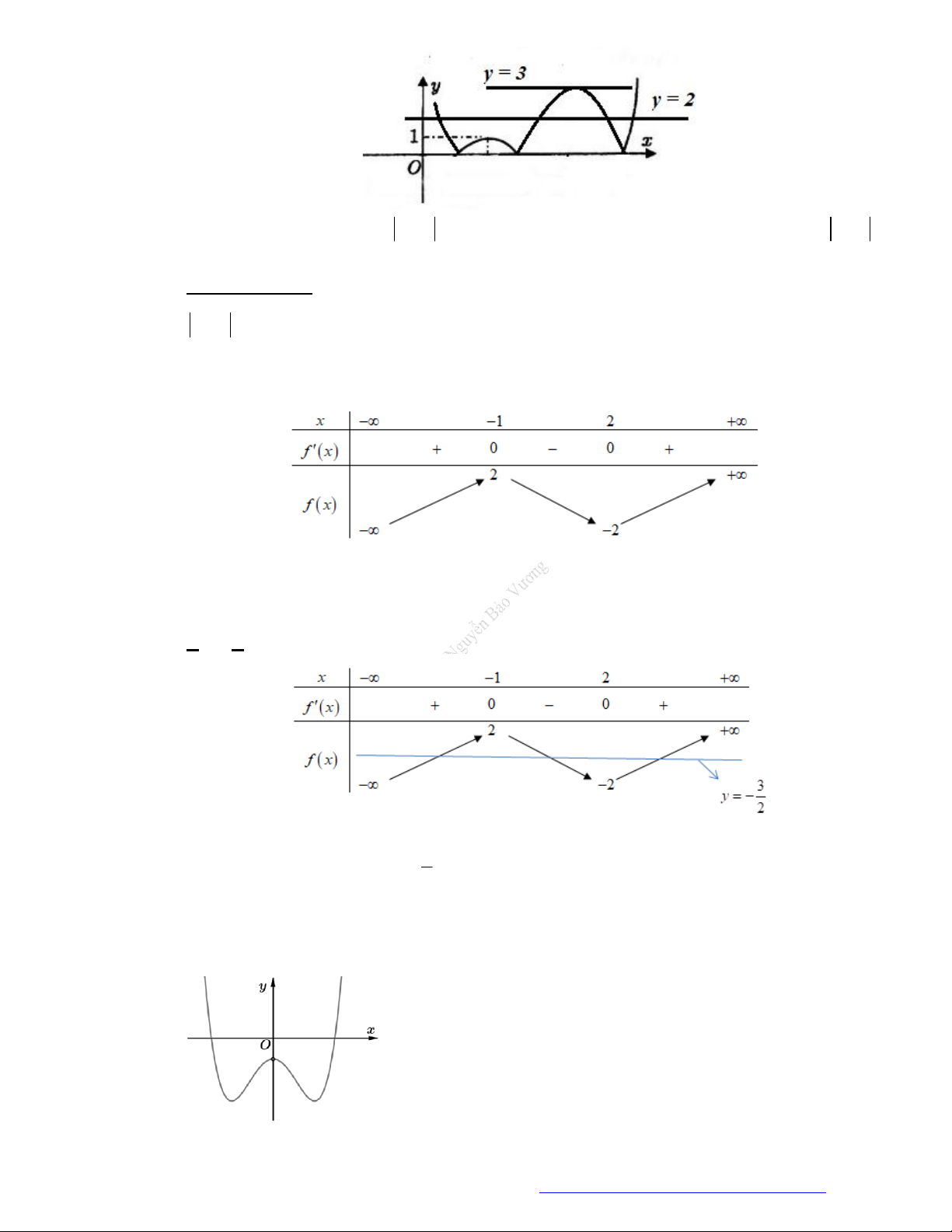
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Số nghiệm của phương trình cũng chính là số giao điểm cũng đồ thị hàm số
và đường thẳng . Dựa vào hình vẽ trên, ta thấy có 4 giao điểm.
*Cách giải khác:
, dựa vào đồ thị suy ra phương trình đã cho có 4 nghiệm
Câu 13. (Mã 104 2019) Cho hàm số có bảng biến thiên như sau:
Số nghiệm thực của phương trình là
A. . B. . C. . D. .
Lời giải
Chọn D
Ta có .
Nhìn bảng biến thiên ta thấy phương trình này có 3 nghiệm.
Câu 14. (Mã 110 2017) Đường cong ở hình bên là đồ thị của hàm số , với là các
số thực. Mệnh đề nào dưới đây đúng?
A. Phương trình vô nghiệm trên tập số thực
B. Phương trình có đúng một nghiệm thực
2
f x
y f x
2
y
( ) 2
2
( ) 2
f x
f x
f x
f x
2 3 0
f x
0
1
2
3
3
2 3 0
2
f x f x
4 2
y ax bx c
, ,a b c
0
y
0
y
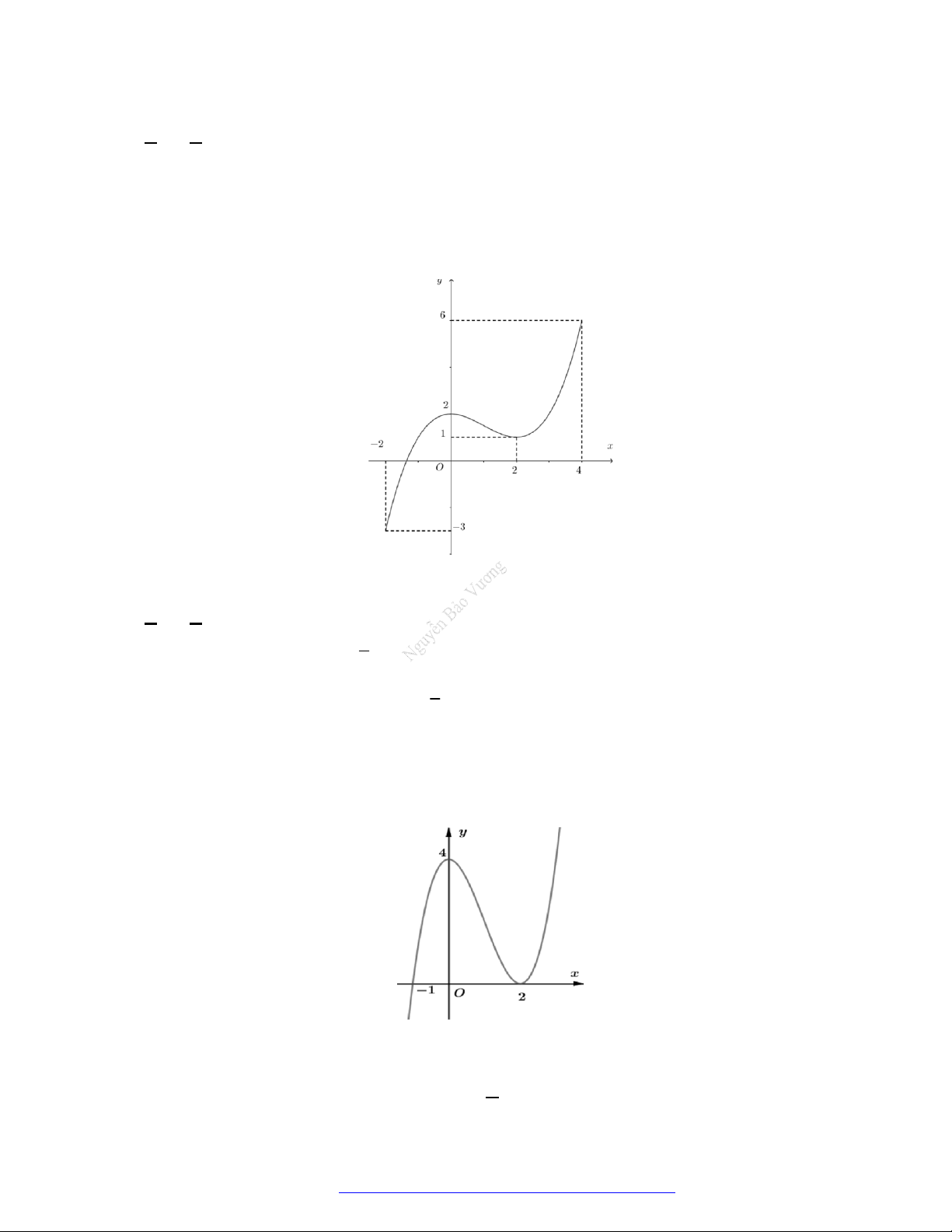
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
C. Phương trình có đúng hai nghiệm thực phân biệt
D. Phương trình có đúng ba nghiệm thực phân biệt
Lời giải
Chọn D
Dựa vào hình dáng của đồ thị hàm số ta thấy đây là đồ thị của hàm số bậc bốn
trùng phương có 3 điểm cực trị nên phương trình có ba nghiệm thực phân biệt.
Câu 15. (Mã 104 2018) Cho hàm số liên tục trên đoạn và có đồ thị như hình vẽ bên. Số
nghiệm thực của phương trình trên đoạn là
A. B. C. D.
Lời giải
Chọn D
Ta có .
Dựa vào đồ thị ta thấy đường thẳng cắt đồ thị hàm số tại ba điểm phân biệt thuộc
đoạn .
Do đó phương trình có ba nghiệm thực.
Câu 16. (THPT Cù Huy Cận 2019) Cho hàm số có đồ thị như hình vẽ.
Số nghiệm thực của phương trình
A. . B. . C. . D. .
Lời giải
0
y
0
y
4 2
y ax bx c
0
y
( )y f x
2;4
3 ( ) 5 0
f x
2;4
2
1
0
3
5
3 ( ) 5 0 ( )
3
f x f x
5
3
y
( )y f x
2;4
3 ( ) 5 0
f x
( )y f x
4 ( ) 7 0
f x
2
4
3
1
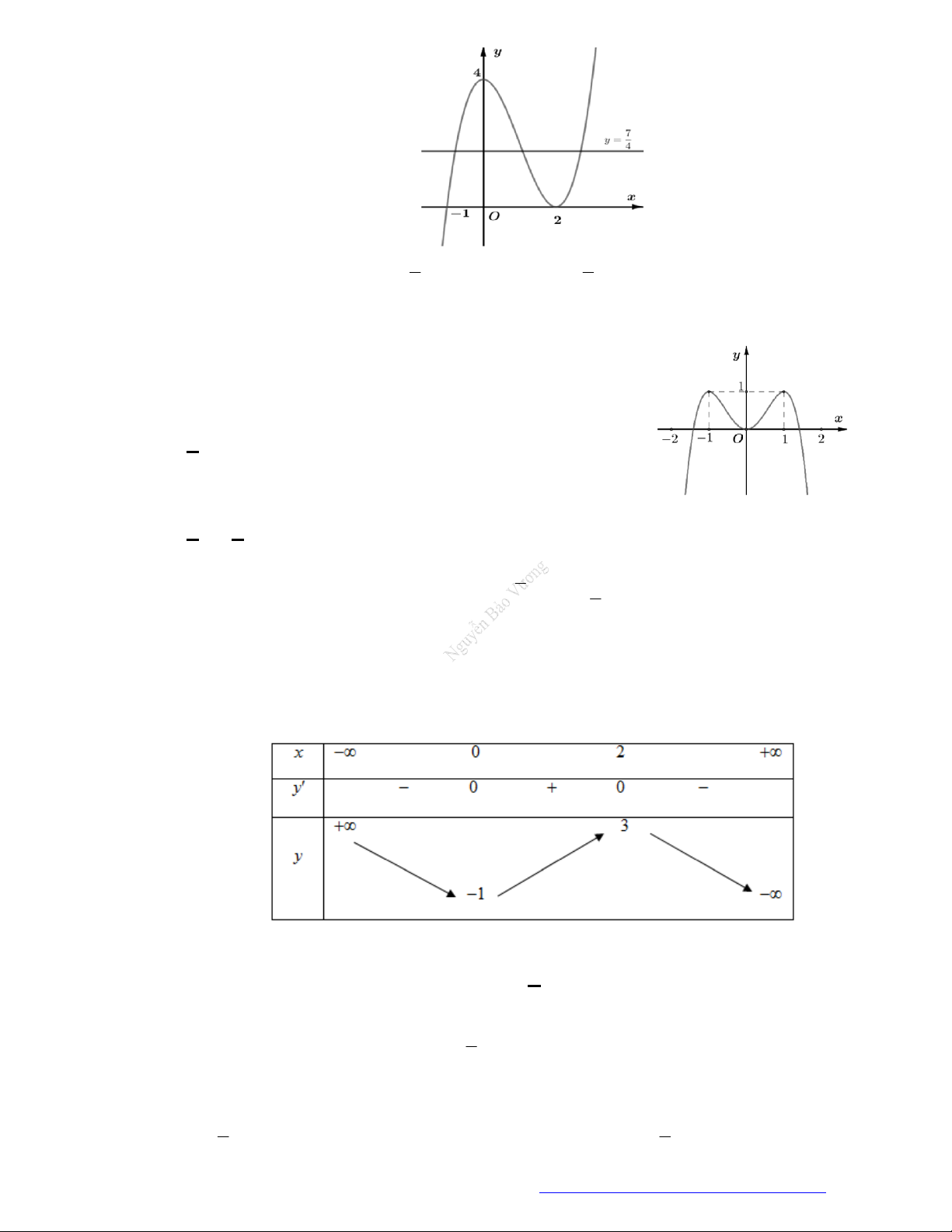
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Ta có: . Do đường thẳng cắt đồ thị hàm số tại điểm
phân biệt nên suy ra phương trình đã cho có nghiệm.
Câu 17. (TRƯỜNG Thpt Lương Tài Số 2 2019) Cho hàm số
có đồ thị như hình vẽ. Phương trình
có tất cả bao nhiêu nghiệm?
A. B.
C. Vô nghiệm D.
Lời giải
Chọn A
Xét phương trình:
Số giao điểm của đường thẳng và đường cong ứng với số nghiệm của phương trình
Theo hình vẽ ta có giao điểm phương trình sẽ có nghiệm phân biệt.
Câu 18. (THPT Yên Phong 1 Bắc Ninh 2019) Cho hàm số có bảng biến thiên sau đây.
Hỏi phương trình có bao nhiêu nghiệm thực?
A. . B. . C. . D. .
Lời giải
Phương trình .
Số nghiệm của phương trình bằng số giao điểm của đồ thị hàm số và đường thẳng
. Nhìn vào bảng biến thiên ta thấy 2 đồ thị và có 3 điểm chung.
7
4 ( ) 7 0 ( )
4
f x f x
7
4
y
y f x
3
3
4 2
( )
y f x ax bx c
1 2. ( ) 0
f x
4
3
2
1
1 2. ( ) 0 1
1
2
2
y f x C
f x f x
y d
d
C
1 .
4
1
4
y f x
2. 5 0
f x
0
1
3
2
5
2. 5 0 *
2
f x f x
*
y f x
5
2
y
y f x
5
2
y
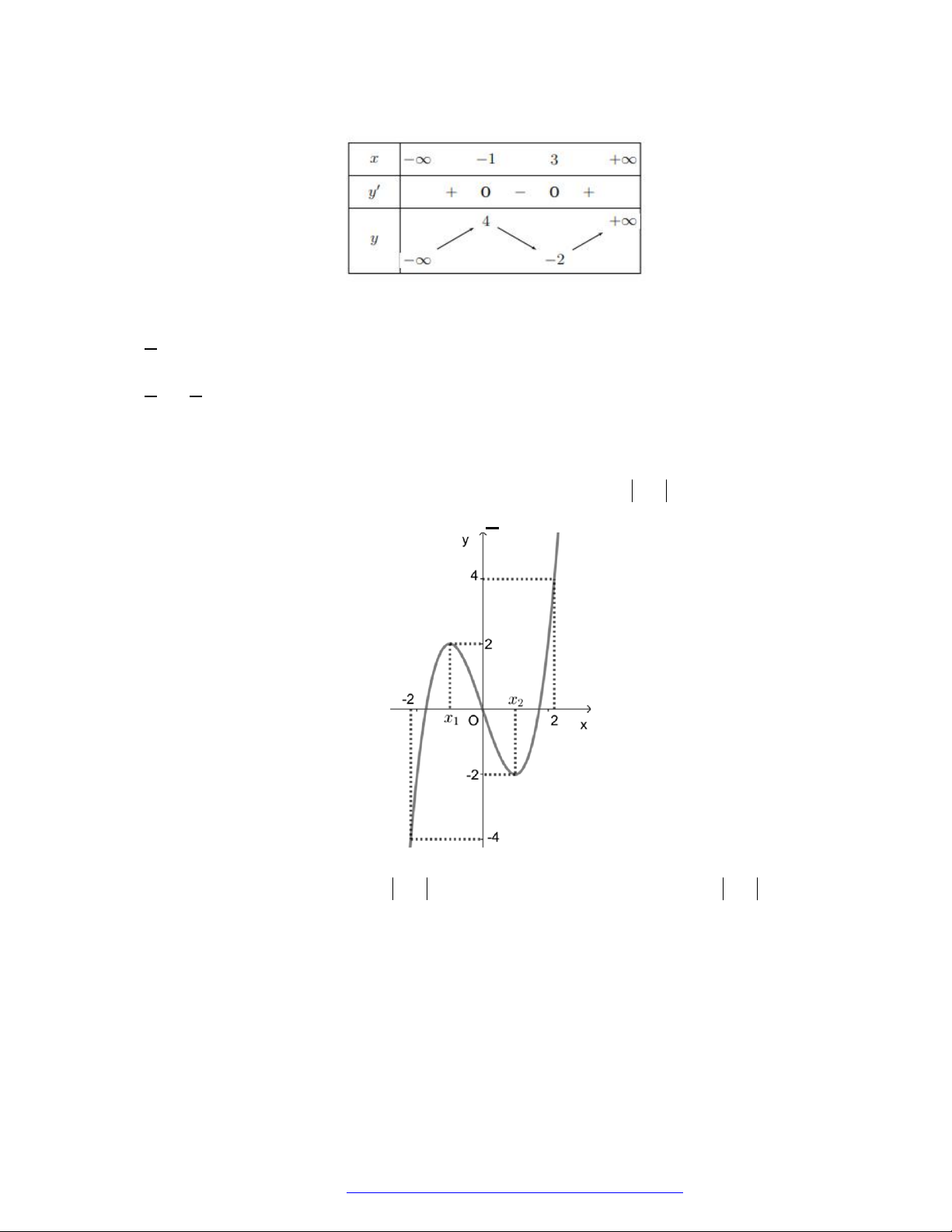
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Vậy phương trình có 3 nghiệm thực.
Câu 19. (THPT Lương Thế Vinh Hà Nội 2019) Cho hàm số có bảng biến thiên như hình bên.
Số nghiệm của phương trình là
A. B. C. D.
Lời giải
Chọn A
Ta có: , theo bảng biến thiên ta có phương trình có 3 nghiệm.
Câu 20. (THPT - Yên Định Thanh Hóa 2019) Cho hàm số liên tục trên đoạn và có đồ
thị là đường cong như hình vẽ bên. Tìm số nghiệm của phương trình trên đoạn .
A. 3. B. 5. C. 6. D. 4.
Lời giải
Ta có số nghiệm của phương trình là số giao điểm của đồ thị hàm số
y f(x)
với
đường thẳng
y 1
.
2. 5 0
f x
y f x
3 0
f x
3
2
1
0
3 0 3
f x f x
y f (x)
2;2
f(x) 1
2;2
f(x) 1
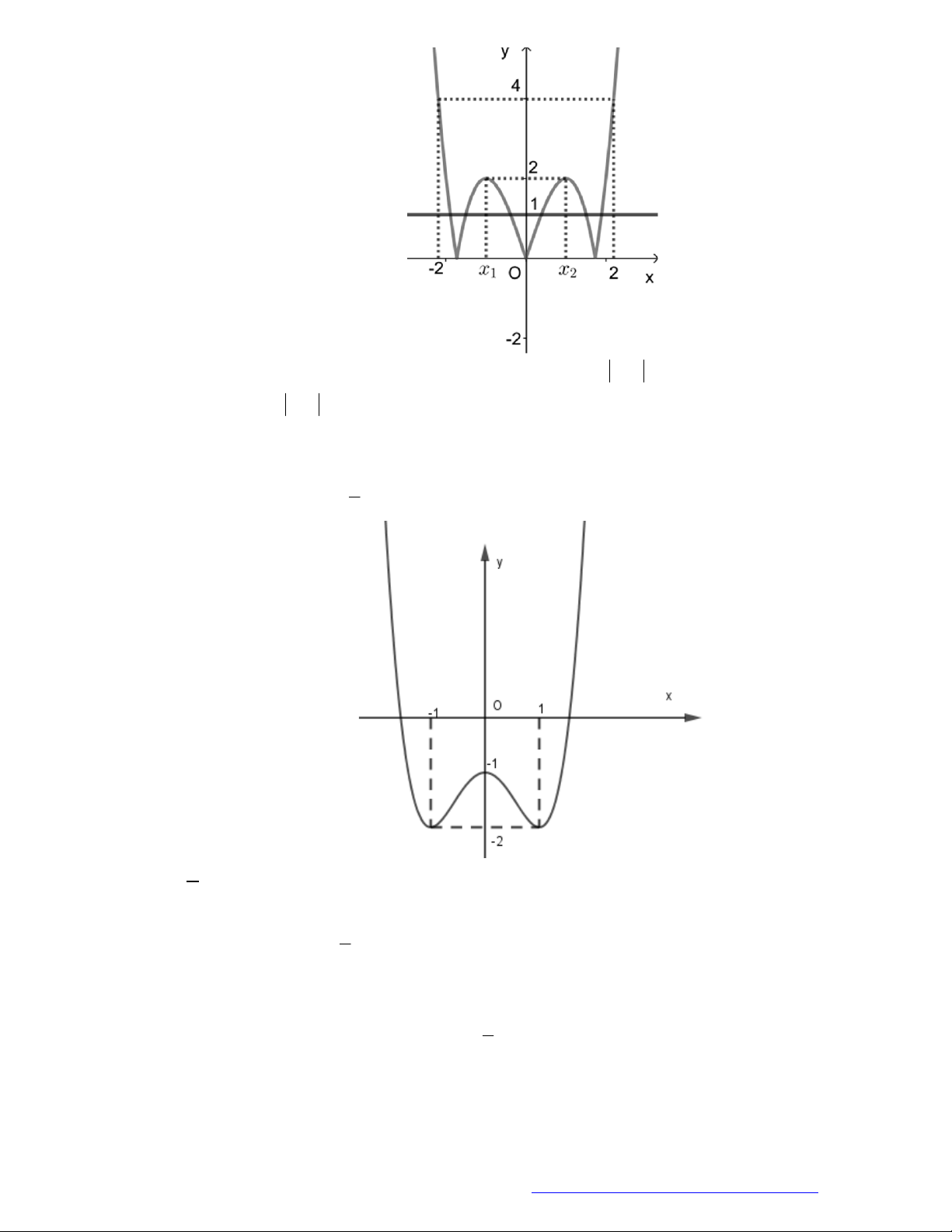
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Từ hình vẽ ta thấy đường thẳng
y 1
cắt đồ thị hàm số
y f(x)
tại 6 điểm. Vậy số nghiệm của
phương trình
f(x) 1
là 6.
Câu 21. (Mã 102 - 2020 Lần 2) Cho hàm số bậc bốn
( )y f x
có đồ thị là đường cong trong hình vẽ bên.
Số nghiệm thực của
phương trình
3
( )
2
f x
là
A.
4
B.
1
C.
3
D.
2
Lời giải
Từ đồ thị ta
3
( )
2
f x
có
4
nghiệm phân biệt
Câu 22. (Mã 103 - 2020 Lần 2) Cho hàm số bậc bốn
y f x
có đồ thị là đường cong trong hình bên.
Số nghiệm thực của phương trình
1
2
f x
là
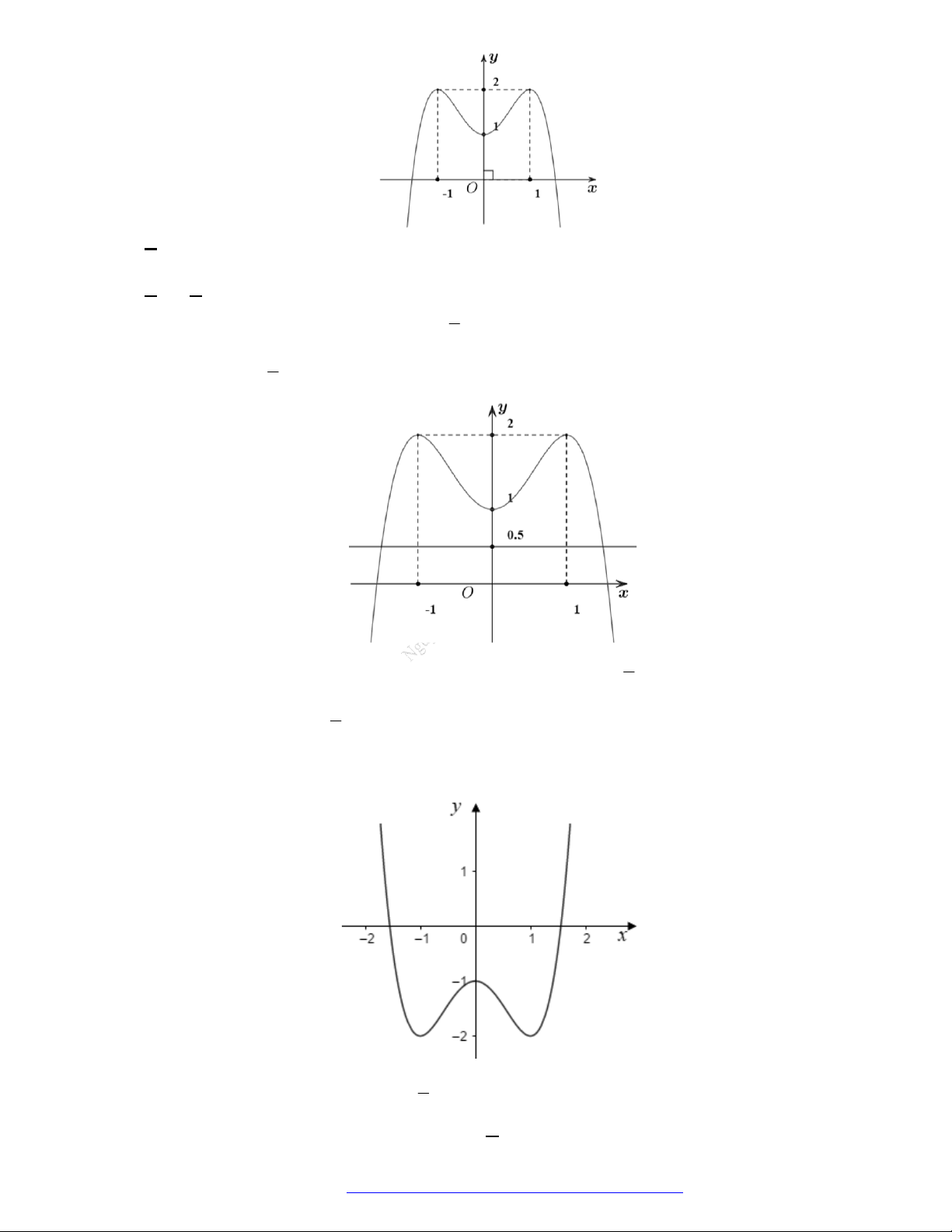
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
2
. B.
4
. C.
1
. D.
3
.
Lời giải
Chọn A
Số nghiệm thực của phương trình
1
2
f x
chính là số giao điểm của đồ thị hàm số
f x
với
đường thẳng
1
2
y
.
Dựa vào hình trên ta thấy đồ thị hàm số
f x
với đường thẳng
1
2
y
có 2 giao điểm.
Vậy phương trình
1
2
f x
có hai nghiệm.
Câu 23. (Mã 101 – 2020 Lần 2) Cho hàm số bậc bốn
y f x
có đồ thị là đường cong trong hình bên.
Số nghiệm của phương trình
1
2
f x
là
A.
3
. B.
4
. C.
2
. D.
1x
.
Lời giải
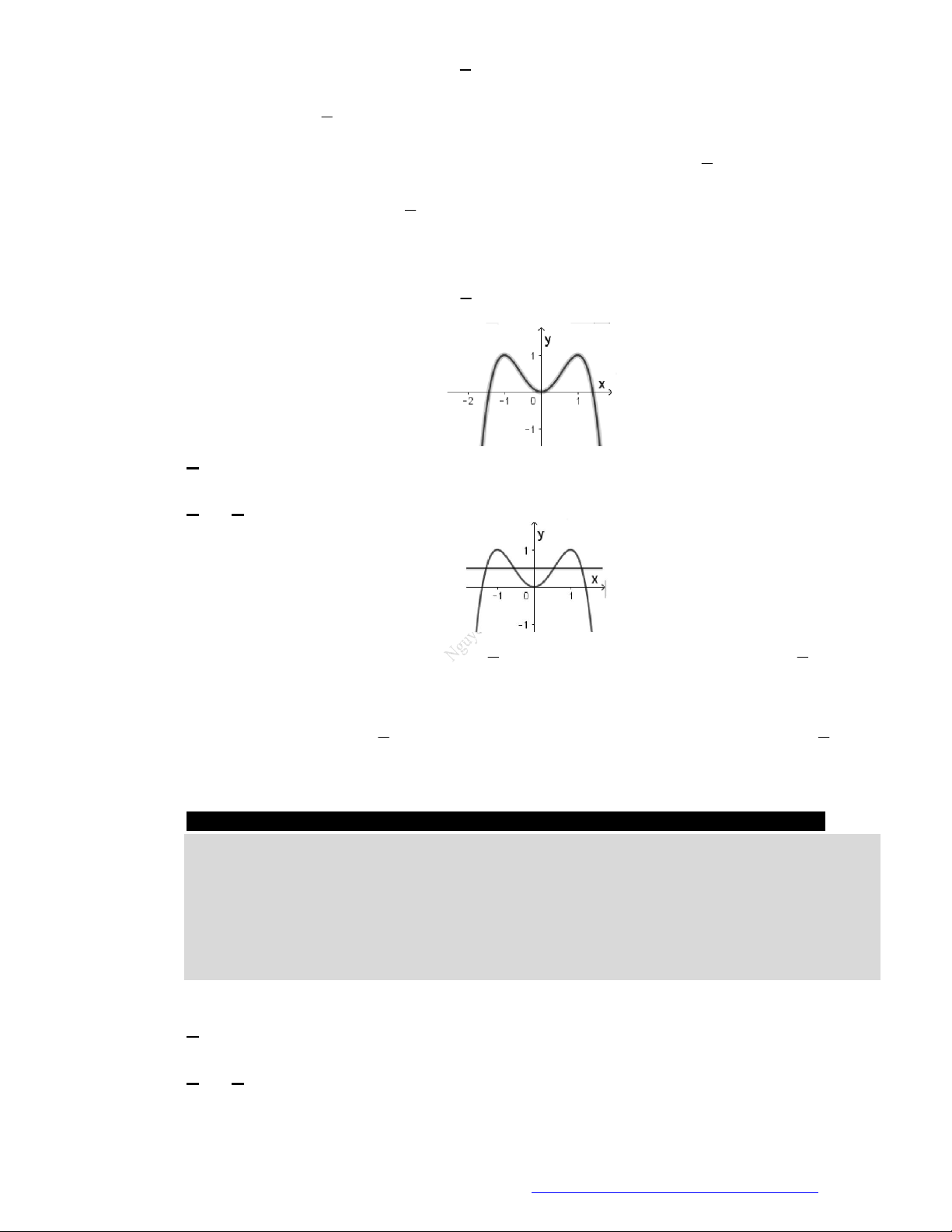
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Số nghiệm của phương trình
1
2
f x
bằng số giao điểm của đồ thị hàm số
y f x
và
đường thẳng
1
2
y
.
Dựa vào đồ thị ta thấy: đồ thị hàm số
y f x
và đường thẳng
1
2
y
cắt nhau tại 2 điểm.
Nên phương trình
1
2
f x
có 2 nghiệm.
Câu 24. (Mã 104 - 2020 Lần 2) Cho hàm số
y f x
có đồ thị là đường cong trong hình bên. Số
nghiệm thực của phương trình
1
2
f x
là
A.
4
. B.
2
. C.
1
. D.
3
.
Lời giải
Chọn A
Số nghiệm thực của phương trình
1
2
f x
bằng số giao điểm của đường thẳng
1
2
y
và có đồ
thị hàm số
y f x
.
Ta thấy đường thẳng
1
2
y
cắt đồ thị hàm số tại
4
điểm nên phương trình
1
2
f x
có
4
nghiệm.
Dạng 2. Bài toán tương giao đồ thị thông qua hàm số cho trước (không chứa tham số)
Cho hai đồ thị
( )y f x
và
( )y g x
.
Bước 1. Giải phương trình
( ) ( )f x g x
.
Bước 2. Tìm
Số giao điểm?
Hoành độ giao điểm?
Tung độ giao điểm?
Câu 25. (Đề Tham Khảo 2020 Lần 2) Số giao điểm của đồ thị hàm số
3
3 1y x x
và trục hoành là
A.
3
. B.
0
. C.
2
. D.
1
.
Lời giải
Chọn A
Tập xác định:
.
Ta có:
2 2
3 3 3 1 ; 0 1y x x y x
.
Bảng biến thiên
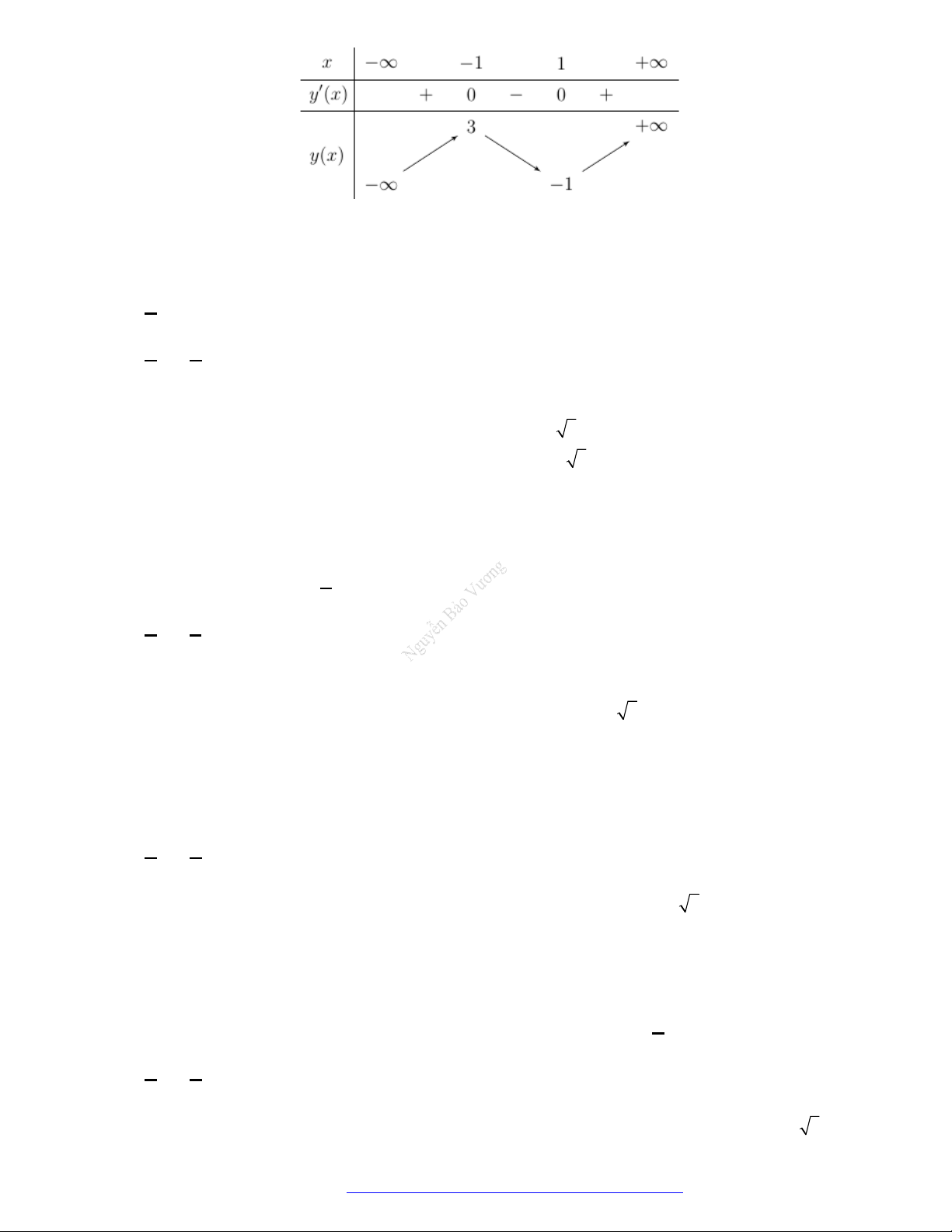
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Từ bảng biến thiên ta thấy đồ thị hàm số cắt trục hoành tại
3
điểm phân biệt.
Câu 26. (Mã 101 - 2020 Lần 1) Số giao điểm của đồ thị hàm số
3 2
3y x x và đồ thị hàm số
2
3 3y x x là
A.
3
. B.
1
. C.
2
. D.
0
.
Lời giải
Chọn A
Phương trình hoành độ giao điểm của hai đồ thị đã cho là:
3 2 2 3 2
0
3 3 3 3 0 3 0 3
3
x
x x x x x x x x x
x
.
Hai đồ thị đã cho cắt nhau tại 3 điểm.
Câu 27. (Mã 102 - 2020 Lần 1) Số giao điểm của đồ thị hàm số
3 2
y x x và đồ thị hàm số
2
5y x x là
A.
2
. B.
3
. C.
1
. D.
0
.
Lời giải
Chọn B
Số giao điểm của đồ thị hàm số
3 2
y x x
và đồ thị hàm số
2
5y x x
chính là số nghiệm
thực của phương trình
3 2 2 3
0
5 5 0
5
x
x x x x x x
x
.
Câu 28. (Mã 103 - 2020 Lần 1) Số giao điểm của đồ thị hàm số
3 2
y x x và đồ thị hàm số
2
5y x x
A.
3.
B.
0
. C.
1.
D.
2.
Lời giải
Chọn A
Phương trình hoành độ giao điểm:
3 2 2 3
0
5 5 0
5
x
x x x x x x
x
.
Vậy số giao điểm của 2 đồ thị là 3.
Câu 29. (Mã 104 - 2020 Lần 1) Số giao điểm của đồ thị hàm số
2
3y x x
và đồ thị hàm số
3 2
y x x
là
A.
1
. B.
0
. C.
2
. D.
3
Lời giải
Chọn D
Phương trình hoành độ giao điểm của hai đồ thị là
3 2 2 3
0
3 3 0
3
x
x x x x x x
x
.
Câu 30. (Mã 102 - 2020 Lần 2) Số giao điểm của đồ thị hàm số
3
7y x x với trục hoành là

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
A.
0
. B.
3
. C.
2
. D.
1
.
Lời giải
Chọn B
Phương trình hoành độ giao điểm của đồ thị và trục hoành là:
3
7 0
x x
2
0
7 0
7
x
x x
x
.
Số giao điểm của đồ thị hàm số
3
7y x x
với trục hoành bằng
3
.
Câu 31. (Mã 103 - 2020 Lần 2) Số giao điểm của đồ thị hàm số
3
3 y x x
với trục hoành là
A.
2
. B.
0
. C.
3
. D.
1
.
Lời giải
Chọn C
Xét phương trình hoành dộ giao điểm
3 2
0
3 0 ( 3) 0
3
x
x x x x
x
.
Vậy có 3 giao điểm.
Câu 32. (Mã 101 – 2020 Lần 2) Số giao điểm của đồ thị hàm số
3
6y x x
với trục hoành là
A.
2
. B.
3
. C.
1
. D.
0
.
Lời giải
Chọn B
Ta có hoành độ giao điểm của đồ thị hàm số
3
6y x x
với trục hoành là nghiệm của phương
trình
3
6 0
x x
(*)
2
6 0
x x
0
6
x
x
.
Phương trình (*) có ba nghiệm phân biệt, do đó đồ thị hàm số
3
6y x x
cắt trục hoành tại ba
điểm phân biệt.
Câu 33. (Mã 104 - 2020 Lần 2) Số giao điểm của đồ thị hàm số
3
5y x x
với trục hoành là:
A.
3
B.
2
C.
0
D.
1
Lời giải
Chọn A.
Ta có
3
5
5 0 5
0
x
x x x
x
Vậy số giao điểm của đồ thị hàm số
3
5y x x
với trục hoành là
3
Câu 34. (Mã 105 2017) Cho hàm số
2
2 1
y x x
có đồ thị
C
. Mệnh đề nào dưới đây đúng?
A.
C
cắt trục hoành tại một điểm. B.
C
cắt trục hoành tại ba điểm.
C.
C
cắt trục hoành tại hai điểm. D.
C
không cắt trục hoành.
Lời giải
Chọn A
Dễ thấy phương trình
2
2 1 0
x x
có 1 nghiệm
2x
C
cắt trục hoành tại một điểm.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 35. (Đề Minh Họa 2017) Biết rằng đường thẳng
2 2y x
cắt đồ thị hàm số
3
2
y x x
tại
điểm duy nhất; kí hiệu
0 0
;x y
là tọa độ của điểm đó. Tìm
0
y
A.
0
4
y
B.
0
0
y
C.
0
2
y
D.
0
1
y
Lời giải
Chọn C
Xét phương trình hoành độ giao điểm:
3 3
2 2 2 3 0 0
x x x x x x
Với
0 0
0 2
x y
.
Câu 36. (THPT - Yên Định Thanh Hóa 2019) Gọi
P
là số giao điểm của hai đồ thị
3 2
1
y x x
và
2
1
y x
. Tìm
P
.
A.
0
P
. B.
2P
. C.
1P
. D.
3
P
.
Lời giải
Xét phương trình hoành độ giao điểm của hai đồ thị
3 2
1
y x x
và
2
1
y x
:
3 2 2 3 2
0
1 1 2 0
2
x
x x x x x
x
Với
0 1x y
.
Với
2 5
x y
.
Nên hai đồ thị trên có hai giao điểm là
0;1
và
2;5
.
Vậy
2P
.
Câu 37. (Đề Tham Khảo 2017) Cho hàm số
3
3 y x x
có đồ thị
C
. Tìm số giao điểm của
C
và
trục hoành.
A.
2
B.
3
C.
1
D.
0
Lời giải
Chọn B
Xét phương trình hoành độ giao điểm của
C
và trục hoành:
3
3 0
x x
0
3
x
x
Vậy số giao điểm của
( )C
và trục hoành là 3.
Câu 38. (THPT Yên Khánh - Ninh Bình 2019) Cho hàm số
4 2
3y x x
có đồ thị
C
. Số giao điểm
của đồ thị
C
và đường thẳng
2
y
là
A.
2
. B.
1
. C.
0
. D.
4
.
Lời giải
Số giao điểm của đồ thị
C
và đường thẳng
2
y
là số nghiệm của phương trình sau:
2
4 2 4 2
2
3 17
3 17
2
3 2 3 2 0
2
3 17
0
2
x
x x x x x
x
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
Phương trình hoành độ giao điểm có 2 nghiệm nên số giao điểm của đồ thị
C
và đường thẳng là
2.
Câu 39. (Chuyên Trần Phú Hải Phòng 2019) Biết rằng đường thẳng
4 5y x
cắt đồ thị hàm số
3
2 1y x x
tại điểm duy nhất; kí hiệu là tọa độ của điểm đó. Tìm .
A.
0
10y
. B.
0
13y
. C.
0
11y
. D.
0
12y
.
Lời giải
Phương trình hoành độ giao điểm là
3 3
2 1 4 5 2 4 0 2x x x x x x
Với
2 13x y
. Vậy
0
13y
Câu 40. (THPT Yên Phong 1 Bắc Ninh 2019) Đồ thị của hàm số
4 2
3 1y x x
cắt trục tung tại
điểm có tung độ bao nhiêu
A. -3. B. 0. C. 1. D. -1.
Lời giải
Trục tung có phương trình:
0x
. Thay
0x
vào
4 2
3 1y x x
được:
1y
.
Câu 41. (THPT Việt Đức Hà Nội 2019) Số giao điểm của đường cong
3 2
2 2 1y x x x
và đường
thẳng
1y x
là
A.
1
B.
2
C.
3
D.
0
Lời giải
Chọn A
Xét phương trình hoành độ giao điểm
3 2
3 2
2
2 2 1 1
2 3 0
2 3 0 0
x x x x
x x x
x x x x
Câu 42. đồ thị hàm số
4 2
3 1y x x
và đồ thị hàm số
2
2 7y x
có bao nhiêu điểm chung?
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn C.
Pthdgd:
2
4 2 2 4 2
2
3
3 1 2 7 6 0 3
2
x
x x x x x x
x
.
Do pt có
2
nghiệm nên đồ thị hai hàm số có
2
điểm chung.
Câu 43. Cho hàm số
3
2 5y x x có đồ thị
C
Tìm số giao điểm của
C
và trục hoành.
A.
2
. B.
3
. C.
1
. D.
0
.
Lời giải
Chọn B.
Pthd của
C
và trục hoành là:
3
0
2 5 0
5
2
x
x x
x
có
3
giao điểm.
Chú ý: Ở bài toán này hoàn toàn có thể giải trực tiếp bằng Casio với phương trình
3
2 5 0x x
,
nhưng chắc chắn thao tác bấm máy sẽ chậm hơn việc tính tay( thậm chí bài này không cần nháp
0 0
;x y
0
y
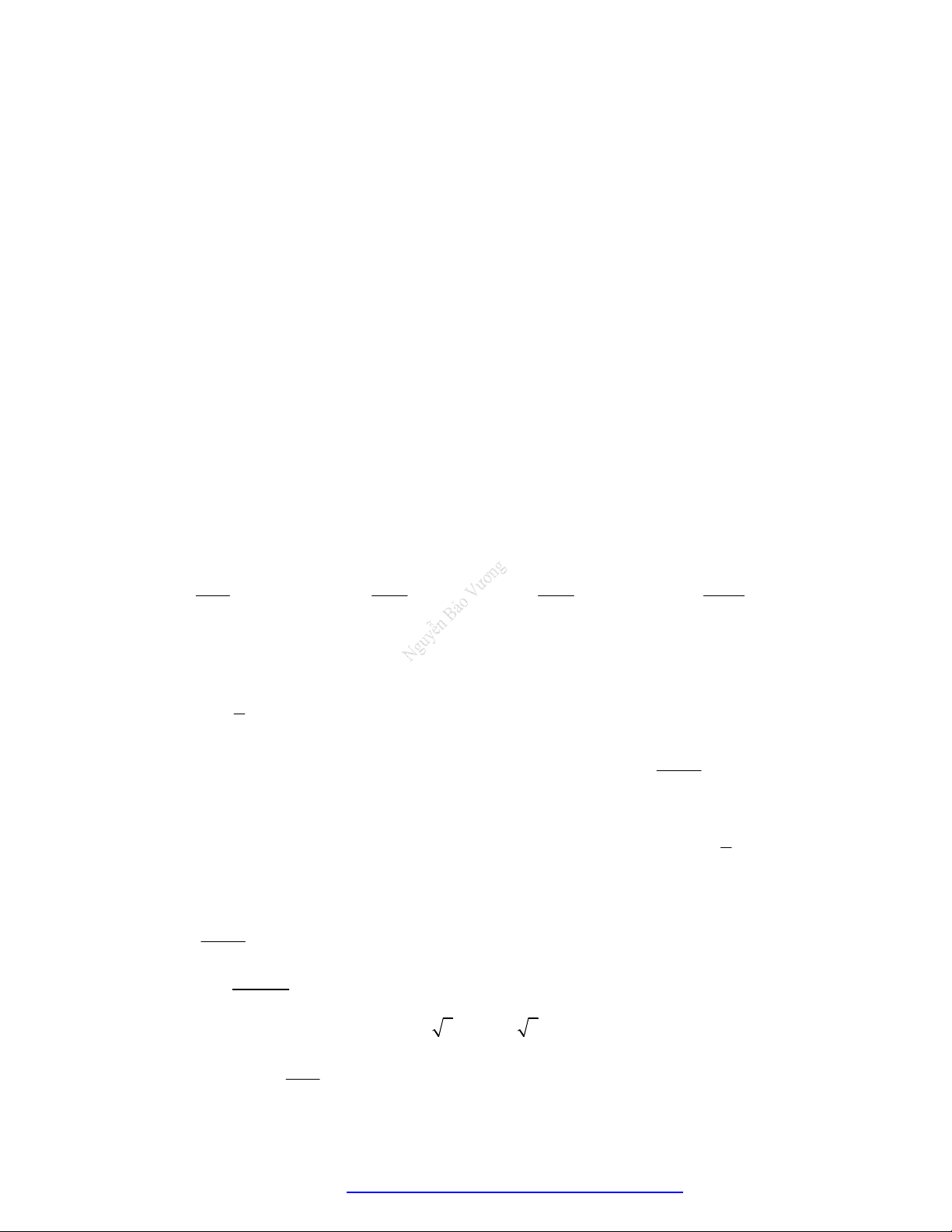
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
khi mà kết quả đã hiện ra luôn khi ta đọc đề xong). Vì vậy, Casio là điều không cần thiết với câu
hỏi này.
Câu 44. Cho hàm số
2
3 2
y x x
có đồ thị
C
. Mệnh đề nào dưới đây đúng?
A.
C
cắt trục hoành tại hai điểm. B.
C
cắt trục hoành tại một điểm.
C.
C
không cắt trục hoành. D.
C
cắt trục hoành tại ba điểm.
Lời giải
Chọn B.
Pthd của
C
và trục hoành là:
2
2
3
3 2 0 3
2
x
x x x
x
nghĩa là
C
cắt trục hoành tại một điểm
Câu 45. Biết rằng đường thẳng
2
y x
cắt đồ thị hàm số
3 2
4
y x x x
tại điểm duy nhất, kí hiệu
0 0
;x y
là tọa độ của điểm đó. Tìm
0
y
.
A.
0
1
y
. B.
0
3
y
. C.
0
2
y
. D.
0
4
y
.
Lời giải
Chọn A.
Pthdgd:
3 2 3 2
0
2 4 2 0 1 1
x x x x x x x y
.
Câu 46. đồ thị hàm số nào sau đây cắt trục tung tại điểm có tung độ âm?
A.
1
3
x
y
x
. B.
1
4
x
y
x
. C.
1
2
x
y
x
. D.
2 1
5
x
y
x
.
Lời giải
Chọn C
Trục tung có phương trình
0
x
, ta thay
0
x
lần lượt vào các phương án thì chỉ có phương án C
cho ta
1
0
2
y
.
Câu 47. Gọi
,M N
là giao điểm của đường thẳng
1y x
và đường cong
2 4
1
x
y
x
. Khi đó hoành độ
I
x
của trung điểm
I
của đoạn
MN
bằng bao nhiêu?
A.
2
I
x
. B.
1
I
x
. C.
5
I
x
. D.
5
2
I
x
.
Lời giải
Chọn B.
Pthdgd
2 4
1 1
1
x
x x
x
2
2 5 0
x x
(*)
Khi đó
1
2
M N
I
x x
x
.
Chú ý: có thể giải (*), tìm được
1 6, 1 6 1
M N I
x x x
Câu 48. Cho hàm số
1
3
x
y
x
có đồ thị
C
và các đường thẳng
1
: 2d y x
,
2
: 2 2
d y x
,
3
: 3 3d y x
,
4
: 3d y x
. Hỏi có bao nhiêu đường thẳng trong bốn đường thẳng
1 2 3 4
, , ,d d d d
đi qua giao điểm của
C
và trục hoành.
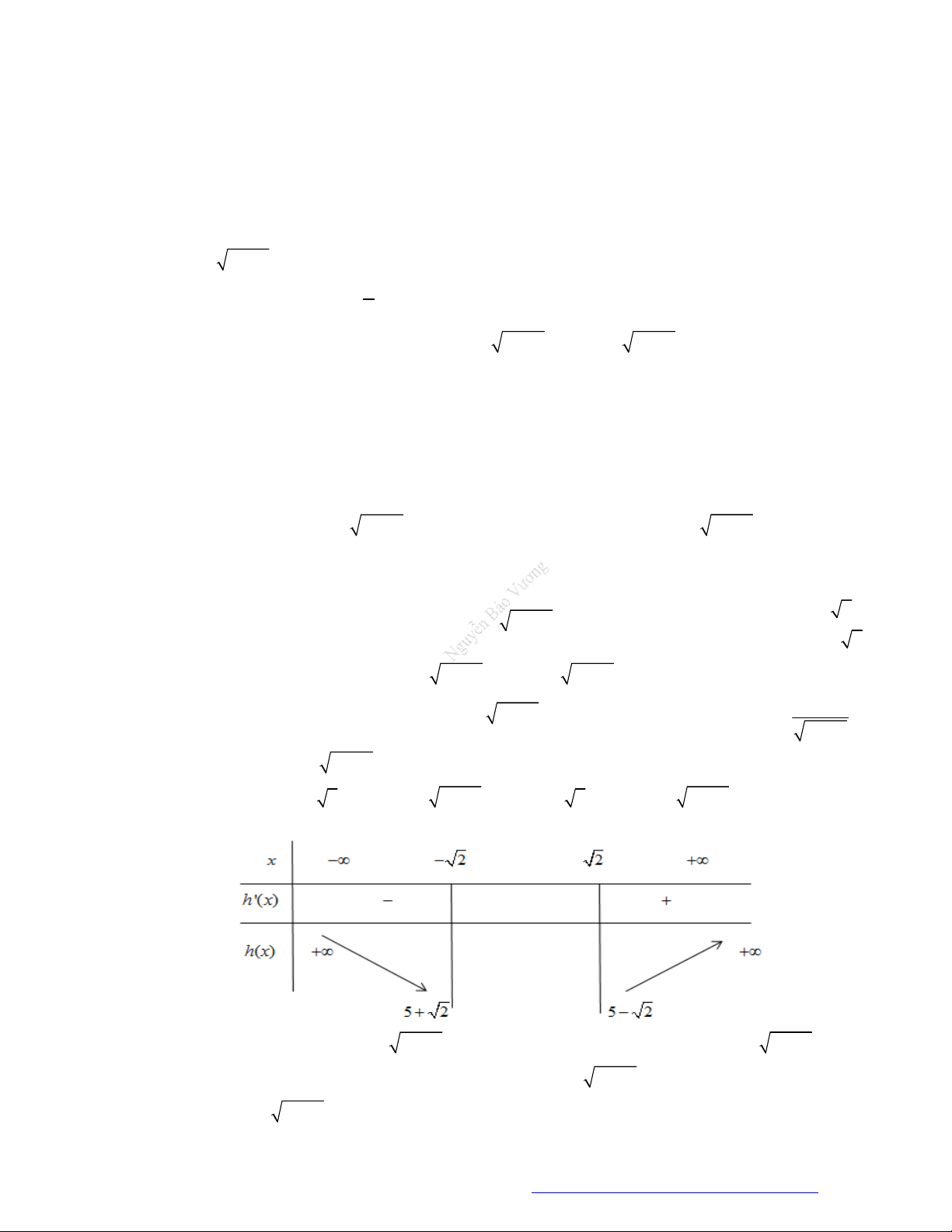
T
ÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
A.
1
. B.
2
. C.
3
. D.
4
.
Lờ
i giải
Chọn A.
Ta có
C
cắt trục hoành
0y
tại điểm
1
;0M
.
Trong các đường thẳng
1
2 3 4
,
, ,d d d d chỉ có
3
M
d , có nghĩa là có
1
đườ
ng thẳng đi qua
1;0M
.
Câu 49. (THPT Quang Trung Đống Đa Hà Nội 2019) Tìm số giao điểm của đồ thị hàm số
4
4
5y x
và đường thẳng
y
x
A.
3
. B.
0
. C.
2
. D.
1
.
Lờ
i giải
Cách 1: Phương trình hoành độ giao điểm
4
4
4 5 4 5x x x x
4
2
5
4 ( 5)
x
x x
4
2
5
10 29 0 (*)
x
x x x
D
o
5x
nê
n
4
2 2 2
(
1) 0x x x x
và
10
29 0x
. Vì vậ
y
(*)
vô nghiệm
Như
vậy phương trình
4
4 5x x
vô
nghiệm hay đồ thị hàm số
4
4 5y x
và
đường
thẳng
y x
khôn
g có giao điểm nào.
Cách 2:
Phương trình hoành độ giao điểm
4
4
5x x
.
Ta có điều kiện xác định
2
2
x
x
Với điều kiện trên ta có
4
4
4
5 4 5 0x x x x
Xé
t hàm số
4
(
) 4 5h x x x
. Ta
có
3
4
2
'
( ) 1
4
x
h x
x
;
3 4
'
( ) 0 2 4h x x x
Với
2x
ta
có
3
4
2 4x x
.
Với
2x
ta
có
3
4
2 4x x
T
a có Bảng biến thiên:
Số nghiệm của phương trình
4
4
5x x
l
à số giao điểm của đồ thị
4
(
) 4 5y h x x x
và
trục hoành
0y
. Dựa và
o BBT ta thấy phương trình
4
4
5x x
vô
nghiệm hay đồ thị
hàm số
4
4
5y x
và đường thẳng
y x
khôn
g có giao điểm nào.
-------------------- HẾT --------------------

T
ÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 1
DẠNG TOÁN DÀNH CHO ĐỐI TƯỢNG HỌC SINH KHÁ MỨC 7+8+9 ĐIỂM
Dạng 1. Bài toán tương giao đường thẳng với đồ thị hàm số bậc 3 (CHỨA THAM SỐ)
Bài
toán tổng quát: Tìmcácgiátrịcủathamsố
m
để
đểđườngthẳng
:d y px q
cắt
đồthịhàmsố
3
2
(
) :C y ax bx cx d tại3điểmphânbiệtthỏađiềukiện
K
?
(dạng có điều kiện)
Phương pháp giải:
Bước
1. Lậpphươngtrìnhhoànhđộgiaođiểmcủa
d
và
(
)C
là:
3
2
ax
bx cx d px q
Đưavềphươngtrìnhbậcbavànhẩmnghiệmđặcbiệt
o
x x đểchiaHoocnerđược:
2
2
(
) ( ) 0
( ) 0
o
o
x
x
x x ax b x c
g x ax b x c
Bước
2. Để
d
cắ
t
(
)C
tạ
i ba điểm phân biệt phương trình
(
) 0g x
c
ó 2 nghiệm phân biệt khác
(
)
0
(
) 0
g
x
o
o
x
g
x
Giả
ihệnày,tìmđượcgiátrị
1
.m
D
Bước 3.Gọi
1
1 2 2
( ; ), ( ; ), ( ; )
o
o
A x px q B x px q C x px q với
1
2
, x x làhainghiệmcủa
(
) 0.g x
T
heoViét,tacó:
1
2
b
x
x
a
và
1
2
c
x
x
a
(1
)
Bước 4.
BiếnđổiđiềukiệnKvềdạngtổngvàtíchcủa
1 2
,
x x (2)
T
hế(1)vào(2)sẽthuđượcphươngtrìnhhoặcbấtphươngtrìnhvớibiếnlà
.m
Giả
ichúngsẽtìmđượcgiátrị
2
.m
D
Kế
tluận:
1
2
.m
D D
Một s
ố công thức tính nhanh “ thường gặp “ liên quan đến cấp số
Tìm điều kiện để đồ thị hàm số
3
2
y ax bx cx d cắt trục hoành tại
3
điểm phân biệt có hoành
độ
lập thành cấp số cộng.
Điề
u kiện cần:
Giả sử
1
2 3
,
,x x x là nghiệm của phương trình
3
2
0a
x bx cx d
Khi đó:
3
2
1 2 3
(
)( )( )ax bx cx d a x x x x x x
, đồng nhất
hệ số ta được
2
3
b
x
a
Thế
2
3
b
x
a
vào phương trình
3
2
0a
x bx cx d
ta được điều kiện ràng buộc về tham số hoặc giá trị của
tham
số.
Điề
u kiện đủ:
T
hử các điều kiện ràng buộc về tham số hoặc giá trị của tham số để phương trình
3 2
0a
x bx cx d
có
3
nghiệm
phân biệt.
Tìm đ
iều kiện để đồ thị hàm số
3
2
y
ax bx cx d
cắt trục hoành tại
3
đ
iểm phân biệt có hoành
độ lập thành cấp số nhân.
Điề
u kiện cần:
Giả sử
1 2 3
,
,x x x là nghiệm của phương trình
3
2
0a
x bx cx d
Khi đó:
3
2
1 2 3
(
)( )( )ax bx cx d a x x x x x x
, đồng nhất
hệ số ta được
3
2
d
x
a
T
hế
3
2
d
x
a
v
ào phương trình
3 2
0a
x bx cx d
t
a được điều kiện ràng buộc về tham số hoặc giá trị
T
ƯƠNG GIAO ĐỒ THỊ HÀM SỐ
Ch
uyên đề 8

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
của tham số.
Điều kiện đủ:
Thử các điều kiện ràng buộc về tham số hoặc giá trị của tham số để phương trình
3 2
0
ax bx cx d
có
3
nghiệm phân biệt.
Câu 1. (Sở Ninh Bình 2020) Chohàmsố
3 2
3 2y x mx m
.Cóbaonhiêugiátrịcủathamsốthực
m
đểđồthịhàmsốcắttrụchoànhtạibađiểmphânbiệtcóhoànhđộlậpthànhcấpsốcộng?
A.
1
. B.
2
. C.
3
. D.
0
.
Lời giải
Chọn B
Phươngtrìnhhoànhđộgiaođiểm:
3 2
3 2 0
x mx m
*
Phươngtrình
3 2
0
ax bx cx d
cóbanghiệmlậpthànhcấpsốcộng
phươngtrìnhcómột
nghiệm
0
3
b
x
a
.
Suyraphươngtrình
*
cómộtnghiệm
.x m
Thay
x m
vàophươngtrình
*
,tađược
3 2 3
1
3 . 2 0 2 2 0
0
m
m m m m m m
m
.
Thửlại:
Với
1
m
,tađược
3 2
1 3
3 2 0 1
1 3
x
x x x
x
.
Dođó
1
m
thỏamãn.
Với
1
m
,tađược
3 2
1 3
3 2 0 1
1 3
x
x x x
x
.
Dođó
1
m
thỏamãn.
Với
0
m
,tađược
3
0 0
x x
.
Dođó
0
m
khôngthỏamãn.
Vậy
1
m
làhaigiátrịcầntìm.
Câu 2. (Cụm Liên Trường Hải Phòng 2019) Tìmtấtcảcácgiátrịthựccủathamsố
m
đểđồthịhàmsố
3 2
3 2
y x x C
cắtđường
thẳng
: ( 1)
d y m x
tạibađiểmphânbiệt
1 2 3
, ,x x x
.
A.
2
m
. B.
2
m
. C.
3
m
. D.
3
m
.
Lời giải
Phươngtrìnhhoànhđộgiaođiểmcủa
C
và
d
là
3 2
3 2 ( 1)
x x m x
(1)
Phươngtrình
(1)
3 2 2
3 2 0 ( 1)( 2 2) 0
x x mx m x x x m
2 2
1 0 1
( ) 2 2 0 ( ) 2 2 0 (2)
x x
f x x x m f x x x m
Phươngtrình
(1)
luôncónghiệm
1
x
,vậyđểphươngtrình
(1)
cóbanghiệmphânbiệtthì
phươngtrình
(2)
phảicóhainghiệmphânbiệtkhác1.
' 1 2 0 3
3
(1) 0 3
m m
m
f m
.
Vậy
3
m
thỏamãnyêucầubàitoán.
Câu 3. (Chuyên Vĩnh Phúc 2019) Đườngthẳng
cóphươngtrình
2 1y x
cắtđồthịcủahàmsố
3
3
y x x
tạihaiđiểm
A
và
B
vớitọađộđượckíhiệulầnlượtlà
;
A A
A x y
và
;
B B
B x y
trongđó
B A
x x
.Tìm
B B
x y
?

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
A.
5
B B
x y
B.
2
B B
x y
C.
4
B B
x y
D.
7
B B
x y
Lời giải
Phươngtrìnhhoànhđộgiaođiểmcủa
và
3
3
y x x
:
3 3
2 3
3 2 1 3 2 0
1 3
x y
x x x x x
x y
Vậy
1;3 ; ( 2; 3) 5
B B
A B x y
Câu 4. (THPT Ba Đình 2019) Cho hàm số
3 2 3
3
y x mx m
có đồ thị
m
C
và đường thẳng
2 3
: 2d y m x m
.Biếtrằng
1 2 1 2
,
m m m m
làhaigiátrịthựccủa
m
đểđườngthẳng
d
cắtđồ
thị
m
C
tại
3
điểmphânbiệtcóhoànhđộ
1 2 3
, ,x x x
thỏamãn
4 4 4
1 2 3
83
x x x
.Phátbiểunào
sauđâylàđúng vềquanhệgiữahaigiátrị
1 2
,m m
?
A.
1 2
0
m m
. B.
2
1 2
2 4
m m
. C.
2
2 1
2 4
m m
. D.
1 2
0
m m
.
Lời giải
Xétphươngtrìnhhoànhđộgiaođiểmcủa
d
và
m
C
3 2 3 2 3
3 2x mx m m x m
3 2 2 3
3 3 0
x mx m x m
3 2 2 3
3 3 0
x m x mx m
2 2 2 2
2 2
3 0
3 0
3
x x m m x m
x m x m
x m
x m
x m
Đểđườngthẳng
d
cắtđồthị
m
C
tại
3
điểmphânbiệtcóhoànhđộ
1 2 3
, ,x x x
0
m
.
Khiđó,
4 4
4 4 4 4
1 2 3
83 3 83
x x x m m m
4
83 83 1
m m
Vậy
1 2
1, 1
m m
hay
1 2
0
m m
.
Câu 5. (THPT Bạch Đằng Quảng Ninh 2019) Tìmtấtcảcácgiátrịthựccủathamsố
m
đểđồthịhàm
số
3 2
3y x x
cắtđườngthẳng
y m
tạibađiểmphânbiệt.
A.
; 4
m
. B.
4;0
m
.
C.
0;m
. D.
; 4 0;m
.
Lời giải
Chọn B
Tacó
3 2 2
0
3 3 6 ; 0
2
x
y x x y x x y
x
Bảngbiếnthiên:
x
0
2
y
0
0
y
0
4

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Dựavàobảngbiếnthiêntathấyđồthịhàmsố
3 2
3y x x
cắtđườngthẳng
y m
tạibađiểm
phânbiệtkhi
4 0
m
Câu 6. (Mã 123 2017) Tìmtấtcảcácgiátrịthựccủathamsố
m
đểđườngthẳng
1y mx m
cắtđồthị
hàmsố
3 2
3 2
y x x x
tạibađiểm
, ,A B C
phânbiệtsao
AB BC
A.
5
;
4
m
B.
2;m
C.
m
D.
; 0 4;m
Lờigiải
Chọn B
Tacóphươngtrìnhhoànhđộgiaođiểmlà:
3 2 3 2
3 2 1 3 1 0 1
x x x mx m x x x mx m
2
2
1
1 2 1 0
2 1 0
x
x x x m
x x m
.Đểđườngthẳngcắtđồthịhàmsốtạiba
điểmphânbiệtthìphươngtrình
2
2 1 0x x m
cóhainghiệmphânbiệtkhác
1
.Hay
1 1 0 2
2
1 2 1 0 2
m m
m
m m
.Với
2m
thìphươngtrình
1
cóbanghiệmphân
biệtlà
1 2
1, ,x x
(
1 2
,x x
lànghiệmcủa
2
2 1 0x x m
).Mà
1 2
x x
1
2
suyrađiểmcóhoành
độx=1luônlàtrungđiểmcủahaiđiểmcònlại.Nênluôncó3điểmA,B,Cthoảmãn
AB BC
Vậy
2m
.
Câu 7. (Sở Cần Thơ - 2019) Tấtcảgiátrịcủathamsố
m
đểđồthịhàmsố
3 2 2
2 2 4
y x m x m
cắtcáctrụctọađộ
,Ox
Oy
lầnlượttại
,A
B
saochodiệntíchtamgiác
OAB
bằng8là
A.
2
m
. B.
1
m
. C.
3
m
. D.
2
m
.
Lời giải
Chọn D
Giaođiểmcủađồthịhàmsốđãchovớitrụctunglà
2
0;2 4
B m
Phươngtrìnhhoànhđộgiaođiểmcủađồthịđãchovớitrụchoànhlà:
3 2 2 2 2
2
2
2
2 2 4 0 2 2 2 0
1 1 0
x
x m x m x x x m
x m vn
Giaođiểmcủađồthịđãchovớitrụchoànhlà
2;0
A
.
Diệntíchtamgiác
ABC
là:
2
1 1
. .2. 2 4 8 2.
2 2
S OA OB m m
Câu 8. (Mã 110 2017) Tìmtấtcảcácgiátrịthựccủathamsố
m
đểđườngthẳng
y mx
cắtđồthịcủa
hàmsố
3 2
3 2
y x x m
tạibađiểmphânbiệt
, ,A B C
saocho
AB BC
.
A.
; 1
m
B.
:m
C.
1:m
D.
;3
m
Lời giải
Chọn D
Hoànhđộgiaođiểmlànghiệmcủaphươngtrình
3 2 2
3 2 1 2 2 0
x x m mx x x x m
2
1
2 2 0
x
x x m
Đặtnghiệm
2
1.
x
Từgiảithiếtbàitoántrởthànhtìm
m
đểphươngtrìnhcó3nghiệmlậpthành
cấpsốcộng.
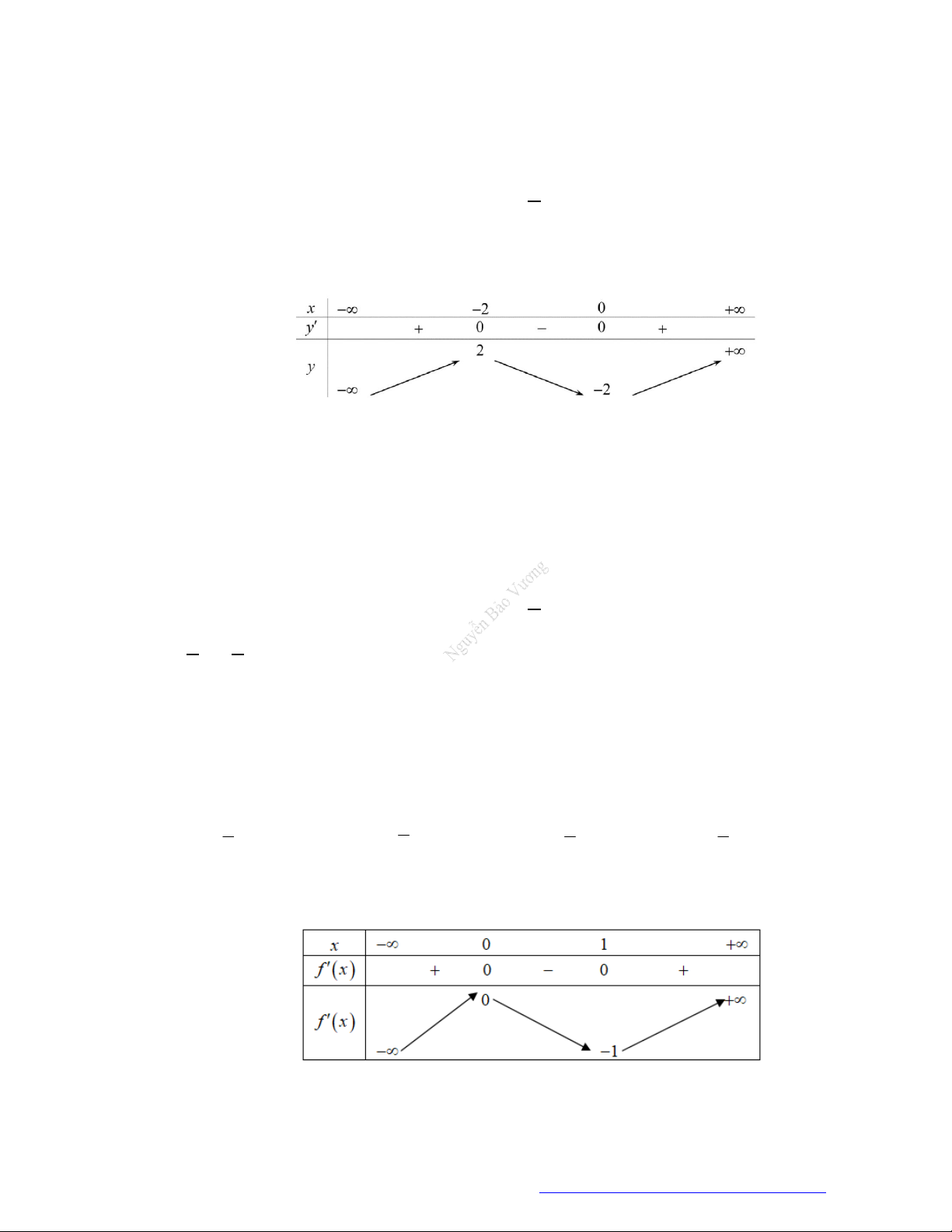
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Khi đó phương trình
2
2 2 0
x x m
phải có 2 nghiệm phân biệt (vì theo Viet rõ ràng
1 3 2
2 2x x x
)
Vậytachỉcần
1 2 0 3m m
Câu 9. (Chuyên Bắc Ninh 2019) Tìmtấtcảcácgiátrịcủathamsố
m
đểphươngtrình
3 2
3 2x x m
cóbanghiệmphânbiệt.
A.
2;m
. B.
; 2m
. C.
2;2m
. D.
2;2m
.
Lời giải
Xéthàmsố
3 2
3 2y x x ,
2
3 6y x x
.
Lậpbảngbiếnthiên
Sốnghiệmcủaphươngtrình
3 2
3 2 *x x m
bằngsốgiaođiểmcủađồthịhàmsố
3 2
3 2y x x
vàđườngthẳng
y m
.
DựavàobảngbiếnthiênsuyraPT(*)có3nghiệmphânbiệtkhi
2 2m
.
Câu 10. (Chuyên Vĩnh Phúc 2019) Đườngthẳng
cóphươngtrình
2 1y x
cắtđồthịcủahàmsố
3
3y x x tạihaiđiểm
A
và
B
vớitọađộđượckíhiệulầnlượtlà
;
A A
A x y
và
;
B B
B x y
trongđó
B A
x x .Tìm
B B
x y ?
A. 5
B B
x y B. 2
B B
x y C. 4
B B
x y D. 7
B B
x y
Lời giải
Chọn C
Hoànhđộgiaođiểmlànghiệmcủaphươngtrình:
3
3 2 1x x x
Giảiphươngtrìnhtađược
1
2
x
x
Vì
B A
x x Vậy 1; 3
B B
x y 4
B B
x y
Câu 11. (ChuyênLêQuýĐônĐiệnBiên2019)Gọi
S
làtậptấtcảcácgiátrịthựccủathamsố
m
để
phươngtrình
3 2
2 3 2 1x x m
cóđúnghainghiệmphânbiệt.Tổngcácphầntửcủa
S
bằng
A.
1
2
. B.
3
2
. C.
5
2
. D.
1
2
.
Lờigiải
Xéthàmsố:
3 2
2 3y x x
2
6 6 0 0 1y x x y x x
.
Bảngbiếnthiên:
Sốnghiệmcủaphươngtrìnhđãchobằngsốgiaođiểmcủahaiđồthị:
3 2
: 2 3
: 2 1
C y x x
d y m

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Nhìnvàobảngbiếnthiêntathấy:Phươngtrìnhđãchocóhainghiệmphân
biệt
1
2 1 1
1
2 1 0
2
m
m
m
m
1
1;
2
S
.
Vậytổngcácphầntửcủa
S
bằng
1 3
1
2 2
.
Câu 12. (THPTMinhKhaiHàTĩnh2019)Tìmtấtcảcácgiátrịthựccủathamsố
m
đểđườngthẳng
5y x
cắtđồthịhàmsố
3 2
2 x 3( 1) 5y x m m x tại3điểmphânbiệt.
A.
1
2
m
m
. B.
2
3
1
2
m
m
m
. C.
2
3
1
2
m
m
m
. D.
1
2
m
m
.
Lờigiải
Phươngtrìnhhoànhđộgiaođiểmchunglà:
3 2
2 x 3( 1) 5 5x m m x x
3 2
2 x (3 2) 0x m m x
2
0
2 3 2 0 (1)
x
x mx m
Đườngthẳng
5y x
cắtđồthịhàmsố
3 2
2 x 3( 1) 5y x m m x tại3điểmphânbiệt
phươngtrình(1)cóhainghiệmphânbiệtkhác
0
.
2
3 2 0
3 2 0
m m
m
2
1
2
3
m
m
m
2
3
1
2
m
m
m
.
Câu 13. (THPTLươngThếVinhHàNội2019)Chohàmsốbậcba
y f x
cóđồthị
C
nhưhình
vẽ, đường thẳng
d
có phương trình
1y x
. Biết phương trình
0f x
có ba nghiệm
1 2 3
x x x
.Giátrịcủa
1 3
x x
bằng
A.
3
. B.
7
3
. C.
2
. D.
5
2
.
Lờigiải
+Tacó:
1
1 1
3
x
f x x x
x
.
f x
làhàmbậcbanên
1 1 1 3f x x a x x x
1 1 3 1f x a x x x x
;
0 2 1f a
.
1 1 3 1f x x x x x
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
+
2
1
0
1 3 1 0 2
x x
f x
x x
.
1 3
,x x
làcácnghiệmcủa
2
nêntacó
1 3
2
x x
.
thẳng
5
2
y
nêntừđồthịtacóphươngtrìnhđãchocó
4
nghiệmphânbiệt.
Câu 14. (ChuyênLêThánhTông2019)Cóbaonhiêugiátrịnguyêncủathamsố
2018;2019
m
để
đồthịhàmsố
3
3 3y x mx
vàđườngthẳng
3 1y x
códuynhấtmộtđiểmchung?
A.
1
. B.
2019
. C.
4038
. D.
2018
.
Lờigiải
Phươngtrìnhhoànhđộgiaođiểm:
3
3 3 3 1x mx x
3
3 2 3x x mx
3
3 2
3
x x
m
x
(1).
Xéthàm
3
2
3 2 2
3
x x
f x x
x x
;
3
2 2
2 2 2
2
x
f x x
x x
;
0 1f x x
.
Bảngbiếnthiên.
Khiđóyêucầubàitoán
0
m
.Mà
m
nguyênvà
2018;2019
m
nêncó
2018
giátrịthỏa
mãn.
Câu 15. (THCS-THPTNguyễnKhuyến2019)Phươngtrình
3 2
6 5 5x mx m
có3nghiệmphânbiệt
lậpthànhcấpsốcộngkhi
A.
0
m
. B.
1 1
m m
. C.
1
m
. D.
m
.
Lờigiải
Phươngtrìnhđãchotươngđương:
3 2
6 5 5 0
x mx m
.
Đặt
3 2
6 5 5y f x x mx m
có
2
3 6f x x m
;
6f x x
.
PTđãchocó3nghiệmphânbiệt
Hàmsố
y f x
cắttrụchoànhtại3điểmphânbiệt
0
f x
có2nghiệmphânbiệt
1
x
,
2
x
thỏamãn
1 2
. 0
f x f x
.
3nghiệmđólậpthànhcấpsốcộngnên
2 1 3 2
x x x x
.
Suyra,
2
x
làhoànhđộcủatâmđốixứnghaylànghiệmcủa
0
f x
.
Cho
0 6 0 0
f x x x
.
Với
0
x
tacó:
2
5 5 0 1
m m
.
Thửlại:
Với
1
m
thìtacó
3 2
0
6 5 5 6 0
6
x
x x x x
x
Với
1
m
thìtacó:
3 2
6 5 5 6 0 0
x x x x x
Câu 16. Tínhtổngtấtcảcácgiátrịcủa
m
biếtđồthịhàmsố
3 2
2 3 4
y x mx m x
vàđườngthẳng
4
y x
cắtnhautạibađiểmphânbiệt
0;4
A
,
B
,
C
saochodiệntíchtamgiác
IBC
bằng
8 2
với
1;3
I
.
A.
3
. B.
8
. C.
1
. D.
5
.
Lờigiải
x
0
1
f x
0
f x
0

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
ChọnC
+)Gọiđồthịhàmsố
3 2
2 3 4
y x mx m x
là
m
C
vàđồthịhàmsố
4
y x
là
d
.
+)Phươngtrìnhhoànhđộgiaođiểmcủa
m
C
và
d
là
3 2
2 3 4 4
x mx m x x
3 2
2 2 0
x mx m x
2
0
2 2 0
x
x mx m
+)Gọi
2
2 2
g x x mx m
.
+)
d
cắt
m
C
tạibađiểmphânbiệt
phươngtrình
cóbanghiệmphânbiệt
phươngtrình
0
g x
cóhainghiệmphânbiệtkhác
0
0
0 0
g
g
2
2 0
2 0
m m
m
1
2
2
m
a
m
m
+)
0
x
làhoànhđộđiểm
A
,hoànhđộđiểm
B
,
C
làhainghiệm
1
x
,
2
x
củaphươngtrình
0
g x
+)
2
2
2
2 1 2 1
4 4
BC x x x x
2
2 1
2
x x
(do
B
,
C
thuộcđườngthẳng
d
2
2 1 1 2
2 4
x x x x
2
8 2
m m
+)Viếtphươngtrìnhđườngthẳng
d
dướidạng
4 0
x y
,tacó
1 3 4
, 2
2
d I d
.
+)
8 2
IBC
S
1
. , 8 2
2
BC d I d
2
2
1
. , 128
4
BC d I d
2
1
8 2 .2 128
4
m m
2
1 137
2
34 0
1 137
2
m
m m
m
(thỏađiềukiện
a
)
+)Vậytổngtấtcảcácgiátrị
m
là
1
.
Câu 17. Cóbaonhiêugiátrịnguyêncủathamsố
2018;2019
m
đểđồthịhàmsố
3
3 3y x mx
và
đườngthẳng
3 1y x
códuynhấtmộtđiểmchung?
A.
1
. B.
2019
. C.
4038
. D.
2018
.
Lời giải
Chọn D
+Phươngtrìnhhoànhđộgiaođiểm:
3
3 3 3 1x mx x
3
3 3 2
mx x x
.
1
+Dễthấy
0
x
khôngthỏa.
+
2
2
1 3 3
m x f x
x
.
+
3
2 2
2 2 2
2 0 1
x
f x x x
x x
.
+Bảngbiếnthiên:
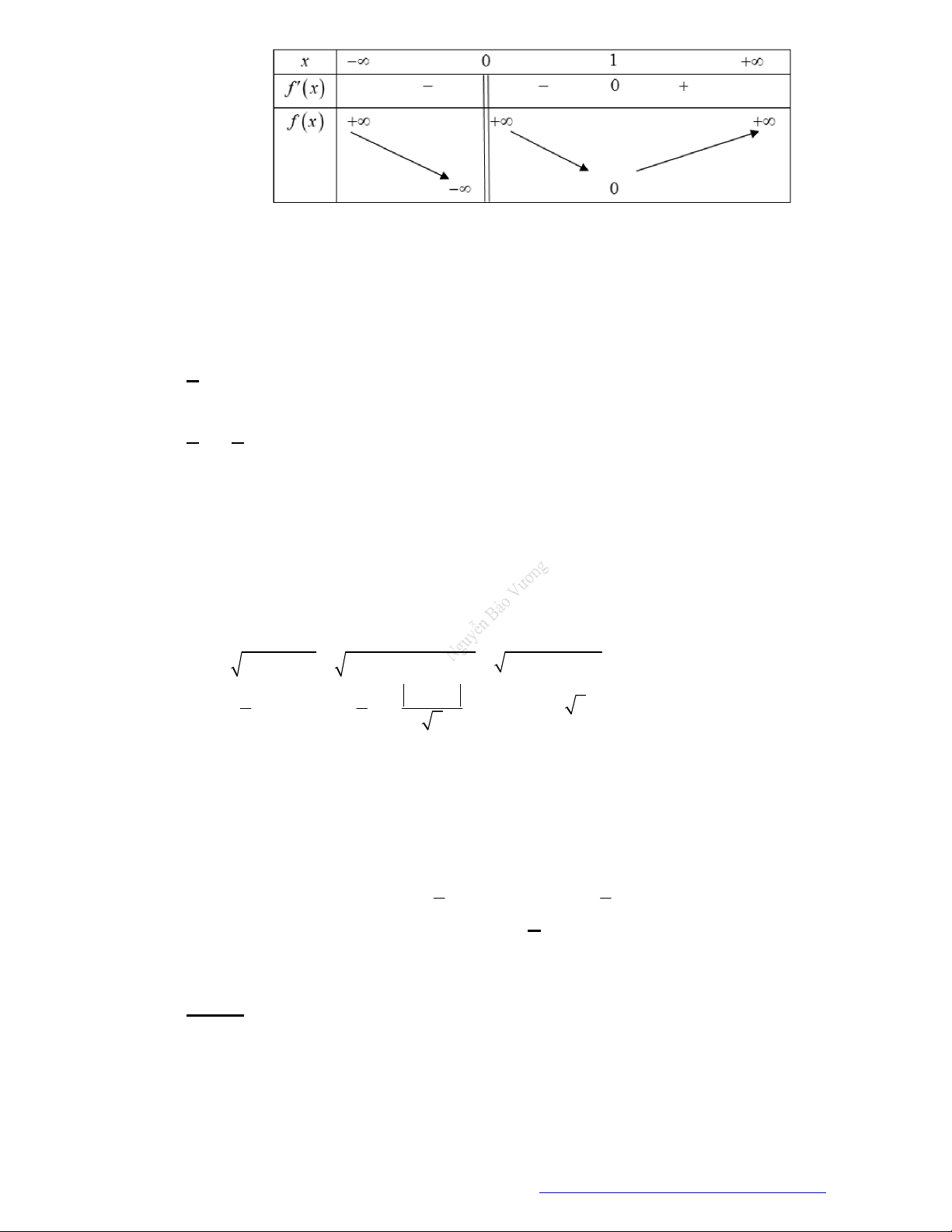
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
+ Đồ thị hàm số
3
3 3y x mx và đường thẳng
3 1y x
có duy nhất một điểm chung
3 0 0m m
.
+Do
m
và
2018;2019m
nêncó
2018
giátrị.
Câu 18. Đườngthẳngd có phươngtrình
4y x
cắtđồ thị hàm số
3 2
2 ( 3) 4y x mx m x
tại3
điểmphânbiệt
(0;4)A
,BvàCsaochodiệntíchcủatamgiácMBCbằng4,với
(1;3)M
.Tìmtất
cảcácgiátrịcủa
m
thỏamãnyêucầubàitoán.
A.
3m
. B.
2m
hoặc
3m
.
C.
2m
hoặc
3m
.D.
2m
hoặc
3m
Lời giải
Chọn A
Hoànhđộgiaođiểmcủahaiđồthịlànghiệmcủaphươngtrình
3 2 3 2
2
0
2 ( 3) 4 4 2 ( 2) 0
2 ( 2) 0 (*)
x
x mx m x x x mx m x
x mx m
.
Đườngthẳngdcắtđồthịhàmsố(1)tại3điểmphânbiệtkhiphươngtrình(*)cóhainghiệmphân
biệtkhác0
2
1
2 0
2
2 0
2
m
m m
m
m
m
.
GiảsửB
1 1
( ; 4)x x
;C
2 2
( ; 4)x x
với
1 2
;x x
lànghiệmcủaphươngtrình(*)khiđó
2 2 2
1 2 1 2 1 2
2( ) 2( ) 8 . 8 8 16BC x x x x x x m m
.
1 3 4
1 1
. ( , ) . . 4 4 2
2 2
2
MBC
S BC d M d BC BC
.
Tacó
2
2
6 0
3
m
m m
m
.
Đốichiếuđiềukiệntacó
3m
.
Câu 19. (THPT Minh Khai - lần 1) Tìmtấtcảcácgiátrịthựccủathamsố
m
đểđườngthẳng
5y x
cắtđồthịhàmsố
3 2
2 3 1 5y x mx m x
tạibađiểmphânbiệt.
A.
1
2
m
m
. B.
2
3
1
2
m
m
m
. C.
2
3
1
2
m
m
m
. D.
1
2
m
m
.
Lời giải
Chọn C
Tacóphươngtrìnhhoànhđộgiaođiểm
3 2
2 3 1 5 5x mx m x x
3 2
2
0
2 3 2 0
2 3 2 0 1
x
x mx m x
x mx m
.
Yêucầubàitoántươngđươngphươngtrình
1
cóhainghiệmphânbiệt,khác
0
.
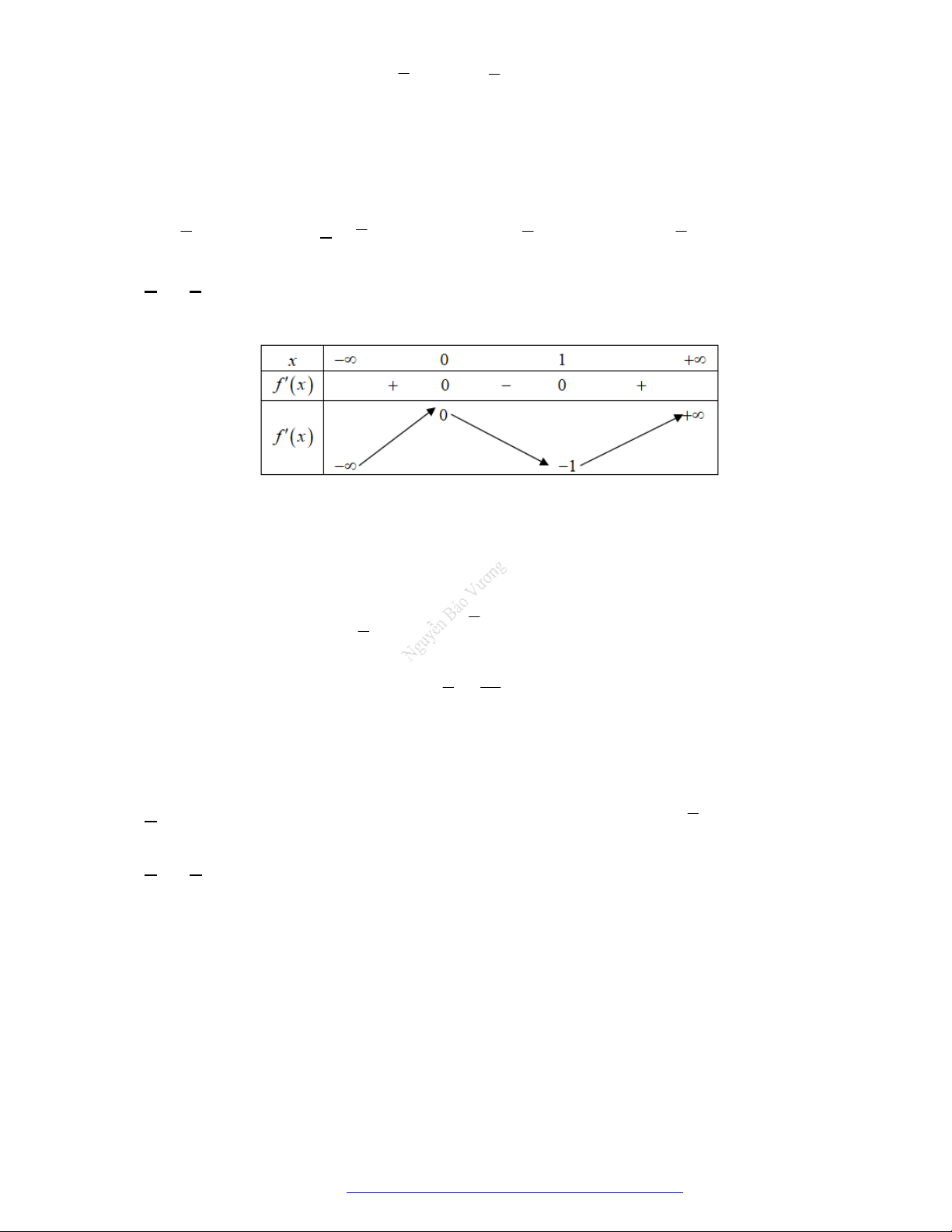
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
2
2
2
3
0 2 .0 3 2 0
3
2 1
3 2 0
1
2
m
m
m m
m m
m m
m
m
.
Câu 20. (Chuyên Lê Quý Đôn Điện Biên 2019) Gọi
S
làtậptấtcảcácgiátrịthựccủathamsố
m
để
phươngtrình
3 2
2 3 2 1x x m
cóđúnghainghiệmphânbiệt.Tổngcácphầntửcủa
S
bằng
A.
1
2
. B.
3
2
. C.
5
2
. D.
1
2
.
Lời giải
Chọn B
Xéthàmsố:
3 2
2 3y x x
2
6 6 0 0 1y x x y x x
.
Bảngbiếnthiên:
Sốnghiệmcủaphươngtrìnhđãchobằngsốgiaođiểmcủahaiđồthị:
3 2
: 2 3
: 2 1
C y x x
d y m
Nhìnvàobảngbiếnthiêntathấy:Phươngtrìnhđãchocóhainghiệmphân
biệt
1
2 1 1
1
2 1 0
2
m
m
m
m
1
1;
2
S
.
Vậytổngcácphầntửcủa
S
bằng
1 3
1
2 2
.
Câu 21. (Kiểm tra năng lực - ĐH - Quốc Tế - 2019) Giá trị lớn nhất của
m
để đường thẳng
: 1d y x m
cắtđồthịhàmsố
3 2
2 2 8 5 5y x m x m x m
tại3điểmphânbiệt
cóhoànhđộ
1 2 3
, ,x x x thỏamãnđiềukiện
2 2 2
1 2 3
20x x x
là
A.
3
. B.
1
. C.
0
. D.
3
2
.
Lời giải
Chọn A
Hoànhđộgiaođiểmcủađườngthẳng
d
vàđồthịhàmsốlànghiệmcủaphươngtrình
3 2
2 2 8 5 5 1x m x m x m x m
2
2 2 2 3 0x x m x m
3
2
2
2 2 3 0 1
x
x m x m
.
Đườngthẳng
d
cắtđồthịhàmsốtại3điểmphânbiệt phươngtrình
1
cóhainghiệmphân
biệt
1 2
;x x khác2
2
1 3 0
4 2 2 .2 3 0
m m
m m
1
2
1
m
m
m
1
2
m
m
(2).
Khiđó,
1 2
1 2
2 2
3
x x m
x x m
.
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Theogiảthiết
2 2 2
1 2 3
20
x x x
2
2
1 2 1 2 3
2 20
x x x x x
2
2 2 2 3 4 20
m m
2
3
2 3 9 0
3
2
m
m m
m
(thỏamãn(2)).
Vậygiátrịlớnnhấtcủa
m
thỏamãnyêucầubàitoánlà
3
.
Câu 22. Cóbaonhiêugiátrịcủa
m
đểđồthịhàmsố
3 2 2 3
2 3 2 2
y x m x m m x
cắttrụchoànhtại
bađiểmphânbiệtcóhoànhđộlàbasốhạngliêntiếpcủamộtcấpsốnhân?
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn C
Hoànhđộgiaođiểmcủađồthịvớitrụchoànhlànghiệmcủaphươngtrình
3 2 2 3
2 3 2 2 0. *
x m x m m x
Giảsửđồthịcắttrụchoànhtại3điểmcóhoànhđộ
1 2 3
, , x x x
.
Khiđótacó
3 2
1 2 3 1 2 3 1 2 2 3 3 1 1 2 3
2 2 2 2 2 .y x x x x x x x x x x x x x x x x x x x x x
Đồngnhấtthứctađược
2
1 2 3
2
1 2 3
3
3
1 2 2 3 3 1 1 2 2 3 3 1
1 2 3
1 2 3
3
1
2
2 3
2
2 2 2
2
2 2
1 3
m
x x x
x x x m
m m
x x x x x x m m x x x x x x
x x x
x x x
Vì
1 2 3
, , x x x
lậpthànhcấpsốnhânnên
2
1 3 2
. 4
x x x
Từ
2
và
3
:
2
1.
x
Thayvàophươngtrình
*
rútrađược
0
1 .
2
m
m
m
Với
0
m
phươngtrình
*
:
3
2 2 0 1x x
(khôngthỏamãn).
Với
1
m
phươngtrình
*
:
1
3 2
2
3
2
2 3 3 2 0 1
1
2
x
x x x x
x
(thỏamãn).
Với
2
m
phươngtrình
*
:
1
3 2
2
3
7 45
2
6 6 1 0 1
7 45
2
x
x x x x
x
(thỏamãn).
Vậycó2giátrị
m
thỏamãn.
Câu 23. (Kinh Môn - Hải Dương 2019) Tìm
m
để đồ thị
C
của
3 2
3 4
y x x
và đường thẳng
y mx m
cắtnhautại3điểmphânbiệt
1;0
A
,
B
,
C
saocho
OBC
códiệntíchbằng
64
.
A.
14
m
. B.
15
m
. C.
16
m
. D.
17
m
.
Lời giải

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Chọn C
2
2 2 2
2
2
2 2
,
1
1
1 4 1 4
1
, . 64 16.
2
B C b c B C
B C B C
OBC
m
d O BC
m
BC x x y y m x x
m x x x x m m
S d O BC BC m m m
Cách 2:
Phươngtrìnhhoànhđộgiaođiểm:
3 2 2
2
1
3 4 1 4 4 0
2
x
x x mx m x x x m
x m
Để
d
cắt
C
tại3điểmphânbiệtphươngtrình
có2nghiệmphânbiệtkhác
0
1
9
m
m
2 2 ;3
2
2 ;3
x m B m m m m
x m
C m m m m
2 ;3 , 2 ;3
OB m m m m OC m m m m
1
, 64 16.
2
OBC
S OB OC m m m
Câu 24. (Sở Bắc Ninh 2019) Chohàmsố
3 2
8 8y x x x
cóđồthị
C
vàhàmsố
2
(8 )
y x a x b
(với
,a b
)cóđồthị
P
.Biếtđồthịhàmsố
C
cắt
P
tạibađiểmcóhoànhđộnằmtrong
1;5
.Khi
a
đạtgiátrịnhỏnhấtthìtích
ab
bằng
A.
729
. B.
375
. C.
225
. D.
384
.
Lời giải
Chọn B
Cách 1:
Phươngtrìnhhoànhđộgiaođiểmlà
3 2 2 3 2
8 8 (8 ) 9 0
x x x x a x b x x ax b
(1).
Gọi
, ,m n p
là3nghiệmcủaphươngtrình(1)tacó
9m n p
mn np pm a
mnp b
Do
C
cắt
P
tạibađiểmcóhoànhđộnằmtrong
1;5
nên
( 1)( 1)( 1) 0 ( ) ( ) 1 0
(5 )(5 )(5 ) 0 5( ) 25( ) 125 0
m n p mnp mn np pm m n p
m n p mnp mn np pm m n p
Cộngvếtheovếcủahệphươngtrìnhtrênta
có
6( ) 24( ) 124 0 15 15.
mn np pm m n p mn np pm a
Dấubằngxảyrakhi
25
25 25
25
mnp
mnp b
mnp
Vậytích
375.
ab
Cách 2:Phươngtrìnhhoànhđộgiaođiểmlà
3 2 2 3 2
8 8 (8 ) 9 0
x x x x a x b x x ax b
(1).
Khiđóphươngtrình(1)có3nghiệmnằmtrong
1;5
.
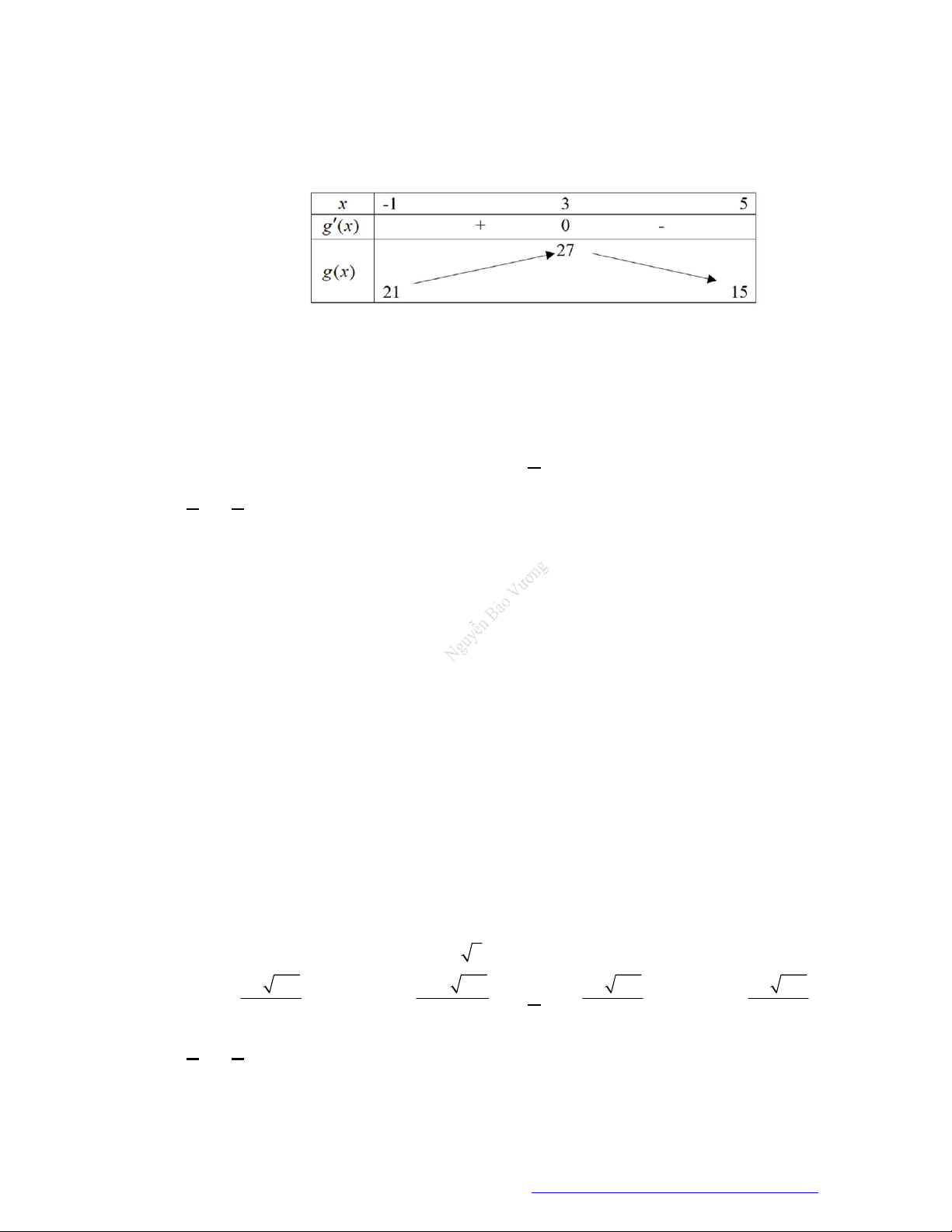
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Đặt
3 2
( ) 9f x x x ax b suyra
2
'( ) 3 18f x x x a .Đểphươngtrình(1)có3nghiệmnằm
trong
1;5
thì
2
'( ) 3 18 0f x x x a cóhainghiệmphânbiệtthuộc
1;5
2
3 18a x x
cóhainghiệmphânbiệtthuộc
1;5
.
Xéthàmsố
2
( ) 3 18g x x x suyra
'( ) 6 18g x x
,tacó
'( ) 0 3g x x
.
Bảngbiếnthiêncủa
( )y g x
TừBBTtacó
15 27a
suyragiátrịnhỏnhấtcủa
a
bằng15khi
5x
,khiđó
25b
.
Vậytích
375.ab
Câu 25. (Sở Quảng Trị 2019) Cóbaonhiêugiátrịnguyêncủathamsố
m
đểđườngthẳng
y mx m
cắt đồ thị hàm số
3 2
y x mx m
tại
3
điểm phân biêt có hoành độ
1 2 3
, ,x x x
thỏa mãn
1 2 3
1 3x x x
?.
A.
6
. B.
5
. C.
2
. D.
3
.
Lờigiải
Chọn C
d y mx m
,
3 2
C y x mx m
.
Phươngtrìnhhoànhđộgiaođiểmcủa
d
và
C
:
3 2
0 1x mx mx
.
2
0
0 2
x
x mx m
Gọi
1 2
,x x
là
2
nghiệmcủaphươngtrình
2
,
3
0x
.
1
có
3
nghiệmphânbiệt
2
có
2
nghiệm
1 2
,x x
phânbiệtvàkhác
0
.
2
0, 4
0
m m
m
;0 4;m
.
1
có
3
nghiệmphânbiệt
1 2 3
, ,x x x
thỏa
1 2 3
1 3x x x
,với
1 2
x x m
,
3
0x
.
1 3m
3 1m
,mà
;0 4;m
,
m
2; 1m
.Vậycó
2
giátrị
m
.
Câu 26. (Chuyên Nguyễn Huệ 2019) Chohàmsố
3 2
2 3 4y x mx m x
m
C
.Tấtcảcácgiátrị
củathamsố
m
đểđườngthẳng
: 4d y x
cắt
m
C
tạibađiểmphânbiệt
0;4A
,
B
,
C
sao
chotamgiác
KBC
códiệntíchbằng
8 2
vớiđiểm
1;3K
là:
A.
1 137
2
m
. B.
1 137
2
m
. C.
1 137
2
m
. D.
1 137
2
m
.
Lời giải
Chọn C
Phươngtrìnhhoànhđộgiaođiểmcủa
m
C
và
d
là:
3 2
2 3 4 4 1x mx m x x
3 2
2 2 0x mx m x
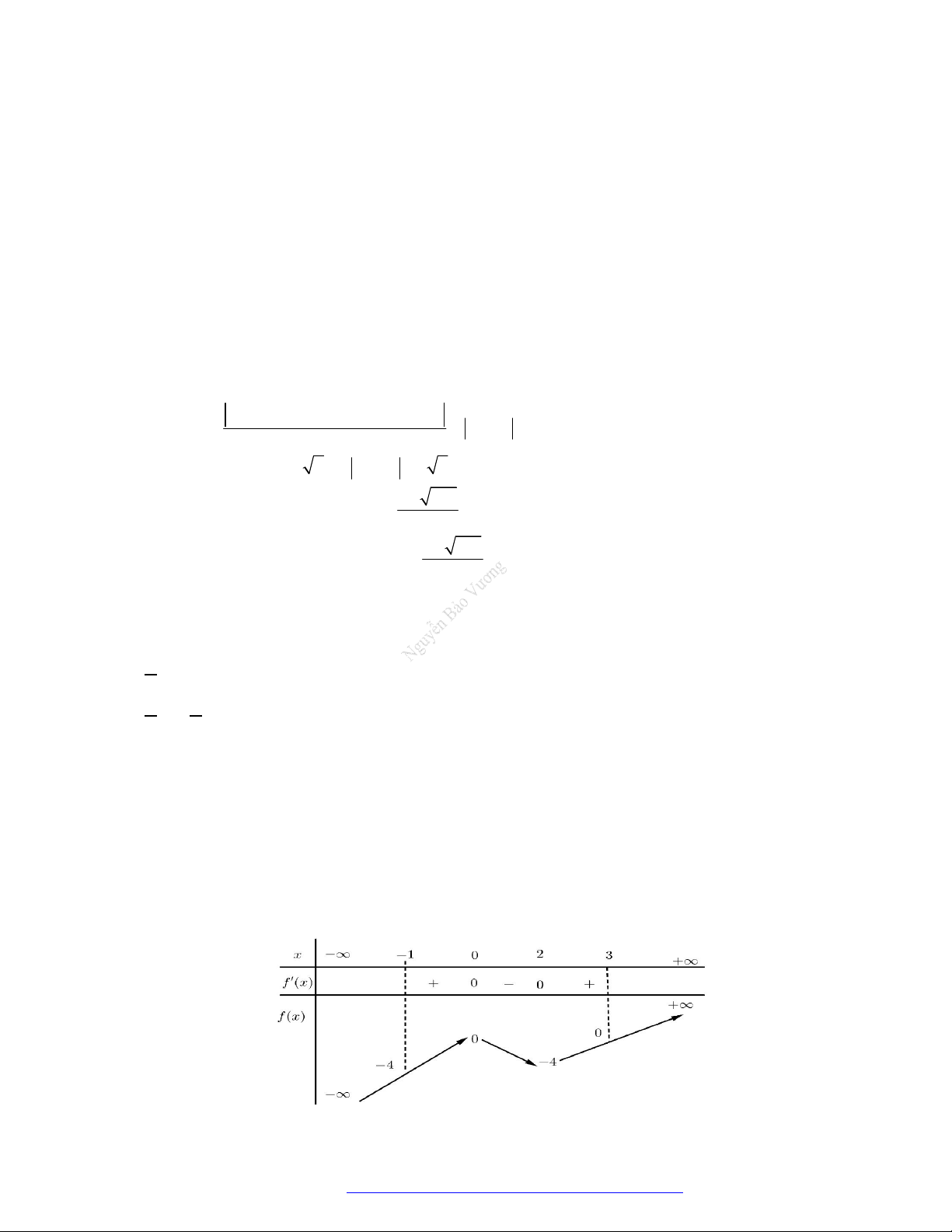
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
. 2 2 0x x mx m
2
0 4
2 2 0 2
x y
x mx m
.
d
cắt
m
C
tạibađiểmphânbiệt
1
cóbanghiệmphânbiệt
2
cóhainghiệmphânbiệtkhác0
2
2
2
2
0
2 0
1 1
0 2 .0 2 0 2 0
2
2
m
m
m m
m m
m m m
m
m
.
Khiđó,
2
cóhainghiệmphânbiệt
1
x và
2
x tươngứngcũnglàhoànhđộcủa
B
và
C
.
1 1
; 4B x x
và
2 2
; 4C x x
.
1 2
1; 1KB x x
và
2 2
1; 1KC x x
.
1 2 2 1
1 2
1 1 1 1
2
KBC
x x x x
S x x
.
Theođềbài:
2
2
1 2 1 2
8 2 8 2 128 4 128
KBC
S x x x x S P
2
1 137
2 4 2 128
2
m m m
(nhận).
Vậytấtcảcácgiátrị
m
thỏađềlà
1 137
2
m
.
Câu 27. (Chuyên Thái Nguyên - 2020) Gọi
T
làtậphợptấtcảcácgiátrịnguyêncủathamsố
m
để
phươngtrình
3 2 3 2
3 3 0x x m m
cóbanghiệmphânbiệt.Tổngtấtcảcácphầntử của
T
bằng
A.
1
. B.
5
. C.
0
. D.
3
.
Lời giải
Chọn A
Cách 1:Tacó
3 2 3 2 3 2 3 2
3 3 0 3 3 ( ) ( )x x m m x x m m f x f m (1)
Xéthàmsố
3 2
( ) 3f x x x .
2
'( ) 3 6 ,f x x x
0
'( ) 0
2
x
f x
x
.
0
( ) 0
3
x
f x
x
.
2
( ) 4
1
x
f x
x
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Dựavàobảngbiếnthiên,suyra(1)cóbanghiệmphânbiệt
4 ( ) 0
f m
1 3
0
2
m
m
m
.
Suyra
1
T
.Vậytổngtấtcảcácphầntửcủa
T
bằng1.
Cách 2:Tacó
3 2 3 2 3 3 2 2
3 3 0 3 0
x x m m x m x m
2 2
3 3 0
x m x m x m m
2 2
3 3 0 *
x m
x m x m m
Phươngtrìnhđãchocó3nghiệmphânbiệt
*
cóhainghiệmphânbiệt,khác
m
2
2
2 2
3 4 3 0
3 3 0
m m m
m m m m m
2
3 3 3 0
3 6 0
m m
m m
1 3
0 1
2
m
m m
m
(vì
m
).
Suyra
1
T
.Vậytổngtấtcảcácphầntửcủa
T
bằng1.
Câu 28. (Đại Học Hà Tĩnh - 2020) Chođồthịhàmsố
3 2
f x x bx cx d
cắttrụchoànhtại3điểm
phânbiệtcóhoànhđộ
1 2 3
, ,x x x
.Tínhgiátrịcủabiểuthức
1 2 3
1 1 1
.
P
f x f x f x
A.
3 2
P b c
. B.
0
P
. C.
P b c d
. D.
1 1
2
P
b c
.
Lời giải
Chọn B
Vì
1 2 3
, ,x x x
làbanghiệmcủaphươngtrìnhbậcba
1 2 3
0
f x f x x x x x x x
Tacó
1 2 2 3 1 3
f x x x x x x x x x x x x x
.
Khiđó:
1 1 2 1 3
2 2 3 2 1
3 3 1 3 2
f x x x x x
f x x x x x
f x x x x x
Suyra
1 2 1 3 2 3 2 1 3 1 3 2
1 1 1
.
P
x x x x x x x x x x x x
2 3 1 3 1 2
1 2 1 3 2 3
0
x x x x x x
x x x x x x
.
Câu 29. (Sở Bắc Ninh - 2020) Cho hàm số bậc ba
y f x
có đồ thị đi qua điểm
1;1 , 2;4 , 3;9
A B C
. Các đường thẳng
, ,AB AC BC
lại cắt đồ thị lần lượt tại các điểm
, ,M N P
(
M
khác
A
và
B
,
N
khác
A
và
C
,
P
khác
B
và
C
.Biếtrằngtổngcáchoànhđộ
của
, ,M N P
bằng5,giátrịcủa
0
f
là
A.
6
. B.
18
. C. 18. D. 6.
Lời giải
Chọn B
Từgiảthuyếtbàitoántagiảsử
2
1 2 3
f x a x x x x
(
0
a
)
Tacó:
: 3 2
AB y x
,
: 4 3AC y x
,
: 5 6BC y x
.
Khiđó:

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Hoành độ của
M
là nghiệm của phương trình:
2
1 2 3 3 2
M M M M M
a x x x x x
1 2 3 1 2 0
M M M M M
a x x x x x
3 1 0
M
a x
1
3
M
x
a
.
Hoành độ của
N
là nghiệm của phương trình:
2
1 2 3 4 3
N N N N N
a x x x x x
1 2 3 1 3 0
N N N N N
a x x x x x
2 1 0
N
a x
1
2
N
x
a
.
Hoành độ của
P
là nghiệm của phương trình:
2
1 2 3 5 6
P P P P P
a x x x x x
1 2 3 2 3 0
P P P P P
a x x x x x
1 1 0
P
a x
1
1
P
x
a
.
Từgiảthuyếttacó;
3
5 6 5 3
M N P
x x x a
a
.
Dođó:
2
3 1 2 3
f x x x x x
0 18
f
.
Câu 30. (Đô Lương 4 - Nghệ An - 2020) Tìm giá trị thực của tham số
m
để đồ thị hàm số
3 2
3 2
y x x
cắtđườngthẳng
: 1
d y m x
tạibađiểmphânbiệtcóhoànhđộ
1
x
,
2
x
,
3
x
thỏamãn
2 2 2
1 2 2
5
x x x
.
A.
3
m
. B.
2
m
C.
3
m
. D.
2
m
.
Lời giải
Chọn D
Phươngtrìnhhoànhđộgiaođiểm:
3 2 3 2
3 2 1 3 2 0
x x m x x x mx m
2
1 2 2 0
x x x m
1
2
1
2 2 0 *
x
g x x x m
.
Đểhaiđồthịcắtnhautạibađiểmphânbiệtthìphươngtrình
*
phảicóhainghiệmphânbiệt
khác
1
2
0
3
1 2 0
3
1 0
3
1 2 2 0
m
m
m
g
m
m
.
Gọi
2
x
,
3
x
làhainghiệmphươngtrình
*
.
TheođịnhlýViéttacó
2 3
2 3
2
. 2
x x
x x m
.
Theobàitacó
2 2 2 2 2 2 2
1 2 3 2 3 2 3
5 1 5 4
x x x x x x x
2
2 3 2 3
2 4
x x x x
4 2 2 4 2
m m
.
Sosánhvớiđiềukiệnởtrênsuyra
2
m
.
Kếtluận:
2
m
thỏamãnyêucầubàitoán.
Câu 31. (Yên Lạc 2 - Vĩnh Phúc - 2020) Gọi
S
làtậptấtcảcácgiátrịcủathamsố
m
đểđồthịhàmsố
3 2
3 9 2 1
y x x x m
vàtrục
Ox
cóđúnghaiđiểmchungphânbiệt.Tínhtổng
T
củacácphầntửthuộctập
S
A.
10
T
. B.
10
T
. C.
12T
. D.
12T
.
Lời giải
Chọn C
Hoànhđộgiaođiểmcủađồthịhàmsố
3 2
3 9 2 1
y x x x m
vàtrục
Ox
lànghiệmcủa
phươngtrình:
3 2 3 2
3 9 2 1 0 3 9 2 1
x x x m x x x m
.
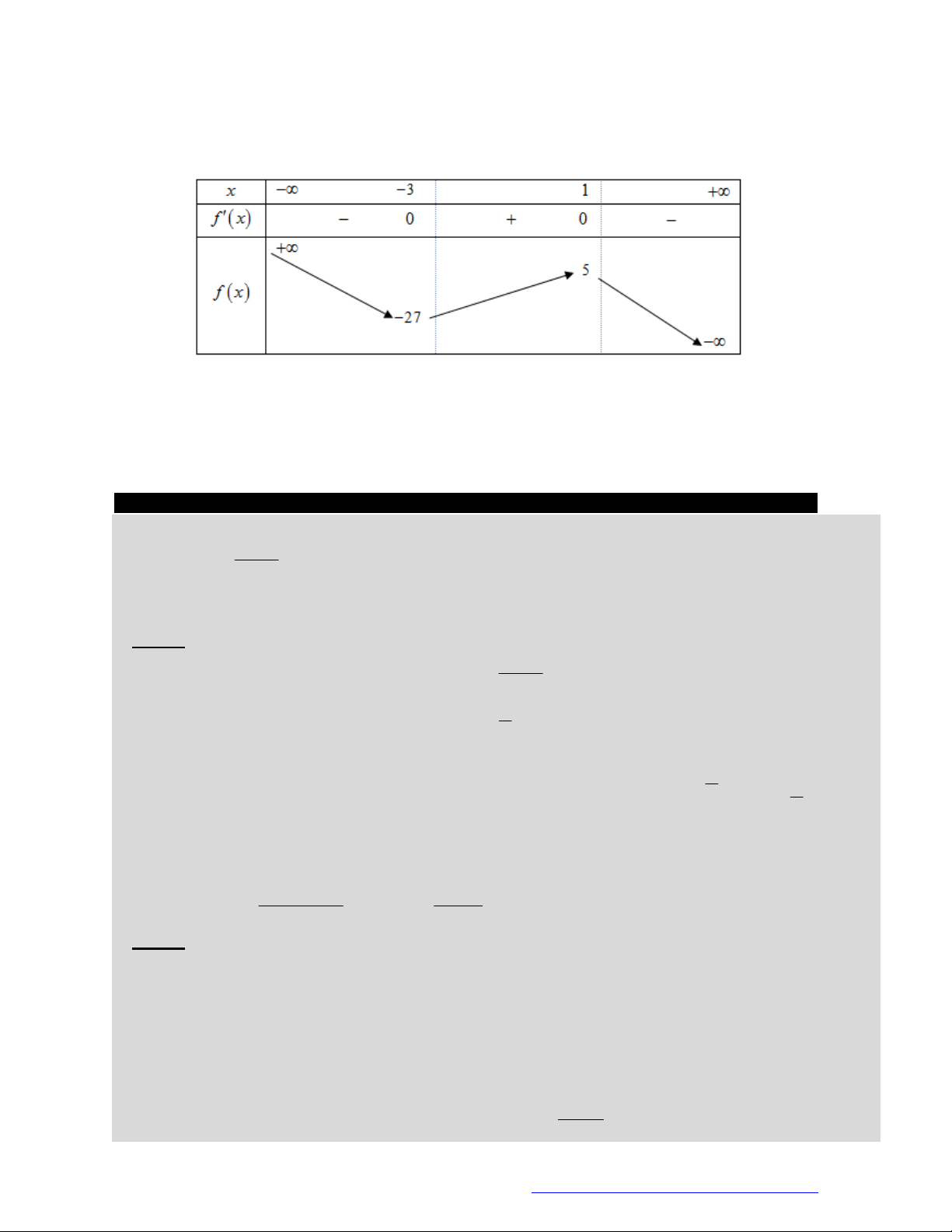
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
Xéthàmsố
3 2
3 9f x x x x
.
Tậpxácđịnh:
D
.
2 2
1
3 6 9, 0 3 6 9 0
3
x
f x x x f x x x
x
.
Bảngbiếnthiên:
Đồthịhàmsố
3 2
3 9 2 1y x x x m cắttrục
Ox
tạihaiđiểmphânbiệtkhivàchỉkhiđường
thẳng
2 1y m
cắtđồthịhàmsố
3 2
3 9f x x x x
tạihaiđiểmphânbiệt.
Từbảngbiếnthiênsuyra:
2 1 5 2
14;2
2 1 27 14
m m
S
m m
.
Tổngcủacácphầntửthuộctập
S
là:
14 2 12T
.
Dạng 2. Bài toán tương giao của đường thẳng với đồ thị hàm số nhất biến (CHỨA THAM SỐ)
Bài toán tổng quát
Chohàmsố
ax b
y
cx d
cóđồthị
C
.Tìmthamsốmđểđườngthẳng
:d y x
cắt
C
tạihaiđiểm
phânbiệt
,A B
thỏamãnđiềukiệnK?
Phương pháp giải
Bước 1.(Bướcnàygiốngnhauởcácbàitoántươnggiaocủahàmnhấtbiến)
Lậpphươngtrìnhhoànhđộgiaođiểmgiữadvà
:C
ax b
x
cx d
2
0,
d
g x cx c d a x d b x
c
.
-Đểdcắt
C
tạihaiđiểmphânbiệt
0g x
cónghiệmnghiệmphânbiệt
d
c
0; 0
0
c
d
g
c
.
Giảihệnày,tasẽtìmđược
1
m D
i
-Gọi
1 1 2 2
; , ;A x x B x y
với
1 2
,x x là
2
nghiệmcủa
0g x
TheoViét:
1 2
;
c d a
S x x
c
1 2
d b
P x x
c
ii
Bước 2.
-BiếnđổiđiềukiệnKchotrướcvềdạngcóchứatổngvàtíchcủa
1 2
,x x
iii
-Thế
ii
vào
iii
sẽthuđượcphươngtrìnhhoặcbấtphươngtrìnhvớibiếnsốlàm.Giảinósẽtìmđược
2
m D
-Từ
1 2
,i m D D
vàkếtluậngiátrịmcầntìm.
Một số công thức tính nhanh “ thường gặp “ liên quan đến tương giao giữa đường thẳng
y kx p
và
đồ thị hàm số
ax b
y
cx d

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Giả sử
:
d y kx p
cắt đồ thị hàm số
ax b
y
cx d
tại
2
điểm phân biệt
,M N
.
Với
ax b
kx p
cx d
cho ta phương trình có dạng:
2
0
Ax Bx C
thỏa điều kiện
0
cx d
, có
2
4
B AC
. Khi đó:
1).
2
1 1 2 2 2 1 2 1
2
( ; ), ( ; ) ( ; ( )) ( 1)
M x kx p N x kx p MN x x k x x MN k
A
Chú ý: khi
min
MN
thì tồn tại
min ,
k const
2).
2 2 2 2 2 2
1 2 1 2
( 1)( ) ( )2 2OM ON k x x x x kp p
3).
2 2
1 2 1 2
. ( . )(1 ) ( )
OM ON x x k x x kp p
4).
2
1 2
( )(1 ) 2 0
OM ON x x k kp
Câu 1. (Sở Ninh Bình 2020) Cótấtcảbaonhiêugiátrịnguyênthuộcđoạn
2020;2020
củathamsố
m
đểđườngthẳng
y x m
cắtđồthịhàmsố
2 3
1
x
y
x
tạihaiđiểmphânbiệt?
A.
4036.
B.
4040.
C.
4038.
D.
4034.
Lời giải
Chọn A
Tacóphươngtrìnhhoànhđộgiaođiểmcủađườngthẳng
y x m
vàđườngcong
2 3
1
x
y
x
2 3
1 2 3 1
1
x
x m x m x x x
x
.
2 2
2 3 3 3 0 *
x mx x m x x m x m
Tacó
2
2 2
3 4 3 6 9 4 12 2 3
m m m m m m m
.
Đểđườngthẳng
y x m
cắtđồthịhàmsố
2 3
1
x
y
x
tạihaiđiểmphânbiệtthìphươngtrình
*
cóhainghiệmphânbiệtkhác
1
.
2
2
0
2 3 0
1
3
1 3 .1 3 0
1 0 đ
m m
m
m
m m
l
.
Theogiảthiết:
2020 2020
m
và
1
3
m
m
nên
2020 1
3 2020
m
m
.
Vì
m
và
2020 1
m
,suyracó
2 2020
1 2019
1
giátrịnguyên
m
.
Vì
m
và
3 2020
m
,suyracó
2020 4
1 2017
1
giátrịnguyên
m
.
Tómlạicótấtcả
2019 2017 4036
giátrịnguyêncủathamsố
m
.
Câu 2. (ĐHQG TPHCM 2019) Đườngthẳng
2y x m
cắtđồthịhàmsố
3
1
x
y
x
tạihaiđiểmphân
biệtkhivàchỉkhi
A.
1
3
m
m
. B.
1
3
m
m
. C.
3
1
m
m
. D.
3 1
m
.
Lờigiải
Phươngtrìnhhoànhđộgiaođiểmcủahaiđồthịhàmsốđãcho

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
3
2
1
x
x m
x
2 1 3
1
x m x x
x
2
2 2 3 0x mx m
*
.(vìkhi
1x
thì
phươngtrìnhtrởthành
0 4
vôlí).
Đểđồthịcủahaihàmsốđãchocắtnhautạihaiđiểmphânbiệtthìphươngtrình
*
phảicóhai
nghiệmphânbiệt.Khiđó
m
phảithoảmãn
*
0
2
1
2 3 0
3
m
m m
m
.
Vậytậphợpcácgiátrịcủathamsố
m
là
1
3
m
m
.
Câu 3. (Gia Lai 2019) Tìmtấtcảcácgiátrịthựccủathamsố
m
đểđườngthẳng
2y x m
cắtđồthị
củahàmsố
3
1
x
y
x
tạihaiđiểmphânbiệt.
A.
;m
. B.
1;m
. C.
2;4m
. D.
; 2m
.
Lời giải
Chọn A
Phươngtrìnhhoànhđộgiaođiểm:
3
2 (*),
1
x
x m
x
vớiđiềukiệnxácđịnh
1x
.
Biếnđổi(*)vềthành:
2
2 ( 1) 3 0 (**)x m x m
.
Theoyêucầuđềbài,phươngtrình(**)cầncóhainghiệmphânbiệtkhác
1
,tứclà:
2
2
1 4.2. 3 0
2. 1 1 . 1 3 0
m m
m m
2
6 25 0
2 0
m m
; .m
Câu 4. Gọi
A
và
B
làhaiđiểmthuộchainhánhkhácnhaucủađồthịhàmsố
2
x
y
x
.Khiđóđộdài
đoạn
AB
ngắnnhấtbằng
A.
4 2
. B.
4
. C.
2 2
. D.
2 2
.
Lờigiải
ChọnB
Hàmsố
2
x
y
x
cóđồthị
C
nhưhìnhvẽ.Gọi
;
2
a
A a
a
và
;
2
b
B b
b
làhaiđiểmthuộc
hainhánhcủa
C
2a b
.
Tacó:
; ;
2 2 2 2
b a b a
AB b a b a
b a b a
.
ÁpdụngBĐTCôsitacó:
2
2 2
4
b a
b a
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Suyra:
2
2
2
2
2 2
b a
AB b a
b a
2
2
64
16
b a
b a
4
AB
.Dấubằngxảyrakhivàchỉkhi
2 2
a
và
2 2
b
.
Vậy
min
4
AB
.
Câu 5. (Chuyên Nguyễn Du ĐăkLăk 2019) Chohàmsố
1
x
y C
x
vàđườngthẳng
: xd
y m
.
Gọi
S
làtậpcácsốthực
m
đểđườngthẳng
d
cắtđồthị
C
tạihaiđiểmphânbiệt
,A B
saocho
tamgiác
OAB
(
O
làgốctọađộ)cóbánkínhđườngtrònngoạitiếpbằng
2 2
.Tổngcácphầntử
của
S
bằng
A.
4
. B.
3
. C.
0
. D.
8
.
Lời giải
Chọn A
Xétphươngtrình
,
1
x
x m
x
(điềukiện
1x
).
Phươngtrìnhtươngđương
2
0
x mx m
1
.
Đồthị
C
vàđườngthẳng
d
cắtnhautạihaiđiểmphânbiệt
A
và
B
khivàchỉkhiphương
trình
1
cóhainghiệmphânbiệt
1x
điềukiệncầnvàđủlà
0 4
m m
.
Khiđóhaigiaođiểmlà
1 1
( ; )A x x m
;
2 2
( ; )B x x m
.
Tacó
2 2 2
2 ; 2 ; 2( 4 )OA m m OB m m AB m m
;
,
2
m
d O d
.
2
1 1 . .
. . , . . 2( 4 )
2 2 4
2
OAB
m
OAOB AB
S AB d O d m m
R
.
Suyra
2 2
2
( 2 ). 2( 4 )
1
. 2( 4 )
2
2 4.2 2
m
m m m m
m m
2
0( )
2 4 6( )
2( )
m l
m m m m n
m n
.
Vậytổngcácphầntừcủa
S
bằng
4
.
Câu 6. Đồthịhàmsố
2 1
1
x
y C
x
vàđườngthẳng
:
d y x m
.Tìmtấtcảcácgiátrịcủathamsố
m
đểđườngthẳng
d
cắtđồthị
C
tại
2
điểmphânbiệt
A.
1
m
. B.
5 1
m
. C.
5
m
. D.
5
m
hoặc
1
m
.
Lời giải
Chọn D
Hàmsố
2 1
1
x
y
x
cótậpxácđịnh
\ 1
D
.
Lậpphươngtrìnhhoànhđộgiaođiểm:
2 1
1
x
x m
x
1
x
2
2
1 1 0
2 1
1
1
x m x m
x x m x mx
x
x
Đườngthẳng
d
cắtđồthị
C
tại
2
điểmphânbiệt

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
phươngtrình
có
2
nghiệmphânbiệt
1x
2
2
0
6 5 0
1 1 1 0
1 0 t/m
m m
m m
5
m
hoặc
1
m
.
Câu 7. (Sở Cần Thơ 2019) Chohàmsố
3
1
x
y
x
cóđồthị
C
vàđườngthẳng
:
d y x m
,với
m
là
thamsốthực.Biếtrằngđườngthẳng
d
cắt
C
tạihaiđiểmphânbiệt
A
và
B
saochođiểm
2; 2
G
làtrọngtâmcủatamgiác
OAB
(
O
làgốctoạđộ).Giátrịcủa
m
bằng
A.
6
. B.
3
. C.
9
. D.
5
.
Lời giải
Chọn A
Hàmsố
3
1
x
y
x
có
2
2
0
1
y
x
,
x D
vàđườngthẳng
:
d y x m
cóhệsố
1 0
a
nên
d
luôncắt
C
tạihaiđiểmphânbiệt
;
A A
A x y
và
;
B B
B x y
vớimọigiátrịcủathamsố
m
.
Phươngtrìnhhoànhđộgiaođiểmcủa
d
và
C
là:
3
1
x
x m
x
2
3 0
x mx m
1
x
.
Suyra
A
x
,
B
x
là2nghiệmcủaphươngtrình
2
3 0
x mx m
.
TheođịnhlíViet,tacó
A B
x x m
.
Mặtkhác,
2; 2
G
làtrọngtâmcủatamgiác
OAB
nên
3
A B O G
x x x x
6
A B
x x
6
m
.
Vậy
6
m
thoảmãnyêucầuđềbài.
Câu 8. (Sở Nam Định 2019) Chohàmsố
3 2
1
x m
y
mx
với
m
làthamsố.Biếtrằngvớimọi
0,
m
đồ
thịhàmsốluôncắtđườngthẳng
: 3 3d y x m
tạihaiđiểmphânbiệt
A
,
.B
Tíchtấtcảcácgiá
trịcủa
m
tìmđượcđểđườngthẳng
d
cắtcáctrục
,Ox
Oy
lầnlượttại
,C
D
saochodiệntích
OAB
bằng2lầndiệntích
OCD
bằng
A.
4
9
. B.
4
. C.
1
. D.
0
.
Lời giải
Chọn A.
Với
0
m
,xétphươngtrình
3 2
3 3
1
x m
x m
mx
2
3 3 1 0
x mx
.(*)
Gọitọađộcácgiaođiểmcủa
d
vớiđồthịhàmsốđãcholà:
1 1
;3 3A x x m
,
2 2
;3 3B x x m
.
Tọađộcácđiểm
C
,
D
là
;0
C m
và
0; 3D m
.
Gọi
,O d
h d
thì
h
làchiềucaocủacáctamgiác
OAB
và
OCD
.
Theogiảthiết: 2
OAB OCD
S S
2 2
1 1
. 2. . 2 4
2 2
AB h CD h AB CD AB CD
2
2 2
2
1 2 1 2
3 4 3x x x x m m
2 2
2 2
1 2 1 2 1 2
10 40 4 4x x m x x x x m
2 2 2
4 4 2
4
3 9 3
m m m m
.
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 22 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Vậytíchcácgiátrịcủa
m
là
4
9
.
Câu 9. (Gia Lai 2019) Cóbaonhiêugiátrịnguyêndươngcủathamsố
m
đểđườngthẳng
3
y x m
cắtđồthịhàmsố
2 1
1
x
y
x
tạihaiđiểmphânbiệt
A
và
B
saochotrọngtâmtamgiác
OAB
(
O
làgốctọađộ)thuộcđườngthẳng
2 2 0
x y
?
A.
2
. B.
1
. C.
0
. D.
3
.
Lời giải
Chọn C
Phươngtrìnhhoànhđộgiaođiểm:
2 1
3
1
x
x m
x
(*)
Vớiđiềukiện
1
x
,(*)
2
3 1 1 0
x m x m
(1)
Đườngthẳng
3
y x m
cắtđồthịhàmsố
2 1
1
x
y
x
tạihaiđiểmphânbiệt
A
và
B
khivà
chỉkhiphươngtrình(1)cóhainghiệmphânbiệtkhác
1
,điềukiện:
2
2
1 12 1 0
3.1 1 .1 1 0
m m
m m
2
10 11 0
3 0
m m
1
11
m
m
.(**)
Khôngmấttínhtổngquát,giảsử
1 1
; 3
A x x m
,
2 2
; 3
B x x m
với
1
x
,
2
x
làhainghiệm
phânbiệtphươngtrình(1).TheoVi-ettacó:
1 2
1
3
m
x x
.
Gọi
M
làtrungđiểm
AB
,tacó:
1 1
;
6 2
m m
M
.Giảsử
;G x y
làtrọngtâmtamgiác
OAB
,
tacó
2
3
OG OM
2 1
.
3 6
2 1
.
3 2
m
x
m
y
1
9
1
3
m
x
m
y
.Vậy
1 1
;
9 3
m m
G
.
Mặtkhác,điểm
G
thuộcđườngthẳng
2 2 0
x y
nêntacó:
1 1
2. 2 0
9 3
m m
11
5
m
(thỏamãn(**)).Dođókhôngcógiátrịnguyêndươngcủa
m
thỏamãnyêucầubài
toán.
Câu 10. Giả sử
b
m
a
,
,a b
,
, 1
a b
là giá trị thực của tham số
m
để đường thẳng
: 3
d y x m
cắtđồthịhàmsố
2 1
1
x
y
x
C
tạihaiđiểmphânbiệt
A
,
B
saochotrọng
tâmtamgiác
OAB
thuộcđườngthẳng
2 2 0
x y
,với
O
làgốctoạđộ.Tính
2a b
.
A.
2
. B.
5
. C.
11
. D.
21
.
Lời giải
Chọn D
Phươngtrìnhhoànhđộgiaođiểm:
2 1
3
1
x
x m
x
,
1
x
.
2
3 1 1 0
x m x m
*
.
Để
C
cắt
d
tạihaiđiểmphânbiệtthì
*
phảicóhainghiệmphânbiệtkhác1.Suyra
2
2
1 12 1 0
1 0
1 12
3.1 1 .1 1 0
m m
m
m
m m
1
11
m
m
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
Khiđó
1 1
; 3
A x x m
,
2 2
; 3
B x x m
,với
1
x
và
2
x
lànghiệmcủaphươngtrình
*
đồng
thờithoảmãn
1 2
1
3
m
x x
.
Gọi
G
làtrọngtâmcủa
OAB
,tacó
1 1
;
9 3
m m
G
.
Mà
G
nên
1 1 11
2 2 0
9 3 5
m m
m
.Suyra
11
5
a
b
.
Vậy
2 21
a b
.
Câu 11. Chohàmsố
3 2
,(C)
2
x
y
x
vàđườngthẳng
: 2 4
d y ax b
.Đườngthẳngdcắt(C)tạiA,
BđốixứngnhauquagốctọađộO,khiđó
T a b
bằng
A.
2T
. B.
5
2
T
. C.
4T
. D.
7
2
T
.
Lời giải
Chọn D
Xétphươngtrìnhhoànhđộ:
3 2
2 4; 2.
2
x
ax b x
x
2
2 2 7 10 0 * .
ax a b x
Đườngthẳngdcắt(C)tạihaiđiểmphânbiệtA,Bkhiphươngtrình(*)cóhainghiệmphân
biệt
2
0
2a 2 7 4 4 10 0 2*
4 0
a
b a b
Gọi
1 1 2 2
; 2 4 ; ; 2 4
A x ax b B x ax b
.
DoA,BđốixứngnhauquagốcOnên
1 2 1 2
0 0
4 8 0 2
x x x x
b b
TheoViétcủaphươngtrình(*)tacó
1 2
7 2 2
.
a b
x x
a
7 2 2 3
0 7 2 2 0 .
2
a b
a b a
a
Thay
3
2
2
a
b
vàođiềukiện(2*)tháythỏamãn.
Vậy
7
.
2
a b
Câu 12. Tìmgiátrịthựccủathamsố
m
đểđườngthẳng
d
:
3
y x m
cắtđồthịhàmsố
2 1
1
x
y
x
tạihaiđiểmphânbiệt
A
,
B
saochotrọngtâm
OAB
thuộcđườngthẳng
:
2 2 0
x y
,
với
O
làgốctọađộ.
A.
11
5
m
. B.
1
5
m
. C.
0
m
. D.
2
m
.
Lời giải
Chọn A
Hoànhđộhaiđiểm
A
,
B
lànghiệmcủaphươngtrình
2 1
3
1
x
x m
x
3 1 2 1x m x x
(vì
1
x
khôngphảilànghiệmcủaphươngtrình).
2
3 1 1 0
x m x m
(*)
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 24 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Điềukiện:
0
2
1 4.3 1 0
m m
1
1 11 0
11
m
m m
m
.
Khiđóphươngtrình
(*)
cóhainghiệmphânbiệt
A
x
,
B
x
thỏamãn
1
3
A B
m
x x
.
Gọi
; 3
A A
A x x m
,
; 3
B B
B x x m
thì trọng tâm của tam giác
OAB
là
3 2
;
3 3
A B
A B
x x m
x x
G
hay
1 1
;
9 3
m m
G
.
G
1 1
2. 2 0
9 3
m m
11
5
m
.
Câu 13. Chohàmsố
2
1
x
y
x
cóđồthịlà
C
.Tìmtậphợptấtcảcácgiátrị
a
đểquađiểm
0;M a
cóthểkẻđượcđườngthẳngcắt
C
tạihaiđiểmphânbiệtđốixứngnhauquađiểm
M
.
A.
;0 2;
. B.
3;
. C.
;0
. D.
; 1 3;
.
Lời giải
Chọn A
Đườngthẳngcóhệsốgóc
k
điquađiểm
0;M a
códạng
y kx a
.
Phươngtrìnhhoànhđộgiaođiểmcủađồthị
C
vàđườngthẳng
y kx a
là:
2
1
2
1
2
x
x
kx a
x
x kx kx ax a
2
1
2 0 *
x
kx a k x a
.
Tacầntìmđiềukiệncủa
a
đểphươngtrình
*
cóhainghiệmphânbiệt
1
x
;
2
x
khác1vàthỏa
mãn
1 2
1 2
0 0
2
x x
x x
.
Điềukiệnnàytươngđươngvới
2
2
1 2
0
2 4 0
.1 2 .1 0
0
k
a k ka
k a k a
x x
2
0
2 4 0
2 0
2
0
k
a k ka
k a
k
0
2
4 2 0
k
k a
a a
2 0
2
;0 2;
a
k a
a
;0 2;a
.
Câu 14. (Đại học Hồng Đức –Thanh Hóa 2019) Cóbaonhiêusốnguyêndương
m
saochođườngthẳng
y x m
cắtđồthịhàmsố
2 1
1
x
y
x
tạihaiđiểmphânbiệt
M
,
N
saocho
10
MN
.
A.
2
. B.
3
. C.
1
. D.
4
.
Lời giải
Chọn D
Điềukiệnxácđịnhcủahàmsố:
1
x
.
Phươngtrìnhhoànhđộgiaođiểm:
2
1 1 0
2 1
1
1
x m x m
x
x m
x
x
.
Đườngthẳng
y x m
cắtđồthịhàmsố
2 1
1
x
y
x
tạihaiđiểmphânbiệt
M
,
N
khivàchỉkhi
phươngtrình
2
1 1 0
x m x m
cóhainghiệmphânbiệtkhác-1
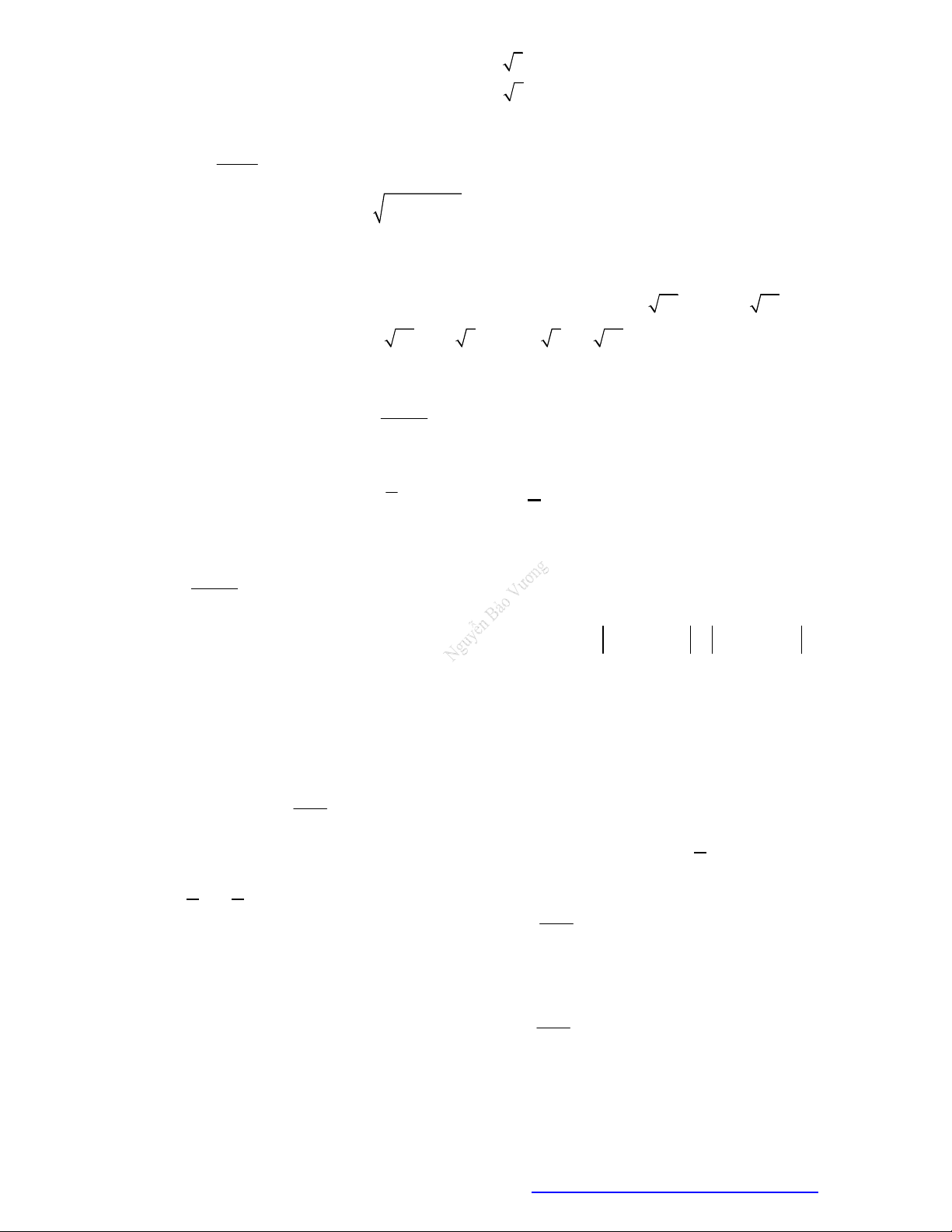
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25
2
0 3 2 3
6 3 0
(*)
1
3 0
3 2 3
m
m m
x
m
.
Gọi
1 1
;
M x x m
,
2 2
;
N x x m
làtọađộgiaođiểmđườngthẳng
y x m
vàđồthịhàmsố
2 1
1
x
y
x
.
Theobàicho
2 2
2 1 1 2 1 2
10 2 10 4 50
MN x x x x x x
ÁpdụngđịnhlíViétchophươngtrình
2
1 1 0
x m x m
tacó:
1 2
1 2
1
. 1
x x m
x x m
.
Tacó
2
2
1 2 1 2
10 4 50 6 53 3 62 3 62
MN x x x x m m m
Kếthợpvới(*)thì
3 62 ;3 2 3 3 2 3 ;3 62
m
.
Cácsốnguyêndương
m
thỏamãnyêucầubàitoánlà
7,8,9,10
m
.
Câu 15. Cholàđồthịhàmsố
x
y
x
2 1
1
.Tìm
k
đểđườngthẳng
d : y kx k 2 1
cắttạihaiđiểm
phânbiệt
A,B
saochokhoảngcáchtừ
A
đếntrụchoànhbằngkhoảngcáchtừ
B
đếntrụchoành.
A. 1. B.
2
5
C.
3
. D.
2
.
Lời giải
Phươngtrìnhhoànhđộgiaođiểm:
x (ld)
x
kx k
kx k x k
x
2
1
2 1
2 1
3 1 2 0 1
1
.
Ycbttươngđươngcóhainghiệmphânbiệt
x ,x
1 2
saocho
kx k kx k
1 2
2 1 2 1
k k
k k k k k .
k k k
k x x k
2 2
1 2
0 0
6 1 0 6 1 0 3
1 3 4 2 0 3
4 2 0
Câu 16. (THPT Lương Thế Vinh Hà Nội 2019) Tìmđiềukiệncủa
m
đểđườngthẳng
1y mx
cắtđồ
thịhàmsố
3
1
x
y
x
tạihaiđiểmphânbiệt.
A.
;0 16;
B.
16;
C.
;0
D.
;0 16;
Lời giải
Chọn D
Hoànhđộgiaođiểmlànghiệmcủaphươngtrình:
3
1
1
x
mx
x
3 1 1
1
x mx x
x
2
4 0 *
1
mx mx
x
Đểđườngthẳng
1y mx
cắtđồthịhàmsố
3
1
x
y
x
tạihaiđiểmphânbiệtthìphươngtrình
*
cóhainghiệmphânbiệtkhác
1
hay
2
0
1 1 4 0
m m
2
16 0
4 0
m m
;0 16;m
.
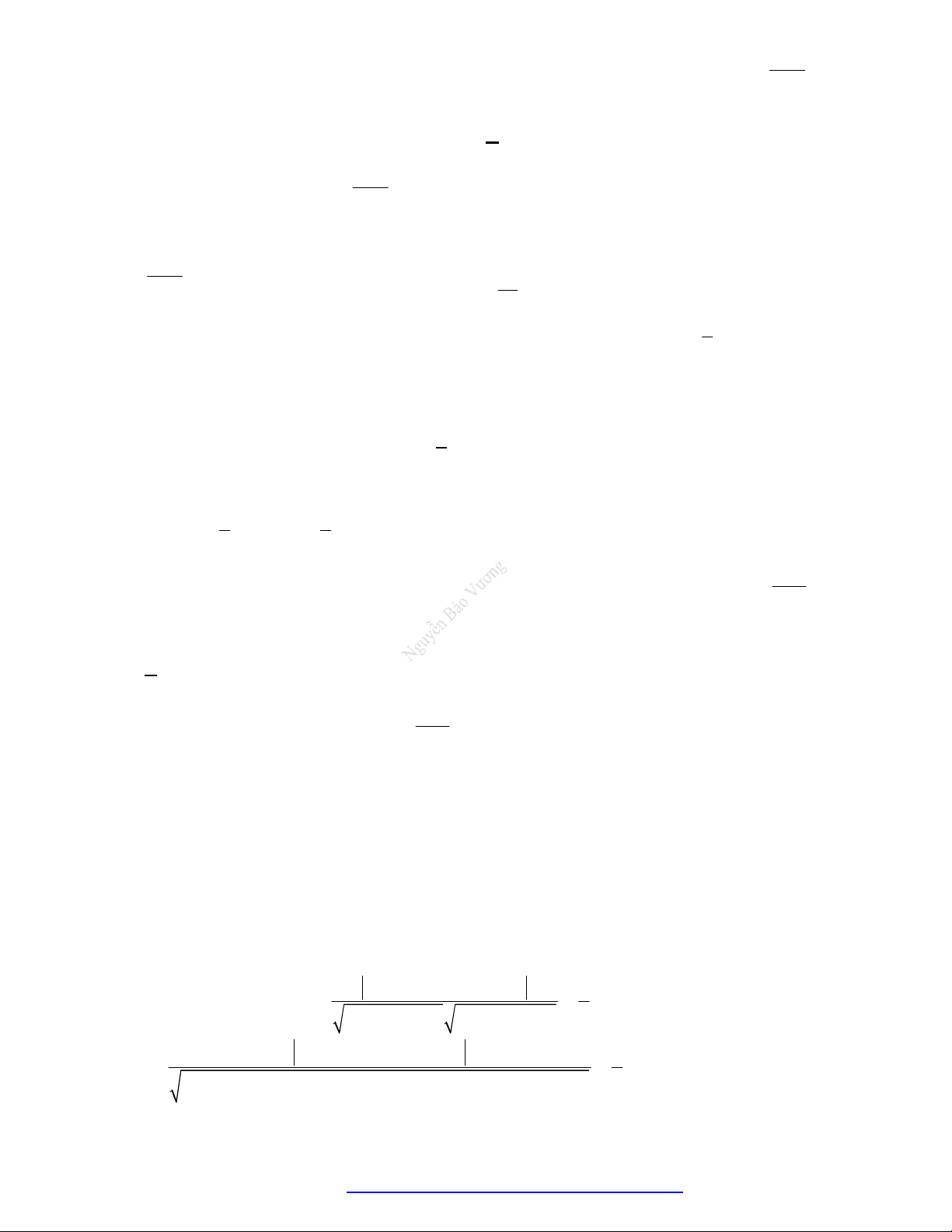
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 26 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 17. (Chuyên Lê Quý Đôn Quảng Trị 2019) Gọi
;M a b
làđiểmtrênđồthịhàmsố
2
x
y
x
sao
chokhoảngcáchtừ
M
đếnđườngthẳng
: 2 6
d y x
nhỏnhất.Tính
2 2
4 5 2 7
a b
.
A.
162
. B.
2
. C.
18
. D.
0
.
Lời giải
Gọi
C
làđồthịhàmsố
2
x
y
x
.
Phươngtrìnhhoànhđộgiaođiểmcủa
C
vàđườngthẳng
d
là:
2
2 6
x
x
x
2
2 5 2 0 0
x x x
2
1
2
x
x
.
Suyrađườngthẳng
d
cắtđồthị
C
tạihaiđiểmphânbiệt
1 2
1
2;2 , ;5
2
M M
.
Tacó
; 0,
d M d M
min ; 0
d M d
khi
M d
.
Mà
M C
M d C
2;2
1
;5
2
M
M
.
Với
2;2
M
2 2
2, 2 4 5 2 7 18
a b a b
.
Với
1
;5
2
M
2 2
1
, 5 4 5 2 7 18
2
a b a b
.
Câu 18. (ToánHọc Tuổi Trẻ 2019) Có bao nhiêu giá trị của
m
để đồ thị củahàm số
1
x
y
x
cắt
đườngthẳng
y x m
tạihaiđiểmphânbiệt
,A B
saochogócgiữahaiđườngthẳng
OA
và
OB
bằng
0
60
(với
O
làgốctọađộ)?
A.
2
B.
1
C.
3
D.
0
Lờigiải
Xétphươngtrìnhhoànhđộgiaođiểm
2
1
0 *
1
x
x
x m
x mx m
x
Đểcóhiađiểmphânbiệt
,A B
thìphươngtrình(*)phảicóhainghiệmphânbiệtkhác
1
2
1 0
4
0
4 0
m m
m
m
m m
Khiđóphươngtrình(*)cóhainghiệmphânbiết
1
x
,
2
x
thỏamãn:
1 2
1 2
x x m
x x m
Giảsử
1 1 2 2
; , ;
A x x m B x x m
,suyra:
1 1 2 2
; , ;
OA x x m OB x x m
Theogiảthiếtgócgiữahaiđườngthẳng
OA
và
OB
bằng
0
60
suyra:
1 2 1 2
0
2 2
2 2
1 1 2 2
1
cos ; cos60
2
x x x m x m
OA OB
x x m x x m
2
1 2 1 2
2
2 2
2 2 2
1 2 1 2 2 1 1 2 1 2
2
1
2
x x m x x m
x x x x mx x x x m x m x m

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27
2 2
2
2 2
2 2
2 1 1 2 1 2
2
1
2
m m m
m m mx m mx x x m x x m
2
2 2
2 2 2
2 1
2
1
2
m
m m mx m mx m m m
2 2
2 1
2 1
2
2 1 1x x
2 2
2 1
2 1 1 16
x x
2
1 2 1 2 1 2
2 2 12
x x x x x x
2
6
4 12 0
2
m
m m
m
Câu 19. (THPT Lê Quy Đôn Điện Biên 2019) Để đường thẳng
: 2
d y x m
cắt đồ thị hàm số
2
1
x
y
x
C
tạihaiđiểmphânbiệt
A
và
B
saochođộdài
AB
ngắnnhấtthìgiátrịcủa
m
thuộckhoảngnào?
A.
4; 2
m
B.
2;4
m
C.
2;0
m
D.
0;2
m
Lờigiải
ChọnD
Phươngtrìnhhoànhđộgiaođiểmcủa
d
và
C
:
2
2
2 1 2 0 *
1
x
x m x m x m
x
(vì
1x
khôngphảilànghiệm).
Đườngthẳng
d
cắt
C
tạihaiđiểmphânbiệt:
Phươngtrình(*)cóhainghiệmphânbiệt
1 2
,x x
.
2 2
1 4 2 1 8 0,m m m m
.
TheođịnhlýVi-ettacó:
1 2
1 2
1
. 2
x x m
x x m
Khiđó
1 1
; 2 ,
A x x m
2 2
; 2
B x x m
.
2 2 2 2
2 1 2 1 2 1 2 1 1 2
2 2 2 2 4
AB x x x m x m x x x x x x
.
2
2 1 8 4
m
.
AB
nhỏnhất
4 1
AB m
.
Câu 20. (THPT Lương Tài Số 2 2019) Biết rằng đường thẳng
2 2y x m
luôn cắt đồ thị hàm số
2
3
1
x
y
x
tạihaiđiểmphânbiệtA, Bvớimọigiátrịcủathamsốm.Tìmhoànhđộtrungđiểm
củaAB?
A.
1
m
B.
1
m
C.
2 2
m
D.
2 1
m
Lờigiải
ChọnC
Phươngtrìnhhoànhđộgiaođiểmcủa
C
và
d
là:
2
3
2 2
1
x
x m
x
2
2 1 2 3 0
x m x m
1
,(
1
x
).
Đườngthẳng
d
cắt
C
tạihaiđiểmphânbiệt
A
,
B
Phươngtrình
1
cóhainghiệmphân
biệtkhác
2

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 28 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2
2
1 2 3 0
1 2 1 . 1 2 3 0
m m
m m
2
4 0,
4 0
m m
.
Khiđó,gọi
1 1
;2 2A x x m
;
2 2
;2 2B x x m
HoànhđộtrungđiểmcủaABlà
1 2
2 2
1
2 2
I
x x m
x m
.
Câu 21. (THPTGiaLộcHảiDương2019) Gọi
H
làđồ thị hàmsố
2 3
1
x
y
x
.Điểm
0 0
;M x y
thuộc
H
cótổngkhoảngcáchđếnhaiđườngtiệmcậnlànhỏnhất,với
0
0
x
khiđó
0 0
x y
bằng
A.
1
. B.
2
. C.
3
. D.
0
.
Lờigiải
TXĐ:
\ 1
D
.
Dễthấyđồthịhàmsốcótiệmcậnđứng
1
: 1
d x
vàtiệmcậnngang
2
: 2
d y
.
Do
0
0
0
2 3
;
1
x
M H M x
x
.
Xét
0
1 2 0 0
0 0
2 3
1
, , 1 2 1 2
1 1
x
d M d d M d x x
x x
.
Đẳngthứcxảyrakhivàchỉkhi
0
0
0
0
0
1
1
2
1
x
x
x
x
.
Theođềbài,tacó
0
0
x
nênnhận
0
2
x
0
1
y
.
Vậy
0 0
1
x y
.
Câu 22. (Chuyên Bến Tre - 2020) Gọi
S
làtậphợptấtcảcácgiátrịnguyêncủathamsố
m
đểđường
thẳng
:
d y x m
cắt đồ thị hàm số
2 1
1
x
y
x
tại hai điểm phân biệt
,A B
sao cho
2 2
AB
.Tổnggiátrịcácphầntửcủa
S
bằng
A.
6
. B.
27
. C.
9
. D.
0
.
Lời giải
Chọn A
Phươngtrìnhhoànhđộgiaođiểm:
2 1
1
x
x m
x
(1)
Điềukiện:
1
x
.
Phươngtrình(1)
2 1
1
x
x m
x
2 1 1
x x m x
2
1 1 0
x m x m
(2).
Đểđườngthẳng
:
d y x m
cắtđồthịhàmsố
2 1
1
x
y
x
tạihaiđiểmphânbiệt
,A B
thì
phươngtrình(2)có2nghiệmphânbiệtkhác
1
2
0
6 3 0.
3 0
m m
; 3 2 3 3 2 3;m
(3).
Gọi
; , ;
A A B B
A x x m B x x m
làtọađộgiaođiểm:
Theođềtacó:
2 2
2 2 2 2
B A B A
AB x x x x

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 29
2
2 8
B A
x x
2 2
2 . 4 0
B A B A
x x x x
2
4 . 4 0
A B A B
x x x x
.
2
1 4 1 4 0
m m
2
6 7 0 7;1
m m m
(4)
Từ(3)và(4)tacó
7; 3 2 2 3 2 2;1
m
.
Vì
6;0
m m
Chọn A.
Câu 23. (Lương Thế Vinh - Hà Nội - 2020) Chohàmsố
2
2
1
x m
y
x
cóđồthị
,
m
C
trongđó
m
là
thamsốthực.Đườngthẳng
:
d y m x
cắt
m
C
tạihaiđiểm
; , ;
A A B B
A x y B x y
với
;
A B
x x
đườngthẳng
': 2
d y m x
cắt
m
C
tạihaiđiểm
; , ;
C C D D
C x y D x y
với
.
C D
x x
Gọi
S
làtậphợptấtcảcácgiátrịcủathamsố
m
để
. 3.
A D
x x
Sốphầntửcủatập
S
là
A.
1.
B.
2.
C.
0.
D.
3.
Lời giải
Chọn B
Hoànhđộđiểm
A
và
B
lànghiệmphươngtrình:
2
2 1
x m x m x
2 2
3 0
x m x m m
suyra
2
. ; 3
A B A B
x x m m x x m
Hoànhđộđiểm
C
và
D
lànghiệmphươngtrình:
2
2 1 2
x m x m x
2 2
1 2 0
x m x m m
suyra
2
. 2; 1
C D C D
x x m m x x m
Mặckhác
A
x
và
D
x
lànghiệmcủaphươngtrình:
2
3
2 3 0
1
A
D
x
x x
x
.Suyra
2 2
0
6 9 5 2 9
2
m
m m m m
m
.
Dạng 3. Bài toán tương giao của đường thẳng với hàm số trùng phương (CHỨA THAM SỐ)
. Bài toán tổng quát: Tìmmđểđườngthẳng
:d y
cắtđồthị
4 2
( ) : ( ; )
C y f x m ax bx c
tạinđiểm
phânbiệtthỏamãnđiềukiệnKchotrước?
Phương pháp giải:
Bước 1. Lậpphươngtrìnhhoànhđộgiaođiểmcủa
d
và
( )C
là:
4 2
0
ax bx c
(1)
Đặt
2
0
t x
thì
2
(1) 0
at bt c
(2)
Tùyvàosốgiaođiểmnmàtabiệnluậnđểtìmgiátrị
1
.m D
Cụthể:
Để
( ) 4
d C n
điểmphânbiệt
(1)
có4nghiệmphânbiệt
(2)
có2nghiệm
1 2
, t t
thỏađiềukiện:
1 2 1
0
0 0 .
0
t t S m D
P
Để
( ) 3
d C n
điểmphânbiệt
(1)
có3nghiệmphânbiệt
(2)
cónghiệm
1 2
, t t
thỏađiềukiện:
1 2 1
0
0 .
0
c
t t m D
b
a
Để
( ) 2
d C n
điểmphânbiệt
(1)
có2nghiệmphânbiệt

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 30 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
(2)
có2nghiệmtráidấuhoặccónghiệmképdương
1
0
.
0
0
ac
m D
S
Để
( ) 1d C n
điểmphânbiệt
(1)
cóđúng1nghiệm
(2)
cónghiệmkép
0
hoặc
1
1
2
0
0
0
.
0 0
0
c
t
m D
b
t c
a
Bước 2.BiếnđổiđiềukiệnKvềdạngcóchứatổngvàtíchcủa
1 2
, t t
(3)
Thếbiểuthứctổng,tíchvào(3)sẽthuđượcphươngtrìnhhoặcbất phươngtrìnhvới biếnsốlà
.m
Giải
chúngtasẽtìmđược
2
.m D
Kếtluận:
1 2
.m D D
Tìm điều kiện để đồ thị hàm số
4 2
y ax bx c
cắt trục hoành tại
4
điểm phân biệt có hoành độ
lập thành cấp số cộng.
Ta có:
4 2
0 (1)
ax bx c
, đặt
2
0
t x
, thì có:
2
0
at bt c
(2)
Để
(1)
có
4
nghiệm phân biệt thì
(2)
có hai nghiệm phân biệt dương, tức là:
1 2
1 2
0
0
. 0
t t
t t
Khi đó
(1)
có
4
nghiệm phân biệt lần lượt là
2 1 1 2
; ; ;t t t t
lập thành cấp số cộng khi và chỉ khi:
2 1 1 1 2 1 2 1
( ) 3 9t t t t t t t t
. Theo định lý Vi – et
1 2
b
t t
a
suy ra
1 2
9
;
10 10
b b
t t
a a
, kết hợp
1 2
.
c
t t
a
nên có:
2 2
9 100
ab a c
Tóm lại: Hàm số
4 2
y ax bx c
cắt trục hoành tại
3
điểm phân biệt có hoành độ lập thành cấp số cộng,
thì điều kiện cần và đủ là:
2
2 2
4 0
0
0
9 100
b ac
b
a
c
a
ab a c
Câu 1. Tậptấtcảcácgiátrịcủathamsố
m
đểphươngtrình
4 2
4 3 0
x x m
có4nghiệmphânbiệt
là
A.
1;3
. B.
3;1
. C.
2;4
. D.
3;0
.
Lời giải
Chọn B
Tacó:
4 2 4 2
4 3 0 4 3
x x m x x m
.
Xéthàmsố
4 2
4 3
y x x
,khiđó:
3
2
4 8 ; 0
0
x
y x x y
x
.
Suyra
1; 3
CD CT
y y
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 31
Vậyđểphươngtrìnhđãchocó4nghiệmphânbiệtthì:
3 1 3;1
m m
.
Câu 2. Tậptấtcảcácgiátrịcủathamsố
m
đểphươngtrình
4 2
2 (2 1) 0x mx m
có4nghiệmthực
phânbiệtlà
A.
1
; \ 1 .
2
B.
(1; )
. C.
1
;
2
. D.
.
Lời giải
Chọn A
Xétphươngtrình:
4 2
2 (2 1) 0x mx m
.
Đặt
2
( 0)x t t
.
Phươngtrìnhđãchotrởthành
2
2 (2 1) 0(*)t mt m
.
Đểphươngtrìnhbanđầucóbốnnghiệmthựcphânbiệtthìphươngtrình
(*)
cóhainghiệmphân
biệtdương
' 2
0 2 1 0 1
1
0 2 0 0
2
1
0 2 1 0 1
2
m m m
m
S m m
m
P m
m
hay
1
; \ 1
2
m
.
Câu 3. (THPT Lương Thế Vinh - Hn - 2018)Chohàmsố
4 2
3 2y x x .Tìmsốthựcdương
m
để
đườngthẳng
y m
cắtđồthịhàmsốtại
2
điểmphânbiệt
A
,
B
saochotamgiác
OAB
vuông
tại
O
,trongđó
O
làgốctọađộ.
A.
2m
. B.
3
2
m
. C.
3m
. D.
1m
.
Lời giải
Hoànhđộgiaođiểmcủahaiđồthịhàmsốlànghiệmcủaphươngtrình:
4 2
3 2x x m
4 2
3 2 0 1x x m
.
Vì
0 2 0m m
hayphươngtrình
1
luôncóhainghiệmphânbiệtthỏamãn:
2
3 4 17
2
m
x
1
3 4 17
2
m
x
và
2
3 4 17
2
m
x
.
Khiđó:
1
;A x m
,
2
;B x m
.
Tacótamgiác
OAB
vuôngtại
O
,trongđó
O
làgốctọađộ
2
1 2
. 0 . 0OAOB x x m
.
2
2
02
2 3 0
4 2
2 3 0
3 4 17
2
2
4 12 4 8 0
m
m
m
m
m m
m m m
.
Vậy
2m
làgiátrịcầntìm.
Câu 4. Đườngthẳng
y m
cắtđồthịhàmsố
4 2
y x x tại
4
điểmphânbiệtkhivàchỉkhi
A.
1
0
4
m
. B.
1
0
4
m
. C.
0m
. D.
1
4
m
Lời giải
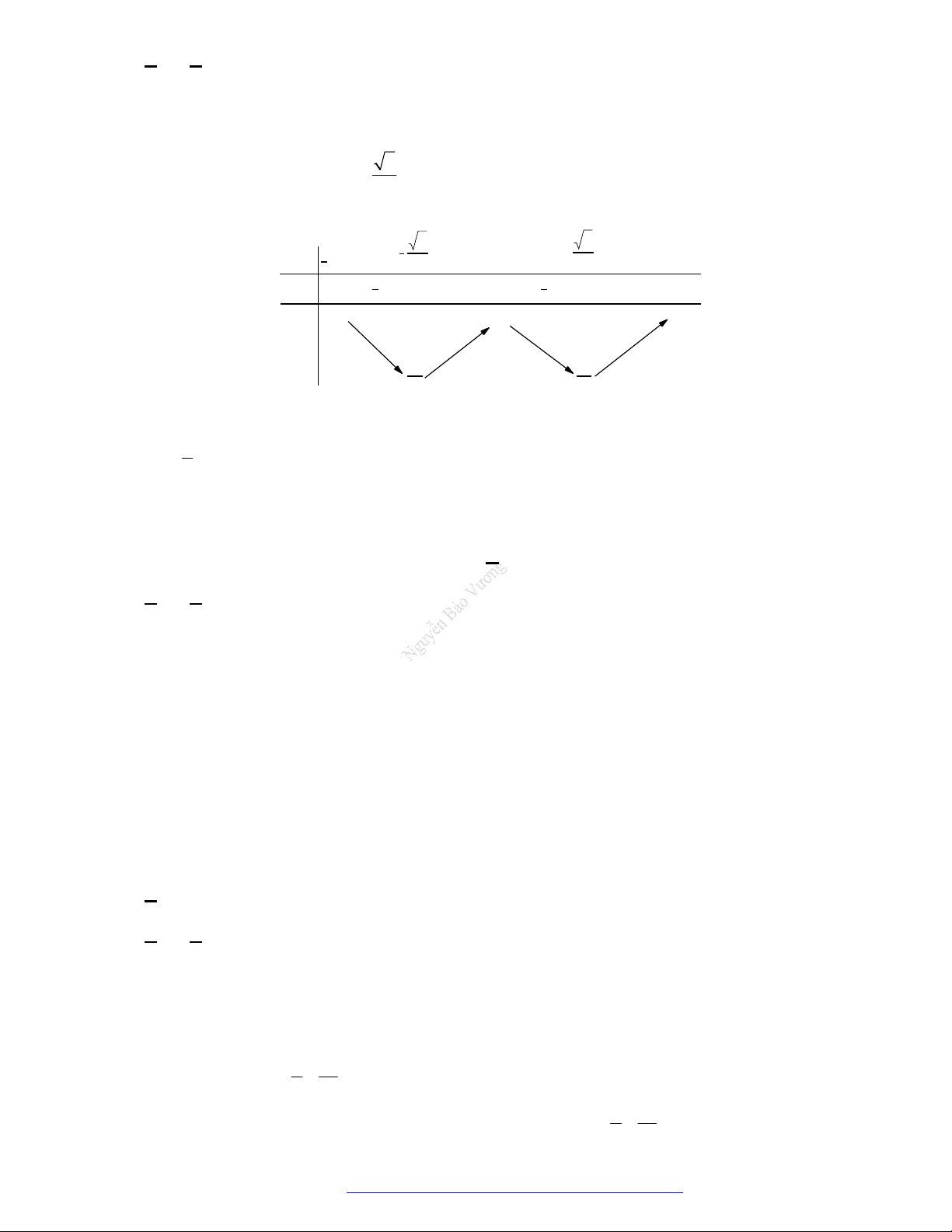
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 32 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Chọn A
Hàmsố
4 2
y x x
cótậpxácđịnh
D
.
3
' 4 2 .y x x
3
0
' 0 4 2 0
2
2
x
y x x
x
.
Bảngbiếnthiên:
Dựavàobảngbiếnthiênđườngthẳng
y m
cắtđồthịhàmsố
4 2
y x x
tại
4
điểmphânbiệt
1
0
4
m
.
Câu 5. (THPT Quỳnh Lưu- Nghệ An- 2019) Mộtđườngthẳngcắtđồthị hàmsố
4 2
2y x x
tại4
điểmphânbiệtcóhoànhđộlà
0, 1,
,m
n
.Tính
2 2
.S m n
A.
1S
. B.
0S
. C.
3S
. D.
2S
.
Lời giải
Chọn C
Tọađộcácgiaođiểmlầnlượtlà
0;0A
,
1; 1B
,
4 2
; 2 ,C m m m
4 2
; 2 .D n n n
Đườngthẳngquacácđiểm
, , ,A B C D
cóphươngtrình:
.y x
Xétphươngtrìnhhoànhđộgiaođiểm:
4 2 4 2
2
0
2 2 0 1
1 0 *
x
x x x x x x x
x x
Vậy ,m n làcácnghiệmcủaphươngtrình
*
.
Khiđó:
2
2 2
2 3.S m n m n mn
Câu 6. Cóbao nhiêugiátrịnguyêncủa
m
để đồthịhàmsố
4 3 2
4 2 8 4y x x m x x
cắttrục
hoànhtạiđúnghaiđiểmcóhoànhđộlớnhơn
1
.
A.
8
. B.
7
. C.
5
. D.
3
.
Lời giải
Chọn A
Phươngtrìnhhoànhđộgiaođiểm
4 3 2
4 2 8 4 0x x m x x
Đồthịhàmsố
4 3 2
4 2 8 4y x x m x x
cắttrụchoànhtạiđúnghaiđiểmcóhoànhđộlớn
hơn
1
cóđúnghainghiệmlớnhơn
1
.
4 3 2
* 4 8 4 2x x x m x
2
2
8 4
2 4m x x
x x
Đâylàphươngtrìnhhoànhđộgiaođiểmcủa
2
2
8 4
: 4 1C y x x x
x x
vớiđườngthẳng
2y m
songsongvớitrụchoành.
+
∞ +
∞
0
+
00
0
x
y'
y
2
2
2
2
+
+
0
∞
∞
-1
4
-1
4
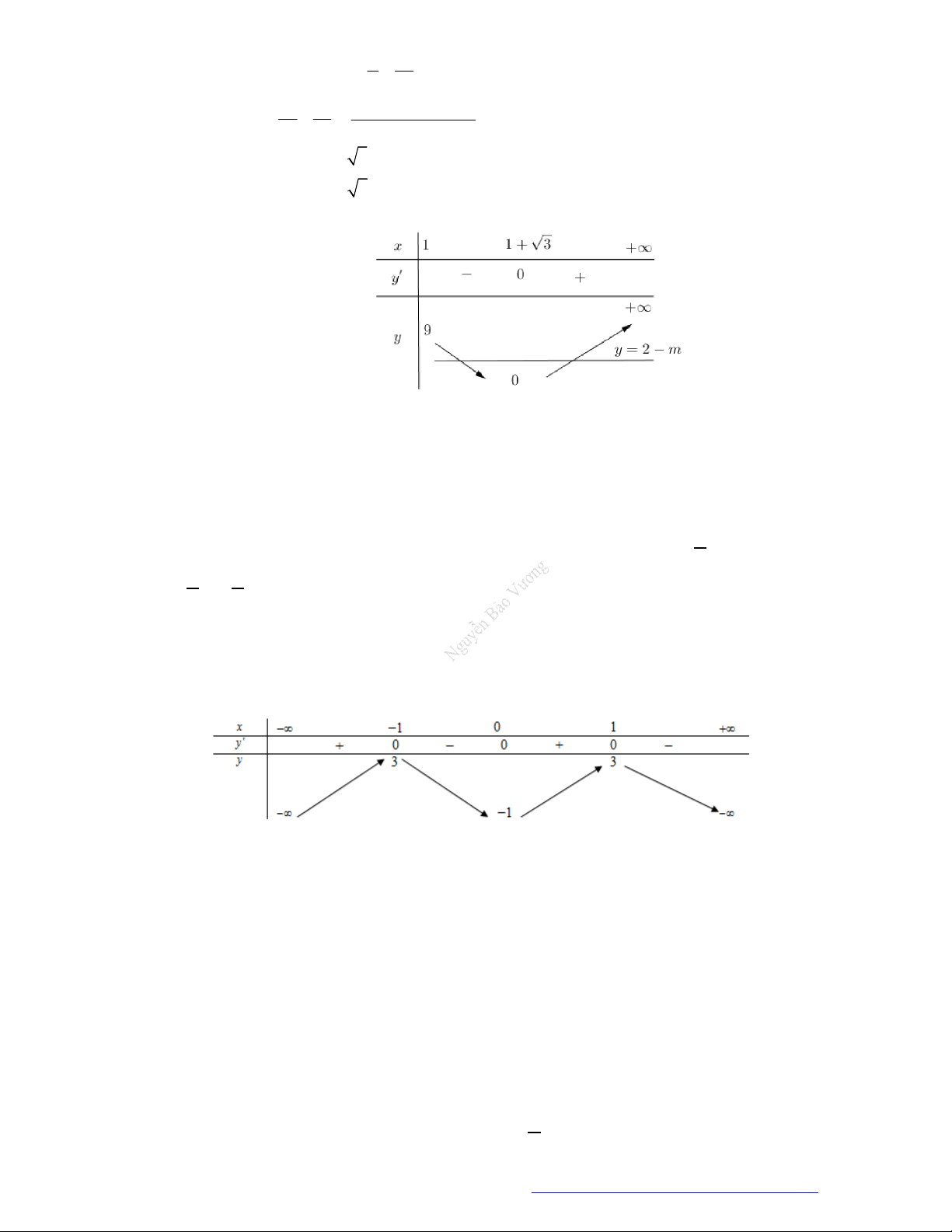
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 33
Xéthàmsố
2
2
8 4
4 1y x x x
x x
.
2 3
8 8
2 4y x
x x
4 3
2
2 4 8 8x x x
x
.
Cho
0y
1 3
1 3
x
x
lo¹i
nhËn
.
Bảngbiếnthiên
Dựavàobảngbiếnthiêntathấy,ycbt
0 2 9m 7 2m
.
Vì
m
nguyênnên
6, 5,...,1m
.
Vậycó
8
giátrịnguyêncủa
m
thỏabàitoán.
Câu 7. (Sở Hà Nam - 2019) Chohàmsố
4 2
4 8 1f x x x
.Cóbaonhiêugiátrịnguyêndươngcủa
m
đểphươngtrình
f x m
cóđúnghainghiệmphânbiệt?
A. 0. B. 2. C. 3. D. 1.
Lời giải
Chọn D
3
0
16 16 0 1
1
x
f x x x x
x
.
Bảngbiếnthiên
Phươngtrình
f x m
làphươngtrìnhhoànhđộgiaođiểmcủađồthịhàmsố
4 2
4 8 1f x x x
C
vàđườngthẳng
y m
.
Phươngtrìnhđãchocó2nghiệmphânbiệt
Đườngthẳng
y m
cắtđồthị
C
tạihaiđiểm
phânbiệt
3
1
m
m
.
Vậycó1giátrịnguyêndươngcủa
m
đểphươngtrình
f x m
cóđúnghainghiệmphânbiệt.
Câu 8. (Sở Thanh Hóa 2018) Chohàmsố
4 2
2y x mx m (với
m
làthamsốthực).Tậptấtcảcácgiá
trịcủathamsố
m
đểđồthịhàmsốđãchocắtđườngthẳng
3y
tạibốnđiểmphânbiệt,trong
đócómộtđiểmcóhoànhđộlớnhơn
2
cònbađiểmkiacóhoànhđộnhỏhơn
1
,làkhoảng
;a b
(với
,a b
,
a
,
b
làphânsốtốigiản).Khiđó,
15ab
nhậngiátrịnàosauđây?
A.
63
. B.
63
. C.
95
. D.
95
.
Lời giải
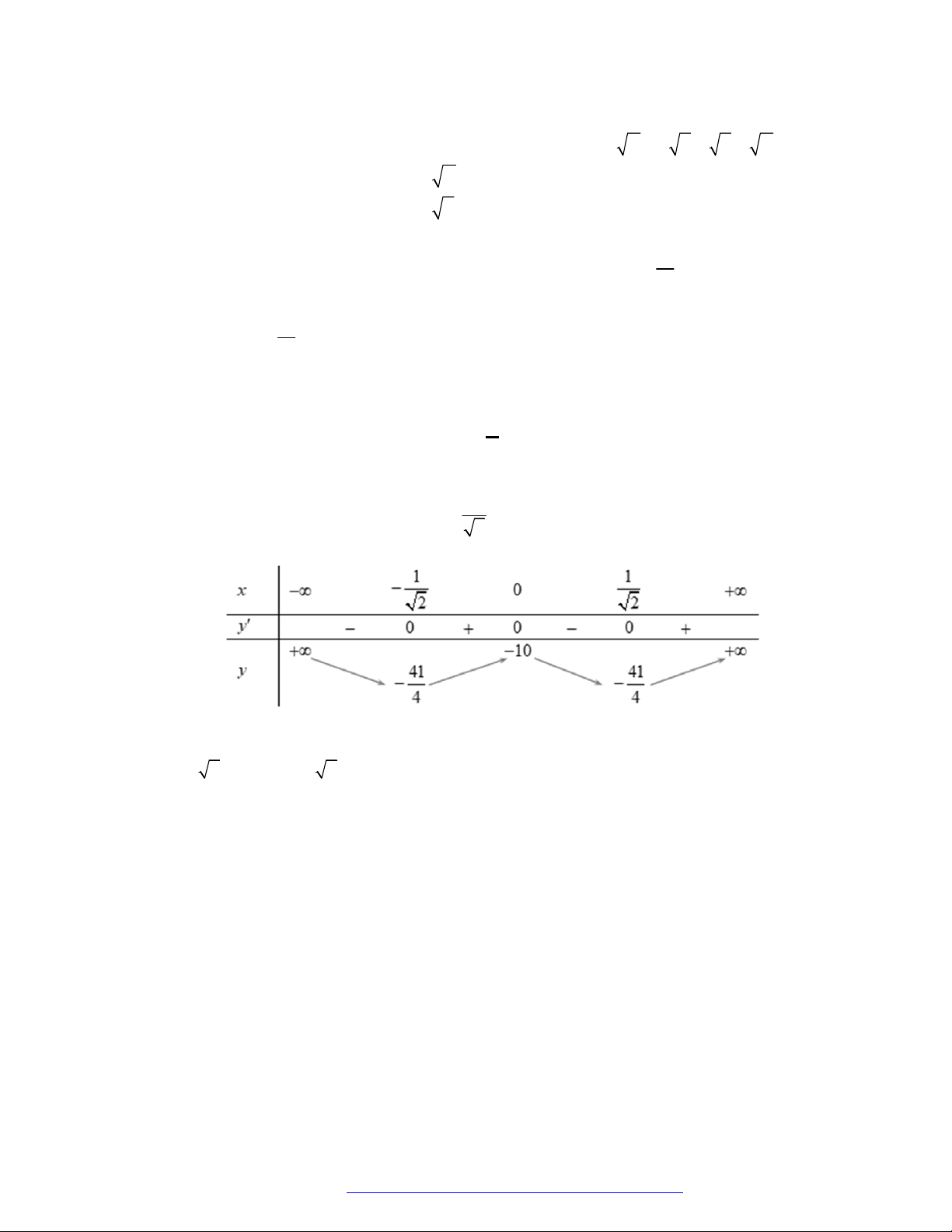
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 34 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Xétphươngtrìnhhoànhđộgiaođiểm
4 2
2 3x mx m
.Đặt
2
x t
,
0t
.Khiđóphươngtrình
trởthành
2
2 3 0t mt m
1
vàđặt
2
2 3f t t mt m
.
Để đồ thị hàm số cắt đường thẳng
3y
tại
4
điểm phân biệt thì phương trình
1
có hai
nghiệmthỏamãn
1 2
0 t t
vàkhiđóhoànhđộbốngiaođiểmlà
2 1 1 2
t t t t .
Dođó,từđiềukiệncủabàitoánsuyra
2
1
2
1
t
t
hay
1 2
0 1 4t t .
Điềunàyxảyrakhivàchỉkhi
0 0
1 0
4 0
f
f
f
3 0
3 4 0
9 19 0
m
m
m
19
3
9
m
.
Vậy
3a
,
19
9
b
nên
15 95ab
.
Câu 9. (Chuyên Hà Tĩnh 2018)Đườngthẳng
2
y m cắtđồthịhàmsố
4 2
10y x x tạihaiđiểm
phânbiệt
A
,
B
saochotamgiác
OAB
vuông(
O
làgốctọađộ).Mệnhđềnàosauđâyđúng?
A.
2
5;7m
. B.
2
3;5m
. C.
2
1;3m
. D.
2
0;1m
.
Lời giải
3 2
4 2 2 2 1y x x x x
;
0
0
1
2
x
y
x
Bảngbiếnthiên
Dựavàobảngbiếnthiên,tathấyđườngthẳng
2
0y m luônphíatrêntrụchoành
Nênnóluôncắtđồthịhàmsốtạihaiđiểmphânbiệt
A
,
B
.
Gọi
2
;A a m và
2
;B a m làgiaođiểmcủahaiđồthịđãcho,với
0a
Tacó
A C
2 2
10 1a a m
Tamgiác
OAB
cântại
O
nêntamgiác
OAB
vuôngtại
O
. 0OAOB
4
m a
2
Từ
1
và
2
tacó
8 4 2
10 0m m m
4 2
10 0t t t
,với
2
0t m
.
3 2
2 2 3 5 0t t t t
2t
2
2 1;3m
.
Câu 10. (Sở Bình Phước 2018) Chohàmsố
4 2
2 3y x x
cóđồthịnhưhìnhvẽbêndưới.Vớigiátrị
nàocủa
m
thìphươngtrình
4 2
2 3 2 4x x m
có
2
nghiệmphânbiệt.
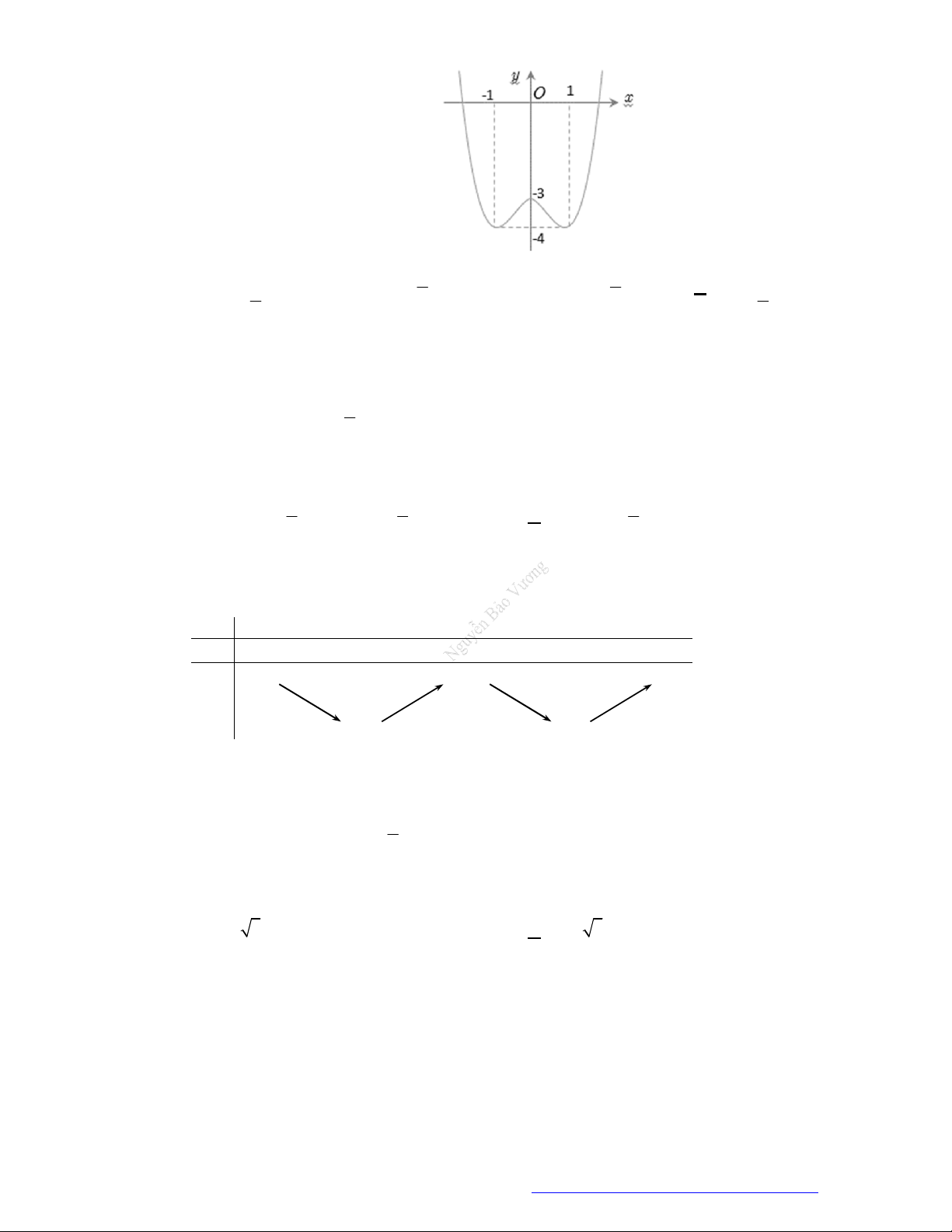
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 35
A.
0
1
2
m
m
. B.
1
2
m
. C.
1
0
2
m
. D.
0
1
2
m
m
.
Lời giải
Dựavàođồthịtathấy,phươngtrình
4 2
2 3 2 4x x m
cóhainghiệmphânbiệtkhi
2 4 4
2 4 3
m
m
0
1
2
m
m
.
Câu 11. (THPT Bình Giang - Hải Dương - 2018) Tìmtấtcảcácgiátrịcủathamsố
m
đểphươngtrình
4 2
2 3 2 0x x m
có
4
nghiệmphânbiệt.
A.
3
2
2
m
. B.
3
2
2
m
. C.
3
2
2
m
. D.
3 4m
.
Lời giải
-Tacó:
4 2 4 2
2 3 2 0 2 3 2x x m x x m
.
-Lậpbảngbiếnthiêncủahàmsố
4 2
2 3y x x .
-Sốnghiệmcủaphươngtrìnhđãcholàsốgiaođiểmcủađồthịhàmsố
4 2
2 3y x x vàđường
thẳng
2y m
.
-TừBBTtathấyphươngtrìnhđãchocó
4
nghiệmphânbiệtkhivàchỉkhi
4 2 3m
3
2
2
m
.
Câu 12. (THPT Vân Nội - Hà Nội - 2018) Tấtcả các giátrịthựccủathamsố
m
,để đồ thịhàmsố
4 2 2
2 2 2 2y x m x m m
khôngcắttrụchoành.
A. 3 1.m B.
3.m
C. 3 1.m D.
3.m
Lời giải
Xétphươngtrìnhhoànhđộgiaođiểm
4 2 2
2 2 2 2 0 1x m x m m
Đặt
2
0t x
.Phươngtrình
1
trởthành
2 2
2 2 2 2 0 2t m t m m
Đồthịhàmsốkhôngcắttrụchoành
1
vônghiệm
2
vônghiệmhoặccónghiệmâm
x
1
0
1
y
0
0
0
y
4
3
4

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 36 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Hay
2
2 6 0
2 6 0
2 0
2 2 0
m
m
m
m m
3
3
2
1 3
1 3
m
m
m
m
m
3
1 3 3
m
m
1 3.
m
Câu 13. (Sở Nam Định - 2018) Tìm tất cả các giá trị của tham số
m
để đồ thị hàm
số
4 2
1 2 2 3 6 5
y m x m x m
cắt trục hoành tại 4 điểm phân biệt có các hoành độ
1 2 3 4
, , ,x x x x
thỏamãn
1 2 3 4
1 . x x x x
A.
5
1;
6
m
. B.
3; 1
m
. C.
3;1
m
. D.
4; 1
m
.
Lời giải
C1:Phươngtrìnhhoànhđộgiaođiểmcủađồthịhàmsốvàtrụchoànhlà
4 2
1 2 2 3 6 5 0 1
m x m x m
Đặt
2
0
t x
pttrởthành
2
1 2 2 3 6 5 0 2
m t m t m
2
1 2 2 3 6 5
g t m t m t m
Đểpt(1)có4nghiệmphânbiệtthìpt(2)phảicó2nghiệmdươngphânbiệt
Hay
2
1 2
1 2
1
1 0
2 3 1 6 5 0
0
6 5
0
. 0
1
0
2 3
0
1
m
m
m m m
m
t t
m
t t
m
m
1
23 561 23 561
4 4
*
5
1
6
3
1
2
m
m
m m
m m
Đểpt(1)có4nghiệmthỏamãn
1 2 3 4
1
x x x x
thìpt(2)phảicó2nghiệmthỏa
1 2
0 1
t t
1
1 2 1 2 1 2
2
1 0
1 1 0 1 0
1 0
t
t t t t t t
t
2 2 3
6 5 3 12
1 0 0 4 1
1 1 1
m
m m
m
m m m
Kếthợpvới(*)tacó
4; 1
m
thỏayêucầubàitoán.
C2:
Phươngtrìnhhoànhđộgiaođiểmcủađồthịhàmsốvàtrụchoànhlà
4 2
1 2 2 3 6 5 0 1
m x m x m
Đặt
2
0
t x
pttrởthành
2
1 2 2 3 6 5 0 2
m t m t m
Đểpt(1)có4nghiệmthỏamãn
1 2 3 4
1
x x x x
thìpt(2)phảicó2nghiệmthỏa
1 2
0 1
t t
Phươngtrình(2)
2
2
6 5
4 6
t t
m
t t
(biểuthức
2
4 6 0,t t t
)
Xéthàmsố
2
2
6 5
4 6
t t
f t
t t
,với
0;t
Tacó
f t
liêntụctrên
0;
vàcó
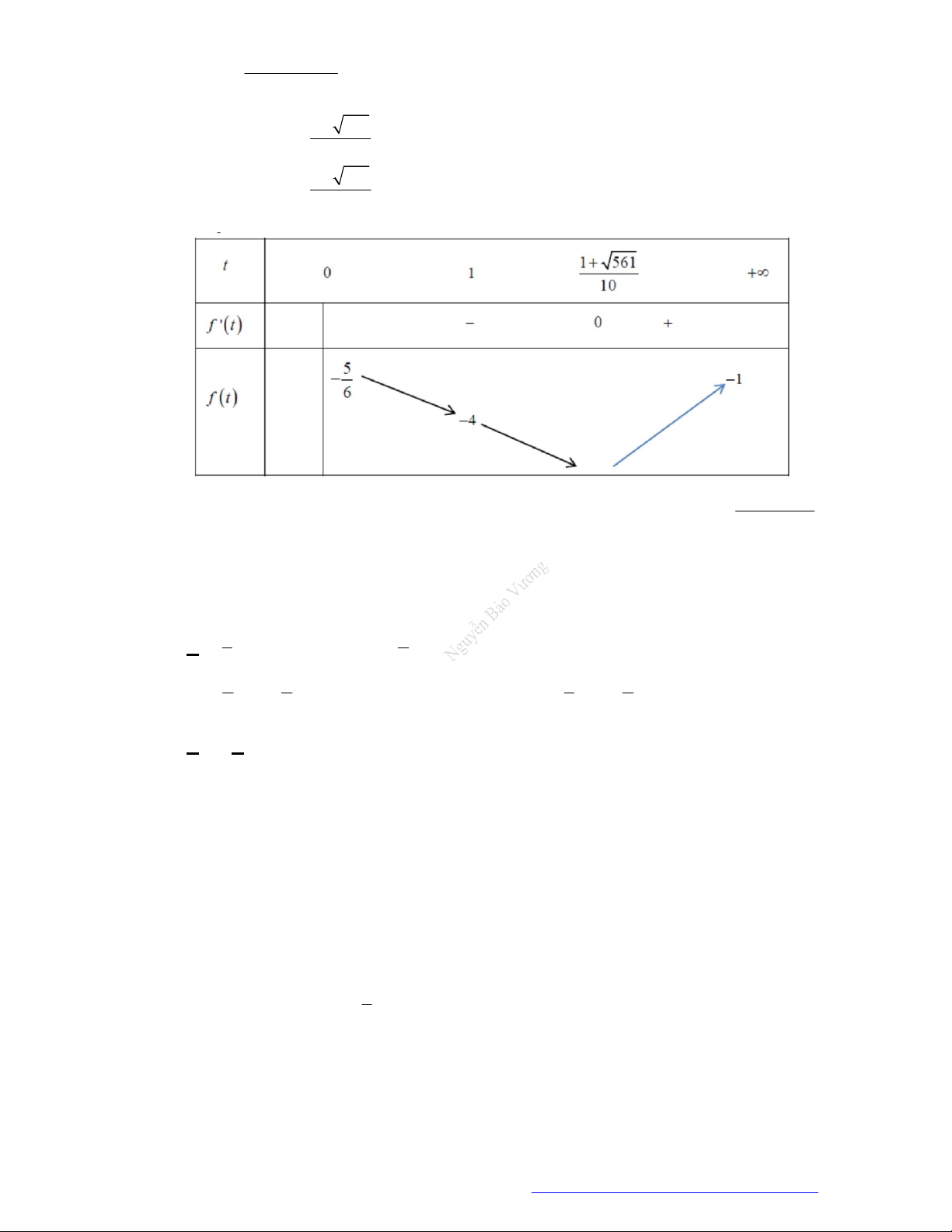
TÀI
LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 37
2
2
2
10
2 56
'
4 6
t t
f t
t t
1 56
1
0
10
' 0
1
561
1
10
t
f t
t
Bảngbiếnthiên
Dựavàobảngbiếnthiêntathấyđườngthẳng
y m
cắtđồth
ịhàmsố
2
2
6 5
4
6
t t
f t
t t
tạihai
giaođiểmcóhoàngđộthỏa
1 2
0 1
t t
khi
4 1m
.
Câu 14.
(ChuyênVĩnhPhúc2019)Chohàmsố
4 2
3 2
3y x m x m
cóđồthịlà ( )
m
C .Tìm
m
để
đườngthẳng
: 1d y
cắtđồthị( )
m
C tại4điểmphânbiệtđềucóhoànhđộnhỏhơn2.
A.
1
1
3
m
và
0m
B.
1
1
2
m
và
0m
C.
1 1
2
2
m
và
0m
D.
1 1
3
2
m
và
0m
Lờigi
ải
ChọnA
Phươ
ng trình hoành độ giao điểm của ( )
m
C và
đường thẳng
d
là
4 2
3 2
3 1x m x m
4 2
3 2
3 1 0x m x m
Đặt
2
t x
,
0t
,phương
trìnhtrởthành
2
3 2
3 1 0t m t m
2
1
3 1
t
t
m
Đườngthẳng
: 1d
y
cắt
đồthị ( )
m
C tại
4
điểm
phânbiệtđềucóhoànhđộnhỏhơn
2
khi
và
chỉkhiphươngtrình
2
cóha
inghiệmdươngphânbiệt
1
t ,
2
t thỏam
ãn
1 2
0 4t
t
0
3 1 1
1
0 3 1 4
1
3
m
m
m
m
-------------------- HẾT --------------------
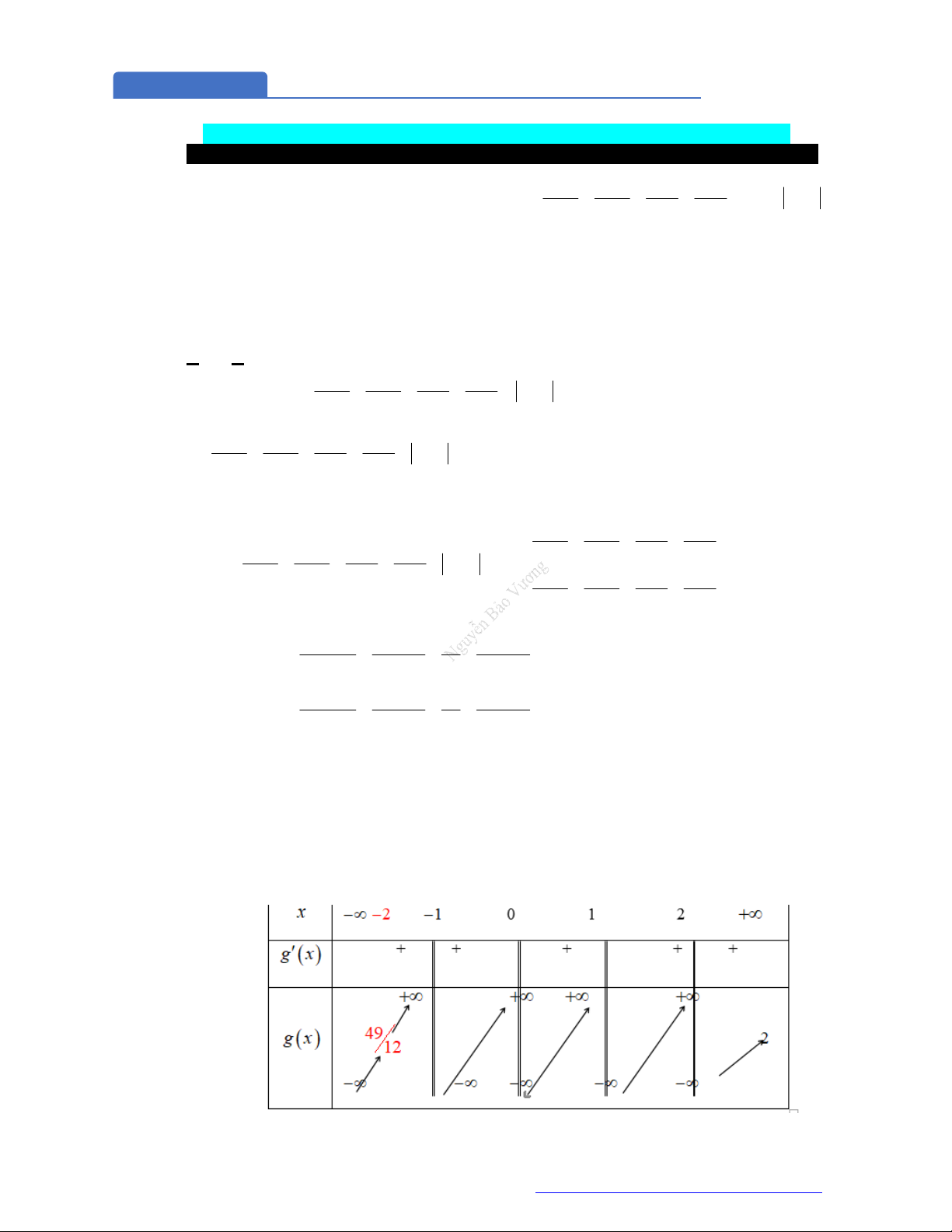
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
DẠNG TOÁN DÀNH CHO ĐỐI TƯỢNG HỌC SINH GIỎI MỨC 9-10 ĐIỂM
Dạng 1. Biện luận m để phương trình có nghiệm thỏa mãn điều kiện k (hàm số khác)
Câu 1. (Mã 101 2019) (Mã đề 001) Cho hai hàm số
3 2 1
2 1 1
x x x x
y
x x x x
và
2y x x m
(
m
là tham số thực) có đồ thị lần lượt là
1
C
và
2
C
. Tập hợp tất cả các giá trị của
m
để
1
C
và
2
C
cắt nhau tại đúng bốn điểm phân biệt là
A.
2;
. B.
;2
. C.
2;
. D.
;2
.
Lời giải
Chọn A
Xét phương trình
3 2 1
2
2 1 1
x x x x
x x m
x x x x
3 2 1
2
2 1 1
x x x x
x x m
x x x x
(1)
Hàm số
3 2 1
2 khi 2
3 2 1
2 1 1
2
3 2 1
2 1 1
2 2 khi 2
2 1 1
x x x x
x
x x x x
x x x x
p x x x
x x x x
x x x x
x x
x x x x
.
Ta có
2 2 2 2
2 2 2 2
1 1 1 1
0, 2; \ 1;0;1;2
2 1 1
1 1 1 1
2 0, 2
2 1 1
x
x
x x x
p x
x
x
x x x
nên hàm số
y p x
đồng biến trên mỗi khoảng
; 1
,
1;0
,
0;1
,
1;2
,
2;
.
Mặt khác ta có
lim 2
x
p x
và
lim
x
p x
.
Bảng biến thiên hàm số
y g x
:
TƯƠNG GIAO ĐỒ THỊ HÀM SỐ
Chuyên đề 8
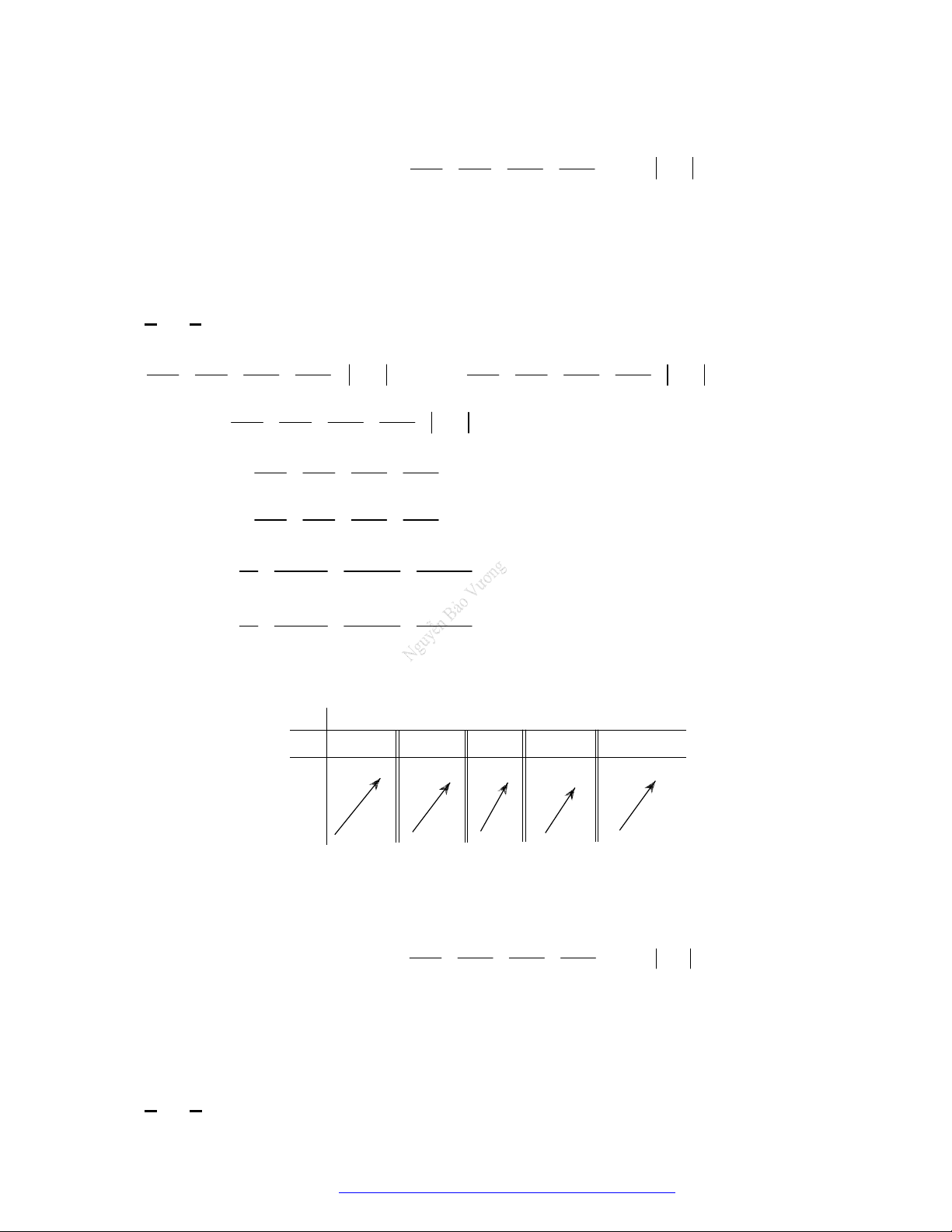
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Do đó để
1
C
và
2
C
cắt nhau tại đúng bốn điểm phân biệt thì phương trình (1) phải có 4
nghiệm phân biệt. Điều này xảy ra khi và chỉ khi đường thẳng
y m
cắt đồ thị hàm số
y p x
tại 4 điểm phân biệt
2m
.
Câu 2. (Mã 103 2019) Cho hai hàm số
1 1 2
1 2 3
x x x x
y
x x x x
và
2y x x m
(
m
là tham
số thực) có đồ thị lần lượt là
1 2
,C C
. Tập hợp tất cả các giá trị của
m
để
1
C
và
2
C
cắt
nhau tại đúng bốn điểm phân biệt là
A.
2;
. B.
; 2
. C.
2;
. D.
; 2
.
Lời giải
Chọn B
Xét phương trình hoành độ giao điểm
1 1 2 1 1 2
2 2 1
1 2 3 1 2 3
x x x x x x x x
x x m x x m
x x x x x x x x
Xét
1 1 2
2 , \ 3; 2; 1;0
1 2 3
x x x x
f x x x x D
x x x x
Ta có
1
2
1 1 2
2, 2;
1 2 3
1 1 2
2 2, ; 2
1 2 3
x x x x
x D D
x x x x
f x
x x x x
x x D D
x x x x
Có
1
2 2 2
2
2
2 2 2
2
1 1 1 1
,
1 2 3
1 1 1 1
2,
1 2 3
x D
x
x x x
f x
x D
x
x x x
Dễ thấy
1 2
0,f x x D D
, ta có bảng biến thiên
Hai đồ thị cắt nhau tại đúng 4 điểm phân biện khi và chỉ khi phương trình
1
có đúng 4 nghiệm
phân biệt, từ bảng biến thiên ta có:
2 2m m
.
Câu 3. (Mã 102 2019) Cho hai hàm số
1 2 3
1 2 3 4
x x x x
y
x x x x
và
1y x x m
(
m
là tham
số thực) có đồ thị lần lượt là
1
C
và
2
C
. Tập hợp tất cả các giá trị của
m
để
1
C
và
2
C
cắt
nhau tại đúng 4 điểm phân biệt là
A.
;3
. B.
;3
. C.
3;
. D.
3;
.
Lời giải
Chọn C
Điều kiện
1;x 2;x
3x
và
4x
.
Ta có phương trình hoành độ giao điểm
-
2
-
-
-
+
+
+
+
-
+
+
+
+
f(x)
f'(x)
+-
x
-3
-2
1 0
+
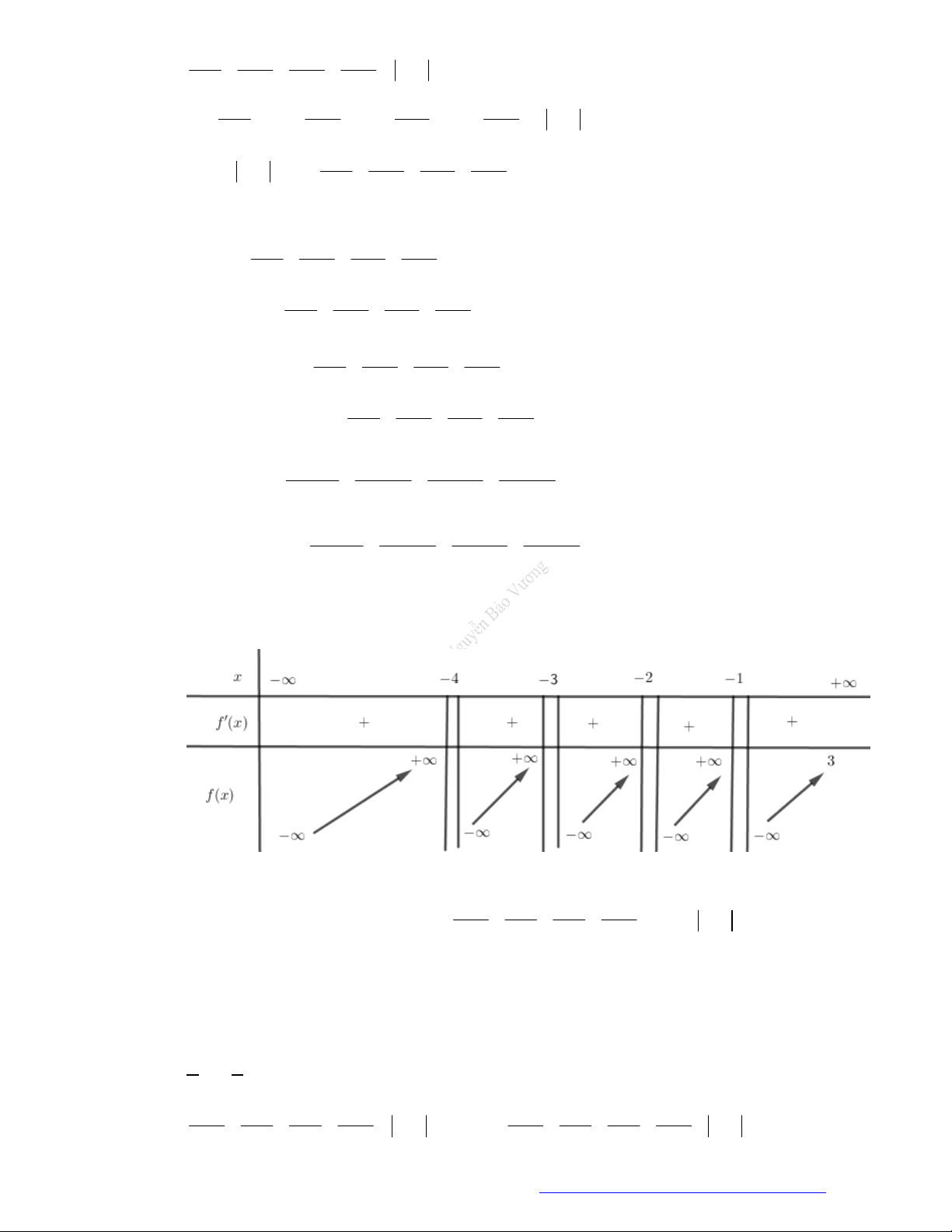
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
1 2 3
1
1 2 3 4
x x x x
x x m
x x x x
1 1 1 1
1 1 1 1 1
1 2 3 4
x x m
x x x x
1 1 1 1
1 4
1 2 3 4
x x m
x x x x
Đặt tập
1
1;D
và
2
( ; 4) 4; 3 ( 3; 2) 2; 1D
.
1
2
1 1 1 1
3 , khi
1 2 3 4
1 1 1 1
2 5 , khi
1 2 3 4
m x D
x x x x
x m x D
x x x x
Đặt
1
2
1 1 1 1
3 , khi
1 2 3 4
1 1 1 1
2 5 , khi
1 2 3 4
x D
x x x x
f x
x x D
x x x x
.
1
2 2 2 2
2
2 2 2 2
1 1 1 1
0, khi
1 2 3 4
1 1 1 1
2 >0, khi
1 2 3 4
x D
x x x x
f x
x D
x x x x
.
Vậy hàm số đồng biến trên từng khoảng xác định
lim 3
x
f x
;
lim
x
f x
nên ta có bảng biến thiên
Do đó để phương trình có 4 nghiệm phân biệt thì
3 3;m m
.
Câu 4. (Mã 104 2019) Cho hai hàm số
2 1 1
1 1 2
x x x x
y
x x x x
và
1y x x m
(
m
là tham
số thực) có đồ thị lần lượt là
1
C
và
2
C
. Tập hợp tất cả các giá trị của
m
để
1
C
và
2
C
cắt
nhau tại đúng bốn điểm phân biệt là
A.
; 3
. B.
3;
. C.
; 3
. D.
3;
.
Lời giải
Chọn B
Xét phương trình hoành độ
2 1 1
1
1 1 2
x x x x
x x m
x x x x
2 1 1
1
1 1 2
x x x x
x x m
x x x x
(1)
Số nghiệm của (1) là số giao điểm của
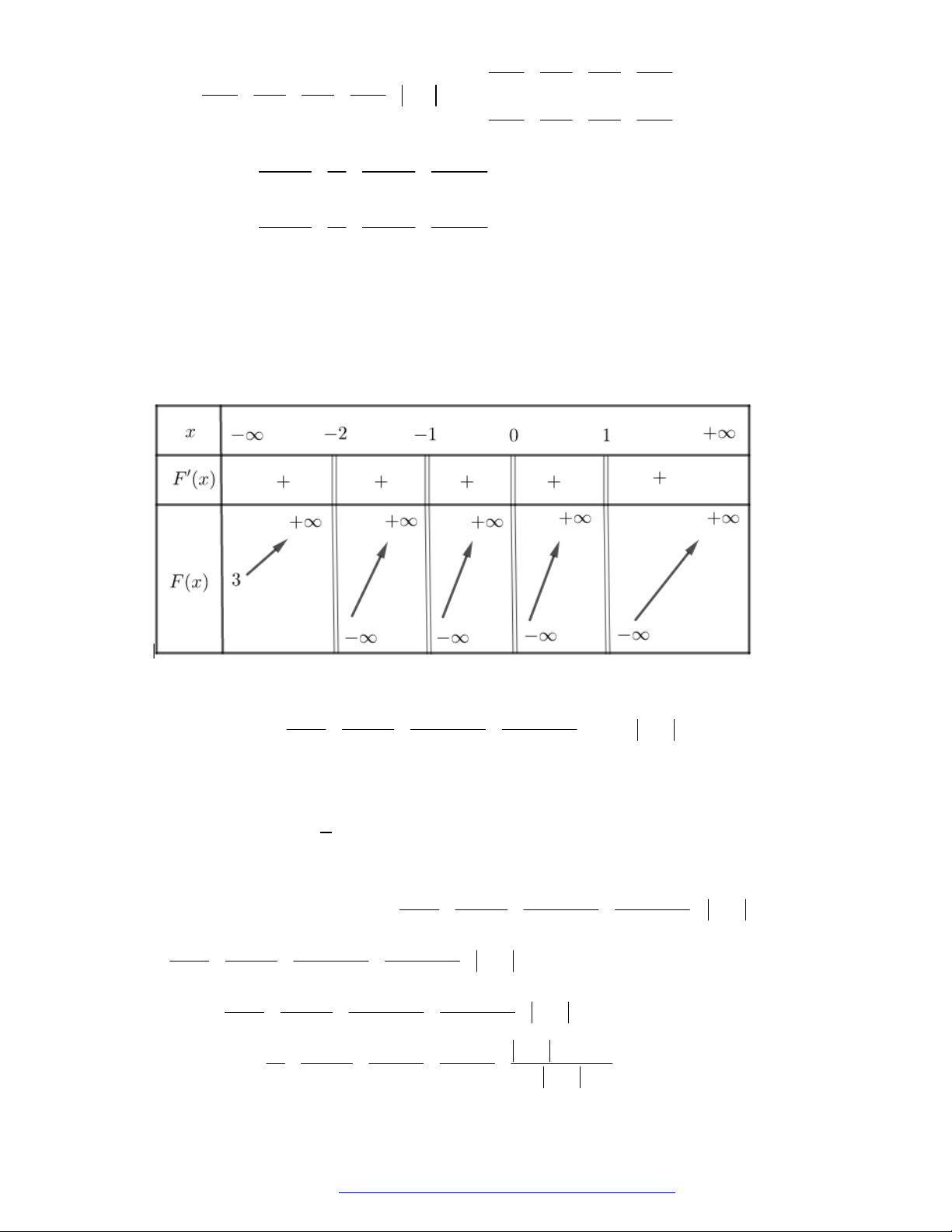
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2 1 1
1 , 1
2 1 1
1 1 2
1
2 1 1
1 1 2
2 1, 1
1 1 2
x x x x
x
x x x x
x x x x
F x x x
x x x x
x x x x
x x
x x x x
Ta có
2 2 2
2
2 2 2
2
1 1 1 1
, 1; \ 0;1
1 1 2
1 1 1 1
2, ; 1 \ 2
1 1 2
x
x
x x x
F x
x
x
x x x
.
Mặt khác
lim ; lim 3
x x
F x F x
2 2 1 1
0 0 1 1
lim ; lim ; lim ; lim
lim ; lim ; lim ; lim
x x x x
x x x x
F x F x F x F x
F x F x F x F x
.
Bảng biến thiên
Để phương trình có 4 nghiệm thì
3 3m m
.
Câu 5. Cho hai hàm số
2 2 2 2
1 2 4 3 6 8
1 2 3
x x x x x x x
y
x x x x
và
2y x x m
( là tham số
thực) có đồ thị lần lượt là
1
( )C
và
2
( )C . Tính tổng tất cả các giá trị nguyên thuộc khoảng
( 15; 20)
của tham số
m
để
1
( )C
và
2
( )C cắt nhau tại nhiều hơn hai điểm phân biệt.
A.
210
. B.
85
. C.
119
. D.
105
.
Lời giải
Chọn B
Xét phương trình hoành độ giao điểm
2 2 2 2
1 2 4 3 6 8
2
1 2 3
x x x x x x x
x x m
x x x x
2 2 2 2
1 2 4 3 6 8
2
1 2 3
x x x x x x x
x x m
x x x x
(1).
Đặt
2 2 2 2
1 2 4 3 6 8
( ) 2
1 2 3
x x x x x x x
g x x x
x x x x
.
Ta có
2
2 2 2
2 ( 2)
1 1 1 1
( ) 4 0
( 1) ( 2) 2
3
x x
g x
x x x x
x
với mọi
x
thuộc các khoảng
sau
; 0
,
0 ;1
,
1; 2
,
2 ; 3
và
3 ;
nên hàm số
( )y g x
đồng biến trên mỗi khoảng đó.
Mặt khác ta có
lim ( )
x
g x
và
lim ( )
x
g x
.
m
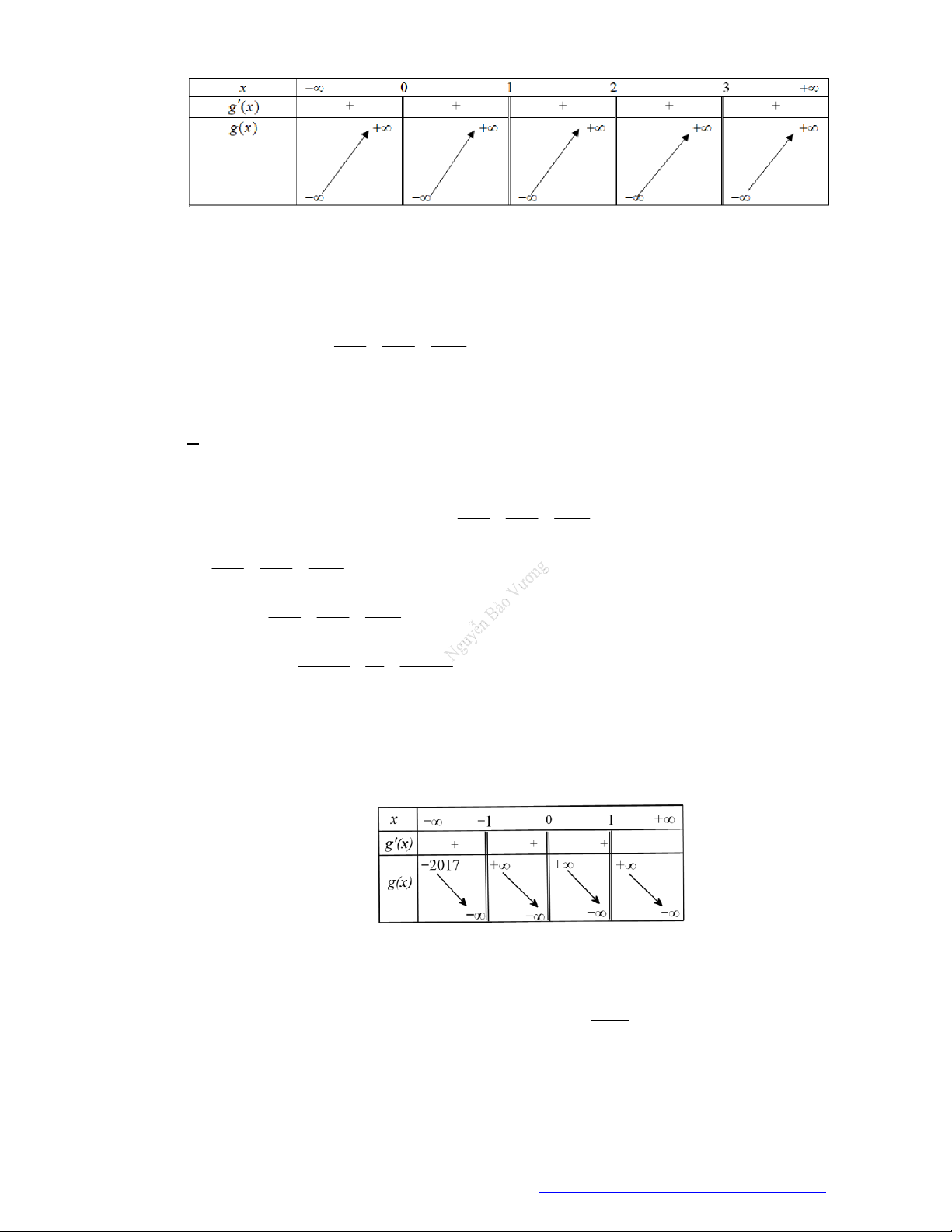
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Bảng biến thiên hàm số
( )y g x
Dựa vào bảng biến thiên ta thấy đường thẳng
y m
luôn cắt đồ thị hàm số
( )y g x
tại năm điểm
phân biệt nên
1
( )C
và
2
( )C luôn cắt nhau tại đúng năm điểm phân biệt với mọi giá trị của
m
. Kết hợp
điều kiện
m
nguyên thuộc
( 15;20)
nên
14; 13;...;18;19m
. Khi đó tổng tất cả các giá trị
m
là
15 16 17 18 19 85S
.
Câu 6. Cho hai hàm số
1 2
1 1
x x x
y
x x x
và
2020 3
x
y e m
(
m
là tham số thực) có đồ thị lần
lượt là
1
( )C và
2
( )C . Có bao nhiêu số nguyên
m
thuộc
( 2019; 2020)
để
1
( )C và
2
( )C cắt nhau
tại 3 điểm phân biệt?
A.
2692
. B.
2691
. C.
2690
. D.
2693
.
Lời giải
Chọn A
Xét phương trình hoành độ giao điểm
1 2
2020 3
1 1
x
x x x
e m
x x x
1 2
2020 3
1 1
x
x x x
e m
x x x
(1).
Đặt
1 2
( ) 2020
1 1
x
x x x
g x e
x x x
.
Ta có
2
2 2
1 1 1
( ) 0
( 1)
1
x
g x e
x x
x
với mọi
x
thuộc các khoảng sau
; 1
,
1;0
,
0;1
và
1;
nên hàm số
( )y g x
nghịch biến trên mỗi khoảng đó.
Mặt khác ta có
lim ( ) 2017
x
g x
và
lim ( )
x
g x
.
Bảng biến thiên hàm số
( )y g x
Do đó để
1
( )C và
2
( )C cắt nhau tại đúng ba điểm phân biệt thì phương trình (1) phải có ba
nghiệm phân biệt. Điều này xảy ra khi và chỉ khi đường thẳng
3y m
cắt đồ thị hàm số
( )y g x
tại ba điểm phân biệt khi và chỉ khi
2017
3 2017 672,3
3
m m
.
Do
m
nguyên thuộc
( 2019; 2020)
nên
672; 671;...;2019m
. Vậy có tất cả 2692 giá trị
m
thỏa mãn.
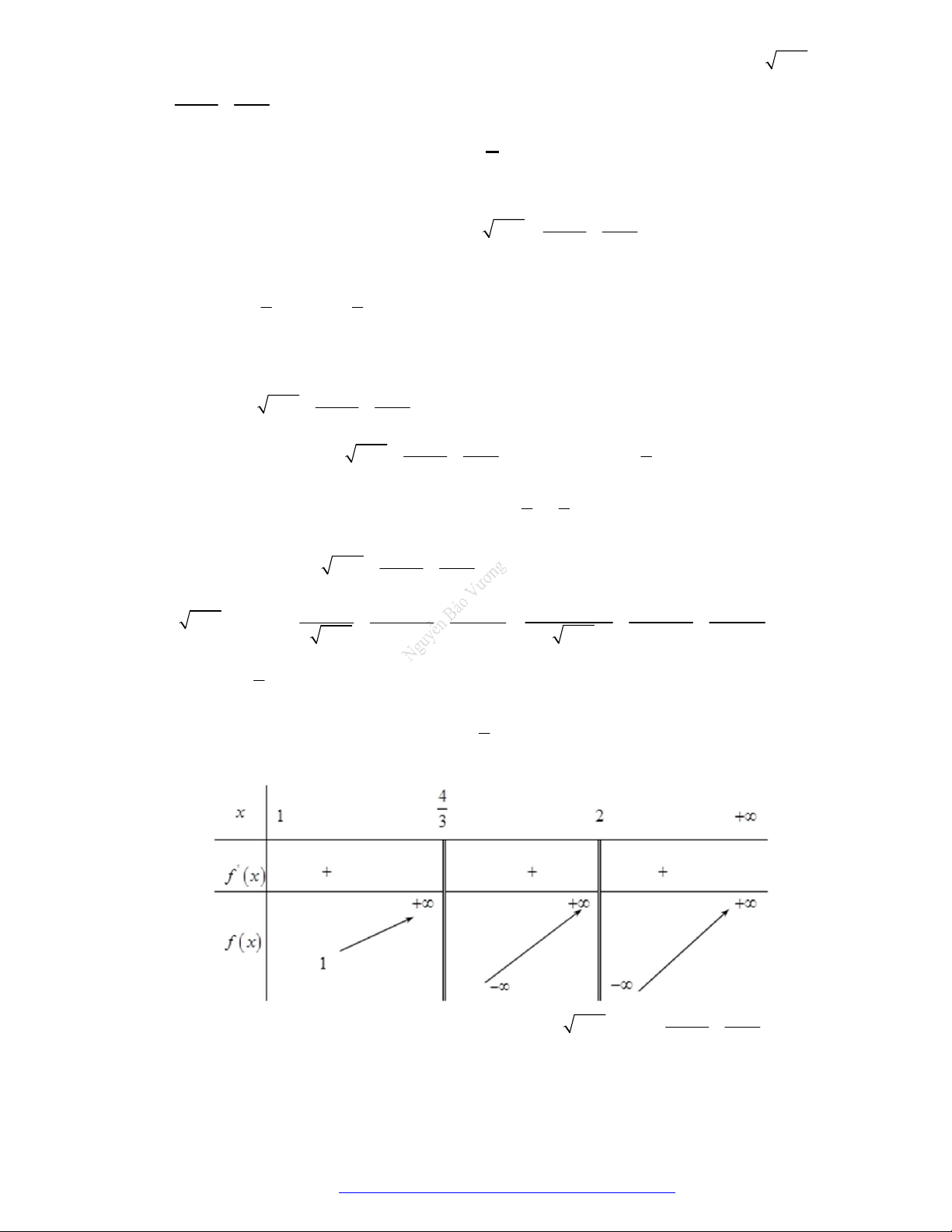
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 7. Tìm tập hợp tất cả các giá trị của tham số
m
để đồ thị hai hàm số
2
2 1 1y x x
và
11 1
11
3 4 2
y m
x x
cắt nhau tại
2
điểm phân biệt?
A.
;0
. B.
;1
. C.
;1
. D.
;2
.
Lời giải
Chọn C
Xét phương trình hoành độ giao điểm:
2
11 1
2 1 1 11 *
3 4 2
x x m
x x
Điều kiện:
1 0 1
4 4
3 3
2 2
x x
x x
x x
Ta có:
*
2
11 1
2 1 1 11
3 4 2
x x m
x x
Xét hàm số
2
11 1
( ) 2 1 1 11
3 4 2
f x x x
x x
trên
4
1; \ ;2
3
Nhận thấy, hàm số
f x
liên tục trên các khoảng
4 4
1; , ;2 , 2;
3 3
Ta có,
2
11 1
( ) 2 1 1 11
3 4 2
f x x x
x x
2
2 2
1 33 1
4 1 2 1
2 1
3 4 2
x x x
x
x x
2
2 2
10 8 1 33 1
0
2 1
3 4 2
x x
x
x x
với
4
1; \ ;2
3
x
Suy ra, hàm số
f x
đồng biến trên
4
1; \ ;2
3
.
Bảng biến thiên
Từ bảng biến thiên ta suy ra đồ thị hai hàm số
2
2 1 1y x x
và
11 1
11
3 4 2
y m
x x
cắt nhau tại
2
điểm phân biệt khi
;1m
.
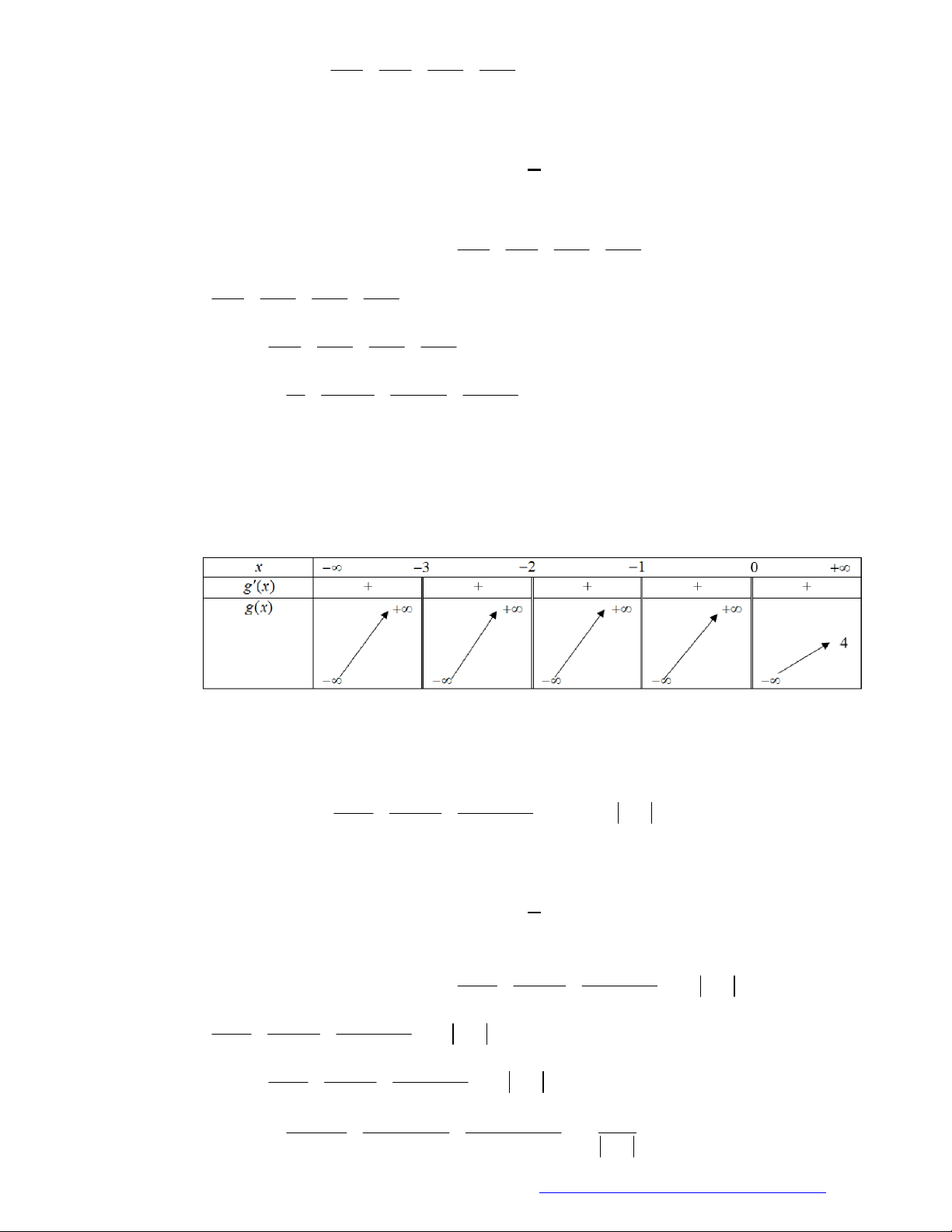
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Câu 8. Cho hai hàm số
1 1 2
1 2 3
x x x x
y
x x x x
và
1
2 2
x
y m
( là tham số thực) có đồ thị lần
lượt là
1
( )C và
2
( )C . Tập hợp tất cả các giá trị của để
1
( )C và
2
( )C cắt nhau tại đúng năm
điểm phân biệt là
A.
2;
. B.
;2
. C.
;2
. D.
;4
.
Lời giải
Chọn C
Xét phương trình hoành độ giao điểm
1
1 1 2
2 2
1 2 3
x
x x x x
m
x x x x
1
1 2 3
2 2
1 2 3 4
x
x x x x
m
x x x x
.
Đặt
1
1 2 3
( ) 2
1 2 3 4
x
x x x x
g x
x x x x
.
Ta có
1
2 2 2
2
1 1 1 1
( ) 2 ln 2 0
1 2 3
x
g x
x
x x x
với mọi
x
thuộc các khoảng sau
; 3
,
3; 2
2; 1
,
1;0
và
0;
nên hàm số
( )y g x
đồng biến trên mỗi khoảng đó
Mặt khác ta có
lim ( ) 4
x
g x
và và
lim ( )
x
g x
.
Bảng biến thiên hàm số
( )y g x
Do đó để và cắt nhau tại đúng năm điểm phân biệt thì phương trình (1) phải có 5
nghiệm phân biệt. Điều này xảy ra khi và chỉ khi đường thẳng
2y m
cắt đồ thị hàm số
( )y g x
tại 5 điểm phân biệt khi và chỉ khi
2 4 2m m
Câu 9. Cho hai hàm số
2 2 2
1 2
1 2 4 3
x x x
y
x x x x x
và
1y x x m
( là tham số thực) có đồ
thị lần lượt là
1
( )C
và
2
( )C
. Số các giá trị
m
nguyên thuộc khoảng
20;20
để
1
( )C
và
2
( )C
cắt
nhau tại năm điểm phân biệt là
A.
22
. B.
39
. C.
21
. D.
20
.
Lời giải
Chọn C
Xét phương trình hoành độ giao điểm
2 2 2
1 2
1
1 2 4 3
x x x
x x m
x x x x x
2 2 2
1 2
1
1 2 4 3
x x x
x x m
x x x x x
(1).
Đặt
2 2 2
1 2
( ) 1
1 2 4 3
x x x
g x x x
x x x x x
.
Ta có
2 2 2
2 2 2
2 2 2
1 2 2 4 5 1
( ) 1
1
1 2 4 3
x x x x x x
g x
x
x x x x x
m
m
1
C
2
C
m
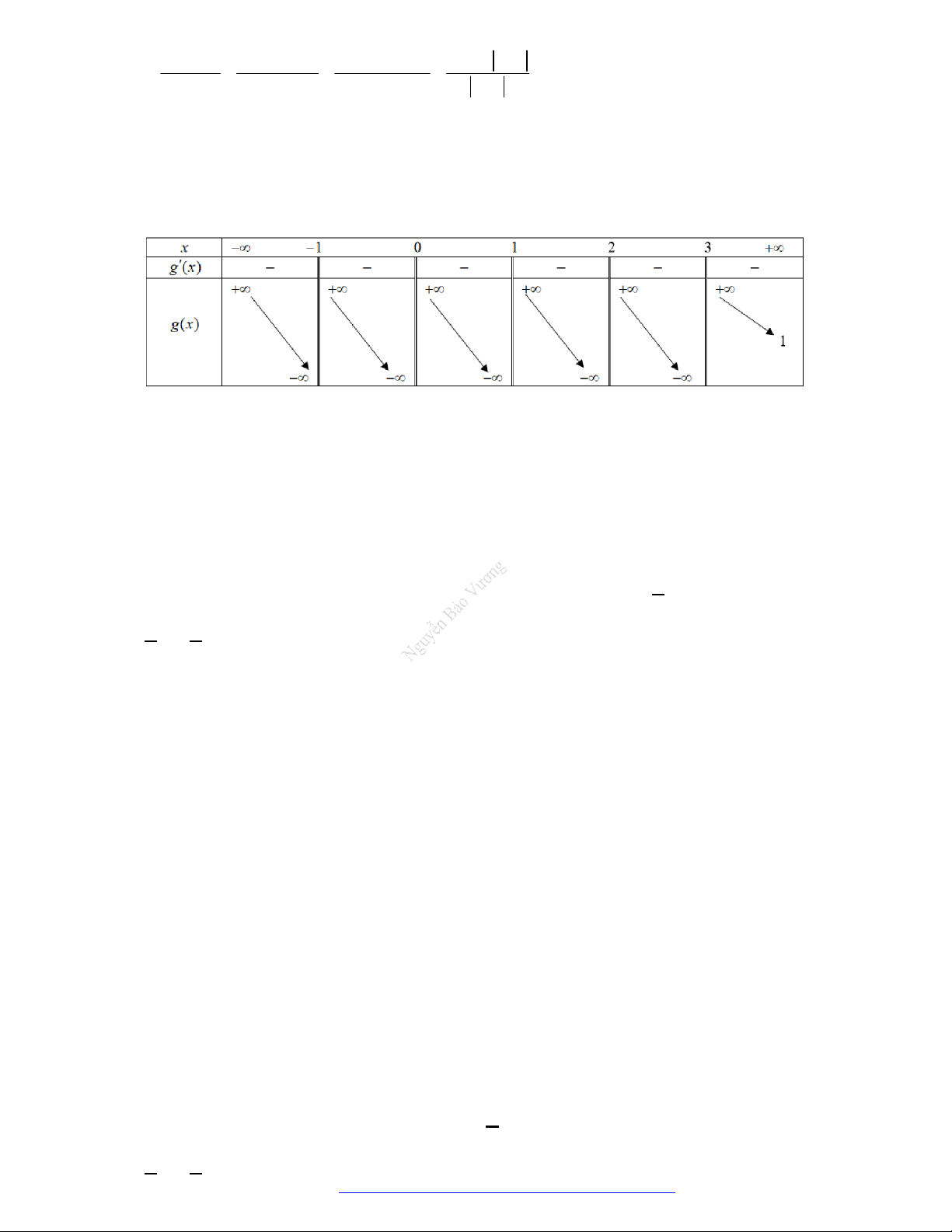
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
2 2 2
2 2 2
2 2 2
1 1
1 ( 1) 1 ( 2) 1
0
1
1 2 4 3
x x
x x x
x
x x x x x
với mọi
x
thuộc các khoảng sau
; 1
,
1;0
,
0;1
,
1;2
,
2;3
và
3;
nên hàm số
( )y g x
nghịch biến trên mỗi khoảng đó.
Mặt khác ta có
lim ( )
x
g x
và và
lim ( ) 1
x
g x
.
Bảng biến thiên hàm số
( )y g x
Do đó để
1
( )C và
2
( )C cắt nhau tại đúng năm điểm phân biệt thì phương trình (1) phải có năm
nghiệm phân biệt. Điều này xảy ra khi và chỉ khi đường thẳng
y m
cắt đồ thị hàm số
( )y g x
tại năm điểm phân biệt khi
1m
, do
m
nguyên thuộc
( 20;20)
nên
19; 18;...;0;1m
. Vậy
có tất cả 21 giá trị
m
thỏa mãn.
Câu 10. Gọi
S
là tập hợp tất cả các giá trị của tham số
m
để bất phương trình
2 4 3 2 2
2 1 0m x m x x m x
nghiệm đúng với mọi
x
. Số phần tử của tập
S
là
A.
3
. B.
2
. C.
0
. D.
1
.
Lời giải
Chọn D
Đặt
2 4 3 2 2
2 1f x m x m x x m x
Ta có
2 4 3 2 2 2 3 2 2
2 1 2 1f x m x m x x m x x m x m x x m
. Giả sử
0x
không phải là nghiệm của phương trình
2 3 2 2
2 1 0g x m x m x x m
thì hàm
số
2 4 3 2 2
2 1f x m x m x x m x
sẽ đổi dấu khi qua điểm
0x
, nghĩa là
2 4 3 2 2
2 1 0m x m x x m x
không có nghiệm đúng với mọi
x
.
Do đó, để yêu cầu bài toán được thỏa mãn thì một điều kiện cần là
2 3 2 2
2 1 0g x m x m x x m
phải có nghiệm
0x
, suy ra
2
1 0 1m m
Điều kiện đủ:
Với
4 3 2 2 2
1, 3 3 1m f x x x x x x x
khi đó
1 1 0f
không thỏa mãn điều kiện
2 4 3 2 2
2 1 0m x m x x m x
nghiệm đúng với mọi
x
. (loại)
Với
4 3 2 2 2
1, 1 0m f x x x x x x x
,
x
.
Vậy
1S
.
Câu 11. Có bao nhiêu cặp số thực
( ; )a b
để bất phương trình
2
1 2 2 0x x ax bx
nghiệm
đúng với mọi
x
A.
3
. B.
2
. C.
0
. D.
1
.
Lời giải
Chọn C

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Đặt
2
1 2 2
f x x x ax bx
Giả sử
1x
không phải là nghiệm của phương trình
2
2 2 0
g x x ax bx
thì hàm số
2
1 2 2
f x x x ax bx
sẽ đổi dấu khi qua điểm
1x
, nghĩa là
2
1 2 2 0
x x ax bx
không có nghiệm đúng với mọi
x
.
Do đó, để yêu cầu bài toán được thỏa mãn thì một điều kiện cần là
2
2 2 0
g x x ax bx
có nghiệm
1x
suy ra
2 0
a b
(1)
Lí luận tương tự có
2
1 2 0
h x x ax bx
cũng phải nhận
2
x
là nghiệm, suy ra
4 2 2 0
a b
(2)
Từ (1) và (2) ta có hệ
2 0 1
4 2 2 0 1
a b a
a b b
Điều kiện đủ:
Với
1
1
a
b
có
2 2
2
1 2 2 1 2 0
f x x x x x x x
,
x
.
Vậy không tồn tại cặp số thực
( ; )a b
nào thỏa mãn yêu cầu bài toán.
Câu 12. Trong số các cặp số thực
;a b
để bất phương trình
2
1 0
x x a x x b
nghiệm đúng
với mọi
x
, tích
ab
nhỏ nhất bằng
A.
1
4
. B.
1
. C.
1
4
. D.
1
.
Lời giải
Chọn C
Đặt
2
1
f x x x a x x b
và
2
g x x a x x b
Giả sử
1x
không phải là nghiệm của phương trình
2
0
g x x a x x b
thì hàm số
2
1
f x x x a x x b
sẽ đổi dấu khi qua điểm
1x
, nghĩa
2
1 0
x x a x x b
không có nghiệm đúng với mọi
x
.
Do đó yêu cầu bài toán được thỏa mãn thì một điều kiện cần là
2
0
g x x a x x b
có
nghiệm
1x
suy ra hoặc
2
1
0,
a
x x b x
hoặc là phương trình
2
0
x x b
có hai
nghiệm
1x
và
x a
Trường hợp 1:
2
1
1
1
1 0
1
0,
1 4 0
4
a
a
a
b
x x b x R
b
Trường hợp 2: phương trình
2
0
x x b
có hai nghiệm
1x
và
x a
Ta thay
1x
vào phương trình
2
0
x x b
có
2
1 1 0 2
b b
. Với
2
b
có phương
trình
2 2
1
0 2 0
2
x
x x b x x
x
Vì
x a
cũng là nghiệm của phương trình nên
2
a
.
Trong trường hợp 1:
1
1
1
4
4
a
ab
b
suy ra tích
ab
nhỏ nhất khi
1
4
ab
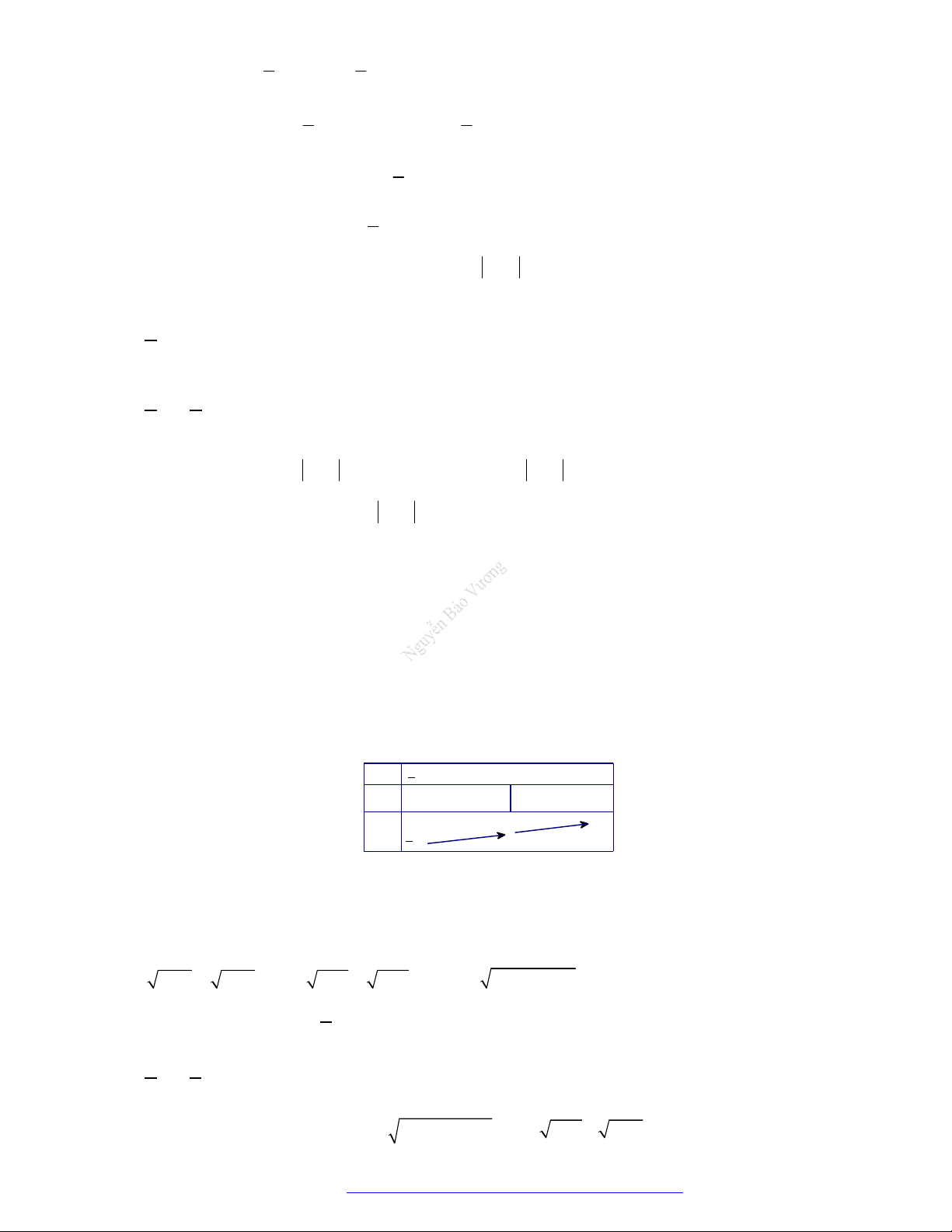
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Và với
1
1,
4
a b
, tích
1
4
ab
thì bất phương trình đã cho tương đương với
2
2
2
1 1
1 1 0 1 0
4 2
x x x x x x
thỏa mãn với mọi
x
(nhận)
Trong trường hợp 2: Tích
1
4
4
ab
Vậy tích
ab
nhỏ nhất khi
1
4
ab
.
Câu 13. Cho 2 hàm số
7 5 3
3 1y x x x m và
2 2y x x m
(
m
là tham số thực) có đồ thị lần
lượt là
1
C
,
2
C
. Tập hợp tất cả các giá trị của
m
để
1
C
cắt
2
C
là
A.
m
. B.
2;m
. C.
;2m
. D.
2;m
.
Lời giải
Chọn A
Xét phương trình hoành độ giao điểm:
7 5 3
3 1 2 2x x x m x x m
7 5 3
2 5 1 (1)x x x x x m
.
Xét hàm số
7 5 3
( ) 2f x x x x x x
.
Ta có
7 5 3
7 5 3
2 khi 2;
( )
2 2 khi ;2
x x x x
f x
x x x x x
.
6 4 2
6 4 2
7 5 3 0 khi 2;
( )
7 5 3 2 0 khi ;2
x x x x
f x
x x x x
.
lim
x
f x
;
lim
x
f x
.
Bảng biến thiên:
Từ bảng biến thiên ta thấy phương trình
1
luôn có nghiệm với mọi
m
.Vậy để
1
C
cắt
2
C
thì
m
.
Câu 14. Có bao nhiêu giá trị nguyên của tham số thực
m
thuộc đoạn
2019;2019
để phương trình
2
3 2 3 1 5 1 2 4 2 3x x m x x m x x
có nghiệm thực?
A.
2019
. B.
4032
. C.
4039
. D.
4033
.
Lời giải
Chọn B
Đk:
3;1x
.
Phương trình đã cho
11 3 4 3 1 2 1 3 0x x x m x x
. (*)
+∞
∞
+
2 +∞
∞
f '(x)
f(x)
x
+
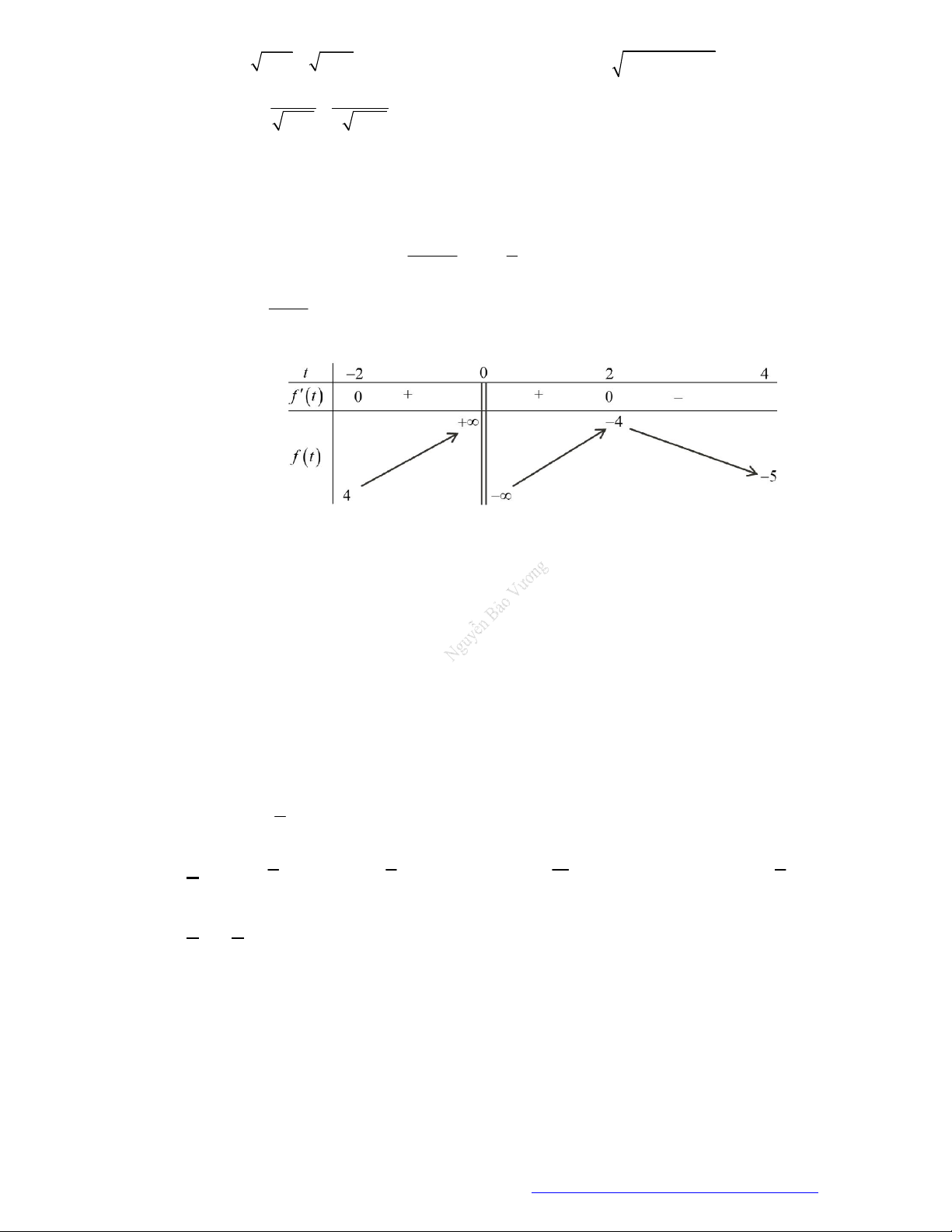
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Đặt
2 1 3t x x g x
, với
2
3;1 11 3 4 3 1 4x x x x t
.
Có
1 1
0, 3;1
1 2 3
g x x
x x
. Suy ra
g x
nghịch biến trên khoảng
3;1
.
3;1
min 1 2g x g
:
3;1
max 3 4 2;4g x g t
.
Từ (*)
2
4 0t mt
.
Nếu
0 0 4 0t
(vô lí).
Nếu
2;4 \{0}t
, ta có
2
4 4t
m t f t
t t
.
Có
2
2
4
, 0 2
t
f t f t t
t
.
Bảng biến thiên
Từ bảng biến thiên, suy ra phương trình có nghiệm thực khi và chỉ khi
4
4
m
m
.
Do đó
2019;2019
4
2019; 2018;....; 4;4;...;2018;2019
4
m
m
m
m
m
.
Vậy có
2019 4 1 .2 4032
giá trị nguyên của tham số thực
m
.
Câu 15. (Chuyên Nguyễn Bỉnh Khiêm - Quảng Nam - 2020) Tập hợp tất cả các số thực của tham số m
để phương trình
6 4 3 3 2 2
6 15 3 6 10 0x x m x m x mx
có đúng hai nghiệm phân biệt
thuộc đoạn
1
;2
2
là:
A.
5
2
2
m
. B.
7
3
5
m
. C.
11
4
5
m
. D.
9
0
4
m
.
Lời giải
Chọn A
Ta có:
6 4 3 3 2 2
3
3
2 2
2
6 15 3 6 10 0
2 3 2 1 3 1
2 1 (*)
x x m x m x mx
x x mx mx
f x f mx
Với
3
3f t t t
. Do
2
' 3 3 0,f t t t
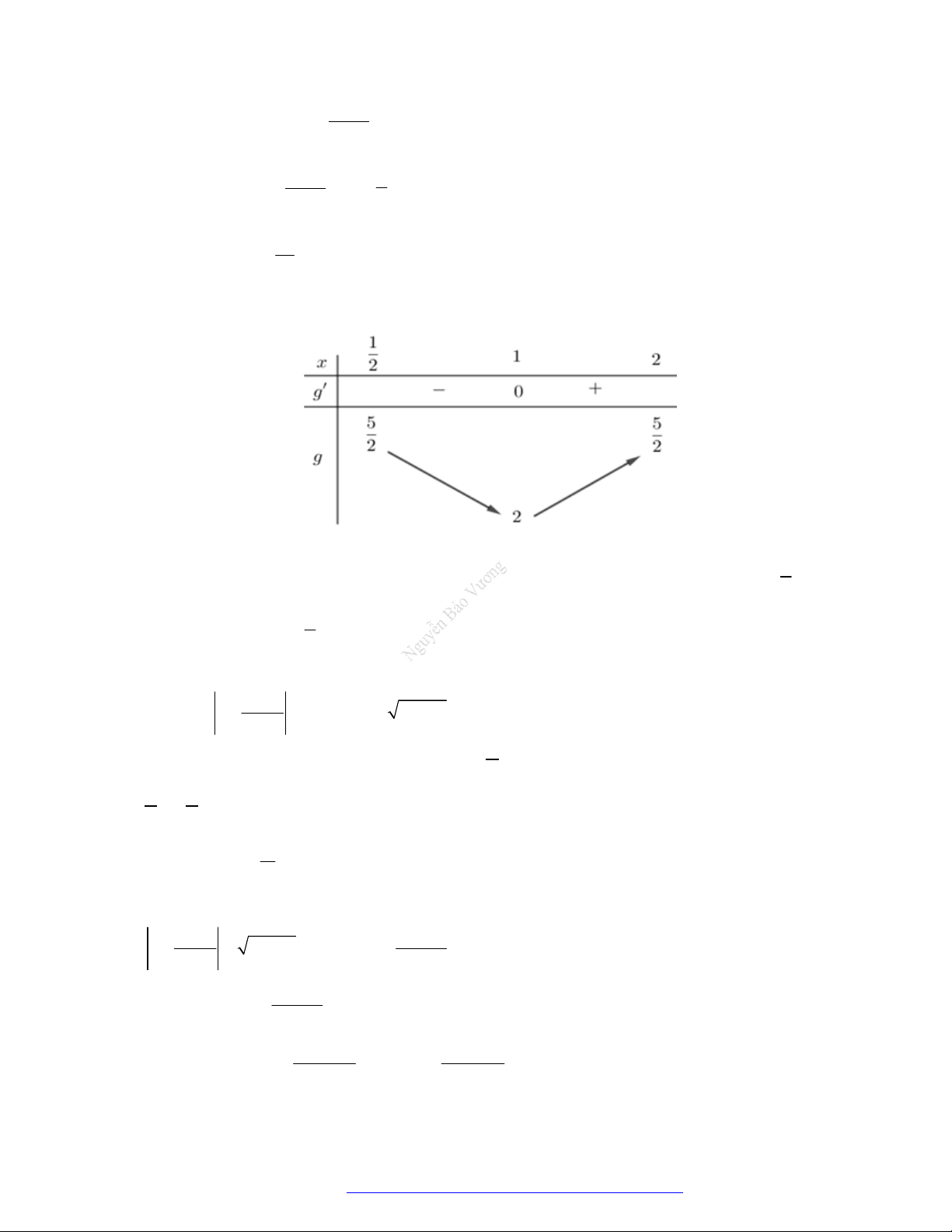
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Hàm số
f t
đồng biến trên
. Nên
2
(*) 2 1x mx
2
2
1
1 0
x
x mx m
x
.
Xét hàm số
2
1x
g x
x
trên
1
;2
2
Ta có:
2
1
' 1 ' 0 1.g x g x x
x
Bảng biến thiên.
Dựa vào bảng biến thiên suy ra phương trình đã cho có đúng hai nghiệm phân biệt thuộc
1
;2
2
khi và chỉ khi
5
2
2
m
.
Câu 16. (Chuyên Hùng Vương - Phú Thọ - 2020) Có bao nhiêu
m
nguyên dương để hai đường cong
1
2
: 2
10
C y
x
và
2
: 4C y x m cắt nhau tại ba điểm phân biệt có hoành độ dương?
A. 35. B. 37. C. 36. D. 34.
Lời giải.
ChọnC
Điều kiện:
10
4
x
m
x
.
Xét trên
0; \ 10
, phương trình hoành độ giao điểm của
1
C
và
2
C
là
2
2 2 18
2 4 4
10 10
x
x m m x
x x
.
Đặt
2
2 18
4
10
x
g x x
x
với
0; \ 10x
.
Ta có:
3
2 18
4 1
10
x
g x
x
;
4
4 34
10
x
g x
x
.
g x
có bảng biến thiên như sau
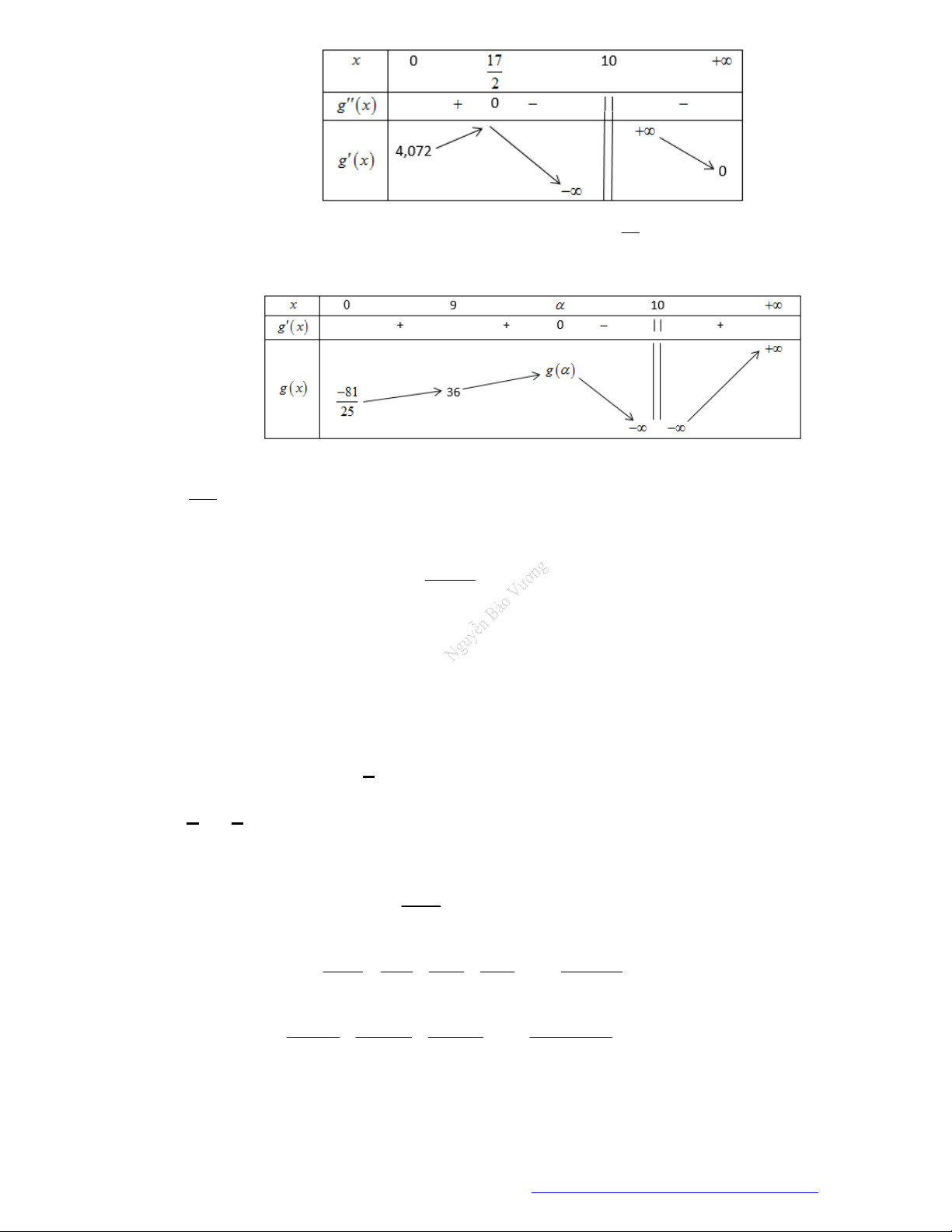
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Suy ra phương trình
0g x
có một nghiệm duy nhất
17
;10
2
. Lại có
9,22 0g
nên
9,22;10
. Ta có bảng biến thiên của
g x
trên
0; \ 10
:
Từ đó suy ra phương trình
m g x
có 3 nghiệm dương phân biệt khi và chỉ khi
81
25
m g
.
Trên khoảng
9,22;10
thì
2
4 40
2 18
3
10
x
x
x
nên
37 36;37g x g
.
Vậy những giá trị
m
nguyên dương thỏa mãn yêu cẩu bài toán là 1; 2; 3; …; 36 hay có 36 giá trị
của
m
cần tìm.
Câu 17. (Chuyên Phan Bội Châu - Nghệ An - 2020) Cho hàm số
( ) ( 1).( 2)...( 2020).f x x x x
Có
bao nhiêu giá trị nguyên của
m
thuộc đoạn
2020;2020
để phương trình
( ) . ( )f x m f x
có 2020 nghiệm phân biệt?
A. 2020. B. 4040. C. 4041. D. 2020.
Lời giải
Chọn B
Ta có nhận xét: khi
( ) 0f x
thì phương trình
( ) . ( )f x m f x
vô nghiệm.
Do đó:
( )
( ) . ( ) .
( )
f x
f x m f x m
f x
Xét hàm số
( ) 1 1 1 1
( )
( ) 1 2 3 2020
f x
g x
f x x x x x
.
Ta có
2 2 2 2
1 1 1 1
( ) 0, \ 1;2;3...;2020
1 2 3 2020
g x x
x x x x
Bảng biến thiên:
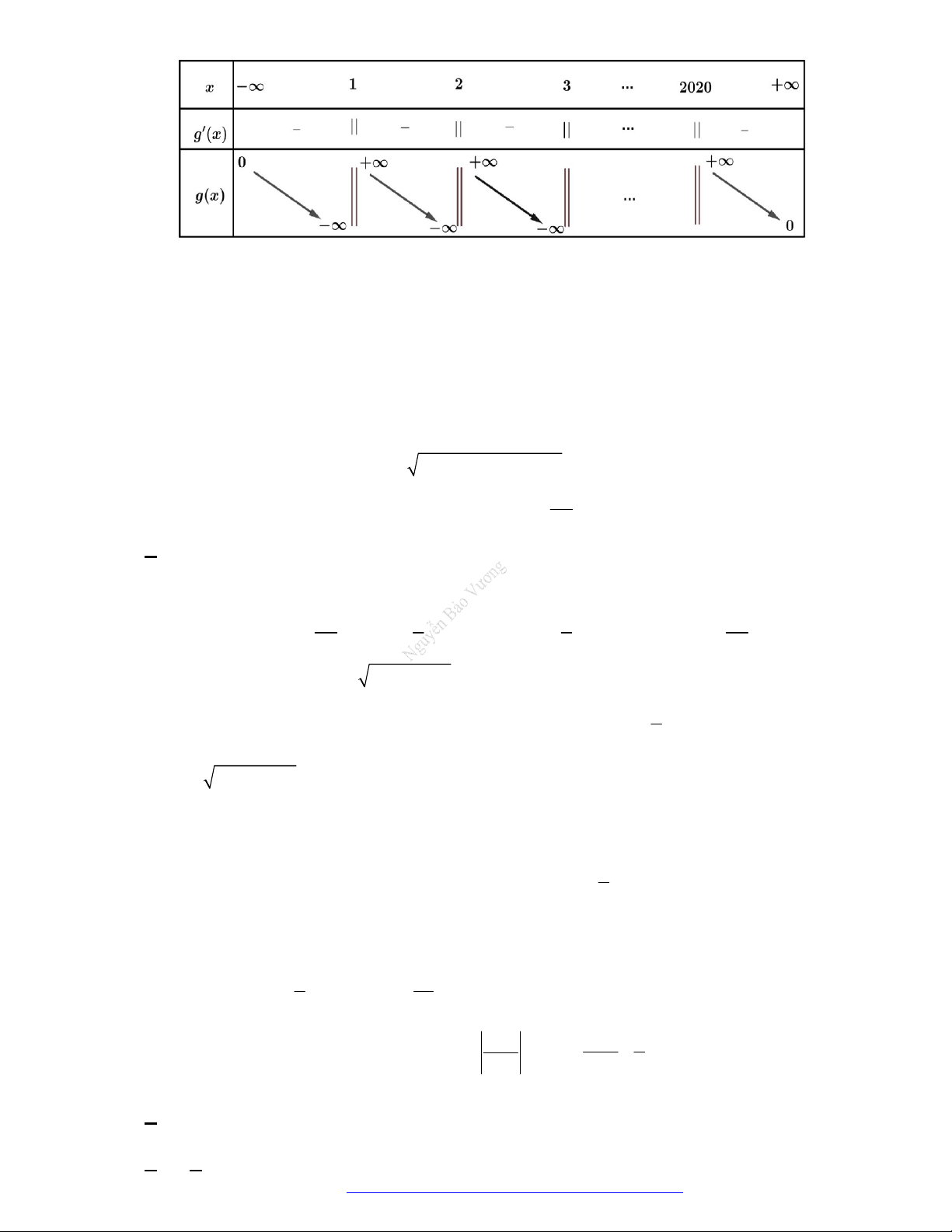
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Dựa vào BBT, phương trình
( ) . ( )f x m f x
có 2020 nghiệm phân biệt khi và chỉ khi
0m
hoặc
0m
.
Kết hợp với điều kiện
m
là số nguyên thuộc
2020;2020
nên
| 2020 2020, 0 .m n n n
Vậy có tất cả 4040 giá trị
m
thỏa yêu cầu bài toán.
Câu 18. (ĐHQG Hà Nội - 2020) Cho phương trình
3
3 2 2
4cos 12 cos 33cos 4 3 3cos 9cosx x x m x x m
. Có bao nhiêu giá trị nguyên của
tham số m để phương trình có nghiệm duy nhất thuộc
2
0;
3
.
A.
15.
B.
16.
C.
17.
D.
18.
Lời giải
Chọn A
Đặt cost x với
2 1
0; ;1
3 2
x t
, với mỗi
1
;1
2
t
chỉ có một
2
0;
3
x
Ta có
3
3 2 2
4 12 33 4 3 3 9 1t t t m t t m
Bài toán trở thành tìm
m
để phương trình (1) có nghiệm duy nhất
1
;1
2
t
Đặt
3 2 3 2
3
2
3 2 3 2
4 12 33 4 3 4 12 33 4 3
3 9
3 9 4 12 36 4
t t t m u t t t m u
u t t m
u t t m u t t m
3 3 2 2 2 2
4 4 3 3 4 4 4 3 0 , 4 4 4 3 0t u u t t u t ut u u t t ut u
Ta tìm
m
để phương trình
3 2
3 9m t t t
có nghiệm duy
1
;1
2
t
Xét
3 2 ' 2 '
1( )
3 9 3 6 9 0
3 ( )
t l
g t t t t g t t t g t
t l
Vậy
1 29
1 11
2 8
g m g m
vậy có 15 giá trị nguyên của m.
Câu 19. (Sở Ninh Bình 2020) Cho hai hàm số
2
ln
x
y
x
và
3 1
4 2020
2
y m
x x
, Tổng tất các
các giá trị nguyên của tham số
m
để đồ thị hai hàm số cắt nhau tại một điểm duy nhất là
A.
506
. B.
1011
. C.
2020
. D.
1010
.
Lời giải
Chọn A
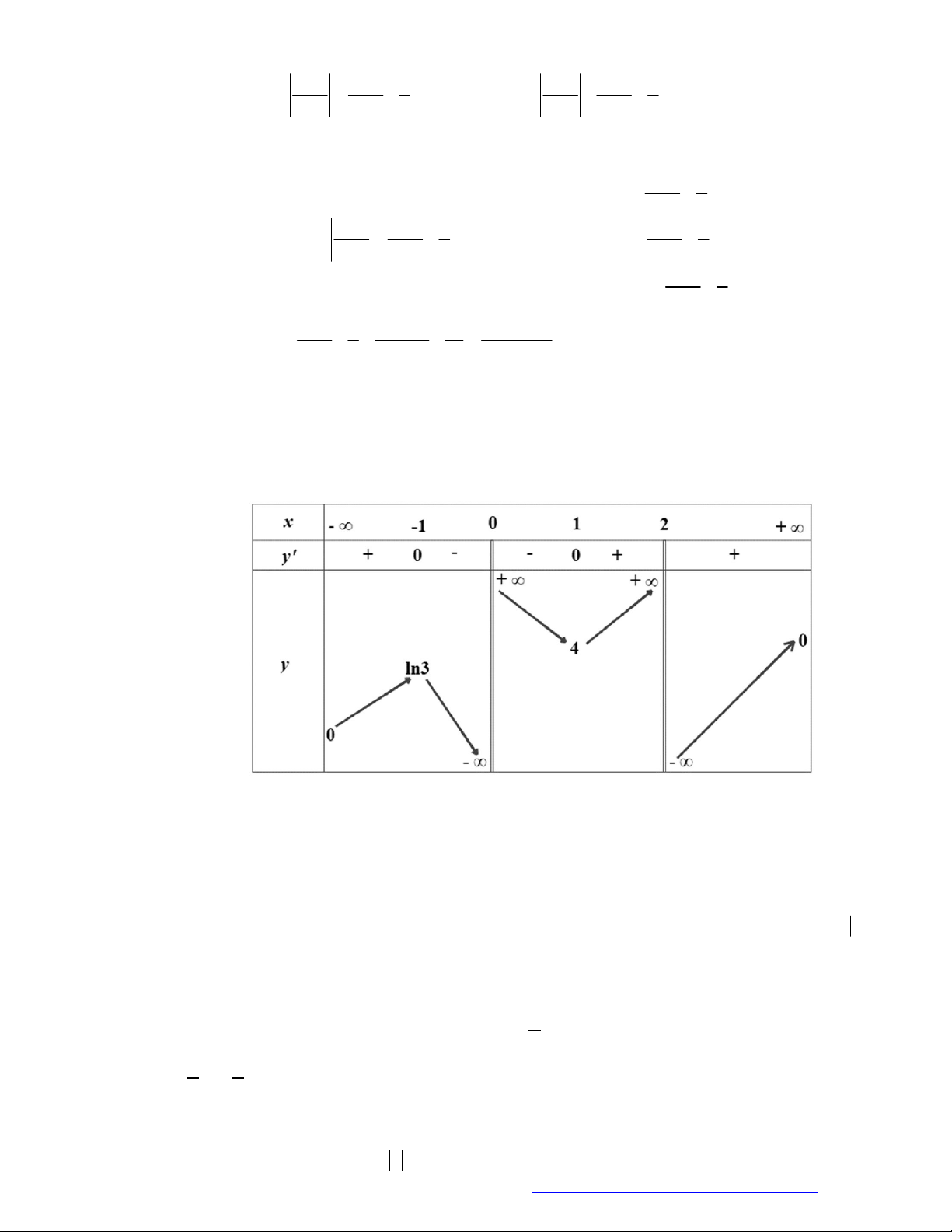
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
+ Phương trình hoành độ điểm chung của hai đồ thị hàm số là
2 3 1 2 3 1
ln 4 2020 ln 4 2020 (*)
2 2
x x
m m
x x x x x x
Đồ thị của hai hàm số đã cho cắt nhau tại một điểm duy nhất khi và chỉ khi (*) có duy nhất một
nghiệm.
+ Xét hàm số
1
2
3
3 1
( ) ln( 2) ln khi 2
2
2 3 1 3 1
ln ( ) ln(2 ) ln khi 0 2
2 2
3 1
( ) ln(2 ) ln( ) khi 0
2
g x x x x
x x
x
y g x x x x
x x x x x
g x x x x
x x
Ta có
2
/
1
2 2 2 2
2
/
2
2 2 2 2
2
/
3
2 2 2 2
1 1 3 1 4( 1)
( ) khi 2
2 ( 2) ( 2)
1 1 3 1 4( 1)
( ) khi 0 2
2 ( 2) ( 2)
1 1 3 1 4( 1)
( ) khi 0
2 ( 2) ( 2)
x
g x x
x x x x x x
x
g x x
x x x x x x
x
g x x
x x x x x x
, do vậy
1
0
1
x
y
x
bảng biến thiên hàm số như sau
+ Qua bảng biến thiên này ta có (*) có nghiệm duy nhất khi và chỉ khi
506
4 2020 4
2020 ln 3
4 2020 ln 3
4
m
m
m
m
+ Tư đây yêu cầu bài toán xãy ra khi và chỉ khi
506m
.
Câu 20. (Đặng Thúc Hứa - Nghệ An - 2020) Cho hai hàm số
1 2 1 3 1 2y x x x m x
;
4 3 2
12 22 10 3y x x x x
có đồ thị lần lượt là
1
C
,
2
C
. Có bao nhiêu giá trị nguyên của
tham số
m
trên đoạn
2020;2020
để
1
C
cắt
2
C
tại 3 điểm phân biệt?
A.
4040
. B.
2020
. C.
2021
. D.
4041
.
Lời giải
Chọn C
Xét phương trình hoành độ giao điểm của hai đồ thị
1
C
và
2
C
:
4 3 2
1 2 1 3 1 2 12 22 10 3x x x m x x x x x
(1)
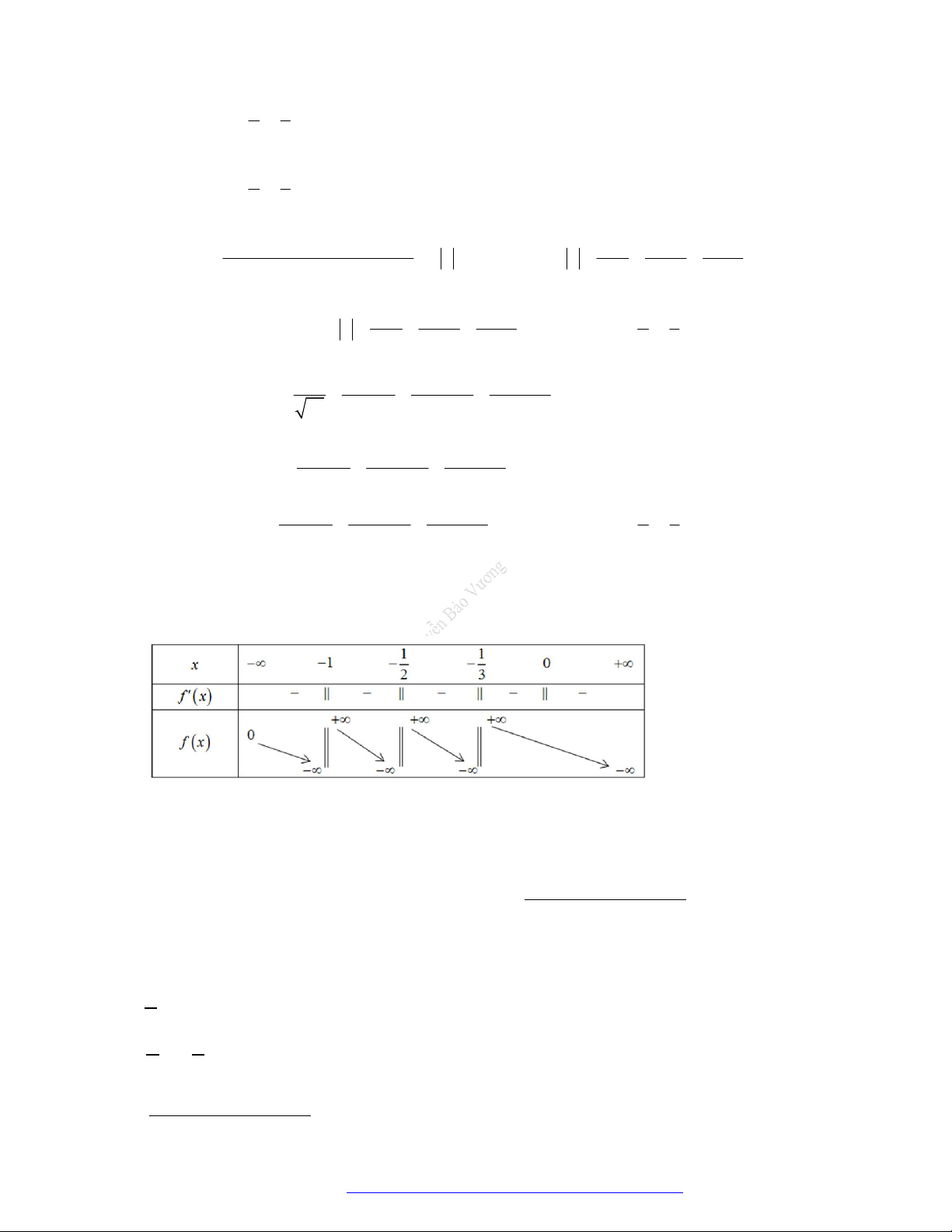
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Để đồ thị
1
C
cắt
2
C
tại 3 điểm phân biệt thì phương trình (1) có 3 nghiệm phân biệt.
Với
1 1
1; ;
2 3
x
: Không là nghiệm của phương trình (1).
Với
1 1
1; ;
2 3
x
ta có:
4 3 2
12 22 10 3 1 1 1
1 2 2 2
1 2 1 3 1 1 2 1 3 1
x x x x
m x m x x
x x x x x x
.
Xét hàm số
1 1 1
2 2
1 2 1 3 1
f x x x
x x x
,
1 1
\ 1; ;
2 3
x
.
Suy ra:
2 2 2
2
2 1 2 3
2
1 2 1 3 1
x
f x
x x x
x
.
Ta có:
2 2 2
2 2 2
1 2 3
4 khi 0;
1 2 1 3 1
1 2 3 1 1
khi ;0 \ 1; ;
2 3
1 2 1 3 1
x
x x x
f x
x
x x x
và
f x
không xác
định tại
0x
.
Bảng biến thiên:
Dựa vào bảng biến thiên ta thấy để phương trình (1) có 3 nghiệm phân biệt thì
0m
. Do đó có
2021 giá trị nguyên của tham số
m
thỏa mãn yêu cầu bài toán.
Câu 21. (Hậu Lộc 2 - Thanh Hóa - 2020) Cho hàm số
2
2
2 3
( )
3
x x m x m
y C
x
và đường thẳng
( ) : 2d y x
( là tham số thực).
Số giá trị nguyên của
15;15m
để đường thẳng
( )d
cắt đồ thị
( )C
tại bốn điểm phân biệt là
A.
15
. B.
30
. C.
16
. D.
17
.
Lời giải
Chọn A
Xét pt hoành độ giao điểm của hai đồ thị:
2
2
2
2 2
2
2 2
2 3
2 2 3 2 6 3
3
2 2 3 3 *
x x m x m
x x x m x m
x x m
x x x
x
x x m x
m

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
Đặt:
2
2
x x m t
ta được hệ:
2 2
2 2 2 2
2 2 0
2 3 2 3 0
x x m t x x t m
t x x m x t x m
2 2
0 1 0
1
t x
x t x t x t x t
t x
Suy ra:
2
2
2 2
3 0 1
2
2 1 1 0 2
x x m
x x m x
x x m x x x m
YCBT
*
phải có 4 nghiệm phân biệt khác 3
1 , 2
đều phải có hai nghiệm pb khác 3 và
các nghiệm của chúng không trùng nhau.
-
1 , 2
đều có hai nghiệm pb khác 3 khi:
3
2
9
9 4 0
4
1, 25
3 3.3 0
0
0 **
1 4 1 0
5
5
4
3 3 1 0
5
m
m
m
m
m
m
m
m
m
m
m
-
1 , 2
không có nghiệm trùng nhau
Hệ:
2
2
3 0
1 0
x x m
x x m
Vô nghiệm
2
2 1 0
3 0
x
x x m
Vô nghiệm
2
1
2
3 0
x
x x m
Vô nghiệm
2
1 1
3. 0
2 2
m
5
***
4
m
Vậy số giá trị nguyên của
15;15
m
đồng thời thỏa mãn
**
và
***
là 15.
Câu 22. (Thanh Chương 1 - Nghệ An - 2020) Cho hai hàm số
6 4 2
6 6 1
y x x x
và
3
15 3 15y x m x m x
có đồ thị lần lượt là
1
C
và
2
C
. Gọi
S
là tập hợp tất cả các giá
trị nguyên của tham số
m
thuộc đoạn
2019;2019
để
1
C
và
2
C
cắt nhau tại hai điểm phân
biệt. Số phần tử của tập hợp
S
bằng
A.
2006
. B.
2005
. C.
2007
. D.
2008
.
Lời giải
Chọn A
Ta biết
1
C
cắt
2
C
tại hai điểm phân biệt khi và chỉ khi phương trình
6 4 2 3
6 6 1 15 3 15 1
x x x x m x m x
có hai nghiệm phân biệt.
Điều kiện:
15 0 15 *
m x m x
.
Nếu
0
x
thì phương trình
1
vô nghiệm. Suy ra
0
x
.
Khi đó
3 2
3
1
1 6 6 15 3 15x x x m x m x
x
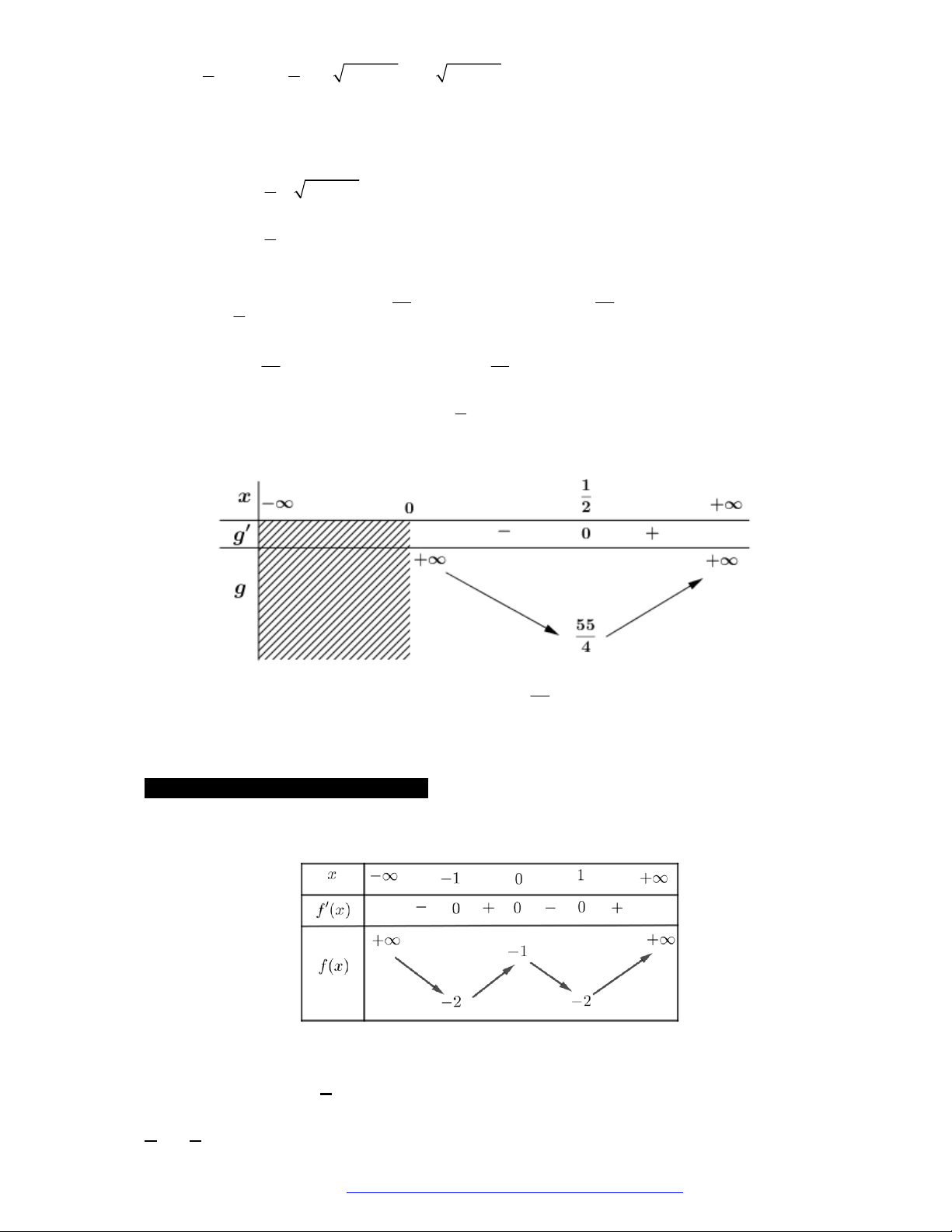
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
3
3
1 1
3 15 3 15x x m x m x
x x
.
Xét hàm số
3
3f t t t
. Tập xác định
D
.
2
3 3 0,f t t t
. Suy ra hàm số
3
3f t t t
đồng biến trên
.
Do đó
1
1 15 2x m x
x
.
Nếu
1
0 0x x
x
Phương trình
2
vô nghiệm
0x
.
Khi đó
0
1
0
m
x
x
nên
2 2
2 2
1 1
2 2 15 2 15x m x m x x
x x
.
Đặt
2
2
1
2 15 , 0g x x x x
x
.
3
2
2 15g x x
x
.
Phương trình
0g x
có một nghiệm
1
2
x
trên khoảng
0;
.
Bảng biến thiên
Suy ra
1
có hai nghiệm phân biệt khi và chỉ khi
55
4
m
( thỏa
0m
).
Kết hợp với
m
nguyên và
2019;2019m
ta có được
m
nguyên và
14;2019m
.
Khi đó
S
có
2019 14 1 2006
phần tử.
Dạng 2. Tương giao hàm hợp, hàm ẩn
Câu 1. (Đề Minh Họa 2020 Lần 1) Cho hàm số
f x
có bảng biến thiên như sau:
Số nghiệm thuộc đoạn
;2
của phương trình
2 sin 3 0f x
là
A.
4
. B.
6
. C.
3
. D.
8
.
Lời giải
Chọn B
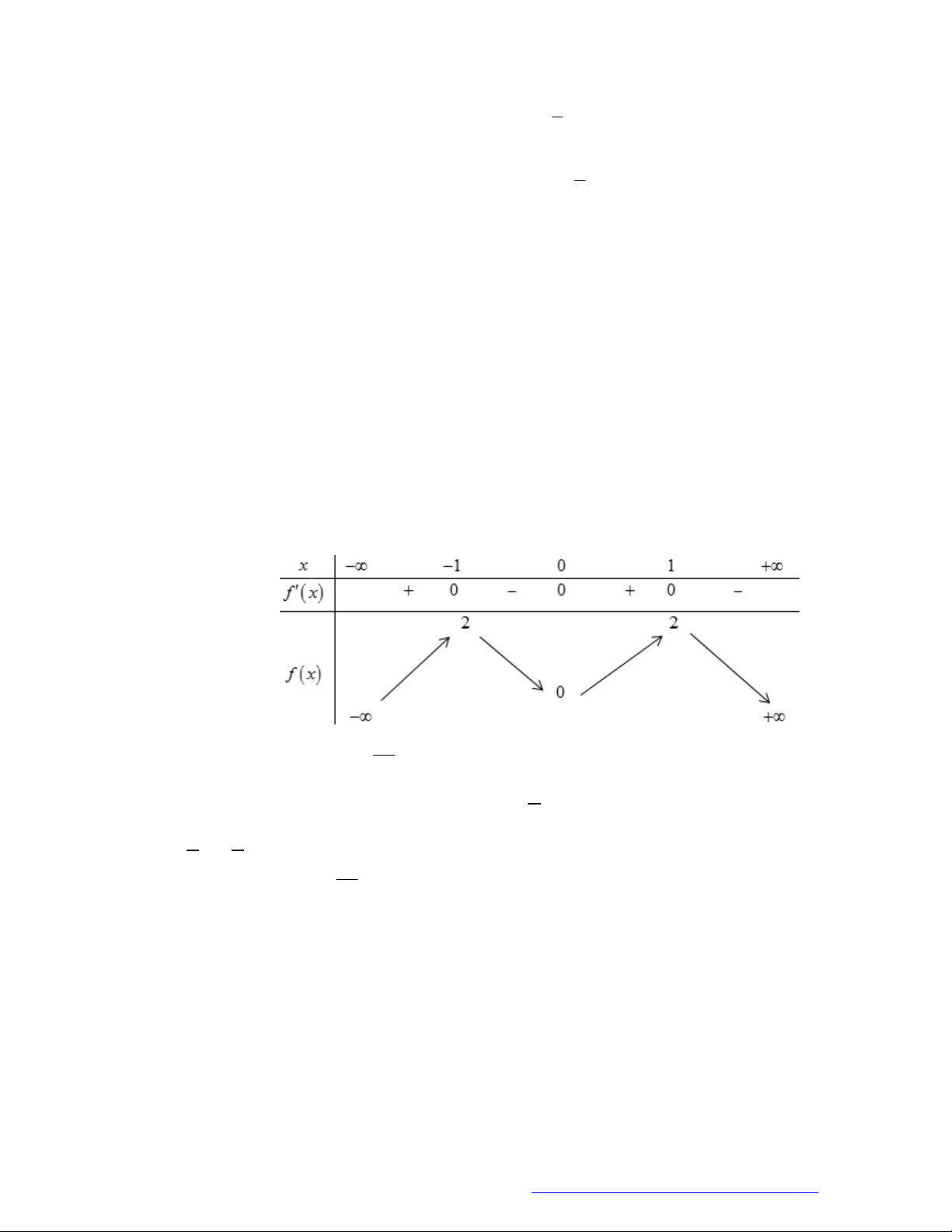
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
Đặt
sint x
. Do
;2x
nên
1;1t
.
Khi đó ta có phương trình
3
2 3 0
2
f t f t
.
Dựa vào bảng biến thiên ta thấy phương trình
3
2
f t
có 2 nghiệm
1;0t a
và
0;1t b
.
Trường hợp 1:
1;0t a
Ứng với mỗi giá trị
1;0t
thì phương trình có 4 nghiệm
1 2 3 4
0 2 .x x x x
Trường hợp 2:
0;1t b
Ứng với mỗi giá trị
0;1t
thì phương trình có 4 nghiệm
5 6
0 .x x
Hiển nhiên cả 6 nghiệm trong 2 trường hợp trên đều khác nhau.
Vậy phương trình đã cho có 6 nghiệm thuộc đoạn
;2
Câu 2. (Đề Tham Khảo 2020 Lần 2) Cho hàm số
f x
có bảng biến thiên như sau
Số nghiệm thuộc đoạn
5
0;
2
của phương trình
sin 1f x
là
A.
7
. B.
4
. C.
5
. D.
6
.
Lời giải
Chọn C
Đặt
sint x
,
5
0; 1;1
2
x t
Khi đó phương trình
sin 1f x
trở thành
1, 1;1f t t
Đây là phương trình hoành độ giao điểm của hàm số
y f t
và đường thẳng
1y
.
Dựa vào bảng biến thiên, ta có
1;0
1
0;1
t a
f t
t b
.
Trường hợp 1:
1;0t a
Ứng với mỗi giá trị
1;0t
thì phương trình
sin x t
có
2
nghiệm
1 2
,x x
thỏa
mãn
1 2
2x x
.
Trường hợp 2:
0;1t b
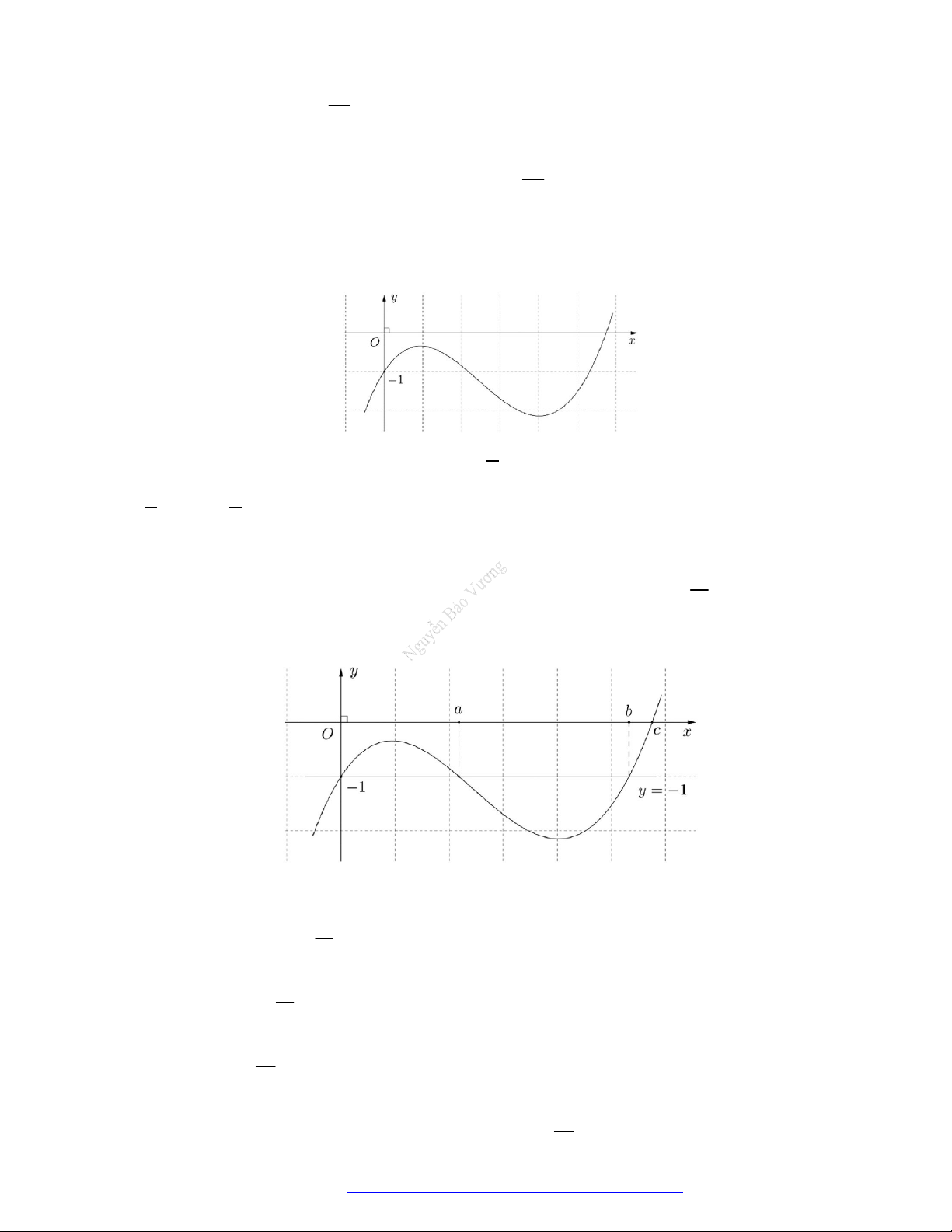
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ứng với mỗi giá trị
0;1t
thì phương trình có
3
nghiệm
1 2 3
, ,x x x
thỏa mãn
3 4 5
5
0 ; 2 ;
2
x x x
Hiển nhiên cả 5 nghiệm trong 2 trường hợp trên đều khác nhau.
Vậy phương trình đã cho có 5 nghiệm thuộc đoạn
5
0;
2
.
Câu 3. (Mã 101 - 2020 Lần 1) Cho hàm số bậc ba
( )y f x
có đồ thị là đường cong trong hình bên. Số
nghiệm thực phân biệt của phương trình
3
( ) 1 0f x f x
là
A.
8
. B.
5
. C.
6
. D.
4
.
Lời giải
Chọn C.
3
3 3 3
3
3
3
0
( ) 0
( ) 0
( ) 1 0 ( ) 1 ( ) 0
( ) (do 0)
( ) 0
( ) (do 0)
x
f x
x f x
a
f x f x f x f x x f x a
f x x
x
x f x b
b
f x x
x
( ) 0f x
có một nghiệm dương
x c
.
Xét phương trình
3
( )
k
f x
x
với
0, 0x k
.
Đặt
3
( ) ( )
k
g x f x
x
.
4
3
( ) '( )
k
g x f x
x
.
Với
x c
, nhìn hình ta ta thấy
( ) 0f x
4
3
( ) ( ) 0
k
g x f x
x

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
( ) 0g x
có tối đa một nghiệm.
Mặt khác
( ) 0
lim ( )
x
g c
g x
và
( )g x
liên tục trên
;c
( ) 0g x
có duy nhất nghiệm trên
;c
.
Với
0 x c
thì
3
( ) 0
k
f x
x
( ) 0g x
vô nghiệm.
Với
0x
, nhìn hình ta ta thấy
( ) 0f x
4
3
( ) ( ) 0
k
g x f x
x
( ) 0g x
có tối đa một nghiệm.
Mặt khác
0
lim ( ) 0
lim ( )
x
x
g x
g x
và
( )g x
liên tục trên
;0
.
( ) 0g x
có duy nhất nghiệm trên
;0
.
Tóm lại
( ) 0g x
có đúng hai nghiệm trên
\ 0
.
Suy ra hai phương trình
3
( )
a
f x
x
,
3
( )
b
f x
x
có 4 nghiệm phân biệt khác 0 và khác
c
.
Vậy phương trình
3
( ) 1 0f x f x
có đúng 6 nghiệm.
Câu 4. (Mã 102 - 2020 Lần 1) Cho hàm số
f x
có đồ thị là đường cong như hình vẽ bên dưới.
Số nghiệm thực phân biệt của phương trình
3
1 0f x f x
là
A.
6
. B.
4
. C.
5
. D.
8
.
Lời giải
Chọn A
Dựa vào đồ thị, ta thấy
3
3 3 3
3
6; 5 1
1 0 1 3; 2 2
0 3
x f x a
f x f x f x f x x f x b
x f x
+ Phương trình
3
tương đương
1 1
0 0
0 , 6 5
x x
f x x x x a
.
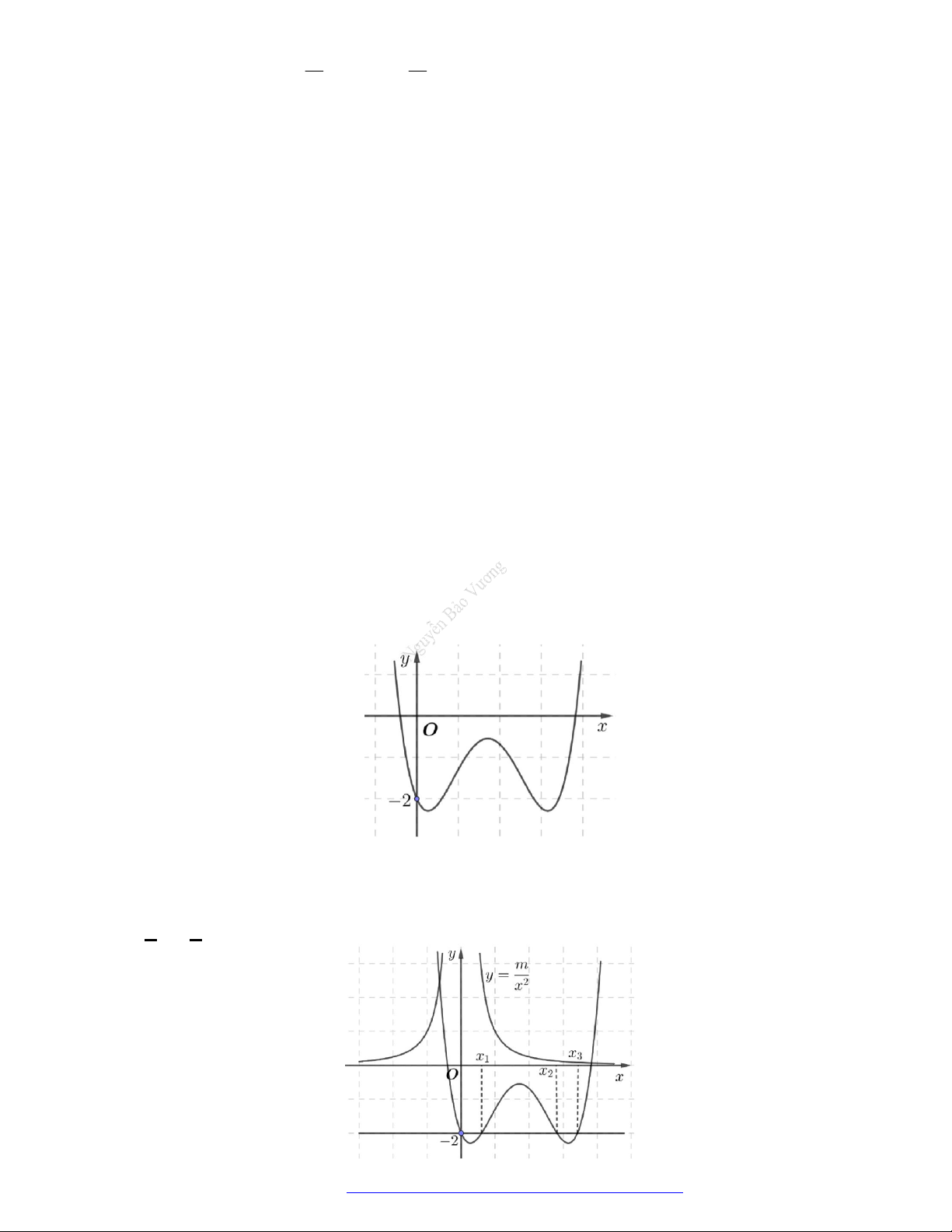
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 22 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
+ Các hàm số
3
a
g x
x
và
3
b
h x
x
đồng biến trên các khoảng
;0
và
0;
, và nhận
xét rằng
0x
không phải là nghiệm của phương trình
1
nên:
1
f x g x
f x h x
.
+ Trên khoảng
;0
, ta có
0
0 0
lim ; lim 1
lim lim 0
lim lim
x
x
x x
x x
f x f x
g x h x
g x h x
nên các phương trình
f x g x
và
f x h x
có nghiệm duy nhất.
+ Trên khoảng
0;
, ta có
0
0 0
lim ; lim 1
lim lim 0
lim lim
x
x
x x
x x
f x f x
g x h x
g x h x
nên các phương trình
f x g x
và
f x h x
có nghiệm duy nhất.
Do đó, phương trình
3
1 0f x f x
có
6
nghiệm phân biệt.
Câu 5. (Mã 103 - 2020 Lần 1) Cho hàm số bậc bốn
y f x
có đồ thị là đường cong trong hình vẽ
bên.
Số nghiệm thực phân biệt của phương trình
2
( ) 2 0f x f x
là
A.
8
. B.
12
. C.
6
. D.
9
.
Lời giải
Chọn D

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
2
2
2
2
2
( ) 0
( ) 1
( ) 2 0
( ) 2
( ) 3
x f x
x f x a
f x f x
x f x b
x f x c
với
0 a b c
.
Xét phương trình
2
( ) 1 0f
m
x m
x
.
Gọi
,
là hoành độ giao điểm của
: ( )C y f x
và
Ox
;
0
.
2
(1) ( ) 0f x
m
x
. Đặt
2
( ) ( )g x f x
x
m
Đạo hàm
3
2
( ) ( )
m
g x f x
x
.
Trường hợp 1:
3
2
; ( ) 0; 0 ( ) 0
m
x f x g x
x
Ta có
2
0li , ( )m
x
m
g x g
. Phương trình
0g x
có một nghiệm thuộc
;
.
Trường hợp 2:
x
( ) 0f x
,
2
0
m
x
suy ra
( ) 0 ( , )g x x
.
Trường hợp 3:
3
2
; ( ) 0; 0 ( ) 0
m
x f x g x
x
Ta có
2
0li , ( )m
x
m
g x g
. Phương trình
0g x
có một nghiệm thuộc
( ; )
.
Vậy phương trình
2
m
f x
x
có hai nghiệm
0m
.
Ta có:
2
( ) 0 0 ( ) 0x f x x f x
: có ba nghiệm.
Vậy phương trình
1
có 9 nghiệm.
Câu 6. (Mã 104 - 2020 Lần 1) Cho hàm số
y f x
có đồ thị là đường cong trong hình vẽ bên.
Số nghiệm thực của phương trình
2
2f x f x
là:
A. 6. B. 12. C. 8. D. 9.
Lời giải
Chọn D
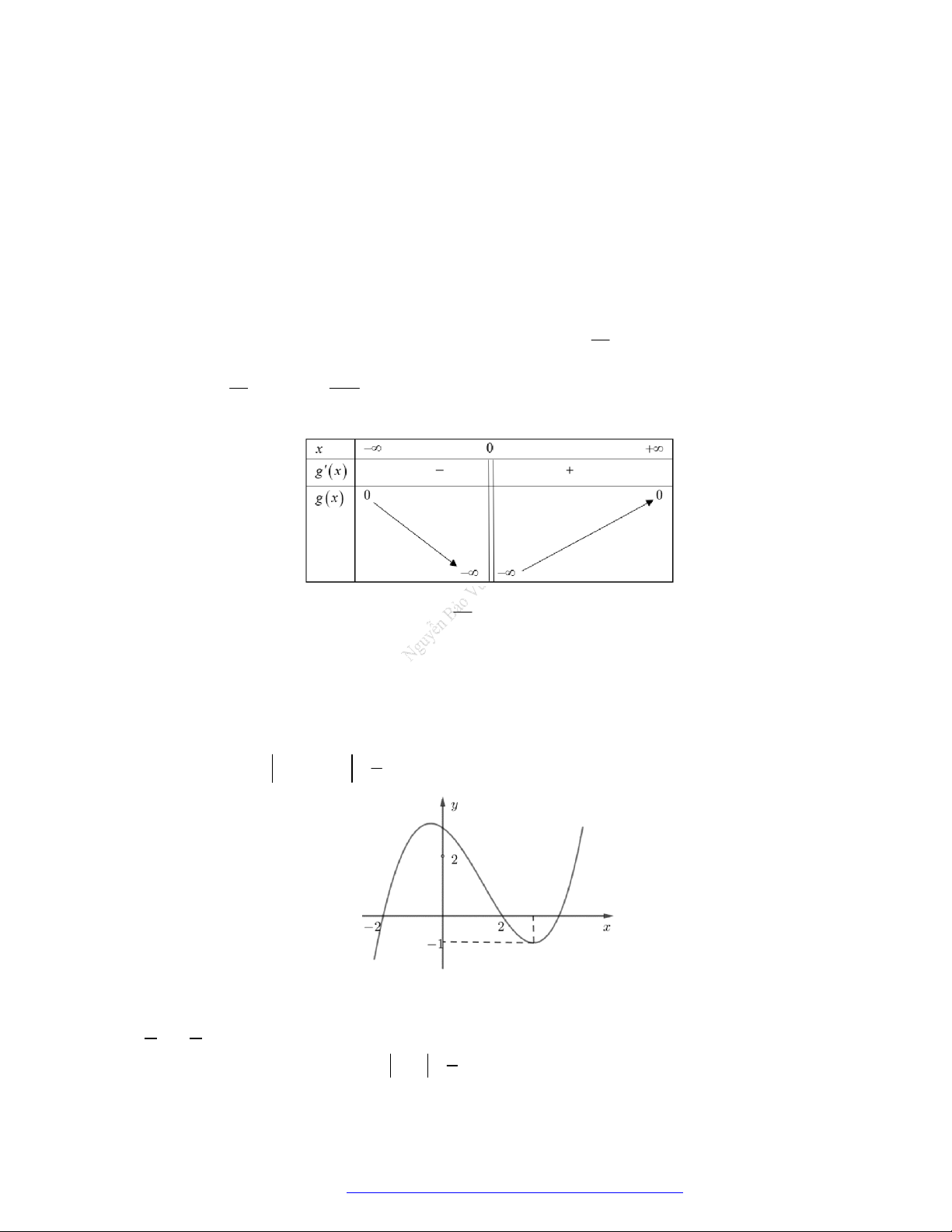
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 24 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta có:
2
2f x f x
2
2
2
2
0
0
0
0
x f x
x f x a
x f x b
x f x c
.
Xét phương trình:
2
0x f x
0
0
x
f x
mà
0f x
có hai nghiệm
2
. 0x f x
có ba
nghiệm.
Xét phương trình:
2
0x f x a
Do
2
0x
;
0x
không là nghiệm của phương trình
2
0
a
f x
x
Xét
2 3
2a a
g x g x
x x
Bảng biến thiên:
Từ bảng biến thiên với
0f x
2
a
f x
x
có 2 nghiệm.
Tương tự:
2
x f x b
và
2
x f x c
, 0b c
mỗi phương trình cũng có hai nghiệm.
Vậy số nghiệm của phương trình
2
2f x f x
là 9 nghiệm.
Câu 7. (Mã 103 2019) Cho hàm số bậc ba
y f x
có đồ thị như hình vẽ dưới đây. Số nghiệm thực
của phương trình
3
3
3
2
f x x
là
A.
7
. B.
3
. C.
8
. D.
4
.
Lời giải
Chọn C
Đặt
3
3t x x
ta có phương trình
3
*
2
f t
.
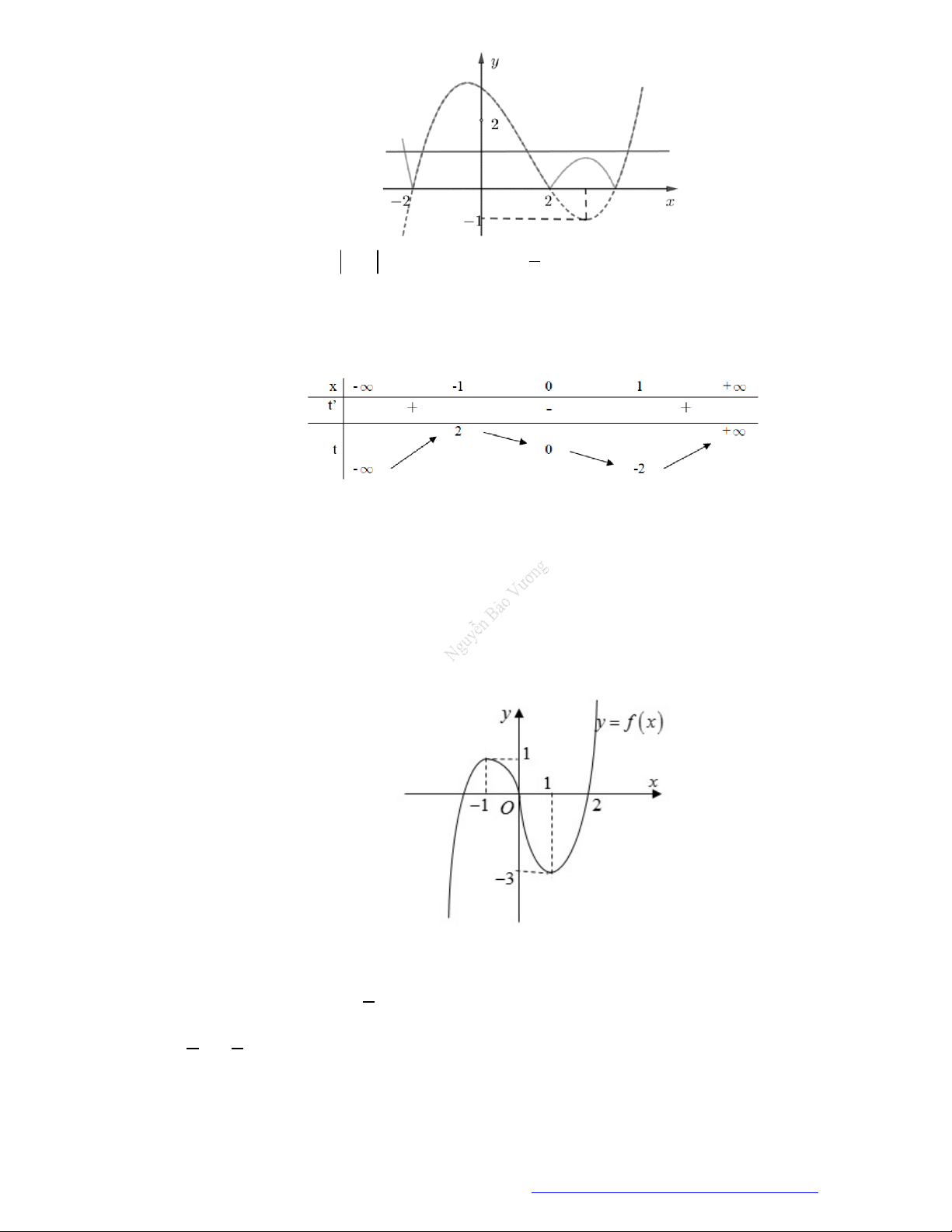
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25
Từ đồ thị hàm số
y f t
và đường thẳng
3
2
y
ta suy ra phương trình
*
có 4 nghiệm
1 2 3 4
2 0 2t t t t
Xét hàm
3
3t x x
. Ta có
2
1
3 3 0
1
x
t x
x
Ta có bảng biến thiên
Với
1
2t phương trình:
3
1
3t x x
cho ta 1 nghiệm.
Với
2
2 0t phương trình:
3
2
3t x x
cho ta 3 nghiệm.
Với
3
0 2t
phương trình:
3
3
3t x x
cho ta 3 nghiệm.
Với
4
2 t phương trình:
3
4
3t x x
cho ta 1 nghiệm.
Vậy phương trình đã cho có tất cả 8 nghiệm. Chọn C
Câu 8. Cho hàm số
y f x
liên tục trên
và có đồ thị như hình vẽ sau
Số nghiệm của phương trình
2 e 1
x
f f là
A.
4
. B.
2
. C.
1
. D.
3
.
Lời giải
Chọn B
Đặt
e 0
x
u
, từ đồ thị suy ra:
3, 0f u u
.
Đặt
2t f u
,
1t
.
Ứng với mỗi nghiệm
1t
, có một nghiệm
1u
.
Ứng với mỗi nghiệm
1;2t
, có hai nghiệm
0;2u
.
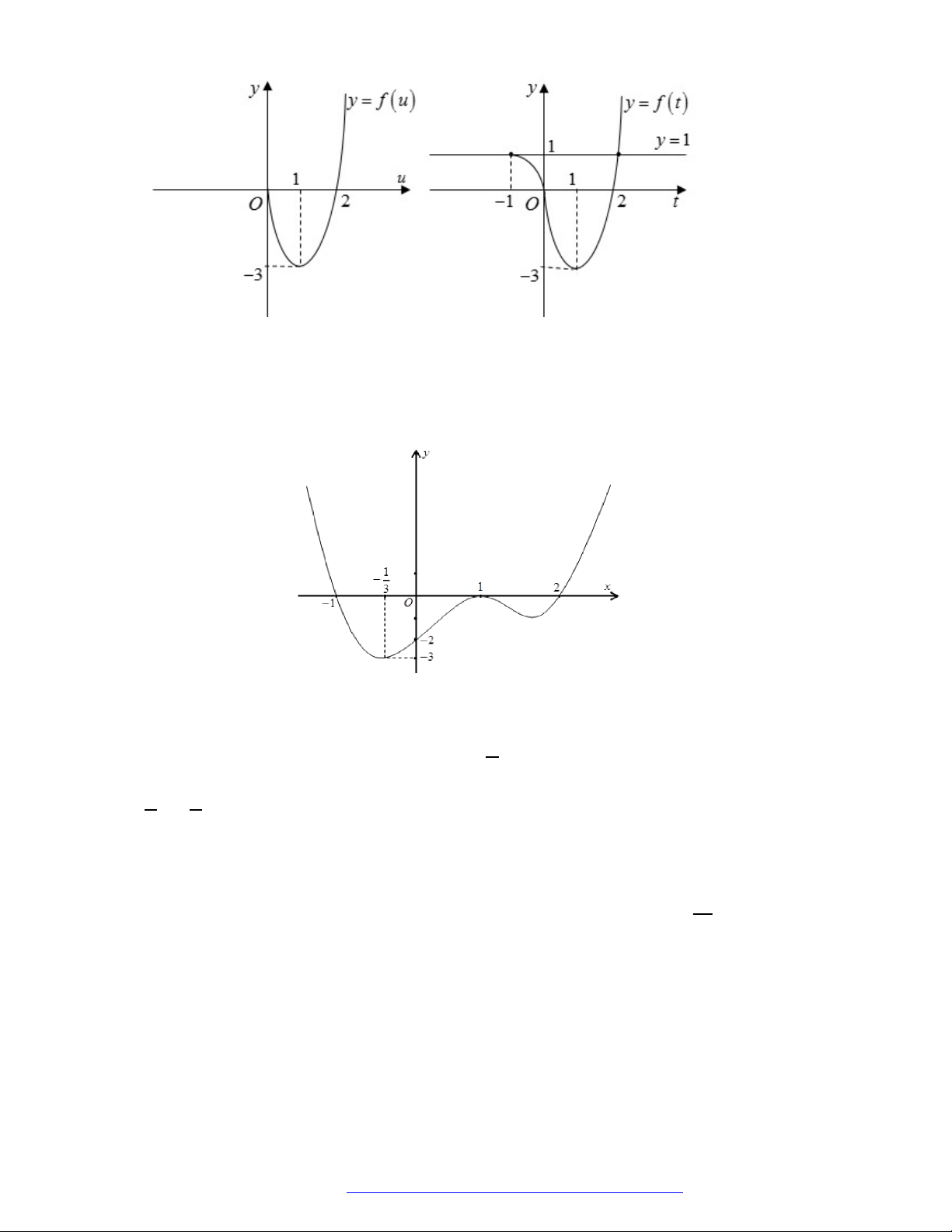
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 26 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ứng với mỗi nghiệm
2t
, có một nghiệm
2u
.
Phương trình
1f t
có một nghiệm
1t
và một nghiệm
2t
.
Vậy phương trình đã cho có hai nghiệm.
Câu 9. Cho hàm số
y f x
có đạo hàm cấp 2 trên
và có đồ thị
f x
là đường cong trong hình vẽ
bên.
Đặt
1 .g x f f x
Gọi
S
là tập nghiệm của phương trình
0.g x
Số phần tử của tập
S
là
A.
8
. B.
10
. C.
9
. D.
6
.
Lời giải
Chọn C
Hàm số
y f x
có đạo hàm cấp 2 trên
nên hàm số
f x
và
f x
xác định trên
.
Do đó, tập xác định của hàm số
g x
là
.D
Ta có:
0
1
3
1
0
1 ; 2
. 1 , 0
1 0
1 1
1 1
1 2
x
x
f x
x x
g x f x f f x g x
f f x
f x
f x
f x
Từ đồ thị ta cũng có:
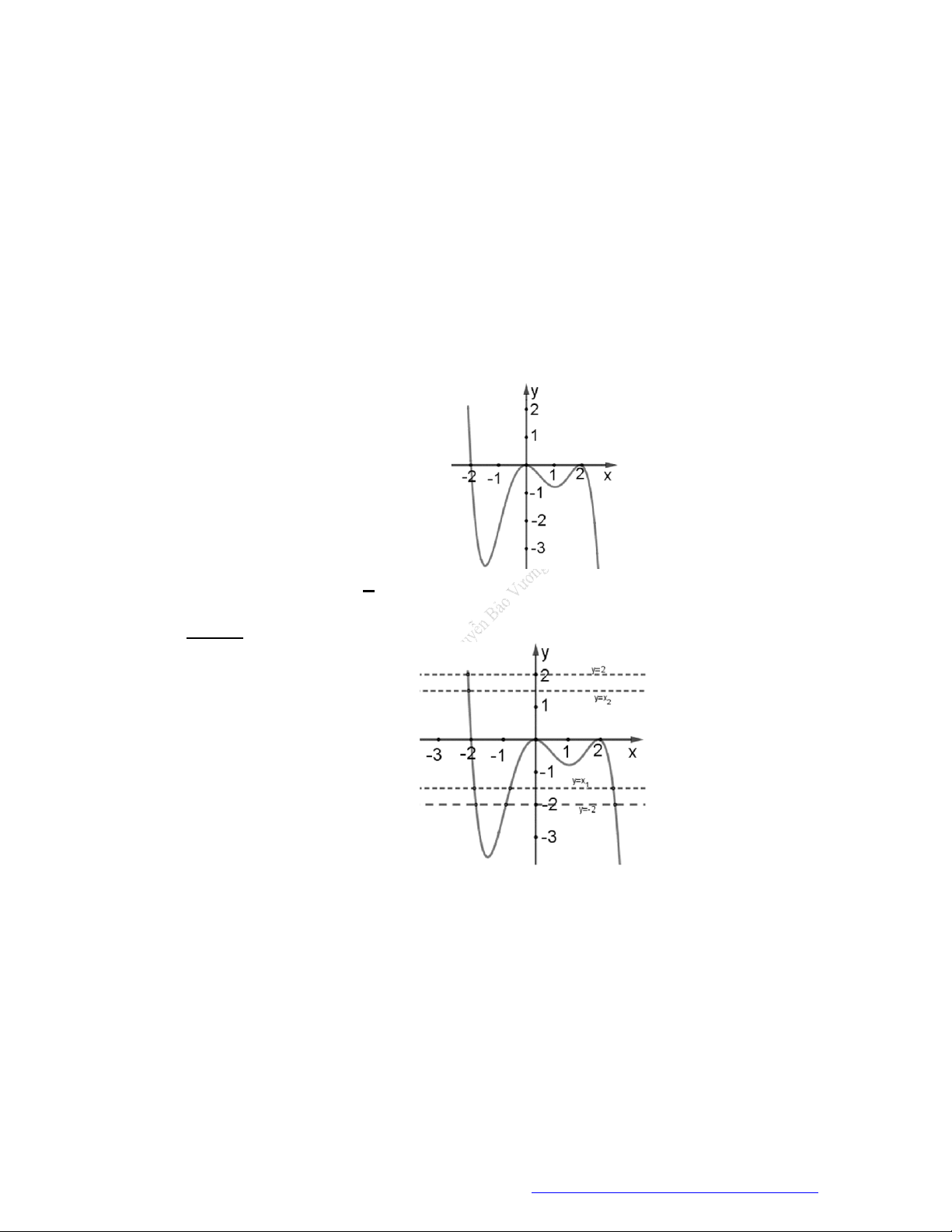
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27
1
1 1 0 1 .
2
x
f x f x x
x
1
2
; -1
1 1 2 .
2 ; +
x x
f x f x
x x
3 1
4 2
;
1 2 3 .
; +
x x x
f x f x
x x x
Vậy phương trình
0g x
có 9 nghiệm.
Câu 10. (THPT Cẩm Bình Hà Tỉnh 2019) Cho hàm số
f x
liên tục trên
và có đồ thị như hình vẽ.
Đặt
g x f f x
. Hỏi phương trình
0g x
có mấy nghiệm thực phân biệt?
A.
14
. B.
10
. C.
8
. D.
12
.
Lời giải
Chọn B
Ta có
.g x f f x f x
0
0
0
f f x
g x
f x
Có
1 1
2 2
, 2 1
0
0
, 1 2
2
x x x
x
f x
x x x
x
;
1
2
0
0
2
f x x
f x
f f x
f x x
f x
Dựa vào đồ thị ta thấy:
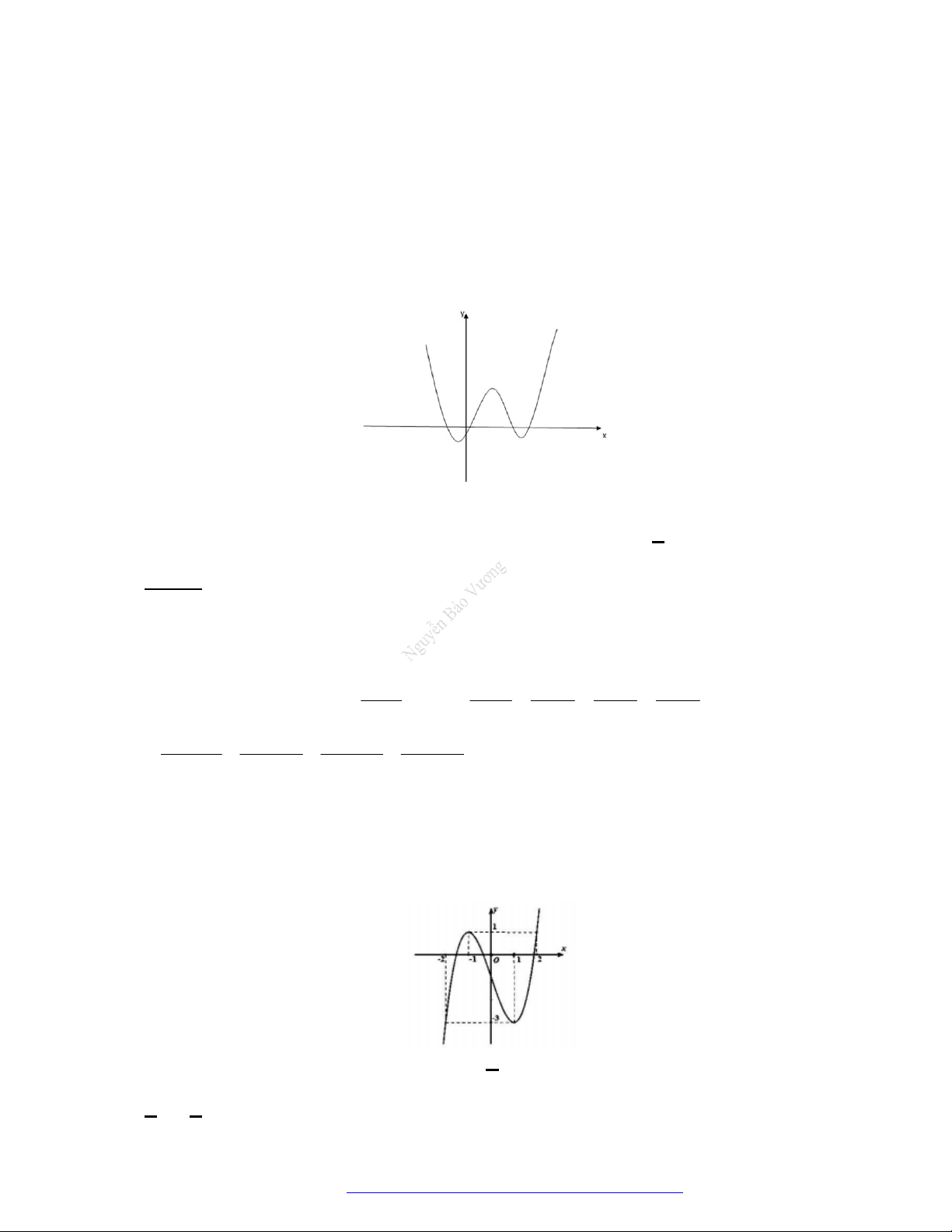
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 28 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
0f x
có
3
nghiệm phân biệt là
2, 0, 2x x x
, trong đó có
2
nghiệm trùng với nghiệm
của
0f x
.
1
f x x
có
3
nghiệm phân biệt
3 4 5
2; 1 , 1;1 , 2;x x x
.
2
f x x
có
1
nghiệm duy nhất
6
; 2x
.
2f x
có
1
nghiệm duy nhất
7
; 2x
.
Cũng từ đồ thị có thể thấy các nghiệm
1 2 3 4 5 6 7
, , , , , , , 2,0,2x x x x x x x
đôi một khác nhau.
Vậy
0g x
có tổng cộng
10
nghiệm phân biệt.
Câu 11. Biết rằng đồ thị hàm số
( )y f x
được cho như hình vẽ sau
Số giao điểm của đồ thị hàm số
2
.y f x f x f x
và trục
Ox
là:
A.
4
. B.
6
. C.
2
. D.
0
.
Lời giải
Chọn D
Đặt
1 2 3 4 1 2 3 4
( ) , 0,f x a x x x x x x x x a x x x x
.
Phương trình hoành độ giao điểm của đồ thị hàm số
2
.y f x f x f x
và trục
Ox
là
2
1 2 3 4
( ) 1 1 1 1
. 0 0 0
( )
f x
f x f x f x
f x x x x x x x x x
2 2 2 2
1 2 3 4
1 1 1 1
0
x x x x x x x x
vô nghiệm.
Vậy số giao điểm của đồ thị hàm số
2
.y f x f x f x
và trục
Ox
là
0
.
Câu 12. (Chuyên Lam Sơn 2019) Cho hàm số
y f x
liên tục trên
và có đồ thị như hình vẽ bên.
Phương trình
1 0f f x
có tất cả bao nhiêu nghiệm thực phân biệt?
A.
6
. B.
5
. C.
7
. D.
4
.
Lời giải
Chọn C

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 29
Ta có
1
2
3
2; 1
0 1;0
1;2
x x
f x x x
x x
Khi đó:
1
2
3
1 2; 1
1 0 1 1;0
1 1;2
f x x
f f x f x x
f x x
1
2
3
1 1;0
1 0;1
1 2;3
f x x
f x x
f x x
+ Ta thấy hai phương trình
1
1 1;0f x x
;
2
1 0;1f x x
đều có ba nghiệm phân
biệt.
Phương trình
3
1 2;3f x x
có một nghiệm.
Vậy phương trình
1 0f f x
có
7
nghiệm.
Câu 13. (Đề tham khảo 2019) Cho hàm số
4 3 2
f x mx nx px qx r
,. Hàm số
y f x
có đồ thị
như hình vẽ bên dưới:
Tập nghiệm của phương trình
f x r
có số phần tử là
A.
4
. B.
3
. C.
1
. D.
2
.
Lời giải
Chọn B
Ta có
3 2
4 3 2
f x mx nx px q
1
Dựa vào đồ thị
y f x
ta thấy phương trình
0
f x
có ba nghiệm đơn là
1
,
5
4
,
3
.
Do đó
1 4 5 3
f x m x x x
và
0m
. Hay
3 2
4 13 2 15
f x mx mx mx m
2
.
Từ
1
và
2
suy ra
13
3
n m
,
p m
và
15q m
.
Khi đó phương trình
f x r
4 3 2
0 mx nx px qx
4 3 2
13
15 0
3
m x x x x
4 3 2
3 13 3 45 0 x x x x
2
3 5 3 0 x x x
5
0 3
3
x x x
.
Vậy tập nghiệm của phương trình
f x r
là
5
;0;3
3
S
.
Câu 14. (Chuyên Bắc Giang 2019) Cho hàm số
4 3 2
y f x mx nx px qx r
, trong đó
, , , ,m n p q r
. Biết rằng hàm số
'y f x
có đồ như hình vẽ dưới.
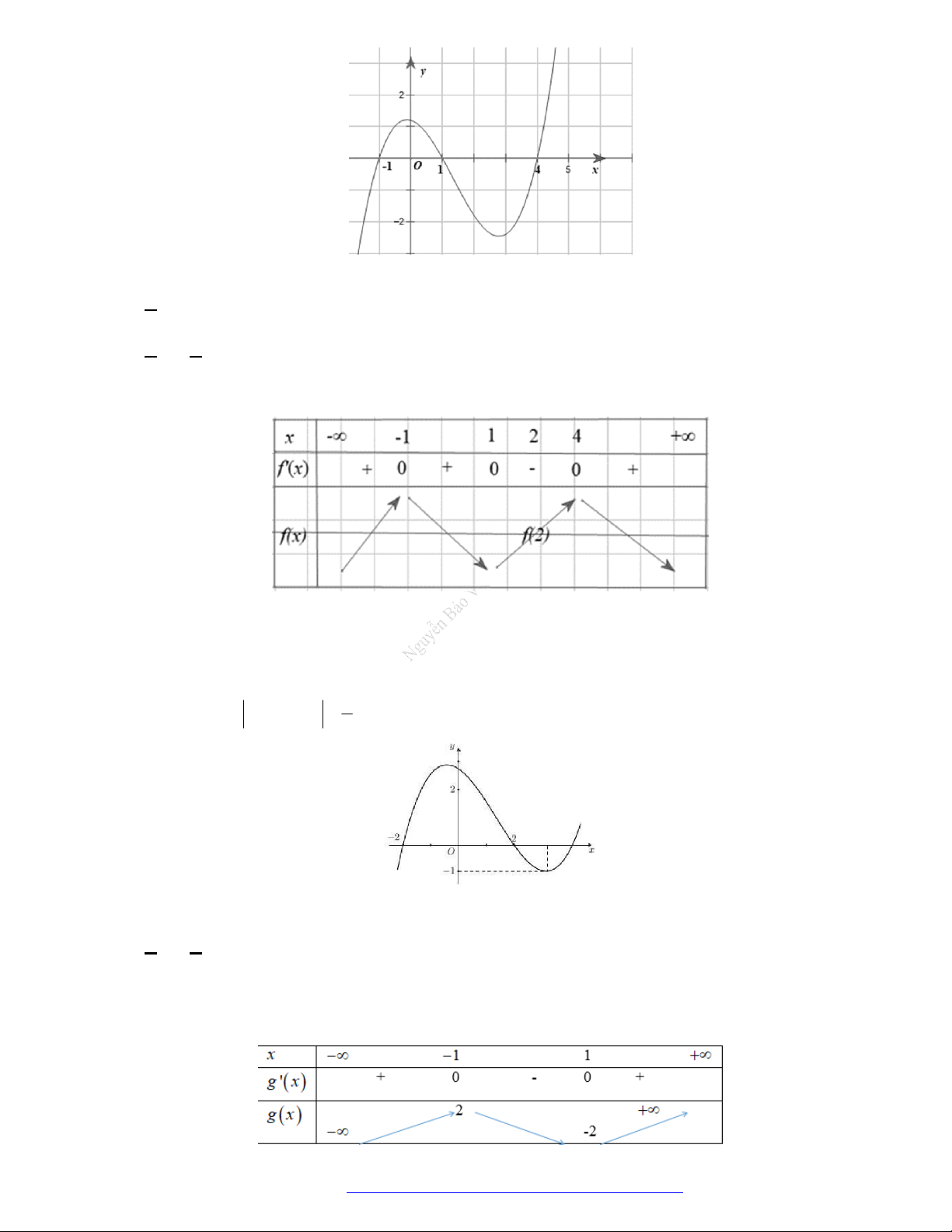
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 30 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Tập nghiệm của phương trình
16 8 4 2f x m n p q r
có tất cả bao nhiêu phần tử.
A.
4
. B.
3
. C.
5
. D.
6
.
Lời giải
Chọn A
Từ đồ thị ta thấy
' 0 1 1 4f x x x x
Ta có bảng biến thiên
Phương trình
16 8 4 2 2f x m n p q r f x f
Từ bảng biến thiên ta thấy phương trình có 4 nghiệm.
Câu 15. (Mã 104 2019) Cho hàm số bậc ba
y f x
có đồ thị như hình vẽ bên. Số nghiệm thực của
phương trình
3
2
3
3
f x x
là
A.
10
B.
3
C.
9
D.
6
Lời giải
Chọn A
Đặt
3
3t g x x x
(1)
Ta có
2
' 3 3 0 1g x x x
Bảng biến thiên
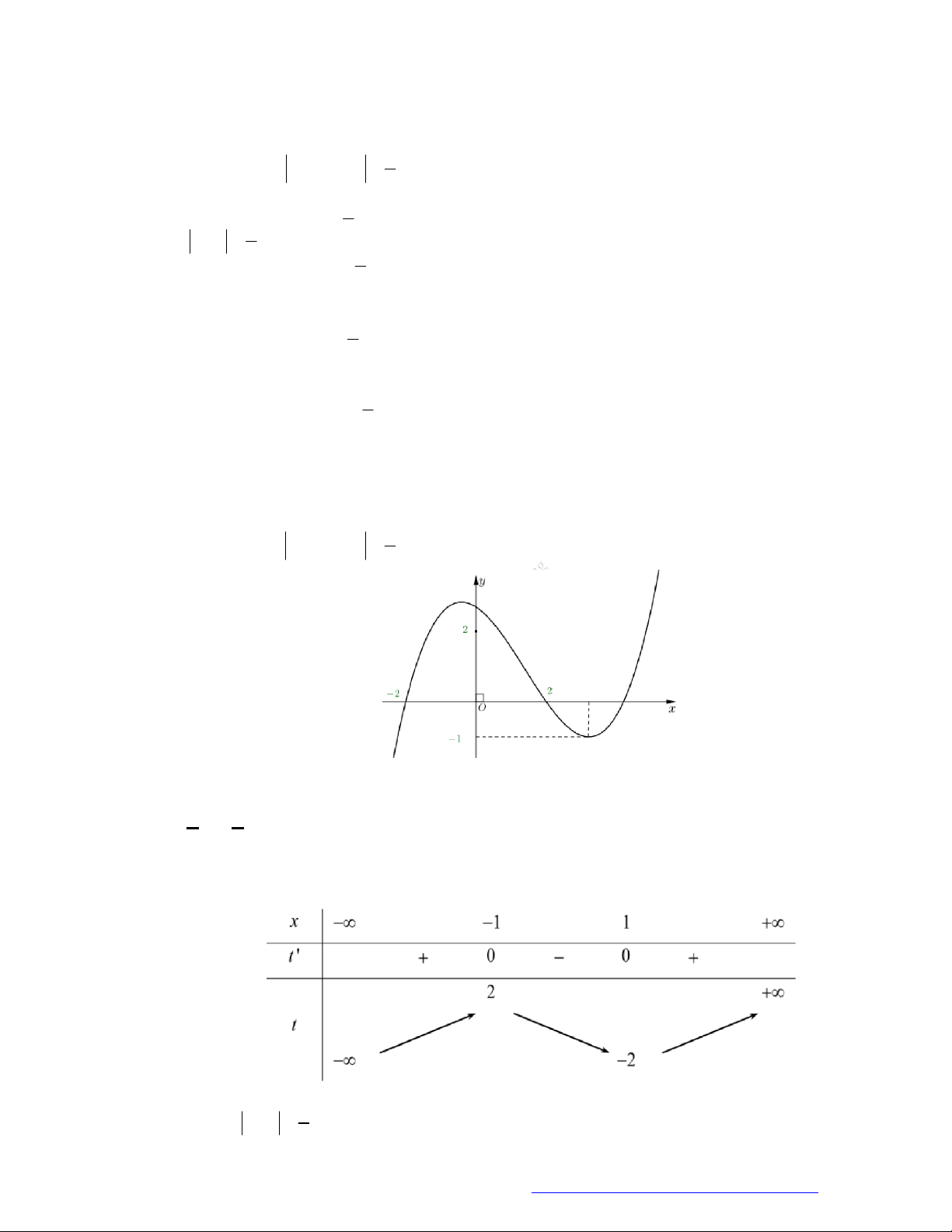
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 31
Dựa vào bảng biến thiên ta có với
2;2t
cho ta 3 giá trị
x
thỏa mãn (1)
2;2t
cho ta 2 giá trị
x
thỏa mãn (1)
; 2 2;t
cho ta 1 giá trị
x
thỏa mãn (1).
Phương trình
3
2
3
3
f x x
(2) trở thành
2
2
3
2
3
3
f t
f t
f t
Dựa vào đồ thị ta có:
+ Phương trình
2
3
f t
có 3 nghiệm thỏa mãn
1 2 3
2 2t t t có 7 nghiệm của phương
trình (2).
+ Phương trình
2
3
f t
có 3 nghiệm thỏa mãn
4 5 6
2 2t t t có 3 nghiệm của phương
trình (2).
Vậy phương trình đã cho có 10 nghiệm.
Câu 16. (Mã 101 2019) Cho hàm số bậc ba
y f x
có đồ thị như hình vẽ bên. Số nghiệm thực của
phương trình
3
4
3
3
f x x
là
A.
7
. B.
4
. C.
3
. D.
8
.
Lời giải
Chọn D
Đặt
3 2
3 3 3t x x t x
. Ta có bảng biến thiên
Khi đó
4
1
3
f t
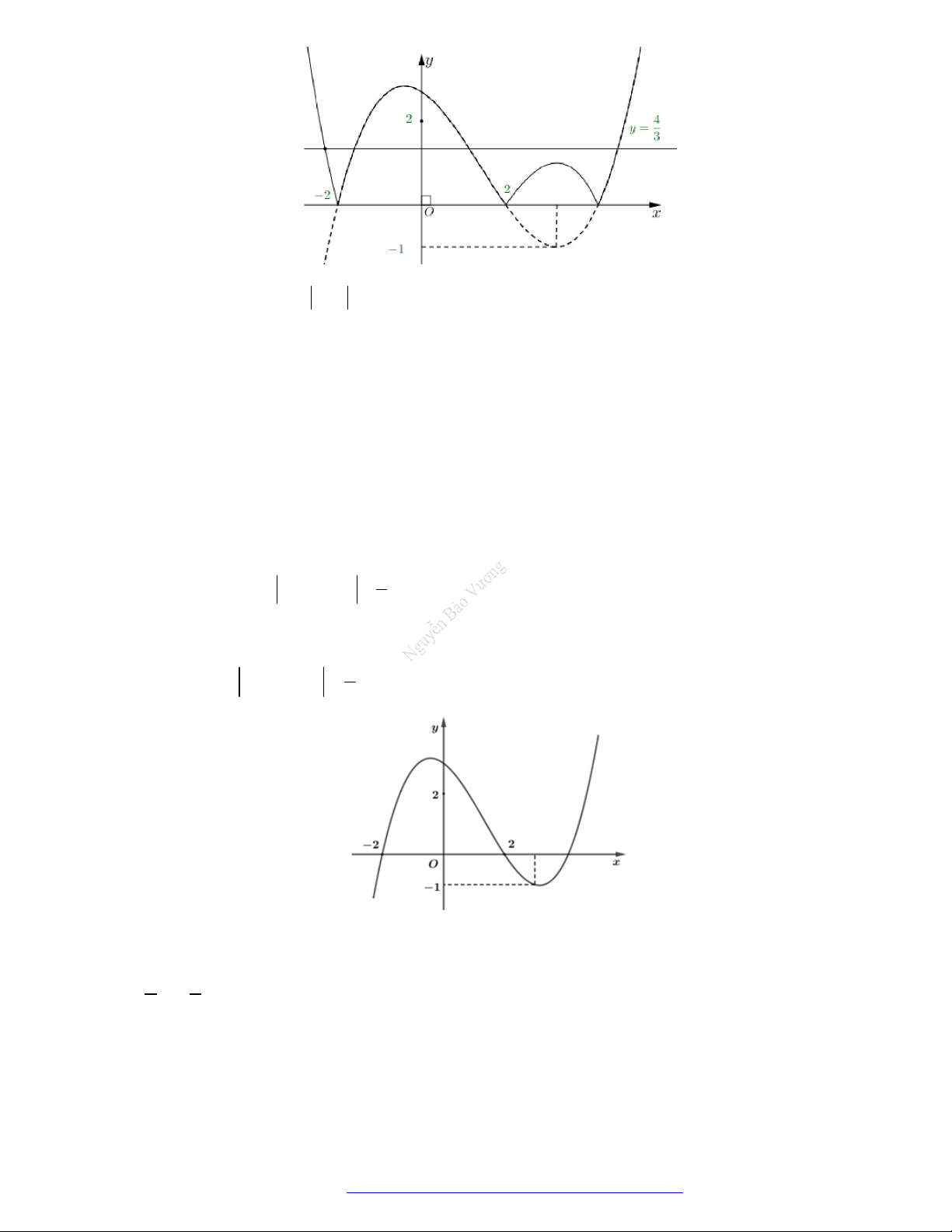
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 32 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Dựa vào đồ thị hàm số
f t
ta thấy phương trình (1) có 4 nghiệm phân biệt
1
2,t
2
2 0,t
3
0 2t ,
4
2t .
Mỗi nghiệm t của phương trình
1
, ta thay vào phương trình
3
3t x x
để tìm nghiệm
x
.
Khi đó
+
1
2t phương trình
3
3t x x
có 1 nghiệm.
+
2
2 0t phương trình
3
3t x x
có 3 nghiệm.
+
3
0 2t
phương trình
3
3t x x
có 3 nghiệm.
+
4
2t
phương trình
3
3t x x
có 1 nghiệm.
Vậy phương trình
3
4
3
3
f x x
có 8 nghiệm.
Câu 17. (Mã 102 2019) Cho hàm số bậc ba
y f x
có đồ thị như hình vẽ bên. Số nghiệm thực của
phương trình
3
1
3
2
f x x
A.
6
. B.
10
. C.
12
. D.
3
.
Lời giải
Chọn B
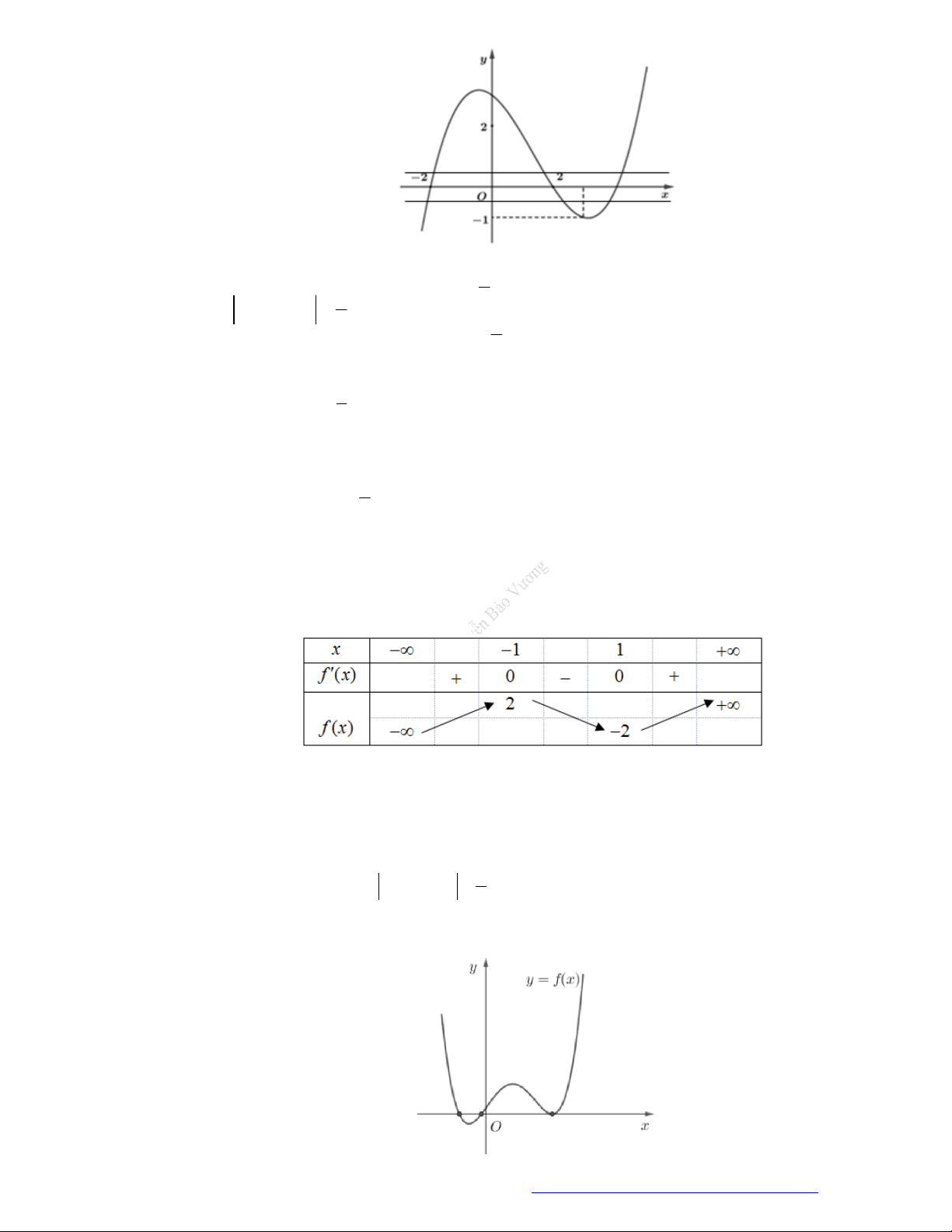
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 33
Ta có
3
3
3
1
3 1
1
2
3
1
2
3 2
2
f x x
f x x
f x x
+)
3
1 1
3 3
2 2
3
3 3
3 2 0
1
1 3 3 0 2
2
3 2
x x
f x x x x
x x
+)
3
4 4
3 3
5 5
3
6 6
3 2
1
2 3 3 2
2
3 2
x x x
f x x x x
x x
Xét hàm số
3
3 ,y x x D
Ta có
2
' 3 3y x
Bảng biến thiên
Dựa vào bảng biến thiên ta có
Phương trình:
3
1
3x x
có
3
nghiệm.
Phương trình:
3
2
3x x
có
3
nghiệm.
Mỗi phương trình
3
3
,
-3x x
3
4
,
-3x x
3
5
-3x x
,
3
6
-3x x
đều có một nghiệm
Từ đó suy ra phương trình
2
1
3
2
f x x
có
10
nghiệm.
Câu 18. Cho
f x
là một hàm đa thức bậc bốn có đồ thị như hình dưới đây.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 34 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Tập nghiệm của phương trình
2
.f x f x f x
có số phần tử là
A.
1.
B.
2.
C.
6.
D.
0.
Lời giải
Chọn A
Xét phương trình
2
. 1f x f x f x
Do
0f x
có ba nghiệm
1 2 2 1 2 3
, ,x x x x x x
và
3
' 0f x
suy ra
3
x là một nghiệm của (1)
Ta có
2
1 2 3
, 0f x a x x x x x x a
Với
3
1 2 3
1 1 2
1 0 0
f x
x x
f x x x x x x x
2 2 2
1 2 3
1 1 2
0
x x x x x x
vô nghiệm.
Vậy, phương trình (1) có đúng một nghiệm
3
.x x
Câu 19. (KTNL GV Thuận Thành 2 Bắc Ninh 2019) Cho hai hàm số
,y f x y g x
có đồ thị như
hình sau:
Khi đó tổng số nghiệm của hai phương trình
0f g x
và
0g f x
là
A.
25
. B.
22
. C.
21
. D.
26
.
Lời giải
Chọn B.
Quan sát đồ thị ta thấy:
1 1
2 2
3 3
4 4
3 2
1
0 1 2
2 3
4 5
x x x
x
f x x x x
x x x
x x x
.
5
y=g(x)
y=f(x)
y
x
-4
-3
-2
-1
4
3
2
1
43
2
1
O
-1
-2-3
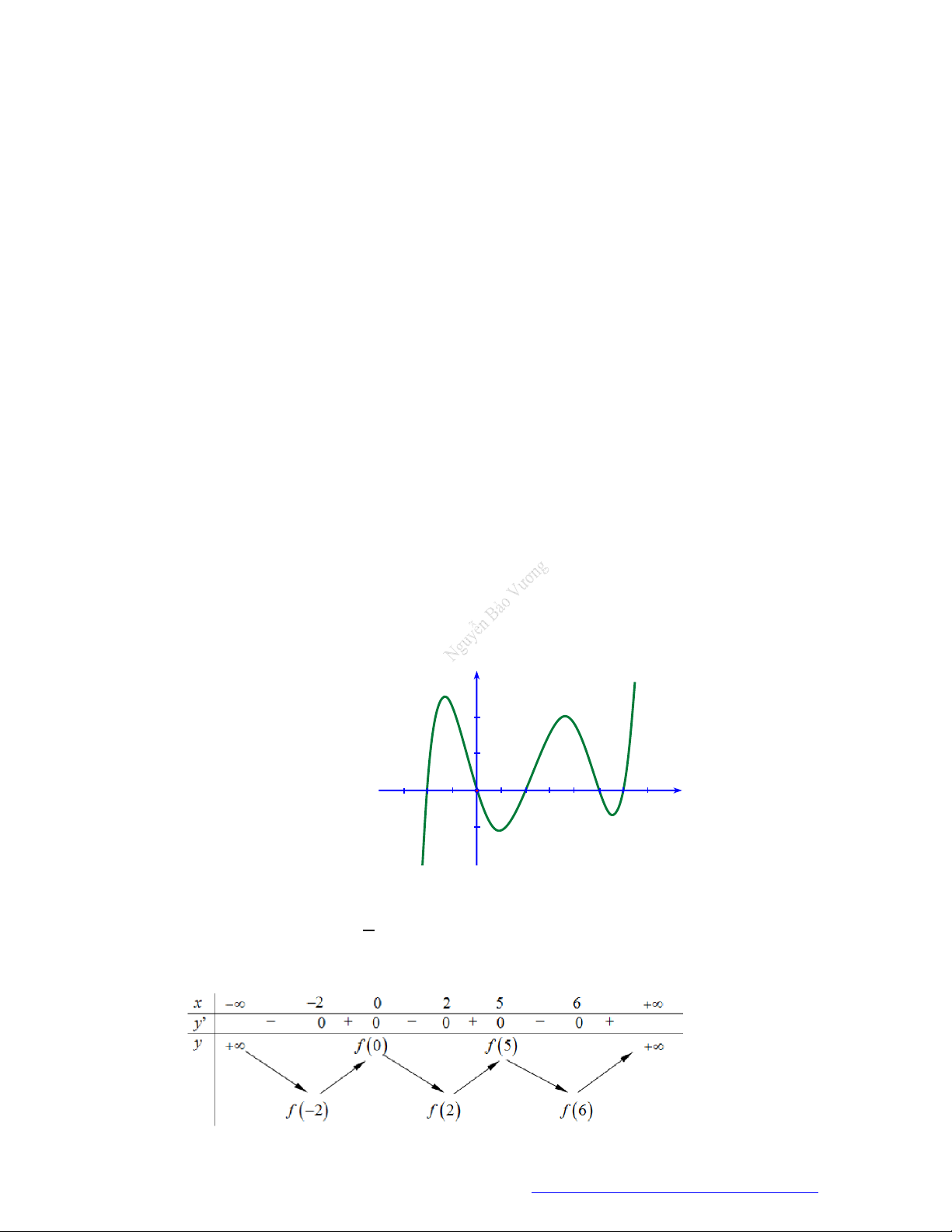
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 35
Do đó:
0f g x
1
2
3
4
1
1 2
3
4
5
g x x
g x
g x x
g x x
g x x
Phương trình
1
có đúng
1
nghiệm; Phương trình
2
có đúng
3
nghiệm; Phương trình
3
có
đúng
3
nghiệm; Phương trình
4
có đúng
3
nghiệm; Phương trình
5
có đúng
1
nghiệm. Tất
cả các nghiệm trên đều phân biệt nên phương trình
0f g x
có đúng
11
nghiệm.
Quan sát đồ thị ta thấy:
0g x
5 5
6 6
2 1
0 1
3
x x x
x x x
x
Do đó
0g f x
5
6
6
7
3 8
f x x
f x x
f x
Phương trình
6
có
5
nghiệm; Phương trình
7
có
5
nghiệm; Phương trình
8
có
1
nghiệm.
Tất cả các nghiệm này đều phân biệt nên phương trình
0g f x
có đúng
11
nghiệm.
Vậy tổng số nghiệm của hai phương trình
0f g x
và
0g f x
là
22
nghiệm.
Câu 20. (THPT Nghĩa Hưng 2019) Cho hàm số
y f x
có đạo hàm liên tục trên
. Hàm số
y f x
có đồ thị như hình vẽ bên dưới:
Số nghiệm thuộc đoạn
2;6
của phương trình
0f x f
là
A. 5 B. 2 C. 3 D. 4
Lời giải
Từ đồ thị của hàm số
'f x
ta có BBT
Gọi
1
S là diện tích hình phẳng giới hạn bởi
' ; 0; 0; 2y f x y x x
O
1
2
3
1
2
3
4
5
6
7
x
y
4
2
2
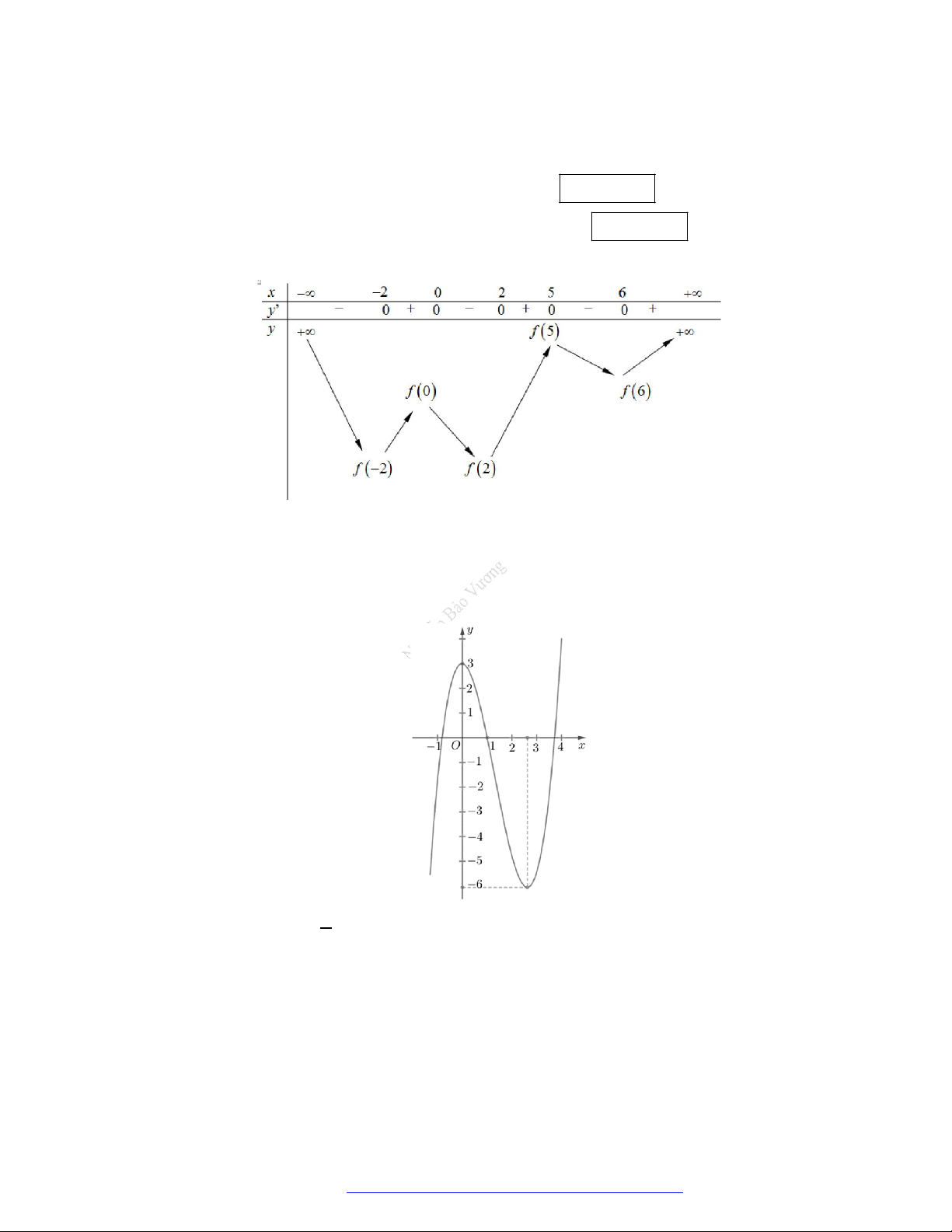
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 36 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Gọi
2
S là diện tích hình phẳng giới hạn bởi
' ; 0; 2; 5y f x y x x
Gọi
3
S là diện tích hình phẳng giới hạn bởi
' ; 0; 5; 6y f x y x x
2
1
0
' 0 2S f x dx f f
;
5
2
2
' 5 2S f x dx f f
;
6
3
5
' 5 6S f x dx f f
Từ đồ thị ta thấy
2 1
5 2 0 2 5 0S S f f f f f f
và
1 3 2
0 2 5 6 5 2 6 0S S S f f f f f f f f
Khi đó ta có BBT chính xác ( dạng đồ thị chính xác ) như sau:
Vậy phương trình
0f x f
có 2 nghiệm thuộc đoạn
2;6
Câu 21. (Chuyên Vĩnh Phúc 2019) Cho hàm số
y f x
có đạo hàm trên
và có đồ thị là đường cong
trong hình vẽ dưới. Đặt
g x f f x
. Tìm số nghiệm của phương trình
0g x
.
.
A.
2
B.
8
C.
4
D.
6
Lời giải.
Ta có:
0
0
0
f x
g x f x f f x
f f x
*
.
Theo đồ thị hàm số suy ra.
1
0
0
x
f x
x a
, với
1
2 3a .
1
0 , 1
0
, 2
f x
f f x
f x a
.

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 37
Phương trình
1
:
0f x
có
3
nghiệm phân biệt khác nghiệm phương trình
*
.
Phương trình
2
:
1
f x a
có 3 nghiệm phân biệt khác nghiệm phương trình
1
và phương
trình
*
.
Vậy phương trình ban đầu có 8 nghiệm phân biệt.
Câu 22. (THPT Hậu Lộc 2 - Thanh Hóa - 2019) Cho hàm số
4 3 2
y f x =ax bx cx dx e
có đồ thị
như hình vẽ bên đây, trong đó a,b,c,d ,e là các hệ số thực. Số nghiệm của phương trình
2 1 0f f x f x f x
là
A. 3. B. 4. C. 2. D. 0.
Lời giải
Chọn B
Từ hình vẽ ta có dạng đồ thị của hàm trùng phương nên
4 2
0b d f x ax cx e
Ta có
3
4 2f x ax cx.
Từ đồ thị
4 2
1 0
4 2 0 1
0 0 0 0 2
1 2
1 1
f
a c a
f e e f x x x .
a c e c
f
2
2f x x x và
2
2f f x f x f x .
Như vậy phương trình
2 1 0f f x f x f x .
2
2 2 1 0f x f x f x f x
với
0f x .
Đặt
0t f x t
ta được phương trình
0g t
với
2
3 2 1g t t t t .
Nhận thấy: Hàm số
g t
liên tục trên đoạn
0 1;
và
0 1 0g .g
0g t
có ít nhất 1 nghiệm thuộc
0 1;
.
Hàm số
g t
liên tục trên đoạn
1 4;
và
1 4 0g .g
0g t
có ít nhất 1 nghiệm thuộc
1 4;
.
Mà
0g t
là phương trình bậc hai chỉ có tối hai nghiệm nên
0g t
có duy nhất một nghiệm thuộc
0 1;
. Suy ra
2 1 0f f x f x f x
có duy nhất một nghiệm
0 1f x ; .
Suy ra
phương trình
f x a
với
0 1a ;
luôn có 4 nghiệm x phân biệt.
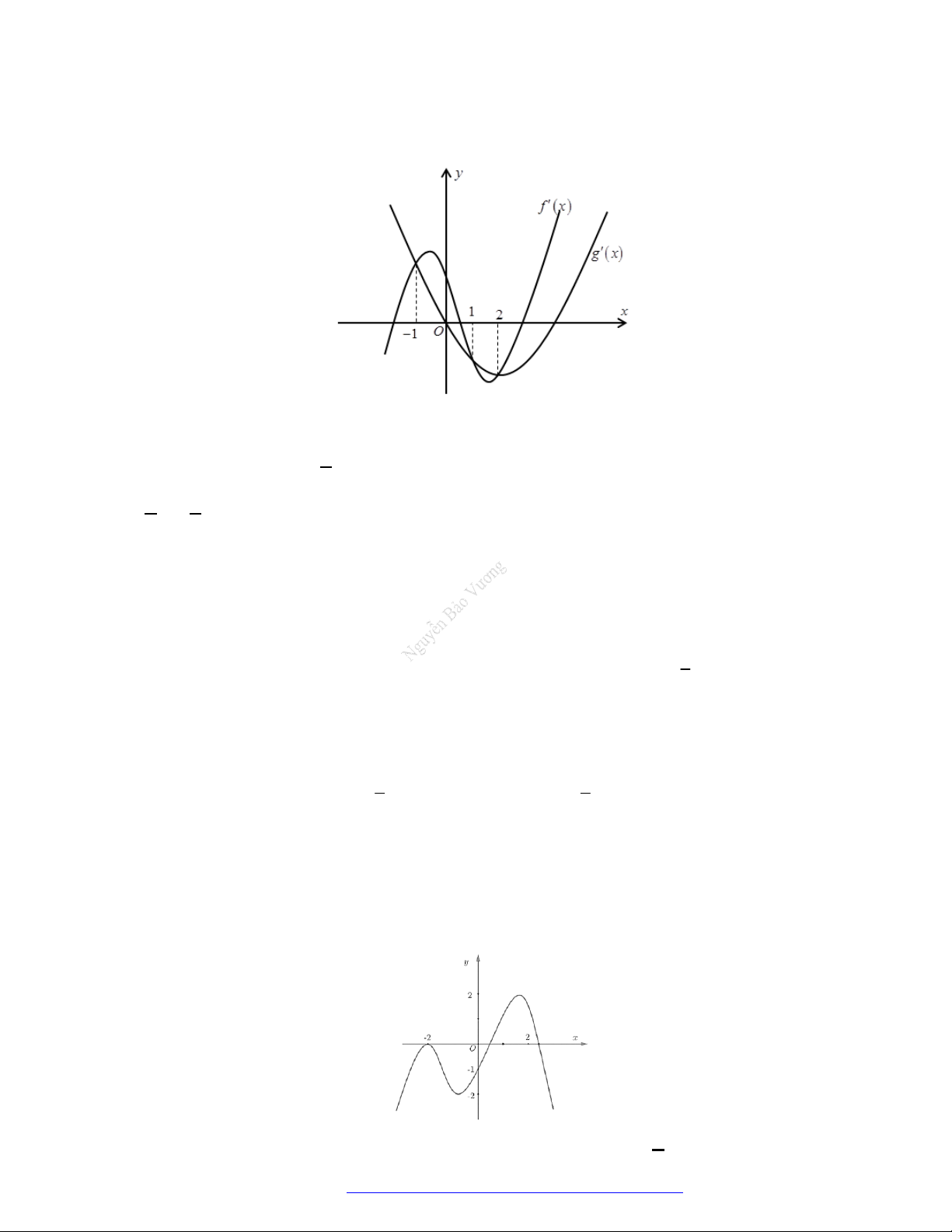
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 38 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 23. (Sở Hưng Yên - 2019) Cho các hàm số
4 3 2
f x mx nx px qx r
và
3 2
g x ax bx cx d
,
, , , , , , , ,n n p q r a b c d
thỏa mãn
0 0f g
. Các hàm số
,f x g x
có đồ thị như hình vẽ dưới đây
Tập nghiệm của phương trình
f x g x
có số phần tử là
A.
4
. B.
2
. C.
1
. D.
3
.
Lời giải
Chọn B
+) Từ giả thiết suy ra
r d
do đó phương trình tương đương với:
3 2
3 2
0
0
0
x
x mx n a x p b x q c
mx n a x p b x q c
+) Từ đồ thị của các hàm số suy ra
0m
và
8
1 1 4 3 2 0
3
1 1 4 3 2 0 2
8
2 2 32 12 4 0
n a m
f g m n a p b q c
f g m n a p b q c p b m
q c m
f g m n a p b q c
.
Từ đó ta có phương trình:
3 2 3 2
8 8
2 8 0 2 8 0
3 3
mx mx mx m x x x
.
Sử dụng máy tính Casio ta được phương trình có 1 nghiệm và nghiệm đó khác
0
.
Vậy tập nghiệm của phương trình có 2 phần tử.
Câu 24. (Sở Hà Tĩnh - 2019) Cho hàm số
y f x
liên tục trên
và có đồ thị như hình vẽ. Tập hợp
nghiệm của phương trình
1 0f f x
có bao nhiêu phần tử?
A.
4
. B.
7
. C.
6
. D.
9
.
0 0
f g
f x g x
,
f x g x
f x g x

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 39
Lời giải
Chọn D.
Dựa vào đồ thị ta có
1 0f f x
1f f x
2
2; 1
0
2
f x a
f x b
f x
f x c
.
+ Với
2f x a
1
2
2
2
x x
x x
.
+ Với
2; 1f x b
3
4
5
6
2
2; 1
1;0
2
x x
x x
x x
x x
.
+ Với
0f x
7
8
9
2
0;1
2;3
x x
x x
x x
.
+ Với
2f x c
vô nghiệm.
Ta thấy hàm số
y f x
đơn điệu trên
; 2
,
1 3
f x a b f x
nên
1 3
x x .
Hàm số
y f x
đơn điệu trên
2;
,
6 9
0f x b f x
nên
6 9
x x .
Vậy phương trình đã cho có 9 nghiệm phân biệt.
Câu 25. (THPT Nguyễn Đức Cảnh - 2019) Cho hàm số
f x
có bảng biến thiên
Phương trình
2
2 3f x x
có bao nhiêu nghiệm?
A. 1. B. 2. C. 3. D. 4.
Lời giải
Chọn B
Trước hết, xét hàm số
2
2t t x x x
,
0;2x
.
Ta có
2
2 2
2 2
x
t x
x x
,
0;2x
.
0 1 0;2t x x
.
Bảng biến thiên của
t x
:
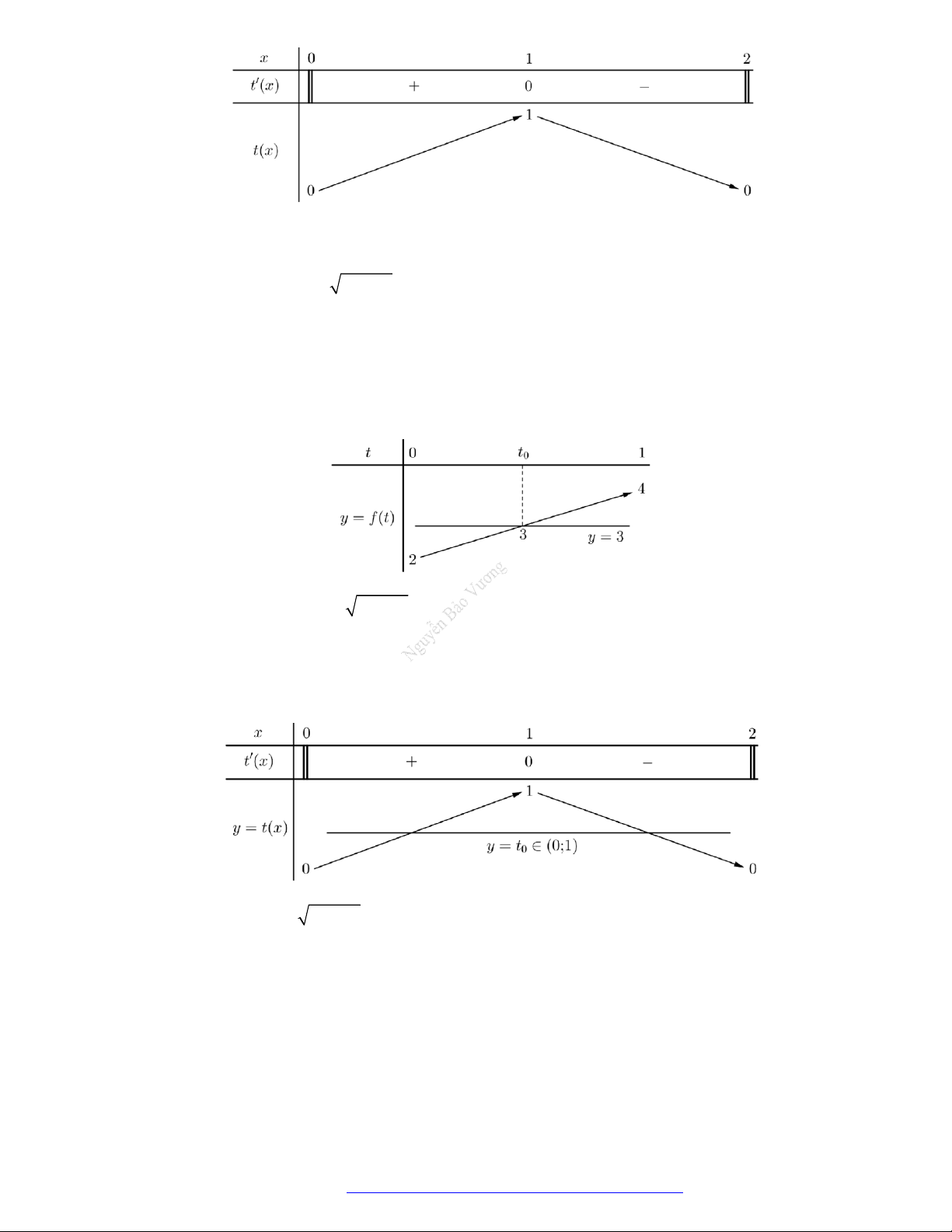
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 40 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
0 1t
,
0;2x
.
Lúc này, phương trình
2
2 3f x x
trở thành
3 1f t
với
0;1t
.
Theo bảng biến thiên của hàm số
f t
trên đoạn
0;1
thì đường thẳng
3y
cắt đồ thị hàm số
y f t
tại đúng 1 điểm có hoành độ thuộc khoảng
0;1
nên phương trình
2
có đúng 1
nghiệm
0
t t với
0
0;1t
.
Khi đó, phương trình
2
0
1 2x x t
2
,
0
0;1t
.
Mặt khác, theo bảng biến thiên của hàm số
t x
, với mỗi
0
0;1t
thì đường thẳng
0
y t cắt đồ
thị hàm số
y t x
tại đúng 2 điểm phân biệt nên phương trình
2
có đúng 2 nghiệm phân biệt.
Vậy phương trình
2
2 3f x x
có đúng 2 nghiệm.
Câu 26. (Chuyên Lam Sơn - 2020) Cho hàm số bậc ba
y f x
có đồ thị như hình vẽ bên.
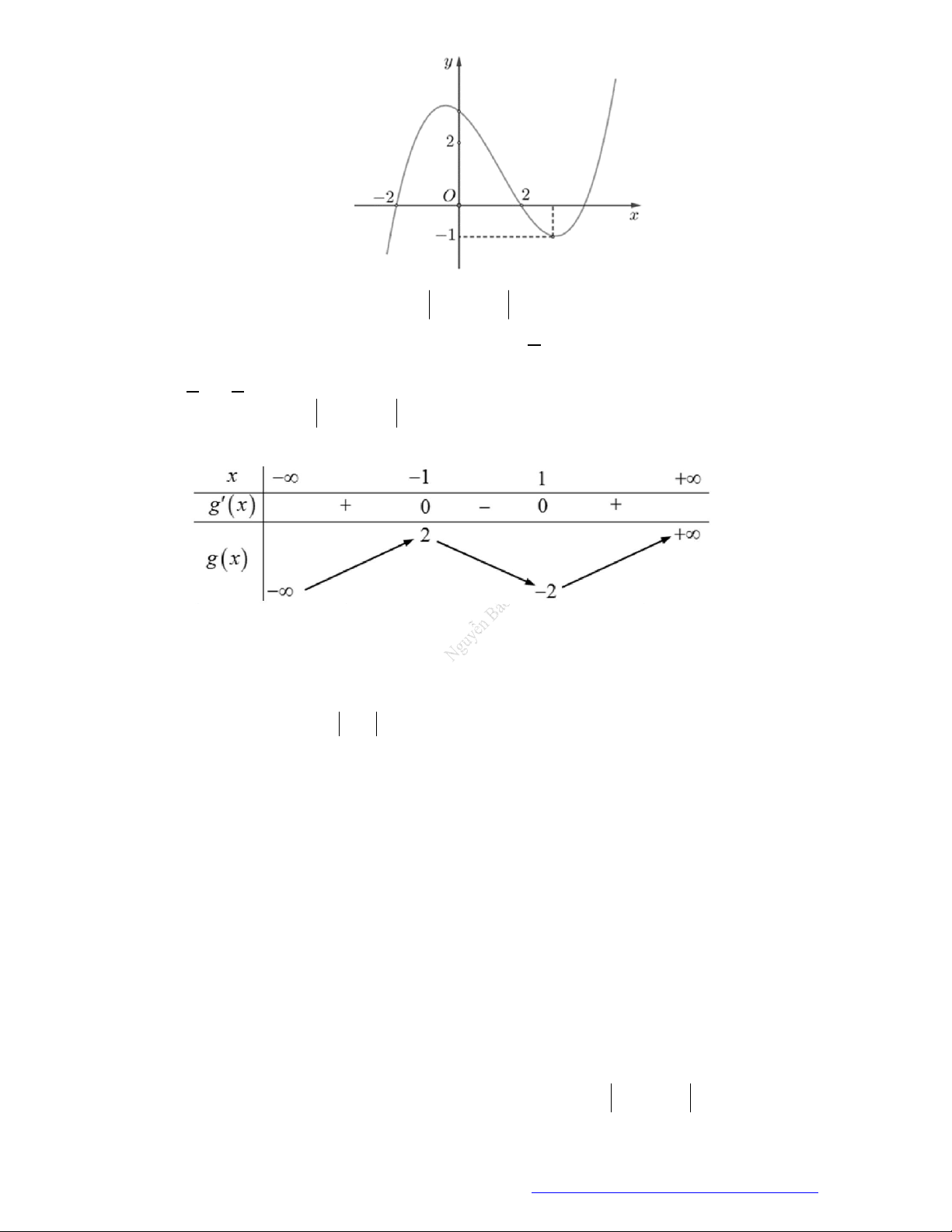
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 41
Số nghiệm thực của phương trình
3
3 1f x x là
A.
10
. B.
8
. C.
9
. D.
7
.
Lời giải
Chọn C
Xét phương trình
3
3 1f x x (1)
Đặt
3
3t x x
, ta có bảng biến thiên của hàm số
3
3t g x x x
như sau:
Từ bảng biến thiên, ta thấy
+ Với mỗi
0
2t hoặc
0
2t , phương trình
3
0
3t x x
có một nghiệm;
+ Với mỗi
0
2 2t
, phương trình
3
0
3t x x
có 3 nghiệm.
Khi đó, (1) trở thành
1
1
1
f t
f t
f t
* TH 1:
1
2
3
2;0
1 0;2
2;
t t
f t t t
t t
+ Với
1
2;0t t
Phương trình
3
1
3t x x
có 3 nghiệm;
+ Với
2
0;2t t
Phương trình
3
2
3t x x
có 3 nghiệm;
+ Với
3
2;t t
Phương trình
3
3
3t x x
có 1 nghiệm;
* TH 2:
4
5
; 2
1
2;
t t
f t
t t
+ Với
4
; 2t t
Phương trình
3
4
3t x x
có 1 nghiệm;
+ Với
5
2;t t
Phương trình
3
5
3t x x
có 1 nghiệm.
Mặt khác, các nghiệm này đều phân biệt. Vậy phương trình
3
3 1f x x có 9 nghiệm phân
biệt.
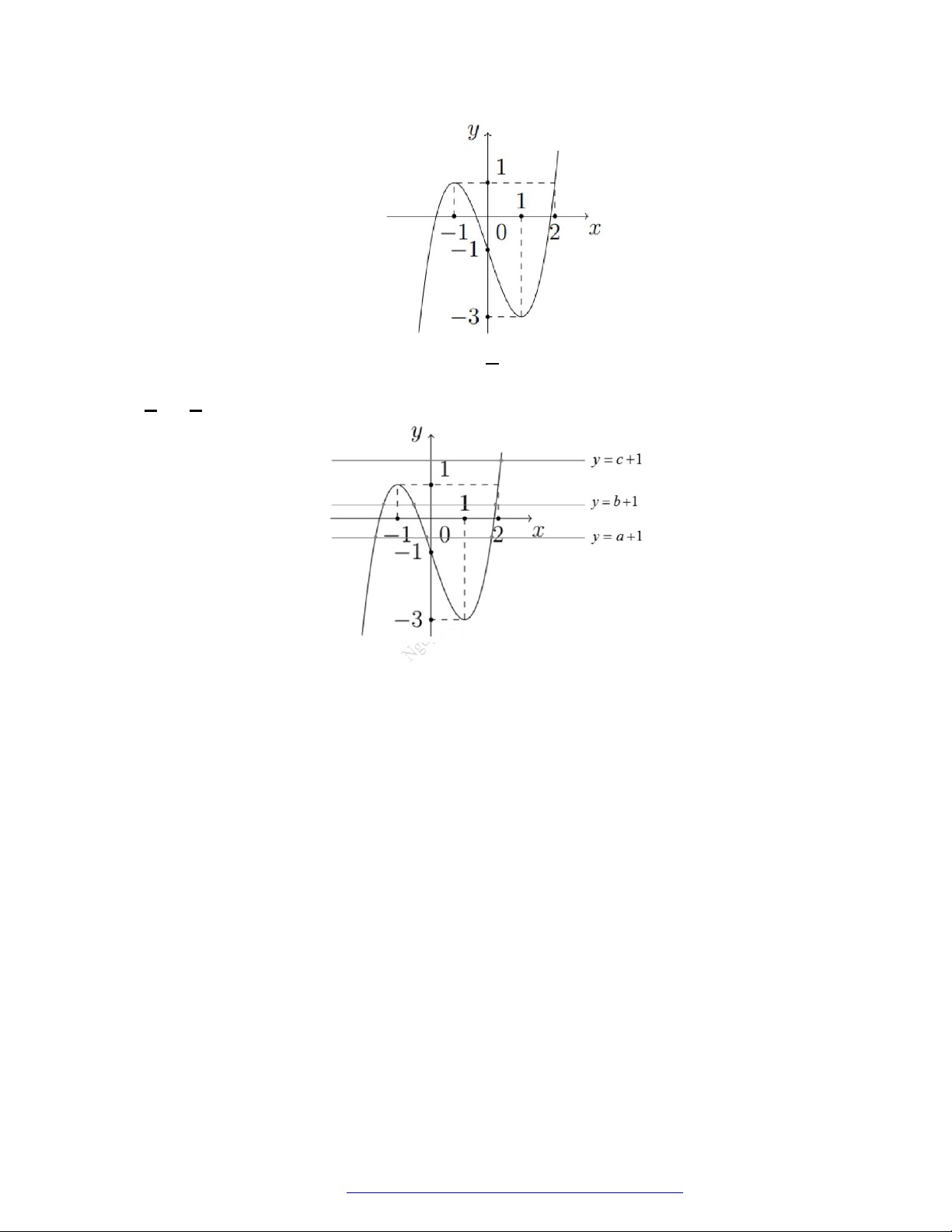
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 42 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 27. (Chuyên Lương Văn Chánh - Phú Yên - 2020) Cho hàm số
f x
có đồ thị như hình bên.
Phương trình
cos 1 0f f x
có bao nhiêu nghiệm thuộc đoạn
0;2
?
A.
2
. B.
5
. C.
4
. D.
6
.
Lời giải
Chọn C
Dựa vào đồ thị hàm số ta thấy:
cos 1 2; 1
cos 1 0 cos 1 1;0
cos 1 1;2
f x a
f f x f x b
f x c
cos 1 1;0
cos 1 0;1
cos 1 2;3
f x a
f x b
f x c
• Xét phương trình
1
2
3
cos 1 1
cos 1 cos 1;0 2
cos 1 3
x
f x a x
x
Vì
cos 1;1x
nên phương trình
,1 3
vô nghiệm và phương trình
2
có 2 nghiệm thuộc
đoạn
; 0 2
.
• Xét phương trình
1
2
3
cos 1 4
cos 1 cos 1;0 5
cos 1 6
x
f x b x
x
Vì
cos 1;1x
nên phương trình
,4 6
vô nghiệm và phương trình
5
có 2 nghiệm thuộc
đoạn
; 0 2
.
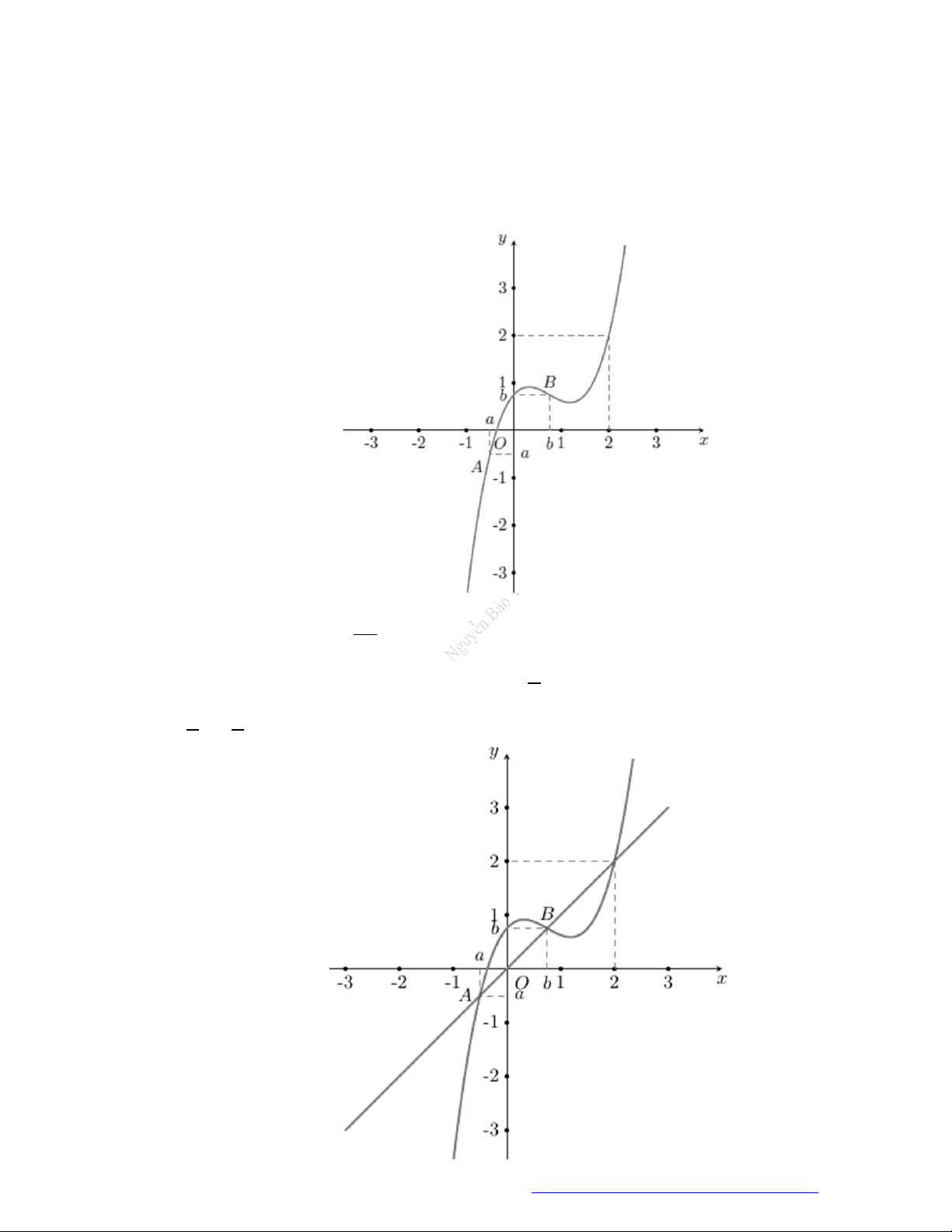
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 43
• Xét phương trình
cos 1 cos 2f x c x t
(vô nghiệm)
Nhận xét hai nghiệm của phương trình
5
không trùng với nghiệm nào của phương trình
2
nên
phương trình
cos 1 0f f x
có 4 nghiệm phận biệt.
Câu 28. (Chuyên Lương Văn Tỵ - Ninh Bình - 2020) Cho hàm số
3 2
f x ax bx bx c
có đồ thị
như hình vẽ:
Số nghiệm nằm trong
;3
2
của phương trình
cos 1 cos 1f x x
là
A.
2
. B.
3
. C. 5. D. 4.
Lời giải
Chọn C
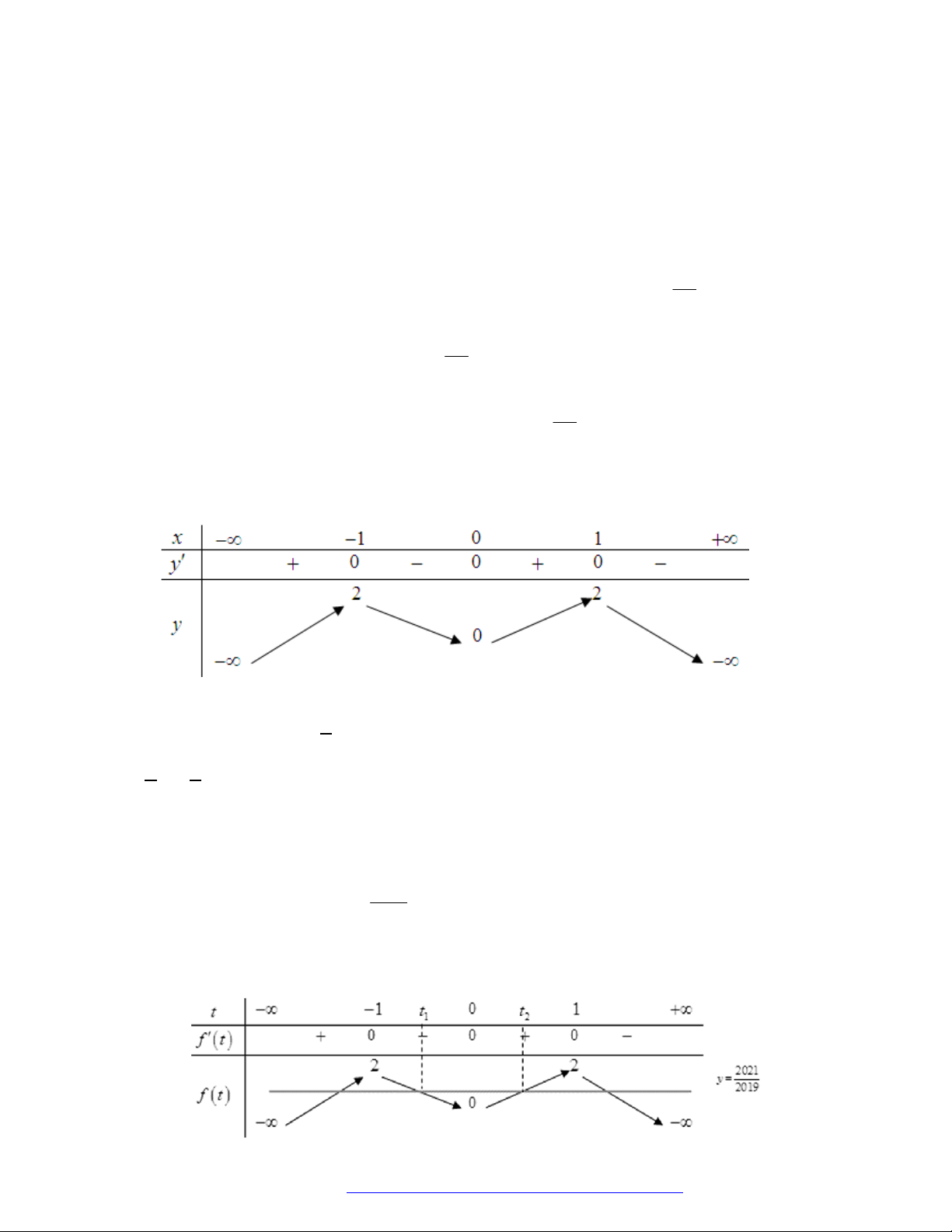
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 44 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Từ đồ thị ta có
;0
0;1
2
x a
f x x x b
x
Do đó
cos 1 ;0
cos 1 cos 1 cos 1 0;1
cos 1 2
x a
f x x x b
x
1
2
cos 1 ; 1 ( )
cos 1 1;0 (1)
cos 1 (2)
x a t VN
x b t
x
Dựa vào đường tròn lượng giác, phương trình (1) có 3 nghiệm nằm trong
;3
2
.
Phương trình (2) có
2
nghiệm nằm trong
;3
2
.
Vậy phương trình ban đầu có tất cả 5 nghiệm nằm trong
;3
2
.
Câu 29. (Chuyên Lê Hồng Phong - Nam Định - 2020) Cho hàm số
f x
liên tục trên
và có bảng
biến thiên như sau:
Số nghiệm thuộc khoảng
;ln 2
của phương trình
2019 1 2021 0
x
f e
là
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn B
Đặt
1
x
t e
;
;ln 2x
1;1t
.
Nhận xét:
ln 1x t
với mỗi giá trị của
1;1t
ta được một giá trị của
;ln2x
.
Phương trình tương đương:
2021
2019
f t
.
Sử dụng bảng biến thiên của
f x
cho
f t
như sau:
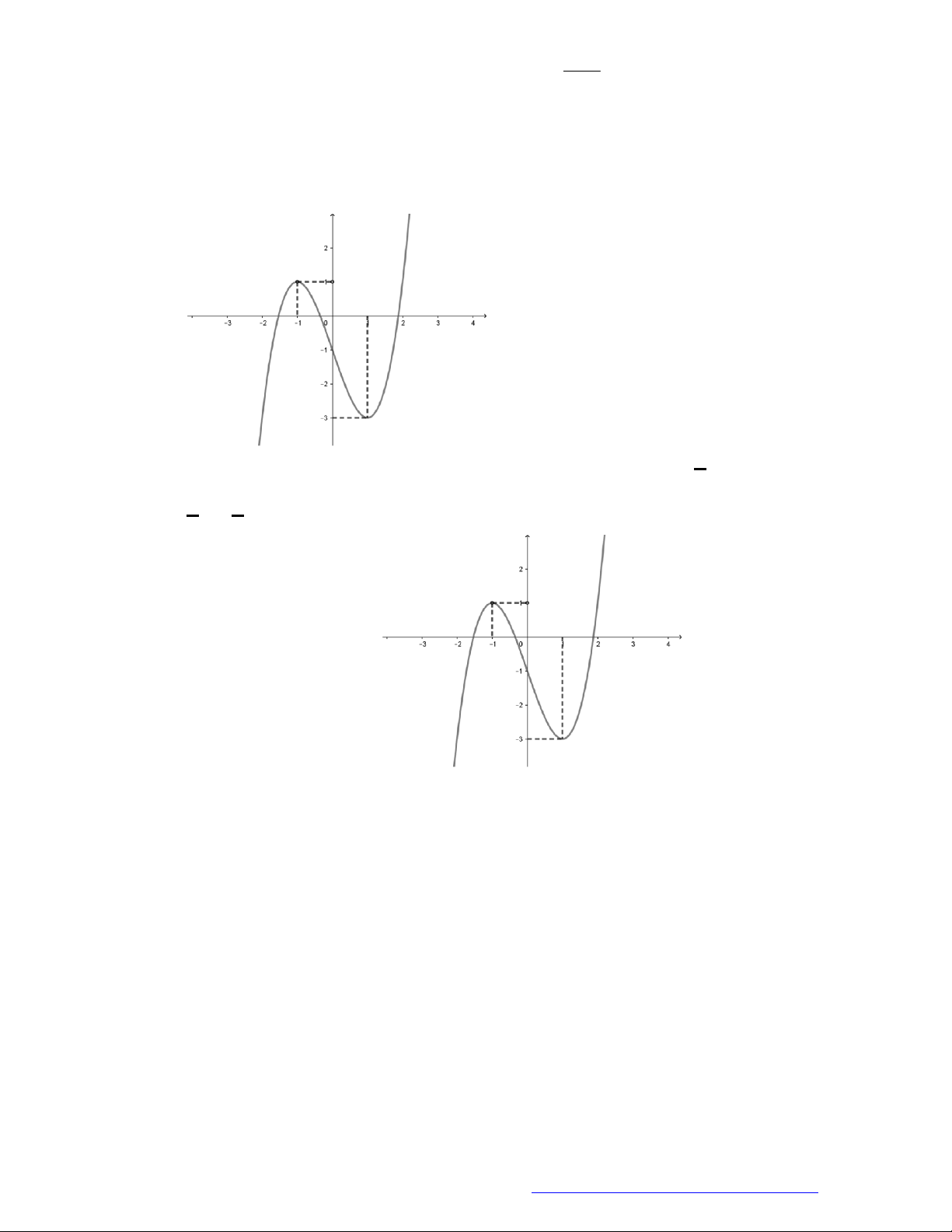
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 45
Dựa vào bảng biến thiên ta thấy phương trình
2021
2019
f t
có 2 nghiệm
1 2
, 1;1t t
.
Vậy phương trình
2019 1 2021 0
x
f e
có 2 nghiệm
;ln 2x
.
Câu 30. (Chuyên Thái Bình - 2020) Cho
y f x
là hàm số đa thức bậc 3 và có đồ thị như hình vẽ bên.
Hỏi phương trình
cos 1 0f f x
có bao nhiêu nghiệm thuộc đoạn
0;3
?
A.
2
. B.
4
. C.
5
. D.
6
.
Lời giải
Chọn D
Đặt cost x , với
0;3 1;1x t
.
Với
1t
, phương trình cost x có hai nghiệm
0;3x
.
Với
1t
, phương trình cost x có hai nghiệm
0;3x
.
Với
1 1t
, phương trình cost x có ba nghiệm
0;3x
.
Thay cost x vào phương trình
cos 1 0f f x
, ta được phương trình:
1 2; 1
1 0 1 1;0
1 1;2
f t a
f f t f t b
f t c
1 1;0 1
1 0;1 2
1 2;3 3
f t a
f t b
f t c
.
Từ đồ thị ta có:
+) Phương trình (1) có 1 nghiệm
1;0t
, suy ra phương trình đã cho có 3 nghiệm.
+) Phương trình (2) có 1 nghiệm
1;0t
, suy ra phương trình đã cho có 3 nghiệm.
+) Phương trình (3) có 1 nghiệm
1t
, suy ra phương trình đã cho vô nghiệm.
Vậy phương trình đã cho có 6 nghiệm.
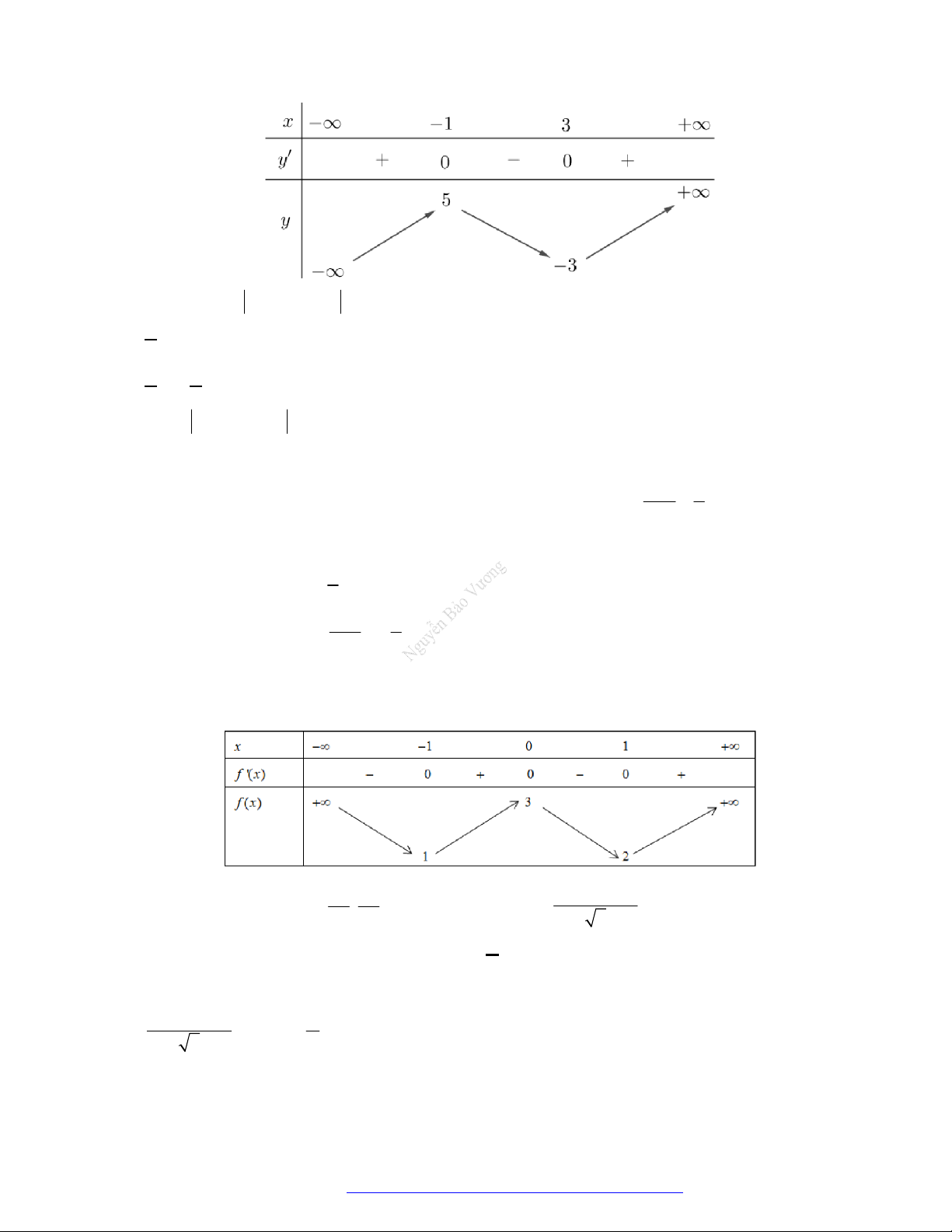
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 46 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 31. (Chuyên Thái Nguyên - 2020) Cho hàm số
y f x
liên tục trên
và có bảng biến thiên như
hình vẽ
Phương trình
3 1 2 5f x
có bao nhiêu nghiệm?
A.
3
. B.
5
. C.
6
. D.
4
.
Lời giải
Chọn A
Ta có
3 1 2 5 3 1 7 1
3 1 2 5
3 1 2 5 3 1 3 2
f x f x
f x
f x f x
.
Dựa vào bảng biến thiên,
+ Phương trình
1
có nghiệm duy nhất thỏa mãn
1 2
3 1 3 .
3 3
a
x a x
+ Phương trình
2
có hai nghiệm phân biệt
1 2
,x x thỏa mãn
1
1
2
2
2
3 1 3
3
.
3 1 1 1 2
3 3
x
x
x b b
x
Vậy phương trình đã cho có
3
nghiệm.
Câu 32. (Sở Bắc Ninh - 2020) Cho hàm số
( )f x
có bảng biến thiên như sau:
Số nghiệm thuộc đoạn
5 5
;
4 4
của phương trình
sin cos
3 7 0
2
x x
f
là:
A.
6.
B.
3.
C.
5.
D.
4.
Lời giải
Chọn C
sin cos
sin
4
2
x x
x
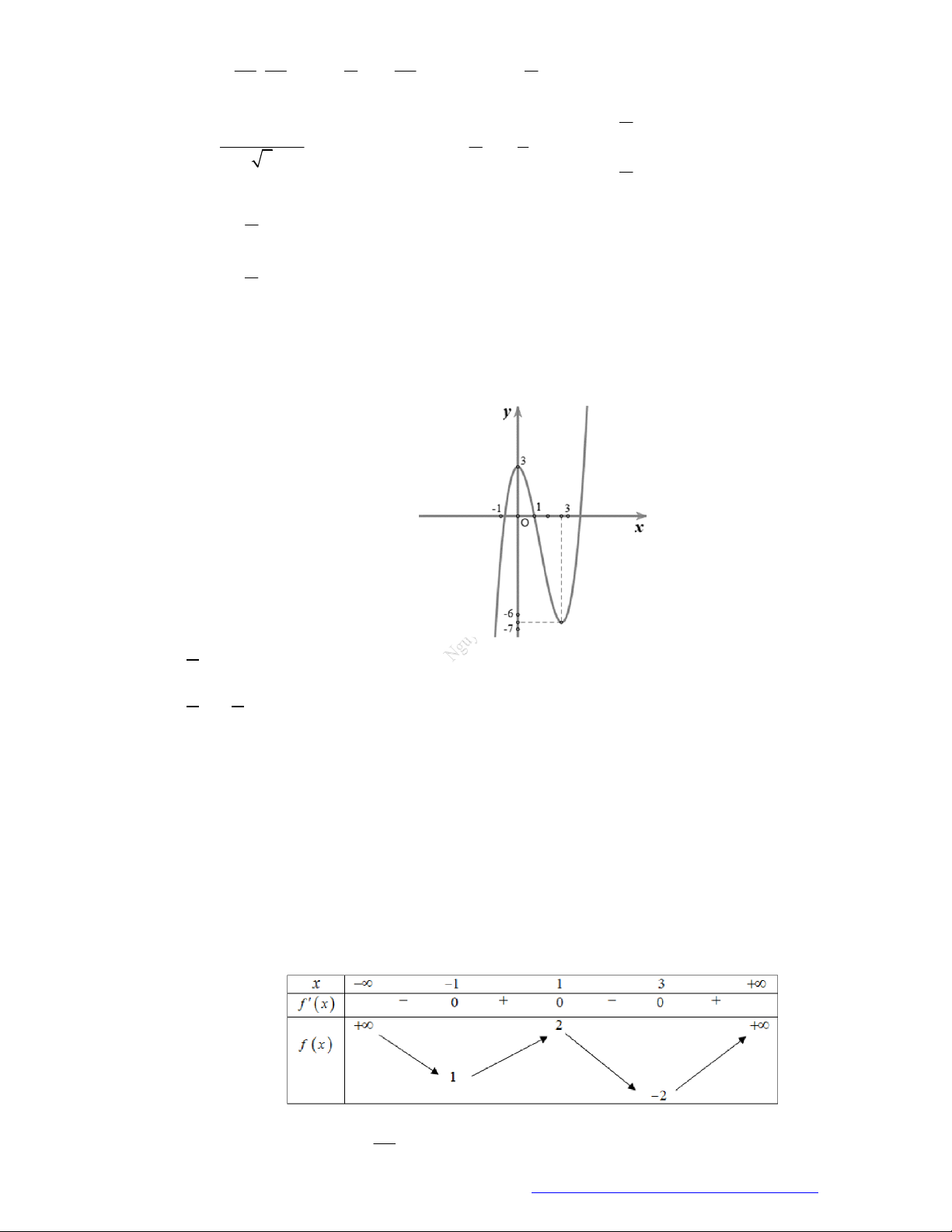
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 47
5 5 3
; ; sin 1;1
4 4 4 2 4
sin ( 1;0)
4
sin cos 7
3 7 0 sin
4 3
2
sin (0;1)
4
x x x
x a
x x
f f x
x b
sin ( 1;0)
4
x a
có 2 nghiệm.
sin (0;1)
4
x b
có 3 nghiệm.
Vậy phương trình có 5 nghiệm.
Câu 33. (Bỉm Sơn - Thanh Hóa - 2020) Cho hàm số có đạo hàm trên và có đồ thị là đường
cong trong hình vẽ bên dưới. Đặt . Tìm số nghiệm của phương trình .
A. . B. . C. . D. .
Lời giải
Chọn A
Ta có .
Phương trình có 2 nghiệm
Phương trình có 3 nghiệm
Phương trình có 3 nghiệm
Vậy phương trình có 8 nghiệm.
Câu 34. (Đặng Thúc Hứa - Nghệ An - 2020) Cho hàm số
f x
có bẳng biến thiên như hình vẽ.
Số nghiệm thuộc đoạn
9
0;
2
của phương trình
2sin 1 1f x
là
y f x
g x f f x
0
g x
8
2
4
6
0
0
' . 0 0
0
1;3
( )
f x
f x
g x f x f f x f x
f f x
f x m
0
f x
0
f x
1;3
f x m
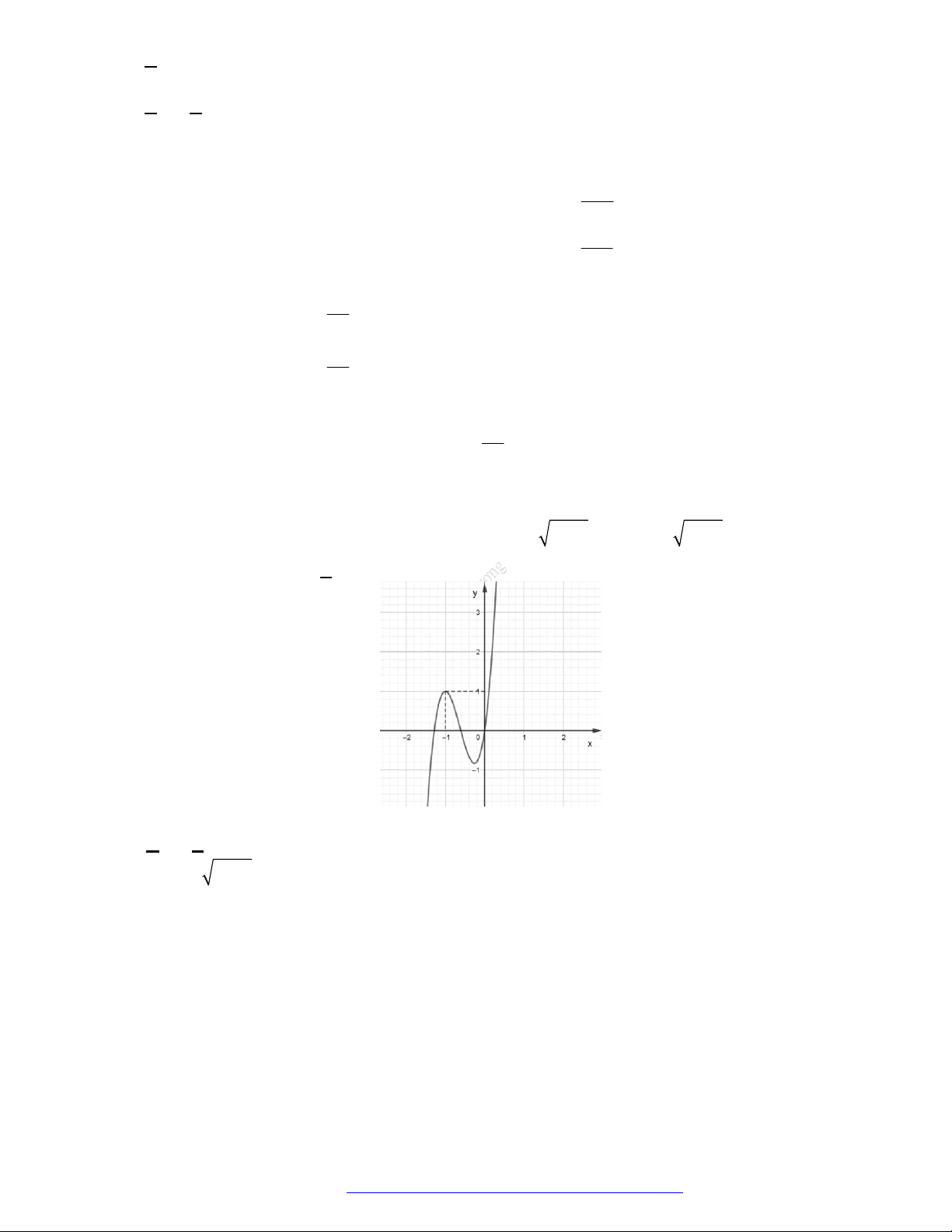
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 48 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
7
. B.
5
. C.
4
. D.
6
.
Lời giải
Chọn A
Ta có
sin 1 (1)
2sin 1 1
1
2sin 1 1 2sin 1 1;3 sin 0;1 (2)
2
2sin 1 3;
1
sin 1; (3)
2
x
x
a
f x x a x
x b
b
x
(1) có 2 nghiệm trong
9
0;
2
.
(2) có 5 nghiệm trong
9
0;
2
.
(3) vô nghiệm.
Vậy phương trình đã cho có 7 nghiệm trong
9
0;
2
.
Câu 35. (Hậu Lộc 2 - Thanh Hóa - 2020) Cho hàm số
3 2
, , ,y f x ax bx cx d a b c d
có đồ
thị như hình vẽ bên. Số nghiệm của phương trình
2 1 0f f f x f x f x f
là
A. 2. B. 3. C. 1. D. 0.
Lời giải
Chọn B
Đặt
t f x
,
0t
.
Ta có:
2
2 1 0f f t t t f
(*).
Xét
0t
:
(*) 0 1 0f f
(không thỏa).
Xét
0t
: Ta có
0f t
và
2
2 0f t t t
Theo đồ thị, hàm
f u
đồng biến trên
0;
.
Do đó, (*)
2 2
2 1 2 1f f t t t f f t t t
2
1 2f t t t
f t g t
(**)(với
2
1 2 , 0g t t t t
)
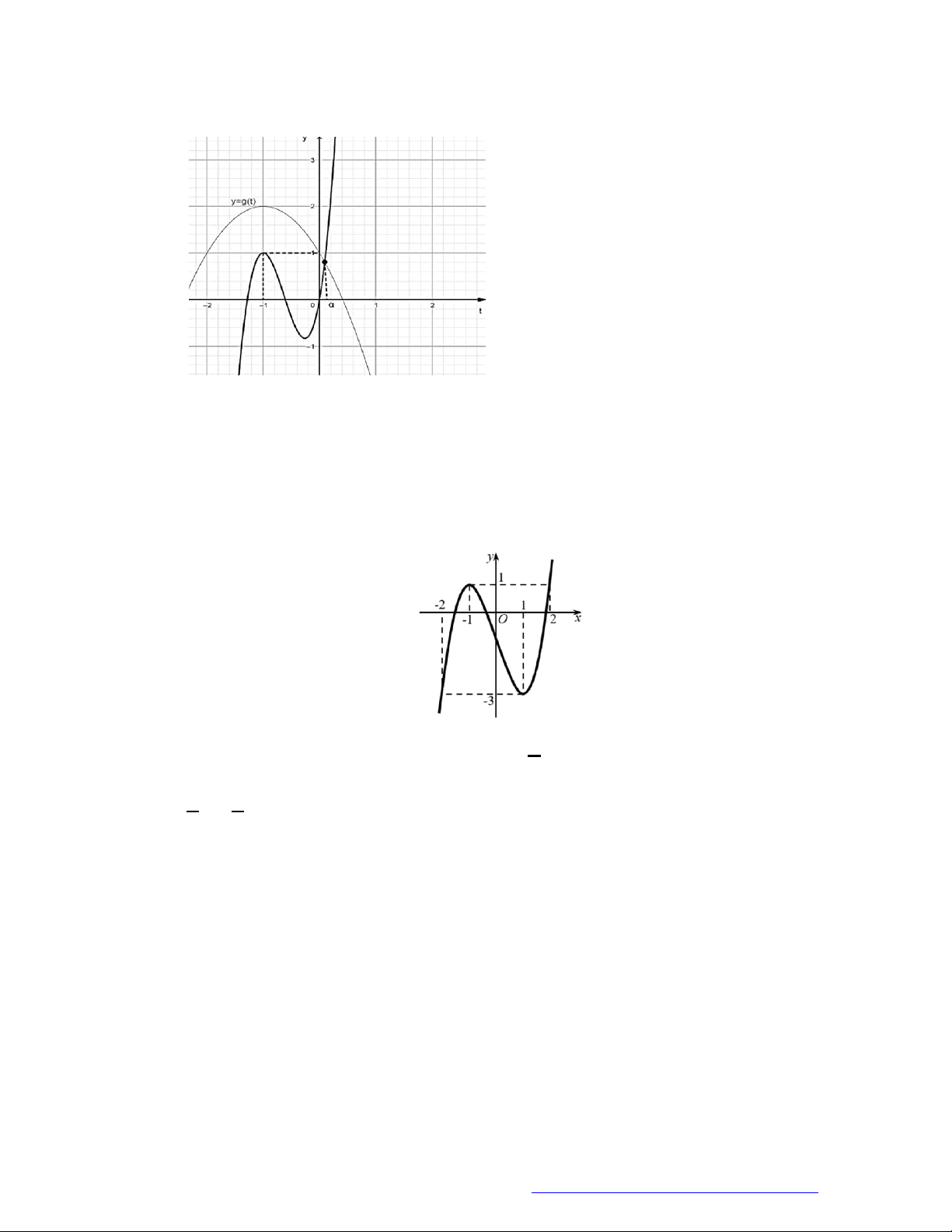
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 49
Vì hàm
f t
đồng biến và
g t
nghịch biến trên
0;
nên phương trình (**) có nghiệm duy
nhất
t
Theo đồ thị hàm
,f t g t
ta có
0;1
.
Khi đó,
2 2
, 0;1t f x
(***).
Vì đồ thị hàm
f x
cắt đường thẳng
2
y
tại 3 điểm phân biệt nên phương trình (***) có 3
nghiệm phân biệt.
Câu 36. (Lý Nhân Tông - Bắc Ninh - 2020) Cho hàm số
y f x
liên tục trên
và có đồ thị như hình
vẽ. Phương trình
1 0 f f x
có tất cả bao nhiêu nghiệm thực phân biệt?
A.
6
. B.
5
. C.
7
. D.
4
.
Lời giải
Chọn C
Từ đồ thị của hàm số
y f x
suy ra
0f x
2; 1
1;0
1;2
x a
x b
x c
Suy ra
1 0 f f x
1
1
1
f x a
f x b
f x c
1
1
1
f x a
f x b
f x c
+ Do
2; 1 1 1;0 a a
Phương trình
1 f x a
có 3 nghiệm phân biệt.
+ Do
1;0 1 0;1 b b
Phương trình
1 f x b
có 3 nghiệm phân biệt.
+ Do
1;2 1 2;3 c c
Phương trình
1 f x c
có 1 nghiệm.
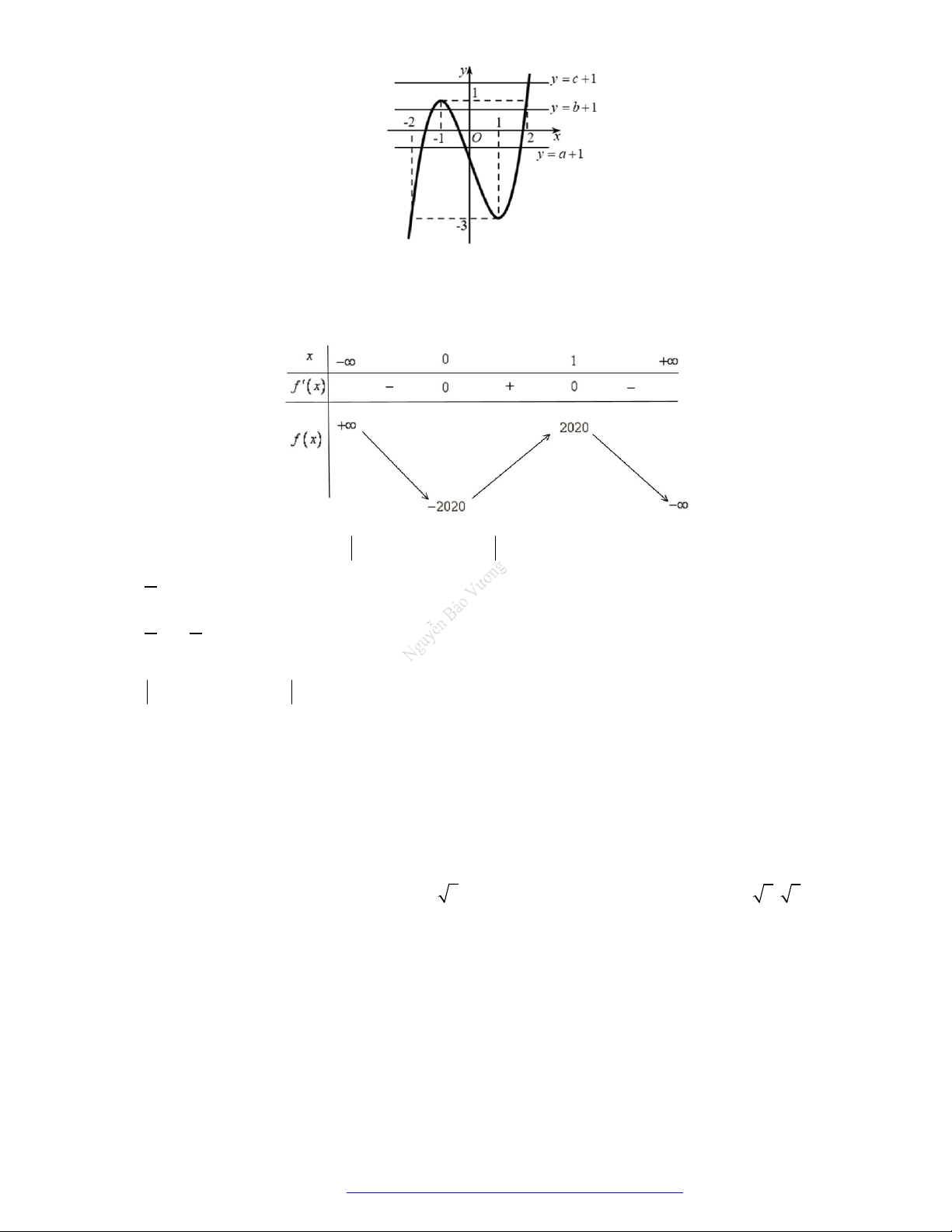
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 50 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Vậy phương trình
1 0 f f x
có
3 3 1 7
nghiệm.
Câu 37. (Nguyễn Huệ - Phú Yên - 2020) Cho hàm số
y f x
có bảng biến thiên như sau:
Số nghiệm của phương trình
2019 2020 2021f x
là
A.
4
. B.
6
. C.
2
. D.
3
.
Lời giải
Chọn A
Ta có :
2019 2020 2021f x
2019 2020 2021 2019 1
2019 2020 2021 2019 4041
f x f x
f x f x
.
Từ bảng biến thiên suy ra:
+) Phương trình:
2019 1f x
có 3 nghiệm.
+) Phương trình:
2019 4041f x
có 1 nghiệm.
Vậy phương trình đã cho có 4 nghiệm.
Câu 38. (Nguyễn Trãi - Thái Bình - 2020) Cho hàm số
y f x
có đồ thị
'y f x
như hình vẽ. Xét
hàm số
3
2 2 4 3 6 5g x f x x x m với
m
là số thực. Để
0, 5; 5g x x
thì
điều kiện của
m
là
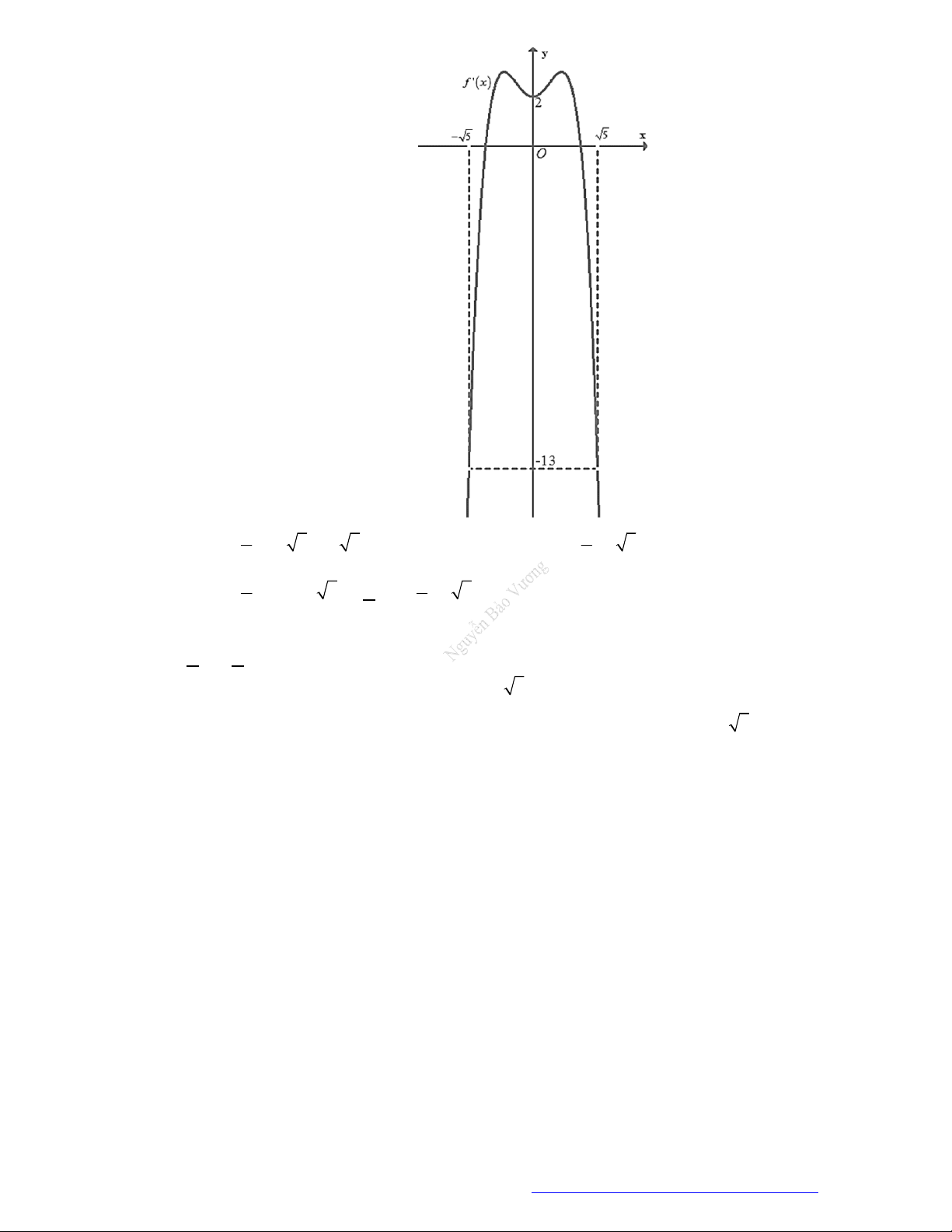
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 51
A.
2
5 4 5
3
m f
. B.
2
5
3
m f
.
C.
2
0 2 5
3
m f
. D.
2
5
3
m f
.
Lời giải
Chọn D
Ta có
3
0 2 2 4 3 6 5g x f x x x m .
Đặt
3
2 2 4h x f x x x
thì bất phương trình
0 3 6 5g x h x m
2 2
' 2 ' 2.3 4 2 ' 3 2h x f x x f x x .
Vẽ đồ thị hàm số
2
3 2y x
trên cùng hệ trục tọa độ với hàm số
'y f x
.
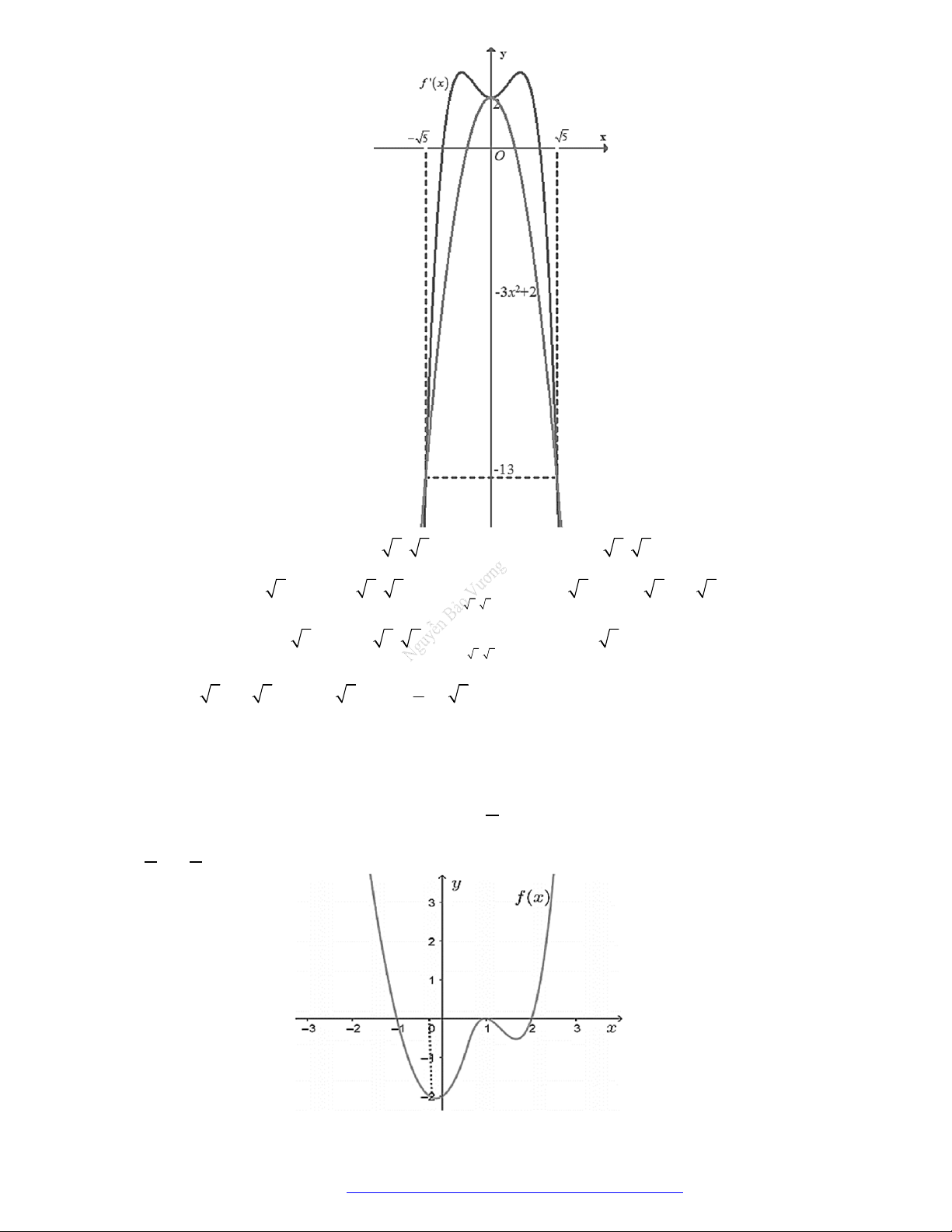
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 52 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta thấy
2
' 3 2f x x
5; 5x
nên
' 0, 5; 5h x x
.
Suy ra
5 , 5; 5h x h x
hay
5; 5
max 5 2 5 6 5h x h f
Do đó
5; 5
3 6 5, 5; 5 max 3 6 5h x m x h x m
2
2 5 6 5 3 6 5 5
3
f m m f
Câu 39. (THPT Nguyễn Viết Xuân - 2020) Cho hàm số
f x
có đồ thị như hình vẽ. Đặt
1g x f f x
. Số nghiệm của phương trình
0g x
là
A.
6
. B.
10
. C.
9
. D.
8
.
Lời giải
Chọn C
Ta có
. 1g x f x f f x
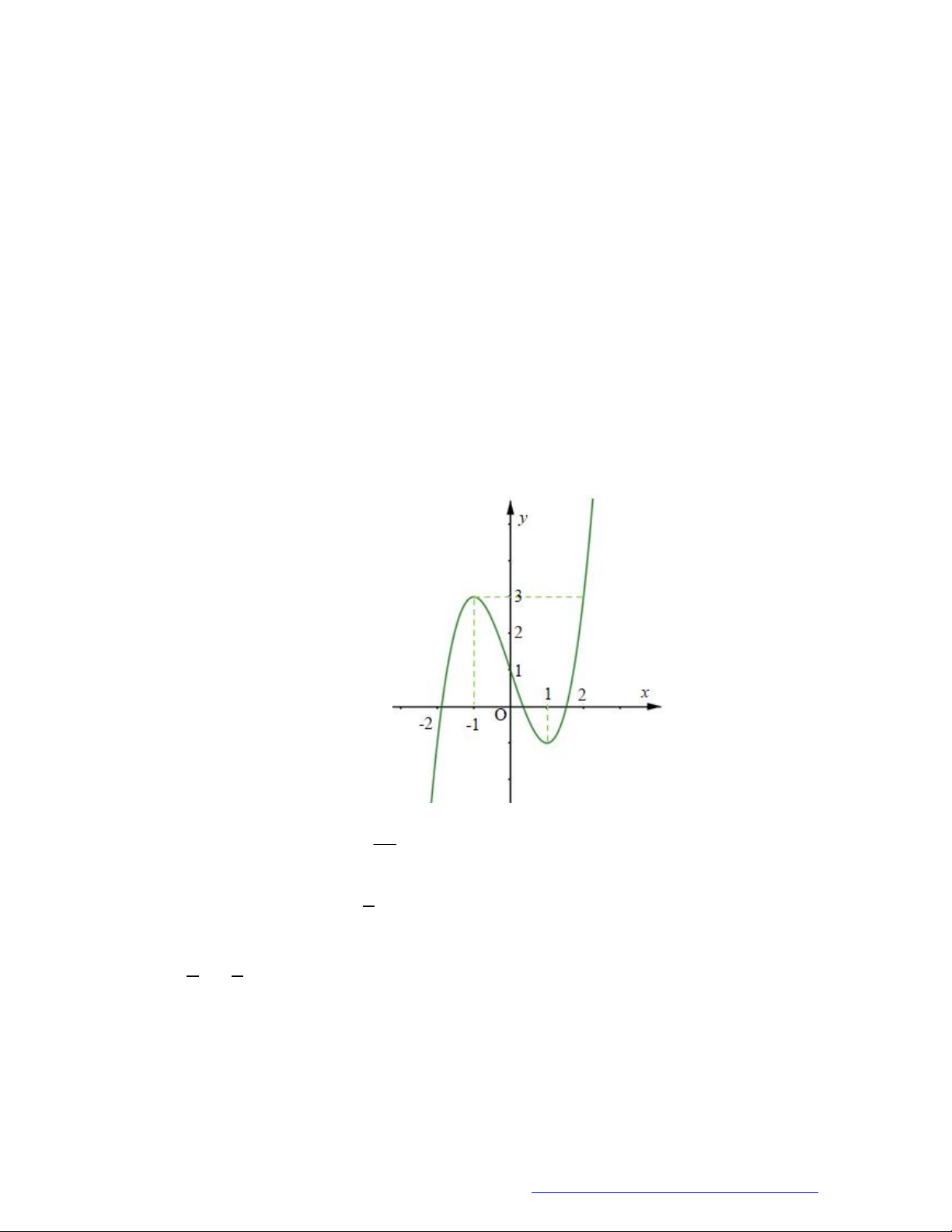
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 53
0
0 . 1 0
1 0
f x
g x f x f f x
f f x
.
+)
1 1
2 2
1;0
0 1
1;2
x a a
f x x
x a a
+)
1 1
2 2
1 1 0;1 1
1 0 1 1 2 2
1 1 2;3 3
f x a f x a
f f x f x f x
f x a f x a
Từ đồ thị suy ra
phương trình (1) có hai nghiệm phân biệt
1 2
2; 1 ; 2;3b b
phương trình (2) có hai nghiệm phân biệt
1 1 2 2
2; ; ;3c b c b
phương trình (3) có hai nghiệm phân biệt
1 1 2 2
2; ; ;3d c d c
Vậy phương trình đã cho có 9 nghiệm phân biệt.
Câu 40. (Tiên Du - Bắc Ninh - 2020) Cho hàm số
( )y f x
liên tục trên
và có đồ thị như hình vẽ bên
Số nghiệm thuộc đoạn
7
0;
2
của phương trình
( (cos )) 0f f x
là
A.
7
. B.
5
. C.
8
. D.
6
.
Lời giải
Chọn B
Đặt
(cos )f x t
ta được phương trình
( ) 0f t
.
Quan sát đồ thị
( )y f x
ta suy ra
1
2
3
( 2; 1)
( ) 0 (0;1) .
t t (1; 2)
t t
f t t t
* Với
1
t t ta có
1
(cos )f x t . Xét tương giao giữa hai đồ thị
( )y f x
và
1 1 1
2; 1 (cos ) cos 1y t f x t x x
nên phương trình vô nghiệm.
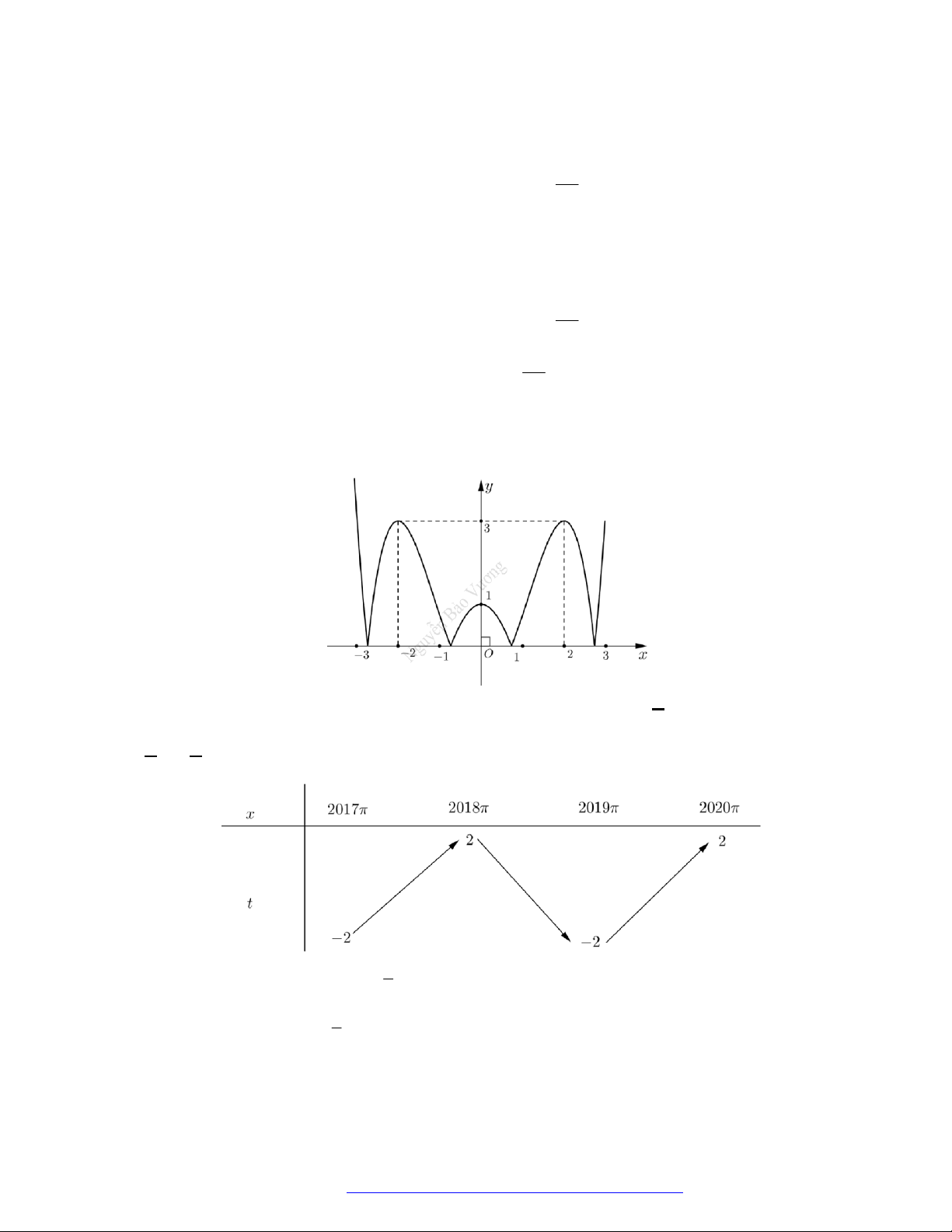
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 54 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
* Với
2
t t ta có
2
(cos )f x t . Xét tương giao giữa hai đồ thị
( )y f x
và
2
2 2 3
4
cos 1
0;1 (cos ) cos (0;1) .
cos (1;2)
x x
y t f x t x x
x x
Chỉ có
3
cos x x thỏa mãn. Khi đó tồn tại 3 giá trị
7
0;
2
x
tương ứng để
3
cos x x .
* Với
3
t t tương tự ta có
5
6
7
cos 1
cos ( 1;0).
cos 1
x x
x x
x x
Chỉ có
6
cos x x thỏa mãn. Khi đó tồn tại 2 giá trị
7
0;
2
x
tương ứng để
6
cos x x .
Vậy phương trình đã cho có 5 nghiệm thuộc đoạn
7
0;
2
.
Câu 41. (Lương Thế Vinh - Hà Nội - 2020) Cho hàm số
y f x
có đồ thị nhưu hình vẽ bên. Tìm số
nghiệm thuộc đoạn
2017 ;2020
của phương trình
3 2cos 8f x
.
A.
8
. B.
3
. C.
4
. D.
6
.
Lời giải
Chọn D
Đặt
2cost x
, ta có bảng biến thiên của t như sau
Khi đó
8
3 2cos 8
3
f x f t
.
Vẽ thêm đường thẳng
8
3
y
trên đồ thị
y f x
đã cho.
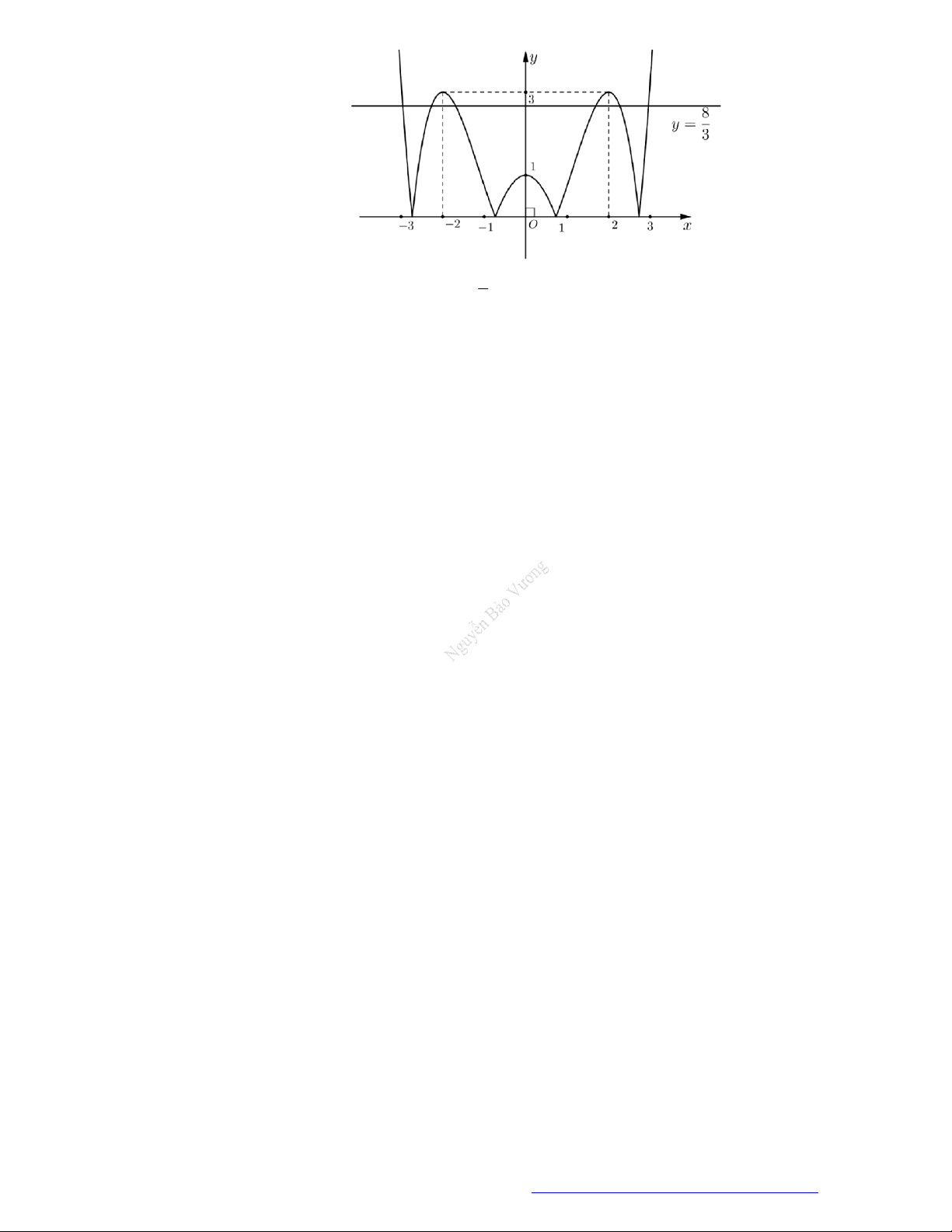
TÀI
LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 55
Xét
trên đoạn
2;
2
, đư
ờng thẳng
8
3
y
cắt
đồ thị hàm số
f t
tại
hai điểm
1
2;
1 t
và
2
1;
2t
.
Từ
bảng biến thiên của t , ứng với giá tị
1
t , ta
tìm được 3 nghiệm
x
thỏa
1
2co
s x t , tươngtự, ta
cũng tìm được 3 nghiệm
x
thỏa
2
2cos x t .
Vậy phương trình
3 2
cos 8f x
có 6 nghi
ệm
x
thu
ộc đoạn
20
17 ; 2020
-------------------- HẾT --------------------
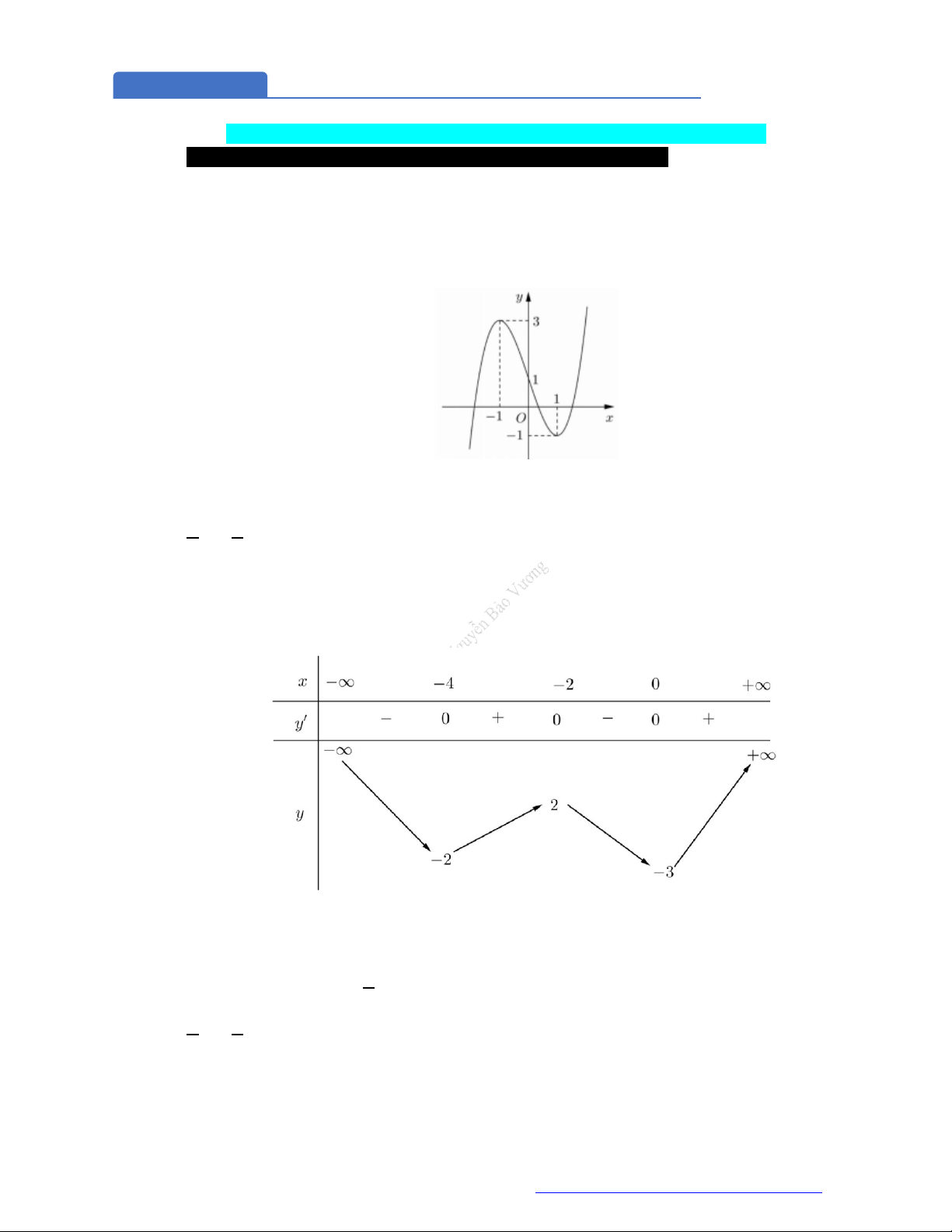
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
DẠNG TOÁN DÀNH CHO ĐỐI TƯỢNG HỌC SINH GIỎI 9-10 ĐIỂM
Dạng 3. Biện luận tương giao hàm hợp, hàm ẩn chứa THAM SỐ
Câu 1. (Đề Tham Khảo 2019) Cho hàm số
y f x
liên tục trên
và có đồ thị như hình vẽ bên. Tập
hợp tất cả các giá trị thực của tham số
m
để phương trình
sinf x m
có nghiệm thuộc khoảng
0;
là
A.
1;3
B.
1;1
C.
1;3
D.
1;1
Lời giải
Chọn B
Đặt
sin 0; 0;1t x x t
Vậy phương trình trở thành
f t m
. Dựa và đồ thị hàm số suy ra
1;1 .m
Câu 2. (Mã 102 - 2020 Lần 2) Cho hàm số
y f x
có bảng biến thiên như hình vẽ:
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
2
6 4f x x m
có ít nhất ba
nghiệm thực phân biệt thuộc khoảng
0;
?
A. 25. B. 30. C. 29. D. 24.
Lời giải
Chọn B
Ta đặt:
2
4g x f x x
.
2
2 4 4g x x f x x
2 2 2
2 2 4 4 4 2 4x x x x x x x
(dựa vào bảng biến thiên)
3
2
2 2 4 2 4x x x x x
.
TƯƠNG GIAO ĐỒ THỊ HÀM SỐ
Chuyên đề 8
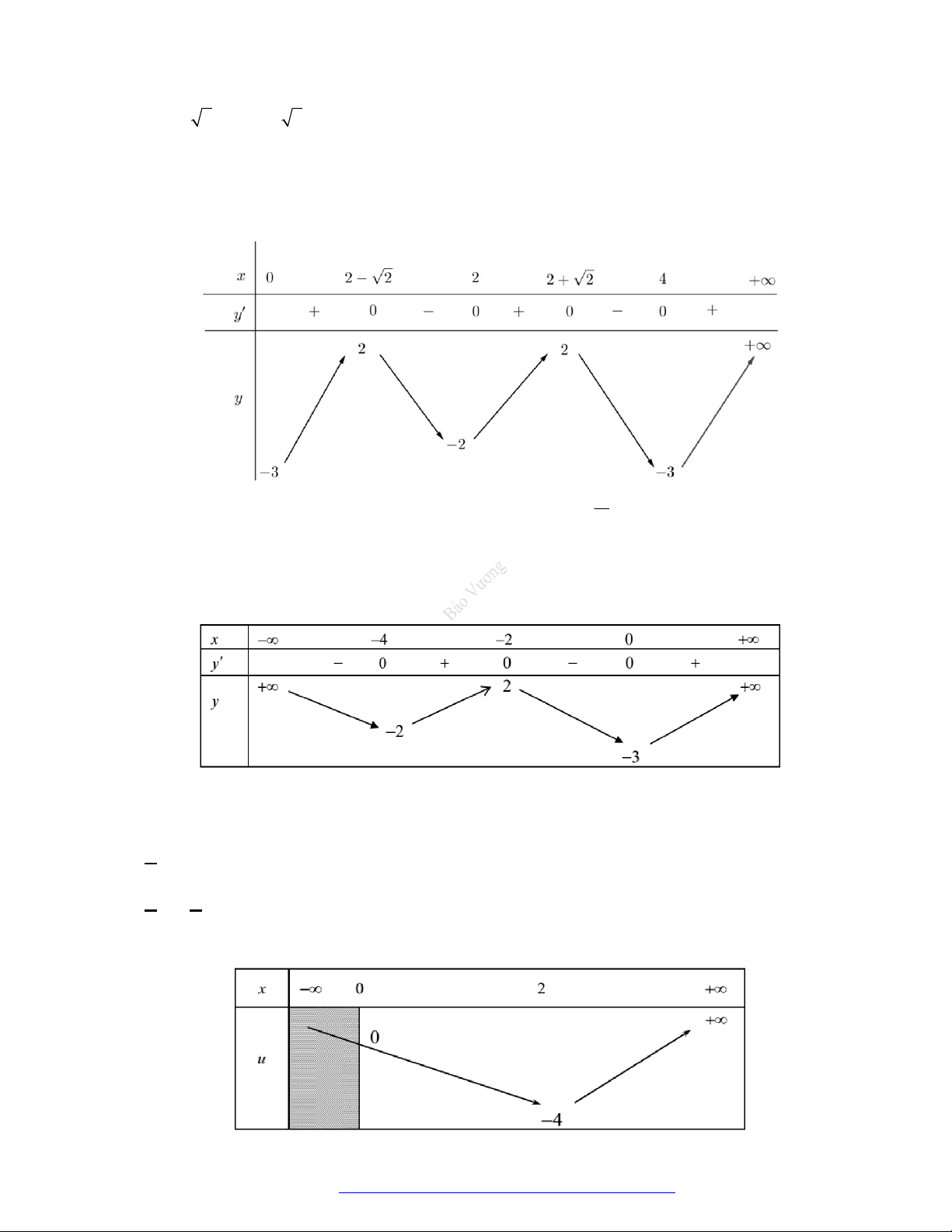
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Mặt khác:
0 0 3g f
;
2 2 2 2 2 2g g f ;
2 4 2g f
;
4 0 3g f
.
Ta có bảng biến thiên:
Từ bảng biến thiên ta được: yêu cầu bài toán tương đương
3 2
6
m
18 12m
.
Vậy có tất cả 30 giá trị của tham số
m
thỏa mãn yêu cầu bài toán.
Câu 3. (Mã 103 - 2020 Lần 2) Cho hàm số
f x
có bảng biến thiên như sau
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
2
3 4f x x m
có ít nhất ba
nghiệm thực phân biệt thuộc khoảng
0;
?
A.
15
. B.
12
. C.
14
. D.
13
.
Lời giải
Chọn A
Đặt
2
4u x x
(1)
Ta có BBT sau:
Ta thấy:
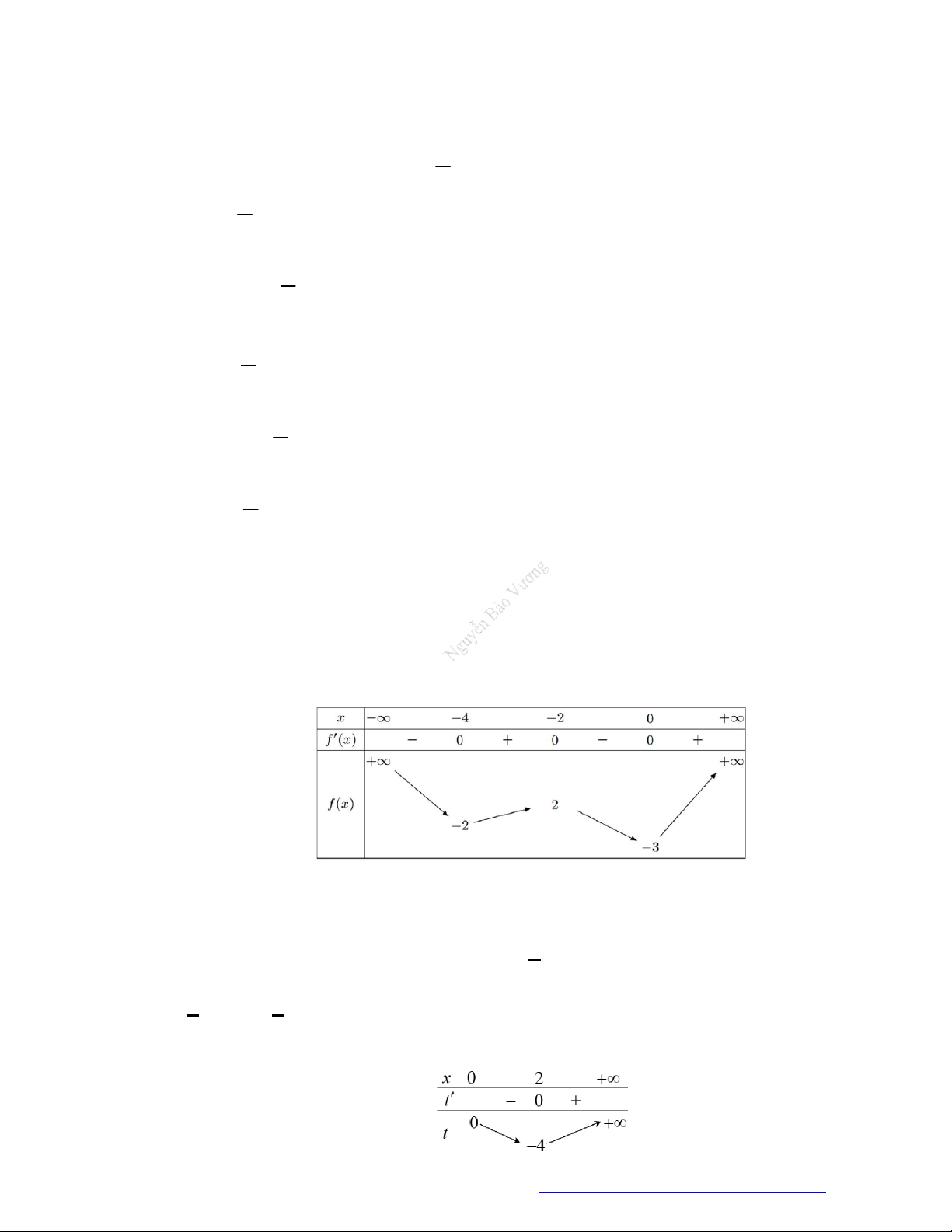
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
+ Với
4u
, phương trình (1) vô nghiệm.
+ Với
4u
, phương trình (1) có một nghiệm
2 0x
.
+ Với
4 0u
, phương trình (1) có hai nghiệm
0x
.
+ Vơi
0u
, phương trình (1) có một nghiệm
0x
Khi đó
2
3 4
3
m
f x x m f u
(2), ta thấy:
+ Nếu
3 9
3
m
m
, phương trình (2) có một nghiệm
0u
nên phương trình đã cho có một
nghiệm
0x
.
+ Nếu
3 2 9 6
3
m
m
, phương trình (2) có một nghiệm
0u
và một nghiệm
2;0u
nên phương trình đã cho có ba ngiệm
0x
.
+ Nếu
2 6
3
m
m
, phương trình (2) có một nghiệm
4u
, một nghiệm
2;0u
và
một nghiệm
0u
nên phương trình đã cho có bốn nghiệm
0x
.
+ Nếu
2 2 6 6
3
m
m
, phương trình (2) có một nghiệm
4u
, hai nghiệm
4;0u
và một nghiệm
0u
nên phương trình đã cho có năm nghiệm
0x
.
+ Nếu
2 6
3
m
m
, phương trình (2) có một nghiệm
4u
, một nghiệm
2u
và một
nghiệm
0u
nên phương trình đã cho có ba nghiệm
0x
.
+ Nếu
2 6
3
m
m
, phương trình (2) có một nghiệm
4u
và một nghiệm
0u
nên phương
trình đã cho có một nghiệm
0x
.
Vậy
9 6m
có
15
giá trị
m
nguyên thỏa ycbt.
Câu 4. (Mã 101 – 2020 Lần 2) Cho hàm số
f x
có bảng biến thiên như sau:
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
2
5 4f x x m
có ít nhất 3 nghiệm
phân biệt thuộc khoảng
0;
A.
24
. B.
21
. C.
25
. D.
20
.
Lời giải
Chọn C.
Đặt
2
4t x x
. Ta có
2 4 0 2t x x
Bảng biến thiên
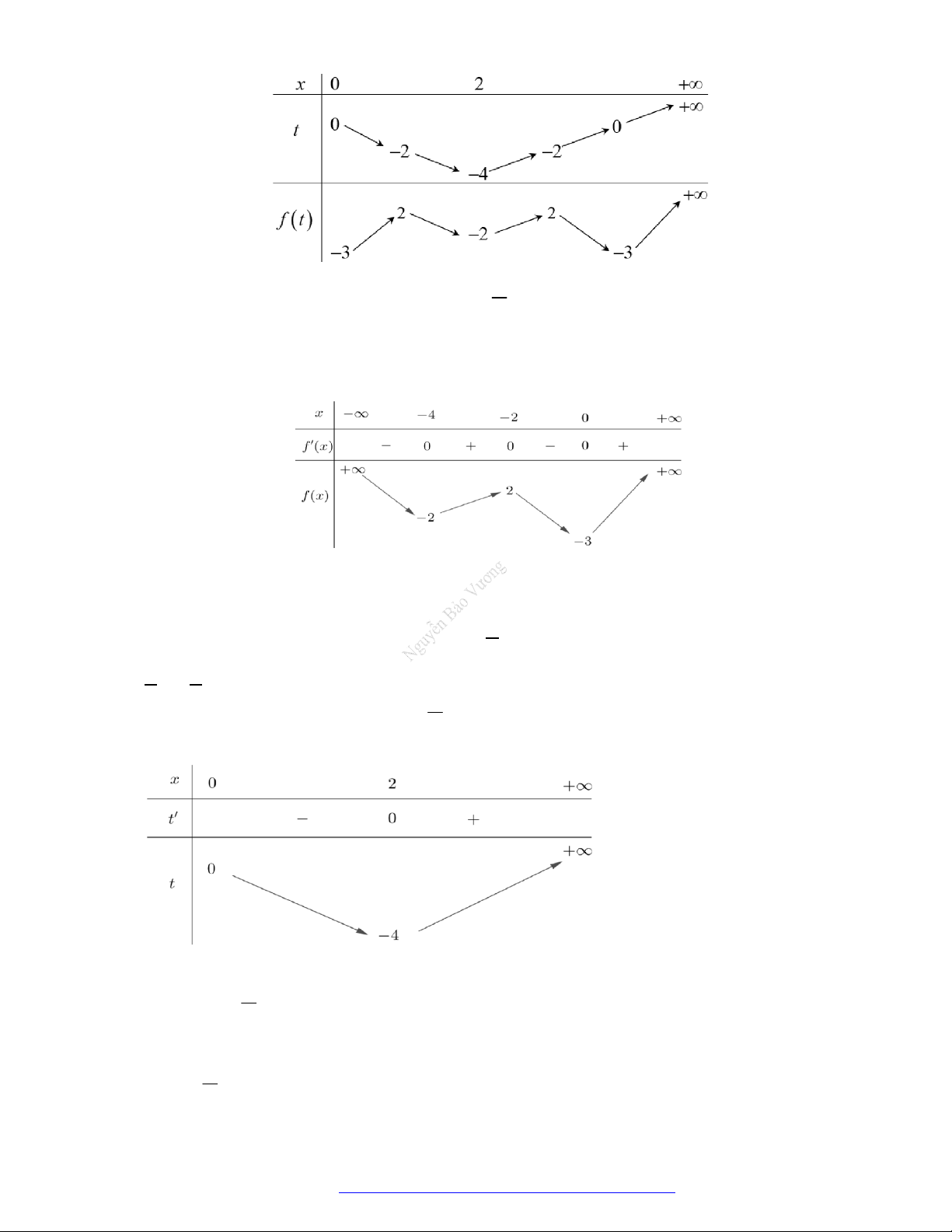
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Với
2
4t x x
.
Dựa vào bảng biến thiên ta có
3 2 15 10
5
m
m
. Vì m nguyên nên
14; 13;....;10m
. Do đó có
25
giá trị nguyên của m thỏa mãn đề bài.
Câu 5. (Mã 104 - 2020 Lần 2) Cho hàm số
f x
có bảng biến thiên như sau:
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
2
4 4f x x m
có ít nhất 3 nghiệm
thực phân biệt thuộc khoảng
0;
?
A.
16
. B.
19
. C.
20
. D.
17
.
Lời giải
Chọn C
Ta có
2 2
4 4 4
4
m
f x x m f x x
Đặt
2
4 2 4 0 2t x x t x x
Vì
0; 4x t
Ta có
4
m
f t
Phương trình đã cho có ít nhất 3 nghiệm phân biệt thuộc khoảng
0;
3 2 12 8
4
m
m
mà
m
nguyên nên
11; 10;...;0;1;...;8m
Vậy có
20
giá trị nguyên của
m
thỏa mãn.
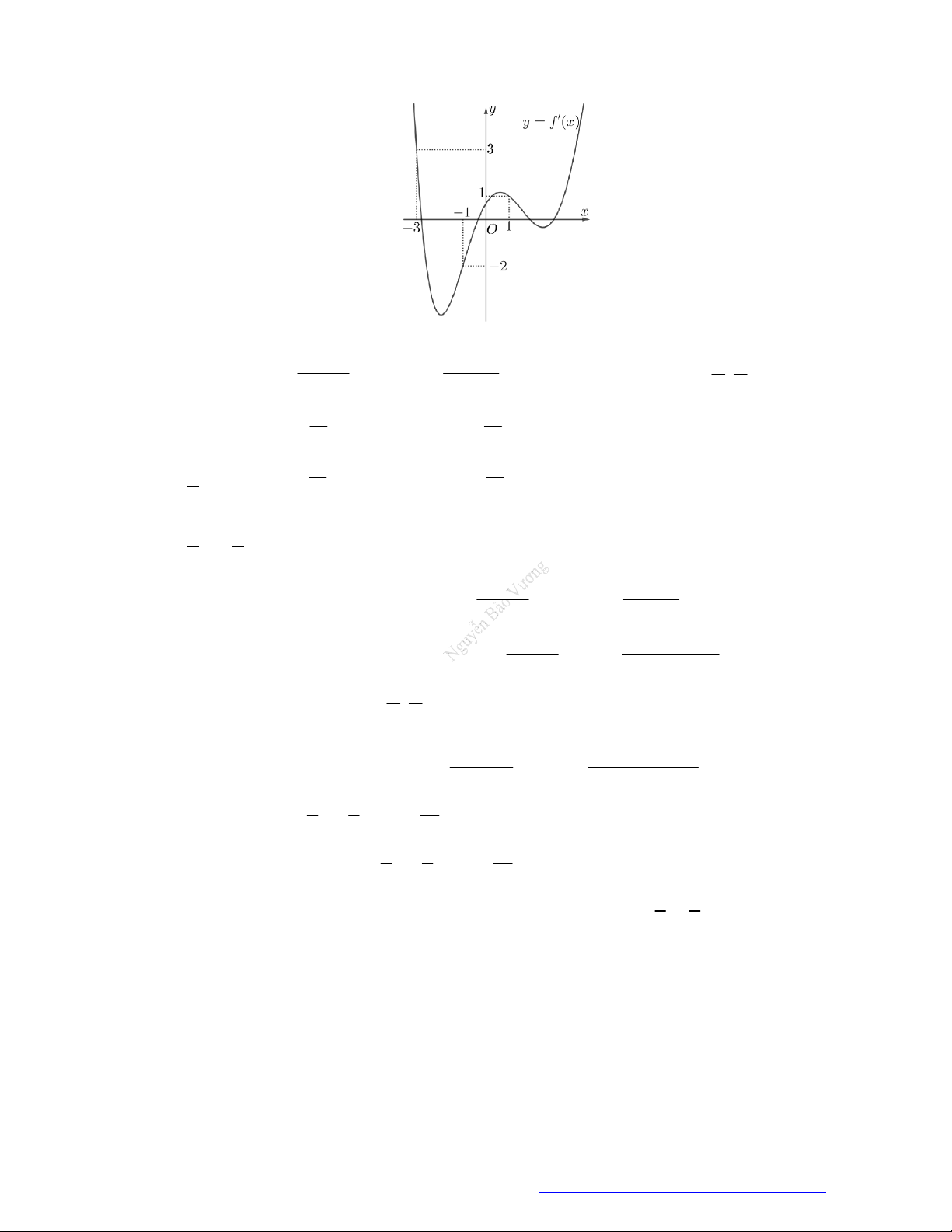
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Câu 6. (Chuyên Biên Hòa - Hà Nam - 2020) Cho hàm số
f x
. Hàm số
y f x
có đồ thị như hình
sau.
Tìm tất cả các giá trị thực của tham số
m
để bất phương trình
3
2sin 5cos2
2 sin 2 sin
3 4
x x
f x x m nghiệm đúng với mọi
;
2 2
x
.
A.
11
2 3 .
12
m f
B.
19
2 1 .
12
m f
C.
19
2 1 .
12
m f
D.
11
2 3 .
12
m f
Lời giải
Chọn C
Ta có
3
2
3
2sin 5cos2
2 sin 2 sin
3 4
5 1 2sin
2sin
2 sin 2 sin
3 4
x x
f x x m
x
x
m f x x
Đặt
sin 2t x
(với
;
2 2
x
thì
3; 1t
, khi đó bất phương trình được viết lại thành:
2
3
5 1 2 2
2 2
2 2
3 4
t
t
m f t t
.
hay
3 2
2 3 65
2 3 *
3 2 12
m f t t t t
.
Xét hàm số
3 2
2 3 65
2 3
3 2 12
g t f t t t t
trên đoạn
3; 1
.
Ta có
2
2 2 3 3g t f t t t
. Do đó
2
3 3
0
2 2
g t f t t t
.
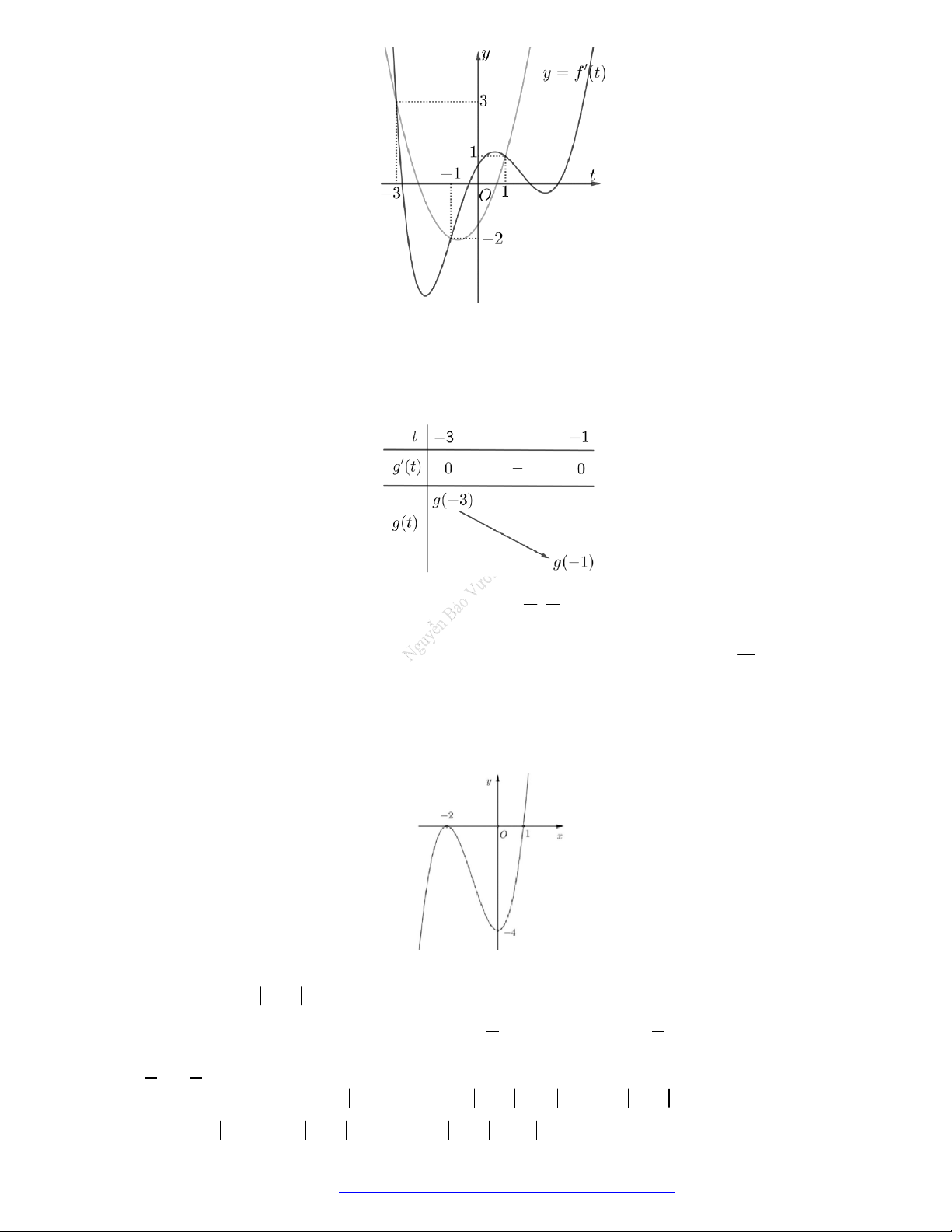
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Dựa vào sự tương giao của đồ thị hàm số
y f t
và parabol
2
3 3
2 2
y t t
trên đoạn
3; 1
thì
0 3; 1g t t
.
Suy ra bảng biến thiên của hàm số
g t
trên đoạn
3; 1
như sau:
Bất phương trình đã cho nghiệm đúng với mọi
;
2 2
x
khi và chỉ khi bất phương trình
*
nghiệm đúng với mọi
3; 1t
. Điều đó tương đương với
19
1 2 1
12
m g f
dựa vào
tính liên tục của hàm số
g t
.
Câu 7. (Chuyên Biên Hòa - Hà Nam - 2020) Cho hàm số
3 2
( )y f x ax bx cx d
có đồ thị như
hình dưới đây
Có tất cả bao nhiêu giá trị nguyên của tham số
5;5m để phương trình
2
( ) ( 4) ( ) 2 4 0f x m f x m
có
6
nghiệm phân biệt
A.
2
. B.
4
. C.
3
. D.
5
.
Lời giải
Chọn C
Ta có:
2
2
( ) ( 4) ( ) 2 4 0 ( ) ( ) 4 ( ) 2 4 0f x m f x m f x m f x f x m
2
( ) 2 ( ) 2 0 ( ) 2 ( ) 2 0f x m f x f x f x m
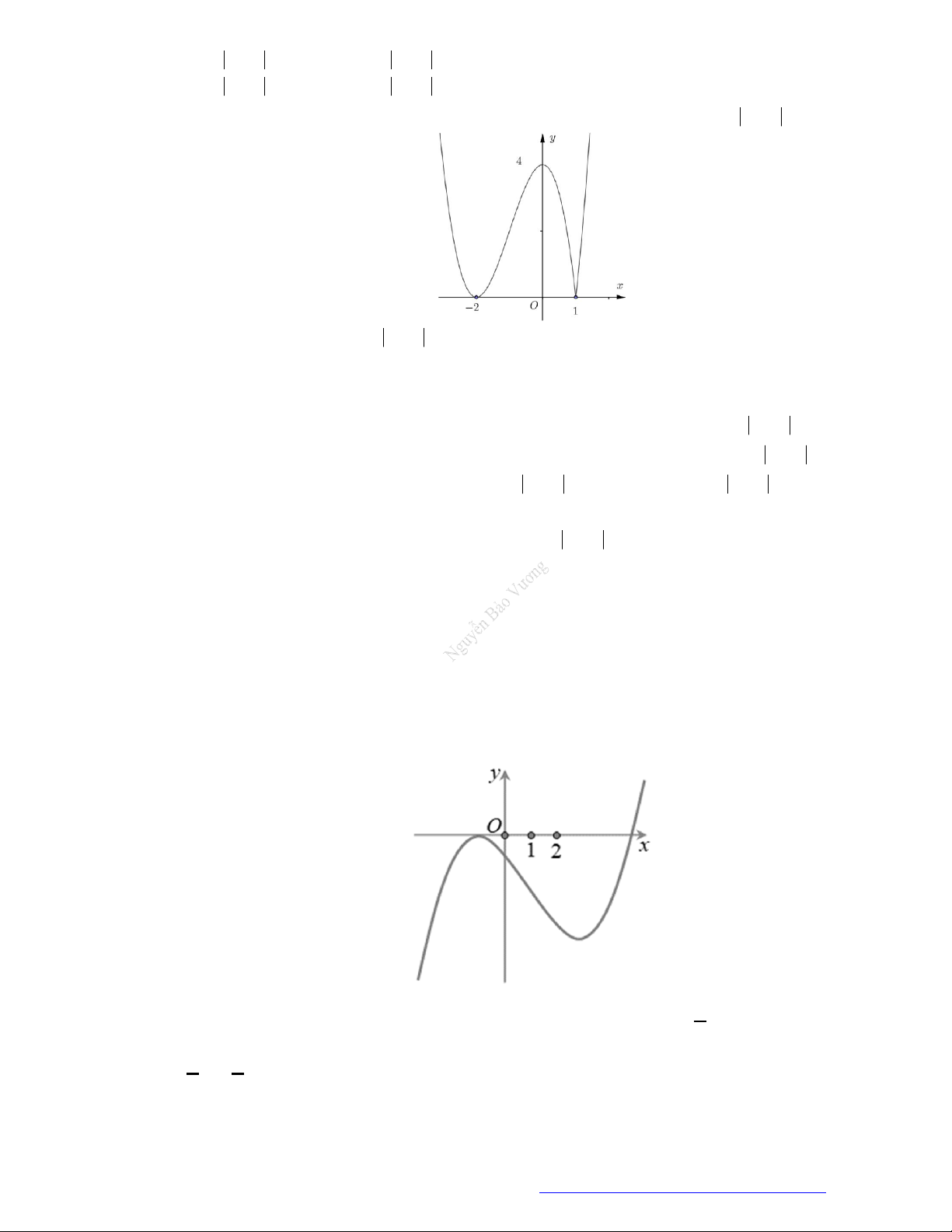
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
( ) 2 1
( ) 2 0
( ) 2 0 ( ) 2 2
f x
f x
f x m f x m
Dựa vào đồ thị hàm số
3 2
( )y f x ax bx cx d
ta có đồ thị hàm số ( )y f x như sau:
Dựa vào đồ thị hàm số ( )y f x suy ra phương trình
1 có 4 nghiệm phân biệt.
Suy ra phương trình đã cho có 6 nghiệm phân biệt
2 có 2 nghiệm phân biệt khác các nghiệm
của phương trình
1 .
Ta có phương trình
2 là phương trình hoành độ giao điểm của hai đường ( )y f x và
2y m
. Số nghiệm phương trình
2 là số giao điểm của 2 đồ thị hàm số ( )y f x và
2y m
. Dựa vào hình vẽ đồ thị hàm số ( )y f x ta được phương trình ( ) 2f x m có 2
nghiệm phân biệt khác các nghiệm của phương trình
( ) 2f x
2 0
2
2 4
2
2 2
m
m
m
m
m
Do
m
và
5;5 2;3;4m m .
Vậy có 3 giá trị nguyên
5;5m thỏa mãn điều kiện bài toán.
Câu 8. (Chuyên Lam Sơn - 2020) Cho hàm số
y f x
, hàm số
y f x
liên tục trên
và có đồ
thị như hình vẽ bên. Bất phương trình
2
2f x x x m
(m là tham số thực) nghiệm đúng với
mọi
1;2x
khi và chỉ khi
A.
2 2m f
. B.
1 1m f
. C.
1 1m f
. D.
2m f
.
Lời giải
Chọn D
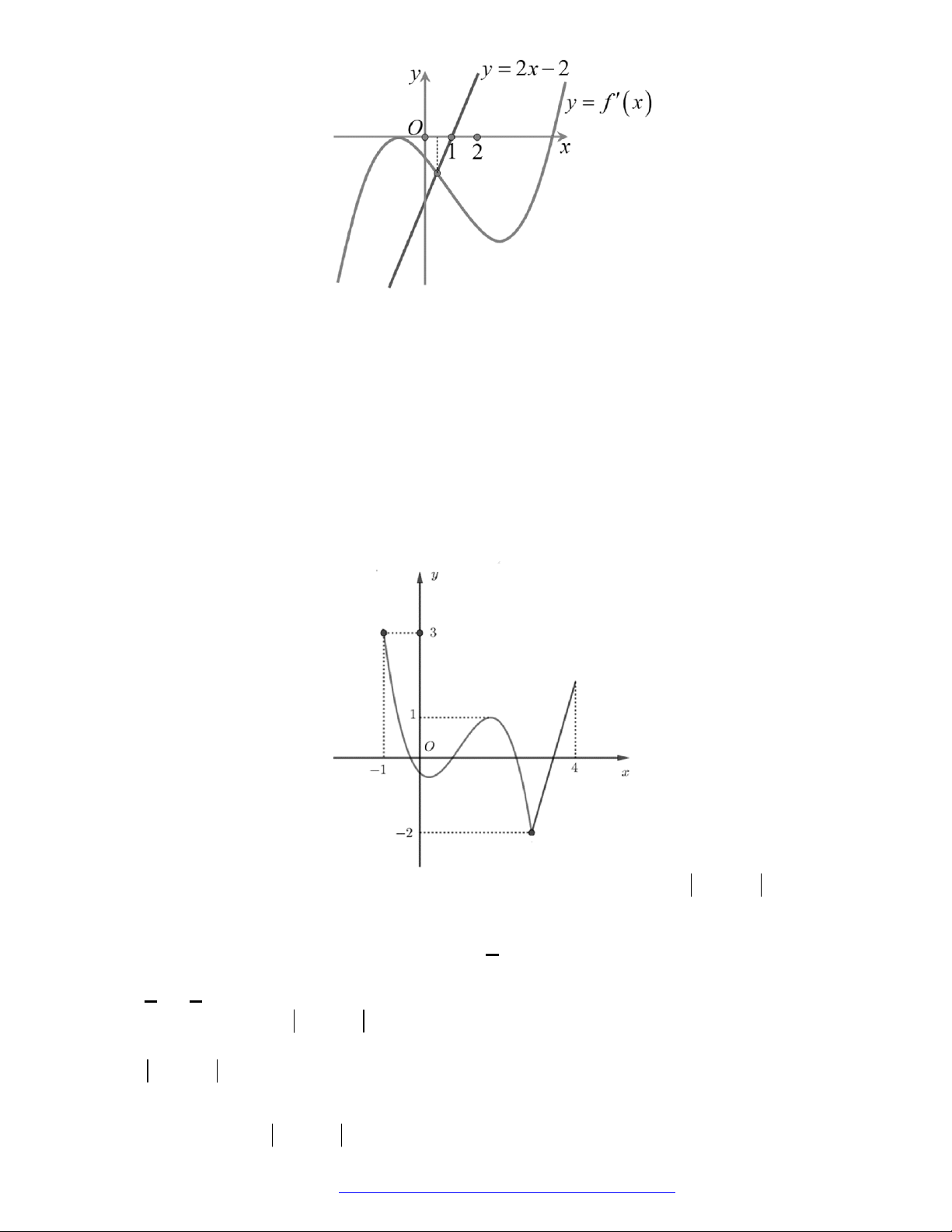
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta có:
2
2 1;2f x x x m x
2
2 1;2 *f x x x m x
.
Gọi
2
2g x f x x x
2 2g x f x x
Theo đồ thị ta thấy
2 2 1;2f x x x
0 1;2g x x
.
Vậy hàm số
y g x
liên tục và nghịch biến trên
1;2
Do đó
*
1;2
min 2 2m g x g f
.
Câu 9. (Chuyên Thái Bình - 2020) Cho hàm số
y f x
liên tục trên đoạn
1; 4
và có đồ thị như
hình vẽ.
Có bao nhiêu giá trị
nguyên của
m
thuộc đoạn
10;10
để bất phương trình
2f x m m
đúng với mọi
x
thuộc đoạn
1; 4
.
A.
6
. B.
5
. C.
7
. D.
8
.
Lời giải
Chọn C
Để bất phương trình
2f x m m
có nghiệm ta suy ra điều kiện
0m
.
2 2 2f x m m m f x m m
3f x m
f x m
.
Bất phương trình
2f x m m
đúng với mọi
x
thuộc đoạn
1; 4
3f x m
f x m
đúng
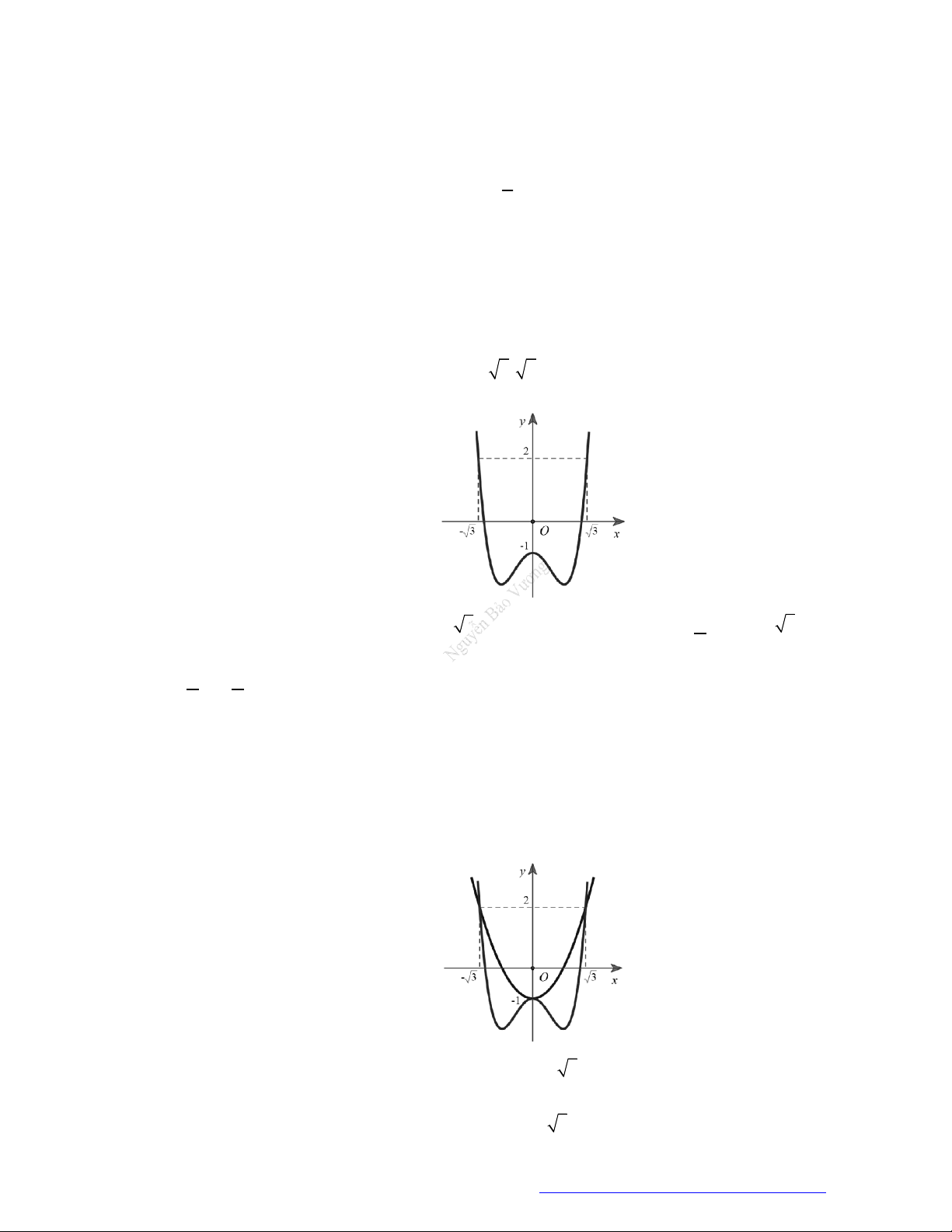
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
với mọi
x
thuộc đoạn
1; 4
1;4
1;4
3 min
max
m f x
m f x
.
Từ đồ thị hàm số
y f x
ta suy ra
1;4
1;4
min 2; max 3f x f x
.
1;4
1;4
2
3 min
3 2
3
3
3
max
3
m f x
m
m
m
m
m f x
m
(thỏa mãn điều kiện
0m
)
Vậy trên đoạn
10;10
có
7
giá trị nguyên của
m
thỏa mãn điều kiện bài toán.
Câu 10. (Chuyên Bến Tre - 2020) Cho hàm số
y f x
. Đồ thị hàm số
'y f x
như hình vẽ. Cho bất
phương trình
3
3 3f x x x m
(
m
là tham số thực). Điều kiện cần và đủ để bất phương trình
3
3 3f x x x m
đúng với mọi
3; 3x
là
A.
3 1m f
. B.
3 3 m f
. C.
3 0m f
. D.
3 3m f
.
Lời giải
Chọn D
Ta có
3 3
3 3 3 3f x x x m f x x x m
Đặt
3
3 3g x f x x x
. Tính
2
' 3 ' 3 3g x f x x
Có
2
' 0 ' 1g x f x x
Nghiệm của phương trình
' 0g x
là hoành độ giao điểm của đồ thị hàm số
'y f x
và
parabol
2
1y x
Dựa vào đồ thị hàm số ta có:
2
3
' 1 0
3
x
f x x x
x
BBT
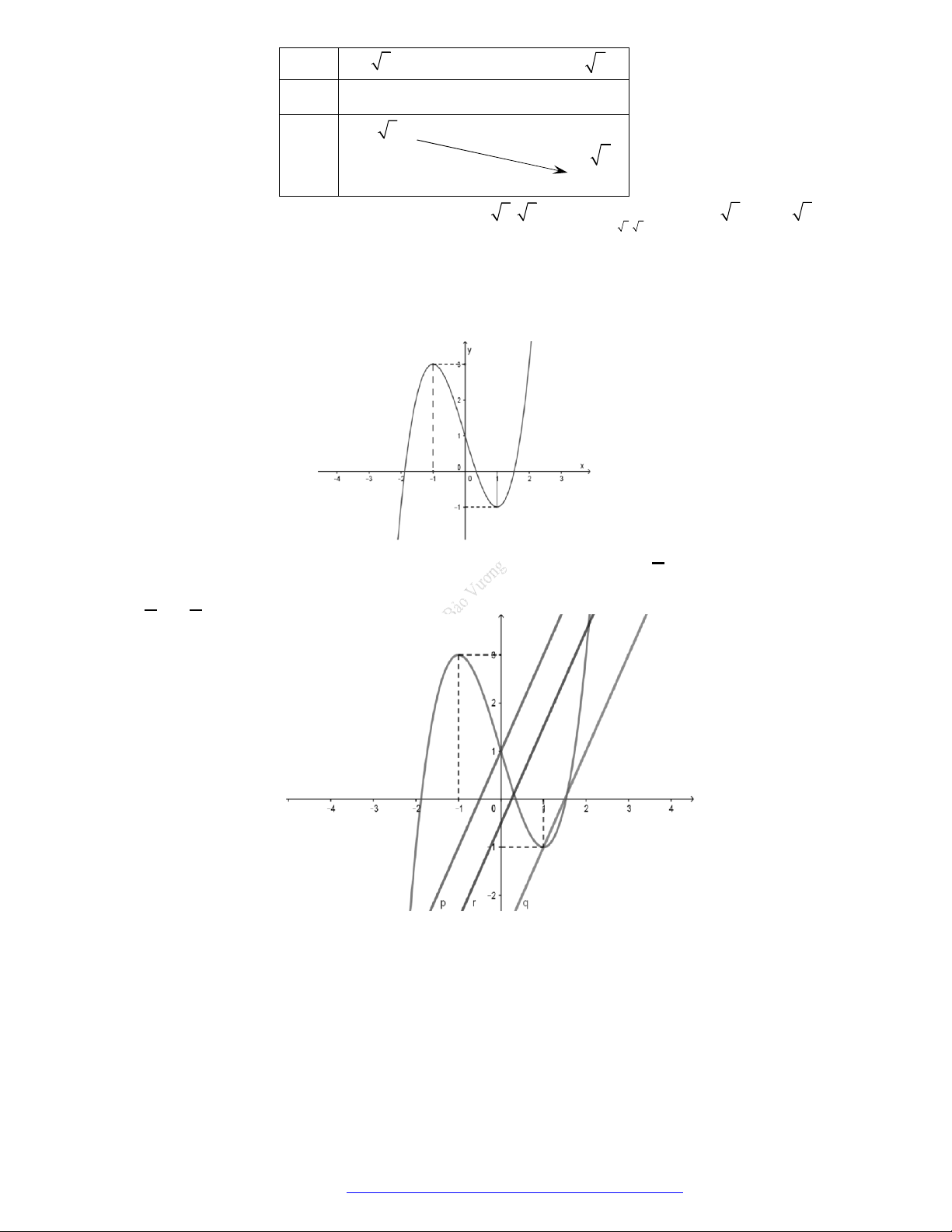
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
x
3
1
3
'
g x
0
0
0
g x
3
g
3
g
Để bất phương trình nghiệm đúng với mọi
3; 3x
thì
3; 3
min 3 3 3m g x g f
.
Câu 11. (Chuyên Hùng Vương - Gia Lai - 2020) Cho hàm số
y f x
liên tục trên
và có đồ thị như
hình vẽ bên dưới. Gọi
S
là tập hợp tất cả giá trị nguyên của tham số
m
để phương trình
sin 2 2sinf x m x
có nghiệm thuộc khoảng
0;
. Tổng các phần tử của
S
bằng
A.
4
. B.
1
. C.
3
. D.
2
.
Lời giải
Chọn D
Đặt
sint x
, với
0;x
0;1t
.
Ta được phương trình:
2 2 2 2f t t m f t t m
(1)
Số nghiệm của phương trình bằng số giao điểm của đồ thị hàm số
y f t
và đường thẳng
2 2y t m r
.
Gọi
: 2 1p y x
song song với đường thẳng
: 2y t
và đi qua điểm
0;1A
.
Gọi
: 2 3q y x
song song với đường thẳng
: 2y t
và đi qua điểm
1; 1B
.
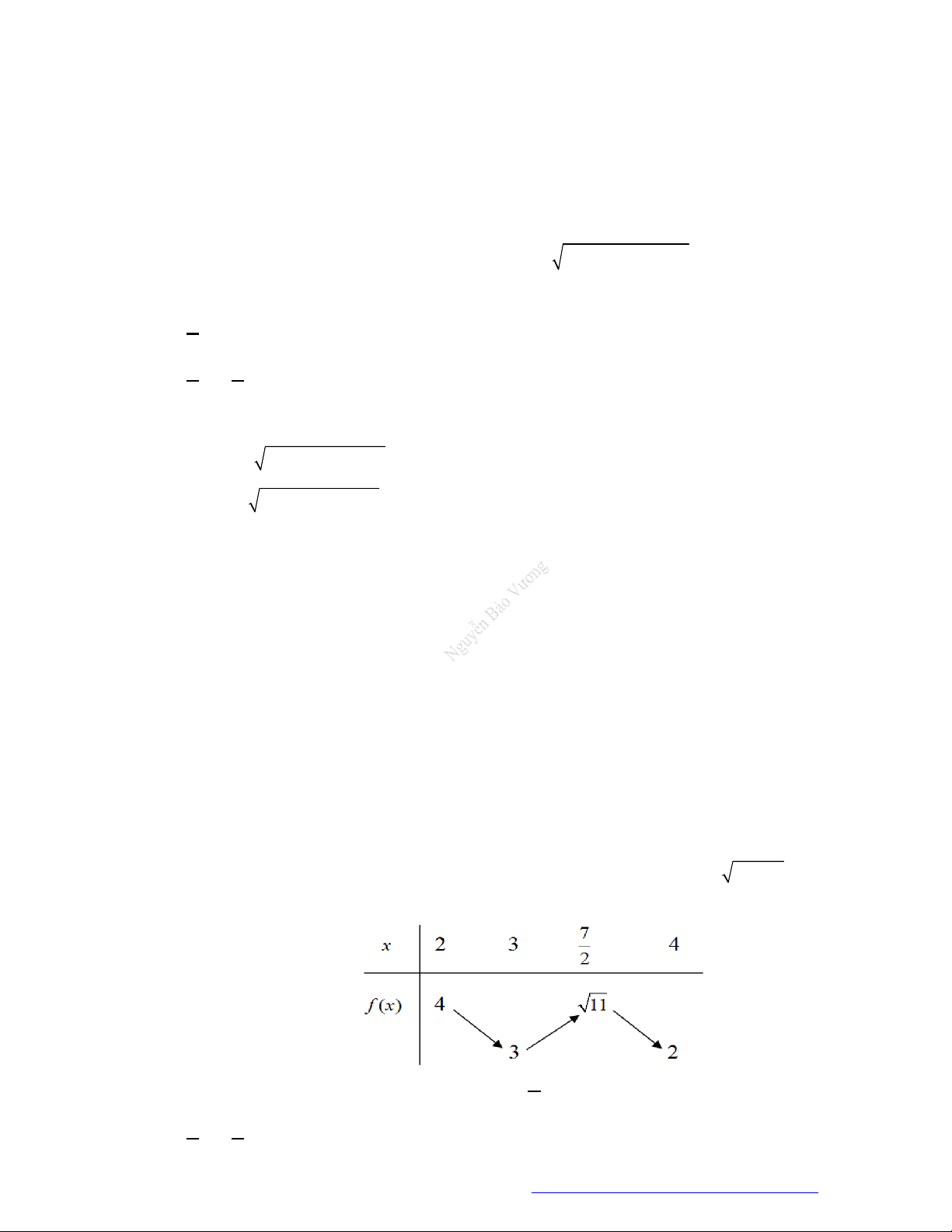
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Để phương trình
sin 2 2sinf x m x
có nghiệm thuộc khoảng
0;
thì phương trình (1)
phải có nghiệm
0;1t
, suy ra đường thẳng
r
nằm trong miền nằm giữa hai đường thẳng
q
và
p
( có thể trùng lên
q
và bỏ
p
)
3 2 1 1 3 1;0;1;2 1;0;1;2m m m S
.
Do đó tổng các phần tử là:
1 0 1 2 2
.
Câu 12. (Chuyên Hùng Vương - Gia Lai - 2020) Cho hàm số
3
2f x x x
. Có tất cả bao nhiêu giá
trị nguyên của tham số
m
để phương trình
3 3
3
2f f x f x m x x
có nghiệm
1;2x
?
A.
1750
. B.
1748
. C.
1747
. D.
1746
.
Lời giải
Chọn A
Xét hàm số
3
( ) 2f t t t , ta có
2
( ) 3 1 0,f t t t
.
Do đó hàm số
f
đồng biến trên
.
Ta có
3
3
( ) ( ) ( )f f x f x m f x
3 3 3
3
( ) ( ) ( ) ( ) 0 (1)x f x f x m f x f x x m
Xét
3 3
( ) ( ) ( )h x f x f x x m trên đoạn
[ 1;2]
.
Ta có
2 2 2 2
( ) 3 ( ) ( ) ( ) 3 ( ) 3 ( ) 1 3 .h x f x f x f x x f x f x x
Ta có
2
( ) 3 1 0, [ 1;2] ( ) 0, [ 1;2]f x x x h x x
.
Hàm số
( )h x
đồng biến trên
[ 1;2]
nên
[ 1;2]
[ 1;2]
min ( ) ( 1) 1, max ( ) (2) 1748.h x h m h x h m
Phương trình
(1)
có nghiệm khi và chỉ khi
[ 1;2]
[ 1;2]
min max 0 1 2
1 1748 0
1748 1.
h x h x h h
m m
m
Do
m
nguyên nên tập các giá trị
m
thỏa mãn là
{ 1748; 1747; ;0;1}S
.
Vậy có tất cả 1750 giá trị nguyên của
m
thỏa mãn.
Câu 13. (Chuyên Quang Trung - 2020) Cho hàm số
( )f x
liên tục trên
2;4
và có bảng biến thiên như
hình vẽ bên. Có bao nhiêu giá trị nguyên của
m
để phương trình
2
2 2 . ( )x x x m f x
có
nghiệm thuộc đoạn
2;4
?
A.
6
. B.
5
. C.
4
. D.
3
.
Lời giải
Chọn C

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Dựa vào bảng biến thiên ta có
2;4
(4) 2Min f x f
và
2;4
(2) 4Max f x f
Hàm số
2
( ) 2 2g x x x x
liên tục và đồng biến trên
2;4
Suy ra
2;4
(2) 2Min g x g
và
2;4
(4) 4 4 2Max g x g
Ta có
2
2
2 2 ( )
2 2 . ( )
( ) ( )
x x x g x
x x x m f x m m
f x f x
Xét hàm số
( )
( )
( )
g x
h x
f x
liên tục trên
2;4
Vì
g x
nhỏ nhất và
f x
lớn nhất đồng thời xảy ra tại
2x
nên
2;4
2;4
2;4
2
1
( ) (2)
2 2
Min g x
g
Min h x h
Max f x f
Vì
g x
lớn nhất và
f x
nhỏ nhất đồng thời xảy ra tại
4x
nên
2;4
2;4
2;4
4
( ) (4) 2 2 2
4
Max g x
g
Max h x h
Min f x f
Từ đó suy ra phương trình
( )h x m
có nghiệm khi và chỉ khi
1
2 2 2
2
m
.
Vậy có 4 giá trị nguyên của m để phương trình có nghiệm.
Câu 14. (Chuyên Sơn La - 2020) Cho hàm số
f x
liên tục trên
và có đồ thị như hình vẽ. Số giá trị
nguyên của tham số
m
để phương trình
2
cos 2019 cos 2020 0f x m f x m
có đúng
6 nghiệm phân biệt thuộc đoạn
0;2
là
A.
1
. B.
3
. C.
2
. D.
5
.
Lời giải
Chọn C
Ta có
2
cos 1
cos 2019 cos 2020 0
cos 2020
f x
f x m f x m
f x m
(1)
* Với
cos 1f x
Dựa vào đồ thị ta có
1 1
cos 0
cos 1
cos 1 ( )
2
x
f x x k
x x x VN
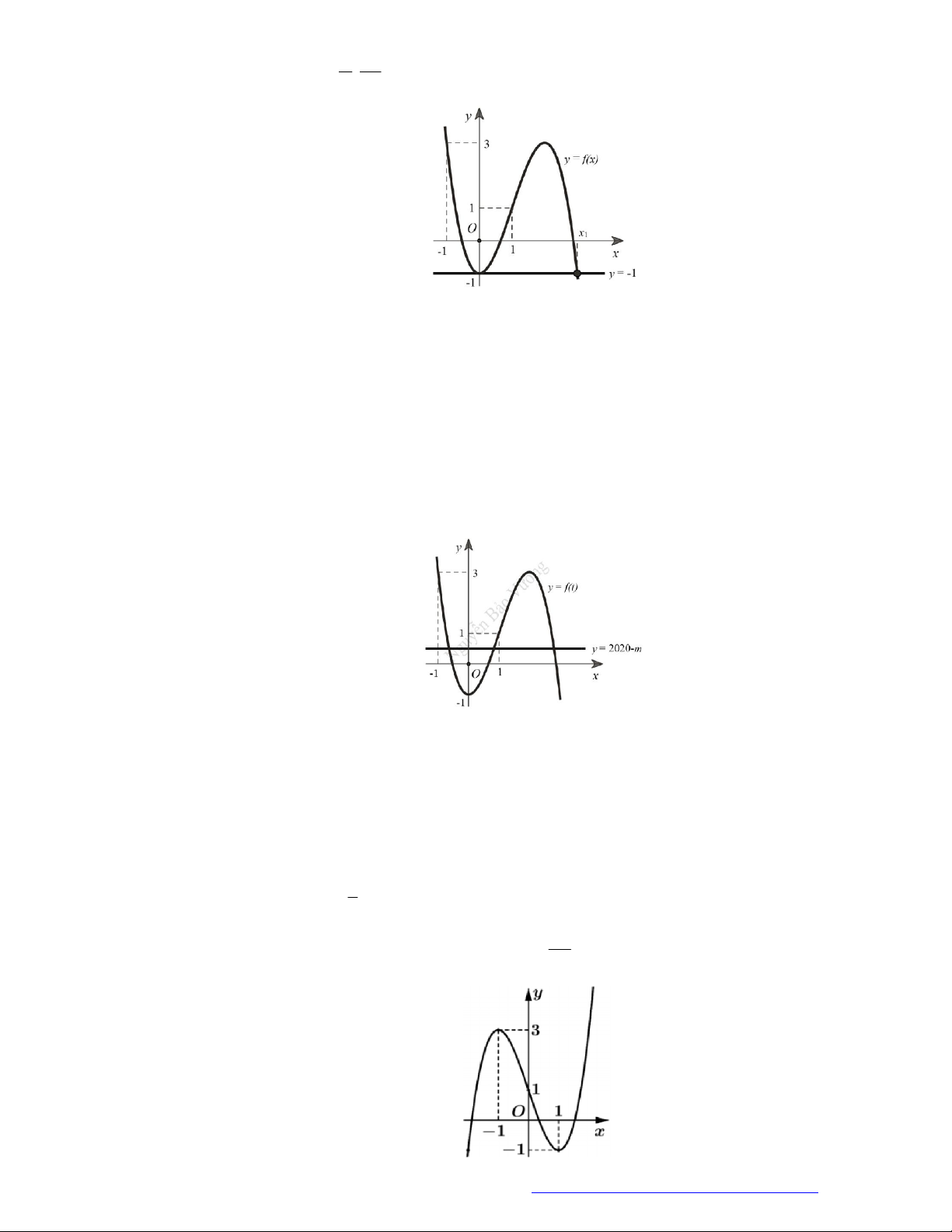
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Vì
3
0;2 ;
2 2
x x
* Với
cos 2020f x m
Đặt
cos 1;1t x t
Với
1;1t
thì phương trình
cost x
có hai nghiệm phân biệt thuộc
0;2
.
Với
1t
thì phương trình
cost x
có một nghiệm thuộc
0;2
Phương trình trở thành
2020f t m
Để phương trình (1) có tất cả 6 nghiệm phân biệt thì phương trình
cos 2020f x m
có 4
nghiệm phân biệt, hay phương trình
2020f t m
có hai nghiệm
1;1t
Dựa vào đồ thị ta có để phương trình
2020f t m
có hai nghiệm
1;1t
thì
1 2020 1 2019 2021m m
Vì
m
nguyên nên
2019;2020m
Vậy có 2 giá trị nguyên của
m
thỏa mãn.
Câu 15. (Chuyên Vĩnh Phúc - 2020) Cho hàm số
( )y f x
. Hàm số
( )y f x
có đồ thị như hình bên.
Biết
f f
e
1
1 1; 2
. Tìm tất cả các giá trị của
m
để bất phương trình
f x x mln
nghiệm đúng với mọi
1
1;x
e
.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
2m
. B.
3m
. C.
2m
. D.
3m
.
Lời giải
Chọn B
Ta có
lnf x x m
lnm f x x
.
Xét hàm số
lng x f x x
trên
1
1;
e
.
Có
1
g x f x
x
.
Trên
1
1;
e
có
0f x
và
1
0
x
nên
1
0, 1;g x x
e
hàm số
g x
đồng biến trên
1
1;
e
.
Vậy nên
lnf x x m
nghiệm đúng với mọi
1
1;x
e
1
, 1;m g x x
e
1
m g
e
3m
.
Câu 16. (Sở Phú Thọ - 2020) Cho hàm số
y f x
liên tục trên
thỏa mãn
1 5, 3 0f f
và
có bảng xét dấu đạo hàm như sau:
Số giá trị nguyên dương của tham số
m
để phương trình
2
3 2 4f x x x m
có nghiệm trong
khoảng
3;5
là
A.
16
. B.
17
. C.
0
. D.
15
.
Lời giải
Chọn D
Đặt
2
3 2 4g x f x x x
với
3;5x
.
Ta có:
2
3 2 1
4
x
g x f x
x
.
Với
3;5x
:
Ta có:
2 3; 1x
nên
2 0f x
suy ra
3 2 0f x
.
Ta có:
2
1
4
x x
x
x
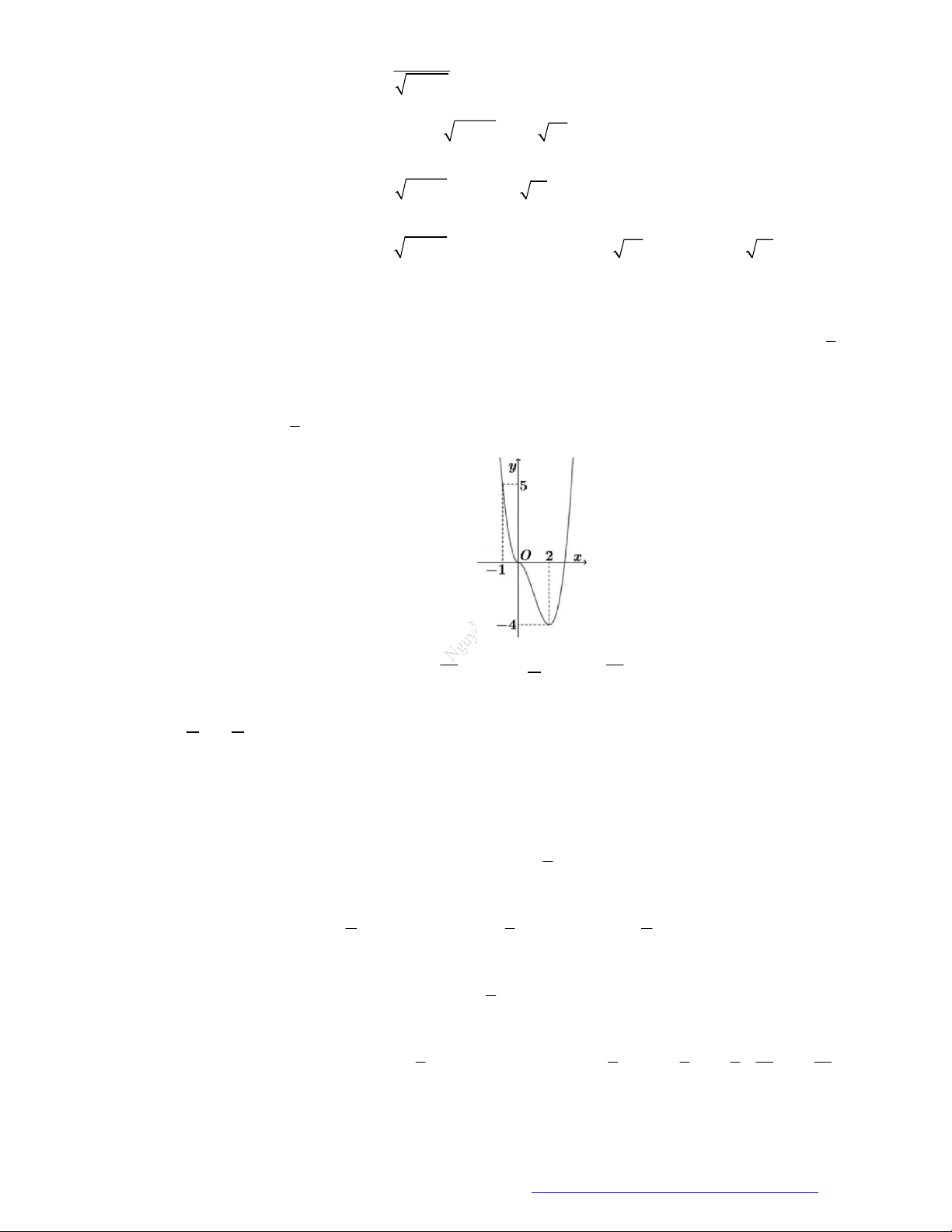
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Suy ra
2
3 2 1 0, 3;5
4
x
g x f x x
x
nên hàm số nghịch biến trên
3;5
.
Suy ra
;
2
3 5
5m 5 3 3 5 5 29in 4g x g f
;
;
2
3 5
3ma 3 3 1 3 4 12x 3 1g x g f
.
Để phương trình
2
3 2 4f x x x m
có nghiệm thì 29 5 12 13m mà
m
nguyên dương nên
1,2,...,15m
tức là có 15 giá trị
Câu 17. (Sở Phú Thọ - 2020) Cho hàm số
y f x
liên tục trên
và thỏa mãn
1
1 1, 2
e
f f
.
Hàm số
f x
có đồ thị như hình vẽ. Bất phương trình
2
lnf x x x m
nghiệm đúng với
mọi
1
1;
e
x
khi và chỉ khi
A.
0m
. B.
2
1
3
e
m
. C.
2
1
3
e
m
. D.
0m
.
Lời giải
Chọn C
Điều kiện:
0 0x x
Bất phương trình đã cho tương đương với
2
lnf x x x m
(*).
Xét hàm số
2
lng x f x x x
trên
1
1;
e
.
Ta có
1
2g x f x x
x
. Với
1
1;
e
x
thì
1
0; 2 0f x x
x
nên
0g x
.
Do đó hàm số
g x
đồng biến trên
1
1;
e
.
Suy ra (*) nghiệm đúng với mọi
1
1;
e
x
khi và chỉ khi
2 2
1 1 1 1 1
ln 3
e e e e e
m g f
.
Câu 18. (Sở Hà Tĩnh - 2020) Cho hàm số
y f x
liên tục trên
và có đồ thị như hình vẽ.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
cosf f x m
có nghiệm thuộc
khoảng
3
;
2 2
?
A. 2. B. 4. C. 5. D. 3.
Lời giải.
Chọn B
Khi
3
;
2 2
x
thì
cos 1;0x
.
Dựa vào đồ thị hàm số
y f x
ta thấy khi
cos 1;0x
thì
cos 1;1f x
; khi đó
cos 1;3f f x
.
Do đó phương trình
cosf f x m
có nghiệm thuộc khoảng
3
;
2 2
khi và chỉ khi
1 3m
.
Vậy có 4 giá trị nguyên của tham số
m
thỏa mãn yêu cầu bài toán.
Câu 19. (Sở Ninh Bình) Cho hàm số bậc ba
y f x
có đồ thị như hình vẽ.
Có tất cả bao nhiêu giá trị nguyên của tham số
m
để phương trình
2
2 sin 6 10f x f m m
có nghiệm?
A. 2. B. 3. C. 4. D. 1.
Lời giải.
Chọn B
Từ đồ thị suy ra hàm số
y f x
đồng biến trên nửa khoảng
0;
.
Do
2
2 sin 0; 6 10 0x m m
nên
2 2
2 sin 6 10 2 sin 6 10f x f m m x m m
.
Mà
0 2 sin 2x
nên yêu cầu bài toán tương đương
2 2
0 6 10 2 6 8 0 4 2m m m m m
.
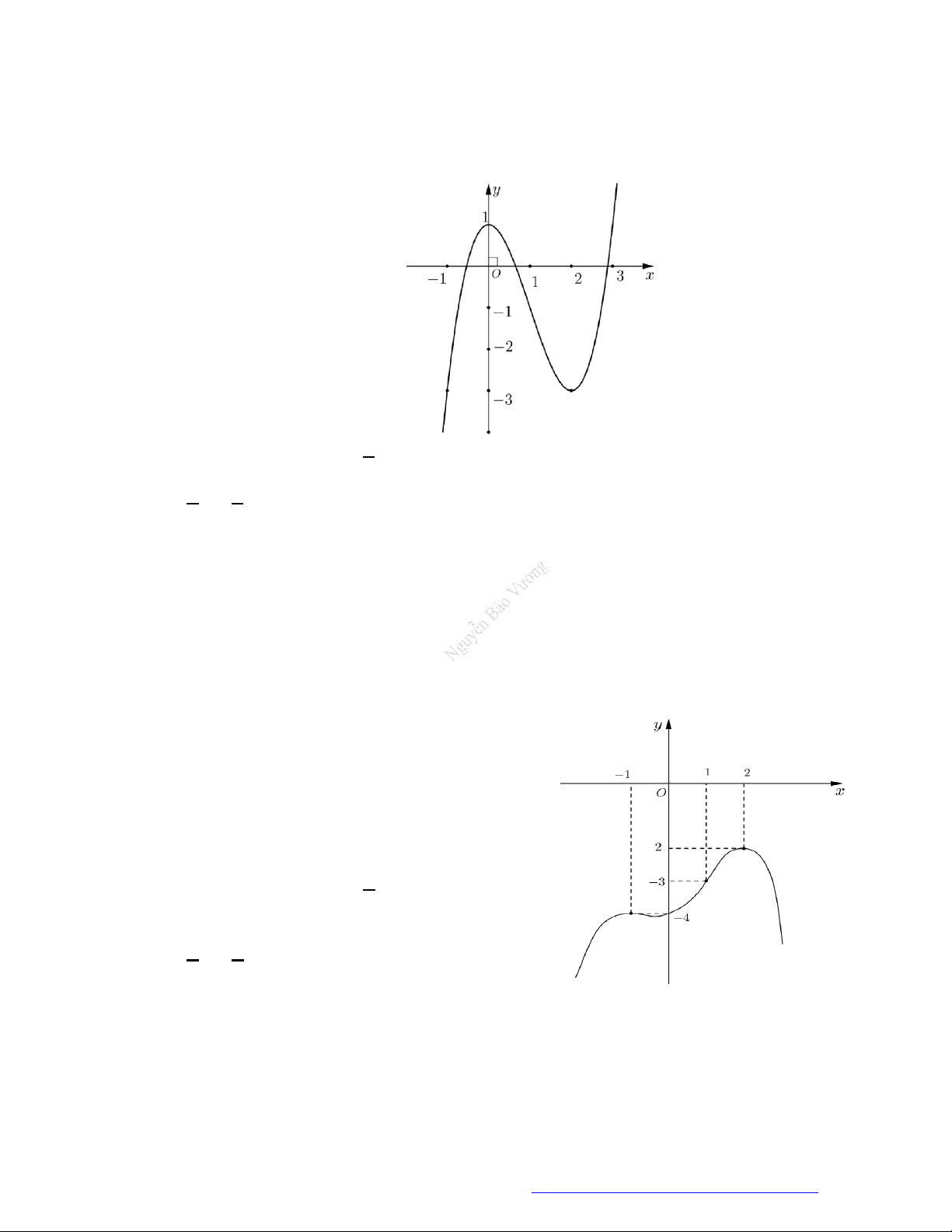
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
Vậy có 3 số nguyên
m
thỏa mãn.
Câu 20. (Sở Yên Bái - 2020) Cho hàm số bậc ba
y f x
có đồ thị như hình vẽ bên. Có tất cả bao nhiêu
giá trị nguyên của tham số
m
để phương trình
3 2
3 3 0 f x x m
có nghiệm thuộc đoạn
1;2
.
A.
7
. B.
8
. C.
10
. D.
5
.
Lời giải
Chọn B
Từ hình vẽ, ta suy ra được hình vẽ là đồ thị của hàm số
3 2
3 1 y x x
.
3 2 3 2
3 3 0 3 3 f x x m f x x m
3 2
3 2
3 1
3 2
x x m
x x m
3 2
3 2
3 1
3 1 3
x x m
x x m
Để phương trình đã cho có nghiệm thuộc đoạn
1; 2
thì
3 1
3 3 1
m
m
1 3
2 6
m
m
.
1;6 m
.
Do
m
nên có 8 giá trị
m
để phương trình đã cho có nghiệm.
Câu 21. (Sở Yên Bái - 2020) Cho hàm số
( )y f x
liên
tục trên
và có đồ thị như hình vẽ bên. Số các
giá trị nguyên của tham số
m
để bất phương trình
( ) 2 ( ) 2 ( )
16.8 ( 5 ).4 ((4 ( )).16
f x f x f x
m m f x
nghiệm đúng với mọi số thực
x
là
A.
3.
B.
5.
C.
1.
D.
4.
Lời giải
Chọn D
( ) 2 ( ) 2 ( ) 2 ( ) 2 ( )
16.8 ( 5 ).4 ((4 ( )).16 5 16.2 (4 ( )).4
f x f x f x f x f x
m m f x m m f x
Vì. nên ta có
( ) 2 ( ) 2
16.2 (4 ( )).4 16.2 0 4
f x f x
f x x
2 2
5 4 5 4 0 1 4m m m m m
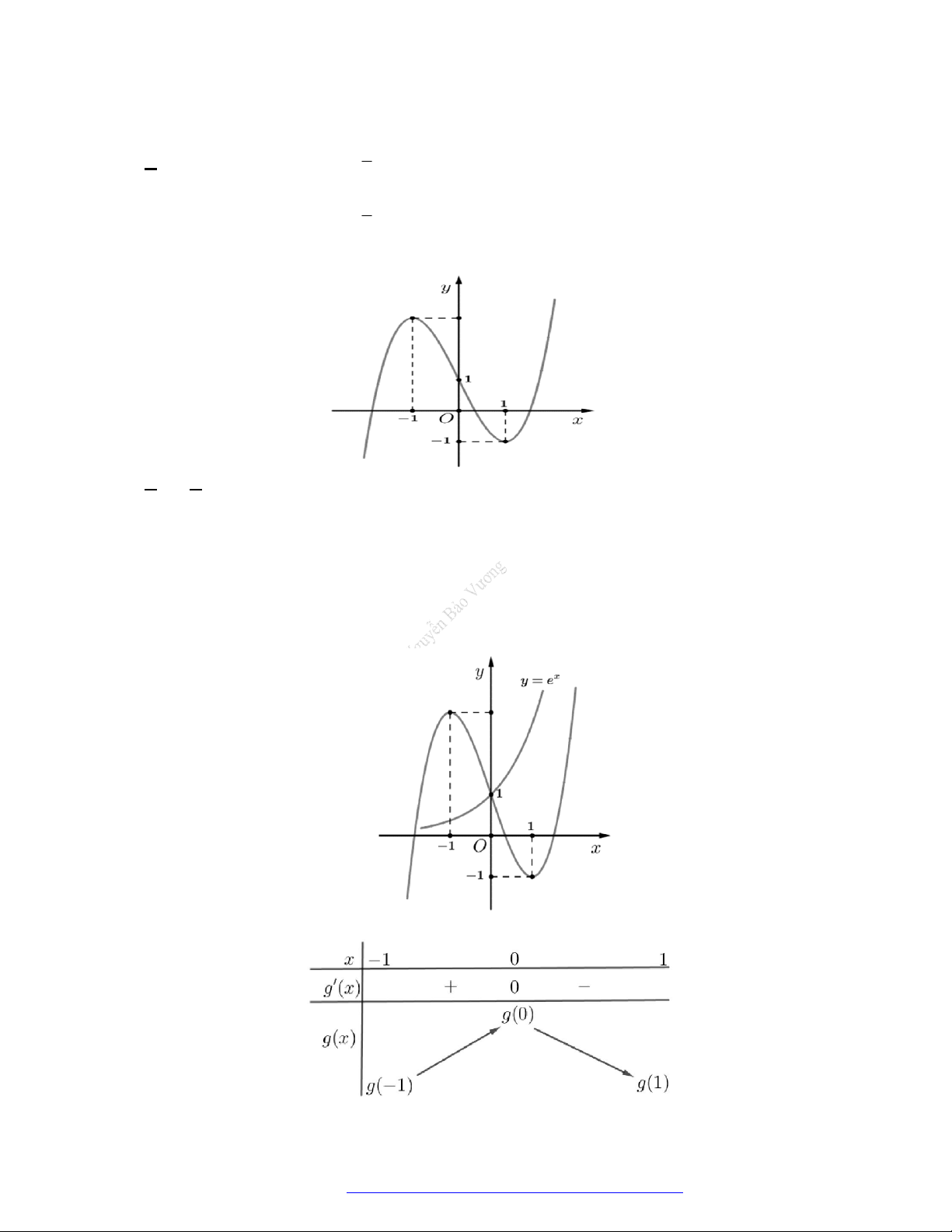
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 22. (Hậu Lộc 2 - Thanh Hóa - 2020) Cho hàm số
y f x
, hàm số
y f x
liên tục trên
và
có đồ thị như hình vẽ bên. Bất phương trình
x
m e f x
có nghiệm với mọi
1;1x
khi và
chỉ khi.
A.
1
min 1 ; 1m f e f
e
. B.
0 1m f
.
C.
1
min 1 ; 1m f e f
e
. D.
0 1m f
.
Lời giải
Chọn A
Ta có:
x x
m e f x m f x e
Xét hàm số
x
g x f x e
với
1;1x
; 0 0
x x x
g x f x e g x f x e f x e
Dễ thấy với
0
1;1 ; 0 1; 1 0x f e x
là nghiệm của phương trình
x
f x e
hơn nữa
là nghiệm duy nhất (Minh họa bằng hình vẽ)
Dựa vào vị trí đồ thị hình vẽ trên ta có bảng biến thiên
Qua bảng biến thiên và chỉ xét trong khoảng
1;1
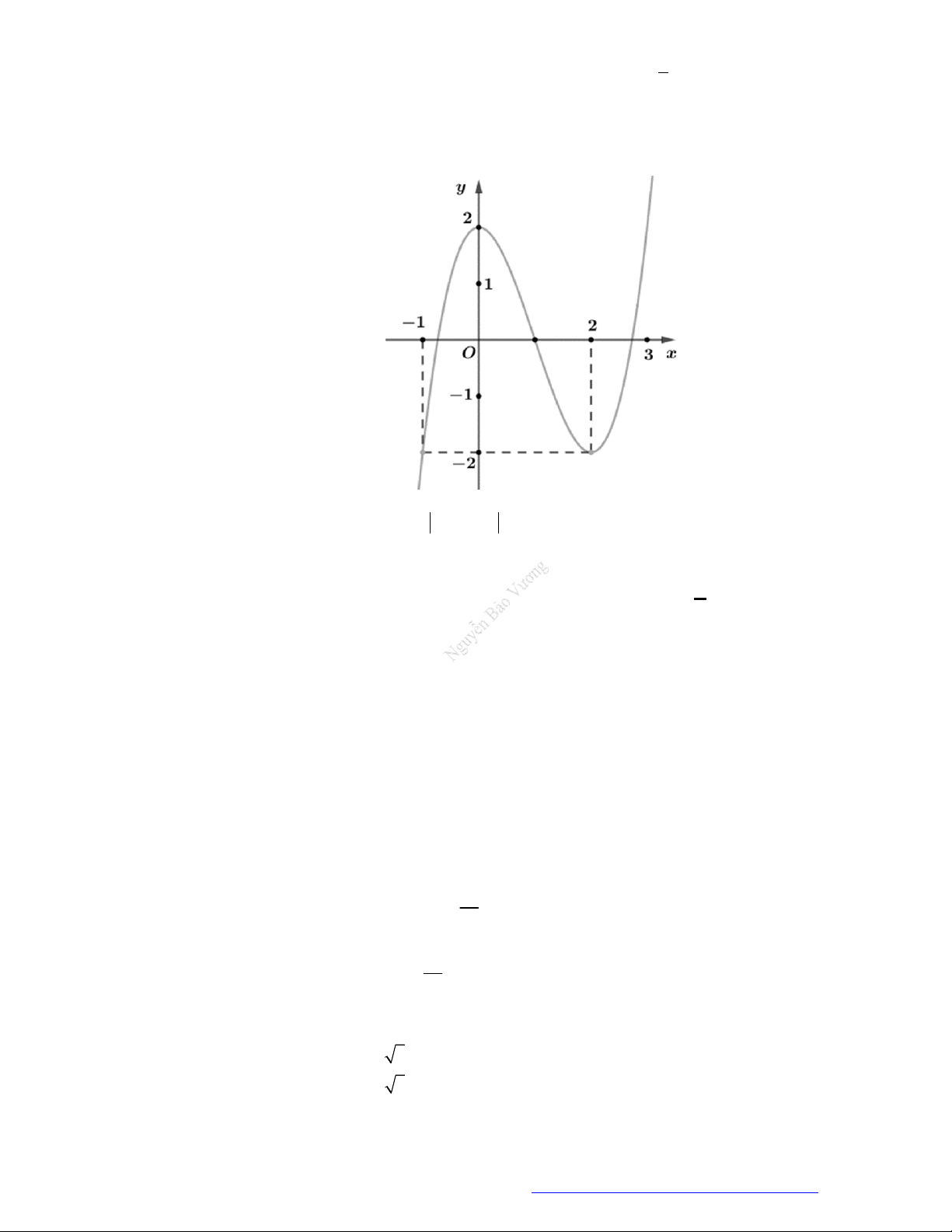
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
1
min 1 ; 1 min 1 ; 1m g x m g g m f e f
e
.
Câu 23. (Liên trường Nghệ An - 2020) Cho hàm số
f x
là hàm số đa thức bậc bốn. Biết
0 0f
và
đồ thị hàm số
y f x
có hình vẽ bên dưới.
Tập nghiệm của phương trình
2sin 1 1f x m
(với
m
là tham số) trên đoạn
0;3
có tất
cả bao nhiêu phần tử?
A.
8
. B.
20
. C.
12
. D.
16
.
Lời giải
Chọn D
Đồ thị đã cho là đồ thị hàm số bậc ba có hai điểm cực trị
0x
và
2x
nên có dạng
3 2
f x ax bx cx d
.
Lần lượt thay thế các dữ kiện từ hình vẽ, ta được
2
3
2
1
0
3
3 2 2 2 0 0
2
2
d
a
c
b
a b c
d
a b d
.
Suy ra
4
3 2 3
3 2 2
4
x
f x x x f x x x C
.
Mà
4
3
0 0 0 2
4
x
f C f x x x .
Ta có
1
0 1 3
1 3
x
f x x
x
.
Suy ra bảng biến thiên
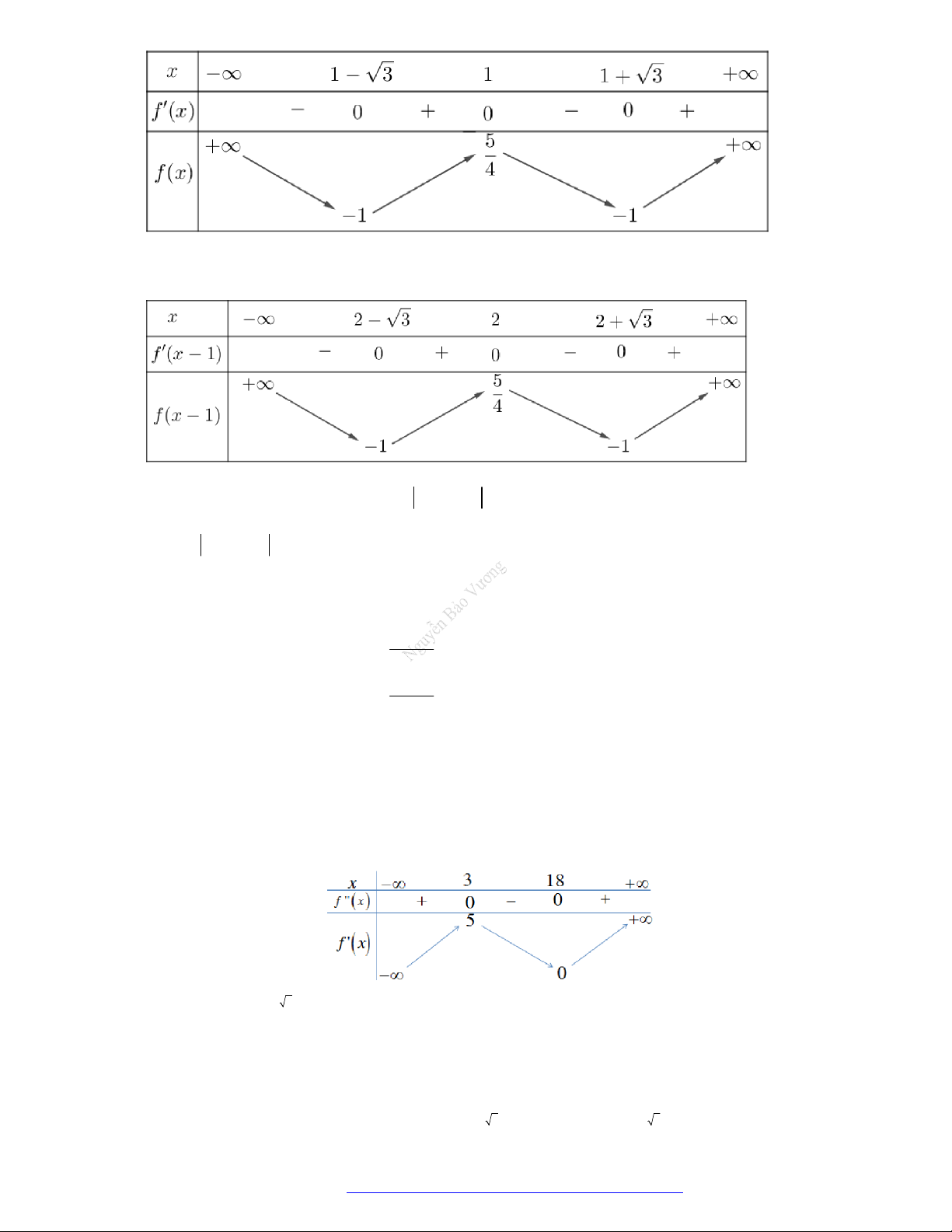
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Từ đó ta có bảng biến thiên của
1f x
Vì
1 sin 1, 0;3x x
nên
0 2sin 1 3x
.
Đặt
2sin 1t x
,
0;3t
Dựa vào bảng biến thiên, suy ra phương trình
1f t m
có tối đa
2
nghiệm
t h
,
t k
.
Do đó
1
sin
2sin 1
2
2sin 1 1
sin
2
h
x
x h
x k k
x
.
Trên
0;3
, mỗi phương trình có nhiều nhất
4
nghiệm, do đó phương trình đã cho có nhiều nhất
16
nghiệm.
Câu 24. (Kìm Thành - Hải Dương - 2020) Cho hàm số
y f x
. Hàm số
'y f x
có bảng biến thiên
như hình vẽ:
Bất phương trình
x
e m f x
có nghiệm
4;16x
khi và chỉ khi:
A.
2
4m f e
. B.
2
4m f e
. C.
2
16m f e
. D.
2
16m f e
.
Lời giải
Chọn B
Từ BBT suy ra
' 0, 4;16f x x
. Ta có:
(*)
x x
e m f x m e f x
.
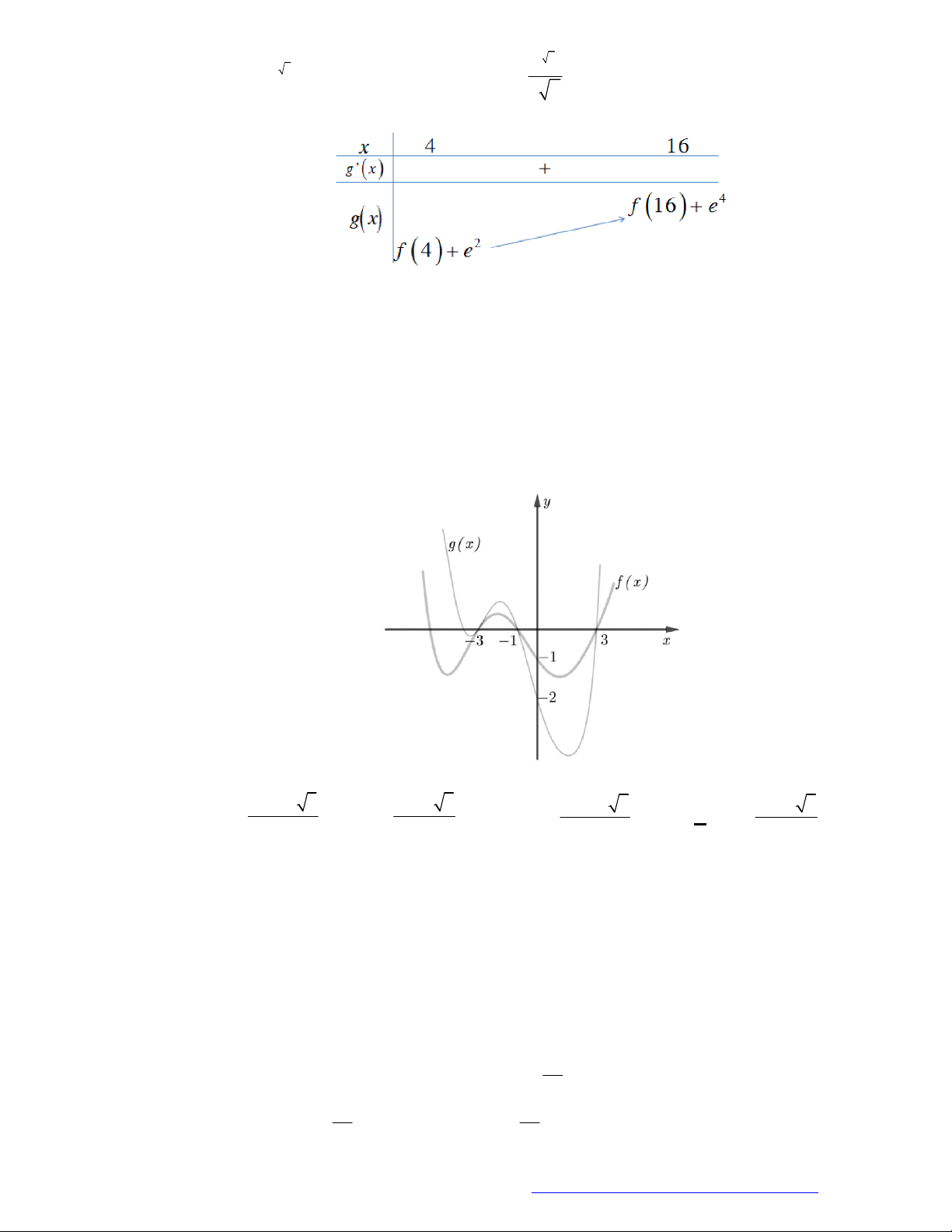
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21
Đặt
x
g x e f x
,
4;16x
' ' 0, 4;16
2
x
e
g x f x x
x
Bảng biến thiên:
(*) thỏa mãn khi
2
4;16
min 4m g x f e
.
Câu 25. (Kìm Thành - Hải Dương - 2020) Cho hàm số đa thức bậc bốn
y f x
và
y g x
có đồ thị
như hình vẽ dưới đây đường đậm hơn là đồ thị hàm số
y f x
. Biết rằng hai đồ thị tiếp xúc với
nhau tại điểm có hoành độ là
3
và cắt nhau tại hai điểm nữa có hoành độ lần lượt là
1
và
3
.
Tìm tập hợp tất các giá trị thực của tham số
m
để bất phương trình
f x g x m
nghiệm
đúng với mọi
3;3x
.
A.
12 10 3
;
9
. B.
12 8 3
;
9
. C.
12 10 3
;
9
. D.
12 8 3
;
9
.
Lời giải
Chọn D
Xét hàm số
h x f x g x
.
Vì đồ thị hàm số
f x
tiếp xúc với đồ thị hàm số
g x
tại điểm có hoành độ
3
và cắt nhau tại
hai điểm nữa có hoành độ lần lượt là
1
và
3
suy ra
2
3 1 3h x f x g x a x x x
.
Nhận xét từ đồ thị khi
x
thì phần đồ thị
f x
nằm dười
g x
nên
0a
.
Mặt khác ta có
1
0 27 2 1 1
27
h a a
Xét hàm
2
4 3 2
1 1
3 1 3 4 6 36 27
27 27
y h x x x x x x x x
.
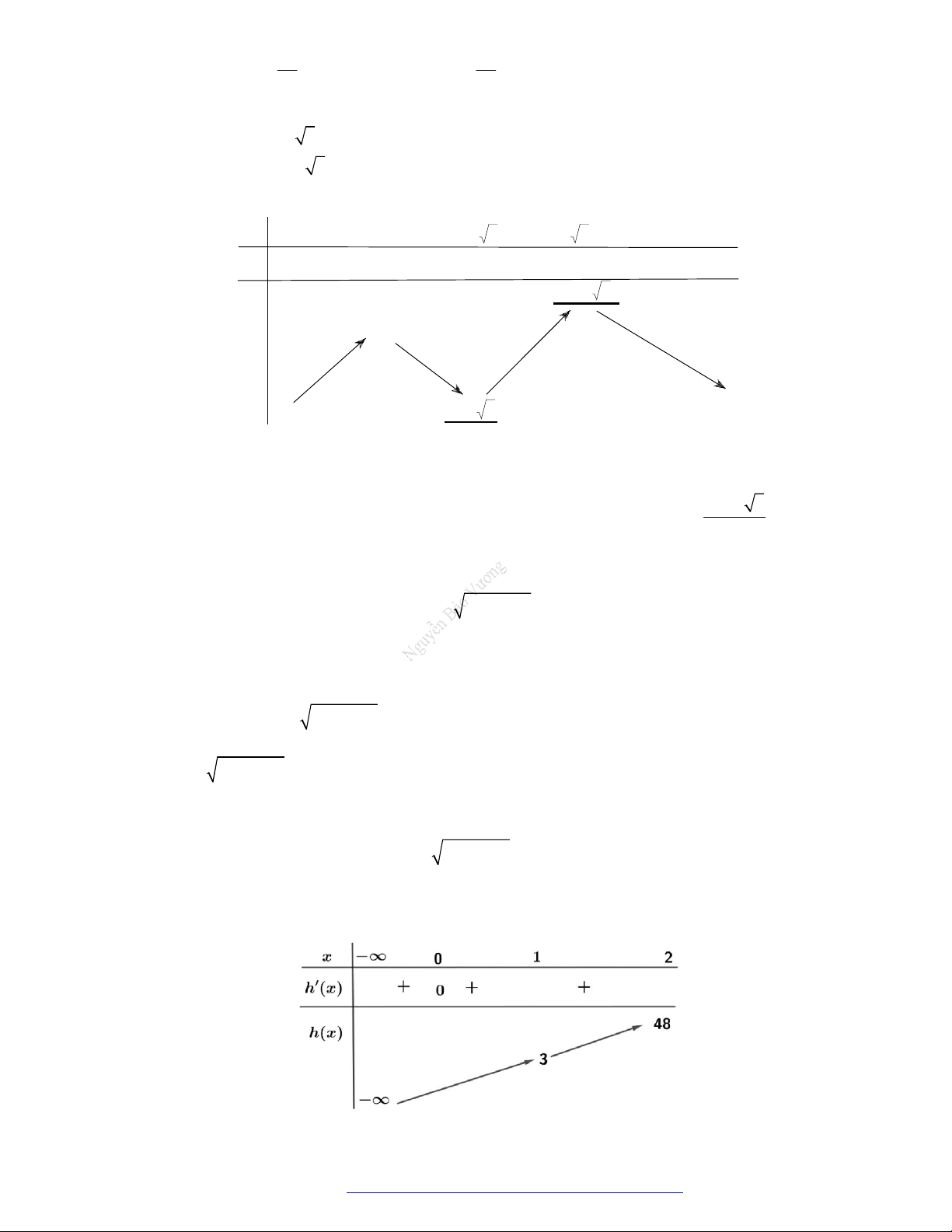
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 22 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ta có
3 2 2
1 1
4 12 12 36 3 4 12
27 27
y h x x x x x x
.
Suy ra
3
0 3
3
x
y x
x
.
Bảng biến thiên
Vây tập hợp tất các giá trị thực của tham số
m
để bất phương trình
f x g x m f x g x m
nghiệm đúng với mọi
3;3x
là
12 8 3
9
m
.
Câu 26. (Kìm Thành - Hải Dương - 2020) Cho hàm số
5 3
3 4f x x x m
. Có bao nhiêu giá trị
nguyên của tham số
m
để phương trình
3
3
f f x m x m
có nghiệm thuộc đoạn
1; 2
?
A.
18
. B.
17
. C.
15
. D.
16
.
Lời giải
Chọn D
Xét phương trình
3
3
f f x m x m
(1)
Đặt . Ta có
3
3
f t x m
f x t m
3 3
f t t f x x
(2)
Xét hàm số
3 2 4 2
3 5 12 0,g u f u u g u f u u u u u
.
Khi đó (2)
g t g x t x
3
3
f x m x x f x m
5 3
2 3x x m
Xét hàm số
5 3 4 2
2 5 6 0,h x x x h x x x x
Ta có bảng biến thiên của hàm số
h x
:
Từ bảng biến thiên suy ra để (1) có nghiệm thuộc đoạn
1; 2
3 3 48 1 16m m
12+8 3
)
9
12-8 3
9
0
0
-∞
-∞
3
3
00
0
-
-
+
+
-3
- 3
h(x)
h'(x)
x
3
t f x m
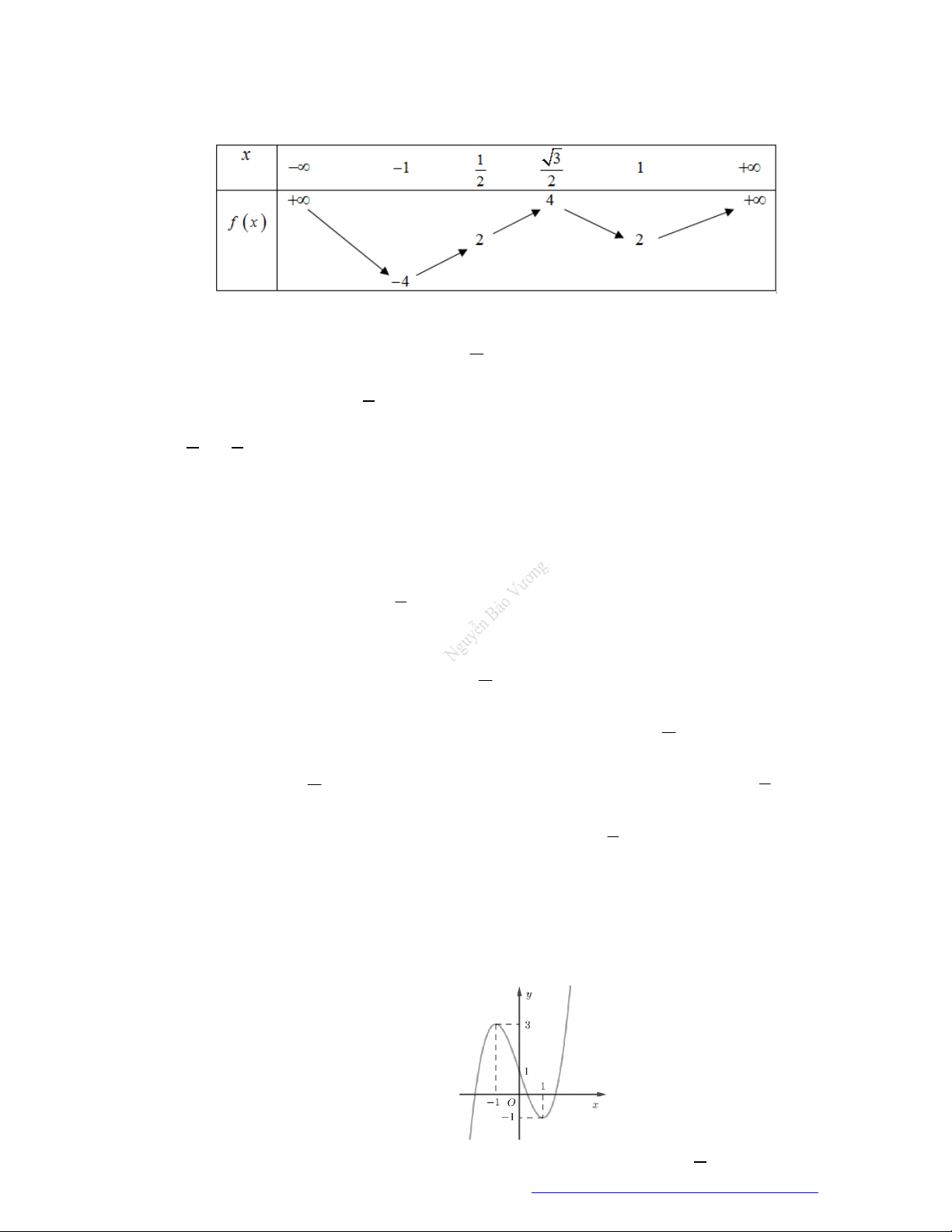
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23
Mà
1;2;3;...;16m m
suy ra có
16
giá trị của
m
thỏa mãn bài toán.
Câu 27. (Tiên Lãng - Hải Phòng - 2020) Cho hàm số
f x
liên tục trên
và có bảng biến thiên như
hình vẽ.
Số giá trị nguyên của tham số
m
để phương trình
2
cos 3 cos 2 10 0f x m f x m
có
đúng 4 nghiệm phân biệt thuộc đoạn
;
3
là
A.
5
. B.
6
. C.
7
. D.
4
.
Lời giải
Chọn B
Xét
2
cos 3 cos 2 10 0f x m f x m
. Ta có
2
7m
.
Do đó
cos 5 (1)
cos 2 (2)
f x m
f x
.
Với
cos 1
1
cos 2 cos
2
cos 1
x a
f x x
x
.
Trường hợp này được 3 nghiệm trong
;
3
.
Để phương trình đã cho có đúng 4 nghiệm phân biệt thuộc đoạn
;
3
thì (1) có đúng 1
nghiệm trong
;
3
và không trùng với nghiệm của các phương trình
1
cos ;cos 1
2
x x
5f t m
với cost x có đúng 1 nghiệm trong
1
1;
2
4 5 2 1 7m m
.
Do m nguyên nên có 6 giá trị của m thỏa mãn.
Câu 28. (Trần Phú - Quảng Ninh - 2020) Cho hàm số
y f x
liên tục trên
và có đồ thị như hình
vẽ. Gọi
S
là tập hợp tất cả các giá trị nguyên của tham số
m
để phương trình
sin 3siny f x x m
có nghiệm thuộc khoảng
0;
. Tổng các phần tử của
S
bằng
A.
5
. B.
8
. C.
6
. D.
10
.
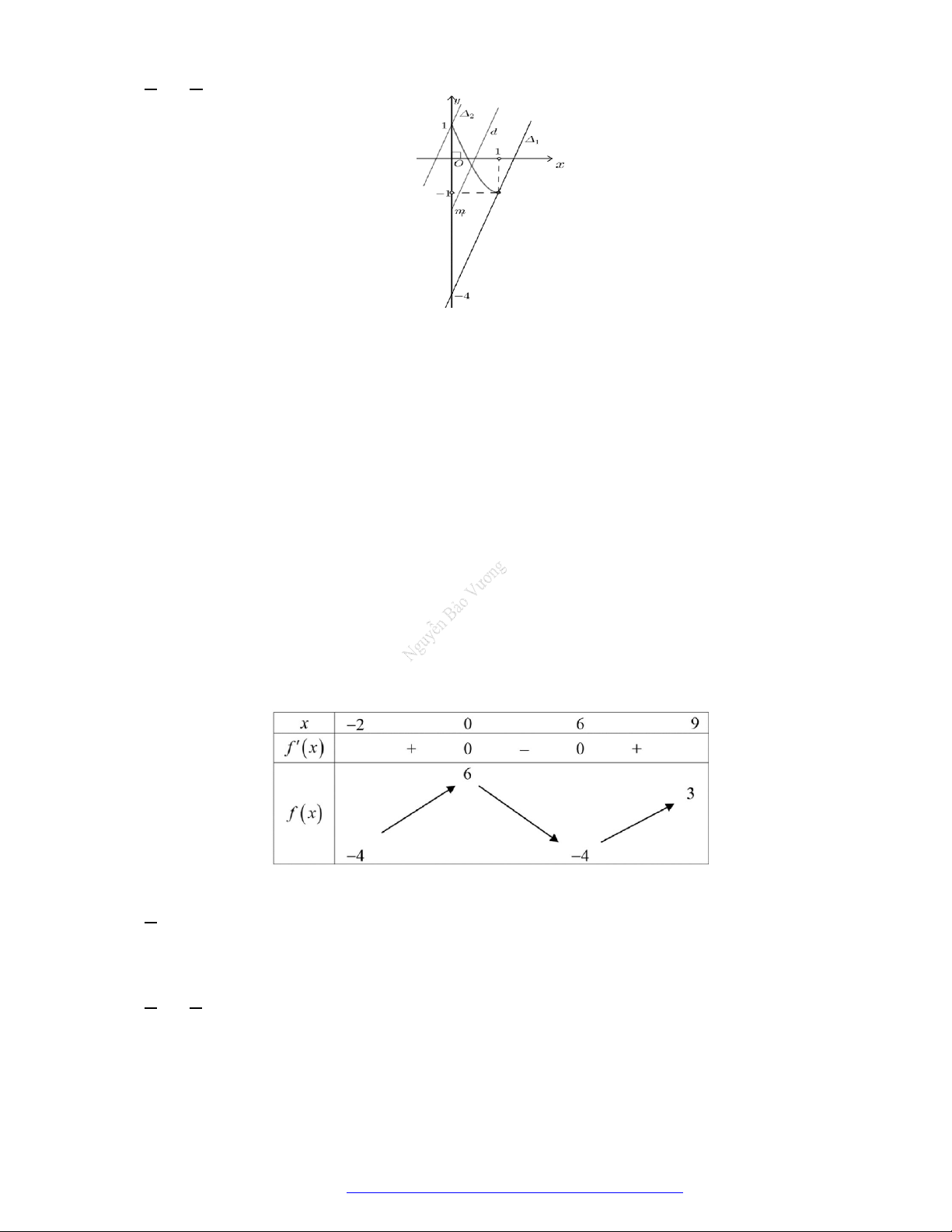
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 24 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Lời giải
Chọn D
Đặt
sint x
,
0; 0;1x t
.
Phương trình
sin 3sinf x x m
có nghiệm thuộc khoảng
0;
khi và chỉ khi phương trình
3f t t m
có nghiệm thuộc
0;1
khi và chỉ khi đồ thị hàm số
y f x
và đường thẳng
: 3d y x m
có điểm chung với hoành độ
0;1x
.
1
: 3 4y x
là đường thẳng qua điểm
1; 1
và
2
: 3 1y x
là đường thẳng qua điểm
0;1
Đồ thị hàm số
y f x
trên
0;1
là phần đường cong nằm giữa hai đường thẳng
1
và
2
.
Vậy phương trình
3f t t m
có nghiệm thuộc nửa khoảng
0;1
khi và chỉ khi
d
dao động
trong miền giới hạn bởi
1
và
2
(không trùng với
2
) khi và chỉ
khi
4 1 4; 3; 2; 1;0m m
.
Vậy tổng các giá trị của
S
bằng
10
.
Câu 29. (NK HCM-2019) Cho
f x
là một hàm số liên tục trên đoạn
2;9 ,
biết
1 2 9 3f f f
và
f x
có bảng biến thiên như sau:
Tìm
m
để phương trình
f x f m
có ba nghiệm phân biệt thuộc đoạn
2;9 .
A.
2;9 \ 1;2 6 .m
B.
2;9 \ 1;2 6 .m
C.
2;9 \ 6 .m
D.
2;9 \ 2;6 .m
Lời giải
Chọn A
Phương trình
f x f m
có ba nghiệm phân biệt thuộc đoạn
2;9
khi
4 3.f m
Trên
2;0 ,
hàm số
f x
đồng biến và
1 3f
nên
4 3 2 1.f m m
Trên
0;6 ,
hàm số
f x
nghịch biến và
2 3f
nên
4 3 6 2.f m m
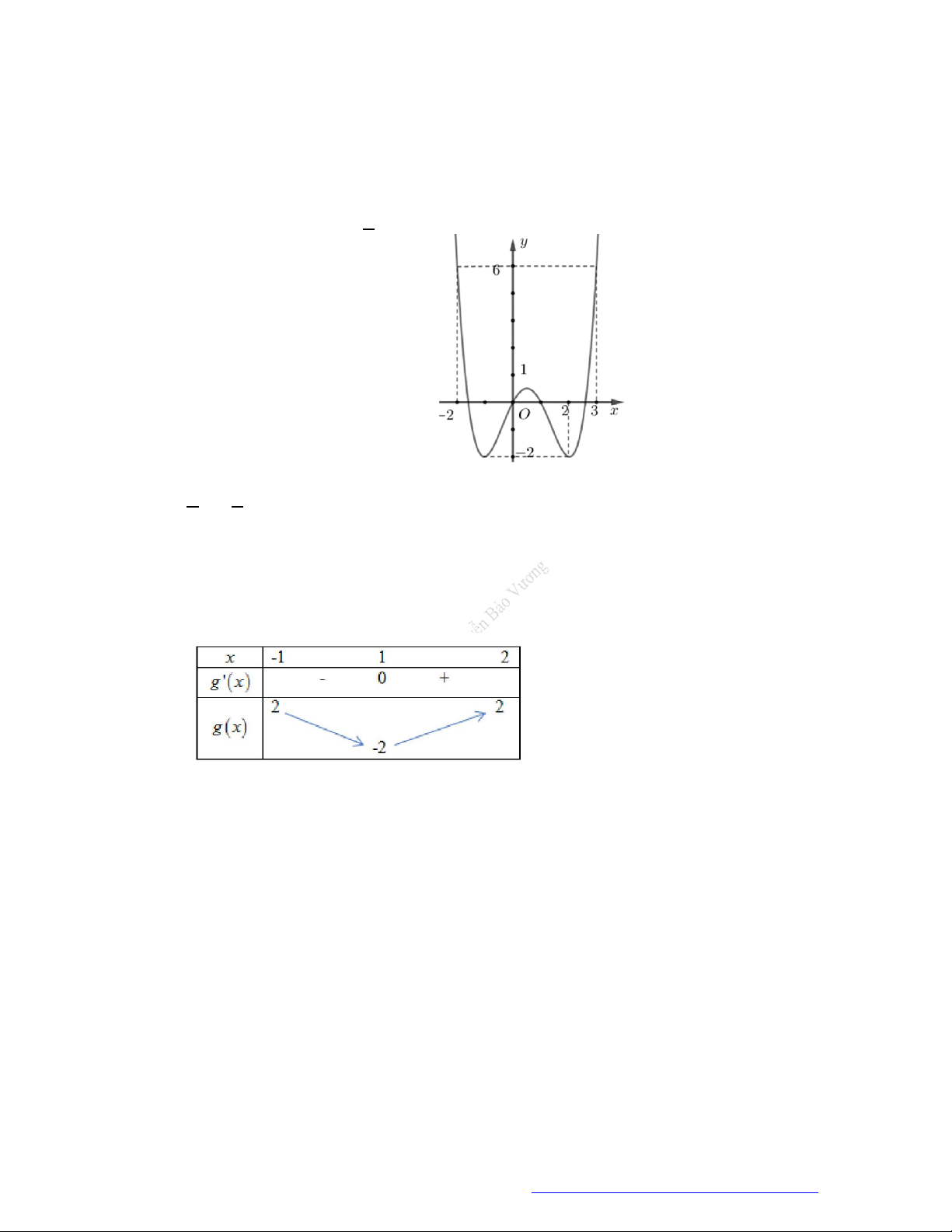
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25
Trên
6;9 ,
hàm số
f x
đồng biến và
9 3f
nên
4 3 6 9.f m m
Vậy điều kiện của
m
là:
2; 1 2;6 6;9 2;9 \ 1;2 6 .m m
Câu 30. (Chuyên Đại học Vinh 2019) Cho hàm số
y f x
có đồ thị như hình vẽ. Có bao nhiêu số
nguyên
m
để phương trình
3
3f x x m
có 6 nghiệm phân biệt thuộc đoạn
1;2
?
A.
3
. B.
2
. C.
6
. D.
7
.
Lời giải
Chọn B
Đặt
3
3 , 1;2t g x x x x
2
1
3 3 0
1
x
g x x
x
Bảng biến thiên của hàm số
g x
trên
1;2
Suy ra với
2t
, có
1
giá trị của
x
thuộc đoạn
1;2
.
2;2t
, có
2
giá trị của
x
thuộc đoạn
1;2
.
Phương trình
3
3f x x m
có
6
nghiệm phân biệt thuộc đoạn
1;2
khi và chỉ khi phương
trình
f t m
có
3
nghiệm phân biệt thuộc
2;2
. (1)
Dựa vào đồ thị hàm số
y f x
và
m
nguyên ta có hai giá trị của
m
thỏa mãn điều kiện (1) là:
0, 1.m m
Câu 31. (Hội 8 trường chuyên ĐBSH 2019) Cho hàm số
y f x
có đồ thị như hình vẽ bên dưới.
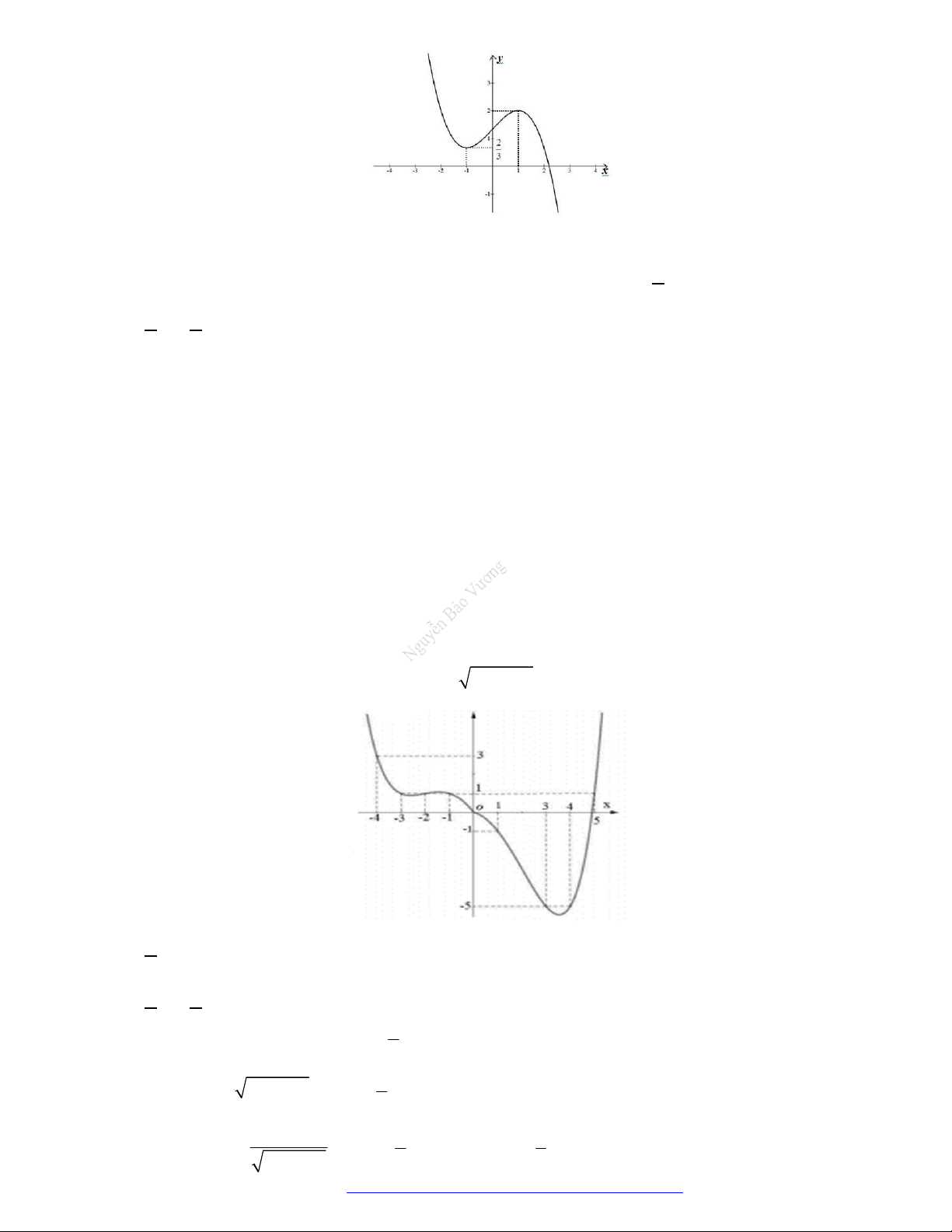
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 26 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Số giá trị nguyên dương của
m
để phương trình
2
4 5 1f x x m
có nghiệm là
A. Vô số. B.
4
. C.
0
. D.
3
.
Lời giải
Chọn D
Đặt
2
4 5t x x
. Ta có
2
2 1 1t x
.
Phương trình
2
4 5 1 1f x x m
trở thành phương trình
1 2f t m
.
Sử dụng các nhận xét ở trên và đồ thị của hàm số
y f x
ta có
1
có nghiệm
2
có nghiệm thuộc
1;
1 2 3m m
Vậy tập hợp các giá trị nguyên dương của
m
thỏa yêu cầu bài toán là
1;2;3
.
Câu 32. Cho hàm số
y f x
xác định, liên tục trên
và có đồ thị như hình vẽ dưới. Có bao nhiêu giá
trị nguyên của
m
để phương trình
2
2 3 4 6 9 3f x x m
có nghiệm
A.
13
. B.
12
. C.
8
. D.
10
.
Lời giải
Chọn A
Điều kiện:
2
2
6 9 0 0
3
x x x
Đặt
2
3 4 6 9t x x
;
2
0
3
x
Ta có:
2
12 3 1
6 9
x
t x
x x
;
2
0
3
x
;
1
0
3
t x t
( nhận ).
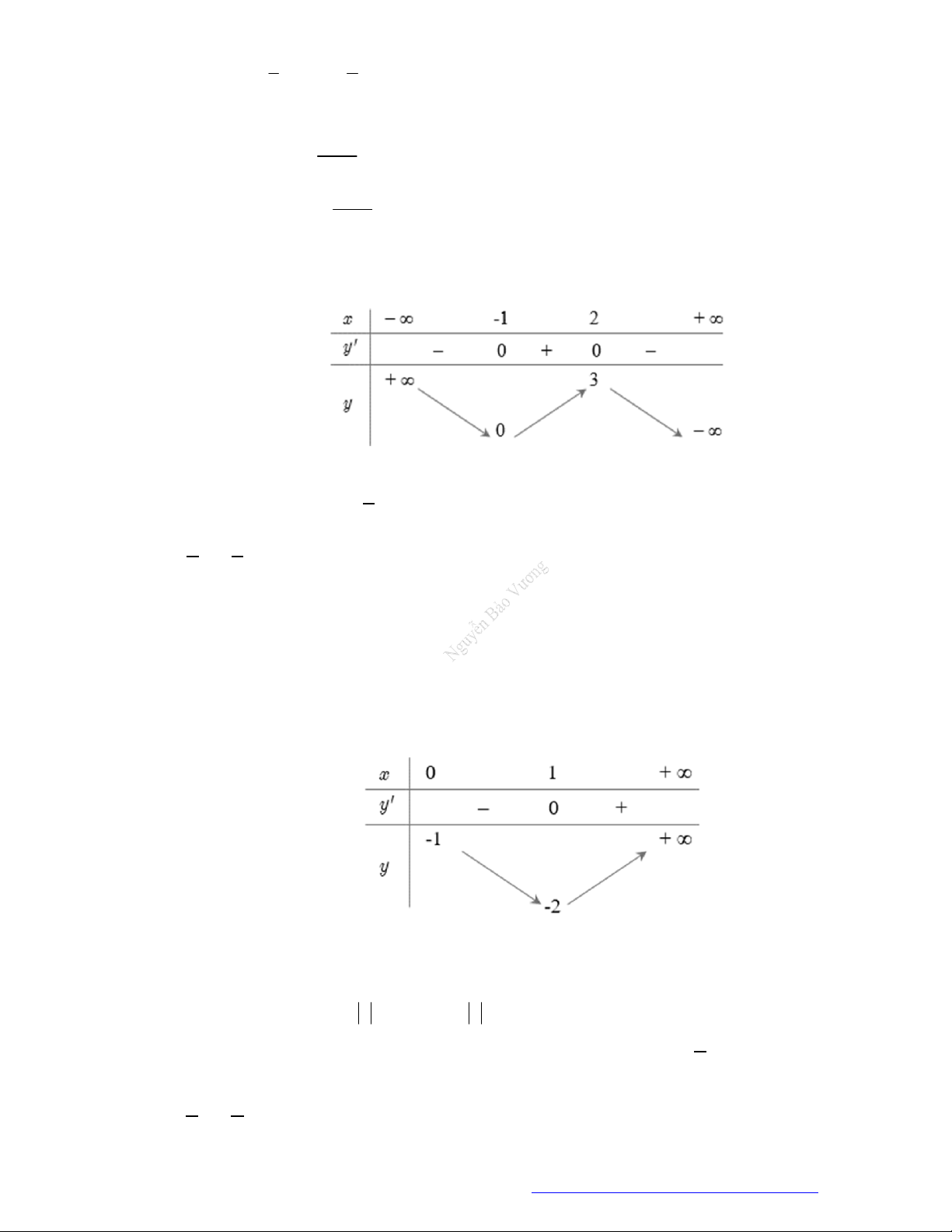
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27
1 2
0 3; 1; 3.
3 3
t t t
Nên
1 3t
.
Mặt khác:
3
2
m
f t
,
1;3t
có nghiệm.
Từ đồ thị ta có
3
5 1 7 5
2
m
m
.
Do
m
nguyên nên có 13 giá trị
m
là
7
,
6
,
5
,
4
,
3
,
2
,
1
,
0
,
1
,
2
,
3
,
4
,
5
.
Câu 33. (Chuyên Bắc Giang 2019) hàm số
y f x
có bảng biến thiên
Tìm
m
để phương trình
2
2 2 2 1 0f x f x m
có nghiệm trên
;1
A.
1;
. B.
2;
. C.
2;
. D.
1;
.
Lời giải
Chọn B
Ta có:
2 2
2 2 2 1 0 2 2 2 1 1f x f x m f x f x m
.
Đặt
t f x
, với
;1x
thì
2 ;2x
, ki đó
2 0;t f x
.
Phương trình
1
trở thành:
2
2 1 2t t m
.
1
có nghiệm trên
;1
tương ứng khi và chỉ khi
2
có nghiệm trên
0;
.
Xét
2
2 1, 0;g t t t t
, có
2 2, 0 1g t t g t t
.
Bảng biến thiên của
g t
:
Từ bảng biến thiên suy ra phương trình
2
có nghiệm
0;t
khi và chỉ khi
2m
.
Câu 34. (Sở Hà Nam - 2019) Cho hàm số
2
4 3f x x x
. Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
2
6 5 0f x m f x m
có
6
nghiệm thực phân biệt?
A.
1
. B.
2
. C.
4
.
D.
3
.
Lời giải
Chọn D
Hàm số
2
4 3f x x x
có bảng biến thiên
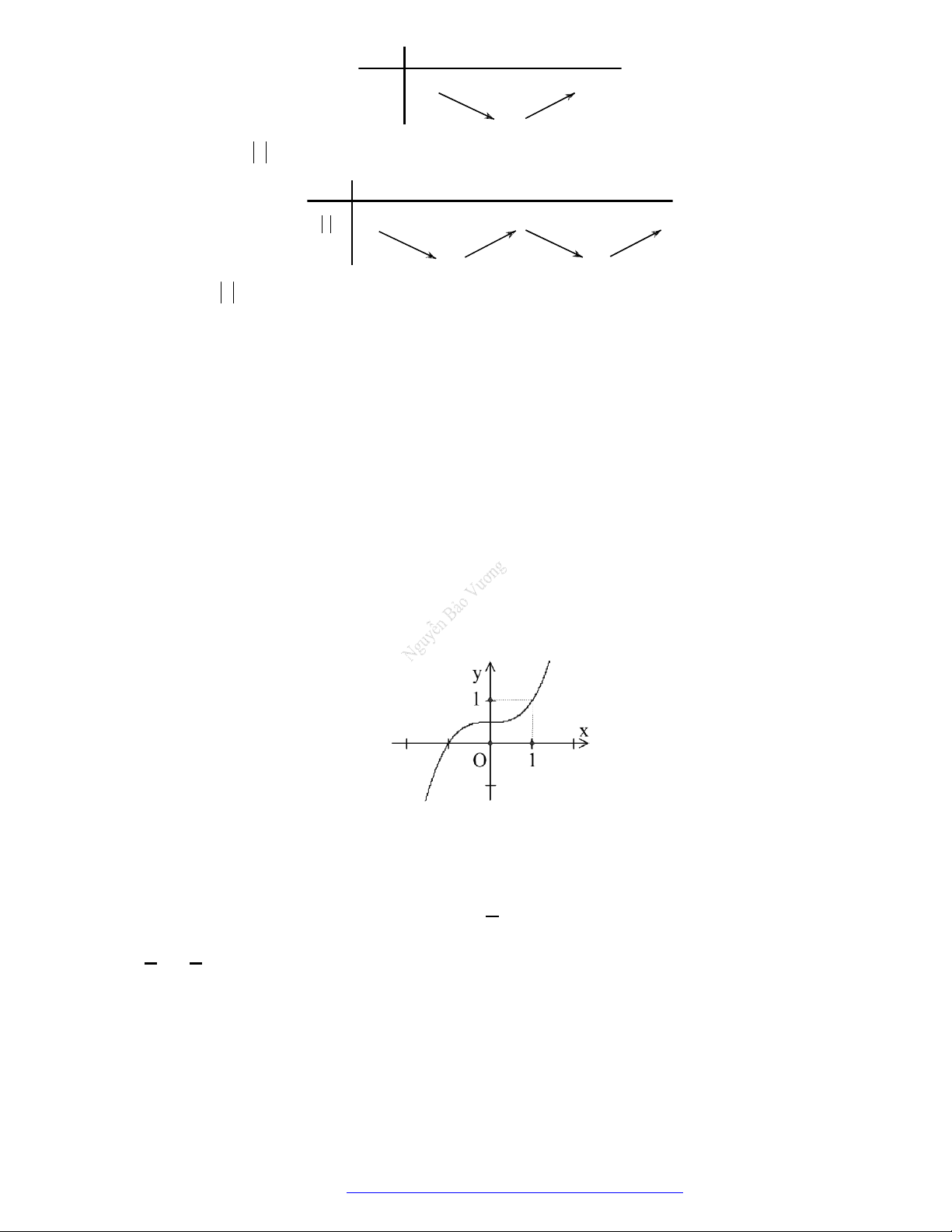
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 28 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Hàm số
y f x
có bảng biến thiên
Đặt
1 *t f x
Nhận xét:
+ với
*
0
1t x
+ với
*
0 0
1; 3t t
2
nghiệm
+ với
*
0
3t
3
nghiệm
+ với
*
0
1;3t
4
nghiệm
Phương trình trở thành
2
6 5 0t m t m
1
5
t
t m
Yêu cầu bài toán suy ra
1 5 3 4 8 5;6;7
m
m m m
.
Câu 35. Cho hàm số
3 2
f x ax bx cx d
có đồ thị như hình vẽ
Gọi
S
là tập hợp các giá trị của
m m
sao cho
3
1 2 1 1 0, .x m f x mf x f x x
Số phần tử của tập
S
là
A.
0.
B.
3.
C.
2
D.
1.
Lời giải
Chọn C
Từ đồ thị ta thấy
f x
=1. Đặt
3
2 1 1g x m f x mf x f x
.
3
1 2 1 1 0, *x m f x mf x f x x
Từ giả thiết ta có điều kiện cần để có
*
là
3 3
0
1 0 1 1 1 1 0 0
1
m
g m f mf f m m
m
Điều kiện đủ:
3
f(x)
-∞
+∞
0
+∞
2
-1
+∞
x
-1
f(
x
)
0
3
2
-∞
+∞
+
∞
-2
-1
+∞
x
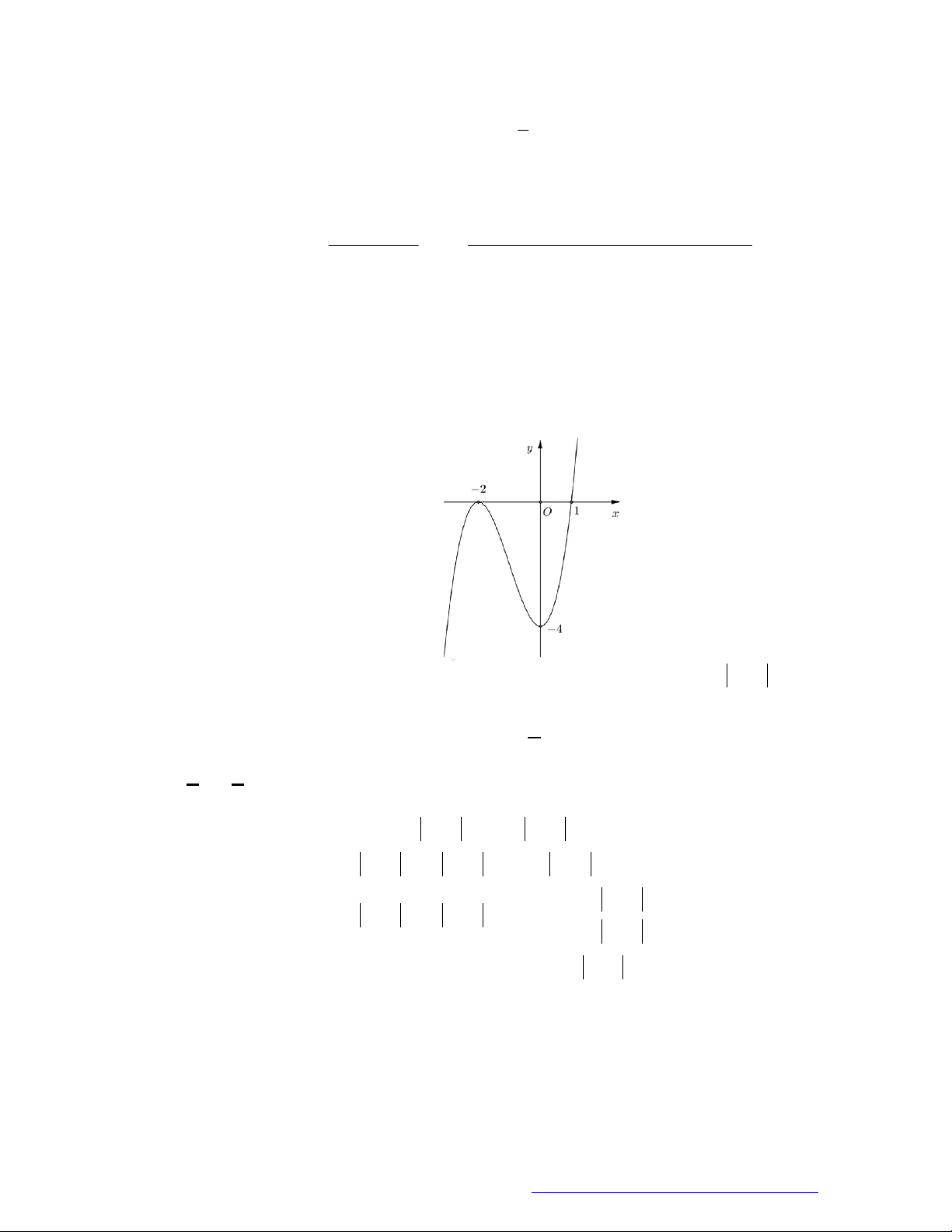
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 29
+)Với
0m
ta có
* 1 1 0g x x f x
đúng với mọi
x
.
Do đó
0m
thỏa mãn.
+)Với
1m
ta có
1
1 2 1 1 2 1 1 2 1 1 0
2
x f x x f x x
. Do đó
1m
thỏa mãn.
+) Với
1m
,
* 1 2 1 2 1 0 **x f x f x
.
Xét
1x
ta có
3 2
3 2
2 1 1 2 1 2 1 2 1 1
lim lim 4 0
2
2
x x
f x a x b x c x d
f x
ax bx cx d
, 1: 2 1 1 2α α f α f α
hay
2 2 1 1 0f α f α
1 2 2 1 1 0α f α f α
( không thỏa mãn
**
).
Do đó
1m
không thỏa mãn
Vậy
S
có
2
phần tử.
Câu 36. Cho hàm số
3 2
y f x ax bx cx d
có đồ thị như hình bên dưới
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
2
5 4 4 0f x m f x m
có
7
nghiệm phân biệt?
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn C
Phương trình tương đương với
2
5 4 4 0
4 1 4 0
4 1
4 1 0 .
1 2
f x f x m f x
f x f x m f x
f x
f x f x m
f x m
Từ đồ thị hàm số
y f x
, ta suy ra đồ thị hàm số
y f x
như sau
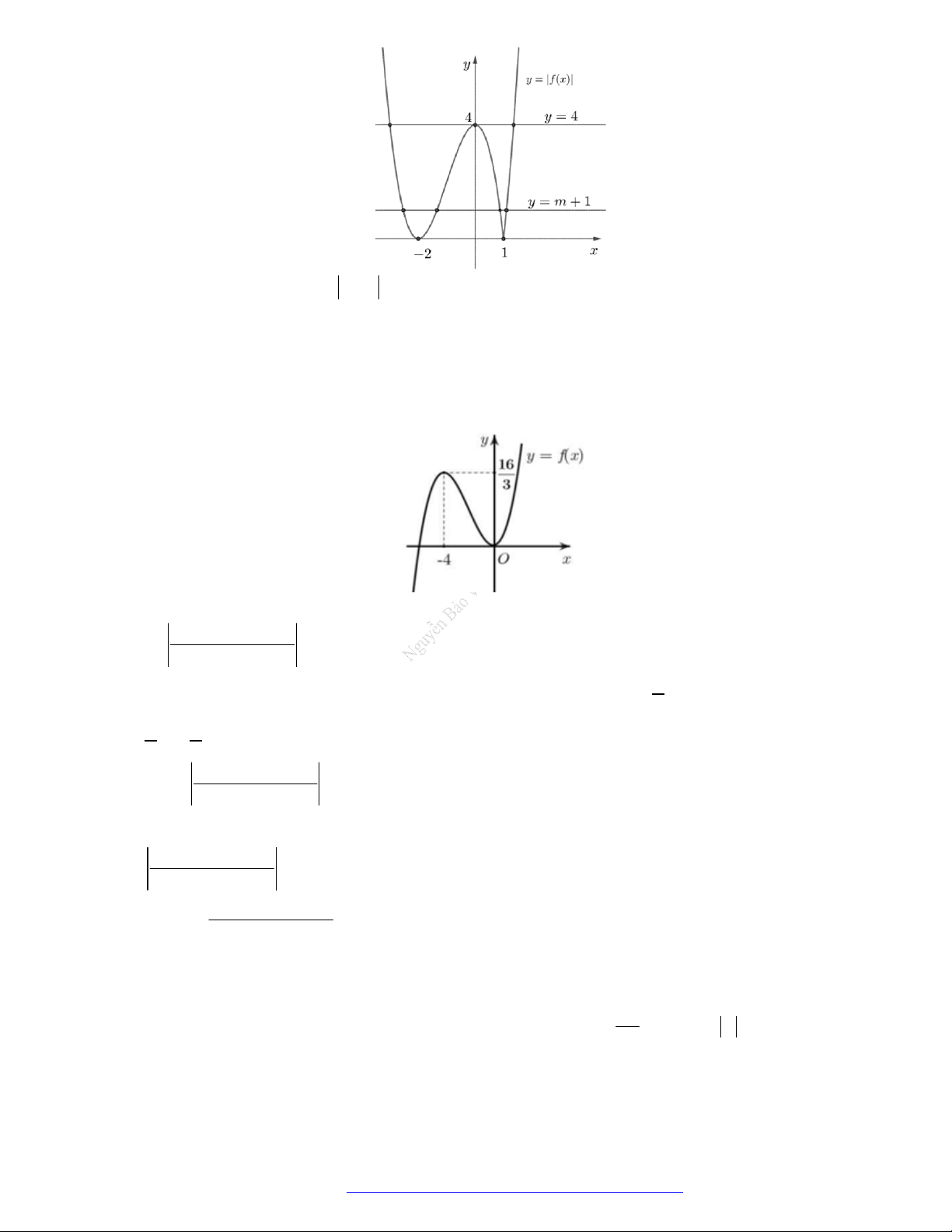
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 30 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Dựa vào đồ thị hàm số
y f x
, suy ra phương trình
1
luôn có
3
nghiệm phân biệt.
Vì vậy, yêu cầu bài toán tương đương với phương trình
2
có
4
nghiệm phân biệt khác
4
.
Suy ra
0 1 4 1 3 0, 1, 2.m m m
Vậy có
3
giá trị nguyên của tham số
m
thỏa bài toán.
Câu 37. Cho hàm số
y f x
liên tục trên
và có đồ thị như hình vẽ
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
2
3sin cos 1
4 4
2cos sin 4
x x
f f m m
x x
có nghiệm.
A.
4
. B.
5
. C. Vô số. D.
3
.
Lời giải
Chọn D
Ta có
3sin cos 1
0
2cos sin 4
x x
x x
,
x
và
2
2
4 4 2 0m m m
,
m
. Nhìn vào đồ thị hàm số
y f x
ta thấy hàm số đã cho đồng biến trên
0;
suy ra phương trình đã cho tương đương
2
3sin cos 1
4 4 1
2cos sin 4
x x
m m
x x
Đặt
3sin cos 1
*
2cos sin 4
x x
P
x x
vì
2cos sin 4 0x x
,
x
nên
* 3 sin 1 2 cos 4 1 2P x P x P
Phương trình
2
có nghiệm
2 2 2
9
4 1 3 1 2 1 1
11
P P P P P
Suy ra phương trình
1
có nghiệm
2
4 4 1 3; 1m m m
Có ba giá trị nguyên của
m
thỏa mãn bài toán.
Câu 38. Cho hàm số
( )y f x
liên tục trên R và có đồ thị như hình bên.
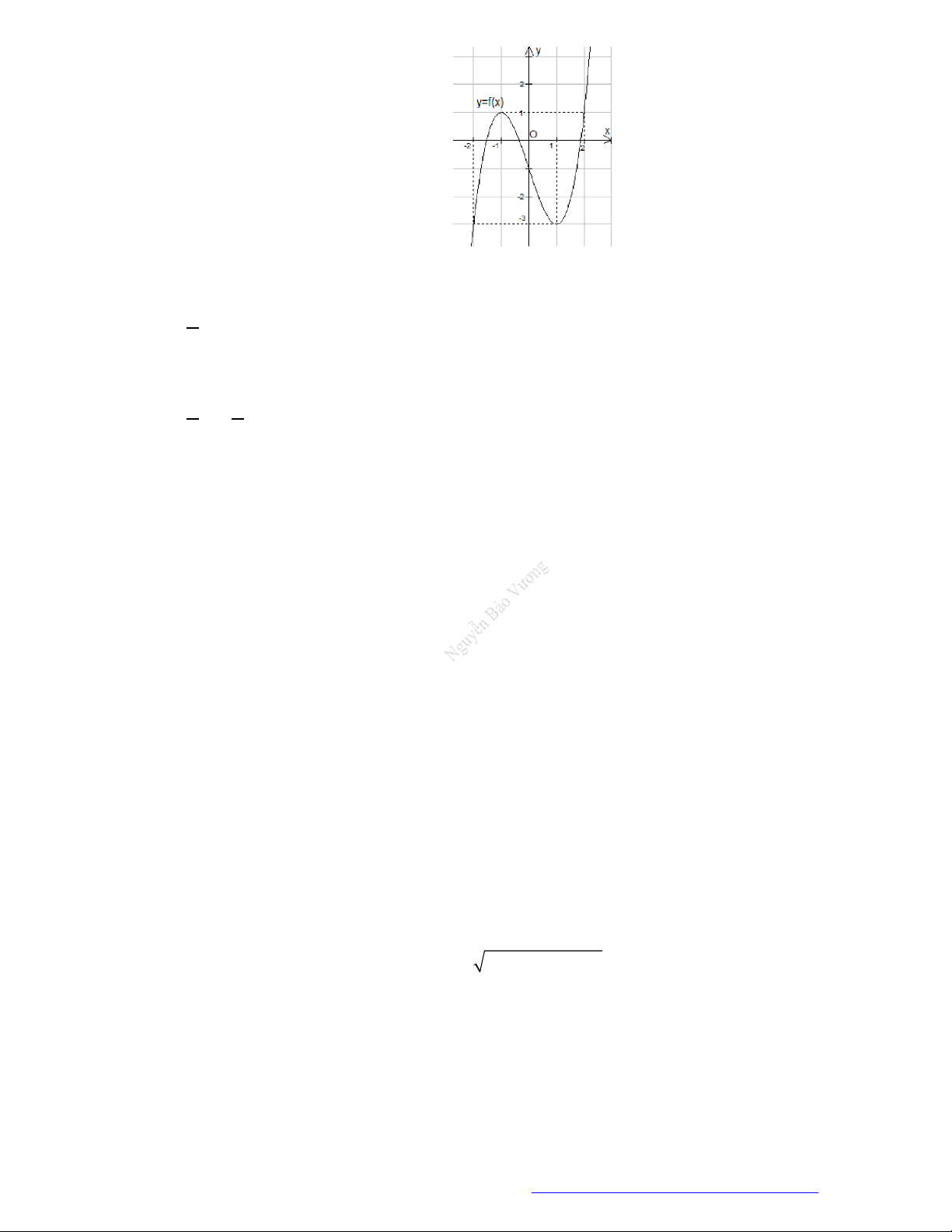
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 31
Phương trình
(2sin )f x m
có đúng ba nghiệm phân biệt thuộc đoạn
;
khi và chỉ khi
A.
3;1 .m
. B.
3;1 .m
.
C.
3;1 .m
. D.
3;1 .m
Lời giải
Chọn A
Đặt
2sint x
(*),
; 2;2 .x t
Khi đó phương trình
(2sin )f x m
trở thành
( )f t m
(1). Số nghiệm của PT(1) bằng số giao
điểm của đồ thị hàm số
( )y f t
và đường thẳng
y m
.
Nhận thấy:
Với
2;2t
thì PT(*) có 1 nghiệm
;x
.
Với
0t
thì PT(*) có 3 nghiệm phân biệt
;x
.
Với
2;2 \ 0t
thì PT(*) có 2 nghiệm phân biệt
;x
.
Do đó, dựa vào đồ thị đã cho ta có:
+) TH 1:
3m
thì phương trình
(1)
có một nghiệm
2t
. Suy ra
3m
bị loại
+) TH 2:
3m
thì PT(1) có hai nghiệm là
1t
và
2t
. Suy ra
3m
là giá trị thỏa mãn.
+) TH 3:
3 1m
thì phương trình
(1)
có ba nghiệm phân biệt thuộc khoảng
( 2;2)
. Suy
ra
3 1m
bị loại.
+) TH 4: Xét trường hợp
1m
thì PT(1) có hai nghiệm là
1t
và
2t
. Suy ra
1m
là giá trị
thỏa mãn.
+) TH 5:
1m
thì phương trình
(1)
có một nghiệm
2t
. Do đó
1m
bị loại.
Vậy các giá trị
m
cần tìm là
3;1 .m
Chọn. A.
Câu 39. Cho hàm số
y f x
xác định và liên tục trên
và có đồ thị như hình vẽ. Có bao nhiêu giá trị
nguyên của m để phương trình
2
302. 3 3 9 2021 19xf x m
có nghiệm.
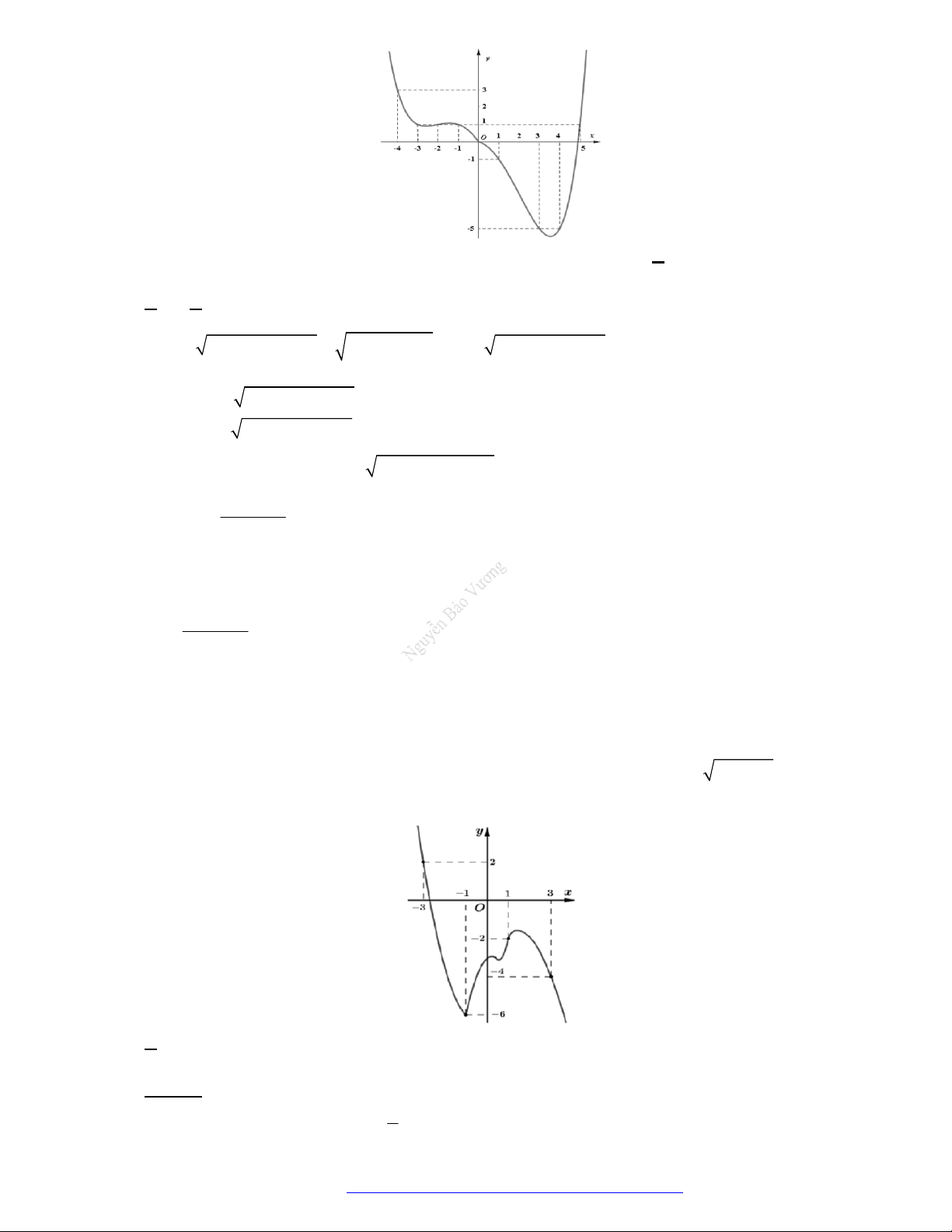
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 32 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
15
. B.
14
. C.
10
. D.
13
.
Lời giải
Chọn D
Ta có:
2
2 2
9 4 3 530 21 30 20 9 1 2x x xx x
2
30 213 3 3 9 3.x x
Đặt
2
3 3 9 ;32 3 .30 1xt x t
Khi đó, phương trình
2
302. 3 3 9 2019 121 xf x m
2 2019f t m
2019
2
2
m
f t
Phương trình
1
có nghiệm khi và chỉ khi phương trình
2
có nghiệm
3;3 .t
Dựa vào đồ thị hàm số
y f x
ta có, phương trình
2
có nghiệm
3;3t
khi và chỉ khi
2019
5 1 10 2019 2 2009 2021
2
m
m m
Vì
m
nên
2009,2010,...,2021m
. Vậy có
13
giá trị
m
nguyên thỏa mãn yêu cầu bài
toán.
Câu 40. (Thi thử cụm Vũng Tàu - 2019) Cho hàm số
y f x
xác định, liên tục trên
và có đồ thị
như hình vẽ bên. Có bao nhiêu giá trị nguyên của
m
để phương trình
2
2 3 4 6 9 3f x x m
có nghiệm.
A.
9
. B.
17
. C.
6
. D.
5
.
Lời giải
Chọn A
Điều kiện:
2
2
6 9 0 0
3
x x x
.
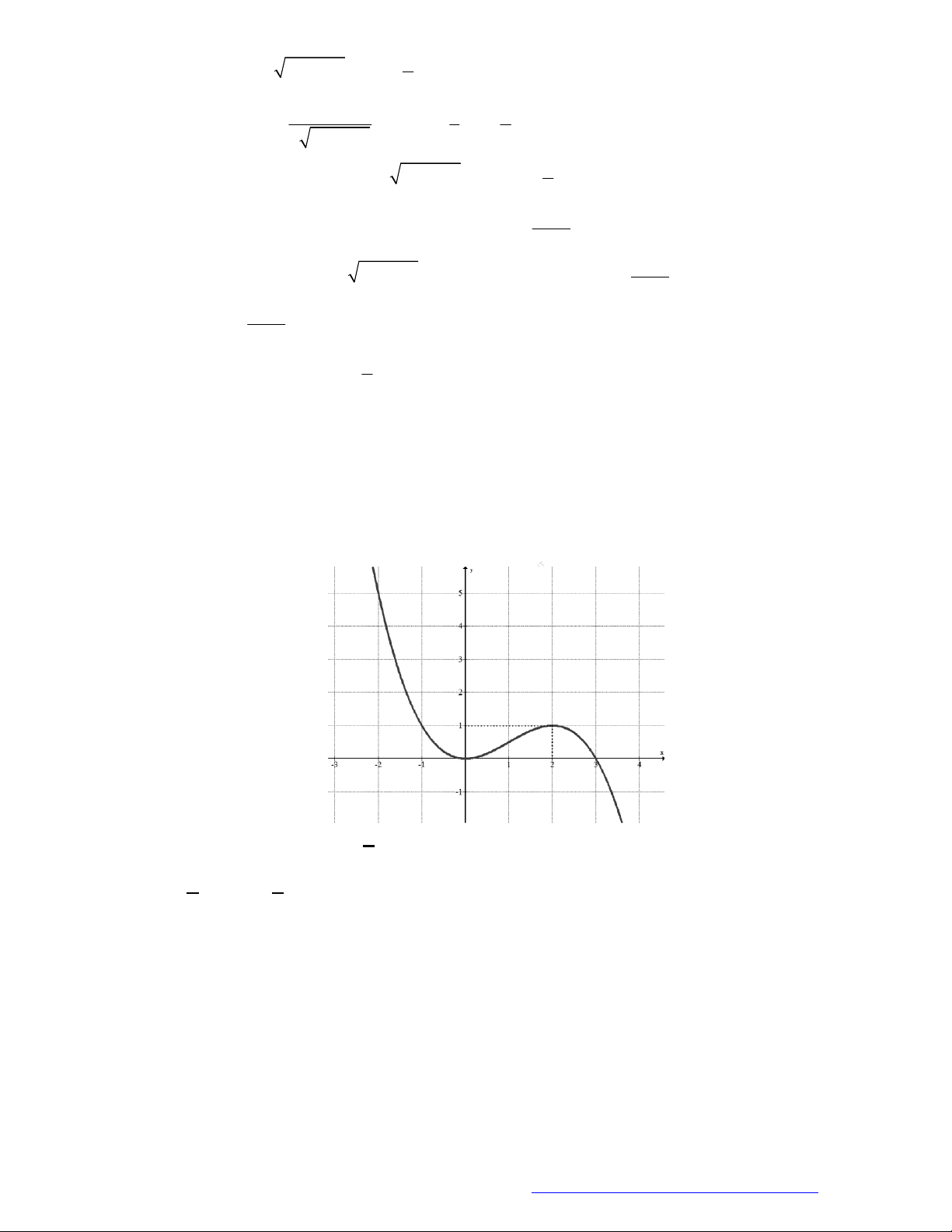
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 33
Đặt
2
2
3 4 6 9 , 0;
3
t x x x
.
Ta có:
2
6 18 1 2
4. 0 0;
3 3
2 6 9
x
t x
x x
.
Bảng biến thiên cho
2
3 4 6 9t x x
.Vì
2
0; 1;3
3
x t
Phương trình trở thành:
3
2 3 , 1;3 . *
2
m
f t m f t t
Phương trình
2
2 3 4 6 9 3f x x m
có nghiệm
3
2
m
f t
có nghiệm
1;3t
3
6 2 12 3 4 2 9 1 2 ,
2
m
a m a m a
với
1;3
1
max 2, 0;
2
f t a a
.
Mà
9; 8; 7;..; 1m m
có 9 giá trị
m
nguyên thỏa ycbt.
Câu 41. (SGD Điện Biên - 2019) Cho hàm số
4 3 2
y f x ax bx cx dx e
với
, , , ,a b c d e
.
Biết hàm số
y f x
có đồ thị như hình vẽ, đạt cực trị tại điểm
0;0O
và cắt trục hoành tại
3;0A
. Có bao nhiêu giá trị nguyên của
m
trên
5;5
để phương trình
2
2f x x m e
có
bốn nghiệm phân biệt.
A.
0
. B.
2
. C.
5
. D.
7
.
Lời giải
Chọn B.
Theo hình vẽ ta có
y f x
là hàm số bậc ba nên
0a
.
3 2
4 3 2f x ax b x cx d
2
12 6 2f x ax bx c
.
Theo giả thiết, ta có:
0 0
0
4
3 0 108 27 6 0
0
0
0 0
f
d
b a
f a b c d
c d
c
f
.
4 3
4f x ax ax e
.
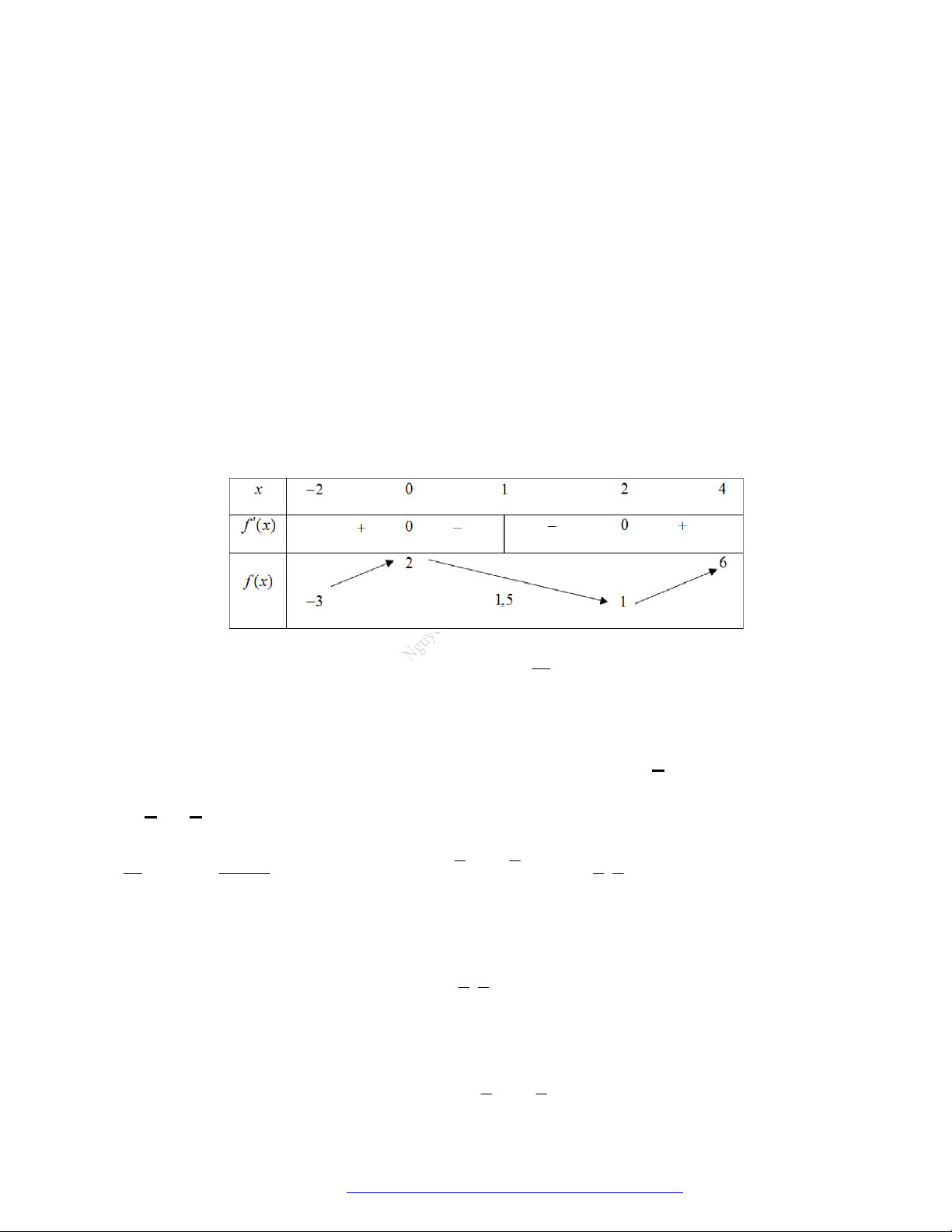
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 34 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
4 3
0
4 0
4
x
f x e ax ax
x
.
Khi đó
2
2 1f x x m e
2
2
2 2
1 1
2 0
2 4
1 3
x m
x x m
x x m
x m
PT
1
có bốn nghiệm phân biệt
1 0
3 0 3
1 3
m
m m
m m
.
Mà
5;5 4;5m m
.
Vậy có
2
giá trị
m
thỏa đề bài.
Câu 42. Cho hàm số
y f x
liên tục và có đạo hàm trên đoạn
2; 4
và có bảng biến thiên như sau
Có bao nhiêu giá trị nguyên của tham số
m
để hệ phương trình
2
3
9
4 0
6 2 1 8 6 0
x
f x x x m
có ba
nghiệm phân biệt?
A.
9
. B.
11
. C.
10
. D.
8
.
Lời giải
Chọn D
Ta có:
2
2
2 2
3 3
9 4 0
9 9 4 3 3
4 0 0 ; \ 0
2 2
2 2
0
0
x
x
x
x
x x
x
x
.
Xét phương trình
3 3
6 2 1 8 6 0 6 2 1 8 6 f x x x m m f x x x
(1)
Xét hàm số
3
6 2 1 8 6 g x f x x x
, với
3 3
; \ 0
2 2
x
.
Ta có
2 2
12 2 1 24 6 6 2 2 1 4 1
g x f x x f x x
Từ giả thiết ta suy ra
2 1 2
1 1
2 1 0
2 1 0
2 2
x
f x x
x
;
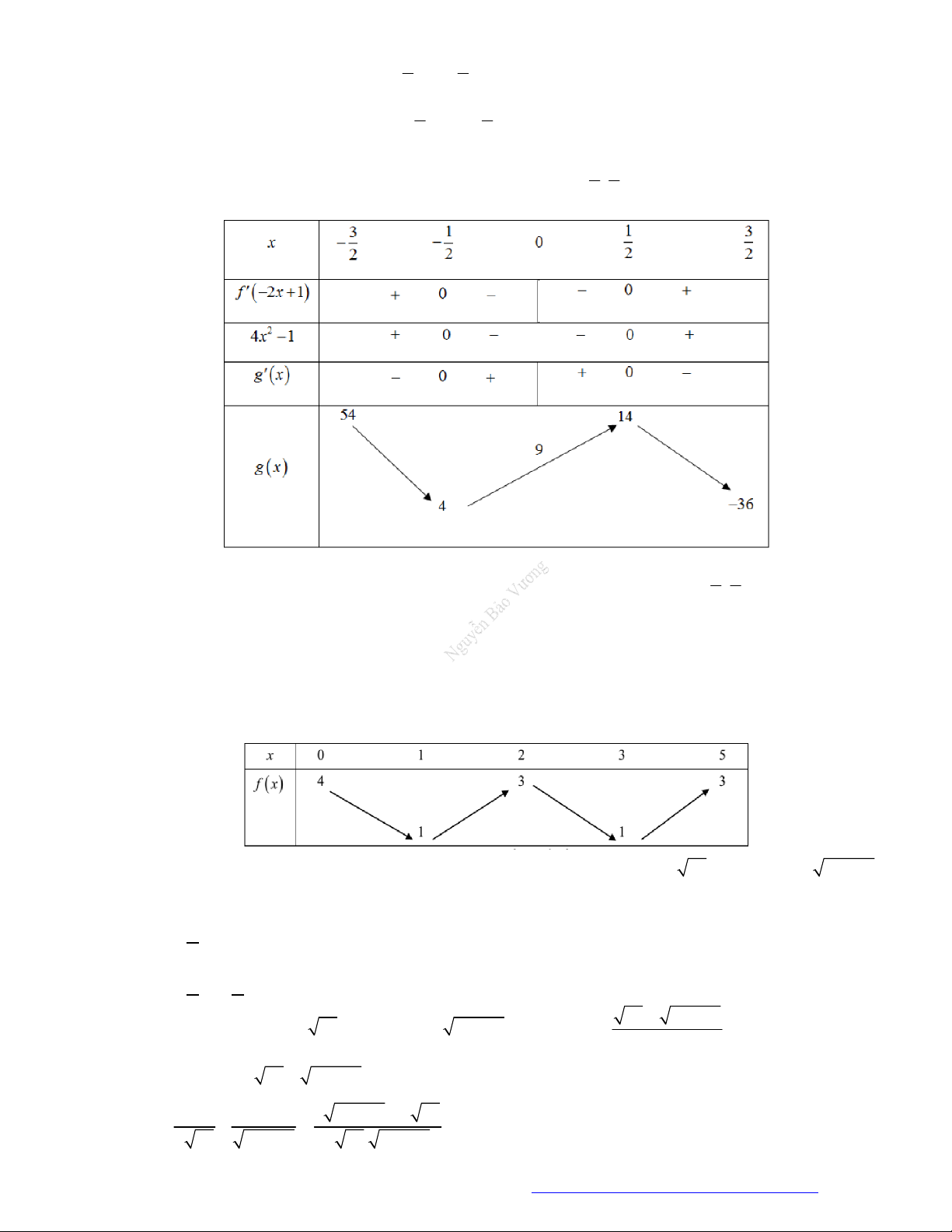
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 35
1 3
2 2 1 0
2 2
2 1 0
2 2 1 4 3 1
2 2
x
x
f x
x
x
.
Bảng biến thiên của hàm số
3
6 2 1 8 6 g x f x x x
trên
3 3
; \ 0
2 2
.
Từ bảng biến thiên ta suy ra hệ có đúng ba nghiệm (1) có đúng ba nghiệm
3 3
; \ 0
2 2
x
4 14
9
m
m
. Vì
5;6;7;8;10;11;12;13 m m
. Vậy có
8
số nguyên
m
.
Câu 43. (Hậu Lộc 2-Thanh Hóa 2019) Cho hàm số
y f x
liên tục trên đoạn
0 5;
và có bảng biến
thiên như hình sau:
Có bao nhiêu giá trị nguyên dương của tham số
m
để bất phương trình
3 2019 10 2mf x x f x x
nghiệm đúng với mọi
0 5x ; .
A. 2014. B. 2015. C. 2019. D. Vô số.
Lời giải
Chọn A
Trên
0 5;
, ta có:
3 10 2
3 2019 10 2 2019
x x
mf x x f x x m .
f x
Xét hàm số
3 10 2g x x x
trên đoạn
0 5; .
3 1 3 10 2 2 3
2 3 10 2 2 3 10 2
x x
g x
x x x. x

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 36 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Cho
0 3 0 5g x x ; .
Do
0 10g
,
3 5g
và
5 15g
nên
0 5
3 5
;
max g x g .
Mặt khác
0 5
3 1
;
min f x f
nên
3 10 2
2019
x x
m
f x
,
0 5x ;
0 5
3 10 2 5
2019 2019 2014
1
;
x x
m min .
f x
Câu 44. (Hậu Lộc 2-Thanh Hóa -2019) Cho hàm số
y f x
liên tục trên
và có đồ thị như hình vẽ
bên. Số giá trị nguyên của tham số
m
để phương trình
2
2018 2019 0f cosx m f cosx m
có đúng 6 nghiệm phân biệt thuộc đoạn
0 2;
là
A. 5. B. 3. C. 2. D. 1.
Lời giải
Chọn C
Ta có
2
2018 2019 0f cosx m f cosx m
1
2019
f cosx
f cosx m.
Dựa vào đồ thị ta có:
0 1
1
1 2
cos x
f cos x
cos x k
PT có 2 nghiệm thỏa mãn, PT vô nghiệm.
Yêu cầu: phương trình
2019 2019 1f cosx m m
có thêm 4 nghiệm thuộc
0 2; .
Nhận xét:
+ Với mỗi
1 1t ;
, phương trình cosx=t vô nghiệm.
+ Với mỗi
1 1t ;
, phương trình cosx=t có 2 nghiệm
0 2x ; .
+ Với
1t
, phương trình cosx t có đúng 1 nghiệm
0 2x ; .
Như vậy,
1 2019 1 2018 2020m m
.
Câu 45. (THPT Gia Lộc Hải Dương 2019) Cho hàm số
y f x
có bảng biến thiên như sau
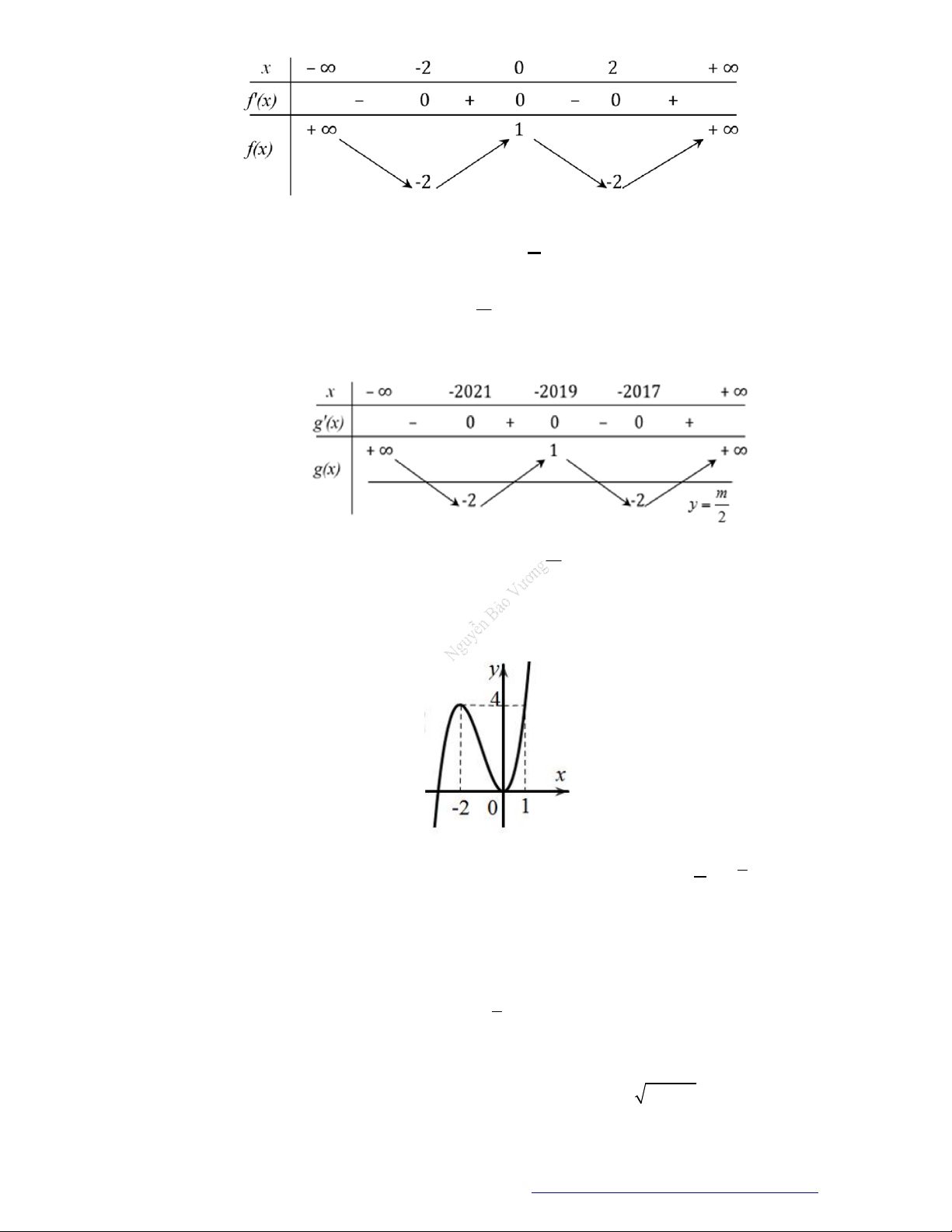
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 37
Tìm
m
để phương trình
2 2019 0 f x m
có
4
nghiệm phân biệt.
A.
0;2m
. B.
2;2 m
. C.
4;2 m
. D.
2;1 m
.
Lời giải
2 2019 0 f x m
2019
2
m
f x
*
.
Ta có bảng biến thiên của hàm số
2019y g x f x
như sau:
Phương trình
*
có
4
nghiệm phân biệt khi
2 1
2
m
4 2 m
.
Câu 46. Cho hàm số
y f x
liên tục trên
R
và có đồ thị như hình vẽ dưới đây. Tập hợp tất cả các giá trị
thực của tham số
m
để phương trình
2
2 2 3 1f x x m
có nghiệm thuộc khoảng
0;1 .
.
A.
0;4
. B.
1;0
. C.
0;1
. D.
1
;1
3
Lời giải
Đặt
2
2 2t x x
. Với
0;1 2;1x t
Phương trình
2
2 2 3 1f x x m
có nghiệm thuộc đoạn
0;1
khi và chỉ khi phương trình
3 1f t m
có nghiệm thuộc
1
2;1 1
3
m
.
Câu 47. (THPT Lê Quý Đôn Đà Nẵng 2019) Cho hàm số
y f x
liên tục trên
và có đồ thị như hình
vẽ. Tập hợp các giá trị thực của tham số
m
để phương trình
2
4 1f x x m
có nghiệm là
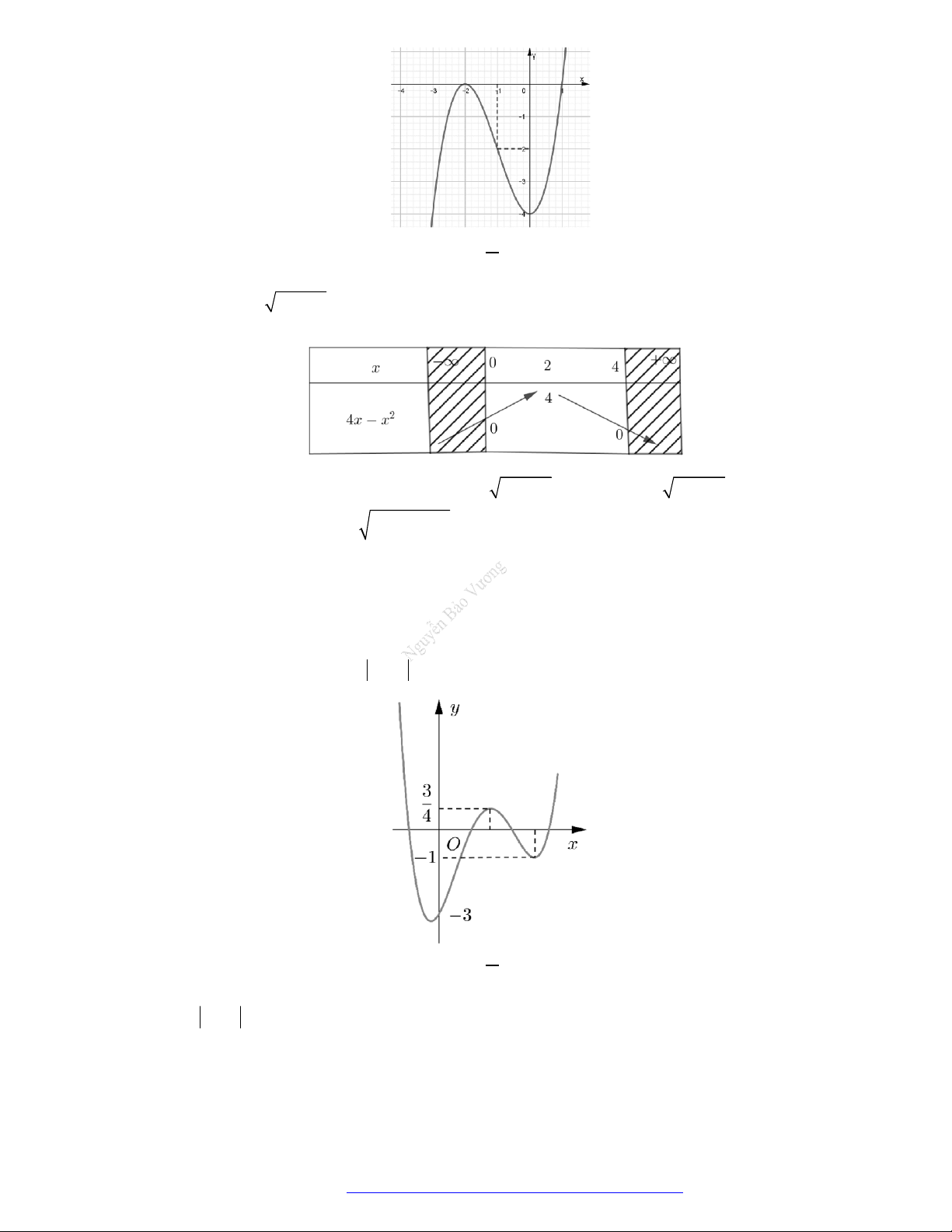
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 38 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
2;0
. B.
4; 2
. C.
4;0
. D.
1;1
.
Lời giải
Phương trình
2
4 1f x x m
có điều kiện
0 4x
. Ta có bảng biến thiên
Từ bảng biến thiên suy ra, với
0 4x
thì
2
1 4 1 1x x
. Đặt
2
4 1t x x
,
1 1t
.(Có thể biến đổi
2
4 2 1t x
1 1t
).
Phương trình đã cho trở thành
f t m
(1). Phương trình đã cho có nghiệm (1) có nghiệm
1;1t
4 0m
.
Câu 48. (Sở Hà Nội 2019) Cho hàm số bậc bốn
y f x
có đồ thị như hình vẽ. Số giá trị nguyên của
tham số
m
để phương trình
f x m m
có
4
nghiệm phân biệt là
A.
2.
B. Vô số. C.
1.
D.
0.
Lời giải
Đặt
0t x m
Với
0t
x m
Với mỗi giá trị
0t
sẽ ứng với
2
giá trị
x
Ta có phương trình
: f t m
0t
*

TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 39
Để phương trình có
4
nghiệm phân biệt thì
*
có
2
nghiệm phân biệt dương
Từ đồ thị của hàm số
y f t
trên miền
0t
3
4
1
m
m
Vậy có 1 giá trị nguyên thỏa mãn
Câu 49. (Chuyen Phan Bội Châu 2019) Cho hàm số
( )y f x
liên tục trên
và có đồ thị như hình vẽ
dưới đây.
Tập hợp tất cả các giá trị thực của tham số m để phương trình
2
( 4 )f x m có nghiệm thuộc
nửa khoảng
[ 2 ; 3)
là:
A.
[-1;3]
. B.
[-1; ( 2)]f
. C.
(-1; ( 2)]f
. D.
(-1;3]
.
Lời giải
Đặt
2
( ) 4t g x x với
[- 2 ; 3)x
.
Suy ra:
2
'( )
4
x
g x
x
.
'( ) 0 0 [ 2 ;3)g x x
.
Ta có:
(0) 2g
,
( 2) 2g
,
( 3) 1g
.
Mà hàm số
( )g x
liên tục trên
[- 2 ; 3)
Suy ra,
(1;2]t
.
Từ đồ thị, phương trình
( )f t m
có nghiệm thuộc khoảng
(1;2]
khi
( 1;3]m
.
Câu 50. (Chuyên Dại Học Vinh 2019) Cho hàm số
y f x
có đồ thị như hình vẽ.
Có bao nhiêu số nguyên
m
để phương trình
1
1
3 2
x
f x m
có nghiệm thuộc đoạn
2;2
?
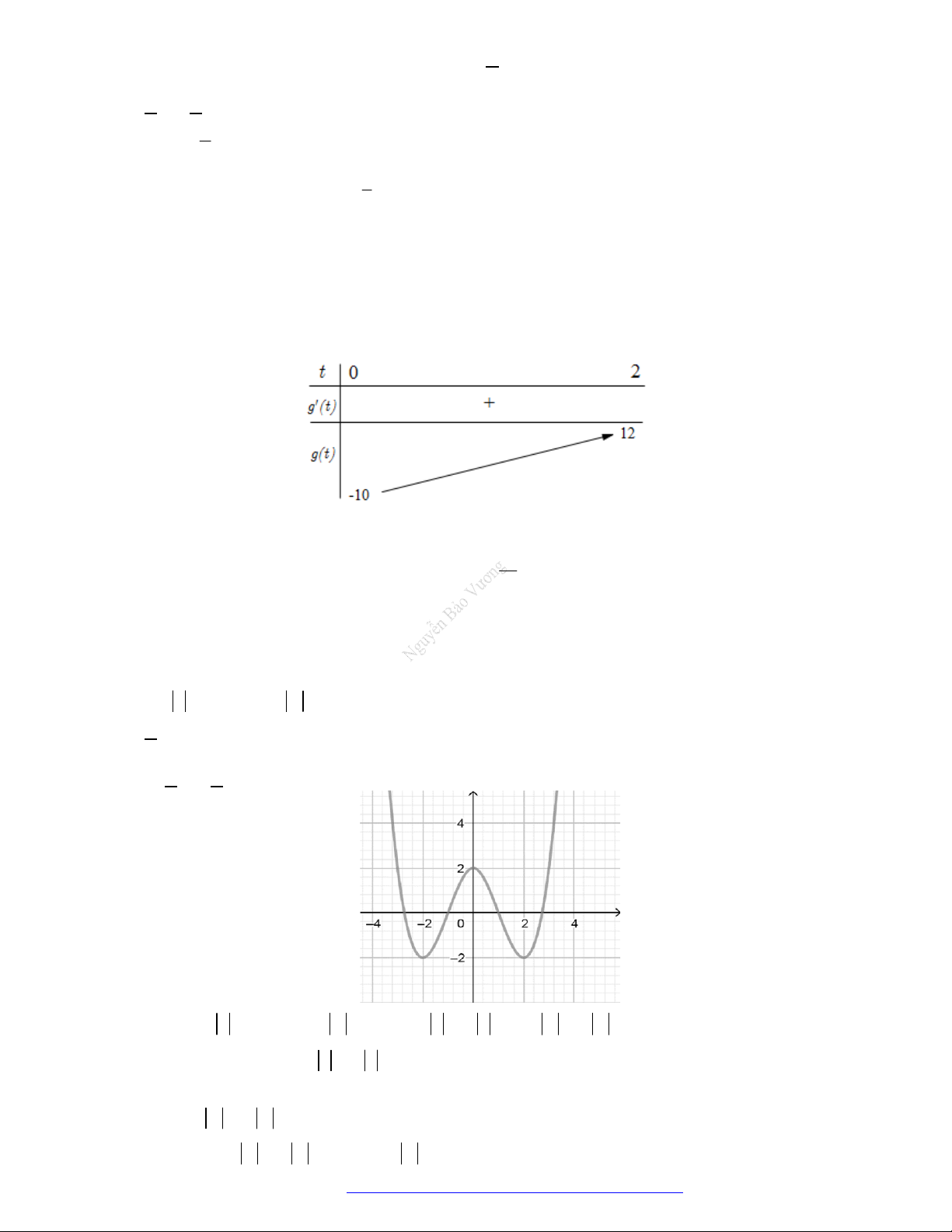
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 40 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
11
B.
9
C.
8
D.
10
Lời giải
Chọn C
Đặt
1
2
x
t
, khi
2 2x
thì
0 2t
.
Phương trình đã cho trở thành
1
2 2
3
f t t m
6 6 3f t t m
.
Xét hàm số
6 6g t f t t
trên đoạn
0;2
.
Ta có
6g t f t
. Từ đồ thị hàm số
y f x
suy ra hàm số
f t
đồng biến trên khoảng
0;2
nên
0, 0;2f t t
0, 0;2g t t
và
0 10g
;
2 12g
.
Bảng biến thiên của hàm số
g t
trên đoạn
0;2
Phương trình đã cho có nghiệm thuộc đoạn
2;2
khi và chỉ khi phương trình
3g t m
có
nghiệm thuộc đoạn
0;2
hay
10 3 12m
10
4
3
m
.
Mặt khác
m
nguyên nên
3; 2; 1;0;1;2;3;4m
.
Vậy có 8 giá trị
m
thoả mãn bài toán.
Câu 51. (THPT Thiệu Hóa – Thanh Hóa 2019) Có bao nhiêu số nguyên
m
để phương trình
2 2
3 2 3 0x x m m
có
4
nghiệm phân biệt.
A.
3
B.
12
C.
7T
D.
5
Lời giải
Chọn A
Ta có
3 2 3 2
2 2
3 2 3 0 3 2 3 *x x m m x x m m
Xét hàm số:
3 2
3 2y f x x x
có đồ thị như hình vẽ:
Từ đồ thị của hàm số ta có: Phương trình (*) có 4 nghiệm phân biệt
3 2
2 3 2m m
Mà
3 2
2
3 3m m m m m
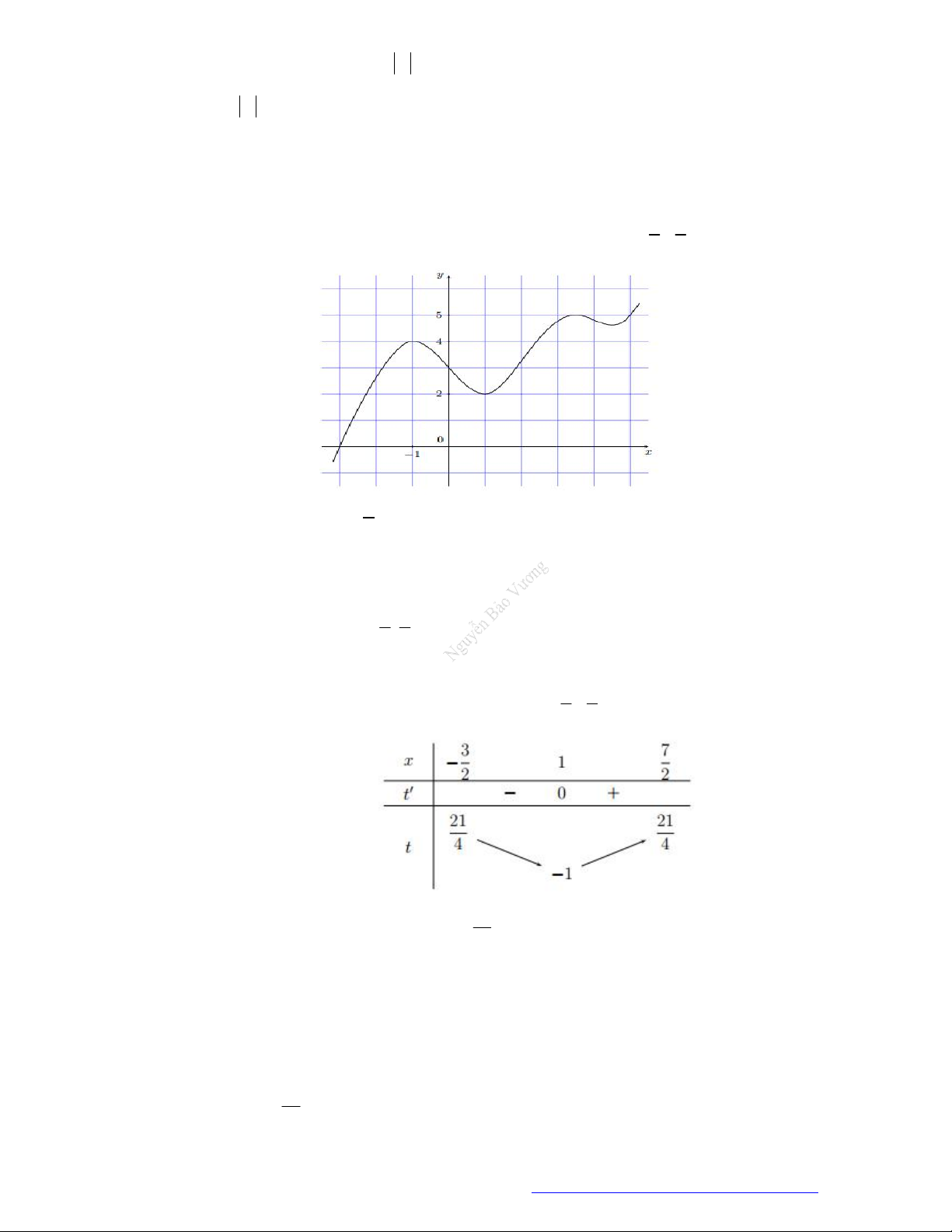
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 41
2
3
0
3
3 1;0;1
1
0
1
m
m
m
m m
m l
m
m l
Câu 52. Cho hàm số
y f x
có đồ thị như hình vẽ. Tìm số giá trị nguyên của
m
để phương trình
2
2f x x m
có đúng
4
nghiệm thực phân biệt thuộc đoạn
3 7
;
2 2
.
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn B
Xét phương trình
2
2f x x m
1
Đặt
2
2t x x
, với
3 7
;
2 2
x
.
Ta có
2 2t x
;
' 0 1t x
.
Bảng biến thiên của hàm số
2
2t x x
trên đoạn
3 7
;
2 2
.
Dựa vào bảng biến thiên suy ra
21
1 ;
4
t
.
Xét
1t
khi đó phương trình
1
thành
1 4f m m
.
Với
4m
phương trình
2
2
2
2 1
2 4 *
2
x x
f x x
x x a
với
2 3a
.
Dễ thấy
*
có tối đa 3 nghiệm (không thỏa mãn yêu cầu).
Xét
0
21
1;
4
t
.
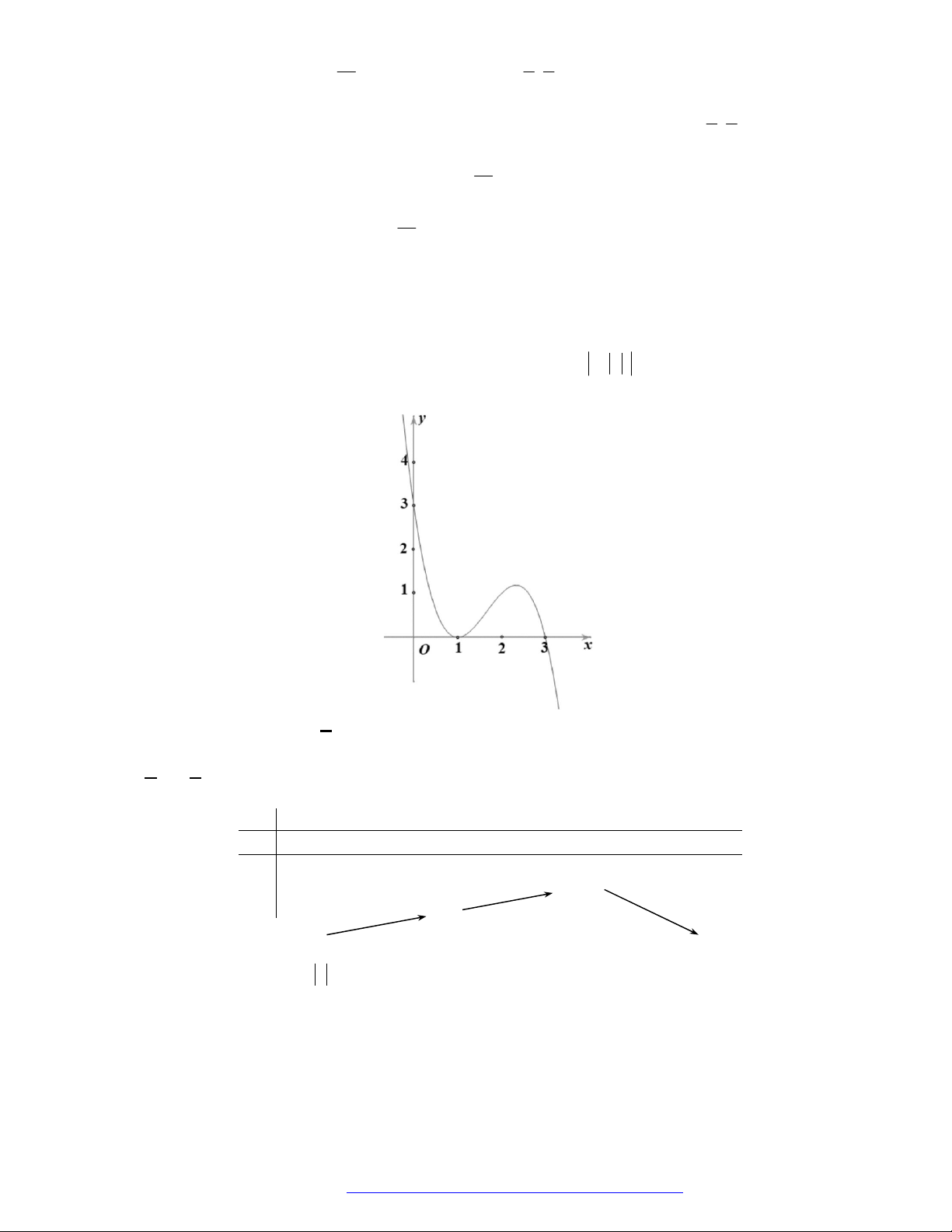
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 42 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Nhận xét với mỗi
0
21
1;
4
t
thì có 2 giá trị
3 7
;
2 2
x
thỏa mãn
2
0
2t x x
.
Do đó phương trình
2
2f x x m
có 4 nghiệm thực phân biệt thuộc đoạn
3 7
;
2 2
khi phương
trình
f t m
có 2 nghiệm phân biệt
21
1;
4
t
. Hay đường thẳng
y m
phải cắt đồ thị hàm
số
y f t
tại 2 điểm với
21
1;
4
t
.
Mà
m
nên từ đồ thị hàm số
y f x
ta có
3; 5m m
thỏa mãn yêu cầu.
KL: Có
2
giá trị nguyên của
m
thỏa mãn yêu cầu bài.
Câu 53. (Chuyên Lam Sơn Thanh Hóa 2019) Cho hàm số
( )y f x
có đạo hàm liên tục trên
. Biết
(0) 0f
và
f x
được cho như hình vẽ bên. Phương trình
( )f x m
( với
m
là tham số) có
nhiều nhất bao nhiêu nghiệm?
A.
8
B.
6
C.
2
D.
4
Lời giải
Chọn B
BBT của hàm số
( )y f x
BBT của hàm số
( )y f x
0
3
y
0
0
y
0
(3)
f
x
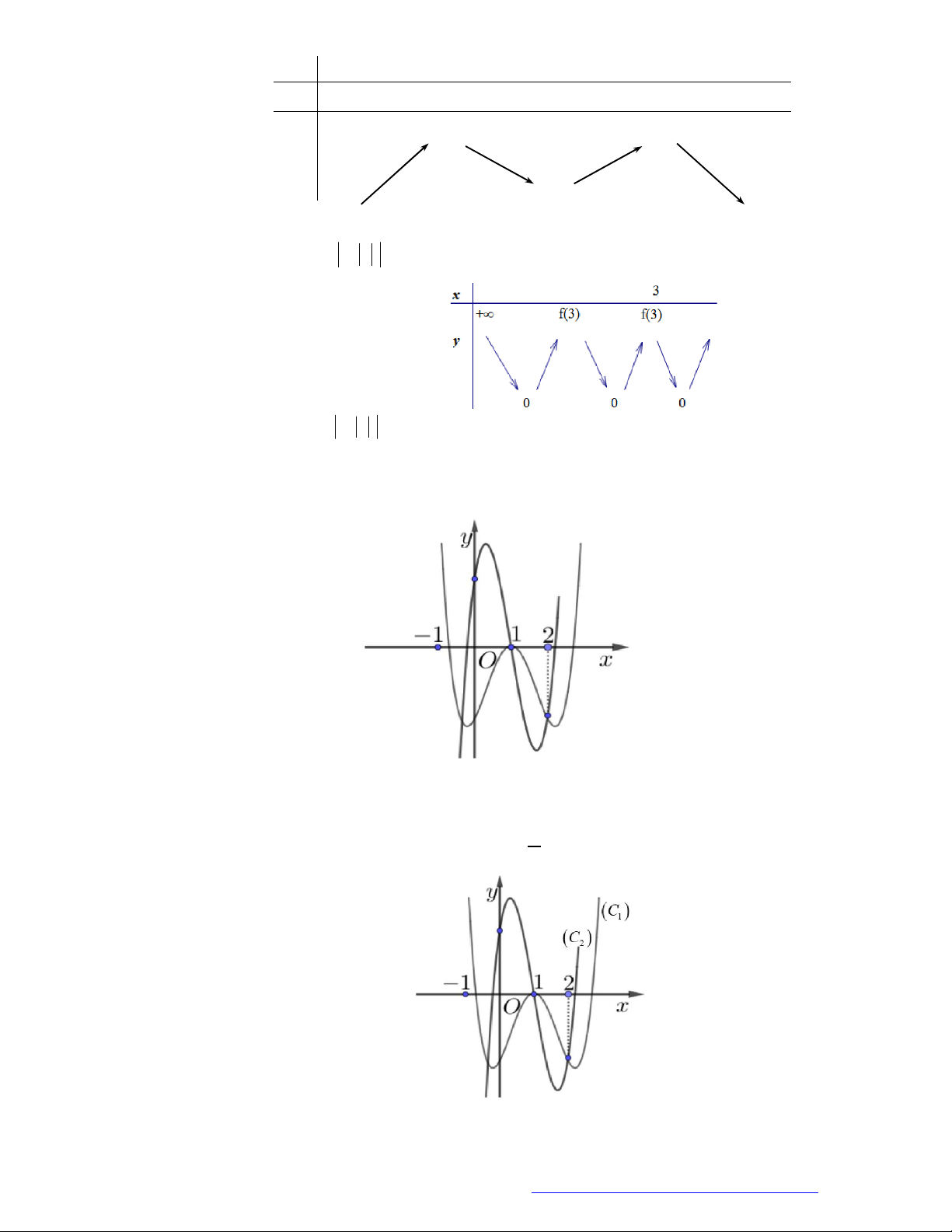
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 43
BBT của hàm số
( )y f x
Suy ra phương trình
( )f x m
có nhiều nhất là
6
nghiệm.
Câu 54. (Thanh Tường Nghệ An 2019) Cho hàm số
y f x
là hàm đa thức với hệ số thực. Hình vẽ
bên dưới là một phần đồ thị của hai hàm số:
y f x
và
y f x
.
Tập các giá trị của tham số
m
để phương trình
x
f x me
có hai nghiệm phân biệt trên
0;2
là
nửa khoảng
;a b
. Tổng
a b
gần nhất với giá trị nào sau đây?
A.
0.81
. B.
0.54
. C.
0.27
. D.
0.27
.
Lời giải
x
3
0
3
y
0
0
0
y
(3)
f
(3)
f
0
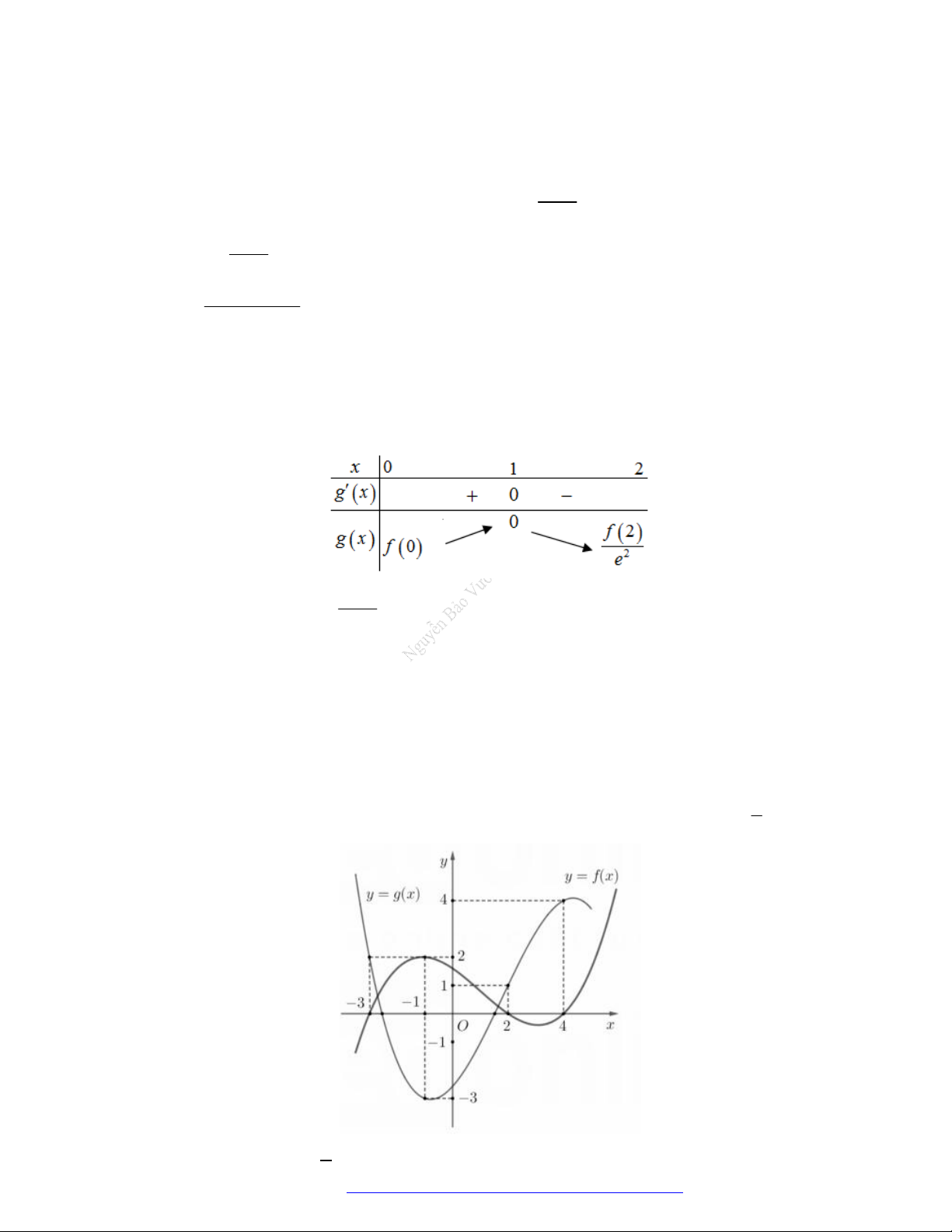
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 44 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Nhận xét: Đồ thị hàm
y f x
cắt trục hoành tại điểm
0
x thì
0
x là điểm cực trị của hàm
y f x
. Dựa vào hai đồ thị đề bài cho, thì
1
C
là đồ thị hàm
y f x
và
2
C
là đồ thị hàm
y f x
.
Xét phương trình hoành độ giao điểm của đồ thị hàm số
y f x
và
x
y me
ta có:
x
f x me
x
f x
m
e
.
Đặt
x
f x
g x
e
ta có:
x
f x f x
g x
e
.
0
1
0 2
1;0
x
g x f x f x x
x x
.
Dựa vào đồ thị của hai hàm số:
y f x
và
y f x
ta được:
Yêu cầu bài toán ta suy ra:
2
2
0
f
m
e
(dựa vào đồ thị ta nhận thấy
0 2 2 f f
)
0,27 0 m
.
Suy ra:
0,27, 0 a b
.
Vậy
0,27 a b
.
Câu 55. (VTED 2019) Cho hai hàm số
y f x
và
y g x
là các hàm xác định và liên tục trên
và
có đồ thị như hình vẽ bên (trong đó đường cong đậm hơn là đồ thị của hàm số
y f x
). Có bao
nhiêu số nguyên
m
để phương trình
1 2 1f g x m
có nghiệm thuộc đoạn
5
1;
2
.
A.
8
B.
3
C.
6
D.
4
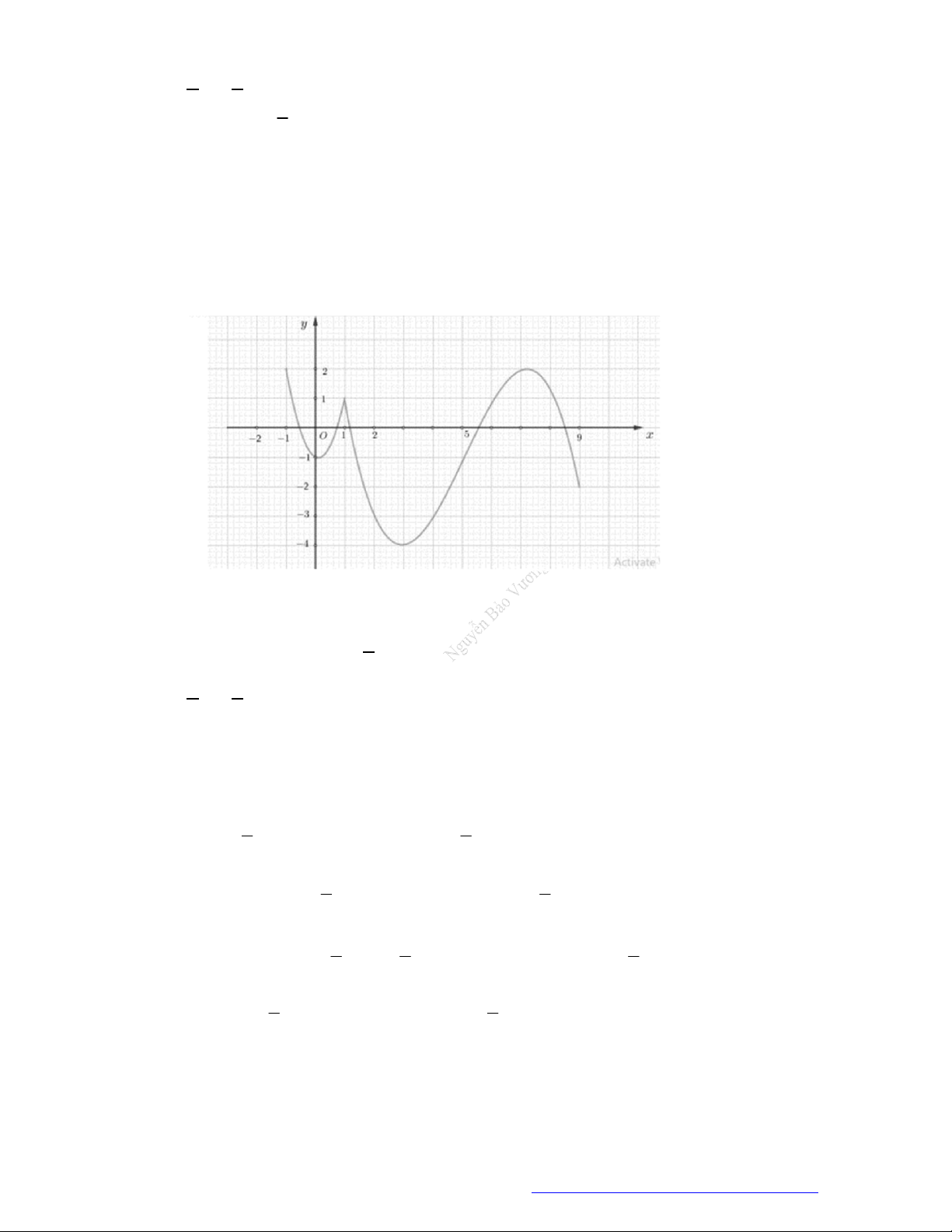
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 45
Lời giải
Chọn B
Với
5
1; 2 1 3;4 2 1 3;4 1 2 1 3;4
2
x x g x t g x
Vậy ta cần tìm
m
để phương trình
f t m
có nghiệm thuộc đoạn
3;4
3;4 3;4
3;4
min max min 2f t m f t f t m
trong đó
3;4
min 1;0f t
. Vậy các số
nguyên cần tìm là
0,1,2a
Câu 56. (THPT Yên Khánh A - Ninh Bình - 2019) Cho hàm số
y f x
liên tục trên đoạn
1;9
và
có đồ thị là đường cong trong hình vẽ dưới đây
Có bao nhiêu giá trị nguyên của tham số
m
để bất phương trình
2 2
16.3 2 8 .4 3 .6
f x f x f x
f x f x m m
nghiệm đúng với mọi giá trị thuộc
1;9
?
A.
32
. B.
31
. C.
5.
D.
6
.
Lời giải
Chọn B
Dễ thấy
4 2, 1;9f x x
(1) nên
4 . 2 0, 1;9f x f x x
.
Do đó
2
2 8 0, 1;9f x f x x
(2).
Ta có
2 2
16.3 2 8 .4 3 .6
f x f x f x
f x f x m m
nghiệm đúng với mọi
1;9x
2 2
1 2
16. 2 8 . 3
2 3
f x f x
f x f x m m
nghiệm đúng với mọi
1;9x
2 2
1; 9
1 2
min 16. 2 8 . 3
2 3
f x f x
x
f x f x m m
(3).
Từ (1) và (2) ta có
2
1 1
2 2
f x
và
2
2
2 8 . 0, 1; 9
3
f x
f x f x x
.
Suy ra
2
1 2
16. 2 8 . 4, 1; 9
2 3
f x f x
f x f x x
.
Dấu “=” xảy ra khi và chỉ khi
2 1 7 8 .f x x x a a
Do đó
4
và (3)
2
4 3 1 4m m m
. Vì
m
nguyên nên
1;0;1;2;3;4m
.
Câu 57. (THPT Yên Khánh A - Ninh Bình - 2019) Cho hàm số
y f x
liên tục trên
1;3
và có đồ
thị như hình vẽ.

NGUYỄN BẢO VƯƠNG - 0946798489
Trang 46 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Bất phương trình
1 7f x x x m
có nghiệm thuộc
1;3
khi và chỉ khi
A.
7m
. B.
7m
. C.
2 2 2m
. D.
2 2 2m
.
Lời giải
Chọn A
Bất phương trình
1 7f x x x m
có nghiệm thuộc
1;3
khi và chỉ khi
1;3
Max 1 7f xm x x
.
Xét hàm số
1 7g x x x
trên đoạn
1;3
.
Ta có
1 1 7 1
2 1 2 7 2 7 . 1
x x
g x
x x x x
.
0g x
7 1 0x x
3x
.
1 8 2 2g
,
3 2 2 4g
.
Suy ra
1;3
Max 4g x
tại
3x
. (1)
Mặt khác, dựa vào đồ thị của
f x
ta có
1;3
Max 3f x
tại
3x
.(2)
Từ (1) và (2) suy ra
1;3
ax 1M 7 7f x x x
tại
3x
.
Vậy bất phương trình đã cho có nghiệm thuộc
1;3
khi và chỉ khi
7m
.
Câu 58. (THPT Yên Khánh A - Ninh Bình - 2019) Cho hàm số
y f x
có đạo hàm liên tục trên đoạn
3;3
và đồ thị hàm số
y f x
như hình vẽ dưới đây
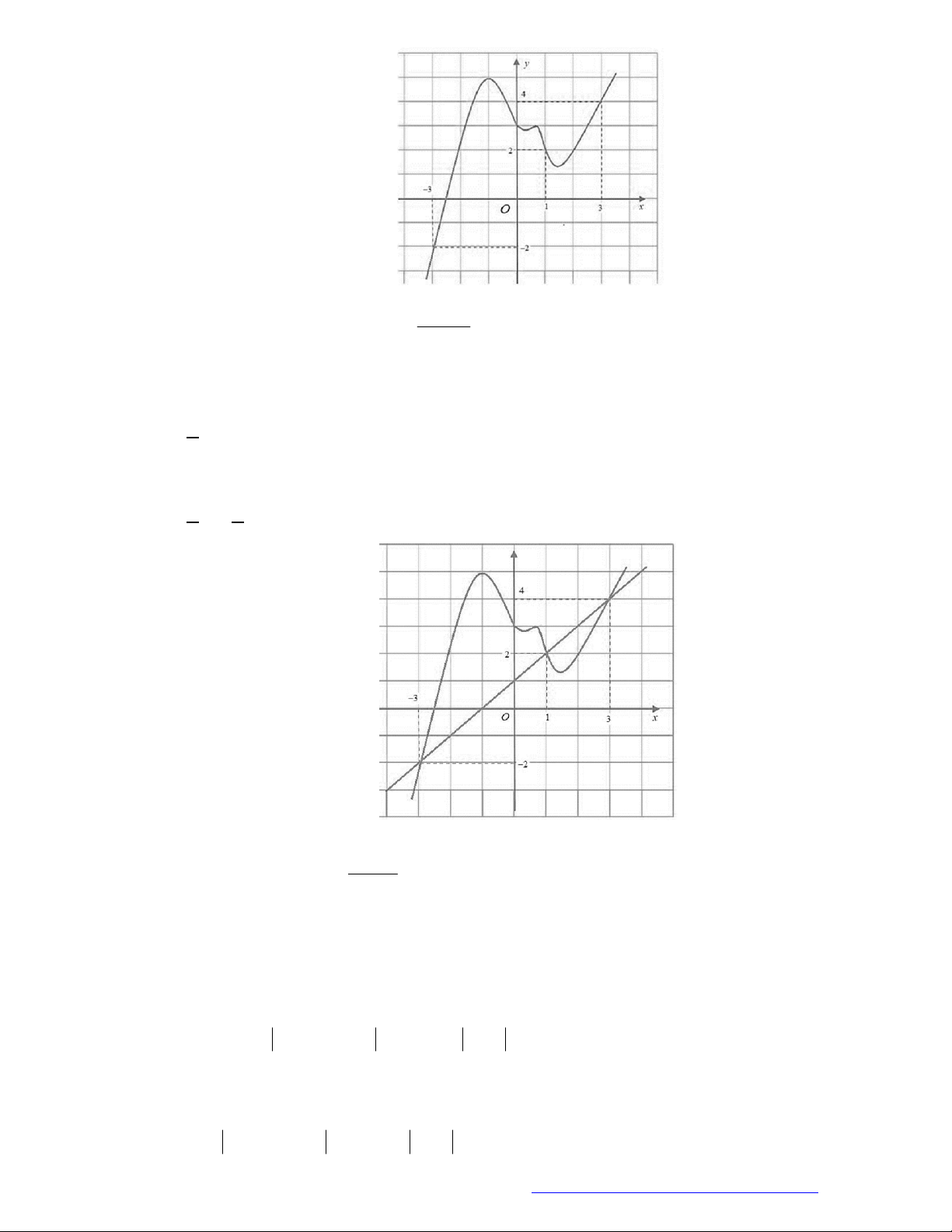
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 47
Biết
1 6f
và
2
1
2
x
g x f x . Mệnh đề nào sau đây là đúng?
A. Phương trình
0g x
có đúng hai nghiệm thuộc đoạn
3;3
.
B. Phương trình
0g x
không có nghiệm thuộc đoạn
3;3
.
C. Phương trình
0g x
có đúng một nghiệm thuộc đoạn
3;3
.
D. Phương trình
0g x
có đúng ba nghiệm thuộc đoạn
3;3
.
Lời giải
Chọn C
Ta có
2
1 1
1 1 1 2 4
2
g f f và
1
g x f x x
. Từ đồ thị hàm số
y f x
và
1 y x
ta có
3
0 1 1
3
x
g x f x x x
x
.
Xét hình phẳng giới hạn bởi đồ thị
; 1; 3; 1
y f x y x x x
có diện tích
1
4S
1 1
3 3
1 4 4 1 3 4 3 1 4 0
f x x dx g x dx g g g g
.
Xét hình phẳng giới hạn bởi đồ thị
; 1; 1; 3
y f x y x x x
có diện tích
2
4S
3 3
1 1
1 4 4 3 1 4 3 1 4 0
f x x dx g x dx g g g g
.
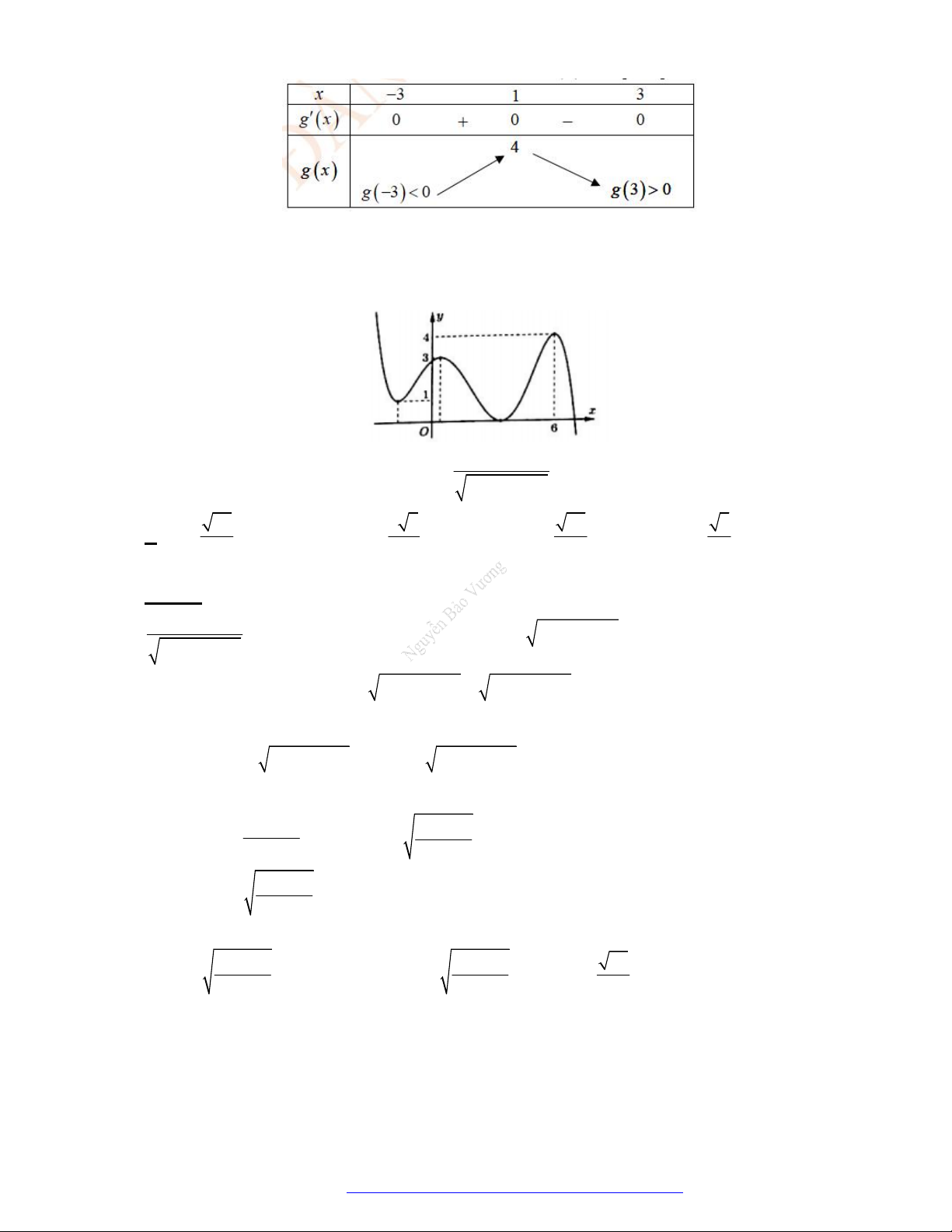
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 48 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Dựa vào đồ thị ta có bảng biến thiên của hàm
y g x
trên
3;3
Từ bảng biến thiên suy ra phương trình
0g x
có đúng một nghiệm thuộc đoạn
3;3
.
Câu 59. (Chuyên Sơn La - Lần 2 - 2019) Cho hàm số
y f x
liên tục trên
và có đồ thị như hình
vẽ.
Các giá trị của tham số
m
để phương trình
3
2
2
4
3
2 5
m m
f x
f x
có ba nghiệm phân biệt là
A.
37
2
m
. B.
3 3
2
m
. C.
37
2
m
. D.
3
2
m
.
Lời giải
Chọn A
3
2 3 2 2
2
3
2 2 2
4
3 4 3 2 5
2 5
2 2 2 5 2 5 2 5
m m
f x m m f x f x
f x
m m f x f x f x
Xét hàm số
3 2
, ' 3 1 0,f t t t t f t t t
2 2
2
2
2
2 2 5 2 2 5
0
0
4 5
4 5
2
2
f m f f x m f x
m
m
m
m
f x
f x
Với
2
4 5
2
m
f x
từ đồ thị ta thấy chỉ có 1 nghiệm.
Vậy để phương trình có 3 nghiệm phân biệt thì phương trình
2
4 5
2
m
f x
phải có hai nghiệm
2
4 5 37
4 , 0
2 2
m
m m
.
Câu 60. (THPT Ngô Quyền - Ba Vì - 2019) Cho hàm số
3 2
f x ax bx cx d
có đồ thị như hình vẽ
sau đây. Hỏi có bao nhiêu giá trị nguyên của tham số thực
m
để phương trình
f f x m
có 4
nghiệm phân biệt thuộc đoạn
1;2
?
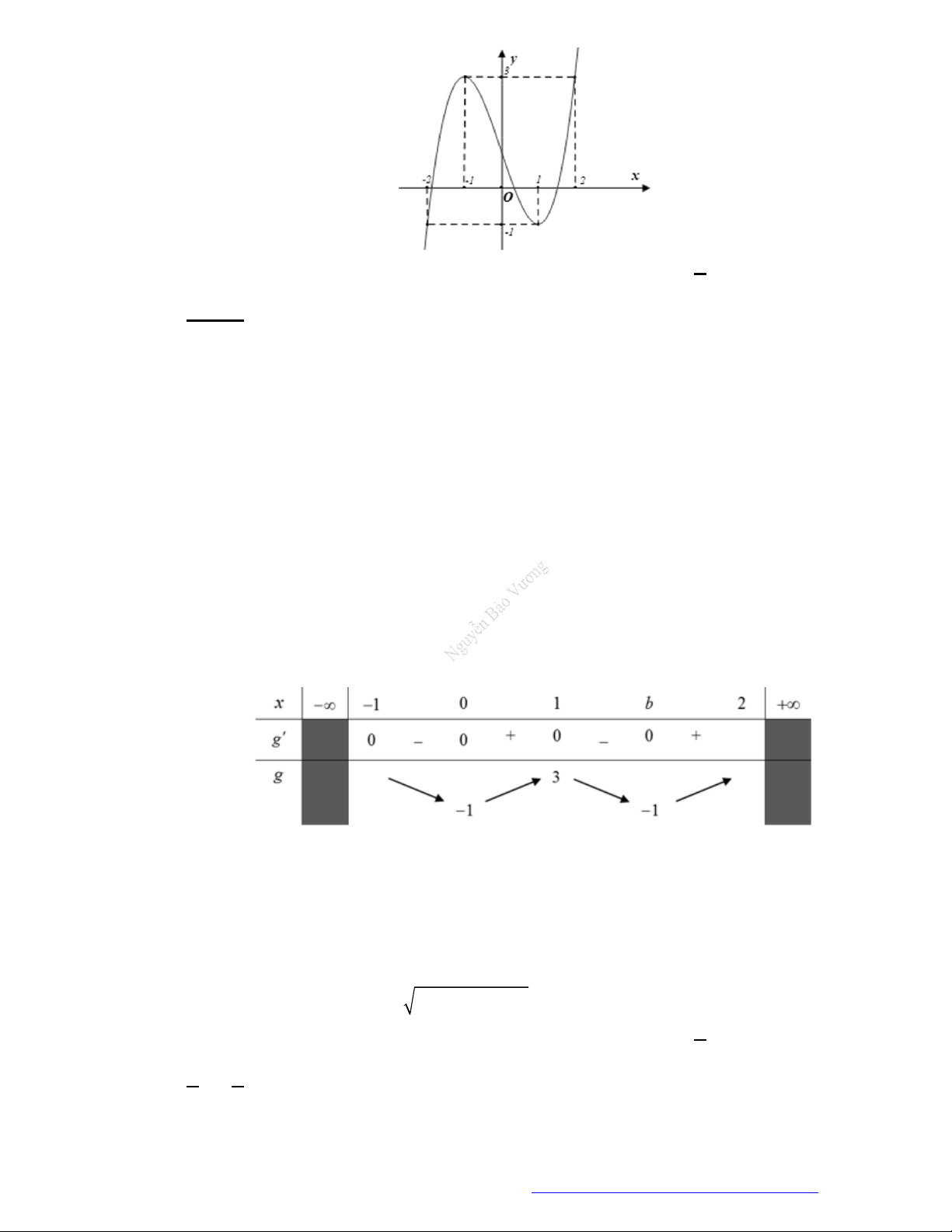
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 49
A.
5
. B.
4
. C.
0
. D.
3
.
Lời giải
Chọn D
Đặt
g x f f x
.
.g x f f x f x
.
Cho
0 . 0g x f f x f x
0
0
f x
f f x
+
1
0
1
x
f x
x
( hoành độ các điểm cực trị ).
+
1
0
1
f x
f f x
f x
Dựa vào đồ thị, ta có:
+ Khi
1 0f x x
;
2; 1x a
;
1;2x b
.
+ Khi
1 1f x x
;
2x
.
Bảng biến thiên
Phương trình
f f x m
có 4 nghiệm phân biệt thuộc đoạn
1;2
1 3m
.
Mà
m
là số nguyên nên
0;1;2m
.
Vậy có 3 giá trị của
m
thỏa đề bài.
Câu 61. (THPT Nguyễn Đức Cảnh - Thái Bình - 2019) Cho hàm số
3 2
2 8g x x x x
. Có bao nhiêu
số nguyên
m
để phương trình
3 2 7g g x m g x
có đúng 6 nghiệm thực phân biệt
A.
7
. B.
8
. C.
24
. D.
25
.
Lời giải
Chọn D
Đặt
3 2 2
3 2 8 3 6 2 8t g x t x x x t x x
.
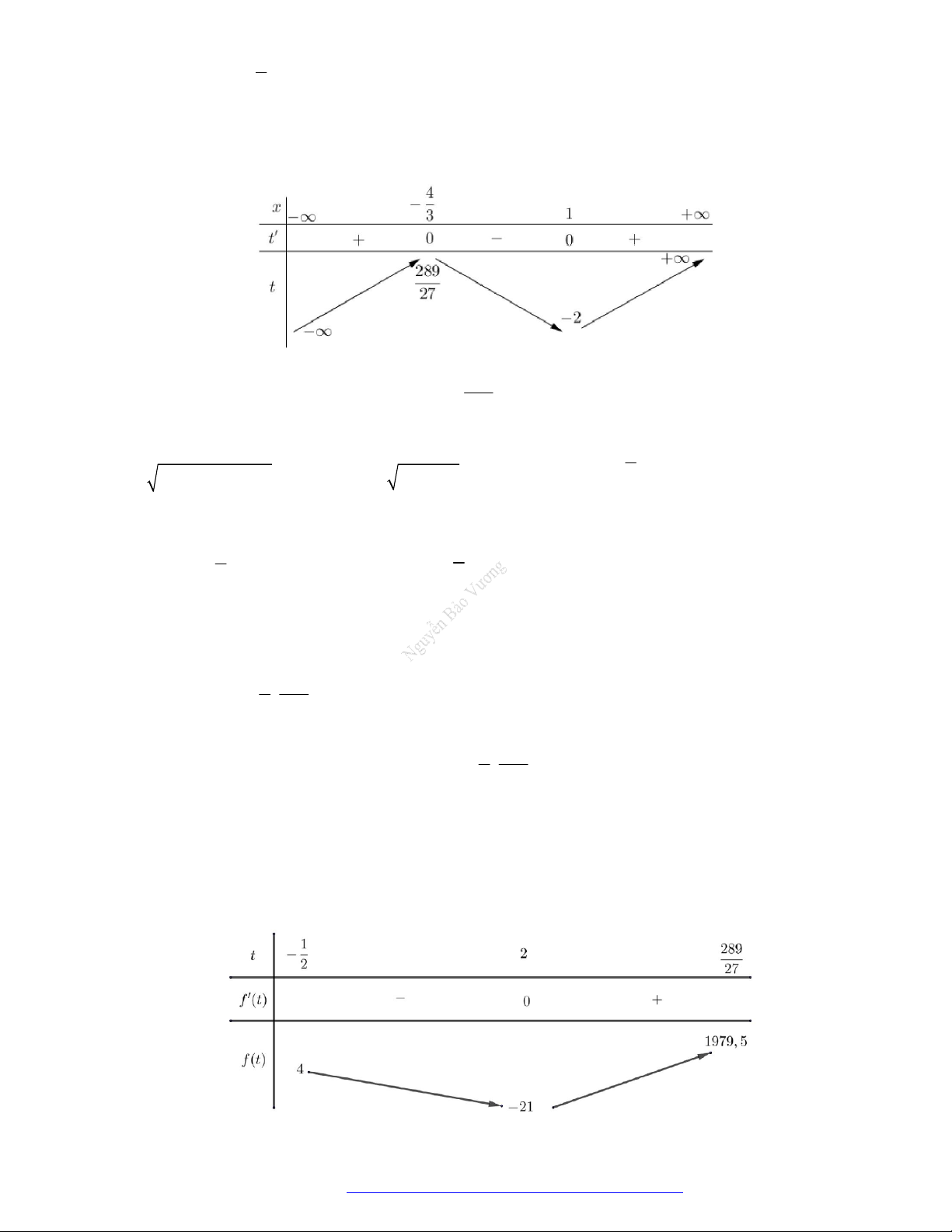
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 50 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
4
0
3
1
x
t
x
.
Ta có bảng biến thiên
Từ bảng biến thiên suy ra mỗi giá trị
289
2;
27
t
sẽ có tương ứng 3 giá trị
x
.
3 2 7g g x m g x
2
1
2
2 3 7
2 1
t
g t m t
g t m t
3 2
3 2 2
1
1
2
2
2 3 12 1 1
2 8 4 4 1
t
t
m t t t
m t t t t t
.
Phương trình đã cho có 6 nghiệm thực phân biệt khi và chỉ khi phương trình
1
có 3 nghiệm
phân biệt
1 289
;
2 27
t
.
Xét hàm số
3 2
2 3 12 1f t t t t
với
1 289
;
2 27
t
.
2
6 6 12f t t t
1
0
2
t
f t
t
.
Ta có bảng biến thiên
Từ bảng biến thiên, phương trình đã cho có 6 nghiệm thực phân biệt
21;4m
.
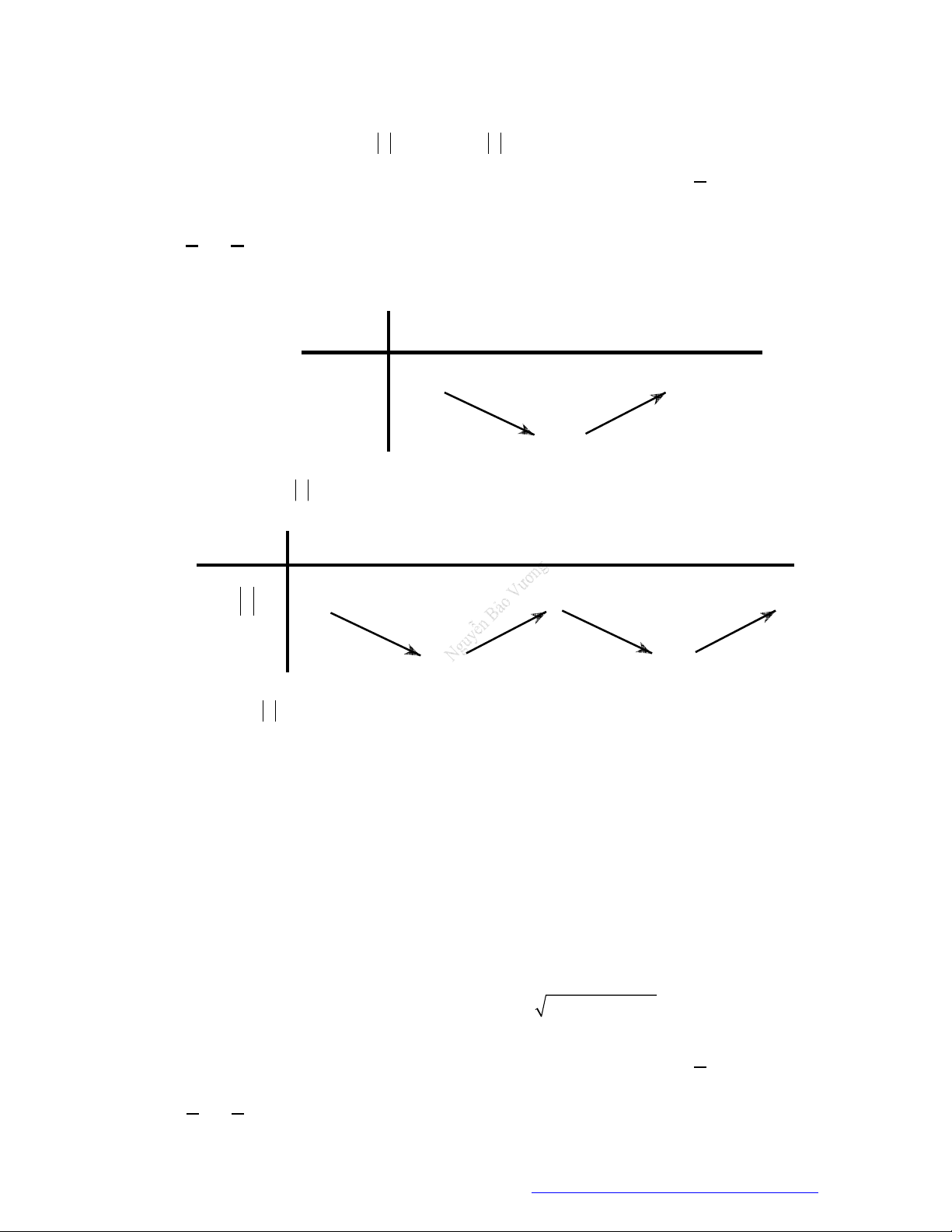
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 51
Mà
20; 19; 18;...;4m m
có 25 số nguyên thỏa mãn.
Câu 62. (THPT Hà Nam - 2019) Cho hàm số
2
4 3f x x x
. Có bao nhiêu giá trị nguyên của tham
số
m
để phương trình
2
6 5 0f x m f x m
có
6
nghiệm thực phân biệt?
A.
1
. B.
2
. C.
4
.
D.
3
.
Lời giải
Chọn D
Hàm số
2
4 3f x x x
có bảng biến thiên
Hàm số
y f x
có bảng biến thiên
Đặt
1 *t f x
Nhận xét:
+ với
*
0
1t x
+ với
*
0 0
1; 3t t
2
nghiệm
+ với
*
0
3t
3
nghiệm + với
*
0
1;3t
4
nghiệm
Phương trình trở thành
2
6 5 0t m t m
1
5
t
t m
Yêu cầu bài toán suy ra
1 5 3 4 8 5;6;7
m
m m m
Câu 63. (Sở GD Bạc Liêu - 2019) Cho hàm số
3 2
( ) 2 8 7 f x x x x
. Gọi
S
là tập hợp tất cả các giá trị
nguyên dương của tham số
m
để phương trình
( ( ) 3) 2 ( ) 5 f f x m f x
có 6 nghiệm thực
phân biệt. Tổng các phần tử của
S
bằng
A.
25
. B.
66
. C.
105
. D.
91
.
Lời giải
Chọn D
Đặt
( ) 3 t f x
.
*
3 2
( ) 3 2 8 4 (1) t f x t x x x
3
f(x)
-∞
+∞
0
+∞
2
-1
+∞
x
-1
f(
x
)
0
3
2
-∞
+∞
+∞
-2
-1
+∞
x
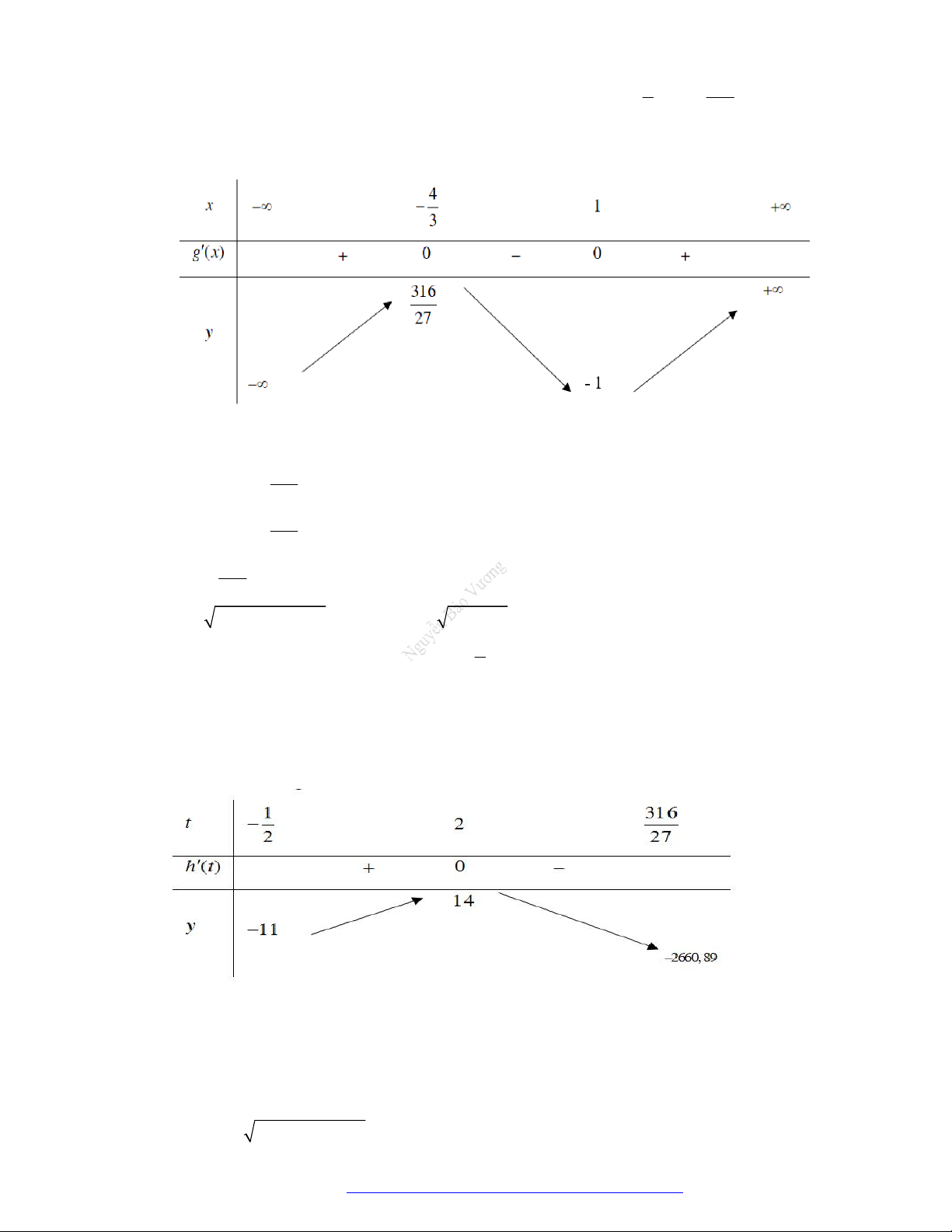
NGUYỄN BẢO VƯƠNG - 0946798489
Trang 52 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Đặt
3 2 2
1 1
( ) 2 8 4 ; ( ) 6 2 8 ; ( ) 0
4 316
3 27
x y
g x x x x g x x x g x
x y
Bảng biến thiên
Số nghiệm của phương trình (1) chính là số giao điểm của đồ thị hàm số
( )y g x
và
y t
Dựa vào bảng biến thiên ta có
+
1 t
hoặc
316
27
t
thì phương trình (1) có 1 nghiệm.
+
1 t
hoặc
316
27
t
thì phương trình (1) có 2 nghiệm.
+
316
1
27
t
thì phương trình (1) có 3 nghiệm phân biệt.
* Ta có
( ( ) 3) 2 ( ) 5 ( ) 2 1 (2) f f x m f x f t m t
Điều kiện để phương trình (2) có nghiệm
1
2
t
2 2 3 2
(2) ( ) 4 4 1 4 4 1 ( ) 2 3 12 6 f t m t t m t t f t m t t t
Đặt
3 2 2
1
( ) 2 3 12 6 ; (t) 6 6 12 ; ( ) 0
2
t
h t t t t h t t h t
t
Bảng biến thiên
Số nghiệm
của phương trình (2) chính là số giao điểm của đồ thị hàm số
( )y h t
và
y m
Dựa vào bảng biến thiên ta có
+
14m
thì phương trình (2) vô nghiệm.
+
14m
hoặc
11 m
thì phương trình (2) có 1 nghiệm.
+
11 14 m
thì phương trình (1) có 2 nghiệm phân biệt.
Phương trình
( ( ) 3) 2 ( ) 5 f f x m f x
có 6 nghiệm thực phân biệt khi phương trình (1) có 3
nghiệm phân biệt và phương trình (2) có 2 nghiệm phân biệt.
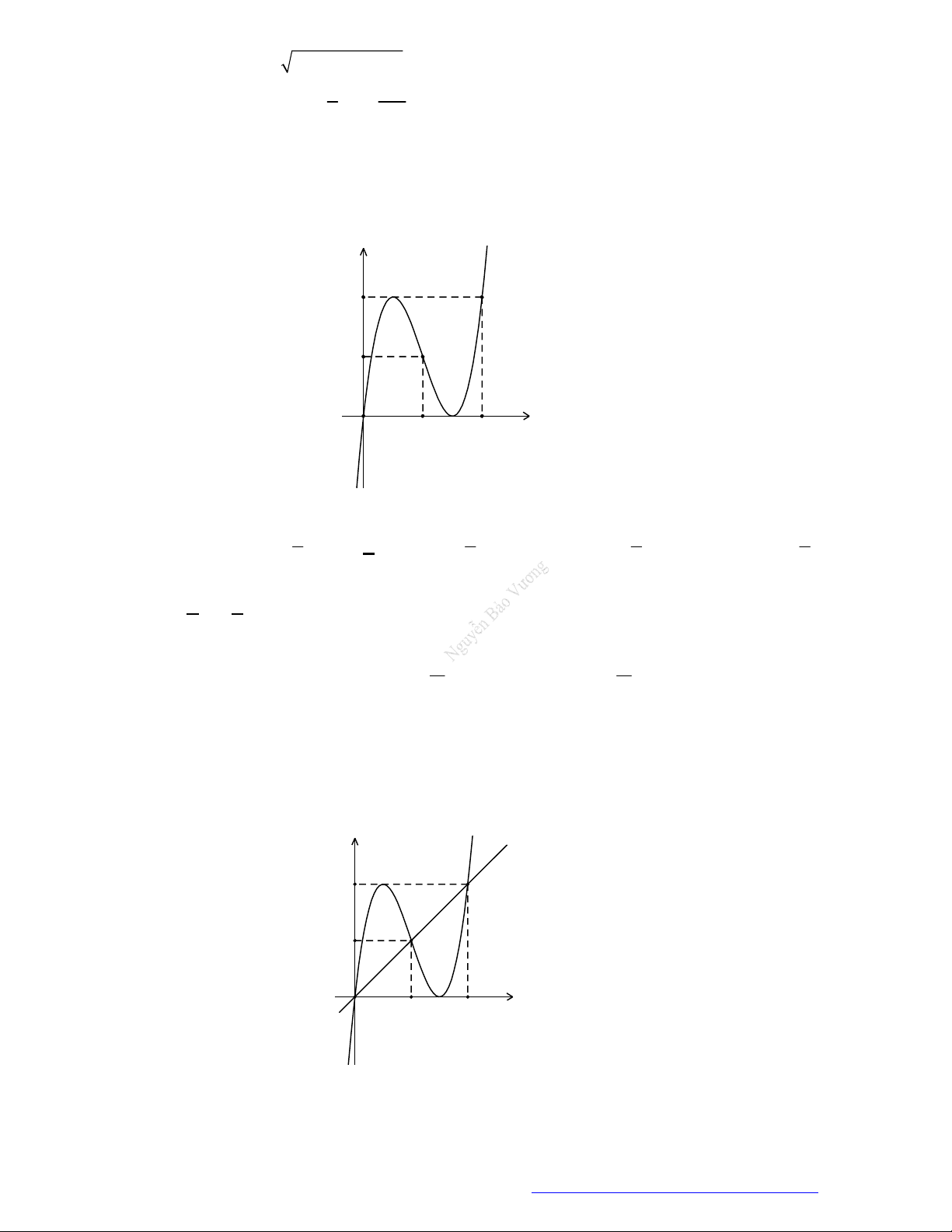
TÀI LIỆU ÔN THI THPTQG 2021
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 53
Vậy phương
( ( ) 3) 2 ( ) 5 f f x m f x
có 6 nghiệm thực phân biệt khi phương trình (2) có hai
nghiệm phân biệt
1 316
2 27
t
.
Dựa vào bảng biến thiên ta được kết quả là
11 14 m
. Suy ra
1;2;...;13S
Tổng các phần tử của
1 ... 11 12 13 91S
.
Câu 64. (Quang Trung - Bình Phước - 2019) Cho hàm số
f x
liên tục trên
. Hàm số
f x
có đồ
thị như hình vẽ:
Bất phương trình
2
2sin 2sinf x x m
đúng với mọi
0;x
khi và chỉ khi
A.
1
0
2
m f
. B.
1
1
2
m f
. C.
1
1
2
m f
. D.
1
0
2
m f
.
Lời giải
Chọn B
Đặt
2sin x t
. Vì
0;x
nên
0;2t
.
Bất phương trình trở thành
2
2
t
f t m
. Đặt
2
2
t
g t f t
với
0;2t
.
Bất phương trình đúng với mọi
0;2t
khi và chỉ khi
0;2
max g t m
.
Ta có
g t f t t
.
0g t f t t
. Nghiệm phương trình này trên khoảng
0;2
là hoành độ giao điểm của đồ
thị
y f t
và đường thẳng
y t
với
0;2t
.
Dựa vào đồ thị ta được nghiệm
1 0;2t
.
Cũng dựa vào đồ thị ta thấy khi
0;1t
thì
f t t
0g t
, khi
1;2t
thì
f t t
0g t
.
2
2
1
1
y
x
O
y
=
t
2
2
1
1
y
x
O
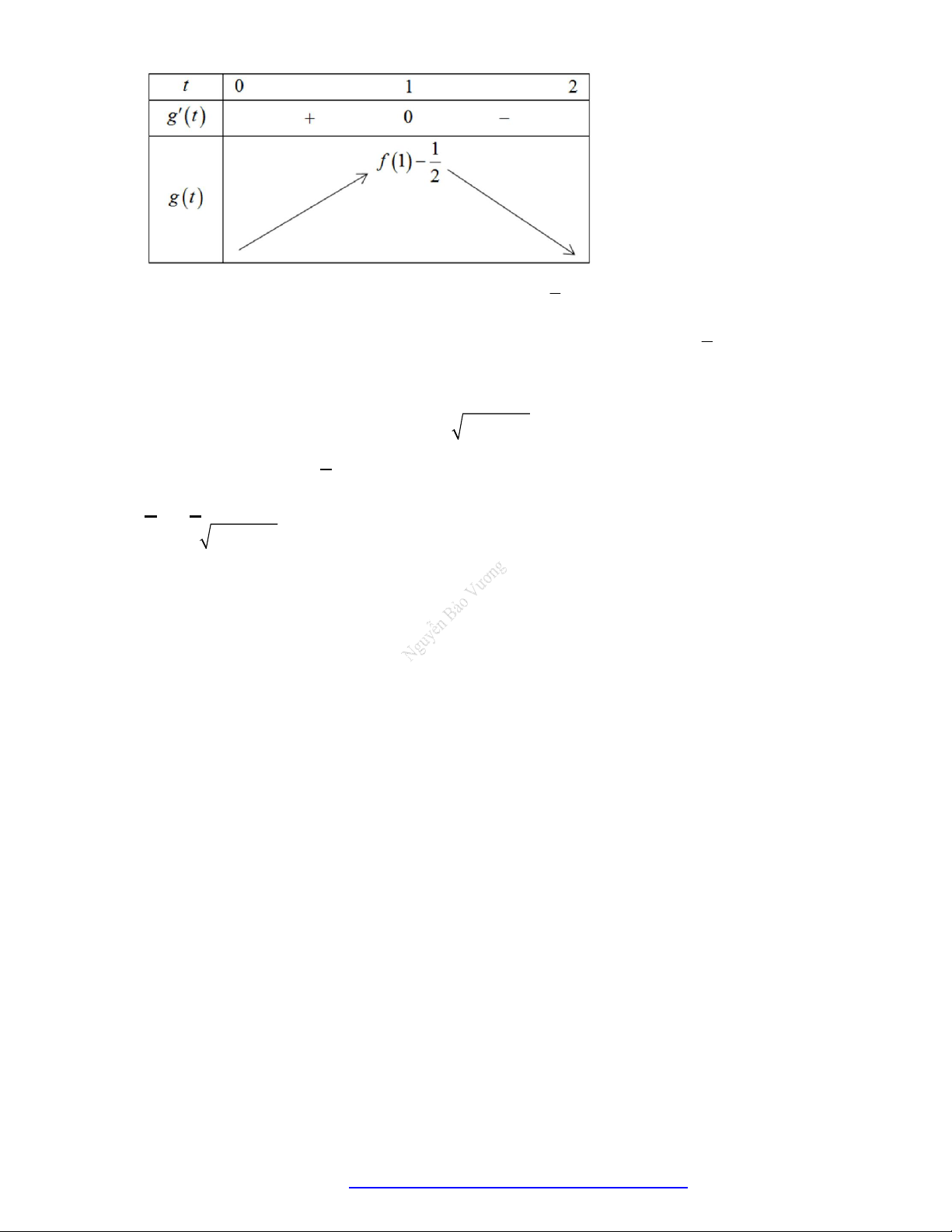
NGUYỄ
N BẢO VƯƠNG - 0946798489
Bảng biến thiên:
Dựa
vào bảng biến thiên ta thấy
0
;2
m
ax 1g t g
1
1
2
f
.
Vậy
bất phương trình đã cho đúng với mọi
0
;x
khi và chỉ khi
1
1
2
m
f
.
Câu 65. (Lương Thế Vinh - Hà Nội - 2019) Cho hàm số
5
3
3 4f x x x m
.
Có bao nhiêu giá trị
nguyên của tham số
m
để phương
trình
3
3
f
f x m x m
có
nghiệm thuộc
1
;2
?
A
.
1
5
. B.
1
6
. C.
1
7
. D.
18
.
Lời giải
Chọn
B
Đặt
3
3
t
f x m t f x m
.
T
a có hệ
3
3
3
3
.
t
f x m
f x x f t t
x f t m
Xét hàm số
3
2
,
1;2 3 0 1;2g x f x x x g x f x x x
.
H
àm số
g x
đồng
biến trên đoạn
1;2
.
V
ì
g
x g t x t
3
f
x x m
5
3 3 5 3
3
4 3 2 1x x m x m m x x
X
ét hàm số
5
3 4 2
2
, 1;2 5 6 0 1;2 .h x x x x h x x x x
Ph
ương trình
1
c
ó nghiệm
1
3 2 3 3 48 1 16h m h m m
.
D
o
1;2;3;4;...;16m Z m
.
Vậy có
16
gi
á trị nguyên của tham số
m
.
-------------------- HẾT --------------------
Trang 54 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Bấm Tải xuống để xem toàn bộ.




