Chuyên đề khoảng cách từ điểm đến mặt phẳng – Trần Mạnh Tường Toán 12

CHUYÊN ĐỀ:
KHOẢNG CÁCH TỪ ĐIỂM ĐẾN MẶT PHẲNG
Tác giả: Trần Mạnh Tường
Nhóm giáo viên Toán tiếp sức Chinh phục kì thi THPT năm 2020 I. KIẾN THỨC CẦN NHỚ: M
1. Khoảng cách giữa điểm và mặt phẳng
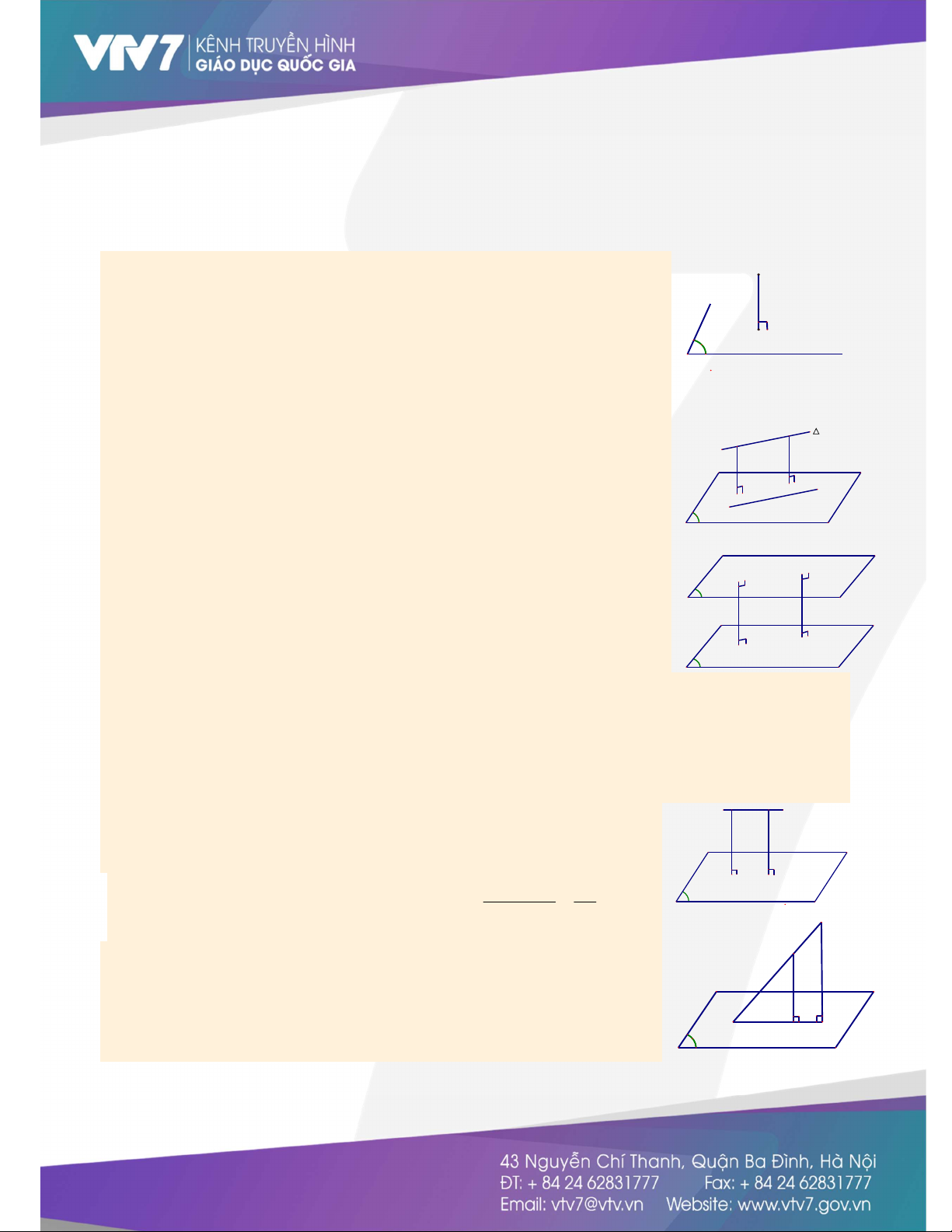
Khoảng cách giữa một điểm và một mặt phẳng là khoảng cách từ điểm đó tới H
hình chiếu vuông góc của nó lên mặt phẳng đó. P
d M ,P  MH (với H là hình chiếu vuông góc của M lên mặt phẳng  ).
2. Khoảng cách giữa một đường thẳng và một mặt phẳng song song N M
Khoảng cách giữa một đường thẳng và một mặt phẳng song song là khoảng cách
từ một điểm bất kì trên đường thẳng này tới mặt phẳng kia. K H
Nếu  / /(P) thì d ,P  d M;(P) với M   P
3. Khoảng cách giữa hai mặt phẳng song song K
Khoảng cách giữa hai mặt phẳng song song là khoảng cách từ một điểm bất kì M P
trên mặt phẳng này tới mặt phẳng kia.
Nếu P / /(Q)thì d P,Q  d M;(Q)  d N;(P) với N H Q M  P, N  Q
4. Các phương pháp thường dùng để tính khoảng cách từ điểm đến mặt phẳng a. Dùng định nghĩa
b. Phương pháp đổi điểm (dùng tỉ số khoảng cách) * Kiến thức cần nhớ: A B
- Nếu đường thẳng AB song song với mặt phẳng P thì d ; A   P d ; B   P d  ; A  P AI H K
- Nếu đường thẳng AB cắt mặt phẳng P tại I thì  P d B;P BI B
Chú ý: Khi sử dụng phương pháp này, ta nên cố gắng đưa việc tính A
khoảng cách từ 1 điểm đến mặt phẳng về việc tính khoảng cách từ chân
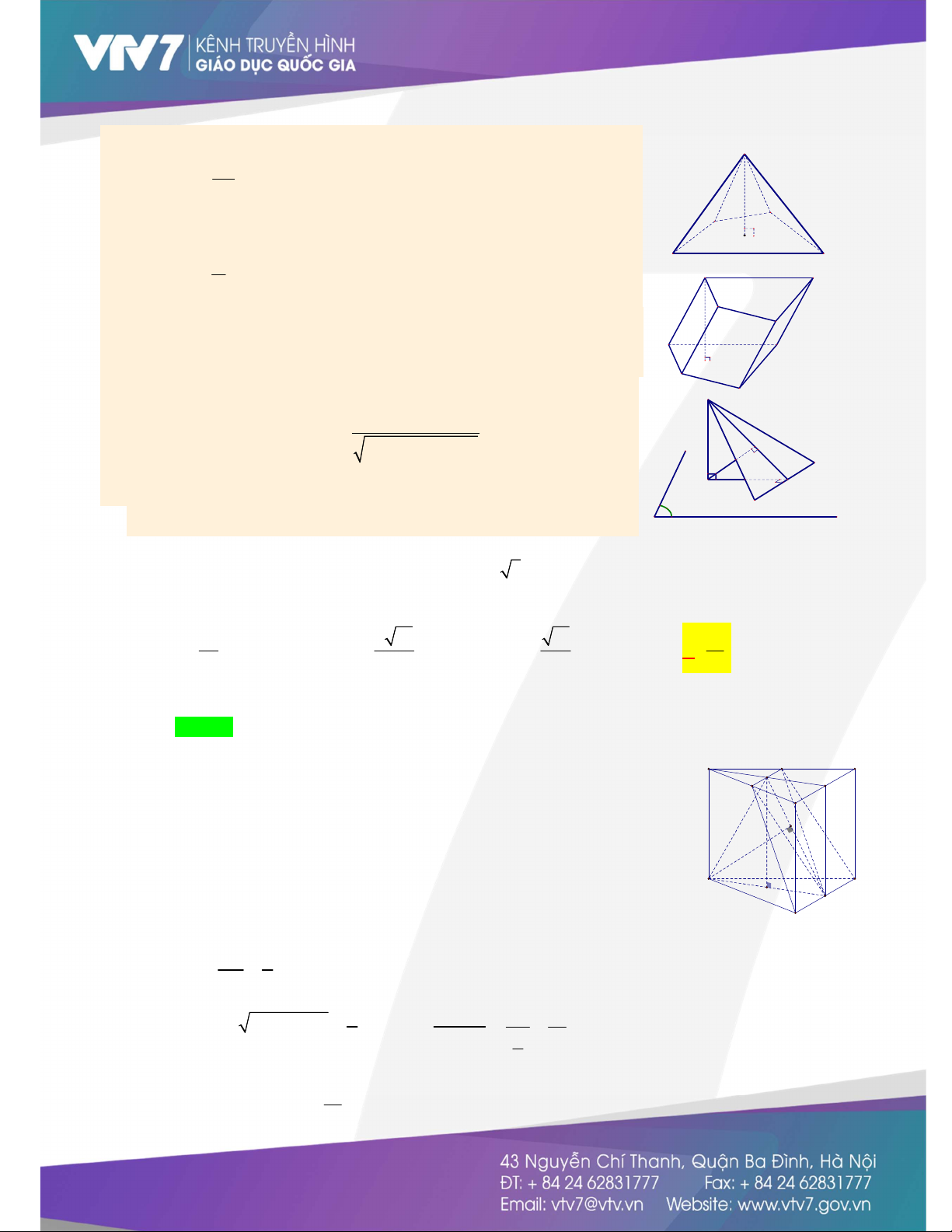
đường cao của hình chóp hoặc lăng trụ đến mặt phẳng I H K P c. Phương pháp thể tích M V * d M P 3 ; 
với V là thể tích của khối chóp có đỉnh là M , S là diện S D
tích của đáy nằm trên mặt phẳng P của khối chóp đó A H V B C
* d M ;P  với V là thể tích của khối lăng trụ có đỉnh là M , S là M S
diện tích của đáy nằm trên mặt phẳng  P của khối lăng trụ đó A D H
d. Một công thức thường dùng trong bài toán tính khoảng cách B S C SI.d I; AB
Nếu SI  IAB thì d I;SAB    2 2 SI  d I; AB H B II. BÀI TẬP VẬN DỤNG I K A 1. Ví dụ minh họa P
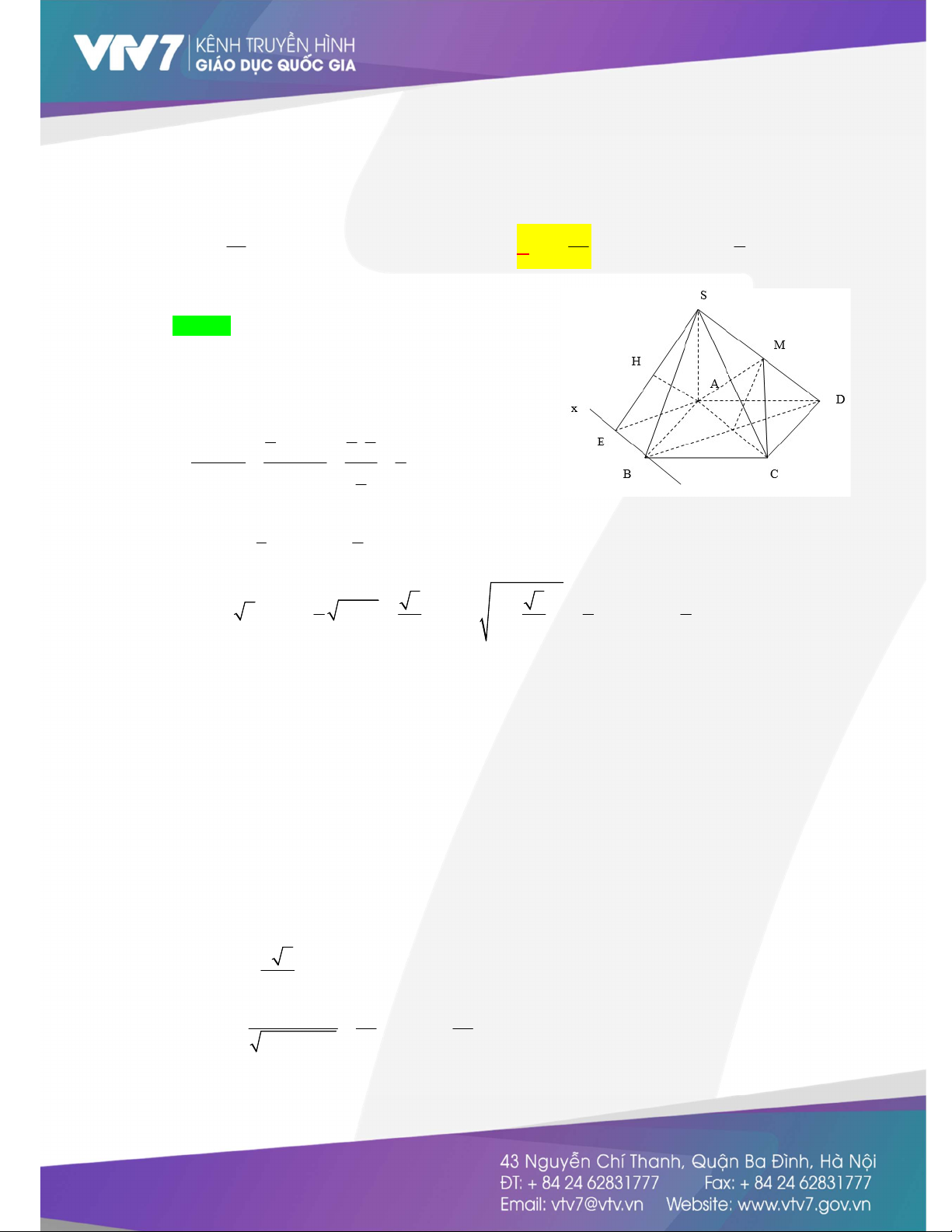
Câu 1. (Khoảng cách từ điểm đến mặt phẳng - Sử dụng phương pháp dùng định nghĩa) Cho hình
lăng trụ tam giác đều ABC.A B  C
  có AB  2 3 và AA  2 . Gọi M , N , P lần lượt là trung
điểm các cạnh AB , A C
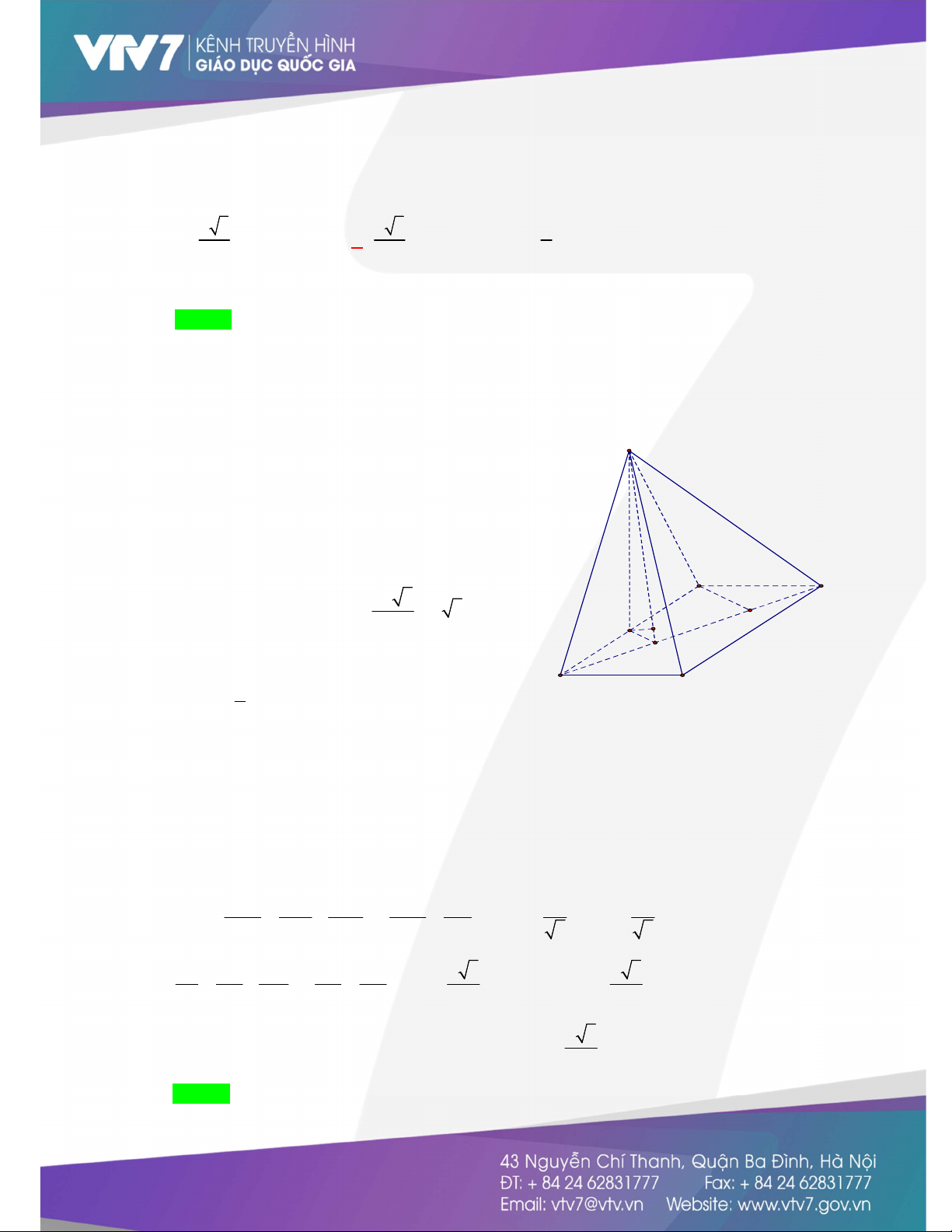
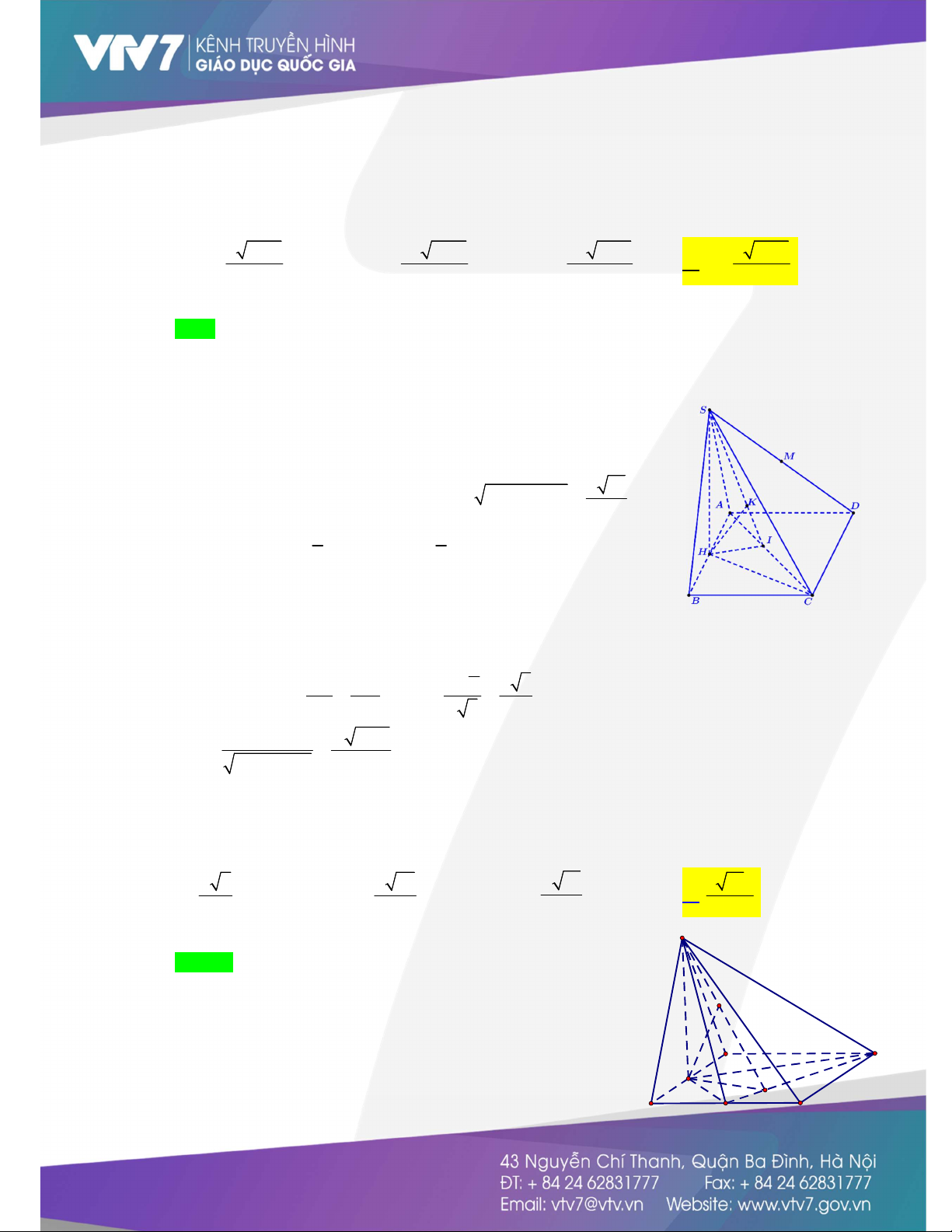
  và BC . Khoảng cách từ A đến MNP bằng 17 6 13 13 12 A. . B. . C. . D. . 65 65 65 5 Lời giải Chọn D MN  AD N A' C'
- Gọi D là trung điểm của B C      MN   ADPA E MN  DP D M B'  MNP   A D  PA H - Gọi E  MN  A D
  EP là giao tuyến của MNP và  ADPA . A C
- Dựng AH  EP  AH  MNP  AH  d  ; A MNP . F P B
- Gọi F là trung điểm của AP  EF  AP và EF  AA  2 , AP 3 FP   2 2 5 EF.AP 2 2
 EP  EF  FP   AH  2.3 12   . 2 EP 5 5 2 Vậy d  A MNP 12 ;  . 5
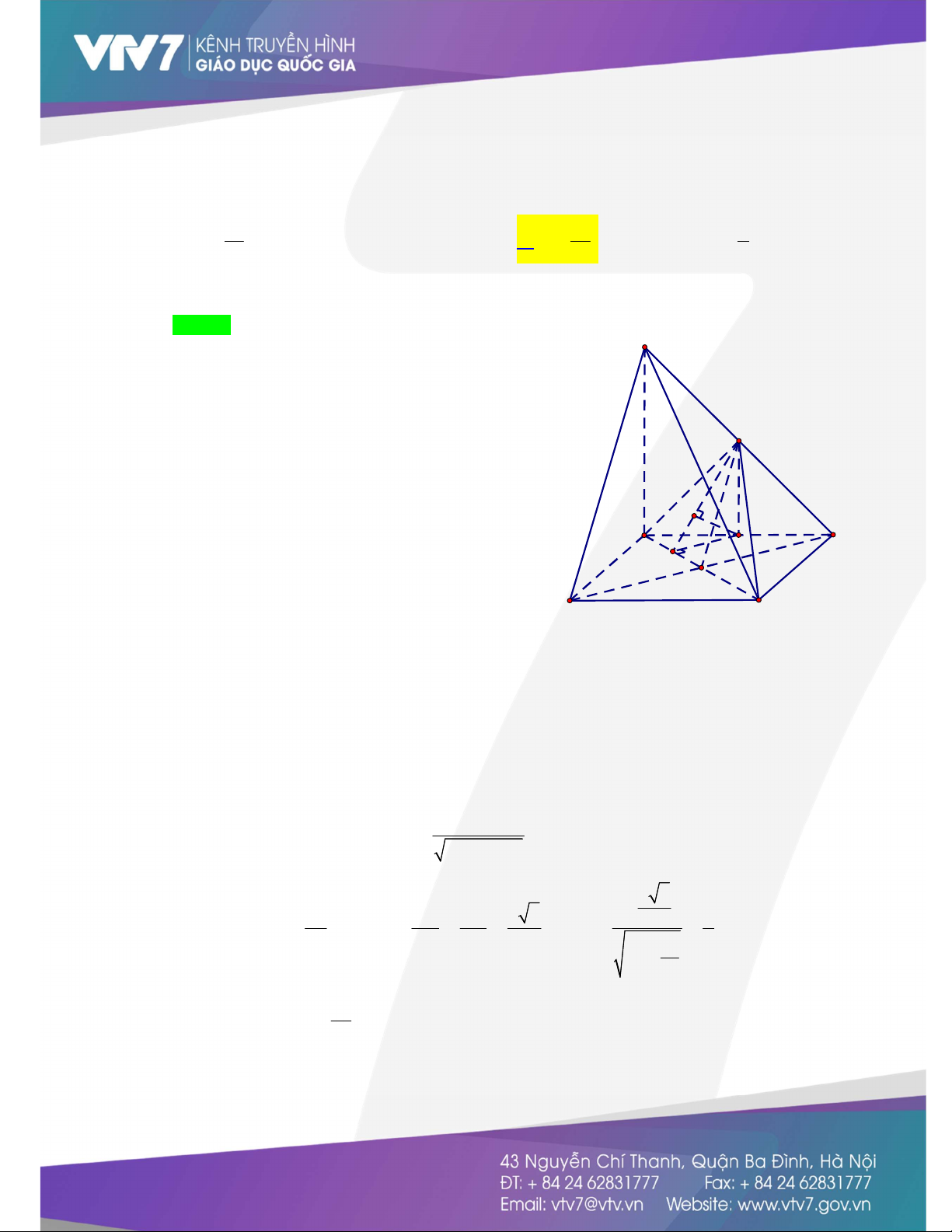
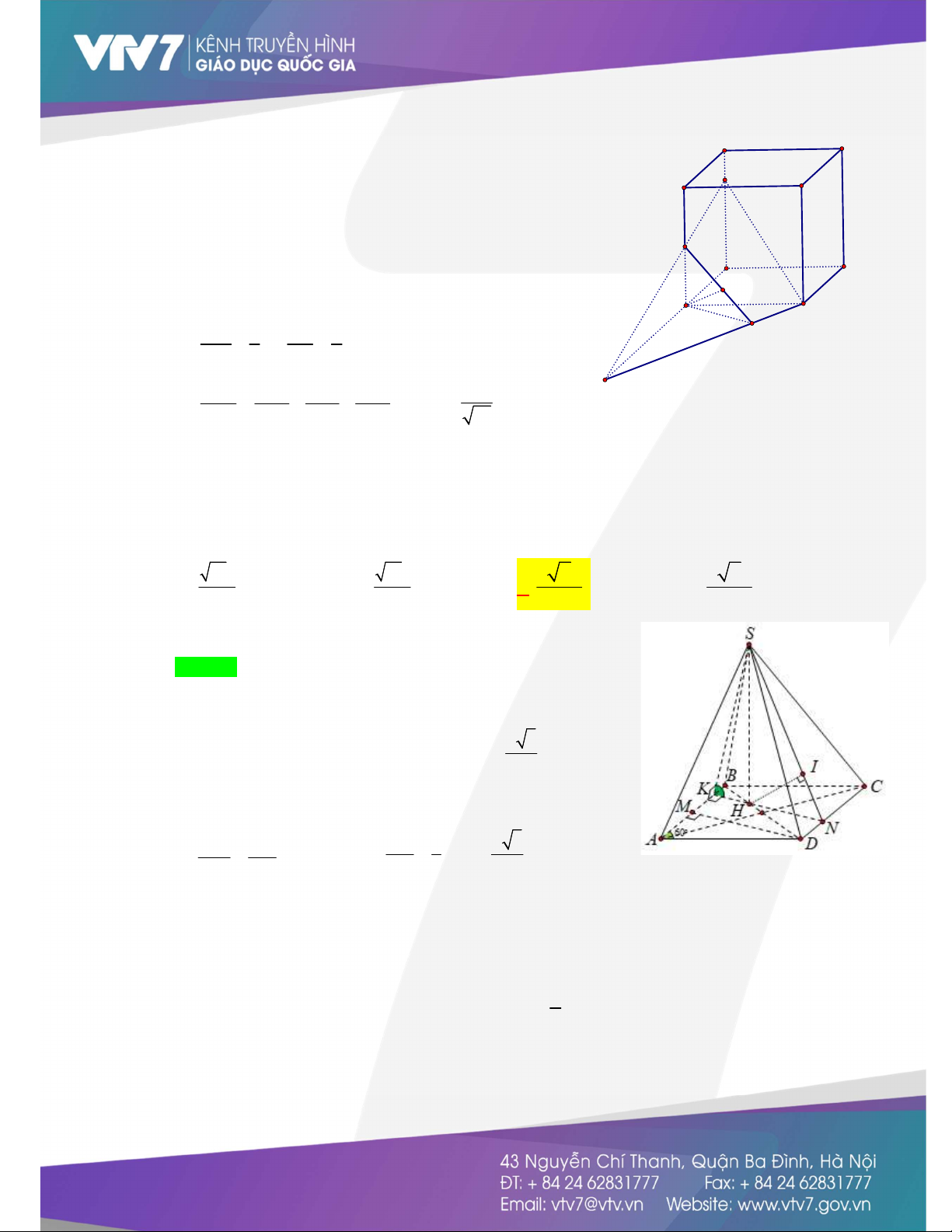
Câu 2. (Khoảng cách từ điểm đến mặt phẳng - Sử dụng phương pháp đổi điểm) Cho hình chóp
S.ABCD có đáy là hình chữ nhật, cạnh AB  2 AD  2a. Tam giác SAB đều và nằm trong mặt
phẳng vuông góc với đáy  ABCD Tính khoảng cách từ điểm A đến mặt phẳng SBD a 3 a 3 a A. . B. . C. . D. a . 4 2 2 Lời giải Chọn B
Phân tích: Gọi I là trung điểm AB , ta sẽ có I là chân đường cao của hình chóp nên ta có ý
tưởng đổi việc tính khoảng cách từ điểm A đến mặt phẳng SBD thành khoảng cách từ điểm
I đến mặt phẳng SBD . * Kẻ SI  A . B S
Do tam giác SAB đều và nằm trong mặt phẳng
vuông góc với đáy  ABCD .
 I là trung điểm của AB và SI   ABCD. A D 2a 3
SAB đều cạnh 2a  SI   a 3. 2 H I J K
* Kẻ IK  BD K  BD, AH  BD H  BD 1 B C  IK  AH 2
Kẻ IJ  SK,  J  SK  (1). IK  BD Ta có 
 BD  SIK   BD  IJ (2). SI    ABCD  SI  BD
* Từ (1) và (2) suy ra IJ  SBD  d I,(SBD)  IJ. 1 1 1 1 5 a a Ta có:     2  AH   IK  . 2 2 2 AH AB AD 2 2 AH 4a 5 5 1 1 1   1 16   a 3  a IJ   d I SBD  3 ,( )  . 2 2 2 IJ SI IK 2 2 IJ 3a 4 4 a
I là trung điểm AB  d  , A (SBD)  d I SBD  3 2 ,( )  . 2 Chọn B Câu 3.
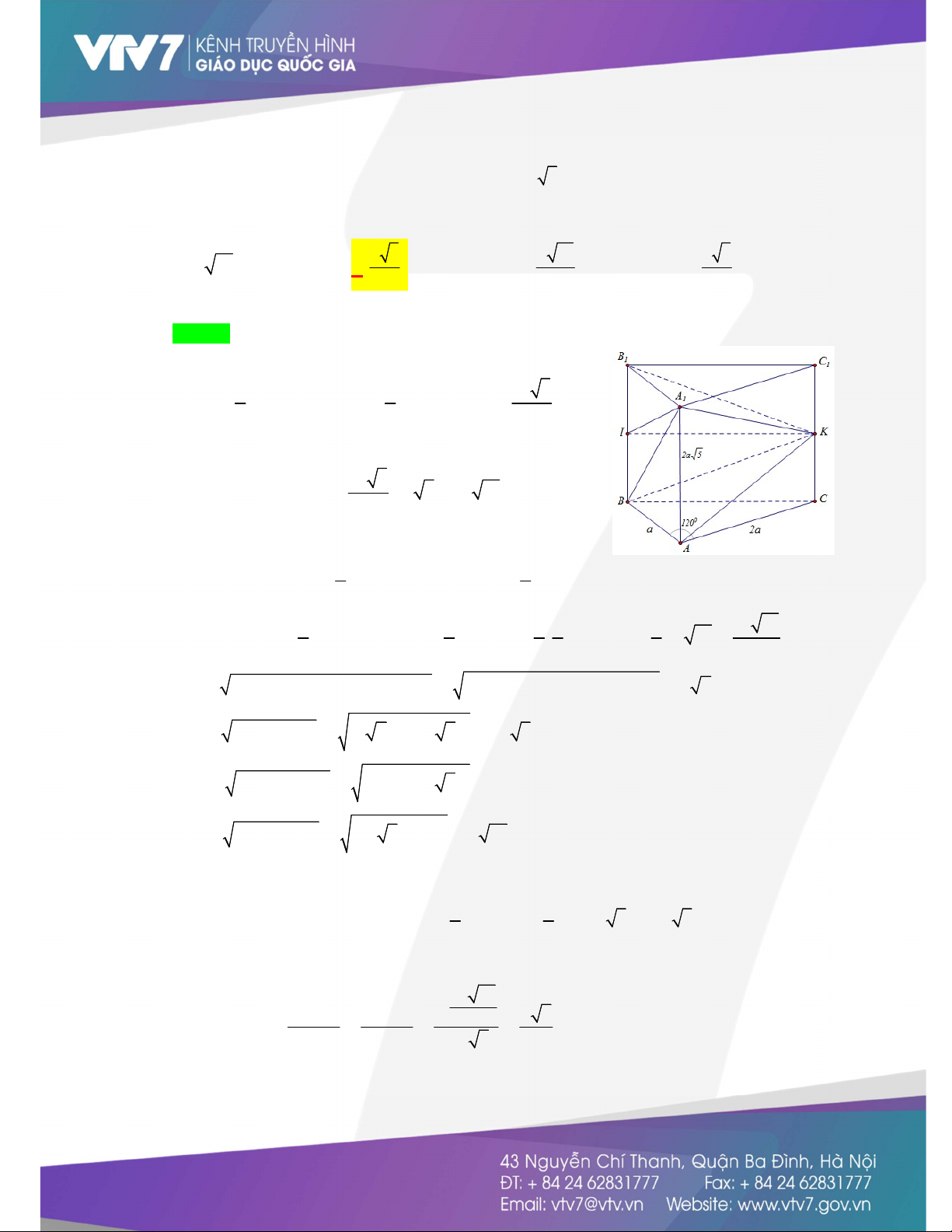
(Khoảng cách từ điểm đến mặt phẳng - Sử dụng phương pháp thể tích) Cho hình lăng trụ đứng AB . C ABC  AC  a BAC  1 1 1 có AB a , 2 , AA  2a 5 và  0
120 . Gọi K, I lần lượt là 1 trung điểm của CC , BB A BK 1
1 . Khoảng cách từ I đến mặt phẳng  bằng 1  a 5 a 15 a 5 A. a 15 . B. . C. . D. . 6 3 3 Lời giải Chọn B Diện tích A  BC là: 1 a S .A . B A . C sin  2 1 3 0 BAC . . a 2 . a sin120 A     BC 2 2 2
Thể tích khối lăng trụ AB . C ABC 1 1 1 là: 2 a 3 3 V  S .AA  .2a 5  a 15 ABC. 1 A 1 B 1 C A  BC 1 2 Dễ thấy V V V V ABC. 1 A 1 B 1 C K. 1 A 1 B 1 C K.ABC K.AB 1 B 1 A 1 2 Mà V V  V nên V  V K . 1 A 1 B 1 C K .ABC ABC. 1 A 1 B 1 6 C K .AB 1 B 1 A ABC. 1 A 1 B 1 3 C 3 1 1 1 2 1 a 15 Ta lại có, 3 S  .S V  .V  . .V  .a 15  1 A BI AB 1 B 1 A K. 1 A BI K.AB 1 B 1 A ABC. 1 A 1 B 1 4 4 4 3 C 6 6 BC  AB  AC  AB AC A  a  a2 2 2 2 0 2 . .cos 2 2.a.2a.cos120  a 7
BK  BC CK  a 2 a 2 2 2 7 5  2a 3
A K  AC C K  2a a 52 2 2 2  3a 1 1 1 1
A B  A A  AB  2a 52 2 2 2 a  a 21 1 1 Xét thấy 2 2 2 2 BK  A A  A B  21a 1 1 1 1 Do đó, A  BK 2 1 vuông tại K  S A K BK a A BK  . .  .3a.2a 3  3 3 1 1 2 2
Khoảng cách từ I đến mặt phằng A BK là: 1  3 a 15 3. d I  3V 3V I A BK A BI a 5 6 , A BK     1  . 1 K. 1 3 S S a A BK A BK 3 3 6 1 1 Câu 4.
(Khoảng cách từ đường thẳng đến mặt phẳng song song - Sử dụng phương pháp thể tích)
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy và SA  2a , M là trung điểm của S .
D Tính khoảng cách d giữa đường thẳng SB và mặt phẳng  ACM  . 3 2 A.  a d . d a . C.  a d . D.  a d 2 B.  3 3 Lời giải Chọn C Cách 1
d( SB,( ACM ))  d( B,( ACM )) 3 3 2 3 V . S .ABCD V 2 M .ABC 4 4 3     . S S 3 3 ACM ACM 4 1 2  V  .S . A S  (a  1) S .ABCD 3 ABCD 3 2 1 5  5  3 3 2  AC  2, AM  1  2  , MC  1      S  2 2  2  2 ACM   4 Cách 2
Theo bài ra ta có SB / /  ACM  .
Qua B ta kẻ đường thẳng x song song với AC, qua A dựng AE  Bx thì ta có SBx / /  ACM  Kẻ AH  SE . EB  AE Lại có   EB  AH EB  SA
Do đó AH  SBx . Khi đó d SB, ACM   d SBx , ACM   d  A,SBx  AH a 2 AE  BO 
; SA  2a (O là tâm hình vuông ABCD) 2  AE.SA 2a 2a AH   . Vậy d  2 2 AE  SA 3 3
Câu 5. (Khoảng cách từ đường thẳng đến mặt phẳng song song - Sử dụng phương pháp đổi điểm)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với đáy và SA  2a .
Gọi M là trung điểm của SD . Tính khoảng cách d giữa đường thẳng SB và mặt phẳng ACM 3a 2a a A. d  . B. d  a . C. d  . D. d  . 2 3 3 Lời giải Chọn D S
+ Gọi O là giao điểm của AC , BD
 MO  SB  SB ACM
 dSB,ACM  dB,ACM  dD,ACM . M
+ Gọi I là trung điểm của AD  H MI SA  MI   ABCD   A  D  . I d
 D,ACM 2dI,ACM K O
+ Trong ABCD: IK  AC (với K  AC ). C B
+ Trong MIK: IH  MK (với H  MK )   1 .
+ Ta có: AC  MI, AC  IK  AC  MIK AC  IH 2. Từ  
1 và 2 suy ra IH ACM dI,ACM  IH . + Tính IH ? IM.IK
- Trong tam giác vuông MIK : IH  . 2 2 IM  IK a 2 SA OD BD a 2 . a a - Mặt khác: MI   a , IK    4  IH   . 2 2 4 4 2 a 3 2 a  8 a Vậy d SB ACM 2 ,  . 3 Câu 6.
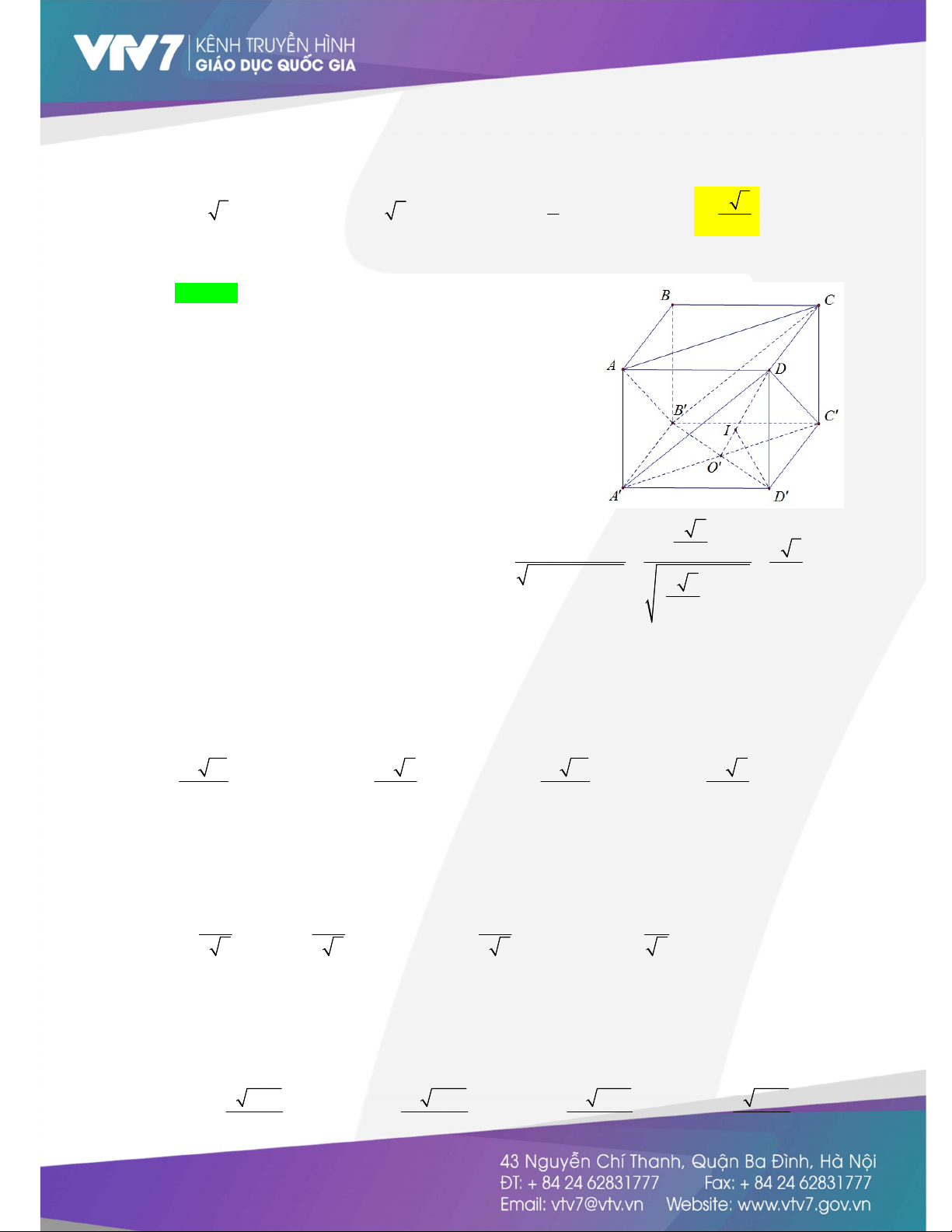
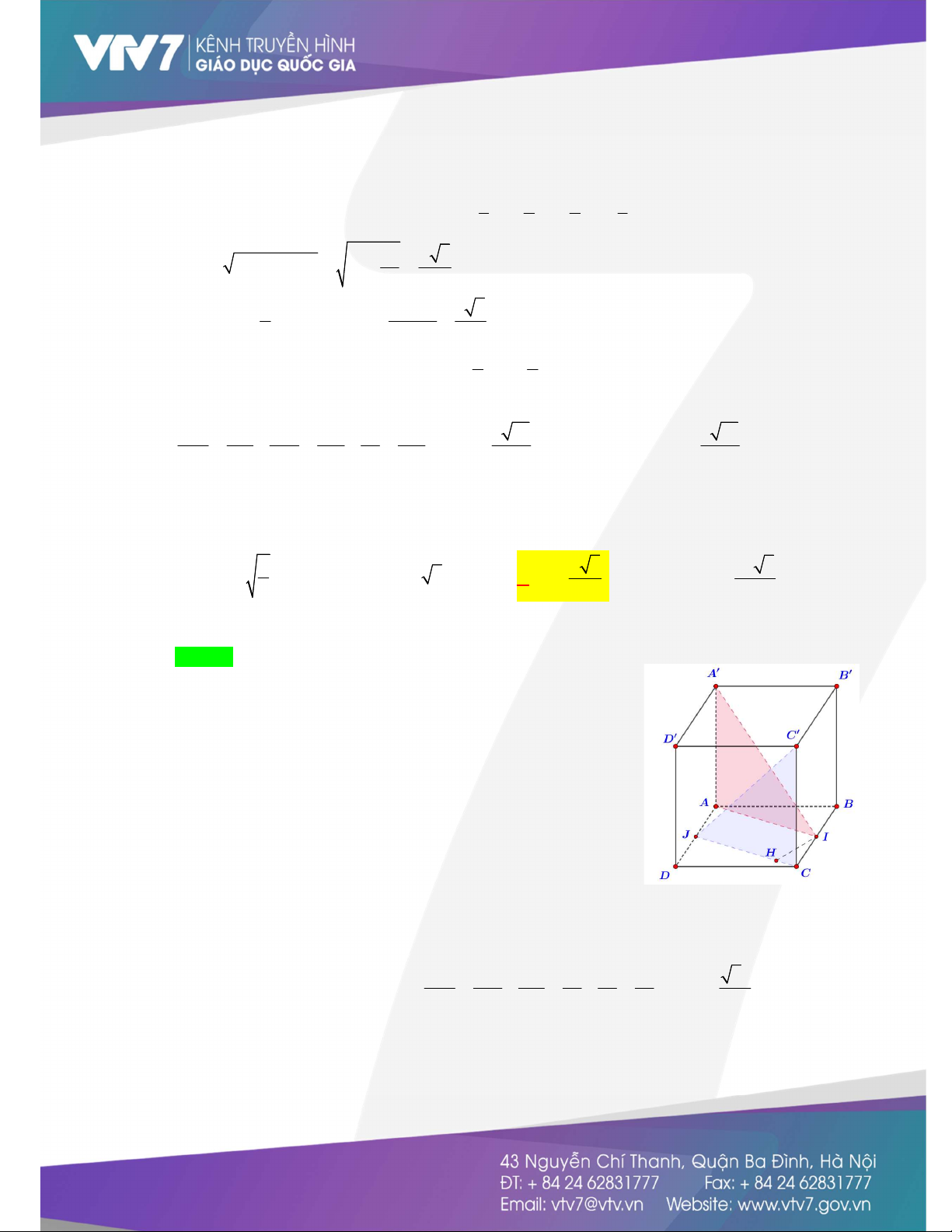
(Khoảng cách giữa hai mặt phẳng song song - Sử dụng phương pháp đổi điểm) Cho hình lập phương ABC . D AB C  D   cạnh .
a Khoảng cách giữa  AB C
  và  ADC bằng : a a 3 A. a 3 . B. a 2 . C. . D. . 3 3 Hướng dẫn giải Chọn D. Ta có d  AB C
 , ADC  d B , ADC  d D , A D  C
Gọi O là tâm của hình vuông AB C  D   . Gọi I là hình . Chiếu của D trên O D
 , suy ra I là hình chiếu của D trên  ADC . a 2 .a     a d AB C
   ADC  d D    ADC D O .D D 3 2 , ,   D I    .  2 2 2 D O    D D  3  a 2  2    a 2   BÀI TẬP TỰ LUYỆN
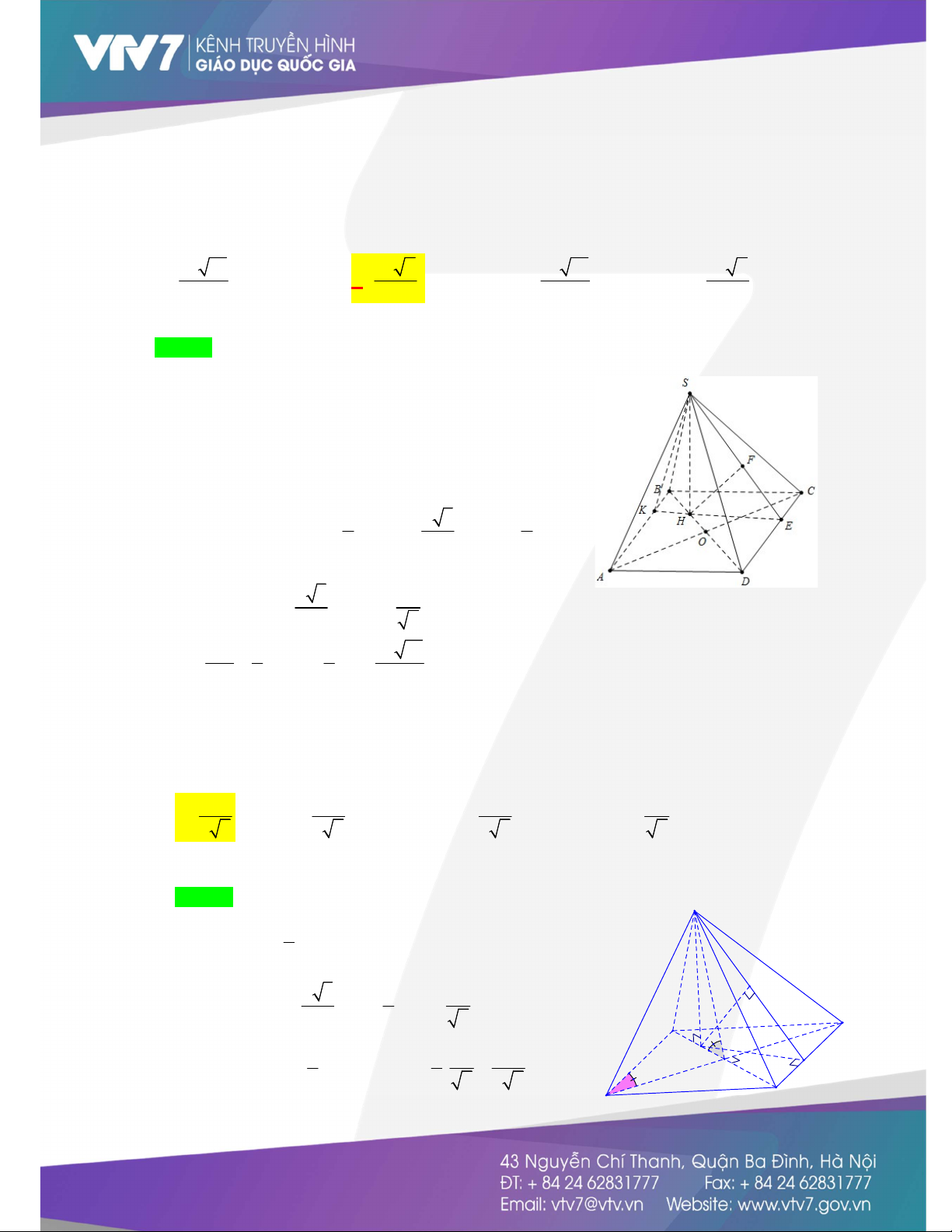
Câu 7. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a. Góc 
BAD có số đo bằng 60 . Hình
chiếu của S lên mặt phẳng  ABCD là trọng tâm tam giác ABC .Góc giữa (ABCD) và SAB bằng
60 . Tính khoảng cách từ B đến mặt phẳng SCD . 3a 17 3a 7 3a 17 3a 7 A. . B. . C. . D. . 14 14 4 4
Câu 8. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc 
BAC  60 , hình chiếu của
đỉnh S trên mặt phẳng  ABCD trùng với trọng tâm tam giác ABC , góc tạo bới hai mặt phẳng
SAC và  ABCD là 60 . Khoảng cách từ B đến mặt phẳng SCD theo a bằng 3a 9a a 3a A. B. C. D. 2 7 2 7 2 7 7
Câu 9. Cho hình chóp S.ABCD có đáy hình chữ nhật, AB  a; AD  2a. Tam giác SAB cân tại S và
nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng SC và mặt phẳng ABCD
bằng 45 . Gọi M là trung điểm của SD . Tính theo a khoảng cách d từ điểm M đến mặt phẳng SAC  . a 1315 A. d  2a 1315 . B. d  2a 1513 . C. d  a 1513 . D. d  . 89 89 89 89
Câu 10.Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , tam giác SAB vuông cân tại S và
nằm trong mặt phẳng vuông góc với đáy. Gọi I là trung điểm của AB và M là trung điểm của
BC . Khoảng cách từ I đến mặt phẳng SMD bằng: a 6 a 30 a 13 3 14a A. . B. . C. . D. . 6 12 26 28
Câu 11.Cho hình lập phương ABC . D AB C  D
  cạnh a . Gọi I , J lần lượt là trung điển của BC và AD .
Tính khoảng cách d giữa hai mặt phẳng  AIA và CJC . 5 a 5 3a 5 A. d  2a . B. d  2a 5 . C. d  . D. d  . 2 5 5
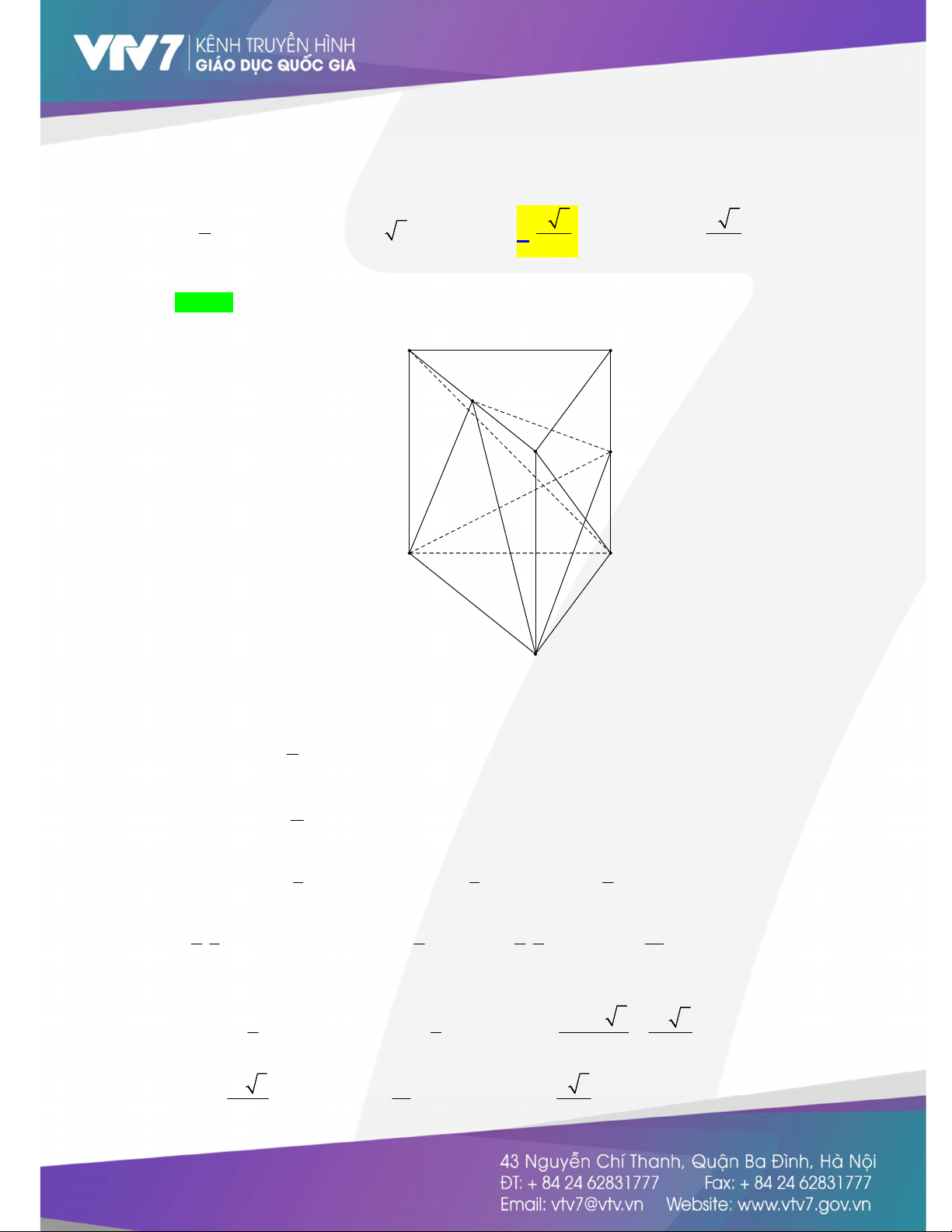
Câu 12.Cho khối lăng trụ ABC. 
A BC có thể tích bằng 3
a . Gọi M , N lần lượt là trung điểm của  A  B
, CC .Tính khoảng cách từ A đến mặt phẳng BMN  biết rằng BMN là tam giác đều cạnh 2a . a a 3 a 3 A. . B. a 3 . C. . D. . 3 3 2
Câu 13.Cho hình lập phương ABC . D A B  C  D
  có cạnh là a . Trên AA , BB lấy lần lượt các điểm M , N 3a a sao cho AM 
, BN  . Khoảng cách từ điểm B đến mặt phẳng (MNC) là 4 2 2a 21 2a 21 a 21 a 41 A. . B. . C. . D. . 21 63 21 8 
Câu 14.Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và BAD  60. Hình chiếu vuông
góc của S trên mặt phẳng  ABC 
D trùng với trọng tâm của tam giác ABC . Góc giữa mặt
phẳng SAB và  ABC 
D bằng 60 . Khoảng cách từ B đến mặt phẳng SCD bằng 21a 21a 3 7a 3 7a A. . B. . C. . D. . 14 7 14 7
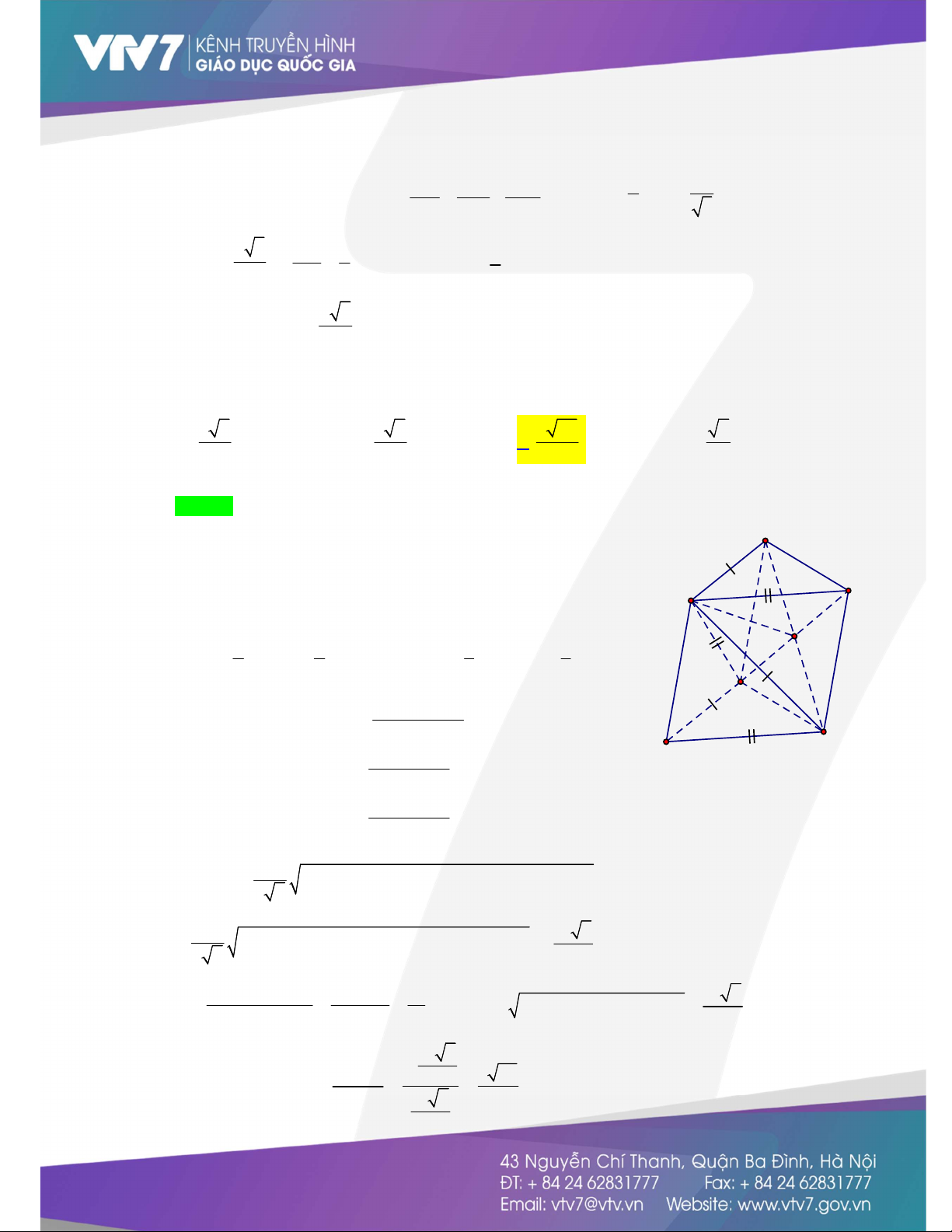
Câu 15.Cho tứ diện ABCD có AB  CD  4 , AC  BD  5 , AD  BC  6 . Tính khoảng cách từ A đến mặt phẳng BCD . 3 6 3 2 3 42 7 A. . B. . C. . D. . 7 5 7 2
ĐÁP ÁN BÀI TẬP LUYỆN TẬP
Câu 7: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a. Góc 
BAD có số đo bằng 60 . Hình
chiếu của S lên mặt phẳng  ABCD là trọng tâm tam giác ABC .Góc giữa (ABCD) và SAB bằng 60 .
Tính khoảng cách từ B đến mặt phẳng SCD . 3a 17 3a 7 3a 17 3a 7 A. . B. . C. . D. . 14 14 4 4 Lời giải Chọn B
Gọi H là trọng tâm ABC Dựng HK  A , B HE  C , D HF  SE
Ta có AB  SHK    SKH  60 Do đó SH  HK tan 60
Mặc khác HK  HB sin 60 ( Do ABD là tam giác đều nên  a a 3 a
ABD  60 ) suy ra HK  sin 60   SH  3 6 2 Lại có a 3  a HE HD tan 60   HF   d H;SCD 3 7 BD 3 3 3a 17 Do đó   d  d  . HD 2 B 2 H 14
Câu 8: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc 
BAC  60 , hình chiếu của
đỉnh S trên mặt phẳng  ABCD trùng với trọng tâm tam giác ABC , góc tạo bới hai mặt phẳng
SAC và  ABCD là 60 . Khoảng cách từ B đến mặt phẳng SCD theo a bằng 3a 9a a 3a A. B. C. D. 2 7 2 7 2 7 7 Lời giải Chọn A S 3 • d  ;
B SCD  d G;SCD 2 K a 3 a a • Tính được: GH  ; SG  ;GK  . 3 2 7 C B 3 3 a 3a G Vậy d  ;
B SCD  d G;SCD  .  . O H 2 2 7 2 7 A a D
Câu 9: Cho hình chóp S.ABCD có đáy hình chữ nhật, AB  a; AD  2a. Tam giác SAB cân tại S và
nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng SC và mặt phẳng ABCD
bằng 45 . Gọi M là trung điểm của SD . Tính theo a khoảng cách d từ điểm M đến mặt phẳng SAC  . a 1315 A. d  2a 1315 . B. d  2a 1513 . C. d  a 1513 . D. d  . 89 89 89 89 Lời giải Chọn D
Phương pháp: Đưa khoảng cách từ M đến SAC  về khoảng cách từ H đến SAC  .
Gọi H là trung điểm của AB  SH   ABCD Ta có SC, ABCD   SC,HC    SCH  45   17 SHC vuông cân tại H 2 2      a SH HC BC BH 2  d M SAC 1  d D SAC 1 ; ;  d  ;
B SAC  d H;SAC 2 2
Trong  ABCD kẻ HI  AC
Trong SHI  kẻ HK  SI  HK  SAC  HK  d H;SAC Ta có a 2 . a HI AH a 5 2 AHI  ACB    HI   BC AC a 5 5 SH.HI A 1513 HK   . 2 2 SH  HI 89
Câu 10: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , tam giác SAB vuông cân tại S và
nằm trong mặt phẳng vuông góc với đáy. Gọi I là trung điểm của AB và M là trung điểm của
BC . Khoảng cách từ I đến mặt phẳng SMD bằng: a 6 a 30 a 13 3 14a A. . B. . C. . D. . 6 12 26 28 Lời giải S Chọn D SAB   ABCD  H  
SAB   ABCD  AB  SI   ABCD. 
SI  AB, SI  SAB  D A I
Kẻ IK  MD K  MD , IH  SK H  SK  . K B M C
Ta có: SI   ABCD, MD   ABCD  SI  MD . Vậy MD  SIK  mà IH  SIK 
 MD  IH . Vậy IH  SMD  d I,SMD  IH . 1 1 1 3 S  S  S  S  S 2 2 2 2 2
 a  a  a  a  a . I  MD ABCD B  IM A  ID C  MD 8 4 4 8 2 a a 5 2 2 2 MD  CD  MD  a   . 4 2 1 2S 3 5 Mà S  IK. IMD MD  IK   a . IMD 2 MD 10 1 1
Tam giác SAB vuông cân tại S nên SI  AB  a . 2 2
Xét tam giác SIK vuông tại I có: 1 1 1 20 4 56      3 14  IH 
a . Vậy d I SMD 3 14 ,  a . 2 2 2 2 2 2 IH SI IK 9a a 9a 28 28
Câu 11: Cho hình lập phương ABC . D A B  C  D
  cạnh a . Gọi I , J lần lượt là trung điển của BC và AD .
Tính khoảng cách d giữa hai mặt phẳng  AIA và CJC . 5 a 5 3a 5 A. d  2a . B. d  2a 5 . C. d  . D. d  . 2 5 5 Lời giải Chọn C
Gọi O là giao điểm của AB và AC . Ta có:
AIA//CJC  d  AIA,CJC  d I,CJC  IH , với
H là hình chiếu vuông góc của I lên JC . Thật vậy, ta có:   JCC   ABCD  
 JCC   ABCD  JC  IH   JCC . IH    ABCD,IH  JC 1 1 1 4 1 5 a
Xét tam giác JIC vuông tại I , có:      5  IH  . 2 2 2 2 2 2 IH IC IJ a a a 5
Câu 12: Cho khối lăng trụ ABC. 
A BC có thể tích bằng 3
a . Gọi M , N lần lượt là trung điểm của 
A B ,CC ',.Tính khoảng cách từ A đến mặt phẳng BMN  biết rằng BMN là tam giác đều cạnh 2a . a a 3 a 3 A. . B. a 3 . C. . D. . 3 3 2 Lời giải Chọn C A' C' M B' N A C B Ta có: V  V  V C.A  A BB C.  A BC ABC.  A BC 1  V  V V C.A  A BB ABC.  A BC ABC. . 3  A BC 2  V  V C.A  A  B B ABC. . 3  A  B C 1 1 1 Ta có: V  .d N; ABM .S  .d C; A  A BB . .S N .ABM    ABM    3 3 2 A  A BB 1 1 3  1 1 2 . .d C; A  A BB.S  .V  . V  a . 2 3 A  A BB C. 2 A  A BB ABC. 2 3  A BC 3 Ta có: 2 1 a  a V d A BMN S d A BMN d A BMN A BMN  2 1 2 3 3 . ; .  . ; .  . ; . .   BMN         3 3 4 3 2 3 a 3 a a 3 Suy ra .d  ; A BMN    d  ; A BMN   . 3 3 3
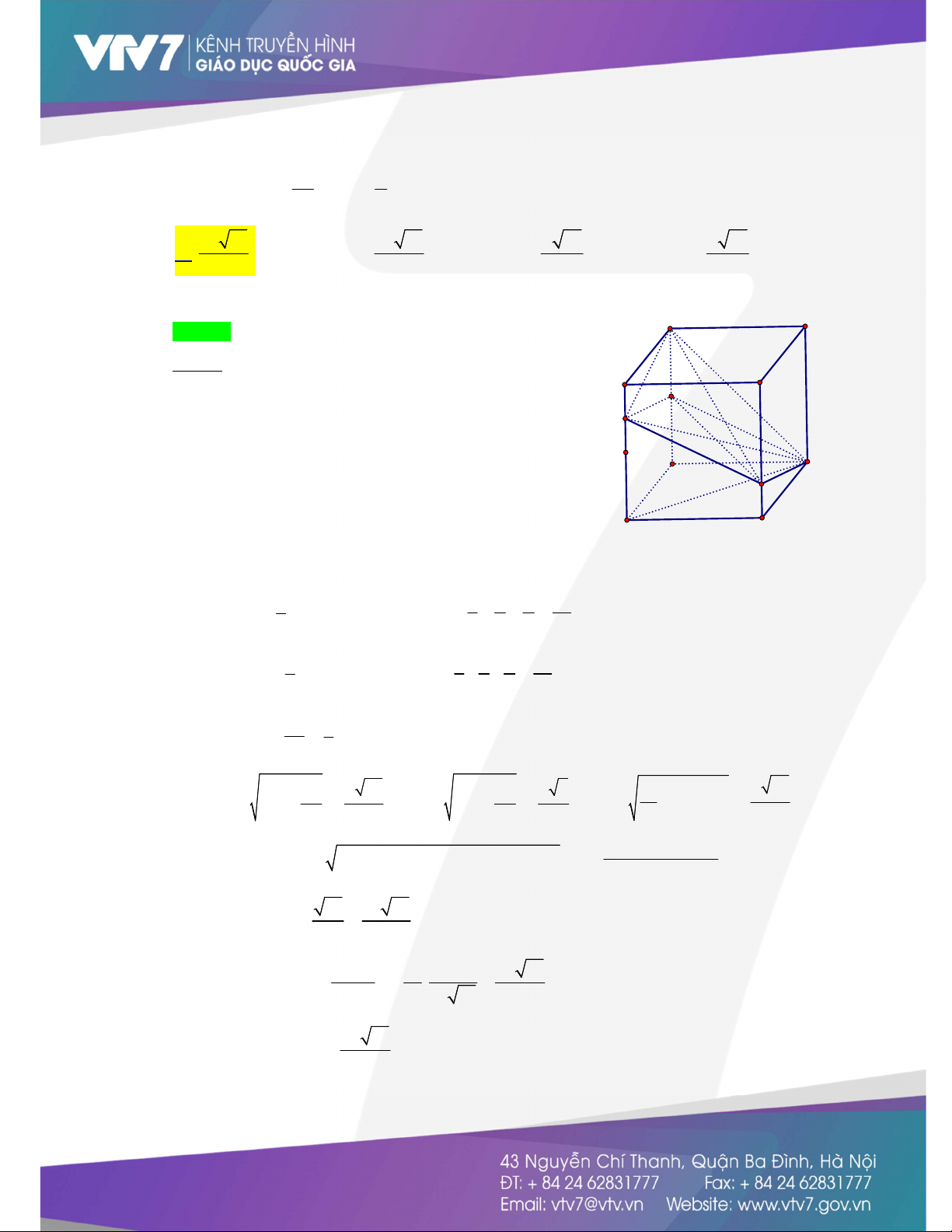
Câu 13: Cho hình lập phương ABC . D AB C  D
  có cạnh là a . Trên AA , BB lấy lần lượt các điểm M , N 3a a sao cho AM 
, BN  . Khoảng cách từ điểm B đến mặt phẳng (MNC) là 4 2 2a 21 2a 21 a 21 a 41 A. . B. . C. . D. . 21 63 21 8 Lời giải C / B / Chọn A Cách 1: D / A/
+Tính d B ,MNC . N M
Mặt phẳng (MNC) cắt các cặp mặt đối của hình hộp theo
các cặp giao tuyến song song. B C Q
Nên thiết diện tạo bởi mp(MNC) và hình hộp là hình bình hành MNCQ. A D V  V  V B '.MNCQ Q.MNB ' Q.B ' NC . 1 3 1 1 a a Có     . a . a  . Q V .MNB' d Q, ABB A .S 3 MNB 3 2 2 12 1 3 1 1 a a Có V  d Q ,CNB .   . ' 3 S Q B NC a a . CNB 3 2 2 12 3  a V 1  d B ,MNCQ B MNCQ  '. .S . 6 3 MNPQ 2 a a 17 2 a a 5 9 a 41 Có 2 2 2 MN  a   , 2 NC  a   , MC  a  2a  . 16 4 4 2 16 4    MN NC MC S  2S
 2 p p  MN  p  NC p  MC , p  . MNCQ MNC 2 2 21 a 21 Suy ra 2 S  2a  . MNCQ 8 4 V 3 a 4 2a 21  d B MNCQ 3 ,   3 .  . S 2 6 a 21 21 MNCQ a
Vậy d B MNCQ 2 21 ,  . 21 Cách 2 A/ D /
Có d B ,CMN   d  , B CMN  M C / B /
Gọi K  MN  AB   ABCD CMN   CK Kẻ BL  CK , LCK , N A D
Kẻ BH  NL , H  NL  d B,CMN   BH . H B C BN 2 KB L Có  2    KB  2BA  2a AM 3 KA 3 K 1 1 1 1 2a Có     BH  2 2 2 2 BH BK BC BN 21 
Câu 14: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và BAD  60. Hình chiếu vuông
góc của S trên mặt phẳng  ABC 
D trùng với trọng tâm của tam giác ABC . Góc giữa mặt
phẳng SAB và  ABC 
D bằng 60 . Khoảng cách từ B đến mặt phẳng SCD bằng 21a 21a 3 7a 3 7a A. . B. . C. . D. . 14 7 14 7 Lời giải Chọn C.
Gọi H là trọng tâm tam giác ABC , M là trung điểm AB a 3
Ta có tam giác ABD là tam giác đều DM  và BD  a 2 Kẻ HK  AB  HK // DM HK BH BH 1 a 3    HK  DM.  DM  DM BD BD 3 6
SABABCD  AB, AB  HK , AB  SK (định lí ba đường vuông góc)  SAB, ABCD     SKH
Tam giác SHK vuông tại H có a SH  HK . tan 60  . 2
Gọi N là giao điểm của HK và CD HN  CD Ta có 
 CD  SHN  ; CDSC  D SC 
D SHN và SHN SCD  SN SH   CD
Trong mặt phẳng SHN kẻ HI  SN thì HI  SCD  HI  d H,SCD 2 a
Tam giác SHN vuông tại H có 1 1 1   , với HN  DM  2 2 2 HI SH HN 3 3 a 7  HI  BD 3    d B SCD 3 ,  d H ,SCD  7 HD 2 2 a Vậy d B SCD 7 ,  . 14
Câu 15: Cho tứ diện ABCD có AB  CD  4 , AC  BD  5 , AD  BC  6 . Tính khoảng cách từ A đến mặt phẳng BCD . 3 6 3 2 3 42 7 A. . B. . C. . D. . 7 5 7 2 Lời giải Chọn C N
Xây dựng bài toán tổng quát
Từ giả thiết ta có: MNDC là hình thoi; các tam giác CAN, n M
DAM là các tam giác cân, suy ra: AI  NC , AI  DM A  AI  (CDMN ) m h 1 1 1 1 I V  V  .4V  2V  I . A IM.IN  . h . m n ABCD . A MNDC . A IMN . 2 2 A IMN 3 3 a b D 2 2 2  a  b  c 2 m   2 2 2 h  m  c 2   C 2 2 2  a  b  c B c Từ 2 2 2 h  n  b 2  n   2 2 2 2 m  n  a   2 2 2  a  b  c 2 h    2 1  V  a b c a b c a b c C  2 2 2     2 2 2    2 2 2   AB D  6 2 1   2 2 2  15 6 4  5  6  2 2 2 4  5  6  2 2 2 4  5  6   . 6 2 4 BC  CD  DB 4  5  6 15 p     S  p p  p  p   BCD     15 7 4 5 6 2 2 2 4 15 6 3. 3V Ta có d  , A  BCD . A BCD  4  3 42  . S 7  15 7 BCD 4