Chuyên đề mặt cầu trong không gian Oxyz – Phạm Văn Long Toán 12

Chuyên đề mặt cầu trong không gian Oxyz – Phạm Văn Long Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

43 22 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ Luyện thi Đại Học 2017

Giáo viên: PHẠM VĂN LONG( TP.Cần Thơ )…0913.518.110… CLB Giáo viên trẻ TP Huế

Giáo viên: PHẠM VĂN LONG

Lớp Toán thầy Long_Thành phố Cần Thơ Số điện thoại: 0913.518.110

CHUYÊN ĐỀ : MẶT CẦU TRONG KHÔNG GIAN OXYZ

I- LÝ THUYẾT:

1/ Định nghĩa

2/ C{c dạng phƣơng trình mặt cầu

Dạng 1 : Phƣơng trình chính tắc

Mặt cầu (S) có tâm

 

;;I a b c

, bán kính

0R 

       

2 2 2

: S x a y b z c R     

Dạng 2 : Phƣơng trình tổng qu{t

2 2 2

( ) : 2 2 2 0 S x y z ax by cz d      

(2)



Điều kiện để phương trình (2) là phương trình

mặt cầu:

2 2 2

0 a b c d   



 

có tâm

 

;;I a b c



 

có bán kính:

2 2 2

R a b c d   

3/ Vị trí tƣơng đối giữa mặt cầu v| mặt phẳng

Cho mặt cầu

 

;S I R

và mặt phẳng

 

. Gọi H là hình chiếu vuông góc của I lên

 

d IH

là

khoảng cách từ I đến mặt phẳng

 

. Khi đó :

+ Nếu

dR

: Mặt cầu và mặt

phẳng không có điểm chung.

+ Nếu

dR

: Mặt phẳng tiếp xúc

mặt cầu. Khi đó (P) là mặt phẳng

tiếp diện của mặt cầu và H là

+ Nếu

dR

: Mặt phẳng (P)

cắt mặt cầu theo thiết diện là

đường tròn có tâm I' và bán

Cho điểm I cố định và một số thực dương R. Tập hợp tất cả

những điểm M trong không gian cách I một khoảng R được gọi là

mặt cầu tâm I, bán kính R.

Kí hiệu:

 

;S I R

   

; / S I R M IM R  

Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ Luyện thi Đại Học 2017

Giáo viên: PHẠM VĂN LONG( TP.Cần Thơ )…0913.518.110… CLB Giáo viên trẻ TP Huế

tiếp điểm.

kính

r R IH

Lưu ý: Khi mặt phẳng

 

đi qua tâm I thì mặt phẳng

 

được gọi là mặt phẳng kính và thiết diện

lúc đó được gọi là đường tròn lớn có diện tích lớn nhất.

4/ Vị trí tƣơng đối giữa mặt cầu v| đƣờng thẳng

Cho mặt cầu

 

;S I R

và đường thẳng



. Gọi H là hình chiếu của I lên



. Khi đó :

IH R



không cắt mặt

cầu.

IH R



tiếp xúc với mặt

cầu.



là tiếp tuyến của (S) và H

là tiếp điểm.

IH R



cắt mặt cầu tại

hai điểm phân biệt.



* Lƣu ý: Trong trường hợp



cắt

 

tại 2 điểm A, B thì bán kính R của (S) được tính như sau:

+ Xác định:

 

;.d I IH

+ Lúc đó:

2 2 2

R IH AH IH



   





5/ Đƣờng tròn trong không gian Oxyz

* Đường tròn

 

trong không gian Oxyz, được xem là giao tuyến của

 

và mặt phẳng

 

2 2 2

: 2 2 2 0 S x y z ax by cz d      

 

: 0P Ax By Cz D   

* Xác định tâm I’ và bán kính r của (C).

+ Tâm

 

'Id





Trong đó

là đường thẳng đi qua

và vuông góc với mp

 

Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ Luyện thi Đại Học 2017

Giáo viên: PHẠM VĂN LONG( TP.Cần Thơ )…0913.518.110… CLB Giáo viên trẻ TP Huế

+ Bán kính

   

 

' ; r R II R d I P



   



5/ Điều kiện tiếp xúc : Cho mặt cầu (S) tâm I, bán kính R.

+ Đường thẳng



là tiếp tuyến của (S)



 

; .d I R

+ Mặt phẳng

 

là tiếp diện của (S)



 

; .d I P R

* Lƣu ý: Tìm tiếp điểm

 

0 0 0 0

;;M x y z

Sử dụng tính chất :

 

IM d

IM a

IM P

IM n





























II. VÍ DỤ MINH HỌA :

Dạng 1: VIẾT PHƢƠNG TRÌNH MẶT CẦU

Phương pháp:

* Thuật to{n 1: Bước 1: Xác định tâm

 

;;I a b c

Bước 2: Xác định bán kính

của (S).

Bước 3: Mặt cầu (S) có tâm

 

;;I a b c

và bán kính

     

2 2 2

( ) : S x a y b z c R     

* Thuật to{n 2: Gọi phương trình

2 2 2

( ) : 2 2 2 0 S x y z ax by cz d      

Phương trình (S) hoàn toàn xác định nếu biết được

, , , .a b c d

(

2 2 2

0a b c d   

)

B|i tập 1 : Viết phương trình mặt cầu (S), trong các trường hợp sau:

 

có tâm

 

2; 2; 3I 

và bán kính

3R 

 

có tâm

 

1;2;0I

và (S) qua

 

2; 2;1P 

 

có đường kính AB với

   

1;3;1 , 2;0;1AB

Bài giải:

a) Mặt cầu tâm

 

2; 2; 3I 

và bán kính

3R 

, có phương trình:

(S):

     

2 2 2

2 2 3 9xyz     

b) Ta có:

 

1; 4;1 3 2IP IP   



Mặt cầu tâm

 

1;2;0I

và bán kính

32R IP

, có phương trình:

(S):

   

1 2 18x y z    

Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ Luyện thi Đại Học 2017

Giáo viên: PHẠM VĂN LONG( TP.Cần Thơ )…0913.518.110… CLB Giáo viên trẻ TP Huế

c) Ta có:

 

3; 3;0 3 2AB AB    



Gọi I là trung điểm AB

; ;1









Mặt cầu tâm

; ;1









và bán kính

R 

, có phương trình:

(S):

 

1 3 9

2 2 2

x y z

   

     

   

   

B|i tập 2 : Viết phương trình mặt cầu (S) , trong các trường hợp sau:

a) (S) qua

   

3;1;0 , 5;5;0AB

và tâm I thuộc trục

b) (S) có tâm O và tiếp xúc mặt phẳng

 

: 16 15 12 75 0x y z



   

c) (S) có tâm

 

1;2; 0I 

và có một tiếp tuyến là đường thẳng

1 1 3





  



Bài giải:

a) Gọi

 

;0;0I a Ox

. Ta có :

   

3 ;1;0 , 5 ; 5;0IA a IB a   

 

Do (S) đi qua A, B

   

3 1 5 25 4 40 10IA IB a a a a           

 

10;0; 0I

và

52IA 

Mặt cầu tâm

 

10;0;0I

và bán kính

52R 

, có phương trình (S) :

 

10 50x y z   

b) Do (S) tiếp xúc với

 



 

d , 3.

O R R



    

Mặt cầu tâm

 

0;0; 0O

và bán kính

3R 

, có phương trình (S) :

2 2 2

9xyz  

c) Chọn

   

1;1;0 0; 1;0A IA    



Đường thẳng



có một vectơ chỉ phương là

 

1;1; 3u



  



. Ta có:

 

, 3; 0; 1IA u













Do (S) tiếp xúc với

 

IA u

I R R







      





Mặt cầu tâm

 

1;2; 0I 

và bán kính

R 

, có phương trình (S) :

   

1 2 .

121

x y z    

B|i tập 3 : Viết phương trình mặt cầu (S) biết :

a) (S) qua bốn điểm

       

1;2; 4 , 1; 3;1 , 2;2; 3 , 1;0; 4A B C D

b) (S) qua

     

0;8;0 , 4;6;2 , 0;12;4A B C

và có tâm I thuộc mặt phẳng (Oyz).

Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ Luyện thi Đại Học 2017

Giáo viên: PHẠM VĂN LONG( TP.Cần Thơ )…0913.518.110… CLB Giáo viên trẻ TP Huế

Bài giải:

a) Cách 1: Gọi

 

;;I x y z

là tâm mặt cầu (S) cần tìm.

Theo giả thiết:

7 2 1

4 1 0

IA IB

IA IB y z x

IA IC IA IC x z y

IA ID y z z

IA ID





  

      



  

        

   

   

   



  



Do đó:

 

2;1;0I 

và

26R IA

. Vậy (S) :

   

2 1 26x y z    

Cách 2: Gọi phương trình mặt cầu (S) :

2 2 2

2 2 2 0x y z ax by cz d      

 

2 2 2

0a b c d   

   

1;2; 4AS  

2 4 8 21a b c d     

(1)

Tương tự:

   

1; 3;1 2 6 2 11B S a b c d        

(2)

   

2;2; 3CS

4 4 6 17a b c d     

(3)

   

1;0; 4 2 8 17D S a c d      

(4)

Giải hệ (1), (2), (3), (4) ta có

, , , a b c d

, suy ra phương trình mặt cầu (S) :

   

2 1 26x y z    

b) Do tâm I của mặt cầu nằm trên mặt phẳng (Oyz)

 

0; ;I b c

Ta có:

IA IB b

IA IB IC

IA IC



  



   









Vậy

 

0;7; 5I

và

26R 

. Vậy (S):

   

7 5 26.x y z    

B|i tập 4: Viết phương trình mặt cầu (S) có tâm I thuộc đường thẳng





  









và (S) tiếp xúc

với hai mặt phẳng

 

: 2 2 3 0xyz



   

và

 

: 2 2 7 0xyz



   

Bài giải:

Gọi

 

; 1;I t t  

là tâm mặt cầu (S) cần tìm.

Theo giả thiết:

 

, , 3

d I d I t







  

     







Suy ra:

 

3; 1; 3I 

và

 





. Vậy (S) :

     

2 2 2

3 1 3

x y z     

Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ Luyện thi Đại Học 2017

Giáo viên: PHẠM VĂN LONG( TP.Cần Thơ )…0913.518.110… CLB Giáo viên trẻ TP Huế

B|i tập 5: Lập phương trình mặt cầu (S) qua 2 điểm

   

2;6;0 , 4;0;8AB

và có tâm thuộc d :

1 2 1

xz





Bài giải:

Ta có

d y t













  



. Gọi

 

1 ; 2 ; 5I t t t d   

là tâm của mặt cầu (S) cần tìm.

Ta có:

   

1 ;6 2 ; 5 , 3 ; 2 ;13IA t t t IB t t t       

 

Theo giả thiết, do (S) đi qua A, B

AI BI

         

2 2 2 2 2

1 6 2 5 3 4 13t t t t t t          

62 32 178 20 12 116

t t t t         

32 58 44

;;

333



  





và

2 233R IA

. Vậy (S):

2 2 2

32 58 44

932

3 3 3

x y z

     

     

     

     

B|i tập 6: Viết phương trình mặt cầu (S) có tâm

 

2; 3; 1I 

và cắt đường thẳng

1 4 1





  



tại hai điểm A, B với

16AB 

Bài giải:

Chọn

   

1;1;0 3; 2;1A IA     



. Đường thẳng



có một vectơ chỉ phương là

 

1; 4;1u







Ta có:

   

, 2; 4;14 d , 2 3

IA u

IA u I









    











Gọi R là bán kính mặt cầu (S). Theo giả thiết :

 

d , 2 19.



   



Vậy (S):

     

2 2 2

2 3 1 76x y z     

B|i tập 7: Cho hai mặt phẳng

   

: 5 4 6 0, : 2 7 0P x y z Q x y z       

và đường thẳng

7 3 2

xz

  



. Viết phương trình mặt cầu (S) có tâm I là giao điểm của (P) và



sao cho (Q)

cắt (S) theo một hình tròn có diện tích là



Bài giải:

Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ Luyện thi Đại Học 2017

Giáo viên: PHẠM VĂN LONG( TP.Cần Thơ )…0913.518.110… CLB Giáo viên trẻ TP Huế

Ta có

















. Tọa độ I là nghiệm của hệ phương trình:

1 7 (1)

3 (2)

1 2 (3)

5 4 6 0 (4)

x y z

  













   



Thay (1), (2), (3) vào (4) ta có:

       

5 1 7 4 3 1 2 6 0 0 1;0;1t t t t I        

Ta có :

 

d I Q 

Gọi r là bán kính đường tròn giao tuyến của (S) và mặt phẳng (Q). Ta có:

20 2 5.rr



  

R là bán kính mặt cầu (S) cần tìm.

Theo giả thiết:

 

330

R d I Q r



  



Vậy (S) :

   

110

x y z    

B|i tập 8: Cho mặt phẳng

( ) : 2 2 2 0P x y z   

và đường thẳng

: 2 1

d y t

  













Viết phương trình mặt cầu (S) có tâm I thuộc

và I cách (P) một khoảng bằng 2 và (S) cắt (P)

theo giao tuyến là đường tròn có bán kính bằng 3.

Bài giải:

Gọi

 

;2 1; 2 :I t t t d   

là tâm của mặt cầu (S) và R là bán kính của (S).

Theo giả thiết :

 

; 4 9 13R d I P r



    



Mặt khác:

 

2 2 1 2 4 2

; 2 2 6 5 6

4 1 4

t t t

d I P t







     

      













* Với

t 

: Tâm

1 2 13

;;

6 3 6









, suy ra

 

2 2 2

1 2 13

: 13

6 3 6

S x y z

     

     

     

     

* Với

t 

: Tâm

11 2 1

;;

6 3 6









, suy ra

 

2 2 2

11 2 1

: 13

6 3 6

S x y z

     

     

     

     

B|i tập 9: Cho điểm

 

1;0; 3I

và đường thẳng

2 1 2







. Viết phương trình mặt cầu

(S) tâm I và cắt

tại hai điểm A, B sao cho

IAB

vuông tại I.

Bài giải :

Đường thẳng

có một vectơ chỉ phương

 

2;1;2u 



và

 

1; 1;1Pd

Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ Luyện thi Đại Học 2017

Giáo viên: PHẠM VĂN LONG( TP.Cần Thơ )…0913.518.110… CLB Giáo viên trẻ TP Huế

Ta có:

 

0; 1; 2IP   



 

, 0; 4; 2u IP



   







. Suy ra:

 

u IP











Gọi R là bán kính của (S). Theo giả thiết,

IAB

vuông tại I

 

2 2 2 2

1 1 1 2 40

2 2d ,

R IH I d

IH IA IB R

       

Vậy (S) :

   

x y z    

B|i tập 10: (Khối A- 2011) Cho mặt cầu (S):

2 2 2

4 4 4 0x y z x y z     

và điểm

 

4; 4; 0A

. Viết

phương trình mặt phẳng (OAB), biết điểm B thuộc (S) và tam giác OAB đều.

Bài giải :

(S) có tâm

 

2; 2; 2 ,I

bán kính

23R 

. Nhận xét: điểm O và A cùng thuộc (S).

Tam giác OAB đều, có bán kính đường tròn ngoại tiếp

R 

Khoảng cách :

 

;

d I P R R  

Mặt phẳng (P) đi qua O có phương trình dạng :

 

2 2 2

0 0 *ax by cz a b c     

Do (P) đi qua A, suy ra:

4 4 0a b b a    

Lúc đó:

 

2 2 2 2 2 2 2

a b c

a b c a c a c



   

   

2 2 2

a c c





   







. Theo (*), suy ra

 

:0P x y z

hoặc

0.xyz  

Chú ý: Kỹ năng xác định tâm và bán kính của đường tròn trong không gian.

Cho mặt cầu (S) tâm I bán kính R. Mặt phẳng (P) cắt (S) theo một đường tròn (C).

Bƣớc 1: Lập phương trình đường thẳng d qua I và vuông góc với mặt phẳng (P).

Bƣớc 2: Tâm H của đường tròn (C) là giao điểm của d và mặt phẳng (P).

Bƣớc 3: Gọi

là bán kính của (C):

 

; r R d I P







B|i tập 11: Chứng minh rằng: Mặt cầu

2 2 2

( ) : 2 3 0S x y z x    

cắt mặt phẳng (P):

20x 

theo giao tuyến là một đường tròn (C). Xác định tâm và bán kính của (C).

Bài giải :

* Mặt cầu (S) có tâm

 

1;0; 0I

và bán kính

2R 

Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ Luyện thi Đại Học 2017

Giáo viên: PHẠM VĂN LONG( TP.Cần Thơ )…0913.518.110… CLB Giáo viên trẻ TP Huế

Ta có :

 

d , 1 2I P R   

mặt phẳng (P) cắt (S) theo giao tuyến là 1 đường tròn. (đ.p.c.m)

* Đường thẳng d qua

 

1;0; 0I

và vuông góc với (P) nên nhận

 

1;0;0

n 



làm 1 vectơ chỉ

phương, có phương trình

















+ Tọa độ tâm

đường tròn là nghiệm của hệ :

 

0 2;0;0

  









  

















+ Ta có:

 

,1d I P 

. Gọi r là bán kính của (C), ta có :

 

, 3.r R d I P



  



Dạng 2 : SỰ TƢƠNG GIAO V\ SỰ TIẾP XÚC

* C{c điều kiện tiếp xúc:

+ Đường thẳng



là tiếp tuyến của (S)



 

; .d I R

+ Mặt phẳng

()



là tiếp diện của (S)



 

; .d I R





* Lưu ý các dạng toán liên quan như tìm tiếp điểm, tương giao.

B|i tập 1: Cho đường thẳng

 

2 1 1



  



và và mặt cầu

 

2 2 2

2 4 1 0x y z x z     

Số điểm chung của

 



và

 

là :

A. 0. B. 1. C. 2. D. 3.

Bài giải:

Đường thẳng

 



đi qua

 

0;1; 2M

và có một vectơ chỉ phương là

 

2;1; 1u 



Mặt cầu

 

có tâm

 

1;0; 2I 

và bán kính

2.R 

Ta có

 

1; 1; 4MI   



và

 

, 5;7; 3u MI



  



 

 

498

u MI





   

 



Vì

 

,d I R

nên

 



không cắt mặt cầu

 

Lựa chọn đáp án A.

B|i tập 2: Cho điểm

 

1; 2; 3I 

. Phương trình mặt cầu tâm I và tiếp xúc với trục Oy là:

     

2 2 2

1 2 3 10.x y z    

     

2 2 2

1 2 3 10.x y z    

Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ Luyện thi Đại Học 2017

Giáo viên: PHẠM VĂN LONG( TP.Cần Thơ )…0913.518.110… CLB Giáo viên trẻ TP Huế

     

2 2 2

1 2 3 10.x y z    

     

2 2 2

1 2 3 9.x y z    

Bài giải:

Gọi M là hình chiếu của

 

1; 2; 3I 

lên Oy, ta có :

 

0; 2; 0M 

   

1;0; 3 , 10IM R d I Oy IM      



là bán kính mặt cầu cần tìm.

Phương trình mặt cầu là :

     

2 2 2

1 2 3 10.x y z    

Lựa chọn đáp án B.

B|i tập 3: Cho điểm

 

1; 2; 3I 

và đường thẳng d có phương trình

2 1 1









. Phương

trình mặt cầu tâm A, tiếp xúc với d là:

     

2 2 2

1 2 3 50.x y z     

     

2 2 2

1 2 3 5 2.x y z     

     

2 2 2

1 2 3 5 2.x y z     

     

2 2 2

1 2 3 50.x y z     

Bài giải:

Đường thẳng

 

đi qua

 

1;2; 3I 

và có VTCP

 

2;1; 1u 



 

, 5 2

u AM

d A d





  

 



Phương trình mặt cầu là :

     

2 2 2

1 2 3 50.x y z    

Lựa chọn đáp án D.

B|i tập 4: Mặt cầu

 

tâm

 

2; 3; 1I 

cắt đường thẳng

11 25

2 1 2







tại 2 điểm A, B sao

cho

16AB 

có phương trình là:

     

2 2 2

2 3 1 17.x y z     

     

2 2 2

2 3 1 289.x y z     

     

2 2 2

2 3 1 289.x y z     

     

2 2 2

2 3 1 280.x y z     

Bài giải:

Đường thẳng

 

đi qua

 

11; 0; 25M 

và có vectơ chỉ phương

 

2;1; 2u 



Gọi H là hình chiếu của I trên (d). Ta có:

 

, 15

u MI

IH d I AB





  

 



R IH



   





Vậy

 

     

2 2 2

2 3 1 289.x y z     

Lựa chọn đáp án C.

Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ Luyện thi Đại Học 2017

Giáo viên: PHẠM VĂN LONG( TP.Cần Thơ )…0913.518.110… CLB Giáo viên trẻ TP Huế

B|i tập 5: Cho đường thẳng

2 2 1









và điểm

(4;1;6)I

. Đường thẳng d cắt mặt cầu

 

có tâm I, tại hai điểm A, B sao cho

6AB 

. Phương trình của mặt cầu

 

là:

     

2 2 2

4 1 6 18.x y z     

     

2 2 2

4 1 6 18.x y z     

     

2 2 2

4 1 6 9.x y z     

     

2 2 2

4 1 6 16.x y z     

Bài giải :

Đường thẳng

đi qua

( 5;7;0)M 

và có vectơ chỉ phương

(2; 2;1)u 



. Gọi H là hình chiếu của I trên (d). Ta có :

 

u MI

IH d I AB





  

 



R IH



   





Vậy

 

     

2 2 2

4 1 6 18.x y z     

Lựa chọn đáp án A.

B|i tập 8: Cho điểm

 

1;0; 0I

và đường thẳng

1 2 1







. Phương trình mặt cầu

 

có

tâm I và cắt đường thẳng d tại hai điểm A, B sao cho tam giác IAB đều là:

 

x y z   

 

x y z   

 

x y z   

 

x y z   

Bài giải:

Đường thẳng

 



đi qua

 

1;1; 2M 

và có vectơ chỉ phương

 

1;2;1u 



Ta có

 

0; 1; 2MI 



và

 

, 5; 2; 1u MI



  



 

Gọi H là hình chiếu của I trên (d). Ta có :

 

u MI

IH d I AB





  

 



Xét tam giác IAB, có

3 2 2 15

IH R R   

Vậy phương trình mặt cầu là:

 

x y z   

Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ Luyện thi Đại Học 2017

Giáo viên: PHẠM VĂN LONG( TP.Cần Thơ )…0913.518.110… CLB Giáo viên trẻ TP Huế

Lựa chọn đáp án A.

B|i tập 9: Cho mặt cầu

2 2 2

( ) : 4 2 6 5 0S x y z x y z      

. Viết phương trình tiếp tuyến của mặt

cầu (S) tại

 

0;0; 5A

biết:

a) Tiếp tuyến có một vectơ chỉ phương

 

1;2; 2u 



b) Vuông góc với mặt phẳng (P) :

3 2 2 3 0.x y z   

Bài giải:

a) Đường thẳng d qua

 

0;0; 5A

và có một vectơ chỉ phương

 

1;2; 2u 



, có phương trình d:

















b) Mặt phẳng (P) có một vectơ pháp tuyến là

 

3; 2; 2

n 



Đường thẳng d qua

 

0;0; 5A

và vuông góc với mặt phẳng (P) nên có một vectơ chỉ phương

 

3; 2; 2

n 



, có phương trình d:

















B|i tập 10: Cho mặt cầu

2 2 2

( ) : 6 6 2 3 0S x y z x y z      

và hai đường thẳng

: 1 2



  



   









2 2 1



  

. Viết phương trình mặt phẳng (P) song song với



và



đồng thời tiếp xúc

với (S).

Bài giải:

Mặt cầu (S) có tâm

 

3;3; 1 , 4IR

Ta có:



có một vectơ chỉ phương là

 

3;2; 2u 





có một vectơ chỉ phương là

 

2; 2;1u 



Gọi



là một vectơ pháp của mặt phẳng (P).

Do:

( ) / /

P n u















chọn

Lúc đó, mặt phẳng (P) có dạng :

2 2 0x y z m    

Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ Luyện thi Đại Học 2017

Giáo viên: PHẠM VĂN LONG( TP.Cần Thơ )…0913.518.110… CLB Giáo viên trẻ TP Huế

Để mặt phẳng (P) tiếp xúc với (S)

 

;( ) 4

d I P R



   

5 12



   







Kết luận: Vậy tồn tại 2 mặt phẳng (P) là :

2 2 7 0; 2 2 17 0x y z x y z         

B|i tập 11: Viết phương trình tiếp diện của mặt cầu

 

2 2 2

: 2 4 6 5 0S x y z x y z      

, biết:

a) qua

 

1;1;1M

b) song song với mặt phẳng (P) :

2 2 1 0x y z   

b) vuông góc với đường thẳng

2 1 2









Bài giải:

Mặt cầu (S) có tâm

 

1;2; 3I 

, bán kính

3R 

a) Để ý rằng,

 

MS

. Tiếp diện tại M có một vectơ pháp tuyến là

 

2; 1; 2IM   



, có phương

trình :

       

: 2 1 1 2 1 0 2 2 1 0.x y z x y z



          

b) Do mặt phẳng

   

// P



nên có dạng :

2 2 0x y z m   

 



tiếp xúc với (S)

 

d , 3 3 9

I R m





  

       







* Với

6m 

suy ra mặt phẳng có phương trình :

2 2 6 0.x y z   

* Với suy ra mặt phẳng có phương trình :

2 2 12 0.x y z   

c) Đường thẳng d có một vectơ chỉ phương là .

Do mặt phẳng

 





nên

 



nhận

 

2;1; 2

u 



làm một vectơ pháp tuyến.

Suy ra mặt phẳng

 



có dạng :

2 2 0x y z m   

 



tiếp xúc với (S)

 

, 3 6 9

d I R m









       







* Với

3m 

suy ra mặt phẳng có phương trình :

2 2 3 0.x y z   

* Với

15m 

suy ra mặt phẳng có phương trình :

2 2 15 0.x y z   

Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ Luyện thi Đại Học 2017

Giáo viên: PHẠM VĂN LONG( TP.Cần Thơ )…0913.518.110… CLB Giáo viên trẻ TP Huế

III. B\I TẬP TRẮC NGHIỆM :

NHẬN BIẾT_THÔNG HIỂU

Câu 1. Phương trình nào sau đây là phương trình mặt cầu ?

2 2 2

2 1 0.x y z x y     

2 2 2

2 0.x y z x   

 

2 2 2

2 2 2 1.x y x y z x     

 

2 1.x y xy z   

Câu 2. Phương trình nào sau đây không phải là phương trình mặt cầu ?

 

2 2 2

2 2 2 1.x y x y z x     

2 2 2

2 0.x y z x   

2 2 2

2 2 1 0.x y z x y     

 

2 1 4 .x y xy z x    

Câu 3. Phương trình nào sau đây không phải là phương trình mặt cầu ?

 

2 3 6 .x y xy z x    

     

2 2 2

1 1 1 6.xyz     

     

2 2 2

2 1 2 1 2 1 6.xyz     

     

2 2 2

1 2 1 1 6.x y z     

Câu 4. Cho các phương trình sau:

 

11x y z   

 

2 1 4x y z   

2 2 2

10xyz   

   

2 1 2 1 4 16x y z    

Số phương trình là phương trình mặt cầu là:

A. 2. B. 3. C. 4. D. 1.

Câu 5. Mặt cầu

     

: 1 2 9S x y z    

có tâm là:

 

1;2;0 .I

 

1;2; 0 .I 

 

1; 2;0 .I 

 

1; 2;0 .I 

Câu 6. Mặt cầu

 

2 2 2

: 8 2 1 0S x y z x y     

có tâm là:

 

4;1;0 .I 

 

4; 1;0 .I 

 

8; 2;0 .I 

 

8; 2; 0 .I 

Câu 7. Mặt cầu

 

2 2 2

: 4 1 0S x y z x    

có tọa độ tâm và bán kính R là:

 

2;0;0 , 3.IR

 

2;0;0 , 3.IR

 

0;2;0 , 3.IR

 

2;0;0 , 3.IR

Câu 8. Phương trình mặt cầu có tâm

 

1;2; 3I 

, bán kính

3R 

là:

     

2 2 2

1 2 3 3.x y z     

     

2 2 2

1 2 3 9.x y z     

     

2 2 2

1 2 3 9.x y z     

     

2 2 2

1 2 3 9.x y z     

Câu 9. Mặt cầu

   

: 2 1 4S x y xy z x    

có tâm là:

Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ Luyện thi Đại Học 2017

Giáo viên: PHẠM VĂN LONG( TP.Cần Thơ )…0913.518.110… CLB Giáo viên trẻ TP Huế

 

2;0; 0 .I

 

4;0; 0 .I

 

4;0; 0 .I 

 

2;0; 0 .I 

Câu 10. Đường kính của mặt cầu

   

: 1 4S x y z   

bằng:

A. 4. B. 2. D. 8. D. 16.

Câu 11. Mặt cầu có phương trình nào sau đây có tâm là

 

1;1;0 ?I

 

2 1 4 .x y xy z x    

2 2 2

2 2 0.x y z x y    

2 2 2

2 2 1 0.x y z x y     

 

2 2 2

2 2 2 1 2 .x y x y z x xy      

Câu 12. Mặt cầu

 

2 2 2

3 3 3 6 12 2 0x y z x y     

có bán kính bằng:

. B.

. C.

. D.

Câu 13. Gọi I là tâm mặt cầu

   

: 2 4S x y z   

. Độ dài



(

là gốc tọa độ ) bằng:

B. 4. C. 1. D. 2.

Câu 14. Phương trình mặt cầu có bán kính bằng 3 và tâm là giao điểm của ba trục toạ độ ?

2 2 2

6 0.x y z x   

2 2 2

6 0.x y z y   

2 2 2

6 0.   x y z z

2 2 2

9.xyz  

Câu 15. Mặt cầu

 

2 2 2

: 2 10 3 1 0S x y z x y z      

đi qua điểm có tọa độ nào sau đây ?

 

2;1;9 .

 

3; 2; 4 .

 

4; 1;0 .

 

1;3; 1 .

Câu 16. Mặt cầu tâm

 

1;2; 3I 

và đi qua điểm

 

2;0; 0A

có phương trình:

     

2 2 2

1 2 3 11.x y z     

     

2 2 2

1 2 3 22.x y z     

     

2 2 2

1 2 3 22.x y z     

     

2 2 2

1 2 3 22.x y z     

Câu 17. Cho hai điểm

 

1;0; 3A 

và

 

3;2;1B

. Phương trình mặt cầu đường kính AB là:

2 2 2

2 6 0.x y z x y z      

2 2 2

4 2 2 0.x y z x y z     

2 2 2

4 2 2 0.x y z x y z     

2 2 2

4 2 2 6 0.      x y z x y z

Câu 18. Nếu mặt cầu

 

đi qua bốn điểm

     

2;2;2 , 4;0;2 , 4;2;0M N P

và

 

4; 2; 2Q

thì tâm

của

 

có toạ độ là:

 

1; 1;0 .

 

3;1;1 .

 

1;1;1 .

 

1;2;1 .

Câu 19. Bán kính mặt cầu đi qua bốn điểm

     

1;0;1 , 1;0;0 , 2;1;0M N P

và

 

1;1;1Q

bằng:

Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ Luyện thi Đại Học 2017

Giáo viên: PHẠM VĂN LONG( TP.Cần Thơ )…0913.518.110… CLB Giáo viên trẻ TP Huế

C. 1. D.

Câu 20. Cho mặt cầu

 

2 2 2

: 4 0S x y z   

và 4 điểm

       

1;2;0 , 0;1;0 , 1;1;1 , 1; 1;2M N P Q 

Trong bốn điểm đó, có bao nhiêu điểm không nằm trên mặt cầu

 

A. 4 điểm. B. 2 điểm. C. 1 điểm. D. 3 điểm.

Câu 21. Mặt cầu

 

tâm

 

1;2; 3I 

và tiếp xúc với mặt phẳng

 

: 2 2 1 0P x y z   

có phương

trình:

     

2 2 2

1 2 3 .

x y z     

     

2 2 2

1 2 3 .

x y z     

     

2 2 2

1 2 3 .

x y z     

     

2 2 2

1 2 3 .

x y z     

Câu 22. Phương trình mặt cầu nào dưới đây có tâm

 

2;1; 3I

và tiếp xúc với mặt phẳng

 

: 2 2 2 0P x y z   

     

2 2 2

2 1 1 4.x y z     

     

2 2 2

2 1 3 16.x y z     

     

2 2 2

2 1 1 25.x y z     

     

2 2 2

2 1 1 9.x y z     

Câu 23. Mặt cầu có tâm

 

3; 3;1I

và đi qua

 

5; 2;1A 

có phương trình:

     

2 2 2

3 3 1 5.x y z     

     

2 2 2

5 2 1 5.     x y z

     

2 2 2

3 3 1 5.x y z     

     

2 2 2

5 2 1 5.x y z     

Câu 24. Phương trình mặt trình mặt cầu có đường kính

với

   

1;3;2 , 3;5;0AB

là:

2 2 2

( 2) ( 4) ( 1) 3.xyz     

2 2 2

( 2) ( 4) ( 1) 2.xyz     

2 2 2

( 2) ( 4) ( 1) 2.xyz     

2 2 2

( 2) ( 4) ( 1) 3.xyz     

Câu 25. Cho

 

1;2; 4I

và mặt phẳng

 

:2 2 1 0   P x y z

. Mặt cầu tâm

và tiếp xúc với mặt

phẳng

 

, có phương trình là:

     

2 2 2

1 2 4 4.x y z     

     

2 2 2

1 2 4 1.x y z     

     

2 2 2

1 2 4 3.x y z     

     

2 2 2

1 2 4 4.x y z     

Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ Luyện thi Đại Học 2017

Giáo viên: PHẠM VĂN LONG( TP.Cần Thơ )…0913.518.110… CLB Giáo viên trẻ TP Huế

VẬN DỤNG

Câu 1. Cho đường thẳng

1 2 1









và điểm

 

5;4; 2A 

. Phương trình mặt cầu đi qua

điểm

và có tâm là giao điểm của

với mặt phẳng

 

Oxy

là:

     

: 1 1 ( 2) 65.S x y z     

     

: 1 1 9.S x y z    

     

: 1 2 64.S x y z    

     

: 1 1 65.S x y z    

Câu 2. Cho ba điểm

(6; 2; 3)A 

(0;1;6)B

(2;0; 1)C 

(4;1;0)O

. Khi đó mặt cầu ngoại tiếp tứ diện

OABC

có phương trình là:

2 2 2

4 2 6 3 0.x y z x y z      

2 2 2

4 2 6 3 0.x y z x y z      

2 2 2

2 3 3 0.x y z x y z      

2 2 2

2 3 3 0.x y z x y z      

Câu 3. Cho ba điểm

     

2;0;1 , 1;0;0 , 1;1;1A B C

và mặt phẳng

 

: 2 0P x y z   

. Phương trình

mặt cầu đi qua ba điểm

,,A B C

và có tâm thuộc mặt phẳng

 

là:

2 2 2

2 1 0.x y z x y     

2 2 2

2 2 1 0.x y z x z     

2 2 2

2 2 1 0.x y z x y     

2 2 2

2 1 0.x y z x z     

Câu 4. Phương trình mặt cầu tâm

 

1; 2; 3I 

và tiếp xúc với trục

là:

     

2 2 2

1 2 3 8.x y z     

     

2 2 2

1 2 3 16.x y z     

     

2 2 2

1 2 3 10.x y z     

     

2 2 2

1 2 3 9.x y z     

Câu 5. Cho các điểm

   

2;4;1 , 2;0;3AB

và đường thẳng

: 1 2

d y t













  



. Gọi

 

là mặt cầu đi

qua

,AB

và có tâm thuộc đường thẳng

. Bán kính mặt cầu

 

bằng:

A. 3. B.

3 3.

2 3.

Câu 6. Cho điểm

 

1; 2; 3A 

và đường thẳng

có phương trình

2 1 1









. Phương

trình mặt cầu tâm

, tiếp xúc với

là:

     

2 2 2

–1 2 – 3 5.x y z   

     

2 2 2

–1 2 – 3 50.x y z   

     

2 2 2

–1 2 – 3 50.x y z   

     

2 2 2

1 2 3 50.x y z     

Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ Luyện thi Đại Học 2017

Giáo viên: PHẠM VĂN LONG( TP.Cần Thơ )…0913.518.110… CLB Giáo viên trẻ TP Huế

Câu 7. Cho đường thẳng d:

3 1 1







và mặt phẳng

 

: 2 2 2 0P x y z   

. Phương trình

mặt cầu

 

có tâm nằm trên đường thẳng d có bán kính nhỏ nhất tiếp xúc với

 

và đi qua

điểm

 

1; 1;1A 

là:

     

2 2 2

3 1 1 1.x y z     

   

4 1 1.x y z    

     

2 2 2

2 2 1 1.xyz     

   

1 1 1.x y z    

Câu 8. Phương trình mặt cầu có tâm

 

1;2; 3I

và tiếp xúc với mặt phẳng

 

Oxz

là:

2 2 2

2 4 6 10 0.x y z x y z      

2 2 2

2 4 6 10 0.x y z x y z      

2 2 2

2 4 6 10 0.x y z x y z      

2 2 2

2 4 6 10 0.x y z x y z      

Câu 9. Mặt phẳng

 

tiếp xúc với mặt cầu tâm

 

1; 3; 2I 

tại điểm

 

7; 1; 5M 

có phương trình là

3 22 0.xyz   

6 2 3 55 0.x y z   

6 2 3 55 0.x y z   

3 22 0.xyz   

Câu 10. Cho mặt cầu

2 2 2

( ) : 2 4 6 2 0S x y z x y z      

và mặt phẳng

( ) : 4 3 12 10 0x y z



   

Mặt phẳng tiếp xúc với

 

và song song với

()



có phương trình là:

4 3 12 78 0x y z   

hoặc

4 3 12 78 0.x y z   

4 3 12 78 0x y z   

hoặc

4 3 12 26 0.x y z   

4 3 12 26 0x y z   

hoặc

4 3 12 26 0.x y z   

4 3 12 78 0x y z   

hoặc

4 3 12 26 0.x y z   

Câu 11. Cho mặt cầu

   

( ) : 2 1 14S x y z    

. Mặt cầu

 

cắt trục

tại

và

( 0)

z 

Phương trình nào sau đây là phương trình tiếp diện của

 

tại

2 3 9 0.x y z   

2 3 9 0.x y z   

2 3 0.x y z   

2 3 0.x y z   

Câu 12. Cho 4 điềm

     

3; 2; 2 , 3;2;0 , 0; 2;1A B C

và

 

1;1; 2D 

. Mặt cầu tâm A và tiếp xúc

với mặt phẳng

 

BCD

có phương trình là:

     

2 2 2

3 2 2 14.xyz     

     

2 2 2

3 2 2 14.x y z     

     

2 2 2

3 2 2 14.xyz     

     

2 2 2

3 2 2 14.x y z     

Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ Luyện thi Đại Học 2017

Giáo viên: PHẠM VĂN LONG( TP.Cần Thơ )…0913.518.110… CLB Giáo viên trẻ TP Huế

Câu 13. Cho mặt phẳng

 

: 2 3 2 0P x y z   

. Mặt cầu

 

có tâm I thuộc trục Oz, bán kính

bằng

và tiếp xúc mặt phẳng (P) có phương trình:

 

x y z   

hoặc

 

x y z   

2 2 2

xyz  

hoặc

 

x y z   

 

   x y z

hoặc

 

x y z   

2 2 2

xyz  

hoặc

 

x y z   

Câu 14. Cho đường thẳng

2 2 1









và điểm

 

4;1;6I

. Đường thẳng d cắt mặt cầu

 

tâm

tại hai điểm A, B sao cho

6AB 

. Phương trình của mặt cầu

 

là:

2 2 2

( 4) ( 1) ( 6) 16.x y z     

2 2 2

( 4) ( 1) ( 6) 12.x y z     

2 2 2

( 4) ( 1) ( 6) 18.x y z     

2 2 2

( 4) ( 1) ( 6) 9.x y z     

Câu 15. Cho hai mặt phẳng

 

có phương trình

 

: 2 1 0P x y z   

và .. Mặt cầu có tâm

nằm trên mặt phẳng

 

và tiếp xúc với mặt phẳng

 

tại điểm

, biết rằng

thuộc mặt

phẳng

 

Oxy

và có hoành độ

x 

, có phương trình là:

     

2 2 2

21 5 10 600.x y z     

     

2 2 2

19 15 10 600.x y z     

     

2 2 2

21 5 10 100.x y z     

     

2 2 2

21 5 10 600.x y z     

Câu 16. Cho hai điểm

 

1;0; 4M

 

1;1; 2N

và mặt cầu

 

2 2 2

: 2 2 2 0.S x y z x y     

Mặt phẳng

 

qua M, N và tiếp xúc với mặt cầu

 

có phương trình:

2 2 6 0.x y z   

4 2 8 0x y z   

hoặc

4 2 8 0.x y z   

2 2 6 0x y z   

hoặc

2 2 2 0.x y z   

Câu 17. Cho hai điểm

   

1; 2;3 , 1;0;1AB

và mặt phẳng

 

: 4 0P x y z   

. Phương trình mặt

cầu

()S

có bán kính bằng

có tâm thuộc đường thẳng

và

()S

tiếp xúc với mặt phẳng

 

là:

Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ Luyện thi Đại Học 2017

Giáo viên: PHẠM VĂN LONG( TP.Cần Thơ )…0913.518.110… CLB Giáo viên trẻ TP Huế

     

2 2 2

4 3 2 .

xyz     

     

2 2 2

4 3 2

xyz     

hoặc

     

2 2 2

6 5 4 .

x y z     

     

2 2 2

4 3 2 .

x y z     

     

2 2 2

4 3 2

x y z     

hoặc

     

2 2 2

6 5 4 .

x y z     

Câu 18. Cho đường thẳng

2 1 2







và hai mặt phẳng

 

: 2 2 2 0;P x y z   

 

: 2 2 1 0P x y z   

. Mặt cầu có tâm

nằm trên

và tiếp xúc với 2 mặt phẳng

   

, PP

, có

phương trình:

       

2 2 2

: 1 2 3 9.S x y z     

       

2 2 2

: 1 2 3 9S x y z     

hoặc

 

2 2 2

19 16 15 9

17 17 17 289

S x y z

     

     

     

     

       

2 2 2

: 1 2 3 9S x y z     

hoặc

 

2 2 2

19 16 15 9

17 17 17 289

S x y z

     

     

     

     

       

2 2 2

: 1 2 3 9.S x y z     

Câu 19. Cho điểm

(1; 3;2)A

, đường thẳng

d y t



  













và mặt phẳng

( ) : 2 2 6 0P x y z   

Phương trình mặt cầu

()S

đi qua A, có tâm thuộc

đồng thời tiếp xúc với

()P

là:

2 2 2

( ) : ( 1) ( 3) ( 2) 16S x y z     

hoặc

2 2 2

83 87 70 13456

( ) : .

13 13 13 169

S x y z

     

     

     

     

2 2 2

( ) : ( 1) ( 3) ( 2) 16S x y z     

hoặc

2 2 2

83 87 70 13456

( ) : .

13 13 13 169

S x y z

     

     

     

     

     

2 2 2

( ) : 1 3 2 16.S x y z     

     

2 2 2

( ) : 1 3 2 4.S x y z     

Câu 20. Cho mặt phẳng

 

: 2 2 10 0P x y z   

và hai đường thẳng

1 1 1

xz

  



1 1 4

xz

  

. Mặt cầu

 

có tâm thuộc



, tiếp xúc với



và mặt phẳng

 

, có

phương trình:

Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ Luyện thi Đại Học 2017

Giáo viên: PHẠM VĂN LONG( TP.Cần Thơ )…0913.518.110… CLB Giáo viên trẻ TP Huế

2 2 2

( 1) ( 1) ( 2) 9x y z     

hoặc

2 2 2

11 7 5 81

2 2 2 4

x y z

     

     

     

     

2 2 2

( 1) ( 1) ( 2) 9x y z     

hoặc

2 2 2

11 7 5 81

2 2 2 4

x y z

     

     

     

     

2 2 2

( 1) ( 1) ( 2) 9.x y z     

2 2 2

( 1) ( 1) ( 2) 3.x y z     

Câu 21. Cho mặt phẳng

 

và mặt cầu

 

có phương trình lần lượt là

 

2 2 2 2

: 2 2 4 5 0; ( ) : 2 2 2 6 0P x y z m m S x y z x y z            

. Giá trị của

để

 

tiếp

xúc

 

là:

1m 

hoặc

5.m 

1m 

hoặc

5.m 

1.m 

5.m 

Câu 22. Cho mặt cầu

 

2 2 2

: 2 4 2 3 0S x y z x y z      

và mặt phẳng

 

: 2 4 0P x y z   

Phương trình đường thẳng

tiếp xúc với mặt cầu

 

tại

 

3; 1;1A 

và song song với mặt

phẳng

 

là:

2 6 .







  





  



1 6 .







  









1 6 .







  















  









Câu 23. Cho điểm

 

2; 5;1A

và mặt phẳng

( ) : 6 3 2 24 0P x y z   

, H là hình chiếu vuông góc

của

trên mặt phẳng

 

. Phương trình mặt cầu

()S

có diện tích

784



và tiếp xúc với mặt

phẳng

 

tại H, sao cho điểm A nằm trong mặt cầu là:

     

2 2 2

16 4 7 196.x y z     

     

2 2 2

8 8 1 196.xyz     

     

2 2 2

8 8 1 196.xyz     

     

2 2 2

16 4 7 196.x y z     

Câu 24. Cho mặt phẳng

 

: 2 5 0P x y z   

và các điểm

   

0;0; 4 , 2;0;0AB

. Phương trình mặt

cầu đi qua

, , O A B

và tiếp xúc với mặt phẳng

 

là:

     

2 2 2

1 1 2 6.xyz     

     

2 2 2

1 1 2 6.xyz     

     

2 2 2

1 1 2 6.x y z     

     

2 2 2

1 1 2 6.xyz     

Câu 25. Cho mặt phẳng

 

: 2 2 2 0P x y z   

và điểm

 

2; 3;0A

. Gọi

là điểm thuộc tia

sao cho mặt cầu tâm

, tiếp xúc với mặt phẳng

 

có bán kính bằng 2. Tọa độ điểm

là:

Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ Luyện thi Đại Học 2017

Giáo viên: PHẠM VĂN LONG( TP.Cần Thơ )…0913.518.110… CLB Giáo viên trẻ TP Huế

 

0; 4;0 .

 

0; 2; 0 .

 

0;2;0

hoặc

 

0; 4;0 .

 

0;1;0 .

Câu 26. Cho hai mă t phăng

( ) : 2 3 2 0,P x y z   

( ) : 2 2 0Q x y z   

. Phương trình mặt cầu

 

tiêp xuc vơi măt phăng

 

tại điểm

 

1; 1;1A 

và có tâm thuộc mặt phẳng

()Q

là:

     

2 2 2

( ): 3 7 3 14.     S x y z

     

2 2 2

( ) : 3 7 3 56.S x y z     

     

2 2 2

( ) : 3 7 3 56.S x y z     

     

2 2 2

( ) : 3 7 3 14.S x y z     

Câu 27. Cho điểm

(0;0; 3)I

và đường thẳng

: 2 .

d y t



  













Phương trình mặt cầu

 

có tâm

và

cắt đường thẳng

tại hai điểm sao cho tam giác

IAB

vuông là:

 

x y z   

 

x y z   

 

x y z   

 

x y z   

Câu 28. Cho đường thẳng

1 1 1

xz

  



và và mặt cầu (S):

2 2 2

4 2 21 0x y z x y     

. Số

giao điểm của

 



và

 

là:

A. 0. B. 1. C. 2. D. 3.

Câu 29. Cho đường thẳng

2 3 2







và mặt cầu (S) :

 

29x y z   

. Tọa độ giao

điểm của

 



và v

là:

 

2; 3;2 .A

 

2; 2; 3 .A 

   

0;0; 2 , 2;2; 3 .AB

 



và

 

không cắt nhau.

Câu 30. Cho đường thẳng

 













  



và mặt cầu

 

2 2 2

2 4 6 67 0x y z x y z      

. Giao

điểm của

 



và

 

là các điểm có tọa độ:

 



và

 

không cắt nhau. B.

   

1;2; 5 , 2;0; 4 .AB

   

2; 2; 5 , 4;0; 3 .AB

   

1;2; 4 , 2; 2; 3 .AB

Cho điểm

 

1;0; 0I

và

đường thẳng

1 2 1







. Phương trình mặt cầu

 

có tâm I và cắt đường thẳng d tại

hai điểm A, B sao cho

4AB 

là:

Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ Luyện thi Đại Học 2017

Giáo viên: PHẠM VĂN LONG( TP.Cần Thơ )…0913.518.110… CLB Giáo viên trẻ TP Huế

 

1 9.x y z   

 

1 3.x y z   

 

1 3.x y z   

 

1 9.x y z   

Câu 31. Cho điểm

 

1;1; 2I

đường thẳng

1 2 1







Phương trình mặt cầu

 

có tâm

I và cắt đường thẳng d tại hai điểm A, B sao cho

6AB 

là:

     

2 2 2

1 1 2 24.xyz     

     

2 2 2

1 1 2 27.xyz     

     

2 2 2

1 1 2 27.xyz     

     

2 2 2

1 1 2 54.xyz     

Câu 32. Cho điểm

 

1;0; 0I

và đường thẳng

1 2 1







. Phương trình mặt cầu

 

có

tâm I và cắt đường thẳng d tại hai điểm A, B sao cho tam giác IAB vuông là:

 

1 12.x y z   

 

1 10.x y z   

 

1 8.x y z   

 

1 16.x y z   

Câu 33. Cho điểm

 

1;0; 0I

và đường thẳng

: 1 2

d y t













  



. Phương trình mặt cầu

 

có tâm I và

cắt đường thẳng d tại hai điểm A, B sao cho tam giác IAB đều là:

 

x y z   

 

x y z   

 

x y z   

 

x y z   

Câu 34. Cho các điểm

 

1;1; 2I 

và đường thẳng

: 3 2

d y t



  













. Phương trình mặt cầu

 

có tâm I

và cắt đường thẳng d tại hai điểm A, B sao cho tam giác IAB vuông là:

     

2 2 2

1 1 2 9.xyz     

     

2 2 2

1 1 2 36.xyz     

     

2 2 2

1 1 2 9.xyz     

     

2 2 2

1 1 2 3.xyz     

Câu 35. Cho điểm

 

1;1; 2I 

đường thẳng

1 2 1







Phương trình mặt cầu

 

có tâm

I và cắt đường thẳng d tại hai điểm A, B sao cho tam giác IAB đều là:

     

2 2 2

1 1 2 24.xyz     

     

2 2 2

1 1 2 24.xyz     

Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ Luyện thi Đại Học 2017

Giáo viên: PHẠM VĂN LONG( TP.Cần Thơ )…0913.518.110… CLB Giáo viên trẻ TP Huế

     

2 2 2

1 1 2 18xyz     

     

2 2 2

1 1 2 18.xyz     

Câu 36. Cho điểm

 

1;1; 2I

đường thẳng

1 2 1







. Phương trình mặt cầu

 

có tâm

I và cắt đường thẳng d tại hai điểm A, B sao cho



IAB 

là:

     

2 2 2

1 1 2 66.xyz     

     

2 2 2

1 1 2 36.xyz     

     

2 2 2

1 1 2 72.xyz     

     

2 2 2

1 1 2 46.xyz     

Câu 37. Phương trình mặt cầu có tâm

 

3; 3; 7I 

và tiếp xúc trục tung là:

 

3 3 7 61.x y z     

 

3 3 7 58.x y z     

 

3 3 7 58.x y z     

 

3 3 7 12.x y z     

Câu 38. Phương trình mặt cầu có tâm

 

5; 3;9I

và tiếp xúc trục hoành là:

 

   

5 3 9 90.x y z     

 

   

5 3 9 14.x y z     

 

   

5 3 9 86.x y z     

 

   

5 3 9 90.x y z     

Câu 39. Phương trình mặt cầu có tâm

 

6; 3; 2 1I   

và tiếp xúc trục Oz là:

     

2 2 2

6 3 2 1 9.xyz      

     

2 2 2

6 3 2 1 9.xyz      

     

2 2 2

6 3 2 1 3.xyz      

     

2 2 2

6 3 2 1 3.xyz      

Câu 40. Phương trình mặt cầu có tâm

 

4;6; 1I 

và cắt trục Ox tại hai điểm A, B sao cho tam giác

IAB vuông là:

     

2 2 2

4 6 1 34.x y z     

     

2 2 2

4 6 1 26.x y z     

     

2 2 2

4 6 1 74.x y z     

     

2 2 2

4 6 1 104.x y z     

Câu 41. Phương trình mặt cầu có tâm

 

3; 3;0I 

và cắt trục Oz tại hai điểm A, B sao cho tam

giác IAB đều là:

   

3 3 8.x y z    

   

3 3 9.x y z    

   

3 3 9.x y z    

   

3 3 8.x y z    

Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ Luyện thi Đại Học 2017

Giáo viên: PHẠM VĂN LONG( TP.Cần Thơ )…0913.518.110… CLB Giáo viên trẻ TP Huế

Câu 42. Phương trình mặt cầu có tâm

 

3;6; 4I 

và cắt trục Oz tại hai điểm A, B sao cho diện tích

tam giác IAB bằng

là:

     

2 2 2

3 6 4 45.xyz     

     

2 2 2

3 6 4 49.xyz     

     

2 2 2

3 6 4 36.xyz     

     

2 2 2

3 6 4 54.     x y z

Câu 43. Mặt cầu

 

có tâm

 

2;1; 1I 

và cắt trục Ox tại hai điểm A, B sao cho tam giác IAB vuông.

Điểm nào sau đây thuộc mặt cầu

 

2;1;1 .

 

2;1;0 .

 

2;0;0 .

 

1;0; 0 .

Câu 44. Gọi

 

là mặt cầu có tâm

 

1; 3;0I 

và cắt trục Ox tại hai điểm A, B sao cho tam giác IAB

đều. Điểm nào sau đây không thuộc mặt cầu

 

3; 3; 2 2 .

 

3; 3; 2 2 .

 

2; 1;1 .

 

1; 3; 2 3 .

Câu 45. Cho các điểm

 

1;0;0I 

và đường thẳng

1 2 1







. Phương trình mặt cầu

 

có tâm I và tiếp xúc d là:

 

1 10.x y z   

 

1 5.x y z   

 

1 10.x y z   

 

1 5.x y z   

Câu 46. Cho điểm

 

1;7; 5I

và đường thẳng

2 1 3







. Phương trình mặt cầu có tâm

và cắt đường thẳng d tại hai điểm A, B sao cho tam giác diện tích tam giác IAB bằng

2 6015

là:

     

2 2 2

1 7 5 2018.x y z     

     

2 2 2

1 7 5 2017.x y z     

     

2 2 2

1 7 5 2016.x y z     

     

2 2 2

1 7 5 2019.x y z     

Câu 47. Cho các điểm

 

1;3;1A

và

 

3;2; 2B

. Mặt cầu đi qua hai điểm A, B và tâm thuộc trục Oz

có đường kính là:

14.

2 14.

2 10.

2 6.

Câu 48. Trong không gian với hệ tọa độ Oxyz, cho các điểm

 

1;2;1A

và

 

0;1;1B

. Mặt cầu đi qua

hai điểm A, B và tâm thuộc trục hoành có đường kính là:

2 6.

2 5.

12.

Câu 49. Cho các điểm

 

2;1; 1A 

và

 

1;0;1B

. Mặt cầu đi qua hai điểm A, B và tâm thuộc trục Oy

có đường kính là:

Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ Luyện thi Đại Học 2017

Giáo viên: PHẠM VĂN LONG( TP.Cần Thơ )…0913.518.110… CLB Giáo viên trẻ TP Huế

4 2.

2 2.

2 6.

Câu 50. Cho các điểm

 

0;1; 3A

và

 

2; 2;1B

và đường thẳng

1 1 2









. Mặt cầu đi

qua hai điểm A, B và tâm thuộc đường thẳng d thì tọa độ tâm là:

6 9 13

; ; .

5 5 5







; ; 2 .







4 2 7

; ; .

333







13 17 12

; ; .

10 10 5







Câu 51. Cho các điểm

 

1;3;0A

và

 

2;1;1B

và đường thẳng

2 1 1





. Mặt cầu

 

đi qua

hai điểm A, B và tâm thuộc đường thẳng d thì tọa độ tâm của

 

là:

 

8;7; 4 .

 

6;6; 3 .

 

4; 5; 2 .

 

4;1; 2 .

Câu 52. Cho các điểm

 

1;1; 3A

và

 

2; 2; 0B

và đường thẳng

1 1 1







. Mặt cầu

 

đi

qua hai điểm A, B và tâm thuộc đường thẳng d thì tọa độ tâm

 

là:

5 7 23

; ; .

6 6 6







11 23 7

; ; .

6 6 6









5 7 25

; ; .

6 6 6







1 9 19

; ; .

6 6 6







Câu 53. Cho đường thẳng

: 1 3

d y t







  









. Phương trình mặt cầu có đường kính là đoạn thẳng

vuông góc chung của đường thẳng d và trục Ox là:

   

1 2 .

x y z    

   

1 2 .

x y z    

 

x y z   

1 1 1

3 2 4

x y z

   

    

   

   

Câu 54. Cho hai đường thẳng

d y t

















và

' : 3 '

d y t

















. Phương trình mặt cầu có đường kính là

đoạn thẳng vuông góc chung của đường thẳng d và d’ là:

 

2 4.x y z   

     

2 2 2

2 1 2 4.x y z     

     

2 2 2

2 1 2 2.x y z     

   

2 1 4.x y z    

Câu 55. Cho các điểm

 

2; 4;1A 

và

 

2;0; 3B

và đường thẳng

2 1 2









. Gọi

 

là

mặt cầu đi qua A, B và có tâm thuộc đường thẳng d. Bán kính mặt cầu

 

bằng:

Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ Luyện thi Đại Học 2017

Giáo viên: PHẠM VĂN LONG( TP.Cần Thơ )…0913.518.110… CLB Giáo viên trẻ TP Huế

967

873

1169

Câu 56. Cho các điểm

 

2; 4; 1A 

và

 

0; 2;1B 

và đường thẳng

d y t

















. Gọi

 

là mặt cầu

đi qua A, B và có tâm thuộc đường thẳng d. Đường kính mặt cầu

 

bằng:

2 19.

2 17.

19.

17.

Câu 57. Mặt cầu tâm

 

2; 4; 6I

và tiếp xúc với mặt phẳng (Oxy) có phương trình:

     

2 2 2

2 4 6 4.xyz     

     

2 2 2

2 4 6 16.xyz     

     

2 2 2

2 4 6 36.xyz     

     

2 2 2

2 4 6 56.xyz     

Câu 58. Mặt cầu tâm

 

2; 4; 6I

và tiếp xúc với mặt phẳng (Oxz) có phương trình:

     

2 2 2

2 4 6 56.xyz     

     

2 2 2

2 4 6 4.xyz     

     

2 2 2

2 4 6 36.xyz     

     

2 2 2

2 4 6 16.xyz     

Câu 59. Phương trình mặt cầu tâm

 

2; 4; 6I

nào sau đây tiếp xúc với trục Ox:

     

2 2 2

2 4 6 52.xyz     

     

2 2 2

2 4 6 40.xyz     

     

2 2 2

2 4 6 20.xyz     

     

2 2 2

2 4 6 56.xyz     

Câu 60. Mặt cầu tâm

 

2; 4; 6I

tiếp xúc với trục Oz có phương trình:

     

2 2 2

2 4 6 40.xyz     

     

2 2 2

2 4 6 20.xyz     

     

2 2 2

2 4 6 52.xyz     

     

2 2 2

2 4 6 56.xyz     

Câu 61. Cho mặt cầu

 

     

2 2 2

1 2 3 9x y z     

. Phương trình mặt cầu nào sau đây

là phương trình của mặt cầu đối xứng với mặt cầu

 

qua mặt phẳng (Oxy):

     

2 2 2

1 2 3 9.x y z     

     

2 2 2

1 2 3 9.x y z     

     

2 2 2

1 2 3 9.x y z     

     

2 2 2

1 2 3 9.x y z     

Câu 62. Cho mặt cầu

 

     

2 2 2

1 1 2 4x y z     

. Phương trình mặt cầu nào sau đây là

phương trình mặt cầu đối xứng với mặt cầu

 

qua trục Oz:

     

2 2 2

1 1 2 4.xyz     

     

2 2 2

1 1 2 4.x y z     

Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ Luyện thi Đại Học 2017

Giáo viên: PHẠM VĂN LONG( TP.Cần Thơ )…0913.518.110… CLB Giáo viên trẻ TP Huế

     

2 2 2

1 1 2 4.xyz     

     

2 2 2

1 1 2 4.x y z     

Câu 63. Đường tròn giao tuyến của

       

2 2 2

: 1 2 3 16S x y z     

khi cắt bởi mặt phẳng

(Oxy) có chu vi bằng :

14 .



27.



HẾT

Xin phép quý thầy cô là những ngƣời sở hữu các câu hỏi có trong tài liệu, cho phép

chúng em biên tập và sử dụng để giúp cho các em học sinh th}n yêu có tƣ liệu học tập. Vì mục

đích không kinh doanh nên mong quý thầy cô đồng ý ạ, chúng em xin chân thành cảm ơn!

CLB sử dụng hệ thống sách chất lƣợng của NXBGD VN 2007, 2008 và các tài liệu tham

khảo chất lƣợng từ Page Toán học Bắc Trung Nam.

P/S: Trong quá trình sưu tầm và biên soạn chắc chắn không tránh khỏi sai sót, kính mong quí thầy

cô và các bạn học sinh thân yêu góp ý để các bản update lần sau hoàn thiện hơn! Xin chân thành cảm ơn.

CLB GI[O VIÊN TRẺ TP HUẾ

Phụ trách chung: LÊ B[ BẢO.

Đơn vị công tác: Trƣờng THPT Đặng Huy Trứ, Thừa Thiên Huế.

Email: lebabaodanghuytru2016@gmail.com Facebook: Lê B{ Bảo

Số điện thoại: 0935.785.115

Bấm Tải xuống để xem toàn bộ.

| 1/28

| | Tải xuống

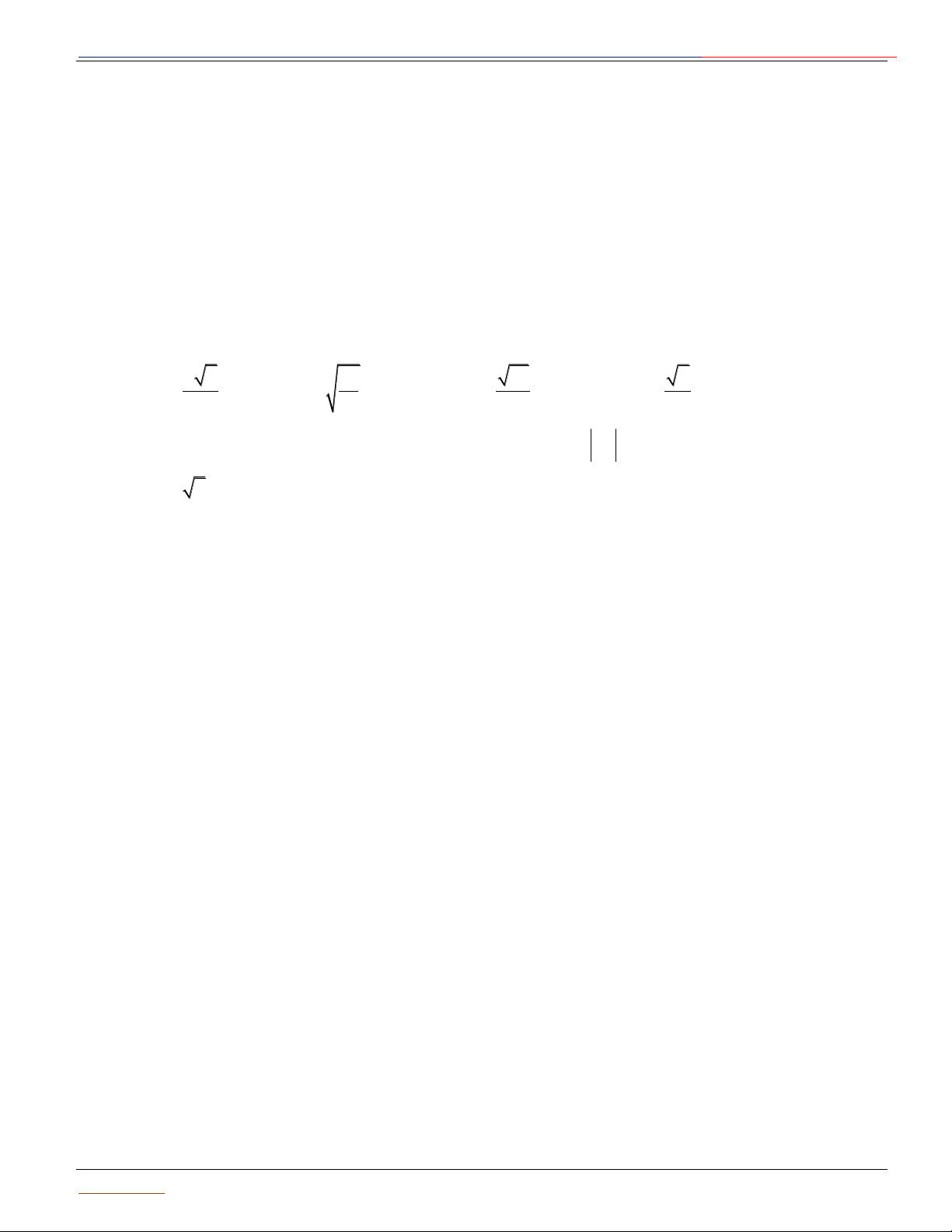
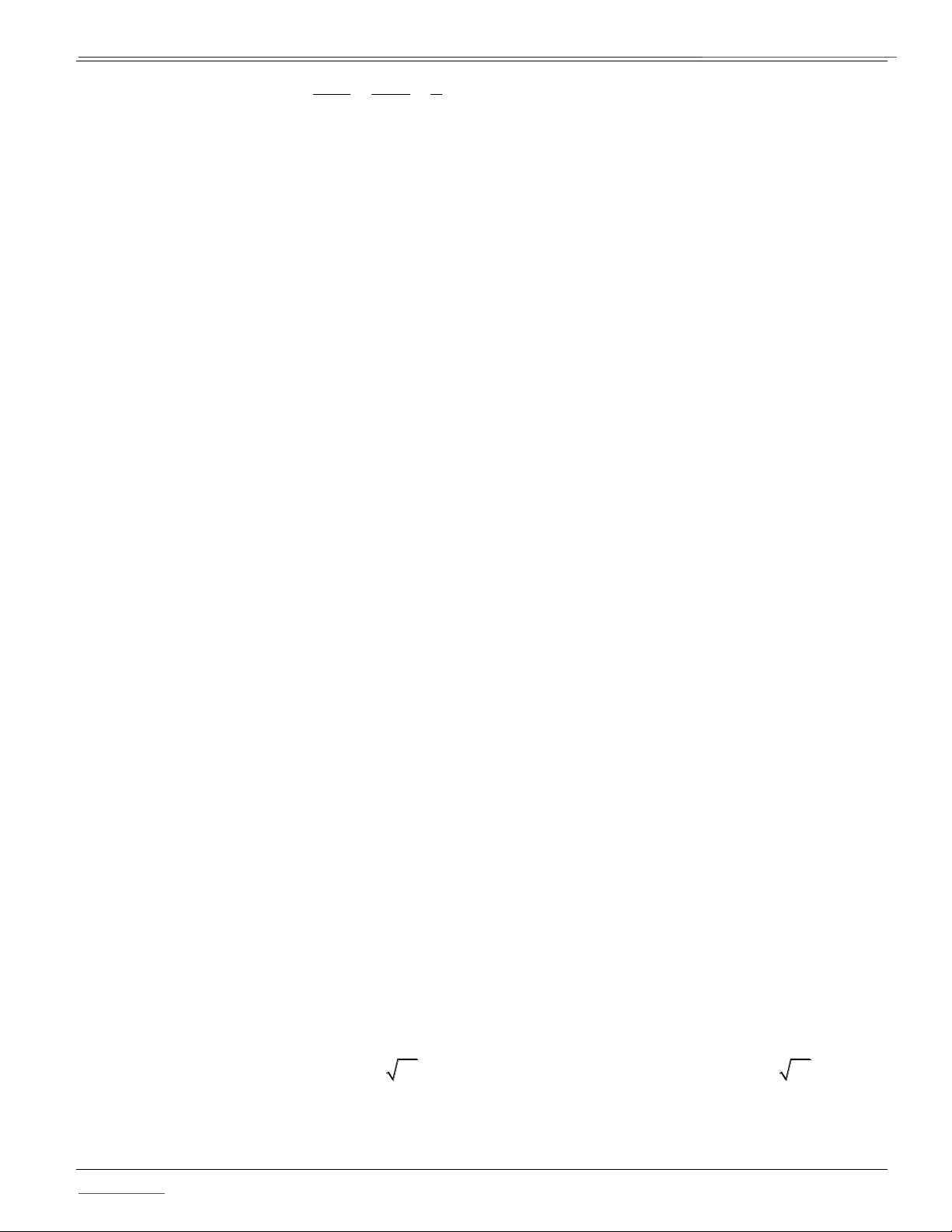
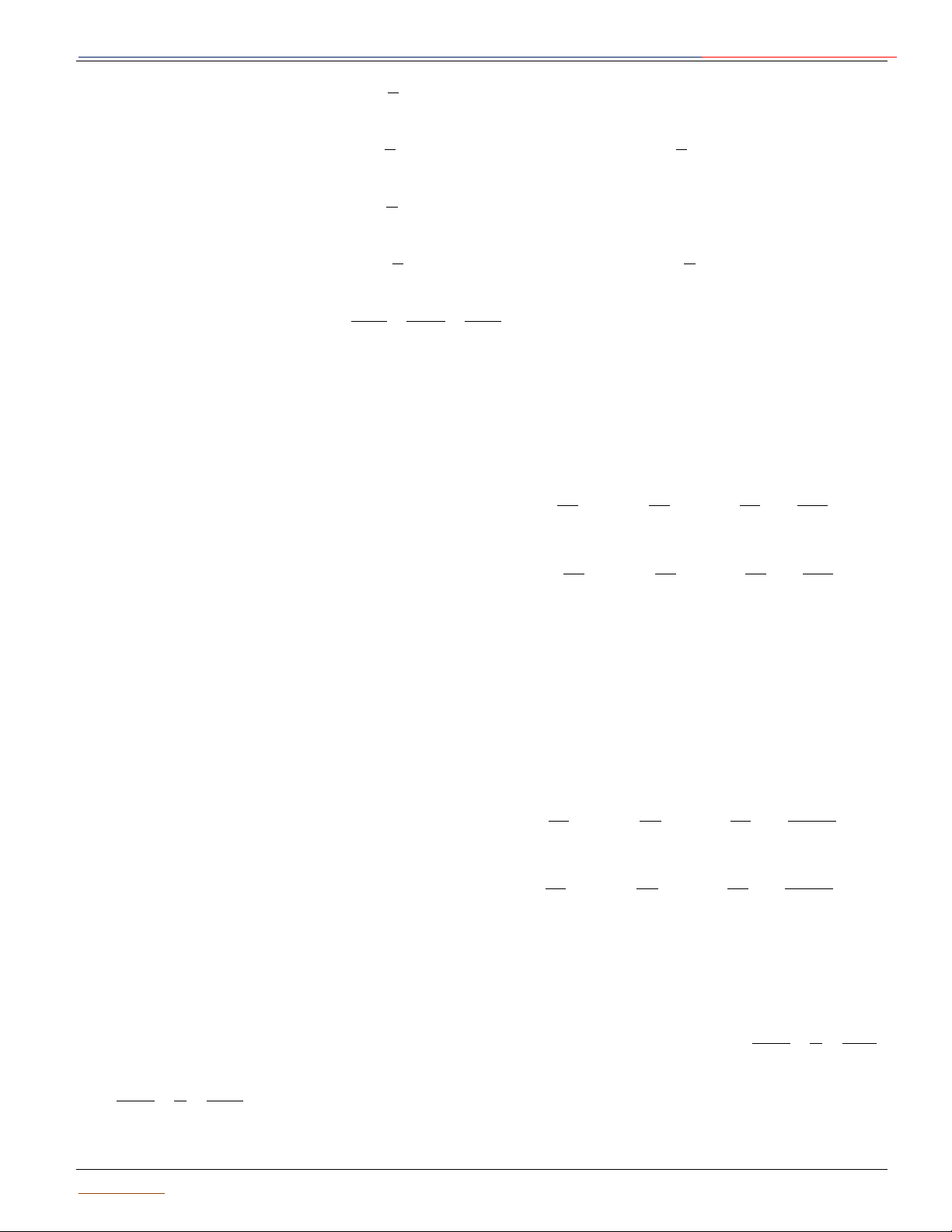
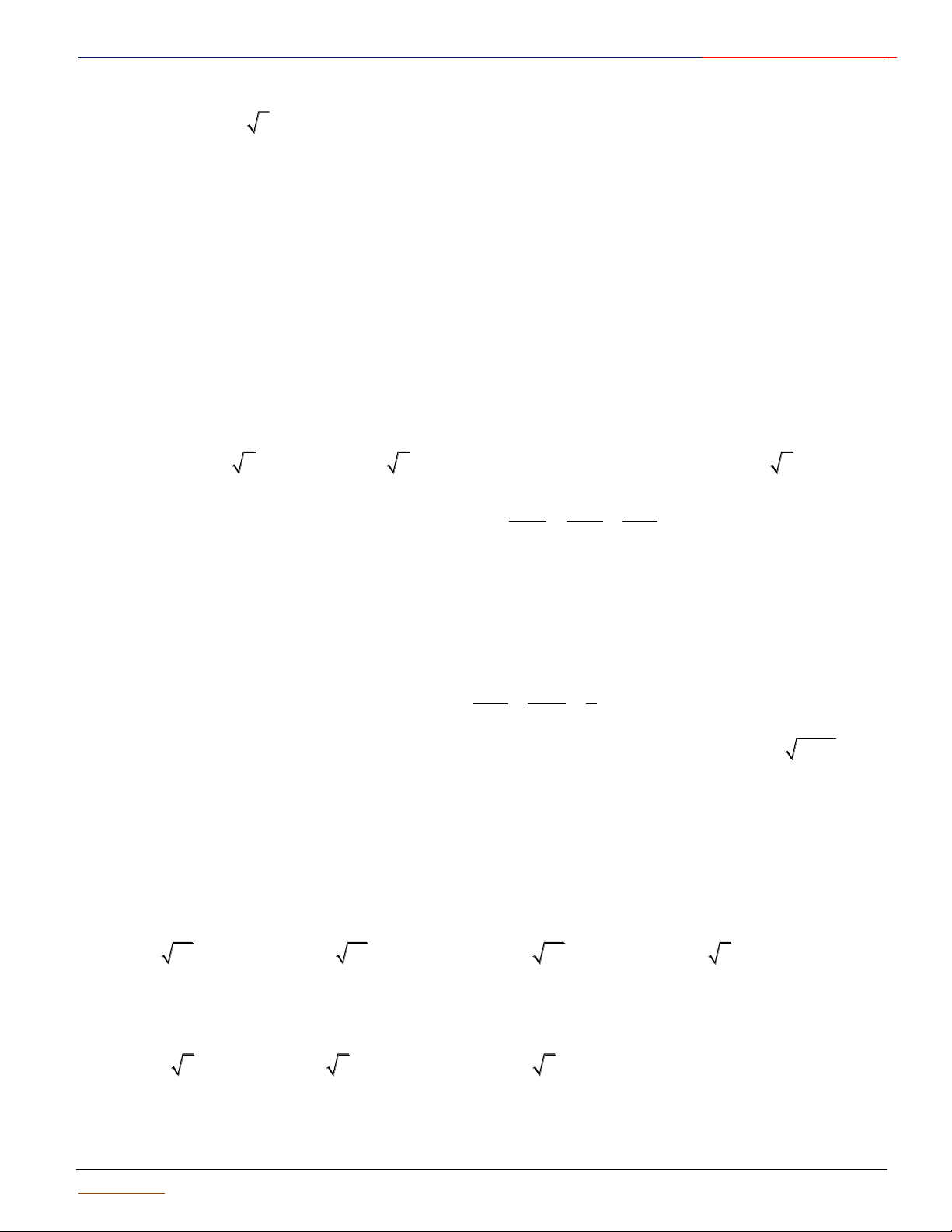
Preview text:

Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ
Luyện thi Đại Học 2017
Giáo viên: PHẠM VĂN LONG
Lớp Toán thầy Long_Thành phố Cần Thơ
Số điện thoại: 0913.518.110
CHUYÊN ĐỀ : MẶT CẦU TRONG KHÔNG GIAN OXYZ I- LÝ THUYẾT: 1/ Định nghĩa
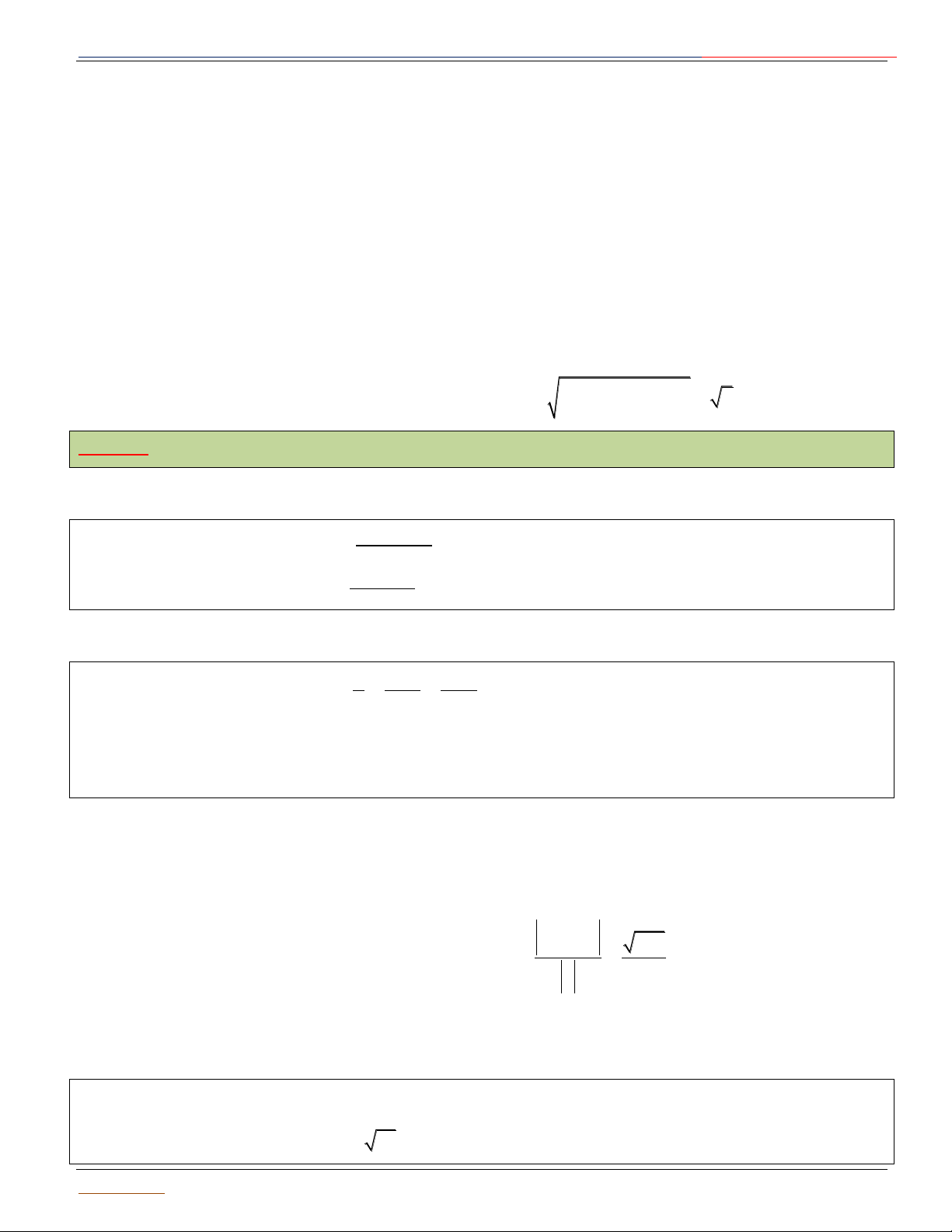
Cho điểm I cố định và một số thực dương R. Tập hợp tất cả R I A
những điểm M trong không gian cách I một khoảng R được gọi là B
mặt cầu tâm I, bán kính R.
Kí hiệu: SI; R  SI; R  M / IM   R
2/ C{c dạng phƣơng trình mặt cầu
Dạng 1 : Phƣơng trình chính tắc
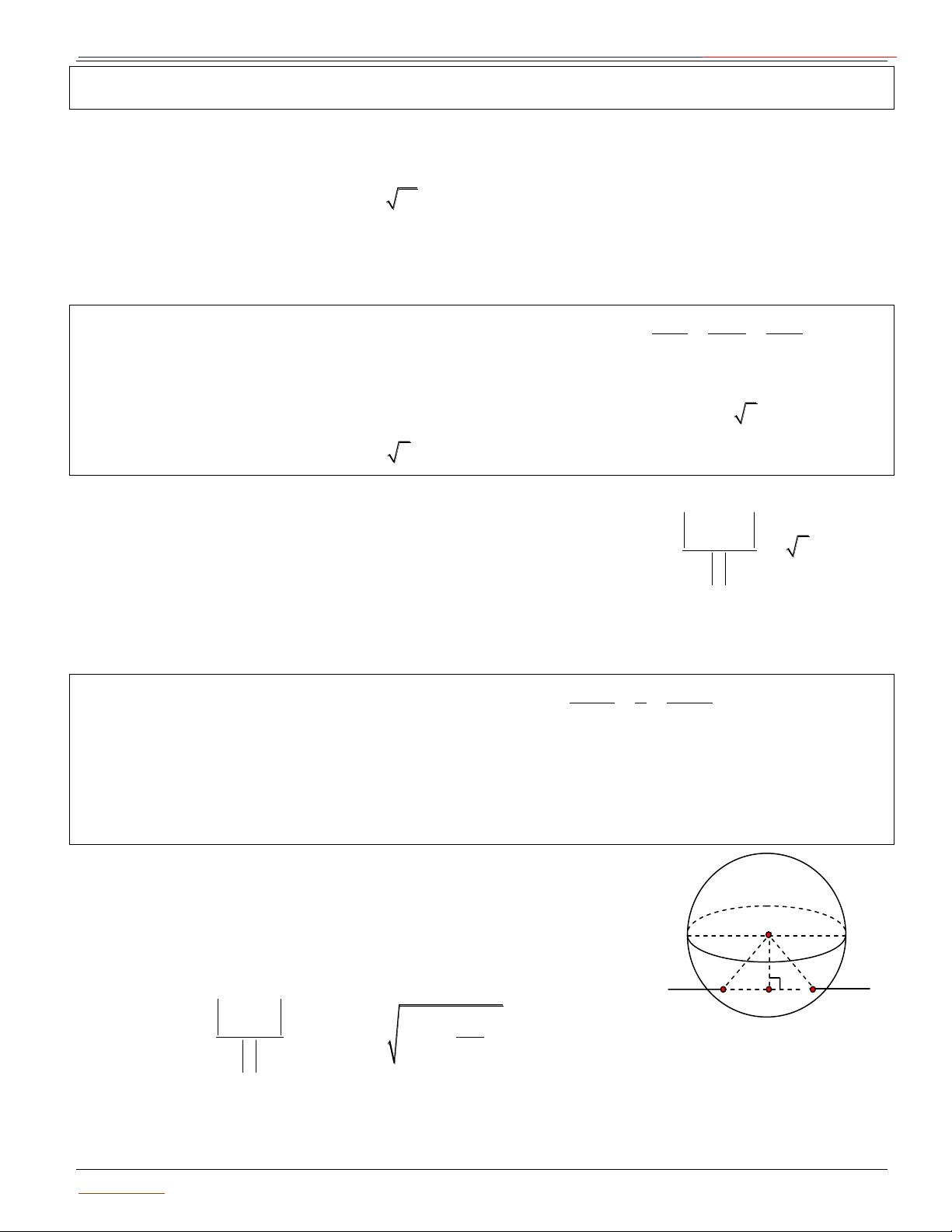
Dạng 2 : Phƣơng trình tổng qu{t 2 2 2 ( )
S : x  y  z  2ax  2by  2cz  d  0 (2)
Mặt cầu (S) có tâm I  ; a ;
b c , bán kính R  0 .  Điều kiện để phương trình (2) là phương trình mặt cầu: 2 2 2
a  b  c  d  0
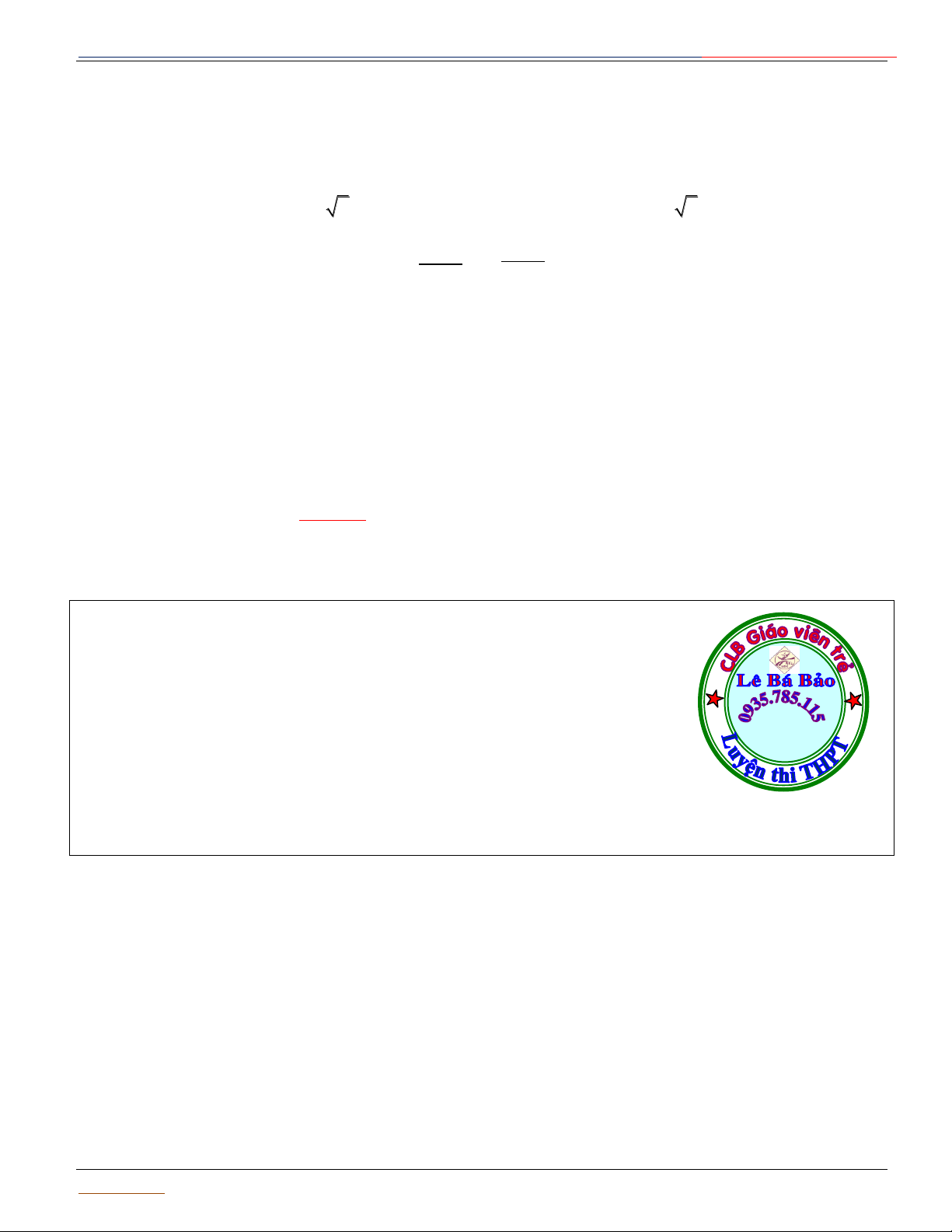
S xa2 yb2 zc2 2 :  R
 S có tâm I  ;a ; b c .
 S có bán kính: 2 2 2
R  a  b  c  d .
3/ Vị trí tƣơng đối giữa mặt cầu v| mặt phẳng
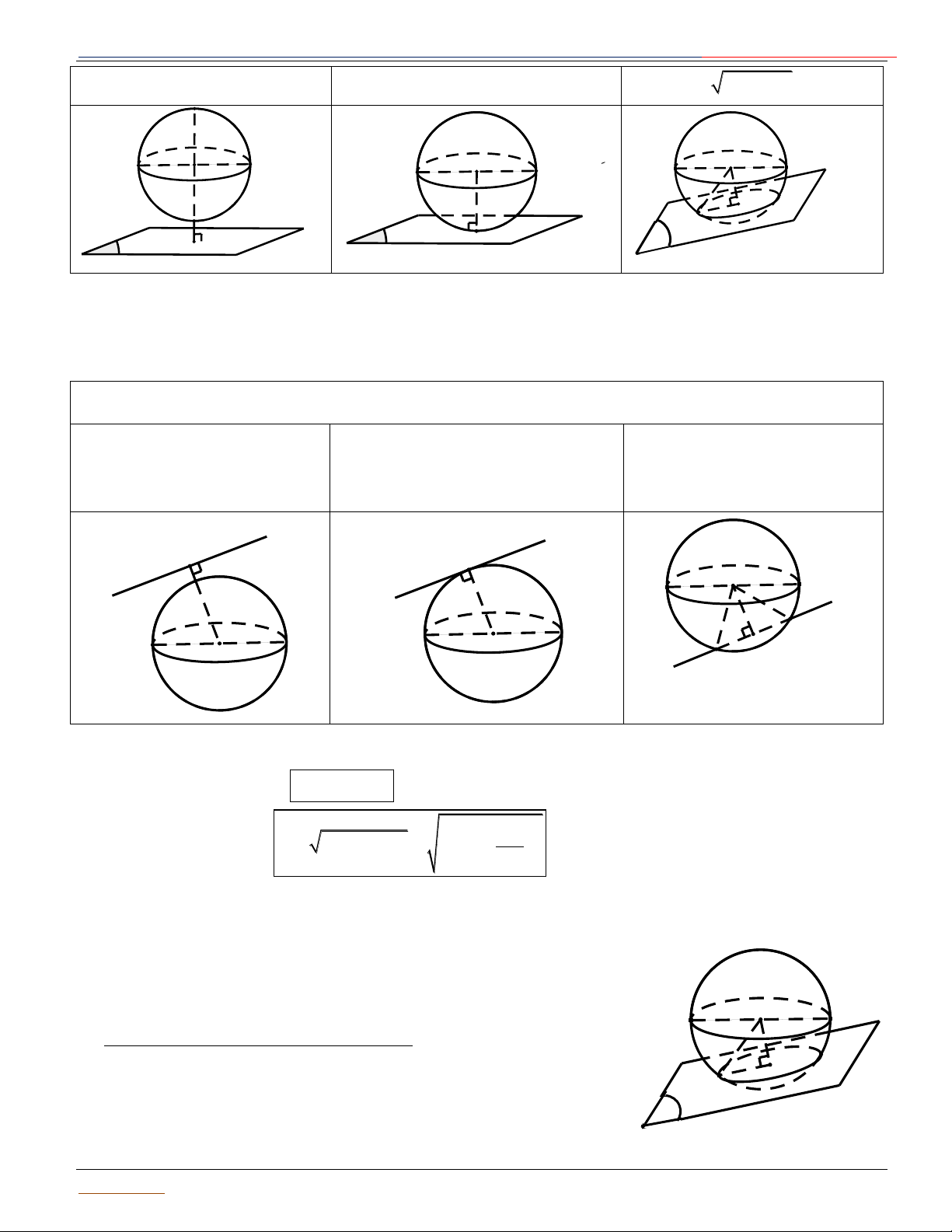
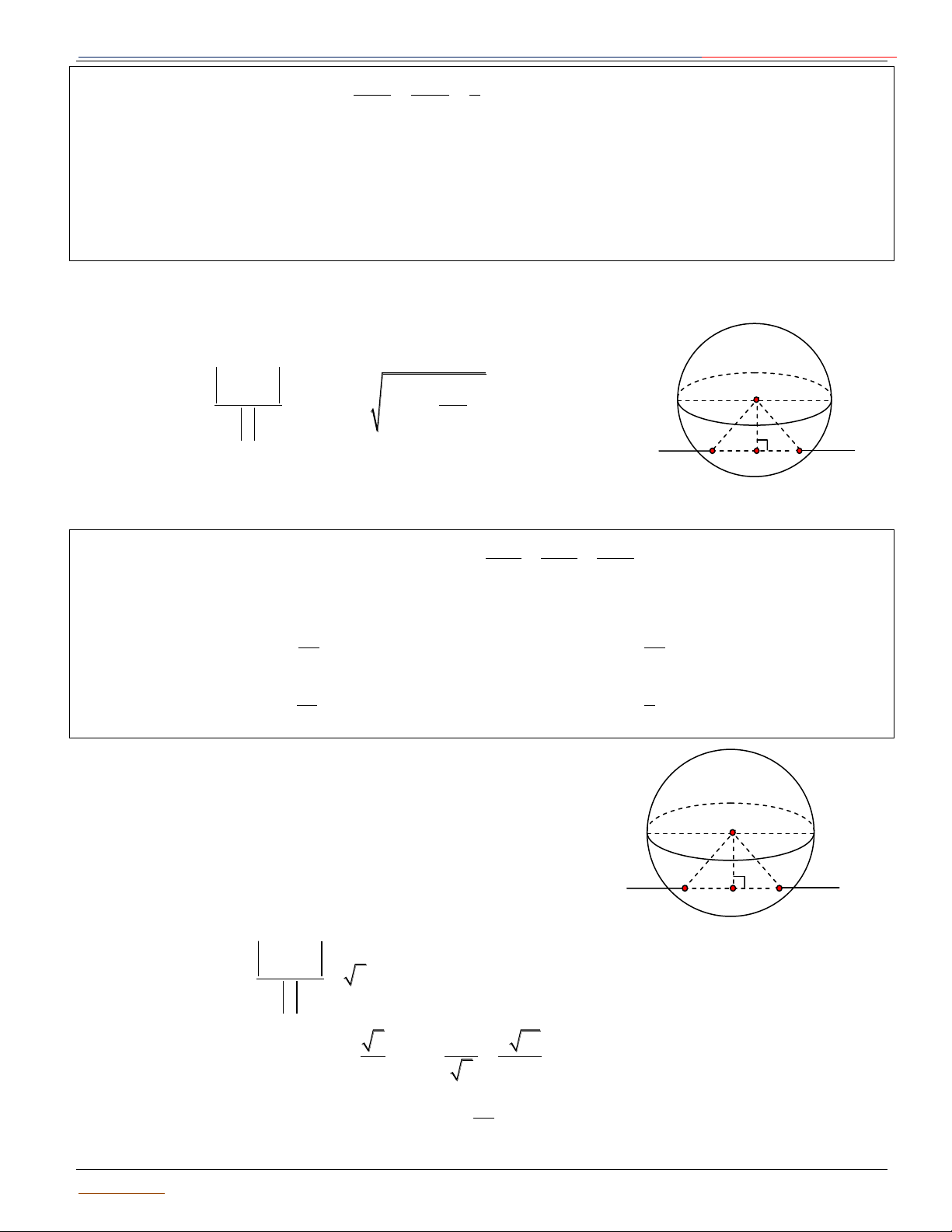
Cho mặt cầu SI; R và mặt phẳng P . Gọi H là hình chiếu vuông góc của I lên P  d  IH là
khoảng cách từ I đến mặt phẳng P . Khi đó :
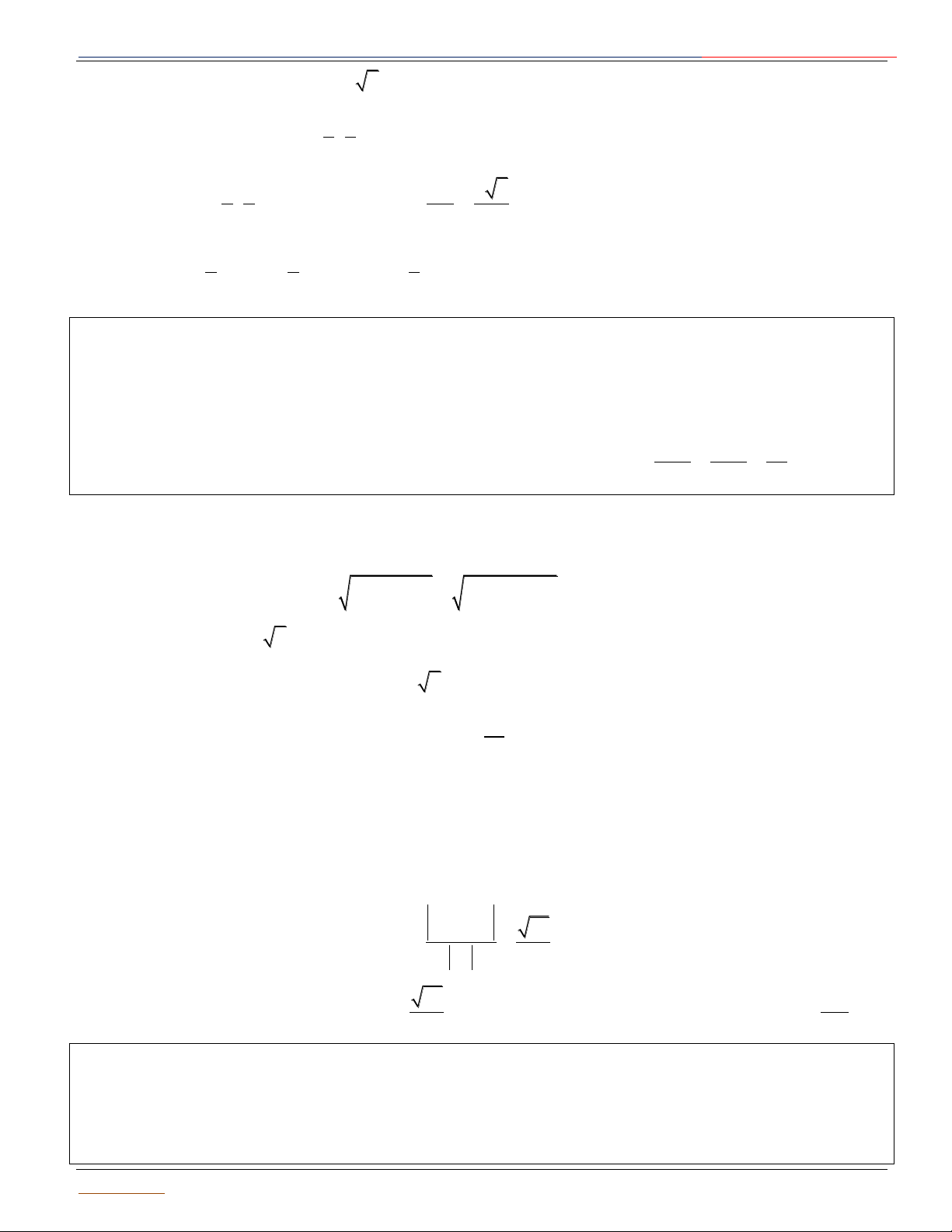
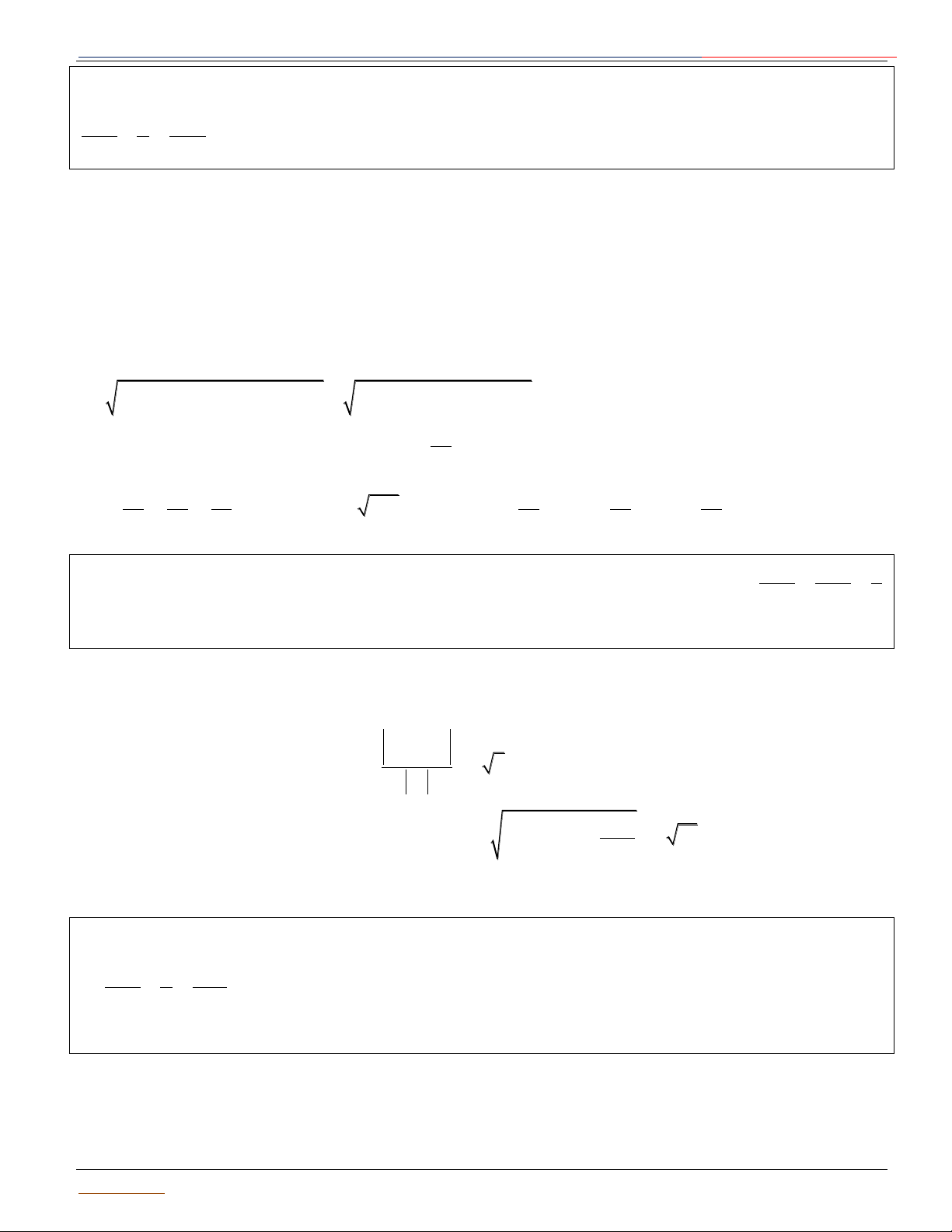
+ Nếu d  R : Mặt cầu và mặt + Nếu d  R : Mặt phẳng tiếp xúc + Nếu d  R : Mặt phẳng (P)
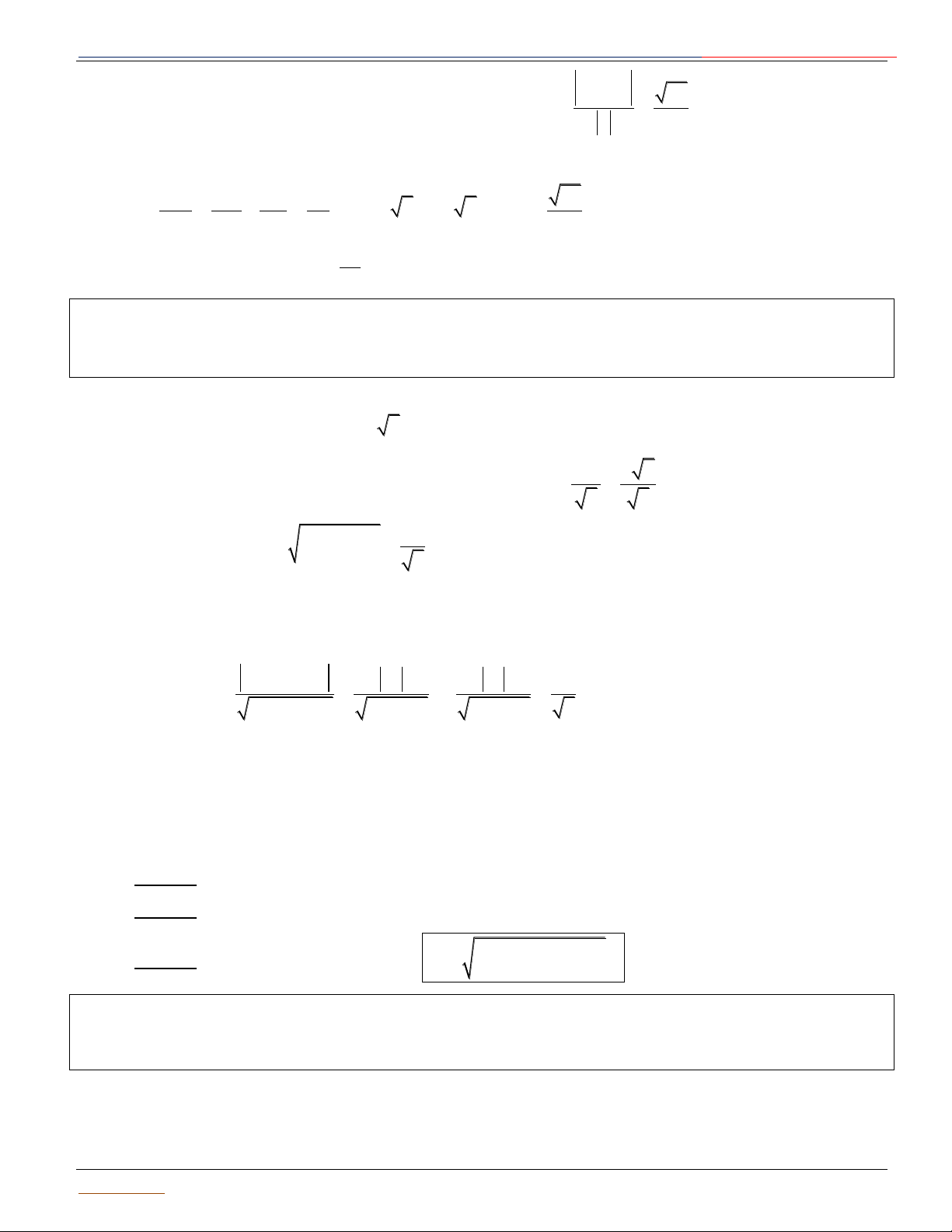
phẳng không có điểm chung. mặt cầu. Khi đó (P) là mặt phẳng cắt mặt cầu theo thiết diện là
tiếp diện của mặt cầu và H là đường tròn có tâm I' và bán Giáo
viên: PHẠM VĂN LONG( TP.Cần Thơ
)…0913.518.110… CLB Giáo viên trẻ TP Huế 1
Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ
Luyện thi Đại Học 2017 tiếp điểm. kính 2 2
r  R  IH M1 R I I I R d M R I' 2 r H H P α P P
Lưu ý: Khi mặt phẳng P đi qua tâm I thì mặt phẳng P được gọi là mặt phẳng kính và thiết diện
lúc đó được gọi là đường tròn lớn có diện tích lớn nhất.
4/ Vị trí tƣơng đối giữa mặt cầu v| đƣờng thẳng
Cho mặt cầu SI; R và đường thẳng  . Gọi H là hình chiếu của I lên  . Khi đó :
+ IH  R :  không cắt mặt + IH  R :  tiếp xúc với mặt + IH  R :  cắt mặt cầu tại cầu.
cầu.  là tiếp tuyến của (S) và H hai điểm phân biệt. là tiếp điểm.   H H I R Δ R R H B I I A
* Lƣu ý: Trong trường hợp  cắt S tại 2 điểm A, B thì bán kính R của (S) được tính như sau:
+ Xác định: dI;   IH. 2  AB  + Lúc đó: 2 2 2
R  IH  AH  IH     2 
5/ Đƣờng tròn trong không gian Oxyz
* Đường tròn C trong không gian Oxyz, được xem là giao tuyến của S và mặt phẳng P . S 2 2 2
: x  y  z  2ax  2by  2cz  d  0
P : Ax  By Cz  D  0 I
* Xác định tâm I’ và bán kính r của (C). R d
+ Tâm I '  d   . I' r
Trong đó d là đường thẳng đi qua I và vuông góc với mp P α P Giáo
viên: PHẠM VĂN LONG( TP.Cần Thơ
)…0913.518.110… CLB Giáo viên trẻ TP Huế 2
Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ
Luyện thi Đại Học 2017
+ Bán kính r  R  II   R  d
 I P 2 2 2 2 ' ;  
5/ Điều kiện tiếp xúc : Cho mặt cầu (S) tâm I, bán kính R.
+ Đường thẳng  là tiếp tuyến của (S)  dI;   . R
+ Mặt phẳng P là tiếp diện của (S)  dI;P  . R
* Lƣu ý: Tìm tiếp điểm M x ; y ; z . 0  0 0 0     IM  d IM  a Sử dụng tính chất : 0     IM   P 0 d   0 IM n  0 P
II. VÍ DỤ MINH HỌA : Dạng 1:
VIẾT PHƢƠNG TRÌNH MẶT CẦU Phương pháp:
* Thuật to{n 1: Bước 1: Xác định tâm I  ; a ; b c .
Bước 2: Xác định bán kính R của (S).
Bước 3: Mặt cầu (S) có tâm I  ; a ;
b c và bán kính R . 2 2 2 S
xa yb zc 2 ( ) :  R
* Thuật to{n 2: Gọi phương trình 2 2 2 ( )
S : x  y  z  2ax  2by  2cz  d  0
Phương trình (S) hoàn toàn xác định nếu biết được a, b, c, . d ( 2 2 2
a  b  c  d  0 )
B|i tập 1 : Viết phương trình mặt cầu (S), trong các trường hợp sau:
a) S có tâm I 2; 2; 3
  và bán kính R  3.
b) S có tâm I 1; 2; 0 và (S) qua P2; 2;  1.
c) S có đường kính AB với A1; 3;  1 , B 2;  0;  1 . Bài giải:
a) Mặt cầu tâm I 2; 2; 3
  và bán kính R  3, có phương trình: 2 2 2
(S): x  2  y  2  z  3  9 
b) Ta có: IP  1; 4;  1 IP  3 2 .
Mặt cầu tâm I 1; 2; 0 và bán kính R  IP  3 2 , có phương trình: 2 2
(S): x    y   2 1 2  z  18 Giáo
viên: PHẠM VĂN LONG( TP.Cần Thơ
)…0913.518.110… CLB Giáo viên trẻ TP Huế 3
Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ
Luyện thi Đại Học 2017  c) Ta có: AB   3  ; 3
 ;0  AB  3 2 .  1 3 
Gọi I là trung điểm AB  I   ; ;1 .  2 2   1 3  AB 3 2 Mặt cầu tâm I  
; ;1 và bán kính R   , có phương trình:  2 2  2 2 2 2  1   3  2 9 (S): x   y   z   1      .  2   2  2
B|i tập 2 : Viết phương trình mặt cầu (S) , trong các trường hợp sau:
a) (S) qua A3;1;0 , B5; 5;0 và tâm I thuộc trục Ox .
b) (S) có tâm O và tiếp xúc mặt phẳng   : 16x 15y 12z  75  0 . x  1 y  1 z
c) (S) có tâm I  1
 ; 2;0 và có một tiếp tuyến là đường thẳng  :   . 1  1 3  Bài giải:   a) Gọi I  ;
a 0; 0Ox . Ta có : IA  3  ;
a 1; 0 , IB  5  ; a 5; 0 . 2 2
Do (S) đi qua A, B  IA  IB  3  a  1  5  a  25  4a  40  a  10
 I 10;0;0 và IA  5 2 .
Mặt cầu tâm I 10; 0; 0 và bán kính R  5 2 , có phương trình (S) : x  2 2 2
10  y  z  50
b) Do (S) tiếp xúc với    O   75 d ,  R  R   3. 25
Mặt cầu tâm O0; 0; 0 và bán kính R  3 , có phương trình (S) : 2 2 2
x  y  z  9  c) Chọn A 1
 ;1;0  IA  0; 1  ;0.   
Đường thẳng  có một vectơ chỉ phương là u        
 1;1; 3 . Ta có: IA,u 3;0; 1   .    IA u    
Do (S) tiếp xúc với   I  , 10 d ,  R  R    . u 11  10 2 2
Mặt cầu tâm I  1
 ; 2;0 và bán kính R 
, có phương trình (S) : x    y   2 10 1 2  z  . 11 121
B|i tập 3 : Viết phương trình mặt cầu (S) biết :
a) (S) qua bốn điểm A1; 2; 4  , B1; 3  ; 
1 , C 2; 2; 3, D1;0; 4 .
b) (S) qua A0;8;0 , B4;6; 2 , C 0;12; 4 và có tâm I thuộc mặt phẳng (Oyz). Giáo
viên: PHẠM VĂN LONG( TP.Cần Thơ
)…0913.518.110… CLB Giáo viên trẻ TP Huế 4
Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ
Luyện thi Đại Học 2017 Bài giải:
a) Cách 1: Gọi I x; y; z là tâm mặt cầu (S) cần tìm. 2 2 IA  IB IA  IB
y  z  1  x  2      Theo giả thiết: 2 2
IA  IC  IA  IC  x  7z  2   y  1 .   2 2   IA  ID IA   ID y  4z  1 z  0    2 2 Do đó: I  2;
 1;0 và R  IA  26 . Vậy (S) : x   y   2 2 1  z  26 .
Cách 2: Gọi phương trình mặt cầu (S) : 2 2 2
x  y  z  2ax  2by  2cz  d  0 ,  2 2 2
a  b  c  d  0. Do A1; 2; 4  S  2
 a  4b  8c  d  2  1 (1) Tương tự: B1; 3  ;  1 S  2
 a  6b  2c  d  1  1 (2)
C 2; 2; 3S  4
 a  4b 6c  d  1  7 (3)
D1;0; 4S  2
 a 8c  d  1  7 (4)
Giải hệ (1), (2), (3), (4) ta có a, b, c, d , suy ra phương trình mặt cầu (S) : 2 2
x  y  2 2 1  z  26 .
b) Do tâm I của mặt cầu nằm trên mặt phẳng (Oyz)  I 0; ; b c . 2 2 IA  IB b   7
Ta có: IA  IB  IC     . 2 2 IA  IC c  5 2 2
Vậy I 0;7; 5 và R  26 . Vậy (S): 2
x  y  7  z  5  26. x  t 
B|i tập 4: Viết phương trình mặt cầu (S) có tâm I thuộc đường thẳng  : y  1 và (S) tiếp xúc z  t  
với hai mặt phẳng   : x  2y  2z  3  0 và   : x  2y  2z  7  0 . Bài giải: Gọi I t; 1  ; t
  là tâm mặt cầu (S) cần tìm.  t  t
  t  t
Theo giả thiết: dI    dI   1 5 1 5 , ,      t  3 . 3 3 1 t  t   5 2 2 2 4 Suy ra: I 3; 1  ; 3
  và R  I   2 d ,
 . Vậy (S) : x  3 y  
1  z  3  . 3 9 Giáo
viên: PHẠM VĂN LONG( TP.Cần Thơ
)…0913.518.110… CLB Giáo viên trẻ TP Huế 5
Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ
Luyện thi Đại Học 2017
B|i tập 5: Lập phương trình mặt cầu (S) qua 2 điểm A2;6;0 , B4;0;8 và có tâm thuộc d : x  1 y z  5   . 1  2 1 Bài giải: x  1 t 
Ta có d : y  2t
. Gọi I 1 t; 2t; 5
  td là tâm của mặt cầu (S) cần tìm. z  5   t   
Ta có: IA  1 t;6  2t; 5 t , IB  3  t; 2
 t;13 t.
Theo giả thiết, do (S) đi qua A, B  AI  BI
  t2   t2  t2   t2  t   t2 2 1 6 2 5 3 4 13 29
 62  32t  178  20t  12t  1  16  t   3  2 2 2 32 58 44         32 58 44 I ;  ;  
 và R  IA  2 233 . Vậy (S): x   y   z         932 .  3 3 3   3   3   3  x  1 y  1 z
B|i tập 6: Viết phương trình mặt cầu (S) có tâm I 2; 3;  
1 và cắt đường thẳng  :   1 4  1
tại hai điểm A, B với AB  16 . Bài giải:   Chọn A 1
 ;1;0  IA   3  ; 2  ; 
1 . Đường thẳng  có một vectơ chỉ phương là u    1; 4; 1 .     IA u      Ta có: IA u           I  , , 2; 4;14 d , 2 3   . u AB
Gọi R là bán kính mặt cầu (S). Theo giả thiết : R   I  2 2 d ,    2 19.  4 2 2 2
Vậy (S): x  2  y  3  z   1  76 .
B|i tập 7: Cho hai mặt phẳng P: 5x  4y  z  6  0, Q : 2x  y  z  7  0 và đường thẳng x  1 y z  1  :  
. Viết phương trình mặt cầu (S) có tâm I là giao điểm của (P) và  sao cho (Q) 7 3 2 
cắt (S) theo một hình tròn có diện tích là 20 . Bài giải: Giáo
viên: PHẠM VĂN LONG( TP.Cần Thơ
)…0913.518.110… CLB Giáo viên trẻ TP Huế 6
Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ
Luyện thi Đại Học 2017     x 1 7t (1) x  1  7t   y  3t (2)
Ta có  : y  3t
. Tọa độ I là nghiệm của hệ phương trình:  
z  1  2t (3)  z  1  2t 
5x  4y  z  6   0 (4)
Thay (1), (2), (3) vào (4) ta có: 51 7t  43t  1 2t  6  0  t  0  I 1;0;  1 .
Ta có : d I Q 5 6 ,  . 3
Gọi r là bán kính đường tròn giao tuyến của (S) và mặt phẳng (Q). Ta có: 2
20  r  r  2 5.
R là bán kính mặt cầu (S) cần tìm. 2 2
Theo giả thiết: R  d 2 110
 I Q 2 2 330 ,   r  . 
Vậy (S) : x  
1  y  z   1  . 3 3 x  t 
B|i tập 8: Cho mặt phẳng ( )
P : 2x  y  2z  2  0 và đường thẳng d : y  2t  1 . z  t  2 
Viết phương trình mặt cầu (S) có tâm I thuộc d và I cách (P) một khoảng bằng 2 và (S) cắt (P)
theo giao tuyến là đường tròn có bán kính bằng 3. Bài giải: Gọi I  t
 ; 2t 1;t  2d : là tâm của mặt cầu (S) và R là bán kính của (S).
Theo giả thiết : R  d
 I P 2 2 ;
  r  4  9  13  .  1  2
  2  1 2  4  2 t t t t 
Mặt khác: d I P 6 ;  2 
 2  6t  5  6   4  1  4  11 t    6 2 2 2 1  1 2 13   1   2   13  * Với t  : Tâm I  ;   ;
 , suy ra S : x   y   z         13 . 1  6 1  6 3 6   6   3   6  2 2 2 11  11 2 1   11   2   1  * Với t   : Tâm I ;  
;  , suy ra S : x   y   z         13 . 2  6 2  6 3 6   6   3   6  x  1 y  1 z  1
B|i tập 9: Cho điểm I 1; 0; 3 và đường thẳng d :  
. Viết phương trình mặt cầu 2 1 2
(S) tâm I và cắt d tại hai điểm A, B sao cho I
 AB vuông tại I. Bài giải : 
Đường thẳng d có một vectơ chỉ phương u  2;1; 2 và P1; 1  ;  1 d . Giáo
viên: PHẠM VĂN LONG( TP.Cần Thơ
)…0913.518.110… CLB Giáo viên trẻ TP Huế 7
Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ
Luyện thi Đại Học 2017        u IP   Ta có: IP  0; 1  ; 2
   u,IP  0; 4;  2     . Suy ra: I d , 20 d ;    . u 3
Gọi R là bán kính của (S). Theo giả thiết, I
 AB vuông tại I 1 1 1 2 40    
 R  2IH  2d I,d  2 2 2 2   IH IA IB R 3 2 2 40
Vậy (S) : x   2
1  y  z  3  . 9
B|i tập 10: (Khối A- 2011) Cho mặt cầu (S): 2 2 2
x  y  z  4x  4y  4z  0 và điểm A4; 4; 0. Viết
phương trình mặt phẳng (OAB), biết điểm B thuộc (S) và tam giác OAB đều. Bài giải :
(S) có tâm I 2; 2; 2 , bán kính R  2 3 . Nhận xét: điểm O và A cùng thuộc (S). OA
Tam giác OAB đều, có bán kính đường tròn ngoại tiếp / 4 2 R   . 3 3
Khoảng cách : dI P  R  R 2 2 / 2 ;  . 3
Mặt phẳng (P) đi qua O có phương trình dạng : ax  by  cz   2 2 2
0 a  b  c  0 *
Do (P) đi qua A, suy ra: 4a  4b  0  b  a  .
2 a  b  c 2c 2c 2
Lúc đó: dI;P       2 2 2 2 2 2 2
a  b  c 2a  c 2a  c 3 c  a 2 2 2
 2a  c  3c  
. Theo (*), suy ra P : x  y  z  0 hoặc x  y  z  0. c  1  
Chú ý: Kỹ năng xác định tâm và bán kính của đường tròn trong không gian.
Cho mặt cầu (S) tâm I bán kính R. Mặt phẳng (P) cắt (S) theo một đường tròn (C).
Bƣớc 1: Lập phương trình đường thẳng d qua I và vuông góc với mặt phẳng (P).
Bƣớc 2: Tâm H của đường tròn (C) là giao điểm của d và mặt phẳng (P).
Bƣớc 3: Gọi r là bán kính của (C): r  R  d
 I P 2 2 ;  
B|i tập 11: Chứng minh rằng: Mặt cầu 2 2 2 ( )
S : x  y  z  2x  3  0 cắt mặt phẳng (P): x  2  0
theo giao tuyến là một đường tròn (C). Xác định tâm và bán kính của (C). Bài giải :
* Mặt cầu (S) có tâm I 1; 0; 0 và bán kính R  2 . Giáo
viên: PHẠM VĂN LONG( TP.Cần Thơ
)…0913.518.110… CLB Giáo viên trẻ TP Huế 8
Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ
Luyện thi Đại Học 2017
Ta có : dI,P  1  2  R  mặt phẳng (P) cắt (S) theo giao tuyến là 1 đường tròn. (đ.p.c.m) 
* Đường thẳng d qua I 1; 0; 0 và vuông góc với (P) nên nhận n  1;0; 0 làm 1 vectơ chỉ P  x  1 t 
phương, có phương trình d : y  0 . z  0  x  1 t  x  2 y  0 
+ Tọa độ tâm H đường tròn là nghiệm của hệ : 
 y  0  H 2;0;0 . z  0  z  0  x  2   0
+ Ta có: dI,P  1. Gọi r là bán kính của (C), ta có : r  R  d
 I P 2 2 ,   3.  Dạng 2 :
SỰ TƢƠNG GIAO V\ SỰ TIẾP XÚC
* C{c điều kiện tiếp xúc:
+ Đường thẳng  là tiếp tuyến của (S)  dI;   . R
+ Mặt phẳng ( ) là tiếp diện của (S)  dI;   . R
* Lưu ý các dạng toán liên quan như tìm tiếp điểm, tương giao. x y  z 
B|i tập 1: Cho đường thẳng  1 2 :  
và và mặt cầu S : 2 2 2
x  y  z  2x  4z  1  0 . 2 1 1 
Số điểm chung của  và S là : A. 0. B. 1. C. 2. D. 3. Bài giải: 
Đường thẳng  đi qua M 0;1; 2 và có một vectơ chỉ phương là u  2;1;   1
Mặt cầu S có tâm I 1; 0;  2 và bán kính R  2.      u MI   Ta có MI  1; 1  ; 4
 và u,MI   5  ;7; 3
   dI, , 498      6 u
Vì dI,  R nên  không cắt mặt cầu S.
Lựa chọn đáp án A.
B|i tập 2: Cho điểm I 1; 2;
 3. Phương trình mặt cầu tâm I và tiếp xúc với trục Oy là: 2 2 2 2 2 2 A. x  
1  y  2 z  3  10. B. x  
1  y  2 z  3  10. Giáo
viên: PHẠM VĂN LONG( TP.Cần Thơ
)…0913.518.110… CLB Giáo viên trẻ TP Huế 9
Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ
Luyện thi Đại Học 2017 2 2 2 2 2 2 C. x  
1  y  2 z  3  10. D. x  
1  y  2 z  3  9. Bài giải:
Gọi M là hình chiếu của I 1; 2;
 3 lên Oy, ta có : M0; 2;  0 .  IM   1  ;0; 3
   R  dI,Oy  IM  10 là bán kính mặt cầu cần tìm. 2 2 2
Phương trình mặt cầu là : x  
1  y  2 z  3  10.
Lựa chọn đáp án B. x  1 y  2 z  3
B|i tập 3: Cho điểm I 1; 2;
 3và đường thẳng d có phương trình   . Phương 2 1 1 
trình mặt cầu tâm A, tiếp xúc với d là: 2 2 2 2 2 2 A. x  
1  y  2  z  3  50. B. x  
1  y  2  z  3  5 2. 2 2 2 2 2 2 C. x  
1  y  2  z  3  5 2. D. x  
1  y  2  z  3  50. Bài giải:    u AM  
Đường thẳng d đi qua I  1  ; 2; 3
  và có VTCP u  2;1; 
1  d  A d , ,    5 2 u 2 2 2
Phương trình mặt cầu là : x  
1  y  2 z  3  50.
Lựa chọn đáp án D. x  11 y z  25
B|i tập 4: Mặt cầu S tâm I 2; 3;  
1 cắt đường thẳng d :  
tại 2 điểm A, B sao 2 1 2 
cho AB  16 có phương trình là: 2 2 2 2 2 2
A. x  2  y  3  z   1  17.
B. x  2  y  3  z   1  289. 2 2 2 2 2 2
C. x  2  y  3  z   1  289.
D. x  2  y  3  z   1  280. Bài giải:
Đường thẳng d đi qua M 11; 0; 2
 5 và có vectơ chỉ phương  I
u  2;1;  2. R
Gọi H là hình chiếu của I trên (d). Ta có: A B d     H 2       AB AB u, MI IH d I ,    15 2  R  IH     17 . u  2  2 2 2
Vậy S : x  2  y  3  z   1  289.
Lựa chọn đáp án C. Giáo
viên: PHẠM VĂN LONG( TP.Cần T
hơ )…0913.518.110… CLB Giáo viê n trẻ TP Huế 10
Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ
Luyện thi Đại Học 2017 x  5 y  7 z
B|i tập 5: Cho đường thẳng d : 
 và điểm I(4;1;6). Đường thẳng d cắt mặt cầu 2 2  1
Scó tâm I, tại hai điểm A, B sao cho AB  6. Phương trình của mặt cầu S là: 2 2 2 2 2 2
A. x  4  y  
1  z  6  18.
B. x  4  y  
1  z  6  18. 2 2 2 2 2 2
C. x  4  y  
1  z  6  9.
D. x  4  y  
1  z  6  16. Bài giải :
Đường thẳng d đi qua ( M 5
 ;7;0) và có vectơ chỉ phương u (2; 2
 ;1). Gọi H là hình chiếu của I trên (d). Ta có :     2      I  AB AB u, MI IH d I,    3 2  R  IH     18 R u  2  A B d 2 2 2
Vậy S : x  4  y  
1  z  6  18. H
Lựa chọn đáp án A. x  1 y  1 z  2
B|i tập 8: Cho điểm I 1; 0; 0 và đường thẳng d :  
. Phương trình mặt cầu S có 1 2 1
tâm I và cắt đường thẳng d tại hai điểm A, B sao cho tam giác IAB đều là: A. x  2 2 2 20
1  y  z  . B. x  2 2 2 20
1  y  z  . 3 3
C. x  2 2 2 16
1  y  z  .
D. x  2 2 2 5
1  y  z  . 4 3 Bài giải:
Đường thẳng  đi qua M  1;1;  2 và có vectơ chỉ phương  I u  1; 2;  1    R Ta có MI  0; 1
 ; 2 và u,MI  5; 2;    1   A B d H
Gọi H là hình chiếu của I trên (d). Ta có :         AB u, MI IH d I,    5 . u 3 2IH 2 15
Xét tam giác IAB, có IH  . R  R   2 3 3
Vậy phương trình mặt cầu là: x  2 2 2 20
1  y  z  . 3 Giáo
viên: PHẠM VĂN LONG( TP.Cần T
hơ )…0913.518.110… CLB Giáo viê n trẻ TP Huế 11
Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ
Luyện thi Đại Học 2017
Lựa chọn đáp án A.
B|i tập 9: Cho mặt cầu 2 2 2 ( )
S : x  y  z  4x  2y  6z  5  0 . Viết phương trình tiếp tuyến của mặt
cầu (S) tại A0; 0; 5 biết: 
a) Tiếp tuyến có một vectơ chỉ phương u  1; 2; 2 .
b) Vuông góc với mặt phẳng (P) : 3x  2y  2z  3  0. Bài giải: 
a) Đường thẳng d qua A0; 0; 5 và có một vectơ chỉ phương u  1; 2; 2 , có phương trình d: x  t  y  2t . z  5 2t  
b) Mặt phẳng (P) có một vectơ pháp tuyến là n  3; 2;  2 . P 
Đường thẳng d qua A0; 0; 5 và vuông góc với mặt phẳng (P) nên có một vectơ chỉ phương x  3t   n  3; 2;
 2 , có phương trình d: y  2  t . P 
z  2t  5  x  1   3t 
B|i tập 10: Cho mặt cầu 2 2 2 ( )
S : x  y  z  6x  6y  2z  3  0 và hai đường thẳng  : y  1   2t 1 z  1 2t  x y  1 z  2  :  
. Viết phương trình mặt phẳng (P) song song với  và  đồng thời tiếp xúc 2 2 2 1 1 2 với (S). Bài giải:
Mặt cầu (S) có tâm I 3; 3;   1 , R  4 . 
Ta có:  có một vectơ chỉ phương là u  3; 2; 2 . 1   1 
 có một vectơ chỉ phương là u  2; 2;1 . 2   2 
Gọi n là một vectơ pháp của mặt phẳng (P).   (  P) / / n  u Do: 1 1      chọn (P) / / n    u 2 2
Lúc đó, mặt phẳng (P) có dạng : 2
 x  y  2z  m  0 . Giáo
viên: PHẠM VĂN LONG( TP.Cần T
hơ )…0913.518.110… CLB Giáo viê n trẻ TP Huế 12
Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ
Luyện thi Đại Học 2017  m
Để mặt phẳng (P) tiếp xúc với (S)  dI P  5 ;( )  R   4 3 m  7
 5  m  12   . m  17  
Kết luận: Vậy tồn tại 2 mặt phẳng (P) là : 2
 x  y  2z 7  0; 2x  y  2z 17  0 .
B|i tập 11: Viết phương trình tiếp diện của mặt cầu S 2 2 2
: x  y  z  2x  4y  6z  5  0 , biết: a) qua M 1;1;  1 .
b) song song với mặt phẳng (P) : x  2y  2z 1  0 . x  3 y  1 z  2
b) vuông góc với đường thẳng d :   . 2 1 2  Bài giải:
Mặt cầu (S) có tâm I  1
 ; 2; 3 , bán kính R  3. 
a) Để ý rằng, M S . Tiếp diện tại M có một vectơ pháp tuyến là IM  2; 1  ; 2  , có phương trình :
: 2x 1y 12z 1  0  2xy2z1 0.
b) Do mặt phẳng   / / P nên có dạng : x  2y  2z  m  0 . m  m  
Do   tiếp xúc với (S)  I   3 6 d ,  R 
 3  m  3  9   . 3 m   12 * Với m  6
 suy ra mặt phẳng có phương trình : x  2y  2z 6  0.
* Với suy ra mặt phẳng có phương trình : x  2y  2z  12  0.
c) Đường thẳng d có một vectơ chỉ phương là . 
Do mặt phẳng    d nên   nhận u  2;1; 2
 làm một vectơ pháp tuyến. d 
Suy ra mặt phẳng   có dạng : 2x  y  2z  m  0 . m  m  
Do   tiếp xúc với (S)  dI   6 3 ,  R 
 3  m  6  9   . 3 m   15 * Với m  3
 suy ra mặt phẳng có phương trình : x  2y  2z  3  0.
* Với m  15 suy ra mặt phẳng có phương trình : x  2y  2z  15  0. Giáo
viên: PHẠM VĂN LONG( TP.Cần T
hơ )…0913.518.110… CLB Giáo viê n trẻ TP Huế 13
Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ
Luyện thi Đại Học 2017
III. B\I TẬP TRẮC NGHIỆM :
NHẬN BIẾT_THÔNG HIỂU
Câu 1. Phương trình nào sau đây là phương trình mặt cầu ? A. 2 2 2
x  y  z  2x  y  1  0. B. 2 2 2
x  y  z  2x  0.
C. x  y  x  y2 2 2 2 2 2
 z  2x 1.
D. x  y2 2
 2xy  z 1.
Câu 2. Phương trình nào sau đây không phải là phương trình mặt cầu ?
A. x  y  x  y2 2 2 2 2 2
 z  2x 1. B. 2 2 2
x  y  z  2x  0. C. 2 2 2
x  y  z  2x  2y  1  0.
D. x  y2 2
 2xy  z 1 4 . x
Câu 3. Phương trình nào sau đây không phải là phương trình mặt cầu ? 2 2 2
A. x  y2 2
 2xy  z  3  6 . x B. x   1  y   1  z   1  6. 2 2 2 2 2 2 C. 2x   1  2y   1  2z   1  6. D. x   1  2y   1  z   1  6.
Câu 4. Cho các phương trình sau: x 2 2 2
1  y  z  1
x   y  2 2 2 2 1  z  4 2 2 2 2 2
x  y  z  1  0
 x   y  2 2 1 2 1  4z  16 .
Số phương trình là phương trình mặt cầu là: A. 2. B. 3. C. 4. D. 1. 2 2
Câu 5. Mặt cầu S x    y   2 : 1
2  z  9 có tâm là: A. I 1; 2; 0. B. I  1  ; 2;0. C. I 1; 2;  0. D. I  1  ; 2;  0.
Câu 6. Mặt cầu S 2 2 2
: x  y  z  8x  2y  1  0 có tâm là: A. I  4;  1;0. B. I 4; 1  ;0. C. I  8;  2;0. D. I 8; 2;  0.
Câu 7. Mặt cầu S 2 2 2
: x  y  z  4x  1  0 có tọa độ tâm và bán kính R là: A. I  2;  0;0, R  3.
B. I 2;0;0 , R  3.
C. I 0; 2;0 , R  3.
D. I 2;0;0 , R  3.
Câu 8. Phương trình mặt cầu có tâm I  1  ; 2; 3
  , bán kính R  3 là: 2 2 2 2 2 2 A.  x  
1   y  2   z  3  3. B. x  
1  y  2  z  3  9. 2 2 2 2 2 2 C. x  
1  y  2  z  3  9. D. x  
1  y  2  z  3  9.
Câu 9. Mặt cầu S x  y2 2 :
 2xy  z 1 4x có tâm là: Giáo
viên: PHẠM VĂN LONG( TP.Cần T
hơ )…0913.518.110… CLB Giáo viê n trẻ TP Huế 14
Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ
Luyện thi Đại Học 2017 A. I 2; 0; 0. B. I 4; 0; 0. C. I  4;  0;0. D. I  2;  0;0.
Câu 10. Đường kính của mặt cầu S x  y  z  2 2 2 : 1  4 bằng: A. 4. B. 2. D. 8. D. 16.
Câu 11. Mặt cầu có phương trình nào sau đây có tâm là I  1  ;1;0 ?
A. x  y2 2
 2xy  z 1 4 . x B. 2 2 2
x  y  z  2x  2y  0. C. 2 2 2
x  y  z  2x  2y  1  0.
D. x  y  x  y2 2 2 2 2 2
 z  2x 1 2x . y
Câu 12. Mặt cầu S : 2 2 2
3x  3y  3z  6x  12y  2  0 có bán kính bằng: 2 7 13 21 7 A. . B. . C. . D. . 3 3 3 3 
Câu 13. Gọi I là tâm mặt cầu S x  y  z  2 2 2 : 2
 4 . Độ dài OI (O là gốc tọa độ ) bằng: A. 2. B. 4. C. 1. D. 2.
Câu 14. Phương trình mặt cầu có bán kính bằng 3 và tâm là giao điểm của ba trục toạ độ ? A. 2 2 2
x  y  z  6x  0. B. 2 2 2
x  y  z  6y  0. C. 2 2 2
x  y  z  6z  0. D. 2 2 2
x  y  z  9.
Câu 15. Mặt cầu S 2 2 2
: x  y  z  2x  10y  3z  1  0 đi qua điểm có tọa độ nào sau đây ? A. 2;1;9. B. 3; 2;  4  . C. 4; 1  ;0. D.  1  ;3;  1 .
Câu 16. Mặt cầu tâm I  1  ; 2; 3
  và đi qua điểm A2;0;0 có phương trình: 2 2 2 2 2 2 A. x  
1  y  2  z  3  11. B. x  
1  y  2  z  3  22. 2 2 2 2 2 2 C. x  
1  y  2  z  3  22. D. x  
1  y  2  z  3  22.
Câu 17. Cho hai điểm A1;0; 3
  và B3;2; 
1 . Phương trình mặt cầu đường kính AB là: A. 2 2 2
x  y  z  2x  y  z  6  0. B. 2 2 2
x  y  z  4x  2y  2z  0. C. 2 2 2
x  y  z  4x  2y  2z  0. D. 2 2 2
x  y  z  4x  2y  2z  6  0.
Câu 18. Nếu mặt cầu S đi qua bốn điểm M 2;2;2, N 4;0;2, P4;2;0 và Q4; 2; 2 thì tâm I
của S có toạ độ là: A.  1  ; 1  ;0. B. 3;1;  1 . C. 1;1;  1 . D. 1; 2;  1 .
Câu 19. Bán kính mặt cầu đi qua bốn điểm M 1;0;1, N 1;0;0, P2;1;0  và Q1;1;  1 bằng: Giáo
viên: PHẠM VĂN LONG( TP.Cần T
hơ )…0913.518.110… CLB Giáo viê n trẻ TP Huế 15
Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ
Luyện thi Đại Học 2017 3 3 A. 3. B. . C. 1. D. . 2 2
Câu 20. Cho mặt cầu S 2 2 2
: x  y  z  4  0 và 4 điểm M 1; 2;0, N 0;1;0, P1;1;1,Q1; 1  ;2 .
Trong bốn điểm đó, có bao nhiêu điểm không nằm trên mặt cầu S ? A. 4 điểm. B. 2 điểm. C. 1 điểm. D. 3 điểm.
Câu 21. Mặt cầu S tâm I  1  ; 2; 3
  và tiếp xúc với mặt phẳng P : x  2y  2z 1  0 có phương trình: 2 2 2 16 2 2 2 4 A. x  
1  y  2  z  3  . B. x  
1  y  2  z  3  . 3 9 2 2 2 4 2 2 2 4 C. x  
1  y  2  z  3  . D. x  
1  y  2  z  3  . 3 9
Câu 22. Phương trình mặt cầu nào dưới đây có tâm I 2;1; 3 và tiếp xúc với mặt phẳng
P: x2y2z2  0 ? 2 2 2 2 2 2
A. x  2  y   1  z   1  4.
B. x  2  y  
1  z  3  16. 2 2 2 2 2 2
C. x  2  y   1  z   1  25.
D. x  2  y   1  z   1  9.
Câu 23. Mặt cầu có tâm I 3; 3  ;  1 và đi qua A5; 2;  1có phương trình: 2 2 2 2 2 2
A. x  3  y  3  z   1  5.
B.  x  5   y  2   z   1  5. 2 2 2 2 2 2
C. x  3  y  3  z   1  5.
D. x  5  y  2  z   1  5.
Câu 24. Phương trình mặt trình mặt cầu có đường kính AB với A1; 3; 2, B3; 5;0  là: A. 2 2 2
(x  2)  (y  4)  (z  1)  3. B. 2 2 2
(x  2)  (y  4)  (z 1)  2. C. 2 2 2
(x  2)  (y  4)  (z  1)  2. D. 2 2 2
(x  2)  (y  4)  (z 1)  3.
Câu 25. Cho I 1; 2; 4 và mặt phẳng P : 2x  2y  z 1  0 . Mặt cầu tâm I và tiếp xúc với mặt
phẳng P , có phương trình là: 2 2 2 2 2 2 A. x  
1  y  2  z  4  4. B. x  
1  y  2  z  4  1. 2 2 2 2 2 2 C.  x  
1   y  2   z  4  3. D. x  
1  y  2  z  4  4. Giáo
viên: PHẠM VĂN LONG( TP.Cần T
hơ )…0913.518.110… CLB Giáo viê n trẻ TP Huế 16
Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ
Luyện thi Đại Học 2017 VẬN DỤNG x y  1 z  1
Câu 1. Cho đường thẳng d :  
và điểm A5; 4; 2
  . Phương trình mặt cầu đi qua 1 2 1 
điểm A và có tâm là giao điểm của d với mặt phẳng Oxy là: 2 2 2 2
A. S x    y   2 : 1
1  (z  2)  65.
B. S x    y   2 : 1 1  z  9. 2 2 2 2
C. S x    y   2 : 1 2  z  64.
D. S x    y   2 : 1 1  z  65.
Câu 2. Cho ba điểm ( A 6; 2  ; 3), ( B 0;1; 6) , ( C 2; 0; 1  ), (
O 4;1; 0) . Khi đó mặt cầu ngoại tiếp tứ diện
OABC có phương trình là: A. 2 2 2
x  y  z  4x  2y  6z  3  0. B. 2 2 2
x  y  z  4x  2y  6z  3  0. C. 2 2 2
x  y  z  2x  y  3z  3  0. D. 2 2 2
x  y  z  2x  y  3z  3  0.
Câu 3. Cho ba điểm A2; 0; 
1 , B1;0;0 ,C 1;1;1 và mặt phẳng P : x  y  z  2  0 . Phương trình
mặt cầu đi qua ba điểm A, B,C và có tâm thuộc mặt phẳng P là: A. 2 2 2
x  y  z  x  2y  1  0. B. 2 2 2
x  y  z  2x  2z  1  0. C. 2 2 2
x  y  z  2x  2y  1  0. D. 2 2 2
x  y  z  x  2z  1  0.
Câu 4. Phương trình mặt cầu tâm I 1; 2;
 3 và tiếp xúc với trục Oy là: 2 2 2 2 2 2 A. x  
1  y  2  z  3  8. B. x  
1  y  2  z  3  16. 2 2 2 2 2 2 C. x  
1  y  2  z  3  10. D. x  
1  y  2  z  3  9. x  1 t 
Câu 5. Cho các điểm A 2;  4; 
1 , B2;0; 3 và đường thẳng d : y  1 2t . Gọi S là mặt cầu đi z  2   t 
qua A, B và có tâm thuộc đường thẳng d . Bán kính mặt cầu S bằng: A. 3. B. 6. C. 3 3. D. 2 3. x  1 y  2 z  3
Câu 6. Cho điểm A1; 2;
 3 và đường thẳng d có phương trình   . Phương 2 1 1 
trình mặt cầu tâm A , tiếp xúc với d là: 2 2 2 2 2 2 A. x – 
1  y  2  z – 3  5. B. x – 
1  y  2  z – 3  50. 2 2 2 2 2 2 C. x – 
1  y  2  z – 3  50. D. x  
1  y  2  z  3  50. Giáo
viên: PHẠM VĂN LONG( TP.Cần T
hơ )…0913.518.110… CLB Giáo viê n trẻ TP Huế 17
Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ
Luyện thi Đại Học 2017 x 1 y  1 z
Câu 7. Cho đường thẳng d: 
 và mặt phẳng P : 2x  y 2z  2  0 . Phương trình 3 1 1
mặt cầu S có tâm nằm trên đường thẳng d có bán kính nhỏ nhất tiếp xúc với P và đi qua điểm A1; 1  ;  1 là: 2 2 2 2 2
A. x  3  y   1  z   1  1. B. x   2
4  y  z   1  1. 2 2 2 2 2
C. x  2  y  2  z   1  1.
D. x    y   2 1 1  z  1.
Câu 8. Phương trình mặt cầu có tâm I 1; 2; 3 và tiếp xúc với mặt phẳng Oxz là: A. 2 2 2
x  y  z  2x  4y  6z  10  0. B. 2 2 2
x  y  z  2x  4y  6z  10  0. C. 2 2 2
x  y  z  2x  4y  6z  10  0. D. 2 2 2
x  y  z  2x  4y  6z  10  0.
Câu 9. Mặt phẳng P tiếp xúc với mặt cầu tâm I 1; 3
 ; 2 tại điểm M7; 1
 ; 5 có phương trình là
A. 3x  y  z  22  0.
B. 6x  2y  3z  55  0.
C. 6x  2y  3z  55  0.
D. 3x  y  z  22  0.
Câu 10. Cho mặt cầu 2 2 2 ( )
S : x  y  z  2x  4y  6z  2  0 và mặt phẳng () : 4x  3y 12z 10  0 .
Mặt phẳng tiếp xúc với S và song song với () có phương trình là:
A. 4x  3y 12z  78  0 hoặc 4x  3y 12z  78  0.
B. 4x  3y 12z  78  0 hoặc 4x  3y 12z  26  0.
C. 4x  3y 12z  26  0 hoặc 4x  3y 12z  26  0.
D. 4x  3y 12z  78  0 hoặc 4x  3y 12z  26  0. 2 2
Câu 11. Cho mặt cầu S x    y   2 ( ) : 2
1  z  14 . Mặt cầu S cắt trục Oz tại A và B (z  0) . A
Phương trình nào sau đây là phương trình tiếp diện của S tại B :
A. 2x  y  3z  9  0.
B. 2x  y  3z  9  0.
C. x  2y  z  3  0.
D. x  2y  z  3  0.
Câu 12. Cho 4 điềm A3; 2  ; 2
 , B3;2;0, C0;2;  1 và D 1
 ;1; 2 . Mặt cầu tâm A và tiếp xúc
với mặt phẳng BCD có phương trình là: 2 2 2 2 2 2
A. x  3  y  2  z  2  14.
B. x  3  y  2  z  2  14. 2 2 2 2 2 2
C. x  3  y  2  z  2  14.
D. x  3  y  2  z  2  14. Giáo
viên: PHẠM VĂN LONG( TP.Cần T
hơ )…0913.518.110… CLB Giáo viê n trẻ TP Huế 18
Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ
Luyện thi Đại Học 2017
Câu 13. Cho mặt phẳng P : 2x  3y  z  2  0 . Mặt cầu S có tâm I thuộc trục Oz, bán kính 2 bằng
và tiếp xúc mặt phẳng (P) có phương trình: 14
A. x  y  z  2 2 2 2 1 
hoặc x  y  z  2 2 2 2 2  . 7 7 B. 2 2 2 2
x  y  z 
hoặc x  y  z  2 2 2 2 4  . 7 7 2
C. x  y   z  32 2 2
 hoặc x  y  z  2 2 2 2 4  . 7 7 D. 2 2 2 2
x  y  z 
hoặc x  y  z  2 2 2 2 1  . 7 7 x  5 y  7 z
Câu 14. Cho đường thẳng d : 
 và điểm I 4;1;6. Đường thẳng d cắt mặt cầu S 2 2  1
tâm I tại hai điểm A, B sao cho AB  6 . Phương trình của mặt cầu S là: A. 2 2 2
(x  4)  (y 1)  (z  6)  16. B. 2 2 2
(x  4)  (y 1)  (z  6)  12. C. 2 2 2
(x  4)  (y 1)  (z  6)  18. D. 2 2 2
(x  4)  (y 1)  (z  6)  9.
Câu 15. Cho hai mặt phẳng P , Q có phương trình P : x  2y  z 1  0 và .. Mặt cầu có tâm
nằm trên mặt phẳng P và tiếp xúc với mặt phẳng Q tại điểm M , biết rằng M thuộc mặt
phẳng Oxy và có hoành độ x  1, có phương trình là: M 2 2 2 2 2 2 A. x  2 
1  y  5  z  10  600.
B. x  19  y  15  z 10  600. 2 2 2 2 2 2 C. x  2 
1  y  5  z  10  100. D. x  2 
1  y  5  z 10  600.
Câu 16. Cho hai điểm M 1; 0; 4 , N 1;1; 2 và mặt cầu S 2 2 2
: x  y  z  2x  2y  2  0. Mặt phẳng
P qua M, N và tiếp xúc với mặt cầu S có phương trình:
A. 2x  2y  z  6  0.
B. 4x  2y  z  8  0 hoặc 4x  2y  z  8  0.
C. 2x  2y  z  6  0 hoặc 2x  2y  z  2  0.
D. 2x  2y  z  2  0.
Câu 17. Cho hai điểm A1; 2;  3, B 1
 ;0;1 và mặt phẳng P : x  y  z  4  0. Phương trình mặt AB
cầu (S) có bán kính bằng
có tâm thuộc đường thẳng AB và (S) tiếp xúc với mặt phẳng P 6 là: Giáo
viên: PHẠM VĂN LONG( TP.Cần T
hơ )…0913.518.110… CLB Giáo viê n trẻ TP Huế 19
Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ
Luyện thi Đại Học 2017 2 2 2 1
A. x  4  y  3  z  2  . 3 2 2 2 1 2 2 2 1
B. x  4  y  3  z  2  hoặc x  6  y  5  z  4  . 3 3 2 2 2 1
C. x  4  y  3  z  2  . 3 2 2 2 1 2 2 2 1
D. x  4  y  3  z  2  hoặc x  6  y  5  z  4  . 3 3 x  1 y  2 z  3
Câu 18. Cho đường thẳng d :  
và hai mặt phẳng P : x  2y  2z 2 0; 1  2 1 2
P : 2xy2z10. Mặt cầu có tâm I nằm trên d và tiếp xúc với 2 mặt phẳng P , P , có 1   2 2  phương trình: 2 2 2
A. S : x  
1  y  2  z  3  9. 2 2 2 2 2 2  19   16   15  9
B. S : x  
1  y  2  z  3  9 hoặc S : x   y   z         .  17   17   17  289 2 2 2 2 2 2  19   16   15  9
C. S : x  
1  y  2  z  3  9 hoặc S : x   y   z         .  17   17   17  289 2 2 2
D. S : x  
1  y  2  z  3  9. x  1   2t  Câu 19. Cho điểm (
A 1; 3; 2) , đường thẳng d : y  4  t và mặt phẳng ( )
P : 2x  2y  z  6  0 . z  2  t 
Phương trình mặt cầu (S) đi qua A, có tâm thuộc d đồng thời tiếp xúc với (P) là: 2 2 2  83   87   70  13456 A. 2 2 2 ( )
S : (x 1)  (y  3)  (z  2)  16 hoặc ( ) S : x   y   z         .  13   13   13  169 2 2 2  83   87   70  13456 B. 2 2 2 ( )
S : (x  1)  (y  3) (z  2)  16 hoặc ( ) S : x   y   z         .  13   13   13  169 2 2 2 C. ( ) S : x  
1  y  3  z  2  16. 2 2 2 D. ( )
S : x 1  y  3  z  2  4. x  2 y z  1
Câu 20. Cho mặt phẳng P : x  2y  2z  10  0 và hai đường thẳng  :   , 1 1 1 1  x  2 y z  3  :  
. Mặt cầu S có tâm thuộc  , tiếp xúc với  và mặt phẳng P , có 2 1 1 4 1 2 phương trình: Giáo
viên: PHẠM VĂN LONG( TP.Cần T
hơ )…0913.518.110… CLB Giáo viê n trẻ TP Huế 20
Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ
Luyện thi Đại Học 2017 2 2 2  11   7   5  81 A. 2 2 2
(x  1)  (y 1)  (z  2)  9 hoặc  x 
   y     z    .  2   2   2  4 2 2 2  11   7   5  81 B. 2 2 2
(x 1)  (y  1)  (z  2)  9 hoặc  x 
   y     z    .  2   2   2  4 C. 2 2 2
(x 1)  (y  1)  (z  2)  9. D. 2 2 2
(x 1)  (y  1) (z  2)  3. Câu 21. Cho mặt phẳng
P và mặt cầu S có phương trình lần lượt là P 2 2 2 2
: 2x  2y  z  m  4m  5  0; ( )
S : x  y  z  2x  2y  2z  6  0 . Giá trị của m để P tiếp xúc S là: A. m  1  hoặc m  5.
B. m  1 hoặc m  5.  C. m  1.  D. m  5.
Câu 22. Cho mặt cầu S 2 2 2
: x  y  z  2x  4y  2z  3  0 và mặt phẳng P : x  y  2z  4  0 .
Phương trình đường thẳng d tiếp xúc với mặt cầu S tại A3; 1  ;  1 và song song với mặt phẳng P là: x  1 4t
x  3  4t
x  3  4t
x  3  2t     A. y  2   6t. B. y  1   6t. C. y  1   6t. D. y  1   t.     z  1   t  z  1  t  z  1  t  z  1  2t 
Câu 23. Cho điểm A2; 5;  1 và mặt phẳng ( )
P : 6x  3y  2z  24  0 , H là hình chiếu vuông góc
của A trên mặt phẳng P . Phương trình mặt cầu (S) có diện tích 784 và tiếp xúc với mặt
phẳng  P tại H, sao cho điểm A nằm trong mặt cầu là: 2 2 2 2 2 2
A. x  16  y  4  z  7  196.
B. x  8  y  8  z   1  196. 2 2 2 2 2 2
C. x  8  y  8  z   1  196.
D. x 16  y  4  z  7  196.
Câu 24. Cho mặt phẳng P : 2x  y  z  5  0 và các điểm A0;0; 4 , B2;0;0 . Phương trình mặt
cầu đi qua O, A, B và tiếp xúc với mặt phẳng P là: 2 2 2 2 2 2 A. x   1  y  
1  z  2  6. B. x   1  y  
1  z  2  6. 2 2 2 2 2 2 C. x   1  y  
1  z  2  6. D. x   1  y  
1  z  2  6.
Câu 25. Cho mặt phẳng P : x  2y  2z  2  0 và điểm A2; 3
 ;0 . Gọi B là điểm thuộc tia Oy
sao cho mặt cầu tâm B , tiếp xúc với mặt phẳng P có bán kính bằng 2. Tọa độ điểm B là: Giáo
viên: PHẠM VĂN LONG( TP.Cần T
hơ )…0913.518.110… CLB Giáo viê n trẻ TP Huế 21
Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ
Luyện thi Đại Học 2017 A. 0; 4;  0. B. 0; 2; 0. C. 0;2;0 hoặc 0; 4  ;0. D. 0;1;0.
Câu 26. Cho hai mặ t phẳng (P) : 2x  3y  z  2  0, ( )
Q : 2x  y  z  2  0 . Phương trình mặt cầu
S tiếp xúc với mặt phẳng P tại điểm  A 1; 1
 ;1 và có tâm thuộc mặt phẳng (Q) là: 2 2 2 2 2 2
A. (S) :  x  3   y  7   z  3 14. B. ( )
S : x  3  y 7  z  3  56. 2 2 2 2 2 2 C. ( )
S : x  3  y  7  z  3  56. D. ( )
S : x  3  y 7  z  3  14. x  1   t 
Câu 27. Cho điểm I(0; 0; 3) và đường thẳng d : y  2t
. Phương trình mặt cầu S có tâm I và z  2 t 
cắt đường thẳng d tại hai điểm sao cho tam giác IAB vuông là:
A. x  y  z  2 2 2 8 3  .
B. x  y  z  2 2 2 3 3  . 3 2
C. x  y  z  2 2 2 2 3  .
D. x  y  z  2 2 2 4 3  . 3 3 x  2 y z  3
Câu 28. Cho đường thẳng  :  
và và mặt cầu (S): 2 2 2
x  y  z  4x  2y  21  0 . Số 1  1 1 
giao điểm của  và S là: A. 0. B. 1. C. 2. D. 3. x  2 y  2 z  3
Câu 29. Cho đường thẳng d :  
và mặt cầu (S) : x  y  z  2 2 2 2  9 . Tọa độ giao 2 3 2
điểm của  và v là: A. A2; 3; 2. B. A 2;  2; 3  .
C. A0;0; 2 , B 2;  2; 3  .
D.  và S không cắt nhau. x  1 t 
Câu 30. Cho đường thẳng  : y  2
và mặt cầu S  : 2 2 2
x  y  z  2x  4y  6z  67  0 . Giao  z  4   7t 
điểm của  và S là các điểm có tọa độ:
A.  và S không cắt nhau.
B. A1; 2; 5 , B 2;  0;4. C. A2; 2;
 5, B4;0;3. D. A1; 2; 4
 , B2;2;3.Cho điểm I 1;0;0 và x  1 y  1 z  2 đường thẳng d :  
. Phương trình mặt cầu S có tâm I và cắt đường thẳng d tại 1 2 1
hai điểm A, B sao cho AB  4 là: Giáo
viên: PHẠM VĂN LONG( TP.Cần T
hơ )…0913.518.110… CLB Giáo viê n trẻ TP Huế 22
Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ
Luyện thi Đại Học 2017 A. x  2 2 2
1  y  z  9. B. x  2 2 2
1  y  z  3. C. x  2 2 2
1  y  z  3. D. x  2 2 2
1  y  z  9. x  1 y  3 z  2
Câu 31. Cho điểm I 1;1; 2
  đường thẳng d :  
. Phương trình mặt cầu S có tâm 1 2 1
I và cắt đường thẳng d tại hai điểm A, B sao cho AB  6 là: 2 2 2 2 2 2 A. x   1  y  
1  z  2  24. B. x   1  y  
1  z  2  27. 2 2 2 2 2 2 C. x   1  y  
1  z  2  27. D. x   1  y  
1  z  2  54. x  1 y  1 z  2
Câu 32. Cho điểm I 1; 0; 0 và đường thẳng d :  
. Phương trình mặt cầu S có 1 2 1
tâm I và cắt đường thẳng d tại hai điểm A, B sao cho tam giác IAB vuông là: A. x  2 2 2
1  y  z  12. B. x  2 2 2
1  y  z  10. C. x  2 2 2
1  y  z  8. D. x  2 2 2
1  y  z  16. x  1 t 
Câu 33. Cho điểm I 1; 0; 0 và đường thẳng d : y  1 2t . Phương trình mặt cầu S có tâm I và z  2   t 
cắt đường thẳng d tại hai điểm A, B sao cho tam giác IAB đều là: A. x  2 2 2 5
1  y  z  . B. x  2 2 2 20
1  y  z  . 3 3 C. x  2 2 2 16
1  y  z  . D. x  2 2 2 20
1  y  z  . 4 3 x  1   t 
Câu 34. Cho các điểm I 1;1; 2
  và đường thẳng d : y  3  2t . Phương trình mặt cầu S có tâm I z  2 t 
và cắt đường thẳng d tại hai điểm A, B sao cho tam giác IAB vuông là: 2 2 2 2 2 2 A. x   1  y  
1  z  2  9. B. x   1  y  
1  z  2  36. 2 2 2 2 2 2 C. x   1  y  
1  z  2  9. D. x   1  y  
1  z  2  3. x  1 y  3 z  2
Câu 35. Cho điểm I 1;1; 2
  đường thẳng d :  
. Phương trình mặt cầu S có tâm 1 2 1
I và cắt đường thẳng d tại hai điểm A, B sao cho tam giác IAB đều là: 2 2 2 2 2 2 A. x   1  y  
1  z  2  24. B. x   1  y  
1  z  2  24. Giáo
viên: PHẠM VĂN LONG( TP.Cần T
hơ )…0913.518.110… CLB Giáo viê n trẻ TP Huế 23
Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ
Luyện thi Đại Học 2017 2 2 2 2 2 2 C. x   1  y  
1  z  2  18 D. x   1  y  
1  z  2  18. x  1 y  3 z  2
Câu 36. Cho điểm I 1;1; 2
  đường thẳng d :  
. Phương trình mặt cầu S  có tâm 1 2 1 
I và cắt đường thẳng d tại hai điểm A, B sao cho 30o IAB  là: 2 2 2 2 2 2 A. x   1  y  
1  z  2  66. B. x   1  y  
1  z  2  36. 2 2 2 2 2 2 C. x   1  y  
1  z  2  72. D. x   1  y  
1  z  2  46.
Câu 37. Phương trình mặt cầu có tâm I 3; 3; 7
  và tiếp xúc trục tung là: 2 2 2 2 2 2
A. x  3  y  3  z  7  61.
B. x  3  y  3  z  7  58. 2 2 2 2 2 2
C. x  3  y  3  z 7  58.
D. x  3  y  3  z  7  12.
Câu 38. Phương trình mặt cầu có tâm I  5; 3;9 và tiếp xúc trục hoành là: 2 2 2 2 2 2
A. x  5  y  3  z  9  90.
B. x  5  y  3  z 9  14. 2 2 2 2 2 2
C. x  5  y  3  z  9  86.
D. x  5  y  3  z 9  90.
Câu 39. Phương trình mặt cầu có tâm I  6; 3; 2  
1 và tiếp xúc trục Oz là: 2 2 2 2 2 2
A. x  6  y  3  z  2  
1  9. B. x  6  y  3  z  2   1  9. 2 2 2 2 2 2
C. x  6  y  3  z  2  
1  3. D. x  6  y  3  z  2   1  3.
Câu 40. Phương trình mặt cầu có tâm I 4; 6;  
1 và cắt trục Ox tại hai điểm A, B sao cho tam giác IAB vuông là: 2 2 2 2 2 2
A. x  4  y  6  z   1  34.
B. x  4  y  6  z   1  26. 2 2 2 2 2 2
C. x  4  y  6  z   1  74.
D. x  4  y  6  z   1  104.
Câu 41. Phương trình mặt cầu có tâm I  3;  3;0 và cắt trục Oz tại hai điểm A, B sao cho tam giác IAB đều là: 2 2 2 2 A. x   y  2 3 3  z  8. B. x   y  2 3 3  z  9. 2 2 2 2 C. x   y  2 3 3  z  9. D. x   y  2 3 3  z  8. Giáo
viên: PHẠM VĂN LONG( TP.Cần T
hơ )…0913.518.110… CLB Giáo viê n trẻ TP Huế 24
Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ
Luyện thi Đại Học 2017
Câu 42. Phương trình mặt cầu có tâm I 3; 6; 4
  và cắt trục Oz tại hai điểm A, B sao cho diện tích
tam giác IAB bằng 6 5 là: 2 2 2 2 2 2
A. x  3  y  6  z  4  45.
B. x  3  y  6  z  4  49. 2 2 2 2 2 2
C. x  3  y  6  z  4  36.
D.  x  3   y  6   z  4  54.
Câu 43. Mặt cầu S có tâm I 2;1;  
1 và cắt trục Ox tại hai điểm A, B sao cho tam giác IAB vuông.
Điểm nào sau đây thuộc mặt cầu S : A. 2;1;  1 . B. 2;1; 0. C. 2; 0; 0. D. 1; 0; 0.
Câu 44. Gọi S là mặt cầu có tâm I 1; 3
 ;0 và cắt trục Ox tại hai điểm A, B sao cho tam giác IAB
đều. Điểm nào sau đây không thuộc mặt cầu S : A. 3; 3  ; 2  2 . B. 3; 3  ; 2 2 . C. 2; 1  ;  1 . D.  1  ; 3  ; 2 3. x  2 y  1 z  1
Câu 45. Cho các điểm I  1
 ;0;0 và đường thẳng d :  
. Phương trình mặt cầu S 1 2 1
có tâm I và tiếp xúc d là: A. x  2 2 2
1  y  z  10. B. x  2 2 2
1  y  z  5. C. x  2 2 2
1  y  z  10. D. x  2 2 2
1  y  z  5. x  1 y  6 z
Câu 46. Cho điểm I 1;7; 5 và đường thẳng d : 
 . Phương trình mặt cầu có tâm I 2 1  3
và cắt đường thẳng d tại hai điểm A, B sao cho tam giác diện tích tam giác IAB bằng 2 6015 là: 2 2 2 2 2 2 A. x  
1  y  7  z  5  2018. B. x  
1  y  7  z  5  2017. 2 2 2 2 2 2 C. x  
1  y  7  z  5  2016. D. x  
1  y  7  z  5  2019.
Câu 47. Cho các điểm A1; 3; 
1 và B3; 2; 2 . Mặt cầu đi qua hai điểm A, B và tâm thuộc trục Oz có đường kính là: A. 14. 2 14. C. 2 10. D. 2 6. B.
Câu 48. Trong không gian với hệ tọa độ Oxyz, cho các điểm A1; 2;  1 và B0;1;  1 . Mặt cầu đi qua
hai điểm A, B và tâm thuộc trục hoành có đường kính là: A. 2 6. B. 6. C. 2 5. D. 12.
Câu 49. Cho các điểm A2;1;   1 và B1; 0; 
1 . Mặt cầu đi qua hai điểm A, B và tâm thuộc trục Oy có đường kính là: Giáo
viên: PHẠM VĂN LONG( TP.Cần T
hơ )…0913.518.110… CLB Giáo viê n trẻ TP Huế 25
Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ
Luyện thi Đại Học 2017 A. 4 2. 2 6. D. 6. B. 2 2. C. x  1 y  2 z  3
Câu 50. Cho các điểm A0;1; 3 và B2; 2; 
1 và đường thẳng d :   . Mặt cầu đi 1 1  2 
qua hai điểm A, B và tâm thuộc đường thẳng d thì tọa độ tâm là:  6 9 13   3 3   4 2 7   13 17 12  A.  ; ; . B.  ; ; 2. C.  ; ; . D.  ; ; .  5 5 5   2 2   3 3 3   10 10 5  x y  3 z
Câu 51. Cho các điểm A1; 3; 0 và B2;1; 
1 và đường thẳng d : 
 . Mặt cầu S đi qua 2 1 1
hai điểm A, B và tâm thuộc đường thẳng d thì tọa độ tâm của S là: A. 8;7; 4. B. 6; 6; 3. C. 4; 5; 2. D.  4;  1; 2  . x y  2 z  3
Câu 52. Cho các điểm A1;1; 3 và B2; 2; 0 và đường thẳng d :  
. Mặt cầu S đi 1 1  1
qua hai điểm A, B và tâm thuộc đường thẳng d thì tọa độ tâm S là:  5 7 23   1  1 23 7   5 7 25   1 9 19  A.  ; ; . B.  ; ; . C.  ; ; . D.  ; ; .  6 6 6   6 6 6   6 6 6   6 6 6  x  t 
Câu 53. Cho đường thẳng d : y  1
  3t . Phương trình mặt cầu có đường kính là đoạn thẳng z  1 
vuông góc chung của đường thẳng d và trục Ox là: 2 2 1 2 2 1 A. x   2
1  y  z  2  . B. x   2
1  y  z  2  . 2 4 2 2  1   1  1 C. x  2 2 2 1
1  y  z  . D. 2 x   y  z       . 2  3   2  4 x  2t ' x  t  
Câu 54. Cho hai đường thẳng d : y  t và d' : y  3  t ' . Phương trình mặt cầu có đường kính là   z  4  z  0 
đoạn thẳng vuông góc chung của đường thẳng d và d’ là: 2 2 2 A. x  2 2 2
2  y  z  4.
B. x  2  y  
1  z  2  4. 2 2 2 2 2
C. x  2  y  
1  z  2  2.
D. x    y   2 2 1  z  4. x  1 y  2 z  3
Câu 55. Cho các điểm A 2;  4; 
1 và B2; 0; 3 và đường thẳng d :   S là 2 1  2  . Gọi  
mặt cầu đi qua A, B và có tâm thuộc đường thẳng d. Bán kính mặt cầu S bằng: Giáo
viên: PHẠM VĂN LONG( TP.Cần T
hơ )…0913.518.110… CLB Giáo viê n trẻ TP Huế 26
Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ
Luyện thi Đại Học 2017 967 873 1169 1169 A. . B. . C. . D. . 2 4 16 4 x  1 2t 
Câu 56. Cho các điểm A2; 4;   1 và B0; 2; 
1 và đường thẳng d : y  2t . Gọi S là mặt cầu  z  1  t 
đi qua A, B và có tâm thuộc đường thẳng d. Đường kính mặt cầu S bằng: A. 2 19. B. 2 17. C. 19. D. 17.
Câu 57. Mặt cầu tâm I 2; 4; 6 và tiếp xúc với mặt phẳng (Oxy) có phương trình: 2 2 2 2 2 2
A. x  2  y  4  z  6  4.
B. x  2  y  4  z  6  16. 2 2 2 2 2 2
C. x  2  y  4  z  6  36.
D. x  2  y  4  z  6  56.
Câu 58. Mặt cầu tâm I 2; 4; 6 và tiếp xúc với mặt phẳng (Oxz) có phương trình: 2 2 2 2 2 2
A. x  2  y  4  z  6  56.
B. x  2  y  4  z  6  4. 2 2 2 2 2 2
C. x  2  y  4  z  6  36.
D. x  2  y  4  z  6  16.
Câu 59. Phương trình mặt cầu tâm I 2; 4; 6 nào sau đây tiếp xúc với trục Ox: 2 2 2 2 2 2
A. x  2  y  4  z  6  52.
B. x  2  y  4  z  6  40. 2 2 2 2 2 2
C. x  2  y  4  z  6  20.
D. x  2  y  4  z  6  56.
Câu 60. Mặt cầu tâm I 2; 4; 6 tiếp xúc với trục Oz có phương trình: 2 2 2 2 2 2
A. x  2  y  4  z  6  40.
B. x  2  y  4  z  6  20. 2 2 2 2 2 2
C. x  2  y  4  z  6  52.
D. x  2  y  4  z  6  56. 2 2 2
Câu 61. Cho mặt cầu S : x  
1  y  2  z  3  9 . Phương trình mặt cầu nào sau đây
là phương trình của mặt cầu đối xứng với mặt cầu S qua mặt phẳng (Oxy): 2 2 2 2 2 2 A. x  
1  y  2  z  3  9. B. x  
1  y  2  z  3  9. 2 2 2 2 2 2 C. x  
1  y  2  z  3  9. D. x  
1  y  2  z  3  9. 2 2 2
Câu 62. Cho mặt cầu S  : x   1  y  
1  z  2  4 . Phương trình mặt cầu nào sau đây là
phương trình mặt cầu đối xứng với mặt cầu S qua trục Oz: 2 2 2 2 2 2 A. x   1  y  
1  z  2  4. B. x   1  y  
1  z  2  4. Giáo
viên: PHẠM VĂN LONG( TP.Cần T
hơ )…0913.518.110… CLB Giáo viê n trẻ TP Huế 27
Chuyên đề: MẶT CẦU TRONG KHÔNG GIAN OXYZ
Luyện thi Đại Học 2017 2 2 2 2 2 2 C. x   1  y  
1  z  2  4. D. x   1  y  
1  z  2  4. 2 2 2
Câu 63. Đường tròn giao tuyến của S : x  
1  y  2  z  3  16 khi cắt bởi mặt phẳng
(Oxy) có chu vi bằng : A. 14 . B. 7 . C. 7 . D. 2 7 . HẾT
Xin phép quý thầy cô là những ngƣời sở hữu các câu hỏi có trong tài liệu, cho phép
chúng em biên tập và sử dụng để giúp cho các em học sinh th}n yêu có tƣ liệu học tập. Vì mục
đích không kinh doanh nên mong quý thầy cô đồng ý ạ, chúng em xin chân thành cảm ơn!
CLB sử dụng hệ thống sách chất lƣợng của NXBGD VN 2007, 2008 và các tài liệu tham
khảo chất lƣợng từ Page Toán học Bắc Trung Nam.
P/S: Trong quá trình sưu tầm và biên soạn chắc chắn không tránh khỏi sai sót, kính mong quí thầy
cô và các bạn học sinh thân yêu góp ý để các bản update lần sau hoàn thiện hơn! Xin chân thành cảm ơn.
CLB GI[O VIÊN TRẺ TP HUẾ
Phụ trách chung: LÊ B[ BẢO.
Đơn vị công tác: Trƣờng THPT Đặng Huy Trứ, Thừa Thiên Huế.
Email: lebabaodanghuytru2016@gmail.com Facebook: Lê B{ Bảo
Số điện thoại: 0935.785.115 Giáo
viên: PHẠM VĂN LONG( TP.Cần T
hơ )…0913.518.110… CLB Giáo viê n trẻ TP Huế 28

Chuyên đề mặt cầu trong không gian Oxyz – Phạm Văn Long Toán 12

Thông tin :

Tài liệu liên quan:

Bài giảng vectơ và hệ trục tọa độ trong không gian Toán 12 KNTTVCS

Toán ứng dụng thực tế vectơ và hệ trục toạ độ trong không gian

Chuyên đề hình học giải tích không gian – Lưu Huy Thưởng Toán 12

Chuyên đề HH giải tích không gian – Trung tâm LTĐH Vĩnh Viễn Toán 12

Bài tập tọa độ không gian phân theo dạng có lời giải chi tiết – Trần Sĩ Tùng Toán 12