Chuyên đề nguyên hàm – tích phân và ứng dụng dành cho học sinh TB – yếu – Dương Minh Hùng Toán 12

Chuyên đề nguyên hàm – tích phân và ứng dụng dành cho học sinh TB – yếu – Dương Minh Hùng được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

23 12 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 3: Nguyên hàm - Tích phân và ứng dụng

Môn: Toán 12

Thông tin:

94 trang 6 tháng trước

Tác giả:

Profile Mai Nguyệt
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 1
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 2
FB: Duong Hung
Bài ❶: NGUYÊN HÀM
.Phương pháp:
. Định nghĩa: Hàm số được gọi là nguyên hàm của hàm số trên nếu
với mọi x thuộc .
. Tính chất:
.
.
.
. Bảng nguyên hàm:
▪
▪
▪
▪
▪
▪
▪
▪
▪
▪
Phương pháp: Casio.
⬧ Xét hiệu: Nhấn shift
⬧ Calc hay ,…. là mệnh đề đúng.
Dạng ①: Nguyên hàm theo định nghĩa và tính chất cơ bản
CHƯƠNG ③:
Full Chuyên
đề 12 new
2020-2021
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 3
A - Bài tập minh họa:
( )
1
23
fx
x
=
+
1
ln 2 3
2
xC++
( )
1
ln 2 3
2
xC++
ln 2 3xC++
1
ln 2 3
ln2
xC++
Lời giải
Chọn A
( ) ( )
1 1 1
d d d 2 3
2 3 2 2 3
1
ln 2 3
2
f x x x x
xx
xC
= = +
++
= + +
PP nhanh trắc nghiệm
Casio:
Calc: x= 2.5
Lưu ý: Gặp ln thì có trị tuyệt đối, rắt dễ chọn
nhằm đáp án B
( )
32
d4f x x x x C= + +
( )
fx
( )
3
4
3
x
f x x Cx= + +
( )
2
12 2f x x x C= + +
( )
2
12 2f x x x=+
( )
3
4
3
x
f x x=+
Lời giải
Chọn B
Ta có:
( ) ( )
( )
( )
3 2 2
d 4 12 2f x f x x x x C x x
= = + + = +
PP nhanh trắc nghiệm
Thử đạo hàm
Casio
Chú ý dễ chọn nhằm câu B
( )
fx
( )
1
'
21
fx
x
=
−
1
2
x
( )
11f =
( )
5f
ln 2
ln3
ln2 1+
ln3 1+
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 4
Lời giải
Chọn D
Ta có:
( ) ( )
'df x x f x C=+
nên
( )
( )
d 2 1
1 1 1
d ln 2 1
2 1 2 2 1 2
x
f x x x C
xx
−
= = = − +
−−

Mặt khác theo đề ra ta có:
( )
11f =
1
ln 2.1 1 1 1
2
CC − + = =
nên
( )
1
ln 2 1 1
2
f x x= − +
Do vậy
( )
11
5 ln 2.5 1 1 ln9 1 ln3 1
22
f = − + = + = +
PP nhanh trắc nghiệm
. Tư duy Casio
( ) ( ) ( )
( ) ( ) ( ) ( )
5
1
55
11
51
5 1 1
f x dx f f
f f f x dx f x dx
=−

= + = +

. Tổng quát:
( ) ( ) ( )
( ) ( ) ( )
( ) ( ) ( )
;
b
a
b
a
b
a
f x dx f b f a
f b f a f x dx
f a f b f x dx
=−
• = +
• = −
B - Bài tập rèn luyện:
Câu 1: Khẳng định nào sau đây là sai?
Ⓐ. Nếu
( ) ( )
f x dx F x C = +
thì
( ) ( )
.f u du F u C = +
Ⓑ. .
( ) ( )
kf x dx k f x dx =
(
k
là hằng số và
0k
).
Ⓒ. Nếu
( )
Fx
và
( )
Gx
đều là nguyên hàm của hàm số
( )
fx
thì
( ) ( )
.F x G x=
Ⓓ.
( ) ( ) ( ) ( )
1 2 1 2
.f x f x dx f x dx f x dx

+ = +

Câu 2: Hàm số nào sau đây không phải là nguyên hàm của hàm số
( ) ( )
4
3f x x=−
?
Ⓐ.
( )
( )
5
3
.
5
x
F x x
−
=+
Ⓑ.
( )
( )
5
3
5
x
Fx
−
=
.
Ⓒ.
( )
( )
5
3
2020
5
x
Fx
−
=+
. Ⓓ.
( )
( )
5
3
1
5
x
Fx
−
=−
.
Câu 3: Trong các khẳng định sau, khẳng định nào sai?
Ⓐ.
0dx C=
(
C
là hằng số). Ⓑ.
1
lndx x C
x
= +
(
C
là hằng số).
Ⓒ.
1
1
x
x dx C
+
= +
+
(
C
là hằng số). Ⓓ.
dx x C = +
(
C
là hằng số).
Câu 4: Cho hai hàm số
( )
fx
,
( )
gx
là hàm số liên tục. Xét các mệnh đề sau:
(I).
( ) ( )
1
.k f x dx f x dx
k
=
với
k
là hằng số thực khác 0 bất kỳ.
(II).
( ) ( ) ( ) ( )
f x g x dx f x dx g x dx

− = −

.
(III).
( ) ( ) ( ) ( )
..f x g x dx f x dx g x dx

=

.
(IV).
( ) ( )
f x dx f x C
= +
.
Số mệnh đề đúng là
Ⓐ.
1
. Ⓑ.
2
. Ⓒ.
3
. Ⓓ.
4
.
Câu 5: Cho hàm số
( )
fx
xác định trên
K
và
( )
Fx
,
( )
Gx
là nguyên hàm của
( )
fx
trên
K
. Khẳng
định nào dưới đây đúng?
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 5
Ⓐ.
( ) ( )
G x F x=
,
.xK
Ⓑ.
( ) ( )
G x f x=
,
.xK
Ⓒ.
( ) ( )
F x G x C=+
,
.xK
Ⓓ.
( ) ( )
F x f x
=
,
xK
.
Câu 6: Mệnh đề nào sau đây sai?
Ⓐ. Nếu
( )
Fx
là một nguyên hàm của
( )
fx
trên
( )
;ab
và
C
là hằng số thì
( ) ( )
df x x F x C=+
Ⓑ. Mọi hàm số liên tục trên
( )
;ab
đều có nguyên hàm trên
( )
;ab
.
Ⓒ.
( )
Fx
là một nguyên hàm của
( )
fx
trên
( ) ( ) ( ) ( )
/
; , ;a b F x f x x a b =
Ⓓ.
( )
( )
( )
/
df x x f x=
Câu 7: Hàm số
( )
1
cos
fx
x
=
có nguyên hàm trên:
Ⓐ.
( )
0;
Ⓑ.
;
22


−


Ⓒ.
( )
;2

Ⓓ.
;
22


−


Câu 8: Hàm số nào sau đây không phải là nguyên hàm của hàm số
( ) ( )
4
3f x x=−
?
Ⓐ.
( )
( )
5
3
5
x
F x x
−
=+
Ⓑ.
( )
( )
5
3
5
x
Fx
−
=
Ⓒ.
( )
( )
5
3
2017
5
x
Fx
−
=+
Ⓓ.
( )
( )
5
3
1
5
x
Fx
−
=−
Câu 9: Hàm số
( )
3
x
F x e=
là một nguyên hàm của hàm số
Ⓐ.
( )
3
x
f x e=
Ⓑ.
( )
3
2
3.
x
f x x e=
Ⓒ.
( )
3
2
3
x
e
fx
x
=
Ⓓ.
( )
3
31
.
x
f x x e
−
=
Câu 10: Nếu
( )
3
d
3
x
x
f x x e C= + +
thì
( )
fx
bằng
Ⓐ.
( )
4
3
x
x
f x e=+
Ⓑ.
( )
2
3
x
f x x e=+
Ⓒ.
( )
4
12
x
x
f x e=+
Ⓓ.
( )
2 x
f x x e=+
Câu 11: Tìm nguyên hàm của hàm số
( )
3
1
f x x
x
=+
Ⓐ.
( )
2
2
1
3f x dx x C
x
= + +
. Ⓑ.
( )
4
ln
4
x
f x dx x C= + +
.
Ⓒ.
( )
2
2
1
3f x dx x C
x
= − +
. Ⓓ.
( )
4
ln
4
x
f x dx x C= + +
.
Câu 12: Trong các khẳng định sau, khẳng định nào sai?
Ⓐ.
1
cos2 d sin 2
2
x x x C=+
. Ⓑ.
1
d
1
e
e
x
x x C
e
+
=+
+
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 6
Ⓒ.
1
d lnx x C
x
=+
. Ⓓ.
1
d
1
e
e
x
x x C
x
+
=+
+
Câu 13: Họ nguyên hàm của hàm số
( )
2
3 sinf x x x=+
là
Ⓐ.
3
cosx x C++
. Ⓑ.
6 cosx x C++
.
Ⓒ.
3
cosx x C−+
. Ⓓ.
6 cosx x C−+
.
Câu 14: Tất cả nguyên hàm của hàm số
( )
1
23
fx
x
=
+
là
Ⓐ.
1
ln 2 3
2
xC++
. Ⓑ.
( )
1
ln 2 3
2
xC++
.
Ⓒ.
ln 2 3xC++
. Ⓓ.
1
ln 2 3
ln2
xC++
.
Câu 15: Giả sử các biểu thức sau đều có nghĩa công thức nào sau đây sai?
Ⓐ.
2
1
tan
cos
dx x C
x
=+
. Ⓑ.
xx
e dx e C=+
.
Ⓒ.
1
lnxdx C
x
=+
. Ⓓ.
sin cosxdx x C= − +
.
Câu 16: Họ nguyên hàm của hàm số
( )
22x
f x e x=+
là
Ⓐ.
( )
23
23
x
ex
F x C= + +
. Ⓑ.
( )
23x
F x e x C= + +
.
Ⓒ.
( )
2
22
x
F x e x C= + +
. Ⓓ.
( )
3
2
3
x
x
F x e C= + +
.
Câu 17: Nguyên hàm của hàm số
( )
3
32f x x x= + +
là hàm số nào trong các hàm số sau ?
Ⓐ.
( )
2
33F x x x C= + +
. Ⓑ.
( )
4
2
32
3
x
F x x x C= + + +
.
Ⓒ.
( )
42
3
2
42
xx
F x x C= + + +
. Ⓓ.
( )
42
2
42
xx
F x x C= + + +
.
Câu 18: Họ nguyên hàm của hàm số
( ) e (3 e )
xx
fx
−
=+
là
Ⓐ.
1
( ) 3e
e
x
x
F x C= − +
. Ⓑ.
( ) 3e
x
F x x C= − +
.
Ⓒ.
( ) 3e e lne
x x x
F x C= + +
. Ⓓ.
( ) 3e
x
F x x C= + +
.
Câu 19: Họ nguyên hàm của hàm số
( )
e cos
x
f x x=+
là
Ⓐ.
e sin
x
xC−+
. Ⓑ.
1
1
e sin
1
x
xC
x
+
++
+
.
Ⓒ.
1
e sin
x
x x C
−
−+
. Ⓓ.
e sin
x
xC++
.
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 7
Câu 20: Nguyên hàm của hàm số
3
x
f x x
là
Ⓐ.
2
3
2 ln3
x
x
F x C
. Ⓑ.
3
1
ln3
x
F x C
.
Ⓒ.
2
3
2
x
x
F x C
. Ⓓ.
2
3 .ln3
2
x
x
F x C
.
BẢNG ĐÁP ÁN
1.C
2.A
3.C
4.B
5.C
6.D
7.D
8.D
9.A
10.C
11.D
12.D
13.C
14.A
15.C
16.A
17.C
18.D
19.D
20.A
A - Bài tập minh họa:
Câu 1: Cho hàm số
( )
fx
có
( )
1
'
21
fx
x
=
−
với mọi
1
2
x
và
( )
11f =
. Khi đó giá trị của
( )
5f
bằng
Ⓐ.
ln 2
. Ⓑ.
ln3
. Ⓒ.
ln2 1+
. Ⓓ.
ln3 1+
.
Lời giải
Chọn D
Ta có:
( ) ( )
'df x x f x C=+
nên
( )
( )
d 2 1
1 1 1
d ln 2 1
2 1 2 2 1 2
x
f x x x C
xx
−
= = = − +
−−

Mặt khác theo đề ra ta có:
( )
11f =
1
ln 2.1 1 1 1
2
CC − + = =
nên
( )
1
ln 2 1 1
2
f x x= − +
Do vậy
( )
11
5 ln 2.5 1 1 ln9 1 ln3 1
22
f = − + = + = +
.
PP nhanh trắc nghiệm
Casio
( ) ( ) ( )
( ) ( ) ( )
( ) ( ) ( )
;
b
a
b
a
b
a
f x dx F b F a
F b F a f x dx
F a F b f x dx
=−
• = +
• = −
-Phương pháp:
Xác định là một nguyên hàm của hàm số sao cho
Tìm nguyên hàm .
Thế điều kiện tìm hằng số C
Kết luận cho bài toán.
Dạng ②: Tìm nguyên hàm của hàm số thỏa mãn điều kiện cho trước
thức chứa lũy thừa.
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 8
Câu 2: Biết
( )
Fx
là một nguyên hàm của hàm số
( )
22
x
f x x=+
thoả mãn
( )
00F =
. Ta có
( )
Fx
bằng
Ⓐ.
2
21
ln2
x
x
−
+
. Ⓑ.
2
12
ln2
x
x
−
+
. Ⓒ.
( )
1 2 1 ln2
x
+−
. Ⓓ.
2
21
x
x +−
.
Lời giải
Chọn A
Ta có:
( )
2
2
2 2 d
ln2
x
x
x x x C+ = + +
. Do đó .
Theo giả thiết
( )
0
2
21
0 0 0 0
ln2 ln2
F C C= + + = = −
.
Vậy
( )
22
2 1 2 1
ln2 ln2 ln2
xx
F x x x
−
= + − = +
.
PP nhanh trắc nghiệm
Casio: Thử đáp án
Câu 3: Tìm nguyên hàm
Fx
của hàm số
sin 2f x x
thỏa mãn
1
2
F
.
Ⓐ.
cos( 2 ) 1
()
22
x
Fx
. Ⓑ.
cos( 2 ) 1
()
22
x
Fx
.
Ⓒ.
cos( 2 )
( ) 1
2
x
Fx
. Ⓓ.
cos( 2 ) 1
()
22
x
Fx
.
Lời giải
Chọn B
cos 2
sin 2 d C
2
x
F x x x
1
11
22
FC
1
2
C
Vậy
cos( 2 ) 1
()
22
x
Fx
PP nhanh trắc nghiệm
Casio: Thử đáp án
B - Bài tập rèn luyện:
Câu 1. Tìm một nguyên hàm
()Fx
của hàm số
3
( ) 4 4 5f x x x= − +
thỏa mãn
(1) 3F =
Ⓐ.
42
( ) 2 5 1F x x x x= − + −
. Ⓑ.
42
( ) 4 5 1F x x x x= − + +
.
Ⓒ.
42
( ) 2 5 3F x x x x= − + +
. Ⓓ.
42
1
( ) 2 5
2
F x x x x= − − +
.
Câu 2. Hàm số
( )
42
5 4 6f x x x= − + −
có một nguyên hàm
( )
Fx
thỏa
( )
31F =
. Tính
( )
3F −
.
Ⓐ.
( )
3 226F −=
. Ⓑ.
( )
3 225F − = −
. Ⓒ.
( )
3 451F −=
. Ⓓ.
( )
3 225F −=
.
Câu 3. Biết
( )
Fx
là một nguyên hàm của hàm số
( )
sin2f x x=
và
1
4
F

=


. Tính
6
PF

=


.
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 9
Ⓐ.
5
4
P =
. Ⓑ.
0P =
. Ⓒ.
1
2
P =
. Ⓓ.
3
4
P =
.
Câu 4. Tìm một nguyên hàm
( )
Fx
của hàm số
( )
2 sin 2cosf x x x x= + +
thỏa mãn
( )
01F =
.
Ⓐ.
( )
2
cos 2sin 2F x x x x= + + −
. Ⓑ.
( )
2
cos 2sinF x x x x= − +
.
Ⓒ.
( )
2 cos 2sinF x x x= + +
. Ⓓ.
( )
2
cos 2sin 2F x x x x= − + +
.
Câu 5. Tìm một nguyên hàm
( )
Fx
của hàm số
( )
2
1
sin
cos
f x x
x
=+
thỏa mãn
2
42
F

=


.
Ⓐ.
( )
cos tanF x x x C= − + +
. Ⓑ.
( )
cos tan 2 1F x x x= − + − +
.
Ⓒ.
( )
cos tan 2 1F x x x= + + −
. Ⓓ.
( )
cos tan 2 1F x x x= − + + −
.
Câu 6. Biết
()Fx
là một nguyên hàm của hàm số
2
( ) e
x
fx=
thỏa
3
(0)
2
F =
Giá trị của
1
2
F



bằng
Ⓐ.
1
2
2
e +
. Ⓑ.
1
1
2
e +
. Ⓒ.
21e+
. Ⓓ.
11
22
e +
Câu 7. Kí hiệu
( )
Fx
là một nguyên hàm của hàm số
( )
( )
2
2
1f x x=+
và
( )
28
1
15
F =
Khẳng định
nào sau đây là đúng?
Ⓐ.
( )
53
2
.
53
xx
F x x= + +
Ⓑ.
( )
53
2
.
53
xx
F x x C= + + +
Ⓒ.
( )
( )
2
4 1 .F x x x=+
Ⓓ.
( )
53
2
1.
53
xx
F x x= + + +
Câu 8. Biết
( )
Fx
là một nguyên hàm của hàm số
( )
1
1
fx
x
=
−
và
( )
2 1.F =
Tính
( )
3.F
Ⓐ.
( )
1
3
2
F =
Ⓑ.
( )
7
3
4
F =
Ⓒ.
( )
3 ln2 1.F =−
Ⓓ.
( )
3 ln2 1.F =+
Câu 9. Tìm nguyên hàm
( )
Fx
của hàm số
( )
2
21
fx
x
=
−
thỏa mãn
( )
57F =
.
Ⓐ.
( )
2 2 1F x x=−
. Ⓑ.
( )
2 2 1 1F x x= − +
.
Ⓒ.
( )
2 1 4F x x= − +
. Ⓓ.
( )
2 1 10F x x= − −
.
Câu 10. Gọi
( )
Fx
là một nguyên hàm của hàm số
( ) ( )
2
23f x x=−
thỏa
( )
1
0
3
F =
. Tính giá trị
của biểu thức
( ) ( )
2
log 3 1 2 2 .T F F=−


Ⓐ.
2T =
. Ⓑ.
4T =
. Ⓒ.
10T =
. Ⓓ.
4T =−
.
BẢNG ĐÁP ÁN
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 10
1.A
2.C
3.D
4.D
5.D
6.B
7.A
8.D
9.B
10.A
A - Bài tập minh họa:
Câu 1: Tìm họ nguyên hàm
2
cos sinx x dx
ta được kết quả là
Ⓐ.
2
cos xC−+
. Ⓑ.
3
1
cos
3
xC+
. Ⓒ.
3
1
cos
3
xC−+
. Ⓓ.
3
1
sin
3
xC+
.
Lời giải
Chọn C
( )
2 2 3
1
cos sin cos cos cos
3
x x dx x d x x C= − = − +

.
PP nhanh trắc nghiệm
Casio: xét hiệu
Câu 2: Nguyên hàm
2
11
cos dx
x
x
bằng
Ⓐ.
1
sin C
x
−+
. Ⓑ.
1
sin C
x
+
. Ⓒ.
1
2sin C
x
−+
. Ⓓ.
1
2sin C
x
+
.
Lời giải
Chọn A
Ta có
2
1 1 1 1 1
cos d cos d sinxC
x x x x
x

= − = − +



.
PP nhanh trắc nghiệm
Casio: xét hiệu
Câu 3: Tính nguyên hàm
1
d
ln 1
Ix
xx
=
+
.
Ⓐ.
3
2
(ln 1)
3
I x C= + +
. Ⓑ.
ln 1I x C= + +
.
Ⓒ.
2
1
(ln 1)
2
I x C= + +
. Ⓓ.
2 ln 1I x C= + +
.
-Định lí: Cho hàm số có đạo hàm và liên tục trên trên và hàm số
liên tục sao cho xác định trên . Khi đó nếu hàm số là một nguyên hàm của
, tức là:
-Phương pháp:
Từ đó ta có hai cách đổi biến số trong việc tính nguyên hàm như sau:
Đặt biến số:
Suy ra: rồi đưa về việc tính nguyên hàm
đơn giản hơn.
Dạng ③: Phương pháp đổi biến số.
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 11
Lời giải
Chọn D
1
2
1
d (ln 1) d(ln 1) 2 ln 1 .
ln 1
x x x x C
xx
−
= + + = + +
+

PP nhanh trắc nghiệm
Casio: xét hiệu
Câu 4: Tìm nguyên hàm của hàm số
sin
()
1 3cos
x
fx
x
=
+
.
Ⓐ.
1
( )d ln 1 3cos
3
f x x x C= + +
. Ⓑ.
( )d ln 1 3cosf x x x C= + +
.
Ⓒ.
( )d 3ln 1 3cosf x x x C= + +
. Ⓓ.
1
( )d ln 1 3cos
3
f x x x C
−
= + +
.
Lời giải
Chọn D
Ta có:
( )
sin 1 1 1
d d 1 3cos ln 1 3cos
1 3cos 3 1 3cos 3
x
x x x C
xx
= − + = − + +
++

PP nhanh trắc nghiệm
Casio: xét hiệu
B - Bài tập rèn luyện:
Câu 1: Biết
( ) ( )
.f u du F u C = +
Mệnh đề nào sau đây đúng?
Ⓐ.
( ) ( )
2 1 2 2 1 .f x dx F x C − = − +
Ⓑ.
( ) ( )
2 1 2 1 .f x dx F x C − = − +
Ⓒ.
( ) ( )
2 1 2 1 .f x dx F x C − = − +
Ⓓ.
( ) ( )
1
2 1 2 1 .
2
f x dx F x C − = − +
Câu 2: Nguyên hàm của hàm số
( )
( )
9
2
1f x x x=+
là
Ⓐ.
( )
10
2
1.xC++
Ⓑ.
( )
10
2
21xC++
.
Ⓒ.
( )
10
2
1
1.
20
xC− + +
Ⓓ.
( )
10
2
1
1.
20
xC++
Câu 3: Nguyên hàm của hàm số
( )
21f x x=−
là
Ⓐ.
( )
1
2 1 .
3
f x dx x C = − − +
Ⓑ.
( )
1
2 1 .
2
f x dx x C = − +
Ⓒ .
( ) ( )
1
2 1 2 1 .
3
f x dx x x C = − − +
Ⓓ.
( ) ( )
2
2 1 2 1 .
3
f x dx x x C = − − +
Câu 4: Nguyên hàm của hàm số
( )
2
x
f x xe=
là
Ⓐ.
2
1
2
x
eC+
Ⓑ.
2
.
x
eC+
Ⓒ.
22
2 .2
xx
e C e C++
Ⓓ.
( )
2
2
2 1 .
x
x e C++
Câu 5: Biết rằng hàm số
( )
Fx
là một nguyên hàm của hàm số
( )
ln x
fx
x
=
và thỏa mãn
( )
2
4.Fe =
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 12
Mệnh đề nào sau đây là đúng?
Ⓐ.
( )
2
ln
3.
2
x
Fx=−
Ⓑ.
( )
2
ln
3.
2
x
Fx=+
Ⓒ.
( )
2
ln
2
2
x
Fx=−
Ⓓ
( )
2
ln
2
2
x
Fx=+
Câu 6: Tìm hàm số
( )
Fx
biết
( )
3
4
d
1
x
F x x
x
=
+
và
( )
01F =
.
Ⓐ.
( )
( )
4
ln 1 1F x x= + +
. Ⓑ.
( )
( )
4
13
ln 1
44
F x x= + +
.
Ⓒ.
( )
( )
4
1
ln 1 1
4
F x x= + +
. Ⓓ.
( )
( )
4
4ln 1 1F x x= + +
.
Câu 7: Họ nguyên hàm của hàm số
sin
()
cos 3
x
fx
x
=
−
là
Ⓐ.
ln cos 3xC− − +
. Ⓑ.
2ln cos 3xC−+
.
Ⓒ.
ln cos 3
2
x
C
−
−+
. Ⓓ.
4ln cos 3xC−+
.
Câu 8: Họ nguyên hàm của hàm số
( )
2
sin
sin 2 .e
x
f x x=
là
Ⓐ.
2
2 sin 1
sin .e
x
xC
−
+
. Ⓑ.
2
sin 1
2
e
sin 1
x
C
x
+
+
+
.
Ⓒ.
2
sin
e
x
C+
. Ⓓ.
2
sin 1
2
e
sin 1
x
C
x
−
+
−
.
Câu 9: Xét nguyên hàm
2
1I x dx=−
với phép đặt
sinxt=
. Khi đó
Ⓐ.
2 cos cosI t tdt=
. Ⓑ.
2
2 sin cosI t tdt=
.
Ⓒ.
cos cosI t tdt=
. Ⓓ.
4 sin cosI t tdt=
.
Câu 10: Xét nguyên hàm
2
4I x dx=−
với phép đặt
2sinxt=
với
0;
2
t



. Khi đó
Ⓐ.
( )
2 1 cos2I t dt=+
Ⓑ.
( )
2 1 cos3I t dt=+
.
Ⓒ.
( )
2 4 cos2I t dt=+
Ⓓ.
( )
2 1 2cos2I t dt=+
BẢNG ĐÁP ÁN
1.D
2.D
3.D
4.A
5.D
6.C
7.A
8.C
9.C
10.A
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 13
A - Bài tập minh họa:
( )
cos2f x x x=
sin2 cos2
24
x x x
C++
cos2
sin 2
2
x
x x C−+
cos2
sin 2
2
x
x x C++
sin2 cos2
24
x x x
C−+
Lời giải
Chọn A
cos2 dI x x x=
.
PP nhanh trắc nghiệm
Casio
-Phương pháp:
Cho hai hàm số 𝑢 và 𝑣 liên tục trên đoạn
ሾ
𝑎; 𝑏
ሿ
và có đạo hàm liên tục trên đoạn
ሾ
𝑎; 𝑏
ሿ
.
Khi đó:∫ 𝑢𝑑𝑣 = 𝑢𝑣 − ∫ 𝑣𝑑𝑢.
ሺ
∗
ሻ
Để tính nguyên hàm ∫ 𝑓
ሺ
𝑥
ሻ
𝑑𝑥 bằng từng phần ta làm như sau:
Bước 1. Chọn 𝑢, 𝑣 sao cho 𝑓
ሺ
𝑥
ሻ
𝑑𝑥 = 𝑢𝑑𝑣 (chú ý 𝑑𝑣 = 𝑣′
ሺ
𝑥
ሻ
𝑑𝑥).
Sau đó tính 𝑣 = ∫ 𝑑𝑣 và 𝑑𝑢 = 𝑢′. 𝑑𝑥.
Bước 2. Thay vào công thức
ሺ
∗
ሻ
và tính ∫ 𝑣𝑑𝑢.
①.Dạng 1. , trong đó là đa thức
⬧.Đặt: .
②. Dạng 2. , trong đó là đa thứ
⬧.Đặt: .
③. Dạng 3. , trong đó là đa thức
⬧.Đặt: .
. Casio: Xét hiệu , calc x= {-5,….,5} một cách thích hợp
Sẽ thu kết quả bảng 0 hoặc xấp xỉ 0 là đáp án đúng.
Dạng ④: Phương pháp từng phần
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 14
Đặt
dd
1
d cos2 d
sin2
2
ux
ux
v x x
vx
=
=

=
=
.
Khi đó
1 1 1 1
sin2 sin2 d sin 2 cos2
2 2 2 4
I x x x x x x x C= − = + +
Calc x=3.5
Chọn A
( )
ln2f x x x=
2
1
ln2
22
x
xC

−+


2
2
ln2
2
x
x x C−+
( )
2
ln 2 1
2
x
xC−+
2
2
ln2
2
x
x x C−+
Lời giải
Chọn A
Đặt
2
1
d
ln2
dd
2
u
ux
x
v x x
x
v
=
=
→

=
=
.
( ) ( )
22
2 2 2
1
d .ln2 . d
22
1
ln2 ln2
2 4 2 2
xx
F x f x x x x
x
x x x
x C x C
= = −

= − + = − +



.
PP nhanh trắc nghiệm
Casio
Calc x=1
Chon A
( )
2
.e
x
f x x=
e
2
11
22
x
F x x C
e
2
22
x
F x x C
e
2
1
2
2
x
F x x C
e
2
1
2
2
x
F x x C
Lời giải
Chọn A
Ta có:
( )
2
.e
x
F x x dx=
.
Đặt
( )
2
2
2 2 2
d
1
e
2
1 1 1 1
e e d e
2 2 2 2
x
x
x x x
du x
ux
v
dv e dx
F x x x x C
=
=

=
=

= − = − +


PP nhanh trắc nghiệm
Casio
Calc: x=2
B - Bài tập rèn luyện:
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 15
Câu 1: Biết rằng hàm số
( )
Fx
là một nguyên hàm của hàm số
( )
lnf x x=
và thỏa mãn
( )
1 3.F =
Giá trị của
( )
2
Fe
bằng
Ⓐ.
4.
Ⓑ.
2
4.e−+
Ⓒ.
2
4e +
. Ⓓ.
2
3 4.e +
Câu 2: Nguyên hàm của hàm
( ) ( )
4 1 lnf x x x=+
là
Ⓐ.
22
2 ln 2 .x x x+
Ⓑ.
22
2 ln 3x x x+
.
Ⓒ.
22
2 lnx x x C++
Ⓓ.
22
2 ln 3 .x x x C++
Câu 3: Biết rằng hàm số
( )
Fx
là một nguyên hàm của hàm số
( ) ( )
1
x
f x x e
−
=−
và thỏa mãn
( )
0 2020.F =
Khẳng định nào sau đây đúng?
Ⓐ.
( )
2019.
x
F x e
−
=+
Ⓑ.
( )
2020
x
F x xe
−
=+
.
Ⓒ.
( )
2020
x
F x xe
−
= − +
. Ⓓ.
( )
2020
x
F x xe= − +
.
Câu 4: Biết rằng hàm số
( )
Fx
là một nguyên hàm của hàm số
( )
2
cos
2
x
f x x=
và thỏa mãn
( )
1
0
2
F =
Giá trị của
( )
F
bằng
Ⓐ.
2
1
22
+
Ⓑ.
2
1
42
−
.
Ⓒ.
2
1
42
+
. Ⓓ.
2
1.
4
+
Câu 5: Nguyên hàm của hàm số
( )
sin
x
f x e x=
là
Ⓐ.
sin sin
xx
e xdx e x C = +
. Ⓑ.
( )
1
sin sin cos
2
x x x
e xdx e x e x C = + +
Ⓒ.
sin cos .
xx
e xdx e x C = +
Ⓓ.
( )
1
sin sin cos
2
x x x
e xdx e x e x C = − +
.
Câu 6: Hàm số
( ) ( 1)sinf x x x=+
có các nguyên hàm là:
Ⓐ.
( ) ( 1)cos sinF x x x x C
. Ⓑ.
( ) ( 1)cos sinF x x x x C
Ⓒ.
( ) ( 1)cos s inF x x x x C
Ⓓ.
( ) ( 1)cos sinF x x x x C= + − +
Câu 7: Tính
cosx xdx
, ta được kết quả là:
Ⓐ.
( )
sin cosF x x x x C= + +
Ⓑ.
( )
sin cosF x x x x C= − +
.
Ⓒ.
( )
sin cosF x x x x C= − + +
. Ⓓ.
( )
sin cosF x x x x C= − − +
Câu 8: Một nguyên hàm của hàm số
( )
2
( ) 2
x
f x x x e=+
Ⓐ.
( ) (2 2).
x
F x x e=+
Ⓑ.
2
()
x
F x x e=
.
Ⓒ.
2
( ) ( ).
x
F x x x e
. Ⓓ.
2
( ) ( 2 ).
x
F x x x e=−
.
Câu 9: Kết quả nào sai trong các kết quả sau ?
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 16
Ⓐ.
3
33
1
39
x
xx
xe
xe dx e C= − +
Ⓑ.
= − +
x x x
xe dx xe e C
.
Ⓒ.
2
.
2
xx
x
xe dx e C
. Ⓓ.
1
x x x
xx
dx C
e e e
−
= − +
.
Câu 10: Cho
0
( ) ln
x
f x tdt=
. Đạo hàm
'( )fx
là hàm số nào dưới đây?
Ⓐ.
1
x
. Ⓑ.
ln x
. Ⓒ.
2
ln x
. Ⓓ.
1
ln
2
x
.
Câu 11: Nguyên hàm của hàm số
( )
sinf x x x=
là
Ⓐ.
– cos sinx x x C++
. Ⓑ.
sin cosx x x C++
.
Ⓒ.
cos sinx x x C++
. Ⓓ.
cos sinx x x C−+
.
Câu 12: Kết quả của
d
x
I xe x=
là
Ⓐ.
2
2
xx
x
I e e C= + +
. Ⓑ.
xx
I e xe C= + +
.
Ⓒ.
2
2
x
x
I e C=+
. Ⓓ.
xx
I xe e C= − +
.
Câu 13: Tính
( ) sin 2F x x xdx=
. Chọn kết quả đúng?
Ⓐ.
1
( ) (2 cos2 sin2 )
4
F x x x x C= + +
. Ⓑ.
1
( ) (2 cos2 sin2 )
4
F x x x x C= − + +
.
Ⓒ.
1
( ) (2 cos2 sin 2 )
4
F x x x x C= − − +
. Ⓓ.
1
( ) (2 cos2 sin2 )
4
F x x x x C= − +
.
Câu 14: Nguyên hàm của hàm số
( ) ( )
1e
x
f x x=+
là
Ⓐ.
e
x
xC+
. Ⓑ.
( )
2e
x
xC++
. Ⓒ.
( )
1e
x
xC−+
. Ⓓ.
2e
x
xC+
.
Câu 15: Họ các nguyên hàm của
( )
lnf x x x=
là
Ⓐ.
2
2
1
ln .
24
x
x x C++
Ⓑ.
22
1
ln .
2
x x x C−+
Ⓒ.
2
2
1
ln .
24
x
x x C−+
Ⓓ.
1
ln .
2
x x x C++
Câu 16: Tìm nguyên hàm của hàm số
( ) ( )
ln 2f x x x=+
.
Ⓐ.
( ) ( )
22
4
d ln 2
22
x x x
f x x x C
+
= + − +
.
Ⓑ.
( ) ( )
22
44
d ln 2
22
x x x
f x x x C
−+
= + − +
.
Ⓒ.
( ) ( )
22
4
d ln 2
24
x x x
f x x x C
+
= + − +
.
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 17
Ⓓ.
( ) ( )
22
44
d ln 2
24
x x x
f x x x C
−−
= + − +
.
Câu 17: Cho hàm số
sin 2 dy x x x=
. Chọn mệnh đề đúng trong các mệnh đề sau
Ⓐ.
3
6 12
y


=


. Ⓑ.
3
66
y


=


.
Ⓒ.
6 12
y


=


. Ⓓ.
6 24
y


=


.
Câu 18: Gọi
( )
Fx
là một nguyên hàm của hàm số
( )
e
x
f x x
−
=
. Tính
( )
Fx
biết
( )
01F =
Ⓐ.
( ) ( )
1 e 2
x
F x x
−
= + +
. Ⓑ.
( ) ( )
1 e 1
x
F x x
−
= − + +
.
Ⓒ.
( ) ( )
1 e 2
x
F x x
−
= − + +
. Ⓓ.
( ) ( )
1 e 1
x
F x x
−
= + +
.
Câu 19: Tìm họ nguyên hàm
( )
Fx
của hàm số
( )
2
.e
x
f x x=
.
Ⓐ.
( ) ( )
2
2e 2
x
F x x C= − +
. Ⓑ.
( ) ( )
2
1
e2
2
x
F x x C= − +
.
Ⓒ.
( )
2
1
2e
2
x
F x x C

= − +


. Ⓓ.
( )
2
11
e
22
x
F x x C

= − +


.
Câu 20: Cho
()Fx
là một nguyên hàm của hàm số
( ) ( )
5 1 e
x
f x x=+
và
( )
03F =
. Tính
( )
1F
.
Ⓐ.
( )
1 e 2F =+
. Ⓑ.
( )
1 11e 3F =−
. Ⓒ.
( )
1 e 3F =+
. Ⓓ.
( )
1 e 7F =+
.
BẢNG ĐÁP ÁN
1.C
2.C
3.C
4.B
5.D
6.B
7.A
8.B
9.C
10.B
11.A
12.D
13.C
14.A
15.C
16.D
17.C
18.C
19.D
20.D
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 18
FB: Duong Hung
A - Bài tập minh họa:
Câu 1: Tính tích phân
d
b
a
x
.
Ⓐ.
ab−
. Ⓑ.
a.b
. Ⓒ.
ba−
. Ⓓ.
ab+
.
Lời giải
Chọn C
Ta có:
d
b
a
b
x x b a
a
= = −
PP nhanh trắc nghiệm
Câu 2: Giá trị của
0
1
1
ed
x
x
+
−
bằng
Ⓐ.
1e−
. Ⓑ.
e1−
. Ⓒ.
e−
. Ⓓ.
e
.
Lời giải
Chọn B
Ta có
0
1
1
ed
x
x
+
−
=
0
1
1
e
x+
−
=
e1−
.
PP nhanh trắc nghiệm
Câu 3: Tích phân
1
2020
0
dI x x=
bằng
Ⓐ.
1
2021
. Ⓑ.
0
. Ⓒ.
1
2019
. Ⓓ.
1
.
Lời giải
PP nhanh trắc nghiệm
Bài 2: TÍCH PHÂN DÙNG ĐỊNH NGHĨA, TÍNH CHẤT
.Phương pháp:
Nhận xét:
Tích phân của hàm số từ a đến b có thể kí hiệu bởi hay Tích phân
đó chỉ phụ thuộc vào f và các cận a, b mà không phụ thuộc vào cách ghi biến số.
. Chú ý: Học thuộc bảng nguyên hàm của các hàm số cơ bản thường gặp.
Dạng ①: Tích phân dùng định nghĩa
CHƯƠNG ③:
Full Chuyên
đề 12 new
2020-2021
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 19
Chọn A
Ta có
1
1
2021
2020
0
0
1
d
2021 2021
x
I x x= = =
.
B - Bài tập rèn luyện:
Câu 1: Biết
( ) ( )
f x dx F x C=+
.Trong các khẳng định sau, khẳng định nào đúng?
Ⓐ.
( ) ( ) ( )
b
a
f x dx F b F a=−
. Ⓑ.
( ) ( ) ( )
.
b
a
f x dx F b F a=
.
Ⓒ.
( ) ( ) ( )
b
a
f x dx F a F b=−
. Ⓓ.
( ) ( ) ( )
b
a
f x dx F b F a=+
.
Câu 2: Trong các phép tính sau đây, phép tính nào sai?
Ⓐ.
( )
2
2
2
1
1
1d
2
x
x x x

+ = +


. Ⓑ.
( )
2
2
cos d sinx x x
=
.
Ⓒ.
( )
2
2
3
3
1
d lnxx
x
−
−
−
−
=
. Ⓓ.
( )
3
3
1
1
d
xx
e x e=
.
Câu 3: Cho hàm số
( )
fx
có đạo hàm trên đoạn
( )
1;3 , 3 5f =
và
( )
3
1
d6f x x
=
. Khi đó
( )
1f
bằng
Ⓐ.
1−
. Ⓑ. 11. Ⓒ.1. Ⓓ. 10.
Câu 4:
( )
Fx
là nguyên hàm của hàm số
( ) ( )
2
23
0f x x
xx
= +
, biết rằng
( )
11F =
. Tính
( )
3F
.
Ⓐ.
( )
3 3ln3 3F =+
. Ⓑ.
( )
3 2ln3 2F =+
. Ⓒ.
( )
3 2ln3 3F =+
. Ⓓ.
( )
33F =
.
Câu 5: Cho hàm số
( )
fx
có đạo hàm trên ,
( )
12f − = −
và
( )
32f =
. Tính
( )
3
1
'.I f x dx
−
=
Ⓐ.
4.I =
Ⓑ.
3.I =
Ⓒ.
0.I =
Ⓓ.
4.I =−
Câu 6: Cho các số thực
a
,
b
( )
ab
. Nếu hàm số
( )
=y f x
có đạo hàm là hàm liên tục trên thì
Ⓐ.
( ) ( ) ( )
d

=−
b
a
f x x f a f b
. Ⓑ.
( ) ( ) ( )
d
=−
b
a
f x x f b f a
.
Ⓒ.
( ) ( ) ( )
d
=−
b
a
f x x f a f b
. Ⓓ.
( ) ( ) ( )
d

=−
b
a
f x x f b f a
.
Câu 7: PT 1.2 Cho
( )
Fx
là một nguyên hàm của hàm số
( )
fx
. Khi đó hiệu số
( ) ( )
12−FF
bằng
Ⓐ.
( )
2
1
d−


f x x
. Ⓑ.
( )
1
2
d
F x x
. Ⓒ.
( )
2
1
d−


F x x
. Ⓓ.
( )
2
1
d
f x x
.
Câu 8: Cho hàm số
( )
fx
có đạo hàm
( )
fx
liên tục trên
;ab
,
( )
5fb=
và
( )
d1
b
a
f x x
=
, khi đó
( )
fa
bằng
Ⓐ.
6−
. Ⓑ.
6
. Ⓒ.
4−
. Ⓓ.
4
.
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 20
Câu 9: Cho hàm số
( )
fx
có đạo hàm liên tục trên
0;1
và thoản mãn
( )
1
0
d3f x x
=−
. Giá trị của
biểu thức
( ) ( )
01ff−
Ⓐ.
2−
. Ⓑ.
1
. Ⓒ.
3
. Ⓓ.
3−
.
Câu 10: Cho hàm số
3
=yx
có một nguyên hàm là
( )
Fx
. Khẳng định nào sau đây là đúng?
Ⓐ.
( ) ( )
2 0 16−=FF
. Ⓑ.
( ) ( )
2 0 1−=FF
. Ⓒ.
( ) ( )
2 0 8−=FF
. Ⓓ.
( ) ( )
2 0 4−=FF
.
Câu 11: Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
1;3
thỏa mãn
( )
12f =
và
( )
3 9.=f
Tính
( )
3
1
dI f x x
=
.
Ⓐ.
11I =
. Ⓑ.
2I =
. Ⓒ.
7I =
. Ⓓ.
18I =
.
Câu 12: Tính tích phân
3
0
d
2
x
I
x
=
+
.
Ⓐ.
21
100
I =−
. Ⓑ.
5
ln
2
I =
. Ⓒ.
5
log
2
I =
. Ⓓ.
4581
5000
I =
.
Câu 13: Tính tích phân
2
1
1
d
21
Ix
x
=
−
.
Ⓐ.
ln3 1I =−
. Ⓑ.
ln 3I =
. Ⓒ.
ln2 1I =+
. Ⓓ.
ln2 1I =−
.
Câu 14: Cho các số thực
( )
,a b a b
. Nếu hàm số
( )
y F x=
là một nguyên hàm của hàm số
( )
y f x=
thì
Ⓐ.
( ) ( ) ( )
d
b
a
f x x F a F b=−
. Ⓑ.
( ) ( ) ( )
d
b
a
F x x f a f b=−
.
Ⓒ.
( ) ( ) ( )
d
b
a
F x x f a f b=−
. Ⓓ.
( ) ( ) ( )
d
b
a
f x x F b F a=−
.
Câu 15: Cho hàm số
( )
fx
liên tục trên tập , một nguyên hàm của
( )
fx
là
( )
Fx
thoả mãn
( )
13F =−
và
( )
01F =
. Giá trị
( )
1
0
df x x
bằng
Ⓐ.
4−
. Ⓑ.
3−
. Ⓒ.
2−
. Ⓓ. 4.
Câu 16: Cho hàm số
( )
fx
thỏa mãn
( )
01f =
,
( )
fx
liên tục trên và
( )
3
0
d9f x x
=
. Giá trị của
( )
3f
là
Ⓐ.
6
. Ⓑ.
3
. Ⓒ.
10
. Ⓓ.
9
.
Câu 17: Cho hàm số
( )
fx
thỏa mãn
( )
01f =
,
( )
fx
liên tục trên và
( )
3
0
d9f x x
=
. Giá trị của
( )
3f
là
Ⓐ.
6
. Ⓑ.
3
. Ⓒ.
10
. Ⓓ.
9
.
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 21
Câu 18: Tích phân
( )
1
2
0
3dx x x+
bằng
Ⓐ. 2. Ⓑ. 1. Ⓒ.
4
7
. Ⓓ.
7
4
.
Câu 19:
2
1
dx
32x −
bằng
Ⓐ.
2ln2
. Ⓑ.
2
ln 2
3
. Ⓒ.
ln 2
. Ⓓ.
1
ln2
3
.
Câu 20: Cho hai số thực
, 0;
2
ab



thỏa mãn
2
1
10
cos
b
a
dx
x
=
. Giá trị của
tan tanab−
bằng
Ⓐ.
10
. Ⓑ.
1
10
−
. Ⓒ.
10−
. Ⓓ.
1
10
.
BẢNG ĐÁP ÁN
1.A
2.C
3.A
4.C
5.A
6.B
7.A
8.D
9.C
10.D
11.C
12.B
13
14.D
15.A
16.C
17.C
18.D
19.B
20.C
A - Bài tập minh họa:
Câu 1: Cho biết
( )
2
0
d3f x x =
và
( )
2
0
d2g x x =−
. Tính tích phân
( ) ( )
2
0
2 2 dI x f x g x x

= + −

.
Ⓐ.
11I =
. Ⓑ.
18I =
. Ⓒ.
5I =
. Ⓓ.
3I =
.
Lời giải
Chọn A
Ta có
( ) ( )
2
0
2 2 dI x f x g x x

= + −

( ) ( )
2 2 2
0 0 0
2 d d 2 dx x f x x g x x= + −
( )
4 3 2. 2 11= + − − =
.
PP nhanh trắc nghiệm
.Phương pháp:
Giả sử cho hai hàm số và liên tục trên là ba số bất kỳ thuộc . Khi đó ta có
①
. ②. .
③
. ④. .
⑤
. .
Dạng ②: Tích phân dùng tính chất
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 22
Câu 2: Cho hàm số
( )
fx
liên tục trên và có
( ) ( )
24
02
d 9; d 4f x x f x x==

. Tính
( )
4
0
dI f x x=
?
Ⓐ.
9
4
I =
. Ⓑ.
36I =
. Ⓒ.
13I =
. Ⓓ.
5I =
.
Lời giải
Chọn C
Ta có
( ) ( ) ( )
4 2 4
0 0 2
d d d 9 4 13f x x f x x f x x= + = + =
.
PP nhanh trắc nghiệm
Câu 3: Cho
( )
1
0
d2f x x =−
và
( )
( )
5
1
2 d 6f x x =
khi đó
( )
5
0
df x x
bằng
Ⓐ.
1
. Ⓑ.
2
. Ⓒ.
4
. Ⓓ.
3
.
Lời giải
Chọn A
( )
( )
( )
55
11
2 d 6 d 3f x x f x x= =

( ) ( ) ( )
5 1 5
0 0 1
d d d 2 3 1f x x f x x f x x= + = − + =
PP nhanh trắc nghiệm
B - Bài tập rèn luyện:
Câu 1: Nếu thì bằng
Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. .
Câu 2: Cho là hai hàm số liên tục trên . Chọn mệnh đề sai trong các mệnh đề sau.
Ⓐ. . Ⓑ. .
Ⓒ. . Ⓓ. .
Câu 3: Cho là hai hàm số liên tục trên . Chọn mệnh đề sai trong các mệnh đề sau?
Ⓐ. .
Ⓑ. .
Ⓒ. .
( ) ( )
25
12
3, 1f x dx f x dx= = −

( )
5
1
f x dx
2
2−
3
4
( ) ( )
,f x g x
( ) ( )
dd
bb
aa
f x x f y y=

( ) ( )
( )
( ) ( )
d d d
b b b
a a a
f x g x x f x x g x x− = −
( )
d0
a
a
f x x =
( ) ( )
( )
( ) ( )
. d d . d
b b b
a a a
f x g x x f x x g x x=
( ) ( )
,f x g x
( ) ( )
bb
aa
f x dx f y dy=

( ) ( )
( )
( ) ( )
b b b
a a a
f x g x dx f x dx g x dx− = −
( )
0
a
a
f x dx =
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 23
Ⓓ. .
Câu 4: Cho và , khi đó bằng
Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. .
Câu 5: Cho và , khi đó bằng
Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. .
Câu 6: Cho và , khi đó bằng
Ⓐ. . Ⓑ. Ⓒ. . Ⓓ. .
Câu 7: Cho , . Tính .
Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. .
Câu 8: Cho và , khi đó bằng
Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. .
Câu 9: Cho hàm số liên tục trên thỏa mãn . Giá trị của
bằng
Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. .
Câu 10: Cho hàm số
()fx
liên tục trên tập và thỏa mãn
( )
2
1
d3f x x =
,
( )
2
0
d5f x x =−
. Giá trị của biểu
thức
( )
1
0
df x x
bằng
Ⓐ.
8
. Ⓑ.
11−
. Ⓒ.
8−
. Ⓓ.
2−
.
Câu 11: Cho hàm số
( )
y f x=
liên tục trên . Mệnh đề nào sau đây đúng?
Ⓐ.
( ) ( )
12
00
1
dd
2
f x x f x x=

. Ⓑ.
( ) ( )
11
10
d 2 df x x f x x
−
=

.
Ⓒ.
( )
1
1
d0f x x
−
=
. Ⓓ.
( ) ( )
11
00
d 1 df x x f x x=−

.
Câu 12: Cho hàm số
( )
=y f x
có đạo hàm liên tục trên đoạn
1;4
, biết
( ) ( )
4 3, 1 1==ff
. Tính
( )
4
1
2d
f x x
( ) ( ) ( ) ( )
.
b b b
a a a
f x g x dx f x dx g x dx=


( )
1
0
d2f x x =
( )
1
0
d5g x x =
( ) ( )
1
0
2df x g x x

+

3−
8−
12
1
( ) ( )
1
0
2 d 12f x g x x−=


( )
1
0
d5g x x =
( )
1
0
df x x
2−
12
22
2
( )
1
1
d2f x x
−
=
( )
1
1
d7g x x
−
=−
( ) ( )
1
1
1
d
7
f x g x x
−

−


3−
3
1
( )
d 50
c
a
f x x =
( )
d 20
c
b
f x x =
( )
d
a
b
f x x
30−
0
70
30
( )
1
0
d2f x x =
( )
1
0
d5g x x =
( ) ( )
1
0
2df x g x x−


3−
12
8−
1
( )
fx
( ) ( ) ( )
6 10 6
0 3 3
7, 8, 9f x dx f x dx f x dx= = =
( )
10
0
I f x dx=
5I =
6I =
7I =
8I =
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 24
Ⓐ.
10
. Ⓑ.
8
. Ⓒ.
4
. Ⓓ.
5
.
Câu 13: Cho các hàm số
( ) ( )
,f x g x
liên tục trên có
( ) ( )
3
1
3 2 d 1f x g x x+=


;
( ) ( )
3
1
2 d 3f x g x x− = −


. Tính
( )
1
0
2 1 df x x+
.
Ⓐ.
5
7
−
. Ⓑ.
10
7
−
. Ⓒ.
11
14
. Ⓓ.
5
14
−
.
Câu 14: Cho và là các hàm số liên tục bất kì trên đoạn . Mệnh đề nào sau đây đúng ?
Ⓐ. . Ⓑ. .
Ⓒ. . Ⓓ. .
Câu 15: Biết
( )
5
2
d3f x x =
,
( )
5
2
d 9.g x x =
Tích phân
( ) ( )
5
2
df x g x x+


bằng
Ⓐ.
10
. Ⓑ.
3
. Ⓒ.
6
. Ⓓ.
12
.
Câu 16: Cho
03
10
( ) 3 ( ) 3f x dx f x dx
−
==

. Tính tích phân
3
1
()f x dx
−
?
Ⓐ.
6
. Ⓑ.
4
. Ⓒ.
2
. Ⓓ.
0
.
Câu 17: Cho
1
0
( ) 2f x dx =−
và
1
0
( ) 5g x dx =−
. Khi đó
1
0
( ) 3 ( )f x g x dx+
bằng
Ⓐ.
10−
. Ⓑ.
12
. Ⓒ.
17−
. Ⓓ.
1
.
Câu 18: Cho
02
20
( )d 2, ( )d 2f x x f x x
−
==

. Tích phân
2
2
( )df x x
−
bằng
Ⓐ.
4
. Ⓑ.
3
. Ⓒ.
6
. Ⓓ.
1
.
Câu 19: Cho
( )
0
1
d1f x x
−
=−
và
( )
4
0
d3f x x =
. Khi đó,
( )
4
1
dI f x x
−
=
bằng
Ⓐ.
4I =−
. Ⓑ.
2I =
. Ⓒ.
4I =
. Ⓓ.
2I =−
.
Câu 20: Cho hàm số
()fx
liên tục trên đoạn
0;3
và
2
0
( )d 1f x x =
,
2
3
( )d 4f x x =
. Tính
3
0
( )dI f x x=
.
Ⓐ.
5I =
. Ⓑ.
3I =−
. Ⓒ.
3I =
. Ⓓ.
4I =
.
BẢNG ĐÁP ÁN
1.A
2.D
3.D
4.C
5.C
6.C
7.A
8.C
9.B
10.C
11.D
12.C
13.D
14.B
15.D
16.B
17.C
18.A
19.B
20.B
( )
fx
( )
gx
;ab
( ) ( ) ( ) ( )
d d d
bb
a
b
a a
x f x x gf x g x xx=−−

( ) ( )
( )
( ) ( )
d d d
bb
a
b
a a
x f x x gf x g x xx=−−

( ) ( )
( )
( ) ( )
d d d
bbb
a aa
x f x x g x xf x g x− =−

( ) ( )
( )
( ) ( )
d d d
bb
a
b
a a
x f x x gf x g x xx=−−

Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 25
-Phương pháp:
①. Dạng 1:I . (với a≠0)
Chú ý: I =
②. Dạng 2: ( với mọi ),é
.
• ,thì
• thì
thì I =
• thì
Đặt
③. Dạng 3: .( liên tục trên đoạn )
• Bằng phương pháp đồng nhất hệ số, ta tìm và sao cho:
• Ta có I=
Tích phân =
Tích phân thuộc dạng 2.
Dạng ③: Tích phân sử dụng định nghĩa chứa tham số a, b, c
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 26
A - Bài tập minh họa:
Câu 1: Cho biết
1
0
13
d ln
22
x
x a b
x
−
=+
+
, với
a
,
b
là các số nguyên. Giá trị của biểu thức
2ab−
bằng
Ⓐ.
6
Ⓑ.
3
. Ⓒ.
5−
. Ⓓ.
7
.
Lời giải
Chọn D
Ta có:
11
00
13
d 1 d
22
x
xx
xx
−

=−

++


( )
1
0
3ln 2xx= − +
( ) ( )
1 3ln3 0 3ln2= − − −
3
1 3ln
2
=−
.
Suy ra
1
3
a
b
=
=−
. Vậy
27ab−=
.
PP nhanh trắc nghiệm
Casio:
Bước 1: Tính tích phân rồi lưu lại là A
.
Bước 2: Rút
3
A ln
2
ab=−
.
Bước 3: Table nhập
( )
3
A ln
2
f x x=−
với Start:
9−
,
End: 9, Step: 1 .
Được cặp số
3x =−
,
( )
1fx=
thỏa
mãn. Suy ra
1a =
,
3b =−
.
Câu 2: Cho
( )
1
2
0
d
ln2 ln3
21
x
a b c
x
x
= + +
+
với
,,abc
là các số hữu tỉ. Giá trị của
abc++
bằng
Ⓐ.
1
12
. Ⓑ.
5
12
. Ⓒ.
1
3
−
. Ⓓ.
1
4
.
Lời giải
Chọn A
( )
( )
( ) ( )
( )
1 1 1
2 2 2
0 0 0
2 1 1
1 1 1 1
21
2 4 2 1
2 1 2
d
d
d
1 2 1
x
x
x
x
x
x x x
x

+−
= = − +


+
+ + +

1
1 1 1 1 1 1
ln 2 1 ln3 1 ln3
0
4 2 1 4 3 4 6
x
x
= + + = + − = −
+
.
Vậy
1 1 1
6 4 12
abc+ + = − + =
.
PP nhanh trắc nghiệm
Đặt
11
2 1 ,
22
d dt
t
t x x x
−
= + = =
3
2
1
3
1 1 1 1 1
ln ln3
1
4 4 4 4 6
t
I dt t
tt
−

= = + = −


Vậy:
1
12
abc+ + =
Câu 3: Cho
3
2
2
15
d ln
9 24 16
x
x a b c
xx
−
=+
−+
, với
,,abc
là các số hữu tỷ. Giá trị của
9 11 22a b c++
bằng
Ⓐ.
15
. Ⓑ.
10−
. Ⓒ.
7
. Ⓓ.
9
.
Lời giải
Chọn C
PP nhanh trắc nghiệm
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 27
Ta có
( )
( )
( )
3 3 3
22
2
2 2 2
5 17
34
1 5 1 5
33
d d d
9 24 16
3 4 3 4
x
xx
x x x
xx
xx
− − −
−−
==
−+
−−
( )
( ) ( )
( )
3 3 5 5
22
2 2 2 2
d 3 4 d 3 4
5 d 17 d 5 17
3 3 4 3 9 3 4 9
3 4 3 4
xx
xx
xx
xx
−−
= − − = − −
−−
−−
5
2
5 17 1 5 2 17
ln 3 4 . ln
9 9 3 4 9 11 22
x
x

= − − + = −

−

5 2 17
,,
9 11 22
5 2 17
9 11 22 9. 11. 22. 10
9 11 22
a b c
a b c
= = = −
+ + = + − = −
B - Bài tập rèn luyện:
Câu 1: Tìm số thực
0a
thỏa mãn
( )
3
1
875
6d
4
a
x x x−=
.
Ⓐ.
4a =−
. Ⓑ.
5a =−
. Ⓒ.
6a =−
. Ⓓ.
3a =−
.
Câu 2: Giá trị của tích phân
2
1
d
25
x
x +
là
1
ln
b
ac
,. Tổng
abc++
bằng
Ⓐ. 18. Ⓑ. 14. Ⓒ.16. Ⓓ. 10.
Câu 3: Giả sử
5
1
ln(b 1)
21
dx
a
x
= + +
−
, với
,ab
là các số nguyên không âm. Tính
T a b=+
?
Ⓐ. 9. Ⓑ. 2. Ⓒ.-1. Ⓓ. 1.
Câu 4: Biết
1
2
0
21
d ln3 ln2
1
x
x a b c
x
−
= + +
+
(
,,abc
là các số nguyên). Giá trị
a b c+−
bằng
Ⓐ.
2
. Ⓑ.
4−
. Ⓒ.
3
. Ⓓ.
1−
.
Câu 5: Cho biết
( )
2
0
4 sin dx x a b
− = +
, với
,ab
là các số nguyên. Giá trị của biểu thức
ab+
bằng
Ⓐ.
4−
. Ⓑ.
6
. Ⓒ.
1
. Ⓓ.
1
.
Câu 6: Cho
8
2
0
cos 2 d
b
I x x
ac
= = +
, với
a
,
b
,
c
là các số nguyên dương,
b
c
tối giản. Tính
P a b c= + +
.
Ⓐ.
15P =
. Ⓑ.
23P =
. Ⓒ.
24P =
. Ⓓ.
25P =
.
Câu 7: Cho
( )
1
2
3
0
2
d ln2
1
xx
x a b
x
+
=+
+
với
a
,
b
là các số hữu tỷ. Giá trị của
16ab+
là
Ⓐ.
17
. Ⓑ.
10
. Ⓒ.
8−
. Ⓓ.
5−
.
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 28
Câu 8: Cho
3
2
1
21
ln2 ln3 ln5, ( , , )
32
x
dx a b c a b c
xx
+
= + +
++
. Giá trị của
a b c++
bằng
Ⓐ. -1 Ⓑ. 4 Ⓒ.1 Ⓓ. 7
Câu 9: Với
,ab
là các tham số thực. Giá trị tích phân
( )
2
0
3 2 1 d
b
x ax x−−
bằng
Ⓐ.
32
b b a b−−
. Ⓑ.
32
b b a b++
. Ⓒ.
23
b ba b−−
. Ⓓ.
2
3 2 1b ab−−
.
Câu 10: Cho
1
0
d ln
1
x
I x a b
x
= = −
+
với
, ab
là các số nguyên dương. Giá trị
ab+
bằng
Ⓐ.
3
. Ⓑ.
4
. Ⓒ.
5
. Ⓓ.
6
.
Câu 11: Có bao nhiêu số thực
(
0;2πa
sao cho
( )
1
2
0
11
cos d
24
ax x
a
=+
.
Ⓐ.
2
. Ⓑ.
4
. Ⓒ.
3
. Ⓓ.
1
.
Câu 12: Cho
3
2
1
3
ln2 ln3 ln5
32
x
dx a b c
xx
+
= + +
++
, với a, b, c là các số nguyên. Giá trị của
abc++
bằng
Ⓐ.
0
. Ⓑ.
2
. Ⓒ.
3
. Ⓓ.
1
.
Câu 13: Cho
( )
1
2
0
d ln2 ln3
2
x
x a b c
x
= + +
+
với
, , a b c
là các số hữu tỷ. Giá trị của
6abc++
bằng
Ⓐ.
4
. Ⓑ.
2−
. Ⓒ.
2
. Ⓓ.
1
.
Câu 14: Biết
3
1
2
d ln
x
I x a b c
x
+
= = +
, với
a
,
b
,
c
,
9c
. Tính tổng
S a b c= + +
.
Ⓐ.
7S =
. Ⓑ.
5S =
. Ⓒ.
8S =
. Ⓓ.
6S =
.
Câu 15: Cho
2
2
1
10
d ln
1
xa
xx
x b b

+ = +

+

với
,ab
. Tính
?P a b=+
Ⓐ.
1P =
. Ⓑ.
5P =
. Ⓒ.
7P =
. Ⓓ.
2P =
.
Câu 16: Giả sử
2
2
0
1
d ln5 ln3
43
x
x a b
xx
−
=+
++
;
,a b Q
. Tính
2
2P a b=−
.
Ⓐ.
10P =
. Ⓑ.
8P =
. Ⓒ.
3P =
. Ⓓ.
1P =
.
Câu 17: Cho
( )
1
2
0
d
ln2 ln3
2
xx
a b c
x
= + +
+
với
,,abc
là các số hữu tỷ. Giá trị của
3abc++
bằng:
Ⓐ.
2−
. Ⓑ.
2
. Ⓒ.
1
. Ⓓ.
1−
.
Câu 18: Cho
( )
4
2
3
1 1 1
d ln
24
a
x
x x b c
=−
+
, với
,,abc
là các số hữu tỷ. Giá trị của
a b c+−
bằng
Ⓐ.
7
. Ⓑ.
5−
. Ⓒ.
14
. Ⓓ.
9
.
BẢNG ĐÁP ÁN
1.C
2.A
3.B
4.D
5.C
6.D
7.D
8.A
9.A
10.A
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 29
11.A
12.B
13.B
14.A
15.B
16.A
17.D
18.B
Hướng dẫn giải
Câu 1:
Ta có
( )
3
1
6d
a
x x x−
4
2
1
3
4
a
x
x

=−


4
2
11
3
44
a
a= − +
.
Từ giả thiết ta có phương trình:
4
2
11 875
3
4 4 4
a
a− + =
42
12 864 0aa − − =
2
2
36
24
a
a
=
=−
.
Do
0a
nên
6a =−
.
Câu 2:
Ta có
( )
( )
22
2
1
11
d 2 5
d 1 1 1 9
ln 2 5 ln
2 5 2 2 5 2 2 7
x
x
x
xx
+
= = + =
++

.
Vậy
2 9 7 18abc+ + = + + =
.
Câu 3:
Ta có
5
5
1
1
11
ln 2 1 (ln9 ln1) ln3 ln(2 1)
2 1 2 2
dx
x
x
= − = − = = +
−
.
Vậy
0, 2 2a b a b= = + =
.
Câu 4:
Ta có:
1
2
0
21
d
1
x
x
x
−
+
1
2
0
3
2d
1
x
x

=−

+

=
( )
1
2
0
2 3ln 1xx−+
3
1 3ln 3ln3 3ln2 1
2
= − = − + +
.
Do đó:
3a =−
,
3b =
,
1c =
. Vậy
1a b c+ − = −
.
Câu 5:
Ta có
2 2 2
22
00
0 0 0
(4 sin )d 4 d sin d 4 cos 2 1x x x x x x x

− = − = + = −
.
Suy ra
2
2 1 1
1
a
ab
b
=
+ = − =
=−
.
Câu 6:
8
2
0
cos 2 dI x x
=
8
0
1 cos4
d
2
x
x
+

=


( )
8
0
1
1 cos4 d
2
xx
=+
11
sin 4
8
24
0
xx

=+


1
16 8
=+
.
16a=
,
1b =
,
8c =
.
Vậy
16 8 1 25P a b c= + + = + + =
.
Câu 7:
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 30
Ta có
( )
( )
( )
( )
( )
1
22
1 1 1 1
2
1
3
33
0
0 0 0 0
0
1 1 1
2 1 3
d d d 1 d ln 1 ln2
1 2 8
11
xx
xx
x x x x x x
x
xx
−
−
+ − +
+
= = − + = + − = − +
+−
++
.
Vậy
3
8
a =−
;
1b =
và
16 5ab+ = −
.
Câu 8:
Ta có:
+
= − = + − + = − −
++
++
3 3 3
33
2
11
1 1 1
2 1 3 1
3ln 2 ln 1 3ln5 3ln3 ln2
21
32
x
dx dx dx x x
xx
xx
Vậy:
1; 3; 3 1a b c a b c= − = − = + + = −
.
Câu 9:
( ) ( )
2 3 2 23
0
0
3 2 1 d
b
b
x ax x x ax x b ab b− − = − − = − −
.
Câu 10:
Ta có:
( )
11
00
1
1
d 1 d x ln 1 1 ln2.
0
11
x
I x x x
xx

= = − = − + = −

++


Vậy:
1, 2 3.a b a b= = + =
Câu 11: Ta có:
( )
( ) ( )
1 1 1 1
2
0 0 0 0
1 cos 2 cos 2
1
cos d d d d
2 2 2
ax ax
ax x x x x
+
= = +
Mà
1
0
11
d
22
x =
và
( )
( ) ( )
1
1
0
0
cos 2
11
d sin 2 sin 2
2 4 4
ax
x ax a
aa
==
.
( ) ( )
1
2
0
11
cos d sin 2
24
ax x a
a
= +
.
Theo đề bài ta có:
( )
1
2
0
11
cos d
24
ax x
a
=+
.
Nên
( )
sin 2 1a =
( )
ππ
22π π,
24
a k a k k = + = +
Do
(
π 1 7
0;2 0 π 2π 0;1 .
4 4 4
a k k k
+ −
Với
π
0
4
ka= =
.
Với
5π
1
4
ka= =
.
Vậy có 2 giá trị
(
0;2πa
thỏa mãn đề bài.
Câu 12:
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 31
( )( )
( )
3 3 3 3
2
1 1 1 1
3 3 2 1
3 2 1 2 1 2
3
2ln 1 ln 2 2ln 2 ln3 ln5
1
xx
dx dx dx dx
x x x x x x
xx
++
= = −
+ + + + + +
= + − + = + −
Suy ra
2 , 1 , 1a b c= = = −
.
Nên
2 1 1 2abc+ + = + − =
.
Câu 13:
Ta có
( ) ( )
1
11
22
00
0
1 2 2 1
d d ln 2 ln2 ln3
2 2 3
22
x
x x x
xx
xx


= − = + + = − − +



++

++


.
Suy ra
1
, 1, 1
3
a b c= − = − =
.
Vậy
62abc+ + = −
.
Câu 14: Ta có
3
1
2
d
x
Ix
x
+
=
3
1
2
1dx
x

=+


( )
3
2ln
1
xx=+
2 2ln3=+
.
Mà
lnI a b c=+
, với
a
,
b
,
c
,
9c
. Suy ra
2a =
,
2b =
,
3c =
.
Vậy
7S a b c= + + =
.
Câu 15:
Ta có
2 2 2
2 2 2
1 1 1
1 1 1
d d 1 d
1 1 1
xx
x x x x x x
x x x
+−
+ = + = + −
+ + +
2
3
1
10 10 2 10
ln 1 ln2 ln3 ln ln
3 3 3 3
xa
xx
bb

= + − + = + − = + = +


.
Suy ra
2; 3ab==
. Vậy
5ab+=
.
Câu 16:
Ta có
22
2
2
0
00
1 1 2
d d ln 1 2ln 3
4 3 1 3
−−


= + = − + + +


+ + + +


x
x x x x
x x x x
2ln5 3ln3=−
.
2a=
,
3b =−
.
Vậy
2
2 10P a b= − =
.
Câu 17:
( ) ( )
1
1 1 1
1
22
0
0
0 0 0
d d d 1 1
2 ln 2 2. ln2 ln3
2 2 3
22
x x x x
x
xx
xx
−
= − = + − = − − +
++
++
.
1
; 1; 1 3 1
3
a b c a b c = − = − = + + = −
.
Câu 18: Ta có:
( )
( )( )
2
22
1
12
22
A Bx C
Ax Bx C x
x x x x
+
= + + + +
++
Khi đó, dùng kỹ thuật đồng nhất hệ số ta được
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 32
( ) ( )
44
22
33
1
4
11
0
1 1 1
42
2 0 d d
4 2 4 2
21
1
2
A
AB
x
B C B x x
x x x x
C
C
=

+=
−+


+ = = − = +


++


=

=

Khi đó ta có:
( )
4
4 4 4 4
22
3 3 3 3
3
11
1 1 d 1 d 1 d 1 2 1
42
d ln
4 2 4 2 4 2 4 2
x
x x x x
x
x x x x x x x

−+

+
+ = − + = −


++



9, 10, 24 5a b c a b c = = = + − = −
.
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 33
FB: Duong Hung
Bài 3: TÍCH PHÂN ĐỔI BIẾN SỐ
.Phương pháp: Cho hàm số liên tục trên đoạn Giả sử hàm số có đạo hàm
liên tục trên đoạn và Giả sử có thể viết với liên
tục trên đoạn Khi đó, ta có
. Để tính tích phân: ta thực hiện các bước:
.Bước 1: Biến đổi để chọn phép đặt
. Bước 2. Thực hiện phép đổi cận:
Với thì ; thì . (Ghi Nhớ : đổi biến phải đổi cận)
. Bước 3. Đưa về dạng đơn giản và dễ tính hơn.
. Dấu hiệu nhận biết và cách đặt.
Dấu hiệu
Có thể đặt
.
Có căn
.
Có ngoặc
.
Có mũ
.
Có
hoặc biểu thức chứa
.
Có
hoặc biểu thức chứa
.
Có
.
Có
.
Có
.
Có
.
Có mẫu:
mẫu
Dạng ①: Phương pháp tích phân bằng cách đổi biến số cơ bản
CHƯƠNG ③:
Full Chuyên
đề 12 new
2020-2021
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 34
A - Bài tập minh họa:
1
24
0
(1 )I x x dx=+
16
5
I =
31
10
I =
1
10
I =
1
10
I =−
Lời giải
Chọn B
Đặt
2
12t x dt xdx= + =
.
Đổi cận
01xt= =
;
12xt= =
Nên
2
4
1
31
2 10
t
I dt==
PP nhanh trắc nghiệm
Casio:
2
2
1
21I x x dx=−
2
1ux=−
3
0
2I udu=
2
1
I udu=
3
0
I udu=
2
1
1
2
I udu=
Lời giải
Chọn C
2
2
1
21I x x dx=−
Đặt
2
12u x du xdx= − =
.
Đổi cận
10xu= =
;
23xu= =
Nên
3
0
I udu=
PP nhanh trắc nghiệm
Casio: xét hiệu bằng 0
Lời giải
Chọn C
Ta có:
3
0
cos .sinI x xdx
=
.
PP nhanh trắc nghiệm
Sử dụng máy tính, tính tích phân hàm lượng
giác phải chuyển về đơn vị radian.
3
0
cos .sin dI x x x
=
4
1
4
I
=−
4
I
=−
0I =
1
4
I =−
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 35
Đặt
cos sin sint x dt xdx dt xdx= = − − =
Đổi cận: với
01xt= =
;với
1xt
= = −
.
Vậy
( )
1
4
11
44
33
11
1
1
1
0
4 4 4
t
I t dt t dt
−
−
−
−
= − = = = − =

.
B - Bài tập rèn luyện:
Câu 1: Cho tích phân
( )
1
5
0
1dI x x x=−
. Mệnh đề nào dưới đây đúng?
Ⓐ.
( )
0
5
1
1dI t t t
−
= − −
. Ⓑ.
( )
0
65
1
dI t t t
−
= − −
.
Ⓒ.
( )
1
5
0
1dI t t t=−
. Ⓓ.
( )
0
65
1
dI t t t
−
= − −
.
Câu 2: Cho
4
0
1 2 dI x x x=+
và
21ux=+
. Mệnh đề nào dưới đây sai?
Ⓐ.
3
53
1
1
2 5 3
uu
I

=−


. Ⓑ.
( )
3
22
1
1dI u u u=−
.
Ⓒ.
( )
3
22
1
1
1d
2
I x x x=−
. Ⓓ.
( )
3
22
1
1
1d
2
I u u u=−
.
Câu 3: Tính
3
2
2
d
1
x
Kx
x
=
−
.
Ⓐ.
ln2K =
. Ⓑ.
18
ln
23
K =
. Ⓒ.
2ln 2K =
. Ⓓ.
8
ln .
3
K =
Câu 4: Tích phân
2
0
cos .sinx xdx
bằng
Ⓐ.
3
2
−
. Ⓑ.
2
3
. Ⓒ.
2
3
−
. Ⓓ.
3
2
.
Câu 5: Cho
2
2
1
2 1dI x x x=−
và
2
1ux=−
. Mệnh đề nào dưới đây sai?
Ⓐ.
3
0
dI u u=
. Ⓑ.
2
27
3
I =
. Ⓒ.
2
1
dI u u=
. Ⓓ.
3
2
2
3
3
I =
.
Câu 6: Cho
3
2
2
4
cot
d
sin
x
Ix
x
=
và
cotux=
. Mệnh đề nào dưới đây đúng
Ⓐ.
2
3
4
dI u u
=
. Ⓑ.
1
3
0
dI u u=
. Ⓒ.
1
3
0
dI u u=−
. Ⓓ.
1
0
dI u u=
.
Câu 7: Cho
( )
ln5
ln2
1
1
xx
x
ee
I dx
e
+
=
−
. Đặt
1
x
te=−
. Chọn mệnh đề đúng.
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 36
Ⓐ.
( )
4
2
1
22I t dt=+
. Ⓑ.
ln5
2
ln2
( 2)I t dt=+
.
Ⓒ.
( )
2
2
1
22I t dt=+
. Ⓓ.
( )
4
2
1
2I t dt=+
.
Câu 8: Cho
4
0
1 2 dI x x x=+
và
21ux=+
. Mệnh đề nào dưới đây sai?
Ⓐ.
3
53
1
1
2 5 3
uu
I

=−


. Ⓑ.
( )
3
22
1
1dI u u u=−
.
Ⓒ.
( )
3
22
1
1
1d
2
I x x x=−
. Ⓓ.
( )
3
22
1
1
1d
2
I u u u=−
.
Câu 9: Tính
3
2
2
d
1
x
Kx
x
=
−
.
Ⓐ.
ln2K =
. Ⓑ.
18
ln
23
K =
. Ⓒ.
2ln 2K =
. Ⓓ.
8
ln .
3
K =
Câu 10: Cho
3
2
2
4
cot
d
sin
x
Ix
x
=
và
cotux=
. Mệnh đề nào dưới đây đúng
Ⓐ.
2
3
4
dI u u
=
. Ⓑ.
1
3
0
dI u u=
. Ⓒ.
1
3
0
dI u u=−
. Ⓓ.
1
0
dI u u=
.
Câu 11: Cho
( )
ln5
ln2
1
1
xx
x
ee
I dx
e
+
=
−
. Đặt
1
x
te=−
. Chọn mệnh đề đúng.
Ⓐ.
( )
4
2
1
22I t dt=+
. Ⓑ.
ln5
2
ln2
( 2)I t dt=+
.
Ⓒ.
( )
2
2
1
22I t dt=+
. Ⓓ.
( )
4
2
1
2I t dt=+
.
Câu 12: Cho
3
2
0
sin cos dI x x x
=
, khẳng định nào sau đây đúng?
Ⓐ.
11
32
I
. Ⓑ.
1
0
3
I
. Ⓒ.
12
23
I
. Ⓓ.
2
1
3
I
.
Câu 13: Cho
1
0
d
2
x
I
xm
=
+
,
m
là số thực dương. Tìm tất cả các giá trị của
m
để
1I
.
Ⓐ.
1
0
4
m
. Ⓑ.
1
4
m
. Ⓒ.
0m
. Ⓓ.
11
84
m
.
Câu 14: Cho tích phân
22
2
0
16 dI x x=−
và
4sinxt=
. Mệnh đề nào sau đây đúng?
Ⓐ.
( )
4
0
8 1 cos2 dI t t
=+
. Ⓑ.
4
2
0
16 sin dI t t
=
.
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 37
Ⓒ.
( )
4
0
8 1 cos2 dI t t
=−
. Ⓓ.
4
2
0
16 cos dI t t
=−
.
BẢNG ĐÁP ÁN
1.C
2.B
3.B
4.B
5.C
6.B
7.C
8.B
9.B
10.B
11.C
12.B
13.A
14.A
A - Bài tập minh họa:
Câu 1: Cho biết
1
2
0
1dx x x+
21a
b
−
=
với
a
,
b
là các số tự nhiên. Giá trị của
22
ab−
bằng
Ⓐ.
5−
. Ⓑ. 5. Ⓒ. 2. Ⓓ.7.
Lời giải
Chọn A
Đặt
2
1xt+=
22
1xt + =
ddx x t t=
.
Ta có
0x =
1t=
,
1x =
2t=
.
Khi đó:
1
2
0
1dx x x+
2
2
1
dtt=
2
3
1
3
t
=
2 2 1
3
−
=
2a=
,
3b =
.
Vậy
22
5ab− = −
.
PP nhanh trắc nghiệm
Tính tích phân rồi lưu lại là A .
Rút
21
A
a
b
−
=
.
table
( )
21
A
x
fx
−
=
với Start:
0
,
End:
18
, Step: 1 .
Được cặp số
2x =
,
( )
3fx=
thỏa mãn. Suy ra
2a =
,
3b =
.
Câu 2: Cho
( )
e
2
1
ln
d ln2 ln3
ln 2
x
x a b c
xx
= + +
+
với
a
,
b
,
c
là các số hữu tỷ. Giá trị của
3abc++
bằng
Ⓐ.
2−
. Ⓑ.
1−
. Ⓒ.
2
. Ⓓ.
1
.
-Phương pháp:
. Để tính tích phân: ta thực hiện các bước:
.Bước 1: Biến đổi để chọn phép đặt
. Bước 2. Thực hiện phép đổi cận:
Với thì ; thì
. Bước 3. Đưa về dạng đơn giản và dễ tính hơn.
Dạng ②: Tích phân đổi biến chứa tham số a, b, c cơ bản
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 38
Lời giải
Chọn B
Đặt
1
ln d dt x t x
x
= =
.
Đổi cận:
10xt= =
;
e1xt= =
.
Khi đó:
( ) ( )
e1
22
10
ln
dd
ln 2 2
xt
I x t
x x t
==
++

( ) ( )
11
22
00
2 2 1 2
dd
2
22
t
tt
t
tt

+−
= = −

+
++



1
0
11
ln 2 2. ln2 ln3
23
t
t

= + + = − − +

+

.
Suy ra:
1
3
a =−
;
1b =−
;
1c =
.
Do đó:
31abc+ + = −
.
PP nhanh trắc nghiệm
Câu 3: Biết
ln6
0
e
d ln2 ln3
1 e 3
x
x
x a b c= + +
++
với
a
,
b
,
c
là các số nguyên. Tính
T a b c= + +
.
Ⓐ.
1T =−
. Ⓑ.
0T =
. Ⓒ.
2T =
. Ⓓ.
1T =
.
Lời giải
Chọn B
Xét
ln6
0
e
d
1 e 3
x
x
Ix=
++
. Đặt
e3
x
t =+
2
e3
x
t = +
2 d e d
x
t t x=
.
Đổi cận
02xt= =
,
ln6 3xt= =
.
Khi đó
3
2
2
d
1
t
It
t
=
+
3
2
2
2d
1
t
t

=−

+

( )
3
2
2 2ln 1tt= − +
2 4ln2 2ln3= − +
.
Suy ra
2a =
,
4b =−
,
2c =
nên
0T a b c= + + =
.
PP nhanh trắc nghiệm
B - Bài tập rèn luyện:
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 39
Câu 1: Tính tích phân
5
1
d
31
x
I
xx
=
+
ta được kết quả
ln3 ln5.I a b=+
Giá trị
22
3S a ab b= + +
là
Ⓐ.
0
. Ⓑ.
4
. Ⓒ.
1
. Ⓓ.
5
.
Câu 2: Cho
( )
2
1
ln
ln3 ln2
3
ln 2
e
xc
I dx a b
xx
= = + +
+
, với
,,abc
. Khẳng định nào sau đâu đúng.
Ⓐ.
2 2 2
1abc+ + =
. Ⓑ.
2 2 2
11abc+ + =
. Ⓒ.
2 2 2
9abc+ + =
. Ⓓ.
2 2 2
3abc+ + =
.
Câu 3: Cho
4
2
3
2 1 3
d ln ln
3 2 2
x
x a b c
xx
+
=+
−−
, với
,,abc
là các số hữu tỷ. Giá trị của
5 15 11a b c+−
bằng
Ⓐ.
12−
. Ⓑ.
15−
. Ⓒ.
14
. Ⓓ.
9
.
Câu 4: Biết
4
2
3
d
ln2 ln3 ln5
x
I a b c
xx
= = + +
+
, trong đó
,,abc
. Tính giá trị của
T a b c= + +
.
Ⓐ.
2T =
. Ⓑ.
3T =
. Ⓒ.
1T =−
. Ⓓ.
5T =
.
Câu 5: Giả sử tích phân
( )
5
1
1
d ln3 ln5 , ,
1 3 1
I x a b c a b c
x
= = + +
++
. Khi đó:
Ⓐ.
8
3
abc+ + =
. Ⓑ.
4
3
abc+ + =
. Ⓒ.
5
3
abc+ + =
. Ⓓ.
7
3
abc+ + =
.
Câu 6: Cho
4
0
2 3tan
d 5 2,
1 cos2
x
x a b
x
+
=+
+
với
,.ab
Tính giá trị biểu thức
.A a b=+
Ⓐ.
1
3
. Ⓑ.
7
12
. Ⓒ.
2
3
. Ⓓ.
4
3
.
Câu 7: Cho
( )
e
2
1
ln
d ln2 ln3
ln 2
x
x a b c
xx
= + +
+
với
a
,
b
,
c
là các số hữu tỷ. Giá trị của
3abc++
bằng
Ⓐ.
2−
. Ⓑ.
1−
. Ⓒ.
2
. Ⓓ.
1
.
Câu 8: Cho
( )
3
2
1
ln
d ln3 ln2
1
xa
xc
b
x
= −
+
với
, , *a b c
và phân số
a
b
tối giản. Giá trị của
abc++
bằng
Ⓐ.
8
. Ⓑ.
7
. Ⓒ.
6
. Ⓓ.
9
.
Câu 9: Biết
ln6
0
e
d ln2 ln3
1 e 3
x
x
x a b c= + +
++
với
a
,
b
,
c
là các số nguyên. Tính
T a b c= + +
.
Ⓐ.
1T =−
. Ⓑ.
0T =
. Ⓒ.
2T =
. Ⓓ.
1T =
.
Câu 10: Cho biết
e
1
ln 3
d3
3
xa
xb
x
+
=+
, với
a
,
b
là các số nguyên. Giá trị của biểu
thức
2
1
log
2
b
a+
bằng
Ⓐ. -1. Ⓑ.
7
2
. Ⓒ. 8. Ⓓ.6.
Câu 11: Cho biết
1
2
0
1dx x x+
21a
b
−
=
với
a
,
b
là các số tự nhiên. Giá trị của
22
ab−
bằng
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 40
Ⓐ.
5−
. Ⓑ. 5. Ⓒ. 2. Ⓓ.7.
BẢNG ĐÁP ÁN
1.D
2.D
3.A
4.A
5.B
6.A
7.B
8.A
9.B
10.C
11.A
A - Bài tập minh họa:
Câu : Biết
( )
fx
là hàm liên tục trên và
( )
9
0
d9f x x =
. Khi đó giá trị của
( )
4
1
3 3 df x x−
là
Ⓐ.
0
. Ⓑ.
27
. Ⓒ.
3
. Ⓓ.
24
.
Lời giải
Chọn C
Đặt
33ux=−
, suy ra
3ddu x=
.
Đổi cận:
1x =
thì
0u =
;
4x =
thì
9u =
.
Ta có:
( ) ( ) ( ) ( )
4 9 9 9
1 0 0 0
1 1 1 1
3 3 d d d d .9 3.
3 3 3 3
f x x f u u f u u f x x− = = = = =
.
Vậy
( )
4
1
3 3 d 3f x x−=
.
PP nhanh trắc nghiệm
Nếu có
( )
m
n
Mf x dx =
thì
( )
;
. , .
f x b dx
n a b m a b
M
a
a

+=
= + = +
Áp dụng:
9
3
3
=
Câu 2: Cho hàm số
()fx
liên tục trên
R
và thỏa mãn
3
( 2 2) 3 1f x x x+ − = −
với
xR
. Tính
tích phân
10
1
()I f x dx=
-Phương pháp:
Tính tích phân .Giả sử được viết dưới dạng
,trong đó hàm số có đạo hàm trên , hàm số y=f(u) liên tục sao cho hàm
hợp xác định trên và là hai số thuộc .
Khi đó
Chú ý: Đối với biến số lấy tích phân, ta có thể chọn bất kì một chữ số thay
cho . Như vậy tích phân không phụ thuộc vào biến tức là
Dạng ③: Tích phân hàm ẩn đổi biến số cơ bản
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 41
Ⓐ.
151
4
. Ⓑ.
27
. Ⓒ.
121
4
. Ⓓ.
105
6
.
Lời giải
Chọn A
Đặt
( )
32
2 2 3 2x t t dx t t dt= + − = +
,
Đổi cận :
3
3
1 2 3 1
10 2 12 2
x t t t
x t t t
= + = =
= + = =
Ta có
( )
( )
( )
22
3 2 2
11
( 2 2). 3 2 3 1 3 2I f t t t t dt t t t dt= + − + = − +

( )
2
32
1
9 3 2t t t dt= + −
2
4
32
1
9 151
44
t
tt

= + − =


PP nhanh trắc nghiệm
Câu 3: Cho Cho hàm số
()fx
liên tục trên
R
và thỏa mãn
2021
0
( ) 2f x dx =
. Tính tích phân
( )
2021
1
2
2
0
. ln( 1) .
1
e
x
I f x dx
x
−
=+
+
Ⓐ.
3
. Ⓑ.
5
. Ⓒ.
1
. Ⓓ.
3−
.
Lời giải
Chọn C
Đặt
( )
2
22
21
ln 1
1 1 2
xx
t x dt dx dx dt
xx
= + = =
++
,
Đổi cận :
2021
00
1 2021
xt
x e t
= =
= − =
Ta có
2021 2021
00
1 1 1
( ) ( ) .2 1
2 2 2
I f t dt f x dx= = = =

PP nhanh trắc nghiệm
B - Bài tập rèn luyện:
Câu 1: Cho
( )
3
1
4f x dx =
, khi đó
( )
1
0
21f x dx+
bằng
Ⓐ.
8
. Ⓑ.
2
. Ⓒ.
1
2
. Ⓓ.
3
2
.
Câu 2: Cho hàm số
( )
fx
liên tục trên
và thỏa mãn
( )
3
1
d2f x x =
. Tính
( )
1
0
2 1 2 1 dI f x x x= + + +


.
Ⓐ.
11I =
. Ⓑ.
3I =
. Ⓒ.
14I =
. Ⓓ.
6I =
.
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 42
Câu 3: Cho
( )
9
4
d 10f x x =
. Tính tích phân
( )
1
0
5 4 dJ f x x=+
.
Ⓐ.
2J =
. Ⓑ.
10J =
. Ⓒ.
50J =
. Ⓓ.
4J =
.
Câu 4: Cho hàm số
( )
fx
liên tục trên và
( )
8
2
d 10f x x =
. Tính
( )
3
1
3
3 1 d
2
I f x x=−
.
Ⓐ.
30
. Ⓑ.
10
. Ⓒ.
20
. Ⓓ.
5
.
Câu 5: Cho
( )
fx
là hàm số chẵn, liên tục trên . Biết rằng
( )
2
1
d8f x x
−
=
và
( )
3
1
2 d 3f x x =
. Tính
tích phân
( )
6
1
df x x
−
.
Ⓐ.
14
. Ⓑ.
11
. Ⓒ.
5
. Ⓓ.
2
.
Câu 6: Cho
4
0
( )d 2018f x x =
. Tính tích phân
2
0
(2 ) (4 2 ) dI f x f x x= + −
Ⓐ.
0I =
. Ⓑ.
2018I =
. Ⓒ.
4036I =
. Ⓓ.
1009I =
.
Câu 7: Biết
( )
4
1
5f x dx =
và
( )
5
4
20f x dx =
. Tính
( )
( )
2 ln2
22
10
43
xx
f x dx f e e dx−−

.
Ⓐ.
15
4
I =
. Ⓑ.
15I =
. Ⓒ.
5
2
I =
. Ⓓ.
25I =
.
Câu 8: Cho
4
0
2018f x dx
. Tính tích phân
2
0
(2 ) (4 2 )I f x f x dx
.
Ⓐ.
0I
. Ⓑ.
2018I
. Ⓒ.
4036I
. Ⓓ.
1009I
.
Câu 9: Giả sử hàm số
( )
fx
liên tục trên đoạn
0;2
thỏa mãn
( )
2
0
d6f x x =
. Tính tích phân
( )
2
0
2sin cos d .I f x x x
=
Ⓐ.
3
. Ⓑ.
3−
. Ⓒ.
6
. Ⓓ.
6−
.
Câu 10: Cho
( )
4
1
d9I f t t==
. Tính tích phân
( )
1
0
3 1 dJ f x x=+
.
Ⓐ. 9. Ⓑ. 27. Ⓒ. 3. Ⓓ.1.
Câu 11: Cho
( )
1
0
d 2019f x x =
. Giá trị của
( )
4
0
cos2 sin2 dI f x x x
=
bằng
Ⓐ.
2019
4
. Ⓑ.
2019
2
−
. Ⓒ.
4038
. Ⓓ.
2019
2
.
Câu 12: Cho tích phân
( )
4
0
d 32.I f x x==
Tính tích phân
( )
2
0
2 d .J f x x=
Ⓐ.
32.=J
Ⓑ.
64.=J
Ⓒ.
8.=J
Ⓓ.
16.=J
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 43
Câu 13 ho hàm số
fx
liên tục trên có
( )
1
0
2 d 2f x x =
và
( )
2
0
1 d 4f x x+=
. Tính
( )
3
0
dI f x x=
.
Ⓐ. I = 5. Ⓑ. I = 4. Ⓒ. I = 6. Ⓓ.I = 7.
Câu 14: Cho hàm số
( )
fx
liên tục trên
và
( )
2
0
d 2018f x x
=
. Tính
( )
2
0
dI xf x x
=
.
Ⓐ.
1008I =
. Ⓑ.
2019I =
. Ⓒ.
2017I =
. Ⓓ.
1009I =
.
Câu 15: Cho hàm số
( )
fx
liên tục trên và có
( ) ( )
13
00
d 2; d 8.f x x f x x==

Tính
( )
1
1
I 2 1 df x x
−
=−
Ⓐ.
6I =
. Ⓑ.
2
3
I =
. Ⓒ.
5I =
. Ⓓ.
3
2
I =
Câu 16: Cho
( )
2
1
d2f x x =
Khi đó
( )
4
1
d
fx
Ix
x
=
bằng
Ⓐ. 4. Ⓑ.
1
2
. Ⓒ. 1. Ⓓ.2.
Câu 17: Cho
( )
8
3
1 d 10f x x+=
. Tính
( )
1
0
5 4 dJ f x x=+
.
Ⓐ.
4J =
. Ⓑ.
10J =
. Ⓒ.
50J =
. Ⓓ.
2J =
BẢNG ĐÁP ÁN
1.B
2.B
3.A
4.D
5.A
6.B
7.A
8.B
9.A
10.C
11.D
12.D
13.A
14.D
15.C
16.A
17.D
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 44
FB: Duong Hung
Bài 5: DIỆN TÍCH HÌNH PHẲNG
. Định lí:
Nếu và là các hàm số có đạo hàm liên tục trên thì:
. Hay
.Phương pháp chung:
• Bước 1: Viết dưới dạng bằng cách chọn một phần thích hợp của
làm và phần còn lại
• Bước 2: Tính
và
• Bước 3: Tính và
.Cách đặt u và dv trong phương pháp tích phân từng phần.
Đặt u theo thứ tự ưu tiên:
Lô-đa-lượng-mũ
u
P(x)
lnx
P(x)
dv
P(x)dx
cosxdx
cosxdx
.Chú ý:
Nên chọn là phần của mà khi lấy đạo hàm thì đơn giản, chọn là
phần của là vi phân một hàm số đã biết hoặc có nguyên hàm dễ tìm.
Dạng ①: Phương pháp tính phân từng phần cơ bản
①. Loại 1:
.Phương pháp:
Đặt: .
Dạng ①: Tích phân chứa đa thức với lượng giác hoặc mũ
CHƯƠNG ③:
Full Chuyên
đề 12 new
2020-2021
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 45
A - Bài tập minh họa:
Câu 1: Tính tích phân
2
1
=
x
I xe dx
.
Ⓐ.
2
=Ie
. Ⓑ.
2
=−Ie
. Ⓒ.
=Ie
. Ⓓ.
2
32=−I e e
.
Lời giải
Chọn A
Đặt
==


==

xx
u x du dx
dv e dx v e
( )
22
2 2 2
11
11
2 2 2
2
2
x x x x
I xe dx xe e dx e e e
e e e e e
= = − = − −
= − − − =

.
PP nhanh trắc nghiệm
Tính tích phân
+ Kiểm tra các đáp án:
2
0Ae−=
(đúng).
Câu 2: Tính tích phân
1
2
0
( 2)
x
I x e dx=−
.
Ⓐ.
2
53
4
e
I
−
=
. Ⓑ.
2
53
4
e
I
−
=
. Ⓒ.
2
53
4
e
I
−
=
. Ⓓ.
2
53
4
e
I
−
=
.
Lời giải
Chọn B
Đặt
2
2
2
1
2
x
x
du dx
ux
ve
dv e dx
=
=−

=
=
(chọn
0C =
)
1
1
2
22
0
0
1 1 5 3
( 2)
2 2 4
xx
e
I x e e dx
−
= − − =
.
PP nhanh trắc nghiệm
Tính tích phân:
+Kiểm tra các đáp án:
Câu 3: Tích phân
( )
2
0
3 2 cos dx x x
+
bằng
Ⓐ.
2
3
4

−
. Ⓑ.
2
3
4

+
. Ⓒ.
2
1
4

+
. Ⓓ.
2
1
4

−
.
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 46
Lời giải
Chọn B
Đặt
( )
2
0
3 2 cos dI x x x
=+
. Ta có:
( )( )
0
1
3 2 1 cos2 d
2
x x x
= + +
( ) ( ) ( )
12
00
11
3 2 d 3 2 cos2 d
22
x x x x x I I


= + + + = +



.
( )
1
0
3 2 dI x x
= + =
22
0
33
22
22
xx


+ = +


.
( )
2
0
3 2 cos2 dI x x x
=+
. Dùng tích phân từng phần
Đặt
d 3d
32
1
d cos2 d
sin2
2
ux
ux
v x x
vx
=
=+

=
=
.
Khi đó
( )
2
0
0
13
3 2 sin2 sin2 d
22
I x x x x
= + −
( )
0
3
0 cos2 0
4
x
= + =
.
Vậy
22
1 3 3
2
2 2 4
I

= + = +


PP nhanh trắc nghiệm
Tính tích phân:
Kiểm tra các đáp án:
B - Bài tập rèn luyện:
Câu 1: Xét tích phân
1
22
0
(2 4)
x
I x e dx=−
Nếu đặt
22
2 4, '
x
u x v e= − =
, ta được tích phân:
1
1
2
0
0
( ) 2
x
I x xe dx
=−
, trong đó:
Ⓐ.
22
( ) ( 2)
x
x x e
=−
. Ⓑ.
22
( ) (2 4)
x
x x e
=−
. Ⓒ.
2
( ) ( 2)
x
x x e
=−
.
Ⓓ.
2
1
( ) (2 4)
2
x
x x e
=−
.
Câu 2: Tính tích phân
2
0
I xcosxdx
=
Ⓐ.
I
2
=
. Ⓑ.
I1
2
=+
. Ⓒ.
I
3
=
. Ⓓ.
1
I
32
=−
.
Câu 3: Tính
1
x
0
xe dx
Ⓐ.
e
. Ⓑ.
e1−
. Ⓒ.
1
. Ⓓ.
1
e1
2
−
.
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 47
Câu 4:
0
L xsinxdx
=
Ⓐ.
L =
. Ⓑ.
L2=−
. Ⓒ.
L0=
. Ⓓ.
L = −
.
Câu 5:
( )
0
x 2 cos2xdx
+
Ⓐ.
0
. Ⓑ.
1
4
−
. Ⓒ.
1
4
. Ⓓ.
1
2
.
Câu 6:
4
0
xcos2xdx
bằng
Ⓐ.
2
8
−
. Ⓑ.
1
4
−
. Ⓒ.
3
2
−
. Ⓓ.
2
2
−
Câu 7: Tính tích phân
1
3
0
( 1)
x
I x e dx=+
Ⓐ.
3
52
.
99
Ie=−
Ⓑ.
3
25
.
99
Ie=−
Ⓒ.
3
25
.
99
Ie=−
Ⓓ.
3
52
.
99
Ie=+
Câu 8: Tính tích phân
1
1
0
x
I xe dx
−
=
Ⓐ.
1
. Ⓑ.
2e−
. Ⓒ.
1 e−
. Ⓓ.
1−
.
Câu 9: Tính tích phân
1
3
0
( 1)
x
I x e dx=+
Ⓐ.
3
52
.
99
Ie=−
Ⓑ.
3
25
.
99
Ie=−
Ⓒ.
3
25
.
99
Ie=−
Ⓓ.
3
52
.
99
Ie=+
Câu 10: Tính tích phân
1
1
0
x
I xe dx
−
=
Ⓐ.
1
. Ⓑ.
2e−
. Ⓒ.
1 e−
. Ⓓ.
1−
.
BẢNG ĐÁP ÁN
1.A
2.C
3.C
4.A
5.A
6.A
7.A
8.D
9.A
10.D
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 48
A - Bài tập minh họa:
Câu 1: Tích phân
e
1
xlnxdx
bằng
Ⓐ.
2
e1
44
+
. Ⓑ.
2
e
1
4
−
. Ⓒ.
2
e1
4
−
. Ⓓ.
2
1e
.
24
−
Lời giải
Chọn D
ee
2 2 2 2
ee
11
11
x x x x e 1
xln xdx ln x dx ( ln x)
2 2 4 2 4
+
= − = − + =

PP nhanh trắc nghiệm
Casio:
Câu 2: Tính tích phân
( ) ( )
5
4
1 ln 3 dI x x x= + −
?
Ⓐ.
10ln2
. Ⓑ.
19
10ln2
4
+
. Ⓒ.
19
10ln2
4
−
. Ⓓ.
19
10ln2
4
−
.
Lời giải
Chọn D
Đặt
( )
2
1
dd
ln 3
3
1
d1
2
ux
ux
x
vx
v x x
=
=−

−

=+
=+
.
( )
2
5
2
4
1
5
1
2
ln 3 d
4
23
xx
I x x x x
x
+

= + − −

−

55
2
44
35 1 9 9 3 3
ln2
2 2 3 3
xx
dx dx
xx
− + − +
= − −
−−

( )
35 1 9
ln2 3 9ln2 1 3ln2
2 2 2

= − + + − +


PP nhanh trắc nghiệm
Casio:
Kiểm tra các đáp án:
②. Loại 2:
-Phương pháp:
.Đặt:
Dạng ②: Tích phân chứa đa thức và ln
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 49
19
10ln2
4
=−
.
Câu 3: Tính
2
1
ln d
e
x x x
Ⓐ.
+
3
21
9
e
. Ⓑ.
−
3
21
9
e
. Ⓒ.
−
3
2
9
e
. Ⓓ.
+
3
2
9
e
.
Lời giải
Chọn A
=
=


=
=

= − = −


−+
= − =
2
3
3 2 3 3
1
1
1
33
3
1
ln
1
3
1 1 1 1
ln
3 3 3 9
1 1 2 1
3 9 9
e
e
e
du dx
ux
x
dv x dx
vx
I x x x dx e x
ee
e
PP nhanh trắc nghiệm
Casio
B - Bài tập rèn luyện:
Câu 1: Tính tích phân
1
( 2)ln
e
I x xdx=+
Ⓐ.
1
2
I =
. Ⓑ.
2
2
2
e
I
−
=
. Ⓒ.
2
1
4
e
I
+
=
. Ⓓ.
2
1
4
e
I
−
=
.
Câu 2. Nếu đặt
( )
ln
21
ux
dv x dx
=
=+
thì tích phân
( )
1
2 1 ln
e
I x xdx=+
trở thành
Ⓐ.
( )
( )
2
1
1
1
e
e
I x x x dx= + − +
. Ⓑ.
( )
2
1
1
ln 1
e
e
I x x x dx= − +
.
Ⓒ.
2
1
1
ln
e
e
I x x xdx=+
. Ⓓ.
( )
( )
2
1
1
ln 1
e
e
I x x x x dx= + + +
.
Câu 3: Tính tích phân
( )
0
0
ln 1J x x dx=+
Ⓐ.
4
ln3
3
J =
. Ⓑ.
5
ln3
3
J =
. Ⓒ.
2
ln3
3
J =
. Ⓓ.
3
ln3
4
J =
.
Câu 4: Tính tích phân
( ) ( )
5
4
1 ln 3 dI x x x= + −
?
Ⓐ.
10ln2
. Ⓑ.
19
10ln2
4
+
. Ⓒ.
19
10ln2
4
−
. Ⓓ.
19
10ln2
4
−
Câu 5: Tích Phân
3
2
2
ln( )=−
I x x dx
là
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 50
Ⓐ.
3ln3
.
Ⓑ.
2ln2
.
Ⓒ.
3ln3 2−
.
Ⓓ.
2 3ln3−
.
Câu 6: Tích phân
2
2
1
ln
=
x
I dx
x
bằng
Ⓐ.
( )
1
1 ln 2
2
+
.
Ⓑ.
( )
1
1 ln2
2
−
.
Ⓒ.
( )
1
ln2 1
2
−
.
Ⓓ.
( )
1
1 ln 2
4
+
.
Câu 7: Cho
1ab −
. Tích phân
( )
ln 1 d
b
a
I x x=+
bằng biểu thức nào sau đây?
Ⓐ.
( ) ( )
1 ln 1
b
a
I x x a b= + + − +
. Ⓑ.
( ) ( )
1 ln 1
b
a
I x x b a= + + − +
.
Ⓒ.
( )
1
1
b
a
I
x
=
+
. Ⓓ.
( )
ln 1 d
1
b
b
a
a
x
I x x x
x
= + +
+
.
BẢNG ĐÁP ÁN
1.C
2.D
3.C
4.D
5.C
6.A
7B
A - Bài tập minh họa:
Câu 1: Cho với , , . Tính .
Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. .
Lời giải
Chọn D
Ta có: nên .
.
PP nhanh trắc nghiệm
Casio
+ Thử C=1,2,3,4,5,6.. giải hệ tìm a,b nguyên.
e
1
ln dI x x x=
2
.eab
c
+
=
a
b
c
T a b c= + +
5
3
4
6
ln
dd
ux
v x x
=
=
2
1
dd
2
ux
x
x
v
=
=
e
1
ln dI x x x=
e
e
2
1
1
1
ln d
22
x
x x x=−
2
e1
4
+
=
-Phương pháp: Tích phân từng phần.
①. ②.
Dạng ③: Tích phân chứa từng phần chứa tham số a, b, c
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 51
.
Vậy .
B - Bài tập rèn luyện:
Câu 1: Cho
3
1
31
ln d
e
a
e
x x x
b
+
=
với
,ab
. Tổng
ab+
bằng
Ⓐ.
20
. Ⓑ.
10
. Ⓒ.
17
. Ⓓ.
12
.
Câu 2: Biết
2
2
1
ln
d = ln2
xb
xa
xc
+
trong đó
a
;
b
,
c
là các số nguyên dương và nguyên tố cùng nhau.
Tính giá trị của
23a b c++
.
Ⓐ.
6
. Ⓑ.
5
. Ⓒ.
4
. Ⓓ.
6−
.
Câu 3: Cho tích phân
2
2
1
ln
ln2
xb
I dx a
xc
= = +
với
a
là số thực,
b
và
c
là các số dương, đồng thời
b
c
là
phân số tối giản. Tính giá trị của biểu thức
23P a b c= + +
.
Ⓐ.
6P =
. Ⓑ.
5P =
. Ⓒ.
6P =−
. Ⓓ.
4P =
.
Câu 4: Cho
( )
2
2
1
1d
x
x e x ae be c+ = + +
với
a
,
b
,
c
là các số nguyên. Tính
abc++
.
Ⓐ. 3. Ⓑ. 4. Ⓒ. 1. Ⓓ. 0.
Câu 5: Biết
23
1
ln d
e
I x x x ae b= = +
với
a
,
b
là các số hữu tỉ. Giá trị của
( )
9 ab+
bằng
Ⓐ.
3
. Ⓑ.
10
. Ⓒ.
9
. Ⓓ.
6
.
Câu 6: Biết
23
1
ln d
e
I x x x ae b= = +
với
a
,
b
là các số hữu tỉ. Giá trị của
( )
9 ab+
bằng
Ⓐ.
3
. Ⓑ.
10
. Ⓒ.
9
. Ⓓ.
6
.
Câu 7: Cho
( )
2
2
1
ln
d ln2 ln
1
xa
I x c
b
x
= = −
+
với
, , a b c
là các số nguyên dương và
a
b
là phân số tối giản.
Tính giá trị của biểu thức
ab
S
c
+
=
.
Ⓐ.
5
.
3
S =
Ⓑ.
8
3
S =
. Ⓒ.
6
5
S =
. Ⓓ.
10
3
S =
.
Câu 8: Biết
( )
2
42
0
2 e e d .e .e
xx
x x a b c+ = + +
với
,,abc
là các số hữu tỉ. Giá trị của
2 3 2a b c++
bằng
Ⓐ. 9. Ⓑ. 10. Ⓒ. 8. Ⓓ. 7.
1
1
4
a
b
c
=
=
=
T a b c= + +
6=
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 52
Câu 9: Biết
2
2
1
ln
ln2=+
xb
dx a
xc
. Giá trị của
23++a b c
bằng.
Ⓐ.
6−
. Ⓑ.
4
. Ⓒ.
5
. Ⓓ.
6
.
Câu 10. Cho
( )
5
2
2
ln d ln5 ln2x x x a b c− = + +
với
a
,
b
,
c
là các số nguyên. Tính
2S a b c= + −
.
Ⓐ.
23S =
. Ⓑ.
20S =
. Ⓒ.
17S =
. Ⓓ.
11S =
.
BẢNG ĐÁP ÁN
1.A
2.C
3.D
4.C
5.A
6.A
7.B
8.B
9.B
10.A
Hướng dẫn giải
Câu 1: Đặt
1
ln d du x u x
x
= =
;
4
3
4
x
dv x dx v= =
.
4 4 4 4 4
34
1
1
1
1 1 1 3 1
ln . d
4 4 4 16 4 16 16 16
e
e
e
x e e e e
I x x x x

+

= − = − = − + =




.
4
20
16
a
ab
b
=
+ =
=
.
Câu 2:
Đặt
2
1
ln
d = d
1
1
d = d
ux
ux
x
vx
v
x
x
=



=−
.
Ta có
2
2
22
22
1
11
1
ln 1 1 1 1 1 1
d = ln d ln2 ln2
2 2 2
x
x x x
x x x x

− + = − − = − +



.
Theo đề ta có
1
2
a =−
,
1b =
,
2c =
.
Do đó
2 3 4a b c+ + =
.
Câu 3:
Đặt
2
2
1
2
ln
22
ln 1 ln 1 1 ln 2
1 1 1
22
dx
ux
du
xx
x
I dx
dx
x x x x
dv
v
x
x
=
=
− − −


= + = + = −


−
=


=
1
1, 2, 2 3 4
2
b c a P a b c
−
= = = = + + =
.
Câu 4:
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 53
Đặt
1
d
x
ux
dv e x
=+
=
ta được
d d ,
x
u x v e==
.
( ) ( )
22
2 2 2
11
11
1 d 1 d 2
x x x x
x e x x e e x xe e e+ = + − = = −

.
2, 1, 0 1a b c a b c = = − = + + =
.
Câu 5:
Đặt
2
ln
dd
ux
v x x
=
=
ta có
3
1
dd
3
ux
x
x
v
=
=
Suy ra
3 2 3 3
3
1
11
ln 2 1
d.
3 3 3 9 9 9
ee
e
x x x e x
I x e= − = − = +
.
Vậy
2
9
a =
,
1
9
b =
nên
( )
93ab+=
.
Câu 6:
Đặt
2
ln
dd
ux
v x x
=
=
ta có
3
1
dd
3
ux
x
x
v
=
=
Suy ra
3 2 3 3
3
1
11
ln 2 1
d.
3 3 3 9 9 9
ee
e
x x x e x
I x e= − = − = +
.
Vậy
2
9
a =
,
1
9
b =
nên
( )
93ab+=
.
Câu 7:
Ta có:
( )
( )
2 2 2 2
2
1 1 1 1
2
ln 1 1 1 1 1 1
d ln d ln d ln2 d
1
1 1 ( 1) 3 1
1
5
2
1 5 8
ln2 ln ln 1 ln2 ln3 3 .
1
3 3 3
3
x
I x x x x x
x x x x x x
x
a
ab
x x b S
c
c
= = − = − + = − + −
+ + + +
+
=
+
= − + − + = − = = =
=
Câu 8:
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 54
Đặt:
2e
d e d
x
x
ux
vx
=+
=
ta được
( )
d 2 e d
e
x
x
ux
v
=+
=
.
Khi đó:
( ) ( ) ( )
22
22
0
00
2 e e d 2 e e 2e e d
x x x x x x
x x x x+ = + − +

( ) ( )
2
2 2 0 0 2
0
1
2.2 e e 2.0 e e 2e e
2
xx

= + − + − +


42
13
e 2e
22
= + +
.
Theo bài ra ta có
13
; 2;
22
a b c= = =
Vậy:
13
2 3 2 2. 3.2 2. 10
22
a b c+ + = + + =
.
Câu 9:
Gọi
2
2
1
ln
=
x
I dx
x
.
Áp dụng phương pháp nguyên hàm từng phần ta có:
Đặt
2
1
ln
1
1
=
=


=

=−
ux
du dx
x
dv dx
v
x
x
2
2
22
2
1
11
1
ln 1 1 ln2 1 1 1 1 1 1 1
. ln2 ln2 1 ln2
2 2 2 2 2 2
= − − − = − + = − − = − − − = −

x
I dx dx
x x x x x
1
; 1; 2
2
= − = =a b c
.
Vậy
2 3 4+ + =a b c
.
Câu 10.
Đặt
( )
2
ln
dd
u x x
vx
=−
=
2
21
dd
x
ux
xx
vx
−
=
−
=
.
Khi đó
( ) ( )
55
22
22
5
21
ln d ln d
2
1
x
x x x x x x x
x
−
− = − −
−

5
2
1
5ln20 2ln 2 2 d
1
x
x

= − − +

−

( )
( )
2
5
5ln 5.2 2ln2 2 ln 1
2
xx= − − + −
( )
5ln5 8ln2 10 4 ln4 ln1= + − − + −
5ln5 6ln2 6= + −
.
Suy ra
5a =
,
6b =
,
6c =−
2 5 2.6 6 23S a b c= + − = + + =
.
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 55
A - Bài tập minh họa:
Câu 1: Cho
( )
fx
là hàm số có đạo hàm trên
1;4
, biết
( )
4
1
d 20f x x =
và
( )
4 16f =
,
( )
17f =
. Tính
( )
4
1
dI xf x x
=
.
Ⓐ.
37I =
. Ⓑ.
47I =
. Ⓒ.
57I =
. Ⓓ.
67I =
.
Lời giải
Chọn A
Xét
( )
4
1
dI xf x x
=
, dùng phương pháp tích phân từng phần :
( ) ( )
dd
dd
u x u x
v f x x v f x
==



==


Do đó:
( ) ( )
4
4
1
1
dI xf x f x x=−
( ) ( ) ( )
4
1
4 4 1 df f f x x= − −
4.16 7 20 37= − − =
PP nhanh trắc nghiệm
Câu 2: Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
0;2
và thỏa mãn
( )
02f =
,
( ) ( )
2
0
2 4 . ' d 4x f x x−=
. Tính tích phân
( )
2
0
dI f x x=
.
Ⓐ.
2I =
. Ⓑ.
2I =−
. Ⓒ.
6I =
. Ⓓ.
6I =−
.
Lời giải
Chọn B
Ta có:
( ) ( )
2
0
2 4 . ' d 4x f x x−=
.
Đặt
( )
24
d ' d
ux
v f x x
=−
=
( )
d 2dux
v f x
=
=
PP nhanh trắc nghiệm
. Phương pháp: Tích phân từng phần.
. Viết dưới dạng bằng các hợp của làm và
phần còn lại
. Tính
và
. Tính và
Dạng ④: Tích phân chứa từng phần hàm ẩn
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 56
Nên
( ) ( ) ( ) ( ) ( )
22
2
0
00
2 4 . ' d 2 4 . 2 dx f x x x f x f x x− = − −

( )
4. 0 2fI=−
82I=−
.
Theo giả thiết ta có:
4 8 2 2 4 2I I I= − = =
.
B - Bài tập rèn luyện:
Câu 1: Cho
( )
fx
có đạo hàm liên tục trên và thỏa mãn
( ) ( )
1
0
2 16, 2 d 6f f x x==
. Tính
( )
2
0
.dI x f x x
=
ta được kết quả
Ⓐ.
14I =
. Ⓑ.
20I =
. Ⓒ.
10I =
. Ⓓ.
4I =
.
Câu 2: Cho
( )
fx
có đạo hàm liên tục trên và thỏa mãn
( ) ( )
1
0
2 16, 2 d 6f f x x==
. Tính
( )
2
0
.dI x f x x
=
ta được kết quả
Ⓐ.
14I =
. Ⓑ.
20I =
. Ⓒ.
10I =
. Ⓓ.
4I =
.
Câu 3: Cho hàm số
( )
fx
có đạo hàm trên và thỏa mãn
( )
3
0
2 4 d 8x f x x
− =
;
( )
22f =
. Tính
( )
1
2
2dI f x x
−
=
.
Ⓐ.
5I =−
. Ⓑ.
10I =−
. Ⓒ.
5I =
. Ⓓ.
10I =
.
Câu 4: Cho hàm số
( )
fx
liên tục trên
0;1
. Biết
( ) ( )
1
0
1
. 1 d
2
x f x f x x

− − =

. Tính
( )
0f
.
Ⓐ.
( )
01f =−
. Ⓑ.
( )
1
0
2
f =
. Ⓒ.
( )
1
0
2
f =−
. Ⓓ.
( )
01f =
.
Câu 5: Cho hàm số
( )
fx
liên tục trên và
( )
3 21f =
,
( )
3
0
d9f x x =
. Tính tích phân
( )
1
0
. 3 dI x f x x
=
.
Ⓐ.
15I =
. Ⓑ.
12I =
. Ⓒ.
9I =
. Ⓓ.
6I =
.
Câu 6: Cho hàm số
( )
y f x=
liên tục và có đạo hàm trên thỏa mãn
( ) ( )
( )
2
5 7 1 3 2f x f x x x− − = −
,
x
. Biết rằng tích phân
( )
1
0
. ' d
a
I x f x x
b
= = −
. Tính
83T a b=−
.
Ⓐ.
1T =
.
Ⓑ.
0T =
.
Ⓒ.
16T =
. Ⓓ.
16T =−
.
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 57
Câu 7: Cho hàm số
( )
fx
có đạo hàm liên tục trên tập hợp thỏa mãn
( )
2
1
3 6 d 3f x x−=
và
( )
32f −=
. Giá trị của
( )
0
3
dx f x x
−
bằng
Ⓐ.
3−
. Ⓑ.
11
. Ⓒ.
6
. Ⓓ.
9
.
Câu 8: Cho hàm số
( )
y f x=
có đạo hàm
( )
fx
liên tục trên
0;2
và
( )
23f =
,
( )
2
0
d3f x x =
.
Tính
( )
2
0
.dx f x x
.
Ⓐ.
3−
. Ⓑ.
3
. Ⓒ.
0
. Ⓓ.
6
.
Câu 9: Cho hàm số
( )
y f x=
có đạo hàm là
( )
'fx
liên tục trên đoạn [0; 1] và
( )
12f =
. Biết
( )
1
0
1f x dx =
, tính tích phân
( )
1
0
.'I x f x dx=
.
Ⓐ.
1I =
. Ⓑ.
1I =−
. Ⓒ.
3I =
. Ⓓ.
3I =−
.
Câu 10: Cho hàm số
( )
fx
thỏa mãn
( ) ( )
1
0
1 ' 10x f x dx+=
và
( ) ( )
2 1 0 2ff−=
. Tính
( )
1
0
I f x dx=
.
Ⓐ.
8I =
. Ⓑ.
8I =−
. Ⓒ.
4I =
. Ⓓ.
4I =−
.
Câu 11: Cho hàm số
( )
fx
có đạo hàm liên tục trên đoạn
0;2
và thỏa mãn
( )
2 16f =
,
( )
2
0
d4f x x =
. Tính tích phân
( )
1
0
. 2 dI x f x x
=
.
Ⓐ.
12I =
. Ⓑ.
7I =
. Ⓒ.
13I =
. Ⓓ.
20I =
.
Câu 12: Cho hàm số có đạo hàm liên tục trên và thỏa mãn , .
Tính .
Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. .
Câu 13: Cho hàm số
y f x
thỏa mãn
3
3 1 3 2, .f x x x x
Tính
5
1
.I x f x dx
.
Ⓐ.
5
4
. Ⓑ.
17
4
. Ⓒ.
33
4
. Ⓓ.
1761−
.
BẢNG ĐÁP ÁN
1.B
2.B
3.B
4.C
5.D
6.B
7.A
8.B
9.A
10.B
11.B
12.B
13.C
Lời giải chi tiết
Câu 1:
Ta có
( ) ( ) ( ) ( )
1 1 2
0 0 0
1
2 d 6 2 d 2 6 d 12
2
f x x f x x f x x= = =
.
( )
y f x=
( )
21f −=
( )
2
1
2 4 d 1f x x−=
( )
0
2
dxf x x
−
1I =
0I =
4I =−
4I =
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 58
Xét
( )
2
0
.dI x f x x
=
Đặt
( ) ( )
dd
dd
u x u x
v f x x v f x
==



==


Khi đó
( ) ( ) ( )
2
0
2
d 2 2 12 20
0
I xf x f x x f= − = − =
.
Câu 2:
Ta có
( ) ( ) ( ) ( )
1 1 2
0 0 0
1
2 d 6 2 d 2 6 d 12
2
f x x f x x f x x= = =
.
Xét
( )
2
0
.dI x f x x
=
Đặt
( ) ( )
dd
dd
u x u x
v f x x v f x
==



==


Khi đó
( ) ( ) ( )
2
0
2
d 2 2 12 20
0
I xf x f x x f= − = − =
.
Câu 3:
Xét
( )
3
0
2 4 d 8J x f x x
= − =
.
Đặt
ux=
và
( ) ( )
1
d 2 4 d d 2 4
2
v f x x f x

= − = −


, ta được
ddux=
và
( )
1
24
2
v f x=−
.
( ) ( )
3
0
3
11
. 2 4 2 4 d
0
22
J x f x f x x = − − −
( ) ( )
3
0
31
2 2 4 d
22
f f x x= − −
( )
2
0
1
3 2 4 d
2
f x x= − −
.
Vì
8J =
( )
3
0
1
3 2 4 d 8
2
f x x − − =
( )
3
0
2 4 d 10f x x − = −
.
Đặt
2 2 4 2d 2d d dt x t x t x= − = =
Đổi cận:
x
0
3
t
2−
1
( ) ( )
11
1
22
2 d 2 d 10I f t t f x x
−−
= = = −

.
Vậy
10I =−
.
Câu 4: Ta có
( ) ( ) ( ) ( )
1 1 1
0 0 0
. 1 d . 1 d dA x f x f x x x f x x f x x


= − − = − −

.
Đặt
( )
1
0
. 1 dI x f x x
=−
.
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 59
Đặt
( ) ( )
dd
d 1 d 1
u x u x
v f x x v f x
==



= − = − −


Khi đó
( ) ( ) ( ) ( )
11
1
0
00
1 . 1 d 0 dI f x x f x x f f x x= − − + − = − +

Do đó
( ) ( ) ( ) ( )
11
00
11
0 d d 0
22
A f f x x f x x f= − + − = = −

.
Câu 5:
Đặt
dd
1
d (3 )d
(3 )
3
ux
ux
v f x x
v f x
=
=

=
=
.
Suy ra
13
00
1
1 1 1 1
. (3 ) (3 )d (3) ( )d 6
0
3 3 3 9
I x f x f x x f f x x= − = − =

.
Vậy
6I =
.
Câu 6:
Ta có :
( ) ( )
( )
2
5 7 1 3 2f x f x x x− − = −
Lần lượt chọn
0, 1xx==
, ta có hệ sau :
( ) ( )
( ) ( )
( )
( )
5
1
5 0 7 1 0
8
5 1 7 0 3
7
0
8
f
ff
ff
f
=
−=


− = −
=
Tính
( )
1
0
. ' dxI x f x=
Đặt :
( )
' dx
ux
dv f x
=
=
Chọn
( )
ddux
v f x
=
=
( ) ( )
1
1
0
0
5
. dx
8
I x f x f x J= − = −
Đặt
1xt=−
( ) ( )
01
10
1 dt 1 dxJ f t f x K = − − = − =

. Suy ra
( )
1
2
0
5 7 3 2 dx 2J K x x− = − = −
Ta có :
1
5 7 2
JK
JK
JK
=
= =
− = −
Vậy
3
53
1
8
88
a
I
b
=
−
= − =
=
8 3 0T a b = − =
Câu 7:
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 60
Đặt
3 6 d 3dt x t x= − =
.
Đổi cận:
13xt= = −
,
20xt= =
.
( ) ( ) ( ) ( )
2 0 0 0
1 3 3 3
1
3 6 d d 3 d 9 d 9
3
f x x f t t f t t f x x
− − −
− = = = =
.
Đặt
( ) ( )
dd
dd
u x u x
v f x x v f x
==



==


Khi đó
( )
0
3
dx f x x
−
( ) ( )
0
0
3
3
dxf x f x x
−
−
=−
( ) ( )
0. 0 3. 3 9 3ff= + − − = −
.
Câu 8:
Ta có
( )
2
0
.dx f x x
( )
( )
2
0
dx f x=
( ) ( )
2
2
0
0
.dx f x f x x=−
( )
2 2 3 3f= − =
.
Câu 9: Ta có:
( )
1
0
.'I x f x dx=
Đặt
u x du dx= =
,
( )
'dv f x dx=
chọn
( ) ( )
'v f x dx f x==
( ) ( ) ( ) ( ) ( )
11
1
0
00
. 1. 1 0. 0 2 1 1I x f x f x dx f f f x dx = − = − − = − =

Chọn A
Câu 10:
( ) ( )
1
0
1'A x f x dx=+
Đặt
1u x du dx= + =
,
( )
'dv f x dx=
chọn
( )
v f x=
( ) ( ) ( ) ( ) ( ) ( )
1 1 1 1
1
0
0 0 0 0
1 . 2 (1) (0) 2 10 8A x f x f x dx f f f x dx f x dx f x dx = + − = − − = − = = −
Câu 11:
Đặt
( )
( )
dd
2
d 2 d
2
ux
ux
fx
v f x x
v
=
=


=
=
.
Khi đó:
( )
( )
( )
( )
12
1
0
00
. 2 2
1 1 16 1
2 d d .4 7
2 2 2 4 2 4
x f x f
I f x x f t t= − = − = − =

.
Câu 12:
Đặt , đổi cận , .
.
Đặt , .
Vậy .
Câu 13:
Đặt
5
5
1
1
u x du dx
I xf x f x dx
dv f x dx v f x
.
Từ
3
5 5 1
3 1 3 2
1 2 0
fx
f x x x
fx
, suy ra
5
1
23 .I f x dx
2 4 d 2dt x t x= − =
12xt= = −
20xt= =
( ) ( )
20
12
1
1 2 4 d d
2
f x x f t t
−
= − =

( )
0
2
d2f t t
−
=
( )
0
2
d2f x x
−
=
ddu x u x= =
( ) ( )
ddv f x x v f x
= =
( )
0
2
dxf x x
−
( ) ( )
0
0
2
2
dxf x f x x
−
−
=−
( )
2 2 2f= − −
2.1 2 0= − =
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 61
Đặt
2
3
33
31
32
dt x dx
t x x
f t x
Đổi cận: Với
3
1 1 3 1 0t x x x
và
3
5 3 1 5 1t x x x
.
Khi đó
51
2
10
33
23 23 3 2 3 3
4
Casio
I f x dx x x dx
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 62
FB: Duong Hung
A - Bài tập minh họa:
Câu 1: Din tch hnh phng gii hn bi đ th hm s
2
cosyx=
, trc honh, đưng thng
0x =
và
x
=
là
Ⓐ.
8
. Ⓑ.
6
. Ⓒ.
4
. Ⓓ.
2
.
Lời giải
Chọn D
Diện tích
S
cần tìm:
2
00
1 cos2 1 sin2
cos
00
2 2 4 2
xx
S xdx dx x


+
= = = + =

.
PP nhanh trắc nghiệm
Casio
Câu 2: Diện tích hình phẳng giới hạn bởi đồ thị hàm số
3
4y x x=−
, trục hoành, đường thẳng
2x =−
và
4x =
là.
Bài 5: DIỆN TÍCH HÌNH PHẲNG
①
. Hình phẳng giới hạn bởi
Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số liên tục trên đoạn ,
trục hoành và hai đường thẳng được tính theo công thức (1)
②. Phương pháp trắc nghiệm:
Tính chất: Hàm số liên tục trên K (khoảng đoạn, nửa khoảng) và là ba số
bất kỳ thuộc K. Khi đó, ta có
Xác định các yếu tố cần thiết như công thức
Sử dụng chức năng tính tích phân có sẵn trong máy tính Casio để tính.
Chú ý: Nếu đề bài chưa cho ( cận tích phân) thì ta cần giải phương trình hoành độ
giao điểm để tìm cận tích phân.
Dạng ①: Ứng dụng của tích phân tính diện tích hình phẳng.
CHƯƠNG ③:
Full Chuyên
đề 12 new
2020-2021
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 63
Ⓐ. 44. Ⓑ.24. Ⓒ. 48. Ⓓ.28.
Lời giải
Chọn A
Diện tích cần tìm
4
3
-2
-4S x xdx=
Ta có:
( )
32
0
4 4 0
2
x
x x x x
x
=
− = − =
=
Vậy
0 2 4
3 3 3
-2 0 2
4 4 4S x x dx x xdx x xdx= − + − + −
4 2 4 2 4 2
0 2 4
4
4 4 44
2 0 2
4 2 4 2 4 2
x x x x x x
= − + − + − =
−
PP nhanh trắc nghiệm
Casio
Câu 3: Diện tích hình phẳng giới hạn bởi đồ thị của hàm số
1
()
x
fx
x
−
=
, trục hoành, hai đường
thẳng
1x =
và
2x =
là.
Ⓐ.
ln2
. Ⓑ.
ln2 1−
. Ⓒ.
ln2 1+
. Ⓓ.
1 ln2−
.
Lời giải
Chọn D
Phương trình hoành độ giao điểm:
1
01
x
x
x
−
= =
Suy ra
( )
2 2 2
1 1 1
2
1 1 1
1 ln 1 ln2
1
xx
S dx dx x x
x x x
−−

= = = − = − = −


.
PP nhanh trắc nghiệm
Casio
B - Bài tập rèn luyện:
Câu 1: Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số
( )
y f x=
liên tục, trục hoành và
hai đường thẳng
, x a x b==
được tính theo công thức:
Ⓐ.
( )
b
a
S f x dx=
. Ⓑ.
( )
b
a
S f x dx=
.
Ⓒ.
( ) ( )
0
0
b
a
S f x dx f x dx=+

. Ⓓ.
( ) ( )
0
0
b
a
S f x dx f x dx=−

.
Câu 2: Diện tích hình phẳng giới hạn bởi các đường
2
, 0, 0y x x y x= − = =
và
2x =
được tính bởi
công thức:
Ⓐ.
( )
2
2
0
x x dx−
. Ⓑ.
( ) ( )
21
22
10
x x dx x x dx− − −

.
Ⓒ.
( ) ( )
12
22
01
x x dx x x dx− + −

. Ⓓ.
( )
1
2
0
x x dx−
.
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 64
Câu 3: Diện tích hình phẳng được giới hạn bởi đồ thị của hàm số
2
yx=
, trục hoành và hai đường
thẳng
1, 3xx= − =
là.
Ⓐ.
28
9
Ⓑ.
28
3
Ⓒ.
1
3
Ⓓ.
4
3
Câu 4: Diện tích hình phẳng giới hạn bởi đồ thị hàm số
sin 1,yx=+
trục hoành và hai đường thẳng
0x =
và
7
6
x
=
là.
Ⓐ.
37
1
26
+−
. Ⓑ.
37
1
26
++
. Ⓒ.
37
1
23
++
. Ⓓ.
37
1
46
+−
.
Câu 5: Diện tích hình phẳng giới hạn bởi hàm số
2
1y x x=+
, trục
Ox
và đường thẳng
1x =
là.
Ⓐ.
2 2+1
3
Ⓑ.
3 2 1
3
−
Ⓒ.
2 2 1
3
−
Ⓓ.
32
3
−
Câu 6: Tính diện tích
S
của hình phẳng được giới hạn bởi đồ thị hàm số
( )
.ln 3 1y x x=+
, trục hoành
và hai đường thẳng
0; 1xx==
Ⓐ.
41
ln2
9 12
S =−
. Ⓑ.
21
ln2
9 12
S =−
. Ⓒ.
71
ln2
9 12
S =−
. Ⓓ.
81
ln2
9 12
S =−
.
Câu 7: Diện tích hình phẳng giới hạn bởi đồ thị hàm số
lnyx=
, trục Ox và đường thẳng
xe=
là.
Ⓐ. 1. Ⓑ.
1
1
e
−
. Ⓒ.
e
. Ⓓ.2.
Câu 8: Diện tích hình phẳng giới hạn bởi đồ thị hàm số
x
ye=
, trục
Ox
, trục
Oy
và đường thẳng
2x =
là.
Ⓐ.
4e+
. Ⓑ.
2
2ee−+
. Ⓒ.
2
3
2
e
+
. Ⓓ.
2
1e −
.
Câu 9: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
42
21y x x−=+
và trục
Ox
Ⓐ.
1S =
. Ⓑ.
2S =
. Ⓒ. S =
1
2
. Ⓓ.S =
16
15
.
Câu 10: Diện tích hình phẳng giới hạn bởi đồ thị hàm số
32
3y x x= − +
và trục hoành là.
Ⓐ.
27
4
. Ⓑ.
5
6
. Ⓒ.
4
9
. Ⓓ.
24
7
.
Câu 11: Diện tích hình phẳng giới hạn bởi đường cong
2
2y x x= − +
và trục hoành là
Ⓐ.
4
3
. Ⓑ.
29
3
. Ⓒ.
8
3
. Ⓓ.
20
3
.
Câu 12: Diện tích hình phẳng giới hạn bởi đồ thị hàm số
4
1yx=−
và trục hoành là
Ⓐ.
7
4
. Ⓑ.
8
5
. Ⓒ.
1
2
. Ⓓ.
1
.
BẢNG ĐÁP ÁN
1.A
2.B
3.B
4.B
5.C
6.D
7.A
8.A
9.D
10.A
11.A
12.B
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 65
A - Bài tập minh họa:
Câu 1:
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
2
2yx=−
và
.yx=
Ⓐ.
9
.
2
Ⓑ.
7
. Ⓒ.
5
. Ⓓ.
11
2
.
Lời giải
Chọn A
Phương trình hoành độ giao điểm của hai đồ thị là
22
2
2 2 0 .
1
x
x x x x
x
=−
− = + − =
=
Diện tích của hình phẳng cần tìm là
11
22
22
1
32
2
2 ( 2)
9
2.
3 2 2
S x x dx x x dx
xx
x
−−
−
= − − + = − − +

= − − + =



PP nhanh trắc nghiệm
Casio:
Câu 2: Gọi
S
là diện tích của hình phẳng giới hạn bởi các đường
2
ln x
y
x
=
,
0y =
,
1x =
,
ex =
. Mệnh
đề nào dưới đây đúng?
-Phương pháp:
Diện tích hình phẳng giới hạn bởi hai đồ thị: , và hai đường
thẳng được xác định bởi công thức: .
Chú ý: Để phá bỏ dấu giá trị tuyệt đối ta thường làm như sau:
* Giải phương trình: tìm nghiệm , .
Tính:
.
Ngoài cách trên, ta có thể dựa vào đồ thị để khử dấu giá trị tuyệt đối.
Dạng ②: Ứng dụng của tích phân tính diện tích hình phẳng.
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 66
Ⓐ.
e
2
1
ln
d
x
Sx
x
=
. Ⓑ.
e
2
1
ln
d
x
Sx
x
=
. Ⓒ.
2
e
2
1
ln
d
x
Sx
x

=


. Ⓓ.
2
e
2
1
ln
d
x
Sx
x

=


.
Lời giải
Chọn B
Ta có
e
2
1
ln
d
x
Sx
x
=
.
Vì
e
22
1
ln ln
[1;e], ln 0 0 d
xx
x x S x
xx
=
.
PP nhanh trắc nghiệm
Casio
Câu 3: Tính diện tích S của hình phẳng giới hạn bởi các đường
( )
1 lny x x=+
, trục hoành và đường
thẳng
xe=
.
Ⓐ.
2
5
4
e
S
+
=
. Ⓑ.
2
7
6
e
S
+
=
. Ⓒ.
2
3
2
e
S
+
=
. Ⓓ.
2
9
8
e
S
+
=
.
Lời giải
Chọn C
Xt phương trình hoành độ giao điểm:
( )
1 ln 0xx+=
(Điều kiện:
0x
).
1 0 1
ln 0 1
xx
xx
+ = = −



==

.
Vì
0x
nên
1x =
.
Ta có:
( ) ( )
11
1 ln d 1 ln d
ee
S x x x x x x= + = +

.
Đặt
( )
2
1
dd
ln
d 1 d
2
ux
ux
x
v x x
x
vx
=
=


=+
=+
.
2 2 2
11
1
2 2 2
1
1
ln d 1 d
2 2 2 2
5
2 4 4
e
ee
e
x x e x
S x x x x e x
x
e x e
ex

= + − + = + − +



+
= + − + =



PP nhanh trắc nghiệm
Casio
B - Bài tập rèn luyện:
Câu 1: Tính diện tích hình phẳng giới hạn bởi đồ thị hai hàm số
2
4yx= − +
và
2yx= − +
?
Ⓐ.
5
7
. Ⓑ.
8
3
. Ⓒ.
9
2
. Ⓓ.
9
.
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 67
Câu 2: Gọi
S
là diện tích hình phẳng giới hạn bởi đồ thị của hàm số
( )
1
:
1
x
Hy
x
−
=
+
và các trục tọa
độ. Khi đó giá trị của
S
bằng
Ⓐ.
2ln 2 1−
. Ⓑ.
ln2 1+
. Ⓒ.
ln2 1−
. Ⓓ.
2ln 2 1+
.
Câu 3: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
2
1yx=+
và đường thẳng
3yx=+
.
Ⓐ.
9
2
. Ⓑ.
13
3
. Ⓒ.
11
3
. Ⓓ.
7
2
.
Câu 4: Tính diện tích hình phẳng giới hạn bởi hai đồ thị hàm số
yx=
;
6yx=−
và trục hoành.
Ⓐ.
22
3
. Ⓑ.
16
3
. Ⓒ.
2
. Ⓓ.
23
3
.
Câu 5: Tính diện tích hình phẳng giới hạn bởi đồ thị các hàm số
2
y x x=−
và
3yx=
.
Ⓐ.
5
3
S =
. Ⓑ.
16
3
S =
. Ⓒ.
9S =
. Ⓓ.
32
3
S =
.
Câu 6: Diện tích hình phẳng giới hạn bởi parabol
( )
2
:2yxP x=−
và đường thẳng
( )
:d yx=
bằng
Ⓐ.
17
6
. Ⓑ.
11
2
. Ⓒ.
9
2
. Ⓓ.
23
6
.
Câu 7: Diện tích hình phẳng giới hạn bởi parabol
2
yx=−
và đường thẳng
2yx= − −
bằng
Ⓐ.
9
2
. Ⓑ.
5
2
. Ⓒ.
11
2
. Ⓓ.
1
2
2
−
.
Câu 8: Diện tích hình phẳng giới hạn bởi đồ thị hàm số
2
yx=
và đường thẳng
2yx=
là
Ⓐ.
4
3
. Ⓑ.
5
3
. Ⓒ.
3
2
. Ⓓ.
23
15
.
Câu 9: Tính diện tích
S
của hình phẳng
()H
giới hạn bởi các đường cong
3
12y x x= − +
và
2
yx=−
.
Ⓐ.
937
12
S =
. Ⓑ.
343
12
S =
. Ⓒ.
793
4
S =
. Ⓓ.
397
4
S =
.
Câu 10: Thể tích khối tròn xoay khi quay hình phẳng
( )
H
xác định bởi các đường
32
1
3
y x x=−
,
0y =
,
0x =
và
3x =
quanh trục
Ox
là
Ⓐ.
81
35
. Ⓑ.
81
35
. Ⓒ.
71
35
. Ⓓ.
71
35
.
Câu 11: Diện tích hình phẳng giới hạn bởi đồ thị các hàm số
22
2 1, 2 4 1y x x y x x= − + + = − +
là
Ⓐ.
8
. Ⓑ.
5
. Ⓒ.
4
. Ⓓ.
10
.
Câu 12: Diện tích hình phẳng giới hạn bởi hai parabol
2
1
2
yx=
và
2
6yx=−
bằng
Ⓐ.
2
2
2
3
6
2
x
dx
−

−


. Ⓑ.
23
2
23
6
2
x
dx
−

−


.
Ⓒ.
2
2
2
3
6
2
x
dx
−

−−


. Ⓓ.
23
2
23
6
2
x
dx
−

−−


.
Câu 13: Diện tích
S
của hình phẳng giới hạn bởi đồ thị hai hàm số
3
yx=−
và
2
2y x x=−
là
Ⓐ.
9
4
S =
. Ⓑ.
7
3
S =
. Ⓒ.
37
12
S =
. Ⓓ.
4
3
S =
.
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 68
Câu 14: Gọi
S
là diện tích hình phẳng giới hạn bởi các đồ thị hàm số:
3
3;y x x y x= − =
. Tính
S
?
Ⓐ.
4S =
. Ⓑ.
8S =
. Ⓒ.
2S =
. Ⓓ.
0S =
.
Câu 15: Hình phẳng giới hạn bởi các đường cong
( )
1y x x=−
và
3
y x x=−
có diện tích bằng
Ⓐ.
37
12
. Ⓑ.
5
12
. Ⓒ.
8
3
. Ⓓ.
9
4
.
Câu 16: Diện tích
S
của hình phẳng giới hạn bởi các đường
2
21y x x= − −
và
2
3yx= − +
là
Ⓐ.
9S =
. Ⓑ.
9S =−
. Ⓒ.
3S =
. Ⓓ.
9
2
S =
.
Câu 17: Tính diện tích
S
của hình phẳng giới hạn bởi đồ thị của hai hàm số
3
32y x x= − +
và
2.yx=+
Ⓐ.
8S =
. Ⓑ.
4S =
. Ⓒ.
12S =
. Ⓓ.
16S =
.
Câu 18: Diện tích hình phẳng giới hạn bởi parabol
2
31y x x= − +
và đường thẳng
1yx=+
được tính
theo công thức nào dưới đây?
Ⓐ.
( )
4
2
0
4dx x x−
. Ⓑ.
( )
4
2
0
4dx x x−+
. Ⓒ.
( )
4
2
0
4dx x x+
. Ⓓ.
( )
4
2
0
2dx x x−−
.
Câu 19: Tính diện tích hình phẳng giới hạn bởi các đường
2
5 0, 3 0y x x y+ − = + − =
.
Ⓐ.
19
6
. Ⓑ.
15
2
. Ⓒ.
37
6
. Ⓓ.
9
2
.
Câu 20: Diện tích hình phẳng giới hạn bởi các đường
3
, 10y x y x= = −
và trục
Ox
là
Ⓐ.
32
. Ⓑ.
26
. Ⓒ.
36
. Ⓓ.
40
.
BẢNG ĐÁP ÁN
1.C
2.A
3.A
4.A
5.D
6.C
7.A
8.A
9.A
10.A
11.C
12.C
13.C
14.B
15.A
16.A
17.A
18.B
19.D
20.C
-Phương pháp:
.Minh họa các dạng thường gặp:
có hai loại dấu trên
. Ghi nhớ: Quan sát hình phẳng mang dấu + hay -
Dạng ③: Diện tích hình phẳng thông qua đồ thị
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 69
A - Bài tập minh họa:
Câu 1: Cho hàm số
( )
y f x=
và
( )
y g x=
có đồ thị
giao nhau tại hai điểm phân biệt có
hoành độ
a
và
b
. Gọi
( )
H
là hình phẳng
được giới hạn bởi đồ thị hai hàm số này
(phần tô đậm ở hình vẽ).
Diện tích của
( )
H
được tính theo công
thức
Ⓐ.
( ) ( )
d
b
a
S f x g x x=−


. Ⓑ.
( ) ( )
d
b
a
S g x f x x=−


.
Ⓒ.
( ) ( )
d
b
a
S f x g x x=+


. Ⓓ.
( ) ( )
d
b
a
S f x g x x= − +


.
Lời giải
Chọn B
Áp dụng công thức
( ) ( )
d
b
a
S f x g x x=−
.
Quan sát hình vẽ ta thấy
( ) ( )
g x f x
trên
,ab
Vậy
( ) ( ) ( ) ( )
( )
dd
bb
aa
S f x g x x g x f x x= − = −

.
PP nhanh trắc nghiệm
Quan sát nhanh
( ) ( )
g x f x
( ) ( )
( )
d
b
a
S g x f x x=−
Câu 2: Cho hàm số
( )
y f x=
liên tục trên đoạn
;ab
. Gọi
D
là diện tích
hình phẳng giới hạn bởi đồ thị
( ) ( )
:C y f x=
, trục hoành, hai
đường thẳng
xa=
,
xb=
(như hình vẽ dưới đây).
Giả sử
D
S
là diện tích hình phẳng
D
. Chọn công thức đúng
trong các phương án
, , ,A B C D
cho dưới đây?
Ⓐ.
( ) ( )
0
0
b
D
a
S f x dx f x dx=+

. Ⓑ.
( ) ( )
0
0
b
D
a
S f x dx f x dx= − +

.
Ⓒ.
( ) ( )
0
0
b
D
a
S f x dx f x dx=−

. Ⓓ.
( ) ( )
0
0
b
D
a
S f x dx f x dx=−

Lời giải
Chọn B
PP nhanh trắc nghiệm
Quan sát dấu của hình phẳng
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 70
( ) ( ) ( )
( ) ( )
0
0
0
0
bb
D
aa
b
a
S f x dx f x dx f x dx
f x dx f x dx
= = +
= − +

Câu 3: Cho hình thang cong
( )
H
giới hạn bởi các đường
x
ye=
,
0y =
,
0x =
,
ln4x =
. Đường thẳng
( )
0 ln4x k k=
chia
( )
H
thành hai phần có diện tích là
1
S
và
2
S
như
hình vẽ bên. Tìm
k
để
12
2SS=
.
Ⓐ.
2
ln4
3
k =
. Ⓑ.
ln2k =
.
Ⓒ.
8
ln
3
k =
. Ⓓ.
ln3k =
.
Lời giải
Chọn D
Ta có
1
0
0
1
k
k
x k k
S e dx e e= = = −
và
ln4
ln4
2
0
4
x x k
k
S e dx e e= = = −
Ta có
( )
12
2 1 2 4 ln3
kk
S S e e k= − = − =
.
PP nhanh trắc nghiệm
Tính Nhập vào máy
0
ln4
A
x
x
k
e dx
e dx
và
CALC với các giá trị của A lần lượt
ở 4 phương án. Giá trị nào cho kết
quả bằng 2 thì chọn.
B - Bài tập rèn luyện:
Câu 1: Cho hàm số
( )
y f x=
có đồ thị như hình dưới đây.
Diện tích hình phẳng giới hạn bởi đồ thị hàm số
( )
y f x=
và
trục
Ox
là
Ⓐ.
S =
( ) ( )
20
01
ddf x x f x x
−
−

.
Ⓑ.
( )
2
1
dS f x x
−
=
.
Ⓒ.
( )
2
1
dS f x x
−
=−
.
Ⓓ.
( ) ( )
02
10
ddS f x x f x x
−
=−

.
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 71
Câu 2: Cho hàm số
( )
y f x=
liên tục trên và có đồ thị
( )
C
là đường cong như hình bên dưới.
Diện tích hình phẳng giới hạn bởi đồ thị
( )
C
, trục hoành và hai đường thẳng
0x =
,
2x =
là
Ⓐ.
( ) ( )
12
01
ddf x x f x x−

.
Ⓑ.
( )
2
0
df x x
.
Ⓒ.
( ) ( )
12
01
ddf x x f x x−+

.
Ⓓ.
( )
2
0
df x x
.
Câu 3: Cho đồ thị hai hàm số
32
33y x x x= − + +
và
2
21y x x= − + +
như hình sau
Diện tích phần hình phẳng được gạch sọc tính theo
công thức nào dưới đây?
Ⓐ.
( ) ( )
12
3 2 3 2
11
2 2 d 2 2 dx x x x x x x x
−
− − + + − + + −

.
Ⓑ.
( )
2
32
1
2 2 dx x x x
−
− − +
.
Ⓒ.
( ) ( )
12
3 2 3 2
11
2 2 d 2 2 dx x x x x x x x
−
− + + − + − − +

.
Ⓓ.
( )
2
32
1
2 2 dx x x x
−
− + + −
.
Câu 4: Cho hàm số
()y f x=
liên tục trên và có đồ thị là đường cong như hình bên. Diện tích hình
phẳng giới hạn bởi đồ thị, trục hoành và hai đường thẳng
0, 2==xx
là
Ⓐ.
12
01
( )d ( )dS f x x f x x= − +

.
Ⓑ.
12
01
( )d ( )dS f x x f x x=−

.
Ⓒ.
2
0
( )dS f x x=
.
Ⓓ.
2
0
( )dS f x x=
.
Câu 5: Diện tích phần hình phẳng gạch chéo trong hình vẽ được tính theo công thức nào dưới đây?
Ⓐ.
( )
2
2
1
2 2 4 dx x x
−
−−
. Ⓑ.
( )
2
1
2 2 dxx
−
−+
.
Ⓒ.
( )
2
1
2 2 dxx
−
−
. Ⓓ.
( )
2
2
1
2 2 4 dx x x
−
− + +
.
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 72
Câu 6: Cho đồ thị hàm số
( )
y f x=
như hình vẽ.Diện tích
S
của hình phẳng được giới hạn bởi đồ
thị hàm số
( )
y f x=
và trục
Ox
được tính bởi công thức
Ⓐ.
( )
3
3
dS f x x
−
=
.
Ⓑ.
( )
3
3
dS f x x
−
=
.
Ⓒ.
( ) ( )
13
31
ddS f x x f x x
−
=−

.
Ⓓ.
( ) ( )
13
31
ddS f x x f x x
−
=+

.
Câu 7: Diện tích hình phẳng giới hạn bởi parabol
2
( 2) ,yx=−
đường
cong
3
yx=
và trục hoành bằng
Ⓐ.
11
.
2
Ⓑ.
73
.
12
Ⓒ.
7
.
12
Ⓓ.
5
.
2
Câu 8: Hình phẳng giới hạn bởi đồ thị hàm số
( )
y f x=
và trục
hoành gồm hai phần, phần nằm phía trên trục hoành có diện
tích
1
8
3
S =
và phần nằm phía dưới trục hoành có diện tích
2
5
12
S =
. Tính
( )
0
1
31I f x dx
−
=+
.
Ⓐ.
5
3
I =
. Ⓑ.
3
4
I =
.
Ⓒ.
37
36
I =
. Ⓓ.
27
4
I =
.
Câu 9: Diện tích phần tô đậm trong hình bên được tính theo công
thức nào trong các công thức sau?
Ⓐ.
( )
1
32
0
3 2 dx x x x− + −
.
Ⓑ.
( )
1
32
0
3 2 dx x x x−+
.
Ⓒ.
( )
2
32
0
3 2 dx x x x− + −
.
Ⓓ.
( )
2
32
0
3 2 dx x x x−+
.
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 73
Câu 10: Gọi
( )
H
là phần hình phẳng gạch chéo trong hình vẽ dưới
đây được giới hạn bởi đồ thị của các hàm số
2
3yx=
,
4yx=−
và trục hoành. Diện tích của
( )
H
là bằng bao
nhiêu?
Ⓐ.
11
2
. Ⓑ.
9
2
.
Ⓒ.
13
2
. Ⓓ.
7
2
.
Câu 11: Cho hàm số
( )
y f x=
liên tục trên và có đồ thị như hình vẽ
dưới đây. Biết diện tích hai phần
A
và
B
lần lượt là
16
3
và
63
4
,
tính
( )
3
2
1
2 1 df x x
−
+
.
Ⓐ.
253
12
. Ⓑ.
253
24
.
Ⓒ.
125
24
−
. Ⓓ.
125
12
−
.
Câu 12: Tính diện tích
S
của hình phẳng (phần gạch sọc) giới hạn bởi hai đồ thị hàm số
( ) ( )
;2f x x g x x= = −
trong hình sau
Ⓐ.
8
3
. Ⓑ.
12
3
.
Ⓒ.
7
3
. Ⓓ.
10
3
.
Câu 12: Gọi S là diện tích hình phẳng
( )
H
giới hạn bởi các đường
( )
y f x=
, trục hoành và 2 đường
thẳng
1, 2xx= − =
trong hình vẽ bên.
Đặt
( ) ( )
02
12
10
d , dS f x x S f x x
−
==

. Mệnh đề nào sau đây
đúng?
Ⓐ.
12
S S S=+
. Ⓑ.
12
S S S= − −
.
Ⓒ.
12
S S S=−
. Ⓓ.
21
S S S=−
.
O
x
4
2
2
y
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 74
Câu 13: Diện tích hình mặt phẳng gạch sọc trong hình vẽ bên bằng
Ⓐ.
3
1
2d
x
x
. Ⓑ.
( )
3
1
2 2 d
x
x−
.
Ⓒ.
( )
3
1
2 2 d
x
x−
. Ⓓ.
( )
3
1
2 2 d
x
x+
.
Câu 14: Diện tích của hình phẳng được giới hạn bởi đồ thị hàm số
( )
y f x=
, trục hoành và hai đường
thẳng
xa=
,
xb=
( )
ab
tính theo công thức nào dưới đây ?
Ⓐ.
( ) ( )
dd
cb
ac
S f x x f x x=+

.
Ⓑ.
( )
d
b
a
S f x x=
.
Ⓒ.
( ) ( )
dd
cb
ac
S f x x f x x= − +

.
Ⓓ.
( )
d
b
a
S f x x=
.
Câu 15: Cho hàm số
( )
y f x=
có đồ thị như hình vẽ dưới đây. Diện tích hình phẳng được tính bằng
công thức nào?
Ⓐ.
0
0
( ) - ( )
b
a
S f x dx f x dx=

.
Ⓑ.
0
0
( ) ( )
b
a
S f x dx f x dx=+

.
Ⓒ.
0
2 ( )
b
S f x dx=
.
Ⓓ.
()
b
a
S f x dx=
.
x
y
a
O
b
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 75
Câu 16: Cho đồ thị hàm số
( )
y f x=
. Diện tích hình phẳng là:
Ⓐ.
( ) ( )
04
-3 0
S f x dx f x dx=+

.
Ⓑ.
( )
4
-3
S f x dx=
.
Ⓒ.
( )
4
-3
S f x dx=
.
Ⓓ.
( ) ( )
04
-3 0
S f x dx f x dx=−

.
Câu 17: Cho đồ thị hàm số
( )
y f x=
trên đoạn
0; 4
như hình vẽ và có
diện tích
12
11 9
,
62
SS==
. Tính tích phân
( )
4
0
I f x dx=
Ⓐ.
8
3
I =−
. Ⓑ.
19
3
I =
.
Ⓒ.
8
3
I =
. Ⓓ.
19
3
I =−
.
Câu 19: Cho đồ thị hàm số
( )
y f x=
trên đoạn
2; 2−
như hình vẽ ở bên và có diện tích
1 2 3
22 76
,
15 15
S S S= = =
. Tính tích phân
( )
2
-2
I f x dx=
Ⓐ.
32
15
I =
. Ⓑ.
8I =
.
Ⓒ.
18
5
I =
. Ⓓ.
32
15
I =−
.
BẢNG ĐÁP ÁN
1.D
2.A
3.A
4.B
5.D
6.C
7.C
8.B
9.B
10.A
11.C
12.D
13.D
14.C
15.C
16.A
17.D
18.D.
19.A
x
y
4
-3
O
1
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 76
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 77
FB: Duong Hung
A - Bài tập minh họa:
Câu 1: Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng
1x =
và
3x =
, biết rằng khi
cắt vật thể bởi mặt phẳng vuông góc với trục
Ox
tại điểm có hoành độ
x
(
13x
) thì
được thiết diện là một hình chữ nhật có độ dài hai cạnh là
3x
và
2
32x −
.
Ⓐ.
32 2 15.V =+
Ⓑ.
124
3
V
=
. Ⓒ.
124
3
V =
. Ⓓ.
(32 2 15) .V
=+
Lời giải
Chọn C
Diện tích thiết diện là:
2
( ) 3 . 3 2S x x x=−
Thể tích vật thể là:
3
2
1
124
3 . 3 2
3
V x x dx= − =
.
PP nhanh trắc nghiệm
Ta nhập biểu thức
3
2
1
3 . 3 2x x dx−
như sau :
y3Q(s3Q(dp2R1E3=
Màn hình hiển thị :
Chọn C
Bài 6: THỂ TÍCH VẬT THỂ TRÒN XOAY
. Phương pháp:
Gọi là phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các điểm a và b;
là diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm ,
. Giả sử là hàm số liên tục trên đoạn .
Khi đó, thể tích của vật thể B được xác định:
Dạng ①: Bài toán Thể tích vật thể:
CHƯƠNG ③:
Full Chuyên
đề 12 new
2020-2021
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 78
Câu 2: Trong không gian với hệ tọa độ
Oxyz
, cho vật thể nằm giữa hai mặt phẳng
0x =
và
3x =
.
Biết rằng thiết diện của vật thể cắt bởi mặt phẳng vuông góc với trục
Ox
tại điểm có hoành
độ
( )
03xx
là một hình vuông cạnh là
2
9 x−
. Tính thể tích
V
của vật thể.
Ⓐ.
171V =
Ⓑ.
171V
=
. Ⓒ.
18V =
. Ⓓ.
18V
=
.
Lời giải
Chọn C
Ta có thể tích của vật thể là
(
)
2
3
2
0
9dV x x=−
( )
3
3
3
2
0
0
9 d 9
3
x
x x x

= − = −


18=
.
PP nhanh trắc nghiệm
Casio
Chú ý: Diện tích hình vuông
B - Bài tập rèn luyện:
Câu 1: Trong không gian với hệ tọa độ
Oxyz
, cho vật thể
( )
H
giới hạn bởi hai mặt phẳng có phương
trình
xa=
,
( )
x b a b=
. Gọi
( )
Sx
là thiết diện của
( )
H
cắt bởi mặt phẳng vuông góc với
trục
Ox
tại điểm có hoành độ là
x
với
a x b
. Giả sử hàm số
( )
y S x=
liên tục trên đoạn
;ab
. Khi đó thể tích
V
của vật thể
( )
H
được cho bởi công thức
Ⓐ.
( )
2
d
b
a
V S x x
=


. Ⓑ.
( )
d
b
a
V S x x
=
. Ⓒ.
( )
2
d
b
a
V S x x=


. Ⓓ.
( )
d
b
a
V S x x=
.
Câu 2: Trong không gian , cho vật thể được giới hạn bởi hai mặt phẳng , vuông góc với
trục lần lượt tại , . Một mặt phẳng tùy ý vuông góc với tại điểm
có hoành độ x,
a x b
cắt vật thể theo thiết diện có diện tích là
Sx
với
y S x
là
hàm số liên tục trên . Thể tích của thể tích đó được tính theo công thức
Ⓐ.
( )
2
b
a
V S x dx=
. Ⓑ.
( )
b
a
V S x dx=
.
Ⓒ.
( )
b
a
V S x dx
=
. Ⓓ.
( )
2
b
a
V S x dx
=
.
Câu 3: Cho phần vật thế
được giới hạn bởi hai mặt phẳng
( )
P
và
( )
Q
vuông góc với trục
Ox
tại
0x =
,
3x =
. Cắt phần vật thể
bởi mặt phẳng vuông góc với trục
Ox
tại điểm có hoành độ
bằng
x
( )
03x
ta được thiết diện là hình chữ nhật có kích thước lần lượt là
x
và
3 x−
.
Thể tích phần vật thể
bằng
Oxyz
( )
P
( )
Q
Ox
xa=
xb=
( )
ab
Ox
;ab
V
O
y
x
z
S(x)
a
x
b
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 79
Ⓐ.
27
4
. Ⓑ.
12 3
5
. Ⓒ.
12 3
5
. Ⓓ.
27
4
.
Câu 4: Cho phần vật thể
( )
giới hạn bởi hai mặt phẳng
có phương trình
0x =
và
2x =
. Cắt phần
vật thể
( )
bởi mặt phẳng vuông góc với trục
Ox
tại điểm có hoành độ
x
( )
02x
, ta
được thiết diện là một tam giác đều có độ dài cạnh bằng
2xx−
. Tính thể tích
V
của phần
vật thể
( )
Ⓐ.
4
.
3
V =
Ⓑ.
3
.
3
V =
Ⓒ.
4 3.V =
Ⓓ.
3.V =
Câu 5: Cho vật thể có mặt đáy là hình tròn có bán kính bằng 1 (hình vẽ). Khi cắt vật thể bởi mặt
phẳng vuông góc với trục
Ox
tại điểm có hoành độ
x
( )
11x−
thì được thiết diện là một
tam giác đều. Tính thể tích
V
của vật thể đó.
Ⓐ.
3V =
. Ⓑ.
33V =
. Ⓒ.
43
3
V =
. Ⓓ.
V
=
.
Câu 6: Cho phần vật thể
B
giới hạn bởi hai mặt phẳng có phương trình
0x =
và
3
x
=
. Cắt phần
vật thể
B
bởi mặt phẳng vuông góc với trục
Ox
tại điểm có hoành độ
x
0
3
x




ta
được thiết diện là một tam giác vuông có độ dài hai cạnh góc vuông lần lượt là
2x
và
cos x
.
Thể tích vật thể
B
bằng
Ⓐ.
33
6
+
. Ⓑ.
33
3
−
. Ⓒ.
33
6
−
. Ⓓ.
3
6
.
Câu 7: Tính thể tích
V
của vật thể nằm giữa hai mặt phẳng
0x =
và
x
=
, biết rằng thiết diện của
vật thể bị cắt bởi mặt phẳng vuông góc với trục
Ox
tại điểm có hoành độ
x
( )
0 x

là
một tam giác đều cạnh
2 sin x
.
Ⓐ.
3V =
. Ⓑ.
3V
=
. Ⓒ.
23V
=
. Ⓓ.
23V =
.
Câu 8. Tính thể tích vật thể giới hạn bởi các mặt phẳng
0x =
và
1x =
, biết thiết diện của vật thể
khi cắt bởi mặt phẳng vuông góc với trục
Ox
tại điểm có hoành độ
x
(0 1)x
là một hình
vuông có độ dài cạnh
( )
1
x
xe−
.
Ⓐ.
2
V
=
. Ⓑ.
1
2
e
V
−
=
. Ⓒ.
1
2
V =
. Ⓓ.
( 1)
2
e
V
−
=
.
Câu 9. Cắt một vật thể
V
bởi hai mặt phẳng song song
P
,
Q
lần lượt vuông góc với trục
Ox
tại
2
x
=−
,
2
x
=
. Một mặt tùy ý vuông góc với trục
Ox
tại điểm
x
22
x


−


cắt
V
theo thiết diện có diện tích là
( )
( )
2
1S x sin x cosx=+
. Tính thể tích vật thể
V
giới hạn bởi
hai mặt phẳng
P
,
Q
.
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 80
Ⓐ.
3,14
. Ⓑ.
8
3
. Ⓒ.
13
6
. Ⓓ.
8
3
.
Câu 10. Tính thể tích của vật thể nằm giữa hai mặt phẳng
1x =−
và
1x =
, biết rằng thiết diện của vật thể
bị cắt bởi mặt phẳng vuông góc với trục
Ox
tại điểm có hoành độ
( )
11xx−
là một tam giác
vuông cân có cạnh huyền bằng
4
1 x−
.
Ⓐ.
3
4
. Ⓑ.
2
5
. Ⓒ.
4
. Ⓓ.
1
4
.
BẢNG ĐÁP ÁN
1.D
2.B
3. C
4.B
5.C
6.C
7.D
8.C
9.B
10.B
Hướng dẫn giải
Lời giải
Câu 3.
Chọn C
Ta có diện tích thiết diện là
( )
3S x x x=−
.
Vậy thể tích phần vật thể
là:
( )
3
0
dV S x x=
3
0
3dx x x=−
12 3
5
=
.
Câu 4.
Lời giải
Chọn B
Diện tích thiết diện:
( )
2
23
4
xx
S
−
=
.
( )
2
2
0
23
d
4
xx
Vx
−
=
( )
2
2
0
3
2d
4
x x x=−
( )
2
2
0
3
2d
4
x x x=−
2
34
0
3 2 1 3
4 3 4 3
xx

= − =


.
Câu 5.
Lời giải
Chọn C
Tại vị trí có hoành độ
x
( )
11x−
thì tam giác thiết diện có cạnh là
2
21 x−
.
Do đó tam giác thiết diện có diện tích
( )
(
)
2
2
3
21
4
S x x=−
( )
2
31 x=−
.
Vậy thể tích
V
của vật thể là
( )
1
2
1
3 1 dxx
−
−
43
3
=
.
Câu 6.
Lời giải
Chọn C
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 81
Thể tích vật thể
B
là
33
3 3 3
0 0 0
00
33
cos d sin sin d sin cos
6
V x x x x x x x x x x

−
= = − = + =

.
Câu 7.
Lời giải
Chọn D
Diện tích tam giác đều
( )
( )
2
3 2 sin
4
x
Sx=
3sin x=
.
Vậy thể tích
( )
0
dV S x x
=
0
3sin dxx
=
23=
.
Câu 8.
Chọn C
Lời giải
Ta có:
( ) ( )
1 1 1
2
0 0 0
( )d 1 d 1 d
xx
V S x x x e x x e x

= = − = −


.
Đặt:
( )
dd
d 1 d
x
x
ux
ux
v e x
v e x
=
=

=−
=−
.
Do đó:
( ) ( )
1
1
2
1
0
0
0
11
d 1 1 1
2 2 2
x x x
x
V x e x e x x e e e e

= − − − = − − − = − − + + =


.
Câu 9.
Chọn B
Lời giải
Ta có thể tích vật thể
V
cần tính là:
( )
( )
22
2
22
= d 1 dV S x x sin x cosx x


−−
=+

.
Đặt
ddt sinx t cosx x= =
.
Đổi cận:
1; 1
22
x t x t

= − = − = =
.
( )
1
1
3
2
1
1
8
= 1 d
33
t
V t t t
−
−

+ = + =


.
Câu 10.
Chọn B
Lời giải
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 82
Ta có diện tích thiết diện được cho bằng:
( )
( )
2
4
4
1 1 1
1
24
2
x
S x x

−
= = −



Ta có diện tích thiết diện được cho bằng:
( )
( )
2
4
4
1 1 1
1
24
2
x
S x x

−
= = −



Thể tích vật thể cần tìm là:
( )
( )
11
4
11
12
.1
45
V S x dx x dx
−−
= = − =

.
A - Bài tập minh họa:
Câu 1: Cho hàm số
()y f x=
liên tục trên đoạn


;ab
. Gọi
D
là hình phẳng giới hạn bởi đồ thị
hàm số
()y f x=
, trục hoành và hai đường thẳng
, ( )x a x b a b= =
. Thể tích khối tròn
xoay tạo thành khi quay
D
quanh trục hoành được tính theo công thức
Ⓐ.
22
()
b
a
V f x dx
=
. Ⓑ.
2
()
b
a
V f x dx
=
. Ⓒ.
2
()
b
a
V f x dx
=
. Ⓓ.
2
2 ( )
b
a
V f x dx
=
.
Lời giải
Chọn B
[a; ]xb
ta có
2
()
b
a
V f x dx
=
PP nhanh trắc nghiệm
Công thức
Câu 2: Tính thể tích của khối tròn xoay được tạo thành khi quay quanh trục hoành hình phẳng giới
hạn bởi đồ thị của các hàm số
2ln , 0, 1,y x y x x e= = = =
.
Ⓐ.
. Ⓑ.
2e−
. Ⓒ.
( )
2e
−
. Ⓓ.
( )
42e
−
.
. Phương pháp:
Tính thể tích vật thể tròn xoay sinh bởi miền giới hạn bởi ; và
khi quay quanh trục .
Phương pháp giải: áp dụng công thức:
Dạng ②: Bài toán Thể tích vật thể tròn xoay quanh trục Ox
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 83
Lời giải
Chọn D
Có
2
1
4 ln d 4 I
e
V x x

==
Đặt
2
1
d 2ln d
ln
dd
u x x
ux
x
vx
vx
=
=

=
=
Suy ra
2
1
1
I ln 2 ln d 2I'
e
e
x x x x e= − = −
Đặt
1
ln
dd
dd
ux
ux
x
vx
vx
=
=

=
=
Suy ra
1
1
I' ln d 1 1
e
e
x x x e e= − = − + =
Suy ra
I2e=−
Vậy
( )
42Ve
=−
PP nhanh trắc nghiệm
Casio
Câu 3: Gọi
( )
H
là hình phẳng giới hạn bởi các đường:
sinyx=
;
Ox
;
0x =
;
x
=
. Quay
( )
H
xung
quanh trục
Ox
ta được khối tròn xoay có thể tích là
Ⓐ.
2
2
. Ⓑ.
2
. Ⓒ.
. Ⓓ.
2
.
Lời giải
Chọn A
Thể tích khối tròn xoay là
( )
2
2
00
1
sin .d 1 2 .d sin2
0
22
s
2
o
2
cV x x x x x x


= = − = − =



.
PP nhanh trắc nghiệm
B - Bài tập rèn luyện:
Câu 1. Gọi
( )
H
là hình phẳng giới hạn bởi các đường
ln ,y x x=
trục
, 1,Ox x x e==
. Tính thể tích
khối tròn xoay được tạo thành khi quay hình phẳng
( )
H
quanh trục
Ox
.
Ⓐ.
( )
2
1
4
e
+
. Ⓑ.
( )
1
3
e
−
. Ⓒ.
( )
1
3
e
+
. Ⓓ.
( )
2
1
4
e
−
.
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 84
Câu 2. Tính thể tích vật thể tròn xoay do hình phẳng giới hạn bởi
lnyx
, trục
Ox
và đường thẳng
2x
quay xung quanh trục
Ox
.
Ⓐ.
2ln2 1
. Ⓑ.
2 ln2
. Ⓒ.
2 ln2
. Ⓓ.
2ln2 1
.
Câu 3. Cho hình phẳng
D
giới hạn với đường cong
2
1yx=+
, trục hoành và các đường thẳng
0, 1xx==
. Khối tròn xoay tạo thành khi quay
D
quanh trục hoành có thể tích
V
bằng bao
nhiêu?
Ⓐ.
4
3
V
=
Ⓑ.
2V
=
Ⓒ.
4
3
V =
Ⓓ.
2V =
Câu 4. Cho hình phẳng
D
giới hạn bởi đường cong
2 sinyx=+
, trục hoành và các đường thẳng
0x =
,
x
=
. Khối tròn xoay tạo thành khi quay
D
quay quanh trục hoành có thể tích
V
bằng bao nhiêu?
Ⓐ.
2
2V
=
. Ⓑ.
( )
21V

=+
. Ⓒ.
2V
=
. Ⓓ.
( )
21V
=+
.
Câu 5. Cho hình phẳng
( )
H
giới hạn bởi các đường
2
3yx=+
,
0y =
,
0x =
,
2x =
. Gọi
V
là thể tích
của khối tròn xoay được tạo thành khi quay
( )
H
xung quanh trục
Ox
. Mệnh đề nào dưới đây
đúng?
Ⓐ.
( )
2
2
2
0
3V x dx
=+
. Ⓑ.
( )
2
2
0
3V x dx
=+
.
Ⓒ.
( )
2
2
2
0
3V x dx=+
. Ⓓ.
( )
2
2
0
3V x dx=+
.
Câu 6: Cho hình phẳng
( )
H
giới hạn bởi các đường thẳng
2
2, 0, 1, 2y x y x x= + = = =
. Gọi
V
là thể
tích của khối tròn xoay được tạo thành khi quay
( )
H
xung quanh trục
Ox
. Mệnh đề nào dưới
đây đúng?
Ⓐ.
( )
2
2
2
1
2dV x x
=+
. Ⓑ.
( )
2
2
2
1
2dV x x=+
. Ⓒ.
( )
2
2
1
2dV x x
=+
. Ⓓ.
( )
2
2
1
2dV x x=+
.
Câu 7: Viết công thức tính thể tích
V
của khối tròn xoay được tạo ra khi quay hình thang cong, giới
hạn bởi đồ thị hàm số
( )
y f x=
, trục
Ox
và hai đường thẳng
( )
,x a x b a b= =
, xung quanh
trục
Ox
.
Ⓐ.
( )
2
b
a
V f x dx
=
. Ⓑ.
( )
2
b
a
V f x dx=
. Ⓒ.
( )
b
a
V f x dx
=
. Ⓓ.
( )
b
a
V f x dx=
.
Câu 8: Kí hiệu
( )
H
là hình phẳng giới hạn bởi đồ thị hàm số
2( 1) ,
x
y x e=−
trục tung và trục hoành.
Tính thể tích
V
của khối tròn xoay thu được khi quay hình
( )
H
xung quanh trục
Ox
Ⓐ.
42Ve=−
. Ⓑ.
( )
42Ve
=−
. Ⓒ.
2
5Ve=−
. Ⓓ.
( )
2
5Ve
=−
.
Câu 9: Tính thể tích của khối tròn xoay được tạo thành khi quay quanh trục hoành hình phẳng giới
hạn bởi đồ thị của các hàm số
2
3 , 0y x x y= − =
.
Ⓐ.
16
15
. Ⓑ.
16
15
. Ⓒ.
81
10
. Ⓓ.
16
15
.
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 85
Câu 10: Tính thể tích của khối tròn xoay được tạo thành khi quay quanh trục hoành hình phẳng giới
hạn bởi đồ thị của các hàm số
3
, 0, 1y x y x= = =
.
Ⓐ.
4
. Ⓑ.
4
7
. Ⓒ.
2
. Ⓓ.
7
.
Câu 11: Tính thể tích của khối tròn xoay được tạo thành khi quay quanh trục hoành hình phẳng giới
hạn bởi đồ thị của các hàm số
9, 0, 1, 3xy y x x= = = =
.
Ⓐ.
54
. Ⓑ.
6
. Ⓒ.
12
. Ⓓ.
6
.
Câu 12: Tính thể tích của khối tròn xoay được tạo thành khi quay quanh trục hoành hình phẳng giới
hạn bởi đồ thị của các hàm số
( )
1
cos , 0, 0,y x y x x
= = = =
.
Ⓐ.
( )
2
8

+
. Ⓑ.
( )
sin 2 2
4
+
. Ⓒ.
sin2 2
4
+
. Ⓓ.
2
8
+
.
Câu 13: Tính thể tích của khối tròn xoay được tạo thành khi quay quanh trục hoành hình phẳng giới
hạn bởi đồ thị của các hàm số
2
cos , 0, 0,y x y x x
= = = =
.
Ⓐ.
2
2
. Ⓑ.
3
8
. Ⓒ.
2
3
8
. Ⓓ.
2
.
BẢNG ĐÁP ÁN
1.D
2.C
3. A
4. B
5. A
6. A
7.A
8.D
9.C
10.D
11.A
12.B
13.C
A - Bài tập minh họa:
. Phương pháp:
Tính thể tích vật thể tròn xoay khi cho hình phẳng giới hạn bởi: ; quay quanh
trục .
Phương pháp giải:
①. Giải phương trình: có nghiệm
②. Khi đó thể tích cần tìm :
③. Casio:
Dạng ③: Bài toán Thể tích vật thể tròn xoay quanh trục Ox
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 86
Câu 1: Thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi Parabol
( )
2
:P y x=
và
đường thẳng
:2d y x=
quay quanh trục
Ox
bằng
Ⓐ.
22
24
00
4x dx x dx

−

. Ⓑ.
( )
2
2
2
0
2x x dx
−
.
Ⓒ.
22
24
00
4x dx x dx

+

. Ⓓ.
( )
2
2
0
2x x dx
−
.
Lời giải
Chọn B
Phương trình hoành độ giao điểm của
( )
P
và
d
là
2
2xx=
0
2
x
x
=
=
.
Thể tích của khối tròn xoay là
( )
( )
2
2
2
2
0
2dx x x

−


22
24
00
4x d dx x x

=−

PP nhanh trắc nghiệm
Câu 2: Thể tích khối tròn xoay sinh bởi hình phẳng giới hạn bởi đồ thị hai hàm số
2
2y x x=−
,
2
4yx=−
khi nó quanh quanh trục hoành là:
Ⓐ.
421
15
. Ⓑ.
27
. Ⓒ.
125
3
. Ⓓ.
30
.
Lời giải
Chọn B
Xt phương trình hoành độ giao điểm:
2 2 2
1
2 4 2 2 4 0
2
x
x x x x x
x
=−
− = − − − =
=
.
Do khi quay quanh trục hoành thì khối sinh bởi hình
phẳng giới hạn bởi đồ thị hàm số
2
2y x x=−
, trục hoành,
0; 2xx==
sẽ nằm trong khối sinh bởi hình phẳng giới
hạn bởi đồ thị hàm số
2
4yx=−
, trục hoành,
0; 2xx==
.
Vậy thể tích cần tính bằng:
( ) ( ) ( )
0 0 2
2 2 2
2 2 2
1 1 0
4 2 4
203 38 256 421
15 15 15 15
V x dx x x dx x dx
−−

= − − − + −


= − + =
PP nhanh trắc nghiệm
Chú ý phần rất dễ thiếu phần
( )
2
2
2
1
0
4V x dx
=−
B - Bài tập tham khảo rèn luyện:
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 87
Câu 1: Cho hình phẳng trong hình (phần tô đậm) quay quanh trục hoành. Thể tích của khối tròn xoay tạo
thành được tính theo công thức nào?
Ⓐ.
( ) ( )
22
12
d
b
a
V f x f x x

=−

.
Ⓑ.
( ) ( )
22
12
d
b
a
V f x f x x

=−

.
Ⓒ.
( ) ( )
22
21
d
b
a
V f x f x x

=−

.
Ⓓ.
( ) ( )
2
12
d
b
a
V f x f x x
=−


.
Lời giải
Chọn B
Do
( ) ( ) ( )
12
;f x f x x a b
nên Chọn B
Câu 2: Tìm công thức tính thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi parabol
( )
2
: =P y x
và đường thẳng
:2=d y x
quay xung quanh trục
Ox
.
Ⓐ.
( )
2
2
2
0
2d
−
x x x
. Ⓑ.
22
24
00
4 d d

−

x x x x
.
Ⓒ.
22
24
00
4 d d

+

x x x x
. Ⓓ.
( )
2
2
0
2d
−
x x x
.
Lời giải
Chọn A
Phương trình hoành độ giao điểm:
2
0
20
2
=
− =
=
x
xx
x
.
Vậy thể tích khối tròn xoay được tính:
( )
2
2
2
0
2d
=−
V x x x
.
Câu 3: Cho hình
( )
H
giới hạn bởi trục hoành, đồ thị của một Parabol
và một đường thẳng tiếp xúc với Parabol đó tại điểm
( )
2;4A
,
như hình vẽ bên. Thể tích vật thể tròn xoay tạo bởi khi hình
( )
H
quay quanh trục
Ox
bằng
Ⓐ.
16
15
. Ⓑ.
32
5
.
Ⓒ.
2
3
. Ⓓ.
22
5
.
Lời giải
Chọn A
Parabol có đỉnh là gốc tọa độ như hình vẽ và đi qua
( )
2;4A
nên có phương trình
2
yx=
.
Tiếp tuyến của Parabol đó tại
( )
2;4A
có phương trình là
( )
4 2 4 4 4y x x= − + = −
.
Suy ra thể tích vật thể tròn xoay cần tìm là
( )
( )
22
2
2
2
01
d 4 4 dV x x x x

= − −

.
( )
2
2
5
2
2
0
0
32
d
55
x
xx==
;
( )
( )
2
22
3
2
22
11
1
16
4 4 d 16 2 1 d 16
33
x
x x x x x x x

− = − + = − + =



.
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 88
Vậy
( )
( )
22
2
2
2
01
32 16 16
d 4 4 d
5 3 15
V x x x x

= − − = − =



.
Câu 4: Gọi
()H
là hình phẳng được giới hạn bởi các đồ thị hàm
số
1
2 , , 0
−
= = =
x
y x y y
x
(phần tô đậm màu đen ở hình vẽ bên).
Thể tích của vật thể tròn xoay tạo thành khi quay
()H
quanh trục
hoành bằng.
Ⓐ.
5
2ln 2
3
V

=−


. Ⓑ.
5
2ln 2
3
V

=+


.
Ⓒ.
2
2ln2
3
V

=−


. Ⓓ.
2
2ln2
3
V

=+


.
Lời giải
Chọn A
Phương trình hoành độ giao điểm của
2yx=
và
1 x
y
x
−
=
là:
1
2
x
x
x
−
=
2
0
2 1 0xx
x
+ − =
0
1
2
1
x
x
x
=
=
−
1
2
x=
.
Phương trình hoành độ giao điểm của
2yx=
và
0y =
là:
20x =
2
0
2 1 0xx
x
+ − =
0x=
.
Phương trình hoành độ giao điểm của
0y =
và
1 x
y
x
−
=
là:
1
0
x
x
−
=
0
10x
x
−=
0
1x
x
=
1x=
.
1
2
1
2
2
1
0
2
1
4 dd
x
V x x x
x

−

=+



1
2
1
3
2
1
0
2
41
.1
3
d
x
x
x


= + −


1
2
1
2
1 1 2
1
6
dx
xx


= + − +


Câu 5: Tính thể tích của khối tròn xoay khi quay hình phẳng giới hạn bởi các đường
2
4yx=−
,
24yx=−
,
0x =
,
2x =
quanh trục
.Ox
Ⓐ.
32π
5
. Ⓑ.
32π
7
. Ⓒ.
32π
15
. Ⓓ.
22π
5
.
Lời giải
Chọn A
Ta có
( )
2
2
2
1
0
256
π 4 d π
15
V x x= − =
,
( )
2
2
2
0
32
π 2 4 d π
3
V x x= − =
.
Vậy thể tích cần tìm
12
32π
5
V V V= − =
.
Câu 6: Cho hình phẳng
( )
H
giới hạn bởi các đường
2
yx=
,
2yx=
. Thể
tích của khối tròn xoay được tạo thành khi quay
( )
H
xung quanh
trục
Ox
bằng:
Ⓐ.
32
15
. Ⓑ.
64
15
.
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 89
Ⓒ.
21
15
. Ⓓ.
16
15
.
Lời giải
Chọn B
Xt phương trình hoành độ giao điểm:
2
20xx−=
0
2
x
x
=
=
.
Khi quay
( )
H
xung quanh trục
Ox
ta được khối tròn xoay giới hạn bởi
2
2
0
2
yx
yx
x
x
=
=
=
=
.
Do đó thể tích của khối tròn xoay là:
( )
( )
2
2
2
2
0
64
2d
15
V x x x
= − =
.
Câu 7: Tính thể tích
V
của vật tròn xoay tạo thành khi quay hình phẳng
( )
H
giới hạn bởi các đường
2
yx=
;
yx=
quanh trục
Ox
.
Ⓐ.
9
10
V
=
. Ⓑ.
3
10
V
=
. Ⓒ.
10
V
=
. Ⓓ.
7
10
V
=
.
Lời giải
Chọn B
Phương trình hoành độ giao điểm
2
xx=
4
0xx − =
( )
( )
2
1 1 0x x x x − + + =
0x=
hoặc
1x =
Khi đó:
Thể tích khối tròn xoay sinh bởi hình
( )
H
là
( )
( )
11
2
2
2
00
3
dd
10
V x x x x

= − =

Câu 8: Cho hình phẳng
D
giới hạn bởi đường cong
1
e
x
y
−
=
, các trục tọa độ và phần đường thẳng
2=−yx
với
1x
. Tính thể tích khối tròn xoay tạo thành khi quay quanh trục hoành.
Ⓐ.
2
2
1 e 1
3 2e
V
−
=+
. Ⓑ.
( )
2
2
5e 3
6e
V
−
=
. Ⓒ.
1 e 1
2e
V
−
=+
. Ⓓ.
2
2
1 e 1
2 2e
V
−
=+
.
Lời giải
Chọn B
Phương trình hoành độ giao điểm của đường cong
1
e
x
y
−
=
và đường
thẳng
2=−yx
:
1
e 2 1
x
xx
−
= − =
. (Vì
1
e
x
y
−
=
là hàm đồng biến và
2yx=−
là hàm nghịch biến trên tập xác định nên phương trình có tối đa
1
nghiệm. Mặt khác
1x =
thỏa mãn pt nên đó là nghiệm duy nhất của pt đó).
Đường thẳng
2=−yx
cắt trục hoành tại
2=x
.
( )
( )
12
2
2
1
01
e d 2 d
x
V x x x

−
= + −

( )
2
2
3
1
22
2
0
1
5e 1
e 2 4
3 6e
x
x
x

−
−

= + − + =


Câu 9: Tính thể tích khối tròn xoay sinh ra khi quay quanh trục
Ox
hình phẳng giới hạn bởi hai đồ thị
2
46y x x= − +
và
2
26y x x= − − +
.
Ⓐ.
. Ⓑ.
1
−
. Ⓒ.
3
. Ⓓ.
2
.
D
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 90
Lời giải
Chọn C
Xt phương trình hoành độ giao điểm
22
4 6 2 6x x x x− + = − − +
2
2 2 0xx − =
0
1
x
x
=
=
.
Thể tích vật thể tròn xoay sinh ra khi quay quanh trục
Ox
hình phẳng giới hạn bởi hai đồ thị là
( ) ( )
1
22
22
0
4 6 2 6 dV x x x x x
= − − − − − +
1
32
0
12 36 24 dx x x x
= − + −
( )
1
32
0
12 36 24 dx x x x
= − + −
( )
1
3 3 2
0
3 12 12x x x
= − + −
3
=
.
Câu 10: Gọi
( )
H
là hình được giới hạn bởi nhánh parabol
2
2yx=
(với
0x
), đường thẳng
3yx= − +
và trục hoành. Thể tích của khối tròn xoay tạo bởi hình
( )
H
khi quay quanh trục
Ox
bằng
Ⓐ.
52
15
V
=
. Ⓑ.
17
5
V
=
. Ⓒ.
51
17
V
=
. Ⓓ.
53
17
V
=
.
Lời giải
Chọn A
Phương trình hoành độ giao điểm:
2
1
23
3
2
x
xx
x
=
= − +
=−
Thể tích khối tròn xoay tạo bởi
( )
H
:
( )
31
2
4
10
52
3 d 4 d
15
V x x x x
= − + + =

.
Câu 11: Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường
20xy+ − =
;
yx=
;
0y =
quay
quanh trục
Ox
bằng
Ⓐ.
5
6
. Ⓑ.
6
5
. Ⓒ.
2
3
. Ⓓ.
5
6
.
Lời giải
Chọn D
Hình phẳng đã cho được chia làm
2
phần sau:
Phần
1
: Hình phẳng giới hạn bởi các đường
yx=
;
0y =
;
0x =
;
1x =
.
Khi quay trục
Ox
phần
1
ta được khối tròn xoay có thể tích
1
2
1
1
0
0
d.
22
x
V x x

= = =
.
Phần
2
: Hình phẳng giới hạn bởi các đường
2yx=−
;
0y =
;
1x =
;
2x =
.
Khi quay trục
Ox
phần
2
ta được khối tròn xoay có thể tích
( )
( )
3
2
2
2
2
1
1
2
2 d .
33
x
V x x

−
= − = =
.
Vậy thể tích khối tròn xoay cần tính là
12
5
6
V V V
= + =
.
Câu 12: Thể tích vật thể tròn xoay sinh ra khi hình phẳng giới hạn bởi các đường
xy=
,
2yx= − +
và
0x =
quay quanh trục
Ox
có giá trị là kết quả nào sau đây?
Ⓐ.
1
3
V
=
. Ⓑ.
3
2
V
=
. Ⓒ.
32
15
V
=
. Ⓓ.
11
6
V
=
.
Lời giải
Chọn C
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 91
Gọi
( )
H
là hình phẳng giới hạn bởi các đường:
2
0
xy
yx
x
=
= − +
=
( )
2
0
2
0
y x x
yx
x
=
= − +
=
Phương trình hoành độ giao điểm:
2
2xx= − +
2
20xx + − =
( )
( )
1
2
x nhaän
x loaïi
=
=−
Thể tích vật tròn xoay sinh ra khi hình
( )
H
quay quanh trục
Ox
là:
( )
( )
(
)
1
2
2
2
0
2dV x x x
= − + −
( )
1
24
0
4 4 dx x x x
= − + −
32
15
=
(đvtt)
Câu 13: Gọi
D
là hình phẳng giới hạn bởi đồ thị hàm số
yx=
, cung tròn có phương trình
2
6yx=−
( )
66x−
và trục hoành (phần tô đậm trong hình vẽ bên). Tính thể tích
V
của vật thể tròn
xoay sinh bởi khi quay hình phẳng
D
quanh trục
Ox
.
Ⓐ.
8 6 2V

=−
. Ⓑ.
22
86
3
V
=+
. Ⓒ.
22
86
3
V
=−
. Ⓓ.
22
46
3
V
=+
.
Lời giải
Chọn D
Cách 1. Cung tròn khi quay quanh
Ox
tạo thành một khối cầu có thể tích
( )
3
4
6 8 6
3
V

==
.
Thể tích nửa khối cầu là
1
46V
=
.
Xt phương trình:
2
6xx=−
2
0
60
x
xx
+ − =
2x=
.
Thể tích khối tròn xoay có được khi quay hình phẳng
( )
H
giới hạn bởi đồ thị các hàm số
yx=
, cung
tròn có phương trình
2
6yx=−
, và hai đường thẳng
0, 2xx==
quanh
Ox
là
( )
2
2
2
0
22
6d
3
V x x x
= − − =
.
Vậy thể tích vật thể tròn xoay cần tìm là
12
22
46
3
V V V
= + = +
.
Cách 2. Cung tròn khi quay quanh
Ox
tạo thành một khối cầu có thể tích
( )
3
1
4
6 8 6
3
V

==
.
Xt phương trình:
2
6xx=−
2
0
60
x
xx
+ − =
2x=
.
Thể tích khối tròn xoay có được khi quay hình phẳng
( )
H
giới hạn bởi đồ thị các hàm số
yx=
, cung
tròn có phương trình
2
6yx=−
và đường thẳng
0y =
quanh
Ox
là
( )
26
2
2
02
d 6 dV x x x x

= + −

12 6 28
2
3

−
=+
22
46
3
=−
.
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 92
Vậy thể tích vật thể tròn xoay cần tìm là
12
V V V=−
22
8 6 4 6
3


= − −


22
46
3
=+
.
Câu 14: Tính thể tích vật thể tròn xoay tạo bởi phép quay xung quanh trục
Ox
hình phẳng giới hạn bởi
các đường
0y =
,
yx=
,
2yx=−
.
Ⓐ.
8
3
. Ⓑ.
16
3
. Ⓒ.
10
. Ⓓ.
8
.
Lời giải
Chọn B
Ta có:
00
0 2 2
24
xx
xx
x x x
= =
= − =
= − =
Dựa vào hoành độ giao điểm của ba đường ta có diện tích hình phẳng gồm hai phần. Phần thứ
nhất giới hạn bởi
yx=
,
0y =
và
0; 2xx==
. Phần thứ hai giới hạn bởi
yx=
,
2yx=−
và
2; 4xx==
.
Thể tích vật thể bằng:
( )
( )
24
2
2
2
02
d 2 dV x x x x x

= + − −

( )
( )
24
2
02
d 2 dx x x x x

= + − −

( )
4
2
3
22
0
2
2
16
2 2 3 3
x
xx


−
= + − =



.
Câu 15: Cho
( )
H
là hình phẳng giới hạn bởi parabol
2
yx=
và đường tròn
22
2xy+=
(phần tô đậm trong hình bên). Tính thể tích
V
của
khối tròn xoay tạo thành khi quay
( )
H
quanh trục hoành.
Ⓐ.
44
15
V
=
. Ⓑ.
22
15
V
=
.
Ⓒ.
5
3
V
=
. Ⓓ.
5
V
=
.
Lời giải
Chọn A
Với
2
yx=
thay vào phương trình đường tròn ta được
2
24
2
11
2
1
2
xx
xx
x
x
==
+ =
=−
=−
.
Hơn nữa
2
22
2
2
2
2
yx
xy
yx
= − −
+ =
=−
.
Thể tích cần tìm chính là thể tích vật thể tròn xoay
( )
2
1
2
1
:
1
yx
x
H
x
Ox
=−
=−
=
quay quanh
Ox
bỏ đi phần thể
tích
( )
2
2
1
:
1
yx
x
H
x
Ox
=
=−
=
quay quanh
Ox
.
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 93
Do đó
(
)
( )
11
2
2
22
11
44
2 d d
15
V x x x x
−−

= − − =



.
Câu 16: Cho hình phẳng
( )
H
(phần gạch chéo trong hình vẽ).
Tính thể tích
V
của khối tròn xoay tạo thành khi
quay hình
( )
H
quanh trục hoành.
Ⓐ.
8V
=
. Ⓑ.
10V
=
.
Ⓒ.
8
3
V
=
. Ⓓ.
16
3
V
=
.
Lời giải
Chọn D
Gọi là hình phẳng giới hạn bởi các đường
0x =
,
4x =
,
( )
f x x=
và trục hoành.
( )
2
D
là hình phẳng giới hạn bởi các đường
2x =
,
4x =
,
( )
2g x x=−
và trục hoành.
Kí hiệu
1
V
,
2
V
tương ứng là thể tích của các khối tròn xoay tạo thành khi quay
( )
1
D
,
( )
2
D
quanh trục hoành.
Khi đó,
12
V V V=−
( ) ( )
44
22
02
ddf x x g x x

=−

( )
44
2
02
d 2 dx x x x

= − −

8
8
3
=−
16
3
=
.
Câu 17: Thể tích
V
của khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi đường tròn
( ) ( )
2
2
: 3 1C x y+ − =
xung quanh trục hoành là
Ⓐ.
2
6
. Ⓑ.
3
6
. Ⓒ.
2
3
. Ⓓ.
6
.
Lời giải
Chọn A
( ) ( ) ( )
22
22
22
22
: 3 1 3 1
3 1 3 1
3 1 3 1
C x y y x
y x y x
y x y x
+ − = − = −

− = − = + −



− = − − = − −

Thể tích
V
của khối tròn xoay được sinh ra khi quay hình
phẳng giới hạn bởi đường tròn
( ) ( )
2
2
: 3 1C x y+ − =
xung quanh trục hoành là
(
)
(
)
22
11
2 2 2
11
3 1 3 1 .6 6V x dx x dx
−−
= + − − − − = =

.
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 94
| 1/94
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 1
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung Full Chuyên đề 12 new 2020-2021 CHƯƠNG ③: FB: Duong Hung
Bài ❶: NGUYÊN HÀM
Dạng ①: Nguyên hàm theo định nghĩa và tính chất cơ bản
.Phương pháp:
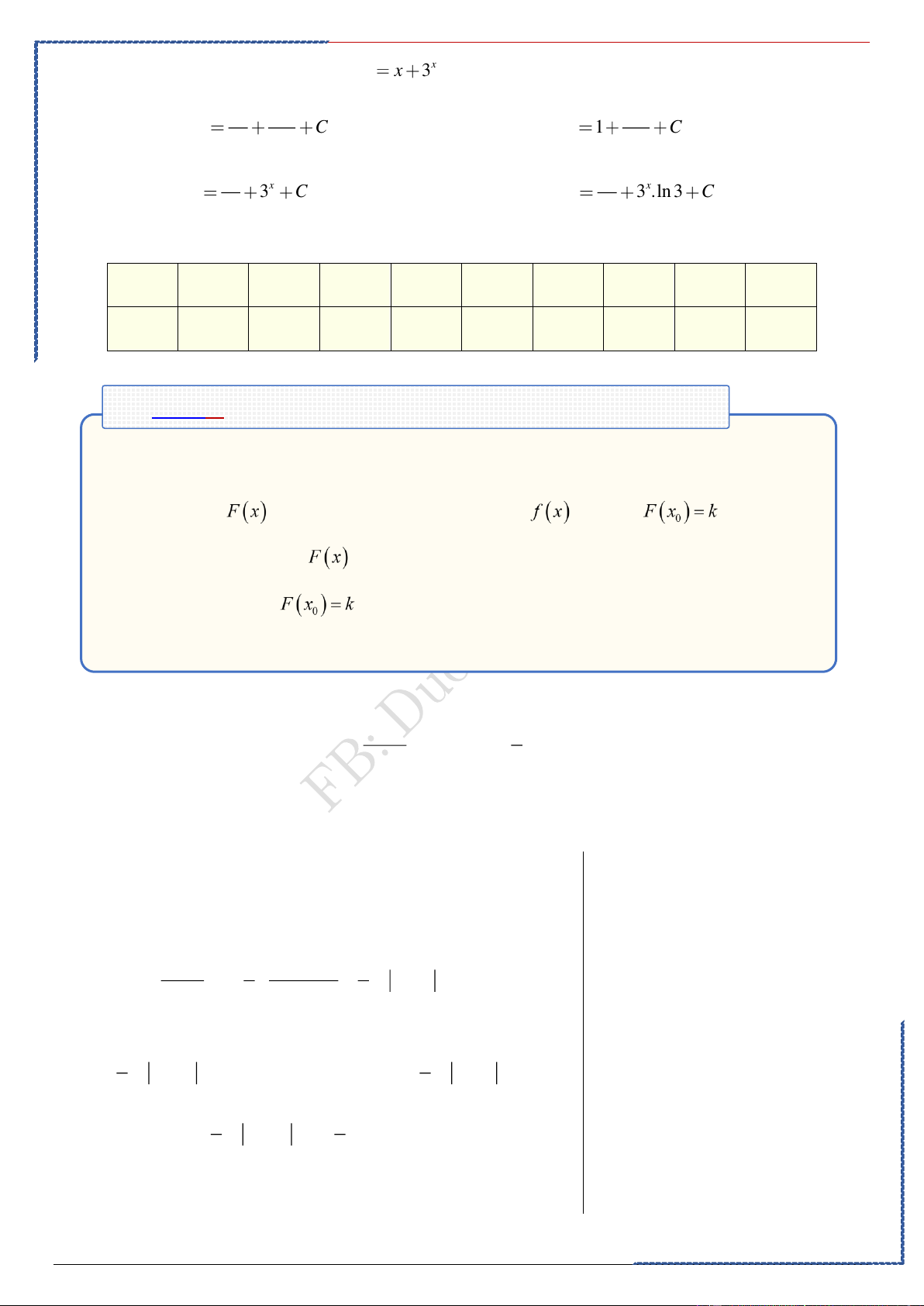
. Định nghĩa: Hàm số
được gọi là nguyên hàm của hàm số trên nếu
với mọi x thuộc . . Tính chất:  .  .  .
. Bảng nguyên hàm:  ▪  ▪  ▪  ▪  ▪   ▪  ▪  ▪   ▪  ▪
Phương pháp: Casio.
⬧ Xét hiệu: Nhấn shift ⬧ Calc hay ,…. là mệnh đề đúng.
St-bs: Duong Hung 2
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
A - Bài tập minh họa:
Câu 1: Tất cả nguyên hàm của hàm số f ( x) 1 = là 2x + 3 Ⓐ. 1 1
ln 2x + 3 + C .
Ⓑ. ln (2x + 3) + C . 2 2
Ⓒ. ln 2x + 3 + C . Ⓓ. 1 ln 2x + 3 + C . ln 2 Lời giải
PP nhanh trắc nghiệm Chọn A Casio: f  (x) 1 1 1 dx = dx = d   (2x +3) + +  2x 3 2 2x 3 1 = ln 2x + 3 + C 2 Calc: x= 2.5
Lưu ý: Gặp ln thì có trị tuyệt đối, rắt dễ chọn nhằm đáp án B
Câu 2: Câu 2: Nếu f  (x) 3 2
dx = 4x + x + C thì hàm số f ( x) bằng Ⓐ. f (x) 3 x 4 = x + + Cx . Ⓑ. f (x) 2
=12x + 2x + C . 3 x
Ⓒ. f ( x) 2 =12x + 2x . Ⓓ. f ( x) 3 4 = x + . 3 Lời giải
PP nhanh trắc nghiệm Chọn B
Thử đạo hàm Ta có:  Casio  
f ( x) = ( f
 (x) x) =( 3 2
x + x + C ) 2 d 4 =12x + 2x
Chú ý dễ chọn nhằm câu B
Câu 3: Cho hàm số f ( x) có f ( x) 1 ' = với mọi 1 x  và f ( )
1 = 1. Khi đó giá trị của f (5) bằng 2x −1 2 Ⓐ. ln 2 . Ⓑ. ln3. Ⓒ. ln 2 +1. Ⓓ. ln3+1.
St-bs: Duong Hung 3
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung Lời giải
PP nhanh trắc nghiệm
Chọn D . Tư duy Casio  Ta có: f '
 (x)dx = f (x)+C nên 5 f
 (x)dx = f (5)− f ( )1 − 1 f ( x) 1 1 d (2x )1 1 = dx = = ln 2x −1 + C   2x −1 2 2x −1 2 5 5
f (5) = f ( ) 1 + f
 (x)dx =1+ f   (x)dx
Mặt khác theo đề ra ta có: f ( ) 1 = 1 1 1 1 
. Tổng quát:
ln 2.1−1 + C = 1  C = 1 nên 2 b f
 (x)dx = f (b)− f (a) f ( x) 1 = ln 2x −1 +1 2 a b Do vậy
 • f (b) = f (a) + f   (x) ; dx a f ( ) 1 1 5 = ln 2.5 −1 +1 = ln 9 +1 = ln 3 +1 2 2 b
• f (a) = f (b) − f   (x)dx a
B - Bài tập rèn luyện:
Câu 1: Khẳng định nào sau đây là sai?
Ⓐ. Nếu  f (x)dx = F (x) + C thì  f (u)du = F (u) + C.
Ⓑ. .  kf (x)dx = k f (x)dx ( k là hằng số và k  0 ).
Ⓒ. Nếu F (x) và G(x) đều là nguyên hàm của hàm số f (x) thì F (x) = G(x).
Ⓓ.   f x + f x dx =  f x dx +  f x d . x  1 ( ) 2 ( ) 1 ( ) 2 ( )
Câu 2: Hàm số nào sau đây không phải là nguyên hàm của hàm số f (x) = ( x − )4 3 ? − − Ⓐ. x F ( x) (x )5 3 = + . x Ⓑ. F (x) ( )5 3 = . 5 5 − − Ⓒ. x x F (x) ( )5 3 = + 2020 .
Ⓓ. F ( x) ( )5 3 = −1. 5 5
Câu 3: Trong các khẳng định sau, khẳng định nào sai?
Ⓐ.  0dx = C ( C là hằng số). Ⓑ. 1
dx = ln x + C (C là hằng số). x  1 + Ⓒ.  xx dx = + C (  = + (  +
C là hằng số).
Ⓓ. dx x C C là hằng số). 1
Câu 4: Cho hai hàm số f ( x) , g (x) là hàm số liên tục. Xét các mệnh đề sau:
(I). k f ( x) 1 . dx =
f (x)dx với k là hằng số thực khác 0 bất kỳ. k (II).   f
 ( x) − g ( x) dx =  f
(x)dx −  g (x)dx. (III).   f
 ( x).g ( x) dx =  f
(x)d .xg (x)dx .
(IV).  f (x)dx = f (x) + C .
Số mệnh đề đúng là Ⓐ. 1. Ⓑ. 2 . Ⓒ. 3 . Ⓓ. 4 .
Câu 5: Cho hàm số f ( x) xác định trên K và F ( x) , G ( x) là nguyên hàm của f ( x) trên K . Khẳng
định nào dưới đây đúng?
St-bs: Duong Hung 4
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
Ⓐ. G(x) = F (x) , x  K.
Ⓑ. G(x) = f (x) , x  K.
Ⓒ. F (x) = G(x) + C , x  K.
Ⓓ. F(x) = f (x) , x   K .
Câu 6: Mệnh đề nào sau đây sai?
Ⓐ. Nếu F ( x) là một nguyên hàm của f (x) trên ( ;
a b) và C là hằng số thì f
 (x)dx = F (x)+C
Ⓑ. Mọi hàm số liên tục trên ( ;
a b) đều có nguyên hàm trên ( ; a b) .
Ⓒ. F ( x) là một nguyên hàm của f (x) trên (a b) / ;
F (x) = f (x), x  ( ; a b) Ⓓ. / ( f
 (x)dx) = f (x)
Câu 7: Hàm số f ( x) 1 = có nguyên hàm trên: cos x Ⓐ. (         0; ) Ⓑ. − ;   Ⓒ. ( ;2 ) Ⓓ. − ;    2 2   2 2 
Câu 8: Hàm số nào sau đây không phải là nguyên hàm của hàm số f ( x) = ( x − )4 3 ? − − Ⓐ. x F ( x) (x )5 3 = + x Ⓑ. F (x) ( )5 3 = 5 5 − − Ⓒ. x x F ( x) ( )5 3 = + 2017 Ⓓ. F (x) ( )5 3 = −1 5 5 Câu 9: Hàm số ( ) 3 x
F x = e là một nguyên hàm của hàm số Ⓐ. ( ) 3 x f x = e Ⓑ. ( ) 3 2 = 3 . x f x x e 3 x Ⓒ. ( ) e f x = Ⓓ. ( ) 3 3 1 . x f x x e − = 2 3x Câu 10: Nếu  ( ) 3 x f x d x x =
+ e + C thì f (x) bằng 3 Ⓐ. f (x) 4 x x = + e Ⓑ. ( ) 2 = 3 x f x x + e 3 Ⓒ. f (x) 4 x x = + e Ⓓ. ( ) 2 x
f x = x + e 12
Câu 11: Tìm nguyên hàm của hàm số f ( x) 1 3 = x + x Ⓐ. x f  (x) 1 2 dx = 3x + + C . Ⓑ. f  (x) 4 dx = + ln x + C . 2 x 4 Ⓒ. x f  (x) 1 2 dx = 3x − + C . Ⓓ. f  (x) 4 dx = + ln x + C . 2 x 4
Câu 12: Trong các khẳng định sau, khẳng định nào sai? e 1 + Ⓐ. 1 x cos 2 d x x = sin 2x + C  . Ⓑ. e x dx = + C  2 e +1
St-bs: Duong Hung 5
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung e 1 + Ⓒ. 1 x
dx = ln x + C  . Ⓓ. e x dx = + Cx x +1
Câu 13: Họ nguyên hàm của hàm số f ( x) 2
= 3x + sin x là Ⓐ. 3
x + cos x + C .
Ⓑ. 6x + cos x +C . Ⓒ. 3
x − cos x + C .
Ⓓ. 6x −cos x +C .
Câu 14: Tất cả nguyên hàm của hàm số f ( x) 1 = là 2x + 3 Ⓐ. 1 1
ln 2x + 3 + C .
Ⓑ. ln (2x + 3) + C . 2 2
Ⓒ. ln 2x + 3 + C .
Ⓓ. 1 ln 2x + 3 + C . ln 2
Câu 15: Giả sử các biểu thức sau đều có nghĩa công thức nào sau đây sai? Ⓐ. 1
dx = tan x + C  . Ⓑ. x x
e dx = e + C  . 2 cos x Ⓒ. 1 lnxdx = + C  .
Ⓓ. sinxdx = −cos x + C. x
Câu 16: Họ nguyên hàm của hàm số f (x) 2 x 2 = e + x là x Ⓐ. ( ) 2 3 e x F x = + + C . Ⓑ. F (x) 2 x 3
= e + x + C . 2 3 Ⓒ. ( ) x 2 = 2 x F x
e + 2x + C .
Ⓓ. F (x) 3 2 x = e + + C . 3
Câu 17: Nguyên hàm của hàm số f ( x) 3
= x + 3x + 2 là hàm số nào trong các hàm số sau ? Ⓐ. x F ( x) 2
= 3x + 3x + C . Ⓑ. F (x) 4 2 =
+ 3x + 2x + C . 3 Ⓒ. ( ) 4 2 x 3x x x F x = + + 2x + C .
Ⓓ. F (x) 4 2 = + + 2x + C . 4 2 4 2
Câu 18: Họ nguyên hàm của hàm số ( ) ex (3 e x f x − = + ) là Ⓐ. x 1 F (x) = 3e − + C . Ⓑ. ( ) = 3ex F x − x + C . ex
Ⓒ. ( ) = 3ex + ex ln ex F x + C . Ⓓ. ( ) = 3ex F x + x + C .
Câu 19: Họ nguyên hàm của hàm số ( ) = ex f x + cos x là Ⓐ. 1 +
ex − sin x + C . Ⓑ. x 1 e
+ sin x + C . x +1 Ⓒ. x 1 e
x − − sin x + C .
Ⓓ. ex + sin x + C .
St-bs: Duong Hung 6
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 20: Nguyên hàm của hàm số 3x f x x là 2 x x Ⓐ. x 3 F x C . Ⓑ. 3 F x 1 C . 2 ln 3 ln 3 2 2 Ⓒ. x x F x 3x C . Ⓓ. F x 3 .
x ln 3 C . 2 2 BẢNG ĐÁP ÁN 1.C 2.A 3.C 4.B 5.C 6.D 7.D 8.D 9.A 10.C 11.D 12.D 13.C 14.A 15.C 16.A 17.C 18.D 19.D 20.A
Dạng ②: Tìm nguyên hàm của hàm số thỏa mãn điều kiện cho trước
thức chứa lũy thừa.
-Phương pháp: Xác định
là một nguyên hàm của hàm số sao cho Tìm nguyên hàm . Thế điều kiện tìm hằng số C
 Kết luận cho bài toán.
A - Bài tập minh họa: 1
Câu 1: Cho hàm số f ( x) có f ( x) 1 ' =
với mọi x  và f ( )
1 = 1. Khi đó giá trị của f (5) bằng 2x −1 2 Ⓐ. ln 2 . Ⓑ. ln3. Ⓒ. ln 2 +1. Ⓓ. ln3+1. Lời giải
PP nhanh trắc nghiệm
Chọn D Casio
Ta có: f '
 (x)dx = f (x)+C nên b f
 (x)dx = F (b)− F (a) − a f ( x) 1 1 d (2x ) 1 1 = dx = = ln 2x −1 + C   2x −1 2 2x −1 2 b
 •F (b) = F (a) + f  (x) ; dx
Mặt khác theo đề ra ta có: f ( ) 1 = 1 a b 1 
• F (a) = F (b) − f  (x)
ln 2.1−1 + C = 1  C = 1 nên f ( x) 1 = ln 2x −1 +1 dx 2 2 a Do vậy f ( ) 1 1 5 = ln 2.5 −1 +1 = ln 9 +1 = ln 3 +1. 2 2
St-bs: Duong Hung 7
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 2: Biết F ( x) là một nguyên hàm của hàm số ( ) = 2 + 2x f x x
thoả mãn F (0) = 0 . Ta có F ( x) bằng x x Ⓐ. 2 −1 1− 2 2 x + . Ⓑ. 2 x + . Ⓒ.1 (2x + − ) 1 ln 2 . Ⓓ. 2 2x x + −1. ln 2 ln 2 Lời giải
PP nhanh trắc nghiệm Chọn A
Casio: Thử đáp án x 2x
Ta có: (2x + 2 ) 2 dx = x + + C . Do đó . ln 2 2 1
Theo giả thiết F (0) 0 2 = 0  0 +
+ C = 0  C = − . ln 2 ln 2 2x 1 2x −1 Vậy F ( x) 2 2 = x + − = x + . ln 2 ln 2 ln 2 
Câu 3: Tìm nguyên hàm F x của hàm số f x sin 
2x thỏa mãn F 1. 2  xx Ⓐ. cos( 2 ) 1 F (x) . Ⓑ. cos( 2 ) 1 F (x) . 2 2 2 2  x cos( 2x) 1 Ⓒ. cos( 2 ) F (x) 1.
Ⓓ. F(x) . 2 2 2 Lời giải
PP nhanh trắc nghiệm Chọn B
Casio: Thử đáp án cos  2x F x sin  2x dx C 2  1  1 F 1 C 1 C 2 2 2 cos( 2x) 1
Vậy F (x) 2 2
B - Bài tập rèn luyện:
Câu 1. Tìm một nguyên hàm F(x) của hàm số 3
f (x) = 4x − 4x + 5 thỏa mãn F(1) = 3 Ⓐ. 4 2
F (x) = x − 2x + 5x −1. Ⓑ. 4 2
F(x) = x − 4x + 5x +1 . Ⓒ. 1 4 2
F (x) = x − 2x + 5x + 3 . Ⓓ. 4 2
F (x) = x − 2x − 5x + . 2
Câu 2. Hàm số f ( x) 4 2 = 5
− x + 4x − 6 có một nguyên hàm F ( x) thỏa F (3) =1. Tính F ( 3 − ) . Ⓐ. F ( 3 − ) = 226 . Ⓑ. F ( 3 − ) = 2 − 25 . Ⓒ. F ( 3 − ) = 451. Ⓓ. F ( 3 − ) = 225.      
Câu 3. Biết F ( x) là một nguyên hàm của hàm số f ( x) = sin 2x và F =1  
. Tính P = F   .  4   6 
St-bs: Duong Hung 8
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung Ⓐ. 5 P = . Ⓑ. P = 0 . Ⓒ. 1 P = . Ⓓ. 3 P = . 4 2 4
Câu 4. Tìm một nguyên hàm F ( x) của hàm số f ( x) = 2x + sin x + 2cos x thỏa mãn F (0) =1. Ⓐ. F (x) 2
= x + cos x + 2sin x − 2 .
Ⓑ. F (x) 2
= x − cos x + 2sin x .
Ⓒ. F (x) = 2 + cos x + 2sin x .
Ⓓ. F (x) 2
= x − cos x + 2sin x + 2 .    2 Câu 5. 1
Tìm một nguyên hàm F ( x) của hàm số f ( x) = sin x + thỏa mãn F =   . 2 cos x  4  2
Ⓐ. F (x) = −cos x + tan x + C .
Ⓑ. F (x) = −cos x + tan x − 2 +1.
Ⓒ. F (x) = cos x + tan x + 2 −1.
Ⓓ. F (x) = −cos x + tan x + 2 −1.  
Câu 6. Biết F(x) là một nguyên hàm của hàm số 2 ( ) e x f x = thỏa 3 F (0) =  Giá trị của 1 F   2  2  bằng Ⓐ. 1 e + 2 . Ⓑ. 1 e +1. Ⓒ. 2e +1. Ⓓ. 1 1 e + 2 2 2 2
Câu 7. Kí hiệu F ( x) là một nguyên hàm của hàm số f (x) = (x + )2 2 1 và F ( ) 28 1 =  Khẳng định 15 nào sau đây là đúng? Ⓐ. ( ) 5 3 x 2x x x F x = + + . x Ⓑ. F (x) 5 3 2 = + + x + C. 5 3 5 3 Ⓒ. x x
F ( x) = x ( 2 4 x + )
1 . Ⓓ. F ( x) 5 3 2 = + + x +1. 5 3
Câu 8. Biết F ( x) là một nguyên hàm của hàm số f ( x) 1 =
và F (2) =1. Tính F (3). x −1 Ⓐ. F ( ) 1 3 =  Ⓑ. F ( ) 7 3 = 
Ⓒ. F (3) = ln 2 −1. Ⓓ. F (3) = ln 2 +1. 2 4
Câu 9. Tìm nguyên hàm F ( x) của hàm số f ( x) 2 =
thỏa mãn F (5) = 7 . 2x −1
Ⓐ. F (x) = 2 2x −1. Ⓑ. F (x) = 2 2x −1+1.
Ⓒ. F (x) = 2x −1+ 4 .
Ⓓ. F (x) = 2x −1−10.
Câu 10. Gọi F ( x) là một nguyên hàm của hàm số f ( x) = ( x − )2 2 3 thỏa F ( ) 1 0 = . Tính giá trị 3
của biểu thức T = log 3F 1 − 2F 2 . 2  ( ) ( ) Ⓐ.T = 2 . Ⓑ. T = 4 . Ⓒ. T =10 . Ⓓ.T = 4 − . BẢNG ĐÁP ÁN
St-bs: Duong Hung 9
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung 1.A 2.C 3.D 4.D 5.D 6.B 7.A 8.D 9.B 10.A
Dạng ③: Phương pháp đổi biến số.
-Định lí: Cho hàm số
có đạo hàm và liên tục trên trên và hàm số liên tục sao cho xác định trên . Khi đó nếu hàm số là một nguyên hàm của , tức là: -Phương pháp:
Từ đó ta có hai cách đổi biến số trong việc tính nguyên hàm như sau:  Đặt biến số:  Suy ra:
rồi đưa về việc tính nguyên hàm  đơn giản hơn.
A - Bài tập minh họa:
Câu 1: Tìm họ nguyên hàm 2 cos x sin x dx  ta được kết quả là Ⓐ. 2 − 1 1 1 cos x + C . Ⓑ. 3 cos x + C . Ⓒ. 3 − cos x + C . Ⓓ. 3 sin x + C . 3 3 3 Lời giải
PP nhanh trắc nghiệm
Chọn C
Casio: xét hiệu 1  2 2
cos x sin x dx = − cos x d   (cos x) 3
= − cos x + C . 3 1 1 Câu 2: Nguyên hàm cos dx  bằng 2 x x Ⓐ. 1 − 1 sin + C . Ⓑ. 1 sin + C . Ⓒ. 1 −2sin + C . Ⓓ. 2sin + C . x x x x Lời giải
PP nhanh trắc nghiệm Chọn A
Casio: xét hiệu 1 1 1  1  1  Ta có cos dx = − cos d = − sin + C     . 2 x x x x x
Câu 3: Tính nguyên hàm 1 I = dx  . x ln x +1 Ⓐ. 2 3 I = (ln x +1) + C .
Ⓑ. I = ln x +1 + C . 3 Ⓒ. 1 2 I = (ln x +1) + C .
Ⓓ. I = 2 ln x +1 + C . 2
St-bs: Duong Hung 10
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung Lời giải
PP nhanh trắc nghiệm Chọn D Casio: xét hiệu 1 − 1  2
dx = (ln x +1) d(ln x +1) = 2 ln x +1 + C.   x ln x +1
Câu 4: Tìm nguyên hàm của hàm số sin x f (x) = 1+ 3cos x . Ⓐ. 1
f (x) dx = ln 1+ 3cos x + C.
Ⓑ. f (x)dx = ln 1+ 3cos x + C. 3 − Ⓒ. 1
f (x) dx = 3ln 1+ 3cos x + C.
Ⓓ. f (x)dx = ln 1+ 3cos x + C  . 3 Lời giải
PP nhanh trắc nghiệm Chọn D Casio: xét hiệu  Ta có: sin x 1 1 x = −   ( + x) 1 d d 1 3cos
= − ln 1+ 3cos x + C 1+ 3cos x 3 1+ 3cos x 3
B - Bài tập rèn luyện:
Câu 1: Biết  f (u)du = F (u) + C. Mệnh đề nào sau đây đúng?
Ⓐ.  f (2x − )
1 dx = 2F (2x − ) 1 + C.
Ⓑ.  f (2x − )
1 dx = 2F ( x) −1+ C. Ⓒ.  1 f (2x − )
1 dx = F (2x − ) 1 + C.
Ⓓ.  f (2x − ) 1 dx = F (2x − ) 1 + C. 2
Câu 2: Nguyên hàm của hàm số f (x) = x(x + )9 2 1 là Ⓐ. (x + )10 2 1 + C. Ⓑ. (x + )10 2 2 1 + C . Ⓒ. 1 − ( 1 x + )10 2 1 + C. Ⓓ. (x + )10 2 1 + C. 20 20
Câu 3: Nguyên hàm của hàm số f (x) = 2x −1 là Ⓐ.  f (x) 1 dx = − 2x −1 + C. Ⓑ.  f (x) 1 dx = 2x −1 + C. 3 2 Ⓒ .  2 f ( x) 1 dx = (2x − ) 1 2x −1 + C. Ⓓ. 
f ( x) dx = (2x − ) 1 2x −1 + C. 3 3
Câu 4: Nguyên hàm của hàm số ( ) 2 x f x = xe là Ⓐ. 2 1 x e + C Ⓑ. 2x e + C. 2 Ⓒ. 2 2 2 x + .2 x e C e + C Ⓓ. ( + ) 2 2 2 1 x x e + C.
Câu 5: Biết rằng hàm số F ( x) là một nguyên hàm của hàm số ( ) ln x f x = và thỏa mãn F ( 2 e ) = 4. x
St-bs: Duong Hung 11
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
Mệnh đề nào sau đây là đúng? Ⓐ. ( ) 2 ln x x F x = − 3. Ⓑ. F (x) 2 ln = + 3. 2 2 Ⓒ. ( ) 2 ln x x F x =
− 2 Ⓓ F (x) 2 ln = + 2 2 2 Câu 6: Tìm hàm số x
F ( x) biết F ( x) 3 = dx  và F (0) =1. 4 x +1 Ⓐ. 1 3 F ( x) = ( 4 ln x + ) 1 +1.
Ⓑ. F (x) = ln ( 4 x + ) 1 + . 4 4 Ⓒ. F (x) 1 = ln ( 4 x + ) 1 +1. Ⓓ. F (x) = ( 4 4 ln x + ) 1 +1. 4
Câu 7: Họ nguyên hàm của hàm số sin x f (x) = là cos x − 3
Ⓐ. −ln cos x − 3 + C .
Ⓑ. 2ln cos x − 3 + C . − Ⓒ. ln cos x 3 −
+ C . Ⓓ. 4ln cos x − 3 + C . 2
Câu 8: Họ nguyên hàm của hàm số ( ) 2 sin = sin 2 .e x f x x là 2 sin x 1 + Ⓐ. 2 e 2 sin 1 sin .e x x − + C . Ⓑ. + C . 2 sin x +1 2 sin x 1 − Ⓒ. 2 e sin e x + C . Ⓓ. + C . 2 sin x −1
Câu 9: Xét nguyên hàm 2 I = 1− x dx
với phép đặt x = sin t . Khi đó
Ⓐ. I = 2 cost costdt  . Ⓑ. 2
I = 2 sin t cos tdt  .
Ⓒ. I = cost costdt
. Ⓓ. I = 4 sin t costdt  .   
Câu 10: Xét nguyên hàm 2 I = 4 − x dx
với phép đặt x = 2sin t với t  0;   . Khi đó  2  Ⓐ. I = 2
 (1+cos2t)dt Ⓑ. I = 2
 (1+cos3t)dt . Ⓒ. I = 2
 (4+cos2t)dt Ⓓ. I = 2
 (1+2cos2t)dt BẢNG ĐÁP ÁN 1.D 2.D 3.D 4.A 5.D 6.C 7.A 8.C 9.C 10.A
St-bs: Duong Hung 12
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
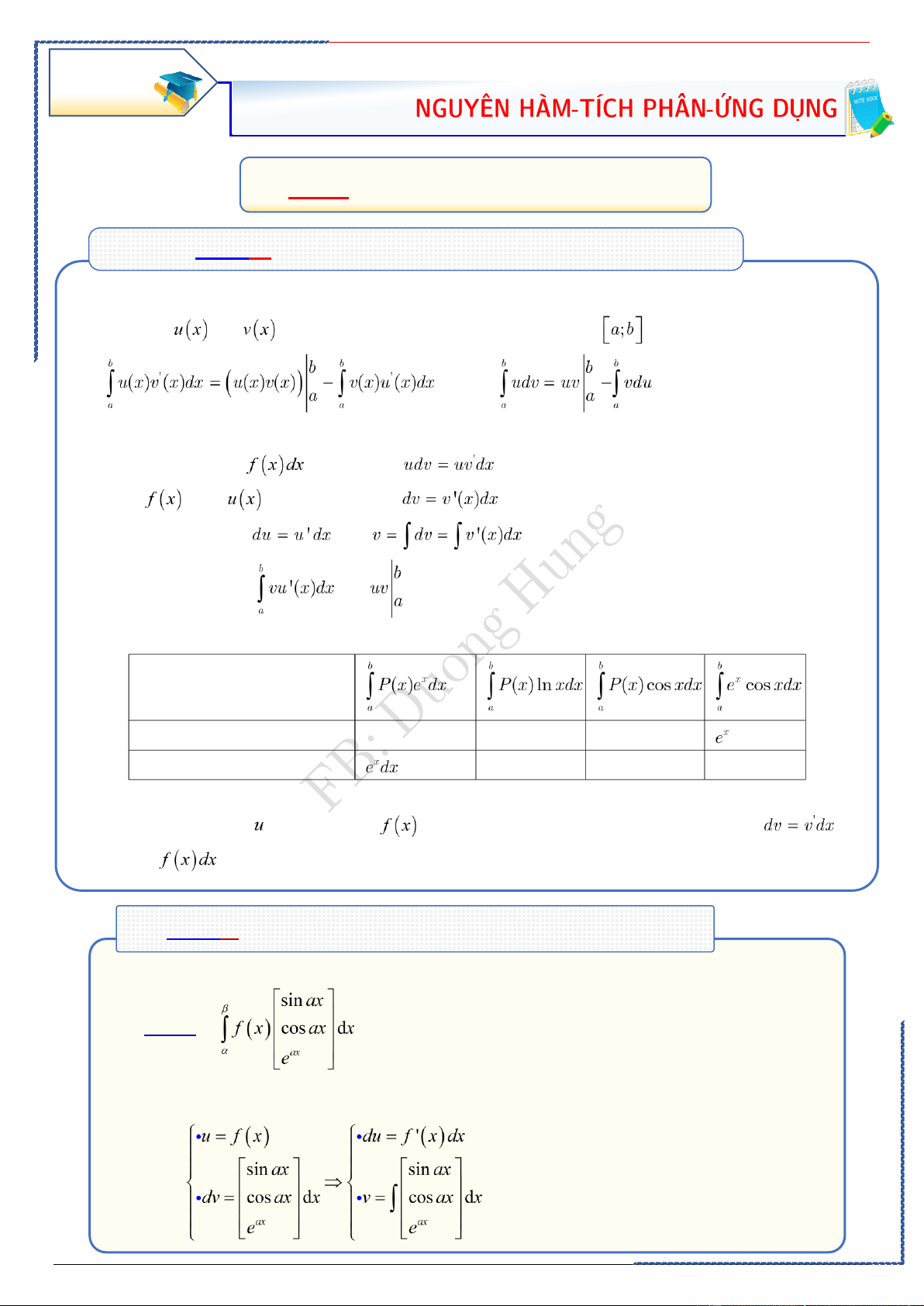
Dạng ④: Phương pháp từng phần
-Phương pháp:
 Cho hai hàm số 𝑢 và 𝑣 liên tục trên đoạn ሾ𝑎; 𝑏ሿ và có đạo hàm liên tục trên đoạn ሾ𝑎; 𝑏ሿ.
 Khi đó:∫ 𝑢𝑑𝑣 = 𝑢𝑣 − ∫ 𝑣𝑑𝑢. ሺ∗ሻ
 Để tính nguyên hàm ∫ 𝑓ሺ𝑥ሻ𝑑𝑥 bằng từng phần ta làm như sau:
Bước 1. Chọn 𝑢, 𝑣 sao cho 𝑓ሺ𝑥ሻ𝑑𝑥 = 𝑢𝑑𝑣 (chú ý 𝑑𝑣 = 𝑣′ሺ𝑥ሻ𝑑𝑥).
 Sau đó tính 𝑣 = ∫ 𝑑𝑣 và 𝑑𝑢 = 𝑢′. 𝑑𝑥.
Bước 2. Thay vào công thức ሺ∗ሻ và tính ∫ 𝑣𝑑𝑢.
①.Dạng 1. , trong đó là đa thức ⬧.Đặt: .
②. Dạng 2. , trong đó là đa thứ ⬧.Đặt: .
③. Dạng 3. , trong đó là đa thức ⬧.Đặt: .
. Casio: Xét hiệu
, calc x= {-5,….,5} một cách thích hợp
Sẽ thu kết quả bảng 0 hoặc xấp xỉ 0 là đáp án đúng.
A - Bài tập minh họa:
Câu 1. Họ nguyên hàm của hàm số f ( x) = x cos 2x là
Ⓐ. xsin 2x cos 2x + + x C . Ⓑ. cos 2 x sin 2x − + C . 2 4 2 Ⓒ. cos 2x x x x x sin 2x + + C . Ⓓ. sin 2 cos 2 − + C . 2 2 4 Lời giải
PP nhanh trắc nghiệm Chọn A
I = x cos 2 d x x  .  Casio
St-bs: Duong Hung 13
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung du = dx Calc x=3.5 u  = x  Đặt    1 . dv = cos 2 d x x v = sin 2x  2 Khi đó 1 1 1 1 I = x sin 2x − sin 2 d x x = x sin 2x + cos 2x + C 2 2 2 4 Chọn A
Câu 2: Họ nguyên hàm của hàm số f ( x) = x ln 2x là 2 x  1  2 x Ⓐ. ln 2x − + C   . Ⓑ. 2 x ln 2x − + C . 2  2  2 2 x 2 x Ⓒ.
(ln 2x − )1 +C . Ⓓ. 2
ln 2x − x + C . 2 2 Lời giải
PP nhanh trắc nghiệm Chọn A  1 Casio du = u  = ln 2x  Đặt x  →  . Calc x=1 2 dv = d x x xv =   2 ( ) =  ( ) 2 2 x 1 x F x f x dx = .ln 2x − . dx  2 x 2  . 2 2 2 x x x  1  = ln 2x − + C = ln 2x − + C   2 4 2  2  Chon A
Câu 3: Tìm nguyên hàm của hàm số ( ) 2 = .e x f x x . 1 x 1 Ⓐ. F x x e2 x C . Ⓑ. F x e2 2 x 2 C . 2 2 1 x 1 Ⓒ. F x x e2 2 x C .
Ⓓ. F x e2 x 2 C . 2 2 Lời giải
PP nhanh trắc nghiệm
Chọn A Ta có: ( ) 2 = .e x F x x dx  .  Casio Calc: x=2 Đặt du = dx u  = x     1 2 x 2 dv = e dx v = e x  2    F (x) 1 x 1 x 1 x 1 2 2 2 = e x − e dx = e x − + C    2 2 2  2 
B - Bài tập rèn luyện:
St-bs: Duong Hung 14
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 1: Biết rằng hàm số F ( x) là một nguyên hàm của hàm số f (x) = ln x và thỏa mãn F ( ) 1 = 3. Giá trị của ( 2 F e ) bằng Ⓐ. 4. Ⓑ. 2 e − + 4. Ⓒ. 2 e + 4 . Ⓓ. 2 3e + 4.
Câu 2: Nguyên hàm của hàm f (x) = 4x(1+ ln x) là Ⓐ. 2 2
2x ln x + 2x . Ⓑ. 2 2
2x ln x + 3x . Ⓒ. 2 2
2x ln x + x + C Ⓓ. 2 2
2x ln x + 3x + . C
Câu 3: Biết rằng hàm số F ( x) là một nguyên hàm của hàm số ( ) ( )1 x f x x e− = − và thỏa mãn
F (0) = 2020. Khẳng định nào sau đây đúng? Ⓐ. ( ) x F x e− = + 2019. Ⓑ. ( ) x F x xe− = + 2020 . Ⓒ. ( ) x F x xe− = − + 2020 . Ⓓ. ( ) x
F x = −xe + 2020 .
Câu 4: Biết rằng hàm số x
F ( x) là một nguyên hàm của hàm số f ( x) 2 = x cos
và thỏa mãn F ( ) 1 0 =  2 2
Giá trị của F ( ) bằng 2  2  Ⓐ. 1 1 +  Ⓑ. − . 2 2 4 2 2  2  Ⓒ. 1 +  . Ⓓ. +1. 4 2 4
Câu 5: Nguyên hàm của hàm số ( ) x
f x = e sin x là Ⓐ. xx 1 sin x e
xdx = e sin x + C . Ⓑ.  sin = ( x sin x e xdx e
x + e cos x) + C 2 Ⓒ. xx 1 sin x e
xdx = e cos x + C. Ⓓ.  sin = ( x sin x e xdx e
x − e cos x) + C . 2
Câu 6: Hàm số f (x) = (x +1)sin x có các nguyên hàm là:
Ⓐ. F(x) (x 1)cos x sinx C . Ⓑ. F(x) (x 1)cosx s inx C Ⓒ.F(x) (x 1)cosx s inx C
Ⓓ. F(x) = (x +1)cos x −sinx + C
Câu 7: Tính x cos xdx
, ta được kết quả là:
Ⓐ. F (x) = xsin x + cos x +C
Ⓑ. F (x) = xsin x − cos x + C .
Ⓒ. F (x) = −xsin x + cos x + C .
Ⓓ. F (x) = −xsin x − cos x + C
Câu 8: Một nguyên hàm của hàm số = ( 2 ( ) + 2 ) x f x x x e Ⓐ. ( ) = (2 + 2). x F x x e Ⓑ. 2 ( ) x F x = x e . Ⓒ. 2 ( ) ( ). x F x x x e . Ⓓ. 2 ( ) = ( − 2 ). x F x x x e .
Câu 9: Kết quả nào sai trong các kết quả sau ?
St-bs: Duong Hung 15
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung 3x Ⓐ. xe x 1 3 3x xe dx = − e + C  Ⓑ. = − +  x x x xe dx xe e C . 3 9 2 Ⓒ. x − x xe dx . x e C . Ⓓ. x x 1 dx = − + C  . 2 x x x e e e x
Câu 10: Cho f (x) = ln tdt
. Đạo hàm f '(x) là hàm số nào dưới đây? 0 Ⓐ. 1 . Ⓑ. ln x . Ⓒ. 2 ln x . Ⓓ. 1 ln x . x 2
Câu 11: Nguyên hàm của hàm số f ( x) = xsin x là
Ⓐ. –xcos x +sin x +C .
Ⓑ. xsin x + cos x +C .
Ⓒ. xcos x +sin x +C .
Ⓓ. xcos x −sin x +C .
Câu 12: Kết quả của x I = xe dx  là 2 x Ⓐ. x x I =
e + e + C . Ⓑ. x x
I = e + xe + C . 2 2 x Ⓒ. x I = e + C . Ⓓ. x x
I = xe − e + C . 2
Câu 13: Tính F(x) = x sin 2xdx
. Chọn kết quả đúng? Ⓐ. 1 F (x) =
(2x cos 2x + sin 2x) + C . Ⓑ. 1 F (x) = −
(2x cos 2x + sin 2x) + C . 4 4 Ⓒ. 1 F (x) = −
(2x cos 2x − sin 2x) + C . Ⓓ. 1 F (x) =
(2x cos 2x − sin 2x) + C . 4 4
Câu 14: Nguyên hàm của hàm số ( ) = ( + ) 1 ex f x x là Ⓐ. ex x + C . Ⓑ. ( + 2)ex x + C . Ⓒ.( − ) 1 ex x + C . Ⓓ. 2 ex x + C .
Câu 15: Họ các nguyên hàm của f ( x) = x ln x là 2 x 1 Ⓐ. 2 1 ln x + x + C. Ⓑ. 2 2 x ln x − x + C. 2 4 2 2 x 1 Ⓒ. 2 ln x − x + C. Ⓓ. 1 x ln x + x + C. 2 4 2
Câu 16: Tìm nguyên hàm của hàm số f ( x) = x ln ( x + 2) . 2 2 x x + 4x Ⓐ. f
 (x)dx = ln(x+ 2)− + C . 2 2 2 2 x − 4 x + 4x Ⓑ. f  (x)dx = ln ( x + 2) − + C . 2 2 2 2 x x + 4x Ⓒ. f
 (x)dx = ln(x+ 2)− + C . 2 4
St-bs: Duong Hung 16
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung 2 2 x − 4 x − 4x Ⓓ. f  (x)dx = ln ( x + 2) − + C . 2 4
Câu 17: Cho hàm số y = x sin 2 d x x
. Chọn mệnh đề đúng trong các mệnh đề sau         Ⓐ. 3 y =   . Ⓑ. 3 y =   .  6  12  6  6         Ⓒ. y =   . Ⓓ. y =   .  6  12  6  24
Câu 18: Gọi F ( x) là một nguyên hàm của hàm số ( ) e x f x x − =
. Tính F ( x) biết F (0) =1 Ⓐ. ( ) ( )1e x F x x − = + + 2. Ⓑ. ( ) ( ) 1 e x F x x − = − + +1. Ⓒ. ( ) ( ) 1 e x F x x − = − + + 2 . Ⓓ. ( ) ( )1e x F x x − = + +1.
Câu 19: Tìm họ nguyên hàm F ( x) của hàm số ( ) 2 = .e x f x x . Ⓐ. ( ) 2 = 1 2e x F x
(x −2)+C . Ⓑ. ( ) 2 = e x F x
(x − 2)+C . 2     Ⓒ. 1 x 1 F ( x) x 1 2 = 2e x − + C   .
Ⓓ. F (x) 2 = e x − + C   .  2  2  2 
Câu 20: Cho F(x) là một nguyên hàm của hàm số ( ) = (5 + ) 1 ex f x x và F (0) = 3. Tính F ( ) 1 . Ⓐ. F ( ) 1 = e + 2 . Ⓑ. F ( ) 1 = 11e − 3 . Ⓒ. F ( ) 1 = e + 3 . Ⓓ. F ( ) 1 = e + 7 . BẢNG ĐÁP ÁN 1.C 2.C 3.C 4.B 5.D 6.B 7.A 8.B 9.C 10.B 11.A 12.D 13.C 14.A 15.C 16.D 17.C 18.C 19.D 20.D
St-bs: Duong Hung 17
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung Full Chuyên đề 12 new 2020-2021 CHƯƠNG ③: FB: Duong Hung
Bài 2: TÍCH PHÂN DÙNG ĐỊNH NGHĨA, TÍNH CHẤT
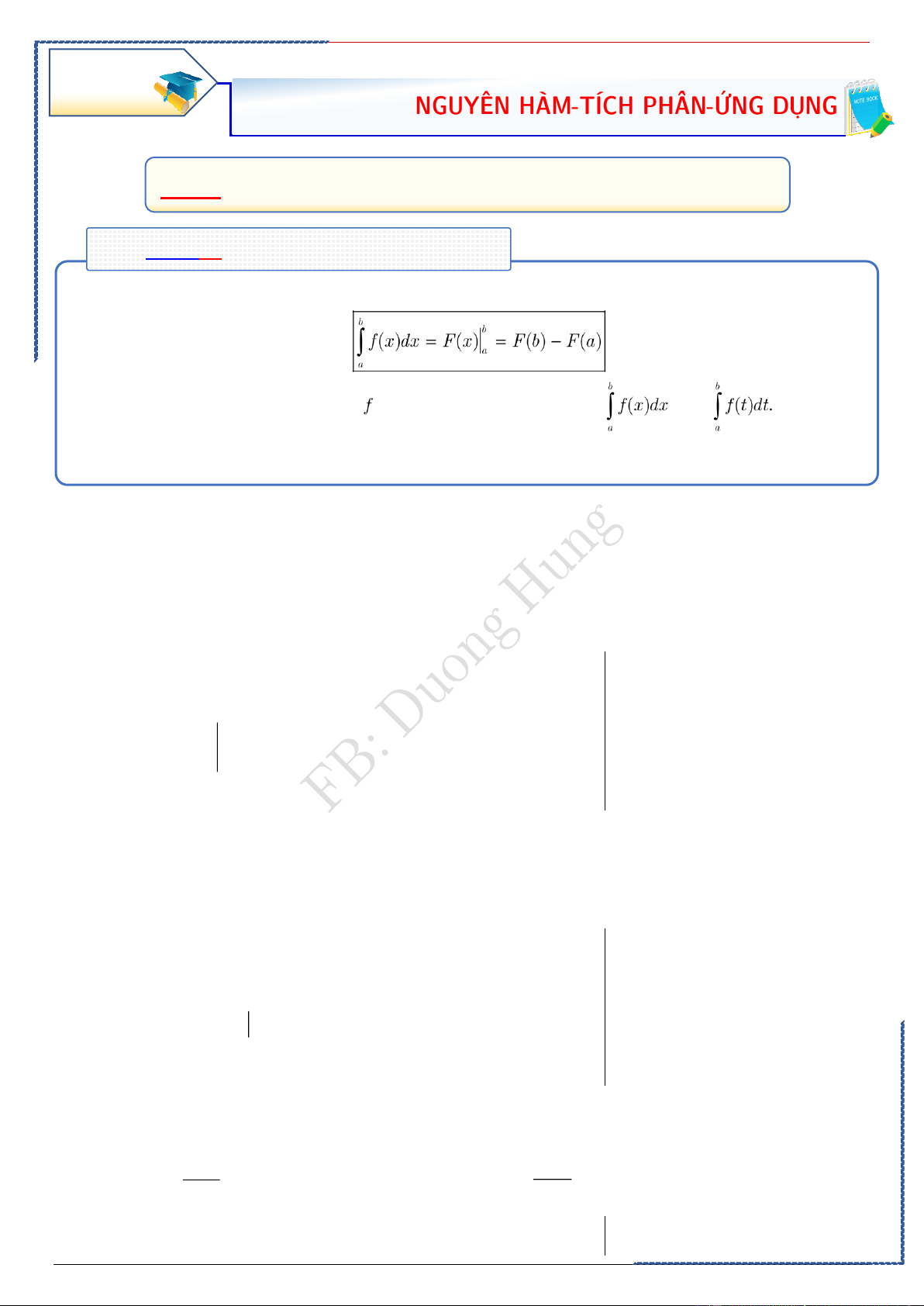
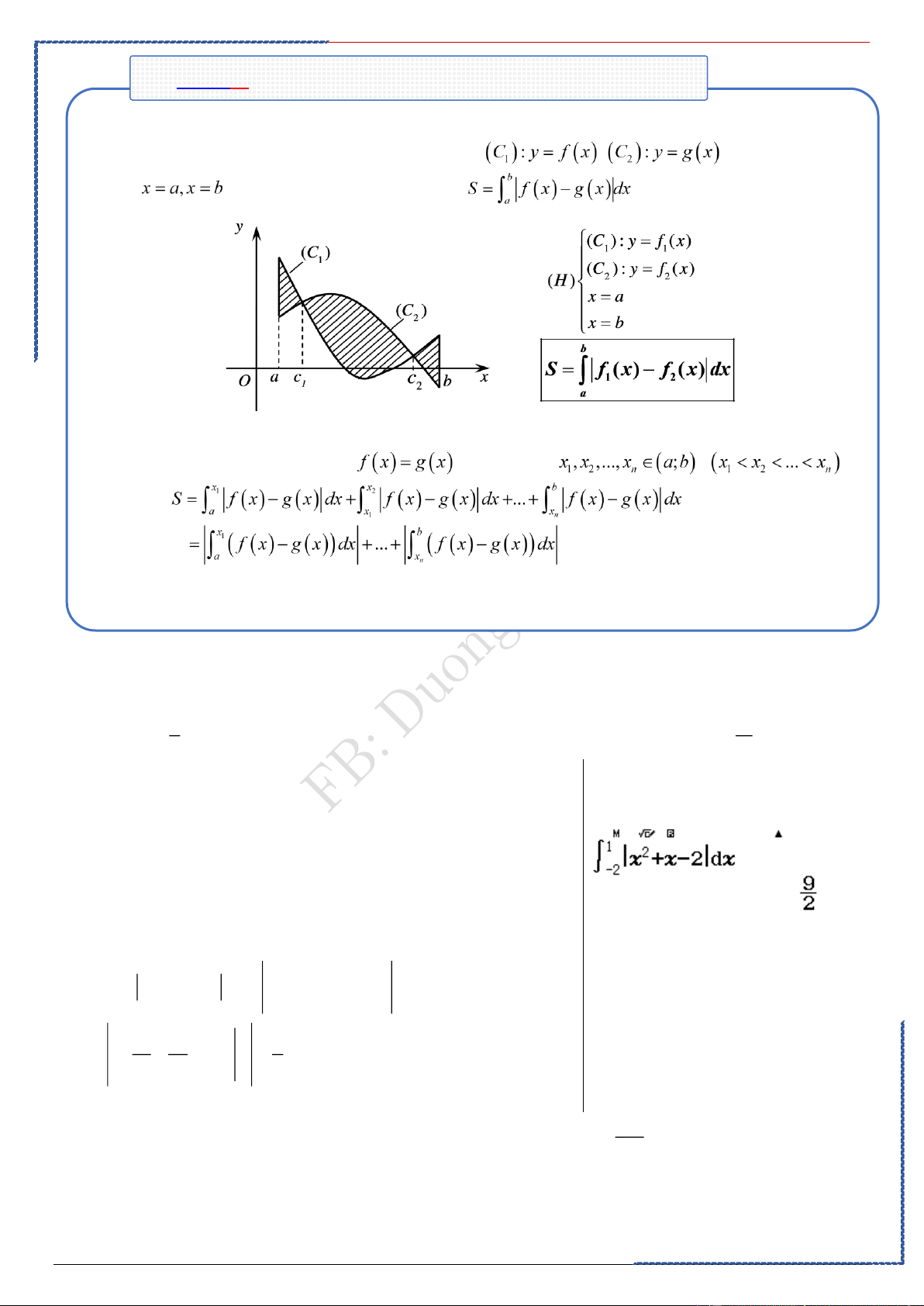
Dạng ①: Tích phân dùng định nghĩa
.Phương pháp:
Nhận xét: Tích phân của hàm số từ a đến b có thể kí hiệu bởi hay Tích phân
đó chỉ phụ thuộc vào f và các cận a, b mà không phụ thuộc vào cách ghi biến số.
. Chú ý: Học thuộc bảng nguyên hàm của các hàm số cơ bản thường gặp.
A - Bài tập minh họa: b
Câu 1: Tính tích phân dx  . a Ⓐ. a −b. Ⓑ. a.b . Ⓒ. b−a . Ⓓ. a + b. Lời giải
PP nhanh trắc nghiệm
Chọn C b b
Ta có: dx = x = b − aa a 0
Câu 2: Giá trị của x 1 e + dx  bằng 1 − Ⓐ. 1−e . Ⓑ. e−1. Ⓒ. −e . Ⓓ. e . Lời giải
PP nhanh trắc nghiệm Chọn B 0  Ta có x 1 e + dx  = 0 1 ex+ = e −1 . −1 1 − 1 Câu 3: Tích phân 2020 I = x dx  bằng 0 Ⓐ. 1 . Ⓑ. 0 . Ⓒ. 1 . Ⓓ. 1. 2021 2019 Lời giải
PP nhanh trắc nghiệm
St-bs: Duong Hung 18
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung Chọn A 1 1 2021 x 1  Ta có 2020 I = x dx = =  . 2021 2021 0 0
B - Bài tập rèn luyện: Câu 1: Biết f
 (x)dx = F(x)+C .Trong các khẳng định sau, khẳng định nào đúng? b b Ⓐ. f
 (x)dx = F (b)−F (a). Ⓑ. f
 (x)dx = F(b).F(a). a a b b Ⓒ. f
 (x)dx = F (a)−F (b). Ⓓ. f
 (x)dx = F (b)+ F (a). a a
Câu 2: Trong các phép tính sau đây, phép tính nào sai? 2 2 2 Ⓐ. 2    ( + ) x 2 x 1 dx =  + x  . Ⓑ. cos d x x =  (sin x) .  2   1 1  2 − 3 Ⓒ. 1 − 3 dx =  (ln x) 2 . Ⓓ. xd =  ( x e x e ) . 3 x − 1 3 − 1 3
Câu 3: Cho hàm số f ( x) có đạo hàm trên đoạn 1; 
3 , f (3) = 5 và f
 (x)dx = 6. Khi đó f ( )1 bằng 1 Ⓐ. 1 − . Ⓑ. 11. Ⓒ.1. Ⓓ. 10. Câu 4: 2 3
F ( x) là nguyên hàm của hàm số f ( x) = +
x  0 , biết rằng F ( )
1 = 1. Tính F (3) . 2 ( ) x x
Ⓐ. F (3) = 3ln3+3 . Ⓑ. F (3) = 2ln3+ 2. Ⓒ. F (3) = 2ln3+3. Ⓓ. F (3) = 3. 3
Câu 5: Cho hàm số f ( x) có đạo hàm trên , f (− ) 1 = 2
− và f (3) = 2 . Tính I = f '
 (x)d .x 1 −
Ⓐ. I = 4.
Ⓑ. I = 3. Ⓒ. I = 0. Ⓓ. I = 4. −
Câu 6: Cho các số thực a , b (a b) . Nếu hàm số y = f ( x) có đạo hàm là hàm liên tục trên thì b b
Ⓐ. f (x)dx = f (a)− f (b).
Ⓑ. f (x)dx = f (b)−  f (a) . a a b b
Ⓒ. f (x)dx = f (a)−  f (b) .
Ⓓ. f (x)dx = f (b)− f (a). a a
Câu 7: PT 1.2 Cho F ( x) là một nguyên hàm của hàm số f ( x) . Khi đó hiệu số F ( ) 1 − F (2) bằng 2 1 2 2 Ⓐ. −  f (x)d  x . Ⓑ. ( )d  F x x . Ⓒ. −  F (x)d  x . Ⓓ. ( )d  f x x . 1 2 1 1 b
Câu 8: Cho hàm số f ( x) có đạo hàm f ( x) liên tục trên a;b, f (b) = 5 và f
 (x)dx =1, khi đó a
f (a) bằng Ⓐ. 6 − . Ⓑ. 6 . Ⓒ. −4. Ⓓ. 4 .
St-bs: Duong Hung 19
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung 1
Câu 9: Cho hàm số f ( x) có đạo hàm liên tục trên 0;  1 và thoản mãn
f ( x)dx = 3 −  . Giá trị của 0
biểu thức f (0) − f ( ) 1 Ⓐ. −2. Ⓑ. 1. Ⓒ.3. Ⓓ. 3 − . Câu 10: Cho hàm số 3
y = x có một nguyên hàm là F ( x) . Khẳng định nào sau đây là đúng?
Ⓐ. F (2)− F (0) =16. Ⓑ. F (2)− F (0) =1. Ⓒ. F (2)− F (0) = 8 . Ⓓ. F (2)− F (0) = 4.
Câu 11: Cho hàm số f ( x) có đạo hàm liên tục trên đoạn 1;  3 thỏa mãn f ( )
1 = 2 và f (3) = 9. Tính 3 I = f
 (x)dx. 1
Ⓐ. I =11. Ⓑ. I = 2 . Ⓒ. I = 7 . Ⓓ. I =18. 3 Câu 12: dx
Tính tích phân I =  . x + 2 0 Ⓐ. 21 5 4581 I = − .
Ⓑ. I = ln . Ⓒ. 5 I = log . Ⓓ. I = . 100 2 2 5000 2 Câu 13: 1
Tính tích phân I = dx  . 2x −1 1
Ⓐ. I = ln3−1.
Ⓑ. I = ln 3 .
Ⓒ. I = ln 2+1.
Ⓓ. I = ln 2−1.
Câu 14: Cho các số thực a,b (a b). Nếu hàm số y = F ( x) là một nguyên hàm của hàm số y = f ( x) thì b b Ⓐ. f
 (x)dx = F(a)−F(b). Ⓑ. F
 (x)dx = f (a)− f (b). a a b b Ⓒ. F
 (x)dx = f (a)− f (b). Ⓓ. f
 (x)dx = F(b)−F(a). a a
Câu 15: Cho hàm số f ( x) liên tục trên tập , một nguyên hàm của f ( x) là F ( x) thoả mãn 1 F ( ) 1 = 3
− và F (0) =1. Giá trị f (x)dx  bằng 0 Ⓐ. −4. Ⓑ. 3 − . Ⓒ. −2. Ⓓ. 4. 3
Câu 16: Cho hàm số f ( x) thỏa mãn f (0) =1, f ( x) liên tục trên và f
 (x)dx = 9. Giá trị của 0 f (3) là Ⓐ. 6 . Ⓑ. 3. Ⓒ.10. Ⓓ. 9. 3
Câu 17: Cho hàm số f ( x) thỏa mãn f (0) =1, f ( x) liên tục trên và f
 (x)dx = 9. Giá trị của 0 f (3) là Ⓐ. 6 . Ⓑ. 3. Ⓒ.10. Ⓓ. 9.
St-bs: Duong Hung 20
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung 1
Câu 18: Tích phân x
 ( 2x +3)dx bằng 0 Ⓐ. 2. Ⓑ. 1. Ⓒ. 4 . Ⓓ. 7 . 7 4 2 dx Câu 19:  bằng 3x − 2 1 Ⓐ. 2ln 2. Ⓑ. 2 ln 2. Ⓒ.ln 2 . Ⓓ. 1 ln 2. 3 3    b Câu 20: 1
Cho hai số thực a,b  0;   thỏa mãn dx = 10 
. Giá trị của tan a − tan b bằng  2  2 cos x a Ⓐ. 10. Ⓑ. 1 − . Ⓒ. 10 − . Ⓓ. 1 . 10 10 BẢNG ĐÁP ÁN 1.A 2.C 3.A 4.C 5.A 6.B 7.A 8.D 9.C 10.D 11.C 12.B 13 14.D 15.A 16.C 17.C 18.D 19.B 20.C
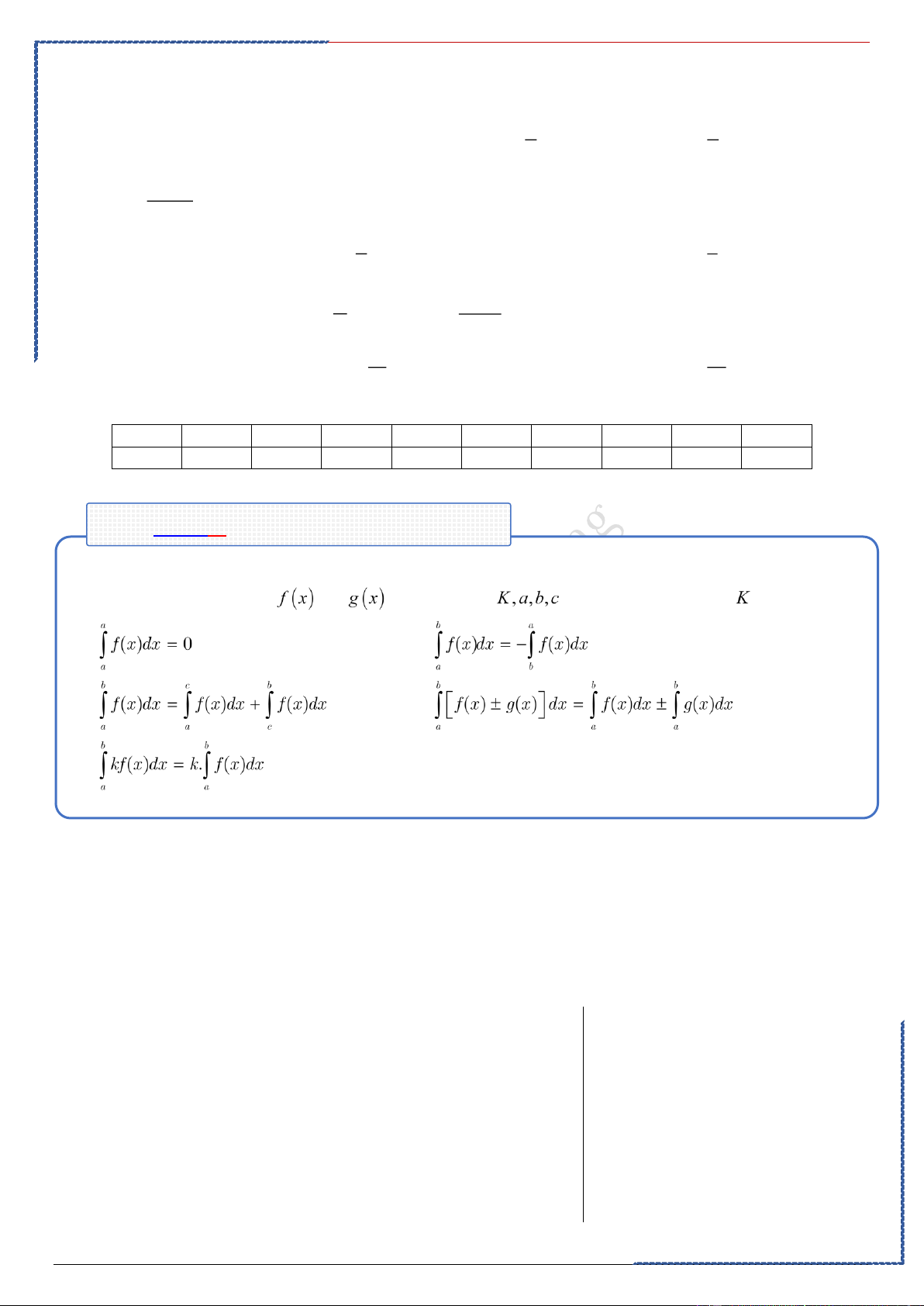
Dạng ②: Tích phân dùng tính chất
.Phương pháp: Giả sử cho hai hàm số và liên tục trên
là ba số bất kỳ thuộc . Khi đó ta có ①. ②. . ③. ④. . ⑤. .
A - Bài tập minh họa: 2 2 2
Câu 1: Cho biết f
 (x)dx = 3 và g(x)dx = 2 − 
. Tính tích phân I = 2x + f 
(x)−2g(x) d  x  . 0 0 0
Ⓐ. I =11. Ⓑ. I =18. Ⓒ. I = 5. Ⓓ. I = 3. Lời giải
PP nhanh trắc nghiệm
Chọn A 2
Ta có I = 2x + f 
(x)−2g(x) d  x  0 2 2 2 = 2 d x x + f
 (x)dx−2 g
 (x)dx = 4+3−2.( 2 − ) =11. 0 0 0
St-bs: Duong Hung 21
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung 2 4 4
Câu 2: Cho hàm số f ( x) liên tục trên và có f
 (x)dx = 9; f
 (x)dx = 4 . Tính I = f
 (x)dx ? 0 2 0 Ⓐ. 9 I = . Ⓑ. I = 36. Ⓒ. I =13. Ⓓ. I = 5. 4 Lời giải
PP nhanh trắc nghiệm Chọn C 4 2 4  Ta có f
 (x)dx = f
 (x)dx + f
 (x)dx = 9+ 4 =13. 0 0 2 1 5 5
Câu 3: Cho f (x)dx = 2 − 
và (2 f (x))dx = 6 khi đó f (x)dx  bằng 0 1 0 Ⓐ. 1. Ⓑ. 2 . Ⓒ.4 . Ⓓ. 3. Lời giải
PP nhanh trắc nghiệm Chọn A  5 5
(2 f (x))dx = 6  f  (x)dx = 3 1 1 5 1 5  f
 (x)dx = f
 (x)dx+ f  (x)dx = 2 − + 3 =1 0 0 1
B - Bài tập rèn luyện: 2 5 5 Câu 1:
Nếu f ( x) dx = 3, f ( x) dx = 1 −   thì f ( x) dx  bằng 1 2 1 Ⓐ. 2 . Ⓑ. −2 . Ⓒ.3 . Ⓓ. 4 . Câu 2:
Cho f ( x), g ( x) là hai hàm số liên tục trên
. Chọn mệnh đề sai trong các mệnh đề sau. b b b b b Ⓐ. f
 (x)dx = f  (y)dy .
Ⓑ. ( f (x)− g(x))dx = f
 (x)dx− g  (x)dx . a a a a a a b b b Ⓒ. f  (x)dx = 0 .
Ⓓ. ( f (x).g(x))dx = f  (x)d .x g  (x)dx . a a a a Câu 3:
Cho f ( x), g ( x) là hai hàm số liên tục trên
. Chọn mệnh đề sai trong các mệnh đề sau? b b Ⓐ. f
 (x)dx = f
 (y)dy . a a b b b
Ⓑ. ( f (x)− g(x))dx = f
 (x)dx− g
 (x)dx . a a a Ⓒ. a f
 (x)dx = 0 . a
St-bs: Duong Hung 22
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung b b b Ⓓ. f
 (x)g(x)dx = f
 (x)d .x g  (x)dx . a a a 1 1 1 Câu 4: Cho f
 (x)dx = 2 và g
 (x)dx = 5 , khi đó  f
 (x)+2g(x)dx bằng  0 0 0 Ⓐ. 3 − . Ⓑ. 8 − . Ⓒ.12 . Ⓓ. 1. 1 1 1 Câu 5: Cho  f
 (x)−2g(x)dx =12  và g
 (x)dx = 5, khi đó f (x)dx  bằng 0 0 0 Ⓐ. −2. Ⓑ. 12. Ⓒ. 22 . Ⓓ. 2 . 1 1 1  1  Câu 6: Cho f
 (x)dx = 2 và g  (x)dx = 7 − , khi đó f
 (x)− g(x) dx bằng    7  1 − 1 − 1 − Ⓐ. 3 − . Ⓑ. Ⓒ.3. Ⓓ. 1. c c a Câu 7: Cho f
 (x)dx =50 , f
 (x)dx = 20 . Tính f  (x)dx . a b b Ⓐ. −30 . Ⓑ. 0 . Ⓒ.70 . Ⓓ. 30 . 1 1 1 Câu 8: Cho f
 (x)dx = 2 và g
 (x)dx = 5 , khi đó  f
 (x)−2g(x)dx  bằng 0 0 0 Ⓐ. 3 − . Ⓑ. 12. Ⓒ. 8 − . Ⓓ. 1. 6 10 6 Câu 9:
Cho hàm số f ( x) liên tục trên thỏa mãn f
 (x)dx = 7, f
 (x)dx =8, f
 (x)dx = 9. Giá trị của 0 3 3 10 I = f
 (x)dx bằng 0 Ⓐ. I = 5 .
Ⓑ. I = 6 . Ⓒ. I = 7 . Ⓓ. I = 8 . 2 2
Câu 10: Cho hàm số f (x) liên tục trên tập và thỏa mãn f
 (x)dx = 3, f (x)dx = 5 −  . Giá trị của biểu 1 0 1 thức f ( x)dx  bằng 0 Ⓐ. 8. Ⓑ. −11. Ⓒ. 8 − . Ⓓ. −2.
Câu 11: Cho hàm số y = f ( x) liên tục trên
. Mệnh đề nào sau đây đúng? 1 2 1 1 Ⓐ. 1 f
 (x)dx = f
 (x)dx. Ⓑ. f
 (x)dx = 2 f
 (x)dx. 2 0 0 1 − 0 1 1 1 Ⓒ. f  (x)dx = 0. Ⓓ. f
 (x)dx = f
 (1− x)dx . 1 − 0 0
Câu 12: Cho hàm số y = f ( x) có đạo hàm liên tục trên đoạn 1; 4 , biết f (4) = 3, f ( ) 1 = 1. Tính 4 2 
f (x)dx 1
St-bs: Duong Hung 23
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung Ⓐ. 10. Ⓑ. 8. Ⓒ. 4 . Ⓓ. 5. 3
Câu 13: Cho các hàm số f ( x), g ( x) liên tục trên có 3 f
 (x)+2g(x)dx =1  ; 1 3 1 2 f
 (x)− g(x)dx = 3 −  . Tính f (2x +  ) 1 dx . 1 0 Ⓐ. −5 10 5 . Ⓑ. − . Ⓒ. 11 . Ⓓ. − . 7 7 14 14
Câu 14: Cho f ( x) và g ( x) là các hàm số liên tục bất kì trên đoạn  ;
a b . Mệnh đề nào sau đây đúng ? b b b b b b Ⓐ. f
 (x)− g(x) dx = f
 (x)dx− g
 (x)dx. Ⓑ. ( f (x)− g(x))dx = f
 (x)dx− g
 (x)dx. a a a a a a b b b b b b
Ⓒ. ( f (x)− g(x)) dx = f
 (x)dx− g
 (x)dx. Ⓓ. ( f (x)− g(x))dx = f
 (x)dx− g  (x)dx . a a a a a a 5 5 5 Câu 15: Biết f
 (x)dx = 3, g
 (x)dx = 9. Tích phân  f
 (x)+ g(x)dx  bằng 2 2 2 Ⓐ. 10. Ⓑ. 3. Ⓒ.6 . Ⓓ. 12. 0 3 3 Câu 16: Cho
f (x)dx = 3 f (x)dx = 3   . Tính tích phân f (x)dx  ? 1 − 0 1 − Ⓐ. 6 . Ⓑ. 4 . Ⓒ. 2 . Ⓓ. 0 . 1 1 1 Câu 17: Cho
f (x)dx = 2 − 
và g(x)dx = 5 − 
. Khi đó  f (x) +3g(x)dx bằng 0 0 0 Ⓐ. 10 − . Ⓑ. 12. Ⓒ. 17 − . Ⓓ. 1. 0 2 2 Câu 18: Cho
f (x)dx = 2, f (x)dx = 2   . Tích phân f (x)dx  bằng 2 − 0 2 − Ⓐ. 4 . Ⓑ. 3. Ⓒ.6 . Ⓓ. 1. 0 4 4 Câu 19: Cho
f ( x) dx = 1 −  và f
 (x)dx = 3. Khi đó, I = f
 (x)dx bằng 1 − 0 1 − Ⓐ. I = 4 − .
Ⓑ. I = 2 . Ⓒ. I = 4 . Ⓓ. I = 2 − . 2 2 3
Câu 20: Cho hàm số f (x) liên tục trên đoạn 0; 
3 và f (x)dx = 1  ,
f (x)dx = 4  . Tính I = f (x)dx  . 0 3 0 Ⓐ. I = 5. Ⓑ. I = 3 − . Ⓒ. I = 3. Ⓓ. I = 4 . BẢNG ĐÁP ÁN 1.A 2.D 3.D 4.C 5.C 6.C 7.A 8.C 9.B 10.C 11.D 12.C 13.D 14.B 15.D 16.B 17.C 18.A 19.B 20.B
St-bs: Duong Hung 24
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
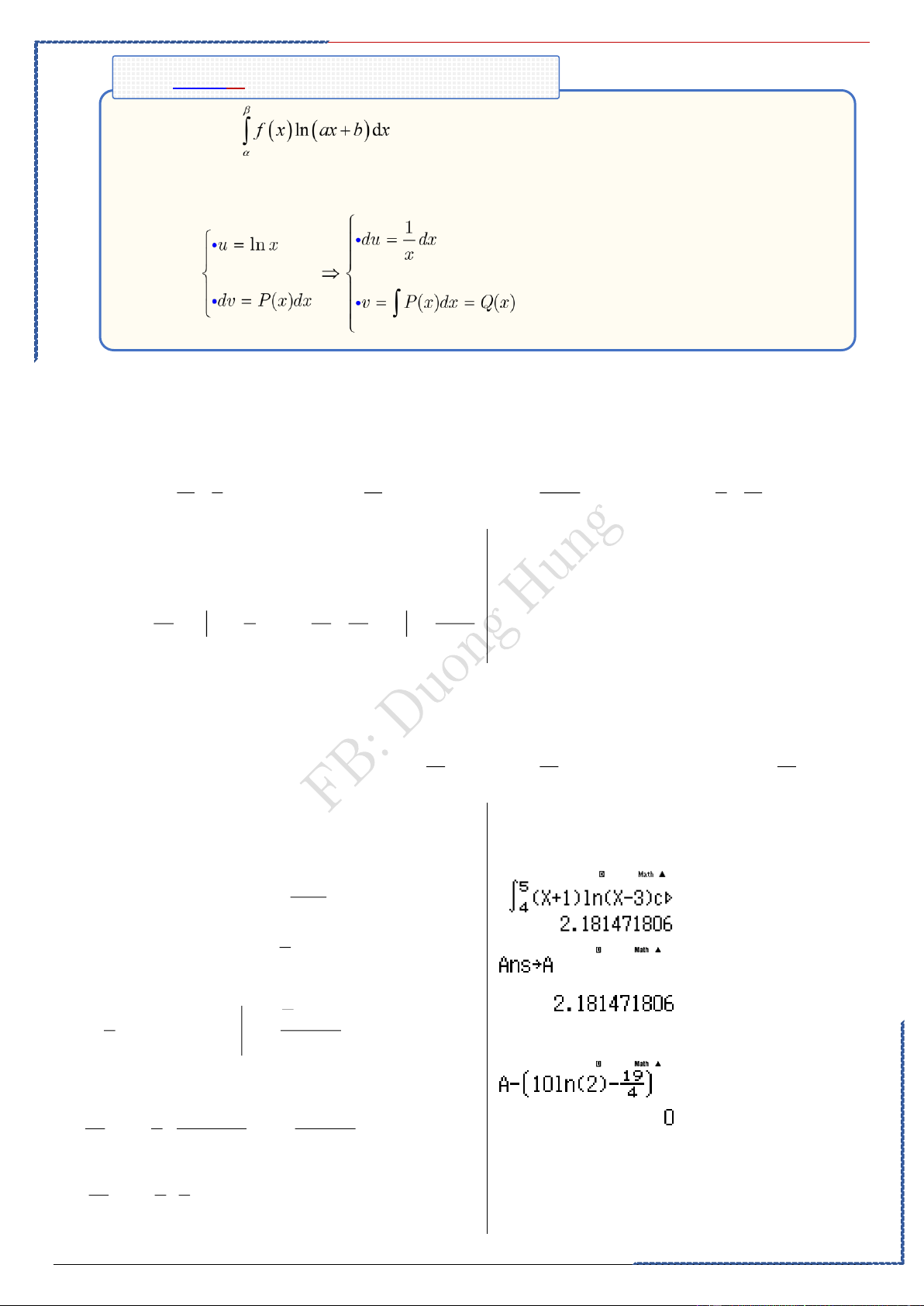
Dạng ③: Tích phân sử dụng định nghĩa chứa tham số a, b, c
-Phương pháp:
①. Dạng 1:I  . (với a≠0) Chú ý: I = ②. Dạng 2: ( với mọi ),é . • ,thì • thì thì I = • thì Đặt ③. Dạng 3: .( liên tục trên đoạn )
• Bằng phương pháp đồng nhất hệ số, ta tìm và sao cho: • Ta có I= Tích phân = Tích phân thuộc dạng 2.
St-bs: Duong Hung 25
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
A - Bài tập minh họa: 1 −
Câu 1: Cho biết x 1 3
dx = a + b ln 
, với a , b là các số nguyên. Giá trị của biểu thức a − 2b bằng x + 2 2 0 Ⓐ. 6 Ⓑ. 3. Ⓒ. 5 − . Ⓓ. 7 . Lời giải
PP nhanh trắc nghiệm
Chọn D Casio: 1 1 −  
Bước 1: Tính tích phân rồi lưu lại là A
Ta có: x 1 3 dx = 1− dx   
= (x −3ln x + 2 )1 . x + 2  x + 2  0 0 0 = (1−3ln3) −(0 − 3 3ln 2) = 1− 3ln . Bước 2: Rút 3 a = A − b ln . 2 2 a =1  Suy ra 
. Vậy a − 2b = 7 .
Bước 3: Table nhập f ( x) 3 = A − x ln b  = 3 − 2 với Start: 9 − , End: 9, Step: 1 .
Được cặp số x = 3
− , f (x) =1 thỏa
mãn. Suy ra a =1, b = 3 − . 1 Câu 2: Cho d x x = + +  với + + bằng ( a b c a, ,
b c là các số hữu tỉ. Giá trị của a b c 2x + ) ln 2 ln 3 2 1 0 Ⓐ. 1 . Ⓑ. 5 . Ⓒ. 1 − . Ⓓ. 1 . 12 12 3 4 Lời giải
PP nhanh trắc nghiệm Chọn A −  Đặt t 1 1
t = 2x +1  x = , dx = dt 2 2 1 1 d x x 1 (2x +1− ) 1 1 dx    1 1 1 = =  − d  2x +1    3 2 2 2 ( ) t −1  1 1  3 2x +1 2 2x +1 4  2x +1 2x +1  1 1 0 ( ) 0 ( ) 0  ( )   I = dt = ln t + = ln 3−    2 4t  4 4t  1 4 6 1 1  1  1 1  1  1 1 = ln 2x +1 + = ln 3 + −1 = ln 3−     . 4  2x +1  0 4  3  4 6 Vậy: 1
a + b + c = 12 Vậy 1 1 1
a + b + c = − + = . 6 4 12 3 1− 5x Câu 3: Cho
dx = a ln b + c  , với a, ,
b c là các số hữu tỷ. Giá trị của 9a +11b + 22c bằng 2 9x − 24x +16 2 Ⓐ. 15. Ⓑ. 10 − . Ⓒ.7 . Ⓓ. 9. Lời giải
PP nhanh trắc nghiệm Chọn C
St-bs: Duong Hung 26
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung Ta có 5 17 − − − 3 3 3 (3x 4) 1− 5x 1− 5x 3 3 dx = dx = dx    2 9x − 24x +16 3x − 4 3x − 4 2 2 ( )2 2 ( )2 3 3 5 5 dx 17 dx 5 d (3x − 4) 5 17 d (3x − 4) = − − = − −     3 3x − 4 3 (3x −4)2 9 3x − 4 9 (3x −4)2 2 2 2 2 5  5 17 1  5 2 17 = − ln 3x − 4 + . = ln −    9 9 3x − 4  9 11 22 2 5 2 17  a = ,b = , c = − 9 11 22 5 2 17
 9a +11b + 22c = 9. +11. − 22. = 1 − 0 9 11 22
B - Bài tập rèn luyện: a Câu 1: 875
Tìm số thực a  0 thỏa mãn ( 3
x − 6x)dx =  . 4 1 Ⓐ. a = 4 − . Ⓑ. a = 5 − . Ⓒ. a = 6 − . Ⓓ. a = 3 − . 2 Câu 2: dx b
Giá trị của tích phân 
là 1 ln ,. Tổng a + b + c bằng 2x + 5 a c 1 Ⓐ. 18. Ⓑ. 14. Ⓒ.16. Ⓓ. 10. 5 Câu 3: dx Giả sử = a + ln(b+1) 
, với a,b là các số nguyên không âm. Tính T = a + b ? 2x −1 1 Ⓐ. 9. Ⓑ. 2. Ⓒ.-1. Ⓓ. 1. 1 2 − Câu 4: 2x 1 Biết
dx = a ln 3 + b ln 2 + c  ( a, ,
b c là các số nguyên). Giá trị a + b − c bằng x +1 0 Ⓐ. 2 . Ⓑ. −4. Ⓒ.3. Ⓓ. 1 − .  2
Câu 5: Cho biết (4−sin x)dx = a +b, với ,a b là các số nguyên. Giá trị của biểu thức a +b bằng 0 Ⓐ. −4. Ⓑ. 6 . Ⓒ.1. Ⓓ. 1.  8  Câu 6: b Cho 2 I = cos 2 d x x = + 
, với a , b , c là các số nguyên dương, b tối giản. Tính P = a + b + c a c c 0 .
Ⓐ. P =15.
Ⓑ. P = 23. Ⓒ. P = 24 . Ⓓ. P = 25 . 1 2 x + 2x Câu 7: Cho = +  + (
với a , b là các số hữu tỷ. Giá trị của 16a b là
x + ) dx a b ln 2 3 1 0 Ⓐ. 17 . Ⓑ. 10. Ⓒ. 8 − . Ⓓ. 5 − .
St-bs: Duong Hung 27
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung 3 2x +1 Câu 8: Cho
dx = aln2 + bln3 + c ln5, ( , a , b c  ) 
. Giá trị của a + b + c bằng 2 x + 3x + 2 1 Ⓐ. -1 Ⓑ. 4 Ⓒ.1 Ⓓ. 7 b
Câu 9: Với a,b là các tham số thực. Giá trị tích phân ( 2 3x − 2ax −  )1dx bằng 0 Ⓐ. 3 2
b − b a − b . Ⓑ. 3 2
b + b a + b . Ⓒ. 3 2
b − ba − b . Ⓓ. 2
3b − 2ab −1. 1 Câu 10: x Cho I =
dx = a − ln b  với ,
a b là các số nguyên dương. Giá trị a + b bằng 0 x +1 Ⓐ. 3. Ⓑ. 4 . Ⓒ.5. Ⓓ. 6 . 1 1 1
Câu 11: Có bao nhiêu số thực a  ( 0;2π  sao cho 2 cos ( ax ) dx = +  . 2 4a 0 Ⓐ. 2 . Ⓑ. 4 . Ⓒ.3. Ⓓ. 1. 3 + Câu 12: x 3 Cho
dx = a ln 2 + b ln 3 + c ln 5 
, với a, b, c là các số nguyên. Giá trị của a + b + c bằng 2 x + 3x + 2 1 Ⓐ. 0 . Ⓑ. 2 . Ⓒ.3. Ⓓ. 1. 1 x Câu 13: Cho = + +  + + ( x a b c với , a ,
b c là các số hữu tỷ. Giá trị của 6a b c bằng x + 2) d ln 2 ln 3 2 0 Ⓐ. 4 . Ⓑ. −2. Ⓒ. 2 . Ⓓ. 1. 3 + Câu 14: x 2 Biết I =
dx = a + b ln c
, với a , b , c  , c  9 . Tính tổng S = a + b + c . x 1
Ⓐ. S = 7.
Ⓑ. S = 5. Ⓒ. S =8.
Ⓓ. S = 6 . 2   Câu 15: x 10 a Cho 2 x + dx = + ln  
với a,b  . Tính P = a + b? x + 1  b b 1 Ⓐ. P =1.
Ⓑ. P = 5. Ⓒ. P = 7 . Ⓓ. P = 2 . 2 − Câu 16: x 1 Giả sử
dx = a ln 5 + b ln 3  ; ,
a b Q . Tính 2
P = a − 2b . 2 x + 4x + 3 0
Ⓐ. P =10.
Ⓑ. P =8. Ⓒ. P = 3. Ⓓ. P =1. 1 Câu 17: Cho d x x = + +  với + + bằng: ( a b c a, ,
b c là các số hữu tỷ. Giá trị của 3a b c x + 2) ln 2 ln 3 2 0 Ⓐ. −2. Ⓑ. 2 . Ⓒ.1. Ⓓ. 1 − . 4 Câu 18: 1 1 a 1 Cho dx = ln −  , với a, ,
b c là các số hữu tỷ. Giá trị của a + b − c bằng 2 x x + 2 4 b c 3 ( ) Ⓐ. 7 . Ⓑ. 5 − . Ⓒ.14. Ⓓ. 9. BẢNG ĐÁP ÁN 1.C 2.A 3.B 4.D 5.C 6.D 7.D 8.A 9.A 10.A
St-bs: Duong Hung 28
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung 11.A 12.B 13.B 14.A 15.B 16.A 17.D 18.B Hướng dẫn giải Câu 1: a a 4   4 Ta có ( x a 11 3
x − 6x)dx 2 =  −3x  2 = − 3a + .  4  4 4 1 1
Từ giả thiết ta có phương trình: 4 a 11 875 2 a = 36 2 − 3a + = 4 2
a −12a −864 = 0   . 4 4 4 2 a = 24 −
Do a  0 nên a = 6 − .
Câu 2: 2 2 dx 1 d (2x + 5) Ta có 1 = =   ( x+ )2 1 9 ln 2 5 = ln . 1 2x + 5 2 2x + 5 2 2 7 1 1
Vậy a + b + c = 2 + 9 + 7 =18. Câu 3: 5 Ta có dx 1 5 1
= ln 2x −1 = (ln 9 − ln1) = ln 3 = ln(2 +1)  . 1 2x −1 2 2 1
Vậy a = 0,b = 2  a + b = 2 . Câu 4: 1 1 2 − 2  3 
Ta có: 2x 1dx  = 2 − dx 
 =(2x −3ln x + 3 1 ) 12 = 1− 3ln = 3 − ln 3 + 3ln 2 +1. x + 1  x + 1  0 2 0 0 Do đó: a = 3
− , b = 3, c =1. Vậy a + b − c = 1 − . Câu 5:    2 2 2   Ta có − = − = 2 + 2 (4 sin x)dx 4 dx sin x dx 4x cos x = 2 −1    . 0 0 0 0 0 a = 2 Suy ra 
a + b = 2 −1 =1. b  = 1 − Câu 6:     8 8  +  8     1 cos 4x 1 1 1 1 2 I = cos 2 d x x  = dx  
= (1+cos4x)dx = x + sin 4x   8 = + .  2  2 2  4  16 8 0 0 0 0
a =16 , b =1, c = 8.
Vậy P = a + b + c =16 +8+1= 25 . Câu 7:
St-bs: Duong Hung 29
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung − 2 x + 2x (x + ) 1 −1 1 − x +1 Ta có 3 dx = dx = dx − x +1 dx = ln x +1 − = − + ln 2     3 3 ( ) 3 1 ( ) 1 2 2 1 1 1 1 (x + ) 1 (x + ) 0 1 x +1 2 − 8 0 0 0 0 0 . Vậy 3
a = − ; b = 1 và 16a + b = 5 − . 8 Câu 8: 3 2x + 3 3 1 3 1 3 3 Ta có: dx = dx −
dx = 3ln x + 2 − ln x +1 = 3ln5−3ln3−  ln2 2   x + 3x + 2 x + 2 x + 1 1 1 1 1 1 Vậy: a = 1 − ;b = 3
− ;c = 3  a + b + c = 1 − . Câu 9: b ( b 2 3x − 2ax − ) 1 dx = ( 3 2
x − ax − x) 3 2
= b − ab −b . 0 0 Câu 10: x  1  1 Ta có: 1 1 I = dx = 1− dx =    
(x−ln x+1) =1−ln2. 0 0 x +1  x +1 0
Vậy: a =1, b = 2  a + b = 3. 1 1 1 1 1 + cos 2ax 1 cos 2ax Câu 11: Ta có: 2 cos ( ax ) ( ) ( ) dx = dx = dx + dx     2 2 2 0 0 0 0 1 1 cos( 2ax ) 1 Mà 1 1 1 1 dx =  và dx = sin ( 2ax ) = sin ( 2a )  . 2 2 2 4a 4a 0 0 0 1 1 1 2
 cos ( ax )dx = + sin ( 2a )  . 2 4a 0 1 1 1 Theo đề bài ta có: 2 cos ( ax ) dx = +  . 2 4a 0 π π
Nên sin( 2a ) = 1  2a = + k2π  a = + π k ,( k  ) 2 4 π 1 7
Do a  ( 0;2   0  + π k  2π  −
k   k 0;  1 . 4 4 4 π
Với k = 0  a = . 4 Với 5π k = 1  a = . 4
Vậy có 2 giá trị a  ( 0;2π  thỏa mãn đề bài. Câu 12:
St-bs: Duong Hung 30
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung 3 3 3 3 x + 3 x + 3 2 1 dx = dx = dx − dx     2 x + 3x + 2 x +1 x + 2 x +1 x + 2 1 1 ( )( )  1 1 = ( x + − x + ) 3 2 ln 1 ln 2 = 2ln 2 + ln 3 − ln 5 1
Suy ra a = 2 , b =1 , c = 1 − .
Nên a + b + c = 2 +1−1 = 2. Câu 13: 1 1 1 x  1 2   2  1 Ta có =  −  = + + = − − +  ( x x x    . x + 2) d d ln 2 ln 2 ln 3 2  x + 2  (x + 2)2   x + 2  3 0 0 0  1
Suy ra a = − , b = 1 − , c =1. 3
Vậy 6a + b + c = 2 − . 3 + 3   Câu 14: Ta có x 2 2 I = dx  = 1+ dx   = ( x + x) 3 2 ln = 2 + 2ln3 . xx  1 1 1
Mà I = a + bln c , với a , b , c  , c  9 . Suy ra a = 2 , b = 2 , c = 3.
Vậy S = a + b + c = 7 . Câu 15: 2 2 2    + −    Ta có x x 1 1 1 2 2 2 x + dx = x + dx = x + 1 − dx        x + 1   x + 1   x + 1  1 1 1 2 3  x  10 10 2 10 a = + x − ln x +1 = + ln 2 − ln 3 = + ln = + ln   .  3  3 3 3 b b 1
Suy ra a = 2;b = 3. Vậy a + b = 5 . Câu 16: 2 2 x −  − 2  Ta có 1 1 2 dx = +
dx = − ln x +1 + 2 ln x + 3     = 2ln5−3ln3. 2   0 x + 4x + 3
x +1 x + 3  0 0
a = 2 , b = 3 − . Vậy 2
P = a − 2b =10 . 1 1 1 1 − Câu 17:  d x x dx dx 1 1 1 = − 2 = ln x + 2 − 2. = − − ln 2 + ln3    . x + 2 x + 2 x + 2 x + 2 3 0 ( )2 0 0 ( )2 0 0 1
  a = − ;b = 1
− ;c = 1 3a + b + c = 1 − . 3 1 A Bx + C Câu 18: Ta có: 2 = +
 1  Ax + Bx + C x + 2 2 x ( x + 2) 2 ( )( ) x + 2 x
Khi đó, dùng kỹ thuật đồng nhất hệ số ta được
St-bs: Duong Hung 31
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung  1 A =  4  + =  1 1 A B 0   4 4 − x +      1 1 1 4 2
2B + C = 0  B = −  dx =   + d  x 2 4 x   (x + 2) 4  ( x + 2) 2 x 3 3  2C = 1   1   C =  2  1 1  4 4 − x + 4 4 4    +  Khi đó ta có: 1 1 dx 1 dx 1 dx 1 x 2 1 4 2  +  x = − + = −      4  ( x + 2) d ln 2 2 x 4 x + 2 4 x 2 x   4 x 2x  3 3 3 3 3  
  a = 9,b =10,c = 24  a + b − c = 5 − .
St-bs: Duong Hung 32
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung Full Chuyên đề 12 new 2020-2021 CHƯƠNG ③: FB: Duong Hung
Bài 3: TÍCH PHÂN ĐỔI BIẾN SỐ
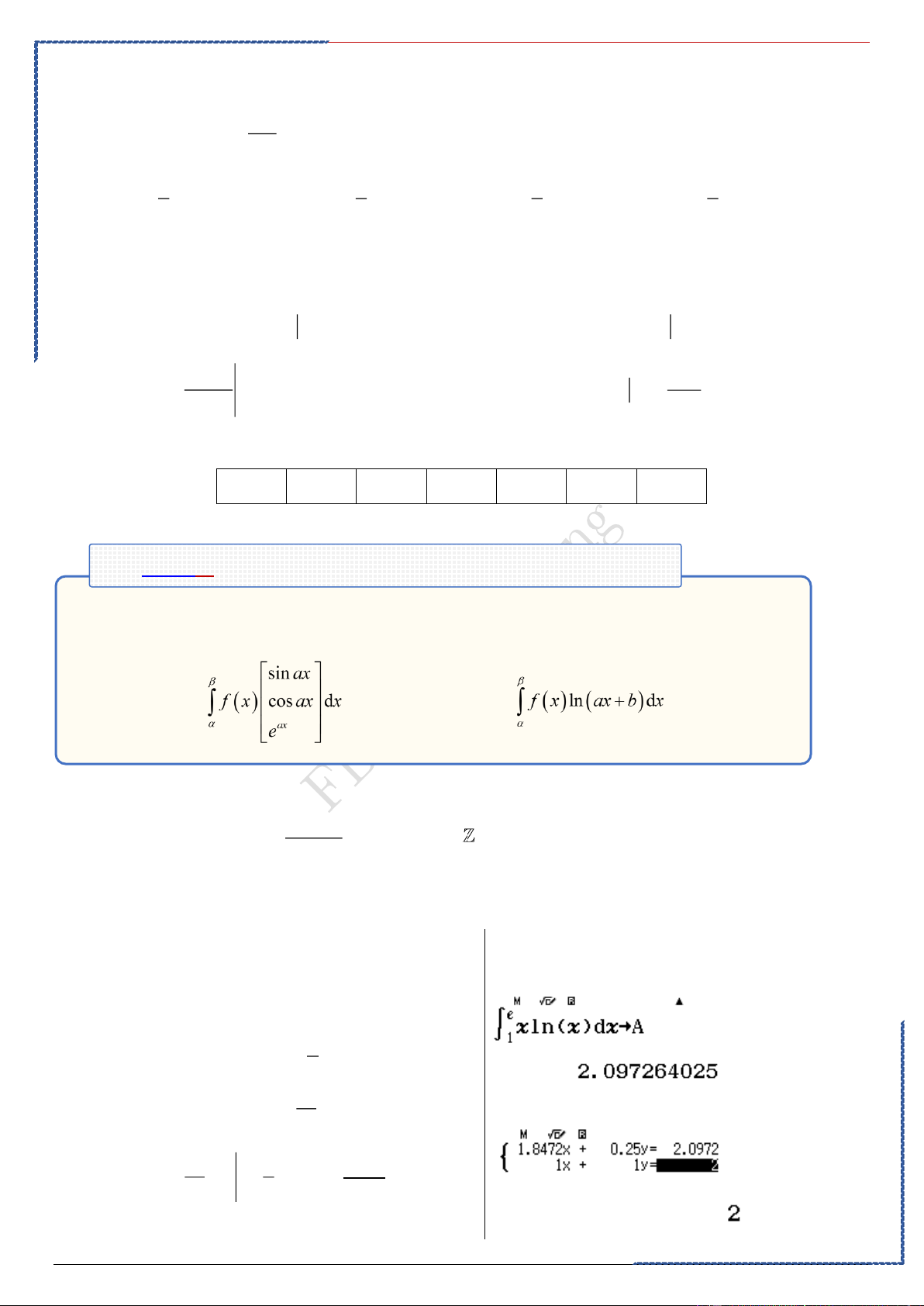
Dạng ①: Phương pháp tích phân bằng cách đổi biến số cơ bản
.Phương pháp: Cho hàm số liên tục trên đoạn Giả sử hàm số có đạo hàm liên tục trên đoạn và Giả sử có thể viết với liên tục trên đoạn Khi đó, ta có
. Để tính tích phân:
ta thực hiện các bước:
.Bước 1: Biến đổi để chọn phép đặt
. Bước 2. Thực hiện phép đổi cận:  Với thì ; thì
. (Ghi Nhớ : đổi biến phải đổi cận)
. Bước 3. Đưa về dạng
đơn giản và dễ tính hơn.
. Dấu hiệu nhận biết và cách đặt. Dấu hiệu Có thể đặt . Có căn . Có ngoặc . Có mũ . Có
hoặc biểu thức chứa . Có
hoặc biểu thức chứa . Có . Có . Có . Có . Có mẫu: mẫu
St-bs: Duong Hung 33
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
A - Bài tập minh họa: 1
Câu 1: Tính tích phân 2 4
I = x(1+ x ) dx 0 Ⓐ. 16 I = Ⓑ. 31 I = Ⓒ. 1 I = Ⓓ. 1 I = − 5 10 10 10 Lời giải
PP nhanh trắc nghiệm Chọn B Casio: Đặt 2
t = 1+ x dt = 2xdx .
Đổi cận x = 0  t =1; x =1 t = 2 2 4 t 31 Nên I = dt =  2 10 1 2
Câu 2: Tính tích phân 2
I = 2x x −1dx  bằng cách đặt 2
u = x −1, mệnh đề nào dưới đây đúng? 1 3 2
Ⓐ. I = 2 udu  Ⓑ. I = udu  0 1 3 2 Ⓒ. 1 I = udu  Ⓓ. I = udu  2 0 1 Lời giải
PP nhanh trắc nghiệm Chọn C
Casio: xét hiệu bằng 0 2  2
I = 2x x −1dx  1 Đặt 2
u = x −1  du = 2xdx .
Đổi cận x =1 u = 0 ; x = 2  u = 3 3 Nên I = udu  0 
Câu 3: Tính tích phân 3 I = cos . x sin d x x . 0 Ⓐ. 1 4 I = −  Ⓑ. 4 I =  − Ⓒ. I = 1 0 Ⓓ. I = − 4 4 Lời giải
PP nhanh trắc nghiệm Chọn C
 Sử dụng máy tính, tính tích phân hàm lượng Ta có: 3 I = cos . x sin xdx  .
giác phải chuyển về đơn vị radian. 0
St-bs: Duong Hung 34
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
Đặt t = cos x dt = −sin xdx d
− t = sin xdx
Đổi cận: với x = 0  t =1;với x =   t = 1 − . 1 − t 1 1 − 3 3 ( )4 1 1 4 4
Vậy I = − t dt = t dt = = − = 0   . 4 4 4 1 1 − 1 −
B - Bài tập rèn luyện: 1 5 Câu 1:
Cho tích phân I = x
 (1− x) dx . Mệnh đề nào dưới đây đúng? 0 0 0 Ⓐ. 5 I = − t
 (1−t)dt .
Ⓑ. I = − ( 6 5
t − t )dt . 1 − 1 − 1 0 Ⓒ. 5 I = t
 (1−t)dt . Ⓓ. I = − ( 6 5
t − t )dt . 0 1 − 4 Câu 2:
Cho I = x 1+ 2x dx  và u =
2x +1 . Mệnh đề nào dưới đây sai? 0 3 5 3   3 Ⓐ. 1 u u I =  −  . Ⓑ. 2 I = u ( 2 u −  )1du . 2  5 3  1 1 3 3 Ⓒ. 1 1 2 I = x ( 2 x −  )1dx. Ⓓ. 2 I = u ( 2 u −  )1du. 2 2 1 1 3 x Câu 3: Tính K = dx  . 2 x −1 2 Ⓐ. 1 8 K = ln 2 .
Ⓑ. K = ln .
Ⓒ. K = 2ln 2 . Ⓓ. 8 K = ln . 2 3 3  Câu 4: Tích phân 2 cos . x sin x dx  bằng 0 Ⓐ. 3 2 2 − . Ⓑ. . Ⓒ. − . Ⓓ. 3 . 2 3 3 2 2 Câu 5: Cho 2
I = 2x x −1dx  và 2
u = x −1. Mệnh đề nào dưới đây sai? 1 3 2 3 Ⓐ. 2 2 I = udu  . Ⓑ. I = 27 . Ⓒ. I = udu  . Ⓓ. 2 I = 3 . 3 3 0 1  2 3 cot x Câu 6: Cho I = dx
và u = cot x . Mệnh đề nào dưới đây đúng 2  sin x 4  2 1 1 1 Ⓐ. 3 I = u du  . Ⓑ. 3 I = u du  . Ⓒ. 3
I = − u du  . Ⓓ. I = d u u  .  0 0 0 4 ln 5 ( x e + ) 1 x e Câu 7: Cho I = dx  . Đặt x
t = e −1 . Chọn mệnh đề đúng. x − ln 2 e 1
St-bs: Duong Hung 35
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung 4 ln 5
Ⓐ. I = 2( 2t + 2)dt . Ⓑ. 2 I = (t + 2)dt  . 1 ln 2 2 4
Ⓒ. I = 2( 2t + 2)dt .
Ⓓ. I = ( 2t + 2)dt . 1 1 4 Câu 8:
Cho I = x 1+ 2x dx  và u =
2x +1 . Mệnh đề nào dưới đây sai? 0 3 5 3   3 Ⓐ. 1 u u I =  −  . Ⓑ. 2 I = u ( 2 u −  )1du . 2  5 3  1 1 3 3 Ⓒ. 1 1 2 I = x ( 2 x −  )1dx. Ⓓ. 2 I = u ( 2 u −  )1du. 2 2 1 1 3 x Câu 9: Tính K = dx  . 2 x −1 2 Ⓐ. 1 8 K = ln 2 .
Ⓑ. K = ln .
Ⓒ. K = 2ln 2 . Ⓓ. 8 K = ln . 2 3 3  2 3 cot x Câu 10: Cho I = dx
và u = cot x . Mệnh đề nào dưới đây đúng 2  sin x 4  2 1 1 1 Ⓐ. 3 I = u du  . Ⓑ. 3 I = u du  . Ⓒ. 3
I = − u du  . Ⓓ. I = d u u  .  0 0 0 4 ln 5 ( x e + ) 1 x e Câu 11: Cho I = dx  . Đặt x
t = e −1 . Chọn mệnh đề đúng. x − ln 2 e 1 4 ln 5
Ⓐ. I = 2( 2t + 2)dt . Ⓑ. 2 I = (t + 2)dt  . 1 ln 2 2 4
Ⓒ. I = 2( 2t + 2)dt .
Ⓓ. I = ( 2t + 2)dt . 1 1  3 Câu 12: Cho 2 I = sin x cos d x x
, khẳng định nào sau đây đúng? 0 Ⓐ. 1 1 1 1 2 I  .
Ⓑ. 0  I  .
Ⓒ. I  . Ⓓ. 2  I  1. 3 2 3 2 3 3 1 dx
Câu 13: Cho I = 
, m là số thực dương. Tìm tất cả các giá trị của m để I  1. 2x + m 0 Ⓐ. 1 1 0  m  .
Ⓑ. m  .
Ⓒ. m  0. Ⓓ. 1 1  m  . 4 4 8 4 2 2
Câu 14: Cho tích phân 2 I = 16 − x dx
và x = 4sin t . Mệnh đề nào sau đây đúng? 0   4 4
Ⓐ. I = 8(1+cos2t)dt . Ⓑ. 2 I = 16 sin d t t  . 0 0
St-bs: Duong Hung 36
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung   4 4
Ⓒ. I = 8(1−cos2t)dt. Ⓓ. 2 I = 1 − 6 cos d t t  . 0 0 BẢNG ĐÁP ÁN 1.C 2.B 3.B 4.B 5.C 6.B 7.C 8.B 9.B 10.B 11.C 12.B 13.A 14.A
Dạng ②: Tích phân đổi biến chứa tham số a, b, c cơ bản
-Phương pháp:
. Để tính tích phân:
ta thực hiện các bước:
.Bước 1: Biến đổi để chọn phép đặt
. Bước 2. Thực hiện phép đổi cận:  Với thì ; thì
. Bước 3. Đưa về dạng
đơn giản và dễ tính hơn.
A - Bài tập minh họa: 1 − Câu 1: Cho biết a 2 x x +1 dx  2 1 =
với a , b là các số tự nhiên. Giá trị của 2 2 a − b bằng b 0 Ⓐ. −5. Ⓑ. 5. Ⓒ. 2. Ⓓ.7. Lời giải
PP nhanh trắc nghiệm Chọn A
Tính tích phân rồi lưu lại là A .  Đặt 2 x +1 = t 2 2
x +1= t xdx = t dt . a − Rút 2 1 b = . A
Ta có x = 0  t =1, x =1  t = 2 . x −  table f ( x) 2 1 = với Start: 1 2 2 3 t − Khi đó: 2 A x x +1 dx  2 = t dt  = 2 2 1 =
a = 2, b = 3. 3 3 0 , End: 18, Step: 1 . 0 1 1 , f (x) = Vậy 2 2
Được cặp số x = 2 3 a − b = 5 − .
thỏa mãn. Suy ra a = 2 , b = 3 . e Câu 2: Cho ln x = + +  với + + ( x a b c
a , b , c là các số hữu tỷ. Giá trị của 3a b c x ln x + 2) d ln 2 ln 3 2 1 bằng Ⓐ. −2 . Ⓑ. 1 − . Ⓒ. 2 . Ⓓ.1.
St-bs: Duong Hung 37
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung Lời giải
PP nhanh trắc nghiệm Chọn B Đặt 1
t = ln x  dt = dx . x
Đổi cận: x =1 t = 0 ; x = e  t =1. Khi đó: e 1 ln x t I = =  ( x tx ln x + 2) d d 2 (t + 2)2 1 0 1 1 t 2 2  1 2  + − = =  −   ( t tt + 2) d d 2 t + 2  (t + 2)2  0 0  1  1  1 = ln t + 2 + 2. = − − ln 2 + ln 3   .  t + 2  3 0 1
Suy ra: a = − ; b = 1 − ; c =1. 3
Do đó: 3a + b + c = 1 − . ln 6 x Câu 3: Biết e
dx = a + b ln 2 + c ln 3 
với a , b , c là các số nguyên. Tính T = a + b + c . x + + 0 1 e 3 Ⓐ. T = 1 − .
Ⓑ. T = 0 .
Ⓒ. T = 2 . Ⓓ.T =1. Lời giải
PP nhanh trắc nghiệm Chọn B ln 6 ex Xét I = dx  . Đặt ex t = + 3 2  = ex t + 3 x + + 0 1 e 3  2 d = ex t t dx .
Đổi cận x = 0  t = 2, x = ln 6  t = 3. 3 2t 3  2  Khi đó I = dt  = 2 − dt  
= (2t − 2ln t +1) 3 t +1  t +1  2 2 2 = 2 − 4ln 2 + 2ln3 .
Suy ra a = 2 , b = 4
− , c = 2 nên T = a +b + c = 0 .
B - Bài tập rèn luyện:
St-bs: Duong Hung 38
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung 5 dx
Câu 1: Tính tích phân I = 
ta được kết quả I = a ln3+ bln5. Giá trị 2 2
S = a + ab + 3b là x 3x +1 1 Ⓐ. 0 . Ⓑ. 4 . Ⓒ. 1. Ⓓ.5. e Câu 2: ln x c Cho I = = + +  , với ( dx a b , a ,
b c  . Khẳng định nào sau đâu đúng. x ln x + 2) ln 3 ln 2 2 3 1 Ⓐ. 2 2 2
a + b + c = 1. Ⓑ. 2 2 2
a + b + c = 11 . Ⓒ. 2 2 2
a + b + c = 9 . Ⓓ. 2 2 2
a + b + c = 3. 4 + Câu 3: 2x 1 3 Cho dx = a ln + bln c  , với a, ,
b c là các số hữu tỷ. Giá trị của 5a +15b −11c bằng 2 3x − x − 2 2 3 Ⓐ. 12 − . Ⓑ. 15 − . Ⓒ. 14 . Ⓓ.9. 4 Câu 4: dx Biết I =
= a ln 2 + bln 3+ cln 5  , trong đó , a , b c
. Tính giá trị của T = a + b + c . 2 x + x 3
Ⓐ. T = 2 .
Ⓑ. T = 3. Ⓒ. T = 1 − . Ⓓ.T = 5 . 5 1
Câu 5: Giả sử tích phân I =
dx = a + b ln 3 + c ln 5 
(a, ,bc  ) . Khi đó: 1 1 + 3x + 1 Ⓐ. 8
a + b + c = . Ⓑ. 4
a + b + c = . Ⓒ. 5
a + b + c = . Ⓓ. 7
a + b + c = . 3 3 3 3  4 + Câu 6: 2 3 tan x Cho
dx = a 5 + b 2, 
với a,b . Tính giá trị biểu thức A = a + . b 1+ cos 2x 0 Ⓐ. 1 . Ⓑ. 7 . Ⓒ. 2 . Ⓓ. 4 . 3 12 3 3 e Câu 7: ln x Cho = + +  với + + bằng ( x a b c
a , b , c là các số hữu tỷ. Giá trị của 3a b c x ln x + 2) d ln 2 ln 3 2 1 Ⓐ. −2 . Ⓑ. 1 − . Ⓒ. 2 . Ⓓ.1. 3 Câu 8: ln x a Cho =  −   với
và phân số a tối giản. Giá trị của + + ( , a , b c  * a b c x + ) dx ln 3 c ln 2 2 1 b b 1 bằng Ⓐ. 8 . Ⓑ. 7 . Ⓒ. 6 . Ⓓ.9 . ln 6 x Câu 9: e Biết
dx = a + b ln 2 + c ln 3 
với a , b , c là các số nguyên. Tính T = a + b + c . x + + 0 1 e 3 Ⓐ. T = 1 − .
Ⓑ. T = 0 .
Ⓒ. T = 2 . Ⓓ.T =1. e + Câu 10: ln x 3 a Cho biết dx = + b 3 
, với a , b là các số nguyên. Giá trị của biểu x 3 1
thức 1 + log a bằng 2 2b Ⓐ. -1. Ⓑ. 7 . Ⓒ. 8. Ⓓ.6. 2 1 − Câu 11: a Cho biết 2 x x +1 dx  2 1 =
với a , b là các số tự nhiên. Giá trị của 2 2 a − b bằng b 0
St-bs: Duong Hung 39
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung Ⓐ. −5. Ⓑ. 5. Ⓒ. 2. Ⓓ.7. BẢNG ĐÁP ÁN 1.D 2.D 3.A 4.A 5.B 6.A 7.B 8.A 9.B 10.C 11.A
Dạng ③: Tích phân hàm ẩn đổi biến số cơ bản
-Phương pháp: Tính tích phân .Giả sử
được viết dưới dạng ,trong đó hàm số
có đạo hàm trên , hàm số y=f(u) liên tục sao cho hàm hợp xác định trên và
là hai số thuộc . Khi đó
Chú ý: Đối với biến số lấy tích phân, ta có thể chọn bất kì một chữ số thay
cho . Như vậy tích phân không phụ thuộc vào biến tức là
A - Bài tập minh họa: 9 4
Câu : Biết f ( x) là hàm liên tục trên và f
 (x)dx =9. Khi đó giá trị của f
 (3x−3)dx là 0 1 Ⓐ. 0 . Ⓑ. 27 . Ⓒ. 3 . Ⓓ. 24 . Lời giải
PP nhanh trắc nghiệm Chọn C m Nếu có f
 (x)dx = M thì
Đặt u = 3x − 3, suy ra du = 3dx . n
Đổi cận: x =1 thì u = 0 ; x = 4 thì u = 9 .  M f  (ax+b)  Ta có: dx = ; a 4 9 9 9  f  ( x− ) 1 x = f  (u) 1 u = f  (u) 1 u = f  (x) 1 3 3 d d d dx = .9 = 3. . n = .
a  + b, m = . a  + b 3 3 3 3 1 0 0 0  Áp dụng: 4  Vậy f
 (3x−3)dx = 3. 9 1 = 3 3
Câu 2: Cho hàm số f (x) liên tục trên R và thỏa mãn 3
f (x + 2x − 2) = 3x −1 với x  R . Tính 10
tích phân I = f (x)dx  1
St-bs: Duong Hung 40
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung Ⓐ. 151. Ⓑ. 27 . Ⓒ. 121 . Ⓓ.105 . 4 4 6 Lời giải
PP nhanh trắc nghiệm
Chọn A Đặt 3
x = t + t −  dx = ( 2 2 2
3t + 2t ) dt , 3
x =1 t + 2t = 3  t =1  Đổi cận :  3
x =10  t + 2t =12  t = 2 2 2 Ta có 3 I =
f (t + 2t − 2).  ( 2
3t + 2t )dt = (3t − ) 1 ( 2
3t + 2t )dt 1 1 2 2 4   = ( 9t 151 3 2
9t + 3t − 2t ) dt 3 2 =  + t − t  =  4  4 1 1 2021
Câu 3: Cho Cho hàm số f (x) liên tục trên R và thỏa mãn
f (x)dx = 2  . Tính tích phân 0 2021 e 1 − x I = . f  ( 2 ln(x +1) .dx 2 ) x +1 0 Ⓐ. 3 . Ⓑ. 5 . Ⓒ. 1. Ⓓ. 3 − . Lời giải
PP nhanh trắc nghiệm Chọn C 2x x 1
Đặt t = ln ( 2 x + ) 1  dt = dx dx = dt , 2 2 x +1 x +1 2
x = 0  t = 0   Đổi cận :  2021 x = e −1  t = 2021 2021 2021 1 1 1  Ta có I = f (t)dt = f (x)dx = .2 = 1   2 2 2 0 0
B - Bài tập rèn luyện: 3 1 Câu 1: Cho f
 (x)dx = 4, khi đó f (2x+  )1dx bằng 1 0 Ⓐ. 1 8 . Ⓑ. 2 . Ⓒ. . Ⓓ. 3 . 2 2 3
Câu 2: Cho hàm số f ( x) liên tục trên và thỏa mãn f
 (x)dx = 2. Tính 1 1 I =  f
 (2x+ )1+2x+1dx  . 0 Ⓐ. I =11.
Ⓑ. I = 3.
Ⓒ. I =14 . Ⓓ. I = 6.
St-bs: Duong Hung 41
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung 9 1 Câu 3: Cho f
 (x)dx =10. Tính tích phân J = f
 (5x + 4)dx . 4 0
Ⓐ. J = 2 .
Ⓑ. J = 10.
Ⓒ. J = 50. Ⓓ. J = 4 . 8 3 Câu 4: 3
Cho hàm số f ( x) liên tục trên và f
 (x)dx =10. Tính I = f (3x−  ) 1 dx . 2 2 1 Ⓐ. 30. Ⓑ. 10. Ⓒ. 20 . Ⓓ.5 . 2 3
Câu 5: Cho f ( x) là hàm số chẵn, liên tục trên . Biết rằng f
 (x)dx = 8 và f
 (2x)dx = 3. Tính 1 − 1 6 tích phân f  (x)dx. 1 − Ⓐ. 14. Ⓑ. 11. Ⓒ. 5 . Ⓓ. 2 . 4 2
Câu 6: Cho f (x)dx = 2018 
. Tính tích phân I =  f (2x) + f (4−2x)dx 0 0 Ⓐ. I = 0. Ⓑ. I = 2018. Ⓒ. I = 4036 . Ⓓ. I =1009 . 4 5 2 ln 2
Câu 7: Biết f
 (x)dx = 5 và f
 (x)dx = 20. Tính (4 −3) −   ( 2x) 2x f x dx f e e dx . 1 4 1 0 Ⓐ. 15 5 I = . Ⓑ. I =15. Ⓒ. I = . Ⓓ. I = 25. 4 2 4 2 Câu 8: Cho f x dx
2018 . Tính tích phân I f (2x) f (4 2x) dx . 0 0
Ⓐ. I 0.
Ⓑ. I 2018.
Ⓒ. I 4036. Ⓓ. I 1009 . 2
Câu 9: Giả sử hàm số f ( x) liên tục trên đoạn 0;2 thỏa mãn f  (x) . Tính tích phân dx = 6 0  2 I = f  (2sin x)cos d x . x 0 Ⓐ. 3 . Ⓑ. 3 − . Ⓒ. 6 . Ⓓ. 6 − . 4 1
Câu 10: Cho I = f
 (t)dt = 9. Tính tích phân J = f (3x+  ) 1 dx . 1 0 Ⓐ. 9. Ⓑ. 27. Ⓒ. 3. Ⓓ.1.  1 4 Câu 11: Cho f
 (x)dx = 2019. Giá trị của I = f  (cos2x)sin2 d x x bằng 0 0
Ⓐ. 2019 . Ⓑ. 2019 − . Ⓒ. 4038 . Ⓓ. 2019 . 4 2 2 4 2
Câu 12: Cho tích phân I = f
 (x)dx = 32. Tính tích phân J = f  (2x)d .x 0 0
Ⓐ. J = 32. Ⓑ. J = 64. Ⓒ. J = 8. Ⓓ. J =16.
St-bs: Duong Hung 42
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung 1 2 3
Câu 13 ho hàm số f x liên tục trên có 2 f
 (x)dx = 2 và f
 (x+ )1dx = 4. Tính I = f  (x)dx . 0 0 0
Ⓐ. I = 5. Ⓑ. I = 4. Ⓒ. I = 6. Ⓓ.I = 7. 2  
Câu 14: Cho hàm số f ( x) liên tục trên và f
 (x)dx = 2018. Tính I = xf
 ( 2x)dx. 0 0
Ⓐ. I =1008.
Ⓑ. I = 2019 . Ⓒ. I = 2017 . Ⓓ. I =1009 . 1 3 1
Câu 15: Cho hàm số f ( x) liên tục trên và có f
 (x)dx = 2; f
 (x)dx =8. Tính I = f
 ( 2x−1)dx 0 0 1 −
Ⓐ. I = 6. Ⓑ. 2 I = .
Ⓒ. I = 5. Ⓓ. 3 I = 3 2 2 4 f ( x ) Câu 16: Cho f
 (x)dx = 2 Khi đó I = dx  bằng x 1 1 Ⓐ. 4. Ⓑ. 1 . Ⓒ. 1. Ⓓ.2. 2 8 1 Câu 17: Cho f
 (x+ )1dx =10. Tính J = f
 (5x+4)dx . 3 0
Ⓐ. J = 4.
Ⓑ. J =10 . Ⓒ. J = 50 . Ⓓ. J = 2 BẢNG ĐÁP ÁN 1.B 2.B 3.A 4.D 5.A 6.B 7.A 8.B 9.A 10.C 11.D 12.D 13.A 14.D 15.C 16.A 17.D
St-bs: Duong Hung 43
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung Full Chuyên đề 12 new 2020-2021 CHƯƠNG ③: FB: Duong Hung
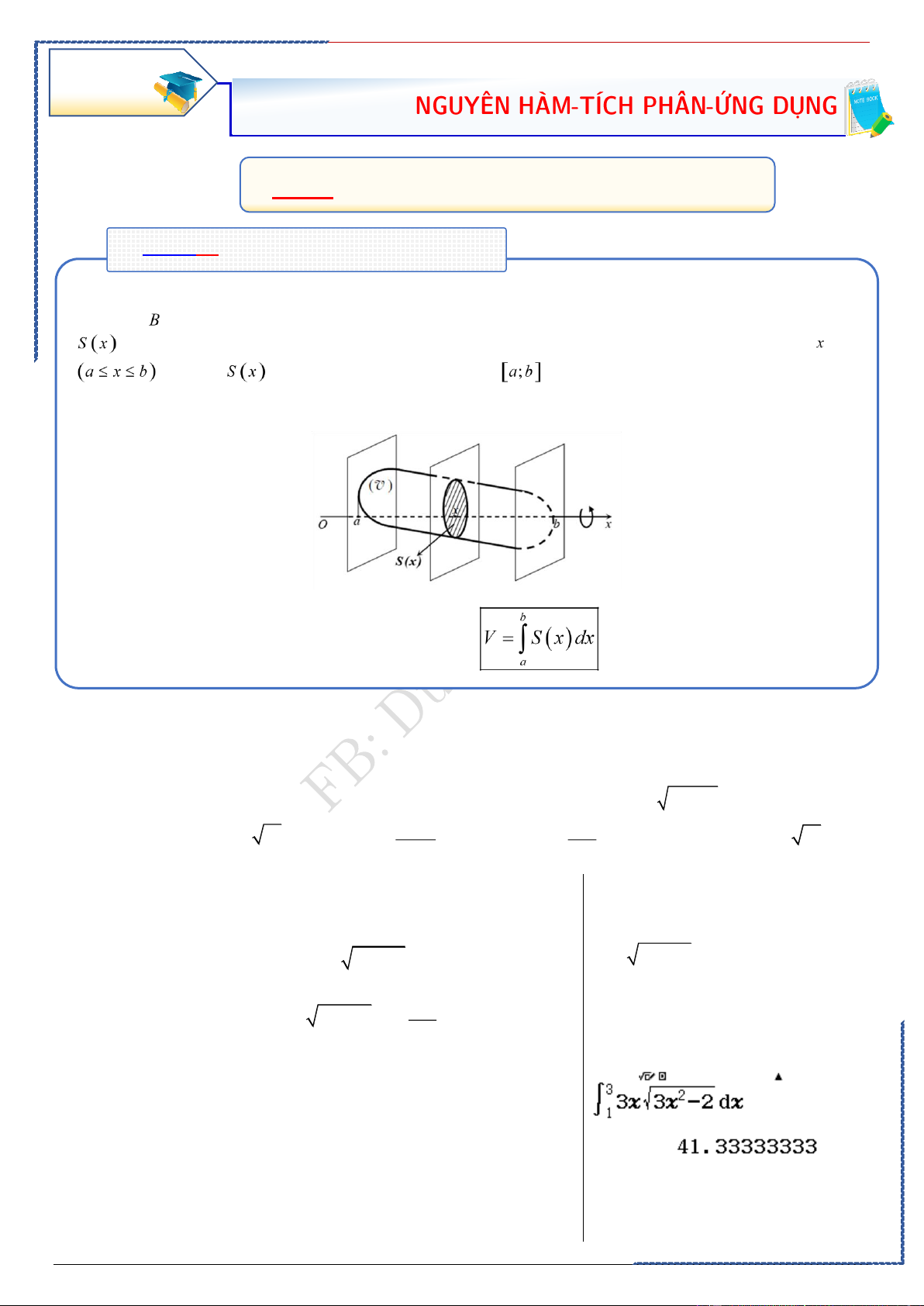
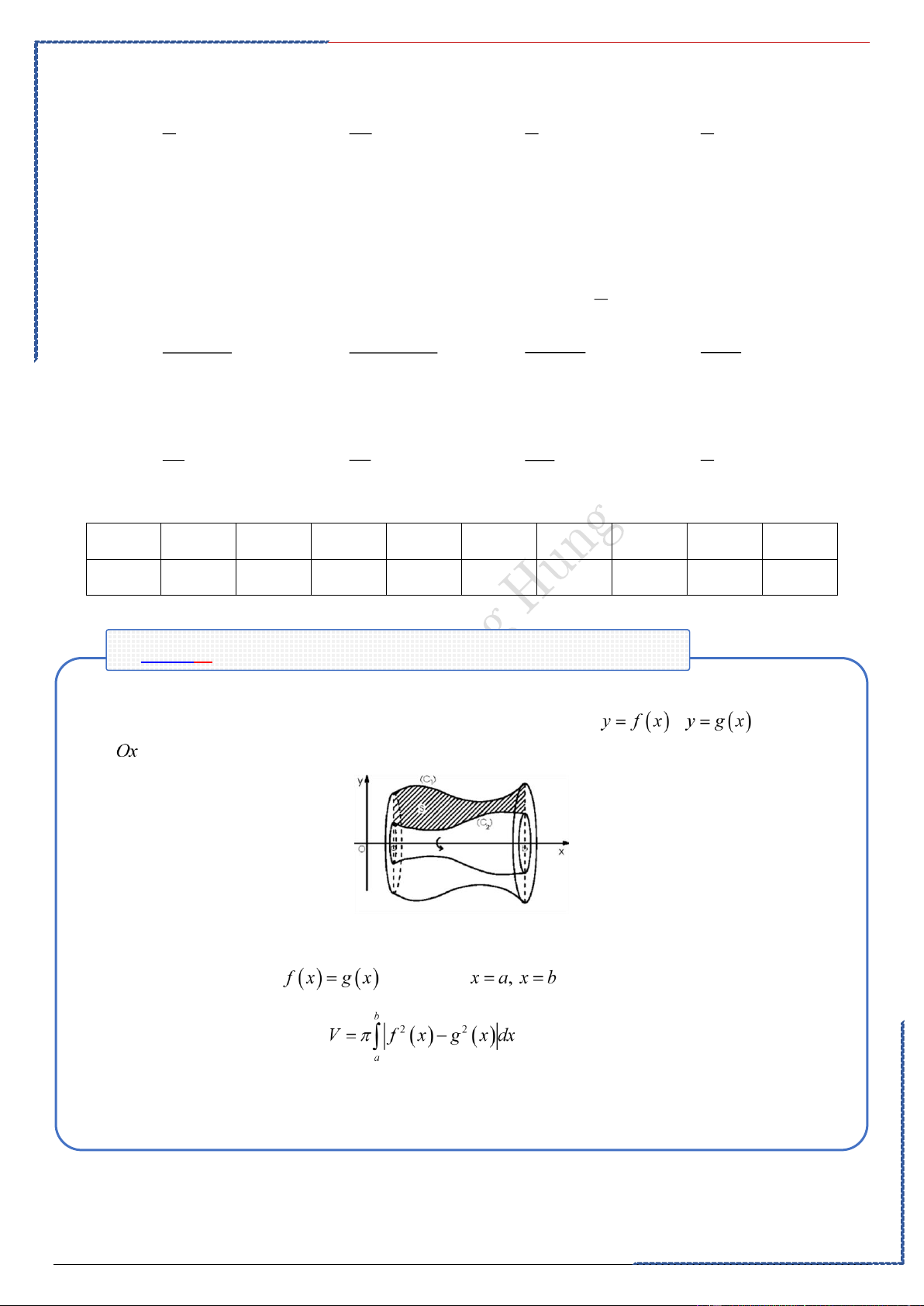
Bài 5: DIỆN TÍCH HÌNH PHẲNG
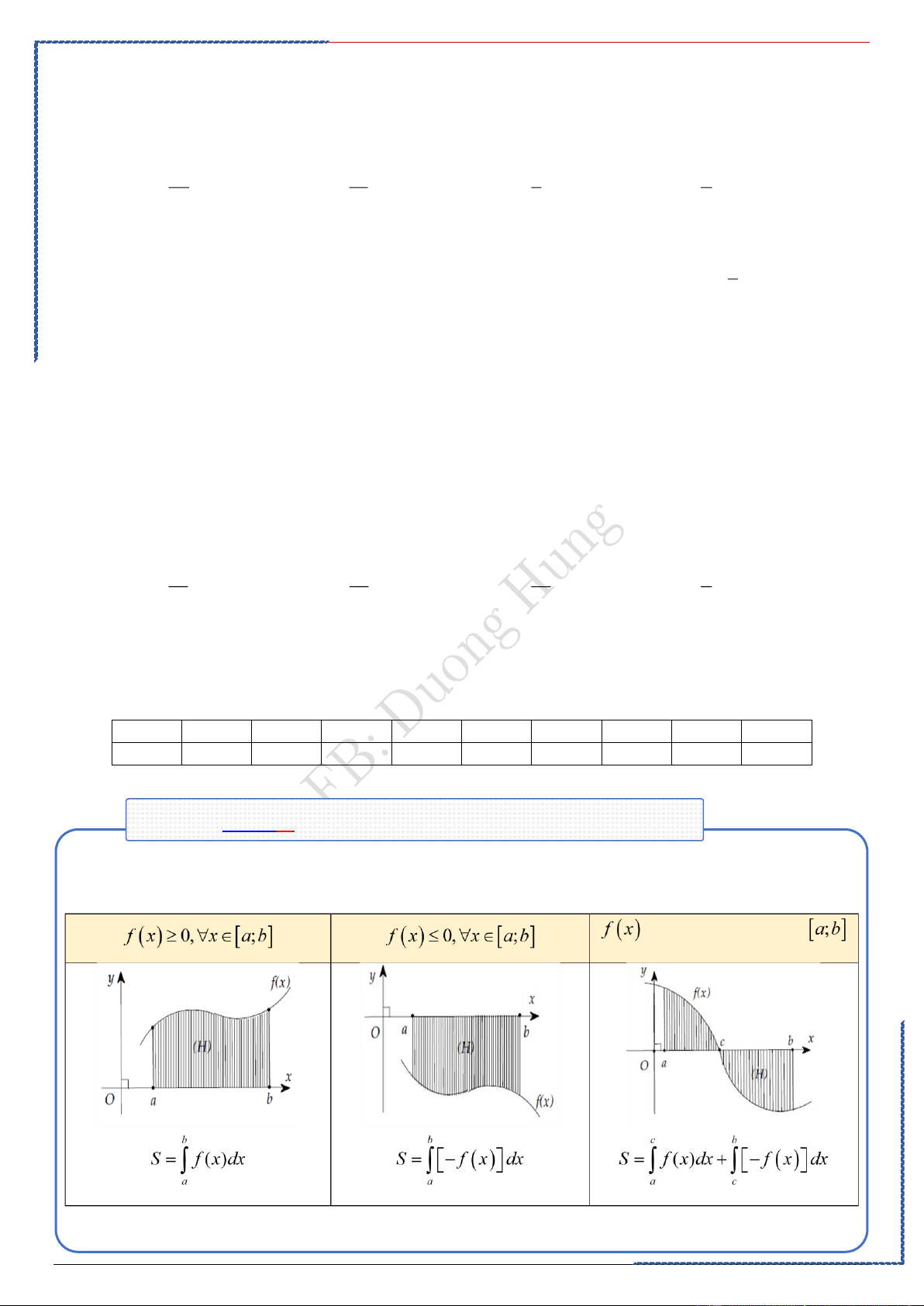
Dạng ①: Phương pháp tính phân từng phần cơ bản
. Định lí:  Nếu và
là các hàm số có đạo hàm liên tục trên thì: . Hay
.Phương pháp chung:
• Bước 1: Viết dưới dạng
bằng cách chọn một phần thích hợp của làm và phần còn lại
• Bước 2: Tính và
• Bước 3: Tính và
.Cách đặt u và dv trong phương pháp tích phân từng phần.
Đặt u theo thứ tự ưu tiên:
Lô-đa-lượng-mũ u P(x) lnx P(x) dv P(x)dx cosxdx cosxdx
.Chú ý: Nên chọn là phần của
mà khi lấy đạo hàm thì đơn giản, chọn là phần của
là vi phân một hàm số đã biết hoặc có nguyên hàm dễ tìm.
Dạng ①: Tích phân chứa đa thức với lượng giác hoặc mũ ①. Loại 1:
.Phương pháp: Đặt: .
St-bs: Duong Hung 44
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
A - Bài tập minh họa: 2
Câu 1: Tính tích phân =  x I xe dx . 1 Ⓐ. 2
I = e . Ⓑ. 2
I = −e . Ⓒ. I = e . Ⓓ. 2
I = 3e − 2e . Lời giải
PP nhanh trắc nghiệm Chọn A
Tính tích phân u = xdu = dx Đặt    dv = x e dxv = x e 2 2 x x 2 x 2 x 2
I = xe dx = xe
− e dx = 2e − e − e   1 1 . 1 1 2
= 2e − e − ( 2 e − e) 2 = e + Kiểm tra các đáp án: 2
A − e = 0 (đúng). 1
Câu 2: Tính tích phân 2 = ( − 2) x I x e dx  . 0 2 − 2 − 2 − 2 − Ⓐ. 5 3e 5 3e 5 3e 5 3e I = . Ⓑ. I = . Ⓒ. I = . Ⓓ. I = . 4 4 4 4 Lời giải
PP nhanh trắc nghiệm Chọn B du = dx Tính tích phân: u  = x − 2  Đặt    1 (chọn C = 0 ) 2 x 2 xdv = e dx v = e  2 1 1 2 1 − e x 1 x 5 3 2 2
I = (x − 2) e − e dx =  . 2 2 4 0 0 +Kiểm tra các đáp án:
Câu 3: Tích phân (3x + 2) 2
cos x dx bằng 0 Ⓐ. 3 3 1 1 2  − . Ⓑ. 2  + . Ⓒ. 2  + . Ⓓ. 2  − . 4 4 4 4
St-bs: Duong Hung 45
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung Lời giải
PP nhanh trắc nghiệm Chọn B   Tính tích phân:
Đặt I = (3x + 2) 2
cos x dx . Ta có: 0  1
= (3x+ 2)(1+cos2x)dx 2 0     1
= ( x + ) x + ( x + ) 1 3 2 d 3
2 cos 2x dx = (I + I . 1 2 ) 2 2 0 0     3  3  I = 3x + 2 dx =  2 2 x + 2x =  + 2   . 1 ( )  2  2 0 0  Kiểm tra các đáp án:  I =
3x + 2 cos 2x dx
. Dùng tích phân từng phần 2 ( ) 0 du = 3dx u  = 3x + 2  Đặt    1 .
dv = cos 2x dx v = sin 2x  2 Khi đó   1 3 I =
3x + 2 sin 2x − sin 2x dx  2 ( ) 2 2 0 0  3 = 0 + (cos 2x) = 0 . 4 0   Vậy 1 3 3 2 2 I =  + 2 =  +   2  2  4
B - Bài tập rèn luyện: 1
Câu 1: Xét tích phân 2 2 = (2 − 4) x I x e dx  Nếu đặt 2 2 = 2 − 4, ' x u x
v = e , ta được tích phân: 0 1 1 2 = ( ) − 2 x I x xe dx  , trong đó: 0 0 Ⓐ. 2 2 ( ) = ( − 2) x x x e . Ⓑ. 2 2 ( ) = (2 − 4) x x x e . Ⓒ. 2 ( ) = ( − 2) x x x e Ⓓ. . 1 2 ( ) = (2 − 4) x x x e . 2  2
Câu 2: Tính tích phân I = x cos xdx  0 Ⓐ.     1 I = . Ⓑ. I = +1. Ⓒ. I = . Ⓓ. I = − . 2 2 3 3 2 1 Câu 3: Tính x xe dx  0 Ⓐ. e . Ⓑ. e−1. Ⓒ. 1. Ⓓ. 1 e −1. 2
St-bs: Duong Hung 46
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung Câu 4: L = x sin xdx  0 Ⓐ. L = . Ⓑ. L = 2 − . Ⓒ. L = 0. Ⓓ. L = − . 
Câu 5: (x + 2)cos2xdx 0 Ⓐ. 0 . Ⓑ. 1 − . Ⓒ. 1 . Ⓓ. 1 . 4 4 2  4 Câu 6: xcos2xdx  bằng 0 Ⓐ.  −  −   2 . Ⓑ. 1 . Ⓒ. 3− . Ⓓ. 2 − 8 4 2 2 1
Câu 7: Tính tích phân 3 = ( +1) x I x e dx 0 Ⓐ. 5 2 2 5 2 5 5 2 3 I = e − . Ⓑ. 3 I = − e . Ⓒ. 3 I = e − . Ⓓ. 3 I = e + . 9 9 9 9 9 9 9 9 1
Câu 8: Tính tích phân 1−x I = xe dx 0 Ⓐ. 1. Ⓑ. e−2. Ⓒ. 1−e. Ⓓ. 1 − . 1
Câu 9: Tính tích phân 3 = ( +1) x I x e dx 0 Ⓐ. 5 2 2 5 2 5 5 2 3 I = e − . Ⓑ. 3 I = − e . Ⓒ. 3 I = e − . Ⓓ. 3 I = e + . 9 9 9 9 9 9 9 9 1
Câu 10: Tính tích phân 1−x I = xe dx 0 Ⓐ. 1. Ⓑ. e−2. Ⓒ. 1−e. Ⓓ. 1 − . BẢNG ĐÁP ÁN 1.A 2.C 3.C 4.A 5.A 6.A 7.A 8.D 9.A 10.D
St-bs: Duong Hung 47
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
Dạng ②: Tích phân chứa đa thức và ln ②. Loại 2:
-Phương pháp: .Đặt:
A - Bài tập minh họa: e
Câu 1: Tích phân x ln xdx  bằng 1 Ⓐ. 2 2 2 − 2 e 1 + . Ⓑ. e − e 1 1 e 1. Ⓒ. . Ⓓ. − . 4 4 4 4 2 4 Lời giải
PP nhanh trắc nghiệm Chọn D Casio: e 2 e 2 2 2 x x x x e +1 e e x ln xdx = ln x − dx = (− + ln x) =   1 1 2 2 4 2 4 1 1 5
Câu 2: Tính tích phân I = (x + )
1 ln ( x − 3)dx ? 4 Ⓐ. 10ln2 . Ⓑ. 19 10 ln 2 + . Ⓒ. 19 −10ln 2 . Ⓓ. 19 10 ln 2 − . 4 4 4 Lời giải
PP nhanh trắc nghiệm Chọn D Casio:  1  = ( = x − ) du dx u ln 3  − Đặt x 3    .  dv = x +1 1 2
v = x + x  2 1 2 5 x + x  1  5 2 I = x + x   (x − ) 2 ln 3 − dx  
Kiểm tra các đáp án: 2  4 x − 3 4 5 2 5 35 1 x − 9 + 9 x − 3 + 3 = ln 2 − dx − dx   2 2 x − 3 x − 3 4 4 35 1  9  = ln 2 − + 3+ 9ln 2 −   (1+ 3ln 2) 2 2  2 
St-bs: Duong Hung 48
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung 19 = 10ln 2 − . 4 e Câu 3: Tính  2 x ln d x x 1 Ⓐ. 3 2e + 3 2e − 3 e − 3 e + 1 . Ⓑ. 1 . Ⓒ. 2 . Ⓓ. 2 . 9 9 9 9 Lời giải
PP nhanh trắc nghiệm Chọn A   Casio du = 1  = ln  dx u x    x dv =  2 x dxv = 1 3  x  3  e e 1  eI = 3 x ln x − 1 2 x dx = 1 3 e − 1    3 x  3  3 3 9 1 1 1 3 1 e − 3 1 2e + = 3 e − = 1 3 9 9
B - Bài tập rèn luyện: e
Câu 1: Tính tích phân I = (x + 2)ln xdx 1 1 2 − 2 + 2 − Ⓐ. e 2 e 1 e 1 I = . Ⓑ. I = . Ⓒ. I = . Ⓓ. I = . 2 2 4 4  u = ln x e
Câu 2. Nếu đặt 
thì tích phân I = (2x +  ) 1 ln xdx trở thành dv = (2x +  ) 1 dx 1 e e e Ⓐ. e I = ( 2
x + x) − ( x +  ) 1 dx . Ⓑ. 2
I = x ln x − ( x +  ) 1 dx . 1 1 1 1 e e e Ⓒ. e 2
I = x ln x + xdx  .
Ⓓ. I = ( 2x + x)ln x + (x +  ) 1 dx . 1 1 1 1 0
Câu 3: Tính tích phân J = x ln (x +  ) 1 dx 0 4 5 2 3
Ⓐ. J = ln3.
Ⓑ. J = ln3.
Ⓒ. J = ln3.
Ⓓ. J = ln3. 3 3 3 4 5
Câu 4: Tính tích phân I = (x + )
1 ln ( x − 3)dx ? 4 Ⓐ. 10ln2 . Ⓑ. 19 10 ln 2 + . Ⓒ. 19 −10ln 2 . Ⓓ. 19 10 ln 2 − 4 4 4 3
Câu 5: Tích Phân 2
I = ln(x − x)  dx là 2
St-bs: Duong Hung 49
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung Ⓐ. 3ln3 . Ⓑ. 2ln 2 . Ⓒ. 3ln3−2. Ⓓ. 2−3ln3. 2 Câu 6: Tích phân ln =  x I dx bằng 2 x 1 Ⓐ. 1 ( 1 1 1 1+ ln 2) . Ⓑ. (1−ln 2) . Ⓒ. (ln 2− ) 1 . Ⓓ. (1+ ln 2) . 2 2 2 4 b
Câu 7: Cho a b  1
− . Tích phân I = ln(x +  )
1 dx bằng biểu thức nào sau đây? a Ⓐ. b I = ( x + ) b 1 ln ( x + ) 1 − a + b . Ⓑ. I = (x + ) 1 ln ( x + ) 1 − b + a . a a b b Ⓒ. 1 b x I = ( .
Ⓓ. I = xln(x + ) 1 + dx  . x + ) 1 a x +1 a a BẢNG ĐÁP ÁN 1.C 2.D 3.C 4.D 5.C 6.A 7B
Dạng ③: Tích phân chứa từng phần chứa tham số a, b, c
-Phương pháp: Tích phân từng phần. ①. ②.
A - Bài tập minh họa: e 2 + Câu 1: Cho .e a b I = x ln d x x =
với a , b , c  . Tính T = a + b + c . c 1 Ⓐ. 5. Ⓑ. 3. Ⓒ. 4 . Ⓓ. 6 . Lời giải
PP nhanh trắc nghiệm Casio
Chọn D  1 du = dx u  = ln x   Ta có:  nên x  . dv = d x x 2 xv =
+ Thử C=1,2,3,4,5,6.. giải hệ tìm a,b nguyên.  2 e e 2 e x 1 2 e + 1 I = x ln d x x = ln x − d x x = .   2 2 4 1 1 1
St-bs: Duong Hung 50
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung a = 1   b  = 1 . c = 4 
Vậy T = a + b + c = 6 .
B - Bài tập rèn luyện: e 3 a e +1 Câu 1: Cho 3 x ln d x x =  với , a b
. Tổng a + b bằng b 1 Ⓐ. 20 . Ⓑ. 10. Ⓒ. 17 . Ⓓ. 12. 2
Câu 2: Biết ln x b dx= + a ln 2 
trong đó a  ; b , c là các số nguyên dương và nguyên tố cùng nhau. 2 x c 1
Tính giá trị của 2a + 3b + c . Ⓐ. 6 . Ⓑ. 5. Ⓒ. 4 . Ⓓ. 6 − . 2 ln x b b
Câu 3: Cho tích phân I = dx = + a ln 2 
với a là số thực, b và c là các số dương, đồng thời là 2 x c c 1
phân số tối giản. Tính giá trị của biểu thức P = 2a + 3b + c .
Ⓐ. P = 6 .
Ⓑ. P = 5. Ⓒ. P = 6 − . Ⓓ. P = 4 . 2
Câu 4: Cho (x + ) x 2
1 e dx = ae + be + c với a , b , c là các số nguyên. Tính a + b + c . 1 Ⓐ. 3. Ⓑ. 4. Ⓒ. 1. Ⓓ. 0. e Câu 5: Biết 2 3 I = x ln d
x x = ae + b
với a , b là các số hữu tỉ. Giá trị của 9(a + b) bằng 1 Ⓐ. 3. Ⓑ. 10. Ⓒ. 9. Ⓓ. 6 . e Câu 6: Biết 2 3 I = x ln d
x x = ae + b
với a , b là các số hữu tỉ. Giá trị của 9(a + b) bằng 1 Ⓐ. 3. Ⓑ. 10. Ⓒ. 9. Ⓓ. 6 . 2 ln x a Câu 7: Cho I = = −  ( với , a ,
b c là các số nguyên dương và a là phân số tối giản. x + ) dx ln 2 ln c 2 1 b b 1 +
Tính giá trị của biểu thức a b S = . c Ⓐ. 5 S = . Ⓑ. 8 S = . Ⓒ. 6 S = . Ⓓ. 10 S = . 3 3 5 3 2
Câu 8: Biết (2x +ex ) x 4 2 e dx = . a e + .
b e + c với a, ,
b c là các số hữu tỉ. Giá trị của 2a + 3b + 2c bằng 0 Ⓐ. 9. Ⓑ. 10. Ⓒ. 8. Ⓓ. 7.
St-bs: Duong Hung 51
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung 2 Câu 9: Biết ln = + ln 2  x b dx a
. Giá trị của 2a + 3b + c bằng. 2 x c 1 Ⓐ. 6 − . Ⓑ. 4 . Ⓒ. 5. Ⓓ. 6 . 5 Câu 10. Cho ln
 ( 2x − x)dx = aln5+bln2+c với a , b , c là các số nguyên. Tính S = a+2b−c. 2
Ⓐ. S = 23.
Ⓑ. S = 20.
Ⓒ. S =17 . Ⓓ. S =11. BẢNG ĐÁP ÁN 1.A 2.C 3.D 4.C 5.A 6.A 7.B 8.B 9.B 10.A Hướng dẫn giải 1 4 Câu 1:  Đặt x
u = ln x  du = dx ; 3
dv = x dx v = . x 4 e 4 4 e e 4 4 4  x  1 e  1  e e 1 3e +1 3 4
I = ln .x  − x dx = − x = − + =    .  4  4 4 16  4 16 16 16 1 1 1  a = 4  
a + b = 20 . b  =16 Câu 2:  1 u  = ln x du = dx    Đặt x  1   . dv = dx 1   2  v x = −  x 2 2 2 2   Ta có ln x 1 1 1 1 1 1 dx= − ln x + dx = − ln 2 − = − ln 2 +     . 2 2 xxx 2 x 2 2 1 1 1 1  1
Theo đề ta có a = − , b =1, c = 2 . 2
Do đó 2a + 3b + c = 4.
Câu 3: dxu = ln x du = 2    x −ln x 2 1  −ln x 1 −  2 Đặt 1 ln 2  dx    I = + dx = + = −    2 dv = 1 − x 1 x    x x  1 2 2 2 1  v x =  x 1 −
b =1,c = 2,a =
P = 2a + 3b + c = 4 . 2
Câu 4:
St-bs: Duong Hung 52
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung u  = x +1 Đặt  ta được d = d , x u
x v = e . x
dv = e dx 2 2
(x+ )1 xedx = (x+ ) x 2 x x 2 2 1 e
− e dx = xe = 2e − e  . 1 1 1 1  a = 2,b = 1
− ,c = 0  a +b + c =1.
Câu 5:  1 du = dx u  = ln x  Đặt  ta có x  2
dv = x dx 3 xv =  3 e e 3 e 2 3 3 Suy ra x ln x x e x 2 1 3 I = − dx = − = .e +  . 3 3 3 9 9 9 1 1 1  1 Vậy 2 a =
, b = nên 9(a + b) = 3. 9 9
Câu 6:  1 du = dx u  = ln x  Đặt  ta có x  2
dv = x dx 3 xv =  3 e e 3 e 2 3 3 Suy ra x ln x x e x 2 1 3 I = − dx = − = .e +  . 3 3 3 9 9 9 1 1 1 1 Vậy 2 a =
, b = nên 9(a + b) = 3. 9 9 Câu 7: Ta có: 2 2 2 2 ln x  1   1  2 1 1  1 1  I = = − = − + = − + −  (         x + ) dx ln d x ln x dx ln 2 dx 2 1  x +1  x +1  1 (x +1)x 3  x x +1 1 1 1 1 a = 5 1 = − + (  + x − x + ) 2 5 a b 8 ln 2 ln ln 1
= ln 2 − ln 3  b = 3  S = = . 3 1 3 c 3 c = 3 
Câu 8:
St-bs: Duong Hung 53
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung u  = 2x + ex
du = (2+ ex )dx Đặt:  ta được  .
dv = exdx v = ex 2 2
Khi đó: (2 +ex )exd = (2 +ex ) x 2 e − ( x 2 2e + e x x x x dx 0 ) 0 0 (   = 1 3 2.2 + e )e − (2.0 + e ) 2 x 1 2 2 0 0 2 e − 2e + e x   4 2 = e + 2e + .  2  2 2 0 Theo bài ra ta có 1 3 a = ; b = 2; c = 2 2 Vậy: 1 3
2a + 3b + 2c = 2. + 3.2 + 2. =10 . 2 2
Câu 9: 2 Gọi ln =  x I dx . 2 x 1
Áp dụng phương pháp nguyên hàm từng phần ta có:  1 u = ln x du =    dx Đặt  x 1   dv = dx 1   2  v = − x  x 2 2 2 2 ln x  1  1 ln 2 1 1 1 1  1  1 1  I = − − − . dx = − + dx = − ln 2 − = − ln 2 − −1 = − ln 2      2 xx x 2 x 2 x 2  2  2 2 1 1 1 1 1
a = − ;b = 1;c = 2 . 2
Vậy 2a + 3b + c = 4 . Câu 10.  2x −1 u  = ( 2 ln x − x) du = dx Đặt   2  x − x . dv = dx v = x 5 5 5 − Khi đó x ln  ( 2 1 2
x − x)dx = x ln ( 2 x − x) − dx  2 x −1 2 2 5  1  = 5 5ln 20 − 2 ln 2 − 2 + dx   = 5ln ( 2
5.2 ) − 2ln 2 − (2x + ln x −1 )  x −1  2 2
= 5ln 5 + 8ln 2 − (10 − 4 + ln 4 − ln ) 1 = 5ln 5 + 6ln 2 − 6 .
Suy ra a = 5 , b = 6, c = 6
−  S = a + 2b −c = 5+ 2.6+ 6 = 23.
St-bs: Duong Hung 54
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
Dạng ④: Tích phân chứa từng phần hàm ẩn
. Phương pháp: Tích phân từng phần. . Viết dưới dạng bằng các hợp của làm và phần còn lại . Tính và . Tính và A - Bài tập minh họa: 4
Câu 1: Cho f ( x) là hàm số có đạo hàm trên 1;4 , biết f
 (x)dx = 20 và f (4) =16 , f ( )1 = 7 . Tính 1 4 I = xf   (x)dx . 1
Ⓐ. I = 37. Ⓑ. I = 47 .
Ⓒ. I = 57. Ⓓ. I = 67 . Lời giải
PP nhanh trắc nghiệm
Chọn A 4
Xét I = xf
 (x)dx , dùng phương pháp tích phân từng phần : 1 u  = x  du = dx     dv = f  
(x)dx v = f  (x) 4 4  4
Do đó: I = xf ( x) − f
 (x)dx = 4 f (4)− f ( )1− f  (x)dx 1 1 1 = 4.16−7 − 20 = 37
Câu 2: Cho hàm số f ( x) có đạo hàm liên tục trên đoạn 0;2 và thỏa mãn f (0) = 2 , 2 2
(2x−4).f '(x)dx = 4. Tính tích phân I = f  (x) dx . 0 0
Ⓐ. I = 2 . Ⓑ. I = 2 − . Ⓒ. I = 6. Ⓓ. I = 6 − . Lời giải
PP nhanh trắc nghiệm Chọn B 2
Ta có: (2x −4).f '(x)dx = 4 . 0 u  = 2x − 4  du = 2dx  Đặt    dv = f '  (x)dxv = f  (x)
St-bs: Duong Hung 55
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung 2 2
Nên (2x −4).f '(x)dx = (2x −4).f (x) 2 −2 f  (x)dx 0 0 0
= 4. f (0) − 2I = 8− 2I .
Theo giả thiết ta có: 4 = 8 − 2I  2I = 4  I = 2 .
B - Bài tập rèn luyện: 1
Câu 1: Cho f ( x) có đạo hàm liên tục trên
và thỏa mãn f (2) =16, f
 (2x)dx = 6. Tính 0 2 I = . x f  
(x)dx ta được kết quả 0 Ⓐ. I =14.
Ⓑ. I = 20 .
Ⓒ. I =10. Ⓓ. I = 4 . 1
Câu 2: Cho f ( x) có đạo hàm liên tục trên
và thỏa mãn f (2) =16, f
 (2x)dx = 6. Tính 0 2 I = . x f  
(x)dx ta được kết quả 0 Ⓐ. I =14.
Ⓑ. I = 20 .
Ⓒ. I =10. Ⓓ. I = 4 . 3
Câu 3: Cho hàm số f ( x) có đạo hàm trên
và thỏa mãn x f  
(2x −4)dx = 8; f (2) = 2 . Tính 0 1 I = f  (2x)dx. 2 − Ⓐ. I = 5 − . Ⓑ. I = 10 − . Ⓒ. I = 5. Ⓓ. I =10. 1 Câu 4: Cho hàm số 1
f ( x) liên tục trên 0;  1 . Biết  . x f  
(1− x)− f (x)dx =   . Tính f (0) . 2 0 Ⓐ. f (0) = 1 − . Ⓑ. f ( ) 1 0 = . Ⓒ. f ( ) 1 0 = − . Ⓓ. f (0) =1. 2 2 3 1
Câu 5: Cho hàm số f ( x) liên tục trên và f ( ) 3 = 21 , f
 (x)dx = 9. Tính tích phânI = .xf   (3x)dx 0 0 .
Ⓐ. I =15.
Ⓑ. I =12. Ⓒ. I = 9. Ⓓ. I = 6.
Câu 6: Cho hàm số y = f ( x) liên tục và có đạo hàm trên thỏa mãn f ( x) − f ( − x) = ( 2 5 7 1 3 x − 2x) 1 , a x
  . Biết rằng tích phân I = .
x f ' ( x)dx = − 
. Tính T = 8a − 3b . b 0 Ⓐ. T =1 .
Ⓑ. T = 0.
Ⓒ. T =16 . Ⓓ. T = 16 − .
St-bs: Duong Hung 56
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung 2
Câu 7: Cho hàm số f ( x) có đạo hàm liên tục trên tập hợp thỏa mãn f
 (3x−6)dx = 3 và f ( 3 − ) = 2 1 0
. Giá trị của x f   (x)dx bằng 3 − Ⓐ. −3. Ⓑ. 11. Ⓒ. 6 . Ⓓ. 9. 2
Câu 8: Cho hàm số y = f ( x) có đạo hàm f ( x) liên tục trên 0;2 và f (2) = 3 , f  (x)dx = 3. 0 2 Tính . x f   (x)dx . 0 Ⓐ. 3 − . Ⓑ. 3. Ⓒ. 0 . Ⓓ. 6 .
Câu 9: Cho hàm số y = f ( x) có đạo hàm là f '( x) liên tục trên đoạn [0; 1] và f ( ) 1 = 2 . Biết 1 1 f
 (x)dx =1, tính tích phân I = .xf '  (x)dx. 0 0
Ⓐ. I =1. Ⓑ. I = 1 − .
Ⓒ. I = 3. Ⓓ. I = 3 − . 1 1
Câu 10: Cho hàm số f ( x) thỏa mãn (x + )
1 f '( x) dx = 10 và 2 f ( )
1 − f (0) = 2 . Tính I = f  (x)dx. 0 0
Ⓐ. I = 8. Ⓑ. I = 8 − .
Ⓒ. I = 4 . Ⓓ. I = 4 − .
Câu 11: Cho hàm số f ( x) có đạo hàm liên tục trên đoạn 0;2 và thỏa mãn f (2) =16 , 2 1 f
 (x)dx = 4. Tính tích phân I = .x f   (2x)dx . 0 0
Ⓐ. I =12.
Ⓑ. I = 7 .
Ⓒ. I =13. Ⓓ. I = 20 . 2
Câu 12: Cho hàm số y = f ( x) có đạo hàm liên tục trên và thỏa mãn f ( 2 − ) =1, f
 (2x−4)dx =1. 1 0 Tính xf
 (x)dx. 2 −
Ⓐ. I =1.
Ⓑ. I = 0. Ⓒ. I = 4 − . Ⓓ. I = 4 . 5
Câu 13: Cho hàm số y f x thỏa mãn 3 f x 3x 1 3x 2, x . Tính I . x f x dx . 1 Ⓐ. 5 17 33 . Ⓑ. . Ⓒ. . Ⓓ. 1761 − . 4 4 4 BẢNG ĐÁP ÁN 1.B 2.B 3.B 4.C 5.D 6.B 7.A 8.B
9.A 10.B 11.B 12.B 13.C
Lời giải chi tiết
Câu 1: 1 1 2 Ta có f  ( x) 1 2 dx = 6  f
 (2x)d(2x) = 6 f  (x)dx =12. 2 0 0 0
St-bs: Duong Hung 57
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung 2 Xét I = . x f   (x)dx 0 u  = x  du = dx  Đặt    dv = f  
(x)dx v = f  (x) 2 2
Khi đó I = xf ( x) − f
 (x)dx = 2 f (2)−12 = 20. 0 0 Câu 2: 1 1 2 Ta có f  ( x) 1 2 dx = 6  f
 (2x)d(2x) = 6 f  (x)dx =12. 2 0 0 0 2 Xét I = . x f   (x)dx 0 u  = x  du = dx  Đặt    dv = f  
(x)dx v = f  (x) 2 2
Khi đó I = xf ( x) − f
 (x)dx = 2 f (2)−12 = 20. 0 0 Câu 3: 3
 Xét J = x f  
(2x −4)dx = 8. 0  1 Đặt  1 
u = x và dv = f (2x − 4)dx = d f
(2x − 4) , ta được du = dx và v = f (2x − 4) .  2  2 3 1 3 2  3 1 1 J =
x f ( x − ) 3 1 . 2 4 − f
 (2x−4)dx = f (2)− f
 (2x−4)dx = 3− f  (2x−4)dx. 2 0 2 2 2 2 0 0 0 3 3 Vì 1 J = 8  3 − f
 (2x−4)dx =8  f
 (2x−4)dx = 1 − 0 . 2 0 0
Đặt 2t = 2x − 4  2dt = 2dx  dt = dx Đổi cận: x 0 3 t −2 1 1 1 I = f 2t dt =
f 2x dx = 1 − 0   . 1 ( ) ( ) 2 − 2 − Vậy I = 10 − . 1 1 1
Câu 4: Ta có A =  . x f
 (1− x)− f (x)dx = .xf  
 (1− x)dx− f  (x)dx . 0 0 0 1 Đặt I = . x f   (1− x)dx. 0
St-bs: Duong Hung 58
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung u  = x  du = dx  Đặt    dv = f  
(1− x)dx v = − f  (1− x) 1 1
Khi đó I = − f (1− x) 1 .x +
f 1− x dx = − f 0 + f x dx   0 ( ) ( ) ( ) 0 0 1 1
Do đó A = − f ( ) + f (x) x − f (x) 1 x =  f ( ) 1 0 d d 0 = −   . 2 2 0 0
Câu 5: du = dx u  = x  Đặt    1 .
dv = f (3x)dx v = f (3x)  3 1 3 1 1 Suy ra 1 1 1 I = . x f (3x) −
f (3x)dx = f (3) −
f (x)dx = 6   . 3 0 3 3 9 0 0 Vậy I = 6. Câu 6:
Ta có : f ( x) − f ( − x) = ( 2 5 7 1 3 x − 2x)
Lần lượt chọn x = 0, x =1 , ta có hệ sau :  5 =
 f ( ) − f ( ) f ( ) 1 5 0 7 1 = 0   8    5  f  ( ) 1 − 7 f (0) = 3 −  f ( ) 7 0 =  8 1 Tính I = . x f '  (x)dx 0  u = x  du = dx Đặt :  Chọn  dv = f '  (x)dx v = f  (x) 1 5  I = .
x f ( x) 1 − f
 (x)dx = − J 0 8 0 0 1 1
Đặt x =1−t J = − f
 (1−t)dt = f
 (1− x)dx = K . Suy ra 5J −7K =3 ( 2x −2x)dx = 2 −  1 0 0  J = K Ta có :   J = K =1 5  J − 7K = 2 − 5 3 − a = 3 Vậy I = −1 =  
T = 8a −3b = 0 8 8 b = 8
Câu 7:
St-bs: Duong Hung 59
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
Đặt t = 3x − 6  dt = 3dx .
Đổi cận: x =1 t = 3
− , x = 2  t = 0. 2 0 0 0  f  ( x− ) 1 3 6 dx = f
 (t)dt =3 f
 (t)dt =9 f  (x)dx =9 . 3 1 3 − 3 − 3 − u  = x  du = dx  Đặt    dv = f  
(x)dx v = f  (x) 0 0 Khi đó 0 x f  
(x)dx = xf (x) − f
 (x)dx = 0.f (0)+3.f ( 3 − ) −9 = 3 − . 3 − 3 − 3 − Câu 8: 2 2 2 2  Ta có . x f   (x)dx = d x
 ( f (x)) = .xf (x) − f
 (x)dx = 2 f (2)−3= 3. 0 0 0 0 1
Câu 9: Ta có: I = . x f '  (x)dx 0
Đặt u = x du = dx , dv = f '( x)dx chọn v = f '
 (x)dx = f (x) 1 1   I = .
x f ( x) 1 − f
 (x)dx =1.f ( )1−0.f (0)− f
 (x)dx = 2−1=1 0 0 0 Chọn A Câu 10: 1  A = (x +  )
1 f '( x) dx Đặt u = x +1 du = dx , dv = f '( x) dx chọn v = f ( x) 0 1 1 1 1
  A = (x + )
1 . f ( x) 1 − f ( x) dx = 2 f (1) − f (0) − f ( x) dx = 2 − f ( x) dx = 10  f ( x) dx = 8 −     0 0 0 0 0 Câu 11: du = dx u  = x   Đặt    f x . dv = f   (2x) (2 ) dxv =  2 . x f (2x) 1 2 1 1 f 2  1 16 1 Khi đó: I = − f  (2x) ( ) dx = − f
 (t)dt = − .4 = 7. 2 0 2 2 4 2 4 0 0 Câu 12:
Đặt t = 2x − 4  dt = 2dx , đổi cận x =1 t = 2
− , x = 2  t = 0. 2 0 0 0  = f  ( x− ) 1 1 2 4 dx = f
 (t)dt f
 (t)dt = 2  f  (x)dx = 2 . 2 1 2 − 2 − 2 −
Đặt u = x  du = dx , dv = f ( x)dx v = f ( x) . 0 0 Vậy 0 xf
 (x)dx = xf (x) − f
 (x)dx = 2 f ( 2
− ) − 2 = 2.1− 2 = 0 . 2 − 2 − 2 − Câu 13: 5 u x du dx Đặt 5 I xf x f x dx . 1 dv f x dx v f x 1 f 5 5 x 1 5 Từ 3 f x 3x 1 3x 2 , suy ra I 23 f x d . x f 1 2 x 0 1
St-bs: Duong Hung 60
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung 2 dt 3x 3 dx Đặt 3 t x 3x 1 f t 3x 2 Đổi cận: Với 3 t 1 1 x 3x 1 x 0 và 3 t 5 x 3x 1 5 x 1. 5 1 Casio Khi đó 33 2 I 23 f x dx 23 3x 2 3x 3 dx 4 1 0
St-bs: Duong Hung 61
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung Full Chuyên đề 12 new 2020-2021 CHƯƠNG ③: FB: Duong Hung
Bài 5: DIỆN TÍCH HÌNH PHẲNG
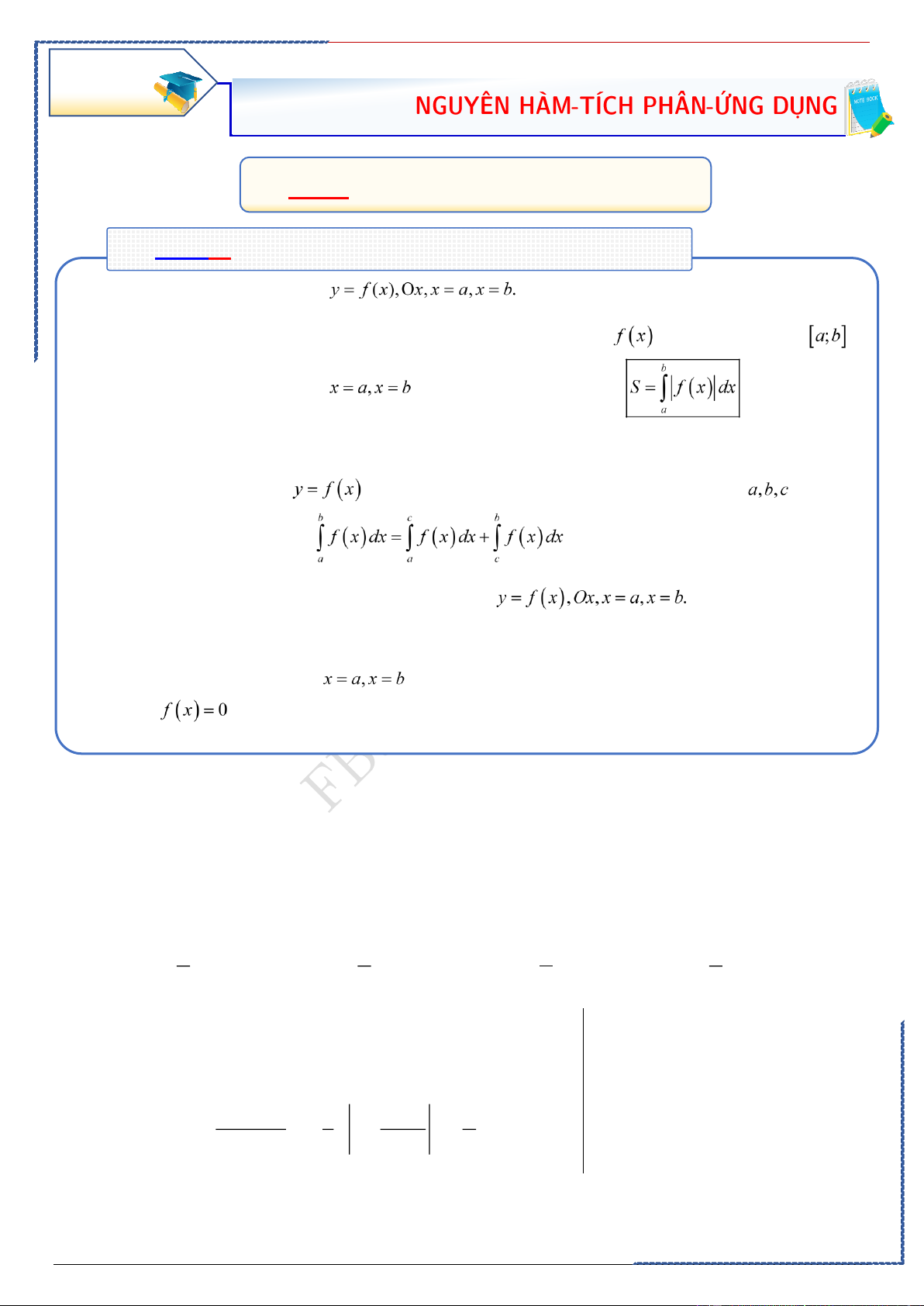
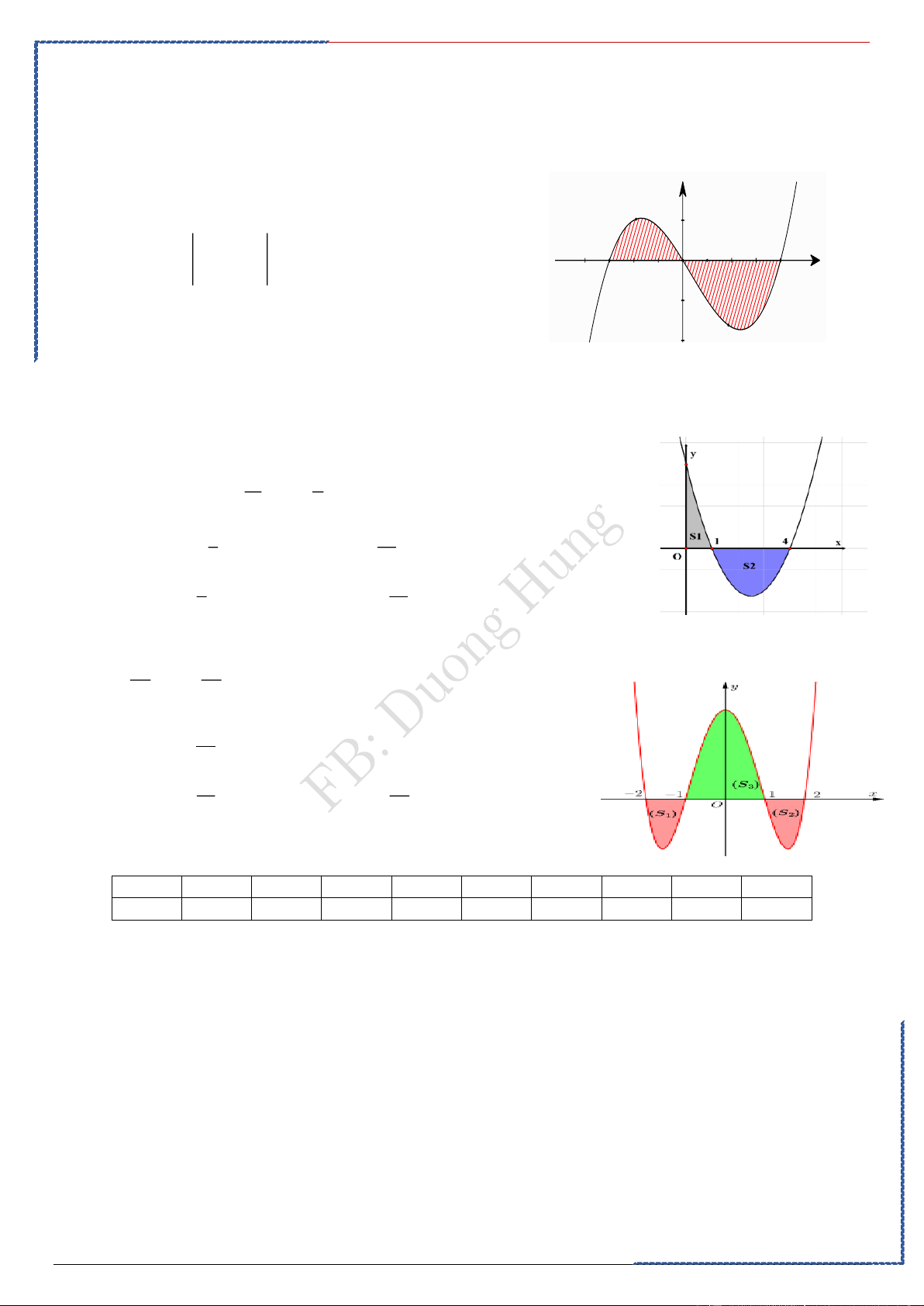
Dạng ①: Ứng dụng của tích phân tính diện tích hình phẳng.
①. Hình phẳng giới hạn bởi
Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số liên tục trên đoạn ,
trục hoành và hai đường thẳng
được tính theo công thức (1)
②. Phương pháp trắc nghiệm: Tính chất: Hàm số
liên tục trên K (khoảng đoạn, nửa khoảng) và là ba số
bất kỳ thuộc K. Khi đó, ta có
 Xác định các yếu tố cần thiết như công thức
Sử dụng chức năng tính tích phân có sẵn trong máy tính Casio để tính.
Chú ý: Nếu đề bài chưa cho
( cận tích phân) thì ta cần giải phương trình hoành độ giao điểm
để tìm cận tích phân.
A - Bài tập minh họa:
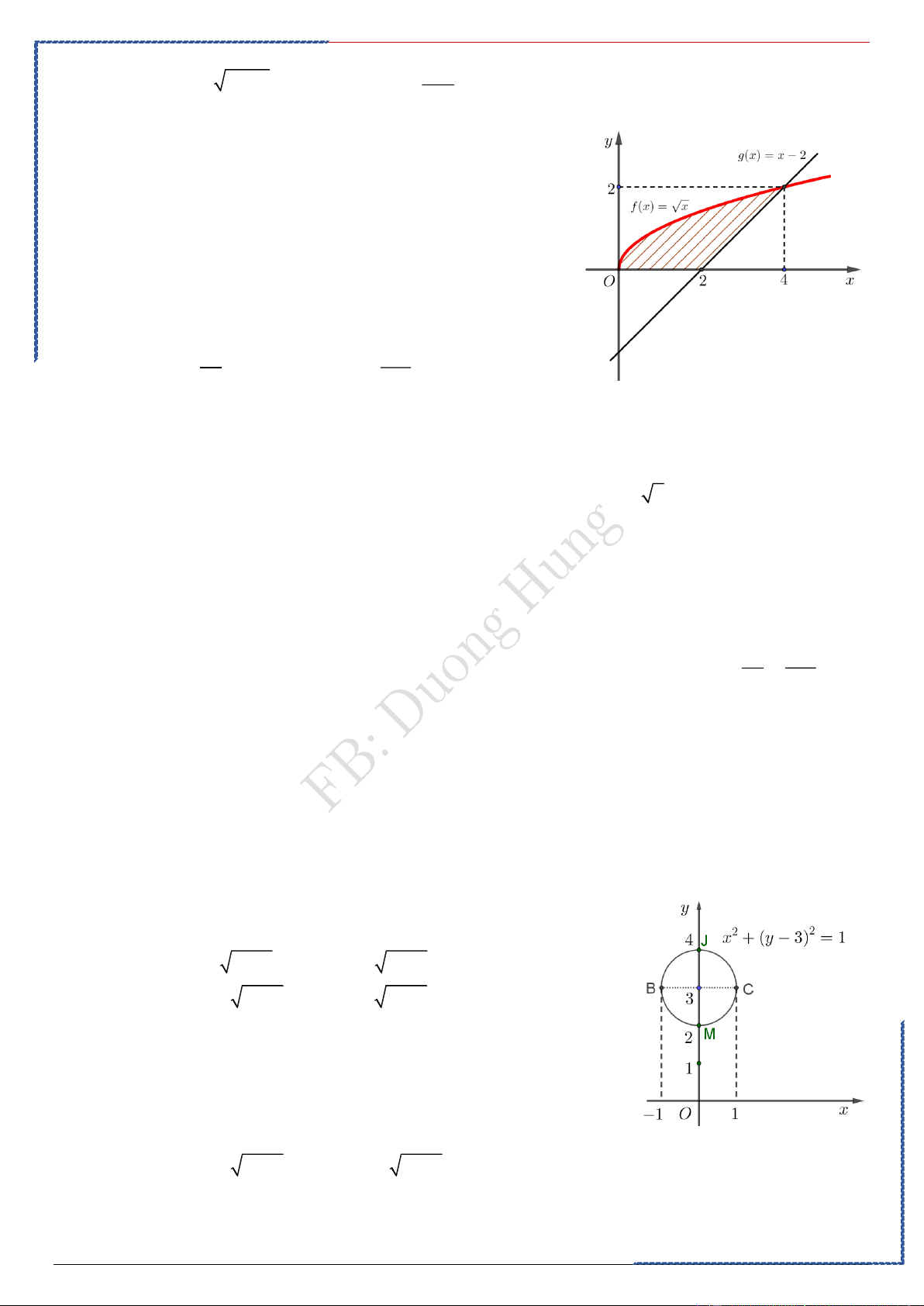
Câu 1: Diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y = cos x , trục hoành, đường thẳng x = 0 và x =  là Ⓐ.     . Ⓑ. . Ⓒ. . Ⓓ. . 8 6 4 2 Lời giải
PP nhanh trắc nghiệm
Chọn D Casio
Diện tích S cần tìm:   1+ cos 2x 1  sin 2x   2 S = cos xdx = dx = x + =   . 0 0 2 2 0 4 0 2
Câu 2: Diện tích hình phẳng giới hạn bởi đồ thị hàm số 3
y = x − 4x , trục hoành, đường thẳng x = 2 − và x = 4 là.
St-bs: Duong Hung 62
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung Ⓐ. 44. Ⓑ.24. Ⓒ. 48. Ⓓ.28. Lời giải
PP nhanh trắc nghiệm Chọn A Casio
Diện tích cần tìm 4 3 S = x - 4x dx  -2  x = 0 Ta có: 3
x − 4x = x ( 2 x − 4) = 0   x = 2  Vậy 0 2 4 3 3 3 S = x − 4x dx + x − 4x dx + x − 4x dx    -2 0 2 4 2 4 2 4 2  x x  0  x 4x  2  x x  4 =  − 4  +  −  +  − 4  = 44 4 2 2 −    4 2 0   4 2 2  x −1
Câu 3: Diện tích hình phẳng giới hạn bởi đồ thị của hàm số f (x) =
, trục hoành, hai đường x
thẳng x =1 và x = 2 là. Ⓐ. ln2 . Ⓑ.ln 2 −1. Ⓒ. ln 2 +1. Ⓓ.1−ln 2 . Lời giải
PP nhanh trắc nghiệm Chọn D Casio x −1
Phương trình hoành độ giao điểm: = 0  x = 1 x Suy ra 2 2 2 x −1 x −1  1  S = dx = dx = 1− =    
(x −ln x) 2 =1−ln 2 . x xx  1 1 1 1
B - Bài tập rèn luyện:
Câu 1: Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số y = f ( x) liên tục, trục hoành và
hai đường thẳng x = a, x = b được tính theo công thức: b b Ⓐ. S = f  (x) dx. Ⓑ. S = f  (x)dx . a a 0 b 0 b
Ⓒ. S = f
 (x)dx+ f  (x)dx . Ⓓ. S = f
 (x)dx− f  (x)dx. a 0 a 0
Câu 2: Diện tích hình phẳng giới hạn bởi các đường 2
y = x − x, y = 0, x = 0 và x = 2 được tính bởi công thức: 2 2 1 Ⓐ. ( 2
x − x ) dx .
Ⓑ. ( 2x − x)dx−( 2x − x)dx. 0 1 0 1 2 1
Ⓒ. ( 2x − x)dx+( 2x − x)dx.
Ⓓ. ( 2x − x)dx. 0 1 0
St-bs: Duong Hung 63
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 3: Diện tích hình phẳng được giới hạn bởi đồ thị của hàm số 2
y = x , trục hoành và hai đường thẳng x = 1 − , x = 3 là. Ⓐ. 28 Ⓑ. 28 Ⓒ. 1 Ⓓ. 4 9 3 3 3
Câu 4: Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = sin x +1, trục hoành và hai đường thẳng 7 x = 0 và x = là. 6 Ⓐ. 3 7    + −1. Ⓑ. 3 7 + +1. Ⓒ. 3 7 + +1. Ⓓ. 3 7 + −1. 2 6 2 6 2 3 4 6
Câu 5: Diện tích hình phẳng giới hạn bởi hàm số 2
y = x x +1 , trục Ox và đường thẳng x = 1 là. Ⓐ. 2 2+1 − − − Ⓑ. 3 2 1 Ⓒ. 2 2 1 Ⓓ. 3 2 3 3 3 3
Câu 6: Tính diện tích S của hình phẳng được giới hạn bởi đồ thị hàm số y = . x ln (3x + ) 1 , trục hoành
và hai đường thẳng x = 0; x =1 Ⓐ. 4 1 7 1 S = ln 2 − . Ⓑ. 2 1 S = ln 2 − .
Ⓒ. S = ln 2 − . Ⓓ. 8 1 S = ln 2 − . 9 12 9 12 9 12 9 12
Câu 7: Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = ln x , trục Ox và đường thẳng x = e là. Ⓐ. 1. Ⓑ. 1 −1. Ⓒ. e . Ⓓ.2. e
Câu 8: Diện tích hình phẳng giới hạn bởi đồ thị hàm số x
y = e , trục Ox , trục Oy và đường thẳng x = 2 là. Ⓐ. 2 e e + 4 . Ⓑ. 2
e − e + 2 . Ⓒ. + 3. Ⓓ. 2 e −1. 2
Câu 9: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 4 2
y = x − 2x +1 và trục Ox Ⓐ. S =1. Ⓑ. S = 2. Ⓒ. S = 1 . Ⓓ.S = 16 . 2 15
Câu 10: Diện tích hình phẳng giới hạn bởi đồ thị hàm số 3 2
y = −x + 3x và trục hoành là. Ⓐ. 27 . Ⓑ. 5 . Ⓒ. 4 . Ⓓ. 24 . 4 6 9 7
Câu 11: Diện tích hình phẳng giới hạn bởi đường cong 2
y = −x + 2x và trục hoành là Ⓐ. 4 . Ⓑ. 29 . Ⓒ. 8 . Ⓓ. 20 . 3 3 3 3
Câu 12: Diện tích hình phẳng giới hạn bởi đồ thị hàm số 4
y = x −1 và trục hoành là Ⓐ. 7 . Ⓑ. 8 . Ⓒ. 1 . Ⓓ.1. 4 5 2 BẢNG ĐÁP ÁN 1.A 2.B 3.B 4.B 5.C 6.D 7.A 8.A 9.D 10.A 11.A 12.B
St-bs: Duong Hung 64
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
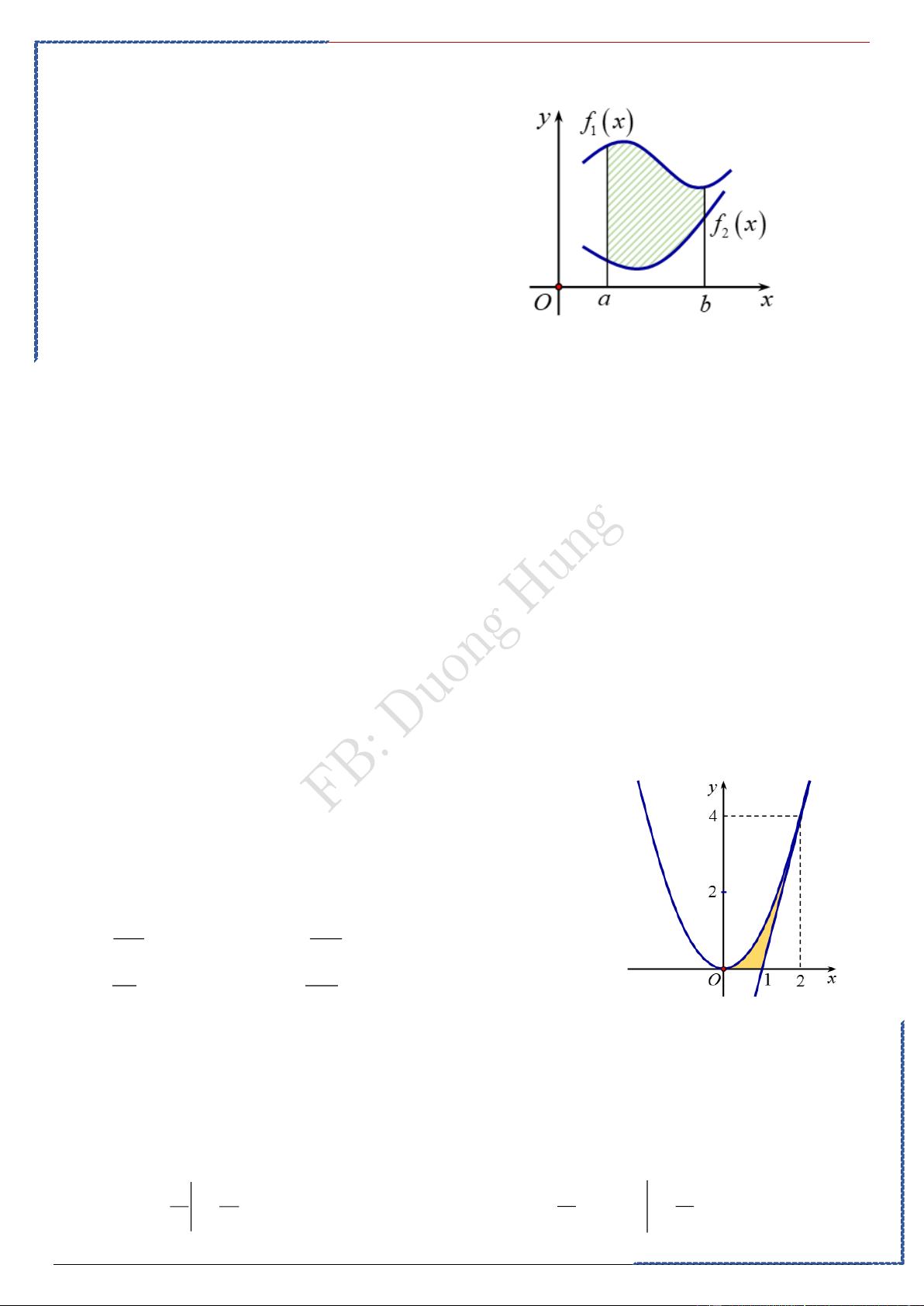
Dạng ②: Ứng dụng của tích phân tính diện tích hình phẳng.
-Phương pháp:
Diện tích hình phẳng giới hạn bởi hai đồ thị: , và hai đường thẳng
được xác định bởi công thức: .
Chú ý: Để phá bỏ dấu giá trị tuyệt đối ta thường làm như sau: * Giải phương trình: tìm nghiệm , . Tính: .
Ngoài cách trên, ta có thể dựa vào đồ thị để khử dấu giá trị tuyệt đối.
A - Bài tập minh họa:
Câu 1: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y = 2 − x và y = . x Ⓐ. 9 .
Ⓑ. 7 . Ⓒ. 5 . Ⓓ. 11 . 2 2 Lời giải
PP nhanh trắc nghiệm
Chọn A Casio:
Phương trình hoành độ giao điểm của hai đồ thị là x = 2 − 2 2
2 − x = x x + x − 2 = 0  .  x =1
Diện tích của hình phẳng cần tìm là 1 1 2 2 S =
−x − x + 2 dx = (−x − x + 2)dx   2 − 2 − 1 3 2  x x  9
= − − + 2x = .  3 2  2 2 − ln x
Câu 2: Gọi S là diện tích của hình phẳng giới hạn bởi các đường y =
, y = 0 , x =1, x = e . Mệnh 2 x
đề nào dưới đây đúng?
St-bs: Duong Hung 65
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung e ln x e ln x e 2   e 2 Ⓐ. ln x ln x S =  dx  . Ⓑ. S = dx  . Ⓒ. S = dx   . Ⓓ. S    = dx   2 x 2 x 2  x  2  x  1 1 1 1 . Lời giải
PP nhanh trắc nghiệm Chọn B Casio e ln x Ta có S = dx  . 2 x 1 e ln x ln x Vì x
 [1;e], ln x  0   0  S = dx  . 2 2 x x 1
Câu 3: Tính diện tích S của hình phẳng giới hạn bởi các đường y = ( x + )
1 ln x , trục hoành và đường thẳng x = e . Ⓐ. 2 e + 5 e + 2 e + 3 e + S = . Ⓑ. 2 7 S = . Ⓒ. S = . Ⓓ. 2 9 S = . 4 6 2 8 Lời giải
PP nhanh trắc nghiệm Chọn C Casio
Xét phương trình hoành độ giao điểm:
(x + )1ln x = 0 (Điều kiện: x  0 ). x +1 = 0 x = 1 −     . ln x = 0 x =1
Vì x  0 nên x =1. e e
Ta có: S = ( x + )
1 ln x dx = ( x +   ) 1 ln d x x . 1 1  1 du = dx u  = ln x     Đặ x t    . dv =  (x + ) 2 1 dx xv = + x  2 e 2 e 2 2  x   x  1 e exS = 
+ xln x −  + x dx = + e− +1 dx    2   2  x 2  2  1 1 1 e 2 2 2 exe + 5 =
+ e −  + x = 2  4  4 1
B - Bài tập rèn luyện:
Câu 1: Tính diện tích hình phẳng giới hạn bởi đồ thị hai hàm số 2
y = −x + 4 và y = −x + 2 ? Ⓐ. 5 . Ⓑ. 8 . Ⓒ. 9 . Ⓓ.9 . 7 3 2
St-bs: Duong Hung 66
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung − Câu 2: x
Gọi S là diện tích hình phẳng giới hạn bởi đồ thị của hàm số ( H ) 1 : y = và các trục tọa x +1
độ. Khi đó giá trị của S bằng Ⓐ. 2ln 2 −1. Ⓑ.ln 2+1. Ⓒ. ln 2−1. Ⓓ.2ln 2+1.
Câu 3: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y = x +1 và đường thẳng y = x + 3 . Ⓐ. 9 . Ⓑ.13 . Ⓒ. 11 . Ⓓ. 7 . 2 3 3 2
Câu 4: Tính diện tích hình phẳng giới hạn bởi hai đồ thị hàm số y = x ; y = 6 − x và trục hoành. Ⓐ. 22 . Ⓑ.16 . Ⓒ. 2 . Ⓓ. 23 . 3 3 3
Câu 5: Tính diện tích hình phẳng giới hạn bởi đồ thị các hàm số 2
y = x − x và y = 3x . Ⓐ. 5 S = . Ⓑ. 16 S = . Ⓒ. S = 9 . Ⓓ. 32 S = . 3 3 3
Câu 6: Diện tích hình phẳng giới hạn bởi parabol (P) 2
: y = x − 2x và đường thẳng (d ) : y = x bằng Ⓐ. 17 9 . Ⓑ.11. Ⓒ. . Ⓓ. 23 . 6 2 2 6
Câu 7: Diện tích hình phẳng giới hạn bởi parabol 2
y = −x và đường thẳng y = −x − 2 bằng Ⓐ. 9 11 . Ⓑ. 5 . Ⓒ. . Ⓓ. 1 − 2 . 2 2 2 2
Câu 8: Diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
y = x và đường thẳng y = 2x là Ⓐ. 4 . Ⓑ. 5 . Ⓒ. 3 . Ⓓ. 23 . 3 3 2 15
Câu 9: Tính diện tích S của hình phẳng (H ) giới hạn bởi các đường cong 3
y = −x +12x và 2 y = −x . Ⓐ. 937 793 S = . Ⓑ. 343 S = . Ⓒ. S = . Ⓓ. 397 S = . 12 12 4 4 1
Câu 10: Thể tích khối tròn xoay khi quay hình phẳng (H ) xác định bởi các đường 3 2 y =
x − x , y = 0 3
, x = 0 và x = 3 quanh trục Ox là Ⓐ. 81 71 . Ⓑ. 81 . Ⓒ. . Ⓓ. 71 . 35 35 35 35
Câu 11: Diện tích hình phẳng giới hạn bởi đồ thị các hàm số 2 2
y = −x + 2x +1, y = 2x − 4x +1 là Ⓐ. 8 . Ⓑ.5 . Ⓒ. 4 . Ⓓ.10 . Câu 12: 1
Diện tích hình phẳng giới hạn bởi hai parabol 2 y = x và 2
y = 6 − x bằng 2 2 2 2 3 Ⓐ.  3x   2    − x 6 dx .
Ⓑ.   −6dx .  2   2  2 − 2 − 3 2 2 2 3 Ⓒ.  3x  2   −   − x 6 dx .
Ⓓ. −   −6dx .  2   2  2 − 2 − 3
Câu 13: Diện tích S của hình phẳng giới hạn bởi đồ thị hai hàm số 3 y = −x và 2
y = x − 2x là Ⓐ. 9 37 S = . Ⓑ. 7 S = . Ⓒ. S = . Ⓓ. 4 S = . 4 3 12 3
St-bs: Duong Hung 67
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 14: Gọi S là diện tích hình phẳng giới hạn bởi các đồ thị hàm số: 3 y = x − 3 ;
x y = x . Tính S ? Ⓐ. S = 4. Ⓑ. S = 8.
Ⓒ. S = 2. Ⓓ. S = 0 .
Câu 15: Hình phẳng giới hạn bởi các đường cong y = x (1− x) và 3
y = x − x có diện tích bằng Ⓐ. 37 . Ⓑ. 5 . Ⓒ. 8 . Ⓓ. 9 . 12 12 3 4
Câu 16: Diện tích S của hình phẳng giới hạn bởi các đường 2
y = x − 2x −1 và 2
y = −x + 3 là Ⓐ. S = 9 . Ⓑ. S = 9 − .
Ⓒ. S = 3. Ⓓ. 9 S = . 2
Câu 17: Tính diện tích S của hình phẳng giới hạn bởi đồ thị của hai hàm số 3
y = x − 3x + 2 và y = x + 2. Ⓐ. S = 8. Ⓑ. S = 4 .
Ⓒ. S =12. Ⓓ. S =16.
Câu 18: Diện tích hình phẳng giới hạn bởi parabol 2
y = x − 3x +1 và đường thẳng y = x +1 được tính
theo công thức nào dưới đây? 4 4 4 4
Ⓐ. ( 2x −4x)dx. Ⓑ. ( 2
−x + 4x)dx . Ⓒ. ( 2x +4x)dx. Ⓓ.( 2
−x − 2x)dx . 0 0 0 0
Câu 19: Tính diện tích hình phẳng giới hạn bởi các đường 2
y + x − 5 = 0, x + y − 3 = 0 . Ⓐ. 19 37 . Ⓑ.15 . Ⓒ. . Ⓓ. 9 . 6 2 6 2
Câu 20: Diện tích hình phẳng giới hạn bởi các đường 3
y = x , y = 10 − x và trục Ox là Ⓐ. 32. Ⓑ. 26 . Ⓒ. 36. Ⓓ. 40 . BẢNG ĐÁP ÁN 1.C 2.A 3.A 4.A 5.D 6.C 7.A 8.A 9.A 10.A 11.C 12.C 13.C 14.B 15.A 16.A 17.A 18.B 19.D 20.C
Dạng ③: Diện tích hình phẳng thông qua đồ thị
-Phương pháp:
.Minh họa các dạng thường gặp: có hai loại dấu trên
. Ghi nhớ: Quan sát hình phẳng mang dấu + hay -
St-bs: Duong Hung 68
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
A - Bài tập minh họa:
Câu 1: Cho hàm số y = f ( x) và y = g ( x) có đồ thị
giao nhau tại hai điểm phân biệt có
hoành độ a và b . Gọi (H ) là hình phẳng
được giới hạn bởi đồ thị hai hàm số này
(phần tô đậm ở hình vẽ).
Diện tích của (H ) được tính theo công thức b b Ⓐ. S =  f
 (x) − g(x) dx  . Ⓑ. S = g
 (x) − f (x) dx  . a a b b Ⓒ. S =  f
 (x) + g(x) dx  .
Ⓓ. S = −  f
  (x) + g(x) dx  . a a Lời giải
PP nhanh trắc nghiệm
Chọn B
Quan sát nhanh g ( x)  f ( x) b
Áp dụng công thức S = f
 (x)− g(x)dx . a
Quan sát hình vẽ ta thấy g ( x)  f ( x) trên a,bb b Vậy S = f
 (x)− g(x)dx = (g(x)− f (x))dx . a a b
S = (g (x)− f (x))dx a
Câu 2: Cho hàm số y = f ( x) liên tục trên đoạn  ;
a b . Gọi D là diện tích
hình phẳng giới hạn bởi đồ thị (C) : y = f (x) , trục hoành, hai
đường thẳng x = a , x = b (như hình vẽ dưới đây).
Giả sử S là diện tích hình phẳng D . Chọn công thức đúng D trong các phương án , A ,
B C, D cho dưới đây? 0 b 0 b
Ⓐ. S = f x dx + f x dx  
. Ⓑ. S = − f x dx + f x dx   D ( ) ( ) D ( ) ( ) a 0 a 0 . 0 b 0 b
Ⓒ. S = f x dx − f x dx  
. Ⓓ. S = f x dx − f x dx   D ( ) ( ) D ( ) ( ) a 0 a 0 Lời giải
PP nhanh trắc nghiệm Chọn B
Quan sát dấu của hình phẳng 
St-bs: Duong Hung 69
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung b 0 b S = f x d x = f x d x + f x d x    D ( ) ( ) ( ) a a 0 0 b = − f
 (x)dx + f  (x)dx a 0
Câu 3: Cho hình thang cong (H ) giới hạn bởi các đường x y = e ,
y = 0 , x = 0 , x = ln 4 . Đường thẳng x = k (0  k  ln 4)
chia (H ) thành hai phần có diện tích là S và S như 1 2
hình vẽ bên. Tìm k để S = 2S . 1 2 Ⓐ. 2 k = ln 4 . Ⓑ. k = ln 2. 3 Ⓒ. 8
k = ln . Ⓓ. k = ln3. 3 Lời giải
PP nhanh trắc nghiệm Chọn D A x e dxk k Ta có x k k
S = e dx = e = e −1  và
Tính Nhập vào máy 0 và ln 4 1 0 x 0 e dxk ln 4 ln 4
CALC với các giá trị của A lần lượt  x x S = e dx = e = 4 k − e  2
ở 4 phương án. Giá trị nào cho kết k 0 quả bằng 2 thì chọn. Ta có = 2 k  −1 = 2 4 k S S e
− e k = ln 3 . 1 2 ( )
B - Bài tập rèn luyện:
Câu 1: Cho hàm số y = f ( x) có đồ thị như hình dưới đây.
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f ( x) và trục Ox là 2 0 Ⓐ. S = f
 (x)dx− f
 (x)dx . 0 1 − 2 Ⓑ. S = f
 (x)dx . 1 − 2
Ⓒ. S = − f  (x)dx . 1 − 0 2 Ⓓ. S = f
 (x)dx− f  (x)dx. 1 − 0
St-bs: Duong Hung 70
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 2: Cho hàm số y = f ( x) liên tục trên và có đồ thị (C) là đường cong như hình bên dưới.
Diện tích hình phẳng giới hạn bởi đồ thị (C ) , trục hoành và hai đường thẳng x = 0 , x = 2 là 1 2 Ⓐ. f
 (x)dx− f
 (x)dx . 0 1 2
Ⓑ. f (x)dx  . 0 1 2 Ⓒ. − f
 (x)dx+ f
 (x)dx. 0 1 2
Ⓓ. f (x)dx  . 0
Câu 3: Cho đồ thị hai hàm số 3 2
y = x − 3x + x + 3 và 2
y = −x + 2x +1 như hình sau
Diện tích phần hình phẳng được gạch sọc tính theo
công thức nào dưới đây? 1 2 Ⓐ. ( 3 2
x − 2x − x + 2)dx + ( 3 2
−x + 2x + x − 2)dx . 1 − 1 2 Ⓑ. ( 3 2
x − 2x − x + 2) dx . 1 − 1 2 Ⓒ. ( 3 2
−x + 2x + x − 2)dx + ( 3 2
x − 2x − x + 2)dx . 1 − 1 2 Ⓓ. ( 3 2
−x + 2x + x − 2)dx . 1 −
Câu 4: Cho hàm số y = f (x) liên tục trên và có đồ thị là đường cong như hình bên. Diện tích hình
phẳng giới hạn bởi đồ thị, trục hoành và hai đường thẳng x = 0, x = 2 là 1 2
Ⓐ. S = − f (x)dx + f (x)dx   . 0 1 1 2
Ⓑ. S = f (x)dx − f (x)dx   . 0 1 2
Ⓒ. S = f (x)dx  . 0 2
Ⓓ. S = f (x)dx  . 0
Câu 5: Diện tích phần hình phẳng gạch chéo trong hình vẽ được tính theo công thức nào dưới đây? 2 2 Ⓐ. ( 2
2x − 2x − 4)dx . Ⓑ.  ( 2
− x + 2)dx . 1 − 1 − 2 2
Ⓒ. (2x−2)dx. Ⓓ.  ( 2 2
− x + 2x + 4)dx . 1 − 1 −
St-bs: Duong Hung 71
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 6: Cho đồ thị hàm số y = f ( x) như hình vẽ.Diện tích S của hình phẳng được giới hạn bởi đồ
thị hàm số y = f ( x) và trục Ox được tính bởi công thức 3 Ⓐ. S = f
 (x)dx . 3 − 3 Ⓑ. S = f  (x)dx. 3 − 1 3
Ⓒ. S = f
 (x)dx− f  (x)dx. 3 − 1 1 3 Ⓓ. S = f
 (x)dx+ f  (x)dx. 3 − 1
Câu 7: Diện tích hình phẳng giới hạn bởi parabol 2
y = (x − 2) , đường cong 3
y = x và trục hoành bằng Ⓐ. 11. Ⓑ. 73. 2 12 Ⓒ. 7 . Ⓓ. 5 . 12 2
Câu 8: Hình phẳng giới hạn bởi đồ thị hàm số y = f ( x) và trục
hoành gồm hai phần, phần nằm phía trên trục hoành có diện 8
tích S = và phần nằm phía dưới trục hoành có diện tích 1 3 5 0 S = . Tính I = f (3x +  )1dx . 2 12 1 − Ⓐ. 5 I = . Ⓑ. 3 I = . 3 4 Ⓒ. 37 I = . Ⓓ. 27 I = . 36 4
Câu 9: Diện tích phần tô đậm trong hình bên được tính theo công
thức nào trong các công thức sau? Ⓐ. 1( 3 2
−x + 3 x − 2 x)dx . 0 Ⓑ. 1( 3 2
x − 3 x + 2 x)dx . 0 Ⓒ. 2 ( 3 2
−x + 3 x − 2 x)dx . 0 Ⓓ. 2( 3 2
x − 3 x + 2 x)dx . 0
St-bs: Duong Hung 72
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 10: Gọi (H ) là phần hình phẳng gạch chéo trong hình vẽ dưới
đây được giới hạn bởi đồ thị của các hàm số 2 y = 3x ,
y = 4 − x và trục hoành. Diện tích của ( H ) là bằng bao nhiêu? Ⓐ. 11 . Ⓑ. 9 . 2 2 Ⓒ. 13 . Ⓓ. 7 . 2 2
Câu 11: Cho hàm số y = f ( x) liên tục trên và có đồ thị như hình vẽ
dưới đây. Biết diện tích hai phần A và B lần lượt là 16 và 63 , 3 4 3 2 tính f (2x +  ) 1 dx . 1 − Ⓐ. 253 . Ⓑ. 253 . 12 24 Ⓒ. 125 − . Ⓓ. 125 − . 24 12
Câu 12: Tính diện tích S của hình phẳng (phần gạch sọc) giới hạn bởi hai đồ thị hàm số
f ( x) = x; g ( x) = x − 2 trong hình sau y 2 Ⓐ. 8 . Ⓑ.12 . 3 3 Ⓒ. 7 . Ⓓ.10 . 3 3 O 2 4 x
Câu 12: Gọi S là diện tích hình phẳng (H ) giới hạn bởi các đường y = f ( x) , trục hoành và 2 đường thẳng x = 1
− , x = 2 trong hình vẽ bên. 0 2
Đặt S = f x d , x S = f x dx   . Mệnh đề nào sau đây 1 ( ) 2 ( ) 1 − 0 đúng?
Ⓐ. S = S + S .
Ⓑ. S = −S − S . 1 2 1 2
Ⓒ. S = S − S .
Ⓓ. S = S − S . 1 2 2 1
St-bs: Duong Hung 73
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 13: Diện tích hình mặt phẳng gạch sọc trong hình vẽ bên bằng 3 3 Ⓐ. 2xdx  .
Ⓑ. (2−2x)dx. 1 1 3 Ⓒ. 3
(2x − 2)dx.
Ⓓ. (2x +2)dx. 1 1
Câu 14: Diện tích của hình phẳng được giới hạn bởi đồ thị hàm số y = f ( x) , trục hoành và hai đường
thẳng x = a , x = b (a b) tính theo công thức nào dưới đây ? c b Ⓐ. S = f
 (x)dx+ f
 (x)dx. a c b Ⓑ. S = f  (x)dx. a c b
Ⓒ. S = − f
 (x)dx+ f
 (x)dx. a c Ⓓ. b S = f  (x)dx . a
Câu 15: Cho hàm số y = f ( x) có đồ thị như hình vẽ dưới đây. Diện tích hình phẳng được tính bằng công thức nào? y 0 b
Ⓐ. S = f (x)dx - f (x)dx   . a 0 0 b
Ⓑ. S = f (x)dx + f (x)dx   . a 0 b a O b x
Ⓒ. S = 2 f (x)dx. 0 b
Ⓓ. S = f (x)dx  . a
St-bs: Duong Hung 74
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 16: Cho đồ thị hàm số y = f ( x) . Diện tích hình phẳng là: 0 4 y Ⓐ. S = f
 (x)dx+ f
 (x)dx. -3 0 4 -3 O 1 4 x Ⓑ. S = f
 (x)dx . -3 4
Ⓒ. S = f
 (x)dx . -3 0 4 Ⓓ. S = f
 (x)dx− f  (x)dx . -3 0
Câu 17: Cho đồ thị hàm số y = f ( x) trên đoạn0; 4 như hình vẽ và có 11 9 4 diện tích S = , S =
. Tính tích phân I = f  (x)dx 1 2 6 2 0 Ⓐ. 8 I = − . Ⓑ. 19 I = . 3 3 Ⓒ. 8 I = . Ⓓ. 19 I = − . 3 3
Câu 19: Cho đồ thị hàm số y = f ( x) trên đoạn  2
− ; 2 như hình vẽ ở bên và có diện tích 22 76 2 S = S = , S =
. Tính tích phân I = f  (x)dx 1 2 3 15 15 -2 Ⓐ. 32 I = . Ⓑ. I = 8. 15 Ⓒ. 18 I = . Ⓓ. 32 I = − . 5 15 BẢNG ĐÁP ÁN 1.D 2.A 3.A 4.B 5.D 6.C 7.C 8.B 9.B 10.A 11.C 12.D 13.D 14.C 15.C 16.A 17.D 18.D. 19.A
St-bs: Duong Hung 75
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 76
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung Full Chuyên đề 12 new 2020-2021 CHƯƠNG ③: FB: Duong Hung
Bài 6: THỂ TÍCH VẬT THỂ TRÒN XOAY
Dạng ①: Bài toán Thể tích vật thể: . Phương pháp:
 Gọi là phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các điểm a và b;
là diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm , . Giả sử
là hàm số liên tục trên đoạn .
Khi đó, thể tích của vật thể B được xác định:
A - Bài tập minh họa:
Câu 1: Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x =1 và x = 3, biết rằng khi
cắt vật thể bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (1 x  3 ) thì
được thiết diện là một hình chữ nhật có độ dài hai cạnh là 3x và 2 3x − 2 . Ⓐ.  V = 32 + 2 15. Ⓑ. 124 V = . Ⓒ. 124 V =
. Ⓓ.V = (32 + 2 15). 3 3 Lời giải
PP nhanh trắc nghiệm
Chọn C
Ta nhập biểu thức 3
Diện tích thiết diện là: 2 2 S(x) = 3 . x 3x − 2 3 .
x 3x − 2dx  như sau : 1 3 124
Thể tích vật thể là: 2 y3Q(s3Q(dp2R1E3= V = 3 .
x 3x − 2dx =  . 3 1  Màn hình hiển thị : Chọn C
St-bs: Duong Hung 77
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 2: Trong không gian với hệ tọa độ Oxyz , cho vật thể nằm giữa hai mặt phẳng x = 0 và x = 3.
Biết rằng thiết diện của vật thể cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành
độ x (0  x  3)là một hình vuông cạnh là 2
9 − x . Tính thể tích V của vật thể. Ⓐ. V =171
Ⓑ. V =171 .
Ⓒ. V =18. Ⓓ.V =18 . Lời giải
PP nhanh trắc nghiệm Chọn C Casio
Ta có thể tích của vật thể là V = ( 9 − x )2 3 2 dx 0 3 3 (  x  = 9 − x ) 3 2 dx = 9x −  =18 .
Chú ý: Diện tích hình vuông  3  0 0
B - Bài tập rèn luyện:
Câu 1: Trong không gian với hệ tọa độ Oxyz , cho vật thể (H ) giới hạn bởi hai mặt phẳng có phương
trình x = a , x = b (a b) . Gọi S (x) là thiết diện của (H ) cắt bởi mặt phẳng vuông góc với
trục Ox tại điểm có hoành độ là x với a x b . Giả sử hàm số y = S (x) liên tục trên đoạn
 ;ab. Khi đó thể tích V của vật thể (H) được cho bởi công thức b b b b
Ⓐ. V =  S
  (x) 2 dx
. Ⓑ. V =  S
 (x)dx . Ⓒ. V = S
  (x) 2 dx  . Ⓓ.V = S  (x)dx . a a a a
Câu 2: Trong không gian Oxyz , cho vật thể được giới hạn bởi hai mặt phẳng ( P) , (Q) vuông góc với
trục Ox lần lượt tại x = a , x = b (a b) . Một mặt phẳng tùy ý vuông góc với Ox tại điểm
có hoành độ x, a x b cắt vật thể theo thiết diện có diện tích là S x với y S x là
hàm số liên tục trên  ;
a b . Thể tích V của thể tích đó được tính theo công thức z
S(x) y O a x b x Ⓐ. b b 2 V = S
 (x)dx. Ⓑ. V = S
 (x)dx . a a b b
Ⓒ. V =  S
 (x)dx . Ⓓ. 2 V =  S  (x)dx . a a
Câu 3: Cho phần vật thế  được giới hạn bởi hai mặt phẳng ( P) và (Q) vuông góc với trục Ox tại
x = 0 , x = 3. Cắt phần vật thể  bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ
bằng x (0  x  3) ta được thiết diện là hình chữ nhật có kích thước lần lượt là x và 3− x .
Thể tích phần vật thể  bằng
St-bs: Duong Hung 78
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung Ⓐ. 27  . Ⓑ. 12 3 . Ⓒ. 12 3 . Ⓓ. 27 . 4 5 5 4
Câu 4: Cho phần vật thể () giới hạn bởi hai mặt phẳng có phương trình x = 0 và x = 2 . Cắt phần
vật thể () bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (0  x  2) , ta
được thiết diện là một tam giác đều có độ dài cạnh bằng x 2 − x . Tính thể tích V của phần vật thể () 3 Ⓐ. 4 V = . Ⓑ. V = .
Ⓒ. V = 4 3. Ⓓ.V = 3. 3 3
Câu 5: Cho vật thể có mặt đáy là hình tròn có bán kính bằng 1 (hình vẽ). Khi cắt vật thể bởi mặt
phẳng vuông góc với trục Ox tại điểm có hoành độ x ( 1 −  x  )
1 thì được thiết diện là một
tam giác đều. Tính thể tích V của vật thể đó. Ⓐ. 4 3 V = 3 .
Ⓑ. V = 3 3 . Ⓒ. V = . Ⓓ.V = . 3 
Câu 6: Cho phần vật thể B giới hạn bởi hai mặt phẳng có phương trình x = 0 và x = . Cắt phần 3   
vật thể B bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x 0  x    ta  3 
được thiết diện là một tam giác vuông có độ dài hai cạnh góc vuông lần lượt là 2x và cos x .
Thể tích vật thể B bằng Ⓐ. 3 + 3 3 − 3 3 − 3  . Ⓑ. . Ⓒ. . Ⓓ. 3 . 6 3 6 6
Câu 7: Tính thể tích V của vật thể nằm giữa hai mặt phẳng x = 0 và x =  , biết rằng thiết diện của
vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (0  x   ) là
một tam giác đều cạnh 2 sin x . Ⓐ. V = 3.
Ⓑ. V = 3 .
Ⓒ. V = 2 3 . Ⓓ.V = 2 3 .
Câu 8. Tính thể tích vật thể giới hạn bởi các mặt phẳng x = 0 và x =1, biết thiết diện của vật thể
khi cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (0  x 1) là một hình vuông có độ dài cạnh ( x x e − ) 1 . Ⓐ.  e −  e − V = . Ⓑ. 1 V = . Ⓒ. 1 V = . Ⓓ. ( 1) V = . 2 2 2 2
Câu 9. Cắt một vật thể V bởi hai mặt phẳng song song P , Q lần lượt vuông góc với trục Ox       tại x = − , x =
. Một mặt tùy ý vuông góc với trục Ox tại điểm x −  x    cắt V 2 2  2 2 
theo thiết diện có diện tích là S ( x) = ( 2
1+ sin x)cosx . Tính thể tích vật thể V giới hạn bởi
hai mặt phẳng P , Q .
St-bs: Duong Hung 79
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung Ⓐ.   3,14 . Ⓑ. 8 . Ⓒ. 13 . Ⓓ. 8 . 3 6 3
Câu 10. Tính thể tích của vật thể nằm giữa hai mặt phẳng x = 1
− và x =1, biết rằng thiết diện của vật thể
bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x ( 1 −  x  ) 1 là một tam giác
vuông cân có cạnh huyền bằng 4 1− x . Ⓐ. 3 . Ⓑ. 2 . Ⓒ.4. Ⓓ. 1 . 4 5 4 BẢNG ĐÁP ÁN 1.D 2.B 3. C 4.B 5.C 6.C 7.D 8.C 9.B 10.B Hướng dẫn giải Lời giải Câu 3. Chọn C
Ta có diện tích thiết diện là S (x) = x 3− x . 3 3
Vậy thể tích phần vật thể  là: V = S
 (x)dx = x 3− xdx  12 3 = . 5 0 0 Câu 4. Lời giải Chọn B 2 x (2 − x) 3
Diện tích thiết diện: S =  . 4 2 2 2 x (2 − x) 3 2 2    3 3 3 2 1 3 V = dx 2 = − 2 = x  (2− x) 3 4 = − = .   x  (2 x)dx dx x x   4 4 4 4  3 4  3 0 0 0 0 Câu 5. Lời giải Chọn C
Tại vị trí có hoành độ x ( 1 −  x  )
1 thì tam giác thiết diện có cạnh là 2 2 1− x .  3
Do đó tam giác thiết diện có diện tích S ( x) = (2 1− x )2 2 4 = ( 2 3 1− x ) . 1  4 3
Vậy thể tích V của vật thể là 3  ( 2 1− x )dx = . 3 1 − Câu 6. Lời giải Chọn C
St-bs: Duong Hung 80
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung   3  3   3 − 3
Thể tích vật thể B là = = 3 − = 3 + 3 V x cos d x x x sin x sin d x x x sin x cos x =   . 0 0 0 6 0 0 Câu 7. Lời giải Chọn D ( x )2 3 2 sin
Diện tích tam giác đều S (x) = = 3 sin x . 4  
Vậy thể tích V = S
 (x)dx = 3sin d x x  = 2 3 . 0 0 Câu 8. Chọn C Lời giải 1 1 1 2 Ta có:   = ( )d =  
( x − )1 d =  ( x V S x x x e x x e − ) 1 dx  .   0 0 0 u  = x  du = dx Đặt:    . dv =  ( xe − )1d x x
v = e − x 1 1 2 1  
Do đó: V = x ( x x
e − x) − ( x e − x) x 1 1
dx = e −1− e −
 = e −1− e + +1 = . 0  2  2 2 0 0 Câu 9. Chọn B Lời giải   2 2
Ta có thể tích vật thể V cần tính là: V = S
 (x)dx =  ( 2 1+ sin x)co d sx x .   − − 2 2
Đặt t = sinx  dt = cosx dx .  
Đổi cận: x = −  t = 1 − ; x =  t = 1. 2 2 1 1 3    t V =  ( 8 2
1+ t )dt = t +  = .  3  3 1 − 1 − Câu 10. Chọn B Lời giải
St-bs: Duong Hung 81
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung 2 4   −  1 1 x 1
Ta có diện tích thiết diện được cho bằng: S ( x) =   = ( 4 1− x ) 2  2  4   2 4   −  1 1 x 1
Ta có diện tích thiết diện được cho bằng: S ( x) =   = ( 4 1− x ) 2  2  4   1 1  1 2
Thể tích vật thể cần tìm là: V =
S ( x).dx = ( 4 1− x )dx =   . 4 5 1 − 1 −
Dạng ②: Bài toán Thể tích vật thể tròn xoay quanh trục Ox . Phương pháp:
 Tính thể tích vật thể tròn xoay sinh bởi miền giới hạn bởi ; và khi quay quanh trục .
Phương pháp giải: áp dụng công thức:
A - Bài tập minh họa:
Câu 1: Cho hàm số y = f (x) liên tục trên đoạn a;b 
 . Gọi D là hình phẳng giới hạn bởi đồ thị
hàm số y = f (x) , trục hoành và hai đường thẳng x = ,
a x = b (a  )
b . Thể tích khối tròn
xoay tạo thành khi quay D quanh trục hoành được tính theo công thức b b b b Ⓐ. 2 2 V =  f (x)dx  . Ⓑ. 2
V =  f (x)dx  . Ⓒ. 2 V =  f (x)dx  . Ⓓ. 2
V = 2 f (x)dx  . a a a a Lời giải
PP nhanh trắc nghiệm
Chọn B
Công thức b x  [a; ] b ta có 2
V =  f (x)dxa
Câu 2: Tính thể tích của khối tròn xoay được tạo thành khi quay quanh trục hoành hình phẳng giới
hạn bởi đồ thị của các hàm số y = 2ln ,
x y = 0, x = 1, x = e . Ⓐ. . Ⓑ.e − 2. Ⓒ. (e− 2) . Ⓓ. 4 (e − 2).
St-bs: Duong Hung 82
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung Lời giải
PP nhanh trắc nghiệm Chọn D Casio e Có 2 V = 4 ln d x x = 4 I  1  1 2 u  = ln x
du = 2ln x dx Đặt    x dv = dx v = x e e Suy ra 2
I = x ln x − 2 ln d x x = e − 2I'  1 1  1 u  = ln x du = dx Đặt    x dv = dx v = x e Suy ra e
I' = x ln x − dx = e − e +1 = 1  1 1
Suy ra I = e − 2
Vậy V = 4 (e − 2)
Câu 3: Gọi (H ) là hình phẳng giới hạn bởi các đường: y = sin x ; Ox ; x = 0 ; x =  . Quay (H ) xung
quanh trục Ox ta được khối tròn xoay có thể tích là 2 Ⓐ.   . Ⓑ. . Ⓒ.  . Ⓓ. 2  . 2 2 Lời giải
PP nhanh trắc nghiệm Chọn A
Thể tích khối tròn xoay là       V    = sin . x dx =  (1−c so2x) 2 1 2 .dx = x − sin 2x =   . 2 2  2  0 2 0 0
B - Bài tập rèn luyện:
Câu 1. Gọi (H ) là hình phẳng giới hạn bởi các đường y = x ln , x trục O ,
x x = 1, x = e . Tính thể tích
khối tròn xoay được tạo thành khi quay hình phẳng (H ) quanh trục Ox .  ( 2e + )  ( 2e − ) Ⓐ. 1  (e − ) 1  (e + ) 1 1 . Ⓑ. . Ⓒ. . Ⓓ. . 4 3 3 4
St-bs: Duong Hung 83
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 2. Tính thể tích vật thể tròn xoay do hình phẳng giới hạn bởi y
ln x , trục Ox và đường thẳng x
2 quay xung quanh trục Ox . Ⓐ. 2ln 2 1.
Ⓑ. 2 ln2  .
Ⓒ. 2 ln2  . Ⓓ. 2ln 2 1.
Câu 3. Cho hình phẳng D giới hạn với đường cong 2 y =
x +1, trục hoành và các đường thẳng
x = 0, x = 1. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu? Ⓐ. 4 V =
Ⓑ. V = 2 Ⓒ. 4 V = Ⓓ.V = 2 3 3
Câu 4. Cho hình phẳng D giới hạn bởi đường cong y = 2 + sin x , trục hoành và các đường thẳng
x = 0 , x =  . Khối tròn xoay tạo thành khi quay D quay quanh trục hoành có thể tích V bằng bao nhiêu? Ⓐ. 2 V = 2 .
Ⓑ. V = 2 ( + ) 1 .
Ⓒ. V = 2 . Ⓓ.V = 2( + ) 1 .
Câu 5. Cho hình phẳng (H ) giới hạn bởi các đường 2
y = x + 3 , y = 0 , x = 0 , x = 2 . Gọi V là thể tích
của khối tròn xoay được tạo thành khi quay (H ) xung quanh trục Ox . Mệnh đề nào dưới đây đúng? 2 2
Ⓐ. V =  (x +3)2 2 dx .
Ⓑ. V =  ( 2x +3)dx. 0 0 2 2
Ⓒ. V = (x +3)2 2 dx .
Ⓓ.V = ( 2x +3)dx. 0 0
Câu 6: Cho hình phẳng (H ) giới hạn bởi các đường thẳng 2
y = x + 2, y = 0, x = 1, x = 2 . Gọi V là thể
tích của khối tròn xoay được tạo thành khi quay (H ) xung quanh trục Ox . Mệnh đề nào dưới đây đúng? 2 2 2 2 Ⓐ. 2
V =  (x + 2)2 2
dx . Ⓑ. V = ( 2
x + 2) dx . Ⓒ. V =  ( 2
x + 2)dx . Ⓓ.V = ( 2 x + 2)dx . 1 1 1 1
Câu 7: Viết công thức tính thể tích V của khối tròn xoay được tạo ra khi quay hình thang cong, giới
hạn bởi đồ thị hàm số y = f ( x) , trục Ox và hai đường thẳng x = a, x = b(a b) , xung quanh trục Ox . b b b b Ⓐ. 2 V =  f
 (x)dx . Ⓑ. 2 V = f
 (x)dx. Ⓒ. V = f
 (x)dx. Ⓓ.V = f  (x)dx . a a a a
Câu 8: Kí hiệu (H ) là hình phẳng giới hạn bởi đồ thị hàm số = 2( −1) x y x
e , trục tung và trục hoành.
Tính thể tích V của khối tròn xoay thu được khi quay hình (H ) xung quanh trục Ox Ⓐ. 2 V = 4 − 2e .
Ⓑ. V = (4− 2e) . Ⓒ. 2 V = e − 5 .
Ⓓ.V = (e −5) .
Câu 9: Tính thể tích của khối tròn xoay được tạo thành khi quay quanh trục hoành hình phẳng giới
hạn bởi đồ thị của các hàm số 2
y = 3x − x , y = 0 . Ⓐ. 16 . Ⓑ.16  . Ⓒ. 81 . Ⓓ. 16 . 15 15 10 15
St-bs: Duong Hung 84
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 10: Tính thể tích của khối tròn xoay được tạo thành khi quay quanh trục hoành hình phẳng giới
hạn bởi đồ thị của các hàm số 3
y = x , y = 0, x = 1 . Ⓐ.     . Ⓑ. 4 . Ⓒ. . Ⓓ. . 4 7 2 7
Câu 11: Tính thể tích của khối tròn xoay được tạo thành khi quay quanh trục hoành hình phẳng giới
hạn bởi đồ thị của các hàm số xy = 9, y = 0, x =1, x = 3 . Ⓐ.54 . Ⓑ.6 . Ⓒ.12 . Ⓓ. 6 .
Câu 12: Tính thể tích của khối tròn xoay được tạo thành khi quay quanh trục hoành hình phẳng giới
hạn bởi đồ thị của các hàm số y = ( x) 1 cos
, y = 0, x = 0, x = .  Ⓐ.  ( + 2)  sin 2 + 2 +  + . Ⓑ. ( ) . Ⓒ. sin 2 2 . Ⓓ. 2 . 8 4 4 8
Câu 13: Tính thể tích của khối tròn xoay được tạo thành khi quay quanh trục hoành hình phẳng giới
hạn bởi đồ thị của các hàm số 2 y = cos ,
x y = 0, x = 0, x =  . 2 2 Ⓐ.     . Ⓑ. 3 . Ⓒ. 3 . Ⓓ. . 2 8 8 2 BẢNG ĐÁP ÁN 1.D 2.C 3. A 4. B 5. A 6. A 7.A 8.D 9.C 10.D 11.A 12.B 13.C
Dạng ③: Bài toán Thể tích vật thể tròn xoay quanh trục Ox . Phương pháp:
 Tính thể tích vật thể tròn xoay khi cho hình phẳng giới hạn bởi: ; quay quanh trục .  Phương pháp giải: ①. Giải phương trình: có nghiệm
②. Khi đó thể tích cần tìm : ③. Casio:
A - Bài tập minh họa:
St-bs: Duong Hung 85
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 1: Thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi Parabol (P) 2 : y = x và
đường thẳng d : y = 2x quay quanh trục Ox bằng 2 2 2 Ⓐ. 2 2 4
 4x dx − x dx  
. Ⓑ.  ( 2x −2x) dx . 0 0 0 2 2 2 Ⓒ. 2 4
 4x dx + x dx   . Ⓓ. ( 2
x − 2x) dx . 0 0 0 Lời giải
PP nhanh trắc nghiệm
Chọn B
Phương trình hoành độ giao điểm của ( P) và d là x = 2 x = 0 2x   . x = 2 2 2
Thể tích của khối tròn xoay là    (  2x)2 − ( 2 x ) dx    0 2 2 2 4
=  4x dx − x dx   0 0
Câu 2: Thể tích khối tròn xoay sinh bởi hình phẳng giới hạn bởi đồ thị hai hàm số 2
y = x − 2x , 2
y = 4 − x khi nó quanh quanh trục hoành là: Ⓐ. 421 125 . Ⓑ. 27 . Ⓒ.  . Ⓓ.30 . 15 3 Lời giải
PP nhanh trắc nghiệm Chọn B
Xét phương trình hoành độ giao điểm: x = 1 −  2 2 2
x − 2x = 4 − x  2x − 2x − 4 = 0   . x = 2
Do khi quay quanh trục hoành thì khối sinh bởi hình
phẳng giới hạn bởi đồ thị hàm số 2
y = x − 2x , trục hoành,
x = 0; x = 2 sẽ nằm trong khối sinh bởi hình phẳng giới
Chú ý phần rất dễ thiếu phần
hạn bởi đồ thị hàm số 2
y = 4 − x , trục hoành, x = 0; x = 2 . 2 V =  4 − x dx  1 ( )2 2
Vậy thể tích cần tính bằng: 0 0  
V =   (4 − x ) 0
dx −   (x − 2x) 2 2
2 dx+ (4− x )2 2 2 2 dx  1− 1 −  0 203 38 256 421 =  −  +  =  15 15 15 15
B - Bài tập tham khảo rèn luyện:
St-bs: Duong Hung 86
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 1: Cho hình phẳng trong hình (phần tô đậm) quay quanh trục hoành. Thể tích của khối tròn xoay tạo
thành được tính theo công thức nào? b Ⓐ. 2 V =  f  (x) 2 − f x  dx  . 1 2 ( ) a b Ⓑ. 2 V =   f  (x) 2 − f x  dx  . 1 2 ( ) a b Ⓒ. 2 V =   f  (x) 2 − f x  dx  . 2 1 ( ) a b
Ⓓ.V =   f
 (x)− f (x) 2 dx. 1 2  a Lời giải Chọn B
Do f x f x x   ;
a b nên Chọn B 1 ( ) 2 ( ) ( )
Câu 2: Tìm công thức tính thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi parabol (P) 2
: y = x và đường thẳng d : y = 2x quay xung quanh trục Ox . 2 2 2
Ⓐ.  (x −2x)2 2 dx . Ⓑ. 2 4
 4x dx − x d   x. 0 0 0 2 2 2 Ⓒ. 2 4
 4x dx + x d   x. Ⓓ. ( 2 2 −  x x )dx. 0 0 0 Lời giải Chọn Ax = 0
Phương trình hoành độ giao điểm: 2
x − 2x = 0   . x = 2 2  2
Vậy thể tích khối tròn xoay được tính: V =  ( 2
x − 2x) dx . 0
Câu 3: Cho hình ( H ) giới hạn bởi trục hoành, đồ thị của một Parabol
và một đường thẳng tiếp xúc với Parabol đó tại điểm A(2; 4) ,
như hình vẽ bên. Thể tích vật thể tròn xoay tạo bởi khi hình
(H ) quay quanh trục Ox bằng Ⓐ. 16 32 . Ⓑ. . 15 5 Ⓒ. 2  . Ⓓ. 22 . 3 5 Lời giải Chọn A
Parabol có đỉnh là gốc tọa độ như hình vẽ và đi qua A(2;4) nên có phương trình 2 y = x .
Tiếp tuyến của Parabol đó tại A(2;4) có phương trình là y = 4( x − 2) + 4 = 4x − 4 . 2 2  2 2
Suy ra thể tích vật thể tròn xoay cần tìm là V =  ( 2
x ) dx − (4x − 4) dx . 0 1 2 2 2 ( 2 2 3   2 x 16 x ) 5 2 x 32 2 dx = = 
; (4x − 4) dx =16( 2 x − 2x + ) 2 1 dx = 16 
− x + x  = . 5 5  3  3 0 0 1 1 1
St-bs: Duong Hung 87
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung 2 2   2 2 32 16 16 Vậy V
 ( 2x) dx (4x 4) dx    = − − = − =   .  5 3  15 0 1
Câu 4: Gọi (H ) là hình phẳng được giới hạn bởi các đồ thị hàm 1− x
số y = 2x, y =
, y = 0 (phần tô đậm màu đen ở hình vẽ bên). x
Thể tích của vật thể tròn xoay tạo thành khi quay (H ) quanh trục hoành bằng. Ⓐ. 5 5 V    = − 2ln 2 
 . Ⓑ. V    = + 2ln 2   .  3   3  Ⓒ. 2 V    = 2 ln 2 −   . Ⓓ. 2 V    = 2 ln 2 +   .  3   3  Lời giải Chọn A −
Phương trình hoành độ 1 x
giao điểm của y = 2x và y = là: xx  0 −   x  0   1 x  1 1 2x =     x =   x = . x 2
2x + x −1 = 0 2  2 x = 1 − x  0
Phương trình hoành độ giao điểm của y = 2x và y = 0 là: 2x = 0    x = 0. 2
2x + x −1 = 0 −
Phương trình hoành độ 1 x
giao điểm của y = 0 và y = là: x 1− xx  0 x  0 = 0      x =1. x 1  − x = 0 x = 1 1 1 2 1 2   3 1 2 1 2  1 x 1 1 2 2 4x 1
V =  4x dx +  − dx     .    = + −1 dx      = + − +1 dx      x  3  x  2 6  x x  0 1 1 0 1 2 2 2
Câu 5: Tính thể tích của khối tròn xoay khi quay hình phẳng giới hạn bởi các đường 2 y = x − 4 ,
y = 2x − 4 , x = 0 , x = 2 quanh trục . Ox Ⓐ. 32π 32π 32π . Ⓑ. . Ⓒ. . Ⓓ. 22π . 5 7 15 5 Lời giải Chọn A 2 2  2 256 2 32 Ta có V = π( 2 x − 4 dx =
π , V = π 2x − 4 dx = π  . 2 ( ) 1 ) 15 3 0 0  32π
Vậy thể tích cần tìm V = V −V = . 1 2 5
Câu 6: Cho hình phẳng ( H ) giới hạn bởi các đường 2
y = x , y = 2x . Thể
tích của khối tròn xoay được tạo thành khi quay ( H ) xung quanh
trục Ox bằng: Ⓐ. 32 64 . Ⓑ. . 15 15
St-bs: Duong Hung 88
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung Ⓒ. 21  . Ⓓ.16 . 15 15 Lời giải Chọn Bx = 0
Xét phương trình hoành độ giao điểm: 2
x − 2x = 0   . x = 2 2  y = x   y = 2x
Khi quay (H ) xung quanh trục Ox ta được khối tròn xoay giới hạn bởi  . x = 0  x = 2 2  Do đó thể 2 2 64
tích của khối tròn xoay là: V =  ( 2
x ) − (2x) dx =  . 15 0
Câu 7: Tính thể tích V của vật tròn xoay tạo thành khi quay hình phẳng ( H ) giới hạn bởi các đường 2
y = x ; y =
x quanh trục Ox . Ⓐ. 9 3   V = . Ⓑ. V = .
Ⓒ. V = . Ⓓ. 7 V = . 10 10 10 10 Lời giải Chọn B
Phương trình hoành độ giao điểm 2 x = x 4  x − x = 0  x(x − )( 2 1 x + x + )
1 = 0  x = 0 hoặc x =1 Khi đó:
Thể tích khối tròn xoay sinh bởi hình (H ) là 1  V =  ( x ) 1 2 dx −  (x )2 3 2 dx =   10 0 0
Câu 8: Cho hình phẳng D giới hạn bởi đường cong 1 ex y − =
, các trục tọa độ và phần đường thẳng
y = 2 − x với x  1. Tính thể tích khối tròn xoay tạo thành khi quay D quanh trục hoành.  ( 2 5e − 3) Ⓐ. 2 1 e −1 1 e −1 1 e −1 V = + . Ⓑ. V = . Ⓒ. V = +  . Ⓓ. 2 V = + . 2 3 2e 2 6e 2 e 2 2 2e Lời giải Chọn B
Phương trình hoành độ giao điểm của đường cong 1 ex y − = và đường
thẳng y = 2 − x : x 1
e − = 2 − x x = 1 . (Vì 1 ex y − = là hàm đồng biến và
y = 2 − x là hàm nghịch biến trên tập xác định
nên phương trình có tối đa
1 nghiệm. Mặt khác x =1 thỏa mãn pt nên đó là nghiệm duy nhất của pt đó).
Đường thẳng y = 2 − x cắt trục hoành tại x = 2 . 1  (ex V − = ) 2
2 dx + (2− x)2 1 dx 0 1 2   − − xx ( 2 3 1 5e 1 2 2 ) =  e
+   − 2x + 4 = 2 0  3  6e 1
Câu 9: Tính thể tích khối tròn xoay sinh ra khi quay quanh trục Ox hình phẳng giới hạn bởi hai đồ thị 2
y = x − 4x + 6 và 2
y = −x − 2x + 6 . Ⓐ.  . Ⓑ.  −1. Ⓒ. 3 . Ⓓ. 2 .
St-bs: Duong Hung 89
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung Lời giải Chọn Cx = 0
Xét phương trình hoành độ giao điểm 2 2
x − 4x + 6 = −x − 2x + 6 2
 2x − 2x = 0   . x =1
Thể tích vật thể tròn xoay sinh ra khi quay quanh trục Ox hình phẳng giới hạn bởi hai đồ thị là 1 1
V =   (x − 4x − 6)2 −(−x − 2x + 6)2 2 2 dx 3 2 =  1
− 2x + 36x − 24x dx  0 0 1 =  ( 3 2 1
− 2x + 36x − 24x)dx =  ( 3
− x +12x −12x )1 3 3 2 = 3 . 0 0
Câu 10: Gọi ( H ) là hình được giới hạn bởi nhánh parabol 2
y = 2x (với x  0 ), đường thẳng y = −x + 3
và trục hoành. Thể tích của khối tròn xoay tạo bởi hình ( H ) khi quay quanh trục Ox bằng Ⓐ. 52 17 51  V = . Ⓑ. V = . Ⓒ. V = . Ⓓ. 53 V = . 15 5 17 17 Lời giải Chọn A x =1
Phương trình hoành độ  giao điểm: 2
2x = −x + 3  3  x = −  2 3 1  2 52
Thể tích khối tròn xoay tạo bởi ( H ) :V =  (−x + 3) 4
dx +  4x dx =   . 15 1 0
Câu 11: Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường x + y − 2 = 0 ; y = x ; y = 0 quay
quanh trục Ox bằng Ⓐ. 5 6 2  . Ⓑ. . Ⓒ. . Ⓓ. 5 . 6 5 3 6 Lời giải Chọn D
Hình phẳng đã cho được chia làm 2 phần sau:
Phần 1: Hình phẳng giới hạn bởi các đường y = x ; y = 0 ; x = 0 ; x =1. 1 2 1   x
Khi quay trục Ox phần 1 ta được khối tròn xoay có thể tích V =  x dx = . =  . 1 2 0 2 0
Phần 2 : Hình phẳng giới hạn bởi các đường y = 2 − x ; y = 0 ; x =1; x = 2 .
Khi quay trục Ox phần 2 ta được khối tròn xoay có thể tích − =  ( xV 2 − x) ( 2)3 2 2 2 dx = . =  . 2 3 1 3 1   5
Vậy thể tích khối tròn xoay cần tính là V = V +V = . 1 2 6
Câu 12: Thể tích vật thể tròn xoay sinh ra khi hình phẳng giới hạn bởi các đường x =
y , y = −x + 2 và
x = 0 quay quanh trục Ox có giá trị là kết quả nào sau đây? Ⓐ. 1 3 32 V =  .
Ⓑ. V =  .
Ⓒ. V =  . Ⓓ. 11 V =  . 3 2 15 6 Lời giải Chọn C
St-bs: Duong Hung 90
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung x = y 2
y = x (x  0)  
Gọi (H ) là hình phẳng giới hạn bởi các đường: y = −x + 2  y = −x + 2   x = 0  x = 0 
x = 1 (nhaän)
Phương trình hoành độ giao điểm: 2 x = −x + 2 2
x + x − 2 = 0   x = −2  (loaïi)
Thể tích vật tròn xoay sinh ra khi hình (H ) quay quanh trục Ox là: 1 1  32
V =  ((−x + 2) −  (x )2 2 2 )dx =( 2 4
x − 4x + 4 − x )dx =  (đvtt) 15 0 0
Câu 13: Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y = x , cung tròn có phương trình 2 y = 6 − x
(− 6  x  6) và trục hoành (phần tô đậm trong hình vẽ bên). Tính thể tích V của vật thể tròn
xoay sinh bởi khi quay hình phẳng D quanh trục Ox . Ⓐ. 22 22 
V = 8 6 − 2 .
Ⓑ. V = 8 6 + .
Ⓒ. V = 8 6 − . Ⓓ. 22 V = 4 6 + . 3 3 3 Lời giải Chọn D
Cách 1. Cung tròn khi quay quanh Ox tạo thành một khối cầu có thể tích V =  ( )3 4 6 = 8 6 . 3
Thể tích nửa khối cầu là V = 4 6 . 1 x  0 Xét phương trình: 2
x = 6 − x    x = 2. 2
x + x − 6 = 0
Thể tích khối tròn xoay có được khi quay hình phẳng (H ) giới hạn bởi đồ thị các hàm số y = x , cung tròn có phương trình 2 y =
6 − x , và hai đường thẳng x = 0, x = 2 quanh Ox là 2  V =  ( 22 2
6 − x − x dx =  . 2 ) 3 0   22
Vậy thể tích vật thể tròn xoay cần tìm là V = V +V = 4 6 + . 1 2 3
Cách 2. Cung tròn khi quay quanh Ox tạo thành một khối cầu có thể tích 4 V =  ( 6)3 = 8 6 . 1 3 x  0 Xét phương trình: 2
x = 6 − x    x = 2. 2
x + x − 6 = 0
Thể tích khối tròn xoay có được khi quay hình phẳng (H ) giới hạn bởi đồ thị các hàm số y = x , cung 2 6 tròn có phương trình 2 y =
6 − x và đường thẳng y = 0 quanh Ox là V =  d x x +    ( 2 6 − x dx 2 ) 0 2 12 6 − 28 = 22 2 +  = 4 6 − . 3 3
St-bs: Duong Hung 91
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung      22
Vậy thể tích vật thể tròn xoay cần tìm là V = V − 22
V = 8 6 − 4 6 − =  + . 1 2   4 6  3  3
Câu 14: Tính thể tích vật thể tròn xoay tạo bởi phép quay xung quanh trục Ox hình phẳng giới hạn bởi
các đường y = 0 , y = x , y = x − 2. Ⓐ. 8 16 . Ⓑ. . Ⓒ. 10 . Ⓓ.8 . 3 3 Lời giải Chọn B
0 = x x = 0 
Ta có: 0 = x − 2  x = 2
x = x −2  x = 4 
Dựa vào hoành độ giao điểm của ba đường ta có diện tích hình phẳng gồm hai phần. Phần thứ
nhất giới hạn bởi y = x , y = 0 và x = 0; x = 2. Phần thứ hai giới hạn bởi y = x , y = x − 2 và x = 2; x = 4 .
Thể tích vật thể bằng: 2 2 4 2 V =  ( x ) 4 2
dx +   (x − 2) 2 2 − x dx =  d x x +  
(x−(x−2) )dx 0 2 0 2 x
x (x − 2) 4 2 3 2 2  16 =  +  −  = . 2  2 3  3 0   2
Câu 15: Cho (H ) là hình phẳng giới hạn bởi parabol 2
y = x và đường tròn 2 2
x + y = 2 (phần tô đậm trong hình bên). Tính thể tích V của
khối tròn xoay tạo thành khi quay (H ) quanh trục hoành. Ⓐ. 44 22 V = . Ⓑ. V = . 15 15 Ⓒ. 5  V = . Ⓓ.V = . 3 5 Lời giải Chọn A 2 x =1 x =1 Với 2
y = x thay vào phương trình đường tròn ta được 2 4
x + x = 2     . 2 x = 2 − x = 1 − 2  = − −  y 2 x Hơn nữa 2 2
x + y = 2   . 2 y = 2− x 2 y = 2 − x   = −  x 1
Thể tích cần tìm chính là thể tích vật thể tròn xoay ( H : 
quay quanh Ox bỏ đi phần thể 1 ) x = 1 Ox  2 y = x  x = 1 − tích ( H :  quay quanh Ox . 2 ) x = 1  Ox 
St-bs: Duong Hung 92
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung 1 1 2   
Do đó V =   ( 2− x ) dx −  (x )2 44 2 2 dx = . 15  1 − 1 − 
Câu 16: Cho hình phẳng (H ) (phần gạch chéo trong hình vẽ).
Tính thể tích V của khối tròn xoay tạo thành khi
quay hình (H ) quanh trục hoành. Ⓐ. V = 8 .
Ⓑ. V =10 . Ⓒ.   8 V = . Ⓓ. 16 V = . 3 3 Lời giải Chọn D
Gọi là hình phẳng giới hạn bởi các đường x = 0 , x = 4 , f (x) = x và trục hoành.
(D là hình phẳng giới hạn bởi các đường x = 2, x = 4, g (x) = x −2 và trục hoành. 2 )
Kí hiệu V , V tương ứng là thể tích của các khối tròn xoay tạo thành khi quay (D , (D 2 ) 1 ) 1 2 quanh trục hoành. 4 4 4 4   Khi đó, 2 8
V = V −V 2 =  f  (x) 2 dx −  g  (x)dx = d x x −  
(x−2) dx = 8 − 16 = . 1 2 3 3 0 2 0 2
Câu 17: Thể tích V của khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi đường tròn
(C) x +( y − )2 2 : 3
=1 xung quanh trục hoành là Ⓐ. 2 6 . Ⓑ. 3 6 . Ⓒ. 2 3 . Ⓓ.6 . Lời giải Chọn A
(C): x +( y −3)2 =1 ( y −3)2 2 2 =1− x 2 2  y 3 1 x  − = − y = 3 + 1− x     2 2
y −3 = − 1− x
y = 3− 1− x
Thể tích V của khối tròn xoay được sinh ra khi quay hình
phẳng giới hạn bởi đường tròn
(C) x +( y − )2 2 : 3
=1 xung quanh trục hoành là 2 2 1 1 V =   ( 2
3 + 1− x ) dx −  ( 2 3 − 1− x ) 2 dx = .6 = 6 . 1 − 1 −
St-bs: Duong Hung 93
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung 94