Chuyên đề phục dựng hình ẩn

Tài liệu gồm 52 trang, được biên soạn bởi quý thầy, cô giáo Nhóm Toán VD – VDC (nay là Nhóm Giáo Viên Toán Việt Nam), tuyển tập 44 bài toán trắc nghiệm chuyên đề phục dựng hình ẩn, có đáp án và lời giải chi tiết.Mời bạn đọc đón xem.

56 28 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Khối đa diện

Môn: Toán 12

Thông tin:

52 trang 8 tháng trước

Tác giả:

Profile Lan Tường
Giáo viên THTP Lương Thế Vinh
Chuyên đề
PHỤC DỰNG
HÌNH ẨN
NĂM HỌC 2021 - 2022
NGUYỄN HOÀNG VIỆT
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 0
DỰ ÁN PHỤC DỰNG HÌNH ẨN
Nhóm biên soạn: Nhóm toán VD - VDC (nay là NHÓM GIÁO VIÊN TOÁN VIỆT NAM)
Qua nhiều bài toán chúng ta gặp phải ở trong các đề thi THPT Quốc gia, thường có các bài
toán về xác định góc, khoảng cách giữa các yếu tố đường thẳng, mặt phẳng và bài toán tính thể
tích các khối chóp, khối lăng trụ,… Trong các bài toán này, dữ kiện đề bài thường cho sẵn một
đường thẳng cụ thể vuông góc với mặt đáy và việc tính toán thường xoay quanh vấn đề đường cao.
Tuy nhiên, trong nhiều bài toán, để tăng mức độ cho câu hỏi về hình học không gian, người
ra đề thường làm ẩn đi các yếu tố này làm cho việc tính toán các yếu tố góc, khoảng cách hay thể
tích khối trở nên khó khăn hơn.
Để giải quyết được bài toán HHKG đã bị ẩn các yếu tố này, ta có thể sử dụng phương pháp
"Phục dựng hình ẩn”.
MỤC LỤC
PHẦN 01. ĐỀ BÀI ....................................................................................... Trang 1
PHẦN 02. BẢNG ĐÁP ÁN ............................................................................ Trang 8
PHẦN 03. ĐÁP ÁN CHI TIẾT ......................................................................... Trang 9
“Nơi nào có ý chí, nơi đó có con đường.”
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 1
ĐỀ BÀI
Câu 1: Tứ diện
ABCD
có
,
4CD
,
90ABC BCD ADC
,
, 60AD BC 
. Cosin của
góc giữa hai mặt phẳng
và
ACD
bằng
Ⓐ.
43
86
. Ⓑ.
4 43
43
. Ⓒ.
43
43
. Ⓓ.
2 43
43
.
Câu 2: Cho hình chóp
.S ABC
có
AB a
,
3AC a
,
2SB a
và
90ABC BAS BCS
. Biết sin
của góc giữa đường thẳng
SB
và mặt phẳng
SAC
bằng
11
11
. Thể tích của khối chóp
.S ABC
bằng
Ⓐ.
3
23
9
a
. Ⓑ.
3
3
9
a
. Ⓒ.
3
6
6
a
. Ⓓ.
3
6
3
a
.
Câu 3: Cho hình chóp
.S ABC
có đáy là tam giác vuông cân tại
B
,
AB a
,
SA AB
,
SC BC
,
2SB a
. Gọi
M
,
N
lần lượt là trung điểm
SA
,
BC
và
là góc giữa
MN
với
ABC
. Giá
trị
cos
bằng
Ⓐ.
2 11
11
. Ⓑ.
6
3
. Ⓒ.
26
5
. Ⓓ.
10
5
.
Câu 4: Cho hình chóp
có đáy là tam giác vuông cân tại
B
,
3AB BC a
,
90SAB SCB
và khoảng cách từ điểm
A
đến
SBC
bằng
2a
. Diện tích của mặt cầu
ngoại tiếp hình chóp
bằng
Ⓐ.
2
2 a
. Ⓑ.
2
8 a
. Ⓒ.
2
16 a
. Ⓓ.
2
12 a
.
Câu 5: (Sở Bắc Ninh lần 2 2018-2019) Cho tứ diện
ABCD
có
90DAB CBDº
;
; 5; 135AB a AC a ABC
. Biết góc giữa hai mặt phẳng
,ABD BCD
bằng
30
.
Thể tích của tứ diện
ABCD
bằng
Ⓐ.
3
23
a
. Ⓑ.
3
2
a
. Ⓒ.
3
32
a
. Ⓓ.
3
6
a
.
Câu 6: (Sở Bắc Ninh lần 2 2018-2019) Trong không gian
Oxyz
, cho điểm
4;0;0 , 0;4;0 , 0;0;A B S c
và đường thẳng
1 1 1
:
112
x y z
d

. Gọi
,AB

lần lượt
là hình chiếu vuông góc của
O
lên
,SA SB
. Khi góc giữa đường thẳng
d
và mặt phẳng
OA B

lớn nhất thì giá trị của số thực
c
thuộc khoảng nào dưới đây?
Ⓐ.
17 15
;
22




. Ⓑ.
9; 8
. Ⓒ.
0;3
. Ⓓ.
8; 6
.
PHẦN 1
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 2
Câu 7: Cho tứ diện
ABCD
có
90ABC BCD CDA
,
,BC CD a
2AD a
. Góc giữa hai
mặt phẳng
và
ACD
bằng
Ⓐ.
60
. Ⓑ.
30
. Ⓒ.
45
. Ⓓ.
90
.
Câu 8: Cho hình chóp
.S ABC
có đáy là tam giác cân tại
A
,
AB a
, các tam giác
,SAB SAC
là tam
giác vuông tại
B
và
C
. Biết độ dài đường cao của hình chóp
.S ABC
gấp hai lần độ dài đường
cao của tam giác
ABC
hạ từ đỉnh
A
. Bán kính mặt cầu ngoại tiếp hình chóp
.S ABC
có giá
trị nhỏ nhất bằng
Ⓐ.
a
. Ⓑ.
3a
. Ⓒ.
2
a
. Ⓓ.
3
2
a
.
Câu 9: Trong không gian cho đoạn thẳng
AB
cố định và có độ dài bằng 4. Qua các điểm
A
và
B
lần
lượt kẻ các tia
Ax
và
By
chéo nhau và hợp nhau góc
30
, đồng thời cùng vuông góc với
đoạn thẳng
AB
. Trên các tia
Ax
và
By
lần lượt lấy các điểm
,MN
sao cho
5MN
. Đặt
AM a
và
BN b
. Biết thể tích khối tứ diện
ABMN
bằng
3
3
. Giá trị biểu thức
2
22
S a b
bằng
Ⓐ.
144
. Ⓑ.
324
. Ⓒ.
100
. Ⓓ.
256
.
Câu 10: Cho hình chóp
có đáy là tam giác vuông cân tại
B
,
,AB a
90SAB SCB
, góc
giữa
AB
và g
SBC
bằng
60
. Thể tích của khối chóp đã cho bằng
Ⓐ.
3
3
.
6
a
Ⓑ.
3
43
.
9
a
Ⓒ.
3
3
.
9
a
Ⓓ.
3
3
.
3
a
Câu 11: Cho hình chóp
có đáy là tam giác cân tại
A
,
AB a
,
,120BAC
90SBA SCA
. Gọi
là góc giữa
SB
và
SAC
thỏa mãn
3
sin
8
, khoảng cách từ
S
đến mặt đáy nhỏ
hơn
2a
. Thể tích của khối chóp
.S ABC
bằng
Ⓐ.
3
3
4
a
. Ⓑ.
3
3
6
a
. Ⓒ.
3
3
12
a
. Ⓓ.
3
3
24
a
.
Câu 12: Cho hình chóp
.S ABC
có SA vuông góc với mặt đáy,
2SA BC
và
120BAC
. Hình chiếu
vuông góc của
A
lên các cạnh
SB
và
SC
lần lượt là
M
và
N
. Góc giữa hai mặt phẳng
ABC
và
AMN
bằng
Ⓐ.
45
. Ⓑ.
60
. Ⓒ.
15
. Ⓓ.
30
.
Câu 13: (VDC) Cho tứ diện
ABCD
có
, 2, 90AB AD a CD a ABC DAB
. Góc giữa hai
đường thẳng
AD
và
BC
bằng
45
. Khoảng cách giữa hai đường thẳng
AC
và
BD
bằng
Ⓐ.
6
.
2
a
Ⓑ.
6
.
3
a
Ⓒ.
6
.
4
a
Ⓓ.
6
.
6
a
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 3
Câu 14: (VDC) Cho hình chóp
.S ABC
có đáy là tam giác vuông tại
A
,
2,AB a AC a
. Các tam giác
,SAB SAC
lần lượt vuông tại
B
và
C
. Biết khoảng cách giữa hai đường thẳng
SA
và
BC
bằng
2
3
a
, cosin của góc giữa
SAB
và
SBC
bằng
Ⓐ.
1
6
. Ⓑ.
3
2
. Ⓒ.
30
6
. Ⓓ.
11
12
.
Câu 15: Cho hình chóp
có đáy là tam giác cân tại
A
,
120BAC 
,
2BC a
và
39
3
a
SA SB SC
. Gọi
G
là trọng tâm của tam giác
SAB
. Thể tích của khối chóp
.G ABC
bằng
Ⓐ.
3
2
9
a
. Ⓑ.
3
a
. Ⓒ.
3
3
a
. Ⓓ.
3
9
a
.
Câu 16: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
2a
,
90SAB SCB
. Gọi
M
là trung
điểm của
SA
. Biết khoảng cách từ
A
đến
MBC
bằng
6
21
a
. Thể tích của khối chóp đã cho
bằng
Ⓐ.
3
8 39
3
a
. Ⓑ.
3
10 3
9
a
. Ⓒ.
3
4 13
3
a
. Ⓓ.
3
23a
.
Câu 17: Cho tứ diện
ABCD
có
90ABC ADC
và
1BC
,
3CD
,
2BD
,
3AB
. Khoảng
cách từ
B
đến
ACD
bằng
Ⓐ.
6
7
. Ⓑ.
42
7
. Ⓒ.
7
7
. Ⓓ.
14
7
.
Câu 18: Cho hình chóp
có
2, 3, 4AB AC BC
,
SA
vuông góc với mặt đáy và
1SA
. Gọi
,HK
lần lượt là hình chiếu của
A
lên
SB
và
SC
. Gọi
là góc giữa hai mặt phẳng
AHK
và
ABC
, giá trị
tan
bằng
Ⓐ.
16 15
15
. Ⓑ.
15
. Ⓒ.
4
. Ⓓ.
6 15
5
.
Câu 19: Cho hình chóp
có
, 3, 150AC a AB a BAC
và
SA
vuông góc với mặt đáy. Gọi
,MN
lần lượt là hình chiếu vuông góc của
A
trên
SB
và
SC
. Thể tích của khối cầu ngoại
tiếp hình chóp
.ABCNM
bằng
Ⓐ.
3
47
3
a
. Ⓑ.
3
44 11
3
a
. Ⓒ.
3
28 7
3
a
. Ⓓ.
3
20 5
3
a
.
Câu 20: Cho hình chóp
có
3SA AB
;
6SB
;
22AC BC
;
5SC
. Khoảng cách
từ
A
đến
SBC
bằng
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 4
Ⓐ.
30
5
. Ⓑ.
5
2
. Ⓒ.
13
6
. Ⓓ.
30
3
.
Câu 21: Cho hình chóp
.S ABC
có đáy là tam giác vuông tại
A
,
2AB a
,
AC a
. Các tam giác
SBA
và
SCA
lần lượt vuông tại
B
và
C
. Biết khoảng cách từ
B
đến mặt phẳng
SAC
bằng
2a
, cosin của góc tạo bởi đường thẳng
SC
và
SAB
bằng
Ⓐ.
1
10
. Ⓑ.
1
3
. Ⓒ.
22
3
. Ⓓ.
3
10
.
Câu 22: Trong không gian
Oxyz
, cho mặt cầu
22
2
: 3 6 45S x y z
và
1;4;5M
. Ba
đường thẳng thay đổi
1 2 3
,,d d d
nhưng đôi một vuông góc tại
O
cắt mặt cầu tại điểm thứ hai
lần lượt là
. Khi khoảng cách từ
M
đến mặt phẳng
ABC
lớn nhất thì phương trình
mặt phẳng
là
Ⓐ.
2 8 0x y z
. Ⓑ.
2 4 0x y z
. Ⓒ.
2 1 0x y z
. Ⓓ.
30x y z
Câu 23: Cho hình chóp đều
có
SA a
. Gọi
,DE
lần lượt là trung điểm của hai cạnh
,SA SC
.
Biết
BD
vuông góc với
AE
, chiều cao của hình chóp
.S ABC
bằng
Ⓐ.
21
3
a
. Ⓑ.
3
6
a
. Ⓒ.
7
3
a
. Ⓓ.
3
a
.
Câu 24: Cho tứ diện
ABCD
có tam giác
ABD
đều cạnh bằng
2
, tam giác
ABC
vuông tại
B
,
3BC
. Khoảng cách giữa hai đường thẳng
AB
và
CD
bằng
3
2
. Thể tích của khối tứ
diện
ABCD
bằng
Ⓐ.
3
2
. Ⓑ.
1
2
. Ⓒ.
3
6
. Ⓓ.
1
6
.
Câu 25: Cho tứ diện
ABCD
có
2AB BC CD
,
1AC BD
,
3AD
. Bán kính mặt cầu ngoại
tiếp tứ diện
ABCD
bằng
Ⓐ.
1
. Ⓑ.
7
3
. Ⓒ.
39
6
. Ⓓ.
23
3
.
Câu 26: Cho hình chóp
có
60 ,ASB 
90 ,BSC 
120CSA 
,
,SA a
2,SB a
3.SC a
Sin của góc giữa hai mặt phẳng
SBC
và
SAB
bằng
Ⓐ.
6
6
. Ⓑ.
6
3
. Ⓒ.
6
4
. Ⓓ.
6
5
.
Câu 27: Cho hình chóp
có
60ASB BSC CSA
và
2, 3, 4.SA SB SC
Thể tích của
khối chóp
bằng
Ⓐ.
43
. Ⓑ.
23
. Ⓒ.
22
. Ⓓ.
42
.
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 5
Câu 28: Cho hình chóp
có
4, 6, 12SA SB SC
và
60 , 90ASB BSC
và
120CSA 
.
Thể tích của khối chóp
.S ABC
bằng
Ⓐ.
36 3
. Ⓑ.
36 2
. Ⓒ.
24 3
. Ⓓ.
24 2
.
Câu 29: Cho tứ diện
ABCD
, có tam giác
BCD
đều, hai tam giác
ABD
và
ACD
vuông cân đáy
AD
.
Điểm
G
là trọng tâm tam giác
ABC
. Gọi
,MN
lần lượt là trung điểm
BC
và
AD
. Gọi
là
góc giữa hai mặt phẳng
CDG
và
MNB
, giá trị
cos
bằng
Ⓐ.
1
11
. Ⓑ.
0
. Ⓒ.
1
11
. Ⓓ.
1
11
.
Câu 30: Ba quả bóng dạng hình cầu có bán kính bằng
1
đôi một tiếp xúc nhau và cùng tiếp xúc với mặt
phẳng
P
. Mặt cầu
S
bán kính bằng
2
tiếp xúc với ba quả bóng trên. Gọi
M
là điểm bất
kỳ trên
S
. Khoảng cách lớn nhất từ điểm M đến mặt phẳng
P
bằng
Ⓐ.
123
3
4
. Ⓑ.
52
9
. Ⓒ.
30
3
2
. Ⓓ.
69
3
3
.
Câu 31: Người ta thả vào bên trong một cái ống nước dạng hình trụ 4 quả bóng tenis có cùng bán kính
bằng
1
. Biết rằng các quả bóng tiếp xúc với nhau và tiếp xúc với các đường sinh của ống hình
trụ. Biết chiều cao của ống bằng
2
. Thể tích của ống nước đó bằng
Ⓐ.
3 2 2
. Ⓑ.
12
. Ⓒ.
6 4 2
. Ⓓ.
2 2 2
.
Câu 32: Cho tứ diện
ABCD
có
10AB CD
,
5AD BC
,
13AC BD
. Gọi
là góc giữa
AB
và
ACD
, giá trị
cos
bằng
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 6
Ⓐ.
6 10
35
. Ⓑ.
865
35
. Ⓒ.
10
10
. Ⓓ.
3 10
10
.
Câu 33: Cho tứ diện
ABCD
có các cạnh
3AD BC
;
4AC BD
;
23AB CD
. Thể tích tứ
diện
ABCD
bằng
Ⓐ.
2470
12
. Ⓑ.
2047
12
. Ⓒ.
2474
12
. Ⓓ.
2740
12
.
Câu 34: Cho hình chóp
.S ABC
có độ dài các cạnh
SA BC x
,
SB AC y
,
SC AB z
thỏa mãn
2 2 2
12 x y z
. Giá trị lớn nhất của thể tích khối chóp
.S ABC
bằng
Ⓐ.
22
3
. Ⓑ.
23
3
. Ⓒ.
2
3
. Ⓓ.
32
2
.
Câu 35: Cho tứ diện
ABCD
có
4; 5; 6AB CD AC BD AD BC
. Thể tích của khối tứ diện
ABCD
bằng
Ⓐ.
15 6
4
. Ⓑ.
15 6
2
. Ⓒ.
45 6
4
. Ⓓ.
45 6
2
.
Câu 36: Xét khối tứ diện
ABCD
có
AB x
và các cạnh còn lại bằng
2 3.
Giá trị của
x
để thể tích của
khối tứ diện
ABCD
lớn nhất là
Ⓐ.
6x
. Ⓑ.
22x
. Ⓒ.
14x
. Ⓓ.
32x
.
Câu 37: Cho tứ diện
có số đo các cạnh lần lượt là
2,AC AF FC a
3,AG a
GF GC a
. Thể tích của khối tứ diện
ACFG
bằng
Ⓐ.
3
6
a
. Ⓑ.
3
3
a
. Ⓒ.
3
12
a
. Ⓓ.
3
15
3
a
.
Câu 38: Cho hình chóp tam giác
.S ABC
có đáy là tam giác vuông cân tại
A
;
;3AB AC a SA a
.
Các tam giác
;SAB SAC
lần lượt vuông tại
;BC
. Gọi
;OM
lần lượt là trung điểm của
;BC SC
. Gọi
là góc giữa hai mặt phẳng
;OMA SAB
, giá trị
tan
bằng
Ⓐ.
1
3
. Ⓑ.
2
2
. Ⓒ.
3
6
. Ⓓ.
3
.
Câu 39: Cho tứ diện
ABCD
có
ABC
là tam giác đều cạnh
2a
,
3AD a
và
AD
vuông góc với
AB
và
AC
. Gọi
,EF
lần lượt là trung điểm của các đoạn thẳng
BC
và
.DE
Góc giữa
AF
với
CD
bằng
Ⓐ.
45
. Ⓑ.
60
. Ⓒ.
90
. Ⓓ.
30
.
Câu 40: Cho tứ diện
ABCD
có
1; 2; 90AB CD ABC DAB
. Góc giữa hai đường thẳng
;AD BC
bằng
30
. Bán kính của mặt cầu ngoại tiếp tứ diện
ABCD
bằng
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 7
Ⓐ.
5
2
. Ⓑ.
2
2
. Ⓒ.
5
. Ⓓ.
2
.
Câu 41: Cho lăng trụ tam giác đều
.ABC A B C
, gọi
I
là trung điểm
AB

và
là góc giữa
AC
với
BIC
. Biết
;2AA a AB a

, giá trị
cos
bằng
Ⓐ.
15
5
. Ⓑ.
10
5
. Ⓒ.
3
5
. Ⓓ.
2
5
.
Câu 42: Cho hình lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác vuông tại
B
,
BA BC a
,
cạnh bên bằng
a
. Khoảng cách giữa hai đường thẳng
AB
và
BC
bằng
Ⓐ.
3
3
a
. Ⓑ.
23
3
a
. Ⓒ.
6
2
a
. Ⓓ.
3
6
a
.
Câu 43: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
a
.
SA
vuông góc với mặt đáy. Góc giữa
SAB
và
SCD
bằng
45
. Gọi
M
là trung điểm của
SB
, khoảng cách giữa
AM
và
SD
bằng
Ⓐ.
2
2
a
. Ⓑ.
3
3
a
. Ⓒ.
2
a
. Ⓓ.
5
4
a
.
Câu 44: Cho tứ diện
ABCD
có
AB CD a
;
AD BC b
;
BD AC c
. Bán kính mặt cầu ngoại
tiếp tứ diện
ABCD
bằng
Ⓐ.
2 2 2
2
abc
. Ⓑ.
2 2 2
8
abc
. Ⓒ.
2 2 2
8
abc
. Ⓓ.
2 2 2
2
abc
.
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 8
BẢNG ĐÁP ÁN
1.D
2.C
3.B
4.D
5.D
6.A
7.A
8.A
9.A
10.A
11.C
12.D
13.D
14.A
15.D
16.B
17.B
18.A
19.C
20.A
21.D
22.A
23.C
24.A
25.C
26.B
27.C
28.D
29.C
30.D
31.C
32.B
33.A
34.A
35.A
36.D
37.A
38.B
39.C
40.A
41.A
42.A
43.B
44.B
PHẦN 2
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 9
LỜI GIẢI CHI TIẾT
Câu 1. Tứ diện
ABCD
có
3BC
,
4CD
,
90ABC BCD ADC
,
, 60AD BC 
. Cosin của
góc giữa hai mặt phẳng
và
ACD
bằng
Ⓐ.
43
86
. Ⓑ.
4 43
43
. Ⓒ.
43
43
. Ⓓ.
2 43
43
.
Lời giải
Chọn D
Cách 1:
Gọi
H
là chân đường cao của tứ diện
ABCD
.
Ta có:
BC AB
BC HB
BC AH

.(1)
Lại có:
CD AD
CD HD
CD AH

.(2)
Mà
90BCD 
.
Từ đây ta suy ra
HBCD
là hình chữ nhật.
Mặt khác:
, , 60AD BC AD HD ADH
. Suy ra:
tan60 3 3AH HD
.
Gọi
K
,
I
lần lượt là hình chiếu vuông góc của
B
lên
AC
và của
H
lên
AD
.
Suy ra:
33
, , sin60
2
d B ACD d H ACD HI HD
.
Tam giác
ABC
vuông tại
B
có:
2 2 2 2 2 2
1 1 1 1 1 52
387BK AB AC AH HB AC
3 559
26
BK
.
Gọi
,ABC ACD
ta có:
,
sin
d B ACD
HI
BK BK

2
2 43
cos 1
43
HI
BK



.
Cách 2:
PHẦN 3
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 10
Gọi
H
là chân đường cao của tứ diện
ABCD
.
Ta có:
BC AB
BC HB
BC AH

.(1)
Lại có:
CD AD
CD HD
CD AH

.(2)
Mà
90BCD 
.
Từ đây ta suy ra
HBCD
là hình chữ nhật.
Mặt khác:
, , 60AD BC AD HD ADH
. Suy ra:
tan60 3 3AH HD
.
Chọn hệ trục
.Oxyz H DBA
như hình vẽ.
Ta có:
0;0;0H
,
0;0;3 3A
,
0;4;0B
,
3;4;0C
,
3;0;0D
.
3; 3; 3 3AD
,
3;4; 3 3AC 
,
0;4; 3 3AB 
.
Gọi
1
n
,
2
n
lần lượt là một véc tơ pháp tuyến của
ABC
và
ABD
.
Suy ra:
1
, 0; 9 3; 12n AB AC


;
2
, 21 3;0;21n AD AC



.
Vậy
12
12
.
cos ,
.
nn
ABC ADC
nn
22
22
22
0.21 3 9 3.0 12.21
2 43
43
0 9 3 12 . 21 3 0 21


.
Câu 2. Cho hình chóp
có
AB a
,
3AC a
,
2SB a
và
90ABC BAS BCS
. Biết
sin của góc giữa đường thẳng
SB
và mặt phẳng
SAC
bằng
11
11
. Thể tích của khối
chóp
bằng
Ⓐ.
3
23
9
a
. Ⓑ.
3
3
9
a
. Ⓒ.
3
6
6
a
. Ⓓ.
3
6
3
a
.
Lời giải
Chọn C
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 11
- Dựng
SD ABC
tại
D
. Ta có:
BA SA
BA SD
BA AD
.
Và:
BC SD
BC CD
BC SC

ABCD
là hình chữ nhật
2DA BC a
,
DC AB a
.
- Sử dụng công thức
,
sin , SAC
d B SAC
SB
SB
.
11
11

;d B SAC
SB
;d D SAC
SB
2
2
1 11
;
SB
d D SAC

1
.
- Lại có :
2 2 2
2
1 1 1 1
;
DS DA DC
d D SAC
2 2 2 2
1 1 1
SB BD DA DC
2 2 2
13
32SB a a

2
.
- Từ
1
và
2
suy ra:
2
11
SB
2 2 2
13
32SB a a

22
22
6
11
3
SB a
SB a
6
11
3
SB a
SB a
Theo giả thiết
2SB a
63SB a SD a
.
Vậy
3
1 1 6
..
3 2 6
SABC
a
V SD BA BC
.
Câu 3. Cho hình chóp
có đáy là tam giác vuông cân tại
B
,
AB a
,
SA AB
,
SC BC
,
2SB a
. Gọi
M
,
N
lần lượt là trung điểm
SA
,
BC
và
là góc giữa
MN
với
ABC
. Giá trị
cos
bằng
Ⓐ.
2 11
11
. Ⓑ.
6
3
. Ⓒ.
26
5
. Ⓓ.
10
5
.
Lời giải
Chọn B
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 12
Dựng
SD ABC
, ta có:
BC SC
BC SD
BC CD
và
AB SA
AB SD
AB AD
.
Mà
ABC
là tam giác vuông cân tại
B
nên
ABCD
là hình vuông.
Gọi
H
là trung điểm của
AD
, ta có
//MH SD
MH ABCD
.
Do đó
HN
là hình chiếu của
MN
lên
ABC
.
,MN ABC

,MN NH
MNH
.
Ta có:
22
SC SB BC
22
4aa
3a
.
Lại có:
22
SD SC DC
22
3aa
2a
.
tan
MH
NH
1
.
2
SD
AB
2
2
a
a
2
2
2
1
cos
1 tan

1
1
1
2
6
3
.
Câu 4. Cho hình chóp
có đáy là tam giác vuông cân tại
B
,
3AB BC a
,
90SAB SCB
và khoảng cách từ điểm
A
đến
SBC
bằng
2a
. Diện tích của mặt
cầu ngoại tiếp hình chóp
.S ABC
bằng
Ⓐ.
2
2 a
. Ⓑ.
2
8 a
. Ⓒ.
2
16 a
. Ⓓ.
2
12 a
.
Lời giải
Chọn D
Gọi H là hình chiếu của S lên (ABC)
a
a
2
a
H
N
M
A
B
D
C
S
S
K
I
J
H
O
A
B
C
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 13
Ta có:
BC SC
HC BC
SH BC

Tương tự
AH AB
Và
ABC
vuông cân tại
B
nên
ABCH
là hình vuông. Gọi
O AC BH
,
O
là tâm
hình vuông. Dựng một đường thẳng
d
qua
O
vuông góc với
ABCH
, dựng mặt
phẳng trung trực của
SA
qua trung điểm
J
cắt
d
tại
II
là tâm mặt cầu ngoại
tiếp.
Ta hoàn toàn có
//IJ SA IJ AB I
là trung điểm
SB
, hay
I d SC
.
Bán kính mặt cầu ngoại tiếp:
22
.
3
;
22
S ABC
a
r AI IJ JA IJ

Do
// , ,AH SBC d A SBC d H SBC HK
(
K
là hình chiếu của
H
lên
SC
và
BC SHC HK SBC
)
2HK a
. Tam giác
SHC
vuông tại
H
6SH a
.
Tam giác
SHA
vuông tại
H
3SA a
.
22
.
3
3 4 12
22
S ABC mc
SA a
JA r AI a S r a

.
Câu 5. (Sở Bắc Ninh lần 2 2018-2019) Cho tứ diện
ABCD
có
90DAB CBDº
;
; 5; 135AB a AC a ABC
. Biết góc giữa hai mặt phẳng
,ABD BCD
bằng
30
.
Thể tích của tứ diện
ABCD
bằng
Ⓐ.
3
23
a
. Ⓑ.
3
2
a
. Ⓒ.
3
32
a
. Ⓓ.
3
6
a
.
Lời giải
Chọn D
Dựng
DH ABC
.
a
a
5
A
B
C
H
D
E
F
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 14
Ta có
BA DA
BA AH
BA DH

. Tương tự
BC DB
BC BH
BC DH

.
Tam giác
AHB
có
AB a
,
o
45ABH
HAB
vuông cân tại
A
AH AB a
.
Áp dụng định lý cosin, ta có
2BC a
.
Vậy
2
1 1 2
sin 2
2 2 2 2
ABC
a
S BA BC CBA a a
.
Dựng
HE DA
HF DB
HE DAB
và
HF DBC
.
Suy ra
,,DBA DBC HE HF EHF
và tam giác
HEF
vuông tại
E
.
Đặt
DH x
, khi đó
22
ax
HE
ax
,
22
2
2
xa
HF
ax
.
Suy ra
22
22
32
cos
4
22
HE x a
EHF x a
HF
xa
.
Vậy
3
1
36
ABCD ABC
a
V DH S
.
Câu 6. (Sở Bắc Ninh lần 2 2018-2019) Trong không gian
Oxyz
, cho điểm
4;0;0 , 0;4;0 , 0;0;A B S c
và đường thẳng
1 1 1
:
112
x y z
d

. Gọi
,AB

lần lượt
là hình chiếu vuông góc của
O
lên
,SA SB
. Khi góc giữa đường thẳng
d
và mặt phẳng
OA B

lớn nhất thì giá trị của số thực
c
thuộc khoảng nào dưới đây?
Ⓐ.
17 15
;
22




. Ⓑ.
9; 8
. Ⓒ.
0;3
. Ⓓ.
8; 6
.
Lời giải
Chọn A
Dựng hình vuông
OACB
, khi đó
4;4;0C
. Dễ chứng minh được
OA SC
SC OA B
OB SC
.
C(4;4;0)
S(0;0;c)
B'
A'
B(0;4;0)
A(4;0;0)
O
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 15
Khi đó
d
tạo với
OA B

góc lớn nhất khi và chỉ khi
1;1;2
d
d OA B u
cùng
phương
4;4;SC c
nên
.
Câu 7. Cho tứ diện
ABCD
có
90ABC BCD CDA
,
,BC CD a
2AD a
. Góc giữa hai
mặt phẳng
ABC
và
ACD
bằng
Ⓐ.
60
. Ⓑ.
30
. Ⓒ.
45
. Ⓓ.
90
.
Lời giải
Chọn A
Gọi
E
là hình chiếu của
A
lên mặt phẳng
BCD
Kết hợp đề bài
BC AB
BC BE
BC AE

;
CD AD
CD ED
CD AE

và
BC CD a
suy ra
tứ giác
BCDE
là hình vuông cạnh
a
.
Khi đó
22
AE AD ED a
Gọi
,HK
lần lượt là hình chiếu của
E
lên
,ABC ACD
thì
,EH ABC EK ACD
nên góc tạo bởi hai mặt phẳng
ABC
và
ACD
là góc
,EH EK
Nhận xét 2 tam giác
SEB
và
SED
là vuông cân tại
E
nên
2
2
a
EH EK
;
2
22
BD a
HK 
suy ra tam giác
EHK
đều.
Vậy số đo góc tạo bởi hai mặt phẳng
ABC
và
ACD
là
60
Câu 8. Cho hình chóp
.S ABC
có đáy là tam giác cân tại
A
,
AB a
, các tam giác
,SAB SAC
là
tam giác vuông tại
B
và
C
. Biết độ dài đường cao của hình chóp
.S ABC
gấp hai lần
độ dài đường cao của tam giác
ABC
hạ từ đỉnh
A
. Bán kính mặt cầu ngoại tiếp hình
chóp
có giá trị nhỏ nhất bằng
a
a
a
2
C
B
D
A
a
2
a
a
K
C
E
D
B
A
H
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 16
Ⓐ.
a
. Ⓑ.
3a
. Ⓒ.
2
a
. Ⓓ.
3
2
a
.
Lời giải
Chọn A
Gọi
H
là hình chiếu của
S
trên mặt phẳng
ABC
. Khi đó ta có
,SBH SCH
là hai tam
giác vuông tại
,BC
. Gọi
E
là trung điểm
BC
, suy ra
AE BC
.
Ta đặt
2 ,0AE h SH h h a
.
+
22
2
.
AB a
AB AE AH AH
AE h
+
4
2
2
42
a
SA h a
h
.
+ Các điểm
, , ,A B C S
cùng nhìn
SA
với một góc vuông, suy ra
SA
là đường kính của
mặt cầu ngoại tiếp hình chóp và trung điểm
I
của
SA
là tâm mặt cầu. Vậy
min
.
2
SA
R a R a
Câu 9. Trong không gian cho đoạn thẳng
AB
cố định và có độ dài bằng 4. Qua các điểm
A
và
B
lần lượt kẻ các tia
Ax
và
By
chéo nhau và hợp nhau góc
30
, đồng thời cùng
vuông góc với đoạn thẳng
AB
. Trên các tia
Ax
và
By
lần lượt lấy các điểm
,MN
sao
cho
5MN
. Đặt
AM a
và
BN b
. Biết thể tích khối tứ diện
ABMN
bằng
3
3
. Giá
trị biểu thức
2
22
S a b
bằng
Ⓐ.
144
. Ⓑ.
324
. Ⓒ.
100
. Ⓓ.
256
.
Lời giải
Chọn A
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 17
AB
là đoạn vuông góc chung của
,AM BN
nên
,4d AM BN AB
Ta có công thức:
1
. . , .sin ,
6
ABMN
V AM BN d AM BN AM BN
0
31
. . .4.sin30 3
36
a b ab
.
Dựng hình chữ nhật
ABNC
. Khi đó:
0
, , 30AM AC AM BN
và
AC BN b
.
Ta có:
AB AM AB AM
AB AMC
AB BN AB AC





.
Mà
||CN AB CN AMC CN CM
. Do đó
22
3CM MN CN
.
Ta có:
2 2 2 2 2
3 9 3
cos cos ,
2 . 2 2
23
AM AC CM a b
MAC AM AC
AM AC
.
22
12ab
. Vậy
144S
.
Câu 10. Cho hình chóp
.S ABC
có đáy là tam giác vuông cân tại
B
,
,AB a
90SAB SCB
,
góc giữa
AB
và g
SBC
bằng
60
. Thể tích của khối chóp đã cho bằng
Ⓐ.
3
3
.
6
a
Ⓑ.
3
43
.
9
a
Ⓒ.
3
3
.
9
a
Ⓓ.
3
3
.
3
a
Lời giải
Chọn A
Dựng hình vuông
ABCD
tâm
O
.
4
a
5
b
N
A
B
C
M
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 18
Do
0
90SAB SCB
nên hình chóp
.S ABC
nội tiếp mặt cầu tâm
I
đường kính
SB
.
Do
O
là tâm đường tròn ngoại tiếp tam giác
ABC
nên
OI
là trục của đường tròn ngoại
tiếp tam giác
ABC
. Suy ra
OI ABC SD ABC
.
, , , 60AB SBC DC SBC CD CS DCS
.
Ta có:
0
.tan60 3SD CD a
.
Từ đây ta suy ra:
23
1 1 3
. . . 3.
3 3 2 6
ABC
aa
V SD S a
.
Câu 11. Cho hình chóp
.S ABC
có đáy là tam giác cân tại
A
,
AB a
,
,120BAC
90SBA SCA
. Gọi
là góc giữa
SB
và
SAC
thỏa mãn
3
sin
8
, khoảng cách
từ
S
đến mặt đáy nhỏ hơn
2a
. Thể tích của khối chóp
.S ABC
bằng
Ⓐ.
3
3
4
a
. Ⓑ.
3
3
6
a
. Ⓒ.
3
3
12
a
. Ⓓ.
3
3
24
a
.
Lời giải
Chọn C
+ Gọi
D
là hình chiếu vuông góc của
S
lên đáy
ABC
, đặt
02SD x x a
.
Ta có
AC SC
AC SDC AC DC
AC SD
. Tương tự ta cũng có
AB DB
.
+ Tam giác
ABC
cân tại
A
và
120CAB 
3BC a
và
60DBC DCB DBC
đều cạnh
3a
.
+ Tam giác
SDC
vuông tại
D
22
3SB a x
+ Kẻ
DK SC
tại
K DK SAC
22
.3
;
3
xa
d D SAC DK
ax
.
+ Gọi
I BD AC
, xét
DIC
vuông tại
C
và
60BDC 
23
DC
DI a
cosBDC
B
là trung điểm của
DI
1
;;
2
d B SAC d D SAC
.
K
C
A
I
B
D
S
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 19
Theo giả thiết
;
;( sin
d B SAC
SB SAC
SB

22
33
8
23
xa
ax

22
3 4 0x a ax
2
4 3 0
xx
aa



3
xa
xa
. So sánh với điều kiện suy ra
xa
.
Vậy
3
.
13
..
3 12
S ABC ABC
a
V S SD

.
Câu 12. Cho hình chóp
có SA vuông góc với mặt đáy,
2SA BC
và
120BAC
. Hình
chiếu vuông góc của
A
lên các cạnh
SB
và
SC
lần lượt là
M
và
N
. Góc giữa hai mặt
phẳng
và
AMN
bằng
Ⓐ.
45
. Ⓑ.
60
. Ⓒ.
15
. Ⓓ.
30
.
Lời giải
Chọn A
Gọi
O
là tâm đường tròn ngoại tiếp tam giác
ABC
có đường kính là
AD
.
Khi đó tam giác
ABD
vuông tại
B
AB BD
.
Ta có
( ) BD AM
AB BD
BD SAB
SA BD
.
Ta có
()
BD AM
AM SBD AM SD
SB AM
.
Tương tự, ta chứng minh được
AN SD
.
Do đó
()SD AMN
suy ra
( );( ) ;ABC AMN SA SD ASD
.
Xét tam giác
SAD
vuông tại A có
tan
AD
ASD
SA
.
Với
3
22
sin120 3
ABC
o
BC
AD R SA
.
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 20
Do đó
3
tan 30
3
o
ASD ASD
( );( ) 30
o
ABC AMN
.
Câu 13. (VDC) Cho tứ diện
ABCD
có
, 2, 90AB AD a CD a ABC DAB
. Góc giữa hai
đường thẳng
AD
và
BC
bằng
45
. Khoảng cách giữa hai đường thẳng
AC
và
BD
bằng
Ⓐ.
6
.
2
a
Ⓑ.
6
.
3
a
Ⓒ.
6
.
4
a
Ⓓ.
6
.
6
a
Lời giải
Chọn D
Gọi H là hình chiếu vuông góc của D lên mặt phẳng
ABC
Ta có
DH AB
AB AH
DA AB

Mà
0
, , 45BC AB AH BC AD BC AD AH DAH
(Vì
DAH
vuông tại H)
2
.
2
a
AH DH
+)
ABD
vuông tại A
22
2BD AB AD a
Suy ra
2DB DC a DBC
cân tại
D
.
Gọi M là trung điểm của BC, ta có
.
DM BC
BC HM
DH BC

AHMB
là hình chữ nhật
1
.
2
AH BM BC
+) Trong hình thang ABCH
AH BC
, gọi
.I AC BH
Theo định lí thalet ta có
11
.
23
IH AH
IH HB
IB BC
+)
AHB
vuông tại A, có
22
6
.
2
a
HB AH AB
Có
2
22
1
.
32
a
HI HB HB AH AI HB
hay
HB AC
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 21
+) Có
AC HB
AC DB
AC DH

Trong tam giác
DHB
dựng
, , .HE DB IF HE IF BD d AC BD IF
DHB
vuông tại H
22
.6
.
4
HB HD a
HE
HB HD
+) Trong
BHE
, có
2 2 6
.
3 3 6
IF BI a
IF HE IF HE
HE BH
Vậy
6
,.
6
a
d AC BD
Câu 14. (VDC) Cho hình chóp
có đáy là tam giác vuông tại
A
,
2,AB a AC a
. Các
tam giác
,SAB SAC
lần lượt vuông tại
B
và
C
. Biết khoảng cách giữa hai đường thẳng
SA
và
BC
bằng
2
3
a
, cosin của góc giữa
SAB
và
SBC
bằng
Ⓐ.
1
6
. Ⓑ.
3
2
. Ⓒ.
30
6
. Ⓓ.
11
12
.
Lời giải
Chọn A
Kẻ
SH ABC SH AB HB AB
(định lý ba đường vuông góc).
Tương tự ta có
AC HC
.
Mà
AB AC
nên tứ giác
là hình chữ nhật
2 , .HC a HB a
Từ
A
kẻ
/ / / /Ax BC BC SAx
12
, , , ,
23
a
d BC SA d BC SAx d I SAx d H SAx
( với
,HK Ax K HK BC I
).
4
,.
3
a
d H SAx HN
(với
N
là hình chiếu vuông góc của
H
trên
SK
).
Ta có
22
.4
2 2. .
5
HB HC a
HK HI
HB HC
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 22
Xét
SHK
vuông tại H có
2 2 2
1 1 1
2.SH a
HN SH HK
Dựng
22
. 2 5
5
HS HB a
HM SB M HM
HS HB
.
Dễ dàng chứng minh được
.CH SHB CM SB
nên
,SAB SBC CMH
.
Ta có
1
cos .
6
MH
CMH
CM

Câu 15. Cho hình chóp
.S ABC
có đáy là tam giác cân tại
A
,
120BAC 
,
2BC a
và
39
3
a
SA SB SC
. Gọi
G
là trọng tâm của tam giác
SAB
. Thể tích của khối chóp
.G ABC
bằng
Ⓐ.
3
2
9
a
. Ⓑ.
3
a
. Ⓒ.
3
3
a
. Ⓓ.
3
9
a
.
Lời giải
Chọn D
Gọi
H
là hình chiếu của
S
trên mặt đáy, vì
SA SB SC
nên
HA HB HC
hay
H
là tâm đường tròn ngoại tiếp tam giác
ABC
23
2sin 3
BC a
HA HB HC
A
.
Gọi
O
là trung điểm
BC
, tam giác
ABC
cân tại
A
nên
60
AO BC
BAO CAO
.
Suy ra
23
3
sin
BO a
AB AC
BAO
.
Diện tích tam giác
ABC
là
2
13
. .sin120
23
ABC
a
S AB AC
.
Đường cao của khối chóp là
22
22
39 12
3
99
aa
SH SA AH a
.
Thể tích khối chóp
là
23
.
13
. . 3
3 3 3
S ABC
aa
Va
.
Do
G
là trọng tâm tam giác
SAB
nên
1
3
GM SM
1
d G, d ,
3
ABC S ABC
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 23
3
..
1
39
G ABC S ABC
a
VV
.
Câu 16. Cho hình chóp
có đáy là tam giác đều cạnh
2a
,
90SAB SCB
. Gọi
M
là
trung điểm của
SA
. Biết khoảng cách từ
A
đến
MBC
bằng
6
21
a
. Thể tích của khối
chóp đã cho bằng
Ⓐ.
3
8 39
3
a
. Ⓑ.
3
10 3
9
a
. Ⓒ.
3
4 13
3
a
. Ⓓ.
3
23a
.
Lời giải
Chọn A
Trong mp
ABC
xác định điểm
D
sao cho tứ giác
ABCD
vuông tại
A
và
C
Khi đó ta có:
AB AD
AB SD
AB SA

;
CB CD
CB SD
CB SC

Vậy
SD ABCD
.
1
.
3
S ABC ABC
V SD S

Có tam giác
ABC
là tam giác đều cạnh
2a
2
3
ABC
Sa

Ta đi tìm
SD
Gọi
I
là trung điểm
AC
vì tam giác
ABC
đều nên
I BD AC BD
Gọi
N
là trung điểm
//BC AN BC AN CD
Gọi
G
là trọng tâm tam giác
ABC
dễ thấy
AGCD
là hình thoi
2
3
CD AG AN
1
Xét hình chóp
.S ANCD
có đáy
ANCD
là hình thang vuông tại C, N. Khoảng cách từ
A
đến mặt phẳng
MNC
bằng
6
21
a
vì
MNC MBC
.
M
G
B
I
D
A
C
S
N
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 24
Trong mp
ANCD
gọi
E CN AD
Trong mp
SAD
kẻ tia
//At SD
gọi
P EM At
Gọi K là hình chiếu của G trên mặt phẳng
CFH
Khi đó ta có
//AP SD AP CN
APN CN
AN CN


Trong mp
APN
kẻ
AH PN
ta có
6
,
21
a
AH d A MCN
Mà tam giác
ABC
là tam giác đều cạnh
2a
3AN a
Từ
2 2 2
1 1 1
AH AP AN

2 2 2 2
1 21 1 1
36 3 4AP a a a
2AP a
Dễ thấy
APM SFM
2SF AP a
2
Xét tam giác
EAN
có
//CD AN
nên
2
3
ED CD
EA AN

(theo
1
)
Xét tam giác
EAP
có
//FD PA
nên
FD ED
PA EA
24
33
FD a
FD
PA
3
Từ
2
và
3
ta có
10
3
a
SD SF FD
Vậy
3
2
.
1 1 10 10 3
. . . 3
3 3 3 9
S ABC ABC
aa
V SD S a
(đpt).
Câu 17. Cho tứ diện
ABCD
có
90ABC ADC
và
1BC
,
3CD
,
2BD
,
3AB
. Khoảng
cách từ
B
đến
ACD
bằng
Ⓐ.
6
7
. Ⓑ.
42
7
. Ⓒ.
7
7
. Ⓓ.
14
7
.
Lời giải
Chọn B
Cách 1:
S
F
P
M
E
D
A
C
N
H
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 25
Gọi
M
là trung điểm của
AC
.
Theo giả thiết
90ABC ADC
1
2
MB MD MA MC AC
M
thuộc trục
đường tròn ngoại tiếp
BCD
(1).
Lại có
1BC
,
3CD
,
2BD
2 2 2
BC DC BD
BCD
vuông tại
C
. Gọi
I
là
trung điểm của
BD
I
là tâm đường tròn ngoại tiếp
BCD
(2).
Từ (1) và (2)
MI BCD
.
Gọi
K
là trung điểm của
CD
//IK BC
IK CD
mà
CD MI
CD MIK
(3).
Kẻ
IH MK
tại
H
. Từ (3)
IH CD
IH MCD
.
Do vậy,
, 2 , 2d B ACD d I MCD IH
.
Ta có
11
22
IK BC
.
2 2 2 2
3 1 10AC AB BC
1 10
22
MC AC
.
1
1
2
IC BD
22
MI MC IC
10 6
1
42
.
2 2 2
1 1 1
IH MI IK

4 28
4
66
6
27
IH
.
Vậy
6 42
,2
7
7
d B ACD IH
.
Cách 2:
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 26
1BC
,
3CD
,
2BD
2 2 2
BC DC BD
BCD
vuông tại
C
.
Dựng hình chữ nhật
BCDE
//BC ED
mà
DC BC DC DE
, lại có
DC AD
DC ADE
DC AE
(1).
Chứng minh tương tự
BC ABE
BC AE
(2).
Từ (1) và (2) suy ra
AE BCDE
.
Kẻ
EH AD
tại
H
. Do
DC ADE
nên
DC EH
EH ACD
.
//BE CD
,,d B ACD d E ACD EH
.
22
AE AB BE
2
2
3 3 6
.
2 2 2
1 1 1
EH EA ED

17
1
66
6 42
7
7
EH
.
Vậy
42
,
7
d B ACD EH
.
Câu 18. Cho hình chóp
có
2, 3, 4AB AC BC
,
SA
vuông góc với mặt đáy và
1SA
.
Gọi
,HK
lần lượt là hình chiếu của
A
lên
SB
và
SC
. Gọi
là góc giữa hai mặt phẳng
AHK
và
ABC
, giá trị
tan
bằng
Ⓐ.
16 15
15
. Ⓑ.
15
. Ⓒ.
4
. Ⓓ.
6 15
5
.
Lời giải
Chọn A
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 27
Gọi
AM
là đường kính của đường tròn ngoại tiếp tam giác
ABC
. Khi đó
BM AB
CM AC
.
Lại có:
BM SA
CM SA
BM SAB
CM SAC
BM AH
CM AK
. Mà
AH SB
AK SC
AH SBM
AK SCM
AH SM
AK SM
SM AHK
.
Mặt khác
SA ABC
nên
,,ABC AHK SA SM SAM
2
tan 2
1
ABC
ABC
R
AM
R
SA
.
Lại có: theo công thức Hê- rông
3 15
4
ABC
S
. . 8 15
4 15
ABC
ABC
AB AC BC
R
S
16 15
tan
15

.
Câu 19. Cho hình chóp
có
, 3, 150AC a AB a BAC
và
SA
vuông góc với mặt đáy.
Gọi
,MN
lần lượt là hình chiếu vuông góc của
A
trên
SB
và
SC
. Thể tích của khối
cầu ngoại tiếp hình chóp
.ABCNM
bằng
Ⓐ.
3
47
3
a
. Ⓑ.
3
44 11
3
a
. Ⓒ.
3
28 7
3
a
. Ⓓ.
3
20 5
3
a
.
Lời giải
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 28
Chọn C
Dựng đường tròn tâm
O
là đường tròn ngoại tiếp tam giác
ABC
. Kẻ đường kính
AQ
Xét tam giác
ACB
:
2 2 2 2 2 2 2
2. . .cos 3 2. . 3.cos150 7 7
7
77
2sin 2.sin150
o
ABC
o
BC AB AC AB AC BAC a a a a BC a
BC a
R a AO a
A
Vì
AQ
là đường kính đường tròn tâm
O
, điểm
B
thuộc đường tròn này nên
QB AB
.
Ta có:
QB AB
QB SAB QB AM
QB SA
Ta có:
AM QB
AM SQB AM QM AMQ
AM SB
vuông tại
M
.
Chứng minh tương tự ta được:
ANQ
vuông tại
N
Ta có các tam giác:
, , ,ABQ AMQ ANQ ACQ
là các tam giác vuông lần lượt ở
, , ,B M N C
Do đó các điểm
, , , ,MA B C N
thuộc mặt cầu đường kính
AQ
Bán kính mặt cầu ngoại tiếp hình chóp
.BCMNA
bằng
7AO a
3
3
3
4 4 28 7
7
3 3 3
a
V R a

.
Câu 20. Cho hình chóp
có
3SA AB
;
6SB
;
22AC BC
;
5SC
. Khoảng
cách từ
A
đến
SBC
bằng
Ⓐ.
30
5
. Ⓑ.
5
2
. Ⓒ.
13
6
. Ⓓ.
30
3
.
Lời giải
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 29
Dựng điểm
D
sao cho
ABCD
là hình chữ nhật.
Áp dụng định lý Pitago ta có các tam giác
;;SAB ABC SBC
lần lượt vuông góc tại
,,A B C
.
Ta có
AB AD
BA SA
1AB SD
BC CD
BC SC
2BC SD
.Từ
1 ; 2
SD ABCD SD BC
. Vậy
SBC SDC
theo giao tuyến
SC
. Kẻ
DH
vuông góc với
SC
tại
H
thì
DH SBC
.
Có
AD SBC
22
. 2. 3 30
,,
5
5
DS DC
d A SBC d D SBC DH
DS DC
.
Câu 21. Cho hình chóp
có đáy là tam giác vuông tại
A
,
2AB a
,
AC a
. Các tam giác
SBA
và
SCA
lần lượt vuông tại
B
và
C
. Biết khoảng cách từ
B
đến mặt phẳng
SAC
bằng
2a
, cosin của góc tạo bởi đường thẳng
SC
và
SAB
bằng
Ⓐ.
1
10
. Ⓑ.
1
3
. Ⓒ.
22
3
. Ⓓ.
3
10
.
Lời giải
Chọn D
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 30
Gọi
,SC SAB
,
sin
d C SAB
SC

.
Gọi
H
là hình chiếu của
S
lên mặt phẳng
ABC
SH AB
,
SH AC
.
Theo giả thiết các tam giác
SBA
và
SCA
lần lượt là các tam giác vuông tại
B
và
C
SB AB
,
SC AC
.
Khi đó
SH AB
SB AB
1HB AB
.
SH AC
SC AC
2HC AC
.
Từ (1) và (2) suy ra
H
là đỉnh thứ tư của hình chữ nhật
BACH
.
Gọi
I
và
K
lần lượt là hình chiếu của
H
lên
SC
và
SB
.
Ta có
//HB SAC
,d B SAC
,2d H SAC HI a
.
Xét tam giác vuông
SHC
:
2 2 2
1 1 1
HI HS HC

2 2 2
1 1 1
HS HI HC
2 2 2
1 1 1
24HS a a

2SH a
.
2 2 2 2 2 2
4 4 8SC SH HC a a a
22SC a
.
Mặt khác
//HB SAC
,d C SAB
,d H SAB HK
.
Xét tam giác vuông
SHB
:
2 2 2
1 1 1
HK HS HB

2
5
a
HK
.
21
sin
5.2 2 10
HK a
SC
a
cosin
13
1
10
10
.
Câu 22. Trong không gian
Oxyz
, cho mặt cầu
22
2
: 3 6 45S x y z
và
1;4;5M
. Ba
đường thẳng thay đổi
1 2 3
,,d d d
nhưng đôi một vuông góc tại
O
cắt mặt cầu tại điểm
thứ hai lần lượt là
. Khi khoảng cách từ
M
đến mặt phẳng
ABC
lớn nhất thì
phương trình mặt phẳng
là
Ⓐ.
2 8 0x y z
. Ⓑ.
2 4 0x y z
. Ⓒ.
2 1 0x y z
. Ⓓ.
30x y z
Lời giải
Chọn A
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 31
Mặt cầu
S
có tâm
0;3;6 , 3 5IR
Nhận xét:
1.
O
thuộc mặt cầu
S
2.
OABC
là một tứ diện vuông nội tiếp mặt cầu
S
nên tồn tại một hình hộp chữ
nhật
.OADBCEFG
nội tiếp mặt cầu
S
.
3. Gọi
H
là trung điểm
AB
,
J OI CH
J
là trọng tâm tam giác
OCD
.
Ta có:
2
0;2;4
3
OJ OI J
.
Mặt phẳng
ABC
luôn qua
J
cố định.
Đánh giá:
,,
Max
d M ABC MJ d M ABC MJ
ABC
qua
J
và nhận
JM
làm vectơ pháp tuyến.
Phương trình có dạng:
2 8 0x y z
.
Câu 23. Cho hình chóp đều
.S ABC
có
SA a
. Gọi
,DE
lần lượt là trung điểm của hai cạnh
,SA SC
. Biết
BD
vuông góc với
AE
, chiều cao của hình chóp
.S ABC
bằng
Ⓐ.
21
3
a
. Ⓑ.
3
6
a
. Ⓒ.
7
3
a
. Ⓓ.
3
a
.
Lời giải
Chọn C
Dựng hình thoi
ABIC
, gọi
K
là trung điểm
BI
.
Khi đó
DE
song song và bằng
BK
nên tứ giác
BDEK
là hình bình hành.
//BD KE AE KE
(Do
AE BD
).
Đặt
AC x
, ta có
2 2 2 2 2
2AK AE EK BD AK
2 2 2 2
76
2
2 4 4 3
x a a x a
x



. Do vậy
2
2
67
.
3
33
aa
ha




Bình luận: Bài toán trên có thể giải bằng nhiều cách dựng thêm hình khác nhau để
khai thác tính chất đường thẳng
AE
vuông góc với đường thẳng
BD
, hoặc có thể
khai thác giả thiết này theo cách sử dụng phương pháp véc tơ, tọa độ hóa.
E
D
K
C
A
B
I
S
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 32
Câu 24. Cho tứ diện
ABCD
có tam giác
ABD
đều cạnh bằng
2
, tam giác
ABC
vuông tại
B
,
3BC
. Khoảng cách giữa hai đường thẳng
AB
và
CD
bằng
3
2
. Thể tích của khối
tứ diện
ABCD
bằng
Ⓐ.
3
2
. Ⓑ.
1
2
. Ⓒ.
3
6
. Ⓓ.
1
6
.
Lời giải
Chọn A
Dựng hình chữ nhật
ABCE
.
Gọi
,MN
lần lượt là trung điểm của
,AB CE
.
Xét
ABD
đều có
DM
là đường trung tuyến nên
3
, . 3.
2
DM AB DM AB
Từ
M
kẻ
MH DN
. Khi đó ta có
//
CE MN
CE DMN CE MH
CE DM CE AB
.
Do đó
3
,,
2
d AB CD d M CDE MH
.
Suy ra
22
22
2 2 2 2
33
3 3 3
22
DN DH HN DM MH MN MH
.
Ta có
CE MH CE DN
2 2 2
3 1 10CD DN NC
Ta có
3
sin , sin , sin
10
DN
AB CD CE CD ECD
DC
Vậy
1 1 3 3 3
. . . , .sin , .2 10. . .
6 6 2 2
10
ABCD
V ABCD d AB CD AB CD
Câu 25. Cho tứ diện
ABCD
có
2AB BC CD
,
1AC BD
,
3AD
. Bán kính mặt cầu
ngoại tiếp tứ diện
ABCD
bằng
Ⓐ.
1
. Ⓑ.
7
3
. Ⓒ.
39
6
. Ⓓ.
23
3
.
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 33
Lời giải
Chọn C
Gọi
,MN
lần lượt là trung điểm của
,BC AD
Ta có
BAD CDA BN CN
. Suy ra
MN
là đường trung trực của
BC
.
Tương tự
MN
là đường trung trực của
AD
.
Khi đó tâm mặt cầu ngoại tiếp tứ diện là điểm
I
sao cho
IB IA
.
Tam giác
ABD
vuông tai
D
nên
2 2 2
37
1
44
BN BD DN
.
2 2 2
2
14 6 3
11
2 4 8 8 4
BN CN BC
MN
.
Ta có
2 2 2 2 2 2
3
12
4
MN R BM R AN R R
.
Từ
1 , 2
ta có
22
33
12
42
RR
.
Sử dụng máy tính được nghiệm là
39
6
R
. ( hoặc dùng phím CACL thử đáp án)
Câu 26. Cho hình chóp
có
60 ,ASB 
90 ,BSC 
120CSA 
,
,SA a
2,SB a
3.SC a
Sin của góc giữa hai mặt phẳng
SBC
và
SAB
bằng
Ⓐ.
6
6
. Ⓑ.
6
3
. Ⓒ.
6
4
. Ⓓ.
6
5
.
Lời giải
Chọn B
M
H
A
B'
C'
S
K
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 34
+ Trên cạnh
,SB SC
lần lượt lấy các điểm
', 'BC
sao cho
''SB SC a
''SA SB SC
. Gọi
H
là chân đường cao của hình chóp
. ' 'S AB C H
là tâm đường tròn ngoại tiếp
tam giác
''AB C
.
Từ giả thiết suy ra
',AB a
' ' 2, ' 3B C a AC a
2 2 2
' ' ' 'AB B C AC
''AB C
vuông tại
'BH
là trung điểm của cạnh
'AC
.
+ Kẻ
''HM B C
(
M
là trung điểm của
''BC
),
''HK SM HK SB C
, ' 'HK d H SB C
Ta có
22
2 2 2 2
3
4 4 2
a a a
SH SA AH a SH SHM
vuông cân tại
2
.
4
a
H HK
+ Tam giác
'SAB
là tam giác đều
3
,'
2
a
d A SB
.
+ Đặt
là góc giữa hai mặt phẳng
SBC
và
SAB
' ' , 'SB C SAB
.
Ta có
2
2.
, ' ' 2 , ' '
6
4
sin
, ' , ' 3
3
2
a
d A SB C d H SB C
d A SB d A SB
a
.
Câu 27. Cho hình chóp
.S ABC
có
60ASB BSC CSA
và
2, 3, 4.SA SB SC
Thể tích của
khối chóp
bằng
Ⓐ.
43
. Ⓑ.
23
. Ⓒ.
22
. Ⓓ.
42
.
Lời giải
Chọn C
Trên tia
,SA SB
lần lượt lấy các điểm
,MN
sao cho
4SM SN
.
Khi đó ta có các tam giác
,SCM SCN
và
SMN
đều
SMNC
là tứ diện đều cạnh
4SC
.
Gọi
H
là hình chiếu vuông góc của
S
trên mặt phẳng
CMN
thì
H
là tâm của tam
giác
CMN
.
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 35
Khi đó ta có
22
2 2 4 3 4 3 4 6
.
3 3 2 3 3
MH MK SH SM MH
.
1
. .sin 4 3
2
CMN
S CM CN MCN

1 16 2
.
33
SCMN CMN
V SH S
.
Mặt khác ta có
.
..
.
33
. . 2 2
88
S ABC
S ABC S MNC
S MNC
V
SA SB SC
VV
V SM SN SC
.
Câu 28. Cho hình chóp
có
4, 6, 12SA SB SC
và
60 , 90ASB BSC
và
120CSA 
. Thể tích của khối chóp
bằng
Ⓐ.
36 3
. Ⓑ.
36 2
. Ⓒ.
24 3
. Ⓓ.
24 2
.
Lời giải
Chọn D
Trên tia
,SA SB
lần lượt lấy cá điểm
,MN
sao cho
12SM SN
. Khi đó ta có :
Tam giác
SMN
đều
12MN
.
Tam giác
SNC
vuông tại
S
nên
2 12 2CN SC
.
Tam giác
SMC
cân tại
S
có
22
2 . .cos 12 3MC SC SM SC SM CSM
.
Từ đó suy ra
2 2 2
MC MN CN
tam giác
CMN
vuông tại
N
.
Gọi
H
là hình chiếu vuông góc của
S
trên mặt phẳng
CMN
.
Vì
12SC SM SN
nên
H
là tâm đường tròn ngoại tiếp tam giác
CMN
H
là
trung điểm của
MC
22
6SH SC CH
.
1
. 72 2
2
CMN
S MN NC
.
1
. . 144 2
3
S CMN CMN
V SH S
.
Mặt khác, ta có
.
.
1
..
6
S ABC
S MNC
V
SA SB SC
V SM SN SC

..
1
24 2
6
S ABC S MNC
VV
.
Câu 29. Cho tứ diện
ABCD
, có tam giác
BCD
đều, hai tam giác
ABD
và
ACD
vuông cân đáy
AD
. Điểm
G
là trọng tâm tam giác
ABC
. Gọi
,MN
lần lượt là trung điểm
BC
và
AD
. Gọi
là góc giữa hai mặt phẳng
CDG
và
MNB
, giá trị
cos
bằng
Ⓐ.
1
11
. Ⓑ.
0
. Ⓒ.
1
11
. Ⓓ.
1
11
.
Lời giải
Chọn C
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 36
Cách1. Ta khôi phục về chóp tứ giác đều tất cả các cạnh bằngnhau\
Gọi
K
là trung điểm
AB
. Thì
I DK BN
I
là trọng tâm tam giác
ABD
,,CDG MNB CDK CNB

.
Rõ ràng
BN ACD
và
ND CN
.
Tứ diện đã cho là nửa chóp tứ giác đều tất cả các cạnh bằng nhau. Chọn cạnh bằng 1
Nên chọn hệ trục toạ độ
0;0;0NO
.
Gọi cạnh
2 2 2AB AD
2CN BN ND NA
2;0;0 , 0; 2;0 , 0;0; 2D C B
2
0;0;
3
I




.
Mặt phẳng
CDK
cắt
,,Ox Oy Oz
lần lượt tại
,,D C I
nên có phương trình dạng:
1
2 2 2 / 3
x y z
, suy ra VTPT của
CDK
là
1;1;3
CDK
n
2;0;0 1;0;0ND BNC ND i
là VTPT của mặt phẳng
BNC
.
1
cos
11
.
CDK
CDK
in
in
Cách 2. Phương pháp khoảng cách để tính góc.
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 37
,
sin
,
d D CNB
d D CI

ND CNB
,ND d D CNB
.
2
,
CDI
S
d D CI
CI
. Từ đó ta cũng tính được
1
cos
11
Cách 3. Phương pháp đa giác chiếu để tính góc.
cos
INC
IDC
S
S
. Từ đó ta cũng tính được
1
cos
11
Cách 4. PP xác định góc để tính góc.
Kẻ
,NE CI E CI
, ta chứng minh được
DE IC
NED

, ta tính được
tan 10
ND
NE

1
cos
11

Câu 30. Ba quả bóng dạng hình cầu có bán kính bằng
1
đôi một tiếp xúc nhau và cùng tiếp xúc
với mặt phẳng
P
. Mặt cầu
S
bán kính bằng
2
tiếp xúc với ba quả bóng trên. Gọi
M
là điểm bất kỳ trên
S
. Khoảng cách lớn nhất từ điểm M đến mặt phẳng
P
bằng
Ⓐ.
123
3
4
. Ⓑ.
52
9
. Ⓒ.
30
3
2
. Ⓓ.
69
3
3
.
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 38
Lời giải
Chọn D
Gọi tâm quả ba quả cầu nhỏ là
A
,
B
,
C
và tâm của quả cầu lớn bên trên là
S
.
Khi đó
là chóp tam giác đều có cạnh đáy là
2
và cạnh bên là
3
.
Gọi
O
là chân dường cao của chóp
.S ABC
. Gọi
H
là hình chiếu của
M
lên mặt phẳng
P
Suy ra
MH
lớn nhất khi
M
,
S
,
O
,
H
thẳng hàng.
max
21MH MS SO OH SO
.
Ta có:
2
2 2 2
2 69
3 . 3
33
SO SA AO



.
Suy ra:
max
69
33
3
MH SO
.
Câu 31. Người ta thả vào bên trong một cái ống nước dạng hình trụ 4 quả bóng tenis có cùng
bán kính bằng
1
. Biết rằng các quả bóng tiếp xúc với nhau và tiếp xúc với các đường
sinh của ống hình trụ. Biết chiều cao của ống bằng
2
. Thể tích của ống nước đó bằng
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 39
Ⓐ.
3 2 2
. Ⓑ.
12
. Ⓒ.
6 4 2
. Ⓓ.
2 2 2
.
Lời giải
Chọn C
Gọi tâm của 4 quả bóng lần lượt là
, , ,A B C D
như hình vẽ.
Khi đó
ABCD
là hình vuông với cạnh bằng
2 2.1 2R 
22AC
.
Do đó bán kính đáy của hình trụ là:
1 2 2 1
12
22
MA AC CN
r


.
Vậy thể tích ống nước đó là:
2
2
. 1 2 .2 6 4 2V r h
.
Câu 32. Cho tứ diện
ABCD
có
10AB CD
,
5AD BC
,
13AC BD
. Gọi
là góc
giữa
AB
và
ACD
, giá trị
cos
bằng
Ⓐ.
6 10
35
. Ⓑ.
865
35
. Ⓒ.
10
10
. Ⓓ.
3 10
10
.
A
E
C
F
B
D
G
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 40
Lời giải
Chọn B
Dựng hình hộp
.AEDF GBHC
.
Do các cạnh đối của tứ diện
ABCD
bằng nhau nên các đường chéo của mỗi mặt của
hình hộp bằng nhau suy ra
.AEDF GBHC
là hình hộp chữ nhật.
Đặt
, , , , 0AE x AF y AG z x y z
.
Ta có hệ:
22
22
22
51
13 2
10 3
x y x
y z y
z x z


Ta thấy:
AB
//
HF
;;AB ACD HF ACD
Gọi
I HF CD
;
sin
F ACD
d
IF

.
Tứ diện
FACD
vuông tại
F
nên:
2
2 2 2
;
1 1 1 1 49
36
F ACD
FA FD FC
d


;
6
7
F ACD
d
.
22
1 1 10
2 2 2
FI FH FC FD
.
6 10 865
sin cos
35 35

.
Câu 33. Cho tứ diện
ABCD
có các cạnh
3AD BC
;
4AC BD
;
23AB CD
. Thể tích tứ
diện
ABCD
bằng
Ⓐ.
2470
12
. Ⓑ.
2047
12
. Ⓒ.
2474
12
. Ⓓ.
2740
12
.
Lời giải
Chọn A
I
F
D
A
H
G
C
B
E
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 41
Từ các đỉnh của tam giác
BCD
ta kẻ các đường thẳng song song với cạnh đối diện
chúng tạo thành tam giác
EFG
có diện tích gấp
4
lần diện tích tam giác
BCD
.
Các tam giác
AEF
,
AFG
,
AGE
là các tam giác vuông tại
A
nên ta có:
2 2 2
64 1AE AF EF
;
2 2 2
36 2AF AG FG
và
2 2 2
48 3AE AG EG
.
Từ
1
,
2
,
3
ta có:
2 2 2
2 148AE AF AG
2 2 2
74AE AF AG
4
.
Từ
1
,
4
ta có:
2
10AG
10AG
.
Từ
2
,
4
ta có:
2
38AE
38AE
.
Từ
3
,
4
ta có:
2
26AF
38AF
.
Thể tích khối chóp
.AEFG
là :
1 1 1
. . 9880 2470
6 6 3
V AE AF AG
.
Do đó thể tích tứ diện
ABCD
là :
1 2470
4 12
VV

.
Câu 34. Cho hình chóp
.S ABC
có độ dài các cạnh
SA BC x
,
SB AC y
,
SC AB z
thỏa
mãn
2 2 2
12 x y z
. Giá trị lớn nhất của thể tích khối chóp
.S ABC
bằng
Ⓐ.
22
3
. Ⓑ.
23
3
. Ⓒ.
2
3
. Ⓓ.
32
2
.
Lời giải
Chọn A
S
A
B
D
C
E
F
x
x
y
y
z
z
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 42
Trong mặt phẳng
dựng
D
,
E
,
F
sao cho
A
,
B
,
C
lần lượt là trung điểm của
DE
,
DF
,
EF
. Khi đó ta có
22DE SA x
;
22DF SB y
;
22SC z
. Suy ra
SD
,
SE
,
SF
đôi một vuông góc.
Ta có
..
1 1 1
. . . .
4 4 6

S ABC S DEF
V V SD SE SF
.
Mặt khác
2 2 2
2 2 2
2 2 2
4
4
4



SD SE x
SD SF y
SE SF z
2 2 2 2
2 2 2 2
2 2 2 2
2
2
2
SD x y z
SE x z y
SF y z x
2
2
2
26
26
26


SD z
SE y
SF x
.
Khi đó
2 2 2
.
1
.8. 6 6 6
24
S ABCD
V x y z
3
2 2 2
1 6 6 6
33



x y z
22
3
.
Vậy
.S ABC
V
đạt giá trị lớn nhất là
22
3
.
Câu 35. Cho tứ diện
ABCD
có
4; 5; 6AB CD AC BD AD BC
. Thể tích của khối tứ
diện
ABCD
bằng
Ⓐ.
15 6
4
. Ⓑ.
15 6
2
. Ⓒ.
45 6
4
. Ⓓ.
45 6
2
.
Lời giải
Chọn A
Dựng tứ diện
AMNK
, sao cho
,,B C D
là trung điểm của các cạnh
,,MN NK KM
. Tứ diện
AMNK
vuông tại
.A
2 2 2
2 2 2
2 2 2
36
64 54
100 10 10
144 90
3 10
AM
AM AN AM
AN AK AN AN
AK AM AK
AK



.
1 1 15 6
. . .3 6 10.3 10 15 6
6 6 4
AMNK ABCD
V AM AN AK V
.
Câu 36. Xét khối tứ diện
ABCD
có
AB x
và các cạnh còn lại bằng
2 3.
Giá trị của
x
để thể
tích của khối tứ diện
ABCD
lớn nhất là
B
C
D
A
M
N
K
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 43
Ⓐ.
6x
. Ⓑ.
22x
. Ⓒ.
14x
. Ⓓ.
32x
.
Lời giải
Chọn D
Gọi
H
là trung điểm của cạnh
AB
, do
ABC
cân tại
C
nên
CH
là đường cao. Tam
giác
ABD
có
23AD BD
nên là tam giác cân tại
D
. Do đó
HD
là đường cao. Khi
đó ta có
CH AB
AB CHD
HD AB

.
Hạ đường cao
CK
xuống
HD
khi đó
.CK AB
Do đó
.CK ABD
Vậy
CK
là đường
cao của tứ diện. Ta có
2
x
HB
. Áp dụng định lý Py-ta-go cho tam giác
HBC
ta có
2
2
2
22
48
23
22
xx
HC BC HB



Tương tự, ta có
2
48
.
2
x
HD
Đặt
y KD
. Áp dụng định lý Py-ta-go cho tam giác
CHK
và
CKD
ta có
2
2 2 2 2 2 2 2
12CK CH HK CD KD CH HD y y
.
2 2 2 2
2
6 12
2 . 12
48
CH HD HD y y y y
HD
x
.
Vì vậy
2
22
2 2 2
2 2 2
2
12 48 12
12 36 12 36
12
D 12
48 48 48
48
x
xx
CK C y CK
x x x
x




Diện tích tam giác
ABD
là
22
1
1 1 48 48
.
2 2 2 4
x x x
S AB HD x

Do đó thể tích tứ diện là
2
2
2
1
2
12 36
1 1 48 1
. . 3. . 36
3 3 48 4 6
x
xx
V CK S x x
x
Áp dụng bất đẳng thức Cô-si cho
2
, 36xx
,
ta có
22
2
36
33
. 36 3 3.
6 6 2
xx
V x x

Dấu bằng xảy ra khi và chỉ khi
2
36 18 3 2x x x
Nhận xét.Chúng ta có thể thay điều kiện các cạnh còn lại bằng
23
bởi điều kiện các
cạnh còn lại bởi một số
0a
nào đó bất kì, để được một bài toán khác nhưng cách làm
tương tự bài này.
Câu 37. Cho tứ diện
ACFG
có số đo các cạnh lần lượt là
2,AC AF FC a
3,AG a
GF GC a
. Thể tích của khối tứ diện
ACFG
bằng
Ⓐ.
3
6
a
. Ⓑ.
3
3
a
. Ⓒ.
3
12
a
. Ⓓ.
3
15
3
a
.
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 44
Lời giải
Chọn A
Dựng hình lập phương như hình vẽ
Khi đó
.ABCD EFGH
là hình lập phương cạnh
a
nên thể tích của hình lập phương là
3
Va
.
Thể tích tứ diện
có được là do ta chia hình lập phương theo các mặt phẳng
ACGE
,
ACF
và
AGF
. Khi đó ta có
3
..
1 1 1
.
3 2 3 6
ACGF ABC EFG ABCD EFGH
a
V V V
Câu 38. Cho hình chóp tam giác
.S ABC
có đáy là tam giác vuông cân tại
A
;
;3AB AC a SA a
.
Các tam giác
;SAB SAC
lần lượt vuông tại
;BC
. Gọi
;OM
lần lượt là trung điểm của
;BC SC
.
Gọi
là góc giữa hai mặt phẳng
;OMA SAB
, giá trị
tan
bằng
Ⓐ.
1
3
. Ⓑ.
2
2
. Ⓒ.
3
6
. Ⓓ.
3
.
Lời giải
Chọn B
Dựng hình vuông
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 45
Ta có:
AC SC
AC SCD AC SD
AC DC
AB DB
AB SBD AB SD
AB SB
SD ABCD
;;OMA SAB DMA SAB

/ / / /
//
DMA OM
SAB SB DM A SAB AE AE SB OM
OM SB
;
sin
;
d D SAB
d D AE

Ta có:
2SC SB a SD a
2DA DE AE a
ADE
đều
6
;
2
a
d D AE
Kẻ
2
;
2
a
DK SB DK SAB d D SAB DK
(
SAD
vuông cân tại
D
)
362
sin cos tan
3 3 2

.
Câu 39. Cho tứ diện
ABCD
có
ABC
là tam giác đều cạnh
2a
,
3AD a
và
AD
vuông góc
với
AB
và
AC
. Gọi
,EF
lần lượt là trung điểm của các đoạn thẳng
BC
và
.DE
Góc
giữa
AF
với
CD
bằng
Ⓐ.
45
. Ⓑ.
60
. Ⓒ.
90
. Ⓓ.
30
.
Lời giải
Chọn C
Dựng thêm từ tứ diện ABCD thành hình hộp.
Ta có
1 1 1
.
2 2 4
AF AD AE AD AB AC
Suy ra
1 1 1
. . . .
2 4 4
AF CD AD CD ABCD AC CD
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 46
1 1 1
2 4 4
AD AD AC AB AD AC AC AD AC
22
2 2 2
1 1 1 3 1
0.
2 4 4 2 2
AD ABAC AC a a a
Vậy số đo góc giữa
AF
và
CD
bằng
90
.
Câu 40. Cho tứ diện
ABCD
có
1; 2; 90AB CD ABC DAB
. Góc giữa hai đường thẳng
;AD BC
bằng
30
. Bán kính của mặt cầu ngoại tiếp tứ diện
ABCD
bằng
Ⓐ.
5
2
. Ⓑ.
2
2
. Ⓒ.
5
. Ⓓ.
2
.
Lời giải
Chọn A
Dựng
AE BC
và
BF AD
ta được lăng trụ đứng
.ADE BFE
Góc
, , 30AD BC AD AE
,
22
1ED CD CE
.
Bán kính mặt cầu ngoại tiếp lăng trụ đứng này là
2
2
4
d
h
RR
21
sin 2sin
dd
ED ED
RR
EAD EAD
suy ra
2
2
15
1
4 4 2
d
h
RR
.
Câu 41. Cho lăng trụ tam giác đều
.ABC A B C
, gọi
I
là trung điểm
AB

và
là góc giữa
AC
với
BIC
. Biết
;2AA a AB a

, giá trị
cos
bằng
Ⓐ.
15
5
. Ⓑ.
10
5
. Ⓒ.
3
5
. Ⓓ.
2
5
.
Lời giải
Chọn A
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 47
AC BIC C

,
là Góc giữa
'AC
và
'BIC
, Ta có
,'
sin
'
d A BIC
AC
.
Ta có
'BIC ABB A

( Vì
C I ABB A
,
'BIC ABB A IB


Gọi
K
là trung điểm
IB
suy ra
B K IB
. Suy ra
''B K BIC
Suy ra
', ' 'd B BIC B K
.
Mặt khác
I
là trung điểm
''AB
nên
', ' ', ' 'd A BIC d B BIC B K
.
Gọi
E
là giao điểm của
'AA
và
BI
suy ra
''E A A BIC
nên
', '
'
,'
d A BIC
EA
EA
d A BIC
.
Mặt khác
' ' 1
/ / '
2
EA A I
Do AB A I
EA AB

.
Suy ra
', '
' 1 2
, ' 2 ', ' 2 ' 2. 2
22
,'
d A BIC
EA a
d A BIC d A BIC B K a
EA
d A BIC
.
22
' ' ' ' 5AC A A A C a
.
,'
2 10
sin
'5
5
d A BIC
a
AC
a
suy ra
15
cosin
5
.
Câu 42. Cho hình lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác vuông tại
B
,
BA BC a
, cạnh bên bằng
a
. Khoảng cách giữa hai đường thẳng
AB
và
BC
bằng
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 48
Ⓐ.
3
3
a
. Ⓑ.
23
3
a
. Ⓒ.
6
2
a
. Ⓓ.
3
6
a
.
Lời giải
Chọn A
Dựng hình lập phương
.ABCD A B C D
. Khi đó
//B C A DB

.
Suy ra
, , , ,d A B B C d B C A BD d C A BD d A A BD
.
Ta thấy
.A A BD
là tứ diện vuông đỉnh
A
nên
2
2 2 2 2
1 1 1 1 3
'
,'
AA AB AD a
d A A BD


.
Vậy
3
,,
3
a
d A B B C d A A BD

.
Câu 43. Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
a
.
SA
vuông góc với mặt đáy. Góc
giữa
SAB
và
SCD
bằng
45
. Gọi
M
là trung điểm của
SB
, khoảng cách giữa
AM
và
SD
bằng
Ⓐ.
2
2
a
. Ⓑ.
3
3
a
. Ⓒ.
2
a
. Ⓓ.
5
4
a
.
D'
A'
B'
D
C'
C
B
A
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 49
Lời giải
Chọn B
Ta có góc giữa
SAB
và
SCD
bằng
45ASD
SA a
.
Dựng hình lập phương
. ' ' 'ABCD SB C D
như hình vẽ
Khi đó
3
; ' ; '
3
a
d AM SD d B AC SC D
.
Câu 44. Cho tứ diện
ABCD
có
AB CD a
;
AD BC b
;
BD AC c
. Bán kính mặt cầu
ngoại tiếp tứ diện
ABCD
bằng
Ⓐ.
2 2 2
2
abc
. Ⓑ.
2 2 2
8
abc
. Ⓒ.
2 2 2
8
abc
. Ⓓ.
2 2 2
2
abc
.
Lời giải
Chọn B
Phục dựng hình ẩn
Nguyễn Hoàng Việt
0905193688
Trang: 50
Dựng hình hộp chữ nhật
.AEBF HCKD
. Đặt
,,AH x AE y ÀF z
.
Ta có hệ
2 2 2
2 2 2
2 2 2 2 2 2 2
2 2 2
2
x y c
abc
x z b x y z AK
y z a
.
Do đó
2 2 2
28
AK a b c
R
.
c
c
b
b
a
a
K
H
F
E
D
C
B
A
| 1/52
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

NGUYỄN HOÀNG VIỆT
Giáo viên THTP Lương Thế Vinh Chuyên đề PHỤC DỰNG HÌNH ẨN NĂM HỌC 2021 - 2022
Phục dựng hình ẩn
DỰ ÁN PHỤC DỰNG HÌNH ẨN
Nhóm biên soạn: Nhóm toán VD - VDC (nay là NHÓM GIÁO VIÊN TOÁN VIỆT NAM)
Qua nhiều bài toán chúng ta gặp phải ở trong các đề thi THPT Quốc gia, thường có các bài
toán về xác định góc, khoảng cách giữa các yếu tố đường thẳng, mặt phẳng và bài toán tính thể
tích các khối chóp, khối lăng trụ,… Trong các bài toán này, dữ kiện đề bài thường cho sẵn một
đường thẳng cụ thể vuông góc với mặt đáy và việc tính toán thường xoay quanh vấn đề đường cao.
Tuy nhiên, trong nhiều bài toán, để tăng mức độ cho câu hỏi về hình học không gian, người
ra đề thường làm ẩn đi các yếu tố này làm cho việc tính toán các yếu tố góc, khoảng cách hay thể
tích khối trở nên khó khăn hơn.
Để giải quyết được bài toán HHKG đã bị ẩn các yếu tố này, ta có thể sử dụng phương pháp "Phục dựng hình ẩn”. MỤC LỤC
 PHẦN 01. ĐỀ BÀI ....................................................................................... Trang 1
 PHẦN 02. BẢNG ĐÁP ÁN ............................................................................ Trang 8
 PHẦN 03. ĐÁP ÁN CHI TIẾT ......................................................................... Trang 9
“Nơi nào có ý chí, nơi đó có con đường.”
Nguyễn Hoàng Việt 0905193688 Trang: 0
Phục dựng hình ẩn ĐỀ BÀI PHẦN 1
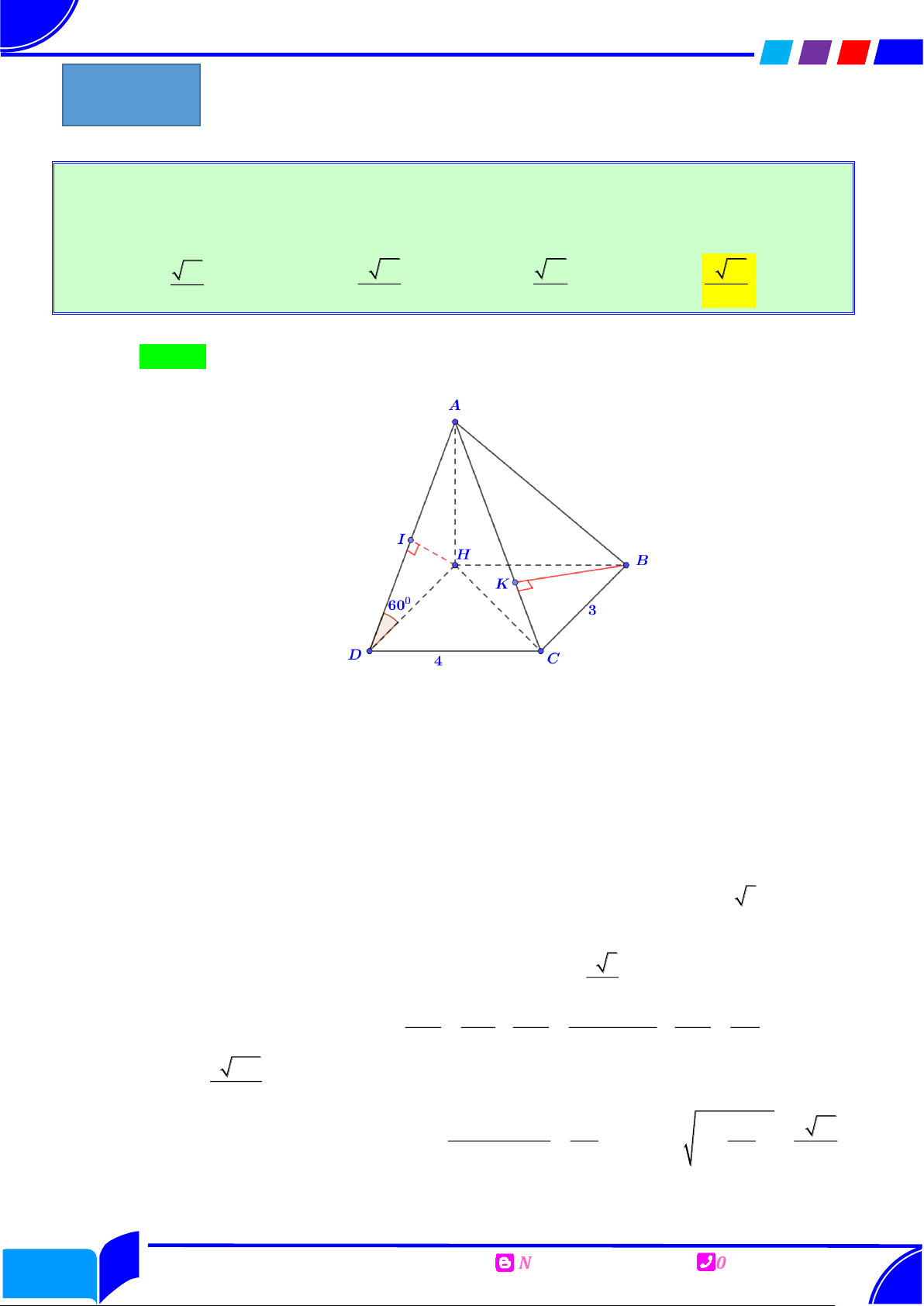
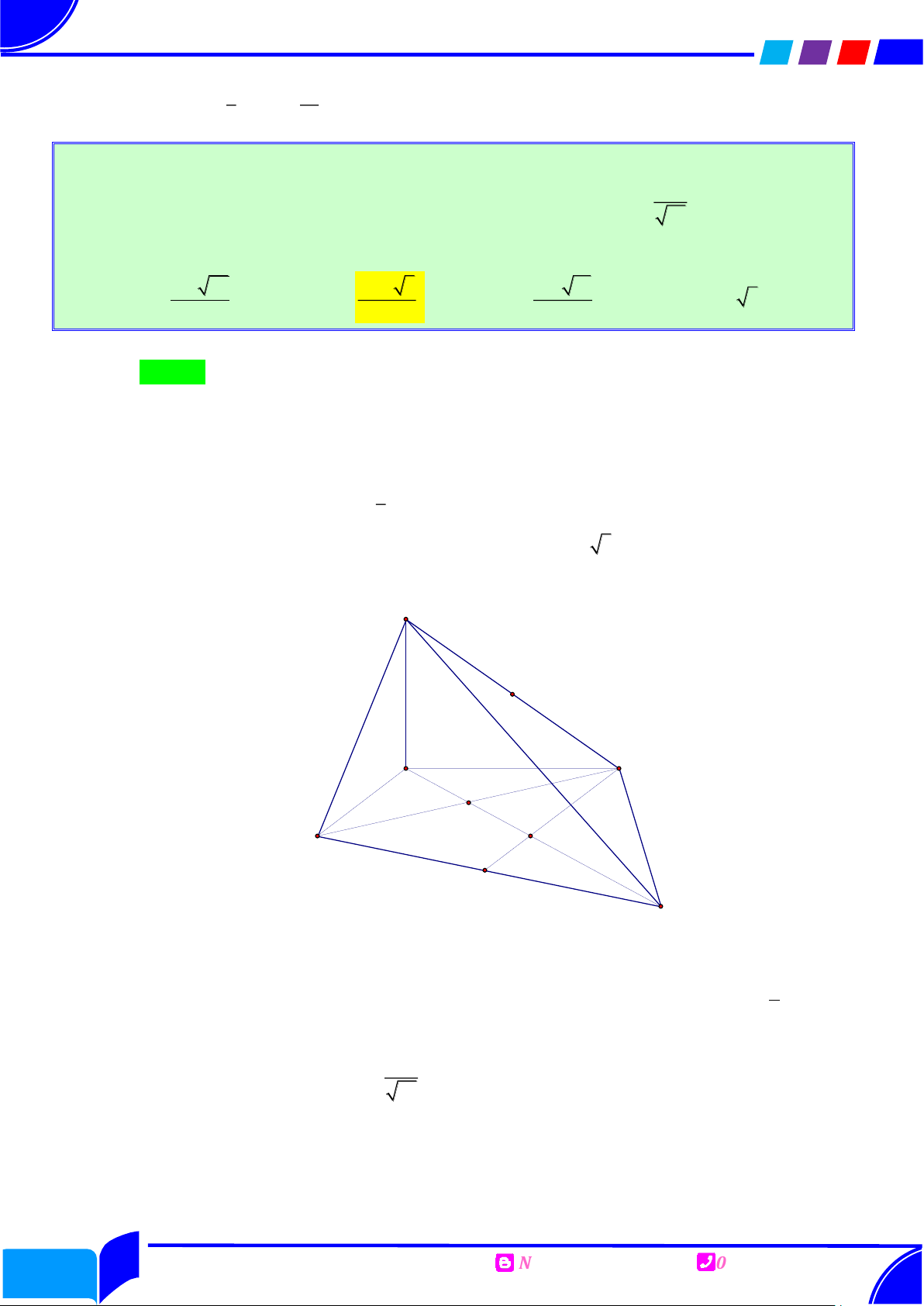
Câu 1: Tứ diện ABCD có BC  3, CD  4, ABC BCD ADC  90 , A ,
D BC   60. Cosin của
góc giữa hai mặt phẳng  ABC và  ACD bằng Ⓐ. 43 4 43 43 2 43 . Ⓑ. . Ⓒ. . Ⓓ. . 86 43 43 43
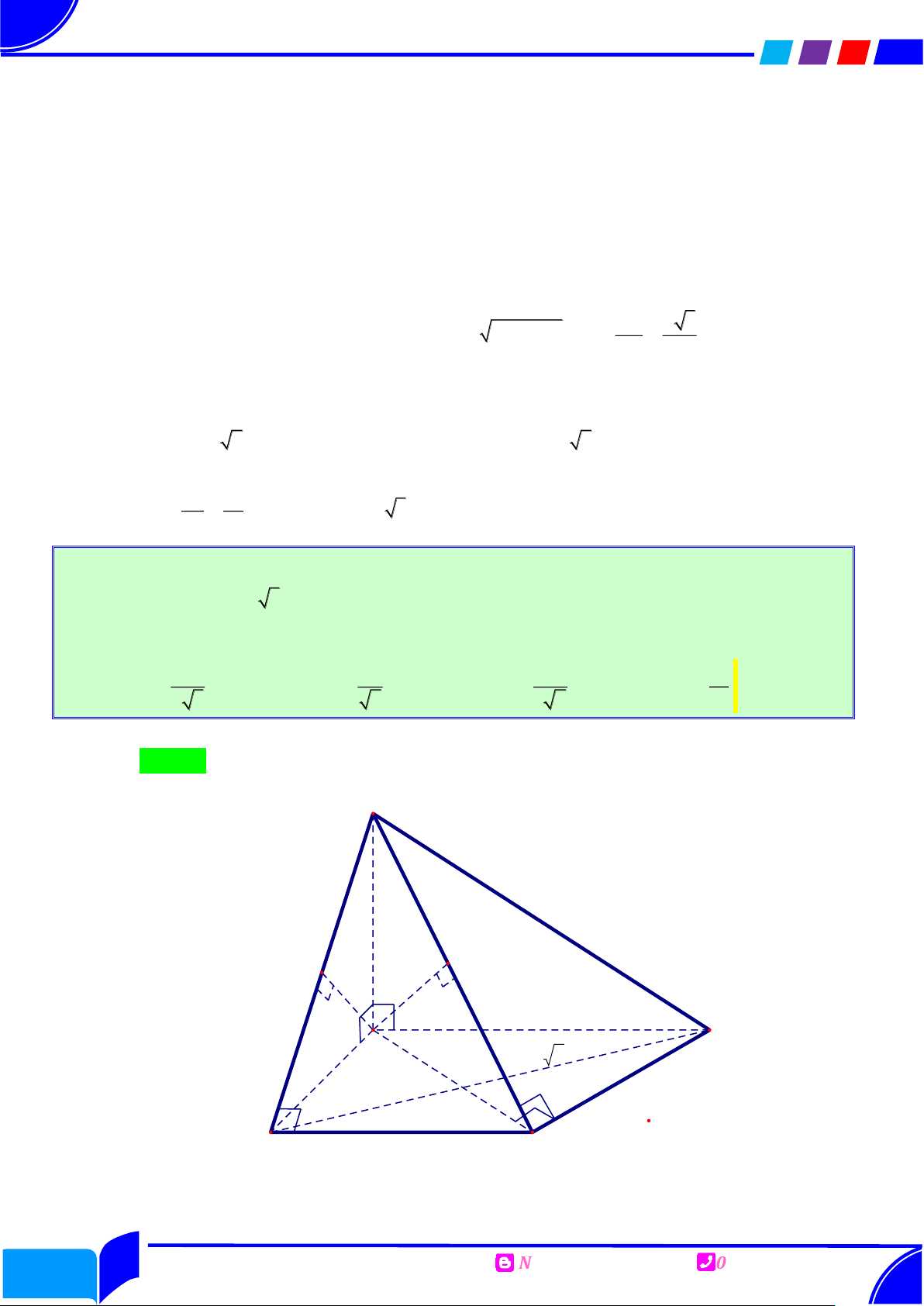
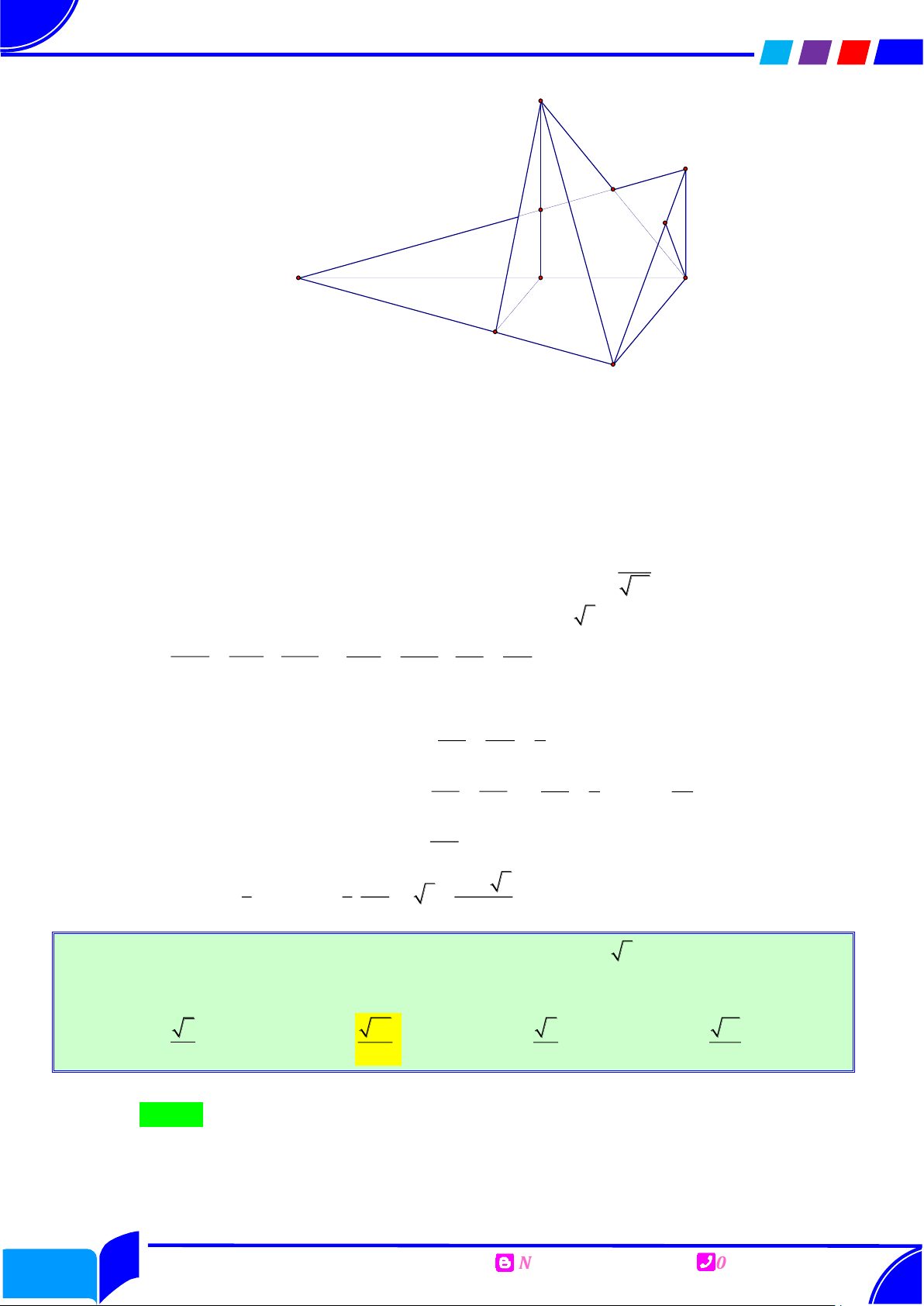
Câu 2: Cho hình chóp S.ABC có AB a , AC a 3 , SB  2a và ABC BAS BCS  90. Biết sin 11
của góc giữa đường thẳng SB và mặt phẳng SAC  bằng
. Thể tích của khối chóp 11 S.ABC bằng 3 3 3 3 Ⓐ. 2a 3 a 3 a 6 a 6 . Ⓑ. . Ⓒ. . Ⓓ. . 9 9 6 3 Câu 3: Cho hình chóp .
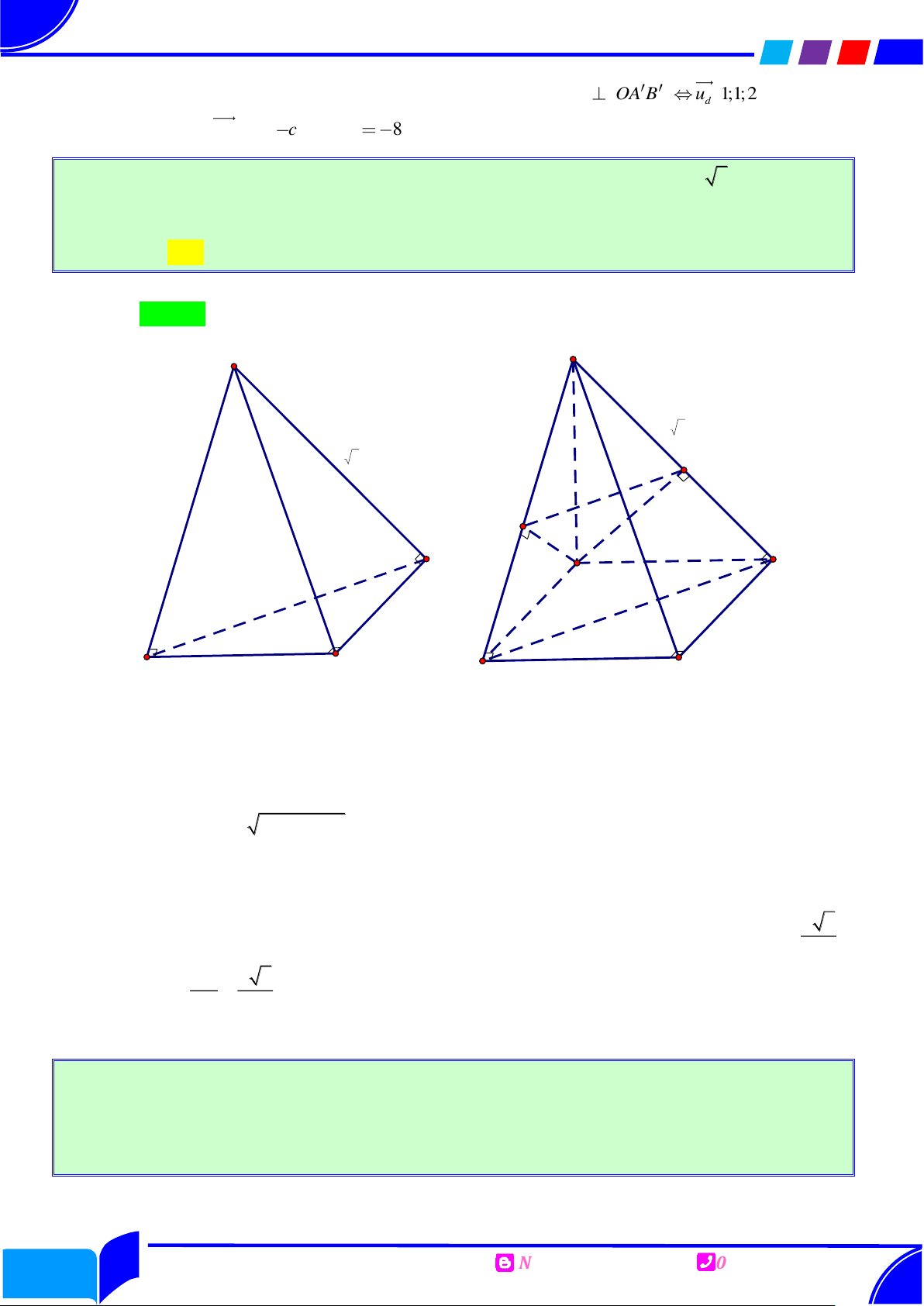
S ABC có đáy là tam giác vuông cân tại B , AB a , SA AB , SC BC ,
SB  2a . Gọi M , N lần lượt là trung điểm SA , BC và  là góc giữa MN với  ABC . Giá trị cos bằng Ⓐ. 2 11 6 2 6 10 . Ⓑ. . Ⓒ. . Ⓓ. . 11 3 5 5
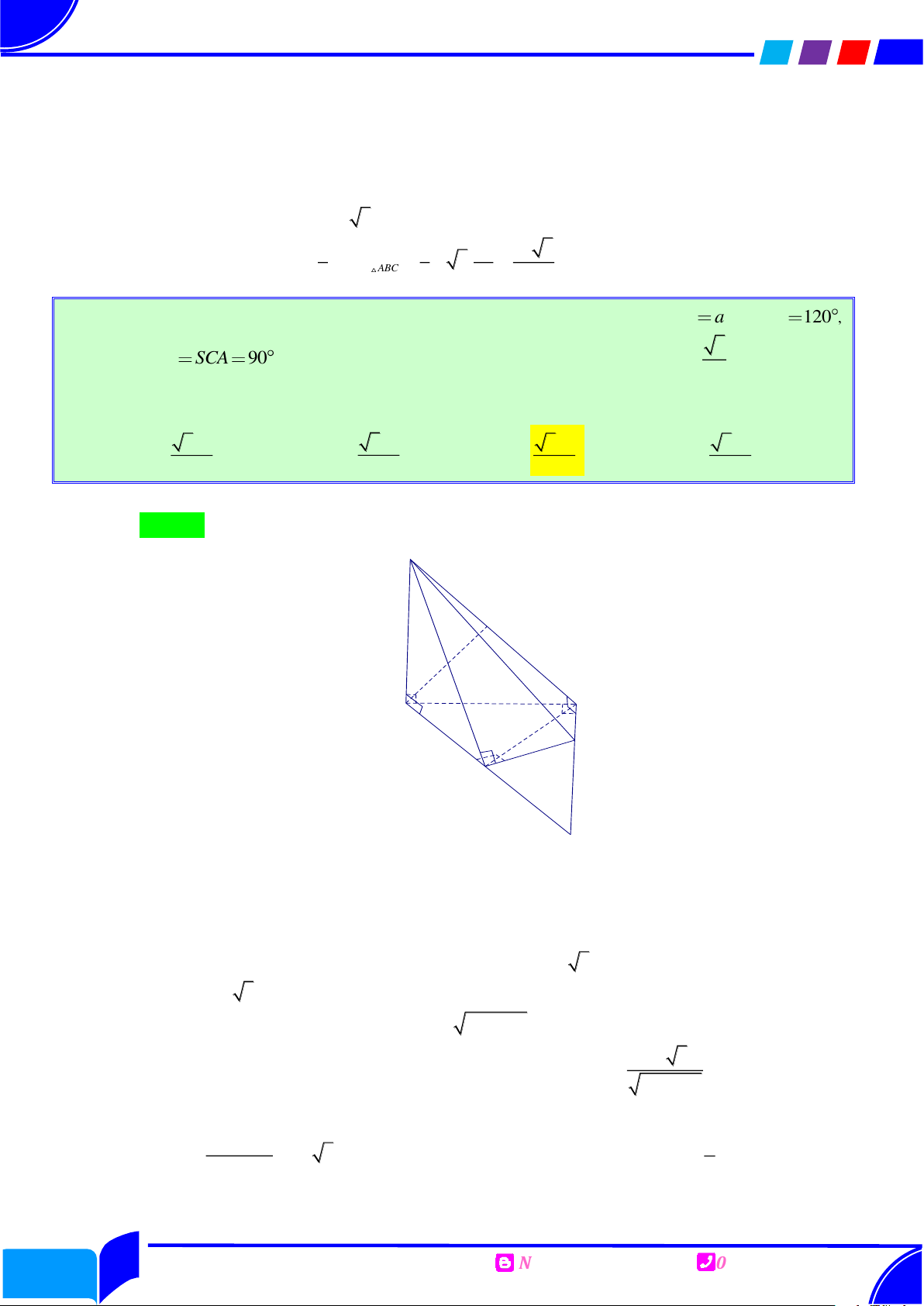
Câu 4: Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B , AB BC a 3 ,
SAB SCB  90 và khoảng cách từ điểm A đến SBC  bằng a 2 . Diện tích của mặt cầu
ngoại tiếp hình chóp S.ABC bằng Ⓐ. 2 2 a . Ⓑ. 2 8 a . Ⓒ. 2 16 a . Ⓓ. 2 12 a .
Câu 5: (Sở Bắc Ninh lần 2 2018-2019) Cho tứ diện ABCD có DAB CBD  90º ; AB  ;
a AC a 5; ABC  135 . Biết góc giữa hai mặt phẳng  ABD,BCD bằng 30 .
Thể tích của tứ diện ABCD bằng 3 3 3 3 Ⓐ. a a a a . Ⓑ. . Ⓒ. . Ⓓ. . 2 3 2 3 2 6
Câu 6: (Sở Bắc Ninh lần 2 2018-2019) Trong không gian Oxyz , cho điểm x 1 y 1 z 1
A4;0;0, B0;4;0, S 0;0;c và đường thẳng d :  
. Gọi A , B lần lượt 1 1 2
là hình chiếu vuông góc của O lên S ,
A SB . Khi góc giữa đường thẳng d và mặt phẳng OA B
  lớn nhất thì giá trị của số thực c thuộc khoảng nào dưới đây? Ⓐ.  17 15   ;    . Ⓑ.  9  ; 8   . Ⓒ. 0;3. Ⓓ.  8  ; 6   .  2 2 
Nguyễn Hoàng Việt 0905193688 Trang: 1
Phục dựng hình ẩn
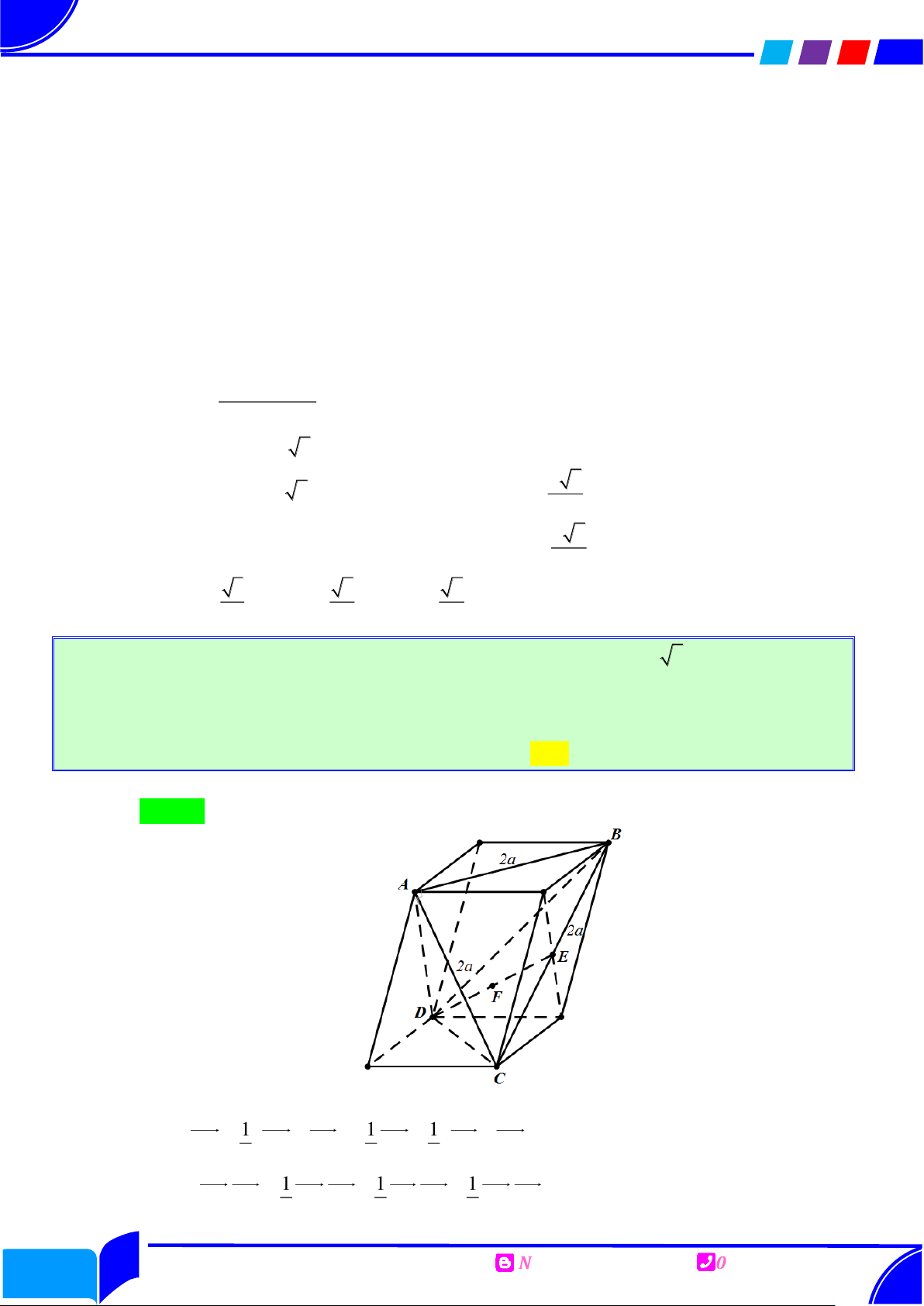
Câu 7: Cho tứ diện ABCD có ABC BCD CDA  90 , BC CD  ,
a AD a 2 . Góc giữa hai
mặt phẳng  ABC  và  ACD bằng Ⓐ. 60. Ⓑ. 30 . Ⓒ. 45. Ⓓ. 90 .
Câu 8: Cho hình chóp S.ABC có đáy là tam giác cân tại A , AB a , các tam giác SA , B SAC là tam
giác vuông tại B và C . Biết độ dài đường cao của hình chóp S.ABC gấp hai lần độ dài đường
cao của tam giác ABC hạ từ đỉnh A . Bán kính mặt cầu ngoại tiếp hình chóp S.ABC có giá trị nhỏ nhất bằng Ⓐ. a a 3 a . Ⓑ. a 3 . Ⓒ. . Ⓓ. . 2 2
Câu 9: Trong không gian cho đoạn thẳng AB cố định và có độ dài bằng 4. Qua các điểm A và B lần
lượt kẻ các tia Ax và By chéo nhau và hợp nhau góc 30 , đồng thời cùng vuông góc với
đoạn thẳng AB . Trên các tia Ax và By lần lượt lấy các điểm M , N sao cho MN  5 . Đặt 3
AM a và BN b . Biết thể tích khối tứ diện ABMN bằng . Giá trị biểu thức 3    2 2 2 S a b bằng Ⓐ. 144. Ⓑ. 324. Ⓒ. 100. Ⓓ. 256 .
Câu 10: Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B , AB  ,
a SAB SCB  90 , góc
giữa AB và g SBC  bằng 60 . Thể tích của khối chóp đã cho bằng 3 3 3 3 Ⓐ. a 3 4a 3 a 3 a 3 . Ⓑ. . Ⓒ. . Ⓓ. . 6 9 9 3
Câu 11: Cho hình chóp S.ABC có đáy là tam giác cân tại A , AB a , BAC 120 , SBA SCA 90 3
. Gọi  là góc giữa SB và SAC  thỏa mãn sin 
, khoảng cách từ S đến mặt đáy nhỏ 8
hơn 2a . Thể tích của khối chóp S.ABC bằng 3 3 3 3 Ⓐ. 3a 3a 3a 3a . Ⓑ. . Ⓒ. . Ⓓ. . 4 6 12 24
Câu 12: Cho hình chóp S.ABC có SA vuông góc với mặt đáy, SA 2BC và BAC 120 . Hình chiếu
vuông góc của A lên các cạnh SB và SC lần lượt là M và N . Góc giữa hai mặt phẳng
ABC vàAMN bằng Ⓐ. 45. Ⓑ. 60. Ⓒ. 15. Ⓓ. 30 .
Câu 13: (VDC) Cho tứ diện ABCD có AB AD  ,
a CD a 2, ABC DAB  90 . Góc giữa hai
đường thẳng AD và BC bằng 45 . Khoảng cách giữa hai đường thẳng AC và BD bằng Ⓐ. a 6 a 6 a 6 a 6 . Ⓑ. . Ⓒ. . Ⓓ. . 2 3 4 6
Nguyễn Hoàng Việt 0905193688 Trang: 2
Phục dựng hình ẩn
Câu 14: (VDC) Cho hình chóp S.ABC có đáy là tam giác vuông tại A , AB  2 ,
a AC a . Các tam giác SA ,
B SAC lần lượt vuông tại B và C . Biết khoảng cách giữa hai đường thẳng SA và BC 2a bằng
, cosin của góc giữa SAB và SBC  bằng 3 Ⓐ. 1 3 30 11 . Ⓑ. . Ⓒ. . Ⓓ. . 6 2 6 12
Câu 15: Cho hình chóp S.ABC có đáy là tam giác cân tại A , BAC 120 , BC  2a và a 39
SA SB SC
. Gọi G là trọng tâm của tam giác SAB . Thể tích của khối chóp . G ABC 3 bằng 3 3 3 Ⓐ. 2a a a . Ⓑ. 3 a . Ⓒ. . Ⓓ. . 9 3 9
Câu 16: Cho hình chóp S.ABC có đáy là tam giác đều cạnh 2a , SAB SCB  90. Gọi M là trung 6a
điểm của SA . Biết khoảng cách từ A đến MBC  bằng
. Thể tích của khối chóp đã cho 21 bằng 3 3 3 Ⓐ. 8a 39 10a 3 4a 13 . Ⓑ. . Ⓒ. . Ⓓ. 3 2a 3 . 3 9 3
Câu 17: Cho tứ diện ABCD có ABC ADC  90 và BC 1, CD  3 , BD  2, AB  3. Khoảng
cách từ B đến  ACD bằng Ⓐ. 6 42 7 14 . Ⓑ. . Ⓒ. . Ⓓ. . 7 7 7 7
Câu 18: Cho hình chóp S.ABC có AB  2, AC  3, BC  4, SA vuông góc với mặt đáy và SA 1. Gọi
H , K lần lượt là hình chiếu của A lên SB và SC . Gọi  là góc giữa hai mặt phẳng  AHK
và  ABC  , giá trị tan bằng Ⓐ. 16 15 6 15 . Ⓑ. 15 . Ⓒ. 4 . Ⓓ. . 15 5
Câu 19: Cho hình chóp S.ABC có AC  ,
a AB a 3, BAC  150 và SA vuông góc với mặt đáy. Gọi
M , N lần lượt là hình chiếu vuông góc của A trên SB và SC . Thể tích của khối cầu ngoại tiếp hình chóp . A BCNM bằng 3 3 3 3 Ⓐ. 4 7 a 44 11 a 28 7 a 20 5 a . Ⓑ. . Ⓒ. . Ⓓ. . 3 3 3 3
Câu 20: Cho hình chóp S.ABC có SA AB  3 ; SB  6 ; AC  2BC  2; SC  5 . Khoảng cách
từ A đến SBC  bằng
Nguyễn Hoàng Việt 0905193688 Trang: 3
Phục dựng hình ẩn Ⓐ. 30 5 13 30 . Ⓑ. . Ⓒ. . Ⓓ. . 5 2 6 3
Câu 21: Cho hình chóp S.ABC có đáy là tam giác vuông tại A , AB  2a , AC a . Các tam giác SBA
và SCA lần lượt vuông tại B và C . Biết khoảng cách từ B đến mặt phẳng SAC  bằng a 2
, cosin của góc tạo bởi đường thẳng SC và SAB bằng Ⓐ. 1 1 2 2 3 . Ⓑ. . Ⓒ. . Ⓓ. . 10 3 3 10 Câu 22: 2 2
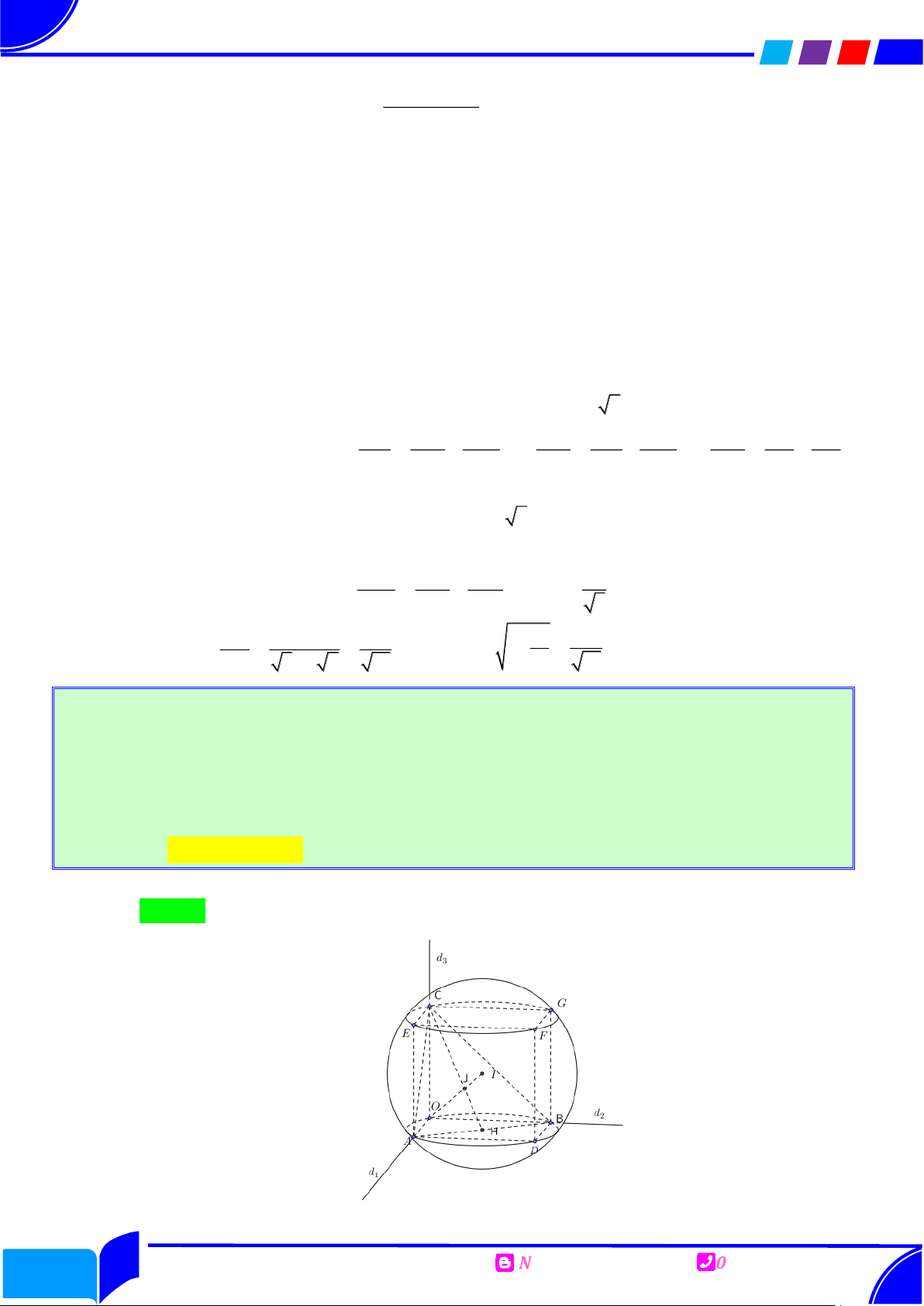
Trong không gian Oxyz , cho mặt cầu S  2
: x   y  3   z  6  45 và M 1; 4;5 . Ba
đường thẳng thay đổi d , d , d nhưng đôi một vuông góc tại O cắt mặt cầu tại điểm thứ hai 1 2 3 lần lượt là , A ,
B C . Khi khoảng cách từ M đến mặt phẳng  ABC lớn nhất thì phương trình
mặt phẳng  ABC  là
Ⓐ. x  2y z 8  0 . Ⓑ. 2x y z  4  0 . Ⓒ. x y  2z 1 0. Ⓓ. x y z 3  0
Câu 23: Cho hình chóp đều S.ABC có SA a. Gọi ,
D E lần lượt là trung điểm của hai cạnh S , A SC .
Biết BD vuông góc với AE , chiều cao của hình chóp S.ABC bằng Ⓐ. a 21 a 3 a 7 a . Ⓑ. . Ⓒ. . Ⓓ. . 3 6 3 3
Câu 24: Cho tứ diện ABCD có tam giác ABD đều cạnh bằng 2 , tam giác ABC vuông tại B , 3
BC  3 . Khoảng cách giữa hai đường thẳng AB và CD bằng
. Thể tích của khối tứ 2 diện ABCD bằng Ⓐ. 3 1 3 1 . Ⓑ. . Ⓒ. . Ⓓ. . 2 2 6 6
Câu 25: Cho tứ diện ABCD có AB BC CD  2 , AC BD 1, AD  3 . Bán kính mặt cầu ngoại
tiếp tứ diện ABCD bằng Ⓐ. 7 39 2 3 1. Ⓑ. . Ⓒ. . Ⓓ. . 3 6 3
Câu 26: Cho hình chóp S.ABC có ASB  60 , BSC  90 , CSA 120 , SA  , a SB  2 , a SC  3 . a
Sin của góc giữa hai mặt phẳng SBC  và SAB bằng Ⓐ. 6 6 6 6 . Ⓑ. . Ⓒ. . Ⓓ. . 6 3 4 5
Câu 27: Cho hình chóp S.ABC có ASB BSC CSA  60 và SA  2,SB  3,SC  4. Thể tích của
khối chóp S.ABC bằng Ⓐ. 4 3 . Ⓑ. 2 3 . Ⓒ. 2 2 . Ⓓ. 4 2 .
Nguyễn Hoàng Việt 0905193688 Trang: 4
Phục dựng hình ẩn
Câu 28: Cho hình chóp S.ABC có SA  4,SB  6,SC 12 và ASB  60 , BSC  90 và CSA 120 .
Thể tích của khối chóp S.ABC bằng Ⓐ. 36 3 . Ⓑ. 36 2 . Ⓒ. 24 3 . Ⓓ. 24 2 .
Câu 29: Cho tứ diện ABCD, có tam giác BCD đều, hai tam giác ABD và ACD vuông cân đáy AD .
Điểm G là trọng tâm tam giác ABC . Gọi M , N lần lượt là trung điểm BC và AD . Gọi  là
góc giữa hai mặt phẳng CDG và MNB , giá trị cos bằng Ⓐ. 1 1 1 . Ⓑ. 0 . Ⓒ. . Ⓓ. . 11 11 11
Câu 30: Ba quả bóng dạng hình cầu có bán kính bằng 1 đôi một tiếp xúc nhau và cùng tiếp xúc với mặt
phẳng  P . Mặt cầu  S  bán kính bằng 2 tiếp xúc với ba quả bóng trên. Gọi M là điểm bất
kỳ trên  S  . Khoảng cách lớn nhất từ điểm M đến mặt phẳng  P bằng Ⓐ. 123 52 30 69 3  . Ⓑ. . Ⓒ. 3 . Ⓓ. 3 . 4 9 2 3
Câu 31: Người ta thả vào bên trong một cái ống nước dạng hình trụ 4 quả bóng tenis có cùng bán kính
bằng 1. Biết rằng các quả bóng tiếp xúc với nhau và tiếp xúc với các đường sinh của ống hình
trụ. Biết chiều cao của ống bằng 2 . Thể tích của ống nước đó bằng
Ⓐ. 3 2 2 . Ⓑ. 1 2 .
Ⓒ. 6 4 2 .
Ⓓ. 2 2 2 .
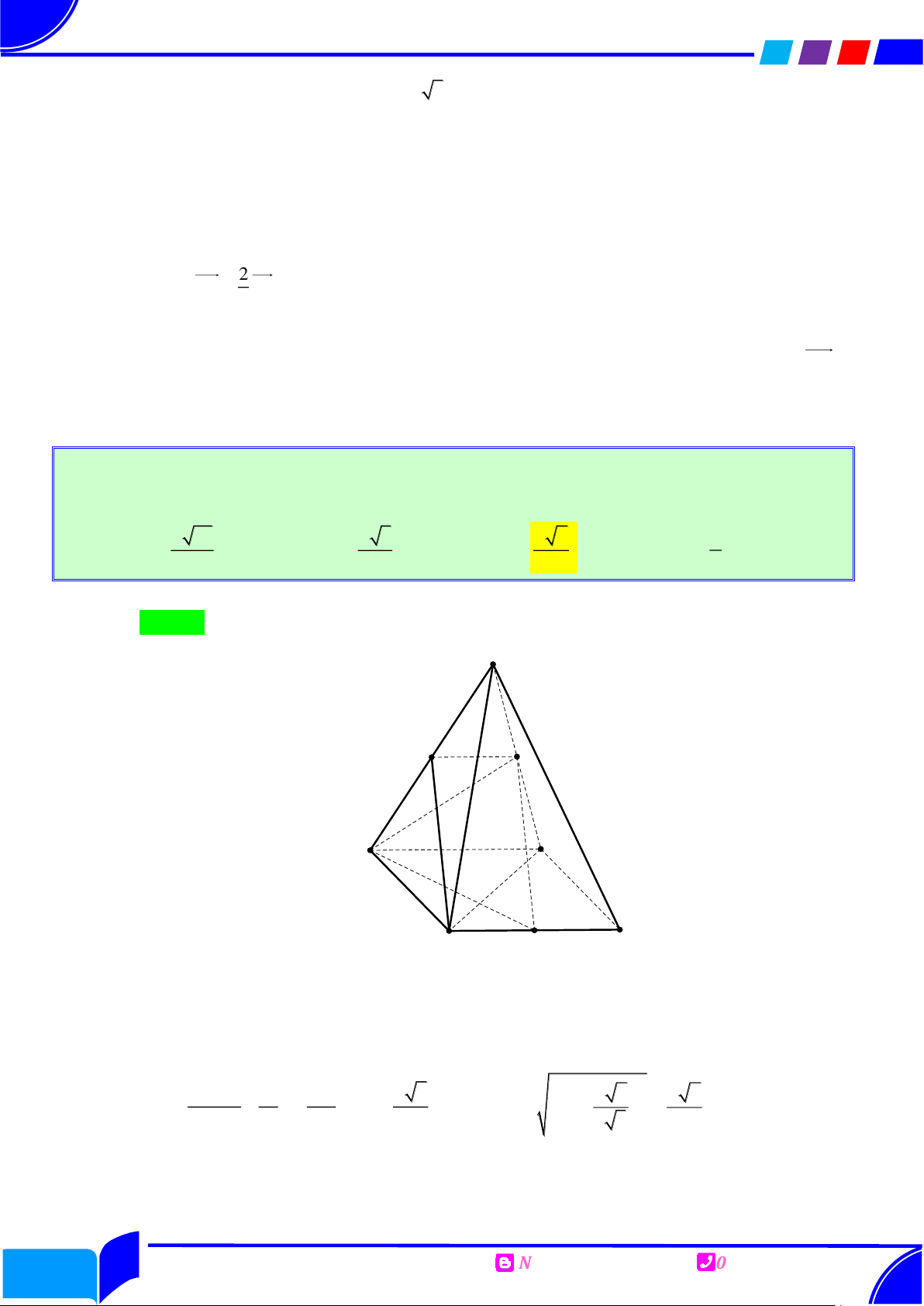
Câu 32: Cho tứ diện ABCD có AB CD  10 , AD BC  5 , AC BD  13 . Gọi  là góc giữa
AB và  ACD , giá trị cos bằng
Nguyễn Hoàng Việt 0905193688 Trang: 5
Phục dựng hình ẩn Ⓐ. 6 10 865 10 3 10 . Ⓑ. . Ⓒ. . Ⓓ. . 35 35 10 10
Câu 33: Cho tứ diện ABCD có các cạnh AD BC  3 ; AC BD  4 ; AB CD  2 3 . Thể tích tứ diện ABCD bằng Ⓐ. 2470 2047 2474 2740 . Ⓑ. . Ⓒ. . Ⓓ. . 12 12 12 12
Câu 34: Cho hình chóp S.ABC có độ dài các cạnh SA BC x , SB AC y , SC AB z thỏa mãn 2 2 2
x y z  12 . Giá trị lớn nhất của thể tích khối chóp S.ABC bằng Ⓐ. 2 2 2 3 2 3 2 . Ⓑ. . Ⓒ. . Ⓓ. . 3 3 3 2
Câu 35: Cho tứ diện ABCD có AB CD  4; AC BD  5; AD BC  6 . Thể tích của khối tứ diện ABCD bằng Ⓐ. 15 6 15 6 45 6 45 6 . Ⓑ. . Ⓒ. . Ⓓ. . 4 2 4 2
Câu 36: Xét khối tứ diện ABCD có AB x và các cạnh còn lại bằng 2 3. Giá trị của x để thể tích của
khối tứ diện ABCD lớn nhất là Ⓐ. x  6 .
Ⓑ. x  2 2 . Ⓒ. x  14 .
Ⓓ. x  3 2 .
Câu 37: Cho tứ diện ACFG có số đo các cạnh lần lượt là AC AF FC a 2, AG a 3,
GF GC a . Thể tích của khối tứ diện ACFG bằng 3 3 3 3 Ⓐ. a a a 15a . Ⓑ. . Ⓒ. . Ⓓ. . 6 3 12 3
Câu 38: Cho hình chóp tam giác S.ABC có đáy là tam giác vuông cân tại A ; AB AC  ; a SA a 3 . Các tam giác SA ;
B SAC lần lượt vuông tại ; B C . Gọi ;
O M lần lượt là trung điểm của
BC; SC . Gọi  là góc giữa hai mặt phẳng OMA;SAB , giá trị tan bằng Ⓐ. 1 2 3 . Ⓑ. . Ⓒ. . Ⓓ. 3 . 3 2 6
Câu 39: Cho tứ diện ABCD có ABC là tam giác đều cạnh 2a , AD a 3 và AD vuông góc với
AB và AC . Gọi E, F lần lượt là trung điểm của các đoạn thẳng BC và DE. Góc giữa AF với CD bằng Ⓐ. 45 . Ⓑ. 60 . Ⓒ. 90. Ⓓ. 30.
Câu 40: Cho tứ diện ABCD có AB 1;CD  2; ABC DAB  90. Góc giữa hai đường thẳng A ;
D BC bằng 30 . Bán kính của mặt cầu ngoại tiếp tứ diện ABCD bằng
Nguyễn Hoàng Việt 0905193688 Trang: 6
Phục dựng hình ẩn Ⓐ. 5 2 . Ⓑ. . Ⓒ. 5 . Ⓓ. 2 . 2 2
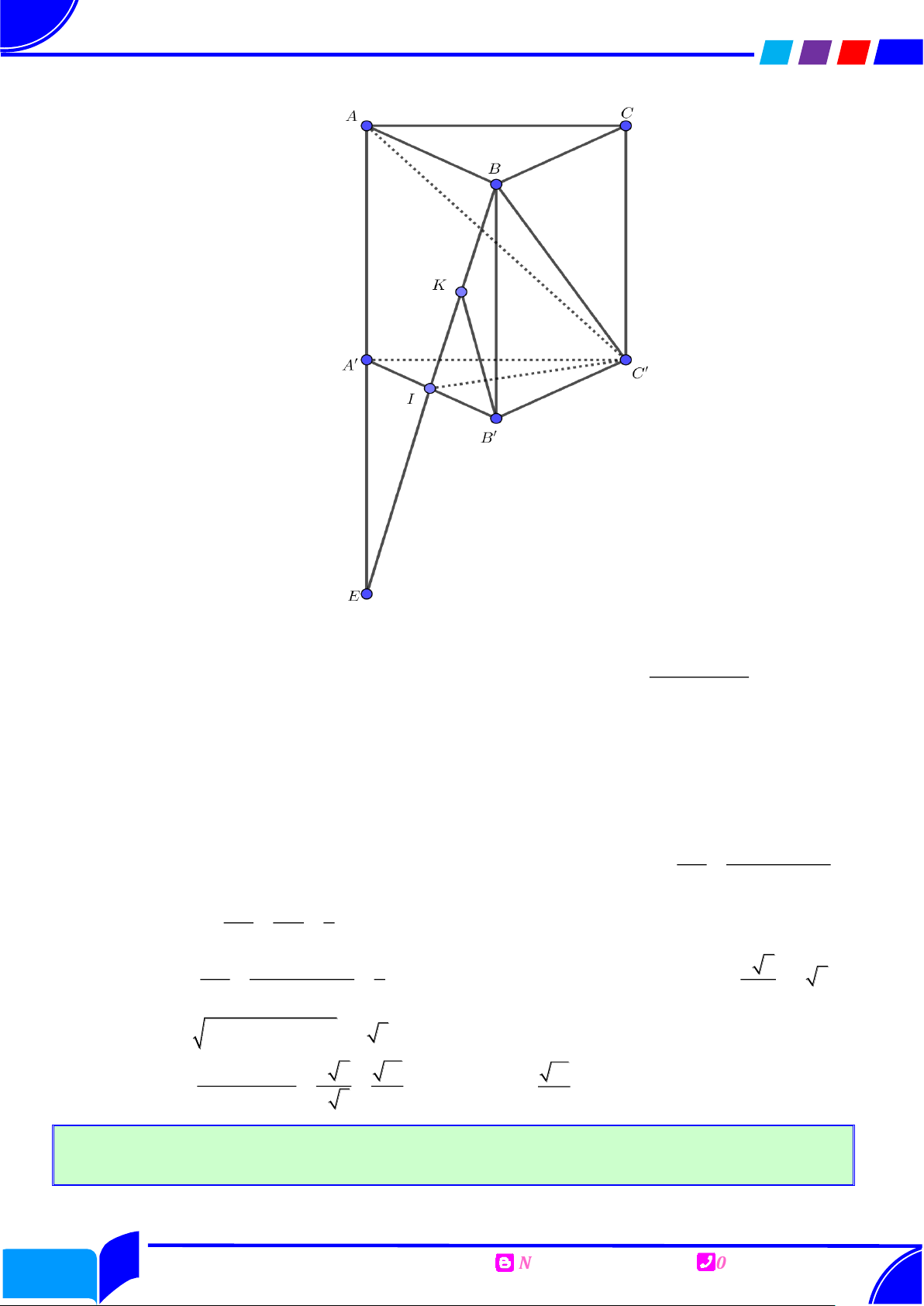
Câu 41: Cho lăng trụ tam giác đều AB . C A BC
 , gọi I là trung điểm A B
  và  là góc giữa AC với
BIC. Biết AA  ;a AB  2a , giá trị cos bằng Ⓐ. 15 10 3 2 . Ⓑ. . Ⓒ. . Ⓓ. . 5 5 5 5
Câu 42: Cho hình lăng trụ đứng AB . C A BC
  có đáy ABC là tam giác vuông tại B , BA BC a,
cạnh bên bằng a . Khoảng cách giữa hai đường thẳng A B  và B C  bằng Ⓐ. a 3 2a 3 a 6 a 3 . Ⓑ. . Ⓒ. . Ⓓ. . 3 3 2 6
Câu 43: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a . SA vuông góc với mặt đáy. Góc giữa
SAB và SCD bằng 45 . Gọi M là trung điểm của SB , khoảng cách giữa AM và SD bằng Ⓐ. a 2 a 3 a a 5 . Ⓑ. . Ⓒ. . Ⓓ. . 2 3 2 4
Câu 44: Cho tứ diện ABCD có AB CD a ; AD BC b; BD AC c . Bán kính mặt cầu ngoại
tiếp tứ diện ABCD bằng 2 2 2 2 2 2   2 2 2 2 2 2 Ⓐ. a b c a b c a b c a b c . Ⓑ. . Ⓒ. . Ⓓ. . 2 8 8 2
Nguyễn Hoàng Việt 0905193688 Trang: 7
Phục dựng hình ẩn BẢNG ĐÁP ÁN PHẦN 2 1.D 2.C 3.B 4.D 5.D 6.A 7.A 8.A 9.A 10.A 11.C 12.D 13.D 14.A 15.D 16.B 17.B 18.A 19.C 20.A 21.D 22.A 23.C 24.A 25.C 26.B 27.C 28.D 29.C 30.D 31.C 32.B 33.A 34.A 35.A 36.D 37.A 38.B 39.C 40.A 41.A 42.A 43.B 44.B
Nguyễn Hoàng Việt 0905193688 Trang: 8
Phục dựng hình ẩn LỜI GIẢI CHI TIẾT PHẦN 3 Câu 1.
Tứ diện ABCD có BC  3, CD  4, ABC BCD ADC  90 ,  A ,
D BC   60. Cosin của
góc giữa hai mặt phẳng  ABC và  ACD bằng 43 4 43 43 2 43 Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. . 86 43 43 43 Lời giải Chọn D Cách 1:
Gọi H là chân đường cao của tứ diện ABCD . BC AB Ta có: 
BC HB .(1) BC AH CD AD Lại có: 
CD HD .(2) CD AH Mà BCD  90 .
Từ đây ta suy ra HBCD là hình chữ nhật. Mặt khác:  A ,
D BC    A ,
D HD  ADH  60. Suy ra: AH HD tan 60  3 3 .
Gọi K , I lần lượt là hình chiếu vuông góc của B lên AC và của H lên AD .
Suy ra: d B ACD  d H ACD 3 3 , ,
HI HDsin 60  . 2 1 1 1 1 1 52
Tam giác ABC vuông tại B có:      2 2 2 2 2 2 BK AB AC AH HB AC 387 3 559  BK  . 26
d B, ACD 2 HI HI 2 43
Gọi    ABC, ACD ta có: sin   cos     1    BK BKBK  43 . Cách 2:
Nguyễn Hoàng Việt 0905193688 Trang: 9
Phục dựng hình ẩn
Gọi H là chân đường cao của tứ diện ABCD . BC AB Ta có: 
BC HB .(1) BC AH CD AD Lại có: 
CD HD .(2) CD AH Mà BCD  90 .
Từ đây ta suy ra HBCD là hình chữ nhật. Mặt khác:  A ,
D BC    A ,
D HD  ADH  60. Suy ra: AH HD tan 60  3 3 .
Chọn hệ trục Oxyz H.DBA như hình vẽ.
Ta có: H 0;0;0 , A0;0;3 3, B0;4;0 , C 3;4;0 , D3;0;0.
AD  3;3;3 3 , AC  3;4;3 3 , AB  0;4;3 3 .
Gọi n , n lần lượt là một véc tơ pháp tuyến của  ABC và  ABD . 1 2
Suy ra: n   A ,
B AC  0;  9 3; 12 ; n   A ,
D AC  21 3;0; 21 . 2     1     n .n
Vậy cos  ABC, ADC 1 2  n . n 1 2 0.21 3  9 3.0 12.21 2 43   .   2    2 2    2 2 2 43 0 9 3 12 . 21 3 0 21 Câu 2.
Cho hình chóp S.ABC có AB a , AC a 3 , SB  2a và ABC BAS BCS  90 . Biết 11
sin của góc giữa đường thẳng SB và mặt phẳng SAC bằng . Thể tích của khối 11
chóp S.ABC bằng 3 2a 3 3 a 3 3 a 6 3 a 6 Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. . 9 9 6 3 Lời giải Chọn C
Nguyễn Hoàng Việt 0905193688 Trang: 10
Phục dựng hình ẩn BA SA
- Dựng SD   ABC tại D . Ta có:   BA AD. BA SDBC SD Và: 
BC CD ABCD là hình chữ nhật DA BC a 2 , DC AB aBC SC . d  , B SAC
- Sử dụng công thức sin  , SB SAC    . SB d  ; B SAC d  ; D SAC  11        1 11    1 . 11 SB SB 2 d  ; D SAC  2 SB - Lại có : 1 1 1 1    1 1 1    1 3   2 . 2 d  ; D SAC  2 2 2 DS DA DC 2 2 2 2 SB BD DA DC 2 2 2 SB  3a 2a 2 2 SB  6aSB a 6 11 1 3   - Từ   1 và 2 suy ra:     2 11  SB 2 2 2 SB  3a 2a 2 2  11 SB a    SB a  3  3
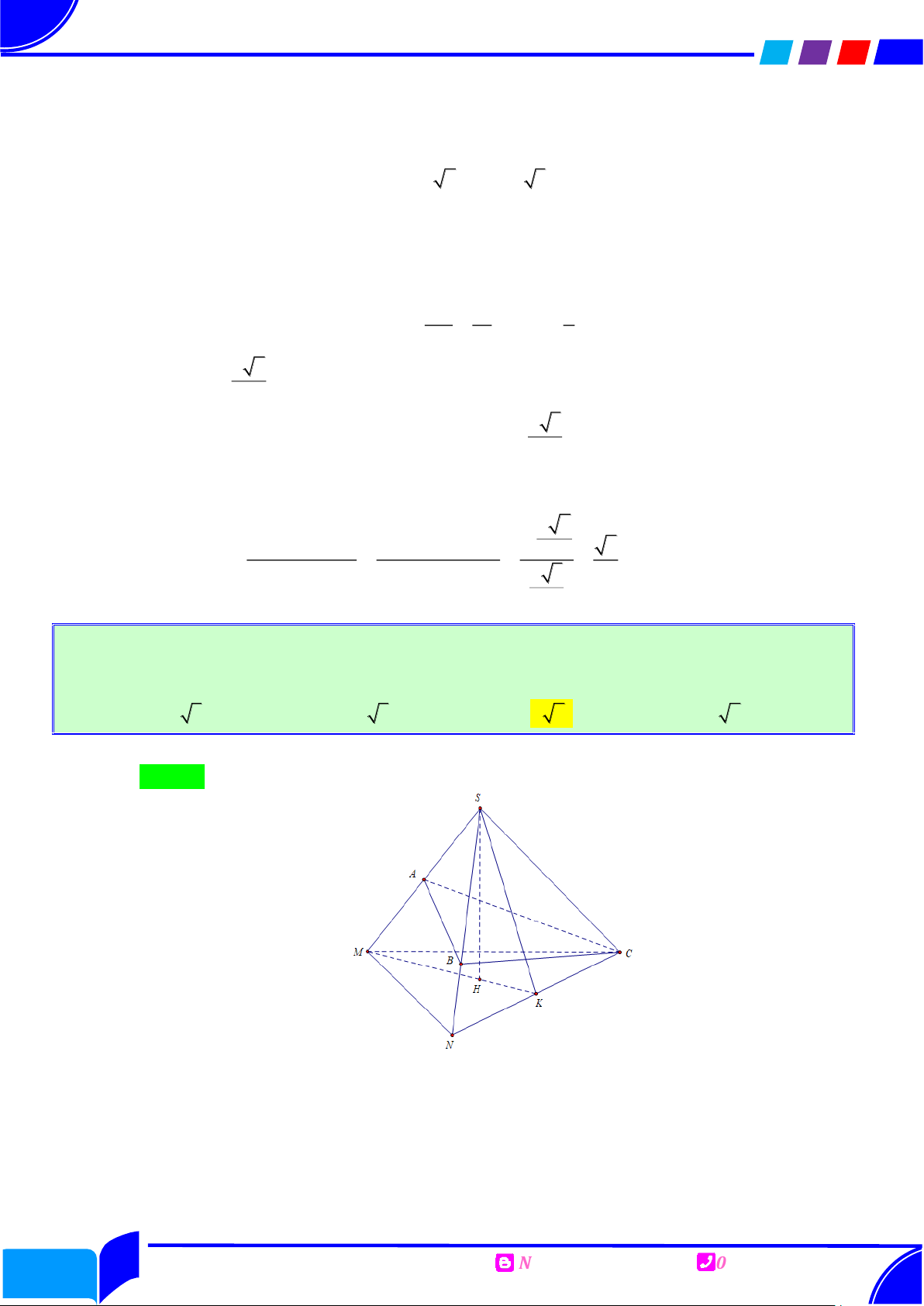
Theo giả thiết SB  2a SB a 6  SD a 3 . 3 1 1 a 6 Vậy VS . D B . A BC  . SABC 3 2 6 Câu 3. Cho hình chóp .
S ABC có đáy là tam giác vuông cân tại B , AB a , SA AB , SC BC
, SB  2a . Gọi M , N lần lượt là trung điểm SA , BC và  là góc giữa MN với  ABC . Giá trị cos bằng 2 11 6 2 6 10 Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. . 11 3 5 5 Lời giải Chọn B
Nguyễn Hoàng Việt 0905193688 Trang: 11
Phục dựng hình ẩn S 2 a M D C H N a A a B
Dựng SD   ABC , ta có: BC SCAB SA
BC CD và 
AB AD . BC SDAB SD
Mà ABC là tam giác vuông cân tại B nên ABCD là hình vuông.
Gọi H là trung điểm của AD , ta có MH // SD MH   ABCD .
Do đó HN là hình chiếu của MN lên  ABC .
  MN,ABC  MN,NH   MNH . Ta có: 2 2
SC SB BC 2 2
 4a a a 3 . Lại có: 2 2
SD SC DC 2 2
 3a a a 2 . 1 a 2 .SD MH 1 1 6 tan  2  2  2   cos    . NH AB a 2 2 1 tan  1 3 1  2 Câu 4.
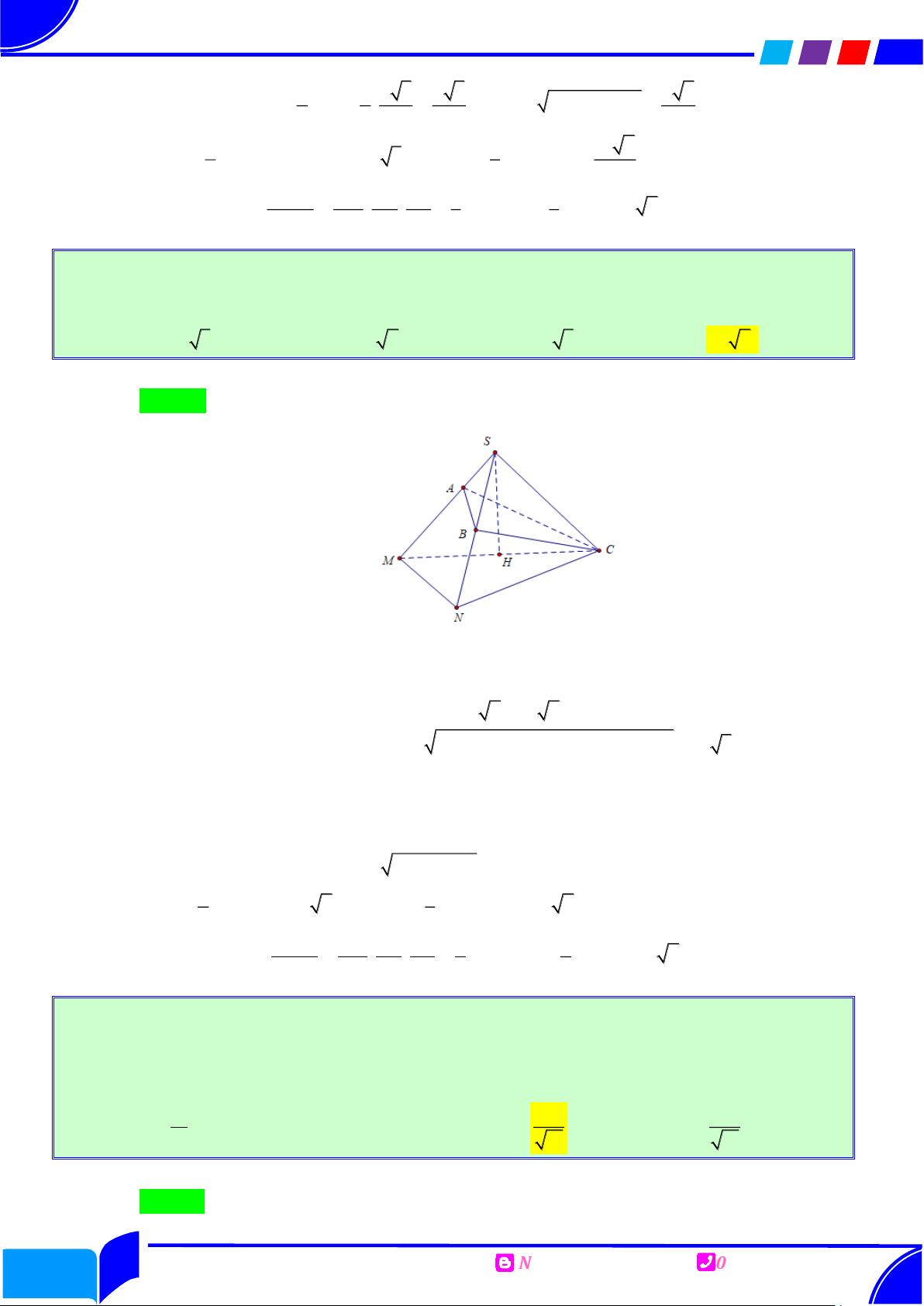
Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B , AB BC a 3 ,
SAB SCB  90 và khoảng cách từ điểm A đến SBC  bằng a 2 . Diện tích của mặt
cầu ngoại tiếp hình chóp S.ABC bằng Ⓐ. 2 2 a . Ⓑ. 2 8 a . Ⓒ. 2 16 a . Ⓓ. 2 12 a . Lời giải Chọn D S K J I C H O A B
Gọi H là hình chiếu của S lên (ABC)
Nguyễn Hoàng Việt 0905193688 Trang: 12
Phục dựng hình ẩn BC SC Ta có:   HC BC SH BC
Tương tự AH AB Và ABC
vuông cân tại B nên ABCH là hình vuông. Gọi O AC BH , O là tâm
hình vuông. Dựng một đường thẳng d qua O vuông góc với  ABCH  , dựng mặt
phẳng trung trực của SA qua trung điểm J cắt d tại I I là tâm mặt cầu ngoại tiếp.
Ta hoàn toàn có IJ SA IJ / / AB I là trung điểm SB , hay I d SC .  a 3
Bán kính mặt cầu ngoại tiếp: 2 2 r
AI IJ JA ; IJ   S .ABC 2 2
Do AH // SBC d  ,
A SBC  d H,SBC  HK
( K là hình chiếu của H lên SC và BC  SHC HK  SBC )
HK a 2 . Tam giác SHC vuông tại H SH a 6 .
Tam giác SHA vuông tại H SA  3a . SA 3a 2 2 JA    r
AI a 3  S  4r 12a . . 2 2 S ABC mc Câu 5.
(Sở Bắc Ninh lần 2 2018-2019) Cho tứ diện ABCD có DAB CBD  90º ; AB  ;
a AC a 5; ABC  135 . Biết góc giữa hai mặt phẳng  ABD,BCD bằng 30 .
Thể tích của tứ diện ABCD bằng 3 a 3 a 3 a 3 a Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. . 2 3 2 3 2 6 Lời giải Chọn D D E F C H a 5 A a B
Dựng DH   ABC .
Nguyễn Hoàng Việt 0905193688 Trang: 13
Phục dựng hình ẩn BA DABC DB Ta có 
BA AH . Tương tự   BC BH . BA DHBC DH
Tam giác AHB có AB a , o ABH  45  H
AB vuông cân tại A AH AB a .
Áp dụng định lý cosin, ta có BC a 2 . 2 1 1 2 a Vậy S
  BABC sinCBA  a a 2   . ABC  2 2 2 2 HE DA Dựng 
HE  DAB và HF  DBC . HF DB
Suy ra DBA,DBC  HE, HF   EHF và tam giác HEF vuông tại E . ax xa 2
Đặt DH x , khi đó HE  , HF  . 2 2 a x 2 2 2a x 2 2 HE 3 x  2a Suy ra cos EHF     x a . 2 2 HF 4 2x  2a 3 1 a Vậy V   DH S  . ABCD  3 ABC 6 Câu 6.
(Sở Bắc Ninh lần 2 2018-2019) Trong không gian Oxyz , cho điểm x 1 y 1 z 1
A4;0;0, B0;4;0, S 0;0;c và đường thẳng d :  
. Gọi A , B lần lượt 1 1 2
là hình chiếu vuông góc của O lên S ,
A SB . Khi góc giữa đường thẳng d và mặt phẳng OA B
  lớn nhất thì giá trị của số thực c thuộc khoảng nào dưới đây?  17 15  Ⓐ.  ;    . Ⓑ.  9  ; 8   . Ⓒ. 0;3 . Ⓓ.  8  ; 6   .  2 2  Lời giải Chọn A S(0;0;c) B' A' B(0;4;0) O A(4;0;0) C(4;4;0)
Dựng hình vuông OACB , khi đó C 4; 4;0 . Dễ chứng minh được OA SC SC OA B . OB SC
Nguyễn Hoàng Việt 0905193688 Trang: 14
Phục dựng hình ẩn
Khi đó d tạo với OA B
  góc lớn nhất khi và chỉ khi d OA B u 1;1; 2 cùng d
phương SC 4;4; c nên c 8. Câu 7.
Cho tứ diện ABCD có ABC BCD CDA  90 , BC CD  ,
a AD a 2 . Góc giữa hai
mặt phẳng  ABC và  ACD bằng Ⓐ. 60 . Ⓑ. 30 . Ⓒ. 45. Ⓓ. 90 . Lời giải Chọn A A A a 2 a 2 K H D D E a a a C B B a C
Gọi E là hình chiếu của A lên mặt phẳng  BCDBC ABCD AD Kết hợp đề bài
  BC BE ;
  CD ED và BC CD a suy ra BC AECD AE
tứ giác BCDE là hình vuông cạnh a . Khi đó 2 2 AE
AD ED a
Gọi H , K lần lượt là hình chiếu của E lên  ABC, ACD thì EH   ABC, EK   ACD
nên góc tạo bởi hai mặt phẳng  ABC và  ACD là góc EH, EK a 2
Nhận xét 2 tam giác SEB và SED là vuông cân tại E nên EH EK  ; 2 BD a 2 HK  
suy ra tam giác EHK đều. 2 2
Vậy số đo góc tạo bởi hai mặt phẳng  ABC và  ACD là 60 Câu 8.
Cho hình chóp S.ABC có đáy là tam giác cân tại A , AB a , các tam giác SA , B SAC là
tam giác vuông tại B và C . Biết độ dài đường cao của hình chóp S.ABC gấp hai lần
độ dài đường cao của tam giác ABC hạ từ đỉnh A . Bán kính mặt cầu ngoại tiếp hình
chóp S.ABC có giá trị nhỏ nhất bằng
Nguyễn Hoàng Việt 0905193688 Trang: 15
Phục dựng hình ẩn a a Ⓐ. a . Ⓑ. a 3 . Ⓒ. . Ⓓ. 3 . 2 2 Lời giải Chọn A
Gọi H là hình chiếu của S trên mặt phẳng  ABC . Khi đó ta có SBH, SCH là hai tam giác vuông tại ,
B C . Gọi E là trung điểm BC , suy ra AE BC .
Ta đặt AE h SH  2 ,
h 0  h a . 2 2 AB a + 2 AB A . E AH AH   AE h 4 a + 2 SA  4h   2a . 2 h + Các điểm , A ,
B C, S cùng nhìn SA với một góc vuông, suy ra SA là đường kính của
mặt cầu ngoại tiếp hình chóp và trung điểm I của SA là tâm mặt cầu. Vậy SA R
a R  . a min 2 Câu 9.
Trong không gian cho đoạn thẳng AB cố định và có độ dài bằng 4. Qua các điểm A
và B lần lượt kẻ các tia Ax và By chéo nhau và hợp nhau góc 30 , đồng thời cùng
vuông góc với đoạn thẳng AB . Trên các tia Ax và By lần lượt lấy các điểm M , N sao 3
cho MN  5 . Đặt AM a và BN b . Biết thể tích khối tứ diện ABMN bằng . Giá 3
trị biểu thức    2 2 2 S a b bằng Ⓐ. 144. Ⓑ. 324. Ⓒ. 100 . Ⓓ. 256 . Lời giải Chọn A
Nguyễn Hoàng Việt 0905193688 Trang: 16
Phục dựng hình ẩn M 5 a C N b A 4 B
AB là đoạn vuông góc chung của AM , BN nên d AM , BN   AB  4 1 Ta có công thức: V
AM.BN.d AM BN AM BN ABMN  , .sin ,  6 3 1 0   . . a .
b 4.sin 30  ab  3 . 3 6
Dựng hình chữ nhật ABNC . Khi đó:  AM AC   AM BN  0 , ,
 30 và AC BN b . AB AMAB AM Ta có:   
AB   AMC. AB BNAB AC
Mà CN || AB CN   AMC  CN CM . Do đó 2 2
CM MN CN  3 .
AM AC CM a b  Ta có: MAC  AM AC 2 2 2 2 2 3 9 3 cos cos ,     . 2AM .AC 2 2 3 2 2 2
a b 12 . Vậy S 144 .
Câu 10. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B , AB  ,
a SAB SCB  90 ,
góc giữa AB và g SBC bằng 60 . Thể tích của khối chóp đã cho bằng 3 a 3 3 4a 3 3 a 3 3 a 3 Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. . 6 9 9 3 Lời giải Chọn A
Dựng hình vuông ABCD tâm O .
Nguyễn Hoàng Việt 0905193688 Trang: 17
Phục dựng hình ẩn Do 0
SAB SCB  90 nên hình chóp S.ABC nội tiếp mặt cầu tâm I đường kính SB .
Do O là tâm đường tròn ngoại tiếp tam giác ABC nên OI là trục của đường tròn ngoại
tiếp tam giác ABC . Suy ra OI   ABC  SD   ABC .
A ,BSBC  DC,SBC  C ,
D CS   DCS  60 . Ta có: 0 SD C .
D tan 60  a 3 . 2 3 1 1 a a 3
Từ đây ta suy ra: V  .S . D S  .a 3.  . 3 ABC 3 2 6
Câu 11. Cho hình chóp S.ABC có đáy là tam giác cân tại A , AB a , BAC 120 , 3 SBA SCA
90 . Gọi  là góc giữa SB và SAC thỏa mãn sin  , khoảng cách 8
từ S đến mặt đáy nhỏ hơn 2a . Thể tích của khối chóp S.ABC bằng 3 3a 3 3a 3 3a 3 3a Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. . 4 6 12 24 Lời giải Chọn C S K C D A B I
+ Gọi D là hình chiếu vuông góc của S lên đáy  ABC  , đặt SD x 0  x  2a  . AC SC Ta có 
AC  SDC  AC DC . Tương tự ta cũng có AB DB . AC SD
+ Tam giác ABC cân tại A và CAB  120  BC a 3 và DBC DCB  60  DBC đều cạnh a 3 .
+ Tam giác SDC vuông tại D 2 2
SB  3a x . x a 3
+ Kẻ DK SC tại K DK  SAC  d  ;
D SAC   DK  . 2 2 3a x
+ Gọi I BD AC , xét D
IC vuông tại C và BDC  60 DC  1 DI
 2a 3  B là trung điểm của DI d  ;
B SAC   d  ;
D SAC  . cosBDC 2
Nguyễn Hoàng Việt 0905193688 Trang: 18
Phục dựng hình ẩn d  ; B SAC  3 xa 3
Theo giả thiết   S ; B (SAC     sin    SB 8 2 2 2 3a x  2   x a 2 2  x x
x  3a  4ax  0   4  3  0    
. So sánh với điều kiện suy ra  a ax  3a x a . 3 1 a 3 Vậy V  .S .SD  . S . ABC  3 ABC 12
Câu 12. Cho hình chóp S.ABC có SA vuông góc với mặt đáy, SA 2BC và BAC 120 . Hình
chiếu vuông góc của A lên các cạnh SB và SC lần lượt là M và N . Góc giữa hai mặt
phẳng  ABC và  AMN  bằng Ⓐ. 45. Ⓑ. 60 . Ⓒ. 15 . Ⓓ. 30 . Lời giải Chọn A
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC có đường kính là AD .
Khi đó tam giác ABD vuông tại B AB BD . AB BD Ta có BD (SAB) BD AM . SA BD BD AM Ta có AM (SBD) AM SD . SB AM
Tương tự, ta chứng minh được AN SD . Do đó SD
(AMN) suy ra (ABC);(AMN) S ; A SD ASD . AD
Xét tam giác SAD vuông tại A có tan ASD . SA BC 3 Với AD 2R 2 SA . ABC sin120o 3
Nguyễn Hoàng Việt 0905193688 Trang: 19
Phục dựng hình ẩn 3 Do đó tan 30o ASD ASD ( );( ) 30o ABC AMN . 3
Câu 13. (VDC) Cho tứ diện ABCD có AB AD  ,
a CD a 2, ABC DAB  90 . Góc giữa hai
đường thẳng AD và BC bằng 45 . Khoảng cách giữa hai đường thẳng AC và BD bằng a 6 a 6 a 6 a Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. 6 . 2 3 4 6 Lời giải Chọn D
Gọi H là hình chiếu vuông góc của D lên mặt phẳng  ABC DH AB Ta có   AB AH DA AB
Mà BC AB AH BC   AD BC   AD AH  0 , ,
DAH  45 (Vì D
AH vuông tại H) a 2
AH DH  . 2 +) ABD  vuông tại A 2 2
BD AB AD a 2
Suy ra DB DC a 2  D
BC cân tại D . DM BC
Gọi M là trung điểm của BC, ta có   BC HM. DH BC  1
AHMB là hình chữ nhật  AH BM BC. 2
+) Trong hình thang ABCH AH BC , gọi I AC BH. IH AH 1 1
Theo định lí thalet ta có 
  IH H . B IB BC 2 3 a 6 +) A
HB vuông tại A, có 2 2 HB AH AB  . 2 2 1 a Có 2 2 HI.HB HB
AH AI HB hay HB AC 3 2
Nguyễn Hoàng Việt 0905193688 Trang: 20
Phục dựng hình ẩn AC HB +) Có   AC DB AC DH Trong tam giác DHB
dựng HE D ,
B IF HE IF BD d AC, BD  IF. H . B HD a 6 DHB
vuông tại HHE   . 2 2  4 HB HD IF BI 2 2 a 6 +) Trong B
HE , có IF HE  
  IF HE  . HE BH 3 3 6 a
Vậy d AC BD 6 ,  . 6
Câu 14. (VDC) Cho hình chóp S.ABC có đáy là tam giác vuông tại A , AB  2 ,
a AC a . Các tam giác SA ,
B SAC lần lượt vuông tại B và C . Biết khoảng cách giữa hai đường thẳng 2a
SA và BC bằng
, cosin của góc giữa SAB và SBC bằng 3 1 3 30 11 Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. . 6 2 6 12 Lời giải Chọn A
Kẻ SH   ABC  SH AB HB AB (định lý ba đường vuông góc).
Tương tự ta có AC HC .
Mà AB AC nên tứ giác ABHC là hình chữ nhật  HC  2 , a HB  . a
Từ A kẻ Ax / /BC BC / / SAx  
SA  d BC SAx  d I SAx 1
d H SAx 2a d BC, , , ,  2 3
( với HK Ax K, HK BC I ).
  SAx 4a d H , 
HN. (với N là hình chiếu vuông góc của H trên SK ). 3 H . B HC 4a
Ta có HK  2HI  2.  . 2 2 HB HC 5
Nguyễn Hoàng Việt 0905193688 Trang: 21
Phục dựng hình ẩn 1 1 1
Xét SHK vuông tại H có    SH  2 . a 2 2 2 HN SH HK HS.HB 2 5a
Dựng HM SB M HM   . 2 2  5 HS HB
Dễ dàng chứng minh được CH  SHB  CM S .
B nên SAB,SBC  CMH . MH 1 Ta có cosCMH   . CM 6
Câu 15. Cho hình chóp S.ABC có đáy là tam giác cân tại A , BAC  120 , BC  2a và a 39
SA SB SC
. Gọi G là trọng tâm của tam giác SAB . Thể tích của khối chóp 3 . G ABC bằng 3 2a 3 a 3 a Ⓐ. . Ⓑ. 3 a . Ⓒ. . Ⓓ. . 9 3 9 Lời giải Chọn D
Gọi H là hình chiếu của S trên mặt đáy, vì SA SB SC nên HA HB HC hay H BC 2a 3
là tâm đường tròn ngoại tiếp tam giác ABC HA HB HC   . 2sin A 3 AO BC
Gọi O là trung điểm BC , tam giác ABC cân tại A nên  .
BAO CAO  60 BO 2a 3
Suy ra AB AC   . sin BAO 3 2 1 a 3
Diện tích tam giác ABC là SA . B AC.sin120  . ABC 2 3 2 2 39a 12a
Đường cao của khối chóp là 2 2
SH SA AH    a 3 . 9 9 2 3 1 a 3 a
Thể tích khối chóp S.ABC là V  . .a 3  . S.ABC 3 3 3 1 1
Do G là trọng tâm tam giác SAB nên GM SM  d G, ABC  dS, ABC 3 3
Nguyễn Hoàng Việt 0905193688 Trang: 22
Phục dựng hình ẩn 3 1 aVV  . G.ABC S . 3 ABC 9
Câu 16. Cho hình chóp S.ABC có đáy là tam giác đều cạnh 2a , SAB SCB  90 . Gọi M là 6a
trung điểm của SA . Biết khoảng cách từ A đến MBC bằng . Thể tích của khối 21 chóp đã cho bằng 3 8a 39 3 10a 3 3 4a 13 Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. 3 2a 3 . 3 9 3 Lời giải Chọn A
Trong mp  ABC xác định điểm D sao cho tứ giác ABCD vuông tại A và C AB AD CB CD Khi đó ta có: 
AB SD ;   CB SD AB SA CB SC 1
Vậy SD   ABCD  VSD.S S.ABC  3 ABC
Có tam giác ABC là tam giác đều cạnh 2a 2  Sa 3 ABC  Ta đi tìm SD S M D A I C G N B
Gọi I là trung điểm AC vì tam giác ABC đều nên I BD AC BD
Gọi N là trung điểm BC AN BC AN / /CD 2
Gọi G là trọng tâm tam giác ABC dễ thấy AGCD là hình thoi  CD AG AN   1 3
Xét hình chóp S.ANCD có đáy ANCD là hình thang vuông tại C, N. Khoảng cách từ A 6a
đến mặt phẳng MNC bằng
vì MNC  MBC . 21
Nguyễn Hoàng Việt 0905193688 Trang: 23
Phục dựng hình ẩn S P M F H E A D C N
Trong mp  ANCD gọi  
E CN AD
Trong mp SAD kẻ tia At / /SD gọi  
P EM At
Gọi K là hình chiếu của G trên mặt phẳng CFH
AP / /SD AP CN Khi đó ta có 
  APN   CN AN CN a
Trong mp  APN  kẻ AH PN ta có AH d A MCN  6 ,  21
Mà tam giác ABC là tam giác đều cạnh 2a AN a 3 1 1 1 1 21 1 1 Từ        AP  2a 2 2 2 AH AP AN 2 2 2 2 AP 36a 3a 4a Dễ thấy APM S
FM SF AP  2a 2 ED CD 2
Xét tam giác EAN có CD / / AN nên   (theo   1 ) EA AN 3 FD ED FD 2 4a
Xét tam giác EAP có FD / /PA nên     FD  3 PA EA PA 3 3 10a
Từ 2 và 3 ta có SD SF FD  3 3 1 1 10a 10a 3 Vậy 2 VSD.S  . .a 3  (đpt). S.ABC  3 ABC 3 3 9
Câu 17. Cho tứ diện ABCD có ABC ADC  90 và BC 1, CD  3 , BD  2, AB  3 . Khoảng
cách từ B đến  ACD bằng 6 42 7 Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. 14 . 7 7 7 7 Lời giải Chọn B Cách 1:
Nguyễn Hoàng Việt 0905193688 Trang: 24
Phục dựng hình ẩn
Gọi M là trung điểm của AC .
Theo giả thiết ABC ADC  1
90  MB MD MA MC
AC M thuộc trục 2
đường tròn ngoại tiếp BCD (1).
Lại có BC 1, CD  3 , BD  2 2 2 2
BC DC BD B
CD vuông tại C . Gọi I là
trung điểm của BD I là tâm đường tròn ngoại tiếp BCD (2).
Từ (1) và (2)  MI  BCD .
Gọi K là trung điểm của CD IK // BC IK CD mà CD MI CD  MIK  (3).
Kẻ IH MK tại H . Từ (3)  IH CD IH  MCD . Do vậy, d  ,
B ACD  2d I,MCD  2IH . 1 1 Ta có IK BC  . 2 2 2 2 2 2 AC
AB BC  3 1  1 10 10  MC AC  . 2 2 1 IC BD  1 2 2
MI MC  10 6 IC  1  . 2 4 2 1 1 1   4 28   4  6  IH  . 2 2 2 IH MI IK 6 6 2 7
Vậy d B ACD 6 42 ,  2IH   . 7 7 Cách 2:
Nguyễn Hoàng Việt 0905193688 Trang: 25
Phục dựng hình ẩn
BC  1, CD  3 , BD  2 2 2 2
BC DC BD B
CD vuông tại C .
Dựng hình chữ nhật BCDE BC // ED mà DC BC DC DE , lại có DC AD
DC   ADE  DC AE (1).
Chứng minh tương tự BC   ABE  BC AE (2).
Từ (1) và (2) suy ra AE  BCDE .
Kẻ EH AD tại H . Do DC   ADE nên DC EH EH   ACD .
BE // CD d  ,
B ACD  d E, ACD  EH . 2 2 AE AB BE    2 2 3 3  6 . 1 1 1   1 7  1  6 42  EH   . 2 2 2 EH EA ED 6 6 7 7
Vậy d B ACD 42 ,  EH  . 7
Câu 18. Cho hình chóp S.ABC có AB  2, AC  3, BC  4 , SA vuông góc với mặt đáy và SA 1.
Gọi H , K lần lượt là hình chiếu của A lên SB và SC . Gọi  là góc giữa hai mặt phẳng
AHK và ABC, giá trị tan bằng 16 15 Ⓐ. . Ⓑ. 15 . Ⓒ. 4 . Ⓓ. 6 15 . 15 5 Lời giải Chọn A
Nguyễn Hoàng Việt 0905193688 Trang: 26
Phục dựng hình ẩn BM AB
Gọi AM là đường kính của đường tròn ngoại tiếp tam giác ABC . Khi đó  . CM   AC Lại có: BM SABM  
SAB BM AHAH SBAH   SBM       . Mà    CM   SA CM   SACCM AKAK SCAK   SCM  AH SM  
SM   AHK  . AK SM
Mặt khác SA   ABC nên    ABC, AHK   S ,
A SM   SAM AM 2R  tan ABC      2R . SA 1 ABC 3 15 A . B AC.BC 8 15
Lại có: theo công thức Hê- rông S   R   ABC   4 ABC 4S 15 ABC  16 15  tan  . 15
Câu 19. Cho hình chóp S.ABC có AC  ,
a AB a 3, BAC  150 và SA vuông góc với mặt đáy.
Gọi M , N lần lượt là hình chiếu vuông góc của A trên SB và SC . Thể tích của khối
cầu ngoại tiếp hình chóp . A BCNM bằng 3 4 7 a 3 44 11 a 3 28 7 a 3 20 5 a Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. . 3 3 3 3 Lời giải
Nguyễn Hoàng Việt 0905193688 Trang: 27
Phục dựng hình ẩn Chọn C
Dựng đường tròn tâm O là đường tròn ngoại tiếp tam giác ABC . Kẻ đường kính AQ Xét tam giác ACB : 2 2 2 2 2 2 o 2
BC AB AC  2.A .
B AC.cos BAC  3a a  2.a . 3.cos150  7a BC a 7 BC a 7 R  
a 7  AO a 7 ABC  2sin A 2.sin150o
Vì AQ là đường kính đường tròn tâm O , điểm B thuộc đường tròn này nên QB AB . QB AB Ta có:
  QB  SAB  QB AM QB SA AM QB Ta có:
  AM  SQB  AM QM A
MQ vuông tại M . AM SB
Chứng minh tương tự ta được: A
NQ vuông tại N
Ta có các tam giác: AB , Q AM , Q AN , Q A
CQ là các tam giác vuông lần lượt ở ,
B M , N,C Do đó các điểm , A ,
B C, N, M thuộc mặt cầu đường kính AQ
 Bán kính mặt cầu ngoại tiếp hình chóp .
A BCMN bằng AO a 7  4 4 28 7 a
V   R   a 7  3 3 3  . 3 3 3
Câu 20. Cho hình chóp S.ABC có SA AB  3 ; SB  6 ; AC  2BC  2 ; SC  5 . Khoảng
cách từ A đến SBC bằng 30 5 13 Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. 30 . 5 2 6 3 Lời giải
Nguyễn Hoàng Việt 0905193688 Trang: 28
Phục dựng hình ẩn
Dựng điểm D sao cho ABCD là hình chữ nhật.
Áp dụng định lý Pitago ta có các tam giác SAB ; ABC ; SBC lần lượt vuông góc tại , A , B C . AB AD Ta có 
AB SD  1 BA SABC CD
BC SD2 .Từ  
1 ;2  SD   ABCD  SD BC . Vậy BC SC
SBC  SDC theo giao tuyến SC . Kẻ DH vuông góc với SC tại H thì
DH  SBC . DS.DC 2. 3 30
Có AD SBC  d  ,
A SBC   d  ,
D SBC   DH    . 2 2 DS DC 5 5
Câu 21. Cho hình chóp S.ABC có đáy là tam giác vuông tại A , AB  2a , AC a . Các tam giác
SBA và SCA lần lượt vuông tại B và C . Biết khoảng cách từ B đến mặt phẳng SAC
bằng a 2 , cosin của góc tạo bởi đường thẳng SC và SAB bằng 1 1 2 2 3 Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. . 10 3 3 10 Lời giải Chọn D
Nguyễn Hoàng Việt 0905193688 Trang: 29
Phục dựng hình ẩn
d C,SAB
Gọi   SC,SAB  sin  . SC
Gọi H là hình chiếu của S lên mặt phẳng  ABC  SH AB , SH AC .
Theo giả thiết các tam giác SBA và SCA lần lượt là các tam giác vuông tại B và C
SB AB , SC AC . SH AB Khi đó 
HB AB  1 . SB ABSH AC
HC AC 2 . SC AC
Từ (1) và (2) suy ra H là đỉnh thứ tư của hình chữ nhật BACH .
Gọi I và K lần lượt là hình chiếu của H lên SC và SB .
Ta có HB// SAC  d  ,
B SAC  d H,SAC  HI a 2 . 1 1 1 1 1 1 1 1 1
Xét tam giác vuông SHC :         2 2 2 HI HS HC 2 2 2 HS HI HC 2 2 2 HS 2a 4aSH  2a . 2 2 2 2 2 2
SC SH HC  4a  4a  8a SC  2a 2 .
Mặt khác HB// SAC  d C,SAB  d H,SAB  HK . 1 1 1 a
Xét tam giác vuông SHB :   2  HK  . 2 2 2 HK HS HB 5 HK 2a 1  sin     1 3 cosin  1  . SC 5.2a 2 10 10 10
Câu 22. Trong không gian 2 2
Oxyz , cho mặt cầu S  2
: x   y  3   z  6  45 và M 1; 4;5 . Ba
đường thẳng thay đổi d , d , d nhưng đôi một vuông góc tại O cắt mặt cầu tại điểm 1 2 3 thứ hai lần lượt là , A ,
B C . Khi khoảng cách từ M đến mặt phẳng  ABC lớn nhất thì
phương trình mặt phẳng  ABC là
Ⓐ. x  2y z 8  0 . Ⓑ. 2x y z  4  0 . Ⓒ. x y  2z 1  0. Ⓓ. x y z 3  0 Lời giải Chọn A
Nguyễn Hoàng Việt 0905193688 Trang: 30
Phục dựng hình ẩn
Mặt cầu S  có tâm I 0;3;6, R  3 5 Nhận xét:
1. O thuộc mặt cầu S
2. OABC là một tứ diện vuông nội tiếp mặt cầu S  nên tồn tại một hình hộp chữ nhật OAD .
B CEFG nội tiếp mặt cầu S  .
3. Gọi H là trung điểm AB , J OI CH J là trọng tâm tam giác OCD . 2
Ta có: OJ OI J 0;2;4 . 3
Mặt phẳng  ABC luôn qua J cố định.
Đánh giá: d M, ABC  MJ d M , ABC
MJ   ABC qua J và nhận JM Max làm vectơ pháp tuyến.
Phương trình có dạng: x  2y z 8  0 .
Câu 23. Cho hình chóp đều S.ABC có SA a . Gọi ,
D E lần lượt là trung điểm của hai cạnh S ,
A SC . Biết BD vuông góc với AE , chiều cao của hình chóp S.ABC bằng a 21 a 3 a 7 a Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. . 3 6 3 3 Lời giải Chọn C S D E C A B K I
Dựng hình thoi ABIC , gọi K là trung điểm BI .
Khi đó DE song song và bằng BK nên tứ giác BDEK là hình bình hành.
BD / /KE AE KE (Do AE BD ).
Đặt AC x , ta có 2 2 2 2 2
AK AE EK  2BD AK 2 2 2 2 2  x a a  7x a 6    a 6 a 7 2     x  . Do vậy 2 h a     .  2 4  4 3   3 3 3  
Bình luận: Bài toán trên có thể giải bằng nhiều cách dựng thêm hình khác nhau để
khai thác tính chất đường thẳng AE vuông góc với đường thẳng BD , hoặc có thể
khai thác giả thiết này theo cách sử dụng phương pháp véc tơ, tọa độ hóa.
Nguyễn Hoàng Việt 0905193688 Trang: 31
Phục dựng hình ẩn
Câu 24. Cho tứ diện ABCD có tam giác ABD đều cạnh bằng 2 , tam giác ABC vuông tại B , 3
BC  3 . Khoảng cách giữa hai đường thẳng AB và CD bằng . Thể tích của khối 2
tứ diện ABCD bằng 3 1 3 Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. 1 . 2 2 6 6 Lời giải Chọn A
Dựng hình chữ nhật ABCE .
Gọi M , N lần lượt là trung điểm của A , B CE . 3 Xét ABD
đều có DM là đường trung tuyến nên DM AB, DM  .AB  3. 2
Từ M kẻ MH DN . Khi đó ta có CE MN   .         ABCEDMNCE MH CE DM CE / /
Do đó d AB CD  d M CDE 3 , ,  MH  . 2 Suy ra    
DN DH HN
DM MH MN MH   3 2 3        3 2 2 2 3 2 2 2 2     3   . 2 2    
Ta có CE MH CE DN 2 2 2
CD DN NC  3 1  10 DN Ta có
AB CD  CE CD 3 sin , sin ,  sin ECD   DC 10 1 1 3 3 3 Vậy V  .A . B C . D d AB CD AB CD   ABCD  , .sin ,  .2 10. . . 6 6 2 10 2
Câu 25. Cho tứ diện ABCD có AB BC CD  2 , AC BD 1, AD  3 . Bán kính mặt cầu
ngoại tiếp tứ diện ABCD bằng 7 39 2 3 Ⓐ. 1. Ⓑ. . Ⓒ. . Ⓓ. . 3 6 3
Nguyễn Hoàng Việt 0905193688 Trang: 32
Phục dựng hình ẩn Lời giải Chọn C
Gọi M , N lần lượt là trung điểm của BC, AD Ta có BAD C
DA BN CN . Suy ra MN là đường trung trực của BC .
Tương tự MN là đường trung trực của AD .
Khi đó tâm mặt cầu ngoại tiếp tứ diện là điểm I sao cho IB IA. 3 7
Tam giác ABD vuông tai D nên 2 2 2
BN BD DN  1  . 4 4 2 2 2 BN CN BC 14 6 3 2 MN   1    1 . 2 4 8 8 4 3 Ta có 2 2 2 2 2 2 MN
R BM R AN R 1  R  2 . 4 3 3 Từ   1 ,2 ta có 2 2 R 1  R  2  . 4 2 39
Sử dụng máy tính được nghiệm là R
. ( hoặc dùng phím CACL thử đáp án) 6
Câu 26. Cho hình chóp S.ABC có ASB  60 ,
BSC  90 , CSA 120 , SA  , a SB  2 , a SC  3 . a
Sin của góc giữa hai mặt phẳng SBC và SAB bằng 6 6 6 Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. 6 . 6 3 4 5 Lời giải Chọn B S K A B' H M C'
Nguyễn Hoàng Việt 0905193688 Trang: 33
Phục dựng hình ẩn + Trên cạnh S ,
B SC lần lượt lấy các điểm B ',C ' sao cho SB '  SC '  a SA SB '  SC '
. Gọi H là chân đường cao của hình chóp S.AB'C '  H là tâm đường tròn ngoại tiếp
tam giác AB 'C ' .
Từ giả thiết suy ra AB '  ,
a B 'C '  a 2, AC '  a 3 2 2 2
AB'  B'C '  AC '  AB'C '
vuông tại B '  H là trung điểm của cạnh AC ' .
+ Kẻ HM B 'C '( M là trung điểm của B 'C ' ), HK SM HK  SB 'C '
HK d H,SB'C ' 2 2 3a a a Ta có 2 2 2 2
SH SA AH a    SH   S
HM vuông cân tại 4 4 2 a 2 H HK  . 4 a
+ Tam giác SAB ' là tam giác đều  d A SB  3 , '  . 2
+ Đặt  là góc giữa hai mặt phẳng SBC và SAB    SB'C ',SAB'.
d A SB C 
d H SB C  a 2 2. , ' ' 2 , ' ' 6 Ta có 4 sin     . d  , A SB ' d  , A SB ' a 3 3 2
Câu 27. Cho hình chóp S.ABC có ASB BSC CSA  60 và SA  2, SB  3, SC  4. Thể tích của
khối chóp S.ABC bằng Ⓐ. 4 3 . Ⓑ. 2 3 . Ⓒ. 2 2 . Ⓓ. 4 2 . Lời giải Chọn C Trên tia S ,
A SB lần lượt lấy các điểm M , N sao cho SM SN  4.
Khi đó ta có các tam giác SCM , SCN và SMN đều  SMNC là tứ diện đều cạnh SC  4 .
Gọi H là hình chiếu vuông góc của S trên mặt phẳng CMN  thì H là tâm của tam giác CMN .
Nguyễn Hoàng Việt 0905193688 Trang: 34
Phục dựng hình ẩn 2 2 4 3 4 3 4 6 Khi đó ta có 2 2 MH MK  . 
SH SM MH  . 3 3 2 3 3 1 S
CM.CN.sin MCN  1 16 2 4 3  VSH.S  . CMN  2 SCMN 3 CMN 3 V SA SB SC 3 3
Mặt khác ta có S.ABC  . .  VV  2 2 . S . ABC S . V SM SN SC 8 8 MNC S .MNC
Câu 28. Cho hình chóp S.ABC có SA  4, SB  6, SC 12 và ASB  60 ,
BSC  90 và CSA 120
. Thể tích của khối chóp S.ABC bằng Ⓐ. 36 3 . Ⓑ. 36 2 . Ⓒ. 24 3 . Ⓓ. 24 2 . Lời giải Chọn D Trên tia S ,
A SB lần lượt lấy cá điểm M , N sao cho SM SN 12 . Khi đó ta có :
Tam giác SMN đều  MN 12 .
Tam giác SNC vuông tại S nên CN SC 2 12 2 .
Tam giác SMC cân tại S có 2 2 MC
SC SM  2S .
C SM.cos CSM  12 3 . Từ đó suy ra 2 2 2
MC MN CN  tam giác CMN vuông tại N .
Gọi H là hình chiếu vuông góc của S trên mặt phẳng CMN  .
Vì SC SM SN 12 nên H là tâm đường tròn ngoại tiếp tam giác CMN H là
trung điểm của MC 2 2
SH SC CH  6 . 1 1 S
MN.NC  72 2 V  .SH.S 144 2 . CMN 2 S .CMN 3 CMN V SA SB SC 1 1
Mặt khác, ta có S.ABC  . .  VV  24 2 . V SM SN SC 6 S .ABC S. 6 MNC S .MNC
Câu 29. Cho tứ diện ABCD , có tam giác BCD đều, hai tam giác ABD và ACD vuông cân đáy
AD . Điểm G là trọng tâm tam giác ABC . Gọi M , N lần lượt là trung điểm BC và AD
. Gọi  là góc giữa hai mặt phẳng CDG và MNB , giá trị cos bằng 1 1 1 Ⓐ. . Ⓑ. 0 . Ⓒ. . Ⓓ. . 11 11 11 Lời giải Chọn C
Nguyễn Hoàng Việt 0905193688 Trang: 35
Phục dựng hình ẩn
Cách1. Ta khôi phục về chóp tứ giác đều tất cả các cạnh bằngnhau\
Gọi K là trung điểm AB . Thì I DK BN I là trọng tâm tam giác ABD
CDG,MNB  CDK,CNB  .
Rõ ràng BN   ACD và ND CN .
Tứ diện đã cho là nửa chóp tứ giác đều tất cả các cạnh bằng nhau. Chọn cạnh bằng 1
Nên chọn hệ trục toạ độ N O0;0;0 .
Gọi cạnh AB  2  AD  2 2  CN BN ND NA  2  2 
D  2;0;0,C 0; 2;0, B0;0; 2   I 0;0;    . 3  
Mặt phẳng CDK  cắt O ,
x Oy,Oz lần lượt tại ,
D C, I nên có phương trình dạng: x y z  
1, suy ra VTPT củaCDK  là n  1;1;3 CDK    2 2 2 / 3
ND   BNC  ND   2;0;0  i  1;0;0 là VTPT của mặt phẳng BNC . i n CDK 1  cos   i .  n CDK 11
Cách 2. Phương pháp khoảng cách để tính góc.
Nguyễn Hoàng Việt 0905193688 Trang: 36
Phục dựng hình ẩn
d D,CNB
 sin  dD,CI
ND  CNB  ND d  ,
D CNB . S 1 d D CI  2 , CDI
. Từ đó ta cũng tính được cos  CI 11
Cách 3. Phương pháp đa giác chiếu để tính góc. S 1 cos INC  
. Từ đó ta cũng tính được cos  S 11 IDC
Cách 4. PP xác định góc để tính góc.
Kẻ NE CI, E CI , ta chứng minh được DE IC    ND 1
NED , ta tính được tan   10  cos  NE 11
Câu 30. Ba quả bóng dạng hình cầu có bán kính bằng 1 đôi một tiếp xúc nhau và cùng tiếp xúc
với mặt phẳng  P . Mặt cầu S  bán kính bằng 2 tiếp xúc với ba quả bóng trên. Gọi
M là điểm bất kỳ trên  S  . Khoảng cách lớn nhất từ điểm M đến mặt phẳng  P bằng 123 52 30 Ⓐ. 3  . Ⓑ. . Ⓒ. 3  . Ⓓ. 69 3  . 4 9 2 3
Nguyễn Hoàng Việt 0905193688 Trang: 37
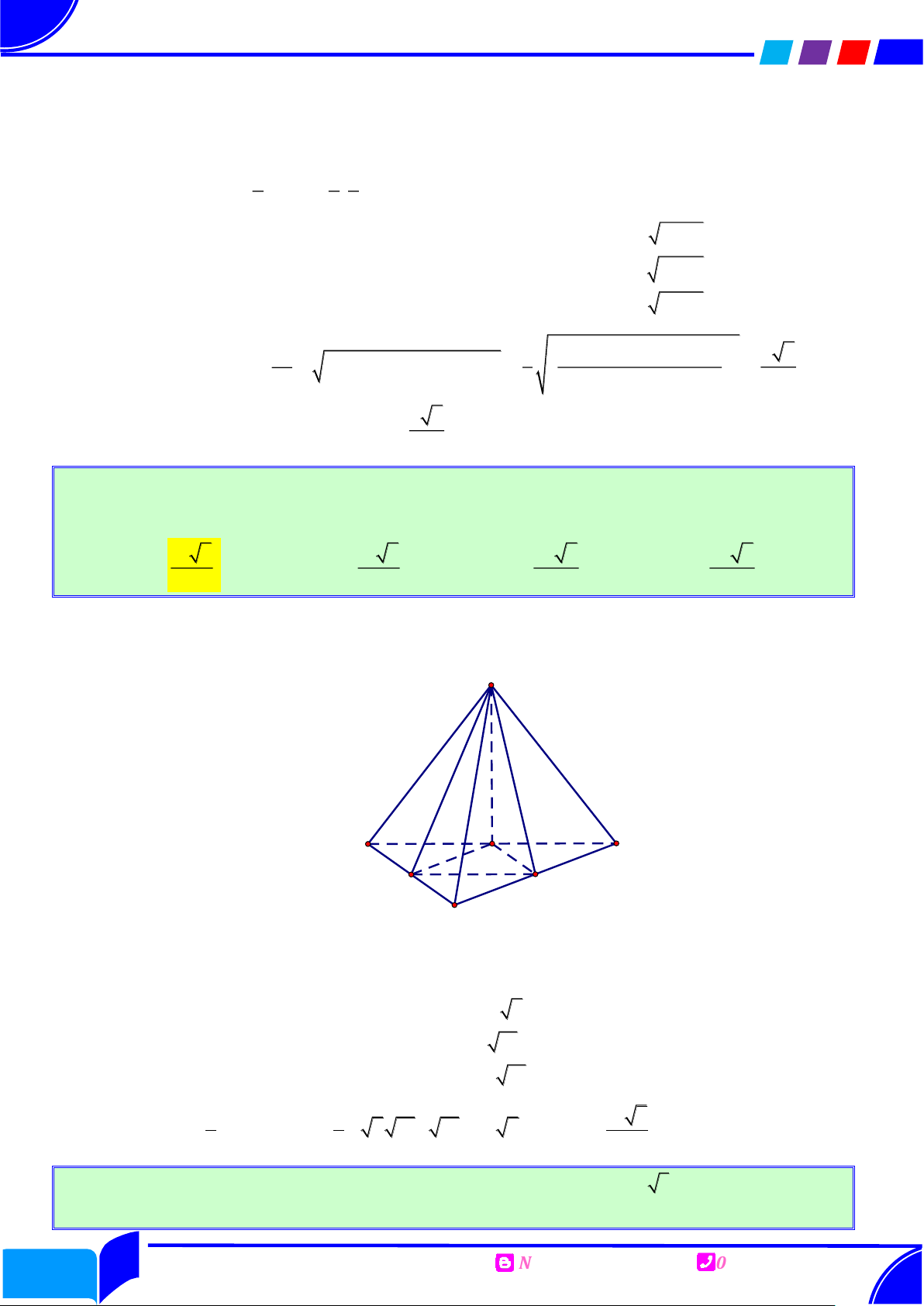
Phục dựng hình ẩn Lời giải Chọn D
Gọi tâm quả ba quả cầu nhỏ là A , B , C và tâm của quả cầu lớn bên trên là S .
Khi đó S.ABC là chóp tam giác đều có cạnh đáy là 2 và cạnh bên là 3 .
Gọi O là chân dường cao của chóp S.ABC . Gọi H là hình chiếu của M lên mặt phẳng P
Suy ra MH lớn nhất khi M , S , O , H thẳng hàng. MH
MS SO OH  2  SO 1. max 2  2  69 Ta có: 2 2 2 SO
SA AO  3  . 3    .  3  3 69 Suy ra: MH  3 SO  3 . max 3
Câu 31. Người ta thả vào bên trong một cái ống nước dạng hình trụ 4 quả bóng tenis có cùng
bán kính bằng 1. Biết rằng các quả bóng tiếp xúc với nhau và tiếp xúc với các đường
sinh của ống hình trụ. Biết chiều cao của ống bằng 2 . Thể tích của ống nước đó bằng
Nguyễn Hoàng Việt 0905193688 Trang: 38
Phục dựng hình ẩn
Ⓐ. 3 2 2 .
Ⓑ. 1 2 .
Ⓒ. 6  4 2 . Ⓓ. 2  2 2 . Lời giải Chọn C
Gọi tâm của 4 quả bóng lần lượt là , A ,
B C, D như hình vẽ.
Khi đó ABCD là hình vuông với cạnh bằng 2R  2.1  2  AC  2 2 .
MAAC CN 1 2 2 1
Do đó bán kính đáy của hình trụ là: r   1 2 . 2 2 2
Vậy thể tích ống nước đó là: 2
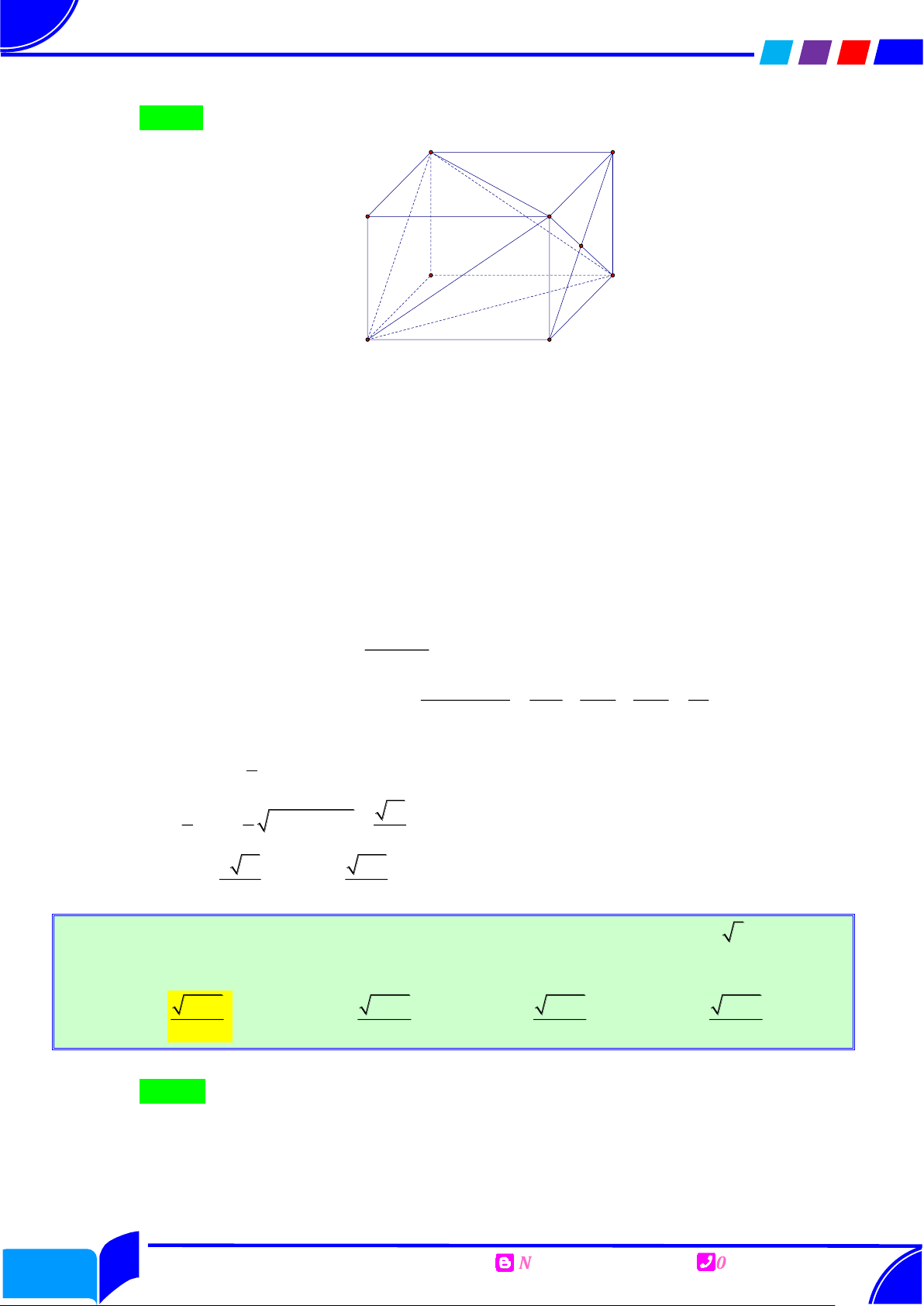
V   r h  .1 2 .2  6  4 2 . A G B D E F C
Câu 32. Cho tứ diện ABCD có AB CD  10 , AD BC  5 , AC BD  13 . Gọi  là góc
giữa AB và  ACD , giá trị cos bằng 6 10 865 10 Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. 3 10 . 35 35 10 10
Nguyễn Hoàng Việt 0905193688 Trang: 39
Phục dựng hình ẩn Lời giải Chọn B A F D E I G C B H
Dựng hình hộp AEDF.GBHC .
Do các cạnh đối của tứ diện ABCD bằng nhau nên các đường chéo của mỗi mặt của
hình hộp bằng nhau suy ra AEDF.GBHC là hình hộp chữ nhật. Đặt AE  ,
x AF y, AG z  ,
x y, z  0 . 2 2
x y  5  x 1   Ta có hệ: 2 2
y z 13  y  2  2 2  z x  10 z  3  
Ta thấy: AB // HF   A ;
B ACD  HF; ACD
dF ;ACD
Gọi I HF CD  sin  . IF 1 1 1 1 49
Tứ diện FACD vuông tại F nên:     2 2 2 2   FA FD FC 36 d
 F ;ACD  6  d  . F  ; ACD 7 1 1 10 2 2 FI FH FC FD  . 2 2 2 6 10 865  sin   cos  . 35 35
Câu 33. Cho tứ diện ABCD có các cạnh AD BC  3 ; AC BD  4; AB CD  2 3 . Thể tích tứ diện ABCD bằng 2470 2047 2474 Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. 2740 . 12 12 12 12 Lời giải Chọn A
Nguyễn Hoàng Việt 0905193688 Trang: 40
Phục dựng hình ẩn
Từ các đỉnh của tam giác BCD ta kẻ các đường thẳng song song với cạnh đối diện
chúng tạo thành tam giác EFG có diện tích gấp 4 lần diện tích tam giác BCD .
Các tam giác AEF , AFG , AGE là các tam giác vuông tại A nên ta có: 2 2 2
AE AF EF  64   1 ; 2 2 2
AF AG FG  36 2 và 2 2 2
AE AG EG  48   3 . Từ  
1 , 2 , 3 ta có:  2 2 2
2 AE AF AG  148 2 2 2
AE AF AG  74 4 . Từ   1 , 4 ta có: 2
AG  10  AG  10 .
Từ 2 , 4 ta có: 2
AE  38  AE  38 .
Từ 3 , 4 ta có: 2
AF  26  AF  38 . 1 1 1 Thể tích khối chóp .
A EFG là : V   A . E AF.AG  9880  2470 . 6 6 3 1 2470
Do đó thể tích tứ diện ABCD là : V V   . 4 12
Câu 34. Cho hình chóp S.ABC có độ dài các cạnh SA BC x , SB AC y , SC AB z thỏa mãn 2 2 2
x y z  12 . Giá trị lớn nhất của thể tích khối chóp S.ABC bằng 2 2 2 3 2 3 2 Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. . 3 3 3 2 Lời giải Chọn A S E x y z A y C z x D F B
Nguyễn Hoàng Việt 0905193688 Trang: 41
Phục dựng hình ẩn
Trong mặt phẳng  ABC dựng D , E , F sao cho A , B , C lần lượt là trung điểm của
DE , DF , EF . Khi đó ta có DE  2SA  2x ; DF  2SB  2y ;  2SC  2z . Suy ra SD ,
SE , SF đôi một vuông góc. 1 1 1 Ta có VV  . .S . D S . E SF . S.ABC S . 4 DEF 4 6 2 2 2 2  2 2 2 
SD  2x y z  2
SD SE  4x SD  2 6  z    Mặt khác 2 2 2
SD SF  4y 2  SE  2 2 2 2
x z y  2
 SE  2 6  y .    2 2 2 SE SF  4  z 2 SF  2 2   2 2 2
y z x  SF  2 6   x 3 1 2 2 2
1  6  x  6  y  6  z  2 2 Khi đó V  .8. x y z     . ABCD  2 6   2 6   2 6  S .  24 3  3  3 2 2 Vậy V
đạt giá trị lớn nhất là . S. ABC 3
Câu 35. Cho tứ diện ABCD có AB CD  4; AC BD  5; AD BC  6 . Thể tích của khối tứ diện ABCD bằng 15 6 15 6 45 6 45 6 Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. . 4 2 4 2 Lời giải Chọn A A M K D B C N
Dựng tứ diện AMNK , sao cho ,
B C, D là trung điểm của các cạnh
MN, NK, KM . Tứ diện AMNK vuông tại . A 2 2 2
AM AN  64 AM  54 AM  3 6    2 2 2
AN AK 100  AN 10  AN  10 .    2 2 2
AK AM  144 AK  90 AK  3 10    1 1 15 6 V
AM.AN.AK  .3 6 10.3 10 15 6 V  . AMNK 6 6 ABCD 4
Câu 36. Xét khối tứ diện ABCD có AB x và các cạnh còn lại bằng 2 3. Giá trị của x để thể
tích của khối tứ diện ABCD lớn nhất là
Nguyễn Hoàng Việt 0905193688 Trang: 42
Phục dựng hình ẩn
Ⓐ. x  6 .
Ⓑ. x  2 2 .
Ⓒ. x  14 .
Ⓓ. x  3 2 . Lời giải Chọn D
Gọi H là trung điểm của cạnh AB , do ABC
cân tại C nên CH là đường cao. Tam
giác ABD có AD BD  2 3 nên là tam giác cân tại D . Do đó HD là đường cao. Khi CH AB đó ta có 
AB  CHD . HD AB
Hạ đường cao CK xuống HD khi đó CK A .
B Do đó CK   ABD. Vậy CK là đường x
cao của tứ diện. Ta có HB
. Áp dụng định lý Py-ta-go cho tam giác HBC ta có 2      x   x HC BC HB 2 3 2 2 2 48 2 2      2  2 2 48  x
Tương tự, ta có HD  . Đặt y
KD . Áp dụng định lý Py-ta-go cho tam giác 2
CHK và CKD ta có
CK CH HK CD KD CH  HD y2 2 2 2 2 2 2 2 12  y . 6 12 2 2 2 2
CH HD  2H .
D y y  12  y y   2 HD 48  x . Vì vậy 12  2
48  x  12 12   2 36  x  12 2 36 12  x 2 2 2  CK  D Cy 12     CK  2 2 2 2  48  x 48  x 48 48  x x 2 2 1 1 48  x x 48  x
Diện tích tam giác ABD là S A . B HD x  1 2 2 2 4 12 2 36 1 1  x  2 x 48  x 1
Do đó thể tích tứ diện là 2 V CK.S  .  3. . x 36  x 1 2 3 3 48  x 4 6
Áp dụng bất đẳng thức Cô-si cho  2 , x 36  x  , 2 x   2 36 3 3  x 2  ta có V  . x 36  x   3 3. 6 6 2
Dấu bằng xảy ra khi và chỉ khi 2
x  36  x x  18  3 2
Nhận xét.Chúng ta có thể thay điều kiện các cạnh còn lại bằng 2 3 bởi điều kiện các
cạnh còn lại bởi một số a  0 nào đó bất kì, để được một bài toán khác nhưng cách làm tương tự bài này.
Câu 37. Cho tứ diện ACFG có số đo các cạnh lần lượt là AC AF FC a 2, AG a 3,
GF GC a . Thể tích của khối tứ diện ACFG bằng 3 a 3 a 3 a 3 15a Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. . 6 3 12 3
Nguyễn Hoàng Việt 0905193688 Trang: 43
Phục dựng hình ẩn Lời giải Chọn A
Dựng hình lập phương như hình vẽ Khi đó ABC .
D EFGH là hình lập phương cạnh a nên thể tích của hình lập phương là 3 V a .
Thể tích tứ diện ACGF có được là do ta chia hình lập phương theo các mặt phẳng 3  1 1 1 a
ACGE  ,  ACF  và  AGF  . Khi đó ta có VV  . VACGF ABC.EFG ABCD. 3 2 3 EFGH 6
Câu 38. Cho hình chóp tam giác S.ABC có đáy là tam giác vuông cân tại A ; AB AC  ; a SA a 3 . Các tam giác SA ;
B SAC lần lượt vuông tại ; B C . Gọi ;
O M lần lượt là trung điểm của BC; SC .
Gọi  là góc giữa hai mặt phẳng OMA;SAB , giá trị tan bằng 1 2 3 Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. 3 . 3 2 6 Lời giải Chọn B
Dựng hình vuông ABDC
Nguyễn Hoàng Việt 0905193688 Trang: 44
Phục dựng hình ẩn AC SC Ta có: 
AC  SCD  AC SD AC DCAB DB
AB SBD  AB SD AB SB
SD   ABCD
OMA;SABDMA;SAB 
DMA  OM  
SAB  SB  DM A SAB  AE AE / /SB / /OM  OM / /SBd  ; D SAB sin  d  ; D AE
Ta có: SC SB a 2  SD a a
DA DE AE a 2  A
DE đều  d D AE 6 ;  2 a
Kẻ DK SB DK  SAB  d D SAB 2 ;  DK  ( S
AD vuông cân tại D ) 2 3 6 2  sin   cos   tan  . 3 3 2
Câu 39. Cho tứ diện ABCD có ABC là tam giác đều cạnh 2a , AD a 3 và AD vuông góc
với AB và AC . Gọi E, F lần lượt là trung điểm của các đoạn thẳng BC và DE. Góc
giữa AF với CD bằng Ⓐ. 45 . Ⓑ. 60 . Ⓒ. 90. Ⓓ. 30. Lời giải Chọn C
Dựng thêm từ tứ diện ABCD thành hình hộp. 1 1 1
Ta có AF   AD AE  AD   AB AC. 2 2 4 1 1 1 Suy ra AF.CD A . D CD A . B CD AC.CD 2 4 4
Nguyễn Hoàng Việt 0905193688 Trang: 45
Phục dựng hình ẩn 1
ADAD AC 1
ABAD AC 1
AC AD AC 2 4 4 2 2 1 1 1 3 1 2 2 2
AD ABAC AC a a a  0. 2 4 4 2 2
Vậy số đo góc giữa AF và CD bằng 90 .
Câu 40. Cho tứ diện ABCD có AB 1;CD  2; ABC DAB  90. Góc giữa hai đường thẳng A ;
D BC bằng 30 . Bán kính của mặt cầu ngoại tiếp tứ diện ABCD bằng 5 2 Ⓐ. . Ⓑ. . Ⓒ. 5 . Ⓓ. 2 . 2 2 Lời giải Chọn A
Dựng AE BC và BF AD ta được lăng trụ đứng AD . E BFE Góc  A ,
D BC   A , D AE  30 , 2 2
ED CD CE  1 . 2 h
Bán kính mặt cầu ngoại tiếp lăng trụ đứng này là 2 R R d 4 ED ED 2  h 1 5 2R R  1 suy ra 2 R R   1  . d d d sin EAD 2sin EAD 4 4 2
Câu 41. Cho lăng trụ tam giác đều AB . C A BC
 , gọi I là trung điểm A B
  và  là góc giữa AC
với  BIC . Biết AA  ;
a AB  2a , giá trị cos bằng 15 10 3 2 Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. . 5 5 5 5 Lời giải Chọn A
Nguyễn Hoàng Việt 0905193688 Trang: 46
Phục dựng hình ẩn d  ,
A BIC '
AC  BIC  C,  là Góc giữa AC ' và  BIC ' , Ta có sin  . AC '
Ta có BIC '   ABB A
  ( Vì C I   ABB A
 , BIC ' ABB A    IB
Gọi K là trung điểm IB suy ra B K
  IB . Suy ra B'K  BIC '
Suy ra d B',BIC '  B' K .
Mặt khác I là trung điểm A' B ' nên d A',BIC '  d B ',BIC '  B ' K . EA'
d A',BIC '
Gọi E là giao điểm của A' A và BI suy ra E A' A BIC ' nên  . EA d  ,
A BIC ' EA' A' I 1 Mặt khác 
 Do AB / /A'I  . EA AB 2 EA'
d A',BIC ' 1 a 2 Suy ra     d  ,
A BIC '   2d A', BIC '   B K   a . EA d ,
A BIC '     2 ' 2. 2 2 2
AC   A A2   A C 2 ' ' ' '  a 5 . d  ,
A BIC ' a 2 10 15 sin    suy ra cosin  . AC ' a 5 5 5
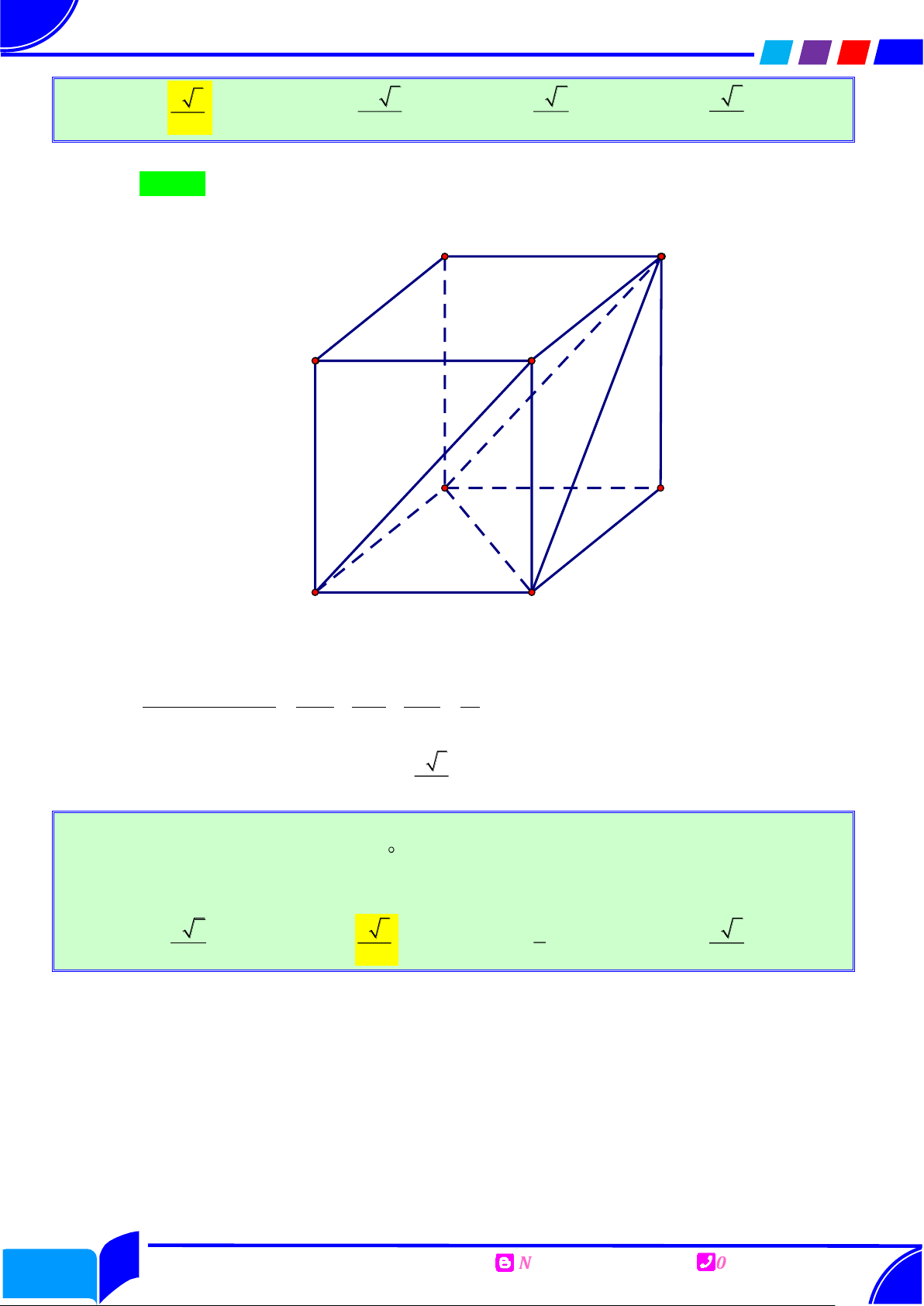
Câu 42. Cho hình lăng trụ đứng AB . C A BC
  có đáy ABC là tam giác vuông tại B , BA BC a
, cạnh bên bằng a . Khoảng cách giữa hai đường thẳng A B  và B C  bằng
Nguyễn Hoàng Việt 0905193688 Trang: 47
Phục dựng hình ẩn a 3 2a 3 a 6 a 3 Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. . 3 3 2 6 Lời giải Chọn A
Dựng hình lập phương ABC . D A BCD   . Khi đó B C  //  A DB. D' A' C' B' D A C B
Suy ra d A , B B C
   d B C  ,A B
D  d C,A B
D  d  , A A BD. Ta thấy . A A BD là tứ diện vuông đỉnh A nên 1 1 1 1 3     .     2 2 2 2 2  ' , ' AA AB AD a d A A BD a Vậy d A BB C
   d A A BD 3 , ,  . 3
Câu 43. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a . SA vuông góc với mặt đáy. Góc
giữa SAB và SCD bằng 45 . Gọi M là trung điểm của SB , khoảng cách giữa AM và SD bằng a 2 a 3 a a Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. 5 . 2 3 2 4
Nguyễn Hoàng Việt 0905193688 Trang: 48
Phục dựng hình ẩn Lời giải Chọn B
Ta có góc giữa SAB và SCD bằng ASD 45 SA a .
Dựng hình lập phương ABC .
D SB 'C ' D ' như hình vẽ a 3
Khi đó d AM ; SD d
B ' AC ; SC ' D . 3
Câu 44. Cho tứ diện ABCD có AB CD
a ; AD BC b ; BD AC c . Bán kính mặt cầu
ngoại tiếp tứ diện ABCD bằng 2 2 2 a b c 2 2 2
a b c 2 2 2 a b c 2 2 2 a b c Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. . 2 8 8 2 Lời giải Chọn B
Nguyễn Hoàng Việt 0905193688 Trang: 49
Phục dựng hình ẩn A E a F c B b b c H C a K D
Dựng hình hộp chữ nhật AEBF.HCKD . Đặt AH , x AE y, ÀF z . 2 2 2 x y c 2 2 2 a b c Ta có hệ 2 2 2 2 2 2 2 x z b x y z AK . 2 2 2 2 y z a 2 2 2 AK a b c Do đó R . 2 8
Nguyễn Hoàng Việt 0905193688 Trang: 50
Document Outline

  • P0-phục dụng hình ẩn
  • P1-phục dụng hình ẩn
  • P2-phục dụng hình ẩn