Chuyên đề phương pháp toạ độ trong không gian ôn thi THPT 2021 – Nguyễn Bảo Vương

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương  https://www.facebook.com/phong.baovuong Trang 1

TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH TRUNG BÌNH MỨC 5-6

Lý thuyết chung

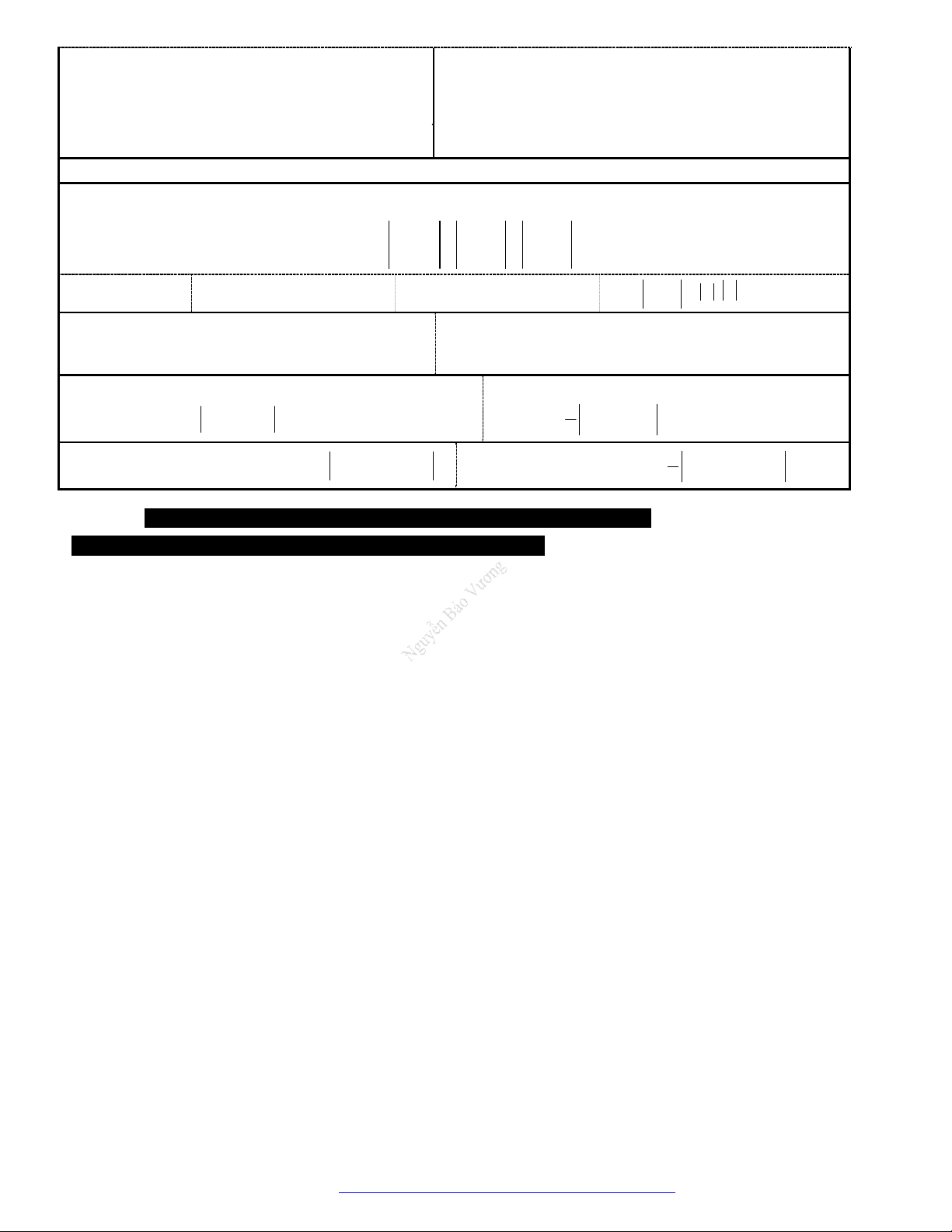
1. Hệ trục tọa độ Oxyz:

Hệ trục gồm ba trục

, ,Ox Oy Oz

đôi một vuông góc nhau.

Trục

:Ox

trục hoành, có vectơ đơn vị

(1;0;0)i





.

Trục

Oy

: trục tung, có vectơ đơn vị

(0;1;0)j





.

Trục

:Oz

trục cao, có vectơ đơn vị

(0;0;1).k





Điểm

(0;0;0)O

là gốc tọa độ.

2. Tọa độ vectơ: Vectơ

( ; ; )u xi y j zk u x y z

    

    

.

Cho

1 2 3 1 2 3

( ; ; ), ( ; ; )a a a a b b b b

 

 

. Ta có:



1 1 2 2 3 3

( ; ; )a b a b a b a b



    



a



cùng phương

b



( )a kb k R

 

  

1 1

3

1 2

2 2 1 2 3

1 2 3

3 3

, ( , , 0).

a kb

a

a a

a kb b b b

b b b

a kb







     











1 2 3

( ; ; )ka ka ka ka







1 1

2 2

3 3

a b

a b a b

a b

 







  











1 1 2 2 3 3

. . . .a b a b a b a b



  



2 2 2

1 2 2

a a a a



  



2

2 2 2 2

1 2 3

a a a a a



   



1 1 2 2 3 3

. 0 0a b a b a b a b a b

   

      



1 1 2 2 3 3

2 2 2 2 2 2

1 2 3 1 2 3

.

cos( , )

.

a b a b a b

a b

a a a b b b



 

 

   

3. Tọa độ điểm:

( ; ; ) ( ; ; )M x y z OM x y z



 

. Cho

( ; ; ) , ( ; ; ) , ( ; ; )

A A A B B B C C C

A x y z B x y z C x y z

, ta có:



( ; ; )

B A B A B A

AB x x y y z z



   



2 2 2

( ) ( ) ( )

B A B A B A

AB x x y y z z     

Toạ độ trung điểm M của đoạn thẳng AB:

; ; .

2 2 2

A B A B A B

x x y y z z

M

  

 

 

 

Toạ độ trọng tâm G của tam giác ABC:

; ; .

3 3 3

A B C A B C A B C

x x x y y y z z z

G

     

 

 

 

QUY TẮC CHIẾU ĐẶC BIỆT

Chiếu điểm trên trục tọa độ Chiếu điểm trên mặt phẳng tọa độ

Điểm

1( )

( ; ; ) ( ;0;0)

Chieáu vaøo Ox

M M M MGiöõ nguyeân x

M x y z M x

  

Điểm

2( )

( ; ; ) (0; ;0)

Chieáu vaøo Oy

M M M MGiöõ nguyeân y

M x y z M y  

Điểm

3

( )

( ; ; ) (0;0; )

Chieáu vaøo Oz

M M M M

Giöõ nguyeân z

M x y z M z  

Điểm

1( , )

( ; ; ) ( ; ;0)

Chieáu vaøo Oxy

M M M M MGiöõ nguyeân x y

M x y z M x y

   

Điểm

2( , )

( ; ; ) (0; ; )

Chieáu vaøo Oyz

M M M M MGiöõ nguyeân y z

M x y z M y z   

Điểm

3

( , )

( ; ; ) ( ;0; )

Chieáu vaøo Oxz

M M M M M

Giöõ nguyeânx z

M x y z M x z   

Đối xứng điểm qua trục tọa độ Đối xứng điểm qua mặt phẳng tọa độ





1( ; , )

( ; ; ) ( ; ; )

Ñoái xöùng qua Ox

M M M M M M

Giöõ nguyeân x ñoåi daáu y z

M x y z M x y z        





2

( ; , )

( ; ; ) ( ; ; )

Ñoái xöùng qua Oy

M M M M M M

Giöõ nguyeân y ñoåi daáu x z

M x y z M x y z         



1

( , ; )

( ; ; ) ( ; ; )

Ñoái xöùng qua Oxy

M M M M M M

Giöõ nguyeân x y ñoåi daáu z

M x y z M x y z       



2

( , ; )

( ; ; ) ( ; ; )

Ñoái xöùng qua Oxz

M M M M M M

Giöõ nguyeân x z ñoåi daáu y

M x y z M x y z       



3( , ; )

( ; ; ) ( ; ; )

Ñoái xöùng qua Oyz

M M M M M MGiöõ nguyeân y z ñoåi daáu x

M x y z M x y z       

HỆ TRỤC TỌA ĐỘ

Chuyên đề 28

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/





3( ; , )

( ; ; ) ( ; ; )

Ñoái xöùng qua Oz

M M M M M M

Giöõ nguyeân z ñoåi daáu x y

M x y z M x y z

        

4. Tích có hướng của hai vectơ:

 Định nghĩa: Cho

1 2 3

( , , )a a a a





,

1 2 3

( , , )b b b b





, tích có hướng của

a



và

b



là:

 

2 3 3 1 1 2

2 3 3 2 3 1 1 3 1 2 2 1

2 3 3 1

1 2

, ; ; ; ;

a a a a

a a

a b a b a b a b a b a b a b

b b b b

b b



 

 

    

  

 

.

 Tính chất:

[ , ]a b a

  



[ , ]a b b

  



 

[ , ] . .sin ,a b a b a b

 



Điều kiện cùng phương của hai vectơ

&a b

 

là

, 0a b

  

 



 

với

0 (0;0;0).





Điều kiện đồng phẳng của ba vectơ

,a b

 

và

c



là

[ , ]. 0.a b c

  



Diện tích hình bình hành

ABCD:

, .

ABCD

S AB AD



 

 



 

Diện tích tam giác ABC:

1

, .

2

ABC

S AB AC

 



 



 

Thể tích khối hộp:

. ' ' ' '

[ , ]. ' .

ABCD A B C D

V AB AD AA

  



Thể tích tứ diện:

1

, .

6

ABCD

V AB AC AD

  

 



 

.

Dạng 1. Tìm tọa độ điểm, véc tơ liên quan đến hệ trục tọa dộ OXYZ

Dạng 1.1 Tìm hình chiếu của điểm lên mặt phẳng, đường thẳng

Câu 1. (Đề Minh Họa 2020 Lần 1) Trong không gian

Oxyz

, hình chiếu vuông góc của điểm

 

2; 2;1M 

trên mặt phẳng

 

Oxy

có tọa độ là

A.

 

2;0;1

. B.

 

2; 2;0

. C.

 

0; 2;1

. D.

 

0;0;1

.

Câu 2. (Đề Tham Khảo 2020 Lần 2) Trong không gian

Oxyz

, hình chiếu vuông góc của điểm

 

2;1; 1M 

trên mặt phẳng

 

Ozx

có tọa độ là

A.

 

0;1;0

. B.

 

2;1;0

. C.

 

0;1; 1

. D.

 

2;0; 1

.

Câu 3. (Mã 102 - 2020 Lần 1) Trong không gian , hình chiếu vuông góc của điểm trên

trục có tọa độ là

A. . B. . C. . D. .

Câu 4. (Mã 101 - 2020 Lần 1) Trong không gian

Oxyz

, hình chiếu vuông góc của điểm

 

3;2;1A

trên

trục

Ox

có tọa độ là:

A.

 

0;2;1

. B.

 

3;0;0

. C.

 

0;0;1

. D.

 

0;2;0

.

Câu 5. (Mã 103 - 2020 Lần 1) Trong không gian

Oxyz

, hình chiếu vuông góc của điểm

 

3;5; 2A

trên

trục

Ox

có tọa độ là

A.

 

0;5;2

. B.

 

0;5;0

. C.

 

3;0;0

. D.

 

0;0;2

.

Câu 6. (Mã 104 - 2020 Lần 1) Trong không gian

Oxyz

,

hình chiếu vuông góc của điểm

(8;1; 2)A

trên

trục

Ox

có tọa độ là

A.

(0;1;0)

. B.

(8;0;0)

. C.

(0;1;2)

. D.

(0;0;2)

.

Oxyz

 

1;2;5

A

Ox

 

0;2;0

 

0;0;5

 

1;0;0

 

0;2;5

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3

Câu 7. (Mã 101 - 2020 Lần 2) Trong không gian

Oxyz

. Điểm nào sau đây là hình chiếu vuông góc của

điểm

(1;4;2)

A

trên mặt phẳng

Oxy

?

A.

(0;4;2)

. B.

(1;4;0)

. C.

(1;0;2)

. D.

(0;0;2)

.

Câu 8. (Mã 103 - 2020 Lần 2) Trong không gian

Oxyz

điểm nào dưới đây là hình chiếu vuông góc của

điểm

 

3;5;2

A

trên mặt phẳng

 

Oxy

?

A.

 

3;0;2

M

B.

 

0;0;2

C.

 

0;5;2

Q

D.

 

3;5;0

N

Câu 9. (Mã 102 - 2020 Lần 2) Trong không gian

Oxyz

, điểm nào dưới đây là hình chiếu vuông góc của

điểm

 

1;2;3

A

trên mặt phẳng

Oxy

.

A.

 

1;0;3

Q

B.

 

1;2;0

P

C.

 

0;0;3

M

D.

 

0;2;3

N

Câu 10. (Mã 104 - 2020 Lần 2) Trong không gian

Oxyz

, điểm nào dưới đây là hình chiếu vuông góc của

điểm

 

3;4;1

A

trên mặt phẳng

 

Oxy

?

A.

 

0;4;1

Q

. B.

 

3;0;1

P

. C.

 

0;0;1

M

. D.

 

3;4;0

N

.

Câu 11. (Mã 104 - 2019) Trong không gian

Oxyz

, hình chiếu vuông góc của điểm

 

3;1; 1

M



trên trục

Oy

có tọa độ là

A.

 

3;0; 1

. B.

 

0;1;0

. C.

 

3;0;0

. D.

 

0;0; 1

.

Câu 12. (Mã 103 - 2019) Trong không gian

Oxyz

, hình chiếu vuông góc của điểm

 

2;1; 1

M



trên trục

Oy

có tọa độ là

A.

 

0;0; 1

. B.

 

2;0; 1

. C.

 

0;1;0

. D.

 

2;0;0

.

Câu 13. (Mã 102 - 2019) Trong không gian

Oxyz

, hình chiếu vuông góc của điểm

 

3; 1;1

M 

trên trục

Oz

có tọa độ là

A.

 

3; 1;0



. B.

 

0;0;1

. C.

 

0; 1;0



. D.

 

3;0;0

.

Câu 14. (Mã 101 - 2019) Trong không gian

Oxyz

, hình chiếu vuông góc của điểm

 

2;1; 1

M



trên trục

Oz

có tọa độ là

A.

 

2;0;0

. B.

 

0;1;0

. C.

 

2;1;0

. D.

 

0;0; 1

.

Câu 15. (Đề Tham Khảo 2018) Trong không gian

Oxyz

, cho điểm

 

3; 1;1

A 

. Hình chiếu vuông góc của

điểm

A

trên mặt phẳng

 

Oyz

là điểm

A.

 

3;0;0

M

B.

 

0; 1;1

N 

C.

 

0; 1;0

P 

D.

 

0;0;1

Q

Câu 16. (Chuyên Lương Thế Vinh Đồng Nai 2019) Trong không gian với hệ tọa độ

Oxyz

, điểm nào sau

đây nằm trên mặt phẳng tọa độ

 

Oyz

?

A.

 

3;4;0

M

. B.

 

2;0;3

P 

. C.

 

2;0;0

Q

. D.

 

0;4; 1

N



.

Câu 17. (Chuyên Hạ Long 2019) Trong không gian với hệ trục tọa độ

Oxyz

cho

 

4;5;6

M

. Hình chiếu

của

M

xuống mặt phẳng

 

Oyz

là

M



. Xác định tọa độ

M



.

A.

 

4;5;0

M



. B.

 

4;0;6

M



. C.

 

4;0;0

M



. D.

 

0;5;6

M



.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 18. (Chuyên Hạ Long 2019) Trong không gian với hệ trục tọa độ

Oxyz

cho điểm

 

; ;M x y z

.

Trong các mệnh đề sau, mệnh đề nào đúng?

A. Nếu

M



đối xứng với

M

qua mặt phẳng

 

Oxz

thì

 

; ;M x y z





.

B. Nếu

M



đối xứng với

M

qua

Oy

thì

 

; ;M x y z





.

C. Nếu

M



đối xứng với

M

qua mặt phẳng

 

Oxy

thì

 

; ;M x y z





.

D. Nếu

M



đối xứng với

M

qua gốc tọa độ

O

thì

 

2 ;2 ;0M x y



.

Câu 19. (THCS - THPT Nguyễn Khuyến 2019) Trong không gian

Oxyz

, tọa độ điểm đối xứng của

 

M ; ;1 2 3

qua mặt phẳng

 

Oyz

là

A.

 

0 2 3; ;

. B.

 

1 2 3; ;  

. C.

 

1 2 3; ;



. D.

 

1 2 3; ;

.

Câu 20. (Chuyên Hạ Long 2018) Trong không gian

Oxyz

, cho điểm

 

2; 3;5

A 

. Tìm tọa độ

A



là điểm

đối xứng với

A

qua trục

Oy

.

A.

 

2;3;5

A



. B.

 

2; 3; 5

A



 

. C.

 

2; 3;5

A



 

. D.

 

2; 3; 5

A



  

.

Dạng 1.2 Xác định tọa độ vectơ, độ dài vec tơ

Câu 21. (Mã 102 2018) Trong không gian

Oxyz

, cho hai điểm

 

1;1; 2

A



và

 

2;2;1

B

. Vectơ

AB



có

tọa độ là

A.

 

1; 1; 3  

B.

 

3;1;1

C.

 

1;1;3

D.

 

3;3; 1

Câu 22. (Đề Tham Khảo 2019) Trong không gian

,Oxyz

cho hai điểm

 

1;1; 1

A



và

 

2;3;2

B

. Vectơ

AB



có tọa độ là

A.

 

1; 2; 3

B.

 

1; 2; 3

 

C.

 

3;5;1

D.

 

3;4;1

Câu 23. (Mã 110 2017) Trong không gian với hệ toạ độ

Oxyz

, cho điểm

 

2;2;1

A

. Tính độ dài đoạn

thẳng

OA

.

A.

5

OA 

B.

5

OA



C.

3

OA



D.

9

OA



Câu 24. (THPT Nguyễn Khuyến 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho ba vecto

     

1;2;3 ; 2;2; 1 ; 4;0; 4

a b c

 



 

. Tọa độ của vecto

2d a b c  

 

là

A.

 

7;0; 4

d

 



B.

 

7;0;4

d 



C.

 

7;0; 4

d





D.

 

7;0;4

d



Câu 25. (THPT Ba Đình 2019) Trong không gian

Oxyz

, cho hai điểm

 

0;1; 1

A



,

 

2;3;2

B

. Vectơ

AB



có tọa độ là

A.

 

2;2;3

. B.

 

1;2;3

. C.

 

3;5;1

. D.

 

3;4;1

.

Câu 26. (THPT Gia Lộc Hải Dương 2019) Trong không gian

Oxyz

cho

 

2;3;2

a 



và

 

1;1; 1

b

 



.

Vectơ

a b



có tọa độ là

A.

 

3;4;1

. B.

 

1; 2;3

 

. C.

 

3;5;1

. D.

 

1;2;3

.

Câu 27. (THPT Hoàng Hoa Thám Hưng Yên 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho

 

2; 3;3

a  



,

 

0;2; 1

b

 



,

 

3; 1;5

c  



. Tìm tọa độ của vectơ

2 3 2u a b c  



  

.

A.

 

10; 2;13



. B.

 

2;2; 7 

. C.

 

2; 2;7

 

. D.

 

2;2;7



.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5

Câu 28. (THPT Hùng Vương Bình Phước 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho

2 3a i j k   

  



. Tọa độ của vectơ

a



là

A.

 

1;2; 3 

. B.

 

2; 3; 1 

. C.

 

2; 1; 3 

. D.

 

3; 2; 1 

.

Câu 29. Trong không gian với hệ tọa độ

Oxyz

, cho

 

2; 3; 3

a  



,

 

0; 2; 1

b

 



,

 

3; 1; 5

c  



. Tìm tọa

độ của vectơ

2 3 2u a b c  

   

.

A.

 

10; 2;13



. B.

 

2; 2; 7 

. C.

 

2; 2; 7

 

. D.

 

2; 2; 7



.

Câu 30. (THPT Minh Khai Hà Tĩnh 2019) Trong không gian với hệ tọa độ

Oxyz

, cho hai vectơ

 

2;1; 3

x

 



và

 

1;0; 1

y

 



. Tìm tọa độ của vectơ

2a x y 

  

.

A.

 

4;1; 1

a

 



. B.

 

3;1; 4

a

 



. C.

 

0;1; 1

a

 



. D.

 

4;1; 5

a

 



.

Câu 31. (THPT - Yên Định Thanh Hóa 2019) Trong không gian

O xyz

, cho

 

2; 1;0

A

và

 

1;1; 3

B

.

Vectơ



AB

có tọa độ là

A.

 

3;0; 3

. B.

 

1;2; 3 

. C.

 

1; 2;3

 

. D.

 

1; 2;3



.

Câu 32. (Sở Hà Nội 2019) Trong không gian

Oxyz

cho

   

2; 2;1 , 1; 1;3 .

A B 

Tọa độ vecto

AB



là:

A.

( 1;1;2).

. B.

( 3;3; 4). 

. C.

(3; 3;4).

. D.

(1; 1; 2) 

Câu 33. (Chuyên Lương Thế Vinh Đồng Nai 2019) Trong không gian

Oxyz

với

, ,i j k

  

lần lượt là các

vecto đơn vị trên các trục

, , .Ox Oy Oz

Tính tọa độ của vecto

.i j k 

  

A.

( 1; 1;1).

i j k    

  

B.

( 1;1;1).

i j k   

  

C.

(1;1; 1).

i j k

   

  

D.

(1; 1;1).

i j k   

  

Câu 34. (THPT Gang Thép Thái Nguyên 2019) Trong không gian với hệ tọa độ

Oxyz

giả sử

2 3

u i j k  

   

, khi đó tọa độ véc tơ

u



là

A.

 

2;3;1



. B.

 

2;3; 1

. C.

 

2; 3; 1 

. D.

 

2;3;1

.

Câu 35. (THPT Lê Quý Đôn Đà Nẵng 2019) Trong không gian

Oxyz

, cho

 

1;2;1

a 



và

 

1;3;0

b  



.

Vectơ

2

c a b 



 

có tọa độ là

A.

 

1;7;2

. B.

 

1;5;2

. C.

 

3;7;2

. D.

 

1;7;3

.

Câu 36. (KTNL GV Thuận Thành 2 Bắc Ninh 2019) Trong không gian với trục hệ tọa độ

Oxyz

, cho

2 3 .a i j k

   

   

Tọa độ của vectơ

a



là:

A.

 

1;2; 3

a

 



. B.

 

2; 3; 1

a

 



. C.

 

3;2; 1

a

 



. D.

 

2; 1; 3

a

 



.

Câu 37. (Sở Thanh Hóa 2019) Trong không gian với hệ tọa độ Oxyz, cho hai điểm A

 

1; 3;1



,

B

 

3;0; 2

. Tính độ dài

AB

.

A. 26. B. 22. C.

26

. D.

22.

Câu 38. (Chuyên - KHTN - Hà Nội - 2019) Trong không gian

Oxyz

, cho hai điểm

 

1; 2; 1

A

 

,

 

1;4;3

B

. Độ dài đoạn thẳng

AB

là

A.

2 13

B.

6

C.

3

D.

2 3

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 39. (Hội 8 trường chuyên 2019) Trong không gian Oxyz, cho

     

2;2;0 , 2;2;0 , 2;2;2

a b c

  

. Giá

trị của

a b c 

  

bằng

A.

6.

B.

11

. C.

2 11

. D.

2 6

.

Câu 40. (Chuyên Nguyễn Du-ĐăkLăk 2019) Trong không gian

Oxyz

, cho 2 điểm

 

1;3;5

A

,

 

2;2;3

B

. Độ dài đoạn

AB

bằng

A.

7

. B.

8

. C.

6

. D.

5

.

Dạng 1.3 Xác định tọa độ điểm

Câu 41. (Mã 101 2018) Trong không gian

Oxyz

, cho hai điểm

 

2; 4;3

A 

và

 

2;2;7

B

. Trung điểm của

đoạn thẳng

AB

có tọa độ là

A.

 

4; 2;10



B.

 

1;3;2

C.

 

2;6;4

D.

 

2; 1;5



Câu 42. (Đề Tham Khảo 2017) Trong không gian với hệ tọa độ

Oxyz

, cho các điểm

 

3; 4;0

A 

,

 

1;1;3

B 

,

 

3,1,0

C

. Tìm tọa độ điểm

D

trên trục hoành sao cho

AD BC

.

A.

 

6;0;0

D

,

 

12;0;0

D

B.

 

0;0;0

D

,

 

6;0;0

D

C.

 

2;1;0

D 

,

 

4;0;0

D 

D.

 

0;0;0

D

,

 

6;0;0

D 

Câu 43. Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm

 

3; 2;3

A

và

 

1;2;5

B

. Tìm tọa độ trung

điểm

I

của đoạn thẳng

AB

.

A.

 

1;0;4

I

. B.

 

2;0;8

I

. C.

 

2; 2; 1 

I

. D.

 

2;2;1

I

.

Câu 44. (THPT Cẩm Giàng 2 2019) Trong không gian với hệ tọa độ

Oxyz

cho hai điểm

 

3; 2;3

A 

và

 

1;2;5

B 

. Tìm tọa độ trung điểm

I

của đoạn thẳng

AB

là :

A.

 

2;2;1

I 

. B.

 

1;0;4

I

. C.

 

2;0;8

I

. D.

 

2; 2; 1

I

 

.

Câu 45. (THPT Hoàng Hoa Thám Hưng Yên 2019) Trong không gian với hệ tọa độ

Oxyz

, cho

 

1;3;2

A

,

 

3; 1;4

B 

. Tìm tọa độ trung điểm

I

của

.AB

A.

 

2; 4;2

I 

. B.

 

4;2;6

I

. C.

 

2; 1; 3

I

  

. D.

 

2;1;3

I

.

Câu 46. Trong không gian cho hệ trục toạ độ

Oxyz

, cho ba điểm

     

1; 2;3 , 1;2;5 , 0;0;1

A B C 

. Tìm

toạ độ trọng tâm

G

của tam giác

ABC

.

A.

 

0;0;3

G

. B.

 

0;0;9

G

. C.

 

1;0;3

G 

. D.

 

0;0;1

G

.

Câu 47. Trong không gian với hệ trục tọa độ

Oxyz

cho

 

1;3;2

A

,

 

3; 1;4

B 

. Tìm tọa độ trung điểm

I

của

AB

.

A.

 

2; 4;2

I 

. B.

 

4;2;6

I

. C.

 

2; 1;3

I  

. D.

 

2;1;3

I

.

Câu 48. (THPT Đoàn Thượng - Hải Dương - 2019) Trong không gian

Oxyz

, cho hai điểm

 

2; 4;3

A 

và

 

2;2;7

B

. Trung điểm của đoạn thẳng

AB

có tọa độ là

A.

 

1;3;2

. B.

 

2; 1;5



. C.

 

2; 1; 5 

. D.

 

2;6;4

.

Câu 49. (THPT Cù Huy Cận 2019) Trong không gian với hệ tọa độ

Oxyz

, cho tam giác

ABC

với

     

1;3; 4 , 2; 1;0 , 3;1;2

A B C

. Tọa độ trọng tâm

G

của tam giác

ABC

là

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7

A.

 

2;1;2

G

. B.

 

6;3;6

G

. C.

2

3; ;3

3

G

 

 

 

. D.

 

2; 1;2

G 

.

Câu 50. (Chuyên Lê Quý Đôn Điện Biên 2019) Trong không gian với hệ tọa độ

Oxyz

cho tam giác

ABC

biết

   

5; 2;0 , 2;3;0

A B 

,

 

0;2;3

C

. Trọng tâm

G

của tam giác

ABC

có tọa độ:

A.

 

1;2;1

. B.

 

2;0; 1

. C.

 

1;1;1

. D.

 

1;1; 2

.

Câu 51. (Chuyên Sơn La 2019) Trong không gian

Oxyz

, cho 2 điểm

 

1; 2;2

M 

và

 

1;0;4

N

. Toạ độ

trung điểm của đoạn thẳng

MN

là:

A.

 

1; 1;3



. B.

 

0;2;2

. C.

 

2; 2;6



. D.

 

1;0;3

.

Câu 52. (KTNL GV Bắc Giang 2019) Trong mặt phẳng với hệ trục tọa độ

Oxy

, cho hai điểm

 

3;4

A 

và

 

5;6

B

. Trung điểm của đoạn thẳng

AB

có tọa độ là

A.

 

1;5

. B.

 

4;1

. C.

 

5;1

. D.

 

8;2

.

Câu 53. (Chuyên Lê Hồng Phong Nam Định 2019) Trong không gian

Oxyz

, cho hai điểm

 

2; 4;3

A 

và

 

2;2;9

B

. Trung điểm của đoạn

AB

có tọa độ là

A.

 

0;3;3

. B.

 

4; 2;12



. C.

 

2; 1;6



. D.

3 3

0; ;

2 2

 

 

 

.

Câu 54. (Liên Trường Thpt Tp Vinh Nghệ An 2019) Trong không gian

Oxyz

, cho hai điểm

 

1;5;2

A 

và

 

3; 3;2

B 

. Tọa độ trung điểm

M

của đoạn thẳng

AB

là

A.

 

1;1;2

M

B.

 

2;2;4

M

C.

 

2; 4;0

M 

D.

 

4; 8;0

M 

Câu 55. (THPT Nghĩa Hưng NĐ- 2019) Trong không gian với hệ tọa độ

Oxyz

cho hai điểm

 

1;5;3

A 

và

 

2;1; 2

M



. Tọa độ điểm

B

biết

M

là trung điểm của

AB

là

A.

1 1

;3;

2 2

B

 

 

 

. B.

 

4;9;8

B 

.

C.

 

5;3; 7

B



. D.

 

5; 3; 7

B

 

.

Dạng 2. Tích vô hướng và ứng dụng

Câu 56. (Mã 105 2017) Trong không gian với hệ trục tọa độ

Oxyz

, cho hai vectơ

 





2; 1; 0

a

và

 

  



1; 0; 2

b

. Tính

 

 

cos ,a b

.

A.

 

 

 

2

cos ,

25

a b

B.

 

 

 

2

cos ,

5

a b

C.

 



 

2

cos ,

25

a b

D.

 



 

2

cos ,

5

a b

Câu 57. (KSCL THPT Nguyễn Khuyến 2019) Trong không gian

,Oxyz

cho vectơ

   

2; 2; 4 , 1; 1;1 .

a b    



Mệnh đề nào dưới đây sai?

A.

 

3; 3; 3

a b

   



B.

a



và

b



cùng phương

C.

3

b 



D.

a b



Câu 58. (THPT Lê Văn Thịnh Bắc Ninh 2019) Trên mặt phẳng toạ độ

Oxy

, cho tam giác

ABC

biết

 

1;3

A

,

 

2; 2

B

 

,

 

3;1

C

. Tính cosin góc

A

của tam giác.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 8 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

A.

2

cos

17

A 

B.

1

cos

17

A 

C.

2

cos

17

A  

D.

1

cos

17

A  

Câu 59. (THPT Quỳnh Lưu 3 Nghệ An 2019) Trong không gian

Oxyz

, góc giữa hai vectơ

i



và

 

3; 0;1

u  



là

A.

120

. B.

60

. C.

150

. D.

30

.

Câu 60. (Chuyên Đại Học Vinh 2019) Trong không gian

Oxyz

, cho

 

3;4;0

a  



,

 

5;0;12

b 



. Côsin

của góc giữa

a



và

b



bằng

A.

3

13

. B.

5

6

. C.

5

6



. D.

3

13



.

Câu 61. (Chuyên Đhsp Hà Nội 2019) Trong không gian tọa độ

Oxyz

góc giữa hai vectơ

i



và

 

3;0;1

u  



là

A.

120

. B.

30

. C.

60

. D.

150

.

Câu 62. (Chuyên Nguyễn Tất Thành Yên Bái 2019) Trong không gian với hệ tọa độ

O

xyz

, cho vectơ

 

3;0;1

u 



và

 

2;1;0

v 



. Tính tích vô hướng

.u v

 

.

A.

. 8

u v



 

. B.

. 6

u v



 

. C.

. 0

u v



 

. D.

. 6

u v

 

 

.

Câu 63. (Chuyên Hưng Yên 2019) Trong không gian tọa độ

Oxyz

, góc giữa hai vectơ

i



và

 

3;0;1

u  



là

A.

0

30

. B.

0

120

. C.

0

60

. D.

0

150

.

Câu 64. (Chuyên Trần Phú Hải Phòng 2019) Trong không gian

,Oxyz

cho ba điểm

( 1; 2;3)

A

 

(0;3;1)

B

,

(4;2;2)

C

. Cosin của góc



BAC

là

A.

9

35

. B.

9

35



. C.

9

2 35



. D.

9

2 35

.

Câu 65. (THPT Ngô Sĩ Liên Bắc Giang 2019) Trong không gian với hệ tọa độ

Oxyz

, cho tam giác

ABC

có

 

1;0;0

A

,

 

0;0;1

B

,

 

2;1;1

C

. Diện tích của tam giác

ABC

bằng:

A.

11

2

B.

7

2

C.

6

2

D.

5

2

Câu 66. (Chuyên Đại học Vinh - 2019) Trong không gian

Oxyz

, cho

 

3;4;0

a  



và

 

5;0;12

b 



.

Côsin của góc giữa

a



và

b



bằng

A.

3

13

. B.

5

6

. C.

5

6



. D.

3

13



.

Câu 67. (Thpt Vĩnh Lộc - Thanh Hóa 2019) Trong hệ tọa độ

Oxy

, cho

3u i j 

  

và

 

2; 1

v

 



. Tính

.u v

 

.

A.

. 1

u v

 

 

. B.

. 1u v 

 

. C.

 

. 2; 3

u v

 

 

. D.

. 5 2

u v 

 

.

Câu 68. (THPT Ngô Quyền - Ba Vì - Hải Phòng 2019) Cho hai véc tơ

 

1; 2;3

a  



,

 

2;1;2

b  



. Khi

đó, tích vô hướng

 

.a b b



  

bằng

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9

A.

12

. B.

2

. C.

11

. D.

10

.

Câu 69. (Kiểm tra năng lực - ĐH - Quốc Tế - 2019) Trong không gian với hệ trục toạ độ

Oxyz

, cho hai

vectơ

 

2;1 ; 3

a

 



,

 

4; 2 ;6

b   



. Phát biểu nào sau đây là sai?

A.

2b a 

 

. B.

. 0

a b



 

. C.

a



ngược hướng với

b



. D.

2b a



 

.

Câu 70. (THPT Mai Anh Tuấn_Thanh Hóa - 2019)

Cho

 

011 ;;u 

,

 

010 ;;v 

, góc giữa hai

véctơ

u

và

v

là

A.

120

. B.

45

. C.

135

. D.

60

.

Câu 71. (Chuyên Lê Hồng Phong - 2018) Trong không gian với hệ toạ độ

Oxyz

, cho tứ diện

ABCD

với

 

0; 0; 3

A

,

 

0; 0; 1

B



,

 

1; 0; 1

C



,

 

0; 1; 1

D



. Mệnh đề nào dưới đây sai?

A.

AB BD

. B.

AB BC

. C.

AB AC

. D.

AB CD

.

Câu 72. (THPT Thanh Miện I - Hải Dương - 2018) Trong không gian

Oxyz

cho

2

véc tơ

2;1

( ); 1

a

 



;

; ;(1 )3 m

b 



. Tìm

m

để

 

; 90

a b

 

 

.

A.

5

m

 

. B.

5

m



. C.

1

m



. D.

2

m

 

Câu 73. (SGD Đồng Tháp - 2018) Trong không gian với hệ trục tọa độ

Oxyz

, cho

 

2; 1;1

u  



và

 

0; 3;

v m  



. Tìm số thực

m

sao cho tích vô hướng

. 1u v 

 

.

A.

4

m



. B.

2

m



. C.

3

m



. D.

2

m

 

.

Câu 74. (CỤM Chuyên Môn 4 - Hải Phòng - 2018) Trong không gian

Oxyz

cho

     

1;2;3 ; 1;2;1 ; 3; 1; 2

A B C

  

. Tính tích vô hướng

.AB AC

 

.

A.

6

. B.

14

. C.

14

. D.

6

.

Câu 75. (THPT Mộ Đức - Quảng Ngãi - 2018) Trong không gian

Oxyz

, cho ba điểm

 

1; 2;3

A  

,

 

0;3;1

B

,

 

4;2;2

C

. Côsin của góc

BAC

bằng

A.

9

35

. B.

9

2 35

. C.

9

2 35



. D.

9

35



.

Dạng 3. Tích có hướng và ứng dụng

Câu 76. (KTNL GV Bắc Giang 2019) Trong không gian với hệ tọa độ

Oxyz

, cho hai vectơ

 

2;1; 2

a

 



và vectơ

 

1;0;2

b 



. Tìm tọa độ vectơ

c



là tích có hướng của

a



và

b



.

A.

 

2;6; 1

c

 



. B.

 

4;6; 1

c

 



. C.

 

4; 6; 1

c

  



. D.

 

2; 6; 1

c

  



.

Câu 77. (Chuyên Nguyễn Du-ĐăkLăk 2019) Trong không gian

Oxyz

, tọa độ một vectơ

n



vuông góc

với cả hai vectơ

 

1;1; 2

a

 



,

 

1;0;3

b 



là

A.

 

2;3; 1

. B.

 

3;5; 2

. C.

 

2; 3; 1 

. D.

 

3; 5; 1 

.

Câu 78. Trong không gian với hệ trục tọa độ

Oxyz

, cho ba véctơ

     

1;2; 1 , 3; 1;0 , 1; 5;2

a b c     

  

.

Câu nào sau đây đúng?

A.

a



cùng phương với

b



. B.

a



,

b



,

c



không đồng phẳng.

C.

a



,

b



,

c



đồng phẳng. D.

a



vuông góc với

b



.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 10 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 79. (Việt Đức Hà Nội 2019) Trong hệ trục tọa độ

Oxyz

, cho bốn điểm

(1; 2;0)

A



,

(2;0;3)

B

,

( 2;1;3)

C



và

(0;1;1)

D

. Thể tích khối tứ diện

ABCD

bằng:

A.

6

. B.

8

. C.

12

. D.

4

.

Câu 80. Trong không gian với hệ toạ độ

Oxyz

, cho

 

1; 2;3

a  



và

 

1;1; 1

b

 



. Khẳng định nào sau đây

sai?

A.

3

a b

 

 

. B.

. 4

a b

 

 

. C.

5

a b

 

 

. D.

 

, 1; 4;3

a b

 

  

 

 

.

Câu 81. (Chuyên Trần Phú Hải Phòng 2019) Trong không gian

,Oxyz

cho hai điểm

   

1;0; 1 , 1; 1;2

 A B

. Diện tích tam giác

OAB

bằng

A.

11.

B.

6

.

2

C.

11

.

2

D.

6.

Câu 82. (Yên Phong 1 - 2018) Trong không gian

Oxyz

, cho 4 điểm

 

2;0;2

A

,

 

1; 1; 2

B

 

,

 

1;1;0

C 

,

 

2;1;2

D 

. Thể tích của khối tứ diện

ABCD

bằng

A.

42

3

. B.

14

3

. C.

21

3

. D.

7

3

.

Câu 83. (SGD và ĐT Đà Nẵng 2019) Trong không gian

Oxyz

, tính diện tích

S

của tam giác

ABC

, biết

   

2;0;0 , 0;3;0

A B

và

 

0;0;4

C

.

A.

61

3

S 

. B.

61

2

S 

. C.

2 61

S 

. D.

61

S 

.

Câu 84. Trong hệ trục tọa độ

Oxyz

, cho

 

0;0;0

O

,

 

0;1; 2

A



,

 

1;2;1

B

,

 

4;3;C m

. Tất cả giá trị của

m

để

4

điểm

, , ,O A B C

đồng phẳng?

A.

14

m



. B.

14

m

 

. C.

7

m



. D.

7

m

 

.

Câu 85. Trong không gian

Oxyz

, cho hình chóp

.

A BCD

có

 

0;1; 1 ,

A



 

1;1;2 ,

B

 

1; 1;0

C 

và

 

0;0;1 .

D

Tính độ dài đường cao của hình chóp

.

A BCD

.

A.

2 2

. B.

3 2

2

. C.

3 2

. D.

2

.

Câu 86. (Chuyên Lê Quý Đôn - Đà Nẵng - 2018) Trong không gian với hệ trục tọa độ, cho hình bình

hành

ABCD

. Biết

 

2;1; 3

A



,

 

0; 2;5

B 

và

 

1;1;3

C

. Diện tích hình bình hành

ABCD

là

A.

2 87

. B.

349

2

. C.

349

. D.

87

.

Câu 87. (SGD - Bình Dương - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho bốn điểm

 

0;1;1

A

,

 

1;0;2

B 

,

 

1;1;0

C 

và điểm

 

2;1; 2

D



. Khi đó thể tích tứ diện

ABCD

là

A.

5

6

V



. B.

5

3

V



. C.

6

5

V



. D.

3

2

V



.

Câu 88. (THPT Mộ Đức - Quảng Ngãi - 2018) Trong không gian

Oxyz

, cho

 

1;2; 1

A



,

 

0; 2;3

B 

.

Tính diện tích tam giác

OAB

.

A.

29

6

. B.

29

2

. C.

78

2

. D.

7

2

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương  https://www.facebook.com/phong.baovuong Trang 1

TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH KHÁ MỨC 7-8 ĐIỂM

Lý thuyết chung

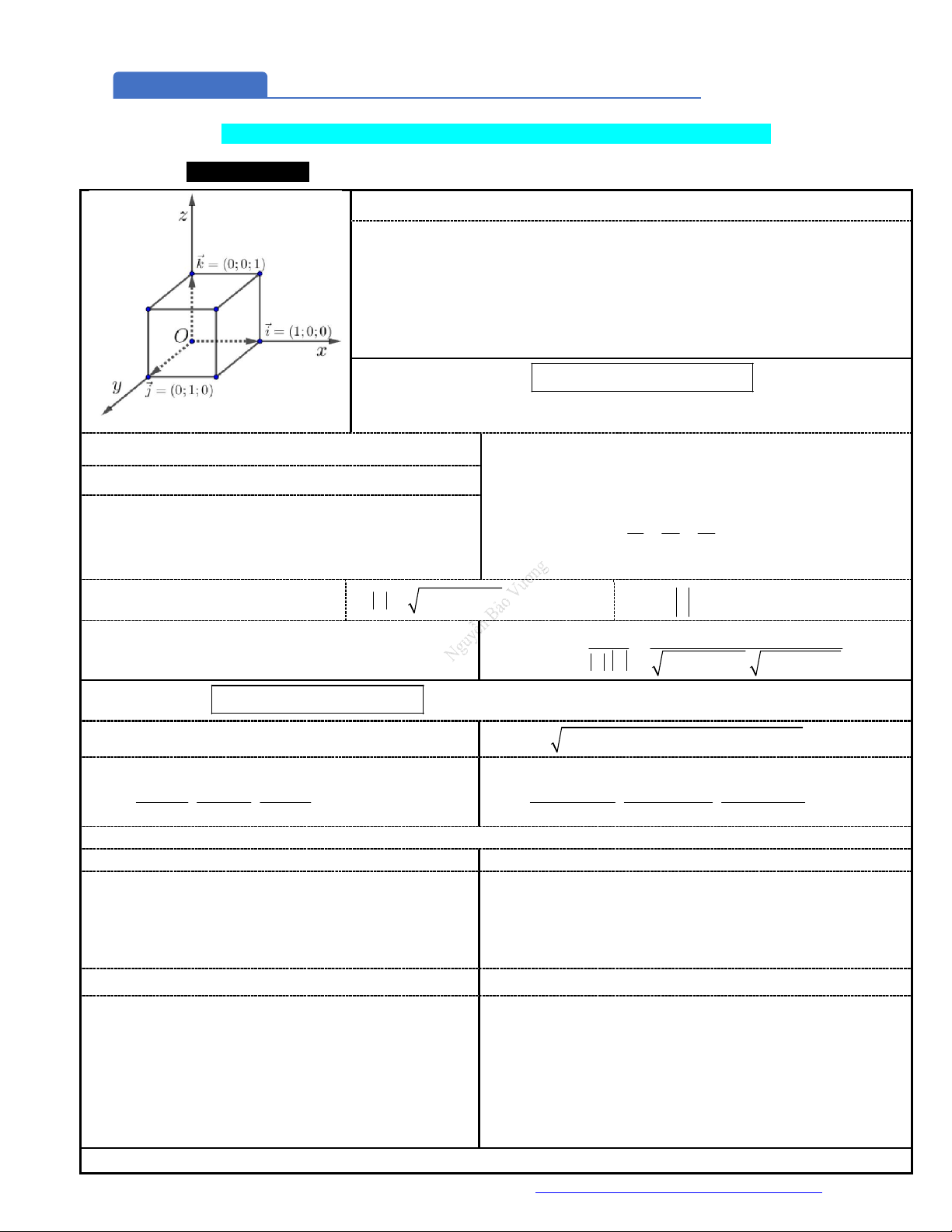
1. Hệ trục tọa độ Oxyz:

 Hệ trục gồm ba trục

, ,Ox Oy Oz

đôi một vuông góc nhau.

 Trục

:Ox

trục hoành, có vectơ đơn vị

(1;0;0)

i





.

 Trục

Oy

: trục tung, có vectơ đơn vị

(0;1;0)j





.

 Trục

:Oz

trục cao, có vectơ đơn vị

(0;0;1).

k





 Điểm

(0;0;0)O

là gốc tọa độ.

2. Tọa độ vectơ: Vectơ

( ; ; )u xi y j zk u x y z

    

    

.

Cho

1 2 3 1 2 3

( ; ; ), ( ; ; )a a a a b b b b

 

 

. Ta có:



1 1 2 2 3 3

( ; ; )a b a b a b a b



    



a



cùng phương

b



( )a kb k R

 

  

1 1

31 2

2 2 1 2 3

1 2 3

3 3

, ( , , 0).

a kb

a

a a

a kb b b b

b b b

a kb







     











1 2 3

( ; ; )ka ka ka ka







1 1

2 2

3 3

a b

a b a b

a b

 







  











1 1 2 2 3 3

. . . .a b a b a b a b



  



2 2 2

1 2 2

a a a a



  



2

2 2 2 2

1 2 3

a a a a a



   



1 1 2 2 3 3

. 0 0a b a b a b a b a b

   

      



1 1 2 2 3 3

2 2 2 2 2 2

1 2 3 1 2 3

.

cos( , )

.

a b a b a b

a b

a a a b b b



 

 

   

3. Tọa độ điểm:

( ; ; ) ( ; ; )M x y z OM x y z



 

. Cho

( ; ; ) , ( ; ; ) , ( ; ; )

A A A B B B C C C

A x y z B x y z C x y z

, ta có:



( ; ; )

B A B A B A

AB x x y y z z



   



2 2 2

( ) ( ) ( )

B A B A B A

AB x x y y z z     

 Toạ độ trung điểm M của đoạn thẳng AB:

; ; .

2 2 2

A B A B A B

x x y y z z

M

  

 

 

 

 Toạ độ trọng tâm G của tam giác ABC:

; ; .

3 3 3

A B C A B C A B C

x x x y y y z z z

G

     

 

 

 

QUY TẮC CHIẾU ĐẶC BIỆT

Chiếu điểm trên trục tọa độ Chiếu điểm trên mặt phẳng tọa độ

 Điểm

1( )

( ; ; ) ( ;0;0)

Chieáu vaøo Ox

M M M MGiöõ nguyeân x

M x y z M x

  

 Điểm

2

( )

( ; ; ) (0; ;0)

Chieáu vaøo Oy

M M M M

Giöõ nguyeân y

M x y z M y 

 Điểm

3( )

( ; ; ) (0;0; )

Chieáu vaøo Oz

M M M MGiöõ nguyeân z

M x y z M z 

 Điểm

1( , )

( ; ; ) ( ; ;0)

Chieáu vaøo Oxy

M M M M MGiöõ nguyeân x y

M x y z M x y

  

 Điểm

2

( , )

( ; ; ) (0; ; )

Chieáu vaøo Oyz

M M M M M

Giöõ nguyeân y z

M x y z M y z  

 Điểm

3( , )

( ; ; ) ( ;0; )

Chieáu vaøo Oxz

M M M M MGiöõ nguyeân x z

M x y z M x z 

Đối xứng điểm qua trục tọa độ Đối xứng điểm qua mặt phẳng tọa độ



1( ; , )

( ; ; ) ( ; ; )

Ñoái xöùng qua Ox

M M M M M M

Giöõ nguyeân x ñoåi daáu y z

M x y z M x y z      



2( ; , )

( ; ; ) ( ; ; )

Ñoái xöùng qua Oy

M M M M M M

Giöõ nguyeân y ñoåi daáu x z

M x y z M x y z

     



3

( ; , )

( ; ; ) ( ; ; )

Ñoái xöùng qua Oz

M M M M M M

Giöõ nguyeân z ñoåi daáu x y

M x y z M x y z

     



1( , ; )

( ; ; ) ( ; ; )

Ñoái xöùng qua Oxy

M M M M M MGiöõ nguyeân x y ñoåi daáu z

M x y z M x y z

     



2( , ; )

( ; ; ) ( ; ; )

Ñoái xöùng qua Oxz

M M M M M MGiöõ nguyeân x z ñoåi daáu y

M x y z M x y z    



3

( , ; )

( ; ; ) ( ; ; )

Ñoái xöùng qua Oyz

M M M M M M

Giöõ nguyeân y z ñoåi daáu x

M x y z M x y z     

4. Tích có hướng của hai vectơ:

HỆ TRỤC TỌA ĐỘ

Chuyên đề 28

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

 Định nghĩa: Cho

1 2 3

( , , )a a a a





,

1 2 3

( , , )b b b b





, tích có hướng của

a



và

b



là:

 

2 3 3 1 1 2

2 3 3 2 3 1 1 3 1 2 2 1

2 3 3 1

1 2

, ; ; ; ;

a a a a

a a

a b a b a b a b a b a b a b

b b b b

b b



 

 

    

  

 

.

 Tính chất:

[ , ]

a b a

  



[ , ]

a b b

  



 

[ , ] . .sin ,a b a b a b

 



 Điều kiện cùng phương của hai vectơ

&a b

 

là

, 0

a b

  

 



 

với

0 (0;0;0).





 Điều kiện đồng phẳng của ba vectơ

,a b

 

và

c



là

[ , ]. 0.

a b c

  



 Diện tích hình bình hành ABCD:

, .

ABCD

S AB AD



 

 



 

 Diện tích tam giác ABC:

1

, .

2

ABC

S AB AC

 



 



 

 Thể tích khối hộp:

. ' ' ' '

[ , ]. ' .

ABCD A B C D

V AB AD AA

  



 Thể tích tứ diện:

1

, .

6

ABCD

V AB AC AD

  

 



 

.

Dạng 1. Tìm tọa độ điểm, véc tơ liên quan đến hệ trục tọa dộ OXYZ

Dạng 1.1 Một số bài toán liên quan đến vectơ, tọa độ vec tơ

Câu 1. (THPT Hùng Vương Bình Phước 2019) Trong không gian với hệ trục

Oxyz

cho ba điểm

     

1;2; 3 , 1;0;2 , ; ; 2

A B C x y

  

thẳng hàng. Khi đó

x y

bằng

A.

1

x y

 

. B.

17

x y

 

. C.

11

5

x y

  

. D.

11

5

x y 

.

Câu 2. (HSG Tỉnh Bắc Ninh 2019) Trong không gian với hệ tọa độ

Oxyz

, cho các vectơ

   

2; 1;3 , 1;3; 2a m b n

   

 

. Tìm

,m n

để các vectơ

,a b

 

cùng hướng.

A.

3

7;

4

m n

  

. B.

4; 3

m n

  

. C.

1; 0

m n

 

. D.

4

7;

3

m n

  

.

Câu 3. (THPT Nguyễn Khuyến -2019) Trong không gian với hệ tọa độ

Oxyz

, cho ba điểm

     

A 2; 1;5 , 5; 5;7 , ; ;1

 

B M x y

. Với giá trị nào của

,x y

thì

, ,A B M

thẳng hàng.

A.

4; 7 

x y

B.

4; 7   

x y

C.

4; 7  

x y

D.

4; 7  

x y

Câu 4. (THPT Quỳnh Lưu 3 Nghệ An -2019) Trong không gian

Oxyz

, cho hai điểm

 

2; 2;1

A 

,

 

0;1;2

B

. Tọa độ điểm

M

thuộc mặt phẳng

 

Oxy

sao cho ba điểm

A

,

B

,

M

thẳng hàng là

A.

 

4; 5;0

M 

. B.

 

2; 3;0

M 

. C.

 

0;0;1

M

. D.

 

4;5;0

M

.

Câu 5. (THPT Yên Khánh - Ninh Bình - 2019) Trong không gian với hệ tọa độ

Oxyz

cho các véc tơ

2 2

u i j k  

   

,

 

;2; 1

v m m

 



với

m

là tham số thực. Có bao nhiêu giá trị của

m

để

u v

 

.

A.

0

. B.

1

. C.

2

. D.

3

.

Câu 6. (Chuyen ĐHSP Hà Nội -2019) Trong không gian với hệ tọa độ

Oxyz

, cho hình hộp

.

ABCD A B C D

   

có

 

0;0;0

A

,

 

;0;0

B a

;

 

0;2 ;0D a

,

 

0;0;2A a



với

0

a



. Độ dài đoạn thẳng

AC



là

A.

a

. B.

2 a

. C.

3 a

. D.

3

2

a

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3

Câu 7. (Chuyên Lê Quý Dôn - Dà Nẵng - 2018) Trong không gian với hệ trục toạ độ

Oxyz

, cho

 

2;3;1

a 



,

 

1;5;2

b  



,

 

4; 1;3

c  



và

 

3;22;5

x  



. Đẳng thức nào đúng trong các đẳng

thức sau?

A.

2 3

x a b c  

   

. B.

2 3

x a b c   

   

.

C.

2 3

x a b c  

   

. D.

2 3

x a b c  

   

.

Câu 8. (Chuyên Thái Bình - 2018) Trong không gian với hệ trục tọa độ

Oxyz

, cho tam giác

ABC

với:

 

1; 2;2

AB  



;

 

3; 4; 6

AC  



. Độ dài đường trung tuyến

AM

của tam giác

ABC

là:

A.

29

. B.

29

. C.

29

2

. D.

2 29

.

Câu 9. (Hồng Quang - Hải Dương - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho các vectơ

 

2; 1;3

a m 



,

 

1;3; 2b n

 



. Tìm

m

,

n

để các vectơ

a



,

b



cùng hướng.

A.

7

m



;

3

4

n

 

. B.

7

m



;

4

3

n

 

. C.

4

m



;

3

n

 

. D.

1

m



;

0

n



.

Câu 10. (THPT Chu Văn An -Thái Nguyên - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho hình

vuông

   

, 3;0;8 , 5; 4;0

ABCD B D  

. Biết đỉnh

A

thuộc mặt phẳng

 

Oxy

và có tọa độ là

những số nguyên, khi đó

CA CB



 

bằng:

A.

10 5

. B.

6 10

. C.

10 6

. D.

5 10

.

Dạng 1.2 Tìm tọa độ điểm

Câu 11. (THPT Cù Huy Cận 2019) Trong không gian với hệ tọa độ

Oxyz

, cho các điểm

 

1;0;3

A

,

 

2;3; 4

B



,

 

3;1;2

C 

. Tìm tọa độ điểm

D

sao cho

ABCD

là hình bình hành.

A.

 

4; 2;9

D  

. B.

 

4;2;9

D 

. C.

 

4; 2;9

D 

. D.

 

4;2; 9

D



.

Câu 12. (THPT - Yên Định Thanh Hóa 2019) Trong không gian

Oxyz

, cho ba điểm

     

1;0;0 , 1;1;0 , 0;1;1

A B C

. Tìm tọa độ điểm

D

sao cho tứ giác

ABCD

(theo thứ tự các đỉnh)

là hình bình hành?

A.

 

2;0;0

D

. B.

 

1;1;1

D

. C.

 

0;0;1

D

. D.

 

0;2;1

D

.

Câu 13. (THPT Nguyễn Khuyến 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho ba điểm

(1; 2; 1), (2; 1;3)

A B

 

và

( 3;5;1)

C



. Tìm tọa độ điểm

D

sao cho tứ giác

ABCD

là hình bình

hành.

A.

( 2;8; 3)

D

 

B.

( 4;8; 5)

D

 

C.

( 2;2;5)

D



D.

( 4;8; 3)

D

 

Câu 14. (THPT Nguyễn Khuyến -2019) Trong mặt phẳng với hệ tọa độ

Oxyz

, Tam giác

ABC

với

 

1; 3;3

A 

;

 

2; 4;5

B 

,

 

; 2;C a b



nhận điểm

 

1; ;3G c

làm trọng tâm của nó thì giá trị của

tổng

a b c 

bằng.

A.

5

B.

3

C.

1

D.

2

Câu 15. (THPT Nguyễn Khuyến 2019) Trong không gian với hệ tọa độ

Oxyz

, cho

2

điểm

 

1;2; 3

B



,

 

7;4; 2

C



Nếu điểm

E

thỏa nãm đẳng thức

2E

CE

B



 

thì tọa độ điẻm

E

là:

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

A.

8 8

3; ;

3 3

 



 

 

B.

8 8

;3;

3 3

 



 

 

. C.

8

3;3;

3

 



 

 

D.

1

1;2;

3

 

 

 

Câu 16. (KTNL Gia Bình 2019) Trong không gian với hệ tọa độ

Oxyz

, cho tam giác

ABC

với

 

1;2; 3

A



,

 

2;5;7

B

,

 

3;1;4

C 

. Điểm

D

để tứ giác

ABCD

là hình bình hành là

A.

 

6;6;0

D

B.

8 8

0; ;

3 3

D

 

 

 

C.

 

0;8;8

D

D.

 

4; 2; 6

D

  

Câu 17. (THPT Lương Thế Vinh Hà Nội 2019) Cho tam giác

ABC

có

 

1; 2;0

A 

,

 

2;1; 2

B



,

 

0;3;4

C

. Tìm tọa độ điểm

D

để tứ giác

ABCD

là hình bình hành.

A.

 

1;0; 6

. B.

 

1;6;2

. C.

 

1;0;6



. D.

 

1;6; 2

.

Câu 18. (Liên Trường Thpt Tp Vinh Nghệ An 2019) Trong không gian

Oxyz

, cho hai điểm

 

3;1; 2

A

,

 

2; 3;5

B

. Điểm

M

thuộc đoạn

AB

sao cho

2MA MB

, tọa độ điểm

M

là

A.

7 5 8

; ;

3 3 3

 



 

 

. B.

 

4;5; 9

. C.

3 17

; 5;

2 2

 



 

 

. D.

 

1; 7;12



.

Câu 19. (THPT Minh Khai Hà Tĩnh 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho hai điểm

 

0;1; 2

A



và

 

3; 1;1

B 

. Tìm tọa độ điểm M sao cho

3AM AB



 

.

A.

 

9; 5;7

M 

. B.

 

9;5;7

M

.

C.

 

9;5; 7

M

 

. D.

 

9; 5; 5

M

 

.

Câu 20. (Chuyên Phan Bội Châu 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho hai điểm

   

1;2; 1 , 1;3;1

A AB 



thì tọa độ của điểm

B

là:

A.

 

2;5;0

B

. B.

 

0; 1; 2

B

 

. C.

 

0;1;2

B

. D.

 

2; 5;0

B  

Câu 21. (Đề Thi Công Bằng Khtn 2019) Trong không gian

Oxyz

, cho hình bình hành

ABCD

. Biết

 

1;0;1

A 

,

 

2;1;2

B 

và

 

1; 1;1

D  

. Tọa độ điểm

C

là

A.

 

2;0;2

. B.

 

2;2;2

. C.

 

2; 2;2



. D.

 

0; 2;0



.

Câu 22. (Sở Phú Thọ -2019) Trong không gian với hệ tọa độ

,Oxyz

cho hai điểm

 

1; 2; 2

A

và

8 4 8

; ;

3 3 3

 

 

 

B

. Biết

 

; ;I a b c

là tâm của đường tròn nội tiếp tam giác

OAB

. Giá trị

 a b c

bằng

A.

1

B.

3

C.

2

D.

0

Câu 23. (Chuyên Đhsp Hà Nội -2019) Trong không gian tọa độ

Oxyz

, cho

     

2;0;0 , 0;2;0 , 0;0;2

A B C

. Có tất cả bao nhiêu điểm

M

trong không gian thỏa mãn

M

không trùng với các điểm

, ,A B C

và



90

AMB BMC CMA

   

?

A.

0

. B.

1

. C.

2

. D.

3

.

Câu 24. Trong không gian

Oxyz

, cho hai điểm

(2;2;1)

M

,

8 4 8

; ;

3 3 3

N

 















 

. Tìm tọa độ tâm đường tròn nội

tiếp tam giác

OMN

.

A.

(1;1;1)

I

. B.

(0;1;1)

I

. C.

(0; 1; 1)

I

 

. D.

(1;0;1)

I

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5

Câu 25. Trong không gian với hệ tọa độ

Oxyz

, cho tam giác

ABC

có

 

1;2; 1

A



,

 

2; 1;3

B



,

 

4;7;5

C



. Gọi

 

; ;D a b c

là chân đường phân giác trong góc

B

của tam giác

ABC

. Giá trị của

2a b c 

bằng

A.

5

. B.

4

. C.

14

. D.

15

.

Câu 26. Trong không gian với hệ tọa độ Oxyz, cho hai điểm

 

2;3;1

A 

và

 

5; 6; 2

B

. Đường thẳng

AB

cắt mặt phẳng

 

Oxz

tại điểm

M

. Tính tỉ số

A M

B M

.

A.

1

2

AM

BM



B.

2

AM

BM



C.

1

3

AM

BM



D.

3

AM

BM



Câu 27. (Bình Giang-Hải Dương 2019) Trong không gian với hệ toạ độ

Oxyz

, cho ba điểm

 

2;3;1

A 

,

 

2;1;0

B

,

 

3; 1;1

C  

. Tìm tất cả các điểm

D

sao cho

ABCD

là hình thang có đáy

AD

và diện

tích tứ giác

ABCD

bằng 3 lần diện tích tam giác

ABC

.

A.

 

12; 1;3

D  

. B.

 

8; 7;1

12;1; 3

D

 









. C.

 

8;7; 1

D



. D.

 

8;7; 1

12; 1;3

D





 





.

Câu 28. (THPT Trần Quốc Tuấn - 2018) Trong không gian với hệ trục tọa độ

Oxyz

cho hình thang

ABCD

vuông tại

A

và

B

. Ba đỉnh

(1;2;1)

A

,

(2;0; 1)

B



,

(6;1;0)

C

Hình thang có diện tích bằng

6 2

. Giả sử đỉnh

( ; ; )D a b c

, tìm mệnh đề đúng?

A.

6

a b c

  

. B.

5

a b c

  

. C.

8

a b c

  

. D.

7

a b c

  

.

Câu 29. (Chuyên Lê Quý Dôn - Dà Nẵng - 2018) Trong không gian với hệ tọa độ

Oxyz

cho hình hộp

.

ABCD A B C D

   

. Biết

 

2;4;0

A

,

 

4;0;0

B

,

 

1;4; 7

C

 

và

 

6;8;10

D



. Tọa độ điểm

B



là

A.

 

8;4;10

B



. B.

 

6;12;0

B



. C.

 

10;8;6

B



. D.

 

13;0;17

B



.

Câu 30. (Chuyên Lương Văn Chánh - Phú Yên - 2018) Trong không gian

Oxyz

, cho hình hộp

.

ABCD A B C D

   

có

 

1;0;1

A

,

 

2;1;2

B

,

 

1; 1;1

D 

,

 

4;5; 5

C





. Tính tọa độ đỉnh

A



của hình

hộp.

A.

 

4;6; 5

A





. B.

 

2;0;2

A



. C.

 

3;5; 6

A





. D.

 

3;4; 6

A





.

Câu 31. (Chuyên Lê Hồng Phong 2018) Trong không gian với hệ toạ độ

Oxyz

, cho hình hộp

.

ABCD A B C D

   

có

 

0; 0; 0

A

,

 

3; 0; 0

B

,

 

0; 3; 0

D

,

 

0; 3; 3

D





. Toạ độ trọng tâm tam

giác

A B C

 

là

A.

 

1; 1; 2

. B.

 

2; 1; 2

. C.

 

1; 2; 1

. D.

 

2; 1; 1

.

Câu 32. (Chuyên Lê Hồng Phong - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho ba điểm

 

1;2; 1

A



,

 

2; 1;3

B 

,

 

4;7;5

C 

. Tọa độ chân đường phân giác trong góc

B

của tam giác

ABC

là

A.

2 11

; ;1

3 3

 



 

 

. B.

11

; 2;1

3

 



 

 

. C.

2 11 1

; ;

3 3 3

 

 

 

. D.

 

2;11;1



.

Câu 33. (Toán Học Và Tuổi Trẻ - 2018) Trong không gian với hệ trục tọa độ

Oxyz

, cho

2 2 2OA i j k  

   

,

 

2; 2;0

B 

và

 

4;1; 1

C



. Trên mặt phẳng

 

Oxz

, điểm nào dưới đây cách

đều ba điểm

A

,

B

,

C

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

A.

3 1

; 0;

4 2

M

 

 

 

. B.

3 1

; 0;

4 2

N

 

 

 

 

. C.

3 1

; 0;

4 2

P



 

 

 

. D.

3 1

; 0;

4 2

Q



 

 

 

.

Câu 34. (SGD Thanh Hóa - 2018) Trong hệ trục tọa độ

Oxyz

, cho hai điểm là

 

1;3; 1A 

,

 

3; 1;5B 

.

Tìm tọa độ của điểm

M

thỏa mãn hệ thức

3MA MB

 

.

A.

5 13

; ;1

3 3

M

 

 

 

. B.

7 1

; ;3

3 3

M

 

 

 

. C.

7 1

; ;3

3 3

M

 

 

 

. D.

 

4; 3;8M 

.

Câu 35. (SGD - Đà Nẵng - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho hình hộp

.ABCD A B C D

   

,

biết rằng

 

3;0;0A 

,

 

0;2;0B

,

 

0;0;1D

,

 

1;2;3A



. Tìm tọa độ điểm

C



.

A.

 

10;4;4C



. B.

 

13;4;4C





. C.

 

13;4;4C



. D.

 

7;4;4C



.

Câu 36. (Đặng Thúc Hứa - Nghệ An - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm

 

0;2; 2A 

,

 

2;2; 4B 

. Giả sử

 

; ;I a b c

là tâm đường tròn ngoại tiếp tam giác

OAB

. Tính

2 2 2

T a b c  

.

A.

8T 

. B.

2T 

. C.

6T 

. D.

14T 

.

Câu 37. (THPT Trần Quốc Tuấn - 2018) Trong không gian với hệ tọa độ

Oxyz

cho hai điểm

 

4; 2; 1A

,

 

2; 1;4B  

. Tìm tọa độ điểm

M

thỏa mãn đẳng thức

2AM MB

 

.

A.

 

0;0;3M

. B.

(0;0; 3)M 

. C.

( 8; 4;7)M  

. D.

(8;4; 7)M 

.

Câu 38. (Chuyên Lê Hồng Phong - TPHCM - 2018) Trong không gian với hệ toạ độ

Oxyz

, cho ba điểm

 

2;3;1A 

,

 

2;1;0B

,

 

3; 1;1C  

. Tìm tất cả các điểm

D

sao cho

ABCD

là hình thang có đáy

AD

và 3

ABCD ABC

S S





A.

 

8;7; 1D 

. B.

 

8; 7;1

12;1; 3

D

 









. C.

 

8;7; 1

12; 1;3

D





 





. D.

 

12; 1;3D  

.

Dạng 2. Tích vô hướng, tích có hướng và ứng dụng

Dạng 2.1 Tích vô hướng và ứng dụng

Câu 1. (Mã 104 2017) Trong không gian với hệ tọa độ

Oxyz

cho ba điểm

 

2;3; 1M 

,

 

1;1;1N 

và

 

1; 1;2P m 

. Tìm

m

để tam giác

MNP

vuông tại

N

.

A. B. C. D.

Câu 2. (THPT Yên Khánh - Ninh Bình - 2019) Trong không gian

Oxyz

cho các điểm

     

5;1;5 ; 4;3;2 ; 3; 2;1A B C  

. Điểm

 

; ;I a b c

là tâm đường tròn ngoại tiếp tam giác

ABC

.

Tính

2a b c 

?

A.

1

. B.

3.

C.

6.

D.

9.

Câu 3. (HSG Bắc Ninh 2019) Trong không gian với hệ tọa độ

Oxyz

, cho véc tơ

   

1;1; 2 , 1;0;u v m  

 

. Tìm tất cả giá trị của

m

để góc giữa

u



,

v



bằng

45



.

A.

2m 

. B. 2 6m   . C. 2 6m   . D. 2 6m   .

Câu 4. (Sở Kon Tum - 2019) Trong không gian

Oxyz

, cho các vec tơ

 

5;3; 2a  



và

 

; 1; 3b m m  



. Có bao nhiêu giá trị nguyên dương của

m

để góc giữa hai vec tơ

a



và

b



là

góc tù?

2

m



6

m

 

0

m



4

m

 

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7

A.

2.

B.

3.

C.

1.

D.

5.

Câu 5. Biết

 

; ;c x y z





khác

0



và vuông góc với cả hai vectơ

   

1;3;4 , 1;2;3

a b  

 

. Khẳng định nào

đúng?

A.

5 0z x 

. B.

7 0x y 

. C.

5 0z x 

. D.

7 0x y 

.

Câu 6. Trong không gian tọa độ

Oxyz

, cho

 

2;0;0

A

,

 

0;2;0

B

,

 

0;0;2

C

. Có tất cả bao nhiêu điểm

M

trong không gian thỏa mãn

M

không trùng với các điểm

, ,A B C

và



90

AMB BMC CMA

   

A.

0

. B.

1

. C.

2

. D.

3

.

Câu 7. (Chuyên Lương Văn Chánh - Phú Yên - 2018) Trong không gian

Oxyz

, cho hai vectơ

u



và

v



tạo với nhau một góc

120

và

2

u





,

5

v





. Tính

u v

 

A.

19

. B.

5

. C.

7

. D.

39

.

Câu 8. (THPT Trần Nhân Tông - 2018) Trong không gian với hệ tọa độ Oxyz, cho ba điểm

 

2;3; 1

M



,

 

1;1;1

N 

và

 

1; 1;2

P m 

. Tìm

m

để tam giác

MNP

vuông tại

N

.

A.

6

m

 

. B.

0

m



. C.

4

m

 

. D.

2

m



.

Dạng 2.2 Tích có hướng và ứng dụng

Câu 9. (Yên Phong 1 - 2018) Trong không gian

Oxyz

, cho 4 điểm

 

2;0;2

A

,

 

1; 1; 2

B

 

,

 

1;1;0

C 

,

 

2;1;2

D 

. Thể tích của khối tứ diện

ABCD

bằng

A.

42

3

. B.

14

3

. C.

21

3

. D.

7

3

.

Câu 10. (SGD Cần Thơ - 2018) Trong không gian

Oxyz

, cho các vectơ

 

5;3; 1  



a

,

 

1;2;1





b

,

 

;3; 1 . 



c m

Giá trị của

m

sao cho

,

 



 

  

a b c

là

A.

1 

m

. B.

2 

m

. C.

1

m

. D.

2

m

.

Câu 11. (SGD - Đà Nẵng - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho hai vectơ

 

4;3;1

m 



,

 

0;0;1

n 



. Gọi

p



là vectơ cùng hướng với

,

 

 

 

m n

(tích có hướng của hai vectơ

m



và

n



). Biết

15

p





, tìm tọa độ vectơ

p



.

A.

 

9; 12;0

p  



. B.

 

45; 60;0

p  



. C.

 

0;9; 12

p  



. D.

 

0;45; 60

p  



.

Câu 12. (THPT Hoàng Hoa Thám - Hưng Yên - 2018)Trong không gian với hệ tọa độ

Oxyz

, cho

 

0; 2;2

A a 

;

 

3; 1;1

B a  

;

 

4; 3;0

C  

;

 

1; 2; 1

D a

  

. Tập hợp các giá trị của

a

để bốn

điểm

A

,

B

,

C

,

D

đồng phẳng là tập con của tập nào sau?

A.

 

7; 2 

. B.

 

3;6

.C.

 

5;8

. D.

 

2;2



.

Câu 13. (Việt Đức Hà Nội 2019) Trong hệ trục tọa độ

Oxyz

, cho tứ diện

ABCD

biết

 

3; 2;A m



,

 

2;0;0

B

,

 

0;4;0

C

,

 

0;0;3

D

. Tìm giá trị dương của tham số

m

để thể tích tứ

diện bằng 8.

A.

8

m



. B.

4

m



. C.

12

m



. D.

6

m



.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 8 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 14. (THPT Nguyễn Khuyến 2019) Trong không gian với hệ tọa độ

Oxyz

, cho

   

1;1;2 , 1; ; 2

u v m m

   

 

. Khi

, 14

u v

 



 

 

thì

A.

1

m



hoặc

11

5

m

 

B.

1

m

 

hoặc

11

3

m

 

C.

1

m



hoặc

3

m

 

D.

1

m

 

Câu 15. (THPT Nguyễn Khuyến 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho tứ diện

ABCD

có

 

2; 1;1

A

,

 

3;0; 1

B

,

 

2; 1;3

C

,

D Oy

và có thể tích bằng

5

. Tính tổng tung độ của các

điểm

D

.

A.

6

B.

2

C.

7

D.

4

Câu 16. (Toán Học Tuổi Trẻ 2019) Trong không gian với hệ tọa độ

Oxyz

, cho điểm

 

1; 2;0

A



,

 

1;0; 1

B



,

 

0; 1;2

C



,

 

2; ;D m n

. Trong các hệ thức liên hệ giữa

m

và

n

dưới đây, hệ thức

nào để bốn điểm

,A

,B

,C

D

đồng phẳng?

A.

2 13

m n

 

. B.

2 13

m n

 

. C.

2 13

m n

 

. D.

2 3 10

m n

 

.

Câu 17. Trong không gian

Oxyz

, cho hai véc tơ

 

4 ; 3 ;1

m 



và

 

0 ; 0 ; 1

n 



. Gọi

p



là véc tơ cùng

hướng với

,m n

 

 

 

và

15

p





. Tọa độ của véc tơ

p



là

A.

 

9 ; 12 ; 0



. B.

 

0 ; 9 ; 12



. C.

 

9 ; 12 ; 0



. D.

 

0 ; 9 ; 12



.

Câu 18. (Việt Đức Hà Nội 2019) Trong hệ trục tọa độ

Oxyz

, cho bốn điểm

       

0; 2;1 ; 1;0; 2 ; 3;1; 2 ; 2; 2; 1

A B C D

     

. Câu nào sau đây sai?

A. Bốn điểm

, , ,A B C D

không đồng phẳng. B. Tam giác

ACD

là tam giác vuông tại

A

.

C. Góc giữa hai véctơ

AB



và

CD



là góc tù. D. Tam giác

ABD

là tam giác cân tại

B

.

Câu 19. (THPT Lương Thế Vinh - 2018) Trong không gian

Oxyz

, cho ba điểm

 

2;3;1

A 

,

 

2;1;0

B

,

 

3; 1;1

C  

. Tìm tất cả các điểm

D

sao cho

ABCD

là hình thang có đáy

AD

và 3

ABCD ABC

S S

.

A.

 

8;7; 1

D



. B.

 

8; 7;1

12;1; 3

D

 









. C.

 

8;7; 1

12; 1;3

D





 





. D.

 

12; 1;3

D  

.

Câu 20. (Bình Giang-Hải Dương 2019) Trong không gian với hệ tọa độ

Oxyz

, cho bốn điểm

 

0;0;2

A

,

 

3;0;5

B

,

 

1;1;0

C

,

 

4;1;2

A

. Độ dài đường cao của tứ diện

ABCD

hạ từ đỉnh

D

xuống mặt

phẳng

ABC

là

A.

11

. B.

1

. C.

11

. D.

11

.

Câu 21. (THPT Hoàng Hoa Thám - Hưng Yên - 2018)Trong không gian với hệ tọa độ

Oxyz

, cho

 

0; 2;2

A a 

;

 

3; 1;1

B a  

;

 

4; 3;0

C  

;

 

1; 2; 1

D a

  

. Tập hợp các giá trị của

a

để bốn

điểm

A

,

B

,

C

,

D

đồng phẳng là tập con của tập nào sau?

A.

 

7; 2 

. B.

 

3;6

.C.

 

5;8

. D.

 

2;2



.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương  https://www.facebook.com/phong.baovuong Trang 1

TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH TRUNG BÌNH MỨC 5-6

Lý thuyết chung

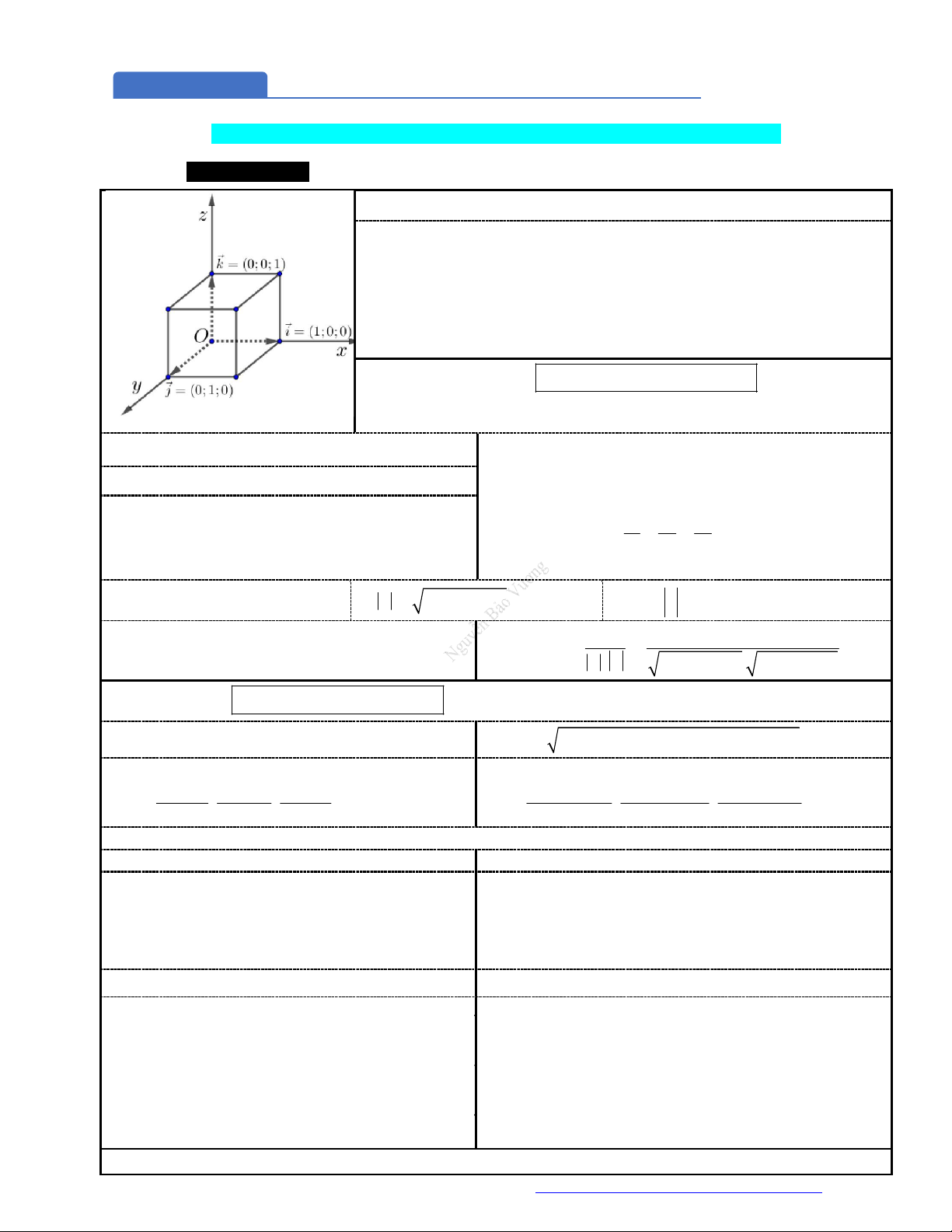
1. Hệ trục tọa độ Oxyz:

 Hệ trục gồm ba trục

, ,Ox Oy Oz

đôi một vuông góc nhau.

 Trục

:Ox

trục hoành, có vectơ đơn vị

(1;0;0)i





.

 Trục

Oy

: trục tung, có vectơ đơn vị

(0;1;0)

j





.

 Trục

:Oz

trục cao, có vectơ đơn vị

(0;0;1).k





 Điểm

(0;0;0)O

là gốc tọa độ.

2. Tọa độ vectơ: Vectơ

( ; ; )u xi y j zk u x y z

    

    

.

Cho

1 2 3 1 2 3

( ; ; ), ( ; ; )a a a a b b b b

 

 

. Ta có:



1 1 2 2 3 3

( ; ; )a b a b a b a b



    



a



cùng phương

b



( )a kb k R

 

  

1 1

31 2

2 2 1 2 3

1 2 3

3 3

, ( , , 0).

a kb

a

a a

a kb b b b

b b b

a kb







     











1 2 3

( ; ; )ka ka ka ka







1 1

2 2

3 3

a b

a b a b

a b

 







  











1 1 2 2 3 3

. . . .a b a b a b a b



  



2 2 2

1 2 2

a a a a



  



2

2 2 2 2

1 2 3

a a a a a



   



1 1 2 2 3 3

. 0 0

a b a b a b a b a b

   

      



1 1 2 2 3 3

2 2 2 2 2 2

1 2 3 1 2 3

.

cos( , )

.

a b a b a b

a b

a a a b b b



 

 

   

3. Tọa độ điểm:

( ; ; ) ( ; ; )M x y z OM x y z



 

. Cho

( ; ; ) , ( ; ; ) , ( ; ; )

A A A B B B C C C

A x y z B x y z C x y z

, ta có:



( ; ; )

B A B A B A

AB x x y y z z



   



2 2 2

( ) ( ) ( )

B A B A B A

AB x x y y z z     

 Toạ độ trung điểm M của đoạn thẳng AB:

; ; .

2 2 2

A B A B A B

x x y y z z

M

  

 

 

 

 Toạ độ trọng tâm G của tam giác ABC:

; ; .

3 3 3

A B C A B C A B C

x x x y y y z z z

G

     

 

 

 

QUY TẮC CHIẾU ĐẶC BIỆT

Chiếu điểm trên trục tọa độ Chiếu điểm trên mặt phẳng tọa độ

 Điểm

1

( )

( ; ; ) ( ;0;0)

Chieáu vaøo Ox

M M M M

Giöõ nguyeân x

M x y z M x

  

 Điểm

2( )

( ; ; ) (0; ;0)

Chieáu vaøo Oy

M M M MGiöõ nguyeân y

M x y z M y  

 Điểm

3( )

( ; ; ) (0;0; )

Chieáu vaøo Oz

M M M MGiöõ nguyeân z

M x y z M z  

 Điểm

1

( , )

( ; ; ) ( ; ;0)

Chieáu vaøo Oxy

M M M M M

Giöõ nguyeân x y

M x y z M x y

   

 Điểm

2( , )

( ; ; ) (0; ; )

Chieáu vaøo Oyz

M M M M MGiöõ nguyeân y z

M x y z M y z    

 Điểm

3( , )

( ; ; ) ( ;0; )

Chieáu vaøo Oxz

M M M M MGiöõ nguyeân x z

M x y z M x z   

Đối xứng điểm qua trục tọa độ Đối xứng điểm qua mặt phẳng tọa độ



1( ; , )

( ; ; ) ( ; ; )

Ñoái xöùng qua Ox

M M M M M M

Giöõ nguyeân x ñoåi daáu y z

M x y z M x y z        



2

( ; , )

( ; ; ) ( ; ; )

Ñoái xöùng qua Oy

M M M M M M

Giöõ nguyeân y ñoåi daáu x z

M x y z M x y z         



3( ; , )

( ; ; ) ( ; ; )

Ñoái xöùng qua Oz

M M M M M M

Giöõ nguyeân z ñoåi daáu x y

M x y z M x y z

        



1

( , ; )

( ; ; ) ( ; ; )

Ñoái xöùng qua Oxy

M M M M M M

Giöõ nguyeân x y ñoåi daáu z

M x y z M x y z

       



2

( , ; )

( ; ; ) ( ; ; )

Ñoái xöùng qua Oxz

M M M M M M

Giöõ nguyeân x z ñoåi daáu y

M x y z M x y z        



3( , ; )

( ; ; ) ( ; ; )

Ñoái xöùng qua Oyz

M M M M M MGiöõ nguyeân y z ñoåi daáu x

M x y z M x y z        

4. Tích có hướng của hai vectơ:

HỆ TRỤC TỌA ĐỘ

Chuyên đề 28

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

 Định nghĩa: Cho

1 2 3

( , , )a a a a





,

1 2 3

( , , )b b b b





, tích có hướng của

a



và

b



là:

 

2 3 3 1 1 2

2 3 3 2 3 1 1 3 1 2 2 1

2 3 3 1 1 2

, ; ; ; ;

a a a a a a

a b a b a b a b a b a b a b

b b b b

b b



 

 

    

 

 

 

.

 Tính chất:

[ , ]a b a

  



[ , ]a b b

  



 

[ , ] . .sin ,a b a b a b

 



 Điều kiện cùng phương của hai vectơ

&a b

 

là

, 0a b

  

 



 

với

0 (0;0;0).





 Điều kiện đồng phẳng của ba vectơ

,a b

 

và

c



là

[ , ]. 0.a b c

  



 Diện tích hình bình hành

ABCD:

, .

ABCD

S AB AD



 

 



 

 Diện tích tam giác ABC:

1

, .

2

ABC

S AB AC

 



 



 

 Thể tích khối hộp:

. ' ' ' '

[ , ]. ' .

ABCD A B C D

V AB AD AA

  



 Thể tích tứ diện:

1

, .

6

ABCD

V AB AC AD

  

 



 

.

Dạng 1. Tìm tọa độ điểm, véc tơ liên quan đến hệ trục tọa dộ OXYZ

Dạng 1.1 Tìm hình chiếu của điểm lên mặt phẳng, đường thẳng

Câu 1. (Đề Minh Họa 2020 Lần 1) Trong không gian

Oxyz

, hình chiếu vuông góc của điểm

 

2; 2;1M 

trên mặt phẳng

 

Oxy

có tọa độ là

A.

 

2;0;1

. B.

 

2; 2;0

. C.

 

0; 2;1

. D.

 

0;0;1

.

Lời giải

Chọn B

Ta có hình chiếu của điểm

 

0 0 0

; ;M x y z

trên mặt phẳng

 

Oxy

là điểm

 

0 0

; ;0M x y



.

Do đó hình chiếu của điểm

 

2; 2;1M 

trên mặt phẳng

 

Oxy

là điểm

 

2; 2;0M





.

Câu 2. (Đề Tham Khảo 2020 Lần 2) Trong không gian

Oxyz

, hình chiếu vuông góc của điểm

 

2;1; 1M 

trên mặt phẳng

 

Ozx

có tọa độ là

A.

 

0;1;0

. B.

 

2;1;0

. C.

 

0;1; 1

. D.

 

2;0; 1

.

Lời giải

Chọn D

Hình chiếu của

 

2;1; 1M 

lên mặt phẳng

 

Ozx

là điểm có tọa độ

 

2;0; 1

.

Câu 3. (Mã 102 - 2020 Lần 1) Trong không gian , hình chiếu vuông góc của điểm trên

trục có tọa độ là

A. . B. . C. . D. .

Lời giải

Chọn C

Hình chiếu vuông góc của điểm trên trục có tọa độ là .

Câu 4. (Mã 101 - 2020 Lần 1) Trong không gian

Oxyz

, hình chiếu vuông góc của điểm

 

3;2;1A

trên

trục

Ox

có tọa độ là:

A.

 

0;2;1

. B.

 

3;0;0

. C.

 

0;0;1

. D.

 

0;2;0

.

Lời giải

Chọn B.

Oxyz

 

1;2;5

A

Ox

 

0;2;0

 

0;0;5

 

1;0;0

 

0;2;5

 

1;2;5

A

Ox

 

1;0;0

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3

Câu 5. (Mã 103 - 2020 Lần 1) Trong không gian

Oxyz

, hình chiếu vuông góc của điểm

 

3;5;2

A

trên

trục

Ox

có tọa độ là

A.

 

0;5; 2

. B.

 

0;5;0

. C.

 

3;0;0

. D.

 

0;0;2

.

Lời giải

Chọn C

Hình chiếu vuông góc của điểm

 

3;5;2

A

trên trục

Ox

có tọa độ là

 

3;0;0

.

Câu 6. (Mã 104 - 2020 Lần 1) Trong không gian

Oxyz

,

hình chiếu vuông góc của điểm

(8;1; 2)

A

trên

trục

Ox

có tọa độ là

A.

(0;1;0)

. B.

(8;0;0)

. C.

(0;1;2)

. D.

(0;0;2)

.

Lời giải

Chọn B

Hình chiếu vuông góc của điểm

(8;1;2)

A

trên trục

Ox

là

(8;0;0)

.

Câu 7. (Mã 101 - 2020 Lần 2) Trong không gian

Oxyz

. Điểm nào sau đây là hình chiếu vuông góc của

điểm

(1;4;2)

A

trên mặt phẳng

Oxy

?

A.

(0;4;2)

. B.

(1;4;0)

. C.

(1;0;2)

. D.

(0;0;2)

.

Lời giải

Chọn B

Ta có hình chiếu của

(1;4;2)

A

trên mặt phẳng

Oxy

là

(1;4;0)

.

Câu 8. (Mã 103 - 2020 Lần 2) Trong không gian

Oxyz

điểm nào dưới đây là hình chiếu vuông góc của

điểm

 

3;5;2

A

trên mặt phẳng

 

Oxy

?

A.

 

3;0;2

M

B.

 

0;0;2

C.

 

0;5;2

Q

D.

 

3;5;0

N

Lời giải

Chọn D

Hình chiếu vuông góc của điểm

 

3;5;2

A

trên mặt phẳng

 

Oxy

là điểm

 

3;5;0

N

.

Câu 9. (Mã 102 - 2020 Lần 2) Trong không gian

Oxyz

, điểm nào dưới đây là hình chiếu vuông góc của

điểm

 

1;2;3

A

trên mặt phẳng

Oxy

.

A.

 

1;0;3

Q

B.

 

1;2;0

P

C.

 

0;0;3

M

D.

 

0;2;3

N

Lời giải

Chọn B

Ta có hình chiếu vuông góc của điểm

 

1;2;3

A

trên mặt phẳng

Oxy

là điểm

 

1;2;0

P

.

Câu 10. (Mã 104 - 2020 Lần 2) Trong không gian

Oxyz

, điểm nào dưới đây là hình chiếu vuông góc của

điểm

 

3;4;1

A

trên mặt phẳng

 

Oxy

?

A.

 

0;4;1

Q

. B.

 

3;0;1

P

. C.

 

0;0;1

M

. D.

 

3;4;0

N

.

Lời giải

Chọn D

Hình chiếu vuông góc của điểm

 

3;4;1

A

trên mặt phẳng

 

Oxy

là điểm

 

3;4;0

N

.

Câu 11. (Mã 104 - 2019) Trong không gian

Oxyz

, hình chiếu vuông góc của điểm

 

3;1; 1

M



trên trục

Oy

có tọa độ là

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

A.

 

3;0; 1

. B.

 

0;1;0

. C.

 

3;0;0

. D.

 

0;0; 1

.

Lời giải

Chọn B

Hình chiếu vuông góc của điểm

 

3;1; 1

M



trên trục

Oy

có tọa độ là

 

0;1;0

.

Câu 12. (Mã 103 - 2019) Trong không gian

Oxyz

, hình chiếu vuông góc của điểm

 

2;1; 1

M



trên trục

Oy

có tọa độ là

A.

 

0;0; 1

. B.

 

2;0; 1

. C.

 

0;1;0

. D.

 

2;0;0

.

Lời giải

Chọn C

Hình chiếu vuông góc của điểm

 

2;1; 1

M



trên trục

Oy

có tọa độ là

 

0;1;0

.

Câu 13. (Mã 102 - 2019) Trong không gian

Oxyz

, hình chiếu vuông góc của điểm

 

3; 1;1

M 

trên trục

Oz

có tọa độ là

A.

 

3; 1;0



. B.

 

0;0;1

. C.

 

0; 1;0



. D.

 

3;0;0

.

Lời giải

Chọn B

Hình chiếu vuông góc của điểm

 

3; 1;1

M 

trên trục

Oz

có tọa độ là

 

0;0;1

Câu 14. (Mã 101 - 2019) Trong không gian

Oxyz

, hình chiếu vuông góc của điểm

 

2;1; 1

M



trên trục

Oz

có tọa độ là

A.

 

2;0;0

. B.

 

0;1;0

. C.

 

2;1;0

. D.

 

0;0; 1

.

Lời giải

Chọn D

Hình chiếu vuông góc của điểm

 

2;1; 1

M



trên trục

Oz

có tọa độ là:

 

0;0; 1

.

Câu 15. (Đề Tham Khảo 2018) Trong không gian

Oxyz

, cho điểm

 

3; 1;1

A 

. Hình chiếu vuông góc của

điểm

A

trên mặt phẳng

 

Oyz

là điểm

A.

 

3;0;0

M

B.

 

0; 1;1

N 

C.

 

0; 1;0

P 

D.

 

0;0;1

Q

Lời giải

Chọn B

Khi chiếu vuông góc một điểm trong không gian lên mặt phẳng

 

Oyz

, ta giữ lại các thành phần

tung độ và cao độ nên hình chiếu của

 

3; 1;1

A 

lên

 

Oyz

là điểm

 

0; 1;1

N 

.

Câu 16. (Chuyên Lương Thế Vinh Đồng Nai 2019) Trong không gian với hệ tọa độ

Oxyz

, điểm nào sau

đây nằm trên mặt phẳng tọa độ

 

Oyz

?

A.

 

3;4;0

M

. B.

 

2;0;3

P 

. C.

 

2;0;0

Q

. D.

 

0;4; 1

N



.

Lời giải

Mặt phẳng tọa độ

 

Oyz

có phương trình là

   

0 0;4; 1

x N Oyz

   

.

Câu 17. (Chuyên Hạ Long 2019) Trong không gian với hệ trục tọa độ

Oxyz

cho

 

4;5;6

M

. Hình chiếu

của

M

xuống mặt phẳng

 

Oyz

là

M



. Xác định tọa độ

M



.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5

A.

 

4;5;0

M



. B.

 

4;0;6

M



. C.

 

4;0;0

M



. D.

 

0;5;6

M



.

Lời giải

Hình chiếu của

 

4;5;6

M

xuống mặt phẳng

 

Oyz

là

 

0;5;6

M



.

Câu 18. (Chuyên Hạ Long 2019) Trong không gian với hệ trục tọa độ

Oxyz

cho điểm

 

; ;M x y z

.

Trong các mệnh đề sau, mệnh đề nào đúng?

A. Nếu

M



đối xứng với

M

qua mặt phẳng

 

Oxz

thì

 

; ;M x y z





.

B. Nếu

M



đối xứng với

M

qua

Oy

thì

 

; ;M x y z





.

C. Nếu

M



đối xứng với

M

qua mặt phẳng

 

Oxy

thì

 

; ;M x y z





.

D. Nếu

M



đối xứng với

M

qua gốc tọa độ

O

thì

 

2 ;2 ;0M x y



.

Lời giải

Nếu

M



đối xứng với

M

qua mặt phẳng

 

Oxz

thì

 

; ;M x y z





. Do đó phương án

A

sai.

Nếu

M



đối xứng với

M

qua

Oy

thì

 

;y;M x z



 

. Do đó phương án

B

sai.

Nếu

M



đối xứng với

M

qua gốc tọa độ

O

thì

 

; y; z

M x



  

. Do đó phương án

D

sai.

Câu 19. (THCS - THPT Nguyễn Khuyến 2019) Trong không gian

Oxyz

, tọa độ điểm đối xứng của

 

M ; ;1 2 3

qua mặt phẳng

 

Oyz

là

A.

 

0 2 3; ;

. B.

 

1 2 3; ;  

. C.

 

1 2 3; ;



. D.

 

1 2 3; ;

.

Lời giải

Gọi

H

là hình chiếu của

M

lên mặt phẳng

   

Oyz H ; ;



0 2 3

Gọi

M '

là điểm đối xứng với

 

M ; ;1 2 3

qua mặt phẳng

 

Oyz

H

là trung điểm của

 

MM ' M ' ; ;

 

1 2 3

.

Câu 20. (Chuyên Hạ Long 2018) Trong không gian

Oxyz

, cho điểm

 

2; 3;5

A 

. Tìm tọa độ

A



là điểm

đối xứng với

A

qua trục

Oy

.

A.

 

2;3;5

A



. B.

 

2; 3; 5

A



 

. C.

 

2; 3;5

A



 

. D.

 

2; 3; 5

A



  

.

Lời giải

Gọi

H

là hình chiếu vuông góc của

 

2; 3;5

A 

lên

Oy

. Suy ra

 

0; 3;0

H 

Khi đó

H

là trung điểm đoạn

AA



.

2 2

2 3

2 5

A H A

x x x

y y y

z z z



   





   





   



 

2; 3; 5

A



   

.

Dạng 1.2 Xác định tọa độ vectơ, độ dài vec tơ

Câu 21. (Mã 102 2018) Trong không gian

Oxyz

, cho hai điểm

 

1;1; 2

A



và

 

2;2;1

B

. Vectơ

AB



có

tọa độ là

A.

 

1; 1; 3  

B.

 

3;1;1

C.

 

1;1;3

D.

 

3;3; 1

Lời giải

Chọn C

 

2 1;2 1;1 2

AB

    



hay

 

1;1;3

AB 



.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 22. (Đề Tham Khảo 2019) Trong không gian

,Oxyz

cho hai điểm

 

1;1; 1

A



và

 

2;3;2

B

. Vectơ

AB



có tọa độ là

A.

 

1; 2; 3

B.

 

1; 2; 3

 

C.

 

3;5;1

D.

 

3;4;1

Lời giải

Chọn A

   

; ; 1;2;3

B A B A B A

AB x x y y z z    



Câu 23. (Mã 110 2017) Trong không gian với hệ toạ độ

Oxyz

, cho điểm

 

2;2;1

A

. Tính độ dài đoạn

thẳng

OA

.

A.

5

OA 

B.

5

OA



C.

3

OA



D.

9

OA



Lời giải

Chọn C

2 2 2

2 2 1 3

OA

   

.

Câu 24. (THPT Nguyễn Khuyến 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho ba vecto

     

1;2;3 ; 2;2; 1 ; 4;0; 4

a b c

 



 

. Tọa độ của vecto

2d a b c  

 

là

A.

 

7;0; 4

d

 



B.

 

7;0;4

d 



C.

 

7;0; 4

d





D.

 

7;0;4

d



Lời giải

Chọn B

Ta có:

   

2 1 2 2.4;2 2 2.0;3 1 2.( 4) 7;0; 4

d a b c

            

 

.

Câu 25. (THPT Ba Đình 2019) Trong không gian

Oxyz

, cho hai điểm

 

0;1; 1

A



,

 

2;3;2

B

. Vectơ

AB



có tọa độ là

A.

 

2;2;3

. B.

 

1;2;3

. C.

 

3;5;1

. D.

 

3;4;1

.

Lời giải

Hai điểm

 

0;1; 1

A



,

 

2;3;2

B

. Vectơ

AB



có tọa độ là

 

2;2;3

.

Câu 26. (THPT Gia Lộc Hải Dương 2019) Trong không gian

Oxyz

cho

 

2;3;2

a 



và

 

1;1; 1

b

 



.

Vectơ

a b



có tọa độ là

A.

 

3;4;1

. B.

 

1; 2;3

 

. C.

 

3;5;1

. D.

 

1;2;3

.

Lời giải

Ta có:

   

2 1;3 1;2 1 1;2;3

a b     



.

Câu 27. (THPT Hoàng Hoa Thám Hưng Yên 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho

 

2; 3;3

a  



,

 

0;2; 1

b

 



,

 

3; 1;5

c  



. Tìm tọa độ của vectơ

2 3 2u a b c  



  

.

A.

 

10; 2;13



. B.

 

2;2; 7 

. C.

 

2; 2;7

 

. D.

 

2;2;7



.

Lời giải

Ta có:

 

2 4; 6;6

a  



,

 

3 0;6; 3

b

 



,

 

2 6;2; 10

c   



 

2 3 2 2;2; 7

u a b c

      



  

.

Câu 28. (THPT Hùng Vương Bình Phước 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho

2 3a i j k   

  



. Tọa độ của vectơ

a



là

A.

 

1;2; 3 

. B.

 

2; 3; 1 

. C.

 

2; 1; 3 

. D.

 

3; 2; 1 

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7

Lời giải

 

2 3 1;2; 3      

  

 

a i j k a

.

Câu 29. Trong không gian với hệ tọa độ

Oxyz

, cho

 

2; 3; 3

a  



,

 

0; 2; 1

b

 



,

 

3; 1; 5

c  



. Tìm tọa

độ của vectơ

2 3 2u a b c  

   

.

A.

 

10; 2;13



. B.

 

2; 2; 7 

. C.

 

2; 2; 7

 

. D.

 

2; 2; 7



.

Lời giải

Có

     

2 4; 6;6 ; 3 0;6; 3 ; 2 6;2; 10

a b c       

  

.

Khi đó:

 

2 3 2 2; 2; 7

u a b c

     

   

.

Câu 30. (THPT Minh Khai Hà Tĩnh 2019) Trong không gian với hệ tọa độ

Oxyz

, cho hai vectơ

 

2;1; 3

x

 



và

 

1;0; 1

y

 



. Tìm tọa độ của vectơ

2a x y 

  

.

A.

 

4;1; 1

a

 



. B.

 

3;1; 4

a

 



. C.

 

0;1; 1

a

 



. D.

 

4;1; 5

a

 



.

Lời giải

Ta có:

 

2 2;0; 2

y

 



.

   

2 2 2;1 0; 3 2 4;1; 5

a x y

        

  

.

Câu 31. (THPT - Yên Định Thanh Hóa 2019) Trong không gian

O xyz

, cho

 

2; 1;0

A

và

 

1;1; 3

B

.

Vectơ



AB

có tọa độ là

A.

 

3;0; 3

. B.

 

1;2; 3 

. C.

 

1; 2;3

 

. D.

 

1; 2;3



.

Lời giải

 

2; 1;0

A

,

 

1;1; 3

B

   

1 2;1 1; 3 0 1;2; 3        



AB

.

Câu 32. (Sở Hà Nội 2019) Trong không gian

Oxyz

cho

   

2; 2;1 , 1; 1;3 .

A B 

Tọa độ vecto

AB



là:

A.

( 1;1; 2).

. B.

( 3;3; 4). 

. C.

(3; 3;4).

. D.

(1; 1; 2) 

Lời giải:

Ta có:

 

1;1;2

AB  



.

Câu 33. (Chuyên Lương Thế Vinh Đồng Nai 2019) Trong không gian

Oxyz

với

, ,i j k

  

lần lượt là các

vecto đơn vị trên các trục

, , .Ox Oy Oz

Tính tọa độ của vecto

.i j k 

  

A.

( 1; 1;1).

i j k    

  

B.

( 1;1;1).

i j k   

  

C.

(1;1; 1).

i j k

   

  

D.

(1; 1;1).

i j k   

  

Lời giải

Ta có

(1;0;0), (0;1;0), (0;0;1).

i j k  

  

Do đó,

(1;1; 1).

i j k

   

  

Câu 34. (THPT Gang Thép Thái Nguyên 2019) Trong không gian với hệ tọa độ

Oxyz

giả sử

2 3

u i j k  

   

, khi đó tọa độ véc tơ

u



là

A.

 

2;3;1



. B.

 

2;3; 1

. C.

 

2; 3; 1 

. D.

 

2;3;1

.

Lời giải

Theo định nghĩa ta có

 

1;0;0

i 



,

 

0;1;0

j 



và

 

0;0;1

k 



.

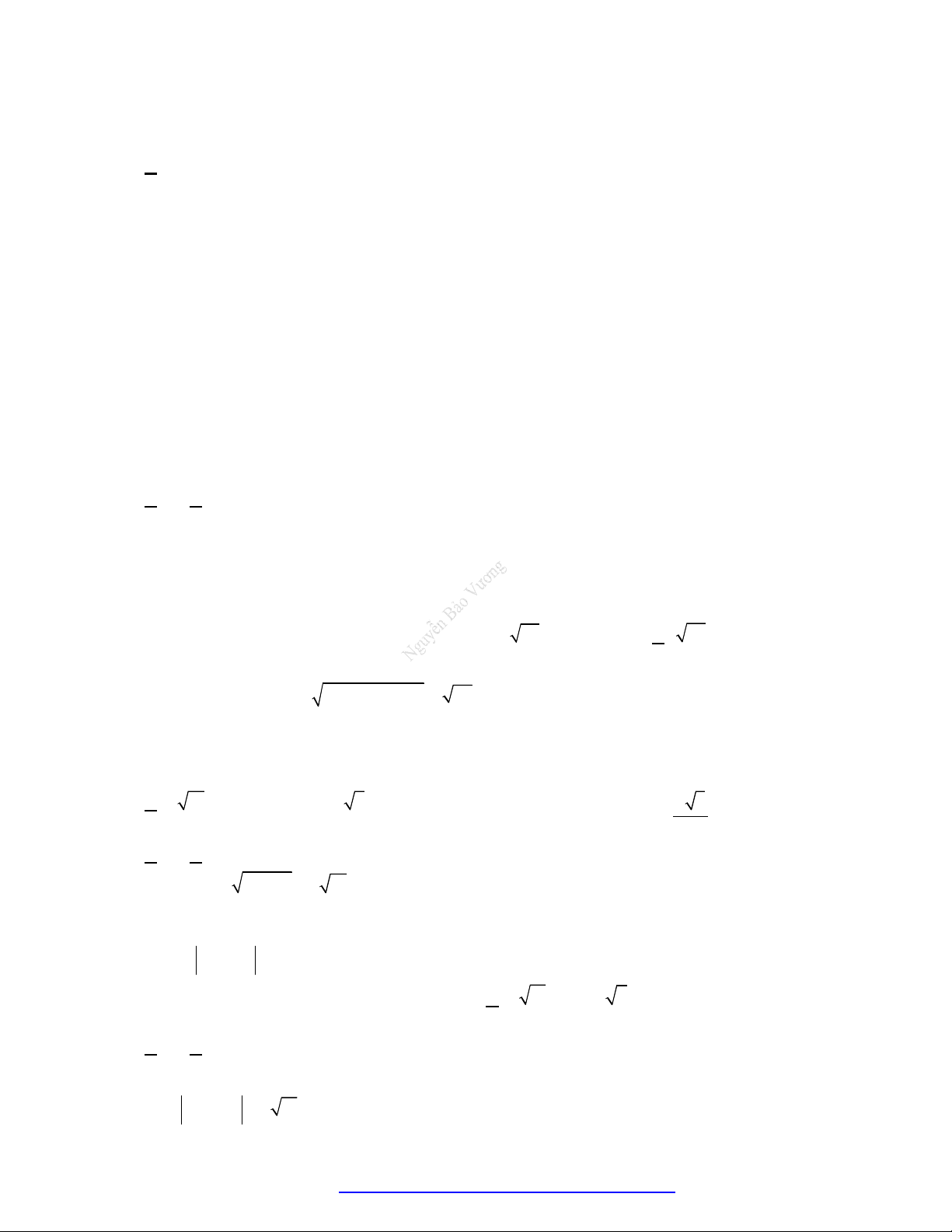
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 8 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Do đó,

 

2 3 2;3; 1

u i j k u

     

    

.

Câu 35. (THPT Lê Quý Đôn Đà Nẵng 2019) Trong không gian

Oxyz

, cho

 

1;2;1

a 



và

 

1;3;0

b  



.

Vectơ

2

c a b 



 

có tọa độ là

A.

 

1;7;2

. B.

 

1;5;2

. C.

 

3;7;2

. D.

 

1;7;3

.

Lời giải

Có

2

c a b 



 

, gọi

 

1 2 3

; ;c c c c





 

1

2

3

2.1 1 1

2.2 3 7

2.1 0 2

c

   





   





  



Vậy

 

1;7;2

c 



Câu 36. (KTNL GV Thuận Thành 2 Bắc Ninh 2019) Trong không gian với trục hệ tọa độ

Oxyz

, cho

2 3 .a i j k

   

   

Tọa độ của vectơ

a



là:

A.

 

1;2; 3

a

 



. B.

 

2; 3; 1

a

 



. C.

 

3;2; 1

a

 



. D.

 

2; 1; 3

a

 



.

Lời giải

Chọn A

+) Ta có

 

; ;a xi y j zk a x y z

   

    

nên

 

1;2; 3 .

a

 



Do đó Chọn A

Câu 37. (Sở Thanh Hóa 2019) Trong không gian với hệ tọa độ Oxyz, cho hai điểm A

 

1; 3;1



,

B

 

3;0; 2

. Tính độ dài

AB

.

A. 26. B. 22. C.

26

. D.

22.

Lời giải

2 2 2

(2;3; 3) 2 3 ( 3) 22.

AB AB       



Câu 38. (Chuyên - KHTN - Hà Nội - 2019) Trong không gian

Oxyz

, cho hai điểm

 

1; 2; 1

A

 

,

 

1;4;3

B

. Độ dài đoạn thẳng

AB

là

A.

2 13

B.

6

C.

3

D.

2 3

Lời giải

Chọn A

Ta có

2 2

6 4 2 13

AB   

.

Câu 39. (Hội 8 trường chuyên 2019) Trong không gian Oxyz, cho

     

2;2;0 , 2;2;0 , 2;2;2

a b c

  

. Giá

trị của

a b c 

  

bằng

A.

6.

B.

11

. C.

2 11

. D.

2 6

.

Lời giải

Chọn C

Ta có:

 

2;6;2

a b c  

  

.

Vậy

2 11

a b c  

  

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9

Câu 40. (Chuyên Nguyễn Du-ĐăkLăk 2019) Trong không gian

Oxyz

, cho 2 điểm

 

1;3;5

A

,

 

2;2;3

B

. Độ dài đoạn

AB

bằng

A.

7

. B.

8

. C.

6

. D.

5

.

Lời giải

Chọn C

     

2 2 2

2 1 2 3 3 5 6

AB       

.

Dạng 1.3 Xác định tọa độ điểm

Câu 41. (Mã 101 2018) Trong không gian

Oxyz

, cho hai điểm

 

2; 4;3

A 

và

 

2;2;7

B

. Trung điểm của

đoạn thẳng

AB

có tọa độ là

A.

 

4; 2;10



B.

 

1;3;2

C.

 

2;6;4

D.

 

2; 1;5



Lời giải

Chọn D

Gọi

I

là trung điểm của

AB

, ta có tọa độ điểm

I

là

2

1

2

5

2

A B

I

A B

I

A B

I

x x

x

y y

y

z z

z





 







  









 





.

Vậy

 

2; 1;5

I 

.

Câu 42. (Đề Tham Khảo 2017) Trong không gian với hệ tọa độ

Oxyz

, cho các điểm

 

3; 4;0

A 

,

 

1;1;3

B 

,

 

3,1,0

C

. Tìm tọa độ điểm

D

trên trục hoành sao cho

AD BC

.

A.

 

6;0;0

D

,

 

12;0;0

D

B.

 

0;0;0

D

,

 

6;0;0

D

C.

 

2;1;0

D 

,

 

4;0;0

D 

D.

 

0;0;0

D

,

 

6;0;0

D 

Lời giải

Chọn B

Gọi

 

;0;0

D x Ox



 

2

0

3 16 5

6

x

AD BC x

x





     







.

Câu 43. Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm

 

3; 2;3

A

và

 

1;2;5

B

. Tìm tọa độ trung

điểm

I

của đoạn thẳng

AB

.

A.

 

1;0;4

I

. B.

 

2;0;8

I

. C.

 

2; 2; 1 

I

. D.

 

2;2;1

I

.

Lời giải

Chọn A

Tọa độ trung điểm

I

của đoạn

AB

với

 

3; 2;3

A

và

 

1;2;5

B

được tính bởi

 

1

2

0 1;0;4

2

4

2



















 











A B

I

A B

I

A B

I

x

y

z

x

y

I

z

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 10 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 44. (THPT Cẩm Giàng 2 2019) Trong không gian với hệ tọa độ

Oxyz

cho hai điểm

 

3; 2;3

A 

và

 

1;2;5

B 

. Tìm tọa độ trung điểm

I

của đoạn thẳng

AB

là :

A.

 

2;2;1

I 

. B.

 

1;0;4

I

. C.

 

2;0;8

I

. D.

 

2; 2; 1

I

 

.

Lời giải

Chọn B

Cho hai điểm

 

3; 2;3

A 

và

 

1;2;5

B 

.

Trung điểm

I

có tọa độ:

 

3 1

1

2 2

0

2 2

3 5

4

2 2

A B

x x

y y

z z

 



 



 





 





 



 





 

1;0;4

I

.

Câu 45. (THPT Hoàng Hoa Thám Hưng Yên 2019) Trong không gian với hệ tọa độ

Oxyz

, cho

 

1;3;2

A

,

 

3; 1;4

B 

. Tìm tọa độ trung điểm

I

của

.AB

A.

 

2; 4;2

I 

. B.

 

4;2;6

I

. C.

 

2; 1; 3

I

  

. D.

 

2;1;3

I

.

Lời giải

Ta có

 

2

1 2;1;3

2

3

2

A B

I

A B

I

A B

I

x x

x

y y

y I

z z

z





 







  









 





.

Câu 46. Trong không gian cho hệ trục toạ độ

Oxyz

, cho ba điểm

     

1; 2;3 , 1;2;5 , 0;0;1

A B C 

. Tìm

toạ độ trọng tâm

G

của tam giác

ABC

.

A.

 

0;0;3

G

. B.

 

0;0;9

G

. C.

 

1;0;3

G 

. D.

 

0;0;1

G

.

Lời giải

Toạ độ trong tâm

G

của tam giác

ABC

bằng

 

1 1 0

0

3 3

2 2 0

0 0;0;3

3 3

3 5 1

3

3 3

A B C

G

A B C

G

A B C

G

x x x

x

y y y

y G

z z z

z

 

 



  



 

  



   





 



  





Câu 47. Trong không gian với hệ trục tọa độ

Oxyz

cho

 

1;3;2

A

,

 

3; 1;4

B 

. Tìm tọa độ trung điểm

I

của

AB

.

A.

 

2; 4;2

I 

. B.

 

4;2;6

I

. C.

 

2; 1;3

I  

. D.

 

2;1;3

I

.

Lời giải

Tọa độ trung điểm

I

của

AB

là

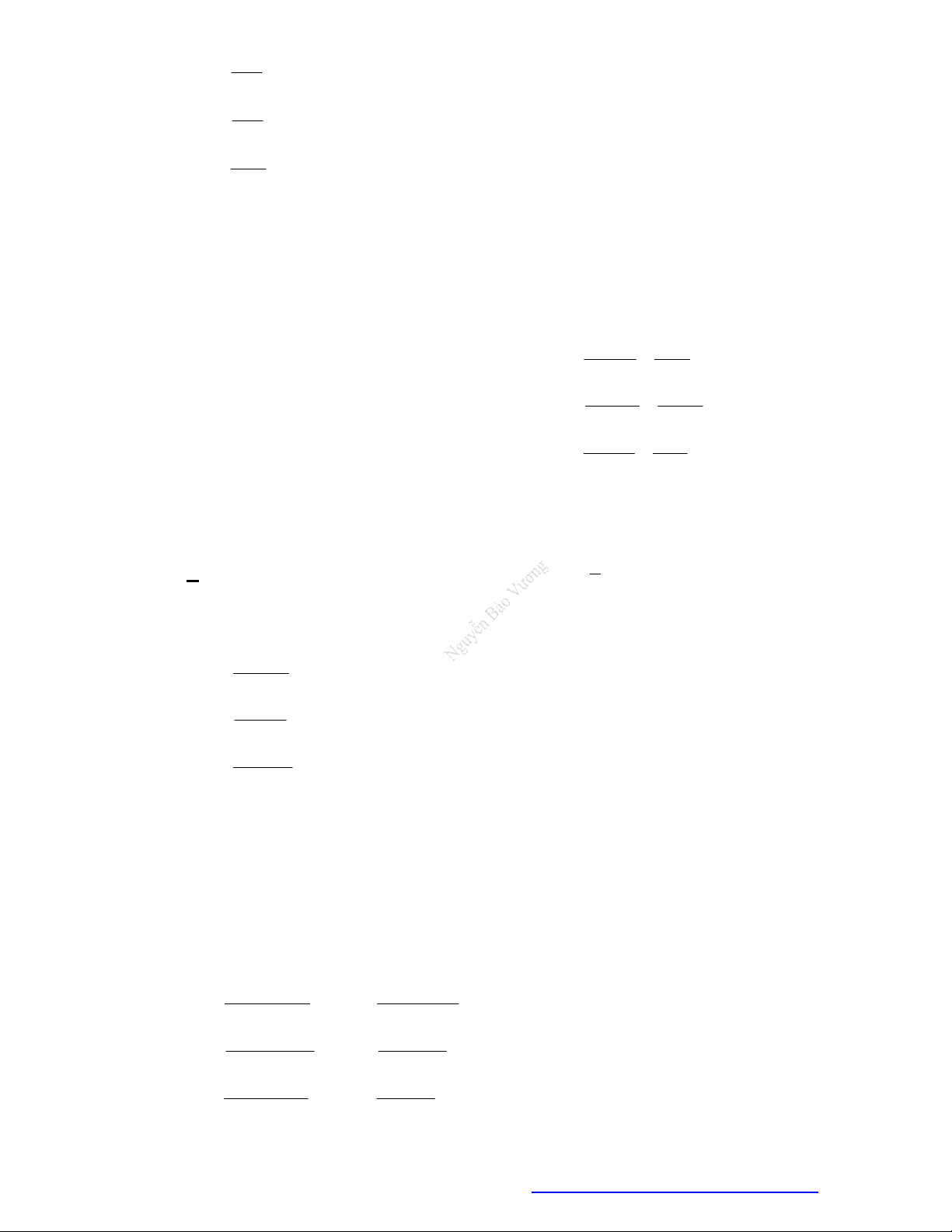
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11

 

1 3

2

3 1

1 2;1;3 .

2

2 4

3

2

I

x

y I

z





 







  









 





Câu 48. (THPT Đoàn Thượng - Hải Dương - 2019) Trong không gian

Oxyz

, cho hai điểm

 

2; 4;3

A 

và

 

2;2;7

B

. Trung điểm của đoạn thẳng

AB

có tọa độ là

A.

 

1;3;2

. B.

 

2; 1;5



. C.

 

2; 1; 5 

. D.

 

2;6;4

.

Lời giải

Gọi

M

là trung điểm của đoạn thẳng

AB

, ta có:

2 2

2

2 2

4 2

1

2 2

3 7

5

2 2

A B

M

A B

M

A B

M

x x

x

y y

y

z z

z

 



  



  



   





 



  







 

2; 1;5

M 

.

Câu 49. (THPT Cù Huy Cận 2019) Trong không gian với hệ tọa độ

Oxyz

, cho tam giác

ABC

với

     

1;3;4 , 2; 1;0 , 3;1;2

A B C

. Tọa độ trọng tâm

G

của tam giác

ABC

là

A.

 

2;1;2

G

. B.

 

6;3;6

G

. C.

2

3; ;3

3

G

 

 

 

. D.

 

2; 1;2

G 

.

Lời giải

Tọa độ trọng tâm

G

là

 

1 2 3

2

3

3 1 1

1 2;1;2 .

3

4 0 2

2

3

G

x

y G

z

 



 



 



  





 



 





Câu 50. (Chuyên Lê Quý Đôn Điện Biên 2019) Trong không gian với hệ tọa độ

Oxyz

cho tam giác

ABC

biết

   

5; 2;0 , 2;3;0

A B 

,

 

0;2;3

C

. Trọng tâm

G

của tam giác

ABC

có tọa độ:

A.

 

1;2;1

. B.

 

2;0; 1

. C.

 

1;1;1

. D.

 

1;1; 2

.

Lời giải

Giả sử

 

, ,G x y z

.

Vì

G

là trọng tâm của tam giác

ABC

suy ra

 

5 2 0

1

3

2 3 2

1 1;1;1

3 3

0 0 3

1

3

A B C

x x x

x

y y y

y y G

z z z

z

  

 





 



 

  

 

    

 

 

   

 

 



 



.

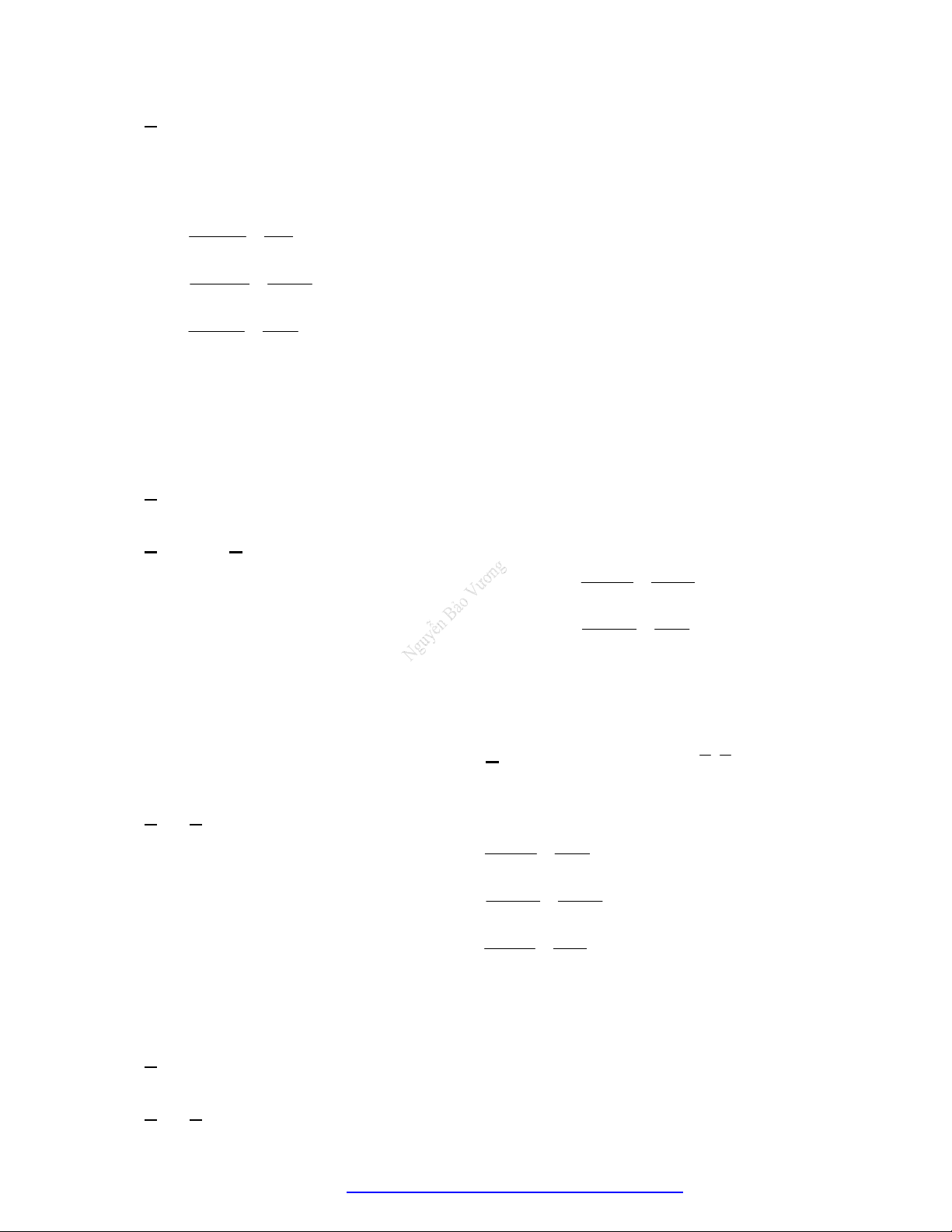
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 12 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 51. (Chuyên Sơn La 2019) Trong không gian

Oxyz

, cho 2 điểm

 

1; 2;2

M 

và

 

1;0;4

N

. Toạ độ

trung điểm của đoạn thẳng

MN

là:

A.

 

1; 1;3



. B.

 

0;2;2

. C.

 

2; 2;6



. D.

 

1;0;3

.

Lời giải

Gọi

I

là trung điểm

MN

. Ta có:

1 1

1

2 2

2 0

1

2 2

2 4

3

2 2

M N

I

M N

I

M N

I

x x

x

y y

y

z z

z





  





 



   









  





Vậy

 

1; 1;3

I 

.

Câu 52. (KTNL GV Bắc Giang 2019) Trong mặt phẳng với hệ trục tọa độ

Oxy

, cho hai điểm

 

3;4

A 

và

 

5;6

B

. Trung điểm của đoạn thẳng

AB

có tọa độ là

A.

 

1;5

. B.

 

4;1

. C.

 

5;1

. D.

 

8;2

.

Lời giải

Chọn A.

Gọi

I

là trung điểm của đoạn thẳng

AB

. Khi đó ta có:

3 5

1

2 2

4 6

5

2 2

A B

I

A B

I

x x

x

y y

y

  



  





 



  





 

1;5

I

.

Câu 53. (Chuyên Lê Hồng Phong Nam Định 2019) Trong không gian

Oxyz

, cho hai điểm

 

2; 4;3

A 

và

 

2;2;9

B

. Trung điểm của đoạn

AB

có tọa độ là

A.

 

0;3;3

. B.

 

4; 2;12



. C.

 

2; 1;6



. D.

3 3

0; ;

2 2

 

 

 

.

Lời giải

Chọn C

Gọi

I

là trung điểm của đoạn

AB

. Ta có

2 2

2

2 2

4 2

1

2 2

3 9

6

2 2

A B

I

A B

I

A B

I

x x

x

y y

y

z z

z





  





 



   









  





 

2; 1;6

I 

.

Câu 54. (Liên Trường Thpt Tp Vinh Nghệ An 2019) Trong không gian

Oxyz

, cho hai điểm

 

1;5;2

A 

và

 

3; 3;2

B 

. Tọa độ trung điểm

M

của đoạn thẳng

AB

là

A.

 

1;1;2

M

B.

 

2;2;4

M

C.

 

2; 4;0

M 

D.

 

4; 8;0

M 

Lời giải

Chọn A

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13

Trung điểm

M

có tọa độ là

 

1 3

1

2 2

5 3

1 1;1;2

2 2

2

2 2

A B

M

A B

M

A B

M

x x

x

y y

y M

z z

z

  



  



 



   





 



  





.

Câu 55. (THPT Nghĩa Hưng NĐ- 2019) Trong không gian với hệ tọa độ

Oxyz

cho hai điểm

 

1;5;3

A 

và

 

2;1; 2

M



. Tọa độ điểm

B

biết

M

là trung điểm của

AB

là

A.

1 1

;3;

2 2

B

 

 

 

. B.

 

4;9;8

B 

.

C.

 

5;3; 7

B



. D.

 

5; 3; 7

B

 

.

Lời giải

Giả sử

 

; ;

B B B

B x y z

.

Vì

M

là trung điểm của

AB

nên ta có:

1

2

2 2

5

1 3

2 2

7

3

2

2 2

A B B

M

B

A B B

M B

B

A B M

M

x x x

x

y y y

y y

z

z z z

z

  

 

 

 





 

 

  

     

  

  

 



 

 

  

 

 

. Vậy

 

5; 3; 7

B

 

.

Dạng 2. Tích vô hướng và ứng dụng

Câu 56. (Mã 105 2017) Trong không gian với hệ trục tọa độ

Oxyz

, cho hai vectơ

 





2; 1; 0

a

và

 

  



1; 0; 2

b

. Tính

 

 

cos ,a b

.

A.

 

 

 

2

cos ,

25

a b

B.

 

 

 

2

cos ,

5

a b

C.

 



 

2

cos ,

25

a b

D.

 



 

2

cos ,

5

a b

Lời giải

Chọn B

Ta có:

 



   

 

. 2 2

cos ,

5

5. 5

.

a b

.

Câu 57. (KSCL THPT Nguyễn Khuyến 2019) Trong không gian

,Oxyz

cho vectơ

   

2; 2; 4 , 1; 1;1 .

a b    



Mệnh đề nào dưới đây sai?

A.

 

3; 3; 3

a b

   



B.

a



và

b



cùng phương

C.

3

b 



D.

a b



Lời giải

Chọn B

 Xét đáp án A:

 

3; 3; 3

a b

   



đúng.

 Xét đáp án B:

   

2 1; 1; 2 1; 1;1

a b     



. Suy ra

a



và

b



không cùng phương.

Đáp án B sai.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 14 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 58. (THPT Lê Văn Thịnh Bắc Ninh 2019) Trên mặt phẳng toạ độ

Oxy

, cho tam giác

ABC

biết

 

1;3

A

,

 

2; 2

B

 

,

 

3;1

C

. Tính cosin góc

A

của tam giác.

A.

2

cos

17

A 

B.

1

cos

17

A 

C.

2

cos

17

A  

D.

1

cos

17

A  

Lời giải

Chọn B

Ta có:

 

3; 5

AB

  



,

 

2; 2

AC

 



.

Khi đó:

 

. 3.2 5.2 1

cos cos ;

.

34.2 2 17

AB AC

A AB AC

AB AC

 

   

 

.

Câu 59. (THPT Quỳnh Lưu 3 Nghệ An 2019) Trong không gian

Oxyz

, góc giữa hai vectơ

i



và

 

3; 0;1

u  



là

A.

120

. B.

60

. C.

150

. D.

30

.

Lời giải

Ta có

 

1; 0; 0

i 



.

Vậy:

 

cos ,i u

 

.

i u



 

 

2

2 2

1. 3 0.0 0.1

1. 3 0 1

  



  

=

3

2



 

, 150

i u

  

 

.

Câu 60. (Chuyên Đại Học Vinh 2019) Trong không gian

Oxyz

, cho

 

3;4;0

a  



,

 

5;0;12

b 



. Côsin

của góc giữa

a



và

b



bằng

A.

3

13

. B.

5

6

. C.

5

6



. D.

3

13



.

Lời giải

Chọn D

Ta có:

 

2

2 2 2 2 2

. 3.5 4.0 0.12 3

os ;

13

.

3 4 0 . 5 0 12

a b

c a b

a b

   

  

    

 

.

Câu 61. (Chuyên Đhsp Hà Nội 2019) Trong không gian tọa độ

Oxyz

góc giữa hai vectơ

i



và

 

3;0;1

u  



là

A.

120

. B.

30

. C.

60

. D.

150

.

Lời giải

Ta có

 

1;0;0

i 





 

. 3

cos ,

2

.

u i



 

 

. Vậy

 

, 150

u i

 

 

.

Câu 62. (Chuyên Nguyễn Tất Thành Yên Bái 2019) Trong không gian với hệ tọa độ

O

xyz

, cho vectơ

 

3;0;1

u 



và

 

2;1;0

v 



. Tính tích vô hướng

.u v

 

.

A.

. 8

u v



 

. B.

. 6

u v



 

. C.

. 0

u v



 

. D.

. 6

u v

 

 

.

Lời giải

Ta có

. 3.2 0.1 1.0 6

u v

   

 

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15

Câu 63. (Chuyên Hưng Yên 2019) Trong không gian tọa độ

Oxyz

, góc giữa hai vectơ

i



và

 

3;0;1

u  



là

A.

0

30

. B.

0

120

. C.

0

60

. D.

0

150

.

Lời giải

Gọi



là góc giữa hai vectơ

i



và

 

3;0;1

u  



, ta có:

0

. 3

cos 150

2

.

i u

 



   

 

.

Câu 64. (Chuyên Trần Phú Hải Phòng 2019) Trong không gian

,Oxyz

cho ba điểm

( 1; 2;3)

A

 

(0;3;1)

B

,

(4;2;2)

C

. Cosin của góc



BAC

là

A.

9

35

. B.

9

35



. C.

9

2 35



. D.

9

2 35

.

Lời giải

Ta có

 

1;5; 2

AB





;

 

5;4; 1

AC





.



. 5 20 2 9

30. 42 2 35

.

AB AC

cosBAC

AB AC

 

  

 

.

Câu 65. (THPT Ngô Sĩ Liên Bắc Giang 2019) Trong không gian với hệ tọa độ

Oxyz

, cho tam giác

ABC

có

 

1;0;0

A

,

 

0;0;1

B

,

 

2;1;1

C

. Diện tích của tam giác

ABC

bằng:

A.

11

2

B.

7

2

C.

6

2

D.

5

2

Lời giải

Chọn C

Ta có:

   

1; 0;1 , 1;1;1

  

 

AB AC

 

1 .1 0.1 1.1 0      

AB AC

.

Nên diện tích tam giác

ABC

là

1 6

.

2 2

 S AB AC

.

Câu 66. (Chuyên Đại học Vinh - 2019) Trong không gian

Oxyz

, cho

 

3;4;0

a  



và

 

5;0;12

b 



.

Côsin của góc giữa

a



và

b



bằng

A.

3

13

. B.

5

6

. C.

5

6



. D.

3

13



.

Lời giải

Chọn D

Ta có:

 

2

2 2 2

. 15 3

cos ;

13

3 4 . 5 12

a b



   

  



.

Câu 67. (Thpt Vĩnh Lộc - Thanh Hóa 2019) Trong hệ tọa độ

Oxy

, cho

3u i j 

  

và

 

2; 1

v

 



. Tính

.u v

 

.

A.

. 1

u v

 

 

. B.

. 1u v 

 

. C.

 

. 2; 3

u v

 

 

. D.

. 5 2

u v 

 

.

Lời giải

Chọn A

Từ

 

3 1;3

u i j u   

   

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 16 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Do đó,

 

. 1.2 3. 1 1

u v

    

 

.

Câu 68. (THPT Ngô Quyền - Ba Vì - Hải Phòng 2019) Cho hai véc tơ

 

1; 2;3

a  



,

 

2;1; 2

b  



. Khi

đó, tích vô hướng

 

.a b b



  

bằng

A.

12

. B.

2

. C.

11

. D.

10

.

Lời giải

Chọn C

 

   

1; 1;5 . 1. 2 1 .1 5.2 11

a b a b b

            

    

.

Câu 69. (Kiểm tra năng lực - ĐH - Quốc Tế - 2019) Trong không gian với hệ trục toạ độ

Oxyz

, cho hai

vectơ

 

2;1 ; 3

a

 



,

 

4; 2 ;6

b   



. Phát biểu nào sau đây là sai?

A.

2b a 

 

. B.

. 0

a b



 

. C.

a



ngược hướng với

b



. D.

2b a



 

.

Lời giải

Chọn B

Dễ thấy

2b a 

 

. Từ đó suy ra vectơ

a



ngược hướng với vectơ

b



và

2b a



 

.

     

. 2. 4 1. 2 3 .6 28 0

a b

        

 

.

Do đó đáp án

B

sai.

Câu 70. (THPT Mai Anh Tuấn_Thanh Hóa - 2019)

Cho

 

011 ;;u 

,

 

010 ;;v 

, góc giữa hai

véctơ u và v là

A.

120

. B.

45

. C.

135

. D.

60

.

Lời giải

Chọn C

Ta có

 

. 1

cos ,

2

.

u v



 

 

 

, 135

u v

  

 

.

Câu 71. (Chuyên Lê Hồng Phong - 2018) Trong không gian với hệ toạ độ

Oxyz

, cho tứ diện

ABCD

với

 

0; 0; 3

A

,

 

0; 0; 1

B



,

 

1; 0; 1

C



,

 

0; 1; 1

D



. Mệnh đề nào dưới đây sai?

A.

AB BD

. B.

AB BC

. C.

AB AC

. D.

AB CD

.

Lời giải

Ta có

 

0; 0; 4

AB

 



,

 

1; 0; 4

AC

 





. 16 0

AB AC

 

 

AB

và

AC

không vuông góc.

A

B

C

D

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17

Câu 72. (THPT Thanh Miện I - Hải Dương - 2018) Trong không gian

Oxyz

cho

2

véc tơ

2;1

( ); 1

a

 



;

; ;(1 )3 m

b 



. Tìm

m

để

 

; 90

a b

 

 

.

A.

5

m

 

. B.

5

m



. C.

1

m



. D.

2

m

 

Lời giải

 

; 90

a b

 

 



. 0

a b



 



5 0

m

 



5

m



.

Câu 73. (SGD Đồng Tháp - 2018) Trong không gian với hệ trục tọa độ

Oxyz

, cho

 

2; 1;1

u  



và

 

0; 3;

v m  



. Tìm số thực

m

sao cho tích vô hướng

. 1u v 

 

.

A.

4

m



. B.

2

m



. C.

3

m



. D.

2

m

 

.

Lời giải

Ta có:

. 1 3 1 2

u v m m

     

 

.

Câu 74. (CỤM Chuyên Môn 4 - Hải Phòng - 2018) Trong không gian

Oxyz

cho

     

1;2;3 ; 1;2;1 ; 3; 1; 2

A B C

  

. Tính tích vô hướng

.AB AC

 

.

A.

6

. B.

14

. C.

14

. D.

6

.

Lời giải

Ta có:

   

2;0; 2 ; 2; 3; 5

AB AC

     

 

. 6

AB AC

 

 

Câu 75. (THPT Mộ Đức - Quảng Ngãi - 2018) Trong không gian

Oxyz

, cho ba điểm

 

1; 2;3

A  

,

 

0;3;1

B

,

 

4;2;2

C

. Côsin của góc

BAC

bằng

A.

9

35

. B.

9

2 35

. C.

9

2 35



. D.

9

35



.

Lời giải

Ta có



cos

BAC 

 

.

cos ,

AB AC



 

với

 

1;5; 2

AB

 



,

 

5;4; 1

AC

 



.

 

  

   

2 2

2 2 2 2

1.5 5.4 2 1

cos ,

1 5 2 5 4 1

AB AC

   



     

 

27

30 42



9

2 35



Dạng 3. Tích có hướng và ứng dụng

Câu 76. (KTNL GV Bắc Giang 2019) Trong không gian với hệ tọa độ

Oxyz

, cho hai vectơ

 

2;1; 2

a

 



và vectơ

 

1;0;2

b 



. Tìm tọa độ vectơ

c



là tích có hướng của

a



và

b



.

A.

 

2;6; 1

c

 



. B.

 

4;6; 1

c

 



. C.

 

4; 6; 1

c

  



. D.

 

2; 6; 1

c

  



.

Lời giải

Chọn D.

Áp dụng công thức tính tích có hướng trong hệ trục tọa độ

Oxyz

ta được:

 

, 2; 6; 1

c a b

 

   

 

  

Vậy chọn đáp án D

Câu 77. (Chuyên Nguyễn Du-ĐăkLăk 2019) Trong không gian

Oxyz

, tọa độ một vectơ

n



vuông góc

với cả hai vectơ

 

1;1; 2

a

 



,

 

1;0;3

b 



là

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 18 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

A.

 

2;3; 1

. B.

 

3;5; 2

. C.

 

2; 3; 1 

. D.

 

3; 5; 1 

.

Lời giải

Chọn D

Ta có

 

, 3; 5; 1

a b

 

  

 

 

.

Câu 78. Trong không gian với hệ trục tọa độ

Oxyz

, cho ba véctơ

     

1;2; 1 , 3; 1;0 , 1; 5;2

a b c     

  

.

Câu nào sau đây đúng?

A.

a



cùng phương với

b



. B.

a



,

b



,

c



không đồng phẳng.

C.

a



,

b



,

c



đồng phẳng. D.

a



vuông góc với

b



.

Lời giải

Chọn C

Ta có:

 

; 1; 3; 7 0

a b

 

    

 

  

. Hai véctơ

a



,

b



không cùng phương.

; . 1 15 14 0

a b c

 

    

 

  

. Ba véctơ

a



,

b



,

c



đồng phẳng.

Câu 79. (Việt Đức Hà Nội 2019) Trong hệ trục tọa độ

Oxyz

, cho bốn điểm

(1; 2;0)

A



,

(2;0;3)

B

,

( 2;1;3)

C



và

(0;1;1)

D

. Thể tích khối tứ diện

ABCD

bằng:

A.

6

. B.

8

. C.

12

. D.

4

.

Lời giải

Ta có:

(1;2;3)

AB 



;

( 3;3;3)

AC  



;

( 1;3;1)

AD  



.

, ( 3; 12;9)

AB AC

 

  

 

 

;

, . ( 3).( 1) ( 12).3 9.1 24

AB AC AD

 

       

 

  

.

1 1

, . 24 4

6 6

ABCD

V AB AC AD

 

   

 

  

.

Câu 80. Trong không gian với hệ toạ độ

Oxyz

, cho

 

1; 2;3

a  



và

 

1;1; 1

b

 



. Khẳng định nào sau đây

sai?

A.

3

a b

 

 

. B.

. 4

a b

 

 

. C.

5

a b

 

 

. D.

 

, 1; 4;3

a b

 

  

 

 

.

Lời giải

Ta có



     

2 2 2

1 1 2 1 3 1 4 1 4 3

a b u

            

  

(đúng).



   

. 1.1 2 .1 3. 1 1 2 3 4

a b

         

 

(đúng).



     

2 2 2

1 1 2 1 3 1 0 9 16 5

a b u

            

  

(đúng).



 

2 3 3 1 1 2

, ; ; 1;4;3

1 1 1 1 1 1

a b

   

 

  

 

 

 

 

 

(sai).

Câu 81. (Chuyên Trần Phú Hải Phòng 2019) Trong không gian

,Oxyz

cho hai điểm

   

1;0; 1 , 1; 1;2

 A B

. Diện tích tam giác

OAB

bằng

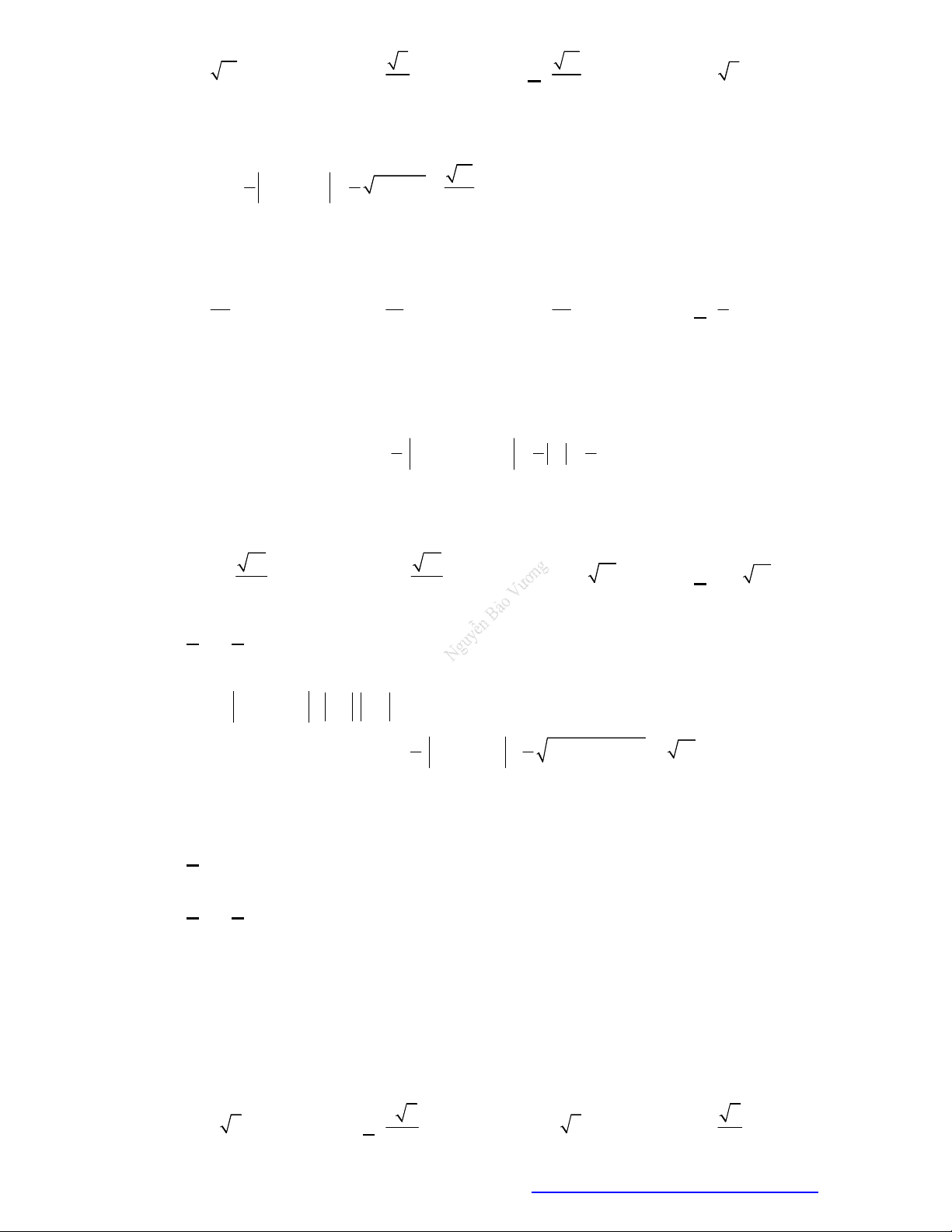
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19

A.

11.

B.

6

.

2

C.

11

.

2

D.

6.

Lời giải

 

, 1; 3; 1

 

   

 

 

OA OB

1 1 11

, 1 9 1

2 2 2



 

    

 

 

OAB

S OA OB

.

Câu 82. (Yên Phong 1 - 2018) Trong không gian

Oxyz

, cho 4 điểm

 

2;0;2

A

,

 

1; 1; 2

B

 

,

 

1;1;0

C 

,

 

2;1;2

D 

. Thể tích của khối tứ diện

ABCD

bằng

A.

42

3

. B.

14

3

. C.

21

3

. D.

7

3

.

Lời giải

     

3;1; 2 ; 1; 1; 4 ; 4;1;0

AC AB AD        

  

.

 

, 6; 10;4

AB AC

 

  

 

 

.

Thể tích khối tứ diện là:

1 1 7

. , . 14

6 6 3

V AB AC AD

 

  

 

  

.

Câu 83. (SGD và ĐT Đà Nẵng 2019) Trong không gian

Oxyz

, tính diện tích

S

của tam giác

ABC

, biết

   

2;0;0 , 0;3;0

A B

và

 

0;0;4

C

.

A.

61

3

S 

. B.

61

2

S 

. C.

2 61

S 

. D.

61

S 

.

Lời giải

Chọn D

 

2;3;0

AB  



,

 

2;0;4

AC  



,

 

, 12;8;6

AB AC

 



 

 

.

Ta có

 

, . .sin , 2AB AC AB AC AB AC S

 

 

 

     

.

Diện tích tam giác

ABC

là

2 2 2

1 1

. , 12 8 6 61

2 2

S AB AC

 

    

 

 

.

Câu 84. Trong hệ trục tọa độ

Oxyz

, cho

 

0;0;0

O

,

 

0;1; 2

A



,

 

1;2;1

B

,

 

4;3;C m

. Tất cả giá trị của

m

để

4

điểm

, , ,O A B C

đồng phẳng?

A.

14

m



. B.

14

m

 

. C.

7

m



. D.

7

m

 

.

Lời giải

Chọn A

Ta có

 

0;1; 2

OA

 



,

 

1;2;1

OB 



,

 

4;3;OC m





. Bốn điểm

, , ,O A B C

đồng phẳng

, . 0

OA OB OC

 

 

 

  

5.4 2.3 1. 0

m

   

14

m

 

.

Vậy

14

m



.

Câu 85. Trong không gian

Oxyz

, cho hình chóp

.

A BCD

có

 

0;1; 1 ,

A



 

1;1;2 ,

B

 

1; 1;0

C 

và

 

0;0;1 .

D

Tính độ dài đường cao của hình chóp

.

A BCD

.

A.

2 2

. B.

3 2

2

. C.

3 2

. D.

2

.

Lời giải

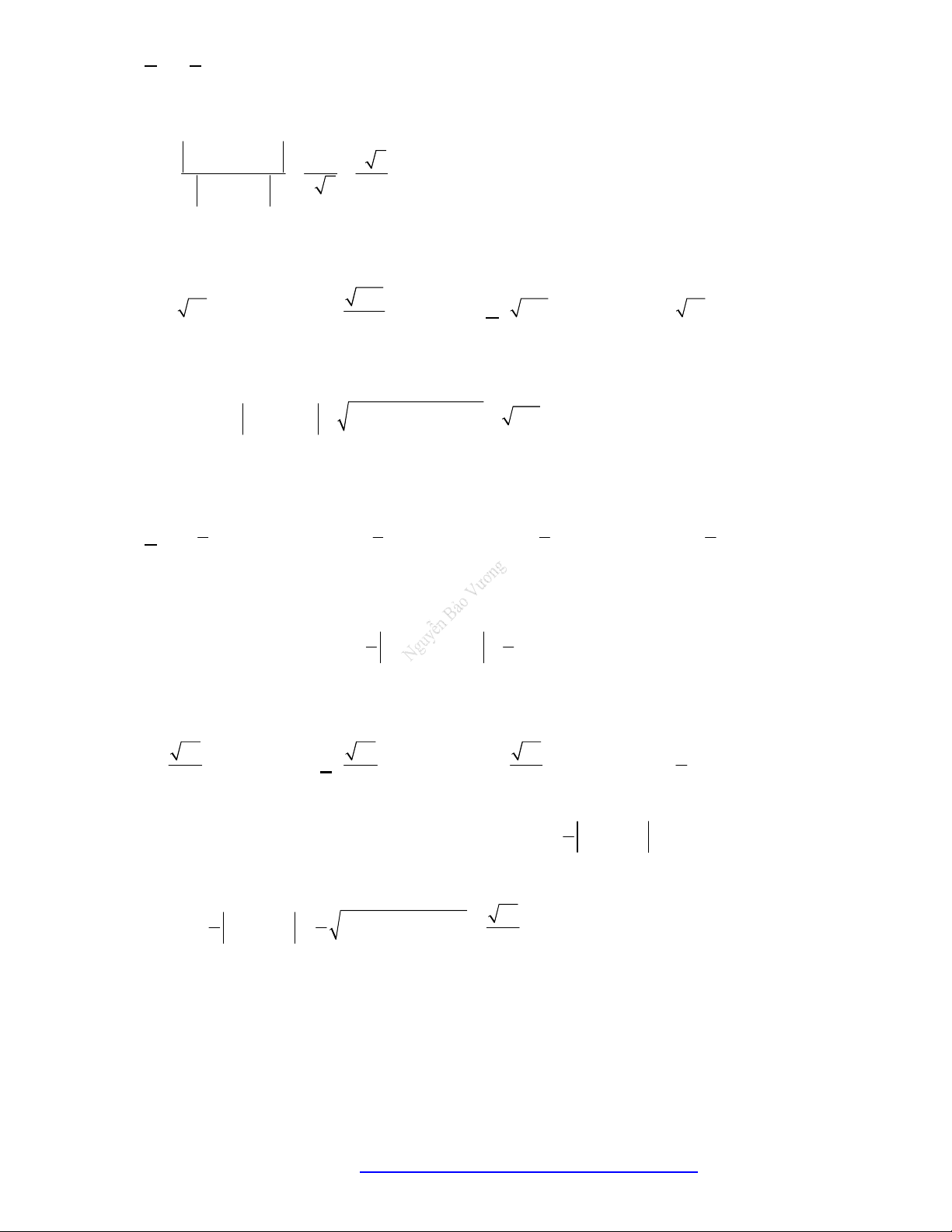
NGUYỄN BẢO VƯƠNG - 0946798489

Chọn B

Có

 

0;

2; 2  



BC

,

 

1;

1; 1   



BD

,

 

1;

0 3  



BA

;

 

, 0

;2; 2 ;

 

 

 



 

BC

BD

, .

6

 



 



  

BC BD

BA

, .

6 3

2

.

2

2 2

,





 

  

 

 



  



 

A

BC

BD BA

h

BC BD

Câu 86.

(Chuyên Lê Quý Đôn - Đà Nẵng - 2018) Trong không gian với hệ trục tọa độ, cho hình bình

hành

AB

CD

. Biết

 

2;1

; 3

A



,

 

0;

2;5

B 

và

 

1;1;

3

C

. Di

ện tích hình bình hành

AB

CD

là

A.

2 87

. B.

349

2

. C.

349

. D.

87

.

Lời giải

Ta

có:

 

2;

3;8

AB 

 





và

 

1;0

;6

AC 







 

, 18

;4; 3

AB AC





 

 

 



 

.

Vậy:

   

2 2

2

, 18

4 3 349

ABCD

S AB

AC

 

      

 



 

.

Câu 87.

(SGD - Bình Dương - 2018) Trong không gian với hệ tọa độ

Oxyz

,

cho bốn điểm

 

0;1

;1

A

,

 

1;

0;2

B 

,

 

1;1

;0

C 

và đi

ểm

 

2;

1; 2

D



. Khi đó thể tích t

ứ diện

AB

CD

là

A.

5

6

V



. B.

5

3

V



. C.

6

5

V



. D.

3

2

V



.

Lời giải

Ta

có

 

1;

1;1

AB 

 





,

 

1;

0; 1

AC

 





,

 

2;

0; 3

AD

 





và

 

, 1

; 2; 1

AB AC





 



 



 

.

Thể

tích tứ diện

AB

CD

là

1 5

, .

6 6

V A

B AC AD

 

 

 



  

.

Câu 88.

(THPT Mộ Đức - Quảng Ngãi - 2018) Trong không gian

Oxyz

, c

ho

 

1;

2; 1

A



,

 

0;

2;3

B 

.

T

ính diện tích tam giác

OA

B

.

A.

29

6

. B.

29

2

. C.

78

2

. D.

7

2

.

Lời giải

Diện tíc

h tam giác

OA

B

được xác định bới công thức:

1

,

2

S O

A OB

 



 



 

Ta có

 

1;

2; 1

OA

 





 

, 0

; 2;3

OB 





 

, 4; 3; 2

OA OB

 

   

 



 

Vậy

1

,

2

S OA

OB

 



 



 

   

2 2

2

1

4 3

2

 

  

29

2



.

Trang 20 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

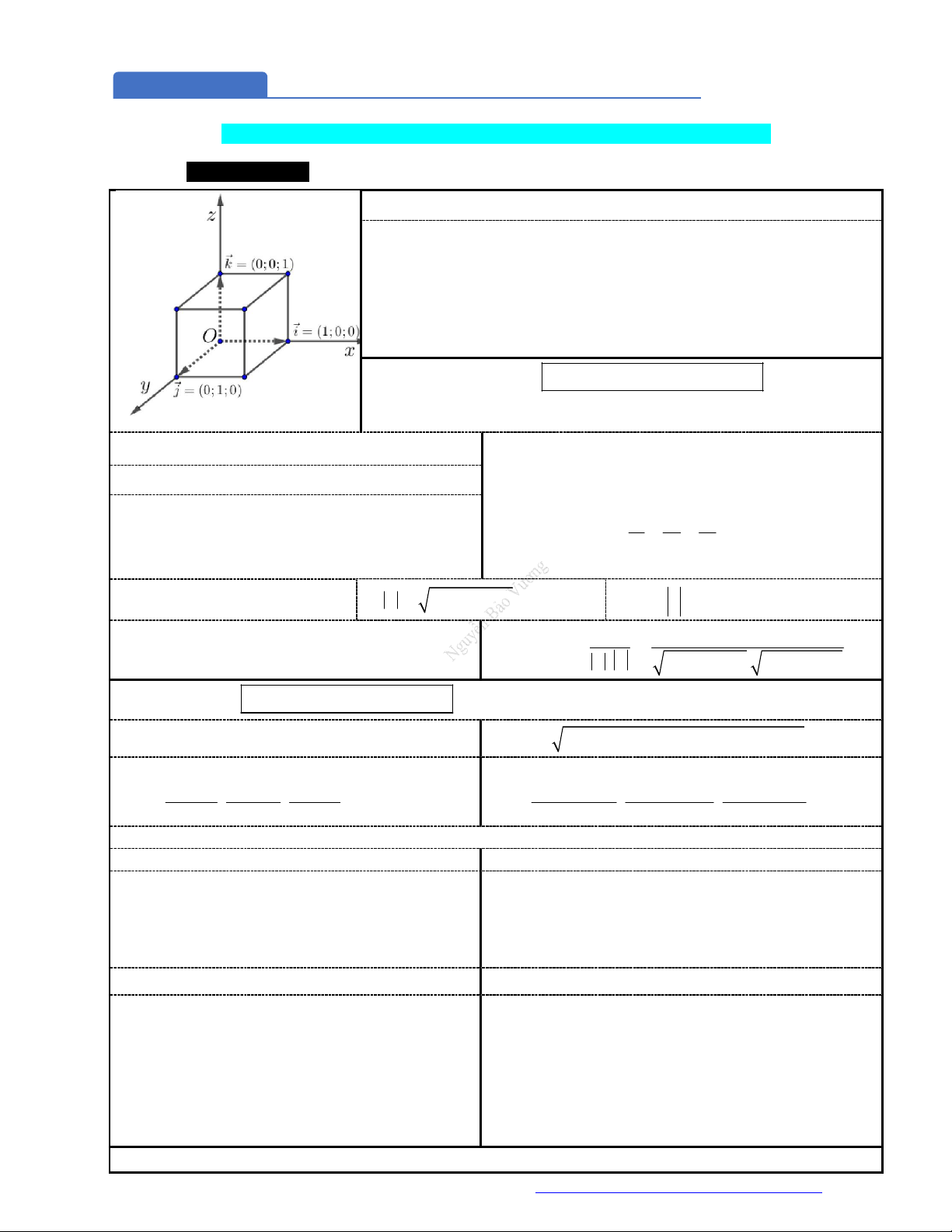
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương  https://www.facebook.com/phong.baovuong Trang 1

TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH KHÁ MỨC 7-8 ĐIỂM

Lý thuyết chung

1. Hệ trục tọa độ Oxyz:

 Hệ trục gồm ba trục

, ,Ox Oy Oz

đôi một vuông góc nhau.

 Trục

:Ox

trục hoành, có vectơ đơn vị

(1;0;0)

i





.

 Trục

Oy

: trục tung, có vectơ đơn vị

(0;1;0)j





.

 Trục

:Oz

trục cao, có vectơ đơn vị

(0;0;1).k





 Điểm

(0;0;0)O

là gốc tọa độ.

2. Tọa độ vectơ: Vectơ

( ; ; )u xi y j zk u x y z

    

    

.

Cho

1 2 3 1 2 3

( ; ; ), ( ; ; )a a a a b b b b

 

 

. Ta có:



1 1 2 2 3 3

( ; ; )a b a b a b a b



    



a



cùng phương

b



( )a kb k R

 

  

1 1

3

1 2

2 2 1 2 3

1 2 3

3 3

, ( , , 0).

a kb

a

a a

a kb b b b

b b b

a kb







     











1 2 3

( ; ; )ka ka ka ka







1 1

2 2

3 3

a b

a b a b

a b

 







  











1 1 2 2 3 3

. . . .a b a b a b a b



  



2 2 2

1 2 2

a a a a



  



2

2 2 2 2

1 2 3

a a a a a



   



1 1 2 2 3 3

. 0 0a b a b a b a b a b

   

      



1 1 2 2 3 3

2 2 2 2 2 2

1 2 3 1 2 3

.

cos( , )

.

a b a b a b

a b

a a a b b b



 

 

   

3. Tọa độ điểm:

( ; ; ) ( ; ; )M x y z OM x y z



 

. Cho

( ; ; ) , ( ; ; ) , ( ; ; )

A A A B B B C C C

A x y z B x y z C x y z

, ta có:



( ; ; )

B A B A B A

AB x x y y z z



   



2 2 2

( ) ( ) ( )

B A B A B A

AB x x y y z z     

 Toạ độ trung điểm M của đoạn thẳng AB:

; ; .

2 2 2

A B A B A B

x x y y z z

M

  

 

 

 

 Toạ độ trọng tâm G của tam giác ABC:

; ; .

3 3 3

A B C A B C A B C

x x x y y y z z z

G

     

 

 

 

QUY TẮC CHIẾU ĐẶC BIỆT

Chiếu điểm trên trục tọa độ Chiếu điểm trên mặt phẳng tọa độ

 Điểm

1( )

( ; ; ) ( ;0;0)

Chieáu vaøo Ox

M M M MGiöõ nguyeân x

M x y z M x

 

 Điểm

2

( )

( ; ; ) (0; ;0)

Chieáu vaøo Oy

M M M M

Giöõ nguyeân y

M x y z M y 

 Điểm

3( )

( ; ; ) (0;0; )

Chieáu vaøo Oz

M M M MGiöõ nguyeân z

M x y z M z 

 Điểm

1( , )

( ; ; ) ( ; ;0)

Chieáu vaøo Oxy

M M M M MGiöõ nguyeân x y

M x y z M x y

  

 Điểm

2

( , )

( ; ; ) (0; ; )

Chieáu vaøo Oyz

M M M M M

Giöõ nguyeân y z

M x y z M y z 

 Điểm

3( , )

( ; ; ) ( ;0; )

Chieáu vaøo Oxz

M M M M MGiöõ nguyeânx z

M x y z M x z 

Đối xứng điểm qua trục tọa độ Đối xứng điểm qua mặt phẳng tọa độ



1( ; , )

( ; ; ) ( ; ; )

Ñoái xöùng qua Ox

M M M M M M

Giöõ nguyeân x ñoåi daáu y z

M x y z M x y z     



2( ; , )

( ; ; ) ( ; ; )

Ñoái xöùng qua Oy

M M M M M M

Giöõ nguyeân y ñoåi daáu x z

M x y z M x y z     



3( ; , )

( ; ; ) ( ; ; )

Ñoái xöùng qua Oz

M M M M M M

Giöõ nguyeân z ñoåi daáu x y

M x y z M x y z

     



1( , ; )

( ; ; ) ( ; ; )

Ñoái xöùng qua Oxy

M M M M M MGiöõ nguyeân x y ñoåi daáu z

M x y z M x y z

     



2( , ; )

( ; ; ) ( ; ; )

Ñoái xöùng qua Oxz

M M M M M MGiöõ nguyeân x z ñoåi daáu y

M x y z M x y z     



3( , ; )

( ; ; ) ( ; ; )

Ñoái xöùng qua Oyz

M M M M M MGiöõ nguyeân y z ñoåi daáu x

M x y z M x y z     

4. Tích có hướng của hai vectơ:

HỆ TRỤC TỌA ĐỘ

Chuyên đề 28

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

 Định nghĩa: Cho

1 2 3

( , , )a a a a





,

1 2 3

( , , )b b b b





, tích có hướng của

a



và

b



là:

 

2 3 3 1 1 2

2 3 3 2 3 1 1 3 1 2 2 1

2 3 3 1

1 2

, ; ; ; ;

a a a a

a a

a b a b a b a b a b a b a b

b b b b

b b



 

 

    

  

 

.

 Tính chất:

[ , ]

a b a

  



[ , ]

a b b

  



 

[ , ] . .sin ,a b a b a b

 



 Điều kiện cùng phương của hai vectơ

&a b

 

là

, 0

a b

  

 



 

với

0 (0;0;0).





 Điều kiện đồng phẳng của ba vectơ

,a b

 

và

c



là

[ , ]. 0.

a b c

  



 Diện tích hình bình hành

ABCD:

, .

ABCD

S AB AD



 

 



 

 Diện tích tam giác ABC:

1

, .

2

ABC

S AB AC

 



 



 

 Thể tích khối hộp:

. ' ' ' '

[ , ]. ' .

ABCD A B C D

V AB AD AA

  



 Thể tích tứ diện:

1

, .

6

ABCD

V AB AC AD

  

 



 

.

Dạng 1. Tìm tọa độ điểm, véc tơ liên quan đến hệ trục tọa dộ OXYZ

Dạng 1.1 Một số bài toán liên quan đến vectơ, tọa độ vec tơ

Câu 1. (THPT Hùng Vương Bình Phước 2019) Trong không gian với hệ trục

Oxyz

cho ba điểm

     

1;2; 3 , 1;0;2 , ; ; 2

A B C x y

  

thẳng hàng. Khi đó

x y

bằng

A.

1

x y

 

. B.

17

x y

 

. C.

11

5

x y

  

. D.

11

5

x y

 

.

Lời giải

Có

   

2; 2;5 , 1; 2;1

AB AC x y

 

    

.

, , A B C

thẳng hàng

, AB AC

 



cùng phương

3

1 2 1

5

1

8

2 2 5

5

x

x y

y





 



 



      















.

Câu 2. (HSG Tỉnh Bắc Ninh 2019) Trong không gian với hệ tọa độ

Oxyz

, cho các vectơ

   

2; 1;3 , 1;3; 2a m b n

   

 

. Tìm

,m n

để các vectơ

,a b

 

cùng hướng.

A.

3

7;

4

m n

  

. B.

4; 3

m n

  

. C.

1; 0

m n

 

. D.

4

7;

3

m n

  

.

Lời giải

a



và

b



cùng hướng

a kb

 

 

 

2 2

0 1 3 7

3

3 2

4

k k

k m k m

k n

n







 



     

 

 

 





 



. Vậy

3

7;

4

m n

  

Câu 3. (THPT Nguyễn Khuyến -2019) Trong không gian với hệ tọa độ

Oxyz

, cho ba điểm

     

A 2; 1;5 , 5; 5;7 , ; ;1

 

B M x y

. Với giá trị nào của

,x y

thì

, ,A B M

thẳng hàng.

A.

4; 7 

x y

B.

4; 7   

x y

C.

4; 7  

x y

D.

4; 7  

x y

Lời giải

Chọn A

Ta có

   

3; 4;2 , 2; 1; 4     

AB AM x y

 

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3

, ,A B M

thẳng hàng

, AB AM

 

cùng phương

4

2 1 4

7

3 4 2

 



  

   









x

x y

y

.

Câu 4. (THPT Quỳnh Lưu 3 Nghệ An -2019) Trong không gian

Oxyz

, cho hai điểm

 

2; 2;1A 

,

 

0;1;2B

. Tọa độ điểm

M

thuộc mặt phẳng

 

Oxy

sao cho ba điểm

A

,

B

,

M

thẳng hàng là

A.

 

4; 5;0M 

. B.

 

2; 3;0M 

. C.

 

0;0;1M

. D.

 

4;5;0M

.

Lời giải

Ta có

   

; ;0M Oxy M x y 

;

   

2;3;1 ; 2; 2; 1AB AM x y     

 

.

Để

A

,

B

,

M

thẳng hàng thì

AB



và

AM



cùng phương, khi đó:

2 2 1

2 3 1

x y  

 



4

5

x

y









 



.

Vậy

 

4; 5;0M 

.

Câu 5. (THPT Yên Khánh - Ninh Bình - 2019) Trong không gian với hệ tọa độ

Oxyz

cho các véc tơ

2 2u i j k  

   

,

 

;2; 1v m m 



với

m

là tham số thực. Có bao nhiêu giá trị của

m

để u v

 

.

A.

0

. B.

1

. C.

2

. D.

3

.

Lời giải

Ta có

 

2; 2;1u  



Khi đó

 

2

2 2

2 2 1 3u     



và

 

2

2 2 2

2 1 2 2 5v m m m m      



Do đó

2

9 2 2 5u v m m    

 

2

1

2 0

2

m

m m

m





    



 



Vậy có 2 giá trị của

m

thỏa yêu cầu bài toán.

Câu 6. (Chuyen ĐHSP Hà Nội -2019) Trong không gian với hệ tọa độ

Oxyz

, cho hình hộp

.ABCD A B C D

   

có

 

0;0;0A

,

 

;0;0B a

;

 

0;2 ;0D a

,

 

0;0;2A a



với

0a 

. Độ dài đoạn thẳng

AC



là

A.

a

. B.

2 a

. C.

3 a

. D.

3

2

a

.

Lời giải

Ta có

 

;0;0AB a



;

 

0;2 ;0AD a



;

 

0;0;2AA a







.

Theo quy tắc hình hộp ta có

AB AD AA AC

 

  

   

 

;2 ;2AC a a a



 



.

Suy ra AC AC



   

2 2

2

2 2 3a a a a   

.

Vậy độ dài đoạn thẳng

3AC a





.

Câu 7. (Chuyên Lê Quý Dôn - Dà Nẵng - 2018) Trong không gian với hệ trục toạ độ

Oxyz

, cho

 

2;3;1a 



,

 

1;5;2b  



,

 

4; 1;3c  



và

 

3;22;5x  



. Đẳng thức nào đúng trong các đẳng

thức sau?

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

A.

2 3

x a b c  

   

. B.

2 3

x a b c   

   

.

C.

2 3

x a b c  

   

. D.

2 3

x a b c  

   

.

Lời giải

Đặt:

. . .x m a n b p c

  

   

,

, ,m n p



.

       

3;22;5 . 2;3;1 . 1;5;2 . 4; 1;3

m n p      

2 4 3

3 5 22

2 3 5

m n p

   





   





  



 

I

.

Giải hệ phương trình

 

I

ta được:

2

3

1

m

n

p













 



.

Vậy

2 3

x a b c  

   

.

Câu 8. (Chuyên Thái Bình - 2018) Trong không gian với hệ trục tọa độ

Oxyz

, cho tam giác

ABC

với:

 

1; 2;2

AB  



;

 

3; 4; 6

AC  



. Độ dài đường trung tuyến

AM

của tam giác

ABC

là:

A.

29

. B.

29

. C.

29

2

. D.

2 29

.

Lời giải

Ta có

 

2

2 2 2

1 2 2 9

AB

    

,

 

2

2 2 2

3 4 6 61

AC

    

,

  

. 1.3 2 4 2.6 23

AC AB

     

 

.

 

2

BC AC AB

 

  

2 2

2. .AC AB AC AB

  

   

61 9 2.23 24   

.

Áp dụng công thức đường trung tuyến ta có:

2 2 2

2

2 4

AB AC BC

AM



 

9 61 24

29

2 4



  

.

Vậy

29

AM  .

Câu 9. (Hồng Quang - Hải Dương - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho các vectơ

 

2; 1;3

a m 



,

 

1;3; 2b n

 



. Tìm

m

,

n

để các vectơ

a



,

b



cùng hướng.

A.

7

m



;

3

4

n

 

. B.

7

m



;

4

3

n

 

. C.

4

m



;

3

n

 

. D.

1

m



;

0

n



.

Lời giải

Các vectơ

a



,

b



cùng hướng khi và chỉ khi tồn tại số thực dương

k

sao cho

a kb



 

 

2

1 3

3 2

k

m k

k n







  





 



 

2

1 6

3 2 2

k

m

n







  





 



2

7

3

4

k

m

n









 













.

Câu 10. (THPT Chu Văn An -Thái Nguyên - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho hình

vuông

   

, 3;0;8 , 5; 4;0

ABCD B D  

. Biết đỉnh

A

thuộc mặt phẳng

 

Oxy

và có tọa độ là

những số nguyên, khi đó

CA CB



 

bằng:

A.

10 5

. B.

6 10

. C.

10 6

. D.

5 10

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5

Lời giải

 

8; 4; 8BD    



12BD 

12

2

AB 

6 2

.

Gọi

M

là trung điểm

AB

3 10MC  .

CA CB

 

2CM



2CM

6 10

.

Dạng 1.2 Tìm tọa độ điểm

Câu 11. (THPT Cù Huy Cận 2019) Trong không gian với hệ tọa độ

Oxyz

, cho các điểm

 

1;0;3A

,

 

2;3; 4B 

,

 

3;1;2C 

. Tìm tọa độ điểm

D

sao cho

ABCD

là hình bình hành.

A.

 

4; 2;9D  

. B.

 

4;2;9D 

. C.

 

4; 2;9D 

. D.

 

4;2; 9D 

.

Lời giải

Gọi

 

; ;D x y z

. Để

ABCD

là hình bình hành

     

4

1;3; 7 3 ;1 ;2 2 4; 2;9

9

x

AB DC x y z y D

z

 





              









 

.

Câu 12. (THPT - Yên Định Thanh Hóa 2019) Trong không gian

Oxyz

, cho ba điểm

     

1;0;0 , 1;1;0 , 0;1;1A B C

. Tìm tọa độ điểm

D

sao cho tứ giác

ABCD

(theo thứ tự các đỉnh)

là hình bình hành?

A.

 

2;0;0D

. B.

 

1;1;1D

. C.

 

0;0;1D

. D.

 

0;2;1D

.

Lời giải

Gọi

 

; ;D x y z

.

Tứ giác

ABCD

là hình bình hành khi và chỉ

AD BC

 

.

Ta có

 

1; ;AD x y z 



và

 

1;0;1BC  



.

Suy ra

0; 0; 1x y z  

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Vậy

 

0;0;1

D

.

Câu 13. (THPT Nguyễn Khuyến 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho ba điểm

(1; 2; 1), (2; 1;3)

A B

 

và

( 3;5;1)

C



. Tìm tọa độ điểm

D

sao cho tứ giác

ABCD

là hình bình

hành.

A.

( 2;8; 3)

D

 

B.

( 4;8; 5)

D

 

C.

( 2;2;5)

D



D.

( 4;8; 3)

D

 

Lời giải

Chọn D

Gọi

( ; ; )

D D D

D x y z

cần tìm

Tứ giác

ABCD

là hình bình hành

AB DC

 

 

2 1 3 4

1 2 5 8

3 ( 1) 1 3

B A C D

D D

B A C D D D

D D

B A C D

x x x x x x

y y y y y y

z z

z z z z

  

     



 

  

          

  

  

     

  

 



.

Suy ra:

( 4;8; 3)

D

 

.

Câu 14. (THPT Nguyễn Khuyến -2019) Trong mặt phẳng với hệ tọa độ

Oxyz

, Tam giác

ABC

với

 

1; 3;3

A 

;

 

2; 4;5

B 

,

 

; 2;C a b



nhận điểm

 

1; ;3G c

làm trọng tâm của nó thì giá trị của

tổng

a b c 

bằng.

A.

5

B.

3

C.

1

D.

2

Lời giải

Chọn D

1 2

1

3

0

3 4 2

1

3

3 5

3

a

c b

c

b

 













  

 

  

 

 

 



 









Vậy

2

a b c

   

Câu 15. (THPT Nguyễn Khuyến 2019) Trong không gian với hệ tọa độ

Oxyz

, cho

2

điểm

 

1;2; 3

B



,

 

7;4; 2

C



Nếu điểm

E

thỏa nãm đẳng thức

2E

CE

B



 

thì tọa độ điẻm

E

là:

A.

8 8

3; ;

3 3

 



 

 

B.

8 8

;3;

3 3

 



 

 

. C.

8

3;3;

3

 



 

 

D.

1

1;2;

3

 

 

 

Lời giải

Chọn A

Gọi

 

; ;E x y z

Ta có:

 

7; 4; 2

CE x y z

   



;

 

2 2 2 ; 4 2 ; 6 2EB x y z

    



3

7 2 2x

8

E 4 4 2

3

2 6 2z

8

3

2

x

B y yC y

z

E







  





 

     

 

 

   





 







 

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7

Câu 16. (KTNL Gia Bình 2019) Trong không gian với hệ tọa độ

Oxyz

, cho tam giác

ABC

với

 

1;2; 3

A



,

 

2;5;7

B

,

 

3;1;4

C 

. Điểm

D

để tứ giác

ABCD

là hình bình hành là

A.

 

6;6;0

D

B.

8 8

0; ;

3 3

D

 

 

 

C.

 

0;8;8

D

D.

 

4; 2; 6

D

  

Lời giải

Chọn D

Tứ giác

ABCD

là hình bình hành

1 3 4

3 1 2

10 4 6

D D

x x

AB DC y y

z z

    

 

 

       

 

 

   

 

 

Vậy

 

4; 2; 6

D

  

.

Câu 17. (THPT Lương Thế Vinh Hà Nội 2019) Cho tam giác

ABC

có

 

1; 2;0

A 

,

 

2;1; 2

B



,

 

0;3;4

C

. Tìm tọa độ điểm

D

để tứ giác

ABCD

là hình bình hành.

A.

 

1;0; 6

. B.

 

1;6;2

. C.

 

1;0;6



. D.

 

1;6; 2

.

Lời giải

Ta có:

ABCD

là hình bình hành

OA OC OB OD

   

   

OD OA OC OB

   

   

D A C B

x x x x

y y y y

z z z z

  





   





  



1 0 2

2 3 1

0 4 2

D

x

y

z

  





    





  



 

1;0;6

D 

.

Câu 18. (Liên Trường Thpt Tp Vinh Nghệ An 2019) Trong không gian

Oxyz

, cho hai điểm

 

3;1; 2

A

,

 

2; 3;5

B

. Điểm

M

thuộc đoạn

AB

sao cho

2MA MB

, tọa độ điểm

M

là

A.

7 5 8

; ;

3 3 3

 



 

 

. B.

 

4;5; 9

. C.

3 17

; 5;

2 2

 



 

 

. D.

 

1; 7;12



.

Lời giải

Gọi

 

;y;z

M x

. Vì M thuộc đoạn AB nên:

 

7

3

3 2 2

5

2 1 2 3

3

2 2 5

8

3

x

x x

MA MB y y y

z z

z







    



          

 

 

    











 

Câu 19. (THPT Minh Khai Hà Tĩnh 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho hai điểm

 

0;1; 2

A



và

 

3; 1;1

B 

. Tìm tọa độ điểm M sao cho

3AM AB



 

.

A.

 

9; 5;7

M 

. B.

 

9;5;7

M

.

C.

 

9;5; 7

M

 

. D.

 

9; 5; 5

M

 

.

Lời giải

Gọi

 

; ;M x y z

. Ta có:

   

; 1; 2 ; 3; 2;3

AM x y z AB    

 

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 8 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

9 9

3 1 6 5

2 9 7

x x

AM AB y y

z z

 

 

 

       

 

 

  

 

 

. Vậy

 

9; 5;7M 

.

Câu 20. (Chuyên Phan Bội Châu 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho hai điểm

   

1;2; 1 , 1;3;1A AB 



thì tọa độ của điểm

B

là:

A.

 

2;5;0B

. B.

 

0; 1; 2B  

. C.

 

0;1;2B

. D.

 

2; 5;0B  

Lời giải

Gọi

 

; ;B x y z

Có

 

1;2; 1A 

 

1;3;1AB 



 

1; 2; 1x y z   

 

2

5 2;5;0

0

x

y B

z







  









Câu 21. (Đề Thi Công Bằng Khtn 2019) Trong không gian

Oxyz

, cho hình bình hành

ABCD

. Biết

 

1;0;1A 

,

 

2;1;2B 

và

 

1; 1;1D  

. Tọa độ điểm

C

là

A.

 

2;0;2

. B.

 

2;2;2

. C.

 

2; 2;2

. D.

 

0; 2;0

.

Lời giải

Gọi tọa độ điểm

C

là

 

; ;x y z

Vì

ABCD

là hình bình hành nên

DC AB

 

Ta có

 

1; 1; 1DC x y z   



và

 

1;1;1AB 



Suy ra

1 1 2

1 1 0

1 1 2

x x

y y

z z

  

 

 

   

 

 

  

 

Vậy tọa độ điểm

C

là

 

2;0;2

.

Câu 22. (Sở Phú Thọ -2019) Trong không gian với hệ tọa độ

,Oxyz

cho hai điểm

 

1; 2; 2A

và

8 4 8

; ;

3 3 3

 

 

 

B

. Biết

 

; ;I a b c

là tâm của đường tròn nội tiếp tam giác

OAB

. Giá trị

 a b c

bằng

A.

1

B.

3

C.

2

D.

0

Lời giải

Chọn D

Ta có

 

1; 2; 2 OA



,

8 4 8

; ;

3 3 3

 



 

 

OB



, do đó

3, 4 OA OB

.

I

D

O

A

B

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9

Gọi

D

là chân đường phân giác trong kẻ từ

O

, ta có

. .   

DA OA

DA DB DB

DB OB

  

, suy ra

3 4. 3.

4 7



   

OA OB

DA DB OD

 

  

. Do đó

12 12

; ; 0

7 7

 

 

 

D

.

Ta có

5 2 15

; ; 2

7 7 7

 

   

 

 

AD AD



.

5

.

7

   

AD

ID IO IO

AO

  

 

7

1; 1; 0

12

  OI OD D

 

Do đó

0  a b c

.

Câu 23. (Chuyên Đhsp Hà Nội -2019) Trong không gian tọa độ

Oxyz

, cho

     

2;0;0 , 0;2;0 , 0;0;2A B C

. Có tất cả bao nhiêu điểm

M

trong không gian thỏa mãn

M

không trùng với các điểm

, ,A B C

và



90AMB BMC CMA   

?

A.

0

. B.

1

. C.

2

. D.

3

.

Lời giải

Gọi

, ,I J K

lần lượt là trung điểm của

, ,AB BC CA

.

Do



90AMB BMC CMA   

nên các tam giác

, ,AMB BMC CMA  

vuông tại

M

.

Khi đó

; ;

2 2 2

AB BC AC

IM JM KM  

. Mặt khác

2 2AB BC AC  

.

Vậy

2MI MJ MK  

. Khi đó

M

thuộc trục của đường tròn ngoại tiếp đáy

IJK

và cách

 

IJK

một khoảng không đổi là

2

. Khi đó có hai điểm

M

thỏa mãn điều kiện trên.

Câu 24. Trong không gian

Oxyz

, cho hai điểm

(2;2;1)M

,

8 4 8

; ;

3 3 3

N

 















 

. Tìm tọa độ tâm đường tròn nội

tiếp tam giác

OMN

.

A.

(1;1;1)I

. B.

(0;1;1)I

. C.

(0; 1; 1)I  

. D.

(1;0;1)I

.

Lời giải

Chọn B

Ta có bài toán bài toán sau

Trong tam giác

ABC

,

I

là tâm đường tròn nột tiếp

ABC

ta có:

a. . . 0IA b IB c IC  

   

.

với

; ; BC a AC b AB c  

.

Thật vậy:

Gọi

A



là chân đường phân giác trong kẻ từ

A

.

I

A'

A

B

C

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 10 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

 

0 1

c

BA A C bBA cCA

b

   

    

   



'

c c b c

IA A I A I A I

ac

A B a

b c



  

  



  



 

0aIA b c IA



   



 

0aIA bIB cIC bBA cCA

 

     

 

   

 

0 1aIA bIB cIC do   

   

.

Áp dụng công thức trong tam giác

OMN

ta được

. . . 0OM IN ON IM MN IO  

   

. . .

0

.y .y .y

1

.z .z .z

1

N M O

I

N M O

I

N M O

I

OM x ON x MN x

x

OM ON MN

y

OM ON MN

z

OM ON MN



 



 



 



 



  





 



 



 



 





.

Vậy điểm

(0;1;1)I

là điểm cần tìm.

Câu 25. Trong không gian với hệ tọa độ

Oxyz

, cho tam giác

ABC

có

 

1;2; 1A 

,

 

2; 1;3B 

,

 

4;7;5C 

. Gọi

 

; ;D a b c

là chân đường phân giác trong góc

B

của tam giác

ABC

. Giá trị của

2a b c 

bằng

A.

5

. B.

4

. C.

14

. D.

15

.

Lời giải

Chọn A

Ta có 26AB  , 104 2 26BC   .

Gọi

 

; ;D x y z

, theo tính chất phân giác ta có

1

2

DA BA

DC BC

 

. Suy ra

 

1

*

2

DA DC 

 

.

Ta có

 

1 ;2 ; 1DA x y z    



và

 

4 ;7 ;5DC x y z    



.

D

A

B

C

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11

Do đó

 

2

1

1 4

3

2

1 11 2 11

* 2 7 ; ;1 2 5

2 3 3 3

1

1 5

2

x

x x

y y y D a b c

z

z z





 

    



 



 





            



 







 

 

 



 

    

 





.

Câu 26. Trong không gian với hệ tọa độ Oxyz, cho hai điểm

 

2;3;1A 

và

 

5; 6; 2B

. Đường thẳng

AB

cắt mặt phẳng

 

Oxz

tại điểm

M

. Tính tỉ số

A M

B M

.

A.

1

2

AM

BM



B.

2

AM

BM



C.

1

3

AM

BM



D.

3

AM

BM



Lời giải

Chọn A

   

;0;M Oxz M x z 

;

 

7;3;1 59AB AB  



;

 

2; 3; 1AM x z   



và

, ,A B M

thẳng hàng

 

. AM k AB k  

 



2 7 9

3 3 1

1 0

x k x

k k

z k z

   

 

 

     

 

 

  

 

 

9;0;0 .M 

   

14; 6; 2 ; 7; 3; 1 2 .         

 

BM BMA ABM

Câu 27. (Bình Giang-Hải Dương 2019) Trong không gian với hệ toạ độ

Oxyz

, cho ba điểm

 

2;3;1A 

,

 

2;1;0B

,

 

3; 1;1C  

. Tìm tất cả các điểm

D

sao cho

ABCD

là hình thang có đáy

AD

và diện

tích tứ giác

ABCD

bằng 3 lần diện tích tam giác

ABC

.

A.

 

12; 1;3D  

. B.

 

8; 7;1

12;1; 3

D

 









. C.

 

8;7; 1D 

. D.

 

8;7; 1

12; 1;3

D





 





.

Lời giải

Chọn A

Ta có:

   

1

. ,

2

ABCD

S AD BC d A BC 

 

2

1

.

2

ABC

ABCD

S

S AD BC

BC



  

.

 

.

3

ABC

AD BC S

S

BC





 

3BC AD BC   2AD BC 

.

Mà

ABCD

là hình thang có đáy

AD

nên

2AD BC

 

 

1

.

 

5; 2;1BC   



,

 

2; 3; 1

D D D

AD x y z   



.

 

1

2 10

3 4

1 2

D

x

y

z

  





   





 



12

1

3

D

x

y

z

 





  









.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 12 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Vậy

 

12; 1;3D  

.

Câu 28. (THPT Trần Quốc Tuấn - 2018) Trong không gian với hệ trục tọa độ

Oxyz

cho hình thang

ABCD

vuông tại

A

và

B

. Ba đỉnh

(1;2;1)A

,

(2;0; 1)B 

,

(6;1;0)C

Hình thang có diện tích bằng

6 2

. Giả sử đỉnh

( ; ; )D a b c

, tìm mệnh đề đúng?

A.

6a b c  

. B.

5a b c  

. C.

8a b c  

. D.

7a b c  

.

Lời giải

Ta có

 

1; 2; 2AB   



3AB 



;

 

4;1;1BC 



3 2BC 



.

Theo giả thiết

ABCD

là hình thang vuông tại

A

và

B

và có diện tích bằng

6 2

nên

 

1

6 2

2

AB AD BC 

 

1

.3. 3 2 6 2

2

AD  

2AD 

1

3

AD BC 

.

Do

ABCD

là hình thang vuông tại

A

và

B

nên

1

3

AD BC

 

.

Giả sử

( ; ; )D a b c

khi đó ta có

4

1

3

1

2

3

1

3

a

b

c



 



 





 





7

3

7

3

4

3

a

b

c







 











6a b c   

.

Câu 29. (Chuyên Lê Quý Dôn - Dà Nẵng - 2018) Trong không gian với hệ tọa độ

Oxyz

cho hình hộp

.ABCD A B C D

   

. Biết

 

2;4;0A

,

 

4;0;0B

,

 

1;4; 7C  

và

 

6;8;10D



. Tọa độ điểm

B



là

A.

 

8;4;10B



. B.

 

6;12;0B



. C.

 

10;8;6B



. D.

 

13;0;17B



.

Lời giải

Giả sử

 

; ;D a b c

,

 

; ;B a b c

   

Gọi

O AC BD 

1 7

;4;

2 2

O



 



 

 

3

8

7

a

b

c

 





 





 



.

C(-1; 4;-7)

B

(4; 0; 0)

A

(2; 4; 0)

C'

A'

B'

D'

(6; 8; 10)

D

O

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13

Vậy

 

9;0;17

DD







,

 

4; ;BB a b c

   

 



. Do

.

ABCD A B C D

   

là hình hộp nên

DD BB

 



 

13

0

17

a

b

c











 











. Vậy

 

13;0;17

B



.

Câu 30. (Chuyên Lương Văn Chánh - Phú Yên - 2018) Trong không gian

Oxyz

, cho hình hộp

.

ABCD A B C D

   

có

 

1;0;1

A

,

 

2;1;2

B

,

 

1; 1;1

D 

,

 

4;5; 5

C





. Tính tọa độ đỉnh

A



của hình

hộp.

A.

 

4;6; 5

A





. B.

 

2;0;2

A



. C.

 

3;5; 6

A





. D.

 

3;4; 6

A





.

Lời giải

Theo quy tắc hình hộp ta có:

AB AD AA AC

 

  

   

.

Suy ra

AA AC AB AD

 

  

   

.

Lại có:

 

3;5; 6

AC



 



,

 

1;1;1

AB 



,

 

0; 1;0

AD  



.

Do đó:

 

2;5; 7

AA



 



.

Suy ra

 

3;5; 6

A





.

Câu 31. (Chuyên Lê Hồng Phong 2018) Trong không gian với hệ toạ độ

Oxyz

, cho hình hộp

.

ABCD A B C D

   

có

 

0; 0; 0

A

,

 

3; 0; 0

B

,

 

0; 3; 0

D

,

 

0; 3; 3

D





. Toạ độ trọng tâm tam

giác

A B C

 

là

A.

 

1; 1; 2

. B.

 

2; 1; 2

. C.

 

1; 2; 1

. D.

 

2; 1; 1

.

Lời giải

Cách 1: Ta có

 

3; 0; 0

AB 



. Gọi

   

; ; ; 3;C x y z DC x y z

  



ABCD

là hình bình hành

     

; ; 3; 3; 0 3; 3; 0

AB DC x y z C    

 

Ta có

 

0; 3; 0

AD 



. Gọi

   

; ; ; 3 ; 3

A x y z A D x y z

        

     



ADD A

 

là hình bình hành

     

; ; 0; 0; 3 0; 0; 3

AD A D x y z A

     

      

 

Gọi

   

0 0 0 0 0 0

; ; ; ; 3

B x y z A B x y z

  

  



ABB A

 

là hình bình hành

     

0 0 0

; ; 3; 0; 3 3; 0; 3

AB A B x y z B

  

      

 

G

là trọng tâm tam giác

ABC

 

0 3 3

2

3

0 0 3

1 2; 1; 2

3

3 3 0

2

3

G

x

y G

z

 



 



 



    





  



  





.

A

B

C

D

A



B



C



D



NGUYỄN BẢO VƯƠNG - 0946798489

Trang 14 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Cách 2: Gọi

I

là trung điểm của đoạn thẳng

BD



.Ta có

3 3 3

; ;

2 2 2

I

 



 

 

.Gọi

 

; ;G a b c

là trọng tâm

tam giác

A B C

 

Ta có:

3DI IG



 

với

3 3 3

; ;

2 2 2

3 3 3

; ;

2 2 2

DI

IG a b c



 

  

 



  



 



   

 



 







. Do đó:

3 3

3

2 2

2

3 3

3 1

2 2

2

3 3

3

2 2

a

b b

c



 

 

 



 









 

    

 

 

 

 

 





 

  



 

 



.

Vậy

 

2;1; 2

G



.

Câu 32. (Chuyên Lê Hồng Phong - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho ba điểm

 

1;2; 1

A



,

 

2; 1;3

B 

,

 

4;7;5

C 

. Tọa độ chân đường phân giác trong góc

B

của tam giác

ABC

là

A.

2 11

; ;1

3 3

 



 

 

. B.

11

; 2;1

3

 



 

 

. C.

2 11 1

; ;

3 3 3

 

 

 

. D.

 

2;11;1



.

Lời giải

Ta có:

   

1; 3;4 26; 6;8;2 2 26

BA BA BC BC        

   

.

Gọi

D

là chân đường phân giác trong kẻ từ

B

lên

AC

của tam giác

ABC

Suy ra :

DA BA

DC BC



2

DC DA

  

 

2 11

; ;1

3 3

D

 

 

 

 

.

Câu 33. (Toán Học Và Tuổi Trẻ - 2018) Trong không gian với hệ trục tọa độ

Oxyz

, cho

2 2 2OA i j k  

   

,

 

2; 2;0

B 

và

 

4;1; 1

C



. Trên mặt phẳng

 

Oxz

, điểm nào dưới đây cách

đều ba điểm

A

,

B

,

C

.

A.

3 1

; 0;

4 2

M

 

 

 

. B.

3 1

; 0;

4 2

N

 

 

 

 

. C.

3 1

; 0;

4 2

P



 

 

 

. D.

3 1

; 0;

4 2

Q



 

 

 

.

Lời giải

Ta có:

 

2;2;2

A

và

3 21

4

PA PB PC  

.

Câu 34. (SGD Thanh Hóa - 2018) Trong hệ trục tọa độ

Oxyz

, cho hai điểm là

 

1;3; 1

A



,

 

3; 1;5

B 

.

Tìm tọa độ của điểm

M

thỏa mãn hệ thức

3

MA MB



 

.

A.

5 13

; ;1

3 3

M

 

 

 

. B.

7 1

; ;3

3 3

M

 

 

 

. C.

7 1

; ;3

3 3

M

 

 

 

. D.

 

4; 3;8

M 

.

Lời giải

Ta có

 

3

4

1 3

3

3 3 4; 3;8

1 3

3

8

1 3

A B

M

A B

M

A B

M

x x

x

y y

MA MB y M

z z

z





 











      











 







 

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15

Câu 35. (SGD - Đà Nẵng - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho hình hộp

.ABCD A B C D

   

,

biết rằng

 

3;0;0A 

,

 

0;2;0B

,

 

0;0;1D

,

 

1;2;3A



. Tìm tọa độ điểm

C



.

A.

 

10;4;4C



. B.

 

13;4;4C





. C.

 

13;4;4C



. D.

 

7;4;4C



.

Lời giải

Gọi

 

; ;C x y z



. Ta có

 

3;2;0AB 



;

 

3;0;1AD 



;

 

4;2;3AA







.

Mà

AC AB AD AA

 

  

   

 

10;4;4AC



 



10 3

4 0

x

y

z

 





  





 



 

13;4;4C





.

Câu 36. (Đặng Thúc Hứa - Nghệ An - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm

 

0;2; 2A 

,

 

2;2; 4B 

. Giả sử

 

; ;I a b c

là tâm đường tròn ngoại tiếp tam giác

OAB

. Tính

2 2 2

T a b c  

.

A.

8T 

. B.

2T 

. C.

6T 

. D.

14T 

.

Lời giải

Ta có

 

0;2; 2OA  



,

 

2;2; 4OB  



.

 

OAB

có phương trình:

0x y z  

 

I OAB

0a b c   

.

 

; 2; 2AI a b c  



,

 

2; 2; 4BI a b c   



,

 

; ;OI a b c



.

Ta có hệ

AI BI

AI OI











     

   

2 2 2

2

2 2

2 2 4

2 2

a c a c

b c b c



     







    





4

2

a c

b c

 







   



Ta có hệ

4

2

0

a c

b c

a b c

 





   





  



4

2

a c

b c

 







   



2

0

2

a

b

c







 





 



.

Vậy

 

2;0; 2I 

2 2 2

8T a b c    

Câu 37. (THPT Trần Quốc Tuấn - 2018) Trong không gian với hệ tọa độ

Oxyz

cho hai điểm

 

4; 2; 1A

,

 

2; 1;4B  

. Tìm tọa độ điểm

M

thỏa mãn đẳng thức

2AM MB

 

.

A.

 

0;0;3M

. B.

(0;0; 3)M 

. C.

( 8; 4;7)M  

. D.

(8;4; 7)M 

.

Lời giải

Gọi điểm

 

; ;M x y z

. Khi đó:

2AM MB

 

 

4 2 2

2 2 1

1 2 4

x x

y y

z z



   



    





  



0

3

x

y

z







 









.

C

B

A

C'

A'

B'

D'

D

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 16 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Vậy

 

0;0;3M

.

Câu 38. (Chuyên Lê Hồng Phong - TPHCM - 2018) Trong không gian với hệ toạ độ

Oxyz

, cho ba điểm

 

2;3;1A 

,

 

2;1;0B

,

 

3; 1;1C  

. Tìm tất cả các điểm

D

sao cho

ABCD

là hình thang có đáy

AD

và 3

ABCD ABC

S S





A.

 

8;7; 1D 

. B.

 

8; 7;1

12;1; 3

D

 











. C.

 

8;7; 1

12; 1;3

D







 





. D.

 

12; 1;3D  

.

Lời giải

Ta có:

   

1

. ,

2

ABCD

S AD BC d A BC 

 

2

1

.

2

ABC

ABCD

S

S AD BC

BC



  

.

 

.

3

ABC

AD BC S

S

BC





 

3BC AD BC   2AD BC 

.

Mà

ABCD

là hình thang có đáy

AD

nên

2AD BC

 

 

1

.

 

5; 2;1BC   



,

 

2; 3; 1

D D D

AD x y z   



.

 

1

2 10

3 4

1 2

D

x

y

z

  





   





 



12

1

3

D

x

y

z

 





  









.

Vậy

 

12; 1;3D  

.

Dạng 2. Tích vô hướng, tích có hướng và ứng dụng

Dạng 2.1 Tích vô hướng và ứng dụng

Câu 1. (Mã 104 2017) Trong không gian với hệ tọa độ

Oxyz

cho ba điểm

 

2;3; 1M 

,

 

1;1;1N 

và

 

1; 1;2P m 

. Tìm

m

để tam giác

MNP

vuông tại

N

.

A. B. C. D.

Lời giải

Chọn C

   

3; 2;2 ; 2; 2;1MN NP m  

 

.

Tam giác

MNP

vuông tại

 

. 0 6 2 2 2 0 2 2 0N MN NP m m m             

 

.

Câu 2. (THPT Yên Khánh - Ninh Bình - 2019) Trong không gian

Oxyz

cho các điểm

     

5;1;5 ; 4;3;2 ; 3; 2;1A B C  

. Điểm

 

; ;I a b c

là tâm đường tròn ngoại tiếp tam giác

ABC

.

Tính

2a b c 

?

A.

1

. B.

3.

C.

6.

D.

9.

Lời giải

Ta có

 

1;2; 3

. 0

7; 5; 1

AB

AB BC

BC



  



  



   







 



tam giác

ABC

vuông tại

B

.

 tâm

I

của đường tròn ngoại tiếp tam giác

ABC

là trung điểm của cạnh huyền

AC

.



1

1; ;3

2

I

 



 

 

. Vậy

2 3.a b c  

2

m



6

m

 

0

m



4

m

 

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17

Câu 3. (HSG Bắc Ninh 2019) Trong không gian với hệ tọa độ

Oxyz

, cho véc tơ

   

1;1; 2 , 1;0;u v m

  

 

. Tìm tất cả giá trị của

m

để góc giữa

u



,

v



bằng

45



.

A.

2

m



. B.

2 6

m   . C.

2 6

m   . D.

2 6

m   .

Lời giải

+

   

2

, 45 cos ,

2

u v u v   

   

. 2

2

.

u v

 

 

2

1 2 1

2

6. 1

m



 



 

2

3 1 1 2m m

   

2 2

1 2 0

3 3 1 4 4

m

m m m

 







   



2

1

2

4 2 0

m

m m













  



2 6

m   .

Câu 4. (Sở Kon Tum - 2019) Trong không gian

Oxyz

, cho các vec tơ

 

5;3; 2

a

 



và

 

; 1; 3

b m m

  



. Có bao nhiêu giá trị nguyên dương của

m

để góc giữa hai vec tơ

a



và

b



là

góc tù?

A.

2.

B.

3.

C.

1.

D.

5.

Lời giải

Chọn A

Ta có

 

2

. 3 9

cos ;

.

38. 2 6 10

a b m

a b

m m



 

 

 

.

Góc giữa hai vec tơ

a



và

b



là góc tù khi và chỉ khi

 

cos ; 0 3 9 0 3

a b m m

     

 

.

Vì

m

nguyên dương nên

 

1; 2

m 

. Vậy có 2 giá trị

m

thỏa mãn yêu cầu bài toán.

Câu 5. Biết

 

; ;c x y z





khác

0



và vuông góc với cả hai vectơ

   

1;3;4 , 1;2;3

a b  

 

. Khẳng định nào

đúng?

A.

5 0z x 

. B.

7 0x y 

. C.

5 0z x 

. D.

7 0x y 

.

Lời giải

Chọn D

Theo giả thiết ta có

 

; ;c x y z





khác

0



và vuông góc với cả hai vectơ

   

1;3;4 , 1;2;3

a b  

 

nên

. 0 1 3 4 0 1 3 4 0

1 2 3 0 5 7 0

. 0

5

1 3 4. 0

7 0

7

5 5 7 0

7

c a x y z x y z

x y z y z

c b

x y y

x y

y z

z y



      

 



 

  

     



 









  



 





 

 

  











 

Câu 6. Trong không gian tọa độ

Oxyz

, cho

 

2;0;0

A

,

 

0;2;0

B

,

 

0;0;2

C

. Có tất cả bao nhiêu điểm

M

trong không gian thỏa mãn

M

không trùng với các điểm

, ,A B C

và



90

AMB BMC CMA

   

A.

0

. B.

1

. C.

2

. D.

3

.

Lời giải

Chọn C

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 18 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Gọi

 

; ;M x y z

.Ta có:



90

AMB BMC CMA

   

. 0

AM BM

BM CM

CM AM







 











 

   

2

2 2 0

x x y y z

x y y z z

x x y z z



    



     





    





2 2 2

2 2 0

x y z x y

x y z y z x z

y z

x y z x z



    



    



       

 

 



    



 

2

0;0;0

3 4 0

4 4 4

; ;

3 3 3

M

x x

x y z

M





 



 



 



 



 



 



.

Câu 7. (Chuyên Lương Văn Chánh - Phú Yên - 2018) Trong không gian

Oxyz

, cho hai vectơ

u



và

v



tạo với nhau một góc

120

và

2

u





,

5

v





. Tính

u v

 

A.

19

. B.

5

. C.

7

. D.

39

.

Lời giải

Ta có :

 

2

u v



 

 

2

u v

 

 

2 2

2

u uv v  

   

 

2 2

2 . cos ;

u u v u v v  

     

2 2

1

2 2.2.5. 5 19

2

 

    

 

 

.

Suy ra

19

u v 

 

.

Câu 8. (THPT Trần Nhân Tông - 2018) Trong không gian với hệ tọa độ Oxyz, cho ba điểm

 

2;3; 1

M



,

 

1;1;1

N 

và

 

1; 1;2

P m 

. Tìm

m

để tam giác

MNP

vuông tại

N

.

A.

6

m

 

. B.

0

m



. C.

4

m

 

. D.

2

m



.

Lời giải

Ta có

 

3;2; 2

NM

 



,

 

2; 2;1

NP m 



.

Tam giác

MNP

vuông tại

N

khi và chỉ khi

. 0

NM NP



 

 

3.2 2. 2 2.1 0

m

    

0

m

 

.

Vậy giá trị cần tìm của

m

là

0

m



.

Dạng 2.2 Tích có hướng và ứng dụng

Câu 9. (Yên Phong 1 - 2018) Trong không gian

Oxyz

, cho 4 điểm

 

2;0;2

A

,

 

1; 1; 2

B

 

,

 

1;1;0

C 

,

 

2;1;2

D 

. Thể tích của khối tứ diện

ABCD

bằng

A.

42

3

. B.

14

3

. C.

21

3

. D.

7

3

.

Lời giải

     

3;1; 2 ; 1; 1; 4 ; 4;1;0

AC AB AD        

  

.

 

, 6; 10;4

AB AC

 

  

 

 

.

Thể tích khối tứ diện là:

1 1 7

. , . 14

6 6 3

V AB AC AD

 

  

 

  

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19

Câu 10. (SGD Cần Thơ - 2018) Trong không gian

Oxyz

, cho các vectơ

 

5;3; 1  



a

,

 

1;2;1





b

,

 

;3; 1 . 



c m

Giá trị của

m

sao cho

,

 



 

  

a b c

là

A.

1 

m

. B.

2 

m

. C.

1

m

. D.

2

m

.

Lời giải

 

, 5; 1;3 2

 

   

 

 

b c m m

Ta có:

1 3

, 2

3 2 1

 



 

   



 

  



  

m

a b c m

m

.

Câu 11. (SGD - Đà Nẵng - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho hai vectơ

 

4;3;1

m 



,

 

0;0;1

n 



. Gọi

p



là vectơ cùng hướng với

,

 

 

 

m n

(tích có hướng của hai vectơ

m



và

n



). Biết

15

p





, tìm tọa độ vectơ

p



.

A.

 

9; 12;0

p  



. B.

 

45; 60;0

p  



. C.

 

0;9; 12

p  



. D.

 

0;45; 60

p  



.

Lời giải

Ta có :

 

; 3; 4;0

m n

 

 

 

 

Do

p



là vectơ cùng hướng với

;m n

 

 

 

nên

;p k m n

 



 

  

,

0

k



Mặt khác:

15

p





. , 15

 

 

 

 

k m n

.5 15

k

 

3

k

 

. Vậy

 

9; 12;0

p  



.

Câu 12. (THPT Hoàng Hoa Thám - Hưng Yên - 2018)Trong không gian với hệ tọa độ

Oxyz

, cho

 

0; 2;2

A a 

;

 

3; 1;1

B a  

;

 

4; 3;0

C  

;

 

1; 2; 1

D a

  

. Tập hợp các giá trị của

a

để bốn

điểm

A

,

B

,

C

,

D

đồng phẳng là tập con của tập nào sau?

A.

 

7; 2 

. B.

 

3;6

.C.

 

5;8

. D.

 

2;2



.

Lời giải

Ta có

 

3;1;a 1

AB a

 



,

 

4; 1;a 2

AC

  



,

 

1;0;2 3

AD a

 



.

 

2

, 2 3; 5 10; 1

AB AC a a a a

 

      

 

 

.

Để bốn điểm

A

,

B

,

C

,

D

đồng phẳng:

   

0

, . 0 2 3 2 3 . 1 0

3

2

a

AB AC AD a a a

a







 

         

 







  

.

Câu 13. (Việt Đức Hà Nội 2019) Trong hệ trục tọa độ

Oxyz

, cho tứ diện

ABCD

biết

 

3; 2;A m



,

 

2;0;0

B

,

 

0;4;0

C

,

 

0;0;3

D

. Tìm giá trị dương của tham số

m

để thể tích tứ

diện bằng 8.

A.

8

m



. B.

4

m



. C.

12

m



. D.

6

m



.

Lời giải

Ta có:

     

3; 2; 3 , 2;0; 3 , 0; 4; 3      

  

DA m DB DC

.

Thể tích tứ diện:

 

6

1 1

, . 8 24 8 3

6

6 6

 



 

     



 





  

m

V DB DC DA m

m

.

Vì

m

dương nên

6.

m



Do đó chọn D.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 20 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 14. (THPT Nguyễn Khuyến 2019) Trong không gian với hệ tọa độ

Oxyz

, cho

   

1;1;2 , 1; ; 2

u v m m

   

 

. Khi

, 14

u v

 



 

 

thì

A.

1

m



hoặc

11

5

m

 

B.

1

m

 

hoặc

11

3

m

 

C.

1

m



hoặc

3

m

 

D.

1

m

 

Lời giải

Chọn C

     

2 2

, 2; ; 1 , 2 1 3 6 5

u v m m m u v m m m m m

   

             

   

   

 

2 2

1

, 14 3 6 5 14 3 6 9 0

3

m

u v m m m m

m





         



 



 

.

Câu 15. (THPT Nguyễn Khuyến 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho tứ diện

ABCD

có

 

2; 1;1

A

,

 

3;0; 1

B

,

 

2; 1;3

C

,

D Oy

và có thể tích bằng

5

. Tính tổng tung độ của các

điểm

D

.

A.

6

B.

2

C.

7

D.

4

Lời giải

Chọn A.

Do

 

0; ;0

 

D Oy D y

, khi đó:

 

2; 1 ;1

  

DA y



,

 

3; ; 1  

DB y



,

 

2; 1 ;3

  

DC y



.

Khi đó

 

, 1 2 ;5; 3

 

  

 

DA DB y y

 

Và

2 6 30 12

1

, . 5

2 6 30 18

6

  

 

 

   

 

 

    

 

ABCD

y y

V DA DB DC

y y

  

.

Vậy

1 2

12 18 6    

y y .

Câu 16. (Toán Học Tuổi Trẻ 2019) Trong không gian với hệ tọa độ

Oxyz

, cho điểm

 

1; 2;0

A



,

 

1;0; 1

B



,

 

0; 1;2

C



,

 

2; ;D m n

. Trong các hệ thức liên hệ giữa

m

và

n

dưới đây, hệ thức

nào để bốn điểm

,A

,B

,C

D

đồng phẳng?

A.

2 13

m n

 

. B.

2 13

m n

 

. C.

2 13

m n

 

. D.

2 3 10

m n

 

.

Lời giải

Ta tính

 

0;2; 1 ;

AB

 



 

1;1;2 ;

AC

 



 

3; 2;AD m n  



;

 

, 5;1;2

AB AC

 



 

 

 

Bốn điểm

,A

,B

,C

D

đồng phẳng

, . 0 2 13

AB AC AD m n

 

    

 

 

  

Câu 17. Trong không gian

Oxyz

, cho hai véc tơ

 

4 ; 3 ;1

m 



và

 

0 ; 0 ; 1

n 



. Gọi

p



là véc tơ cùng

hướng với

,m n

 

 

 

và

15

p





. Tọa độ của véc tơ

p



là

A.

 

9 ; 12 ; 0



. B.

 

0 ; 9 ; 12



. C.

 

9 ; 12 ; 0



. D.

 

0 ; 9 ; 12



.

Lời giải

Ta có:

 

, 3 ; 4 ; 0

m n

 

 

 

 

.

Vì

p



là véc tơ cùng hướng với

,m n

 

 

 

nên

 

. , 3 ; 4 ;0 , 0

p k m n k k k

 

   

 

  

.

Ta có:

2 2

3

15 9 16 15

3

k

p k k

k

 



    









.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21

So sánh với điều kiện

0 3

k k

  

 

9 ; 12 ; 0

p  



.

Câu 18. (Việt Đức Hà Nội 2019) Trong hệ trục tọa độ

Oxyz

, cho bốn điểm

       

0; 2;1 ; 1;0; 2 ; 3;1; 2 ; 2; 2; 1

A B C D

     

. Câu nào sau đây sai?

A. Bốn điểm

, , ,A B C D

không đồng phẳng. B. Tam giác

ACD

là tam giác vuông tại

A

.

C. Góc giữa hai véctơ

AB



và

CD



là góc tù. D. Tam giác

ABD

là tam giác cân tại

B

.

Lời giải

   

 

1;2; 3 ; 5; 3;1

3;3; 3 ; 3; 2;1

2;0; 2

AB CD

AC BD

AD

    

  

 



Ta có:

 

, 3; 6; 3

AB AC

 

  

 

 

    

, . 2 .3 0.6 2 3 0

AB AC AD

 

       

 

  

.

, ,AB AC AD



  

đồng phẳng hay bốn điểm

, , ,A B C D

đồng phẳng. Vậy đáp án A sai.

Lại có

     

. 3. 2 3.0 3 . 2 0

AC AD AC AD

        

 

.



tam giác

ACD

là tam giác vuông tại

A

. Vậy đáp án B đúng.

Mặt khác:

     

   

. 1. 5 2. 3 3 .1 14 0 , 0 ,

AB CD cos AB CD AB CD

           

     

là góc tù.

Vậy đáp án C đúng.

14

AB BD hay AB BD

  

 



tam giác

ABD

là tam giác cân tại

B

. Vậy đáp án D đúng.

Câu 19. (THPT Lương Thế Vinh - 2018) Trong không gian

Oxyz

, cho ba điểm

 

2;3;1

A 

,

 

2;1;0

B

,

 

3; 1;1

C  

. Tìm tất cả các điểm

D

sao cho

ABCD

là hình thang có đáy

AD

và

3

ABCD ABC

S S

.

A.

 

8;7; 1

D



. B.

 

8; 7;1

12;1; 3

D

 









. C.

 

8;7; 1

12; 1;3

D





 





. D.

 

12; 1;3

D  

.

Lời giải

Ta có

//

AD BC AD

nhận

 

5;2; 1

CB

 



là một VTCP.

Kết hợp với

AD

qua

 

2;3;1

A 

2 5

: 3 2

1

x t

AD y t

z t

  





  





 



 

t 



 

5 2;2 3;1

D t t t   

.

Biến đổi 3

ABCD ABC

S S

2

ACD ABC

S S 

 

1

Ta có

 

4; 2; 1

; 4;1; 18

1; 4;0

; 4 ; ;18

5 ;2 ;

AB

AB AC

AC

AC AD t t t

AD t t t



  



 

  



  

   

 

 

 

 

 



 







 



 



   

     

2 2

2

2 2 2

1 1 341

; 4 1 18

2 2 2

341

1 1

; 4 18

2 2 2

ABC

ACD

S AB AC

t

S AC AD t t t



 

      



 









 

     



 



 

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 22 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Kết hợp với

 

1

ta được

 

2 8;7; 1

341

2

2 12; 1;3

t D

t

t D

  

 



    





Với

   

8;7; 1 10;4; 2 2 2

D AD CB BC

      

  

.

Với

   

12; 1;3 10; 4;2 2 2

D AD CB BC

        

  

.

Hình thang

ABCD

có đáy

AD

thì

AD k BC



 

với

0

k



.

Do đó chỉ có

 

12; 1;3

D  

thỏa mãn.

Câu 20. (Bình Giang-Hải Dương 2019) Trong không gian với hệ tọa độ

Oxyz

, cho bốn điểm

 

0;0;2

A

,

 

3;0;5

B

,

 

1;1;0

C

,

 

4;1;2

A

. Độ dài đường cao của tứ diện

ABCD

hạ từ đỉnh

D

xuống mặt

phẳng

ABC

là

A.

11

. B.

1

. C.

11

. D.

11

.

Lời giải

Chọn A

Gọi

DH

là độ dài đường cao của tứ diện

ABCD

hạ từ đỉnh

D

xuống mặt phẳng

ABC

.

Công thức tính thể tích tứ diện

ABCD

là:

1

, .

6

ABCD

V AB AC AD

 



 

  

.

Công thức tính diện tích tam giác

ABC

S



là:

1

,

2

ABC

S AB AC



 



 

 

.

Mặt khác

1

3

ABCD ABC

V S DH



  

nên

, .

1 1 1

, . ,

6 3 2

,

AB AC AD

AB AC AD AB AC DH DH

AB AC

 

 

   

      

   

 

 

  

    

 

Ta có:

     

 

3;0;3 ; 1;1; 2 ; 4;1;0

, 3;9;3 ; , . 3.

AB AC AD

AB AC AB AC AD

   

   

    

   

  

    

Nên

 

2

2 2

, .

3 11

11

,

3 9 3

AB AC AD

DH

AB AC

 

 

   

 

  

 

  

 

Câu 21. (THPT Hoàng Hoa Thám - Hưng Yên - 2018)Trong không gian với hệ tọa độ

Oxyz

, cho

 

0; 2;2

A a 

;

 

3; 1;1

B a  

;

 

4; 3;0

C  

;

 

1; 2; 1

D a

  

. Tập hợp các giá trị của

a

để bốn

điểm

A

,

B

,

C

,

D

đồng phẳng là tập con của tập nào sau?

A.

 

7; 2 

. B.

 

3;6

.C.

 

5;8

. D.

 

2;2



.

Lời giải

Ta có

 

3;1;a 1

AB a

 



,

 

4; 1;a 2

AC

  



,

 

1;0;2 3

AD a

 



.

 

2

, 2 3; 5 10; 1

AB AC a a a a

 

      

 

 

.

Để bốn điểm

A

,

B

,

C

,

D

đồng phẳng:

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23

   

0

,

. 0 2 3 2 3 . 1 0

3

2

a

A

B AC AD a a a

a







 

         

 









  

.

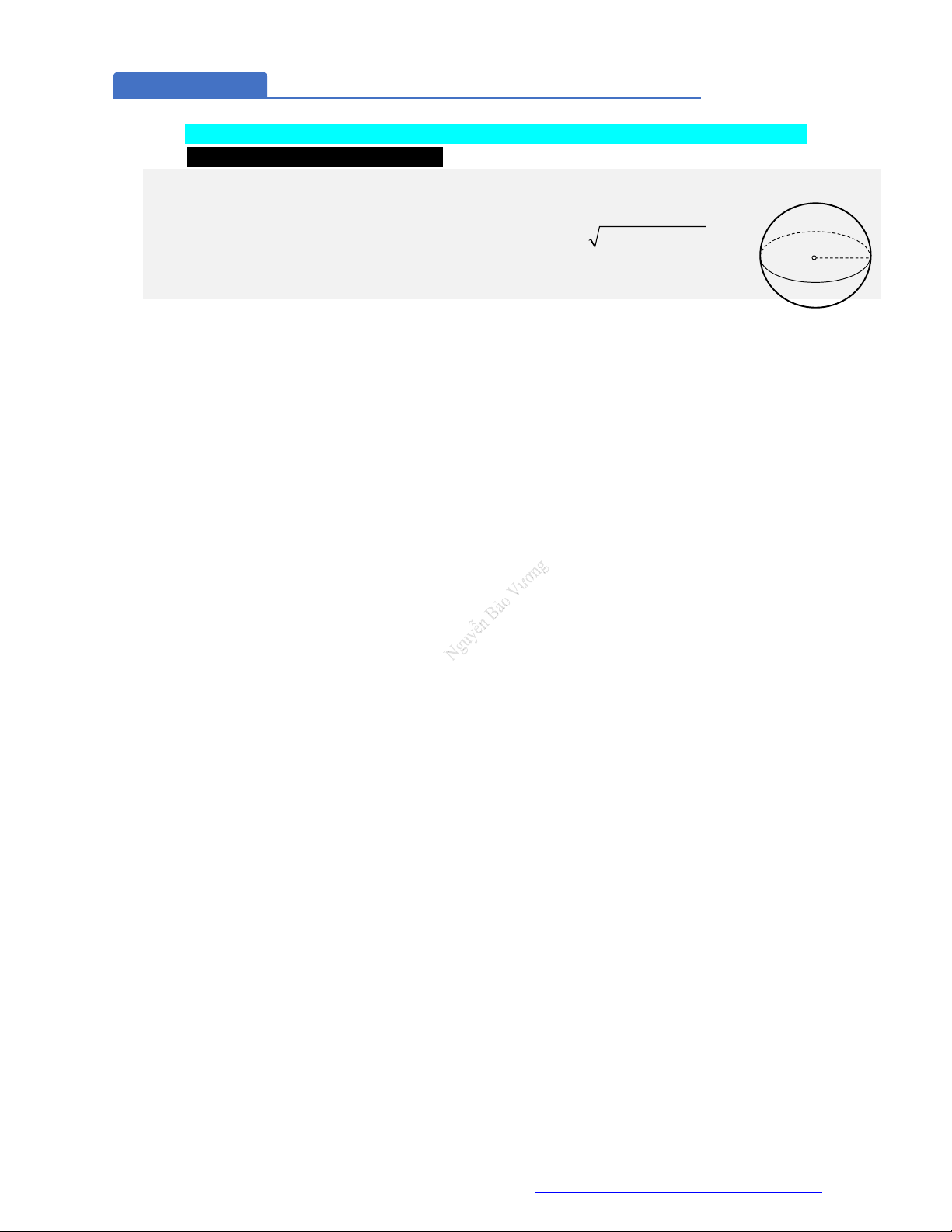
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương  https://www.facebook.com/phong.baovuong Trang 1

TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH TRUNG BÌNH MỨC 5-6 ĐIỂM

Dạng 1. Xác định tâm và bán kính



Mặt cầu tâm

( ; ; )I a b c

và có bán kính

R

có phương trình

2 2 2 2

( ) : ( ) ( ) ( ) .S x a y b z c R     



Phương trình

2 2 2

2 2 2 0x y z ax by cz d      

với

2 2 2

0a b c d   

là phương trình của mặt cầu có tâm

( ; ; )I a b c

và bán kính

2 2 2

.R a b c d   

 Để một phương trình là một phương trình mặt cầu, cần thỏa mãn hai điều kiện:

Hệ số trước

2 2 2

, , x y z phải bằng nhau và

2 2 2

0.a b c d   

Câu 1. (Đề Minh Họa 2020 Lần 1) Trong không gian

Oxyz

, cho mặt cầu

       

2 2 2

: 1 2 3 16S x y z     

. Tâm của

 

S

có tọa độ là

A.

 

1; 2; 3  

. B.

 

1;2;3

. C.

 

1;2; 3 

. D.

 

1; 2;3

.

Câu 2. (Đề Tham Khảo 2020 Lần 2) Trong không gian

Oxyz

, cho mặt cầu

       

2 2 2

: 2 4 1 9S x y z     

. Tâm của

 

S

có tọa độ là

A.

 

2;4; 1 

. B.

 

2; 4;1

. C.

 

2;4;1

. D.

 

2; 4; 1  

.

Câu 3. (Mã 102 - 2020 Lần 1) Trong không gian , cho mặt cầu . Bán

kính của bằng

A. . B. . C. . D. .

Câu 4. (Mã 101 - 2020 Lần 1) Trong không gian

Oxyz

, cho mặt cầu

   

2

2 2

: 2 9S x y z   

. Bán

kính của

 

S

bằng

A.

6

. B.

18

. C.

9

. D.

3

.

Câu 5. (Mã 103 - 2020 Lần 1) Trong không gian

Oxyz

, cho mặt cầu

2 2 2

( ): ( 1) 16S x y z    . Bán

kính của

( )S

là:

A.

32

B.

8

C.

4

D.

16

Câu 6. (Mã 104 - 2020 Lần 1) Trong không gian

,Oxyz

cho mặt cầu

   

2

2 2

: 2 16S x y z   

. Bán

kính của mặt cầu

 

S

bằng

A.

4

. B.

32

. C.

16

. D.

8

.

Câu 7. (Mã 101- 2020 Lần 2) Trong không gian

Oxyz

, cho mặt cầu

       

2 2 2

: 1 2 3 4S x y z     

. Tâm của

 

S

có tọa độ là

A.

 

1; 2; 3 

. B.

 

2; 4;6

. C.

 

1; 2;3

. D.

 

2; 4; 6 

.

Câu 8. (Mã 103 - 2020 Lần 2) Trong không gian

Oxyz

, cho mặt cầu

       

2 2 2

: 1 2 3 4S x y z     

. Tâm của

 

S

có tọa độ là

A.

 

1;2;3

. B.

 

2; 4; 6 

. C.

 

2;4;6

. D.

 

1; 2; 3 

.

Câu 9. (Mã 102 - 2020 Lần 2) Trong không gian

Oxyz

, cho mặt

cầu

2 2 2

( ) : ( 1) ( 2) ( 3) 9S x y z     

. Tâm của

( )S

có tọa độ là:

PHƯƠNG TRÌNH MẶT CẦU

Chuyên đề 29

Oxyz

   

2

2 2

: 2 9

S x y z

   

 

S

6

18

3

9

I

R

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

A.

( 2; 4;6) 

. B.

(2;4; 6)

. C.

( 1; 2;3) 

. D.

(1;2; 3)

.

Câu 10. (Mã 104 - 2020 Lần 2) Trong không gian

Oxyz

, cho mặt cầu

 

S

:

     

2 2 2

1 2 3 9

x y z

     

. Tâm của

 

S

có tọa độ là

A.

 

1; 2;3

 

. B.

 

2; 4;6

 

. C.

 

1;2; 3

. D.

 

2;4; 6

.

Câu 11. (Mã 104 2017) Trong không gian với hệ toạ độ

Oxyz

, cho mặt cầu

     

2 2

2

: 2 2 8

S x y z

    

. Tính bán kính

R

của

 

S

.

A.

2 2

R 

B.

64

R



C.

8

R



D.

4R 

Câu 12. (Mã 104 2018) Trong không gian

Oxyz

, mặt cầu

       

2 2 2

: 5 1 2 3

S x y z

     

có bán

kính bằng

A.

9

B.

2 3

C.

3

D.

3

Câu 13. (Mã 105 2017) Trong không gian với hệ toạ độ

Oxyz

, cho mặt cầu

       

     

2 2 2

: 5 1 2 9

S x y z . Tính bán kính

R

của

 

S

.

A.

 6R

B.

 3R

C.

 18R

D.

 9R

Câu 14. (Mã 103 2018) Trong không gian

Oxyz

, cho mặt cầu

       

2 2 2

: 3 1 1 2

S x y z

     

. Tâm

của

 

S

có tọa độ là

A.

 

3; 1;1



B.

 

3; 1;1

 

C.

 

3;1; 1 

D.

 

3;1; 1

Câu 15. (Đề Tham Khảo 2017) Trong không gian với hệ trục tọa độ

Oxyz

, tìm tọa độ tâm

I

và bán kính

R

của mặt cầu

     

2 2 2

1 2 4 20

x y z

     

.

A.

 

1;2; 4 , 2 5

I R  

B.

 

1; 2;4 , 20

I R

 

C.

 

1; 2;4 , 2 5

I R 

D.

 

1;2; 4 , 5 2

I R  

Câu 16. (Mã 101 - 2019) Trong không gian

Oxyz

, cho mặt cầu

 

2 2 2

: 2 2 7 0

S x y z x z

     

. Bán

kính của mặt cầu

đã cho bằng

A.

3

. B.

15

. C.

7

. D.

9

.

Câu 17. (Mã 104 - 2019) Trong không gian

Oxyz

, cho mặt cầu

 

2 2 2

: 2 2 7 0     

S x y z y z

. Bán

kính của mặt cầu đã cho bằng

A.

15

. B.

7

. C.

9

. D.

3

.

Câu 18. (Mã 102 - 2019) Trong không gian

Oxyz

, cho mặt cầu

 

2 2 2

: 2 2 7 0.

S x y z x y

     

Bán

kính của mặt cầu đã cho bằng

A.

7

. B.

9

. C.

15

. D.

3

.

Câu 19. (Mã 103 - 2019) Trong không gian

Oxyz

, cho mặt cầu

2 2 2

( ) : 2 2 7 0.

S x y z y z

     

Bán

kính của mặt cầu đã cho bằng

A.

7

. B.

3

. C. 9. D.

15

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3

Câu 20. (THPT Hoàng Hoa Thám Hưng Yên 2019) Trong không gian với hệ tọa độ

Oxyz

, cho mặt cầu

 

2 2 2

: 8 2 1 0

S x y z x y

     

. Tìm tọa độ tâm và bán kính của mặt cầu

 

S

.

A.

 

–4;1;0 .

,

2

I R



B.

 

–4;1;0 .

,

4

I R



C.

 

4; –1;0 , 2.

I R



D.

 

4; –1;0 , 4.

I R



Câu 21. (THPT Lương Thế Vinh Hà Nội 2019) Cho mặt cầu

 

2 2 2

: 2 4 2 3 0

S x y z x y z

      

.

Tính bán kính

R

của mặt cầu

 

S

.

A.

3

R 

. B.

3

R



. C.

9

R



. D.

3 3

R 

.

Câu 22. Trong không gian vơi hệ tọa độ

Oxyz

, cho mặt cầu

 

2 2 2

: 8 2 1 0

S x y z x y

     

. Tìm tọa độ

tâm và bán kính mặt cầu

 

S

:

A.

 

4;1;0 , 2

I R

 

. B.

 

4;1;0 , 4

I R

 

. C.

 

4; 1;0 , 2

I R

 

. D.

 

4; 1;0 , 4

I R

 

.

Câu 23. (THPT Đoàn Thượng - Hải Dương -2019) Trong không gian

Oxyz

, cho mặt cầu

       

2 2 2

: 3 1 1 2

S x y z

     

. Xác định tọa độ tâm của mặt cầu

 

S

A.

 

3;1; 1

I

 

. B.

 

3;1; 1

I



. C.

 

3; 1;1

I  

. D.

 

3; 1;1

I 

.

Câu 24. (Sở Hà Nội 2019) Trong không gian

Oxyz

, cho mặt cầu

 

2 2 2

: 2 4 2 3 0

S x y z x y z

      

.

Tọa độ tâm

I

của mặt cầu

 

S

là:

A.

 

1; 2; 1



. B.

 

2; 4; 2 

. C.

 

1; 2; 1 

. D.

 

2;4;2



.

Câu 25. (Chuyên Lê Quý Đôn Quảng Trị 2019) Trong không gian

Oxyz

, cho mặt cầu

 

2 2 2

: 8 10 6 49 0

S x y z x y z

      

. Tính bán kính

R

của mặt cầu

 

S

.

A.

1R 

. B.

7

R



. C.

151

R 

. D.

99

R 

.

Câu 26. Trong không gian

Oxyz

, mặt cầu

 

2 2 2

: 4 2 6 1 0

S x y z x y z

      

có tâm là

A.

 

4;2; 6 

B.

 

2; 1;3



C.

 

2;1; 3 

D.

 

4; 2;6



Câu 27. (THPT Gang Thép Thái Nguyên 2019) Trong không gian với hệ tọa độ

Oxyz

, cho mặt cầu có

phương trình

     

2 2 2

1 2 3 4

x y z

     

. Tìm tọa độ tâm

I

và bán kính

R

của mặt cầu đó.

A.

 

1;2; 3

I

 

;

2R 

. B.

 

1;2; 3

I

 

;

4R 

.

C.

 

1; 2;3

I 

;

2R 

. D.

 

1; 2;3

I 

;

4R 

.

Câu 28. (KTNL GV Bắc Giang 2019) Trong không gian với hệ tọa độ

Oxyz

, cho mặt cầu

( )S

có

phương trình

2 2 2

4 2 4 0

x y z x y

     

.Tính bán kính

R

của

( ).S

A.

1

. B.

9

. C.

2

. D.

3

.

Câu 29. (Chuyên Lê Hồng Phong Nam Định 2019) Trong không gian

Oxyz

, cho mặt cầu

       

2 2 2

: 3 1 1 4

S x y z

     

. Tâm của

 

S

có tọa độ là

A.

 

3;1; 1 

. B.

 

3; 1;1

. C.

 

3; 1; 1 

. D.

 

3;1; 1

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Dạng 2. Viết phương trình mặt cầu

 Dạng 1. Cơ bản

2 2 2 2

( ) : ( ): ( ) ( ) ( ) .

( ; )

:

;

âm I a bT

S S x a y b z c R

BK R

c



      







 Dạng 2. Viết phương trình mặt cầu

( )S

có tâm

I

và đi qua điểm

.A

Phương pháp:

( ) :

:

âm IT

S

BK R IA











(dạng 1)

 Dạng 3. Viết phương trình mặt cầu

( )S

có đường kính

,AB

với

, A B

cho trước.

Phương pháp:

( ) :

1

:

2

R

âmT

S

BK AB

I















Câu 1. (Đề Minh Họa 2020 Lần 1) Trong không gian

Oxyz

, cho mặt cầu

 

S

có tâm

 

0;0; 3

I



và đi

qua điểm

 

4;0;0

M

. Phương trình của

 

S

là

A.

 

2

2 2

3 25

x y z

   

. B.

 

2

2 2

3 5

x y z

   

.

C.

 

2

2 2

3 25

x y z

   

. D.

 

2

2 2

3 5

x y z

   

.

Câu 2. (Mã 110 2017) Trong không gian hệ tọa độ

Oxyz

, tìm tất cả các giá trị của

m

để phương trình

2 2 2

2 2 4 0

x y z x y z m

      

là phương trình của một mặt cầu.

A.

6

m



B.

6

m



C.

6

m



D.

6

m



Câu 3. (Đề Tham Khảo 2019) Trong không gian

Oxyz

cho hai điểm

 

1;1;1

I

và

 

1;2;3

A

. Phương

trình mặt cầu có tâm I và đi qua A là

A.

     

2 2 2

1 1 1 5

x y z

     

B.

     

2 2 2

1 1 1 29

x y z

     

C.

     

2 2 2

1 1 1 5

x y z

     

D.

     

2 2 2

1 1 1 25

x y z

     

Câu 4. (THPT Cù Huy Cận 2019) Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm

   

1; 2;7 , 3;8; 1

A B

  

. Mặt cầu đường kính

AB

có phương trình là

A.

     

2 2 2

1 3 3 45

x y z     

. B.

     

2 2 2

1 3 3 45

x y z

     

.

C.

     

2 2 2

1 3 3 45

x y z     

. D.

     

2 2 2

1 3 3 45

x y z

     

.

Câu 5. (THPT - Yên Định Thanh Hóa 2019) Trong không gian với hệ tọa độ

Oxyz

, viết phương trình

mặt cầu có tâm

 

1; 4;3

I 

và đi qua điểm

 

5; 3;2

A 

.

A.

     

2 2 2

1 4 3 18

x y z

     

. B.

     

2 2 2

1 4 3 16

x y z

     

.

C.

     

2 2 2

1 4 3 16

x y z

     

. D.

     

2 2 2

1 4 3 18

x y z

     

.

Câu 6. (Chuyên Sơn La -2019) Trong không gian

Oxyz

, cho hai điểm

 

1;1;1

A

và

 

1; 1;3

B 

. Phương

trình mặt cầu có đường kính

AB

là

A.

   

2 2

2

1 2 8

x y z

    

. B.

   

2 2

2

1 2 2

x y z

    

.

C.

   

2 2

2

1 2 2

x y z

    

. D.

   

2 2

2

1 2 8

x y z

    

.

Câu 7. (Sở Thanh Hóa 2019) Trong không gian Oxyz, cho hai điểm A(2;4;1), B

 

2;2; 3 

. Phương trình

mặt cầu đường kính AB là

là trung điểm của

.AB

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5

A.

   

2 2

2

3 1 36.

x y z    

B.

   

2 2

2

3 1 9.

x y z

    

C.

   

2 2

2

3 1 9.

x y z

    

D.

   

2 2

2

3 1 36.

x y z    

Câu 8. (Chuyên Bắc Giang 2019) Trong không gian với hệ tọa độ Oxyz, hỏi trong các phương trình sau

phương trình nào là phương trình của mặt cầu?

A.

2 2 2

2 4 1 0

x y z x z

     

B.

2 2

3 2 4 1 0

x z x y z

     

C.

2 2 2

2 4 4 1 0

x y z xy y z

      

D.

2 2 2

2 2 4 8 0

x y z x y z

      

Câu 9. Trong không gian

Oxyz

, cho hai điểm

 

2; 1; 3 

A

;

 

0;3; 1

B

. Phương trình của mặt cầu

đường kính

AB

là :

A.

     

2 2 2

1 1 2 6     

x y z

B.

     

2 2 2

1 1 2 24     

x y z

C.

     

2 2 2

1 1 2 24     

x y z

D.

     

2 2 2

1 1 2 6     

x y z

Câu 10. (Chuyên KHTN 2019) Trong không gian với hệ tọa độ

Oxyz

phương trình nào sau đây không

phải là phương trình của một mặt cầu?

A.

2 2 2

2 4 3 0

x y z x y z

      

. B.

2 2 2

2 2 2 0

x y z x y z

     

.

C.

2 2 2

2 2 2 4 8 6 3 0

x y z x y z

      

. D.

2 2 2

2 4 4 10 0

x y z x y z

      

.

Câu 11. (Chuyên Phan Bội Châu Nghệ An 2019) Trong không gian với hệ trục tọ độ

Oxyz

, cho hai

điểm

   

1;2;3 , 5;4; 1

A B



. Phương trình mặt cầu đường kính

AB

là

A.

     

2 2 2

3 3 1 36

x y z

     

. B.

     

2 2 2

3 3 1 9

x y z

     

.

C.

     

2 2 2

3 3 1 6

x y z

     

. D.

     

2 2 2

3 3 1 9

x y z

     

.

Câu 12. (Việt Đức Hà Nội 2019) Trong hệ trục tọa độ

Oxyz

, phương trình mặt cầu tâm

 

2;1; 2

I



bán

kính

2R 

là:

A.

     

2 2 2

2

2 1 2 2

x y z

     

. B.

2 2 2

4 2 4 5 0

x y z x y z

      

.

C.

2 2 2

4 2 4 5 0

x y z x y z

      

. D.

     

2 2 2

2 1 2 2

x y z

     

.

Câu 13. (Việt Đức Hà Nội 2019) Phương trình nào sau đây là phương trình mặt cầu

 

S

tâm

 

2;1;0

A

,

đi qua điểm

 

0;1;2

B

?

A.

     

2 2

2

: 2 1 8

S x y z

    

. B.

     

2 2

2

: 2 1 8

S x y z

    

.

C.

     

2 2

2

: 2 1 64

S x y z

    

. D.

     

2 2

2

: 2 1 64

S x y z

    

.

Câu 14. (Chuyên Lam Sơn 2019) Trong không gian Oxyz cho điểm

(2;3;4)

I

và

 

1; 2;3

A

. Phương trình

mặt cầu tâm I và đi qua A có phương trình là:

A.

2 2 2

( 2) ( 3) ( 4) 3

x y z

     

. B.

   

2 2

2

( 2) 3 4 9

x y z

     

.

C.

   

2 2

2

( 2) 3 4 45

x y z

     

. D.

   

2 2

2

( 2) 3 4 3

x y z

     

.

Câu 15. (Thpt Vĩnh Lộc - Thanh Hóa 2019) Trong không gian

Oxyz

, cho hai điểm

 

1;1;1

I

và

 

1;2;3

A

. Phương trình của mặt cầu có tâm

I

và đi qua

A

là

A.

     

2 2 2

1 1 1 29

x y z

     

. B.

     

2 2 2

1 1 1 5

x y z

     

.

C.

     

2 2 2

1 1 1 25

x y z

     

. D.

     

2 2 2

1 1 1 5

x y z

     

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu

16. (THPT Phan Bội Châu - Nghệ An - 2019) Trong không gian với hệ trục tọa độ

O

xyz

,

cho hai

điểm

 

1

;2;3

A

,

 

5

;4; 1

B

. P

hương trình mặt cầu đường kính

AB

là

A.

     

2 2 2

3 3 1 9     

x y z

. B.

     

2 2 2

3 3 1 6     

x y z

.

C.

     

2 2 2

3

3 1 9     

x

y z

. D

.

     

2 2 2

3

3 1 36     

x

y z

.

Câu

17. (Lý Nhân Tông - Bắc Ninh 1819) Trong không gian

Oxy

z

,

cho hai điểm

 

7; 2;2

A 

v

à

 

1

;2;4

B

.

Phương trình nào dưới đây là phương trình mặt cầu đường kính

A

B

?

A.

   

2

4

3 14

x

y z



   

. B.

   

2

4

3 2 14

x

y z    

.

C.

     

2

2 2

7 2 2 14

x y z

     

. D.

   

2

4 3 56

x y z

    

.

Câu

18. (Bình Phước - 2019) Trong không gian

Oxyz

,

cho hai điểm

 

3

; 2;5

M 

,

 

1

;6; 3

N



.

Mặt cầu

đường kính

M

N

c

ó phương trình là:

A.

     

2

2 2

1

2 1 6

x

y z



    

. B.

     

2

2 2

1

2 1 6

x

y z



    

.

C.

     

2

2 2

1

2 1 36

x

y z



    

. D.

     

2

2 2

1

2 1 36

x

y z



    

.

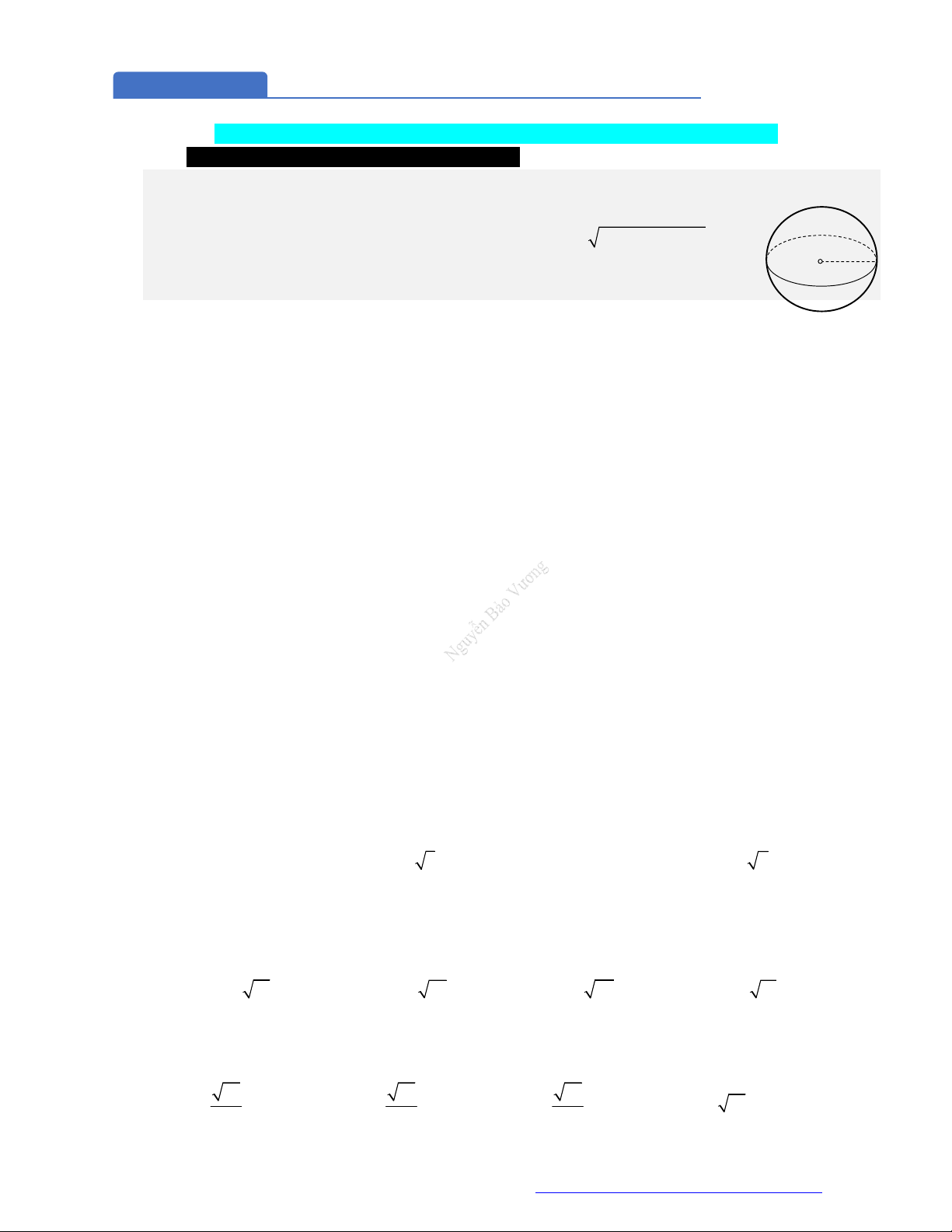
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương  https://www.facebook.com/phong.baovuong Trang 1

TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH KHÁ – MỨC 7-8 ĐIỂM

Dạng 1. Xác định tâm, bán kính của mặt cầu



Mặt cầu tâm

( ; ; )I a b c

và có bán kính

R

có phương trình

2 2 2 2

( ) : ( ) ( ) ( ) .S x a y b z c R     

 Phương trình

2 2 2

2 2 2 0x y z ax by cz d       với

2 2 2

0a b c d   

là phương trình của mặt cầu có tâm

( ; ; )I a b c

và bán kính

2 2 2

.R a b c d   

 Để một phương trình là một phương trình mặt cầu, cần thỏa mãn hai điều kiện:

Hệ số trước

2 2 2

, , x y z phải bằng nhau và

2 2 2

0.a b c d   

Câu 1. (Sở Phú Thọ 2019) Trong không gian

Oxyz

, có tất cả bao nhiêu giá nguyên của

m

để

   

2 2 2 2

2 2 2 1 3 5 0        x y z m x m z m

là phương trình một mặt cầu?

A.

4

B.

6

C.

5

D.

7

Câu 2. Trong không gian với hệ trục tọa độ

Oxyz

, tìm tất cả các giá trị của

m

để phương trình

 

2 2 2

2 2 4 19 6 0       x y z m x my m

là phương trình mặt cầu.

A.

1 2 m

. B.

1m

hoặc

2m

. C.

2 1  m

. D.

2 m

hoặc

1m

.

Câu 3. (Chuyên Lê Quý Đôn Điện Biên 2019) Trong không gian

Oxyz

có tất cả bao nhiêu giá trị

nguyên

m

để phương trình

2 2 2 2

4 2 2 9 28 0x y z mx my mz m       

là phương trình mặt cầu?

A.

7

. B.

8

. C.

9

. D.

6

.

Câu 4. Trong không gian

Oxyz

, xét mặt cầu

 

S

có phương trình dạng

2 2 2

4 2 2 10 0x y z x y az a      

. Tập hợp các giá trị thực của

a

để

 

S

có chu vi đường tròn

lớn bằng

8

là

A.

 

1;10

. B.

 

2; 10

. C.

 

1;11

. D.

 

1; 11

.

Câu 5. (Chuyên Lê Quý Dôn - Dà Nẵng - 2018) Trong không gian với hệ trục tọa độ

Oxyz

, cho ba

điểm

 

1;0;0A

,

 

0;0;3C

,

 

0;2;0B

. Tập hợp các điểm

M

thỏa mãn

2 2 2

MA MB MC 

là mặt

cầu có bán kính là:

A.

2R 

. B.

3R 

. C.

3R 

. D.

2R 

.

Câu 6. (Toán Học Và Tuổi Trẻ 2018) Trong không gian với hệ trục tọa độ

Oxyz

, cho ba điểm

 

1;2; 4A 

,

 

1; 3;1B 

,

 

2;2;3C

. Tính đường kính

l

của mặt cầu

 

S

đi qua ba điểm trên và có

tâm nằm trên mặt phẳng

 

Oxy

.

A. 2 13l  . B.

2 41l 

. C. 2 26l  . D.

2 11l 

.

Câu 7. (Chuyên ĐHSPHN - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho

 

1;0;0A 

,

 

0;0;2B

,

 

0; 3;0C 

. Bán kính mặt cầu ngoại tiếp tứ diện

OABC

là

A.

14

3

. B.

14

4

. C.

14

2

. D.

14

.

PHƯƠNG TRÌNH MẶT CẦU

Chuyên đề 29

I

R

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 8. (THPT Lương Thế Vinh Hà Nội -2019) Gọi

 

S

là mặt cầu đi qua

4

điểm

       

2;0;0 , 1;3;0 , 1;0;3 , 1;2;3

A B C D

. Tính bán kính

R

của

 

S

.

A.

2 2

R 

.

B.

3

R



. C.

6

R



.

D.

6

R 

.

Câu 9. (Sở Hà Nội 2019) Cho hai điểm

,A B

cố định trong không gian có độ dài

AB

là

4

. Biết rằng tập

hợp các điểm

M

trong không gian sao cho

3

MA MB

là một mặt cầu. Bán kính mặt cầu đó bằng

A.

3

. B.

9

2

. C.

1

. D.

3

2

.

Câu 10. (Sở Bình Phước - 2018) Trong không gian với hệ trục

Oxyz

, cho phương trình

 

2 2 2 2

2 2 4 2 5 9 0

x y z m x my mz m

        

. Tìm các giá trị của

m

để phương trình trên

là phương trình của một mặt cầu.

A.

5

m

 

hoặc

1

m



. B.

5 1

m

  

. C.

5

m

 

. D.

1

m



.

Câu 11. (Yên Phong 1 - 2018) Trong không gian

Oxyz

. Cho tứ diện đều

ABCD

có

 

0;1;2

A

và hình

chiếu vuông góc của

A

trên mặt phẳng

 

BCD

là

 

4; 3; 2

H

 

. Tìm tọa độ tâm

I

của mặt cầu

ngoại tiếp tứ diện

ABCD

.

A.

 

3; 2; 1

I

 

. B.

 

2; 1;0

I 

. C.

 

3; 2;1

I 

. D.

 

3; 2;1

I  

.

Câu 12. (Kiểm tra năng lực - ĐH - Quốc Tế - 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho mặt

cầu

 

S

có tâm nằm trên mặt phẳng

Oxy

và đi qua ba điểm

 

1;2; 4

A



,

 

1; 3;1

B 

,

 

2;2;3

C

.

Tọa độ tâm

 

I

của mặt cầu là

A.

 

2; 1;0



. B.

 

2;1;0



. C.

 

0;0; 2

. D.

 

0;0;0

.

Câu 13. Trong không gian tọa độ

Oxyz

, mặt cầu

 

S

đi qua điểm

O

và cắt các tia

, ,Ox Oy Oz

lần lượt tại

các điểm

, ,A B C

khác

O

thỏa mãn tam giác

ABC

có trọng tâm là điểm

 

6; 12;18

G  

. Tọa độ

tâm của mặt cầu

 

S

là

A.

 

9;18; 27



. B.

 

3; 6;9

 

. C.

 

3;6; 9

. D.

 

9; 18; 27

 

.

Câu 14. Trong hệ trục tọa độ

Oxyz

, cho mặt cầu

       

2 2 2

: cos cos cos 4

S x y z

  

     

với

,

 

và



lần lượt là ba góc tạo bởi tia

Ot

bất kì với

3

tia

,Ox Oy

và

Oz

. Biết rằng mặt cầu

 

S

luôn tiếp xúc với hai mặt cầu cố định. Tổng diện tích của hai mặt cầu cố định đó bằng

A.

40



. B.

4



. C.

20



. D.

36



.

Câu 15. Cho phương trình

      

2 2 2 2

4 2 3 2 0

x y z x my m m

với

m

là tham số. Tính tổng tất cả các

giá trị nguyên của

m

để phương trình đã cho là phương trình mặt cầu.

A.

0

. B.

1

. C.

2

. D.

3

.

Câu 16. (Sở Kon Tum 2019) Trong không gian

Oxyz

, cho điểm

 

3;0;0

A

,

 

0; 2;0

B 

,

 

0;0; 4

C



.

Mặt cầu ngoại tiếp tứ diện

OABC

có diện tích bằng

A.

116



. B.

29

4



. C.

29



. D.

16



.

Câu 17. (Chuyên Lê Hồng Phong-Nam Định -2019) Trong không gian với hệ tọa độ

Oxyz

, cho ba điểm

 

1;2; 4

A



,

 

1; 3;1

B 

,

 

2;2;3

C

. Tính bán kính

R

của mặt cầu

 

S

đi qua ba điểm trên và có

tâm nằm trên mặt phẳng

 

Oxy

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3

A.

41

R 

. B.

15

R 

. C.

13

R 

. D.

26

R 

.

Câu 18. (THPT Thăng Long-Hà Nội- 2019) Trong không gian

Oxyz

, gọi

 

S

là mặt cầu đi qua điểm

 

0;1;2

D

và tiếp xúc với các trục

Ox

,

Oy

,

Oz

tại các điểm

 

;0;0

A a

,

 

0; ;0B b

,

 

0;0;C c

trong đó

 

, , \ 0;1

a b c



. Bán kính của

 

S

bằng

A.

5

. B.

5

2

. C.

3 2

2

. D.

5 2

.

Câu 19. Trong không gian với hệ trục tọa độ

Oxyz

, cho mặt cầu

       

2 2 2

: 1 2 3 25

S x y z

     

và

hình nón

 

H

có đỉnh

 

3;2; 2

A



và nhận

AI

làm trục đối xứng với

I

là tâm mặt cầu. Một

đường sinh của hình nón

 

H

cắt mặt cầu tại

, M N

sao cho

3

AM AN

. Viết phương trình mặt

cầu đồng tâm với mặt cầu

 

S

và tiếp xúc với các đường sinh của hình nón

 

H

.

A.

     

2 2 2

71

1 2 3

3

x y z     

. B.

     

2 2 2

70

1 2 3

3

x y z     

.

C.

     

2 2 2

74

1 2 3

3

x y z     

. D.

     

2 2 2

76

1 2 3

3

x y z     

.

Câu 20. (Chuyên Hà Tĩnh - 2018) Trong không gian

Oxyz

, gọi

 

; ;I a b c

là tâm mặt cầu đi qua điểm

 

1; 1; 4

A 

và tiếp xúc với tất cả các mặt phẳng tọa độ. Tính

P a b c  

.

A.

6

P



. B.

0

P



. C.

3

P



. D.

9

P



.

Câu 21. (THPT Mộ Đức - Quảng Ngãi - 2018) Trong mặt phẳng tọa độ

Oxyz

, cho bốn điểm

 

0; 1;2

A 

,

 

2; 3;0

B 

,

 

2;1;1

C 

,

 

0; 1;3

D 

. Gọi

 

L

là tập hợp tất cả các điểm

M

trong không gian thỏa

mãn đẳng thức

. . 1

MA MB MC MD

 

   

. Biết rằng

 

L

là một đường tròn, đường tròn đó có bán

kính

r

bằng bao nhiêu?

A.

11

2

r 

. B.

7

2

r 

. C.

3

2

r 

. D.

5

2

r 

.

Dạng 2. Viết phương trình mặt cầu

 Dạng 1. Cơ bản

2 2 2 2

( ) : ( ): ( ) ( ) ( ) .

( ; )

:

;

âm I a bT

S S x a y b z c R

BK R

c



      







 Dạng 2. Viết phương trình mặt cầu

( )S

có tâm

I

và đi qua điểm

.A

Phương pháp:

( ) :

:

âm IT

S

BK R IA











(dạng 1)

 Dạng 3. Viết phương trình mặt cầu

( )S

có đường kính

,AB

với

, A B

cho trước.

Phương pháp:

( ) :

1

:

2

R

âmT

S

BK AB

I















 Dạng 4. Viết phương trình mặt cầu

( )S

có tâm

I

và tiếp xúc với các trục và mp tọa độ.

Phương pháp:

( ) :

:

âm IT

S

BK R IM











 Dạng 5. Viết phương trình mặt cầu

( )S

có tâm

I

và tiếp xúc với mặt phẳng

( ).P

Phương pháp:

 

( ) :

;( )

:

T

S

B I

âm I

K R d P















là trung điểm của

.AB

với M là hình chiếu của

I

lên trục hoặc mp tọa

độ.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/



Khoảng cách từ điểm

( ; ; )

M M M

M x y z

đến mặt phẳng

( ) : 0

P ax by cz d

   

được xác định bởi

công thức:

2 2 2

( ;( ))

M M M

ax by cz d

d M P

a b c

  

 

 

 Dạng 6. Viết phương trình mặt cầu

( )S

đi qua bốn điểm

, , , .A B C D

Phương pháp: Gọi

2 2 2

( ) : 2 2 2 0

S x y z ax by cz d

      

Vì

, , , ( )A B C D S

nên tìm được 4 phương trình

, , , ( ).a b c d S 

 Dạng 7. Viết phương trình mặt cầu

( )S

đi qua 3 điểm

, , A B C

và tâm thuộc mp

( ).P

Phương pháp: Gọi

2 2 2

( ) : 2 2 2 0

S x y z ax by cz d

      

Vì

, , ( )A B C S

nên tìm được 3 phương trình và

( ; ; ) ( )I a b c P

là phương trình thứ tư.

Giải hệ bốn phương trình này

, , , ( ).a b c d S 

 Dạng 8. Viết phương trình mặt cầu

( )S

có tâm

I

và cắt mặt phẳng

( )P

theo giao tuyến là một

đường tròn có bán kính

.r

(dạng này mình sẽ đưa vào bài phương trình mặt phẳng, các bạn

học cũng có thể tự tìm để hiểu hơn)

Phương pháp: Dựa vào mối liên hệ

2 2 2

[ ;( )]I P

R d r 

và cần nhớ

2

C

r





và

2

t

.S r





đ

Câu 1. (Mã 123 2017) Trong không gian với hệ tọa độ

Oxyz

, cho điểm

 



1; 2; 3

M

. Gọi

I

là hình

chiếu vuông góc của

M

trên trục

Ox

. Phương trình nào dưới đây là phương trình mặt cầu tâm

I

bán kính

IM

?

A.

 

   

2

2 2

1 13

x y z B.

 

   

2

2 2

1 17

x y z

C.

 

   

2

2 2

1 13

x y z D.

 

   

2

2 2

1 13

x y z

Câu 2. (THPT Đoàn Thượng - Hải Dương -2019) Trong không gian Oxyz, cho điểm

(1; 2;3)

I



. Viết

phương trình mặt cầu tâm I, cắt trục

Ox

tại hai điểm

A

và

B

sao cho

2 3

AB 

A.

2 2 2

( 1) ( 2) ( 3) 16.

x y z     

B.

2 2 2

( 1) ( 2) ( 3) 20.

x y z     

C.

2 2 2

( 1) ( 2) ( 3) 25.

x y z     

D.

2 2 2

( 1) ( 2) ( 3) 9.

x y z

     

Câu 3. (Sgd Cần Thơ - 2018) Trong không gian

Oxyz

, giá trị dương của

m

sao cho mặt phẳng

 

Oxy

tiếp xúc với mặt cầu

   

2 2

3 2 1

x y z m

     

là

A.

5m 

. B.

3

m 

. C.

3m 

. D.

5

m 

.

Câu 4. (THPT Đoàn Thượng - Hải Dương - 2019) Trong không gian

Oxyz

, cho điểm

 

1; 2;3

M 

.

Gọi

I

là hình chiếu vuông góc của

M

trên trục

Ox

. Phương trình nào sau đây là phương trình

mặt cầu tâm

I

bán kính

IM

?

A.

 

2

2 2

1 13

x y z   

. B.

 

2

2 2

1 13

x y z

   

.

C.

 

2

2 2

1 13

x y z

   

. D.

 

2

2 2

1 17

x y z

   

.

Câu 5. (Sở Bắc Giang 2019) Trong không gian với hệ tọa độ

Oxyz

, trong các mặt cầu dưới đây, mặt cầu

nào có bán kính

2R 

?

A.

 

2 2 2

: 4 2 2 3 0

S x y z x y z

      

. B.

 

2 2 2

: 4 2 2 10 0

S x y z x y z

      

.

C.

 

2 2 2

: 4 2 2 2 0

S x y z x y z

      

. D.

 

2 2 2

: 4 2 2 5 0

S x y z x y z

      

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5

Câu 6. (THPT Gang Thép Thái Nguyên 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho điểm

   

1;1;2 , 3;2; 3

A B



. Mặt cầu

 

S

có tâm

I

thuộc

Ox

và đi qua hai điểm

,A B

có phương

trình.

A.

2 2 2

8 2 0

x y z x

    

. B.

2 2 2

8 2 0

x y z x

    

.

C.

2 2 2

4 2 0

x y z x

    

. D.

2 2 2

8 2 0

x y z x

    

.

Câu 7. Trong không gian

Oxyz

, mặt cầu có tâm

 

1;1;1

I

và diện tích bằng

4



có phương trình là

A.

     

2 2 2

1 1 1 4

x y z

     

B.

     

2 2 2

1 1 1 1

x y z

     

C.

     

2 2 2

1 1 1 4

x y z

     

D.

     

2 2 2

1 1 1 1

x y z

     

Câu 8. (Việt Đức Hà Nội 2019) Trong không gian với hệ tọa độ

Oxyz

, mặt cầu

 

S

qua bốn điểm

 

3;3;0

A

,

 

3;0;3

B

,

 

0;3;3

C

,

 

3;3;3

D

. Phương trình mặt cầu

 

S

là

A.

2 2 2

3 3 3 3 3

2 2 2 2

x y z

     

     

     

     

.

B.

2 2 2

3 3 3 27

2 2 2 4

x y z

     

     

     

     

.

C.

2 2 2

3 3 3 27

2 2 2 4

x y z

     

     

     

     

.

D.

2 2 2

3 3 3 27

2 2 2 4

x y z

     

     

     

     

.

Câu 9. (THPT Trần Phú - Đà Nẵng - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho tứ diện

ABCD

có tọa độ đỉnh

 

2; 0; 0

A

,

 

0; 4; 0

B

,

 

0; 0; 6

C

,

 

2; 4; 6

A

. Gọi

 

S

là mặt cầu ngoại tiếp

tứ diện

ABCD

. Viết phương trình mặt cầu

 

S



có tâm trùng với tâm của mặt cầu

 

S

và có bán

kính gấp

2

lần bán kính của mặt cầu

 

S

.

A.

     

2 2 2

1 2 3 56

x y z

     

. B.

2 2 2

2 4 6 0

x y z x y z

     

.

C.

     

2 2 2

1 2 3 14

x y z

     

. D.

2 2 2

2 4 6 12 0

x y z x y z

      

.

Câu 10. (Trần Phú - Hà Tĩnh - 2018) Trong không gian với hệ tọa độ

Oxyz

, mặt cầu tâm

 

2;1; 3

I



và

tiếp xúc với trục

Oy

có phương trình là

A.

     

2 2 2

2 1 3 4

x y z

     

. B.

     

2 2 2

2 1 3 13

x y z

     

.

C.

     

2 2 2

2 1 3 9

x y z

     

. D.

     

2 2 2

2 1 3 10

x y z

     

.

Câu 11. (THPT

Phan Đình Phùng - Hà Tĩnh - 2018)

Trong không gian với hệ tọa độ

Oxyz

cho mặt

cầu

 

S

có tâm

 

1;4;2

I 

và có thể tích bằng

256

3



. Khi đó phương trình mặt cầu

 

S

là

A.

     

2 2 2

1 4 2 16

x y z

     

. B.

     

2 2 2

1 4 2 4

x y z

     

.

C.

     

2 2 2

1 4 2 4

x y z

     

. D.

     

2 2 2

1 4 2 4

x y z

     

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu

12. (Chuyên Nguyễn Đình Triểu - Đồng Tháp - 2018) Trong không gian

O

xyz

,

cho mặt cầu

     

2

:

1 1 4.

S

x y z



   

Một

mặt cầu

 

S



có

tâm

 

9

;1;6

I



và

tiếp xúc ngoài với mặt cầ

u

 

.S

Phương trình mặt cầu

 

S



là

A.

     

2

2 2

9 1 6 64

x y z

     

. B.

     

2

2 2

9 1 6 144

x y z     

.

C.

     

2

2 2

9

1 6 36

x

y z



    

. D

.

     

2

2 2

9

1 6 25

x

y z



    

.

Câu

13. (THPT Hai Bà Trưng - Huế - 2018) Trong không gian

Ox

yz

,

viết phương trình mặt cầu đi qua

điểm

 

1

; 1;4

A 

và

tiếp xúc với các mặt phẳng tọa độ.

A.

     

2

2 2

3

3 3 16

x

y z



    

. B.

     

2

2 2

3

3 3 9

x

y z



    

.

C.

     

2

2 2

3

3 3 36

x

y z



    

. D

.

     

2

2 2

3

3 3 49

x

y z



    

.

Câu

14. (Kim Liên - Hà Nội – 2018) Trong không gian

O

xyz

,

cho hai điểm

 

2

;2;1

M

,

8

4 8

; ;

3 3 3

N



 

 

 

.

Viết

phương trình mặt cầu có tâm là tâm của đường tròn nội tiếp tam giác

OMN

và

tiếp xúc với

mặt phẳng

 

Oxz

.

A.

   

2

1

1 1

x

y z



   

. B.

   

2

1

1 1

x

y z



   

.

C.

   

2

1

1 1

x

y z



   

. D

.

   

2

1

1 1

x

y z



   

.

Câu

15. (Toán Học Tuổi Trẻ 2018) Trong không gian

Oxyz

,

cho điểm

 

1

;2; 2

H



.

Mặt phẳng

 



đi

qua

H

và

cắt các trục

O

x

,

Oy

,

Oz

tại

A

,

B

,

C

s

ao cho

H

l

à trực tâm tam giác

AB

C

.

Viết

phương trình mặt cầu tâm

O

và t

iếp xúc với mặt phẳng

 



.

A.

2

2 2

81

x

y z



 

. B.

2

2 2

1

x

y z



 

. C

.

2

2 2

9

x

y z



 

. D

.

2

2 2

25

x

y z



 

.

Câu

16. (THPT Hai Bà Trưng - Huế - 2018) Trong không gian

O

xyz

,

viết phương trình mặt cầu đi qua

điểm

 

1

; 1;4

A 

và t

iếp xúc với các mặt phẳng tọa độ.

A.

     

2 2 2

3

3 3 16

x

y z



    

. B.

     

2 2 2

3

3 3 9

x

y z



    

.

C.

     

2 2 2

3

3 3 36

x

y z



    

. D.

     

2 2 2

3

3 3 49

x

y z



    

.

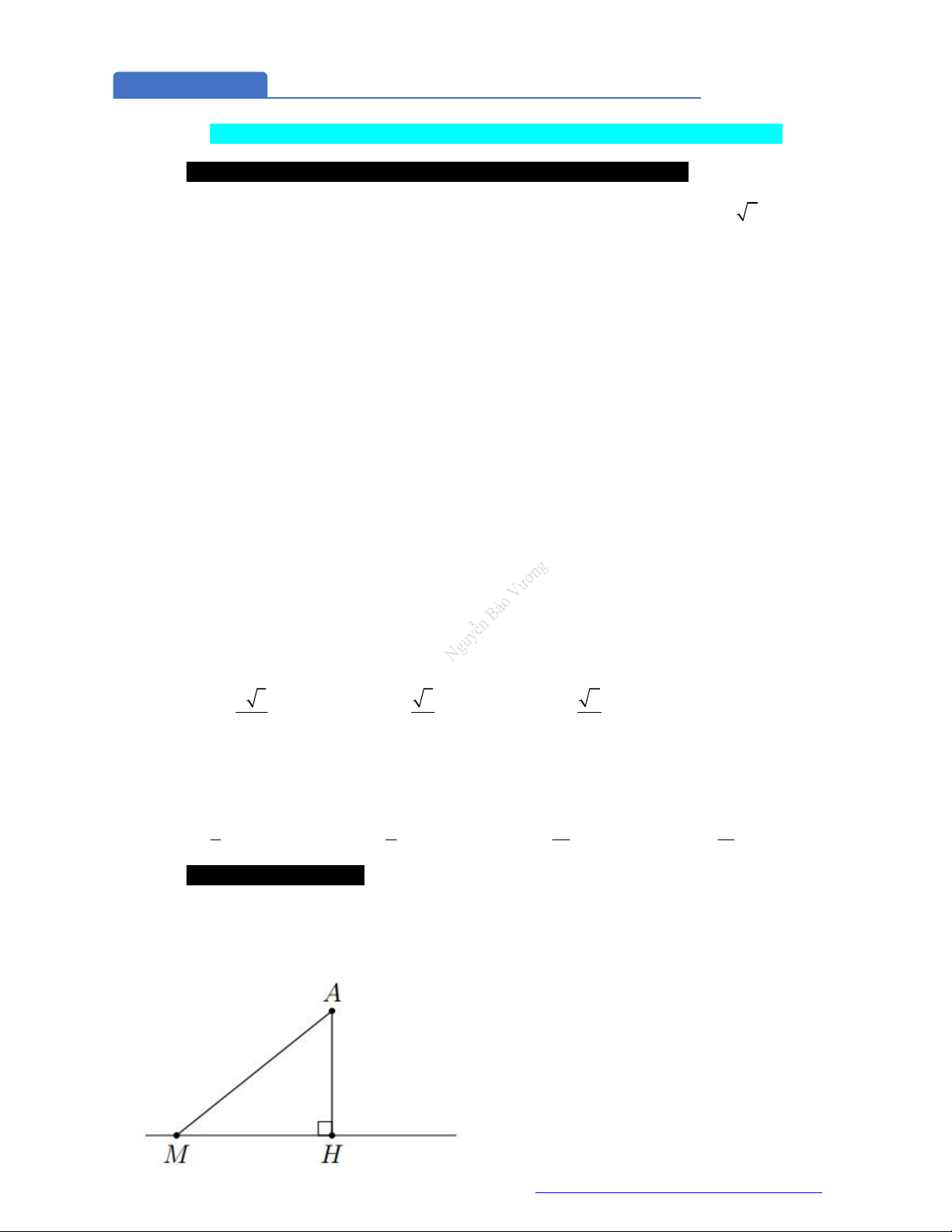
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương  https://www.facebook.com/phong.baovuong Trang 1

TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH GIỎI – MỨC 9-10 ĐIỂM

Dạng 1. Một số bài toán liên quan đến tiếp tuyến (tiếp xúc) mặt cầu

Câu 1. (Mã 102 - 2019) Trong không gian

Oxyz

, cho mặt cầu

 

2

2 2

: 2 3S x y z    . Có tất cả

bao nhiêu điểm

 

; ;A a b c

(

, ,a b c

là các số nguyên) thuộc mặt phẳng

 

Oxy

sao cho có ít nhất

hai tiếp tuyến của

 

S

đi qua

A

và hai tiếp tuyến đó vuông góc với nhau?

A.

8

. B.

16

. C.

12

. D.

4

.

Câu 2. (Mã 104 - 2019) Trong không gian

Oxyz

, cho mặt cầu

   

2

2 2

: 1 5S x y z   

. Có tất cả bao

nhiêu điểm

 

, ,A a b c

(

, ,a b c

là các số nguyên) thuộc mặt phẳng

 

Oxy

sao cho có ít nhất hai tiếp

tuyến của

 

S

đi qua

A

và hai tiếp tuyến đó vuông góc với nhau?

A. 20 B. 8 C. 12 D. 16

Câu 3. (Mã 103 - 2019) Trong không gian

Oxyz

, cho mặt cầu:

   

2

2 2

: 1 5S x y z   

. Có tất cả bao

nhiêu điểm

 

; ;A a b c

( , , a b c

là các số nguyên) thuộc mặt phẳng

 

Oxy

sao cho có ít nhất hai

tiếp tuyến của

 

S

đi qua

A

và hai tiếp tuyến đó vuông góc nhau?

A.

20

. B.

8

. C.

12

. D.

16

.

Câu 4. (THPT Chuyên Ngữ - Hà Nội - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho mặt cầu

     

2 2

2

: 1 1 4S x y z    

và một điểm

 

2;3;1M

. Từ

M

kẻ được vô số các tiếp tuyến tới

 

S

, biết tập hợp các tiếp điểm là đường tròn

 

C

. Tính bán kính

r

của đường tròn

 

C

.

A.

2 3

3

r 

. B.

3

r 

. C.

2

3

r 

. D.

 

2

.

Câu 5. (THPT Chuyên Hạ Long - 2018) Trong không gian, cho bốn mặt cầu có bán kính lần lượt là

2

,

3

,

3

,

2

(đơn vị độ dài) tiếp xúc ngoài với nhau. Mặt cầu nhỏ nhất tiếp xúc ngoài với cả bốn mặt

cầu nói trên có bán kính bằng

A.

5

9

. B.

3

7

. C.

7

15

. D.

6

11

.

Dạng 2. Bài toán cực trị

1. Một số bất đẳng thức cơ bản

Kết quả 1. Trong một tam giác, cạnh đối diện với góc lớn thì lớn hơn

Kết quả 2. Trong các đường xiên và đường vuông góc kẻ từ một điểm nằm ngoài đường thẳng đến đường

thẳng đó thì đường vuông góc là đường ngắn nhất. Như trong hình vẽ ta luôn có

AM AH

PHƯƠNG TRÌNH MẶT CẦU

Chuyên đề 29

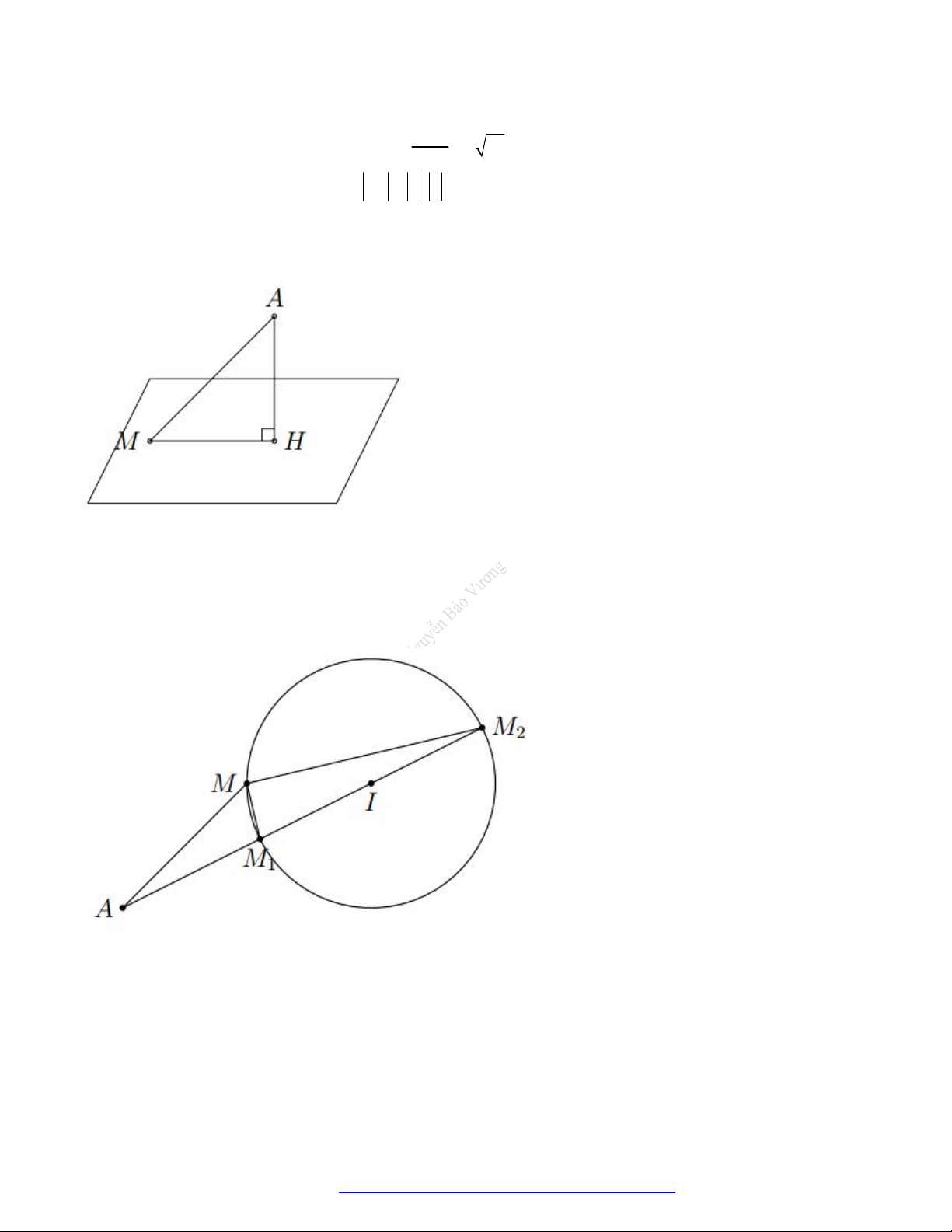
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Kết quả 3. Với ba điểm

, ,A B C

bất kì ta luôn có bất đẳng thức

.AB BC AC 

Tổng quát hơn ta có bất đẳng thức của đường gấp khúc: Với

n

điểm

1 2

, ,....

n

A A A ta luôn có

1 2 2 3 1 1

...

n n n

A A A A A A A A



   

Kết quả 4. Với hai số không âm

,x y

ta luôn có

2

x y

xy





. Đẳng thức xảy ra khi và chỉ khi

x y

Kết quả 5. Với hai véc tơ

,a b

 

ta luôn có . .a b a b

   

. Đẳng thức xảy ra khi

,a kb k 

 



2. Một số bài toán thường gặp

Bài toán 1. Cho điểm

A

cố định và điểm

M

di động trên hình

 

H

(

 

H

là đường thẳng, mặt phẳng). Tìm

giá trị nhỏ nhất của

AM

Lời giải: Gọi

H

là hình chiếu vuông góc của

A

lên hình

 

H

. Khi đó, trong tam giác

AHM

Vuông tại .

M

ta có

.AM AH

Đẳng thức xảy ra khi

M H

. Do đó

AM

nhỏ nhất khi

M

là hình chiếu của

A

lên

 

H

Bài toán 2. Cho điểm

A

và mặt cầu

 

S

có tâm

,I

bán kính

,R

M

là điểm di động trên

 

S

. Tìm giá trị

nhỏ nhất và giá trị lớn nhất của

AM

.

Lời giải. Xét

A

nằm ngoài mặt cầu

( ).S

Gọi

1 2

,M M lần lượt là giao điểm của đường thẳng

AI

với mặt

cầu

 

1 2

( )S AM AM

và

( )



là mặt phẳng đi qua

M

và đường thẳng

.AI

Khi đó

( )



cắt

( )S

theo một

đường tròn lớn

( ).C

Ta có



1 2

90 ,M MM



 nên



2

AMM và



1

AM M là các góc tù, nên trong các tam giác

1

AMM và

2

AMM ta có

1 2

AI R AM AM AM AI R     

Tương tự với

A

nằm trong mặt cầu ta có

R AI AM R AI   

Vậy

min | |,maxAM AI R AM R AI   

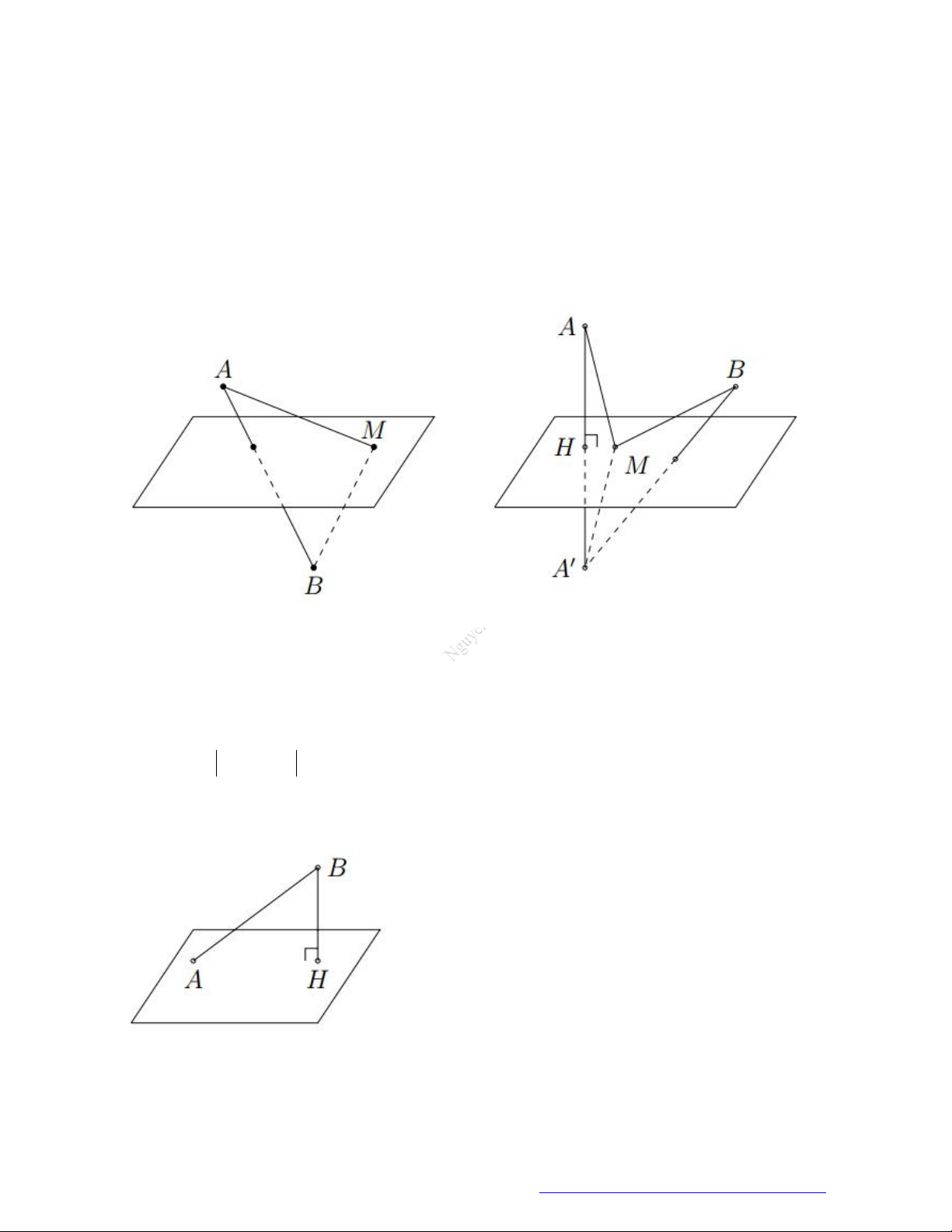
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3

Bài toán 3. Cho măt phẳng

( )P

và hai điểm phân biệt

, .A B

Tìm điểm

M

thuộc

( )P

sao cho

1.

MA MB

nhỏ nhất.

2.

| |MA MB

lớn nhất.

Lời giải.

1. Ta xét các trường hợp sau

- TH 1: Nếu

A

và

B

nằm về hai phía so với

( )P

. Khi đó

AM BM AB 

Đẳng thức xảy ra khi

M

là giao điểm của

AB

với

( )P

.

- TH 2: Nếu

A

và

B

nằm cùng một phía so với

( )P

. Gọi A



đối xứng với

A

qua

( )P

. Khi đó

AM BM A M BM A B

 

   

Đẳng thức xảy ra khi

M

là giao điểm của A B



với

( )P

.

2. Ta xét các trường hợp sau

- TH 1: Nếu

A

và

B

nằm cùng một phía so với

( )P

. Khi đó

| |AM BM AB 

Đẳng thức xảy ra khi

M

là giao điểm của

AB

với

( )P

.

- TH 2: Nếu

A

và

B

nằm khác phía so với

( )P

. Gọi

'A

đối xứng với

A

qua

 

P

, Khi đó

| |AM BM A M BM A B

 

   

Đẳng thức xảy ra khi

M

là giao điểm của

A B



với

( )P

.

Bài toán 4. Viết phương trinh măt phẳng

( )P

di qua

A

và cách

B

một khoảng lớn nhất.

Lời giải. Gọi

H

là hình chiếu của

B

lên mặt phẳng

( ),P

khi đó

d( ,( ))B P BH BA 

Do đó

 

P

là mặt phẳng đi qua

A

vuông góc với

AB

Bài toán 5. Cho các số thực dương

,

 

và ba điểm

, ,A B

C. Viết phương trình măt phẳng

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

( )P

đi qua

C

và

d( ,( )) d( ,( ))T A P B P

 

 

nhỏ nhất.

Lời giải.

1. Xét

,A B

nằm về cùng phía so với

( )P

.

- Nếu ( )AB P‖ thì

( )d( ,( )) ( )P A P AC

   

   

- Nếu đường thẳng

AB

cắt

( )P

tại

.I

Gọi

D

là điểm thỏa mãn IB ID







 

và

E

là trung điểm

.BD

Khi đó

d( ,( )) d( ,( )) 2 d( ,( )) 2( )

IB

P A P D P E P EC

ID

    

      

2. Xét

,A B

nằm về hai phía so với

( )P

. Gọi

I

là giao điểm của

AB

và ( ),P B



là điểm đối xứng với

B

qua

I

. Khi đó

 

d( ,( )) d ,( )P A P B P

 



 

Đến đây ta chuyển về trường hợp trên.

So sánh các kết quả ở trên ta chọn kết quả lớn nhất.

Bài toán 6. Trong không gian cho

n

điểm

1 2

, , ,

n

A A A và diểm

.A

Viết phương trình mặt phẳng

( )P

đi

qua

A

và tổng khoảng cách từ các điểm

( 1,

i

A i n

) lớn nhất.

Lời giải.

- Xét

n

điểm

1 2

, , ,

n

A A A nằm cùng phía so với

( ).P

Gọi

G

là trọng tâm của

n

điểm đã cho. Khi đó

 

1

d ,( ) d( ,( ))

n

i

A P n G P nGA



 



- Trong

n

điểm trên có

m

điểm nằm về một phía và

k

điểm nằm về phía khác

(m k n 

). Khi đó, gọi

1

G

là trọng tâm của

m

điểm,

2

G là trọng tâm của

k

điểm

3

G đối xứng với

1

G qua

.A

Khi dó

   

3 2

md ,( ) d ,( )P G P k G P 

Đến đây ta chuyển về bài toán trên.

Bài toán 7.Viết phương trình mặt phẳng

 

P

đi qua đường thẳng



và cách

A

một khoảng lớn nhất

Lời giải. Gọi

,H K

lần lượt là hình chiếu của

A

lên mặt phẳng

( )P

và đường thẳng

.

Khi đó

d( ,( ))A P AH AK 

Do đó

( )P

là mặt phẳng đi qua

K

và vuông góc vói

.AK

Bài toán 8. Trong không gian

Oxyz,

cho các điểm

1 2

, , , .

n

A A A Xét véc tơ

1 1 2 2 n n

w MA M A M A

  

   

  





Trong đó

1 2

; ...

n

  

là các số thực cho trước thỏa mãn

1 2

... 0

n

  

    . Tìm điểm

M

thuôc măt phẳng

( )P

sao cho

| |w



có đô dài nhỏ nhất.

Lời giải. Gọi

G

là điểm thỏa mãn

1 1 2 2

0

n n

GA GA GA

  

   

   



(điểm

G

hoàn toàn xác định).

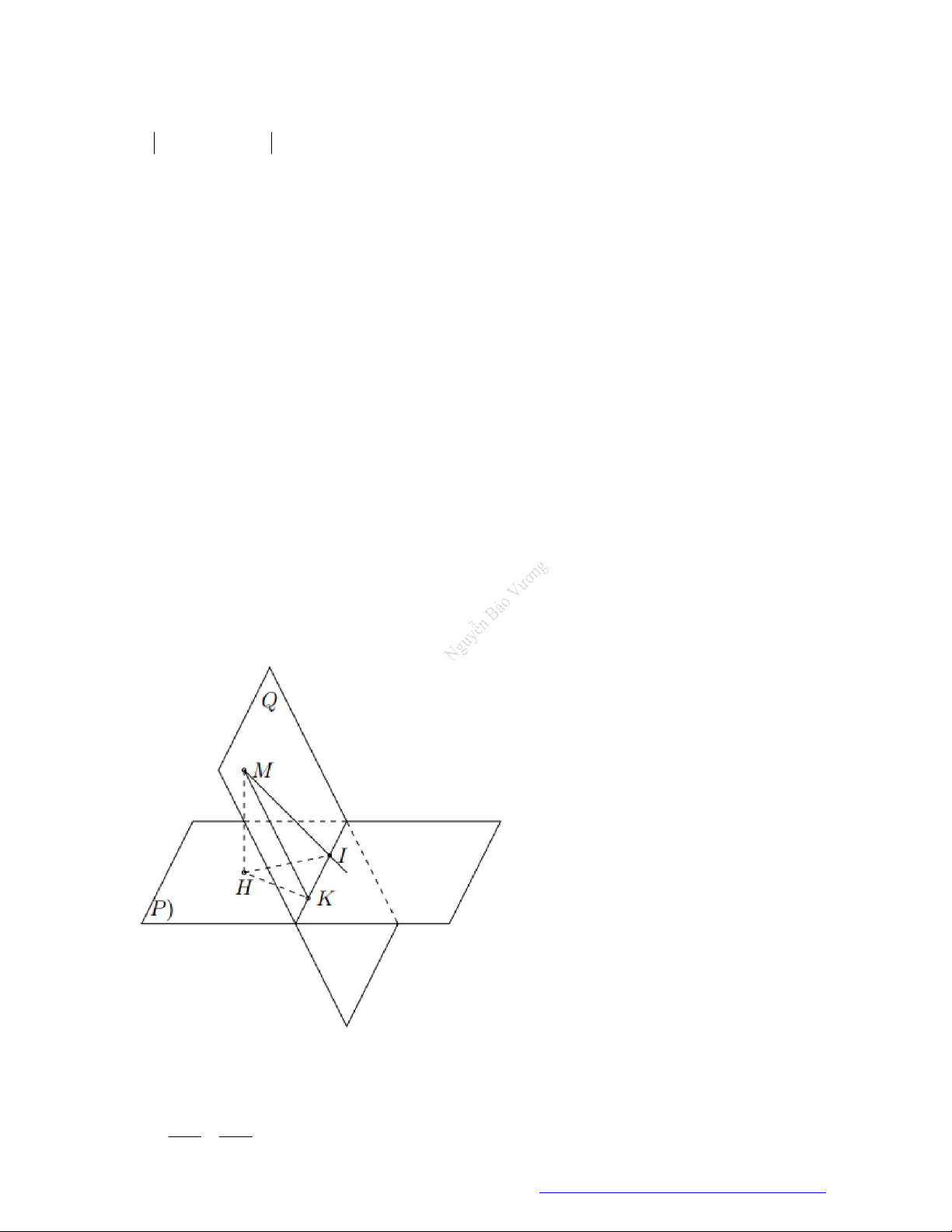
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5

Ta có

k

MA MG GA 





vói

1;2; ; ,k n 

nên

   

1 2 1 1 2 2 1 2

w

n n n n

MG GA GA GA MG

        

         

 

  





Do đó

1 2

| | | |

n

w MG

  

    





Vi

1 2 n

  

   là hằng số khác không nên

| |w



có giá trị nhỏ nhất khi và chỉ khi

MG

nhỏ nhất, mà

( )M P

nên điểm

M

cần tìm là hình chiếu của

G

trên mặt phẳng

( )P

.

Bài toán 9. Trong không gian Oxy

,z

cho các diểm

1 2

, , , .

n

A A A Xét biểu thức:

2 2 2

1 1 2 2 n n

T MA MA MA

  

   

Trong đó

1 2

, , ,

n

  

 là các số thực cho trước. Tìm điểm M thuộc măt phẳng

( )P

sao cho

1.

T

giá trị nhỏ nhất biết

1 2

0

n

  

   .

2. T có giá trị lớn nhất biết

1 2

0

n

  

   .

Lời giải. Gọi

G

là điểm thỏa mãn

1 1 2 2

0

n n

GA GA GA

  

   

   



Ta có

k

MA MG GA 





với

1;2; ; ,k n 

nên

 

2

2 2 2

2

k k k k

MA MG GA MG MG GA GA     

 

 

Do đó

 

2 2 2 2

1 2 1 1 2 2n n n

T MG GA GA GA

     

      

Vì

2 2 2

1 1 2 2 n n

GA GA GA

  

  

không đổi nên

•

với

1 2

0

n

  

   thì

T

đạt giá trị nhỏ nhất khi và chỉ khi

MG

nhỏ nhất.

•

với

1 2

0

n

  

   thì

T

đạt giá trị lớn nhất khi và chỉ khi

MG

nhỏ nhất.

Mà

( )M P

nên

MG

nhỏ nhất khi điểm

M

là hình chiếu của

G

trên mặt phẳng

( )P

.

Bài toán 10. Trong không gian Oxyz, cho đường thẳng d và mặt phẳng

( )P

cắt nhau. Viết phương trình của

mặt phẳng

( )Q

chứa

d

và tạo với mặt phẳng

( )P

một góc nhỏ nhất.

Lời giải. Gọi

I

là giao điểm của đường thẳng

d

với mặt phẳng

( )P

và lấy điểm

,M d M I 

. Gọi

,H K

lầ lượt là hình chiếu của

M

lên

( )P

và giao tuyến



của

( )P

và

( )Q

.

Đặt



là góc giữa

( )P

và

( ),Q

ta có



,MKH





do đó

tan

HM HM

HK HI



 

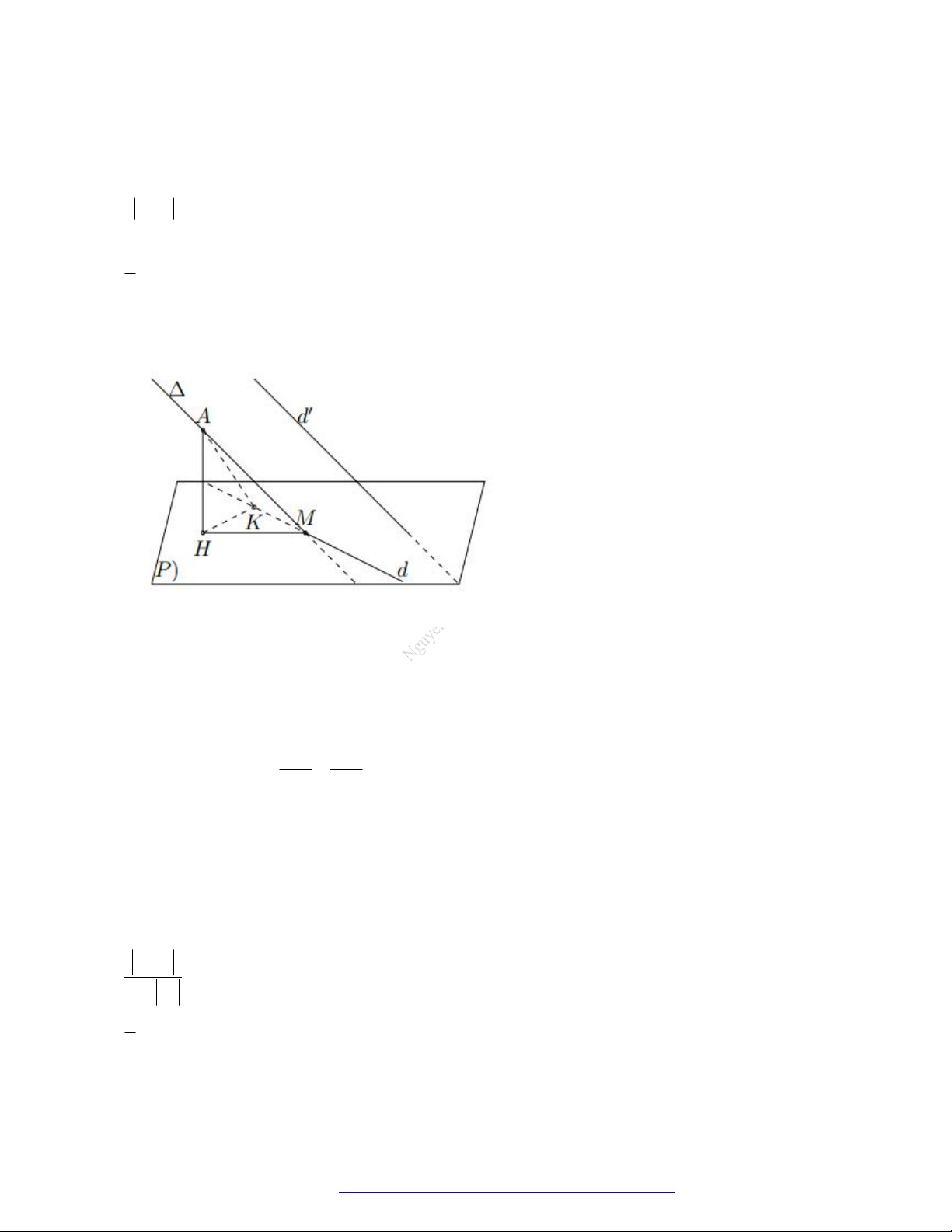
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Do đó

( )Q

là mặt phẳng đi qua

d

và vuông góc với mặt phẳng

( ),MHI

nên

( )Q

đi qua

M

và nhận

 

P d d

n u u 

  

làm VTPT.

Chú ý. Ta có thể giải bài toán trên bằng phương pháp đai số như sau:

- Goi

2 2 2

( ; ; ), 0n a b c a b c   



là một VTPT của mặt phẳng

( ).Q

Khi đó 0

d

n u 

 

từ đây ta rút được

a

theo

,b c

(hoặc

b

theo

,a c

hoặc

c

theo

,a b

).

- Gọi



là góc giữa

( )P

và

( ),Q

ta có

cos ( )

| |

P

n n

f t

n n





 



 

với

, 0.

b

t c

c

 

Khảo sát

( )f t

ta tìm được max của

( )f t

Bài toán 11. Trong không gian Oxyz, cho hai đường thẳng

d

và

d



chéo nhau. Viết phương trinh mặt

phẳng

( )P

chứa

d

và tạo với

d



một góc lớn nhất.

Lời giải. Trên đường thẳng

d

, lấy điểm

M

và dựng đường thẳng



đi qua

M

song song với

d



. Khi đó

góc giữa



và

( )P

chính là góc giữa

d



và

( )P

.

Trên đường thẳng



, lấy điểm

A

. Gọi

H

và

K

lần lượt là hình chiếu của

A

lên

( )P

và

,d



là góc giữa



và

( )P

.

Khi đó



AMH





và

cos

HM KM

AM AM



 

Suy ra

( )P

là mặt phẳng chứa

d

và vuông góc với mặt phẳng

( ).AMK

Do dó

( )P

đi qua

M

và nhận

 

d d

d

u u u



 

  

làm VTPT.

Chú ý. Ta có thể giải bài toán trên bằng phương pháp đại số như sau:

- Goi

2 2 2

( ; ; ), 0n a b c a b c   



là một VTPT của măt phẳng

( ).P

Khi đó 0

d

n u 

 

từ đây ta rút được

a

theo

,b c

(hoặc

b

theo

,a c

hoặc

c

theo

,a b

).

- Gọi



là góc giữa

( )P

và ,d



ta có

sin ( )

| |

d

n u

f t

n u







 



 

với

, 0.

b

t c

c

 

Khảo sát

( )f t

ta tìm được max của

( )f t

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7

Câu 6. (THPT Nguyễn Khuyến 2019) Trong không gian với hệ trục

Oxyz

, cho các điểm

   

1;2;3 , 6; 5;8

A B 

và

. .OM a i b k

 

  

trong đó

,a b

là cá số thực luôn thay đổi. Nếu

2

MA MB



 

đạt giác trị nhỏ nhất thì giá trị

a b

bằng

A.

25

B.

13

C.

0

D.

26

Câu 7. (Sở Hà Nội 2019) Trong không gian

Oxyz

, cho hai điểm

 

1;2;1

A

;

 

2; 1;3

B 

và điểm

 

; ;0

M a b

sao cho

2 2

MA MB

nhỏ nhất. Giá trị của

a b

là

A.

2

. B.

2

. C.

3

. D.

1

.

Câu 8. (THPT Gang Thép Thái Nguyên 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho

4

điểm

 

2;4; 1

A



,

 

1;4; 1

B



,

 

2;4;3

C

,

 

2;2; 1

D



, biết

 

; ;M x y z

để

2 2 2 2

MA MB MC MD

  

đạt giá trị nhỏ nhất thì

x y z 

bằng

A.

6

. B.

21

4

. C.

8

. D.

9

.

Câu 9. Trong không gian

Oxyz

, cho hai điểm

 

1;2;1

A

,

 

2; 1;3

B 

,

 

3;1; 5

C



. Tìm điểm

M

trên mặt phẳng

 

Oyz

sao cho

2 2 2

2

MA MB MC

 

lớn nhất.

A.

3 1

; ;0

2 2

M

 

















 

. B.

1 3

; ; 0

2 2

M

 



















 

. C.

 

0; 0;5

M

. D.

 

3; 4; 0

M



.

Câu 10. (THPT Nghĩa Hưng Nđ- 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho tam giác

ABC

với

 

2;1;3

A

,

 

1; 1;2

B 

,

 

3; 6;1

C 

. Điểm

 

; ;M x y z

thuộc mặt phẳng

 

Oyz

sao cho

2 2 2

MA MB MC

 

đạt giá trị nhỏ nhất. Tính giá trị biểu thức

P x y z  

.

A.

0

P



. B.

2P 

. C.

6

P



. D.

2P  

.

Câu 11. Trong không gian với hệ tọa độ

Oxyz

, cho ba điểm

     

4;2;2 , 1;1; 1 , 2; 2; 2

A B C

  

. Tìm tọa

độ điểm

M

thuộc mặt phẳng

 

Oyz

sao cho

2

MA MB MC

 

  

nhỏ nhất

A.

 

2;3;1

M

. B.

 

0;3;1

M

. C.

 

0; 3;1

M 

. D.

 

0;1;2

M

.

Câu 12. (Chuyên Lê Quý Đôn - Đà Nẵng - 2018) Trong không gian với hệ trục tọa độ

Oxyz

, cho bốn

điểm

 

2; 3;7

A 

,

 

0;4;1

B

,

 

3;0;5

C

và

 

3;3;3

D

. Gọi

M

là điểm nằm trên mặt phẳng

 

Oyz

sao cho biểu thức

MA MB MC MD

  

   

đạt giá trị nhỏ nhất. Khi đó tọa độ của

M

là:

A.

 

0;1; 4

M



. B.

 

2;1;0

M

. C.

 

0;1; 2

M



. D.

 

0;1;4

M

.

Câu 13. (Toán Học Tuổi Trẻ - 2018) Trong không gian cho ba điểm

 

1;1;1

A

,

 

1;2;1

B 

,

 

3;6; 5

C



.

Điểm

M

thuộc mặt phẳng

Oxy

sao cho

2 2 2

MA MB MC

 

đạt giá trị nhỏ nhất là

A.

 

1;2;0

M

. B.

 

0;0; 1

M



. C.

 

1;3; 1

M



. D.

 

1;3;0

M

.

Câu 14. (Lê Quý Đôn - Hải Phòng - 2018) Trong không gian với hệ tọa độ

Oxyz

cho

 

3;2;1

A

,

 

2;3;6

B 

. Điểm

 

; ;

M M M

M x y z

thay đổi thuộc mặt phẳng

 

Oxy

. Tìm giá trị của biểu thức

M M M

T x y z  

khi

3

MA MB



 

nhỏ nhất.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 8 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

A.

7

2



. B.

7

2

. C.

2

. D.

2

.

Câu 15. (Chuyen Phan Bội Châu Nghệ An 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho mặt

cầu

2 2 2

( ):( 1) ( 2) ( 1) 9

S x y z

     

và

hai điểm

(4;3;1)

A

,

(3;1;3)

B

;

M

là điểm thay đổi trên

( )S

. Gọi

,m n

lần lượt là giá trị lớn

nhất và giá trị nhỏ nhất của biểu thức

2 2

2P MA MB 

. Xác định

( )m n

.

A.

64

. B.

68

. C.

60

. D.

48

.

Câu 16. (Chuyên Vĩnh Phúc - 2018) Trong không gian với hệ trục tọa độ

Oxyz

, cho mặt cầu

 

S

có

phương trình là

2 2 2

2 2 6 7 0

x y z x y z

      

. Cho ba điểm

A

,

M

,

B

nằm trên mặt cầu

 

S

sao cho



90

AMB

 

. Diện tích tam giác

AMB

có giá trị lớn nhất bằng?

A.

4

. B.

2

. C.

4

. D. Không tồn tại.

Câu 17. (Phan Đình Phùng - Hà Tĩnh - 2018) Cho

, , , , ,a b c d e f

là các số thực thỏa mãn

     

   

2 2 2

2 2

2

1 2 3 1

.

3 2 9

d e f

a b c



     





    





Gọi giá trị lớn nhất, giá trị nhỏ nhất của biểu thức

     

2 2 2

F a d b e c f

     

lần lượt là

, .M m

Khi đó,

M m

bằng

A.

10

. B.

10

. C.

8

. D.

2 2

.

Câu 18. (THPT Lê Xoay - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm

 

2;2; 2

A

 

;

 

3; 3;3

B 

. Điểm

M

trong không gian thỏa mãn

2

3

MA

MB



. Khi đó độ dài

OM

lớn nhất bằng

A.

6 3

. B.

12 3

. C.

5 3

2

. D.

5 3

.

Câu 19. Trong không gian

Oxyz

, cho ba điểm

(1;1;1)

A

,

( 2;3;4)

B



và

( 2;5;1)

C



. Điểm

( ; ;0)M a b

thuộc

mặt phẳng

 

Oxy

sao cho

2 2 2

MA MB MC

 

đạt giá trị nhỏ nhất. Tổng

2 2

T a b 

bằng

A.

10

T



. B.

25

T



. C.

13

T



. D.

17

T



.

Câu 20. (THPT Đoàn Thượng – Hải Dương 2019) Trong không gian

Oxyz

cho

 

1; 1;2

A 

,

 

2;0;3

B 

,

 

0;1; 2

C



. Gọi

 

; ;M a b c

là điểm thuộc mặt phẳng

 

Oxy

sao cho biểu thức

. 2 . 3 .S MA MB MB MC MC MA

  

     

đạt giá trị nhỏ nhất. Khi đó

12 12

T a b c  

có giá trị là

A.

3

T



. B.

3

T

 

. C.

1T 

. D.

1T  

.

Câu 21. (Chuyên - Vĩnh Phúc - 2019) Trong không gian

Oxyz

, lấy điểm

C

trên tia

Oz

sao cho

1

OC



.

Trên hai tia

,Ox Oy

lần lượt lấy hai điểm

,A B

thay đổi sao cho

OA OB OC 

. Tìm giá trị nhỏ

nhất của bán kính mặt cầu ngoại tiếp tứ diện

.

O ABC

?

A.

6

.

2

B.

6.

C.

6

.

3

D.

6

.

4

Câu 22. (THPT Ngô Quyền - Ba Vì - Hải Phòng 2019) Trong không gian với hệ tọa độ

Oxyz

, gọi điểm

 

; ;M a b c

(với

a

,

b

,

c

là các phân số tối giản) thuộc mặt cầu

 

2 2 2

: 2 4 4 7 0

S x y z x y z

      

sao cho biểu thức

2 3 6T a b c  

đạt giá trị lớn nhất. Khi

đó giá trị biểu thức

2

P a b c  

bằng

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9

A.

12

7

. B.

8

. C.

6

. D.

51

7

.

Câu 23. (THPT Ngô Quyền - Ba Vì - Hải Phòng 2019) Trong không gian với hệ tọa độ Oxyz, Cho điểm

 

2 ;2 ;0A t t

,

 

0;0;B t

(với

0t 

). Điểm

P

di động thỏa mãn

. . . 3

OP AP OP BP AP BP

  

     

. Biết

rằng có giá trị

a

t

b



với

,a b

nguyên dương và

a

b

tối giản sao cho

OP

đạt giá trị lớn nhất bằng

3. Khi đó giá trị của

2

Q a b 

bằng

A.

5

B.

13

. C.

11

. D.

9

.

Câu 24. (HSG Nam Định-2019) Trong không gian với hệ trục tọa độ

,Oxyz

cho các điểm

     

4;1;5 , 3;0;1 , 1;2;0

A B C

và điểm

 

; ;M a b c

thỏa mãn

. 2 . 5 .

 

     

MA MB MB MC MC MA

lớn

nhất. Tính

2 4 .  P a b c

A.

23

P

. B.

31

P

. C.

11P

. D.

13.

P

Câu 25. Trong không gian với hệ trục tọa độ

Oxyz

, cho hai điểm

 

2; 2;4

A 

,

 

3;3; 1

B

 

và mặt cầu

       

2 2 2

: 1 3 3 3

S x y z

     

. Xét điểm

M

thay đổi thuộc mặt cầu

 

S

, giá trị nhỏ nhất

của

2 2

2 3

MA MB



bằng

A.

103

. B.

108

. C.

105

. D.

100

.

Câu 26. (Kim Liên - Hà Nội 2019) Trong không gian

Oxyz

, cho mặt cầu

 

2 2 2

9

: 2 4 2 0

2

S x y z x y z

      

và hai điểm

 

0;2;0

A

,

 

2; 6; 2

B

 

. Điểm

 

; ;M a b c

thuộc

 

S

thỏa mãn

.MA MB

 

có giá trị nhỏ nhất. Tổng

a b c 

bằng

A.

1

. B.

1

. C.

3

. D.

2

.

Câu 27. Trong không gian tọa độ

Oxyz

, cho 5 điểm

 

1;0;0

A

,

 

1;1;0

B 

,

 

0; 1;0

C 

,

 

0;1;0

D

,

 

0;3;0

E

.

M

là điểm thay đổi trên mặt cầu

2 2 2

( ) : ( 1) 1

S x y z

   

. Giá trị lớn nhất của biểu

thức 2 3

P MA MB MC MD ME

    

    

là:

A.

12

. B.

12 2

. C.

24

. D.

24 2

.

Câu 28. Trong không gian với hệ trục tọa độ

Oxyz

, cho các điểm

 

0; 1;3

A 

,

 

2; 8; 4

B

  

,

 

2; 1;1

C 

và mặt cầu

       

2 2 2

: 1 2 3 14

S x y z

     

. Gọi

 

; ;

M M M

M x y z

là điểm trên

 

S

sao cho biểu thức 3 2

MA MB MC

 

  

đạt giá trị nhỏ nhất. Tính

M M

P x y 

.

A.

P 0

. B.

P 6

. C.

P 14



. D.

P 3 14



.

Câu 29. Trong không gian

Oxyz

cho

   

0 ; 0 ; 2 , 1 ; 1; 0

A B

và mặt cầu

   

2

2 2

1

: 1

4

S x y z

   

. Xét

điểm

M

thay đổi thuộc

 

S

. Giá trị nhỏ nhất của biểu thức

2 2

2MA MB

bằng

A.

1

2

. B.

3

4

. C.

19

4

. D.

21

4

.

Câu 30. Trong không gian tọa độ

Oxyz

, cho 2 điểm A, B thay đổi trên mặt cầu

2 2 2

( 1) 25

x y z

   

thỏa

mãn

6

AB



. Giá trị lớn nhất của biểu thức

2 2

OA OB



là

A. 12. B. 6. C. 10. D. 24.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 10 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 31. Trong không gian

Oxyz

, cho ba điểm

 

1;4;5

A

,

 

3;4;0

B

,

 

2; 1;0

C 

. Gọi

 

; ;M a b c

là

điểm sao cho

2 2 2

3

MA MB MC

 

đạt giá trị nhỏ nhất. Tổng

a b c 

có giá trị bằng

A. 2. B. 3. C. 4. D.

4

.

Câu 32. Trong không gian với hệ trục

Oxyz

, cho mặt cầu

     

2 2

2

: 1 4 8

S x y z

    

và điểm

   

3;0;0 ; 4;2;1

A B

. Điểm

M

thay đổi nằm trên mặt cầu, tìm giá trị nhỏ nhất của biểu thức

2P MA MB 

.

A.

2 2

P 

. B.

3 2

P 

. C.

4 2

P 

. D.

6 2

P 

.

Câu 33. Trong không gian

Oxyz

,cho mặt cầu

 

2 2 2

: 2 2 2 0

S x y z x z

     

và các điểm

 

0;1;1

A

,

 

1; 2; 3

B

  

,

 

1;0; 3

C



. Điểm

D

thuộc mặt cầu

 

S

. Thể tích tứ diện

ABCD

lớn nhất bằng:

A.

9

. B.

8

3

. C.

7

. D.

16

3

.

Câu 34. (THPT Thuận Thành 3 - Bắc Ninh 2019) Trong không gian với hệ trục

Oxyz

, cho mặt cầu

     

2 2

2

: 1 4 8

S x y z

    

và điểm

 

3 ; 0 ;0

A

,

 

4 ; 2 ;1

B

. Điểm

M

thay đổi nằm trên

mặt cầu, tìm giá trị nhỏ nhất của biểu thức

2P MA MB 

.

A.

2 2

P 

. B.

3 2

P 

. C.

4 2

P 

. D.

6 2

P 

.

Câu 35. (Kinh Môn - Hải Dương 2019) Trong không gian với hệ tọa độ

Oxyz

cho hai điểm

 

4;2; 2

A

,

 

1;1; 1

B



,

 

2; 2; 2

C

 

. Tìm tọa độ điểm M thuộc

 

Oxy

sao cho

2

MA MB MC

 

  

nhỏ nhất.

A.

 

2; 3;0

M

. B.

 

1; 3;0

M

. C.

 

2; 3; 0

M 

. D.

 

2;3;1

M

.

Câu 36. Trong không gian

Oxyz

cho mặt cầu

 

S

có phương trình

2 2 2

4 2 2 3 0

x y z x y z

      

và

điểm

 

5;3; 2

A



. Một đường thẳng

d

thay đổi luôn đi qua

A

và luôn cắt mặt cầu tại hai điểm

phân biệt

,M N

. Tính giá trị nhỏ nhất của biểu thức

4

S AM AN 

.

A.

min

30

S



. B.

min

20

S



. C.

min

34 3

S

 

.

D.

min

5 34 9

S

 

.

Câu 37. Trong không gian

Oxyz

, cho mặt cầu

     

2 2

2

: 1 2 10

S x y z

    

và hai điểm

 

1;2; 4

A



và

 

1;2;14

B

. Điểm

M

thay đổi trên mặt cầu

 

S

. Giá trị nhỏ nhất của

 

2

MA MB



bằng

A.

2 82

. B.

3 79

. C.

5 79

. D.

3 82

.

Câu 38. Trong không gian với hệ trục tọa độ

Oxyz

, cho hai mặt cầu

 

2 2 2

1

: 1

S x y z

  

,

   

2

2 2

2

: 4 4

S x y z

   

và các điểm

 

4;0;0

A

,

1

;0;0

4

B

 

 

 

,

 

1;4;0

C

,

 

4;4;0

D

. Gọi

M

là

điểm thay đổi trên

 

1

S

,

N

là điểm thay đổi trên

 

2

S

. Giá trị nhỏ nhất của biểu thức

2 4 4

Q MA ND MN BC   

là

A.

2 265

. B.

265

. C.

3 265

. D.

4 265

.

Câu 39. Trong không gian với hệ tọa độ

Oxyz

, cho

 

2;3; 1

A



,

 

2;3;2

B

,

 

1;0;2

C 

.Tìm tọa độ điểm

M

thuộc mặt phẳng

 

Oxz

để

4

S MA MC MA MB MC

    

    

nhỏ nhất.

A.

7

1;0;

3

M

 



 

 

. B.

 

0;3;0

M

. C.

7

1;0;

3

M

 

 

 

. D.

1

;0;2

2

M

 



 

 

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11

Câu 40. Tr

ong không gian với hệ tọa độ

O

xyz

,

cho mặt cầu

2

2 2

( ): 2 4 4 0

S x y z x y

     

và

hai

điểm

(

4;2;4), (1; 4;2)

A

B

.

M

N

là dây cung của mặt cầu thỏa mãn

M

N



cùng hướng với

(

0;1;1)

u





và

4

2

M

N 

. Tí

nh giá trị lớn nhất của

A

M BN



.

A.

4

1

. B.

4

2

. C.

7

. D.

17

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương  https://www.facebook.com/phong.baovuong Trang 1

TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH TRUNG BÌNH MỨC 5-6 ĐIỂM

Dạng 1. Xác định tâm và bán kính



Mặt cầu tâm

( ; ; )I a b c

và có bán kính

R

có phương trình

2 2 2 2

( ) : ( ) ( ) ( ) .S x a y b z c R     



Phương trình

2 2 2

2 2 2 0x y z ax by cz d      

với

2 2 2

0a b c d   

là phương trình của mặt cầu có tâm

( ; ; )I a b c

và bán kính

2 2 2

.R a b c d   

 Để một phương trình là một phương trình mặt cầu, cần thỏa mãn hai điều kiện:

Hệ số trước

2 2 2

, , x y z phải bằng nhau và

2 2 2

0.a b c d   

Câu 1. (Đề Minh Họa 2020 Lần 1) Trong không gian

Oxyz

, cho mặt cầu

       

2 2 2

: 1 2 3 16S x y z     

. Tâm của

 

S

có tọa độ là

A.

 

1; 2; 3  

. B.

 

1;2;3

. C.

 

1;2; 3 

. D.

 

1; 2;3

.

Lời giải

Chọn D

Mặt cầu

       

2 2 2

2

:S x a y b z c R     

có tâm là

 

; ;I a b c

.

Suy ra, mặt cầu

       

2 2 2

: 1 2 3 16S x y z     

có tâm là

 

1; 2;3I 

.

Câu 2. (Đề Tham Khảo 2020 Lần 2) Trong không gian

Oxyz

, cho mặt cầu

       

2 2 2

: 2 4 1 9S x y z     

. Tâm của

 

S

có tọa độ là

A.

 

2;4; 1 

. B.

 

2; 4;1

. C.

 

2;4;1

. D.

 

2; 4; 1  

.

Lời giải

Chọn B

Tâm của mặt cầu

 

S

có tọa độ là

 

2; 4;1

.

Câu 3. (Mã 102 - 2020 Lần 1) Trong không gian , cho mặt cầu . Bán

kính của bằng

A. . B. . C. . D. .

Lời giải

Chọn C

Bán kính của là .

Câu 4. (Mã 101 - 2020 Lần 1) Trong không gian

Oxyz

, cho mặt cầu

   

2

2 2

: 2 9S x y z   

. Bán

kính của

 

S

bằng

A.

6

. B.

18

. C.

9

. D.

3

.

Lời giải

Chọn D.

Câu 5. (Mã 103 - 2020 Lần 1) Trong không gian

Oxyz

, cho mặt cầu

2 2 2

( ): ( 1) 16S x y z    . Bán

kính của

( )S

là:

A.

32

B.

8

C.

4

D.

16

PHƯƠNG TRÌNH MẶT CẦU

Chuyên đề 29

Oxyz

   

2

2 2

: 2 9

S x y z

   

 

S

6

18

3

9

 

S

9 3

R

 

I

R

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Lời giải

Chọn C

Từ phương trình mặt cầu

2 2 2

( ) : ( 1) 16

S x y z

   



Bán kính

16 4

R

 

Câu 6. (Mã 104 - 2020 Lần 1) Trong không gian

,Oxyz

cho mặt cầu

   

2

2 2

: 2 16

S x y z

   

. Bán

kính của mặt cầu

 

S

bằng

A.

4

. B.

32

. C.

16

. D.

8

.

Lời giải

Chọn A

Bán kính của mặt cầu

   

2

2 2

: 2 16

S x y z

   

là

16 4

R

 

.

Câu 7. (Mã 101- 2020 Lần 2) Trong không gian

Oxyz

, cho mặt cầu

       

2 2 2

: 1 2 3 4

S x y z

     

. Tâm của

 

S

có tọa độ là

A.

 

1; 2; 3 

. B.

 

2; 4;6



. C.

 

1; 2;3



. D.

 

2; 4; 6 

.

Lời giải

Chọn A

Tâm mặt cầu

 

S

có tọa độ là

 

1; 2; 3 

.

Câu 8. (Mã 103 - 2020 Lần 2) Trong không gian

Oxyz

, cho mặt cầu

       

2 2 2

: 1 2 3 4

S x y z

     

. Tâm của

 

S

có tọa độ là

A.

 

1;2;3



. B.

 

2; 4; 6 

. C.

 

2;4;6



. D.

 

1; 2; 3 

.

Lời giải

Chọn D

Tâm của mặt cầu

 

S

có tọa độ là

 

1; 2; 3 

.

Câu 9. (Mã 102 - 2020 Lần 2) Trong không gian

Oxyz

, cho mặt

cầu

2 2 2

( ) : ( 1) ( 2) ( 3) 9

S x y z

     

. Tâm của

( )S

có tọa độ là:

A.

( 2; 4;6) 

. B.

(2;4; 6)

. C.

( 1; 2;3) 

. D.

(1;2; 3)

.

Lời giải

Chọn C

Tâm của

( )S

có tọa độ là:

( 1; 2;3) 

Câu 10. (Mã 104 - 2020 Lần 2) Trong không gian

Oxyz

, cho mặt cầu

 

S

:

     

2 2 2

1 2 3 9

x y z

     

. Tâm của

 

S

có tọa độ là

A.

 

1; 2;3

 

. B.

 

2; 4;6

 

. C.

 

1;2; 3

. D.

 

2;4; 6

.

Lời giài

Chọn C

Tâm của mặt cầu

 

S

đã cho là:

 

1;2; 3

I



.

Câu 11. (Mã 104 2017) Trong không gian với hệ toạ độ

Oxyz

, cho mặt cầu

     

2 2

2

: 2 2 8

S x y z

    

. Tính bán kính

R

của

 

S

.

A.

2 2

R 

B.

64

R



C.

8

R



D.

4R 

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3

Lời giải

Chọn A

Phương trình mặt cầu tổng quát:

     

2 2 2

2

2 2

x a y b z c R R       

.

Câu 12. (Mã 104 2018) Trong không gian

Oxyz

, mặt cầu

       

2 2 2

: 5 1 2 3

S x y z

     

có bán

kính bằng

A.

9

B.

2 3

C.

3

D.

3

Lời giải

Chọn D

Câu 13. (Mã 105 2017) Trong không gian với hệ toạ độ

Oxyz

, cho mặt cầu

       

     

2 2 2

: 5 1 2 9

S x y z . Tính bán kính

R

của

 

S

.

A.

 6R

B.

 3R

C.

 18R

D.

 9R

Lời giải

Chọn B

Phương trình mặt cầu tâm

 

; ;I a b c

, bán kính

R

có dạng:

     

       

2 2 2

2

3

x a y b z c R R .

Câu 14. (Mã 103 2018) Trong không gian

Oxyz

, cho mặt cầu

       

2 2 2

: 3 1 1 2

S x y z

     

. Tâm

của

 

S

có tọa độ là

A.

 

3; 1;1



B.

 

3; 1;1

 

C.

 

3;1; 1 

D.

 

3;1; 1

Lời giải

Chọn B

Tâm của

 

S

có tọa độ là

 

3; 1;1

 

.

Câu 15. (Đề Tham Khảo 2017) Trong không gian với hệ trục tọa độ

Oxyz

, tìm tọa độ tâm

I

và bán kính

R

của mặt cầu

     

2 2 2

1 2 4 20

x y z

     

.

A.

 

1;2; 4 , 2 5

I R  

B.

 

1; 2;4 , 20

I R

 

C.

 

1; 2;4 , 2 5

I R 

D.

 

1;2; 4 , 5 2

I R  

Lời giải

Chọn C

Trong không gian với hệ trục tọa độ

Oxyz

, mặt cầu

       

2 2 2

2

:

S x a y b z c R     

có tâm

 

; ;I a b c

và bán kính

R

.

Nên mặt cầu

     

2 2 2

1 2 4 20

x y z

     

có tâm và bán kính là

 

1; 2;4 , 2 5.

I R 

Câu 16. (Mã 101 - 2019) Trong không gian

Oxyz

, cho mặt cầu

 

2 2 2

: 2 2 7 0

S x y z x z

     

. Bán

kính của mặt cầu

đã cho bằng

A.

3

. B.

15

. C.

7

. D.

9

.

Lời giải

Chọn A

2 2 2 2 2 2

2 2 7 0 2.( 1). 2.0. 2.1. 7 0

x y z x z x y z x y z

              

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

1, 0, 1, -7

a b c d

     

.



Tâm mặt cầu

 

1;0;1

I 

bán kính

 

2

2 2 2 2 2

1 0 1 7 3

R a b c d

         

.

Câu 17. (Mã 104 - 2019) Trong không gian

Oxyz

, cho mặt cầu

 

2 2 2

: 2 2 7 0     

S x y z y z

. Bán

kính của mặt cầu đã cho bằng

A.

15

. B.

7

. C.

9

. D.

3

.

Lời giải

Chọn D

Ta có

   

2

1 1 7 3     

R

.

Câu 18. (Mã 102 - 2019) Trong không gian

Oxyz

, cho mặt cầu

 

2 2 2

: 2 2 7 0.

S x y z x y

     

Bán

kính của mặt cầu đã cho bằng

A.

7

. B.

9

. C.

15

. D.

3

.

Lời giải

Chọn D

Ta có

     

2 2

2 2 2 2

: 2 2 7 0 1 1 9

S x y z x y x y z

           

Vậy bán kính của mặt cầu bằng

3.

Câu 19. (Mã 103 - 2019) Trong không gian

Oxyz

, cho mặt cầu

2 2 2

( ) : 2 2 7 0.

S x y z y z

     

Bán

kính của mặt cầu đã cho bằng

A.

7

. B.

3

. C. 9. D.

15

.

Lời giải

Chọn B

Mặt cầu đã cho có phương trình dạng

2 2 2

2 2 2 0

x y z ax by cz d

      

có bán kính là

2 2 2 2 2

1 1 7 3

a b c d

      

Câu 20. (THPT Hoàng Hoa Thám Hưng Yên 2019) Trong không gian với hệ tọa độ

Oxyz

, cho mặt cầu

 

2 2 2

: 8 2 1 0

S x y z x y

     

. Tìm tọa độ tâm và bán kính của mặt cầu

 

S

.

A.

 

–4;1;0 .

,

2

I R



B.

 

–4;1;0 .

,

4

I R



C.

 

4; –1;0 , 2.

I R



D.

 

4; –1;0 , 4.

I R



Lời giải

Ta có:

   

2 2

2 2 2 2

8 2 1 0 4 1 16.

x y z x y x y z           

Vậy mặt cầu

 

S

có tâm

 

4; –1;0

I

và bán kính

4.

R



Câu 21. (THPT Lương Thế Vinh Hà Nội 2019) Cho mặt cầu

 

2 2 2

: 2 4 2 3 0

S x y z x y z

      

.

Tính bán kính

R

của mặt cầu

 

S

.

A.

3

R 

. B.

3

R



. C.

9

R



. D.

3 3

R 

.

Lời giải

 

2 2 2

: 2 4 2 3 0

S x y z x y z

      

     

2 2 2

1 2 1 9

x y z

      

.

Vậy bán kính của mặt cầu

 

S

là

3

R



.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5

Câu 22. Trong không gian vơi hệ tọa độ

Oxyz

, cho mặt cầu

 

2 2 2

: 8 2 1 0

S x y z x y

     

. Tìm tọa độ

tâm và bán kính mặt cầu

 

S

:

A.

 

4;1;0 , 2

I R

 

. B.

 

4;1;0 , 4

I R

 

. C.

 

4; 1;0 , 2

I R

 

. D.

 

4; 1;0 , 4

I R

 

.

Lời giải

 

2 2 2

: 8 2 1 0

S x y z x y

     

 

4; 1;0

I 

4R 

.

Câu 23. (THPT Đoàn Thượng - Hải Dương -2019) Trong không gian

Oxyz

, cho mặt cầu

       

2 2 2

: 3 1 1 2

S x y z

     

. Xác định tọa độ tâm của mặt cầu

 

S

A.

 

3;1; 1

I

 

. B.

 

3;1; 1

I



. C.

 

3; 1;1

I  

. D.

 

3; 1;1

I 

.

Lời giải

Mặt cầu

 

S

có tâm là

 

3; 1;1

I  

.

Câu 24. (Sở Hà Nội 2019) Trong không gian

Oxyz

, cho mặt cầu

 

2 2 2

: 2 4 2 3 0

S x y z x y z

      

.

Tọa độ tâm

I

của mặt cầu

 

S

là:

A.

 

1; 2; 1



. B.

 

2; 4; 2 

. C.

 

1; 2; 1 

. D.

 

2;4;2



.

Lời giải

Ta có:

     

2 2 2

2 4 2 3 0 1 2 1 9

x y z x y z x y z

             

.

Từ đó suy ra mặt cầu

 

S

có tâm là:

 

1;2;1



.

Câu 25. (Chuyên Lê Quý Đôn Quảng Trị 2019) Trong không gian

Oxyz

, cho mặt cầu

 

2 2 2

: 8 10 6 49 0

S x y z x y z

      

. Tính bán kính

R

của mặt cầu

 

S

.

A.

1R 

. B.

7

R



. C.

151

R 

. D.

99

R 

.

Lời giải

Phương trình mặt cầu:

2 2 2

2 2 2 0

x y z ax by cz d

      

 

2 2 2

0

a b c d

   

có tâm

 

; ;I a b c

, bán kính

2 2 2

R a b c d   

.

Ta có

4

a



,

5

b

 

,

3

c



,

49

d



. Do đó

2 2 2

1

R a b c d

    

.

Câu 26. Trong không gian

Oxyz

, mặt cầu

 

2 2 2

: 4 2 6 1 0

S x y z x y z

      

có tâm là

A.

 

4;2; 6 

B.

 

2; 1;3



C.

 

2;1; 3 

D.

 

4; 2;6



Lời giải

Chọn B

Từ phương trình mặt cầu suy ra tâm của mặt cầu là

 

2; 1;3



.

Câu 27. (THPT Gang Thép Thái Nguyên 2019) Trong không gian với hệ tọa độ

Oxyz

, cho mặt cầu có

phương trình

     

2 2 2

1 2 3 4

x y z

     

. Tìm tọa độ tâm

I

và bán kính

R

của mặt cầu đó.

A.

 

1;2; 3

I

 

;

2R 

. B.

 

1;2; 3

I

 

;

4R 

.

C.

 

1; 2;3

I 

;

2R 

. D.

 

1; 2;3

I 

;

4R 

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Lời giải

Mặt cầu đã cho có tâm

 

1; 2;3

I 

và bán kính

2R 

.

Câu 28. (KTNL GV Bắc Giang 2019) Trong không gian với hệ tọa độ

Oxyz

, cho mặt cầu

( )S

có

phương trình

2 2 2

4 2 4 0

x y z x y

     

.Tính bán kính

R

của

( ).S

A.

1

. B.

9

. C.

2

. D.

3

.

Lời giải

Chọn D.

Giả sử phương trình mặt cầu

2 2 2 2 2 2

( ) : 2 2 2 0 ( 0)

S x y z ax by cz d a b c d

          

Ta có:

2, 1, 0, 4

a b c d

      

Bán kính

2 2 2

3

R a b c d

    

.

Câu 29. (Chuyên Lê Hồng Phong Nam Định 2019) Trong không gian

Oxyz

, cho mặt cầu

       

2 2 2

: 3 1 1 4

S x y z

     

. Tâm của

 

S

có tọa độ là

A.

 

3;1; 1 

. B.

 

3; 1;1

. C.

 

3; 1; 1 

. D.

 

3;1; 1

.

Lời giải

Chọn B

Tâm của

 

S

có tọa độ là

 

3; 1;1

.

Dạng 2. Viết phương trình mặt cầu

 Dạng 1. Cơ bản

2 2 2 2

( ) : ( ): ( ) ( ) ( ) .

( ; )

:

;

âm I a bT

S S x a y b z c R

BK R

c



      







 Dạng 2. Viết phương trình mặt cầu

( )S

có tâm

I

và đi qua điểm

.A

Phương pháp:

( ) :

:

âm IT

S

BK R IA











(dạng 1)

 Dạng 3. Viết phương trình mặt cầu

( )S

có đường kính

,AB

với

, A B

cho trước.

Phương pháp:

( ) :

1

:

2

R

âmT

S

BK AB

I















Câu 1. (Đề Minh Họa 2020 Lần 1) Trong không gian

Oxyz

, cho mặt cầu

 

S

có tâm

 

0;0; 3

I



và đi

qua điểm

 

4;0;0

M

. Phương trình của

 

S

là

A.

 

2

2 2

3 25

x y z

   

. B.

 

2

2 2

3 5

x y z

   

.

C.

 

2

2 2

3 25

x y z

   

. D.

 

2

2 2

3 5

x y z

   

.

Lời giải

Chọn A

Phương trình mặt cầu

 

S

có tâm

 

0;0; 3

I



và bán kính

R

là:

 

2

2 2 2

3

x y z R   

.

Ta có:

   

2

2 2 2 2

4 0 0 3 25

M S R R

       

.

Vậy phương trình cần tìm là:

 

2

2 2

3 25

x y z

   

.

Câu 2. (Mã 110 2017) Trong không gian hệ tọa độ

Oxyz

, tìm tất cả các giá trị của

m

để phương trình

2 2 2

2 2 4 0

x y z x y z m

      

là phương trình của một mặt cầu.

A.

6

m



B.

6

m



C.

6

m



D.

6

m



là trung điểm của

.AB

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7

Lời giải

Chọn A

Phương trình

2 2 2

2 2 4 0

x y z x y z m

      

là một phương trình mặt cầu

2 2 2

1 1 2 0

m

    



6

m



.

Câu 3. (Đề Tham Khảo 2019) Trong không gian

Oxyz

cho hai điểm

 

1;1;1

I

và

 

1;2;3

A

. Phương

trình mặt cầu có tâm I và đi qua A là

A.

     

2 2 2

1 1 1 5

x y z

     

B.

     

2 2 2

1 1 1 29

x y z

     

C.

     

2 2 2

1 1 1 5

x y z

     

D.

     

2 2 2

1 1 1 25

x y z

     

lời giải

Chọn C

Ta có

     

2 2 2

1 1 2 1 3 1 5

R IA       

vậy phương trình mặt cầu tâm

I

và đi qua điểm

A

có phương trình là

           

2 2 2 2 2 2

2

1 1 1 5

I I I

x x y y z z R x y z

            

Câu 4. (THPT Cù Huy Cận 2019) Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm

   

1; 2;7 , 3;8; 1

A B

  

. Mặt cầu đường kính

AB

có phương trình là

A.

     

2 2 2

1 3 3 45

x y z     

. B.

     

2 2 2

1 3 3 45

x y z

     

.

C.

     

2 2 2

1 3 3 45

x y z     

. D.

     

2 2 2

1 3 3 45

x y z

     

.

Lời giải

Gọi

I

là trung điểm

AB

ta có

 

1;3;3

I 

là tâm mặt cầu.

Bán kính

     

2 2 2

1 1 2 3 7 3 45.

R IA        

Vậy phương trình mặt cầu cần tìm là

     

2 2 2

1 3 3 45

x y z

     

.

Câu 5. (THPT - Yên Định Thanh Hóa 2019) Trong không gian với hệ tọa độ

Oxyz

, viết phương trình

mặt cầu có tâm

 

1; 4;3

I 

và đi qua điểm

 

5; 3;2

A 

.

A.

     

2 2 2

1 4 3 18

x y z

     

. B.

     

2 2 2

1 4 3 16

x y z

     

.

C.

     

2 2 2

1 4 3 16

x y z

     

. D.

     

2 2 2

1 4 3 18

x y z

     

.

Lời giải

Mặt cầu có tâm

 

1; 4;3

I 

và đi qua điểm

 

5; 3;2

A 

nên có bán kính

3 2

R IA 

Vậy phương trình mặt cầu cần tìm là:

     

2 2 2

1 4 3 18

x y z

     

.

Câu 6. (Chuyên Sơn La -2019) Trong không gian

Oxyz

, cho hai điểm

 

1;1;1

A

và

 

1; 1;3

B 

. Phương

trình mặt cầu có đường kính

AB

là

A.

   

2 2

2

1 2 8

x y z

    

. B.

   

2 2

2

1 2 2

x y z

    

.

C.

   

2 2

2

1 2 2

x y z

    

. D.

   

2 2

2

1 2 8

x y z

    

.

Lời giải

Gọi

I

là tâm của mặt cầu đường kính

AB

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 8 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Khi đó

 

1;0;2

I

.

Bán kính của mặt cầu là:

     

2 2 2

1 1

1 1 1 1 3 1 2

2 2

R AB        

.

Vậy phương trình mặt cầu là:

   

2 2

2

1 2 2

x y z

    

.

Câu 7. (Sở Thanh Hóa 2019) Trong không gian Oxyz, cho hai điểm A(2;4;1), B

 

2;2; 3 

. Phương trình

mặt cầu đường kính AB là

A.

   

2 2

2

3 1 36.

x y z    

B.

   

2 2

2

3 1 9.

x y z

    

C.

   

2 2

2

3 1 9.

x y z

    

D.

   

2 2

2

3 1 36.

x y z    

Lời giải

Gọi I là trung điểm của AB

(0;3; 1).

I

 

2 2 2

(2;1;2) 2 1 2 3.

IA IA

     



Mặt cầu đã cho có tâm I, đường kính AB nên có phương trình là

   

2 2

2

3 1 9.

x y z

    

Câu 8. (Chuyên Bắc Giang 2019) Trong không gian với hệ tọa độ Oxyz, hỏi trong các phương trình sau

phương trình nào là phương trình của mặt cầu?

A.

2 2 2

2 4 1 0

x y z x z

     

B.

2 2

3 2 4 1 0

x z x y z

     

C.

2 2 2

2 4 4 1 0

x y z xy y z

      

D.

2 2 2

2 2 4 8 0

x y z x y z

      

Lời giải

Chọn A

Đáp án B vì không có số hạng

2

y

. Đáp án C loại vì có số hạng

2xy

. Đáp án D loại vì

2 2 2

1 1 4 8 2 0

a b c d

         

.

Đáp án A thỏa mãn vì

2 2 2

1 0 4 1 6 0

a b c d

        

.

Câu 9. Trong không gian

Oxyz

, cho hai điểm

 

2; 1; 3 

A

;

 

0;3; 1

B

. Phương trình của mặt cầu

đường kính

AB

là :

A.

     

2 2 2

1 1 2 6     

x y z

B.

     

2 2 2

1 1 2 24     

x y z

C.

     

2 2 2

1 1 2 24     

x y z

D.

     

2 2 2

1 1 2 6     

x y z

Lờigiải

Chọn D

Tâm

I

mặt cầu là trung điểm của

AB

 

1;1; 2

I

bán kính

1 1 1

4 16 4 24

2 2 2

    R AB

     

2 2 2

1 1 2 6     

x y z

Câu 10. (Chuyên KHTN 2019) Trong không gian với hệ tọa độ

Oxyz

phương trình nào sau đây không

phải là phương trình của một mặt cầu?

A.

2 2 2

2 4 3 0

x y z x y z

      

. B.

2 2 2

2 2 2 0

x y z x y z

     

.

C.

2 2 2

2 2 2 4 8 6 3 0

x y z x y z

      

. D.

2 2 2

2 4 4 10 0

x y z x y z

      

.

Lời giải

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9

Phương trình

2 2 2

2 2 2 0

x y z ax by cz d

      

là phương trình của một mặt cầu nếu

2 2 2

0

a b c d

   

.

Câu 11. (Chuyên Phan Bội Châu Nghệ An 2019) Trong không gian với hệ trục tọ độ

Oxyz

, cho hai

điểm

   

1;2;3 , 5;4; 1

A B



. Phương trình mặt cầu đường kính

AB

là

A.

     

2 2 2

3 3 1 36

x y z

     

. B.

     

2 2 2

3 3 1 9

x y z

     

.

C.

     

2 2 2

3 3 1 6

x y z

     

. D.

     

2 2 2

3 3 1 9

x y z

     

.

Lời giải.

Tọa độ tâm mặt cầu là

 

3;3;1

I

, bán kính

3

R IA

 

.

Câu 12. (Việt Đức Hà Nội 2019) Trong hệ trục tọa độ

Oxyz

, phương trình mặt cầu tâm

 

2;1; 2

I



bán

kính

2R 

là:

A.

     

2 2 2

2

2 1 2 2

x y z

     

. B.

2 2 2

4 2 4 5 0

x y z x y z

      

.

C.

2 2 2

4 2 4 5 0

x y z x y z

      

. D.

     

2 2 2

2 1 2 2

x y z

     

.

Lời giải

Phương trình mặt cầu tâm

 

2;1; 2

I



bán kính

2R 

có hai dạng:

Chính tắc:

     

2 2 2

2

2 1 2 2

x y z

     

Tổng quát:

2 2 2

4 2 4 5 0

x y z x y z

      

.

Vậy đáp án đúng là B.

Câu 13. (Việt Đức Hà Nội 2019) Phương trình nào sau đây là phương trình mặt cầu

 

S

tâm

 

2;1;0

A

,

đi qua điểm

 

0;1;2

B

?

A.

     

2 2

2

: 2 1 8

S x y z

    

. B.

     

2 2

2

: 2 1 8

S x y z

    

.

C.

     

2 2

2

: 2 1 64

S x y z

    

. D.

     

2 2

2

: 2 1 64

S x y z

    

.

Lời giải

Vì mặt cầu

 

S

có tâm

 

2;1;0

A

, đi qua điểm

 

0;1;2

B

nên mặt cầu

 

S

có tâm

 

2;1;0

A

và

nhận độ dài đoạn thẳng

AB

là bán kính.

Ta có:

 

2 :0;2

AB  



.

 

2

2 2

2 0 2 2 2

AB AB     



. Suy ra:

2 2

R 

.

Vậy:

     

2 2

2

: 2 1 8

S x y z

    

.

Vậy chọn đáp án B

Câu 14. (Chuyên Lam Sơn 2019) Trong không gian Oxyz cho điểm

(2;3;4)

I

và

 

1;2;3

A

. Phương trình

mặt cầu tâm I và đi qua A có phương trình là:

A.

2 2 2

( 2) ( 3) ( 4) 3

x y z

     

. B.

   

2 2

2

( 2) 3 4 9

x y z

     

.

C.

   

2 2

2

( 2) 3 4 45

x y z

     

. D.

   

2 2

2

( 2) 3 4 3

x y z

     

.

Lời giải

Chọn D

Bán kính mặt cầu là

3

R IA  .

Phương trình mặt cầu tâm

(2;3;4)

I

và

3

R IA  là

   

2 2

2

( 2) 3 4 3

x y z

     

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 10 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 15. (Thpt Vĩnh Lộc - Thanh Hóa 2019) Trong không gian

Oxyz

, cho hai điểm

 

1;1;1

I

và

 

1;2;3

A

. Phương trình của mặt cầu có tâm

I

và đi qua

A

là

A.

     

2 2 2

1 1 1 29

x y z

     

. B.

     

2 2 2

1 1 1 5

x y z

     

.

C.

     

2 2 2

1 1 1 25

x y z

     

. D.

     

2 2 2

1 1 1 5

x y z

     

.

Lời giải

Chọn B

Bán kính của mặt cầu:

2 2 2

0 1 2 5

r IA    

.

Phương trình mặt cầu:

     

2 2 2

1 1 1 5

x y z

     

.

Câu 16. (THPT Phan Bội Châu - Nghệ An - 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho hai

điểm

 

1;2;3

A

,

 

5;4; 1

B

. Phương trình mặt cầu đường kính

AB

là

A.

     

2 2 2

3 3 1 9     

x y z

. B.

     

2 2 2

3 3 1 6     

x y z

.

C.

     

2 2 2

3 3 1 9     

x y z

. D.

     

2 2 2

3 3 1 36     

x y z

.

Lời giải

Chọn A

+ Gọi

I

là trung điểm của

AB

 

3;3;1

 I

.

 

4;2; 4 16 4 16 6     



AB AB

+ Mặt cầu đường kính

AB

có tâm

 

3;3;1

I

, bán kính

3

2

 

AB

R

có phương trình là:

     

2 2 2

3 3 1 9     

x y z

.

Câu 17. (Lý Nhân Tông - Bắc Ninh 1819) Trong không gian

Oxyz

, cho hai điểm

 

7; 2;2

A 

và

 

1;2;4

B

. Phương trình nào dưới đây là phương trình mặt cầu đường kính

AB

?

A.

   

2 2

2

4 3 14

x y z

    

. B.

   

2 2

2

4 3 2 14

x y z    

.

C.

     

2 2 2

7 2 2 14

x y z

     

. D.

   

2 2

2

4 3 56

x y z

    

.

Lời giải

Chọn D

Mặt cầu nhận

AB

làm đường kính, do đó mặt cầu nhận trung điểm

 

4;0;3

I

của

AB

làm tâm

và có bán kính

56

2

AB

R  

.

Suy ra phương trình mặt cầu cần tìm là

   

2 2

2

4 3 56

x y z

    

.

Câu 18. (Bình Phước - 2019) Trong không gian

Oxyz

, cho hai điểm

 

3; 2;5

M 

,

 

1;6; 3

N

 

. Mặt cầu

đường kính

MN

có phương trình là:

A.

     

2 2 2

1 2 1 6

x y z

     

. B.

     

2 2 2

1 2 1 6

x y z

     

.

C.

     

2 2 2

1 2 1 36

x y z

     

. D.

     

2 2 2

1 2 1 36

x y z

     

.

Lời giải

Chọn D

Tâm

I

của mặt cầu là trung điểm đoạn

MN



 

1;2;1

I

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11

Bán kính mặt

cầu

     

2

2 2

1

3 6 2 3 5

6

2

M

N

R

      



 

.

Vậy phương trình mặt

cầu là

     

2

2 2

1

2 1 36

x

y z



    

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương  https://www.facebook.com/phong.baovuong Trang 1

TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH KHÁ MỨC 7-8 ĐIỂM

Dạng 1. Xác định tâm, bán kính của mặt cầu



Mặt cầu tâm

( ; ; )I a b c

và có bán kính

R

có phương trình

2 2 2 2

( ) : ( ) ( ) ( ) .S x a y b z c R     



Phương trình

2 2 2

2 2 2 0x y z ax by cz d      

với

2 2 2

0a b c d   

là phương trình của mặt cầu có tâm

( ; ; )I a b c

và bán kính

2 2 2

.R a b c d   

 Để một phương trình là một phương trình mặt cầu, cần thỏa mãn hai điều kiện:

Hệ số trước

2 2 2

, , x y z phải bằng nhau và

2 2 2

0.a b c d   

Câu 1. (Sở Phú Thọ 2019) Trong không gian

Oxyz

, có tất cả bao nhiêu giá nguyên của

m

để

   

2 2 2 2

2 2 2 1 3 5 0        x y z m x m z m

là phương trình một mặt cầu?

A.

4

B.

6

C.

5

D.

7

Lời giải

Chọn D

Phương trình đã cho là phương trình mặt cầu khi và chỉ khi

   

2 2

2

2 1 3 5 0

2 10 0

1 11 1 11

     

   

     

m m m

m m

m

Theo bài ra





2; 1;0;1;2;3;4     m m

có

7

giá trị của

m

nguyên thỏa mãn bài toán.

Câu 2. Trong không gian với hệ trục tọa độ

Oxyz

, tìm tất cả các giá trị của

m

để phương trình

 

2 2 2

2 2 4 19 6 0       x y z m x my m

là phương trình mặt cầu.

A.

1 2 m

. B.

1m

hoặc

2m

. C.

2 1  m

. D.

2 m

hoặc

1m

.

Lời giải

Điều kiện để phương trình

 

2 2 2

2 2 4 19 6 0       x y z m x my m

là phương trình mặt cầu

là:

 

2

2 2

2 4 19 6 0 5 15 10 0        m m m m m

1 m

hoặc

2m

.

Câu 3. (Chuyên Lê Quý Đôn Điện Biên 2019) Trong không gian

Oxyz

có tất cả bao nhiêu giá trị

nguyên

m

để phương trình

2 2 2 2

4 2 2 9 28 0x y z mx my mz m       

là phương trình mặt cầu?

A.

7

. B.

8

. C.

9

. D.

6

.

Lời giải

Ta có

2 2 2 2

4 2 2 9 28 0x y z mx my mz m       

     

2 2 2

2

2 28 3x m y m z m m       

 

1

.

 

1

là phương trình mặt cầu

2

28 28

28 3 0

3 3

m m      

.

Do

m

nguyên nên

 

3; 2; 1;0;1; 2;3m   

.

Vậy có

7

giá trị của

m

thỏa mãn yêu cầu bài toán.

PHƯƠNG TRÌNH MẶT CẦU

Chuyên đề 29

I

R

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 4. Trong không gian

Oxyz

, xét mặt cầu

 

S

có phương trình dạng

2 2 2

4 2 2 10 0

x y z x y az a

      

. Tập hợp các giá trị thực của

a

để

 

S

có chu vi đường tròn

lớn bằng

8

là

A.

 

1;10

. B.

 

2; 10



. C.

 

1;11



. D.

 

1; 11



.

Lời giải

Đường tròn lớn có chu vi bằng

8

nên bán kính của

 

S

là

8

4

2







.

Từ phương trình của

 

S

suy ra bán kính của

 

S

là

2 2 2

2 1 10a a

  

.

Do đó:

2 2 2

1

2 1 10 4

11

a

a a

a

 



    







.

Câu 5. (Chuyên Lê Quý Dôn - Dà Nẵng - 2018) Trong không gian với hệ trục tọa độ

Oxyz

, cho ba

điểm

 

1;0;0

A

,

 

0;0;3

C

,

 

0;2;0

B

. Tập hợp các điểm

M

thỏa mãn

2 2 2

MA MB MC

 

là mặt

cầu có bán kính là:

A.

2R 

. B.

3

R  . C.

3

R



. D.

2

R 

.

Lời giải

Giả sử

 

; ;M x y z

.

Ta có:

 

2

2 2 2

1

MA x y z   

;

 

2

2 2 2

2

MB x y z   

;

 

2

2 2 2

3

MC x y z   

.

2 2 2

MA MB MC

 

     

2 2 2

2 2 2 2 2 2

1 2 3

x y z x y z x y z           

   

2 2

2

2 1 2 3

x y x z       

     

2 2 2

1 2 3 2

x y z

      

.

Vậy tập hợp các điểm

M

thỏa mãn

2 2 2

MA MB MC

 

là mặt cầu có bán kính là

2

R 

.

Câu 6. (Toán Học Và Tuổi Trẻ 2018) Trong không gian với hệ trục tọa độ

Oxyz

, cho ba điểm

 

1;2; 4

A



,

 

1; 3;1

B 

,

 

2;2;3

C

. Tính đường kính

l

của mặt cầu

 

S

đi qua ba điểm trên và có

tâm nằm trên mặt phẳng

 

Oxy

.

A.

2 13

l  . B.

2 41

l 

. C.

2 26

l  . D.

2 11

l 

.

Lời giải

Gọi tâm mặt cầu là:

 

; ; 0

I x y

.

       

2 2 2 2

2 2

2 2 2 2

2 2

1 2 4 1 3 1

1 2 4 2 2 3

x y x y

IA IB

IA IC

x y x y



        









 







        



   

2 2

2 4 3 1

2 1 16 4 4 9

y y

x x x x



    







      





10 10 2

2 4 1

y x

x y

  

 

 

 

  

 

   

2 2

2

2 2 3 1 4 2 26

l R       

.

Câu 7. (Chuyên ĐHSPHN - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho

 

1;0;0

A 

,

 

0;0;2

B

,

 

0; 3;0

C 

. Bán kính mặt cầu ngoại tiếp tứ diện

OABC

là

A.

14

3

. B.

14

4

. C.

14

2

. D.

14

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3

Lời giải

Gọi

 

S

là mặt cầu ngoại tiếp tứ diện

OABC

.

Phương trình mặt cầu

 

S

có dạng:

2 2 2

2 2 2 0x y z ax by cz d       .

Vì

O

,

A

,

B

,

C

thuộc

 

S

nên ta có:

0

1 2 0

4 4 0

9 6 0

d

a d

c d

b d







  





  



  



1

2

3

2

1

0

a

b

c

d



 



 















.

Vậy bán kính mặt cầu

 

S

là:

2 2 2

R a b c d   

1 9

1

4 4

  

14

2



.

Câu 8. (THPT Lương Thế Vinh Hà Nội -2019) Gọi

 

S

là mặt cầu đi qua

4

điểm

       

2;0;0 , 1;3;0 , 1;0;3 , 1;2;3A B C D

. Tính bán kính

R

của

 

S

.

A.

2 2R 

.

B.

3R



. C.

6R



.

D.

6R 

.

Lời giải

Gọi

 

; ;I a b c

là tâm mặt cầu đi qua bốn điểm

, , ,A B C D

. Khi đó:

     

       

2 2 2

2 2

2 2 2

2 2 2 2 2

2 2

2 2 2 2

2 2

2 1 3

2 1 2 3

a b c a b c

AI BI

AI CI a b c a b c

AI DI

a b c a b c



       







         

 

 



        







 

3 3 0

1 1 0;1;1

2 3 5 1

a b a

a c b I

a b c c

   

 

 

      

 

 

    

 

Bán kính:

2 2 2

2 1 1 6R IA    

.

Câu 9. (Sở Hà Nội 2019) Cho hai điểm

,A B

cố định trong không gian có độ dài

AB

là

4

. Biết rằng tập

hợp các điểm

M

trong không gian sao cho

3MA MB

là một mặt cầu. Bán kính mặt cầu đó bằng

A.

3

. B.

9

2

. C.

1

. D.

3

2

.

Lời giải

Ta có:

2 2

3 9MA MB MA MB  

 

   

2 2

9MI IA MI IB   

   

 

2 2 2

9 2 9 8 1IA IB MI IA IB MI    

  

Gọi

I

thỏa mãn

1

9 0

8

IA IB BI AB   

    

nên

1 9

;

2 2

IB IA 

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Từ

 

1

suy ra

2

3

8 18

2

MI MI

   

suy ra

3

; .

2

M S I

 



 

 

Câu 10. (Sở Bình Phước - 2018) Trong không gian với hệ trục

Oxyz

, cho phương trình

 

2 2 2 2

2 2 4 2 5 9 0

x y z m x my mz m

        

. Tìm các giá trị của

m

để phương trình trên

là phương trình của một mặt cầu.

A.

5

m

 

hoặc

1

m



. B.

5 1

m

  

. C.

5

m

 

. D.

1

m



.

Lời giải

Ta có điều kiện xác định mặt cầu là

2 2 2

a b c 



 

2

2 2 2

2 4 5 9 0

m m m m

     

2

4 5 0

m m

   

5

1

m

 











.

Câu 11. (Yên Phong 1 - 2018) Trong không gian

Oxyz

. Cho tứ diện đều

ABCD

có

 

0;1;2

A

và hình

chiếu vuông góc của

A

trên mặt phẳng

 

BCD

là

 

4; 3; 2

H

 

. Tìm tọa độ tâm

I

của mặt cầu

ngoại tiếp tứ diện

ABCD

.

A.

 

3; 2; 1

I

 

. B.

 

2; 1;0

I 

. C.

 

3; 2;1

I 

. D.

 

3; 2;1

I  

.

Lời giải

Gọi

     

; ; ;1 ;2 ; 4 ; 3 ; 2

I a b c IA a b c IH a b c          

 

ABCD

là tứ diện đều nên tâm

I

của mặt cầu ngoại tiếp trùng với trọng tâm tứ diện

3IA IH

  

 

 

3 4

3

1 3 3 2

1

2 3 2

a a

a

b b b

c

c c



   







        

 

 

 

    



 

3; 2; 1

I

  

.

Câu 12. (Kiểm tra năng lực - ĐH - Quốc Tế - 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho mặt

cầu

 

S

có tâm nằm trên mặt phẳng

Oxy

và đi qua ba điểm

 

1;2; 4

A



,

 

1; 3;1

B 

,

 

2;2;3

C

.

Tọa độ tâm

 

I

của mặt cầu là

A.

 

2; 1;0



. B.

 

2;1;0



. C.

 

0;0; 2

. D.

 

0;0;0

.

Lời giải

Chọn B

Gọi tâm

 

; ;I a b c

và phương trình mặt cầu

 

2 2 2

: 2 2 2 0

S x y z ax by cz d

      

Do

   

2 2 2

0 : 2 2 0

I Oxy c S x y z ax by d

         

.

Ta có:

 

2 4 - 21 2

2 - 6 - 11 1

4 4 - 17 21

A S

a b d a

B S a b d b

a b d d

C S



   

 



 

    

  

  

   



 



.

Vậy

 

2;1;0

I 

.

Câu 13. Trong không gian tọa độ

Oxyz

, mặt cầu

 

S

đi qua điểm

O

và cắt các tia

, ,Ox Oy Oz

lần lượt tại

các điểm

, ,A B C

khác

O

thỏa mãn tam giác

ABC

có trọng tâm là điểm

 

6; 12;18

G  

. Tọa độ

tâm của mặt cầu

 

S

là

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5

A.

 

9;18; 27

. B.

 

3; 6;9 

. C.

 

3;6; 9

. D.

 

9; 18;27 

.

Lời giải

Chọn D

Gọi tọa độ các điểm trên ba tia

, ,Ox Oy Oz

lần lượt là

     

;0;0 , 0; ;0 , 0;0;A a B b C c

với

, , 0a b c 

.

Vì

G

là trọng tâm tam giác

ABC

nên

6

3

18

12 36

3

54

18

3

a

b

c



 



 





 

    

 

 













.

Gọi phương trình mặt cầu

 

S

cần tìm là:

2 2 2

2 2 2 0x y z mx ny pz q       . Vì

 

S

qua các

điểm

, , ,O A B C

nên ta có hệ:

2

0

9

36 18

18

27

72 36

0

108 54

q

m

m q

n

p

n q

q

p q





 





  

 

 



 



  

 



   



.

Vậy tọa độ tâm mặt cầu

 

S

là

 

9; 18;27 

.

Câu 14. Trong hệ trục tọa độ

Oxyz

, cho mặt cầu

       

2 2 2

: cos cos cos 4S x y z

  

     

với

,

 

và



lần lượt là ba góc tạo bởi tia

Ot

bất kì với

3

tia

,Ox Oy

và

Oz

. Biết rằng mặt cầu

 

S

luôn tiếp xúc với hai mặt cầu cố định. Tổng diện tích của hai mặt cầu cố định đó bằng

A.

40



. B.

4



. C.

20



. D.

36



.

Lời giải

Chọn A

Ta dễ dàng chứng minh được:

2 2 2

cos cos cos 1

  

  

Mặt cầu

 

S

có tâm

 

cos ;cos ;cosI

  

.

Suy ra tâm

I

thuộc mặt cầu

 

S



có tâm

 

2 2 2

O 0;0;0 , R cos cos cos 1

  

   

Mặt cầu

 

S

luôn tiếp xúc với hai mặt cầu

   

1 2

,S S

.

Mặt cầu

 

1

S

có tâm là

O

, bán kính

1

1 2 1R OI R    

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Mặt cầu

 

2

S

có tâm là

O

, bán kính

2

1 2 3

R OI R

    

.

Vậy tổng diện tích hai mặt cầu bằng

   

2 2 2 2

1 2

4 4 1 3 40

R R

  

   

.

Câu 15. Cho phương trình

      

2 2 2 2

4 2 3 2 0

x y z x my m m

với

m

là tham số. Tính tổng tất cả các

giá trị nguyên của

m

để phương trình đã cho là phương trình mặt cầu.

A.

0

. B.

1

. C.

2

. D.

3

.

Lời giải

Chọn B

Giả sử

      

2 2 2 2

4 2 3 2 0

x y z x my m m

là phương trình mặt cầu.

Khi đó tâm mặt cầu là

 



2; ;0

I m

, và bán kính

 

    

 

2 22

3 2

4 2 2 4

R m m mm m

. với

điều kiện

 

      

2

2 2 4 0 1;2

m m m

.

Do

 

  

 0;1

m m

.

Vậy tổng tất cả các giá trị nguyên của

m

bằng 1.

Câu 16. (Sở Kon Tum 2019) Trong không gian

Oxyz

, cho điểm

 

3;0;0

A

,

 

0; 2;0

B 

,

 

0;0; 4

C



.

Mặt cầu ngoại tiếp tứ diện

OABC

có diện tích bằng

A.

116



. B.

29

4



. C.

29



. D.

16



.

Lời giải

Chọn B

Cách 1:

Giả sử mặt cầu

 

S

ngoại tiếp tứ diện

OABC

có phương trình

2 2 2

2 2 2 0

x y z ax by cz d

      

.

 

S

đi qua

4

điểm

O

,

A

,

B

,

C

nên ta có hệ phương trình:

3

0

2

9 6 0

1

4 4 0

2

16 8 0

0

d

a

a d

b

b d

c

c d

d









  

 

 



 

  

 

 

 

  









.

Suy ra mặt cầu

 

S

có tâm

3

; 1; 2

2

I

 

 

 

 

, bán kinh

2 2 2

29

2

R a b c d    

.

Vậy diện tích mặt cầu

 

S

bằng

29

4



.

Cách 2:

Khối tứ diện

OABC

có 3 cạnh

OA

,

OB

,

OC

đôi một vuông góc tại

O

. Khi đó mặt cầu ngoại

tiếp khối tứ diện

OABC

có bán kính

2 2 2

29

2 2

OA OB OC

R

 

 

.

Vậy diện tích mặt cầu ngoại tiếp

OABC

bằng

29

4



.

Câu 17. (Chuyên Lê Hồng Phong-Nam Định -2019) Trong không gian với hệ tọa độ

Oxyz

, cho ba điểm

 

1;2; 4

A



,

 

1; 3;1

B 

,

 

2;2;3

C

. Tính bán kính

R

của mặt cầu

 

S

đi qua ba điểm trên và có

tâm nằm trên mặt phẳng

 

Oxy

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7

A.

41

R 

. B.

15

R 

. C.

13

R 

. D.

26

R 

.

Lời giải

Chọn D

Gọi phương trình mặt cầu

 

S

có dạng

2 2 2

2 2 2 0

x y z ax by cz d

      

, với tọa độ tâm

 

; ;I a b c

.

Ta có:

   

; ; 0

I a b c Oxy c

  

;

 

2 4 21 2

2 6 11 1

4 4 17 21

A S

a b d a

B S a b d b

a b d d

C S



      

 



 

        

  

  

      



 



;

2 2 2

4 1 0 21 26

R a b c d        

.

Câu 18. (THPT Thăng Long-Hà Nội- 2019) Trong không gian

Oxyz

, gọi

 

S

là mặt cầu đi qua điểm

 

0;1;2

D

và tiếp xúc với các trục

Ox

,

Oy

,

Oz

tại các điểm

 

;0;0

A a

,

 

0; ;0B b

,

 

0;0;C c

trong đó

 

, , \ 0;1

a b c



. Bán kính của

 

S

bằng

A.

5

. B.

5

2

. C.

3 2

2

. D.

5 2

.

Lời giải

Chọn D

Gọi

I

là tâm của mặt cầu

 

S

. Vì

 

S

tiếp xúc với các trục

Ox

,

Oy

,

Oz

tại các điểm

 

;0;0

A a

,

 

0; ;0B b

,

 

0;0;C c

nên ta có

IA Ox

,

IB Oy

,

IC Oz

hay

A

,

B

,

C

tương

ứng là hình chiếu của

I

trên

Ox

,

Oy

,

Oz

 

; ;I a b c



.



Mặt cầu

 

S

có phương trình:

2 2 2

2 2 2 0

x y z ax by cz d

      

với

2 2 2

0

a b c d

   

.

Vì

 

S

đi qua

A

,

B

,

C

,

D

nên ta có:

 

2 2 2

1

5 2 4 0 2

a b c d

b c d



  





   





.

Vì

 

, , \ 0;1

a b c



nên

0 1

d

 

. Mặt khác, từ

 

2 2 2

1 2R a b c d d

     

.

TH1: Từ

 

1

b c d

  

. Thay vào

 

*

:

5 6 0 25

d d d

    

(nhận).

2.25 5 2

R   .

TH2: Từ

 

1

b c d

   

. Thay vào

 

*

:

5 6 0

d d

  

(vô nghiệm).

TH3: Từ

 

1

b d

 

,

c d

 

. Thay vào

 

*

:

5 2 0

d d

  

(vô nghiệm).

TH4: Từ

 

1

b d

  

,

c d

 . Thay vào

 

*

:

5 2 0

d d

  

(vô nghiệm).

Vậy mặt cầu

 

S

có bán kính

5 2

R 

.

Câu 19. Trong không gian với hệ trục tọa độ

Oxyz

, cho mặt cầu

       

2 2 2

: 1 2 3 25

S x y z

     

và

hình nón

 

H

có đỉnh

 

3;2; 2

A



và nhận

AI

làm trục đối xứng với

I

là tâm mặt cầu. Một

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 8 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

đường sinh của hình nón

 

H

cắt mặt cầu tại

, M N

sao cho

3AM AN

. Viết phương trình mặt

cầu đồng tâm với mặt cầu

 

S

và tiếp xúc với các đường sinh của hình nón

 

H

.

A.

     

2 2 2

71

1 2 3

3

x y z     

. B.

     

2 2 2

70

1 2 3

3

x y z     

.

C.

     

2 2 2

74

1 2 3

3

x y z     

. D.

     

2 2 2

76

1 2 3

3

x y z     

.

Lời giải

Chọn A

Gọi hình chiếu vuông góc của

I

trên

MN

là

K

.

Dễ thấy

1

3

AN NK AM 

, mặt cầu

 

S

có tâm

 

1;2;3I

và bán kính

5R 

Có

2 2 2 2 2

4 2 3 213

. 4

3 3 3

AM AN AI R AN KN AN IK IN KN           

.

Nhận thấy mặt cầu đồng tâm với mặt cầu

 

S

và tiếp xúc với các đường sinh của hình nón

 

H

chính là mặt cầu tâm

 

1; 2;3I

có bán kính

213

3

IK 

.

Vậy phương trình mặt cầu cần tìm là:

     

2 2 2

71

1 2 3

3

x y z     

.

Câu 20. (Chuyên Hà Tĩnh - 2018) Trong không gian

Oxyz

, gọi

 

; ;I a b c

là tâm mặt cầu đi qua điểm

 

1; 1;4A 

và tiếp xúc với tất cả các mặt phẳng tọa độ. Tính

P a b c  

.

A.

6P 

. B.

0P 

. C.

3P 

. D.

9P 

.

Lời giải

Vì mặt cầu tâm

I

tiếp xúc với các mặt phẳng tọa độ nên

 

, , ,d I Oyz d I Ozx d I Oxy 

a b c  

a b c

 





  







  



   



Nhận thấy chỉ có trường hợp

a b c  

thì phương trình

 

,AI d I Oxy

có nghiệm, các

trường hợp còn lại vô nghiệm.

Thật vậy:

Với

a b c  

thì

 

; ;I a a a

 

,AI d I Oyx

     

2 2 2

2

1 1 4a a a a      

2

6 9 0a a   

3a 

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9

Khi đó

9

P a b c

   

.

Câu 21. (THPT Mộ Đức - Quảng Ngãi - 2018) Trong mặt phẳng tọa độ

Oxyz

, cho bốn điểm

 

0; 1;2

A 

,

 

2; 3;0

B 

,

 

2;1;1

C 

,

 

0; 1;3

D 

. Gọi

 

L

là tập hợp tất cả các điểm

M

trong không gian thỏa

mãn đẳng thức

. . 1

MA MB MC MD

 

   

. Biết rằng

 

L

là một đường tròn, đường tròn đó có bán

kính

r

bằng bao nhiêu?

A.

11

2

r 

. B.

7

2

r 

. C.

3

2

r 

. D.

5

2

r 

.

Lời giải

Gọi

 

; ;M x y z

là tập hợp các điểm thỏa mãn yêu cầu bài toán. Ta có

 

; 1; 2

AM x y z

  



,

 

2; 3;BM x y z

  



,

 

2; 1; 1

CM x y z

   



,

 

; 1; 3

DM x y z

  



.

Từ giả thiết:

. 1

. . 1

. 1

MA MB

MA MB MC MD

MC MD







  









 

   

 

      

       

2 1 3 2 1

2 1 1 1 3 1

x x y y z z

      







       





2 2 2

2 4 2 2 0

2 4 1 0

x y z x y z

x y z x z



      







     





Suy ra quỹ tích điểm

M

là đường tròn giao tuyến của mặt cầu tâm

 

1

1; 2;1

I 

,

1

2

R



và mặt cầu

tâm

 

2

1;0;2

I 

,

2

R



.

Ta có:

1 2

5

I I 

.

Dễ thấy:

2

1 2

1

5 11

4

2 4 2

I I

r R

 

    

 

 

.

Dạng 2. Viết phương trình mặt cầu

 Dạng 1. Cơ bản

2 2 2 2

( ) : ( ): ( ) ( ) ( ) .

( ; )

:

;

âm I a bT

S S x a y b z c R

BK R

c



      







 Dạng 2. Viết phương trình mặt cầu

( )S

có tâm

I

và đi qua điểm

.A

Phương pháp:

( ) :

:

âm IT

S

BK R IA











(dạng 1)

 Dạng 3. Viết phương trình mặt cầu

( )S

có đường kính

,AB

với

, A B

cho trước.

Phương pháp:

( ) :

1

:

2

R

âmT

S

BK AB

I















 Dạng 4. Viết phương trình mặt cầu

( )S

có tâm

I

và tiếp xúc với các trục và mp tọa độ.

Phương pháp:

( ) :

:

âm IT

S

BK R IM











 Dạng 5. Viết phương trình mặt cầu

( )S

có tâm

I

và tiếp xúc với mặt phẳng

( ).P

Phương pháp:

 

( ) :

;( )

:

T

S

B I

âm I

K R d P















1

I

2

I

M

là trung điểm của

.AB

với M là hình chiếu của

I

lên trục hoặc mp tọa

độ.

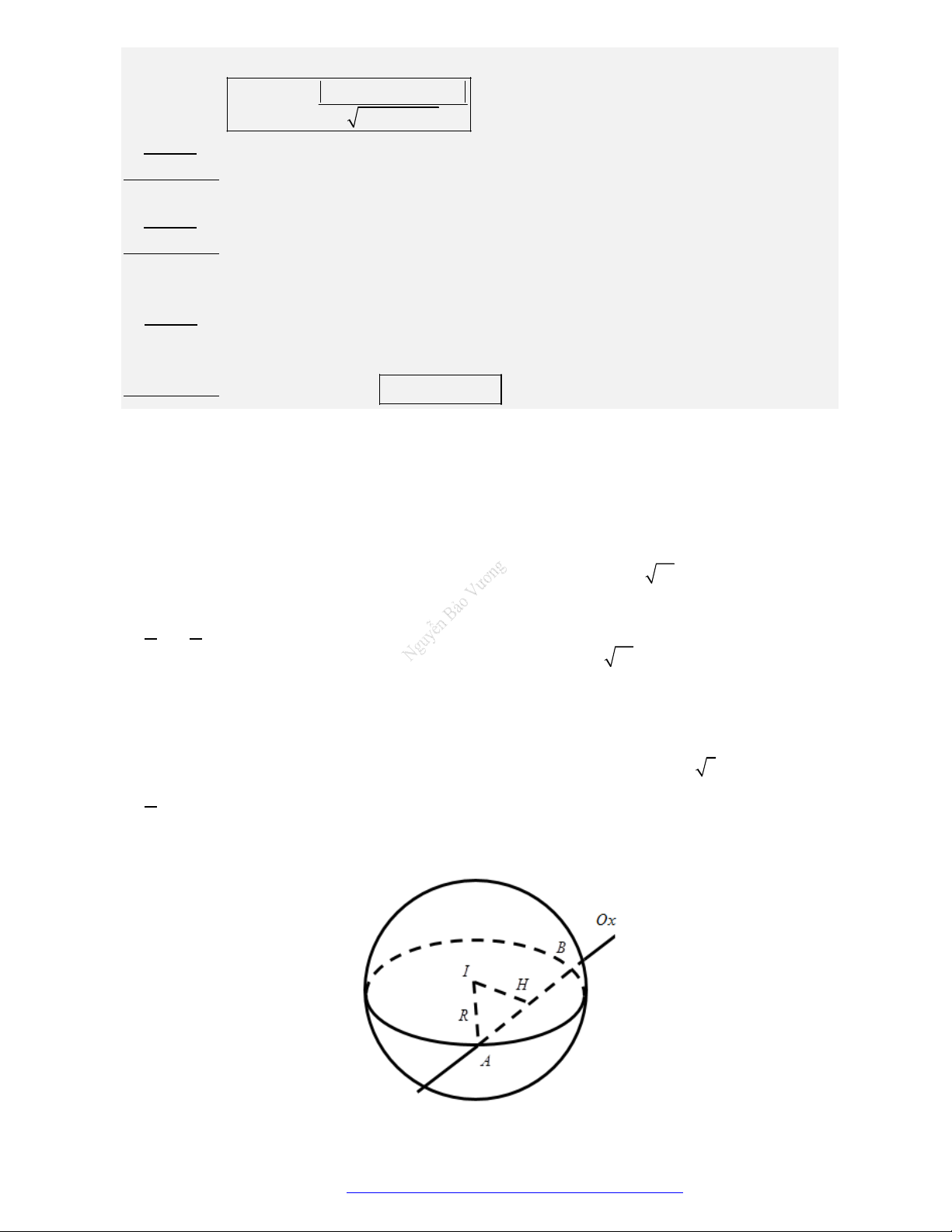
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 10 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

 Khoảng cách từ điểm ( ; ; )

M M M

M x y z đến mặt phẳng

( ) : 0P ax by cz d   

được xác định bởi

công thức:

2 2 2

( ;( ))

M M M

ax by cz d

d M P

a b c

  

 

 

 Dạng 6. Viết phương trình mặt cầu

( )S

đi qua bốn điểm

, , , .A B C D

Phương pháp: Gọi

2 2 2

( ) : 2 2 2 0S x y z ax by cz d      

Vì

, , , ( )A B C D S

nên tìm được 4 phương trình

, , , ( ).a b c d S 

 Dạng 7. Viết phương trình mặt cầu

( )S

đi qua 3 điểm

, , A B C

và tâm thuộc mp

( ).P

Phương pháp: Gọi

2 2 2

( ) : 2 2 2 0S x y z ax by cz d      

Vì

, , ( )A B C S

nên tìm được 3 phương trình và

( ; ; ) ( )I a b c P

là phương trình thứ tư.

Giải hệ bốn phương trình này

, , , ( ).a b c d S 

 Dạng 8. Viết phương trình mặt cầu

( )S

có tâm

I

và cắt mặt phẳng

( )P

theo giao tuyến là một

đường tròn có bán kính

.r

(dạng này mình sẽ đưa vào bài phương trình mặt phẳng, các bạn

học cũng có thể tự tìm để hiểu hơn)

Phương pháp: Dựa vào mối liên hệ

2 2 2

[ ;( )]I P

R d r 

và cần nhớ

2C r





và

2

t

.S r





đ

Câu 1. (Mã 123 2017) Trong không gian với hệ tọa độ

Oxyz

, cho điểm

 

1; 2; 3M

. Gọi

I

là hình

chiếu vuông góc của

M

trên trục

Ox

. Phương trình nào dưới đây là phương trình mặt cầu tâm

I

bán kính

IM

?

A.

 

   

2

2 2

1 13x y z B.

 

   

2

2 2

1 17x y z

C.

 

   

2

2 2

1 13x y z D.

 

   

2

2 2

1 13x y z

Lời giải

Chọn A

Hình chiếu vuông góc của

M

trên trục

Ox

là

 

 1; 0; 0 13I IM

.Suy ra phương trình mặt

cầu tâm

I

bán kính

IM

là:

 

   

2

2 2

1 13x y z .

Câu 2. (THPT Đoàn Thượng - Hải Dương -2019) Trong không gian Oxyz, cho điểm

(1; 2;3)I 

. Viết

phương trình mặt cầu tâm I, cắt trục

Ox

tại hai điểm

A

và

B

sao cho

2 3AB 

A.

2 2 2

( 1) ( 2) ( 3) 16.x y z     

B.

2 2 2

( 1) ( 2) ( 3) 20.x y z     

C.

2 2 2

( 1) ( 2) ( 3) 25.x y z     

D.

2 2 2

( 1) ( 2) ( 3) 9.x y z     

Lời giải.

Gọi

H

là trung điểm

AB

suy ra

H

là hình chiếu vuông góc của

I

lên

Ox

nên

 

1;0;0H

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11

2 2

13 4

IH R IA IH AH

     

.

Phương trình mặt cầu là:

     

2 2 2

1 2 3 16

x y z

     

.

Câu 3. (Sgd Cần Thơ - 2018) Trong không gian

Oxyz

, giá trị dương của

m

sao cho mặt phẳng

 

Oxy

tiếp xúc với mặt cầu

   

2 2

3 2 1

x y z m

     

là

A.

5m 

. B.

3

m 

. C.

3m 

. D.

5

m 

.

Lời giải

Mặt cầu

 

S

:

   

2 2

3 2 1

x y z m

     

có tâm

 

3;0;2

I

, bán kính

2

1

R m

 

.

 

S

tiếp xúc với

 

Oxy

 

,

d I Oxy R 

2

2 1

m

  

2

3m 

3

m 

(do

m

dương).

Câu 4. (THPT Đoàn Thượng - Hải Dương - 2019) Trong không gian

Oxyz

, cho điểm

 

1; 2;3

M 

.

Gọi

I

là hình chiếu vuông góc của

M

trên trục

Ox

. Phương trình nào sau đây là phương trình

mặt cầu tâm

I

bán kính

IM

?

A.

 

2

2 2

1 13

x y z   

. B.

 

2

2 2

1 13

x y z

   

.

C.

 

2

2 2

1 13

x y z

   

. D.

 

2

2 2

1 17

x y z

   

.

Lời giải

Với điểm

 

1; 2;3

M 

thì hình chiếu vuông góc của

M

trên trục

Ox

là

 

1;0;0

I

Có

13

IM 

vậy phương trình mặt cầu tâm

 

1;0;0

I

bán kính

IM

là:

 

2

2 2

1 13

x y z

   

Câu 5. (Sở Bắc Giang 2019) Trong không gian với hệ tọa độ

Oxyz

, trong các mặt cầu dưới đây, mặt cầu

nào có bán kính

2R 

?

A.

 

2 2 2

: 4 2 2 3 0

S x y z x y z

      

. B.

 

2 2 2

: 4 2 2 10 0

S x y z x y z

      

.

C.

 

2 2 2

: 4 2 2 2 0

S x y z x y z

      

. D.

 

2 2 2

: 4 2 2 5 0

S x y z x y z

      

.

Lời giải

Ta có mặt cầu

 

2 2 2

: 2 2 2 0

S x y z ax by cz d

      

có bán kính là

2 2 2

R a b c d   

Trong đáp án C ta có:

2 2 2

2

1

4 2

1

2

a

b

R a b c d

c

d







 



      



 







.

Câu 6. (THPT Gang Thép Thái Nguyên 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho điểm

   

1;1;2 , 3;2; 3

A B



. Mặt cầu

 

S

có tâm

I

thuộc

Ox

và đi qua hai điểm

,A B

có phương

trình.

A.

2 2 2

8 2 0

x y z x

    

. B.

2 2 2

8 2 0

x y z x

    

.

C.

2 2 2

4 2 0

x y z x

    

. D.

2 2 2

8 2 0

x y z x

    

.

Lời giải

Gọi

 

;0;0

I a Ox



   

1 ;1;2 ; 3 ;2; 3

IA a IB a

   

 

.

Do

 

S

đi qua hai điểm

,A B

nên

   

2 2

1 5 3 13

IA IB a a

      

4 16 4

a a

   

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 12 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

 

S



có tâm

 

4;0;0

I

, bán kính

14

R IA 

.

   

2

2 2 2 2 2

: 4 14 8 2 0.

S x y z x y z x

          

Câu 7. Trong không gian

Oxyz

, mặt cầu có tâm

 

1;1;1

I

và diện tích bằng

4



có phương trình là

A.

     

2 2 2

1 1 1 4

x y z

     

B.

     

2 2 2

1 1 1 1

x y z

     

C.

     

2 2 2

1 1 1 4

x y z

     

D.

     

2 2 2

1 1 1 1

x y z

     

Lời giải

Ta có:

2

4 4 1

S R R

 

   

Vậy

 

S

tâm

 

1;1;1

I

bán kính

1R 

có pt:

     

2 2 2

1 1 1 1

x y z

     

Câu 8. (Việt Đức Hà Nội 2019) Trong không gian với hệ tọa độ

Oxyz

, mặt cầu

 

S

qua bốn điểm

 

3;3;0

A

,

 

3;0;3

B

,

 

0;3;3

C

,

 

3;3;3

D

. Phương trình mặt cầu

 

S

là

A.

2 2 2

3 3 3 3 3

2 2 2 2

x y z

     

     

     

     

.

B.

2 2 2

3 3 3 27

2 2 2 4

x y z

     

     

     

     

.

C.

2 2 2

3 3 3 27

2 2 2 4

x y z

     

     

     

     

.

D.

2 2 2

3 3 3 27

2 2 2 4

x y z

     

     

     

     

.

Lời giải

Gọi phương trình mặt cầu

 

2 2 2 2 2 2

: 2 2 2 0 0

S x y z ax by cz d a b c d

          

Vì mặt cầu đi qua 4 điểm nên:

18 6 6 0

27 6 6 6 0

a b d

a c d

b c d

a b c d

   





   





   



    



6 6 18

6 6 6 27

a b d

a c d

b c d

a b c d

    





    







    



     



3

2

3

2

3

2

0

a

b

c

d

























Suy ra tâm

3 3 3

; ;

2 2 2

I

 

 

 

bán kính

2 2 2

3 3 3 3 3

2 2 2 2

R

     

   

     

     

.

Vậy phương trình mặt cầu

2 2 2

3 3 3 27

2 2 2 4

x y z

     

     

     

     

.

Câu 9. (THPT Trần Phú - Đà Nẵng - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho tứ diện

ABCD

có tọa độ đỉnh

 

2; 0; 0

A

,

 

0; 4; 0

B

,

 

0; 0; 6

C

,

 

2; 4; 6

A

. Gọi

 

S

là mặt cầu ngoại tiếp

tứ diện

ABCD

. Viết phương trình mặt cầu

 

S



có tâm trùng với tâm của mặt cầu

 

S

và có bán

kính gấp

2

lần bán kính của mặt cầu

 

S

.

A.

     

2 2 2

1 2 3 56

x y z

     

. B.

2 2 2

2 4 6 0

x y z x y z

     

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13

C.

     

2 2 2

1 2 3 14

x y z

     

. D.

2 2 2

2 4 6 12 0

x y z x y z

      

.

Lời giải

Gọi phương trình mặt cầu

 

S

có dạng:

2 2 2

2 2 2 0

x y z ax by cz d

      

.

Vì

 

S

là mặt cầu ngoại tiếp tứ diện

ABCD

nên ta có:

2 2 2

2 0 0 2. .2 2. .0 2. .0 0

0 4 0 2. .0 2. .4 2. .0 0

0 0 6 2. .0 2. .0 2. .6 0

2 4 6 2. .2 2. .4 2. .6 0

a b c d



      



      





      



      





4 4

8 16

12 36

4 8 12 56

a d

b d

c d

a b c d

   





   





   



     





1

2

3

0

a

b

c

d























2 2 2

2 4 6 0

x y z x y z

     



 

1; 2; 3

I

và

14

R 



2 14

R





.

Vậy: mặt cầu

 

S



có tâm

 

1; 2; 3

I

và

2 14

R





:

     

2 2 2

1 2 3 56

x y z

     

.

Câu 10. (Trần Phú - Hà Tĩnh - 2018) Trong không gian với hệ tọa độ

Oxyz

, mặt cầu tâm

 

2;1; 3

I



và

tiếp xúc với trục

Oy

có phương trình là

A.

     

2 2 2

2 1 3 4

x y z

     

. B.

     

2 2 2

2 1 3 13

x y z

     

.

C.

     

2 2 2

2 1 3 9

x y z

     

. D.

     

2 2 2

2 1 3 10

x y z

     

.

Lời giải

Gọi

M

là hình chiếu của

I

trên

Oy

 

0;1;0

M

Mặt cầu

 

S

tâm

 

2;1; 3

I



và tiếp xúc với trục

Oy

có bán kính

13

IM 

.

Vậy

 

S

có phương trình

     

2 2 2

2 1 3 13

x y z

     

.

Câu 11. (THPT

Phan Đình Phùng - Hà Tĩnh - 2018)

Trong không gian với hệ tọa độ

Oxyz

cho mặt

cầu

 

S

có tâm

 

1;4;2

I 

và có thể tích bằng

256

3



. Khi đó phương trình mặt cầu

 

S

là

A.

     

2 2 2

1 4 2 16

x y z

     

. B.

     

2 2 2

1 4 2 4

x y z

     

.

C.

     

2 2 2

1 4 2 4

x y z

     

. D.

     

2 2 2

1 4 2 4

x y z

     

.

Lời giải

Thể tích mặt cầu là

3

4

3

V R





.

Theo đề bài ta có

3

4 256

3 3

R





4

R

 

.

Phương trình mặt cầu

 

S

tâm

 

1;4;2

I 

và bán kính

4R 

là

     

2 2 2

1 4 2 16

x y z

     

.

Câu 12. (Chuyên Nguyễn Đình Triểu - Đồng Tháp - 2018) Trong không gian

Oxyz

, cho mặt cầu

     

2 2

2

: 1 1 4.

S x y z

    

Một mặt cầu

 

S



có tâm

 

9;1;6

I



và tiếp xúc ngoài với mặt cầu

 

.S

Phương trình mặt cầu

 

S



là

A.

     

2 2 2

9 1 6 64

x y z

     

. B.

     

2 2 2

9 1 6 144

x y z     

.

C.

     

2 2 2

9 1 6 36

x y z

     

. D.

     

2 2 2

9 1 6 25

x y z

     

.

Lời giải

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 14 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Chọn A

Gọi

 

1;1;0 , 2.

I R



10

II





.

Gọi

R



là bán kính của mặt cầu

 

S



. Theo giả thiết, ta có

8

R R II R II R

   

     

.

Khi đó phương trình mặt cầu

 

S



:

     

2 2 2

9 1 6 64

x y z

     

.

Câu 13. (THPT Hai Bà Trưng - Huế - 2018) Trong không gian

Oxyz

, viết phương trình mặt cầu đi qua

điểm

 

1; 1;4

A 

và tiếp xúc với các mặt phẳng tọa độ.

A.

     

2 2 2

3 3 3 16

x y z

     

. B.

     

2 2 2

3 3 3 9

x y z

     

.

C.

     

2 2 2

3 3 3 36

x y z

     

. D.

     

2 2 2

3 3 3 49

x y z

     

.

Lời giải

Gọi

 

; ;I a b c

là tâm của mặt cầu

 

S

. Mặt cầu

 

S

tiếp xúc với các mặt phẳng tọa độ

 

, , ,

d I Oxy d I Oyz d I Oxz

 

a b c R   

 

1

Mặt cầu

 

S

đi qua

 

1; 1;4

A 

0; 0; 0

IA R

a c b









  



2 2

0; 0; 0

IA R

a c b









  



     

 

2 2 2

2

1 1 4

0 ( 1 )

a b c R

a c b R do



     







    





     

2 2 2

2

1 1 4

0

a a a a

a c b R



      







    





2

2 12 18 0

0

a a

a c b R



  





    



2

6 9 0

0

a a

a c b R



  





    



3

a c

b

R

 





  









       

2 2 2

: 3 3 3 9

S x y z

      

.

Câu 14. (Kim Liên - Hà Nội – 2018) Trong không gian

Oxyz

, cho hai điểm

 

2;2;1

M

,

8 4 8

; ;

3 3 3

N



 

 

 

.

Viết phương trình mặt cầu có tâm là tâm của đường tròn nội tiếp tam giác

OMN

và tiếp xúc với

mặt phẳng

 

Oxz

.

A.

   

2 2

2

1 1 1

x y z

    

. B.

   

2 2

2

1 1 1

x y z

    

.

C.

   

2 2

2

1 1 1

x y z

    

. D.

   

2 2

2

1 1 1

x y z

    

.

Lời giải

Gọi

I

là tâm đường tròn nội tiếp tam giác

OMN

.

Ta áp dụng tính chất sau : “Cho tam giác

OMN

với

I

là tâm đường tròn nội tiếp, ta có

. . . 0

a IO b IM c IN

  

   

, với

a MN

,

b ON

,

c OM

”.

Ta có

2 2 2

2 2 1 3

OM

   

,

2 2 2

8 4 8

4

3 3 3

ON



     

   

     

     

.

2 2 2

8 4 8

2 2 1 5

3 3 3

MN



     

      

     

     

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15

8

5.0 4.2 3.

3

0

3 4 5

4

5.0 4.2 3.

3

5. 4. 3. 0 1

3 4 5

8

5.0 4.2 3.

3

1

3 4 5

I

x

IO IM IN y

z

 

 

 

 



 



 

 



 

 



 



 

     



 



 

 

 



 



 

 





   

.

Mặt phẳng

 

Oxz

có phương trình

0

y



.

Mặt cầu tiếp xúc với mặt phẳng

 

Oxz

nên mặt cầu có bán kính

 

, 1

R d I Oxz

 

.

Vậy phương trình mặt cầu là:

   

2 2

2

1 1 1

x y z

    

.

Câu 15. (Toán Học Tuổi Trẻ 2018) Trong không gian

Oxyz

, cho điểm

 

1;2; 2

H



. Mặt phẳng

 



đi

qua

H

và cắt các trục

Ox

,

Oy

,

Oz

tại

A

,

B

,

C

sao cho

H

là trực tâm tam giác

ABC

. Viết

phương trình mặt cầu tâm

O

và tiếp xúc với mặt phẳng

 



.

A.

2 2 2

81

x y z

  

. B.

2 2 2

1

x y z

  

. C.

2 2 2

9

x y z

  

. D.

2 2 2

25

x y z

  

.

Lời giải

Ta có

H

là trực tâm tam giác

ABC

 

OH ABC

 

.

Thật vậy :

OC OA

OC AB

OC OB





 







(1)

Mà

CH AB

(vì

H

là trực tâm tam giác

ABC

) (2)

Từ (1) và (2) suy ra

 

AB OHC



AB OH 

(*)

Tương tự

 

BC OAH



BC OH 

. (**)

Từ (*) và (**) suy ra

 

OH ABC



.

Khi đó mặt cầu tâm

O

tiếp xúc mặt phẳng

 

ABC

có bán kính

3

R OH

 

.

Vậy mặt cầu tâm

O

và tiếp xúc với mặt phẳng

 



là

 

2 2 2

: 9

S x y z

  

.

O

A

B

C

K

H

z

y

x

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 16 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu

16. (THPT Hai Bà Trưng - Huế - 2018) Trong không gian

Oxy

z

,

viết phương trình mặt cầu đi qua

điểm

 

1; 1;4

A 

và t

iếp xúc với các mặt phẳng tọa độ.

A.

     

2

2 2

3

3 3 16

x

y z



    

. B.

     

2

2 2

3

3 3 9

x

y z



    

.

C.

     

2

2 2

3

3 3 36

x

y z



    

. D.

     

2

2 2

3

3 3 49

x

y z



    

.

Lời giải

Gọi

 

;

;I a b c

là tâm của mặt cầu

 

S

. Mặt cầu

 

S

tiếp xúc với các mặt phẳng tọa độ

 

, , ,

d I Oxy d I Oyz d I Oxz

 

a b c R   

 

1

Mặt cầ

u

 

S

đi

qua

 

1

; 1;4

A 

0; 0; 0

IA R

a c b









  



2

0

; 0; 0

IA R

a c b











 



     

 

2 2 2

2

1

1 4

0 ( 1 )

a

b c R

a

c b R do



     







    





     

2

2 2

2

1 1 4

0

a a a a

a

c b R



      







    





2

12 18 0

0

a

a c b R





 







   



2

6

9 0

0

a

a c b R



  







   



3

a c

b

R

 







 









       

2 2 2

:

3 3 3 9

S

x y z



     

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương  https://www.facebook.com/phong.baovuong Trang 1

TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH GIỎI – MỨC 9-10 ĐIỂM

Dạng 1. Một số bài toán liên quan đến tiếp tuyến (tiếp xúc) mặt cầu

Câu 1. (Mã 102 - 2019) Trong không gian

Oxyz

, cho mặt cầu

 

2

2 2

: 2 3S x y z    . Có tất cả

bao nhiêu điểm

 

; ;A a b c

(

, ,a b c

là các số nguyên) thuộc mặt phẳng

 

Oxy

sao cho có ít nhất

hai tiếp tuyến của

 

S

đi qua

A

và hai tiếp tuyến đó vuông góc với nhau?

A.

8

. B.

16

. C.

12

. D.

4

.

Lời giải

Chọn C

Mặt cầu

 

S

có tâm

 

0;0; 2I và bán kính

3R 

;

 

A Oxy

 

; ;0A a b

.

* Xét trường hợp

 

A S

, ta có

2 2

1a b 

. Lúc này các tiếp tuyến của

 

S

thuộc tiếp diện của

 

S

tại

A

nên có vô số các tiếp tuyến vuông góc nhau.

Trường hợp này ta có 4 cặp giá trị của

 

;a b

là

0 0 1 1

; ; ;

1 1 0 0

a a a a

b b b b

     

   

   

    

   

.

* Xét trường hợp

A

ở ngoài

 

S

. Khi đó, các tiếp tuyến của

 

S

đi qua

A

thuộc mặt nón đỉnh

A

. Nên các tiếp tuyến này chỉ có thể vuông góc với nhau tại

A

.

Điều kiện để có ít nhất 2 tiếp tuyến vuông góc là góc ở đỉnh của mặt nón lớn hơn hoặc bằng

90

.

Giả sử

;A N A M

 

là các tiếp tuyến của

 

S

thỏa mãn

AN AM

(

;N M

là các tiếp điểm)

Dễ thấy

A NIM



là hình vuông có cạnh

3IN R 

và

3. 2 6IA



 

.

Điều kiện phải tìm là

6

IA R

IA IA











 





2 2

1

4

a b



 







 





Vì

,a b

là các số nguyên nên ta có các cặp nghiệm

 

;a b

là

               

0;2 , 0; 2 , 2;0 , 2;0 , 1;1 , 1; 1 , 1;1 , 1; 1     

.

Vậy có

12

điểm

A

thỏa mãn yêu cầu.

Câu 2. (Mã 104 - 2019) Trong không gian

Oxyz

, cho mặt cầu

   

2

2 2

: 1 5S x y z   

. Có tất cả bao

nhiêu điểm

 

, ,A a b c

(

, ,a b c

là các số nguyên) thuộc mặt phẳng

 

Oxy

sao cho có ít nhất hai tiếp

tuyến của

 

S

đi qua

A

và hai tiếp tuyến đó vuông góc với nhau?

A. 20 B. 8 C. 12 D. 16

PHƯƠNG TRÌNH MẶT CẦU

Chuyên đề 29

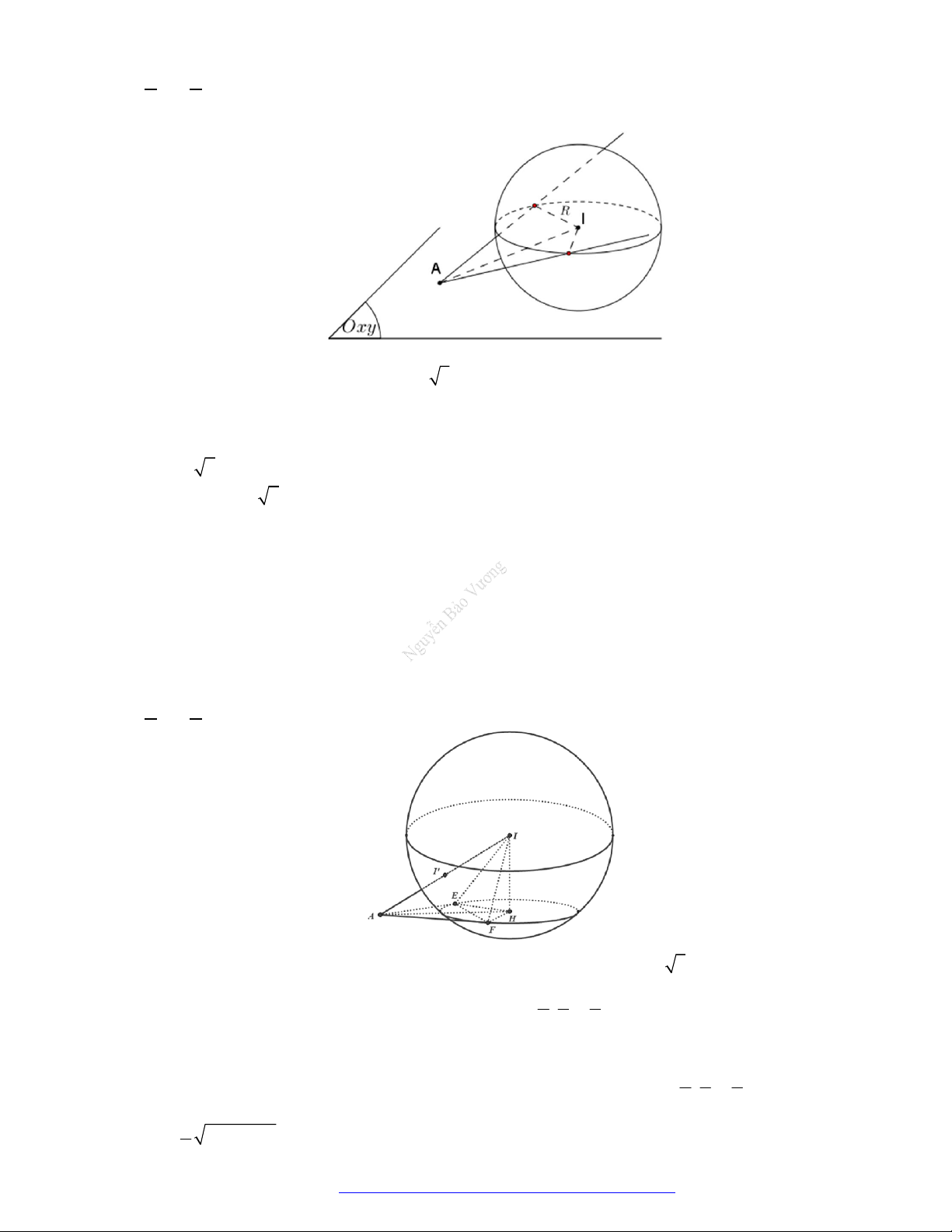
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Lời giải

Chọn A

Mặt cầu có tâm

 

0;0;1I

, bán kính

5R 

.

Vì

 

A Oxy

nên

0c 

. Các giao tuyến của

A

đến mặt cầu (nếu

IA R

) tạo nên một mặt nón

tâm

A

, để mặt nón này có hai đường sinh vuông góc thì góc của mặt nón này phải

90 

hay

2IA R

.

Vậy

2 2 2 2

2 5 1 10 4 9R IA R a b a b          

Ta có các bộ số thõa mãn

             

0; 2 ; 0; 3 ; 1; 2 ; 2; 2 ; 2; 1 ; 2;0 ; 3;0         

, 20 bộ số.

Câu 3. (Mã 103 - 2019) Trong không gian

Oxyz

, cho mặt cầu:

   

2

2 2

: 1 5S x y z   

. Có tất cả bao

nhiêu điểm

 

; ;A a b c

( , , a b c

là các số nguyên) thuộc mặt phẳng

 

Oxy

sao cho có ít nhất hai

tiếp tuyến của

 

S

đi qua

A

và hai tiếp tuyến đó vuông góc nhau?

A.

20

. B.

8

. C.

12

. D.

16

.

Lời giải

Chọn A

Mặt cầu

 

2 2 2

: ( 1) 5S x y z   

có tâm

 

0;0; 1I 

và có bán kính 5R 

   

; ;0A a b Oxy

, Gọi

I



là trung điểm của

1

; ;

2 2 2

a b

AI I

 



 

 

 

Gọi

,E F

lần lượt là hai tiếp điểm của tiếp tuyến đi qua

A

sao cho

AE AF

.

Ta có:

,E F

cùng thuộc mặt cầu

 

S



đường kính

IA

có tâm

1

; ;

2 2 2

a b

I

 





 

 

, bán kính

2 2

1

2

R a b



  

.

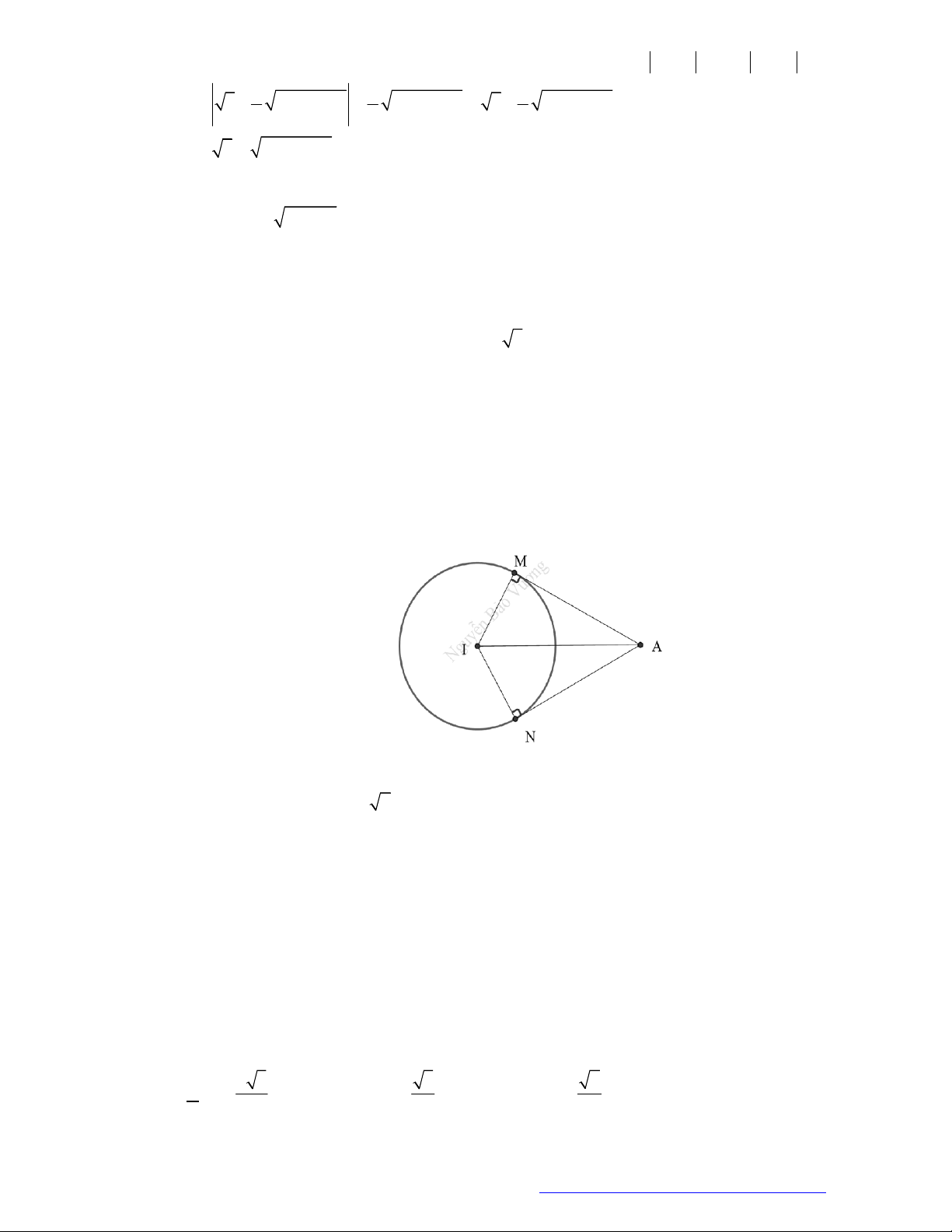
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3

Đề tồn tại

,E F

thì hai mặt cầu

 

S

và

 

S



phải cắt nhau suy ra

R R II R R

  

   

2 2 2 2 2 2

1 1 1

5 1 1 5 1

2 2 2

a b a b a b          

 

2 2 2 2

5 1 4 1a b a b      

Gọi

H

là hình chiếu của

I

trên

 

AEF

khi đó tứ giác

AEHF

là hình vuông có cạnh

2

5AE HF AI  

.

Ta có

 

2 2 2 2 2 2 2 2 2

5 5 10 0 1 10 9 2IH R HF AI AI a b a b              

Từ

 

1

và

 

2

ta có

2 2

4 9a b   mà

, , a b c  

nên có

20

điểm thỏa bài toán.

Cách khác:

Mặt cầu

 

S

có tâm

 

0,0, 1I 

bán kính 5R  . Ta có

 

1

I Oxy

d R  

mặt cầu

 

S

cắt mặt

phẳng

 

Oxy

. Để có tiếp tuyến của

 

S

đi qua

 

1A AI R 

.

Có

     

2 2

, , , ,0 , 1A a b c Oxy A a b IA a b    

.

Quỹ tích các tiếp tuyến đi qua

A

của

 

S

là một mặt nón nếu

AI R

và là một mặt phẳng nếu

AI R

.

Trong trường hợp quỹ tích các tiếp tuyến đi qua

A

của

 

S

là một mặt nón gọi

,AM AN

là hai

tiếp tuyến sao cho

, , ,A M I N

đồng phẳng.

Tồn tại ít nhất hai tiếp tuyến của

 

S

đi qua

A

và hai tiếp tuyến đó vuông góc với nhau khi và chỉ

khi



 

90 2 2

o

MAN IA R  

.

Từ

   

2 2

1 , 2 4 9a b   

. Vì

,a b 

2

0

9

a

b

















hoặc

2

9

0

a

b















hoặc

2

4

0

a

b















hoặc

2

0

4

a

b















hoặc

2

1

4

a

b















hoặc

2

4

1

a

b















hoặc

2

4

a

b















.

Bốn hệ phương trình đầu tiên có hai nghiệm, ba hệ sau có 4 nghiệm suy ra số điểm

A

thỏa mãn là

4.2 3.4 20 

.

Câu 4. (THPT Chuyên Ngữ - Hà Nội - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho mặt cầu

     

2 2

2

: 1 1 4S x y z    

và một điểm

 

2;3;1M

. Từ

M

kẻ được vô số các tiếp tuyến tới

 

S

, biết tập hợp các tiếp điểm là đường tròn

 

C

. Tính bán kính

r

của đường tròn

 

C

.

A.

2 3

3

r 

. B.

3

r 

. C.

2

3

r 

. D.

 

2

.

Lời giải

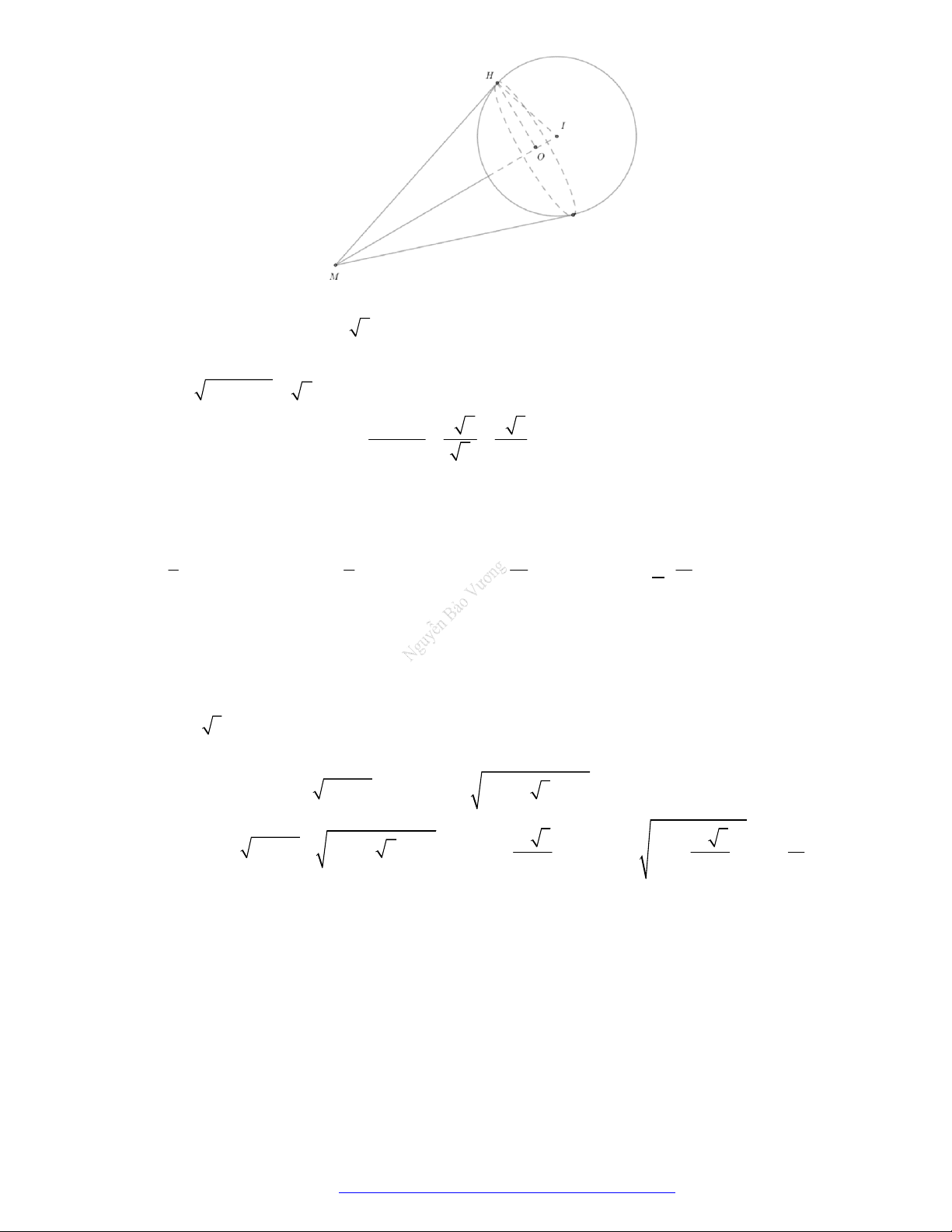
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Mặt cầu

 

S

có tâm

 

1;1;0I

và bán kính

2R 

.

Ta có

 

1;2;1IM 



và 6IM  .

Gọi

H

là một tiếp điểm tùy ý khi kẻ tiếp tuyến từ

Oxyz

đến mặt cầu, khi đó

2 2

2MH IM R  

. Gọi

O

là tâm của đường tròn

 

C

khi đó

IM HO

và

HO r

.

Ta có

. .HI HM HO IM

. 2 2 2 3

3

6

HI HM

r

IM

    .

Câu 5. (THPT Chuyên Hạ Long - 2018) Trong không gian, cho bốn mặt cầu có bán kính lần lượt là

2

,

3

,

3

,

2

(đơn vị độ dài) tiếp xúc ngoài với nhau. Mặt cầu nhỏ nhất tiếp xúc ngoài với cả bốn mặt

cầu nói trên có bán kính bằng

A.

5

9

. B.

3

7

. C.

7

15

. D.

6

11

.

Lời giải

Cách 1:

Gọi

, , ,A B C D

là tâm bốn mặt cầu, không mất tính tổng quát ta giả sử

4AB 

,

5AC BD AD BC   

. Gọi

,M N

lần lượt là trung điểm của

,AB CD

. Dễ dàng tính được

2 3MN  . Gọi

I

là tâm mặt cầu nhỏ nhất với bán kính

r

tiếp xúc với bốn mặt cầu trên. Vì

,IA IB IC ID 

nên

I

nằm trên đoạn

MN

.

Đặt

IN x

, ta có

2 2

3 3IC x r   

,

 

2

2 2 3 2IA x r    

Từ đó suy ra

 

2

2 2 2

12 3

3 2 2 2 1

11

x x x      

, suy ra

2

12 3 6

3 3

11 11

r

 

   

 

 

Cách 2

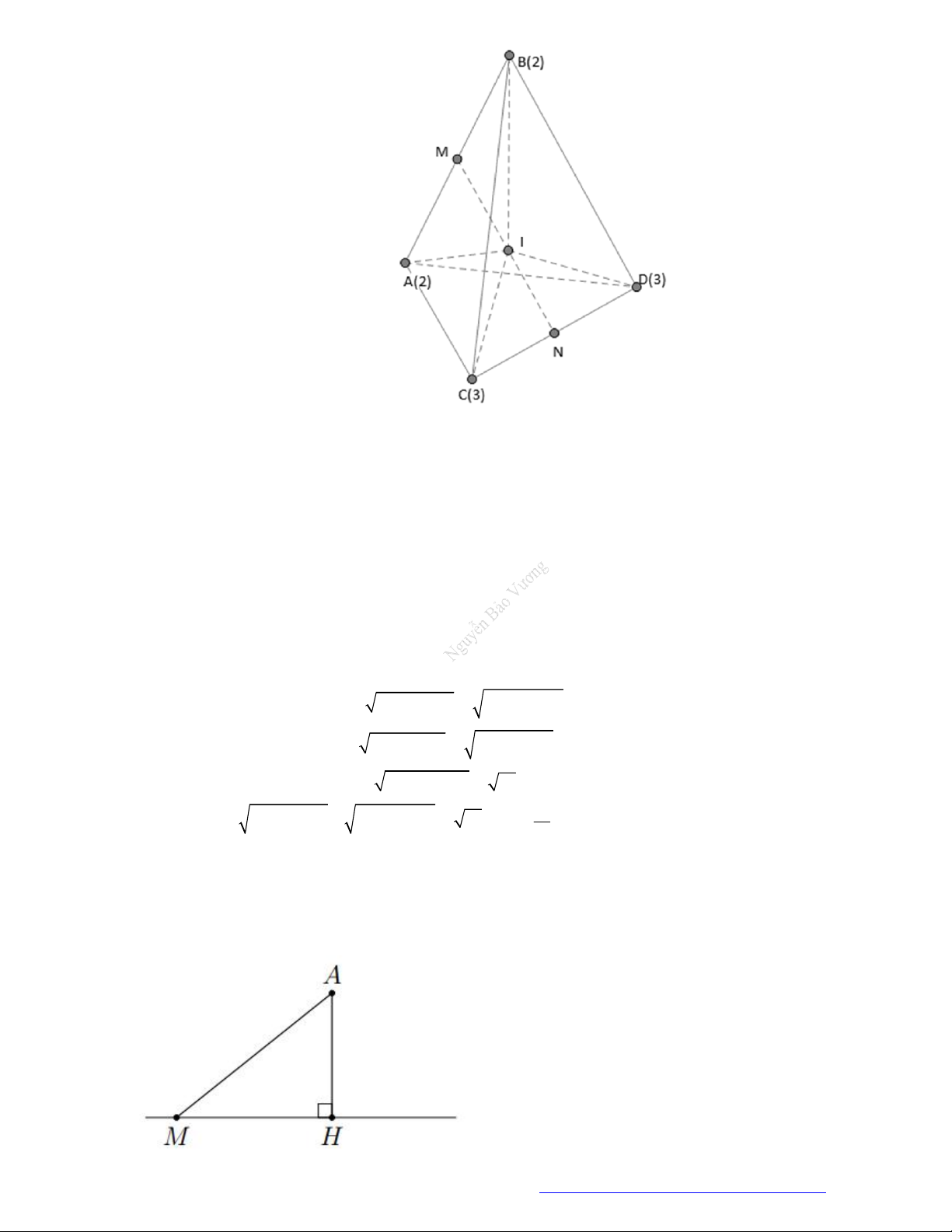
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5

Gọi

,A B

là tâm quả cầu bán kính bằng

2

.

,C D

là tâm quả cầu bán kính bằng

3

.

I

là tâm quả

cầu bán kính

x

.

Mặt cầu

 

I

tiếp xúc ngoài với

4

mặt cầu tâm

, , ,A B C D

nên

2, 3IA IB x IC ID x     

.

Gọi

 

P

,

 

Q

lần lượt là các mặt phẳng trung trực đoạn

AB

và

CD

.

 

     

1

IA IB I P

I P Q

IC ID I Q

  





  



  





.

Tứ diện

ABCD

có

5DA DB CA CB   

suy ra

MN

là đường vuông góc chung của

AB

và

CD

, suy ra

   

MN P Q 

(2).

Từ

 

1

và

 

2

suy ra

I MN

Tam giác

IAM

có

 

2

2 2

2 4IM IA AM x    

.

Tam giác

CIN

có

 

2

2 2

3 9IN IC CN x    

.

Tam giác

ABN

có

2 2

12NM NA AM  

.

Suy ra

   

2 2

6

3 9 2 4 12

11

x x x       

.

Dạng 2. Bài toán cực trị

1. Một số bất đẳng thức cơ bản

Kết quả 1. Trong một tam giác, cạnh đối diện với góc lớn thì lớn hơn

Kết quả 2. Trong các đường xiên và đường vuông góc kẻ từ một điểm nằm ngoài đường thẳng đến đường

thẳng đó thì đường vuông góc là đường ngắn nhất. Như trong hình vẽ ta luôn có

AM AH

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Kết quả 3. Với ba điểm

, ,A B C

bất kì ta luôn có bất đẳng thức

.AB BC AC 

Tổng quát hơn ta có bất đẳng thức của đường gấp khúc: Với

n

điểm

1 2

, ,....

n

A A A ta luôn có

1 2 2 3 1 1

...

n n n

A A A A A A A A



   

Kết quả 4. Với hai số không âm

,x y

ta luôn có

2

x y

xy





. Đẳng thức xảy ra khi và chỉ khi

x y

Kết quả 5. Với hai véc tơ

,a b

 

ta luôn có . .a b a b

   

. Đẳng thức xảy ra khi

,a kb k 

 



2. Một số bài toán thường gặp

Bài toán 1. Cho điểm

A

cố định và điểm

M

di động trên hình

 

H

(

 

H

là đường thẳng, mặt phẳng). Tìm

giá trị nhỏ nhất của

AM

Lời giải: Gọi

H

là hình chiếu vuông góc của

A

lên hình

 

H

. Khi đó, trong tam giác

AHM

Vuông tại .

M

ta có

.AM AH

Đẳng thức xảy ra khi

M H

. Do đó

AM

nhỏ nhất khi

M

là hình chiếu của

A

lên

 

H

Bài toán 2. Cho điểm

A

và mặt cầu

 

S

có tâm

,I

bán kính

,R

M

là điểm di động trên

 

S

. Tìm giá trị

nhỏ nhất và giá trị lớn nhất của

AM

.

Lời giải. Xét

A

nằm ngoài mặt cầu

( ).S

Gọi

1 2

,M M lần lượt là giao điểm của đường thẳng

AI

với mặt

cầu

 

1 2

( )S AM AM

và

( )



là mặt phẳng đi qua

M

và đường thẳng

.AI

Khi đó

( )



cắt

( )S

theo một

đường tròn lớn

( ).C

Ta có



1 2

90 ,M MM



 nên



2

AMM và



1

AM M là các góc tù, nên trong các tam giác

1

AMM và

2

AMM ta có

1 2

AI R AM AM AM AI R     

Tương tự với

A

nằm trong mặt cầu ta có

R AI AM R AI   

Vậy

min | |,maxAM AI R AM R AI   

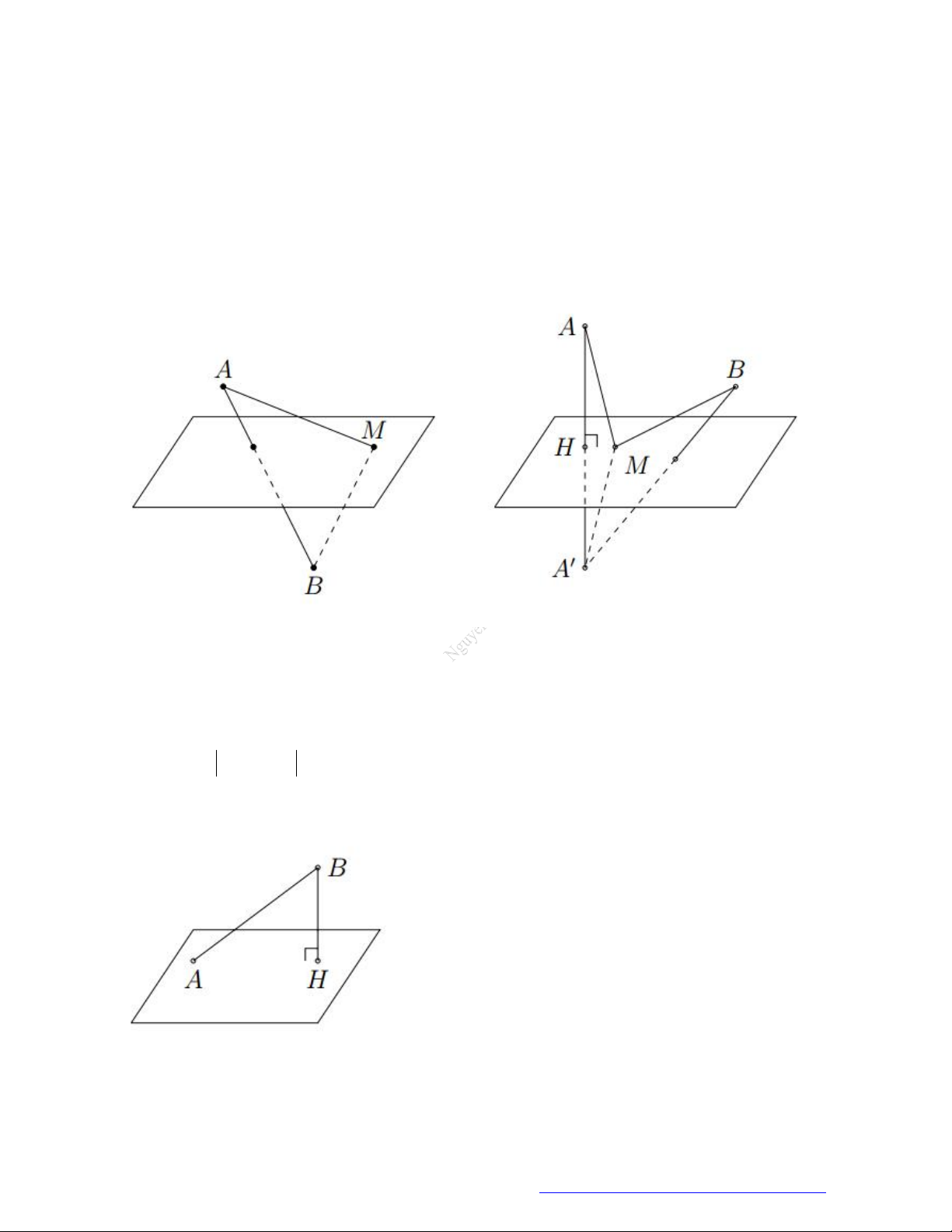
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7

Bài toán 3. Cho măt phẳng

( )P

và hai điểm phân biệt

, .A B

Tìm điể

M

thuộc

( )P

sao cho

1.

MA MB

nhỏ nhất.

2.

| |MA MB

lớn nhất.

Lời giải.

1. Ta xét các trường hợp sau

- TH 1: Nếu

A

và

B

nằm về hai phía so với

( )P

. Khi đó

AM BM AB 

Đẳng thức xảy ra khi

M

là giao điểm của

AB

với

( )P

.

- TH 2: Nếu

A

và

B

nằm cùng một phía so với

( )P

. Gọi A



đối xứng với

A

qua

( )P

. Khi đó

AM BM A M BM A B

 

   

Đẳng thức xảy ra khi

M

là giao điểm của A B



với

( )P

.

2. Ta xét các trường hợp sau

- TH 1: Nếu

A

và

B

nằm cùng một phía so với

( )P

. Khi đó

| |AM BM AB 

Đẳng thức xảy ra khi

M

là giao điểm của

AB

với

( )P

.

- TH 2: Nếu

A

và

B

nằm khác phía so với

( )P

. Gọi

'A

đối xứng với

A

qua

 

P

, Khi đó

| |AM BM A M BM A B

 

   

Đẳng thức xảy ra khi

M

là giao điểm của

A B



với

( )P

.

Bài toán 4. Viết phương trinh măt phẳng

( )P

di qua

A

và cách

B

một khoảng lớn nhất.

Lời giải. Gọi

H

là hình chiếu của

B

lên mặt phẳng

( ),P

khi đó

d( ,( ))B P BH BA 

Do đó

 

P

là mặt phẳng đi qua

A

vuông góc với

AB

Bài toán 5. Cho các số thực dương

,

 

và ba điểm

, ,A B

C. Viết phương trình măt phẳng

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 8 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

( )P

đi qua

C

và

d( ,( )) d( ,( ))T A P B P

 

 

nhỏ nhất.

Lời giải.

1. Xét

,A B

nằm về cùng phía so với

( )P

.

- Nếu ( )AB P‖ thì

( )d( ,( )) ( )P A P AC

   

   

- Nếu đường thẳng

AB

cắt

( )P

tại

.I

Gọi

D

là điểm thỏa mãn IB ID







 

và

E

là trung điểm

.BD

Khi đó

d( ,( )) d( ,( )) 2 d( ,( )) 2( )

IB

P A P D P E P EC

ID

    

      

2. Xét

,A B

nằm về hai phía so với

( )P

. Gọi

I

là giao điểm của

AB

và ( ),P B



là điểm đối xứng với

B

qua

I

. Khi đó

 

d( ,( )) d ,( )P A P B P

 



 

Đến đây ta chuyển về trường hợp trên.

So sánh các kết quả ở trên ta chọn kết quả lớn nhất.

Bài toán 6. Trong không gian cho

n

điểm

1 2

, , ,

n

A A A và diểm

.A

Viết phương trình mặt phẳng

( )P

đi

qua

A

và tổng khoảng cách từ các điểm

( 1,

i

A i n

) lớn nhất.

Lời giải.

- Xét

n

điểm

1 2

, , ,

n

A A A nằm cùng phía so với

( ).P

Gọi

G

là trọng tâm của

n

điểm đã cho. Khi đó

 

1

d ,( ) d( ,( ))

n

i

A P n G P nGA



 



- Trong

n

điểm trên có

m

điểm nằm về một phía và

k

điểm nằm về phía khác

(m k n 

). Khi đó, gọi

1

G

là trọng tâm của

m

điểm,

2

G là trọng tâm của

k

điểm

3

G đối xứng với

1

G qua

.A

Khi dó

   

3 2

md ,( ) d ,( )P G P k G P 

Đến đây ta chuyển về bài toán trên.

Bài toán 7.Viết phương trình mặt phẳng

 

P

đi qua đường thẳng



và cách

A

một khoảng lớn nhất

Lời giải. Gọi

,H K

lần lượt là hình chiếu của

A

lên mặt phẳng

( )P

và đường thẳng

.

Khi đó

d( ,( ))A P AH AK 

Do đó

( )P

là mặt phẳng đi qua

K

và vuông góc vói

.AK

Bài toán 8. Trong không gian

Oxyz,

cho các điểm

1 2

, , , .

n

A A A Xét véc tơ

1 1 2 2 n n

w MA M A M A

  

   

  





Trong đó

1 2

; ...

n

  

là các số thực cho trước thỏa mãn

1 2

... 0

n

  

    . Tìm điểm

M

thuôc măt phẳng

( )P

sao cho

| |w



có đô dài nhỏ nhất.

Lời giải. Gọi

G

là điểm thỏa mãn

1 1 2 2

0

n n

GA GA GA

  

   

   



(điểm

G

hoàn toàn xác định).

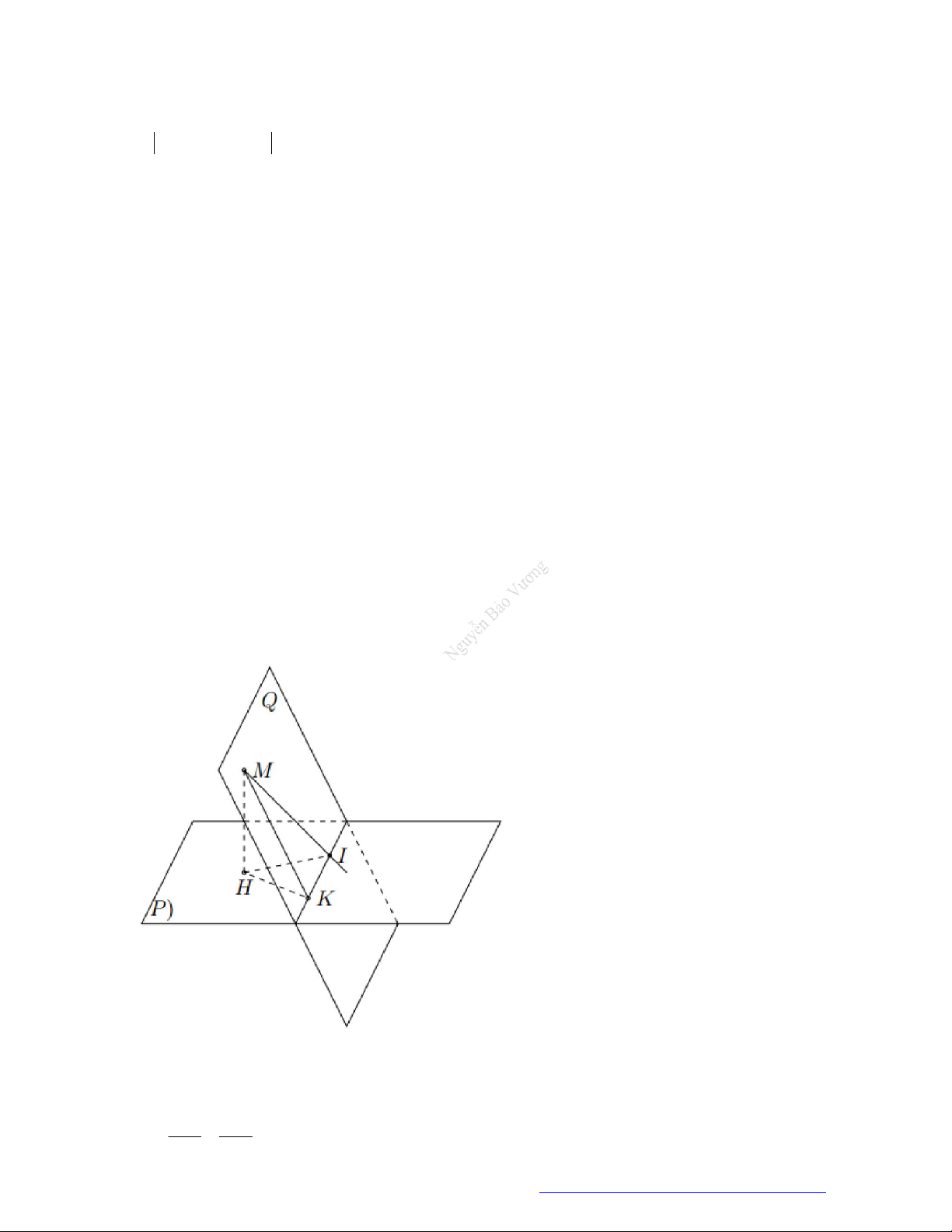
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9

Ta có

k

MA MG GA 





vói

1;2; ; ,k n 

nên

   

1 2 1 1 2 2 1 2

w

n n n n

MG GA GA GA MG

        

         

 

  





Do đó

1 2

| | | |

n

w MG

  

    





Vi

1 2 n

  

   là hằng số khác không nên

| |w



có giá trị nhỏ nhất khi và chỉ khi

MG

nhỏ nhất, mà

( )M P

nên điểm

M

cần tìm là hình chiếu của

G

trên mặt phẳng

( )P

.

Bài toán 9. Trong không gian Oxy

,z

cho các diểm

1 2

, , , .

n

A A A Xét biểu thức:

2 2 2

1 1 2 2 n n

T MA MA MA

  

   

Trong đó

1 2

, , ,

n

  

 là các số thực cho trước. Tìm điểm M thuộc măt phẳng

( )P

sao cho

1.

T

giá trị nhỏ nhất biết

1 2

0

n

  

   .

2. T có giá trị lớn nhất biết

1 2

0

n

  

   .

Lời giải. Gọi

G

là điểm thỏa mãn

1 1 2 2

0

n n

GA GA GA

  

   

   



Ta có

k

MA MG GA 





với

1;2; ; ,k n 

nên

 

2

2 2 2

2

k k k k

MA MG GA MG MG GA GA     

 

 

Do đó

 

2 2 2 2

1 2 1 1 2 2n n n

T MG GA GA GA

     

      

Vì

2 2 2

1 1 2 2 n n

GA GA GA

  

  

không đổi nên

•

với

1 2

0

n

  

   thì

T

đạt giá trị nhỏ nhất khi và chỉ khi

MG

nhỏ nhất.

•

với

1 2

0

n

  

   thì

T

đạt giá trị lớn nhất khi và chỉ khi

MG

nhỏ nhất.

Mà

( )M P

nên

MG

nhỏ nhất khi điểm

M

là hình chiếu của

G

trên mặt phẳng

( )P

.

Bài toán 10. Trong không gian Oxyz, cho đường thẳng d và mặt phẳng

( )P

cắt nhau. Viết phương trình của

mặt phẳng

( )Q

chứa

d

và tạo với mặt phẳng

( )P

một góc nhỏ nhất.

Lời giải. Gọi

I

là giao điểm của đường thẳng

d

với mặt phẳng

( )P

và lấy điểm

,M d M I 

. Gọi

,H K

lầ lượt là hình chiếu của

M

lên

( )P

và giao tuyến



của

( )P

và

( )Q

.

Đặt



là góc giữa

( )P

và

( ),Q

ta có



,MKH





do đó

tan

HM HM

HK HI



 

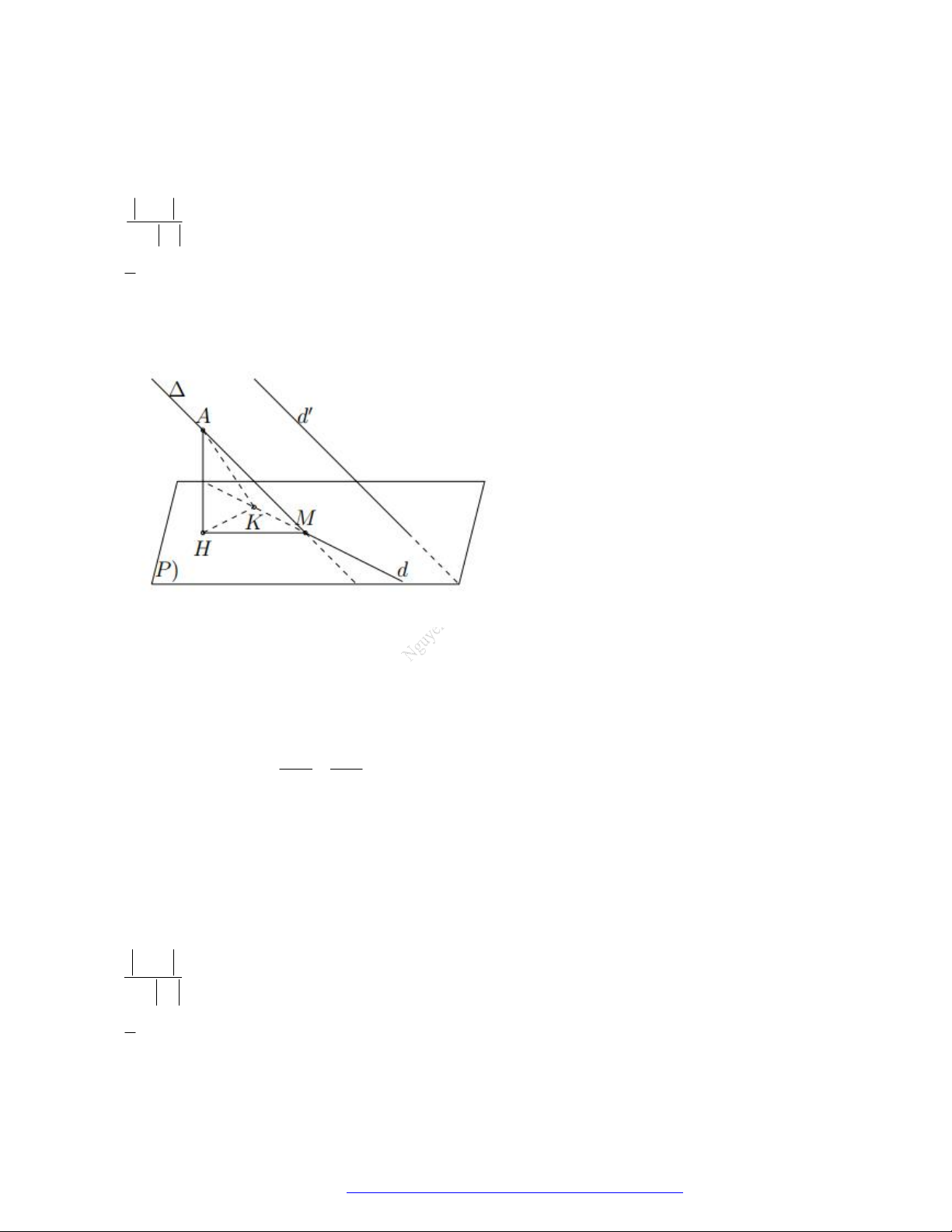
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 10 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Do đó

( )Q

là mặt phẳng đi qua

d

và vuông góc với mặt phẳng

( ),MHI

nên

( )Q

đi qua

M

và nhận

 

P d d

n u u 

  

làm VTPT.

Chú ý. Ta có thể giải bài toán trên bằng phương pháp đai số như sau:

- Goi

2 2 2

( ; ; ), 0n a b c a b c   



là một VTPT của mặt phẳng

( ).Q

Khi đó 0

d

n u 

 

từ đây ta rút được

a

theo

,b c

(hoặc

b

theo

,a c

hoặc

c

theo

,a b

).

- Gọi



là góc giữa

( )P

và

( ),Q

ta có

cos ( )

| |

P

n n

f t

n n





 



 

với

, 0.

b

t c

c

 

Khảo sát

( )f t

ta tìm được max của

( )f t

Bài toán 11. Trong không gian Oxyz, cho hai đường thẳng

d

và

d



chéo nhau. Viết phương trinh mặt

phẳng

( )P

chứa

d

và tạo với

d



một góc lớn nhất.

Lời giải. Trên đường thẳng

d

, lấy điểm

M

và dựng đường thẳng



đi qua

M

song song với

d



. Khi đó

góc giữa



và

( )P

chính là góc giữa

d



và

( )P

.

Trên đường thẳng



, lấy điểm

A

. Gọi

H

và

K

lần lượt là hình chiếu của

A

lên

( )P

và

,d



là góc giữa



và

( )P

.

Khi đó



AMH





và

cos

HM KM

AM AM



 

Suy ra

( )P

là mặt phẳng chứa

d

và vuông góc với mặt phẳng

( ).AMK

Do dó

( )P

đi qua

M

và nhận

 

d d

d

u u u



 

  

làm VTPT.

Chú ý. Ta có thể giải bài toán trên bằng phương pháp đại số như sau:

- Goi

2 2 2

( ; ; ), 0n a b c a b c   



là một VTPT của măt phẳng

( ).P

Khi đó 0

d

n u 

 

từ đây ta rút được

a

theo

,b c

(hoặc

b

theo

,a c

hoặc

c

theo

,a b

).

- Gọi



là góc giữa

( )P

và ,d



ta có

sin ( )

| |

d

n u

f t

n u







 



 

với

, 0.

b

t c

c

 

Khảo sát

( )f t

ta tìm được max của

( )f t

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11

Câu 6. (THPT Nguyễn Khuyến 2019) Trong không gian với hệ trục

Oxyz

, cho các điểm

   

1;2;3 , 6; 5;8

A B 

và

. .OM a i b k

 

  

trong đó

,a b

là cá số thực luôn thay đổi. Nếu

2

MA MB



 

đạt giác trị nhỏ nhất thì giá trị

a b

bằng

A.

25

B.

13

C.

0

D.

26

Lời giải

Chọn C

Ta có:

 

. . ;0;OM a i b k M a b

  

  

     

1 a;2;3 ; 6 ; 5;8 2 12 2 ;10; 16 2MA b MB a b MB a b

              

  

 

2 13;12; 13

MA MB a b    

 

   

2 2

2

2 13 12 13 12

MA MB a b

       

 

Vậy

min

13

2 12

13

a

MA MB

b





  







 

. Do đó

0

a b

 

Câu 7. (Sở Hà Nội 2019) Trong không gian

Oxyz

, cho hai điểm

 

1;2;1

A

;

 

2; 1;3

B 

và điểm

 

; ;0

M a b

sao cho

2 2

MA MB

nhỏ nhất. Giá trị của

a b

là

A.

2

. B.

2

. C.

3

. D.

1

.

Lời giải

Ta thấy

   

; ;0

M a b Oxy



.

Gọi

3 1

; ;2

2 2

I

 

 

 

là trung điểm của đoạn thẳng

AB

, ta có

2 2

MA MB MA MB  

 

   

2 2

IA IM IB IM

   

   









2 2 2 2

2 . 2 .

IA IM IA IM IB IM IB IM

     

       

 

2

2 2 2 2

2 2 7

2

AB

IM IA IM IA IB IM IM

       

  

.

Bởi vậy

2 2

MA MB

nhỏ nhất



IM

ngắn nhất



M

là hình chiếu vuông góc của

I

trên mặt

phẳng

 

Oxy

. Bởi vậy

3 1

; ;0

2 2

M

 

 

 

. Như vậy

3 1 3 1

, 2

2 2 2 2

a b a b

      

.

Câu 8. (THPT Gang Thép Thái Nguyên 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho

4

điểm

 

2;4; 1

A



,

 

1;4; 1

B



,

 

2;4;3

C

,

 

2;2; 1

D



, biết

 

; ;M x y z

để

2 2 2 2

MA MB MC MD

  

đạt giá trị nhỏ nhất thì

x y z 

bằng

A.

6

. B.

21

4

. C.

8

. D.

9

.

Lời giải

Xét điểm

 

; ;I a b c

thỏa mãn

0

IA IB IC ID

   

    

. Khi đó

7 7

; ;0

4 2

I

 

 

 

.

Ta có

2 2 2 2

MA MB MC MD

  

       

2 2 2 2

MI IA MI IB MI IC MI ID

       

       

 

2 2 2 2 2

4 2

MI MI IA IB IC ID IA IB IC ID

        

    

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 12 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

2 2 2 2 2 2 2 2 2

4

MI IA IB IC ID IA IB IC ID

        

( vì

2

0

MI



với mọi điểm

M

)

Dấu

" "

xảy ra

M I 

tức là

7 7 7 7

; ;0

4 2 4 2

M x y z

 

    

 

 

21

4



.

Câu 9. Trong không gian

Oxyz

, cho hai điểm

 

1;2;1

A

,

 

2; 1;3

B 

,

 

3;1; 5

C



. Tìm điểm

M

trên mặt phẳng

 

Oyz

sao cho

2 2 2

2

MA MB MC

 

lớn nhất.

A.

3 1

; ;0

2 2

M

 

















 

. B.

1 3

; ;0

2 2

M

 



















 

. C.

 

0;0;5

M

. D.

 

3; 4; 0

M



.

Lời giải

Gọi điểm

E

thỏa

2 0EA EB 

 



. Suy ra

B

là trung điểm của

AE

, suy ra

 

3; 4; 5

E



.

Khi đó:

2 2

2MA MB 

   

2 2

2

ME EA ME EB

  

   

2 2 2

2ME EA EB   

.

Do đó

2 2

2MA MB

lớn nhất



ME

nhỏ nhất



M

là hình chiếu của

 

3; 4; 5

E



lên

 

Oxy

 

3; 4; 0

M

 

.

Chú ý: Ta có thể làm trắc nghiệm như sau

+ Loại C vì

 

0;0; 5

M

không thuộc

 

Oxy

.

+ Lần lượt thay

3 1

; ;0

2 2

M

 

















 

,

1 3

; ;0

2 2

M

 



















 

,

 

3; 4; 0

M



vào biểu thức

2 2

2MA MB

thì

 

3; 4; 0

M



cho giá trị lớn nhất nên ta chọn

 

3; 4; 0

M



.

Câu 10. (THPT Nghĩa Hưng Nđ- 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho tam giác

ABC

với

 

2;1;3

A

,

 

1; 1;2

B 

,

 

3; 6;1

C 

. Điểm

 

; ;M x y z

thuộc mặt phẳng

 

Oyz

sao cho

2 2 2

MA MB MC

 

đạt giá trị nhỏ nhất. Tính giá trị biểu thức

P x y z  

.

A.

0

P



. B.

2P 

. C.

6

P



. D.

2P  

.

Lời giải

Gọi

I

là điểm thỏa

0

IA IB IC

  

   

 

2; 2;2

I 

.

2 2 2

MA MB MC

 

     

2 2 2

MI IA MI IB MI IC

     

     

 

2 2 2 2

3 2 .

MI IA IB IC MI IA IB IC

      

   

2 2 2 2

3

MI IA IB IC

   

.

Mà

 

M Oyz



2 2 2

MA MB MC

  

đạt giá trị nhỏ nhất



M

là hình chiếu của

I

lên

 

Oyz

 

0; 2;2

M 

.

Vậy

0 2 2 0

P

   

.

Câu 11. Trong không gian với hệ tọa độ

Oxyz

, cho ba điểm

     

4;2;2 , 1;1; 1 , 2; 2; 2

A B C

  

. Tìm tọa

độ điểm

M

thuộc mặt phẳng

 

Oyz

sao cho

2

MA MB MC

 

  

nhỏ nhất

A.

 

2;3;1

M

. B.

 

0;3;1

M

. C.

 

0; 3;1

M 

. D.

 

0;1;2

M

.

Lời giải

Gọi

 

; ;I x y z

là điểm thỏa

2 0

IA IB IC

  

   

.

Khi đó

     

2 0 2 0

IA IB IC OA OI OB OI OC OI

         

          

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13

 

   

1

2 2;3;1 2;3;1

2

OI OA OB OC I     

   

.

Ta có

     

2 2

MA MB MC MI IA MI IB MI IC

       

        

2 2 2 2MI IA IB IC MI MI

     

    

.

2

MA MB MC

 

  

nhỏ nhất khi và chỉ khi

MI

ngắn nhất, khi đó

M

là hình chiếu của

 

2;3;1

I

lên mặt phẳng

 

Oyz

. Suy ra

 

0;3;1

M

.

Câu 12. (Chuyên Lê Quý Đôn - Đà Nẵng - 2018) Trong không gian với hệ trục tọa độ

Oxyz

, cho bốn

điểm

 

2; 3;7

A 

,

 

0;4;1

B

,

 

3;0;5

C

và

 

3;3;3

D

. Gọi

M

là điểm nằm trên mặt phẳng

 

Oyz

sao cho biểu thức

MA MB MC MD

  

   

đạt giá trị nhỏ nhất. Khi đó tọa độ của

M

là:

A.

 

0;1; 4

M



. B.

 

2;1;0

M

. C.

 

0;1; 2

M



. D.

 

0;1;4

M

.

Lời giải

Ta có:

 

2;7; 6

AB

  



,

 

1;3; 2

AC

 



,

 

1;6; 4

AD

 



nên

, . 4 0

AB AC AD

 

  

 

  

.

Suy ra:

AB



,

AC



,

AD



không đồng phẳng.

Gọi

G

là trọng tâm tứ diện

ABCD

. Khi đó

 

2;1;4

G

.

Ta có:

4 4

MA MB MC MD MG MG

    

    

.

Do đó

MA MB MC MD

  

   

nhỏ nhất khi và chỉ khi

MG

ngắn nhất.

Vậy

M

là hình chiếu vuông góc của

G

lên mặt phẳng

 

Oyz

nên

 

0;1;4

M

.

Câu 13. (Toán Học Tuổi Trẻ - 2018) Trong không gian cho ba điểm

 

1;1;1

A

,

 

1;2;1

B 

,

 

3;6; 5

C



.

Điểm

M

thuộc mặt phẳng

Oxy

sao cho

2 2 2

MA MB MC

 

đạt giá trị nhỏ nhất là

A.

 

1;2;0

M

. B.

 

0;0; 1

M



. C.

 

1;3; 1

M



. D.

 

1;3;0

M

.

Lời giải

Lấy

 

1;3; 1

G



là trọng tâm của tam giác

ABC

.

Ta có:

2 2 2

MA MB MC

 

     

2 2 2

MG GA MG GB MG GC

     

     

2 2 2 2

3

MG GA GB GC

   

.

Do đó

2 2 2

MA MB MC

 

bé nhất khi

MG

bé nhất.

Hay

M

là hình chiếu của điểm

G

lên mặt phẳng

Oxy

.

Vậy

 

1;3;0

M

.

Câu 14. (Lê Quý Đôn - Hải Phòng - 2018) Trong không gian với hệ tọa độ

Oxyz

cho

 

3;2;1

A

,

 

2;3;6

B 

. Điểm

 

; ;

M M M

M x y z

thay đổi thuộc mặt phẳng

 

Oxy

. Tìm giá trị của biểu thức

M M M

T x y z  

khi

3

MA MB



 

nhỏ nhất.

A.

7

2



. B.

7

2

. C.

2

. D.

2

.

Lời giải

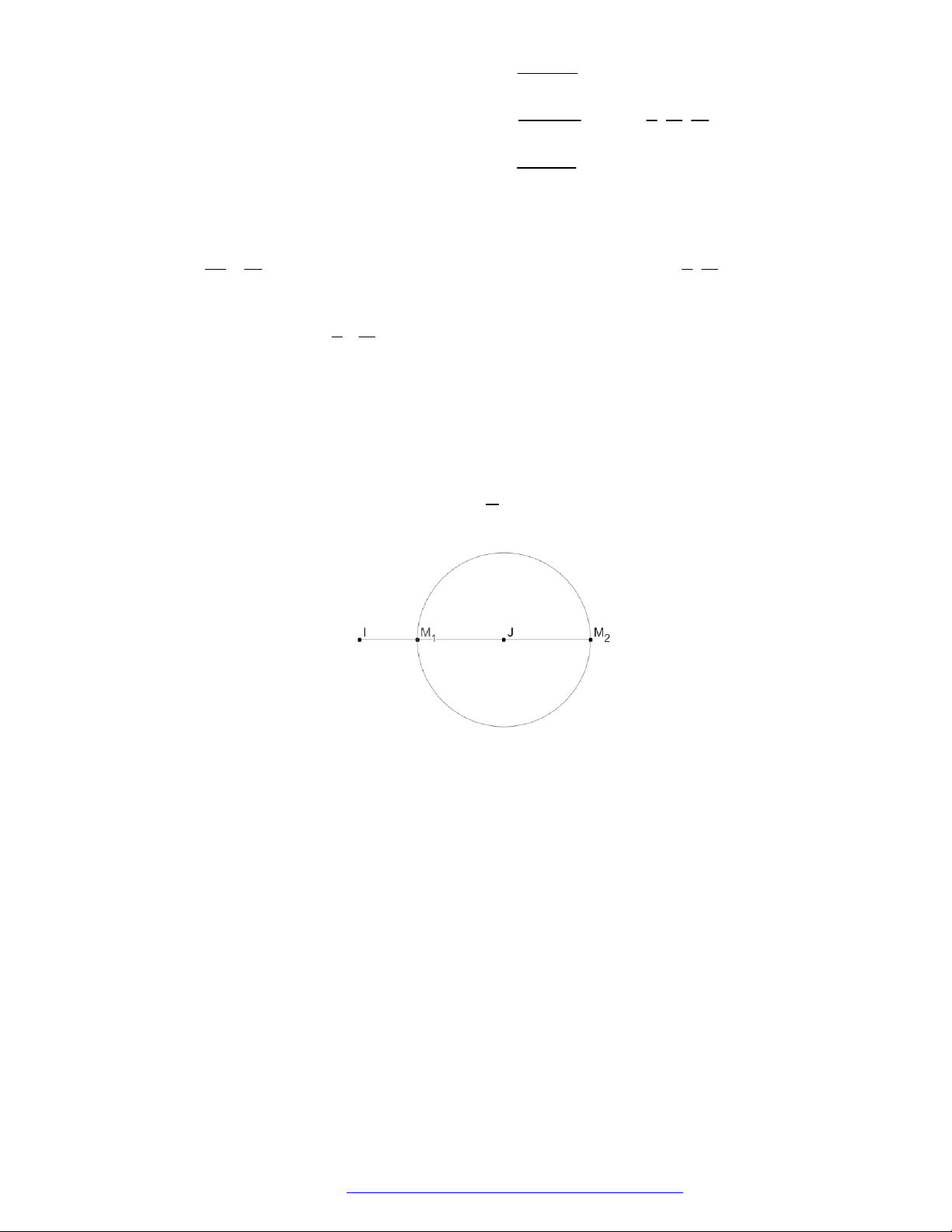
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 14 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Gọi điểm

H

thỏa mãn

3 0HA HB 

  

khi đó:

3

1 3

3

1 3

3

1 3

A B

H

A B

H

A B

H

x x

x

y y

y

z z

z





































3 11 19

; ;

4 4 4

H

 

 

 

 

.

Phương trình mặt phẳng

 

Oxy

là

0z 

.

Xét

19

1 4

H

z

T  

do đó tọa độ điểm

M

cần tìm là:

M H

x x aT

y y bT

z z cT

 





 





 



3 11

; ;0

4 4

M

 

 

 

 

.

Vậy

M M M

T x y z  

3 11

0 2

4 4

    

.

Câu 15. (Chuyen Phan Bội Châu Nghệ An 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho mặt

cầu

2 2 2

( ) :( 1) ( 2) ( 1) 9S x y z     

và

hai điểm

(4;3;1)A

,

(3;1;3)B

;

M

là điểm thay đổi trên

( )S

. Gọi

,m n

lần lượt là giá trị lớn

nhất và giá trị nhỏ nhất của biểu thức

2 2

2P MA MB 

. Xác định

( )m n

.

A.

64

. B.

68

. C.

60

. D.

48

.

Lời giải

Gọi

I

là điểm thỏa mãn

2 0IA IB 

  

(2 ;2 ;2 )

A B A B A B

I x x y y z z   

(5;5; 1)I 

.

Suy ra

I

là điểm cố định.

Suy ra P đạt giá trị nhỏ nhất khi

MI

đạt giá trị nhỏ nhất, P đạt giá trị lớn nhất khi

MI

đạt giá trị

lớn nhất.

2 2 2

( ) :( 1) ( 2) ( 1) 9S x y z     

có tâm

(1;2; 1)J 

và bán kính

3R 

Suy ra

5IJ 

Mà

M

là điểm thay đổi trên

( )S

Do đó:

min

1

5 3 2MI IM JI R     

max

2

5 3 8MI IM JI R     

Suy ra

2 2

8 2 60m n   

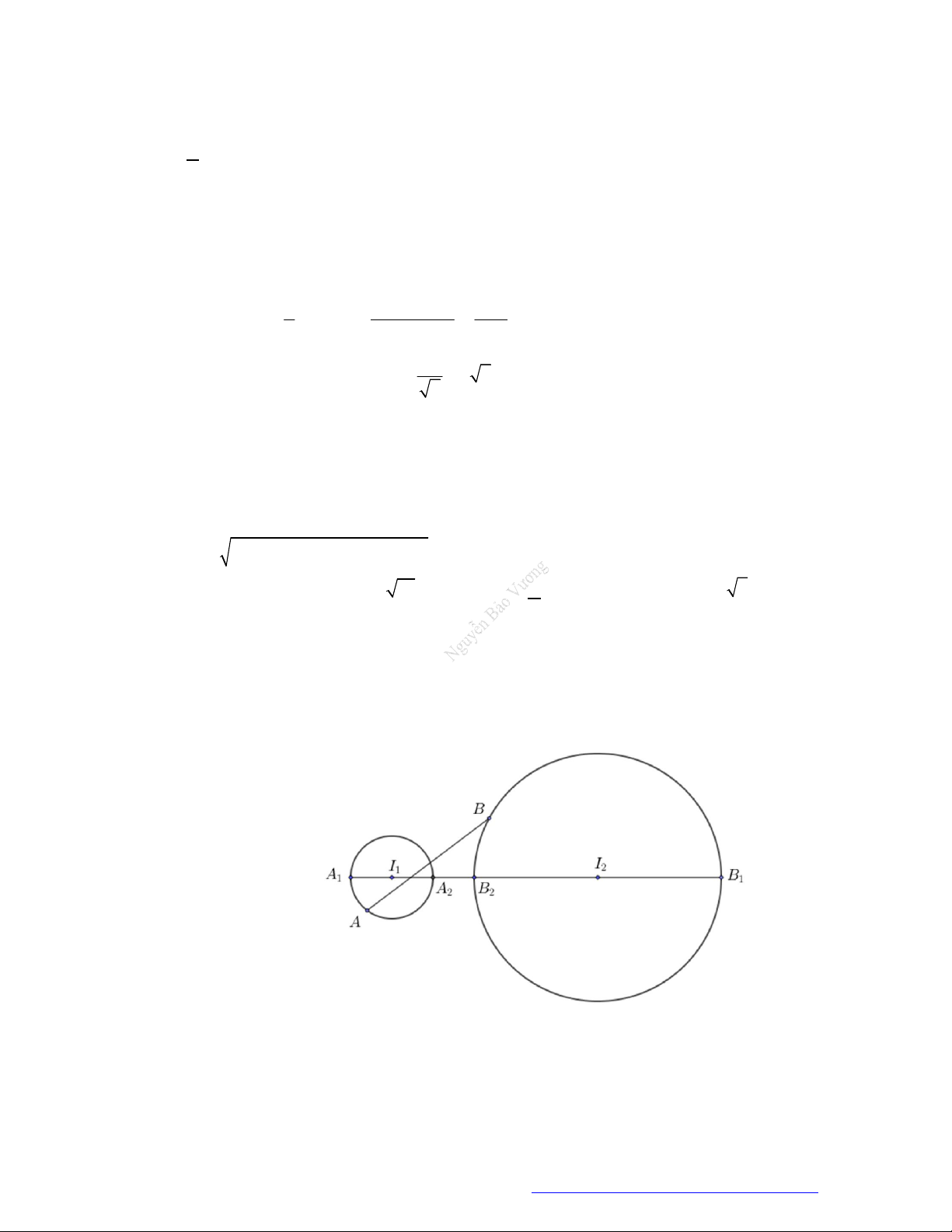
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15

Câu 16. (Chuyên Vĩnh Phúc - 2018) Trong không gian với hệ trục tọa độ

Oxyz

, cho mặt cầu

 

S

có

phương trình là

2 2 2

2 2 6 7 0x y z x y z       . Cho ba điểm

A

,

M

,

B

nằm trên mặt cầu

 

S

sao cho



90AMB   . Diện tích tam giác

AMB

có giá trị lớn nhất bằng?

A.

4

. B.

2

. C.

4

. D. Không tồn tại.

Lời giải

Ta có

       

2 2 2

: 1 1 3 4S x y z     

 

S

có tâm

 

1;1;3I

và bán kính

2R 

.

Bài ra

A

,

M

,

B

nằm trên mặt cầu

 

S

và



90AMB  

AB

qua

2 4I AB R  

.

Ta có

1

.

2

AMB

S MA MB

2 2

4

MA MB



2

4

AB

  .

Dấu

" "

xảy ra

2 2

2

AB

MA MB   

và

4AB 

.

Do đó diện tích tam giác

AMB

có giá trị lớn nhất bằng

4

.

Câu 17. (Phan Đình Phùng - Hà Tĩnh - 2018) Cho

, , , , ,a b c d e f

là các số thực thỏa mãn

     

   

2 2 2

2 2

2

1 2 3 1

.

3 2 9

d e f

a b c



     





    





Gọi giá trị lớn nhất, giá trị nhỏ nhất của biểu thức

     

2 2 2

F a d b e c f     

lần lượt là

, .M m

Khi đó,

M m

bằng

A.

10

. B. 10 . C.

8

. D.

2 2

.

Lời giải

Gọi

 

, ,A d e f

thì

A

thuộc mặt cầu

       

2 2 2

1

: 1 2 3 1S x y z     

có tâm

 

1

1;2;3I

, bán

kính

1

1R  ,

 

, ,B a b c

thì

B

thuộc mặt cầu

     

2 2

2

: 3 2 9S x y z    

có tâm

 

2

3;2;0I 

,

bán kính

2

3R  . Ta có

1 2 1 2

5I I R R  

 

1

S

và

 

2

S

không cắt nhau và ở ngoài nhau.

Dễ thấy

F AB

,

AB

max khi

1 1

,A A B B   Giá trị lớn nhất bằng

1 2 1 2

9I I R R   .

AB

min khi

2 2

,A A B B   Giá trị nhỏ nhất bằng

1 2 1 2

1I I R R   .

Vậy

8M m 

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 16 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 18. (THPT Lê Xoay - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm

 

2;2; 2

A

 

;

 

3; 3;3

B 

. Điểm

M

trong không gian thỏa mãn

2

3

MA

MB



. Khi đó độ dài

OM

lớn nhất bằng

A.

6 3

. B.

12 3

. C.

5 3

2

. D.

5 3

.

Lời giải

Gọi

 

; ;M x y z

.

Ta có

2

3

MA

MB



3 2

MA MB 

2 2

9 4

MA MB

 

           

2 2 2 2 2 2

9 2 2 2 4 3 3 3

x y z x y z

   

           

   

2 2 2

12 12 12 0

x y z x y z

      

     

2 2 2

6 6 6 108

x y z      

.

Như vậy, điểm

M

thuộc mặt cầu

 

S

tâm

 

6;6; 6

I

 

và bán kính

108 6 3

R   .

Do đó

OM

lớn nhất bằng

   

2 2

2

6 6 6 6 3 12 3

OI R       

.

Câu 19. Trong không gian

Oxyz

, cho ba điểm

(1;1;1)

A

,

( 2;3;4)

B



và

( 2;5;1)

C



. Điểm

( ; ;0)M a b

thuộc

mặt phẳng

 

Oxy

sao cho

2 2 2

MA MB MC

 

đạt giá trị nhỏ nhất. Tổng

2 2

T a b 

bằng

A.

10

T



. B.

25

T



. C.

13

T



. D.

17

T



.

Lời giải

Chọn A

Ta có

 

1;3;2

G 

là trọng tâm tam giác

ABC

.

Khi đó

     

 

2 2 2

2 2 2 2

3 2

3

G

MA MB MC MA MB MC

MG GA MG MG

GA GB GC MG GA GB GC

G

B GC

MG

MG A GB GC

    

    

    

  

 

  

     

   

Do đó

2 2 2

MA MB MC

 

nhỏ nhất khi và chỉ khi

MG

nhỏ nhất



M là hình chiếu của G lên

mặt phẳng

 

Oxy

. Do hình chiếu vuông góc của G lên mặt phẳng

 

Oxy

có tọa độ

 

1;3;0



Vậy

 

1;3;0

M 

. Từ đó

 

2

1 10

3T 

  

.

Câu 20. (THPT Đoàn Thượng – Hải Dương 2019) Trong không gian

Oxyz

cho

 

1; 1;2

A 

,

 

2;0;3

B 

,

 

0;1; 2

C



. Gọi

 

; ;M a b c

là điểm thuộc mặt phẳng

 

Oxy

sao cho biểu thức

. 2 . 3 .S MA MB MB MC MC MA

  

     

đạt giá trị nhỏ nhất. Khi đó

12 12

T a b c  

có giá trị là

A.

3

T



. B.

3

T

 

. C.

1T 

. D.

1T  

.

Lời giải:

Chọn D

Xét

. 2 . 3 .S MA MB MB MC MC MA

  

     

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17

( )( ) 2( )( ) 3( )( )MI IA MI IB MI IB MI IC MI IC MI IA

        

           

2

6 (4 3 5 ) 2 3MI MI IA IB IC IAIB IBIC IC IA      

         

Gọi I là điểm thỏa mãn

4 3 5

12

4 3 5

2 1 7

4 3 5 0 ( , , )

12 12 12 12

4 3 5

12

A B C

I

A B c

I

A B C

I

x x x

x

y y y

IA IB IC y I

x z z

z





 







  





     





 









   

.

Mà:

(4 3 5 ) 0

IA IB IC

  

  



.

2 3

IAIB IBIC IC IA const

  

    

. Nên

min min

S MI

Suy ra M là hình chiếu của I lên mặt Oxy.

2 1

( , ,0)

12 12

M





.

12 12 1

T a b c

     

Câu 21. (Chuyên - Vĩnh Phúc - 2019) Trong không gian

Oxyz

, lấy điểm

C

trên tia

Oz

sao cho

1

OC



.

Trên hai tia

,Ox Oy

lần lượt lấy hai điểm

,A B

thay đổi sao cho

OA OB OC 

. Tìm giá trị nhỏ

nhất của bán kính mặt cầu ngoại tiếp tứ diện

.

O ABC

?

A.

6

.

2

B.

6.

C.

6

.

3

D.

6

.

4

Lời giải

Chọn D

Đặt:

; ( 0, 0)

OA a OB b a b

   

1

a b

  

2 2

1 2a b ab

   

Bán kính cầu:

R

2 2 2

1

2

a b c  

 

2

1 2 1

4

ab

R

 

 

 

2 2 1

4

a a 



2

2 2 2

4

a a

 



2

1

2

a a 



2

1 3

4 4

2

a

 

 

 

 



2

3 6

8 4

R R  

. Vậy

min

6

4

R 

Câu 22. (THPT Ngô Quyền - Ba Vì - Hải Phòng 2019) Trong không gian với hệ tọa độ

Oxyz

, gọi điểm

 

; ;M a b c

(với

a

,

b

,

c

là các phân số tối giản) thuộc mặt cầu

 

2 2 2

: 2 4 4 7 0

S x y z x y z

      

sao cho biểu thức

2 3 6T a b c  

đạt giá trị lớn nhất. Khi

đó giá trị biểu thức

2

P a b c  

bằng

A.

12

7

. B.

8

. C.

6

. D.

51

7

.

Lời giải

Chọn C

     

2 2 2

2 4 4 7 0 1 2 2 16

x y z x y z x y z

             

.

         

2 2 2

; ; 1 2 2 16

M a b c S a b c

       

.

Ta có:

     

 

     

2 2 2

2 1 3 2 6 2 2 3 6 . 1 2 2

a b c a b c

 

            

 

.

2 3 6 20 28

a b c

    

2 3 6 20 28

a b c

    

2 3 6 48

a b c

   

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 18 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Dấu

" "

xảy ra khi:

15

2 3 6 48

7

2 3 6 48

1 2 26

3 2 1

2 3 7

3 1

1 2 38

2 6 7

a

a b c

a b

a b b

a c

c







  





 

  

      

  

  

 



 

 

 

 



Vậy

15 26 38

2 2. 6

7 7 7

P a b c

      

.

Câu 23. (THPT Ngô Quyền - Ba Vì - Hải Phòng 2019) Trong không gian với hệ tọa độ Oxyz, Cho điểm

 

2 ;2 ;0A t t

,

 

0;0;B t

(với

0t 

). Điểm

P

di động thỏa mãn

. . . 3

OP AP OP BP AP BP

  

     

. Biết

rằng có giá trị

a

t

b



với

,a b

nguyên dương và

a

b

tối giản sao cho

OP

đạt giá trị lớn nhất bằng

3. Khi đó giá trị của

2

Q a b 

bằng

A.

5

B.

13

. C.

11

. D.

9

.

Lời giải

Chọn C

Gọi

 

; ;P x y z

, ta có:

 

; ;OP x y z





,

 

2 ; 2 ;AP x t y t z

  



,

 

; ;

BP x y z t 



Vì

 

; ;P x y z

thỏa mãn

. . . 3

OP AP OP BP AP BP

  

     

2 2 2 2 2 2

4 4 2

3 3 3 4 4 2 3 0 1 0

3 3 3

x y z tx ty tz x y z tx ty tz

               

Nên

P

thuộc mặt cầu tâm

2

2 2

; ; , 1

3 3 3

t t t

I R t

 

 

 

 

.

Ta có

OI t R 

nên O thuộc phần không gian phía trong mặt cầu.

Để

max

OP

thì

, ,P I O

thẳng hàng và

OP OI R 

.

Suy ra

2

max

3 1

OP OI R t t

     

. Từ đó tìm được

4

3

t



Suy ra

4, 3

a b

 

Vậy,

2 11

Q a b

  

.

Câu 24. (HSG Nam Định-2019) Trong không gian với hệ trục tọa độ

,Oxyz

cho các điểm

     

4;1;5 , 3;0;1 , 1;2;0

A B C

và điểm

 

; ;M a b c

thỏa mãn

. 2 . 5 .

 

     

MA MB MB MC MC MA

lớn

nhất. Tính

2 4 .  P a b c

A.

23

P

. B.

31

P

. C.

11P

. D.

13.

P

Lời giải

Chọn D

+ Đặt

. 2 . 5 .

  

     

Q MA MB MB MC MC MA

.

 

2

2 2 2 2 2

1

2 . .

2

       

     

MA MB MA MB MA MB MA MB MA MB AB

.

 

2

2 2 2 2 2

2 . 2 .       

     

MB MC MB MC MB MC MB MC MB MC BC

.

 

2

2 2 2 2 2

1

2 . .

2

       

     

MC MA MC MA MC MA MC MA MC MA AC

.

. 2 . 5 .

   

     

Q MA MB MB MC MC MA

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19

   

2 2 2 2 2 2 2 2 2

1 5

2 2

        MA MB AB MB MC BC MC MA AC

2 2 2 2 2 2

3 3 1 5

2

2 2 2 2

      MA MB MC AB BC AC

.

2 2 2

1 5

2 2

  AB BC AC

không đổi nên

Q

lớn nhất khi

2 2 2

3 3

2

2 2

   T MA MB MC

đạt giá trị

lớn nhất.

+

2 2 2

3 3

2

2 2

   T MA MB MC

.

Gọi

E

là điểm thỏa mãn

3 3

2 0

2 2

   

   

EA EB EC

.

3

4 3 3 0 4 3

4

        

       

EA EB EC EA CB EA CB

.

5 17

1; ;

2 4

 



 

 

E

.

     

2 2 2

3 3 3 3

2 2

2 2 2 2

          

     

T MA MB MC ME EA ME EB ME EC

2 2 2 2 2 2 2

3 3 3 3

2 2 2

2 2 2 2

        ME EA EB EC EA EB EC

.

Vì

2 2 2

3 3

2

2 2

  EA EB EC

không đổi nên

T

đạt giá trị lớn nhất khi

0  ME M E

.

5 17

1; ;

2 4

 



 

 

M

.

5 17

2 4 1 2. 4. 13

2 4

      P a b c

.

Câu 25. Trong không gian với hệ trục tọa độ

Oxyz

, cho hai điểm

 

2; 2;4A 

,

 

3;3; 1B  

và mặt cầu

       

2 2 2

: 1 3 3 3S x y z     

. Xét điểm

M

thay đổi thuộc mặt cầu

 

S

, giá trị nhỏ nhất

của

2 2

2 3MA MB

bằng

A.

103

. B.

108

. C.

105

. D.

100

.

Lời giải

Chọn C

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 20 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Mặt cầu

 

S

có tâm

 

1;3;3

I

bán kính

3

R  .

Gọi

E

là điểm thỏa mãn:

2 3 0

EA EB

 

  

. Suy ra

 

1;1;1

E 

.

Xét

   

2 2

2 2 2 2 2

2 3 2 3 5 2 3

P MA MB ME EA ME EB ME EA EB

        

   

.

P

đạt giá trị nhỏ nhất khi và chỉ khi

ME

đạt giá trị nhỏ nhất.

2 3

IE R 

suy ra điểm

E

nằm ngoài mặt cầu nên

ME

nhỏ nhất bằng

2 3 3 3

IE R   

.

Vậy

2 2 2 2 2

2 3 5 2 3 105

P MA MB ME EA EB     

.

Câu 26. (Kim Liên - Hà Nội 2019) Trong không gian

Oxyz

, cho mặt cầu

 

2 2 2

9

: 2 4 2 0

2

S x y z x y z

      

và hai điểm

 

0;2;0

A

,

 

2; 6; 2

B

 

. Điểm

 

; ;M a b c

thuộc

 

S

thỏa mãn

.MA MB

 

có giá trị nhỏ nhất. Tổng

a b c 

bằng

A.

1

. B.

1

. C.

3

. D.

2

.

Lời giải

Chọn B

 

2 2 2

9

: 2 4 2 0

2

S x y z x y z

      

       

2 2 2

3

: 1 2 1

2

S x y z

      

.

Mặt cầu

 

S

có tâm

 

1;2;1

I 

, bán kính

6

2

R 

.

Vì

2

IA R 

và

82

IB R 

nên hai điểm

A

,

B

nằm ngoài mặt cầu

 

S

.

Gọi

K

là trung điểm đoạn thẳng

AB

thì

 

1; 2; 1

K

 

và

K

nằm ngoài mặt cầu

 

S

.

Ta có:

.MA MB

 

   

.

MK KA MK KB

  

   

 

2

. .MK MK KA KB KA KB

   

    

2 2

MK KA 

.

Suy ra

.MA MB

 

nhỏ nhất khi

2

MK

nhỏ nhất, tức là

MK

nhỏ nhất.

Đánh giá:

IM MK IK R MK IK MK     

IK R 

.

Suy ra

MK

nhỏ nhất bằng

IK R

, xảy ra khi

I

,

M

,

K

thẳng hàng và

M

nằm giữa hai điểm

I

,

K

. Như vậy

M

là giao điểm của đoạn thẳng

IK

và mặt cầu

 

S

.

Có

 

2; 4; 2

IK

  



,

   

2 2

2

2 4 2 2 6 4 4

IK R IM

       

.

Suy ra

4IK IM

 

 

2 4 1

4 4 2

2 4 1

a

b

c

 



   





  



1

2

1

2

a

b

c



 



 









.

Vậy

1a b c  

.

Câu 27. Trong không gian tọa độ

Oxyz

, cho 5 điểm

 

1;0;0

A

,

 

1;1;0

B 

,

 

0; 1;0

C 

,

 

0;1;0

D

,

 

0;3;0

E

.

M

là điểm thay đổi trên mặt cầu

2 2 2

( ) : ( 1) 1

S x y z

   

. Giá trị lớn nhất của biểu

thức 2 3

P MA MB MC MD ME

    

    

là:

A.

12

. B.

12 2

. C.

24

. D.

24 2

.

Lời giải

Chọn B

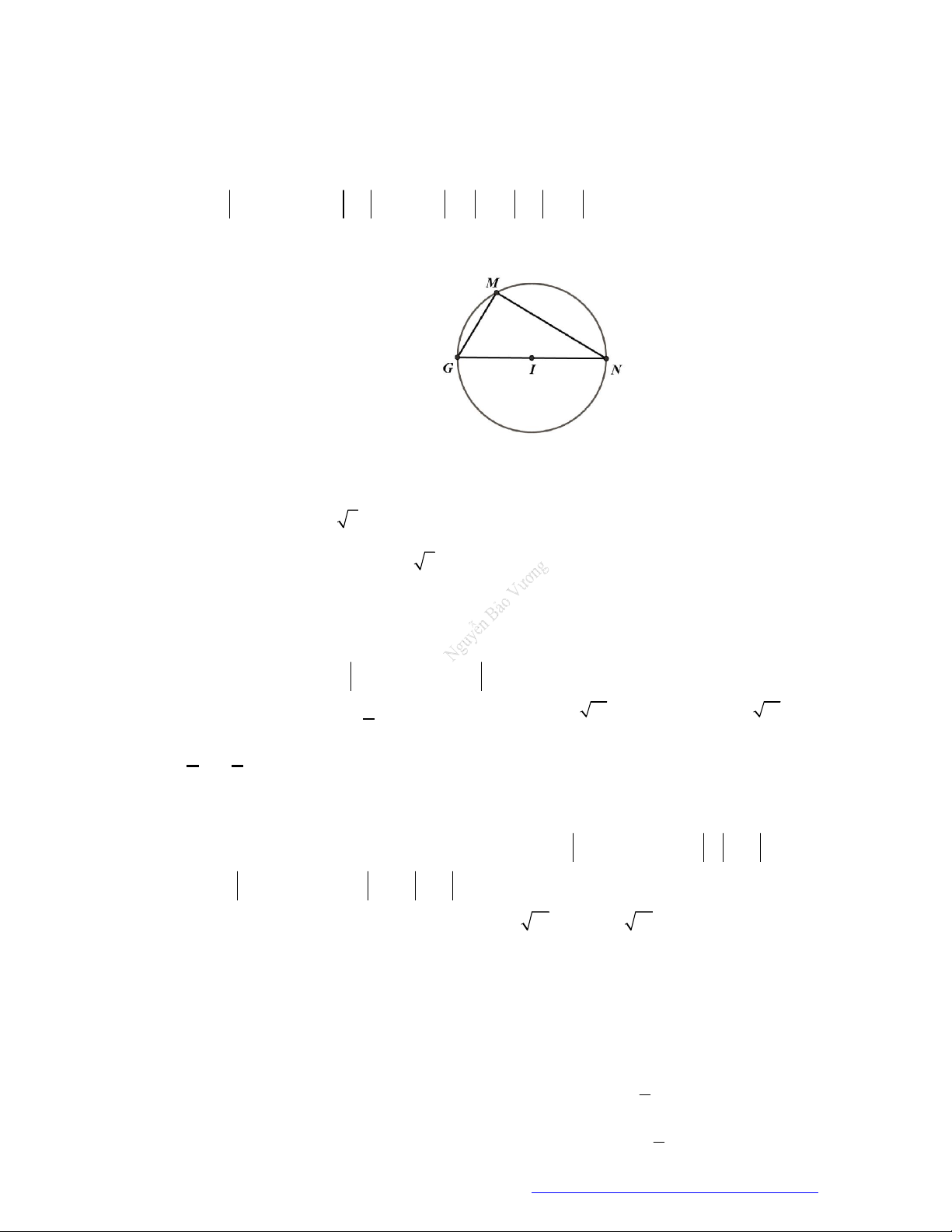
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21

Mặt cầu

 

S

: tâm

 

0;1;0I

bán kính

1R 

Gọi trọng tâm tam giác

ABC

là

 

0;0;0G

, trung điểm

DE

là

 

0;2;0N

do

,G N

đều nằm trên

 

S

và

I

là trung điểm

GN

nên

GN

là đường kính của

 

S

 

2 3 2 3 3 2

6 6 6

P MA MB MC MD ME MG MN

MG MN MG MN

      

   

      

Ta có:

 

2

2 2 2

2 2 8MG MN MG MN GN    

Suy ra

2 2MG MN 

Vậy giá trị lớn nhất của

P

là

12 2

.

Câu 28. Trong không gian với hệ trục tọa độ

Oxyz

, cho các điểm

 

0; 1;3A 

,

 

2; 8; 4B   

,

 

2; 1;1C 

và mặt cầu

       

2 2 2

: 1 2 3 14S x y z     

. Gọi

 

; ;

M M M

M x y z

là điểm trên

 

S

sao cho biểu thức 3 2MA MB MC 

  

đạt giá trị nhỏ nhất. Tính

M M

P x y  .

A.

P 0

. B.

P 6

. C.

P 14

. D.

P 3 14

.

Lời giải

Chọn B

Gọi

J

là điểm thỏa mãn

3 2 0JA JB JC  

   

2 3 2 0JO OA OB OC    

    

2 3 2OJ OA OB OC   

   

(3;6;9)J

.

Mà

 

3 2 2 3 2MA MB MC MJ JA JB JC     

      

nên 3 2 2MA MB MC MJ  

   

Do đó

min min

3 2 2MA MB MC MJ  

   

.

Mặt khác:

 

S

có tâm

 

1;2;3I

, bán kính

14R 

và

2 14IJ R 



điểm

J

nằm ngoài mặt

cầu nên

IJ

cắt mặt cầu

 

S

tại hai điểm

1 2

,M M .

Phương trình đường thẳng

 

1 2

: 2 4 ,

3 6

x t

IJ y t t

z t

 





  





 





.

Xét hệ phương trình:

     

2 2 2

1 2

2 4

3 6

1 2 3 14

x t

y t

z t

x y z

 





 





 



     



1

2

1

2

1

2

t











 





.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 22 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Suy ra

   

1 2

2;4;6 , 0;0;0

M M

,

1 2

14; 3 14

M J M J 

.

Vậy

min min

3 2 2

MA MB MC MJ

  

   

1

M M 

.

2 4 6

M M

P x y

    

.

Câu 29. Trong không gian

Oxyz

cho

   

0 ; 0 ; 2 , 1 ; 1; 0

A B

và mặt cầu

   

2

2 2

1

: 1

4

S x y z

   

. Xét

điểm

M

thay đổi thuộc

 

S

. Giá trị nhỏ nhất của biểu thức

2 2

2MA MB

bằng

A.

1

2

. B.

3

4

. C.

19

4

. D.

21

4

.

Lời giải

Chọn C

Mặt cầu

 

S

có tâm

 

0 ; 0 ; 1

I

, bán kính

1

.

2

R



Gọi

K

là điểm thỏa mãn

2 2 2

2 0 ; ; .

3 3 3

KA KB K

 

  

 

 

  

Ta có

   

 

2 2

2 2 2 2 2 2

2 2

3 2 2 2 3 2 .

MA MB MK KA MK KB

MK KA KB MK KA KB MK KA KB

    

       

   

  

Biểu thức

2 2

2MA MB

đạt GTNN khi và chỉ khi

MK

đạt giá trị nhỏ nhất.

Với

M

thay đổi thuộc

 

S

ta có

min

1 1

1 .

2 2

MK KI R

    

Vậy

 

2 2 2 2 2

min

3 8 4 19

2 3 2 .

4 3 3 4

MA MB MK KA KB       

Câu 30. Trong không gian tọa độ

Oxyz

, cho 2 điểm A, B thay đổi trên mặt cầu

2 2 2

( 1) 25

x y z

   

thỏa

mãn

6

AB



. Giá trị lớn nhất của biểu thức

2 2

OA OB



là

A. 12. B. 6. C. 10. D. 24.

Lời giải

Chọn A

Mặt cầu

2 2 2

( 1) 25

x y z

   

có tâm

 

0;0;1

I

.

Vì

A

,

B

cùng thuộc mặt cầu tâm

I

nên

IA IB

.

       

2 2 2 2

2 2

OA OB OA OB OI IA OI IB

      

     

 

2 2 . 2 . .cos

OI IA IB OI BA OI BA



   

    

, với

 

,

OI BA





 

.

Suy ra biểu thức

2 2

OA OB



đạt GTLN khi và chỉ khi

0





.

Vậy

 

2 2

max 2.1.6.cos0 12

OA OB

  

.

Câu 31. Trong không gian

Oxyz

, cho ba điểm

 

1;4;5

A

,

 

3;4;0

B

,

 

2; 1;0

C 

. Gọi

 

; ;M a b c

là

điểm sao cho

2 2 2

3

MA MB MC

 

đạt giá trị nhỏ nhất. Tổng

a b c 

có giá trị bằng

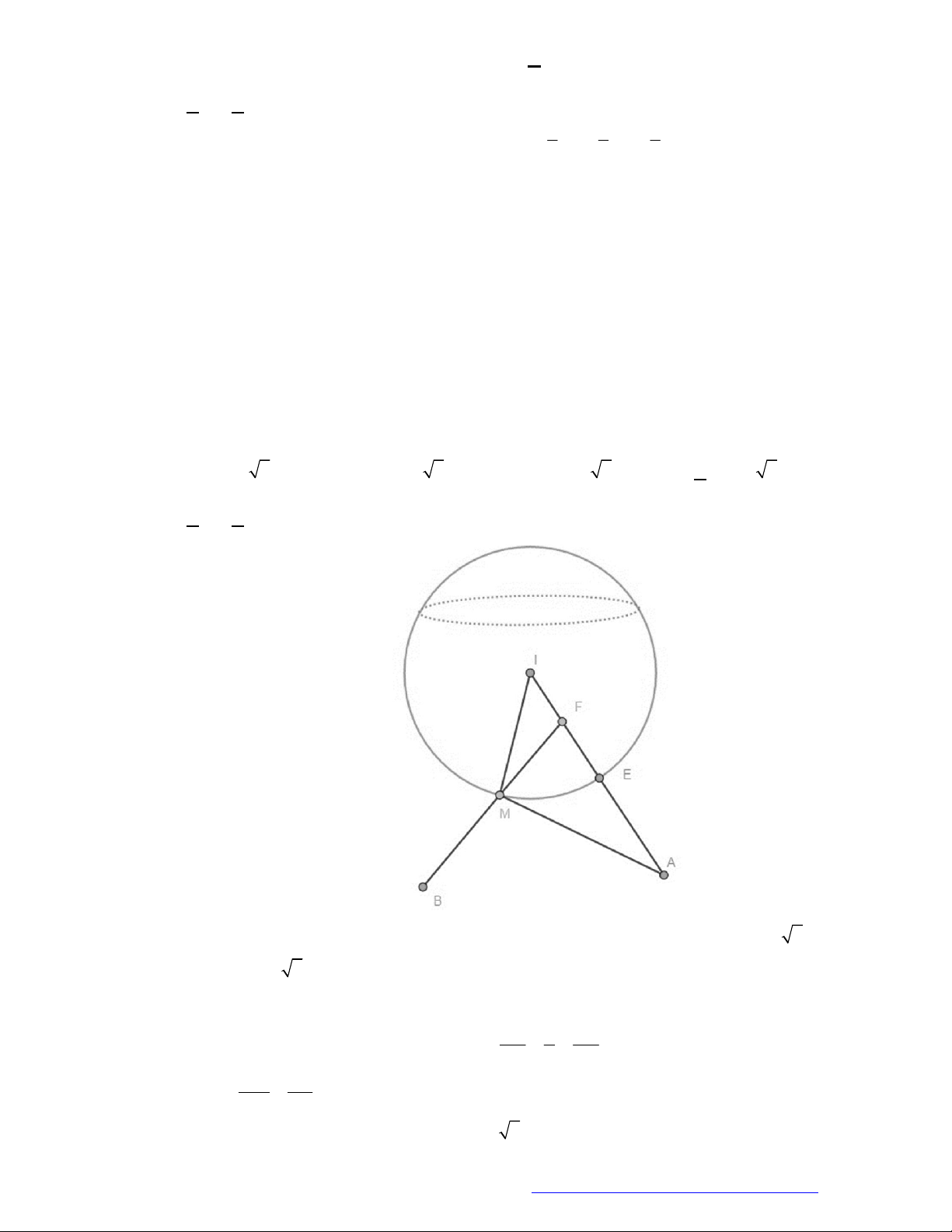
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23

A. 2. B. 3. C. 4. D.

4

.

Lời giải

Chọn C

Gọi

I

là điểm thỏa mãn

   

1 1 3

3 0 2;1;1 2;1;1

5 5 5

IA IB IC OI OA OB OC I        

       

.

Khi đó,

     

2 2 2

3 3T MA MB MC MI IA MI IB MI IC        

     

 

2 2 2 2

5 2 . 3 3MI MI IA IB IC IA IB IC      

   

2 2 2 2

5 3MI IA IB IC   

(vì

3 0IA IB IC  

   

)

Vì

I

,

A

,

B

,

C

cố định

2 2 2

3IA IB IC  

không đổi nên

T

nhỏ nhất

MI

nhỏ nhất

 

2;1;1 2M I a   

,

1b c 

.

Vậy

4a b c  

.

Câu 32. Trong không gian với hệ trục

Oxyz

, cho mặt cầu

     

2 2

2

: 1 4 8S x y z    

và điểm

   

3;0;0 ; 4;2;1A B

. Điểm

M

thay đổi nằm trên mặt cầu, tìm giá trị nhỏ nhất của biểu thức

2P MA MB 

.

A.

2 2P 

. B.

3 2P 

. C.

4 2P 

. D.

6 2P 

.

Lời giải

Chọn D

Nhận xét: điểm

,A B

nằm ngoài mặt cầu

 

S

. Mặt cầu

 

S

có tâm

 

1;4;0 , 2 2I R  .

Ta có:

   

4 2 2 , 1;2;0IA R E IA S E    

.

Gọi

F

là trung điểm của

 

0;3;0IE F

.

Tam giác

IFM

và

IMA

có



AIM

chung và

1

2

IF IM

AIM MIF

IM IA

    

.

Suy ra

2 2

MA AI

MA MF

FM MI

   

.

Ta có:

 

2 2 2 6 2MA MB MF MB FB     .

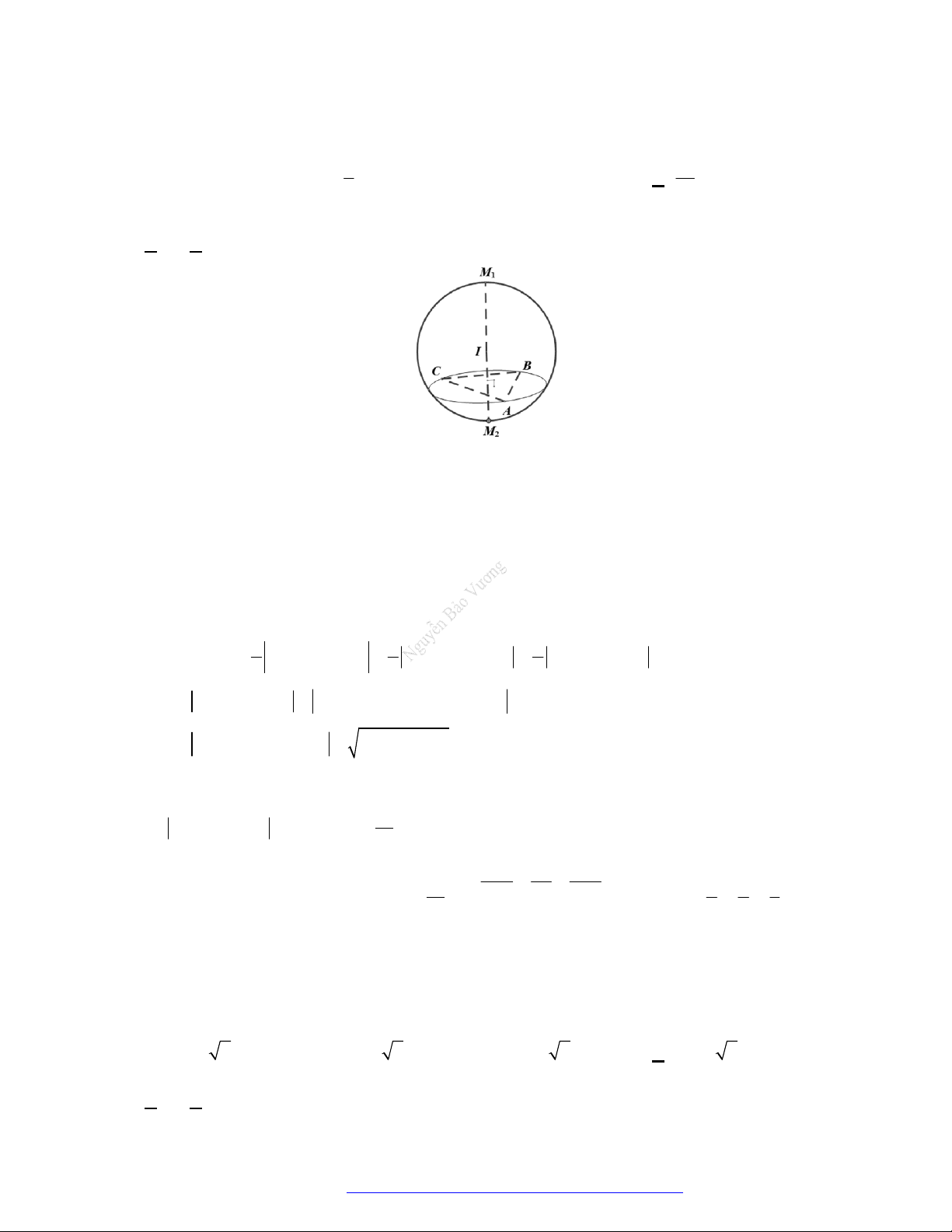
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 24 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Vì

F

nằm trong

 

S

và

B

nằm ngoài

 

S

nên dấu

'' ''

xảy ra khi

 

M BF S 

.

Câu 33. Trong không gian

Oxyz

,cho mặt cầu

 

2 2 2

: 2 2 2 0S x y z x z     

và các điểm

 

0;1;1A

,

 

1; 2; 3B   

,

 

1;0; 3C 

. Điểm

D

thuộc mặt cầu

 

S

. Thể tích tứ diện

ABCD

lớn nhất bằng:

A.

9

. B.

8

3

. C.

7

. D.

16

3

.

Lời giải

Chọn D

Cách 1:Ta có

     

2 2

2

: 1 1 4S x y z    

.

Ta có:

 

1; 3; 4

, 8; 8;4 .

1; 1; 4

AB

AB AC

AC



   



 

  



 

  







 



Gọi

   

 

2 2

2

1 1 4

; ; .

; 1; 1

x y z

D x y z S

AD x y z



    



 



  







Ta có:

1 1 2

, . 8 8 4 4 2 2 1

6 6 3

ABCD

V AB AC AD x y z x y z

 

        

 

  

.

Ta có:

   

2 2 1 2. 1 2. 1. 1 2x y z x y z        

Ta có:

 

   

2 2

2 2 2 2

2 1 2 1 2 2 1 1 1 6x y z x y z

 

           

 

 

6 2 1 2 1 6 4 2 2 1 8x y z x y z              

16

2 2 1 8

3

ABCD

x y z V      

Suy ra: Giá trị lớn nhất của

ABCD

V

bằng

   

2 2

2

1 1

0

16 7 4 1

2 2 1

; ;

3 3 3 3

1 1 4

x y z

D

x y z

 



  



 



   



 

 



    



.

Câu 34. (THPT Thuận Thành 3 - Bắc Ninh 2019) Trong không gian với hệ trục

Oxyz

, cho mặt cầu

     

2 2

2

: 1 4 8S x y z    

và điểm

 

3 ; 0 ;0A

,

 

4 ; 2 ;1B

. Điểm

M

thay đổi nằm trên

mặt cầu, tìm giá trị nhỏ nhất của biểu thức

2P MA MB 

.

A.

2 2P 

. B.

3 2P 

. C.

4 2P 

. D.

6 2P 

.

Lời giải

Chọn D

Giả sử

 

; ;M x y z

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25

Ta có:

 

3 ; y ;AM x z

 



,

 

4 ; y 2 ; 1

BM x z

   



.

Và

   

2 2

2

1 4 8

x y z

    

   

2 2

2

3 1 4 8 0

x y z

 

      

 

.

Ta có:

2P MA MB 

       

2 2 2 2

2 2

3 2 4 2 1

x y z x y z         

           

2 2 2 2 2 2

2 2 2

3 3 1 4 8 2 4 2 1

x y z x y z x y z

 

               

 

     

2 2 2

4 4 24 4 36 2 4 2 1

x y y z x y z          

       

2 2 2 2

2 2

2 3 4 2 1

x y z x y z

 

         

 

 

       

2 2 2 2

2 2

2 3 4 2 1

x y z x y z

 

         

 

 

Áp dụng bất đẳng thức Minkowxki:

2 2 2 2 2 2

a b c d e f

    

     

2 2 2

a d b e c f

     

.

Dấu bằng xảy ra khi:

0

a b a

d e f

  

.

         

2 2 2 2 2

2

2 4 3 2 1 2 4 1 1 6 2

P x x y y z z               

.

Dấu bằng xảy ra khi:

   

2 2

2

3

0

4 2 1

1 4 8

x y z

t

x y z





   



  





    



2 2 2

4

1

2 3

1

5 1 2 1

8

1 1 1

t

x

t

y

t

z

t

t t t



































  

     



  

     

  



     



2

4

1

2 3

1

22 2 6 0

t

x

t

y

t

z

t

t t



































  



4 4 133

23 133

34 133

23 133

1 133

23 133

1 133

22

x

y

z

t















 





























.

Vậy giá trị nhỏ nhất của biểu thức là

6 2

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 26 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 35. (Kinh Môn - Hải Dương 2019) Trong không gian với hệ tọa độ

Oxyz

cho hai điểm

 

4;2; 2A

,

 

1;1; 1B 

,

 

2; 2; 2C  

. Tìm tọa độ điểm M thuộc

 

Oxy

sao cho 2MA MB MC 

  

nhỏ nhất.

A.

 

2; 3;0M

. B.

 

1; 3;0M

. C.

 

2; 3; 0M 

. D.

 

2;3;1M

.

Lời giải

Chọn A

Cách 1

Gọi

; ;D E F

lần lượt là trung điểm của

; ;AB AC ME

. Ta có:

2 2. 2. 2. 2 2. 4.MA MB MC MA MB MB MC MD CB MD ED FD FD           

           

Ta lại có:

   

5 3 1 3

; ;0 ; ; ; ; 3;0;0 ; ; ;0

2 2 2 2 2

x y

M x y D E F



   

   

   

min

FD 

F

là hình chiếu của

D

trên

 

mp Oxy

 

2; 3 2;3;0x y M   

Cách 2

Gọi

I

là điểm thỏa mãn:

   

2 0 2 0IA IB IC IO OA IO OB IO OC         

          

 

1

2 0 2;3;1

2

OI OA OB C I    

   

2 2 2 2.MA MB MC MI IA IB IC MI      

      

2MA MB MC 

  

nhỏ nhất 

MI

nhỏ nhất 

M

là hình chiếu của

I

trên

 

mp Oxy

.

Vì

   

2;3;1 2;3;0I M

Cách 3

Gọi

 

; ;0M x y

. Ta có:

 

2 2

2 4 2 ;6 2 ; 1 2 4 4 16 24 53MA MB MC x y MA MB MC x y x y             

     

Thế tọa độ điểm

M

ở đáp án A vào ta được 2 1MA MB MC  

  

Thế tọa độ điểm

M

ở đáp án B vào ta được 2 17MA MB MC  

  

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27

Thế tọa độ điểm

M

ở đáp án C vào ta được 2 145MA MB MC  

  

Điểm

M

ở đáp án D không thuộc

 

Oxy

nên bị loại.

Cách 4

Gọi

 

; ;0M x y

. Ta có:

 

2 2

2 4 2 ;6 2 ; 1 2 4 4 16 24 53MA MB MC x y MA MB MC x y x y             

     

Ta có:

   

2 2

4 4 16 24 53 2 4 2 6 1 1x y x y x y         

Dấu

" "

xảy ra

2; 3x y  

. Khi đó

 

2;3;0M

.

Câu 36. Trong không gian

Oxyz

cho mặt cầu

 

S

có phương trình

2 2 2

4 2 2 3 0x y z x y z      

và

điểm

 

5;3; 2A 

. Một đường thẳng

d

thay đổi luôn đi qua

A

và luôn cắt mặt cầu tại hai điểm

phân biệt

,M N

. Tính giá trị nhỏ nhất của biểu thức

4S AM AN 

.

A.

min

30S  . B.

min

20S  . C.

min

34 3S  

.

D.

min

5 34 9S  

.

Lời giải

Chọn D

Mặt cầu

 

S

có tâm

 

2; 1;1I 

, bán kính

3R 

.

34AI R  

A

nằm ngoài mặt cầu

 

S

.

Do hai điểm

,M N

nằm ở vị trí hai đầu một dây cung nên để

min

S

thì

N

nằm giữa

A

và

M

.

Gọi

H

là trung điểm

MN

1

,

2

IH MN NH MN  

 

4 5 3S AH NH AH NH AH NH     

2 2 2 2 2 2

5 3 5 34 3 9 ,S AI IH R IH x x x IH        

Xét hàm số

   

2 2

5 34 3 9 , 0 3f x x x x     

 

2 2 2 2 2 2

5 3 5 3

34 3 34 3

x x

f x x

x x x x

 

 



   

 

   

 

N

H

I

A

M

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 28 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Xét

2 2

5 3

0

34 9x x

 



 

 

 

 

2 2

5 9 3 34

x x

   

2 2 2

225 25 9 34 9 16 81 0.x x x      

(luôn đúng )

Suy ra

    

0 0 3 0 0

; , ; ,f x x f x x

 

     





 

f x



đồng biến trên



0 3;





Suy ra



   

0 3

0 5 34 9

;

min .

f x f





  

Câu 37. Trong không gian

Oxyz

, cho mặt cầu

     

2 2

2

: 1 2 10

S x y z

    

và hai điểm

 

1;2; 4

A



và

 

1;2;14

B

. Điểm

M

thay đổi trên mặt cầu

 

S

. Giá trị nhỏ nhất của

 

2

MA MB



bằng

A.

2 82

. B.

3 79

. C.

5 79

. D.

3 82

.

Lời giải

Chọn D

 

S

có tâm

 

1;0;2

I

và bán kính

10

R  .

Ta có

2 10 2IA R

  nên tồn tại điểm

C

cố định sao cho

2

MA MC

 

M S

 

 

1

.

Thật vậy, gọi

 

; ;a b c

là tọa độ điểm

C

. Khi đó, với mọi điểm

   

2 2 2

; ; 2 4 5M x y z S x y z x z      

, ta có:

     

2 2 2

2 2 2 2

1 2 4 2 4 8 21

MA x y z x y z x y z

            

2 4 5 2 4 8 21 4 12 26

x z x y z y z

          

.

     

2 2 2

2 2 2 2 2 2 2

2 2 2

MC x a y b z c x y z ax by cz a b c              

   

2 2 2 2 2 2

2 4 5 2 2 2 2 2 2 4 2 5

x z ax by cz a b c a x by c z a b c

                 

.

Nên

 

2 2

1 4

MA MC

 

 

M S

 

   

2 2 2

4 12 26 4 2 2 2 4 2 5

y z a x by c z a b c

 

            

 

, ,x y z

 

2 2 2

1

4 2 2 0

2

4 2 4

1 1

1 1; ;

4 4 2 12

2 2

1

4 5 26

2

a

b

a C

c

a b c

 







  



 

   

 

 

 

 

 



   



.

Lúc này,

10

2 37

2

IC R IB   

nên

C

nằm trong

 

S

còn

B

nằm ngoài

 

S

và

 

2 2 2 2 2 3 82

MA MB MC MB MC MB BC      

.

Đẳng thức xảy ra

M

là giao điểm của đoạn

BC

và mặt cầu

 

S

.

Vậy

 

min 2 3 82

MA MB 

.

Câu 38. Trong không gian với hệ trục tọa độ

Oxyz

, cho hai mặt cầu

 

2 2 2

1

: 1

S x y z

  

,

   

2

2 2

2

: 4 4

S x y z

   

và các điểm

 

4;0;0

A

,

1

;0;0

4

B

 

 

 

,

 

1;4;0

C

,

 

4;4;0

D

. Gọi

M

là

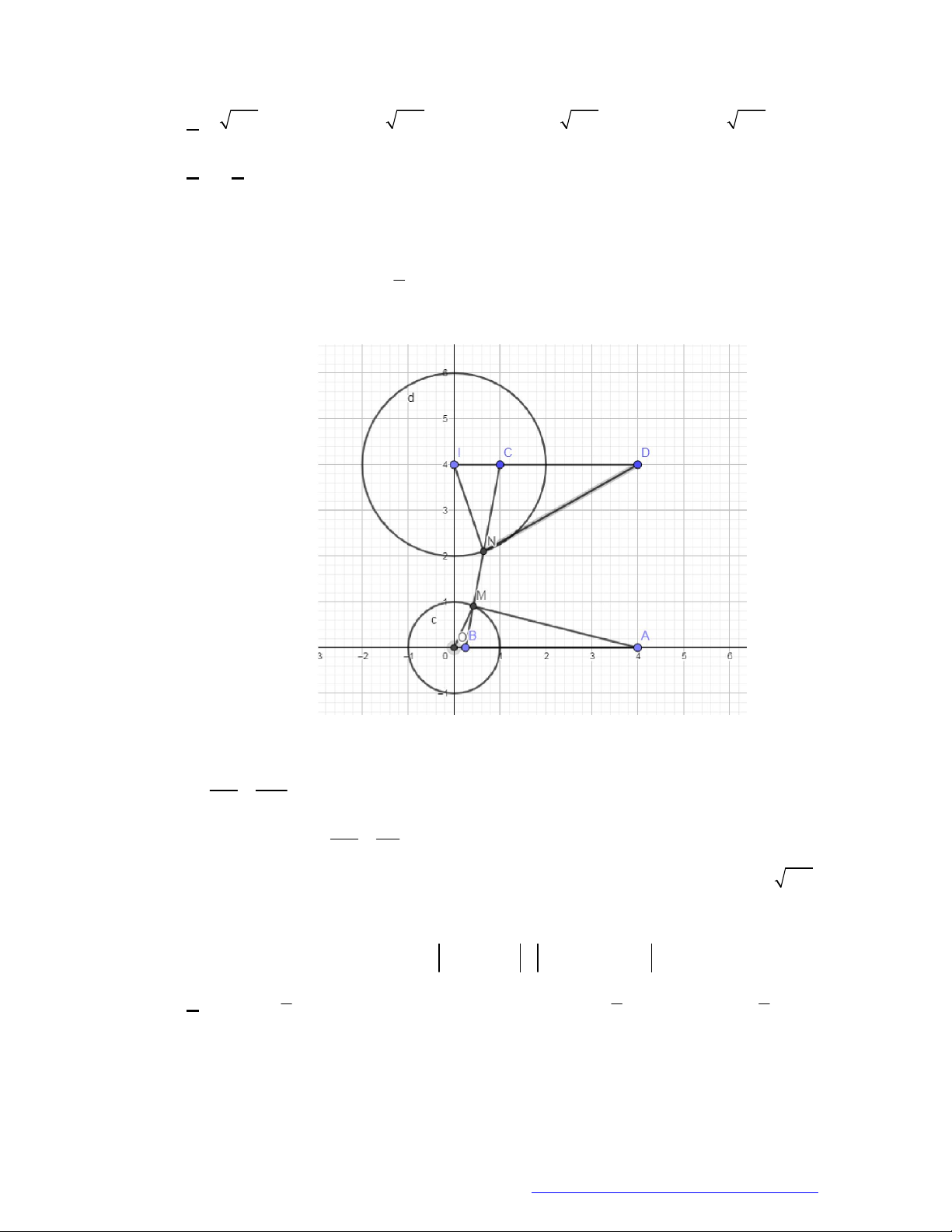
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 29

điểm thay đổi trên

 

1

S

,

N

là điểm thay đổi trên

 

2

S

. Giá trị nhỏ nhất của biểu thức

2 4 4Q MA ND MN BC   

là

A. 2 265 . B. 265 . C. 3 265 . D. 4 265 .

Lời giải

Chọn A

 

2 2 2

1

: 1S x y z  

nên

 

1

S

có tâm

 

0;0;0O

và bán kính

1

1R 

   

2

2 2

2

: 4 4S x y z   

nên

 

2

S

có tâm

 

0;4;0I

và bán kính

2

2R 

Vậy các điểm

 

4;0;0A

,

1

;0;0

4

B

 

 

 

,

 

1;4;0C

,

 

4;4;0D

,

 

0;0;0O

và

 

0;4;0I

cùng thuộc

 

Oxy

Nhận thấy

2

.OB OA OM

suy ra

OM

là tiếp tuyến của đường tròn ngoại tiếp tam giác

MAB

Do đó

MOB

đồng dạng

AOM

4 4

MA OA

MA MB

MB OM

    

Hoàn tòan tương tự

2 2

ND DI

ND NC

NC NI

   

 

2 4 4 4 4 4 4 8 2 265Q MA ND MN BC MB NC MN BC BC BC BC           

Câu 39. Trong không gian với hệ tọa độ

Oxyz

, cho

 

2;3; 1A 

,

 

2;3;2B

,

 

1;0;2C 

.Tìm tọa độ điểm

M

thuộc mặt phẳng

 

Oxz

để 4S MA MC MA MB MC    

    

nhỏ nhất.

A.

7

1;0;

3

M

 



 

 

. B.

 

0;3;0M

. C.

7

1;0;

3

M

 

 

 

. D.

1

;0;2

2

M

 



 

 

.

Lời giải

Chọn A

Gọi

G

là trọng tâm tam giác

ABC

, suy ra

 

1;2;1G

.

Gọi

 

; ;H x y z

là điểm thỏa mãn

4 0HA HC 

  

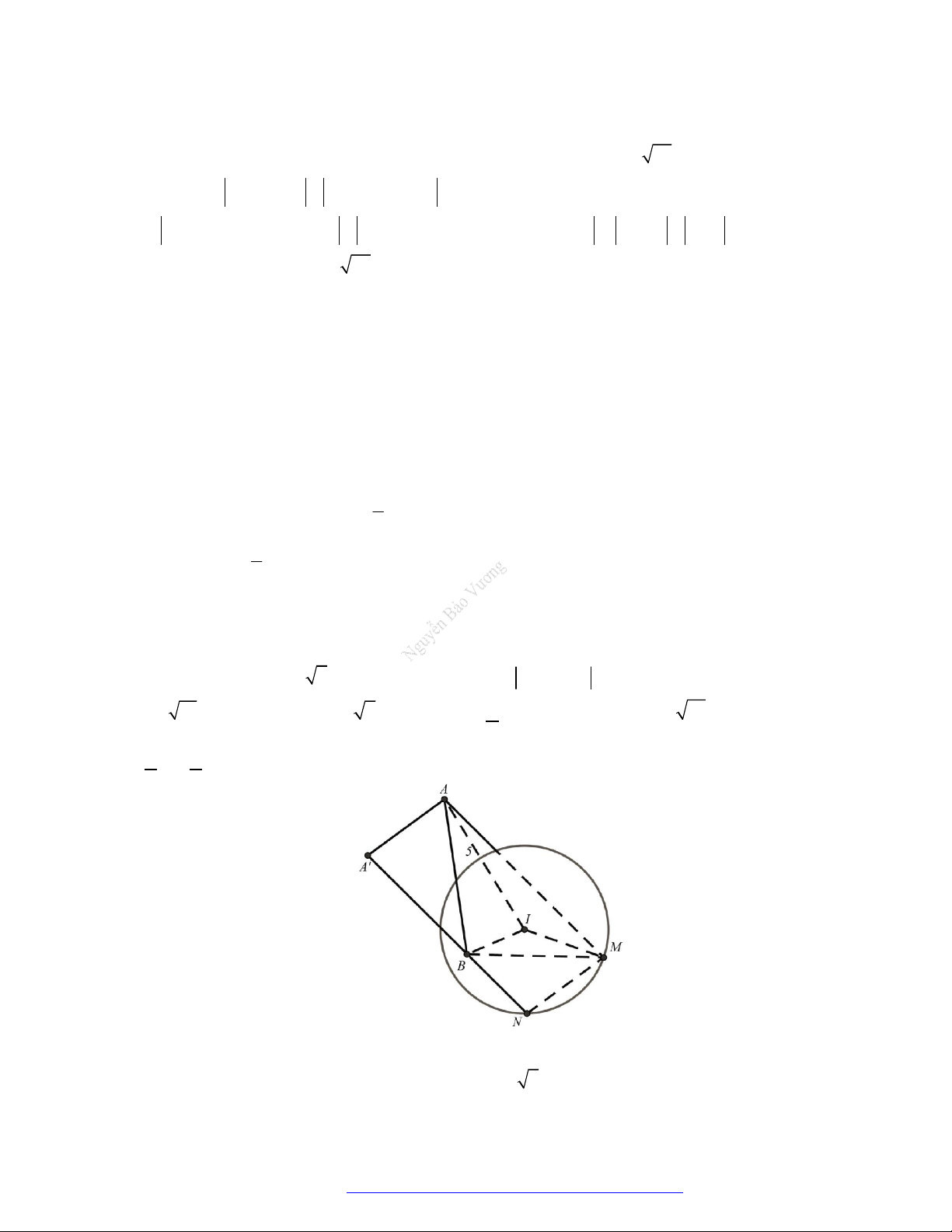
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 30 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

 

2 4 1

3 4 0

1 4 2

x x

y y

z z

   





   





   



2

1

3

x

y

z

 





  









 

2; 1;3H  

.

Nhận thấy

G

và

H

nằm về hai phía đối với mặt phẳng

 

Oxz

;

22HG 

.

Ta có: 4S MA MC MA MB MC    

    

4 4MH HA MH HC MG GA MG GB MG GC         

         

3 3MH MG  

 

 

3 MH MG 

3GH

3 22

.

Đẳng thức xảy ra khi và chỉ khi

H

,

M

,

G

thẳng hàng theo thứ tự.

Lại do

 

M Oxz

nên

S

đạt giá trị nhỏ nhất khi và chỉ khi

M

là giao điểm của đường thẳng

GH

với mặt phẳng

 

Oxz

.

Đường thẳng

GH

có phương trình

1 3

2 3

1 2

x t

y t

z t

 





 





 



; mặt phẳng

 

Oxz

có phương trình

0y 

.

 

1 3 ; 2 3 ;1 2M GH M t t t    

.

 

2

2 3 0

3

M Oxz t t      

.

Vậy

7

1;0;

3

M

 



 

 

.

Câu 40. Trong không gian với hệ tọa độ

Oxyz

, cho mặt cầu

2 2 2

( ): 2 4 4 0S x y z x y     

và hai

điểm

(4;2;4), (1;4;2)A B

.

MN

là dây cung của mặt cầu thỏa mãn

MN



cùng hướng với

(0;1;1)u 



và

4 2MN 

. Tính giá trị lớn nhất của

AM BN

.

A.

41

. B.

4 2

. C.

7

. D.

17

.

Lời giải

Chọn C

Tâm

(1; 2;0)I

, bán kính

3R 

.

Ta có

(3;0;4) 5IA IA  



,

(0;2;2) 2 2IB IB  



nên điểm

(4;2;4)A

nằm ngoài mặt cầu

( )S

và điểm

(1;4;2)B

nằm trong mặt cầu

( )S

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 31

Do

M

N



cùng hướng với

(

0;1;1)

u





suy ra

 

0

; ; , 0

MN

k k k







do

4

2

M

N 

s

uy ra

 

0

;4;4

M

N 





.

Gọi

(

)

M

N

A

T A









, suy ra

(

4;6;8)

A





. Khi đó

AMNA



là hình bình hành nên

AM A N





Ta

có

A

M BN A N BN A B

 



  

, dấu bằ

ng xảy ra khi

,

,A N B



thẳng hàng



N

là

gia

o

điểm của mặt cầu với đường thẳng

A

B



. (Điểm

N

luôn tồn tại).

( 3; 2; 6)

A B



   



suy ra

2

2 2

(

3) ( 2) ( 6) 7

A

B





     

. Vậ

y

m

in

7

AM BN A B



  

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương  https://www.facebook.com/phong.baovuong Trang 1

TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH TRUNG BÌNH MỨC 5-6 ĐIỂM

Dạng 1. Xác định véc tơ pháp tuyến

 Véctơ pháp tuyến

n



của mặt phẳng

( )P

là véctơ có giá vuông góc với

( ).P

Nếu

n



là một véctơ pháp

tuyến của

( )P

thì

.k n



cũng là một véctơ pháp tuyến của

( ).P

 Nếu mặt phẳng

( )P

có cặp véctơ chỉ phương là

1 2

, u u

 

thì

( )P

có véctơ pháp tuyến là

1 2

[ , ].n u u

  



Mặt phẳng

( ) : 0P ax by cz d   

có một véctơ pháp tuyến là

( ; ; ).n a b c



Câu 1. (Đề Minh Họa 2020 Lần 1) Trong không gian

Oxyz

, cho mặt phẳng

 

: 3 2 4 1 0x y z



   

.

Vectơ nào dưới đây là một vectơ pháp tuyến của

 



?

A.

 

2

3;2;4n 



. B.

 

3

2; 4;1n  



. C.

 

1

3; 4;1n  



. D.

 

4

3;2; 4n  



.

Câu 2. (Đề Tham Khảo 2020 Lần 2) Trong không gian

Oxyz

, cho mặt phẳng

 

: 2 3 2 0P x y z   

.

Véctơ nào dưới đây là một véctơ pháp tuyến của

 

P

?

A.

 

3

2;3;2n



. B.

 

1

2;3;0n



. C.

 

2

2;3;1n



. D.

 

4

2;0;3n



.

Câu 3. (Mã 101 2020 Lần 2) Trong không gian

Oxyz

, cho mặt phẳng

 

: 2 4 3 0x y z



   

. Véctơ

nào sau đây là véc tơ pháp tuyến của

 



?

A.

 

1

2;4; 1n  



. B.

 

2

2; 4;1n  



. C.

 

3

2;4;1n  



. D.

 

1

2;4;1n 



.

Câu 4. (Mã 102 - 2020 Lần 2) Trong không gian

Oxyz

, cho mặt phẳng

 

: 2 3 4 1 0x y z



   

. Vectơ

nào dưới đây là một vectơ pháp tuyến của

 



?

A.

 

3

2; 3; 4n  



. B.

 

2

2; 3; 4n  



. C.

 

1

2; 3; 4n 



. D.

 

4

2; 3; 4n  



.

Câu 5. (Mã 103 - 2020 Lần 2) Trong không gian

Oxyz

, Cho mặt phẳng

 

: 2 3 5 0x y z



   

. Vectơ

nào dưới đây là một vectơ pháp tuyến của

 



?

A.

 

3

2;1;3 .n  



B.

 

4

2;1; 3 .n  



C.

 

2

2; 1;3 .n  



D.

 

1

2;1;3 .n 



Câu 6. (Mã 104 - 2020 Lần 2) Trong không gian

Oxyz

, cho mặt phẳng

 

: 2 4 1 0x y z



   

.Vectơ

nào dưới đây là một vectơ pháp tuyến của mặt phẳng

 



?

A.

 

3

1; 2;4n



 

. B.

 

1

1;2; 4n



 

. C.

 

2

1;2;4n





. D.

 

4

1;2;4n



 

Câu 7. (Đề Minh Họa 2017) Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

 

:3 2 0P x z  

.

Vectơ nào dưới đây là một vectơ pháp tuyến của

 

P

?

A.

 

2

3;0; 1n  



B.

 

1

3; 1;2n  



C.

 

3

3; 1;0n  



D.

 

4

1;0; 1n   



Câu 8. (Mã 104 2018) Trong không gian

Oxyz

, mặt phẳng

 

: 2 3 1 0P x y z   

có một vectơ pháp

tuyến là:

A.

 

3

2;1;3n 



B.

 

2

1;3;2n  



C.

 

4

1;3;2n 



D.

 

1

3;1;2n 



PHƯƠNG TRÌNH MẶT PHẲNG

Chuyên đề 30

P

n



2

u



2

u



NGUYỄN BẢO VƯƠNG - 0946798489

Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 9. (Mã 101 - 2019) Trong không gian

Oxyz

, cho mặt phẳng

( ) : 2 3 1 0.

P x y z

   

Vectơ nào dưới

đây là một vectơ pháp tuyến của

( )P

?

A.

 

3

1;2; 1 .

n

 



B.

 

4

1;2;3 .

n 



C.

 

1

1;3; 1 .

n

 



D.

 

2

2;3; 1 .

n

 



Câu 10. (Mã 103 2018) Trong không giam

,Oxyz

mặt phẳng

 

: 2 3 1 0

P x y z

   

có một vectơ pháp

tuyến là

A.

 

1

2;3; 1

n 





B.

 

3

1;3;2

n 



C.

 

4

2;3;1

n 



D.

 

2

1;3;2

n 



Câu 11. (Mã 102 - 2019) Trong không gian

Oxyz

, cho mặt phẳng

 

: 2 3 1 0

P x y z

   

. Vectơ nào

dưới đây là một vectơ pháp tuyến của

 

P

?

A.

 

3

2;3;1

n 



. B.

 

1

2; 1; 3

n

  



. C.

 

4

2;1;3

n 



. D.

 

2

2; 1;3

n  



.

Câu 12. (Mã 103 -2019) Trong không gian

Oxyz

, cho mặt phẳng

 

: 2 3 2 0

P x y z

   

. Véctơ nào sau

đây là một véctơ pháp tuyến của

 

P

A.

 

1

2; 3;1

n  



. B.

 

4

2;1; 2

n

 



. C.

 

3

3;1; 2

n

  



. D.

 

2

2; 3; 2

n

  



.

Câu 13. (Mã 104 - 2019) Trong không gian

Oxyz

, cho mặt phẳng

 

: 4 3 1 0

P x y z

   

. Véctơ nào sau

đây là một véctơ pháp tuyến của

 

P

A.

 

4

3;1; 1

n

 



. B.

 

3

4;3;1

n 



. C.

 

2

4; 1;1

n  



. D.

 

1

4;3; 1

n

 



.

Câu 14. (Mã 102 2018) Trong không gian

Oxyz

, mặt phẳng

 

:3 2 4 0

P x y z

   

có một vectơ pháp

tuyến là

A.

 

2

3;2;1

n 



B.

 

1

1;2;3

n 



C.

 

3

1;2;3

n  



D.

 

4

1;2; 3

n

 



Câu 15. (Mã 101 2018) Trong không gian

Oxyz

cho mặt phẳng

 

: 2 3 5 0

P x y z

   

có một véc tơ

pháp tuyến là

A.

 

3

1;2;3

n  



B.

 

4

1;2; 3

n

 



C.

 

2

1;2;3

n 



D.

 

1

3;2;1

n 



Câu 16. (Mã 123 2017) Trong không gian với hệ tọa độ

Oxyz

, vectơ nào dưới đây là một véctơ pháp

tuyến của mặt phẳng

 

Oxy

?

A.

 





1; 0; 0

i B.

 





1;1;1

m C.

 





0; 1; 0

j D.

 





0; 0;1

k

Câu 17. (THPT Lý Thái Tổ 2019) Cho mặt phẳng

 

: 2 3 4 1 0

x y z



   

. Khi đó, một véc tơ pháp

tuyến của

 



A.

 

2;3; 4

n

 



. B.

 

2; 3;4

n  



. C.

 

2;3;4

n  



. D.

 

2;3;1

n  



.

Câu 18. Trong không gian

Oxyz

, cho mặt phẳng

 

:3 – 2 0

P x z

 

. Vectơ nào dưới đây là một vectơ pháp

tuyến của

 

P

?

A.

4

( 1;0; 1)

n

  



B.

1

(3; 1;2)

n  



C.

3

(3; 1;0)

n  



D.

2

(3;0; 1)

n

 



Câu 19. Trong không gian

Oxyz

, véctơ nào dưới đây có giá vuông góc với mặt phẳng

 

: 2 3 1 0?



  

x y

A.

 

2; 3;1

 



a

B.

 

2;1; 3 



b

C.

 

2; 3; 0

 



c

D.

 

3; 2; 0





d

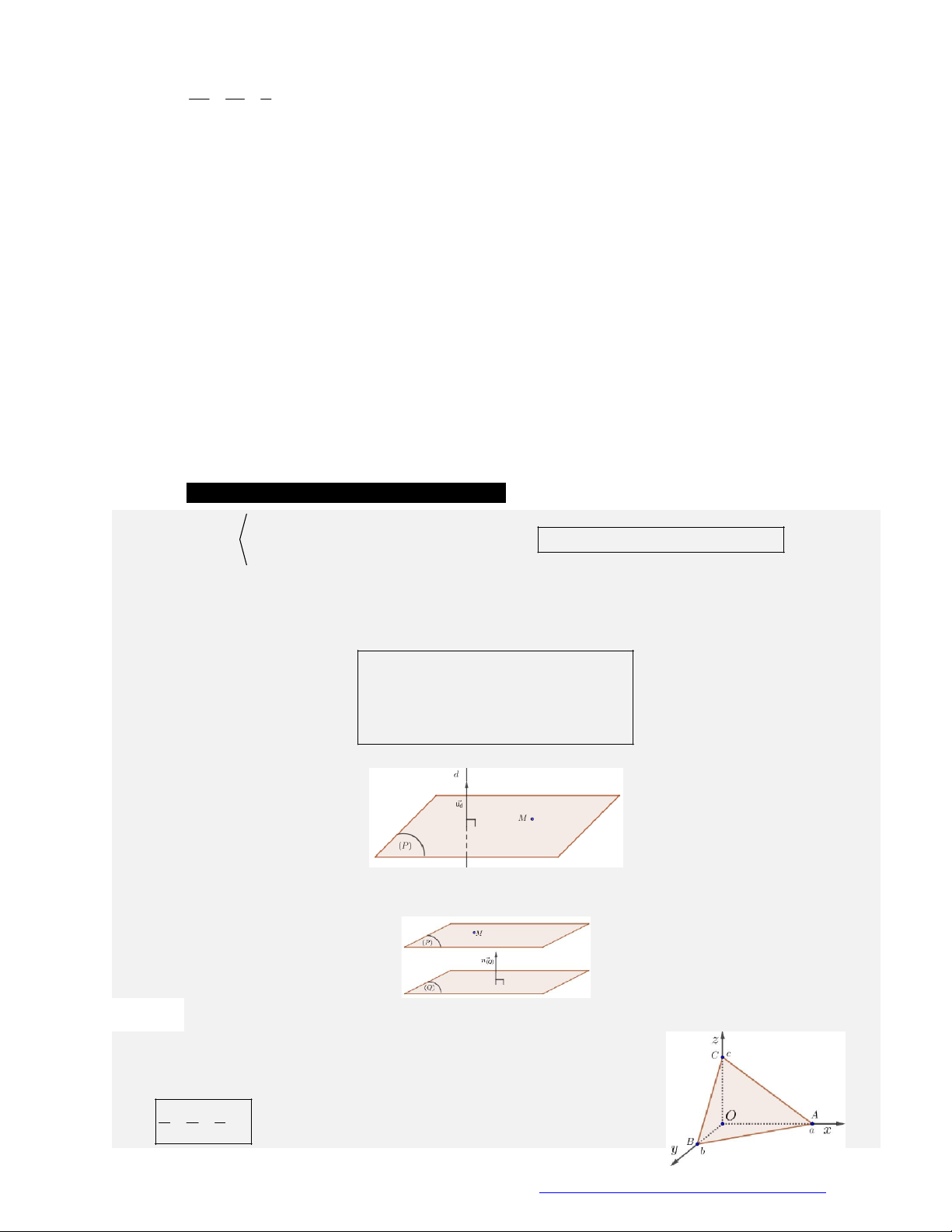
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3

Câu 20. (THPT Nghĩa Hưng NĐ- 2019) Trong không gian

Oxyz

, một vectơ pháp tuyến của mặt phẳng

1

2 1 3

x y z

  

 

là

A.

(3;6; 2)n  



B.

(2; 1;3)n  



C.

( 3; 6; 2)n    



D.

( 2; 1;3)n   



Câu 21. (THPT Ba Đình 2019) Trong mặt phẳng tọa độ

Oxyz

, cho phương trình tổng quát của mặt phẳng

 

: 2 6 8 1 0P x y z   

. Một véc tơ pháp tuyến của mặt phẳng

 

P

có tọa độ là:

A.

 

1; 3; 4 

B.

 

1; 3; 4

C.

 

1; 3; 4 

D.

 

1; 3; 4

Câu 22. (Chuyên KHTN 2019) Trong không gian

Oxyz

, vectơ nào dưới đây là một vectơ pháp tuyến

của mặt phẳng

 

: 2 3 1 0P y z  

?

A.

 

4

2;0; 3u  



. B.

 

2

0;2; 3u  



. C.

 

1

2; 3;1u  



. D.

 

3

2; 3;0u  



.

Câu 23. (THPT Lương Thế Vinh Hà Nội 2019) Cho mặt phẳng

 

:3 2 0P x y  

. Véc tơ nào trong

các véctơ dưới đây là một véctơ pháp tuyến của mặt phẳng

 

P

?

A.

 

3; 1;2

. B.

 

1;0; 1 

. C.

 

3;0; 1

. D.

 

3; 1;0

.

Dạng 2. Xác định phương trình mặt phẳng

Mặt phẳng

0 0 0

qua ( ; ; )

( )

( ; ; )

M x y z

P

VTPT n a b c





thì phương trình

0 0 0

( ) : ( ) ( ) ( ) 0P a x x b y y c z z     

(*)

Ngược lại, một mặt phẳng bất kỳ đều có phương trình dạng

0ax by cz d   

, mặt phẳng này có

( ; ; )VTPT n a b c





với

2 2 2

0a b c  

.

Các mặt phẳng cơ bản

( )

( ) : 0 (1;0;0)

( ) : 0 (0;1;0)

( ) : 0 (0;0;1)

VTPT

Oyz

VTPT

Oxz

VTPT

Oxy

mp Oyz x n

mp Oxz y n

mp Oxy z n

  



1. Viết phương trình mặt phẳng (P) qua M và vuông góc với với đường thẳng AB cho trước.

Mặt phẳng (P) qua M , có VTPT

( )P

n AB

 

nên phương trình được viết theo (*).

2. Viết phương trình mặt phẳng (P) qua M và song song với mặt phẳng (Q) cho trước.

Mặt phẳng (P) qua M, có VTPT là

( ) ( )P Q

n n

 



nên phương trình được viết theo (*).

3. Viết phương trình mặt phẳng cắt Ox, Oy, Oz lần lượt tại

( ;0;0), (0; ;0),A a B b (0;0; )C c

với

. . 0a b c 

.

Phương trình mặt phẳng được viết theo đoạn chắn

( ) : 1.

x y z

P

a b c

  

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 24. (Đề Tham Khảo 2019) Trong không gian

Oxyz

, mặt phẳng

 

Oxz

có phương trình là:

A.

0

x



B.

0

z



C.

0

x y z

  

D.

0

y



Câu 25. (Mã 110 2017) Trong không gian với hệ toạ độ

Oxyz

, phương trình nào dưới đây là phương trình

của mặt phẳng

 

Oyz

?

A.

0

y



B.

0

x



C.

0

y z

 

D.

0

z



Câu 26. (Sở Thanh Hóa 2019) Trong không gian

Oxyz

, mặt phẳng

 

Oyz

có phương trình là

A.

0

z



. B.

0

x y z

  

. C.

0

x



. D.

0

y



.

Câu 27. (Chuyên Hưng Yên 2019) Trong không gian với hệ tọa độ

,Oxyz

phương trình nào sau đây là phương

trình của mặt phẳng

Ozx

?

A.

0.

x



B.

1 0.

y

 

C.

0.

y



D.

0.

z



Câu 28. (Chuyên Quang Trung- Bình Phước 2019) Trong không gian

Oxyz

, mặt phẳng

 

Oxy

có

phương trình là

A.

0

z



. B.

0

x



. C.

0

y



. D.

0

x y

 

.

Câu 29. (Mã 104 2017) Trong không gian với hệ tọa độ

Oxyz

, phương trình nào dưới đây là phương

trình mặt phẳng đi qua điểm

 

1;2; 3

M



và có một vectơ pháp tuyến

 

1; 2;3

n  



.

A.

2 3 12 0

x y z

   

B.

2 3 6 0

x y z

   

C.

2 3 12 0

x y z

   

D.

2 3 6 0

x y z

   

Câu 30. (Đề Minh Họa 2017) Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm

 

0;1;1

A

) và

 

1;2;3

B

. Viết phương trình của mặt phẳng

 

P

đi qua

A

và vuông góc với đường thẳng

AB

.

A.

2 3 0

x y z

   

B.

2 6 0

x y z

   

C.

3 4 7 0

x y z

   

D.

3 4 26 0

x y z

   

Câu 31. (Mã 104 2018) Trong không gian

,Oxyz

Cho hai điểm

 

5; 4;2

A 

và

 

1;2;4 .

B

Mặt phẳng đi

qua

A

và vuông góc với đường thẳng

AB

có phương trình là

A.

2 3 20 0

x y z

   

B.

3 3 25 0

x y z

   

C.

2 3 8 0

x y z

   

D.

3 3 13 0

x y z

   

Câu 32. (Đề Tham Khảo 2018) Trong không gian

,Oxyz

cho hai điểm

 

1;2;1

A

và

 

2;1;0 .

B

Mặt

phẳng qua

A

và vuông góc với

AB

có phương trình là

A.

3 5 0   

x y z

B.

3 6 0   

x y z

C.

3 6 0   

x y z

D.

3 6 0   

x y z

Câu 33. (Mã 103 2018) Trong không gian

Oxyz

, cho ba điểm

 

1;1;1

A 

,

 

2;1;0

B

 

1; 1;2

C 

. Mặt

phẳng đi qua

A

và vuông góc với đường thẳng

BC

có phương trình là

A.

3 2 1 0

x z

  

B.

2 2 1 0

x y z

   

C.

2 2 1 0

x y z

   

D.

3 2 1 0

x z

  

Câu 34. (Chuyên Lê Hồng Phong Nam Định 2019) Trong không gian

Oxyz

, cho 2 điểm

(5; 4;2)

A



và

B(1;2;4)

. Mặt phẳng đi qua

A

và vuông góc với đường thẳng

AB

là?

A.

3 3 25 0

x y z

   

B.

2 3 8 0

x y z

   

C.

3 3 13 0

x y z

   

D.

2 3 20 0

x y z

   

Câu 35. (Chuyên Đại Học Vinh 2019) Trong không gian

Oxyz

, mặt phẳng

 

P

đi qua điểm

 

3; 1;4

M 

đồng thời vuông góc với giá của vectơ

 

1; 1;2

a  



có phương trình là

A.

3 4 12 0

x y z

   

. B.

3 4 12 0

x y z

   

. C.

2 12 0

x y z

   

. D.

2 12 0

x y z

   

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5

Câu 36. (THPT Lương Thế Vinh Hà Nội 2019) Cho ba điểm

     

2;1; 1 , 1;0;4 , 0; 2; 1

A B C

   

.

Phương trình mặt phẳng đi qua

A

và vuông góc với

BC

là

A.

2 5 5 0

x y z

   

. B.

2 5 5 0

x y z

   

. C.

2 5 0

x y

  

. D.

2 5 5 0

x y z

   

.

Câu 37. (Sở Bắc Giang 2019) Trong không gian

Oxyz

, cho hai điểm

 

1;1;2

A

và

 

2;0;1

B

. Mặt phẳng

đi qua

A

và vuông góc với

AB

có phương trình là

A.

0

x y z

  

. B.

2 0

x y z

   

. C.

4 0

x y z

   

. D.

2 0

x y z

   

.

Câu 38. (Chuyên - KHTN - Hà Nội - 2019) Trong không gian

,Oxyz

cho hai điểm

 

1;2;0

A

và

 

2;3; 1 .

B



Phương trình mặt phẳng qua

A

và vuông góc với

AB

là

A.

2 3 0.

x y z

   

B.

3 0.

x y z

   

C.

3 0.

x y z

   

D.

3 0.

x y z

   

Câu 39. (Chuyên Đại học Vinh 2019) Trong không gian

Oxyz

, mặt phẳng

 

P

đi qua điểm

 

3; 1;4

M 

đồng thời vuông góc với giá của vectơ

 

1; 1;2

a  



có phương trình là

A.

3 4 12 0

x y z

   

. B.

3 4 12 0

x y z

   

.

C.

2 12 0

x y z

   

. D.

2 12 0

x y z

   

.

Câu 40. (THPT Thuận Thành 3 - Bắc Ninh 2019) Trong không gian với hệ trục tọa độ

,Oxyz

phương

trình mặt phẳng đi qua điểm

 

1;2; 3

A



có véc tơ pháp tuyến

 

2; 1;3

n



 

là

A.

2 3 9 0

x y z

   

. B.

2 3 4 0

x y z

   

.

C.

2 4 0

x y

  

. D.

2 3 4 0

x y z

   

.

Câu 41. (SGD Điện Biên - 2019) Trong không gian

Oxyz

phương trình mặt phẳng đi qua điểm

(1; 2;3)

A



và vuông góc với giá của véctơ

( 1;2;3)

v  



là

A.

2 3 4 0.

x y z

   

B.

2 3 4 0.

x y z

   

C.

2 3 4 0.

x y z

   

D.

2 3 4 0.

x y z

    

Câu 42. (SGD Cần Thơ 2019) Trong không gian

Oxyz

, phương trình của mặt phẳng đi qua điểm

 

3;0; 1

A



và có véctơ pháp tuyến

 

4; 2; 3

n

  



là

A.

4 2 3 9 0

x y z

   

. B.

4 2 3 15 0

x y z

   

.

C.

3 15 0

x z

  

. D.

4 2 3 15 0

x y z

   

.

Câu 43. Trong không gian với hệ tọa độ

Oxyz

, phương trình mặt phẳng qua

 

1;1; 2

A

 

và có vectơ

pháp tuyến

 

1; 2; 2

n

  



là

A.

2 2 1 0

x y z

   

. B.

2 1 0

x y z

    

. C.

2 2 7 0

x y z

   

. D.

2 1 0

x y z

    

.

Câu 44. (Nguyễn Huệ- Ninh Bình- 2019)Trong không gian

Oxyz

, cho 2 điểm

   

1;0;1 , 2;1;0

A B

.

Viết phương trình mặt phẳng

 

P

đi qua

A

và vuông góc với

AB

.

A.

 

:3 4 0

P x y z

   

. B.

 

: 3 4 0

P x y z

   

.

C.

 

:3 0

P x y z

  

. D.

 

: 2 1 0

P x y z

   

.

Câu 45. (Chuyên Lê Hồng Phong-Nam Định- 2019) Trong không gian với hệ tọa độ

Oxyz

, cho các

điểm

 

0;1;2

A

,

 

2; 2;1

B 

,

 

2;0;1

C 

. Phương trình mặt phẳng đi qua

A

và vuông góc với

BC

là

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

A.

2 5 0

y z

  

. B.

2 1 0

x y

  

. C.

2 1 0

x y

  

. D.

2 5 0

y z

   

.

Câu 46. (Mã 101 2020 Lần 2) Trong không gian

Oxyz

, cho điểm

 

2; 1;4

M 

và mặt phẳng

 

:3 2 1 0

P x y z

   

. Phương trình của mặt phẳng đi qua

M

và song song với mặt phẳng

 

P

là

A.

2 2 4 21 0

x y z

   

. B.

2 2 4 21 0

x y z

   

C.

3 2 12 0

x y z

   

. D.

3 2 12 0

x y z

   

.

Câu 47. (Mã 102 - 2020 Lần 2) Trong không gian

Oxyz

, cho điểm

 

2;1; 2

M



và mặt phẳng

 

:3 2 1 0

P x y z

   

. Phương trình của mặt phẳng đi qua

M

và song song với

 

P

là:

A.

2 2 9 0

x y x

   

. B.

2 2 9 0

x y z

   

C.

3 2 2 0

x y z

   

. D.

3 2 2 0

x y z

   

.

Câu 48. (Mã 103 - 2020 Lần 2) Trong không gian

Oxyz

, cho điểm

 

2; 1;3

M 

và mặt phẳng

 

:3 2 1 0

P x y z

   

. Phương trình mặt phẳng đi qua

M

và song song với

 

P

là

A.

3 2 11 0

x y z

   

. B.

2 3 14 0

x y z

   

.

C.

3 2 11 0

x y z

   

. D.

2 3 14 0

x y z

   

.

Câu 49. (Mã 104 - 2020 Lần 2) Trong không gian

Oxyz

, cho điểm

 

2;1; 3

M



và mặt phẳng

 

:3 2 3 0

P x y z

   

. Phương trình của mặt phẳng đi qua

M

và song song với

( )P

là

A.

3 2 1 0

x y z

   

. B.

3 2 1 0

x y z

   

. C.

2 3 14 0

x y z

   

. D.

2 3 14 0

x y z

   

Câu 50. (Mã 105 2017) Trong không gian với hệ toạ độ

Oxyz

, cho điểm

 

3; 1; 2

M

 

và mặt phẳng

 

:3 2 4 0

x y z



   

. Phương trình nào dưới đây là phương trình mặt phẳng đi qua

M

và song

song với

 



?

A.

3 2 6 0

x y z

   

B.

3 2 6 0

x y z

   

C.

3 2 6 0

x y z

   

D.

3 2 14 0

x y z

   

Câu 51. (Mã 101 2018) Trong không gian

Oxyz

, mặt phẳng đi qua điểm

 

2; 1;2

A 

và song song với

mặt phẳng

 

: 2 3 2 0

P x y z

   

có phương trình là

A.

2 3 11 0

x y z

   

B.

2 3 11 0

x y z

   

C.

2 3 11 0

x y z

   

D.

2 3 9 0

x y z

   

Câu 52. (THPT Cẩm Giàng 2 -2019) Trong không gian với hệ trục

,Oxyz

mặt phẳng đi qua điểm

 

1;3; 2

A



và song song với mặt phẳng

 

: 2 3 4 0

P x y z

   

là:

A.

2 3 7 0

x y z

   

. B.

2 3 7 0

x y z

   

.

C.

2 3 7 0

x y z

   

. D.

2 3 7 0

x y z

   

.

Câu 53. Trong không gian

Oxyz

, mặt phẳng qua điểm

 

1;1;2

A 

và song song với mặt phẳng

 

: 2 2 1 0

x y z



   

có phương trình là

A.

2 2 2 0

x y z

   

B.

2 2 0

x y z

  

C.

2 2 6 0

x y z

   

D.

 

: 2 2 2 0

x y z



   

Câu 54. Trong không gian

Oxyz

, cho điểm

 

2; 1; 3

A

 

và mặt phẳng

 

:3 2 4 5 0

P x y z

   

. Mặt

phẳng

 

Q

đi qua

A

và song song với mặt phẳng

 

P

có phương trình là

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7

A.

 

:3 2 4 4 0.Q x y z   

B.

 

:3 2 4 4 0.Q x y z   

C.

 

:3 2 4 5 0.Q x y z   

D.

 

:3 2 4 8 0.Q x y z   

Câu 55. (Chuyên Quốc Học Huế 2019) Trong không gian với hệ tọa độ

Oxyz

cho điểm

 

1;0;6M

và

mặt phẳng

 



có phương trình

2 2 1 0x y z   

. Viết phương trình mặt phẳng

 



đi qua

M

và song song với mặt phẳng

 



.

A.

 

: 2 2 13 0x y z



   

. B.

 

: 2 2 15 0x y z



   

.

C.

 

: 2 2 15 0x y z



   

. D.

 

: 2 2 13 0x y z



   

.

Câu 56. (Mã 101 - 2020 Lần 1) Trong không gian

Oxyz

, cho ba điểm

 

3;0;0A

,

 

0;1;0B

và

 

0;0; 2C 

. Mặt phẳng

 

ABC

có phương trình là:

A.

1

3 1 2

x y z

  



. B.

1

3 1 2

x y z

  



.

C.

1

3 1 2

x y z

  

. D.

1

3 1 2

x y z

  



.

Câu 57. (Mã 102 - 2020 Lần 1) Trong không gian , cho ba điểm , và

. Mặt phẳng có phương trình là

A. . B. . C. . D. .

Câu 58. (Mã 103 - 2020 Lần 1) Trong không gian

Oxyz

, cho 3 điểm

 

1;0;0A 

,

 

0;2;0B

và

 

0;0;3C

. Mặt phẳng

 

ABC

có phương trình là

A.

1

1 2 3

x y z

  



. B.

1

1 2 3

x y z

  



. C.

1

1 2 3

x y z

  



. D

1

1 2 3

x y z

  

.

Câu 59. (Mã 104 - 2020 Lần 1) Trong không gian

Oxyz

, cho ba điểm

 

2;0;0A

,

 

0; 1;0B 

,

 

0;0;3C

.

Mặt phẳng

 

ABC

có phương trình là

A.

1

2 1 3

x y z

  



. B.

1

2 1 3

x y z

  



. C.

1

2 1 3

x y z

  

. D.

1

2 1 3

x y z

  



.

Câu 60. (Đề Tham Khảo 2018) Trong không gian

Oxyz

, cho ba điểm

 

2;0;0M

,

 

0; 1;0N

,

 

0;0;2P

.

Mặt phẳng

 

MNP

có phương trình là:

A.

1

2 1 2

   



x y z

. B.

1

2 1 2

  

x y z

. C.

1

2 1 2

  



x y z

D.

0

2 1 2

  



x y z

.

Câu 61. (Đề thử nghiệm THPT QG 2017) Trong không gian với hệ tọa độ

Oxyz

, cho

3

điểm

 

1;0;0A

;

 

0; 2;0B

;

 

0;0;3C

. Phương trình nào dưới dây là phương trình mặt phẳng

 

ABC

?

A.

1

3 2 1

  



x y z

. B.

1

2 1 3

  



x y z

. C.

1

1 2 3

  



x y z

. D.

1

3 1 2

  



x y z

.

Câu 62. (SGD Bắc Ninh 2019) Trong không gian với hệ tọa độ

Oxyz

, phương trình mặt phẳng

 



đi

qua điêm

 

0; 1;0A 

,

 

2;0;0B

,

 

0;0;3C

là

Oxyz

 

2;0;0

A 

 

0;3;0

B

 

0;0; 4

C

 

ABC

1

2 3 4

x y z

  



1

2 3 4

x y z

  

1

2 3 4

x y z

  



1

2 3 4

x y z

  



NGUYỄN BẢO VƯƠNG - 0946798489

Trang 8 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

A.

1

2 1 3

x y z

  

. B.

0

2 1 3

x y z

  



. C.

1

1 2 3

x y z

  



. D.

1

2 1 3

x y z

  



.

Câu 63. (Lômônôxốp - Hà Nội 2019) Trong không gian

Oxyz

, cho ba điểm

 

1;0;0

M

,

 

0;2;0

N

,

 

0;0;3

P

. Mặt phẳng

 

MNP

có phương trình là:

A.

6 3 2 6 0

x y z

   

. B.

6 3 2 1 0

x y z

   

.

C.

6 3 2 1 0

x y z

   

. D.

6 0

x y z

   

.

Câu 64. (THPT Hoàng Hoa Thám - Hưng Yên 2019) Trong không gian với hệ tọa độ Oxyz, cho ba

điểm

(2;0;0), B(0;-1;0), C(0;0;-3).

A

Viết phương trình mặt phẳng

( ).ABC

A.

3 6 2 6 0

x y z

    

. B.

3 6 2 6 0

x y z

    

.

C.

3 6 2 6 0

x y z

    

. D.

3 6 2 6 0

x y z

    

.

Câu 65. (Chuyên - KHTN - Hà Nội - 2019) Trong không gian

Oxyz

, phương trình mặt phẳng đi qua ba

điểm

 

3;0;0

A 

,

 

0;4;0

B

,

 

0;0; 2

C



là

A.

4 3 6 12 0

x y z

   

. B.

4 3 6 12 0

x y z

   

.

C.

4 3 6 12 0

x y z

   

. D.

4 3 6 12 0

x y z

   

.

Câu 66. (THPT Ngô Sĩ Liên Bắc Giang 2019) Trong không gian

Oxyz

, cho ba điểm

( 2;0;0)

A



,

(0;0;7)

B

và

(0;3;0)

C

. Phương trình mặt phẳng

( )ABC

là

A.

1

2 7 3

x y z

  



B.

0

2 3 7

x y z

  



C.

1

2 3 7

x y z

  



D.

1 0

2 3 7

x y z

   



Câu 67. Trong không gian

Oxyz

, mặt phẳng qua ba điểm

 

1;0;0

A 

,

 

0;2;0

B

,

 

0;0; 3

C



có phương

trình là

A.

1

1 2 3

x y z

   

 

. B.

1

1 2 3

x y z

  



. C.

1

1 2 3

x y z

  

 

. D.

1

1 2 3

x y z

  



.

Câu 68. (Chuyên Thái Bình -2019) Trong không gian

Oxyz

, cho điểm

 

1;2;3

M

. Gọi

, ,A B C

lần lượt

là hình chiếu vuông góc của điểm

M

lên các trục

, ,Ox Oy Oz

. Viết phương trình mặt phẳng

 

ABC

.

A.

1

1 2 3

x y z

  

. B.

1

1 2 3

x y z

  

. C.

0

1 2 3

x y z

  

. D.

1

1 2 3

x y z

   

.

Câu 69. (Đề Thi Công Bằng KHTN 2019) Trong không gian

O

xyz

, phương trình mặt phẳng đi qua ba

điểm

 

3;0;0

A  ;

 

0;4;0

B và

 

0;0; 2

C



là.

A.

4 3 6 12 0

x y z

   

. B.

4 3 6 12 0

x y z

   

.

C.

4 3 6 12 0

x y z

   

. D.

4 3 6 12 0

x y z

   

.

Câu 70. (THPT Gang Thép Thái Nguyên 2019) Trong không gian với hệ trục tọa độ

Oxyz

, mặt phẳng

qua các điểm

 

1;0;0

A

,

 

0;3;0

B

,

 

0;0;5

C

có phương trình là

A.

15 5 3 15 0.

x y z

   

B.

1 0.

1 3 5

x y z

   

C.

3 5 1.

x y z

  

D.

1.

1 3 5

x y z

  

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9

Câu 71. (Chuyên Sơn La 2019) Trong không gian

Oxyz

, phương trình mặt phẳng đi qua ba điểm

 

1;0;0

A

,

 

0; 2;0

B

và

 

0;0;3

C

là

A.

1

1 2 3

x y z

  



. B.

1

1 2 3

x y z

   



. C.

0

1 2 3

x y z

  



. D.

1

1 2 3

x y z

  

.

Câu 72. (THPT Hoàng Hoa Thám Hưng Yên 2019) Trong không gian với hệ tọa độ

Oxyz

, cho ba điểm

 

2;0;0

A

,

 

0; 1;0

B 

,

 

0;0; 3

C



. Viết phương trình mặt phẳng

 

ABC

.

A.

3 6 2 6 0

x y z

    

. B.

3 6 2 6 0

x y z

    

.

C.

3 6 2 6 0

x y z

    

. D.

3 6 2 6 0

x y z

    

.

Câu 73. (Chuyên Lê Quý Đôn Điện Biên 2019) Trong không gian với hệ tọa độ

Oxyz

, cho 3 điểm

     

1;0;0 , 0;3;0 , 0;0;4

A B C

. Phương trình nào dưới đây là phương trình của mặt phẳng

 

ABC

?

A.

1

1 3 4

x y z

  

. B.

1

1 3 4

x y z

  

. C.

1

4 3 1

x y z

  



. D.

1

1 3 4

x y z

   

.

Dạng 3. Điểm thuộc mặt phẳng

Một mặt phẳng bất kỳ đều có phương trình dạng

 

: 0

P ax by cz d

   

, và điểm

 

; ;

M M M

M x y z

.

Nếu

 

0

M M M

ax by cz d M P

     

Nếu

 

0

M M M

ax by cz d M P

     

Câu 74. (Mã 105 2017) Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

 

: 6 0

x y z



   

.

Điểm nào dưới đây không thuộc

 



?

A.

 

3;3;0

Q

B.

 

2;2;2

N

C.

 

1;2;3

P

D.

 

1; 1;1

M 

Câu 75. (Mã 123 2017) Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

 

: 2 5 0.

P x y z

   

Điểm nào dưới đây thuộc

 

P

?

A.

 

0;0; 5

P



B.

 

1;1;6

M

C.

 

2; 1;5

Q 

D.

 

5;0;0

N 

Câu 76. Trong không gian

Oxyz

, mặt phẳng

 

: 3 0

P x y z

   

đi qua điểm nào dưới đây?

A.

 

1; 1; 1

M

  

B.

 

1;1;1

N

C.

 

3;0;0

P 

D.

 

0;0; 3

Q



Câu 77. (THPT Cẩm Giàng 2 2019) Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

 

:2 3 0

P x y z

   

. Điểm nào trong các phương án dưới đây thuộc mặt phẳng

 

P

A.

 

2;1;0

M

. B.

 

2; 1;0

M 

. C.

 

1; 1;6

M  

. D.

 

1; 1;2

M  

.

Câu 78. (Chuyên Bắc Ninh 2019) Trong không gian

Oxyz

, điểm nào dưới đây nằm trên mặt phẳng

 

: 2 2 0

P x y z

   

.

A.

 

1; 2; 2

Q 

. B.

 

2; 1; 1

P

 

. C.

 

1;1; 1

M



. D.

 

1; 1; 1

N

 

.

Câu 79. (Hậu Lộc 2-Thanh Hóa- 2019) Trong không gian

Oxyz

, mặt phẳng

 

: 1

1 2 3

x y z

P

  

không

đi qua điểm nào dưới đây?

A.

 

0;2;0

P

. B.

 

1;2;3

N

. C.

 

1;0;0

M

. D.

 

0;0;3

Q

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 10 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 80. (Chuyên Lê Hồng Phong Nam Định 2019) Trong không gian

Oxyz

, mặt phẳng nào dưới đây

đi qua gốc tọa độ?

A.

20 0

x

 

. B.

2019 0

x

 

. C.

5 0

y

 

. D.

2 5 8 0

x y z

  

.

Câu 81. (Chuyên Lê Quý Đôn – Điện Biên 2019) Trong không gian Oxyz, cho mặt phẳng

( )



:

2 2z 3 0.

x y

   

Điểm nào sau đây nằm trên mặt phẳng

( )



?

A.

(2; 0;1).

M

B.

(2;1;1).

Q

C.

(2; 1;1).

P



D.

(1; 0;1).

N

Câu 82. (SGD Bình Phước - 2019) Trong không gian

Oxyz

,mặt phẳng

 

: 2 3 0

x y z



   

đi qua

điểm nào dưới đây?

A.

3

1;1;

2

M

 

 

 

. B.

3

1; 1;

2

N

 

 

 

 

. C.

 

1;6;1

P

. D.

 

0;3;0

Q

.

Câu 83. (Sở Kon Tum - 2019) Trong không gian

Oxyz

, mặt phẳng

 

: 2 4 0

x y z



   

đi qua điểm

nào sau đây

A.

 

1; 1;1

Q 

. B.

 

0;2;0

N

. C.

 

0;0; 4

P



. D.

 

1;0;0

M

.

Câu 84. (SGD Bến Tre 2019) Trong không gian

Oxyz

cho mặt phẳng

 

: 2 1 0

P x y z

   

. Điểm nào

dưới đây thuộc

 

P

?

A.

 

0;1; 2

N



. B.

 

2; 1;1

M 

. C.

 

1; 2;0

P 

. D.

 

1; 3; 4

Q

 

.

Dạng 4. Khoảng cách từ điểm đến mặt



Khoảng cách từ điểm

( ; ; )

M M M

M x y z

đến mặt phẳng

( ) : 0

P ax by cz d

   

được xác định bởi công

thức:

2 2 2

( ;( ))

M M M

ax by cz d

d M P

a b c

  

 

 

Câu 85. (Đề Minh Họa 2017) Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng cho mặt phẳng

 

P

có phương trình

3 4 2 4 0

x y z

   

và điểm

 

1; 2;3

A 

. Tính khoảng cách

d

từ

A

đến

 

P

A.

5

29

d 

B.

5

29

d 

C.

5

3

d 

D.

5

9

d



Câu 86. (THPT Ba Đình 2019) Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

 

P

có phương

trình:

3 4 2 4 0

x y z

   

và điểm

 

1; 2;3

A 

. Tính khoảng cách

d

từ

A

đến

 

P

.

A.

5

9

d



. B.

5

29

d 

. C.

5

29

d 

. D.

5

3

d 

.

Câu 87. (THPT Gia Lộc Hải Dương 2019) Trong không gian

Oxyz

, tính khoảng cách từ

 

1;2; 3

M



đến mặt phẳng

 

: 2 2 10 0

P x y z

   

.

A.

11

3

. B.

3

. C.

7

3

. D.

4

3

.

Câu 88. (Sở Hà Nội 2019) Trong không gian

Oxyz

, cho mặt phẳng

 

: 2 2 1 0

P x y z

   

. Khoảng cách

từ điểm

 

1;2;0

M 

đến mặt phẳng

 

P

bằng

A.

5

. B.

2

. C.

5

3

. D.

4

3

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11

Câu 89. (C

huyên Lê Quý Đôn Quảng Trị 2019) Trong không gian với hệ tọa độ

O

xyz

,

cho mặt phẳng

 

:

2 2 4 0

P

x y z



  

. Tí

nh khoảng cách

d

từ điểm

 

1

;2;1

M

đến mặt phẳng

 

P

.

A.

3

d



. B.

4

d



. C.

1

d



. D.

1

3

d



.

Câu 90. (Sở Bắc Giang 2019) Trong không gian

O

xyz

,

cho mặt phẳng

 

:

2 2 1 0

Q

x y z



  

và

điểm

 

1; 2;1

M 

. K

hoảng cách từ điểm

M

đến mặt

phẳng

 

Q

bằng

A.

4

3

. B.

1

3

. C.

2

3

. D.

2

6

3

.

Câu 91.

(Kiểm tra năng lực - ĐH - Quốc Tế - 2019) Trong không gian với hệ trục tọa độ

Oxyz

,

gọi

H

là

hình chiếu vuông góc của điểm

 

1

; 2;3

A 

lê

n mặt phẳng

 

:

2 2 5 0

P

x y z



  

.

Độ dài đoạn

thẳng

AH

là

A.

3

. B.

7

. C.

4

. D.

1

.

Câu 92.

(SGD Cần Thơ 2019) Trong không gian

O

xyz

, cho điểm

 

1

;2 3

M



và mặt phẳng

 

: 2 2 5 0

P x y z

   

. Khoảng cách từ điểm

M

đến mặt phẳng

 

P

bằng

A.

4

3

. B.

1

3

. C.

2

3

. D.

4

9

.

Câu 93.

(Cần Thơ - 2019) Trong không gian

O

xyz

,

cho mặt phẳng

 

:

2 2 5 0

P

x y z



  

và

điểm

 

1;3; 2

A

 

. Khoảng cá

ch từ

A

đến mặt

 

P

l

à

A.

1

4

7

.

B.

3

14

. C.

2

3

. D.

1

.

Câu 94.

(Sở Kon Tum - 2019) Trong không gian

O

xyz

, cho mặt phẳng

 

:

2 2 4 0

P

x y z



  

. Khoảng

cách từ điểm

 

3

;1; 2

M



đến

mặt phẳng

 

P

bằng

A.

2

. B.

1

3

. C.

1

. D.

3

.

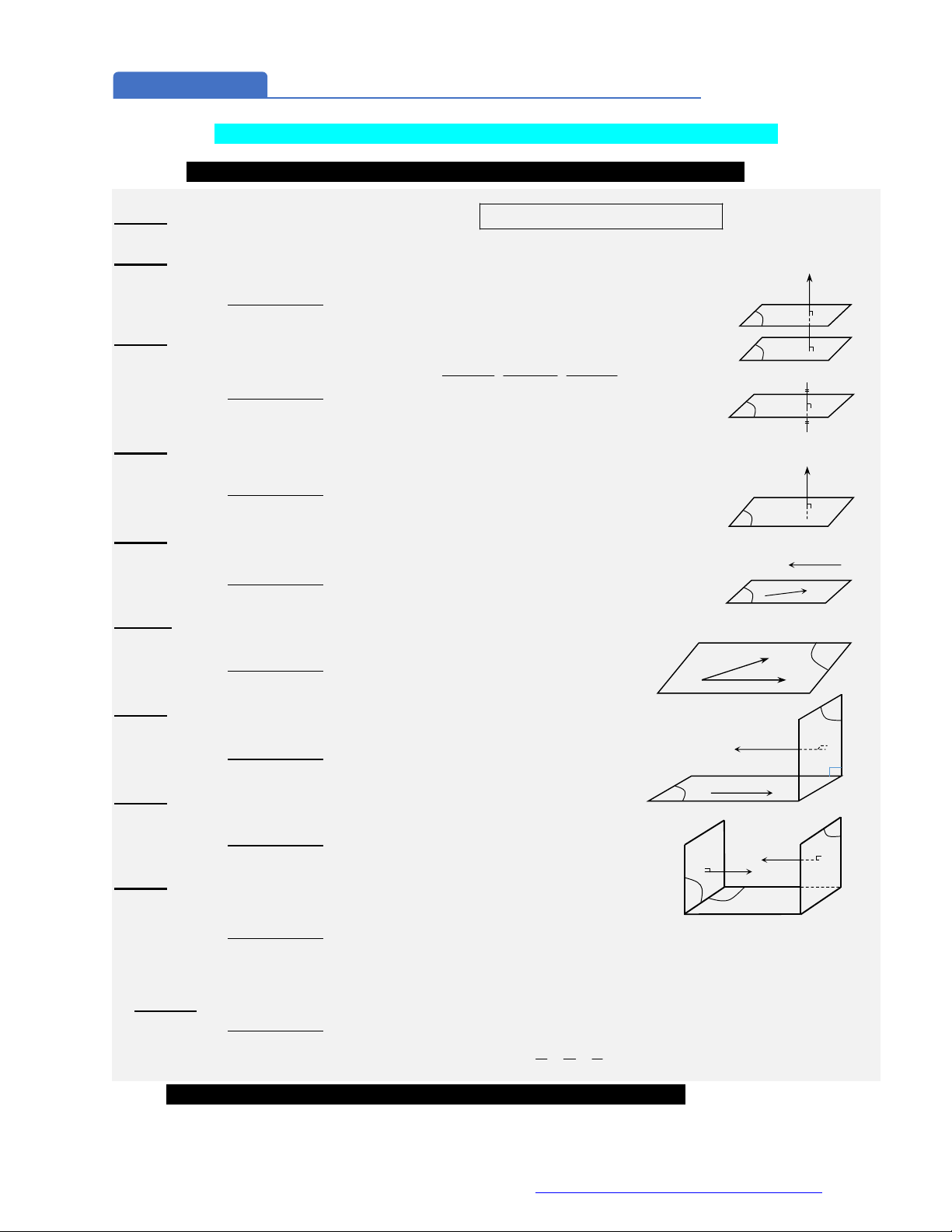
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương  https://www.facebook.com/phong.baovuong Trang 1

TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH KHÁ – MỨC 7-8 ĐIỂM

Dạng 1. Xác định phương trình mặt phẳng (không chứa yếu tố đường thẳng)

Dạng 1. Mặt

( )

( ; ; )

( ) : ( ) : ( ) ( ) ( ) 0 .

: ( ; ; )

P

Qua A x y z

P P a x x b y y c z z

VTPT n a b c



      







  







Dạng 2. Viết phương trình

( )P

qua ( ; ; )A x y z

  

và

( ) ( ) : 0.P Q ax by cz d   

Phương pháp.

( ) ( )

( , , )

( ) :

: ( ; ; )

P Q

A x y z

P

VT

u

PT n n b

a

a c

Q





 



  



 



Dạng 3. Viết phương trình mặt phẳng trung trực

( )P

của đoạn thẳng

.AB

Phương pháp.

( )

2

(

;

:

) :

;

2 2

A B A B A B

P

x x y y z z

Qua I

VTPT n AB

P



  

 

 























Dạng 4. Viết phương trình mặt phẳng

( )P

qua

M

và vuông góc với đường thẳng

.d AB

Phương pháp.

( )

( ; ; )

( ) :

:

P d

M x y z

P

VTPT n u

u

AB

Q a







 





  





 



Dạng 5. Viết phương trình mặt phẳng

( )P

qua điểm

M

và có cặp véctơ chỉ phương

, .a b



Phương pháp.

( )

( ; ; )

( ) :

]

: [ ,

P

M x y z

P

VTPT n a b

Qua













  





 



Dạng 6. Viết phương trình mặt phẳng

( )P

đi qua ba điểm

, , A B C

không thẳng hàng.

Phương pháp.

( )

, ( )

( ) :

: ,

ABC

P

VTP A

Qua A hay B hay C

T n AB C







 





 





 





Dạng 7. Viết phương trình mặt phẳng

( )P

đi qua

, A B

và

( ) ( ).P Q

Phương pháp.

( ) ( )

, ( )

( ) :

: ,

P Q

Q A hay B

P

VTPT n AB n

ua







 





 







 



Dạng 8. Viết phương trình mp

( )P

qua

M

và vuông góc với hai mặt

( ), ( ).

 

Phương pháp.

( ) ( ) ( )

(

;

) :

: ,

( ; )

P

Q

P

VTPT

ua

n

M x y z

n n

 







 





 



  



  



Dạng 9. Viết

( )P

đi qua

M

và giao tuyến

d

của hai mặt phẳng:

1 1 1 1

( ) : 0Q a x b y c z d    và

2 2 2 2

( ): 0.T a x b y c z d   

Phương pháp: Khi đó mọi mặt phẳng chứa

d

đều có dạng:

2 2

1 1 1 1 2 2 2 2

( ) : ( ) ( ) 0, 0.P m a x b y c z d n a x b y c z d m n         

Vì

( )M P 

mối liên hệ giữa

m

và

.n

Từ đó chọn m n sẽ tìm được

( ).P

Dạng 10. Viết phương trình mặt phẳng đoạn chắn

Phương pháp: Nếu mặt phẳng

( )P

cắt ba trục tọa độ lần lượt tại các điểm

( ;0;0),A a

(0; ;0),B b

(0;0; )C c

với

( 0)abc 

thì

( ) : 1

x y z

P

a b c

  

gọi là mặt phẳng đoạn chắn.

Dạng 1.1 Xác định phương trình mặt phẳng khi biết yếu tố vuông góc

Câu 1. (Mã 104 - 2019) Trong không gian Oxyz, cho hai điểm

 

4;0;1A

và

 

2;2;3 .B

Mặt phẳng trung

trực của đoạn thẳng AB có phương trình là

PHƯƠNG TRÌNH MẶT PHẲNG

Chuyên đề 30

P

Q

( ) ( )

P Q

n n



 

: là trung điểm

.

AB

P

A

B

I

P

( )P d

AB

n u

 



 

d

M

P

a



b



A

C

B

P

B

A

P

Q

( )

Q

n







( )

n





( )

n





P

M

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

A.

3 0.  

x y z

B.

3 6 0.   

x y z

C.

2 6 0.   

x y z

D.

6 2 2 1 0.   

x y z

Câu 2. (Mã 102 - 2019) Trong không gian

Oxyz

, cho hai điểm

 

1;2;0

A 

và

 

3;0;2

B

. Mặt phẳng

trung trực của đoạn thẳng

AB

có phương trình là

A.

3 0

x y z

   

. B.

2 2 0

x y z

   

. C.

2 4 0

x y z

   

. D.

2 2 0

x y z

   

.

Câu 3. (Mã 110 2017) Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm

 

4;0;1

A

và

 

2;2;3

B 

.

Phương trình nào dưới đây là phương trình mặt phẳng trung trực của đoạn thẳng

AB

?

A.

3 6 0

x y z

   

B.

3 0

x y z

  

C.

6 2 2 1 0

x y z

   

D.

3 1 0

x y z

   

Câu 4. (Mã 101 2019) Trong không gian

Oxyz

, cho hai điểm

 

1;3;0

A

và

 

5;1; 1

B



. Mặt phẳng trung

trực của đoạn thẳng

AB

có phương trình là:

A.

2 3 0

x y z

   

. B.

3 2 14 0

x y z

   

. C.

2 5 0

x y z

   

. D.

2 5 0

x y z

   

.

Câu 5. (Mã 103 - 2019) Trong không gian

Oxyz

, cho hai điểm

(2;1;2)

A

và

(6;5; 4)

B



. Mặt phẳng

trung trực của đoạn thẳng

AB

có phương trình là

A.

2 2 3 17 0

x y z

   

. B.

4 3 26 0

x y z

   

.

C.

2 2 3 17 0

x y z

   

. D.

2 2 3 11 0

x y z

   

.

Câu 6. (Chuyên Thái Bình 2019) Trong không gian

Oxyz

, cho hai điểm

 

1;3; 4

A



và

 

1;2;2

B 

.

Viết phương trình mặt phẳng trung trực

 



của đoạn thẳng

AB

.

A.

 

: 4 2 12 7 0

x y z



   

. B.

 

: 4 2 12 17 0

x y z



   

.

C.

 

: 4 2 12 17 0

x y z



   

. D.

 

: 4 2 12 7 0

x y z



   

.

Câu 7. (THPT An Lão Hải Phòng 2019) Trong không gian hệ tọa độ

Oxyz

, cho

 

1;2; 1

A



;

 

1;0;1

B 

và mặt phẳng

 

: 2 1 0

P x y z

   

. Viết phương trình mặt phẳng

 

Q

qua

,A B

và vuông góc

với

 

P

A.

 

:2 3 0

Q x y

  

B.

 

: 0

Q x z

 

C.

 

: 0

Q x y z

   

D.

 

:3 0

Q x y z

  

Câu 8. (THPT Gia Lộc Hải Dương 2019) Trong không gian

Oxyz

, cho hai điểm

   

2;4;1 1;1;3

A ,B 

và mặt phẳng

 

: 3 2 5 0

P x y z

   

. Lập phương trình mặt phẳng

 

Q

đi qua hai điểm

A

,

B

và

vuông góc với mặt phẳng

 

P

.

A.

2 3 11 0

y z

  

. B.

2 3 11 0

x y

  

. C.

3 2 5 0

x y z

   

. D.

3 2 11 0

y z

  

.

Câu 9. (Chuyên KHTN 2019) Trong không gian

Oxyz

, cho hai điểm

 

1; 1;2

A

và

 

3;3;0

B

. Mặt

phẳng trung trực của đoạn thẳng

AB

có phương trình là

A.

2 0   

x y z

. B.

2 0   

x y z

. C.

2 3 0   

x y z

. D.

2 3 0   

x y z

.

Câu 10. (Chuyên Sơn La 2019) Trong không gian

Oxyz

, mặt phẳng

 

P

đi qua hai điểm

 

0;1;0

A

,

 

2;3;1

B

và vuông góc với mặt phẳng

 

: 2 0  

Q x y z

có phương trình là

A.

4 3 2 3 0

x y z

   

. B.

4 3 2 3 0

x y z

   

. C.

2 3 1 0

x y z

   

. D.

4 2 1 0

x y z

   

.

Câu 11. (KTNL GV Lý Thái Tổ 2019) Cho hai mặt phẳng

   

:3 2 2 7 0, : 5 4 3 1 0

x y z x y z

 

       

. Phương trình mặt phẳng đi qua gốc tọa độ

O

đồng thời vuông góc với cả

 



và

 



là:

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3

A.

2 2 0.

x y z

  

B.

2 2 0.

x y z

  

C.

2 2 0.

x y z

  

D.

2 2 1 0.

x y z

   

Câu 12. (Chuyên Lê Hồng Phong Nam Định 2019) Trong không gian với hệ tọa độ

Oxyz

, cho điểm

   

2;4;1 ; 1;1;3

A B 

và mặt phẳng

 

: 3 2 5 0

P x y z

   

. Một mặt phẳng

 

Q

đi qua hai điểm

,A B

và vuông góc với mặt phẳng

 

P

có dạng

11 0

ax by cz

   

. Khẳng định nào sau đây là

đúng?

A.

5

a b c

  

. B.

15

a b c

  

. C.

5

a b c

   

. D.

15

a b c

   

.

Câu 13. (THPT Yên Phong Số 1 Bắc Ninh 2019) Trong không gian với hệ tọa độ

Oxyz

, cho

   

1; 1;2 ; 2;1;1

A B

và mặt phẳng

 

: 1 0

P x y z

   

. Mặt phẳng

 

Q

chứa

,A B

và vuông

góc với mặt phẳng

 

P

. Mặt phẳng

 

Q

có phương trình là:

A.

3 2 3 0

x y z

   

. B.

2 0

x y z

   

. C.

0

x y

  

. D.

3 2 3 0

x y z

   

.

Câu 14. (Chuyên Đại Học Vinh 2019) Trong không gian

,Oxyz

cho hai mặt phẳng

 

: 3 2 1 0,

P x y z

   

 

: 2 0

Q x z

  

. Mặt phẳng

 



vuông góc với cả

 

P

và

 

Q

đồng

thời cắt trục

Ox

tại điểm có hoành độ bằng

3.

Phương trình của mp

 



là

A.

3 0

x y z

   

B.

3 0

x y z

   

C.

2 6 0

x z

   

D.

2 6 0

x z

   

Câu 15. (Chuyên Lam Sơn Thanh Hóa 2019) Trong không gian với hệ tọa độ

Oxyz

cho hai mặt phẳng

 

: 3 2 2 7 0

x y z



   

và

 

: 5 4 3 1 0

x y z



   

. Phương trình mặt phẳng đi qua

O

đồng

thời vuông góc với cả

 



và

 



có phương trình là

A.

2 2 1 0

x y z

   

. B.

2 2 0

x y z

  

. C.

2 2 0

x y z

  

. D.

2 2 0

x y z

  

.

Câu 16. (HSG Bắc Ninh 2019) Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

 

: 1 0

P x y z

   

và hai điểm

   

1; 1;2 ; 2;1;1

A B

. Mặt phẳng

 

Q

chứa

,A B

và vuông góc

với mặt phẳng

 

P

, mặt phẳng

 

Q

có phương trình là:

A.

3 2 3 0

x y z

   

. B.

2 0

x y z

   

. C.

3 2 3 0

x y z

   

. D.

0

x y

  

.

Câu 17. (Đề Thi Công Bằng KHTN 2019) Trong không gian

Oxyz

, phương trình mặt phẳng đi qua hai

điểm

   

0;1;0 , 2;0;1

A B

và vuông góc với mặt phẳng

 

: 1 0

P x y

  

là:

A.

3 1 0

x y z

   

. B.

2 2 5 2 0

x y z

   

.

C.

2 6 2 0

x y z

   

. D.

1 0

x y z

   

.

Câu 18. (Chuyên Lam Sơn 2019) Trong không gian

Oxyz

, cho hai mặt phẳng

 

: 3 2 2 7 0

x y z



   

và

 

: 5 4 3 1 0.

x y z

   



Phương trình mặt phẳng qua

O

, đồng thời vuông góc với cả

 



và

 



có phương trình là

A.

2 2 0

x y z

  

. B.

2 2 1 0

x y z

   

. C.

2 2 0

x y z

  

. D.

2 2 0

x y z

  

.

Câu 19. (SGD Bến Tre 2019) Trong không gian

Oxyz

,

cho điểm

 

1; 1;2

A 

;

 

2;1;1

B

và mặt phẳng

 

: 1 0

P x y z

   

.

Mặt phẳng

 

Q

chứa

A

,

B

và vuông góc với mặt phẳng

 

P

.

Mặt phẳng

 

Q

có phương trình là

A.

3 2 3 0

x y z

   

. B.

0

x y

  

. C.

2 0

x y z

   

. D.

3 2 3 0

x y z

   

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 20. Trong không gian với hệ trục tọa độ

Oxyz

, cho mặt phẳng

 

: 9 0

P ax by cz

   

chứa hai điểm

 

3;2;1

A

,

 

3;5;2

B 

và vuông góc với mặt phẳng

 

:3 4 0

Q x y z

   

. Tính tổng

S a b c  

.

A.

12

S

 

. B.

2

S



. C.

4

S

 

. D.

2

S

 

.

Câu 21. (Thi thử hội 8 trường chuyên 2019) Trong không gian

,Oxyz

cho ba mặt phẳng

 

: 1 0,

P x y z

   

 

: 2 5 0

Q y z

  

và

 

: 2 0.

R x y z

   

Gọi

 



là mặt phẳng qua giao

tuyến của

 

P

và

 

,Q

đồng thời vuông góc với

 

.R

Phương trình của

 



là

A.

2 3 5 5 0.

x y z

   

B.

3 2 6 0.

x y z

   

C.

3 2 6 0.

x y z

   

D.

2 3 5 5 0.

x y z

   

Câu 22. (THPT Lương Thế Vinh - HN - 2018) Trong không gian

Oxyz

, phương trình của mặt phẳng

 

P

đi qua điểm

 

2;1; 3

B



, đồng thời vuông góc với hai mặt phẳng

 

: 3 0

Q x y z

  

,

 

: 2 0

R x y z

  

là

A.

4 5 3 22 0

x y z

   

. B.

4 5 3 12 0

x y z

   

.

C.

2 3 14 0

x y z

   

. D.

4 5 3 22 0

x y z

   

.

Câu 23. (Chuyên Nguyễn Quang Diêu - Đồng Tháp - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho

hai điểm

 

2;4;1

A

,

 

1;1;3

B 

và mặt phẳng

 

P

:

3 2 5 0

x y z

   

. Một mặt phẳng

 

Q

đi qua

hai điểm

A

,

B

và vuông góc với

 

P

có dạng là

11 0

ax by cz

   

. Tính

a b c 

.

A.

10

a b c

  

. B.

3

a b c

  

. C.

5

a b c

  

. D.

7

a b c

   

.

Câu 24. (Chuyên Trần Phú - Hải Phòng - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho điểm

 

1;1;1

A

và hai mặt phẳng

 

: 2 3 1 0

P x y z

   

,

 

: 0

Q y



. Viết phương trình mặt phẳng

 

R

chứa

A

, vuông góc với cả hai mặt phẳng

 

P

và

 

Q

.

A.

3 2 4 0

x y z

   

. B.

3 2 2 0

x y z

   

. C.

3 2 0

x z

 

. D.

3 2 1 0

x z

  

.

Câu 25.

(THPT

Lý

Thái

Tổ

-

Bắc

Ninh

-

2018)

Cho hai mặt phẳng

 



:

3 2 2 7 0

x y z

   

và

 



:

5 4 3 1 0

x y z

   

. Phương trình mặt phẳng

 

P

đi qua gốc tọa độ đồng thời vuông góc

 



và

 



là:

A.

2 0

x y z

  

. B.

2 2 0

x y z

  

. C.

2 2 1 0

x y z

   

. D.

2 2 0

x y z

  

.

Câu 26. (Toán Học Tuổi Trẻ 2018) Trong không gian với hệ tọa độ

Oxyz

cho hai điểm

 

2;4;1

A

,

 

1;1;3

B



và mặt phẳng

 

: 3 2 5 0

P x y z

   

. Một mặt phẳng

 

Q

đi qua hai điểm

A

,

B

và

vuông góc với

 

P

có dạng:

11 0

ax by cz

   

. Khẳng định nào sau đây là đúng?

A.

a b c 

. B.

5

a b c

  

. C.

 

;a b c



. D.

a b c 

.

Câu 27. (Chuyên ĐHSPHN - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho các điểm

 

0;1; 2

A

,

 

2; 2;0

B 

,

 

2;0;1

C 

. Mặt phẳng

 

P

đi qua

A

, trực tâm

H

của tam giác

ABC

và vuông góc

với mặt phẳng

 

ABC

có phương trình là

A.

4 2 4 0

x y z

   

. B.

4 2 4 0

x y z

   

. C.

4 2 4 0

x y z

   

. D.

4 2 4 0

x y z

   

.

Dạng 1.2 Xác định phương trình mặt phẳng đoạn chắn

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5

Câu 28. (Thpt Vĩnh Lộc - Thanh Hóa 2019) Trong không gian

Oxyz

cho điểm

 

1;2;3

M

. Viết phương

trình mặt phẳng

 

P

đi qua điểm

M

và cắt các trục tọa độ

, , Ox Oy Oz

lần lượt tại

A

,

B

,

C

sao cho

M

là trọng tâm của tam giác

ABC

.

A.

 

: 6 3 2 18 0

P x y z

   

. B.

 

: 6 3 2 6 0

P x y z

   

.

C.

 

: 6 3 2 18 0

P x y z

   

. D.

 

: 6 3 2 6 0

P x y z

   

.

Câu 29. (Chuyên Thái Bình - 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho điểm

 

1;2;3

M

.

Gọi

, ,A B C

lần lượt là hình chiếu vuông góc của

M

trên các trục

, ,Ox Oy Oz

. Viết phương trình

mặt phẳng

 

ABC

.

A.

1

1 2 3

  

x y z

. B.

1

1 2 3

  

x y z

. C.

0

1 2 3

  

x y z

. D.

1

1 2 3

   

x y z

.

Câu 30. (Chu Văn An - Hà Nội - 2019) Trong không gian với hệ trục tọa độ

,Oxyz

cho điểm

 

1;4;3 .

G

Mặt phẳng nào sau đây cắt các trục

, ,Ox Oy Oz

lần lượt tại

, ,A B C

sao cho

G

là trọng tâm tứ

diện

?OABC

A.

1

3 12 9

x y z

  

. B.

12 3 4 48 0

x y z

   

.C.

0

4 16 12

x y z

  

. D.

12 3 4 0

x y z

  

.

Câu 31. (THPT An Lão Hải Phòng 2019) Trong không gian với hệ tọa độ

Oxyz

, viết phương trình mặt

phẳng

 

P

đi qua

 

1;1;1

A

và

 

0;2;2

B

đồng thời cắt các tia

Ox

,

Oy

lần lượt tại hai điểm

,M N

( không trùng với gốc tọa độ

O

) sao cho

2

OM ON

A.

 

:3 2 6 0

P x y z

   

B.

 

: 2 3 4 0

P x y z

   

C.

 

: 2 4 0

P x y z

   

D.

 

: 2 2 0

P x y z

   

Câu 32. (THCS - THPT Nguyễn Khuyến 2019) Trong không gian

Oxyz

, nếu ba điểm

, ,A B C

lần lượt

là hình chiếu vuông góc của điểm

 

1;2;3

M

lên các trục tọa độ thì phương trình mặt phẳng

 

ABC

là

A.

1 2 3

1

x y z

  

. B.

1

1 2 3

x y z

  

. C.

1 2 3

0

x y z

  

. D.

0

1 2 3

x y z

  

.

Câu 33. (Chuyên Trần Phú Hải Phòng 2019) Trong không gian

,Oxyz

cho điểm

(8; 2;4)

M



. Gọi

, B, C

A

lần lượt là hình chiếu của

M

trên các trục

, , Ox Oy Oz

. Phương trình mặt phẳng đi qua

ba điểm

, A B

và

C

là

A.

4 2 8 0

x y z

   

B.

4 2 18 0

x y z

   

C.

4 2 8 0

x y z

   

D.

4 2 8 0

x y z

   

Câu 34. (Chuyên Hạ Long 2019) Viết phương trình mặt phẳng

 



đi qua

 

2;1; 3

M



, biết

 



cắt trục

, ,Ox Oy Oz

lần lượt tại

, ,A B C

sao cho tam giác

ABC

nhận

M

làm trực tâm

A.

2 5 6 0.

x y z

   

B.

2 6 23 0.

x y z

   

C.

2 3 14 0.

x y z

   

D.

3 4 3 1 0.

x y z

   

Câu 35. (Việt Đức Hà Nội 2019) Trong hệ trục tọa độ Oxyz, cho điểm

 

2;1;1

H

. Gọi các điểm

, ,A B C

lần lượt ở trên các trục tọa độ

, ,Ox Oy Oz

sao cho

H

là trực tâm của tam giác

ABC

. Khi đó

hoành độ điểm

A

là:

A.

3

. B.

5

. C. 3. D. 5

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 36. Trong không gian

Oxyz

, cho mặt phẳng

 



đi qua điểm

 

1;2;3

M

và cắt các trục

,Ox

,Oy

Oz

lần lượt tại

,A

,B

C

(khác gốc tọa độ

O

) sao cho

M

là trực tâm tam giác

ABC

. Mặt phẳng

 



có phương trình dạng

14 0

ax by cz

   

. Tính tổng

T a b c  

.

A.

8

. B.

14

. C.

6

T



. D.

11

.

Câu 37. (THPT Lương Thế Vinh Hà Nội 2019) Cho điểm

 

1;2;5

M

. Mặt phẳng

 

P

đi qua điểm

M

cắt các trục tọa độ

, ,Ox Oy Oz

tại

,A

,B

C

sao cho

M

là trực tâm tam giác

ABC

. Phương trình

mặt phẳng

 

P

là

A.

8 0

x y z

   

. B.

2 5 30 0

x y z

   

. C.

0

5 2 1

x y z

  

. D.

1

5 2 1

x y z

  

.

Câu 38. Trong không gian

Oxyz

, cho hai mặt phẳng

 

: 4 2 6 0

P x y z

   

,

 

: 2 4 6 0

Q x y z

   

.

Mặt phẳng

 



chứa giao tuyến của

   

,P Q

và cắt các trục tọa độ tại các điểm

, ,A B C

sao cho

hình chóp

.

O ABC

là hình chóp đều. Phương trình mặt phẳng

 



là

A.

6 0

x y z

   

. B.

6 0

x y z

   

. C.

3 0

x y z

   

. D.

6 0

x y z

   

.

Câu 39. (Chuyên Lê Quý Đôn Điện Biên 2019) Trong không gian với hệ tọa độ

Oxyz

cho mặt phẳng

 

P

đi qua điểm

 

9;1;1

M

cắt các tia

, ,Ox Oy Oz

tại

, ,A B C

(

, ,A B C

không trùng với gốc tọa độ ).

Thể tích tứ diện

OABC

đạt giá trị nhỏ nhất là bao nhiêu?

A.

81

2

. B.

243

2

. C.

81

6

. D.

243

.

Câu 40. (Chuyên Nguyễn Trãi Hải Dương 2019) Trong không gian

Oxyz

cho các điểm

(2;0;0), (0;4;0), (0;0;6), (2;4;6)

A B C D

. Gọi

( )P

là mặt phẳng song song với mặt phẳng

( )ABC

,

( )P

cách đều

D

và mặt phẳng

( )ABC

. Phương trình của mặt phẳng

( )P

là

A.

6 3 2 24 0

x y z

   

. B.

6 3 2 12 0

x y z

   

.

C.

6 3 2 0

x y z

  

. D.

6 3 2 36 0

x y z

   

.

Câu 41. (Kiểm tra năng lực - ĐH - Quốc Tế - 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho ba

điểm

 

;0;0

A a

,

 

0; ;0B b

,

 

0;0;C c

với

a

,

b

,

c

là ba số thực dương thay đổi, thỏa mãn điều

kiện:

1 1 1

2017

a b c

  

. Khi đó, mặt phẳng

 

ABC

luôn đi qua có một điểm có tọa độ cố định là

A.

1 1 1

; ;

3 3 3

 

 

 

. B.

 

1;1;1

.

C.

1 1 1

; ;

2017 2017 2017

 

 

 

. D.

 

2017;2017; 2017

.

Câu 42. Trong không gian

Oxyz

cho điểm

 

1;2;3

M

. Phương trình mặt phẳng

 

P

đi qua

M

cắt các trục

tọa độ

Ox

,

Oy

,

Oz

lần lượt tại

A

,

B

,

C

sao cho

M

là trọng tâm của tam giác

ABC

là

A.

 

: 6 3 2 18 0

P x y z

   

. B.

 

: 6 3 2 6 0

P x y z

   

.

C.

 

: 6 3 2 18 0

P x y z

   

. D.

 

: 6 3 2 6 0

P x y z

   

.

Câu 43. Cho điểm

 

1;2;5

M

. Mặt phẳng

 

P

đi qua

M

cắt các trục

, ,Ox Oy Oz

lần lượt tại

, ,A B C

sao

cho

M

là trực tâm tam giác

ABC

. Phương trình mặt phẳng

 

P

là

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7

A.

8 0

x y z

   

. B.

2 5 30 0

x y z

   

. C.

0

5 2 1

x y z

  

. D.

1

5 2 1

x y z

  

.

Câu 44. Trong không gian

Oxyz

, cho điểm

 

1;2;5

M

. Số mặt phẳng

 



đi qua

M

và cắt các trục

, ,Ox Oy Oz

lần lượt tại

, ,A B C

mà

0

OA OB OC

  

là

A.

1.

B.

2.

C.

3.

D.

4.

Câu 45. Trong không gian

Oxyz

, cho điểm

 

1 1 2M ; ;

. Hỏi có bao nhiêu mặt phẳng

 

P

đi qua

M

và cắt

các trục

x'Ox,y'Oy,z'Oz

lần lượt tại các điểm

A,B,C

sao cho

0

OA OB OC

  

?

A.

3

B.

1

C.

4

D.

8

Câu 46. Trong không gian với hệ tọa độ

Oxyz

, có bao nhiêu mặt phẳng qua

 

2;1;3

M

,

 

0;0;4

A

và cắt

hai trục

Ox

,

Oy

lần lượt tại

B

,

C

khác

O

thỏa mãn diện tích tam giác

OBC

bằng

1

?

A.

0

. B.

3

. C.

2

. D.

4

.

Câu 47. (Đồng Tháp - 2018) Trong không gian với hệ trục tọa độ

Oxyz

, cho điểm

 

3;2;1

M

. Mặt phẳng

 

P

qua

M

và cắt các trục

Ox

,

Oy

,

Oz

lần lượt tại

A

,

B

,

C

sao cho

M

là trực tâm tam giác

ABC

. Phương trình mặt phẳng

 

P

là

A.

6 0

x y z

   

. B.

0

3 2 1

x y z

  

. C.

1

3 2 1

x y z

  

. D.

3 2 14 0

x y z

   

.

Câu 48. (Chuyên Trần Phú - Hải Phòng - 2018) Trong không gian với hệ tọa độ

Oxyz

, viết phương

trình mặt phẳng

 

P

chứa điểm

 

1;3; 2

M



, cắt các tia

Ox

,

Oy

,

Oz

lần lượt tại

A

,

B

,

C

sao

cho

1 2 4

OA OB OC

 

.

A.

2 1 0

x y z

   

. B.

2 4 1 0

x y z

   

. C.

4 2 1 0

x y z

   

. D.

4 2 8 0

x y z

   

.

Câu 49. (Sở Nam Định - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho mặt cầu

   

2 2 2

: 2 2 3 0

S x y z x y z

     

. Gọi

, ,A B C

lần lượt là giao điểm (khác gốc tọa độ

O

) của

mặt cầu

 

S

và các trục

Ox

,

Oy

,

Oz

. Phương trình mặt phẳng

 

ABC

là:

A.

6 3 2 12 0

x y z

   

. B.

9 3 2 12 0

x y z

   

.

C.

6 3 2 12 0

x y z

   

. D.

6 3 2 12 0

x y z

   

.

Câu 50. (THPT Thực Hành - TPHCM - 2018) Trong không gian tọa độ

Oxyz

, cho mặt phẳng

 



đi

qua

 

1; 3; 8

M 

và chắn trên

Oz

một đoạn dài gấp đôi các đoạn chắn trên các tia

Ox

,

Oy

. Giả sử

 

: 0

ax by cz d



   

(

,a

,b

,c

d

là các số nguyên). Tính

a b c

S

d

 



.

A.

3

. B.

3

. C.

5

4

. D.

5

4



.

Dạng 1.3 Phương trình mặt phẳng qua 3 điểm

Câu 51. (THCS - THPT Nguyễn Khuyến 2019) Trong không gian

Oxyz

, gọi

M

,

N

,

P

lần lượt là

hình chiếu vuông góc của

 

2; 3;1

A 

lên các mặt phẳng tọa độ. Phương trình mặt phẳng

 

MNP

là

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 8 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

A.

1

2 3 1

x y z

  

. B.

3 2 6 6

x y z

  

. C.

0

2 3 1

x y z

  

. D.

3 2 6 12 0

x y z

   

.

Câu 52. (Chuyên KHTN 2019) Trong không gian

Oxyz

, cho các điểm

   

1;2;1 , 2; 1;4

A B 

và

 

1;1;4

C

. Đường thẳng nào dưới đây vuông góc với mặt phẳng

 

ABC

?

A.

1 1 2

x y z

 



. B.

2 1 1

x y z

 

. C.

1 1 2

x y z

 

. D.

2 1 1

x y z

 



.

Câu 53. (THPT Nghĩa Hưng NĐ-2019) Trong không gian với hệ tọa độ

Oxyz

, cho ba điểm

     

0;1;2 ,B 2; 2;1 , 2;1;0

A C 

. Khi đó, phương trình mặt phẳng

 

ABC

là

0

ax y z d

   

.

Hãy xác định

a

và

d

.

A.

1, 1a d 

. B.

6, 6

a d

  

. C.

1, 6

a d

   

. D.

6, 6

a d

  

.

Câu 54. (Lý Nhân Tông - Bắc Ninh 2019) Trong không gian

Oxyz

, cho điểm

 

3;5;2

A

, phương trình

nào dưới đây là phương trình mặt phẳng đi qua các điểm là hình chiếu của điểm

A

trên các mặt

phẳng tọa độ?

A.

3 5 2 60 0

x y z

   

. B.

10 6 15 60 0

x y z

   

.

C.

10 6 15 90 0

x y z

   

. D.

1

3 5 2

x y z

  

.

Câu 55. (Thi thử cụm Vũng Tàu - 2019) Trong không gian

Oxyz

, cho ba

điểm

 

3; 2; 2

A

 

,

 

3;2;0

B

,

 

0;2;1

C

. Phương trình mặt phẳng

 

ABC

là

A.

2 3 6 12 0

x y z

   

. B.

2 3 6 12 0

x y z

   

.

C.

2 3 6 0

x y z

  

. D.

2 3 6 12 0

x y z

   

.

Câu 56. Trong không gian với hệ tọa độ

Oxyz

, mặt phẳng đi qua 3 điểm

 

1;2;3

A

,

 

4;5;6

B

,

 

1;0;2

C

có phương trình là

A.

2 5 0

x y z

   

. B.

2 3 4 0

x y z

   

. C.

3 3 0

x y z

  

. D.

2 3 0

x y z

   

.

Câu 57. (SGD - Bình Dương - 2018) Trong không gian với hệ tọa độ

Oxyz

, mặt phẳng đi qua ba điểm

 

2; 3; 5

A

,

 

3; 2; 4

B

và

 

4; 1; 2

C

có phương trình là

A.

5 0

x y

  

. B.

5 0

x y

  

. C.

2 0

y z

  

. D.

2 7 0

x y

  

.

Câu 58. (Lê Quý Đôn - Hải Phòng - 2018) Trong không gian với hệ tọa độ

Oxyz

, viết phương trình mặt

phẳng đi qua ba điểm

 

1;1;4

A

,

 

2;7;9

B

,

 

0;9;13

C

.

A.

2 1 0

x y z

   

. B.

4 0

x y z

   

. C.

7 2 9 0

x y z

   

. D.

2 2 0

x y z

   

.

Câu 59. (SGD - Bình Dương - 2018) Trong không gian với hệ trục tọa độ

Oxyz

, cho bốn điểm

 

1;6;2

S 

,

 

0;0;6

A

,

 

0;3;0

B

,

 

2;0;0

C 

. Gọi

H

là chân đường cao vẽ từ

S

của tứ diện

.

S ABC

. Phương trình mặt phẳng đi qua ba điểm

S

,

B

,

H

là

A.

3 0

x y z

   

. B.

3 0

x y z

   

. C.

5 7 15 0

x y z

   

. D.

7 5 4 15 0

x y z

   

.

Dạng 2. Một số bài toán liên đến khoảng cách - góc

Dạng 2.1 Khoảng cách từ điểm đến mặt, khoảng cách giữa hai mặt

Khoảng cách từ một điểm đến mặt phẳng, khoảng cách giữa hai mặt phẳng song song

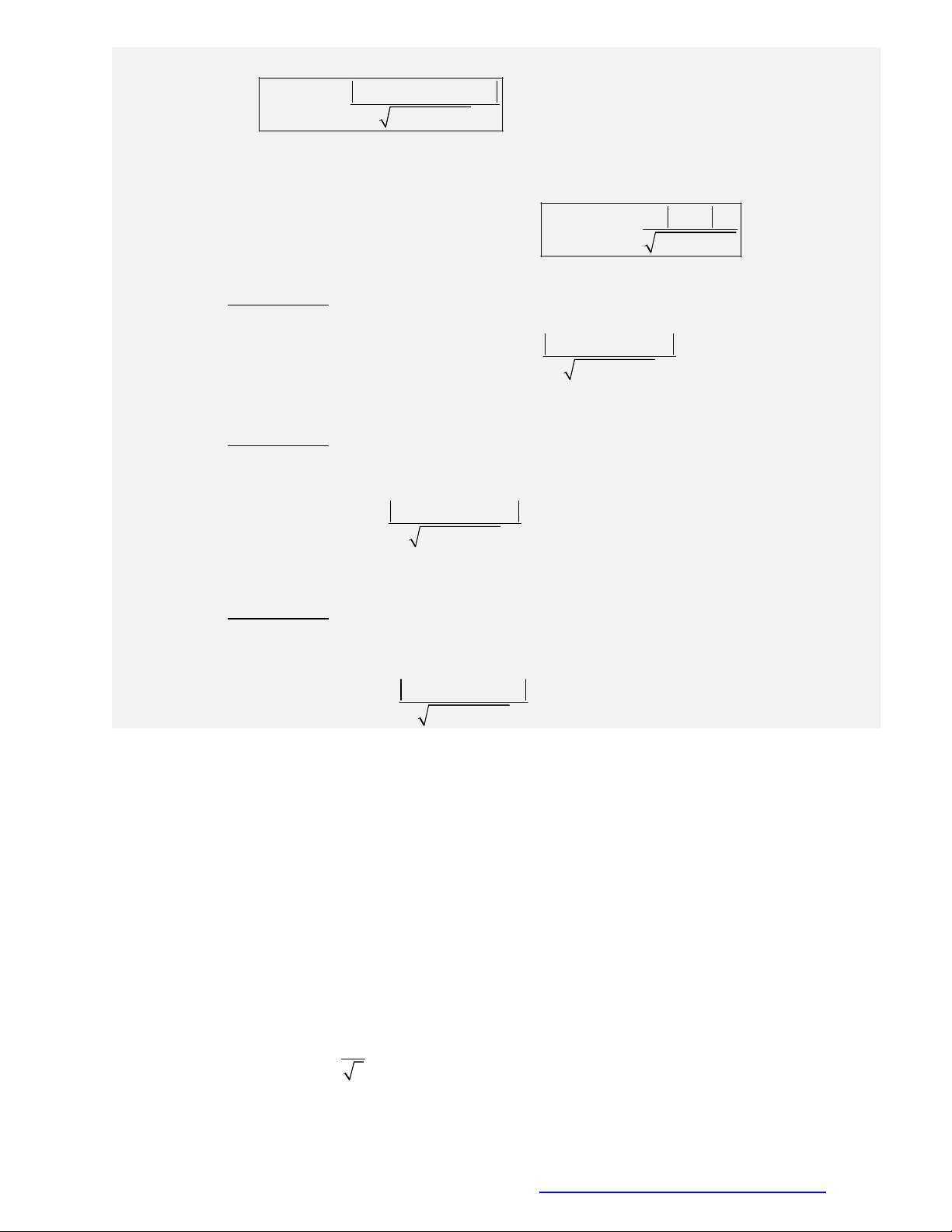
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9



Khoảng cách từ điểm

( ; ; )

M M M

M x y z

đến mặt phẳng

( ) : 0

P ax by cz d

   

được xác định bởi

công thức:

2 2 2

( ;( ))

M M M

ax by cz d

d M P

a b c

  

 

 

Khoảng cách giữa đường thẳng và mặt phẳng song song là khoảng cách từ một điểm thuộc đường

thẳng đến mặt phẳng



Cho hai mặt phẳng song song

( ) : 0

P ax by cz d

   

và

( ) : 0

Q ax by cz d



   

có cùng véctơ

pháp tuyến, khoảng cách giữa hai mặt phẳng đó là

 

2 2 2

( ),( )

d d

d Q P

a b c





 

 

Viết phương trình

( ) ( ) : 0

P Q ax by cz d

   

và cách

( ; ; )M x y z

  

khoảng

.k

Phương pháp:



Vì

( ) ( ) : 0 ( ): 0.

P Q ax by cz d P ax by cz d



        



Sử dụng công thức khoảng cách

 

,( )

2 2 2

.

M P

ax by cz d

d k d

a b c



  



  

 

  

Viết phương trình mặt phẳng

( ) ( ) : 0

P Q ax by cz d

   

và

( )P

cách mặt phẳng

( )Q

một khoảng

k

cho trước.

Phương pháp:



Vì

( ) ( ) : 0 ( ): 0.

P Q ax by cz d P ax by cz d



        



Chọn một điểm

( ; ; ) ( )M x y z Q

  

và sử dụng công thức:

   

( );( ) ,( )

2 2 2

.

Q P M P

ax by cz d

d d k d

a b c



  



   

 

  

Viết phương trình mặt phẳng

( )P

vuông góc với hai mặt phẳng

( ), ( ),

 

đồng thời

( )P

cách điểm

( ; ; )M x y z

  

một khoảng bằng

k

cho trước.

Phương pháp:



Tìm

( ) ( )

, .n n

 

 

Từ đó suy ra

( ) ( ) ( )

, ( ; ; ).

P

n n n a b c

 

 

 

 

  



Khi đó phương trình

( )P

có dạng

( ) : 0,

P ax by cz d

   

(cần tìm

).d



Ta có:

 

;( )

2 2 2

.

M P

ax by cz d

d k k d

a b c

  

   

 

  

Câu 1. (Chuyên Hùng Vương Gia Lai 2019) Trong không gian

Oxyz

, điểm

M

thuộc trục

Oy

và cách

đều hai mặt phẳng:

 

: 1 0

P x y z

   

và

 

: 5 0

Q x y z

   

có tọa độ là

A.

 

0; 3;0

M 

. B.

 

0;3;0

M

. C.

 

0; 2;0

M 

. D.

 

0;1;0

M

.

Câu 2. Trong không gian với hệ trục tọa độ

Oxyz

, cho

(1; 2;3)

A

,

 

3;4;4

B

. Tìm tất cả các giá trị của

tham số

m

sao cho khoảng cách từ điểm

A

đến mặt phẳng

2 1 0   

x y mz

bằng độ dài đoạn

thẳng

AB

.

A.

2

m

. B.

2 

m

. C.

3 

m

. D.

2 

m

.

Câu 3. (Chuyên Trần Phú Hải Phòng 2019) Trong không gian

,Oxyz

cho 3 điểm

     

1;0;0 , 0; 2;3 , 1;1;1

A B C

. Gọi

 

P

là mặt phẳng chứa

, A B

sao cho khoảng cách từ

C

tới

mặt phẳng

 

P

bằng

2

3

. Phương trình mặt phẳng

 

P

là

A.

2 3 1 0

3 7 6 0

x y z



   



   



B.

2 1 0

2 3 6 13 0

x y z



   



    



NGUYỄN BẢO VƯƠNG - 0946798489

Trang 10 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

C.

2 1 0

2 3 7 23 0

x y z



   



    



D.

1 0

23 37 17 23 0

x y z



   



    



Câu 4. Trong không gian

Oxyz

cho

       

2;0;0 , 0;4;0 , 0;0;6 , 2;4;6

A B C D

. Gọi

 

P

là mặt phẳng

song song với

 

mp ABC

,

 

P

cách đều

D

và mặt phẳng

 

ABC

. Phương trình của

 

P

là

A.

6 3 2 24 0

x y z

   

B.

6 3 2 12 0

x y z

   

C.

6 3 2 0

x y z

  

D.

6 3 2 36 0

x y z

   

Câu 5. (Chuyên Phan Bội Châu Nghệ An 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho hai

điểm

 

1;2;3

A

,

 

5; 4; 1

B

 

và mặt phẳng

 

P

qua

Ox

sao cho

 

; 2 ;

d B P d A P



,

 

P

cắt

AB

tại

 

; ;I a b c

nằm giữa

AB

. Tính

a b c 

.

A.

12

. B.

6

. C.

4

. D.

8

.

Câu 6. (Đề Tham Khảo 2019) Trong không gian

Oxyz

, Khoảng cách giữa hai mặt phẳng

 

: 2 2 10 0

P x y z

   

và

 

: 2 2 3 0

Q x y z

   

bằng:

A.

4

3

B.

8

3

. C.

7

3

. D.

3

.

Câu 7. (Sở Thanh Hóa 2019) Trong không gian

Oxyz

cho hai mặt phẳng song song

 

P

và

 

Q

lần

lượt có phương trình

2 0

x y z

  

và

2 7 0

x y z

   

. Khoảng cách giữa hai mặt phẳng

 

P

và

 

Q

bằng

A.

7

. B.

7 6

. C.

6 7

. D.

7

6

.

Câu 8. Trong không gian

Oxyz

, khoảng cách giữa hai mặt phẳng

 

: 2 2 8 0

P x y z

   

và

 

: 2 2 4 0

Q x y z

   

bằng

A. 1. B.

4

3

. C. 2. D.

7

3

.

Câu 9. Trong không gian

Oxyz

, khoảng cách giữa hai mặt phẳng

 

: 2 2 16 0

P x y z

   

và

 

: 2 2 1 0

Q x y z

   

bằng

A. 5. B.

17

.

3

C. 6. D.

5

3

.

Câu 10. (Chuyên Lam Sơn Thanh Hóa 2019) Trong không gian

Oxyz

khoảng cách giữa hai mặt phẳng

 

: 2 3 1 0

P x y z

   

và

 

: 2 3 6 0

Q x y z

   

là

A.

7

14

B.

8

14

C.

14

D.

5

14

Câu 11. Trong không gian

Oxyz

, khoảng cách giữa hai mặt phẳng

 

: 6 3 2 1 0

P x y z

   

và

 

1 1

: 8 0

2 3

Q x y z

   

bằng

A.

7

. B.

8

. C.

9

. D.

6

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11

Câu 12. (Chuyên Lam Sơn-2019) Trong không gian

Oxyz

khoảng cách giữa hai mặt phẳng

 

: 2 3 1 0

P x y z

   

và

 

: 2 3 6 0

Q x y z

   

là:

A.

7

14

. B.

8

14

. C.

14

. D.

5

14

.

Câu 13. (Chuyên Bắc Giang 2019) Trong không gian với hệ tọa độ

Oxyz

, tính khoảng cách giữa hai mặt

phẳng song song

 

: 2 2 4 0

x y z



   

và

 

: 2 2 7 0

x y z



    

.

A.

0

. B.

3

. C.

1

. D.

1

.

Câu 14. (THPT Đông Sơn 1 - Thanh Hóa 2019) Trong không gian với hệ tọa độ

,Oxyz

cho mặt cầu

 

2 2 2

: 2 2 2 22 0

S x y z x y z

      

và mặt phẳng

 

:3 2 6 14 0.

P x y z

   

Khoảng cách từ

tâm

I

của mặt cầu

 

S

đến mặt phẳng

 

P

bằng

A. 2. B. 4. C. 3. D. 1.

Câu 15. (SGD Bến Tre 2019) Trong không gian

Oxyz

cho hai mặt phẳng

 

: 2 2 9 0

P x y z

   

và

 

: 4 2 4 6 0.

Q x y z

   

Khoảng cách giữa hai mặt phẳng

 

P

và

 

Q

bằng

A.

0

. B.

2

. C.

1

. D.

3

.

Câu 16. (SP Đồng Nai - 2019) Trong không gian

Oxyz

, cho hai mặt phẳng

( ) : 2 2 6 0

P x y z

   

và

( ) : 2 2 3 0

Q x y z

   

. Khoảng cách giữa hai mặt phẳng

( )P

và

( )Q

bằng

A.

3

. B.

1

. C.

9

. D.

6

.

Câu 17. (Đà Nẵng 2019) Trong không gian

Oxyz

, cho mặt phẳng

 

:3 4 12 5 0

P x y z

   

và điểm

 

2;4; 1

A



. Trên mặt phẳng

 

P

lấy điểm

M

. Gọi

B

là điểm sao cho

3.

AB AM



 

. Tính khoảng

cách

d

từ

B

đến mặt phẳng

 

P

.

A.

6

d



. B.

30

13

d 

. C.

66

13

d 

. D.

9

d



.

Câu 18. (Chu Văn An - Hà Nội - 2019) Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

 

: 2 2 1 0

P x y z

   

. Mặt phẳng nào sau đây song song với

 

P

và cách

 

P

một khoảng bằng

3?

A.

 

: 2 2 10 0

Q x y z

   

. B.

 

: 2 2 4 0

Q x y z

   

.

C.

 

: 2 2 8 0

Q x y z

   

. D.

 

: 2 2 8 0

Q x y z

   

.

Câu 19. (SGD Bến Tre 2019) Tìm trên trục

Oz

điểm

M

cách đều điểm

 

2;3;4

A

và mặt

phẳng

 

: 2 3 17 0

P x y z

   

.

A.

 

0;0; 3

M



. B.

 

0;0;3

M

. C.

 

0;0; 4

M



. D.

 

0;0;4

M

.

Câu 20. (SGD Bắc Ninh 2019) Trong mặt phẳng với hệ tọa độ

Oxyz

, cho hai điểm

   

1;2;1 , 3;4;0

A B

,

mặt phẳng

 

: 46 0

P ax by cz

   

. Biết rằng khoảng cách từ

,A B

đến mặt phẳng

 

P

lần lượt

bằng

6

và

3

. giá trị của biểu thức

T a b c  

bằng

A.

3

. B.

6

. C.

3

. D.

6

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 12 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 21. (Chuyên Quang Trung- Bình Phước 2019) Trong không gian

Oxyz

, cho mặt phẳng

 

: 2 2 10 0

P x y z

   

. Phương trình mặt phẳng

 

Q

với

 

Q

song song với

 

P

và khoảng

cách giữa hai mặt phẳng

 

P

và

 

Q

bằng

7

3

là.

A.

2 2 3 0; 2 2 17 0

x y z x y z

       

B.

2 2 3 0; 2 2 17 0

x y z x y z

       

C.

2 2 3 0; 2 2 17 0

x y z x y z

       

D.

2 2 3 0; 2 2 17 0

x y z x y z

       

Câu 22. (SGD Hưng Yên 2019) Trong không gian hệ toạ độ

Oxyz

, lập phương trình các mặt phẳng song

song với mặt phẳng

 

: 3 0

x y z



   

và cách

 



một khoảng bằng

3

.

A.

6 0

x y z

   

;

0

x y z

  

. B.

6 0

x y z

   

.

C.

6 0

x y z

   

;

0

x y z

  

. D.

6 0

x y z

   

;

0

x y z

  

.

Câu 23. (THPT Hàm Rồng - Thanh Hóa - 2018) Trong hệ trục tọa độ

Oxyz

cho

3

điểm

 

4;2;1

A

,

 

0;0;3

B

,

 

2;0;1

C

. Viết phương trình mặt phẳng chứa

OC

và cách đều

2

điểm

,A B

.

A.

2 2 0  

x y z

hoặc

4 2 0

x y z

  

. B.

2 2 0  

x y z

hoặc

4 2 0

x y z

  

.

C.

2 2 0  

x y z

hoặc

4 2 0

x y z

  

. D.

2 2 0  

x y z

hoặc

4 2 0

x y z

  

.

Câu 24. (THPT Nguyễn Tất Thành - Yên Bái - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho tam

giác

ABC

có

(1;0;0), (0; 2;3), (1;1;1).

A B C



Phương trình mặt phẳng

 

P

chứa

,A B

sao cho

khoảng cách từ

C

tới

 

P

bằng

2

3

là

A.

1 0

x y z

   

hoặc

23 37 17z 23 0

x y

    

.

B.

2 1 0

x y z

   

hoặc

23 3 7 23 0.

x y z

    

C.

2 1 0

x y z

   

hoặc

13 3 6 13 0.

x y z

    

D.

2 3 1 0

x y z

   

hoặc

3 7 3 0.

x y z

   

Câu 25. (THPT Quang Trung Đống Đa Hà Nội 2019) Trong không gian với hệ tọa độ

Oxyz

, cho mặt

phẳng

 

: 2 2 5 0

P x y z

   

. Viết phương trình mặt phẳng

 

Q

song song với mặt phẳng

 

P

,

cách

 

P

một khoảng bằng 3 và cắt trục

Ox

tại điểm có hoành độ dương.

A.

 

: 2 2 4 0

Q x y z

   

. B.

 

: 2 2 14 0

Q x y z

   

.

C.

 

: 2 2 19 0

Q x y z

   

. D.

 

: 2 2 8 0

Q x y z

   

.

Câu 26. (Chuyên Phan Bội Châu -2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho mặt phẳng

 

Q

:

2 2 3 0

x y z

   

, mặt phẳng

 

P

không qua

O

, song song với mặt phẳng

 

Q

và

   

 

, 1

d P Q



. Phương trình mặt phẳng

 

P

là

A.

2 2 1 0

x y z

   

B.

2 2 0

x y z

  

C.

2 2 6 0

x y z

   

D.

2 2 3 0

x y z

   

Câu 27. (Chuyên Nguyễn Trãi Hải Dương 2019) Trong không gian

Oxyz

, cho

 

2;0;0

A

,

 

0;4;0

B

,

 

0;0;6

C

,

 

2;4;6

D

. Gọi

 

P

là mặt phẳng song song với

 

mp ABC

,

 

P

cách đều

D

và mặt

phẳng

 

ABC

. Phương trình của

 

P

là

A.

6 3 2 24 0

x y z

   

. B.

6 3 2 12 0

x y z

   

.

C.

6 3 2 0

x y z

  

. D.

6 3 2 36 0

x y z

   

.

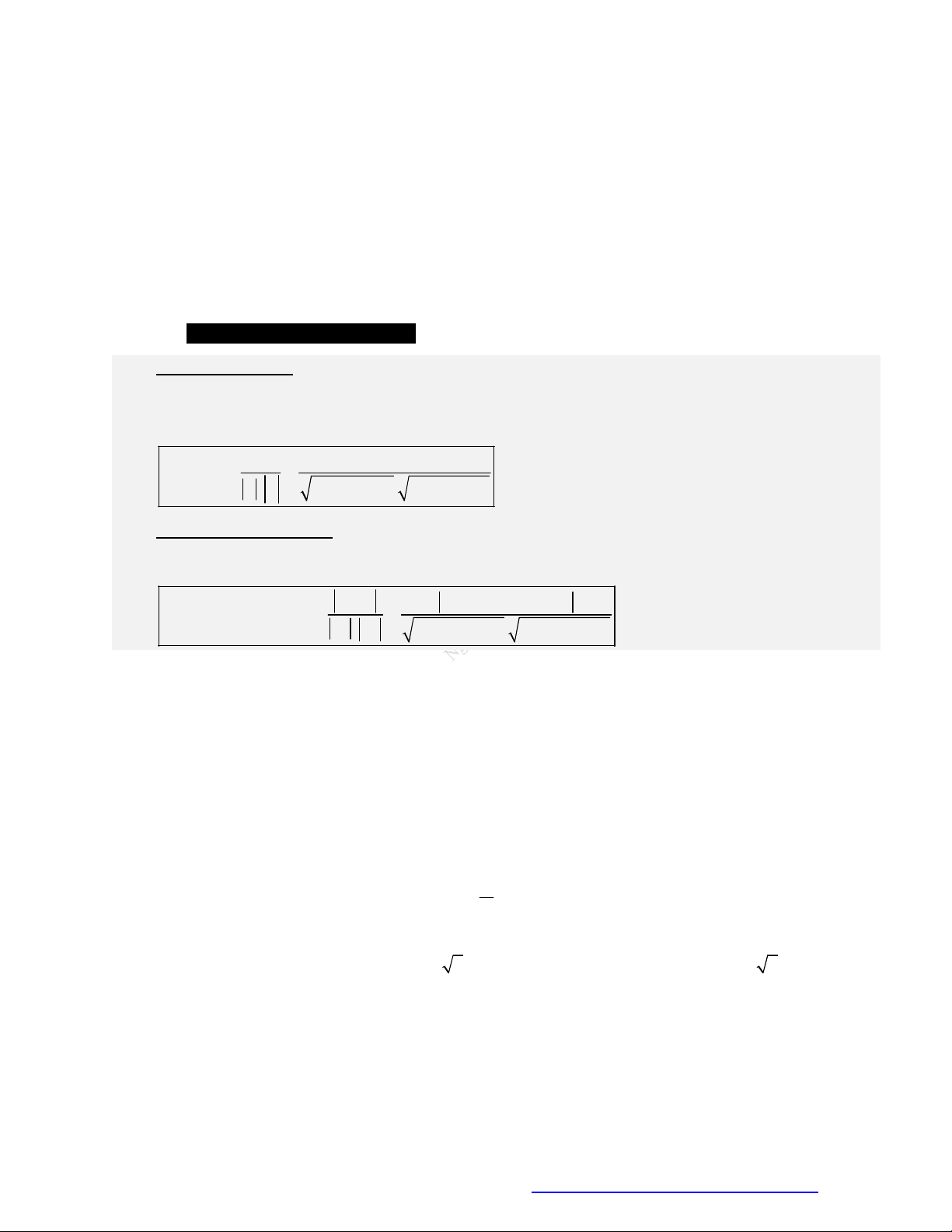
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13

Câu 28. (Ngô Quyền - Hải Phòng 2019) Trong không gian

Oxyz

, cho ba điểm

 

2;0;0

A

,

 

0;3;0

B

,

 

0;0; 1

C



. Phương trình của mặt phẳng

 

P

qua

 

1;1;1

D

và song song với mặt phẳng

 

ABC

là

A.

2 3 6 1 0

x y z

   

. B.

3 2 6 1 0

x y z

   

.

C.

3 2 5 0

x y z

  

. D.

6 2 3 5 0

x y z

   

.

Câu 29. (Chuyên Nguyễn Đình Triểu - Đồng Tháp - 2018) Trong không gian

Oxyz

, cho

 

1;1;0

A

,

 

0;2;1

B

,

 

1;0;2

C

,

 

1;1;1

D

. Mặt phẳng

 



đi qua

 

1;1;0

A

,

 

0;2;1

B

,

 



song song với

đường thẳng

CD

. Phương trình mặt phẳng

 



là

A.

2 3 0

x y

   

. B.

2 2 0

x y z

   

. C.

2 3 0

x y z

   

. D.

2 0

x y

  

.

Dạng 2.2 Góc của 2 mặt phẳng

1. Góc giữa hai véctơ

Cho hai véctơ

1 2 3

( ; ; )a a a a



và

1 2 3

( ; ; ).b b b b





Khi đó góc giữa hai véctơ

a



và

b



là góc nhợn hoặc

tù.

1 1 2 2 3 3

2 2 2 2 2 2

1 2 3 1 2 3

.

cos( ; )

.

a b a b a b

a b

a a a b b b

 

 

   



với

0 180 .



   

2. Góc giữa hai mặt phẳng

Cho hai mặt phẳng

1 1 1 1

( ) : 0

P A x B y C z D

   

và

2 2 2 2

( ) : 0.

Q A x B y C z D

   

 

1 2 1 2 1 2

2 2 2 2 2 2

1 1 1 2 2 2

.

cos ( ),( ) cos

.

P Q

n n

A A B B C C

P Q

n n

A B C A B C



 

  

   

 

với

0 90 .



   

Câu 30. (THPT Nguyễn Khuyến 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho điểm

 

2;1; 2

H

,

H

là hình chiếu vuông góc của gốc tọa độ

O

xuống mặt phẳng

 

P

, số đo góc giữa mặt

 

P

và

mặt phẳng

 

: 11 0

Q x y

  

A.

0

60

B.

0

30

C.

0

45

D.

0

90

Câu 31. (THPT Quang Trung Đống Đa 2019) Trong không gian

Oxyz

, cho mặt phẳng

( )P

có phương

trình

2 2 5 0

x y z

   

. Xét mặt phẳng

( ) : (2 1) 7 0

Q x m z

   

, với

m

là tham số thực. Tìm tất

cả giá trị của

m

để

( )P

tạo với

( )Q

góc

4



.

A.

1

4

m











. B.

2

2 2

m







 



. C.

2

4

m











. D.

4

2

m











.

Câu 32. (THPT Ba Đình 2019) Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

 

P

có phương

trình:

1 0

ax by cz

   

với

0

c



đi qua

2

điểm

 

0;1;0

A

,

 

1;0;0

B

và tạo với

 

Oyz

một góc

60

. Khi đó

a b c 

thuộc khoảng nào dưới đây?

A.

 

5;8

. B.

 

8;11

. C.

 

0;3

. D.

 

3;5

.

Câu 33. (Chuyên Bắc Giang -2019) Trong không gian với hệ tọa độ

O

xyz

, cho hai mặt phẳng

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 14 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

( ) : 2 2 1 0,

P x y z

   

( ) : ( 1) 2019 0

Q x my m z

    

. Khi hai mặt phẳng

 

P

,

 

Q

tạo với

nhau một góc nhỏ nhất thì mặt phẳng

 

Q

đi qua điểm

M

nào sau đây?

A.

(2019; 1;1)

M



B.

(0; 2019;0)

M



C.

( 2019;1;1)

M



D.

(0;0; 2019)

M



Câu 34. (THPT Thăng Long-Hà Nội- 2019) Trong không gian

Oxyz

, cho hai mặt phẳng

 

: 2 2 5 0

P x y z

   

và

 

: 2 0

Q x y

  

. Trên

 

P

có tam giác

ABC

; Gọi

, ,A B C

  

lần

lượt là hình chiếu của

, ,A B C

trên

 

Q

. Biết tam giác

ABC

có diện tích bằng

4

, tính diện tích

tam giác

A B C

  

.

A.

2

. B.

2 2

. C.

2

. D.

4 2

.

Câu 35. (Chuyên Nguyễn Du-ĐăkLăk 2019) Trong không gian

Oxyz

, biết hình chiếu của

O

lên mặt

phẳng

 

P

là

 

2; 1; 2

H

 

. Số đo góc giữa mặt phẳng

 

P

với mặt phẳng

 

: 5 0

Q x y

  

là

A.

30

. B.

45

. C.

60

. D.

90

.

Câu 36. Trong hệ trục toạ độ

Oxyz

, cho điểm

 

2; 1; 2

H

. Điểm

H

là hình chiếu vuông góc của gốc toạ

độ

O

xuống mặt phẳng

 

P

, số đo góc giữa mặt phẳng

 

P

và mặt phẳng

 

: 11 0

Q x y

  

là

A.

90

. B.

30

. C.

60

. D.

45

.

Câu 37. (Chuyên Trần Phú Hải Phòng -2019) Trong không gian

,Oxyz

cho hai điểm

   

3;0;1 , 6; 2;1

A B 

. Phương trình mặt phẳng

 

P

đi qua

, A B

và tạo với mặt phẳng

 

Oyz

một

góc



thỏa mãn

2

cos

7





là

A.

2 3 6 12 0

2 3 6 0

x y z

   





  



B.

2 3 6 12 0

2 3 6 0

x y z

   





  



C.

2 3 6 12 0

2 3 6 1 0

x y z

   





   



D.

2 3 6 12 0

2 3 6 1 0

x y z

   





   



Câu 38. (Toán Học Tuổi Trẻ 2018) Trong không gian với hệ tọa độ

Oxyz

, biết mặt phẳng

 

: 0

P ax by cz d

   

với

0

c



đi qua hai điểm

 

0;1;0

A

,

 

1;0;0

B

và tạo với mặt phẳng

 

yOz

một góc

60

. Khi đó giá trị

a b c 

thuộc khoảng nào dưới đây?

A.

 

0;3

. B.

 

3;5

. C.

 

5;8

. D.

 

8;11

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15

Dạng 3. Vị trí tương đối

Dạng 3.1 Vị trí tương đối mặt phẳng với mặt cầu

Vị trí tương đối giữa mặt phẳng (P) và mặt cầu (S)

Cho mặt cầu

( ; )S I R

và mặt phẳng

( ).P

Gọi

H

là hình chiếu vuông góc của

I

lên

( )P

và có

d IH

là khoảng cách từ I đến mặt phẳng

( ).P

Khi đó:

 Nếu

:d R

Mặt cầu và mặt phẳng không có điểm chung.



Nếu

:d R

Mặt phẳng tiếp xúc mặt cầu.

Lúc đó

( )P

là mặt phẳng tiếp diện của

( )S

và

H

là tiếp điểm.



Nếu

:d R

mặt phẳng

( )P

cắt mặt cầu theo thiết diện

là đường tròn có tâm

H

và bán kính

2 2

.r R IH 

Viết phương trình mặt

( ) ( ) : 0P Q ax by cz d   

và tiếp xúc với mặt cầu

( ).S

Phương pháp:

 Vì

( ) ( ) : 0 ( ) : 0.P Q ax by cz d P ax by cz d



        

 Tìm tâm

I

và bán kính

R

của mặt cầu.



Vì

( )P

tiếp xúc

( )S

nên có

 

;( )

.

I P

d R d



 

Câu 1. (Đề Tham Khảo 2017) Trong không gian với hệ tọa độ

Oxyz

, cho mặt cầu

 

S

có tâm

 

3;2; 1I 

và đi qua điểm

 

2;1;2A

. Mặt phẳng nào dưới đây tiếp xúc với

 

S

tại

A

?

A.

3 9 0x y z   

B.

3 3 0x y z   

C.

3 8 0x y z   

D.

3 3 0x y z   

Câu 2. (Chuyên Quốc Học Huế -2019) Trong không gian với hệ trục tọa độ

Oxyz

cho mặt phẳng

 



có phương trình

2 1 0x y z   

và mặt cầu

 

S

có phương trình

     

2 2 2

1 1 2 4x y z     

. Xác định bán kính

r

của đường tròn là giao tuyến của mặt phẳng

 



và mặt cầu

 

S

.

A.

2 42

3

r 

. B.

2 3

3

r 

C.

2 15

3

r 

. D.

2 7

3

r 

Câu 3. (Chuyên Lê Quý Đôn Điện Biên 2019) Trong không gian

Oxyz

, viết phương trình mặt cầu có

tâm

 

2;1; 4I 

và tiếp xúc với mặt phẳng

 

: 2 2 7 0x y z



   

.

A.

2 2 2

4 2 8 4 0x y z x y z      

. B.

2 2 2

4 2 8 4 0x y z x y z      

.

C.

2 2 2

4 2 8 4 0x y z x y z      

. D.

2 2 2

4 2 8 4 0x y z x y z      

.

Câu 4. (SGD Bình Phước - 2019) Trong không gian

Oxyz

, cho mặt phẳng

 

: 2 2 3 0P x y z   

và

mặt cầu

 

S

có tâm

 

0; 2;1I 

. Biết mặt phẳng

 

P

cắt mặt cầu

 

S

theo giao tuyến là một

đường tròn có diện tích

2



. Mặt cầu

 

S

có phương trình là

A.

   

2 2

2

2 1 2x y z    

. B.

   

2 2

2

2 1 3x y z    

.

C.

   

2 2

2

2 1 3x y z    

. D.

   

2 2

2

2 1 1x y z    

.

H

I

A

R

r

d

P

M

2

M

1

H

I

R

I

H

P

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 16 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 5. (Bình Giang-Hải Dương 2019) Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

 

: 2 2 2 0

P x y z

   

và điểm

 

1;2; 1

I

 

. Viết phương trình mặt cầu

 

S

có tâm

I

và cắt

mặt phẳng

 

P

theo giao tuyến là đường tròn có bán kính bằng

5

.

A.

       

2 2 2

: 1 2 1 25

S x y z

     

. B.

       

2 2 2

: 1 2 1 16

S x y z

     

.

C.

       

2 2 2

: 1 2 1 34

S x y z

     

. D.

       

2 2 2

: 1 2 1 34

S x y z

     

.

Câu 6. Trong không gian với hệ tọa độ

Oxyz

, mặt cầu

 

S

có tâm

 

1;2;1

I 

và tiếp xúc với mặt

phẳng

 

P

:

2 2 2 0

x y z

   

có phương trình là

A.

     

2 2 2

1 2 1 3

x y z

     

. B.

     

2 2 2

1 2 1 9

x y z

     

.

C.

     

2 2 2

1 2 1 9

x y z

     

. D.

     

2 2 2

1 2 1 3

x y z

     

.

Câu 7. (Chuyên Nguyễn Huệ- 2019) Phương trình mặt cầu tâm

 

3; 2;4

I 

và tiếp xúc với

 

: 2 2 4 0

P x y z

   

là:

A.

     

2 2 2

20

3 2 4

3

x y z     

. B.

     

2 2 2

400

3 2 4

9

x y z     

.

C.

     

2 2 2

20

3 2 4

3

x y z     

. D.

     

2 2 2

400

3 2 4

9

x y z     

.

Câu 8. Trong không gian

Oxyz

, cho điểm

 

3;1; 1

I

và mặt phẳng

 

: 2 2 3 0   

P x y z

. Phương

trình mặt cầu

 

S

có tâm

I

và tiếp xúc với mặt phẳng

 

P

là

A.

     

2 2 2

3 1 1 4     

x y z

. B.

     

2 2 2

3 1 1 16     

x y z

.

C.

     

2 2 2

3 1 1 4     

x y z

. D.

     

2 2 2

3 1 1 16     

x y z

.

Câu 9. (Đà Nẵng 2019) Trong không gian

Oxyz

, cho mặt cầu

 

S

có tâm

 

1;2;1

I

và cắt mặt phẳng

 

:2 2 7 0

P x y z

   

theo một đường tròn có đường kính bằng

8

. Phương trình mặt cầu

 

S

là

A.

     

2 2 2

1 2 1 81

x y z

     

. B.

     

2 2 2

1 2 1 5

x y z

     

.

C.

     

2 2 2

1 2 1 9

x y z

     

. D.

     

2 2 2

1 2 1 25

x y z

     

.

Câu 10. (Thpt Vĩnh Lộc - Thanh Hóa 2019) Cho mặt cầu

 

S

có phương trình

     

2 2 2

3 2 1 100

x y z     

và mặt phẳng

 



có phương trình

2 2 9 0

x y z

   

. Tính

bán kính của đường tròn

 

C

là giao tuyến của mặt phẳng

 



và mặt cầu

 

S

.

A.

8

. B.

4 6

. C.

10

. D.

6

.

Câu 11. (chuyên Hùng Vương Gia Lai -2019) Trong không gian

Oxyz

, cho mặt cầu

 

2 2 2

: 4 2 2 10 0

S x y z x y z

      

, mặt phẳng

 

: 2 2 10 0

P x y z

   

. Mệnh đề nào dưới

đây đúng?

A.

 

P

tiếp xúc với

 

S

.

B.

 

P

cắt

 

S

theo giao tuyến là đường tròn khác đường tròn lớn.

C.

 

P

và

 

S

không có điểm chung.

D.

 

P

cắt

 

S

theo giao tuyến là đường tròn lớn.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17

Câu 12. (Chuyên Bắc Giang 2019) Trong không gian với hệ tọa độ

Oxyz

, cho mặt cầu

 

2 2 2

1

:S x y z

  

và mặt phẳng

 

2 2 1 0

:P x y z

   

. Tìm bán kính

r

đường tròn giao

tuyến của

 

S

và

 

P

.

A.

1

3

r



. B.

2 2

3

r 

. C.

1

2

.

r



D.

2

r 

.

Câu 13. (Kinh Môn - Hải Dương 2019) Trong không gian với hệ trục toạ độ

Oxyz

, phương trình nào

dưới đây là phương trình của mặt cầu có tâm

 

3;1;0

I

và tiếp xúc với mặt phẳng

 

: 2 2 1 0

P x y z

   

?

A.

   

2 2

2

3 1 3

x y z

    

. B.

   

2 2

2

3 1 9

x y z

    

.

C.

   

2 2

2

3 1 3

x y z

    

. D.

   

2 2

2

3 1 9

x y z

    

.

Câu 14. (SGD Bến Tre 2019) Trong không gian

Oxyz

cho mặt cầu

 

2 2 2

: 2 4 6 0

S x y z x y z

     

.

Đường tròn giao tuyến của

 

S

với mặt phẳng

 

Oxy

có bán kính là

A.

3

r

. B.

5

r . C.

6

r . D.

14

r

.

Câu 15. Trong không gian với hệ tọa độ

Oxyz

, cho mặt cầu

 

S

có tâm

 

2;1;1

I

và mặt

phẳng

 

: 2 2 2 0

P x y z

   

. Biết mặt phẳng

 

P

cắt mặt cầu

 

S

theo giao tuyến là một đường

tròn có bán kính bằng 1. Viết phương trình của mặt cầu

 

S

A.

       

2 2 2

: 2 1 1 8

S x y z

     

B.

       

2 2 2

: 2 1 1 10

S x y z

     

C.

       

2 2 2

: 2 1 1 8

S x y z

     

D.

       

2 2 2

: 2 1 1 10

S x y z

     

Câu 16. (Mã 104 2017) Trong không gian với hệ trục tọa độ

Oxyz

, phương trình nào dưới đây là phương

trình mặt cầu đi qua ba điểm

 

2;3;3

M

,

 

2; 1; 1

N

 

,

 

2; 1;3

P  

và có tâm thuộc mặt phẳng

 

: 2 3 2 0

x y z



   

.

A.

2 2 2

4 2 6 2 0

x y z x y z

      

B.

2 2 2

2 2 2 2 0

x y z x y z

      

C.

2 2 2

2 2 2 10 0

x y z x y z

      

D.

2 2 2

4 2 6 2 0

x y z x y z

      

Câu 17. Trong không gian với hệ tọa độ

,Oxyz

xét các điểm

 

0;0;1

A

,

 

;0;0

B m

,

 

0; ;0C n

,

 

1;1;1

D

với

0; 0

m n

 

và

1. 

m n

Biết rằng khi

m

,

n

thay đổi, tồn tại một mặt cầu cố định tiếp xúc

với mặt phẳng

 

ABC

và đi qua

D

. Tính bán kính

R

của mặt cầu đó?

A.

1R

. B.

2

R

. C.

3

2



R

. D.

3

2

R

.

Câu 18. Trong không gian

O

xyz

, cho mặt cầu

 

S

:

     

2 2 2

2 4 1 4

x y z

     

và mặt phẳng

 

P

:

3 1 0

x my z m

    

. Tìm tất cả các giá trị thực của tham số

m

để mặt phẳng

 

P

cắt mặt cầu

 

S

theo giao tuyến là đường tròn có đường kính bằng

2

.

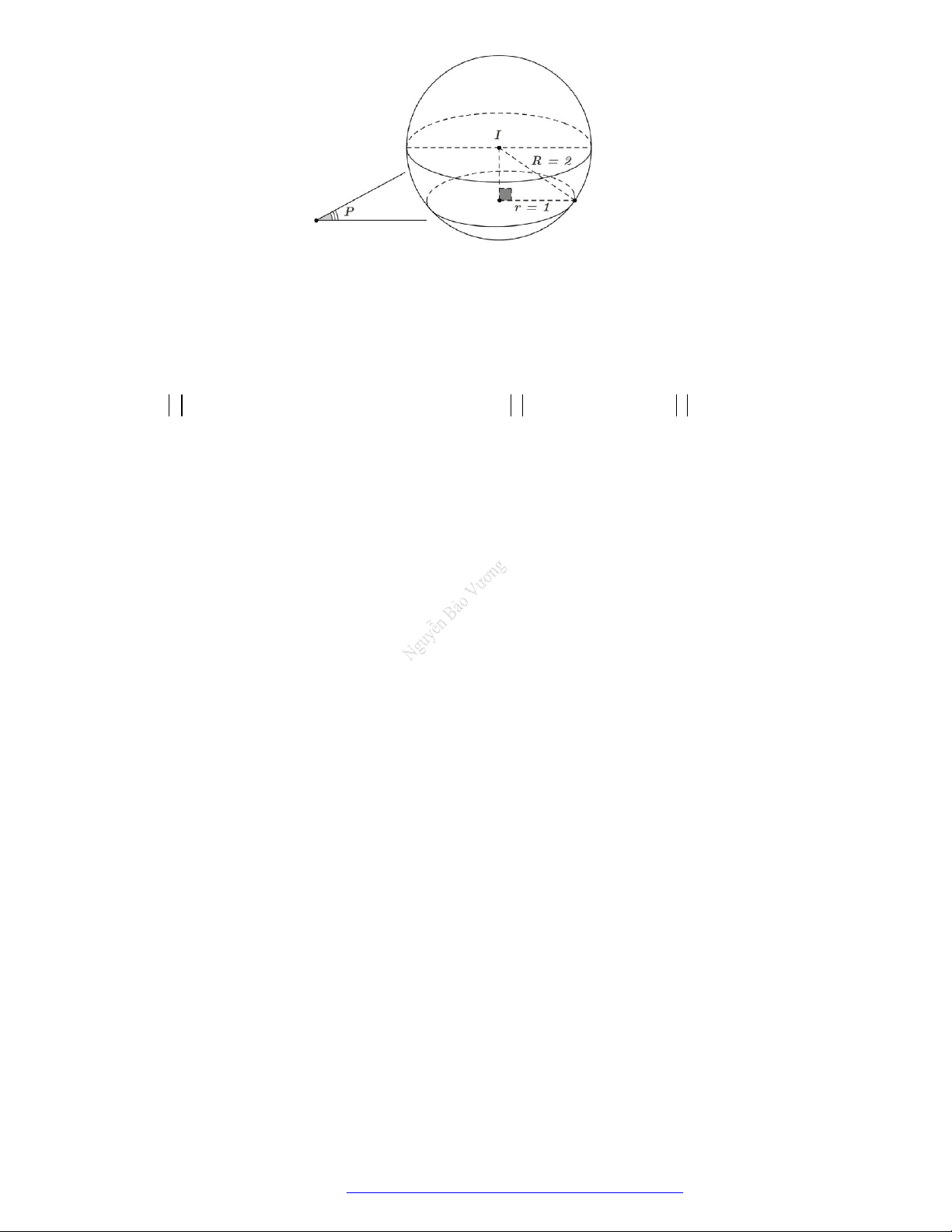
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 18 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

A.

1m 

. B.

1m  

hoặc

2m  

.

C.

1m 

hoặc

2m 

. D.

1m  

Câu 19. (THPT Đoàn Thượng - Hải Dương -2019) Trong không gian

Oxyz

, cho mặt cầu

 

S

tâm

( ; ; )I a b c

bán kính bằng

1

, tiếp xúc mặt phẳng

 

.Oxz

Khẳng định nào sau đây luôn đúng?

A.

1a 

. B.

1a b c  

. C.

1b 

. D.

1c 

.

Câu 20. (Sở Hà Nội 2019) Trong không gian

Oxyz

cho mặt cầu

 

2 2 2

: 2 4 6 5 0S x y z x y z      

.

Mặt phẳng tiếp xúc với

 

S

và song song với mặt phẳng

 

: 2 2 11 0P x y z   

có phương trình

là:

A.

2 2 7 0x y z   

. B.

2 2 9 0x y z   

.

C.

2 2 7 0x y z   

. D.

2 2 9 0x y z   

.

Câu 21. (Sở Hà Nội 2019) Trong không gian

Oxyz

cho hai mặt phẳng

 

: 2 2 0P x y z   

và

 

: 2 1 0Q x y z   

. Số mặt cầu đi qua

 

1; 2;1A 

và tiếp xúc với hai mặt phẳng

   

,P Q

là

A.

0

. B.

1

. C. Vô số. D.

2

.

Câu 22. Trong không gian tọa độ

Oxyz

, cho mặt cầu

 

S

có đường kính

AB

với

 

6;2; 5A 

,

 

4;0;7B 

.

Viết phương trình mặt phẳng

 

P

tiếp xúc với mặt cầu

 

S

tại

A

.

A.

 

:5 6 62 0P x y z   

. B.

 

:5 6 62 0P x y z   

.

C.

 

:5 6 62 0P x y z   

. D.

 

:5 6 62 0P x y z   

.

Câu 23. (Chuyên Lê Hồng Phong Nam Định 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho mặt

phẳng

2

( ) : 2 x 2 y z m 3 0P m    

và mặt cầu

     

2 2 2

( ) : 1 1 1 9S x y z     

. Tìm tất cả

các giá trị của

m

để

( )P

tiếp xúc với

( )S

.

A.

2

5

m

 









. B.

2

5

m







 



. C.

2m 

. D.

5m  

.

Câu 24. (THPT Ngô Sĩ Liên Bắc Giang 2019) Trong không gian với hệ trục tọa độ

0xyz

, cho mặt cầu

       

2 2 2

: 1 1 1 25S x y z     

có tâm

I

và mặt phẳng

 

: 2 2 7 0P x y z   

. Thể tích của

khối nón đỉnh

I

và đường tròn đáy là giao tuyến của mặt cầu

 

S

và mặt phẳng

 

P

bằng

A.

12



B.

48



C.

36



D.

24



Câu 25. (Chuyên Ngữ Hà Nội 2019) Trong không gian với hệ tọa độ

Oxyz

cho hai mặt cầu

   

1 2

,S S

lần lượt có phương trình là

2 2 2

2 2 2 22 0x y z x y z      

,

2 2 2

6 4 2 5 0x y z x y z      

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19

Xét các mặt phẳng

 

P

thay đổi nhưng luôn tiếp xúc cả hai mặt cầu đã cho. Gọi

 

; ;A a b c

là

điểm mà tất cả các mặt phẳng

 

P

đi qua. Tính tổng

S a b c  

.

A.

5

.

2

S



B.

5

.

2

S

 

C.

9

.

2

S



D.

9

.

2

S

 

Câu 26. (Sở Kon Tum - 2019) Trong không gian

Oxyz

, cho mặt cầu

       

2 2 2

: 1 2 1 45

S x y z

     

và mặt phẳng

 

: 13 0

P x y z

   

. Mặt cầu

 

S

cắt mặt

phẳng

 

P

theo giao tuyến là đường tròn có tâm

 

; ;I a b c

thì giá trị của

a b c 

bằng

A.

11

. B.

5

. C.

2

. D.

1

.

Câu 27. (Sở Hà Nam - 2019) Trong không gian

Oxyz

, cho mặt phẳng

 

: 2 7 0

P x y z

   

và mặt cầu

 

2 2 2

: 2 4 10 0

S x y z x z

     

. Gọi

 

Q

là mặt phẳng song song với mặt phẳng

 

P

và cắt

mặt cầu

 

S

theo một giao tuyến là đường tròn có chu vi bằng

6



. Hỏi

 

Q

đi qua điểm nào

trong số các điểm sau?

A.

 

6;0;1

. B.

 

3;1;4



. C.

 

2; 1;5

 

. D.

 

4; 1; 2 

.

Câu 28. (Chuyên Lam Sơn Thanh Hóa 2019) Trong không gian

Oxyz

, cho mặt cầu

 

2 2 2

: 2 4 6 2 0

S x y z x y z

      

và mặt phẳng

 

: 4 3 12 10 0

x y z



   

. Lập phương

trình mặt phẳng

 



thỏa mãn đồng thời các điều kiện: tiếp xúc với

 

S

; song song với

 



và cắt

trục

Oz

ở điểm có cao độ dương.

A.

4 3 12 78 0

x y z

   

. B.

4 3 12 26 0

x y z

   

.

C.

4 3 12 78 0

x y z

   

. D.

4 3 12 26 0

x y z

   

.

Câu 29. (THPT Yên Phong 1 Bắc Ninh 2019) Trong không gian

Oxyz

, cho mặt phẳng

 

:2 2 1 0

P x y z

   

và điểm

 

1; 2;0

M 

. Mặt cầu

tâm

M

, bán kính bằng

3

cắt phẳng

 

P

theo giao tuyến là đường tròn có bán kính bằng bao

nhiêu?

A.

2

. B.

2

. C.

2 2

. D.

3 1

.

Câu 30. (Chuyên Lê Hồng Phong Nam Định 2019) Trong không gian với hệ tọa độ

Oxyz

cho mặt phẳng

 

: 2 5 0

Q x y z

   

và mặt cầu

     

2 2

2

: 1 2 15

S x y z

    

. Mặt phẳng

 

P

song song với

mặt phẳng

 

Q

và cắt mặt cầu

 

S

theo giao tuyến là một đường tròn có chu vi bằng

6



đi qua

điểm nào sau đây?

A.

 

2; 2;1



. B.

 

1; 2;0



. C.

 

0; 1; 5 

. D.

 

2;2; 1 

.

Câu 31. (Việt Đức Hà Nội 2019) Cho mặt cầu

2 2 2

( ) :( 1) ( 2) ( 4) 9

S x y z

     

. Phương trình mặt

phẳng

( )



tiếp xúc với mặt cầu

( )S

tại điểm

(0;4; 2)

M



là

A.

6 6 37 0

x y z

   

B.

2 2 4 0

x y z

   

C.

2 2 4 0

x y z

   

D.

6 6 37 0

x y z

   

Câu 32. Trong không gian

O

xyz

, cho mặt cầu

 

S

:

     

2 2 2

2 1 2 4

x y z

     

và mặt phẳng

 

P

:

4 3 0

x y m

  

. Tìm tất cả các giá trị thực của tham số

m

để mặt phẳng

 

P

và mặt cầu

 

S

có

đúng

1

điểm chung.

A.

1

m



. B.

1

m

 

hoặc

21

m

 

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 20 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

C.

1

m



hoặc

21

m



. D.

9

m

 

hoặc

31

m



.

Câu 33. (THPT Ba Đình -2019) Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng

 

P : mx 2y z 1 0   

(

m

là tham số). Mặt phẳng

 

P

cắt mặt cầu

     

2 2

2

S : x 2 y 1 z 9    

theo một đường tròn có bán kính bằng

2

. Tìm tất cả các giá trị

thực của tham số

m

?

A.

m 1 

. B.

m 2 5

   . C.

m 4 

. D.

m 6 2 5

  .

Câu 34. (Yên Định Thanh Hóa 2019) Trong không gian

Oxyz

, cho mặt cầu

 

2 2 2

: 2 4 2 3 0

S x y z x y z

      

. Viết phương trình mặt phẳng

 

Q

chứa trục

Ox

và cắt

 

S

theo một đường tròn bán kính bằng

3

.

A.

 

: 3 0

Q y z

 

. B.

 

: 2 0

Q x y z

  

. C.

 

: 0

Q y z

 

. D.

 

: 2 0

Q y z

 

.

Câu 35. (THPT An Lão Hải Phòng 2019) Trong không gian với hệ tọa độ Oxyz, cho điểm

1;

( )2;1

I



và

mặt phẳng

( )P

có phương trình

2 2 8 0

x y z

   

. Viết phương trình mặt cầu tâm

I

và tiếp xúc

với mặt phẳng

( )P

:

A.

2 2 2

( 1) ( 2) ( 1) 9

x y z

     

B.

2 2 2

( ) ( ) (

1 2 1 3

)x y z

     

C.

2 2 2

( ) ( ) (

1 2 1 4

)x y z

     

D.

2 2 2

( ) ( ) (

1 2 1 9

)x y z

     

Câu 36. Trong không gian với hệ tọa độ

Oxyz

, phương trình nào dưới đây là phương trình của mặt cầu có

tâm

 

0;1;3

I

và tiếp xúc với mặt phẳng

( ) :2 2 2 0?

P x y z

   

A.

   

2 2

2

1 3 9

x y z

    

. B.

   

2 2

2

1 3 9

x y z

    

.

C.

   

2 2

2

1 3 3

x y z

    

. D.

   

2 2

2

1 3 3

x y z

    

.

Câu 37. (Sở Bắc Giang 2019) Trong không gian

Oxyz

, phương trình mặt cầu

 

S

tâm

 

1;2;5

I 

và tiếp

xúc với mặt phẳng

 

: 2 2 4 0

P x y z

   

là

A.

 

2 2 2

: 2 4 10 21 0

S x y z x y z

      

. B.

 

2 2 2

: 2 4 10 21 0

S x y z x y z

      

.

C.

 

2 2 2

: 2 4 10 21 0

S x y z x y z

      

. D.

 

2 2 2

: 2 5 21 0

S x y z x y z

      

.

Câu 38. (THPT Yên Khánh - Ninh Bình - 2019) Trong không gian

Oxyz

cho điểm

 

1; 2;3

I 

và mặt

phẳng

 

: 2 2 1 0

P x y z

   

. Mặt cầu

 

S

tâm

I

tiếp xúc với

 

P

có phương trình là:

A.

     

2 2 2

1 2 3 9.     

x y z

B.

     

2 2 2

1 2 3 3.     

x y z

C.

     

2 2 2

1 2 3 3.     

x y z

D.

     

2 2 2

1 2 3 9.     

x y z

Câu 39. (THPT Ngô Sĩ Liên Bắc Giang 2019) Trong không gian với hệ tọa độ

Oxyz

, cho điểm

( 3;0;1)

I



. Mặt cầu

( )S

có tâm

I

và cắt mặt phẳng

( ) : 2 2 1 0

P x y z

   

theo một thiết diện là một

hình tròn. Diện tích của hình tròn này bằng



. Phương trình mặt cầu

( )S

là

A.

2 2 2

( 3) ( 1) 4.

x y z

    

B.

2 2 2

( 3) ( 1) 25.

x y z    

C.

2 2 2

( 3) ( 1) 5.

x y z

    

D.

2 2 2

( 3) ( 1) 2.

x y z

    

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21

Câu 40. (Chuyên Nguyễn Tất Thành Yên Bái 2019) Trong không gian với hệ tọa độ

,Oxyz

cho mặt

phẳng

 

: 2 2 2 0   

P x y z

và điểm

 

1; 2; 1

I

 

. Viết phương trình mặt cầu

 

S

có tâm

I

và cắt mặt phẳng

 

P

theo giao tuyến là đường tròn có bán kính bằng

5.

A.

       

2 2 2

: 1 2 1 25.

     S x y z

B.

       

2 2 2

: 1 2 1 16.

     S x y z

C.

       

2 2 2

: 1 2 1 34.

     S x y z

D.

       

2 2 2

: 1 2 1 34.

     S x y z

Câu 41. (Đà Nẵng 2019) Trong không gian

Oxyz

, cho mặt cầu

 

2 2 2

: 2 2 0

S x y z z

    

và điểm

 

2;2;0

K

. Viết phương trình mặt phẳng chứa tất cả các tiếp điểm của các tiếp tuyến vẽ từ

K

đến

mặt cầu

 

S

.

A.

2 2 4 0

x y z

   

. B.

6 6 3 8 0

x y z

   

.

C.

2 2 2 0

x y z

   

D.

6 6 3 3 0

x y z

   

.

Câu 42. Trong không gian với hệ trục toạ độ

Oxyz

, cho mặt cầu có phương trình

 

2 2 2

: 2 4 6 3 0

S x y z x y z m

       

. Tìm số thực của tham số

m

để mặt phẳng

 

: 2 2 8 0

x y z



   

cắt

 

S

theo một đường tròn có chu vi bằng

8



.

A.

3

m

 

. B.

1

m

 

. C.

2

m

 

. D.

4

m

 

.

Câu 43. (THPT Kinh Môn - HD - 2018) Trong không gian

Oxyz

, cho mặt cầu

 

2 2 2

: 2 6 4 2 0

S x y z x y z

      

và mặt phẳng

 

: 4 -11 0

x y z



  

. Viết phương trình

mặt phẳng

 

P

, biết

 

P

song song với giá của vectơ

 

1;6;2

v 



, vuông góc với

 



và tiếp xúc

với

 

S

.

A.

2 3 0

2 21 0

x y z

   





   



B.

3 4 1 0

3 4 2 0

x y z

   





   



.

C.

4 3 5 0

4 3 27 0

x y z

   





   



. D.

2 2 3 0

2 2 21 0

x y z

   





   



.

Câu 44. (SGD - Đà Nẵng - 2018) Trong không gian với hệ trục tọa độ

Oxyz

, cho mặt phẳng

 

P

có

phương trình

2 2 5 0

x y z

   

và mặt cầu

 

S

có phương trình

     

2 2 2

1 2 3 4

x y z

     

.

Tìm phương trình mặt phẳng song song với mặt phẳng

 

P

và đồng thời tiếp xúc với mặt cầu

 

S

.

A.

2 2 1 0

x y z

   

. B.

2 2 5 0

x y z

    

.

C.

2 2 23 0

x y z

   

. D.

2 2 17 0

x y z

    

.

Câu 45. (Chuyên Lam Sơn - Thanh Hóa - 2018) Trong không gian với hệ trục tọa độ

Oxyz

cho mặt cầu

 

2 2 2

: 2 6 4 2 0

S x y z x y z

      

, mặt phẳng

 

: 4 11 0

x y z



   

. Gọi

 

P

là mặt phẳng

vuông góc với

   

, P



song song với giá của vecto

 

1;6;2

v 



và

 

P

tiếp xúc với

 

S

. Lập

phương trình mặt phẳng

 

P

.

A.

2 2 2 0

x y z

   

và

2 21 0

x y z

   

. B.

2 2 3 0

x y z

   

và

2 21 0

x y z

   

.

C.

2 2 3 0

x y z

   

và

2 2 21 0

x y z

   

. D.

2 2 5 0

x y z

   

và

2 2 2 0

x y z

   

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 22 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 46. (Hồng Lĩnh - Hà Tĩnh – 2018) Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm

 

1;0;0

A

,

 

0;0; 2

B

và mặt cầu

 

2 2 2

: 2 2 1 0

S x y z x y

     

. Số mặt phẳng chứa hai điểm

A

,

B

và

tiếp xúc với mặt cầu

 

S

là

A.

1

mặt phẳng. B.

2

mặt phẳng. C.

0

mặt phẳng. D. Vô số mặt phẳng.

Câu 47. (THPT Nam Trực - Nam Định - 2018) Trong không gian

Oxyz

, cho mặt phẳng

 

Q

song với

mặt phẳng

 

: 2 2 7 0

P x y z

   

. Biết

 

mp Q

cắt mặt cầu

     

2 2

2

: 2 1 25

S x y z

    

theo một đường tròn có bán kính

3

r



. Khi đó mặt phẳng

 

Q

có phương trình là:

A.

2 7 0

x y z

   

. B.

2 2 7 0

x y z

   

.

C.

2 2 17 0

x y z

   

. D.

2 2 17 0

x y z

   

.

Dạng 3.2 Vị trí tương đối hai mặt

Vị trí tương đối giữa hai mặt phẳng (P) và (Q)

Cho hai mặt phẳng

1 1 1 1

( ) : 0

P A x B y C z D

   

và

2 2 2 2

( ) : 0.

Q A x B y C z D

   

( )P

cắt

1 1 1 1

2 2 2 2

( )

A B C D

Q

A B C D

    

1 1 1 1

2 2 2 2

( ) ( )

A B C D

P Q

A B C D

    

 

1 1 1 1

2 2 2 2

( ) ( )

A B C D

P Q

A B C D

     



1 2 1 2 1 2

( ) ( ) 0.

P Q A A B B C C

    

Câu 48. (THPT - Yên Định Thanh Hóa 2019) Trong không gian với hệ tọa độ

Oxyz

, cho hai mặt phẳng

 

: 2 3 5 0

P x my z

   

và

 

: 8 6 2 0

Q nx y z

   

, với

,m n



. Xác định m, n để

 

P

song

song với

 

Q

.

A.

4

m n

  

. B.

4; 4

m n

  

. C.

4; 4

m n

  

. D.

4

m n

 

.

Câu 49. (Chuyên Trần Phú Hải Phòng 2019) Trong không gian

,Oxyz

cho hai mặt phẳng

 

: – 2 2 – 3 0

P x y z

 

và

 

: – 2 1 0

Q mx y z

  

. Với giá trị nào của m thì hai mặt phẳng đó

vuông góc với nhau?

A.

1

m



B.

1

m

 

C.

6

m

 

D.

6

m



Câu 50. (THPT Hai Bà Trưng - Huế - 2018) Trong không gian

Oxyz

, tìm tập hợp các điểm cách đều

cặp mặt phẳng sau đây:

4 2 3 0

x y z

   

,

4 2 5 0

x y z

   

.

A.

4 2 6 0

x y z

   

. B.

4 2 4 0

x y z

   

. C.

4 2 1 0

x y z

   

. D.

4 2 2 0

x y z

   

.

Câu 51. (THPT Yên Khánh - Ninh Bình - 2019) Trong không gian

Oxyz

, cho hai mặt phẳng

 

: 2 3 0

P x y z

   

;

 

: 2 1 0

Q x y z

   

. Mặt phẳng

 

R

đi qua điểm

 

1;1;1

M

chứa giao

tuyến của

 

P

và

 

Q

; phương trình của

     

: 2 3 2 1 0

R m x y z x y z

       

. Khi đó giá

trị của

m

là

A.

3

. B.

1

3

. C.

1

3



. D.

3

.

Câu 52. (THPT Gia Lộc Hải Dương 2019) Trong không gian

Oxyz

, mặt phẳng

 

: 2 2 0

P x y z

   

vuông góc với mặt phẳng nào dưới đây?

A.

2 2 0

x y z

   

. B.

2 0

x y z

   

. C.

2 0

x y z

   

. D.

2 2 0

x y z

   

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23

Câu 53. (Chuyên Hùng Vương Gia Lai 2019) Trong không gian Oxyz, cho 3 điểm

     

1;0;0 , 0; ;0 , 0;0;A B b C c

trong đó

. 0

b c



và mặt phẳng

 

: 1 0

P y z

  

. Mối liên hệ giữa

,b c

để mặt phẳng

( )ABC

vuông góc với mặt phẳng

( )P

là

A.

2

b c

. B.

2b c

. C.

b c

. D.

3 .b c

Câu 54. (THPT Yên Phong 1 Bắc Ninh 2019) Trong không gian

Oxyz

, cho

 

: 2 5 0

P x y z

   

và

   

: 4 2 3 0

Q x m y mz

    

,

m

là tham số thực. Tìm tham số

m

sao cho mặt phẳng

 

Q

vuông góc với mặt phẳng

 

P

.

A.

3

m

 

. B.

2

m

 

. C.

3

m



. D.

2

m



.

Câu 55. (Chuyên Lê Quý Đôn – Điện Biên 2019) Trong không gian

Oxyz

, cho mặt phẳng

 

: 2 0

ax y z b



   

đi qua giao tuyến của hai mặt phẳng

 

: 1 0

P x y z

   

và

 

: 2 1 0

Q x y z

   

. Tính

4a b

.

A.

16

. B.

8

. C.

0

. D.

8

.

Câu 56. (SGD Bến Tre 2019) Trong không gian

Oxyz

cho hai mặt phẳng

 

: 2 1 0

x y z



   

và

 

: 2 4 2 0.

x y mz



   

Tìm

m

để hai mặt phẳng

 



và

 



song song với nhau.

A.

1

m



. B. Không tồn tại

m

. C.

2

m

 

. D.

2

m



.

Câu 57. (Chuyên Lê Hồng Phong-Nam Định-2019) Trong không gian toạ độ

Oxyz

, cho mặt phẳng

( ) : 2 2 1 0

P x y z

   

, mặt phẳng nào dưới đây song song với

 

P

và cách

 

P

một khoảng

bằng

3

.

A.

( ): 2 2 8 0

Q x y z

   

. B.

 

: 2 2 5 0

Q x y z

   

.

C.

( ): 2 2 1 0

Q x y z

   

. D.

 

: 2 2 2 0

Q x y z

   

.

Câu 58. (Cụm 5 Trường Chuyên - ĐBSH - 2018) Trong không gian với hệ tọa độ

Oxyz

có bao nhiêu

mặt phẳng song song với mặt phẳng

 

: 3 0

Q x y z

   

, cách điểm

 

3;2;1

M

một khoảng

bằng

3 3

biết rằng tồn tại một điểm

 

; ;X a b c

trên mặt phẳng đó thỏa mãn

2

a b c

   

?

A.

1

. B. Vô số. C.

2

. D.

0

.

Câu 59. (Chuyên Thái Bình - 2018) Trong không gian với hệ trục tọa độ

Oxyz

, cho hai mặt phẳng

 

1

:3 4 2 0

Q x y z

   

và

 

2

:3 4 8 0

Q x y z

   

. Phương trình mặt phẳng

 

P

song song và

cách đều hai mặt phẳng

 

1

Q

và

 

2

Q

là:

A.

 

:3 4 10 0

P x y z

   

. B.

 

:3 4 5 0

P x y z

   

.

C.

 

:3 4 10 0

P x y z

   

. D.

 

:3 4 5 0

P x y z

   

.

Câu 60. (THPT Lương Thế Vinh Hà Nội 2019) Gọi

m,n

là hai giá trị thực thỏa mãn giao tuyến của hai

mặt phẳng

 

: 2 1 0   

m

P mx y nz

và

 

: 2 0   

m

Q x my nz

vuông góc với mặt phẳng

 

: 4 6 3 0



   

x y z

. Tính

m n

.

A.

0 

m n

. B.

2 

m n

. C.

1 m n

. D.

3 

m n

.

Câu 61. (Chuyên KHTN 2019) Biết rằng trong không gian với hệ tọa độ

Oxyz

có hai mặt phẳng

 

P

và

 

Q

cùng thỏa mãn các điều kiện sau: đi qua hai điểm

 

1;1;1

A

và

 

0; 2;2

B 

, đồng thời cắt các

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 24 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

tr

ục tọa độ

,Ox Oy

tại

hai điểm cách đều

O

.

Giả sử

 

P

có

phương trình

1 1

1

0

x b

y c z d

 

 

và

 

Q

có

phương trình

2 2 2

0

x b

y c z d

 

 

. Tính giá tr

ị biểu thức

1 2 1 2

b b

c c

.

A. 7. B. -9. C. -

7. D. 9.

Câu 62. (Toán Học Và Tuổi Trẻ 2018) Trong không gian với hệ tọa độ

,Oxyz

cho

điểm

 

3;

2;1

M

.

Mặt

phẳng

 

P

đi qua

M

và c

ắt các trục tọa độ

Ox

,

Oy

,

Oz

lần lư

ợt tại các điểm

A

,

B

,

C

không

trùng

với gốc tọa độ sao cho

M

là

trực tâm tam giác

ABC

.

Trong các mặt phẳng sau, tìm mặt

phẳng song song với mặt phẳng

 

P

.

A.

3 2

14 0

x y

z

 

 

. B.

2 3

9 0

x y

z

 

 

. C.

3 2

14 0

x y

z

 

 

. D.

2 9

0

x y

z

 

 

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương  https://www.facebook.com/phong.baovuong Trang 1

TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH GIỎI MỨC 9-10 ĐIỂM

Dạng 1. Một số bài toán liên khác quan điểm – mặt phẳng – mặt cầu

Câu 1. (Mã 103 2018) Trong không gian

Oxyz

, cho mặt cầu

2 2 2

( ) : ( 1) ( 2) ( 3) 1S x y z     

và điểm

(2;3;4)A

. Xét các điểm

M

thuộc

( )S

sao cho đường thẳng

AM

tiếp xúc với

( )S

,

M

luôn thuộc

mặt phẳng có phương trình là

A.

2 2 2 15 0x y z   

B.

7 0x y z   

C.

2 2 2 15 0x y z   

D.

7 0x y z   

Câu 2. (Sở Bắc Giang Năm 2019) Trong không gian với hệ trục

Oxyz

, cho điểm

 

2; 2;2A 

và mặt

cầu

   

2

2 2

: 2 1S x y z   

. Điểm

M

di chuyển trên mặt cầu

 

S

đồng thời thỏa mãn

. 6OM AM 

 

. Điểm

M

thuộc mặt phẳng nào sau đây?

A.

2 2 6 9 0x y z   

. B.

2 2 6 9 0x y z   

.

C.

2 2 6 9 0x y z   

. D.

2 2 6 9 0x y z   

.

Câu 3. Trong không gian với hệ trục

Oxyz

, cho điểm

 

2; 2;2A 

và mặt cầu

   

2

2 2

: 2 1S x y z   

.

Điểm

M

di chuyển trên mặt cầu

 

S

đồng thời thỏa mãn

. 6OM AM 

 

. Điểm

M

luôn thuộc mặt

phẳng nào dưới đây?

A.

2x 2 6z 9 0y   

. B.

2 2 6z 9 0x y   

.

C.

2x 2 6z 9 0y   

. D.

2x 2 6z 9 0y   

.

Câu 4. (Chuyên Lê Quý Đôn Điện Biên 2019) Trong không gian

Oxyz

, cho mặt

cầu

       

2 2 2

: 1 1 1 1S x y z     

và điểm

(2;2;2)A

. Xét các điểm

M

thuộc

( )S

sao cho

đường thẳng

AM

luôn tiếp xúc với

( )S

.

M

luôn thuộc một mặt phẳng cố định có phương trình

là

A.

– 6 0x y z  

. B.

4 0x y z   

. C.

3 3 3 –8 0x y z  

. D.

3 3 3 – 4 0x y z  

.

Câu 5. (Đề Tham Khảo 2018) Trong không gian

Oxyz

, cho ba điểm

 

1;2;1A

,

 

3; 1;1B 

và

 

1; 1;1C  

. Gọi

 

1

S

là mặt cầu có tâm

A

, bán kính bằng

2

;

 

2

S

và

 

3

S

là hai mặt cầu có

tâm lần lượt là

B

,

C

và bán kính đều bằng

1

. Hỏi có bao nhiêu mặt phẳng tiếp xúc với cả ba mặt

cầu

 

1

S

,

 

2

S

,

 

3

S

.

A.

8

B.

5

C.

7

D.

6

Câu 6. Trong không gian

,Oxyz

cho

       

2 2 2

: 3 2 5 36S x y z     

, điểm

 

7;1;3M

. Gọi



là

đường thẳng di động luôn đi qua

M

và tiếp xúc với mặt cầu

 

S

tại

N

. Tiếp điểm

N

di động

trên đường tròn

 

T

có tâm

 

, ,J a b c

. Gọi

2 5 10k a b c  

, thì giá trị của

k

là

A.

45

. B.

50

. C.

45

. D.

50

.

PHƯƠNG TRÌNH MẶT PHẲNG

Chuyên đề 30

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 7. (Chuyên Đại Học Vinh 2019) Trong không gian

Oxyz

, cho các điểm

     

2;1;4 , 5;0;0 , 1; 3;1

M N P 

. Gọi

 

; ;I a b c

là tâm của mặt cầu tiếp xúc với mặt phẳng

 

Oyz

đồng thời đi qua các điểm

, ,M N P

. Tìm

c

biết rằng

5

a b c

  

A. 3 B. 2 C. 4 D. 1

Câu 8. (Chuyên KHTN 2019) Trong không gian với hệ tọa độ

Oxyz

, cho điểm

 

1;2; 2

H



. Mặt phẳng

 



đi qua

H

và cắt các trục

, ,Ox Oy Oz

lần lượt tại các điểm

, ,A B C

sao cho

H

là trực tâm của

tam giác

ABC

. Tính diện tích mặt cầu ngoại tiếp tứ diện

OABC

.

A.

243



. B.

81



. C.

81

2



. D.

243

2



.

Câu 9. ( HSG Bắc Ninh 2019) Trong không gian với hệ tọa độ

Oxyz

, cho ba điểm

 

6;0;0

M

,

 

0;6;0

N

,

 

0;0;6

P

. Hai mặt cầu có phương trình

 

2 2 2

1

: 2 2 1 0     

S x y z x y

và

 

2 2 2

2

: 8 2 2 1 0

S x y z x y z

      

cắt nhau theo đường tròn

 

C

. Hỏi có bao nhiêu mặt cầu

có tâm thuộc mặt phẳng chứa

 

C

và tiếp xúc với ba đường thẳng

, ,

MN NP PM

.

A.

1

. B.

3

. C. Vô số. D.

4

.

Câu 10. Trong không gian với hệ tọa độ

Oxyz

cho

   

3;1;1 , 1; 1;5

 A B

và mặt phẳng

 

: 2 2 11 0.   

P x y z

Mặt cầu

 

S

đi qua hai điểm

,A B

và tiếp xúc với

 

P

tại điểm

C

. Biết

C

luôn thuộc một đường tròn

 

T

cố định. Tính bán kính

r

của đường tròn

 

T

.

A.

4r

. B.

2r

. C.

3

r

. D.

2

r

.

Câu 11. (THPT Lê Quý Đôn Đà Nẵng 2019) Trong không gian

Oxyz

, cho hai điểm

5 3 7 3

; ;3

2 2

A

 

 

 

 

,

5 3 7 3

; ;3

2 2

B

 

 

 

 

và mặt cầu

2 2 2

( ) : ( 1) ( 2) ( 3) 6

S x y z

     

. Xét

mặt phẳng

( ) : 0

P ax by cz d

   

,

 

, , , : 5

a b c d d

  

là mặt phẳng thay đổi luôn đi qua hai

điểm

,A B

. Gọi

( )N

là hình nón có đỉnh là tâm của mặt cầu

( )S

và đường tròn đáy là đường tròn

giao tuyến của

( )P

và

( )S

. Tính giá trị của

T a b c d   

khi thiết diện qua trục của hình nón

( )N

có diện tích lớn nhất.

A.

4T 

. B.

6

T



. C.

2T 

. D.

12T 

.

Câu 12. Trong không gian

Oxyz

, xét số thực

 

0;1

m 

và hai mặt phẳng

 

: 2 2 10 0

x y z

    

và

 

: 1

1 1

x y z

m m

   



. Biết rằng, khi

m

thay đổi có hai mặt cầu cố định tiếp xúc đồng thời với cả

hai mặt phẳng

   

, 

. Tổng bán kính của hai mặt cầu đó bằng

A.

6

B.

3

C.

9

D.

12

Câu 13. Trong không gian

Oxyz

, mặt cầu

 

S

đi qua điểm

 

2; 2;5

A 

và tiếp xúc với ba mặt phẳng

   

: 1, : 1

P x Q y

  

và

 

: 1R z 

có bán kính bằng

A.

3

. B.

1

. C.

2 3

. D.

3 3

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3

Câu 14. (Đề Tham Khảo 2018) Trong không gian

Oxyz

, cho điểm

 

1 1 2M ; ;

. Hỏi có bao nhiêu mặt

phẳng

 

P

đi qua

M

và cắt các trục

x'Ox, y'Oy,z'Oz

lần lượt tại các điểm

A,B,C

sao cho

0

OA OB OC

  

?

A.

8

B.

1

C.

4

D.

3

Câu 15. (Hoàng Hoa Thám Hưng Yên 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho hai điểm

 

3;1;7

A

,

 

5;5;1

B

và mặt phẳng

 

: 2 4 0

P x y z

   

. Điểm

M

thuộc

 

P

sao cho

35

MA MB 

. Biết

M

có hoành độ nguyên, ta có

OM

bằng

A.

2 2

. B.

2 3

. C.

3 2

. D.

4

.

Câu 16. (Cụm 5 Trường Chuyên - ĐBSH - 2018) Trong không gian với hệ trục tọa độ

Oxyz

, cho ba

điểm

 

;0;0

A a

,

 

0; ;0B b

,

 

0;0;C c

với

, , 0

a b c



. Biết rằng

 

ABC

đi qua điểm

1 2 3

; ;

7 7 7

M

 

 

 

và tiếp xúc với mặt cầu

       

2 2 2

72

: 1 2 3

7

S x y z     

. Tính

2 2 2

1 1 1

a b c

 

.

A.

14

. B.

1

7

. C.

7

. D.

7

2

.

Câu 17. (Chuyên Đại học Vinh - 2019) Trong không gian

Oxyz

, cho các điểm

 

2;1;4

M

,

 

5;0;0

N

,

 

1; 3;1

P 

. Gọi

 

; ;I a b c

là tâm của mặt cầu tiếp xúc với mặt phẳng

 

Oyz

đồng thời đi qua các

điểm

M

,

N

,

P

. Tìm

c

biết rằng

5

a b c

  

.

A.

3

. B.

2

. C.

4

. D.

1

.

Câu 18. (Sở Nam Định - 2019) Trong không gian

Oxyz

, cho mặt cầu

   

2

2 2

: 1 4

S x y z

   

và điểm

 

2;2;2

A

. Từ

A

kẻ ba tiếp tuyến

AB

,

AC

,

AD

với

B

,

C

,

D

là các tiếp điểm. Viết phương

trình mặt phẳng

 

.BCD

A.

2 2 1 0

x y z

   

. B.

2 2 3 0

x y z

   

.

C.

2 2 1 0

x y z

   

. D.

2 2 5 0

x y z

   

.

Câu 19. (Hội 8 Trường Chuyên 2019) Trong không gian

,Oxyz

cho hai mặt cầu

 

S

:

 

2

2 2

1 25

x y z

   

và

 

S



:

     

2 2 2

1 2 3 1.

x y z

     

Mặt phẳng

 

P

tiếp xúc

 

S



và

cắt

 

S

theo giao tuyến là một đường tròn có chu vi bằng

6 .



Khoảng cách từ

O

đến

 

P

bằng

A.

14

3

. B.

17

7

. C.

8

9

. D.

19

2

.

Câu 20. (Chuyên Nguyễn Du-ĐăkLăk 2019) Trong không gian

Oxyz

, cho điểm

 

2;11; 5

A



và mặt

phẳng

 

   

2 2

: 2 1 1 10 0

P mx m y m z

     

. Biết rằng khi

m

thay đổi, tồn tại hai mặt cầu cố

định tiếp xúc với mặt phẳng

 

P

và cùng đi qua

A

. Tổng bán kính của hai mặt cầu đó bằng

A.

10 2

. B.

12 3

. C.

12 2

. D.

10 3

.

Câu 21. (Chuyên Lê Quý Đôn – Điện Biên 2019) Trong không gian với hệ tọa độ

Oxyz

, cho mặt cầu

       

2 2 2

: 1 1 1 1

S x y z

     

và điểm

 

2;2;2

A

. Xét các điểm

M

thuộc mặt cầu

 

S

sao

cho đường thẳng

AM

luôn tiếp xúc với

 

S

.

M

luôn thuộc mặt phẳng cố định có phương trình là

A.

6 0

x y z

   

. B.

4 0

x y z

   

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

C.

3 3 3 8 0x y z   

. D.

3 3 3 4 0x y z   

.

Câu 22. Trong không gian với hệ tọa độ

Oxyz

, cho mặt cầu

 

2 2 2

: 4 4 2 7 0S x y z x y z      

và

đường thẳng

m

d là giao tuyến của hai mặt phẳng

 

1 2 4 4 0x m y mz    

và

 

2 2 1 8 0x my m z    

. Khi đó

m

thay đổi các giao điểm của

m

d và

 

S

nằm trên một

đường tròn cố định. Tính bán kính

r

của đường tròn đó.

A.

142

15

r 

. B.

92

3

r 

. C.

23

3

r 

. D.

586

15

r 

.

Câu 23. (Chuyên Quốc Học Huế 2019) Trong không gian với hệ tọa độ Oxyz cho mặt cầu

 

S

có

phương trình

     

2 2 2

2 4 2 2 0x y z a b x a b c y b c z d          

, tâm

I

nằm trên mặt

phẳng

 



cố định. Biết rằng

4 2 4a b c  

. Tìm khoảng cách từ điểm

 

1;2; 2D 

đến mặt

phẳng

 



.

A.

15

23

. B.

1

915

. C.

9

15

. D.

1

314

.

Câu 24. (THPT Ngô Sĩ Liên Bắc Giang 2019) Trong không gian với hệ trục toạ độ

,Oxyz

điểm

 

, ,M a b c

thuộc mặt phẳng

 

: 6 0P x y z   

và cách đều các điểm

     

1;6;0 , 2;2; 1 , 5; 1;3 .A B C  

Tích

abc

bằng

A.

6

B.

6

C.

0

D.

5

Dạng 2. Cực trị

1. Một số bất đẳng thức cơ bản

Kết quả 1. Trong một tam giác, cạnh đối diện với góc lớn thì lớn hơn

Kết quả 2. Trong các đường xiên và đường vuông góc kẻ từ một điểm nằm ngoài đường thẳng đến đường

thẳng đó thì đường vuông góc là đường ngắn nhất. Như trong hình vẽ ta luôn có

AM AH

Kết quả 3. Với ba điểm

, ,A B C

bất kì ta luôn có bất đẳng thức

.AB BC AC 

Tổng quát hơn ta có bất đẳng thức của đường gấp khúc: Với

n

điểm

1 2

, ,....

n

A A A ta luôn có

1 2 2 3 1 1

...

n n n

A A A A A A A A



   

Kết quả 4. Với hai số không âm

,x y

ta luôn có

2

x y

xy





. Đẳng thức xảy ra khi và chỉ khi

x y

Kết quả 5. Với hai véc tơ

,a b

 

ta luôn có . .a b a b

   

. Đẳng thức xảy ra khi

,a kb k 

 



2. Một số bài toán thường gặp

Bài toán 1. Cho điểm

A

cố định và điểm

M

di động trên hình

 

H

(

 

H

là đường thẳng, mặt phẳng). Tìm

giá trị nhỏ nhất của

AM

Lời giải: Gọi

H

là hình chiếu vuông góc của

A

lên hình

 

H

. Khi đó, trong tam giác

AHM

Vuông tại .

M

ta có

.AM AH

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5

Đẳng thức xảy ra khi

M H

. Do đó

AM

nhỏ nhất khi

M

là hình chiếu của

A

lên

 

H

Bài toán 2. Cho điểm

A

và mặt cầu

 

S

có tâm

,I

bán kính

,R

M

là điểm di động trên

 

S

. Tìm giá trị

nhỏ nhất và giá trị lớn nhất của

AM

.

Lời giải. Xét

A

nằm ngoài mặt cầu

( ).S

Gọi

1 2

,M M lần lượt là giao điểm của đường thẳng

AI

với mặt

cầu

 

1 2

( )S AM AM

và

( )



là mặt phẳng đi qua

M

và đường thẳng

.AI

Khi đó

( )



cắt

( )S

theo một

đường tròn lớn

( ).C

Ta có



1 2

90 ,M MM



 nên



2

AMM và



1

AM M là các góc tù, nên trong các tam giác

1

AMM và

2

AMM ta có

1 2

AI R AM AM AM AI R     

Tương tự với

A

nằm trong mặt cầu ta có

R AI AM R AI   

Vậy

min | |,maxAM AI R AM R AI   

Bài toán 3. Cho măt phẳng

( )P

và hai điểm phân biệt

, .A B

Tìm điể

M

thuộc

( )P

sao cho

1.

MA MB

nhỏ nhất.

2.

| |MA MB

lớn nhất.

Lời giải.

1. Ta xét các trường hợp sau

- TH 1: Nếu

A

và

B

nằm về hai phía so với

( )P

. Khi đó

AM BM AB 

Đẳng thức xảy ra khi

M

là giao điểm của

AB

với

( )P

.

- TH 2: Nếu

A

và

B

nằm cùng một phía so với

( )P

. Gọi

A



đối xứng với

A

qua

( )P

. Khi đó

AM BM A M BM A B

 

   

Đẳng thức xảy ra khi

M

là giao điểm của A B



với

( )P

.

2. Ta xét các trường hợp sau

- TH 1: Nếu

A

và

B

nằm cùng một phía so với

( )P

. Khi đó

| |AM BM AB 

Đẳng thức xảy ra khi

M

là giao điểm của

AB

với

( )P

.

- TH 2: Nếu

A

và

B

nằm khác phía so với

( )P

. Gọi

'A

đối xứng với

A

qua

 

P

, Khi đó

| |AM BM A M BM A B

 

   

Đẳng thức xảy ra khi

M

là giao điểm của A B



với

( )P

.

Bài toán 4. Viết phương trinh măt phẳng

( )P

di qua

A

và cách

B

một khoảng lớn nhất.

Lời giải. Gọi

H

là hình chiếu của

B

lên mặt phẳng

( ),P

khi đó

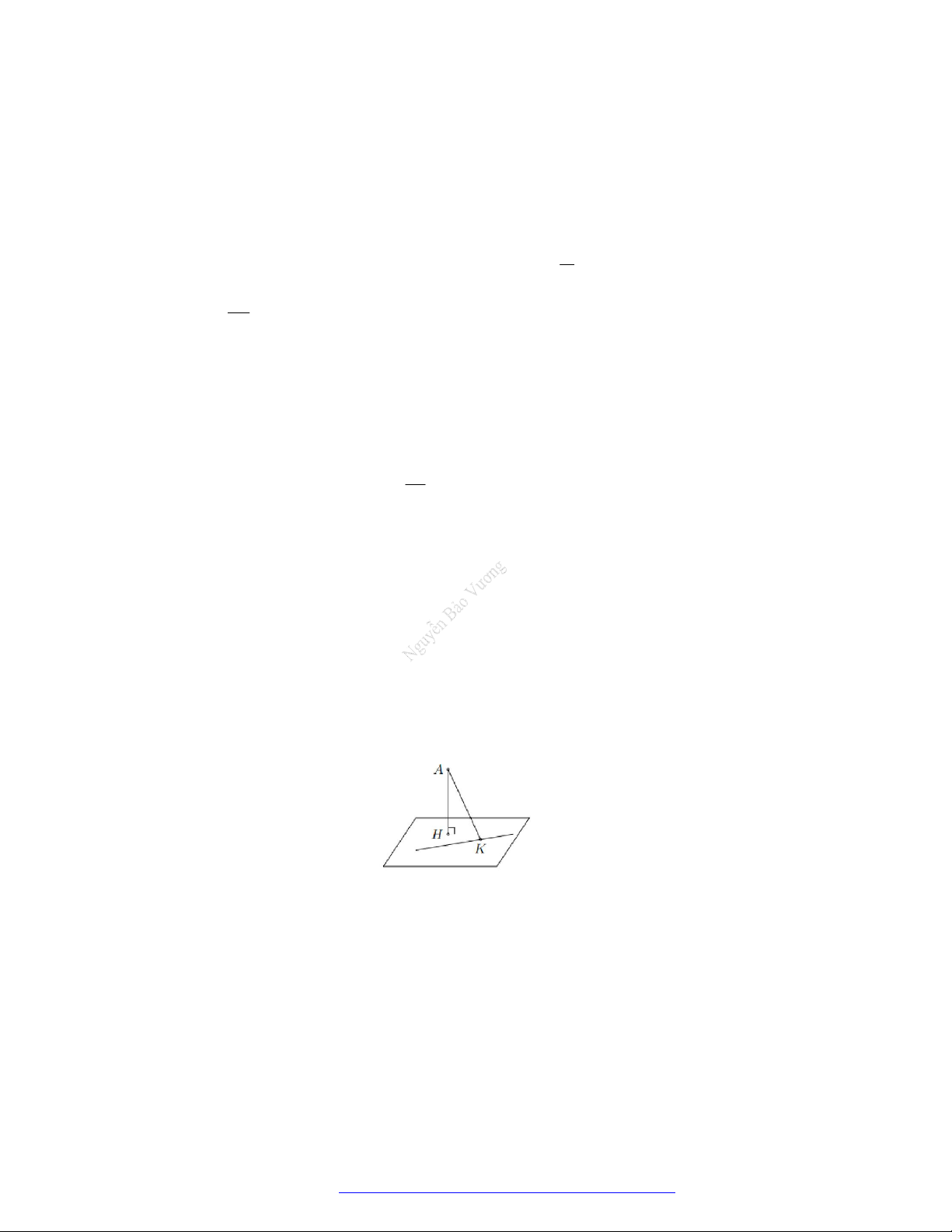
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

d( ,( ))B P BH BA 

Do đó

 

P

là mặt phẳng đi qua

A

vuông góc với

AB

Bài toán 5. Cho các số thực dương

,

 

và ba điểm

, ,A B

C. Viết phương trình măt phẳng

( )P

đi qua

C

và

d( ,( )) d( ,( ))T A P B P

 

 

nhỏ nhất.

Lời giải.

1. Xét

,A B

nằm về cùng phía so với

( )P

.

- Nếu ( )AB P‖ thì

( )d( ,( )) ( )P A P AC

   

   

- Nếu đường thẳng

AB

cắt

( )P

tại

.I

Gọi

D

là điểm thỏa mãn IB ID







 

và

E

là trung điểm

.BD

Khi đó

d( ,( )) d( ,( )) 2 d( ,( )) 2( )

IB

P A P D P E P EC

ID

    

      

2. Xét

,A B

nằm về hai phía so với

( )P

. Gọi

I

là giao điểm của

AB

và ( ),P B



là điểm đối xứng với

B

qua

I

. Khi đó

 

d( ,( )) d ,( )P A P B P

 



 

Đến đây ta chuyển về trường hợp trên.

So sánh các kết quả ở trên ta chọn kết quả lớn nhất.

Bài toán 6. Trong không gian cho

n

điểm

1 2

, , ,

n

A A A và diểm

.A

Viết phương trình mặt phẳng

( )P

đi

qua

A

và tổng khoảng cách từ các điểm

( 1,

i

A i n

) lớn nhất.

Lời giải.

- Xét

n

điểm

1 2

, , ,

n

A A A

nằm cùng phía so với

( ).P

Gọi

G

là trọng tâm của

n

điểm đã cho. Khi đó

 

1

d ,( ) d( ,( ))

n

i

A P n G P nGA



 



- Trong

n

điểm trên có

m

điểm nằm về một phía và

k

điểm nằm về phía khác

(m k n 

). Khi đó, gọi

1

G

là trọng tâm của

m

điểm,

2

G là trọng tâm của

k

điểm

3

G đối xứng với

1

G qua

.A

Khi dó

   

3 2

md ,( ) d ,( )P G P k G P 

Đến đây ta chuyển về bài toán trên.

Bài toán 7.Viết phương trình mặt phẳng

 

P

đi qua đường thẳng



và cách

A

một khoảng lớn nhất

Lời giải. Gọi

,H K

lần lượt là hình chiếu của

A

lên mặt phẳng

( )P

và đường thẳng

.

Khi đó

d( ,( ))A P AH AK 

Do đó

( )P

là mặt phẳng đi qua

K

và vuông góc vói

.AK

Bài toán 8. Trong không gian

Oxyz,

cho các điểm

1 2

, , , .

n

A A A

Xét véc tơ

1 1 2 2 n n

w MA M A M A

  

   

  





Trong đó

1 2

; ...

n

  

là các số thực cho trước thỏa mãn

1 2

... 0

n

  

    . Tìm điểm

M

thuôc măt phẳng

( )P

sao cho

| |w



có đô dài nhỏ nhất.

Lời giải. Gọi

G

là điểm thỏa mãn

1 1 2 2

0

n n

GA GA GA

  

   

   



(điểm

G

hoàn toàn xác định).

Ta có

k

MA MG GA 





vói

1;2; ; ,k n 

nên

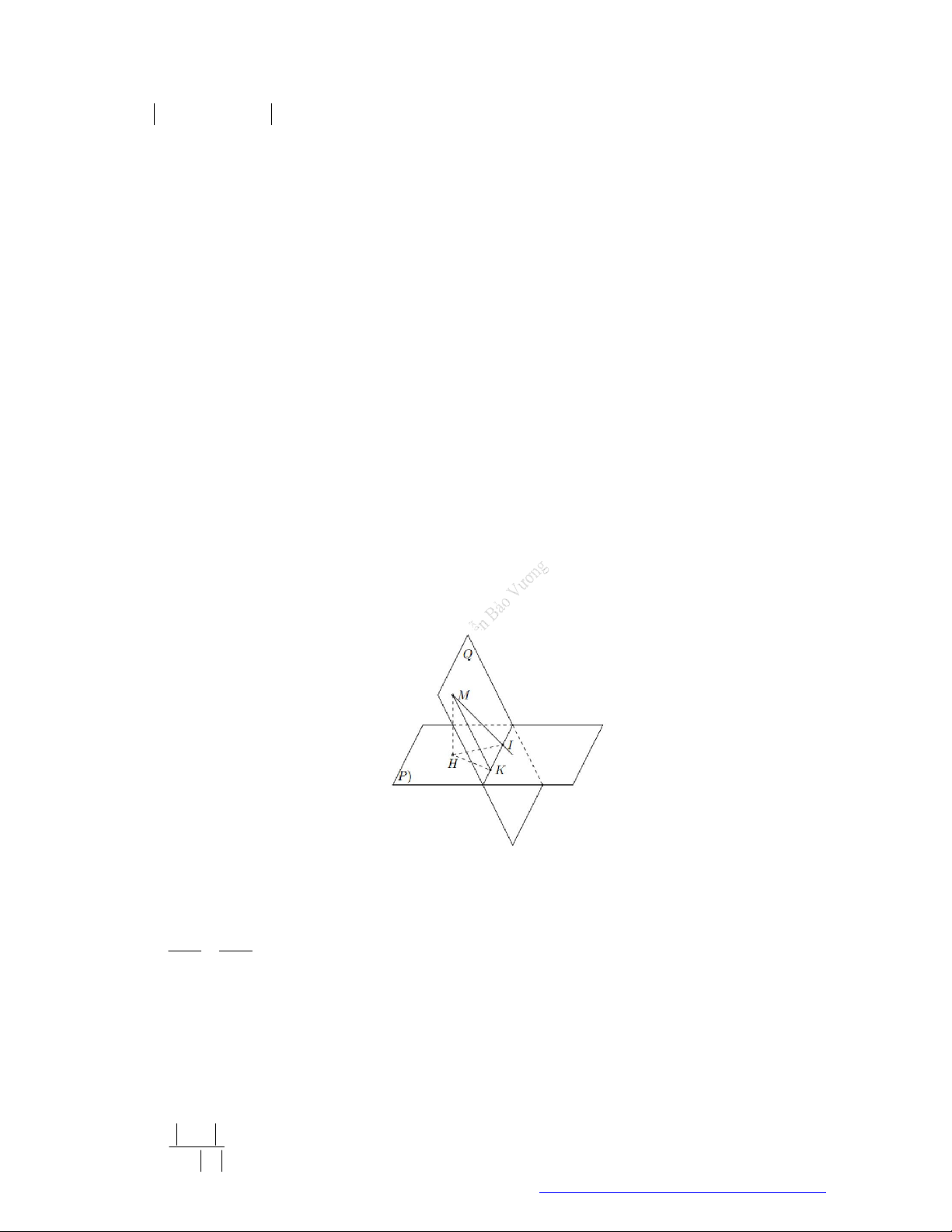
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7

   

1 2 1 1 2 2 1 2

w

n n n n

MG GA GA GA MG

        

         

 

  





Do đó

1 2

| | | |

n

w MG

  

    





Vi

1 2 n

  

   là hằng số khác không nên

| |w



có giá trị nhỏ nhất khi và chỉ khi

MG

nhỏ nhất, mà

( )M P

nên điểm

M

cần tìm là hình chiếu của

G

trên mặt phẳng

( )P

.

Bài toán 9. Trong không gian Oxy

,z

cho các diểm

1 2

, , , .

n

A A A Xét biểu thức:

2 2 2

1 1 2 2 n n

T MA MA MA

  

   

Trong đó

1 2

, , ,

n

  

 là các số thực cho trước. Tìm điểm M thuộc măt phẳng

( )P

sao cho

1.

T

giá trị nhỏ nhất biết

1 2

0

n

  

   .

2. T có giá trị lớn nhất biết

1 2

0

n

  

   .

Lời giải. Gọi

G

là điểm thỏa mãn

1 1 2 2

0

n n

GA GA GA

  

   

   



Ta có

k

MA MG GA 





với

1;2; ; ,k n 

nên

 

2

2 2 2

2

k k k k

MA MG GA MG MG GA GA     

 

 

Do đó

 

2 2 2 2

1 2 1 1 2 2n n n

T MG GA GA GA

     

      

Vì

2 2 2

1 1 2 2 n n

GA GA GA

  

  

không đổi nên

•

với

1 2

0

n

  

   thì

T

đạt giá trị nhỏ nhất khi và chỉ khi

MG

nhỏ nhất.

•

với

1 2

0

n

  

   thì

T

đạt giá trị lớn nhất khi và chỉ khi

MG

nhỏ nhất.

Mà

( )M P

nên

MG

nhỏ nhất khi điểm

M

là hình chiếu của

G

trên mặt phẳng

( )P

.

Bài toán 10. Trong không gian Oxyz, cho đường thẳng d và mặt phẳng

( )P

cắt nhau. Viết phương trình của

mặt phẳng

( )Q

chứa

d

và tạo với mặt phẳng

( )P

một góc nhỏ nhất.

Lời giải. Gọi

I

là giao điểm của đường thẳng

d

với mặt phẳng

( )P

và lấy điểm

,M d M I 

. Gọi

,H K

lầ lượt là hình chiếu của

M

lên

( )P

và giao tuyến



của

( )P

và

( )Q

.

Đặt



là góc giữa

( )P

và

( ),Q

ta có



,MKH





do đó

tan

HM HM

HK HI



 

Do đó

( )Q

là mặt phẳng đi qua

d

và vuông góc với mặt phẳng

( ),MHI

nên

( )Q

đi qua

M

và nhận

 

P d d

n u u 

  

làm VTPT.

Chú ý. Ta có thể giải bài toán trên bằng phương pháp đai số như sau:

- Goi

2 2 2

( ; ; ), 0n a b c a b c   



là một VTPT của mặt phẳng

( ).Q

Khi đó 0

d

n u 

 

từ đây ta rút được

a

theo

,b c

(hoặc

b

theo

,a c

hoặc

c

theo

,a b

).

- Gọi



là góc giữa

( )P

và

( ),Q

ta có

cos ( )

| |

P

n n

f t

n n





 



 

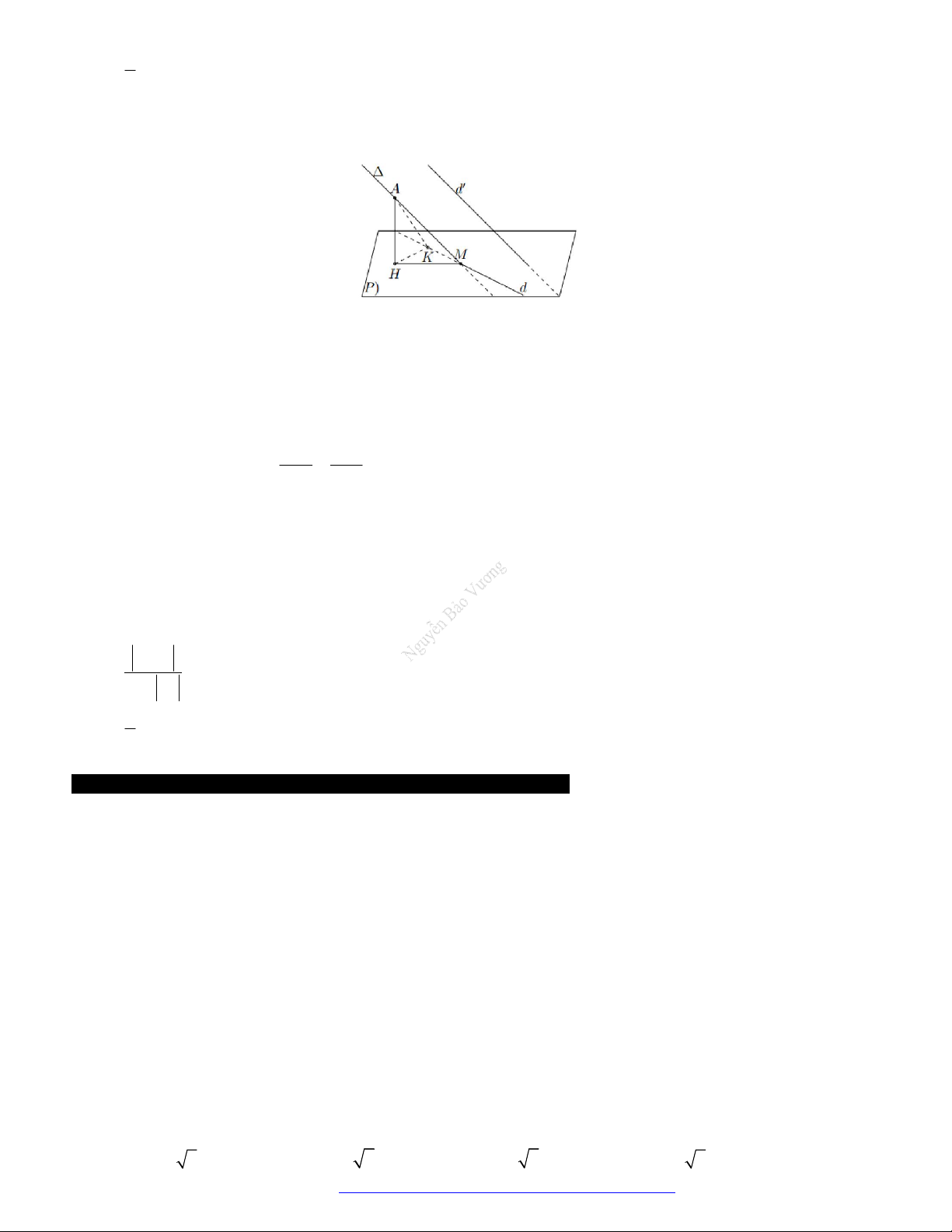
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 8 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

với

, 0.

b

t c

c

 

Khảo sát

( )f t

ta tìm được max của

( )f t

Bài toán 11. Trong không gian Oxyz, cho hai đường thẳng

d

và

d



chéo nhau. Viết phương trinh mặt

phẳng

( )P

chứa

d

và tạo với

d



một góc lớn nhất.

Lời giải. Trên đường thẳng

d

, lấy điểm

M

và dựng đường thẳng



đi qua

M

song song với

d



. Khi đó

góc giữa



và

( )P

chính là góc giữa

d



và

( )P

.

Trên đường thẳng



, lấy điểm

A

. Gọi

H

và

K

lần lượt là hình chiếu của

A

lên

( )P

và

,d



là góc giữa



và

( )P

.

Khi đó



AMH





và

cos

HM KM

AM AM



 

Suy ra

( )P

là mặt phẳng chứa

d

và vuông góc với mặt phẳng

( ).AMK

Do dó

( )P

đi qua

M

và nhận

 

d d

d

u u u



 

  

làm VTPT.

Chú ý. Ta có thể giải bài toán trên bằng phương pháp đại số như sau:

- Goi

2 2 2

( ; ; ), 0n a b c a b c   



là một VTPT của măt phẳng

( ).P

Khi đó 0

d

n u 

 

từ đây ta rút được

a

theo

,b c

(hoặc

b

theo

,a c

hoặc

c

theo

,a b

).

- Gọi



là góc giữa

( )P

và ,d



ta có

sin ( )

| |

d

n u

f t

n u







 



 

với

, 0.

b

t c

c

 

Khảo sát

( )f t

ta tìm được max của

( )f t

Dạng 2.1. Cực trị liên quan đến bán kính, diện tích, chu vi, thể tích

Câu 1. (Mã 105 2017) Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm

   

3; 2;6 , 0;1;0A B

và mặt

cầu

       

2 2 2

: 1 2 3 25S x y z     

. Mặt phẳng

 

: 2 0P ax by cz   

đi qua

,A B

và cắt

 

S

theo giao tuyến là đường tròn có bán kính nhỏ nhất. Tính

T a b c  

A.

3T 

B.

4T 

C.

5T 

D.

2T 

Câu 2. (THPT Gia Lộc Hải Dương 2019) Mặt phẳng

 

P

đi qua điểm

 

1;1;1M

cắt các tia

Ox

,

Oy

,

Oz

lần lượt tại

 

;0;0A a

,

 

0; ;0B b

,

 

0;0;C c

sao cho thể tích khối tứ diện

OABC

nhỏ nhất. Khi

đó

2 3a b c 

bằng

A.

12

. B.

21

. C.

15

. D.

18

.

Câu 3. Trong không gian với hệ tọa độ

Oxyz

, cho

 

2;0;0A

,

 

1;1;1M

. Mặt phẳng

 

P

thay đổi qua

AM

và cắt các tia

Oy

,

Oz

lần lượt tại

B

,

C

. Khi mặt phẳng

 

P

thay đổi thì diện tích tam giác

ABC

đạt giá trị nhỏ nhất bằng bao nhiêu?

A. 5 6 . B.

4 6

. C.

3 6

. D. 2 6 .

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9

Câu 4. Trong không gian với hệ toạ độ

Oxyz

, cho mặt cầu

       

2 2 2

: 1 2 3 9     

S x y z

, điểm

 

0;0; 2

A

. Mặt phẳng

 

P

qua

A

và cắt mặt cầu

 

S

theo thiết diện là hình tròn

 

C

có diện

tích nhỏ nhất, phương trình

 

P

là:

A.

 

: 2 3 6 0   

P x y z

. B.

 

: 2 3 6 0   

P x y z

.

C.

 

:3 2 2 4 0   

P x y z

. D.

 

: 2 2 0   

P x y z

.

Câu 5. (Bỉm Sơn - Thanh Hóa - 2019) Trong không gian

Oxyz

cho mặt cầu

     

2 2 2

( ) : 1 2 3 27

S x y z

     

. Gọi

 



là mặt phẳng đi qua 2 điểm

 

0;0; 4

A



,

 

2;0;0

B

và cắt

 

S

theo giao tuyến là đường tròn

 

C

sao cho khối nón có đỉnh là tâm của

 

S

, là hình

tròn

 

C

có thể tích lớn nhất. Biết mặt phẳng

 



có phương trình dạng

0

ax by z c

   

, khi đó

a b c 

bằng:

A. 8. B. 0. C. 2. D. -4.

Câu 6. Trong không gian

Oxyz

, cho hai điểm

5 3 7 3

; ;3

2 2

A

 

 

 

 

,

5 3 7 3

; ;3

2 2

B

 

 

 

 

và mặt cầu

2 2 2

( ) :( 1) ( 2) ( 3) 6

S x y z

     

. Xét mặt phẳng

( ) : 0

P ax by cz d

   

,

 

, , , : 5

a b c d d

  

là mặt phẳng thay đổi luôn đi qua hai điểm

,A

B

. Gọi

( )N

là hình nón có

đỉnh là tâm của mặt cầu

( )S

và đường tròn đáy là đường tròn giao tuyến của

( )P

và

( )S

. Tính

giá trị của

T a b c d   

khi thiết diện qua trục của hình nón

( )N

có diện tích lớn nhất.

A.

4T 

. B.

6

T



. C.

2T 

. D.

12T 

.

Câu 7. (Nho Quan A - Ninh Bình - 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho hai điểm

   

0; 1; 1 , 1; 3;1

A B   

. Giả sử

,C D

là hai điểm di động trên mặt phẳng

 

:2 2 1 0

P x y z

   

sao cho

4

CD



và

, ,A C D

thẳng hàng. Gọi

1 2

,S S

lần lượt là diện tích

lớn nhất và nhỏ nhất của tam giác

BCD

. Khi đó tổng

1 2

S S

có giá trị bằng bao nhiêu?

A.

34

3

. B.

37

3

. C.

11

3

. D.

17

3

.

Câu 8. (Chuyên Lê Quý Đôn Quảng Trị 2019) Trong không gian

Oxyz

cho mặt phẳng (P):

2 1 0

x y z

   

và các điểm

   

0;1;1 ; 1;0;0

A B

(

A

và

B

nằm trong mặt phẳng

 

P

) và mặt

cầu

       

2 2 2

: 2 1 2 4

S x y z

     

.

CD

là đường kính thay đổi của

 

S

sao cho

CD

song

song với mặt phẳng

 

P

và bốn điểm

, , ,A B C D

tạo thành một tứ diện. Giá trị lớn nhất của tứ

diện đó là

A.

2 6

. B.

2 5

. C.

2 2

. D.

2 3

.

Câu 9. Trong không gian với hệ trục tọa độ

Oxyz

, cho tứ diện

ABCD

có điểm

 

1;1;1 ,

A

 

2;0;2 ,

B

 

 

1; 1;0 ,

C

 

0;3;4

D

. Trên các cạnh

, ,AB AC AD

lần lượt lấy các điểm

, ,B C D

  

thỏa

4

AB AC AD

  

  

. Viết phương trình mặt phẳng

 

B C D

  

biết tứ diện

AB C D

  

có thể

tích nhỏ nhất?

A.

16 40 44 39 0   

x y z

B.

16 40 44 39 0   

x y z

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 10 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

C.

16 40 44 39 0   

x y z

D.

16 40 44 39 0   

x y z

Câu 10. Trong không gian

Oxyz

, cho hai điểm

   

1;2;4 , 0;0;1

A B

và mặt cầu

     

2 2

2

: 1 1 4

S x y z

    

. Mặt phẳng

 

:a 4 0

P x by cz

   

đi qua

,A B

và cắt

 

S

theo

giao tuyến là một đường tròn có bán kính nhỏ nhất. Tính

?T a b c  

A.

1

5

T



. B.

3

4

T



. C.

1T 

. D.

2T  

.

Câu 11. (Chuyên Lê Quý Đôn Quảng Trị 2019) Trong không gian

Oxyz

, cho mặt phẳng

 

P

:

2 0

x y

  

và hai điểm

 

1;2;3

A

,

 

1;0;1

B

. Điểm

   

; ; 2

C a b P

 

sao cho tam giác

ABC

có

diện tích nhỏ nhất. Tính

a b

A. 0. B.

3

. C. 1. D. 2.

Câu 12. (THPT Ngô Sĩ Liên Bắc Giang 2019) Trong không gian với hệ trục toạ độ

,Oxyz

mặt phẳng

 

P

đi qua điểm

 

1;2;1

M

cắt các tia

, ,Ox Oy Oz

lần lượt tại các điểm

, ,A B C

(

, ,A B C

không trùng

với gốc

O

) sao cho tứ diện

OABC

có thể tích nhỏ nhất. Mặt phẳng

 

P

đi qua điểm nào trong

các điểm dưới đây?

A.

 

0;2;2

N

B.

 

0;2;1

M

C.

 

2;0;0

P

D.

 

2;0; 1

Q

Câu 13. (Chuyên Lê Quý Đôn Điện Biên 2019) Trong không gian với hệ tọa độ

Oxyz

cho mặt phẳng

 

P

đi qua điểm

 

9;1;1

M

cắt các tia

, ,Ox Oy Oz

tại

, ,A B C

(

, ,A B C

không trùng với gốc tọa độ ). Thể

tích tứ diện

OABC

đạt giá trị nhỏ nhất là bao nhiêu?

A.

81

2

. B.

243

2

. C.

81

6

. D.

243

.

Câu 14. (THPT Quang Trung Đống Đa Hà Nội 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho

mặt cầu

 

2 2 2

: 3

S x y z

  

. Một mặt phẳng

 



tiếp xúc với mặt cầu

 

S

và cắt các tia

Ox

,

O y

,

Oz

lần lượt tại

A

,

B

,

C

thỏa mãn

2 2 2

27

OA OB OC

  

. Diện tích tam giác

ABC

bằng

A.

3 3

2

. B.

9 3

2

. C.

3 3

. D.

9 3

.

Dạng 2.2. Cực trị liên quan đến giá trị biểu thức

Câu 15. (Đề Tham Khảo 2019) Trong không gian

Oxyz

, cho hai điểm

 

2; 2;4

A 

,

 

3;3; 1

B

 

và mặt

phẳng

 

: 2 2 8 0

P x y z

   

. Xét M là điểm thay đổi thuộc

 

P

, giá trị nhỏ nhất của

2 2

2 3

MA MB



bằng

A.

145

B.

135

C.

105

D.

108

Câu 16. Trong không gian

Oxyz

, cho ba điểm

     

     2; 2; 4 , 3; 3; 1 , 1; 1; 1

A B C

và mặt phẳng

 

   : 2 2 8 0

P x y z

. Xét điểm

M

thay đổi thuộc

 

P

, tìm giá trị nhỏ nhất của biểu thức

  

2 2 2

2T MA MB MC

.

A. 102. B. 105. C. 30. D. 35.

Câu 17. (Chuyên Quang Trung- Bình Phước 2019) Trong không gian

Oxyz

, cho

     

0;1;2 , 1;1;0 , 3;0;1

A B C

và mặt phẳng

 

: 5 0

Q x y z

   

. Xét điểm

M

thay đổi thuộc

 

Q

. Giá trị nhỏ nhất của biểu thức

2 2 2

MA MB MC 

bằng

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11

A.

34

3

. B.

22

3

. C.

0

. D.

26

3

.

Câu 18. (Chuyên Lam Sơn 2019) Trong hệ trục tọa độ

Oxyz

cho điểm

 

( 1;3;5); (2;6; 1); 4; 12;5

A B C   

và mặt phẳng

 

: 2 2 5 0

P x y z

   

. Gọi

M

là điểm di

động trên

 

P

. Giá trị nhỏ nhất của biểu thức

S MA MB MC

  

  

là

A.

42

B.

14

. C.

14 3

. D.

14

3

.

Câu 19. Trong không gian

Oxyz

cho các điểm

 

1; 1;3

A 

,

 

2;1;0

B

,

 

3; 1; 3

C

  

và mặt phẳng

 

: 4 0

P x y z

   

. Gọi

 

, ,M a b c

là điểm thuộc mặt phẳng

 

P

sao cho biểu thức

3 2

T MA MB MC

  

  

đạt giá trị nhỏ nhất. Tính giá trị của biểu thức

S a b c  

.

A.

3

S



. B.

1

S

 

. C.

2

S



. D.

1

S



.

Câu 20. (Ngô Quyền - Hải Phòng 2019) Trong không gian

Oxyz

, cho ba điểm

     

1;1;1 , 1;2;0 , 3; 1;2

A B C 

và điểm

M

thuộc mặt phẳng

 

: 2 2 7 0

x y z



   

. Tính giá

trị nhỏ nhất của

3 5 7

P MA MB MC

  

  

.

A.

min

20

P



. B.

min

5

P



. C.

min

25

P



. D.

min

27

P



.

Câu 21. (SGD Hưng Yên 2019) Trong không gian với hệ tọa độ

Oxyz

, cho ba điểm

 

1;4;5

A

,

 

3;4;0

B

,

 

2; 1;0

C 

và mặt phẳng

 

: 3 3 2 29 0

P x y z

   

. Gọi

 

; ;M a b c

là điểm thuộc

 

P

sao cho biểu thức

2 2 2

3

T MA MB MC

  

đạt GTNN. Tính tổng

a b c 

.

A. 8. B. 10. C.

10

. D.

8

.

Câu 22. Trong không gian

Oxyz

, cho ba điểm

     

0;0;1 , 1;1;0 , 1;0; 1

A B C

 

. Điểm

M

thuộc mặt

phẳng

 

: 2 2 2 0

P x y z

   

sao cho

2 2 2

3 2

MA MB MC

 

đạt giá trị nhỏ nhất. Giá trị nhỏ nhất

đó bằng

A.

13

6

. B.

17

2

. C.

61

6

. D.

23

2

.

Câu 23. Trong không gian

Oxyz

, cho hai điểm

 

3;1; 3

A



,

 

0; 2;3

B



và mặt cầu

   

2 2

2

( ) : 1 3 1

S x y z

    

. Xét điểm

M

thay đổi luôn thuộc mặt cầu

( )S

, giá trị lớn nhất

của

2 2

2

MA MB

bằng

A.

102

. B.

78

. C.

84

. D.

52

.

Câu 24. (Hậu Lộc 2-Thanh Hóa -2019) Trong không gian

Oxyz

, cho các điểm

 

A 0;0;2

và

 

B 3;4;1

.

Gọi

 

P

là mặt phẳng chứa đường tròn giao tuyến của hai mặt cầu

       

2 2 2

1

: 1 1 3 25

S x y z

     

với

 

2 2 2

2

: x 2 2 14 0

S y z x y

     

.

M

,

N

là hai điểm

thuộc

 

P

sao cho

1

MN



. Giá trị nhỏ nhất của

AM BN

là

A.

34 1

. B.

5

. C.

34

. D.

3

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 12 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 25. (SGD Điện Biên - 2019) Trong không gian

Oxyz

, cho ba điểm

 

2; 2;4

A 

,

 

3;3; 1

B

 

,

 

1; 1; 1

C

  

và mặt phẳng

 

: 2 2 8 0

P x y z

   

. Xét điểm

M

thay đổi thuộc

 

P

, tìm giá trị

nhỏ nhất của biểu thức

2 2 2

2

T MA MB MC

  

.

A. 102. B. 105. C. 30. D. 35.

Câu 26. (THPT Cẩm Giàng 2 2019) Trong không gian

Oxyz

, cho ba điểm

 

10; 5;8

A  

,

 

2;1; 1

B



,

 

2;3;0

C

và mặt phẳng

 

: 2 2 9 0

P x y z

   

. Xét

M

là điểm thay đổi trên

 

P

sao cho

2 2 2

2 3

MA MB MC

 

đạt giá trị nhỏ nhất. Tính

2 2 2

2 3

MA MB MC

 

.

A.

54

.

B.

282

.

C.

256

.

D.

328

.

Câu 27. Trong không gian

Oxyz

, cho

     

4; 2;6 ; 2;4;2 ; : 2 3 7 0

A B M x y z



     

sao cho

.MA MB

 

nhỏ nhất, khi đó tọa độ của

M

là

A.

29 58 5

; ;

13 13 13

 

 

 

B.

 

4;3;1

C.

 

1;3;4

D.

37 56 68

; ;

3 3 3



 

 

 

Câu 28. (Chuyên Lam Sơn Thanh Hóa 2019) Trong hệ trục

,Oxyz

cho điểm

 

1;3;5 ,

A

 

2;6; 1 ,

B

 

4; 12;5

 C

và mặt phẳng

 

: 2 2 5 0.   

P x y z

Gọi

M

là điểm di động trên

 

.P

Gía trị

nhỏ nhất của biểu thức

  

  

S MA MB MC

là

A.

42.

B.

14.

C.

14 3.

D.

14

.

3

Câu 29. (Chuyên Lê Hồng Phong Nam Định 2019) Trong không gian với hệ tọa độ

Oxyz

, cho ba điểm

 

1;2;5

A 

,

 

3; 1;0

B 

,

 

4;0; 2

C

 

. Gọi

I

là điểm trên mặt phẳng

 

Oxy

sao cho biểu thức

2 3IA IB IC

 

  

đạt giá trị nhỏ nhất. Tính khoảng cách từ

I

đến mặt phẳng

 

: 4 3 2 0

P x y

  

.

A.

17

5

. B.

6

. C.

12

5

. D.

9

.

Câu 30. Trong không gian tọa độ

,Oxyz

cho hai điểm

   

3; 2;2 , 2;2;0

A B 

và mặt phẳng

 

: 2 2 3 0.

P x y z

   

Xét các điểm

,M N

di động trên

 

P

sao cho

1.

MN



Giá trị nhỏ nhất

của biểu thức

2 2

2 3

AM BN



bằng

A.

49,8.

B.

45.

C.

53.

D.

55,8.

Câu 31. (THPT Nghĩa Hưng NĐ- 2019) Trong không gian với hệ tọa độ

Oxyz

, cho điểm

 

; ;A a b c

với

a

,

b

,

c

là các số thực dương thỏa mãn

 

2 2 2

5 9 2    

a b c ab bc ca

và

 

3

2 2

1

 



 

a

Q

b c

a b c

có giá trị lớn nhất. Gọi

M

,

N

,

P

lần lượt là hình chiếu vuông góc của

A

lên các tia

Ox

,

Oy

,

Oz

. Phương trình mặt phẳng

 

MNP

là

A.

4 4 12 0   

x y z

. B.

3 12 12 1 0   

x y z

.

C.

4 4 0  

x y z

. D.

3 12 12 1 0   

x y z

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13

Câu 32. (Sở Bắc Giang 2019) Cho

, , , , ,x y z a b c

là các số thực thay đổi thỏa mãn

     

2 2 2

1 1 2 1

x y z

     

và

3.

a b c

  

Tìm giá trị nhỏ nhất của

     

2 2 2

.P x a y b z c

     

A.

3 1.

B.

3 1.

C.

4 2 3.



D.

4 2 3.



Câu 33. (Chuyên Sơn La 2019) Trong không gian

Oxyz

, cho hai điểm

 

1;0;0

A

và

 

2;3;4

B

. Gọi

 

P

là mặt phẳng chứa đường tròn giao tuyến của hai mặt cầu

     

2 2

2

1

: 1 1 4    

S x y z

và

 

2 2 2

2

: 2 2 0    

S x y z y

. Xét

M

,

N

là hai điểm bất kỳ thuộc mặt phẳng

 

P

sao cho

1

MN



. Giá trị nhỏ nhất của

AM BN

bằng

A. 5. B. 3. C. 6. D. 4.

Câu 34. (THPT Yên Khánh - Ninh Bình - 2019) Trong không gian

Oxyz

cho mặt cầu

 

2 2 2

: 1

S x y z

  

. Điểm

 

M S



có tọa độ dương; mặt phẳng

 

P

tiếp xúc với

 

S

tại

M

cắt

các tia

Ox

;

Oy

;

Oz

tại các điểm

A

,

B

,

C

. Giá trị nhỏ nhất của biểu thức

   

2 2 2

1 1 1

T OA OB OC

   

là:

A. 24. B. 27. C. 64. D. 8.

Dạng 2.3. Cực trị liên quan đến góc, khoảng cách

Câu 35. Trong không gian với hệ tọa độ

Oxyz

, cho ba điểm

     

,0,0 , 0, ,0 , 0,0,A a B b C c

với

, ,a b c

là

những số dương thay đổi thỏa mãn

2 2 2

4 16 49

a b c

  

. Tính tổng

2 2 2

S a b c  

khi khoảng

cách từ

O

đến mặt phẳng

 

ABC

đạt giá trị lớn nhất.

A.

51

5

S 

. B.

49

4

S 

. C.

49

5

S 

. D.

51

4

S 

.

Câu 36. (Chuyên Lê Hồng Phong Nam Định 2019) Trong không gian với hệ tọa độ

Oxyz

, cho bốn

điểm

 

1;0;0

A

,

 

2;1;3

B

,

 

0;2; 3

C



,

 

2;0; 7

D

. Gọi

M

là điểm thuộc mặt cầu

     

2 2

2

: 2 4 39

S x y z

    

thỏa mãn

2

2 . 8

MA MB MC

 

 

. Biết rằng đoạn thẳng

MD

đạt

giá trị lớn nhất. Tìm giá trị lớn nhất đó?

A.

7

. B.

2 7

. C.

3 7

. D.

4 7

.

Câu 37. (Bình Giang-Hải Dương 2019) Cho

 

0;8;2

A

và mặt cầu

       

2 2 2

: 5 3 7 72

S x y z

     

và điểm

 

9; 7;23

A 

. Viết phương trình mặt phẳng

 

P

đi

qua A và tiếp xúc với mặt cầu

 

S

sao cho khoảng cách từ B đến mặt phẳng

 

P

là lớn nhất. Giải

sử

 

1; ;n m n





là một vectơ pháp tuyến của

 

P

. Lúc đó

A.

. 4

m n



. B.

. 2

m n



. C.

. 4

m n

 

. D.

. 2

m n

 

.

Câu 38. Cho

, ,x y z

là ba số thực thỏa

2 2 2

4 6 2 11 0

x y z x y z

      

. Tìm giá trị lớn nhất của

2 2

P x y z  

.

A.

max 20

P



. B.

max 18

P

 

. C.

max 18

P



. D.

max 12

P



.

Câu 39. (Sở Nam Định - 2019) Trong không gian

Oxyz

, cho các điểm

     

;0;0 , 0; ; 0 , 0;0;M m N n P p

không trùng với gốc tọa độ và thỏa mãn

2 2 2

3

m n p

  

.

Tìm giá trị lớn nhất của khoảng cách từ

O

đến mặt phẳng

 

MNP

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 14 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

A.

1

3

. B.

3

. C.

1

3

. D.

1

27

.

Câu 40. Trong không gian với hệ tọa độ

,Oxyz

cho mặt phẳng

 

: 2 2 3 0

P x y z

   

và mặt cầu

 

2 2 2

: 2 4 2 5 0.

S x y z x y z

      

Giả sử

 

M P



và

 

N S



sao cho



MN

cùng phương

với vectơ

 

1;0;1

u



và khoảng cách giữa

M

và

N

lớn nhất. Tính

.MN

A.

3

MN

B.

1 2 2

 MN

C.

3 2

MN

D.

14

MN

Câu 41. Trong không gian

Oxyz

, cho bốn điểm

 

2;0;1

A

,

 

3;1;5

B

,

 

1;2;0

C

,

 

4;2;1

D

. Gọi

 



là mặt phẳng đi qua

D

sao cho ba điểm

A

,

B

,

C

nằm cùng phía đối với

 



và tổng khoảng

cách từ các điểm

A

,

B

,

C

đến mặt phẳng

 



là lớn nhất. Giả sử phương trình

 



có dạng:

2 0

x my nz p

   

. Khi đó,

T m n p  

bằng:

A. 9. B. 6. C. 8. D. 7.

Câu 42. Trong không gian với hệ tọa độ

Oxyz

gọi

( ) : y z 3 0P ax b c   

(

, ,a b c

là các số nguyên

không đồng thời bằng

0

) là phương trình mặt phẳng đi qua hai điểm

   

0; 1;2 , 1;1;3

M N

 

và

không đi qua

 

0;0;2

H

. Biết rằng khoảng cách từ

 

0;0;2

H

đến mặt phẳng

( )P

đạt giá trị lớn

nhất. Tổng

2 3 12P a b c   

bằng

A.

8

. B.

16

. C.

12

. D.

16

.

Câu 43. (Chu Văn An - Hà Nội - 2019) Trong không gian với hệ trục toạ độ

Oxyz

, cho mặt phẳng

 

: 2z 0

P x y

  

. Phương trình mặt phẳng

 

Q

chứa trục hoành và tạo với

 

P

một góc nhỏ

nhất là

A.

2z 0.

y

 

B.

0.

y z

 

C.

2 0.

y z

 

D.

0.

x z

 

Câu 44. (Việt Đức Hà Nội 2019) Trong hệ trục tọa độ

O

xyz

, mặt phẳng

 

P

đi qua điểm

 

1;7;2

A

và

cách

 

2;4; 1

M

 

một khoảng lớn nhất có phương trình là

A.

 

:3 3 3 10 0

P x y z

   

. B.

 

: 1 0

P x y z

   

.

C.

 

: 10 0

P x y z

   

. D.

 

: 10 0

P x y z

   

.

Câu 45. (HSG Bắc Ninh 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho ba điểm

( ;0;0), (0; ;0), (0;0; )A a B b C c

, trong đó

, ,a b c

là các số thực thỏa mãn

2 2 1

1

a b c

  

. Khoảng

cách từ gốc tọa độ

O

đến mặt phẳng

 

ABC

có giá trị lớn nhất bằng:

A.

3

B.

4

C.

2

D.

1

Câu 46. (Chuyên Trần Phú Hải Phòng 2019) Trong không gian

,Oxyz

cho mặt phẳng

( ) : 2 2 3 0

P x y z

   

và hai điểm

   

1;2;3 , B 3;4;5

A

. Gọi

M

là một điểm di động trên

( )P

.

Giá trị lớn nhất của biểu thức

2 3

MA

MB



bằng

A.

3 3 78



. B.

54 6 78



. C.

8 2

. D.

6 3

.

Câu 47. (Chuyên Hạ Long 2019) Cho

   

4;5;6 ; 1;1;2

A B

,

M

là một điểm di động trên mặt phẳng

 

:2 2 1 0

P x y z

   

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15

Khi đó

M

A MB



nhận gi

á trị lớn nhất là?

A.

7

. B.

41

. C.

7

. D.

85

.

Câu 48. Tr

ong không gian

Ox

yz

,

cho điểm

 

1;1

;2

A

và

mặt phẳng

   

:

1 1 0

P

m x y mz



   

,

với

m

là

tham số. Biết khoảng cách từ điểm

A

đến mặt phẳng

 

P

lớn nhất. Khẳng định đúng trong bốn

khẳng định dưới đây là

A.

2 6

m

 

. B.

6

m



. C.

2 2

m

  

. D.

6 2

m

  

.

Câu 49. (Chu

yên Lê Quý Đôn Điện Biên 2019) Trong không gian

Oxyz

,

cho hai điểm

   

1

;2; 1 , 3;0;3

A

B

.

Biết mặt phẳng

 

P

đi

qua điểm

A

và

cách

B

một

khoảng lớn nhất.

Phương trình mặt phẳng

 

P

là:

A.

2

2 5 0

x

y z



  

. B.

2

3 0

x

y z



  

.

C.

2

2 4 3 0

x

y z



  

. D

.

2

2 0

x

y z



 

.

Câu 50. (Sở Bắc Giang 2019) T

rong không gian

Oxyz

,

cho điểm

 

1

;4;9

M

.

Gọi

 

P

là

mặt phẳng đi

qua

M

và

cắt 3 tia

,

, Ox Oy Oz

lần

lượt tại các điểm

,

,A B C

(khá

c

O

)

sao cho

O

A OB OC 

đạt

giá trị nhỏ nhất. Tính khoảng cách

d

từ gốc

tọa độ

O

đến

mặt phẳng

 

P

.

A.

3

6

7

d 

. B.

2

4

5

d 

. C.

8

3

d



. D.

2

6

14

d 

.

Câu 51. Tr

ong không gian

,O

xyz

cho

điểm

(

1;4;9)

M

.

Gọi (P) là mặt phẳng đi qua M và cắt 3 tia Ox, Oy,

Oz lần lượt tại các điểm A, B, C (khác O) sao cho

OA

OB OC 

đạt

giá trị nhỏ nhất. Tính khoảng

cách d từ gốc tọa độ O đến mặt phẳng (P).

A.

36

7

d 

B.

24

5

d 

C.

8

3

d



D.

2

6

14

d 

Câu 52. (THPT Ba Đìn

h -2019) Trong không gian với hệ tọa độ

,Oxyz

cho

mặt phẳng

 

:

2 2 3 0

P

x y z



  

và

mặt cầu

 

2

2 2

:

2 4 2 5 0

S

x y z x y z



     

.

Giả sử

 

M

P



và

 

N S



s

ao cho

M

N



cùng

phương với vectơ

 

1

;0;1

u 



và

khoảng cách giữa

M

và

N

lớn

nhất. Tính

.M

N

A.

3

MN



. B.

1

2 2

M

N  

. C.

3

2

M

N 

. D.

14

MN



.

Câu 53. (C

huyên Lê Hồng Phong Nam Định 2019) Trong không gian với hệ tọa độ

Oxy

z

c

ho bốn điểm

(

1;0;0)

A

,

(

2;1;3)

B

,

(

0;2; 3)

C



,

(2;0; 7)

D

.

Gọi

M

là

điểm thuộc mặt cầu

2

2 2

(

) : ( 2) ( 4) 39

S

x y z



   

thỏa

mãn:

2

2 . 8

MA MB MC

 

 

.

Biết độ dài đoạn thẳng

MD

đạt

giá trị lớn nhất. Tính giá trị lớn nhất đó.

A.

2

7

. B.

7

. C.

3

7

. D.

4

7

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương  https://www.facebook.com/phong.baovuongTrang 1



TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH TRUNG BÌNH MỨC 5-6 ĐIỂM

Dạng1.Xácđịnhvéctơpháptuyến

 Véctơ pháp tuyến

n



của mặt phẳng

( )P

là véctơ có giá vuông góc với

( ).P

Nếu

n



là một véctơ pháp

tuyến của

( )P

thì

.k n



cũng là một véctơ pháp tuyến của

( ).P

 Nếu mặt phẳng

( )P

có cặp véctơ chỉ phương là

1 2

, u u

 

thì

( )P

có véctơ pháp tuyến là

1 2

[ , ].n u u

  



Mặt phẳng

( ) : 0P ax by cz d   

có một véctơ pháp tuyến là

( ; ; ).n a b c





Câu 1. (Đề Minh Họa 2020 Lần 1) Trongkhônggian

Oxyz

,chomặtphẳng

 

: 3 2 4 1 0x y z



   

.

Vectơnàodướiđâylàmộtvectơpháptuyếncủa

 



?

A.

 

2

3;2;4n 



. B.

 

3

2; 4;1n  



. C.

 

1

3; 4;1n  



. D.

 

4

3;2; 4n  



.

Lời giải

Chọn D

Mặtphẳng

 

: 3 2 4 1 0x y z



   

cóvectơpháptuyến

 

3;2; 4n  





Câu 2. (Đề Tham Khảo 2020 Lần 2) Trongkhônggian

Oxyz

,chomặtphẳng

 

: 2 3 2 0P x y z   

.

Véctơnàodướiđâylàmộtvéctơpháptuyếncủa

 

P

?

A.

 

3

2;3;2n



. B.

 

1

2;3;0n



. C.

 

2

2;3;1n



. D.

 

4

2;0;3n



.

Lời giải

Chọn C

Véctơpháptuyếncủa

 

P

là

 

2

2;3;1n



.

Câu 3. (Mã 101 2020 Lần 2)Trongkhônggian

Oxyz

,chomặtphẳng

 

: 2 4 3 0x y z



   

.Véctơ

nàosauđâylàvéctơpháptuyếncủa

 



?

A.

 

1

2;4; 1n  



. B.

 

2

2; 4;1n  



. C.

 

3

2;4;1n  



. D.

 

1

2;4;1n 



.

Lời giải

Chọn A

Mặtphẳng

 

: 2 4 3 0x y z



   

cómộtvéctơpháptuyếnlà

 

2;4; 1n  



.

Câu 4. (Mã 102 - 2020 Lần 2) Trongkhônggian

Oxyz

,chomặtphẳng

 

: 2 3 4 1 0x y z



   

.Vectơ

nàodướiđâylàmộtvectơpháptuyếncủa

 



?

A.

 

3

2; 3; 4n  



. B.

 

2

2; 3; 4n  



. C.

 

1

2; 3; 4n 



. D.

 

4

2; 3; 4n  



.

Lời giải

Chọn A

Vectơpháptuyếncủamặtphẳng

 

: 2 3 4 1 0x y z



   

là

 

3

2; 3; 4n  



.

Câu 5. (Mã 103 - 2020 Lần 2) Trongkhônggian

Oxyz

,Chomặtphẳng

 

: 2 3 5 0x y z



   

.Vectơ

nàodướiđâylàmộtvectơpháptuyếncủa

 



?

PHƯƠNG TRÌNH MẶT PHẲNG

Chuyên đề 30



P



n





2

u





2

u





NGUYỄN BẢO VƯƠNG - 0946798489

Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

A.

 

3

2;1;3 .

n  



B.

 

4

2;1; 3 .

n

 



C.

 

2

2; 1;3 .

n  



D.

 

1

2;1;3 .

n 





Lời giải

Chọn C

Câu 6. (Mã 104 - 2020 Lần 2) Trongkhônggian

Oxyz

,chomặtphẳng

 

: 2 4 1 0

x y z



   

.Vectơ

nàodướiđâylàmộtvectơpháptuyếncủamặtphẳng

 



?

A.

 

3

1; 2;4

n



 

. B.

 

1

1;2; 4

n



 

. C.

 

2

1;2;4

n





. D.

 

4

1;2;4

n



 



Lời giải

Chọn A.

Câu 7. (ĐềMinhHọa2017)Trongkhônggianvớihệtọađộ

O

xyz

,chomặtphẳng

 

:3 2 0

P x z

  

.

Vectơnàodướiđâylàmộtvectơpháptuyếncủa

 

P

?

A.

 

2

3;0; 1

n

 



B.

 

1

3; 1;2

n  



C.

 

3

3; 1;0

n  



D.

 

4

1;0; 1

n

  





Lờigiải

ChọnA

Vectơpháptuyếncủamặtphẳng

 

:3 2 0

P x z

  

là

 

2

3;0; 1

n

 



.

Câu 8. (Mã1042018)Trongkhônggian

Oxyz

,mặtphẳng

 

: 2 3 1 0

P x y z

   

cómộtvectơpháp

tuyếnlà:

A.

 

3

2;1;3

n 



B.

 

2

1;3;2

n  



C.

 

4

1;3;2

n 



D.

 

1

3;1;2

n 





Lờigiải

ChọnA

Mặtphẳng

 

: 2 3 1 0

P x y z

   

cómộtvectơpháptuyếnlà

 

2;1;3

.

Câu 9. (Mã101-2019)Trongkhônggian

Oxyz

,chomặtphẳng

( ) : 2 3 1 0.

P x y z

   

Vectơnàodưới

đâylàmộtvectơpháptuyếncủa

( )P

?

A.

 

3

1;2; 1 .

n

 



B.

 

4

1;2;3 .

n 



C.

 

1

1;3; 1 .

n

 



D.

 

2

2;3; 1 .

n

 





Lờigiải

ChọnB

Từphươngtrìnhmặtphẳng(P)suyramộtvectơpháptuyếncủamặtphẳnglà

 

4

1;2;3 .

n 



Câu 10. (Mã1032018)Trongkhônggiam

,Oxyz

mặtphẳng

 

: 2 3 1 0

P x y z

   

cómộtvectơpháp

tuyếnlà

A.

 

1

2;3; 1

n 





B.

 

3

1;3;2

n 



C.

 

4

2;3;1

n 



D.

 

2

1;3;2

n 





Lờigiải

ChọnC

Mặtphẳng

 

: 2 3 1 0

P x y z

   

cómộtvectơpháptuyếnlà

 

4

2;3;1

n 



.

Câu 11. (Mã102 - 2019) Trongkhông gian

Oxyz

,cho mặt phẳng

 

: 2 3 1 0

P x y z

   

.Vectơ nào

dướiđâylàmộtvectơpháptuyếncủa

 

P

?

A.

 

3

2;3;1

n 



. B.

 

1

2; 1; 3

n

  



. C.

 

4

2;1;3

n 



. D.

 

2

2; 1;3

n  



.

Lờigiải

ChọnD

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3

Mặtphẳng

 

: 2 3 1 0

P x y z

   

cómộtvectơpháptuyếnlà

 

2

2; 1;3

n  



Câu 12. (Mã103-2019)Trongkhônggian

Oxyz

,chomặtphẳng

 

: 2 3 2 0

P x y z

   

.Véctơnàosau

đâylàmộtvéctơpháptuyếncủa

 

P



A.

 

1

2; 3;1

n  



. B.

 

4

2;1; 2

n

 



. C.

 

3

3;1; 2

n

  



. D.

 

2

2; 3; 2

n

  



.

Lờigiải

ChọnA

 

: 2 3 2 0

P x y z

   

.Véctơ

 

1

2; 3;1

n  



làmộtvéctơpháptuyếncủa

 

P

.

Câu 13. (Mã104-2019)Trongkhônggian

Oxyz

,chomặtphẳng

 

: 4 3 1 0

P x y z

   

.Véctơnàosau

đâylàmộtvéctơpháptuyếncủa

 

P

A.

 

4

3;1; 1

n

 



. B.

 

3

4;3;1

n 



. C.

 

2

4; 1;1

n  



. D.

 

1

4;3; 1

n

 



.

Lờigiải

ChọnB

 

: 4 3 1 0

P x y z

   

.

Véctơ

 

3

4;3;1

n 



làmộtvéctơpháptuyếncủa

 

P

.

Câu 14. (Mã1022018)Trongkhônggian

Oxyz

,mặtphẳng

 

:3 2 4 0

P x y z

   

cómộtvectơpháp

tuyếnlà

A.

 

2

3;2;1

n 



B.

 

1

1;2;3

n 



C.

 

3

1;2;3

n  



D.

 

4

1;2; 3

n

 



Lờigiải

ChọnA

Mặtphẳng

 

:3 2 4 0

P x y z

   

cómộtvectơpháptuyếnlà

 

2

3;2;1

n 



.

Câu 15. (Mã1012018)Trongkhônggian

Oxyz

chomặtphẳng

 

: 2 3 5 0

P x y z

   

cómộtvéctơ

pháptuyếnlà

A.

 

3

1;2;3

n  



B.

 

4

1;2; 3

n

 



C.

 

2

1;2;3

n 



D.

 

1

3;2;1

n 





Lờigiải

ChọnC

Véctơpháptuyếncủamặtphẳng

 

: 2 3 5 0

P x y z

   

là:

 

2

1;2;3

n 



.

Câu 16. (Mã1232017)Trongkhônggianvớihệtọađộ

Oxyz

,vectơnàodướiđâylàmộtvéctơpháp

tuyếncủamặtphẳng

 

Oxy

?

A.

 





1; 0; 0

i B.

 





1;1;1

m C.

 





0; 1; 0

j D.

 





0; 0; 1

k 

Lờigiải

ChọnD

Domặtphẳng

 

Oxy



vuônggócvớitrục



Oz



nênnhậnvéctơ

 





0; 0; 1

k



làmmộtvéctơ



pháp

tuyến

Câu 17. (THPTLý TháiTổ 2019)Chomặt phẳng

 

: 2 3 4 1 0

x y z



   

.Khi đó,mộtvéctơpháp

tuyếncủa

 





A.

 

2;3; 4

n

 



. B.

 

2; 3;4

n  



. C.

 

2;3;4

n  



. D.

 

2;3;1

n  



.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Lờigiải

ChọnC

Mặtphẳng

 

: 2 3 4 1 0

x y z



   

cómộtvéctơpháptuyến

 

0

2; 3; 4

n

  



.

Nhậnthấy

 

0

2;3;4

n n   

 

,hay

n



cùngphươngvới

0

n



.

Dođóvéctơ

 

2;3;4

n  



cũnglàmộtvéctơpháptuyếncủamặtphẳng

 





Câu 18. Trongkhônggian

Oxyz

,chomặtphẳng

 

:3 – 2 0

P x z

 

.Vectơnàodướiđâylàmộtvectơpháp

tuyếncủa

 

P

?

A.

4

( 1;0; 1)

n

  



B.

1

(3; 1;2)

n  



C.

3

(3; 1;0)

n  



D.

2

(3;0; 1)

n

 





Lờigiải

ChọnD

Câu 19. Trong không gian

Oxyz

, véctơ nào dưới đây có giá vuông góc với mặt phẳng

 

: 2 3 1 0?



  

x y



A.

 

2; 3;1

 



a

 B.

 

2;1; 3 



b

 C.

 

2; 3; 0

 



c

 D.

 

3; 2; 0





d



Lờigiải

ChọnC

Mặtphẳng

 



cómộtVTPTlà

 

2; 3; 0

  

 

n c

.

Câu 20. (THPTNghĩaHưngNĐ-2019)Trongkhônggian

Oxyz

,mộtvectơpháptuyếncủamặtphẳng

1

2 1 3

x y z

  

 

là

A.

(3;6; 2)

n

 



B.

(2; 1;3)

n  



C.

( 3; 6; 2)

n

   



D.

( 2; 1;3)

n   



Lờigiải

Phươngtrình

1 1

1 1 0. 3 6 2 6 0.

2 1 3 2 3

x y z

x y z x y z

             

 



Mộtvectơpháptuyếncủamặtphẳng

(3;6; 2)

n

 



.

Câu 21. (THPTBaĐình2019)Trongmặtphẳngtọađộ

Oxyz

,chophươngtrìnhtổngquátcủamặtphẳng

 

: 2 6 8 1 0

P x y z

   

.Mộtvéctơpháptuyếncủamặtphẳng

 

P

cótọađộlà:

A.

 

1; 3;4

 

 B.

 

1;3;4

 C.

 

1; 3; 4 

 D.

 

1; 3;4





Lờigiải

Phươngtrìnhtổngquátcủamặtphẳng

 

: 2 6 8 1 0

P x y z

   

nênmộtvéctơpháptuyếncủamặt

phẳng

 

P

cótọađộlà

 

2; 6; 8 

hay

 

1; 3; 4 

.

Câu 22. (ChuyênKHTN2019)Trongkhônggian

Oxyz

,vectơnàodướiđâylàmộtvectơpháptuyến

củamặtphẳng

 

: 2 3 1 0

P y z

  

?

A.

 

4

2;0; 3

u

 



. B.

 

2

0;2; 3

u

 



. C.

 

1

2; 3;1

u  



. D.

 

3

2; 3;0

u  



.

Lờigiải

Tacó

 

2

0;2; 3

u

 



làmộtvectơpháptuyếncủamặtphẳng

 

: 2 3 1 0

P y z

  

.

Câu 23. (THPTLươngThếVinhHàNội2019)Chomặtphẳng

 

:3 2 0

P x y

  

.Véctơnàotrong

cácvéctơdướiđâylàmộtvéctơpháptuyếncủamặtphẳng

 

P

?

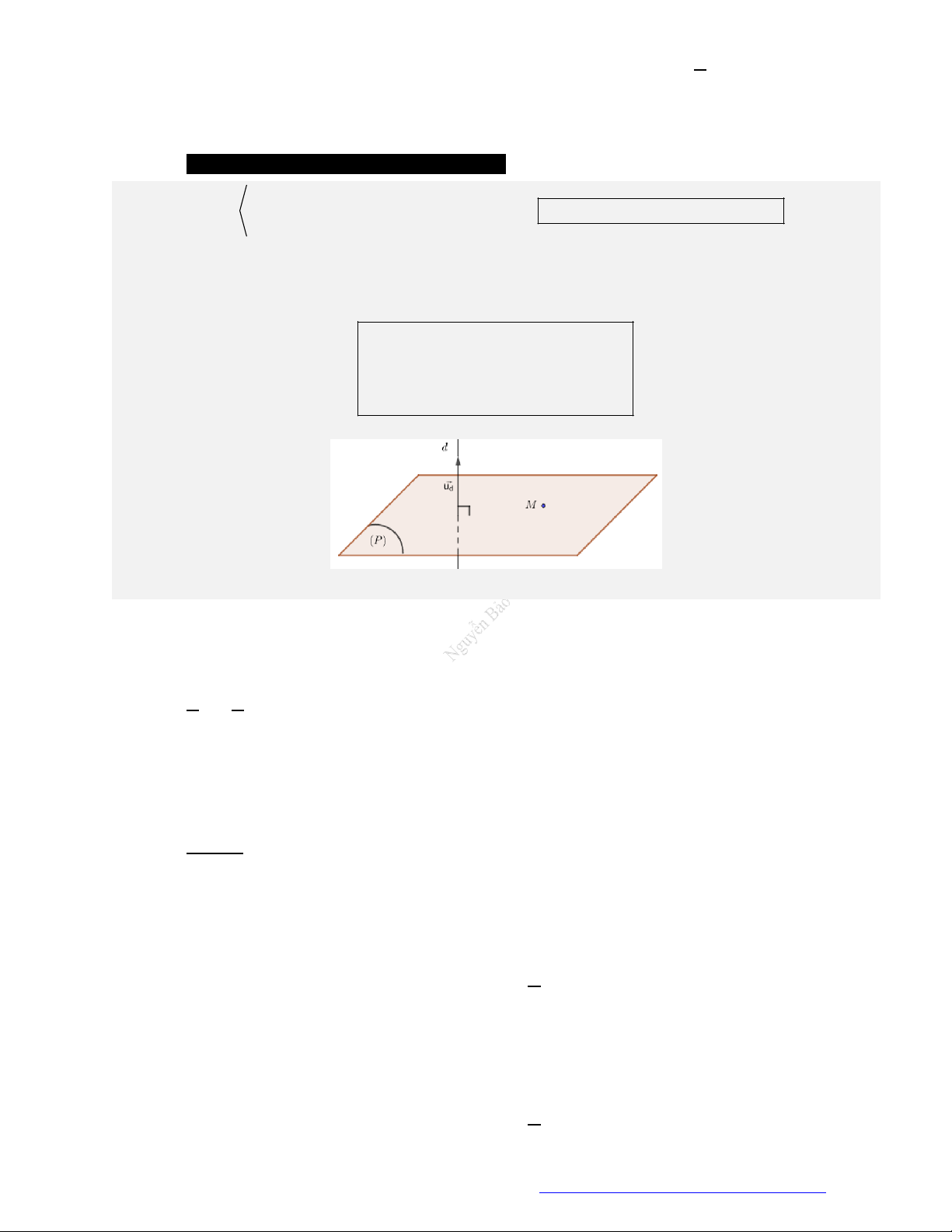
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5

A.

 

3; 1;2

. B.

 

1;0; 1 

. C.

 

3;0; 1

. D.

 

3; 1;0

.

Lờigiải

Mộtvéctơpháptuyếncủamặtphẳng

 

:3 2 0P x y  

là

 

3; 1;0

.

Dạng2.Xácđịnhphươngtrìnhmặtphẳng

 Mặtphẳng

0 0 0

qua ( ; ; )

( )

( ; ; )

M x y z

P

VTPT n a b c





thìphươngtrình

0 0 0

( ) : ( ) ( ) ( ) 0P a x x b y y c z z     

(*)

Ngượclại,mộtmặtphẳngbấtkỳđềucóphươngtrìnhdạng

0ax by cz d   

,mặtphẳngnàycó

( ; ; )VTPT n a b c





với

2 2 2

0a b c  

.

 Cácmặtphẳngcơbản

( )

( ) : 0 (1;0;0)

( ) : 0 (0;1;0)

( ) : 0 (0;0;1)

VTPT

Oyz

VTPT

Oxz

VTPT

Oxy

mp Oyz x n

mp Oxz y n

mp Oxy z n

  





Viết phương trình mặt phẳng (P) qua M và vuông góc với với đường thẳng AB cho trước.



Mặtphẳng(P)quaM,cóVTPT

( )P

n AB

 

nênphươngtrìnhđượcviếttheo(*).

Câu 24. (ĐềThamKhảo2019)Trongkhônggian

Oxyz

,mặtphẳng

 

Oxz

cóphươngtrìnhlà:

A.

0x 

B.

0z 

C.

0x y z  

D.

0y 



Lờigiải

ChọnD

Câu 25. (Mã1102017)Trongkhônggianvớihệtoạđộ

Oxyz

,phươngtrìnhnàodướiđâylàphươngtrình

củamặtphẳng

 

Oyz

?

A.

0y 

B.

0x 

C.

0y z 

D.

0z 

Lờigiải

Chọn B

Mặtphẳng

 

Oyz

điquađiểm

 

0;0;0O

vàcóvectơpháptuyếnlà

 

1;0;0i 



nêntacóphương

trìnhmặtphẳng

 

Oyz

là:

     

1 0 0 0 0 0 0 0x y z x       

.

Câu 26. (SởThanhHóa2019)Trongkhônggian

Oxyz

,mặtphẳng

 

Oyz

cóphươngtrìnhlà

A.

0z 

. B.

0x y z  

. C.

0x 

. D.

0y 

.

Lờigiải

Chọn C.

Câu 27. (ChuyênHưngYên2019)Trongkhônggianvớihệtọađộ

,Oxyz

phươngtrìnhnàosauđâylàphương

trìnhcủamặtphẳng

Ozx

?

A.

0.x 

B.

1 0.y  

C.

0.y 

D.

0.z 

Lờigiải

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Tacómặtphẳng

Ozx

điquađiểm

 

0;0;0

O

vàvuônggócvớitrục

Oy

nêncóVTPT

 

0;1;0

n 



.Do

đóphươngtrìnhcủamặtphẳng

Ozx

là

0.

y



Câu 28. (Chuyên Quang Trung- Bình Phước 2019) Trong không gian

Oxyz

, mặt phẳng

 

Oxy

 có

phươngtrìnhlà

A.

0

z



. B.

0

x



. C.

0

y



. D.

0

x y

 

.

Lời giải

Chọn A

Mặtphẳng

 

Oxy

điquagốctọađộ

 

0;0;0

O

,nhậnvectơđơnvị

 

0;0;1

k





làvectơpháptuyến



Phươngtrìnhtổngquát:

     

0. 0 0. 0 1. 0 0

x y z

     



 

: 0

Oxy z



.

Câu 29. (Mã1042017)Trong khônggianvớihệtọađộ

Oxyz

,phươngtrìnhnàodướiđâylàphương

trìnhmặtphẳngđiquađiểm

 

1;2; 3

M



vàcómộtvectơpháptuyến

 

1; 2;3

n  



.

A.

2 3 12 0

x y z

   

B.

2 3 6 0

x y z

   

C.

2 3 12 0

x y z

   

D.

2 3 6 0

x y z

   

Lờigiải

ChọnA

Phươngtrìnhmặtphẳngđiquađiểm

 

1;2; 3

M



vàcómộtvectơpháptuyến

 

1; 2;3

n  



là

     

1 1 2 2 3 3 0

x y z

     

2 3 12 0

x y z

    

.

Câu 30. (Đề Minh Họa 2017) Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm

 

0;1;1

A

 ) và

 

1;2;3

B

.Viếtphươngtrìnhcủamặtphẳng

 

P

điqua

A

vàvuônggócvớiđườngthẳng

AB

.

A.

2 3 0

x y z

   

B.

2 6 0

x y z

   

C.

3 4 7 0

x y z

   

D.

3 4 26 0

x y z

   

Lờigiải

ChọnA

Mặtphẳng

 

P

điqua

 

0;1;1

A

vànhậnvecto

 

1;1;2

AB 



làvectơpháptuyến

       

:1 0 1 1 2 1 0 2 3 0

P x y z x y z

          

.

Câu 31. (Mã1042018)Trongkhônggian

,Oxyz

Chohaiđiểm

 

5; 4;2

A 

và

 

1;2;4 .

B

Mặtphẳngđi

qua

A

vàvuônggócvớiđườngthẳng

AB

cóphươngtrìnhlà

A.

2 3 20 0

x y z

   

B.

3 3 25 0

x y z

   

C.

2 3 8 0

x y z

   

D.

3 3 13 0

x y z

   

Lờigiải

ChọnA

( 4;6;2) 2(2; 3; 1)

AB

     





 

P

điqua

 

5; 4;2

A 

nhận

(2; 3; 1)

n

  



làmVTPT

 

:P



2 3 20 0

x y z

   

Câu 32. (Đề Tham Khảo2018) Trong không gian

,Oxyz

 cho hai điểm

 

1;2;1

A

 và

 

2;1;0 .

B

 Mặt

phẳngqua

A

vàvuônggócvới

AB

cóphươngtrìnhlà

A.

3 5 0   

x y z

B.

3 6 0   

x y z

C.

3 6 0   

x y z

D.

3 6 0   

x y z



Lờigiải

ChọnD

 

3; 1; 1 . 



AB

Domặtphẳng

 



cầntìmvuônggócvới

AB

nên

 



nhận

 

3; 1; 1 



AB

làm

vtpt.Suyra,phươngtrìnhmặtphẳng

       

:3 1 2 1 0 3 6 0.          

x y z x y z



TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7

Câu 33. (Mã 103 2018) Trong không gian

Oxyz

, cho ba điểm

 

1;1;1

A 

,

 

2;1;0

B

 

1; 1;2

C 

. Mặt

phẳngđiqua

A

vàvuônggócvớiđườngthẳng

BC

cóphươngtrìnhlà

A.

3 2 1 0

x z

  

B.

2 2 1 0

x y z

   

C.

2 2 1 0

x y z

   

D.

3 2 1 0

x z

  



Lờigiải

ChọnB

Tacó

 

1; 2;2

BC   



làmộtvéctơpháptuyếncủamặtphẳng

 

P

cầntìm.

 

1;2; 2

n BC

   

 

cũnglàmộtvéctơpháptuyếncủamặtphẳng

 

P

.

Vậyphươngtrìnhmặtphẳng

 

P

là

2 2 1 0

x y z

   

.

Câu 34. (ChuyênLêHồngPhongNamĐịnh2019)Trongkhônggian

Oxyz

,cho2điểm

(5; 4;2)

A



và

B(1;2;4)

.Mặtphẳngđiqua

A

vàvuônggócvớiđườngthẳng

AB

là?

A.

3 3 25 0

x y z

   

 B.

2 3 8 0

x y z

   

 C.

3 3 13 0

x y z

   

 D.

2 3 20 0

x y z

   



Lờigiải

ChọnD

Mặtphẳngvuônggócvớiđườngthẳng

AB

nênnhận

AB



làmvectơpháptuyến,

( 4;6;2)

AB  





Mặtphẳngđiqua

(5; 4;2)

A



vàcóvectơpháptuyến,

( 4;6;2)

AB  



cóphươngtrình

4( 5) 6(y 4) 2(z 2) 0

x

      

hay

2 3 y z 20 0

x

   

.Vậychọn D.

Câu 35. (Chuyên Đại Học Vinh 2019) Trong không gian

Oxyz

, mặt phẳng

 

P

 đi qua điểm

 

3; 1;4

M 

đồngthờivuônggócvớigiácủavectơ

 

1; 1;2

a  



cóphươngtrìnhlà

A.

3 4 12 0

x y z

   

. B.

3 4 12 0

x y z

   

.C.

2 12 0

x y z

   

. D.

2 12 0

x y z

   

.

Lờigiải

ChọnC

 

P

códạng:

     

1. 3 1 1 2 4 0

x y z

     

 2 12 0

x y z

   

.

Câu 36. (THPT Lương Thế Vinh Hà Nội 2019) Cho ba điểm

     

2;1; 1 , 1;0;4 , 0; 2; 1

A B C

   

.

Phươngtrìnhmặtphẳngđiqua

A

vàvuônggócvới

BC

là

A.

2 5 5 0

x y z

   

. B.

2 5 5 0

x y z

   

. C.

2 5 0

x y

  

. D.

2 5 5 0

x y z

   

.

Lờigiải

Domặtphẳngvuônggócvới

BC

nên

 

1; 2; 5

BC

  



làvectơpháptuyếncủamặtphẳng.

Vìvậyphươngtrìnhmặtphẳnglà:

     

1 2 2 1 5 1 0 2 5 5 0

x y z x y z

          

.

Câu 37. (SởBắcGiang2019)Trongkhônggian

Oxyz

,chohaiđiểm

 

1;1;2

A

và

 

2;0;1

B

.Mặtphẳng

điqua

A

vàvuônggócvới

AB

cóphươngtrìnhlà

A.

0

x y z

  

. B.

2 0

x y z

   

. C.

4 0

x y z

   

. D.

2 0

x y z

   

.

Lờigiải

Tacó:

 

1; 1; 1

AB

  



.

Phươngtrìnhmặtphẳngđiqua

A

vàvuônggócvới

AB

cóphươngtrìnhlà:

     

1 1 2 0 2 0

x y z x y z

          

.

Câu 38. (Chuyên - KHTN - Hà Nội - 2019) Trong không gian

,Oxyz

 cho hai điểm

 

1;2;0

A

 và

 

2;3; 1 .

B



Phươngtrìnhmặtphẳngqua

A

vàvuônggócvới

AB

là

A.

2 3 0.

x y z

   

B.

3 0.

x y z

   

C.

3 0.

x y z

   

D.

3 0.

x y z

   

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 8 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Lời giải

Chọn C



 

1;1; 1 .

AB







 Mặtphẳngqua

A

vàvuônggócvới

AB

nhận

AB



làmvectơpháptuyếncóphươngtrìnhlà

1 2 0 3 0.

x y z x y z

         



Câu 39. (Chuyên Đại học Vinh 2019) Trong không gian

Oxyz

, mặt phẳng

 

P

 đi qua điểm

 

3; 1;4

M 

đồngthờivuônggócvớigiácủavectơ

 

1; 1;2

a  



cóphươngtrìnhlà

A.

3 4 12 0

x y z

   

. B.

3 4 12 0

x y z

   

.

C.

2 12 0

x y z

   

. D.

2 12 0

x y z

   

.

Lời giải

Chọn C

Mặtphẳng

 

P

điquađiểm

 

3; 1;4

M 

đồngthờivuônggócvớigiácủa

 

1; 1;2

a  



nênnhận

 

1; 1;2

a  



làmvectơpháptuyến.Dođó,

 

P

cóphươngtrìnhlà

     

1 3 1 1 2 4 0 2 12 0

x y z x y z

          

.

Vậy,tachọn

C.

Câu 40. (THPT Thuận Thành 3 - Bắc Ninh 2019) Trongkhônggianvớihệtrụctọađộ

,Oxyz

phương

trìnhmặtphẳngđiquađiểm

 

1;2; 3

A



cóvéctơpháptuyến

 

2; 1;3

n



 

là

A.

2 3 9 0

x y z

   

. B.

2 3 4 0

x y z

   

.

C.

2 4 0

x y

  

. D.

2 3 4 0

x y z

   

.

Lời giải

Chọn A

Phươngtrìnhmặtphẳngđiquađiểm

 

1;2; 3

A



cóvéctơpháptuyến

 

2; 1;3

n



 

là

     

2. 1 1. 2 3. 3 0

2 2 2 3 9 0

2 3 9 0.

x y z

     

      

    



Câu 41. (SGD Điện Biên - 2019) Trong không gian

Oxyz

 phương trình mặt phẳng đi qua điểm

(1; 2;3)

A



vàvuônggócvớigiácủavéctơ

( 1;2;3)

v  





là

A.

2 3 4 0.

x y z

   



B.

2 3 4 0.

x y z

   



C.

2 3 4 0.

x y z

   



D.

2 3 4 0.

x y z

    



Lời giải

Chọn C

Phươngtrìnhmặtphẳngđiquađiểm

(1; 2;3)

A



vàvuônggócvớigiácủavéctơ

( 1;2;3)

v  





là:

1( 1) 2( 2) 3( 3) 0 2 3 4 0 2 3 4 0.

x y z x y z x y z

                 



Câu 42. (SGD Cần Thơ 2019) Trong không gian

Oxyz

, phương trình của mặt phẳng đi qua điểm

 

3;0; 1

A



vàcóvéctơpháptuyến

 

4; 2; 3

n

  



là

A.

4 2 3 9 0

x y z

   

. B.

4 2 3 15 0

x y z

   

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9

C.

3 15 0

x z

  

. D.

4 2 3 15 0

x y z

   

.

Lời giải

Chọn B

Mặtphẳngđiquađiểm

 

3;0; 1

A



vàcóvéctơpháptuyến

 

4; 2; 3

n

  



cóphươngtrình:

     

4 3 2 0 3 1 0 4 2 3 15 0

x y z x y z

          

.

Câu 43. Trongkhônggianvớihệtọađộ

Oxyz

,phươngtrìnhmặtphẳngqua

 

1;1; 2

A

 

vàcóvectơ

pháptuyến

 

1; 2; 2

n

  



là

A.

2 2 1 0

x y z

   

. B.

2 1 0

x y z

    

. C.

2 2 7 0

x y z

   

. D.

2 1 0

x y z

    

.

Lời giải

Chọn A

Mặtphẳng

 

P

điqua

 

1;1; 2

A

 

vàcóvectơpháptuyến

 

1; 2; 2

n

  



nêncóphươngtrình

     

1 2 1 2 2 0 2 2 1 0

x y z x y z

          

.

Vậymặtphẳngcầntìmcóphươngtrình:

2 2 1 0

x y z

   

.

Câu 44. (Nguyễn Huệ- Ninh Bình- 2019)Trongkhông gian

Oxyz

,cho2 điểm

   

1;0;1 , 2;1;0

A B

.

Viếtphươngtrìnhmặtphẳng

 

P

điqua

A

vàvuônggócvới

AB

.

A.

 

:3 4 0

P x y z

   

. B.

 

: 3 4 0

P x y z

   

.

C.

 

:3 0

P x y z

  

. D.

 

: 2 1 0

P x y z

   

.

Lời giải

Chọn A

Tacó:

 

3;1; 1

AB

 



.

Mặtphẳng

 

P

quađiểm

 

1;0;1

A 

vàvuônggócvớiđườngthẳng

AB

nêncó1véctơpháp

tuyến

 

3;1; 1

AB

 







       

:3 1 1 0 1 1 0 3 4 0

P x y z x y z

          

.

Câu 45. (Chuyên Lê Hồng Phong-Nam Định- 2019) Trongkhônggianvớihệtọađộ

Oxyz

,chocác

điểm

 

0;1;2

A

,

 

2; 2;1

B 

,

 

2;0;1

C 

.Phươngtrìnhmặtphẳngđiqua

A

vàvuônggócvới

BC



là

A.

2 5 0

y z

  

. B.

2 1 0

x y

  

. C.

2 1 0

x y

  

. D.

2 5 0

y z

   

.

Lời giải

Chọn C

Tacóvectơpháptuyếncủamặtphẳng:

 

4;2;0

BC  



.

Phươngtrìnhmặtphẳng:

     

4 0 2 1 0 2 0

x y z

      

4 2 2 0

x y

    

2 1 0

x y

   

.

Câu 46. (Mã 101 2020 Lần 2) Trong không gian

Oxyz

, cho điểm

 

2; 1;4

M 

 và mặt phẳng

 

:3 2 1 0

P x y z

   

.Phươngtrìnhcủamặtphẳngđiqua

M

vàsongsongvớimặtphẳng

 

P



là

A.

2 2 4 21 0

x y z

   

.B.

2 2 4 21 0

x y z

   



C.

3 2 12 0

x y z

   

. D.

3 2 12 0

x y z

   

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 10 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Lời giải

Chọn C

Phươngtrìnhcủamặtphẳngđiqua

M

vàsongsongvớimặtphẳng

 

P

là

     

3 2 2 1 4 0

x y z

     

3 2 12 0

x y z

    

.

Câu 47. (Mã 102 - 2020 Lần 2) Trong không gian

Oxyz

, cho điểm

 

2;1; 2

M



 và mặt phẳng

 

:3 2 1 0

P x y z

   

.Phươngtrìnhcủamặtphẳngđiqua

M

vàsongsongvới

 

P

là:

A.

2 2 9 0

x y x

   

. B.

2 2 9 0

x y z

   



C.

3 2 2 0

x y z

   

. D.

3 2 2 0

x y z

   

.

Lời giải

Chọn D

Phươngtrìnhmặtphẳng

 

Q

songsongmặtphẳng

 

P

códạng:

3 2 0

x x z D

   

.

Mặtphẳng

 

Q

quađiểm

 

2;1; 2

M



,dođó:

 

3.2 2.1 2 0 2

D D

       

.

Vậy

 

:3 2 2 0

Q x y z

   

.

Câu 48. (Mã 103 - 2020 Lần 2) Trong không gian

Oxyz

, cho điểm

 

2; 1;3

M 

 và mặt phẳng

 

:3 2 1 0

P x y z

   

.Phươngtrìnhmặtphẳngđiqua

M

vàsongsongvới

 

P

là

A.

3 2 11 0

x y z

   

. B.

2 3 14 0

x y z

   

.

C.

3 2 11 0

x y z

   

. D.

2 3 14 0

x y z

   

.

Lời giải

Chọn C

 

P

nhận

 

3; 2;1

n  



làmvectơpháptuyến

Mặtphẳngđãchosongsongvới

 

P

nêncũngnhậnnhận

 

3; 2;1

n  



làmvectơpháptuyến

Vậymặtphẳngđiqua

M

vàsongsongvới

 

P

cóphươngtrìnhlà

     

3 2 2 1 3 0

x y z

     

3 2 11 0

x y z

    



Câu 49. (Mã 104 - 2020 Lần 2) Trong không gian

Oxyz

, cho điểm

 

2;1; 3

M



 và mặt phẳng

 

:3 2 3 0

P x y z

   

.Phươngtrìnhcủamặtphẳngđiqua

M

vàsongsongvới

( )P

là

A.

3 2 1 0

x y z

   

. B.

3 2 1 0

x y z

   

. C.

2 3 14 0

x y z

   

.D.

2 3 14 0

x y z

   



Lời giải

Chọn B

Mặtphẳng

( )Q

cầntìmsongsongvớimặtphẳng

 

:3 2 3 0

P x y z

   

nêncóphươngtrình

dạng

 

:3 2 0,  3

Q x y z m m

     



Vì

( )M Q

nên

 

:3.2 2.1 ( 3) 0 1

Q m m

       



Vậy

 

:3 2 1 0

Q x y z

   

.

Câu 50. (Mã1052017)Trong khônggianvớihệtoạđộ

Oxyz

,chođiểm

 

3; 1; 2

M

 

và mặtphẳng

 

:3 2 4 0

x y z



   

.Phươngtrìnhnàodướiđâylàphươngtrìnhmặtphẳngđiqua

M

vàsong

songvới

 



?

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11

A.

3 2 6 0

x y z

   

B.

3 2 6 0

x y z

   

C.

3 2 6 0

x y z

   

D.

3 2 14 0

x y z

   



Lờigiải

ChọnA

Gọi

 

//

 

,PTcódạng

 

:3 2 0

x y z D



   

(điềukiện

4D 

);

Tacó:

 



qua

 

3; 1; 2

M

 

nên

   

3.3 1 2. 2 0

D

     



6

D

  

(thoảđk);

Vậy

 

:3 2 6 0

x y z



   

Câu 51. (Mã1012018)Trongkhônggian

Oxyz

,mặtphẳngđiquađiểm

 

2; 1;2

A 

vàsongsongvới

mặtphẳng

 

: 2 3 2 0

P x y z

   

cóphươngtrìnhlà

A.

2 3 11 0

x y z

   

B.

2 3 11 0

x y z

   

C.

2 3 11 0

x y z

   

D.

2 3 9 0

x y z

   



Lờigiải

ChọnC

Gọi

 

Q

làmặtphẳngđiquađiểm

 

2; 1;2

A 

vàsongsongvớimặtphẳng

 

P

.

Do

 

//

Q P

nênphươngtrìnhcủa

 

Q

códạng

2 3 0

x y z d

   

(

2

d



).

Do

 

2; 1;2

A Q

 

nên

 

2.2 1 3.2 0

d

    

11

d

  

(nhận).

Vậy

 

: 2 3 11 0

Q x y z

   

.

Câu 52. (THPT Cẩm Giàng 2 -2019) Trong không gian với hệ trục

,Oxyz

 mặt phẳng đi qua điểm

 

1;3; 2

A



vàsongsongvớimặtphẳng

 

: 2 3 4 0

P x y z

   

là:

A.

2 3 7 0

x y z

   

. B.

2 3 7 0

x y z

   

.

C.

2 3 7 0

x y z

   

. D.

2 3 7 0

x y z

   

.

Lờigiải

Gọi

 



làmặtphẳngcầntìm.Vì

     

( ) ( )

// 2; 1;3

P

P n n



   

 



Tacó:

 



điqua

 

1;3; 2

A



vàcóvéctơpháptuyếnlà

 

( )

2; 1;3

n



 



.

Dođóphươngtrìnhtổngquátcủamặtphẳng

 



là:

     

2 1 1 3 3 2 0

x y z

     



hay

2 3 7 0

x y z

   

.

Câu 53. Trong không gian

Oxyz

, mặt phẳng qua điểm

 

1;1;2

A 

 và song song với mặt phẳng

 

: 2 2 1 0

x y z



   

cóphươngtrìnhlà

A.

2 2 2 0

x y z

   

 B.

2 2 0

x y z

  



C.

2 2 6 0

x y z

   

 D.

 

: 2 2 2 0

x y z



   



Lờigiải

ChọnA

Có

 

P

songsong

 

: 2 2 1 0

x y z



   

nên

 

: 2 2 0

P x y z m

   

,với

1

m

 

.

Do

 

P

điquađiểm

 

1;1;2

A 

nên

2 2 2 0 2

m m

      

(nhận)

Vậymătphẳngcầntìmlà

 

: 2 2 2 0

P x y z

   

.

Câu 54. Trong không gian

Oxyz

, cho điểm

 

2; 1; 3

A

 

và mặt phẳng

 

:3 2 4 5 0

P x y z

   

. Mặt

phẳng

 

Q

điqua

A

vàsongsongvớimặtphẳng

 

P

cóphươngtrìnhlà

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 12 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

A.

 

:3 2 4 4 0.Q x y z   

B.

 

:3 2 4 4 0.Q x y z   

C.

 

:3 2 4 5 0.Q x y z   

D.

 

:3 2 4 8 0.Q x y z   

Lời giải

Chọn B

Domặtphẳng

 

Q

songsongvớimặtphẳng

 

P

nêncóvectơpháptuyếnlà

 

3; 2;4n  



.

Phươngtrìnhmặtphẳng

 

Q

:

     

3 2 2 1 4 3 0x y z     



3 2 4 4 0x y z    

.

Câu 55. (Chuyên Quốc Học Huế 2019) Trongkhônggianvớihệtọađộ

Oxyz

chođiểm

 

1;0;6M

và

mặtphẳng

 



cóphươngtrình

2 2 1 0x y z   

.Viếtphươngtrìnhmặtphẳng

 



điqua

M



vàsongsongvớimặtphẳng

 



.

A.

 

: 2 2 13 0x y z



   

. B.

 

: 2 2 15 0x y z



   

.

C.

 

: 2 2 15 0x y z



   

. D.

 

: 2 2 13 0x y z



   

.

Lời giải

Chọn A

Mặtphẳng

 



songsongvớimặtphẳng

 



nêncódạng

 

2 2 0 1x y z m m     

.

Do

 

M





nêntacó:

1 2.0 2.6 0 13 0 13m m m         

(thỏamãn).

Vậy

 

: 2 2 13 0x y z



   

.

Câu 56. (Mã 101 - 2020 Lần 1) Trong không gian

Oxyz

, cho ba điểm

 

3;0;0A

,

 

0;1;0B

 và

 

0;0; 2C 

.Mặtphẳng

 

ABC

cóphươngtrìnhlà:

A.

1

3 1 2

x y z

  



. B.

1

3 1 2

x y z

  



.

C.

1

3 1 2

x y z

  

. D.

1

3 1 2

x y z

  



.

Lời giải

Chọn B.

 

: 1

x y z

ABC

a b c

  

hay

 

: 1

3 1 2

x y z

ABC   



.

Câu 57. (Mã 102 - 2020 Lần 1) Trong không gian , cho ba điểm ,  và

.Mặtphẳng cóphươngtrìnhlà

A. . B. . C. . D. .

Lời giải

Chọn A

Mặtphẳng cóphươngtrìnhlà .

Câu 58. (Mã 103 - 2020 Lần 1) Trong không gian

Oxyz

, cho 3 điểm

 

1;0;0A 

,

 

0;2;0B

 và

 

0;0;3C

.Mặtphẳng

 

ABC

cóphươngtrìnhlà

Oxyz

 

2;0;0

A 

 

0;3;0

B

 

0;0;4

C

 

ABC

1

2 3 4

x y z

  



1

2 3 4

x y z

  

1

2 3 4

x y z

  



1

2 3 4

x y z

  



 

ABC

1

2 3 4

x y z

  



TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13

A.

1

1 2 3

x y z

  



. B.

1

1 2 3

x y z

  



. C.

1

1 2 3

x y z

  



. D

1

1 2 3

x y z

  

.

Lời giải

Chọn C

Câu 59. (Mã 104 - 2020 Lần 1) Trongkhônggian

Oxyz

,chobađiểm

 

2;0;0

A

,

 

0; 1;0

B 

,

 

0;0;3

C

.

Mặtphẳng

 

ABC

cóphươngtrìnhlà

A.

1

2 1 3

x y z

  



. B.

1

2 1 3

x y z

  



. C.

1

2 1 3

x y z

  

. D.

1

2 1 3

x y z

  



.

Lời giải

Chọn D

Phươngtrìnhmặtphẳngquabađiểm

 

;0;0

A a

,

 

0; ;0B b

,

 

0;0;C c

(với

0)

abc



códạng

1

x y z

a b c

  



Câu 60. (ĐềThamKhảo2018)Trongkhônggian

Oxyz

,chobađiểm

 

2;0;0

M

,

 

0; 1;0

N

,

 

0;0;2

P

.

Mặtphẳng

 

MNP

cóphươngtrìnhlà:

A.

1

2 1 2

   



x y z

. B.

1

2 1 2

  

x y z

. C.

1

2 1 2

  



x y z

D.

0

2 1 2

  



x y z

.

Lờigiải

ChọnC

Tacó:

 

2;0;0

M

,

 

0; 1;0

N

,

 

0;0;2

P



 

: 1

2 1 2

   



x y z

MNP



Câu 61. (Đề thử nghiệm THPT QG 2017) Trongkhônggianvớihệtọađộ

Oxyz

,cho

3

điểm

 

1;0;0

A

;

 

0; 2;0

B

;

 

0;0;3

C

.Phươngtrìnhnàodướidâylàphươngtrìnhmặtphẳng

 

ABC

?

A.

1

3 2 1

  



x y z

. B.

1

2 1 3

  



x y z

. C.

1

1 2 3

  



x y z

. D.

1

3 1 2

  



x y z

.

Lời giải

Chọn C

Phươngtrìnhmặtphẳngtheođoạnchắnđiqua3điểm

A

,

B

,

C

là

1.

1 2 3

x y z

  





Câu 62. (SGD Bắc Ninh 2019) Trongkhônggianvớihệtọađộ

Oxyz

,phươngtrìnhmặtphẳng

 



đi

quađiêm

 

0; 1;0

A 

,

 

2;0;0

B

,

 

0;0;3

C

là

A.

1

2 1 3

x y z

  

. B.

0

2 1 3

x y z

  



. C.

1

1 2 3

x y z

  



. D.

1

2 1 3

x y z

  



.

Lời giải

Chọn D

Vì

, ,

A Oy B Ox C Oz  

nênphươngtrìnhmặtphẳng

 



là

1

2 1 3

x y z

  



.

Câu 63. (Lômônôxốp - Hà Nội 2019) Trong không gian

Oxyz

,cho ba điểm

 

1;0;0

M

,

 

0;2;0

N

,

 

0;0;3

P

.Mặtphẳng

 

MNP

cóphươngtrìnhlà:

A.

6 3 2 6 0

x y z

   

. B.

6 3 2 1 0

x y z

   

.

C.

6 3 2 1 0

x y z

   

. D.

6 0

x y z

   

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 14 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Lời giải

Chọn A

Mặtphẳng

 

MNP

cóphươngtrìnhlà:

1

1 2 3

x y z

  

6 3 2 6 0

x y z

    

.

Câu 64. (THPT Hoàng Hoa Thám - Hưng Yên 2019) Trongkhông gianvớihệtọađộOxyz,cho ba

điểm

(2;0;0), B(0;-1;0),C(0;0;-3).

A

Viếtphươngtrìnhmặtphẳng

( ).ABC



A.

3 6 2 6 0

x y z

    

.B.

3 6 2 6 0

x y z

    

.

C.

3 6 2 6 0

x y z

    

.D.

3 6 2 6 0

x y z

    

.

Lời giải

Chọn C

Mặtphẳng

 

ABC

điquabađiểm

     

2;0;0 , 0; 1;0 , 0;0; 3

A B C

 

suyramặtphẳng

 

ABC

có

phươngtrìnhđoạnchắnlà:

1 3 6 2 6 0

2 1 3

x y z

        

 



Câu 65. (Chuyên - KHTN - Hà Nội - 2019) Trongkhônggian

Oxyz

,phươngtrìnhmặtphẳngđiquaba

điểm

 

3;0;0

A 

,

 

 0;4;0

B

,

 

0;0; 2

C



là

A.

4 3 6 12 0

x y z

   

. B.

4 3 6 12 0

x y z

   

.

C.

4 3 6 12 0

x y z

   

. D.

4 3 6 12 0

x y z

   

.

Lời giải

Chọn A

Phươngtrìnhmặtphẳngđiquabađiểm

 

3;0;0

A 

,

 

 0;4;0

B

,

 

0;0; 2

C



là

1

3 4 2

x y z

  

 

4 3 6 12 0

x y z

    

.

Câu 66. (THPT Ngô Sĩ Liên Bắc Giang 2019) Trong không gian

Oxyz

, cho ba điểm

( 2;0;0)

A



,

(0;0;7)

B

và

(0;3;0)

C

.Phươngtrìnhmặtphẳng

( )ABC

là

A.

1

2 7 3

x y z

  



 B.

0

2 3 7

x y z

  



 C.

1

2 3 7

x y z

  



 D.

1 0

2 3 7

x y z

   





Lờigiải

ChọnC

Phươngtrìnhmặtphẳng

( )ABC

điquabađiểm

( 2;0;0)

A



,

(0;0;7)

B

và

(0;3;0)

C

là

1

2 3 7

x y z

  



Câu 67. Trongkhônggian

Oxyz

,mặtphẳngquabađiểm

 

1;0;0

A 

,

 

0;2;0

B

,

 

0;0; 3

C



cóphương

trìnhlà

A.

1

1 2 3

x y z

   

 

. B.

1

1 2 3

x y z

  



. C.

1

1 2 3

x y z

  

 

. D.

1

1 2 3

x y z

  



.

Lờigiải

Tacóphươngtrìnhmặtphẳngtheođoạnchắn:

1

1 2 3

x y z

  

 



TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15

Câu 68. (ChuyênTháiBình-2019)Trongkhônggian

Oxyz

,chođiểm

 

1;2;3

M

.Gọi

, ,A B C

lầnlượt

là hình chiếu vuông góc của điểm

M

lên các trục

, ,Ox Oy Oz

. Viết phương trình mặt phẳng

 

ABC

.

A.

1

1 2 3

x y z

  

. B.

1

1 2 3

x y z

  

. C.

0

1 2 3

x y z

  

. D.

1

1 2 3

x y z

   

.

Lờigiải

Tacó

     

1;0;0 , 0;2;0 , 0;0;3

A B C

lầnlượtlàhìnhchiếucủa

M

lên

, ,Ox Oy Oz

.

Phươngtrìnhđoạnchắncódạng:

1

1 2 3

x y z

  

.

Câu 69. (ĐềThiCôngBằngKHTN2019)Trongkhônggian

O

xyz

,phươngtrìnhmặtphẳngđiquaba

điểm

 

3;0;0

A 

;

 

0;4;0

B

và

 

0;0; 2

C



là.

A.

4 3 6 12 0

x y z

   

.B.

4 3 6 12 0

x y z

   

.

C.

4 3 6 12 0

x y z

   

.D.

4 3 6 12 0

x y z

   

.

Lờigiải

Phươngtrìnhmặtphẳng

 

ABC

:

1

3 4 2

x y z

  

 

4 3 6 12 0

x y z

    

.

Câu 70. (THPTGangThépTháiNguyên2019)Trongkhônggianvớihệtrụctọađộ

Oxyz

,mặtphẳng

quacácđiểm

 

1;0;0

A

,

 

0;3;0

B

,

 

0;0;5

C

cóphươngtrìnhlà

A.

15 5 3 15 0.

x y z

   

 B.

1 0.

1 3 5

x y z

   



C.

3 5 1.

x y z

  

 D.

1.

1 3 5

x y z

  



Lờigiải

Sửdụngphươngtrìnhmặtphẳngtheođoạnchắn,tacóphươngtrìnhmặtphẳngquacácđiểm

 

1;0;0

A

,

 

0;3;0

B

,

 

0;0;5

C

là

1.

1 3 5

x y z

  



Câu 71. (Chuyên Sơn La 2019) Trong không gian

Oxyz

, phương trình mặt phẳng đi qua ba điểm

 

1;0;0

A

,

 

0; 2;0

B

và

 

0;0;3

C

là

A.

1

1 2 3

x y z

  



. B.

1

1 2 3

x y z

   



. C.

0

1 2 3

x y z

  



. D.

1

1 2 3

x y z

  

.

Lờigiải

Tacóphươngtrìnhmặtphẳngđiquabađiểm

 

1;0;0

A

,

 

0; 2;0

B 

và

 

0;0;3

C

là:

1

1 2 3

x y z

  



.

Câu 72. (THPTHoàngHoaThámHưngYên2019)Trongkhônggianvớihệtọađộ

Oxyz

,chobađiểm

 

2;0;0

A

,

 

0; 1;0

B 

,

 

0;0; 3

C



.Viếtphươngtrìnhmặtphẳng

 

ABC

.

A.

3 6 2 6 0

x y z

    

.B.

3 6 2 6 0

x y z

    

.

C.

3 6 2 6 0

x y z

    

.D.

3 6 2 6 0

x y z

    

.

Lờigiải

Phươngtrìnhmặtphẳng

 

ABC



(theođoạnchắn)là

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 16 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

1 3 6 2 6 0

2 1 3

x y z

        

 

.

Câu 73. (Chuyên Lê Quý Đôn Điện Biên 2019) Trongkhông gian với hệtọa độ

Oxyz

,cho 3 điểm

     

1;0;0 , 0;3;0 , 0;0;4

A B C

. Phương trình nào dưới đây là phương trình của mặt phẳng

 

ABC

?

A.

1

1 3 4

x y z

  

. B.

1

1 3 4

x y z

  

. C.

1

4 3 1

x y z

  



. D.

1

1 3 4

x y z

   

.

Lời giải

Chọn D

Mặtphẳng

 

ABC

cóphươngtrìnhđoạnchắnlà

1 1

1 3 4 1 3 4

x y z x y z

       



.

Dạng3.Điểmthuộcmặtphẳng

Mộtmặtphẳngbấtkỳđềucóphươngtrìnhdạng

 

: 0

P ax by cz d

   

,vàđiểm

 

; ;

M M M

M x y z

.

Nếu

 

0

M M M

ax by cz d M P

     



Nếu

 

0

M M M

ax by cz d M P

     



Câu 74. (Mã 105 2017) Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

 

: 6 0

x y z



   

.

Điểmnàodướiđâykhôngthuộc

 



?

A.

 

3;3;0

Q

B.

 

2;2;2

N

C.

 

1;2;3

P

D.

 

1; 1;1

M 



Lờigiải

ChọnD

Tacó:

 

1 1 1 6 5 0 1; 1;1

M       

làđiểmkhôngthuộc

 



.

Câu 75. (Mã123 2017) Trongkhông gian với hệtọađộ

Oxyz

,chomặt phẳng

 

: 2 5 0.

P x y z

   



Điểmnàodướiđâythuộc

 

P

?

A.

 

0;0; 5

P



B.

 

1;1;6

M

C.

 

2; 1;5

Q 

D.

 

5;0;0

N 



Lờigiải

ChọnB

Tacó

1 2.1 6 5 0   

nên

 

1;1;6

M

thuộcmặtphẳng

 

P

.

Câu 76. Trongkhônggian

Oxyz

,mặtphẳng

 

: 3 0

P x y z

   

điquađiểmnàodướiđây?

A.

 

1; 1; 1

M

  

 B.

 

1;1;1

N

 C.

 

3;0;0

P 

 D.

 

0;0; 3

Q





Lờigiải

Điểm

 

1;1;1

N

cótọađộthỏamãnphươngtrìnhmặtphẳng

 

P

nên

 

N P



.

Câu 77. (THPT Cẩm Giàng 2 2019) Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

 

:2 3 0

P x y z

   

.Điểmnàotrongcácphươngándướiđâythuộcmặtphẳng

 

P



A.

 

2;1;0

M

. B.

 

2; 1;0

M 

. C.

 

1; 1;6

M  

. D.

 

1; 1;2

M  

.

Lờigiải

Tacó:

   

2.2 1 0 3 0 2;1;0 :2 3 0

M P x y z

         

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17

Câu 78. (Chuyên Bắc Ninh 2019) Trong không gian

Oxyz

, điểm nào dưới đây nằm trên mặt phẳng

 

: 2 2 0

P x y z

   

.

A.

 

1; 2; 2

Q 

. B.

 

2; 1; 1

P

 

. C.

 

1;1; 1

M



. D.

 

1; 1; 1

N

 

.

Lờigiải

+Thaytoạđộđiểm

Q

vàophươngtrìnhmặtphẳng

 

P

tađược

 

2.1 2 2 2 4 0     

nên

 

Q P



.

+Thaytoạđộđiểm

P

vàophươngtrìnhmặtphẳng

 

P

tađược

   

2.2 1 1 2 2 0      

nên

 

P P



.

+Thaytoạđộđiểm

M

vàophươngtrìnhmặtphẳng

 

P

tađược

 

2.1 1 1 2 2 0      

nên

 

M P



.

+Thaytoạđộđiểm

N

vàophươngtrìnhmặtphẳng

 

P

tađược

   

2.1 1 1 2 0     

nên

 

N P



.

Câu 79. (Hậu Lộc 2-Thanh Hóa- 2019) Trongkhônggian

Oxyz

,mặtphẳng

 

: 1

1 2 3

x y z

P

  

không

điquađiểmnàodướiđây?

A.

 

0;2;0

P

. B.

 

1;2;3

N

. C.

 

1;0;0

M

. D.

 

0;0;3

Q

.

Lời giải

Chọn B

Thếtọađộđiểm

N

vàophươngtrìnhmặtphẳng

 

P

tacó:

1 2 3

1

1 2 3

  

.

Vậymặtphẳng

 

: 1

1 2 3

x y z

P

  

khôngđiquađiểm

 

1;2;3

N

.

Câu 80. (Chuyên Lê Hồng Phong Nam Định 2019) Trongkhônggian

Oxyz

,mặtphẳngnàodướiđây

điquagốctọađộ?

A.

20 0

x

 

. B.

2019 0

x

 

. C.

5 0

y

 

. D.

2 5 8 0

x y z

  

.

Lời giải

Chọn D

Cách 1:

Dựavàonhậnxétmặtphẳngcóphươngtrình

0

Ax By Cz D

   

điquagốctọađộthì

0.

D





Vậychọnđápán D.

Cách 2:Thaytọađộđiểm

 

0;0;0

O

lầnlượtvàocácphươngtrìnhđểkiểmtra.

Câu 81. (Chuyên Lê Quý Đôn – Điện Biên 2019) Trong không gian Oxyz, cho mặt phẳng

( )



:

2 2z 3 0.

x y

   

Điểmnàosauđâynằmtrênmặtphẳng

( )



?

A.

(2; 0;1).

M



B.

(2;1;1).

Q



C.

(2; 1;1).

P





D.

(1; 0;1).

N



Lời giải

Chọn D

Tacó:

1.1 2.0 2.1 3 0.   

Tọađộđiểm

(1;0;1)

N

thỏamãnphươngtrìnhmặtphẳng

( )



nênN

nằmtrênmặtphẳng

( )



.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 18 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 82. (SGD Bình Phước - 2019) Trong không gian

Oxyz

,mặt phẳng

 

: 2 3 0

x y z



   

đi qua

điểmnàodướiđây?

A.

3

1;1;

2

M

 

 

 

. B.

3

1; 1;

2

N

 

 

 

 

. C.

 

1;6;1

P

. D.

 

0;3;0

Q

.

Lời giải

Chọn A

Xétđiểm

3

1;1;

2

M

 

 

 

,tacó:

3

1 1 2. 3 0

2

   

đúngnên

 

M





nênAđúng.

Xétđiểm

3

1; 1;

2

N

 

 

 

 

,tacó:

3

1 1 2. 3 0

2

 

    

 

 

sainên

 

N





nênB sai.

Xétđiểm

 

1;6;1

P

,tacó:

1 6 2.1 3 0   

sainên

 

P





nênC sai.

Xétđiểm

 

0;3;0

Q

,tacó:

0 3 2.0 3 0   

sainên

 

Q





nênD sai.

Câu 83. (Sở Kon Tum - 2019) Trongkhônggian

Oxyz

,mặtphẳng

 

:  2 4 0

x y z



   

điquađiểm

nàosauđây

A.

 

1; 1;1

Q 

. B.

 

0;2;0

N

. C.

 

0;0; 4

P



. D.

 

1;0;0

M

.

Lời giải

Chọn A

Thaytọađộ

Q

vàophươngtrìnhmặtphẳng

 



tađược:

 

1 2 1 1 4 0    

.

Thaytọađộ

N

vàophươngtrìnhmặtphẳng

 



tađược:

0 2.2 0 4 8 0      

LoạiB

Thaytọađộ

P

vàophươngtrìnhmặtphẳng

 



tađược:

0 2.0 4 4 8 0      

LoạiC

Thaytọađộ

M

vàophươngtrìnhmặtphẳng

 



tađược:

1 2.0 0 4 3 0      

LoạiD

Câu 84. (SGD Bến Tre 2019) Trongkhônggian

Oxyz

chomặtphẳng

 

: 2 1 0

P x y z

   

.Điểmnào

dướiđâythuộc

 

P

?

A.

 

0;1; 2

N



. B.

 

2; 1;1

M 

. C.

 

1; 2;0

P 

. D.

 

1; 3; 4

Q

 

.

Lời giải

Chọn D

Nhậnthấy

   

2.1 3 4 1 0     

nên

 

1; 3; 4

Q

 

thuộc

 

P

.

Dạng4.Khoảngcáchtừđiểmđếnmặt



Khoảng cách từ điểm

( ; ; )

M M M

M x y z

đến mặt phẳng

( ) : 0

P ax by cz d

   

được xác định bởi công

thức:

2 2 2

( ;( ))

M M M

ax by cz d

d M P

a b c

  

 

 

Câu 85. (ĐềMinhHọa2017)Trongkhônggianvớihệtọađộ

Oxyz

,chomặtphẳngchomặtphẳng

 

P



cóphươngtrình

3 4 2 4 0

x y z

   

vàđiểm

 

1; 2;3

A 

.Tínhkhoảngcách

d

từ

A

đến

 

P

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19

A.

5

29

d 

B.

5

29

d 

C.

5

3

d 

D.

5

9

d





Lờigiải

ChọnB

Khoảngcáchtừđiểm

A

đến

 

P

là

 

2 2 2

3.1 4. 2 2.3 4

5

29

3 4 2

d

   

  

 



Câu 86. (THPTBaĐình2019)Trongkhônggianvớihệtọađộ

Oxyz

,chomặtphẳng

 

P

cóphương

trình:

3 4 2 4 0

x y z

   

vàđiểm

 

1; 2;3

A 

.Tínhkhoảngcách

d

từ

A

đến

 

P

.

A.

5

9

d



. B.

5

29

d 

. C.

5

29

d 

. D.

5

3

d 

.

Lờigiải

Khoảngcách

d

từ

A

đến

 

P

là

2 2 2

3 4 2 4 3 8 6 4

( ,( ))

29

3 4 2

A A A

x y z

d A P

     

 

 



5

( ,( ))

29

d A P 



Câu 87. (THPTGiaLộcHảiDương2019)Trongkhônggian

Oxyz

,tínhkhoảngcáchtừ

 

1;2; 3

M





đếnmặtphẳng

 

: 2 2 10 0

P x y z

   

.

A.

11

3

. B.

3

. C.

7

3

. D.

4

3

.

Lờigiải

 

2 2 2

1 2 2 2 3 10

11

;

3 3

1 2 2

. .

d M P

   



  

 

.

Câu 88. (Sở Hà Nội 2019) Trong không gian

Oxyz

, cho mặt phẳng

 

: 2 2 1 0

P x y z

   

. Khoảng cách

từ điểm

 

1;2;0

M 

đến mặt phẳng

 

P

bằng

A.

5

. B.

2

. C.

5

3

. D.

4

3

.

Lờigiải

Tacó

 

2

2 2

2. 1 2.2 0 1

5

,

3

2 2 1

d M P

   

 

  

.

Câu 89. (ChuyênLêQuýĐônQuảngTrị2019)Trongkhônggianvớihệtọađộ

Oxyz

,chomặtphẳng

 

: 2 2 4 0

P x y z

   

.Tínhkhoảngcách

d

từđiểm

 

1;2;1

M

đếnmặtphẳng

 

P

.

A.

3

d



. B.

4

d



. C.

1

d



. D.

1

3

d



.

Lờigiải

Khoảngcách

d

từđiểm

 

1;2;1

M

đếnmp

 

P

là

 

2

2 2

2.1 2.2 1 4

, 1

2 2 1

d d M P

  

  

  

.

Câu 90. (SởBắcGiang2019)Trongkhônggian

Oxyz

,chomặtphẳng

 

: 2 2 1 0

Q x y z

   

vàđiểm

 

1; 2;1

M 

.Khoảngcáchtừđiểm

M

đếnmặtphẳng

 

Q

bằng

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 20 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

A.

4

3

. B.

1

3

. C.

2

3

. D.

2 6

3

.

Lờigiải

Khoảngcáchtừđiểm

M

đếnmặtphẳng

 

Q

bằng

 

2

1 2 2 2.1 1

4

,

3

1 2 2

d M Q

   

  

  



Câu 91. (Kiểm tra năng lực - ĐH - Quốc Tế - 2019) Trongkhônggianvớihệtrụctọađộ

Oxyz

,gọi

H



làhìnhchiếuvuônggóccủađiểm

 

1; 2;3

A 

lênmặtphẳng

 

: 2 2 5 0

P x y z

   

.Độdàiđoạn

thẳng

AH

là

A.

3

. B.

7

. C.

4

. D.

1

.

Lời giải

Chọn D

 

   

2 2

2

2 2 6 5

, 1

2 1 2

AH d A P

  

  

   

.

Câu 92. (SGD Cần Thơ 2019) Trong không gian

Oxyz

, cho điểm

 

1;2 3

M

 

 và mặt phẳng

 

: 2 2 5 0

P x y z

   

.Khoảngcáchtừđiểm

M

đếnmặtphẳng

 

P

bằng

A.

4

3

. B.

1

3

. C.

2

3

. D.

4

9

.

Lời giải

Chọn A

Khoảngcáchtừđiểm

M

đếnmặtphẳng

 

P

:

 

   

 

2

2 2

2. 1 2.2 1. 3 5

4

,

3

2 2 1

d M P

    

 

  

.

Câu 93. (Cần Thơ - 2019) Trong không gian

Oxyz

, cho mặt phẳng

 

: 2 2 5 0

P x y z

   

 và điểm

 

1;3; 2

A

 

.Khoảngcáchtừ

A

đếnmặt

 

P

là

A.

14

7

.

 B.

3 14

14

. C.

2

3

. D.

1

.

Lời giải

Chọn C

Tacókhoảngcáchtừ

A

Ađếnmặtphẳng

 

P

là

 

   

2 2

2

| 1 2.3 2. 2 5 |

2

,

3

1 2 2

d A P

    

 

   

.

Câu 94. (Sở Kon Tum - 2019) Trongkhônggian

Oxyz

,chomặtphẳng

 

: 2 2 4 0

P x y z

   

.Khoảng

cáchtừđiểm

 

3;1; 2

M



đếnmặtphẳng

 

P

bằng

A.

2

. B.

1

3

. C.

1

. D.

3

.

Lời giải

Chọn C

Khoảngcáchtừđiểm

 

3;1; 2

M



đếnmặtphẳng

 

P

:

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21

 

2

2.3

1 2. 2 4

, 1

2

1 2

d M P

   

 



 

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương  https://www.facebook.com/phong.baovuong Trang 1

TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH KHÁ – MỨC 7-8 ĐIỂM

Dạng 1. Xác định phương trình mặt phẳng (không chứa yếu tố đường thẳng)

Dạng 1. Mặt

( )

( ; ; )

( ) : ( ) : ( ) ( ) ( ) 0 .

: ( ; ; )

P

Qua A x y z

P P a x x b y y c z z

VTPT n a b c



      







  







Dạng 2. Viết phương trình

( )P

qua ( ; ; )A x y z

  

và

( ) ( ): 0.P Q ax by cz d   

Phương pháp.

( ) ( )

( , , )

( ) :

: ( ; ; )

P Q

A x y z

P

VT

u

PT n n b

a

a c

Q





 



  



 



Dạng 3. Viết phương trình mặt phẳng trung trực

( )P

của đoạn thẳng

.AB

Phương pháp.

( )

2

(

;

:

) :

;

2 2

A B A B A B

P

x x y y z z

Qua I

VTPT n AB

P



  

 

 























Dạng 4. Viết phương trình mặt phẳng

( )P

qua

M

và vuông góc với đường thẳng

.d AB

Phương pháp.

( )

( ; ; )

( ) :

:

P d

M x y z

P

VTPT n u

u

AB

Q a







 





  





 



Dạng 5. Viết phương trình mặt phẳng

( )P

qua điểm

M

và có cặp véctơ chỉ phương

, .a b



Phương pháp.

( )

( ; ; )

( ) :

]

: [ ,

P

M x y z

P

VTPT n a b

Qua













  





 



Dạng 6. Viết phương trình mặt phẳng

( )P

đi qua ba điểm

, , A B C

không thẳng hàng.

Phương pháp.

( )

, ( )

( ) :

: ,

ABC

P

VTP A

Qua A hay B hay C

T n AB C







 





 





 





Dạng 7. Viết phương trình mặt phẳng

( )P

đi qua

, A B

và

( ) ( ).P Q

Phương pháp.

( ) ( )

, ( )

( ) :

: ,

P Q

Q A hay B

P

VTPT n AB n

ua







 





 







 



Dạng 8. Viết phương trình mp

( )P

qua

M

và vuông góc với hai mặt

( ), ( ).

 

Phương pháp.

( ) ( ) ( )

(

;

) :

: ,

( ; )

P

Q

P

VTPT

ua

n

M x y z

n n

 







 





 



  



  



Dạng 9. Viết

( )P

đi qua

M

và giao tuyến

d

của hai mặt phẳng:

1 1 1 1

( ) : 0Q a x b y c z d    và

2 2 2 2

( ): 0.T a x b y c z d   

Phương pháp: Khi đó mọi mặt phẳng chứa

d

đều có dạng:

2 2

1 1 1 1 2 2 2 2

( ) : ( ) ( ) 0, 0.P m a x b y c z d n a x b y c z d m n         

Vì

( )M P 

mối liên hệ giữa

m

và

.n

Từ đó chọn m n sẽ tìm được

( ).P

Dạng 10. Viết phương trình mặt phẳng đoạn chắn

Phương pháp: Nếu mặt phẳng

( )P

cắt ba trục tọa độ lần lượt tại các điểm

( ;0;0),A a

(0; ;0),B b

(0;0; )C c

với

( 0)abc 

thì

( ) : 1

x y z

P

a b c

  

gọi là mặt phẳng đoạn chắn.

Dạng 1.1 Xác định phương trình mặt phẳng khi biết yếu tố vuông góc

Câu 1. (Mã 104 - 2019) Trong không gian Oxyz, cho hai điểm

 

4;0;1A

và

 

2;2;3 .B

Mặt phẳng trung

trực của đoạn thẳng AB có phương trình là

PHƯƠNG TRÌNH MẶT PHẲNG

Chuyên đề 30

: là trung điểm

.

AB

P

Q

( ) ( )

P Q

n n



 

P

A

B

I

P

( )P d

AB

n u

 



 

d

M

P

a



b



A

C

B

P

B

A

P

Q

( )

Q

n







( )

n





( )

n





P

M

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

A.

3 0.  

x y z

B.

3 6 0.   

x y z

C.

2 6 0.   

x y z

D.

6 2 2 1 0.   

x y z

Lời giải

Chọn A

Mặt phẳng trung trực của đoạn thẳng AB có véctơ pháp tuyến là

 

6;2;2

 



AB

và đi qua trung

điểm

 

1;1;2

I

của đoạn thẳng AB. Do đó, phương trình mặt phẳng đó là:

     

6 1 2 1 2 2 0 6 2 2 0 3 0.               

x y z x y z x y z

Câu 2. (Mã 102 - 2019) Trong không gian

Oxyz

, cho hai điểm

 

1;2;0

A 

và

 

3;0;2

B

. Mặt phẳng

trung trực của đoạn thẳng

AB

có phương trình là

A.

3 0

x y z

   

. B.

2 2 0

x y z

   

. C.

2 4 0

x y z

   

. D.

2 2 0

x y z

   

.

Lời giải

Chọn D

Gọi

I

là trung điểm của đoạn thẳng

AB

. Suy ra

 

1;1;1

I

.

Ta có

 

4; 2;2

AB  



.

Phương trình mặt phẳng trung trực của đoạn thẳng

AB

đi qua trung điểm

I

của

AB

và nhận

AB



làm vtpt, nên có phương trình là

 

: 2 2 0

x y z



   

.

Câu 3. (Mã 110 2017) Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm

 

4;0;1

A

và

 

2;2;3

B 

.

Phương trình nào dưới đây là phương trình mặt phẳng trung trực của đoạn thẳng

AB

?

A.

3 6 0

x y z

   

B.

3 0

x y z

  

C.

6 2 2 1 0

x y z

   

D.

3 1 0

x y z

   

Lời giải

Chọn B

Gọi

I

là trung điểm của đoạn thẳng

AB

. Gọi

 



là mặt phẳng trung trực của đoạn thẳng

AB

 



đi qua

 

1;1;2

I

và nhận

 

6;2;2

AB  



làm một VTPT.



       

: 6 1 2 1 2 2 0

x y z



      

 





:

3 0

x y z

  

.

Câu 4. (Mã 101 2019) Trong không gian

Oxyz

, cho hai điểm

 

1;3;0

A

và

 

5;1; 1

B



. Mặt phẳng trung

trực của đoạn thẳng

AB

có phương trình là:

A.

2 3 0

x y z

   

. B.

3 2 14 0

x y z

   

. C.

2 5 0

x y z

   

. D.

2 5 0

x y z

   

.

Lời giải

Chọn D

Mặt phẳng trung trực của đoạn thẳng

AB

đi qua trung điểm

 

3;2; 1

I



, có vec tơ pháp tuyến

 

1

2; 1; 1

2

n AB

   

 

có phương trình:

     

2 3 1 2 1 1 0 2 5 0

x y z x y z

          

.

Chọn đáp án B.

Câu 5. (Mã 103 - 2019) Trong không gian

Oxyz

, cho hai điểm

(2;1;2)

A

và

(6;5; 4)

B



. Mặt phẳng

trung trực của đoạn thẳng

AB

có phương trình là

A.

2 2 3 17 0

x y z

   

. B.

4 3 26 0

x y z

   

.

C.

2 2 3 17 0

x y z

   

. D.

2 2 3 11 0

x y z

   

.

Lời giải

Chọn A

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3

Mặt phẳng trung trực của đoạn thẳng

AB

đi qua trung điểm của

AB

là

(4;3; 1)

M



và có véctơ

pháp tuyến là

(4; 4; 6)

AB

 



nên có phương trình là

4( 4) 4( 3) 6( 1) 0

x y z

     

2( 4) 2( 3) 3( 1) 0

2 2 3 17 0

x y z

      

    

Câu 6. (Chuyên Thái Bình 2019) Trong không gian

Oxyz

, cho hai điểm

 

1;3; 4

A



và

 

1;2;2

B 

.

Viết phương trình mặt phẳng trung trực

 



của đoạn thẳng

AB

.

A.

 

: 4 2 12 7 0

x y z



   

. B.

 

: 4 2 12 17 0

x y z



   

.

C.

 

: 4 2 12 17 0

x y z



   

. D.

 

: 4 2 12 7 0

x y z



   

.

Lời giải

Gọi

5

0; ; 1

2

I

 



 

 

là trung điểm của

AB

;

 

2; 1;6

AB   



.

Mặt phẳng

 



qua

5

0; ; 1

2

I

 



 

 

và có VTPT

 

2; 1;6

n   



nên có

PT:

     

5

: 2 6 1 0 4 2 12 17 0

2

x y z x y z



 

          

 

 

.

Câu 7. (THPT An Lão Hải Phòng 2019) Trong không gian hệ tọa độ

Oxyz

, cho

 

1;2; 1

A



;

 

1;0;1

B 

và mặt phẳng

 

: 2 1 0

P x y z

   

. Viết phương trình mặt phẳng

 

Q

qua

,A B

và vuông góc

với

 

P

A.

 

:2 3 0

Q x y

  

B.

 

: 0

Q x z

 

C.

 

: 0

Q x y z

   

D.

 

:3 0

Q x y z

  

Lời giải

Chọn B

     

2; 2;2 2 1;1; 1 , 1;1; 1

AB u

       





 

1;2; 1

P

n

 



   

 

, 1;0;1

Q P

n AB n

 

 

 

  

Vậy

 

: 0

Q x z

 

.

Câu 8. (THPT Gia Lộc Hải Dương 2019) Trong không gian

Oxyz

, cho hai điểm

   

2;4;1 1;1;3

A ,B 

và mặt phẳng

 

: 3 2 5 0

P x y z

   

. Lập phương trình mặt phẳng

 

Q

đi qua hai điểm

A

,

B

và

vuông góc với mặt phẳng

 

P

.

A.

2 3 11 0

y z

  

. B.

2 3 11 0

x y

  

. C.

3 2 5 0

x y z

   

. D.

3 2 11 0

y z

  

.

Lời giải

Ta có:

 

3; 3;2

AB   



, vectơ pháp tuyến của mp

 

P

là

 

1; 3;2

P

n  



.

Từ giả thiết suy ra

 

0;8;12

P

n AB,n

 

 

 

  

là vectơ pháp tuyến của mp

 

Q

.

Mp

 

Q

đi qua điểm

 

2;4;1

A

suy ra phương trình tổng quát của mp

 

Q

là:

     

0 2 8 4 12 1 0 2 3 11 0

x y z y z

         

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 9. (Chuyên KHTN 2019) Trong không gian

Oxyz

, cho hai điểm

 

1; 1;2

A

và

 

3;3;0

B

. Mặt

phẳng trung trực của đoạn thẳng

AB

có phương trình là

A.

2 0   

x y z

. B.

2 0   

x y z

. C.

2 3 0   

x y z

. D.

2 3 0   

x y z

.

Lời giải

Ta có

 

2 1;2; 1

AB

 



.

Gọi

I

là trung điểm của

 

2;1;1

AB I

.

+ Mặt phẳng trung trực

 



của đoạn thẳng

AB

đi qua

I

và nhận

 

1

1;2; 1

2

  

 

n AB

làm vectơ

pháp tuyến có phương trình là

   

2 2 1 1 0 2 3 0          

x y z x y z

.

Vậy mặt phẳng trung trực của đoạn thẳng

AB

là

2 3 0   

x y z

.

Câu 10. (Chuyên Sơn La 2019) Trong không gian

Oxyz

, mặt phẳng

 

P

đi qua hai điểm

 

0;1;0

A

,

 

2;3;1

B

và vuông góc với mặt phẳng

 

: 2 0  

Q x y z

có phương trình là

A.

4 3 2 3 0

x y z

   

. B.

4 3 2 3 0

x y z

   

. C.

2 3 1 0

x y z

   

. D.

4 2 1 0

x y z

   

.

Lời giải

Ta có

 

2;2;1

AB 



, vectơ pháp tuyến mặt phẳng

 

Q

:

 

1;2; 1

Q

n

 



.

Theo đề bài ta có vectơ pháp tuyến mặt phẳng

 

P

:

 

4; 3; 2

P Q

n n AB

    

  

.

Phương trình mặt phẳng

 

P

có dạng

4 3 2 0

x y z C

   

.

Mặt phẳng

 

P

đi qua

 

0;1;0

A

nên:

3 0 3

C C

    

.

Vậy phương trình mặt phẳng

 

P

là

4 3 2 3 0

x y z

   

.

Câu 11. (KTNL GV Lý Thái Tổ 2019) Cho hai mặt phẳng

   

:3 2 2 7 0, :5 4 3 1 0

x y z x y z

 

       

. Phương trình mặt phẳng đi qua gốc tọa độ

O

đồng thời vuông góc với cả

 



và

 



là:

A.

2 2 0.

x y z

  

B.

2 2 0.

x y z

  

C.

2 2 0.

x y z

  

D.

2 2 1 0.

x y z

   

Lời giải

Chọn C

Véc tơ pháp tuyến của hai mặt phẳng lần lượt là

 

3; 2;2

n



 



,

 

5; 4;3

n



 



.

 

; 2;1; 2

n n

 

 

  

 

 

Phương trình mặt phẳng đi qua gốc tọa độ

O

,VTPT

 

2;1; 2

n

 



:

2 2 0.

x y z

  

Câu 12. (Chuyên Lê Hồng Phong Nam Định 2019) Trong không gian với hệ tọa độ

Oxyz

, cho điểm

   

2;4;1 ; 1;1;3

A B 

và mặt phẳng

 

: 3 2 5 0

P x y z

   

. Một mặt phẳng

 

Q

đi qua hai điểm

,A B

và vuông góc với mặt phẳng

 

P

có dạng

11 0

ax by cz

   

. Khẳng định nào sau đây là

đúng?

A.

5

a b c

  

. B.

15

a b c

  

. C.

5

a b c

   

. D.

15

a b c

   

.

Lời giải

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5

Chọn A

Vì

 

Q

vuông góc với

 

P

nên

 

Q

nhận vtpt

 

1; 3;2

n  



của

 

P

làm vtcp

Mặt khác

 

Q

đi qua

A

và

B

nên

 

Q

nhận

 

3; 3;2

AB   



làm vtcp

 

Q

nhận

 

, 0;8;12

Q

n n AB

 

 

 

  

làm vtpt

Vậy phương trình mặt phẳng

 

:0( 1) 8( 1) 12( 3) 0

x y zQ

     

, hay

 

: 2 3 11 0

y zQ

  

Vậy

5

a b c

  

. Chọn A.

Câu 13. (THPT Yên Phong Số 1 Bắc Ninh 2019) Trong không gian với hệ tọa độ

Oxyz

, cho

   

1; 1;2 ; 2;1;1

A B

và mặt phẳng

 

: 1 0

P x y z

   

. Mặt phẳng

 

Q

chứa

,A B

và vuông

góc với mặt phẳng

 

P

. Mặt phẳng

 

Q

có phương trình là:

A.

3 2 3 0

x y z

   

. B.

2 0

x y z

   

. C.

0

x y

  

. D.

3 2 3 0

x y z

   

.

Lời giải

Chọn A

Ta có

 

1;2; 1

AB

 



Từ

 

P

suy ra vec tơ pháp tuyến của

 

P

là

 

1;1;1

P

n 



Gọi vec tơ pháp tuyến của

 

Q

là

Q

n



Vì

 

Q

chứa

,A B

nên

 

1

Q

n AB

 

Mặt khác

   

Q P



nên

 

2

Q P

n n

 

Từ

   

1 , 2

ta được

 

, 3; 2; 1

Q P

n AB n

 

   

 

  

 

Q

đi qua

 

1; 1;2

A 

và có vec tơ pháp tuyến

 

3; 2; 1

Q

n

  



nên

 

Q

có phương trình là

     

3 1 2 1 2 0

x y z

     

3 2 3 0

x y z

    

.

Câu 14. (Chuyên Đại Học Vinh 2019) Trong không gian

,Oxyz

cho hai mặt phẳng

 

: 3 2 1 0,

P x y z

   

 

: 2 0

Q x z

  

. Mặt phẳng

 



vuông góc với cả

 

P

và

 

Q

đồng

thời cắt trục

Ox

tại điểm có hoành độ bằng

3.

Phương trình của mp

 



là

A.

3 0

x y z

   

B.

3 0

x y z

   

C.

2 6 0

x z

   

D.

2 6 0

x z

   

Lời giải

Chọn A

 

P

có vectơ pháp tuyến

 

1; 3;2

P

n  



,

 

Q

có vectơ pháp tuyến

 

1;0; 1

Q

n

 



.

Vì mặt phẳng

 



vuông góc với cả

 

P

và

 

Q

nên

 



có một vectơ pháp tuyến là

   

, 3;3;3 3 1;1;1

P Q

n n

 

 

 

 

.

Vì mặt phẳng

 



cắt trục

Ox

tại điểm có hoành độ bằng 3 nên

 



đi qua điểm

 

3;0;0

M

.

Vậy

 



đi qua điểm

 

3;0;0

M

và có vectơ pháp tuyến

 

1;1;1

n







nên

 



có phương trình:

3 0.

x y z

   

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 15. (Chuyên Lam Sơn Thanh Hóa 2019) Trong không gian với hệ tọa độ

Oxyz

cho hai mặt phẳng

 

: 3 2 2 7 0

x y z



   

và

 

: 5 4 3 1 0

x y z



   

. Phương trình mặt phẳng đi qua

O

đồng

thời vuông góc với cả

 



và

 



có phương trình là

A.

2 2 1 0

x y z

   

. B.

2 2 0

x y z

  

. C.

2 2 0

x y z

  

. D.

2 2 0

x y z

  

.

Lời giải

Gọi mặt phẳng phải tìm là

 

P

. Khi đó véc tơ pháp tuyến của

 

P

là:

 

, 2; 1; 2

P

n n n

 

 

  

 

  

.

Phương trình của

 

P

là

2 - 2 0

x y z

 

.

Câu 16. (HSG Bắc Ninh 2019) Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

 

: 1 0

P x y z

   

và hai điểm

   

1; 1;2 ; 2;1;1

A B

. Mặt phẳng

 

Q

chứa

,A B

và vuông góc

với mặt phẳng

 

P

, mặt phẳng

 

Q

có phương trình là:

A.

3 2 3 0

x y z

   

. B.

2 0

x y z

   

. C.

3 2 3 0

x y z

   

. D.

0

x y

  

.

Lờigiải

Mặt phẳng

 

P

có 1 véc tơ pháp tuyến là

(1;1;1)

p

n 



. Véc tơ

(1;2; 1)

AB

 



.

Gọi

n



là một véc tơ pháp tuyến của

 

Q

, do

 

Q

vuông góc với

 

P

nên

n



có giá vuông góc với

p

n



, mặt khác véc tơ

AB



có giá nằm trong mặt phẳng

 

Q

nên

n



cũng vuông góc với

AB



Mà

p

n



và

AB



không cùng phương nên ta có thể chọn

n



=

 

, 3;2;1

P

n AB

 

 

 

 

, mặt khác

 

Q

đi

qua

 

1; 1;2

A 

nên phương trình của mặt phẳng

 

Q

là:

   

3 1 2 1 1( 2) 0 3 2 3 0

x y z x y z

           

.

Câu 17. (Đề Thi Công Bằng KHTN 2019) Trong không gian

Oxyz

, phương trình mặt phẳng đi qua hai

điểm

   

0;1;0 , 2;0;1

A B

và vuông góc với mặt phẳng

 

: 1 0

P x y

  

là:

A.

3 1 0

x y z

   

. B.

2 2 5 2 0

x y z

   

.

C.

2 6 2 0

x y z

   

. D.

1 0

x y z

   

.

Lời giải

Ta có:

 

2; 1;1

AB  



. Mặt phẳng

 

P

có 1 véctơ pháp tuyến là:

 

1; 1;0

P

n  



.

Gọi

n



là véctơ pháp tuyến của mặt phẳng cần tìm. Khi đó

 

; 1;1; 1

P

n AB

n AB n

n n







 

   



 







 

  

 

.

Vậy phương trình mặt phẳng cần tìm là:

     

1 0 1 1 1 0 0 1 0

x y z x y z

          

.

Câu 18. (Chuyên Lam Sơn 2019) Trong không gian

Oxyz

, cho hai mặt phẳng

 

: 3 2 2 7 0

x y z



   

và

 

: 5 4 3 1 0.

x y z

   



Phương trình mặt phẳng qua

O

, đồng thời vuông góc với cả

 



và

 



có phương trình là

A.

2 2 0

x y z

  

. B.

2 2 1 0

x y z

   

. C.

2 2 0

x y z

  

. D.

2 2 0

x y z

  

.

Lời giải

Chọn C

Mặt phẳng

 



có một vectơ pháp tuyến là

 

1

3; 2;2

n  



.

Mặt phẳng

 



có một vectơ pháp tuyến là

 

2

5; 4;3

n  



.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7

Giả sử mặt phẳng

 



có vectơ pháp tuyến là

n



.

Do mặt phẳng

 



vuông góc với cả

 



và

 



nên ta có:

1

2

n n















 

 

1 2

, 2;1; 2

n n n

 

   

 

  

.

Mặt phẳng

 



đi qua

 

0;0;0

O

và có vectơ pháp tuyến

 

2;1; 2

n

 



có phương trình là:

2 2 0

x y z

  

.

Câu 19. (SGD Bến Tre 2019) Trong không gian

Oxyz

,

cho điểm

 

1; 1;2

A 

;

 

2;1;1

B

và mặt phẳng

 

: 1 0

P x y z

   

.

Mặt phẳng

 

Q

chứa

A

,

B

và vuông góc với mặt phẳng

 

P

.

Mặt phẳng

 

Q

có phương trình là

A.

3 2 3 0

x y z

   

. B.

0

x y

  

. C.

2 0

x y z

   

. D.

3 2 3 0

x y z

   

.

Lời giải

Chọn A

Ta có:

 

1 ;2 ; 1

AB

 



, mặt phẳng

 

P

có một véc tơ pháp tuyến là

 

1;1;1

m 



.

Vì mặt phẳng

( )Q

chứa

A

,

B

và vuông góc với mặt phẳng

 

P

nên mặt phẳng

 

Q

có một véc

tơ pháp tuyến là

,n AB m

 



 

  

 

3 ; 2 ; 1  

.

Mặt phẳng

 

Q

có phương trình là

       

: 3 1 2 1 2 0

Q x y z

     

3 2 3 0

x y z

    

.

Câu 20. Trong không gian với hệ trục tọa độ

Oxyz

, cho mặt phẳng

 

: 9 0

P ax by cz

   

chứa hai điểm

 

3;2;1

A

,

 

3;5;2

B 

và vuông góc với mặt phẳng

 

:3 4 0

Q x y z

   

. Tính tổng

S a b c  

.

A.

12

S

 

. B.

2

S



. C.

4

S

 

. D.

2

S

 

.

Lời giải

Chọn C

 

6;3;1

AB  



.

 

3;1;1

Q

n 



là VTPT của mp

 

Q

.

Mp

 

P

chứa hai điểm

 

3;2;1

A

,

 

3;5; 2

B 

và vuông góc với mặt phẳng

 

Q

.

   

 

, 2;9; 15

p Q

n AB n

 

   

 

  

là VTPT của mp

 

P

   

3;2;1

A P



 

: 2 9 15 9 0

P x y z

    

hoặc

 

: 2 9 15 9 0

P x y z

    

Mặt khác

 

: 9 0

P ax by cz

   

2; 9; 15

a b c

    

.

Vậy

 

2 9 15 4

S a b c

        

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 8 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 21. (Thi thử hội 8 trường chuyên 2019) Trong không gian

,Oxyz

cho ba mặt phẳng

 

: 1 0,

P x y z

   

 

: 2 5 0

Q y z

  

và

 

: 2 0.

R x y z

   

Gọi

 



là mặt phẳng qua giao

tuyến của

 

P

và

 

,Q

đồng thời vuông góc với

 

.R

Phương trình của

 



là

A.

2 3 5 5 0.

x y z

   

B.

3 2 6 0.

x y z

   

C.

3 2 6 0.

x y z

   

D.

2 3 5 5 0.

x y z

   

Lời giải

Chọn B

Tọa độ mọi điểm thuộc giao tuyến của 2 mặt phẳng

 

P

và

 

Q

thỏa mãn hệ phương

trình:

1 0

2 5 0

x y z

y z

   





  



Cho

1z 

ta được

 

2;2;1

A 

, cho

5

z



ta được

 

4;0;5

B 

thuộc giao tuyến,

 

2; 2;4

AB  



.

Mặt phẳng

 

R

có vec tơ pháp tuyến

 

1; 1;1

R

n  



.

Mặt phẳng

 



đi qua

 

2;2;1

A 

và có vec tơ pháp tuyến

 

1

, 1;3;2

2

R

n AB n

 

 

 

  

.

Phương trình của

 



là:

     

2 3 2 2 1 0 3 2 6 0

x y z x y z

          

.

Câu 22. (THPT Lương Thế Vinh - HN - 2018) Trong không gian

Oxyz

, phương trình của mặt phẳng

 

P

đi qua điểm

 

2;1; 3

B



, đồng thời vuông góc với hai mặt phẳng

 

: 3 0

Q x y z

  

,

 

: 2 0

R x y z

  

là

A.

4 5 3 22 0

x y z

   

. B.

4 5 3 12 0

x y z

   

.

C.

2 3 14 0

x y z

   

. D.

4 5 3 22 0

x y z

   

.

Lời giải

Mặt phẳng

 

: 3 0

Q x y z

  

,

 

: 2 0

R x y z

  

có các vectơ pháp tuyến lần lượt là

 

1

1;1;3

n 



và

 

2

2; 1;1

n  



.

Vì

 

P

vuông góc với hai mặt phẳng

 

Q

,

 

R

nên

 

P

có vectơ pháp tuyến là

 

1 2

, 4;5; 3

n n n

 

  

 

  

.

Ta lại có

 

P

đi qua điểm

 

2;1; 3

B



nên

       

: 4 2 5 1 3 3 0

P x y z

     

4 5 3 22 0

x y z

    

.

Câu 23. (Chuyên Nguyễn Quang Diêu - Đồng Tháp - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho

hai điểm

 

2;4;1

A

,

 

1;1;3

B 

và mặt phẳng

 

P

:

3 2 5 0

x y z

   

. Một mặt phẳng

 

Q

đi qua

hai điểm

A

,

B

và vuông góc với

 

P

có dạng là

11 0

ax by cz

   

. Tính

a b c 

.

A.

10

a b c

  

. B.

3

a b c

  

. C.

5

a b c

  

. D.

7

a b c

   

.

Lời giải

Ta có

 

3; 3; 2

AB   



,

 

P

có vtpt

 

1; 3;2

n  



,

 

Q

có vtpt

,k AB n

 



 





 

0;8;12





 

Q

có dạng:

   

2 4 3 1 0

y z

   

2 3 11 0

y z

   

.

Vậy

5

a b c

  

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9

Câu 24. (Chuyên Trần Phú - Hải Phòng - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho điểm

 

1;1;1

A

và hai mặt phẳng

 

: 2 3 1 0

P x y z

   

,

 

: 0

Q y



. Viết phương trình mặt phẳng

 

R

chứa

A

, vuông góc với cả hai mặt phẳng

 

P

và

 

Q

.

A.

3 2 4 0

x y z

   

. B.

3 2 2 0

x y z

   

. C.

3 2 0

x z

 

. D.

3 2 1 0

x z

  

.

Lời giải

 

: 2 3 1 0

P x y z

   

có véctơ pháp tuyến

 

2; 1;3

P

n  



.

 

: 0

Q y



có véctơ pháp tuyến

 

0;1;0

Q

n 



.

Do mặt phẳng

 

R

vuông góc với cả hai mặt phẳng

 

P

và

 

Q

nên có véctơ pháp tuyến

     

,

R P Q

n n n

 



 

  

.

 

3;0;2

R

n  



.

Vậy phương trình mặt phẳng

 

R

là:

3 2 1 0

x z

   

3 2 1 0

x z

   

.

Câu 25.

(THPT

Lý

Thái

Tổ

-

Bắc

Ninh

-

2018)

Cho hai mặt phẳng

 



:

3 2 2 7 0

x y z

   

và

 



:

5 4 3 1 0

x y z

   

. Phương trình mặt phẳng

 

P

đi qua gốc tọa độ đồng thời vuông góc

 



và

 



là:

A.

2 0

x y z

  

. B.

2 2 0

x y z

  

. C.

2 2 1 0

x y z

   

. D.

2 2 0

x y z

  

.

Lời giải

Gọi

P

n



là vectơ pháp tuyến của

 

P

. Ta có

P

n n





 

và

P

n n





 

với

 

3; 2;2

n



 



và

 

5; 4;3

n



 



. Chọn

;

P

n n n

 

 



 

  

 

2;1; 2 

.

Mặt phẳng

 

P

đi qua gốc tọa độ nên

 

P

:

2 2 0

x y z

  

.

Câu 26. (Toán Học Tuổi Trẻ 2018) Trong không gian với hệ tọa độ

Oxyz

cho hai điểm

 

2;4;1

A

,

 

1;1;3

B



và mặt phẳng

 

: 3 2 5 0

P x y z

   

. Một mặt phẳng

 

Q

đi qua hai điểm

A

,

B

và

vuông góc với

 

P

có dạng:

11 0

ax by cz

   

. Khẳng định nào sau đây là đúng?

A.

a b c 

. B.

5

a b c

  

. C.

 

;a b c



. D.

a b c 

.

Lời giải

Ta có:

 

2;4;1

A

,

 

1;1;3

B



 

3; 3;2

AB   



.

Véc tơ pháp tuyến của

 

P

là:

 

1; 3;2

n  



.

Do mặt phẳng

 

Q

đi qua

AB

và vuông góc với

 

P

nên

 

Q

nhận véc tơ

 

, 0; 8; 12

AB n

 

  

 

 

 

làm một véc tơ pháp tuyến nên phương trình của

 

Q

sẽ là:

   

2 4 3 1 0

y z

   

2 3 11 0

y z

  

.

Suy ra

0

a



,

2

b



,

3

c



5

a b c

   

.

Câu 27. (Chuyên ĐHSPHN - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho các điểm

 

0;1;2

A

,

 

2; 2;0

B 

,

 

2;0;1

C 

. Mặt phẳng

 

P

đi qua

A

, trực tâm

H

của tam giác

ABC

và vuông góc

với mặt phẳng

 

ABC

có phương trình là

A.

4 2 4 0

x y z

   

. B.

4 2 4 0

x y z

   

. C.

4 2 4 0

x y z

   

. D.

4 2 4 0

x y z

   

.

Lời giải

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 10 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Ta có

 

2; 3; 2

AB

  



,

 

2; 1; 1

AC

   



nên

 

, 1;6; 8

AB AC

 

 

 

 

.

Phương trình mặt phẳng

 

ABC

là:

6 8 10 0

x y z

   

.

Phương trình mặt phẳng qua

B

và vuông góc với

AC

là:

2 2 0

x y z

   

.

Phương trình mặt phẳng qua

C

và vuông góc với

AB

là:

2 3 2 6 0

x y z

   

.

Giao điểm của ba mặt phẳng trên là trực tâm

H

của tam giác

ABC

nên

22 70 176

; ;

101 101 101

H

 



 

 

.

Mặt phẳng

 

P

đi qua

A

,

H

nên

 

22 31 26 1

; ; 22;31;26

101 101 101 101

P

n AH

 

      

 

 

 

.

Mặt phẳng

   

P ABC



nên

 

1;6; 8

ABC

P

n n

  

 

.

Vậy

 

; 404; 202; 101

ABC AH

n u

 

  

 

 

là một vectơ pháp tuyến của

 

P

.

Chọn

 

4; 2; 1

P

n

  



nên phương trình mặt phẳng

 

P

là

4 2 4 0

x y z

   

.

Dạng 1.2 Xác định phương trình mặt phẳng đoạn chắn

Câu 28. (Thpt Vĩnh Lộc - Thanh Hóa 2019) Trong không gian

Oxyz

cho điểm

 

1;2;3

M

. Viết phương

trình mặt phẳng

 

P

đi qua điểm

M

và cắt các trục tọa độ

, , Ox Oy Oz

lần lượt tại

A

,

B

,

C

sao cho

M

là trọng tâm của tam giác

ABC

.

A.

 

: 6 3 2 18 0

P x y z

   

. B.

 

: 6 3 2 6 0

P x y z

   

.

C.

 

: 6 3 2 18 0

P x y z

   

. D.

 

: 6 3 2 6 0

P x y z

   

.

Lời giải

Chọn C

Theo giả thiết

, ,

A Ox B Oy C Oz  

nên ta có thể đặt

     

;0;0 , 0; ;0 , 0;0;A a B b C c

.

Vì

 

1;2;3

M

là trọng tâm tam giác

ABC

nên

3

6

9

a

b

c

















.

Từ đó ta có phương trình mặt phẳng theo đoạn chắn là:

 

: 1 6 3 2 18 0

3 6 9

x y z

P x y z

       

.

Câu 29. (Chuyên Thái Bình - 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho điểm

 

1;2;3

M

.

Gọi

, ,A B C

lần lượt là hình chiếu vuông góc của

M

trên các trục

, ,Ox Oy Oz

. Viết phương trình

mặt phẳng

 

ABC

.

A.

1

1 2 3

  

x y z

. B.

1

1 2 3

  

x y z

. C.

0

1 2 3

  

x y z

. D.

1

1 2 3

   

x y z

.

Lời giải

Chọn A

+

A

là hình chiếu vuông góc của

M

trên trục

Ox

 

1;0;0

 A

.

B

là hình chiếu vuông góc của

M

trên trục

Oy

 

0;2;0

 B

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11

C

là hình chiếu vuông góc của

M

trên trục

Oz

 

0;0;3

 C

.

+ Phương trình mặt phẳng

 

ABC

là

1

1 2 3

  

x y z

.

Câu 30. (Chu Văn An - Hà Nội - 2019) Trong không gian với hệ trục tọa độ

,Oxyz

cho điểm

 

1;4;3 .

G

Mặt phẳng nào sau đây cắt các trục

, ,Ox Oy Oz

lần lượt tại

, ,A B C

sao cho

G

là trọng tâm tứ

diện

?OABC

A.

1

3 12 9

x y z

  

. B.

12 3 4 48 0

x y z

   

.

C.

0

4 16 12

x y z

  

. D.

12 3 4 0

x y z

  

.

Lời giải

Chọn B

Mp(P) cắt các trục

, ,Ox Oy Oz

lần lượt tại

, ,A B C

nên

     

;0;0 , 0; ;0 , 0;0; .A a B b C c

Vì

G

là trọng tâm tứ diện

OABC

nên

4 4

4

16

4 4

12

4 4

A B C O

G

A B C O

G

A B C O

G

x x x x

a

x

a

y y y y

b

y b

c

z z z z

c

z

  



 









  

 

   

 

 





  



 





.

Khi đó mp(P) có phương trình là

1

4 16 12

x y z

  

hay

12 3 4 48 0

x y z

   

.

Vậy mp(P) thỏa mãn là

12 3 4 48 0

x y z

   

.

Câu 31. (THPT An Lão Hải Phòng 2019) Trong không gian với hệ tọa độ

Oxyz

, viết phương trình mặt

phẳng

 

P

đi qua

 

1;1;1

A

và

 

0;2;2

B

đồng thời cắt các tia

Ox

,

Oy

lần lượt tại hai điểm

,M N

( không trùng với gốc tọa độ

O

) sao cho

2

OM ON

A.

 

:3 2 6 0

P x y z

   

B.

 

: 2 3 4 0

P x y z

   

C.

 

: 2 4 0

P x y z

   

D.

 

: 2 2 0

P x y z

   

Lời giải

Chọn D

Cách 1.

Giả sử

 

P

đi qua 3 điểm

 

;0;0

M a

,

 

0; ;0N b

,

 

0;0;P c

Suy ra

 

: 1

x y z

P

a b c

  

Mà

 

P

đi qua

 

1;1;1

A

và

 

0;2;2

B

nên ta có hệ

1 1 1

2

1

2 2

1

a

a b c

b c





  





 



 

 

 

 







Theo giả thuyết ta có

2 2 1

OM ON a b b

    

TH1.

1b 

2

c

  

suy ra

 

: 2 2 0

P x y z

   

TH1.

1

b

 

2

3

c

  

suy ra

 

: 2 3 2 0

P x y z

   

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 12 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 32. (THCS - THPT Nguyễn Khuyến 2019) Trong không gian

Oxyz

, nếu ba điểm

, ,A B C

lần lượt

là hình chiếu vuông góc của điểm

 

1;2;3

M

lên các trục tọa độ thì phương trình mặt phẳng

 

ABC

là

A.

1 2 3

1

x y z

  

. B.

1

1 2 3

x y z

  

. C.

1 2 3

0

x y z

  

. D.

0

1 2 3

x y z

  

.

Lời giải

Gọi

, ,A B C

lần lượt là hình chiếu vuông góc của điểm

 

1;2;3

M

lên

, ,Ox Oy Oz

.

Suy ra:

     

1;0;0 , 0;2;0 , 0;0;3

A B C

.

Vậy phương trình mặt phẳng

 

ABC

theo đoạn chắn là

1

1 2 3

x y z

  

.

Câu 33. (Chuyên Trần Phú Hải Phòng 2019) Trong không gian

,Oxyz

cho điểm

(8; 2;4)

M



. Gọi

, B, C

A

lần lượt là hình chiếu của

M

trên các trục

, , Ox Oy Oz

. Phương trình mặt phẳng đi qua

ba điểm

, A B

và

C

là

A.

4 2 8 0

x y z

   

B.

4 2 18 0

x y z

   

C.

4 2 8 0

x y z

   

D.

4 2 8 0

x y z

   

Lời giải

(8; 2;4)

M



chiếu lên

, , Ox Oy Oz

lần lượt là

(8;0;0), (0; 2;0), (0;0;4)

A B C



Phương trình đoạn chắn qua

, B, C

A

là:

1 4 2 8 0

8 2 4

x y z

       



Câu 34. (Chuyên Hạ Long 2019) Viết phương trình mặt phẳng

 



đi qua

 

2;1; 3

M



, biết

 



cắt trục

, ,Ox Oy Oz

lần lượt tại

, ,A B C

sao cho tam giác

ABC

nhận

M

làm trực tâm

A.

2 5 6 0.

x y z

   

B.

2 6 23 0.

x y z

   

C.

2 3 14 0.

x y z

   

D.

3 4 3 1 0.

x y z

   

Lời giải

Giả sử

     

;0;0 , 0; ;0 , 0;0; , 0.

A a B b C c abc



Khi đó mặt phẳng

 



có dạng:

1

x y z

a b c

  

.

Do

   

2 1 3

1 1

M

a b c



    

Ta có:

       

2 ;1; 3 , 2;1 ; 3 , 0; ; , ;0;AM a BM b BC b c AC a c

         

   

Do

M

là trực tâm tam giác

ABC

nên:

 

3

. 0 3 0

2

3

2 3 0

. 0

2

b c

AM BC b c

c

a c

a

BM AC

 



   



 

 

  

  

 









 

Thay

 

2

vào

 

1

ta có:

4 1 3 14

1 7, 14.

3 3 3

c a b

c c c

         

Do đó

 

3

: 1 2 3 14 0.

7 14 14

x y z



       

Câu 35. (Việt Đức Hà Nội 2019) Trong hệ trục tọa độ Oxyz, cho điểm

 

2;1;1

H

. Gọi các điểm

, ,A B C

lần lượt ở trên các trục tọa độ

, ,Ox Oy Oz

sao cho

H

là trực tâm của tam giác

ABC

. Khi đó

hoành độ điểm

A

là:

A.

3

. B.

5

. C. 3. D. 5

Lời giải

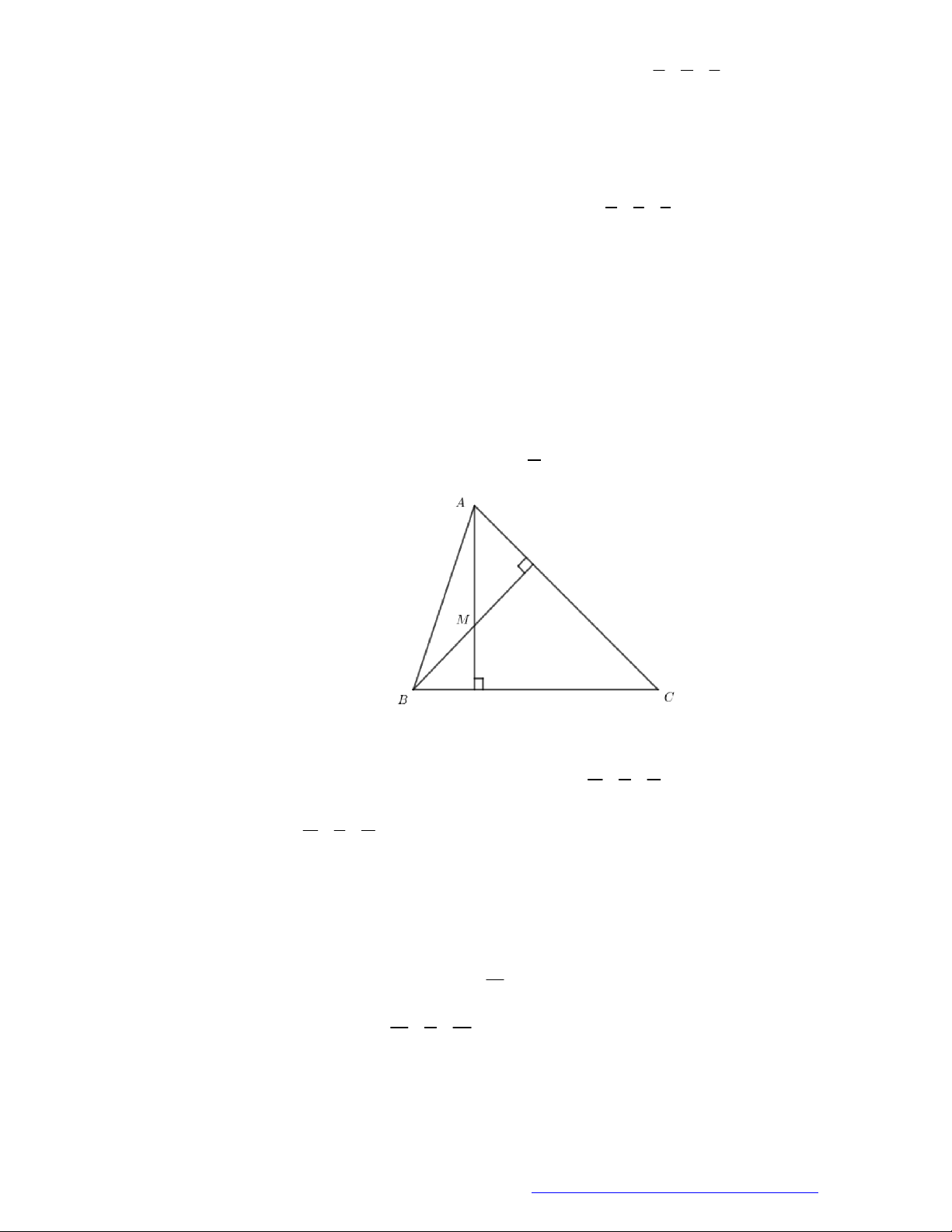
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13

Giả sử

     

;0;0 ; 0; ;0 ; 0;0;A a B b C c

. Khi đó mặt phẳng

 

: 1

x y z

ABC

a b c

  

Ta có:

   

2 ;1;1 ; 2;1 ;1

0; ; ; ;0;

AH a BH b

BC b c AC a c

   

 

Vì

H

là trực tâm của tam giác

ABC

nên

 

2 1 1

1

3

. 0 0 6

2 0 6

. 0

H ABC

a

a b c

AH BC b c b

a c c

BH AC



  













 

      

  

  

   









 

Vậy

 

3;0;0A

Câu 36. Trong không gian

Oxyz

, cho mặt phẳng

 



đi qua điểm

 

1;2;3M

và cắt các trục

,Ox

,Oy

Oz

lần lượt tại

,A

,B

C

(khác gốc tọa độ

O

) sao cho

M

là trực tâm tam giác

ABC

. Mặt phẳng

 



có phương trình dạng

14 0ax by cz   

. Tính tổng

T a b c  

.

A.

8

. B.

14

. C.

6T 

. D.

11

.

Lời giải

Mặt phẳng

 



cắt các trục

,Ox

,Oy

Oz

lần lượt tại

 

;0;0 ,A m

 

0; ;0 ,B n

 

0;0;C p

,

, , 0m n p 

. Ta có phương trình mặt phẳng

 



có dạng

1

x y z

m n p

  

.

Mà

 

1 2 3

1M

m n p



     .

 

1

Ta có

 

1 ;2;3 ,AM m 



 

1;2 ;3 ,BM n 



 

0; ; ,BC n p 



 

;0;AC m p 



.

M

là trực tâm tam giác

ABC

. 0 3 2 0

3 0

. 0

AM BC p n

p m

BM AC



  





 

 

 









 

.

 

2

Từ

 

1

và

 

2

suy ra:

14;m 

7;n 

14

3

p 

.

Suy ra

 



có phương trình

3

1 2 3 14 0

14 7 14

x y z

x y z       

.

Vậy

1 2 3 6T a b c      

.

Câu 37. (THPT Lương Thế Vinh Hà Nội 2019) Cho điểm

 

1;2;5M

. Mặt phẳng

 

P

đi qua điểm

M

cắt các trục tọa độ

, ,Ox Oy Oz

tại

,A ,B

C

sao cho

M

là trực tâm tam giác

ABC

. Phương trình

mặt phẳng

 

P

là

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 14 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

A.

8 0

x y z

   

. B.

2 5 30 0

x y z

   

. C.

0

5 2 1

x y z

  

. D.

1

5 2 1

x y z

  

.

Lời giải

Cách 1 :

Ta có tính chất hình học sau : tứ diện

OABC

có ba cạnh

, ,OA OB OC

đôi một vuông góc thì điểm

M

là trực tâm của tam giác

ABC

khi và chỉ khi

M

là hình chiếu vuông góc của điểm

O

lên mặt

phẳng

 

ABC

.

Do đó mặt phẳng

 

P

đi qua điểm

 

1;2;5

M

và có véc tơ pháp tuyến

 

1;2;5

OM



.

Phương trình mặt phẳng

 

P

là

     

1 2 2 5 5 0 2 5 30 0.

x y z x y z

          

Cách 2:

Giả sử

     

;0;0 ; 0; ;0 ; 0;0;A a B b C c

Khi đó phương trình mặt phẳng

 

P

có dạng

1

x y z

a b c

  

.

Theo giả thiết ta có

 

M P



nên

 

1 2 5

1 1

a b c

  

.

Ta có

       

1 ;2;5 ; 0; ; ; 1;2 ;5 ; ;0;AM a BC b c BM b AC a c

     

   

Mặt khác

M

là trực tâm tam giác

ABC

nên

 

. 0 2 5

2

5

. 0

AM BC b c

a c

BM AC



 







 









 

Từ

 

1

và

 

2

ta có

30; 15; 6

a b c

  

.

Phương trình mặt phẳng

 

P

là

1 2 5 30 0.

30 15 6

x y z

       

Câu 38. Trong không gian

Oxyz

, cho hai mặt phẳng

 

: 4 2 6 0

P x y z

   

,

 

: 2 4 6 0

Q x y z

   

.

Mặt phẳng

 



chứa giao tuyến của

   

,P Q

và cắt các trục tọa độ tại các điểm

, ,A B C

sao cho

hình chóp

.

O ABC

là hình chóp đều. Phương trình mặt phẳng

 



là

A.

6 0

x y z

   

. B.

6 0

x y z

   

. C.

3 0

x y z

   

. D.

6 0

x y z

   

.

Lời giải

Mặt phẳng

 

: 4 2 6 0

P x y z

   

có véctơ pháp tuyến

 

1;4; 2

P

n

 



.

Mặt phẳng

 

: 2 4 6 0

Q x y z

   

có véctơ pháp tuyến

 

1; 2;4

Q

n  



.

Ta có

 

; 12; 6; 6

P Q

n n

 

  

 

 

, cùng phương với

 

2; 1; 1

u

  



.

Gọi

   

d P Q

 

. Ta có đường thẳng

d

có véctơ chỉ phương là

 

2; 1; 1

u

  



và đi qua điểm

 

6;0;0

M

.

Mặt phẳng

 



cắt các trục tọa độ tại các điểm

 

;0;0

A a

,

 

0; ;0B b

,

 

0;0;C c

với

0

abc



.

Phương trình mặt phẳng

 

: 1

x y z

a b c



  

.

Mặt phẳng

 



có véctơ pháp tuyến

1 1 1

; ;

n

a b c

 



 

 



.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15

Mặt phẳng

 



chứa

d

 

n u

M



















 

 

2 1 1

6

0

1 1 1

6

1

3

a

a b c

b c

a





  





 

 

 

  

 









.

Ta lại có hình chóp

.

O ABC

là hình chóp đều

OA OB OC a b c     

6

b c

  

Kết hợp với điều kiện

 



ta được

6

b c

 

.

Vậy phương trình của mặt phẳng

 

: 1 6 0

6 6 6

x y z



       

.

Câu 39. (Chuyên Lê Quý Đôn Điện Biên 2019) Trong không gian với hệ tọa độ

Oxyz

cho mặt phẳng

 

P

đi qua điểm

 

9;1;1

M

cắt các tia

, ,Ox Oy Oz

tại

, ,A B C

(

, ,A B C

không trùng với gốc tọa độ ).

Thể tích tứ diện

OABC

đạt giá trị nhỏ nhất là bao nhiêu?

A.

81

2

. B.

243

2

. C.

81

6

. D.

243

.

Lời giải

Giả sử

     

;0;0 , 0; ;0 , 0;0;A a B b C c

với

, , 0

a b c



.

Mặt phẳng

 

P

có phương trình ( theo đoạn chắn):

1

x y z

a b c

  

.

Vì mặt phẳng

 

P

đi qua điểm

 

9;1;1

M

nên

9 1 1

1

a b c

  

.

Ta có

3

9 1 1 9

1 3 . . 243

. .

a b c

a b c a b c

     

.

1 243 81

. . .

6 6 2

OABC

V a b c  

Vậy thể tích tứ diện

OABC

đạt giá trị nhỏ nhất là

81

2

.

Câu 40. (Chuyên Nguyễn Trãi Hải Dương 2019) Trong không gian

Oxyz

cho các điểm

(2;0;0), (0;4;0), (0;0;6), (2;4;6)

A B C D

. Gọi

( )P

là mặt phẳng song song với mặt phẳng

( )ABC

,

( )P

cách đều

D

và mặt phẳng

( )ABC

. Phương trình của mặt phẳng

( )P

là

A.

6 3 2 24 0

x y z

   

. B.

6 3 2 12 0

x y z

   

.

C.

6 3 2 0

x y z

  

. D.

6 3 2 36 0

x y z

   

.

Lời giải

Chọn A

Phương trình mặt phẳng

( )ABC

là:

1 6 3 2 12 0

2 4 6

x y z

       

+

( )P

song song với mặt phẳng

( )ABC

nên

( )P

có dạng:

6 3 2 0 ( -12)

x y z D D

    

+

( ;( )) (( ),( )) ( ;( )) ( ,( ))d D P d ABC P d D P d A P  

36 12 24

D D D

      

.

Vậy

( )P

là:

6 3 2 24 0

x y z

   

.

Câu 41. (Kiểm tra năng lực - ĐH - Quốc Tế - 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho ba

điểm

 

;0;0

A a

,

 

0; ;0B b

,

 

0;0;C c

với

a

,

b

,

c

là ba số thực dương thay đổi, thỏa mãn điều

kiện:

1 1 1

2017

a b c

  

. Khi đó, mặt phẳng

 

ABC

luôn đi qua có một điểm có tọa độ cố định là

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 16 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

A.

1 1 1

; ;

3 3 3

 

 

 

. B.

 

1;1;1

.

C.

1 1 1

; ;

2017 2017 2017

 

 

 

. D.

 

2017;2017; 2017

.

Lời giải

Chọn C

Phương trình mặt phẳng

 

: 1

x y z

ABC

a b c

  

.

Dựa vào điều kiện, chọn

 

; ;M m m m

cố định nằm trên

 

ABC

.

Ta có:

 

1 1 1 1

1 .2017 1

2017

M ABC m m m

a b c

 

        

 

 

.

Vậy

1 1 1

; ;

2017 2017 2017

 

 

 

là điểm cố định.

Câu 42. Trong không gian

Oxyz

cho điểm

 

1;2;3

M

. Phương trình mặt phẳng

 

P

đi qua

M

cắt các trục

tọa độ

Ox

,

Oy

,

Oz

lần lượt tại

A

,

B

,

C

sao cho

M

là trọng tâm của tam giác

ABC

là

A.

 

: 6 3 2 18 0

P x y z

   

. B.

 

: 6 3 2 6 0

P x y z

   

.

C.

 

: 6 3 2 18 0

P x y z

   

. D.

 

: 6 3 2 6 0

P x y z

   

.

Lời giải

Chọn A

Gọi tọa độ các điểm

 

;0;0

A a Ox



,

 

0; ;0

B b Oy



và

 

0;0;

C c Oz



.

M

là trọng tâm của tam giác

ABC

nên ta có hệ sau:

3

3 6

9

3

M A B C

x x x x

a

y y y y b

c

y z z z

  





 

    

 

 



  



Do đó phương trình mặt phẳng

 

P

là

1 6 3 2 18 0

3 6 9

x y z

       

.

Câu 43. Cho điểm

 

1;2;5

M

. Mặt phẳng

 

P

đi qua

M

cắt các trục

, ,Ox Oy Oz

lần lượt tại

, ,A B C

sao

cho

M

là trực tâm tam giác

ABC

. Phương trình mặt phẳng

 

P

là

A.

8 0

x y z

   

. B.

2 5 30 0

x y z

   

.

C.

0

5 2 1

x y z

  

. D.

1

5 2 1

x y z

  

.

Lời giải

Chọn B

Cách 1: Gọi

     

;0;0 , 0; ;0 , 0;0;A a B b C c

. Phương trình mặt phẳng

 

P

là

1

x y z

a b c

  

.

Mặt phẳng

 

P

đi qua

M

nên

1 2 5

1(*)

a b c

  

.

Ta có

   

; ;0 , ;0;AB a b AC a c   

 

,

   

1;2 ;5 , 1;2;5

BM b CM c   

 

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17

Do

M

là trực tâm tam giác

ABC

nên

. 0

2

. 0

5

a

b

AB CM

a

AC BM

c

















 

 



 









 

.

Thay vào (*) ta có

1 4 25

1 30 15, 6

a b c

a a a

       

.

Phương trình mặt phẳng

 

P

là

1 2 5 30 0

30 15 6

x y z

       

.

Câu 44. Trong không gian

Oxyz

, cho điểm

 

1;2;5

M

. Số mặt phẳng

 



đi qua

M

và cắt các trục

, ,Ox Oy Oz

lần lượt tại

, ,A B C

mà

0

OA OB OC

  

là

A.

1.

B.

2.

C.

3.

D.

4.

Lời giải

Chọn D

Giả sử

     

;0;0 ,B 0;b;0 ,C 0;0;c

A a

với

0

abc



 

: 1

x y z

ABC

a b c

   

Mà

0

OA OB OC

  

b a

c a

 

 





 

 

 









Trường hợp 1:

;

b a c a 

 

: 1

x y z

ABC

a a a

   

mà

 

1 2 5

(1;2;5) 1 8

M ABC a

a a a

      

Trường hợp 2:

;

b a c a  

 

: 1

x y z

ABC

a a a

   

mà

 

1 2 5

(1;2;5) 1 2

M ABC a

a a a

       

Trường hợp 3:

;

b a c a  

 

: 1

x y z

ABC

a a a

   

mà

 

1 2 5

(1;2;5) 1 4

M ABC a

a a a

       

Trường hợp 4:

;

b a c a   

 

: 1

x y z

ABC

a a a

   

mà

 

1 2 5

(1;2;5) 1 6

M ABC a

a a a

       

Vậy có

4

mặt phẳng

 



Câu 45. Trong không gian

Oxyz

, cho điểm

 

1 1 2M ; ;

. Hỏi có bao nhiêu mặt phẳng

 

P

đi qua

M

và cắt

các trục

x'Ox,y'Oy,z'Oz

lần lượt tại các điểm

A,B,C

sao cho

0

OA OB OC

  

?

A.

3

B.

1

C.

4

D.

8

Lời giải

Chọn A

Mặt phẳng

 

P

đi qua

M

và cắt các trục

x'Ox,y'Oy,z'Oz

lần lượt tại các

điểm

     

0 0 0 0 0 0A a; ; ,B ;b; ,C ; ;c

. Khi đó phương trình mặt phẳng

 

P

có dạng:

1

x y z

a b c

  

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 18 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Theo bài mặt phẳng

 

P

đi qua

 

1 1 2M ; ;

và

OA OB OC 

nên ta có hệ:

 

1 1 2

1 1

2

a b c



  







 



. Ta có:

 

2

a b c

a c b

b c a

 





  







  



  



- Với

 a b c

thay vào

 

1

được

4  

a b c

- Với

  a b c

thay vào

 

1

được

0 1

.

- Với

  a c b

thay vào

 

1

được

2   

a c b

.

- Với

  b c a

thay vào

 

1

được

2   

b c a

.

Vậy có ba mặt phẳng thỏa mãn bài toán là:

     

1 2 3

1 1 1

4 4 4 2 2 2 2 2 2

x y z x y z x y z

P : ; P : ; P :

        

 

Câu 46. Trong không gian với hệ tọa độ

Oxyz

, có bao nhiêu mặt phẳng qua

 

2;1;3

M

,

 

0;0;4

A

và cắt

hai trục

Ox

,

Oy

lần lượt tại

B

,

C

khác

O

thỏa mãn diện tích tam giác

OBC

bằng

1

?

A.

0

. B.

3

. C.

2

. D.

4

.

Lời giải

Chọn C

Gọi

 

;0;0

B a

,

 

0; ;0C b

lần lượt là giao điểm của

 

P

với các trục

,Ox Oy

.

Phương trình mặt phẳng

 

: 1

4

x y z

P

a b

  

.

Vì

 

2;1;3

M

thuộc

 

P

nên ta có

2 1 3

1

4a b

  

2 1 1

4 8

4

a b ab

a b

     

.

Diện tích tam giác

1 1 1

. . 1

2 2 2

OBC

S OB OC a b ab



   

2

ab

 

Xét hệ phương trình

 

4 8

,

2

a b ab

I

ab

 









4 8 2 2 4 1

2 2 4

a b a b

ab ab

   

 

 

 

 

 

 

2

2 1 4

1 4 4

4 4 0,

a b

b b

b b vn

 



 

 

 

 

  





. Hệ vô nghiệm.

Xét hệ phương trình

4 8

2

a b ab

ab

 





 



4 8 2 2 4 1

2 2 4

a b a b

ab ab

     

 

 

 

   

 

 

2

2 1 4

1 4 4

4 4 0

a b

b b

  





 

 

   

  





. Hệ có hai

nghiệm.

Vậy có hai mặt phẳng thỏa yêu cầu bài toán.

Câu 47. (Đồng Tháp - 2018) Trong không gian với hệ trục tọa độ

Oxyz

, cho điểm

 

3;2;1

M

. Mặt phẳng

 

P

qua

M

và cắt các trục

Ox

,

Oy

,

Oz

lần lượt tại

A

,

B

,

C

sao cho

M

là trực tâm tam giác

ABC

. Phương trình mặt phẳng

 

P

là

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19

A.

6 0

x y z

   

. B.

0

3 2 1

x y z

  

.

C.

1

3 2 1

x y z

  

. D.

3 2 14 0

x y z

   

.

Lời giải

Giả sử

     

A ;0;0 , 0; ;0 , 0;0;a B b C c

, khi đó phương trình mặt phẳng

 

: 1

x y z

ABC

a b c

  

.

Ta có

   

0; ; , ;0;BC b c CA a c   

 

và

   

3 ;2;1 , 3;2 ;1AM a BM b

   

 

.

Vì

M

là trực tâm tam giác

ABC

nên ta có hệ

. 0

AM BC

BM CA















 

2 0

3a 0

b c

c

  







 



2

3a

c b

c













.

Hơn nữa vì

M

thuộc

 

ABC

nên

3 2 1

1

a b c

  

3 2 1

1

3a

2

a

   

14

3

a

 

.

Ta được

14

a

3



,

7

b



,

14

c



hay

 

:ABC

1

14

7 14

3

x y z

  

.

Ta chọn

 

:ABC

3 2 14 0

x y z

   

.

Câu 48. (Chuyên Trần Phú - Hải Phòng - 2018) Trong không gian với hệ tọa độ

Oxyz

, viết phương

trình mặt phẳng

 

P

chứa điểm

 

1;3; 2

M



, cắt các tia

Ox

,

Oy

,

Oz

lần lượt tại

A

,

B

,

C

sao

cho

1 2 4

OA OB OC

 

.

A.

2 1 0

x y z

   

. B.

2 4 1 0

x y z

   

. C.

4 2 1 0

x y z

   

. D.

4 2 8 0

x y z

   

.

Lời giải

Phương trình mặt chắn cắt tia

Ox

tại

 

;0;0

A a

, cắt tia

Oy

tại

 

0; ;0B b

, cắt tia

Oz

tại

 

0;0;C c

có dạng là

 

P

:

1

x y z

a b c

  

(với

0

a



,

0

b



,

0

c



).

Theo đề:

1 2 4

OA OB OC

 

1 2 4

a b c

  

2

b

a

c b

















.

Vì

 

1;3; 2

M



nằm trên mặt phẳng

 

P

nên ta có:

1 3 2

1

2

b

b b



  

4

1

b

 

4

b

 

.

Khi đó

2

a



,

8

c



.

Vậy phương trình mặt phẳng

 

P

là:

1

2 4 8

x y z

  

4 2 8 0

x y z

    

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 20 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 49. (Sở Nam Định - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho mặt cầu

   

2 2 2

: 2 2 3 0

S x y z x y z

     

. Gọi

, ,A B C

lần lượt là giao điểm (khác gốc tọa độ

O

) của

mặt cầu

 

S

và các trục

Ox

,

Oy

,

Oz

. Phương trình mặt phẳng

 

ABC

là:

A.

6 3 2 12 0

x y z

   

. B.

9 3 2 12 0

x y z

   

.

C.

6 3 2 12 0

x y z

   

. D.

6 3 2 12 0

x y z

   

.

Lời giải

Giả sử

     

;0;0 , 0; ;0 , 0;0;

A a Ox B b Oy C c Oz

  

. Theo giả thiết ta có

, , 0

a b c



.

Vì

 

A S



nên ta có:

0

2

2 0 2

a

a a a



   

. Vậy

 

2;0;0

A

.

Vì

 

B S



nên ta có:

0

2

4 0 4

b

b a b



   

. Vậy

 

0;4;0

B

.

Vì

 

C S



nên ta có:

0

2

6 0 6

c

c c c



   

. Vậy

 

0;0;6

C

.

Khi đó phương trình mặt phẳng

 

ABC

là:

1 6 3 2 12 0

2 4 6

x y z

       

.

Câu 50. (THPT Thực Hành - TPHCM - 2018) Trong không gian tọa độ

Oxyz

, cho mặt phẳng

 



đi

qua

 

1; 3; 8

M 

và chắn trên

Oz

một đoạn dài gấp đôi các đoạn chắn trên các tia

Ox

,

Oy

. Giả sử

 

: 0

ax by cz d



   

(

,a

,b

,c

d

là các số nguyên). Tính

a b c

S

d

 



.

A.

3

. B.

3

. C.

5

4

. D.

5

4



.

Lời giải

Giả sử mặt phẳng

 



cắt các tia

,Ox

,Oy

Oz

lần lượt tại

 

; 0; 0

A m

,

 

0; ; 0B n

,

 

0; 0;C p

(với

, , 0

m n p



)

Theo giả thiết có

2 2OC OA OB 

 

2 2 1

p m n  

.

Phương trình mặt phẳng

 



có dạng

1

x y z

m n p

  

.

Do mặt phẳng

 



đi qua

 

1; 3; 8

M 

nên

 

1 3 8

1 2

m n p

  

Thay

 

1

vào

 

2

ta được

1 3 8

1

2m m m

  

2

1

m

 

2

m

 

2, 4

m n p

   

Phương trình mặt phẳng

 



có dạng

1

2 2 4

x y z

  

2 2 4 0

x y z

    

Từ đó suy ra

 

2 , 2 , , 4 0

a t b t c t d t t

     

Vậy

5

4

a b c

S

d

 

  

.

Dạng 1.3 Phương trình mặt phẳng qua 3 điểm

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21

Câu 51. (THCS - THPT Nguyễn Khuyến 2019) Trong không gian

Oxyz

, gọi

M

,

N

,

P

lần lượt là

hình chiếu vuông góc của

 

2; 3;1

A 

lên các mặt phẳng tọa độ. Phương trình mặt phẳng

 

MNP

là

A.

1

2 3 1

x y z

  

. B.

3 2 6 6

x y z

  

.

C.

0

2 3 1

x y z

  

. D.

3 2 6 12 0

x y z

   

.

Lời giải

Không mất tính tổng quát, ta giả sử

M

,

N

,

P

lần lượt là hình chiếu vuông góc của

 

2; 3;1

A 

lên các mặt phẳng tọa độ

 

Oxy

,

 

Oxz

,

 

Oyz

.

Khi đó,

 

2; 3;0

M 

,

 

2;0;1

N

và

 

0; 3;1

P 

 

0;3;1

MN 



và

 

2;0;1

MP  



.

Ta có,

MN



và

MP



là cặp vectơ không cùng phương và có giá nằm trong

 

MNP

Do đó,

 

MNP

có một vectơ pháp tuyến là

 

, 3; 2;6

n MN MP

 

  

 

  

.

Mặt khác,

 

MNP

đi qua

 

2; 3;0

M 

nên có phương trình là:

     

3 2 2 3 6 0 0 3 2 6 12 0

x y z x y z

          

.

Câu 52. (Chuyên KHTN 2019) Trong không gian

Oxyz

, cho các điểm

   

1;2;1 , 2; 1;4

A B 

và

 

1;1;4

C

. Đường thẳng nào dưới đây vuông góc với mặt phẳng

 

ABC

?

A.

1 1 2

x y z

 



. B.

2 1 1

x y z

 

. C.

1 1 2

x y z

 

. D.

2 1 1

x y z

 



.

Lời giải

Ta có

   

3; 3;3 ; 2; 1;3

AB AC   

 

.

Suy ra

 

; 6; 3;3

AB AC

 

  

 

 

.

Đường thẳng vuông góc với mặt phẳng

 

ABC

có vecto chỉ phương

u



vuông góc với

;AB AC

 

nên

u



cùng phương với

,

AB AC

 

 

 

do đó chọn

(2;1; 1)

u





.

Câu 53. (THPT Nghĩa Hưng NĐ-2019) Trong không gian với hệ tọa độ

Oxyz

, cho ba điểm

     

0;1;2 ,B 2; 2;1 , 2;1;0

A C 

. Khi đó, phương trình mặt phẳng

 

ABC

là

0

ax y z d

   

.

Hãy xác định

a

và

d

.

A.

1, 1a d 

. B.

6, 6

a d

  

. C.

1, 6

a d

   

. D.

6, 6

a d

  

.

Lời giải

Ta có:

 

2; 3; 1

AB

  



;

 

2;0; 2

AC

  



.

 

3 1 1 2 2 3

, ; ; 6;6; 6

0 2 2 2 2 0

AB AC

     

 

  

 

 

   

 

 

.

Chọn

 

1

; 1;1; 1

6

n AB AC

 

  

 

  

là một VTPT của

 

mp ABC

. Ta có pt

 

mp ABC

là:

1 2 0 1 0

x y z x y z

         

. Vậy

1, 1a d 

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 22 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 54. (Lý Nhân Tông - Bắc Ninh 2019) Trong không gian

Oxyz

, cho điểm

 

3;5;2

A

, phương trình

nào dưới đây là phương trình mặt phẳng đi qua các điểm là hình chiếu của điểm

A

trên các mặt

phẳng tọa độ?

A.

3 5 2 60 0

x y z

   

. B.

10 6 15 60 0

x y z

   

.

C.

10 6 15 90 0

x y z

   

. D.

1

3 5 2

x y z

  

.

Lời giải

Chọn B

Gọi

1 2 3

, ,A A A

lần lượt là hình chiếu của điểm

A

lên các mặt phẳng

     

, ,

Oxy Oyz Oxz

.

Ta có

     

1 2 3

3;5;0 , 0;5;2 , 3;0;2

A A A

.

   

1 2 1 3

3;0;2 , 0; 5;2

A A A A   

 

.

Mặt phẳng qua

1

A

có vectơ pháp tuyến

 

1 2 1 3

, 10;6;15

n A A A A

 

 

 

  

có phương trình là

10 6 15 60 0

x y z

   

.

Câu 55. (Thi thử cụm Vũng Tàu - 2019) Trong không gian

Oxyz

, cho ba

điểm

 

3; 2; 2

A

 

,

 

3;2;0

B

,

 

0;2;1

C

. Phương trình mặt phẳng

 

ABC

là

A.

2 3 6 12 0

x y z

   

. B.

2 3 6 12 0

x y z

   

.

C.

2 3 6 0

x y z

  

. D.

2 3 6 12 0

x y z

   

.

Lời giải

Chọn C

Cách 1:

Ta có:

 

0;4;2

AB 



,

 

3;4;3

AC  



,

 

; 4; 6;12

 

  

 

 



n AB AC

.

Ta có

 

4; 6;12

n  



cùng phương

 

1

2; 3;6

n  



Mặt phẳng

 

ABC

đi qua điểm

 

0;2;1

C

và có một vectơ pháp tuyến

 

1

2; 3;6

n  



nên

 

ABC

có phương trình là:

     

2 0 3 2 6 1 0

x y z

     

2 3 6 0

x y z

   

.

Vậy phương trình mặt phẳng cần tìm là:

2 3 6 0

x y z

  

.

Cách 2:

Vì phương trình mặt phẳng

 

ABC

đi qua 3 điểm A, B, C nên thay tọa độ điểm

 

0;2;1

C

lần

lượt vào các đáp án. Loại đáp án A, B, D. Còn lại đáp án C thỏa.

Vậy phương trình mặt phẳng cần tìm là:

2 3 6 0

x y z

  

.

Câu 56. Trong không gian với hệ tọa độ

Oxyz

, mặt phẳng đi qua 3 điểm

 

1;2;3

A

,

 

4;5;6

B

,

 

1;0;2

C

có phương trình là

A.

2 5 0

x y z

   

. B.

2 3 4 0

x y z

   

.

C.

3 3 0

x y z

  

. D.

2 3 0

x y z

   

.

Lời giải

Chọn D

Ta có:

 

3;3;3

AB 



,

 

0; 2; 1

AC

  



TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23

Mặt phẳng đi qua 3 điểm

 

1;2;3

A

,

 

4;5;6

B

,

 

0;1;2

C

nhận

 

3;3; 6

,

AB AC

n

 

 



 

  

làm

véctơ pháp tuyến.

Nên phương trình mặt phẳng đi qua 3 điểm

 

1;2;3

A

,

 

4;5;6

B

,

 

1;0;2

C

có phương trình là

3 3 6 9 0

x y z

   

hay

2 3 0

x y z

   

Câu 57. (SGD - Bình Dương - 2018) Trong không gian với hệ tọa độ

Oxyz

, mặt phẳng đi qua ba điểm

 

2; 3; 5

A

,

 

3; 2; 4

B

và

 

4; 1; 2

C

có phương trình là

A.

5 0

x y

  

. B.

5 0

x y

  

. C.

2 0

y z

  

. D.

2 7 0

x y

  

.

Lời giải

Vì

AB



;

AC



 

ABC



nên

 

ABC

sẽ nhận

,

n AB AC

 



 

  

làm một vectơ pháp tuyến.

Ta có

 

1; 1; 1

AB

  



,

 

2; 2; 3

AC

  



suy ra

 

, 1; 1; 0

n AB AC

 

 

 

  

.

Hiển nhiên

 

ABC

đi qua

 

2; 3; 5

A

nên ta có phương trình của

 

ABC

là

     

1 2 1 3 0 5 0

x y z

     

5 0

x y

   

.

Câu 58. (Lê Quý Đôn - Hải Phòng - 2018) Trong không gian với hệ tọa độ

Oxyz

, viết phương trình mặt

phẳng đi qua ba điểm

 

1;1;4

A

,

 

2;7;9

B

,

 

0;9;13

C

.

A.

2 1 0

x y z

   

. B.

4 0

x y z

   

. C.

7 2 9 0

x y z

   

. D.

2 2 0

x y z

   

.

Lời giải

Ta có

 

1;6;5

AB 



,

 

1;8;9

AC  



,

 

ABC

đi qua

 

1;1;4

A

có vtpt

,

n AB AC

 



 

 



 

14; 14;14

 

 

14 1; 1;1

 

có dạng

4 0

x y z

   

.

Câu 59. (SGD - Bình Dương - 2018) Trong không gian với hệ trục tọa độ

Oxyz

, cho bốn điểm

 

1;6;2

S 

,

 

0;0;6

A

,

 

0;3;0

B

,

 

2;0;0

C 

. Gọi

H

là chân đường cao vẽ từ

S

của tứ diện

.

S ABC

. Phương trình mặt phẳng đi qua ba điểm

S

,

B

,

H

là

A.

3 0

x y z

   

. B.

3 0

x y z

   

.

C.

5 7 15 0

x y z

   

. D.

7 5 4 15 0

x y z

   

.

Lời giải

Phương trình Mặt phẳng

 

: 1

2 3 6

x y z

ABC

  



3 2 6 0

x y z

     

.

H

là chân đường cao vẽ từ

S

của tứ diện

.

S ABC

nên

H

là hình chiếu vuông góc của

S

lên mặt

phẳng

 

ABC

19 31 17

; ;

14 7 14

H

 



 

 

Mặt phẳng

 

0;3;0

:

11 55 11 11

, ; ; 1;5; 7

14 14 2 14

qua B

SBH

vtpt BH SB







 

 

   

 



 

 



 

.

Phương trình Mặt phẳng

   

: 5 3 7 0

SBH x y z

   

5 7 15 0

x y z

    

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 24 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Dạng 2. Một số bài toán liên đến khoảng cách - góc

Dạng 2.1 Khoảng cách từ điểm đến mặt, khoảng cách giữa hai mặt

Khoảng cách từ một điểm đến mặt phẳng, khoảng cách giữa hai mặt phẳng song song



Khoảng cách từ điểm

( ; ; )

M M M

M x y z

đến mặt phẳng

( ) : 0

P ax by cz d

   

được xác định bởi

công thức:

2 2 2

( ;( ))

M M M

ax by cz d

d M P

a b c

  

 

 

Khoảng cách giữa đường thẳng và mặt phẳng song song là khoảng cách từ một điểm thuộc đường

thẳng đến mặt phẳng



Cho hai mặt phẳng song song

( ) : 0

P ax by cz d

   

và

( ) : 0

Q ax by cz d



   

có cùng véctơ

pháp tuyến, khoảng cách giữa hai mặt phẳng đó là

 

2 2 2

( ),( )

d d

d Q P

a b c





 

 

Viết phương trình

( ) ( ) : 0

P Q ax by cz d

   

và cách

( ; ; )M x y z

  

khoảng

.k

Phương pháp:



Vì

( ) ( ) : 0 ( ): 0.

P Q ax by cz d P ax by cz d



        



Sử dụng công thức khoảng cách

 

,( )

2 2 2

.

M P

ax by cz d

d k d

a b c



  



  

 

  

Viết phương trình mặt phẳng

( ) ( ) : 0

P Q ax by cz d

   

và

( )P

cách mặt phẳng

( )Q

một khoảng

k

cho trước.

Phương pháp:



Vì

( ) ( ) : 0 ( ): 0.

P Q ax by cz d P ax by cz d



        



Chọn một điểm

( ; ; ) ( )M x y z Q

  

và sử dụng công thức:

   

( );( ) ,( )

2 2 2

.

Q P M P

ax by cz d

d d k d

a b c



  



   

 

  

Viết phương trình mặt phẳng

( )P

vuông góc với hai mặt phẳng

( ), ( ),

 

đồng thời

( )P

cách điểm

( ; ; )M x y z

  

một khoảng bằng

k

cho trước.

Phương pháp:



Tìm

( ) ( )

, .n n

 

 

Từ đó suy ra

( ) ( ) ( )

, ( ; ; ).

P

n n n a b c

 

 

 

 

  



Khi đó phương trình

( )P

có dạng

( ) : 0,

P ax by cz d

   

(cần tìm

).d



Ta có:

 

;( )

2 2 2

.

M P

ax by cz d

d k k d

a b c

  

   

 

  

Câu 1. (Chuyên Hùng Vương Gia Lai 2019) Trong không gian

Oxyz

, điểm

M

thuộc trục

Oy

và cách

đều hai mặt phẳng:

 

: 1 0

P x y z

   

và

 

: 5 0

Q x y z

   

có tọa độ là

A.

 

0; 3;0

M 

. B.

 

0;3;0

M

. C.

 

0; 2;0

M 

. D.

 

0;1;0

M

.

Lời giải

Ta có

 

0; ;0M Oy M y

 

.

Theo giả thiết:

 

1 5

3

3 3

y y

d M P d M Q y

  

     

.

Vậy

 

0; 3;0

M 

Câu 2. Trong không gian với hệ trục tọa độ

Oxyz

, cho

(1; 2;3)

A

,

 

3;4;4

B

. Tìm tất cả các giá trị của

tham số

m

sao cho khoảng cách từ điểm

A

đến mặt phẳng

2 1 0   

x y mz

bằng độ dài đoạn

thẳng

AB

.

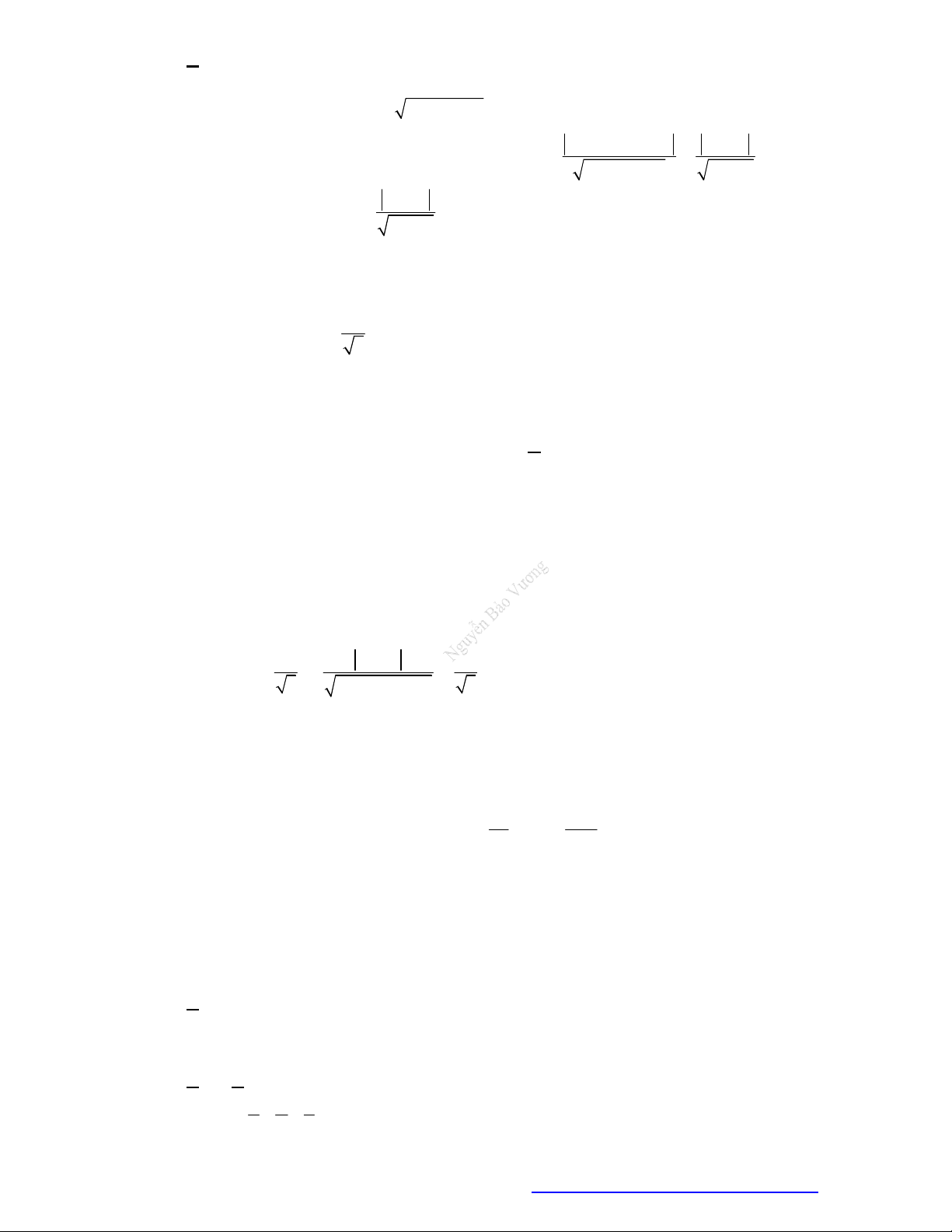
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25

A.

2

m

. B.

2 

m

. C.

3 

m

. D.

2 

m

.

Lời giải

Ta có

 

2;2;1





AB



 

2 2 2

2 2 1 3 1

   AB

.

Khoảng cách từ

A

đến mặt phẳng

 

P

:

 

2 2 2

2.1 2 .3 1

,

2 1

  



 

m

d A P

m

 

2

3 3

2

5

m







.

Để

 

2

3 3

, 3

5

m

AB d A P

m



  



 

2

9 5 9 1

m m

   

2

m

 

.

Câu 3. (Chuyên Trần Phú Hải Phòng 2019) Trong không gian

,Oxyz

cho 3 điểm

     

1;0;0 , 0; 2;3 , 1;1;1

A B C

. Gọi

 

P

là mặt phẳng chứa

, A B

sao cho khoảng cách từ

C

tới

mặt phẳng

 

P

bằng

2

3

. Phương trình mặt phẳng

 

P

là

A.

2 3 1 0

3 7 6 0

x y z



   



   



B.

2 1 0

2 3 6 13 0

x y z



   



    



C.

2 1 0

2 3 7 23 0

x y z



   



    



D.

1 0

23 37 17 23 0

x y z



   



    



Lời giải

Gọi

(1;0;0)

( ) :

( ; ; ) 0

qua A

P

VTPT n A B C









 





 

( ) : .( 1) 0

( ) : 2 3 0 2 3 (1)

P A x By Cz

B P A B C A B C

   

        

2 2 2 2 2

2 2 2

2 2

( ;( )) 3( 2 ) 4( )

3 3

6 4 0 (2)

B C

d C P B C BC A B C

A B C

B C BC A



        

 

    

Thay

(1)

vào

(2)

ta có:

2 2 2 2 2

6 4( 2 3 ) 0 17 54 37 0

B C BC B C B BC C

         

Cho

2

1 1

1: 17 54 37 0

37 23

17 17

B A

C B B

B A



  



    





  





( ) : 1 0

( ) : 23 37 17 23 0

P x y x

P x y z

   

    

Câu 4. Trong không gian

Oxyz

cho

       

2;0;0 , 0;4;0 , 0;0;6 , 2;4;6

A B C D

. Gọi

 

P

là mặt phẳng

song song với

 

mp ABC

,

 

P

cách đều

D

và mặt phẳng

 

ABC

. Phương trình của

 

P

là

A.

6 3 2 24 0

x y z

   

B.

6 3 2 12 0

x y z

   

C.

6 3 2 0

x y z

  

D.

6 3 2 36 0

x y z

   

Lời giải

Chọn A

 

: 1 6 3 2 12 0

2 4 6

x y z

ABC x y z

       

.

       

// : 6 3 2 0 12

P ABC P x y z m m      

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 26 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

 

P

cách đều

D

và mặt phẳng

   

 

, ,

ABC d D P d A P

 

2 2 2 2 2 2

36 12

6.2 3.4 2.6 6.2 3.0 2.0

36 12

6 3 2 6 3 2

m m

  

     



      



   

   



24

m

  

(nhận).

Vậy phương trình của

 

P

là

6 3 2 24 0

x y z

   

.

Câu 5. (Chuyên Phan Bội Châu Nghệ An 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho hai

điểm

 

1;2;3

A

,

 

5; 4; 1

B

 

và mặt phẳng

 

P

qua

Ox

sao cho

 

; 2 ;

d B P d A P



,

 

P

cắt

AB

tại

 

; ;I a b c

nằm giữa

AB

. Tính

a b c 

.

A.

12

. B.

6

. C.

4

. D.

8

.

Lời giải.

Vì

 

; 2 ;

d B P d A P



và

 

P

cắt đoạn

AB

tại

I

nên

 

7

5 2 1

3

2 4 2 2 0 4

5

1 2 3

3

a

a a

BI AI b b b a b c

c c

c





   



            

 

 

   



 



 

.

Câu 6. (Đề Tham Khảo 2019) Trong không gian

Oxyz

, Khoảng cách giữa hai mặt phẳng

 

: 2 2 10 0

P x y z

   

và

 

: 2 2 3 0

Q x y z

   

bằng:

A.

4

3

B.

8

3

. C.

7

3

. D.

3

.

Lời giải

Chọn C

Lấy

   

2;1;3

A P



.Do

 

P

song song với

 

Q

nên Ta có

   

 

2 2 2

2 2.1 2.3 3

7

, ,

3

1 2 2

d P Q d A Q

  

  

 

Câu 7. (Sở Thanh Hóa 2019) Trong không gian

Oxyz

cho hai mặt phẳng song song

 

P

và

 

Q

lần

lượt có phương trình

2 0

x y z

  

và

2 7 0

x y z

   

. Khoảng cách giữa hai mặt phẳng

 

P

và

 

Q

bằng

A.

7

. B.

7 6

. C.

6 7

. D.

7

6

.

Lời giải

Mặt phẳng

 

P

đi qua điểm

 

0;0;0

O

.

Do mặt phẳng

 

P

song song mặt phẳng

 

Q

nên khoảng cách giữa hai mặt phẳng

 

P

và

 

Q

bằng:

   

 

7

, ,

6 6

d P Q d O Q



   

Câu 8. Trong không gian

Oxyz

, khoảng cách giữa hai mặt phẳng

 

: 2 2 8 0

P x y z

   

và

 

: 2 2 4 0

Q x y z

   

bằng

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27

A. 1. B.

4

3

. C. 2. D.

7

3

.

Lời giải

Ta có

   

 

2 2 2

/ /

8 2.0 2.0 4

4

; ; .

3

8;0;0

1 2 2

P Q

d P Q d A Q

A P



  



   





 





Nhận xét:

Nếu mặt phẳng

 

:

P ax by cz d  

và

 

: 'Q ax by cz d  

 

2 2 2

0

a b c

  

song song với

nhau

 

'd d



thì

   

 

2 2 2

'

; .

d d

d P Q

a b c





 

.

Câu 9. Trong không gian

Oxyz

, khoảng cách giữa hai mặt phẳng

 

: 2 2 16 0

P x y z

   

và

 

: 2 2 1 0

Q x y z

   

bằng

A. 5. B.

17

.

3

C. 6. D.

5

3

.

Lời giải

Ta có

   

 

2 2 2

/ /

16 2.0 2.0 1

; ; 5.

16;0;0

1 2 2

P Q

d P Q d A Q

A P



  



   





 





Câu 10. (Chuyên Lam Sơn Thanh Hóa 2019) Trong không gian

Oxyz

khoảng cách giữa hai mặt phẳng

 

: 2 3 1 0

P x y z

   

và

 

: 2 3 6 0

Q x y z

   

là

A.

7

14

B.

8

14

C.

14

D.

5

14

Lời giải

 

: 2 3 1 0

P x y z

   

 

: 2 3 6 0

Q x y z

   

. Ta có:

1 2 3 1

1 2 3 6



  

Các giải trắc nghiệm:

Công thức tính nhanh:

   

1 2

: 0; 0

P Ax By Cz D Q Ax By Cz D

       

d

   

 

;

P Q

=

2 1

2 2 2

D D

A B C



 

 

P

//

 

Q

áp dụng công thức: d

   

 

;

P Q

2 2 2

1 6

14

2

1 2 3

 

 

 

.

Câu 11. Trong không gian

Oxyz

, khoảng cách giữa hai mặt phẳng

 

: 6 3 2 1 0

P x y z

   

và

 

1 1

: 8 0

2 3

Q x y z

   

bằng

A.

7

. B.

8

. C.

9

. D.

6

.

Lời giải

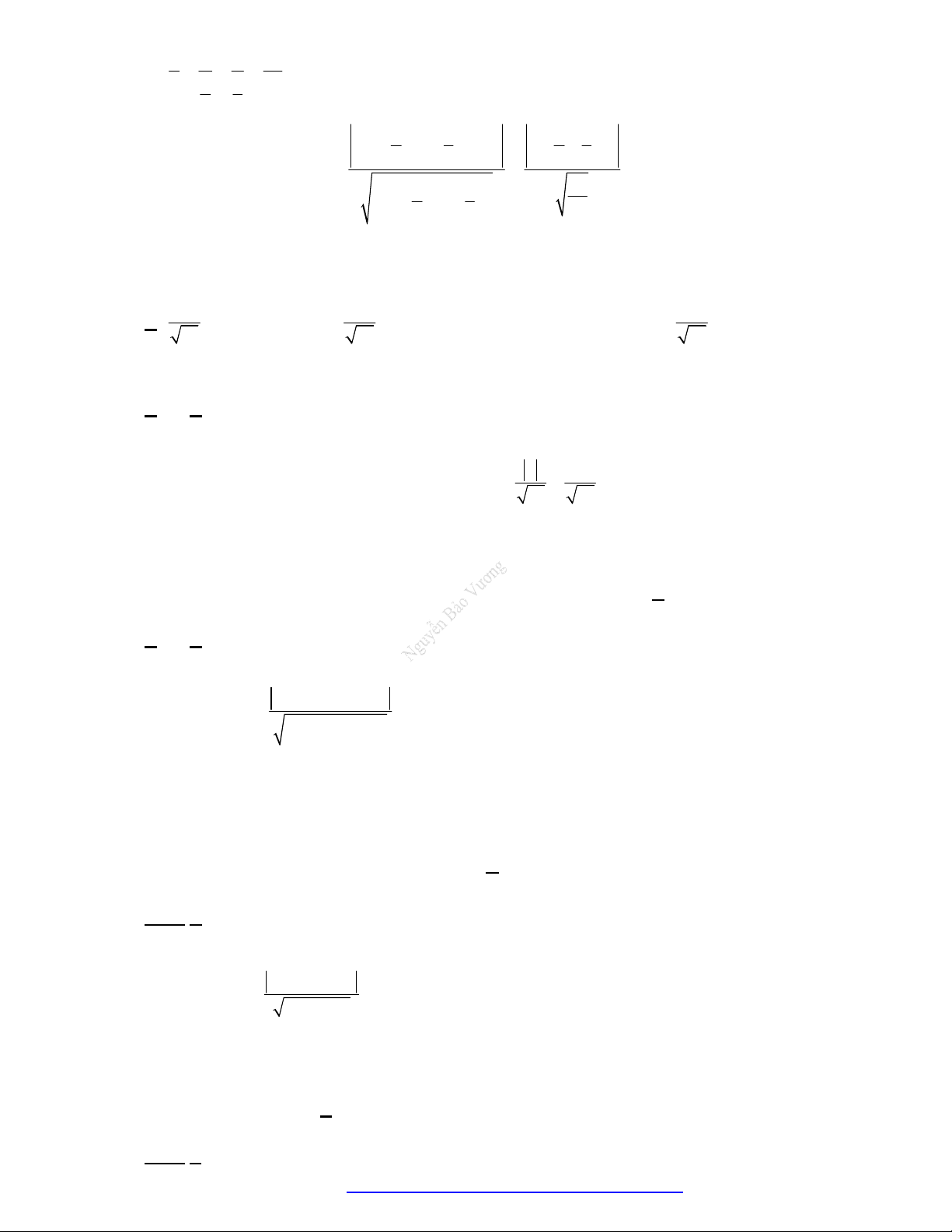
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 28 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Vì

6 3 2 1

1 1

1 8

2 3



   

   

//

P Q

nên

   

 

; ;

d P Q d M Q



với

   

0;1; 1

M P

 

   

 

2 2

2

1 1 1 1

8 0 8

2 3 2 3

; ; 7

49

1 1

1

36

2 3

M M M

x y z

d P Q d M Q

     

   

   

 

   

   

.

Câu 12. (Chuyên Lam Sơn-2019) Trong không gian

Oxyz

khoảng cách giữa hai mặt phẳng

 

: 2 3 1 0

P x y z

   

và

 

: 2 3 6 0

Q x y z

   

là:

A.

7

14

. B.

8

14

. C.

14

. D.

5

14

.

Lời giải

Chọn A

Có

       

 

/ / , ,

P Q d P Q d A Q

 

với

A

bất kì thuộc

 

P

.

Chọn

   

1;0;0

A P



có

   

 

7

, ,

14 14

d P Q d A Q  

.

Câu 13. (Chuyên Bắc Giang 2019) Trong không gian với hệ tọa độ

Oxyz

, tính khoảng cách giữa hai mặt

phẳng song song

 

: 2 2 4 0

x y z



   

và

 

: 2 2 7 0

x y z



    

.

A.

0

. B.

3

. C.

1

. D.

1

.

Lời giải

Chọn D

Ta có

   

0;1;1M





, khoảng cách giữa hai mặt phẳng

   

,

 

là:

 

2

2 2

0 2.1 2.1 7

, 1

1 2 2

h d M



   

  

  

.

Câu 14. (THPT Đông Sơn 1 - Thanh Hóa 2019) Trong không gian với hệ tọa độ

,Oxyz

cho mặt cầu

 

2 2 2

: 2 2 2 22 0

S x y z x y z

      

và mặt phẳng

 

:3 2 6 14 0.

P x y z

   

Khoảng cách từ

tâm

I

của mặt cầu

 

S

đến mặt phẳng

 

P

bằng

A. 2. B. 4. C. 3. D. 1.

Lời giải

Chọn C

Mặt cầu

 

S

có tâm

 

1;1;1 .

I

Vậy

 

3 2 6 14

, 3.

9 4 36

d I P

  

 

 

.

Câu 15. (SGD Bến Tre 2019) Trong không gian

Oxyz

cho hai mặt phẳng

 

: 2 2 9 0

P x y z

   

và

 

: 4 2 4 6 0.

Q x y z

   

Khoảng cách giữa hai mặt phẳng

 

P

và

 

Q

bằng

A.

0

. B.

2

. C.

1

. D.

3

.

Lời giải

Chọn B

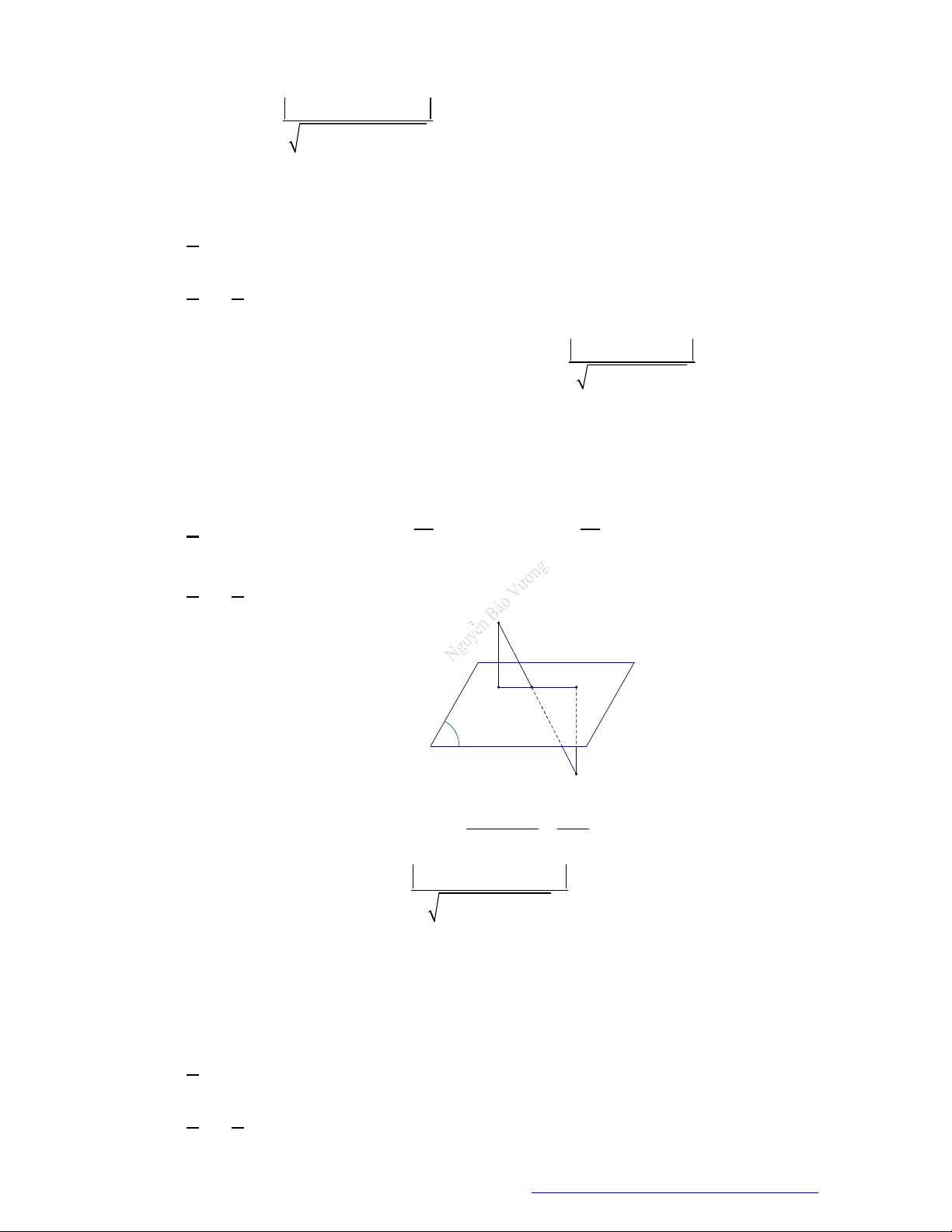
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 29

Trong mặt phẳng

 

P

ta chọn điểm

 

0; 9;0M 

. Tính khoảng cách từ

M

đến

 

Q

ta có:

 

   

2 2

2

4.0 2.( 9) 4.0 6

, 2

4 2 4

d M Q

   

 

   

. Vậy

   

 

, , 2d P Q d M Q 

.

Câu 16. (SP Đồng Nai - 2019) Trong không gian

Oxyz

, cho hai mặt phẳng

( ) : 2 2 6 0P x y z   

và

( ) : 2 2 3 0Q x y z   

. Khoảng cách giữa hai mặt phẳng

( )P

và

( )Q

bằng

A.

3

. B.

1

. C.

9

. D.

6

.

Lời giải

Chọn A

Nhận xét hai mặt phẳng

( )P

và

( )Q

song song với nhau.

Lấy

(6;0;0) ( )M P

ta có

   

2 2 2

1.6 2.0 2.0 3

( );( ) ;( ) 3

1 2 ( 2)

d P Q d M Q

  

  

  

.

Câu 17. (Đà Nẵng 2019) Trong không gian

Oxyz

, cho mặt phẳng

 

:3 4 12 5 0P x y z   

và điểm

 

2;4; 1A 

. Trên mặt phẳng

 

P

lấy điểm

M

. Gọi

B

là điểm sao cho

3.AB AM

 

. Tính khoảng

cách

d

từ

B

đến mặt phẳng

 

P

.

A.

6d 

. B.

30

13

d 

. C.

66

13

d 

. D.

9d 

.

Lời giải

Chọn A

Ta có:

3. 2.AB AM BM AM  

 



 

,

2

,

d B P

BM

AM

d A P

 

 

2

2 2

3.2 4.4 12. 1 5

, 2. , 2. 2.3 6

3 4 12

d B P d A P

   

    

  

.

Câu 18. (Chu Văn An - Hà Nội - 2019) Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

 

: 2 2 1 0P x y z   

. Mặt phẳng nào sau đây song song với

 

P

và cách

 

P

một khoảng bằng

3?

A.

 

: 2 2 10 0Q x y z   

. B.

 

: 2 2 4 0Q x y z   

.

C.

 

: 2 2 8 0Q x y z   

. D.

 

: 2 2 8 0Q x y z   

.

Lời giải

Chọn C

Mặt phẳng

 

P

đi qua điểm

 

0;0; 1M 

và có một vectơ pháp tuyến

 

2;2; 1n  



.

(P)

M

H

K

B

A

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 30 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Mặt phẳng

 

Q

song song với

 

P

và cách

 

P

một khoảng bằng 3 nên có dạng

   

: 2 2 0, 1

Q x y z d d

     

.

Mặt khác ta có

 

8

1

, 3 3 1 9

10

4 4 1

d

d M Q d

d







      



 

 



(thỏa mãn).

Do đó

 

: 2 2 8 0

Q x y z

   

hoặc

 

: 2 2 10 0

Q x y z

   

.

Câu 19. (SGD Bến Tre 2019) Tìm trên trục

Oz

điểm

M

cách đều điểm

 

2;3;4

A

và mặt

phẳng

 

: 2 3 17 0

P x y z

   

.

A.

 

0;0; 3

M



. B.

 

0;0;3

M

. C.

 

0;0; 4

M



. D.

 

0;0;4

M

.

Lời giải

Chọn B

Vì

M Oz



 

0;0;M m

. Ta có:

 

2

2 2

2 3 4

MA m

   

;

 

17

,

14

m

d M P





.

M

cách đều điểm

 

2;3;4

A

và mặt phẳng

 

: 2 3 17 0

P x y z

   

khi và chỉ khi

   

2 2

17

2 3 4 13 3 0 3

14

m

m m m



        

. Vậy

 

0;0;3

M

.

Câu 20. (SGD Bắc Ninh 2019) Trong mặt phẳng với hệ tọa độ

Oxyz

, cho hai điểm

   

1;2;1 , 3;4;0

A B

,

mặt phẳng

 

: 46 0

P ax by cz

   

. Biết rằng khoảng cách từ

,A B

đến mặt phẳng

 

P

lần lượt

bằng

6

và

3

. giá trị của biểu thức

T a b c  

bằng

A.

3

. B.

6

. C.

3

. D.

6

.

Lời giải

Chọn B

Ta có

3 (B,( ))AB d P 

suy ra

,A B

nằm cùng phía đối với mặt phẳng

 

P

.

Gọi

,H K

lần lượt là hình chiếu của

,A B

xuống mặt phẳng

 

P

.

Ta có

6 6

AH BK AK AH

    

. Do đó

, , ,A B H K

thẳng hàng.

Từ đó suy ra

( )AB P

và B là trung điểm của AH nên

(5;6; 1)

H



,

(2;2; 1)

AB





.

Phương trình mặt phẳng

 

: 2( 5) 2( 6) 1( 1) 0 2 2 23 0 4 4 2 46 0

P x y z x y z x y z

                

.

Vậy

6

a b c

   

.

Câu 21. (Chuyên Quang Trung- Bình Phước 2019) Trong không gian

Oxyz

, cho mặt phẳng

 

: 2 2 10 0

P x y z

   

. Phương trình mặt phẳng

 

Q

với

 

Q

song song với

 

P

và khoảng

cách giữa hai mặt phẳng

 

P

và

 

Q

bằng

7

3

là.

A.

2 2 3 0; 2 2 17 0

x y z x y z

       

B.

2 2 3 0; 2 2 17 0

x y z x y z

       

C.

2 2 3 0; 2 2 17 0

x y z x y z

       

D.

2 2 3 0; 2 2 17 0

x y z x y z

       

Lời giải

Chọn D

Vì

 

Q

song song với

 

P

nên phương trình mặt phẳng

 

Q

có dạng

 

: 2 2 0

Q x y z c

   

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 31

Lấy

     

 

7

0;0;5 ,

3

M P M d M Q

   

. Khi đó ta có

 

2 2 2

10 7 3

2.5

7

,

10 7 17

3

1 2 2

c c

c

d M Q

c c

 

   



 

   

 

    

 

 

Vậy ta có các mặt phẳng

 

Q

là

   

: 2 2 3 0; : 2 2 17 0

Q x y z Q x y z

       

Câu 22. (SGD Hưng Yên 2019) Trong không gian hệ toạ độ

Oxyz

, lập phương trình các mặt phẳng song

song với mặt phẳng

 

: 3 0

x y z



   

và cách

 



một khoảng bằng

3

.

A.

6 0

x y z

   

;

0

x y z

  

. B.

6 0

x y z

   

.

C.

6 0

x y z

   

;

0

x y z

  

. D.

6 0

x y z

   

;

0

x y z

  

.

Lời giải

Chọn A

Gọi mặt phẳng

 



cần tìm.

Vì

   

 

//

nên phương trình

 



có dạng :

0

x y z c

   

với

 

\ 3

c



.

Lấy điểm

   

1; 1;1I



  

.

Vì khoảng cách từ

 



đến

 



bằng

3

nên ta có :

 

1 1 1

, 3 3

3

c

d I



   

  

3

c 

 

0

6

c













. (thỏa điều kiện

 

\ 3

c



).

Vậy phương trình

 



là:

6 0

x y z

   

;

0

x y z

  

.

Câu 23. (THPT Hàm Rồng - Thanh Hóa - 2018) Trong hệ trục tọa độ

Oxyz

cho

3

điểm

 

4;2;1

A

,

 

0;0;3

B

,

 

2;0;1

C

. Viết phương trình mặt phẳng chứa

OC

và cách đều

2

điểm

,A B

.

A.

2 2 0  

x y z

hoặc

4 2 0

x y z

  

. B.

2 2 0  

x y z

hoặc

4 2 0

x y z

  

.

C.

2 2 0  

x y z

hoặc

4 2 0

x y z

  

. D.

2 2 0  

x y z

hoặc

4 2 0

x y z

  

.

Lời giải

Gọi

 

2 2 2

: 0 0

Ax By Cz D A B C



      

.

 

O





nên ta có:

0

D



 

1

 

C





nên ta có:

2 0

Ax By Cz A C

    

 

2

Từ

   

1 , 2 2C A  

.

Theo đề bài:

 

, ,d A d B

 



.

2 2 6A B A

   

 

2 *

2 6

4 **

B A

A B A

B A



 



 



  

 







Từ

 

* :

Chọn

1 2, 2

A B C

    

 

: 2 2 0

x y z



   

.

Từ

 

** :

Chọn

1 4, 2

A B C

     

 

: 4 2 0

x y z



   

.

Câu 24. (THPT Nguyễn Tất Thành - Yên Bái - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho tam

giác

ABC

có

(1;0;0), (0; 2;3), (1;1;1).

A B C



Phương trình mặt phẳng

 

P

chứa

,A B

sao cho

khoảng cách từ

C

tới

 

P

bằng

2

3

là

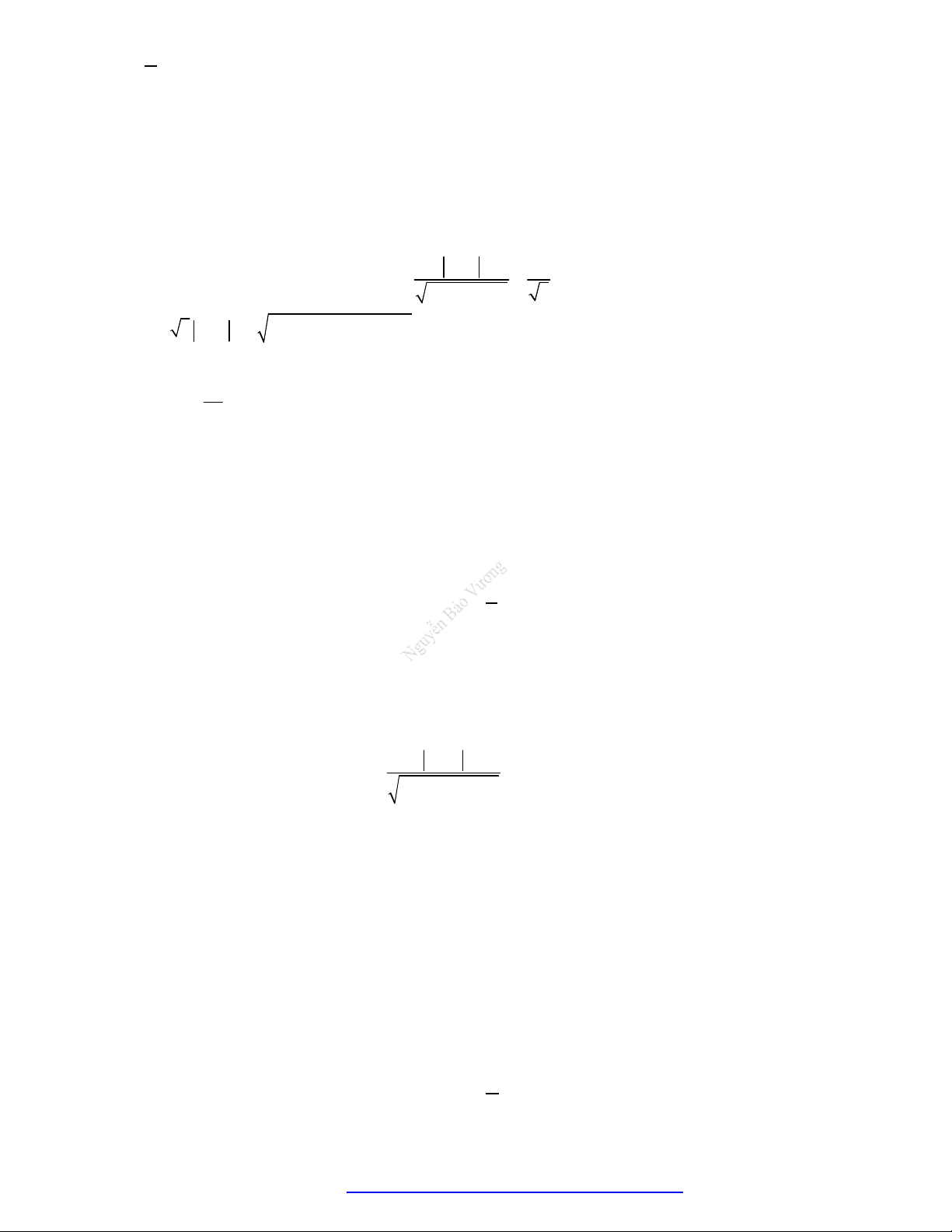
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 32 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

A.

1 0

x y z

   

hoặc

23 37 17z 23 0

x y

    

.

B.

2 1 0

x y z

   

hoặc

23 3 7 23 0.

x y z

    

C.

2 1 0

x y z

   

hoặc

13 3 6 13 0.

x y z

    

D.

2 3 1 0

x y z

   

hoặc

3 7 3 0.

x y z

   

Lời giải

Giả sử

 

; ;n a b c





là véc tơ pháp tuyến của mặt phẳng

 

P

.

Ta có

 

1; 2;3 2 3 0 2 3 .n AB a b c a b c            

 

 

2 2 2

2

:ax by cz a 0 ( ;( ))

3

b c

P d C P

a b c



      

 

.

 

2

2 2 2 2

3 2 2 3 17 54 37 0

b c b c b c b bc c

          

.

1

37

17, 37

17

b c

c b

b c





 





 



 





TH1:

1 1 ( ): x y z 1 0

b c a P

        

.

TH2:

37, 17 23 ( ) : 23x 37 y 17z 23 0

b c a P

          

.

Câu 25. (THPT Quang Trung Đống Đa Hà Nội 2019) Trong không gian với hệ tọa độ

Oxyz

, cho mặt

phẳng

 

: 2 2 5 0

P x y z

   

. Viết phương trình mặt phẳng

 

Q

song song với mặt phẳng

 

P

,

cách

 

P

một khoảng bằng 3 và cắt trục

Ox

tại điểm có hoành độ dương.

A.

 

: 2 2 4 0

Q x y z

   

. B.

 

: 2 2 14 0

Q x y z

   

.

C.

 

: 2 2 19 0

Q x y z

   

. D.

 

: 2 2 8 0

Q x y z

   

.

Lời giải

Ta có,

 

Q

song song

 

P

nên phương trình mặt phẳng

 

: 2 2 0

Q x y z C

   

;

5

C

 

Chọn

   

0;0;5

M P



Ta có

   

 

2

2 2

5

; ; 3

2 2 1

C

d P Q d M Q



  

  

4

14

C









 



 

4 : 2 2 4 0

C Q x y z

     

khi đó

 

Q

cắt

Ox

tại điểm

 

1

2;0;0

M 

có hoành độ âm nên

trường hợp này

 

Q

không thỏa đề bài.

 

14 : 2 2 14 0

C Q x y z

      

khi đó

 

Q

cắt

Ox

tại điểm

 

2

7;0;0

M

có hoành độ dương

do đó

 

: 2 2 14 0

Q x y z

   

thỏa đề bài.

Vậy phương trình mặt phẳng

 

: 2 2 14 0

Q x y z

   

.

Câu 26. (Chuyên Phan Bội Châu -2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho mặt phẳng

 

Q

:

2 2 3 0

x y z

   

, mặt phẳng

 

P

không qua

O

, song song với mặt phẳng

 

Q

và

   

 

, 1

d P Q



. Phương trình mặt phẳng

 

P

là

A.

2 2 1 0

x y z

   

B.

2 2 0

x y z

  

C.

2 2 6 0

x y z

   

D.

2 2 3 0

x y z

   

Lời giải

Vì mặt phẳng

 

P

song song với mặt phẳng

 

Q

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 33

 

1;2;2

P Q

vtptn vtptn  

 

Phương trình mặt phẳng

 

P

có dạng

2 2 0

x y z D

   

Gọi

   

3;0;0

A Q



   

 

,

, 1

d P Q d A P



3 3 0 ( ),

3

1

3 3 6 ( )

3

D D l quaO

D

D D n

  



 

   

 

    

 

Câu 27. (Chuyên Nguyễn Trãi Hải Dương 2019) Trong không gian

Oxyz

, cho

 

2;0;0

A

,

 

0;4;0

B

,

 

0;0;6

C

,

 

2;4;6

D

. Gọi

 

P

là mặt phẳng song song với

 

mp ABC

,

 

P

cách đều

D

và mặt

phẳng

 

ABC

. Phương trình của

 

P

là

A.

6 3 2 24 0

x y z

   

. B.

6 3 2 12 0

x y z

   

.

C.

6 3 2 0

x y z

  

. D.

6 3 2 36 0

x y z

   

.

Lời giải

Phương trình

 

mp ABC

:

1

2 4 6

x y z

  

6 3 2 12 0

x y z

    

.

Mặt phẳng

 

P

song song với mặt phẳng

 

ABC

nên phương trình có dạng:

6 3 2 0

x y z d

   

,

12

d

 

.

Mặt phẳng

 

P

cách đều

D

và mặt phẳng

 

ABC

   

 

, ,

d ABC P d D P

 

 

, ,

d A P d D P

 

2 2 2 2 2 2

6.2 6.2 3.4 2.6

6 3 2 6 3 2

d d   

 

   

12 36

d d

   

24

d

  

(thỏa mãn).

Vậy phương trình mặt phẳng

 

P

:

6 3 2 24 0

x y z

   

.

Câu 28. (Ngô Quyền - Hải Phòng 2019) Trong không gian

Oxyz

, cho ba điểm

 

2;0;0

A

,

 

0;3;0

B

,

 

0;0; 1

C



. Phương trình của mặt phẳng

 

P

qua

 

1;1;1

D

và song song với mặt phẳng

 

ABC

là

A.

2 3 6 1 0

x y z

   

. B.

3 2 6 1 0

x y z

   

.

C.

3 2 5 0

x y z

  

. D.

6 2 3 5 0

x y z

   

.

Lời giải

Chọn B

Phương trình đoạn chắn của mặt phẳng

 

ABC

là:

1

2 3 1

x y z

  



.

Mặt phẳng

 

P

song song với mặt phẳng

 

ABC

nên

 

:P

 

1 1

0 1

2 3

x y z m m

     

.

Do

   

1;1;1

D P



có:

1 1 1 1

.1 .1 1 0 0

2 3 6 6

m m m

        

.

Vậy

 

1 1 1

: 0 3 2 6 1 0

2 3 6

P x y z x y z

        

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 34 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 29. (Chuyên Nguyễn Đình Triểu - Đồng Tháp - 2018) Trong không gian

Oxyz

, cho

 

1;1;0

A

,

 

0;2;1

B

,

 

1;0;2

C

,

 

1;1;1

D

. Mặt phẳng

 



đi qua

 

1;1;0

A

,

 

0;2;1

B

,

 



song song với

đường thẳng

CD

. Phương trình mặt phẳng

 



là

A.

2 3 0

x y

   

. B.

2 2 0

x y z

   

. C.

2 3 0

x y z

   

. D.

2 0

x y

  

.

Lời giải

 

1;1;1

AB  



,

 

0;1; 1

CD

 



 

, 2; 1; 1

AB CD

 

    

 

 

.

 



đi qua

 

1;1;0

A

và có một VTPT là

 

2;1;1

n



 

: 2 3 0

x y z



    

.

Dạng 2.2 Góc của 2 mặt phẳng

1. Góc giữa hai véctơ

Cho hai véctơ

1 2 3

( ; ; )a a a a



và

1 2 3

( ; ; ).b b b b





Khi đó góc giữa hai véctơ

a



và

b



là góc nhợn hoặc

tù.

1 1 2 2 3 3

2 2 2 2 2 2

1 2 3 1 2 3

.

cos( ; )

.

a b a b a b

a b

a a a b b b

 

 

   



với

0 180 .



   

2. Góc giữa hai mặt phẳng

Cho hai mặt phẳng

1 1 1 1

( ) : 0

P A x B y C z D

   

và

2 2 2 2

( ) : 0.

Q A x B y C z D

   

 

1 2 1 2 1 2

2 2 2 2 2 2

1 1 1 2 2 2

.

cos ( ),( ) cos

.

P Q

n n

A A B B C C

P Q

n n

A B C A B C



 

  

   

 

với

0 90 .



   

Câu 30. (THPT Nguyễn Khuyến 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho điểm

 

2;1; 2

H

,

H

là hình chiếu vuông góc của gốc tọa độ

O

xuống mặt phẳng

 

P

, số đo góc giữa mặt

 

P

và

mặt phẳng

 

: 11 0

Q x y

  

A.

0

60

B.

0

30

C.

0

45

D.

0

90

Lời giải

Chọn C

 

P

qua O và nhận

 

2;1; 2

OH 



làm VTPT

 

: 11 0

Q x y

  

có VTPT

 

1;1; 0

n 



Ta có

   







   

 



0

.

1

cos , , 45

2

.

OH n

P Q P Q

OH n

   

 



Câu 31. (THPT Quang Trung Đống Đa 2019) Trong không gian

Oxyz

, cho mặt phẳng

( )P

có phương

trình

2 2 5 0

x y z

   

. Xét mặt phẳng

( ) : (2 1) 7 0

Q x m z

   

, với

m

là tham số thực. Tìm tất

cả giá trị của

m

để

( )P

tạo với

( )Q

góc

4



.

A.

1

4

m











. B.

2

2 2

m







 



. C.

2

4

m











. D.

4

2

m











.

Lời giải

Mặt phẳng

( )P

,

( )Q

có vectơ pháp tuyến lần lượt là

 

1; 2;2

p

n  



,

 

1;0; 2 1

Q

n m

 



TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 35

Vì

( )P

tạo với

( )Q

góc

4



nên

 

2

1 2(2 1)

1

cos cos ;

4

2

3. 1 (2 1)

2 4 1 9 4 4 2

4 20 16 0

1

.

4

p Q

m

n n

m

m m m

m m

m



 

  

 

    

   













 

Câu 32. (THPT Ba Đình 2019) Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

 

P

có phương

trình:

1 0

ax by cz

   

với

0

c



đi qua

2

điểm

 

0;1;0

A

,

 

1;0;0

B

và tạo với

 

Oyz

một góc

60

. Khi đó

a b c 

thuộc khoảng nào dưới đây?

A.

 

5;8

. B.

 

8;11

. C.

 

0;3

. D.

 

3;5

.

Lời giải.

Mặt phẳng

 

P

đi qua hai điểm

A

,

B

nên

1 0

1

1 0

b

a b

a

 



  



 



.

Và

 

P

tạo với

 

Oyz

góc

60

nên

   

 

2 2 2

1

cos ,

2

. 1

a

P Oyz

a b c

 

 

(*).

Thay

1

a b

 

vào phương trình được

2

2 2 2

c c

    

.

Khi đó

 

2 2 0;3

a b c    

.

Câu 33. (Chuyên Bắc Giang -2019) Trong không gian với hệ tọa độ

O

xyz

, cho hai mặt phẳng

( ) : 2 2 1 0,

P x y z

   

( ) : ( 1) 2019 0

Q x my m z

    

. Khi hai mặt phẳng

 

P

,

 

Q

tạo với

nhau một góc nhỏ nhất thì mặt phẳng

 

Q

đi qua điểm

M

nào sau đây?

A.

(2019; 1;1)

M



B.

(0; 2019;0)

M



C.

( 2019;1;1)

M



D.

(0;0; 2019)

M



Lời giải

Chọn C

Gọi



là góc giữa hai mặt phẳng

 

P

và

 

Q

.

Khi đó:

2 2 2 2 2 2 2 2

1.1 2. 2.( 1)

1 1 1

cos

3

1 2 ( 2) . 1 ( 1) 3 2 2 2

1 3

3

3. 2

2

2 2

m m

m m m m

m

  

    

       

 

 

 

 

Góc



nhỏ nhất



cos

lớn nhất

1

2

m

 

.

Khi

1

2

m



thì

 

1 1

: 2019 0

2 2

x zQ y

   

, đi qua điểm

( 2019;1;1)

M



.

Câu 34. (THPT Thăng Long-Hà Nội- 2019) Trong không gian

Oxyz

, cho hai mặt phẳng

 

: 2 2 5 0

P x y z

   

và

 

: 2 0

Q x y

  

. Trên

 

P

có tam giác

ABC

; Gọi

, ,A B C

  

lần

lượt là hình chiếu của

, ,A B C

trên

 

Q

. Biết tam giác

ABC

có diện tích bằng

4

, tính diện tích

tam giác

A B C

  

.

A.

2

. B.

2 2

. C.

2

. D.

4 2

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 36 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Lời giải

Chọn B

Gọi



là góc giữa hai mặt phẳng

 

P

và

 

Q

.

 

   

2 2

2 2 2 2

2.1 1. 1 2.0

1

cos

2

2 1 2 . 1 1 0



  

  

     

.

Ta có:

1

.cos 4. 2 2

2

A B C ABC

S S



  

  

.

Câu 35. (Chuyên Nguyễn Du-ĐăkLăk 2019) Trong không gian

Oxyz

, biết hình chiếu của

O

lên mặt

phẳng

 

P

là

 

2; 1; 2

H

 

. Số đo góc giữa mặt phẳng

 

P

với mặt phẳng

 

: 5 0

Q x y

  

là

A.

30

. B.

45

. C.

60

. D.

90

.

Lời giải

Chọn B

Mặt phẳng

 

Q

có một vectơ pháp tuyến là

 

1; 1;0

Q

n  



.

Hình chiếu của

O

lên mặt phẳng

 

P

là

 

2; 1; 2

H

 

 

P



qua

H

và nhận

 

2; 1; 2

OH

  



làm vectơ pháp tuyến.

Gọi



là góc giữa hai mặt phẳng

 

P

và

 

Q

.

 

2 1 0

2

cos cos ,

2

4 1 4. 1 1 0

Q

OH n



 

  

   

 

45



  

.

Câu 36. Trong hệ trục toạ độ

Oxyz

, cho điểm

 

2; 1; 2

H

. Điểm

H

là hình chiếu vuông góc của gốc toạ

độ

O

xuống mặt phẳng

 

P

, số đo góc giữa mặt phẳng

 

P

và mặt phẳng

 

: 11 0

Q x y

  

là

A.

90

. B.

30

. C.

60

. D.

45

.

Lời giải

Ta có

H

là hình chiếu vuông góc của

O

xuống mặt phẳng

 

P

nên

 

OH P



. Do đó

 

2; 1; 2

OH 



là một vectơ pháp tuyến của mặt phẳng

 

P

.

Mặt phẳng

 

Q

có một vectơ pháp tuyến là

 

1; 1; 0

n 



.

Gọi



là góc giữa hai mặt phẳng

   

,

P Q

.

Ta có

2 2 2 2 2 2

.

2.1 1.1 2.0

2

cos 45

2

.

2 1 2 . 1 1 0

OH n

 

 

     

   

 

.

Vây góc giữa hai mặt phẳng

   

,

P Q

là

45

.

Câu 37. (Chuyên Trần Phú Hải Phòng -2019) Trong không gian

,Oxyz

cho hai điểm

   

3;0;1 , 6; 2;1

A B 

. Phương trình mặt phẳng

 

P

đi qua

, A B

và tạo với mặt phẳng

 

Oyz

một

góc



thỏa mãn

2

cos

7





là

A.

2 3 6 12 0

2 3 6 0

x y z

   





  



B.

2 3 6 12 0

2 3 6 0

x y z

   





  



C.

2 3 6 12 0

2 3 6 1 0

x y z

   





   



D.

2 3 6 12 0

2 3 6 1 0

x y z

   





   



Lời giải

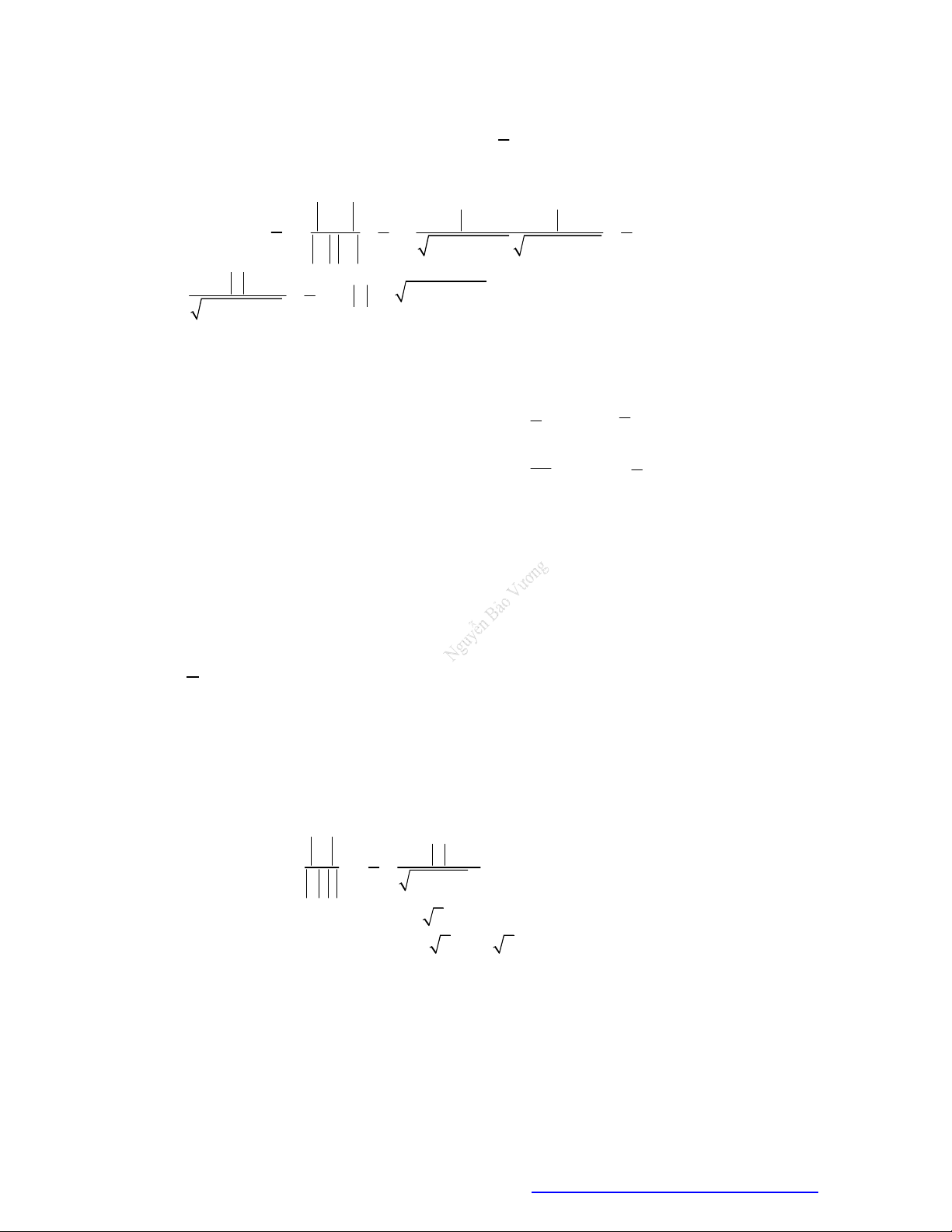
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 37

Giả sử

 

P

có VTPT

 

1

; ;n a b c





 

P

có VTCP

 

3; 2;0

AB  



suy ra

1 1

. 0

n AB n AB

  

   

   

2

3 2 0. 0 3 2 0 1

3

a b c a b a b         

 

Oyz

có phương trình

0

x



nên có VTPT

 

2

1;0;0

n 



Mà

2

cos

7





1 2

2 2 2 2 2 2

1 2

.

.1 .0 .0

2 2

7 7

.

. 1 0 0

n n

a b c

n n

a b c

 

   

   

 

2 2 2

2

7 2

7

.

a

a a b c

a b c

    

 

 

2 2 2 2

49 4

a a b c

   

 

2 2 2

45 4 4 0 2

a b c   

Thay

 

1

vào

 

2

ta được

2 2

4 0

b c

 

Chọn

2

c



ta có

2 2

2

;1;2

1

3

4 2 0

1 2

2

; 1;2

3

n

a

b

a

n



 





 







 



    



   

 







  



 





 





hay

 

2;3;6

2;3; 6

n







 





Vậy

 

P

2 3 6 12 0

2 3 6 0

x y z

   





  



Câu 38. (Toán Học Tuổi Trẻ 2018) Trong không gian với hệ tọa độ

Oxyz

, biết mặt phẳng

 

: 0

P ax by cz d

   

với

0

c



đi qua hai điểm

 

0;1;0

A

,

 

1;0;0

B

và tạo với mặt phẳng

 

yOz

một góc

60

. Khi đó giá trị

a b c 

thuộc khoảng nào dưới đây?

A.

 

0;3

. B.

 

3;5

. C.

 

5;8

. D.

 

8;11

.

Lời giải

Ta có:

 

,

A B P



nên

0

b d

a d

 





 



. Suy ra

 

P

có dạng

0

ax ay cz a

   

có vectơ pháp tuyến là

 

; ;n a a c





.

Măt phẳng

 

yOz

có vectơ pháp tuyến là

 

1;0;0

i 



.

Ta có:

.

cos60

.

n i

 

 

2 2

1

2

2 .1

a

a c

 



2 2 2

2 4a c a

  

2 2

2 0

a c

  

.

Chọn

1

a



, ta có:

2

2 2

c c   

do

0

c



.

Ta có:

 

1 1 2 2 2 0;3

a b c a a c          

.

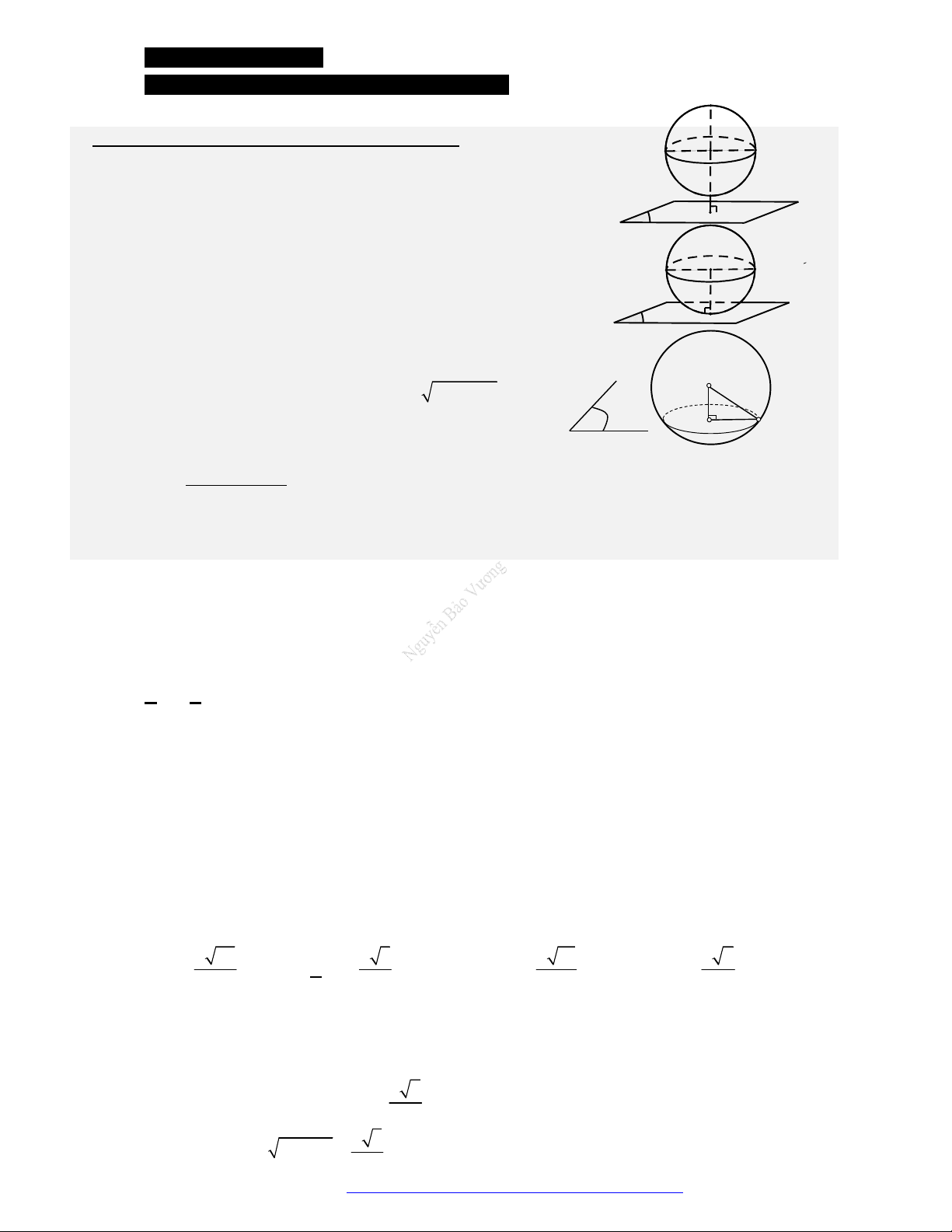
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 38 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Dạng 3. Vị trí tương đối

Dạng 3.1 Vị trí tương đối mặt phẳng với mặt cầu

Vị trí tương đối giữa mặt phẳng (P) và mặt cầu (S)

Cho mặt cầu

( ; )S I R

và mặt phẳng

( ).P

Gọi

H

là hình chiếu vuông góc của

I

lên

( )P

và có

d IH

là khoảng cách từ I đến mặt phẳng

( ).P

Khi đó:

 Nếu

:d R

Mặt cầu và mặt phẳng không có điểm chung.



Nếu

:d R

Mặt phẳng tiếp xúc mặt cầu.

Lúc đó

( )P

là mặt phẳng tiếp diện của

( )S

và

H

là tiếp điểm.



Nếu

:d R

mặt phẳng

( )P

cắt mặt cầu theo thiết diện

là đường tròn có tâm

H

và bán kính

2 2

.r R IH 

Viết phương trình mặt

( ) ( ) : 0P Q ax by cz d   

và tiếp xúc với mặt cầu

( ).S

Phương pháp:

 Vì

( ) ( ) : 0 ( ) : 0.P Q ax by cz d P ax by cz d



        



Tìm tâm

I

và bán kính

R

của mặt cầu.



Vì

( )P

tiếp xúc

( )S

nên có

 

;( )

.

I P

d R d



 

Câu 1. (Đề Tham Khảo 2017) Trong không gian với hệ tọa độ

Oxyz

, cho mặt cầu

 

S

có tâm

 

3;2; 1I 

và đi qua điểm

 

2;1;2A

. Mặt phẳng nào dưới đây tiếp xúc với

 

S

tại

A

?

A.

3 9 0x y z   

B.

3 3 0x y z   

C.

3 8 0x y z   

D.

3 3 0x y z   

Lời giải

Chọn B

Gọi

 

P

là mặt phẳng cần tìm. Khi đó,

 

P

tiếp xúc với

 

S

tại

A

khi chỉ khi

 

P

đi qua

 

2;1;2A

và nhận vectơ

 

1; 1;3IA   



làm vectơ pháp tuyến. Phương trình mặt phẳng

 

P

là

3 3 0 3 3 0x y z x y z         

.

Câu 2. (Chuyên Quốc Học Huế -2019) Trong không gian với hệ trục tọa độ

Oxyz

cho mặt phẳng

 



có phương trình

2 1 0x y z   

và mặt cầu

 

S

có phương trình

     

2 2 2

1 1 2 4x y z     

. Xác định bán kính

r

của đường tròn là giao tuyến của mặt phẳng

 



và mặt cầu

 

S

.

A.

2 42

3

r 

. B.

2 3

3

r 

C.

2 15

3

r 

. D.

2 7

3

r 

Lời giải

Chọn B

Mặt cầu

 

S

có tâm

 

1;1; 2I 

và bán kính

2R 

. Gọi

d

là khoảng cách từ tâm

I

đến mặt

phẳng

 



. Ta có

 

2 6

,

3

d d I



 

.

Khi đó ta có:

2 2

2 3

3

r R d  

.

P

M

2

M

1

H

I

R

I

H

P

H

I

A

R

r

d

P

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 39

Câu 3. (Chuyên Lê Quý Đôn Điện Biên 2019) Trong không gian

Oxyz

, viết phương trình mặt cầu có

tâm

 

2;1; 4

I



và tiếp xúc với mặt phẳng

 

: 2 2 7 0

x y z



   

.

A.

2 2 2

4 2 8 4 0

x y z x y z

      

. B.

2 2 2

4 2 8 4 0

x y z x y z

      

.

C.

2 2 2

4 2 8 4 0

x y z x y z

      

. D.

2 2 2

4 2 8 4 0

x y z x y z

      

.

Lời giải

Chọn C

Mặt cầu cần tìm có bán kính

 

2

2 2

2 2.1 2. 4 7

, 5

1 2 2

R d I



   

  

  

.

Phương trình mặt cầu cần tìm là

     

2 2 2

2 1 4 25

x y z

     

2 2 2

4 2 8 4 0

x y z x y z

       

.

Câu 4. (SGD Bình Phước - 2019) Trong không gian

Oxyz

, cho mặt phẳng

 

: 2 2 3 0

P x y z

   

và

mặt cầu

 

S

có tâm

 

0; 2;1

I 

. Biết mặt phẳng

 

P

cắt mặt cầu

 

S

theo giao tuyến là một

đường tròn có diện tích

2



. Mặt cầu

 

S

có phương trình là

A.

   

2 2

2

2 1 2

x y z

    

. B.

   

2 2

2

2 1 3

x y z

    

.

C.

   

2 2

2

2 1 3

x y z

    

. D.

   

2 2

2

2 1 1

x y z

    

.

Lời giải

Chọn B

Gọi

,R r

lần lượt là bán kính của mặt cầu và đường tròn giao tuyến. Theo giải thiết ta có:

2 2

r r

 

  

Mặt khác

 

d , 1

I P



nên

 

2

2 2

, 3

R r d I P

 

  

 

.

Vậy phương trình mặt cầu là

   

2 2

2

2 1 3

x y z

    

.

Câu 5. (Bình Giang-Hải Dương 2019) Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

 

: 2 2 2 0

P x y z

   

và điểm

 

1;2; 1

I

 

. Viết phương trình mặt cầu

 

S

có tâm

I

và cắt

mặt phẳng

 

P

theo giao tuyến là đường tròn có bán kính bằng

5

.

A.

       

2 2 2

: 1 2 1 25

S x y z

     

. B.

       

2 2 2

: 1 2 1 16

S x y z

     

.

C.

       

2 2 2

: 1 2 1 34

S x y z

     

. D.

       

2 2 2

: 1 2 1 34

S x y z

     

.

Lời giải

Chọn D

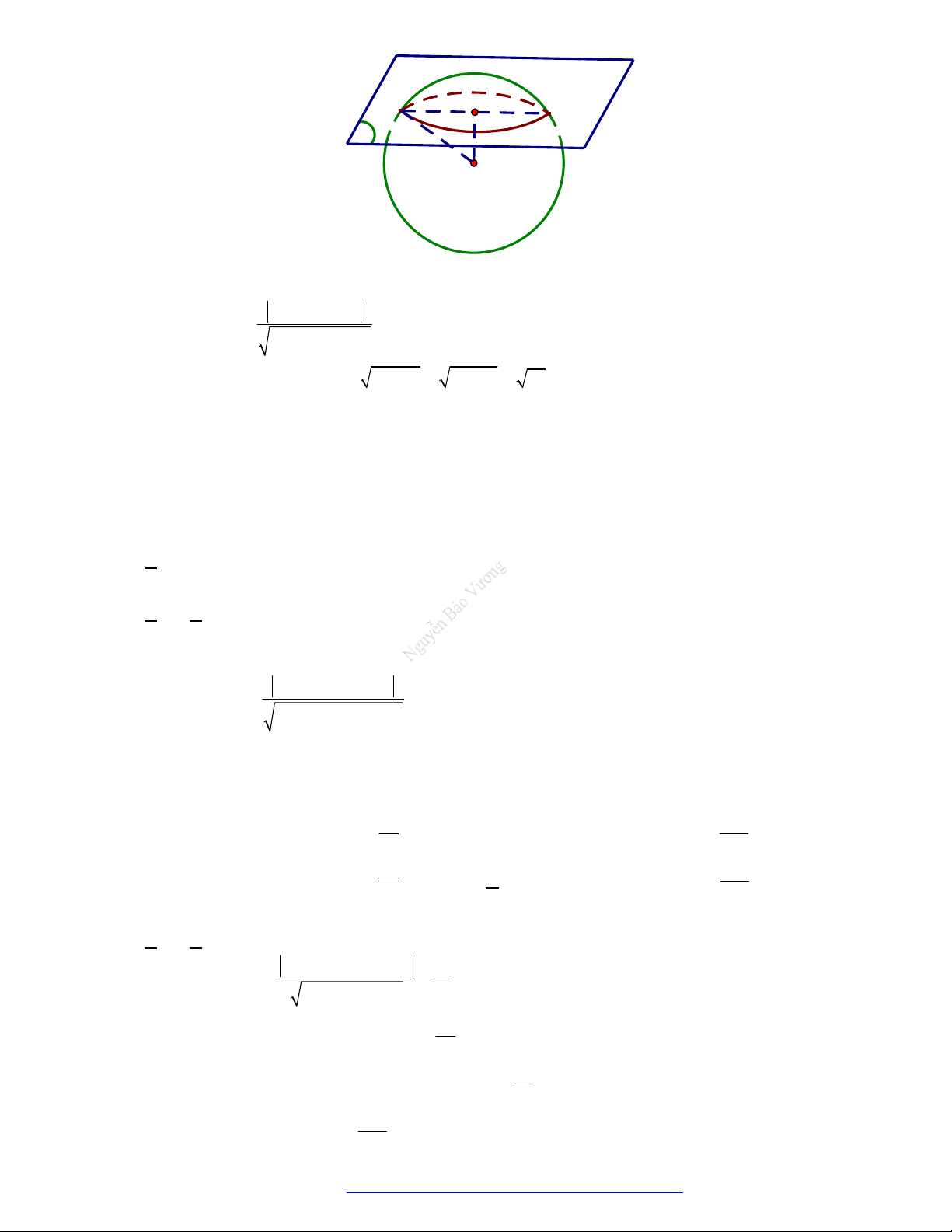
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 40 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Gọi

h

là khoảng cách từ tâm

I

đến mặt phẳng

 

P

ta có:

 

2

2 2

1 4 2 2

; 3

1 2 2

h d I P

   

  

  

.

Bán kính mặt cầu

 

S

là:

2 2 2 2

5 3 34R r h    

.

Phương trình mặt cầu

 

S

là:

     

2 2 2

1 2 1 34x y z     

.

Câu 6. Trong không gian với hệ tọa độ

Oxyz

, mặt cầu

 

S

có tâm

 

1;2;1I 

và tiếp xúc với mặt

phẳng

 

P

:

2 2 2 0x y z   

có phương trình là

A.

     

2 2 2

1 2 1 3x y z     

. B.

     

2 2 2

1 2 1 9x y z     

.

C.

     

2 2 2

1 2 1 9x y z     

. D.

     

2 2 2

1 2 1 3x y z     

.

Lời giải

Chọn C

Vì mặt cầu tâm

 

1;2;1I 

tiếp xúc với mặt phẳng

 

P

:

2 2 2 0x y z   

nên bán kính

 

   

2 2

2

1 2.2 2.1 2

, 3

1 2 2

R d I P

   

  

   

       

2 2 2

: 1 2 1 9S x y z      

.

Câu 7. (Chuyên Nguyễn Huệ- 2019) Phương trình mặt cầu tâm

 

3; 2; 4I 

và tiếp xúc với

 

: 2 2 4 0P x y z   

là:

A.

     

2 2 2

20

3 2 4

3

x y z     

. B.

     

2 2 2

400

3 2 4

9

x y z     

.

C.

     

2 2 2

20

3 2 4

3

x y z     

. D.

     

2 2 2

400

3 2 4

9

x y z     

.

Lời giải

Chọn D

Ta có:

 

2 2 2

2.3 ( 2) 2.4 4

20

,( ) .

3

2 ( 1) 2

d I P

   

 

  

Suy ra mặt cầu tâm

 

3; 2;4I 

và tiếp xúc với

 

: 2 2 4 0P x y z   

có bán kính

20

.

3

R 

Phương trình mặt cầu tâm

 

3; 2; 4 ,I 

bán kính

20

3

R 

là:

     

2 2 2

400

3 2 4 .

9

x y z     

H

B

A

P

r

h

R

I

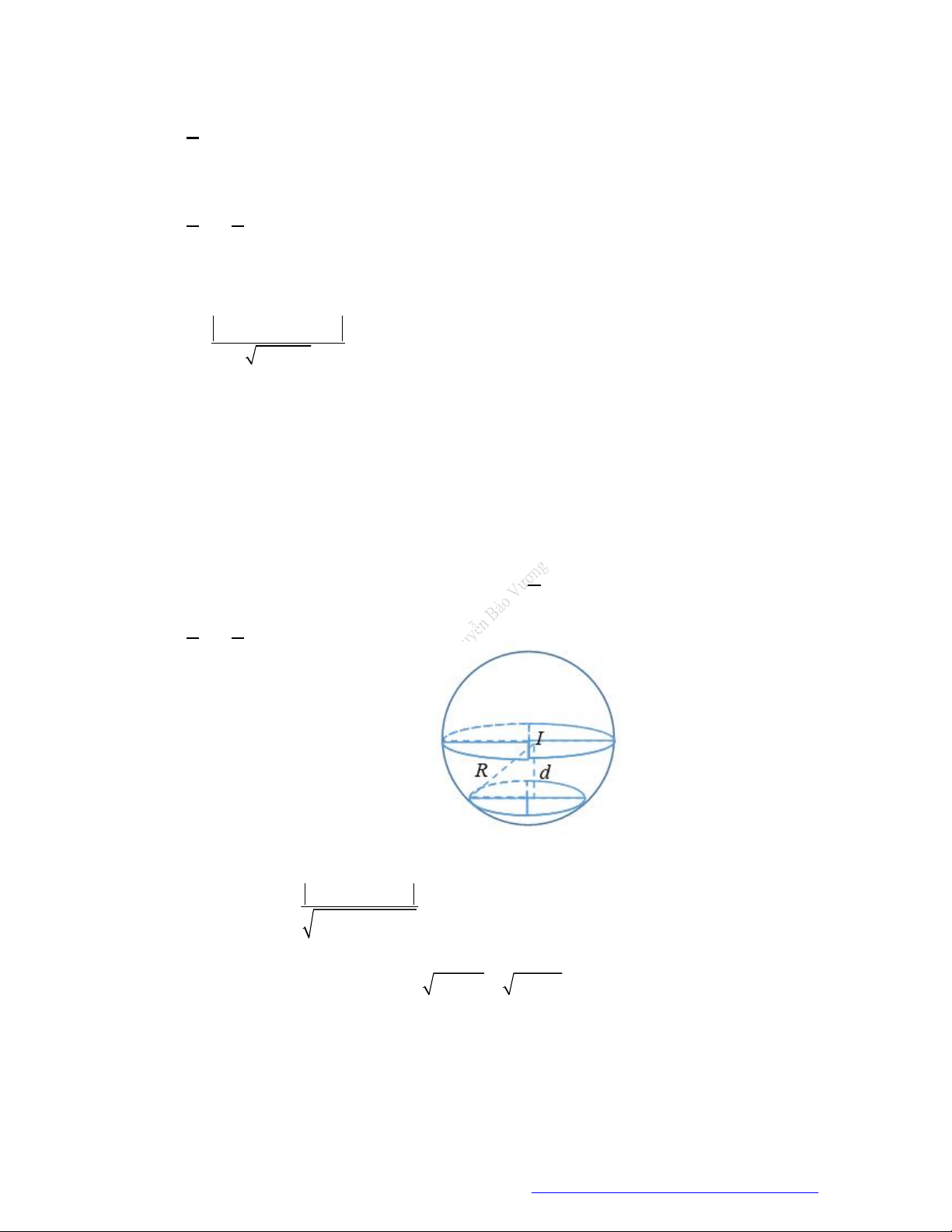
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 41

Câu 8. Trong không gian

Oxyz

, cho điểm

 

3;1; 1I

và mặt phẳng

 

: 2 2 3 0   P x y z

. Phương

trình mặt cầu

 

S

có tâm

I

và tiếp xúc với mặt phẳng

 

P

là

A.

     

2 2 2

3 1 1 4     x y z

. B.

     

2 2 2

3 1 1 16     x y z

.

C.

     

2 2 2

3 1 1 4     x y z

. D.

     

2 2 2

3 1 1 16     x y z

.

Lời giải

Chọn A

Gọi bán kính của mặt cầu

 

S

là

R

.

Mặt cầu

 

S

có tâm

I

và tiếp xúc với mặt phẳng

 

P

 

; d I P R

 

3 2.1 2. 1 3

2

1 4 4

   

   

 

R R

.

Vậy phương trình mặt cầu

 

S

tâm

I

và tiếp xúc với mặt phẳng

 

P

là:

     

2 2 2

3 1 1 4     x y z

.

Câu 9. (Đà Nẵng 2019) Trong không gian

Oxyz

, cho mặt cầu

 

S

có tâm

 

1;2;1I

và cắt mặt phẳng

 

:2 2 7 0P x y z   

theo một đường tròn có đường kính bằng

8

. Phương trình mặt cầu

 

S

là

A.

     

2 2 2

1 2 1 81x y z     

. B.

     

2 2 2

1 2 1 5x y z     

.

C.

     

2 2 2

1 2 1 9x y z     

. D.

     

2 2 2

1 2 1 25x y z     

.

Lời giải

Chọn D

Khoảng cách từ tâm

I

đến mặt phẳng

 

P

là

 

2

2 2

2.1 2 2.1 7

, 3

2 1 2

d d I P

  

  

  

.

Đường tròn giao tuyến có đường kính bằng

8

nên bán kính đường tròn là

4r 

.

Bán kính của mặt cầu

 

S

là

2 2 2 2

3 4 5R d r    

.

Vậy phương trình mặt cầu

 

S

là

     

2 2 2

1 2 1 25x y z     

.

Câu 10. (Thpt Vĩnh Lộc - Thanh Hóa 2019) Cho mặt cầu

 

S

có phương trình

     

2 2 2

3 2 1 100x y z     

và mặt phẳng

 



có phương trình

2 2 9 0x y z   

. Tính

bán kính của đường tròn

 

C

là giao tuyến của mặt phẳng

 



và mặt cầu

 

S

.

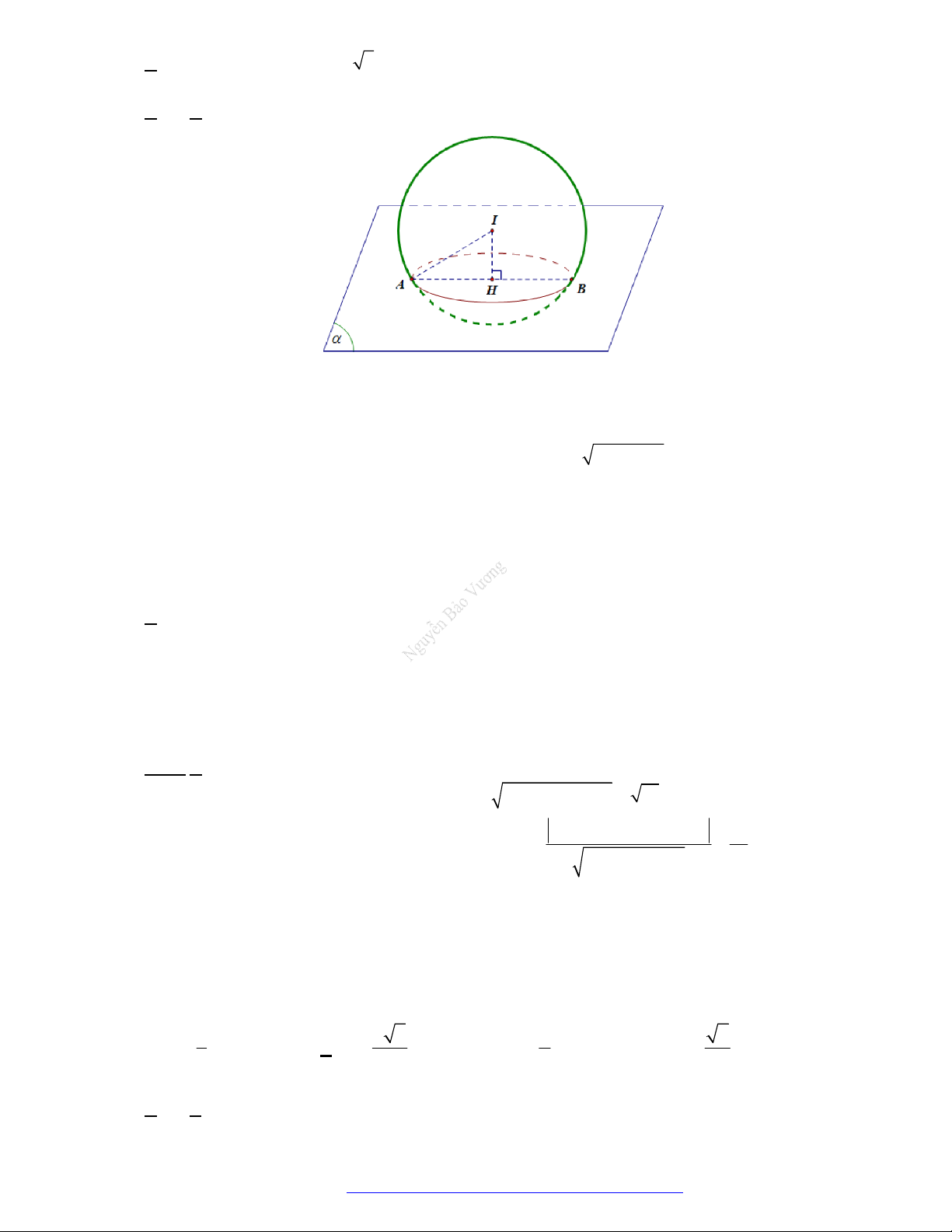
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 42 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

A.

8

. B.

4 6

. C.

10

. D.

6

.

Lời giải

Chọn A

Gọi

I

là tâm mặt cầu

 

S

,

H

là hình chiếu vuông góc của

I

lên mặt phẳng

 



và

AB

là một

đường kính của đường tròn

 

C

.

Dễ thấy

 

3; 2;1I 

,

10IA 

,

 

, 6IH d I



 

suy ra

2 2

8HA IA IH  

.

Vậy bán kính đường tròn

 

C

bằng 8.

Câu 11. (chuyên Hùng Vương Gia Lai -2019) Trong không gian

Oxyz

, cho mặt cầu

 

2 2 2

: 4 2 2 10 0S x y z x y z      

, mặt phẳng

 

: 2 2 10 0P x y z   

. Mệnh đề nào dưới

đây đúng?

A.

 

P

tiếp xúc với

 

S

.

B.

 

P

cắt

 

S

theo giao tuyến là đường tròn khác đường tròn lớn.

C.

 

P

và

 

S

không có điểm chung.

D.

 

P

cắt

 

S

theo giao tuyến là đường tròn lớn.

Lời giải

Chọn A

Mặt cầu

 

S

có tâm

 

2; 1; 1I   

, bán kính

 

4 1 1 10 16 4R       

Khoảng cách từ tâm

I

đến mặt phẳng

 

P

là:

 

   

 

2

2 2

2 2. 1 2 1 10

12

, 4

3

1 2 2

d I P

    

  

  

Ta thấy:

 

,d I P R

, vậy

 

P

tiếp xúc với

 

S

.

Câu 12. (Chuyên Bắc Giang 2019) Trong không gian với hệ tọa độ

Oxyz

, cho mặt cầu

 

2 2 2

1:S x y z  

và mặt phẳng

 

2 2 1 0:P x y z   

. Tìm bán kính

r

đường tròn giao

tuyến của

 

S

và

 

P

.

A.

1

3

r 

. B.

2 2

3

r 

. C.

1

2

.r 

D.

2

r 

.

Lời giải

Chọn B

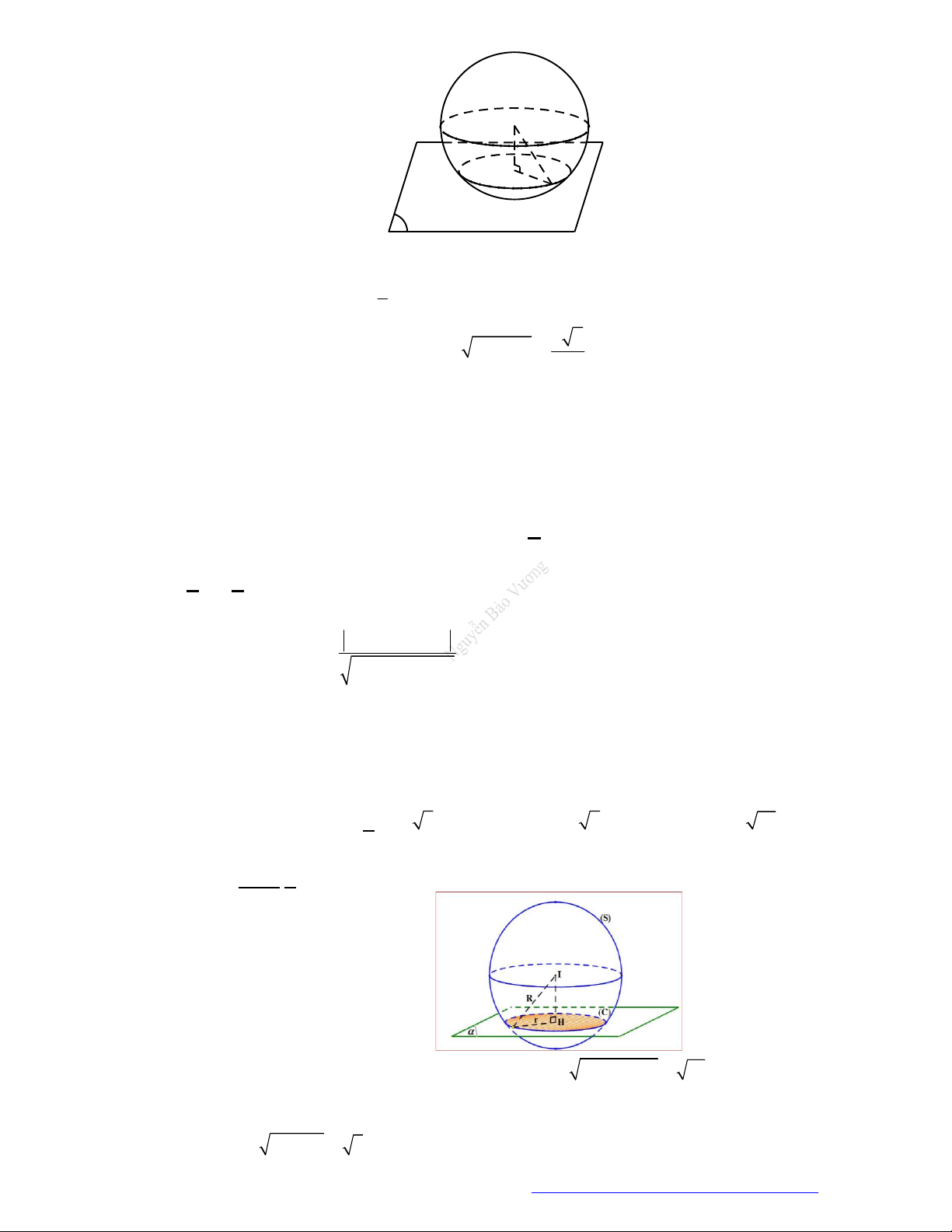
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 43

Mặt cầu có tâm

 

0 0 0; ;O

, bán kính

1R 

.

Khoảng cách

 

1

3

,d O P 

.

Bán kính đường tròn giao tuyến là

2 2

3

.r R d  

Câu 13. (Kinh Môn - Hải Dương 2019) Trong không gian với hệ trục toạ độ

Oxyz

, phương trình nào

dưới đây là phương trình của mặt cầu có tâm

 

3;1;0I

và tiếp xúc với mặt phẳng

 

: 2 2 1 0P x y z   

?

A.

   

2 2

2

3 1 3x y z    

. B.

   

2 2

2

3 1 9x y z    

.

C.

   

2 2

2

3 1 3x y z    

. D.

   

2 2

2

3 1 9x y z    

.

Lời giải

Chọn D

Gọi

 

S

là mặt cầu có tâm

I

và tiếp xúc với

 

P

có

R

là bán kính. Khi đó ta có:

 

2

2 2

2.3 2.1 0 1

, 3

2 2 1

d I P R R R

  

    

  

.

Vậy phương trình của

 

S

là

   

2 2

2

3 1 9x y z    

.

Câu 14. (SGD Bến Tre 2019) Trong không gian

Oxyz

cho mặt cầu

 

2 2 2

: 2 4 6 0S x y z x y z     

.

Đường tròn giao tuyến của

 

S

với mặt phẳng

 

Oxy

có bán kính là

A.

3r

. B. 5r . C. 6r . D.

14r

.

Lời giải

Chọn B

Mặt cầu

 

S

có tâm

 

1;2;3I

và bán kính

2 2 2

1 2 3 14R     .

Khoảng cách từ tâm

I

đến mặt phẳng

 

Oxy

là

3d 

, suy ra bán kính đường tròn giao tuyến cần

tìm là

2 2

5r R d  

.

d

R

r

P

O

H

M

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 44 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 15. Trong không gian với hệ tọa độ

Oxyz

, cho mặt cầu

 

S

có tâm

 

2;1;1

I

và mặt

phẳng

 

: 2 2 2 0

P x y z

   

. Biết mặt phẳng

 

P

cắt mặt cầu

 

S

theo giao tuyến là một đường

tròn có bán kính bằng 1. Viết phương trình của mặt cầu

 

S

A.

       

2 2 2

: 2 1 1 8

S x y z

     

B.

       

2 2 2

: 2 1 1 10

S x y z

     

C.

       

2 2 2

: 2 1 1 8

S x y z

     

D.

       

2 2 2

: 2 1 1 10

S x y z

     

Lời giải

Chọn D

Gọi

,R r

lần lượt là bán kính của mặt cầu

 

S

và đường tròn giao tuyến

Ta có

 

2

2 2

2.2 1.1 2.1 2

, 1 10

2 1 2

R r d I P

 

  

    

 

 

 

Mặt cầu

 

S

tâm

 

2;1;1

I

bán kính

10

R 

là

     

2 2 2

2 1 1 10

x y z

     

.

Câu 16. (Mã 104 2017) Trong không gian với hệ trục tọa độ

Oxyz

, phương trình nào dưới đây là phương

trình mặt cầu đi qua ba điểm

 

2;3;3

M

,

 

2; 1; 1

N

 

,

 

2; 1;3

P  

và có tâm thuộc mặt phẳng

 

: 2 3 2 0

x y z



   

.

A.

2 2 2

4 2 6 2 0

x y z x y z

      

B.

2 2 2

2 2 2 2 0

x y z x y z

      

C.

2 2 2

2 2 2 10 0

x y z x y z

      

D.

2 2 2

4 2 6 2 0

x y z x y z

      

Lời giải

Chọn D

Giả sử phương trình mặt cầu

 

S

có dạng

2 2 2

2 2 2 0

x y z ax by cz d

      

.

Điều kiện:

 

2 2 2

0 *

a b c d   

Vì mặt cầu

 

S

đi qua 3 điểm

 

2;3;3

M

,

 

2; 1; 1

N

 

,

 

2; 1;3

P  

và có tâm

I

thuộc

 

mp P

nên ta có hệ phương trình

 

4 6 6 22 2

4 2 2 6 1

: / *

4 2 6 14 3

2 3 2 2

a b c d a

a b c d b

T m

a b c d c

a b c d

    

 

 

     

 



 

     

 

     

 

Vậy phương trình mặt cầu là:

2 2 2

4 2 6 2 0.

x y z x y z

      

Câu 17. Trong không gian với hệ tọa độ

,Oxyz

xét các điểm

 

0;0;1

A

,

 

;0;0

B m

,

 

0; ;0C n

,

 

1;1;1

D

với

0; 0

m n

 

và

1. 

m n

Biết rằng khi

m

,

n

thay đổi, tồn tại một mặt cầu cố định tiếp xúc

với mặt phẳng

 

ABC

và đi qua

D

. Tính bán kính

R

của mặt cầu đó?

A.

1R

. B.

2

R

. C.

3

2



R

. D.

3

2

R

.

Lời giải

Chọn A

Gọi

 

1;1;0

I

là hình chiếu vuông góc của

D

lên mặt phẳng

( )Oxy

Ta có: Phương trình theo đoạn chắn của mặt phẳng

( )ABC

là:

1  

x y

z

m n

Suy ra phương trình tổng quát của

( )ABC

là

0   

nx my mnz mn

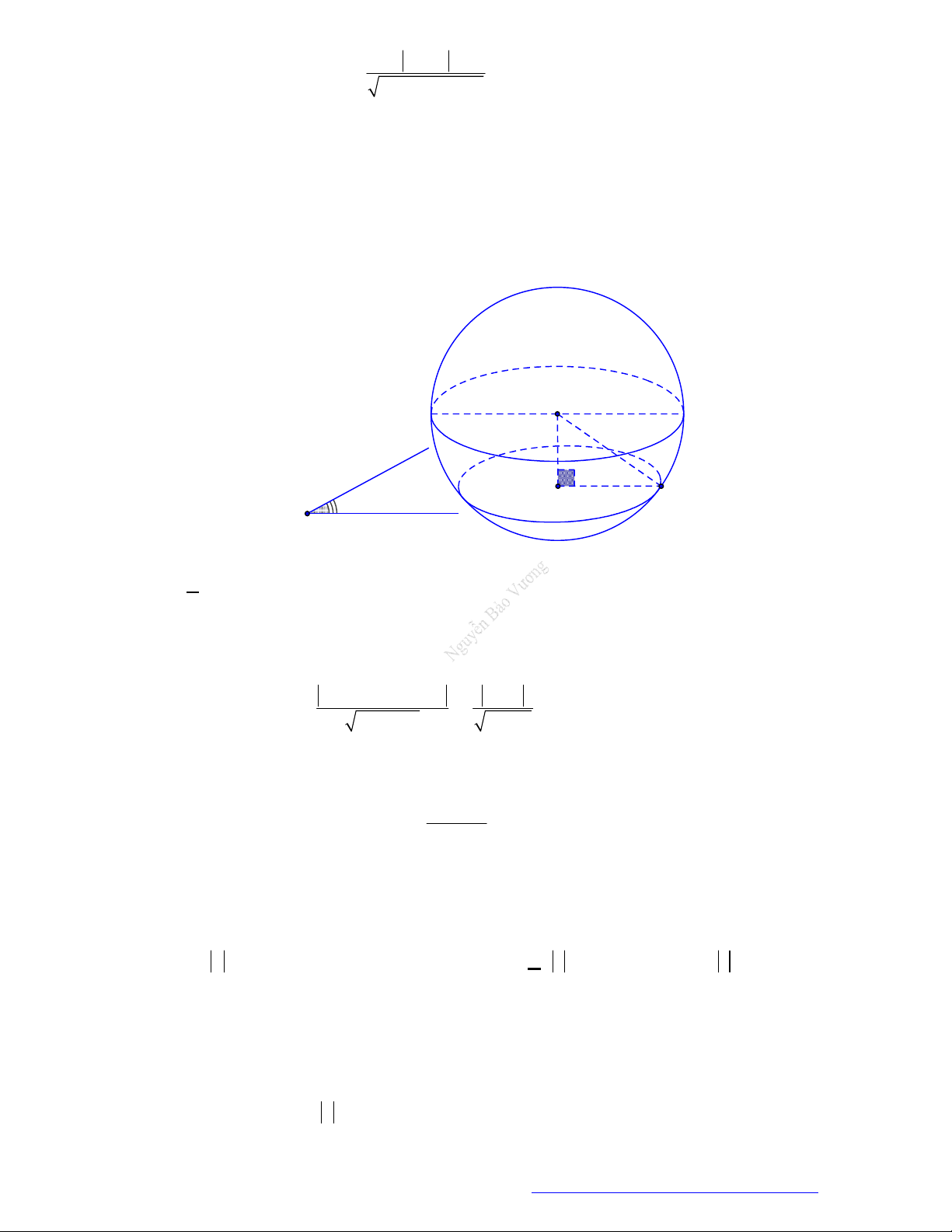
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 45

Mặt khác

 

2 2 2 2

1

; 1



 

 

mn

d I ABC

m n m n

(vì

1 m n

) và

 

1 ( ; . ID d I ABC

Nên tồn tại mặt cầu tâm

I

(là hình chiếu vuông góc của

D

lên mặt phẳng

Oxy

) tiếp xúc với

( )ABC

và đi qua

D

. Khi đó

1R

.

Câu 18. Trong không gian

Oxyz

, cho mặt cầu

 

S

:

     

2 2 2

2 4 1 4x y z     

và mặt phẳng

 

P

:

3 1 0x my z m    

. Tìm tất cả các giá trị thực của tham số

m

để mặt phẳng

 

P

cắt mặt cầu

 

S

theo giao tuyến là đường tròn có đường kính bằng

2

.

A.

1m 

. B.

1m  

hoặc

2m  

.

C.

1m 

hoặc

2m 

. D.

1m  

Lời giải

Mặt cầu :

     

2 2 2

2 4 1 4x y z     

có tâm

 

2; 4;1I

, bán kính .

Ta có

 

2

2 4 1 3 1

,

1 1

m m

d I P

m

   



 

2

m







Mặt phẳng

 

P

cắt mặt cầu

 

S

theo giao tuyến là đường tròn có đường kính bằng

2

nên bán

kính đường tròn giao tuyến

1r 

.

Ta có

 

2 2 2

,R d I P r 

 

2

4 1

2

m



  



 

2 2

4 4 3 2m m m    

2

2 4 2 0m m   

1m 

.

Câu 19. (THPT Đoàn Thượng - Hải Dương -2019) Trong không gian

Oxyz

, cho mặt cầu

 

S

tâm

( ; ; )I a b c

bán kính bằng

1

, tiếp xúc mặt phẳng

 

.Oxz

Khẳng định nào sau đây luôn đúng?

A.

1a 

. B.

1a b c  

. C.

1b 

. D.

1c 

.

Lời giải

Phương trình mặt phẳng

 

Oxz

:

0y 

.

Vì mặt cầu

 

S

tâm

( ; ; )I a b c

bán kính bằng

1

tiếp xúc với

 

Oxz

nên ta có:

 

; 1 1d I Oxz b  

.

P

R = 2

r = 1

I

 

S

2R 

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 46 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 20. (Sở Hà Nội 2019) Trong không gian

Oxyz

cho mặt cầu

 

2 2 2

: 2 4 6 5 0

S x y z x y z

      

.

Mặt phẳng tiếp xúc với

 

S

và song song với mặt phẳng

 

: 2 2 11 0

P x y z

   

có phương trình

là:

A.

2 2 7 0

x y z

   

. B.

2 2 9 0

x y z

   

.

C.

2 2 7 0

x y z

   

. D.

2 2 9 0

x y z

   

.

Lời giải

Ta gọi phương trình mặt phẳng song song với mặt phẳng

 

: 2 2 11 0

P x y z

   

có dạng :

   

: 2 2 0, 11

Q x y z D D     

.

Mặt cầu

 

S

có tâm

 

1;2;3

I 

, bán kính

 

2

2 2

1 2 3 5 3

R

     

Vì mặt phẳng tiếp xúc với

 

S

nên ta có :

 

2

2 2

2. 1 2 2.3

2

, 3 3

3

2 1 2

D

d I Q R

   



    

  

.

2 9 7

2 9 11

D D

  

 

 

 

    

 

. Do

11 7

D D

   

.

Vậy mặt phẳng cần tìm là

2 2 7 0

x y z

   

.

Câu 21. (Sở Hà Nội 2019) Trong không gian

Oxyz

cho hai mặt phẳng

 

: 2 2 0

P x y z

   

và

 

: 2 1 0

Q x y z

   

. Số mặt cầu đi qua

 

1; 2;1

A 

và tiếp xúc với hai mặt phẳng

   

,

P Q

là

A.

0

. B.

1

. C. Vô số. D.

2

.

Lời giải

Ta có

       

 

6

0;0;2 ; M;

2

M P d P Q d Q   

 

   

 

6

A; ; A; 6 A; A; ;

2

d P d Q d Q d P d Q P

    

Vậy không có mặt cầu thỏa yêu cầu bài toán

Câu 22. Trong không gian tọa độ

Oxyz

, cho mặt cầu

 

S

có đường kính

AB

với

 

6;2; 5

A



,

 

4;0;7

B 

.

Viết phương trình mặt phẳng

 

P

tiếp xúc với mặt cầu

 

S

tại

A

.

A.

 

:5 6 62 0

P x y z

   

. B.

 

:5 6 62 0

P x y z

   

.

C.

 

:5 6 62 0

P x y z

   

. D.

 

:5 6 62 0

P x y z

   

.

Lời giải

Gọi

I

là trung điểm của

AB

 

1;1;1

I

.

Mặt cầu

 

S

có đường kính

AB

nên có tâm là điểm

I

.

Mặt phẳng

 

P

tiếp xúc với mặt cầu

 

S

tại

A

nên mặt phẳng

 

P

đi qua

A

và nhận

 

5;1; 6

IA

 



là vectơ pháp tuyến.

Phương trình mặt phẳng

 

P

:

     

5 6 1 2 6 5 0 5 6 62 0

x y z x y z

          

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 47

Câu 23. (Chuyên Lê Hồng Phong Nam Định 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho mặt

phẳng

2

( ) : 2 x 2 y z m 3 0

P m

    

và mặt cầu

     

2 2 2

( ) : 1 1 1 9

S x y z

     

. Tìm tất cả

các giá trị của

m

để

( )P

tiếp xúc với

( )S

.

A.

2

5

m

 









. B.

2

5

m







 



. C.

2

m



. D.

5

m

 

.

Lời giải

Chọn B

Ta có

 

1; 1;1

( ) :

3

I

S

R















.

Để

( )P

tiếp xúc với

( )S

thì

 

2

1 3

3 10 0 2

; 3

5

3

3 8 0

m m

m m m

d I P R

m

m m

 



   



    



 

  



.

Câu 24. (THPT Ngô Sĩ Liên Bắc Giang 2019) Trong không gian với hệ trục tọa độ

0

xyz

, cho mặt cầu

       

2 2 2

: 1 1 1 25

S x y z

     

có tâm

I

và mặt phẳng

 

: 2 2 7 0

P x y z

   

. Thể tích của

khối nón đỉnh

I

và đường tròn đáy là giao tuyến của mặt cầu

 

S

và mặt phẳng

 

P

bằng

A.

12



B.

48



C.

36



D.

24



Lời giải

Chọn A

Mặt cầu

 

S

có tâm

 

1;1;1

I

và bán kính

5

R



Ta có chiều cao của khối nón

 

2 2 2

1 2 2 7

,( ) 4

1 2 2

h d I P

  

  

 

Bán kính đáy của hình nón là

2 2

25 16 3

r R h

    

Thể tích của khối nón

2 3

1 1

.3 .4 12 .

3 3

V r h

  

  

Câu 25. (Chuyên Ngữ Hà Nội 2019) Trong không gian với hệ tọa độ

Oxyz

cho hai mặt cầu

   

1 2

,

S S

lần lượt có phương trình là

2 2 2

2 2 2 22 0

x y z x y z

      

,

2 2 2

6 4 2 5 0

x y z x y z

      

.

Xét các mặt phẳng

 

P

thay đổi nhưng luôn tiếp xúc cả hai mặt cầu đã cho. Gọi

 

; ;A a b c

là

điểm mà tất cả các mặt phẳng

 

P

đi qua. Tính tổng

S a b c  

.

A.

5

.

2

S



B.

5

.

2

S

 

C.

9

.

2

S



D.

9

.

2

S

 

Lời giải

Chọn D

Mặt cầu

 

1

S

có tâm

 

1;1;1

I

và bán kính

1

5

R



Mặt cầu

 

2

S

có tâm

 

3; 2; 1

J

 

và bán kính

2

3

R



Ta có

 

1 2 1 2

2; 3; 2 IJ 17 IJ< .IJ R R R R

       



Vậy

   

1 2

,

S S

là hai mặt cầu cắt nhau.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 48 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Gọi

A

là tâm tỉ cự của hai mặt cầu ta có

5 5

AJ 3 5AJ

AJ 3 3

5 3 13 9

6; ; 4

2 2 2

AI ID

AI AI

JE

OJ OI

OA A a b c

     



 

         

 

 

   

 



Câu 26. (Sở Kon Tum - 2019) Trong không gian

Oxyz

, cho mặt cầu

       

2 2 2

: 1 2 1 45S x y z     

và mặt phẳng

 

: 13 0P x y z   

. Mặt cầu

 

S

cắt mặt

phẳng

 

P

theo giao tuyến là đường tròn có tâm

 

; ;I a b c

thì giá trị của

a b c 

bằng

A.

11

. B.

5

. C.

2

. D.

1

.

Lời giải

Chọn B

Mặt cầu

 

S

có tâm

 

1;2; 1A 

và bán kính 3 5R  .

Mặt cầu

 

S

cắt mặt phẳng

 

P

theo giao tuyến là đường tròn có tâm

 

; ;I a b c



I

là hình

chiếu của

A

lên mp

 

P

 

P

I P

IA kn

 













 

     

13 0

1

1 2 1 13 0 3

2

1

a b c

a k

k k k k

b k

c k

   





 



            



 



   



 

4;5; 4I 

.

Vậy

5a b c  

.

Câu 27. (Sở Hà Nam - 2019) Trong không gian

Oxyz

, cho mặt phẳng

 

: 2 7 0P x y z   

và mặt cầu

 

2 2 2

: 2 4 10 0S x y z x z     

. Gọi

 

Q

là mặt phẳng song song với mặt phẳng

 

P

và cắt

mặt cầu

 

S

theo một giao tuyến là đường tròn có chu vi bằng

6



. Hỏi

 

Q

đi qua điểm nào

trong số các điểm sau?

A.

 

6;0;1

. B.

 

3;1;4

. C.

 

2; 1;5 

. D.

 

4; 1; 2 

.

Lời giải

Chọn C

Mặt cầu

 

S

có tâm

 

1;0; 2I 

, bán kính

15R 

.

Gọi

r

là bán kính của đường tròn giao tuyến. Ta có

2 6 3r r

 

  

.

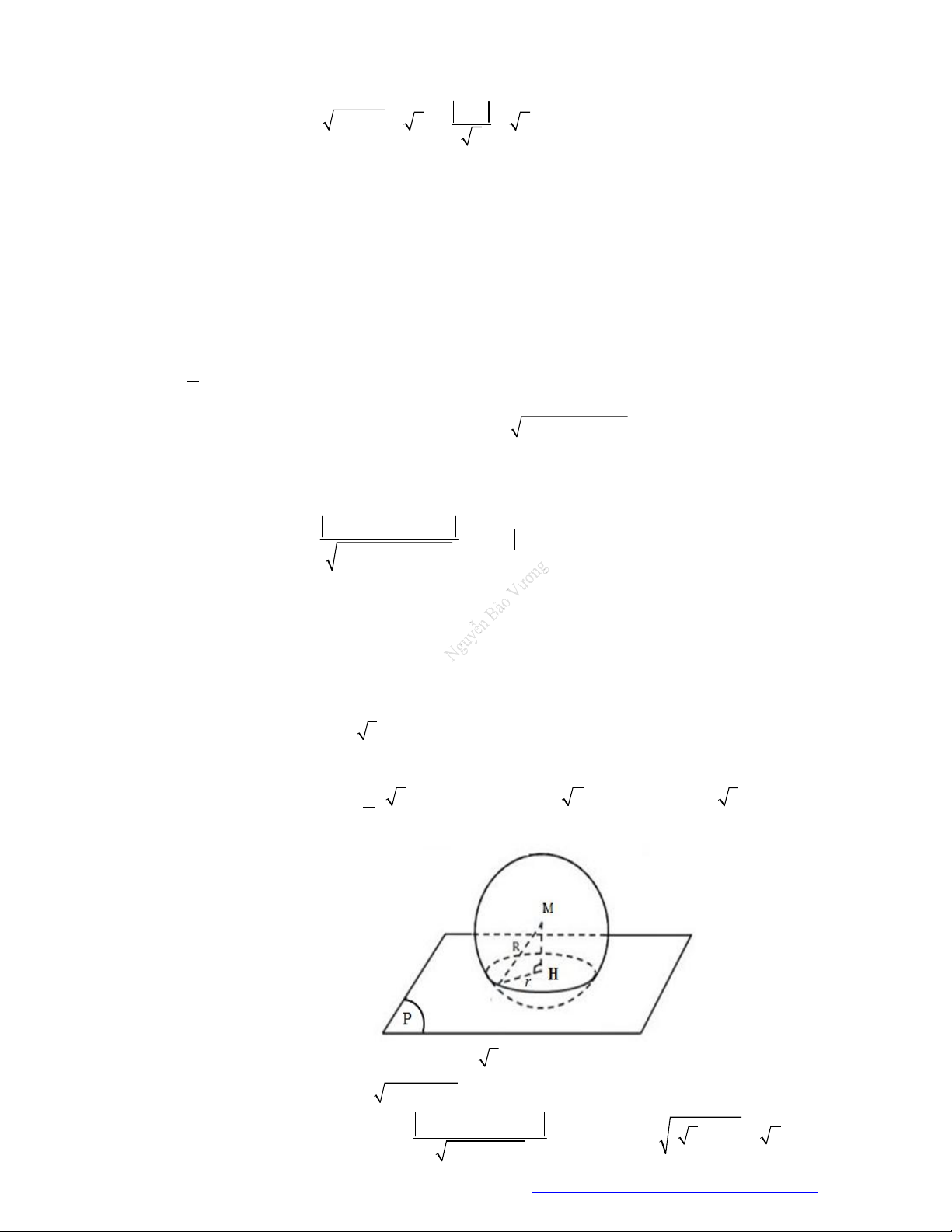
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 49

Do

   

//Q P

   

: 2 0 7Q x y z d d     

.

Ta có:

 

2 2

7

1

, 6 6

5

6

d

d I Q R r

d





     



 





loaïi

nhaän

Vậy

 

: 2 5 0Q x y z   

. Thay tọa độ

 

2; 1;5 

vào

 

Q

thấy thỏa mãn.

Câu 28. (Chuyên Lam Sơn Thanh Hóa 2019) Trong không gian

Oxyz

, cho mặt cầu

 

2 2 2

: 2 4 6 2 0S x y z x y z      

và mặt phẳng

 

: 4 3 12 10 0x y z



   

. Lập phương

trình mặt phẳng

 



thỏa mãn đồng thời các điều kiện: tiếp xúc với

 

S

; song song với

 



và cắt

trục

Oz

ở điểm có cao độ dương.

A.

4 3 12 78 0x y z   

. B.

4 3 12 26 0x y z   

.

C.

4 3 12 78 0x y z   

. D.

4 3 12 26 0x y z   

.

Lời giải

Mặt cầu

 

S

có: tâm

 

1;2;3I

, bán kính

2 2 2

1 2 3 2 4R     

.

Vì

   

 



nên phương trình mp

 



có dạng:

 

4 3 12 0, 10x y z d d    

.

Vì

 



tiếp xúc mặt cầu

 

S

nên:

 

,

2

2 2

4.1 3.2 12.3

26

4 26 52

78

4 3 12

I

d

d R d

d



  

 



      







  

.

Do

 



cắt trục

Oz

ở điểm có cao độ dương nên chọn

78d 

.

Vậy mp

 



:

4 3 12 78 0x y z   

.

Câu 29. (THPT Yên Phong 1 Bắc Ninh 2019) Trong không gian

Oxyz

, cho mặt phẳng

 

:2 2 1 0P x y z   

và điểm

 

1; 2;0M 

. Mặt cầu

tâm

M

, bán kính bằng 3 cắt phẳng

 

P

theo giao tuyến là đường tròn có bán kính bằng bao

nhiêu?

A.

2

. B.

2

. C.

2 2

. D. 3 1 .

Lời giải

Mặt cầu tâm tâm

M

, bán kính bằng 3R  cắt phẳng

 

P

theo giao tuyến là đường tròn tâm

H

, bán kính

r

suy ra

2 2

r R MH 

.

Với

 

2 2 2

2.1 2 2.0 1

, 1

2 1 2

MH d M P

   

  

 

. Suy ra

 

2

3 1 2r    .

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 50 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 30. (Chuyên Lê Hồng Phong Nam Định 2019) Trong không gian với hệ tọa độ

Oxyz

cho mặt phẳng

 

: 2 5 0Q x y z   

và mặt cầu

     

2 2

2

: 1 2 15S x y z    

. Mặt phẳng

 

P

song song với

mặt phẳng

 

Q

và cắt mặt cầu

 

S

theo giao tuyến là một đường tròn có chu vi bằng

6



đi qua

điểm nào sau đây?

A.

 

2; 2;1

. B.

 

1; 2;0

. C.

 

0; 1; 5 

. D.

 

2;2; 1 

.

Lời giải

Mặt cầu

 

S

có tâm

 

1;0; 2I 

và bán kính 15R  .

Đường tròn có chu vi bằng

6



nên có bán kính

6

3

2

r



 

.

Mặt phẳng

 

P

song song với mặt phẳng

 

Q

nên phương trình mặt phẳng

 

P

có dạng:

2 0x y z D   

,

5D  

.

Vì mặt phẳng

 

P

cắt mặt cầu

 

S

theo giao tuyến là một đường tròn có chu vi bằng

6



nên

 

2 2

; ; 6d I P R r d I P   

 

2

2 2

1 6 7

1 2.0 2

6 1 6

1 6 5

1 2 1

D D

D

D D

  

  

 

      

 

    

 

  

.

Đối chiếu điều kiện ta được

7D 

. Do đó phương trình mặt phẳng

 

: 2 7 0P x y z   

.

Nhận thấy điểm có tọa độ

 

2;2; 1 

thuộc mặt phẳng

 

P

.

Câu 31. (Việt Đức Hà Nội 2019) Cho mặt cầu

2 2 2

( ) : ( 1) ( 2) ( 4) 9S x y z      . Phương trình mặt

phẳng

( )



tiếp xúc với mặt cầu

( )S

tại điểm

(0;4; 2)M 

là

A.

6 6 37 0x y z   

B.

2 2 4 0x y z   

C.

2 2 4 0x y z   

D.

6 6 37 0x y z   

Lời giải

Mặt cầu

2 2 2

( ) :( 1) ( 2) ( 4) 9S x y z     

có tâm

(1;2; 4).I 

( 1;2;2).IM  



Phương trình mặt phẳng

( )



đi qua

(0;4; 2)M 

nhận

( 1;2;2)IM  



làm véc-tơ pháp tuyến là

1( 0) 2( 4) 2( 2) 0 2 2 4 0x y z x y z           

.

Câu 32. Trong không gian

Oxyz

, cho mặt cầu

 

S

:

     

2 2 2

2 1 2 4x y z     

và mặt phẳng

 

P

:

4 3 0x y m  

. Tìm tất cả các giá trị thực của tham số

m

để mặt phẳng

 

P

và mặt cầu

 

S

có

đúng

1

điểm chung.

A.

1m 

. B.

1m  

hoặc

21m  

.

C.

1m 

hoặc

21m 

. D.

9m  

hoặc

31m 

.

Lời giải

Ta có mặt cầu : có tâm , bán kính .

Mặt phẳng và mặt cầu có đúng điểm chung khi và chỉ khi mặt phẳng tiếp xúc với

mặt cầu .

Câu 33. (THPT Ba Đình -2019) Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng

 

P : mx 2y z 1 0   

(

m

là tham số). Mặt phẳng

 

P

cắt mặt cầu

 

S

     

2 2 2

2 1 2 4

x y z

     

 

2; 1; 2

I

 

2R 

 

P

 

S

1

 

P

 

S

 

,

d I P R 

 

2 2

4.2 3. 1

2

4 3

m  

 



11 10

m

  

1

21

m













TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 51

     

2 2

2

S : x 2 y 1 z 9    

theo một đường tròn có bán kính bằng

2

. Tìm tất cả các giá trị

thực của tham số

m

?

A.

m 1 

. B.

m 2 5  

. C.

m 4 

. D.

m 6 2 5 

.

Lời giải

Từ

     

2 2

2

S : x 2 y 1 z 9    

ta có tâm

 

2;1;0I 

bán kính

3R 

. Gọi

H

là hình chiếu vuông góc của

I

trên

 

P

và

     

;P S C H r 

với

2r 

Ta có

 

;IH d I P



2 2

2 2 0 1 2 3

4 1 5

m m

IH

m m

   

 

  

Theo yêu cầu bài toán ta có

2 2 2

R IH r 



 

2

2 3

9 4

5

m



 





2

6 2 5

12 16 0

6 2 5

m

m m

m



 

   



 





.

Câu 34. (Yên Định Thanh Hóa 2019) Trong không gian

Oxyz

, cho mặt cầu

 

2 2 2

: 2 4 2 3 0S x y z x y z      

. Viết phương trình mặt phẳng

 

Q

chứa trục

Ox

và cắt

 

S

theo một đường tròn bán kính bằng

3

.

A.

 

: 3 0Q y z 

. B.

 

: 2 0Q x y z  

. C.

 

: 0Q y z 

. D.

 

: 2 0Q y z 

.

Lời giải

 

Q

chứa trục

Ox

nên có dạng

0By Cz 

 

2 2

0B C 

.

 

S

có tâm

 

1; 2; 1I  

và bán kính

3R 

.

Bán kính đường tròn giao tuyến

3r 

.

Vì

R r

nên

 

I Q

.

2 0B C   

vì

,B C

không đồng thời bằng 0 nên chọn

1 2B C   

.

Vậy

 

: 2 0Q y z 

.

Câu 35. (THPT An Lão Hải Phòng 2019) Trong không gian với hệ tọa độ Oxyz, cho điểm

1;( )2;1I 

và

mặt phẳng

( )P

có phương trình

2 2 8 0x y z   

. Viết phương trình mặt cầu tâm

I

và tiếp xúc

với mặt phẳng

( )P

:

A.

2 2 2

( 1) ( 2) ( 1) 9x y z      B.

2 2 2

( ) ( ) (1 2 1 3)x y z     

C.

2 2 2

( ) ( ) (1 2 1 4)x y z      D.

2 2 2

( ) ( ) (1 2 1 9)x y z     

Lời giải

Chọn D

Vì mặt cầu tâm

I

tiếp xúc với mặt phẳng

( )P

:

 

1 4 2 8

;( ) 3

1 4 4

R d I P

   

   

 

Vậy:

2 2 2

( ) : ( ) ( ) 9)1(1 2x yS z     

A

I

H

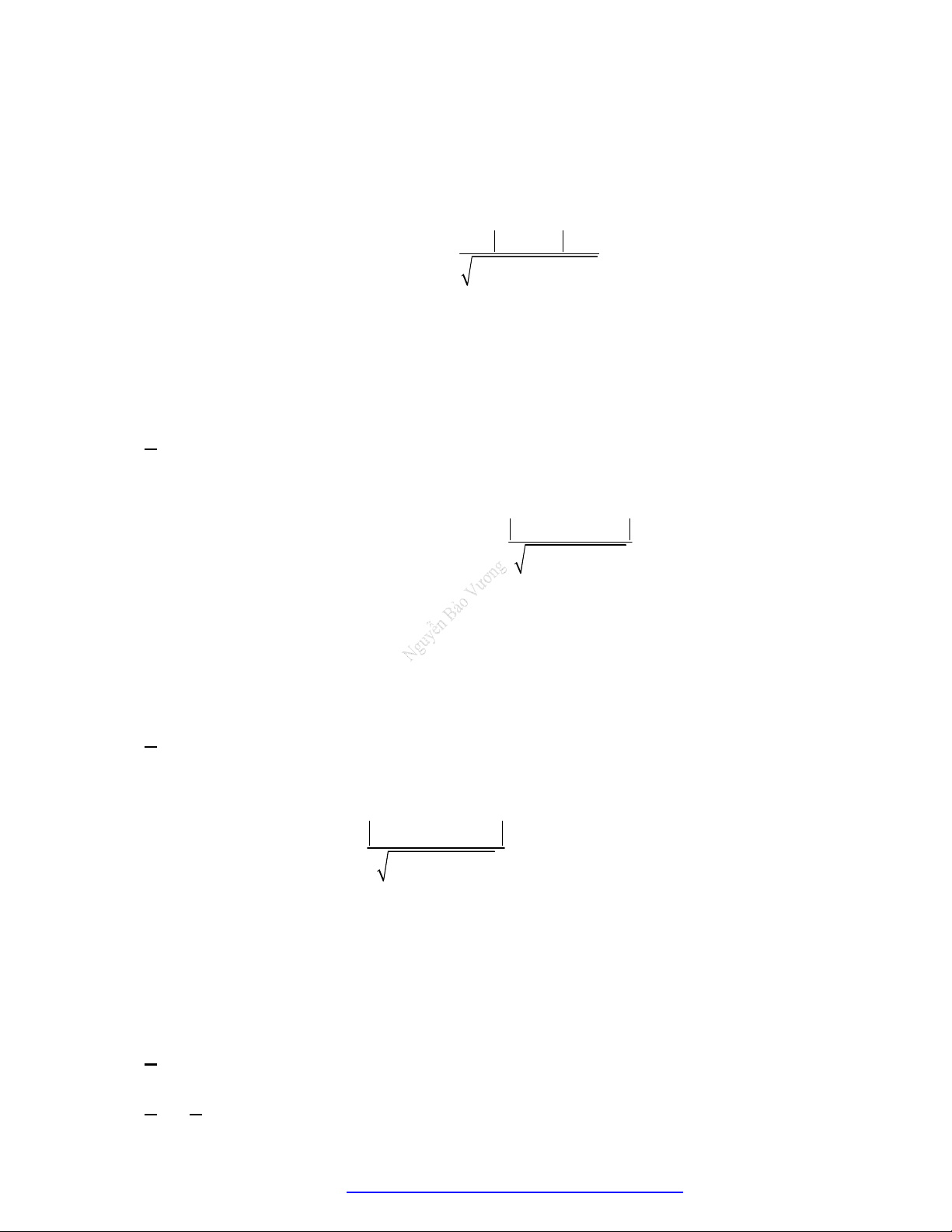
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 52 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 36. Trong không gian với hệ tọa độ

Oxyz

, phương trình nào dưới đây là phương trình của mặt cầu có

tâm

 

0;1;3

I

và tiếp xúc với mặt phẳng

( ) :2 2 2 0?

P x y z

   

A.

   

2 2

2

1 3 9

x y z

    

. B.

   

2 2

2

1 3 9

x y z

    

.

C.

   

2 2

2

1 3 3

x y z

    

. D.

   

2 2

2

1 3 3

x y z

    

.

Lời giải

Ta có: Bán kính mặt cầu là:

 

;

R d I P



   

2 2

2

1 6 2

3

2 1 2

  

 

   

.

Phương trình mặt cầu là:

   

2 2

2

1 3 9

x y z

    

.

Câu 37. (Sở Bắc Giang 2019) Trong không gian

Oxyz

, phương trình mặt cầu

 

S

tâm

 

1;2;5

I 

và tiếp

xúc với mặt phẳng

 

: 2 2 4 0

P x y z

   

là

A.

 

2 2 2

: 2 4 10 21 0

S x y z x y z

      

. B.

 

2 2 2

: 2 4 10 21 0

S x y z x y z

      

.

C.

 

2 2 2

: 2 4 10 21 0

S x y z x y z

      

. D.

 

2 2 2

: 2 5 21 0

S x y z x y z

      

.

Lời giải

Ta có bán kính của mặt cầu

 

S

là

 

2

2 2

1 2.2 2.5 4

; 3

1 2 2

R d I P

   

  

  

.

Vậy mặt cầu

 

S

có tâm

 

1;2;5

I 

và bán kính của

3

R



suy ra phương trình mặt cầu

 

S

là

     

2 2 2

2 2 2 2

1 2 5 3 2 4 10z 21 0

x y z x y z x y

             

.

Câu 38. (THPT Yên Khánh - Ninh Bình - 2019) Trong không gian

Oxyz

cho điểm

 

1; 2;3

I 

và mặt

phẳng

 

: 2 2 1 0

P x y z

   

. Mặt cầu

 

S

tâm

I

tiếp xúc với

 

P

có phương trình là:

A.

     

2 2 2

1 2 3 9.     

x y z

B.

     

2 2 2

1 2 3 3.     

x y z

C.

     

2 2 2

1 2 3 3.     

x y z

D.

     

2 2 2

1 2 3 9.     

x y z

Lời giải

Theo giả thiết

 

,

R d I P



 

2

2 2

2 1 2 2 3 1

3

2 1 2

. .   

 

  

Vậy

 

:S

     

2 2 2

1 2 3 9.     

x y z

Câu 39. (THPT Ngô Sĩ Liên Bắc Giang 2019) Trong không gian với hệ tọa độ

Oxyz

, cho điểm

( 3;0;1)

I



. Mặt cầu

( )S

có tâm

I

và cắt mặt phẳng

( ) : 2 2 1 0

P x y z

   

theo một thiết diện là một

hình tròn. Diện tích của hình tròn này bằng



. Phương trình mặt cầu

( )S

là

A.

2 2 2

( 3) ( 1) 4.

x y z

    

B.

2 2 2

( 3) ( 1) 25.

x y z    

C.

2 2 2

( 3) ( 1) 5.

x y z

    

D.

2 2 2

( 3) ( 1) 2.

x y z

    

Lời giải

Chọn C

Gọi

S

,

r

lần lượt là diện tích hình tròn và bán kính hình tròn.

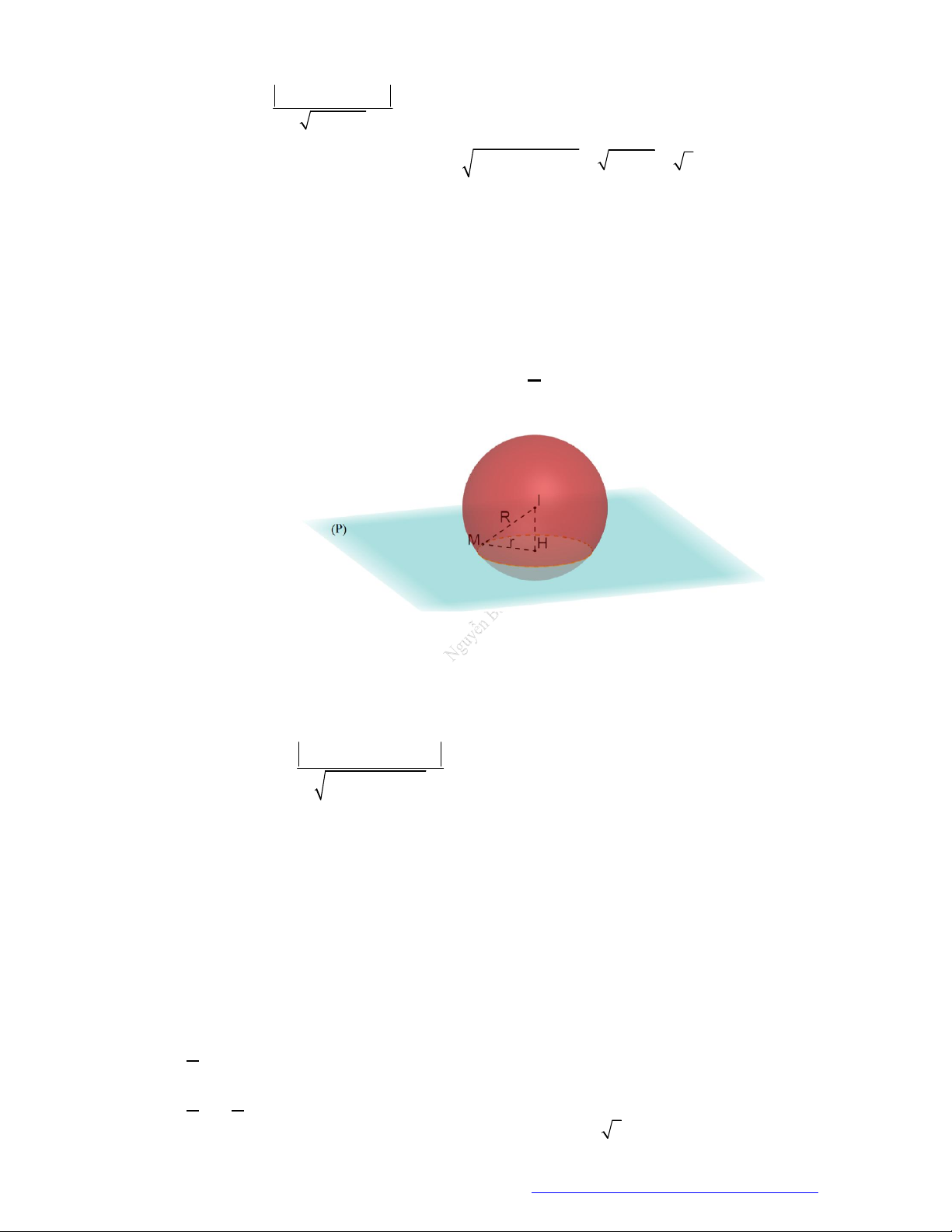
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 53

Ta có:

2

S r

 

 

1r 

 

3 2.0 2.1 1

; 2

1 4 4

d I P

   

 

 

( )S

có tâm

( 3;0;1)I 

và bán kính

 

2 2 2 2

; 2 1 5R d I P r    

Phương trình mặt cầu

( )S

là:

2 2 2

( 3) ( 1) 5.x y z    

Câu 40. (Chuyên Nguyễn Tất Thành Yên Bái 2019) Trong không gian với hệ tọa độ

,Oxyz

cho mặt

phẳng

 

: 2 2 2 0   P x y z

và điểm

 

1; 2; 1I  

. Viết phương trình mặt cầu

 

S

có tâm

I

và cắt mặt phẳng

 

P

theo giao tuyến là đường tròn có bán kính bằng

5.

A.

       

2 2 2

: 1 2 1 25.     S x y z

B.

       

2 2 2

: 1 2 1 16.     S x y z

C.

       

2 2 2

: 1 2 1 34.     S x y z

D.

       

2 2 2

: 1 2 1 34.     S x y z

Lời giải

Gọi

M

là điểm nằm trên đường tròn giao tuyến của

 

S

và

 

.P

Ta có

.IM R

Áp dụng công

thức tính bán kính mặt cầu trong trường hợp mặt cầu

 

S

giao với mặt phẳng

 

P

theo giao tuyến

là đường tròn có bán kính

r

là

 

2 2 2 2

;

*

I P

IM R d r  

Ta có:

 

;

2

2 2

1 2.2 2. 1 2

3 .

1 2 2

    

  

  

I P

d IH

Từ

 

2 2 2

* 3 5 34R   

.

Vậy phương trình mặt cầu

 

S

thỏa mãn yêu cầu đề bài là

     

2 2 2

1 2 1 34.     x y z

Câu 41. (Đà Nẵng 2019) Trong không gian

Oxyz

, cho mặt cầu

 

2 2 2

: 2 2 0S x y z z    

và điểm

 

2;2;0K

. Viết phương trình mặt phẳng chứa tất cả các tiếp điểm của các tiếp tuyến vẽ từ

K

đến

mặt cầu

 

S

.

A.

2 2 4 0x y z   

. B.

6 6 3 8 0x y z   

.

C.

2 2 2 0x y z   

D.

6 6 3 3 0x y z   

.

Lời giải

Chọn C

   

2

2 2

: 1 3S x y z   

 mặt cầu tâm

 

0;0; 1 , 3I R  .

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 54 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Do

 

2;2;1 , 3

IK IK

 



R 

K

nằm ngoài mặt cầu. Suy ra từ

K

vẽ được vô số tiếp tuyến đến

mặt cầu và khoảng cách từ

K

đến các tiếp điểm bẳng nhau.

Gọi

E

là

1

tiếp điểm

IE EK IKE   

vuông tại

E 

2 2

6

KE IK IE  



E

thuộc

mặt cầu tâm

K

bán kính

6

R





.

Tọa độ điểm

E

thỏa mãn hệ

   

2 2 2

2 2

2 2 2 2

2 2

2

2 2 0

2 2 2 2 6

2 2 6

x y z z

x y z z x y z

x y z



    



          



    





4 4 2 4 0 2 2 2 0.

x y z x y z

         

Câu 42. Trong không gian với hệ trục toạ độ

Oxyz

, cho mặt cầu có phương trình

 

2 2 2

: 2 4 6 3 0

S x y z x y z m

       

. Tìm số thực của tham số

m

để mặt phẳng

 

: 2 2 8 0

x y z



   

cắt

 

S

theo một đường tròn có chu vi bằng

8



.

A.

3

m

 

. B.

1

m

 

. C.

2

m

 

. D.

4

m

 

.

Lời giải

Chọn B

Ta có

       

2 2 2

: 2 4 6 3 0 1 2 3 17

S x y z x y z m x y z m               

.

 

S

là phương trình của mặt cầu thì

17 0 17

m m

   

.

Khi đó

 

1;2;3 ; 17

I R m  

lần lượt là tâm và bán kính của

 

S

.

Để mặt phẳng

 

: 2 2 8 0

x y z



   

cắt

 

S

theo thiết diện là một đường tròn có chu vi bằng

8



thì đường tròn đó có bán kính

4r 

.

Ta có

 

2 2 2

, 17 16 2 1

R d I r m m



        

(TMĐK).

Câu 43. (THPT Kinh Môn - HD - 2018) Trong không gian

Oxyz

, cho mặt cầu

 

2 2 2

: 2 6 4 2 0

S x y z x y z

      

và mặt phẳng

 

: 4 -11 0

x y z



  

. Viết phương trình

mặt phẳng

 

P

, biết

 

P

song song với giá của vectơ

 

1;6;2

v 



, vuông góc với

 



và tiếp xúc

với

 

S

.

A.

2 3 0

2 21 0

x y z

   





   



B.

3 4 1 0

3 4 2 0

x y z

   





   



.

C.

4 3 5 0

4 3 27 0

x y z

   





   



. D.

2 2 3 0

2 2 21 0

x y z

   





   



.

Lời giải

Mặt cầu

 

S

có tâm

 

1; 3;2

I 

và bán kính

4R 

.

Vì mặt phẳng (P) song song với giá của vectơ

 

1;6;2

v 



, vuông góc với

 



nên có vec tơ pháp

tuyến

 

,n n v



 



 

  

 

2; 1;2

 

.

Mặt phẳng

 

: 2 2 0

P x y z D

   

.

Vì

 

P

tiếp xúc với mặt cầu

 

S

nên ta có:

 

;

d I P R

 

2

2 2

2.1 3 2.2

4

2 1 2

D  

 

  

21

9 12

3

D

 



   







.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 55

Vậy phương trình mặt phẳng

 



là:

2 2 3 0

2 2 21 0

x y z

   





   



Câu 44. (SGD - Đà Nẵng - 2018) Trong không gian với hệ trục tọa độ

Oxyz

, cho mặt phẳng

 

P

có

phương trình

2 2 5 0

x y z

   

và mặt cầu

 

S

có phương trình

     

2 2 2

1 2 3 4

x y z

     

.

Tìm phương trình mặt phẳng song song với mặt phẳng

 

P

và đồng thời tiếp xúc với mặt cầu

 

S

.

A.

2 2 1 0

x y z

   

. B.

2 2 5 0

x y z

    

.

C.

2 2 23 0

x y z

   

. D.

2 2 17 0

x y z

    

.

Lời giải

Mặt cầu

 

S

có tâm

 

1; 2; 3

I

 

và bán kính

2R 

.

Gọi

 

Q

là mặt phẳng song song với mặt phẳng

 

P

và đồng thời tiếp xúc với mặt cầu

 

S

.

Phương trình

 

Q

có dạng:

2 2 0

x y z D

   

 

5

D

 

.

 

Q

tiếp xúc với

 

S

khi và chỉ khi

 

,

d I Q R

   

2 2 2

1 2. 2 2. 3

2

1 2 2

D    

 

 

11 6

D

  

11 6

D

 







  



5

17

D

 







 



.

Đối chiếu điều kiện suy ra

17

D

 

.

Vậy phương trình của

 

Q

là

2 2 17 0 2 2 17 0

x y z x y z

         

.

Câu 45. (Chuyên Lam Sơn - Thanh Hóa - 2018) Trong không gian với hệ trục tọa độ

Oxyz

cho mặt cầu

 

2 2 2

: 2 6 4 2 0

S x y z x y z

      

, mặt phẳng

 

: 4 11 0

x y z



   

. Gọi

 

P

là mặt phẳng

vuông góc với

   

, P



song song với giá của vecto

 

1;6;2

v 



và

 

P

tiếp xúc với

 

S

. Lập

phương trình mặt phẳng

 

P

.

A.

2 2 2 0

x y z

   

và

2 21 0

x y z

   

. B.

2 2 3 0

x y z

   

và

2 21 0

x y z

   

.

C.

2 2 3 0

x y z

   

và

2 2 21 0

x y z

   

. D.

2 2 5 0

x y z

   

và

2 2 2 0

x y z

   

.

Lời giải

 

S

có tâm

 

1; 3;2

I 

và bán kính

4R 

. Véc tơ pháp tuyến của

 



là

 

1;4;1

n







.

Suy ra VTPT của

 

P

là

,

P

n n v



 



 

  

 

2; 1;2

 

.

Do đó

 

P

có dạng:

2 2 0

x y z d

   

.

Mặt khác

 

P

tiếp xúc với

 

S

nên

 

, 4

d I P



Hay

 

2

2 2

2 3 4

4

2 1 2

d  



  

21

3

d

 











.

Câu 46. (Hồng Lĩnh - Hà Tĩnh – 2018) Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm

 

1;0;0

A

,

 

0;0;2

B

và mặt cầu

 

2 2 2

: 2 2 1 0

S x y z x y

     

. Số mặt phẳng chứa hai điểm

A

,

B

và

tiếp xúc với mặt cầu

 

S

là

A.

1

mặt phẳng. B.

2

mặt phẳng. C.

0

mặt phẳng. D. Vô số mặt phẳng.

Lời giải

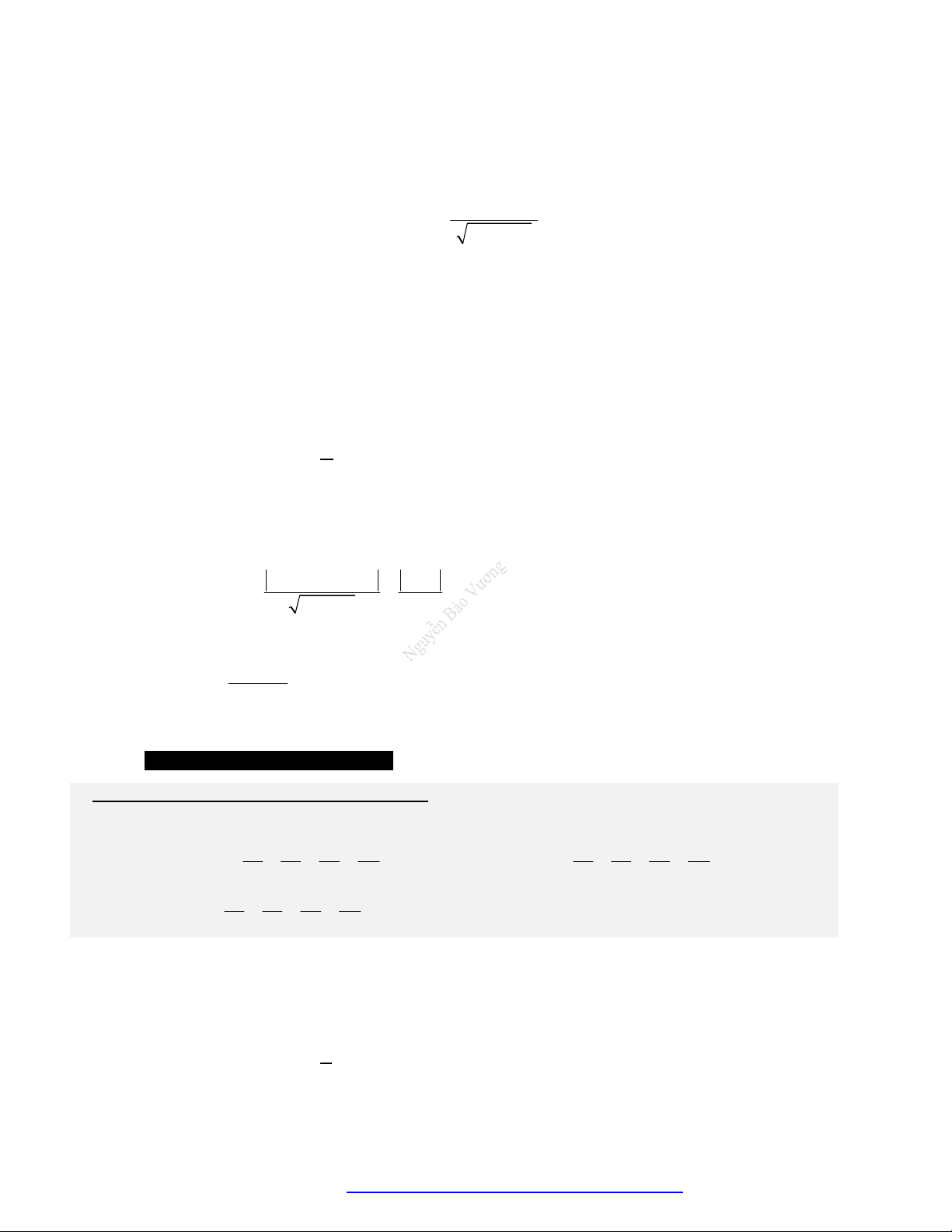
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 56 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Gọi phương trình mặt phẳng là:

 

2 2 2

: 0 0

P Ax By Cz D A B C

      

.

Theo đề bài, mặt phẳng qua

,A B

nên ta có:

0 2

2 0 2

A D A C

C D D C

  

 



 

   

 

. Vậy mặt phẳng

 

P

có dạng:

2 2 0

Cx By Cz C

   

.

 

S

có tâm

 

1,1,0

I

và

1R 

.

Vì

 

P

tiếp xúc với

 

S

nên

 

2 2 2

I,

2 2

1 5 0

5

P

C B C

d R B C B C

C B

 

       



.

Suy ra

0

A D

 

.

Vậy phương trình mặt phẳng

 

: 0

P y



.

Câu 47. (THPT Nam Trực - Nam Định - 2018) Trong không gian

Oxyz

, cho mặt phẳng

 

Q

song với

mặt phẳng

 

: 2 2 7 0

P x y z

   

. Biết

 

mp Q

cắt mặt cầu

     

2 2

2

: 2 1 25

S x y z

    

theo một đường tròn có bán kính

3

r



. Khi đó mặt phẳng

 

Q

có phương trình là:

A.

2 7 0

x y z

   

. B.

2 2 7 0

x y z

   

.

C.

2 2 17 0

x y z

   

. D.

2 2 17 0

x y z

   

.

Lời giải

Do mặt phẳng

   

// : 2 2 7 0

Q P x y z

   

, suy ra

   

: 2 2 0, 7

Q x y z m m

     

.

Ta có

     

2 2

2

: 2 1 25

S x y z

    

có tâm

 

0;2; 1

I



bán kính

5

R



.

Gọi

 

;

2.0 2.2 1 5

3

4 4 1

I Q

m m

h d

   

  

 

.

Do

 

Q

cắt mặt cầu

 

S

theo một đường tròn có bán kính

3

r



, suy ra:

2 2 2

R r h 

 

2

17

5 12

5

25 9 5 144

7 loai

5 12

9

m





 





       



 

  



.

Vậy

 

mp Q

có phương trình:

2 2 17 0

x y z

   

.

Dạng 3.2 Vị trí tương đối hai mặt

Vị trí tương đối giữa hai mặt phẳng (P) và (Q)

Cho hai mặt phẳng

1 1 1 1

( ) : 0

P A x B y C z D

   

và

2 2 2 2

( ) : 0.

Q A x B y C z D

   

( )P

cắt

1 1 1 1

2 2 2 2

( )

A B C D

Q

A B C D

    

1 1 1 1

2 2 2 2

( ) ( )

A B C D

P Q

A B C D

    

 

1 1 1 1

2 2 2 2

( ) ( )

A B C D

P Q

A B C D

     



1 2 1 2 1 2

( ) ( ) 0.

P Q A A B B C C

    

Câu 48. (THPT - Yên Định Thanh Hóa 2019) Trong không gian với hệ tọa độ

Oxyz

, cho hai mặt phẳng

 

: 2 3 5 0

P x my z

   

và

 

: 8 6 2 0

Q nx y z

   

, với

,m n



. Xác định m, n để

 

P

song

song với

 

Q

.

A.

4

m n

  

. B.

4; 4

m n

  

. C.

4; 4

m n

  

. D.

4

m n

 

.

Lời giải

Mặt phẳng

 

P

có véc tơ pháp tuyến

 

1

2; ;3

n m



TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 57

Mặt phẳng

 

Q

có véc tơ pháp tuyến

 

2

; 8; 6

n n



 

Mặt phẳng

   

1 2

1

2

/ / ( ) 8 4

3 6 4

k

kn

P Q n k n k m k m

k n

 



 







 

       

 

 

   









Nên chọn đáp án B

Câu 49. (Chuyên Trần Phú Hải Phòng 2019) Trong không gian

,Oxyz

cho hai mặt phẳng

 

: – 2 2 – 3 0

P x y z

 

và

 

: – 2 1 0

Q mx y z

  

. Với giá trị nào của m thì hai mặt phẳng đó

vuông góc với nhau?

A.

1

m



B.

1

m

 

C.

6

m

 

D.

6

m



Lời giải

Hai mặt phẳng

   

,P Q

vuông góc với nhau khi và chỉ khi

 

1. 2.1 2. 2 0 6

m m

     

Câu 50. (THPT Hai Bà Trưng - Huế - 2018) Trong không gian

Oxyz

, tìm tập hợp các điểm cách đều

cặp mặt phẳng sau đây:

4 2 3 0

x y z

   

,

4 2 5 0

x y z

   

.

A.

4 2 6 0

x y z

   

. B.

4 2 4 0

x y z

   

. C.

4 2 1 0

x y z

   

. D.

4 2 2 0

x y z

   

.

Lời giải

Gọi điểm

   

0; 3;0 4 2 3 0 A x y z



     

và

   

0; 5;0 4 2 5 0 B x y z



     

.

Mặt phẳng cách đều hai mp trên có dạng:

 

4 2 0

x y z m



   

.

Để mp

 



cách đều hai mp trên thì

 

; 2 ;d A d A

 



2

3 1

4

m

 



   



 



.

Mặt khác điểm hai điểm

A

,

B

phải nằm về hai phía của mp

 



.

Do đó:

+) Với

2

m

 

ta có:

  

4.0 3 2.0 2 4.0 5 2.0 2 0      

nên

;A B

cùng phía.

+) Với

4

m

 

ta có:

  

4.0 3 2.0 4 4.0 5 2.0 4 0      

nên

;A B

khác phía.

Vậy phương trình mặt phẳng cần tìm là

 

4 2 4 0

x y z



   

.

Câu 51. (THPT Yên Khánh - Ninh Bình - 2019) Trong không gian

Oxyz

, cho hai mặt phẳng

 

: 2 3 0

P x y z

   

;

 

: 2 1 0

Q x y z

   

. Mặt phẳng

 

R

đi qua điểm

 

1;1;1

M

chứa giao

tuyến của

 

P

và

 

Q

; phương trình của

     

: 2 3 2 1 0

R m x y z x y z

       

. Khi đó giá

trị của

m

là

A.

3

. B.

1

3

. C.

1

3



. D.

3

.

Lời giải

Vì

     

: 2 3 2 1 0

R m x y z x y z

       

đi qua điểm

 

1;1;1

M

nên ta có:

   

1 2.1 1 3 2.1 1 1 1 0

m

       

3

m

  

.

Câu 52. (THPT Gia Lộc Hải Dương 2019) Trong không gian

Oxyz

, mặt phẳng

 

: 2 2 0

P x y z

   

vuông góc với mặt phẳng nào dưới đây?

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 58 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

A.

2 2 0

x y z

   

. B.

2 0

x y z

   

. C.

2 0

x y z

   

. D.

2 2 0

x y z

   

.

Lời giải

Mặt phẳng

 

P

có một vectơ pháp tuyến

 

2;1;1

P

n 



.

Mặt phẳng

 

: 2 0

Q x y z

   

có một vectơ pháp tuyến

 

1; 1; 1

Q

n

  



.

Mà

. 2 1 1 0

P Q

n n

   

 

   

P Q

n n P Q

   

 

.

Vậy mặt phẳng

2 0

x y z

   

là mặt phẳng cần tìm.

Câu 53. (Chuyên Hùng Vương Gia Lai 2019) Trong không gian Oxyz, cho 3 điểm

     

1;0;0 , 0; ;0 , 0;0;A B b C c

trong đó

. 0

b c



và mặt phẳng

 

: 1 0

P y z

  

. Mối liên hệ giữa

,b c

để mặt phẳng

( )ABC

vuông góc với mặt phẳng

( )P

là

A.

2

b c

. B.

2b c

. C.

b c

. D.

3 .b c

Lời giải

• Phương trình

 

ABC

:

 

1

x y z

ABC

b c

   

có VTPT:

1 1

1; ;

n

b c

 



 

 



.

• Phương trình

 

: 1 0

P y z

  

 

P



có VTPT:

 

' 0;1; 1

n

 



.

•

   

1 1

. ' 0 0

ABC P n n b c

b c

       

 

.

Câu 54. (THPT Yên Phong 1 Bắc Ninh 2019) Trong không gian

Oxyz

, cho

 

: 2 5 0

P x y z

   

và

   

: 4 2 3 0

Q x m y mz

    

,

m

là tham số thực. Tìm tham số

m

sao cho mặt phẳng

 

Q

vuông góc với mặt phẳng

 

P

.

A.

3

m

 

. B.

2

m

 

. C.

3

m



. D.

2

m



.

Lời giải

Mặt phẳng

 

P

có véctơ pháp tuyến là

 

1;1; 2

P

n

 



.

Mặt phẳng

 

Q

có véctơ pháp tuyến là

 

4;2 ;

Q

n m m

 



.

Ta có:

   

       

. 0 4.1 2 2 0 2

P Q P Q

P Q n n n n m m m

           

   

.

Nên

2

m



.

Câu 55. (Chuyên Lê Quý Đôn – Điện Biên 2019) Trong không gian

Oxyz

, cho mặt phẳng

 

: 2 0

ax y z b



   

đi qua giao tuyến của hai mặt phẳng

 

: 1 0

P x y z

   

và

 

: 2 1 0

Q x y z

   

. Tính

4a b

.

A.

16

. B.

8

. C.

0

. D.

8

.

Lời giải

Chọn A

Trên giao tuyến



của hai mặt phẳng

   

,P Q

ta lấy lần lượt 2 điểm

,A B

như sau:

Lấy

 

; ;1A x y



, ta có hệ phương trình:

 

0

0 0;0;1

2 0

x y

x y A

x y

 



   



 



.

Lấy

 

1; ;B y z

 

, ta có hệ phương trình:

 

0 2

1;2; 2

2 2 2

y z y

B

y z z

  

 

   

 

   

 

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 59

Vì

 



 

nên

 

,A B





. Do đó ta có:

2 0 8

6 0 2

b a

a b b

   

 



 

     

 

.

Vậy

 

4 8 2. 2 16.

a b

     

Câu 56. (SGD Bến Tre 2019) Trong không gian

Oxyz

cho hai mặt phẳng

 

: 2 1 0

x y z



   

và

 

: 2 4 2 0.

x y mz



   

Tìm

m

để hai mặt phẳng

 



và

 



song song với nhau.

A.

1

m



. B. Không tồn tại

m

. C.

2

m

 

. D.

2

m



.

Lời giải

Chọn B

Ta có vec tơ pháp tuyến của

 



là

 

1

1;2; 1

n

 



, vec tơ pháp tuyến của

 



là

 

2

2;4;

n m 



.

Hai mặt phẳng

 



và

 



song song khi

2 4 2

1 2 1 1

m

 

  

 

Vậy không có giá trị nào của

m

thỏa mãn điều kiện trên.

Câu 57. (Chuyên Lê Hồng Phong-Nam Định-2019) Trong không gian toạ độ

Oxyz

, cho mặt phẳng

( ): 2 2 1 0

P x y z

   

, mặt phẳng nào dưới đây song song với

 

P

và cách

 

P

một khoảng

bằng

3

.

A.

( ): 2 2 8 0

Q x y z

   

. B.

 

: 2 2 5 0

Q x y z

   

.

C.

( ): 2 2 1 0

Q x y z

   

. D.

 

: 2 2 2 0

Q x y z

   

.

Lời giải

Chọn A

+ Ta có:

( ) : 2 2 1 0

P x y z

   

, chọn

   

1;0;0

A P



.

+ Xét đáp án A, ta có

 

2

2 2

1 8

; 3.

1 2 2

d A Q



 

  

Vậy đáp án A thoả mãn.

Câu 58. (Cụm 5 Trường Chuyên - ĐBSH - 2018) Trong không gian với hệ tọa độ

Oxyz

có bao nhiêu

mặt phẳng song song với mặt phẳng

 

: 3 0

Q x y z

   

, cách điểm

 

3;2;1

M

một khoảng

bằng

3 3

biết rằng tồn tại một điểm

 

; ;X a b c

trên mặt phẳng đó thỏa mãn

2

a b c

   

?

A.

1

. B. Vô số. C.

2

. D.

0

.

Lời giải

Ta có mặt phẳng cần tìm là

 

: 0

P x y z d

   

với

3

d



.

Mặt phẳng

 

P

cách điểm

 

3;2;1

M

một khoảng bằng

3 3

6

3 3

3

d

 

3

15

d









 



đối

chiếu điều kiện suy ra

15

d

 

. Khi đó

 

: 15 0

P x y z

   

.

Theo giả thiết

   

; ;

X a b c P



15 2

a b c

     

không thỏa mãn

2

a b c

   

.

Vậy không tồn tại mặt phẳng

 

P

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 60 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 59. (Chuyên Thái Bình - 2018) Trong không gian với hệ trục tọa độ

Oxyz

, cho hai mặt phẳng

 

1

:3 4 2 0

Q x y z

   

và

 

2

:3 4 8 0

Q x y z

   

. Phương trình mặt phẳng

 

P

song song và

cách đều hai mặt phẳng

 

1

Q

và

 

2

Q

là:

A.

 

:3 4 10 0

P x y z

   

. B.

 

:3 4 5 0

P x y z

   

.

C.

 

:3 4 10 0

P x y z

   

. D.

 

:3 4 5 0

P x y z

   

.

Lời giải

Mặt phẳng

 

P

có dạng

3 4 0

x y z D

   

.

Lấy

   

1

0;2;0

M Q



và

   

2

0;8;0

N Q



. Do

   

1 2

//

Q Q

trung điểm

 

0;5;0

I

của

MN

phải

thuộc vào

 

P

nên ta tìm được

5

D



.

Vậy

 

:3 4 5 0

P x y z

   

.

Câu 60. (THPT Lương Thế Vinh Hà Nội 2019) Gọi

m,n

là hai giá trị thực thỏa mãn giao tuyến của hai

mặt phẳng

 

: 2 1 0   

m

P mx y nz

và

 

: 2 0   

m

Q x my nz

vuông góc với mặt phẳng

 

: 4 6 3 0



   

x y z

. Tính

m n

.

A.

0 

m n

. B.

2 

m n

. C.

1 m n

. D.

3 

m n

.

Lời giải

+

 

: 2 1 0   

m

P mx y nz

có vectơ pháp tuyến

 

1

;2;



n m n

.

 

: 2 0   

m

Q x my nz

có vectơ pháp tuyến

 

2

1; ;





n m n

.

 

: 4 6 3 0



   

x y z

có vectơ pháp tuyến

 

4; 1; 6



 



n

.

+ Giao tuyến của hai mặt phẳng

 

m

P

và

 

m

Q

vuông góc với mặt phẳng

 



nên

   

1 1

2 2

. 0

4 2 6 0 2

.

4 6 0 1

. 0

 



 





 

   

 

  

   

    

   



 

 



 



 

   

   

m

P

n n n n

m n m

m n n

Q

n n n n

Vậy

3 

m n

.

Câu 61. (Chuyên KHTN 2019) Biết rằng trong không gian với hệ tọa độ

Oxyz

có hai mặt phẳng

 

P

và

 

Q

cùng thỏa mãn các điều kiện sau: đi qua hai điểm

 

1;1;1

A

và

 

0; 2;2

B 

, đồng thời cắt các

trục tọa độ

,Ox Oy

tại hai điểm cách đều

O

. Giả sử

 

P

có phương trình

1 1 1

0

x b y c z d

   

và

 

Q

có phương trình

2 2 2

0

x b y c z d

   

. Tính giá trị biểu thức

1 2 1 2

b b c c

.

A. 7. B. -9. C. -7. D. 9.

Lời giải

Cách 1

Xét mặt phẳng

 



có phương trình

0

x by cz d

   

thỏa mãn các điều kiện: đi qua hai điểm

 

1;1;1

A

và

 

0; 2;2

B 

, đồng thời cắt các trục tọa độ

,Ox Oy

tại hai điểm cách đều

O

.

Vì

 



đi qua

 

1;1;1

A

và

 

0; 2;2

B 

nên ta có hệ phương trình:

 

1 0

*

2 2 0

b c d

   





   



Mặt phẳng

 



cắt các trục tọa độ

,Ox Oy

lần lượt tại

 

;0;0 , 0; ;0

d

M d N

b



 



 

 

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 61

Vì

,M N

cách đều

O

nên

OM ON

. Suy ra:

d

b



.

Nếu

0

d



thì chỉ tồn tại duy nhất một mặt phẳng thỏa mãn yêu cầu bài toán (mặt phẳng này sẽ đi

qua điểm

O

).

Do đó để tồn tại hai mặt phẳng thỏa mãn yêu cầu bài toán thì:

1

d

d b

b

   

.

 Với

1b 

,

 

2 4

*

2 2 6

c d c

c d d

   

 

 

 

   

 

. Ta được mặt phẳng

 

P

:

4 6 0

x y z

   

 Với

1

b

 

,

 

0 2

*

2 2 2

c d c

c d d

   

 

 

 

   

 

. Ta được mặt phẳng

 

Q

:

2 2 0

x y z

   

Vậy:

   

1 2 1 2

1. 1 4. 2 9

bb c c

      

.

Cách 2

 

1; 3;1

AB   



Xét mặt phẳng

 



có phương trình

0

x by cz d

   

thỏa mãn các điều kiện: đi qua hai điểm

 

1;1;1

A

và

 

0; 2;2

B 

, đồng thời cắt các trục tọa độ

,Ox Oy

tại hai điểm cách đều

O

lần lượt tại

,M N

. Vì

,M N

cách đều

O

nên ta có 2 trường hợp sau:

TH1:

( ;0;0), (0; ;0)M a N a

với

0

a



khi đó

 



chính là

 

P

. Ta có

( ; ;0)MN a a

 



, chọn

1

( 1;1;0)

u  



là một véc tơ cùng phương với

MN



. Khi đó

1

, ( 1; 1; 4)

P

n AB u

 

    

 

  

,

suy ra

 

1

: 4 0

P x y z d

   

TH2:

( ;0;0), (0; ;0)M a N a

với

0

a



khi đó

 



chính là

 

Q

. Ta có

( ; ;0)MN a a





, chọn

2

(1;1;0)

u 



là một véc tơ cùng phương với

MN



. Khi đó

2

, ( 1;1;2)

Q

n AB u

 

  

 

  

,

suy ra

 

2

: 2 0

Q x y z d

   

Vậy:

   

1 2 1 2

1. 1 4. 2 9

bb c c

      

.

Câu 62. (Toán Học Và Tuổi Trẻ 2018) Trong không gian với hệ tọa độ

,Oxyz

cho điểm

 

3;2;1

M

. Mặt

phẳng

 

P

đi qua

M

và cắt các trục tọa độ

Ox

,

Oy

,

Oz

lần lượt tại các điểm

A

,

B

,

C

không

trùng với gốc tọa độ sao cho

M

là trực tâm tam giác

ABC

. Trong các mặt phẳng sau, tìm mặt

phẳng song song với mặt phẳng

 

P

.

A.

3 2 14 0

x y z

   

. B.

2 3 9 0

x y z

   

. C.

3 2 14 0

x y z

   

. D.

2 9 0

x y z

   

.

Lời giải

Gọi

     

;0;0 ; 0; ;0 ; 0;0;A a B b C c

Phương trình mặt phẳng

 

P

có dạng:

 

1 . . 0

x y z

a b c

   

Vì

 

P

qua

M

nên

 

3 2 1

1 1

a b c

  

Ta có:

       

3; 2; 1 ; 3; 2; 1 ; 0; ; ; ;0;MA a MB b BC b c AC a c

           

   

Vì M là trực tâm của tam giác

ABC

nên:

 

. 0 2

2

3

. 0

MA BC b c

a c

MB AC



 







 









 

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 62 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Từ

 

1

và

 

2

suy ra

14

;

; 14

3 2

a

b c



 

. Khi đó phương trì

nh

 

P

:

3 2 14 0

x y z

   

Vậy mặt phẳng

song song với

 

P

là

:

3

2 14 0.

x

y z



  

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương  https://www.facebook.com/phong.baovuong Trang 1

TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH GIỎI MỨC 9-10 ĐIỂM

Dạng 1. Một số bài toán liên khác quan điểm – mặt phẳng – mặt cầu

Câu 1. (Mã 103 2018) Trong không gian

Oxyz

, cho mặt cầu

2 2 2

( ) : ( 1) ( 2) ( 3) 1S x y z     

và điểm

(2;3;4)A

. Xét các điểm

M

thuộc

( )S

sao cho đường thẳng

AM

tiếp xúc với

( )S

,

M

luôn thuộc

mặt phẳng có phương trình là

A.

2 2 2 15 0x y z   

B.

7 0x y z   

C.

2 2 2 15 0x y z   

D.

7 0x y z   

Lời giải

Chọn D

Dễ thấy

A

nằm ngoài mặt cầu

( )S

. Tâm mặt cầu là

(1;2;3)I

.

Đường thẳng

AM

tiếp xúc với

( ) . 0S AM IM AM IM   

 

( 2)( 1) ( 3)( 2) ( 4)( 3) 0x x y y z z         

( 1 1)( 1) ( 2 1)( 2) ( 3 1)( 3) 0x x y y z z            

2 2 2

( 1) ( 2) ( 3) ( 7) 0x y z x y z          

2 2 2

7 0 ( ( 1) ( 2) ( 3) 0)x y z Do x y z           .

Câu 2. (Sở Bắc Giang Năm 2019) Trong không gian với hệ trục

Oxyz

, cho điểm

 

2; 2;2A 

và mặt

cầu

   

2

2 2

: 2 1S x y z   

. Điểm

M

di chuyển trên mặt cầu

 

S

đồng thời thỏa mãn

. 6OM AM 

 

. Điểm

M

thuộc mặt phẳng nào sau đây?

A.

2 2 6 9 0x y z   

. B.

2 2 6 9 0x y z   

.

C.

2 2 6 9 0x y z   

. D.

2 2 6 9 0x y z   

.

Lời giải

Giả sử

 

; ;M x y z

thì

 

; ;OM x y z



,

 

2; 2; 2AM x y z   



.

Vì

 

M S

và

. 6OM AM 

 

nên ta có hệ

     

 

2

2 2

2 2 2 6

2 1

x x y y z z

x y z

     





   





2 2 2

2 2 2 6

4 4 1

x y z x y z

x y z z



     







    





2 2 6 9 0x y z    

.

Vậy điểm

M

thuộc mặt phẳng có phương trình:

2 2 6 9 0x y z   

.

Câu 3. Trong không gian với hệ trục

Oxyz

, cho điểm

 

2; 2;2A 

và mặt cầu

   

2

2 2

: 2 1S x y z   

.

Điểm

M

di chuyển trên mặt cầu

 

S

đồng thời thỏa mãn

. 6OM AM 

 

. Điểm

M

luôn thuộc mặt

phẳng nào dưới đây?

A.

2x 2 6z 9 0y   

. B.

2 2 6z 9 0x y   

.

C.

2x 2 6z 9 0y   

. D.

2x 2 6z 9 0y   

.

Lời giải

Chọn D

Gọi điểm

   

; ;M x y z S

là điểm cần tìm.

PHƯƠNG TRÌNH MẶT PHẲNG

Chuyên đề 30

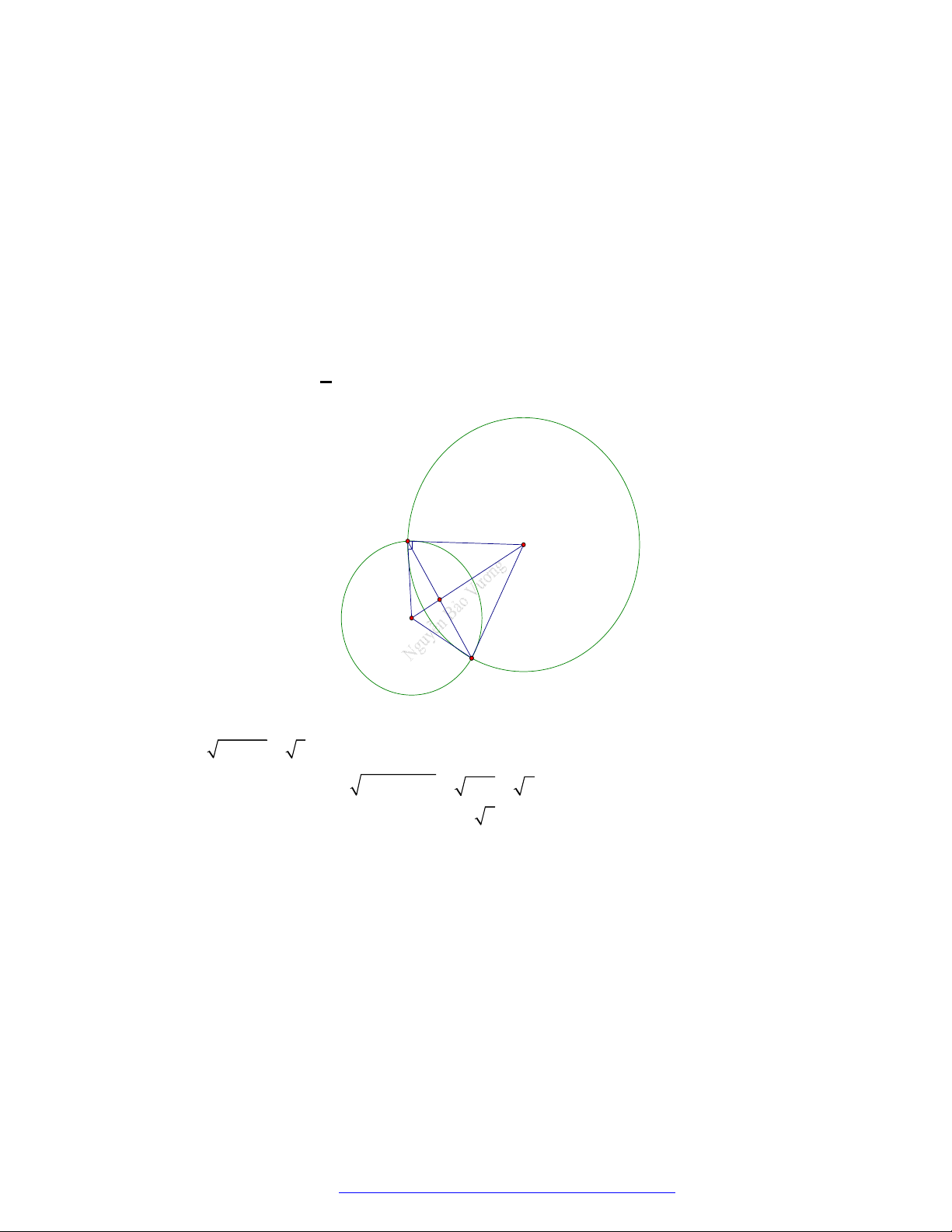
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Khi đó:

 

2

2 2

2 1x y z   

2 2 2

4 4 1x y z z     

 

2 2 2

4 3 1x y z z     

Ta có:

 

; ;OM x y z



và

 

2; 2; 2AM x y z   



.

Suy ra

. 6OM AM 

 

     

2 2 2 6x x y y z z      

 

2 2 2

2 2 2 6 2x y z x y z      

Thay

 

1

vào

 

2

ta được

4 3 2 2 2 6 0z x y z       2 2 6 9 0x y z    

.

Câu 4. (Chuyên Lê Quý Đôn Điện Biên 2019) Trong không gian

Oxyz

, cho mặt

cầu

       

2 2 2

: 1 1 1 1S x y z     

và điểm

(2;2;2)A

. Xét các điểm

M

thuộc

( )S

sao cho

đường thẳng

AM

luôn tiếp xúc với

( )S

.

M

luôn thuộc một mặt phẳng cố định có phương trình

là

A.

– 6 0x y z  

. B.

4 0x y z   

. C.

3 3 3 – 8 0x y z  

. D.

3 3 3 – 4 0x y z  

.

Lời giải

 

S

có tâm

 

1;1;1I

và bán kính

1R 

.

Do

1 1 1 3IA R    

nên điểm

A

nằm ngoài mặt cầu

 

S

.

AMI

vuông tại

M

:

2 2

3 1 2AM AI IM    

.

M

thuộc mặt cầu

 

S



có tâm

A

bán kính

2

.

Ta có phương trình

 

S



     

2 2 2

: 2 2 2 2x y z     

.

Ta có

   

M S S



 

.

Tọa độ của

M

thỏa hệ phương trình

     

 

2 2 2

1 1 1 1

2 2 2 2

x y z

I

x y z



     





     





.

Ta có

 

2 2 2

2 2 2 2 0

4 4 4 10 0

x y z x y z

I

x y z x y z



      







      





2 2 2 8 0x y z     4 0x y z    

Suy ra

 

: 4 0M P x y z    

.

Câu 5. (Đề Tham Khảo 2018) Trong không gian

Oxyz

, cho ba điểm

 

1;2;1A

,

 

3; 1;1B 

và

 

1; 1;1C  

. Gọi

 

1

S

là mặt cầu có tâm

A

, bán kính bằng

2

;

 

2

S

và

 

3

S

là hai mặt cầu có

I

A

M

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3

tâm lần lượt là

B

,

C

và bán kính đều bằng

1

. Hỏi có bao nhiêu mặt phẳng tiếp xúc với cả ba mặt

cầu

 

1

S

,

 

2

S

,

 

3

S

.

A.

8

B.

5

C.

7

D.

6

Lời giải

Chọn C

Gọi phương trình mặt phẳng

 

P

tiếp xúc với cả ba mặt cầu đã cho có phương trình là:

0

ax by cz d

   

( đk:

2 2 2

0

a b c

  

).

Khi đó ta có hệ điều kiện sau:

 

; 2

; 1

d A P

d B P

d C P



















2 2 2

2

3

1

a b c d

a b c

a b c d

a b c

a b c d

a b c



  





 



  



 



 



   







 



2 2 2

2 2

3

a b c d a b c



     



      





      





.

Khi đó ta có:

3

a b c d a b c d       

3

a b c d a b c d

       







      



0

a

a b c d









   



.

với

0

a



thì ta có

2 2

b c d b c

b c d b c d



   





     





2 2

4 0

0

b c d b c

b c d

c d



   







  







 





0 0, 0

4 , 2 2

c d c d b

c d b c b

     







   



do đó có 3

mặt phẳng.

Với

0

a b c d

   

thì ta có

2 2 2

3 2

2

b a b c

a a b c



  







  





2 2 2

3 4

2

b a

a a b c

 







  





4

3

11

3

b a

c a



















do đó có 4 mặt phẳng thỏa mãn bài toán.Vậy có

7

mặt phẳng thỏa mãn bài toán.

Câu 6. Trong không gian

,Oxyz

cho

       

2 2 2

: 3 2 5 36

S x y z

     

, điểm

 

7;1;3

M

. Gọi



là

đường thẳng di động luôn đi qua

M

và tiếp xúc với mặt cầu

 

S

tại

N

. Tiếp điểm

N

di động

trên đường tròn

 

T

có tâm

 

, ,J a b c

. Gọi

2 5 10k a b c  

, thì giá trị của

k

là

A.

45

. B.

50

. C.

45

. D.

50

.

Lời giải

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Mặt cầu

       

2 2 2

: 3 2 5 36S x y z     

có tâm

 

3;2;5I 

, bán kính

6R 

.

Có 25 16 4 3 5 6IM R      , nên

M

thuộc miền ngoài của mặt cầu

 

S

.

Có

MN

tiếp xúc mặt cầu

 

S

tại

N

, nên

MN IN

tại

N

.

Gọi

J

là điểm chiếu của

N

lên

MI

.

Có

2

.IN IJ IM . Suy ra

2

36 12 5

5

3 5

IN

IJ

IM

  

(không đổi), I cố định.

Suy ra

N

thuộc

 

P

cố định và mặt cầu

 

S

, nên

N

thuộc đường tròn

 

C

tâm

J

.

Gọi

 

; ;N x y z

, có

IJ

IJ IM

IM



 

12 5 1 4

5 5

3 5

IM IM 

 

3 8

4

2

5

2

5

x

y

z





 



   





  





6 23

5; ;

5 5

N

 



 

 

,

2 5 10 50k a b c   

. Vậy

50k 

.

Câu 7. (Chuyên Đại Học Vinh 2019) Trong không gian

Oxyz

, cho các điểm

     

2;1;4 , 5;0;0 , 1; 3;1M N P 

. Gọi

 

; ;I a b c

là tâm của mặt cầu tiếp xúc với mặt phẳng

 

Oyz

đồng thời đi qua các điểm

, ,M N P

. Tìm

c

biết rằng

5a b c  

A. 3 B. 2 C. 4 D. 1

Lời giải

Chọn B

Phương trình mặt cầu

 

S

tâm

 

; ;I a b c

là

2 2 2

2 2 2 0x y z ax by cz d      

Đk:

2 2 2

0a b c d   

 

S

đi qua các điểm

, ,M N P

và tiếp xúc với mặt phẳng

 

Oyz

4 2 8 21

10 25

2 6 2 11

a b c d

a d

a b c d

R a

     





   







     







N

I

J

M

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5

2 2 2 2

4 2 8 10 25 21

10 25

2 6 2 10 25 11

a b c a

d a

a b c a

a b c d a

      





 







      



   



2 2

6 2 8 4

10 25

8 6 2 14

0

a b c

d a

a b c

b c d

  





 







  



  



2 2

6 2 8 4

10 25

32 24 8 56

0

a b c

d a

a b c

b c d

  





 







  



  



2 2

6 2 8 4

10 25

26 26 52

0

a b c

d a

a b

b c d

  





 







 



  



2 2

1

10 25

2

0

c a

d a

b a

b c d

 





 







  



  



   

2 2

2 1 10 25 0

a a a

       

2

2 16 30 0

a a

   

3 5

3 1 3

5 2 4

5 25

a a

a b b

hay

a c c

d d

 

 

 

    



 

 

 



  



 

 

 

Vì

5

a b c

  

nên chọn

2

c



.

Câu 8. (Chuyên KHTN 2019) Trong không gian với hệ tọa độ

Oxyz

, cho điểm

 

1;2; 2

H



. Mặt phẳng

 

a

đi qua

H

và cắt các trục

, ,Ox Oy Oz

lần lượt tại các điểm

, ,A B C

sao cho

H

là trực tâm của

tam giác

ABC

. Tính diện tích mặt cầu ngoại tiếp tứ diện

OABC

.

A.

243



. B.

81



. C.

81

2



. D.

243

2



.

Lời giải

Mặt phẳng

 

a

cắt các trục

, ,Ox Oy Oz

lần lượt tại các điểm

 

;0;0

A a

,

 

0; ;0

B b

,

 

0;0;C c

. Do

H

là trực tâm tam giác

ABC

nên

, , 0

a b c



.

Khi đó phương trình mặt phẳng

 

a

:

1

x y z

a b c

  

.

Mà

   

1;2; 2H

a

 

nên:

1 2 2

1

a b c

  

 

1

.

Ta có:

 

1 ;2; 2

AH a

  



,

 

1;2 ; 2

BH b

  



,

 

0; ;BC b c

 



,

 

;0;AC a c

 



.

Lại có

H

là trực tâm tam giác

ABC

, suy ra

. 0

AH BC

BH AC















 

hay

2

b c

a c

 





 



(2)

.

Thay

 

2

vào

 

1

ta được:

1 2 2 9

1

2 2

c

c c c

     

 

, khi đó

9

9,

2

a b

 

.

Vậy

 

9;0;0

A

,

9

0; ;0

2

B

 

 

 

,

9

0;0;

2

C

 



 

 

.

Khi đó, giả sử mặt cầu ngoại tiếp tứ diện

OABC

có phương trình là:

2 2 2

2 2 2 0

x y z a x b y c z d

  

      

. Với

     

2 2 2

0

a b c d

  

   

Vì 4 điểm

, , ,O A B C

thuộc mặt cầu nên ta có hệ phương trình:

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

0

9

18 81

2

81

9

4

81

9

4

d

a d

a

b d

b

c d

c













   





 





 

   





 



  

 



 







.

Phương trình mặt cầu ngoại tiếp tứ diện

OABC

là:

2 2 2

9 9

9 0

2 2

x y z x y z

     

, có tâm

9 9 9

; ;

2 4 4

I

 



 

 

và bán kính

2 2 2

9 9 9 9 6

0

2 4 4 4

R

     

    

     

     

.

Vậy diện tích mặt cầu ngoại tiếp tự diện

OABC

là

2

9 6 243

4 4 .

4 2

S R



 

 

  

 

 

.

Câu 9. ( HSG Bắc Ninh 2019) Trong không gian với hệ tọa độ

Oxyz

, cho ba điểm

 

6;0;0

M

,

 

0;6;0

N

,

 

0;0;6

P

. Hai mặt cầu có phương trình

 

2 2 2

1

: 2 2 1 0     

S x y z x y

và

 

2 2 2

2

: 8 2 2 1 0

S x y z x y z

      

cắt nhau theo đường tròn

 

C

. Hỏi có bao nhiêu mặt cầu

có tâm thuộc mặt phẳng chứa

 

C

và tiếp xúc với ba đường thẳng

, ,

MN NP PM

.

A.

1

. B.

3

. C. Vô số. D.

4

.

Lời giải

 Giả sử mặt cầu

 

S

có tâm

 

I C



và tiếp xúc với ba đường thẳng

, ,

MN NP PM

.

Gọi

H

là hình chiếu vuông góc của

I

trên

 

MNP

.

Ta có:

 

S

tiếp xúc với ba đường thẳng

, ,

MN NP PM

     

, , ,

d I MN d I NP d I PM

  

     

, , ,

d H MN d H NP d H PM

  

H

là tâm đường tròn nội tiếp hoặc tâm đường tròn bàng tiếp của tam giác

MNP

.



 

MNP

có phương trình là

1

6 6 6

x y z

  

hay

6 0

x y z

   

.



     

1 2

C S S

 



Tọa độ các điểm thuộc trên

 

C

thỏa mãn hệ phương trình:

2 2 2

2 2 1 0

8 2 2 1 0

x y z x y

x y z x y z



     





      





3 2 0

x y z

   

.

Do đó, phương trình chứa mặt phẳng chứa

 

C

là

 

:3 2 0

x y z

a

  

.

 Vì

   

1.3 1. 2 1. 1 0    

   

MNP

a

 

.

 

1

 Ta có:

6 2

MN NP PM  

MNP 

đều.

Gọi

G

là trọng tâm tam giác

MNP

 

2;2;2

G

và

G

là tâm đường tròn nội tiếp tam giác

MNP

. Thay tọa độ của điểm

G

vào phương trình mặt phẳng

 

a

, ta có:

 

G

a



.

 Gọi



là đường thẳng vuông góc với

 

MNP

tại

G

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7

Vì

   

 

MNP

G

a















 

a

  

.

Khi đó:

I  

   

, ,d I MN d I NP 

 

,d I PM r 

 Mặt cầu tâm

I

bán kính

r

tiếp xúc với ba đường thẳng

MN

,

NP

,

PM

.

Vậy có vô số mặt cầu có tâm thuộc mặt phẳng chứa

 

C

và tiếp xúc với ba đường thẳng

, ,MN MP PM

.

Câu 10. Trong không gian với hệ tọa độ

Oxyz

cho

   

3;1;1 , 1; 1;5 A B

và mặt phẳng

 

: 2 2 11 0.   P x y z

Mặt cầu

 

S

đi qua hai điểm

,A B

và tiếp xúc với

 

P

tại điểm

C

. Biết

C

luôn thuộc một đường tròn

 

T

cố định. Tính bán kính

r

của đường tròn

 

T

.

A.

4r

. B.

2r

. C.

3r

. D.

2r

.

Lời giải

Ta có

 

4; 2; 4 



AB

và mp

 

P

có vec tơ pháp tuyến

 

2; 1; 2 



n

. Do đó

AB

vuông góc với

 

P

.

Giả sử mặt cầu

 

S

có phương trình

2 2 2

2 2 2 0      x y z ax by cz d

. Mặt cầu

 

S

đi qua hai

điểm

,A B

nên ta có

9 1 1 6 2 2 0 6 2 2 11

1 1 25 2 2 10 0 2 2 10 27

           

 



 

          

 

a b c d a b c d

.

Suy ra

8 4 8 16 2 2 4.      a b c a b c

Mặt cầu

 

S

tiếp xúc với

 

P

nên ta có

 

2 2 11

, 5.

3

  

 

a b c

d I P

Ta có

 

4; 2;4 16 4 16 6.      



AB AB

Goi

M

là trung điểm

AB

ta có

 

2 2

, 5 3 4.   d C AB IM

Vậy

C

luôn thuộc một đường tròn

 

T

cố định có bán kính

4.r

.

Câu 11. (THPT Lê Quý Đôn Đà Nẵng 2019) Trong không gian

Oxyz

, cho hai điểm

5 3 7 3

; ;3

2 2

A

 

 

 

 

,

5 3 7 3

; ;3

2 2

B

 

 

 

 

và mặt cầu

2 2 2

( ) : ( 1) ( 2) ( 3) 6S x y z      . Xét

mặt phẳng

( ) : 0P ax by cz d   

,

 

, , , : 5a b c d d  

là mặt phẳng thay đổi luôn đi qua hai

điểm

,A B

. Gọi

( )N

là hình nón có đỉnh là tâm của mặt cầu

( )S

và đường tròn đáy là đường tròn

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 8 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

giao tuyến của

( )P

và

( )S

. Tính giá trị của

T a b c d   

khi thiết diện qua trục của hình nón

( )N

có diện tích lớn nhất.

A.

4T 

. B.

6T 

. C.

2T 

. D.

12T 

.

Lời giải

Mặt cầu

( )S

có tâm

 

1;2;3I

, bán kính

6R 

.

Có 6IA IB  nên

,A B

thuộc mặt cầu

( )S

.

 

3; 3;0 3 1; 1;0 3AB a      

 

,

5 7

; ;3

2 2

M

 

 

 

là trung điểm của

AB

.

Gọi

(1; 1;0) 



a

và

( ; ; )



n a b c

với

2 2 2

0a b c  

là vectơ pháp tuyến của mặt phẳng

( )P

Vì

, ( )A B P

nên có

5 7

( )

6 3

3 0

2 2

. 0

0

I P

d a c

a b c d

a b

a n

a b







  

   



 

 

  









 



 

.

Gọi

 

,( )h d I P

,

( ) ( ) ( )C P S 

,

r

là bán kính đường tròn

( )C

.

2 2 2

6r R h h   

.

Diện tích thiết diện qua trục của hình nón

( )N

.

2 2

2

1 6

. .2 . 6 3

2 2

h h

S h r h h

 

     .

3MaxS 

khi

2 2

6 3h h h    .

 

2 2 2

2 3

,( ) 3

a b c d

h d I P

a b c

  

  

 

.

2 2

a c





  



 



.

Nếu

a c

thì

; 9b a d a  

và

( ) : - 9 0 9 0P ax ay az a x y z       

(nhận).

Nếu

a c 

thì

; 3b a d a  

và

( ) : - 3 0 3 0P ax ay az a x y z       

(loại).

Vây

6T a b c d    

.

Câu 12. Trong không gian

Oxyz

, xét số thực

 

0;1m 

và hai mặt phẳng

 

: 2 2 10 0x y za    

và

 

: 1

1 1

x y z

m m

   



. Biết rằng, khi

m

thay đổi có hai mặt cầu cố định tiếp xúc đồng thời với cả

hai mặt phẳng

   

,a 

. Tổng bán kính của hai mặt cầu đó bằng

A.

6

B.

3

C.

9

D.

12

Lời giải

Chọn C

h

r

R

I

B

A

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9

Gọi

 

; ;I a b c

là tâm mặt cầu.

Theo giả thiết ta có

 

, ,R d I d I

 a  

.

Mà

 

2

1

,

1 1

1

a b

c

m m

d I

m

  



 

 



Ta có

 

   

 

2

1 1 1 1 1 1

1 2 . 1

1 1

1

1 1 1 1

2 . 1 1(do 0;1

1 1 1

m m m m m

m

m m m m m m

 

     

 

 

 



 

     

 

  

 

Nên

     

 

     

2 2

2

2 2 2

2

1 1 1

1

1 1 0 1

1 1 0 2

a m bm cm m m m

m m

R

m m

a am bm cm cm m m

R

m m

R Rm Rm a am bm cm cm m m

m R c m a b c R R a

m R c m b c a R R a

     







     

 

 



        





         





         





         





Xét (1) do mặt cầu tiếp xúc với tiếp xúc đồng thời với cả hai mặt phẳng

   

,a 

với mọi

 

0;1

m 

nên pt (1) nghiệm đúng với mọi

 

0;1

m 

.

 

1 0

1 0 ; ;1

0 1

R c a R

a b c R b R I R R R

R a c R

   

 

 

         

 

 

   

 

.

Mà

 

2 2 1 10

3

, 3 12

6( )

3

R R R

R

R d I R R R

R l

   





 a      



 



Xét (2) tương tự ta được

 

1 0

1 0 ; ; 1

0 1

R c a R

b c a R b R I R R R

R a c R

    

 

 

            

 

 

   

 

Mà

 

2 2 1 10

6

, 3 12

3( )

3

R R R

R

R d I R R R

R l

    





 a      



 



.

Vậy

1 2

9

R R

 

.

Câu 13. Trong không gian

Oxyz

, mặt cầu

 

S

đi qua điểm

 

2; 2;5

A 

và tiếp xúc với ba mặt phẳng

   

: 1, : 1

P x Q y

  

và

 

: 1R z 

có bán kính bằng

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 10 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

A.

3

. B.

1

. C.

2 3

. D.

3 3

.

Lời giải

Gọi

 

; ;I a b c

và

R

là tâm và bán kính của

 

S

. Khi đó ta có

 

1

; ; ; 1 1 1 1 1

1 1

IA a

R IA d I P d I Q d I R IA a b c a b

a c

  



               





   



TH1:

     

2 2 2 2

2

1

2 2

1 1

2 12 28 0

2 5 1

IA a

b a b a

a b c a c a

a c

a a

a a a a



  



   



 

      

  

  

  

  

     







(vô nghiệm)

TH2:

       

2 2 2 2 2

1

4

1 1 4 1

1 1 4

2 16 32 0

2 2 5 1

IA a

b a b a a

a b c a c a b R

a c c

a a

a a a a



  



    





  

            

   

   

   

  



       







TH3:

     

2 2 2 2

2

1

2

1 1 2

1 1

2 4 12 0

2 3 1

IA a

b a b a

a b c a c a

a c

a a

a a a a



  



   



 

       

  

  

   

  

     







(vô nghiệm)

TH4:

       

2 2 2 2 2

1

1 1 2

1 1

2 12 0

2 2 3 1

IA a

b a b a

a b c a c a

a c

a

a a a a



  



   



 

        

  

  

   

 

       







(vô nghiệm)

Vậy mặt cầu có bán kính

1R 

Câu 14. (Đề Tham Khảo 2018) Trong không gian

Oxyz

, cho điểm

 

1 1 2M ; ;

. Hỏi có bao nhiêu mặt

phẳng

 

P

đi qua

M

và cắt các trục

x'Ox, y'Oy,z'Oz

lần lượt tại các điểm

A,B,C

sao cho

0

OA OB OC

  

?

A.

8

B.

1

C.

4

D.

3

Lời giải

Chọn D

Mặt phẳng

 

P

đi qua

M

và cắt các trục

x'Ox, y'Oy,z'Oz

lần lượt tại các

điểm

     

0 0 0 0 0 0A a; ; ,B ;b; ,C ; ;c

. Khi đó phương trình mặt phẳng

 

P

có dạng:

1

x y z

a b c

  

.

Theo bài mặt phẳng

 

P

đi qua

 

1 1 2M ; ;

và

OA OB O C 

nên ta có hệ:

 

1 1 2

1 1

2

a b c



  







 



. Ta có:

 

2

a b c

a c b

b c a

 





  







  



  



- Với

 a b c

thay vào

 

1

được

4  

a b c

- Với

  a b c

thay vào

 

1

được

0 1

(loại).

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11

- Với

  a c b

thay vào

 

1

được

2   

a c b

.

- Với

  b c a

thay vào

 

1

được

2   

b c a

.

Vậy có ba mặt phẳng thỏa mãn bài toán là:

     

1 2 3

1 1 1

4 4 4 2 2 2 2 2 2

x y z x y z x y z

P : ; P : ; P :

        

 

Câu 15. (Hoàng Hoa Thám Hưng Yên 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho hai điểm

 

3;1;7

A

,

 

5;5;1

B

và mặt phẳng

 

: 2 4 0

P x y z

   

. Điểm

M

thuộc

 

P

sao cho

35

MA MB 

. Biết

M

có hoành độ nguyên, ta có

OM

bằng

A.

2 2

. B.

2 3

. C.

3 2

. D.

4

.

Lời giải

Gọi

 

; ;M a b c

với

a



,

b



,

c



.

Ta có:

 

3; 1; 7

AM a b c

   



và

 

5; 5; 1

BM a b c

   



.

Vì

 

35

M P

MA MB







 





 

2 2

2

35

M P

MA MB

MA





 









nên ta có hệ phương trình sau:

           

     

2 2 2 2 2 2

2 2 2

2 4 0

3 1 7 5 5 1

3 1 7 35

a b c

a b c a b c

a b c



   



          





     





     

2 2 2

2 4

4 8 12 8

3 1 7 35

a b c



   



    





     





     

2 2 2

2

3 1 7 35

b c

c a

a b c







  





     





2

3 14 0

b a

c a

a a



 



  





 



0

2

a

b

c







 









, (do

a



).

Ta có

 

2;2;0

M

. Suy ra

2 2

OM 

.

Câu 16. (Cụm 5 Trường Chuyên - ĐBSH - 2018) Trong không gian với hệ trục tọa độ

Oxyz

, cho ba

điểm

 

;0;0

A a

,

 

0; ;0B b

,

 

0;0;C c

với

, , 0

a b c



. Biết rằng

 

ABC

đi qua điểm

1 2 3

; ;

7 7 7

M

 

 

 

và tiếp xúc với mặt cầu

       

2 2 2

72

: 1 2 3

7

S x y z     

. Tính

2 2 2

1 1 1

a b c

 

.

A.

14

. B.

1

7

. C.

7

. D.

7

2

.

Lời giải

Phương trình đoạn chắn của mặt phẳng

 

ABC

là:

1

x y z

a b c

  

.

Vì điểm

1 2 3

, ,

7 7 7

M

 

 

 

thuộc mặt phẳng

 

ABC

1 2 3

1 2 3 1 2 3

7 7 7

1 1 7

7 7 7a b c a b c a b c

     

     

     

           

Mặt khác mặt phẳng

 

ABC

tiếp xúc với

       

2 2 2

72

: 1 2 3

7

S x y z     

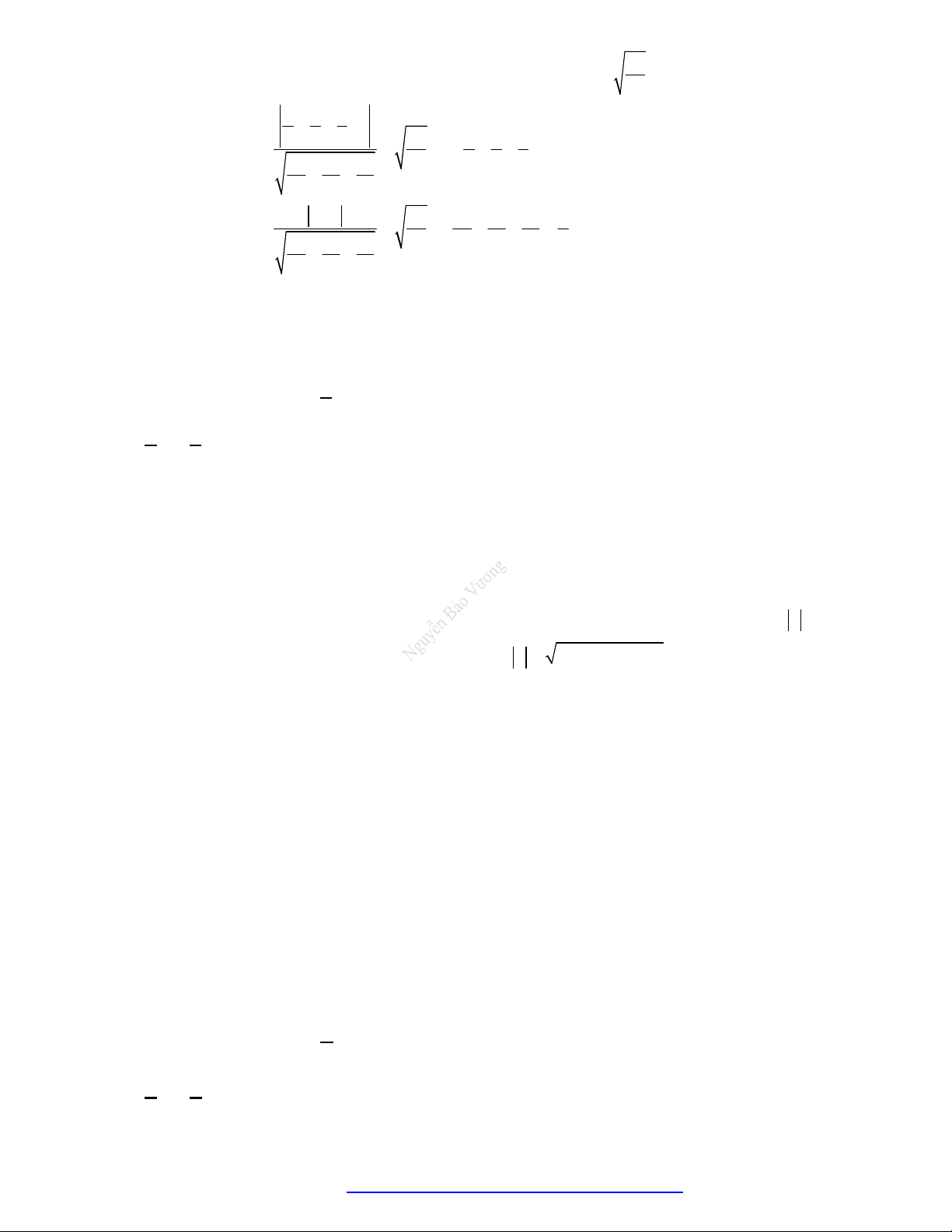
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 12 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/



khoảng cách từ tâm

 

1,2,3

I

của cầu tới mặt phẳng

 

ABC

là

72

7

 

2 2 2

1 2 3

1

72

,

7

1 1 1

a b c

d I ABC

a b c

  

  

 

mà

1 2 3

7

a b c

  

 

2 2 2

7 1

72 1 1 1 7

,

7 2

1 1 1

d I ABC

a b c



      

 

.

Câu 17. (Chuyên Đại học Vinh - 2019) Trong không gian

Oxyz

, cho các điểm

 

2;1;4

M

,

 

5;0;0

N

,

 

1; 3;1

P 

. Gọi

 

; ;I a b c

là tâm của mặt cầu tiếp xúc với mặt phẳng

 

Oyz

đồng thời đi qua các

điểm

M

,

N

,

P

. Tìm

c

biết rằng

5

a b c

  

.

A.

3

. B.

2

. C.

4

. D.

1

.

Lời giải

Chọn B

Giả sử mặt cầu

 

S

đã cho có phương trình dạng:

2 2 2

2 2 2 0

x y z ax by cz d

      

.

Từ đề bài ta có:

     

2;1;4 4 2 8 21 1

M S a b c d       

     

5;0;0 10 25 2

N S a d     

.

     

1; 3;1 2 6 2 11 3

P S a b c d        

.

Hình chiếu của điểm

 

; ;I a b c

lên mặt phẳng

 

Oyz

là

   

0; ; ;0;0

H b c HI a HI a   



.

Mặt cầu

 

S

tiếp xúc với mặt phẳng

   

2 2 2 2 2

0 4

Oyz IH a a b c d b c d         

.

Từ (1); (2); (3) ta có:

2

1

10 25

b a

c a

d a

 





 





 



.

Thế vào phương trình (4) ta được:

2

8 15 0 5 3

a a a a

      

.

Trường hợp 1:

5 3, 4 6 5

a b c a b c

          

loại.

Trường hợp 1:

3 1, 2 4 5

a b c a b c

          

nhận.

Vậy

2

c



thỏa yêu cầu đề.

Câu 18. (Sở Nam Định - 2019) Trong không gian

Oxyz

, cho mặt cầu

   

2

2 2

: 1 4

S x y z

   

và điểm

 

2;2;2

A

. Từ

A

kẻ ba tiếp tuyến

AB

,

AC

,

AD

với

B

,

C

,

D

là các tiếp điểm. Viết phương

trình mặt phẳng

 

.BCD

A.

2 2 1 0

x y z

   

. B.

2 2 3 0

x y z

   

.

C.

2 2 1 0

x y z

   

. D.

2 2 5 0

x y z

   

.

Lời giải

Chọn D

Mặt cầu

 

S

có tâm

 

0;0;1

I

, bán kính

2R 

.

Có

 

2;2;1

IA 



3

IA

 

.

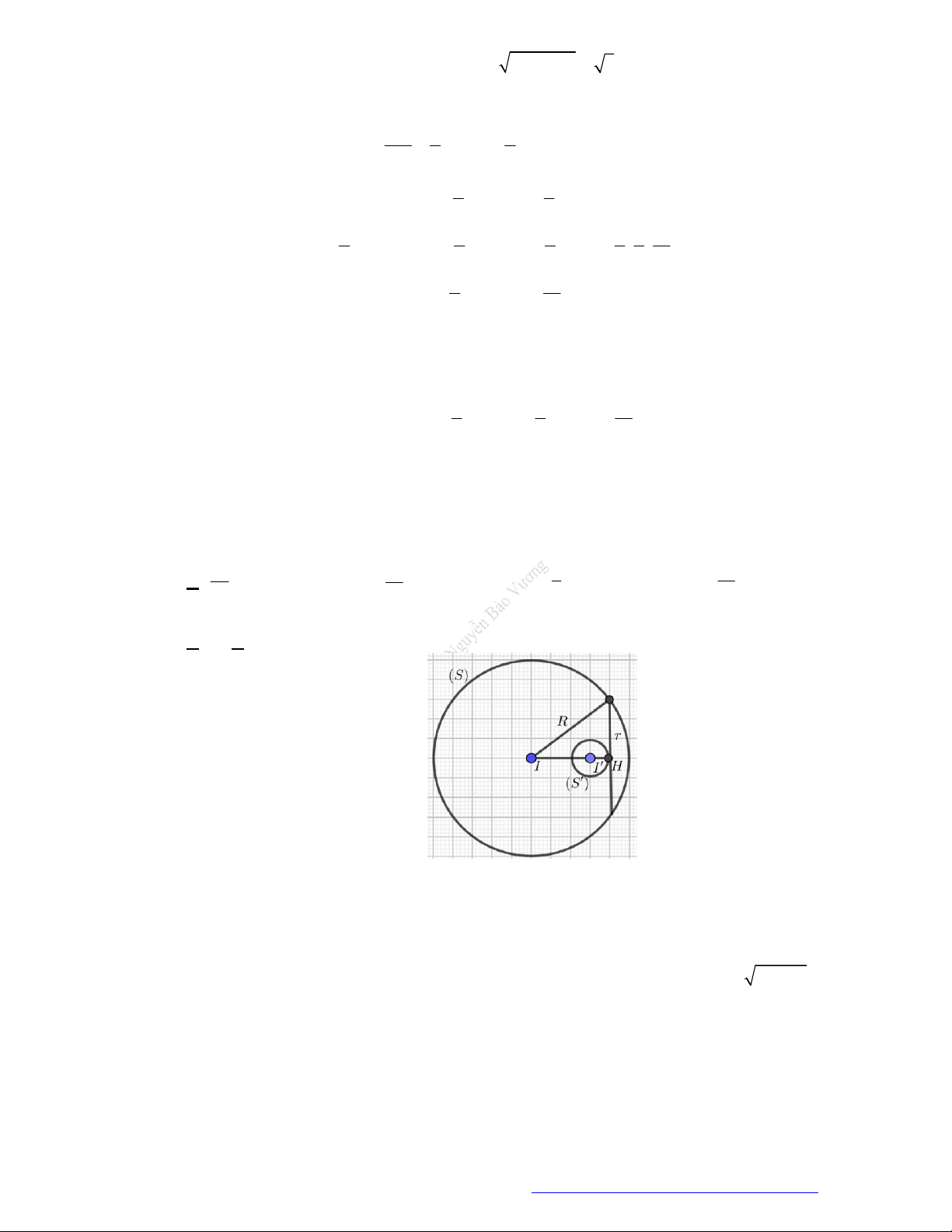
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13

Tam giác

ABI

vuông tại

B

nên ta có

2 2

5AB IA IB  

.

Gọi

 

; ;H x y z

là chân đường cao kẻ từ

B

của tam giác

ABI

.

Ta có:

2

4 4

. .

3 9

IB

IB IH IA IH IH IA

IA

     

.

Từ suy ra được

4

0 .2

9

4 4

0 .2

9 9

4

1 .1

9

x

IH IA y

z



 



   





 





 

8

9

8

9

13

9

x

y

z







 











8 8 13

; ;

9 9 9

H

 



 

 

.

Mặt phẳng

 

BCD

vuông góc với đường thẳng

IA

nên nhận

 

2;2;1IA 



làm vectơ pháp tuyến.

Hơn nữa mặt phẳng

 

BCD

đi qua điểm

H

.

Vậy

 

BCD

có phương trình:

8 8 13

2. 2. 1. 0

9 9 9

x y z

     

     

     

     

2 2 5 0x y z    

.

Câu 19. (Hội 8 Trường Chuyên 2019) Trong không gian

,Oxyz

cho hai mặt cầu

 

S

:

 

2

2 2

1 25x y z   

và

 

S



:

     

2 2 2

1 2 3 1.x y z     

Mặt phẳng

 

P

tiếp xúc

 

S



và

cắt

 

S

theo giao tuyến là một đường tròn có chu vi bằng

6 .



Khoảng cách từ

O

đến

 

P

bằng

A.

14

3

. B.

17

7

. C.

8

9

. D.

19

2

.

Lời giải

Chọn A

Mặt cầu

 

S

có tâm

 

0;0;1I

, bán kính

5R 

, mặt cầu

 

S



có tâm

 

1;2;3I



, bán kính

1R





Vì

3 4I I R R

 

   

nên mặt cầu

 

S



nằm trong mặt cầu

 

S

.

Mặt phẳng

 

P

tiếp xúc

 

S



 

, 1d I P R

 

  

;

 

P

cắt

 

S

theo giao tuyến là một đường

tròn có chu vi bằng

6



( suy ra bán kính đường tròn là

3r 

) nên

 

2 2

, 4d I P R r  

.

Nhận thấy

 

, ,d I P d I P I I

 

 

nên tiếp điểm

H

của

 

P

và

 

S



cũng là tâm đường tròn

giao của

 

P

và

 

S

. Khi đó,

 

P

là mặt phẳng đi qua

H

, nhận

 

1;2;2II







làm vecto pháp

tuyến.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 14 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Ta có:

4

3

4 8 4 8 11

; ;

3 3 3 3 3

11

3

H

x

IH II y H

z







 



   



 

 









 

.

Phương trình mặt phẳng

 

P

:

4 8 11

2 2 0

3 3 3

x y z

   

     

   

   

2 2 14 0

x y z

    

.

Khoảng cách từ

O

đến

 

P

là

 

14

,

3

d O P



.

Câu 20. (Chuyên Nguyễn Du-ĐăkLăk 2019) Trong không gian

Oxyz

, cho điểm

 

2;11; 5

A



và mặt

phẳng

 

   

2 2

: 2 1 1 10 0

P mx m y m z

     

. Biết rằng khi

m

thay đổi, tồn tại hai mặt cầu cố

định tiếp xúc với mặt phẳng

 

P

và cùng đi qua

A

. Tổng bán kính của hai mặt cầu đó bằng

A.

10 2

. B.

12 3

. C.

12 2

. D.

10 3

.

Lời giải

Chọn C

Gọi

 

0 0 0

; ;I x y z

là tâm của mặt cầu

 

S

cố định và

R

là bán kính của mặt cầu

 

S

.

Ta có:

 

   

2 2

0 0 0

2 2

2 2 2

2 1 1 10

,

4 1 1

mx m y m z

R d I P

m m m

    

 

   

   

 

2 2

0 0 0

2

2 1 1 10

2 1

mx m y m z

m

    





     

2 2 2

0 0 0

2 2 2

0 0 0

2 1 1 10 2 1

mx m y m z R m



      







       



đúng với mọi

m

  

.

 

2 2

0 0 0 0 0

2 2

0 0 0 0 0

2 10 2 2

y z m mx y z R m R



      





       





đúng với mọi

m

  

.

 

0 0

0

0 0

0

0 0

2

0

10 2

2

0

10 2

y z R

x

I

y z R

x

II

y z R





 















  











  















    





Từ hệ

 

I

suy ra

0 0 0

0; 5 2; 5

x y R z

    

Do đó tâm mặt cầu là

 

0;5 2; 5

I R

 

Ta có:

 

2

2 2 2

4 2 6

R IA R R    

suy ra

2 2

R 

và

10 2

R 

Hệ

 

II

suy ra

0 0 0

0; 5 2, 5

x y R z

    

Như vậy, ta có:

 

2

2 2 2 2

4 2 6

R IA R R    

, phương trình không có giá trị

R

thỏa mãn nên

loại.

Vậy tổng hai bán kính của hai mặt cầu là:

12 2

.

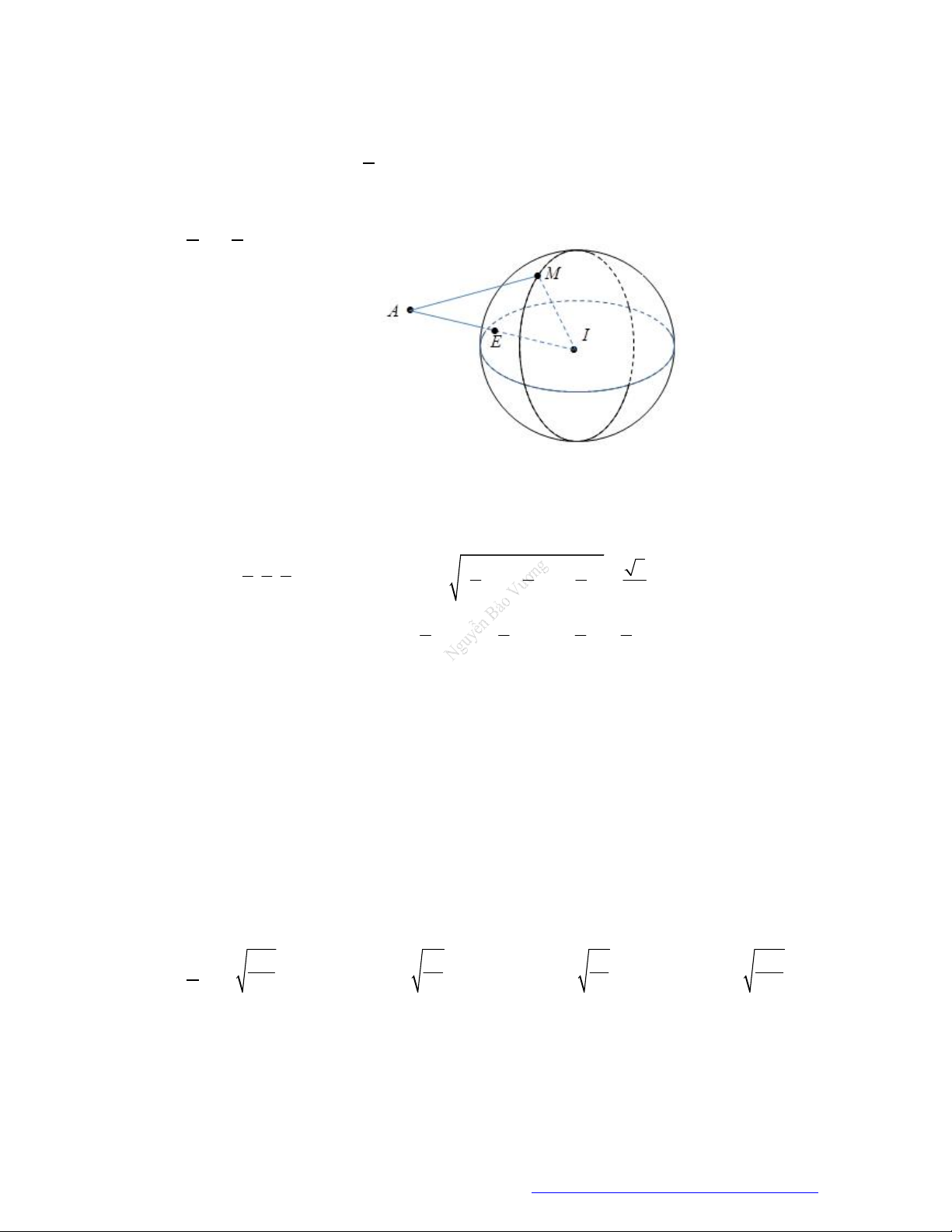
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15

Câu 21. (Chuyên Lê Quý Đôn – Điện Biên 2019) Trong không gian với hệ tọa độ

Oxyz

, cho mặt cầu

       

2 2 2

: 1 1 1 1S x y z     

và điểm

 

2;2;2A

. Xét các điểm

M

thuộc mặt cầu

 

S

sao

cho đường thẳng

AM

luôn tiếp xúc với

 

S

.

M

luôn thuộc mặt phẳng cố định có phương trình là

A.

6 0x y z   

. B.

4 0x y z   

C.

3 3 3 8 0x y z   

. D.

3 3 3 4 0x y z   

.

Lời giải

Chọn B

Mặt cấu

 

S

có tâm

 

1;1;1I

, bán kính

1R 

.

 

2;2;2A

Ta luôn có



o

90AMI 

, suy ra điểm

M

thuộc mặt cầu

 

1

S

tâm

E

là trung điểm của

AI

đường

kính

AI

.

Với

3 3 3

; ;

2 2 2

E

 

 

 

, bán kính

2 2 2

1

1 1 1 3

2 2 2 2

R IE

     

    

     

     

.

Phương trình mặt cầu

 

1

S

:

2 2 2

3 3 3 3

2 2 2 4

x y z

     

     

     

     

2 2 2

3 3 3 6 0x y z x y z       

.

Vậy điểm

M

có tọa độ thỏa mãn hệ:

     

2 2 2

2 2 2 2 0

1 1 1 1

3 3 3 6 0

x y z x y z

x y z

x y z x y z



      

     

 



 

      



      





Trừ theo vế hai phương trình cho nhau ta được:

4 0x y z   

.

Câu 22. Trong không gian với hệ tọa độ

Oxyz

, cho mặt cầu

 

2 2 2

: 4 4 2 7 0S x y z x y z      

và

đường thẳng

m

d là giao tuyến của hai mặt phẳng

 

1 2 4 4 0x m y mz    

và

 

2 2 1 8 0x my m z    

. Khi đó

m

thay đổi các giao điểm của

m

d và

 

S

nằm trên một

đường tròn cố định. Tính bán kính

r

của đường tròn đó.

A.

142

15

r 

. B.

92

3

r 

. C.

23

3

r 

. D.

586

15

r 

.

Lời giải

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 16 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Giả sử đường thẳng

m

d cắt mặt cầu tại hai điểm ,A B .

Mặt cầu

 

S

có tâm

 

2; 2;1I 

, bán kính

4R 

.

Đường thẳng

 

;

m

M x y d

thỏa

 

1 2 4 4 0

5 2 20 0

2 2 1 8 0

x m y mz

x y z

x my m z

    





    



    





nên các

giao điểm của

 

S

và

m

d thuộc đường tròn giao tuyến giữa

 

S

và

 

: 5 2 20 0P x y z   

.

 

14

,

30

d I P 

nên

 

2

2 2 2

14 142

, 4

30 15

r R d I P     .

Câu 23. (Chuyên Quốc Học Huế 2019) Trong không gian với hệ tọa độ Oxyz cho mặt cầu

 

S

có

phương trình

     

2 2 2

2 4 2 2 0x y z a b x a b c y b c z d          

, tâm

I

nằm trên mặt

phẳng

 

a

cố định. Biết rằng

4 2 4a b c  

. Tìm khoảng cách từ điểm

 

1;2; 2D 

đến mặt

phẳng

 

a

.

A.

15

23

. B.

1

915

. C.

9

15

. D.

1

314

.

Lời giải

Chọn B

Mặt cầu

 

S

có tâm

 

4 ; ;I a b a b c b c     

.

Giả sử mặt phẳng

 

a

có phương trình

0Ax By Cz D   

.

Vì

 

I  a

nên ta có

     

4 0A a b B a b c C b c D         

     

4A B a A B C b B C c D         

(1).

Theo bài ra ta có

4 2 4a b c  

(2).

Đồng nhất (1) và (2) ta có hệ phương trình

Q

P

N

B

A

I

K

H

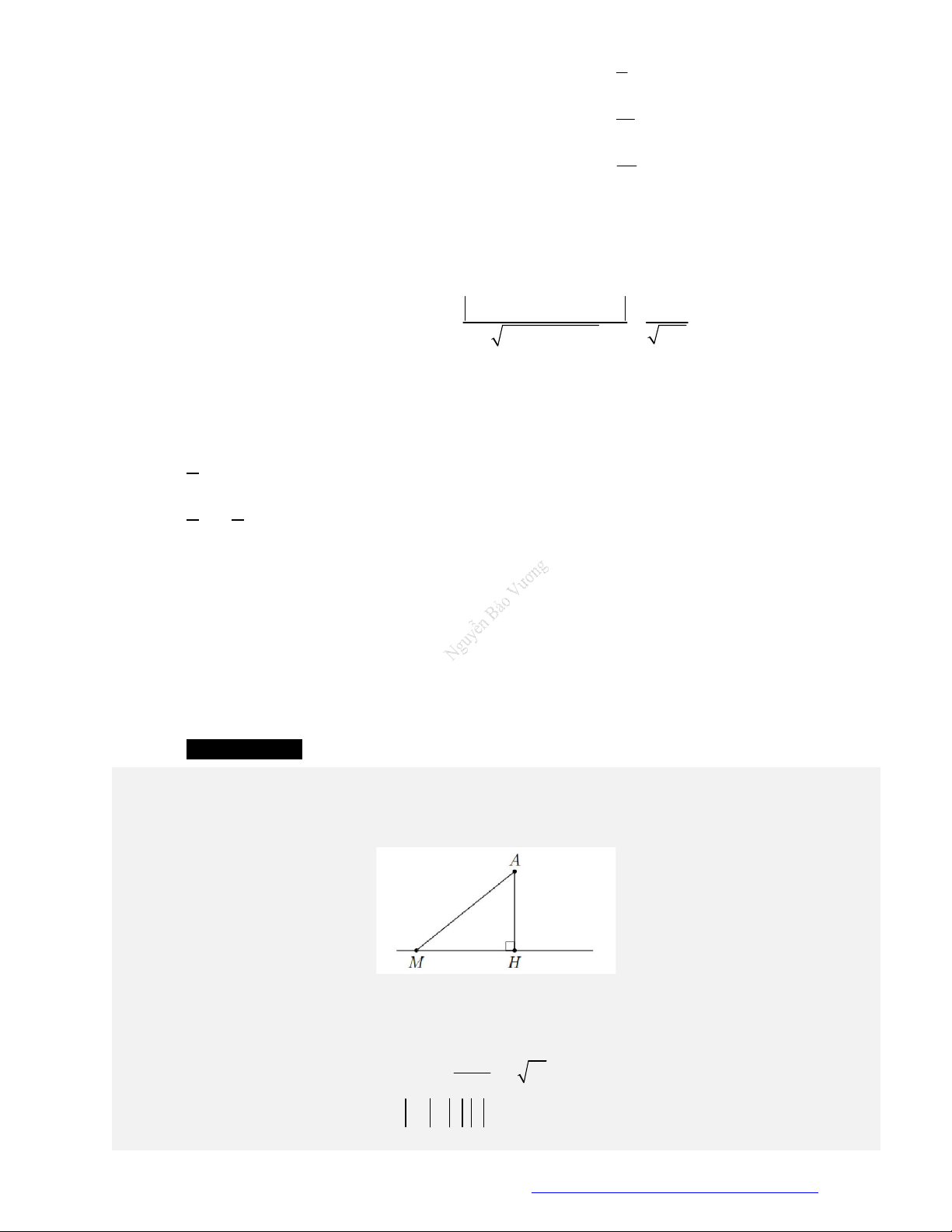
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17

1

4

17

4 1

4

2

25

4

A

A B

A B C

B

B C

C

D



 



 





  

 

 



 

   

 

 

 

 





 



Suy ra

 

a

có phương trình

17 25 16 0x y z   

.

Vậy, khảng cách từ điểm

 

1;2; 2D 

đến

 

a

bằng

 

2 2 2

1 17.2 25. 2 16

1

,

915

1 17 25

d D

   

a  

 

.

Câu 24. (THPT Ngô Sĩ Liên Bắc Giang 2019) Trong không gian với hệ trục toạ độ

,Oxyz

điểm

 

, ,M a b c

thuộc mặt phẳng

 

: 6 0P x y z   

và cách đều các điểm

     

1;6;0 , 2;2; 1 , 5; 1;3 .A B C  

Tích

abc

bằng

A.

6

B.

6

C.

0

D.

5

Lời giải

Chọn A

Ta có:

         

2 2 2 2 2

2 2 2

2 2

2 2 2 2 2

2

6

1 6 2 2 1

1 6 5 1 3

a b c

MA MB a b b a b c

MA MC

a b c a b c



  





           

 

 



         







6 1

3 4 14 2 6.

4 7 3 1 3

a b c a

a b c b abc

a b b c

   

 

 

       

 

 

    

 

Dạng 2. Cực trị

1. Một số bất đẳng thức cơ bản

Kết quả 1. Trong một tam giác, cạnh đối diện với góc lớn thì lớn hơn

Kết quả 2. Trong các đường xiên và đường vuông góc kẻ từ một điểm nằm ngoài đường thẳng đến đường

thẳng đó thì đường vuông góc là đường ngắn nhất. Như trong hình vẽ ta luôn có

AM AH

Kết quả 3. Với ba điểm

, ,A B C

bất kì ta luôn có bất đẳng thức

.AB BC AC 

Tổng quát hơn ta có bất đẳng thức của đường gấp khúc: Với

n

điểm

1 2

, ,....

n

A A A ta luôn có

1 2 2 3 1 1

...

n n n

A A A A A A A A



   

Kết quả 4. Với hai số không âm

,x y

ta luôn có

2

x y

xy





. Đẳng thức xảy ra khi và chỉ khi

x y

Kết quả 5. Với hai véc tơ

,a b

 

ta luôn có . .a b a b

   

. Đẳng thức xảy ra khi

,a kb k 

 



2. Một số bài toán thường gặp

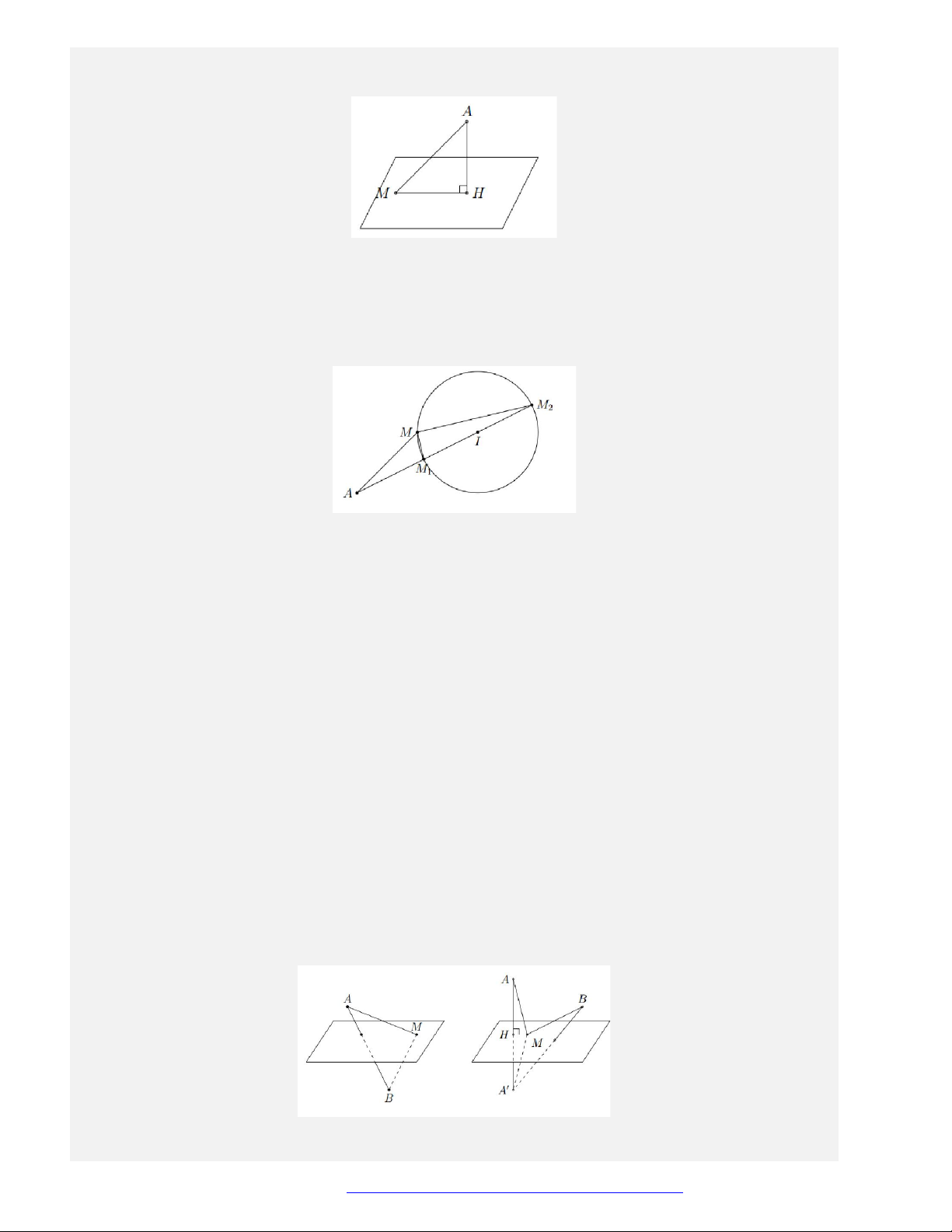
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 18 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Bài toán 1. Cho điểm

A

cố định và điểm

M

di động trên hình

 

H

(

 

H

là đường thẳng, mặt phẳng). Tìm

giá trị nhỏ nhất của

AM

Lời giải: Gọi

H

là hình chiếu vuông góc của

A

lên hình

 

H

. Khi đó, trong tam giác

AHM

Vuông tại .

M

ta có

.AM AH

Đẳng thức xảy ra khi

M H

. Do đó

AM

nhỏ nhất khi

M

là hình chiếu của

A

lên

 

H

Bài toán 2. Cho điểm

A

và mặt cầu

 

S

có tâm

,I

bán kính

,R

M

là điểm di động trên

 

S

. Tìm giá trị

nhỏ nhất và giá trị lớn nhất của

AM

.

Lời giải. Xét

A

nằm ngoài mặt cầu

( ).S

Gọi

1 2

,M M lần lượt là giao điểm của đường thẳng

AI

với mặt

cầu

 

1 2

( )S AM AM

và

( )

a

là mặt phẳng đi qua

M

và đường thẳng

.AI

Khi đó

( )

a

cắt

( )S

theo một

đường tròn lớn

( ).C

Ta có



1 2

90 ,M MM



 nên



2

AMM và



1

AM M là các góc tù, nên trong các tam giác

1

AMM và

2

AMM ta có

1 2

AI R AM AM AM AI R     

Tương tự với

A

nằm trong mặt cầu ta có

R AI AM R AI   

Vậy

min | |,maxAM AI R AM R AI   

Bài toán 3. Cho măt phẳng

( )P

và hai điểm phân biệt

, .A B

Tìm điể

M

thuộc

( )P

sao cho

1.

MA MB

nhỏ nhất.

2.

| |MA MB

lớn nhất.

Lời giải.

1. Ta xét các trường hợp sau

- TH 1: Nếu

A

và

B

nằm về hai phía so với

( )P

. Khi đó

AM BM AB 

Đẳng thức xảy ra khi

M

là giao điểm của

AB

với

( )P

.

- TH 2: Nếu

A

và

B

nằm cùng một phía so với

( )P

. Gọi A



đối xứng với

A

qua

( )P

. Khi đó

AM BM A M BM A B

 

   

Đẳng thức xảy ra khi

M

là giao điểm của A B



với

( )P

.

2. Ta xét các trường hợp sau

- TH 1: Nếu

A

và

B

nằm cùng một phía so với

( )P

. Khi đó

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19

| |AM BM AB 

Đẳng thức xảy ra khi

M

là giao điểm của

AB

với

( )P

.

- TH 2: Nếu

A

và

B

nằm khác phía so với

( )P

. Gọi

'A

đối xứng với

A

qua

 

P

, Khi đó

| |AM BM A M BM A B

 

   

Đẳng thức xảy ra khi

M

là giao điểm của A B



với

( )P

.

Bài toán 4. Viết phương trinh măt phẳng

( )P

di qua

A

và cách

B

một khoảng lớn nhất.

Lời giải. Gọi

H

là hình chiếu của

B

lên mặt phẳng

( ),P

khi đó

d( ,( ))B P BH BA 

Do đó

 

P

là mặt phẳng đi qua

A

vuông góc với

AB

Bài toán 5. Cho các số thực dương

,

a 

và ba điểm

, ,A B

C. Viết phương trình măt phẳng

( )P

đi qua

C

và

d( ,( )) d( ,( ))T A P B P

a 

 

nhỏ nhất.

Lời giải.

1. Xét

,A B

nằm về cùng phía so với

( )P

.

- Nếu ( )AB P‖ thì

( )d( ,( )) ( )P A P AC

a  a 

   

- Nếu đường thẳng

AB

cắt

( )P

tại

.I

Gọi

D

là điểm thỏa mãn IB ID

a





 

và

E

là trung điểm

.BD

Khi đó

d( ,( )) d( ,( )) 2 d( ,( )) 2( )

IB

P A P D P E P EC

ID

a  a a 

      

2. Xét

,A B

nằm về hai phía so với

( )P

. Gọi

I

là giao điểm của

AB

và ( ),P B



là điểm đối xứng với

B

qua

I

. Khi đó

 

d( ,( )) d ,( )P A P B P

a 



 

Đến đây ta chuyển về trường hợp trên.

So sánh các kết quả ở trên ta chọn kết quả lớn nhất.

Bài toán 6. Trong không gian cho

n

điểm

1 2

, , ,

n

A A A và diểm

.A

Viết phương trình mặt phẳng

( )P

đi

qua

A

và tổng khoảng cách từ các điểm

( 1,

i

A i n

) lớn nhất.

Lời giải.

- Xét

n

điểm

1 2

, , ,

n

A A A nằm cùng phía so với

( ).P

Gọi

G

là trọng tâm của

n

điểm đã cho. Khi đó

 

1

d ,( ) d( ,( ))

n

i

A P n G P nGA



 



- Trong

n

điểm trên có

m

điểm nằm về một phía và

k

điểm nằm về phía khác

(m k n 

). Khi đó, gọi

1

G

là trọng tâm của

m

điểm,

2

G là trọng tâm của

k

điểm

3

G đối xứng với

1

G qua

.A

Khi dó

   

3 2

md ,( ) d ,( )P G P k G P 

Đến đây ta chuyển về bài toán trên.

Bài toán 7.Viết phương trình mặt phẳng

 

P

đi qua đường thẳng



và cách

A

một khoảng lớn nhất

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 20 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Lời giải. Gọi

,H K

lần lượt là hình chiếu của

A

lên mặt phẳng

( )P

và đường thẳng

.

Khi đó

d( ,( ))A P AH AK 

Do đó

( )P

là mặt phẳng đi qua

K

và vuông góc vói

.AK

Bài toán 8. Trong không gian

Oxyz,

cho các điểm

1 2

, , , .

n

A A A Xét véc tơ

1 1 2 2 n n

w MA M A M A

a a a

   

  





Trong đó

1 2

; ...

n

a a a

là các số thực cho trước thỏa mãn

1 2

... 0

n

a a a

    . Tìm điểm

M

thuôc măt phẳng

( )P

sao cho

| |w



có đô dài nhỏ nhất.

Lời giải. Gọi

G

là điểm thỏa mãn

1 1 2 2

0

n n

GA GA GA

a a a

   

   



(điểm

G

hoàn toàn xác định).

Ta có

k

MA MG GA 





vói

1;2; ; ,k n 

nên

   

1 2 1 1 2 2 1 2

w

n n n n

MG GA GA GA MG

a a a a a a a a a

         

 

  





Do đó

1 2

| | | |

n

w MG

a a a

    





Vi

1 2 n

a a a

   là hằng số khác không nên

| |w



có giá trị nhỏ nhất khi và chỉ khi

MG

nhỏ nhất, mà

( )M P

nên điểm

M

cần tìm là hình chiếu của

G

trên mặt phẳng

( )P

.

Bài toán 9. Trong không gian Oxy

,z

cho các diểm

1 2

, , , .

n

A A A Xét biểu thức:

2 2 2

1 1 2 2 n n

T MA MA MA

a a a

   

Trong đó

1 2

, , ,

n

a a a

 là các số thực cho trước. Tìm điểm M thuộc măt phẳng

( )P

sao cho

1.

T

giá trị nhỏ nhất biết

1 2

0

n

a a a

   .

2. T có giá trị lớn nhất biết

1 2

0

n

a a a

   .

Lời giải. Gọi

G

là điểm thỏa mãn

1 1 2 2

0

n n

GA GA GA

a a a

   

   



Ta có

k

MA MG GA 





với

1;2; ; ,k n 

nên

 

2

2 2 2

2

k k k k

MA MG GA MG MG GA GA     

 

 

Do đó

 

2 2 2 2

1 2 1 1 2 2n n n

T MG GA GA GA

a a a a a a

      

Vì

2 2 2

1 1 2 2 n n

GA GA GA

a a a

  

không đổi nên

•

với

1 2

0

n

a a a

   thì

T

đạt giá trị nhỏ nhất khi và chỉ khi

MG

nhỏ nhất.

•

với

1 2

0

n

a a a

   thì

T

đạt giá trị lớn nhất khi và chỉ khi

MG

nhỏ nhất.

Mà

( )M P

nên

MG

nhỏ nhất khi điểm

M

là hình chiếu của

G

trên mặt phẳng

( )P

.

Bài toán 10. Trong không gian Oxyz, cho đường thẳng d và mặt phẳng

( )P

cắt nhau. Viết phương trình của

mặt phẳng

( )Q

chứa

d

và tạo với mặt phẳng

( )P

một góc nhỏ nhất.

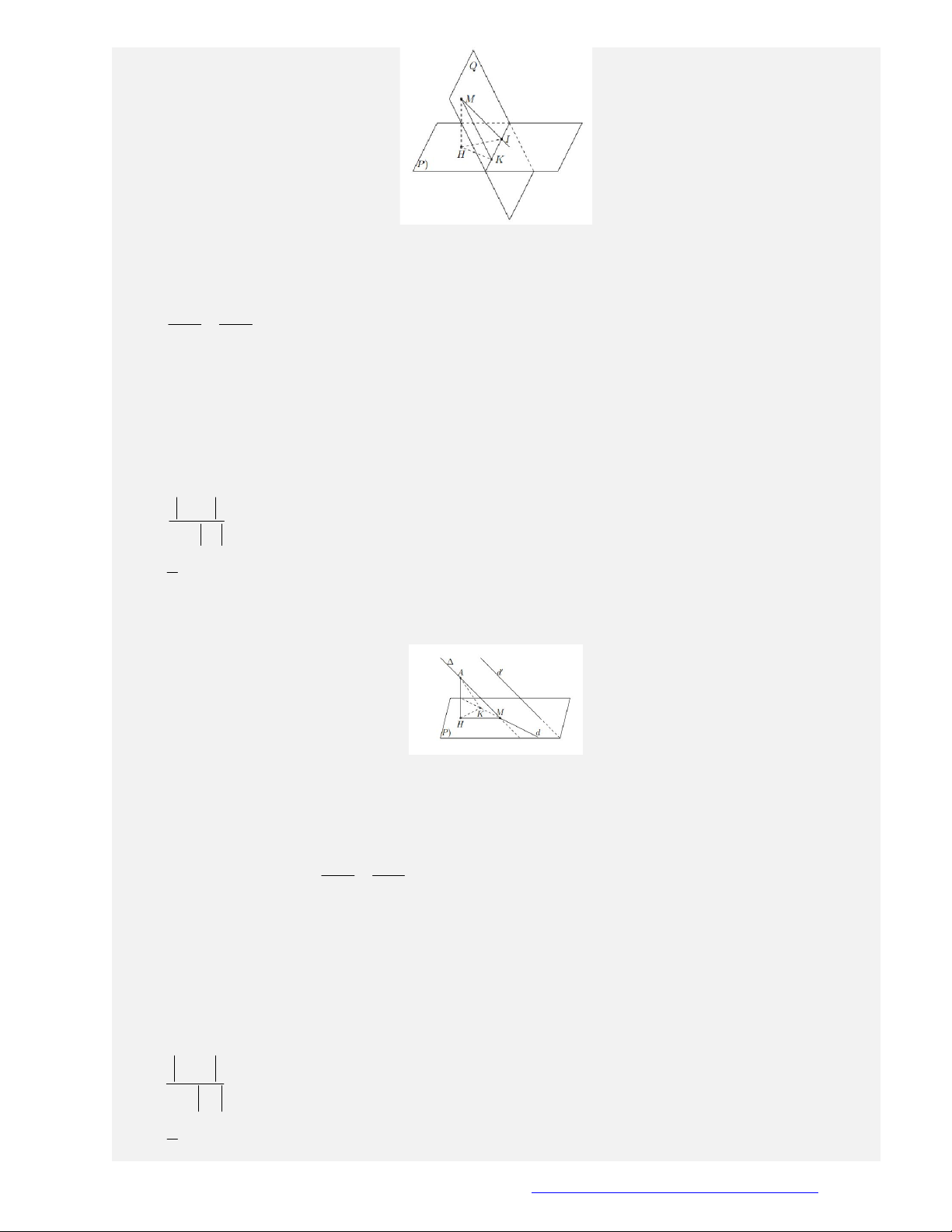
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21

Lời giải. Gọi

I

là giao điểm của đường thẳng

d

với mặt phẳng

( )P

và lấy điểm

,M d M I 

. Gọi

,H K

lầ lượt là hình chiếu của

M

lên

( )P

và giao tuyến



của

( )P

và

( )Q

.

Đặt



là góc giữa

( )P

và

( ),Q

ta có



,MKH





do đó

tan

HM HM

HK HI



 

Do đó

( )Q

là mặt phẳng đi qua

d

và vuông góc với mặt phẳng

( ),MHI

nên

( )Q

đi qua

M

và nhận

 

P d d

n u u 

  

làm VTPT.

Chú ý. Ta có thể giải bài toán trên bằng phương pháp đai số như sau:

- Goi

2 2 2

( ; ; ), 0n a b c a b c   



là một VTPT của mặt phẳng

( ).Q

Khi đó 0

d

n u 

 

từ đây ta rút được

a

theo

,b c

(hoặc

b

theo

,a c

hoặc

c

theo

,a b

).

- Gọi



là góc giữa

( )P

và

( ),Q

ta có

cos ( )

| |

P

n n

f t

n n





 



 

với

, 0.

b

t c

c

 

Khảo sát

( )f t

ta tìm được max của

( )f t

Bài toán 11. Trong không gian Oxyz, cho hai đường thẳng

d

và

d



chéo nhau. Viết phương trinh mặt

phẳng

( )P

chứa

d

và tạo với

d



một góc lớn nhất.

Lời giải. Trên đường thẳng

d

, lấy điểm

M

và dựng đường thẳng



đi qua

M

song song với

d



. Khi đó

góc giữa



và

( )P

chính là góc giữa

d



và

( )P

.

Trên đường thẳng



, lấy điểm

A

. Gọi

H

và

K

lần lượt là hình chiếu của

A

lên

( )P

và

,d



là góc giữa



và

( )P

.

Khi đó



AMH





và

cos

HM KM

AM AM



 

Suy ra

( )P

là mặt phẳng chứa

d

và vuông góc với mặt phẳng

( ).AMK

Do dó

( )P

đi qua

M

và nhận

 

d d

d

u u u



 

  

làm VTPT.

Chú ý. Ta có thể giải bài toán trên bằng phương pháp đại số như sau:

- Goi

2 2 2

( ; ; ), 0n a b c a b c   



là một VTPT của măt phẳng

( ).P

Khi đó 0

d

n u 

 

từ đây ta rút được

a

theo

,b c

(hoặc

b

theo

,a c

hoặc

c

theo

,a b

).

- Gọi



là góc giữa

( )P

và

,d



ta có

sin ( )

| |

d

n u

f t

n u







 



 

với

, 0.

b

t c

c

 

Khảo sát

( )f t

ta tìm được max của

( )f t

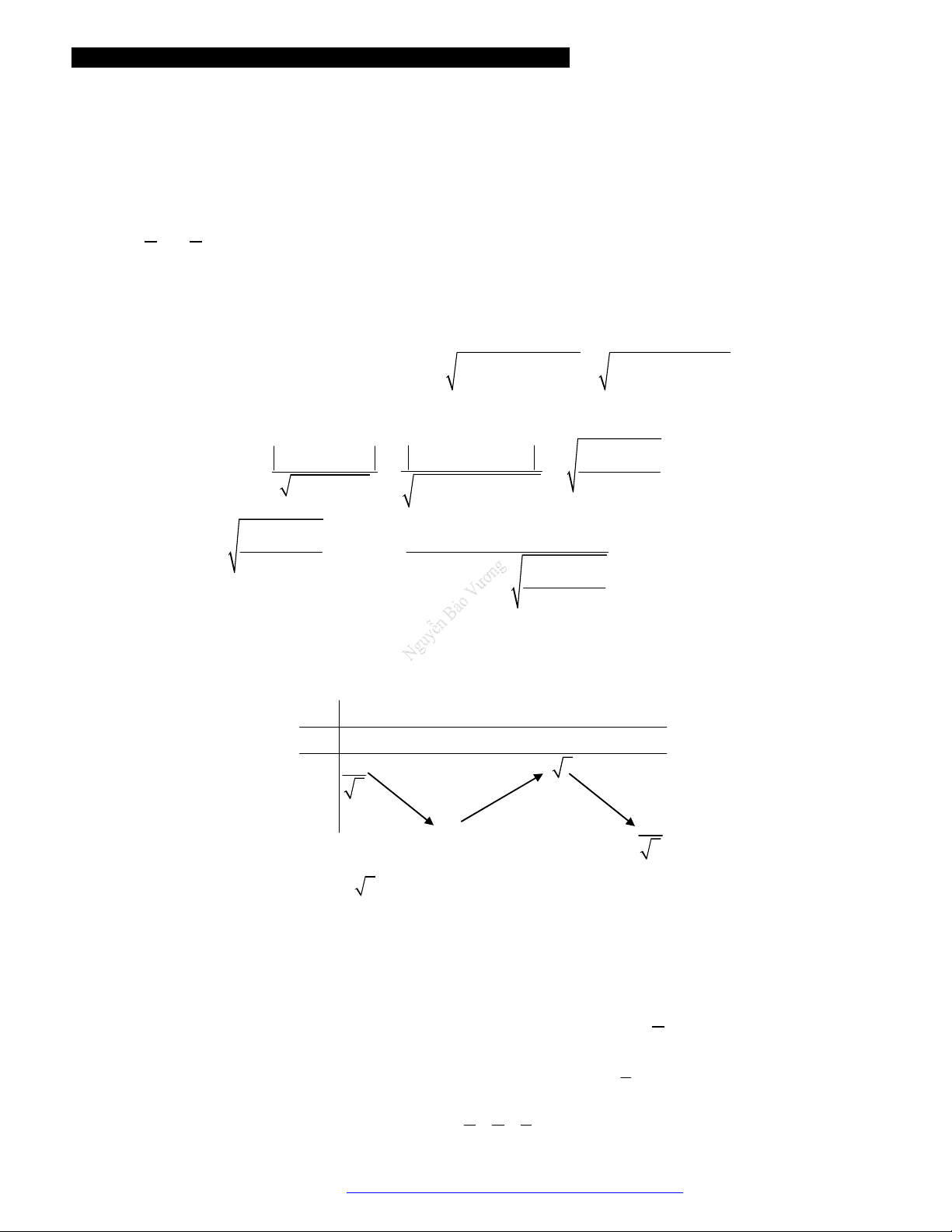
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 22 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Dạng 2.1. Cực trị liên quan đến bán kính, diện tích, chu vi, thể tích

Câu 1. (Mã 105 2017) Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm

   

3; 2;6 , 0;1;0A B

và mặt

cầu

       

2 2 2

: 1 2 3 25S x y z     

. Mặt phẳng

 

: 2 0P ax by cz   

đi qua

,A B

và cắt

 

S

theo giao tuyến là đường tròn có bán kính nhỏ nhất. Tính

T a b c  

A.

3T 

B.

4T 

C.

5T 

D.

2T 

Lời giải

Chọn A

Mặt cầu

 

S

có tâm

 

1; 2; 3I

và bán kính

 5R

Ta có

 





    





 

 









3 2 6 2 0

2 0

A P

a b c

b

B P

  









2 2

2

a c

b

Bán kính của đường tròn giao tuyến là

 

   

   

   

2 2

2

; 25 ;r R d I P d I P

Bán kính của đường tròn giao tuyến nhỏ nhất khi và chỉ khi

 

;d I P lớn nhất

Ta có

 

  



 

2 2 2

2 3 2

,

a b c

d I P

a b c

 

   



  

2

2 2

2 2 4 3 2

2 2 2

c c

 





 

2

4

5 8 8

c

c c

Xét

 





 

2

4

5 8 8

c

f c

c c

 

  



 



 

2

48 144 192

4

5 8 8

c c

f c

c

c c

 

 



 



 



1

0

4

c

f c

c

Bảng biến thiên

Vậy

 

;d I P lớn nhất bằng

5

khi và chỉ khi

       1 0, 2 3c a b a b c

.

Câu 2. (THPT Gia Lộc Hải Dương 2019) Mặt phẳng

 

P

đi qua điểm

 

1;1;1M

cắt các tia

Ox

,

Oy

,

Oz

lần lượt tại

 

;0;0A a

,

 

0; ;0B b

,

 

0;0;C c

sao cho thể tích khối tứ diện

OABC

nhỏ nhất. Khi

đó

2 3a b c 

bằng

A.

12

. B.

21

. C.

15

. D.

18

.

Lời giải

Từ giả thiết ta có

0, 0, 0a b c  

và thể tích khối tứ diện

OABC

là

1

6

OABC

V abc

.

Ta có phương trình đoạn chắn mặt phẳng

 

P

có dạng

1

x y z

a b c

  

.

0

y

x

'y





4

0

1

5

1

5



1

0



TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23

Mà

 

1 1 1

1

M P

a b c

    

.

Áp dụng bất đẳng thức côsi cho ba số ta có:

3

1 1 1 1

1 3 27

abc

a b c abc

     

.

Do đó

1 9

6 2

 

OABC

V abc

. Đẳng thức xảy ra khi và chỉ khi

3

a b c

  

.

Vậy

9

min 3

2

OABC

V

a b c

    

. Khi đó

2 3 18

a b c

  

.

Câu 3. Trong không gian với hệ tọa độ

Oxyz

, cho

 

2;0;0

A

,

 

1;1;1

M

. Mặt phẳng

 

P

thay đổi qua

AM

và cắt các tia

Oy

,

Oz

lần lượt tại

B

,

C

. Khi mặt phẳng

 

P

thay đổi thì diện tích tam giác

ABC

đạt giá trị nhỏ nhất bằng bao nhiêu?

A.

5 6

. B.

4 6

. C.

3 6

. D.

2 6

.

Lời giải

Chọn B

Đặt

 

0; ;0B b

,

 

0;0;C c

với

, 0

b c



.

Phương trình của mặt phẳng

 

P

là

1

2

x y z

b c

  

.

 

1 1 1 1 1 1

1

2 2

M P

b c b c

       

.

Suy ra

1 1 1 2

16

2

bc

b c

bc

    

.

2 2 2 2

2 2

1 1

; 4 4

2 2

1

8

2

ABC

S AB AC b c b c

b c bc

 

   

 

 

 

2

1

16 8.16 4 6

2

  

.

Vậy

min 4 6

ABC

S 

, đạt được khi

4

b c

 

.

Câu 4. Trong không gian với hệ toạ độ

Oxyz

, cho mặt cầu

       

2 2 2

: 1 2 3 9     

S x y z

, điểm

 

0;0; 2

A

. Mặt phẳng

 

P

qua

A

và cắt mặt cầu

 

S

theo thiết diện là hình tròn

 

C

có diện

tích nhỏ nhất, phương trình

 

P

là:

A.

 

: 2 3 6 0   

P x y z

. B.

 

: 2 3 6 0   

P x y z

.

C.

 

:3 2 2 4 0   

P x y z

. D.

 

: 2 2 0   

P x y z

.

Lời giải

Chọn D

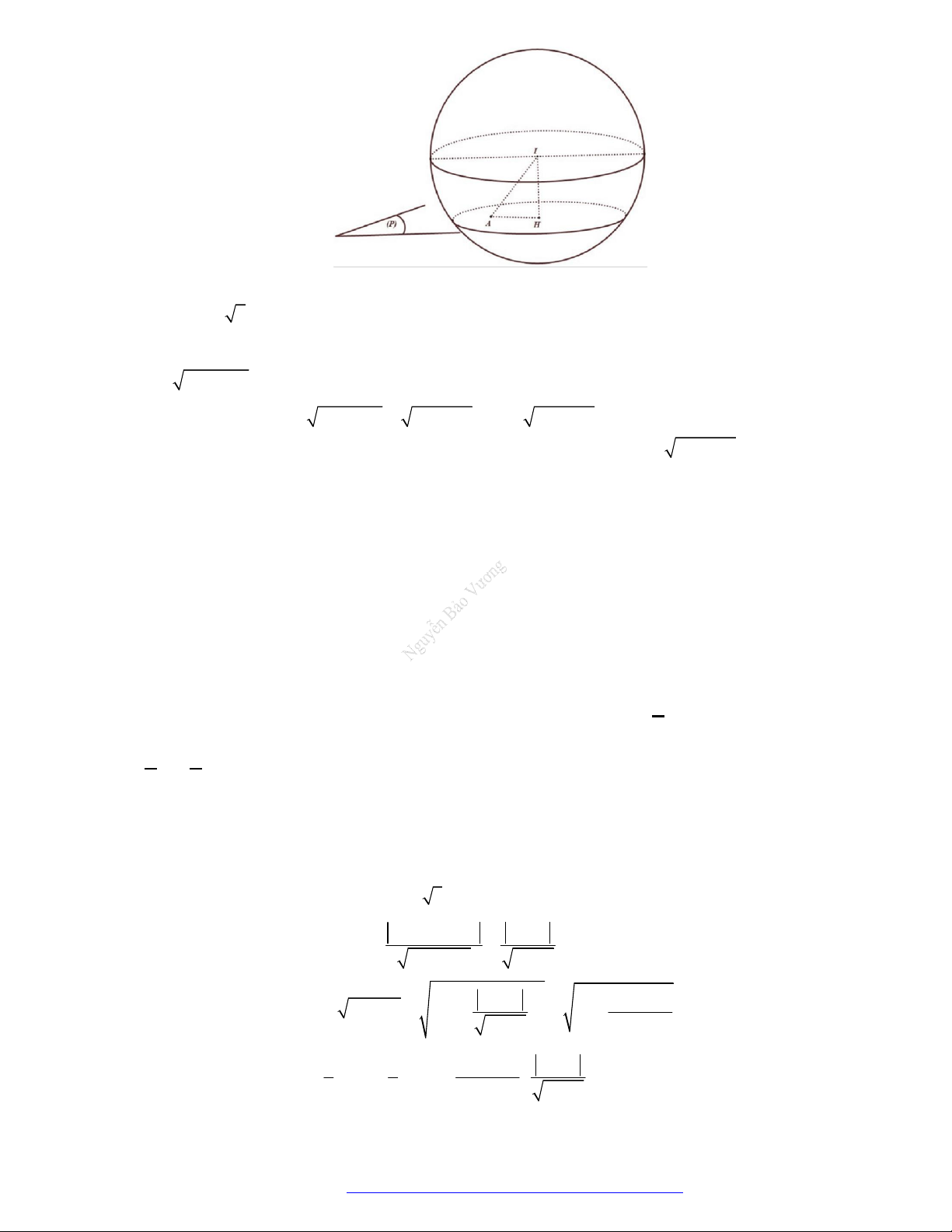
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 24 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Mặt cầu

 

S

có tâm

 

1;2;3I

, bán kính

3R

.

Ta có

6 IA R

 A

nằm trong mặt cầu

 

S

.

Do đó mặt phẳng

 

P

qua

A

luôn cắt mặt cầu

 

S

theo thiết diện là hình tròn

 

C

có bán kính

2 2

 r R IH

(với

H

là hình chiếu của

 

1;2;3I

trên

 

P

).

Ta luôn có

2 2 2 2 2 2

       IA IH R IH R IA r R IA

.

Diện tích của hình tròn

 

C

nhỏ nhất khi bán kính

r

nhỏ nhất, tức là

2 2

   r R IA H A

.

Khi đó

 

IA P

mặt phẳng

 

P

nhận

 

1; 2; 1   



IA

làm một VTPT.

Vậy phương trình mặt phẳng

 

P

:

 

2 2 0 2 2 0.         x y z x y z

.

Câu 5. (Bỉm Sơn - Thanh Hóa - 2019) Trong không gian

Oxyz

cho mặt cầu

     

2 2 2

( ) : 1 2 3 27S x y z     

. Gọi

 

a

là mặt phẳng đi qua 2 điểm

 

0;0; 4A 

,

 

2;0;0B

và cắt

 

S

theo giao tuyến là đường tròn

 

C

sao cho khối nón có đỉnh là tâm của

 

S

, là hình

tròn

 

C

có thể tích lớn nhất. Biết mặt phẳng

 

a

có phương trình dạng

0ax by z c   

, khi đó

a b c 

bằng:

A. 8. B. 0. C. 2. D. -4.

Lời giải

Chọn D

+ Vì

 

a

qua A ta có:

( 4) 0 4c c      

.

+ Vì

 

a

qua B ta có:

2 0 2a c a   

.



 

a

:

2 4 0x by z   

.

+ Mặt cầu

( )S

có tâm

 

1; 2;3I 

,

3 3R 

.

+ Chiều cao khối nón:

 

,

2 2

2 2 3 4 2 5

4 1 5

I

b b

h d

b b

a

   

  

  

.

+Bán kính đường tròn:

 

2

2 2

2

2 5 2 5

27 27

5

b b

r R h

b

 

 

     

 



 

.

+ Thể tích khối nón:

 

2

2 52 5

1 1

27

3 3 5

5

bb

V r h

b

 

 



  

 



 

+ Tới đây ta có thể Thử các trường hợp đáp án.

Hoặc ta làm tự luận như sau:

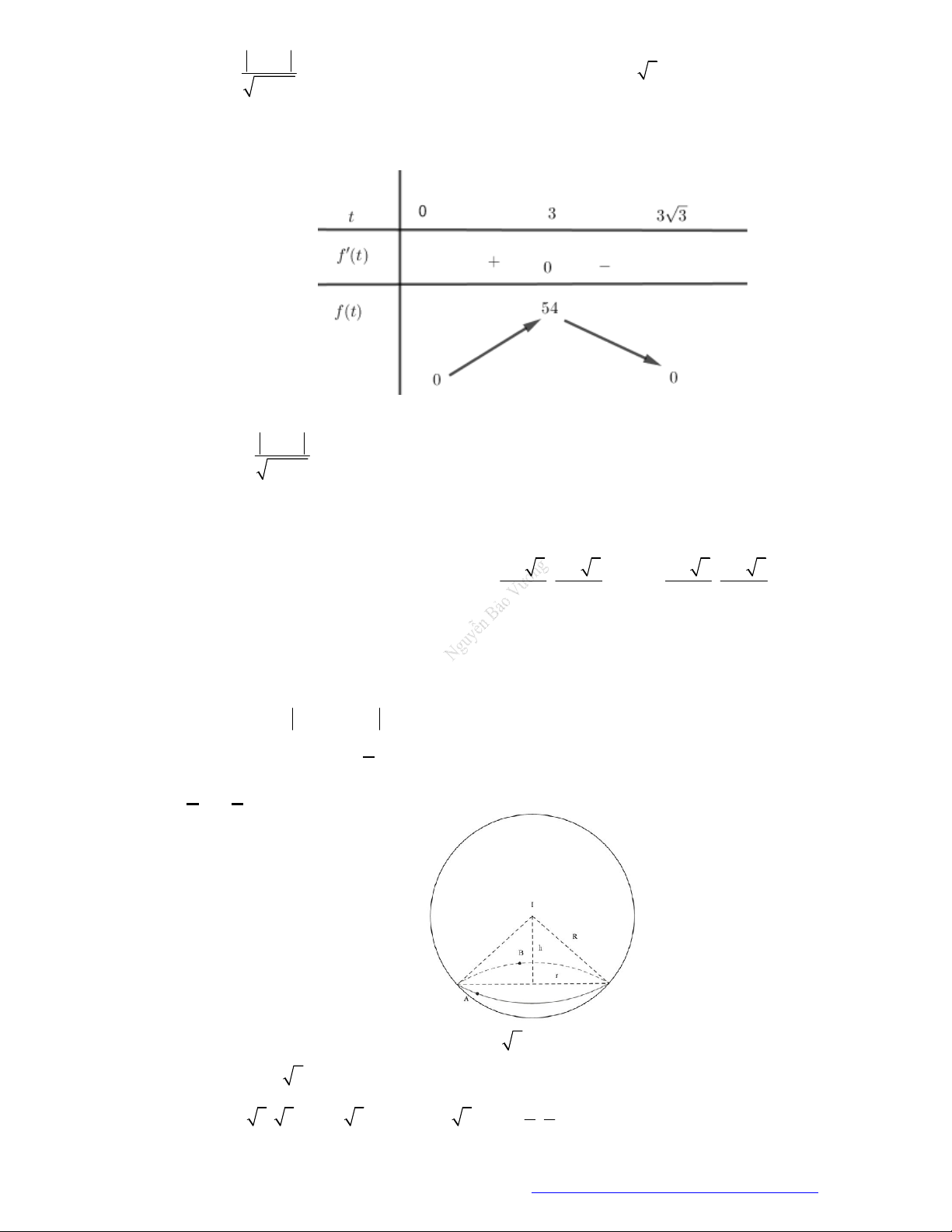
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25

Đặt

2

2 5

5

b

t

b







và xét hàm số

 

2

27f t t t 

trên đoạn 0;3 3

 

 

.

Ta có:

 

2

27 3f t t



 

;

 

3

0

3

t

f t

t l







 



 



. Ta có bảng biến thiên:

Do đó thể tích khối nón lớn nhất khi và chỉ khi

2

2 2 2

2

2 5

3 3 4 20 25 9 45

5

b

t b b b

b

 



       

 



 

2

5 20 20 0 2b b b     

.

Vì vậy

4a b c   

.

Câu 6. Trong không gian

Oxyz

, cho hai điểm

5 3 7 3

; ;3

2 2

A

 

 

 

 

,

5 3 7 3

; ;3

2 2

B

 

 

 

 

và mặt cầu

2 2 2

( ) :( 1) ( 2) ( 3) 6S x y z     

. Xét mặt phẳng

( ) : 0P ax by cz d   

,

 

, , , : 5a b c d d  

là mặt phẳng thay đổi luôn đi qua hai điểm

,A

B

. Gọi

( )N

là hình nón có

đỉnh là tâm của mặt cầu

( )S

và đường tròn đáy là đường tròn giao tuyến của

( )P

và

( )S

. Tính

giá trị của

T a b c d   

khi thiết diện qua trục của hình nón

( )N

có diện tích lớn nhất.

A.

4T 

. B.

6T 

. C.

2T 

. D.

12T 

.

Lời giải

Chọn B

Mặt cầu

( )S

có tâm

 

1;2;3I

, bán kính

6R 

.

Có

6IA IB 

nên

,A B

thuộc mặt cầu

( )S

.

 

3; 3;0 3 1; 1;0 3AB a      

 

,

5 7

; ;3

2 2

M

 

 

 

là trung điểm của

AB

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 26 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Gọi

(1; 1;0)

 



a

và

( ; ; )





n a b c

với

2 2 2

0

a b c

  

là vectơ pháp tuyến của mặt phẳng

( )P

Vì

, ( )A B P

nên có

5 7

( )

6 3

3 0

2 2

. 0

0

I P

d a c

a b c d

a b

a n

a b







  

   



 

 

  









 



 

.

Gọi

 

,( )h d I P



,

( ) ( ) ( )C P S 

,

r

là bán kính đường tròn

( )C

.

2 2 2

6

r R h h   

.

Diện tích thiết diện qua trục của hình nón

( )N

.

2 2

2

1 6

. .2 . 6 3

2 2

h h

S h r h h

 

    

.

max 3

S



khi

2 2

6 3

h h h   

.

 

2 2 2

2 3

,( ) 3

a b c d

h d I P

a b c

  

  

 

2 2

a c





  



 



.

Nếu

a c

thì

; 9b a d a  

và

( ) : - 9 0 9 0

P ax ay az a x y z

       

(nhận).

Nếu

a c 

thì

; 3b a d a  

và

( ) : - 3 0 3 0

P ax ay az a x y z

       

(loại).

Vây

6

T a b c d

    

.

Câu 7. (Nho Quan A - Ninh Bình - 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho hai điểm

   

0; 1; 1 , 1; 3;1

A B   

. Giả sử

,C D

là hai điểm di động trên mặt phẳng

 

:2 2 1 0

P x y z

   

sao cho

4

CD



và

, ,A C D

thẳng hàng. Gọi

1 2

,S S

lần lượt là diện tích

lớn nhất và nhỏ nhất của tam giác

BCD

. Khi đó tổng

1 2

S S

có giá trị bằng bao nhiêu?

A.

34

3

. B.

37

3

. C.

11

3

. D.

17

3

.

Lời giải

Chọn A

Ta có

 

1; 2;2

AB   



Gọi

H

là hình chiếu của

B

trên

CD

ta có

BH BA

nên

BCD

S



lớn nhất khi

H A

.

Vậy

1

1 1

. .3.4 6

2 2

S BACD

  

.

Gọi

1

H

là hình chiếu của

B

trên mặt phẳng

 

P

khi đó

 

1

1 1

. ; .

2 2

BCD

S BH CD d B P CD



 

điều này xảy ra khi

1

, , ,A C D H

thẳng hàng.

Vậy

 

2

2 3 2 1

1 1 16

, . .4

2 2 3

9

S d B P CD

   

  

.

Khi đó

1 2

16 34

6

3 3

S S   

.

Câu 8. (Chuyên Lê Quý Đôn Quảng Trị 2019) Trong không gian

Oxyz

cho mặt phẳng (P):

2 1 0

x y z

   

và các điểm

   

0;1;1 ; 1;0;0

A B

(

A

và

B

nằm trong mặt phẳng

 

P

) và mặt

cầu

       

2 2 2

: 2 1 2 4

S x y z

     

.

CD

là đường kính thay đổi của

 

S

sao cho

CD

song

song với mặt phẳng

 

P

và bốn điểm

, , ,A B C D

tạo thành một tứ diện. Giá trị lớn nhất của tứ

diện đó là

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27

A.

2 6

. B.

2 5

. C.

2 2

. D.

2 3

.

Lời giải

Chọn C

Mặt cầu

 

S

có tâm

 

2; 1;2

I 

, mặt phẳng

 

P

có VTPT

(1; 1;2)

n  



. Gọi điểm

 

; ;C x y z

, ta có

( )C S

nên

     

2 2 2

2 1 2 4

x y z

     

(1).

Do

CD

là đường kính của mặt cầu (S) nên

I

là trung điểm của

CD

, suy ra

 

4 ; 2;4

D x y z   

.

Mà theo đề có

CD

song song với mặt phẳng

 

P

nên

. 0 2 ( 1) 2( 2) 0

IC n IC n x y z

         

   

(2).

Ta có:

     

1; 1; 1 ; ; 1; 1 ; 4 ; 3;3

AB AC x y z AD x y z          

  

.

 

; 2 4 6; 2 4 4; 4 4 4

AC AD y z x z x y

 

        

 

 

.

 

; 2 4 6 ( 1). 2 4 4 ( 1).( 4 4 4)

6 6 6.

AB AC AD y z x z x y

x y

 

            

 

  

  

Thể tích khối tứ diện

ABCD

là:

1

; 1 .

6

V AB AC AD x y

 

   

 

  

Đặt

2

1

2

x a

y b

z c

 





 





 



. Từ (1) và (2) ta có hệ:

2 2 2

2

4

4 5

2 0

2

a b c

c

a b c

ab

  



  





 



  









2

2 2 2

1 2 1 ( ) 4

4 2(4 5 ) 8 6 2 2.

V x y x y a b a b ab

c c c

           

     

Vậy GTLN của

V

là

2 2

khi

     

2 2 2

2 0

2 2; y 1 2; 2

2 1

2 2; y 1 2; 2

2 1 2 4

z

x z

x y

x z

x y z



 





     



   





     







     





.

Câu 9. Trong không gian với hệ trục tọa độ

Oxyz

, cho tứ diện

ABCD

có điểm

 

1;1;1 ,

A

 

2;0;2 ,

B

 

 

1; 1;0 ,

C

 

0;3;4

D

. Trên các cạnh

, ,AB AC AD

lần lượt lấy các điểm

, ,B C D

  

thỏa

4

AB AC AD

  

  

. Viết phương trình mặt phẳng

 

B C D

  

biết tứ diện

AB C D

  

có thể

tích nhỏ nhất?

A.

16 40 44 39 0   

x y z

B.

16 40 44 39 0   

x y z

C.

16 40 44 39 0   

x y z

D.

16 40 44 39 0   

x y z

Lời giải

Chọn C

Đặt

, ,

AB AC AD

x y z

AB AC AD

  

  

. Ta có

4

AB AC AD

  

  

. Suy ra

3

1 1 1 1 27

4 3

64

xyz

x y z xyz

     

. Dấu

" "

xảy ra khi

x y z 

.

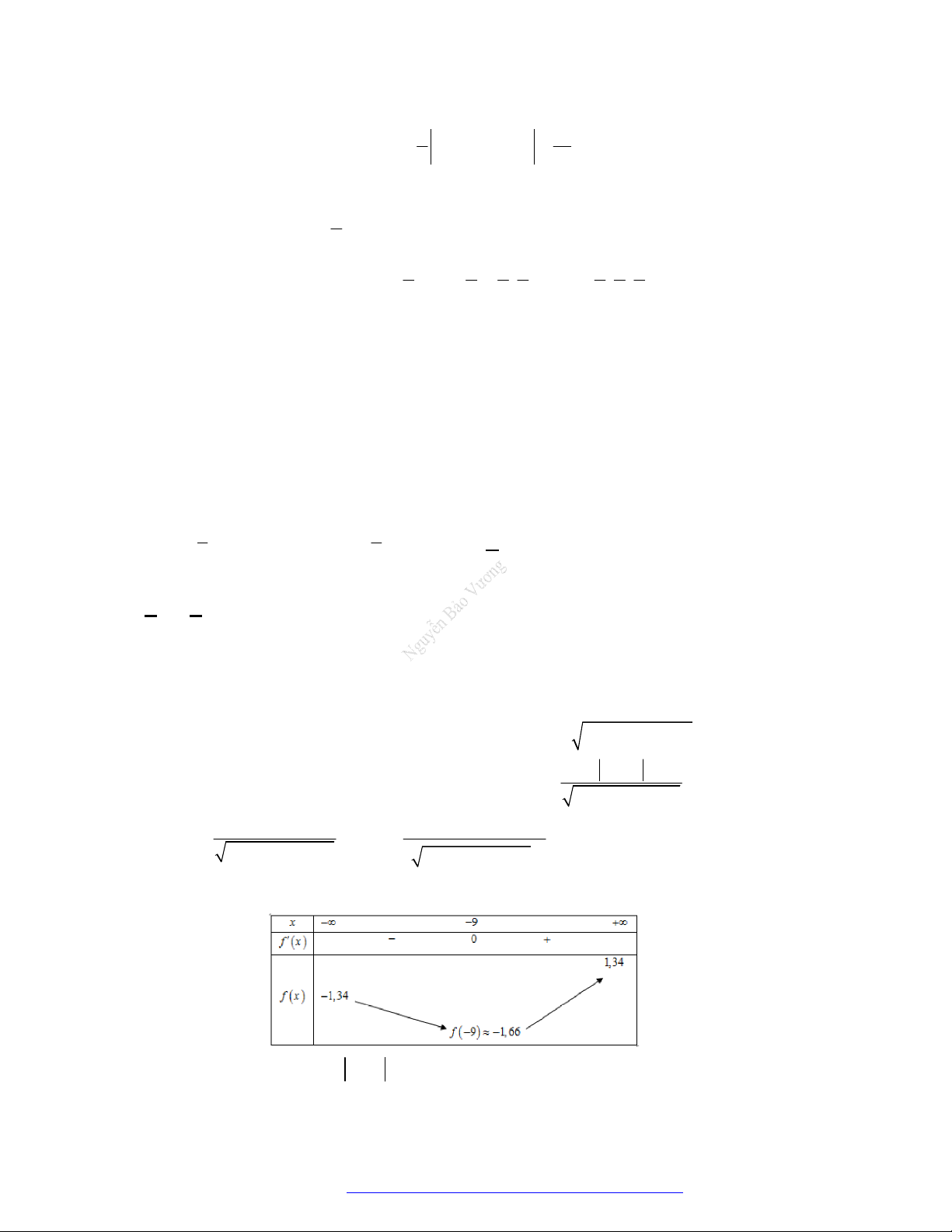
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 28 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

 

   

1; 1;1 ;

; 3; 1; 4 ; 1;2;3

2; 2; 1

AB

AB AC AD

AC



 



 

     



 

   







  



.

Thể tích của tứ diện ABCD là

1 17

; .

6 6

ABCD

V AB AC AD

 

 

 

  

Lại có

AB C D ABCD

V xyzV

  

 

tứ diện

AB C D

  

có thể tích nhỏ nhất khi

xyz

nhỏ nhất

Khi và chỉ khi

3

4

x y z    Mặt phẳng mặt phẳng

 

B C D

  

song song với mặt phẳng

 

BCD

và đi qua điểm

B



. Vì

3 3 3 3

; ;

4 4 4 4

AB AB

 



  

 

 

 

nên

7 1 7

; ;

4 4 4

B

 



 

 

 

   

3; 1; 2 ;

; 4;10; 11

2;3;2

BC

BC BD B C D

BD



   



 

  

   



 

 







 



nhận VTPT là

 

4;10; 11n  



Suy ra phương trình mặt phẳng

 

:B C D

  

16 40 44 39 0   x y z

Câu 10. Trong không gian

Oxyz

, cho hai điểm

   

1;2;4 , 0;0;1A B

và mặt cầu

     

2 2

2

: 1 1 4S x y z    

. Mặt phẳng

 

:a 4 0P x by cz   

đi qua

,A B

và cắt

 

S

theo

giao tuyến là một đường tròn có bán kính nhỏ nhất. Tính

?T a b c  

A.

1

5

T 

. B.

3

4

T 

. C.

1T 

. D.

2T  

.

Lời giải

Chọn C

Ta có:

 

S

có tâm

 

1;1;0I 

và bàn kính

2.R 

Do

     

2 4 4 0 2 12

, : 2 6 4 4 0.

4 0 4

a b c a b

A B P P b x by z

c c

      

 

         

 

  

 

Gọi

r

là bán kính của đường tròn là giao tuyến của

 

P

và

 

S

 

2 2

,r R d I P   , để

r

đạt giá trị

nhỏ nhất

 

,d I P

đạt giá trị lớn nhất. Mà

 

2

3 8

,

5 48 160

b

d I P

b b





 

.

Xét hàm số

   





 

3

2

3 8 32 288

; ; 0 9.

5 48 160

x x

f x f x f x x

x x

 

 

     

 

Bảng xét biến thiên:

suy ra bảng biến thiên của hàm số

 

y f x

là

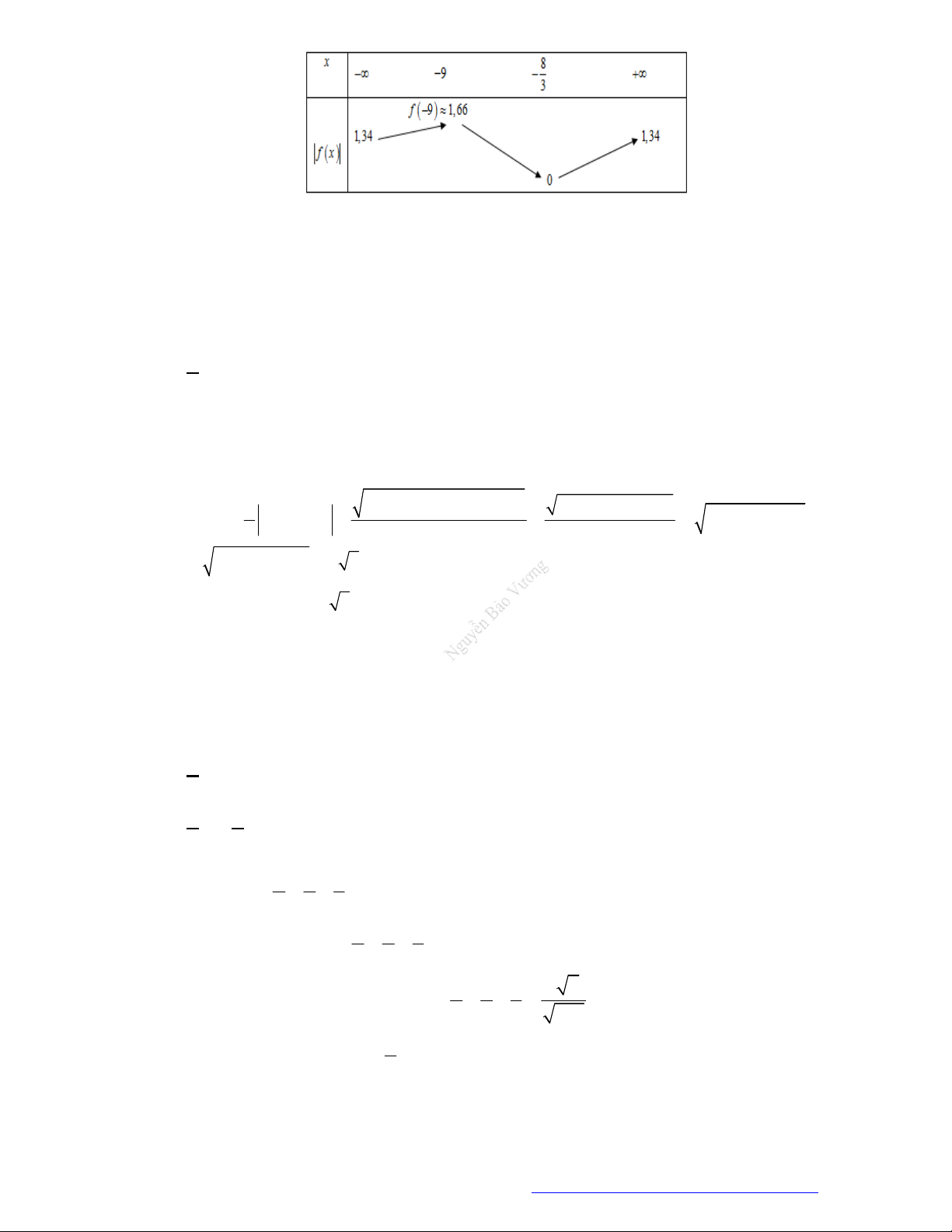
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 29

Dựa vào bảng biến thiên, ta có:

9 9 6 1.x b a T        

Kết luận:

1.T 

Câu 11. (Chuyên Lê Quý Đôn Quảng Trị 2019) Trong không gian

Oxyz

, cho mặt phẳng

 

P

:

2 0x y  

và hai điểm

 

1;2;3A

,

 

1;0;1B

. Điểm

   

; ; 2C a b P 

sao cho tam giác

ABC

có

diện tích nhỏ nhất. Tính

a b

A. 0. B.

3

. C. 1. D. 2.

Lời giải

   

; ; 2C a b P 

 

2 0 2 ; 2; 2a b b a C a a         

.

 

0; 2; 2AB   



,

 

1; ; 5AC a a  



 

, 10 2 ; 2 2;2 2AB AC a a a

 

     

 

 

.

   

2 2

2

2 10 2 2 2

1 12 24 108

,

2 2 2

ABC

a a

S AB AC



  

 

 

  

 

 

 

2

3 2 9a a  

 

2

3 1 24a  

2 6

với

a

.

Do đó

min 2 6

ABC

S





khi

1a  

. Khi đó ta có

 

1;1; 2C  

0a b  

.

Câu 12. (THPT Ngô Sĩ Liên Bắc Giang 2019) Trong không gian với hệ trục toạ độ

,Oxyz

mặt phẳng

 

P

đi qua điểm

 

1;2;1M

cắt các tia

, ,Ox Oy Oz

lần lượt tại các điểm

, ,A B C

(

, ,A B C

không trùng

với gốc

O

) sao cho tứ diện

OABC

có thể tích nhỏ nhất. Mặt phẳng

 

P

đi qua điểm nào trong

các điểm dưới đây?

A.

 

0;2;2N

B.

 

0;2;1M

C.

 

2;0;0P

D.

 

2;0; 1Q

Lời giải

Chọn A

Gọi

 

P

cắt các tia

, ,Ox Oy Oz

lần lượt tại các điểm

       

;0;0 ; 0; ;0 ; 0;0;c , , 0A a B b C a b c 

Ta có

 

: 1

x y z

P

a b c

  

Vì

 

M P

nên ta có

1 2 1

1

a b c

  

Áp dụng bất đẳng thức côsi ta có

3

1 2 1 3 2

1 54abc

a b c

abc

     

Thể tích khối chóp

1

9

6

OABC

V abc 

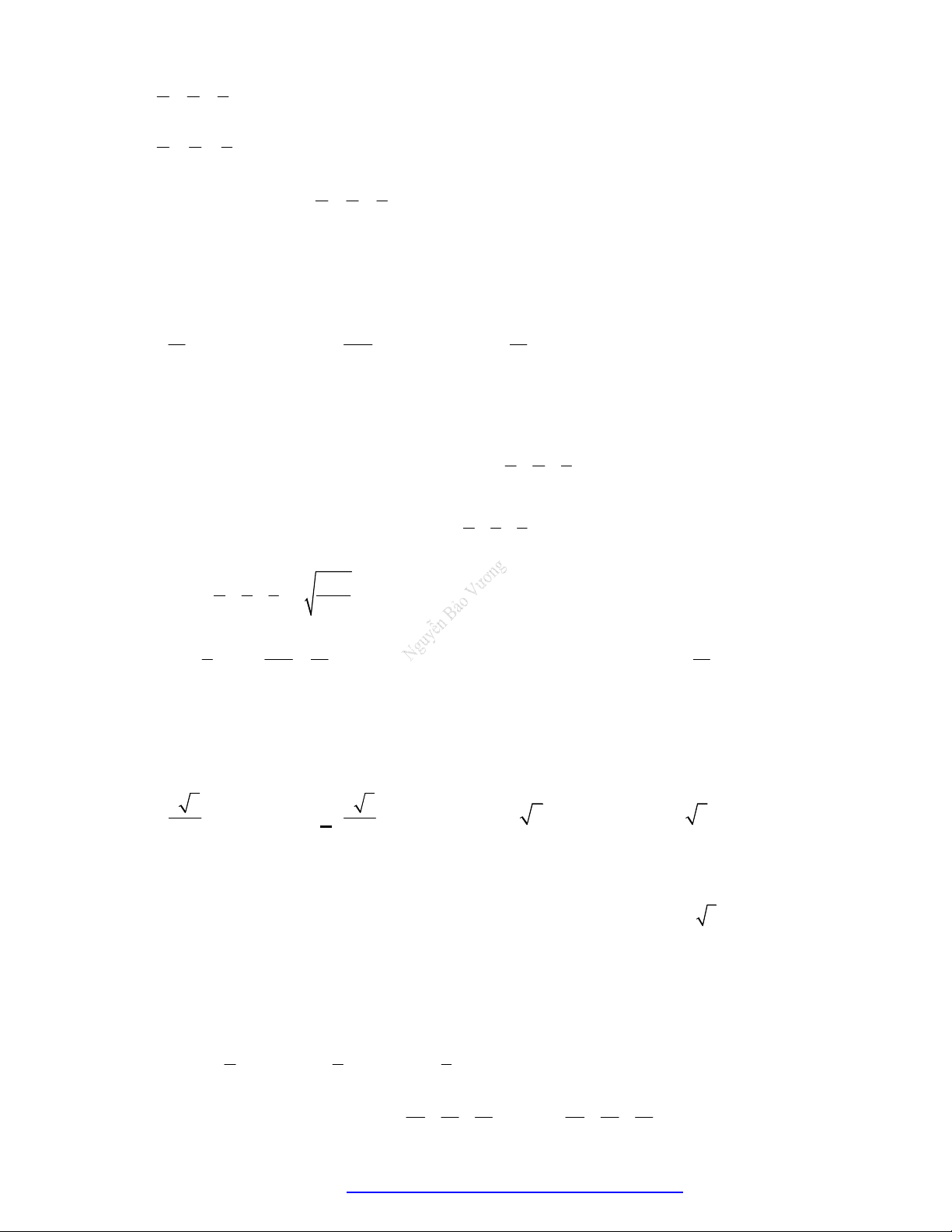
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 30 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Dấu bằng xảy ra khi các số tham gia cô si bằng nhau nghĩa là

1 2 1

1

3; 6; 3

1 2 1

a b c



  



   





 





Vây pt mặt phẳng

     

: 1 0;2;2

3 6 3

x y z

P N P

    

Câu 13. (Chuyên Lê Quý Đôn Điện Biên 2019) Trong không gian với hệ tọa độ

Oxyz

cho mặt phẳng

 

P

đi qua điểm

 

9;1;1

M

cắt các tia

, ,Ox Oy Oz

tại

, ,A B C

(

, ,A B C

không trùng với gốc tọa độ ). Thể

tích tứ diện

OABC

đạt giá trị nhỏ nhất là bao nhiêu?

A.

81

2

. B.

243

2

. C.

81

6

. D.

243

.

Lời giải

Giả sử

     

;0;0 , 0; ;0 , 0;0;A a B b C c

với

, , 0

a b c



.

Mặt phẳng

 

P

có phương trình ( theo đoạn chắn):

1

x y z

a b c

  

.

Vì mặt phẳng

 

P

đi qua điểm

 

9;1;1

M

nên

9 1 1

1

a b c

  

.

Ta có

3

9 1 1 9

1 3 . . 243

. .

a b c

a b c a b c

     

.

1 243 81

. . .

6 6 2

OABC

V a b c  

Vậy thể tích tứ diện

OABC

đạt giá trị nhỏ nhất là

81

2

.

Câu 14. (THPT Quang Trung Đống Đa Hà Nội 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho

mặt cầu

 

2 2 2

: 3

S x y z

  

. Một mặt phẳng

 

a

tiếp xúc với mặt cầu

 

S

và cắt các tia

Ox

,

O y

,

Oz

lần lượt tại

A

,

B

,

C

thỏa mãn

2 2 2

27

OA OB OC

  

. Diện tích tam giác

ABC

bằng

A.

3 3

2

. B.

9 3

2

. C.

3 3

. D.

9 3

.

Lời giải

Gọi

 

; ;H a b c

là tiếp điểm của mặt phẳng

 

a

và mặt cầu

 

S

. Từ giả thiết ta có

a

,

b

,

c

là

các số dương. Mặt khác,

 

H S



nên

2 2 2

3

a b c

  

hay

2

3 3

OH OH  

. (1)

Mặt phẳng

 

a

đi qua điểm

H

và vuông góc với đường thẳng

OH

nên nhận

 

; ;OH a b c





làm

véctơ pháp tuyến. Do đó, mặt phẳng

 

a

có phương trình là

     

0

a x a b y b c z c

     



 

2 2 2

0

ax by cz a b c

     



3 0

ax by cz

   

Suy ra:

3

;0;0

A

a

 

 

 

,

3

0; ;0

B

b

 

 

 

,

3

0;0;

C

c

 

 

 

.

Theo đề:

2 2 2

27

OA OB OC

  



2 2 2

9 9 9

27

a b c

  



2 2 2

1 1 1

3

a b c

  

(2)

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 31

Từ (1) và (2) ta có:

 

2 2 2

1 1 1

9

a b c

 

    

 

 

.

Mặt khác, ta có:

 

2 2 2

1 1 1

9

a b c

 

    

 

 

và dấu

" "

xảy ra khi

1a b c  

. Suy ra,

3

OA OB OC

  

và

.

. . 9

.

6 2

O ABC

OA OB OC

V

 

Lúc đó:

.

3

9 3

2

O ABC

ABC

V

S

OH



 

.

Dạng 2.2. Cực trị liên quan đến giá trị biểu thức

Câu 15. (Đề Tham Khảo 2019) Trong không gian

Oxyz

, cho hai điểm

 

2; 2;4

A 

,

 

3;3; 1

B

 

và mặt

phẳng

 

: 2 2 8 0

P x y z

   

. Xét M là điểm thay đổi thuộc

 

P

, giá trị nhỏ nhất của

2 2

2 3

MA MB



bằng

A.

145

B.

135

C.

105

D.

108

Lời giải

Chọn B

Gọi

 

; ;I x y z

là điểm thỏa mãn

2 3 0

MA MB

 

 



suy ra

 

1;1;1

I 

2

27

IA



;

2

12IB 

;

 

, 3

d I P



2 2

2 3

MA MB



   

2 2

2 3

MI IA MI IB

   

   

2 2 2

5 2 3MI IA IB

  

  

2

5 90

MI

 

Mà

2 2

2 3

MA MB



nhỏ nhất



MI

nhỏ nhất

Suy ra

 

, 3

MI d I P

 

Vậy

2 2

2 3 5.9 90 135

MA MB   

Câu 16. Trong không gian

Oxyz

, cho ba điểm

     

     2; 2; 4 , 3; 3; 1 , 1; 1; 1

A B C

và mặt phẳng

 

   : 2 2 8 0

P x y z

. Xét điểm

M

thay đổi thuộc

 

P

, tìm giá trị nhỏ nhất của biểu thức

  

2 2 2

2T MA MB MC

.

A. 102. B. 105. C. 30. D. 35.

Lời giải

Chọn A

Gọi

I

là điểm thỏa

  

   

2 0IA IB IC

 



 

 



 



   





 



 





2

1

2

0 1; 0; 4

2

4

2

A B C

I

A B C

I

A B C

I

x x x

x

y y y

y I

z z z

z

.

Ta có:

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 32 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

     

   

        

 

 

          

 

 



     

   



2 2 2

2 2 2 2 2 2 2 2

0

2 2

2 2 . 2 2 2 2

T MA MB MC MI IA MI IB MI IC

MI MI IA IB IC IA IB IC MI IA IB IC

Để

T

nhỏ nhất thì

2

2MI

nhỏ nhất

 MI

ngắn nhất

M

là hình chiếu của điểm

 

/

I P

. Khi đó

 

      

2 2 2

, 6; 2 30 min 102

MI d I P IA IB IC T

Câu 17. (Chuyên Quang Trung- Bình Phước 2019) Trong không gian

Oxyz

, cho

     

0;1;2 , 1;1;0 , 3;0;1

A B C

và mặt phẳng

 

: 5 0

Q x y z

   

. Xét điểm

M

thay đổi thuộc

 

Q

. Giá trị nhỏ nhất của biểu thức

2 2 2

MA MB MC 

bằng

A.

34

3

. B.

22

3

. C.

0

. D.

26

3

.

Lời giải

Chọn A

Gọi điểm

G

thỏa mãn

0

GA GB GC

  

   

, suy ra

4 2

; ;1

3 3

G

 













 

. Khi đó

     

 

2 2 2

2 2 2 2

2

2 2

2

2 2 2

3 2 .

3

3 , .

P MG GA MG GB MG GC

MG MG GA GB GC GA GB GC

MG GA GB GC

d G Q GA GB G

MA M C

C

B M      

      

   

 

   





 





     

   

Dấu bằng xảy ra khi

M

là hình chiếu của

G

lên mặt phẳng

 

Q

.

Ta có

 

4 2

1 5

2

3 3

,

3 3

d G Q

  

 

2

4 1 26

; ;1

3 3 9

GA GA

 





   









 



;

2

1 1 11

; ; 1

3 3 9

GB GB

 





    









 



;

2

5 2 29

; ;0

3 3 9

GC GC

 





   









 



.

Vậy

4 26 11 29 34

min 3.

3 9 9 9 3

P     

khi

M

là hình chiếu của

G

lên mặt phẳng

 

Q

.

Câu 18. (Chuyên Lam Sơn 2019) Trong hệ trục tọa độ

Oxyz

cho điểm

 

( 1;3;5); (2;6; 1); 4; 12;5

A B C   

và mặt phẳng

 

: 2 2 5 0

P x y z

   

. Gọi

M

là điểm di

động trên

 

P

. Giá trị nhỏ nhất của biểu thức

S MA MB MC

  

  

là

A.

42

B.

14

. C.

14 3

. D.

14

3

.

Lời giải

Chọn B

Gọi G là trọng tâm tam giác

ABC

nên

( 1; 1;3)

G

 

và

3 3

S MA MB MC MG MG

    

   

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 33

Vì

( )G P

nên

GM GH

với H là chân đường vuông góc từ G đến mp(P)

 

min

;

2

2 2

1 2 6 5

3 3 3 14

1 2 2

G P

S GH d

   

   

  

Câu 19. Trong không gian

Oxyz

cho các điểm

 

1; 1;3

A 

,

 

2;1;0

B

,

 

3; 1; 3

C

  

và mặt phẳng

 

: 4 0

P x y z

   

. Gọi

 

, ,M a b c

là điểm thuộc mặt phẳng

 

P

sao cho biểu thức

3 2

T MA MB MC

  

  

đạt giá trị nhỏ nhất. Tính giá trị của biểu thức

S a b c  

.

A.

3

S



. B.

1

S

 

. C.

2

S



. D.

1

S



.

Lời giải

Chọn C

Gọi

 

; ;I x y z

là điểm thỏa mãn

3 2 0

IA IB IC

  

   

Ta có

   

1 ; 1 ;3 3 3 3 ; 3 3 ;9 3IA x y z IA x y z

          

 

   

2 ;1 ; 2 4 2 ;2 2 ; 2IB x y z IB x y z

        

 

 

3 ; 1 ; 3

IC x y z      



Khi đó

 

3 2 2 4; 2 6; 2 6 0

IA IB IC x y z

         

   

2 4 0 2

2 6 0 3

x x

y y

z z

    

 

 

      

 

 

   

 

. Vậy

 

2; 3;3

I  

Ta có

     

3 2 3 2 2

T MA MB MC MI IA MI IB MI IC MI

         

        

Suy ra

min

T MI





khi và chỉ khi

M

là hình chiếu của

I

lên mặt phẳng

 

P

Đường thẳng

MI

đi qua

 

2; 3;3

I  

và vuông góc với mặt phẳng

 

P

có phương trình tham số

là

2

: 3

3

x t

MI y t

z t

  





  





 



. Lấy

 

2 ; 3 ;3

M t t t MI

     

Mặt khác

       

2 3 3 4 0 4M P t t t t            

Suy ra

 

2;1; 1

M



. Vậy

2

a b c

  

Câu 20. (Ngô Quyền - Hải Phòng 2019) Trong không gian

Oxyz

, cho ba điểm

     

1;1;1 , 1;2;0 , 3; 1;2

A B C 

và điểm

M

thuộc mặt phẳng

 

: 2 2 7 0

x y z

a

   

. Tính giá

trị nhỏ nhất của

3 5 7

P MA MB MC

  

  

.

A.

min

20

P



. B.

min

5

P



. C.

min

25

P



. D.

min

27

P



.

Lời giải

Chọn D

Gọi

I

là điểm thỏa mãn:

3 5 7 0

IA IB IC

  

   

     

3 5 7 0

OA OI OB OI OC OI

      

      

3 5 7

OI OA OB OC

   

   



Tọa độ điểm

 

23; 20; 11

I   

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 34 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Khi đó:

3 5 7

u MA MB MC

  

   

     

3 5 7

IA IM IB IM IC IM

     

     

 

3 5 7

IM IA IB IC

    

   

IM 



.

Nên:

3 5 7

P MA MB MC

  

  

IM

 



IM

 

,d I

a



.

Vậy:

 

min

,P d I

a



   

2 2 2

2. 23 20 2 11 7

27

2 1 2

    

 

 

.

Câu 21. (SGD Hưng Yên 2019) Trong không gian với hệ tọa độ

Oxyz

, cho ba điểm

 

1;4;5

A

,

 

3; 4;0

B

,

 

2; 1;0

C 

và mặt phẳng

 

: 3 3 2 29 0

P x y z

   

. Gọi

 

; ;M a b c

là điểm thuộc

 

P

sao cho biểu thức

2 2 2

3

T MA MB MC

  

đạt GTNN. Tính tổng

a b c 

.

A. 8. B. 10. C.

10

. D.

8

.

Lời giải

Chọn A

Gọi

I

là điểm thỏa mãn hệ thức:

3 0

IA IB IC

  

   

 

*

.

Khi đó,

     

1 1 3

* 2;1;1 2;1;1

5 5 5

OI OA OB OC I     

   

.

Mặt khác, áp dụng tính chất tâm tỉ cự của hệ điểm

2 2 2 2

5 3

T MI IA IB IC

    

.

Vì

2 2 2

3

IA IB IC

 

là hằng số nên suy ra

T

đạt GTNN

MI

đạt GTNN

M

là hình chiếu vuông góc của

I

trên

 

P

 





  





  

   

  

  

 



 



 

 



 

5

3 3 2 29

4

2 1 1

cïng ph¬ng

1

3 3 2

P

a

a b c

M P

b

a b c

IM n

c

.

Vậy

8

a b c

  

.

Câu 22. Trong không gian

Oxyz

, cho ba điểm

     

0;0;1 , 1;1;0 , 1;0; 1

A B C

 

. Điểm

M

thuộc mặt

phẳng

 

: 2 2 2 0

P x y z

   

sao cho

2 2 2

3 2

MA MB MC

 

đạt giá trị nhỏ nhất. Giá trị nhỏ nhất

đó bằng

A.

13

6

. B.

17

2

. C.

61

6

. D.

23

2

.

Lời giải

Chọn C

Gọi

I

là điểm thảo mãn

3 2

1

6 6

3 2

1 1 1 1

3 2 0 ; ;

6 3 6 3 3

3 2

1

6 3

A B C

I

A B C

I

A B C

I

x x x

x

y y y

IA IB IC y I

z z z

z

 



  



 



 

       



 

 



 



 





   

.

Ta có

     

2 2 2

3 2 3 2

MA MB MC IA IM IB IM IC IM

       

     

 

2 2 2 2

3 2 6 2 3 2

IA IB IC IM MI IA IB IC

      

   

2 2 2 2

3 2 6

IA IB IC IM

   

.

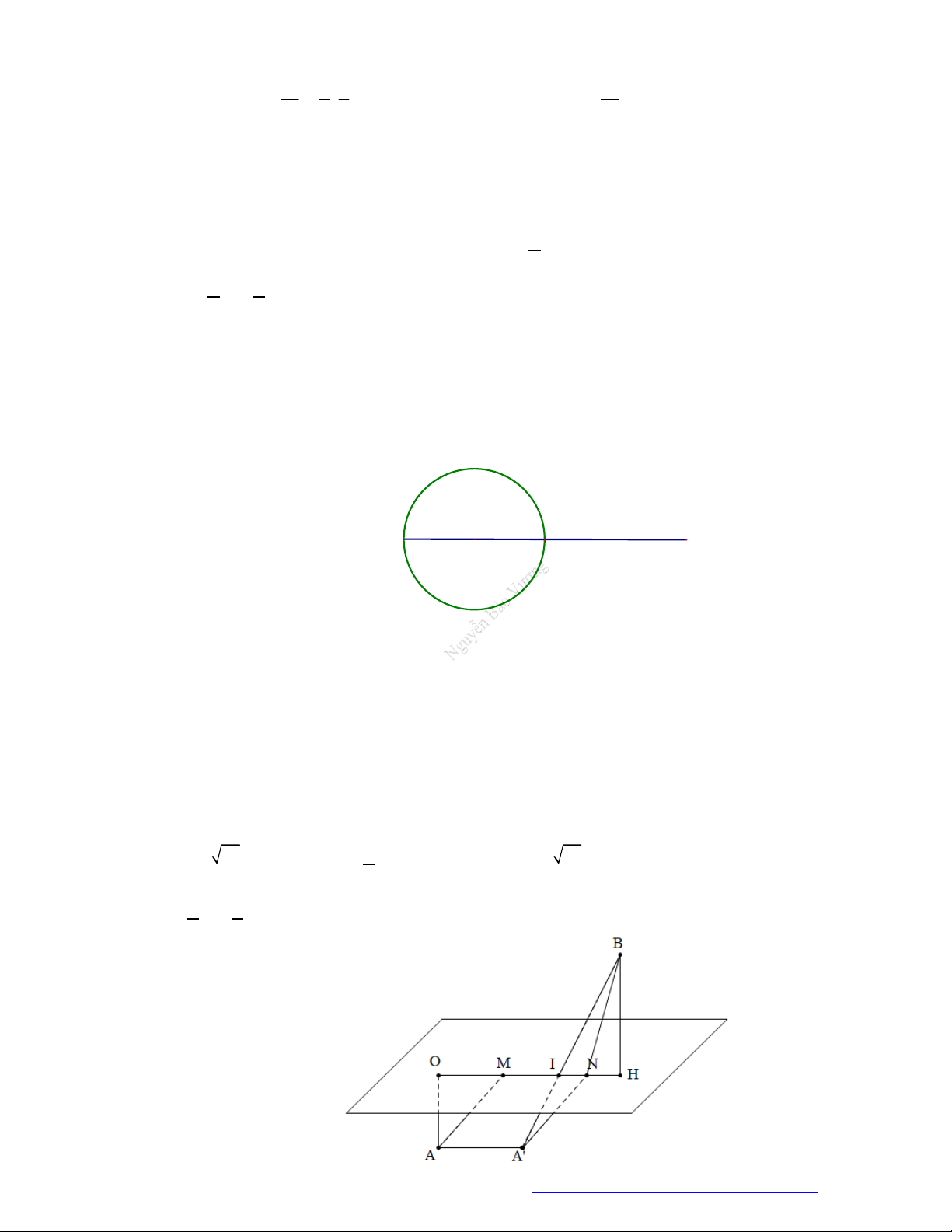
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 35

Do đó

2 2 2

3 2MA MB MC 

nhỏ nhất khi và chỉ khi

IM

nhỏ nhất

M

là hình chiếu của

I

trên

 

P

11 1 5

; ;

18 9 9

M

 

  

 

 

 

2 2 2

61

min 3 2

6

MA MB MC   

Câu 23. Trong không gian

Oxyz

, cho hai điểm

 

3;1; 3A 

,

 

0; 2;3B 

và mặt cầu

   

2 2

2

( ) : 1 3 1S x y z    

. Xét điểm

M

thay đổi luôn thuộc mặt cầu

( )S

, giá trị lớn nhất

của

2 2

2MA MB

bằng

A.

102

. B.

78

. C.

84

. D.

52

.

Lời giải

Chọn C

Gọi

I

là điểm thỏa mãn hệ thức

 

2 0 1; 1;1IA IB I   

  

.

Ta có

   

2 2

2 2 2T MA MB MA MB MI IA MI IB       

     

2 2 2 2

3 2 3 36MI IA IB MI    

.

Mặt cầu

( )S

có tâm

 

1;0;3J 

, bán kính

1R 

.

Ta có:

IJ R I 

nằm ngoài mặt cầu

( )S

.

Ta có:

T

lớn nhất

IM

lớn nhất.

Mà

max

3 1 4IM IJ R     .

Do đó:

2

max

3.4 36 84.T   

Câu 24. (Hậu Lộc 2-Thanh Hóa -2019) Trong không gian

Oxyz

, cho các điểm

 

A 0;0; 2

và

 

B 3;4;1

.

Gọi

 

P

là mặt phẳng chứa đường tròn giao tuyến của hai mặt cầu

       

2 2 2

1

: 1 1 3 25S x y z     

với

 

2 2 2

2

: x 2 2 14 0S y z x y     

.

M

,

N

là hai điểm

thuộc

 

P

sao cho

1MN 

. Giá trị nhỏ nhất của

AM BN

là

A.

34 1

. B.

5

. C.

34

. D.

3

.

Lời giải

Chọn B

J

I

M

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 36 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Từ

         

   

2 2 2

1

2 2 2

2

: 1 1 3 25 1

: x 2 2 14 0 2

S x y z

S y z x y



     





     





Lấy

 

1

trừ

 

2

, ta được

6 0

z



hay

 

: 0

P z



tức là

   

.P Oxy



Dễ thấy

A

,

B

nằm khác phía đối với

 

P

, hình chiếu của

A

trên

 

P

là

O

, hình chiếu của

B

trên

 

P

là

 

3;4;0 .

H

Lấy

'A

sao cho

.AA MN





 

Khi đó

AM BN A N BN A B

 

   

và cực trị chỉ xảy ra khi

MN



cùng phương

.OH



Lấy

3 4

; ;0 .

5 5

OH

MN

OH

 

 

 

 







Khi đó vì

AA MN





 

nên

3 4

; ;0 .

5 5

A

 



 

 

Do đó

5.

AM BN A N BN A B

 

    

Câu 25. (SGD Điện Biên - 2019) Trong không gian

Oxyz

, cho ba điểm

 

2; 2;4

A 

,

 

3;3; 1

B

 

,

 

1; 1; 1

C

  

và mặt phẳng

 

: 2 2 8 0

P x y z

   

. Xét điểm

M

thay đổi thuộc

 

P

, tìm giá trị

nhỏ nhất của biểu thức

2 2 2

2

T MA MB MC

  

.

A. 102. B. 105. C. 30. D. 35.

Lời giải

Chọn A

Gọi

I

là điểm thỏa mãn:

2 0

IA IB IC

  

   

     

2 0

OA OI OB OI OC OI

      

      

 

1 1

1;0;4

2 2

OI OA OB OC    

   

 

1;0;4

I

.

Khi đó, với mọi điểm

   

; ;

M x y z P



, ta luôn có:

     

2 2 2

2

T MI IA MI IB MI IC

     

     

 

2 2 2 2

2 2 . 2 2

MI MI IA IB IC IA IB IC

      

       

2 2 2 2

2 2

MI IA IB IC

   

.

Ta tính được

2 2 2

2 30

IA IB IC

  

.

Do đó,

T

đạt GTNN

MI

đạt GTNN

 

MI P

 

.

Lúc này,

 

2

2 2

2.1 0 2.4 8

, 6

2 1 2

IM d I P

  

  

  

.

Vậy

2

min

2.6 30 102

T   

.

Câu 26. (THPT Cẩm Giàng 2 2019) Trong không gian

Oxyz

, cho ba điểm

 

10; 5;8

A  

,

 

2;1; 1

B



,

 

2;3;0

C

và mặt phẳng

 

: 2 2 9 0

P x y z

   

. Xét

M

là điểm thay đổi trên

 

P

sao cho

2 2 2

2 3

MA MB MC

 

đạt giá trị nhỏ nhất. Tính

2 2 2

2 3

MA MB MC

 

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 37

A.

54

.

B.

282

.

C.

256

.

D.

328

.

Lời giải

Gọi

 

; ;I x y z

là điểm thỏa mãn

2 3 0

IA IB IC

  

   

.

Ta có

 

10 ; 5 ;8

IA x y z     



,

 

2 ;1 ; 1

IB x y z    



,

 

2 ;3 ;

IC x y z   



.

Khi đó,

     

10 2 2 3 2 0

5 2 1 3 3 0

8 2 1 3 0

x x x

y y y

z z z

      





      





      



0

1

x

y

z







 











 

0;1;1

I

.

Với điểm

M

thay đổi trên

 

P

, ta có

2 2 2

2 3

MA MB MC

 

     

2 2 2

2 3

MI IA MI IB MI IC

     

     

 

2 2 2 2

6 2 3 2 2 3

MI IA IB IC MI IA IB IC

      

   

2 2 2 2

6 2 3

MI IA IB IC

   

(Vì

2 3 0

IA IB IC

  

   

).

Ta lại có

2 2 2

2 3

IA IB IC

 

185 2.8 3.9  

228

.

Do đó,

2 2 2

2 3

MA MB MC

 

đạt giá trị nhỏ nhất



MI

đạt giá trị nhỏ nhất



M

là hình chiếu vuông góc của

I

trên

 

P

.

Khi đó,

 

, 3

MI d I P

 

.

Vậy giá trị nhỏ nhất của

2 2 2

2 3

MA MB MC

 

bằng

2

6 228

MI 

6.9 228 

282

.

Giá trị nhỏ nhất của

2 2 2

2 3

MA MB MC

 

đạt được khi và chỉ khi

M

là hình chiếu vuông góc

của

I

trên

 

P

.

Câu 27. Trong không gian

Oxyz

, cho

     

4; 2;6 ; 2;4;2 ; : 2 3 7 0

A B M x y z

a

     

sao cho

.MA MB

 

nhỏ nhất, khi đó tọa độ của

M

là

A.

29 58 5

; ;

13 13 13

 

 

 

B.

 

4;3;1

C.

 

1;3;4

D.

37 56 68

; ;

3 3 3



 

 

 

Lời giải

Chọn B.

Gọi

   

; ; 2 3z 7 0

M x y z x y

a

     

 

4 ; 2 ;6

MA x y z    



;

 

2 ;4 ;2

MB x y z   



        

. 4 2 2 4 6 2

MA MB x x y y z z         

 

2 2 2

6 2 8 12

x y z x y z

      

     

2 2 2

3 1 4 12

x y z

      

Áp dụng bđt B. C. S:

           

2

2 2 2 2

2 2

1 2 3 3 1 4 3 2 1 3 4

x y z x y z

   

             

 

 

   

     

 

2

2 2 2

14 3 1 4 2 3 7

x y z x y z

 

         

 

     

 

2

2 2 2

7 7

3 1 4

14

x y z



      

     

2 2 2

3 1 4 12 2

x y z

       

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 38 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

 

. 2

Min MA MB



 

xảy ra khi và chỉ khi

4

2 3z 7 0

3

3 1 4

1

1 2 3

x

x y

y

x y z

z





   



 

 

   

 

 







.

Câu 28. (Chuyên Lam Sơn Thanh Hóa 2019) Trong hệ trục

,Oxyz

cho điểm

 

1;3;5 ,

A

 

2;6; 1 ,

B

 

4; 12;5

 C

và mặt phẳng

 

: 2 2 5 0.   

P x y z

Gọi

M

là điểm di động trên

 

.P

Gía trị

nhỏ nhất của biểu thức

  

  

S MA MB MC

là

A.

42.

B.

14.

C.

14 3.

D.

14

.

3

Lời giải

Gọi

 

1 1 1

; ;G x y z

là trọng tâm tam giác

.ABC

Vì

G

là trọng tâm tam giác

ABC

và

M

là điểm tùy ý nên

3 .

  

   

MA MB MG MG

Vậy

3 3 .

    

   

S MA MB MC MG MG

Do

G

là trọng tâm tam giác

ABC

nên

 

1

1 2 4

1

3 3

3 6 12

1 1; 1;3 .

3 3

5 1 5

3

3 3

 

  



   



 

 



      





 

 



  





A B C

x x x

x

y y y

y G

z z z

z

Vì

G

cố định nên

3

S MG

đạt giá trị nhỏ nhất khi và chỉ khi

MG

nhỏ nhất. Tức là

 

.



MG P

Ta có:

 

2

2 2

1.1 2. 1 2.3 5

14

, .

3

1 2 2

    

  

  

d G P MG

Vậy giá trị nhỏ nhất

14

3 3 3. 14.

3

      

   

S MA MB MC MG MG

Câu 29. (Chuyên Lê Hồng Phong Nam Định 2019) Trong không gian với hệ tọa độ

Oxyz

, cho ba điểm

 

1;2;5

A 

,

 

3; 1;0

B 

,

 

4;0; 2

C

 

. Gọi

I

là điểm trên mặt phẳng

 

Oxy

sao cho biểu thức

2 3IA IB IC

 

  

đạt giá trị nhỏ nhất. Tính khoảng cách từ

I

đến mặt phẳng

 

: 4 3 2 0

P x y

  

.

A.

17

5

. B.

6

. C.

12

5

. D.

9

.

Lời giải

Gọi

 

; ;M a b c

là điểm thỏa mãn

2 3 0

MA MB MC

  

   

.

Khi đó:

   

1 2 3 3 4 0

2 2 1 3 0 0

5 2 0 3 2 0

a a a

b b b

c c c

       





      





      



19

2

1

2

a

b

c



 



 





 



19 1

;2;

2 2

M

 

  

 

 

.

Ta có:

2 3IA IB IC

 

  

2 2 3 3

IM MA IM MB IM MC

     

     

 

2 2 3

IM MA MB MC

   

   

2 2

IM IM

 



.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 39

Biểu thức

2 3IA IB IC

 

  

đạt giá trị nhỏ nhất

IM

nhỏ nhất



I

là hình chiếu vuông góc của

M

lên

 

Oxy

19

;2;0

2

I

 

 

 

 

.

Khoảng cách từ điểm

I

đến mặt phẳng

 

P

là:

 

2 2

19

4. 3.2 2

2

; 6

4 3

d I P

 

  

 

 

 



.

Câu 30. Trong không gian tọa độ

,Oxyz

cho hai điểm

   

3; 2;2 , 2;2;0

A B 

và mặt phẳng

 

: 2 2 3 0.

P x y z

   

Xét các điểm

,M N

di động trên

 

P

sao cho

1.

MN



Giá trị nhỏ nhất

của biểu thức

2 2

2 3

AM BN



bằng

A.

49,8.

B.

45.

C.

53.

D.

55,8.

Lời giải

Gọi

,H K

lần lượt là hình chiếu của

,A B

trên mặt phẳng

 

P

   

3, 1; 1;0 , 0;1;2 , 3.

AH BK H K HK

    

Đặt

HM t

ta có:

3 2HM MN NK HK NB t      

 

2

2 2 2 2 2 2 2

2 3 2 2 3 3 45 2 2 49,8

AM BN AH HM BK KN t t         

Dấu bằng xảy ra khi

,

M N 

đoạn thẳng

.HK

Vậy Giá trị nhỏ nhất của biểu thức

2 2

2 3

AM BN



bằng

49,8

Câu 31. (THPT Nghĩa Hưng NĐ- 2019) Trong không gian với hệ tọa độ

Oxyz

, cho điểm

 

; ;A a b c

với

a

,

b

,

c

là các số thực dương thỏa mãn

 

2 2 2

5 9 2    

a b c ab bc ca

và

 

3

2 2

1

 



 

a

Q

b c

a b c

có giá trị lớn nhất. Gọi

M

,

N

,

P

lần lượt là hình chiếu vuông góc của

A

lên các tia

Ox

,

Oy

,

Oz

. Phương trình mặt phẳng

 

MNP

là

A.

4 4 12 0   

x y z

. B.

3 12 12 1 0   

x y z

.

C.

4 4 0  

x y z

. D.

3 12 12 1 0   

x y z

.

Lời giải

Đặt

 t b c

 

0

t

;

2

2 2

2

 

t

b c

;

2

4



t

bc

.

 

2 2 2

5 9 2

a b c ab bc ca

    

   

2

5 5 9 28

     

a b c a b c bc

2 2 2

5 5 9 7

   

a t at t

  

5 2 0   

a t a t

2 a t

.

Vậy

 

3

4 1

27

  

Q f t

t t

với

0t

.

Ta có

 

2 4

4 1

0

9



   

f t

t t

1

6

 

t

(vì

0t

).

Ta có bảng biến thiên

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 40 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Vậy 16

max

Q

1

3

 a

;

1

12

 b c

.

Suy ra tọa độ điểm

1 1 1

; ;

3 12 12

 

 

 

A

; tọa độ các điểm

1

;0;0

3

 

 

 

M

;

1

0; ;0

12

 

 

 

N

;

1

0;0;

12

 

 

 

P

.

Phương trình mặt phẳng

 

MNP

1

1 1 1

3 12 12

  

x y z

3 12 12 1 0    x y z

.

Câu 32. (Sở Bắc Giang 2019) Cho

, , , , ,x y z a b c

là các số thực thay đổi thỏa mãn

     

2 2 2

1 1 2 1x y z     

và

3.a b c  

Tìm giá trị nhỏ nhất của

     

2 2 2

.P x a y b z c     

A.

3 1.

B.

3 1.

C.

4 2 3.

D.

4 2 3.

Lời giải

Chọn C

Gọi

 

; ;M x y z M

thuộc mặt cầu

 

S

tâm

 

1; 1;2I  

bán kính

1R 

Gọi

 

; ;H a b c H

thuộc mặt phẳng

 

: 3 0P x y z   

Ta có

 

1 1 2 3

, 3

3

d I P R

   

   

 

P

và

 

S

không có điểm chung

     

2 2 2

2

P x a y b z c MH      

đạt giá trị nhỏ nhất khi vị trí của

M

và

H

như hình vẽ

Khi đó

 

, 3 3 1HI d I P HM HI R      

Do đó

 

2

min

3 1 4 2 3P    

.

Câu 33. (Chuyên Sơn La 2019) Trong không gian

Oxyz

, cho hai điểm

 

1;0;0A

và

 

2;3;4B

. Gọi

 

P

là mặt phẳng chứa đường tròn giao tuyến của hai mặt cầu

     

2 2

2

1

: 1 1 4    S x y z

và

 

2 2 2

2

: 2 2 0    S x y z y

. Xét

M

,

N

là hai điểm bất kỳ thuộc mặt phẳng

 

P

sao cho

1MN 

. Giá trị nhỏ nhất của

AM BN

bằng

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 41

A. 5. B. 3. C. 6. D. 4.

Lời giải

 Xét hệ

   

2 2

2

2 2 2

1 1 4

2 2 0

x y z

x y z y



    





    





2 2 2

2 2 2 0

2 2 0

x y z x y

x y z y



     







    





0x 

Vậy

 

: 0P x 

 



P

chính là mặt phẳng

 



Oyz

.

Gọi

 

0;0;0C

và

 

0;3;4D

lần lượt là hình chiếu vuông góc của

 

1;0;0A 

và

 

2;3;4B

trên

mặt phẳng

 

P

. Suy ra

1AC 

,

2BD 

,

5CD 

.

 Áp dụng bất đẳng thức

   

2 2

2 2 2 2

a b c d a c b d      

, ta được

   

 

2 2 2 2

2 2

2

9

AM BN AC CM BD DN

AC BD CM DN

CM DN

    

   

  

Lại có

5CM MN ND CD   

nên suy ra

4CM ND 

. Do đó

5AM BN 

.

Đẳng thức xảy ra khi

C

,

M

,

N

,

D

thẳng hàng theo thứ tự đó và

AC BD

CM DN



, tức là

4 16

0; ;

5 15

M

 

 

 

và

7 28

0; ;

5 15

N

 

 

 

.

Vậy giá trị nhỏ nhất của

AM BN

là 5.

Câu 34. (THPT Yên Khánh - Ninh Bình - 2019) Trong không gian

Oxyz

cho mặt cầu

 

2 2 2

: 1S x y z  

. Điểm

 

M S

có tọa độ dương; mặt phẳng

 

P

tiếp xúc với

 

S

tại

M

cắt

các tia

Ox

;

Oy

;

Oz

tại các điểm

A

,

B

,

C

. Giá trị nhỏ nhất của biểu thức

   

2 2 2

1 1 1T OA OB OC   

là:

A. 24. B. 27. C. 64. D. 8.

Lời giải

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 42 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

 

S

có tâm

 

O

và bán kính

1R 

.

Theo đề bài ta có

       

,0,0 ; 0, ,0 ; 0,0, ; , , 0A a B b C c a b c 

khi đó phương trình mặt phẳng

 

P

là:

1

x y z

a b c

  

.

 

P

tiếp xúc với

 

S

tại

 

M S

 

2 2 2

1

; 1 1

1 1 1

d O P

a b c

   

 

 

32 2 2 2 2 2 4 4 4

3 3 3 1abc a b b c c a a b c abc      

vì

 

, , 0a b c 

.

Khi đó:

       

2 2 2 2 2 2

1 1 1 1 1 1T OA OB OC a b c       

2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2

1 1 2T a b c a b b c c a a b c a b c a b c             

Mặt khác

 

32 2 2 2 2 2 2 2 2 2 2 2

1 2 1 3 2 64 2 64a b c a b c a b c a b c T         

.

Vậy giá trị nhỏ nhất của T là 64 khi

 

1

và

 

2

xảy ra dấu bằng 3a b c    .

Dạng 2.3. Cực trị liên quan đến góc, khoảng cách

Câu 35. Trong không gian với hệ tọa độ

Oxyz

, cho ba điểm

     

,0,0 , 0, ,0 , 0,0,A a B b C c

với

, ,a b c

là

những số dương thay đổi thỏa mãn

2 2 2

4 16 49a b c  

. Tính tổng

2 2 2

S a b c  

khi khoảng

cách từ

O

đến mặt phẳng

 

ABC

đạt giá trị lớn nhất.

A.

51

5

S 

. B.

49

4

S 

. C.

49

5

S 

. D.

51

4

S 

.

Lời giải

Chọn B

Dựng

   

 

;OH ABC H ABC 

vì OABC là tứ diện vuông nên ta có:

M

z

x

y

I

O

C

A

B

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 43

2 2

2 2 2 2 2 2 2 2 2 2

1 1 1 1 1 1 1 1 2 4

4 16OH OA OB OC a b c a b c

        

Áp dụng bất đẳng thức Schwarz:

 

2

2 2

2 2 2 2 2 2 2

1 2 4

1 1 2 4

1 1

4 16 4 16

OH

OH a b c a b c

 

      

 

Vậy khoảng cách từ

O

đến mặt phẳng

 

ABC

đạt giá trị lớn nhất là 1 khi:

2

2 2 2 2 2 2

2

7

1 2 4 1 2 4 1 7 49

4 16 4 16 7 2 4

7

4

a

b S

a b c a b c

c









 



       



 









Câu 36. (Chuyên Lê Hồng Phong Nam Định 2019) Trong không gian với hệ tọa độ

Oxyz

, cho bốn

điểm

 

1;0;0A

,

 

2;1;3B

,

 

0;2; 3C 

,

 

2;0; 7D . Gọi

M

là điểm thuộc mặt cầu

     

2 2

2

: 2 4 39S x y z    

thỏa mãn

2

2 . 8MA MB MC 

 

. Biết rằng đoạn thẳng

MD

đạt

giá trị lớn nhất. Tìm giá trị lớn nhất đó?

A. 7 . B. 2 7 . C. 3 7 . D. 4 7 .

Lời giải

Chọn B

Giả sử

 

; ;M x y z

, ta có:

 

2 2 2 2

2 . 8 2 2 7 0 1MA MB MC x y z x y        

 

.

Mà

 

M S

nên ta có:

 

2 2 2

4 8 19 0 2x y z x y     

Trừ

   

1 , 2

theo vế ta được:

2 0x y  

.

Suy ra

M

thuộc đường tròn

 

T

là giao của

 

S

với mặt phẳng

 

: 2 0P x y  

.

Thay tọa độ của

D

vào phương trình của

 

P

và của

 

S

thấy thỏa mãn nên

 

D T

, suy ra giá

trị lớn nhất của

MD

bằng đường kính của

 

T

.

 

S

có tâm

 

2;4;0I

và bán kính 39R  .

Khoảng cách từ

I

với

 

P

là

 

; 4 2h d I P  .

Bán kính của

 

T

là

2 2

7r R h  

. Suy ra max 2 2 7MD r  .

Câu 37. (Bình Giang-Hải Dương 2019) Cho

 

0;8;2A

và mặt cầu

       

2 2 2

: 5 3 7 72S x y z     

và điểm

 

9; 7;23A 

. Viết phương trình mặt phẳng

 

P

đi

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 44 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

qua A và tiếp xúc với mặt cầu

 

S

sao cho khoảng cách từ B đến mặt phẳng

 

P

là lớn nhất. Giải

sử

 

1; ;n m n





là một vectơ pháp tuyến của

 

P

. Lúc đó

A.

. 4

m n



. B.

. 2

m n



. C.

. 4

m n

 

. D.

. 2

m n

 

.

Lời giải

Chọn C

 

P

đi qua điểm

 

0;8;2

A

và có vectơ pháp tuyến

 

1; ;n m n





 

: 8 2 0

P x my nz m n

     

.

 

P

tiếp xúc với mặt cầu

 

S

2 2

5 11 5

6 2

1

m n

 

 

 

.

 

2 2 2 2

9 15 21 5 11 5 4 4 16

;

1 1

m n m n m n

d d B P

m n m n

      

  

   

.

2 2 2 2

5 11 5 1 4

4

1 1

m n m n

   

 

   

.

 

2

2 2 2 2

2 2

1 1 4 . 1

6 2 4

1

m n

    

 

 

(Buinhiacôpxki).

18 2



.

max

1

1 1 4

18 2 . 4

4

1

m

d m n

n

m n

 





        







Câu 38. Cho

, ,x y z

là ba số thực thỏa

2 2 2

4 6 2 11 0

x y z x y z

      

. Tìm giá trị lớn nhất của

2 2

P x y z  

.

A.

max 20

P



. B.

max 18

P

 

. C.

max 18

P



. D.

max 12

P



.

Lời giải

Chọn D

Ta có:

 

2 2 2 2 0 1

P x y z x y z P       

.

Lại có:

       

2 2 2

4 6 2 11 0 2 3 1 25 2

x y z x y z x y z             

Xét trong hệ trục tọa độ

Oxyz

, ta thấy

 

1

là phương trình của một mặt phẳng, gọi là

 

mp

a

và

 

2

là phương trình của một mặt cầu

 

S

tâm

 

2; 3;1

I 

, bán kính

5

R



.

Giá trị lớn nhất của

2 2

P x y z  

là giá trị lớn nhất của

P

để

 

a

và

 

S

có điểm chung, điều

này tương đương với

 

2

2 2

2.2 2. 3 1.1

, 5 3 15 18 12.

2 2 1

P

d I R P P

a

   

         

  

Vậy

max 12

P



.

Câu 39. (Sở Nam Định - 2019) Trong không gian

Oxyz

, cho các điểm

     

;0;0 , 0; ;0 , 0;0;M m N n P p

không trùng với gốc tọa độ và thỏa mãn

2 2 2

3

m n p

  

.

Tìm giá trị lớn nhất của khoảng cách từ

O

đến mặt phẳng

 

MNP

.

A.

1

3

. B.

3

. C.

1

3

. D.

1

27

.

Lời giải

Chọn C

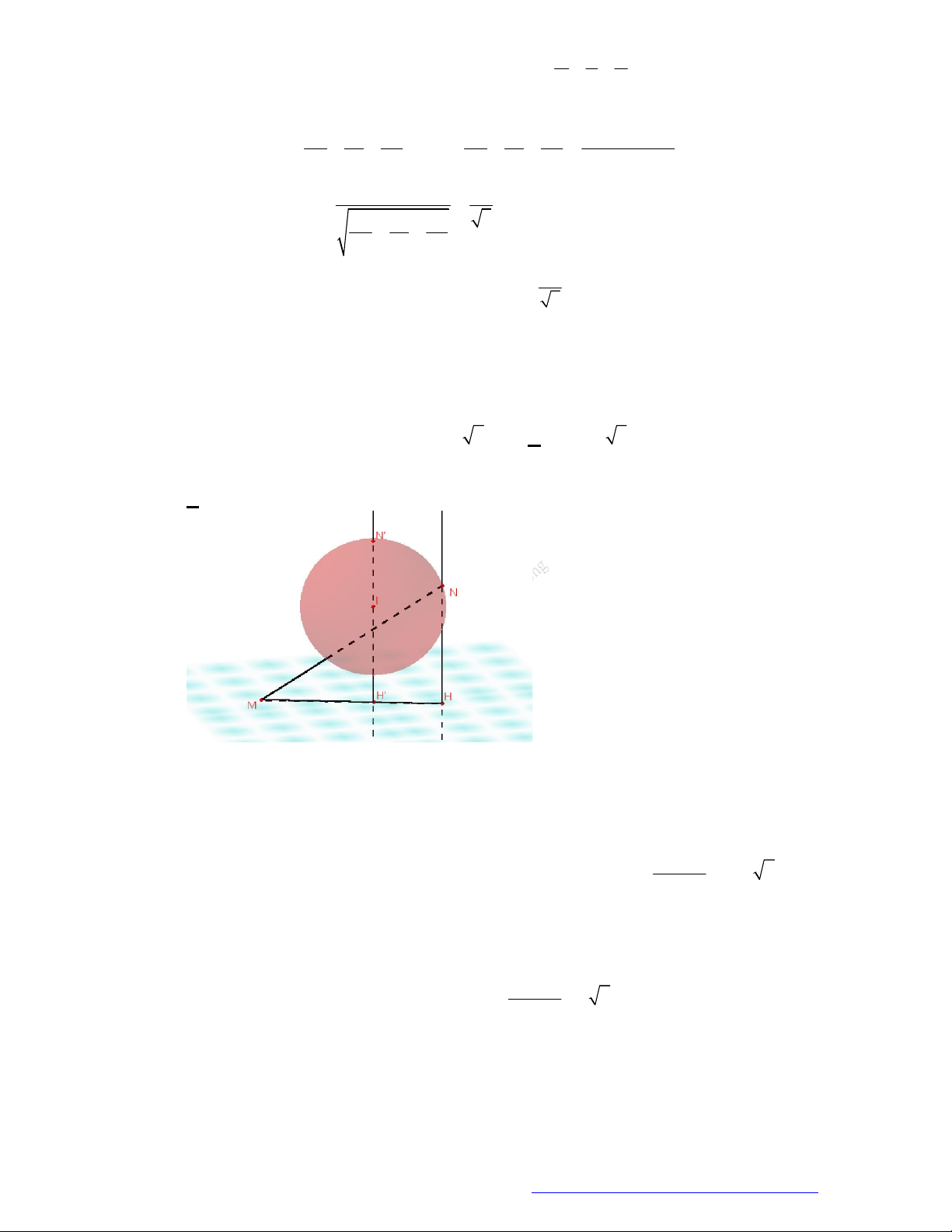
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 45

Phương trình mặt phẳng

 

MNP

có phương trình là

1

x y z

m n p

  

.

Theo bất đẳng thức Bunhia-Copsky ta có:

 

2 2 2

2 2 2 2 2 2 2 2 2

1 1 1 1 1 1 9

9 3m n p

m n p m n p m n p

 

         

 

 

 

Khi đó:

 

2 2 2

1 1

;

1 1 1 3

d O P

m n p

 

 

. Dấu bằng xảy ra khi

1m n p  

.

Vậy khoảng cách lớn nhất từ

O

đến

 

MNP

bằng

1

3

.

Câu 40. Trong không gian với hệ tọa độ

,Oxyz

cho mặt phẳng

 

: 2 2 3 0P x y z   

và mặt cầu

 

2 2 2

: 2 4 2 5 0.S x y z x y z      

Giả sử

 

M P

và

 

N S

sao cho



MN

cùng phương

với vectơ

 

1;0;1u



và khoảng cách giữa

M

và

N

lớn nhất. Tính

.MN

A.

3MN

B.

1 2 2 MN

C.

3 2MN

D.

14MN

Lời giải

Chọn C

Mặt phẳng có vtpt

 

1; 2; 2n  



. Mặt cầu

 

S

có tâm

 

1; 2; 1I 

và bán kính

1r 

. Nhận

thấy rằng góc giữa

u



và

n



bằng

ο

45

. Vì

 

; 2 1d I P r   nên

 

P

không cắt

 

S

.

Gọi

H

là hình chiếu của

N

lên

 

P

thì



ο

45NMH 

và

ο

2

sin 45

NH

MN NH 

nên

MN

lớn

nhất khi và chỉ khi

NH

lớn nhất. Điều này xảy ra khi

N N





và

H H





với

N



là giao điểm

của đường thẳng

d

qua

I

, vuông góc

 

P

và

H



là hình chiếu của

I

lên

 

.P

Lúc đó

 

max

; 3NH N H r d I P

 

    và

max

ο

3 2

sin 45

NH

MN   .

Câu 41. Trong không gian

Oxyz

, cho bốn điểm

 

2;0;1A

,

 

3;1;5B

,

 

1;2;0C

,

 

4;2;1D

. Gọi

 

a

là mặt phẳng đi qua

D

sao cho ba điểm

A

,

B

,

C

nằm cùng phía đối với

 

a

và tổng khoảng

cách từ các điểm

A

,

B

,

C

đến mặt phẳng

 

a

là lớn nhất. Giả sử phương trình

 

a

có dạng:

2 0x my nz p   

. Khi đó,

T m n p  

bằng:

 

P

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 46 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

A. 9. B. 6. C. 8. D. 7.

Lời giải

Chọn A

Vì mặt phẳng

 

a

đi qua

 

4;2;1

D

nên phương trình

 

a

có dạng:

     

. 4 . 2 . 1 0

a x b y c z

     

Đặt

     

2 2 2

2 2 4 3

, , ,

a b a b c a c

S d A d B d C

a b c

a a a

        

        

     

 

.

Theo giả thiết,

A

,

B

,

C

nằm cùng phía đối với

 

a

nên không mất tính tổng quát, ta giả sử:

2 2 0

4 0

3 0

a b

a b c

a c

  





   





  



.

Khi đó,

2 2 2 2 2 2

2 2 4 3 6 3 3a b a b c a c a b c

S

a b c a b c

         

 

   

.

Áp dụng bất đẳng thức

. .B C S

cho hai bộ số

 

6; 3;3

 

và

 

; ;a b c

, ta được:

   

2 2 2 2 2 2

6 3 3 6 3 3 6 3 3 .

a b c a b c a b c

           

3 6

S 

.

Đẳng thức xảy ra

6 3 3 0

6 3 3

a b c

   









 



 



. Ta chọn

2

1

a

b

c

 





 









.

 

: 2 9 0

x y z

a

     

hay

 

: 2 9 0

x y z

a

   

1

m

 

,

1

n

 

,

9

p



.

Vậy

9

T m n p

   

.

Câu 42. Trong không gian với hệ tọa độ

Oxyz

gọi

( ) : y z 3 0P ax b c   

(

, ,a b c

là các số nguyên

không đồng thời bằng

0

) là phương trình mặt phẳng đi qua hai điểm

   

0; 1;2 , 1;1;3

M N

 

và

không đi qua

 

0;0;2

H

. Biết rằng khoảng cách từ

 

0;0;2

H

đến mặt phẳng

( )P

đạt giá trị lớn

nhất. Tổng

2 3 12P a b c   

bằng

A.

8

. B.

16

. C.

12

. D.

16

.

Lời giải

Chọn B

Mặt phẳng

( )P

đi qua hai điểm

   

0; 1;2 , 1;1;3

M N

 

nên ta có

2 3 0 2 3

3 3 0 5 6

b c b c

a b c a c





     





 

 

      

 







(*).

Mặt khác

 

2 2 2

2 3

;( )

c

d H P

a b c





 

(**).

Thay (*) vào (**) ta được

 

2 2 2 2

2 3 2 3

;( )

30 72 45

c c

d H P

a b c c c

 

 

   

.

Xét hàm số

2

2 3

30 72 45

c

y

c c





 

có tập xác định

D  

.

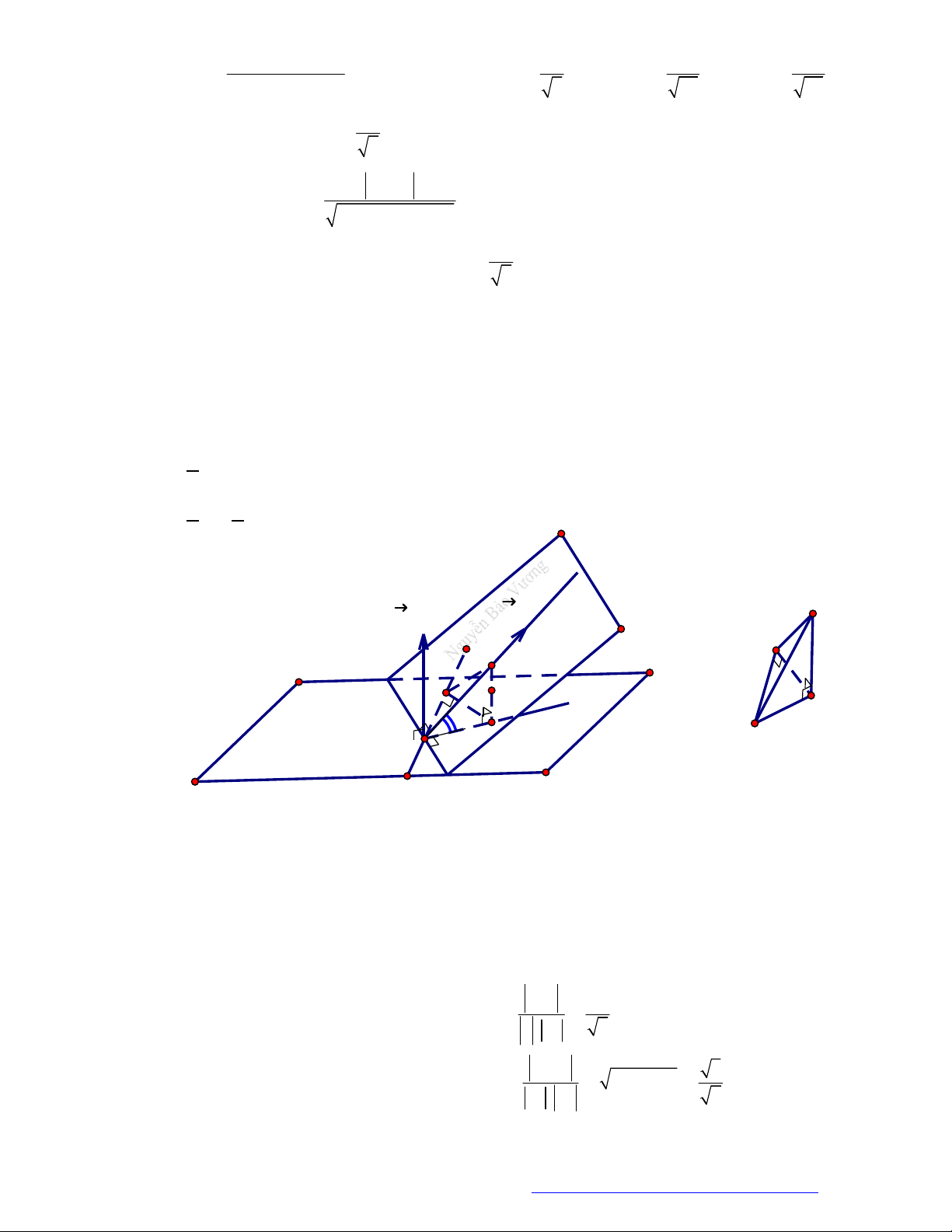
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 47

2

18 18 1

' ; ' 0 1

30 72 45

3

c

y y c y

c c



      

 

và

2 2

;

30 30

c c

limy limy

 

  

1

(1)

3

D

y

miny

   

.

Xét hàm số

2

2 3

( )

30 72 45

c

g c

c c





 

Từ đó suy ra

1

g(c) (1) (1)

3

f g

max

  



đạt tại

1c 

.

Với

1 1; 1c a b    

.

Vậy

2 3 12 16P a b c    

Câu 43. (Chu Văn An - Hà Nội - 2019) Trong không gian với hệ trục toạ độ

Oxyz

, cho mặt phẳng

 

: 2z 0P x y  

. Phương trình mặt phẳng

 

Q

chứa trục hoành và tạo với

 

P

một góc nhỏ

nhất là

A.

2z 0.y  

B.

0.y z 

C.

2 0.y z 

D.

0.x z 

Lời giải

Chọn A

Chứng minh góc giữa (P) và (Q) bé nhất là góc giữa Ox và (P).

Giả sử (Q)



(AKI). Ta có

   

 



,P Q AKI

,

 



,Ox P AIH

Xét

,AHI AHK 

là tam giác vuông chung cạnh AH.





, 90 A 90 90IHK K HK HI K H IAH AKH AIH AKH AIH            

Ox

có VTCP

 

1;0;0i



 

P

có VTPT

 

1; 1;2

P

n  



Góc giữa

Ox

và mặt phẳng

 

P

là



:

.

1

sin

6

.

P

i n

  



Góc giữa

 

Q

và mặt phẳng

 

P

thoả:

2

.

5

cos 1 sin

.

6

P Q

n n

     

 

.

Phương trình mặt phẳng

 

: 0Q By Cz 

a

(Q

P)

a

d'

Ox

i

n

P

H

I

H

A

K

A

K

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 48 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Ta có:

2 2

2

5

2 5 5

6

. 6

4 4 0 2

B C

B C B C

B C

B BC C C B

 

     



      

Chọn B = 1, C = -2.

Câu 44. (Việt Đức Hà Nội 2019) Trong hệ trục tọa độ

O

xyz

, mặt phẳng

 

P

đi qua điểm

 

1;7;2

A

và

cách

 

2;4; 1

M

 

một khoảng lớn nhất có phương trình là

A.

 

:3 3 3 10 0

P x y z

   

. B.

 

: 1 0

P x y z

   

.

C.

 

: 10 0

P x y z

   

. D.

 

: 10 0

P x y z

   

.

Lời giải

Ta có:

 

,

d M P MA



Nên

 

ax

,

m

d M P MA



khi

A

là hình chiếu của

M

trên mặt phẳng

 

P

.

Suy ra

   

3; 3; 3

AM P AM

     



là vectơ pháp tuyến của

 

P

.

 

P

đi qua

 

1;7;2

A

và nhận

 

3; 3; 3

AM

   



là vectơ pháp tuyến nên có phương trình

     

3 1 3 7 3 2 0 10 0

x y z x y z

           

.

Câu 45. (HSG Bắc Ninh 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho ba điểm

( ;0;0), (0; ;0), (0;0; )A a B b C c

, trong đó

, ,a b c

là các số thực thỏa mãn

2 2 1

1

a b c

  

. Khoảng

cách từ gốc tọa độ

O

đến mặt phẳng

 

ABC

có giá trị lớn nhất bằng:

A.

3

B.

4

C.

2

D.

1

Lời giải

Phương trình mặt phẳng

 

ABC

:

1

x y z

a b c

  

.

Nhận thấy, điểm

 

(2; 2;1)

M ABC

 

;

 

2; 2;1 , 3

OM OM

  



.

Ta có:

 

;( )

d O ABC OH OM

 



khoảng cách từ gốc tọa độ

O

đến mặt phẳng

 

ABC

có giá

trị lớn nhất khi

( )OM ABC

( )

1 1

2

1 1

. ,( 0) 2

2

1 1

ABC

k a

a k

n k OM k k b

b k

k c

c k

 

 

 

        

 

 

 

 

 

 

.

Mà

2 2 1

1

a b c

  

nên

2 2 1 1

1 9 1

1 1 1

9

2 2

k k

k k k

      



. Do đó

9 9

; ; 9

2 2

a b c

   

.

Vậy

 

max

;( ) 3

d O ABC OM

 

khi

9 9

; ; 9

2 2

a b c

   

.

Câu 46. (Chuyên Trần Phú Hải Phòng 2019) Trong không gian

,Oxyz

cho mặt phẳng

( ) : 2 2 3 0

P x y z

   

và hai điểm

   

1;2;3 , B 3;4;5

A

. Gọi

M

là một điểm di động trên

( )P

.

Giá trị lớn nhất của biểu thức

2 3

MA

MB



bằng

A.

3 3 78



. B.

54 6 78



. C.

8 2

. D.

6 3

.

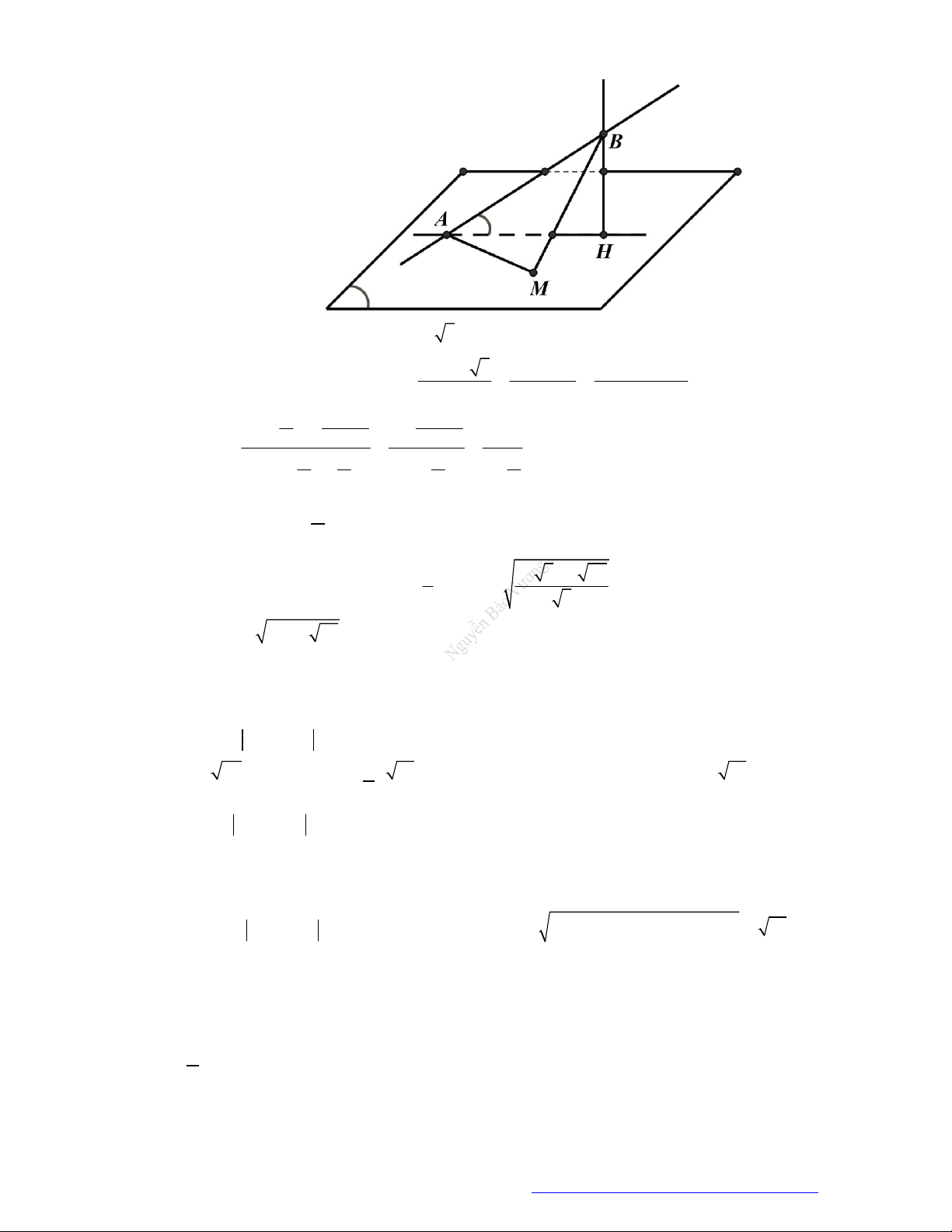
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 49

Lời giải

+) Nhận xét:

   

2;2;2 2 3; .AB AB A P  



+) Xét tam giác

MAB

ta có

2 3 sin sin

sinA

MA MA AB B M

P

MB MB

  

  

2cos cos cos

1

2 2 2

2cos sin sin sin

2 2 2 2

A B M B M

P

A A A A

 

   

+) Để

max

sin

2

A

P 

min, dấu bằng xảy ra khi



AB AM

ABM ABH















 

/ P

2 24 3 8 26

( ) : 2 2 3 0

3

B

P x y z d BM



       

max

54 6 78P  

.

Câu 47. (Chuyên Hạ Long 2019) Cho

   

4;5;6 ; 1;1;2A B

, M là một điểm di động trên mặt phẳng

 

:2 2 1 0P x y z   

.

Khi đó

MA MB

nhận giá trị lớn nhất là?

A. 77 . B.

41

. C.

7

. D. 85 .

Lời giải

Ta có

MA MB AB 

với mọi điểm

 

M P

Vì

   

2.4 5 2.6 1 . 2.1 1 2.2 1 208 0       

nên hai điểm

,A B

nằm cùng phía với

 

P

Dấu

" "

xảy ra khi và chỉ khi

 

M AB P 

Khi đó,

MA MB

nhận giá trị lớn nhất là:

     

2 2 2

4 1 5 1 6 2 41AB       

.

Câu 48. Trong không gian

Oxyz

, cho điểm

 

1;1;2A

và mặt phẳng

   

: 1 1 0P m x y mz    

, với

m

là tham số. Biết khoảng cách từ điểm

A

đến mặt phẳng

 

P

lớn nhất. Khẳng định đúng trong bốn

khẳng định dưới đây là

A.

2 6m 

. B.

6m 

. C.

2 2m  

. D.

6 2m  

.

Lời giải

Cách 1:

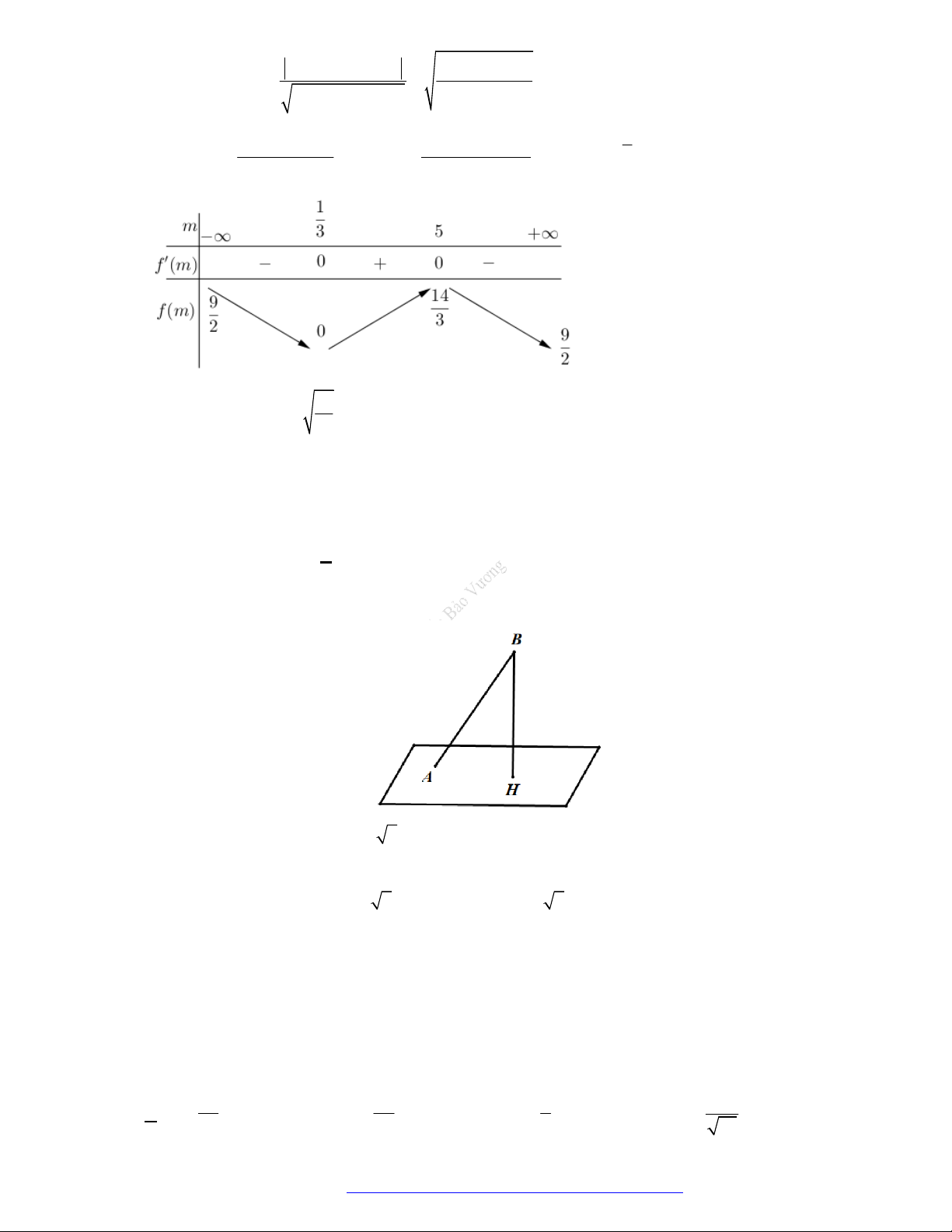
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 50 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Ta có

 

2

1 1 2 1

3 1

;

2 1

1 1

m m

m

d A P

m m

   



 

 

  

.

Xét

 

  

 

2

1

3 1 5 3 1

0

3

2 1

5

m m m

m

f m f m

m m

m



  







    



 





.

Vậy

 

14

max ;

3

d A P 

khi

 

5 2;6m  

.

Câu 49. (Chuyên Lê Quý Đôn Điện Biên 2019) Trong không gian

Oxyz

, cho hai điểm

   

1;2; 1 , 3;0;3A B

. Biết mặt phẳng

 

P

đi qua điểm

A

và cách

B

một khoảng lớn nhất.

Phương trình mặt phẳng

 

P

là:

A.

2 2 5 0x y z   

. B.

2 3 0x y z   

.

C.

2 2 4 3 0x y z   

. D.

2 2 0x y z  

.

Lời giải

Ta có

 

2; 2;4 2 6AB AB   



.

Gọi

H

là hình chiếu vuông góc của

B

trên mặt phẳng

 

P

.

Ta có

 

, 2 6 , 2 6d B P BH BA maxd B P    

, đạt được khi

H A

.

Khi đó mặt phẳng

 

P

đi qua

A

và nhận

 

2; 2;4AB  



là véctơ pháp tuyến.

Suy ra phương trình mặt phẳng

 

P

là

     

2 1 2 2 4 1 0 2 3 0x y z x y z          

.

Câu 50. (Sở Bắc Giang 2019) Trong không gian

Oxyz

, cho điểm

 

1;4;9M

. Gọi

 

P

là mặt phẳng đi

qua

M

và cắt 3 tia

, , Ox Oy Oz

lần lượt tại các điểm

, ,A B C

(khác

O

) sao cho

OA OB OC 

đạt giá trị nhỏ nhất. Tính khoảng cách

d

từ gốc tọa độ

O

đến mặt phẳng

 

P

.

A.

36

7

d 

. B.

24

5

d 

. C.

8

3

d 

. D.

26

14

d 

.

Lời giải

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 51

Giả sử

     

;0;0 , 0; ;0 , 0;0;A a B b C c

với

, , 0.

a b c



Phương trình mặt phẳng

 

: 1

x y z

P

a b c

  

.

   

1 4 9

1; 4;9 1

M P

a b c

    

.

Áp dụng BĐT

Bunhiacopxki:

 

     

 

2 2 2

2

1 4 9 1 4 9

1 2 3 .

a b c a b c

 

     

 

 

           

     

 

     

 

 

     

 

49.

a b c

   

Dấu “



” xảy ra khi

49

1 4 9

6

1

12.

1 2 3

18

a b c

a

a b c

b

c

a b c

  







  



 

 

 

 

 









Nên

 

: 1.

6 12 18

x y z

P

  

Vậy

36

.

7

d 

Câu 51. Trong không gian

,Oxyz

cho điểm

(1; 4;9)

M

. Gọi (P) là mặt phẳng đi qua M và cắt 3 tia Ox, Oy,

Oz lần lượt tại các điểm A, B, C (khác O) sao cho

OA OB OC 

đạt giá trị nhỏ nhất. Tính khoảng

cách d từ gốc tọa độ O đến mặt phẳng (P).

A.

36

7

d 

B.

24

5

d 

C.

8

3

d



D.

26

14

d 

Lời giải

Chọn A

Gọi mặt phẳng

 

P

đi qua điểm

 

1;4;9

M

cắt các tia tại

     

;0;0 , 0; ;0 , 0;0;A a B b C c

với

, , 0

a b c



ta có

 

: 1

x y z

P

a b c

  

suy ra

1 4 9

1

a b c

  

và

OA OB OC a b c    

đạt giá trị

nhỏ nhất khi

 

2

2 2 2

1 2 3

1 4 9 1 2 3

1 36

a b c

a b c a b c a b c

 

          

 

Dấu bằng xảy ra khi và chỉ khi

6

12

18

a

b

c

















 

: 1

6 12 18

x y z

P

   

Nên

 

2 2 2

0 0 0

1

36

6 12 18

;

7

1 1 1

6 12 18

d o p

  

 

     

 

     

     

Câu 52. (THPT Ba Đình -2019) Trong không gian với hệ tọa độ

,Oxyz

cho mặt phẳng

 

: 2 2 3 0

P x y z

   

và mặt cầu

 

2 2 2

: 2 4 2 5 0

S x y z x y z

      

. Giả sử

 

M P



và

 

N S



sao cho

MN



cùng phương với vectơ

 

1;0;1

u 



và khoảng cách giữa

M

và

N

lớn

nhất. Tính

.MN

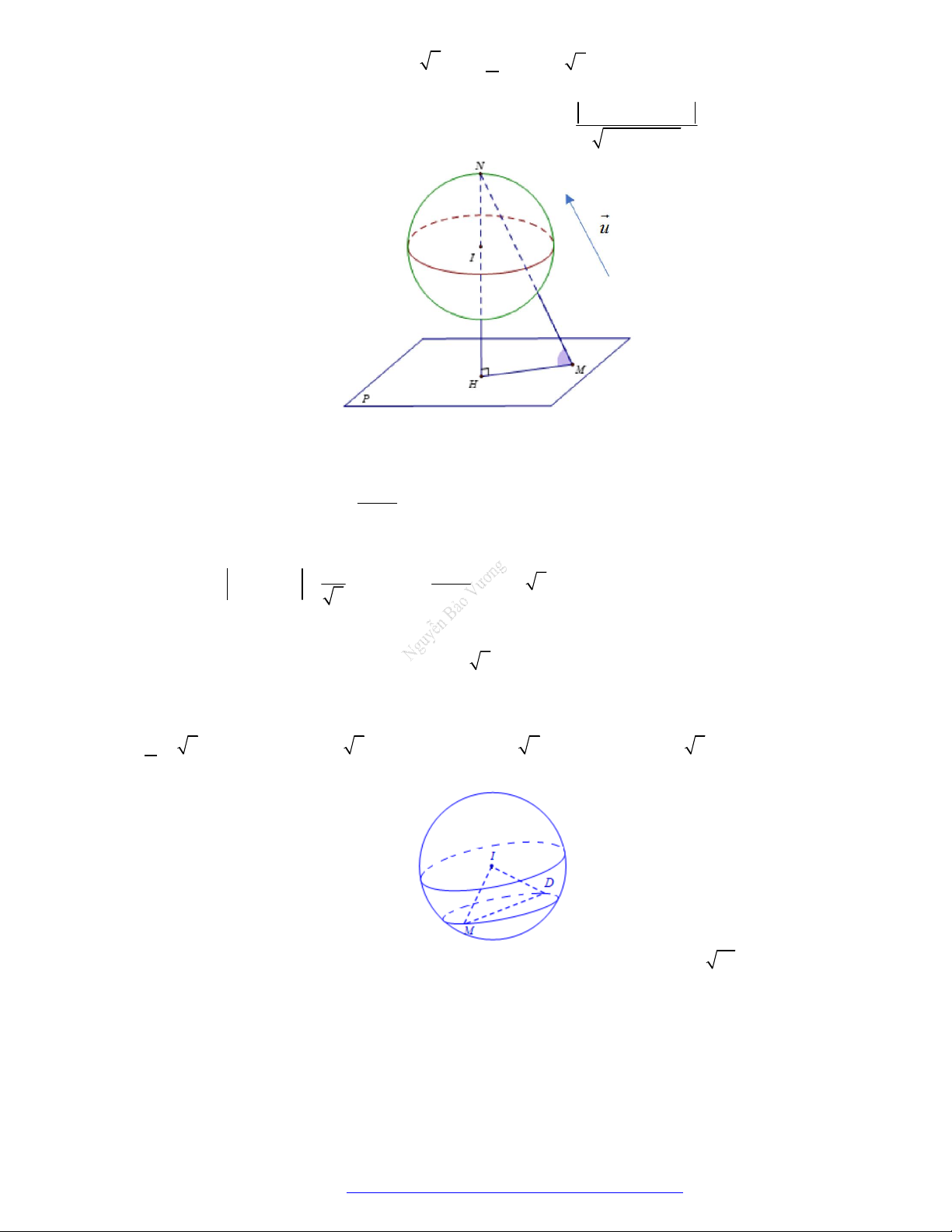
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 52 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

A.

3MN 

. B.

1 2 2MN  

. C.

3 2MN 

. D.

14MN 

.

Lời giải.

 

S

có tâm

 

1;2;1I 

và bán kính

1R 

. Ta có:

 

2 2 2

1 2.2 2.1 3

d , 2

1 2 2

I P R

   

  

 

.

Gọi

H

là hình chiếu vuông góc của

N

trên mặt phẳng

 

P

và

a

là góc giữa

MN

và

NH

.

Vì

MN



cùng phương với

u



nên góc

a

có số đo không đổi,



HNM

a



.

Có

1

.cos .

cos

HN MN MN HN

a

  

nên

MN

lớn nhất



HN

lớn nhất



 

, 3HN d I P R  

.

Có

 

1

cos cos ,

2

P

u n

a

 

 

nên

1

3 2

cos

MN HN

a

 

.

Câu 53. (Chuyên Lê Hồng Phong Nam Định 2019) Trong không gian với hệ tọa độ

Oxyz

cho bốn điểm

(1;0;0)A

,

(2;1;3)B

,

(0;2; 3)C 

,

(2;0; 7)D

. Gọi

M

là điểm thuộc mặt cầu

2 2 2

( ): ( 2) ( 4) 39S x y z    

thỏa mãn:

2

2 . 8MA MB MC 

 

. Biết độ dài đoạn thẳng

MD

đạt

giá trị lớn nhất. Tính giá trị lớn nhất đó.

A. 2 7 . B. 7 . C. 3 7 . D. 4 7 .

Lời giải

+) Mặt cầu

2 2 2

( ) : ( 2) ( 4) 39S x y z     có tâm là

 

2;4;0I 

, bán kính

39R 

.

Gọi

( , , ) ( )M x y z S

. Ta có:

2 2 2

19 4 8x y z x y     .

2 2 2 2

( 1) 20 6 8MA x y z x y       .

(2 ;1 ;3 )MB x y z   



;

( ; 2 ; 3 )MC x y z    



.

2 2 2

. 2 2 3 9MB MC x x y y z       

 

19 4 8 2 3 7x y x y     

6 5 12x y   

.

Suy ra

2

2 .MA MB MC

 

18 18 44x y   

.

Theo giả thiết

2

2 . 8MA MB MC 

 

18 18 44 8x y     2 0x y    

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 53

Do đó

(

) : 2 0

M

P x y



   

.

Ta

có

8

(

;( )) 32 39

2

d

I P   

nê

n mặt phẳng

(

)P

cắt

mặt cầu

(

)S

the

o giao tuyến là đường

tròn

 

C

c

ó bán kính

1

R

với

2 2

1

3

9 32 7

R

R d    

.

Mặ

t khác ta có

 

,

D M P

D M S















,

(C)

D

M



. Do

đó độ dài

M

D

lớ

n nhất bằng

1

2

2 7

R 

.

Vậ

y chọn A.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương  https://www.facebook.com/phong.baovuong Trang 1

TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH TRUNG BÌNH MỨC 5-6 ĐIỂM

Dạng 1. Xác định VTCP

 Véctơ chỉ phương

u



của đường thẳng

d

là véctơ có giá song song hoặc trùng với đường thẳng

.d

Nếu

d

có một véctơ chỉ phương là

u



thì

.k u



cũng là một véctơ chỉ phương của

.d

 Nếu có hai véctơ

1

n



và

2

n



cùng vuông góc với

d

thì

d

có một véctơ chỉ phương là

1 2

[ , ].u n n

  



Để viết phương trình đường thẳng

,d

ta cần tìm điểm đi qua và một véctơ chỉ phương.

Nếu đường thẳng

1 2 3

( ; ; )

:

: ( ; ; )

d

Qua M x y z

d

VTCP u a a a









  



thì ta có hai dạng phương trình đường thẳng:

Phương trình đường thẳng

d

dạng tham số

1

2

3

, ( ).

x x a t

y y a t t

z z a t

 





  





 







Phương trình đường thẳng

d

dạng chính tắc

1 2 3

, ( 0).

x x y y z z

a a a

  

  

  

Câu 1. (Mã 101 - 2020 Lần 1) Trong không gian

Oxyz

, cho đường thẳng

3 4 1

:

2 5 3

x y z

d

  

 



.

Vecto nào dưới đây là một vecto chỉ phương của

d

?

A.

 

2

2;4; 1u 



. B.

 

1

2; 5;3u 



. C.

 

3

2;5;3u



. D.

 

4

3;4;1u



.

Câu 2. (Mã 102 - 2020 Lần 1) Trong không gian , cho đường thẳng .

Vectơ nào dưới đây là một vectơ chỉ phương của ?

A. . B. . C. . D. .

Câu 3. (Mã 103 - 2020 Lần 1) Trong không gian

Oxyz

, cho đường thẳng

3 1 2

:

4 2 3

x y z

d

  

 



.

Vecto nào dưới đây là một vecto chỉ phương của

d

A.

 

3

3; 1; 2u   



. B.

 

4

4;2;3u 



. C.

 

2

4; 2;3u  



. D.

 

1

3;1;2u 



.

Câu 4. (Mã 104 - 2020 Lần 1) Trong không gian

Oxyz

, cho đường thẳng

4 2 3

:

3 1 2

x y z

d

  

 

 

.

Vectơ nào dưới đây là một vectơ chỉ phương của

d

?

A.

 

2

4; 2;3u  



. B.

 

4

4;2; 3u  



. C.

 

3

3; 1; 2u   



. D.

 

1

3;1;2u 



.

Câu 5. (Mã 101 2018) Trong không gian

Oxyz

, đường thẳng

2

: 1 2

3

x t

d y t

z t

 





 





 



có một vectơ chỉ phương là:

A.

 

1

1;2;3u  



B.

 

3

2;1;3u 



C.

 

4

1;2;1u  



D.

 

2

2;1;1u 



Câu 6. (Mã 102 - 2019) Trong không gian

Oxyz

, cho đường thẳng

1 3 2

:

2 5 3

x y z

d

  

 



. Vectơ nào

dưới đây là vectơ chỉ phương của đường thẳng

d

A.

 

1;3; 2u  



. B.

 

2;5;3u 



. C.

 

2; 5;3u  



. D.

 

1;3;2u 



.

Câu 7. (Mã 104 2017) Trong không gian với hệ toạ độ

Oxyz

, cho hai điểm

 

1;1;0A

và

 

0;1;2B

.

Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng

AB

.

PHƯƠNG TRÌNH ĐƯỜNG THẲNG

Chuyên đề 31

Oxyz

2 5 2

:

3 4 1

x y z

d

  

 



d

 

2

3;4; 1

u

 



 

1

2; 5;2

u  



 

3

2;5; 2

u

 



 

3

3;4;1

u 



u



.k u



d

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

A.

 

1;1;2

d  



B.

 

1;0; 2

a

  



C.

 

1;0;2

b  



D.

 

1;2;2

c 



Câu 8. (Mã 102 2018) Trong không gian

Oxyz

, đường thẳng

3 1 5

:

1 1 2

x y z

d

  

 



có một vectơ chỉ

phương là

A.

 

1

3; 1;5

u  



B.

 

4

1; 1;2

u  



C.

 

2

3;1;5

u  



D.

 

3

1; 1; 2

u

  



Câu 9. (Mã 103 - 2019) Trong không gian

Oxyz

, cho đường thẳng

2 1 3

: .

1 3 2

x y z

d

  

 



Vectơ nào

dưới đây là một vectơ chỉ phương của

?d

A.

 

4

1;3;2 .

u 



B.

 

3

2;1;3 .

u  



C.

 

1

2;1; 2 .

u  



D.

 

2

1; 3;2 .

u  



Câu 10. (Đề Tham Khảo 2018) Trong không gian

,Oxyz

cho đường thẳng

2 1

: .

1 2 1

x y z

d

 

 



Đường

thẳng

d

có một vectơ chỉ phương là

A.

 

4

1;2;0

u  



B.

 

2

2;1; 0

u 



C.

 

3

2;1;1

u 



D.

 

1

1;2;1

u  



Câu 11. (Mã 104 - 2019) Trong không gian

Oxyz

cho đường thẳng

3 1 5

:

1 2 3

x y z

d

  

 



. Vectơ nào

sau đây là một vectơ chỉ phương của đường thẳng

d

?

A.

2

(1; 2;3)

u  



B.

3

(2;6; 4)

u

 



. C.

4

( 2; 4;6)

u   



. D.

1

(3; 1;5)

u  



.

Câu 12. (Mã 101 - 2019) Trong không gian

Oxyz

, cho đường thẳng

2 1 3

:

1 2 1

  

 



x y z

d

. Vectơ nào

dưới đây là một vectơ chỉ phương của

d

?

A.

4

(1;2; 3) 



u . B.

3

( 1;2;1) 



u . C.

1

(2;1; 3) 



u . D.

2

(2;1;1)



u .

Câu 13. (Đề Tham Khảo 2019) Trong không gian

Oxyz

, đường thẳng

1 2 3

:

2 1 2

x y z

d

  

 



đi qua

điểm nào dưới đây?

A.

 

2; 1;2

Q 

B.

 

1; 2; 3

M

  

C.

 

1;2;3

P

D.

 

2;1; 2

N

 

Câu 14. (Mã 104 2017) Trong không gian với hệ tọa độ

Oxyz

, cho điểm

 

1;2;3

M

. Gọi

1

M

,

2

M

lần

lượt là hình chiếu vuông góc của

M

lên các trục

Ox

,

Oy

. Vectơ nào dưới đây là một véctơ chỉ

phương của đường thẳng

1 2

M M

?

A.

 

4

1;2;0

u  



B.

 

1

0;2;0

u 



C.

 

2

1;2;0

u 



D.

 

3

1;0;0

u 



Câu 15. Trong không gian với hệ tọa độ

Oxyz

, cho đường thẳng

4 3

:

1 2 3

x y z

d

 

 



. Hỏi trong các

vectơ sau, đâu không phải là vectơ chỉ phương của

d

?

A.

 

1

1; 2;3

u  



. B.

 

2

3; 6; 9

u

  



. C.

 

3

1; 2; 3

u

  



. D.

 

4

2;4;3

u  



.

Câu 16. (Sở Bình Phước 2019) Trong không gian với hệ tọa độ

Oxyz

, đường thẳng nào sau đây nhận

 

2;1;1

u 



là một vectơ chỉ phương?

A.

2 1 1

1 2 3

x y z  

 

B.

1 2

2 1 1

x y z

 

 



C.

1 1

2 1 1

x y z 

 

  

D.

2 1 1

x y z

  

 



Câu 17. (Chuyen Phan Bội Châu Nghệ An 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho đường

thẳng

1 2 1

:

2 1 2

x y z

d

  

 

nhận véc tơ

 

;2;u a b



làm véc tơ chỉ phương. Tính

a b

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3

A.

8

. B.

8

. C.

4

. D.

4

.

Câu 18. (THPT Lê Quý Đôn Đà Nẵng 2019) Trong không gian

,Oxyz

tọa độ nào sau đây là tọa độ của

một véctơ chỉ phương của đường thẳng

 

2 4

: 1 6 , ?

9

x t

y t t

z t

 





   











A.

1 1 3

; ;

3 2 4



 

 

 

. B.

1 1 3

; ;

3 2 4

 

 

 

. C.

 

2;1;0

. D.

 

4; 6;0



.

Câu 19. (Chuyên KHTN 2019) Vectơ nào sau đây là một vectơ chỉ phương của đường thẳng

2 1 3

3 2 1

x y z  

 

 

A.

 

2;1; 3 

. B.

 

3;2;1



. C.

 

3; 2;1



. D.

 

2;1;3

.

Câu 20. (Chuyên Thái Bình 2019) Trong không gian với hệ tọa độ

Oxyz

, đường thẳng

 

1 3 7

:

2 4 1

x y z

d

  

 



nhận vectơ nào dưới đây là một vectơ chỉ phương?

A.

 

2; 4;1

 

. B.

 

2;4;1

. C.

 

1; 4;2



. D.

 

2; 4;1



.

Câu 21. (Đề Thi Công Bằng KHTN 2019) Trong không gian

O

xyz

véc tơ nào dưới đây là một véc tơ chỉ

phương của đường thẳng

d

:

1

4

3 2

x t

y

z t

 











 



,

A.

(1;4;3)

u 



. B.

(1;4; 2)

u

 



. C.

(1;0; 2)

u

 



. D.

(1;0;2)

u 



.

Dạng 2. Viết phương trình đường thẳng

Dạng 1. Viết phương trình đường thẳng

d

dạng tham số và dạng chính tắc (nếu có), biết

d

đi qua điểm

( ; ; )M x y z

  

và có véctơ chỉ phương

1 2 3

( ; ; ).

d

u a a a



Phương pháp. Ta có:

1 2 3

( ; ; )

:

: ( ; ; )

d

Qua M x y z

d

VTCP u a a a









  







Phương trình đường thẳng

d

dạng tham số

1

2

3

: , ( ).

x x a t

d y y a t t

z z a t

 





  





 







Phương trình đường thẳng

d

dạng chính tắc

1 2 3

: , ( 0).

x x y y z z

d a a a

a a a

  

  

  

Dạng 2. Viết phương trình tham số và chính tắc (nếu có) của đường thẳng

d

đi qua

A

và

.B

Phương pháp. Đường thẳng

( )

:

d

Qua A hay B

d

VTCP u AB





















(dạng 1)

Dạng 3. Viết phương trình đường thẳng

d

dạng tham số và chính tắc (nếu có), biết

d

đi qua điểm

M

và song song với đường thẳng

.

Phương pháp. Ta có

Qua ( ; ; )

:

d

M x y z

d

VTCP u u















  



 



(dạng 1)

Dạng 4. Viết phương trình đường thẳng

d

dạng tham số và chính tắc (nếu có), biết

d

đi qua điểm

M

và vuông góc với mặt phẳng

( ) : 0.

P ax by cz d

   

Phương pháp. Ta có

( )

:

: ( ; ; )

d P

Qua M

d

VTCP u n a b c





 





 



(dạng 1)

A

B

d

M



d

u





P

u n

d P



 

d

M

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Dạng 4. Viết phương trình đường thẳng

d

qua

M

và song song với hai mặt phẳng

( ), ( ).P Q

Phương pháp. Ta có

:

: , ]

[

d P Q

d

VTCP u n

Qua M

n











  



(dạng 1)

Dạng 2.1 Xác định phương trình đường thẳng cơ bản

Câu 22. (Đề Tham Khảo 2020 Lần 2) Trong không gian Oxyz, cho hai điểm

(1;0;1)

M

và

(3;2; 1)

N

.

Đường thẳng MN có phương trình tham số là

A.

1 2

2 .

1

 











 



x t

y t

z t

B.

1

.

1

 











 



x t

y t

z t

C.

1

.

1

 











 



x t

y t

z t

D.

1

.

1

 











 



x t

y t

z t

Câu 23. (Đề Tham Khảo 2017) Trong không gian tọa độ

Ox ,yz

phương trình nào dưới đây là phương

trình chính tắc của đường thẳng

1 2

: 3 ?

2

x t

d y t

z t

 











  



A.

1 2

2 3 1

x y z

 

 

B.

1 2

1 3 2

x y z

 

 



C.

1 2

2 3 2

x y z

 

 



D.

1 2

2 3 1

x y z

 

 

Câu 24. Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm

 

1; 2;1

M 

,

 

0;1; 3

N

. Phương trình đường

thẳng qua hai điểm

M

,

N

là

A.

1 2 1

1 3 2

x y z  

 



. B.

1 3 2

1 2 1

x y z

  

 



.

C.

1 3

1 3 2

x y z

 

 



. D.

1 3

1 2 1

x y z 

 



.

Câu 25. Trong không gian Oxyz, phương trình tham số của đường thẳng đi qua điểm

 

2;0; 1

M



và có

véctơ chỉ phương

 

2; 3;1

a  



là

A.

4 2

6 .

2

x t

y

z t

 





 





 



B.

2 2

3 .

1

x t

y t

z t

  





 





 



C.

2 4

6 .

1 2

x t

y t

z t

  





 





 



D.

2 2

3 .

1

x t

y t

z t

 





 





  



Câu 26. (Chuyên Đại Học Vinh 2019) Trong không gian

Oxyz

, cho

( 1;0;2)

E



và

(2;1; 5)

F



. Phương

trình đường thẳng

EF

là

A.

1 2

3 1 7

x y z

 

 



B.

1 2

3 1 7

x y z

 

 



C.

1 2

1 1 3

x y z

 

 



D.

1 2

1 1 3

x y z

 

 

Câu 27. Trong không gian

Oxyz

, cho đường thẳng



đi qua điểm

 

2;0; 1

M



và có một vectơ chỉ

phương

 

4; 6;2

a  



.Phương trình tham số của



là

A.

2 4

6

1 2

x t

y t

z t

  











 



. B.

2 2

3

1

x t

y t

z t

 





 





  



. C.

4 2

6

2

x t

y

z t

 





 





 



. D.

2 2

3

1

x t

y t

z t

  











 



.

Câu 28. (THPT Yên Phong 1 Bắc Ninh 2019) Trong không gian

Oxyz

, viết phương trình đường thẳng

đi qua hai điểm

 

1;1; 1

P



và

 

2;3;2

Q

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5

A.

1 1 1

2 3 2

x y z  

 

. B.

1 1 1

1 2 3

x y z  

 

.

C.

1 2 3

1 1 1

x y z

  

 



. D.

2 3 2

1 2 3

x y z

  

 

.

Câu 29. (Chuyên Lê Hồng Phong Nam Định 2019) Trong không gian

Oxyz

, phương trình đường thẳng

đi qua hai điểm

 

1;2;3

A

và

 

5;4; 1

B



là

A.

5 4 1

2 1 2

x y z  

 

. B.

1 2 3

4 2 4

x y z  

 



.

C.

1 2 3

4 2 4

x y z

  

 

. D.

3 3 1

2 1 2

x y z  

 

 

.

Câu 30. Trong không gian

Oxyz

, đường thẳng

Oy

có phương trình tham số là

A.

 

x t

y t t

z t







 











. B.

 

0

2

0

x

y t t

z







  











. C.

 

0

x

y t

z t







 











. D.

 

0

x t

y t

z







 











.

Câu 31. (THPT An Lão Hải Phòng 2019) Trong không gian

Oxyz

có đường thẳng có phương trình

tham số là

1 2

( ) : 2

3

x t

d y t

z t

 





 





  



. Khi đó phương trình chính tắc của đường thẳng

d

là

A.

1 2 3

2 1 1

x y z

  

 



B.

1 2 3

2 1 1

x y z

  

 



C.

1 2 3

2 1 1

x y z

  

 

D.

1 2 3

2 1 1

x y z  

 



Câu 32. (Chuyên Đại học Vinh - 2019) Trong không gian

Oxyz

, cho

 

1;0;2

E 

và

 

2;1; 5

F



. Phương

trình đường thẳng

EF

là

A.

1 2

3 1 7

x y z

 

 



. B.

1 2

3 1 7

x y z

 

 



. C.

1 2

1 1 3

x y z

 

 



. D.

1 2

1 1 3

x y z

 

 

.

Câu 33. (THPT Phan Bội Châu - Nghệ An 2019) Trong không gian với hệ trục tọa độ

Oxyz

, phương

trình tham số trục

Oz

là

A.

0

z



. B.

0

x

y t

z

















. C.

0

x t

y

z

















. D.

0

x

y

z t

















.

Câu 34. (THPT Cẩm Bình 2019) Trong không gian

Oxyz

, trục

Ox

có phương trình tham số

A.

0.

x



B.

0.

y z

 

C.

0

0.

x

y

z t

















D.

0.

0

x t

y

z

















Câu 35. (Ngô Quyền - Hải Phòng 2019) Trong không gian

Oxyz

, phương trình tham số của đường thẳng

d

đi qua điểm

 

1;2;3

M

và có véctơ chỉ phương

 

1; 4; 5

a

 



là

A.

1 2 3

1 4 5

x y z

  

 

 

. B.

1

4 2

5 3

x t

y t

z t

 





  





  



.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

C.

1 4 5

1 2 3

x y z  

 

. D.

1

2 4

3 5

x t

y t

z t

 





 





 



.

Câu 36. (Chuyên Nguyễn Huệ 2019) Trong không gian với hệ trục tọa độ

Oxyz

, phương trình tham số

của đường thẳng

d

đi qua gốc tọa độ

O

và có vectơ chỉ phương

 

1;3;2

u 



là

A.

0

: 3

2

x

d y t

z t

















. B.

1

: 3

2

x

d y

z

















. C.

: 3

2

x t

d y t

z t

















. D.

: 2

3

x t

d y t

z t

 





 





 



.

Câu 37. (Đà Nẵng 2019) Trong không gian

Oxyz

, viết phương trình đường thẳng đi qua điểm

 

1;2;3

A

và có vectơ chỉ phương

 

2; 1; 2

u

  



.

A.

2 1 2

1 2 3

x y z

  

 

. B.

1 2 3

2 1 2

x y z  

 

 

.

C.

2 1 2

1 2 3

x y z

  

 

. D.

1 2 3

2 1 2

x y z

  

 

 

.

Câu 38. (Sở Bình Thuận 2019) Trong không gian

Oxyz

, cho đường thẳng

d

đi qua điểm

 

0; 1;4

M 

và nhận vectơ

 

3; 1;5

u  



làm vectơ chỉ phương. Hệ phương trình nào sau đây là phương trình

tham số của

d

?

A.

3

1

4 5

x t

y t

z t







 





 



. B.

3

1

5 4

x

y t

z t







  





 



. C.

3

1

4 5

x t

y t

z t







  





 



. D.

3

1

4 5

x t

y t

z t







 





  



.

Câu 39. (Sở GD Nam Định - 2019) Trong không gian

Oxyz

, đường thẳng



đi qua

 

1;2; 3

M



nhận

vectơ

 

1;2;1

u  



làm vectơ chỉ phương có phương trình là

A.

1 2 3

1 2 1

x y z  

 



. B.

1 2 3

1 2 1

x y z

  

 



.

C.

1 2 3

1 2 1

x y z

  

 



. D.

1 2 3

1 2 1

x y z

  

 



.

Dạng 2.2 Xác định phương trình đường thẳng khi biết yếu tố vuông góc

Câu 40. (Mã 101 2020 Lần 2) Trong không gian

Oxyz

, cho điểm

 

1; 2;3

M



và mặt phẳng

 

: 2 3 1 0

P x y z

   

. Phương trình của đường thẳng đi qua

M

và vuông góc với

 

P

là

A.

1 2

2

3 3

x t

y t

z t

 





  





 



. B.

1 2

2

3 3

x t

y t

z t

  





 





  



. C.

2

1 2

3 3

x t

y t

z t

 





  





 



. D.

1 2

2

3 3

x t

y t

z t

 





  





 



.

Câu 41. (Mã 102 - 2020 Lần 2) Trong không gian

Oxyz

, cho

 

1;2; 3

M



và mặt phẳng

( ) : 2 3 1 0

P x y z

   

. Phương trình của đường thẳng đi qua điểm

M

và vuông góc với

( )P

là

A.

2

1 2

3 3

x t

y t

z t

 





  





 



. B.

1 2

2

3 3

x t

y t

z t

  





  





 



. C.

1 2

2

3 3

x t

y t

z t

 





 





  



. D.

1 2

2

3 3

x t

y t

z t

 





 





  



.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7

Câu 42. (Mã 103 - 2020 Lần 2) Trong không gian

Oxyz

, cho điểm

 

1; 2;2

M 

và mặt phẳng

 

: 2 3 1 0

P x y z

   

. Phương trình của đường thẳng qua

M

và vuông góc với mặt phẳng

 

P

là

A.

1 2

2

2 3

x t

y t

z t

 





  





 



. B.

1

2 2

2

x t

y t

z t

 





  





 



. C.

2

1 2

3 2

x t

y t

z t

 





 





  



. D.

1 2

2

2 3

x t

y t

z t

  





 





  



.

Câu 43. (Mã 104 - 2020 Lần 2) Trong không gian

Oxyz

, cho điểm

 

1;2; 2

M



và mặt phẳng

 

: 2 3 1 0

P x y z

   

. Phương trình của đường thẳng đi qua

M

và vuông góc với

 

P

là:

A.

1 2

2

2 3

x t

y t

z t

  





  





 



. B.

1 2

2

2 3

x t

y t

z t

 





 





  



. C.

1 2

2

2 3

x t

y t

z t

 





 





  



. D.

2

1 2

3 2

x t

y t

z t

 





 





  



Câu 44. (Mã 123 2017) Trong không gian với hệ tọa độ

Oxyz

, phương trình nào dưới đây là phương

trình của đường thẳng đi qua

 

2; 3; 0

A

và vuông góc với mặt phẳng

 

   

: 3 5 0 ?

P x y z

A.

  



 





 



1

1 3

1

x t

y t

z t

B.

  









 



1

3

1

x t

y t

z t

C.

  



 





 



1 3

1

x t

y t

z t

D.

  



 





 



1 3

1

x t

y t

z t

Câu 45. (THPT Yên Phong Số 1 Bắc Ninh 2019) Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

 

: 2 1x y z



  

. Trong các đường thẳng sau, đường thẳng nào vuông góc với

 



.

A.

1

:

1 1 2

x y z

d



 



. B.

2

1

:

1 1 1

x y z

d



 

 

. C.

3

1

:

1 1 1

x y z

d



 

 

. D.

4

2

: 0

x t

d y

z t













 



Câu 46. (THCS - THPT Nguyễn Khuyến 2019) Trong không gian

Oxyz

, đường thẳng đi qua điểm

 

1;1;1

A

và vuông góc với mặt phẳng tọa độ

 

Oxy

có phương trình tham số là:

A.

1

x t

y

z

 















. B.

1

x

y

z t













 



. C.

1

x t

y

z

 















. D.

1

x t

y t

z

 





 









.

Câu 47. Trong không gian với hệ trục

Oxyz

, cho điểm

 

1; 3; 2

M 

và mặt phẳng

 

: 3 2 1 0

P x y z

   

. Tìm phương trình đường thẳng

d

qua

M

và vuông góc với

 

P

.

A.

1 3 2

x y z

  

 



. B.

1 3 2

x y z

  

 



.

C.

1 3 2

x y z

 



. D.

1 3 2

x y z

  

 



.

Câu 48. (Sở Thanh Hóa 2019) Trong không gian với hệ tọa độ

,Oxyz

cho điểm

 

1;0;2

A

và đường thẳng

1 1

:

1 1 2

x y z

d

 

 

. Đường thẳng



đi qua

A

, vuông góc và cắt

d

có phương trình là

A.

2 1 1

:

1 1 1

x y z  

  



. B.

1 2

:

1 1 1

x y z

 

  

.

C.

2 1 1

:

2 2 1

x y z  

  

. D.

1 2

:

1 3 1

x y z

 

  



.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 8 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 49. (Đà Nẵng 2019) Trong không gian

Oxyz

, đường thẳng đi qua điểm

 

3;1;2

A

và vuông góc với

mặt phẳng

3 5 0

x y z

   

có phương trình là

A.

3 1 2

.

1 1 3

x y z

  

 

B.

1 1 3

.

3 1 2

x y z

  

 

C.

1 1 3

.

3 1 2

x y z

  

 

D.

3 1 2

.

1 1 3

x y z

  

 

Câu 50. Trong không gian

,Oxyz

cho điểm

(3; 2; 1)M 

và mặt phẳng

( ) : 2 0.P x z  

Đường thẳng đi

qua

M

và vuông góc với

( )P

có phương trình là

A.

3

2 .

1

x t

y

z t

  









  



B.

3

2 .

1

x t

y t

z

  



 





 



C.

3

2 .

1

x t

y t

z t

  









 



D.

3

1 2 .

x t

y t

z t

  



 





 



Câu 51. (SGD Bắc Ninh 2019) Trong không gian với hệ trục tọa độ

oxyz

, phương trình đường thẳng

d

đi

qua điểm

 

1;2;1

A

và vuông góc với mặt phẳng

 

: 2 1 0

P x y z

   

có dạng

A.

1 2 1

:

1 2 1

x y z

d

  

 



. B.

2 2

:

1 2 1

x y z

d

 

 



.

C.

1 2 1

:

1 2 1

x y z

d

  

 

. D.

2 2

:

2 4 2

x y z

d

 

 



.

Câu 52. (Nguyễn Huệ- Ninh Bình- 2019)Trong không gian với hệ tọa độ

Oxyz

, cho

 

: 2 5 1 0

P x y z

   

và

 

1;2; 1

A



. Đường thẳng



qua

A

và vuông góc với

 

P

có phương

trình là

A.

2

5 2

1

x t

y t

z t

 





  





 



. B.

3 2

3 5

1

x t

y t

z t

 





  





 



. C.

1 2

2 5

1

x t

y t

z t

 





 





 



. D.

3 2

3 5

x t

y t

z t

 





  





 



.

Câu 53. Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

 

: 2 3 0

P x y z

   

và điểm

 

1; 2;1 .

A 

Phương trình đường thẳng

d

đi qua

A

và vuông góc với

 

P

là

A.

1 2

: 2

1

x t

d y t

z t

 





  





 



. B.

1 2

: 2 4

1 3

x t

d y t

z t

 





  





 



. C.

2

1 2

1

x t

y t

z t

 





  





 



. D.

1 2

: 2

1 3

x t

d y t

z t

 





  





 



.

Câu 54. Trong không gian với hệ tọa độ

Oxyz

, phương trình đường thẳng

d

đi qua điểm

 

1;2;1

A

và

vuông góc với mặt phẳng

 

: 2 1 0

P x y z

   

có dạng

A.

2

:

1 2 1

x y z

d



 

 

. B.

1 2 1

:

1 2 1

x y z

d

  

 

.

C.

1 2 1

:

1 2 1

x y z

d

  

 

 

. D.

2

:

2 4 2

x y z

d



 

 

.

Câu 55. (Chu Văn An - Hà Nội - 2019) Trong không gian với hệ tọa độ

Oxyz

, đường thẳng



đi qua

điểm

 

2;4;3

A 

và vuông góc với mặt phẳng

 

:2 3 6 19 0

x y z

    

có phương trình là

A.

2 3 6

2 4 3

x y z

  

 



. B.

2 4 3

2 3 6

x y z  

 



.

C.

2 3 6

2 4 3

x y z

  

 



. D.

2 4 3

2 3 6

x y z  

 



.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9

Dạng 2.3 Xác định phương trình đường thẳng khi biết yếu tố song song

Câu 56. (Mã 101 - 2020 Lần 1) Trong không gian

Oxyz

, cho ba điểm

 

1;0;1A

,

 

1;1;0B

và

 

3;4; 1C 

. Đường thẳng đi qua

A

và song song với

BC

có phương trình là

A.

1 1

4 5 1

x y z 

 



. B.

1 1

2 3 1

x y z 

 



. C.

1 1

2 3 1

x y z 

 



. D.

1 1

4 5 1

x y z 

 



.

Câu 57. (Mã 102 - 2020 Lần 1) Trong không gian , cho ba điểm .

Đường thẳng đi qua và song song với

có phương trình là

A. . B. .

C. . D. .

Câu 58. (Mã 103 - 2020 Lần 1) Trong không gian

Oxyz

, cho ba điểm

(1;2;0), (1;1;2)A B

và

(2;3;1)C

.

Đường thẳng đi qua

A

và song song với

BC

có phương trình là

A.

1 2

.

1 2 1

x y z 

 



B.

1 2

.

3 4 3

x y z 

 

C.

1 2

.

3 4 3

x y z 

 

D.

1 2

.

1 2 1

x y z 

 



Câu 59. (Mã 104 - 2020 Lần 1) Trong không gian

Oxyz

, cho ba điểm

     

1;1;0 , 1;0;1 , 3;1;0A B C

.

Đường thẳng đi qua A và song song với BC có phương trình là:

A.

1 1

2 1 1

x y z 

 

. B.

1 1

4 1 1

z y z 

 

.

C.

1 1

2 1 1

x y z 

 



. D.

1 1

4 1 1

x y z 

 

.

Câu 60. (Mã 110 2017) Trong không gian với hệ tọa độ

Oxyz

, cho ba điểm

 

0; 1;3A 

,

 

1;0;1B

,

 

1;1;2C 

. Phương trình nào dưới đây là phương trình chính tắc của đường thẳng đi qua

A

và

song song với đường thẳng

BC

?

A.

2 0x y z  

. B.

2

1

3

x t

y t

z t

 





  





 



.

C.

1 3

2 1 1

x y z 

 



. D.

1 1

2 1 1

x y z 

 



.

Câu 61. (Mã 105 2017) Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm

 

 1; 2; 3A

;

 

1; 4; 1B

và

đường thẳng



 

 



2

2 3

:

1 1 2

y

x z

d

. Phương trình nào dưới đây là phương trình của đường

thẳng đi qua trung điểm của đoạn

AB

và song song với

d

?

A.





 

1

1 1 2

y

x z

B.





 



1

1 1 2

y

x z

C.



 

 



1

1 1

1 1 2

y

x z

D.





 



2

1 1 2

y

x z

Câu 62. Trong không gian với hệ toạ độ

Oxyz

, cho điểm

 

1; 2; 3A

và hai mặt phẳng

 

   : 1 0P x y z

,

 

   : 2 0Q x y z

. Phương trình nào dưới đây là phương trình đường

thẳng đi qua

A

, song song với

 

P

và

 

Q

?

Oxyz

     

1;2;3 , 1;1;1 , 3;4;0

A B C

A

BC

1 2 3

4 5 1

x y z  

 

1 2 3

4 5 1

x y z

  

 

1 2 3

2 3 1

x y z

  

 



1 2 3

2 3 1

x y z  

 



NGUYỄN BẢO VƯƠNG - 0946798489

Trang 10 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

A.

 



 





 



1

2

3 2

x

y

z t

B.

   









  



1

2

3

x t

y

z t

C.

  



 





 



1 2

2

3 2

x t

y

z t

D.

  



 





 



1

2

3

x t

y

z t

Câu 63. Trong không gian với hệ tọa độ

Oxyz

cho ba điểm

 



0; 1; 3

A

,

 

1; 0;1

B

,

 



1;1; 2

C

. Phương

trình nào dưới đây là phương trình chính tắc của đường thẳng đi qua

A

và song song với đường

thẳng

BC

?

A.

  



  





 



2

1

3

x t

y t

z t

. B.





 



1

3

2 1 1

y

x z

.

C.

 

 



1 1

2 1 1

y

x z

. D.

  2 0x y z

.

Câu 64. Trong không gian

Oxyz

, cho điểm

 

2;0; 1

A



và mặt phẳng

 

: 1 0

P x y

  

. Đường thẳng đi

qua

A

đồng thời song song với

 

P

và mặt phẳng

 

Oxy

có phương trình là

A.

  









 



3

2

1

x t

y t

z t

. B.

  



 





 



2

1

x t

y t

z

. C.

  



 





 



1 2

1

x t

y

z t

. D.

  



 





 



3

1 2

x t

y t

z t

.

Câu 65. Trong không gian với hệ tọa độ

Oxyz

, cho điểm

 

2;3; 1

M

 

,

 

1;2;3

N 

và

 

2; 1;1

P 

.

Phương trình đường thẳng

d

đi qua

M

và song song với

NP

là

A.

1 3

2 3

3 2

x t

y t

z t

  





 





 



. B.

2 3

1 3

1 2

x t

y t

z t

 





  





 



. C.

2 3

3 3

1 2

x t

y t

z t

  





 





  



. D.

3 2

3 3

2

x t

y t

z t

 





  





  



.

Câu 66. (Đà Nẵng 2019) Trong không gian

Oxyz

, cho đường thẳng

1 1 2

: .

1 2 1

x y z

d

  

 

 

Đường

thẳng đi qua điểm

 

2;1; 1

M



và song song với đường thẳng

d

có phương trình là:

A.

2 1 1

.

1 2 1

x y z

  

 

 

B.

5 3

.

1 2 1

x y z

 

 



C.

1 2 1

.

2 1 1

x y z

  

 



D.

2 1 1

.

1 1 2

x y z

  

 



Câu 67. (Nho Quan A - Ninh Bình - 2019) Trong không gian với hệ tọa độ

Oxyz

, cho ba điểm

   

(0; 0; 1),B 1; 2;0 , 2;1; 1

A C

  

. Đường thẳng



đi qua

C

và song song với

AB

có phương

trình là

A.

 

2

1 2 ,

1

x t

y t t R

z t

 





  





  



. B.

 

2

1 2 ,

1

x t

y t t R

z t

 





  





  



.

C.

 

2

1 2 ,

1

x t

y t t R

z t

 





  





  



. D.

 

2

1 2 ,

1

x t

y t t R

z t

 





  





  



.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11

Câu 68. (Chu Văn An - Hà Nội - 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho hai mặt phẳng

 

: 2 1 0

x y z



   

,

 

: 2 0

x y z



  

và điểm

 

1;2; 1

A



. Đường thẳng



đi qua điểm

A

và

song song với cả hai mặt phẳng

   

,

 

có phương trình là

A.

1 2 1

2 4 2

x y z  

 

 

. B.

1 2 1

1 3 5

x y z  

 

.

C.

1 2 1

x y z  

 

 

. D.

2 3

1 2 1

x y z

 

 

.

Dạng 3 Bài toán liên quan điểm (hình chiếu) thuộc đường, giao điểm đường với mặt phẳng

Câu 69. (Đề Minh Họa 2020 Lần 1) Trong không gian

Oxyz

, điểm nào dưới đây thuộc đường thẳng

1 2 1

:

1 3 3

x y z

d

  

 



?

A.

 

1;2;1

P 

. B.

 

1; 2; 1

Q

 

. C.

 

1;3;2

N 

. D.

 

1;2;1

P

.

Câu 70. (Đề Tham Khảo 2020 Lần 2) Trong không gian

,Oxyz

cho đường thẳng

1 2 1

: .

2 3 1

x y z

d

  

 



Điểm nào sau đây thuộc

?d

A.

 

1;2; 1 .

P



B.

 

1; 2;1 .

M  

C.

 

2;3; 1 .

N



D.

 

2; 3;1 .

Q  

Câu 71. (Mã 101 2020 Lần 2) Trong không gian Oxyz, cho đường thẳng

x 2 y 1 z 3

d :

4 2 1

  

 



. Điểm

nào dưới đây thuộc d?

A.

 

4; 2;1 .

Q 

B.

 

4;2;1 .

N

C.

 

2;1; 3 .

P



D.

 

2;1;3 .

M

Câu 72. (Mã 102 - 2020 Lần 2) Trong không gian

Oxyz

, cho đường thẳng

4 2 1

:

2 5 1

x z z

d

  

 



. Điểm

nào sau đây thuộc

d

?

A.

(4;2; 1)

N



. B.

(2;5;1)

Q

. C.

(4;2;1)

M

. D.

(2; 5;1)

P



.

Câu 73. (Mã 103 - 2020 Lần 2) Trong không gian

Oxyz

, cho đường thẳng

3 1 2

:

2 4 1

x y z

d

  

 



. Điểm

nào dưới đây thuộc

d

?

A.

 

3; 1; 2

N

 

B.

 

2;4;1

Q

C.

 

2;4; 1

P



D.

 

3;1;2

M

Câu 74. (Mã 104 - 2020 Lần 2) Trong không gian

Oxyz

, cho đường thẳng

3 1 5

:

2 2 1

x y z

d

  

 



. Điểm

nào dưới đây thuộc

d

?

A.

 

3;1;5

M

. B.

 

3;1; 5

N



. C.

 

2;2; 1

P



. D.

 

2;2;1

Q

.

Câu 75. (Mã đề 104 BGD&ĐT NĂM 2018) Trong không gian

Oxyz

, điểm nào dưới đây thuộc đường

thẳng

d

:

1

5

2 3

x t

y t

z t

 





 





 



?

A.

 

1;5;2

N

B.

 

1;1;3

Q 

C.

 

1;1;3

M

D.

 

1;2;5

P

Câu 76. (Mã 103 2018) Trong không gian

Oxyz

, điểm nào dưới đây thuộc đường thằng

2 1 2

:

1 1 2

x y z

d

  

 

.

A.

 

2; 1;2

N 

B.

 

2;1; 2

Q

 

C.

 

2; 2;1

M  

D.

 

1;1;2

P

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 12 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 77. (Chuyên Hùng Vương Gia Lai 2019) Trong không gian

Oxyz

, đường thẳng

1 2

: 3

1

x t

d y t

z t

 





 





 



đi

qua điểm nào dưới đây?

A.

 

1;3; 1

M



. B.

 

3;5;3

M 

. C.

 

3;5;3

M

. D.

 

1;2; 3

M



.

Câu 78. (THPT Hùng Vương Bình Phước 2019) Trong không gian với hệ tọa độ

Oxyz

. Đường thẳng

1

2

x t

d y t

z t







 





 



đi qua điểm nào sau sau đây?

A.

 

1; 1;1

K 

. B.

 

1;1;2

E

. C.

 

1;2;0

H

. D.

 

0;1;2

F

.

Câu 79. (Chuyên KHTN 2019) Trong không gian

Oxyz

, điểm nào dưới đây thuộc đường thẳng

1 1 2

2 1 3

x y z

  

 



?

A.

 

2;1; 3

Q

 

. B.

 

2; 1;3

P 

. C.

 

1;1; 2

M

 

. D.

 

1; 1;2

N 

.

Câu 80. (Chuyên KHTN 2019) Trong không gian

Oxyz

, gọi

d

là đường thẳng qua

 

1;0;2

A

, cắt và

vuông góc với đường thẳng

1

1 5

:

1 1 2

 

 



x y z

d

. Điểm nào dưới đây thuộc

d

?

A.

 

2; 1;1

P

. B.

 

0; 1;1

Q

. C.

 

0; 1;2

N

. D.

 

1; 1;1

 M

.

Câu 81. Trong không gian

Oxyz

, điểm nào dưới đây thuộc đường thẳng

1

: 5

2 3

 





 





 



x t

d y t

z t

?

A.

 

1;1; 3

Q

B.

 

1; 2; 5

P

C.

 

1; 5; 2

N

D.

 

1;1; 3

M

Câu 82. Trong không gian

Oxyz

, đường thẳng

1 2 3

:

2 1 2

x y z

d

  

 

 

đi qua điểm nào dưới đây?

A.

(2; 1; 2)

Q

 

. B.

(1; 2; 3)

M

 

. C.

( 1;2; 3)

P

 

. D.

N(2; 1; 2) 

.

Câu 83. (KTNL GV THPT Lý Thái Tổ 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho đường

thẳng

1 2 3

:

3 4 5

  

 

 

x y z

d

. Hỏi

d

đi qua điểm nào trong các điểm sau:

A.

 

3;4;5

C

. B.

 

3; 4; 5 

D

. C.

 

1;2; 3 

B

. D.

 

1; 2;3

A

.

Câu 84. (Sở Thanh Hóa 2019) Trong không gian

Oxyz

, cho điểm

 

3; 2;1

A 

. Đường thẳng nào sau đây

đi qua

A

?

A.

3 2 1

1 1 2

x y z  

 

. B.

3 2 1

4 2 1

x y z  

 

 

.

C.

3 2 1

1 1 2

x y z  

 

. D.

3 2 1

4 2 1

x y z  

 

 

.

Câu 85. Trong không gian

Oxyz

, điểm nào dưới đây thuộc đường thẳng

1

: 5

2 3

 





 





 



x t

d y t

z t

?

A.

 

1;1; 3

Q

B.

 

1; 2; 5

P

C.

 

1; 5; 2

N

D.

 

1;1; 3

M

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13

Câu 86. (Chuyên Nguyễn Tất Thành Yên Bái 2019) Trong không gian với hệ tọa độ

Oxyz

, cho đường

thẳng

d

có phương trình

1 2 3

3 2 4

x y z  

 



. Điểm nào sau đây không thuộc đường thẳng

d

?

A.

 

7;2;1

P

. B.

 

2; 4;7

Q  

. C.

 

4;0; 1

N



. D.

 

1; 2;3

M 

.

Câu 87. (THPT Cẩm Bình 2019) Giao điểm của mặt phẳng

 

: 2 0

P x y z

   

và đường thẳng

2

:

3 3

x t

d y t

z t

 





 





 



A.

 

1;1;0

. B.

 

0;2;4

. C.

 

0;4;2

. D.

 

2;0;3

.

Câu 88. (Thpt Vĩnh Lộc - Thanh Hóa 2019) Trong không gian

,Oxyz

cho đường

thẳng

1 2

: 3 ,

1

x t

d y t

z t

 





 





 



t  

và mặt phẳng

 

: 2 3 2 0.

P x y z

   

Tìm tọa độ của điểm

A

là giao

điểm của đường thẳng

d

và mặt phẳng

 

.P

A.

 

3;5;3

A

. B.

 

1;3;1

A

. C.

 

3;5;3

A 

. D.

 

1;2; 3

A



.

Câu 89. (Hùng Vương Gia Lai2019) Trong không gian

Oxyz

, giao điểm của mặt phẳng

 

: 3 5 2 0

P x y z

   

và đường thẳng

12 9 1

:

4 3 1

x y z  

  

là điểm

 

0 0 0

; ;M x y z

. Giá trị

tổng

0 0 0

x y z 

bằng

A.

1

. B.

2

. C.

5

. D.

2

.

Câu 90. Trong không gian với hệ trục tọa độ

Oxyz

, hình chiếu vuông góc của điểm

 

4;5;2

M 

lên mặt

phẳng

 

: 1 0

P y

 

là điểm có tọa độ

A.

 

4; 1;2

 

. B.

 

4;1;2



. C.

 

0; 1;0



. D.

 

0;1;0

.

Câu 91. (Chuyên Bắc Giang 19) Trong không gian với hệ trục tọa độ

Oxyz

, cho đường thẳng

12 9 1

:

4 3 1

x y z

d

  

 

và mặt phẳng

 

:3 5 2 0

P x y z

   

. Tìm tọa độ giao điểm của

d

và

 

P

.

A.

 

1;0;1

. B.

 

0;0; 2

. C.

 

1;1;6

. D.

 

12;9;1

.

Câu 92. (Kon Tum - 2019) Trong không gian

Oxyz

, cho đường thẳng

4 2

: 3

1

x t

d y t

z t

 





  





 



, giao điểm của

d

với mặt phẳng

 

Oxy

có tọa độ là

A.

 

4; 3;0



. B.

 

2; 2;0



. C.

 

0; 1; 1 

. D.

 

2;0; 2 

.

Câu 93. (Kinh Môn - Hải Dương 2019) Trong không gian với hệ toạ độ

Oxyz

, cho 3 điểm

 

1;0;0

A

,

 

0;2;0

B

,

 

0;0;3

C

và đường thẳng

: 2

3

x t

d y t

z t

 





 





 



. Gọi

 

; ;M a b c

là toạ độ giao điểm của

đường thẳng

d

với mặt phẳng

 

ABC

. Tính tổng

S a b c  

.

A.

6

. B.

5

.

C.

7

. D.

11

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 14 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 94. (Bến Tre 2019) Trong không gian

Oxyz

, cho đường thẳng

3 1 3

:

2 1 1

x y z

d

  

 

và mặt phẳng

 

: 2 5 0

P x y z

   

. Tìm tọa độ giao điểm

M

của đường thẳng

d

và mặt phẳng

 

P

.

A.

 

1;0;4

M 

. B.

 

5; 2;2

M  

. C.

 

0;0;5

M

. D.

 

3; 1;3

M  

.

Câu 95. (Đà Nẵng 2019) Trong không gian

Oxyz

, cho điểm

 

2;3;5 .

A

Tìm tọa độ điểm

'A

là hình

chiếu vuông góc của

A

lên trục

.Oy

A.

 

' 2;0;0 .

A

B.

 

' 0;3;0 .

A

C.

 

' 2;0;5 .

A

D.

 

' 0;3;5 .

A

Dạng 4. Bài toán liên quan khoảng cách, góc

1. Khoảng cách từ một điểm đến đường thẳng – Khoảng cách giữa hai đường thẳng



Khoảng cách từ điểm

M

đến một đường thẳng

d

qua điểm

M



có véctơ chỉ phương

d

u



được xác

định bởi công thức

,

( , )

d

M M u

d M d

u

 

 

 







Khoảng cách giữa hai đường thẳng song song là khoảng cách từ một điểm thuộc đường thẳng này

đến đường thẳng kia.



Khoảng cách giữa hai đường thẳng chéo nhau:

d

đi qua điểm

M

và có véctơ chỉ phương

u



và

d



đi qua điểm

M



và có véctơ chỉ phương

u





là

 

, .

( , )

,

u u M M

d d d

u u



 







 

2. Góc giữa hai đường thẳng

Góc giữa hai đường thẳng

1

d

và

2

d

có véctơ chỉ phương

1 1 1 1

( ; ; )u a b c



và

2 2 2 2

( ; ; ).u a b c



1 2 1 2 1 2 1 2

1 2

2 2 2 2 2 2

1 2

1 1 1 2 2 2

.

cos( ; ) cos

.

u u a a b b c c

d d

u u

a b c a b c



 

  

   

 

với

0 90 .



   

3. Góc giữa đường thẳng và mặt phẳng

Góc giữa đường thẳng

d

có véctơ chỉ phương

( ; ; )

d

u a b c



và mặt phẳng

( )P

có véctơ pháp tuyến

( )

( ; ; )

P

n A B C



được xác định bởi công thức:

( )

2 2 2 2 2 2

( )

.

sin cos( ; )

.

d P

P d

d P

u n

aA bB cC

n u

u n

a b c A B C



 

  

   

 

với

0 90 .



   

Câu 96. (Đề Tham Khảo 2017) Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

 

: 2 2 1 0

P x y z

   

và đường thẳng

1 2 1

:

2 1 2

x y z  

  

. Tính khoảng cách

d

giữa



và

 

P

.

A.

2

d



B.

5

3

d



C.

2

3

d



D.

1

3

d



Câu 97. (Chuyên Sơn La 2019) Trong không gian

Oxyz

, khoảng cách giữa đường thẳng

1

:

1 1 2

x y z

d



 



và mặt phẳng

 

: 2 0

P x y z

   

bằng:

A.

2 3.

B.

3

.

3

C.

2 3

.

3

D.

3.

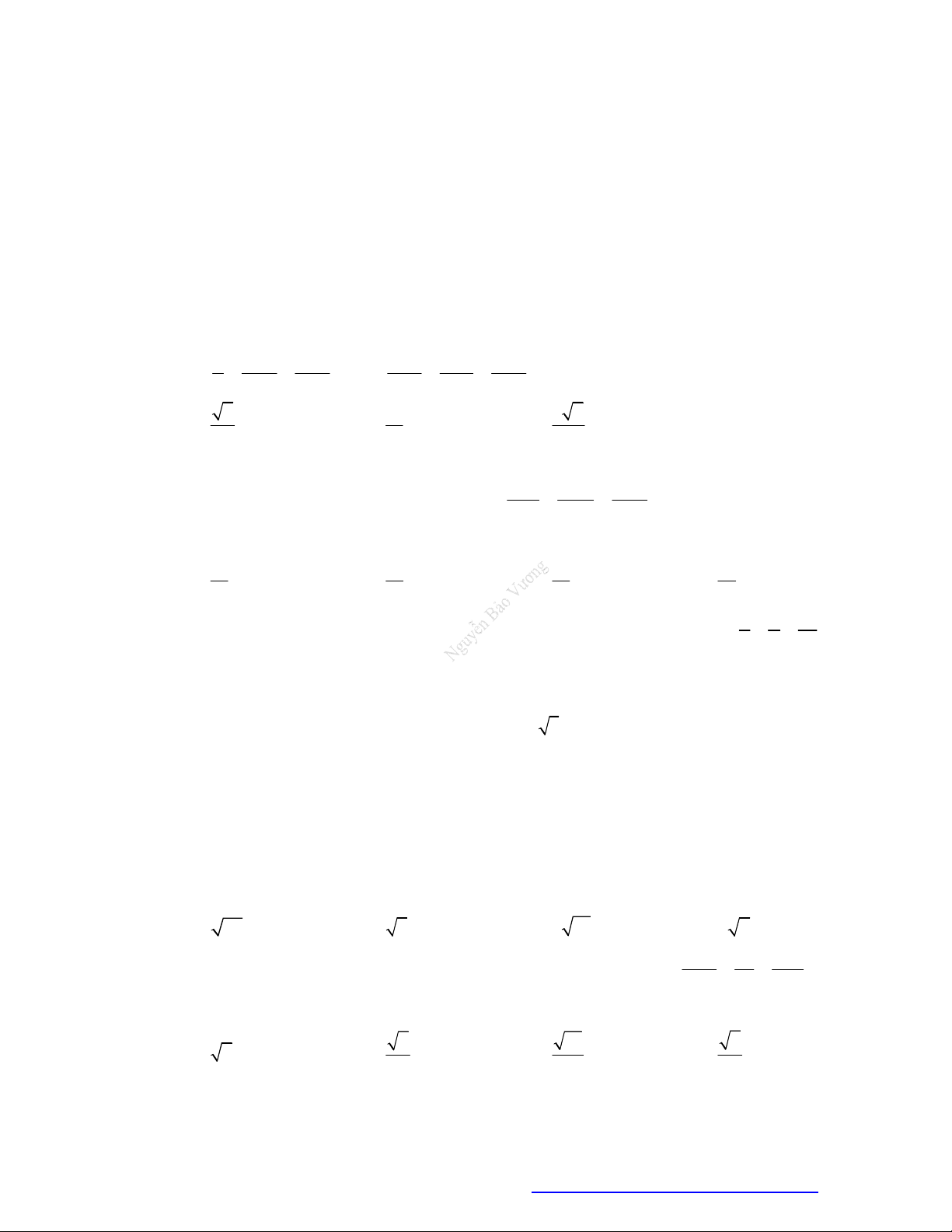
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15

Câu 98. (THPT Lê Quý Đôn Dà Nẵng 2019) Trong không gian với hệ tọa độ

Oxyz

, khoảng cách giữa

đường thẳng

2

: 5 4

2

x t

y t

z t

 





  





 



,

 

t 



và mặt phẳng

 

: 2 2 0

P x y z

  

bằng

A.

1

. B.

0

. C.

2

. D.

3

.

Câu 99. (Chuyên Bắc Giang 2019) Trong không gian với hệ tọa độ Oxyz cho đường thẳng

1

: 2 2

3

x t

d y t

z t

 





 





 



và mặt phẳng (P):

3 0

x y

  

. Tính số đo góc giữa đường thẳng d và mặt phẳng (P).

A.

0

60

B.

0

30

C.

120

o

D.

0

45

Câu 100. (Chuyên Trần Đại Nghĩa - TPHCM - 2018) Tính khoảng cách giữa hai đường thẳng

1

d

:

3 2

1 2 1

x y z

 

 

và

2

d

:

3 1 2

1 2 1

x y z

  

 



A.

2

3

. B.

12

5

. C.

3 2

2

. D.

3

.

Câu 101. (Chuyên Lê Quý Đôn Quảng Trị 2019) Trong không gian tọa độ

Oxyz

, cho mặt phẳng

 

: 4 3 1 0

P x y z

   

và đường thẳng

1 6 4

:

4 3 1

x y z

d

  

 

, sin của góc giữa đường thẳng

d

và mặt phẳng

 

P

bằng

A.

5

13

. B.

8

13

. C.

1

13

. D.

12

13

.

Câu 102. (Chuyên ĐH Vinh -2019) Trong không gian

Oxyz

cho đường thẳng

:

1 2 1

x y z

  



và mặt

phẳng

 

: 2 0

x y z



  

. Góc giữa đường thẳng



và mặt phẳng

 



bằng

A.

30

. B.

60

. C.

150

. D.

120

.

Câu 103. Trong không gian

Oxyz

, cho mặt phẳng (P):

3 1 0

x y

   

. Tính góc tạo bởi

( )P

với trục

Ox

?

A.

0

60

. B.

0

30

. C.

0

120

. D.

0

150

.

Câu 104. (Bình Phước - 2019) Trong không gian

Oxyz

, khoảng cách từ điểm

 

2; 4; 1

M

 

tới đường

thẳng

: 2

3 2

x t

y t

z t







  





 



bằng

A.

14.

.

B.

6.

.

C.

2 14.

.

D.

2 6.

Câu 105. Trong không gian với hệ tọa độ

Oxyz

, cho đường thẳng

 

3 1

:

2 1 1

x y z

d

 

 

 

và điểm

(2; 1;0)

A



. Khoảng cách từ điểm

A

đến đường thẳng

 

d

bằng

A.

7

. B.

7

2

. C.

21

3

. D.

7

3

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 16 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 106. (Chuyên Bắc Giang -2019) Cho

1

3 1

: 3 , ' :

3 1 1

2 2

x t

x y z

d y t d

z t

 



 



    







 



. Khi đó khoảng cách giữa

d

và

'd

là

A.

13 30

30

. B.

30

3

. C.

9 30

10

. D.

0

.

Câu 107. Trong không gian

Oxyz

, khoảng cách giữa đường thẳng

1

:

1 1 2

x y z

d



 



và mặt phẳng

 

: 2 0P x y z   

bằng

A.

2 3

. B.

3

. C.

2 3

3

. D.

3

.

Câu 108. Trong không gian với hệ tọa độ Oxyz, khoảng cách giữa đường thẳng

1 3 2

:

2 2 1

x y z

d

  

 

và mặt phẳng

( ) : 2 2 4 0P x y z   

A. 1. B. 0. C. 3. D. 2.

Dạng 5. Xác định phương trình mặt phẳng có yếu tố đường thẳng

Dạng 1. Viết phương trình mặt phẳng

( )P

qua

M

và vuông góc với đường thẳng

.d AB

Phương pháp.

( )

( ; ; )

( ) :

:

P d

M x y z

P

VTPT n u

u

AB

Q a







 





  





 



Dạng 2. Viết phương trình mặt phẳng qua M và chứa đường thẳng d với

M d

.

Bước 1: Chọn điểm

A d

và một VTCP

.

d

u



Tính ,

d

AM u

 

 

 

.

Bước 2: Phương trình

qua

mp( )

VTPT ,

d

M

P

n AM u

 



 

  

Câu 109. (Mã 101 - 2020 Lần 1) Trong không gian

Oxyz

, cho điểm

 

2; 2;3M 

và đường thẳng

d

:

1 2 3

3 2 1

x y z  

 



. Mặt phẳng đi qua điểm

M

và vuông góc với đường thẳng

d

có phương

trình là

A.

3 2 1 0x y z   

. B.

2 2 3 17 0x y z   

.

C.

3 2 1 0x y z   

. D.

2 2 3 17 0x y z   

.

Câu 110. (Đề Minh Họa 2020 Lần 1) Trong không gian

Oxyz

, mặt phẳng đi qua điểm

 

1;1; 1M 

và

vuông góc với đường thẳng

1 2 1

:

2 2 1

x y z  

  

có phương trình là

A.

2 2 3 0x y z   

. B.

2 0x y z  

. C.

2 2 3 0x y z   

. D.

2 2 0x y z   

.

Câu 111. (Đề Tham Khảo 2020 Lần 2) Trong không gian Oxyz, cho điểm

( 2;1;0)M

và đường thẳng

3 1 1

: .

1 4 2

  

  



x y z

Mặt phẳng đi qua M và vuông góc với



có phương trình là

A.

3 7 0   x y z

. B.

4 2 6 0   x y z

.

P

( )P d

AB

n u

 



 

d

M

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17

C.

4 2 6 0   x y z

. D.

3 7 0   x y z

.

Câu 112. (Mã 102 - 2020 Lần 1) Trong không gian cho điểm

và đường thẳng

. Mặt phẳng đi qua

và vuông góc với

có phương trình là

A. . B. .

C. . D. .

Câu 113. (Mã 103 - 2020 Lần 1) Trong không gian

Oxyz

, cho điểm

(2; 1;2)M 

và đường thẳng

1 2 3

:

2 3 1

x y z

d

  

 

. Mặt phẳng đi qua điểm qua

M

và vuông góc với

d

có phương trình là

A.

2 3 3 0.x y z   

B.

2 2 9 0.x y z   

C.

2 3 3 0.x y z   

D.

2 2 9 0.x y z   

Câu 114. (Mã 104 - 2020 Lần 1) Trong gian gian

,Oxyz

cho điểm

 

3; 2;2M 

và đường thẳng

3 1 1

:

1 2 2

x y z

d

  

 



. Mặt phẳng đi qua

M

và vuông góc với

d

có phương trình là

A.

2 2 5 0x y z   

. B.

3 2 2 17 0x y z   

.

C.

3 2 2 17 0x y z   

. D.

2 2 5 0x y z   

.

Câu 115. (Mã 102 2018) Trong không gian

Oxyz

, mặt phẳng đi qua điểm

 

1;2; 2A 

và vuông góc với

đường thẳng

1 2 3

:

2 1 3

x y z  

  

có phương trình là

A.

2 3 2 0x y z   

. B.

2 3 1 0x y z   

.

C.

2 3 2 0x y z   

. D.

3 2 5 0x y z   

.

Câu 116. (Mã 123 2017) Trong không gian với hệ tọa độ

Oxyz

cho điểm

 

3; 1;1M

. Phương trình nào

dưới đây là phương trình mặt phẳng đi qua điểm

M

và vuông góc với đường thẳng



 

  



2

1 3

: ?

3 2 1

y

x z

A.

   3 2 8 0x y z

B.

   3 2 12 0x y z

C.

   3 2 12 0x y z

D.

   2 3 3 0x y z

Câu 117. (THPT Hùng Vương Bình Phước 2019) Trong không gian với hệ trục tọa độ

Oxyz

, phương

trình nào dưới đây là phương trình mặt

phẳng đi qua

 

1; 1;2M 

và vuông góc với đường thẳng

1 2

:

2 1 3

x y z 

  



.

A.

2 3 9 0x y z   

. B.

2 3 9 0x y z   

. C.

2 3 9 0x y z   

. D.

2 3 6x y z  

.

Câu 118. (THPT Yên Khánh - Ninh Bình - 2019) Trong không gian

Oxyz

cho đường thẳng

1 2 3

:

2 1 2

x y z

d

  

 



. Mặt phẳng

 

P

vuông góc với

d

có một vectơ pháp tuyến là:

A.

 

1;2;3n 



. B.

 

2; 1;2n  



. C.

 

1;4;1n 



. D.

 

2;1;2n 



.

Câu 119. (THCS - THPT Nguyễn Khuyến 2019) Trong không gian

Oxyz

, phương trình mặt phẳng đi qua

gốc tọa độ và vuông góc với đường thẳng

( ) :

1 1 1

x y z

d  

là:

A.

1 0x y z   

. B.

1x y z  

. C.

1x y z  

. D.

0x y z  

.

Câu 120. (THCS - THPT Nguyễn Khuyến 2019) Trong không gian

Oxyz

, mặt phẳng đi qua điểm

 

0;1;0A

và chứa đường thẳng

 

2 1 3

:

1 1 1

x y z  

  



có phương trình là:

Oxyz

(1;1; 2)

M



1 2

:

1 2 3

x y z

d

 

 



M

d

2 3 9 0

x y z

   

2 6 0

x y z

   

2 3 9 0

x y z

   

2 6 0

x y z

   

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 18 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

A.

1 0

x y z

   

. B.

3 2 1 0

x y z

   

. C.

1 0

x y z

   

. D.

3 2 1 0

x y z

   

.

Câu 121. (Chuyên Hưng Yên 2019) Trong không gian

Oxyz

, cho đường thẳng

1 2 2

:

1 2 1

x y z

d

  

 



.

Mặt phẳng nào sau đây vuông góc với đường thẳng

d

.

A.

 

: 2 1 0

T x y z

   

. B.

 

: 2 1 0

P x y z

   

.

C.

 

: 2 1 0

Q x y z

   

. D.

 

: 1 0

R x y z

   

.

Câu 122. (Đề Thi Công Bằng KHTN 2019) Trong không gian

Oxyz

cho điểm

 

0; 3;1

A 

và đường

thẳng

1 1 3

:

3 2 1

x y z

d

  

 



. Phương trình mặt phẳng đi qua

A

và vuông góc với đường thẳng

d

là:

A.

3 2 5 0

x y z

   

. B.

3 2 7 0

x y z

   

.

C.

3 2 10 0

x y z

   

. D.

3 2 5 0

x y z

   

.

Câu 123. Trong không gian với hệ tọa độ

Oxyz

cho điểm

 



3; 1;1

M

. Phương trình nào dưới đây là

phương trình mặt phẳng đi qua điểm

M

và vuông góc với đường thẳng



 

  



2

1 3

: ?

3 2 1

y

x z

A.

   2 3 3 0x y z

B.

   3 2 8 0x y z

C.

   3 2 12 0x y z

D.

   3 2 12 0x y z

Câu 124. (Chuyên - KHTN - Hà Nội - 2019) Trong không gian

Oxyz

cho điểm

 

0; 3;1

A 

và đường

thẳng

1 1 3

:

3 2 1

x y z

d

  

 



. Phương trình mặt phẳng đi qua

A

và vuông góc với đường thẳng

d

là

A.

3 2 5 0

x y z

   

. B.

3 2 7 0

x y z

   

.

C.

3 2 10 0

x y z

   

. D.

3 2 5 0

x y z

   

.

Câu 125. Trong không gian với hệ trục tọa độ

Oxyz

, cho điểm

 

1;3; 2

A 

và đường thẳng

d

có phương

trình

1 4

2

x t

y t

z t

 











 



. Mặt phẳng

 

P

chứa điểm

A

và đường thẳng

d

có phương trình nào dưới đây?

A.

2 2 1 0.

x y z

   

. B.

0.

x y z

  

.

C.

3 2 10 23 0.

x y z

    

. D.

2 3 4 0.

x y z

   

Câu 126. Trong không gian

Oxyz

, cho điểm

 

1;2;0

A

và đường thẳng

1 2

:

1

x t

d y t

z t

  











 



. Tìm phương trình

mặt phẳng

 

P

đi qua điểm

A

và vuông góc với

.d

A.

2 4 0

x y z

   

. B.

2 4 0

x y z

   

. C.

2 4 0

x y z

   

. D.

2 4 0

x y z

   

.

Câu 127. (THPT Thuận Thành 3 - Bắc Ninh 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho điểm

 

1;3;2

A 

và đường thẳng

d

có phương trình

1 4

2

x t

y t

z t

 











 



. Mặt phẳng

 

P

chứa điểm

A

và

đường thẳng

d

có phương trình nào dưới đây?

A.

2 2 1 0

x y z

   

. B.

0

x y z

  

.

C.

3 2 10 23 0

x y z

    

. D.

2 3 4 0

x y z

   

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19

Câu 128. Tr

ong không gian

O

xyz

,

mặt phẳng

 

P

đi

qua điểm

 

1

;2;0

A

và

vuông góc với đường thẳng

1

2 1 1

x y z 

 



có phương trình là

A.

2 4 0

x y z

   

. B.

2 4 0

x y z

   

.

C.

2 4 0

x y z

   

. D

.

2 4 0

x y z

   

.

Câu 129. Tr

ong không gian

O

xyz

,

viết phương trình mặt phẳng đi qua

 

2

; 3;0

A 

và

vuông góc với

đường thẳng

d

có phương

trình:

3 4 7

1 2 5

x y z

  

 

.

A.

2

5 10 0

x

y z



  

. B.

2

5 8 0

x

y z



  

.

C.

2 3 4 0

x y

  

. D

.

2

5 4 0

x

y z



  

.

Câu 130. (Bắc Giang - 2018) Tr

ong không gian với hệ tọa độ

Oxy

z

,

cho đường thẳng

1

2

:

1

1 2

x y z

d





 



.

Mặt phẳng

 

P

đi

qua điểm

 

2;0; 1

M



và

vuông góc với

d

c

ó phư

ơng

trình là ?

A.

 

:

2 0

P

x y z



 

. B.

 

:

2 0

P

x y z



 

. C.

 

:

2 0

P

x y z



 

. D.

 

:

2 2 0

P

x y



 

.

Câu 131. (C

huyên Vĩnh Phúc - 2018) Trong không gian

O

xyz

,

cho đường thẳng

3

2 1

:

1 1 2

x y z

d



 





.

Viết

phương trình mặt phẳng

 

P

đi qua điểm

 

2

;0; 1

M



và

vuông góc với

d

.

A.

 

:

2 0

P

x y z



 

. B.

 

:

2 2 0

P

x y



 

. C.

 

:

2 0

P

x y z



 

. D.

 

:

2 0

P

x y z



 

.

Câu 132. (S

GD&ĐT Đồng Tháp - 2018) Trong không gian với hệ tọa độ

O

xy

,

cho đường thẳng

 

2 2 3

:

1

1 2

x y z

d

  

 



và

điểm

 

1

; 2;3

A 

.

Mặt phẳng qua

A

và

vuông góc với đường thẳng

 

d

c

ó phương trình là:

A.

2

9 0

x

y z



  

. B.

2

3 14 0

x

y z



  

.

C.

2 9 0

x y z

   

. D.

2 3 9 0

x y z

   

.

Câu 133. (THP

T Thái Phiên - Hải Phòng 2018) Trong không gian với hệ trục

Oxyz

, c

ho điểm

 

0;0;3

A

và

đường thẳng

1

:

.

2 1 1







y

x

z

d

Phươn

g trình mặt phẳng đi qua điểm

A

và

vuông góc vớ

i

đường thẳng

d

là

A.

2

3 0   x y z

. B.

2

2 6 0   x y z

. C.

2

3 0   x y z

. D.

2

3 0   x y z

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương  https://www.facebook.com/phong.baovuong Trang 1

TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH KHÁ – MỨC 7-8 ĐIỂM

Dạng 1. Xác định phương trình đường thẳng

1. Dạng 1. Viết phương trình đường thẳng

d

dạng tham số và dạng chính tắc (nếu có), biết

d

đi qua

điểm ( ; ; )M x y z

  

và có véctơ chỉ phương

1 2 3

( ; ; ).

d

u a a a



Phương pháp. Ta có:

1 2 3

( ; ; )

:

: ( ; ; )

d

Qua M x y z

d

VTCP u a a a









  







Phương trình đường thẳng

d

dạng tham số

1

2

3

: , ( ).

x x a t

d y y a t t

z z a t

 





  





 







Phương trình đường thẳng

d

dạng chính tắc

1 2 3

: , ( 0).

x x y y z z

d a a a

a a a

  

  

  

2. Dạng 2. Viết phương trình tham số và chính tắc (nếu có) của đường thẳng

d

đi qua

A

và

.B

Phương pháp. Đường thẳng

( )

:

d

Qua A hay B

d

VTCP u AB





















(dạng 1)

3. Dạng 3. Viết phương trình đường thẳng

d

dạng tham số và chính tắc (nếu có), biết

d

đi qua điểm

M

và song song với đường thẳng

.

Phương pháp. Ta có

Qua ( ; ; )

:

d

M x y z

d

VTCP u u















  



 



(dạng 1)

4. Dạng 4. Viết phương trình đường thẳng

d

dạng tham số và chính tắc (nếu có), biết

d

đi qua điểm

M

và vuông góc với mặt phẳng

( ) : 0.P ax by cz d   

Phương pháp. Ta có

( )

:

: ( ; ; )

d P

Qua M

d

VTCP u n a b c





 





 



(dạng 1)

5. Dạng 5. Viết phương trình tham số và chính tắc của đường thẳng

d

là giao tuyến của hai mặt

phẳng

( )P

và

( )Q

cho trước.

Phương pháp. Ta có

( ) ( )

:

: [ , ]

( ) ( )

d P Q

d

VTCP u n n

Qua A P Q









 

  



(dạng 1)

6. Dạng 6. Viết phương trình tham số và chính tắc (nếu có) của đường thẳng

d

đi qua điểm

M

và

vuông góc với hai đường thẳng

1 2

, d d cho trước.

Phương pháp. Ta có

1 2

:

[ , ]

d d d

d

C

Qua M

VT P u u u











  



(dạng 1)

7. Dạng 7. Viết phương trình đường thẳng

d

qua

M

và song song với hai mặt phẳng

( ), ( ).P Q

Phương pháp. Ta có

:

: , ]

[

d P Q

d

VTCP u n

Qua M

n











  



(dạng 1)

8. Dạng 8. Viết phương trình đường thẳng

d

qua

,M

vuông góc đường

d



và song song mặt

( ).P

Phương pháp. Ta có

:

: , ]

[

d d P

d

VTCP u u n

Qua M













  



(dạng 1)

PHƯƠNG TRÌNH ĐƯỜNG THẲNG

Chuyên đề 31

A

B

d

M



d

u





P

u n

d P



 

d

M

d

A

1

d

u



d

1

d

2

d

2

d

u



NGUYỄN BẢO VƯƠNG - 0946798489

Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

9. Dạng 9. Viết phương trình đường thẳng

d

nằm trong mặt

( ),P

song song mặt

( )Q

và qua

.M

Phương pháp. Ta có

:

: , ]

[

d P Q

d

VTCP u n

Qua M

n











  



(dạng 1)

10. Dạng 10. Viết phương trình đường thẳng

d

đi qua điểm

,A

vuông góc và cắt đường thẳng

.d



Phương pháp.

Viết phương trình mặt phẳng

( )P

qua

,A

vuông góc

.d



Nghĩa là mặt phẳng

( ) :

:

P d

Qua A

P

VTPT n u















 



Tìm

( ).B d P



 

Suy ra đường thẳng

d

qua

A

và

B

(dạng 1)

Lưu ý: Trường hợp

d



là các trục tọa độ thì

,d AB

với

B

là hình chiếu của

A

lên trục.

11. Dạng 11. Viết phương trình tham số và chính tắc (nếu có) của đường thẳng

d

đi qua điểm

M

và

cắt đường thẳng

1

d

và vuông góc

2

d

cho trước.

Phương pháp. Giả sử

1 1

, ( , )d d H H d H d   

1 1 2 2 3 2 1

( ; ; ) .H x a t x a t x a t d    

Vì

2

. 0 .

d

MH d MH u t H

    

 

Suy ra đường thẳng

:

d

Qua M

d

VTCP u MH





















(dạng 1)

Dạng 12.

d

đi qua điểm

0 0 0 0

( ; ; )M x y z

và cắt hai đường thẳng

1 2

d , d

:

 Cách 1: Gọi

1 1 2 2

M d , M d 

Từ điều kiện

1 2

M, M , M

thẳng hàng ta tìm được

1 2

M , M

. Từ đó

suy ra phương trình đường thẳng

d

.

 Cách 2: Gọi

 

P 

0 1

( , )M d

,

 

0 2

( , )Q M d



. Khi đó

d



 

P



 

Q

, do đó, một VTCP của

d

có thể

chọn là

,

P Q

a n n



 

 

  

.

Dạng 13.

d

nằm trong mặt phẳng

 

P

và cắt cả hai đường thẳng

1 2

d , d

:

Tìm các giao điểm

   

1 2

A d P , B d P .

   

Khi đó

d

chính là đường thẳng

AB

.

Dạng 14.

d

song song với



và cắt cả hai đường thẳng

1 2

d , d

:

Viết phương trình mặt phẳng

 

P

chứa



và

1

d

, mặt phẳng

 

Q

chứa



và

2

d

.

Khi đó

d



 

P



 

Q

.

Dạng 15.

d

là đường vuông góc chung của hai đường thẳng

1 2

d , d

chéo nhau:

 Cách 1: Gọi

1 2

M d , N d . 

Từ điều kiện

1

2

MN d











, ta tìm được

,M N

.

Khi đó,

d

là đường thẳng

MN

.

 Cách 2:

– Vì

1

d d

và

2

d d

nên một VTCP của

d

có thể là:

1 2

,

d d

a a a



 

 

  

.

– Lập phương trình mặt phẳng

 

P

chứa

d

và

1

d

, bằng cách:

+ Lấy một điểm

A

trên

1

d

.

+ Một VTPT của

 

P

có thể là:

1

,

P d

n a a



 

 

  

.

– Tương tự lập phương trình mặt phẳng

 

Q

chứa

d

và

1

d

.

Khi đó

d



 

P



 

Q

.

Dạng 16. Viết phương trình đường thẳng

d

là hình chiếu vuông góc của đường thẳng



lên mặt

( ).P

Phương pháp: Xét vị trí tương đối của đường thẳng



và

( ).P



Nếu

( ).P 

Chọn một điểm

M

trên

.

Tìm

H

là hình chiếu của

M

lên

( ).P

A

B

d



d

P

2

d

u



2

d

H

M

d

1

d

M

H

P



d

M



TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3

Hình chiếu

Qua

:

VTCP :

d

H

d

u u













 



Nếu

( ) .P I  

Chọn một điểm

M I

trên

.

Tìm

H

là hình chiếu của

M

lên

( ).P

Hình chiếu vuông góc của



lên

( )P

là

.d IH

Dạng 17. Viết đường thẳng

d

là đường thẳng đối xứng với đường thẳng



qua mặt phẳng

( ).P

Phương pháp: Xét vị trí tương đối của đường thẳng



và

( ).P



Nếu

( ).P 

Chọn một điểm

M

trên

.

Tìm

H

là hình chiếu của

M

lên

( ).P

Tìm

M



đối xứng với

M

qua

( ).P

Đường thẳng đối xứng

Qua

:

VTCP :

d

M

d

u u















 



Nếu

( ) .P I  

Chọn một điểm

M

trên

.

Tìm

H

là hình chiếu của

M

lên

( ).P

Tìm

M



đối xứng với

M

qua

( ).P

Đường thẳng đối xứng

Qua

: .

VTCP :

d

M

d

u IM





















Dạng 1.1 Xác định phương trình đường thẳng khi biết yếu tố vuông góc

Câu 1. (Mã 101 2018) Trong không gian

Oxyz

cho điểm

 

1;2;3

A

và đường thẳng

3 1 7

:

2 1 2

x y z

d

  

 



. Đường thẳng đi qua

A

, vuông góc với

d

và cắt trục

Ox

có phương trình

là

A.

1 2

2

x t

y t

z t

  





 









B.

1

2 2

3 3

x t

y t

z t

 





 





 



C.

1 2

2

3

x t

y t

z t

  















D.

1

2 2

3 2

x t

y t

z t

 





 





 



Câu 2. (Mã 102 - 2019) Trong không gian

,Oxyz

cho các điểm

     

1;0;2 , 1;2;1 , 3;2;0

A B C

và

 

1;1;3 .

D

Đường thẳng đi qua A và vuông góc với mặt phẳng

 

BCD

có phương trình là

A.

1

4 .

2 2

x t

y t

z t



 









 





B.

1

4 .

2 2

x t

y

z t



 









 





C.

2

4 4 .

4 2

x t

y t

z t



 



 





 





D.

1

2 4

2 2

x t

y t

z t



 



 





 





Câu 3. (Đề Tham Khảo 2018) Trong không gian

Oxyz

, cho hai đường thẳng

1

3 3 2

:

1 2 1

x y z

d

  

 

 

;

2

5 1 2

:

3 2 1

x y z

d

  

 



và mặt phẳng

 

: 2 3 5 0

P x y z

   

. Đường thẳng vuông góc với

 

P

,

cắt

1

d

và

2

d

có phương trình là

A.

1 1

3 2 1

x y z 

 

B.

2 3 1

1 2 3

x y z  

 

C.

3 3 2

1 2 3

x y z

  

 

D.

1 1

1 2 3

x y z 

 

M

H

P



d

M



M



M

H

P



d

I

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 4. (Mã 101 - 2019) Trong không gian

Oxyz

, cho các điểm

       

1;2;0 , 2;0;2 , 2; 1;3 , 1;1;3

A B C D



. Đường thẳng đi qua

C

và vuông góc với mặt

phẳng

 

ABD

có phương trình là

A.

2 4

4 3

2

x t

y t

z t

  





  





 



. B.

4 2

3

1 3

x t

y t

z t

 





 





 



. C.

2 4

2 3

2

x t

y t

z t

  





  





 



. D.

2 4

1 3

3

x t

y t

z t

 





  





 



.

Câu 5. (Mã 104 - 2019) Trong không gian

Oxyz

, cho các điểm

 

2; 1;0

A

,

 

1;2;1

B

,

 

3; 2;0

C

,

 

1;1; 3

D

. Đường thẳng đi qua

D

và vuông góc với mặt phẳng

 

ABC

có phương trình là:

A.

1

2 3

 





 





  



x t

y t

z t

.

B.

1

3 2

 





 





  



x t

y t

z t

.

C.

1 2













  



x t

y t

z t

.

D.

1 2













 



x t

y t

z t

.

Câu 6. (Mã 102 2018) Trong không gian

Oxyz

, cho điểm

 

2;1;3

A

và đường thẳng

1 1 2

:

1 2 2

x y z

d

  

 



. Đường thẳng đi qua

A

, vuông góc với

d

và cắt trục

Oy

có phương

trình là.

A.

2

3 4

3

x t

y t

z t







  









B.

2 2

1

3 3

x t

y t

z t

 





 





 



C.

2 2

1 3

3 2

x t

y t

z t

 





 





 



D.

2

3 3

2

x t

y t

z t







  









Câu 7. (Mã 103 - 2019) Trong không gian

Oxyz

cho

     

0;0;2 , 2;1;0 , 1;2; 1

A B C



và

 

2;0; 2

D



. Đường thẳng đi qua

A

và vuông góc với

 

BCD

có phương trình là

A.

3

2

1 2

x

y

z t













  



. B.

3 3

2 2

1

x t

y t

z t

 





 





 



. C.

3

2

x t

y t

z t













 



. D.

3 3

2 2

1

x t

y t

z t

 





  





 



.

Câu 8. (Đề Minh Họa 2017) Trong không gian với hệ tọa độ

Oxyz

cho điểm

 

1;0;2

A

và đường thẳng

d

có phương trình:

1 1

1 1 2

 

 

x y z

. Viết phương trình đường thẳng



đi qua

A

, vuông góc và

cắt

d

.

A.

1 2

2 2 1

 

 

x y z

B.

1 2

1 3 1

 

 



x y z

C.

1 2

1 1 1

 

 

x y z

D.

1 2

1 1 1

 

 



x y z

Câu 9. (Đề Tham Khảo 2018) Trong không gian

Oxyz

, cho hai điểm

8 4 8

(2;2;1), ( ; ; )

3 3 3

A B 

. Đường

thẳng qua tâm đường tròn nội tiếp tam giác

OAB

và vuông góc với mặt phẳng

( )OAB

có phương

trình là:

A.

2 2 5

9 9 9

1 2 2

x y z

  

 



B.

1 8 4

1 2 2

x y z

  

 



C.

1 5 11

3 3 6

1 2 2

x y z

  

 



D.

1 3 1

1 2 2

x y z  

 



TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5

Câu 10. (Mã 103 2018) Trong không gian Oxyz, cho đường thẳng

1 2

:

2 1 2

x y z

d

 

 



và mặt phẳng

( ) : 1 0

P x y z

   

. Đường thẳng nằm trong mặt phẳng

( )P

đồng thời cắt và vuông góc với

d

có

phương trình là:

A.

1

4

3

x t

y t

z t

  





 





 



B.

3

2 4

2

x t

y t

z t

 





  





 



C.

3

2 4

2 3

x t

y t

z t

 





  





 



D.

3 2

2 6

2

x t

y t

z t

 





  





 



Câu 11. (Mã 123 2017) Trong không gian

Oxyz

cho điểm

 



1; 1; 3

M

và hai đường thẳng



 

  

3

1 1

:

3 2 1

y

x z

,





  



1

:

1 3 2

y

x z

. Phương trình nào dưới đây là phương trình đường

thẳng đi qua

M

và vuông góc với



và





.

A.

   



 





 



1

1 3

x t

y t

z t

B.

  



 





 



1

3

x t

y t

z t

C.

   



 





 



1

3

x t

y t

z t

D.

   



 





 



1

3

x t

y t

z t

Câu 12. (Mã 104 2018) Trong không gian

Oxyz

cho đường thẳng

1 1

:

1 2 1

x y z 

  

và mặt phẳng

 

: 2 y z 3 0

P x

   

. Đường thẳng nằm trong

 

P

đồng thời cắt và vuông góc với



có

phương trình là:

A.

1 2

1

2

x t

y t

z

 





 









B.

3

2

x

y t

z t

 





 









C.

1

1 2

2 3

x t

y t

z t

 





 





 



D.

1

2 2

x

y t

z t







 





 



Câu 13. (Mã 123 2017) Trong không gian với hệ tọa độ

Oxyz

, cho hai đường thẳng

  



  









1

1 3

: 2

2

x t

d y t

z

,





 



2

1

:

2 1 2

y

x z

d

và mặt phẳng

 

  : 2 2 3 0.

P x y z

Phương trình nào dưới đây là phương

trình mặt phẳng đi qua giao điểm của

1

d

và

 

P

, đồng thời vuông góc với

2

d

?

A.

   2 2 13 0x y z

B.

   2 2 22 0x y z

C.

   2 2 13 0x y z

D.

   2 2 22 0x y z

Câu 14. (Chuyên Lương Thế Vinh Đồng Nai -2019) Trong không gian với hệ tọa độ

Oxyz

cho

 

1; 1; 3

A



và hai đường thẳng

1

4 2 1

: ,

1 4 2

x y z

d

  

 



2

2 1 1

:

1 1 1

x y z

d

  

 



. Phương

trình đường thẳng qua

A

, vuông góc với

1

d

và cắt

2

d

là

A.

1 1 3

2 1 3

x y z

  

 

. B.

1 1 3

4 1 4

x y z

  

 

.

C.

1 1 3

1 2 3

x y z

  

 



. D.

1 1 3

2 1 1

x y z

  

 

 

.

Câu 15. (Chuyên Lê Quý Đôn Điện Biên 2019) Trong không gian

Oxyz

, cho điểm

 

1;0;1

M

và đường

thẳng

1 2 3

:

1 2 3

x y z

d

  

 

. Đường thẳng đi qua

M

, vuông góc với

d

và cắt

Oz

có phương

trình là

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

A.

1 3

0

1

x t

y

z t

 











 



. B.

1 3

0

1

x t

y

z t

 











 



. C.

1 3

1

x t

y t

z t

 











 



. D.

1 3

0

1

x t

y

z t

 











 



.

Câu 16. (Kinh Môn - Hải Dương 2019) Trong không gian với hệ tọa độ Oxyz cho điểm

 

1; 1;3A 

và

hai đường thẳng

1

3 2 1

:

3 3 1

x y z

d

  

 



, . Phương trình đường thẳng

d

đi qua

A

, vuông góc với đường thẳng

1

d và cắt thẳng

2

d .

A.

1 1 3

5 4 2

x y z  

 



. B.

1 1 3

3 2 3

x y z  

 



.

C.

1 1 3

6 5 3

x y z  

 



. D.

1 1 3

2 1 3

x y z  

 



.

Câu 17. (Hội 8 trường chuyên 2019) Trong không gian

,Oxyz

cho điểm

 

1; 1;2M 

và hai đường thẳng

: 1 4 ,

6 6

x t

d y t

z t







  





 



1 2

: .

2 1 5

x y z

d

 



 



Phương trình nào dưới đây là phương trình đường thẳng đi

qua

,M

vuông góc với

d

và

d



?

A.

1 1 2

.

17 14 9

x y z  

 

B.

1 1 2

.

14 17 9

x y z  

 

C.

1 1 2

.

17 9 14

x y z  

 

D.

1 1 2

.

14 17 9

x y z  

 

Câu 18. Cho hai đường thẳng

 

1

2

:

1

x t

d

y t

z t

 





 





 



và

 

2

7

:

1 3 1

x y z

d



 

 

. Đường thẳng

 



là đường vuông

góc chung của

 

1

d

và

 

2

d

. Phương trình nào sau đâu là phương trình của

 



A.

2 1 2

1 1 2

x y z  

 



. B.

2 1 1

1 1 2

x y z  

 



.

C.

1 4 1

1 1 2

x y z  

 



. D.

3 2 3

1 1 2

x y z  

 

 

.

Câu 19. Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

 

:3 0P x y z  

và đường thẳng

1 3

:

1 2 2

x y z

d

 

 



. Gọi



là đường thẳng nằm trong

 

P

, cắt và vuông góc với

d

. Phương

trình nào sau đây là phương trình tham số của



?

A.

2 4

3 5

3 7

x t

y t

z t

  





 





 



. B.

3 4

5 5

4 7

x t

y t

z t

  





 





 



. C.

1 4

1 5

4 7

x t

y t

z t

 





 





  



. D.

3 4

7 5

2 7

x t

y t

z t

  





 





 



.

Câu 20. Trong không gian với hệ tọa độ

Oxyz

, cho điểm

 

1; 1;3A 

và hai đường thẳng:

1 2

4 2 1 2 1 1

: , :

1 4 2 1 1 1

x y z x y z

d d

     

   

 

. Viết phương trình đường thẳng

d

đi qua

A

,

vuông góc với đường thẳng

1

d và cắt đường thẳng

2

d .

A.

1 1 3

2 1 1

x y z  

 

 

. B.

1 1 3

6 1 5

x y z  

 

.

2

2 1 1

:

1 1 1

x y z

d

  

 



TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7

C.

1 1 3

6 4 1

x y z  

 

 

. D.

1 1 3

2 1 3

x y z  

 

.

Câu 21. Trong không gian

Oxyz

, cho đường thẳng

3 2

2 1 3

:

x y z

d

 

 



và mặt phẳng

 

2 6 0

:P x y z

   

. Đường thẳng nằm trong

 

P

cắt và vuông góc với

d

có phương trình

là?

A.

2 2 5

.

1 7 3

  

 

x y z

B.

2 2 5

.

1 7 3

  

 

x y z

C.

2 4 1

.

1 7 3

  

 

x y z

D.

2 4 1

.

1 7 3

  

 

x y z

Câu 22. Trong không gian

Oxyz

, cho mặt phẳng

 

: 2 3 7 0

P x y z

   

và hai đường thẳng

1 2

3 2 2 1 1 2

: ; :

2 1 4 3 2 3

x y z x y z

d d

     

   

 

. Đường thẳng vuông góc mặt phẳng

 

P

và cắt

cả hai đường thẳng

1 2

;d d

có phương trình là

A.

7 6

1 2 3

x y z

 

 

B.

5 1 2

1 2 3

x y z

  

 

C.

4 3 1

1 2 3

x y z  

 

D.

3 2 2

1 2 3

x y z

  

 

Câu 23. Trong không gian

Oxyz

, cho hai đường thẳng

1

1 1

:

2 1 1

x y z

d

 

 



và

2

1

: 1

x t

d y

z t



  



 





 





và mặt

phẳng

 

: 1 0

P x y z

   

. Đường thẳng vuông góc với

 

P

cắt

1

d

và

2

d

có phương trình là

A.

13 9 4

5 5 5

1 1 1

x y z

  

 

. B.

1 3 2

5 5 5

1 1 1

x y z

  

 

.

C.

7 2

1

5 5

1 1 1

x z

y

 



 

. D.

1 1 1

x y z

 

.

Câu 24. Trong không gian với hệ trục tọa độ

Oxyz

, cho đường thẳng

 



đi qua điểm

 

0;1;1

M

, vuông

góc với đường thẳng

   

1

: 1

1

x t

d y t t

z







  





 





và cắt đường thẳng

 

2

1

:

2 1 1

x y z

d



 

. Phương trình

của

 



là?

A.

0

1

x

y t

z t













 



. B.

0

1

x

y

z t













 



. C.

0

1

x

y t

z







 









. D.

0

1

x

y

z t













 



.

Câu 25. Trong không gian với hệ tọa độ

Oxyz

cho điểm

 

1;0;2

A

và đường thẳng

d

có phương trình:

1 1

1 1 2

 

 

x y z

. Viết phương trình đường thẳng



đi qua

A

, vuông góc và cắt

d

.

A.

1 2

1 1 1

 

 

x y z

B.

1 2

1 1 1

 

 



x y z

C.

1 2

2 2 1

 

 

x y z

D.

1 2

1 3 1

 

 



x y z

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 8 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 26. (Chuyên Lê Quý Đôn – Điện Biên 2019) Trong không gian

,Oxyz

cho điểm

(1;0;1)

M

và đường

thẳng

1 2 3

: .

1 2 3

x y z

d

  

 

Đường thẳng đi qua

,M

vuông góc với

d

và cắt

Oz

có phương

trình là

A.

1 3

0

1

x t

y

z t

 











 



. B.

1 3

0

1

x t

y

z t

 











 



. C.

1 3

1

x t

y t

z t

 











 



. D.

1 3

0

1

x t

y

z t

 











 



.

Câu 27. Trong không gian với hệ trục

Oxyz

, đường vuông góc chung của hai đường thẳng chéo nhau

1

2 3 4

:

2 3 5

x y z

d

  

 



và

2

1 4 4

:

3 2 1

x y z

d

  

 

 

có phương trình

A.

2 2 3

2 3 4

x y z  

 

. B.

2 3

2 3 1

x y z

 

 



.

C.

2 2 3

2 2 2

x y z  

 

. D.

1

1 1 1

x y z 

 

.

Câu 28. (Chuyên Nguyễn Huệ- 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho mặt phẳng

 

: 2 2 9 0

P x y z

   

và đường thẳng

1 3 3

:

1 2 1

x y z

d

  

 



. Phương trình tham số của đường

thẳng

Δ

đi qua

 

0; 1;4

A 

, vuông góc với

d

và nằm trong

 

P

là:

A.

5

Δ : 1

4 5

x t

y t

z t







  





 



. B.

2

Δ :

4 2

x t

y t

z t













 



. C.

Δ : 1

4

x t

y

z t







 





 



. D.

Δ : 1 2

4

x t

y t

z t

 





  





 



.

Câu 29. (Đại học Hồng Đức –Thanh Hóa 2019) Trong không gian

Oxyz

, cho mặt phẳng

 

: 2 4 0

P x y z

   

và đường thẳng

1 2

:

2 1 3

x y z

d

 

 

. Phương trình đường thằng



nằm

trong mặt phẳng

 

P

, đồng thời cắt và vuông góc với đường thẳng

d

là

A.

1 1 2

5 1 2

x y z

  

 



. B.

1 3 1

5 1 3

x y z  

 



.

C.

1 1 1

5 1 3

x y z  

 



. D.

1 1 1

5 1 3

x y z  

 

 

.

Câu 30. (Sở Hà Nam - 2019) Trong không gian

Oxyz

, cho đường thẳng

3 1

:

2 1 1

x y z

d

 

 



và mặt

phẳng

 

: 3 2 0

P x y z

   

. Gọi

'd

là đường thẳng nằm trong mặt phẳng

 

P

, cắt và vuông

góc với

d

. Đường thẳng

'd

có phương trình là

A.

1 1

2 5 1

x y z 

 

 

. B.

1 1

2 5 1

x y z 

 

. C.

1 1

2 5 1

x y z 

 



. D.

1 1

2 5 1

x y z 

 

 

.

Câu 31. Trong không gian với hệ tọa độ

Oxyz

, cho hai đường thẳng

1

1 2 1

:

2 1 1

x y z  

  

và

2

2 1 2

:

4 1 1

x y z  

  

 

. Đường thẳng chứa đoạn vuông góc chung của

1



và

2



đi qua điểm

nào sau đây?

A.

 

0; 2; 5 

M

. B.

 

1; 1; 4 

N

. C.

 

2;0;1

P

. D.

 

3;1; 4

Q

.

Dạng 1.2 Xác định phương trình đường thẳng khi biết yếu tố song song

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9

Câu 32. (Mã 110 2017) Trong không gian với hệ toạ độ

Oxyz

, cho điểm

 

1; 2;3

A 

và hai mặt phẳng

 

: 1 0

P x y z

   

,

 

: 2 0

Q x y z

   

. Phương trình nào dưới đây là phương trình đường

thẳng đi qua

A

, song song với

 

P

và

 

Q

?

A.

1

2

3

x t

y

z t

 





 





 



B.

1

2

3

x t

y

z t

  











  



C.

1 2

2

3 2

x t

y

z t

 





 





 



D.

1

2

3 2

x

y

z t







 





 



Câu 33. (Chuyên Nguyễn Tất Thành Yên Bái 2019) Trong không gian với hệ toạ độ

Oxyz

, cho điểm

 

1; 3;4

M 

, đường thẳng

d

có phương trình:

2 5 2

3 5 1

x y z

  

 

 

và mặt phẳng

 

P

:

2 2 0

x z

  

. Viết phương trình đường thẳng



qua

M

vuông góc với

d

và song song với

 

P

.

A.



:

1 3 4

1 1 2

x y z

  

 

 

. B.



:

1 3 4

1 1 2

x y z

  

 

  

.

C.



:

1 3 4

1 1 2

x y z

  

 



. D.



:

1 3 4

1 1 2

x y z

  

 



.

Câu 34. Trong không gian

O

xyz

, cho mặt phẳng

 

: 2 2 3 0

P x y z

   

và hai đường thẳng

1

1 1

:

3 1 1

x y z

d

 

 



;

2

2 1 3

:

1 2 1

x y z

d

  

 



. Xét các điểm

,A B

lần lượt di động trên

1

d

và

2

d

sao cho

AB

song song với mặt phẳng

 

P

. Tập hợp trung điểm của đoạn thẳng

AB

là

A. Một đường thẳng có vectơ chỉ phương

 

9;8; 5

u

  



B. Một đường thẳng có vectơ chỉ phương

 

5;9;8

u  



C. Một đường thẳng có vectơ chỉ phương

 

1; 2; 5

u

  



D. Một đường thẳng có vectơ chỉ phương

 

1;5; 2

u

 



Câu 35. (THPT Lương Văn Can - 2018) Trong không gian

Oxyz

, cho điểm

 

3; 2; 4

A

 

và mặt phẳng

 

:3 2 3 7 0

P x y z

   

, đường thẳng

2 4 1

:

3 2 2

x y z

d

  

 



. Phương trình nào sau đây là

phương trình đường thẳng



đi qua

A

, song song

 

P

và cắt đường thẳng

d

?

A.

3 11

2 54

4 47

x t

y t

z t

 





 





  



. B.

3 54

2 11

4 47

x t

y t

z t

 





 





  



. C.

3 47

2 54

4 11

x t

y t

z t

 





 





  



. D.

3 11

2 47

4 54

x t

y t

z t

 





 





  



.

Câu 36. Trong không gian với hệ toạ độ

Oxyz

, cho điểm

 

1; 3;4

M 

, đường thẳng

2 5 2

:

3 5 1

x y z

d

  

 

 

và mặt phẳng

 

P

:

2 2 0

x z

  

. Viết phương trình đường thẳng



qua

M

vuông góc với

d

và song song với

 

P

.

A.

1 3 4

:

1 1 2

x y z

  

  

 

. B.

1 3 4

:

1 1 2

x y z

  

  

  

.

C.

1 3 4

:

1 1 2

x y z

  

  



. D.

1 3 4

:

1 1 2

x y z

  

  



.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 10 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 37. Trong không gian với hệ toạ độ

Oxyz

, cho điểm

 



1; 2; 3

A

và hai mặt phẳng

 

   : 1 0

P x y z

,

 

   : 2 0

Q x y z

. Phương trình nào dưới đây là phương trình đường

thẳng đi qua

A

, song song với

 

P

và

 

Q

?

A.

 



 





 



1

2

3 2

x

y

z t

B.

   









  



1

2

3

x t

y

z t

C.

  



 





 



1 2

2

3 2

x t

y

z t

D.

  



 





 



1

2

3

x t

y

z t

Câu 38. Trong không gian

Oxyz

, cho điểm

 

2;0; 1

A



và mặt phẳng

 

: 1 0

P x y

  

. Đường thẳng đi

qua

A

đồng thời song song với

 

P

và mặt phẳng

 

Oxy

có phương trình là

A.

  









 



3

2

1

x t

y t

z t

. B.

  



 





 



2

1

x t

y t

z

. C.

  



 





 



1 2

1

x t

y

z t

. D.

  



 





 



3

1 2

x t

y t

z t

.

Câu 39. (Chuyên Lê Quý Đôn Quảng Trị 2019) Trong không gian tọa độ

Oxyz

, viết phương trình chính

tắc của đường thẳng đi qua điểm

 

3; 1;5

A 

và cùng song song với hai mặt phẳng

 

: 4 0

P x y z

   

,

 

: 2 4 0

Q x y z

   

.

A.

3 1 5

:

2 1 3

x y z

d

  

 



. B.

3 1 5

2 1 3

x y z  

 

 

.

C.

3 1 5

2 1 3

x y z

  

 



. D.

3 1 5

2 1 3

x y z

  

 

 

.

Câu 40. (Chu Văn An - Hà Nội - 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho hai mặt phẳng

 

: 2 1 0

x y z



   

,

 

: 2 0

x y z



  

và điểm

 

1;2; 1

A



. Đường thẳng



đi qua điểm

A

và

song song với cả hai mặt phẳng

   

,

 

có phương trình là

A.

1 2 1

2 4 2

x y z  

 

 

. B.

1 2 1

1 3 5

x y z  

 

.

C.

1 2 1

x y z  

 

 

. D.

2 3

1 2 1

x y z

 

 

.

Câu 41. Trong không gian

Oxyz

, cho ba điểm

 

1;0;0

A

,

 

0;2;0

B

,

 

0;0;3

C

. Đường thẳng đi qua tâm

đường tròn ngoại tiếp tam giác

ABC

, song song với mặt phẳng

 

Oxy

và vuông góc với

AB

.

A.

13

98

40

2

49

135

98

x t

y t

z



 



  











. B.

13

2

98

40

49

135

98

x t

y t

z



 



 











. C.

13

2

98

40

49

135

98

x t

y t

z



 



 











. D.

13

98

40

2

49

135

98

x t

y t

z



  



 











.

Câu 42. (THPT Cẩm Bình 2019) Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

 

: 2 6 0

x z

   

và đường thẳng

1

: 3

1

x t

d y t

z t

 





 





  



. Viết phương trình đường thẳng



nằm trong

mặt phẳng

 



cắt đồng thời vuông góc với

.d

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11

A.

2 4 2

2 1 1

x y z

  

 

. B.

2 4 2

2 1 1

x y z

  

 



.

C.

2 3 2

2 1 1

x y z

  

 



. D.

2 4 2

2 1 1

x y z

  

 



.

Câu 43. Trong không gian Oxyz, cho ba đường thẳng

1

3 1 2

:

2 1 2

x y z

d

  

 



;

2

1 4

:

3 2 1

x y z

d

 

 

 

và

3

3 2

:

4 1 6

x y z

d

 

 



. Đường thẳng song song với d

3

, cắt d

1

và d

2

có phương trình là

A.

3 1 2

4 1 6

x y z

  

 

. B.

3 1 2

4 1 6

x y z

  

 

 

.

C.

1 4

4 1 6

x y z

 

 



. D.

1 4

4 1 6

x y z

 

 



.

Câu 44. (SGD Cần Thơ 2019) Trong không gian

Oxyz

, cho các đường thẳng

1 2

1 3

3 1 2

: , : 2

2 1 2

4

x t

x y z

d d y t

z t

  



  



   







  



,

3

3 2

:

4 1 6

x y z

d

 

 



. Đường thẳng song song với

3

d

và cắt đồng thời

1

d

và

2

d

có phương trình là:

A.

1 4

4 1 6

x y z

 

 



. B.

1 4

4 1 6

x y z

 

 



.

C.

3 1 2

4 1 6

x y z

  

 

. D.

3 1 2

4 1 6

x y z

  

 

 

.

Câu 45. Trong không gian với hệ tọa độ

Oxyz

, viết phương trình tham số của đường thẳng đi qua điểm

 

1;3; 2

M



, đồng thời song song với giao tuyến của hai mặt phẳng

 

: 3 0

P x y

  

và

 

: 2 3 0

Q x y z

   

.

A.

1 3

3

2

x t

y t

z t

 





 





  



. B.

1 3

3

2

x t

y t

z t

 





 





  



. C.

1

3

2 3

x t

y t

z t

 





 





  



. D.

1

3

2 3

x t

y t

z t

 





 





  



.

Câu 46. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng

1 2

:

1 2 2

x y z

d

 

 

, mặt phẳng

( ) :2 2 5 0

P x y z

   

và điểm

 

1;1; 2

A



. Phương trình chính tắc của đường thẳng



đi qua

điểm

A

song song với mặt phẳng

( )P

và vuông góc với

d

là:

A.

1 1 2

:

1 2 2

x y z

  

  



. B.

1 1 2

:

2 1 2

x y z

  

  



.

C.

1 1 2

:

2 2 3

x y z

  

  



. D.

1 1 2

:

1 2 2

x y z

  

  

.

Câu 47. (SP Đồng Nai - 2019) Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

 

: 9 0,

P x y z

   

đường thẳng

3 3

:

1 3 2

x y z

d

 

 

và điểm

 

1;2; 1 .

A



Viết phương trình

đường thẳng



đi qua điểm

A

cắt

d

và song song với mặt phẳng

 

P

.

A.

1 2 1

x y z  

 



. B.

1 2 1

x y z  

 



.

C.

1 2 1

x y z  

 

. D.

1 2 1

x y z  

 

 

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 12 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 48. (THPT Thăng Long-Hà Nội- 2019) Trong không gian, cho mặt phẳng

 

: 4 0

P x y z

   

và

điểm

 

2; 1;3

A 

. Gọi



là đường thẳng đi qua

A

và song song với

 

P

, biết



có một vectơ chỉ

phương là

 

; ;u a b c





, đồng thời



đồng phẳng và không song song với

Oz

. Tính

a

c

.

A.

2

a

c



. B.

2

a

c

 

. C.

1

2

a

c

 

. D.

1

2

a

c



.

Dạng 1.3 Phương trình đường thẳng hình chiếu, đối xứng

Câu 49. (Đề Tham Khảo 2017) Trong không gian với hệ tọa độ

Oxyz

, cho đường thẳng

1 5 3

:

2 1 4

x y z

d

  

 



. Phương trình nào dưới đây là phương trình hình chiếu vuông góc của

d

trên mặt phẳng

3 0

x

 

?

A.

3

5 2

3

x

y t

z t

 





  





 



B.

3

6

7 4

x

y t

z t

 





  





 



C.

3

5

3 4

x

y t

z t

 





  





  



D.

3

5

3 4

x

y t

z t

 





  





 



Câu 50. (Đề Tham Khảo 2019) Trong không gian Oxyz, cho mặt phẳng

 

: 3 0

x yP z

   

và đường

thẳng

1 2

:

1 2 1

x y z

d

 

 



. Hình chiếu vuông góc của

d

trên

 

P

có phương trình là

A.

1 1 1

1 4 5

x y z  

 



B.

1 4 5

1 1 1

x y z

  

 

C.

1 1 1

1 4 5

x y z  

 

 

D.

1 1 1

3 2 1

x y z  

 

 

Câu 51. Trong không gian

Oxyz

, cho mặt phẳng

 

: 2 3 0

x y z



   

và đường thẳng

4 3 2

:

3 6 1

x y z

d

  

 

 

. Viết phương trình đường thẳng

'd

đối xứng với đường thẳng

d

qua

mặt phẳng

 



.

A.

5 4

11 17 2

x y z

 

 

 

. B.

5 4

11 17 2

x y z

 

 

 

.

C.

5 4

11 17 2

x y z

 

 

 

. D.

5 4

11 17 2

x y z

 

 



.

Câu 52. (Chuyen Phan Bội Châu Nghệ An 2019) Trong không gian với hệ tọa độ

Oxyz

, cho đường

thẳng

1 2 1

:

2 1 3

x y z

d

  

 

và mặt phẳng

 

: 3 0

P x y z

   

. Đường thẳng

d



là hình chiếu

của

d

theo phương

Ox

lên

 

P

,

d



nhận

 

; ;2019

u a b



là một vectơ chỉ phương. Xác định

tổng

 

.a b



A.

2019

. B.

2019

. C.

2018

. D.

2020

.

Câu 53. Trong không gian

Oxyz

, cho mặt phẳng

 

: 6 0

x y z



   

và đường thẳng

1 4

:

2 3 5

x y z

d

 

 

. Hình chiếu vuông góc của

d

trên

 



có phương trình là

A.

1 4 1

2 3 5

x y z  

 

. B.

5 1

2 3 5

x y z

 

 

.

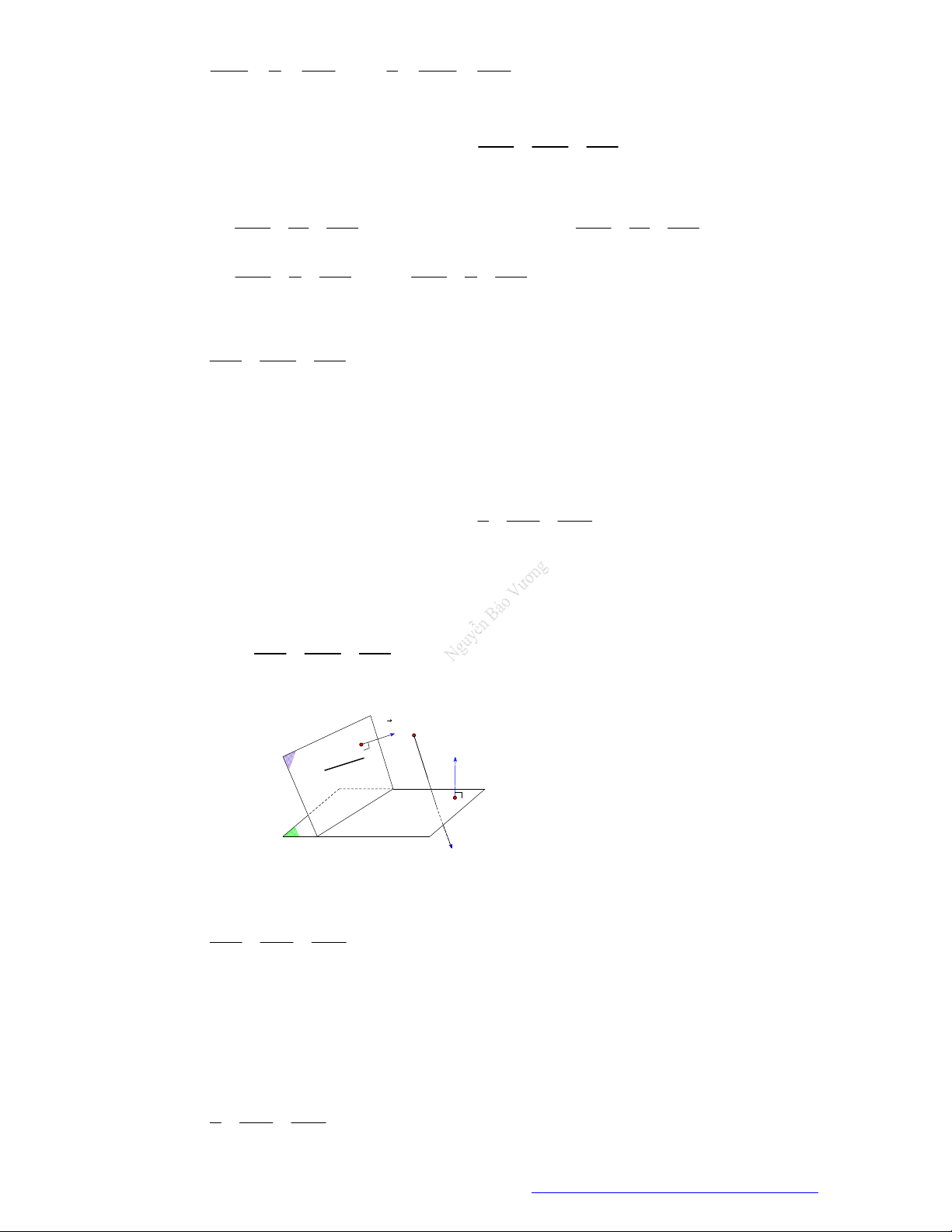
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13

C.

5 1

2 3 5

x y z 

 

. D.

5 1

2 3 5

x y z 

 

.

Câu 54. (KTNL GV Bắc Giang 2019) Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

 

: 1 0P x y z   

và đường thẳng

2 4 1

:

2 2 1

x y z

d

  

 



. Viết phương trình đường thẳng

d



là hình chiếu vuông góc của

d

trên

 

P

.

A.

2 1

:

7 5 2

x y z

d

 



 



. B.

2 1

:

7 5 2

x y z

d

 



 



.

C.

2 1

:

7 5 2

x y z

d

 



 

. D.

2 1

:

7 5 2

x y z

d

 



 

.

Câu 55. (Chuyên Phan Bội Châu 2019) Trong không gian với hệ tọa độ

Oxyz

, cho đường thẳng

1 2 1

:

2 1 3

x y z

d

  

 

và mặt phẳng

( ) : 3 0P x y z   

. Đường thẳng

'd

là hình chiếu của

d

theo phương

Ox

lên

( )P

;

'd

nhận

 

; ;2019u a b



làm một véctơ chỉ phương. Xác định tổng

a b

.

A.

2019

B.

2019

C.

2018

D.

2020

Câu 56. (THPT Đông Sơn 1 - Thanh Hóa 2019) Trong không gian với hệ tọa độ

,Oxyz

cho mặt phẳng

 

: 3 0P x y z   

và đường thẳng

1 2

:

1 2 1

x y z

d

 

 



. Hình chiếu của

d

trên

 

P

có

phương

trình là đường thẳng

d



. Trong các điểm sau điểm nào thuộc đường thẳng

d



:

A.

 

2;5; 4M 

. B.

 

1;3; 1P 

. C.

 

1; 1;3N 

. D.

 

2;7; 6Q 

.

Câu 57. (THPT Phan Bội Châu - Nghệ An - 2019) Trong không gian với hệ tọa độ

Oxyz

, cho đường

thẳng

1 2 1

:

2 1 3

x y z

d

  

 

và mặt phẳng

 

: 3 0P x y z   

. Đường thẳng

d



là hình chiếu

của

d

theo phương

Ox

lên

 

P

,

d



nhận

 

; ;2019u a b



là một vectơ chỉ phương. Xác định

tổng

 

.a b

A.

2019

. B.

2019

. C.

2018

. D.

2020

.

Câu 58. (SGD Bắc Ninh 2019) Trong không gian với hệ tọa độ

Oxyz

, cho đường thẳng

1 1 2

:

1 2 1

x y z

d

  

 



và mặt phẳng

 

: 2 2 1 0P x y z   

. Gọi

d



là hình chiếu của đường

thẳng

d

lên mặt phẳng

 

P

, véc tơ chỉ phương của đường thẳng

d



là

A.

 

3

5; 6; 13u   



. B.

 

2

5; 4; 3u   



.

C.

 

4

5;16;13u 



. D.

 

1

5;16; 13u  



.

Câu 59. Trong không gian

Oxyz

cho mặt phẳng

 

: 3 0   P x y z

và đường thẳng

1 2

: .

1 2 1

x y z

d

 

 



Hình chiếu vuông góc của

d

trên

 

P

có

phương trình là

n

Q

P

d

x

O

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 14 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

A.

1 1 1

1 4 5

  

 

 

x y z

. B.

1 1 1

3 2 1

  

 

 

x y z

.

C.

1 1 1

1 4 5

  

 



x y z

. D.

1 4 5

1 1 1

  

 

x y z

.

Dạng 1.4 Xác định một số phương trình đường thẳng đặc biệt (phân giác, trung tuyến, giao

tuyến…)

Hai đường thẳng

1 2

,d d

cắt nhau tại điểm

 

0 0 0

; ;A x y z

và có vécto chỉ phương |ân lượt là

   

1 1 1 1 2 2 2 2

; ; , ; ;u a b c u a b c

 

Đường thẳng phân giác của góc tạo bởi hai đường thẳng này có vécto chỉ phương được xác định theo công

thức

   

1 2 1 1 1 2 2 2

2 2 2 2 2 2

1 2

1 1 1 2 2 2

1 1 1 1

; ; ; ;u u u a b c a b c

u u

a b c a b c

     

   

 



Chi tiết có hai phân giác:

Nếu

1 2 1 2

1 2

1 1

0

u u u u u

u u

     

  



là vécto chỉ phương của phân

giác tạo bởi góc nhọn giữa hai đường thẳng và

1 2

1 1

u u u

u u

   

 



là vécto chỉ phương của phân giác tạo

bởi góc tù giữa hai đường thẳng.

Nếu

1 2 1 2

1 2

1 1

0

u u u u u

u u

     

  



là vécto chỉ phương của phân

giác tạo bởi góc tù giữa hai đường thẳng và

1 2

1 1

u u u

u u

   

 



là vécto chỉ phương của phân giác tạo bởi

góc nhọn giữa hai đường thẳng.

Câu 60. (Mã 102 2018) Trong không gian

Oxyz

, cho đường thẳng

1 3

: 3

5 4

 





 





 



x t

d y

z t

. Gọi



là đường thẳng

đi qua điểm

 

1; 3;5

A

và có vectơ chỉ phương

 

1;2; 2



u

. Đường phân giác của góc nhọn tạo bởi

d

và



có phương trình là

A.

1 2

2 5

6 11

  





 





 



x t

y t

z t

B.

1 2

2 5

6 11

  





 





  



x t

y t

z t

C.

1 7

3 5

5

 





  





 



x t

y t

z t

D.

1

3

5 7

 





 





 



x t

y

z t

Câu 61. (Mã 101 2018) Trong không gian

Oxyz

, cho đường thẳng

1 7

: 1 4

1

x t

d y t

z

 





 









. Gọi



là đường thẳng

đi qua điểm

 

1;1;1

A

và có vectơ chỉ phương

 

1; 2;2

u



 

. Đường phân giác của góc nhọn tạo

bởi

d

và



có phương trình là.

A.

1 2

10 11

6 5

x t

y t

z t

  





  





  



B.

1 2

10 11

6 5

x t

y t

z t

  





  





 



C.

1 3

1 4

1 5

x t

y t

z t

  





 





 



D.

1 7

1

1 5

x t

y t

z t

 





 





 



Câu 62. (Mã 104 2018) Trong không gian

Oxyz

, cho đường thẳng

1 3

: 1 4

1

x t

d y t

z

 





 









. Gọi



là đường thẳng

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15

đi qua điểm

 

1;1;1

A

và có vectơ chỉ phương

 

2;1;2

u  



. Đường phân giác của góc nhọn tạo

bởi

d

và



có phương trình là.

A.

1 27

1

x t

y t

z t

 





 





 



B.

18 19

6 7

11 10

x t

y t

z t

  





  





 



C.

18 19

6 7

11 10

x t

y t

z t

  





  





  



D.

1

1 17

1 10

x t

y t

z t

 





 





 



Câu 63. (Mã 103 2018) Trong không gian

Oxyz

, cho đường thẳng

1

: 2 .

3

x t

d y t

z

 





 









Gọi



là đường thẳng

đi qua điểm

(1;2;3)

A

và có vectơ chỉ phương

(0; 7; 1).

u

  



Đường phân giác của góc nhọn tạo

bởi

d

và



có phương trình là

A.

1 5

2 2 .

3

x t

y t

z t

 





 





 



B.

1 6

2 11 .

3 8

x t

y t

z t

 





 





 



C.

4 5

10 12 .

2

x t

y t

z t

  





  





 



D.

4 5

10 12 .

2

x t

y t

z t

  





  





  



Câu 64. (THPT An Lão Hải Phòng 2019) Trong không gian với hệ tọa độ

Oxyz

, cho tam giác

ABC

có

     

1;3;2 2;0;5 , ;,

0 2;1

A B C 

. Viết phương trình đường trung tuyến

AM

của tam giác

ABC

.

A.

1 3 2

:

2 4 1

x y z

AM

  

 



B.

1 3 2

:

2 4 1

x y z

AM

  

 



C.

1 3 2

:

2 4 1

x y z

AM

  

 



D.

2 4 1

:

1 1 3

x y z

AM

  

 



Câu 65. (THPT Yên Phong 1 Bắc Ninh 2019) Trong không gian

Oxyz

, cho

 

2;0;0

A

, đường thẳng

d

đi qua

A

cắt chiều âm trục

Oy

tại điểm

B

sao cho diện tích tam giác

OAB

bằng 1. Phương trình

tham số đường thẳng

d

là

A.

1 2

0

x t

y t

z

 















. B.

2 2

0

x t

y t

z

 





 









. C.

2 2

0

x t

y t

z

 





 









. D.

2 2

1

x t

y t

z

 















.

Câu 66. Trong không gian

Oxyz

cho hai điểm

8 4 8

(2;2;1), ( ; ; )

3 3 3

A B



. Đường phân giác trong của tam giác

OAB

có phương trình là

A.

0

x

y t

z t

















B.

4x t

y t

z t













 



C.

14

2

5

x t

y t

z t













 



D.

2

14

13

x t

y t

z t

















Câu 67. (Chuyên Hạ Long 2019) Trong không gian với hệ trục tọa độ

Oxyz

cho hai đường thẳng

1

4

6 2

x t

d y t

z t

 





  





 



;

2

5 11 5

:

2 4 2

x y z

d

  

 

. Đường thẳng

d

đi qua

 

5; 3;5

A 

cắt

1 2

;d d

lần lượt ở

,B C

.Tính tỉ sô

AB

AC

.

A.

2

. B.

3

. C.

1

2

. D.

1

3

.

Câu 68. (THPT Gang Thép Thái Nguyên -2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho

2

điểm

   

1;2;3 , 2;4;4

M A

và hai mặt phẳng

 

: 2 1 0

P x y z

   

,

 

: 2 4 0.

Q x y z

   

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 16 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Viết phương trình đường thẳng



đi qua

M

, cắt

( ), ( )P Q

lần lượt tại

,B C

sao cho tam giác

ABC

cân tại

A

và nhận

AM

làm đường trung tuyến.

A.

1 2 3

1 1 1

x y z

  

 

 

. B.

1 2 3

2 1 1

x y z

  

 



.

C.

1 2 3

1 1 1

x y z

  

 



. D.

1 2 3

1 1 1

x y z

  

 

 

.

Câu 69. (Chuyên Bắc Giang 2019) Trong không gian với hệ tọa độ Oxyz cho tam giác ABC

biết

(2;1;0), (3;0;2), (4;3; 4)

A B C



. Viết phương trình đường phân giác trong góc A.

A.

2

1

0

x

y t

z







 









B.

2

1

x

y

z t

















C.

2

1

0

x t

y

z

 















D.

2

1

x t

y

z t

 















Câu 70. (Chuyên Nguyễn Tất Thành Yên Bái 2019) Trong không gian với hệ tọa độ

Oxyz

, cho đường

thẳng

1 2

:

2 1 1

x y z

d

 

 

, mặt phẳng

 

: 2 5 0

P x y z

   

và

 

1; 1;2

A 

. Đường thẳng



cắt

d

và

 

P

lần lượt tại

M

và

N

sao cho

A

là trung điểm của đoạn thẳng

MN

. Một vectơ chỉ

phương của



là

A.

 

4; 5; 13

u  



. B.

 

2; 3; 2

u 



. C.

 

1; 1; 2

u  



. D.

 

3; 5; 1

u  



.

Câu 71. (THPT Phan Đình Phùng - Hà Tĩnh - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho hình

vuông

ABCD

biết

 

1;0;1

A

,

 

1;0; 3

B



và điểm

D

có hoành độ âm. Mặt phẳng

 

ABCD

đi qua

gốc tọa độ

O

. Khi đó đường thẳng

d

là trục đường tròn ngoại tiếp hình vuông

ABCD

có phương

trình

A.

1

:

1

x

d y t

z

 











 



. B.

1

:

1

x

d y t

z













 



. C.

1

:

1

x

d y t

z

 















. D.

: 1

x t

d y

z t

















.

Câu 72. (THPT Nghen - Hà Tĩnh - 2018) Trong không gian với hệ toạ độ

Oxyz

, cho hai đường thẳng

1

1 2 1

:

1 2 3

x y z  

  

và

2

1 2 1

:

1 2 3

x y z  

  



cắt nhau và cùng nằm trong mặt phẳng

 

P

.

Lập phương trình đường phân giác

d

của góc nhọn tạo bởi

1



,

2



và nằm trong mặt phẳng

 

P

.

A.

 

1

: 2 ,

1

x

d y t

z t

 





 





  





. B.

 

1

: 2 ,

1 2

x t

d y t

z t

  





 





  





.

C.

 

1

: 2 2 ,

1

x t

d y t t

z t

  





  





  





. D.

 

1

: 2 2 ,

1

x t

d y t t

z

  





  





 





Câu 73. (Quảng Xương - Thanh Hóa - 2018) Trong không gian tọa độ

Oxyz

, cho tam giác

ABC

biết

 

1;0; 1

A



,

 

2;3; 1

B



,

 

2;1;1

C 

. Phương trình đường thẳng đi qua tâm đường tròn ngoại tiếp

của tam giác

ABC

và vuông góc với mặt phẳng

 

ABC

là:

A.

3 1 5

x y z  

 



. B.

2

3 1 5

x y z

 

.

C.

1 1

1 2 2

x y z 

 



. D.

3 2 5

3 1 5

x y z  

 



.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17

Câu 74. (SGD Bắc Giang - 2018) Trong không gian

Oxyz

, cho tam giác nhọn

ABC

có

 

2;2;1

H

,

8 4 8

; ;

3 3 3

K

 



 

 

,

O

lần lượt là hình chiếu vuông góc của

A

,

B

,

C

trên các cạnh

BC

,

AC

,

AB

.

Đường thẳng

d

qua

A

và vuông góc với mặt phẳng

 

ABC

có phương trình là

A.

4 1 1

:

1 2 2

x y z

d

  

 



. B.

8 2 2

3 3 3

:

1 2 2

x y z

d

  

 



.

C.

4 17 19

9 9 9

:

1 2 2

x y z

d

  

 



. D.

6 6

:

1 2 2

x y z

d

 

 



.

Câu 75. (Chuyên Vinh - 2018) Trong không gian

Oxyz

, cho tam giác

ABC

có

 

2;3;3

A

, phương trình

đường trung tuyến kẻ từ

B

là

3 3 2

1 2 1

x y z

  

 

 

, phương trình đường phân giác trong của góc

C

là

2 4 2

2 1 1

x y z

  

 

 

. Đường thẳng

AB

có một véc-tơ chỉ phương là

A.

 

3

2;1; 1

u

 



. B.

 

2

1; 1;0

u  



. C.

 

4

0;1; 1

u

 



. D.

 

1

1;2;1

u 



.

Câu 76. (Chuyên Quang Trung- Bình Phước 2019) Trong không gian

Oxyz

, cho mặt phẳng

 

: 3 0

P x y z

   

và đường thẳng

1 2

:

1 2 1

x y z

d

 

 



. Đường thẳng

'd

đối xứng với

d

qua mặt phẳng

 

P

có phương trình là

A.

1 1 1

1 2 7

x y z  

 



. B.

1 1 1

1 2 7

x y z  

 

.

C.

1 1 1

1 2 7

x y z

  

 

. D.

1 1 1

1 2 7

x y z

  

 



.

Câu 77. Trong không gian

Oxyz

, cho đường thẳng

1 3

: 3

5 4

 





 





 



x t

d y

z t

. Gọi



là đường thẳng đi qua điểm

 

1; 3;5

A

và có vectơ chỉ phương

 

1;2; 2



u

. Đường phân giác của góc nhọn tạo bởi

d

và



có

phương trình là

A.

1 2

2 5

6 11

  





 





 



x t

y t

z t

. B.

1 2

2 5

6 11

  





 





  



x t

y t

z t

. C.

1 7

3 5

5

 





  





 



x t

y t

z t

. D.

1

3

5 7

 





 





 



x t

y

z t

.

Câu 78. (THPT Ninh Bình-Bạc Liêu-2019) Trong không gian

Oxyz

, cho mặt phẳng

 

: 2 10 0

P x y z

   

, điểm

 

1;3;2

A

và đường thẳng

2 2

: 1

1

x t

d y t

z t

  





 





 



. Tìm phương trình

đường thẳng



cắt

 

P

và

d

lần lượt tại hai điểm

M

và

N

sao cho

A

là trung điểm của đoạn

MN

.

A.

6 1 3

7 4 1

x y z  

 



. B.

6 1 3

7 4 1

x y z

  

 



.

C.

6 1 3

7 4 1

x y z

  

 

 

. D.

6 1 3

7 4 1

x y z  

 

 

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 18 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 79. (Chuyên Bắc Giang 2019) Trong không gian với hệ tọa độ

Oxyz

viết phương trình đường thẳng

giao tuyến của hai mặt phẳng

 

: 3 1 0

x y z

    

,

 

: 2 7 0

x y z

    

.

A.

2 3

2 3 7

x y z 

 

 

B.

2 3

2 3 7

x y z

 

 



C.

3 10

2 3 7

x y z

 

 

 

D.

2 3

2 3 7

x y z

 

 



Câu 80. Đường thẳng



là giao tuyến của 2 mặt phẳng:

5 0

x z

  

và

2 3 0

x y z

   

thì có phương

trình là

A.

2 1

1 3 1

x y z 

 



B.

2 1

1 2 1

x y z 

 



C.

2 1 3

1 1 1

x y z

  

 



D.

2 1 3

1 2 1

x y z

  

 



Câu 81. (Chuyên KHTN 2019) Trong không gian với hệ tọa độ

Oxyz

, gọi

 



là mặt phẳng chứa đường

thẳng

2 3

( ) :

1 1 2

x y z

d

 

 

và vuông góc với mặt phẳng

 

: 2z 1 0

x y



   

. Hỏi giao tuyến

của

 



và

 



đi qua điểm nào?

A.

 

0;1;3

. B.

 

2;3;3

. C.

 

5;6;8

D.

 

1; 2;0



Câu 82. (Chuyên Nguyễn Trãi Hải Dương 2019) Đường thẳng



là giao của hai mặt phẳng

5 0

x z

  

và

2 3 0

x y z

   

thì có phương trình là

A.

2 1

1 3 1

x y z 

 



. B.

2 1

1 2 1

x y z 

 



.

C.

2 1 3

1 1 1

x y z

  

 



. D.

2 1 3

1 2 1

x y z

  

 



.

Câu 83. (Mã 105 2017) Trong không gian với hệ tọa độ

Oxyz

, cho hai đường thẳng

  



  





 



2 3

: 3

4 2

x t

d y t

z t

và







 



1

4

:

3 1 2

y

x z

d

. Phương trình nào dưới đây là phương trình đường thẳng thuộc mặt phẳng

chứa

d

và



d

, đồng thời cách đều hai đường thẳng đó.

A.



 

 



2

3 2

3 1 2

y

x z

B.



 

 



2

3 2

3 1 2

y

x z

.

C.



 

 



2

3 2

3 1 2

y

x z

D.



 

 



2

3 2

3 1 2

y

x z

Câu 84. (THPT Nghen - Hà Tĩnh - 2018) Trong không gian với hệ tọa độ

Oxyz

cho hai đường thẳng

2

: 1 2

4 2

x t

d y t

z t

 





 





 



và

4 1

:

1 2 2

x y z

d

 



 



. Phương trình nào dưới đây là phương trình đường thẳng

thuộc mặt phẳng chứa

d

và

d



đồng thời cách đều hai đường thẳng đó.

A.

2 1 4

3 1 2

x y z

  

 



. B.

3 2 2

1 2 2

x y z

  

 



.

C.

3 2

1 2 2

x y z

 

 



. D.

3 2 2

1 2 2

x y z

  

 

 

.

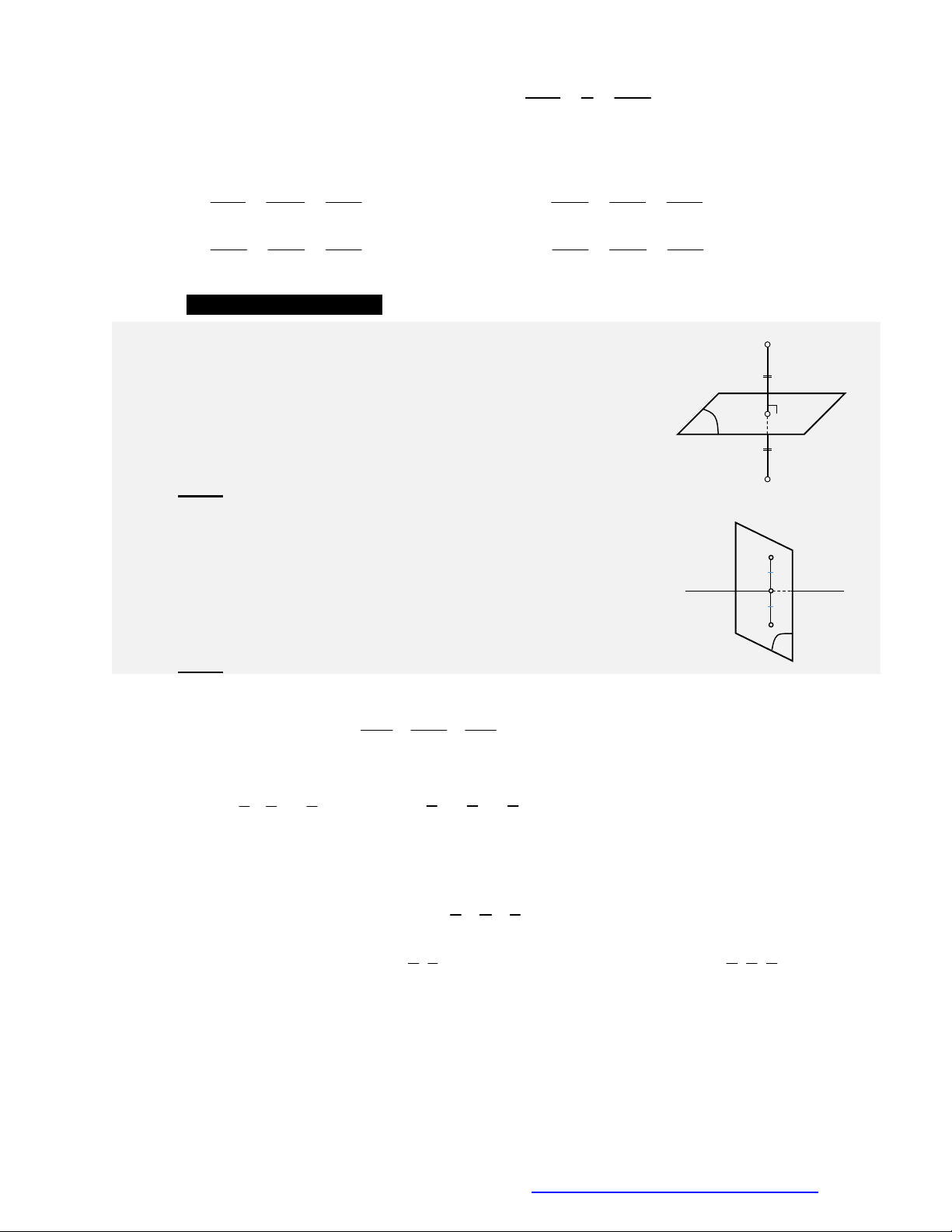
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19

Câu 85. (Toán Học Tuổi Trẻ 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho đường thẳng

d

và

mặt phẳng

 

P

lần lượt có phương trình

1 2

2 1 1

x y z

 

 

và

2 8 0

x y z

   

, điểm

 

2; 1;3

A



. Phương trình đường thẳng



cắt

d

và

 

P

lần lượt tại

M

và

N

sao cho

A

là trung

điểm của đoạn thẳng

MN

là:

A.

1 5 5

3 4 2

x y z

  

 

B.

2 1 3

6 1 2

x y z

  

 

C.

5 3 5

6 1 2

x y z

  

 

D.

5 3 5

3 4 2

x y z

  

 

Dạng 2. Bài toán tìm điểm

 Tìm hình chiếu

H

của điểm

M

lên mặt phẳng

( ) : 0

P ax by cz d

   

Viết phương trình đường thẳng

MH

qua

M

và vuông góc với

( ),P

khi đó:

( )H d P 

thỏa

1

2

3

?

? .

?

0

x x a t

x

y y a t

t y H

z z a t

z

ax by cz d

 









 

 

   

 

 

 







   





 Lưu ý: Để tìm điểm đối xứng

M



của điểm

M

qua

( )

P



H

là trung điểm

.MM



 Tìm hình chiếu

H

của điểm

M

lên đường thẳng

.d

Viết phương trình mặt phẳng

( )P

qua

M

và vuông góc với

,d

khi đó:

( )H d P 

thỏa

1

2

3

?

? .

?

0

x x a t

x

y y a t

t y H

z z a t

z

ax by cz d

 









 

 

   

 

 

 







   





 Lưu ý: Để tìm điểm đối xứng

M



của điểm

M

qua

d 

H

là trung điểm

.MM



Câu 1. (Mã 104 2017) Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm

 

1; 1; 2

A 

,

 

1; 2; 3

B 

và đường thẳng

1 2 1

:

1 1 2

x y z

d

  

 

. Tìm điểm

 

; ; M a b c

thuộc

d

sao cho

2 2

28

MA MB

 

, biết

0

c



.

A.

1 7 2

; ;

6 6 3

 



 

 

M

B.

1 7 2

; ;

6 6 3

M

 

  

 

 

C.

 

1; 0; 3 

M

D.

 

2; 3; 3

M

Câu 2. (THCS - THPT Nguyễn Khuyến 2019) Trong không gian

Oxyz

, tọa độ hình chiếu vuông góc

của

 

1;0;1

M

lên đường thẳng

 

:

1 2 3

x y z

  

là

A.

 

2;4;6

. B.

1 1

1; ;

2 3

 

 

 

. C.

 

0;0;0

. D.

2 4 6

; ;

7 7 7

 

 

 

.

Câu 3. Trong không gian với hệ tọa độ Oxyz, cho điểm

( 4;0;0)

M

và đường thẳng

1

: 2 3

2

 





   





 



x t

y t

z t

. Gọi

( ; ;c)H a b

là hình chiếu của

M

lên



. Tính a+b+c.

A.

5

. B.

1

. C.

3

. D.

7

.

P

M



M

H

M



H

d

P

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 20 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 4. (THPT Yên Phong 1 Bắc Ninh 2019) Trong không gian Oxyz, tìm tọa độ hình chiếu H của

 

1;1;1

A

lên đường thẳng

d :

1

x t

y t

z t

 













.

A.

H

4 4 1

( ; ; ).

3 3 3

B.

 

1;1;1 .

H

C.

(0 ; 0 ; -1).

H

D.

(1 ; 1 ; 0).

H

Câu 5. (THPT Quang Trung Dống Da Hà Nội 2019) Trong không gian với hệ tọa độ

Oxyz

, cho điểm

 

1;1;1

A

và đường thẳng

 

6 4

: 2

1 2

x t

d y t

z t

 





  





  



. Tìm tọa độ hình chiếu

A



của

A

trên

 

d

.

A.

(2;3;1)

A



. B.

( 2;3;1)

A





. C.

(2; 3;1)

A





. D.

(2; 3; 1)

A



 

.

Câu 6. Trong không gian

Oxyz

, cho hình thang cân

ABCD

có đáy là

AB

và

CD

. Biết

 

3;1; 2

A



,

 

1;3;2

B 

,

 

6;3;6

C 

và

 

; ;D a b c

với

, ,a b c



. Giá trị của

a b c 

bằng

A.

3

. B.

1

. C.

3

. D.

1

.

Câu 7. (THPT Chuyên Đại Học Vinh 2019) Trong không gian

Oxyz

, cho đường thẳng

1 2

:

2 1 1

x y z

d

 

 



và hai điểm

 

1;3;1

A 

;

 

0;2; 1

B



. Gọi

 

; ;C m n p

là điểm thuộc đường

thẳng

d

sao cho diện tích tam giác

ABC

bằng

2 2

. Giá trị của tổng

m n p 

bằng

A.

1

B.

2

C.

3

D.

5

Câu 8. (Chuyên Hà Tĩnh - 2018) Trong không gian

Oxyz

, cho đường thẳng

1 3 2

:

1 2 2

x y z

d

  

 

và

điểm

 

3;2;0

A

. Điểm đối xứng của điểm

A

qua đường thẳng

d

có tọa độ là

A.

 

1;0;4



. B.

 

7;1; 1

. C.

 

2;1; 2

. D.

 

0;2; 5

.

Câu 9. (Sở Bình Phước -2019) Trong không gian

Oxyz

, khoảng cách từ điểm

 

2; 4; 1

M

 

tới đường

thẳng

: 2

3 2

x t

y t

z t







  





 



bằng

A.

14

B.

6

C.

2 14

D.

2 6

Câu 10. Trong không gian với hệ trục tọa độ

Oxyz

, Gọi

 

; ; M a b c

thuộc đường thẳng

1 2

:

1 2 3

x y z

 

  

. Biết điểm

M

có tung độ âm và cách mặt phẳng

 

Oyz

một khoảng bằng 2.

Xác định giá trị

T a b c  

.

A.

1T  

. B.

11T 

. C.

13

T

 

. D.

1T 

.

Câu 11. Trong không gian

Oxyz

, cho

 

2;0;0

A

, đường thẳng

d

đi qua

A

cắt chiều âm trục

Oy

tại

điểm

B

sao cho diện tích tam giác

OAB

bằng 1. Phương trình tham số đường thẳng

d

là

A.

1 2

0

x t

y t

z

 















. B.

2 2

0

x t

y t

z

 





 









. C.

2 2

0

x t

y t

z

 





 









. D.

2 2

1

x t

y t

z

 















.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21

Câu 12. (Bắc Ninh 2019) Trong không gian với hệ tọa độ

Oxyz

, cho đường thẳng

2 1

:

3 1 2

x y z 

  



.

Gọi

M

là giao điểm của



với mặt phẳng

 

: 2 3 2 0P x y z   

. Tọa độ điểm

M

là

A.

 

2;0; 1M 

. B.

 

5; 1; 3M  

. C.

 

1;0;1M

. D.

 

1;1;1M 

.

Câu 13. (THCS - THPT Nguyễn Khuyến 2019) Trong không gian

Oxyz

, tọa độ hình chiếu vuông góc

của điểm

 

3;2; 1A 

lên mặt phẳng

 

: 0x y z



  

là:

A.

 

2;1;1

. B.

5 2 7

; ;

3 3 3

 



 

 

. C.

 

1;1; 2

. D.

1 1 1

; ;

2 4 4

 

 

 

.

Câu 14. (THCS - THPT Nguyễn Khuyến 2019) Trong không gian với hệ trục tọa độ

Oxyz

, hình chiếu

của điểm

 

1;0;3M

theo phương véctơ

 

1; 2;1 



v

trên mặt phẳng

 

: 2 0   P x y z

có

tọa độ là

A.

 

2; 2; 2 

. B.

 

1;0;1

. C.

 

2;2;2

. D.

 

1;0; 1

.

Câu 15. (Chuyên Hùng Vương Gia Lai 2019) Trong không gian

Oxyz

, giao điểm của mặt phẳng

 

: 3 5 2 0P x y z   

và đường thẳng

12 9 1

:

4 3 1

x y z  

  

là điểm

 

0 0 0

; ;M x y z

. Giá trị

tổng

0 0 0

x y z 

bằng

A.

1

. B.

2

. C.

5

. D.

2

.

Câu 16. Trong không gian với hệ tọa độ

Oxyz

, cho 3 điểm

     

1;0;0 , 0;2;0 , 0;0;3A B C

và

Gọi

( ; ; )M a b c

là tọa độ giao điểm của d và mặt phẳng . Tổng

S a b c  

là:

A. -7. B. 11. C. 5. D. 6.

Câu 17. (Đề Tham Khảo 2017) Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

 

:6 2 35 0P x y z   

và điểm

 

1;3;6 .A

Gọi

'A

là điểm đối xứng với

A

qua

 

P

, tính

'.OA

A.

5 3OA





B.

46OA





C.

186OA





D.

3 26OA





Câu 18. (KTNL GV Thuận Thành 2 Bắc Ninh 2019) Trong không gian với hệ tọa độ

Oxyz

, xác định tọa độ

điểm

M



là hình chiếu vuông góc của điểm

 

2;3;1M

lên mặt phẳng

 

: 2 0x y z



  

.

A.

5

2; ;3

2

M

 



 

 

. B.

 

1;3;5M



. C.

5 3

;2;

2 2

M

 



 

 

. D.

 

3;1;2M



.

Câu 19. (Chuyên Lê Hồng Phong Nam Định 2019) Trong không gian

Oxyz

, điểm

M



đối xứng với

điểm

 

1;2;4M

qua mặt phẳng

 

: 2 2 3 0x y z



   

có tọa độ là

A.

 

3;0;0

. B.

 

1;1;2

. C.

 

1; 2; 4  

. D.

 

2;1;2

.

Câu 20. (KSCL THPT Nguyễn Khuyến 2019) Trong không gian

Oxyz

, cho điểm

 

1;2; 1A 

,đường

thẳng

1 1 2

:

2 1 1

x y z

d

  

 



và mặt phẳng

 

: 2 1 0P x y z   

. Điểm

B

thuộc mặt phẳng

 

P

thỏa mãn đường thẳng

AB

vuông góc và cắt đường thẳng

d

. Tọa độ điểm

B

là

A.

(6; 7;0)

B.

(3; 2; 1) 

C.

( 3;8; 3) 

D.

(0;3; 2)



 



 





 



: 2 .

3

x t

d y t

z t

 

ABC

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 22 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 21. Trong không gian với hệ tọa độ

Oxyz

, gọi

d

là đường thẳng qua

 

1;0;2

A

, cắt và vuông góc

với đường thẳng

1

1 5

:

1 1 2

x y z

d

 

 



. Điểm nào dưới đây thuộc

d

?

A.

 

2; 1;1

P



. B.

 

0; 1;1

Q



. C.

 

0; 1;2

N



. D.

 

1; 1;1

M

 

.

Câu 22. Trong không gian

Oxyz

, cho tam giác đều

ABC

với

 

6;3;5

A

và đường thẳng

BC

có phương

trình tham số

1

2

x t

y t

z t

 





 









. Gọi



là đường thẳng qua trọng tâm

G

của tam giác

ABC

và vuông

góc với mặt phẳng

 

ABC

. Điểm nào dưới đây thuộc đường thẳng



?

A.

 

1; 12;3

M  

. B.

 

3; 2;1

N 

. C.

 

0; 7;3

P 

. D.

 

1; 2;5

Q 

.

Câu 23. (Chuyên Đại học Vinh - 2019) Trong không gian

Oxyz

, cho đường thẳng

1 2

:

2 1 1

x y z

d

 

 



và hai điểm

 

1;3;1

A 

,

 

0;2; 1

B



. Gọi

 

; ;C m n p

là điểm thuộc

d

sao cho diện tích tam giác

ABC

bằng

2 2

. Giá trị của tổng

m n p 

bằng

A.

1

. B. 2. C. 3. D.

5

.

Câu 24. (Đà Nẵng 2019) Trong không gian

 

Oxyz

cho hai đường thẳng

2 4

1 1 2

x y z 

 



và

3 1 2

2 1 1

x y z

  

 

 

. Gọi

M

là trung điểm đoạn vuông góc chung của hai đường thẳng trên. Tính

đoạn

OM

.

A.

14

2

OM 

. B.

5

OM 

. C.

2 35

OM 

. D.

35

OM 

.

Câu 25. (Kinh Môn - Hải Dương 2019) Trong không gian với hệ tọa độ

Oxyz

, cho

 

: 2 0

P x y z

  

và đường thẳng

1 2

:

2 1 1

x y z

d

 

 



. Đường thẳng

d

cắt

 

P

tại điểm

A

. Điểm

 

; ;M a b c

thuộc

đường thẳng

d

và có hoành độ dương sao cho

6

AM  . Khi đó tổng

2016

S a b c  

là

A.

2018

. B.

2019

. C.

2017

. D.

2020

.

Câu 26. Trong không gian

Oxyz

, cho hai đường thẳng

1

1 1

:

1 1 2

x y z

d

 

 



,

2

1

:

1 2 1

x y z

d



 

. Đường

thẳng

d

đi qua

 

5; 3;5

A 

lần lượt cắt

1

d

,

2

d

tại

B

và

.C

Độ dài

BC

là

A.

19

. B.

19

. C.

3 2

. D.

2 5

.

Câu 27. Trong không gian với hệ tọa độ

Oxyz

, cho điểm

 

3;3; 2

M



và hai đường thẳng

1

1 2

:

1 3 1

x y z

d

 

 

;

2

1 1 2

:

1 2 4

x y z

d

  

 



. Đường thẳng

d

đi qua

M

căt

1 2

,d d

lần lượt tại

A

và

B

. Độ dài đoạn thẳng

AB

bằng

A.

3

. B.

6

. C.

4

. D.

2

.

Câu 28. Cho ba điểm

 

1;1;1

A

,

 

0;0;2

B

,

 

2;3; 2

C



và đường thẳng

2

: 1

x t

y t

z t

 





  









.

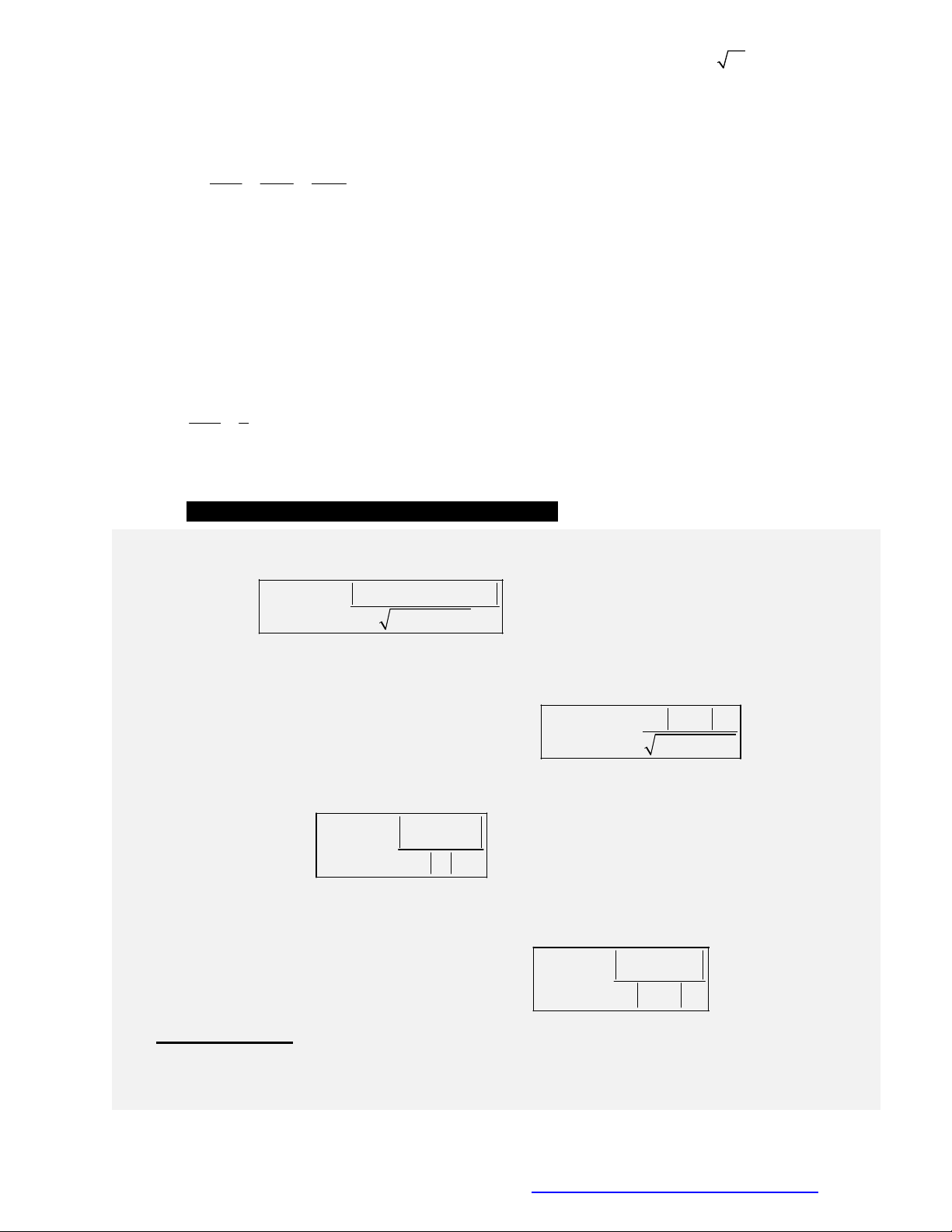
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23

Biết điểm

 

; ;M a b c

với

0

a



thuộc mặt phẳng

 

ABC

sao cho

AM  

và

14

AM 

. Tính giá trị của

biểu thức

T a b c  

.

A.

1T  

. B.

5

T



. C.

7

T



. D.

6

T

 

.

Câu 29. (Chuyên Đh Vinh - 2018) Trong không gian

Oxyz

, cho điểm

 

1;2; 1

A



, đường thẳng

1 1 2

:

2 1 1

x y z

d

  

 



và mặt phẳng

 

: 2 1 0

P x y z

   

. Điểm

B

thuộc mặt phẳng

 

P

thỏa

mãn đường thẳng

AB

vuông góc và cắt đường thẳng

d

. Tọa độ điểm

B

là

A.

 

3; 2; 1 

. B.

 

3;8; 3 

. C.

 

0;3; 2

. D.

 

6; 7;0



.

Câu 30. (SGD Bạc Liêu - 2018) Trong không gian với hệ trục tọa độ

Oxyz

, cho đường thẳng

 

3

: 1 ,

2

x t

y t t

z t

 





    





  





, điểm

 

1;2; 1

M



và mặt cầu

 

2 2 2

: 4 10 14 64 0

S x y z x y z

      

.

Gọi





là đường thẳng đi qua

M

cắt đường thẳng



tại

A

, cắt mặt cầu tại

B

sao cho

1

3

AM

AB



và điểm

B

có hoành độ là số nguyên. Mặt phẳng trung trực đoạn

AB

có phương trình là

A.

2 4 4 19 0

x y z

   

. B.

3 6 6 62 0

x y z

   

.

C.

2 4 4 43 0

x y z

   

. D.

3 6 6 31 0

x y z

   

.

Dạng 3. Bài toán liên quan đến góc – khoảng cách

1. Khoảng cách từ một điểm đến mặt phẳng, khoảng cách giữa hai mặt phẳng song song



Khoảng cách từ điểm

( ; ; )

M M M

M x y z

đến mặt phẳng

( ) : 0

P ax by cz d

   

được xác định bởi

công thức:

2 2 2

( ;( ))

M M M

ax by cz d

d M P

a b c

  

 

 

Khoảng cách giữa đường thẳng và mặt phẳng song song là khoảng cách từ một điểm thuộc đường

thẳng đến mặt phẳng



Cho hai mặt phẳng song song

( ) : 0

P ax by cz d

   

và

( ) : 0

Q ax by cz d



   

có cùng véctơ

pháp tuyến, khoảng cách giữa hai mặt phẳng đó là

 

2 2 2

( ),( )

d d

d Q P

a b c





 

 

2. Khoảng cách từ một điểm đến đường thẳng – Khoảng cách giữa hai đường thẳng



Khoảng cách từ điểm

M

đến một đường thẳng

d

qua điểm

M



có véctơ chỉ phương

d

u



được xác

định bởi công thức

,

( , )

d

M M u

d M d

u

 

 

 







Khoảng cách giữa hai đường thẳng song song là khoảng cách từ một điểm thuộc đường thẳng này

đến đường thẳng kia.



Khoảng cách giữa hai đường thẳng chéo nhau:

d

đi qua điểm

M

và có véctơ chỉ phương

u



và

d



đi qua điểm

M



và có véctơ chỉ phương

u





là

 

, .

( , )

,

u u M M

d d d

u u



 







 

3. Góc giữa hai véctơ

Cho hai véctơ

1 2 3

( ; ; )a a a a



và

1 2 3

( ; ; ).b b b b





Khi đó góc giữa hai véctơ

a



và

b



là góc nhợn hoặc

tù.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 24 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

1 1 2 2 3 3

2 2 2 2 2 2

1 2 3 1 2 3

.

cos( ; )

.

a b a b a b

a b

a a a b b b

 

 

   



với

0 180 .



   

4. Góc giữa hai mặt phẳng

Cho hai mặt phẳng

1 1 1 1

( ) : 0

P A x B y C z D

   

và

2 2 2 2

( ) : 0.

Q A x B y C z D

   

 

1 2 1 2 1 2

2 2 2 2 2 2

1 1 1 2 2 2

.

cos ( ),( ) cos

.

P Q

n n

A A B B C C

P Q

n n

A B C A B C



 

  

   

 

với

0 90 .



   

5. Góc giữa hai đường thẳng

Góc giữa hai đường thẳng

1

d

và

2

d

có véctơ chỉ phương

1 1 1 1

( ; ; )u a b c



và

2 2 2 2

( ; ; ).u a b c



1 2 1 2 1 2 1 2

1 2

2 2 2 2 2 2

1 2

1 1 1 2 2 2

.

cos( ; ) cos

.

u u a a b b c c

d d

u u

a b c a b c



 

  

   

 

với

0 90 .



   

6. Góc giữa đường thẳng và mặt phẳng

Góc giữa đường thẳng

d

có véctơ chỉ phương

( ; ; )

d

u a b c



và mặt phẳng

( )P

có véctơ pháp tuyến

( )

( ; ; )

P

n A B C



được xác định bởi công thức:

( )

2 2 2 2 2 2

( )

.

sin cos( ; )

.

d P

P d

d P

u n

aA bB cC

n u

u n

a b c A B C



 

  

   

 

với

0 90 .



   

Câu 31. Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

 

: 4 7 25 0

P x y z

   

và đường thẳng

1

1 1

:

1 2 1

x y z

d

 

 



. Gọi

1

'd

là hình chiếu vuông góc của

1

d

lên mặt phẳng

 

P

. Đường thẳng

2

d

nằm trên

 

P

tạo với

1 1

, 'd d

các góc bằng nhau,

2

d

có vectơ chỉ phương

 

2

; ;u a b c



. Tính

2a b

c



.

A.

2 2

3

a b

c





. B.

2

0

a b

c





. C.

2 1

3

a b

c





. D.

2

1

a b

c





.

Câu 32. Trong không gian với hệ tọa độ

,Oxyz

cho hai điểm

   

3;1;7 , 5;5;1

A B

và mặt phẳng

 

:2 4 0

P x y z

   

. Điểm

M

thuộc

 

P

sao cho

35.

MA MB 

Biết

M

có hoành độ

nguyên, ta có

OM

bằng

A.

2 2

. B.

2 3

. C.

3 2

. D.

4

.

Câu 33. (Chuyen Phan Bội Châu Nghệ An 2019) Trong không gian với hệ tọa độ

Oxyz

, cho hai đường

thẳng

1

1 2 1

: ,

2 2 1

x y z

d

  

 

 

2

: 0 .

x t

d y

z t













 



Mặt phẳng

 

P

qua

1

d

tạo với

2

d

một góc

0

45

và

nhận vectơ

 

1; ;n b c





làm một vectơ pháp tuyến. Xác định tích

.bc

A.

4

hoặc

0.

B.

4

hoặc

0.

C.

4

. D.

4

.

Câu 34. (Chuyên Phan Bội Châu 2019) Trong không gian với hệ tọa độ

O

xyz

, cho hai đường thẳng

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25

1

1 2 1

:

2 2 1

x y z

d

  

 

 

và

2

: 0

x t

d y

z t













 



. Mặt phẳng

 

P

qua

1

d

tạo với

2

d

một góc

o

45

và nhận

véctơ

 

1; ;n b c



làm một véctơ pháp tuyến. Xác định tích

bc

.

A.

4

hoặc

0

B.

4

hoặc

0

C.

4

D.

4

Câu 35. (Chuyên Phan Bội Châu Nghệ An 2019) rong không gian

Oxyz

, cho hai đường thẳng

1

1 2 1

:

2 2 1

x y z

d

  

 

 

và

2

: 0

x t

d y

z t













 



. Mặt phẳng

 

P

qua

1

d

, tạo với

2

d

một góc

45

và nhận

vectơ

 

1; ;n b c



làm một vec tơ pháp tuyến. Xác định tích

.b c

.

A.

4

. B.

4

. C.

4

hoặc

0

. D.

4

hoặc

0

.

Câu 36. Trong không gian tọa độ

O

xyz

cho đường thẳng

3 2 1

:

2 1 1

x y z

d

  

 



, mặt phẳng

( ) : 2 0

P x y z

   

. Gọi

M

là giao điểm của

d

và

( )P

. Gọi



là đường thẳng nằm trong

( )P

vuông góc với

d

và cách

M

một khoảng

42

. Phương trình đường thẳng



là

A.

5 2 4

2 3 1

x y z

  

 



. B.

1 1 1

2 3 1

x y z  

 

 

.

C.

3 4 5

2 3 1

x y z

  

 



. D. Đáp án khác.

Câu 37. (THPT Lê Quý Đôn Đà Nẵng 2019) Trong không gian

Oxyz

, đường thẳng

: 1 2 , ,

2

x t

d y t t

z t







   





 





cắt mặt phẳng

 

: 3 0

P x y z

   

tại điểm

I

. Gọi



là đường thẳng

nằm trong mặt phẳng

 

P

sao cho

d 

và khoảng cách từ điểm

I

đến đường thẳng



bằng

42

. Tìm tọa độ hình chiếu

 

; ;M a b c

( với

a b c 

) của điểm

I

trên đường thẳng



.

A.

 

2;5; 4

M



. B.

 

6; 3;0

M 

. C.

 

5;2; 4

M



. D.

 

3;6;0

M 

.

Câu 38. (Chuyên Đại Học Vinh 2019) Trong không gian

Oxyz

cho ba đường thẳng

1

: ,

1 1 2

x y z

d



 



1

3 1

: ,

2 1 1

x y z

 

  

2

1 2

:

1 2 1

x y z 

  

. Đường thẳng



vuông góc với

d

đồng thời cắt

1 2

, 

tương ứng tại

,H K

sao cho độ dài

HK

nhỏ nhất. Biết rằng



có một vectơ

chỉ phương

 

; ;1 .

u h k



Giá trị

h k

bằng

A.

0.

B.

4.

C.

6.

D.

2.

Câu 39. (Hội 8 trường chuyên 2019) Trong không gian

,Oxyz

gọi

d

là đường thẳng đi qua

,O

thuộc

mặt phẳng

 

Oyz

và cách điểm

 

1; 2;1

M 

một khoảng nhỏ nhất. Côsin của góc giữa

d

và trục

tung bằng

A.

2

5

. B.

1

5

. C.

1

5

. D.

2

5

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 26 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 40. (Sở Cần Thơ - 2019) Trong không gian

Oxyz

, cho điểm

 

2;1;1

A

, mặt phẳng

 

: 1 0  

P x z

và đường thẳng

 

1

: 2

2

 











  



x t

d y

z t

. Gọi

1 2

;d d

là các đường thẳng đi qua

A

, nằm trong

 

P

và đều

có khoảng cách đến đường thẳng

d

bằng

6

. Côsin của góc giữa

1

d

và

2

d

bằng

A.

1

3

. B.

2

3

. C.

3

. D.

2

3

.

Câu 41. (Chuyên Bắc Giang 2019) Trong không gian với hệ tọa độ

Oxyz

, cho đường thẳng

 

3 3

: ,

1 3 2

x y z

d

 

 

mặt phẳng

 

: 3 0

P x y z

   

và điểm

 

1; 2; 1

A



. Cho đường thẳng

 



đi qua

A

, cắt

 

d

và song song với mặt phẳng

 

P

. Tính khoảng cách từ gốc tọa độ

O

đến

 



A.

3

. B.

16

3

. C.

2 3

3

. D.

4 3

3

.

Câu 42. (Kim Liên - Hà Nội 2019) Trong không gian

Oxyz

, cho hai đường thẳng

1

1 2

:

2 1 1

x y z

d

 

 



và

2

1 4

: 1 2

2 2

x t

d y t

z t

 





  





 



.

Khoảng cách giữa hai đường thẳng đã cho bằng?

A.

87

6

. B.

174

6

. C.

174

3

. D.

87

3

.

Câu 43. Trong không gian

Oxyz

, cho hai điểm

 

3;1;2

A

,

 

3; 1;0

B  

và mặt phẳng

 

: 3 14 0

P x y z

   

. Điểm

M

thuộc mặt phẳng

 

P

sao cho

MAB

vuông tại

M

. Tính

khoảng cách từ điểm

M

đến mặt phẳng

 

Oxy

.

A. 5. B. 4. C. 3. D. 1.

Câu 44. Trong không gian với hệ trục tọa độ

Oxyz

, cho 4 điểm

     

2;0;0 , 0;3;0 , 0;0;6

A B C

và

 

1;1;1

D

. Gọi



là đường thẳng qua

D

và thỏa mãn tổng khoảng cách từ các điểm

, ,A B C

đến



là lớn nhất. Khi đó



đi qua điểm nào dưới đây?

A.

 

4;3;7

. B.

 

1; 2;1

 

. C.

 

7;5;3

. D.

 

3;4;3

.

Câu 45. (Nguyễn Huệ- Ninh Bình- 2019)Tính khoảng cách từ giao điểm của hai đường thẳng

1 2

;d d

tới

mặt phẳng

 

P

trong đó:

 

1 2

1 1 1 1

: ; : ; : 2 4 4 3 0

2 3 3 2 1 1

x y z x y z

d d P x y z

    

       

.

A.

4

3

. B.

7

6

. C.

13

6

. D.

5

3

.

Câu 46. (THPT Hậu Lộc 2 2019) Trong không gian

Oxyz

, cho mặt phẳng

 

: 2 2 3 0

P x y z

   

và

đường thẳng

 

1 1 1

:

2 2 1

x y x  

  



. Khoảng cách giữa

 



và

 

P

là

A.

2

3

B.

8

3

C.

2

9

D.

1

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27

Câu 47. Trong không gian với hệ tọa độ

Oxyz

,cho đường thẳng

0

: 3

x

d y t

z t







 









.Gọi

 

P

là mặt phẳng chứa

đường thẳng

d

và tạo với mặt phẳng

 

Oxy

một góc

45

.Điểm nào sau đây thuộc mặt phẳng

 

P

?

A.

 

3;2;1

M

. B.

 

3;2; 1

N



. C.

 

3; 1;2

P 

. D.

 

3; 1; 2

M

 

.

Câu 48. (Chuyên Hà Tĩnh 2019)) Trong không gian với hệ tọa độ

Oxyz

cho đường thẳng

5 7 12

:

2 2 1

  

 



x y z

d

và mặt phẳng

 

: 2 3 3 0   

x y z



. Gọi

M

là giao điểm của

d

và

 



,

A

thuộc

d

sao cho

14

AM

. Tính khoảng cách từ

A

đến mặt phẳng

 



.

A.

2

. B.

3

. C.

6

. D.

14

.

Câu 49. (Hội 8 trường chuyên 2019) Trong không gian

,Oxyz

cho

2

đường thẳng

1

1 2 1

:

1 1 2

x y z

d

  

 

và

2

1 1 2

: .

2 1 1

x y z

d

  

 

Mặt phẳng

   

: 0 0

P x ay bz c c

    

song song với

1 2

,d d

và khoảng cách từ

1

d

đến

 

P

bằng 2 lần khoảng cách từ

2

d

đến

 

.P

Giá

trị của

a b c 

bằng

A.

14

. B.

6

. C.

4.

D.

6

.

Câu 50. Trong không gian với hệ trục toạ độ

Oxyz

, cho hai điểm

   

3;3;1 , 0;2;1

A B

và mặt phẳng

 

: 7 0

P x y z

   

. Đường thẳng

d

nằm trong

 

P

sao cho mọi điểm của

d

cách đều hai

điểm

,A B

có phương trình là:

A.

2

7 3

x t

y t

z t







 









. B.

7 3

2

x t

y t

z t







 









. C.

7 3

2

x t

y t

z t







 









. D.

7 3

4

x t

y t

z t

 





 









.

Câu 51. (Chuyên ĐH Vinh- 2019) Trong không gian

Oxyz

, cho tam giác

ABC

vuông tại

A

,



0

30

ABC  ,

3 2

BC 

, đường thẳng

BC

có phương trình

4 5 7

1 1 4

x y z

  

 



, đường thẳng

AB

nằm

trong mặt phẳng

 

: 3 0

x z



  

. Biết đỉnh

C

có cao độ âm. Tính hoành độ đỉnh A.

A.

3

2

. B.

3

. C.

9

2

. D.

5

2

.

Dạng 4. Viết phương trình mặt phẳng liên quan đến đường thẳng

Dạng 1. Viết phương trình mp

 

P

đi qua

,M

vuông góc mp

 

Q

và

 

//

mp P



:

 

   

• , ,

:

• :

,

Đ

o o o

PP

P Q

M x y z

mp P

VT n

i q

PT

u

n u

a











 





 



  

Dạng 2. Viết phương trình mặt phẳng

 

P

đi qua M và vuông góc với đường thẳng d đi qua hai

điểm A và B, với:

 

•

:

•

Đ

:

PP

d

P

M

mp P

VTPT n

i qua

u AB









 





  

u





Δ

P

Q

 

Q

n



P

 

P d

n u AB

 

  

d

M

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 28 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Dạng 3. Viết phương trình của mặt phẳng

 

P

đi qua điểm M và chứa đường thẳng



:

PP



Trên đường thẳng Δ lấy điểm A và xác định VTCP

u





Khi đó

 

•

:

• : ,

Đ

P

M

m

V

i qua

p P

TPT n AM u









 





 



  

Dạng 4. Viết phương trình của mặt phẳng

 

P

đi qua hai đường thẳng song song

1 2

,  

:

 

1 2

• ,

:

•

Đ

: ,

PP

P

M hay M

mp P

VTPT n u u

i qua

 

 









 





 



  

Dạng 5. Viết phương trình của mặt phẳng

 

P

đi qua hai đường thẳng cắt nhau

1 2

, : 

 

1 2

• ,

:

•

Đ

: ,

PP

P

M hay M

mp P

VTPT n u u

i qua

 

 









 





 



  

Dạng 6. Cho 2 đường thẳng chéo nhau

1 2

,  

. Hãy viết phương trình

 

P

chứa

1



và song song

2



 

1 2

• ,

:

•

Đ

: ,

PP

P

M hay M

mp P

VTPT n u u

i qua

 

 









 





 



  

Dạng 7. Viết phương trình mặt phẳng

 

P

đi qua điểm M và giao tuyến của hai mặt phẳng

   

,

 

PP



Chọn

,A B

thuộc giao tuyến hai mặt phẳng

 



và

 



 

,

A B P

 

. Cụ thể:

Cho:

 

   

1 1 1 1

2 2 2 2

...

...;...;...

...

o

A x B y C z D

x

z z A P

y

A x B y C z D

   







    

 



   







Cho:

 

   

1 1 1 1

2 2 2 2

...

...;...;...

...

o

B y C z A x D

y

x x B P

z

B y C z A x D

   







    

 



   







Khi đó

 

Đ •

:

• : ,

P

m

V

i qua M

p P

TPT n AB AM







 





 



  

Câu 52. (Đề Minh Họa 2017) Trong không gian với hệ tọa độ

Oxyz

, cho đường thẳng



có phương

trình:

10 2 2

5 1 1

x y z

  

 

. Xét mặt phẳng

 

:10 2 11 0

P x y mz

   

,

m

là tham số thực. Tìm tất cả

các giá trị của

m

để mặt phẳng

 

P

vuông góc với đường thẳng



.

A.

2

m



B.

52

m

 

C.

52

m



D.

2

m

 

M

Δ

A

u





P

M

Δ

1

u





P

2

u





Δ

2

M

Δ

1

u





P

2

u





Δ

2

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 29

Câu 53. Trong không gian với hệ tọa độ

Oxyz

, cho đường thẳng

1 2

:

1 2 3

x y z 

  

 

và mặt phẳng

 

: 3 0

P x y z

   

. Phương trình mặt phẳng

 



đi qua

O

, song song với



và vuông góc với

mặt phẳng

 

P

là

A.

2 0

x y z

  

. B.

2 0

x y z

  

. C.

2 4 0

x y z

   

. D.

2 4 0

x y z

   

.

Câu 54. (Toán Học Tuổi Trẻ 2019) Trong không gian với hệ tọa độ

Oxyz

, cho đường thẳng

1

d

có véctơ

chỉ phương

 

1;0; 2

u

 



và đi qua điểm

 

1; 3;2

M



,

2

3 1 4

:

1 2 3

x y z

d

  

 



. Phương trình

mặt phẳng

 

P

cách đều hai đường thẳng

1

d

và

2

d

có dạng

11 0

ax by cz

   

. Giá trị

2 3a b c 

bằng

A.

42

. B.

32

. C.

11

. D.

20

.

Câu 55. Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng

 

P

song song và cách đều

hai đường thẳng

1

2

:

1 1 1

x y z

d



 



và

2

1 2

:

2 1 1

x y z

d

 

 

 

A.

 

:2 2 1 0

xP z

  

B.

 

:2 2 1 0

yP z

  

C.

 

:2 2 1 0

xP y

  

D.

 

:2 2 1 0

yP z

  

Câu 56. (SGD Cần Thơ - 2018) Trong không gian

Oxyz

, mặt phẳng chứa hai đường thẳng cắt nhau

1 2 4

2 1 3

  

 



x y z

và

1 2

1 1 3

 

 



x y z

có phương trình là

A.

2 9 36 0    

x y z

. B.

2 0  

x y z

.

C.

6 9 8 0   

x y z

. D.

6 9 8 0   

x y z

.

Câu 57. (Hồng Bàng - Hải Phòng - 2018) Trong không gian tọa độ

,Oxyz

cho điểm

 

0;1;0 ,

A

mặt

phẳng

 

: 4 6 0

Q x y z

   

và đường thẳng

3

: 3

5

x

d y t

z t







 





 



. Phương trình mặt phẳng

 

P

qua

A

,

song song với

d

và vuông góc với

 

Q

là :

A.

3 1 0

x y z

   

. B.

3 1 0

x y z

   

. C.

3 3 0

x y z

   

. D.

1 0

x y z

   

.

Câu 58. (Toán Học Tuổi Trẻ - 2018) Trong không gian với hệ tọa độ Descartes

Oxyz

, cho điểm

 

3; 1;0

A 

và đường thẳng

2 1 1

:

1 2 1

x y z

d

  

 



. Mặt phẳng

 



chứa

d

sao cho khoảng cách

từ

A

đến

 



lớn nhất có phương trình là

A.

0

x y z

  

. B.

2 0

x y z

   

. C.

1 0

x y z

   

. D.

2 5 0

x y z

    

.

Câu 59. (SGD&ĐT BRVT - 2018) Trong không gian

Oxyz

, cho hai đường thẳng chéo nhau

1

2 6 2

:

2 2 1

x y z

d

  

 



và

2

4 1 2

:

1 3 2

x y z

d

  

 



. Phương trình mặt phẳng

 

P

chứa

1

d

và

 

P

song song với đường thẳng

2

d

là

A.

 

: 5 8 16 0

P x y z

   

. B.

 

: 5 8 16 0

P x y z

   

.

C.

 

: 4 6 12 0

P x y z

   

. D.

 

: 2 6 0

P x y

  

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 30 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 60. (Chuyên Thăng Long - Đà Lạt - 2018) Trong không gian

Oxyz

, phương trình mặt phẳng chứa

hai đường thẳng:

 

2

: 3 1

2 1

x t

d y t

z t

 





 





 



và

 

3

: 3 2

2 1

x m

y m

z m

 





  





 



có dạng

0

x ay bz c

   

. Tính

2 3P a b c  

.

A.

10

P

 

. B.

4P 

. C.

8

P

 

. D.

0

P



.

Câu 61. (Chuyên Trần Đại Nghĩa - 2018) Tìm tất cả các mặt phẳng

 



chứa đường thẳng

d

:

1 1 3

x y z

 

 

và tạo với mặt phẳng

 

P

:

2 1 0

x z

  

góc

45

.

A.

 



:

3 0

x z

 

. B.

 



:

3 0

x y z

  

.

C.

 



:

3 0

x z

 

. D.

 



:

3 0

x z

 

hay

 



:

8 5 0

x y z

  

.

Câu 62. (Quảng Nam - 2018) Trong không gian với hệ trục tọa độ

Oxyz

, cho hai điểm

 

1;1;0

A

,

 

0; 1;2

B 

. Biết rằng có hai mặt phẳng cùng đi qua hai điểm

A

,

O

và cùng cách

B

một khoảng

bằng

3

. Véctơ nào trong các véctơ dưới đây là một véctơ pháp tuyến của một trong hai mặt

phẳng đó.

A.

 

1; 1; 1

n

  



. B.

 

1; 1; 3

n

  



. C.

 

1; 1;5

n  



. D.

 

1; 1; 5

n

  



.

Câu 63. (Sở Bình Phước - 2018) Trong không gian với hệ toạ độ

Oxyz

, cho hai đường thẳng

1 2

,d d

lần

lượt có phương trình

1

2 2 3

:

2 1 3

x y z

d

  

 

,

2

1 2 1

:

2 1 4

x y z

d

  

 



. Mặt phẳng cách đều hai

đường thẳng

1 2

,d d

có phương trình là

A.

14 4 8 1 0.

x y z

   

B.

14 4 8 3 0.

x y z

   

C.

14 4 8 3 0.

x y z

   

D.

14 4 8 1 0.

x y z

   

Câu 64. (THPT Thực Hành - TPHCM - 2018) Trong không gian tọa độ

Oxyz

, cho điểm

 

1;0;0

A

và

đường thẳng

1 2 1

:

2 1 2

x y z

d

  

 

. Viết phương trình mặt phẳng chứa điểm

A

và đường thẳng

d

?

A.

 

:5 2 4 5 0

P x y z

   

. B.

 

: 2 1 2 1 0

P x y z

   

.

C.

 

:5 2 4 5 0

P x y z

   

. D.

 

: 2 1 2 2 0

P x y z

   

.

Câu 65. (Chuyên Nguyễn Đình Triểu - Đồng Tháp - 2018) Trong không gian

Oxyz

, cho hai đường

thẳng

1 2

,d d

lần lượt có phương trình

1 2

2 2 3 1 2 1

: , :

2 1 3 2 1 4

x y z x y z

d d

     

   



. Viết

phương trình mặt phẳng cách đều hai đường thẳng

1 2

,d d

.

A.

14 4 8 13 0

x y z

   

. B.

14 4 8 17 0

x y z

   

.

C.

14 4 8 13 0

x y z

   

. D.

14 4 8 17 0

x y z

   

.

Câu 66. (Chuyên KHTN - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho hai đường thẳng

1

2

:

1 1 1

x y z

d



 



và

2

1 2

:

2 1 1

x y z

d

 

 



. Phương trình mặt phẳng

 

P

song song và cách đều

hai đường thẳng

1 2

;d d

là:

A.

2 2 1 0

y z

  

. B.

2 2 1 0

y z

  

.

C.

2 2 1 0

x z

  

. D.

2 2 1 0

x z

  

.

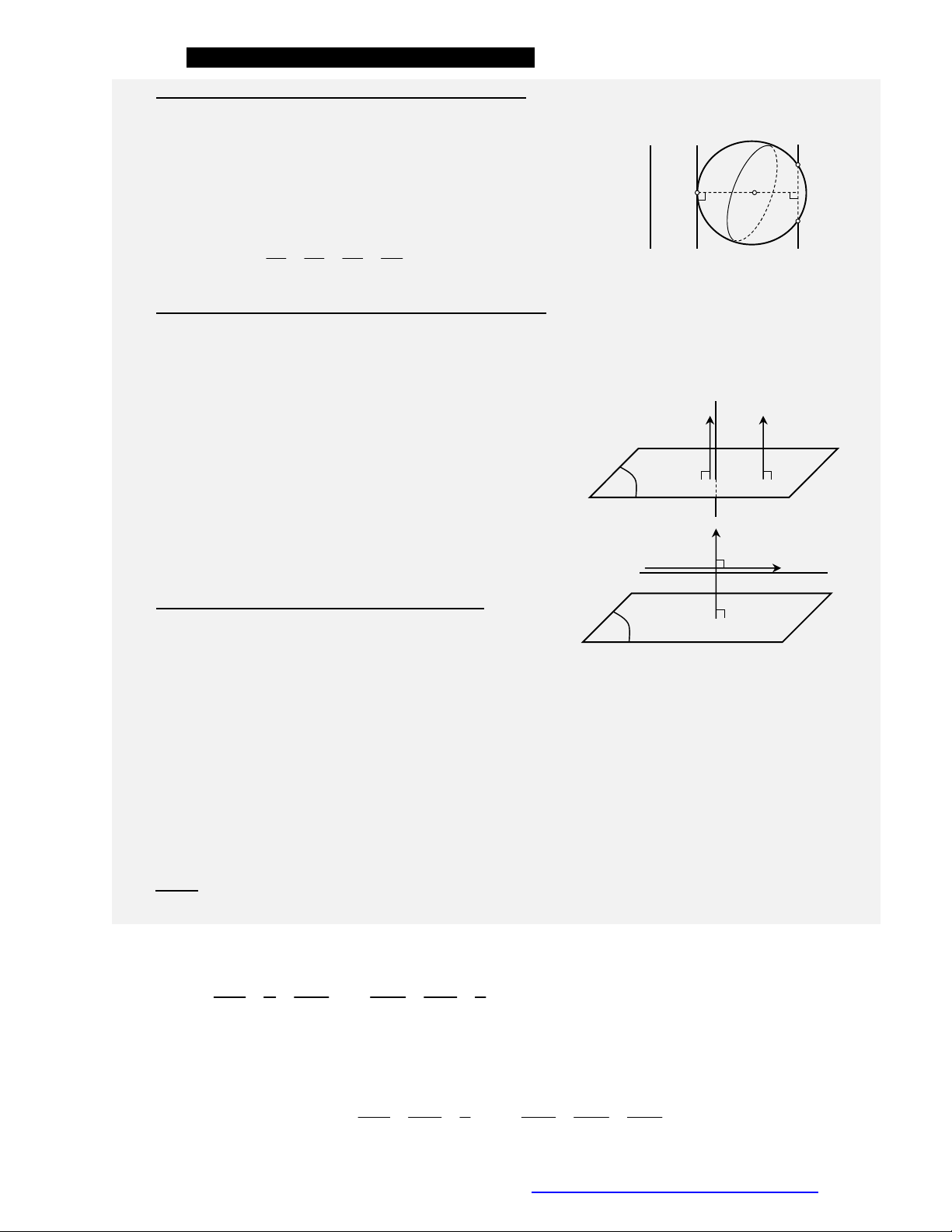
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 31

Dạng 5. Bài toán liên quan đến vị trí tương đối

1. Vị trí tương đối giữa đường thẳng d và mặt cầu (S)

Cho mặt cầu

( )S

có tâm

,I

bán kính

R

và đường thẳng

.

Để xét vị trí tương đối giữa



và

( )S

ta

tính

( , )d I 

rồi so sánh với bán kính

.R



Nếu

( , ) :

d I R

  

không cắt

( ).S



Nếu

( , ) :

d I R

  

tiếp xúc với

( )S

tại

.H



Nếu

( , ) :

d I R

  

cắt

( )S

tại hai điểm phân biệt

, .A B

1 1 1 1

2 2 2 2

( ) ( )

A B C D

P Q

A B C D

     



1 2 1 2 1 2

( ) ( ) 0.

P Q A A B B C C

    

2. Vị trí tương đối giữa đường thẳng d và mặt phẳng (P)

Cho đường thẳng

1

2

3

:

x x a t

d y y a t

z z a t

 





 





 





và mặt phẳng

( ) : 0

Ax By Cz D



   

Xét hệ phương trình:

1

2

3

(1)

(2)

(3)

0 (4)

x x a t

y y a t

z z a t

Ax By Cz D

 





 





 



   





( )



Nếu

( )

có nghiệm duy nhất

d

cắt

( ).





Nếu

( )

có vô nghiệm

( ).

d



 



Nếu

( )

vô số nghiệm

( ).

d



 

3. Vị trí tương đối giữa hai đường thẳng d và d’

Cho hai đường thẳng:

1

2

3

:

x x a t

d y y a t

z z a t

 





 





 





và

1

2

3

:

x x a t

d y y a t

z z a t

  

 





  

 





 

 





lần lượt qua điểm hai điểm

, M N

và có

véctơ chỉ phương lần lượt là

, .

d d

a a



 



d

song song

.

d d

a ka

d

M d



















 



d

trùng

.

d d

a ka

d

M d



















 



d

cắt

d





 

, . 0

d d

a ko a

a a MN



















 



 



d

chéo

 

, . 0.

d d

d a a MN



 



 

Lưu ý: Nếu

d

cắt

d



ta tìm tọa độ giao điểm bằng giải hệ phương trình:

1 1

2 2

3 3

.

x a t x a t

y a t y a t

z a t z a t

  

  





  

  





  

  



 

Câu 67. (Chuyên Bắc Giang 2019) Trong không gian với hệ tọa độ

Oxyz

cho hai đường thẳng

1

1 2

:

2 1 2

x y z

d

 

 



,

2

2 1

:

2 1 2

x y z

d

 

 

 

. Xét vị trí tương đói của hai đường thẳng đã cho.

A. Chéo nhau B. Trùng nhau C. Song song D. Cắt nhau

Câu 68. (Chuyên Lương Thế Vinh Đồng Nai 2019) Trong không gian tọa độ

Oxyz

, xét vị trí tương đối

của hai đường thẳng

1 2

1 1 3 3 2

: , :

2 2 3 1 2 1

x y z x y z

    

     

 

A.

1



song song với

2



. B.

1



chéo với

2



. C.

1



cắt

2



. D.

1



trùng với

2



.

A

B

I

H

d

R

P

d

u



P

n



P

n



d

u



d

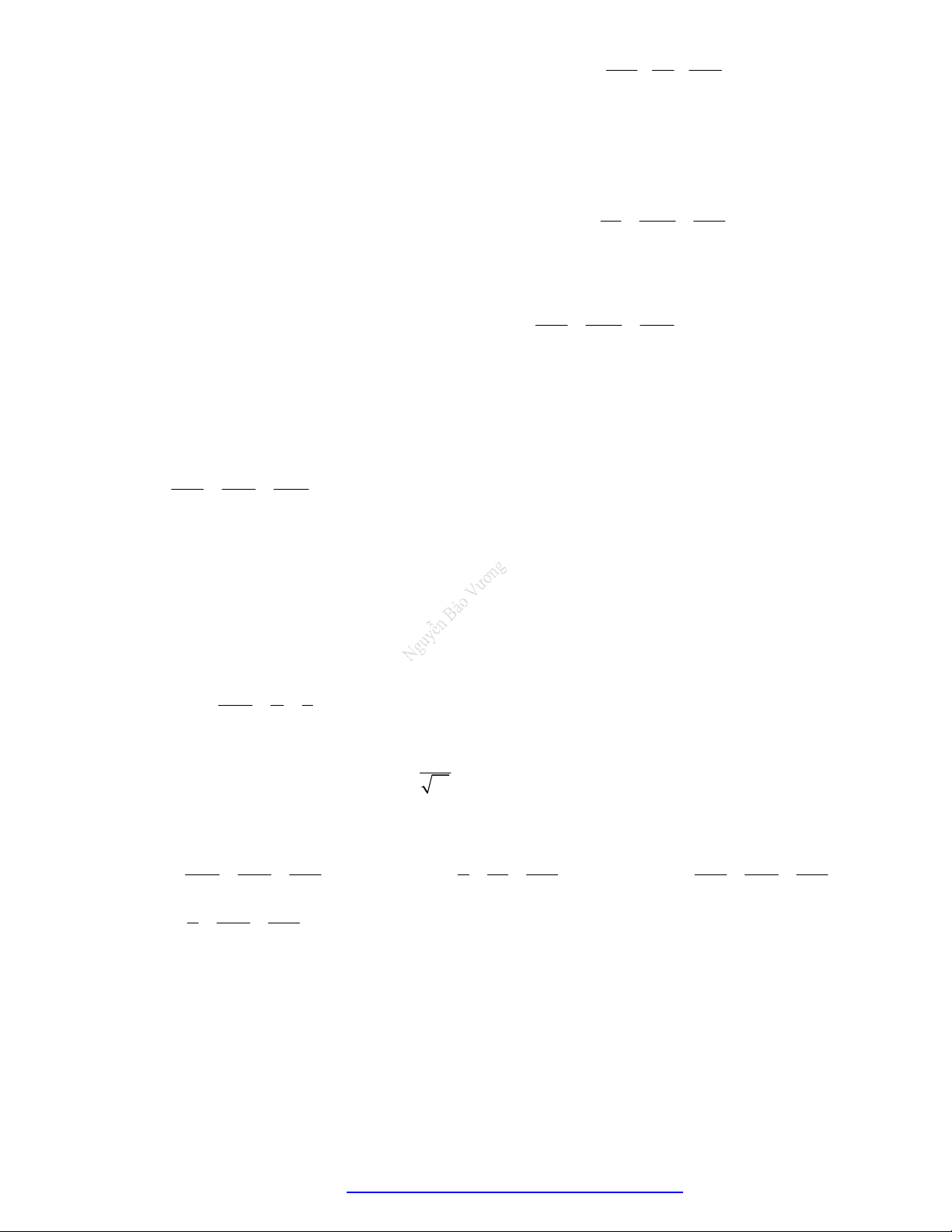
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 32 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 69. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng

1 5

:

1 3 1

x y z

d

 

 

 

và mặt phẳng

 

:3 3 2 6 0

P x y z

   

. Mệnh đề nào dưới đây đúng?

A.

d

cắt và không vuông góc với

 

.P

B.

d

vuông góc với

 

.P

C.

d

song song với

 

.P

D.

d

nằm trong

 

.P

Câu 70. Trong không gian với hệ tọa độ

Oxyz

, cho đường thẳng

2 1

:

2 1 3

x y z 

  



và mặt phẳng

 

:11 16 0

P x my nz

   

. Biết

 

P

 

, tính giá trị của

T m n 

.

A.

2T 

. B.

2T  

. C.

14T 

. D.

14T  

.

Câu 71. Trong không gian tọa độ

Oxyz

, cho đường thẳng

1 2 9

1 3 1

:

y z

d

x

  

 



và mặt phẳng

 



có

phương trình

2

2 19 0

m x my z

   

với

m

là tham số. Tập hợp các giá trị

m

thỏa mãn

 

//d



là

A.

 

1

. B.



. C.

 

1;2

. D.

 

2

.

Câu 72. Trong không gian với hệ trục toạ độ

Oxyz

, tìm tất cả các giá trị của tham số

m

để đường thẳng

d

:

1 1 2

1 1 1

x y z

  

 



song song với mặt phẳng

 

2

: 2 0

P x y m z m

   

A.

1

m



. B.

m



C.

 

1;1

m 

. D.

1

m

 

Câu 73. Gọi

,m n

là hai giá trị thực thỏa mãn: giao tuyến của hai mặt phẳng

 

: 2 1 0

m

P mx y nz

   

và

 

: 2 0

m

Q x my nz

   

vuông góc với mặt phẳng

 

: 4 6 3 0

x y z



   

.

A.

0

m n

 

. B.

2

m n

 

. C.

1

m n

 

. D.

3

m n

 

.

Câu 74. (THPT Gang Thép Thái Nguyên 2019) Trong không gian với hệ tọa độ

Oxyz

, cho hai đường

thẳng

1 2

1

: ; : 2

2 1 3

x t

x y z

d d y t

z m

 







   









. Gọi

S

là tập tất cả các số

m

sao cho

1

d

và

2

d

chéo

nhau và khoảng cách giữa chúng bằng

5

19

. Tính tổng các phần tử của

S

.

A.

11

. B.

12

. C.

12

. D.

11

.

Câu 75.

(Chuyên Vĩnh Phúc - 2018) Trong không gian

Oxyz

, cho bốn đường thẳng:

 

1

3 1 1

:

1 2 1

x y z

d

  

 



,

 

2

1

:

1 2 1

x y z

d



 



,

 

3

1 1 1

:

2 1 1

x y z

d

  

 

,

 

4

1 1

:

1 1 1

x y z

d

 

 



. Số đường thẳng trong không gian cắt cả bốn đường thẳng trên là:

A.

0

. B.

2

. C. Vô số. D.

1

.

Câu 76. (Mã 105 2017) Trong không gian với hệ tọa độ

Oxyz

, cho điểm

 

1; 2; 3

I

và mặt phẳng

 

   : 2 2 4 0

P x y z

. Mặt cầu tâm

I

tiếp xúc với

 

P

tại điểm

H

. Tìm tọa độ điểm

H

.

A.

 



1; 1; 0

H

B.

 

 3; 0; 2

H

C.

 



1; 4; 4

H

D.

 

3; 0; 2

H

Câu 77. Trong không gian

Oxyz

, biết mặt cầu

 

S

có tâm

O

và tiếp xúc với mặt phẳng

 

2 2 9 0

:P x y z

   

tại điểm

 

; ;H a b c

. Giá trị của tổng

a b c 

bằng

A.

2

. B.

1

. C.

1.

D.

2

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 33

Câu 78. (Chuyên Lê Hồng Phong-Nam Định- 2019) Trong không gian

Oxyz

, cho điểm

 

1;0;2

I

và

đường thẳng

1

:

2 1 1

x y z

d



 



. Gọi

 

S

là mặt cầu có tâm

I

, tiếp xúc với đường thẳng

d

. Bán

kính của

 

S

bằng

A.

5

3

. B.

2 5

3

. C.

30

3

. D.

4 2

3

.

Câu 79. Trong không gian

Oxyz

, cho mặt cầu

       

2 2 2

: 1 2 3 1

S x y z

     

, đường thẳng

6 2 2

:

3 2 2

x y z

  

  



và điểm

 

4;3;1

M

. Trong các mặt phẳng sau mặt phẳng nào đi qua

M

,

song song với



và tiếp xúc với mặt cầu

 

S

?

A.

2 2 5 22 0

x y z

   

. B.

2 2 13 0

x y z

   

.

C.

2 2 1 0

x y z

   

. D.

2 2 7 0

x y z

   

.

Câu 80. (Mã 104 2018) Trong không gian Oxyz, cho mặt cầu

       

2 2 2

: 2 3 1 16

S x y z

     

và

điểm

 

1; 1; 1 .

A

  

Xét các điểm M thuộc

 

S

sao cho đường thẳng AM tiếp xúc với

 

.S

M

luôn thuộc một mặt phẳng cố định có phương trình là

A.

6 8 11 0

x y

  

B.

6 8 11 0

x y

  

C.

3 4 2 0

x y

  

D.

3 4 2 0

x y

  

Câu 81. (Mã 110 2017) Trong không gian với hệ tọa độ

Oxyz

, cho mặt cầu

       

2 2 2

: 1 1 2 2

S x y z

     

và hai đường thẳng

2 1

:

1 2 1

x y z

d

 

 



;

1

:

1 1 1

x y z 

  



.

Phương trình nào dưới đây là phương trình của một mặt phẳng tiếp xúc với

 

S

, song song với

d

và



?

A.

3 0

y z

  

B.

1 0

x z

  

C.

1 0

x y

  

D.

1 0

x z

  

Câu 82. Trong không gian

Oxyz

, cho mặt phẳng

(P)

chứa đường thẳng

4 4

:

3 1 4

x y z

d

 

 



và tiếp xúc

với mặt cầu

       

2 2 2

: 3 3 1 9

S x y z

     

. Khi đó

 

P

song song với mặt phẳng nào sau

đây?

A.

3x 2z 0

y

  

. B.

2x 2 4 0

y z

    

.

C.

x 0

y z

  

D. Đáp án khác.

Câu 83. (Chuyên Bắc Giang 2019) Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng

tiếp xúc với mặt cầu

2 2 2

( 1) ( 2) 6

x y z

    

đồng thời song song với hai đường thẳng

1

2 1

:

3 1 1

x y z

d

 

 

 

,

2

2 2

:

1 1 1

x y z

d

 

 



.

A.

2 3 0

2 9 0

x y z

   





   



B.

2 3 0

2 9 0

x y z

   





   



C.

2 9 0

x y z

   

D.

2 9 0

x y z

   

Câu 84. (Đề Tham Khảo 2019) Trong không gian

,Oxyz

cho điểm

 

2;1;3

E

, mặt phẳng

 

: 2 2 3 0

P x y z

   

và mặt cầu

       

2 2 2

: 3 2 5 36

S x y z

     

. Gọi



là đường thẳng

đi qua

E

, nằm trong mặt phẳng

 

P

và cắt

 

S

tại hai điểm có khoảng cách nhỏ nhất. Phương

trình của



là

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 34 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

A.

2 9

1 9

3 8

x t

y t

z t

 





 





 



B.

2 5

1 3

3

x t

y t

z

 





 









C.

2

1

3

x t

y t

z

 





 









D.

2 4

1 3

3 3

x t

y t

z t

 





 





 



Câu 85. Trong không gian

Oxyz

, cho hai mặt cầu

 

1

S

,

 

2

S

có phương trình lần lượt là

 

2 2 2

1

: 25

S x y z  

,

   

2

2 2

2

: 1 4

S x y z

   

. Một đường thẳng

d

vuông góc với véc tơ

 

1; 1;0

u  



tiếp xúc với mặt cầu

 

2

S

và cắt mặt cầu

 

1

S

theo một đoạn thẳng có độ dài bằng

8

. Hỏi véc tơ nào sau đây là véc tơ chỉ phương của

d

?

A.

 

1

1;1; 3

u 



B.

 

2

1;1; 6

u 



C.

 

3

1;1;0

u 



D.

 

4

1;1; 3

u  



Câu 86. (Chuyên Bắc Giang 2019) Trong không gian với hệ tọa độ

Oxyz

, cho điểm

 

1;1;1

E

, mặt cầu

 

2 2 2

: 4

S x y z

  

và mặt phẳng

 

: 3 5 3 0

P x y z

   

. Gọi



là đường thẳng đi qua

E

,

nằm trong

 

P

và cắt mặt cầu

 

S

tại hai điểm

,A B

sao cho tam giác

OAB

là tam giác đều.

Phương trình của đường thẳng



là

A.

1 1 1

2 1 1

x y z  

 

 

. B.

1 1 1

2 1 1

x y z  

 



.

C.

1 1 1

2 1 1

x y z  

 

. D.

1 1 1

2 1 1

x y z  

 

 

.

Câu 87. Trong không gian

Oxyz

, cho đường thẳng

1

1 2 3

:

1 2 1

x y z

d

  

 



và điểm

 

1;0; 1

A



. Gọi

2

d

là

đường thẳng đi qua điểm

A

và có vectơ chỉ phương

 

;1;2

v a



. Giá trị của

a

sao cho đường

thẳng

1

d

cắt đường thẳng

2

d

là

A.

1

a

 

. B.

2

a



. C.

0

a



. D.

1

a



.

Câu 88. Trong không gian

Oxyz

, cho ba mặt cầu

       

2 2 2

1

: 3 2 4 1

S x y z

     

,

     

2 2

2

: 2 4 4

S x y z

    

và

 

2 2 2

3

: 4 4 1 0

S x y z x y

     

. Hỏi có bao nhiêu mặt phẳng tiếp xúc với cả ba mặt cầu

 

1

S

,

 

2

S

,

 

3

S

?

A.

2

. B.

4

. C.

6

. D.

8

.

Câu 89. Trong không gian với hệ tọa độ

Oxyz

cho đường thẳng

1 2

:

2 1 1

x y z

d

 

 



. Gọi

 

S

là mặt

cầu có bán kính

5

R



, có tâm

I

thuộc đường thẳng

d

và tiếp xúc với trục

Oy

. Biết rằng

I

có

tung độ dương. Điểm nào sau đây thuộc mặt cầu

 

S

?

A.

 

1; 2;1

M  

. B.

 

1;2; 1

N



.

C.

 

5;2; 7

P

 

. D.

 

5; 2;7

Q 

.

Câu 90. Trong không gian

Oxyz

, cho mặt cầu

 

2 2 2

: 4 6 0

S x y z x y m

     

(

m

là tham số) và

đường thẳng

4 2

: 3

3 2

x t

y t

z t

 





  





 



. Biết đường thẳng



cắt mặt cầu

 

S

tại hai điểm phân biệt

,A B

sao cho

8

AB



. Giá trị của

m

là

A.

5

m



. B.

12

m



. C.

12

m

 

. D.

10

m

 

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 35

Câu 91.

(SGD Bến Tre 2019) Trong không gian

O

xyz

c

ho hai đường thẳng chéo nhau

1

2

4 2 1

:

,( ), : ' ,( ' )

3

'

x t x

d y t t d y t t

z z t

  

 

 

   

 

 

  

 



.

P

hương trình mật cầu có bán kính nhỏ nhất tiếp xúc với cả hai đường thẳng

   

1

2

,

d

l

à:

A.

 

2

3

9

2

4

x

y z

 



   

 

 

. B.

 

2

3

2

x

y z

 



   

 

 

.

C.

 

2

3

9

2

4

x

y z

 



   





 

. D.

 

2

3

2

x

y z

 



   





 

.

Câu 92.

Trong không gian

Ox

yz

,

cho hai đường thẳng

1

4

1 5

3 1 2

:

x

y z  



 

 

v

à

2

3

1

3 1

:

x

y z







 

.

Trong tất cả mặt cầu tiếp xúc với cả hai đường thẳng

1



và

2



.

Gọi

(

)S

là mặt cầu

có bán kính nhỏ nhất. Bán kính của mặt cầu

(

)S

là

A.

1

2

. B.

6

. C.

2

4

. D.

3

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương  https://www.facebook.com/phong.baovuong Trang 1

TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH GIỎI MỨC 9-10 ĐIỂM

Dạng 1. Bài toán liên quan đến mặt cầu – mặt phẳng – đường thẳng

Câu 1. (Mã 110 2017) Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm

 

4;6;2A

và

 

2; 2;0B 

và

mặt phẳng

 

: 0P x y z  

. Xét đường thẳng

d

thay đổi thuộc

 

P

và đi qua

B

, gọi

H

là hình

chiếu vuông góc của

A

trên

d

. Biết rằng khi

d

thay đổi thì

H

thuộc một đường tròn cố định.

Tính bán kính

R

của đường tròn đó.

A.

3R 

B.

2R 

C.

1R 

D.

6R 

Câu 2. Trong không gian

Oxyz

mặt phẳng

 

: 2 6 3 0P x y z   

cắt trục

Oz

và đường thẳng

5 6

:

1 2 1

x y z

d

 

 



lần lượt tại

A

và

B

. Phương trình mặt cầu đường kính

AB

là:

A.

     

2 2 2

2 1 5 36.x y z     

B.

     

2 2 2

2 1 5 9.x y z     

C.

     

2 2 2

2 1 5 9.x y z     

D.

     

2 2 2

2 1 5 36.x y z     

Câu 3. Trong không gian

Oxyz

, cho mặt cầu

 

2 2 2

: 4 6 0S x y z x y m     

(

m

là tham số) và

đường thẳng

4 2

: 3

3 2

x t

y t

z t

 





  





 



. Biết đường thẳng



cắt mặt cầu

 

S

tại hai điểm phân biệt

,A B

sao

cho

8AB 

. Giá trị của

m

là

A.

5m 

. B.

12m 

. C.

12m  

. D.

10m  

.

Câu 4. Trong không gian

Oxyz

, cho đường thẳng

 

3 2

:

2 1 1

x y z

d

 

 

và hai mặt phẳng

 

: 2 2 0P x y z  

;

 

: 2 3 5 0Q x y z   

. Mặt cầu

 

S

có tâm

I

là giao điểm của đường

thẳng

 

d

và mặt phẳng

 

P

. Mặt phẳng

 

Q

tiếp xúc với mặt cầu

 

S

. Viết phương trình mặt

cầu

 

S

.

A.

       

2 2 2

: 2 4 3 1S x y z     

. B.

       

2 2 2

: 2 4 3 6S x y z     

.

C.

       

2 2 2

2

: 2 4 3

7

S x y z     

. D.

       

2 2 2

: 2 4 4 8S x y z     

.

Câu 5. Trong không gian

Oxyz

, cho mặt cầu

       

2 2 2

: 2 3 4 14S x y z     

và mặt phẳng

 

: 3 2 5 0x y z



   

. Biết đường thẳng



nằm trong

 



, cắt trục

Ox

và tiếp xúc với

 

S

.

Vectơ nào sau đây là vectơ chỉ phương của



?

A.

 

4; 2;1u  



. B.

 

2;0; 1v  



. C.

 

3;1;0m  



. D.

 

1; 1;1n  



.

Câu 6. (Bình Dương - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

 

: 2 2 9 0P x y z   

và mặt cầu

       

2 2 2

: 3 2 1 100S x y z     

. Mặt phẳng

 

P

cắt

mặt cầu

 

S

theo một đường tròn

 

C

. Tìm tọa độ tâm

K

và bán kính

r

của đường tròn

 

C

là

A.

 

3; 2;1K 

,

10r 

. B.

 

1;2;3K 

,

8r 

. C.

 

1; 2;3K 

,

8r 

. D.

 

1; 2;3K

,

6r 

.

PHƯƠNG TRÌNH ĐƯỜNG THẲNG

Chuyên đề 31

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 7. (Chuyên Thái Bình 2019) Trong không gian hệ tọa độ

Oxyz

, cho hai điểm

   

1;1;1 , 2;2;1

A B

và mặt phẳng

 

: 2 0

P x y z

  

. Mặt cầu

 

S

thay đổi qua

,A B

và tiếp xúc với

 

P

tại

H

. Biết

H

chạy trên 1 đường tròn cố định. Tìm bán kính của đường tròn đó.

A.

3 2

. B.

2 3

. C.

3

. D.

3

2

Câu 8. (Chuyên Lam Sơn 2019) Trong không gian

Oxyz

cho mặt cầu

 

2 2 2

: 2 4 6 2 0

S x y z x y z

      

và mặt phẳng

 

: 4 3 12 10 0

x y z

   



. Lập phương

trình mặt phẳng

 



thỏa mãn đồng thời các điều kiện: Tiếp xúc với

 

S

; song song với

 



và

cắt trục

Oz

ở điểm có cao độ dương.

A.

4 3 12 78 0

x y z

   

. B.

4 3 12 26 0

x y z

   

.

C.

4 3 12 78 0

x y z

   

. D.

4 3 12 26 0

x y z

   

.

Câu 9. (Chuyên Nguyễn Trãi Hải Dương 2019) Trong không gian

Oxyz

, cho mặt cầu

2 2 2

9

x y z

  

và điểm

 

0 0 0

1

; ; : 1 2

2 3

x t

M x y z d y t

z t

 





  





 



. Ba điểm

A

,

B

,

C

phân biệt cùng thuộc mặt cầu sao cho

MA

,

MB

,

MC

là tiếp tuyến của mặt cầu. Biết rằng mặt phẳng

 

ABC

đi qua điểm

 

1;1;2

D

.

Tổng

2 2 2

0 0 0

T x y z  

bằng

A.

30

. B.

26

. C.

20

. D.

21

.

Câu 10. Trong không gian với hệ trục tọa độ

Oxyz

, cho mặt cầu

 

2 2 2

: 2 2 1 0

S x y z x z

     

và

đường thẳng

2

:

1 1 1

x y z

d



 



. Hai mặt phẳng

   

, 'P P

chứa

d

và tiếp xúc với

( )S

tại

T

,

'T

.

Tìm tọa độ trung điểm

H

của

'.TT

A.

7 1 7

; ;

6 3 6

H

 



 

 

. B.

5 2 7

; ;

6 3 6

H

 



 

 

. C.

5 1 5

; ;

6 3 6

H

 



 

 

. D.

5 1 5

; ;

6 3 6

H

 



 

 

.

Câu 11. Trong không gian

Oxyz

, cho điểm

 

2;1;3

E

, mặt phẳng

 

: 2 2 3 0   

P x y z

và mặt cầu

       

2 2 2

: 3 2 5 36     

S x y z

. Gọi



là đường thẳng đi qua

E

, nằm trong

 

P

và cắt

 

S

tại hai điểm có khoảng cách nhỏ nhất. Phương trình của



là

A.

2 9

1 9

3 8

 





 





 



x t

y t

z t

. B.

2 5

1 3

3

 





 









x t

y t

z

. C.

2

1

3

 





 









x t

y t

z

. D.

2 4

1 3

3 3

 





 





 



x t

y t

z t

.

Câu 12. (Chuyên Lê Quý Đôn – Điện Biên 2019) Trong không gian

Oxyz

cho mặt cầu

   

2 2

2

3 1 4

x y z

    

và đường thẳng

1 2

: 1 ,

x t

d y t t

z t

 





   





 





. Mặt phẳng chứa

d

và cắt

( )S

theo một đường tròn có bán kính nhỏ nhất có phương trình là

A.

1 0

y z

  

. B.

3 5 2 0

x y z

   

. C.

2 3 0

x y

  

. D.

3 2 4 8 0

x y z

   

.

Câu 13. (Đại học Hồng Đức –Thanh Hóa 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho

điểm

 

1;1;1

E

, mặt phẳng

 

: 3 5 3 0

P x y z

   

và mặt cầu

 

2 2 2

: 4

S x y z

  

. Gọi



là

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3

đường thẳng qua

E

, nằm trong mặt phẳng

 

P

và cắt

 

S

tại 2 điểm phân biệt

,A B

sao cho

2AB 

. Phương trình đường thẳng



là

A.

1 2

2

1

x t

y t

z t

 





 





 



. B.

1 2

1

x t

y t

z t

 





 





 



. C.

1 2

3

5

x t

y t

z t

 





  





 



. D.

1 2

1

x t

y t

z t

 





 





 



.

Câu 14. (SGD Cần Thơ 2019) Trong không gian

Oxyz

, cho điểm

 

0;1; 2

A

, mặt phẳng

 

: 1 0   

P x y z

và mặt cầu

 

2 2 2

: 2 4 7 0     

S x y z x y

. Gọi



là đường thẳng đi qua

A

và



nằm trong mặt phẳng

 

P

và cắt mặt cầu

 

S

tại hai điểm

B

,

C

sao cho tam giác

IBC

có diện tích lớn nhất, với

I

là tâm của mặt cầu

 

S

. Phương trình của đường thẳng



là

A.

1

2













  



x t

y

z t

. B.

1

2







 





  



x t

y t

z t

. C.

1

2







 





 



x t

y t

z

. D.

1

2







 





 



x t

y t

z

.

Câu 15. Trong không gian với hệ tọa độ

Oxyz

cho mặt phẳng

 

: 2 0

P z

 

,

 

0;0; 2

K



, đường thẳng

:

1 1 1

x y z

d

 

. Phương trình mặt cầu tâm thuộc đường thẳng

d

và cắt mặt phẳng

 

P

theo thiết

diện là đường tròn tâm

K

, bán kính

5

r  là

A.

 

2

2 2

2 16

x y z

   

. B.

2 2 2

16

x y z

  

.

C.

 

2

2 2

2 9

x y z

   

. D.

2 2 2

9

x y z

  

.

Câu 16. Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

 

: 3 0

P x y z

   

và hai điểm

 

1;1;1

M

,

 

3; 3; 3

N

  

. Mặt cầu

 

S

đi qua M, N và tiếp xúc với mặt phẳng

 

P

tại điểm

Q

.

Biết rằng

Q

luôn thuộc một đường tròn cố định. Tìm bán kính của đường tròn đó.

A.

2 11

3

R 

. B.

6

R



. C.

2 33

3

R 

. D.

4R 

.

Câu 17. (Nguyễn Huệ- Ninh Bình- 2019)Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

 

: 2 2 3 0

P x y z

   

và mặt cầu

     

2 2

2

: 1 3 9

S x y z

    

và đường thẳng

2 1

:

2 1 2

x y z

d

 

 



. Cho các phát biểu sau đây:

I. Đường thẳng

d

cắt mặt cầu

 

S

tại 2 điểm phân biệt.

II. Mặt phẳng

 

P

tiếp xúc với mặt cầu

 

S

.

III. Mặt phẳng

 

P

và mặt cầu

 

S

không có điểm chung.

IV. Đường thẳng

d

cắt mặt phẳng

 

P

tại một điểm.

Số phát biểu đúng là:

A.

4

. B.

1

. C.

2

. D.

3

.

Câu 18. (Chuyên Hoàng Văn Thụ-Hòa Bình-2019)Trong không gian Oxyz, cho mặt cầu

       

2 2 2

2

: 1 2 1 3

S x y z

     

, mặt phẳng

 

: 3 0

P x y z

   

và điểm

 

1;0; 4

N



thuộc

 

P

. Một đường thẳng



đi qua N nằm trong

 

P

cắt

 

S

tại hai điểm A, B thỏa mãn

4AB 

.

Gọi

 

1; ;u b c



,

 

0

c



là một vecto chỉ phương của



, tổng

b c

bằng

A.

1

. B.

3

. C.

1

. D.

45

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 19. (Chuyên Hạ Long 2019) Trong không gian với hệ trục

Oxyz

cho hai đường thẳng

1

1 1 1

:

2 1 2

x y z  

  

và

2

1 1 1

:

2 2 1

x y z  

  

. Tính diện tích mặt cầu có bán kính nhỏ

nhất, đồng thời tiếp xúc với cả hai đường thẳng

1



và

2



.

A.

16

17



(đvdt). B.

4

17



(đvdt). C.

16

17



(đvdt). D.

4

17



(đvdt).

Câu 20. (THPT Quang Trung Đống Đa Hà Nội 2019) Trong không gian với hệ tọa độ

Oxyz

, cho hai

đường thẳng

1

2

:

4

x t

d y t

z

















và

2

3 '

: '

0

x t

d y t

z

 















. Viết phương trình mặt cầu

 

S

có bán kính nhỏ nhất

tiếp xúc với cả hai đường thẳng

1

d

và

2

.d

A.

       

2 2 2

: 2 1 2 4.

S x y z

     

B.

       

2 2 2

: 2 1 2 16.

S x y z     

C.

     

2 2

2

: 2 1 ( 2) 4.

S x y z

     

D.

   

2

2 2

: 2 ( 1) ( 2) 16.

S x y z     

Câu 21. (KTNL GV Thuận Thành 2 Bắc Ninh 2019) Trong không gian với hệ trục

,Oxyz

cho mặt cầu

 

2 2 2

: 2 4 6 13 0

S x y z x y z

      

và đường thẳng

1 2 1

:

1 1 1

x y z

d

  

 

. Điểm

   

; ; , 0

M a b c a



nằm trên đường thẳng

d

sao cho từ

M

kẻ được ba tiếp tuyến

, ,

MA MB MC

đến mặt cầu

 

S

(

, ,A B C

là các tiếp điểm) và



0

60

AMB 

,



0

60

BMC 

,



0

120

CMA 

. Tính

3 3 3

a b c 

.

A.

3 3 3

173

9

a b c  

. B.

3 3 3

112

9

a b c  

. C.

3 3 3

8

a b c

   

. D.

3 3 3

23

9

a b c  

.

Câu 22. (Chuyên Nguyễn Tất Thành Yên Bái 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho

điểm

 

3;3; 3

M

 

thuộc mặt phẳng

 

: 2 2 15 0

x y z



   

và mặt cầu

       

2 2 2

: 2 3 5 100

S x y z     

. Đường thẳng



qua

M

, nằm trên mặt phẳng

 



cắt

 

S

tại

,A B

sao cho độ dài

AB

lớn nhất. Viết phương trình đường thẳng



.

A.

3 3 3

1 1 3

x y z

  

 

. B.

3 3 3

1 4 6

x y z

  

 

.

C.

3 3 3

16 11 10

x y z

  

 



. D.

3 3 3

5 1 8

x y z

  

 

.

Câu 23. (Mã 104 2017) Trong không gian với hệ tọa độ

Oxyz

, cho ba điểm

 

2;0;0

A 

,

 

0; 2;0

B 

,

 

0;0; 2

C



. Gọi

D

là điểm khác

O

sao cho

DA

,

DB

,

DC

đôi một vuông góc nhau và

 

; ;I a b c

là tâm mặt cầu ngoại tiếp tứ diện

ABCD

. Tính

S a b c  

.

A.

4

S

 

B.

1

S

 

C.

2

S

 

D.

3

S

 

Câu 24. (Chuyên Hạ Long 2019) Trong không gian

Oxyz

, cho

 

:2 2 1 0

P x y z

   

,

   

0;0;4 , 3;1;2

A B

. Một mặt cầu

 

S

luôn đi qua

,A B

và tiếp xúc với

 

P

tại

C

. Biết rằng,

C

luôn thuộc một đường tròn cố định bán kính

r

. Tính bán kính

r

của đường tròn đó.

A. Đáp án khác. B.

4

2 244651

3

r 

. C.

2 244651

9

r 

. D.

2024

3

r 

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5

Câu 25. (KTNL GV Thuận Thành 2 Bắc Ninh 2019) Trong không gian với hệ tọa độ

Oxyz

, cho hình

chóp

.S ABCD

với

 

1; 1;6S 

,

 

1;2;3A

,

 

3;1;2B

,

 

4;2;3C

,

 

2;3;4D

. Gọi

I

là tâm mặt cầu

 

S

ngoại tiếp hình chóp. Tính khoảng cách

d

từ

I

đến mặt phẳng

 

SAD

.

A.

3 3

2

d 

. B.

6

2

d 

. C.

21

2

d 

. D.

3

2

d 

.

Câu 26. Trong không gian

Oxyz

, xét số thực

 

0;1m

và hai mặt phẳng

 

: 2 2 10 0x y z    

và

 

: 1

1 1

x y z

m m

   



. Biết rằng, khi

m

thay đổi có hai mặt cầu cố định tiếp xúc đồng thời với cả

hai mặt phẳng

   

, 

. Tổng bán kính của hai mặt cầu đó bằng

A.

6

B.

3

C.

9

D.

12

Câu 27. (Chuyên Lê Hồng Phong Nam Định 2019) Trong không gian với hệ tọa độ

Oxyz

, cho mặt

phẳng

 

: 2 2 3 0P x y z   

và mặt cầu

 

S

tâm

 

5; 3;5I 

, bán kính 2 5R  . Từ một điểm

A

thuộc mặt phẳng

 

P

kẻ một đường thẳng tiếp xúc với mặt cầu

 

S

tại

B

. Tính

OA

biết

4AB 

.

A.

11OA 

. B.

5OA 

. C.

3OA 

. D.

6OA 

.

Câu 28. Trong không gian cho mặt cầu

2 2 2

9x y z   và điểm

 

0 0 0

; ;M x y z

thuộc

1

: 1 2

2 3

x t

d y t

z t

 





 





 



. Ba điểm

A

,

B

,

C

phân biệt cùng thuộc mặt cầu sao cho

MA

,

MB

,

MC

là tiếp

tuyến của mặt cầu. Biết rằng mặt phẳng

 

ABC

đi qua

 

1;1;2D

. Tổng

2 2 2

0 0 0

T x y z  

bằng

A.

30

B.

26

C.

20

D. 21

Câu 29. (Chuyên KHTN 2019) Trong không gian với hệ tọa độ

Oxyz

cho hai điểm

   

0;0;3 , 2;0;1A B 

và mặt phẳng

 

: 2 2 8 0x y z



   

. Hỏi có bao nhiêu điểm

C

trên mặt

phẳng

 



sao cho tam giác

ABC

đều?

A.

2

. B.

1

. C.

0

. D. Vô số.

Câu 30. (Chuyên Nguyễn Trãi Hải Dương 2019) Trong không gian

Oxyz

, cho mặt cầu

2 2 2

9x y z  

và điểm

 

0 0 0

; ; M x y z

thuộc đường thẳng

1

: 1 2 .

2 3

x t

d y t

z t

 





 





 



Ba điểm

,A

,B

C

phân biệt cùng

thuộc mặt cầu sao cho

,MA

,MB

MC

là tiếp tuyến của mặt cầu. Biết rằng mặt phẳng

 

ABC

đi

qua

 

1; 1; 2D

. Tổng

2 2 2

0 0 0

T x y z  

bằng

A.

30

. B.

26

. C.

20

. D.

21

.

Câu 31. (Tỉnh Bắc Ninh 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho mặt cầu

( ) :S

2 2 2

2 2 1 0x y z x z     

và đường thẳng

2

:

1 1 1

x y z

d



 



. Hai mặt phẳng

( )P

,

( )P



chứa

d

và tiếp xúc với

( )S

tại

T

,

T



. Tìm tọa độ trung điểm

H

của

TT



.

A.

7 1 7

; ;

6 3 6

H

 



 

 

. B.

5 2 7

; ;

6 3 6

H

 



 

 

. C.

5 1 5

; ;

6 3 6

H

 



 

 

. D.

5 1 5

; ;

6 3 6

H

 



 

 

.

,Oxyz

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 32. Cho hai đường thẳng

2

:

2 2

x

d y t

z t

 











 



 

t 



,

3 1 4

:

1 1 1

x y z

  

  



và mặt phẳng

 

: 2 0

P x y z

   

. Gọi

d



,





lần lượt là hình chiếu của

d

và



lên mặt phẳng

 

P

. Gọi

 

; ;M a b c

là giao điểm của hai đường thẳng

d



và





. Biểu thức

.a b c

bằng

A.

4

. B.

5

. C.

3

. D.

6

.

Câu 33. (Thpt Vĩnh Lộc - Thanh Hóa 2019) Trong không gian với hệ tọa độ

Oxyz

, cho đường thẳng

d

là giao tuyến của hai mặt phẳng

 

: 2 1 0

x my z m



    

và

 

: 2 0

mx y mz m



    

. Gọi



là hình chiếu vuông góc của

d

lên mặt phẳng

 

Oxy

. Biết rằng với mọi số thực

m

thay đổi thì

đường thẳng



luôn tiếp xúc với một đường tròn cố định. Tính bán kính

R

của đường tròn đó.

A.

2

. B.

1

. C.

4

. D.

3

.

Câu 34. Trong không gian với hệ tọa độ

Oxyz

, cho ba điểm

 

6; 0; 0

M

,

 

0; 6; 0

N

,

 

0; 0; 6

P

. Hai

mặt cầu có phương trình

 

2 2 2

1

: 2 2 1 0

S x y z x y

     

và

 

2 2 2

2

: 8 2 2 1 0

S x y z x y z

      

cắt nhau theo đường tròn

 

C

. Hỏi có bao nhiêu mặt cầu

có tâm thuộc mặt phẳng chứa

 

C

và tiếp xúc với ba đường thẳng

MN

,

NP

,

PM

?

A.

1

. B.

3

. C. Vô số. D.

4

.

Câu 35. Trong không gian cho mặt phẳng

 

: 6 0

P x z

  

và hai mặt cầu

 

2 2 2

1

: 25

S x y z

  

,

 

2

:S

2 2 2

4 4 7 0

x y z x z

     

. Biết rằng tập hợp tâm

I

các mặt cầu tiếp xúc với cả hai mặt

cầu

 

1

S

,

 

2

S

và tâm

I

nằm trên

 

P

là một đường cong. Tính diện tích hình phẳng giới hạn

bởi đường cong đó.

A.

7

3



. B.

7

9



. C.

9

7



. D.

7

6



.

Câu 36. Trong không gian với hệ tọa độ

,Oxyz

cho phương trình mặt

cầu:

   

2 2 2

: 2 2 2 3 0

m

S x y z m x my mz m

        

.

Biết rằng với mọi số thực

m

thì

 

m

S

luôn chứa một đường tròn cố định. Tính bán kính

r

của

đường tròn đó.

A.

2

3

r 

. B.

4 2

3

r 

. C.

1

3

r



. D.

3

r  .

Câu 37. Trong không gian với hệ trục tọa độ

Oxyz

, cho mặt câu

 

2 2

: 2 4 6 13 0

S x y x y z

     

và

đường thẳng

1 2 1

:

1 1 1

x y z

d

  

 

. Điểm

  

; ; 0

M a b c a



nằm trên đường thẳng

d

sao cho

từ

M

kẻ được ba tiếp tuyến

, ,

MA MB MC

đến mặt cầu

 

S

(

, ,A B C

là các tiếp điểm) thỏa mãn



60

AMB

 

,



90

BMC

 

,



120

CMA

 

.Tính

Q a b c  

.

A.

3

Q



. B.

10

3

Q



. C.

2

Q



. D.

1

Q



.

Dạng 2 Bài toán cực trị

1. Một số bất đẳng thức cơ bản

Kết quả 1. Trong một tam giác, cạnh đối diện với góc lớn thì lớn hơn

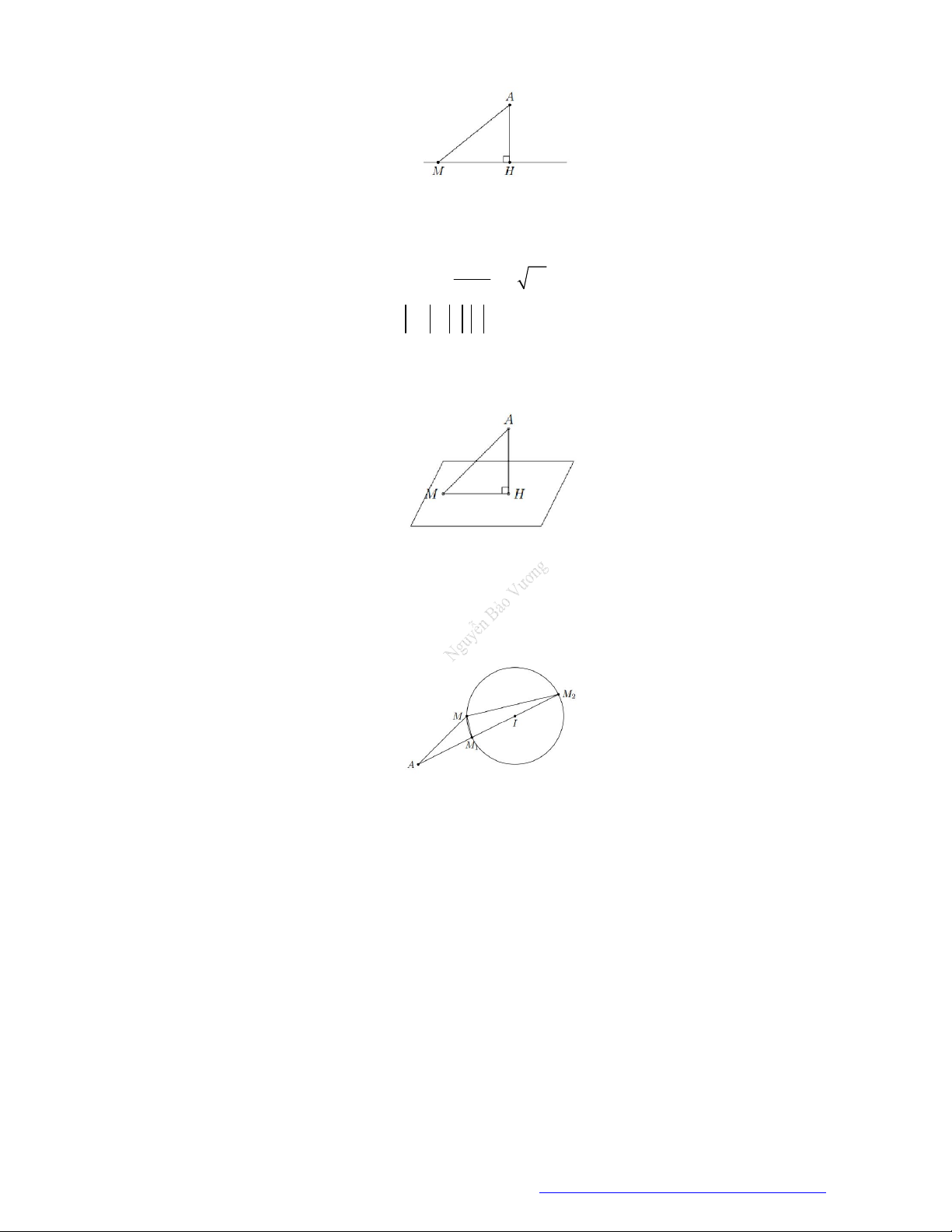
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7

Kết quả 2. Trong các đường xiên và đường vuông góc kẻ từ một điểm nằm ngoài đường thẳng đến đường

thẳng đó thì đường vuông góc là đường ngắn nhất. Như trong hình vẽ ta luôn có

AM AH

Kết quả 3. Với ba điểm

, ,A B C

bất kì ta luôn có bất đẳng thức

.AB BC AC 

Tổng quát hơn ta có bất đẳng thức của đường gấp khúc: Với

n

điểm

1 2

, ,....

n

A A A ta luôn có

1 2 2 3 1 1

...

n n n

A A A A A A A A



   

Kết quả 4. Với hai số không âm

,x y

ta luôn có

2

x y

xy





. Đẳng thức xảy ra khi và chỉ khi

x y

Kết quả 5. Với hai véc tơ

,a b

 

ta luôn có . .a b a b

   

. Đẳng thức xảy ra khi

,a kb k 

 



2. Một số bài toán thường gặp

Bài toán 1. Cho điểm

A

cố định và điểm

M

di động trên hình

 

H

(

 

H

là đường thẳng, mặt phẳng). Tìm

giá trị nhỏ nhất của

AM

Lời giải: Gọi

H

là hình chiếu vuông góc của

A

lên hình

 

H

. Khi đó, trong tam giác

AHM

Vuông tại .

M

ta có

.AM AH

Đẳng thức xảy ra khi

M H

. Do đó

AM

nhỏ nhất khi

M

là hình chiếu của

A

lên

 

H

Bài toán 2. Cho điểm

A

và mặt cầu

 

S

có tâm

,I

bán kính

,R

M

là điểm di động trên

 

S

. Tìm giá trị

nhỏ nhất và giá trị lớn nhất của

AM

.

Lời giải. Xét

A

nằm ngoài mặt cầu

( ).S

Gọi

1 2

,M M lần lượt là giao điểm của đường thẳng

AI

với mặt

cầu

 

1 2

( )S AM AM

và

( )



là mặt phẳng đi qua

M

và đường thẳng

.AI

Khi đó

( )



cắt

( )S

theo một

đường tròn lớn

( ).C

Ta có



1 2

90 ,M MM



 nên



2

AMM và



1

AM M là các góc tù, nên trong các tam giác

1

AMM và

2

AMM ta có

1 2

AI R AM AM AM AI R     

Tương tự với

A

nằm trong mặt cầu ta có

R AI AM R AI   

Vậy

min | |,maxAM AI R AM R AI   

Bài toán 3. Cho măt phẳng

( )P

và hai điểm phân biệt

, .A B

Tìm điể

M

thuộc

( )P

sao cho

1.

MA MB

nhỏ nhất.

2.

| |MA MB

lớn nhất.

Lời giải.

1. Ta xét các trường hợp sau

- TH 1: Nếu

A

và

B

nằm về hai phía so với

( )P

. Khi đó

AM BM AB 

Đẳng thức xảy ra khi

M

là giao điểm của

AB

với

( )P

.

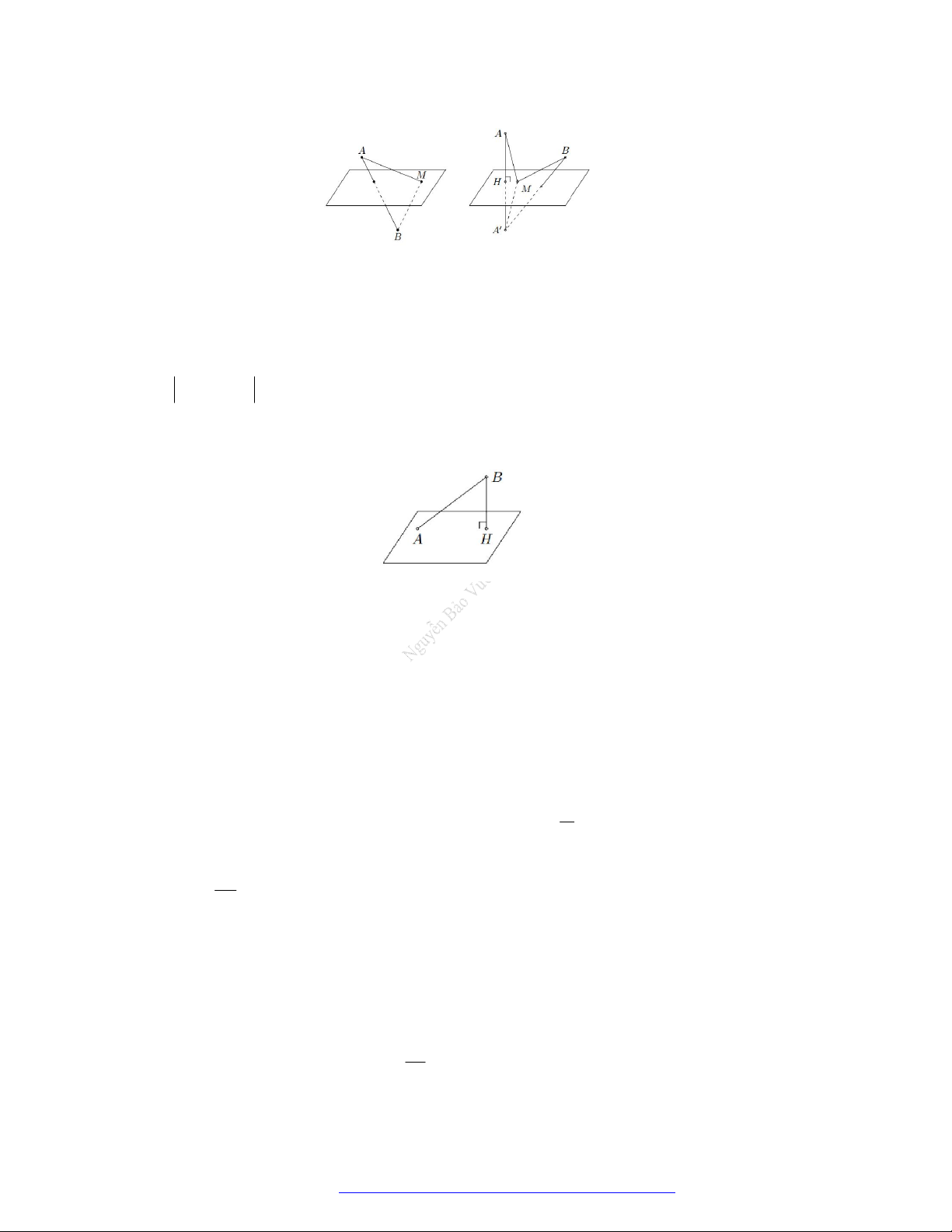
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 8 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

- TH 2: Nếu

A

và

B

nằm cùng một phía so với

( )P

. Gọi A



đối xứng với

A

qua

( )P

. Khi đó

AM BM A M BM A B

 

   

Đẳng thức xảy ra khi

M

là giao điểm của A B



với

( )P

.

2. Ta xét các trường hợp sau

- TH 1: Nếu

A

và

B

nằm cùng một phía so với

( )P

. Khi đó

| |AM BM AB 

Đẳng thức xảy ra khi

M

là giao điểm của

AB

với

( )P

.

- TH 2: Nếu

A

và

B

nằm khác phía so với

( )P

. Gọi

'A

đối xứng với

A

qua

 

P

, Khi đó

| |AM BM A M BM A B

 

   

Đẳng thức xảy ra khi

M

là giao điểm của

A B



với

( )P

.

Bài toán 4. Viết phương trinh măt phẳng

( )P

di qua

A

và cách

B

một khoảng lớn nhất.

Lời giải. Gọi

H

là hình chiếu của

B

lên mặt phẳng

( ),P

khi đó

d( ,( ))B P BH BA 

Do đó

 

P

là mặt phẳng đi qua

A

vuông góc với

AB

Bài toán 5. Cho các số thực dương

,

 

và ba điểm

, ,A B

C. Viết phương trình măt phẳng

( )P

đi qua

C

và

d( ,( )) d( ,( ))T A P B P

 

 

nhỏ nhất.

Lời giải.

1. Xét

,A B

nằm về cùng phía so với

( )P

.

- Nếu ( )AB P‖ thì

( )d( ,( )) ( )P A P AC

   

   

- Nếu đường thẳng

AB

cắt

( )P

tại

.I

Gọi

D

là điểm thỏa mãn IB ID







 

và

E

là trung điểm

.BD

Khi đó

d( ,( )) d( ,( )) 2 d( ,( )) 2( )

IB

P A P D P E P EC

ID

    

      

2. Xét

,A B

nằm về hai phía so với

( )P

. Gọi

I

là giao điểm của

AB

và ( ),P B



là điểm đối xứng với

B

qua

I

. Khi đó

 

d( ,( )) d ,( )P A P B P

 



 

Đến đây ta chuyển về trường hợp trên.

So sánh các kết quả ở trên ta chọn kết quả lớn nhất.

Bài toán 6. Trong không gian cho

n

điểm

1 2

, , ,

n

A A A và diểm

.A

Viết phương trình mặt phẳng

( )P

đi

qua

A

và tổng khoảng cách từ các điểm

( 1,

i

A i n

) lớn nhất.

Lời giải.

- Xét

n

điểm

1 2

, , ,

n

A A A nằm cùng phía so với

( ).P

Gọi

G

là trọng tâm của

n

điểm đã cho. Khi đó

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9

 

1

d ,( ) d( ,( ))

n

i

A P n G P nGA



 



- Trong

n

điểm trên có

m

điểm nằm về một phía và

k

điểm nằm về phía khác

(m k n 

). Khi đó, gọi

1

G là trọng tâm của

m

điểm,

2

G là trọng tâm của

k

điểm

3

G đối xứng với

1

G qua

.A

Khi dó

   

3 2

md ,( ) d ,( )P G P k G P 

Đến đây ta chuyển về bài toán trên.

Bài toán 7.Viết phương trình mặt phẳng

 

P

đi qua đường thẳng



và cách

A

một khoảng lớn nhất

Lời giải. Gọi

,H K

lần lượt là hình chiếu của

A

lên mặt phẳng

( )P

và đường thẳng

.

Khi đó

d( ,( ))A P AH AK 

Do đó

( )P

là mặt phẳng đi qua

K

và vuông góc vói

.AK

Bài toán 8. Trong không gian

Oxyz,

cho các điểm

1 2

, , , .

n

A A A Xét véc tơ

1 1 2 2 n n

w MA M A M A

  

   

  





Trong đó

1 2

; ...

n

  

là các số thực cho trước thỏa mãn

1 2

... 0

n

  

    . Tìm điểm

M

thuôc măt phẳng

( )P

sao cho

| |w



có đô dài nhỏ nhất.

Lời giải. Gọi

G

là điểm thỏa mãn

1 1 2 2

0

n n

GA GA GA

  

   

   



(điểm

G

hoàn toàn xác định).

Ta có

k

MA MG GA 





vói

1;2; ; ,k n 

nên

   

1 2 1 1 2 2 1 2

w

n n n n

MG GA GA GA MG

        

         

 

  





Do đó

1 2

| | | |

n

w MG

  

    





Vi

1 2 n

  

   là hằng số khác không nên

| |w



có giá trị nhỏ nhất khi và chỉ khi

MG

nhỏ nhất, mà

( )M P

nên điểm

M

cần tìm là hình chiếu của

G

trên mặt phẳng

( )P

.

Bài toán 9. Trong không gian Oxy

,z

cho các diểm

1 2

, , , .

n

A A A Xét biểu thức:

2 2 2

1 1 2 2 n n

T MA MA MA

  

   

Trong đó

1 2

, , ,

n

  



là các số thực cho trước. Tìm điểm M thuộc măt phẳng

( )P

sao cho

1.

T

giá trị nhỏ nhất biết

1 2

0

n

  

   .

2. T có giá trị lớn nhất biết

1 2

0

n

  

   .

Lời giải. Gọi

G

là điểm thỏa mãn

1 1 2 2

0

n n

GA GA GA

  

   

   



Ta có

k

MA MG GA 





với

1;2; ; ,k n 

nên

 

2

2 2 2

2

k k k k

MA MG GA MG MG GA GA     

 

 

Do đó

 

2 2 2 2

1 2 1 1 2 2n n n

T MG GA GA GA

     

      

Vì

2 2 2

1 1 2 2 n n

GA GA GA

  

  

không đổi nên

•

với

1 2

0

n

  

   thì

T

đạt giá trị nhỏ nhất khi và chỉ khi

MG

nhỏ nhất.

•

với

1 2

0

n

  

   thì

T

đạt giá trị lớn nhất khi và chỉ khi

MG

nhỏ nhất.

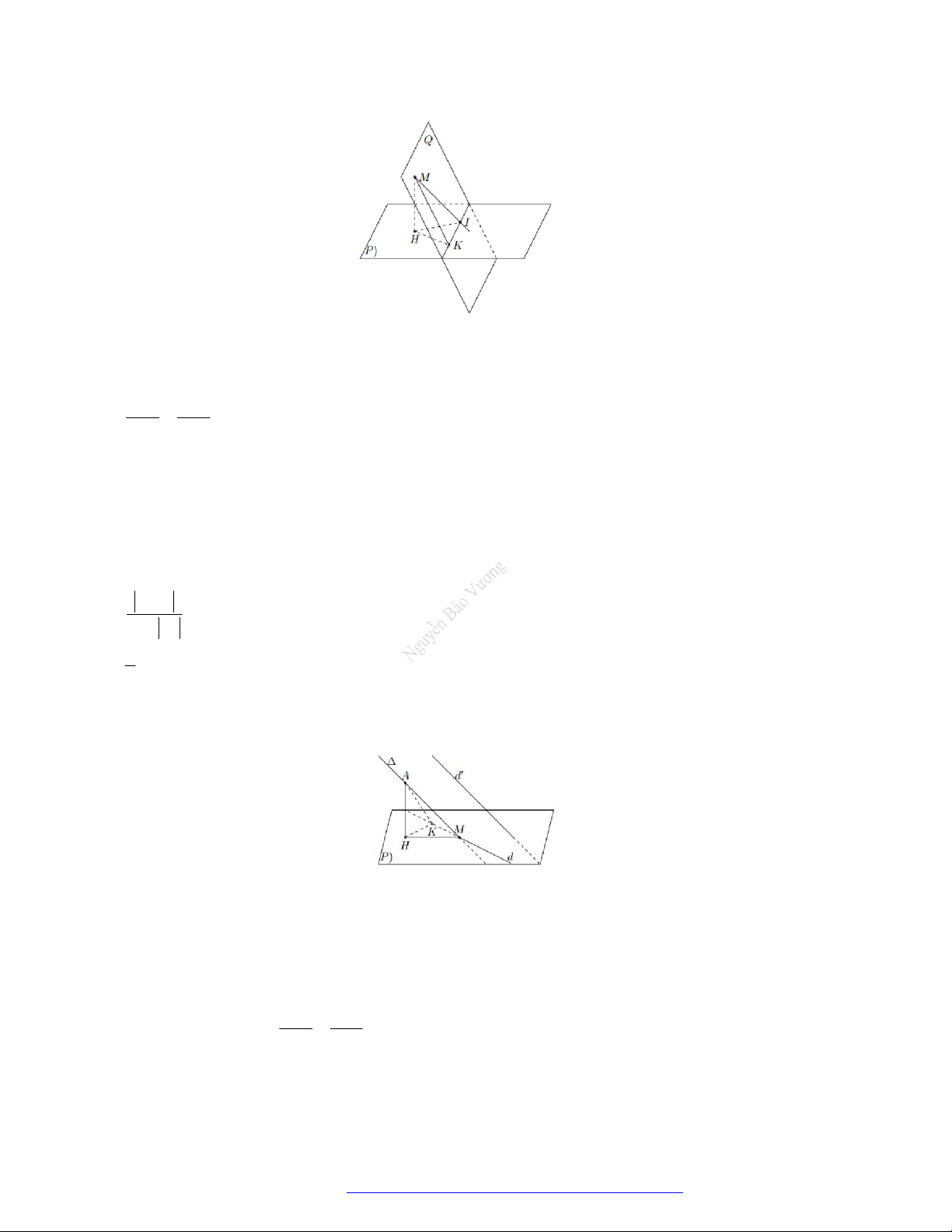
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 10 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Mà

( )M P

nên

MG

nhỏ nhất khi điểm

M

là hình chiếu của

G

trên mặt phẳng

( )P

.

Bài toán 10. Trong không gian Oxyz, cho đường thẳng d và mặt phẳng

( )P

cắt nhau. Viết phương trình của

mặt phẳng

( )Q

chứa

d

và tạo với mặt phẳng

( )P

một góc nhỏ nhất.

Lời giải. Gọi

I

là giao điểm của đường thẳng

d

với mặt phẳng

( )P

và lấy điểm

,M d M I 

. Gọi

,H K

lầ lượt là hình chiếu của

M

lên

( )P

và giao tuyến



của

( )P

và

( )Q

.

Đặt



là góc giữa

( )P

và

( ),Q

ta có



,MKH





do đó

tan

HM HM

HK HI



 

Do đó

( )Q

là mặt phẳng đi qua

d

và vuông góc với mặt phẳng

( ),MHI

nên

( )Q

đi qua

M

và nhận

 

P d d

n u u 

  

làm VTPT.

Chú ý. Ta có thể giải bài toán trên bằng phương pháp đai số như sau:

- Goi

2 2 2

( ; ; ), 0n a b c a b c   



là một VTPT của mặt phẳng

( ).Q

Khi đó 0

d

n u 

 

từ đây ta rút được

a

theo

,b c

(hoặc

b

theo

,a c

hoặc

c

theo

,a b

).

- Gọi



là góc giữa

( )P

và

( ),Q

ta có

cos ( )

| |

P

n n

f t

n n





 



 

với

, 0.

b

t c

c

 

Khảo sát

( )f t

ta tìm được max của

( )f t

Bài toán 11. Trong không gian Oxyz, cho hai đường thẳng

d

và

d



chéo nhau. Viết phương trinh mặt

phẳng

( )P

chứa

d

và tạo với

d



một góc lớn nhất.

Lời giải. Trên đường thẳng

d

, lấy điểm

M

và dựng đường thẳng



đi qua

M

song song với

d



. Khi đó

góc giữa



và

( )P

chính là góc giữa

d



và

( )P

.

Trên đường thẳng



, lấy điểm

A

. Gọi

H

và

K

lần lượt là hình chiếu của

A

lên

( )P

và

,d



là góc giữa



và

( )P

.

Khi đó



AMH





và

cos

HM KM

AM AM



 

Suy ra

( )P

là mặt phẳng chứa

d

và vuông góc với mặt phẳng

( ).AMK

Do dó

( )P

đi qua

M

và nhận

 

d d

d

u u u



 

  

làm VTPT.

Chú ý. Ta có thể giải bài toán trên bằng phương pháp đại số như sau:

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11

- Goi

2 2 2

( ; ; ), 0

n a b c a b c

   



là một VTPT của măt phẳng

( ).P

Khi đó

0

d

n u

 

 

từ đây ta rút được

a

theo

,b c

(hoặc

b

theo

,a c

hoặc

c

theo

,a b

).

- Gọi



là góc giữa

( )P

và

,d



ta có

sin ( )

| |

d

n u

f t

n u







 



 

với

, 0.

b

t c

c

 

Khảo sát

( )f t

ta tìm được max của

( )f t

Dạng 2.1. Cực trị liên quan đến khoảng cách, góc

Câu 1. (Mã 101 - 2019) Trong không gian

Oxyz

, cho điểm

 

0;4; 3

A



. Xét đường thẳng

d

thay đổi,

song song với trục

Oz

và cách trục

Oz

một khoảng bằng

3

. Khi khoảng cách từ

A

đến

d

nhỏ

nhất,

d

đi qua điểm nào dưới đây?

A.

 

0;5; 3 .

Q



B.

 

3;0; 3 .

P

 

C.

 

0; 3; 5 .

M

 

D.

 

0;3; 5 .

N



Câu 2. (Mã 103 2019) Trong không gian Oxyz, cho điểm

 

0;3; 2

A



. Xét đường thẳng

d

thay đổi

song song với Oz và cách Oz một khoảng bằng 2. Khi khoảng cách từ

A

đến

d

nhỏ nhất.

d

đi

qua điểm nào dưới đây?

A.

 

0;2; 5

Q



. B.

 

0;4; 2

M



. C.

 

2;0; 2

P

 

. D.

 

0; 2; 5

N

 

.

Câu 3. (Mã 102 - 2019) Trong không gian

Oxyz

, cho điểm

 

0;4; 3

A



. Xét đường thẳng

d

thay đổi,

song song với trục

Oz

và cách trục

Oz

một khoảng bằng 3. Khi khoảng cách từ

A

đến

d

lớn

nhất,

d

đi qua điểm nào dưới đây?

A.

 

0;3; 5

N



. B.

 

0; 3; 5

M

 

. C.

 

3;0; 3

P

 

. D.

 

0;11; 3

Q



.

Câu 4. (Mã 104 2019) Trong không gian

,Oxyz

cho điểm

 

0;3; 2 .

A 

Xét đường thẳng

d

thay đổi,

song song với trục

Oz

và cách trục

Oz

một khoảng bằng

2.

Khi khoảng cách từ

A

đến

d

lớn

nhất,

d

đi qua điểm nào dưới đây?

A.

 

0;8; 5

M



. B.

 

0;2; 5

N



. C.

 

0; 2; 5

P

 

. D.

 

2;0; 3

Q

 

.

Câu 5. (THCS - THPT Nguyễn Khuyến 2019) Trong không gian

Oxyz

, cho đường thẳng

:

2 2 1

x y z

  

và mặt phẳng

 

: 2 2 0

P x y z

  

. Gọi

 

Q

là mặt phẳng chứa



sao cho góc

giữa hai mặt phẳng

 

P

và

 

Q

là nhỏ nhất. Phương trình mặt phẳng

 

Q

là

A.

2 0

x y z

  

. B.

22 10 0

x y z

  

. C.

2 0

x y z

  

. D.

10 22 0

x y z

  

.

Câu 6. Trong không gian

Oxyz

, cho điểm

 

1;1;2

A

và mặt phẳng

   

: 1 1 0

P m x y mz

    

, với

m

là tham số. Biết khoảng cách từ điểm

A

đến mặt phẳng

 

P

lớn nhất. Khẳng định đúng trong bốn

khẳng định dưới đây là

A.

2 6

m

 

. B.

6

m



. C.

2 2

m

  

. D.

6 2

m

  

.

Câu 7. (THPT Quang Trung Đống Đa Hà Nội 2019) Trong không gian với hệ tọa độ

Oxyz

, cho hai

điểm

(1;1;1)

A

,

(2;0;1)

B

và mặt phẳng

( ) : 2 2 0.

P x y z

    

Viết phương trình chính tắc của

đường thẳng

d

đi qua

A

, song song với mặt phẳng

( )P

sao cho khoảng cách từ

B

đến

d

lớn

nhất.

A.

1 1 1

:

3 1 2

x y z

d

  

  



. B.

2

:

2 2 2

x y z

d



  



.

C.

2 2

:

1 1 1

x y z

d

 

  



. D.

1 1 1

:

3 1 1

x y z

d

  

  

 

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 12 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 8. (KTNL GV THPT Lý Thái Tổ 2019) Trong không gian với hệ tọa độ

Oxyz

, cho đường thẳng

1 2

:

1 2 1

x y z

d

 

 



. Gọi

 

P

là mặt phẳng chứa đường thẳng

d

và tạo với mặt phẳng

 

: 2 2 2 0

Q x y z

   

một góc có số đo nhỏ nhất. Điểm

 

1;2;3

A

cách mặt phẳng

 

P

một

khoảng bằng:

A.

3

. B.

5 3

3

. C.

7 11

11

. D.

4 3

3

.

Câu 9. (Chuyên Bắc Giang 2019) Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm

 

1;2; 3

A



,

 

2; 2;1

B  

và mặt phẳng

 



:

2 2 9 0

x y z

   

. Gọi

M

là điểm thay đổi trên mặt phẳng

 



sao cho

M

luôn nhìn đoạn

AB

dưới một góc vuông. Xác định phương trình đường thẳng

MB

khi

MB

đạt giá trị lớn nhất.

A.

2

2 2

1 2

x t

y t

z t

  





  





 



B.

2 2

2

1 2

x t

y t

z t

  





  





 



C.

2

1 2

x t

y

z t

  





 





 



D.

2

1

x t

y t

z

  





  









Câu 10. -(Chuyên Nguyễn Tất Thành Yên Bái 2019) Viết phương trình đường thẳng

a

đi qua

 

4; 2; 1

M 

, song song với mặt phẳng

( ) : 3 4 12 0

x y z

   



và cách

 

2; 5; 0

A 

một

khoảng lớn nhất.

A.

4

2

1

x t

y t

z t

 





  





 



. B.

4

2

1

x t

y t

z t

 





  





  



. C.

1 4

1 2

1

x t

y t

z t

 





 





  



. D.

4

2

1

x t

y t

z t

 





  





 



.

Câu 11. (Chuyên Nguyễn Trãi Hải Dương 2019) Đường thẳng



đi qua điểm

 

3;1;1

M

, nằm trong mặt

phẳng

 

: 3 0

x y z



   

và tạo với đường thẳng

1

: 4 3

3 2

x

d y t

z t







 





  



một góc nhỏ nhất thì phương trình

của



là

A.

1

2

x

y t

z t









 











. B.

8 5

3 4

2

x t

y t

z t



 







  







 



. C.

1 2

1

3 2

x t

y t

z t



 







 







 



. D.

1 5

1 4

3 2

x t

y t

z t



 







 







 



.

Câu 12. (Chuyên Thái Bình 2019) Trong không gian

Oxyz

, cho điểm

 

1;1;1

A

và mặt phẳng

( ) : 2 0

P x y

 

. Gọi



là đường thẳng đi qua

A

, song song với

( )P

và cách điểm

 

1;0;2

B 

một khoảng ngắn nhất. Hỏi



nhận vecto nào dưới đây là vecto chỉ phương ?

A.

 

6;3; 5

u

 



. B.

 

6; 3;5

u  



. C.

 

6;3;5

u 



. D.

 

6; 3; 5

u

  



.

Câu 13. Trong không gian với hệ tọa độ

Oxyz

cho điểm

 

2; 1; 2

A

 

và đường thẳng

 

d

có phương

trình

1 1 1

x y z  

 



. Gọi

 

P

là mặt phẳng đi qua điểm

A

, song song với đường thẳng

 

d

và khoảng cách từ

d

tới mặt phẳng

 

P

là lớn nhất. Khi đó mặt phẳng

 

P

vuông góc với mặt

phẳng nào sau đây?

A.

6 0

x y

  

. B.

3 2 10 0

x y z

   

.

C.

2 3 1 0

x y z

   

. D.

3 2 0

x z

  

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13

Câu 14. Trong không gian với hệ toạ độ

Oxyz

, gọi

 

P

là mặt phẳng đi qua hai điểm

 

1; 7; 8

A

 

,

 

2; 5; 9

B

 

sao cho khoảng cách từ điểm

 

7; 1; 2

M

 

đến

 

P

đạt giá trị lớn nhất. Biết

 

P

có

một véctơ pháp tuyến là

 

; ;4n a b





, khi đó giá trị của tổng

a b

là

A.

1

. B.

3

. C.

6

. D.

2

.

Câu 15. Trong không gian với hệ tọa độ

Oxyz

, cho điểm

 

3; 1;0

A 

và đường thẳng

2 1 1

:

1 2 1

x y z

d

  

 



. Mặt phẳng

 



chứa

d

sao cho khoảng cách từ

A

đến

 



lớn nhất có

phương trình là

A.

2 0

x y z

   

. B.

0

x y z

  

.

C.

1 0

x y z

   

. D.

2 5 0

x y z

    

.

Câu 16. Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm

 

3;0;1

A 

,

 

1; 1;3

B 

và mặt phẳng

 

: 2 2 5 0

P x y z

   

. Viết phương trình chính tắc của đường thẳng

d

đi qua

A

, song song với

mặt phẳng

 

P

sao cho khoảng cách từ

B

đến

d

nhỏ nhất.

A.

3 1

:

26 11 2

x y z

d

 

 



. B.

3 1

:

26 11 2

x y z

d

 

 



.

C.

3 1

:

26 11 2

x y z

d

 

 

. D.

3 1

:

26 11 2

x y z

d

 

 

 

.

Câu 17. (Sở Thanh Hóa 2019) Trong không gian

Oxyz

, cho điểm

 

2;5;3

A

và đường thẳng

1 2

:

2 1 2

x y z

d

 

 

. Gọi

 

P

là mặt phẳng chứa

d

sao cho khoảng cách từ

A

đến

 

P

là lớn

nhất. Khoảng cách từ gốc tọa độ

O

đến

 

P

bằng

A.

2

. B.

3

6

. C.

11 2

6

. D.

1

2

.

Câu 18. (Chuyên Phan Bội Châu 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho hai điểm

   

1;2;3 , 5; 4; 1

A B

 

và mặt phẳng

 

P

qua

Ox

sao cho

 

, ,

2 ,

B P A P

d d P



cắt

AB

tại

 

; ;I a b c

nằm giữa

AB

. Tính

a b c 

A.

8

B.

6

C.

12

D.

4

Câu 19. (Đề Thi Công Bằng KHTN -2019) Trong không gian Oxyz, cho đường thẳng

1 1

:

2 1 1

x y z

d

 

 



và điểm

(1;2;3)

A

. Gọi

( )P

là mặt phẳng chứa d và cách điểm A một khoảng

cách lớn nhất. Vectơ nào dưới đây là một vectơ pháp tuyến của

( )P

.

A.

(1;0;2)

n 



. B.

(1;0; 2)

n

 



. C.

(1;1;1)

n 



. D.

(1;1; 1)

n

 



.

Câu 20. (Chuyên Thái Bình - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm

 

3;0;1

A 

,

 

1; 1;3

B 

và mặt phẳng

 

: 2 2 5 0

P x y z

   

. Viết phương trình chính tắc của đường thẳng

d

đi qua

A

, song song với mặt phẳng

 

P

sao cho khoảng cách từ

B

đến

d

nhỏ nhất.

A.

3 1

:

26 11 2

x y z

d

 

 



. B.

3 1

:

26 11 2

x y z

d

 

 



.

C.

3 1

:

26 11 2

x y z

d

 

 

. D.

3 1

:

26 11 2

x y z

d

 

 

 

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 14 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 21. (Sở Quảng Nam - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

 

: 4 0

P x y z

  

, đường thẳng

1 1 3

:

2 1 1

x y z

d

  

 



và điểm

 

1; 3; 1

A

thuộc mặt phẳng

 

P

. Gọi



là đường thẳng đi qua

A

, nằm trong mặt phẳng

 

P

và cách đường thẳng

d

một

khoảng cách lớn nhất. Gọi

 

; ; 1u a b





là một véc tơ chỉ phương của đường thẳng



. Tính

2a b

.

A.

2 3

a b

  

. B.

2 0

a b

 

. C.

2 4

a b

 

. D.

2 7

a b

 

.

Câu 22. ( Bắc Giang 2018) Trong không gian với hệ tọa độ

Oxyz

cho điểm

 

2;1;3

A

và mặt phẳng

   

: 2 1 2 0

P x my m z m

     

,

m

là tham số. Gọi

 

; ;H a b c

là hình chiếu vuông góc của

điểm

A

trên

 

P

. Tính

a b

khi khoảng cách từ điểm

A

đến

 

P

lớn nhất ?

A.

1

2

a b

  

. B.

2

a b

 

. C.

0

a b

 

. D.

3

2

a b

 

.

Câu 23. (Đề Tham Khảo 2017) Trong không gian với hệ tọa độ

,Oxyz

cho mặt phẳng

 

: 2 2 3 0

P x y z

   

và mặt cầu

 

2 2 2

: 2 4 2 5 0.

S x y z x y z

      

Giả sử

 

M P



và

 

N S



sao cho



MN

cùng phương với vectơ

 

1;0;1

u



và khoảng cách giữa

M

và

N

lớn nhất.

Tính

.MN

A.

3

MN

B.

1 2 2

 MN

C.

3 2

MN

D.

14

MN

Câu 24. (SGD&ĐT Đồng Tháp - 2018) Trong không gian với hệ trục tọa độ

Oxyz

, cho mặt cầu

     

2 2

2

: 1 2 4

S x y z

    

có tâm

I

và mặt phẳng

 

: 2 2 2 0

P x y z

   

. Tìm tọa độ điểm

M

thuộc

 

P

sao cho đoạn

IM

ngắn nhất.

A.

1 4 4

; ;

3 3 3

 

  

 

 

. B.

11 8 2

; ;

9 9 9

 

  

 

 

C.

 

1; 2;2



. D.

 

1; 2; 3 

.

Câu 25. (THPT Ba Đình 2019) Trong không gian với hệ tọa độ

,Oxyz

cho mặt phẳng

 

: 2 2 3 0

P x y z

   

và mặt cầu

 

2 2 2

: 2 4 2 5 0

S x y z x y z

      

. Giả sử

 

M P



và

 

N S



sao cho

MN



cùng phương với vectơ

 

1;0;1

u 



và khoảng cách giữa

M

và

N

lớn

nhất. Tính

.MN

A.

3

MN



. B.

1 2 2

MN  

. C.

3 2

MN 

. D.

14

MN



.

Câu 26. (HSG Bắc Ninh 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho mặt cầu

2 2 2

( ) : 2 4 2 3 0

S x y z x y z

      

và mặt phẳng

( ) : 2 2 14 0

P x y z

   

. Điểm

M

thay đổi

trên

 

S

, điểm

N

thay đổi trên

( )P

. Độ dài nhỏ nhất của

MN

bằng

A.

1

B.

2

C.

1

2

D.

3

2

Câu 27. Trong không gian với hệ tọa độ

Oxyz

, cho mặt cầu

 

S

tâm

 

1; 2;1

I 

; bán kính

4R 

và đường

thẳng

1 1

:

2 2 1

x y z

d

 

 

 

. Mặt phẳng

 

P

chứa

d

và cắt mặt cầu

 

S

theo một đường tròn có

diện tích nhỏ nhất. Hỏi trong các điểm sau điểm nào có khoảng cách đến mặt phẳng

 

P

lớn nhất.

A.

 

0;0;0

O

. B.

3 1

1; ;

5 4

A

 



 

 

. C.

 

1; 2; 3

B

  

. D.

 

2;1;0

C

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15

Câu 28. (Sở Thanh Hóa 2019) Trong không gian

Oxyz

cho mặt phẳng

 

: 1 0

P y

 

, đường thẳng

1

: 2

1

x

d y t

z







 









và hai điểm

 

1; 3;11

A  

,

1

;0;8

2

B

 

 

 

. Hai điểm

M

,

N

thuộc mặt phẳng

 

P

sao

cho

 

, 2

d M d



và

2

NA NB

. Tìm giá trị nhỏ nhất của đoạn

MN

.

A.

min

1

MN



. B.

min

2

MN 

. C.

min

2

MN 

. D.

min

2

.

3

MN



Câu 29. (THPT Yên Phong Số 1 Bắc Ninh 2019) Trong không gian với hệ tọa độ

Oxyz

, cho các điểm

 

1; 0; 0

A

,

 

3;2;0

B

,

 

1;2; 4

C



. Gọi

M

là điểm thay đổi sao cho đường thẳng

MA

,

MB

,

MC

hợp với mặt phẳng

 

ABC

các góc bằng nhau;

N

là điểm thay đổi nằm trên mặt cầu

       

2 2 2

1

: 3 2 3

2

S x y z

     

. Tính giá trị nhỏ nhất của độ dài đoạn

MN

.

A.

3 2

2

. B.

2

. C.

2

. D.

5

.

Câu 30. (Sở Bình Phước - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho điểm

 

1; 2; 3

A



và mặt

phẳng

 

: 2 2 9 0

P x y z

   

. Đường thẳng

d

đi qua

A

và có vectơ chỉ phương

 

3; 4; 4

u

 



cắt

 

P

tại điểm

B

. Điểm

M

thay đổi trong

 

P

sao cho

M

luôn nhìn đoạn

AB

dưới góc

90

.

Khi độ dài

MB

lớn nhất, đường thẳng

MB

đi qua điểm nào trong các điểm sau?

A.

 

3;2;7

J 

. B.

 

3;0;15

K

. C.

 

2; 1;3

H  

. D.

 

1; 2;3

I  

.

Câu 31. (Sở Bạc Liêu - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho mặt cầu

 

S

có tâm

 

1;2;3

I

và có bán kính

2r 

. Xét đường thẳng

 

1

:

1

x t

d y mt t

z m t



 



  





 





,

m

là tham số thực. Giả sử

   

,P Q

là mặt phẳng chứa

d

và tiếp xúc với

 

S

lần lượt tại

,M N

. Khi đó đoạn

MN

ngắn

nhất hãy tính khoảng cách từ điểm

 

1;0;4

B

đến đường thẳng

d

.

A.

5

. B.

5 3

3

. C.

4 237

21

. D.

4 273

21

.

Câu 32. (Hậu Lộc 2-Thanh Hóa 2019) Trong không gian

O

xyz

, cho mặt phẳng

 

: 2 2 9 0

P x y z

   

và điểm

 

1;2; 3

A



. Đường thẳng

d

đi qua

A

và có véc tơ chỉ phương

 

3;4; 4

u

 



cắt

 

P

tại

B

. Điểm

M

thay đổi trên

 

P

sao cho

M

luôn nhìn đoạn

AB

dưới một góc

90

. Độ dài đoạn

MB

lớn nhất bằng

A.

36

5

. B.

41

. C.

6

. D.

5

.

Câu 33. (Chuyên Nguyễn Trãi Hải Dương 2019) Đường thẳng



đi qua điểm

 

3;1;1

M

, nằm trong mặt

phẳng

 

: 3 0

x y z



   

và tạo với đường thẳng

1

: 4 3

3 2

x

d y t

z t







 





  



một góc nhỏ nhất thì phương

trình của



là:

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 16 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

A.

1

2

x

y t

z t









 











. B.

8 5

3 4

2

x t

y t

z t



 







  







 



. C.

1 2

1

3 2

x t

y t

z t



 







 







 



. D.

1 5

1 4

3 2

x t

y t

z t



 







 







 



.

Câu 34. (THPT Ngô Quyền - Ba Vì - Hải Phòng 2019) Trong không gian

Oxyz

, cho điểm

 

2; 5; 3

A

và

đường thẳng

d

:

1 2

2 1 2

x y z

 

 

. Biết rằng

 

P

:

3 0

ax by cz

   

 

, ,a b c 



là mặt phẳng

chứa

d

và khoảng cách từ

A

đến

 

P

lớn nhất. Khi đó tổng

T a b c  

bằng

A.

3

. B.

3

. C.

2

. D.

5

.

Câu 35. (ĐH - Quốc Tế - 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho hai điểm

 

2;1; 3

A



,

 

3;2;1

B 

. Gọi

 

d

là đường thẳng đi qua

 

1;2;3

M

sao cho tổng khoảng cách từ

A

đến

 

d

và

từ

B

đến

 

d

là lớn nhất. Khi đó phương trình đường thẳng

 

d

là

A.

1

2

5 4

x z

y



  



. B.

1 2 3

3 2 1

x y z

  

 



.

C.

1 2 3

1 13 2

x y z

  

 



. D.

1 2 3

3 2 2

x y z

  

 



.

Câu 36. (Chuyên Ngữ Hà Nội 2019) Trong không gian với hệ tọa độ

,Oxyz

cho đường thẳng

:

x y z

d

 

 



1 2

1 2 1

và mặt phẳng

 

:P x y z

   2 2 2 0

.

 

Q

là mặt phẳng chứa

d

và tạo

với mp

 

P

một góc nhỏ nhất. Gọi

 

; ;

Q

n a b



1



là một vectơ pháp tuyến của

 

Q

. Đẳng thức nào

đúng?

A.

.

a b

  1

B.

.

a b

  2

C.

.

a b

  1

D.

.

a b

  0

Câu 37. (Chuyên Bắc Giang 2019)Trong không gian với hệ tọa độ

Oxyz

, cho đường thẳng

1 1

:

2 1 1

x y z

d

 

 



,

 

2;1;0

M

. Gọi

 

; ;H a b c

là điểm thuộc

d

sao cho

MH

có độ dài nhỏ

nhất. Tính

2 2 2

T a b c  

.

A.

6

T



. B.

12T 

. C.

5

T 

. D.

21T 

.

Câu 38. (SGD Điện Biên - 2019) Trong không gian

Oxyz

, cho điểm

 

1;2; 3

A



và mp

 

:P

2 2 9 0

x y z

   

. Đường thẳng

d

qua

A

và vuông góc với mp

 

:Q

3 4 4 5 0

x y z

   

, cắt

mp

 

P

tại

B

. Điểm

M

nằm trong mp

 

P

sao cho

M

luôn nhìn

AB

dưới góc vuông. Tính độ

dài lớn nhất của

MB

.

A.

41

2

M 

. B.

5

2

MB 

. C.

5

MB 

. D.

41

MB 

.

Câu 39. (SP Đồng Nai - 2019) Trong không gian

Oxyz

, cho bốn điểm

     

3;0;0 , 0;2;0 , 0;0;6

A B C

và

 

1;1;1

D

. Gọi



là đường thẳng đi qua

D

và thỏa mãn tổng khoảng cách từ các điểm

, ,A B C

đến



là lớn nhất. Hỏi



đi qua điểm nào trong các điểm dưới đây?

A.

 

5;7;3

M

. B.

 

1; 2;1

M  

. C.

 

3;4;3

M

. D.

 

7;13;5

M

.

Câu 40. (Chuyên - KHTN - Hà Nội - 2019) Trong không gian

Oxyz

, cho đường thẳng

d

:

1 1

2 1 1

x y z 

 



và điểm

 

1;2;3

A

. Gọi

 

P

là mặt phẳng chứa

d

và cách điểm

A

một khoảng

cách lớn nhất. Véc-tơ nào dưới đây là một véc-tơ pháp tuyến của

 

P

?

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17

A.

 

1;0;2

n 



. B.

 

1;0; 2

n

 



. C.

 

1;1;1

n 



. D.

 

1;1; 1

n

 



.

Câu 41. (Chuyên Quang Trung- Bình Phước2019) Trong không gian

Oxyz

cho hai đường thẳng

1

:

1 1 1

x y z 

  

và

1

'

1 2 1

x y z

   

. Xét điểm

M

thay đổi. Gọi

,a b

lần lượt là khoảng

cách từ M đến



và

'

. Biểu thức

2 2

2a b

đạt giá trị nhỏ nhất khi và chỉ

khi

 

0 0 0 0

, ,M M x y z

. Khi đó giá trị

0 0

x y

bằng

A.

4

3

. B.

0

. C.

2

3

. D.

2

.

Câu 42. (Chuyên Thái Bình - 2019) Trong không gian với hệ tọa độ

Oxyz

, cho điểm

 

1;1;1

A

và mặt

phẳng

 

: 2 0

P x y

 

. Gọi



là đường thẳng đi qua

A

song song với

 

P

và cách

 

1;0;2

B



một khoảng nhỏ nhất. Hỏi



nhận vectơ nào dưới đây làm vecto chỉ phương?

A.

 

6;3; 5

u

 



. B.

 

6; 3;5

u  



. C.

 

6;3;5

u 



. D.

 

6; 3; 5

u

  



.

Câu 43. (Chuyên Nguyễn Huệ-HN-2019) Trong không gian với hệ trục toạ độ

,Oxyz

gọi

 

P

là mặt

phẳng chứa đường thẳng

1 2

:

1 1 2

x y z

d

 

 

 

và tạo với trục

Oy

góc có số đo lớn nhất. Điểm

nào sau đây thuộc mặt phẳng

 

P

?

A.

 

3;0;4 .

E 

B.

 

3;0;2 .

M

C.

 

1; 2; 1 .

N

  

D.

 

1;2;1 .

F

Câu 44. (Chuyên Lê Quý Đôn Quảng Trị 2019) Trong không gian

,Oxyz

cho mặt cầu

2 2 2

5

( ) : ( 1) ( 1)

6

    

S x y z

, mặt phẳng

( ) : 1 0   

P x y z

và đường thẳng

:

1 1 1

  

x y z

. Điểm

M

thay đổi trên đường tròn giao tuyến của

( )P

và

( )S

. Giá trị lớn nhất của

( ; )

d M

là

A.

3 2

.

2

B.

2 2.

C.

2.

D.

2

.

2

Câu 45. (SP Đồng Nai - 2019) Trong không gian với hệ tọa độ

Oxyz

, cho hình lăng trụ đứng

.

ABC A B C

  

có

 

0

;0;0

A x

 

0

;0;0

B x

,

 

0;1;0

C

và

 

0 0

;0;B x y





trong đó

0 0

;x y

là các số

thực dương và thỏa mãn

0 0

4

x y

 

. Khi khoảng cách giữa hai đường thẳng

AC



và

B C



lớn

nhất thì bán kính

R

của mặt cầu ngoại tiếp hình lăng trụ

.

ABC A B C

  

bằng bao nhiêu?

A.

29

2

R 

. B.

29

4

R 

. C.

41

4

R 

. D.

3 6

2

R 

.

Câu 46. (Chu Văn An - Hà Nội - 2019) Trong không gian

Oxyz

, cho hai điểm

 

2;1; 2

A



,

 

5;1;1

B

và

mặt cầu

 

2 2 2

: 6 12 9 0

S x y z y z

     

. Xét đường thẳng

d

đi qua

A

và tiếp xúc với

 

S

sao cho khoảng cách từ

B

đến

d

nhỏ nhất. Phương trình của đường thẳng

d

là

A.

2

1

2 2

x

y t

z t







 





  



. B.

2

1 4

2

x

y t

z t







 





  



. C.

2 2

1 2

2

x t

y t

z t

 





 





  



. D.

2

1 4

2

x t

y t

z t

 





 





  



.

Dạng 2.2. Cực trị lên quan đến giá trị biểu thức

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 18 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 47. (THPT - Yên Định Thanh Hóa 2019) Trong không gian

Oxyz

, cho đường thẳng

d

có phương

trình

1

2

x t

y t

z t

 





 





 



và ba điểm

 

6;0;0

A

,

 

0;3;0

B

,

 

0;0;4

C

. Gọi

 

; ;M a b c

là điểm thuộc

d

sao

cho biểu thức

2 2 2

2 3

P MA MB MC

  

đạt giá trị nhỏ nhất, khi đó

a b c 

bằng

A.

3

. B.

4

. C.

1

. D.

2

.

Câu 48. (Lê Quý Đôn - Quảng Trị - 2018) Trong không gian

Oxyz

, cho

2

điểm

 

3; 2;3

A 

,

 

1;0;5

B

và đường thẳng

1 2 3

:

1 2 2

x y z

d

  

 



. Tìm tọa độ điểm

M

trên đường thẳng

d

để

2 2

MA MB

đạt giá trị nhỏ nhất.

A.

 

1;2;3

M

. B.

 

2;0;5

M

. C.

 

3; 2;7

M 

. D.

 

3;0;4

M

.

Câu 49. (THPT Chu Văn An - Hà Nội - 2018) Trong không gian

Oxyz

, cho đường thẳng

1

:

1 1 1

x y z

  

và hai điểm

 

1;2; 5

A



,

 

1;0;2

B 

. Biết điểm

M

thuộc



sao cho biểu thức

MA MB



đạt giá trị lớn nhất

max

T

. Khi đó,

max

T

bằng bao nhiêu?

A.

max

57

T 

. B.

max

3

T



. C.

max

2 6 3

T

 

. D.

max

3 6

T 

.

Câu 50. Trong không gian với hệ tọa độ

Oxyz

, cho đường thẳng

2 1

:

1 2 3

x y z

d

 

 

và hai điểm

 

2;0;3

A

,

 

2; 2; 3

B

 

. Biết điểm

 

0 0 0

; ;M x y z

thuộc

d

thỏa mãn

4 4

MA MB

nhỏ nhất. Tìm

0

x

.

A.

0

1

x



. B.

0

3

x



. C.

0

x



. D.

0

2

x



.

Câu 51. (Chuyên Hà Tĩnh - 2018) Trong không gian

Oxyz

, cho ba điểm

 

1;0;1

A 

,

 

3;2;1

B

,

 

5;3;7

C

. Gọi

 

; ;M a b c

là điểm thỏa mãn

MA MB

và

MB MC

đạt giá trị nhỏ nhất. Tính

P a b c  

A.

4P 

. B.

0

P



. C.

2P 

. D.

5

P



.

Câu 52. (THPT An Lão Hải Phòng 2019) Trong không gian với hệ tọa độ Oxyz, cho 3 điểm

     

1;2;3 , 0;1;1 , 1;0; 2

A B C



và mặt phẳng

 

: 2 0

P x y z

   

. Gọi M là điểm thuộc mặt

phẳng (P) sao cho giá trị của biểu thức

2 2 2

2 3

T MA MB MC

  

nhỏ nhất. Tính khoảng cách từ M

đến mặt phẳng

 

:2 2 3 0

Q x y z

   

?

A.

2 5

3

B.

121

54

C.

24

D.

91

54

Câu 53. (THPT Cẩm Giàng 2 2019) Trong không gian

Oxyz

, cho ba điểm

 

10; 5;8

A  

,

 

2;1; 1

B



,

 

2;3;0

C

và mặt phẳng

 

: 2 2 9 0

P x y z

   

. Xét

M

là điểm thay đổi trên

 

P

sao cho

2 2 2

2 3

MA MB MC

 

đạt giá trị nhỏ nhất. Tính

2 2 2

2 3

MA MB MC

 

.

A.

54

.

B.

282

.

C.

256

.

D.

328

.

Câu 54. Trong không gian

Oxyz

cho mặt phẳng

 

: 3 0

P x y z

   

và ba điểm

 

3;1;1

A

,

 

7;3;9

B

và

 

2;2;2

C

. Điểm

 

; ;M a b c

trên

 

P

sao cho

2 3

MA MB MC

 

  

đạt giá trị nhỏ nhất. Tính

2 10

a b c 

.

A.

62

9

. B.

27

9

. C.

46

9

. D.

43

9

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19

Câu 55. (THPT Lê Quý Dôn Dà Nẵng 2019) Trong không gian

Oxyz

, cho 3 điểm

( 8;1;1)

A



,

(2;1;3)

B

và

(6;4;0)

C

. Một điểm

M

di động trong không gian sao cho

. . 34

MA MC MA MB

 

   

. Cho biết

MA MB



đạt giá trị lớn nhất khi điểm

M

trùng với điểm

0 0 0 0

( ; ; )M x y z

. Tính tích số

0 0 0

x y z

.

A.

16.

B.

18.

C.

14.

D.

12.

Câu 56. Trong không gian với hệ tọa độ

Oxyz

, cho tam giác

ABC

với

 

2;1; 3 ,

A

 

1; 1;2 ,

B



 

3; 6; 0 ,

C



 

2; 2; 1 .

D  

Điểm

 

; ;M x y z

thuộc mặt phẳng

 

: 2 0

P x y z

   

sao cho

2 2 2 2

S MA MB MC MD   

đạt giá trị nhỏ nhất. Tính giá trị của biểu thức

  

2 2 2

P x y z

.

A.

 6P

. B.

2P 

. C.

 0P

. D.

2P  

.

Câu 57. (Chuyên Nguyễn Trãi Hải Dương 2019) Trong không gian

Oxyz

cho

 

4; 2;6

A 

,

 

2;4;2

B

,

 

: 2 3 7 0

M x y z



    

sao cho

.MA MB

 

nhỏ nhất. Tọa độ của

M

bằng

A.

29 58 5

; ;

13 13 13

 

 

 

. B.

 

4;3;1

. C.

 

1;3;4

. D.

37 56 68

; ;

3 3 3



 

 

 

.

Câu 58. Trong không gian với hệ tọa độ

Oxyz

,cho hai điểm

(1;0;2), (3;1; 1).

A B



và mặt phẳng

( ) : 1 0.

P x y z

   

Gọi

( ; ; ) ( )M a b c P

sao cho

3 2

MA MB



 

đạt giá trị nhỏ nhất. Tính

9a 3 6 .S b c  

A.

4.

B.

3.

C.

2.

D.

1.

Câu 59. (KTNL GV THPT Lý Thái Tổ 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho ba điểm

     

1;4;5 , 3;4;0 , 2; 1;0

A B C

và mặt phẳng

 

:3 3 2 12 0.   

x y z



Gọi

 

; ;M a b c

thuộc

 



sao cho

2 2 2

3 

MA MB MC

đạt giá trị nhỏ nhất. Tính tổng

.  S a b c

A.

3

. B.

2

. C.

2

. D.

1

.

Câu 60. (Dề Thi Công Bằng KHTN 2019) Trong không gian

Oxyz

cho các điểm

(1;2;0), (1; 1;3), (1; 1; 1)

A B C

  

và mặt phẳng

( ) :3 3 2 15 0

P x y z

   

. Xét

( ; ; )M a b c

thuộc mặt

phẳng

( )P

sao cho

2 2 2

2

MA MB MC

 

nhỏ nhất. Giá trị của

a b c 

bằng

A.

3

. B.

7

. C.

2

. D.

1

.

Câu 61. (Trần Phú - Hà Tĩnh - 2018) Trong không gian

Oxyz

, cho ba điểm

 

1; 2;1

A 

,

 

5; 0; 1

B



,

 

3;1; 2

C

và mặt phẳng

 

:3 3 0

Q x y z

   

. Gọi

 

; ;M a b c

là điểm thuộc

 

Q

thỏa mãn

2 2 2

2

MA MB MC

 

nhỏ nhất. Tính tổng

5a b c 

.

A.

11

. B.

9

. C.

15

. D.

14

.

Câu 62. (Lê Quý Đôn - Quảng Trị - 2018) Trong không gian với hệ trục tọa độ

Oxyz

cho 3 điểm

 

1;1;1

A

,

 

0;1;2

B

,

 

2;1;4

C 

và mặt phẳng

 

: 2 0   

P x y z

. Tìm điểm

 

N P



sao cho

2 2 2

2

S NA NB NC

  

đạt giá trị nhỏ nhất.

A.

4 4

;2;

3 3

N

 



 

 

. B.

 

2;0;1

N 

. C.

1 5 3

; ;

2 4 4

N

 



 

 

. D.

 

1;2;1

N 

.

Câu 63. (Chuyên Phan Bội Châu 2019) Trong không gian với hệ trục tọa độ

Ox ,yz

cho mặt cầu

       

2 2 2

: 1 2 1 9

S x y z

     

và hai điểm

 

4;3;1

A

,

 

3;1;3

B

; M là điểm thay đổi trên

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 20 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

 

S

. Gọi

,m n

là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức

2 2

2P MA MB 

. Xác định

 

.m n



A.

64

. B.

68

. C.

60

. D.

48

.

Câu 64. (Chuyên KHTN 2019) Trong không gian với hệ tọa độ

O

xyz

cho ba điểm

     

8;5; 11 , 5;3; 4 , 1;2; 6

A B C

  

và mặt cầu

       

2 2 2

: 2 4 1 9

S x y z

     

. Gọi điểm

 

; ;M a b c

là điểm trên

 

S

sao cho

MA MB MC

 

  

đạt giá trị nhỏ nhất. Hãy tìm

a b

.

A.

6

. B.

2

. C.

4

. D. 9.

Câu 65. Cho mặt cầu

       

2 2 2

: 2 1 3 9

S x y z

     

và hai điểm

 

1 ; 1 ; 3

A

,

 

21 ; 9 ; 13

B 

.

Điểm

 

; ; M a b c

thuộc mặt cầu

 

S

sao cho

2 2

3

MA MB



đạt giá trị nhỏ nhất. Khi đó giá trị

của biểu thức

. .T a b c

bằng

A.

3

. B.

8

. C.

6

. D.

18

.

Câu 66. Trong không gian

Oxyz

cho đường thẳng

1 2 3

:

2 3 4

x y z

d

  

 

và mặt cầu

 

S

:

     

2 2 2

3 4 5 729

x y z     

. Cho biết điểm

 

2; 2; 7

A

  

, điểm

B

thuộc giao tuyến của

mặt cầu

 

S

và mặt phẳng

 

: 2 3 4 107 0

P x y z

   

. Khi điểm

M

di động trên đường thẳng

d

giá trị nhỏ nhất của biểu thức

MA MB

bằng

A.

5 30

. B.

27

. C.

5 29

. D.

742

.

Câu 67. (THPT Chuyên Thái Bình - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

 

: 1 0

P x y z

   

, đường thẳng

 

15 22 37

:

1 2 2

x y z

d

  

 

và mặt cầu

 

2 2 2

: 8 6 4 4 0

S x y z x y z

      

. Một đường thẳng

 



thay đổi cắt mặt cầu

 

S

tại hai

điểm

,A B

sao cho

8

AB



. Gọi

A



,

B



là hai điểm lần lượt thuộc mặt phẳng

 

P

sao cho

AA



,

BB



cùng song song với

 

d

. Giá trị lớn nhất của biểu thức

AA BB

 



là

A.

8 30 3

9



. B.

24 18 3

5



. C.

12 9 3

5



. D.

16 60 3

9



.

Câu 68. (Đại học Hồng Đức –Thanh Hóa 2019) Trong không gian với hệ tọa độ

Oxyz

, cho

 

3;1;1

A 

,

 

5;1;1

B

và hai mặt phẳng

 

: 2 4 0

P x y z

   

,

 

: 1 0

Q x y z

    

. Gọi

 

; ;M a b c

là

điểm nằm trên hai mặt phẳng

 

P

và

 

Q

sao cho

MA MB

đạt giá trị nhỏ nhất. Tính

2 2 2

T a b c  

.

A.

5

. B.

29

. C.

13

. D.

3

.

Dạng 2.3. Cực trị liên quan đến chu vi, diện tích, bán kính, thể tích

Câu 69. (Chuyên Hùng Vương Gia Lai 2019) Trong không gian

Oxyz

, cho hình hộp chữ nhật

.

ABCD A B C D

   

có

A

trùng với gốc tọa độ

O

, các đỉnh

( ;0;0)

B a

,

(0; ;0)D a

,

(0;0; )A b



với

, 0

a b



và

2

a b

 

. Gọi

M

là trung điểm của cạnh

CC



. Thể tích của khối tứ diện

BDA M



có

giá trị lớn nhất bằng

A.

64

27

. B.

32

27

. C.

8

27

. D.

4

27

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21

Câu 70. (THPT Nguyễn Huệ - Huế - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho đường thẳng

 

1 2

: 1

2

x t

d y t

z t

  





 









và hai điểm

 

1;5;0

A

,

 

3;3;6

B

. Gọi

 

; ;M a b c

là điểm trên

 

d

sao cho chu

vi tam giác

MAB

đạt giá trị nhỏ nhất. Tính

P a b c  

.

A.

1P 

. B.

3

P

 

. C.

3

P



. D.

1P  

.

Câu 71. (Hoàng Hoa Thám Hưng Yên 2019) Trong không gian với hệ tọa độ

Oxyz

, cho tứ diện

ABCD

có

 

1;1;6

A 

,

 

3; 2; 4

B

  

,

 

1;2; 1

C



,

 

2; 2;0

D 

. Điểm

 

; ;M a b c

thuộc đường thẳng

CD

sao cho tam giác

ABM

có chu vi nhỏ nhất. Tính

a b c 

.

A.

1

. B.

2

. C.

3

. D.

0

.

Câu 72. Trong không gian với hệ tọa độ

Oxyz

cho tứ diện

ABCD

có

 

1;1;6

A 

,

 

3; 2; 4

B

  

,

 

1;2; 1

C



,

 

2; 2;0

D 

. Điểm

 

; ;M a b c

thuộc đường thẳng

CD

sao cho tam giác

ABM

có chu

vi nhỏ nhất. Tính

.a b c 

A.

1

. B.

2

. C.

3

. D.

0

.

Câu 73. (Chuyên Lê Hồng Phong Nam Định 2019) Trong không gian với hệ tọa độ

Oxyz

, cho mặt

phẳng

 

: 2 0

P x y z

   

và hai điểm

   

3;4;1 ; 7; 4; 3

A B

 

. Điểm

  

; ; 2

M a b c a



thuộc

 

P

sao cho tam giác

ABM

vuông tại

M

và có diện tích nhỏ nhất. Khi đó giá trị biểu thức

T a b c  

bằng:

A.

6

T



. B.

8

T



. C.

4T 

. D.

0

T



.

Câu 74. (Chuyên Lê Quý Đôn Điện Biên 2019) Trong không gian

Oxyz

, cho mặt cầu

   

2 2

2

( ) : 3 1 4

S x y z

    

và đường thẳng

1 2

: 1 ,( )

x t

d y t t

z t

 





   





 





. Mặt phẳng chứa

d

và cắt

( )S

theo một đường tròn có bán kính nhỏ nhất có phương trình là

A.

1 0

y z

  

. B.

3 5 2 0

x y z

   

.

C.

2 3 0

x y

  

. D.

3 2 4 8 0

x y z

   

.

Câu 75. Trong không gian với hệ tọa độ Oxyz, cho hai điểm

(3; 2;6), (0;1;0)

A B



và mặt cầu

2 2 2

( ) : ( 1) ( 2) ( 3) 25

S x y z

     

. Mặt phẳng

( ) : 2 0

P ax by cz

   

đi qua A, B và cắt theo

giao tuyến là đường tròn có bán kính nhỏ nhất. Tính

T a b c  

.

A.

3

T



B.

5

T



C.

2T 

D.

4T 

Câu 76. Trong không gian

,Oxyz

cho mặt cầu

       

2 2 2

: 1 2 3 48

S x y z

     

Gọi

 



là mặt

phẳng đi qua hai điểm

   

0;0; 4 , 2;0;0

A B

và cắt mặt cầu

 

S

theo giao tuyến là đường tròn

 

C

. Khối nón

 

N

có đỉnh là tâm của

 

S

, đường tròn đáy là

 

C

có thể tích lớn nhất bằng

A.

128

3



B.

39



C.

88

3



C.

215

3



Câu 77. (Chuyên Hùng Vương Gia Lai 2019) Trong không gian

Oxyz

, cho hình hộp chữ nhật

.

ABCD A B C D

   

có

A

trùng với gốc tọa độ

O

, các đỉnh

( ;0;0)

B a

,

(0; ;0)D a

,

(0;0; )A b



với

, 0

a b



và

2

a b

 

. Gọi

M

là trung điểm của cạnh

CC



. Thể tích của khối tứ diện

BDA M



có giá trị lớn nhất bằng

A.

64

27

. B.

32

27

. C.

8

27

. D.

4

27

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 22 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu

78. Trong không gian

O

xyz

,

cho đường thẳng

4

3

: 3 4

0

x

t

d y t

z





















.

Gọi

A

là

hình chiếu vuông góc của

O

t

rên

d

. Điểm

M

di động trên tia

O

z

, điểm

N

di động trên đường thẳng

d

sao cho

MN OM AN 

.

Gọi

I

là

trung điểm đoạn thẳng

OA

.

Trong trường hợp diện tích tam giác

I

MN

đạt

giá trị nhỏ nhất, một vectơ pháp tuyến của mặt phẳng

 

,M

d

c

ó tọa độ là

A.

 

4

;3;5 2

. B.

 

4

;3;10 2

. C

.

 

4

;3;5 10

. D

.

 

4

;3;10 10

.

Câu

79. Trong không gian

O

xyz

,

cho điểm

1

3

;

;0

2

M





 

 

và

mặt cầu

 

2

2 2

:

8

S

x y z



 

.

Đường thẳng

d

thay

đổi, đi qua điểm

,M

cắt

mặt cầu

 

S

tại

hai điểm phân biệt

,A

B

.

Tính diện tích lớn nhất

S

của

tam giác

OAB

.

A.

7

S 

. B.

4

S



. C

.

2 7

S 

. D

.

2

S 

.

Câu

80. Trong không gian

Ox

yz

,

cho điểm

 

1;4;3

A

và

mặt phẳng

 

: 2 0

P y z

 

.

Biết điểm

B

thuộc

 

P

, điểm

C

thuộc

 

O

xy

sao c

ho chu vi tam giác

A

BC

nhỏ

nhất. Hỏi giá trị nhỏ nhất đó là

A.

6

5

. B.

2

5

. C.

4

5

. D.

5

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương  https://www.facebook.com/phong.baovuong Trang 1

TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH TRUNG BÌNH MỨC 5-6 ĐIỂM

Dạng 1. Xác định VTCP

 Véctơ chỉ phương

u



của đường thẳng

d

là véctơ có giá song song hoặc trùng với đường thẳng

.d

Nếu

d

có một véctơ chỉ phương là

u



thì

.k u



cũng là một véctơ chỉ phương của

.d

 Nếu có hai véctơ

1

n



và

2

n



cùng vuông góc với

d

thì

d

có một véctơ chỉ phương là

1 2

[ , ].u n n

  



Để viết phương trình đường thẳng

,d

ta cần tìm điểm đi qua và một véctơ chỉ phương.

Nếu đường thẳng

1 2 3

( ; ; )

:

: ( ; ; )

d

Qua M x y z

d

VTCP u a a a









  



thì ta có hai dạng phương trình đường thẳng:

Phương trình đường thẳng

d

dạng tham số

1

2

3

, ( ).

x x a t

y y a t t

z z a t

 





  





 







Phương trình đường thẳng

d

dạng chính tắc

1 2 3

, ( 0).

x x y y z z

a a a

  

  

  

Câu 1. (Mã 101 - 2020 Lần 1) Trong không gian

Oxyz

, cho đường thẳng

3 4 1

:

2 5 3

x y z

d

  

 



.

Vecto nào dưới đây là một vecto chỉ phương của

d

?

A.

 

2

2;4; 1u 



. B.

 

1

2; 5;3u 



. C.

 

3

2;5;3u



. D.

 

4

3;4;1u



.

Lời giải

Chọn B.

Câu 2. (Mã 102 - 2020 Lần 1) Trong không gian , cho đường thẳng .

Vectơ nào dưới đây là một vectơ chỉ phương của ?

A. . B. . C. . D. .

Lời giải

Chọn A

Đường thẳng có một vectơ chỉ phương là .

Câu 3. (Mã 103 - 2020 Lần 1) Trong không gian

Oxyz

, cho đường thẳng

3 1 2

:

4 2 3

x y z

d

  

 



.

Vecto nào dưới đây là một vecto chỉ phương của

d

A.

 

3

3; 1; 2u   



. B.

 

4

4;2;3u 



. C.

 

2

4; 2;3u  



. D.

 

1

3;1;2u 



.

Lời giải

Chọn C

Một vectơ chỉ phương của đường thẳng

d

là

 

2

4; 2;3u 



.

Câu 4. (Mã 104 - 2020 Lần 1) Trong không gian

Oxyz

, cho đường thẳng

4 2 3

:

3 1 2

x y z

d

  

 

 

.

Vectơ nào dưới đây là một vectơ chỉ phương của

d

?

A.

 

2

4; 2;3u  



. B.

 

4

4;2; 3u  



. C.

 

3

3; 1; 2u   



. D.

 

1

3;1;2u 



.

PHƯƠNG TRÌNH ĐƯỜNG THẲNG

Chuyên đề 31

Oxyz

2 5 2

:

3 4 1

x y z

d

  

 



d

 

2

3;4; 1

u

 



 

1

2; 5;2

u  



 

3

2;5; 2

u

 



 

3

3;4;1

u 



2 5 2

:

3 4 1

x y z

d

  

 



 

2

3;4; 1

u

 



u



.k u



d

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Lời giải

Chọn C

Câu 5. (Mã 101 2018) Trong không gian

Oxyz

, đường thẳng

2

: 1 2

3

x t

d y t

z t

 





 





 



có một vectơ chỉ phương là:

A.

 

1

1;2;3

u  



B.

 

3

2;1;3

u 



C.

 

4

1;2;1

u  



D.

 

2

2;1;1

u 



Lời giải

Chọn C

2

: 1 2

3

x t

d y t

z t

 





 





 



có một vectơ chỉ phương là

 

4

1;2;1

u  



.

Câu 6. (Mã 102 - 2019) Trong không gian

Oxyz

, cho đường thẳng

1 3 2

:

2 5 3

x y z

d

  

 



. Vectơ nào

dưới đây là vectơ chỉ phương của đường thẳng

d

A.

 

1;3; 2

u

 



. B.

 

2;5;3

u 



. C.

 

2; 5;3

u  



. D.

 

1;3;2

u 



.

Lời giải

Chọn C

Dựa vào phương trình đường thẳng suy ra một vectơ chỉ phương của

d

là

 

2; 5;3

u  



Câu 7. (Mã 104 2017) Trong không gian với hệ toạ độ

Oxyz

, cho hai điểm

 

1;1;0

A

và

 

0;1;2

B

.

Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng

AB

.

A.

 

1;1;2

d  



B.

 

1;0; 2

a

  



C.

 

1;0;2

b  



D.

 

1;2;2

c 



Lời giải.

Chọn C

Ta có

 

1;0;2

AB  



suy ra đường thẳng

AB

có VTCP là

 

1;0;2

b  



.

Câu 8. (Mã 102 2018) Trong không gian

Oxyz

, đường thẳng

3 1 5

:

1 1 2

x y z

d

  

 



có một vectơ chỉ

phương là

A.

 

1

3; 1;5

u  



B.

 

4

1; 1;2

u  



C.

 

2

3;1;5

u  



D.

 

3

1; 1; 2

u

  



Lời giải

Chọn B

Đường thẳng

3 1 5

:

1 1 2

x y z

d

  

 



có một vectơ chỉ phương là

 

4

1; 1;2

u  



.

Câu 9. (Mã 103 - 2019) Trong không gian

Oxyz

, cho đường thẳng

2 1 3

: .

1 3 2

x y z

d

  

 



Vectơ nào

dưới đây là một vectơ chỉ phương của

?d

A.

 

4

1;3;2 .

u 



B.

 

3

2;1;3 .

u  



C.

 

1

2;1;2 .

u  



D.

 

2

1; 3;2 .

u  



Lời giải

Chọn D

Đường thẳng

2 1 3

:

1 3 2

x y z

d

  

 



có một vectơ chỉ phương là

 

2

1; 3;2 .

u  



TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3

Câu 10. (Đề Tham Khảo 2018) Trong không gian

,Oxyz

cho đường thẳng

2 1

: .

1 2 1

x y z

d

 

 



Đường

thẳng

d

có một vectơ chỉ phương là

A.

 

4

1;2; 0

u  



B.

 

2

2;1; 0

u 



C.

 

3

2;1;1

u 



D.

 

1

1;2;1

u  



Lời giải

Chọn D

Câu 11. (Mã 104 - 2019) Trong không gian

Oxyz

cho đường thẳng

3 1 5

:

1 2 3

x y z

d

  

 



. Vectơ nào

sau đây là một vectơ chỉ phương của đường thẳng

d

?

A.

2

(1; 2;3)

u  



B.

3

(2;6; 4)

u

 



. C.

4

( 2; 4;6)

u   



. D.

1

(3; 1;5)

u  



.

Lời giải

Chọn A

Ta thấy đường thẳng d có một vectơ chỉ phương có tọa độ

2

(1; 2;3)

u  



.

Câu 12. (Mã 101 - 2019) Trong không gian

Oxyz

, cho đường thẳng

2 1 3

:

1 2 1

  

 



x y z

d

. Vectơ nào

dưới đây là một vectơ chỉ phương của

d

?

A.

4

(1;2; 3) 



u . B.

3

( 1;2;1) 



u . C.

1

(2;1; 3) 



u . D.

2

(2;1;1)



u .

Lời giải

Chọn B

Một vectơ chỉ phương của

d

là:

( 1;2;1) 



u

.

Câu 13. (Đề Tham Khảo 2019) Trong không gian

Oxyz

, đường thẳng

1 2 3

:

2 1 2

x y z

d

  

 



đi qua

điểm nào dưới đây?

A.

 

2; 1;2

Q 

B.

 

1; 2; 3

M

  

C.

 

1;2;3

P

D.

 

2;1; 2

N

 

Lời giải

Chọn C

Câu 14. (Mã 104 2017) Trong không gian với hệ tọa độ

Oxyz

, cho điểm

 

1;2;3

M

. Gọi

1

M

,

2

M

lần

lượt là hình chiếu vuông góc của

M

lên các trục

Ox

,

Oy

. Vectơ nào dưới đây là một véctơ chỉ

phương của đường thẳng

1 2

M M

?

A.

 

4

1;2;0

u  



B.

 

1

0;2;0

u 



C.

 

2

1;2;0

u 



D.

 

3

1;0;0

u 



Lời giải

Chọn A

1

M

là hình chiếu của

M

lên trục

 

1

1;0;0

Ox M

.

2

M

là hình chiếu của

M

lên trục

 

2

0;2;0

Oy M

.

Khi đó:

 

1 2

1;2;0

M M  



là một vectơ chỉ phương của

1 2

M M

.

Câu 15. Trong không gian với hệ tọa độ

Oxyz

, cho đường thẳng

4 3

:

1 2 3

x y z

d

 

 



. Hỏi trong các

vectơ sau, đâu không phải là vectơ chỉ phương của

d

?

A.

 

1

1; 2;3

u  



. B.

 

2

3; 6; 9

u

  



. C.

 

3

1; 2; 3

u

  



. D.

 

4

2;4;3

u  



.

Lời giải

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Ta có một vectơ chỉ phương của

d

là

 

1

1; 2;3

u  



.

2 1

3u u 

 

,

3 1

u u 

 



các vectơ

2 3

,u u

 

cũng là vectơ chỉ phương của

d

.

Không tồn tại số

k

để

4 1

.u k u



 

nên

 

4

2;4;3

u  



không phải là vectơ chỉ phương của

d

.

Câu 16. (Sở Bình Phước 2019) Trong không gian với hệ tọa độ

Oxyz

, đường thẳng nào sau đây nhận

 

2;1;1

u 



là một vectơ chỉ phương?

A.

2 1 1

1 2 3

x y z  

 

B.

1 2

2 1 1

x y z

 

 



C.

1 1

2 1 1

x y z 

 

  

D.

2 1 1

x y z

  

 



Lời giải

Chọn C

Xét đường thẳng được cho ở câu C, có một vectơ chỉ phương là

   

2; 1; 1 2;1;1

    

(thỏa đề

bài).

Câu 17. (Chuyen Phan Bội Châu Nghệ An 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho đường

thẳng

1 2 1

:

2 1 2

x y z

d

  

 

nhận véc tơ

 

;2;u a b



làm véc tơ chỉ phương. Tính

a b

.

A.

8

. B.

8

. C.

4

. D.

4

.

Lời giải

Đường thẳng

d

có một véc tơ chỉ phương là

 

2;1;2

v



.

 

;2;u a b



làm véc tơ chỉ phương của

d

suy ra

u



và

v



cùng phương nên

4

2

4

2 1 2

a

a b

b





  







Câu 18. (THPT Lê Quý Đôn Đà Nẵng 2019) Trong không gian

,Oxyz

tọa độ nào sau đây là tọa độ của

một véctơ chỉ phương của đường thẳng

 

2 4

: 1 6 , ?

9

x t

y t t

z t

 





   











A.

1 1 3

; ;

3 2 4



 

 

 

. B.

1 1 3

; ;

3 2 4

 

 

 

. C.

 

2;1;0

. D.

 

4; 6;0



.

Lời giải

Cách 1: Từ phương trình



suy ra véctơ chỉ phương của



là

 

1 1 3

4; 6;9 12 ; ; .

3 2 4

u



 

  

 

 



Câu 19. (Chuyên KHTN 2019) Vectơ nào sau đây là một vectơ chỉ phương của đường thẳng

2 1 3

3 2 1

x y z  

 

 

A.

 

2;1; 3 

. B.

 

3;2;1



. C.

 

3; 2;1



. D.

 

2;1;3

.

Lời giải

Vectơ chỉ phương của đường thẳng là

   

3; 2; 1 1 3;2;1

u      



nên

 

1

3;2;1

u  



cũng là

một vectơ chỉ phương của đường thẳng.

Câu 20. (Chuyên Thái Bình 2019) Trong không gian với hệ tọa độ

Oxyz

, đường thẳng

 

1 3 7

:

2 4 1

x y z

d

  

 



nhận vectơ nào dưới đây là một vectơ chỉ phương?

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5

A.

 

2; 4;1

 

. B.

 

2;4;1

. C.

 

1; 4;2



. D.

 

2; 4;1



.

Lời giải

Từ phương trình chính tắc của đường thẳng

d

ta có vectơ chỉ phương là

 

2; 4;1

d

u  



.

Câu 21. (Đề Thi Công Bằng KHTN 2019) Trong không gian

O

xyz

véc tơ nào dưới đây là một véc tơ chỉ

phương của đường thẳng

d

:

1

4

3 2

x t

y

z t

 











 



,

A.

(1;4;3)

u 



. B.

(1;4; 2)

u

 



. C.

(1;0; 2)

u

 



. D.

(1;0;2)

u 



.

Lời giải

Từ phương trình tham số của đường thẳng

d

, ta suy ra một véc tơ chỉ phương của đường thẳng

d

là

(1;0; 2)

u

 



.

Dạng 2. Viết phương trình đường thẳng

Dạng 1. Viết phương trình đường thẳng

d

dạng tham số và dạng chính tắc (nếu có), biết

d

đi qua điểm

( ; ; )M x y z

  

và có véctơ chỉ phương

1 2 3

( ; ; ).

d

u a a a



Phương pháp. Ta có:

1 2 3

( ; ; )

:

: ( ; ; )

d

Qua M x y z

d

VTCP u a a a









  







Phương trình đường thẳng

d

dạng tham số

1

2

3

: , ( ).

x x a t

d y y a t t

z z a t

 





  





 







Phương trình đường thẳng

d

dạng chính tắc

1 2 3

: , ( 0).

x x y y z z

d a a a

a a a

  

  

  

Dạng 2. Viết phương trình tham số và chính tắc (nếu có) của đường thẳng

d

đi qua

A

và

.B

Phương pháp. Đường thẳng

( )

:

d

Qua A hay B

d

VTCP u AB





















(dạng 1)

Dạng 3. Viết phương trình đường thẳng

d

dạng tham số và chính tắc (nếu có), biết

d

đi qua điểm

M

và song song với đường thẳng

.

Phương pháp. Ta có

Qua ( ; ; )

:

d

M x y z

d

VTCP u u















  



 



(dạng 1)

Dạng 4. Viết phương trình đường thẳng

d

dạng tham số và chính tắc (nếu có), biết

d

đi qua điểm

M

và vuông góc với mặt phẳng

( ) : 0.

P ax by cz d

   

Phương pháp. Ta có

( )

:

: ( ; ; )

d P

Qua M

d

VTCP u n a b c





 





 



(dạng 1)

Dạng 4. Viết phương trình đường thẳng

d

qua

M

và song song với hai mặt phẳng

( ), ( ).P Q

Phương pháp. Ta có

:

: , ]

[

d P Q

d

VTCP u n

Qua M

n











  



(dạng 1)

Dạng 2.1 Xác định phương trình đường thẳng cơ bản

Câu 22. (Đề Tham Khảo 2020 Lần 2) Trong không gian Oxyz, cho hai điểm

(1;0;1)

M

và

(3;2; 1)

N

.

Đường thẳng MN có phương trình tham số là

A

B

d

M



d

u





P

u n

d P



 

d

M

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

A.

1 2

2 .

1

 











 



x t

y t

z t

B.

1

.

1

 











 



x t

y t

z t

C.

1

.

1

 











 



x t

y t

z t

D.

1

.

1

 











 



x t

y t

z t

Lời giải

Chọn D

Đường thẳng MN nhận

(2;2; 2) 



MN

hoặc

(1;1; 1)



u

là véc tơ chỉ phương nên ta loại ngay

phương án A, B và C.

Thay tọa độ điểm

(1;0;1)

M

vào phương trình ở phương án D ta thấy thỏa mãn.

Câu 23. (Đề Tham Khảo 2017) Trong không gian tọa độ

Ox ,yz

phương trình nào dưới đây là phương

trình chính tắc của đường thẳng

1 2

: 3 ?

2

x t

d y t

z t

 











  



A.

1 2

2 3 1

x y z

 

 

B.

1 2

1 3 2

x y z

 

 



C.

1 2

2 3 2

x y z

 

 



D.

1 2

2 3 1

x y z

 

 

Lời giải

Chọn D

Do đường thẳng

1 2

: 3

2

x t

d y t

z t

 











  



đi qua điểm

(1;0; 2)

M



và có véc tơ chỉ phương

(2;3;1)

u



nên có

phương trình chính tắc là

1 2

.

2 3 1

x y z

 

 

Câu 24. Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm

 

1; 2;1

M 

,

 

0;1; 3

N

. Phương trình đường

thẳng qua hai điểm

M

,

N

là

A.

1 2 1

1 3 2

x y z  

 



. B.

1 3 2

1 2 1

x y z

  

 



.

C.

1 3

1 3 2

x y z

 

 



. D.

1 3

1 2 1

x y z 

 



.

Lời giải

 

1; 3; 2

MN  



.

Đường thẳng

MN

qua

N

nhận

 

1; 3; 2

MN  



làm vectơ chỉ phương có phương trình

1 3

1 3 2

x y z

 

 



.

Câu 25. Trong không gian Oxyz, phương trình tham số của đường thẳng đi qua điểm

 

2;0; 1

M



và có

véctơ chỉ phương

 

2; 3;1

a  



là

A.

4 2

6 .

2

x t

y

z t

 





 





 



B.

2 2

3 .

1

x t

y t

z t

  





 





 



C.

2 4

6 .

1 2

x t

y t

z t

  





 





 



D.

2 2

3 .

1

x t

y t

z t

 





 





  



Lời giải

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7

Theo lý thuyết về dường thẳng trong không gian Oxyz, ta có phương trình tham số của đường

thẳng đi qua điểm

 

0 0 0

; ;M x y z

và có véctơ chỉ phương

 

1 2 3

; ;a a a a





là

 

0 1

0 2

0 3

, .

x x a t

y y a t t

z z a t

 





  





 





Do đó, đáp án D đúng.

Câu 26. (Chuyên Đại Học Vinh 2019) Trong không gian

Oxyz

, cho

( 1;0;2)

E



và

(2;1; 5)

F



. Phương

trình đường thẳng

EF

là

A.

1 2

3 1 7

x y z

 

 



B.

1 2

3 1 7

x y z

 

 



C.

1 2

1 1 3

x y z

 

 



D.

1 2

1 1 3

x y z

 

 

Lời giải

Chọn B

Ta có:

(3;1; 7)

EF

 



. Đường thẳng

EF

đi qua điểm

( 1;0;2)

E



và có VTCP

(3;1; 7)

u EF

  

 

có phương trình:

1 2

3 1 7

x y z

 

 



.

Câu 27. Trong không gian

Oxyz

, cho đường thẳng



đi qua điểm

 

2;0; 1

M



và có một vectơ chỉ

phương

 

4; 6;2

a  



.Phương trình tham số của



là

A.

2 4

6

1 2

x t

y t

z t

  











 



. B.

2 2

3

1

x t

y t

z t

 





 





  



. C.

4 2

6

2

x t

y

z t

 





 





 



. D.

2 2

3

1

x t

y t

z t

  











 



.

Lời giải

   

4; 6;2 2 2; 3;1

a    



\

Do đó đường thẳng



có một vectơ chỉ phương là

 

2; 3;1

u  



. Vậy phương trình tham số của



đi qua

 

2;0; 1

M



và có một vectơ chỉ phương là

 

2; 3;1

u  



là:

2 2

3

1

x t

y t

z t

 





 





  



.

Câu 28. (THPT Yên Phong 1 Bắc Ninh 2019) Trong không gian

Oxyz

, viết phương trình đường thẳng

đi qua hai điểm

 

1;1; 1

P



và

 

2;3;2

Q

A.

1 1 1

2 3 2

x y z  

 

. B.

1 1 1

1 2 3

x y z  

 

.

C.

1 2 3

1 1 1

x y z

  

 



. D.

2 3 2

1 2 3

x y z

  

 

.

Lời giải

Ta có

 

1;2;3

PQ 



. Gọi

d

là đường thẳng đi qua hai điểm

,P Q

Khi đó

d

có một vec tơ chỉ phương là

 

1;2;3

d

u PQ 

 

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 8 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Phương trình đường thẳng

d

đi qua điểm

 

1;1; 1

P



là

1 1 1

:

1 2 3

x y z

d

  

 

.

Câu 29. (Chuyên Lê Hồng Phong Nam Định 2019) Trong không gian

Oxyz

, phương trình đường thẳng

đi qua hai điểm

 

1;2;3

A

và

 

5;4; 1

B



là

A.

5 4 1

2 1 2

x y z  

 

. B.

1 2 3

4 2 4

x y z  

 



.

C.

1 2 3

4 2 4

x y z

  

 

. D.

3 3 1

2 1 2

x y z  

 

 

.

Lời giải

Ta có

 

4;2; 4

AB





. Suy ra

AB



cùng phương với

 

2; 1;2

u  



.

Phương trình đường thẳng

AB

đi qua

 

5;4; 1

B



nhận

 

2; 1;2

u  



làm vectơ chỉ phương là:

 

5 4 1

, 1

2 1 2

x y z

  

 

 

. Do đó loại A, C.

Có tọa độ

 

1; 2; 3

C

  

không thỏa mãn phương trình

 

1

nên phương án B.

Lại có tọa độ

 

3;3;1

D

thỏa mãn phương trình

 

1

nên phương trình đường thẳng

AB

cũng được

viết là:

3 3 1

2 1 2

x y z  

 

 

.

Câu 30. Trong không gian

Oxyz

, đường thẳng

Oy

có phương trình tham số là

A.

 

x t

y t t

z t







 











. B.

 

0

2

0

x

y t t

z







  











. C.

 

0

x

y t

z t







 











. D.

 

0

x t

y t

z







 











.

Lời giải

Đường thẳng

Oy

đi qua điểm

 

0 ; 2 ; 0

A

và nhận vectơ đơn vị

 

0; 1; 0

j 



làm vectơ chỉ

phương nên có phương trình tham số là

   

0 0. 0

2 1. 2

0 0. 0

x t x

y t t y t t

z t z

  

 

 

      

 

 

  

 

 

.

Câu 31. (THPT An Lão Hải Phòng 2019) Trong không gian

Oxyz

có đường thẳng có phương trình

tham số là

1 2

( ) : 2

3

x t

d y t

z t

 





 





  



. Khi đó phương trình chính tắc của đường thẳng

d

là

A.

1 2 3

2 1 1

x y z

  

 



B.

1 2 3

2 1 1

x y z

  

 



C.

1 2 3

2 1 1

x y z

  

 

D.

1 2 3

2 1 1

x y z  

 



Lời giải

Chọn A

Đường thẳng

d

đi qua điểm

(1;2; 3)

M



nhận véc tơ

 

2; 1;1

u  



nên có phương trình dạng chính

tắc là

1 2 3

2 1 1

x y z

  

 



TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9

Câu 32. (Chuyên Đại học Vinh - 2019) Trong không gian

Oxyz

, cho

 

1;0;2

E 

và

 

2;1; 5

F



. Phương

trình đường thẳng

EF

là

A.

1 2

3 1 7

x y z

 

 



. B.

1 2

3 1 7

x y z

 

 



. C.

1 2

1 1 3

x y z

 

 



. D.

1 2

1 1 3

x y z

 

 

.

Lời giải

Chọn B

Đường thẳng

EF

có véctơ chỉ phương là

 

3;1; 7

EF

 



và đi qua

 

1;0;2

E 

nên có phương

trình:

1 2

3 1 7

x y z

 

 



.

Câu 33. (THPT Phan Bội Châu - Nghệ An 2019) Trong không gian với hệ trục tọa độ

Oxyz

, phương

trình tham số trục

Oz

là

A.

0

z



. B.

0

x

y t

z

















. C.

0

x t

y

z

















. D.

0

x

y

z t

















.

Lời giải

Chọn D

Trục

Oz

đi qua gốc tọa độ

 

0;0;0

O

và nhận vectơ đơn vị

 

0;0;1

k 



làm vectơ chỉ phương nên

có phương trình tham số

0

x

y

z t

















.

Câu 34. (THPT Cẩm Bình 2019) Trong không gian

Oxyz

, trục

Ox

có phương trình tham số

A.

0.

x



B.

0.

y z

 

C.

0

0.

x

y

z t

















D.

0.

0

x t

y

z

















Lời giải

Chọn D

Trục

Ox

đi qua

 

0;0;0

O

và có véctơ chỉ phương

 

1;0;0

i



nên có phương trình tham số là:

0 1.

0 0. 0.

0 0. 0

x t x t

y t y

z t z

  

 

 

   

 

 

  

 

Vậy trục

Ox

có phương trình tham số

0

x t

y

z

















.

Câu 35. (Ngô Quyền - Hải Phòng 2019) Trong không gian

Oxyz

, phương trình tham số của đường thẳng

d

đi qua điểm

 

1;2;3

M

và có véctơ chỉ phương

 

1; 4; 5

a

 



là

A.

1 2 3

1 4 5

x y z

  

 

 

. B.

1

4 2

5 3

x t

y t

z t

 





  





  



.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 10 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

C.

1 4 5

1 2 3

x y z  

 

. D.

1

2 4

3 5

x t

y t

z t

 





 





 



.

Lời giải

Chọn D

Đường thẳng

d

có véctơ chỉ phương

 

1; 4; 5

a

 



, do

a v 

 

với

 

1;4;5

v 



nên

d

cũng nhận

véctơ

 

1;4;5

v 



làm véctơ chỉ phương do đó phương trình tham số của đường thẳng

d

là

1

2 4 .

3 5

x t

y t

z t

 





 





 



.

Câu 36. (Chuyên Nguyễn Huệ 2019) Trong không gian với hệ trục tọa độ

Oxyz

, phương trình tham số

của đường thẳng

d

đi qua gốc tọa độ

O

và có vectơ chỉ phương

 

1;3;2

u 



là

A.

0

: 3

2

x

d y t

z t

















. B.

1

: 3

2

x

d y

z

















. C.

: 3

2

x t

d y t

z t

















. D.

: 2

3

x t

d y t

z t

 





 





 



.

Lời giải

Chọn C

Đường thẳng

d

đi qua gốc tọa độ

 

0;0;0

O

và nhận vectơ

 

1;3;2

u 



làm vectơ chỉ phương có

phương trình tham số là

: 3

2

x t

d y t

z t

















.

Câu 37. (Đà Nẵng 2019) Trong không gian

Oxyz

, viết phương trình đường thẳng đi qua điểm

 

1;2;3

A

và có vectơ chỉ phương

 

2; 1; 2

u

  



.

A.

2 1 2

1 2 3

x y z

  

 

. B.

1 2 3

2 1 2

x y z  

 

 

.

C.

2 1 2

1 2 3

x y z

  

 

. D.

1 2 3

2 1 2

x y z

  

 

 

.

Lời giải

Chọn D

Câu 38. (Sở Bình Thuận 2019) Trong không gian

Oxyz

, cho đường thẳng

d

đi qua điểm

 

0; 1;4

M 

và nhận vectơ

 

3; 1;5

u  



làm vectơ chỉ phương. Hệ phương trình nào sau đây là phương trình

tham số của

d

?

A.

3

1

4 5

x t

y t

z t







 





 



. B.

3

1

5 4

x

y t

z t







  





 



. C.

3

1

4 5

x t

y t

z t







  





 



. D.

3

1

4 5

x t

y t

z t







 





  



.

Lời giải

Chọn C

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11

Đường thẳng

d

đi qua điểm

 

0; 1;4

M 

và nhận vectơ

 

3; 1;5

u  



làm vectơ chỉ phương.

Phương trình tham số của

d

là:

3

1

4 5

x t

y t

z t







  





 



.

Câu 39. (Sở GD Nam Định - 2019) Trong không gian

Oxyz

, đường thẳng



đi qua

 

1;2; 3

M



nhận

vectơ

 

1;2;1

u  



làm vectơ chỉ phương có phương trình là

A.

1 2 3

1 2 1

x y z  

 



. B.

1 2 3

1 2 1

x y z

  

 



.

C.

1 2 3

1 2 1

x y z

  

 



. D.

1 2 3

1 2 1

x y z

  

 



.

Lời giải

Chọn D

Đường thẳng



đi qua

 

1;2; 3

M



nhận vectơ

 

1;2;1

u  



làm vectơ chỉ phương có phương

trình là

1 2 3

1 2 1

x y z

  

 





Dạng 2.2 Xác định phương trình đường thẳng khi biết yếu tố vuông góc

Câu 40. (Mã 101 2020 Lần 2) Trong không gian

Oxyz

, cho điểm

 

1; 2;3

M



và mặt phẳng

 

: 2 3 1 0

P x y z

   

. Phương trình của đường thẳng đi qua

M

và vuông góc với

 

P

là

A.

1 2

2

3 3

x t

y t

z t

 





  





 



. B.

1 2

2

3 3

x t

y t

z t

  





 





  



. C.

2

1 2

3 3

x t

y t

z t

 





  





 



. D.

1 2

2

3 3

x t

y t

z t

 





  





 



.

Lời giải

Chọn A

Đường thẳng cần tìm đi qua

 

1; 2;3

M



, vuông góc với

 

P

nên nhận

 

2; 1;3

P

n

 



là véc tơ

chỉ phương. Phương trình đường thẳng cần tìm là

1 2

2

3 3

x t

y t

z t

 





  





 



.

Câu 41. (Mã 102 - 2020 Lần 2) Trong không gian

Oxyz

, cho

 

1;2; 3

M



và mặt phẳng

( ) : 2 3 1 0

P x y z

   

. Phương trình của đường thẳng đi qua điểm

M

và vuông góc với

( )P

là

A.

2

1 2

3 3

x t

y t

z t

 





  





 



. B.

1 2

2

3 3

x t

y t

z t

  





  





 



. C.

1 2

2

3 3

x t

y t

z t

 





 





  



. D.

1 2

2

3 3

x t

y t

z t

 





 





  



.

Lời giải

Chọn C

Ta có một vectơ pháp tuyến của mặt phẳng

( ) : 2 3 1 0

P x y z

   

là

 

2; 1;3

n  



.

Đường thẳng đi qua điểm

 

1;2; 3

M



và và vuông góc với

( )P

có phương trình là

1 2

2

3 3

x t

y t

z t

 





 





  



.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 12 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 42. (Mã 103 - 2020 Lần 2) Trong không gian

Oxyz

, cho điểm

 

1; 2;2

M 

và mặt phẳng

 

: 2 3 1 0

P x y z

   

. Phương trình của đường thẳng qua

M

và vuông góc với mặt phẳng

 

P

là

A.

1 2

2

2 3

x t

y t

z t

 





  





 



. B.

1

2 2

2

x t

y t

z t

 





  





 



. C.

2

1 2

3 2

x t

y t

z t

 





 





  



. D.

1 2

2

2 3

x t

y t

z t

  





 





  



.

Lời giải

Chọn A

Đường thẳng đi qua điểm

M

và vuông góc với mặt phẳng

 

P

nhận véc tơ pháp tuyến của mặt

phẳng

 

P

làm véc tơ chỉ phương có phương trình tham số là

1 2

2

2 3

x t

y t

z t

 





  





 



.

Câu 43. (Mã 104 - 2020 Lần 2) Trong không gian

Oxyz

, cho điểm

 

1;2; 2

M



và mặt phẳng

 

: 2 3 1 0

P x y z

   

. Phương trình của đường thẳng đi qua

M

và vuông góc với

 

P

là:

A.

1 2

2

2 3

x t

y t

z t

  





  





 



. B.

1 2

2

2 3

x t

y t

z t

 





 





  



. C.

1 2

2

2 3

x t

y t

z t

 





 





  



. D.

2

1 2

3 2

x t

y t

z t

 





 





  



Lời giải

Chọn B

Mặt phẳng

 

: 2 3 1 0

P x y z

   

có vectơ pháp tuyến

 

2;1; 3

n

 



đường thẳng đi qua

 

1;2; 2

M



và vuông góc với

 

P

nên nhận

 

2;1; 3

n

 



làm vectơ chỉ

phương. Vậy phương trình tham số là

1 2

2

2 3

x t

y t

z t

 





 





  



.

Câu 44. (Mã 123 2017) Trong không gian với hệ tọa độ

Oxyz

, phương trình nào dưới đây là phương

trình của đường thẳng đi qua

 

2; 3; 0

A

và vuông góc với mặt phẳng

 

   

: 3 5 0 ?

P x y z

A.

  



 





 



1

1 3

1

x t

y t

z t

B.

  









 



1

3

1

x t

y t

z t

C.

  



 





 



1 3

1

x t

y t

z t

D.

  



 





 



1 3

1

x t

y t

z t

Lời giải

Chọn B

Vectơ chỉ phương của đường thẳng là

 

 



1; 3; 1

u

nên suy ra chỉ đáp án A hoặc B đúng. Thử tọa

độ điểm

 

2; 3; 0

A

vào ta thấy đáp án B thỏa mãn

Câu 45. (THPT Yên Phong Số 1 Bắc Ninh 2019) Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

 

: 2 1

x y z



  

. Trong các đường thẳng sau, đường thẳng nào vuông góc với

 



.

A.

1

:

1 1 2

x y z

d



 



. B.

2

1

:

1 1 1

x y z

d



 

 

. C.

3

1

:

1 1 1

x y z

d



 

 

. D.

4

2

: 0

x t

d y

z t













 



Lời giải

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13

Chọn A

Gọi VTCP của đường thẳng cần tìm là

 

1 2 3

; ;a a a a





với

2 2 2

1 2 3

0

a a a

  

.

Đường thẳng vuông góc với

 



a





cùng phương

n



1 2 3

1 1 2

a a a

  



Chọn

1

a



thì

2

1

a

 

và

3

2

a



.

Câu 46. (THCS - THPT Nguyễn Khuyến 2019) Trong không gian

Oxyz

, đường thẳng đi qua điểm

 

1;1;1

A

và vuông góc với mặt phẳng tọa độ

 

Oxy

có phương trình tham số là:

A.

1

x t

y

z

 















. B.

1

x

y

z t













 



. C.

1

x t

y

z

 















. D.

1

x t

y t

z

 





 









.

Lời giải

Đường thẳng

d

vuông góc với mặt phẳng tọa độ

 

Oxy

nên nhận

 

0;0;1

k 



làm vectơ chỉ

phương. Mặt khác

d

đi qua

 

1;1;1

A

nên:



Đường thẳng

d

có phương trình là:

1

x

y

z t













 



.

Câu 47. Trong không gian với hệ trục

Oxyz

, cho điểm

 

1; 3; 2

M 

và mặt phẳng

 

: 3 2 1 0

P x y z

   

. Tìm phương trình đường thẳng

d

qua

M

và vuông góc với

 

P

.

A.

1 3 2

x y z

  

 



. B.

1 3 2

x y z

  

 



.

C.

1 3 2

x y z

 



. D.

1 3 2

x y z

  

 



.

Lời giải

Chọn B

Mặt phẳng

 

P

có VTPT là

 

1; 3;2

n  



.

Vì

d

vuông góc với

 

P

nên

d

nhận

 

1; 3;2

n  



là VTCP.

Đường thẳng

d

qua

M

và nhận

 

1; 3;2

n  



là VTCP có phương trình:

1 3 2

x y z

  

 



.

Câu 48. (Sở Thanh Hóa 2019) Trong không gian với hệ tọa độ

,Oxyz

cho điểm

 

1;0;2

A

và đường thẳng

1 1

:

1 1 2

x y z

d

 

 

. Đường thẳng



đi qua

A

, vuông góc và cắt

d

có phương trình là

A.

2 1 1

:

1 1 1

x y z  

  



. B.

1 2

:

1 1 1

x y z

 

  

.

C.

2 1 1

:

2 2 1

x y z  

  

. D.

1 2

:

1 3 1

x y z

 

  



.

Lời giải

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 14 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Gọi giao điểm của



và

d

là

 

1; ;2 1

B t t t

 

. Khi đó

 

, , 2 3

u AB t t t



  

 

.

Vì đường thẳng



vuông góc với đường thẳng

d

có

 

1,1, 2

d

u 



thì:

   

2 2 3 0 1 1,1, 1

t t t t u



        



.

Phương trình đường thẳng



thỏa mãn yêu cầu bài toán là

2 1 1

:

1 1 1

x y z  

  



Câu 49. (Đà Nẵng 2019) Trong không gian

Oxyz

, đường thẳng đi qua điểm

 

3;1;2

A

và vuông góc với

mặt phẳng

3 5 0

x y z

   

có phương trình là

A.

3 1 2

.

1 1 3

x y z

  

 

B.

1 1 3

.

3 1 2

x y z

  

 

C.

1 1 3

.

3 1 2

x y z

  

 

D.

3 1 2

.

1 1 3

x y z

  

 

Lời giải

Chọn A

Vì đường thẳng vuông góc với mặt phẳng

3 5 0

x y z

   

nên nó có véc tơ chỉ phương là

 

1;1;3

u 



. Vậy phương trình đường thẳng cần tìm là

3 1 2

.

1 1 3

x y z

  

 

Câu 50. Trong không gian

,Oxyz

cho điểm

(3; 2; 1)M 

và mặt phẳng

( ) : 2 0.P x z  

Đường thẳng đi

qua

M

và vuông góc với

( )P

có phương trình là

A.

3

2 .

1

x t

y

z t

  









  



B.

3

2 .

1

x t

y t

z

  



 





 



C.

3

2 .

1

x t

y t

z t

  









 



D.

3

1 2 .

x t

y t

z t

  



 





 



Lời giải

Chọn A

Ta có mặt phẳng

  ( ) : 2 0P x z



Mặt phẳng

 

P

có véc tơ pháp tuyến là

 

1;0;1

P

n 



Gọi đường thẳng cần tìm là



. Vì đường thẳng



vuông góc với

 

P

nên véc tơ pháp tuyến của

mặt phẳng

 

P

là véc tơ chỉ phương của đường thẳng



.

 

1;0;1

P

u n



  

 

Vậy phương trình đường thẳng



đi qua

(3; 2; 1)M 

và có véc tơ chỉ phương

 

1;0;1

u







là:

  









  



3

2 .

1

x t

y

z t

Câu 51. (SGD Bắc Ninh 2019) Trong không gian với hệ trục tọa độ

oxyz

, phương trình đường thẳng

d

đi

qua điểm

 

1;2;1

A

và vuông góc với mặt phẳng

 

: 2 1 0

P x y z

   

có dạng

A.

1 2 1

:

1 2 1

x y z

d

  

 



. B.

2 2

:

1 2 1

x y z

d

 

 



.

C.

1 2 1

:

1 2 1

x y z

d

  

 

. D.

2 2

:

2 4 2

x y z

d

 

 



.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15

Lời giải

Chọn D

Mặt phẳng

 

P

có vecto pháp tuyến

 

1; 2;1

P

n  



. Vì

 

d P



nên

 

1; 2;1

P

n  



cũng là vecto

chỉ phương của đường thẳng

d

. Suy ra phương trình đường thẳng

d

thường gặp là

1 2 1

x y z  

 



. So với đáp án không có, nên đường thẳng

d

theo bài là đường có vecto chỉ

phương cùng phương với

P

n



và đi qua điểm

 

1;2;1

A

. Thay tọa độ điểm

 

1;2;1

A

vào 3 đáp án

A, B, D thấy đáp án D thỏa mãn.

Câu 52. (Nguyễn Huệ- Ninh Bình- 2019)Trong không gian với hệ tọa độ

Oxyz

, cho

 

: 2 5 1 0

P x y z

   

và

 

1;2; 1

A



. Đường thẳng



qua

A

và vuông góc với

 

P

có phương

trình là

A.

2

5 2

1

x t

y t

z t

 





  





 



. B.

3 2

3 5

1

x t

y t

z t

 





  





 



. C.

1 2

2 5

1

x t

y t

z t

 





 





 



. D.

3 2

3 5

x t

y t

z t

 





  





 



.

Lời giải

Chọn D

Mặt phẳng

 

P

có một vectơ pháp tuyến là

 

2; 5;1

n  



.

Đường thẳng



vuông góc với

 

P

nên có một vectơ chỉ phương là

 

2;5; 1

u n

    

 

.



đi qua

A

nên có phương trình

1 2

2 5

1

x t

y t

z t

 





 





  



.

Cho

1

t

 

ta được điểm

 

3; 3;0B

 

.

Vì thế



có phương trình

3 2

3 5

x t

y t

z t

 





  





 



.

Câu 53. Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

 

: 2 3 0

P x y z

   

và điểm

 

1; 2;1 .

A 

Phương trình đường thẳng

d

đi qua

A

và vuông góc với

 

P

là

A.

1 2

: 2

1

x t

d y t

z t

 





  





 



. B.

1 2

: 2 4

1 3

x t

d y t

z t

 





  





 



. C.

2

1 2

1

x t

y t

z t

 





  





 



. D.

1 2

: 2

1 3

x t

d y t

z t

 





  





 



.

Lời giải

Chọn A

Mặt phẳng

 

P

có một vectơ pháp tuyến là

 

2; 1;1

n  



.

Đường thẳng

d

vuông góc với mặt phẳng

 

P

nên nhận

 

2; 1;1

n  



làm vectơ chỉ phương. Mà

d

đi qua

 

1; 2;1

A 

nên có phương trình:

1 2

2

1

x t

y t

z t

 





  





 



(

t 

).

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 16 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 54. Trong không gian với hệ tọa độ

Oxyz

, phương trình đường thẳng

d

đi qua điểm

 

1;2;1A

và

vuông góc với mặt phẳng

 

: 2 1 0P x y z   

có dạng

A.

2

:

1 2 1

x y z

d



 

 

. B.

1 2 1

:

1 2 1

x y z

d

  

 

.

C.

1 2 1

:

1 2 1

x y z

d

  

 

 

. D.

2

:

2 4 2

x y z

d



 

 

.

Lời giải

Chọn D

 

: 2 1 0P x y z   

có

 

1; 2; 1

P

n   



Vì

 

d P

nên

d

có một VTCP là

 

1; 2; 1a    



chọn A, C, D

Thay tọa độ điểm A vào các câu đã chọn, ta thấy câu D thỏa yêu cầu.

1 2 2 1

:

2 4 2

d



 

 

Câu 55. (Chu Văn An - Hà Nội - 2019) Trong không gian với hệ tọa độ

Oxyz

, đường thẳng



đi qua

điểm

 

2;4;3A 

và vuông góc với mặt phẳng

 

:2 3 6 19 0x y z    

có phương trình là

A.

2 3 6

2 4 3

x y z  

 



. B.

2 4 3

2 3 6

x y z  

 



.

C.

2 3 6

2 4 3

x y z  

 



. D.

2 4 3

2 3 6

x y z  

 



.

Lời giải

Chọn B

Mặt phẳng

 

:2 3 6 19 0x y z    

có vectơ pháp tuyến là

 

2; 3;6n  



.

Đường thẳng



đi qua điểm

 

2;4;3A 

và vuông góc với mặt phẳng

 



nhận

 

2; 3;6n  



làm vectơ chỉ phương, khi đó phương trình đường thẳng



là:

2 4 3

.

2 3 6

x y z  

 



Dạng 2.3 Xác định phương trình đường thẳng khi biết yếu tố song song

Câu 56. (Mã 101 - 2020 Lần 1) Trong không gian

Oxyz

, cho ba điểm

 

1;0;1A

,

 

1;1;0B

và

 

3;4; 1C 

. Đường thẳng đi qua

A

và song song với

BC

có phương trình là

A.

1 1

4 5 1

x y z 

 



. B.

1 1

2 3 1

x y z 

 



. C.

1 1

2 3 1

x y z 

 



. D.

1 1

4 5 1

x y z 

 



.

Lời giải

Chọn C

Đường thẳng

d

đi qua

A

và song song với

BC

nhận

 

2;3; 1BC  



làm một véc tơ chỉ

phương.

Phương trình của đường thẳng

d

:

1 1

2 3 1

x y z 

 



.

Câu 57. (Mã 102 - 2020 Lần 1) Trong không gian , cho ba điểm .

Đường thẳng đi qua và song song với

có phương trình là

A. . B. .

C. . D. .

Oxyz

     

1;2;3 , 1;1;1 , 3;4;0

A B C

A

BC

1 2 3

4 5 1

x y z  

 

1 2 3

4 5 1

x y z

  

 

1 2 3

2 3 1

x y z

  

 



1 2 3

2 3 1

x y z  

 



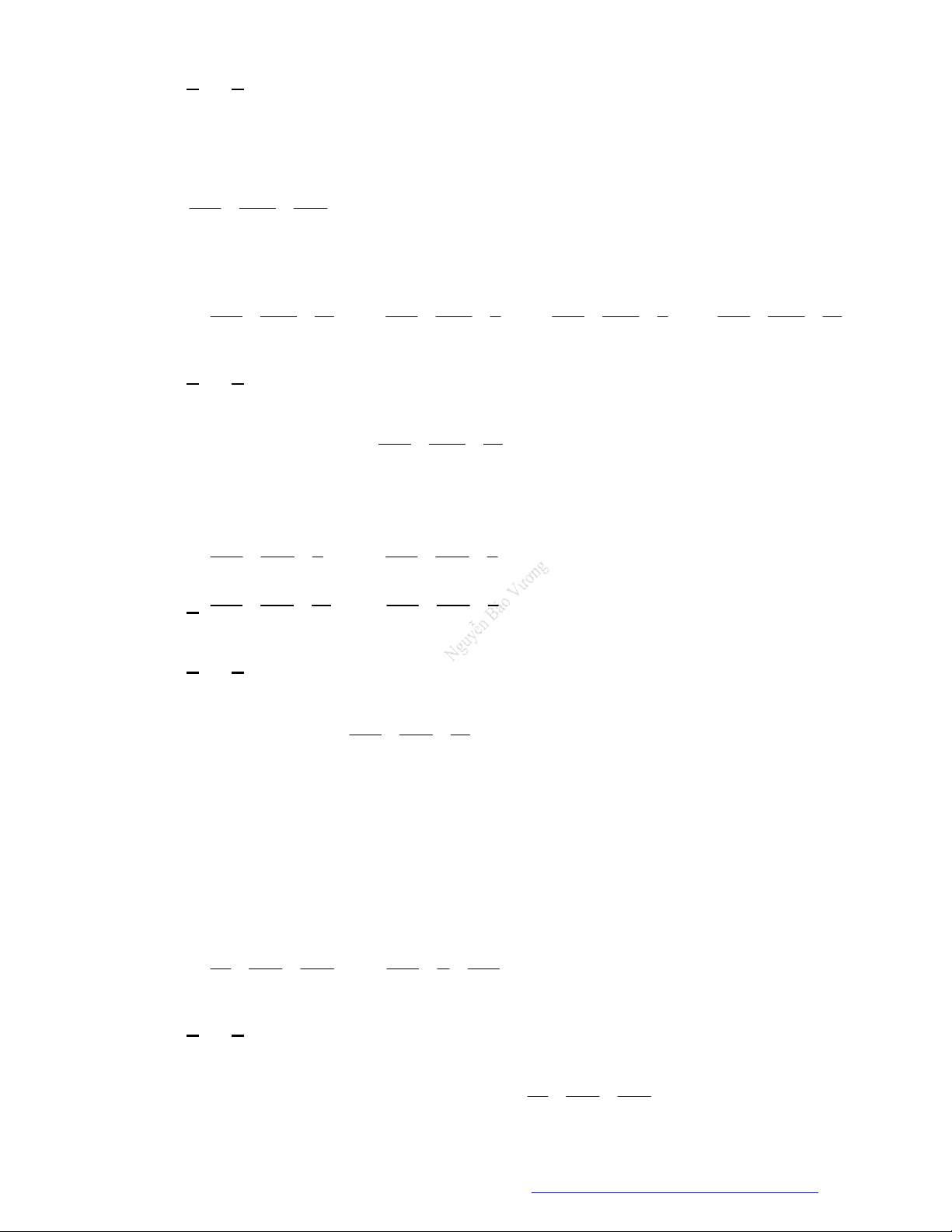
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17

Lời giải

Chọn C

Ta có , đường thẳng song song nên có vec tơ chỉ phương cùng phương với

.

Do vậy đường thẳng đi qua và song song với

có phương trình là

Câu 58. (Mã 103 - 2020 Lần 1) Trong không gian

Oxyz

, cho ba điểm

(1;2;0), (1;1;2)A B

và

(2;3;1)C

.

Đường thẳng đi qua

A

và song song với

BC

có phương trình là

A.

1 2

.

1 2 1

x y z 

 



B.

1 2

.

3 4 3

x y z 

 

C.

1 2

.

3 4 3

x y z 

 

D.

1 2

.

1 2 1

x y z 

 



Lời giải

Chọn A

Gọi

d

là phương trình đường thẳng qua

 

1;2;0A

và song song với

BC

.

Ta có

 

1;2; 1BC  



1 2

:

1 2 1

x y z

d

 

  



.

Câu 59. (Mã 104 - 2020 Lần 1) Trong không gian

Oxyz

, cho ba điểm

     

1;1;0 , 1;0;1 , 3;1;0A B C

.

Đường thẳng đi qua A và song song với BC có phương trình là:

A.

1 1

2 1 1

x y z 

 

. B.

1 1

4 1 1

z y z 

 

.

C.

1 1

2 1 1

x y z 

 



. D.

1 1

4 1 1

x y z 

 

.

Lời giải

Chọn C

Đường thẳng đi qua

 

1;1;0A

, song song với BC nên nhận

 

2;1; 1BC  



là véc tơ chỉ phương do

đó có phương trình là:

1 1

2 1 1

x y z 

 



.

Câu 60. (Mã 110 2017) Trong không gian với hệ tọa độ

Oxyz

, cho ba điểm

 

0; 1;3A 

,

 

1;0;1B

,

 

1;1;2C 

. Phương trình nào dưới đây là phương trình chính tắc của đường thẳng đi qua

A

và

song song với đường thẳng

BC

?

A.

2 0x y z  

. B.

2

1

3

x t

y t

z t

 





  





 



.

C.

1 3

2 1 1

x y z 

 



. D.

1 1

2 1 1

x y z 

 



.

Lời giải

Chọn C

Đường thẳng



đi qua

A

và song song

BC

nhận

 

2;1;1BC  



làm vectơ chỉ phương

 Phương trình chính tắc của đường thẳng



:

1 3

2 1 1

x y z 

 



.

Chú ý: Đáp án A không nhận được, vì đó là phương trình tham số của đường thẳng cần tìm, chứ

không phải phương trình chính tắc.

 

2;3; 1

BC

 



 

2;3; 1

BC

 



A

BC

1 2 3

2 3 1

x y z

  

 



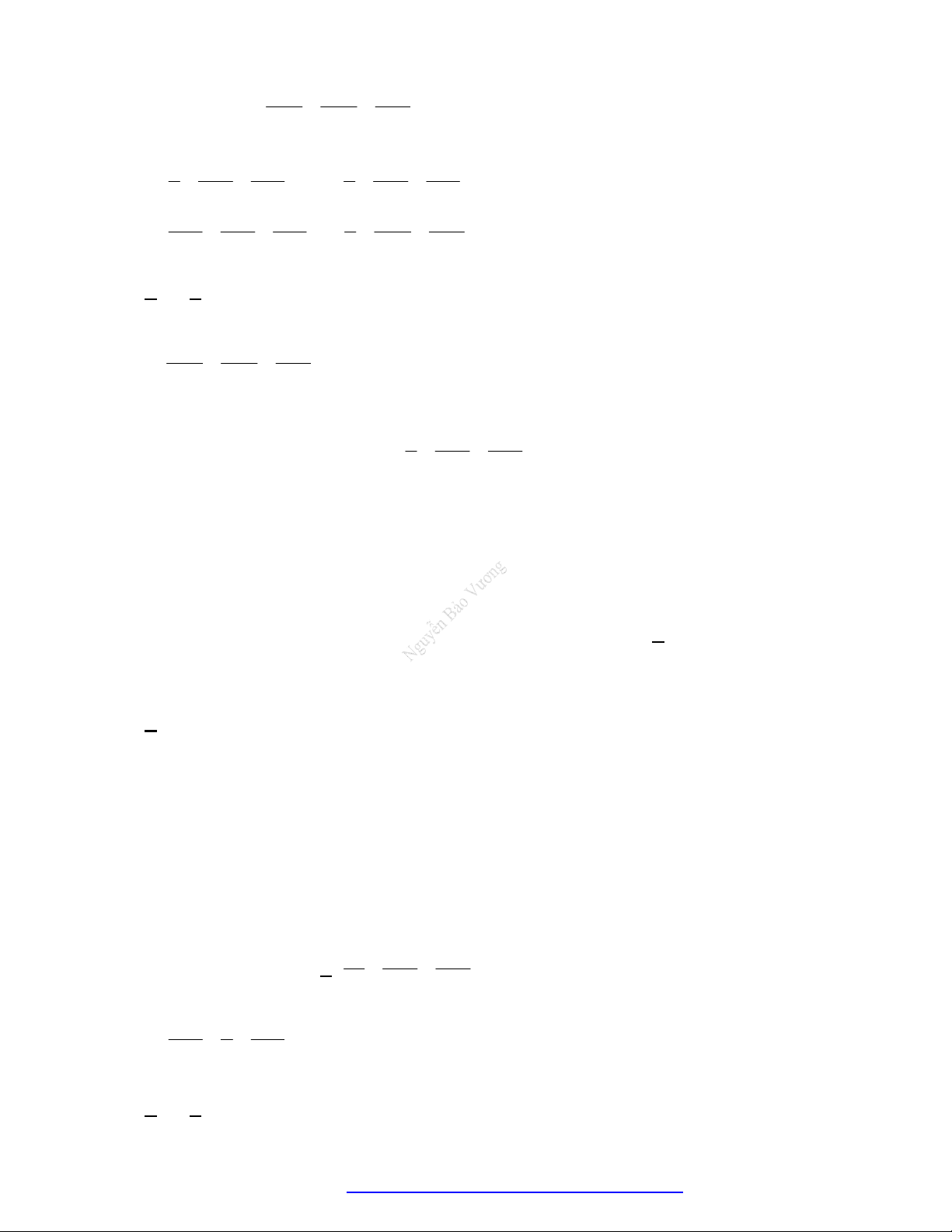
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 18 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 61. (Mã 105 2017) Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm

 

 1; 2; 3

A

;

 



1; 4;1

B

và

đường thẳng



 

 



2

2 3

:

1 1 2

y

x z

d

. Phương trình nào dưới đây là phương trình của đường

thẳng đi qua trung điểm của đoạn

AB

và song song với

d

?

A.





 

1

1 1 2

y

x z

B.





 



1

1 1 2

y

x z

C.



 

 



1

1 1

1 1 2

y

x z

D.





 



2

1 1 2

y

x z

Lời giải

Chọn B

Trung điểm của

AB

là

 

0;1; 1

I



 

 



2

2 3

:

1 1 2

y

x z

d

có VTCP là

 





1; 1; 2

u

nên đường thẳng



cần tìm cũng có VTCP

 





1; 1; 2

u .

Suy ra phương trình đường thẳng





  



1

: .

1 1 2

y

x x

Câu 62. Trong không gian với hệ toạ độ

Oxyz

, cho điểm

 



1; 2; 3

A

và hai mặt phẳng

 

   : 1 0

P x y z

,

 

   : 2 0

Q x y z

. Phương trình nào dưới đây là phương trình đường

thẳng đi qua

A

, song song với

 

P

và

 

Q

?

A.

 



 





 



1

2

3 2

x

y

z t

B.

   









  



1

2

3

x t

y

z t

C.

  



 





 



1 2

2

3 2

x t

y

z t

D.

  



 





 



1

2

3

x t

y

z t

Lời giải

Chọn D

Ta có

 









 







1;1;1

1; 1; 1

P

Q

n

và

   

 

   

 

 

, 2;0; 2 2 1; 0; 1

P Q

n n

. Vì đường thẳng

d

song song với

hai mặt phẳng, nên nhận véc tơ

 

1; 0; 1

làm véc tơ chỉ phương.

Câu 63. Trong không gian với hệ tọa độ

Oxyz

cho ba điểm

 



0; 1; 3

A

,

 

1; 0;1

B

,

 



1;1; 2

C

. Phương

trình nào dưới đây là phương trình chính tắc của đường thẳng đi qua

A

và song song với đường

thẳng

BC

?

A.

  



  





 



2

1

3

x t

y t

z t

. B.





 



1

3

2 1 1

y

x z

.

C.

 

 



1 1

2 1 1

y

x z

. D.

  2 0x y z

.

Lời giải

Chọn B

Đường thẳng đi qua

A

và song song

BC

nhận

 

 



2;1;1

BC làm vecto chỉ phương

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19



Phương trình đường thẳng cần tìm:





 



1

3

2 1 1

y

x z

.

Chú ý: Đáp án A không nhận được, vì đó là phương trình tham số của đường thẳng cần tìm, chứ

không phải phương trình chính tắc.

Câu 64. Trong không gian

Oxyz

, cho điểm

 

2;0; 1

A



và mặt phẳng

 

: 1 0

P x y

  

. Đường thẳng đi

qua

A

đồng thời song song với

 

P

và mặt phẳng

 

Oxy

có phương trình là

A.

  









 



3

2

1

x t

y t

z t

. B.

  



 





 



2

1

x t

y t

z

. C.

  



 





 



1 2

1

x t

y

z t

. D.

  



 





 



3

1 2

x t

y t

z t

.

Lời giải

Chọn B

Ta có:

 

1;1;0

Oxy

n 



,

 

0;0;1

Oxy

n 



.

Gọi

d

là đường thẳng đi qua

A

đồng thời song song với

 

P

và mặt phẳng

 

Oxy

. Khi đó:

 

   

 

(Oxy)

, 1; 1;0

d P

d P Oxy

d

u n

u n n

u n







 

   



 







 

  

 

. Vậy

2

:

1

x t

d y t

z

 





 





 



.

Câu 65. Trong không gian với hệ tọa độ

Oxyz

, cho điểm

 

2;3; 1

M

 

,

 

1;2;3

N 

và

 

2; 1;1

P 

.

Phương trình đường thẳng

d

đi qua

M

và song song với

NP

là

A.

1 3

2 3

3 2

x t

y t

z t

  





 





 



. B.

2 3

1 3

1 2

x t

y t

z t

 





  





 



. C.

2 3

3 3

1 2

x t

y t

z t

  





 





  



. D.

3 2

3 3

2

x t

y t

z t

 





  





  



.

Lời giải

Chọn C

Phương trình đường thẳng

d

đi qua

M

và song song với

NP

nên có vectơ chỉ phương là:

 

3; 3; 2

NP

  



.

Vậy phương trình đưởng thẳng

d

là:

2 3

3 3

1 2

x t

y t

z t

  





 





  



Câu 66. (Đà Nẵng 2019) Trong không gian

Oxyz

, cho đường thẳng

1 1 2

: .

1 2 1

x y z

d

  

 

 

Đường

thẳng đi qua điểm

 

2;1; 1

M



và song song với đường thẳng

d

có phương trình là:

A.

2 1 1

.

1 2 1

x y z

  

 

 

B.

5 3

.

1 2 1

x y z

 

 



C.

1 2 1

.

2 1 1

x y z

  

 



D.

2 1 1

.

1 1 2

x y z

  

 



Lời giải

Chọn B

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 20 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Vì đường thẳng song song với đường thẳng

d

nên nó có vectơ chỉ phương là

 

1; 2; 1

u

  



hoặc

 

1; 2;1

u  



nên loại phương án C và D.

Vì điểm

 

2;1; 1

M



thuộc đường thẳng

5 3

1 2 1

x y z

 

 



nên chọn phương án B.

Vậy phương trình của đường thẳng là

5 3

.

1 2 1

x y z

 

 



Câu 67. (Nho Quan A - Ninh Bình - 2019) Trong không gian với hệ tọa độ

Oxyz

, cho ba điểm

   

(0; 0; 1),B 1; 2;0 , 2;1; 1

A C

  

. Đường thẳng



đi qua

C

và song song với

AB

có phương

trình là

A.

 

2

1 2 ,

1

x t

y t t R

z t

 





  





  



. B.

 

2

1 2 ,

1

x t

y t t R

z t

 





  





  



.

C.

 

2

1 2 ,

1

x t

y t t R

z t

 





  





  



. D.

 

2

1 2 ,

1

x t

y t t R

z t

 





  





  



.

Lời giải

Chọn A

 

1; 2; 1

AB

  



nên chọn là véc tơ chỉ phương của



là

 

1;2;1

u



.

Do đó phương trình của



là

 

2

1 2 ,

1

x t

y t t R

z t

 





  





  



Câu 68. (Chu Văn An - Hà Nội - 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho hai mặt phẳng

 

: 2 1 0

x y z



   

,

 

: 2 0

x y z



  

và điểm

 

1;2; 1

A



. Đường thẳng



đi qua điểm

A

và

song song với cả hai mặt phẳng

   

,

 

có phương trình là

A.

1 2 1

2 4 2

x y z  

 

 

. B.

1 2 1

1 3 5

x y z  

 

.

C.

1 2 1

x y z  

 

 

. D.

2 3

1 2 1

x y z

 

 

.

Lời giải

Chọn B

mp

 



có véc tơ pháp tuyến là

 

1

1; 2;1

n  



, mp

 



có véc tơ pháp tuyến là

 

2

2;1; 1

n

 



.

Đường thẳng



có véc tơ chỉ phương là

 

1 2

; 1;3;5

u n n

 

 

 

  

.

Phương trình của đường thẳng

1 2 1

:

1 3 5

x y z  

  

.

Dạng 3 Bài toán liên quan điểm (hình chiếu) thuộc đường, giao điểm đường với mặt phẳng

Câu 69. (Đề Minh Họa 2020 Lần 1) Trong không gian

Oxyz

, điểm nào dưới đây thuộc đường thẳng

1 2 1

:

1 3 3

x y z

d

  

 



?

A.

 

1;2;1

P 

. B.

 

1; 2; 1

Q

 

. C.

 

1;3;2

N 

. D.

 

1;2;1

P

.

Lời giải

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21

Chọn A

Thay tọa độ các điểm vào phương trình đường thẳng ta thấy điểm

 

1;2;1

P 

thỏa

1 1 2 2 1 1

0

1 3 3

   

  



. Vậy điểm

 

1;2;1

P 

thuộc đường thẳng yêu cầu.

Câu 70. (Đề Tham Khảo 2020 Lần 2) Trong không gian

,Oxyz

cho đường thẳng

1 2 1

: .

2 3 1

x y z

d

  

 



Điểm nào sau đây thuộc

?d

A.

 

1;2; 1 .

P



B.

 

1; 2;1 .

M  

C.

 

2;3; 1 .

N



D.

 

2; 3;1 .

Q  

Lời giải

Chọn A

Thay tọa độ điểm

 

1;2; 1

P



vào phương trình đường thẳng

d

thấy thỏa mãn nên đường thẳng

d

đi qua điểm

 

1;2; 1 .

P



Câu 71. (Mã 101 2020 Lần 2) Trong không gian Oxyz, cho đường thẳng

x 2 y 1 z 3

d :

4 2 1

  

 



. Điểm

nào dưới đây thuộc d?

A.

 

4; 2;1 .

Q 

B.

 

4;2;1 .

N

C.

 

2;1; 3 .

P



D.

 

2;1;3 .

M

Lời giải

Chọn C

Thay tọa độ điểm

 

2;1; 3

P



vào

2 1 3

:

4 2 1

x y z

d

  

 



ta được

2 2 1 1 3 3

0 0 0

4 2 1

   

    



đúng. Vậy điểm

 

P d



.

Câu 72. (Mã 102 - 2020 Lần 2) Trong không gian

Oxyz

, cho đường thẳng

4 2 1

:

2 5 1

x z z

d

  

 



. Điểm

nào sau đây thuộc

d

?

A.

(4;2; 1)

N



. B.

(2;5;1)

Q

. C.

(4;2;1)

M

. D.

(2; 5;1)

P



.

Lời giải

Chọn A

Thế điểm

(4;2; 1)

N



vào

d

ta thấy thỏa mãn nên chọn A.

Câu 73. (Mã 103 - 2020 Lần 2) Trong không gian

Oxyz

, cho đường thẳng

3 1 2

:

2 4 1

x y z

d

  

 



. Điểm

nào dưới đây thuộc

d

?

A.

 

3; 1; 2

N

 

B.

 

2;4;1

Q

C.

 

2;4; 1

P



D.

 

3;1;2

M

Lời giải

Chọn A

Ta có:

3 3 1 1 2 2

0

2 4 1

    

  



. Vậy

 

3; 1; 2

N

 

thuộc

d

.

Câu 74. (Mã 104 - 2020 Lần 2) Trong không gian

Oxyz

, cho đường thẳng

3 1 5

:

2 2 1

x y z

d

  

 



. Điểm

nào dưới đây thuộc

d

?

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 22 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

A.

 

3;1;5

M

. B.

 

3;1; 5

N



. C.

 

2;2; 1

P



. D.

 

2;2;1

Q

.

Lời giải

Chọn B

Ta có

3 3 1 1 5 5

0

2 2 1

   

  



nên điểm

 

3;1; 5

N d 

.

Câu 75. (Mã đề 104 BGD&ĐT NĂM 2018) Trong không gian

Oxyz

, điểm nào dưới đây thuộc đường

thẳng

d

:

1

5

2 3

x t

y t

z t

 





 





 



?

A.

 

1;5;2

N

B.

 

1;1;3

Q 

C.

 

1;1;3

M

D.

 

1;2;5

P

Lời giải

Chọn A

Cách 1. Dựa vào lý thuyết: Nếu

d

qua

 

0 0 0

; ;z

M x y

, có véc tơ chỉ phương

 

; ;



u a b c

thì phương

trình đường thẳng

d

là:

0

x x at

y y bt

z z ct

 





 





 



, ta chọn đáp án

B.

Cách 2. Thay tọa độ các điểm

M

vào phương trình đường thẳng

d

, ta có:

1 1 0

2 5 3

5 2 3 1

t t

  

 

 

    

 

 

  

 

(Vô lý). Loại đáp án A.

Thay tọa độ các điểm

N

vào phương trình đường thẳng

d

, ta có:

1 1

5 5 0

2 2 3

t

t t

t

 





   





 



. Nhận đáp án B.

Câu 76. (Mã 103 2018) Trong không gian

Oxyz

, điểm nào dưới đây thuộc đường thằng

2 1 2

:

1 1 2

x y z

d

  

 

.

A.

 

2; 1;2

N 

B.

 

2;1; 2

Q

 

C.

 

2; 2;1

M  

D.

 

1;1;2

P

Lời giải

Chọn B

Đường thằng

2 1 2

:

1 1 2

x y z

d

  

 

đi qua điểm

 

2;1; 2 

.

Câu 77. (Chuyên Hùng Vương Gia Lai 2019) Trong không gian

Oxyz

, đường thẳng

1 2

: 3

1

x t

d y t

z t

 





 





 



đi

qua điểm nào dưới đây?

A.

 

1;3; 1

M



. B.

 

3;5;3

M 

. C.

 

3;5;3

M

. D.

 

1;2; 3

M



.

Lời giải

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23

Với

2

t

 

, ta có

 

1 2 2 3

3 2 5

1 2 3

x

y

z

    





   





   



.

Vậy

 

3;5;3

M d 

.

Câu 78. (THPT Hùng Vương Bình Phước 2019) Trong không gian với hệ tọa độ

Oxyz

. Đường thẳng

1

2

x t

d y t

z t







 





 



đi qua điểm nào sau sau đây?

A.

 

1; 1;1

K 

. B.

 

1;1;2

E

. C.

 

1;2;0

H

. D.

 

0;1;2

F

.

Lời giải

Thay tọa độ của

 

1; 1;1

K 

vào PTTS của

d

ta được

1 1

1 1 2 :

1 2 1

t t

 

 

 

    

 

 

   

 

không tồn tại t.

Do đó,

.K d

Thay tọa độ của

 

1;1;2

E

vào PTTS của

d

ta được

1 1

1 1 0 :

2 2 0

t t

 

 

 

   

 

 

  

 

không tồn tại t.

Do đó,

.E d

Thay tọa độ của

 

1;2;0

H

vào PTTS của

d

ta được

1 1

2 1 1 :

0 2 2

t t

 

 

 

    

 

 

   

 

không tồn tại t.

Do đó,

.H d

Thay tọa độ của

 

0;1;2

F

vào PTTS của

d

ta được

0 0

1 1 0 0.

2 2 0

t t

t t t

t t

 

 

 

     

 

 

  

 

Câu 79. (Chuyên KHTN 2019) Trong không gian

Oxyz

, điểm nào dưới đây thuộc đường thẳng

1 1 2

2 1 3

x y z

  

 



?

A.

 

2;1; 3

Q

 

. B.

 

2; 1;3

P 

. C.

 

1;1; 2

M

 

. D.

 

1; 1;2

N 

.

Lời giải

Xét điểm

 

1; 1;2

N 

ta có

1 1 1 1 2 2

2 1 3

   

 



nên điểm

 

1; 1; 2

N

 

thuộc đường thẳng đã cho.

Câu 80. (Chuyên KHTN 2019) Trong không gian

Oxyz

, gọi

d

là đường thẳng qua

 

1;0;2

A

, cắt và

vuông góc với đường thẳng

1

1 5

:

1 1 2

 

 



x y z

d

. Điểm nào dưới đây thuộc

d

?

A.

 

2; 1;1

P

. B.

 

0; 1;1

Q

. C.

 

0; 1;2

N

. D.

 

1; 1;1

 M

.

Lời giải

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 24 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Phương trình tham số đường thẳng

 

1

:

5 2

 





 





 





x t

d y t t

z t

, với vectơ chỉ phương

 

1;1; 2 



u

.

Giả sử đường thẳng

d

cắt đường thẳng

1

d

tại

B

. Khi đó

 

1 ; ;5 2

 

B t t t

.

 

; ;3 2

 



AB t t t

Vì đường thẳng

d

vuông góc với đường thẳng

1

d

nên

1

. 0  

 

AB d AB u

  

3 2 2 0 1       t t t t

.

Khi đó

 

2;1;3

B

.

Phương trình đường thẳng

d

đi qua

 

1;0;2

A

và có vectơ chỉ phương

 

1;1;1





AB

là:

1 2

1 1 1

 

 

x y z

.

Nhận thấy

 

0; 1;1

 Q d

.

Câu 81. Trong không gian

Oxyz

, điểm nào dưới đây thuộc đường thẳng

1

: 5

2 3

 





 





 



x t

d y t

z t

?

A.

 

1;1; 3

Q

B.

 

1; 2; 5

P

C.

 

1; 5; 2

N

D.

 

1;1; 3

M

Lời giải

Chọn C

Với

 

1

0 5 1; 5; 2

2







    









x

t y N d

z

.

Câu 82. Trong không gian

Oxyz

, đường thẳng

1 2 3

:

2 1 2

x y z

d

  

 

 

đi qua điểm nào dưới đây?

A.

(2; 1; 2)

Q

 

. B.

(1; 2; 3)

M

 

. C.

( 1;2; 3)

P

 

. D.

N(2; 1; 2) 

.

Lời giải

Đáp án A nhầm vectơ chỉ phương.

Đáp án B nhầm dấu tọa độ điểm.

Đáp án D nhầm vectơ chỉ phương.

Câu 83. (KTNL GV THPT Lý Thái Tổ 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho đường

thẳng

1 2 3

:

3 4 5

  

 

 

x y z

d

. Hỏi

d

đi qua điểm nào trong các điểm sau:

A.

 

3;4;5

C

. B.

 

3; 4; 5 

D

. C.

 

1;2; 3 

B

. D.

 

1; 2;3

A

.

Lời giải

Chọn D

Đường thẳng

1 2 3

:

3 4 5

  

 

 

x y z

d

đi qua điểm

 

1; 2;3

A

.

Câu 84. (Sở Thanh Hóa 2019) Trong không gian

Oxyz

, cho điểm

 

3; 2;1

A 

. Đường thẳng nào sau đây

đi qua

A

?

A.

3 2 1

1 1 2

x y z  

 

. B.

3 2 1

4 2 1

x y z  

 

 

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25

C.

3 2 1

1 1 2

x y z  

 

. D.

3 2 1

4 2 1

x y z  

 

 

.

Lời giải

Xét đáp án A. Thay tọa độ điểm

 

3; 2;1

A 

vào phương trình đường thẳng ta được

0 0 0

1 1 2

 

đúng. Suy ra đường thẳng

3 2 1

1 1 2

x y z  

 

đi qua điểm

 

3; 2;1

A 

.

Câu 85. Trong không gian

Oxyz

, điểm nào dưới đây thuộc đường thẳng

1

: 5

2 3

 





 





 



x t

d y t

z t

?

A.

 

1;1; 3

Q

B.

 

1; 2; 5

P

C.

 

1; 5; 2

N

D.

 

1;1; 3

M

Lời giải

Chọn C

Với

 

1

0 5 1; 5; 2

2







    









x

t y N d

z

.

Câu 86. (Chuyên Nguyễn Tất Thành Yên Bái 2019) Trong không gian với hệ tọa độ

Oxyz

, cho đường

thẳng

d

có phương trình

1 2 3

3 2 4

x y z  

 



. Điểm nào sau đây không thuộc đường thẳng

d

?

A.

 

7;2;1

P

. B.

 

2; 4;7

Q  

. C.

 

4;0; 1

N



. D.

 

1; 2;3

M 

.

Lời giải

Thay tọa độ điểm

 

7; 2;1

P

vào phương trình đường thẳng

d

ta có

7 1 2 2 1 3

3 2 4

  

 



nên điểm

 

7;2;1

P d

.

Câu 87. (THPT Cẩm Bình 2019) Giao điểm của mặt phẳng

 

: 2 0

P x y z

   

và đường thẳng

2

:

3 3

x t

d y t

z t

 





 





 



A.

 

1;1;0

. B.

 

0;2;4

. C.

 

0;4;2

. D.

 

2;0;3

.

Lời giải

Chọn A

Gọi

 

; ;A x y z

là giao điểm của đường thẳng d và mặt phẳng

 

P

.

Ta có:

 

2 3 3 2 0 3 3 0 1

t t t t t

            

.

 

1

1 1;1;0

0

x

y A

z







  









.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 26 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 88. (Thpt Vĩnh Lộc - Thanh Hóa 2019) Trong không gian

,Oxyz

cho đường

thẳng

1 2

: 3 ,

1

x t

d y t

z t

 





 





 



t  

và mặt phẳng

 

: 2 3 2 0.

P x y z

   

Tìm tọa độ của điểm

A

là giao

điểm của đường thẳng

d

và mặt phẳng

 

.P

A.

 

3;5;3

A

. B.

 

1;3;1

A

. C.

 

3;5;3

A 

. D.

 

1;2; 3

A



.

Lời giải

Chọn C

Vì

A

là giao điểm của đường thẳng

d

và mặt phẳng

 

P

nên

+

 

1 2 ;3 ;1 .A d A t t t    

+

       

1 2 2 3 3 1 2 0 2.

A P t t t t

           

Vậy tọa độ điểm

 

3;5;3 .

A 

Câu 89. (Hùng Vương Gia Lai2019) Trong không gian

Oxyz

, giao điểm của mặt phẳng

 

: 3 5 2 0

P x y z

   

và đường thẳng

12 9 1

:

4 3 1

x y z  

  

là điểm

 

0 0 0

; ;M x y z

. Giá trị

tổng

0 0 0

x y z 

bằng

A.

1

. B.

2

. C.

5

. D.

2

.

Lời giải

Chọn D

 

12 4 ;9 3 ;1

M M t t t     

.

       

3 12 4 5 9 3 1 2 0 3

M P t t t t

           

.

 

0 0 0

0;0; 2 2

M x y z

     

.

Câu 90. Trong không gian với hệ trục tọa độ

Oxyz

, hình chiếu vuông góc của điểm

 

4;5;2

M 

lên mặt

phẳng

 

: 1 0

P y

 

là điểm có tọa độ

A.

 

4; 1;2

 

. B.

 

4;1;2



. C.

 

0; 1;0



. D.

 

0;1;0

.

Lời giải

Chọn A

Gọi

H

à hình chiếu vuông góc của

M

lên

 

P

4

: 5

2

x

MH y t

z

 





  









 

4;5 ;2H MH H t

   

   

5 1 0 6 4; 1;2

H P t t H          

Câu 91. (Chuyên Bắc Giang 19) Trong không gian với hệ trục tọa độ

Oxyz

, cho đường thẳng

12 9 1

:

4 3 1

x y z

d

  

 

và mặt phẳng

 

:3 5 2 0

P x y z

   

. Tìm tọa độ giao điểm của

d

và

 

P

.

A.

 

1;0;1

. B.

 

0;0; 2

. C.

 

1;1;6

. D.

 

12;9;1

.

Lời giải

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27

Chọn B

Ta có

12 9 1

:

4 3 1

x y z

d

  

 



12 4

: 9 3

1

x t

d y t

z t

 





 





 



 

t 



.

Thay

12 4x t 

,

9 3y t 

,

1z t 

vào

 

:3 5 2 0

P x y z

   

, ta được:

     

3 12 4 5 9 3 1 2 0

t t t

      



3

t

 

.

Với

3

t

 



0

x



,

0

y



,

2z  

.

Vậy tọa độ giao điểm của

d

và

 

P

là

 

0;0; 2

.

Câu 92. (Kon Tum - 2019) Trong không gian

Oxyz

, cho đường thẳng

4 2

: 3

1

x t

d y t

z t

 





  





 



, giao điểm của

d

với mặt phẳng

 

Oxy

có tọa độ là

A.

 

4; 3;0



. B.

 

2; 2;0



. C.

 

0; 1; 1 

. D.

 

2;0; 2 

.

Lời giải

Chọn B

Mặt phẳng

 

Oxy

có phương trình

0

z



.

Gọi

 

4 2 ; 3 ;1

M m m m   

là giao điểm của

d

với mặt phẳng

 

Oxy

thì ta có:

1 0 1

m m

   

.

Vậy

 

2; 2;0

M 

.

Câu 93. (Kinh Môn - Hải Dương 2019) Trong không gian với hệ toạ độ

Oxyz

, cho 3 điểm

 

1;0;0

A

,

 

0;2;0

B

,

 

0;0;3

C

và đường thẳng

: 2

3

x t

d y t

z t

 





 





 



. Gọi

 

; ;M a b c

là toạ độ giao điểm của

đường thẳng

d

với mặt phẳng

 

ABC

. Tính tổng

S a b c  

.

A.

6

. B.

5

.

C.

7

. D.

11

.

Lời giải

Chọn C

Phương trình mặt phẳng

 

ABC

có dạng:

1 6 3 2 6 0

1 2 3

x y z

       

Điểm

   

;2 ;3

M d M t t t    

. Lại vì

 

M d ABC

 

nên ta có

       

6 3 2 2 3 6 0 6 6 6;8;9

t t t t t M              

Vậy ta có

6 8 9 7

S a b c

        

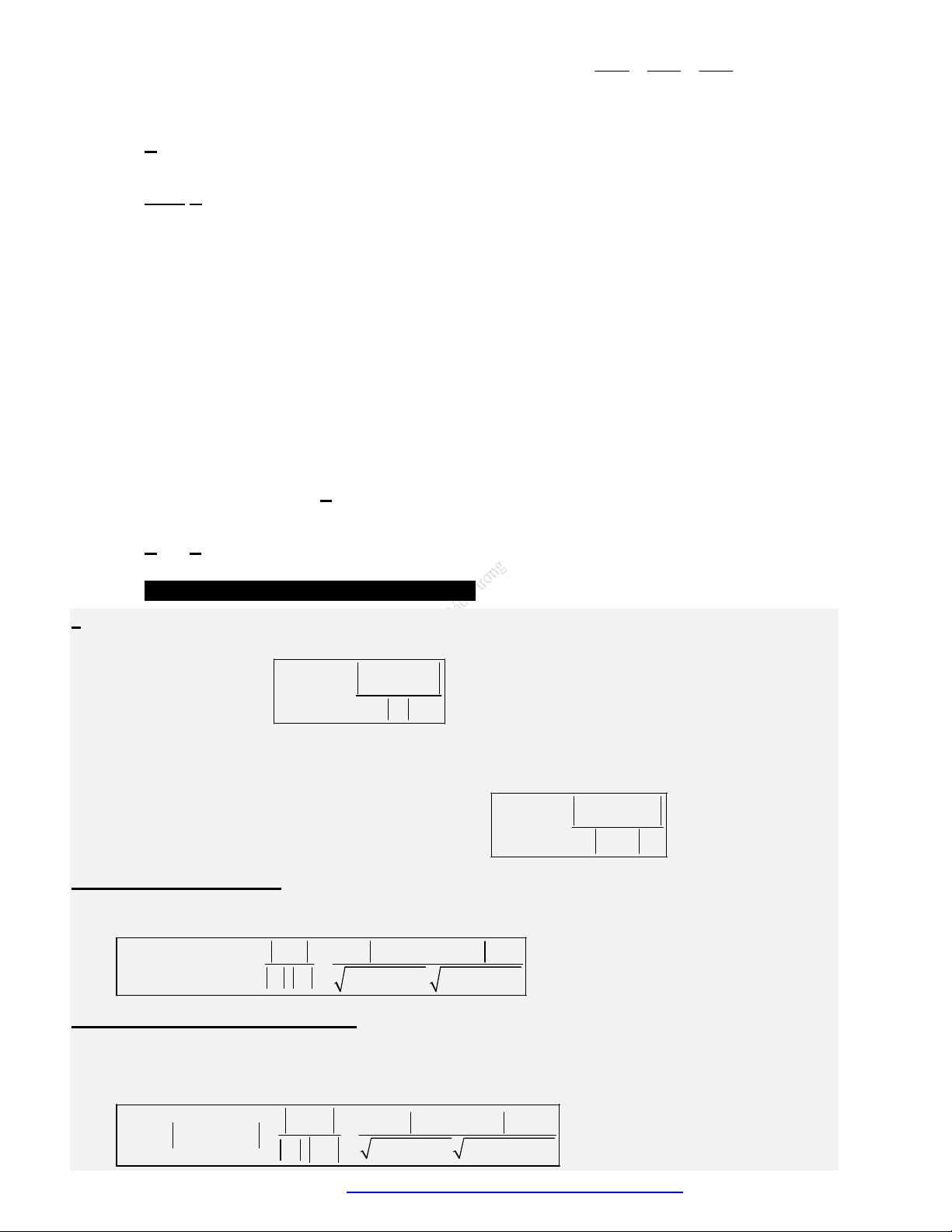
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 28 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 94. (Bến Tre 2019) Trong không gian

Oxyz

, cho đường thẳng

3 1 3

:

2 1 1

x y z

d

  

 

và mặt phẳng

 

: 2 5 0

P x y z

   

. Tìm tọa độ giao điểm

M

của đường thẳng

d

và mặt phẳng

 

P

.

A.

 

1;0;4

M 

. B.

 

5; 2;2

M  

. C.

 

0;0;5

M

. D.

 

3; 1;3

M  

.

Lời giải

Chọn A

Phương trình tham số của đường thẳng

d

:

3 2

1

3

x t

y t

z t

  





  





 



.

Xét phương trình

   

3 2 2 1 3 5 0

t t t

        

3 3 1t t   

.



Đường thẳng

d

cắt mặt phẳng

 

P

tại điểm

 

1;0;4

M 

.

Câu 95. (Đà Nẵng 2019) Trong không gian

Oxyz

, cho điểm

 

2;3;5 .

A

Tìm tọa độ điểm

'A

là hình

chiếu vuông góc của

A

lên trục

.Oy

A.

 

' 2;0;0 .

A

B.

 

' 0;3;0 .

A

C.

 

' 2;0;5 .

A

D.

 

' 0;3;5 .

A

Lời giải

Chọn B

Dạng 4. Bài toán liên quan khoảng cách, góc

1. Khoảng cách từ một điểm đến đường thẳng – Khoảng cách giữa hai đường thẳng



Khoảng cách từ điểm

M

đến một đường thẳng

d

qua điểm

M



có véctơ chỉ phương

d

u



được xác

định bởi công thức

,

( , )

d

M M u

d M d

u

 

 

 







Khoảng cách giữa hai đường thẳng song song là khoảng cách từ một điểm thuộc đường thẳng này

đến đường thẳng kia.



Khoảng cách giữa hai đường thẳng chéo nhau:

d

đi qua điểm

M

và có véctơ chỉ phương

u



và

d



đi qua điểm

M



và có véctơ chỉ phương

u





là

 

, .

( , )

,

u u M M

d d d

u u



 







 

2. Góc giữa hai đường thẳng

Góc giữa hai đường thẳng

1

d

và

2

d

có véctơ chỉ phương

1 1 1 1

( ; ; )u a b c



và

2 2 2 2

( ; ; ).u a b c



1 2 1 2 1 2 1 2

1 2

2 2 2 2 2 2

1 2

1 1 1 2 2 2

.

cos( ; ) cos

.

u u a a b b c c

d d

u u

a b c a b c



 

  

   

 

với

0 90 .



   

3. Góc giữa đường thẳng và mặt phẳng

Góc giữa đường thẳng

d

có véctơ chỉ phương

( ; ; )

d

u a b c



và mặt phẳng

( )P

có véctơ pháp tuyến

( )

( ; ; )

P

n A B C



được xác định bởi công thức:

( )

2 2 2 2 2 2

( )

.

sin cos( ; )

.

d P

P d

d P

u n

aA bB cC

n u

u n

a b c A B C



 

  

   

 

với

0 90 .



   

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 29

Câu 96. (Đề Tham Khảo 2017) Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

 

: 2 2 1 0

P x y z

   

và đường thẳng

1 2 1

:

2 1 2

x y z  

  

. Tính khoảng cách

d

giữa



và

 

P

.

A.

2

d



B.

5

3

d



C.

2

3

d



D.

1

3

d



Lời giải

Chọn A

( )P

có vecto pháp tuyến

 



(2; 2; 1)

n

và đường thẳng



có vecto chỉ phương

(2;1; 2)

u



thỏa mãn

. 0n u 

 

nên

//( )P

hoặc

( )P 

.

Do đó: lấy

  (1; 2;1)A

ta có:

2.1 2.( 2) 1 1

( ( )) ( ; ( )) 2

4 4 1

d P d A P

   

   

 

.

Câu 97. (Chuyên Sơn La 2019) Trong không gian

Oxyz

, khoảng cách giữa đường thẳng

1

:

1 1 2

x y z

d



 



và mặt phẳng

 

: 2 0

P x y z

   

bằng:

A.

2 3.

B.

3

.

3

C.

2 3

.

3

D.

3.

Lời giải

Đường thẳng

d

qua

 

1;0;0

M

và có vec-tơ chỉ phương

 

1;1; 2

a

 



.

Mặt phẳng

 

P

có vec-tơ pháp tuyến

 

1;1;1

n 



.

Ta có:

 

. 1.1 1.1 2.1 0

/ / .

a n

d P

M P



   













 

 

2 2 2

1 0 0 2

, , 3.

1 1 1

d d P d M P

  

  

 

Câu 98. (THPT Lê Quý Đôn Dà Nẵng 2019) Trong không gian với hệ tọa độ

Oxyz

, khoảng cách giữa

đường thẳng

2

: 5 4

2

x t

y t

z t

 





  





 



,

 

t 



và mặt phẳng

 

: 2 2 0

P x y z

  

bằng

A.

1

. B.

0

. C.

2

. D.

3

.

Lời giải

Xét phương trình

     

2 2 5 4 2 2 0 0 3 0

t t t t

        

.

Phương trình này vô nghiệm nên

 

//

P



.

Chọn

 

2;5;2M



.

Khi đó:

 

2

2 2

2.2 5 2.2

, , 1.

2 1 2

d P d M P

 

   

  

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 30 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 99. (Chuyên Bắc Giang 2019) Trong không gian với hệ tọa độ Oxyz cho đường thẳng

1

: 2 2

3

x t

d y t

z t

 





 





 



và mặt phẳng (P):

3 0

x y

  

. Tính số đo góc giữa đường thẳng d và mặt phẳng (P).

A.

0

60

B.

0

30

C.

120

o

D.

0

45

Lời giải

Chọn A.

Đường thẳng

d

có véc tơ chỉ phương là

 

1;2;1

u  



Mặt phẳng

 

P

có véc tơ pháp tuyến là

 

1; 1;0

n  



Gọi



là góc giữa Đường thẳng

d

và Mặt phẳng

 

P

. Khi đó ta có

 

   

2 2

2 2 2 2

.

1.1 2. 1 1.0

3 3

sin

2

2 3

1 2 1 . 1 1 0

u n

   

    

     

 

Do đó

0

60

 

Câu 100. (Chuyên Trần Đại Nghĩa - TPHCM - 2018) Tính khoảng cách giữa hai đường thẳng

1

d

:

3 2

1 2 1

x y z

 

 

và

2

d

:

3 1 2

1 2 1

x y z

  

 



A.

2

3

. B.

12

5

. C.

3 2

2

. D.

3

.

Lời giải

1

d

qua

 

0;3;2

M

có vtcp

 

1;2;1

u 



,

2

d

qua

 

3; 1;2

N 

có vtcp

 

1; 2;1

v  



.

 

 

, 4;0; 4

u v

 

 

,

 

3; 4;0

MN  



.

 

1 2

,d d d



 

, .

,

u v MN

u v





 

12 3 2

2

4 2

 .

Câu 101. (Chuyên Lê Quý Đôn Quảng Trị 2019) Trong không gian tọa độ

Oxyz

, cho mặt phẳng

 

: 4 3 1 0

P x y z

   

và đường thẳng

1 6 4

:

4 3 1

x y z

d

  

 

, sin của góc giữa đường thẳng

d

và mặt phẳng

 

P

bằng

A.

5

13

. B.

8

13

. C.

1

13

. D.

12

13

.

Lời giải

Chọn D

Mặt phẳng

 

: 4 3 1 0

P x y z

   

có một vectơ pháp tuyến là

 

4;3; 1

n

 



.

Đường thẳng

1 6 1

:

4 3 1

x y z

d

  

 

có một vectơ chỉ phương là

 

4;3;1

u 



.

Gọi



là góc giữa đường thẳng

d

và mặt phẳng

 

P

.

Khi đó

 

sin cos ;n u





 

.n u

n u



 

 

2

2 2 2 2 2

4.4 3.3 1 1

4 3 1 . 4 3 1

  



    

12

13



.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 31

Câu 102. (Chuyên ĐH Vinh -2019) Trong không gian

Oxyz

cho đường thẳng

:

1 2 1

x y z

  



và mặt

phẳng

 

: 2 0

x y z



  

. Góc giữa đường thẳng



và mặt phẳng

 



bằng

A.

30

. B.

60

. C.

150

. D.

120

.

Lời giải

Chọn A

Đường thẳng



có vectơ chỉ phương

 

1;2; 1

u

 



, mặt phẳng

 



có vectơ pháp tuyến

 

1; 1;2

n  



. Gọi



là góc giữa đường thẳng



và mặt phẳng

 



, khi đó

 

.

1 2 2

1

sin cos , 30

2

6. 6

.

u n

 

 

      

 

.

Câu 103. Trong không gian

Oxyz

, cho mặt phẳng (P):

3 1 0

x y

   

. Tính góc tạo bởi

( )P

với trục

Ox

?

A.

0

60

. B.

0

30

. C.

0

120

. D.

0

150

.

Lời giải

Chọn A

Mặt phẳng

( )P

có VTPT

( 3;1;0)

n  



Trục

Ox

có VTCP

(1;0;0)

i 



Góc tạo bởi

( )P

với trục

Ox

3.1 1.0 0.0

.

3

sin((P); ) cos((P); ) =

2

3 1. 1

.

n i

Ox Ox

n i

  

  



 

Vậy góc tạo bởi

( )P

với trục

Ox

bằng

0

60

.

Câu 104. (Bình Phước - 2019) Trong không gian

Oxyz

, khoảng cách từ điểm

 

2; 4; 1

M

 

tới đường

thẳng

: 2

3 2

x t

y t

z t







  





 



bằng

A.

14.

.

B.

6.

.

C.

2 14.

.

D.

2 6.

Lời giải

Chọn C

Đường thẳng



đi qua

 

0;2;3

N

, có véc tơ chỉ phương

 

1; 1; 2

u  



   

2;6;4 ; , 16;8; 4

MN MN u

 

   

 

  

.

 

,

336

, 2 14.

6

MN u

d M

u

 

 

   

 



.

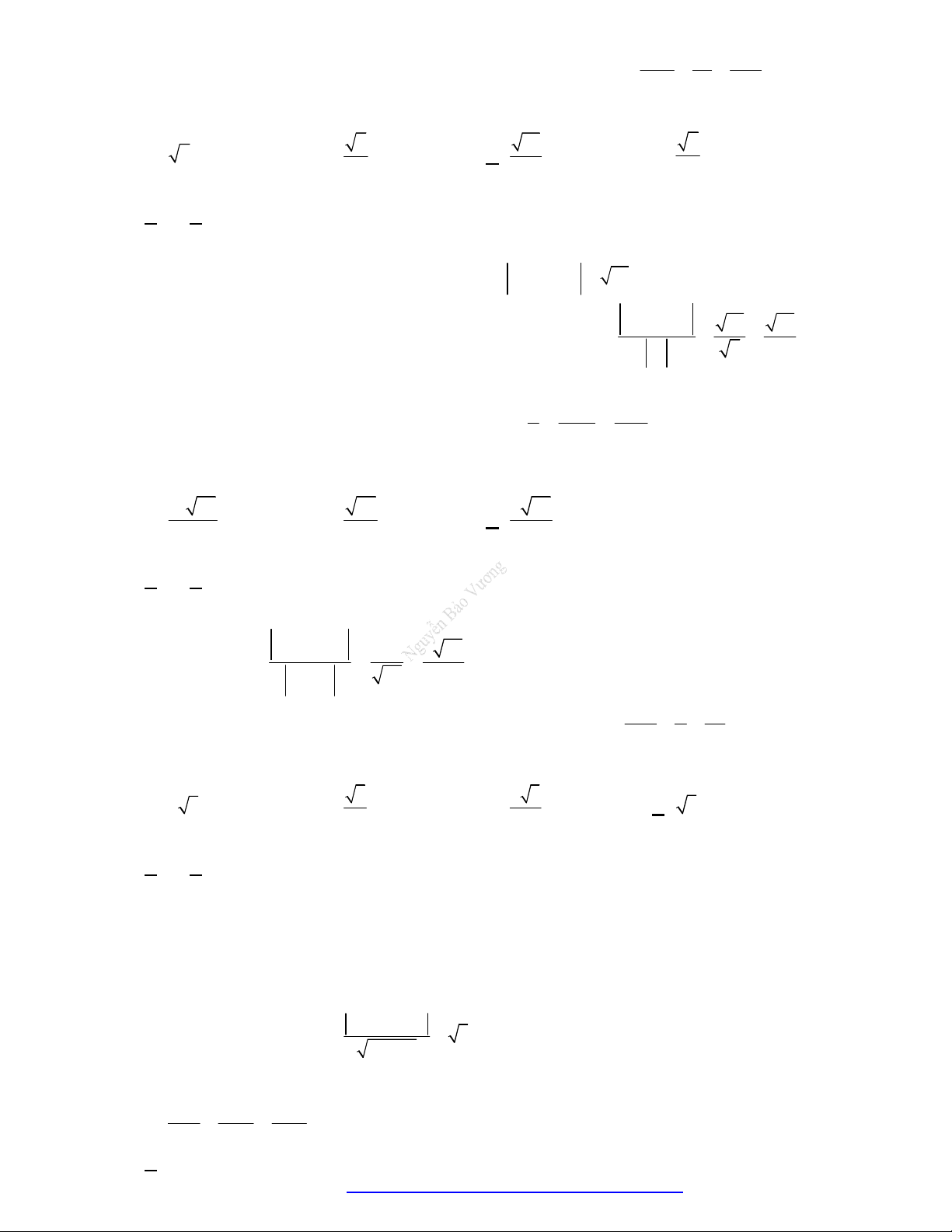
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 32 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 105. Trong không gian với hệ tọa độ

Oxyz

, cho đường thẳng

 

3 1

:

2 1 1

x y z

d

 

 

 

và điểm

(2; 1;0)

A



. Khoảng cách từ điểm

A

đến đường thẳng

 

d

bằng

A.

7

. B.

7

2

. C.

21

3

. D.

7

3

.

Lời giải

Chọn C

Gọi

 

3;0;1

M d

.

 

(1;1;1); ( 2; 1;1) ; 2; 3;1 ; 14

d d d

AM u AM u AM u

   

      

   

     

.

Vậy khoảng cách từ điểm

A

đến đường thẳng

 

d

bằng

;

14 21

( , )

3

6

d

AM u

d A d

u

 

 

  

 



Câu 106. (Chuyên Bắc Giang -2019) Cho

1

3 1

: 3 , ' :

3 1 1

2 2

x t

x y z

d y t d

z t

 



 



    







 



. Khi đó khoảng cách giữa

d

và

'd

là

A.

13 30

30

. B.

30

3

. C.

9 30

10

. D.

0

.

Lời giải

Chọn C

Ta có

   

1; 3;2 , 0;3;1 'A d B d  

và

   

1; 1;2 , ' 3; 1;1

u u 

 

lần lượt là vectơ chỉ phương của

d,d'

Ta có

 

, ' .

27 9 30

, '

10

30

, '

u u AB

d d d

u u

 

 

  

 

 

  

 

Câu 107. Trong không gian

Oxyz

, khoảng cách giữa đường thẳng

1

:

1 1 2

x y z

d



 



và mặt phẳng

 

: 2 0

P x y z

   

bằng

A.

2 3

. B.

3

. C.

2 3

3

. D.

3

.

Lời giải

Chọn D

Đường thẳng

d

đi qua điểm

 

1;0;0

M

và có véc tơ chỉ phương

 

1;1; 2

u

 



.

Mặt phẳng

 

P

có véc tơ pháp tuyến

 

1;1;1

n 



.

Ta có

 

. 0

/ /

u n

d P

M P

















 

.

 

1 0 0 2

d , d , 3

1 1 1

d P M P

  

   

 

.

Câu 108. Trong không gian với hệ tọa độ Oxyz, khoảng cách giữa đường thẳng

1 3 2

:

2 2 1

x y z

d

  

 

và mặt phẳng

( ) : 2 2 4 0

P x y z

   

A. 1. B. 0. C. 3. D. 2.

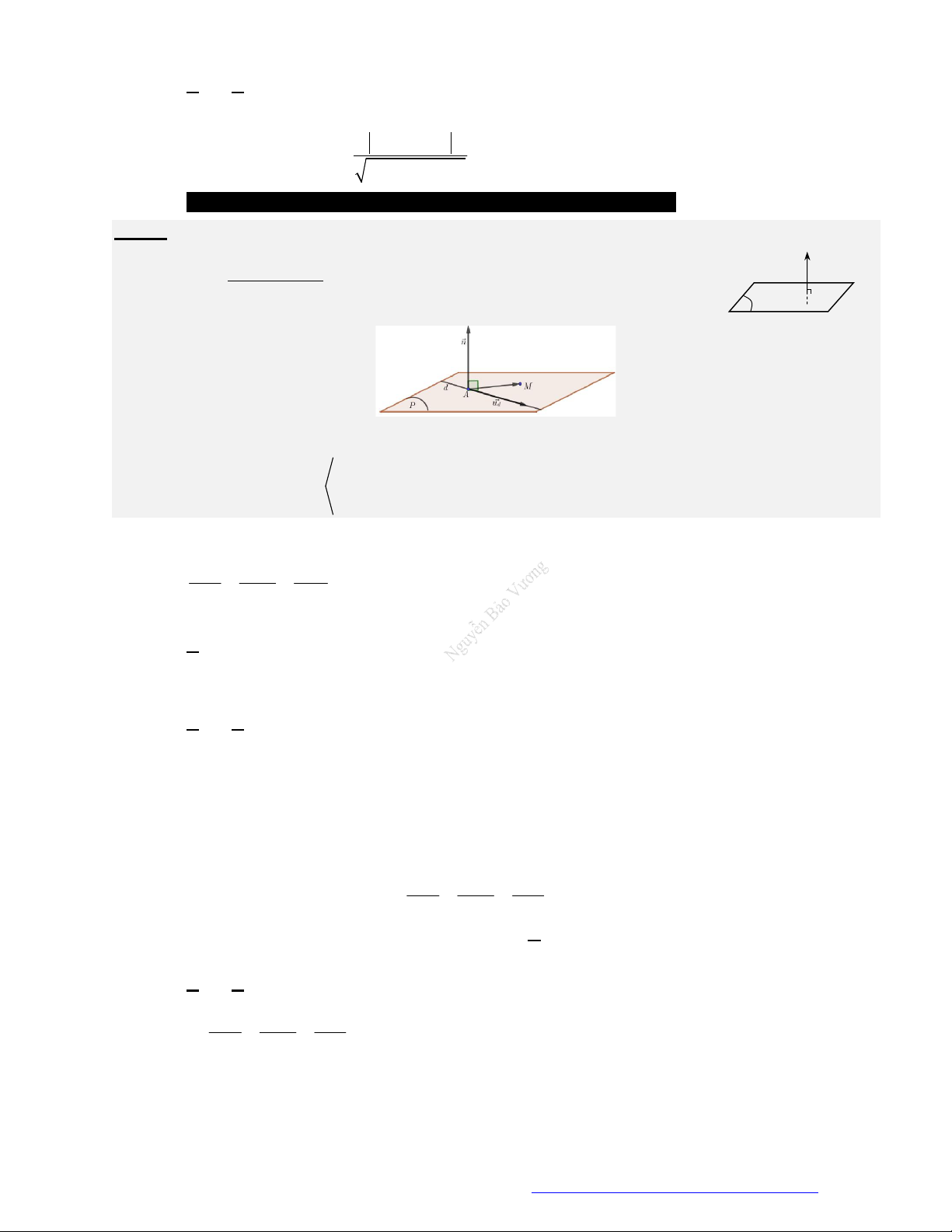
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 33

Lời giải

Chọn A

Vì đường thẳng

d

song song với mặt phẳng (P) nên : Chọn

(1;3;2)M d

2 2 2

1 6 4 4

( ;( )) (M;(P)) 1

1 ( 2) 2

d d P d

  

  

  

Dạng 5. Xác định phương trình mặt phẳng có yếu tố đường thẳng

Dạng 1. Viết phương trình mặt phẳng

( )P

qua

M

và vuông góc với đường thẳng

.d AB

Phương pháp.

( )

( ; ; )

( ) :

:

P d

M x y z

P

VTPT n u

u

AB

Q a







 





  





 



Dạng 2. Viết phương trình mặt phẳng qua M và chứa đường thẳng d với

M d

.

 Bước 1: Chọn điểm

A d

và một VTCP

.

d

u



Tính ,

d

AM u

 

 

 

.

Bước 2: Phương trình

qua

mp( )

VTPT ,

d

M

P

n AM u

 



 

  

Câu 109. (Mã 101 - 2020 Lần 1) Trong không gian

Oxyz

, cho điểm

 

2; 2;3M 

và đường thẳng

d

:

1 2 3

3 2 1

x y z  

 



. Mặt phẳng đi qua điểm

M

và vuông góc với đường thẳng

d

có phương

trình là

A.

3 2 1 0x y z   

. B.

2 2 3 17 0x y z   

.

C.

3 2 1 0x y z   

. D.

2 2 3 17 0x y z   

.

Lời giải

Chọn A

Gọi

 

P

là mặt phẳng đi qua

M

và vuông góc với đường thẳng

d

.

Ta có:

 

3;2; 1

P d

n u  

 

là một véc tơ pháp tuyến của mặt phẳng

 

P

.

Phương trình mặt phẳng

 

P

là:

     

3 2 2 2 1 3 0 3 2 1 0x y z x y z          

.

Câu 110. (Đề Minh Họa 2020 Lần 1) Trong không gian

Oxyz

, mặt phẳng đi qua điểm

 

1;1; 1M 

và

vuông góc với đường thẳng

1 2 1

:

2 2 1

x y z  

  

có phương trình là

A.

2 2 3 0x y z   

. B.

2 0x y z  

. C.

2 2 3 0x y z   

. D.

2 2 0x y z   

.

Lời giải

Chọn C

1 2 1

:

2 2 1

x y z  

  

thì



có một vec-tơ chỉ phương là

 

2; 2;1u 



.

Gọi

 



là mặt phẳng cần tìm.

Có

 



 

, nên

 

2;2;1u 



là một vec-tơ pháp tuyến của

 



.

P

( )P d

AB

n u

 



 

d

M

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 34 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Mặt phẳng

 



qua điểm

 

1;1; 1M 

và có một vec-tơ pháp tuyến

 

2;2;1u 



.

Nên phương trình

 



là

2 2 3 0x y z   

.

Câu 111. (Đề Tham Khảo 2020 Lần 2) Trong không gian Oxyz, cho điểm

( 2;1;0)M

và đường thẳng

3 1 1

: .

1 4 2

  

  



x y z

Mặt phẳng đi qua M và vuông góc với



có phương trình là

A.

3 7 0   x y z

. B.

4 2 6 0   x y z

.

C.

4 2 6 0   x y z

. D.

3 7 0   x y z

.

Lời giải

Chọn C

Đường thẳng

3 1 1

:

1 4 2

  

  



x y z

nhận véc tơ

(1;4; 2)



u

là một véc tơ chỉ phương.

Mặt phẳng đi qua M và vuông góc với



nhận véc tơ chỉ phương

(1;4; 2)



u

của



là véc tơ pháp

tuyến.

Vậy phương trình mặt phẳng phải tìm là:

     

1. 2 4 1 2 0 0 4 2 6 0          x y z x y z

.

Câu 112. (Mã 102 - 2020 Lần 1) Trong không gian cho điểm

và đường thẳng

. Mặt phẳng đi qua

và vuông góc với

có phương trình là

A. . B. .

C. . D. .

Lời giải

Chọn A

Mặt phẳng đi qua

và vuông góc với

nhận véc tơ

làm véc tơ pháp tuyến

nên có phương trình:

Câu 113. (Mã 103 - 2020 Lần 1) Trong không gian

Oxyz

, cho điểm

(2; 1;2)M 

và đường thẳng

1 2 3

:

2 3 1

x y z

d

  

 

. Mặt phẳng đi qua điểm qua

M

và vuông góc với

d

có phương trình là

A.

2 3 3 0.x y z   

B.

2 2 9 0.x y z   

C.

2 3 3 0.x y z   

D.

2 2 9 0.x y z   

Lời giải

Chọn A

Đường thẳng

d

có một vecto chỉ phương là

 

2;3;1u 



Mặt phẳng

 

P

vuông góc với

d

nên nhận

u



làm vecto pháp tuyến

Phương trình mặt phẳng cần tìm là:

     

2 2 3 1 1 2 0 2 3 3 0x y z x y z          

.

Câu 114. (Mã 104 - 2020 Lần 1) Trong gian gian

,Oxyz

cho điểm

 

3; 2; 2M 

và đường thẳng

3 1 1

:

1 2 2

x y z

d

  

 



. Mặt phẳng đi qua

M

và vuông góc với

d

có phương trình là

A.

2 2 5 0x y z   

. B.

3 2 2 17 0x y z   

.

C.

3 2 2 17 0x y z   

. D.

2 2 5 0x y z   

.

Oxyz

(1;1; 2)

M



1 2

:

1 2 3

x y z

d

 

 



M

d

2 3 9 0

x y z

   

2 6 0

x y z

   

2 3 9 0

x y z

   

2 6 0

x y z

   

(1;1; 2)

M



d

(1;2; 3)

n





1 2( 1) 3( 2) 0

x y z

     

2 3 9 0

x y z

    

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 35

Lời giải

Chọn A

Mặt phẳng nhận vectơ nhận

 

1;2; 2

là vecto pháp tuyến và đáp án cần chọn là A.

Câu 115. (Mã 102 2018) Trong không gian

Oxyz

, mặt phẳng đi qua điểm

 

1;2; 2

A



và vuông góc với

đường thẳng

1 2 3

:

2 1 3

x y z

  

  

có phương trình là

A.

2 3 2 0

x y z

   

. B.

2 3 1 0

x y z

   

.

C.

2 3 2 0

x y z

   

. D.

3 2 5 0

x y z

   

.

Lời giải

Chọn A

Mặt phẳng qua

 

1;2; 2

A



và nhận

 

2;1;3

u







làm VTPT

Vậy phương trình của mặt phẳng là:

     

2 1 2 3 2 0

x y z

     

2 3 2 0

x y z

    

.

Câu 116. (Mã 123 2017) Trong không gian với hệ tọa độ

Oxyz

cho điểm

 



3; 1;1

M

. Phương trình nào

dưới đây là phương trình mặt phẳng đi qua điểm

M

và vuông góc với đường thẳng



 

  



2

1 3

: ?

3 2 1

y

x z

A.

   3 2 8 0x y z

B.

   3 2 12 0x y z

C.

   3 2 12 0x y z

D.

   2 3 3 0x y z

Lời giải

Chọn C

Mặt phẳng cần tìm đi qua

 



3; 1;1

M

và nhận VTCP của



là

 



 



3; 2;1

u làm VTPT nên có

phương trình:

   3 2 12 0.x y z

Câu 117. (THPT Hùng Vương Bình Phước 2019) Trong không gian với hệ trục tọa độ

Oxyz

, phương

trình nào dưới đây là phương trình mặt

phẳng đi qua

 

1; 1;2

M 

và vuông góc với đường thẳng

1 2

:

2 1 3

x y z 

  



.

A.

2 3 9 0

x y z

   

. B.

2 3 9 0

x y z

   

. C.

2 3 9 0

x y z

   

. D.

2 3 6x y z  

.

Lời giải

Mặt phẳng

 

P

vuông góc với



nên

 

P

nhận vtcp của



là

 

2; 1;3

u







làm vtpt



Phương trình mặt phẳng

 

P

là:

     

2 1 1 1 3 2 0

x y z

     

hay

2 3 9 0

x y z

   

.

Câu 118. (THPT Yên Khánh - Ninh Bình - 2019) Trong không gian

Oxyz

cho đường thẳng

1 2 3

:

2 1 2

x y z

d

  

 



. Mặt phẳng

 

P

vuông góc với

d

có một vectơ pháp tuyến là:

A.

 

1;2;3

n 



. B.

 

2; 1;2

n  



. C.

 

1;4;1

n 



. D.

 

2;1;2

n 



.

Lời giải

Ta có: Đường thẳng

1 2 3

:

2 1 2

x y z

d

  

 



có vectơ chỉ phương là

 

2; 1;2

d

a  



NGUYỄN BẢO VƯƠNG - 0946798489

Trang 36 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Vì

 

P d

nên vectơ pháp tuyến của mặt phẳng

 

P

là

( )P

n



=

 

2; 1;2

d

a  



Câu 119. (THCS - THPT Nguyễn Khuyến 2019) Trong không gian

Oxyz

, phương trình mặt phẳng đi qua

gốc tọa độ và vuông góc với đường thẳng

( ) :

1 1 1

x y z

d

 

là:

A.

1 0

x y z

   

. B.

1

x y z

  

. C.

1

x y z

  

. D.

0

x y z

  

.

Lời giải

Mặt phẳng

( )P

vuông góc với đường thẳng

( ) :

1 1 1

x y z

d

 

nên nhận véc tơ chỉ phương

 

1;1;1

d

u 



làm véc tơ pháp tuyến, suy ra phương trình mặt phẳng

( )P

có

dạng:

0

x y z D

   

, mặt khác

( )P

đi qua gốc tọa độ nên

0

D



.

Vậy phương trình

( )P

là:

0

x y z

  

.

Câu 120. (THCS - THPT Nguyễn Khuyến 2019) Trong không gian

Oxyz

, mặt phẳng đi qua điểm

 

0;1;0

A

và chứa đường thẳng

 

2 1 3

:

1 1 1

x y z

  

  



có phương trình là:

A.

1 0

x y z

   

. B.

3 2 1 0

x y z

   

. C.

1 0

x y z

   

. D.

3 2 1 0

x y z

   

.

Lời giải

Ta lấy điểm

   

 

2;0;3

2;1;3 , 3;1; 2

1; 1;1

AM

M n AM u

vtcpu









 

      



 

 







  



Mặt phẳng cần tìm qua

 

0;1;0

A

và nhận

 

3;1; 2

n

 



làm véc-tơ pháp tuyến có phương trình là:

     

3. 0 1. 1 2. 0 0 3 2 1 0

x y z x y z

          

.

Câu 121. (Chuyên Hưng Yên 2019) Trong không gian

Oxyz

, cho đường thẳng

1 2 2

:

1 2 1

x y z

d

  

 



.

Mặt phẳng nào sau đây vuông góc với đường thẳng

d

.

A.

 

: 2 1 0

T x y z

   

. B.

 

: 2 1 0

P x y z

   

.

C.

 

: 2 1 0

Q x y z

   

. D.

 

: 1 0

R x y z

   

.

Lời giải

Đường thẳng vuông góc với mặt phẳng nếu vectơ chỉ phương của đường thẳng cùng phương với

vectơ pháp tuyến của mặt phẳng.

Đường thẳng

d

có một vectơ chỉ phương là

 

1 ; 2 ; 1

u  



.

Mặt phẳng

 

T

có một vectơ pháp tuyến là

 

1 ; 1 ; 2

T

n 



. Do

1 2 1

1 1 2



 

nên

u



không cùng

phương với

T

n



. Do đó

d

không vuông góc với

 

T

.

Mặt phẳng

 

P

có một vectơ pháp tuyến là

 

1 ; -2 ; 1

P

n 



. Do

1 2 1



 



nên

u



cùng phương

với

P

n



. Do đó

d

vuông góc với

 

P

.

Mặt phẳng

 

Q

có một vectơ pháp tuyến là

 

1 ; -2 ; -1

Q

n 



. Do

1 2 1



 

 

nên

u



không cùng

phương với

Q

n



. Do đó

 

d

không vuông góc với

 

Q

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 37

Mặt phẳng

 

R

có một vectơ pháp tuyến là

 

1 ; 1 ; 1

R

n 



. Do

1 2 1

1 1 1



 

nên

u



không cùng

phương với

R

n



. Do đó

 

d

không vuông góc với

 

R

.

Câu 122. (Đề Thi Công Bằng KHTN 2019) Trong không gian

Oxyz

cho điểm

 

0; 3;1

A 

và đường

thẳng

1 1 3

:

3 2 1

x y z

d

  

 



. Phương trình mặt phẳng đi qua

A

và vuông góc với đường thẳng

d

là:

A.

3 2 5 0

x y z

   

. B.

3 2 7 0

x y z

   

.

C.

3 2 10 0

x y z

   

. D.

3 2 5 0

x y z

   

.

Lời giải

Chọn véc tơ pháp tuyến của mặt phẳng cần tìm là:

 

3; 2;1

d

n u  

 

. Mặt khác mặt phẳng này đi

qua

A

nên có phương trình là:

     

3 0 2 3 1 0

3 2 7 0

x y z

     

    

.

Câu 123. Trong không gian với hệ tọa độ

Oxyz

cho điểm

 



3; 1;1

M

. Phương trình nào dưới đây là

phương trình mặt phẳng đi qua điểm

M

và vuông góc với đường thẳng



 

  



2

1 3

: ?

3 2 1

y

x z

A.

   2 3 3 0x y z

B.

   3 2 8 0x y z

C.

   3 2 12 0x y z

D.

   3 2 12 0x y z

Lời giải

Chọn D

Mặt phẳng cần tìm đi qua

 



3; 1;1

M

và nhận VTCP của



là

 



 



3; 2; 1

u

làm VTPT nên có

phương trình:

   3 2 12 0 .x y z

Câu 124. (Chuyên - KHTN - Hà Nội - 2019) Trong không gian

Oxyz

cho điểm

 

0; 3;1

A 

và đường

thẳng

1 1 3

:

3 2 1

x y z

d

  

 



. Phương trình mặt phẳng đi qua

A

và vuông góc với đường thẳng

d

là

A.

3 2 5 0

x y z

   

. B.

3 2 7 0

x y z

   

.

C.

3 2 10 0

x y z

   

. D.

3 2 5 0

x y z

   

.

Lời giải

Chọn B

Phương trình mặt phẳng đi qua

 

0; 3;1

A 

và vuông góc với đường thẳng

d

nên có VTPT

 

3; 2;1

d

n u  

 

.

Phương trình tổng quát:

     

3 0 2 3 1 0 3 2 7 0

x y z x y z

          

.

Câu 125. Trong không gian với hệ trục tọa độ

Oxyz

, cho điểm

 

1;3; 2

A 

và đường thẳng

d

có phương

trình

1 4

2

x t

y t

z t

 











 



. Mặt phẳng

 

P

chứa điểm

A

và đường thẳng

d

có phương trình nào dưới đây?

A.

2 2 1 0.

x y z

   

. B.

0.

x y z

  

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 38 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

C.

3 2 10 23 0.

x y z

    

. D.

2 3 4 0.

x y z

   

Lời giải

Chọn C

Đường thẳng

d

đi qua điểm

 

1;0;2

M

và có vectơ chỉ phương

 

4;1;1

u  



.

Ta có:

 

2; 3;0

AM  



;

 

, 3; 2; 10

AM u

 

   

 





.

Mặt phẳng

( )P

chứa điểm

A

và đường thẳng

d

có vectơ pháp tuyến

 

, 3; 2; 10

AM u

 

   

 





.

Vậy phương trình mặt phẳng

( )P

là

     

3 1 2 3 10 2 0

x y z

      

3 2 10 23 0

x y z

     

.

Câu 126. Trong không gian

Oxyz

, cho điểm

 

1;2;0

A

và đường thẳng

1 2

:

1

x t

d y t

z t

  











 



. Tìm phương trình

mặt phẳng

 

P

đi qua điểm

A

và vuông góc với

.d

A.

2 4 0

x y z

   

. B.

2 4 0

x y z

   

. C.

2 4 0

x y z

   

. D.

2 4 0

x y z

   

.

Lời giải

Chọn D

Do

 

P

vuông góc với

d

nên ta có

 

2;1; 1

d

P

n u

  

 

.

Phương trình mặt phẳng

 

P

là

     

2 1 1 2 1 0 0 2 4 0.          

x y z x y z

Câu 127. (THPT Thuận Thành 3 - Bắc Ninh 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho điểm

 

1;3;2

A 

và đường thẳng

d

có phương trình

1 4

2

x t

y t

z t

 











 



. Mặt phẳng

 

P

chứa điểm

A

và

đường thẳng

d

có phương trình nào dưới đây?

A.

2 2 1 0

x y z

   

. B.

0

x y z

  

.

C.

3 2 10 23 0

x y z

    

. D.

2 3 4 0

x y z

   

.

Lời giải

Chọn C

Đường thẳng

d

đi qua điểm

 

1;0;2

B

và có VTCP

 

4;1;1

u  



.

Ta có

   

2; 3;0

AB P

  



có VTPT

 

, 3; 2; 10

n AB u

 

    

 

  

.

Mà

 

P

đi qua

 

1;3;2

A 

nên

 

P

có phương trình:

3 2 10 23 0

x y z

    

.

Câu 128. Trong không gian

Oxyz

, mặt phẳng

 

P

đi qua điểm

 

1;2;0

A

và vuông góc với đường thẳng

1 1

2 1 1

x y z 

 



có phương trình là

A.

2 4 0

x y z

   

. B.

2 4 0

x y z

   

.

C.

2 4 0

x y z

   

. D.

2 4 0

x y z

   

.

Lời giải

Chọn A

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 39

Mặt phẳng

 

P

vuông góc với đường thẳng

1 1

2 1 1

x y z 

 



suy ra nó có một vectơ pháp tuyến

là

 

2,1, 1

n

 



.

Vậy mặt phẳng

 

P

đi qua điểm

 

1;2;0

A

và nhận

 

2,1, 1

n

 



làm vectơ pháp tuyến có

phương trình là:

2( 1) 1( 2) 1( 0) 0 2 4 0

x y z x y z

          

.

Câu 129. Trong không gian

Oxyz

, viết phương trình mặt phẳng đi qua

 

2; 3;0

A 

và vuông góc với

đường thẳng

d

có phương trình:

3 4 7

1 2 5

x y z

  

 

.

A.

2 5 10 0

x y z

   

. B.

2 5 8 0

x y z

   

.

C.

2 3 4 0

x y

  

. D.

2 5 4 0

x y z

   

.

Lời giải

Chọn B

Ta viết lại phương trình đường thẳng

d

là:

3 4 7

1 2 5

x y z

  

 





đường thẳng

d

có vectơ chỉ phương

 

1; 2;5

d

u  



.

Mặt phẳng

 

P

đi qua

 

2; 3;0

A 

và vuông góc với đường thẳng

d



Mp

 

P

qua

A

và nhận vectơ

 

1; 2;5

d

u  



làm vectơ pháp tuyến



Phương trình của mặt phẳng

 

: 2 5 8 0

P x y z

   

.

Câu 130. (Bắc Giang - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho đường thẳng

1 2

:

1 1 2

x y z

d

 

 



. Mặt phẳng

 

P

đi qua điểm

 

2;0; 1

M



và vuông góc với

d

có phương

trình là ?

A.

 

: 2 0

P x y z

  

. B.

 

: 2 0

P x y z

  

. C.

 

: 2 0

P x y z

  

. D.

 

: 2 2 0

P x y

  

.

Lời giải

d

có VTCP

 

1; 1;2

u  



.

 

P d 

 

P

có VTPT

 

1; 1;2

n u  

 

.

Vậy phương trình mặt phẳng

     

: 2 0 2 1 0 2 0

P x y z x y z

         

.

Câu 131. (Chuyên Vĩnh Phúc - 2018) Trong không gian

Oxyz

, cho đường thẳng

3 2 1

:

1 1 2

x y z

d

  

 



.

Viết phương trình mặt phẳng

 

P

đi qua điểm

 

2;0; 1

M



và vuông góc với

d

.

A.

 

: 2 0

P x y z

  

. B.

 

: 2 2 0

P x y

  

. C.

 

: 2 0

P x y z

  

. D.

 

: 2 0

P x y z

  

.

Lời giải

Mặt phẳng

 

P

vuông góc với đường thẳng

d

nên

 

P

có VTPT

 

1; 1;2

P d

n u  

 

.

Nên phương trình mặt phẳng

 

P

có dạng:

     

2 0 2 1 0 2 0

x y z x y z

         

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 40 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu

132. (SGD&ĐT Đồng Tháp - 2018) Trong không gian với hệ tọa độ

O

xy

,

cho đường thẳng

 

2

2 3

:

1

1 2

x y z

d



 





và

điểm

 

1

; 2;3

A 

.

Mặt phẳng qua

A

và

vuông góc với đường thẳng

 

d

có phương trình là:

A.

2

9 0

x

y z



  

. B.

2

3 14 0

x

y z



  

.

C.

2 9 0

x y z

   

. D

.

2 3 9 0

x y z

   

.

Lời giải

Đường t

hẳng

d

có vec

tơ chỉ phương:

 

1

; 1;2

u 





.

Vì mặt phẳng

 

P

đi

qua

A

và vuông góc vớ

i đường thẳng

 

d

nên

 

P

c

ó vectơ pháp tuyến:

 

1

; 1; 2

n 





.



P

hương trình mặt phẳng

 

P

là

:

     

1

2 2 3 0

x

y z



    

2

9 0

x

y z



   

.

Câu

133. (THPT Thái Phiên - Hải Phòng 2018) Trong không gian với hệ trục

O

xyz

, cho điểm

 

0;0;3

A

và

đường thẳng

1

:

.

2 1 1







y

x z

d

P

hương trình mặt phẳng đi qua điểm

A

và

vuông góc với

đường thẳng

d

l

à

A.

2

3 0   x y z

. B.

2

2 6 0   x y z

. C

.

2

3 0   x y z

. D

.

2

3 0   x y z

.

Lời giải

Mặt phẳng

cần tìm đi qua điểm

 

0

;0;3

A

và

vuông góc với đường thẳng

d

nên nhận v

éc tơ chỉ

phương của đường thẳng

d

là

 

2

; 1;1







u

làm

véc tơ pháp tuyến. Do đó phương trình mặt phẳng

cần tìm là:

2

3 0.   x y z

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương  https://www.facebook.com/phong.baovuong Trang 1

TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH KHÁ – MỨC 7-8 ĐIỂM

Dạng 1. Xác định phương trình đường thẳng

1. Dạng 1. Viết phương trình đường thẳng

d

dạng tham số và dạng chính tắc (nếu có), biết

d

đi qua

điểm ( ; ; )M x y z

  

và có véctơ chỉ phương

1 2 3

( ; ; ).

d

u a a a



Phương pháp. Ta có:

1 2 3

( ; ; )

:

: ( ; ; )

d

Qua M x y z

d

VTCP u a a a









  







Phương trình đường thẳng

d

dạng tham số

1

2

3

: , ( ).

x x a t

d y y a t t

z z a t

 





  





 







Phương trình đường thẳng

d

dạng chính tắc

1 2 3

: , ( 0).

x x y y z z

d a a a

a a a

  

  

  

2. Dạng 2. Viết phương trình tham số và chính tắc (nếu có) của đường thẳng

d

đi qua

A

và

.B

Phương pháp. Đường thẳng

( )

:

d

Qua A hay B

d

VTCP u AB





















(dạng 1)

3. Dạng 3. Viết phương trình đường thẳng

d

dạng tham số và chính tắc (nếu có), biết

d

đi qua điểm

M

và song song với đường thẳng

.

Phương pháp. Ta có

Qua ( ; ; )

:

d

M x y z

d

VTCP u u















  



 



(dạng 1)

4. Dạng 4. Viết phương trình đường thẳng

d

dạng tham số và chính tắc (nếu có), biết

d

đi qua điểm

M

và vuông góc với mặt phẳng

( ) : 0.P ax by cz d   

Phương pháp. Ta có

( )

:

: ( ; ; )

d P

Qua M

d

VTCP u n a b c





 





 



(dạng 1)

5. Dạng 5. Viết phương trình tham số và chính tắc của đường thẳng

d

là giao tuyến của hai mặt

phẳng

( )P

và

( )Q

cho trước.

Phương pháp. Ta có

( ) ( )

:

: [ , ]

( ) ( )

d P Q

d

VTCP u n n

Qua A P Q









 

  



(dạng 1)

6. Dạng 6. Viết phương trình tham số và chính tắc (nếu có) của đường thẳng

d

đi qua điểm

M

và

vuông góc với hai đường thẳng

1 2

, d d cho trước.

Phương pháp. Ta có

1 2

:

[ , ]

d d d

d

C

Qua M

VT P u u u











  



(dạng 1)

7. Dạng 7. Viết phương trình đường thẳng

d

qua

M

và song song với hai mặt phẳng

( ), ( ).P Q

Phương pháp. Ta có

:

: , ]

[

d P Q

d

VTCP u n

Qua M

n











  



(dạng 1)

8. Dạng 8. Viết phương trình đường thẳng

d

qua

,M

vuông góc đường

d



và song song mặt

( ).P

Phương pháp. Ta có

:

: , ]

[

d d P

d

VTCP u u n

Qua M













  



(dạng 1)

PHƯƠNG TRÌNH ĐƯỜNG THẲNG

Chuyên đề 31

d

A

1

d

u



d

1

d

2

d

2

d

u



A

B

d

M



d

u





P

u n

d P



 

d

M

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

9. Dạng 9. Viết phương trình đường thẳng

d

nằm trong mặt

( ),P

song song mặt

( )Q

và qua

.M

Phương pháp. Ta có

:

: , ]

[

d P Q

d

VTCP u n

Qua M

n











  



(dạng 1)

10. Dạng 10. Viết phương trình đường thẳng

d

đi qua điểm

,A

vuông góc và cắt đường thẳng

.d



Phương pháp.

Viết phương trình mặt phẳng

( )P

qua

,A

vuông góc

.d



Nghĩa là mặt phẳng

( ) :

:

P d

Qua A

P

VTPT n u















 



Tìm

( ).B d P



 

Suy ra đường thẳng

d

qua

A

và

B

(dạng 1)

Lưu ý: Trường hợp

d



là các trục tọa độ thì

,d AB

với

B

là hình chiếu của

A

lên trục.

11. Dạng 11. Viết phương trình tham số và chính tắc (nếu có) của đường thẳng

d

đi qua điểm

M

và

cắt đường thẳng

1

d

và vuông góc

2

d

cho trước.

Phương pháp. Giả sử

1 1

, ( , )d d H H d H d   

1 1 2 2 3 2 1

( ; ; ) .H x a t x a t x a t d    

Vì

2

. 0 .

d

MH d MH u t H

    

 

Suy ra đường thẳng

:

d

Qua M

d

VTCP u MH





















(dạng 1)

Dạng 12.

d

đi qua điểm

0 0 0 0

( ; ; )M x y z

và cắt hai đường thẳng

1 2

d , d

:

 Cách 1: Gọi

1 1 2 2

M d , M d 

Từ điều kiện

1 2

M, M , M

thẳng hàng ta tìm được

1 2

M , M

. Từ đó

suy ra phương trình đường thẳng

d

.

 Cách 2: Gọi

 

P 

0 1

( , )M d

,

 

0 2

( , )Q M d



. Khi đó

d



 

P



 

Q

, do đó, một VTCP của

d

có thể

chọn là

,

P Q

a n n



 

 

  

.

Dạng 13.

d

nằm trong mặt phẳng

 

P

và cắt cả hai đường thẳng

1 2

d , d

:

Tìm các giao điểm

   

1 2

A d P , B d P .

   

Khi đó

d

chính là đường thẳng

AB

.

Dạng 14.

d

song song với



và cắt cả hai đường thẳng

1 2

d , d

:

Viết phương trình mặt phẳng

 

P

chứa



và

1

d

, mặt phẳng

 

Q

chứa



và

2

d

.

Khi đó

d



 

P



 

Q

.

Dạng 15.

d

là đường vuông góc chung của hai đường thẳng

1 2

d , d

chéo nhau:

 Cách 1: Gọi

1 2

M d , N d . 

Từ điều kiện

1

2

MN d











, ta tìm được

,M N

.

Khi đó,

d

là đường thẳng

MN

.

 Cách 2:

– Vì

1

d d

và

2

d d

nên một VTCP của

d

có thể là:

1 2

,

d d

a a a



 

 

  

.

– Lập phương trình mặt phẳng

 

P

chứa

d

và

1

d

, bằng cách:

+ Lấy một điểm

A

trên

1

d

.

+ Một VTPT của

 

P

có thể là:

1

,

P d

n a a



 

 

  

.

– Tương tự lập phương trình mặt phẳng

 

Q

chứa

d

và

1

d

.

Khi đó

d



 

P



 

Q

.

Dạng 16. Viết phương trình đường thẳng

d

là hình chiếu vuông góc của đường thẳng



lên mặt

( ).P

Phương pháp: Xét vị trí tương đối của đường thẳng



và

( ).P



Nếu

( ).P 

Chọn một điểm

M

trên

.

Tìm

H

là hình chiếu của

M

lên

( ).P

2

d

u



2

d

H

M

d

1

d

A

B

d



d

P

M

H

P



d

M



TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3

Hình chiếu

Qua

:

VTCP :

d

H

d

u u













 



Nếu

( ) .P I  

Chọn một điểm

M I

trên

.

Tìm

H

là hình chiếu của

M

lên

( ).P

Hình chiếu vuông góc của



lên

( )P

là

.d IH

Dạng 17. Viết đường thẳng

d

là đường thẳng đối xứng với đường thẳng



qua mặt phẳng

( ).P

Phương pháp: Xét vị trí tương đối của đường thẳng



và

( ).P



Nếu

( ).P 

Chọn một điểm

M

trên

.

Tìm

H

là hình chiếu của

M

lên

( ).P

Tìm

M



đối xứng với

M

qua

( ).P

Đường thẳng đối xứng

Qua

:

VTCP :

d

M

d

u u















 



Nếu

( ) .P I  

Chọn một điểm

M

trên

.

Tìm

H

là hình chiếu của

M

lên

( ).P

Tìm

M



đối xứng với

M

qua

( ).P

Đường thẳng đối xứng

Qua

: .

VTCP :

d

M

d

u IM





















Dạng 1.1 Xác định phương trình đường thẳng khi biết yếu tố vuông góc

Câu 1. (Mã 101 2018) Trong không gian

Oxyz

cho điểm

 

1;2;3

A

và đường thẳng

3 1 7

:

2 1 2

x y z

d

  

 



. Đường thẳng đi qua

A

, vuông góc với

d

và cắt trục

Ox

có phương trình

là

A.

1 2

2

x t

y t

z t

  





 









B.

1

2 2

3 3

x t

y t

z t

 





 





 



C.

1 2

2

3

x t

y t

z t

  















D.

1

2 2

3 2

x t

y t

z t

 





 





 



Lời giải

Chọn C

Gọi



là đường thẳng cần tìm.

Gọi

M Ox  

. Suy ra

 

;0;0

M a

.

 

1; 2; 3

AM a

   



.

d

có VTCP:

 

2;1; 2

d

u

 



.

Vì

d 

nên

. 0

d

AM u



 

2 2 2 6 0

a

    

1

a

  

.

Vậy



qua

 

1;0;0

M 

và có VTCP

   

2; 2; 3 2;2;3

AM      



nên



có phương trình:

1 2

2

3

x t

y t

z t

  















.

M

H

P



d

M



M



M

H

P



d

I

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 2. (Mã 102 - 2019) Trong không gian

,Oxyz

cho các điểm

     

1;0;2 , 1;2;1 , 3;2;0

A B C

và

 

1;1;3 .

D

Đường thẳng đi qua A và vuông góc với mặt phẳng

 

BCD

có phương trình là

A.

1

4 .

2 2

x t

y t

z t



 









 





B.

1

4 .

2 2

x t

y

z t



 









 





C.

2

4 4 .

4 2

x t

y t

z t



 



 





 





D.

1

2 4

2 2

x t

y t

z t



 



 





 





Lời giải

Chọn C

Đường thẳng đi qua A và vuông góc với mặt phẳng

 

BCD

nhận vectơ pháp tuyến của

 

BCD

là

vectơ chỉ phương

Ta có

   

2;0; 1 , 0; 1;2

BC BD   

 

 

; 1; 4; 2

d BCD

u n BC BD

 

      

 

 

   

Khi đó ta loại đáp án A và B

Thay điểm

 

1;0;2

A

vào phương trình ở phương án C ta có

1 2 1

0 4 4 1

2 4 2 1

t t

 

   

 

    

 

 

   

 

 

.

Suy ra đường thẳng có phương trình tham số ở phương án C đi qua điểm

A

nên C là phương án

đúng

Câu 3. (Đề Tham Khảo 2018) Trong không gian

Oxyz

, cho hai đường thẳng

1

3 3 2

:

1 2 1

x y z

d

  

 

 

;

2

5 1 2

:

3 2 1

x y z

d

  

 



và mặt phẳng

 

: 2 3 5 0

P x y z

   

. Đường thẳng vuông góc với

 

P

,

cắt

1

d

và

2

d

có phương trình là

A.

1 1

3 2 1

x y z 

 

B.

2 3 1

1 2 3

x y z  

 

C.

3 3 2

1 2 3

x y z

  

 

D.

1 1

1 2 3

x y z 

 

Lời giải

Chọn D

Phương trình

1

1 1

1

3

: 3 2

2

x t

d y t

z t

 





 





  



và

2

2 2

2

5 3

: 1 2

2

x t

d y t

z t

 





  





 



.

Gọi đường thẳng cần tìm là



.

Giả sử đường thẳng



cắt đường thẳng

1

d

và

2

d

lần lượt tại

A

,

B

.

Gọi

 

1 1 1

3 ;3 2 ; 2

A t t t   

,

 

2 2 2

5 3 ; 1 2 ;2

B t t t   

.

 

2 1 2 1 2 1

2 3 ; 4 2 2 ;4

AB t t t t t t       



.

Vectơ pháp tuyến của

 

P

là

 

1;2;3

n 



.

Do

AB



và

n



cùng phương nên

2 1 2 1 2 1

2 3 4 2 2 4

1 2 3

t t t t t t      

 

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5

2 1 2 1

2 3 4 2 2

1 2

4 2 2 4

2 3

t t t t

    











    









1

2

1

t













. Do đó

 

1; 1;0

A 

,

 

2; 1;3

B 

.

Phương trình đường thẳng



đi qua

 

1; 1;0

A 

và có vectơ chỉ phương

 

1;2;3

n 



là

1 1

1 2 3

x y z 

 

.

Câu 4. (Mã 101 - 2019) Trong không gian

Oxyz

, cho các điểm

       

1;2;0 , 2;0;2 , 2; 1;3 , 1;1;3

A B C D



. Đường thẳng đi qua

C

và vuông góc với mặt

phẳng

 

ABD

có phương trình là

A.

2 4

4 3

2

x t

y t

z t

  





  





 



. B.

4 2

3

1 3

x t

y t

z t

 





 





 



. C.

2 4

2 3

2

x t

y t

z t

  





  





 



. D.

2 4

1 3

3

x t

y t

z t

 





  





 



.

Lời giải

Chọn A

 

1; 2;2

0; 1;3

AB

AD

 



 

4; 3; 1

AB AD

    

 

Đường thẳng qua

 

2; 1;3

C



và vuông góc với mặt phẳng

 

ABD

có phương trình

2 4

1 3

3

x t

y t

z t

 





  





 



Điểm

 

2; 4;2

E

 

thuộc đường thẳng trên, suy ra đường thẳng cần tìm trùng với đường thẳng

có phương trình

2 4

4 3

2

x t

y t

z t

  





  





 



Chọn đáp án đúng là đáp án C

Câu 5. (Mã 104 - 2019) Trong không gian

Oxyz

, cho các điểm

 

2; 1;0

A

,

 

1;2;1

B

,

 

3; 2;0

C

,

 

1;1; 3

D

. Đường thẳng đi qua

D

và vuông góc với mặt phẳng

 

ABC

có phương trình là:

A.

1

2 3

 





 





  



x t

y t

z t

.

B.

1

3 2

 





 





  



x t

y t

z t

.

C.

1 2













  



x t

y t

z t

.

D.

1 2













 



x t

y t

z t

.

Lời giải

Chọn C

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Ta có

 

1;3;1

 



AB

;

 

1; 1;0

 



AC

;

 

,

 



 

 



ABC

n AB AC

 

1;1; 2 

.

Đường thẳng đi qua

D

và vuông góc với mặt phẳng

 

ABC

nên có véc tơ chỉ phương

là

 

1;1; 2

ABC

n

 



, phương trình tham số là:

1

3 2

x t

y t

z t

 





 





  



.

Câu 6. (Mã 102 2018) Trong không gian

Oxyz

, cho điểm

 

2;1;3

A

và đường thẳng

1 1 2

:

1 2 2

x y z

d

  

 



. Đường thẳng đi qua

A

, vuông góc với

d

và cắt trục

Oy

có phương

trình là.

A.

2

3 4

3

x t

y t

z t







  









B.

2 2

1

3 3

x t

y t

z t

 





 





 



C.

2 2

1 3

3 2

x t

y t

z t

 





 





 



D.

2

3 3

2

x t

y t

z t







  









Lời giải

Chọn A

Gọi đường thẳng cần tìm là



1 1 2

:

1 2 2

x y z

d

  

 



có VTCP

 

1; 2;2

u  



.

Gọi

 

0; ;0

M m Oy



, ta có

 

2; 1; 3

AM m

   



Do

d 

. 0

AM u

 





 

2 2 1 6 0

m

     

3

m

  

Ta có



có VTCP

 

2; 4; 3

AM

   



nên có phương trình

2

3 4

3

x t

y t

z t







  









.

Câu 7. (Mã 103 - 2019) Trong không gian

Oxyz

cho

     

0;0;2 , 2;1;0 , 1;2; 1

A B C



và

 

2;0; 2

D



. Đường thẳng đi qua

A

và vuông góc với

 

BCD

có phương trình là

A.

3

2

1 2

x

y

z t













  



. B.

3 3

2 2

1

x t

y t

z t

 





 





 



. C.

3

2

x t

y t

z t













 



. D.

3 3

2 2

1

x t

y t

z t

 





  





 



.

Lời giải

Chọn B

Gọi

d

là đường thẳng đi qua

A

và vuông góc với

 

.BCD

Ta có

   

1;1; 1 ; 0; 1; 2

BC BD

     

 

.

Mặt phẳng

 

BCD

có vec tơ pháp tuyến là

 

, 3;2; 1 .

BCD

n BD BC

 

  

 

  

Gọi

d

u



là vec tơ chỉ phương của đường thẳng

d

.

Vì

 

d BCD



nên

 

3;2; 1

BCD

d

u n

  

 

.

Đáp A và C có VTCP

 

3;2; 1

d

u

 



nên loại B và

D.

Ta thấy điểm

 

0;0;2

A

thuộc đáp án C nên loại A.

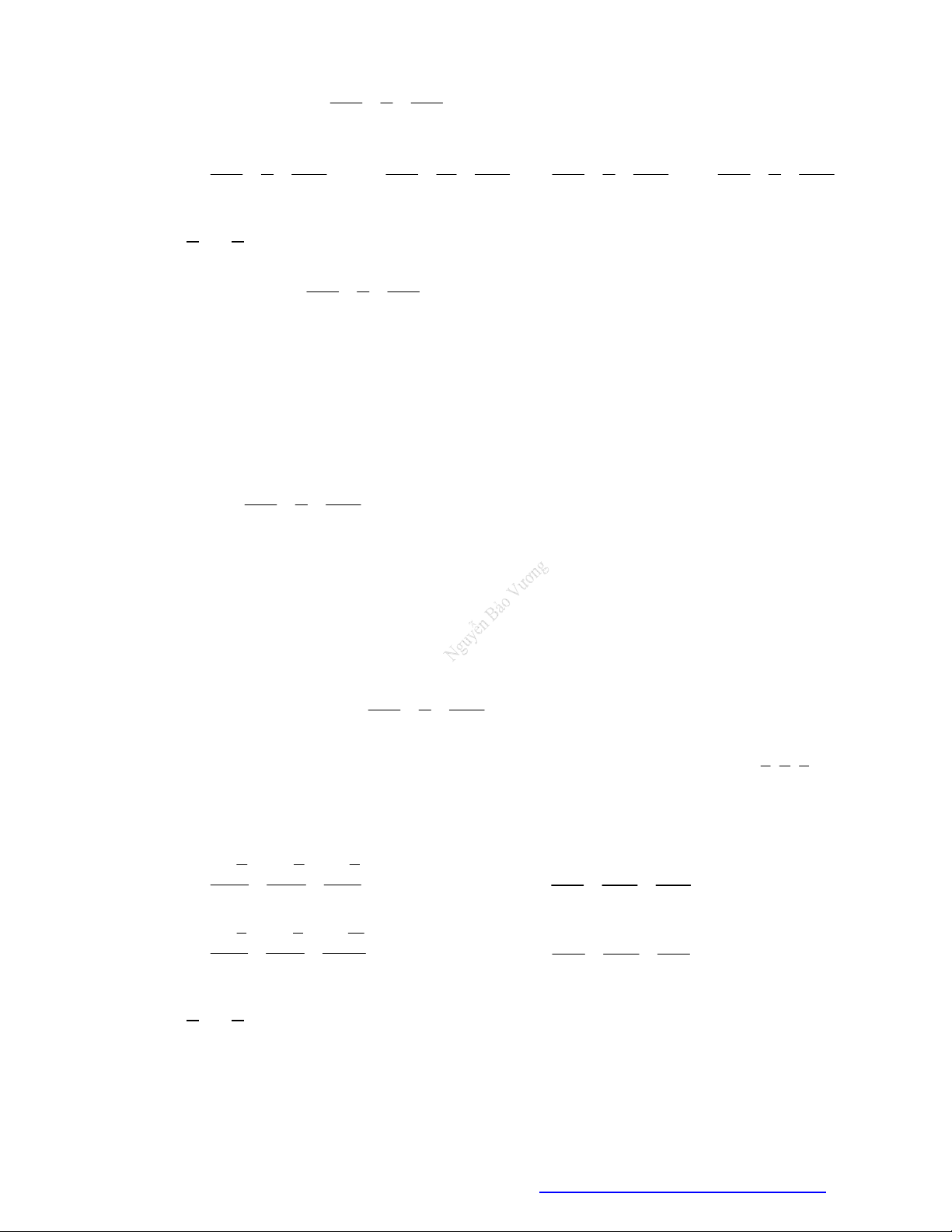
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7

Câu 8. (Đề Minh Họa 2017) Trong không gian với hệ tọa độ

Oxyz

cho điểm

 

1;0;2

A

và đường thẳng

d

có phương trình:

1 1

1 1 2

 

 

x y z

. Viết phương trình đường thẳng



đi qua

A

, vuông góc và

cắt

d

.

A.

1 2

2 2 1

 

 

x y z

B.

1 2

1 3 1

 

 



x y z

C.

1 2

1 1 1

 

 

x y z

D.

1 2

1 1 1

 

 



x y z

Lời giải

Chọn D

Cách 1:

Đường thẳng

1 1

:

1 1 2

 

 

x y z

d

có véc tơ chỉ phương

 

1;1;2





u

Gọi

 

P

là mặt phẳng qua điểm

A

và vuông góc với đường thẳng

d

, nên nhận véc tơ chỉ phương

của

d

là vecto pháp tuyến

     

:1 1 2 2 0 2 5 0         

P x y z x y z

Gọi

B

là giao điểm của mặt phẳng

 

P

và đường thẳng

 

1 ; ; 1 2

   

d B t t t

Vì

       

1 2 1 2 5 0 1 2;1;1

           B P t t t t B

Ta có đường thẳng



đi qua

A

và nhận vecto

 

1;1; 1 



AB

là véc tơ chỉ phương có

dạng

1 2

:

1 1 1

 

  



x y z

.

Cách 2:

Gọi

 

1 ; ; 1 2

     

d B B t t t

 

; ; 3 2

  



AB t t t

, Đường thẳng

d

có VTCP là

 

1;1;2





d

u

Vì

 

d

nên

 

. 0 2 3 2 0 1          

   

d d

AB u AB u t t t t

Suy ra

 

1;1; 1 



AB

.Ta có đường thẳng



đi qua

 

1;0;2

A

và nhận véc tơ

 

1;1; 1 



AB

là véc

tơ chỉ phương có dạng

1 2

:

1 1 1

 

  



x y z

.

Câu 9. (Đề Tham Khảo 2018) Trong không gian

Oxyz

, cho hai điểm

8 4 8

(2;2;1), ( ; ; )

3 3 3

A B 

. Đường

thẳng qua tâm đường tròn nội tiếp tam giác

OAB

và vuông góc với mặt phẳng

( )OAB

có phương

trình là:

A.

2 2 5

9 9 9

1 2 2

x y z

  

 



B.

1 8 4

1 2 2

x y z

  

 



C.

1 5 11

3 3 6

1 2 2

x y z

  

 



D.

1 3 1

1 2 2

x y z  

 



Lời giải.

Chọn D

Ta có:

 

; 4; 8;8

OA OB

 

 

 

 

Gọi

d

là đường thẳng thỏa mãn khi đó

d

có VTCP

 

1; 2;2

u  



Ta có

3, 4, 5

OA OB AB

  

. Gọi

( ; ; )I x y z

là tâm đường tròn nội tiếp tam giác

OAB

Áp dụng hệ thức

. . . 0

OB IA OA IB AB IO

  

   

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 8 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

 

1

4.( ) 3.( ) 5. 0 4 3 0;1;1

12

OA OI OB OI IO OI OA OB I         

        

Suy ra

: 1 2

1 2

x t

d y t

z t







 





 



cho

1

t d  

đi qua điểm

( 1;3; 1)

M

 

Do đó

d

đi qua

( 1;3; 1)

M

 

có VTCP

(1; 2;2)

u  



nên đường thẳng có phương trình

1 3 1

1 2 2

x y z  

 



Câu 10. (Mã 103 2018) Trong không gian Oxyz, cho đường thẳng

1 2

:

2 1 2

x y z

d

 

 



và mặt phẳng

( ) : 1 0

P x y z

   

. Đường thẳng nằm trong mặt phẳng

( )P

đồng thời cắt và vuông góc với

d

có

phương trình là:

A.

1

4

3

x t

y t

z t

  





 





 



B.

3

2 4

2

x t

y t

z t

 





  





 



C.

3

2 4

2 3

x t

y t

z t

 





  





 



D.

3 2

2 6

2

x t

y t

z t

 





  





 



Lời giải

Chọn C

d

:

1 2

2 2

x t

y t

z t

  





 





  



Gọi



là đường thẳng nằm trong

( )P

vuông góc với

d

.

; ( 1;4;3)

d P

u u n



 

  

 

  

Gọi A là giao điểm của

d

và

( )P

. Tọa độ A là nghiệm của phương trình:

( 1 2 ) ( t) ( 2 2 t) 1 0 t 2 (3; 2;2)

t A

            

Phương trình



qua

(3; 2;2)

A



có vtcp

u ( 1;4;3)



 



có dạng:

3

2 4

2 3

x t

y t

z t

 





  





 



Câu 11. (Mã 123 2017) Trong không gian

Oxyz

cho điểm

 



1; 1; 3

M

và hai đường thẳng



 

  

3

1 1

:

3 2 1

y

x z

,





  



1

:

1 3 2

y

x z

. Phương trình nào dưới đây là phương trình đường

thẳng đi qua

M

và vuông góc với



và





.

A.

   



 





 



1

1 3

x t

y t

z t

B.

  



 





 



1

3

x t

y t

z t

C.

   



 





 



1

3

x t

y t

z t

D.

   



 





 



1

3

x t

y t

z t

Lời giải

Chọn D

+) VTCP của



 ,

lần lượt là

 





3; 2;1

u

và

 

 



1; 3; 2

v

;

 

   

 

 

, 7; 7; 7

u v

+) Vì

d

vuông góc với



và





nên

 

 



1;1;1

d

u

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9

+)

d

đi qua

 



1; 1; 3

M

nên

   



 





 



1

: 1

3

x t

d y t

z t

.

Câu 12. (Mã 104 2018) Trong không gian

Oxyz

cho đường thẳng

1 1

:

1 2 1

x y z 

  

và mặt phẳng

 

: 2 y z 3 0

P x

   

. Đường thẳng nằm trong

 

P

đồng thời cắt và vuông góc với



có

phương trình là:

A.

1 2

1

2

x t

y t

z

 





 









B.

3

2

x

y t

z t

 





 









C.

1

1 2

2 3

x t

y t

z t

 





 





 



D.

1

2 2

x

y t

z t







 





 



Lời giải

Chọn D

Ta có

1 1

:

1 2 1

x y z 

  

: 1 2

1

x t

y t

z t







    





 



Gọi

 

M P

  

 

;2 1; 1

M M t t t

     

     

2 2 1 1 3 0

M P t t t

       

4 4 0 1t t    

 

1;1;2

M

Véc tơ pháp tuyến của mặt phẳng

 

P

là

 

1; 2; 1

n

  



Véc tơ chỉ phương của đường thẳng



là

 

1;2;1

u 



Đường thẳng

d

nằm trong mặt phẳng

 

P

đồng thời cắt và vuông góc với





Đường thẳng

d

nhận

 

1

, 0; 1;2

2

n u

 

 

 

 

làm véc tơ chỉ phương và

 

1;1;2

M d



Phương trình đường thẳng

1

: 1

2 2

x

d y t

z t







 





 



Câu 13. (Mã 123 2017) Trong không gian với hệ tọa độ

Oxyz

, cho hai đường thẳng

  



  









1

1 3

: 2

2

x t

d y t

z

,





 



2

1

:

2 1 2

y

x z

d

và mặt phẳng

 

  : 2 2 3 0.

P x y z

Phương trình nào dưới đây là phương

trình mặt phẳng đi qua giao điểm của

1

d

và

 

P

, đồng thời vuông góc với

2

d

?

A.

   2 2 13 0x y z

B.

   2 2 22 0x y z

C.

   2 2 13 0x y z

D.

   2 2 22 0x y z

Lời giải:

Chọn C

Tọa độ giao điểm của

1

d

và

 

P

là

 



4; 1; 2

A

Mặt phẳng cần tìm đi qua

A

và nhận

 





2

2; 1; 2

u

làm VTCP có phương trình

   2 2 13 0.x y z

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 10 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 14. (Chuyên Lương Thế Vinh Đồng Nai -2019) Trong không gian với hệ tọa độ

Oxyz

cho

 

1; 1; 3A 

và hai đường thẳng

1

4 2 1

: ,

1 4 2

x y z

d

  

 



2

2 1 1

:

1 1 1

x y z

d

  

 



. Phương

trình đường thẳng qua

A

, vuông góc với

1

d và cắt

2

d là

A.

1 1 3

2 1 3

x y z  

 

. B.

1 1 3

4 1 4

x y z  

 

.

C.

1 1 3

1 2 3

x y z  

 



. D.

1 1 3

2 1 1

x y z  

 

 

.

Lời giải

Gọi

d

là đường thẳng qua

A

và

d

cắt

2

d tại

K

. Khi đó

 

2 ; 1 ; 1K t t t   

.

Ta có

 

1 ; ; 2AK t t t   



.

Đường

1

AK d

1

. 0AK u 

 

, với

 

1

1; 4; 2u  



là một vectơ chỉ phương của

1

d .

Do đó

1 4 2 4 0 1t t t t      

, suy ra

 

2; 1; 1AK   



.

Vậy phương trình đường thẳng

1 1 3

:

2 1 1

x y z

d

  

 

 

.

Câu 15. (Chuyên Lê Quý Đôn Điện Biên 2019) Trong không gian

Oxyz

, cho điểm

 

1;0;1M

và đường

thẳng

1 2 3

:

1 2 3

x y z

d

  

 

. Đường thẳng đi qua

M

, vuông góc với

d

và cắt

Oz

có phương

trình là

A.

1 3

0

1

x t

y

z t

 











 



. B.

1 3

0

1

x t

y

z t

 











 



. C.

1 3

1

x t

y t

z t

 











 



. D.

1 3

0

1

x t

y

z t

 











 



.

Lời giải

Đường thẳng

d

có một vectơ chỉ phương là

 

1;2;3u 



.

Gọi



là đường thẳng đi qua

M

, vuông góc với

d

và cắt

Oz

.

Gọi

 

0;0;N t Oz  

 

1;0; 1MN t   



.

. 0d MN u   

 

4

3

t 

1

1;0;

3

MN

 

  

 

 



. Khi đó

MN



cùng phương với

 

1

3;0;1u  



Đường thẳng



đi qua điểm

 

1;0;1M

và có một vectơ chỉ phương

 

3;0;1

nên có phương

Câu 16. (Kinh Môn - Hải Dương 2019) Trong không gian với hệ tọa độ Oxyz cho điểm

 

1; 1;3A 

và

hai đường thẳng

1

3 2 1

:

3 3 1

x y z

d

  

 



, . Phương trình đường thẳng

d

đi qua

A

, vuông góc với đường thẳng

1

d và cắt thẳng

2

d .

A.

1 1 3

5 4 2

x y z  

 



. B.

1 1 3

3 2 3

x y z  

 



.

C.

1 1 3

6 5 3

x y z  

 



. D.

1 1 3

2 1 3

x y z  

 



.

Lời giải

Chọn C

Gọi

 

2

2 ; 1 ;1M t t t d d     

với

t 

.

2

2 1 1

:

1 1 1

x y z

d

  

 



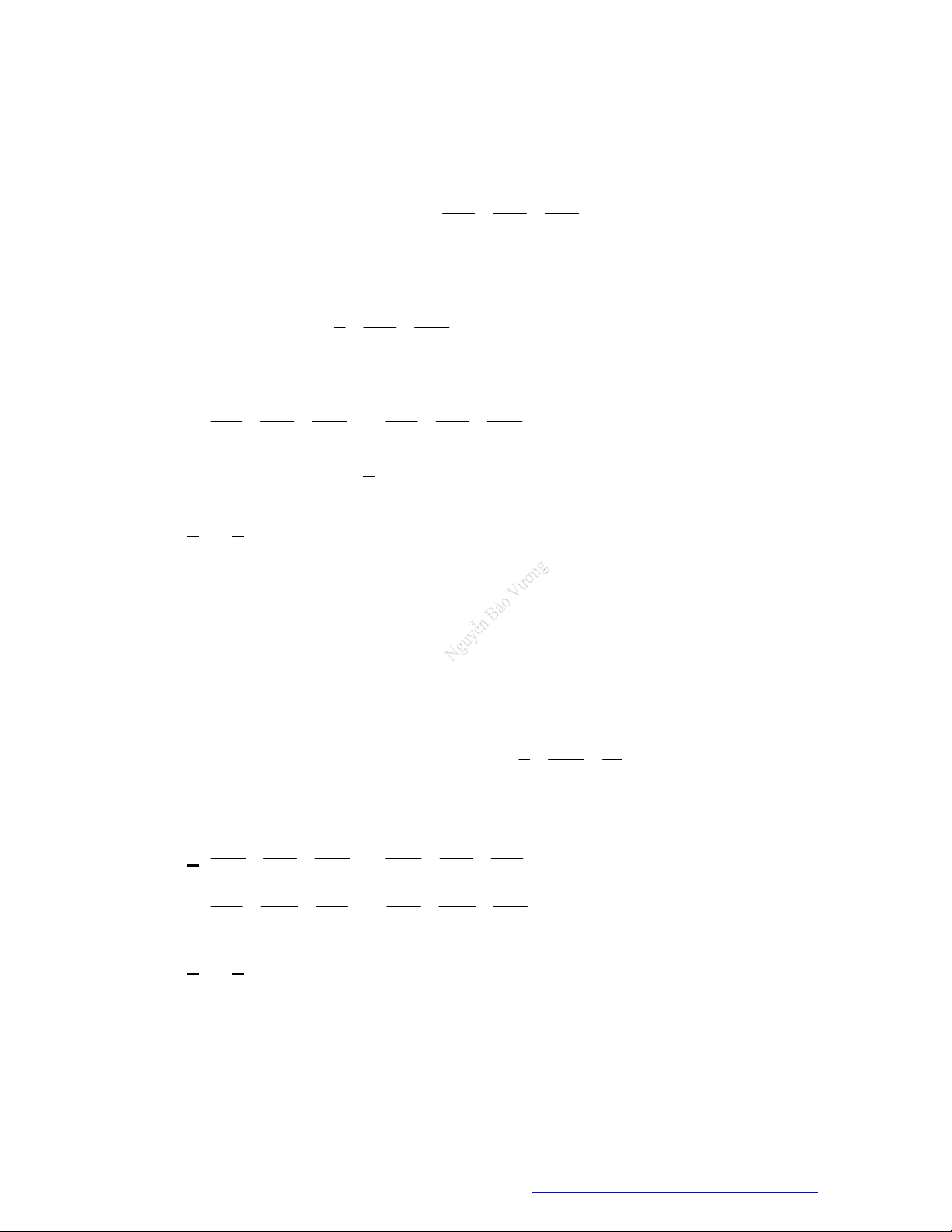
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11

Ta có

 

1 ; ; 2

AM t t t    



và

 

1

3;3; 1

u

 



là vectơ chỉ phương của

1

d

Mặt khác

1

. 0

AM u



 

nên

 

3.(1 ) 3.( ) 1. 2 0 5t t t t        

(6; 5;3)

AM  



là 1 vectơ chỉ phương của

d

.

Vậy phương trình đường thẳng

d

:

1 1 3

6 5 3

x y z

  

 



.

Câu 17. (Hội 8 trường chuyên 2019) Trong không gian

,Oxyz

cho điểm

 

1; 1;2

M 

và hai đường thẳng

: 1 4 ,

6 6

x t

d y t

z t







  





 



1 2

: .

2 1 5

x y z

d

 



 



Phương trình nào dưới đây là phương trình đường thẳng đi

qua

,M

vuông góc với

d

và

d



?

A.

1 1 2

.

17 14 9

x y z

  

 

B.

1 1 2

.

14 17 9

x y z

  

 

C.

1 1 2

.

17 9 14

x y z

  

 

D.

1 1 2

.

14 17 9

x y z

  

 

Lời giải

Chọn D

Đường thẳng

d

có một vectơ chỉ phương

 

1; 4;6

u  



.

Đường thẳng

d



có một vectơ chỉ phương

 

2;1; 5

u



 



.

Gọi



là đường thẳng qua

,M

vuông góc với

d

và

d



nên có một vectơ chỉ phương là:

 

, 14;17;9

u u u



 



 

 

  

.

Vậy phương trình đường thẳng



:

1 1 2

.

14 17 9

x y z

  

 

Câu 18. Cho hai đường thẳng

 

1

2

:

1

x t

d

y t

z t

 





 





 



và

 

2

7

:

1 3 1

x y z

d



 

 

. Đường thẳng

 



là đường vuông

góc chung của

 

1

d

và

 

2

d

. Phương trình nào sau đâu là phương trình của

 



A.

2 1 2

1 1 2

x y z

  

 



. B.

2 1 1

1 1 2

x y z  

 



.

C.

1 4 1

1 1 2

x y z  

 



. D.

3 2 3

1 1 2

x y z

  

 

 

.

Lời giải

Chọn A

Lấy điểm

 

1

M d



:

 

1 1 1

2 ;1 ;1

M t t t  

 

2

:N d



 

2 2 2

;7 3 ;

N t t t 

 

2 1 2 1 2 1

2; 3 6; 1

MN t t t t t t

        



Đường thẳng

MN

là đường vuông góc chung

1

2

. 0

MN u

















 

 

2 1 2

2 1 1

1 2

11 3 19 1

t t t



  





 

 

   





Suy ra

   

1;0;0 , 2;1; 2

M N



và

 

1;1; 2

MN





NGUYỄN BẢO VƯƠNG - 0946798489

Trang 12 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Phương trình đường thẳng

 



đi qua

,M N

là:

2 1 2

1 1 2

x y z

  

 



Câu 19. Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

 

:3 0

P x y z

  

và đường thẳng

1 3

:

1 2 2

x y z

d

 

 



. Gọi



là đường thẳng nằm trong

 

P

, cắt và vuông góc với

d

. Phương

trình nào sau đây là phương trình tham số của



?

A.

2 4

3 5

3 7

x t

y t

z t

  





 





 



. B.

3 4

5 5

4 7

x t

y t

z t

  





 





 



. C.

1 4

1 5

4 7

x t

y t

z t

 





 





  



. D.

3 4

7 5

2 7

x t

y t

z t

  





 





 



.

Lời giải

Chọn B

Do



nằm trong nằm trong

 

P

và vuông góc với

d

nên



có véctơ chỉ phương là

 

, 4; 5; 7

d

P

u n u



 

   

 

  

Gọi

A d  

thì

   

1;0; 3

A P d A

   

Vậy phương trình tham số của



là

1 4

0 5

3 7

x t

y t

z t

 





 





  



hay

3 4

5 5

4 7

x t

y t

z t

  





 





 



Câu 20. Trong không gian với hệ tọa độ

Oxyz

, cho điểm

 

1; 1;3

A 

và hai đường thẳng:

1 2

4 2 1 2 1 1

: , :

1 4 2 1 1 1

x y z x y z

d d

     

   

 

. Viết phương trình đường thẳng

d

đi qua

A

,

vuông góc với đường thẳng

1

d

và cắt đường thẳng

2

d

.

A.

1 1 3

2 1 1

x y z  

 

 

. B.

1 1 3

6 1 5

x y z  

 

.

C.

1 1 3

6 4 1

x y z  

 

 

. D.

1 1 3

2 1 3

x y z  

 

.

Lời giải

Ta có:

 

1

1;4; 2

d

u

 



2

2 1 1

:

1 1 1

x y z

d

  

 



nên phương trình tham số của

 

2

: 1

1

x t

d y t t

z t

 





   





 





Gọi đường thẳng

d

cắt đường thẳng

2

d

tại

 

2 ; 1 ;1

M t t t   

Ta có:

 

1 ; ; 2

AM t t t

   



Đường thẳng

d

đi qua

;A M

nên vectơ chỉ phương

 

1 ; ; 2

d

u t t t

   



Theo đề bài

d

vuông góc

1

d

     

1 1

. 0 1. 1 4 2 2 0 1

d d d d

u u u u t t t t            

   

 

2; 1; 1

d

u

   



Phương trình đường thẳng

d

đi qua

 

1; 1;3

A 

và có

 

2; 1; 1

d

u

  



có dạng:

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13

1 1 3

2 1 1

x y z  

 

 

.

Câu 21. Trong không gian

Oxyz

, cho đường thẳng

3 2

2 1 3

:

x y z

d

 

 



và mặt phẳng

 

2 6 0

:P x y z

   

. Đường thẳng nằm trong

 

P

cắt và vuông góc với

d

có phương trình

là?

A.

2 2 5

.

1 7 3

  

 

x y z

B.

2 2 5

.

1 7 3

  

 

x y z

C.

2 4 1

.

1 7 3

  

 

x y z

D.

2 4 1

.

1 7 3

  

 

x y z

Lời giải

 

1 1 2; ; ,

P

n  



 

2 1 3; ;

d

u

 



, Gọi

 

I d P

 

,

 

2 3 2 3

; ;

I d I t t t

   

 

I P



   

2 3 2 2 3 6 0

t t t

      

1t  

 

2 2 5; ;

I 

Gọi



là đường thẳng cần tìm.

Theo giả thiết

d

P

u u

u n

















 

 

1 7 3, ; ;

P d

u n u



 

  

 

  

Và đường thẳng



đi qua điểm

I

. Vậy

:

2 2 5

.

1 7 3

  

 

x y z

Câu 22. Trong không gian

Oxyz

, cho mặt phẳng

 

: 2 3 7 0

P x y z

   

và hai đường thẳng

1 2

3 2 2 1 1 2

: ; :

2 1 4 3 2 3

x y z x y z

d d

     

   

 

. Đường thẳng vuông góc mặt phẳng

 

P

và cắt

cả hai đường thẳng

1 2

;d d

có phương trình là

A.

7 6

1 2 3

x y z

 

 

B.

5 1 2

1 2 3

x y z

  

 

C.

4 3 1

1 2 3

x y z  

 

D.

3 2 2

1 2 3

x y z

  

 

Lời giải

Gọi



là đường thẳng cần tìm

1

d M  

nên

 

3 2 ; 2 ; 2 4M t t t

     

2

d N  

nên

 

1 3 ; 1 2 ;2 3N u u u

    

 

2 3 2 ;1 2 ;4 3 4MN u t u t u t

      



Ta có

MN



cùng phương với

 

P

n



Nên

2 3 2 1 2 4 3 4

1 2 3

u t u t u t     

 

ta giải hệ phương trình tìm được

2

1

u

t

 





 



Khi đó tọa độ điểm

 

5; 1;2

M  

và VTCP

   

2; 4 6 2 1;2;3

MN      



Phương trình tham số



là

5 1 2

1 2 3

x y z

  

 

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 14 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 23. Trong không gian

Oxyz

, cho hai đường thẳng

1

1 1

:

2 1 1

x y z

d

 

 



và

2

1

: 1

x t

d y

z t



  



 





 





và mặt

phẳng

 

: 1 0

P x y z

   

. Đường thẳng vuông góc với

 

P

cắt

1

d

và

2

d

có phương trình là

A.

13 9 4

5 5 5

1 1 1

x y z

  

 

. B.

1 3 2

5 5 5

1 1 1

x y z

  

 

.

C.

7 2

1

5 5

1 1 1

x z

y

 



 

. D.

1 1 1

x y z

 

.

Lời giải

Chọn B

Giả sử đường thẳng

 

d

vuông góc với

 

P

cắt

1

d

và

2

d

tai

,M N

Ta có:

 

1 2 ; 1 ;M a a a  

,

 

1 ; 1;N t t   

,

 

2 2; ;

NM a t a a t    



.

Mặt phẳng

 

P

có vectơ pháp tuyến là

 

1;1;1

n



Vì

MN

vuông góc với mặt phẳng

 

P

nên

NM



cùng phương

n



2

1 1 1

a t a a t  

  

2 1 3 2

; ;

5 5 5 5

4

5

a M

t



 









    



 







 









 





Đường thẳng

 

d

qua điểm

M

nhận

n



làm vec tơ chỉ phương

Phương trình

1 3 2

5 5 5

:

1 1 1

x y z

d

  

 

.

Câu 24. Trong không gian với hệ trục tọa độ

Oxyz

, cho đường thẳng

 



đi qua điểm

 

0;1;1

M

, vuông

góc với đường thẳng

   

1

: 1

1

x t

d y t t

z







  





 





và cắt đường thẳng

 

2

1

:

2 1 1

x y z

d



 

. Phương trình

của

 



là?

A.

0

1

x

y t

z t













 



. B.

0

1

x

y

z t













 



. C.

0

1

x

y t

z







 









. D.

0

1

x

y

z t













 



.

Lời giải

Chọn B

Gọi

   

2

2 ;1 ;

A t t t d

  

 

là giao điểm giữa đường thẳng

 



và đường thẳng

 

2

d

Ta có vecto chỉ phương

 

1

1; 1;0

d

u  



,

 

2 ; ; 1

MA t t t

  

 



Theo đề bài:

1

. 0 2 0 0

d

u MA t t t

  

     

 

Suy ra

 

0;1;0

A

Khi đó vecto chỉ phương của đường thẳng

 



là

 

0;0;1

u AM



 

 

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15

Phương trình đường thẳng

 



qua

 

0;1;1

M

có vecto chỉ phương

 

0;0;1

u







có dạng:

0

1

x

y

z t













 



Câu 25. Trong không gian với hệ tọa độ

Oxyz

cho điểm

 

1;0;2

A

và đường thẳng

d

có phương trình:

1 1

1 1 2

 

 

x y z

. Viết phương trình đường thẳng



đi qua

A

, vuông góc và cắt

d

.

A.

1 2

1 1 1

 

 

x y z

B.

1 2

1 1 1

 

 



x y z

C.

1 2

2 2 1

 

 

x y z

D.

1 2

1 3 1

 

 



x y z

Lời giải

Chọn B

Đường thẳng

1 1

:

1 1 2

 

 

x y z

d

có véc tơ chỉ phương

 

1;1;2





u

Gọi

 

P

là mặt phẳng qua điểm

A

và vuông góc với đường thẳng

d

, nên nhận véc tơ chỉ phương

của

d

là vecto pháp tuyến

     

:1 1 2 2 0 2 5 0         

P x y z x y z

Gọi

B

là giao điểm của mặt phẳng

 

P

và đường thẳng

 

1 ; ; 1 2

   

d B t t t

Vì

       

1 2 1 2 5 0 1 2;1;1

           B P t t t t B

Ta có đường thẳng



đi qua

A

và nhận vecto

 

1;1; 1 



AB

là véc tơ chỉ phương có

dạng

1 2

:

1 1 1

 

  



x y z

.

Câu 26. (Chuyên Lê Quý Đôn – Điện Biên 2019) Trong không gian

,Oxyz

cho điểm

(1;0;1)

M

và đường

thẳng

1 2 3

: .

1 2 3

x y z

d

  

 

Đường thẳng đi qua

,M

vuông góc với

d

và cắt

Oz

có phương

trình là

A.

1 3

0

1

x t

y

z t

 











 



. B.

1 3

0

1

x t

y

z t

 











 



. C.

1 3

1

x t

y t

z t

 











 



. D.

1 3

0

1

x t

y

z t

 











 



.

Lời giải

Chọn A

Gọi



là đường thẳng cần tìm và

.N Oz 

Ta có

(0;0; ).N c

Vì



qua

,M N

và

M Oz

nên

( 1;0; 1)

MN c

 



là VTCP của

.

d

có 1 VTCP

(1; 2; 3)

u



và

d 

nên

4 1

0 1 3( 1) 0 ( 1;0; ).

3 3

MN u c c MN          

 



Chọn

( 3; 0;1)

v





là 1 VTCP của



, phương trình tham số của đường thẳng



là

1 3

0

1

x t

y

z t

 











 



.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 16 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 27. Trong không gian với hệ trục

Oxyz

, đường vuông góc chung của hai đường thẳng chéo nhau

1

2 3 4

:

2 3 5

x y z

d

  

 



và

2

1 4 4

:

3 2 1

x y z

d

  

 

 

có phương trình

A.

2 2 3

2 3 4

x y z  

 

. B.

2 3

2 3 1

x y z

 

 



.

C.

2 2 3

2 2 2

x y z  

 

. D.

1

1 1 1

x y z 

 

.

Lời giải

Chọn D

Gọi



là đường thẳng cần tìm.

Gọi

   

1 2

; 2 2 ;3 3 ; 4 5 , 1 3 ;4 2 ;4

A d B d A t t t B t t t

  

              

Ta có:

 

3 2 3; 2 3 1; 5 8

AB t t t t t t

  

        



.

Gọi

   

1 2

, 2;3; 5 , 3; 2; 1

d d

u u u



    

  

lần lượt là véc tơ chỉ phương của

1 2

, ,d d

ta có:

1

2

d

u u

















 

.Chọn

   

1 2

, 13; 13; 13 13 1;1;1 13

d d

u u u u



 

        

 

   

.

Vì

,AB u

 

đều là véc tơ chỉ phương của



nên ta có:

3 2 3 3 2 3 1

2 3 1 2 3 1 1

5 8 5 8 2

t t k t t k t

AB ku t t k t t k t

t t k t t k k

  

      

  

  

 

              

  

  

 

         

  

 

 

0;0;1

A

.

1

:

1 1 1

x y z 

   

.

Câu 28. (Chuyên Nguyễn Huệ- 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho mặt phẳng

 

: 2 2 9 0

P x y z

   

và đường thẳng

1 3 3

:

1 2 1

x y z

d

  

 



. Phương trình tham số của đường

thẳng

Δ

đi qua

 

0; 1;4

A 

, vuông góc với

d

và nằm trong

 

P

là:

A.

5

Δ : 1

4 5

x t

y t

z t







  





 



. B.

2

Δ :

4 2

x t

y t

z t













 



. C.

Δ : 1

4

x t

y

z t







 





 



. D.

Δ : 1 2

4

x t

y t

z t

 





  





 



.

Lời giải

Chọn C

 

d

P

u u

d

P

u n







 



 



 

 











 

 

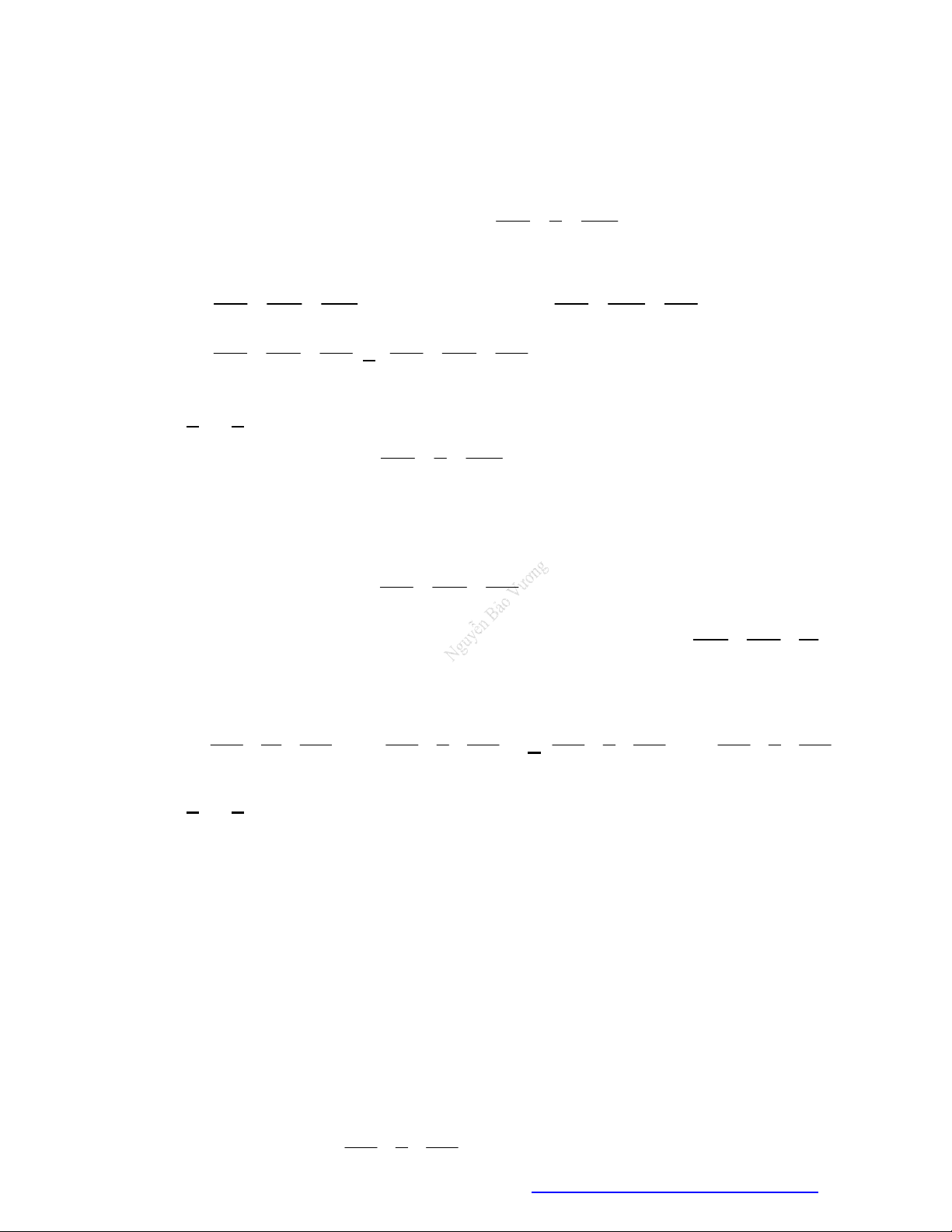
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17

 

, 5;0;5

d

P

u n

 



 

 

. Do đó một vectơ chỉ phương của đường thẳng

Δ

là

 

1;0;1

u







: 1

4

x t

y

z t







   





 



Câu 29. (Đại học Hồng Đức –Thanh Hóa 2019) Trong không gian

Oxyz

, cho mặt phẳng

 

: 2 4 0

P x y z

   

và đường thẳng

1 2

:

2 1 3

x y z

d

 

 

. Phương trình đường thằng



nằm

trong mặt phẳng

 

P

, đồng thời cắt và vuông góc với đường thẳng

d

là

A.

1 1 2

5 1 2

x y z

  

 



. B.

1 3 1

5 1 3

x y z  

 



.

C.

1 1 1

5 1 3

x y z  

 



. D.

1 1 1

5 1 3

x y z  

 

 

.

Lời giải

Chọn D

Gọi

 

1 2

: 2 1; ;3 2

2 1 3

x y z

M d M d M t t t

 

         

.

     

: 2 4 0 2 1 2 3 2 4 0 1 1;1;1

M P M P x y z t t t t M                 

.

Vì

d 

và

 

P

  



có vectơ chỉ phương

 

; 5; 1; 3

d

u n u

 

   

 

  

.

Vậy phương trình



là

1 1 1

:

5 1 3

x y z  

  

 

.

Câu 30. (Sở Hà Nam - 2019) Trong không gian

Oxyz

, cho đường thẳng

3 1

:

2 1 1

x y z

d

 

 



và mặt

phẳng

 

: 3 2 0

P x y z

   

. Gọi

'd

là đường thẳng nằm trong mặt phẳng

 

P

, cắt và vuông

góc với

d

. Đường thẳng

'd

có phương trình là

A.

1 1

2 5 1

x y z 

 

 

. B.

1 1

2 5 1

x y z 

 

. C.

1 1

2 5 1

x y z 

 



. D.

1 1

2 5 1

x y z 

 

 

.

Lời giải

Chọn C

Phương trình tham số của

3 2

: 1

x t

d y t

z t

  





  





 



.

Tọa độ giao điểm của

d

và

 

P

là nghiệm của hệ:

   

3 2 3 2 1

1 1 1

1;0; 1

0

3 2 0 3 2 1 3 2 0 1

x t x t t

y t y t x

d P M

z t z t y

x y z t t t z

      

  

  

       

  

      

  

    

  

            

  

.

Vì

'd

nằm trong mặt phẳng

 

P

, cắt và vuông góc với

d

nên

'd

đi qua

M

và có véc tơ chỉ

phương

 

'

2; 5; 1

d P d

u n u

    

  

hay

'd

nhận véc tơ

 

2;5;1

v  



làm véc tơ chỉ phương.

Phương trình của

'd

:

1 1

2 5 1

x y z 

 



.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 18 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 31. Trong không gian với hệ tọa độ

Oxyz

, cho hai đường thẳng

1

1 2 1

:

2 1 1

x y z  

  

và

2

2 1 2

:

4 1 1

x y z  

  

 

. Đường thẳng chứa đoạn vuông góc chung của

1



và

2



đi qua điểm

nào sau đây?

A.

 

0; 2; 5 

M

. B.

 

1; 1; 4 

N

. C.

 

2;0;1

P

. D.

 

3;1; 4

Q

.

Lời giải

Gọi

 

1 2 ; 2 ;1

A t t t    

và

 

2 4 ;1 ; 2

B t t t

  

    

là hai điểm lần lượt thuộc

1



và

2



.

 

1 2 4 ;3 ; 3

AB t t t t t t

  

        



.

1



có VTCP

 

2;1;1

u 



;

2



có VTCP

 

4;1; 1

u



  



.

AB

là đoạn vuông góc chung của

1



và

2



. 0

AB u



















 

 

     

2 1 2 4 3 3 0

6 8 2 1

8 18 10 1

4 1 2 4 3 3 0

t t t t t t

t t t

t t t t t t

  

          



   

 



  

  

 

    

  

           

 





Suy ra

 

1; 1;2

A 

và

 

1;1; 3

AB

 



.

Phương trình đường thẳng chứa đoạn vuông góc chung của

1



và

2



là:

1

2 3

x t

y t

z t

 





  





 



.

Chỉ có điểm

 

3;1; 4

Q

có tọa độ thỏa mãn phương trình.

Dạng 1.2 Xác định phương trình đường thẳng khi biết yếu tố song song

Câu 32. (Mã 110 2017) Trong không gian với hệ toạ độ

Oxyz

, cho điểm

 

1; 2;3

A 

và hai mặt phẳng

 

: 1 0

P x y z

   

,

 

: 2 0

Q x y z

   

. Phương trình nào dưới đây là phương trình đường

thẳng đi qua

A

, song song với

 

P

và

 

Q

?

A.

1

2

3

x t

y

z t

 





 





 



B.

1

2

3

x t

y

z t

  











  



C.

1 2

2

3 2

x t

y

z t

 





 





 



D.

1

2

3 2

x

y

z t







 





 



Lời giải

Chọn A

Ta có

 

1;1;1

1; 1;1

P

Q

n







 







và

   

 

, 2;0; 2

P Q

n n

 

 

 

 

. Vì đường thẳng

d

song song với hai mặt

phẳng

 

P

và

 

Q

, nên

d

có véctơ chỉ phương

 

1;0; 1

u

 



.

Đường thẳng

d

đi qua

 

1; 2;3

A 

nên có phương trình:

1

2

3

x t

y

z t

 





 





 



Câu 33. (Chuyên Nguyễn Tất Thành Yên Bái 2019) Trong không gian với hệ toạ độ

Oxyz

, cho điểm

 

1; 3;4

M 

, đường thẳng

d

có phương trình:

2 5 2

3 5 1

x y z

  

 

 

và mặt phẳng

 

P

:

2 2 0

x z

  

. Viết phương trình đường thẳng



qua

M

vuông góc với

d

và song song với

 

P

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19

A.



:

1 3 4

1 1 2

x y z

  

 

 

. B.



:

1 3 4

1 1 2

x y z

  

 

  

.

C.



:

1 3 4

1 1 2

x y z

  

 



. D.



:

1 3 4

1 1 2

x y z

  

 



.

Lời giải

Ta có

(3; 5; 1)

d

u

  



là véc tơ chỉ phương của

d

.

 

( )

2;0;1

P

n 



là véc tơ pháp tuyến của

 

P

.

 

, 5; 5;10

d

p

u n

 

  

 



.

Do



vuông góc với

d

và song song với

 

P

nên

 

1;1; 2

u

 



là véctơ chỉ phương của



.

Khi đó, phương trình của



là

1 3 4

1 1 2

x y z

  

 



.

Câu 34. Trong không gian

O

xyz

, cho mặt phẳng

 

: 2 2 3 0

P x y z

   

và hai đường thẳng

1

1 1

:

3 1 1

x y z

d

 

 



;

2

2 1 3

:

1 2 1

x y z

d

  

 



. Xét các điểm

,A B

lần lượt di động trên

1

d

và

2

d

sao cho

AB

song song với mặt phẳng

 

P

. Tập hợp trung điểm của đoạn thẳng

AB

là

A. Một đường thẳng có vectơ chỉ phương

 

9;8; 5

u

  



B. Một đường thẳng có vectơ chỉ phương

 

5;9;8

u  



C. Một đường thẳng có vectơ chỉ phương

 

1; 2; 5

u

  



D. Một đường thẳng có vectơ chỉ phương

 

1;5; 2

u

 



Lời giải

Chọn A

 

1

3 ;1 ; 1

A d A a a a    

;

 

2

2 ;1 2 ; 3

B d B b b b     

.

 

2 3 ; 2 ; 2

AB b a b a b a      



;

 

2; 1;2

P

n  



.

Do

 

//

AB P

nên

2

. 0

3

P

AB n a b

  





.

Tọa độ trung điểm của đoạn thẳng

AB

là

3 2 2 2 4

; ;

2 2 2

a b b a a b

I

      

 

 

 

hay

3 8 5

1 ;1 ; 2

2 6 6

I b b b

 

   

 

 

Suy ra tập hợp trung điểm của đoạn thẳng

AB

là một đường thẳng có vectơ chỉ phương

 

9;8; 5

u

  



.

Câu 35. (THPT Lương Văn Can - 2018) Trong không gian

Oxyz

, cho điểm

 

3; 2; 4

A

 

và mặt phẳng

 

:3 2 3 7 0

P x y z

   

, đường thẳng

2 4 1

:

3 2 2

x y z

d

  

 



. Phương trình nào sau đây là

phương trình đường thẳng



đi qua

A

, song song

 

P

và cắt đường thẳng

d

?

A.

3 11

2 54

4 47

x t

y t

z t

 





 





  



. B.

3 54

2 11

4 47

x t

y t

z t

 





 





  



. C.

3 47

2 54

4 11

x t

y t

z t

 





 





  



. D.

3 11

2 47

4 54

x t

y t

z t

 





 





  



.

Lời giải

Gọi

 

3; 2; 3

P

n  



 

là vectơ pháp tuyến của mặt phẳng

 

P

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 20 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Đường thẳng

d

đi qua điểm

 

2; 4;1

M 

 

và có vectơ chỉ phương

 

3; 2; 2

d

u  



 

.

Giả sử

d M  

nên

 

2 3 ; 4 2 ;1 2M t t t

   

khi đó vectơ chỉ phương của đường thẳng



là

 

3 1; 2 6;2 5

u AM t t t



     

 

.

Ta có

   

. 0

P P

AM n AM n

  

   

nên

     

6

3 3 1 2 2 6 3 2 5 0

7

t t t t

        

.

Suy ra

11 54 47

; ;

7 7 7

AM

 

 

 

 



 

Chọn vectơ chỉ phương của đường thẳng



có tọa độ là

 

11; 54; 47



 

do đó phương trình đường

thẳng cần tìm là

3 11

2 54

4 47

x t

y t

z t

 





 





  



.

Câu 36. Trong không gian với hệ toạ độ

Oxyz

, cho điểm

 

1; 3;4

M 

, đường thẳng

2 5 2

:

3 5 1

x y z

d

  

 

 

và mặt phẳng

 

P

:

2 2 0

x z

  

. Viết phương trình đường thẳng



qua

M

vuông góc với

d

và song song với

 

P

.

A.

1 3 4

:

1 1 2

x y z

  

  

 

. B.

1 3 4

:

1 1 2

x y z

  

  

  

.

C.

1 3 4

:

1 1 2

x y z

  

  



. D.

1 3 4

:

1 1 2

x y z

  

  



.

Lời giải

Chọn C

Đường thẳng

2 5 2

:

3 5 1

x y z

d

  

 

 

có vec tơ chỉ phương

 

3; 5; 1

d

u

  



Mặt phẳng

 

P

:

2 2 0

x z

  

có vec tơ pháp tuyến

 

( )

2;0;1

P

n 



Đường thẳng



vuông góc với

d

nên vec tơ chỉ phương

d

u u





 

,

Đường thẳng



song song với

 

P

nên

( )P

u n





 

Ta có

( )P

d

u n



 

=

 

5; 5;10 .

 

Chọn vec tơ chỉ phương

 

1;1; 2

u



 



Vậy phương trình đường thẳng



qua

M

vuông góc với

d

và song song với

 

P

là

1 3 4

1 1 2

x y z

  

 



.

Câu 37. Trong không gian với hệ toạ độ

Oxyz

, cho điểm

 



1; 2; 3

A

và hai mặt phẳng

 

   : 1 0

P x y z

,

 

   : 2 0

Q x y z

. Phương trình nào dưới đây là phương trình đường

thẳng đi qua

A

, song song với

 

P

và

 

Q

?

A.

 



 





 



1

2

3 2

x

y

z t

B.

   









  



1

2

3

x t

y

z t

C.

  



 





 



1 2

2

3 2

x t

y

z t

D.

  



 





 



1

2

3

x t

y

z t

Lời giải

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21

Chọn D

Ta có

 









 







1;1;1

1; 1; 1

P

Q

n

và

   

 

   

 

 

, 2;0; 2 2 1; 0; 1

P Q

n n

. Vì đường thẳng

d

song song với

hai mặt phẳng, nên nhận véc tơ

 

1; 0; 1

làm véc tơ chỉ phương.

Câu 38. Trong không gian

Oxyz

, cho điểm

 

2;0; 1

A



và mặt phẳng

 

: 1 0

P x y

  

. Đường thẳng đi

qua

A

đồng thời song song với

 

P

và mặt phẳng

 

Oxy

có phương trình là

A.

  









 



3

2

1

x t

y t

z t

. B.

  



 





 



2

1

x t

y t

z

. C.

  



 





 



1 2

1

x t

y

z t

. D.

  



 





 



3

1 2

x t

y t

z t

.

Lời giải

Chọn B

Ta có:

 

1;1;0

Oxy

n 



,

 

0;0;1

Oxy

n 



.

Gọi

d

là đường thẳng đi qua

A

đồng thời song song với

 

P

và mặt phẳng

 

Oxy

. Khi đó:

 

   

 

(Oxy)

, 1; 1;0

d P

d P Oxy

d

u n

u n n

u n







 

   



 







 

  

 

. Vậy

2

:

1

x t

d y t

z

 





 





 



.

Câu 39. (Chuyên Lê Quý Đôn Quảng Trị 2019) Trong không gian tọa độ

Oxyz

, viết phương trình chính

tắc của đường thẳng đi qua điểm

 

3; 1;5

A 

và cùng song song với hai mặt phẳng

 

: 4 0

P x y z

   

,

 

: 2 4 0

Q x y z

   

.

A.

3 1 5

:

2 1 3

x y z

d

  

 



. B.

3 1 5

2 1 3

x y z  

 

 

.

C.

3 1 5

2 1 3

x y z

  

 



. D.

3 1 5

2 1 3

x y z

  

 

 

.

Lời giải

Chọn B

Mặt phẳng

 

P

có một vectơ pháp tuyến là

 

1; 1;1

P

n  



; mặt phẳng

 

Q

có một vectơ pháp

tuyến là

 

2;1;1

Q

n 



.

Nhận thấy

 

A P



và

 

A Q



.

Gọi đường thẳng cần lập là

d

và

u



là một vectơ chỉ phương của nó.

Ta chọn

 

, 2; 1; 3

Q P

u n n

 

   

 

  

.

Mặt khác,

d

qua

 

3; 1;5

A 

nên có phương trình chính tắc là

3 1 5

2 1 3

x y z  

 

 

.

Câu 40. (Chu Văn An - Hà Nội - 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho hai mặt phẳng

 

: 2 1 0

x y z



   

,

 

: 2 0

x y z



  

và điểm

 

1;2; 1

A



. Đường thẳng



đi qua điểm

A

và

song song với cả hai mặt phẳng

   

,

 

có phương trình là

A.

1 2 1

2 4 2

x y z  

 

 

. B.

1 2 1

1 3 5

x y z  

 

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 22 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

C.

1 2 1

x y z  

 

 

. D.

2 3

1 2 1

x y z

 

 

.

Lời giải

Chọn B

mp

 



có véc tơ pháp tuyến là

 

1

1; 2;1

n  



, mp

 



có véc tơ pháp tuyến là

 

2

2;1; 1

n

 



.

Đường thẳng



có véc tơ chỉ phương là

 

1 2

; 1;3;5

u n n

 

 

 

  

.

Phương trình của đường thẳng

1 2 1

:

1 3 5

x y z  

  

.

Câu 41. Trong không gian

Oxyz

, cho ba điểm

 

1;0;0

A

,

 

0;2;0

B

,

 

0;0;3

C

. Đường thẳng đi qua tâm

đường tròn ngoại tiếp tam giác

ABC

, song song với mặt phẳng

 

Oxy

và vuông góc với

AB

.

A.

13

98

40

2

49

135

98

x t

y t

z



 



  











. B.

13

2

98

40

49

135

98

x t

y t

z



 



 











. C.

13

2

98

40

49

135

98

x t

y t

z



 



 











. D.

13

98

40

2

49

135

98

x t

y t

z



  



 











.

Lời giải

Chọn C

Gọi

( ; ; )I x y z

là tâm đường tròn ngoại tiếp tam giác

ABC

, ta có:

   

2 2

2 2 2 2

2 2

2 2 2 2

1 2

1 3

( )

1

1 2 3

x y z x y z

AI BI

AI CI x y z x y z

I ABC

x y z



      









        

 

 







  



13

98

2 4 3

40 13 40 135

2 6 8 ; ;

49 98 49 98

6 3 2 6

135

98

x

x y

x z y I

x y z

z







  





 

 

      

 

 

 

 

  











.

Ta có:

( 1;2;0)

AB  



.

Mặt phẳng

( )Oxy

có 1 véc tơ pháp tuyến

 

0;0;1

k 



.

Theo giả thiết đường thẳng



cần tìm có 1 véc tơ chỉ phương là

 

, 2;1;0

u AB k

 

 

 



  

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23

Phương trình tham số của đường thẳng

:

13

2

98

40

49

135

98

x t

y t

z



 



 











.

Câu 42. (THPT Cẩm Bình 2019) Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

 

: 2 6 0x z   

và đường thẳng

1

: 3

1

x t

d y t

z t

 





 





  



. Viết phương trình đường thẳng



nằm trong

mặt phẳng

 



cắt đồng thời vuông góc với

.d

A.

2 4 2

2 1 1

x y z  

 

. B.

2 4 2

2 1 1

x y z  

 



.

C.

2 3 2

2 1 1

x y z  

 



. D.

2 4 2

2 1 1

x y z  

 



.

Lời giải

Chọn B

Giao điểm

I

của

d

và

 



là nghiệm của hệ

 

1

3

2;4; 2 .

1

2 6 0

x t

y t

I

z t

x z

 





 



 



  



  



Mặt phẳng

 



có một vectơ pháp tuyến

 

1;0; 2 ;n  



đường thẳng

d

có một vectơ chỉ phương

 

1;1; 1u  



.

Khi đó đường thẳng



có một vectơ chỉ phương là

 

 

, 2; 1;1 .n u  

 

Đường thẳng



qua điểm

 

2;4; 2I 

và có một vectơ chỉ phương

 

 

, 2; 1;1n u  

 

nên có

phương trình chính tắc:

2 4 2

.

2 1 1

x y z  

 



Câu 43. Trong không gian Oxyz, cho ba đường thẳng

1

3 1 2

:

2 1 2

x y z

d

  

 



;

2

1 4

:

3 2 1

x y z

d

 

 

 

và

3

3 2

:

4 1 6

x y z

d

 

 



. Đường thẳng song song với d

3

, cắt d

1

và d

2

có phương trình là

A.

3 1 2

4 1 6

x y z  

 

. B.

3 1 2

4 1 6

x y z  

 

 

.

C.

1 4

4 1 6

x y z 

 



. D.

1 4

4 1 6

x y z 

 



.

I

d

α

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 24 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Lời giải

Chọn B

Từ

1 1

3 2

3 1 2

: : 1

2 1 2

2 2

x t

x y z

d d y t

z t

 



  



     







 



; từ

2

(3; 2; 1)

1 4

:

3 2 1

( 1;0; 4)

u

x y z

d

A



  

 



  



 







;

Từ

3 3

3 2

:

4 1 6

x y z

d u

 

   





(4; –1; 6)

Gọi (P) là mặt phẳng chứa d

2

và song song với d

3

2 3

2 1 1 3 3 2

; ; ; ( 13; 22;5)

1 6 6 4 4 1

( 1;0; 4) (P)

P

n u u

A



 

   

 

    



 

 



 



 



  



  

( ) : 13( 1) 22 5( 4) 0 ( ) :13 22 5 7 0

P x y z P x y z

           

Gọi B là giao điểm của (P) và d

1

. Đường thẳng đi qua B và song song với d

3

chính là đường thẳng

cần tìm.

Gọi B(3+ 2t; –1 + t; 2 – 2t). Thay tọa độ B vào (P): 13(3 + 2t) + 22(–1 + t) – 5(2 – 2t) – 7 = 0



t = 0



B (3; –1; 2)

Vì đường thẳng cần tìm song song với (d

3

) nên có các véc tơ chỉ phương là

3

.n u



(

0;n n

 

)

Như vậy chỉ có đáp án B là hợp lý.

Câu 44. (SGD Cần Thơ 2019) Trong không gian

Oxyz

, cho các đường thẳng

1 2

1 3

3 1 2

: , : 2

2 1 2

4

x t

x y z

d d y t

z t

  



  



   







  



,

3

3 2

:

4 1 6

x y z

d

 

 



. Đường thẳng song song với

3

d

và cắt đồng thời

1

d

và

2

d

có phương trình là:

A.

1 4

4 1 6

x y z

 

 



. B.

1 4

4 1 6

x y z

 

 



.

C.

3 1 2

4 1 6

x y z

  

 

. D.

3 1 2

4 1 6

x y z

  

 

 

.

Lời giải

Chọn D

Gọi



đường thẳng song song với

3

d

và cắt

1

d

và

2

d

.

3

;u u



 

lần lượt là véctơ chỉ phương của



và

3

d

.

Ta có

 

1

2 3; 1; 2 2

d A A x x x

       

;

 

2

1 3 ; 2 ; 4

d B B y y y        

.

 

3 2 4; 2 1; 2 6

AB y x y x y x

        



.

Vì

3

3 2 4 2 1 2 6

/ /

4 1 6

y x y x y x

d u ku



       

     



 

.

2 3 4 8 4 4 6 5 0

0

12 6 6 2 6 13 4 0

x y y x x y

x y

y x y x y x

       

 

    

 

        

 

.

Từ đó suy ra:

     

3; 1;2 ; 1;0; 4 4;1; 6

A B AB

      



là véctơ chỉ phương của



.

Phương trình



là:

3 1 2

4 1 6

x y z

  

 

 

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25

Câu 45. Trong không gian với hệ tọa độ

Oxyz

, viết phương trình tham số của đường thẳng đi qua điểm

 

1;3; 2

M



, đồng thời song song với giao tuyến của hai mặt phẳng

 

: 3 0

P x y

  

và

 

: 2 3 0

Q x y z

   

.

A.

1 3

3

2

x t

y t

z t

 





 





  



. B.

1 3

3

2

x t

y t

z t

 





 





  



. C.

1

3

2 3

x t

y t

z t

 





 





  



. D.

1

3

2 3

x t

y t

z t

 





 





  



.

Lời giải

Chọn C

Hai mặt phẳng

 

: 3 0

P x y

  

và

 

: 2 3 0

Q x y z

   

có vectơ pháp tuyến lần lượt là:

   

1;1;0 ; 2; 1;1

P Q

n n  

 

.

Giao tuyến của hai mặt phẳng

 

P

và

 

Q

có vectơ chỉ phương:

 

; 1; 1; 3 .

P Q

u n n

 

   

 

  

Đường thẳng đi qua điểm

 

1;3; 2

M



, đồng thời song song với giao tuyến của hai mặt phẳng

 

: 3 0

P x y

  

và

 

: 2 3 0

Q x y z

   

nhận vectơ

u



làm vectơ chỉ phương có phương trình

tham số là:

1

3

2 3

x t

y t

z t

 





 





  



.

Câu 46. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng

1 2

:

1 2 2

x y z

d

 

 

, mặt phẳng

( ) :2 2 5 0

P x y z

   

và điểm

 

1;1; 2

A



. Phương trình chính tắc của đường thẳng



đi qua

điểm

A

song song với mặt phẳng

( )P

và vuông góc với

d

là:

A.

1 1 2

:

1 2 2

x y z

  

  



. B.

1 1 2

:

2 1 2

x y z

  

  



.

C.

1 1 2

:

2 2 3

x y z

  

  



. D.

1 1 2

:

1 2 2

x y z

  

  

.

Lời giải

Chọn C

1 2

:

1 2 2

x y z

d

 

 

d

có một vectơ chỉ phương là

 

1;2;2

u



.

( ) :2 2 5 0

P x y z

   

( )P

có một vectơ pháp tuyến là

 

2;1;2

n



.

Đường thẳng



song song với mặt phẳng

( )P

và vuông góc với

d

 

có một vectơ chỉ phương là

 

, 2;2; 3

v u n

 

  

 

  

, và đường thẳng



đi qua điểm

 

1;1; 2

A





Phương trình chính tắc của đường thẳng



là:

1 1 2

2 2 3

x y z

  

 



.

Câu 47. (SP Đồng Nai - 2019) Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

 

: 9 0,

P x y z

   

đường thẳng

3 3

:

1 3 2

x y z

d

 

 

và điểm

 

1;2; 1 .

A



Viết phương trình

đường thẳng



đi qua điểm

A

cắt

d

và song song với mặt phẳng

 

P

.

A.

1 2 1

x y z  

 



. B.

1 2 1

x y z  

 



.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 26 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

C.

1 2 1

x y z  

 

. D.

1 2 1

x y z  

 

 

.

Lời giải

Chọn A

Cách 1:

Ta có:

 

P

có vectơ pháp tuyến là:

 

1;1; 1

n

 



.

d

có vectơ chỉ phương là:

 

1;3;2

u 



và

 

3;3;0

B d

.



có vectơ chỉ phương là:

 

; ;u a b c







và

 

1;2; 1A

 

(trong đó

2 2 2

0

a b c

  

).

   

2;1;1 ; . 0 0

AB d P u n a b c c a b



          

  



 

; ; .u a b a b



  



Do

d

cắt



, . 0 2 0 2 .AB u u a b b a



 

       

 

  

Chọn

 

1 2 1

1 2 1 1;2;1 : .

1 2 1

x y z

a b c u



  

            





Kết luận:

1 2 1

: .

1 2 1

x y z

  

  



Cách 2:

Ta có:

 

P

có vectơ pháp tuyến là:

 

1;1; 1

n

 



.



có vectơ chỉ phương là:

 

; ;u a b c







và

 

1;2; 1A

 

(trong đó

2 2 2

0

a b c

  

).

Do



song song với mặt phẳng

 

. 0

P u n



 

 

.

Nhận xét đáp án A:

. 0

u n





 

.

Nhận xét đáp án B:

. 4 0

u n



  

 

loại đáp án B.

đáp án C:

. 2 0

u n



  

 

loại đáp án C.

đáp án D:

. 2 0

u n



  

 

loại đáp án D.

Kết luận: Chọn đáp án A.

Câu 48. (THPT Thăng Long-Hà Nội- 2019) Trong không gian, cho mặt phẳng

 

: 4 0

P x y z

   

và

điểm

 

2; 1;3

A 

. Gọi



là đường thẳng đi qua

A

và song song với

 

P

, biết



có một vectơ chỉ

phương là

 

; ;u a b c





, đồng thời



đồng phẳng và không song song với

Oz

. Tính

a

c

.

A.

2

a

c



. B.

2

a

c

 

. C.

1

2

a

c

 

. D.

1

2

a

c



.

Lời giải

Chọn A

 

P

có một vectơ pháp tuyến là

 

1;1; 1

n

 



.



đi qua điểm

 

2; 1;3

A 

và có một vectơ chỉ phương là

 

; ;u a b c





.

Oz

đi qua điểm

 

0;0;0

O

và có một vectơ chỉ phương là

 

0;0;1

k 



.



không song song với

Oz



: : 0 : 0 :1

a b c



.



đồng phẳng với

Oz



Ba vectơ

; ;

u k OA

  

đồng phẳng

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27



, 0

k OA u

 



 

  



2 0

a b

 



2a b 

.

Do

 

/ /

P





u n

 

. 0

u n

 

  

0

a b c

   

c b  

. Suy ra

2

a

c



.

Dạng 1.3 Phương trình đường thẳng hình chiếu, đối xứng

Câu 49. (Đề Tham Khảo 2017) Trong không gian với hệ tọa độ

Oxyz

, cho đường thẳng

1 5 3

:

2 1 4

x y z

d

  

 



. Phương trình nào dưới đây là phương trình hình chiếu vuông góc của

d

trên mặt phẳng

3 0

x

 

?

A.

3

5 2

3

x

y t

z t

 





  





 



B.

3

6

7 4

x

y t

z t

 





  





 



C.

3

5

3 4

x

y t

z t

 





  





  



D.

3

5

3 4

x

y t

z t

 





  





 



Lời giải

Chọn B

Cách 1: Đường thẳng

d

đi qua điểm

0

(1; 5;3)

M 

và có VTCP

 

2; 1;4

d

u  



Gọi

 

Q

là mặt phẳng chứa

d

và vuông góc với

 

: 3 0

P x

 

.

Suy ra mặt phẳng

 

Q

đi qua điểm

0

(1; 5;3)

M 

và có VTPT là

 

 

; 0;4;1

P d

n u 

 

 

: 4 17 0

Q y z

   

.

Phương trình hình chiếu vuông góc của

d

trên mặt phẳng

 

P

là

4 17 0

3 0

y z

x

  





 



hay

3

6

7 4

x

y t

z t

 





  





 



Cách 2: Ta có

 

1 2 ; 5 ;3 4M d M t t t

     

. Gọi

M



là hình chiếu của

M

trên

 

: 3 0

P x

 

. Suy ra

 

3; 5 ;3 4M t t



   

. Suy ra

3

: 5

3 4

x

d y t

z t

 







  





 



So sánh với các phương án, ta chọn D là đáp án đúng.

Câu 50. (Đề Tham Khảo 2019) Trong không gian Oxyz, cho mặt phẳng

 

: 3 0

x yP z

   

và đường

thẳng

1 2

:

1 2 1

x y z

d

 

 



. Hình chiếu vuông góc của

d

trên

 

P

có phương trình là

A.

1 1 1

1 4 5

x y z  

 



B.

1 4 5

1 1 1

x y z

  

 

C.

1 1 1

1 4 5

x y z  

 

 

D.

1 1 1

3 2 1

x y z  

 

 

Lời giải

Chọn A

Gọi

M

là giao điểm của

d

với

 

P

.

Tọa độ của

M

là nghiệm của hệ:

3 1

3 0

2 1 1

1 2

2 1

1 2 1

x y z x

x y z

x y y

x y z

x z z

   

 

   



  

    

  

 

 

  

  

 

 

 

1;1;1

M

Lấy điểm

 

0; 1;2

N d 

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 28 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Một vec tơ pháp tuyến của mặt phẳng

 

P

là:

 

1;1;1

n 



.

Gọi



là đường thẳng đi qua

N

và nhận

 

1;1;1

n 



làm vec tơ chỉ phương.

Phương trình đường thẳng

1 2

:

1 1 1

x y z

 

  

Gọi

N



là giao điểm của



với

 

P

.

Tọa độ của

N



là nghiệm của hệ:

2

3

3 0

1

1 2

3

2

1 1 1

8

3

x

x y z

x y y

x y z

x z

z







  



   



  

     

   

 

  

  











2 1 8

; ;

3 3 3

N

 





 

 

 

1 4 5 1

; ; 1;4; 5

3 3 3 3

MN u

 



     

 

 

 

Đường thẳng cần tìm đi qua điểm

 

1;1;1

M

và nhận

 

1;4; 5

u

 



làm vec tơ chỉ phương nên có

phương trinh

1 1 1

1 4 5

x y z  

 



.

Câu 51. Trong không gian

Oxyz

, cho mặt phẳng

 

: 2 3 0

x y z



   

và đường thẳng

4 3 2

:

3 6 1

x y z

d

  

 

 

. Viết phương trình đường thẳng

'd

đối xứng với đường thẳng

d

qua

mặt phẳng

 



.

A.

5 4

11 17 2

x y z

 

 

 

. B.

5 4

11 17 2

x y z

 

 

 

.

C.

5 4

11 17 2

x y z

 

 

 

. D.

5 4

11 17 2

x y z

 

 



.

Lời giải

Mặt phẳng

 

: 2 3 0

x y z



   

có vectơ pháp tuyến

 

2;1;1

n



.

Gọi tọa độ giao điểm của

d

và

 



là

I

thì

 

22;39;8

I 

.

Lấy

 

4;3;2

A d 

. Gọi



là đường thẳng đi qua

A

và vuông góc với

 



.

Suy ra phương trình đường thẳng



là

4 2

3

2

x t

y t

z t

  





 





 



Gọi

H

là hình chiếu của

A

lên

 



thì

 

H



  

 

2;4;3

H 

.

'A

đối xứng với

A

qua

 





H

là trung điểm

'AA

 

' 0;5;4

A

.

Đường thẳng

'd

đối xứng với đường thẳng

d

qua mặt phẳng

 



'd

đi qua điểm

, 'I A

có

vectơ chỉ phương

   

' 22; 34; 4 2 11; 17; 2

A I

     



có phương trình là:

5 4

11 17 2

x y z

 

 

 

.

Câu 52. (Chuyen Phan Bội Châu Nghệ An 2019) Trong không gian với hệ tọa độ

Oxyz

, cho đường

thẳng

1 2 1

:

2 1 3

x y z

d

  

 

và mặt phẳng

 

: 3 0

P x y z

   

. Đường thẳng

d



là hình chiếu

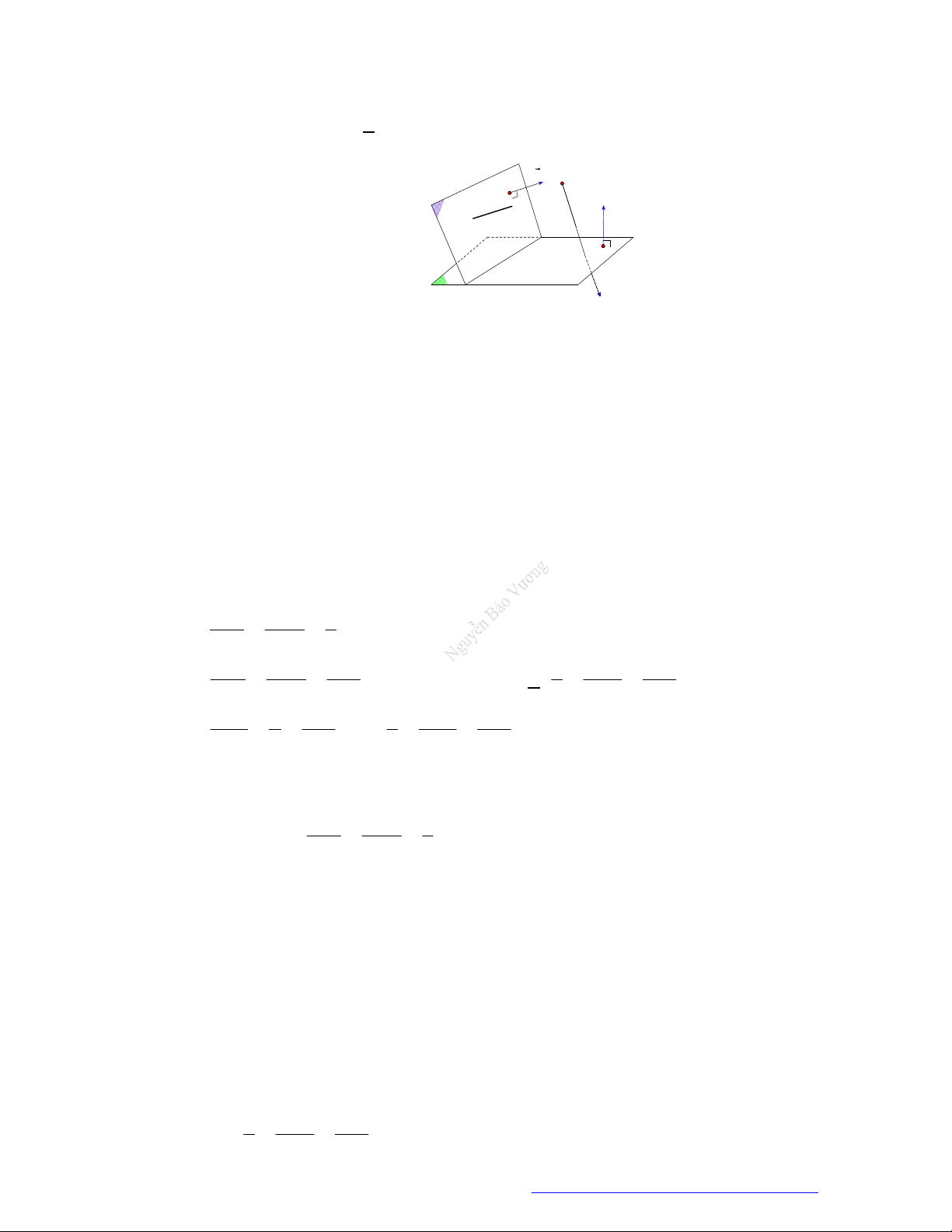
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 29

của

d

theo phương

Ox

lên

 

P

,

d



nhận

 

; ;2019u a b



là một vectơ chỉ phương. Xác định

tổng

 

.a b

A.

2019

. B.

2019

. C.

2018

. D.

2020

.

Lời giải

Chọn

     

1;2; 1 ; 2;1;3 ; , 0;3; 1 .

d

A d u u i

 

    

 



 

Ta thấy

; . 7 0

d

u i OA d

 

  

 





và

Ox

chéo nhau.

Gọi

 

Q

là mặt phẳng chứa

d

và song song với

.Ox

Một vectơ pháp tuyến của mặt phẳng

 

Q

là

 

; 0;3; 1 .

Q d

n u i

 

  

 



 

Hình chiếu

d



của

d

trên mặt phẳng

 

P

là đường giao tuyến giữa hai mặt phẳng

 

P

và

 

.Q

d



có một vectơ chỉ phương là

   

; 4;1;3 673 ; 2692;673;2019

Q P Q P

n n u n n

   

     

   

    

cũng

là một vectơ chỉ phương.

Vậy

2019.a b  

Câu 53. Trong không gian

Oxyz

, cho mặt phẳng

 

: 6 0x y z



   

và đường thẳng

1 4

:

2 3 5

x y z

d

 

 

. Hình chiếu vuông góc của

d

trên

 



có phương trình là

A.

1 4 1

2 3 5

x y z  

 

. B.

5 1

2 3 5

x y z 

 

.

C.

5 1

2 3 5

x y z 

 

. D.

5 1

2 3 5

x y z 

 

.

Lời giải

Mặt phẳng

 

: 1 0x y z



   

có vectơ pháp tuyến

 

1;1; 1n 



.

Đường thẳng

1 4

:

2 3 5

x y z

d

 

 

có vectơ chỉ phương

 

2;3;5u



.

Vì

 

. 1.2 1.3 1 .5 0n u     

 

nên

 

/ /d



.

Gọi

'd

là hình chiếu vuông góc của

d

trên

 



'/ /d d

.

Lấy

 

1; 4;0A d 

. Gọi



là đường thẳng đi qua

A

và vuông góc với

 



.

Suy ra phương trình đường thẳng



là

1

4

x t

y t

z t

 





  





 



.

Gọi

'A

là hình chiếu của

A

lên

 



thì

 

'A



  

 

' 0; 5;1A 

.

Đường thẳng

'd

là đường thẳng đi qua

 

' 0; 5;1A 

, có vectơ chỉ phương

 

2;3;5u



có phương

trình là

5 1

2 3 5

x y z 

 

.

n

Q

P

d

x

O

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 30 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 54. (KTNL GV Bắc Giang 2019) Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

 

: 1 0P x y z   

và đường thẳng

2 4 1

:

2 2 1

x y z

d

  

 



. Viết phương trình đường thẳng

d



là hình chiếu vuông góc của

d

trên

 

P

.

A.

2 1

:

7 5 2

x y z

d

 



 



. B.

2 1

:

7 5 2

x y z

d

 



 



.

C.

2 1

:

7 5 2

x y z

d

 



 

. D.

2 1

:

7 5 2

x y z

d

 



 

.

Lời giải

Chọn B.

+) Phương trình tham số của

2 2

: 4 2

1

x t

d y t

z t

  





 





  



,

t R

. Gọi

 

2 2 ;4 2 ; 1M t t t     

là giao điểm

của

d

và

 

P

     

2 2 4 2 1 1 0t t t         

2t 

 

2;0;1M 

.

+) Mặt phẳng

 

P

có 1 vector pháp tuyến là

 

1;1; 1

P

n  



. Điểm

 

0;2;0N 

d

.

Gọi



là đường thẳng qua

 

0;2;0N

và vuông góc với mặt phẳng

 

P





nhận vector

 

1;1; 1

P

n  



làm vector chỉ phương. Suy ra phương trình của



là:

   

0 2 0

: : 2

1 1 1

x c

x y z

y c

z c





  



      







 



,

c R

. Gọi

 

;2 ;M c c c



  

là giao điểm của



với mặt phẳng

 

P

   

1

2 1 0

3

c c c c         

1 5 1

; ;

3 3 3

M

 



 

 

 

.

+)

7 5 2

; ;

3 3 3

MM

 



  

 

 



, đường thẳng

d



là hình chiếu vuông góc của

d

trên mặt phẳng

 

P

nên

d



chính là đường thẳng

'MM

, suy ra

d



đi qua

 

2;0;1M

và nhận vector

 

3 7; 5;2u MM



   

 

làm vector chỉ phương nên phương trình của

d



là:

2 1

:

7 5 2

x y z

d

 



 



.

Câu 55. (Chuyên Phan Bội Châu 2019) Trong không gian với hệ tọa độ

Oxyz

, cho đường thẳng

1 2 1

:

2 1 3

x y z

d

  

 

và mặt phẳng

( ) : 3 0P x y z   

. Đường thẳng

'd

là hình chiếu của

d

d'

d

P

M

N

M'

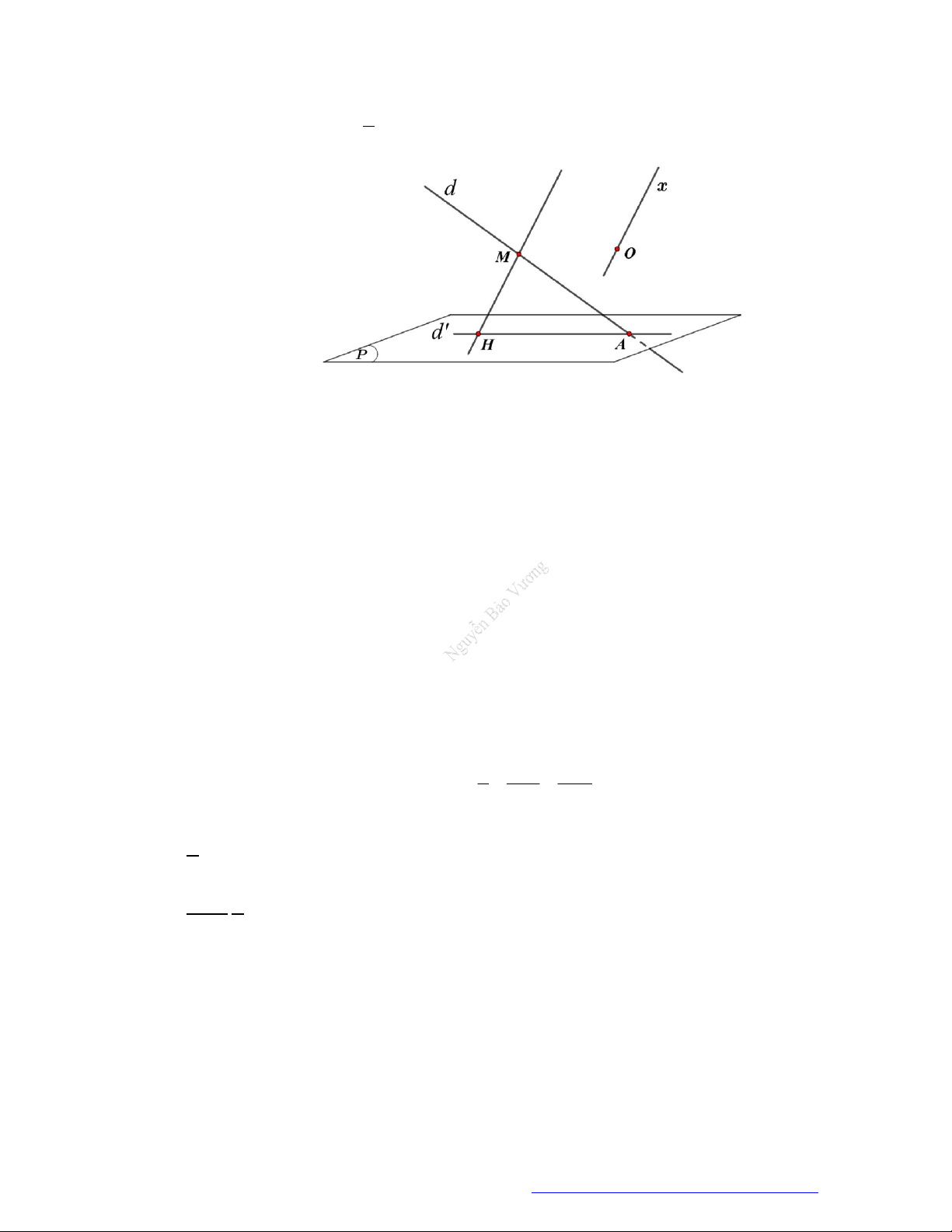
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 31

theo phương

Ox

lên

( )P

;

'd

nhận

 

; ;2019u a b



làm một véctơ chỉ phương. Xác định tổng

a b

.

A.

2019

B.

2019

C.

2018

D.

2020

Lời giải

 Mặt phẳng

 

P

có véctơ pháp tuyến

 

1;1;1

P

n 



.

Đường thẳng

d

có véctơ chỉ phương là

 

2;1;3

d

u 



, đường thẳng chứa trục

Ox

có có véctơ chỉ

phương

 

1;0;0i 



.

 Gọi

 

Q

là mặt phẳng chứa đường thẳng

d

và song song (hoặc chứa) trục

Ox

.

Khi đó

 

Q

có véctơ pháp tuyến

 

, 0;3; 1

d

Q

n u i

 

  

 



 

.

 Đường thẳng

'd

chính là giao tuyến của

 

P

và

 

Q

.

 Vectơ chỉ phương của

'd

là

   

 

1

, 4;1;3

P Q

u n n

 

  

 

  

.

Suy ra:

 

2692;673;2019u 



cũng là chỉ phương của

'd

.

Ta có:

2692 673 2019a b     

.

Câu 56. (THPT Đông Sơn 1 - Thanh Hóa 2019) Trong không gian với hệ tọa độ

,Oxyz

cho mặt phẳng

 

: 3 0P x y z   

và đường thẳng

1 2

:

1 2 1

x y z

d

 

 



. Hình chiếu của

d

trên

 

P

có

phương

trình là đường thẳng

d



. Trong các điểm sau điểm nào thuộc đường thẳng

d



:

A.

 

2;5; 4M 

. B.

 

1;3; 1P 

. C.

 

1; 1;3N 

. D.

 

2;7; 6Q 

.

Lời giải

Chọn A

Gọi

 

A d P 

. Vì

 

: 1 2 ; 1 2 ;2

2

x t

A d y t A t t t

z t







       





 



.

Mặt khác

 

1 2 2 3 0 1A P t t t t         

. Vậy

 

1;1;1A

.

Lấy

 

0; 1;2B d 

. Gọi



là đường thẳng qua

B

và vuông góc

 

P

.

Thì

: 1

2

x t

y t

z t











   







 



. Gọi

C

là hình chiếu của

B

lên

 

P

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 32 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Suy ra

 

; 1 ;2C C t t t

  

    

.

Mặt khác

 

2

1 2 3 0

3

C P t t t t

   

         

. Vậy

2 1 8

; ;

3 3 3

C



 

 

 

.

Lúc này

d



qua

 

1;1;1A

và có một vectơ chỉ phương là

1 4 5

; ;

3 3 3

AC

 

 



 

 



. Hay

d



nhận

 

1;4; 5u  



làm một vectơ chỉ phương.

Suy ra

1

: 1 4

1 5

x s

d y s

z s

 







 





 



. Vậy điểm thuộc đường thẳng

d



là

 

2;5; 4M 

.

Câu 57. (THPT Phan Bội Châu - Nghệ An - 2019) Trong không gian với hệ tọa độ

Oxyz

, cho đường

thẳng

1 2 1

:

2 1 3

x y z

d

  

 

và mặt phẳng

 

: 3 0P x y z   

. Đường thẳng

d



là hình chiếu

của

d

theo phương

Ox

lên

 

P

,

d



nhận

 

; ;2019u a b



là một vectơ chỉ phương. Xác định

tổng

 

.a b

A.

2019

. B.

2019

. C.

2018

. D.

2020

.

Lời giải

Chọn B

Chọn

     

1;2; 1 ; 2;1;3 ; , 0;3; 1 .

d

A d u u i

 

    

 



 

Ta thấy

; . 7 0

d

u i OA d

 

  

 





và

Ox

chéo nhau.

Gọi

 

Q

là mặt phẳng chứa

d

và song song với

.Ox

Một vectơ pháp tuyến của mặt phẳng

 

Q

là

 

; 0;3; 1 .

Q d

n u i

 

  

 



 

Hình chiếu

d



của

d

trên mặt phẳng

 

P

là đường giao tuyến giữa hai mặt phẳng

 

P

và

 

.Q

d



có một vectơ chỉ phương là

   

; 4;1;3 673 ; 2692;673;2019

Q P Q P

n n u n n

   

     

   

    

cũng

là một vectơ chỉ phương.

Vậy

2019.a b  

.

Câu 58. (SGD Bắc Ninh 2019) Trong không gian với hệ tọa độ

Oxyz

, cho đường thẳng

1 1 2

:

1 2 1

x y z

d

  

 



và mặt phẳng

 

: 2 2 1 0P x y z   

. Gọi

d



là hình chiếu của đường

thẳng

d

lên mặt phẳng

 

P

, véc tơ chỉ phương của đường thẳng

d



là

A.

 

3

5; 6; 13u   



. B.

 

2

5; 4; 3u   



.

C.

 

4

5;16;13u 



. D.

 

1

5;16; 13u  



.

Lời giải

Chọn D

Đường thẳng

d

đi qua điểm

 

1;1;2A

và có 1 véc tơ chỉ phương

 

1;2; 1

d

u  



.

n

Q

P

d

x

O

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 33

Mặt phẳng

 

P

có 1 véc tơ pháp tuyến

 

2;1;2

P

n 



.

Gọi

d

u





là một véc tơ chỉ phương của đường thẳng

d



.

Gọi

 

Q

là mặt phẳng chứa đường thẳng

d

và vuông góc với mặt phẳng

 

P

. Khi đó

 

Q

đi qua

điểm

 

1;1;2

A

và có 1 véc tơ pháp tuyến

   

 

, 5; 4; 3

d

Q P

n u n

 

   

 

  

.

d



là hình chiếu của đường thẳng

d

trên mặt phẳng

     

P d P Q



  

nên

 

d

P

d Q

u n

















 

 

. Véc

tơ chỉ phương của đường thẳng

d



là

   

 

, 5;16; 13

d

P Q

u n n



 

  

 

  

.

Câu 59. Trong không gian

Oxyz

cho mặt phẳng

 

: 3 0   

P x y z

và đường thẳng

1 2

: .

1 2 1

x y z

d

 

 



Hình chiếu vuông góc của

d

trên

 

P

có

phương trình là

A.

1 1 1

1 4 5

  

 

 

x y z

. B.

1 1 1

3 2 1

  

 

 

x y z

.

C.

1 1 1

1 4 5

  

 



x y z

. D.

1 4 5

1 1 1

  

 

x y z

.

Lời giải

Chọn C

Cách 1: Đường thẳng

d

đi qua điểm

 

0; 1;2

M 

và có một vectơ chỉ phương là

 

1;2; 1

d

u

 



.

Gọi

 

Q

là mặt phẳng chứa

d

và vuông góc với

 

P

.

 

Q

đi qua điểm

 

0; 1;2

M 

và có một vectơ pháp tuyến là

 

, 3; 2; 1

Q d P

n u n

 

   

 

  

.

 

:3 2 0   

Q x y z

.

Gọi



là hình chiếu vuông góc của

d

trên

 

P

, khi đó tập hợp các điểm thuộc



là nghiệm của

hệ phương trình

 

3 2 0

.

3 0

x y z

I

x y z

  





   



Trong hệ

 

I

cho

1z 

, ta được

1, 1x y 

. Vậy điểm

 

1;1;1

A

thuộc



.



là đường thẳng đi qua điểm

 

1;1;1

A

và có một vectơ chỉ phương

 

, 1;4; 5

P Q

u n n



 

  

 

 



nên

có phương trình chính tắc là

1 1 1

1 4 5

  

 



x y z

.

Cách 2: Gọi

 

A d P

 

.

 

; 1 2 ;2

A d A t t t    

.

       

1 2 2 3 0 2 2 0 1 1;1;1

A P t t t t t A              

.

Lấy điểm

 

0; 1;2

M d 

. Gọi



là đường thẳng đi qua

M

và vuông góc với

 

P

. Khi đó



có

phương trình tham số là

1

2

x t

y t

z t







  





 



.

Gọi

 

B P

  

.

 

; 1 ;2

B B t t t     

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 34 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

     

2 2 1 8

1 2 3 0 3 2 0 ; ;

3 3 3 3

B P t t t t t B



 

              

 

 

.

Phương trình hình chiếu vuông góc của

d

trên mặt phẳng

 

P

là đường thẳng

AB

đi qua điểm

 

1;1;1

A

và có một vectơ chỉ phương

 

1 4 5

3. 3. ; ; 1;4; 5

3 3 3

u AB

 

 

     

 

 





nên có phương

trình chính tắc là

1 1 1

1 4 5

  

 



x y z

.

Dạng 1.4 Xác định một số phương trình đường thẳng đặc biệt (phân giác, trung tuyến, giao

tuyến…)

Hai đường thẳng

1 2

,d d

cắt nhau tại điểm

 

0 0 0

; ;A x y z

và có vécto chỉ phương |ân lượt là

   

1 1 1 1 2 2 2 2

; ; , ; ;u a b c u a b c

 

Đường thẳng phân giác của góc tạo bởi hai đường thẳng này có vécto chỉ phương được xác định theo công

thức

   

1 2 1 1 1 2 2 2

2 2 2 2 2 2

1 2

1 1 1 2 2 2

1 1 1 1

; ; ; ;u u u a b c a b c

u u

a b c a b c

     

   

 



Chi tiết có hai phân giác:

Nếu

1 2 1 2

1 2

1 1

0

u u u u u

u u

     

  



là vécto chỉ phương của phân

giác tạo bởi góc nhọn giữa hai đường thẳng và

1 2

1 1

u u u

u u

   

 



là vécto chỉ phương của phân giác tạo

bởi góc tù giữa hai đường thẳng.

Nếu

1 2 1 2

1 2

1 1

0

u u u u u

u u

     

  



là vécto chỉ phương của phân

giác tạo bởi góc tù giữa hai đường thẳng và

1 2

1 1

u u u

u u

   

 



là vécto chỉ phương của phân giác tạo bởi

góc nhọn giữa hai đường thẳng.

Câu 60. (Mã 102 2018) Trong không gian

Oxyz

, cho đường thẳng

1 3

: 3

5 4

 





 





 



x t

d y

z t

. Gọi



là đường thẳng

đi qua điểm

 

1; 3;5

A

và có vectơ chỉ phương

 

1;2; 2



u

. Đường phân giác của góc nhọn tạo bởi

d

và



có phương trình là

A.

1 2

2 5

6 11

  





 





 



x t

y t

z t

B.

1 2

2 5

6 11

  





 





  



x t

y t

z t

C.

1 7

3 5

5

 





  





 



x t

y t

z t

D.

1

3

5 7

 





 





 



x t

y

z t

Lời giải

Chọn B

Ta có điểm

 

1; 3;5

A

thuộc đường thẳng

d

, nên

 

1; 3;5

A

là giao điểm của

d

và



.

Một vectơ chỉ phương của đường thẳng

d

là

 

3;0; 4 



v

. Ta xét:

1

.



 



u u

u

 

1

1;2; 2

3

 

1 2 2

; ;

3 3 3

 

 

 

 

;

1

.



 



v v

v

 

1

3;0; 4

5

  

3 4

;0;

5 5

 

  

 

 

.

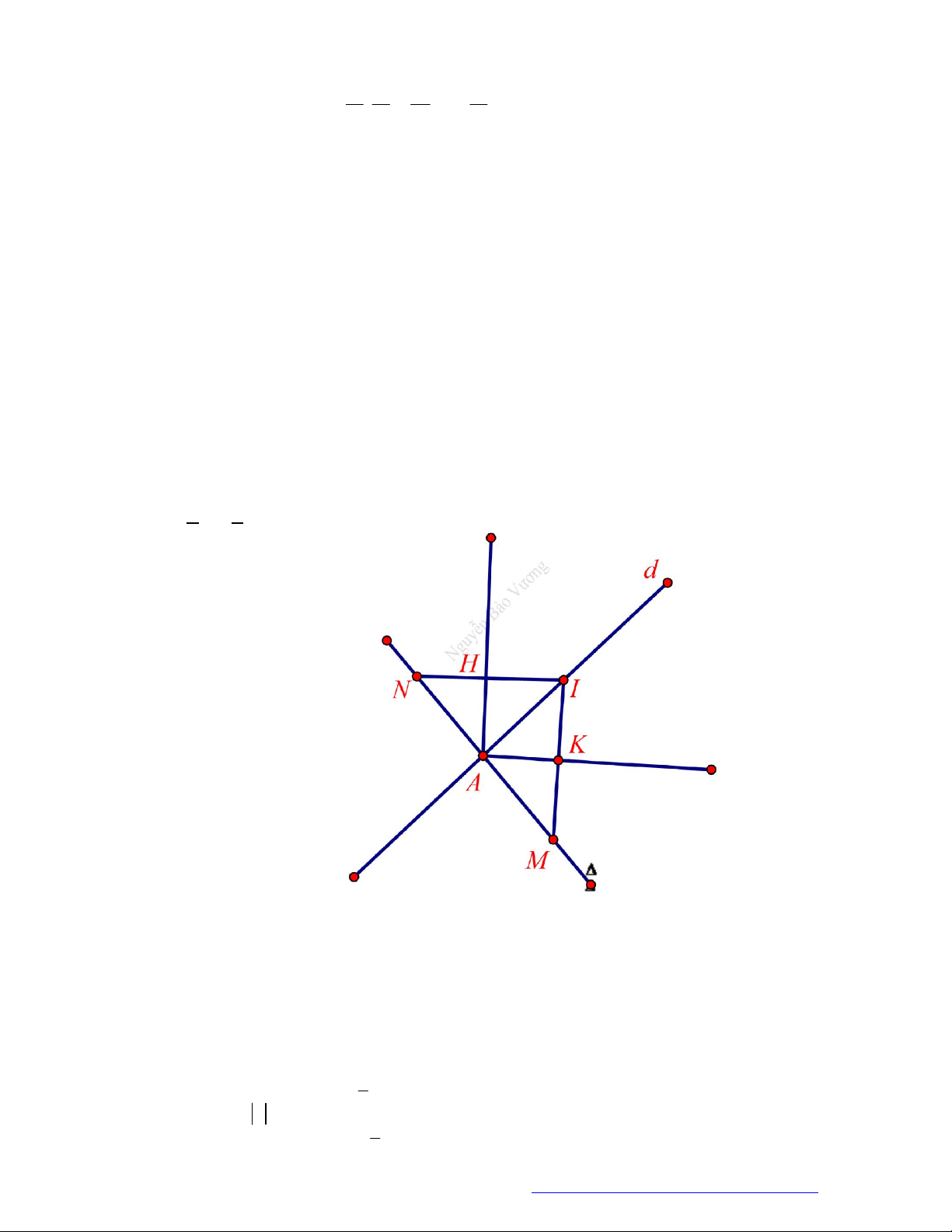
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 35

Nhận thấy

1 1

. 0

 

u v

, nên góc tạo bởi hai vectơ

1



u

,

1



v

là góc nhọn tạo bởi

d

và



.

Ta có

1 1

w  

  

u v

4 10 22

; ;

15 15 15

 

  

 

 

 

15

2; 5;11

2

  

là vectơ chỉ phương của đường phân giác

của góc nhọn tạo bởi

d

và



hay đường phân giác của góc nhọn tạo bởi

d

và



có vectơ chỉ

phương là

 

1

w 2; 5;11 



. Do đó có phương trình:

1 2

2 5

6 11

  





 





  



x t

y t

z t

.

Câu 61. (Mã 101 2018) Trong không gian

Oxyz

, cho đường thẳng

1 7

: 1 4

1

x t

d y t

z

 





 









. Gọi



là đường thẳng

đi qua điểm

 

1;1;1A

và có vectơ chỉ phương

 

1; 2;2u



  . Đường phân giác của góc nhọn tạo

bởi

d

và



có phương trình là.

A.

1 2

10 11

6 5

x t

y t

z t

  





  





  



B.

1 2

10 11

6 5

x t

y t

z t

  





  





 



C.

1 3

1 4

1 5

x t

y t

z t

  





 





 



D.

1 7

1

1 5

x t

y t

z t

 





 





 



Lời giải

Chọn B

Phương trình

1 '

: 1 2 '

1 2 '

x t

y t

z t

 





  





 



.

Ta có

 

1;1;1d A  

. Lấy

 

4;5;1I d

 

3;4;0 5AI AI



   

.

Gọi

 

1 ';1 2 ';1 2 'M t t t    

sao cho

AM AI

.

Khi đó

5

'

3

3 ' 5

5

'

3

t







 



 





.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 36 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Với

5

'

3

t



8 7 13

; ;

3 3 3

M

 

 

 

 

5 10 10 15

; ;

3 3 3 3

AM AM





 

   

 

 

.

Khi đó

 

0

1

cos 90

3

IAM IAM   



trong trường hợp này

 

0

; 90

d  

( loại)

Với

5

'

3

t

 

2 13 7

; ;

3 3 3

N



 

 

 

 

5 10 10 15

; ;

3 3 3 3

AN AN



 

     

 

 

.

Khi đó



0

1

cos 90

3

IAN IAM  



trong trường hợp này

 

0

; 90

d  

(thỏa mãn)

Gọi

H

là trung điểm của

 

5 14 2 1

; ; 2;11; 5

3 3 3 3

NI H AH





 

   

 

 

.

Khi đó đường phân giác của góc nhọn tạo bởi

d

và



đi qua

5 14 2

; ;

3 3 3

H



 

 

 

hoặc

 

1;1;1

A

và nhận làm

 

2;11; 5

u



 

VTCP



phương trình phân giác là

1 2

10 11

6 5

x t

y t

z t

  





  





 



.

Câu 62. (Mã 104 2018) Trong không gian

Oxyz

, cho đường thẳng

1 3

: 1 4

1

x t

d y t

z

 





 









. Gọi



là đường thẳng

đi qua điểm

 

1;1;1

A

và có vectơ chỉ phương

 

2;1; 2

u  



. Đường phân giác của góc nhọn tạo

bởi

d

và



có phương trình là.

A.

1 27

1

x t

y t

z t

 





 





 



B.

18 19

6 7

11 10

x t

y t

z t

  





  





 



C.

18 19

6 7

11 10

x t

y t

z t

  





  





  



D.

1

1 17

1 10

x t

y t

z t

 





 





 



Lời giải

Chọn B

A d

  

Phương trình tham số của đường thẳng

1 2

: 1 1

1 2

x t

y t

z t

 





  





 



.

Chọn điểm

 

1;2;3 , 3

B AB

  

.

Gọi

C d

thỏa mãn

AC AB

14 17

; ;1

5 5

C

 



 

 

hoặc

4 7

; ;1

5 5

C

 

 

 

 

Kiểm tra được điểm

4 7

; ;1

5 5

C

 

 

 

 

thỏa mãn

BAC

là góc nhọn.

Trung điểm của

BC

là

9 3

; ;2

10 10

I

 



 

 

.Đường phân giác cần tìm là

AI

có vectơ chỉ phương là

 

19;7; 10

u  



có phương trình là

1 19

1 7

1 10

x t

y t

z t

 





 





 



. Tọa độ điểm của đáp án B thuộc

AI

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 37

Câu 63. (Mã 103 2018) Trong không gian

Oxyz

, cho đường thẳng

1

: 2 .

3

x t

d y t

z

 





 









Gọi



là đường thẳng

đi qua điểm

(1;2;3)

A

và có vectơ chỉ phương

(0; 7; 1).

u

  



Đường phân giác của góc nhọn tạo

bởi

d

và



có phương trình là

A.

1 5

2 2 .

3

x t

y t

z t

 





 





 



B.

1 6

2 11 .

3 8

x t

y t

z t

 





 





 



C.

4 5

10 12 .

2

x t

y t

z t

  





  





 



D.

4 5

10 12 .

2

x t

y t

z t

  





  





  



Lời giải

Chọn C

Đường thẳng

d

đi qua

(1;2;3)

A

và có VTCP

(1;1;0)

a





.

Ta có

. 1.0 1.( 7) 0.( 1) 7 0 ( , ) 90 .

a u a u



         

   

Đường phân giác của góc nhọn tạo bởi

d

và



có VTCP:

   

1

5;12;1 // 5;12;1

5 2

u a

b

u a

   

 



 

.

Phương trình đường thẳng cần tìm là

4 5

10 12 .

2

x t

y t

z t

  





  





 



Câu 64. (THPT An Lão Hải Phòng 2019) Trong không gian với hệ tọa độ

Oxyz

, cho tam giác

ABC

có

     

1;3;2 2;0;5 , ;,

0 2;1

A B C 

. Viết phương trình đường trung tuyến

AM

của tam giác

ABC

.

A.

1 3 2

:

2 4 1

x y z

AM

  

 



B.

1 3 2

:

2 4 1

x y z

AM

  

 



C.

1 3 2

:

2 4 1

x y z

AM

  

 



D.

2 4 1

:

1 1 3

x y z

AM

  

 



Lời giải

Chọn A

Gọi

 

; ;M x y z

là trung điểm

BC

. Khi đó

 

1; 1;3

M 

Ta có

 

2; 4;1

AM vtcpu  

 

PTĐT

1 3 2

:

2 4 1

x y z

AM

  

 



Câu 65. (THPT Yên Phong 1 Bắc Ninh 2019) Trong không gian

Oxyz

, cho

 

2;0;0

A

, đường thẳng

d

đi qua

A

cắt chiều âm trục

Oy

tại điểm

B

sao cho diện tích tam giác

OAB

bằng 1. Phương trình

tham số đường thẳng

d

là

A.

1 2

0

x t

y t

z

 















. B.

2 2

0

x t

y t

z

 





 









. C.

2 2

0

x t

y t

z

 





 









. D.

2 2

1

x t

y t

z

 















.

Lời giải

Gọi

 

0; ;0B b

là giao điểm của

d

với trục

Oy

. (Điều kiện

0

b



)

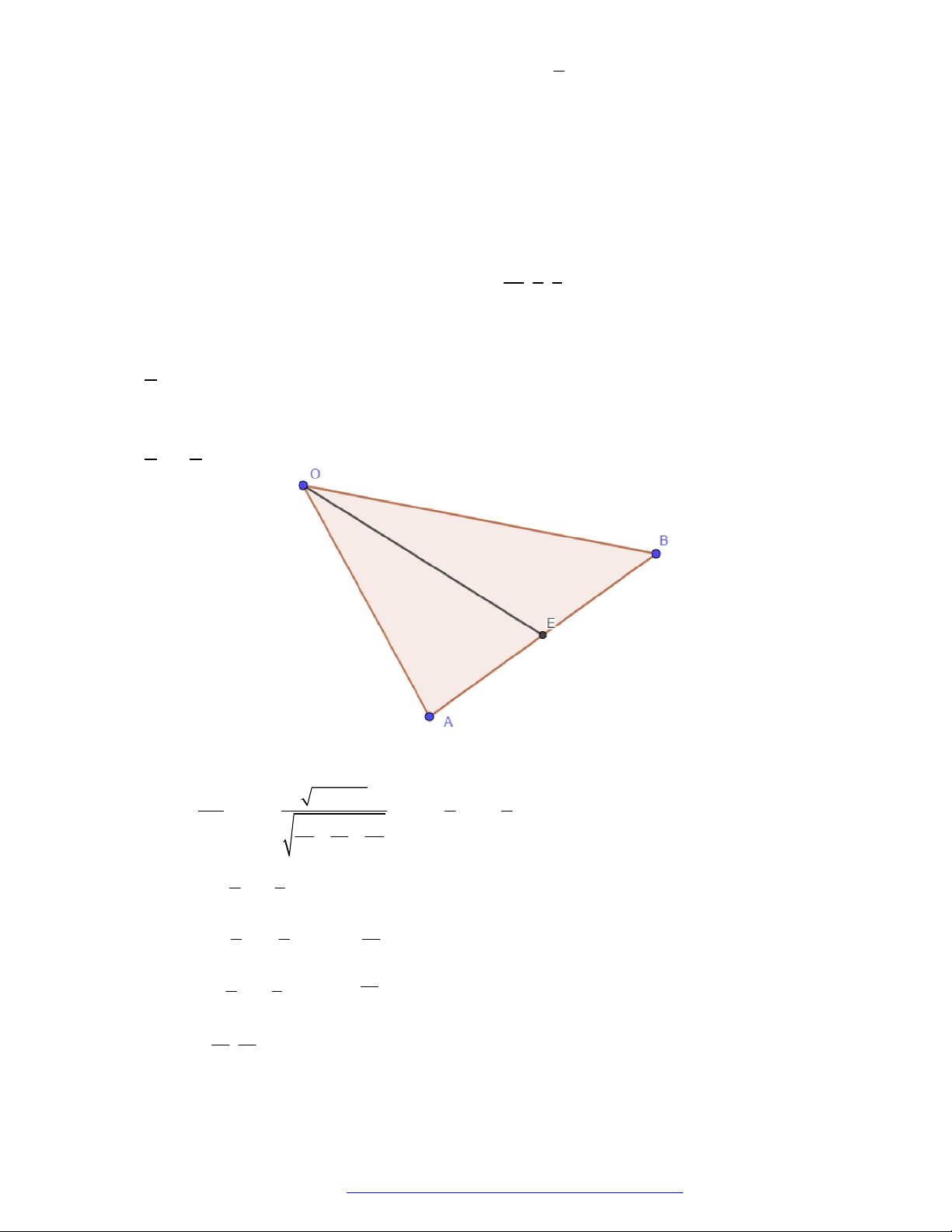
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 38 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Ta có

2OA 

và tam giác

OAB

vuông tại

O

nên

1

. 1 1

2

OAB

S OAOB OB



   

Suy ra

 

0; 1;0B 

. Ta có

 

2; 1;0AB   



là một vec tơ chỉ phương của

d

.

Và đường thẳng

d

đi qua điểm

 

2;0;0A

nên

2 2

0

x t

y t

z

 





 









.

Câu 66. Trong không gian

Oxyz

cho hai điểm

8 4 8

(2;2;1), ( ; ; )

3 3 3

A B



. Đường phân giác trong của tam giác

OAB

có phương trình là

A.

0x

y t

z t

















B.

4x t

y t

z t













 



C.

14

2

5

x t

y t

z t













 



D.

2

14

13

x t

y t

z t

















Lời giải

Chọn A

Ta có:

4 4 1 3 3

. . . .

4 4

64 16 64

9 9 9

3 8

2 x

4 3

0

3 4 12

2

4 3 7

12

3 8

1

7

4 3

OA

EA EB EB EB BE

OB

x

y y y

z

z z

 

      

 



 



  

 





 



 

     

 

 

 

 

 



  

 

 



 



    

12 12

0; ; (0;1;1)

7 7

O

:

0

:

OE u

qua

VTCP u

x

y t

z t

 

  

 

 













 















 



TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 39

Câu 67. (Chuyên Hạ Long 2019) Trong không gian với hệ trục tọa độ

Oxyz

cho hai đường thẳng

1

4

6 2

x t

d y t

z t

 





  





 



;

2

5 11 5

:

2 4 2

x y z

d

  

 

. Đường thẳng

d

đi qua

 

5; 3;5

A 

cắt

1 2

;d d

lần lượt ở

,B C

.Tính tỉ sô

AB

AC

.

A.

2

. B.

3

. C.

1

2

. D.

1

3

.

Lời giải

 

1

4 ; 4 ;6 2B d B t t t

     

. PT tham số của

2

5 2

: 11 4

5 2

x s

d y s

z s

 





 





 



.

 

2

5 2 ;11 4s;5 2C d C s s

    

. Khi đó:

(1 ; 1 ;2 1); (2s;4s 14;2s)

AB t t t AC      

 

.

Do

, ,A B C

thẳng hàng

,AB AC





cùng phương

:

k AB k AC

   

 



1 2 2

1 4 14 3

2 1 2 1

2

t ks t

t ks k s

t ks

k





   





       

 

 

 









. Do đó:

1 1

.

2 2

AB

AB AC

AC

  

 

Câu 68. (THPT Gang Thép Thái Nguyên -2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho

2

điểm

   

1;2;3 , 2;4;4

M A

và hai mặt phẳng

 

: 2 1 0

P x y z

   

,

 

: 2 4 0.

Q x y z

   

Viết phương trình đường thẳng



đi qua

M

, cắt

( ), ( )P Q

lần lượt tại

,B C

sao cho tam giác

ABC

cân tại

A

và nhận

AM

làm đường trung tuyến.

A.

1 2 3

1 1 1

x y z

  

 

 

. B.

1 2 3

2 1 1

x y z

  

 



.

C.

1 2 3

1 1 1

x y z

  

 



. D.

1 2 3

1 1 1

x y z

  

 

 

.

Lời giải

Điểm

B

thuộc mặt

( )P

nên

 

2 1; ;B c b b c

 

vì

 

1;2;3

M

là trung điểm

BC

nên

 

3 2 ;4 ;6

C c b b c   

. Do

C

thuộc mặt

(Q)

nên

3 7 0 3 7

c c c b

     

. Khi đó

(5 15; ;3 7)

B b b b

 

,

( 5 17;4 ;13 3 )C b b b   

.

( 10 32; 2 4; 6 20)

BC b b b     



.

ABC

cân tại

A

nên

. 0 20 60 0 3 (0;3;2) .

BC AM b b B      

 

Đường thẳng



đi qua

(1;2;3)

M

và

(0;3;2)

B

có phương trình là

1 2 3

1 1 1

x y z

  

 



.

Câu 69. (Chuyên Bắc Giang 2019) Trong không gian với hệ tọa độ Oxyz cho tam giác ABC biết

(2;1;0), (3;0;2), (4;3; 4)

A B C



. Viết phương trình đường phân giác trong góc A.

A.

2

1

0

x

y t

z







 









B.

2

1

x

y

z t

















C.

2

1

0

x t

y

z

 















D.

2

1

x t

y

z t

 















Lời giải

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 40 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Chọn C

Ta có

 

1; 1; 2AB  



và

 

2; 2; 4AC  



.

Gọi

M

là trung điểm

AC

, ta có

 

3; 2; 2M 

,

 

1; 1; 2AM  



.

Do đó

ABM

cân tại

A

. Gọi

K

là điểm thỏa mãn

 

2; 0; 0AK AM AB  

  

. Khi đó

AK

là tia

phân giác trong góc



BAC .

Vậy phương trình đường phân giác trong góc



BAC là

2

1 ,

0

x t

y t

z

 





 











.

Câu 70. (Chuyên Nguyễn Tất Thành Yên Bái 2019) Trong không gian với hệ tọa độ

Oxyz

, cho đường

thẳng

1 2

:

2 1 1

x y z

d

 

 

, mặt phẳng

 

: 2 5 0P x y z   

và

 

1; 1;2A 

. Đường thẳng



cắt

d

và

 

P

lần lượt tại

M

và

N

sao cho

A

là trung điểm của đoạn thẳng

MN

. Một vectơ chỉ

phương của



là

A.

 

4; 5; 13u  



. B.

 

2; 3; 2u 



. C.

 

1; 1; 2u  



. D.

 

3; 5; 1u  



.

Lời giải

Ta có

1 2

:

2 1 1

2

x t

x y z

d y t

z t

  



 



   





 



. Do đó

M d

 

1 2 ; ;2M t t t   

.

Vì

 

1; 1;2A 

là trung điểm

MN

 

3 2 ; 2 ;2N t t t    

.

Mặt khác

 

N P

 

3 2 2 2 2 5 0t t t       

 

2 3;2;4t M  

 

2;3; 2AM 



là một

vectơ chỉ phương của



.

Câu 71. (THPT Phan Đình Phùng - Hà Tĩnh - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho hình

vuông

ABCD

biết

 

1;0;1A

,

 

1;0; 3B 

và điểm

D

có hoành độ âm. Mặt phẳng

 

ABCD

đi qua

K

C

M

B

A

d



P

M

N

A

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 41

gốc tọa độ

O

. Khi đó đường thẳng

d

là trục đường tròn ngoại tiếp hình vuông

ABCD

có phương

trình

A.

1

:

1

x

d y t

z

 











 



. B.

1

:

1

x

d y t

z













 



. C.

1

:

1

x

d y t

z

 















. D.

: 1

x t

d y

z t

















.

Lời giải

Ta có

   

0;0; 4 4 0;0;1

AB    



. Hay

AB

có véc-tơ chỉ phương

 

0;0;1

k 



.

Mặt phẳng

 

ABCD

có một véc-tơ pháp tuyến:

   

; 0;4;0 4 0;1;0

OA OB

 

 

 

 

, hay

 

0;1;0

j 



là một véc-tơ pháp tuyến của mặt phẳng

 

ABCD

.

Vì

 

AD AB

AD ABCD















nên

AD k

AD j















 

. Đường thẳng

AD

có véc-tơ chỉ phương là

 

; 1;0;0

j k

 



 

 

.

Phương trình đường thẳng

AD

là:

1

0

1

x t

y

z

 















.

Do đó

 

1 ;0;1

D t

.

Mặt khác

 

2

2 2

4

0 1 1 4

4

t

AD AB t

t





      



 



.

Vì điểm

D

có hoành độ âm nên

 

3;0;1

D 

.

Vì tâm

I

của hình vuông

ABCD

là trung điểm

BD

, nên

 

1;0; 1

I

  

.

Đường thẳng

d

là trục đường tròn ngoại tiếp hình vuông

ABCD

có véc-tơ pháp tuyến là

 

0;1;0

j 



, nên phương trình đường thẳng

d

là:

1

:

1

x

d y t

z

 











 



.

Câu 72. (THPT Nghen - Hà Tĩnh - 2018) Trong không gian với hệ toạ độ

Oxyz

, cho hai đường thẳng

1

1 2 1

:

1 2 3

x y z  

  

và

2

1 2 1

:

1 2 3

x y z  

  



cắt nhau và cùng nằm trong mặt phẳng

 

P

.

Lập phương trình đường phân giác

d

của góc nhọn tạo bởi

1



,

2



và nằm trong mặt phẳng

 

P

.

A.

 

1

: 2 ,

1

x

d y t

z t

 





 





  





. B.

 

1

: 2 ,

1 2

x t

d y t

z t

  





 





  





.

C.

 

1

: 2 2 ,

1

x t

d y t t

z t

  





  





  





. D.

 

1

: 2 2 ,

1

x t

d y t t

z

  





  





 





Lời giải

Nhận thấy

 

1;2; 1

A

 

là giao điểm của

1



và

2



.

1



có VTCP là

 

1

1;2;3

u 



2



có VTCP là

 

2

1;2; 3

u

 



.

   

1 2

; 12;6;0 6 2; 1;0

u u

 

    

 

 

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 42 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Phương trình mặt phẳng

 

P

:

2 4 0

x y

  

.

Gọi

 

; ;u a b c





là VTCP của

d

cần tìm.

Ta có

d

nằm trong mặt phẳng

 

P

chứa hai đường thẳng

1



,

2



1 2

;u u u

 

 

 

  

2 0

a b

  

2b a 

Lại có

d

là phân giác của

1



,

2



   

1 2

cos , cos ,

d d

   

2 2 2 2 2 2

2 3 2 3

. 14 . 14

a b c a b c

   

 

   

2 3 2 3

a b c a b c

    







     



 

0 1

2 0 2

c

a b







 





.

Xét

 

1

,

0

c



,

2b a

   

,2 ,0 1;2;0

u a a  



.

1

: 2 2 ,

1

x t

d y t t

z

  





   





 





.

 

1

1.1 2.2

70

cos ;

14

14. 5

d



  

 

1

; 53 18'

d

   

.

Xét

 

2

:

2 0

0

2

a b

b a

 



  







   

0;0; 0;0;1

u c c  



1

: 2 ,

1

x

d y t

z t

 





  





  





.

 

1

3

cos ,

14.1 14

d



  

 

1

, 36 42'

d

   

.

Do

d

là đường phân giác của góc nhọn nên

 

1

, 45

d

  

.

Vậy đường thẳng

d

cần tìm là

1

: 2 ,

1

x

d y t

z t

 





 





  





.

Nhận xét: Có thể làm đơn giản hơn bằng cách: ta thấy

 

1

1;2;3

u 



;

 

2

1;2; 3

u

 



là hai véc tơ có

độ dài bằng nhau và

 

1 2 1 2

. 0 , 90

u u u u

   

   

. Vậy

 

1 2

u u



 

chính là véc tơ chỉ phương của

d

.

Câu 73. (Quảng Xương - Thanh Hóa - 2018) Trong không gian tọa độ

Oxyz

, cho tam giác

ABC

biết

 

1;0; 1

A



,

 

2;3; 1

B



,

 

2;1;1

C 

. Phương trình đường thẳng đi qua tâm đường tròn ngoại tiếp

của tam giác

ABC

và vuông góc với mặt phẳng

 

ABC

là:

A.

3 1 5

x y z  

 



. B.

2

3 1 5

x y z

 

.

C.

1 1

1 2 2

x y z 

 



. D.

3 2 5

3 1 5

x y z  

 



.

Lời giải

Ta có:

 

1;3;0

AB 



;

 

4; 2;2

BC   



,

 

3;1;2

AC  



2

10

AB

 

,

2

24

BC



,

2

14

AC



ABC 

vuông tại

A

.

Tâm

I

của đường tròn ngoại tiếp tam giác là trung điểm của

BC

 

0;2;0

I

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 43

Đường thẳng

d

cần tìm đi qua

 

0;2;0I

và nhận vectơ

1

,

2

u AB AC

 



 

  

 

3; 1;5 

làm véc tơ

chỉ phương. Phương trình chính tắc của đường thẳng

d

là:

3 1 5

x y z  

 



.

Câu 74. (SGD Bắc Giang - 2018) Trong không gian

Oxyz

, cho tam giác nhọn

ABC

có

 

2;2;1H

,

8 4 8

; ;

3 3 3

K

 



 

 

,

O

lần lượt là hình chiếu vuông góc của

A

,

B

,

C

trên các cạnh

BC

,

AC

,

AB

.

Đường thẳng

d

qua

A

và vuông góc với mặt phẳng

 

ABC

có phương trình là

A.

4 1 1

:

1 2 2

x y z

d

  

 



. B.

8 2 2

3 3 3

:

1 2 2

x y z

d

  

 



.

C.

4 17 19

9 9 9

:

1 2 2

x y z

d

  

 



. D.

6 6

:

1 2 2

x y z

d

 

 



.

Lời giải

Ta có tứ giác

BOKC

là tứ giác nội tiếp đường tròn ( vì có hai góc vuông

K

,

O

cùng nhìn

BC

dưới một góc vuông) suy ra

 

 

1OKB OCB

Ta có tứ giác

KDHC

là tứ giác nội tiếp đường tròn ( vì có hai góc vuông

K

,

H

cùng nhìn

DC

dưới một góc vuông) suy ra



 

2DKH OCB

Từ

 

1

và

 

2

suy ra



DKH OKB

do đó

BK

là đường phân giác trong của góc



OKH và

AC

là đường phân giác ngoài của góc



OKH .

Tương tự ta chứng minh được

OC

là đường phân giác trong của góc



KOH và

AB

là đường

phân giác ngoài của góc



KOH .

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 44 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Ta có

4

OK



;

3

OH



;

5

KH



.

Gọi

I

,

J

lần lượt là chân đường phân giác ngoài của góc



OKH

và



KOH

.

Ta có

I AC HO 

ta có

4

5

IO KO

IH KH

 

4

5

IO IH

 

 

 

8; 8; 4

I

   

.

Ta có

J AB KH 

ta có

4

3

JK OK

JH OH

 

 

4

16;4; 4

3

JK JH J

   

 

.

Đường thẳng

IK

qua

I

nhận

 

16 28 20 4

; ; 4;7;5

3 3 3 3

IK

 

 

 

 



làm vec tơ chỉ phương có phương

trình

 

8 4

: 8 7

4 5

x t

IK y t

z t

  





  





  



Đường thẳng

OJ

qua

O

nhận

   

16;4; 4 4 4;1; 1

OJ

   



làm vec tơ chỉ phương có phương

trình

 

4

:

x t

OJ y t

z t



















 



Khi đó

A IK OJ 

, giải hệ ta tìm được

 

4; 1;1

A  

.

Ta có

 

4;7;5

IA 



và

 

24;12;0

IJ 



, ta tính

   

, 60;120; 120 60 1; 2;2

IA IJ

 

     

 

 

.

Khi đó đường thẳng đi qua

A

và vuông góc với mặt phẳng

 

ABC

có véc tơ chỉ phương

 

1; 2;2

u  



nên có phương trình

4 1 1

1 2 2

x y z  

 



.

Nhận xét:

 Mấu chốt của bài toán trên là chứng minh trực tâm

D

của tam giác

ABC

là tâm đường tròn

nội tiếp tam giác

OHK

. Khi đó, ta tìm tọa độ điểm

D

dựa vào tính chất quen thuộc sau: “Cho

tam giác

ABC

với

I

là tâm đường tròn nội tiếp, ta có

. . . 0

a IA b IB c IC

  

   

, với

a BC

,

b CA

,

c AB

”. Sau khi tìm được

D

, ta tìm được

A

với chú ý rằng

A DH

và

OA DA

.

 Ta cũng có thể tìm ngay tọa độ điểm

A

bằng cách chứng minh

A

là tâm đường tròn bàng tiếp

góc

H

của tam giác

OHK

. Khi đó, ta tìm tọa độ điểm

D

dựa vào tính chất quen thuộc sau: “Cho

tam giác

ABC

với

J

là tâm đường tròn bàng tiếp góc

A

, ta có

. . . 0

a JA b JB c JC

   

   

, với

a BC

,

b CA

,

c AB

”.

Câu 75. (Chuyên Vinh - 2018) Trong không gian

Oxyz

, cho tam giác

ABC

có

 

2;3;3

A

, phương trình

đường trung tuyến kẻ từ

B

là

3 3 2

1 2 1

x y z

  

 

 

, phương trình đường phân giác trong của góc

C

là

2 4 2

2 1 1

x y z

  

 

 

. Đường thẳng

AB

có một véc-tơ chỉ phương là

A.

 

3

2;1; 1

u

 



. B.

 

2

1; 1;0

u  



. C.

 

4

0;1; 1

u

 



. D.

 

1

1;2;1

u 



.

Lời giải

Phương trình tham số của đường phân giác trong góc

C

là

2 2

: 4

2

x t

CD y t

z t

 





 





 



.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 45

Gọi

 

2 2 ; 4 ;2

C t t t   

, suy ra tọa độ trung điểm

M

của

AC

là

7 5

2 ; ;

2 2

t t

M t

 

 

 

 

 

. Vì

M BM

nên:

 

7 5

3 2

2 3

2 2

1 2 1

t t

t

 

   

 

   

 

   

 

 

1 1 1

1

1 4 2

t t t

t

  

    

 

.

Do đó

 

4;3;1

C 

.

Phương trình mặt phẳng

 

P

đi qua

A

và vuông góc

CD

là

     

2. 2 1. 3 1. 3 0

x y z

     

hay

2 2 0

x y z

   

.

Tọa độ giao điểm

H

của

 

P

và

CD

là nghiệm

 

; ;x y z

của hệ

2 2

4

2

2 2 0

x t

y t

z t

x y z

 





 





 



   



     

2 2

4

2

2 2 2 4 2 2 0

x t

y t

z t

t t t

 





 







 



      



2

4

2

0

x

y

z

t























 

2;4;2

H

.

Gọi

A



là điểm đối xứng với

A

qua đường phân giác

CD

, suy ra

H

là trung điểm

AA



, bởi vậy:

2 2.2 2 2

2 2.4 3 5

2 2.2 3 1

A H A

x x x

y y y

x z z



    





    





    



 

2;5;1

A





.

Do

A BC





nên đường thẳng

BC

có véc-tơ chỉ phương là

   

2;2;0 2 1;1;0

CA



   



, nên

phương trình đường thẳng

BC

là

4

3

1

x t

y t

z

 





 









.

Vì

B BM BC 

nên tọa độ

B

là nghiệm

 

; ;x y z

của hệ

4

2

3

5

1

3 3

2

1

1 2

x t

x

y t

y

z

x y

t

 









 





 



 



 

 

 



 





 

 

2;5;1

B A



 

.

Đường thẳng

AB

có một véc-tơ chỉ phương là

   

0;2; 2 2 0;1; 1

AB

   



; hay

 

4

0;1; 1

u

 



là

một véc-tơ chỉ của phương đường thẳng

AB

.

Câu 76. (Chuyên Quang Trung- Bình Phước 2019) Trong không gian

Oxyz

, cho mặt phẳng

 

: 3 0

P x y z

   

và đường thẳng

1 2

:

1 2 1

x y z

d

 

 



. Đường thẳng

'd

đối xứng với

d

qua mặt phẳng

 

P

có phương trình là

A.

1 1 1

1 2 7

x y z  

 



. B.

1 1 1

1 2 7

x y z  

 

.

C.

1 1 1

1 2 7

x y z

  

 

. D.

1 1 1

1 2 7

x y z

  

 



.

Lời giải

Chọn A

+

d

không vuông góc với

 

P

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 46 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Phương trình tham số của đường thẳng

: 1 2

2

x t

d y t

z t







  





 





.

Tọa độ giao điểm

I

của

d

và mặt phẳng

 

P

là nghiệm của hệ phương

trình

 

1

1 2

1 1;1;1

2

1

3 0

x t

x

y t

y I

z t

z

x y z













  



  

 

 

 

 



 







   





.

+ Lấy điểm

 

0; 1;2

M d 

.

Đường thẳng



qua

M

và vuông góc với

 

P

có phương trình

1

2

x t

y t

z t







  





 





.

 

2 1 8

; ;

3 3 3

P H H

 





   









 

.

'M

đối xứng với

M

qua

 

P H

là trung điểm của

4 1 10

' ' ; ; .

3 3 3

MM M

 















 

+ Đường thẳng

'd

đối xứng với

d

qua mặt phẳng

 

P

'd

đi qua

 

1;1;1

I

và

4 1 10

' ; ;

3 3 3

M

 













 

có vectơ chỉ phương

 

1 2 7 1

' ; ; 1; 2;7

3 3 3 3

IM

 





   









 



,

phương trình

'd

là

1 1 1

1 2 7

x y z  

 



.

Câu 77. Trong không gian

Oxyz

, cho đường thẳng

1 3

: 3

5 4

 





 





 



x t

d y

z t

. Gọi



là đường thẳng đi qua điểm

 

1; 3;5

A

và có vectơ chỉ phương

 

1;2; 2



u

. Đường phân giác của góc nhọn tạo bởi

d

và



có

phương trình là

A.

1 2

2 5

6 11

  





 





 



x t

y t

z t

. B.

1 2

2 5

6 11

  





 





  



x t

y t

z t

. C.

1 7

3 5

5

 





  





 



x t

y t

z t

. D.

1

3

5 7

 





 





 



x t

y

z t

.

Lời giải

Chọn B

Ta có điểm

 

1; 3;5

A

thuộc đường thẳng

d

, nên

 

1; 3;5

A

là giao điểm của

d

và



.

Một vectơ chỉ phương của đường thẳng

d

là

 

3;0; 4 



v

. Ta xét:

1

.



 



u u

u

 

1

1;2; 2

3

 

1 2 2

; ;

3 3 3

 

 

 

 

;

1

.



 



v v

v

 

1

3;0; 4

5

  

3 4

;0;

5 5

 

  

 

 

.

Nhận thấy

1 1

. 0

 

u v

, nên góc tạo bởi hai vectơ

1



u

,

1



v

là góc nhọn tạo bởi

d

và



.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 47

Ta có

1 1

w

 

  

u v

4 10 22

; ;

15 15 15

 

  

 

 

 

15

2; 5;11

2

  

là vectơ chỉ phương của đường phân giác

của góc nhọn tạo bởi

d

và



hay đường phân giác của góc nhọn tạo bởi

d

và



có vectơ chỉ

phương là

 

1

w 2; 5;11

 



. Do đó có phương trình:

1 2

2 5

6 11

  





 





  



x t

y t

z t

.

Câu 78. (THPT Ninh Bình-Bạc Liêu-2019) Trong không gian

Oxyz

, cho mặt phẳng

 

: 2 10 0

P x y z

   

, điểm

 

1;3;2

A

và đường thẳng

2 2

: 1

1

x t

d y t

z t

  





 





 



. Tìm phương trình

đường thẳng



cắt

 

P

và

d

lần lượt tại hai điểm

M

và

N

sao cho

A

là trung điểm của đoạn

MN

.

A.

6 1 3

7 4 1

x y z  

 



. B.

6 1 3

7 4 1

x y z

  

 



.

C.

6 1 3

7 4 1

x y z

  

 

 

. D.

6 1 3

7 4 1

x y z  

 

 

.

Lời giải

Chọn A

Theo giả thiết:

 

2 2; 1;1

N d N t t t    

.

Mà

A

là trung điểm

 

4 2 ;5 ;3

MN M t t t   

.

Mặt khác,

       

2 4 2 5 3 10 0 2

M P t t t t

           

.

   

6; 1;3 7;4; 1

N NA

     



.

Đường thẳng



đi qua

 

6; 1;3

N  

và có một VTCP là

 

7;4; 1

u NA

  

 

nên có phương trình

chính tắc là:

6 1 3

7 4 1

x y z  

 



.

Câu 79. (Chuyên Bắc Giang 2019) Trong không gian với hệ tọa độ

Oxyz

viết phương trình đường thẳng

giao tuyến của hai mặt phẳng

 

: 3 1 0

x y z

    

,

 

: 2 7 0

x y z

    

.

A.

2 3

2 3 7

x y z 

 

 

B.

2 3

2 3 7

x y z

 

 



C.

3 10

2 3 7

x y z

 

 

 

D.

2 3

2 3 7

x y z

 

 



Lời giải

Chọn D

Tọa độ các điểm thuộc giao tuyến

d

của hai mặt phẳng thỏa mãn hệ phương trình:

3 1 0

2 7 0

x y z

   





   



.

Với

0

y



 

1 2

2;0;3

2 7 3

x z x

A d

x z z

   

 

   

 

  

 

Với

 

10 0

3 0;3;10

2 10 10

x z x

y B d

x z z

   

 

    

 

  

 

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 48 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Vậy đường thẳng

d

đi qua

 

2;0;3

A

và nhận

 

2;3;7

AB  



làm vecto chỉ phương có phương

trình chính tắc là:

2 3

2 3 7

x y z

 

 



.

Câu 80. Đường thẳng



là giao tuyến của 2 mặt phẳng:

5 0

x z

  

và

2 3 0

x y z

   

thì có phương

trình là

A.

2 1

1 3 1

x y z 

 



B.

2 1

1 2 1

x y z 

 



C.

2 1 3

1 1 1

x y z

  

 



D.

2 1 3

1 2 1

x y z

  

 



Lời giải

Chọn C

 

: 5 0

P x z

  

có 1 vtpt

 

1

1;0;1

n 



 

: 2 3 0

Q x y z

   

có 1 vtpt

 

2

1; 2; 1

n

  



Gọi



là giao tuyến của 2 mặt phẳng thì



có 1 vtcp

 

1 2

, 2;2; 2

u n n

 

  

 

  

.

Câu 81. (Chuyên KHTN 2019) Trong không gian với hệ tọa độ

Oxyz

, gọi

 



là mặt phẳng chứa đường

thẳng

2 3

( ) :

1 1 2

x y z

d

 

 

và vuông góc với mặt phẳng

 

: 2z 1 0

x y



   

. Hỏi giao tuyến

của

 



và

 



đi qua điểm nào?

A.

 

0;1;3

. B.

 

2;3;3

. C.

 

5;6;8

D.

 

1; 2;0



Lời giải

(1;1;2)

d

u



là một VTCP của đường thẳng d

(1;1; 2)

n







là một VTPT của

 



; ( 4;4;0)

d

n u n

 

 

   

 

  

 

(2;3;0)A d A



  

Phương trình mặt phẳng

( ) : 4( 2) 4( 3) 0( 0) 0 4x 4 4 0 1 0

x y z y x y



               

.

Giả sử

   

( ; ; )M x y z

 

 

. Khi đó tọa độ M thỏa mãn hệ

x- 1 0

2z 1 0

y

x y

 





   



Thay các đáp án vào hệ trên ta thấy

(2;3;3)

M

thỏa mãn. Chọn đáp án B

Câu 82. (Chuyên Nguyễn Trãi Hải Dương 2019) Đường thẳng



là giao của hai mặt phẳng

5 0

x z

  

và

2 3 0

x y z

   

thì có phương trình là

A.

2 1

1 3 1

x y z 

 



. B.

2 1

1 2 1

x y z 

 



.

C.

2 1 3

1 1 1

x y z

  

 



. D.

2 1 3

1 2 1

x y z

  

 



.

Lời giải

 

: 5 0

P x z

  

có vectơ pháp tuyến

 

1

1;0;1

n 



.

 

: 2 3 0

Q x y z

   

có vectơ pháp tuyến

 

2

1; 2; 1

n

  



.

Ta có:

 

1 2

, 2;2; 2

n n

 

 

 

 

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 49

Gọi

u



là một vectơ chỉ phương của



, thì

1

u n





và

2

u n





.

Suy ra

u



cùng phương với

1 2

,n n

 

 

 

. Chọn

 

1;1; 1

u

 



.

Lấy

 

2;1;3

M

thuộc mặt phẳng

 

P

và

 

Q

.

Đường thẳng



đi qua

 

2;1;3

M

có một véctơ chỉ phương

 

1;1; 1

u

 



.

Vậy phương trình



là:

2 1 3

1 1 1

x y z

  

 



.

Câu 83. (Mã 105 2017) Trong không gian với hệ tọa độ

Oxyz

, cho hai đường thẳng

  



  





 



2 3

: 3

4 2

x t

d y t

z t

và







 



1

4

:

3 1 2

y

x z

d

. Phương trình nào dưới đây là phương trình đường thẳng thuộc mặt phẳng

chứa

d

và



d

, đồng thời cách đều hai đường thẳng đó.

A.



 

 



2

3 2

3 1 2

y

x z

B.



 

 



2

3 2

3 1 2

y

x z

.

C.



 

 



2

3 2

3 1 2

y

x z

D.



 

 



2

3 2

3 1 2

y

x z

Lời giải

Chọn D

Ta thấy hai đường thẳng

d

và



d

có cùng véctơ chỉ phương hay



/ /d d

Vậy đường thẳng cần tìm có véctơ chỉ phương là

 

 



3;1; 2

u

và đi qua trung điểm

 



3; 2; 2

I

của

AB

với

 

 

2; 3; 4

A d

và

 



 

4; 1; 0

B d

Vậy phương trình đường thẳng cần tìm là



 

 



2

3 2

3 1 2

y

x z

.

Câu 84. (THPT Nghen - Hà Tĩnh - 2018) Trong không gian với hệ tọa độ

Oxyz

cho hai đường thẳng

2

: 1 2

4 2

x t

d y t

z t

 





 





 



và

4 1

:

1 2 2

x y z

d

 



 



. Phương trình nào dưới đây là phương trình đường thẳng

thuộc mặt phẳng chứa

d

và

d



đồng thời cách đều hai đường thẳng đó.

A.

2 1 4

3 1 2

x y z

  

 



. B.

3 2 2

1 2 2

x y z

  

 



.

C.

3 2

1 2 2

x y z

 

 



. D.

3 2 2

1 2 2

x y z

  

 

 

.

Lời giải

d

đi qua

 

2;1;4

A

và có véc tơ chỉ phương

 

1

1;2; 2

u

  



.

d



đi qua

 

4; 1;0

B 

có véc tơ chỉ phương

 

2

1; 2;2

u  



.

Ta có

1 2

u u 

 

và

2 4 1 1 4

1 2 2

 

 



nên

//d d



.

NGUYỄN BẢO VƯƠNG - 0946798489

Đường thẳng



thuộc mặt phẳng chứa

d

và

d



đồng thời cách đều hai đường thẳng đó khi và chỉ

khi

   

// //

, ,

d d

d d d

d













  





hay



qua trung điểm

 

3;0;2

I

và có một véc tơ chỉ phương là

 

1; 2

;2

u  



. Khi đ

ó phương trình của



:

3 2

1 2 2

x y z

 

 



.

Câu 85. (Toán H

ọc Tuổi Trẻ 2019) Trong không gian với hệ trục tọa độ

Oxyz

, c

ho đường thẳng

d

và

mặ

t phẳng

 

P

lần lượt có phương trình

1 2

2 1

1

x y z

 

 

và

2 8 0

x y z

  



, điểm

 

2; 1

;3

A



. Phương

trình đường thẳng



cắt

d

và

 

P

lần lượ

t tại

M

và

N

sao c

ho

A

là

trung

điểm của đoạn thẳng

MN

là:

A.

1 5 5

3

4 2

x y z

  

 

B.

2 1 3

6

1 2

x y z

  

 

C.

5 3 5

6 1 2

x y z

  

 

D.

5 3 5

3 4 2

x y z

  

 

Lời giải

Đường thẳng

d

có phương trì

nh tham số:

1 2

2

x t

y t

z t



 











 





Điểm

M

thuộc đư

ờng thẳng

d

nên

 

1 2 ;

;2

M t t

t  

.

Điểm

A

là trung điểm của

MN

nên:

 

2; 1

;3

2 5 2

2 2 5 2 ; 2 ;4

2 4

N A M

N

A M

N A M

A

x x x

t

y y y

t N t t t

z z z

t





  





  

      





   







Mặt khác điể

m

 

N P

nên:

5 2 2

8 2 8 0 3

t t t

t

  

     

Suy ra:

 

5;3

;5

M

.

Đường thẳ

ng



có

véc tơ chỉ phương

 

3;4

;2

AM





và đi

qua điểm

 

5;3

;5

M

nên

có phương

trình:

5 3 5

3

4 2

x y z

  

 

Trang 50 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

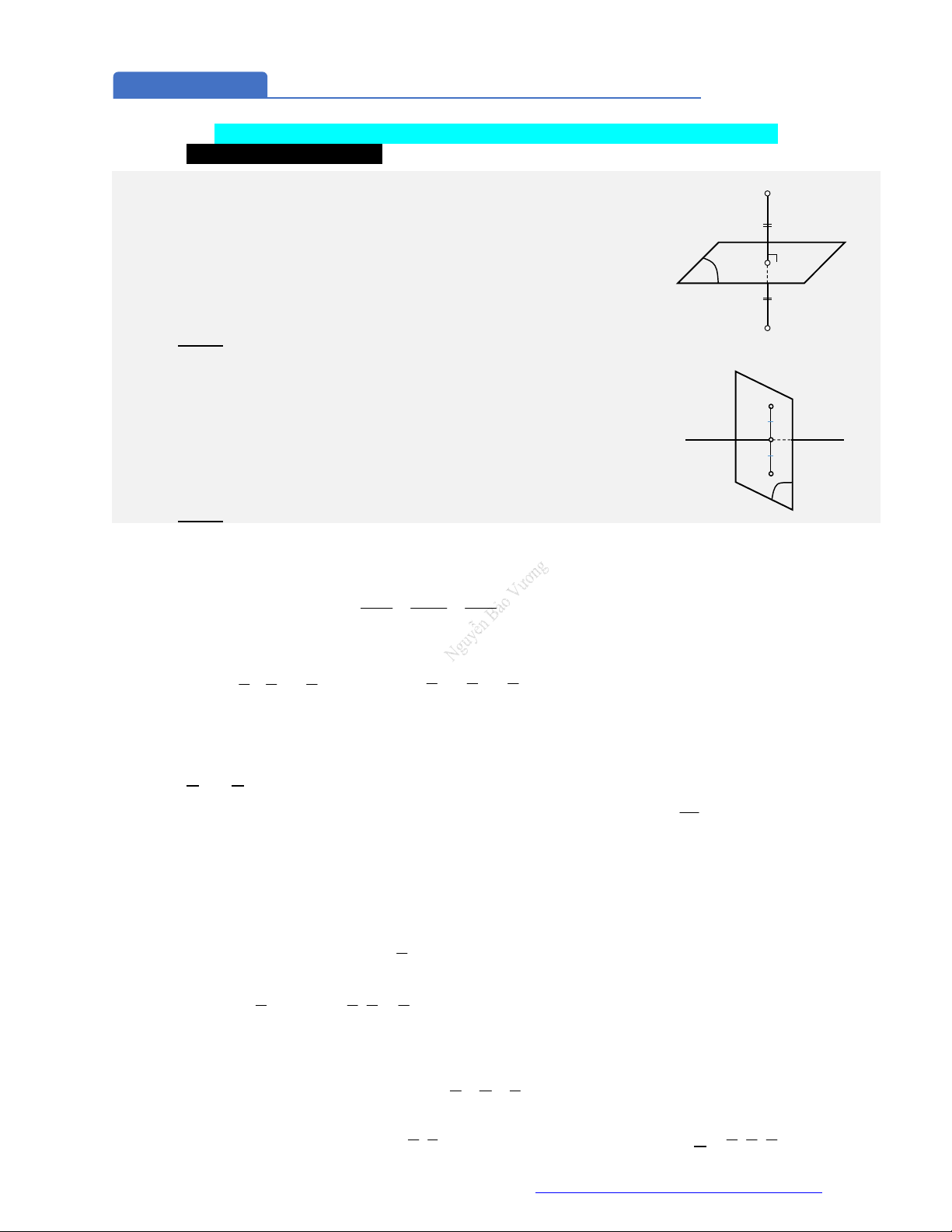
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương  https://www.facebook.com/phong.baovuong Trang 1

TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH KHÁ – MỨC 7-8 ĐIỂM

Dạng 2. Bài toán tìm điểm

 Tìm hình chiếu

H

của điểm

M

lên mặt phẳng

( ) : 0P ax by cz d   

Viết phương trình đường thẳng

MH

qua

M

và vuông góc với

( ),P

khi đó:

( )H d P 

thỏa

1

2

3

?

? .

?

0

x x a t

x

y y a t

t y H

z z a t

z

ax by cz d

 









 

 

   

 

 

 







   





 Lưu ý: Để tìm điểm đối xứng

M



của điểm

M

qua

( )P 

H

là trung điểm

.MM



 Tìm hình chiếu

H

của điểm

M

lên đường thẳng

.d

Viết phương trình mặt phẳng

( )P

qua

M

và vuông góc với

,d

khi đó:

( )H d P 

thỏa

1

2

3

?

? .

?

0

x x a t

x

y y a t

t y H

z z a t

z

ax by cz d

 









 

 

   

 

 

 







   





 Lưu ý: Để tìm điểm đối xứng

M



của điểm

M

qua

d 

H

là trung điểm

.MM



Câu 1. (Mã 104 2017) Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm

 

1; 1; 2A 

,

 

1; 2; 3B 

và đường thẳng

1 2 1

:

1 1 2

x y z

d

  

 

. Tìm điểm

 

; ; M a b c

thuộc

d

sao cho

2 2

28MA MB 

, biết

0c 

.

A.

1 7 2

; ;

6 6 3

 



 

 

M

B.

1 7 2

; ;

6 6 3

M

 

  

 

 

C.

 

1; 0; 3 M

D.

 

2; 3; 3M

Lời giải

Chọn A

Ta có :

M d

nên

 

: 1 ; 2 ; 1 2t M t t t    

.Đk :

 

1

1 2 0 *

2

t t



   

2 2

28MA MB 

           

2 2 2 2 2 2

3 1 2 2 2 2 28t t t t t t              

2

12 2 10 0t t   

 

1

5

/

6

t L

t T m

 







 





Với

5

6

t  

, ta có

1 7 2

; ;

6 6 3

M

 



 

 

.

Câu 2. (THCS - THPT Nguyễn Khuyến 2019) Trong không gian

Oxyz

, tọa độ hình chiếu vuông góc

của

 

1;0;1M

lên đường thẳng

 

:

1 2 3

x y z

  

là

A.

 

2;4;6

. B.

1 1

1; ;

2 3

 

 

 

. C.

 

0;0;0

. D.

2 4 6

; ;

7 7 7

 

 

 

.

PHƯƠNG TRÌNH ĐƯỜNG THẲNG

Chuyên đề 31

P

M



M

H

M



H

d

P

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Lời giải

Đường thẳng



có vtcp

 

1;2 ;3

u 



và có phương trình tham số là:

 

2

3

x t

y t t

z t







 











.

Gọi

 

;2 ;3N t t t



là hình chiếu vuông góc của

M

lên



, khi đó:

2 2 4 6

. 0 ( 1) (2 0).2 (3 1).3 0 14 4 0 ; ; .

7 7 7 7

MN u t t t t t N

 

             

 

 

 

Câu 3. Trong không gian với hệ tọa độ Oxyz, cho điểm

( 4;0;0)

M

và đường thẳng

1

: 2 3

2

 





   





 



x t

y t

z t

. Gọi

( ; ;c)H a b

là hình chiếu của

M

lên



. Tính a+b+c.

A.

5

. B.

1

. C.

3

. D.

7

.

Lời giải

Chọn B

Gọi

H

là hình chiếu của

M

lên



nên tọa độ của H có dạng

(1 ; 2 3 ; 2 )   H t t t

và





 

MH u

11 3 5 22

. 0 14 11 0 ( ; ; ) 1

14 14 14 14





           

 

MH u t t H a b c

Câu 4. (THPT Yên Phong 1 Bắc Ninh 2019) Trong không gian Oxyz, tìm tọa độ hình chiếu H của

 

1;1;1

A

lên đường thẳng

d :

1

x t

y t

z t

 













.

A.

H

4 4 1

( ; ; ).

3 3 3

B.

 

1;1;1 .

H

C.

(0 ; 0 ; 1).

H

D.

(1 ; 1 ; 0).

H

Lời giải

Đường thẳng d có vectơ chỉ phương là

u = (1 ; 1 ; 1).



Do

H(1+ t ; 1+ t ; t)

H d

 

.

Ta có:

= (t ; t ;t 1).

AH



Do H là hình chiếu của điểm A lên đường thẳng d nên suy ra

1 4 4

. = 0 t + t + t 1 = 0 t = ( ; ;1).

3 3 3

AH u AH u H    

   

Câu 5. (THPT Quang Trung Dống Da Hà Nội 2019) Trong không gian với hệ tọa độ

Oxyz

, cho điểm

 

1;1;1

A

và đường thẳng

 

6 4

: 2

1 2

x t

d y t

z t

 





  





  



. Tìm tọa độ hình chiếu

A



của

A

trên

 

d

.

A.

(2;3;1)

A



. B.

( 2;3;1)

A





. C.

(2; 3;1)

A





. D.

(2; 3; 1)

A



 

.

Lời giải

Ta có

 

A d





nên gọi

 

6 4 ; 2 ; 1 2A t t t



    

;

 

5 4 ; 3 ; 2 2AA t t t



     



;

đường thẳng

 

d

có vectơ chỉ phương

 

4; 1;2

u   



.

           

. 0 5 4 . 4 3 . 1 2 2 .2 0 1AA d AA u t t t t

 

               

 

.

 

2; 3;1

A



 

.

Vậy

 

2; 3;1

A





.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3

Câu 6. Trong không gian

Oxyz

, cho hình thang cân

ABCD

có đáy là

AB

và

CD

. Biết

 

3;1; 2

A



,

 

1;3;2

B 

,

 

6;3;6

C 

và

 

; ;D a b c

với

, ,a b c



. Giá trị của

a b c 

bằng

A.

3

. B.

1

. C.

3

. D.

1

.

Lời giải

Phương trình đường thẳng

d

qua

 

6;3;6

C 

và song song với đường thẳng

AB

là

6 3 6

2 1 2

x y z

  

 



Điểm

D

thuộc đường thẳng

d

nên gọi tọa độ

D

là

 

6 2 ;3 ;6 2D t t t

   

.

Tứ giác

ABCD

là hình thang cân nên ta có:

AD BC



 

2

8 12 0

t t

   

2

6

t

 







 



.

Với

2

t

 

 

1

2;1;2

D 

, tứ giác là hình bình hành nên loại.

Với

6

t

 

 

2

6; 3; 6

D

  

thỏa mãn, nên

6 3 6 3   

.

Câu 7. (THPT Chuyên Đại Học Vinh 2019) Trong không gian

Oxyz

, cho đường thẳng

1 2

:

2 1 1

x y z

d

 

 



và hai điểm

 

1;3;1

A 

;

 

0;2; 1

B



. Gọi

 

; ;C m n p

là điểm thuộc đường

thẳng

d

sao cho diện tích tam giác

ABC

bằng

2 2

. Giá trị của tổng

m n p 

bằng

A.

1

B.

2

C.

3

D.

5

Lời giải

Chọn C

Phương trình tham số của đường thẳng

1 2

:

2

x t

d y t

z t

  











 



Vì

 

1 2

: 1 2 ;

2

x t

C d y t c t t

z t

  





    





 



Ta có

   

1; 1; 2 ; 1 2 ; ;2

AB AC t t t      

 

 

, 3 7; 3 1;3 3

AB AC t t t

 

     

 

 

Diện tích tam giác

ABC

là

2

1 1

, 27 54 59

2 2

ABC

S AB AC t t

 

   

 

 

2

1

2 2 27 54 59 2 2

2

ABC

S t t    

1t 

 

1;1;1

C

3

m n p

   

Câu 8. (Chuyên Hà Tĩnh - 2018) Trong không gian

Oxyz

, cho đường thẳng

1 3 2

:

1 2 2

x y z

d

  

 

và

điểm

 

3;2;0

A

. Điểm đối xứng của điểm

A

qua đường thẳng

d

có tọa độ là

A.

 

1;0;4



. B.

 

7;1; 1

. C.

 

2;1; 2

. D.

 

0;2; 5

.

Lời giải

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Gọi

 

P

là mặt phẳng đi qua

A

và vuông góc với đường thẳng

d

. Phương trình của mặt phẳng

 

P

là:

     

1 3 2 2 2 0 0

x y z

     

2 2 7 0

x y z

    

.

Gọi

H

là hình chiếu của

A

lên đường thẳng

d

, khi đó

 

H d P

 

Suy ra

 

1 ; 3 2 ; 2 2H d H t t t

       

, mặt khác

 

H P



1 6 4 4 4 7 0

t t t

        

2

t

 

. Vậy

 

1;1;2

H

.

Gọi

A



là điểm đối xứng với

A

qua đường thẳng

d

, khi đó

H

là trung điểm của

AA



suy ra

 

1;0;4

A





.

Câu 9. (Sở Bình Phước -2019) Trong không gian

Oxyz

, khoảng cách từ điểm

 

2; 4; 1

M

 

tới đường

thẳng

: 2

3 2

x t

y t

z t







  





 



bằng

A.

14

B.

6

C.

2 14

D.

2 6

Lời giải

Chọn C

Đường thẳng



đi qua

 

0;2;3

N

, có véc tơ chỉ phương

 

1; 1;2

u  



   

2;6;4 ; , 16;8; 4

MN MN u

 

   

 

  

.

 

,

336

, 2 14.

6

MN u

d M

u

 

 

   

 



Câu 10. Trong không gian với hệ trục tọa độ

Oxyz

, Gọi

 

; ; M a b c

thuộc đường thẳng

1 2

:

1 2 3

x y z

 

  

. Biết điểm

M

có tung độ âm và cách mặt phẳng

 

Oyz

một khoảng bằng 2.

Xác định giá trị

T a b c  

.

A.

1T  

. B.

11T 

. C.

13

T

 

. D.

1T 

.

Lời giải

 

; 1 2 ; 2 3M M t t t

    

.

Ta có

 

2 1 2 5

; 2

2 1 2 2

t t

d M Oyz t

t t

   



  



     



.

Suy ra

2

t

 

. Do đó

 

2; 3; 8

M

  

.

Vậy

2; 3; 8 13

a b c T a b c

           

.

trình

1 2

2 3 0

x t

y t

z t

x y

  











 



  



1

3

t

x

y

z























. Do đó

 

1;1;3

M

,

5

a b c

  

.

Câu 11. Trong không gian

Oxyz

, cho

 

2;0;0

A

, đường thẳng

d

đi qua

A

cắt chiều âm trục

Oy

tại

điểm

B

sao cho diện tích tam giác

OAB

bằng 1. Phương trình tham số đường thẳng

d

là

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5

A.

1 2

0

x t

y t

z

 















. B.

2 2

0

x t

y t

z

 





 









. C.

2 2

0

x t

y t

z

 





 









. D.

2 2

1

x t

y t

z

 















.

Lời giải

Chọn C

Gọi

 

0; ;0B b

là giao điểm của

d

với trục

Oy

. (Điều kiện

0

b



)

Ta có

2

OA



và tam giác

OAB

vuông tại

O

nên

1

. 1 1

2

OAB

S OAOB OB



   

Suy ra

 

0; 1;0

B 

. Ta có

 

2; 1;0

AB   



là một vec tơ chỉ phương của

d

.

Và đường thẳng

d

đi qua điểm

 

2;0;0

A

nên

2 2

0

x t

y t

z

 





 









.

Câu 12. (Bắc Ninh 2019) Trong không gian với hệ tọa độ

Oxyz

, cho đường thẳng

2 1

:

3 1 2

x y z 

  



.

Gọi

M

là giao điểm của



với mặt phẳng

 

: 2 3 2 0

P x y z

   

. Tọa độ điểm

M

là

A.

 

2;0; 1

M



. B.

 

5; 1; 3

M

 

. C.

 

1;0;1

M

. D.

 

1;1;1

M 

.

Lời giải

Tọa độ của điểm

M

là nghiệm của hệ:

2

3 1

1

1 2

2 3 2 0

x y

y z

x y z























   





3 2

2 1

2 3 2

x y

y z

x y z

 





  





   



1

x

y

z

 





 









Vậy

 

1;1;1

M 

.

Câu 13. (THCS - THPT Nguyễn Khuyến 2019) Trong không gian

Oxyz

, tọa độ hình chiếu vuông góc

của điểm

 

3;2; 1

A



lên mặt phẳng

 

: 0

x y z



  

là:

A.

 

2;1;1



. B.

5 2 7

; ;

3 3 3

 



 

 

. C.

 

1;1; 2

. D.

1 1 1

; ;

2 4 4

 

 

 

.

Lời giải

Gọi

H

là hình chiếu của

 

3;2; 1

A



lên mặt phẳng

 

: 0

x y z



  

. Khi đó:

AH

nhận

 

1;1;1

n



là vectơ chỉ phương suy ra phương trình

3 2 1

:

1 1 1

x y z

AH

  

 

.

Do

 

3 ; 2 ; 1

H AH H t t t     

.

Do

 

4 5 2 7

3 2 1 0 ; ;

3 3 3 3

H t t t t H



 

            

 

 

.

Câu 14. (THCS - THPT Nguyễn Khuyến 2019) Trong không gian với hệ trục tọa độ

Oxyz

, hình chiếu

của điểm

 

1;0;3

M

theo phương véctơ

 

1; 2;1

 



v

trên mặt phẳng

 

: 2 0   

P x y z

có

tọa độ là

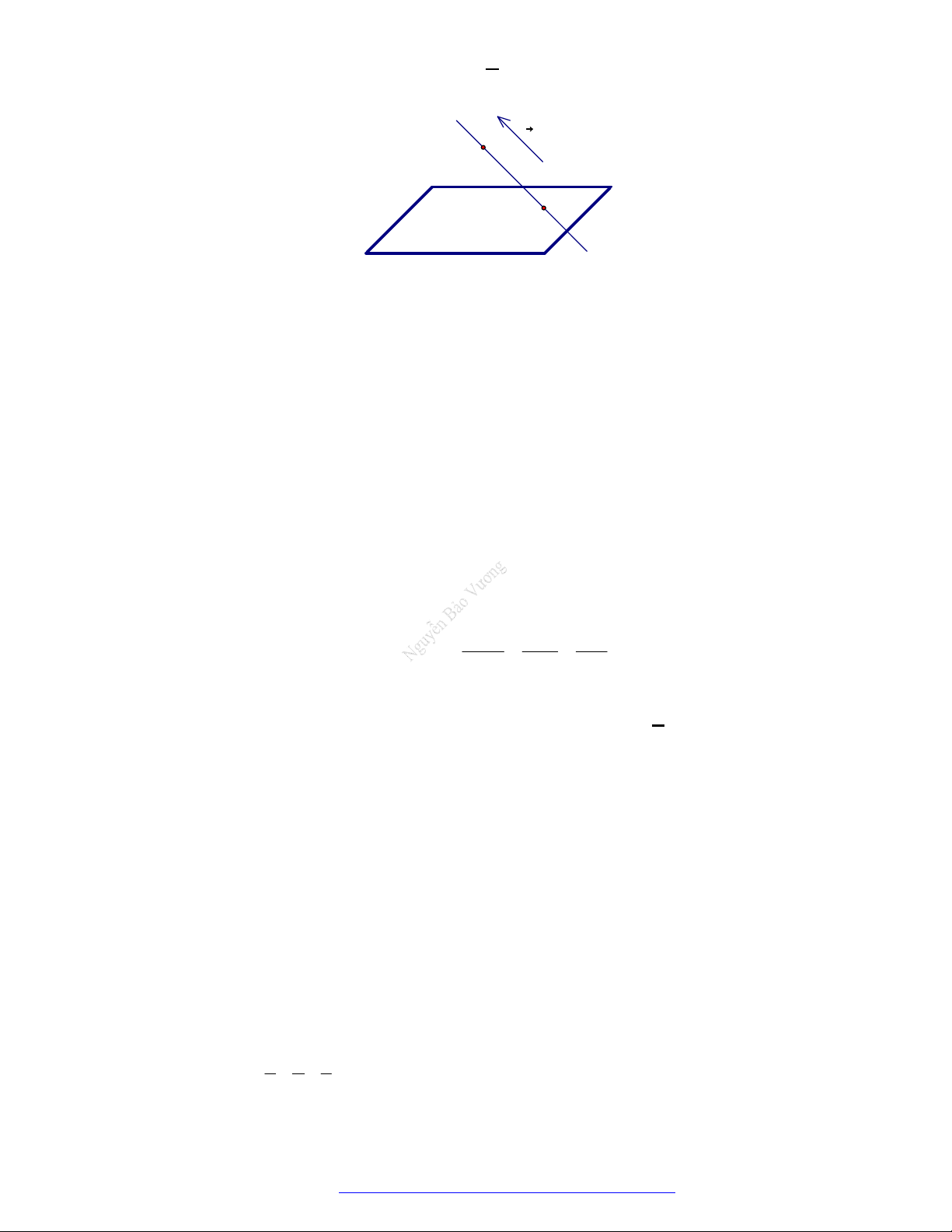
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

A.

 

2; 2; 2 

. B.

 

1;0;1

. C.

 

2;2;2

. D.

 

1;0; 1

.

Lời giải

Đường thẳng

d

đi qua

 

1;0;3M

, có véctơ chỉ phương

 

1; 2;1 



v

có phương trình tham số là

1

2

3

  





 





 



x t

y t

z t

.

Gọi

M



là hình chiếu của điểm

 

1;0;3M

theo phương véctơ

 

1; 2;1 



v

trên mặt phẳng

 

: 2 0   P x y z

.

 

M d P



   

tọa độ

M



là nghiệm của hệ phương trình:

 

1 1 2

2 2 2

2;2;2

3 3 2

2 0 1 2 3 2 0 1

x t x t x

y t y t y

M

z t z t z

x y z t t t t

       

  

  

    

  



   

  

    

  

            

  

.

Câu 15. (Chuyên Hùng Vương Gia Lai 2019) Trong không gian

Oxyz

, giao điểm của mặt phẳng

 

:3 5 2 0P x y z   

và đường thẳng

12 9 1

:

4 3 1

x y z  

  

là điểm

 

0 0 0

; ;M x y z

. Giá trị

tổng

0 0 0

x y z  bằng

A.

1

. B.

2

. C.

5

. D.

2

.

Lời giải

 

12 4 ;9 3 ;1M M t t t    

.

       

3 12 4 5 9 3 1 2 0 3M P t t t t           

.

 

0 0 0

0;0; 2 2M x y z     

.

Câu 16. Trong không gian với hệ tọa độ

Oxyz

, cho 3 điểm

     

1;0;0 , 0;2;0 , 0;0;3A B C

và

Gọi

( ; ; )M a b c

là tọa độ giao điểm của d và mặt phẳng . Tổng

S a b c  

là:

A. 7. B. 11. C. 5. D. 6.

Lời giải

Mặt phẳng

( )ABC

qua các điểm

     

1;0;0 , 0;2;0 , 0;0;3A B C

nằm trên các trục

Ox

,

Oy

,

Oz

có

phương trình là:

1

1 2 3

x y z

  

.

Điểm

( ; ; )M a b c

là tọa độ giao điểm của của d và mặt phẳng .

d

P

M'

M

v



 



 





 



: 2 .

3

x t

d y t

z t

 

ABC

 

ABC

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7

Suy ra

2 3

1 6

1 2 3

t t t

t

  

    

suy ra

6

8

9

a

b

c

 















.

Vậy

6 8 9 11.

S

    

Câu 17. (Đề Tham Khảo 2017) Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

 

:6 2 35 0

P x y z

   

và điểm

 

1;3;6 .

A

Gọi

'A

là điểm đối xứng với

A

qua

 

P

, tính

'.OA

A.

5 3

OA





B.

46

OA





C.

186

OA





D.

3 26

OA





Lời giải

Chọn C

+

A



đối xứng với

A

qua

 

P

nên

AA



vuông góc với

 

P

+Suy ra phương trình đường thẳng

AA



:

1 6

3 2

6

x t

y t

z t

  





 





 



+Gọi

H

là giao điểm của

AA



và mặt phẳng

 

P

 

1 6 ;3 2t;6 t

H t

    

+ Do

H

thuộc

 

P

     

6 1 6 2 3 2 1 6 35 0        

t t t

 

41 41 0 1 5;1;7

     t t H

+

A



đối xứng với

A

qua

 

P

nên

H

là trung điểm của

AA



   

2

2 2

11; 1;8 11 1 8 186

A OA

 

       

Câu 18. (KTNL GV Thuận Thành 2 Bắc Ninh 2019) Trong không gian với hệ tọa độ

Oxyz

, xác định tọa độ

điểm

M



là hình chiếu vuông góc của điểm

 

2;3;1

M

lên mặt phẳng

 

: 2 0

x y z



  

.

A.

5

2; ;3

2

M

 



 

 

. B.

 

1;3;5

M



. C.

5 3

;2;

2 2

M

 



 

 

. D.

 

3;1;2

M



.

Lời giải

Chọn C

Gọi



là đường thẳng qua

M

và vuông góc với

 



.



Phương trình tham số của



là:

2

3 2

1

x t

y t

z t

 





 





 



. Ta có

 

M





  

.

Xét phương trình:

 

2 2 3 2 1 0

t t t

     

1

2

t

 

.

Vậy

5 3

;2;

2 2

M

 



 

 

.

Câu 19. (Chuyên Lê Hồng Phong Nam Định 2019) Trong không gian

Oxyz

, điểm

M



đối xứng với

điểm

 

1;2;4

M

qua mặt phẳng

 

: 2 2 3 0

x y z



   

có tọa độ là

A.

 

3;0;0



. B.

 

1;1;2



. C.

 

1; 2; 4  

. D.

 

2;1;2

.

Lời giải

Mặt phẳng

 



có vectơ pháp tuyến là

 

2;1;2

n 



.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 8 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

MM



vuông góc với mặt phẳng

 



nên đường thẳng

MM



nhận

 

2;1;2

n 



làm vectơ chỉ

phương. Phương trình đường thẳng

MM



là:

1 2

2

4 2

x t

y t

z t

 





 





 



.

Gọi

H

là giao điểm của đường thẳng

MM



và mặt phẳng

 



.

H MM





 

1 2 ;2 ;4 2H t t t

   

.

 

H





   

2 1 2 2 2 4 2 3 0

t t t

       

9 9 0

t

  

1

t

  

 

1;1;2

H 

.

M



đối xứng với điểm

M

qua mặt phẳng

 



nên

H

là trung điểm của

MM



 

3;0;0

M



 

.

Câu 20. (KSCL THPT Nguyễn Khuyến 2019) Trong không gian

Oxyz

, cho điểm

 

1;2; 1

A



,đường

thẳng

1 1 2

:

2 1 1

x y z

d

  

 



và mặt phẳng

 

: 2 1 0

P x y z

   

. Điểm

B

thuộc mặt phẳng

 

P

thỏa mãn đường thẳng

AB

vuông góc và cắt đường thẳng

d

. Tọa độ điểm

B

là

A.

(6; 7;0)

B.

(3; 2; 1) 

C.

( 3;8; 3) 

D.

(0;3; 2)

Lời giải

Chọn D

Ta gọi

AB

cắt

d

tại điểm

 

1 2 ; 1 ;2

M m m m d    

 

2 ; 3;3

AM m m m 



, theo yêu cầu bài toán

AB

vuông góc

d

, ta có

. 0 2.2 3 3 0 1 (2; 2;2)

d

AM u m m m m AM           

  

Đường thẳng

AB

đi qua

A

nhận

 

1

1; 1;1

2

u AM  





là VTCP, ta có phương trình

AB

là

1 2 1

:

1 1 1

x y z

AB

  

 



. Gọi

 

1 ;2 ; 1

B t t t AB

    

Lại có điểm

( ) 1 2 2( 1 ) 1 0 1

B P t t t t

            

. Vậy

(0;3; 2)

B



.

Câu 21. Trong không gian với hệ tọa độ

Oxyz

, gọi

d

là đường thẳng qua

 

1;0;2

A

, cắt và vuông góc

với đường thẳng

1

1 5

:

1 1 2

x y z

d

 

 



. Điểm nào dưới đây thuộc

d

?

A.

 

2; 1;1

P



. B.

 

0; 1;1

Q



. C.

 

0; 1;2

N



. D.

 

1; 1;1

M

 

.

Lời giải

Chọn B

Đường thẳng

1

d

có VTCP là

 

1;1; 2

u

 



.

Gọi

H

là giao điểm của đường thẳng

d

và đường thẳng

1

d

. Vì

 

1

: 1 ; ;5 2H d H t t t  

.

Ta có:

 

; ;3 2AH t t t 



.

d

vuông góc với

1

d



 

. 0 2 3 2 0 6 6 1u AH t t t t t         

 

.

Lúc đó, đường thẳng

d

qua

 

1;0;2

A

và có VTCP

 

1;1;1

AH





có phương trình:

1

2

x t

y t

z t



 









 





.

Lúc đó, điểm

 

0; 1;1

Q



thuộc đường thẳng

d

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9

Câu 22. Trong không gian

Oxyz

, cho tam giác đều

ABC

với

 

6;3;5

A

và đường thẳng

BC

có phương

trình tham số

1

2

x t

y t

z t

 





 









. Gọi



là đường thẳng qua trọng tâm

G

của tam giác

ABC

và vuông

góc với mặt phẳng

 

ABC

. Điểm nào dưới đây thuộc đường thẳng



?

A.

 

1; 12;3

M  

. B.

 

3; 2;1

N 

. C.

 

0; 7;3

P 

. D.

 

1; 2;5

Q 

.

Lời giải

Chọn D

Đường thẳng

BC

đi qua

 

0

1;2;0

M

và có vecto chỉ phương

 

1;1;2

u  



.

Mp

 

ABC

có vecto pháp tuyến

0

,

n u M A

 



 

  

 

3;15; 6 

cùng phương

 

1;5; 2

n



 



.

 

ABC

 





có vecto chỉ phương

 

1;5; 2

n



 



Gọi

H

là trung điểm của

BC



AH BC

và

 

1 ;2 ;2H t t t

 

.

 

5 ; 1 ;2 5

AH t t t

     



. Ta có

AH BC

AH u 

 

. 0

AH u

 

 

6 6 0

t

  



1t 

.

Suy ra

 

0;3;2

H

.

G

là trọng tâm tam giác

ABC

2

3

AG AH

 

 

3 2

AG AH

 

 

   

3 2

OG OA OH OA

   

   

 

1

2

3

OG OH OA

  

  

 

2;3;3

OG 



 

2;3;3

G 

.



đi qua

G

, có vecto chỉ phương

 

1;5; 2

n



 





phương trình tham số của



là:

2

3 5

3 2

x t

y t

z t

 





 





 



. Vậy

Q



.

Câu 23. (Chuyên Đại học Vinh - 2019) Trong không gian

Oxyz

, cho đường thẳng

1 2

:

2 1 1

x y z

d

 

 



và hai điểm

 

1;3;1

A 

,

 

0;2; 1

B



. Gọi

 

; ;C m n p

là điểm thuộc

d

sao cho diện tích tam giác

ABC

bằng

2 2

. Giá trị của tổng

m n p 

bằng

A.

1

. B. 2. C. 3. D.

5

.

Lời giải

Chọn C

Ta có

   

; ; 1 2 ; ;2

C m n p d C t t t    

.

Suy ra

 

1; 1; 2

, 3 7; 3 1;3 3

2 ; 3;1

AB

AB AC t t t

AC t t t



  



 

     



 

  







 



.

Diện tích tam giác

ABC

:

2

1 1

, 27 54 59

2 2

ABC

S AB AC t t



 

   

 

 

.

Theo đề ta có

2

1

27 54 59 2 2

2

t t  

2

27 54 27 0 1t t t     

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 10 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Suy ra

 

1;1;1

C

.

Vậy

3

m n p

  

.

Câu 24. (Đà Nẵng 2019) Trong không gian

 

Oxyz

cho hai đường thẳng

2 4

1 1 2

x y z 

 



và

3 1 2

2 1 1

x y z

  

 

 

. Gọi

M

là trung điểm đoạn vuông góc chung của hai đường thẳng trên. Tính

đoạn

OM

.

A.

14

2

OM 

. B.

5

OM 

. C.

2 35

OM 

. D.

35

OM 

.

Lời giải

Chọn B

Đường thẳng

2

: 4

2

x t

d y t

z t

 





 





 



nhận véctơ

 

1;1; 2

u

 



làm véctơ chỉ phương.

Đường thẳng

3 2

: 1

2

x m

d y m

z m

 







  





  



nhận véctơ

 

2; 1; 1

v

  



làm véctơ chỉ phương.

Gọi

AB

là đoạn vuông góc chung với

A d

và

B d





.

Khi đó

 

2 ;4 ; 2A t t t  

và

 

3 2 ; 1 ; 2

B m m m

    

.

Suy ra

 

2 1; 5; 2 2

AB m t m t m t

        



.

Ta có

. 0 3 6 0 2

6 3 9 1

. 0

AB u AB u m t m

m t t

AB v AB v

 

     

 

 

  

   

    

 

 

 

 

   

. Suy ra

 

1;3;2

A

và

 

1;1;0

B 

.

Suy ra trung điểm của

AB

là

 

0;2;1

M

. Vậy

5

OM 

.

Câu 25. (Kinh Môn - Hải Dương 2019) Trong không gian với hệ tọa độ

Oxyz

, cho

 

: 2 0

P x y z

  

và đường thẳng

1 2

:

2 1 1

x y z

d

 

 



. Đường thẳng

d

cắt

 

P

tại điểm

A

. Điểm

 

; ;M a b c

thuộc

đường thẳng

d

và có hoành độ dương sao cho

6

AM  . Khi đó tổng

2016

S a b c  

là

A.

2018

. B.

2019

. C.

2017

. D.

2020

.

Lời giải

Chọn A

Tìm

A

từ hệ

2 0 1

2 0

2 1 1

1 2

2 1

2 1 1

x y z x

x y z

x y y

x y z

y z z

    

 

  



  

     

   

 

  

    

 

 



 

1; 1; 1

A

  

.

Gọi

 

1

1 2 ; ; 2 ,

2

M t t t t



   

ta có

2

6 12 6 6 0; 2

AM t t t t

       

Với

 

0 1;0; 2 1; 0; 2 2018.

t M a b c S         

Câu 26. Trong không gian

Oxyz

, cho hai đường thẳng

1

1 1

:

1 1 2

x y z

d

 

 



,

2

1

:

1 2 1

x y z

d



 

. Đường

thẳng

d

đi qua

 

5; 3;5

A 

lần lượt cắt

1

d

,

2

d

tại

B

và

.C

Độ dài

BC

là

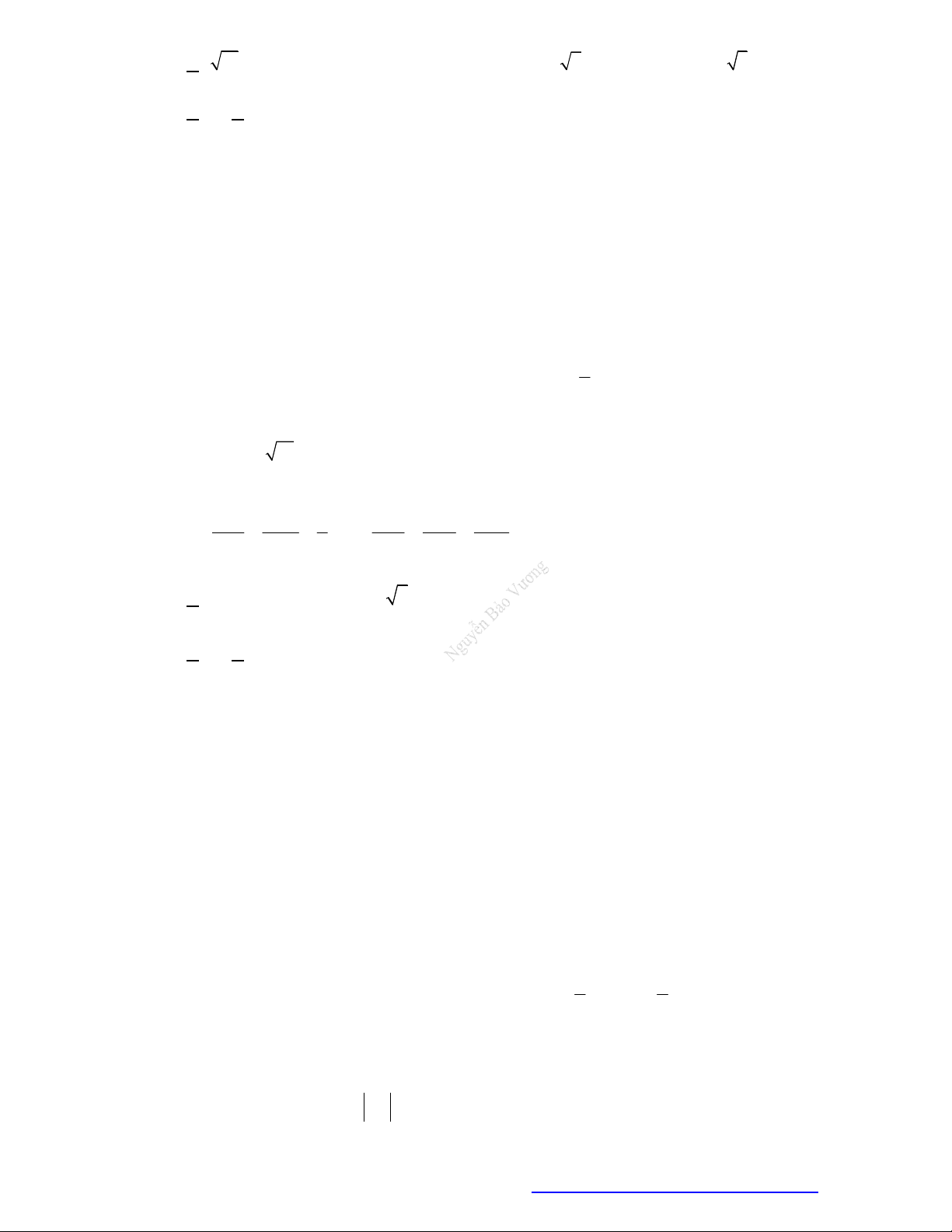
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11

A.

19

. B.

19

. C.

3 2

. D.

2 5

.

Lời giải

Chọn A

Ta có:

1 1 1 1

(1 ; 1 ;2 )d d B B t t t

     

.

2 2 2 2

( ;1 2 ; )d d C C t t t

   

.

Khi đó:

 

1 1 1

4; 2;2 5

AB t t t

    



và

 

2 2 2

5;2 4; 5

AC t t t

   



.

Vì

2

A d



0

AC



 

.

Ba điểm

A

,

B

,

C

cùng thuộc đường thẳng

d



AB



và

AC



cùng phương



:

k AB k AC

  

 



 

1 2

1

1 2 2

1 2

4 5

1

2 2 4 1

1

2 5 5

2

t k t

t

t k t t

t k t

k



  







       

 

 

  









.

Do đó

 

2; 2;2

B 

,

 

1; 1; 1

C

  

 

3;1; 3

BC

   



.

Vậy

19

BC 

.

Câu 27. Trong không gian với hệ tọa độ

Oxyz

, cho điểm

 

3;3; 2

M



và hai đường thẳng

1

1 2

:

1 3 1

x y z

d

 

 

;

2

1 1 2

:

1 2 4

x y z

d

  

 



. Đường thẳng

d

đi qua

M

căt

1 2

,d d

lần lượt tại

A

và

B

. Độ dài đoạn thẳng

AB

bằng

A.

3

. B.

6

. C.

4

. D.

2

.

Lời giải

Chọn A

Ta có:

phương trình tham số của

1

1 1 1

1

: 2 3 ;

x t

d y t t

z t

 





  











,

 

1 1 1 1

1 ;2 3 ;A d A t t t

   

;

phương trình tham số của

2

2 2 2

2

1

: 1 2 ;

2 4

x t

d y t t

z t

  





  





 





,

 

2 2 2 2

1 ;1 2 ;2 4B d B t t t

     

;

   

1 1 1 2 2 2

2;3 1; 2 ; 4 4 ; 2 2 ;4 4MA t t t MB t t t

         

 

.

Vì

, ,A B M

thẳng hàng nên

,MA kMB k

 

 



1 2 1 2

2 4 4 2

3 1 2 2 3 2 2 1

2 4 4 4 4 2

t k kt t k kt

      

 

 

        

 

 

      

 

1 1

2 2

0 0

1 1

2 2

0 0

t t

k k

kt t

 

 

 

   

 

 

 

 

 

.

Vậy,

 

1;2;0

A

và

   

1;1;2 2; 1;2

B AB    



.

Độ dài đoạn thẳng

3

AB AB

 



.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 12 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 28. Cho ba điểm

 

1;1;1

A

,

 

0;0;2

B

,

 

2;3; 2

C



và đường thẳng

2

: 1

x t

y t

z t

 





  









.

Biết điểm

 

; ;M a b c

với

0

a



thuộc mặt phẳng

 

ABC

sao cho

AM  

và

14

AM 

. Tính giá trị của

biểu thức

T a b c  

.

A.

1T  

. B.

5

T



. C.

7

T



. D.

6

T

 

.

Lời giải

Chọn C

Ta có



có một vectơ chỉ phương là

 

1; 1;1

u



 



.

 

1; 1;1

AB   



,

 

1;2; 3

AC

 



 

, 1; 2; 1

AB AC

 

   

 

 

.

Mặt phẳng

 

ABC

nhận vectơ

 

, 1; 2; 1

ABC

n AB AC

 

   

 

  

làm vectơ pháp tuyến.

Gọi

 

Q

là mặt phẳng qua

A

và vuông góc với đường thẳng





mặt phẳng

 

Q

nhận vectơ

 

1; 1;1

Q

n u



  

 

làm vectơ pháp tuyến.

Khi đó

   

AM AM Q M Q

     

.

Mặt khác theo giả thiết

 

M ABC



M 

giao tuyến

d

của hai mặt phẳng

 

ABC

và

 

Q

.

Đường thẳng

d

nhận vectơ

 

, 3;2; 1

Q

ABC

n n

 

 

 

 

làm vectơ chỉ phương, đồng thời đi qua

A



PT

1 3

: 1 2

1

x t

d y t

z t

 





 





 



.

Ta có

 

1 3 ;1 2 ;1

M d M t t t     

.

Theo giả thiết

     

2 2 2

2 2

1

14 3 2 14 14 14

1

t

AM t t t t

t

 



        







.

Với

 

1 2; 1;2

t M     

(loại).

Với

 

1 4;3;0

t M  

(nhận)

Khi đó

4; 3; 0

a b c

  

.

Vậy

7

a b c

  

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13

Câu 29. (Chuyên Đh Vinh - 2018) Trong không gian

Oxyz

, cho điểm

 

1;2; 1

A



, đường thẳng

1 1 2

:

2 1 1

x y z

d

  

 



và mặt phẳng

 

: 2 1 0

P x y z

   

. Điểm

B

thuộc mặt phẳng

 

P

thỏa

mãn đường thẳng

AB

vuông góc và cắt đường thẳng

d

. Tọa độ điểm

B

là

A.

 

3; 2; 1 

. B.

 

3;8; 3 

. C.

 

0;3; 2

. D.

 

6; 7;0



.

Lời giải

Đường thẳng

d

có một VTCP là

 

2;1; 1

d

u

 



.

Gọi

 

1 2 ; 1 ;2

M AB d M t t t      



 

2 ; 3;3

AM t t t  



.

. 0

AB d AM u

  

 

4 3 3 0t t t     

1t 

 

2; 2;2

AM  



 

2 1; 1;1

 

Đường thẳng

AB

đi qua điểm

 

1;2; 1

A



, có một VTCP là

 

1; 1;1

u  



 

1

: 2

1

x t

AB y t t

z t

 





   





  





.

Ta có:

 

B AB P

 

nên tọa độ của

B

là nghiệm của hệ

1

2

1

2 1 0

x t

y t

z t

x y z

 





 





  



   



1

0

3

2

t

x

y

z

 

















 



 

0;3; 2

B

 

.

Câu 30. (SGD Bạc Liêu - 2018) Trong không gian với hệ trục tọa độ

Oxyz

, cho đường thẳng

 

3

: 1 ,

2

x t

y t t

z t

 





    





  





, điểm

 

1;2; 1

M



và mặt cầu

 

2 2 2

: 4 10 14 64 0

S x y z x y z

      

.

Gọi





là đường thẳng đi qua

M

cắt đường thẳng



tại

A

, cắt mặt cầu tại

B

sao cho

1

3

AM

AB



và điểm

B

có hoành độ là số nguyên. Mặt phẳng trung trực đoạn

AB

có phương trình là

A.

2 4 4 19 0

x y z

   

. B.

3 6 6 62 0

x y z

   

.

C.

2 4 4 43 0

x y z

   

. D.

3 6 6 31 0

x y z

   

.

Lời giải





là đường thẳng đi qua

M

cắt đường thẳng



tại

A

suy ra tọa độ

 

3 ; 1 ; 2

A a a a    

.

1

3

AM

AM AB

AB

   

 

Trường hợp 1:

 

3 2 3

3 3 3 1

3 1 2

a x a

AM AB a y a

a z a

    





     





   



 

3 2

8 2

1 2

x a

y a

z a

  





  





 



suy ra

 

3 2 ;8 2 ;1 2B a a a

   

Do

 

B S



nên

           

2 2 2

3 2 8 2 1 2 4 3 2 10 8 2 14 1 2 64 0

a a a a a a

              

2

12 40 244 0

a a

   

, phương trình vô nghiệm

Trường hợp 2:

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 14 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

   

3 2 3

3 3 3 1

3 1 2

a x a

AM AB a y a

a z a

     





       





    



 

9 4

10 4

5 4

x a

y a

z a

 





   





  



Suy ra

 

9 4 ; 10 4 ; 5 4B a a a

    

Do

 

B S



nên

           

2 2 2

9 4 10 4 5 4 4 9 4 10 10 4 14 5 4 64 0

a a a a a a

                

2

1

48 112 64 0

4

3

a

a a

a

 





    



 



.

Điểm

B

có hoành độ là số nguyên nên

 

5; 6; 9

B

 

;

 

2;0; 3

A



.

Mặt phẳng trung trực đoạn

AB

đi qua trung điểm

7

; 3; 6

2

I

 

 

 

 

và có một véc tơ pháp tuyến

 

1;2;2

n  



nên có phương trình

   

7

2 3 2 6 0 2 4 4 43 0

2

x y z x y z

 

          

 

 

Dạng 3. Bài toán liên quan đến góc – khoảng cách

1. Khoảng cách từ một điểm đến mặt phẳng, khoảng cách giữa hai mặt phẳng song song



Khoảng cách từ điểm

( ; ; )

M M M

M x y z

đến mặt phẳng

( ) : 0

P ax by cz d

   

được xác định bởi

công thức:

2 2 2

( ;( ))

M M M

ax by cz d

d M P

a b c

  

 

 

Khoảng cách giữa đường thẳng và mặt phẳng song song là khoảng cách từ một điểm thuộc đường

thẳng đến mặt phẳng



Cho hai mặt phẳng song song

( ) : 0

P ax by cz d

   

và

( ) : 0

Q ax by cz d



   

có cùng véctơ

pháp tuyến, khoảng cách giữa hai mặt phẳng đó là

 

2 2 2

( ),( )

d d

d Q P

a b c





 

 

2. Khoảng cách từ một điểm đến đường thẳng – Khoảng cách giữa hai đường thẳng



Khoảng cách từ điểm

M

đến một đường thẳng

d

qua điểm

M



có véctơ chỉ phương

d

u



được xác

định bởi công thức

,

( , )

d

M M u

d M d

u

 

 

 







Khoảng cách giữa hai đường thẳng song song là khoảng cách từ một điểm thuộc đường thẳng này

đến đường thẳng kia.



Khoảng cách giữa hai đường thẳng chéo nhau:

d

đi qua điểm

M

và có véctơ chỉ phương

u



và

d



đi qua điểm

M



và có véctơ chỉ phương

u





là

 

, .

( , )

,

u u M M

d d d

u u



 







 

3. Góc giữa hai véctơ

Cho hai véctơ

1 2 3

( ; ; )a a a a



và

1 2 3

( ; ; ).b b b b





Khi đó góc giữa hai véctơ

a



và

b



là góc nhợn hoặc

tù.

1 1 2 2 3 3

2 2 2 2 2 2

1 2 3 1 2 3

.

cos( ; )

.

a b a b a b

a b

a a a b b b

 

 

   



với

0 180 .



   

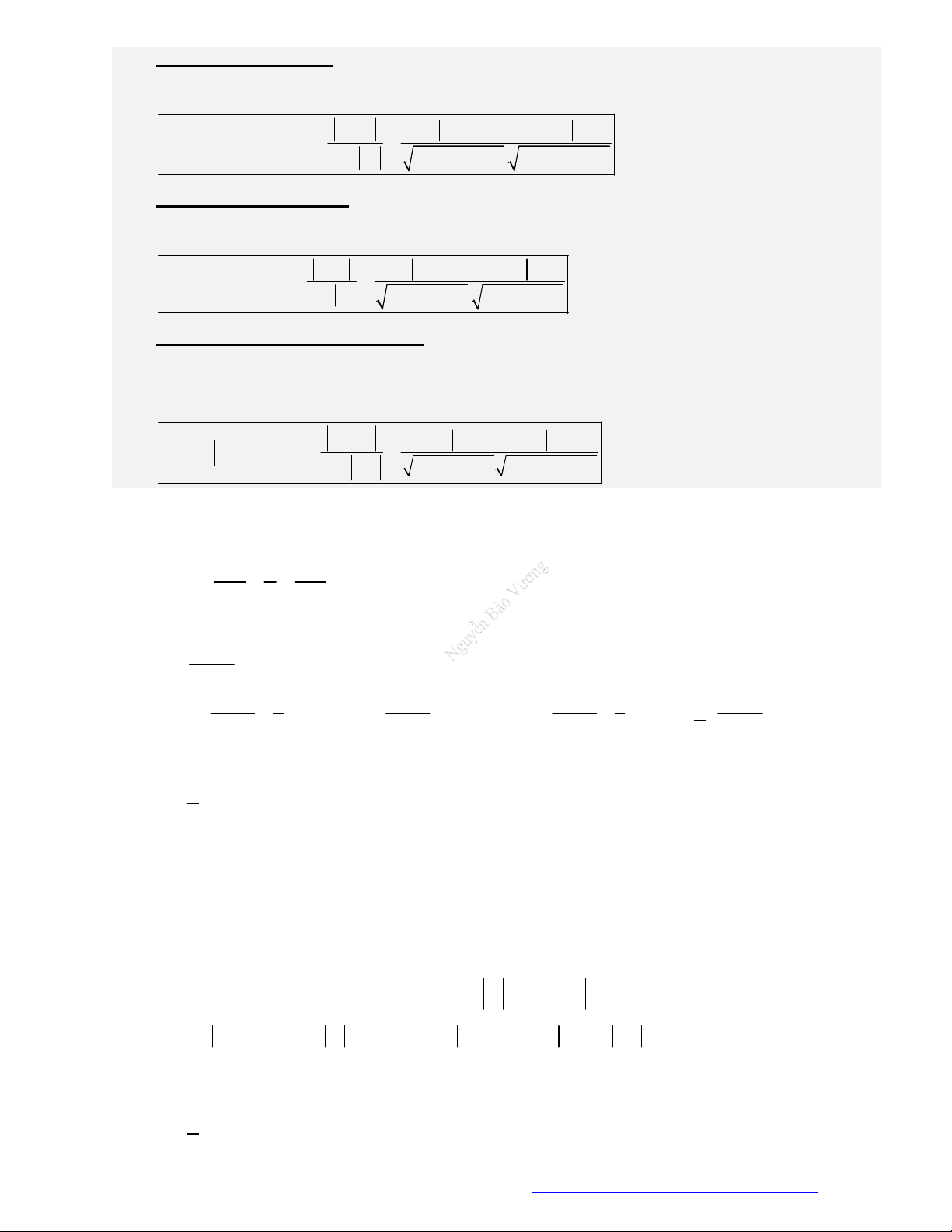
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15

4. Góc giữa hai mặt phẳng

Cho hai mặt phẳng

1 1 1 1

( ) : 0

P A x B y C z D

   

và

2 2 2 2

( ) : 0.

Q A x B y C z D

   

 

1 2 1 2 1 2

2 2 2 2 2 2

1 1 1 2 2 2

.

cos ( ),( ) cos

.

P Q

n n

A A B B C C

P Q

n n

A B C A B C



 

  

   

 

với

0 90 .



   

5. Góc giữa hai đường thẳng

Góc giữa hai đường thẳng

1

d

và

2

d

có véctơ chỉ phương

1 1 1 1

( ; ; )u a b c



và

2 2 2 2

( ; ; ).u a b c



1 2 1 2 1 2 1 2

1 2

2 2 2 2 2 2

1 2

1 1 1 2 2 2

.

cos( ; ) cos

.

u u a a b b c c

d d

u u

a b c a b c



 

  

   

 

với

0 90 .



   

6. Góc giữa đường thẳng và mặt phẳng

Góc giữa đường thẳng

d

có véctơ chỉ phương

( ; ; )

d

u a b c



và mặt phẳng

( )P

có véctơ pháp tuyến

( )

( ; ; )

P

n A B C



được xác định bởi công thức:

( )

2 2 2 2 2 2

( )

.

sin cos( ; )

.

d P

P d

d P

u n

aA bB cC

n u

u n

a b c A B C



 

  

   

 

với

0 90 .



   

Câu 31. Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

 

: 4 7 25 0

P x y z

   

và đường thẳng

1

1 1

:

1 2 1

x y z

d

 

 



. Gọi

1

'd

là hình chiếu vuông góc của

1

d

lên mặt phẳng

 

P

. Đường thẳng

2

d

nằm trên

 

P

tạo với

1 1

, 'd d

các góc bằng nhau,

2

d

có vectơ chỉ phương

 

2

; ;u a b c



. Tính

2a b

c



.

A.

2 2

3

a b

c





. B.

2

0

a b

c





. C.

2 1

3

a b

c





. D.

2

1

a b

c





.

Lời giải

Cách 1:

Gọi

   

1 1

, 'Q d d



khi đó

 

Q

có vectơ pháp tuyến

 

1

, 5;5;15

Q

P

n n u

 

 

 

  

.

Đường thẳng

1

'd

có vectơ chỉ phương

 

1 1

' , 22;11; 11

P

u n u

 

  

 

  

hay một vecto chỉ phương

khác

 

2;1; 1

u

 



.

Vì

 

2 2

. 0 4 7 0 7 4 ; ;7 4

p

n u a b c c b a u a b b a

          

  

.

Ta lại có

   

1 2 1 2 1 2 1 2

; '; cos , cos ',d d d d u u u u

  

   

2 4 7 2 4 7 5 5 6 6 0

a b a b a b a b a b a b a b a b                

Chọn

2

1 1, 3 1

a b

a b c

c



     

.

Cách 2:

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 16 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Gọi

   

1 1

, 'Q d d



khi đó

   

P Q



. Các đường thẳng nằm trong

 

P

mà vuông góc với

 

Q

thì

vuông góc với tất cả các đường thẳng trong

 

Q

hay chúng cùng tạo với

1 1

, 'd d

các góc

90



. Do

đó, các đường thẳng này thỏa mãn yêu cầu đề bài. Chúng có vectơ chỉ phương

 

2

1;1;3 1

Q

a b

u n

c



  

 

.

Câu 32. Trong không gian với hệ tọa độ

,Oxyz

cho hai điểm

   

3;1;7 , 5;5;1

A B

và mặt phẳng

 

:2 4 0

P x y z

   

. Điểm

M

thuộc

 

P

sao cho

35.

MA MB  Biết

M

có hoành độ

nguyên, ta có

OM

bằng

A.

2 2

. B.

2 3

. C.

3 2

. D.

4

.

Lời giải

* Ta có :

   

2;4; 6 2 1;2; 3

AB

   



Gọi

 

4;3;4

I

là trung điểm của

AB

Phương trình mặt phẳng trung trực

 

Q

của

AB

là :

     

4 2 3 3 4 0

x y z

     

2 3 2 0

x y z

    

Gọi

   

d P Q

 

. Đường thẳng

d

có

1

vpcp là

   

 

, 1;1;1

P Q

u n n

 

 

 

  

và đi qua điểm

 

2;0;0

N 

, có phương trình là

2

:

x t

d y t

z t

  















* Gọi

 

:

M P MA MB

 

. Khi đó

d

M



và

 

2 ; ;M t t t

 

Theo giả thiết, ta có :

35

MA 

     

2 2 2

5 1 7 35

t t t      

2

3 26 40 0

t t

   

 

20

3

2 0;2;2

t

t M











 





Vậy

2 2

OM 

Câu 33. (Chuyen Phan Bội Châu Nghệ An 2019) Trong không gian với hệ tọa độ

Oxyz

, cho hai đường

thẳng

1

1 2 1

: ,

2 2 1

x y z

d

  

 

 

2

: 0 .

x t

d y

z t













 



Mặt phẳng

 

P

qua

1

d

tạo với

2

d

một góc

0

45

và

nhận vectơ

 

1; ;n b c





làm một vectơ pháp tuyến. Xác định tích

.bc

A.

4

hoặc

0.

B.

4

hoặc

0.

C.

4

. D.

4

.

Lời giải

Ta có vectơ chỉ phương của

1 2

, d d

lần lượt là

 

1

2; 2; 1

u

  



và

 

2

1;0; 1

u

 



.

Mặt phẳng

 

P

qua

 

1 1

. 0 2 2 0. 1

d n u b c     

 

 

2

2 2 2

2

2 2

2

. 1

2

sin , sin 45 1 1 2 0. 2

. 2

1. 2

u n c

d P c b c b c

u n

b c



            

 

 

Từ

 

1

và

 

2

2 . 4.

2

b

b c

c





   



 



TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17

Câu 34. (Chuyên Phan Bội Châu 2019) Trong không gian với hệ tọa độ

O

xyz

, cho hai đường thẳng

1

1 2 1

:

2 2 1

x y z

d

  

 

 

và

2

: 0

x t

d y

z t













 



. Mặt phẳng

 

P

qua

1

d

tạo với

2

d

một góc

o

45

và nhận

véctơ

 

1; ;n b c



làm một véctơ pháp tuyến. Xác định tích

bc

.

A.

4

hoặc

0

B.

4

hoặc

0

C.

4

D.

4

Lời giải

Đường thẳng

1

d

và

2

d

có véctơ chỉ phương lần lượt là

 

1

2; 2; 1

u

  



và

 

2

1;0; 1

u

 



.

Mặt phẳng

 

P

có véctơ pháp tuyến là

 

1; ;n b c





.

Từ giả thiết ta có:

1

o

2

.

sin 45

| |.| |

u n















 



1

2 2 2 2 2 2

. 0

1.1 0. ( 1). 2

2

1 0 ( 1) . 1

u n

b c







  







    





 



 

2

2 2

2 2 0

2 2

2

2 0

1 1

b c

b

c

b c

c b c

  

 



 





 

  

   

 

 

   











Vậy

. 4

b c

 

.

Câu 35. (Chuyên Phan Bội Châu Nghệ An 2019) rong không gian

Oxyz

, cho hai đường thẳng

1

1 2 1

:

2 2 1

x y z

d

  

 

 

và

2

: 0

x t

d y

z t













 



. Mặt phẳng

 

P

qua

1

d

, tạo với

2

d

một góc

45

và nhận

vectơ

 

1; ;n b c



làm một vec tơ pháp tuyến. Xác định tích

.b c

.

A.

4

. B.

4

. C.

4

hoặc

0

. D.

4

hoặc

0

.

Lời giải.

   

1 2

2; 2; 1 , 1;0; 1

u u

    

 

lần lượt là vectơ chỉ phương của

1 2

,d d

. Theo bài ra ta có

 

1

2 2

. 0

cos ; sin ;

n u

n u d P















 

 

   

 

2 2

2.1 2 1 0

1.1 0. 1

1

2

1 . 2

b c

    







  







 



 

2

2 2

1 1

c b

c b c

 









   





2

b

c









 



.

Câu 36. Trong không gian tọa độ

O

xyz

cho đường thẳng

3 2 1

:

2 1 1

x y z

d

  

 



, mặt phẳng

( ) : 2 0

P x y z

   

. Gọi

M

là giao điểm của

d

và

( )P

. Gọi



là đường thẳng nằm trong

( )P

vuông góc với

d

và cách

M

một khoảng

42

. Phương trình đường thẳng



là

A.

5 2 4

2 3 1

x y z

  

 



. B.

1 1 1

2 3 1

x y z  

 

 

.

C.

3 4 5

2 3 1

x y z

  

 



. D. Đáp án khác.

Lời giải

Chọn D

Gọi

( )M d P 

. Suy ra

(3 2 ; 2 ; 1 ); ( ) 1 (1; 3;0)

M d M t t t M P t M

            

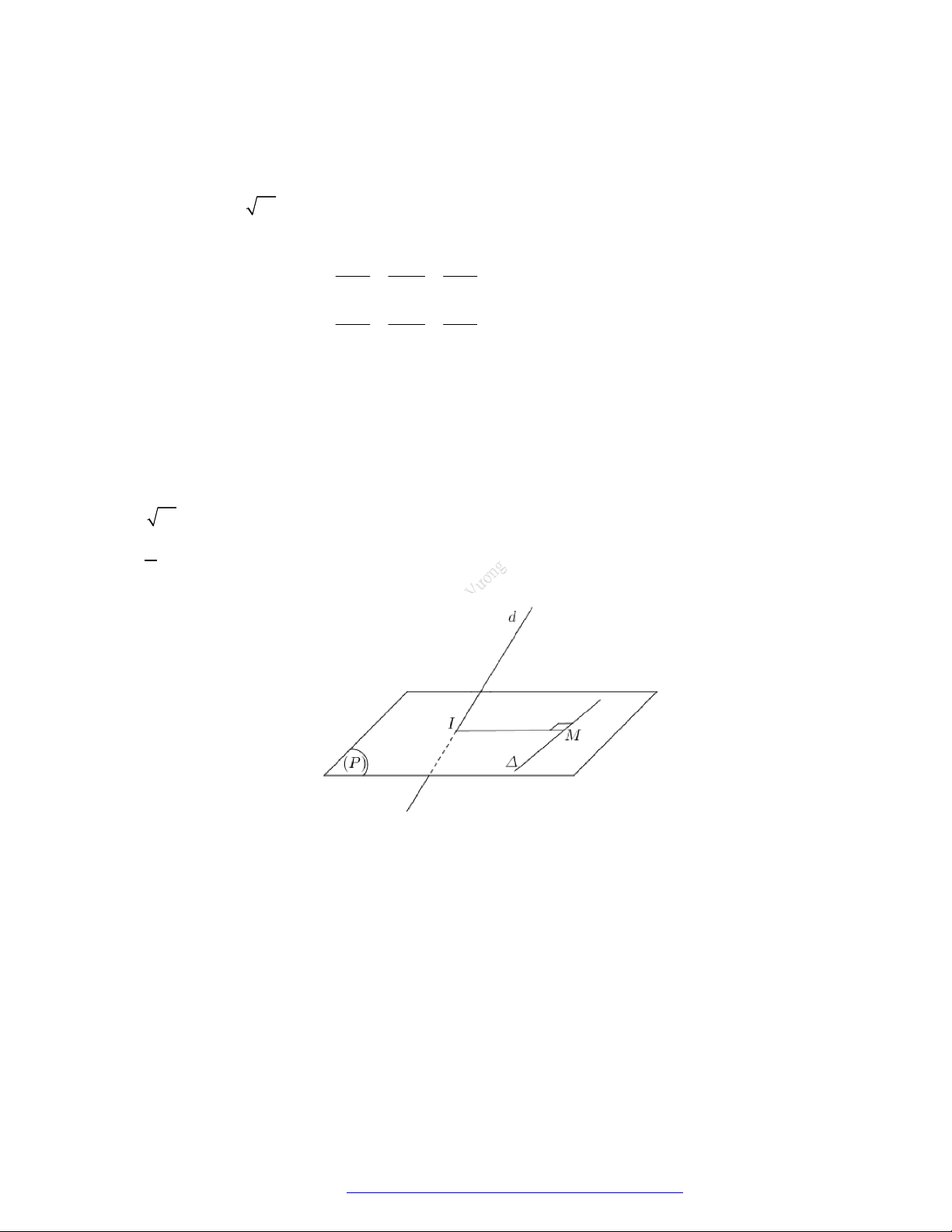
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 18 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

( )P

có véc tơ pháp tuyến là (1;1;1)

P

n 



.

d

có véc tơ chỉ phương (2;1; 1)

d

a  



.



có véc tơ chỉ

phương

 

, (2; 3;1)

d P

a a n



  

  

. Gọi

( ; ; )N x y z

là hình chiếu vuông góc của

M

trên



, khi đó

( 1; 3; )MN x y z  

.

Ta có

2 2 2

2 3 11 0

( ) 2 0

( 1) ( 3) 42

42

MN a x y z

N P x y z

x y z

MN





    





     

 

 

    





 

.

Giải hệ ta tìm được

(5; 2; 5)N  

và

( 3; 4;5)N  

.

Với

(5; 2; 5)N  

, ta có

5 2 5

:

2 3 1

x y z  

  



.

Với

( 3; 4;5)N  

, ta có

3 4 5

:

2 3 1

x y z  

  



.

Câu 37. (THPT Lê Quý Đôn Đà Nẵng 2019) Trong không gian

Oxyz

, đường thẳng

: 1 2 , ,

2

x t

d y t t

z t







   





 





cắt mặt phẳng

 

: 3 0P x y z   

tại điểm

I

. Gọi



là đường thẳng

nằm trong mặt phẳng

 

P

sao cho

d 

và khoảng cách từ điểm

I

đến đường thẳng



bằng

42

. Tìm tọa độ hình chiếu

 

; ;M a b c

( với

a b c 

) của điểm

I

trên đường thẳng



.

A.

 

2;5; 4M 

. B.

 

6; 3;0M 

. C.

 

5;2; 4M 

. D.

 

3;6;0M 

.

Lời giải

 

P

có véctơ pháp tuyến

 

1;1;1n 



và

d

có véctơ chỉ phương

 

1;2; 1u  



.

   

1;1;1I d P I  

.

Vì

 

;P d     

có véctơ chỉ phương

 

, 3;2;1u n u

 

  

 



  

.

M

là hình chiếu của

I

trên



nên

M

thuộc mặt phẳng

 

Q

đi qua

I

và vuông góc với



.

Mặt phẳng

 

Q

nhận

 

3;2;1u  





làm véctơ pháp tuyến nên ta có phương trình của

       

: 3 1 2 1 1 1 0 3 2 0Q x y z x y z          

.

Gọi

   

1 1

d P Q d  

có véctơ chỉ phương

 

, 1;4; 5v u n

 

  

 



  

và

1

d đi qua

I

, phương trình

của

1

: 1 4

1 5

x t

d y t

z t

 





 





 



.

Mặt khác

 

1

M M P M d    

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19

Giả sử

   

1 ;1 4 ;1 5 ;4 ; 5M t t t IM t t t     



.

Ta có:

2 2 2

42 16 25 42 1

IM t t t t

       

.

+) Với

 

1 2;5; 4

t M

  

.

+) Với

 

1 0; 3;6

t M   

.

Vì

 

; ;M a b c

( với

a b c 

) nên

 

2;5; 4

M



.

Cách 2: Vì

 

; ;M a b c

là hình chiếu vuông góc của

I

lên



.

Khi đó ta có

 

     

2 2 2

3 0

3 1 2 1 1 0 3 2 0

42

1 1 1 42

M P

a b c

IM u a b c a b c

IM

a b c









   



  

             

  

  



     





 

           

2 2 2 2 2 2

4 3 4 3

3 0 5 6

1 1 1 42 1 1 1 42

a b b a

a b c c a

a b c a b c

 

   

 

        

 

 

           

 

 

0

3

6

2

5

4

a

b

c

a

b

c

 







 





































 





Vì

 

; ;M a b c

( với

a b c 

) nên

 

2;5; 4

M



.

Câu 38. (Chuyên Đại Học Vinh 2019) Trong không gian

Oxyz

cho ba đường thẳng

1

: ,

1 1 2

x y z

d



 



1

3 1

: ,

2 1 1

x y z

 

  

2

1 2

:

1 2 1

x y z 

  

. Đường thẳng



vuông góc với

d

đồng thời cắt

1 2

, 

tương ứng tại

,H K

sao cho độ dài

HK

nhỏ nhất. Biết rằng



có một vectơ

chỉ phương

 

; ;1 .

u h k



Giá trị

h k

bằng

A.

0.

B.

4.

C.

6.

D.

2.

Lời giải

Chọn A

 

1

3 2 ; ;1

H H t t t   

.

 

2

1 ;2 2 ;K K m m m

   

.

Ta có

 

2 2;2 2; 1

HK m t m t m t

      



.

Đường thẳng

d

có một VTCP là

 

1;1; 2

d

u

 



.

d

  

. 0

d

u HK



 

 

2 0 2 4; 2; 3 .

m t m t HK t t

            



Ta có

       

2 2 2 2

2

4 2 3 2 1 27 27,

HK t t t t             

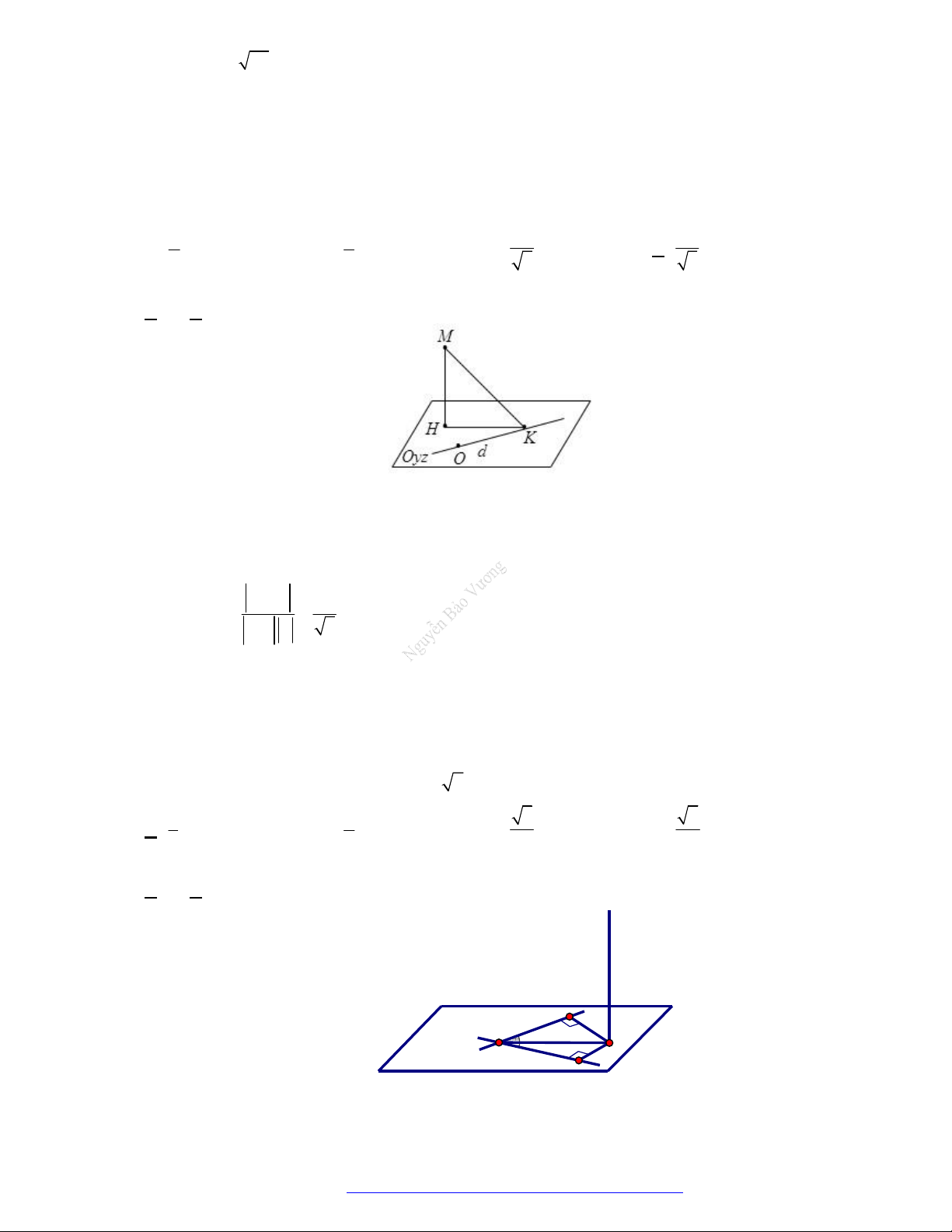
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 20 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

27,minHK 

đạt được khi

1t  

.

Khi đó ta có

 

3; 3; 3HK    



, suy ra

 

1;1;1 1 0.u h k h k     



Câu 39. (Hội 8 trường chuyên 2019) Trong không gian

,Oxyz

gọi

d

là đường thẳng đi qua

,O

thuộc

mặt phẳng

 

Oyz

và cách điểm

 

1; 2;1M 

một khoảng nhỏ nhất. Côsin của góc giữa

d

và trục

tung bằng

A.

2

5

. B.

1

5

. C.

1

5

. D.

2

5

.

Lời giải

Chọn D

Gọi

,H K

lần lượt là hình chiếu của

M

trên mặt phẳng

 

Oyz

và trên đường thẳng

d

.

Ta có:

 

, 1d M d MK MH  

,

 

0; 2;1H 

.

Suy ra

 

,d M d

nhỏ nhất khi

K H

. Khi đó

d

có một vecto chỉ phương là

 

0; 2;1OH  



.

 

.

2

cos ,

5

OH j

d Oy

OH j

 









.

Câu 40. (Sở Cần Thơ - 2019) Trong không gian

Oxyz

, cho điểm

 

2;1;1A

, mặt phẳng

 

: 1 0  P x z

và đường thẳng

 

1

: 2

2

 











  



x t

d y

z t

. Gọi

1 2

;d d là các đường thẳng đi qua

A

, nằm trong

 

P

và đều

có khoảng cách đến đường thẳng

d

bằng 6 . Côsin của góc giữa

1

d và

2

d bằng

A.

1

3

. B.

2

3

. C.

3

. D.

2

3

.

Lời giải

Chọn A

* Ta có:

   

d

1;0; 1 , 1;0;1   

 

P

n u

 

 d P

và

   

0;2; 1  d P M

 

2; 1;2 3    



MA MA

d

2

d

1

P)

A

M

H

K

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21

* Gọi

; H K

lần lượt là hình chiếu vuông góc của

M

lên

1

d

và

2

d

, ta có

       

1 1 2 2

; ; , ; ; 6

      d d d d M d MH d d d d M d MK MH MK



6

sin sin

3

   

HM

MAK MAH

AM

 



 



2

1 2

4 1

cos ; cos 2. 1 2sin 1

3 3

      

d d MAH MAH

.

Câu 41. (Chuyên Bắc Giang 2019) Trong không gian với hệ tọa độ

Oxyz

, cho đường thẳng

 

3 3

: ,

1 3 2

x y z

d

 

 

mặt phẳng

 

: 3 0

P x y z

   

và điểm

 

1;2; 1

A



. Cho đường thẳng

 



đi qua

A

, cắt

 

d

và song song với mặt phẳng

 

P

. Tính khoảng cách từ gốc tọa độ

O

đến

 



A.

3

. B.

16

3

. C.

2 3

3

. D.

4 3

3

.

Lời giải

Chọn D

Gọi

        

3;3 3;2 2;3 1;2 1

M d M t t t t R AM t t t

           



.

Gọi

 

1;1; 1

n





là vectơ pháp tuyến của mặt phẳng

 

P

.

Ta có

   

/ / . 0 2 3 1 2 1 0 1

P AM n AM n t t t t

              

   

   

,

4 3

1; 2; 1 ;

3

AM OA

AM d O

AM

 

 

      

 



Câu 42. (Kim Liên - Hà Nội 2019) Trong không gian

Oxyz

, cho hai đường thẳng

1

1 2

:

2 1 1

x y z

d

 

 



và

2

1 4

: 1 2

2 2

x t

d y t

z t

 





  





 



.

Khoảng cách giữa hai đường thẳng đã cho bằng?

A.

87

6

. B.

174

6

. C.

174

3

. D.

87

3

.

Lời giải

Chọn B

Ta có: Đường thẳng

1

d

đi qua điểm

(1; 2;0)

M



và nhận

 

1

2; 1;1

u  



làm VTCP.

Đường thẳng

2

d

đi qua điểm

(1; 1;2)

N



và nhận

 

2

4; 2;2

u  



làm VTCP.

Dễ thấy:

2 1

2.u u



 

nên đường thẳng

1

d

song song hoặc trùng với đường thẳng

2

d

.

Lại có điểm

 

1

1; 2;0

M d 

nhưng

 

2

1; 2;0

M d 

nên suy ra

1 2

// d d

.

Vậy khoảng cách giữa hai đường thẳng đã cho bằng khoảng cách từ điểm

 

1; 2;0

M 

đến

đường thẳng

2

d

.

 

2

d ;

MN u

M d

u





 



.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 22 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Ta có

 

0;1;2

MN 



,

 

2

6;8;4

MN u 

 

.

 

2

2 2

2 1 2

2

2 2

6 8 4

174 174

; ( ; ) .

6 6

4 2 2

d M d d d d

  

    

  

Câu 43. Trong không gian

Oxyz

, cho hai điểm

 

3;1;2

A

,

 

3; 1;0

B  

và mặt phẳng

 

: 3 14 0

P x y z

   

. Điểm

M

thuộc mặt phẳng

 

P

sao cho

MAB

vuông tại

M

. Tính

khoảng cách từ điểm

M

đến mặt phẳng

 

Oxy

.

A. 5. B. 4. C. 3. D. 1.

Lời giải

Chọn B

Gọi

 

; ;M x y z

là điểm cần tìm.

 

3; 1; 2

AM x y z

   



,

 

3; 1;BM x y z

  



.

Vì

MAB

vuông tại

M

nên

       

. 0 3 3 1 1 2 0

AM BM x x y y z z

         

 

 

2

2 2 2 2 2

9 1 2 0 1 11

x y z z x y z

           

.

M

thuộc mặt cầu

 

S

có tâm

 

0;0;1

I

và bán kính

11

R 

.

Nhận xét thấy

 

2 2 3

0 0 3.1 14

, 11

1 1 3

d I P R

  

  

 

.

 

P



tiếp xúc với

 

S

tại

M

M

là hình chiếu vuông góc của

I

trên

 

P

 

1

3 14

1 1;1;4

1

cïng ph¬ng

4

1 1 3

P

x

x y z

M P

y M

x y z

IM n

z





  



 

  

    

  

 

  







 

.

Vậy

 

, 4 4

d M Oxy

 

.

Câu 44. Trong không gian với hệ trục tọa độ

Oxyz

, cho 4 điểm

     

2;0;0 , 0;3;0 , 0;0;6

A B C

và

 

1;1;1

D

. Gọi



là đường thẳng qua

D

và thỏa mãn tổng khoảng cách từ các điểm

, ,A B C

đến



là lớn nhất. Khi đó



đi qua điểm nào dưới đây?

A.

 

4;3;7

. B.

 

1; 2;1

 

. C.

 

7;5;3

. D.

 

3;4;3

.

Lời giải

Chọn C

Phương trình mặt phẳng

 

: 1 3 2 6 0

2 3 6

x y z

ABC x y z

       

, dễ thấy

 

D ABC



.

Ta thấy

     

, , ,

P d A d B d C AD BD CD

        

.

Vậy

P

lớn nhất khi và chỉ khi các hình chiếu vuông góc của các điểm

, ,A B C

trên



trùng

D

hay

 

ABC

 

tại

D

.

Phương trình đường thẳng



là

1 3

1 2

1

x t

y t

z t

 





 





 



, ta thấy



đi qua điểm có tọa độ

 

7;5;3

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23

Câu 45. (Nguyễn Huệ- Ninh Bình- 2019)Tính khoảng cách từ giao điểm của hai đường thẳng

1 2

;d d

tới

mặt phẳng

 

P

trong đó:

 

1 2

1 1 1 1

: ; : ; : 2 4 4 3 0

2 3 3 2 1 1

x y z x y z

d d P x y z

    

       

.

A.

4

3

. B.

7

6

. C.

13

6

. D.

5

3

.

Lời giải

Chọn A

Phương trình tham số của hai đường thẳng

1 2

,d d

như sau:

1 2

1 2 1 2

: 3 , :

1 3 1

x t x t

d y t d y t

z t z t



    

 

 



 

 

 



   

 

.

Xét hệ phương trình:

1

1 2 1 2 2 2 2

4

3 3 0

3

1 3 1 3 0

4

t t t t

t

t t t t

t

t t t t



 

     

 





  

 

    

  

  





 

    

 





.

Suy ra giao điểm của

1 2

,d d

là

1 3 7

; ;

2 4 4

A

 



 

 

.

Khoảng cách từ

A

đến mặt phẳng

 

P

là:

 

2

2 2

1 3 7

2. 4. 4. 3

2 4 4

4

;

3

2 4 4

d A P

     

   

     

     

 

  

.

Câu 46. (THPT Hậu Lộc 2 2019) Trong không gian

Oxyz

, cho mặt phẳng

 

: 2 2 3 0

P x y z

   

và

đường thẳng

 

1 1 1

:

2 2 1

x y x  

  



. Khoảng cách giữa

 



và

 

P

là

A.

2

3

B.

8

3

C.

2

9

D.

1

Lời giải

Chọn A

Mặt phẳng

 

: 2 2 3 0

P x y z

   

có véc tơ pháp tuyến là

 

2; 1; 2

n  



.

Đường thẳng

 

1 1 1

:

2 2 1

x y z  

  



có véc tơ chỉ phương là

 

2;2; 1

u

 



và đi qua điểm

 

1; 1;1

M  

.

Ta có

 

. 0

n u

M P















 

suy ra

 



song song với

 

P

.

Khi đó

   

 

2

2 2

2 1 2 3

2

, ,

3

2 2 1

d P d M P

  

   

  

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 24 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 47. Trong không gian với hệ tọa độ

Oxyz

,cho đường thẳng

0

: 3

x

d y t

z t







 









.Gọi

 

P

là mặt phẳng chứa

đường thẳng

d

và tạo với mặt phẳng

 

Oxy

một góc

45

.Điểm nào sau đây thuộc mặt phẳng

 

P

?

A.

 

3;2;1

M

. B.

 

3;2; 1

N



. C.

 

3; 1;2

P 

. D.

 

3; 1; 2

M

 

.

Lời giải

Chọn A

Ta viết phương trình đường thẳng

d

:

0

3 0

x

y z







  



.

Mặt phẳng

 

P

chứa đường thẳng

d

nên có dạng:

 

2 2

3 0, 0

mx n y z m n

     

 

3 0

mx ny nz n P

     

có một véc tơ pháp tuyến là

 

; ;

P

n m n n





.

Mặt phẳng

 

Oxy

có một véc tơ pháp tuyến là

 

0;0;1

k 



.

Ta có:

   

 

2 2 2

.

1

cos ; cos ; cos45

2

.

P

n k

n

P Oxy n k

n k

m n n

     

 

 

2 2 2

2 2 0 0

m n n m m

      

.

Chọn

 

1 : 3 0

n P y z

    

.

Do đó:

   

3;2;1

M P



.

Bình luận: Đối với những bài toán viết phương trình mặt phẳng chứa đường thẳng cho trước ta

nên sử dụng khái niệm chùm mặt phẳng như sau: Mặt phẳng

 



qua giao tuyến của hai mặt

phẳng

 

1 1 1 1

: 0

P a x b y c z d

   

và

 

2 2 2 2

: 0

Q a x b y c z d

   

có phương trình dạng

   

2 2

1 1 1 1 2 2 2 2

0, 0

m a x b y c z d n a x b y c z d m n

         

.

Câu 48. (Chuyên Hà Tĩnh 2019)) Trong không gian với hệ tọa độ

Oxyz

cho đường thẳng

5 7 12

:

2 2 1

  

 



x y z

d

và mặt phẳng

 

: 2 3 3 0   

x y z



. Gọi

M

là giao điểm của

d

và

 



,

A

thuộc

d

sao cho

14

AM

. Tính khoảng cách từ

A

đến mặt phẳng

 



.

A.

2

. B.

3

. C.

6

. D.

14

.

Lời giải

Chọn B

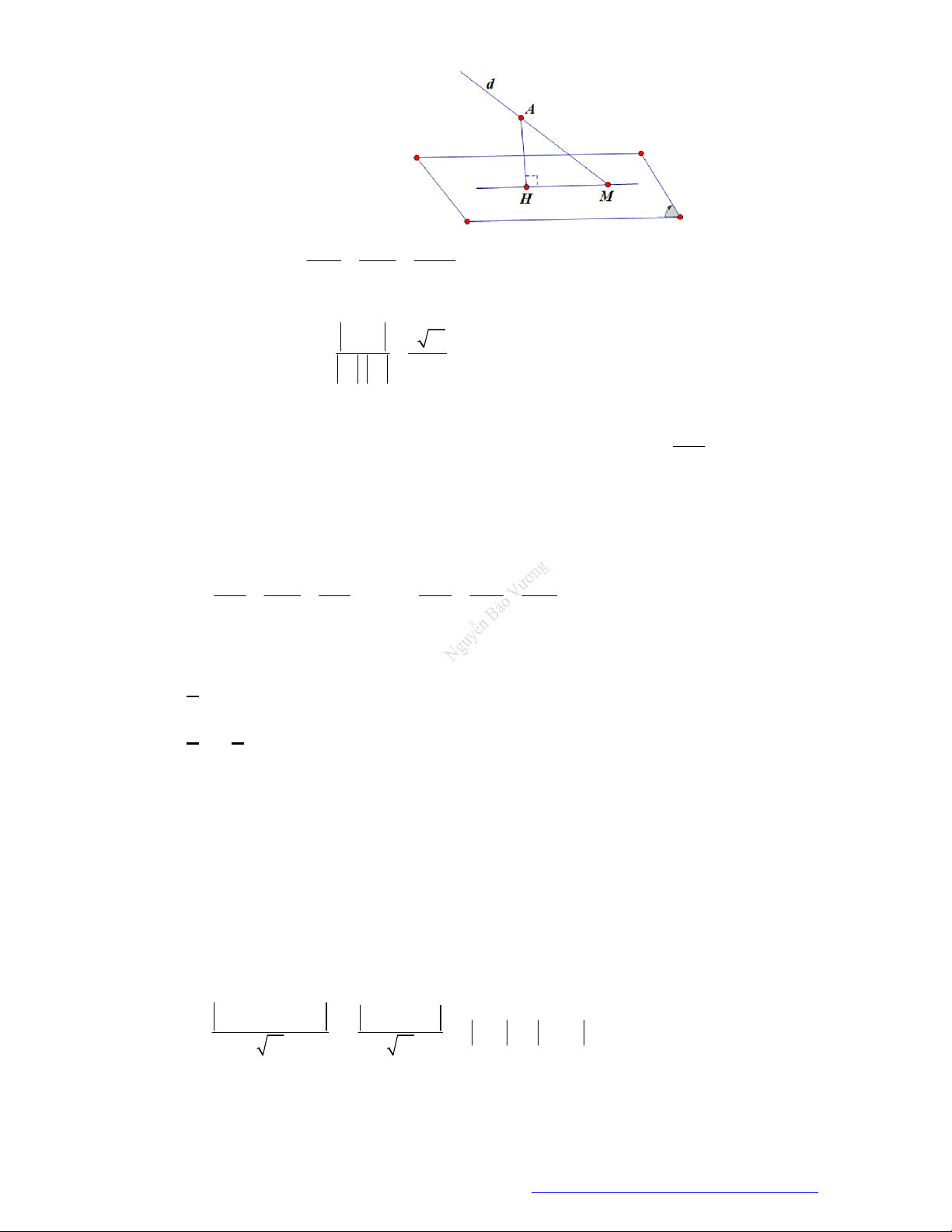
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25

Đường thẳng

5 7 12

:

2 2 1

  

 



x y z

d

có một vectơ chỉ phương là

 

2;2; 1 



u .

Mặt phẳng

 

: 2 3 3 0   x y z



có một vectơ pháp tuyến là

 

1;2; 3 



n .

Ta có:

 

.

3 14

sin ;

14

.

 

 

d

u n

d

u n



.

Gọi

H

là hình chiếu vuông góc của

A

lên mặt phẳng

 



.

Khi đó tam giác

MAH

vuông tại

H

nên

 



sin ; sin 

AH

d AMH

AM



.

 

.sin ; 3  AH AM d



.

Vậy khoảng cách từ

A

đến mặt phẳng

 



bằng

3

.

Câu 49. (Hội 8 trường chuyên 2019) Trong không gian

,Oxyz

cho

2

đường thẳng

1

1 2 1

:

1 1 2

x y z

d

  

 

và

2

1 1 2

: .

2 1 1

x y z

d

  

 

Mặt phẳng

   

: 0 0P x ay bz c c    

song song với

1 2

,d d

và khoảng cách từ

1

d

đến

 

P

bằng 2 lần khoảng cách từ

2

d

đến

 

.P

Giá

trị của

a b c 

bằng

A.

14

. B.

6

. C.

4.

D.

6

.

Lời giải

Chọn A

Gọi

 

1

1;1;2u 



,

 

2

2;1;1u 



lần lượt là một vectơ chỉ phương của

1

d

,

2

d

.

Gọi

 

1 1 2

, 1;3; 1n u u

 

   

 

  

, có

1

n



cùng phương

 

2

1; 3;1n  



.

 

1; ;n a b



là một vectơ chỉ phương của

 

P

.

Do

 

P

song song với

1 2

,d d

nên chọn

 

1; 3;1n  



.

Suy ra phương trình mặt phẳng

 

P

có dạng:

3 0x y z c   

.

Lấy

 

1 1

1; 2;1M d 

,

 

2 2

1;1; 2M d 

Có

 

1 2

; 2 ;d d P d d P

 

1 2

; 2 ;d M P d M P 

 

1 3 2 1

1 3 2

2

11 11

c

   

  

 

8 2 4c c    

 

8 2 4

c c



   





  





 

16 nhaän

0 loaïi

c















.

Nên

 

: 3 16 0P x y z   

, suy ra

3a  

,

1b 

,

16c 

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 26 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Vậy

14  

a b c

.

Câu 50. Trong không gian với hệ trục toạ độ

Oxyz

, cho hai điểm

   

3;3;1 , 0;2;1

A B

và mặt phẳng

 

: 7 0

P x y z

   

. Đường thẳng

d

nằm trong

 

P

sao cho mọi điểm của

d

cách đều hai

điểm

,A B

có phương trình là:

A.

2

7 3

x t

y t

z t







 









. B.

7 3

2

x t

y t

z t







 









. C.

7 3

2

x t

y t

z t







 









. D.

7 3

4

x t

y t

z t

 





 









.

Lời giải

Chọn C

+ Các điểm cách đều hai điểm

,A B

thì nằm trên mặt phẳng

 



là mặt phẳng trung trực của đoạn

AB

.

+ Gọi

I

là trung điểm của

AB

3 5

; ;1

2 2

I

 



 

 

+ Phương trình mặt phẳng

 



là

3 7 0

x y

  

.

Do đó đường thẳng

d

là giao tuyến của

2

mặt phẳng

 

P

và

 



Phương trình đường thẳng

d

đi qua điểm

     

0;7;0M P



 

và nhận

 

( ) ( )

, 1; 3;2

P

u n n



 

  

 

  

làm một vectơ chỉ phương là

7 3

2

x t

y t

z t







 









.

Câu 51. (Chuyên ĐH Vinh- 2019) Trong không gian

Oxyz

, cho tam giác

ABC

vuông tại

A

,



0

30

ABC  ,

3 2

BC 

, đường thẳng

BC

có phương trình

4 5 7

1 1 4

x y z

  

 



, đường thẳng

AB

nằm trong mặt phẳng

 

: 3 0

x z



  

. Biết đỉnh

C

có cao độ âm. Tính hoành độ đỉnh A.

A.

3

2

. B.

3

. C.

9

2

. D.

5

2

.

Lời giải

Chọn C

Vì

C BC

nên

 

4 ;5 ; 7 4C t t t

   

.

BC

có véc tơ chỉ phương

 

1;1; 4

u

 



. Mặt phẳng

 



có véc tơ pháp tuyến

 

1;0;1

n 



.

Gọi



là góc giữa

BC

và

 



. Ta có

 

0

1

sin cos ; 30

2

u n

 

   

 

. Tức là

A

là hình chiếu

của

C

lên

 



.

Vậy

 

3;4; 3

1

4 7 4 3

3 2

;

3

2

1;2;5

2

C

t

t t

CA d C

t

C







 

   



    



 







Mà

C

có cao độ âm, suy ra

 

1;2;5

C

.

Lúc này

AC

qua

 

1;2;5

C

và có véc tơ chỉ phương

 

1;0;1

n 



. Nên

 

3 ;4; 3

A t t  

.

Mặt khác

A

nằm trong mặt phẳng

 

3 9

: 3 0

2 2

A

x z t x



      

.

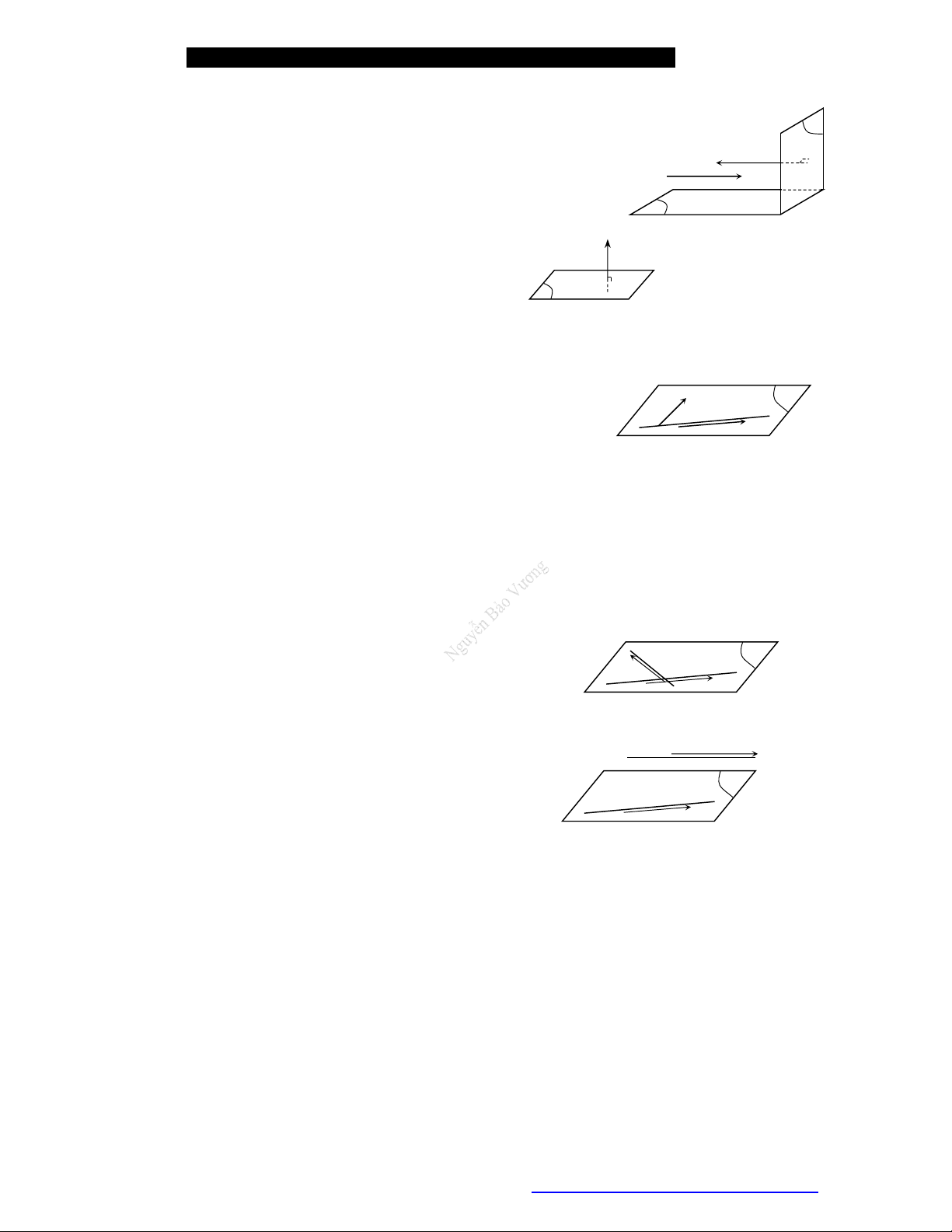
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27

Dạng 4. Viết phương trình mặt phẳng liên quan đến đường thẳng

Dạng 1. Viết phương trình mp

 

P

đi qua

,M

vuông góc mp

 

Q

và

 

//

mp P



:

 

   

• , ,

:

• :

,

Đ

o o o

PP

P Q

M x y z

mp P

VT n

i q

PT

u

n u

a











 





 



  

Dạng 2. Viết phương trình mặt phẳng

 

P

đi qua M và vuông góc với đường thẳng d đi qua hai

điểm A và B, với:

 

•

:

•

Đ

:

PP

d

P

M

mp P

VTPT n

i qua

u AB









 





  

Dạng 3. Viết phương trình của mặt phẳng

 

P

đi qua điểm M và chứa đường thẳng



:

PP



Trên đường thẳng Δ lấy điểm A và xác định VTCP

u





Khi đó

 

•

:

• : ,

Đ

P

M

m

V

i qua

p P

TPT n AM u









 





 



  

Dạng 4. Viết phương trình của mặt phẳng

 

P

đi qua hai đường thẳng song song

1 2

,  

:

 

1 2

• ,

:

•

Đ

: ,

PP

P

M hay M

mp P

VTPT n u u

i qua

 

 









 





 



  

Dạng 5. Viết phương trình của mặt phẳng

 

P

đi qua hai đường thẳng cắt nhau

1 2

, : 

 

1 2

• ,

:

•

Đ

: ,

PP

P

M hay M

mp P

VTPT n u u

i qua

 

 









 





 



  

Dạng 6. Cho 2 đường thẳng chéo nhau

1 2

,  

. Hãy viết phương trình

 

P

chứa

1



và song song

2



 

1 2

• ,

:

•

Đ

: ,

PP

P

M hay M

mp P

VTPT n u u

i qua

 

 









 





 



  

Dạng 7. Viết phương trình mặt phẳng

 

P

đi qua điểm M và giao tuyến của hai mặt phẳng

   

,

 

PP



Chọn

,A B

thuộc giao tuyến hai mặt phẳng

 



và

 



 

,

A B P

 

. Cụ thể:

Cho:

 

   

1 1 1 1

2 2 2 2

...

...;...;...

...

o

A x B y C z D

x

z z A P

y

A x B y C z D

   







    

 



   







Cho:

 

   

1 1 1 1

2 2 2 2

...

...;...;...

...

o

B y C z A x D

y

x x B P

z

B y C z A x D

   







    

 



   







Khi đó

 

Đ •

:

• : ,

P

m

V

i qua M

p P

TPT n AB AM







 





 



  

u





Δ

P

Q

 

Q

n



P

 

P d

n u AB

 

  

d

M

Δ

A

u





P

M

Δ

1

u





P

2

u





Δ

2

M

Δ

1

u





P

2

u





Δ

2

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 28 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 52. (Đề Minh Họa 2017) Trong không gian với hệ tọa độ

Oxyz

, cho đường thẳng



có phương

trình:

10 2 2

5 1 1

x y z

  

 

. Xét mặt phẳng

 

:10 2 11 0

P x y mz

   

,

m

là tham số thực. Tìm tất cả

các giá trị của

m

để mặt phẳng

 

P

vuông góc với đường thẳng



.

A.

2

m



B.

52

m

 

C.

52

m



D.

2

m

 

Lời giải

Chọn A

Đường thẳng

10 2 2

:

5 1 1

x y z

  

  

có vectơ chỉ phương

 

5;1;1

u 



Mặt phẳng

 

:10 2 11 0

P x y mz

   

có vectơ pháp tuyến

 

10;2;n m





Để mặt phẳng

 

P

vuông góc với đường thẳng



thì

u



phải cùng phương với

n



5 1 1

2

10 2

m

    

.

Câu 53. Trong không gian với hệ tọa độ

Oxyz

, cho đường thẳng

1 2

:

1 2 3

x y z 

  

 

và mặt phẳng

 

: 3 0

P x y z

   

. Phương trình mặt phẳng

 



đi qua

O

, song song với



và vuông góc với

mặt phẳng

 

P

là

A.

2 0

x y z

  

. B.

2 0

x y z

  

. C.

2 4 0

x y z

   

. D.

2 4 0

x y z

   

.

Lời giải



có VTCP

 

1;2; 3

u

  



và

 

P

có VTPT là

 

1; 1;1

n  



.

 



qua

O

và nhận

 

; 1;2;1

n u n

 



  

 

  

Suy ra

 

: 2 0

x y z



  

.

Câu 54. (Toán Học Tuổi Trẻ 2019) Trong không gian với hệ tọa độ

Oxyz

, cho đường thẳng

1

d

có véctơ

chỉ phương

 

1;0; 2

u

 



và đi qua điểm

 

1; 3;2

M



,

2

3 1 4

:

1 2 3

x y z

d

  

 



. Phương trình

mặt phẳng

 

P

cách đều hai đường thẳng

1

d

và

2

d

có dạng

11 0

ax by cz

   

. Giá trị

2 3a b c 

bằng

A.

42

. B.

32

. C.

11

. D.

20

.

Lời giải

Đường thẳng

2

d

có véctơ chỉ phương

 

1; 2;3

v

 



và đi qua điểm

 

3;1; 4

N

 

Ta có:

 

, 4;5;2 0

v u

 

 

 

 

  

;

 

4;4; 6

MN

  



;

, . 16 20 12 8 0

v u MN

 

      

 

 

  



1

d

và

2

d

chéo nhau.

Mặt phẳng

 

P

cách đều hai đường thẳng

1

d

và

2

d

nên

 

P

nhận

 

, 4;5;2

v u

 



 

 

 

làm một vectơ

pháp tuyến và đi qua trung điểm

 

1; 1; 1

I

  

của đoạn

MN

Suy ra phương trình của

 

P

:

     

4 1 5 1 2 1 0 4 5 2 11 0

x y z x y z

          

4; 5; 2

a b c

   

2 3 20

a b c

   

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 29

Câu 55. Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng

 

P

song song và cách đều

hai đường thẳng

1

2

:

1 1 1

x y z

d



 



và

2

1 2

:

2 1 1

x y z

d

 

 

 

A.

 

:2 2 1 0

xP z

  

B.

 

:2 2 1 0

yP z

  

C.

 

:2 2 1 0

xP y

  

D.

 

:2 2 1 0

yP z

  

Lời giải

Chọn B

Ta có:

1

d

đi qua điểm

 

2;0;0

A

và có VTCP

 

1

1;1;1

u  



2

d

đi qua điểm

 

0;1;2

B

và có VTCP

 

2

2; 1; 1

u

  



Vì

 

P

song song với hai đường thẳng

1

d

và

2

d

nên VTPT của

 

P

là

 

1 2

[ , ] 0;1; 1

n u u

  

  

Khi đó

 

P

có dạng

0

y z D

  



loại đáp án A và C

Lại có

 

P

cách đều

1

d

và

2

d

nên

 

P

đi qua trung điểm

1

0; ;1

2

M

 

 

 

của

AB

Do đó

 

:2 2 1 0

yP z

  

Câu 56. (SGD Cần Thơ - 2018) Trong không gian

Oxyz

, mặt phẳng chứa hai đường thẳng cắt nhau

1 2 4

2 1 3

  

 



x y z

và

1 2

1 1 3

 

 



x y z

có phương trình là

A.

2 9 36 0    

x y z

. B.

2 0  

x y z

.

C.

6 9 8 0   

x y z

. D.

6 9 8 0   

x y z

.

Lời giải

Đường thẳng

1

1 2 4

:

2 1 3

  

 



x y z

d

đi qua điểm

 

1; 2; 4

M

, có một VTCP là

 

1

2;1;3

 



u

.

Đường thẳng

2

1 2

:

1 1 3

 

 



x y z

d

có một VTCP là

 

2

1; 1;3

 



u

.

Mặt phẳng

 

P

chứa hai đường thẳng cắt nhau

1 2

,d d



 

P

qua điểm

 

1; 2;4 ,

M

có một

VTPT là

 

1 2

, 6;9;1

 

 

 

  

n u u

. Phương trình mặt phẳng

 

P

là :

       

: 6 1 9 2 4 0 6 9 8 0          

P x y z x y z

.

Câu 57. (Hồng Bàng - Hải Phòng - 2018) Trong không gian tọa độ

,Oxyz

cho điểm

 

0;1;0 ,

A

mặt

phẳng

 

: 4 6 0

Q x y z

   

và đường thẳng

3

: 3

5

x

d y t

z t







 





 



. Phương trình mặt phẳng

 

P

qua

A

,

song song với

d

và vuông góc với

 

Q

là :

A.

3 1 0

x y z

   

. B.

3 1 0

x y z

   

. C.

3 3 0

x y z

   

. D.

1 0

x y z

   

.

Lời giải

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 30 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Mặt phẳng

 

Q

có VTPT

 

1;1; 4

Q

n

 



.

Đường thẳng

d

có VTCP

 

0;1; 1

d

u

 



.

Gọi VTPT của mặt phẳng

 

P

là

P

n



.

Ta có:

P Q

n n



 

và

P d

n u

 

nên chọn

 

, 3;1;1

P Q d

n n u

 

 

 

  

.

 

P

đi qua điểm

 

0;1;0 ,

A

VTPT

 

3;1;1

P

n 



có phương trình là:

3 1 0

x y z

   

.

Câu 58. (Toán Học Tuổi Trẻ - 2018) Trong không gian với hệ tọa độ Descartes

Oxyz

, cho điểm

 

3; 1;0

A 

và đường thẳng

2 1 1

:

1 2 1

x y z

d

  

 



. Mặt phẳng

 



chứa

d

sao cho khoảng cách

từ

A

đến

 



lớn nhất có phương trình là

A.

0

x y z

  

. B.

2 0

x y z

   

. C.

1 0

x y z

   

. D.

2 5 0

x y z

    

.

Lời giải

Gọi

H

là hình chiếu của

A

đến

d

. Khi đó

 

2 ; 1 2 ;1

H t t t   

 

1 ;2 ;1

AH t t t    



.

Do

AH d

 

1 2.2 1 0

t t t

       

1

3

t

  

. Khi đó

2 2 2

; ;

3 3 3

AH

 

  

 

 



.

Mặt phẳng

 



chứa

d

sao cho khoảng cách từ

A

đến

 



lớn nhất khi

 

AH





.

Do đó

 



có vectơ pháp tuyến là

 

1;1; 1

n

 



.

Vậy

 

:



     

1 2 1 1 1 1 0

x y z

     

0

x y z

   

.

Câu 59. (SGD&ĐT BRVT - 2018) Trong không gian

Oxyz

, cho hai đường thẳng chéo nhau

1

2 6 2

:

2 2 1

x y z

d

  

 



và

2

4 1 2

:

1 3 2

x y z

d

  

 



. Phương trình mặt phẳng

 

P

chứa

1

d

và

 

P

song song với đường thẳng

2

d

là

A.

 

: 5 8 16 0

P x y z

   

. B.

 

: 5 8 16 0

P x y z

   

.

C.

 

: 4 6 12 0

P x y z

   

. D.

 

: 2 6 0

P x y

  

.

Lời giải

Đường thẳng

1

d

đi qua

 

2;6; 2

A



và có một véc tơ chỉ phương

 

1

2; 2;1

u  



.

Đường thẳng

2

d

có một véc tơ chỉ phương

 

2

1;3; 2

u

 



.

Gọi

n



là một véc tơ pháp tuyến của mặt phẳng

 

P

. Do mặt phẳng

 

P

chứa

1

d

và

 

P

song

song với đường thẳng

2

d

nên

 

1 2

, 1;5;8

n u u

 

 

 

  

.

Vậy phương trình mặt phẳng

 

P

đi qua

 

2;6; 2

A



và có một véc tơ pháp tuyến

 

1;5;8

n 



là

5 8 16 0

x y z

   

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 31

Câu 60. (Chuyên Thăng Long - Đà Lạt - 2018) Trong không gian

Oxyz

, phương trình mặt phẳng chứa

hai đường thẳng:

 

2

: 3 1

2 1

x t

d y t

z t

 





 





 



và

 

3

: 3 2

2 1

x m

y m

z m

 





  





 



có dạng

0

x ay bz c

   

. Tính

2 3P a b c  

.

A.

10

P

 

. B.

4P 

. C.

8

P

 

. D.

0

P



.

Lời giải

Ta có

//

d



.

Chọn

       

2; 1;1 , 3; 2;1A d B

    

.

 

1; 1;0

AB  



Phương trình mặt phẳng chứa hai đường thẳng

 

d

và

 



qua

 

2; 1;1

A 

và có VTPT

 

   

, 2; 2;4 2 1;1; 2

d

n AB u

 

      

 

  

là:

     

1 2 1 1 2 1 0 2 1 0

x y z x y z

          

.

 

1

2 2 3 1 2. 2 3.1 0

1

a

b P a b c

c







           









.

Câu 61. (Chuyên Trần Đại Nghĩa - 2018) Tìm tất cả các mặt phẳng

 



chứa đường thẳng

d

:

1 1 3

x y z

 

 

và tạo với mặt phẳng

 

P

:

2 1 0

x z

  

góc

45

.

A.

 



:

3 0

x z

 

. B.

 



:

3 0

x y z

  

.

C.

 



:

3 0

x z

 

. D.

 



:

3 0

x z

 

hay

 



:

8 5 0

x y z

  

.

Lời giải

d

đi qua điểm

 

0;0;0

O

có vtcp

 

1; 1; 3

u

  



.

 



qua

O

có vtpt

 

; ;n a b c





có dạng

0

ax by cz

  

, do

. 0

n u



 

3 0

a b c

   

.

 

P

:

2 1 0

x z

  

vtpt

 

2;0; 1

k

 



.

Ta có

.

cos45 



n k

 

2 2 2

2

5

a c

a b c





 

2



 

2

2 2 2

10 4 2a b c a c

    

 

2

2 2 2 2

10 6 9 4 12 2b bc c b c b c c

       

 

2

2 2

10 2 6 10 4 10b bc c b c

    

2

4 20 0

b bc

  

0

5

b

b c













.

+

0

b



3a c 

 





:

3 0

x z

 

.

+

5b c

, chọn

1c 

5

b

 

,

8

a



 





:

8 5 0

x y z

  

.

Câu 62. (Quảng Nam - 2018) Trong không gian với hệ trục tọa độ

Oxyz

, cho hai điểm

 

1;1;0

A

,

 

0; 1;2

B 

. Biết rằng có hai mặt phẳng cùng đi qua hai điểm

A

,

O

và cùng cách

B

một khoảng

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 32 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

bằng

3

. Véctơ nào trong các véctơ dưới đây là một véctơ pháp tuyến của một trong hai mặt

phẳng đó.

A.

 

1; 1; 1

n

  



. B.

 

1; 1; 3

n

  



. C.

 

1; 1;5

n  



. D.

 

1; 1; 5

n

  



.

Lời giải

Phương trình đường thẳng qua hai điểm

A

,

O

có dạng

0

x t

x y

y t

z





 





 

 











.

Gọi

 

P

là mặt phẳng cùng đi qua hai điểm

A

,

O

nên

 

P

:

 

0

m x y nz

  

,

2 2

0

m n

 

. Khi

đó véctơ pháp tuyến của

 

P

có dạng

 

; ;n m m n

 



.

Ta có

 

2 2 2

2

, 3 3

m n

d B P

m m n



  

 

2 2

1

2 4 0

1

5

m

n

m mn n

m

n







    









.

Vậy một véctơ pháp tuyến của một trong hai mặt phẳng đó là

 

1 1

; ; 1; 1;5

5 5 5

n

n n n n



 

  

 

 



.

Câu 63. (Sở Bình Phước - 2018) Trong không gian với hệ toạ độ

Oxyz

, cho hai đường thẳng

1 2

,d d

lần

lượt có phương trình

1

2 2 3

:

2 1 3

x y z

d

  

 

,

2

1 2 1

:

2 1 4

x y z

d

  

 



. Mặt phẳng cách đều hai

đường thẳng

1 2

,d d

có phương trình là

A.

14 4 8 1 0.

x y z

   

B.

14 4 8 3 0.

x y z

   

C.

14 4 8 3 0.

x y z

   

D.

14 4 8 1 0.

x y z

   

Lời giải

Ta có

 

2;1;3

a 



và

 

2; 1;4

b  



là véc tơ chỉ phương của

1 2

,d d

Nên

 

7; 2; 4

n a b

    

  

là véc tơ pháp tuyến của mặt phẳng

 

P

.

Do đó

 

: 7 2 4 0

P x y z D

   

Lấy

 

1

2;2;3

M d

và

 

2

1;2;1

N d

.

Do

 

P

cách đều

1

d

và

2

d

nên

 

, ,

d M P d N P



.

2 2 2 2 2 2

7.2 2.2 4.3 7.1 2.2 4.1

7 2 4 7 2 4

D D     

 

   

3

2 1

2

D D D

     

.

Vậy

   

3

:7 2 4 0 :14 4 8 3 0

2

P x y z P x y z

        

.

Câu 64. (THPT Thực Hành - TPHCM - 2018) Trong không gian tọa độ

Oxyz

, cho điểm

 

1;0;0

A

và

đường thẳng

1 2 1

:

2 1 2

x y z

d

  

 

. Viết phương trình mặt phẳng chứa điểm

A

và đường thẳng

d

?

A.

 

:5 2 4 5 0

P x y z

   

. B.

 

: 2 1 2 1 0

P x y z

   

.

C.

 

:5 2 4 5 0

P x y z

   

. D.

 

: 2 1 2 2 0

P x y z

   

.

Lời giải

VTCP của

d

là

 

2;1;2

a 



và

 

1; 2;1

B d 

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 33

Khi đó:

 

0; 2;1

AB  



.

Do đó véc tơ pháp tuyến của mặt phẳng là

 

, 5, 2; 4

n AB a

 

   

 

  

.

Từ đó suy ra phương trình mặt phẳng cần tìm là

     

5 1 2 0 4 0 0

x y z

     

hay

5 2 4 5 0

x y z

   

.

Câu 65. (Chuyên Nguyễn Đình Triểu - Đồng Tháp - 2018) Trong không gian

Oxyz

, cho hai đường

thẳng

1 2

,d d

lần lượt có phương trình

1 2

2 2 3 1 2 1

: , :

2 1 3 2 1 4

x y z x y z

d d

     

   



. Viết

phương trình mặt phẳng cách đều hai đường thẳng

1 2

,d d

.

A.

14 4 8 13 0

x y z

   

. B.

14 4 8 17 0

x y z

   

.

C.

14 4 8 13 0

x y z

   

. D.

14 4 8 17 0

x y z

   

.

Lời giải

Chọn B

1 2

,d d

lần lượt có vectơ chỉ phương là

   

1 2

2;1;3 , 2; 1;4

n n 

 

.

Vectơ pháp tuyến của mặt phẳng cần tìm là

 

1 2

, 7; 2; 4

n u u

 

   

 

  

.

Gọi

   

1 2

2;2;3 , 1; 2; 1

A d B d   

.

Gọi phương trình mặt phẳng

 

: 7 2 4 0

P x y z d

   

.

Do mặt phẳng

 

P

cần tìm cách đều

1 2

,d d

nên

 

2 2 2 2 2 2

2 15

, ,

7 2 4 7 2 4

d d

d A P d B P

 

  

   

2 15

d d   

13

2 15

2

d d d

       

.

Vậy

 

13

:7 2 4 0 14 4 8 13 0.

2

P x y z x y z

        

Câu 66. (Chuyên KHTN - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho hai đường thẳng

1

2

:

1 1 1

x y z

d



 



và

2

1 2

:

2 1 1

x y z

d

 

 



. Phương trình mặt phẳng

 

P

song song và cách đều

hai đường thẳng

1 2

;d d

là:

A.

2 2 1 0

y z

  

. B.

2 2 1 0

y z

  

.

C.

2 2 1 0

x z

  

. D.

2 2 1 0

x z

  

.

Lời giải

Ta có: Đường thẳng

1

d

đi qua điểm

 

2;0;0

A

có VTCP là

 

1

1;1;1

u  



và đường thẳng

2

d

đi

qua điểm

 

0;1;2

A

có VTCP là

 

1

2;1;1

u  



Mặt phẳng

 

P

song song

1 2

;d d

nên

 

P

có VTPT là

 

1 2

; 0; 1;1

n u u

 

  

 

 

Do đó: Mặt phẳng

 

P

có dạng

0

y z m

  

Mặt khác:

 

P

cách đều hai đường thẳng

1 2

;d d

nên

 

1 2

1

; ; ; ; 1

2

d d P d d P d A P d B P m m m

       

Vậy

 

P

:

1

0 2 2 1 0

2

y z y z

      

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 34 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Dạng 5. Bài toán liên quan đến vị trí tương đối

1. Vị trí tương đối giữa đường thẳng d và mặt cầu (S)

Cho mặt cầu

( )S

có tâm

,I

bán kính

R

và đường thẳng

.

Để xét vị trí tương đối giữa



và

( )S

ta

tính

( , )d I 

rồi so sánh với bán kính

.R



Nếu

( , ) :

d I R

  

không cắt

( ).S



Nếu

( , ) :

d I R

  

tiếp xúc với

( )S

tại

.H



Nếu

( , ) :

d I R

  

cắt

( )S

tại hai điểm phân biệt

, .A B

1 1 1 1

2 2 2 2

( ) ( )

A B C D

P Q

A B C D

     



1 2 1 2 1 2

( ) ( ) 0.

P Q A A B B C C

    

2. Vị trí tương đối giữa đường thẳng d và mặt phẳng (P)

Cho đường thẳng

1

2

3

:

x x a t

d y y a t

z z a t

 





 





 





và mặt phẳng

( ) : 0

Ax By Cz D



   

Xét hệ phương trình:

1

2

3

(1)

(2)

(3)

0 (4)

x x a t

y y a t

z z a t

Ax By Cz D

 





 





 



   





( )



Nếu

( )

có nghiệm duy nhất

d

cắt

( ).





Nếu

( )

có vô nghiệm

( ).

d



 



Nếu

( )

vô số nghiệm

( ).

d



 

3. Vị trí tương đối giữa hai đường thẳng d và d’

Cho hai đường thẳng:

1

2

3

:

x x a t

d y y a t

z z a t

 





 





 





và

1

2

3

:

x x a t

d y y a t

z z a t

  

 





  

 





 

 





lần lượt qua điểm hai điểm

, M N

và có

véctơ chỉ phương lần lượt là

, .

d d

a a



 



d

song song

.

d d

a ka

d

M d



















 



d

trùng

.

d d

a ka

d

M d



















 



d

cắt

d





 

, . 0

d d

a ko a

a a MN



















 



 



d

chéo

 

, . 0.

d d

d a a MN



 



 

Lưu ý: Nếu

d

cắt

d



ta tìm tọa độ giao điểm bằng giải hệ phương trình:

1 1

2 2

3 3

.

x a t x a t

y a t y a t

z a t z a t

  

  





  

  





  

  



 

Câu 67. (Chuyên Bắc Giang 2019) Trong không gian với hệ tọa độ

Oxyz

cho hai đường thẳng

1

1 2

:

2 1 2

x y z

d

 

 



,

2

2 1

:

2 1 2

x y z

d

 

 

 

. Xét vị trí tương đói của hai đường thẳng đã cho.

A. Chéo nhau B. Trùng nhau C. Song song D. Cắt nhau

Lời giải

A

B

I

H

d

R

P

d

u



P

n



P

n



d

u



d

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 35

Chọn C

1

1 2

:

2 1 2

x y z

d

 

 



 

1

2;1; 2

u

  



;

2

2 1

:

2 1 2

x y z

d

 

 

 

 

2

2; 1;2

u   



1 2 1 2 1 2

/ /

u u d d d d    

 

Điểm

 

1

1;0; 2 d

M

 

;

2

M d

nên

1 2

/ /d d

Câu 68. (Chuyên Lương Thế Vinh Đồng Nai 2019) Trong không gian tọa độ

Oxyz

, xét vị trí tương đối

của hai đường thẳng

1 2

1 1 3 3 2

: , :

2 2 3 1 2 1

x y z x y z

    

     

 

A.

1



song song với

2



. B.

1



chéo với

2



. C.

1



cắt

2



. D.

1



trùng với

2



.

Lời giải

Vì

2 2

1 2



 

nên vectơ chỉ phương

 

1

2;2;3

u 



của đường thẳng

1



không cùng phương với

vectơ chỉ phương

 

2

1; 2;1

u   



của

2



. Tức là

1



chéo với

2



hoặc

1



cắt

2



.

Lấy

 

1

1; 1;0M

 

,

 

2

3;3; 2N

 

. Ta có:

 

2;4; 2

MN

 



.

Khi đó:

1 2

; . 0

u u MN

 



 

  

. Suy ra

1 2

, ,

u u MN

  

đồng phẳng.

Vậy

1



cắt

2



.

Câu 69. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng

1 5

:

1 3 1

x y z

d

 

 

 

và mặt phẳng

 

:3 3 2 6 0

P x y z

   

. Mệnh đề nào dưới đây đúng?

A.

d

cắt và không vuông góc với

 

.P

B.

d

vuông góc với

 

.P

C.

d

song song với

 

.P

D.

d

nằm trong

 

.P

Lời giải

Chọn A

Đường thẳng

d

có vtcp

 

1; 3; 1

u

 



Mặt phẳng

 

P

có vtpt

 

3; 3;2

n 



Ta có

. 3 9 2 10 0

u n

    

 

nên loại trường hợp

 

/ /

d P

và

 

d P



.

Lại có

u



và

n



không cùng phương nên loại trường hợp

 

d P



.

Vậy

d

cắt và không vuông góc với

 

.P

Câu 70. Trong không gian với hệ tọa độ

Oxyz

, cho đường thẳng

2 1

:

2 1 3

x y z 

  



và mặt phẳng

 

:11 16 0

P x my nz

   

. Biết

 

P

 

, tính giá trị của

T m n 

.

A.

2T 

. B.

2T  

. C.

14T 

. D.

14T  

.

Lời giải

Cách 1: Lấy

 

0;2; 1

2;3;2

A

B

 







  





Mà

 

P

 

 

A P

B P















 

2 16 0

10

11. 2 3 2 16 0

4

m n

m

m n

n

  









 

 

    







NGUYỄN BẢO VƯƠNG - 0946798489

Trang 36 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

14

T m n

   

.

Cách 2: Đường thẳng



đi qua

 

0;2; 1

A



có VTCP

 

2;1;3

u  



.

Mặt phẳng

 

P

có VTPT

 

11; ;n m n





.

 

0

A P

P

n.u





  









 

2 16 0 10

22 3 0 4

m n m

m n n

   

 

 

 

    

 

.

14

T m n

   

.

Câu 71. Trong không gian tọa độ

Oxyz

, cho đường thẳng

1 2 9

1 3 1

:

y z

d

x

  

 



và mặt phẳng

 



có

phương trình

2

2 19 0

m x my z

   

với

m

là tham số. Tập hợp các giá trị

m

thỏa mãn

 

//d



là

A.

 

1

. B.



. C.

 

1;2

. D.

 

2

.

Lời giải

Chọn D

Đường thẳng

d

có vectơ chỉ phương là

 

1;3; 1

u

 



.

Mặt phẳng

 



có vectơ pháp tuyến là

 

2

; ; 2

n m m

  



.

Để

 

//d



thì

   

. 0

1;2;9

u n

M

















 

2

1

3 2 0

2

2 18 19 0

1

m

m m

m

m m

m

 





  

 



   



 



   











.

Câu 72. Trong không gian với hệ trục toạ độ

Oxyz

, tìm tất cả các giá trị của tham số

m

để đường thẳng

d

:

1 1 2

1 1 1

x y z

  

 



song song với mặt phẳng

 

2

: 2 0

P x y m z m

   

A.

1

m



. B.

m



C.

 

1;1

m 

. D.

1

m

 

Lời giải

Chọn D

Một véctơ chỉ phương của

:d

 

1; 1;1

u  



;

 

1; 1;2

A d 

.

Một véctơ pháp tuyến của

 

:P

 

2

2;1;

n m

 



.

 

2

1 2 1 1 1 0

/ /

2 1 1 2 0

m

u n

d P

A P

m m



     



 

 

 



    





 

2

1

1 0

1

1 2 0

m

m m

 



 





    

 

  





.

Câu 73. Gọi

,m n

là hai giá trị thực thỏa mãn: giao tuyến của hai mặt phẳng

 

: 2 1 0

m

P mx y nz

   

và

 

: 2 0

m

Q x my nz

   

vuông góc với mặt phẳng

 

: 4 6 3 0

x y z



   

.

A.

0

m n

 

. B.

2

m n

 

. C.

1

m n

 

. D.

3

m n

 

.

Lời giải

Chọn D

 

: 2 1 0

m

P mx y nz

   

có VTPT

 

;2;

P

n m n



.

 

: 2 0

m

Q x my nz

   

có VTPT

 

1; ;

Q

n m n 



.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 37

 

: 4 6 3 0

x y z



   

có VTPT

 

4; 1; 6

n



  



.

Do giao tuyến của

 

m

P

và

 

n

Q

vuông góc với

 



   

4 2 6 0 4 6 2 2

4 6 0 6 4 1

m

P

n

Q

P

n n

m n m n m

m n m n n

Q

n n











  

     

  



   

    

    

    

      



  

  

 







 

Vậy

3

m n

 

.

Câu 74. (THPT Gang Thép Thái Nguyên 2019) Trong không gian với hệ tọa độ

Oxyz

, cho hai đường

thẳng

1 2

1

: ; : 2

2 1 3

x t

x y z

d d y t

z m

 







   









. Gọi

S

là tập tất cả các số

m

sao cho

1

d

và

2

d

chéo

nhau và khoảng cách giữa chúng bằng

5

19

. Tính tổng các phần tử của

S

.

A.

11

. B.

12

. C.

12

. D.

11

.

Lời giải

1

d

đi qua điểm

 

1;0;0

M

, có vectơ chỉ phương

 

1

2;1;3

u 



.

2

d

đi qua điểm

 

1;2;N m

, có vectơ chỉ phương

 

2

1;1;0

u 



.

 

 

1 2

, 3;3;1

u u  

 

;

 

0;2;MN m





.

1

d

và

2

d

chéo nhau khi và chỉ khi

 

1 2

, . 0 6

u u MN m

   



 

.

Mặt khác

 

1 2

5

,

19

d d d 

 

1 2

, .

5

,

19

u u MN

u u

 



 

6

5

19 19

m 

 

1

11

m

 







 



.

Khi đó tổng các phần tử của

m

là

12

.

Câu 75.

(Chuyên Vĩnh Phúc - 2018) Trong không gian

Oxyz

, cho bốn đường thẳng:

 

1

3 1 1

:

1 2 1

x y z

d

  

 



,

 

2

1

:

1 2 1

x y z

d



 



,

 

3

1 1 1

:

2 1 1

x y z

d

  

 

,

 

4

1 1

:

1 1 1

x y z

d

 

 



. Số đường thẳng trong không gian cắt cả bốn đường thẳng trên là:

A.

0

. B.

2

. C. Vô số. D.

1

.

Lời giải

Đường thẳng

1

d

đi qua điểm

 

1

3; 1; 1

M

  

và có một véctơ chỉ phương là

 

1

1; 2;1

u  



.

Đường thẳng

2

d

đi qua điểm

 

2

0;0;1

M 

và có một véctơ chỉ phương là

 

2

1; 2;1

u  



.

Do

2

1

u u

 

và

1 1

M d

nên hai đường thẳng

1

d

và

2

d

song song với nhau.

Ta có

 

1 2

3;1;2

M M  



,

 

1

1 2

, 5; 5; 5

u M M

 

   

 

 

 

5 1;1;1;

 

Gọi

 



là mặt phẳng chứa

1

d

và

2

d

khi đó

 



có một véctơ pháp tuyến là

 

1;1;1

n 



. Phương

trình mặt phẳng

 



là

1 0

x y z

   

.

Gọi

 

3

A d



 

thì

 

1; 1;1

A 

. Gọi

 

4

B d



 

thì

 

1;2;0

B 

.

Do

 

2;3; 1

AB

  



không cùng phương với

 

1

1; 2;1

u  



nên đường thẳng

AB

cắt hai đường

thẳng

1

d

và

2

d

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 38 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 76. (Mã 105 2017) Trong không gian với hệ tọa độ

Oxyz

, cho điểm

 

1; 2; 3

I

và mặt phẳng

 

   : 2 2 4 0

P x y z

. Mặt cầu tâm

I

tiếp xúc với

 

P

tại điểm

H

. Tìm tọa độ điểm

H

.

A.

 



1; 1; 0

H

B.

 

 3; 0; 2

H

C.

 



1; 4; 4

H

D.

 

3; 0; 2

H

Lời giải

Chọn D

Tọa độ điểm

H

là hình chiếu của điểm

I

trên mặt phẳng

 

P

.

Phương trình đường thẳng

d

qua

I

và vuông góc với mặt phẳng

 

P

là:

  



 





 



1 2

2 2

3

x t

y t

z t

.

Tọa độ điểm

H

là giao điểm của

d

và

 

P

, ta có:

     

        2 1 2 2 2 2 3 4 0 1t t t t

Vậy

 

3; 0; 2

H

.

Câu 77. Trong không gian

Oxyz

, biết mặt cầu

 

S

có tâm

O

và tiếp xúc với mặt phẳng

 

2 2 9 0

:P x y z

   

tại điểm

 

; ;H a b c

. Giá trị của tổng

a b c 

bằng

A.

2

. B.

1

. C.

1.

D.

2

.

Lời giải

 

1 2 2; ;

P

n  



là véc tơ chỉ phương của đường thẳng

OH

2

:

x t

OH y t

z t







  









 

2 2; ;H t t t

 

 

H P



 

2 2 2 2 9 0

. .t t t

     

1t  

 

1 2 2; ;

H

  

1a b c    

Câu 78. (Chuyên Lê Hồng Phong-Nam Định- 2019) Trong không gian

Oxyz

, cho điểm

 

1;0;2

I

và

đường thẳng

1

:

2 1 1

x y z

d



 



. Gọi

 

S

là mặt cầu có tâm

I

, tiếp xúc với đường thẳng

d

. Bán

kính của

 

S

bằng

A.

5

3

. B.

2 5

3

. C.

30

3

. D.

4 2

3

.

Lời giải

Chọn C

Gọi

 

1 2 ; ;H t t t

 

là hình chiếu của

I

trên đường thẳng

d

.

Có

 

2 ; ; 2

IH t t t

  



; vectơ chỉ phương của

d

là

 

2; 1;1

u  



.

Vì

H

là hình chiếu vuông góc của

I

trên

d

nên

. 0

IH u IH u

  

   

     

2 .2 . 1 2 .1 0

t t t

      

1

3

t

 

2 1 5

; ;

3 3 3

IH

 

   

 

 



30

3

IH 

.

Bán kính của mặt cầu

 

S

là

30

3

R IH 

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 39

Câu 79. Trong không gian

Oxyz

, cho mặt cầu

       

2 2 2

: 1 2 3 1

S x y z

     

, đường thẳng

6 2 2

:

3 2 2

x y z

  

  



và điểm

 

4;3;1

M

. Trong các mặt phẳng sau mặt phẳng nào đi qua

M

,

song song với



và tiếp xúc với mặt cầu

 

S

?

A.

2 2 5 22 0

x y z

   

. B.

2 2 13 0

x y z

   

.

C.

2 2 1 0

x y z

   

. D.

2 2 7 0

x y z

   

.

Lời giải

Cách 1:

Gọi

 

2 ; ;n a b c





là véctơ pháp tuyến của mặt phẳng

 

P

cần lập,

2 2 2

0

a b c

  

.

Đường thẳng



có vectơ chỉ phương là

 

3;2;2

u  



.

Mặt phẳng

 

P

song song với



nên ta có

. 0 6 2 2 0

n u a b c

     

 

3

c a b  

.

Mặt phẳng

 

P

đi qua

M

và có vectơ pháp tuyến

n



nên phương trình có dạng:

      

2 4 3 3 1 0

a x b y a b z

      

 

2 3 11 2 0

ax by a b z a b

      

 

*

Mặt cầu

 

S

có tâm

 

1;2;3

I

và bán kính

1R 

.

Mặt phẳng

 

P

tiếp xúc với mặt cầu

 

S

 

2

2 2

3

, 1 1

4 3

b

d I P

a b a b

   

  

2 2

3

1 3 13 2 6

13 2 6

b

b a b ab

a b ab

     

 

.

2 2 2 2 2

9 13 2 6 13 6 7 0

b a b ab a ab b

       

  

13 7 0

13 7

a b

a b a b

a b





    



 



.

Với

a b

, chọn

1, 1

a b

 

, thay vào

 

*

ta được pt

 

1

: 2 2 13 0

P x y z

   

.

Ta có

 

6;2;2N



. Dễ thấy

 

1

N P



, suy ra

 

1

: 2 2 13 0

P x y z

   

song song với



.

Với

13 7a b 

, chọn

7, 13

a b

  

, thay vào

 

*

ta được pt

 

2

:14 13 34 51 0

P x y z

   

.

Ta có

 

6;2;2N



, dễ thấy

 

2

N P



, suy ra

 

2

:14 13 34 51 0

P x y z

   

song song với



.

Vậy chọn B.

Cách 2: ( Trắc nghiệm)

Gọi

 

P

là mặt phẳng thỏa mãn yêu cầu bài toán và có vectơ pháp tuyến là

n



.

Vì

 

P

đi qua

 

4;3;1

M

nên phương án A, C bị loại.

Đường thẳng



có vectơ chỉ phương

 

3;2;2

u  



.

 

P

song song với đường thẳng



nên

. 0

n u



 

. Do đó phương án D bị loại.

Vậy phương án B là phương án thỏa mãn yêu cầu bài toán.

Câu 80. (Mã 104 2018) Trong không gian Oxyz, cho mặt cầu

       

2 2 2

: 2 3 1 16

S x y z

     

và

điểm

 

1; 1; 1 .

A

  

Xét các điểm M thuộc

 

S

sao cho đường thẳng AM tiếp xúc với

 

.S

M

luôn thuộc một mặt phẳng cố định có phương trình là

A.

6 8 11 0

x y

  

B.

6 8 11 0

x y

  

C.

3 4 2 0

x y

  

D.

3 4 2 0

x y

  

Lời giải

Chọn C

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 40 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

 

S

có tâm

 

2;3; 1 ;I 

bán kính

4R 

   

1; 1; 1 3; 4;0A IA      



, tính được

5IA 

.

Mặt phẳng cố định đi qua điểm H là hình chiếu của M xuống IA và nhận

 

3; 4;0IA   



làm

vectơ pháp tuyến.

Do hai tam giác MHI và AMI đồng dạng nên tính được

2

16

.

5

IM

IM IH IA IH

IA

    , từ đó

tính được

16

25

IH IA

 

tìm được

2 11

; ; 1

25 25

H

 



 

 

Mặt phẳng cần tìm có phương trình là:

2 11

3 4 0 3 4 2 0.

25 25

x y x y

   

        

   

   

Câu 81. (Mã 110 2017) Trong không gian với hệ tọa độ

Oxyz

, cho mặt cầu

       

2 2 2

: 1 1 2 2S x y z     

và hai đường thẳng

2 1

:

1 2 1

x y z

d

 

 



;

1

:

1 1 1

x y z 

  



.

Phương trình nào dưới đây là phương trình của một mặt phẳng tiếp xúc với

 

S

, song song với

d

và



?

A.

3 0y z  

B.

1 0x z  

C.

1 0x y  

D.

1 0x z  

Lời giải.

Chọn B

Mặt cầu

 

S

có tâm

 

1;1 2I  

;

2R 

.

Véctơ chỉ phương của

d

:

 

1;2; 1

d

u  



. Véctơ chỉ phương của



:

 

1;1; 1u



 



.

Gọi

 

P

là mặt phẳng cần viết phương trình.

Ta có

 

, 1;0; 1

d

u u



 

  

 

 

nên chọn một véctơ pháp tuyến của

 

P

là

 

1;0;1n 



.

Mặt phẳng

 

P

có phương trình tổng quát dạng:

0x z D  

.

Do

 

P

tiếp xúc với

 

S

nên

 

1 2

; 2

2

D

d I P R

  

  

5

3 2

1

D





   







.

Chọn

 

P

:

1 0x z  

.

Câu 82. Trong không gian

Oxyz

, cho mặt phẳng

(P)

chứa đường thẳng

4 4

:

3 1 4

x y z

d

 

 



và tiếp xúc

với mặt cầu

       

2 2 2

: 3 3 1 9S x y z     

. Khi đó

 

P

song song với mặt phẳng nào sau

đây?

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 41

A.

3x 2z 0

y

  

. B.

2x 2 4 0

y z

    

.

C.

x 0

y z

  

D. Đáp án khác.

Lời giải

Chọn D

Véc tơ chỉ phương của

d

là

 

3;1; 4

u

 



, véc tơ pháp tuyến của mặt phẳng

 

P

là

n



.

Mặt cầu

 

S

có tâm

 

3; 3;1

I 

và bán kính

3

R



.

Vì

 

P

chứa

d

nên

. 0

u n



 

và

 

P

tiếp xúc với

 

S

nên

 

; 3

d I P



.

Ta chỉ xét phương trình

. 0

u n



 

. Lấy hai điểm nằm trên đường thẳng

d

là

 

4;0; 4

M



và

 

1; 1;0

N 

.

Ta nhận thấy:

 

4;0; 4

M



và

 

1; 1;0

N 

không thỏa mãn đáp án

; ;A B C

.

Vây, đáp án là

D

.

Câu 83. (Chuyên Bắc Giang 2019) Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng

tiếp xúc với mặt cầu

2 2 2

( 1) ( 2) 6

x y z

    

đồng thời song song với hai đường thẳng

1

2 1

:

3 1 1

x y z

d

 

 

 

,

2

2 2

:

1 1 1

x y z

d

 

 



.

A.

2 3 0

2 9 0

x y z

   





   



B.

2 3 0

2 9 0

x y z

   





   



C.

2 9 0

x y z

   

D.

2 9 0

x y z

   

Lời giải

Chọn B

Đường thẳng

1

d

có vtcp

 

1

3; 1; 1

u

 



, đường thẳng

2

d

có vtcp

 

2

1;1; 1

u





. Gọi

n



là vtpt của mặt

phẳng

 



cần tìm. Do

 



song song với hai đường thẳng

1 2

,d d

nên

1

n u

 

và

2

n u

 

, từ đó ta

chọn

 

1 2

, 2;2;4

n u u

 

 

 

  

. Suy ra

 

: 2 0x y z c    

.

Mặt cầu

 

S

có tâm

 

1;0; 2

I



, bán kính

6

R 

.

 



tiếp xúc với

   

 

3 6 9

3

; 6 6

3 6 3

6

c c

c

S d I

c c

  



 

      

 

   

 

.

Câu 84. (Đề Tham Khảo 2019) Trong không gian

,Oxyz

cho điểm

 

2;1;3

E

, mặt phẳng

 

: 2 2 3 0

P x y z

   

và mặt cầu

       

2 2 2

: 3 2 5 36

S x y z

     

. Gọi



là đường thẳng

đi qua

E

, nằm trong mặt phẳng

 

P

và cắt

 

S

tại hai điểm có khoảng cách nhỏ nhất. Phương

trình của



là

A.

2 9

1 9

3 8

x t

y t

z t

 





 





 



B.

2 5

1 3

3

x t

y t

z

 





 









C.

2

1

3

x t

y t

z

 





 









D.

2 4

1 3

3 3

x t

y t

z t

 





 





 



Lời giải

Chọn C

Ta có tâm và bán kính mặt cầu

 

S

là

 

3;2;5 ; 6

I R



1 1 4 6

IE R    

Gọi



là đường thẳng đi qua

E

Gọi

H

là hình chiếu vuông góc của

I

lên



NGUYỄN BẢO VƯƠNG - 0946798489

Trang 42 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Dây cung càng nhỏ khi khoảng cách từ tâm tới đường thẳng



càng lớn

Ta có

 

,d I IH IE  

Vậy dây cung nhỏ nhất khi đường thẳng



vuông góc với

 

1; 1;; 2IE    



Dựa vào các đáp án ta thấy trong các vecto chỉ phương

 

1

9;9;8u 



 

3

5;3;0u  



 

3

1; 1;0u  



 

4

4;3; 3u  



Thì chỉ có

3

. 0u IE 

 

Nhận xét: ta hoàn toàn có thể viết được pt đường thẳng



bằng cách viết pt mặt phẳng

 

Q

đi

qua

E

nhận

 

1; 1;; 2IE    



làm một vecto pháp tuyến, khi đó

   

P Q  

Câu 85. Trong không gian

Oxyz

, cho hai mặt cầu

 

1

S

,

 

2

S

có phương trình lần lượt là

 

2 2 2

1

: 25S x y z  

,

   

2

2 2

2

: 1 4S x y z   

. Một đường thẳng

d

vuông góc với véc tơ

 

1; 1;0u  



tiếp xúc với mặt cầu

 

2

S

và cắt mặt cầu

 

1

S

theo một đoạn thẳng có độ dài bằng

8

. Hỏi véc tơ nào sau đây là véc tơ chỉ phương của

d

?

A.

 

1

1;1; 3u 



B.

 

2

1;1; 6u 



C.

 

3

1;1;0u 



D.

 

4

1;1; 3u  



Lời giải

Mặt cầu

 

1

S

có tâm

 

0;0;0O

, bán kính

1

5R  .

Mặt cầu

 

2

S

có tâm

 

0;0;1I

, bán kính

2

2R  .

Có

1 2

1OI R R   nên

 

2

S

nằm trong mặt cầu

 

1

S

.

Giả sử

d

tiếp xúc với

 

2

S

tại

H

và cắt mặt cầu

 

1

S

tại

M

,

N

. Gọi

K

là trung điểm

MN

.

(

S

2

)

(

S

1

)

M

N

H

O

I

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 43

Khi đó

2

2IH R  và

OH OK

.

Theo giả thiết

8 4MN MK  

2 2 2 2

1

5 4 3OK R MK     

.

Có

1OI 

,

2IH 

OK OI IH OH OK    

. Do đó

OH OK

, suy ra

H K

, tức

d

vuông

góc với đường thẳng

OI

.

Đường thẳng

d

cần tìm vuông góc với véc tơ

 

1; 1;0u  



và vuông góc với

 

0;0;1OI 



nên có

véc tơ chỉ phương

 

3

, 1;1;0u OI u

 

 

 



 

.

Câu 86. (Chuyên Bắc Giang 2019) Trong không gian với hệ tọa độ

Oxyz

, cho điểm

 

1;1;1E

, mặt cầu

 

2 2 2

: 4S x y z  

và mặt phẳng

 

: 3 5 3 0P x y z   

. Gọi



là đường thẳng đi qua

E

,

nằm trong

 

P

và cắt mặt cầu

 

S

tại hai điểm

,A B

sao cho tam giác

OAB

là tam giác đều.

Phương trình của đường thẳng



là

A.

1 1 1

2 1 1

x y z  

 

 

. B.

1 1 1

2 1 1

x y z  

 



.

C.

1 1 1

2 1 1

x y z  

 

. D.

1 1 1

2 1 1

x y z  

 

 

.

Lời giải

Chọn D

Mặt cầu

 

S

có tâm

 

0; 0;0O

bán kính

2R 

. Tam giác

OAB

là tam giác đều có cạnh bằng 2.

Gọi

M

là trung điểm

AB

ta có

2 3

3

2

OM  

, mặt khác

 

1;1;1 3OE OE 



. Vậy điểm

M

trùng điểm

E

. Gọi

u



là vectơ chỉ phương của



ta có:

u OE

 

và

u n

 

( với

 

1; 3;5n 



là

vectơ pháp tuyến của

 

P

vì

 

P 

).

 

, 8;4;4n OE

 

 

 

 

, chọn

 

1

, 2; 1; 1

4

u n OE

 

    

 

  

.

Vậy đường thẳng



đi qua

E

, có vectơ chỉ phương

 

2; 1; 1u  



có phương trình là:

1 1 1

2 1 1

x y z  

 

 

.

Câu 87. Trong không gian

Oxyz

, cho đường thẳng

1

1 2 3

:

1 2 1

x y z

d

  

 



và điểm

 

1;0; 1

A



. Gọi

2

d

là

đường thẳng đi qua điểm

A

và có vectơ chỉ phương

 

;1;2v a



. Giá trị của

a

sao cho đường

thẳng

1

d

cắt đường thẳng

2

d

là

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 44 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

A.

1

a

 

. B.

2

a



. C.

0

a



. D.

1

a



.

Lời giải

Chọn C

Phương trình tham số của đường thẳng

1

d

là:

1

2 2

3

x t

y t

z t

 





 





 



.

Phương trình tham số đường thẳng

2

d

qua điểm

A

và có vectơ chỉ phương

 

;1;2

v a



là:

2

1

: 0

1 2

x at

d y t

z t



 







 







  



1

d

nhận

 

1; 2;1

u  



làm vectơ chỉ phương và

2

d

nhận

 

;1;2

v a



làm vectơ chỉ phương

Đường thẳng

1

d

cắt đường thẳng

2

d

khi và chỉ khi hệ phương trình

1 1

2 2 0

3 1 2

t at

t t



  







  







   



có đúng

một nghiệm.

Ta có:

1 1 0 0 0

2 2 0 2 2 2 2

3 1 2 2 4 0 .2 0 0

t at t at t t

t t t t t t

t t t t a a

 

      

   

   

   

            

   

   

 

         

   

Vậy

0

a



.

Câu 88. Trong không gian

Oxyz

, cho ba mặt cầu

       

2 2 2

1

: 3 2 4 1

S x y z

     

,

     

2 2

2

: 2 4 4

S x y z

    

và

 

2 2 2

3

: 4 4 1 0

S x y z x y

     

. Hỏi có bao nhiêu mặt phẳng tiếp xúc với cả ba mặt cầu

 

1

S

,

 

2

S

,

 

3

S

?

A.

2

. B.

4

. C.

6

. D.

8

.

Lời giải

Chọn A

Ta có:

 

1

3;2;4

:

1

I

S

R









,

 

2

0;2;4

:

2

I

S

R









,

 

3

2

2;2;0

:

3

I

S

R









1 2 1 2

3

I I R R   

   

1 2

,

S S



tiếp xúc với nhau tại

M

.

Ta có

 

2 1 1 2

2

2 2;2;4

3

MI I M I I M   

  

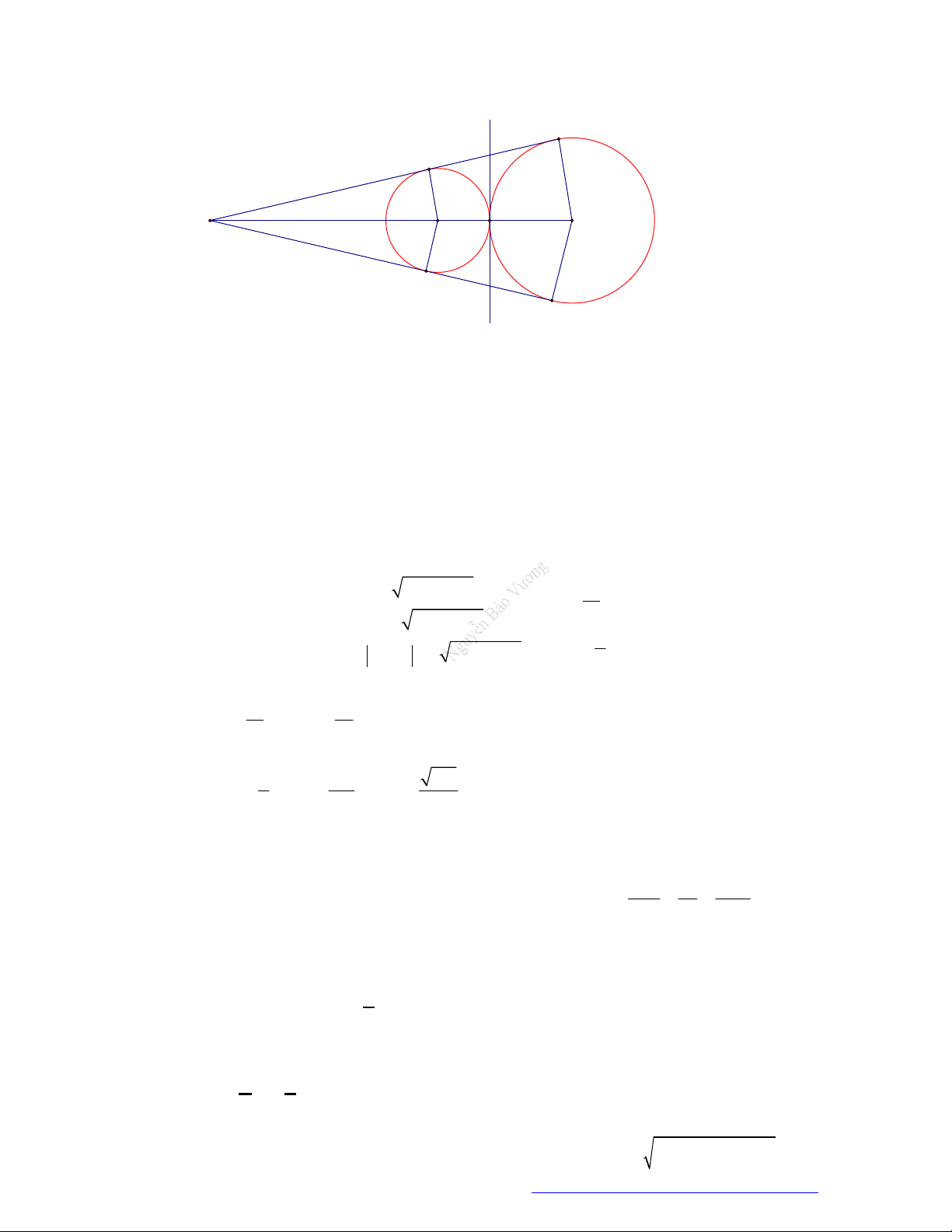
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 45

Cắt hai mặt cầu

   

1 2

,S S

theo phương chứa đường nối tâm của chúng ta có thiết diện là hai

đường tròn lớn

   

1 2

,C C

.

Trường hợp 1: Mặt phằng qua

M

vuông góc với

1 2

I I có phương trình là

 

: 2 0x



 

mà

 

3

; 0d I





 





không tiếp xúc với

 

3

S



LOẠI.

Trường hợp 2:

N

là tâm vị tự ngoài của

   

1 2

,C C

 

2 1 1 2

2 2 6;2;4NI NI I I N   

  

.

Gọi

 

P

là mặt phẳng tiếp xúc với 3 mặt cầu.

 

P

qua

N

và có vtpt là

 

1; ;n a b



     

: 6 2 4 0P x a y b z      

 

: 2 4 6 0P x ay bz a b      

.

Có:

 

1

2

3

;( ) 1

;( ) 2

;( ) 3

d I P















2 2

13

3 1

4

6 2 1

5

4 4 3 1

4

a b

b

a b

b

b a b



   









    









 

   









Với

2

13 41

4 16

b a   

(loại)

Với

2

5 103 103

4 16 4

b a a      

Vậy có 2 mặt phẳng tiếp xúc với 3 mặt cầu

 

1

S

,

 

2

S

,

 

3

S

.

Câu 89. Trong không gian với hệ tọa độ

Oxyz

cho đường thẳng

1 2

:

2 1 1

x y z

d

 

 



. Gọi

 

S

là mặt

cầu có bán kính

5R 

, có tâm

I

thuộc đường thẳng

d

và tiếp xúc với trục

Oy

. Biết rằng

I

có

tung độ dương. Điểm nào sau đây thuộc mặt cầu

 

S

?

A.

 

1; 2;1M  

. B.

 

1;2; 1N 

.

C.

 

5;2; 7P  

. D.

 

5; 2;7Q 

.

Lời giải

Chọn B

Điểm

I

thuộc đường thẳng

d

nên có tọa độ dang:

 

1 2 ; ; 2I t t t   

Vì mặt cầu

 

S

tiếp xúc với trục

Oy

nên

     

2 2

, 1 2 2 5d I Oy R t t      

(C

1

)

(C

2

)

I

2

I

1

M

N

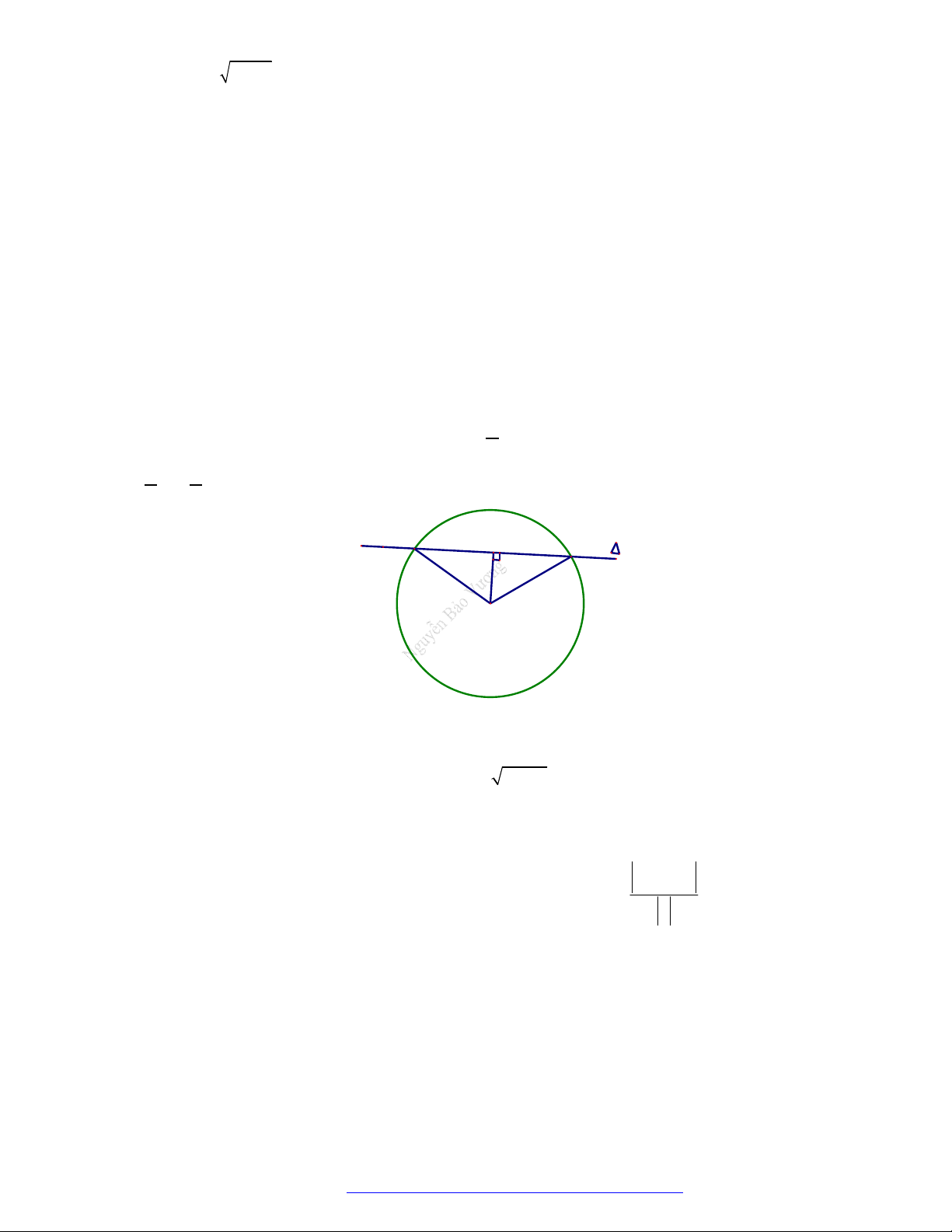
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 46 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

2

5 5 5t  

2

t













Với

2t 

ta có

 

5; 2;0I 

(Loại).

Với

2t  

ta có

 

3;2; 4I  

(Thỏa mãn).

Nên mặt cầu

 

S

có phương trình là:

     

2 2 2

3 2 4 25x y z     

.

Thay tọa độ các điểm trong các phương án vào phương trình mặt cầu, nhận thấy điểm

 

1;2; 1N 

thỏa mãn.

Câu 90. Trong không gian

Oxyz

, cho mặt cầu

 

2 2 2

: 4 6 0S x y z x y m     

(

m

là tham số) và

đường thẳng

4 2

: 3

3 2

x t

y t

z t

 





  





 



. Biết đường thẳng



cắt mặt cầu

 

S

tại hai điểm phân biệt

,A B

sao cho

8AB 

. Giá trị của

m

là

A.

5m 

. B.

12m 

. C.

12m  

. D.

10m  

.

Lời giải

Chọn C

Gọi

H

là trung điểm đoạn thẳng

, 4AB IH AB HA  

.

Mặt cầu

 

S

có tâm

 

2 ; 3 ; 0I 

, bán kính

 

13 , 13R m m  

.

Đường thẳng



đi qua

 

4 ; 3 ; 3M

và có 1 véc tơ chỉ phương

 

2 ; 1 ; 2u 



.

Ta có:

     

,

6 ; 0 ; 3 , 3; 6 ; 6 , 3

IM u

IM IM u IH d I

u

 

 

 

         

 

 

  



.

Ta có:

2 2 2 2 2

13 3 4 12R IH HA m m        

.

Câu 91. (SGD Bến Tre 2019) Trong không gian

Oxyz

cho hai đường thẳng chéo nhau

1 2

4 2 1

: ,( ), : ' ,( ' )

3 '

x t x

d y t t d y t t

z z t

  

 

 

   

 

 

  

 

 

.

Phương trình mật cầu có bán kính nhỏ nhất tiếp xúc với cả hai đường thẳng

   

1 2

,d d

là:

R

B

I

A

H

M

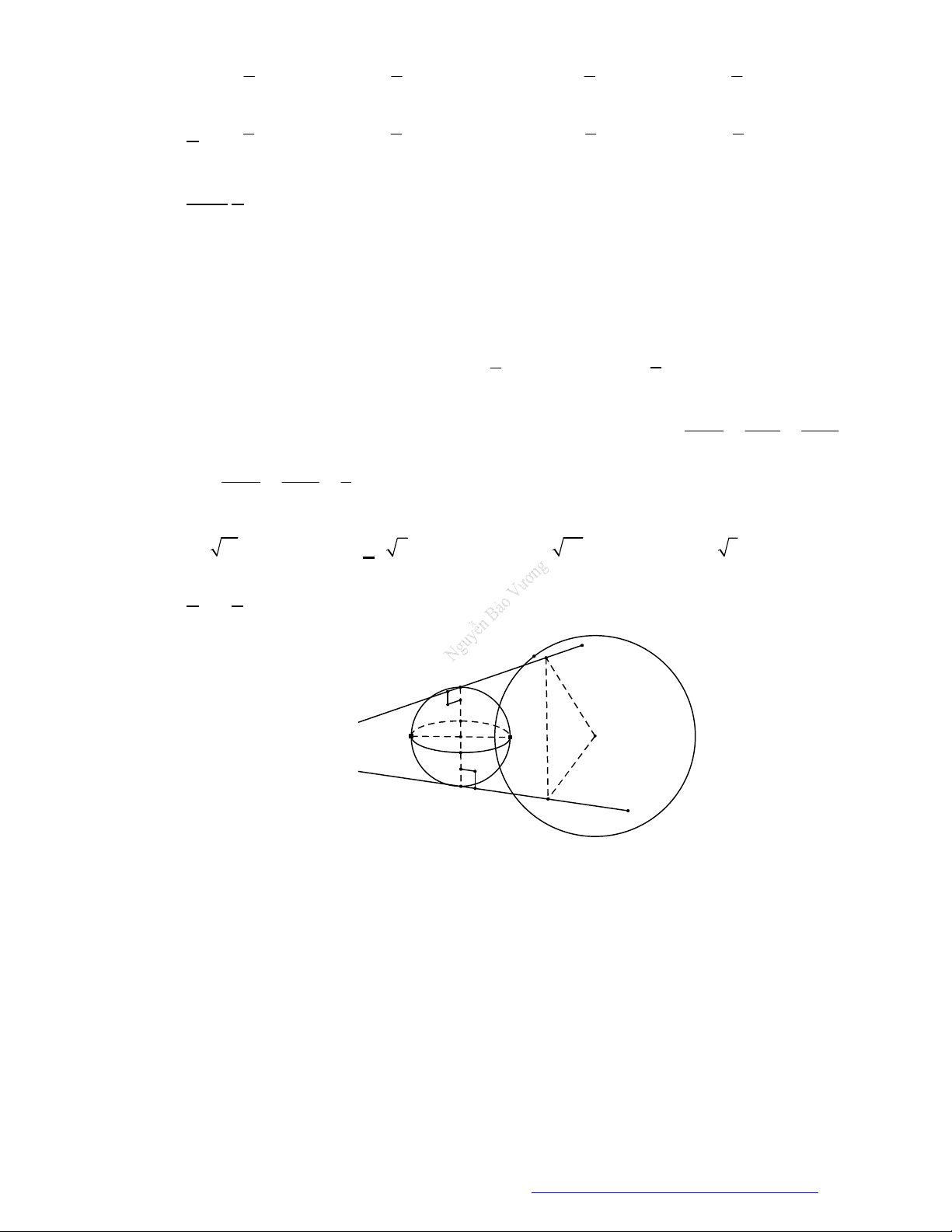
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 47

A.

 

2

3 9

2

2 4

x y z

 

    

 

 

. B.

 

2

3 3

2

2 2

x y z

 

    

 

 

.

C.

 

2

3 9

2

2 4

x y z

 

    

 

 

. D.

 

2

3 3

2

2 2

x y z

 

    

 

 

.

Lời giải

Chọn C

Mặt cầu có bán kính nhỏ nhất tiếp xúc với

   

1 2

,d d

là mặt cầu có đường kính là đoạn vuông góc

chung của

   

1 2

,d d

. Lấy

   

1 2

4 2 ; ;3 ; 1; '; 'A t t d B t t d   

.

,A B

là đoạn vuông góc chung khi

và chỉ khi

1

2

. 0

5 ' 6 1

2 ' 3 ' 1

. 0

d

AB u

t t t

AB u





    

 



 

  

     



 





 

.

Khi đó

 

2;1;3 ; (1; 1;1)A B 

. Suy ra tâm

3

;0;2

2

I

 

 

 

, bán kính

3

2

R 

.

Câu 92. Trong không gian

Oxyz

, cho hai đường thẳng

1

4 1 5

3 1 2

:

x y z  

  

 

và

2

2 3

1 3 1

:

x y z 

   . Trong tất cả mặt cầu tiếp xúc với cả hai đường thẳng

1



và

2



. Gọi

( )S

là mặt cầu có bán kính nhỏ nhất. Bán kính của mặt cầu

( )S

là

A.

12

. B. 6 . C.

24

. D. 3 .

Lời giải

Chọn B

Ta có

1 2

1 1 2 2 1 2

1 2

4 3 2

1 3 3

5 2

: , : ( , )

x t x t

y t y t t t

z t z t

 

   

 

       

 

 

   

 



, gọi

1 2

3 1 2 1 3 1( ; ; ), ( ; ; )u u 

 

lần lượt là

véc tơ chỉ phương của hai đường thẳng.

Gọi

1 1 1 1 2 2 2 2

4 3 1 5 2 2 3 3( ; ; ); ( ; ; )M M t t t N N t t t           

.

Suy

2 1 2 1 2 1

3 2 3 4 2 5( ; ; )MN t t t t t t      



.

MN

là đoạn vuông góc chung khi và chỉ khi:

1

2

1 2 1

1 2 2

0 7 6 1

2 11 9 1

0

.



 

     

  

 

  

  



 



 



 

MN u t t t

t t t

MN u

.

Δ

2

Δ

1

I

N

M

J

A

B

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 48 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

2

2 4 2 6( ; ; ) .MN MN



  





Giả sử

(

)S

l

à mặt cầu tâm

J

đườ

ng kính

d

tiếp xúc

với lần lượt

1



,

2



tạ

i

,A

B

.

Khi

đó

J

A JB AB 

. Ha

y

d

AB MN d MN   

. Vậ

y đường kính

d

nhỏ

nhất khi

d

MN

. S

uy

ra mặt cầu

(

)S

c

ó bán kính nhỏ nhất

6

2

MN

r 



.

Cách khác

Hai mặ

t phẳng song song và lần lượt chứa

1



,

2



là

(

)P

,

( )Q

. Mặt cầu có bán kính nhỏ nhất tiếp

xúc với

cả hai đường thẳng

1



và

2



sẽ

tiếp xúc với

(

),( )P Q

nê

n đường kính cầu là khoảng cá

ch

giữa hai mặt phẳng

(

),( )P Q

hay là khoảng cách từ

2



đến

( )P

.

Gọi

1

2

3 1 2 1 3 1( ; ; ), ( ; ; )u u

 



lần

lượt là véc tơ chỉ phương của hai đường thẳng,

2

3 0

(

; ; )  N

.

 

1

2

5

5 10 1 1 2, ( ; ; ) ; ;

p

u

u n

 

    

 



 

, phươ

ng trình

2

7 0( ) :    P x y z

.

2

2 2

2 3 7

2

6

1

1 2

(( ),( )) ( ,( )) ( ,( ))

( )

 

    

  

d P Q d P d N P

. S

uy ra bán kính cần tìm là

6

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương  https://www.facebook.com/phong.baovuong Trang 1

TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH GIỎI MỨC 9-10 ĐIỂM

Dạng 1. Bài toán liên quan đến mặt cầu – mặt phẳng – đường thẳng

Câu 1. (Mã 110 2017) Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm

 

4;6;2A

và

 

2; 2;0B 

và

mặt phẳng

 

: 0P x y z  

. Xét đường thẳng

d

thay đổi thuộc

 

P

và đi qua

B

, gọi

H

là hình

chiếu vuông góc của

A

trên

d

. Biết rằng khi

d

thay đổi thì

H

thuộc một đường tròn cố định.

Tính bán kính

R

của đường tròn đó.

A.

3R 

B.

2R 

C.

1R 

D.

6R 

Lời giải

Chọn D

Gọi

I

là trung điểm của

AB

 

3;2;1I

 

3 2 1

; 2 3

3

d I P

 

 

Gọi

 

S

là mặt cầu có tâm

 

3;2;1I

và bán kính

3 2

2

AB

R



 

Ta có

 

H S

. Mặt khác

 

H P

nên

     

H C S P  

Bán kính của đường tròn

 

C

là

   

 

   

2 2

2

; 3 2 2 3 6R R d I P



    

.

Câu 2. Trong không gian

Oxyz

mặt phẳng

 

: 2 6 3 0P x y z   

cắt trục

Oz

và đường thẳng

5 6

:

1 2 1

x y z

d

 

 



lần lượt tại

A

và

B

. Phương trình mặt cầu đường kính

AB

là:

A.

     

2 2 2

2 1 5 36.x y z     

B.

     

2 2 2

2 1 5 9.x y z     

C.

     

2 2 2

2 1 5 9.x y z     

D.

     

2 2 2

2 1 5 36.x y z     

Lời giải

Chọn B

   

0;0;3P Oz A 

Tọa độ của

B

là nghiệm của hệ phương trình:

 

2 6 3 0 4

2 6 3 0

2 10 0 2 4; 2;7 .

5 6

2 12 0 7

1 2 1

x y z x

x y z

x y y B

x y z

y z z

    

 

   



  

        

   

 

  

   



 

Gọi

I

là trung điểm của

 

2; 1;5 4 1 4 3.AB I IA      

Phương trình mặt cầu đường kính

AB

là:

     

2 2 2

2 1 5 9.x y z     

Câu 3. Trong không gian

Oxyz

, cho mặt cầu

 

2 2 2

: 4 6 0S x y z x y m     

(

m

là tham số) và

đường thẳng

4 2

: 3

3 2

x t

y t

z t

 





  





 



. Biết đường thẳng



cắt mặt cầu

 

S

tại hai điểm phân biệt

,A B

sao

cho

8AB 

. Giá trị của

m

là

PHƯƠNG TRÌNH ĐƯỜNG THẲNG

Chuyên đề 31

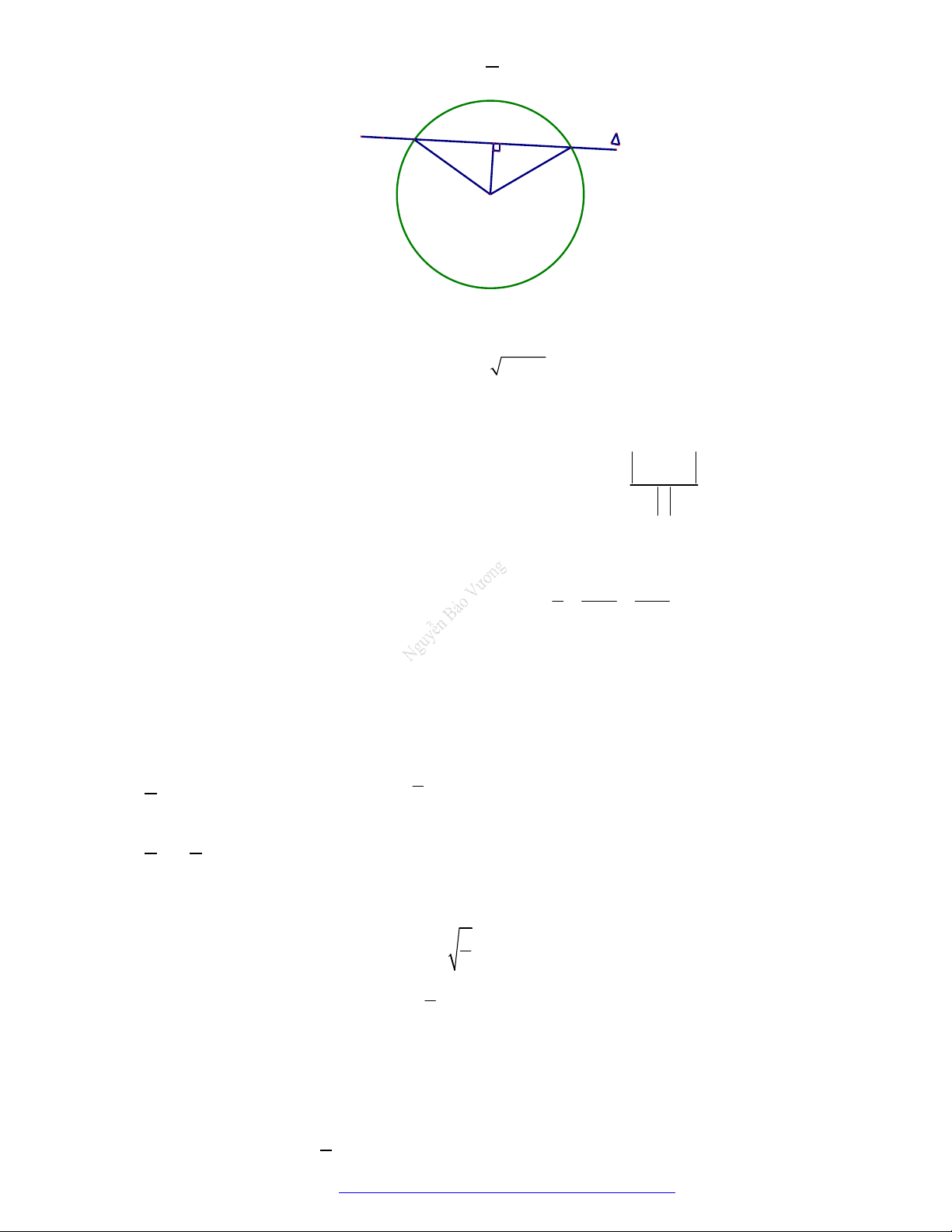
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

A.

5m 

. B.

12m 

. C.

12m  

. D.

10m  

.

Lời giải

Gọi

H

là trung điểm đoạn thẳng

, 4AB IH AB HA  

.

Mặt cầu

 

S

có tâm

 

2 ; 3 ; 0I 

, bán kính

 

13 , 13R m m  

.

Đường thẳng



đi qua

 

4 ; 3 ; 3M

và có 1 véc tơ chỉ phương

 

2 ; 1 ; 2u 



.

Ta có:

     

,

6 ; 0 ; 3 , 3; 6 ; 6 , 3

IM u

IM IM u IH d I

u

 

 

 

         

 

 

  



.

Ta có:

2 2 2 2 2

13 3 4 12R IH HA m m        

.

Câu 4. Trong không gian

Oxyz

, cho đường thẳng

 

3 2

:

2 1 1

x y z

d

 

 

và hai mặt phẳng

 

: 2 2 0P x y z  

;

 

: 2 3 5 0Q x y z   

. Mặt cầu

 

S

có tâm

I

là giao điểm của đường

thẳng

 

d

và mặt phẳng

 

P

. Mặt phẳng

 

Q

tiếp xúc với mặt cầu

 

S

. Viết phương trình mặt

cầu

 

S

.

A.

       

2 2 2

: 2 4 3 1S x y z     

. B.

       

2 2 2

: 2 4 3 6S x y z     

.

C.

       

2 2 2

2

: 2 4 3

7

S x y z     

. D.

       

2 2 2

: 2 4 4 8S x y z     

.

Lời giải

Chọn C

Ta có:

 

I d

 

2 ;3 ;2I t t t  

.

         

: 2 2 3 2 2 0 1 2;4;3I P P t t t t I         

 

Q

tiếp xúc với

 

S

nên

 

2

,

7

R d I Q 

.

Vậy

       

2 2 2

2

: 2 4 3

7

S x y z     

.

Câu 5. Trong không gian

Oxyz

, cho mặt cầu

       

2 2 2

: 2 3 4 14S x y z     

và mặt phẳng

 

: 3 2 5 0x y z



   

. Biết đường thẳng



nằm trong

 



, cắt trục

Ox

và tiếp xúc với

 

S

.

Vectơ nào sau đây là vectơ chỉ phương của



?

A.

 

4; 2;1u  



. B.

 

2;0; 1v  



. C.

 

3;1;0m  



. D.

 

1; 1;1n  



.

R

B

I

A

H

M

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3

Lời giải

Chọn B

Mặt cầu

 

S

có tâm

 

2;3;4I

và bán kính

14R 

.

Ta có

 

, 14d I R

 

   tiếp xúc với

 

S

.

Gọi

H

là hình chiếu vuông góc của

I

lên

   

1;0;2H





Gọi

 

;0;0A Ox A a   

và

 

1;0; 2AH a  



Đường thẳng



nằm trong

 



, cắt trục

Ox

và tiếp xúc với

 

S

nên

AH n





 

. Tức là

 

1 0 4 0 5 4;0; 2a a AH        



cùng phương với

 

2;0; 1v  



.

Câu 6. (Bình Dương - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

 

: 2 2 9 0P x y z   

và mặt cầu

       

2 2 2

: 3 2 1 100S x y z     

. Mặt phẳng

 

P

cắt

mặt cầu

 

S

theo một đường tròn

 

C

. Tìm tọa độ tâm

K

và bán kính

r

của đường tròn

 

C

là

A.

 

3; 2;1K 

,

10r 

. B.

 

1;2;3K 

,

8r 

. C.

 

1; 2;3K 

,

8r 

. D.

 

1; 2;3K

,

6r 

.

Lời giải

 Mặt cầu

 

S

có tâm

 

3; 2;1I 

;

10R 

.

 Khoảng cách từ

I

đến

 

P

là

 

6 4 1 9

; 6

3

IK d I P

  

   .

 Đường thẳng qua

 

3; 2;1I 

vuông góc với

 

P

có phương trình tham số là

3 2

2 2

1

x t

y t

z t

 





  





 



khi đó

Tọa độ tâm

K

là nghiệm của hệ phương trình

 

3 2

2 2

1;2;3

1

2 2 9 0

x t

y t

K

z t

x y z

 





  



 



 



   



.

 Bán kính:

2 2

100 36 8r R IK    

.

Câu 7. (Chuyên Thái Bình 2019) Trong không gian hệ tọa độ

Oxyz

, cho hai điểm

   

1;1;1 , 2;2;1A B

và mặt phẳng

 

: 2 0P x y z  

. Mặt cầu

 

S

thay đổi qua ,A B và tiếp xúc với

 

P

tại H . Biết

H chạy trên 1 đường tròn cố định. Tìm bán kính của đường tròn đó.

A.

3 2

. B. 2 3 . C. 3 . D.

3

2

Lời giải

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Có

(1;1;1), (2;2;1)

A B



Phương trình AB:

1

x t

y t

z

 





 









Gọi

K

là giao điểm của

AB

và

 

P



 

1; 1;1

K  

Có Mặt cầu

 

S

tiếp xúc với

 

P

tại

H

.



HK

là tiếp tuyến của

 

S



2

. 12 2 3

KH KA KB KH   

 

không đổi



Biết

H

chạy trên 1 đường tròn bán kính

2 3

không đổi

Câu 8. (Chuyên Lam Sơn 2019) Trong không gian

Oxyz

cho mặt cầu

 

2 2 2

: 2 4 6 2 0

S x y z x y z

      

và mặt phẳng

 

: 4 3 12 10 0

x y z

   



. Lập phương

trình mặt phẳng

 



thỏa mãn đồng thời các điều kiện: Tiếp xúc với

 

S

; song song với

 



và

cắt trục

Oz

ở điểm có cao độ dương.

A.

4 3 12 78 0

x y z

   

. B.

4 3 12 26 0

x y z

   

.

C.

4 3 12 78 0

x y z

   

. D.

4 3 12 26 0

x y z

   

.

Lời giải

Chọn C

Mặt cầu

 

S

có tâm

 

1; 2; 3

I

, bán kính

4.

R



Mặt phẳng

 



song song với

 



nên có phương trình dạng

 

4 3 12 0 10

x y z c c    

.

 



tiếp xúc với

 

S



 

2 2 2

4.1 3.2 12.3 26

; 4 4

13

4 3 12

c c

d I R

    

    

 



26 52 78

26 52 26

c c

   

 

 

 

     

 

Nếu

78

c



thì

 

: 4 3 12 78 0

x y z

   



. Mặt phẳng

 



cắt trục

Oz

ở điểm

13

0; 0;

2

M

 

 

 

có

cao độ dương.

Nếu

26

c

 

thì

 

: 4 3 12 26 0

x y z

   



. Mặt phẳng

 



cắt trục

Oz

ở điểm

13

0; 0;

6

M

 



 

 

có cao độ âm.

Vậy

 

: 4 3 12 78 0

x y z

   



.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5

Câu 9. (Chuyên Nguyễn Trãi Hải Dương 2019) Trong không gian

Oxyz

, cho mặt cầu

2 2 2

9x y z  

và điểm

 

0 0 0

1

; ; : 1 2

2 3

x t

M x y z d y t

z t

 





  





 



. Ba điểm

A

,

B

,

C

phân biệt cùng thuộc mặt cầu sao cho

MA

,

MB

,

MC

là tiếp tuyến của mặt cầu. Biết rằng mặt phẳng

 

ABC

đi qua điểm

 

1;1;2D

.

Tổng

2 2 2

0 0 0

T x y z  

bằng

A.

30

. B.

26

. C.

20

. D.

21

.

Lời giải

Chọn B

* Ta có:

 

0 0 0 0 0 0

1

; ; : 1 2 4

2 3

x t

M x y z d y t x y z

z t

 





      





 



.

* Mặt cầu có phương trình

2 2 2

9x y z    tâm

 

0;0;0O

, bán kính

3R 

.

*

MA

,

MB

,

MC

là tiếp tuyến của mặt cầu

 

.MO ABC 



 

ABC

đi qua

 

1;1;2D

có véc tơ pháp tuyến

 

0 0 0

; ;OM x y z



có phương trình dạng:

     

0 0 0

1 1 2 0x x y y z z     

.

*

MA

là tiếp tuyến của mặt cầu tại

A

MOA 

vuông tại

2 2

. 9A OH OM OA R   

.

Gọi

H

là hình chiếu của

O

lên

 

ABC

 

OH OM HM 

, ta có:

 

0 0 0 0 0 0 0 0

0

2 2 2 2 2 2

0 0 0 0 0 0

2 4

; . 4

x y z x y z z z

d O ABC OH OH OM z

OM

x y z x y z

      

      

   

.

0 0 0

4 9 5 13z z z       

.

* Với

0

5z  

 

0; 1;5 26M T  

nhận do:

0

4

9

26;

26

z

OM OH

OM



  

;

   

 

17

: 5 9 0 ;

26

pt ABC y z MH d M ABC       .

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

OH HM OM  

.

* Với

 

0

13 6;11; 13z M

    

loại do:

9

326;

326

OM OH 

;

   

 

335

:6 11 13 9 0 ;

326

ABC x y z MH d M ABC      

.

OH HM OM  

.

Câu 10. Trong không gian với hệ trục tọa độ

Oxyz

, cho mặt cầu

 

2 2 2

: 2 2 1 0

S x y z x z

     

và

đường thẳng

2

:

1 1 1

x y z

d



 



. Hai mặt phẳng

   

, 'P P

chứa

d

và tiếp xúc với

( )S

tại

T

,

'T

.

Tìm tọa độ trung điểm

H

của

'.TT

A.

7 1 7

; ;

6 3 6

H

 



 

 

. B.

5 2 7

; ;

6 3 6

H

 



 

 

. C.

5 1 5

; ;

6 3 6

H

 



 

 

. D.

5 1 5

; ;

6 3 6

H

 



 

 

.

Lời giải

Chọn C

Mặt cầu

 

S

có tâm

 

1;0; 1

I



, bán kính

1R 

.

Đường thẳng

d

có vectơ chỉ phương

 

1;1; 1

d

u

 



.

Gọi

K

là hình chiếu của

I

trên

d

, ta có

   

;2 ; 1;2 ; 1

K t t t IK t t t

       



.

Vì

IK d

nên

   

. 0 1 2 1 0 0 1;2;1

d

u IK t t t t IK            

  

.

Phương trình tham số của đường thẳng

IK

là

1 '

2 '

1 '

x t

y t

z t

 











  



Khi đó, trung điểm

H

của

'TT

nằm trên

IK

nên

   

1 ';2 '; 1 ' ';2 '; 'H t t t IH t t t

     



. Mặt

khác, ta có:

2

1

. . 1 ' 4 ' ' 1 '

6

IH IK IT IH IK t t t t

        

   

5 1 5

; ; .

6 3 6

H

 

 

 

 

Câu 11. Trong không gian

Oxyz

, cho điểm

 

2;1;3

E

, mặt phẳng

 

: 2 2 3 0   

P x y z

và mặt cầu

       

2 2 2

: 3 2 5 36     

S x y z

. Gọi



là đường thẳng đi qua

E

, nằm trong

 

P

và cắt

 

S

tại hai điểm có khoảng cách nhỏ nhất. Phương trình của



là

A.

2 9

1 9

3 8

 





 





 



x t

y t

z t

. B.

2 5

1 3

3

 





 









x t

y t

z

. C.

2

1

3

 





 









x t

y t

z

. D.

2 4

1 3

3 3

 





 





 



x t

y t

z t

.

Lời giải

Chọn C

Mặt cầu

 

S

có tâm

 

3;2;5

I

và bán kính

6

R

.

2 2 2

1 1 2 6

    IE R



điểm

E

nằm trong mặt cầu

 

S

.

Gọi

H

là hình chiếu của

I

trên mặt phẳng

 

P

,

A

và

B

là hai giao điểm của



với

 

S

.

Khi đó,

AB

nhỏ nhất

 AB OE

, mà

AB IH

nên

 



AB HIE

 AB IE

.

Suy ra:

   

; 5; 5;0 5 1; 1;0



 

    

 

  

P

u n EI .

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7

Vậy phương trình của



là

2

1

3

 





 









x t

y t

z

.

Câu 12. (Chuyên Lê Quý Đôn – Điện Biên 2019) Trong không gian

Oxyz

cho mặt cầu

   

2 2

2

3 1 4x y z    

và đường thẳng

1 2

: 1 ,

x t

d y t t

z t

 





   





 





. Mặt phẳng chứa

d

và cắt

( )S

theo một đường tròn có bán kính nhỏ nhất có phương trình là

A.

1 0y z  

. B.

3 5 2 0x y z   

. C.

2 3 0x y  

. D.

3 2 4 8 0x y z   

.

Lời giải

Chon A

Gọi

H

là hình chiếu vuông góc của tâm cầu

 

3;1;0I

lên

d

, từ đó ta tìm được

 

3;0; 1H 

. Thấy

IH R

nên

d

cắt

( )S

. Vậy mặt phẳng cần tìm nhận

 

0; 1; 1IH   



làm VTPT nên pt mặt

phẳng là

1 0y z  

.

Câu 13. (Đại học Hồng Đức –Thanh Hóa 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho

điểm

 

1;1;1E

, mặt phẳng

 

: 3 5 3 0P x y z   

và mặt cầu

 

2 2 2

: 4S x y z  

. Gọi



là

đường thẳng qua

E

, nằm trong mặt phẳng

 

P

và cắt

 

S

tại 2 điểm phân biệt

,A B

sao cho

2AB 

. Phương trình đường thẳng



là

A.

1 2

2

1

x t

y t

z t

 





 





 



. B.

1 2

1

x t

y t

z t

 





 





 



. C.

1 2

3

5

x t

y t

z t

 





  





 



. D.

1 2

1

x t

y t

z t

 





 





 



.

Lời giải

Chọn D

 

2 2 2

: 4S x y z   

Tâm

 

0;0;0I

; bán kính

2R 

.

 

: 3 5 3 0P x y z    

véctơ pháp tuyến của

   

: 1; 3; 5

P

P n  



.

Gọi H là hình chiếu của I lên

1

2

AB

AH BH    

.

Xét

IAH

vuông tại

2 2

4 1 3H IH IA AH     

.

Mặt khác ta có

 

1;1;1 3IE IE IH    



H E IE   

.

Đường thẳng



đi qua

 

1;1;1E

; vuông góc với

IE

và chứa trong

 

P

nên:

Véctơ chỉ phương của



:

 

; 8;4;4

P

n n IE



 

  

 

  

.

véctơ

 

2; 1; 1u   



cũng là véctơ chỉ phương của



.

Δ

R

H

B

A

I

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 8 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Phương trình đường thẳng



là:

1 2

1

x t

y t

z t

 





 





 



.

Câu 14. (SGD Cần Thơ 2019) Trong không gian

Oxyz

, cho điểm

 

0;1; 2A

, mặt phẳng

 

: 1 0   P x y z

và mặt cầu

 

2 2 2

: 2 4 7 0     S x y z x y

. Gọi



là đường thẳng đi qua

A

và



nằm trong mặt phẳng

 

P

và cắt mặt cầu

 

S

tại hai điểm

B

,

C

sao cho tam giác

IBC

có diện tích lớn nhất, với

I

là tâm của mặt cầu

 

S

. Phương trình của đường thẳng



là

A.

1

2













  



x t

y

z t

. B.

1

2







 





  



x t

y t

z t

. C.

1

2







 





 



x t

y t

z

. D.

1

2







 





 



x t

y t

z

.

Lời giải

Chọn C

 

S

có tâm

 

1;2;0I

và bán kính

2 2

1 2 7 2 3   R

.

 

1;1;2



AI

6  AI R

 A

nằm trong mặt cầu

 

S

và

A

nằm trên dây cung

BC

 

1

.



1

. .sin

2





IBC

S IB IC BIC



2 2

sin

2 2

 

R R

BIC

nên diện tích

IBC

đạt giá trị lớn nhất là

2

R



sin 1 BIC



90  BIC

 IBC

vuông cân tại

I

2 BC IC

2 2 6 R

Gọi

J

là trung điểm của

BC

. Ta có

IJ BC

và

6

2

 

BC

IJ

 

2

.

AIJ

vuông tại

J

AI IJ

, kết hợp thêm với

 

1

và

 

2

ta có

IJ AI  A J

 A

là

trung điểm của

BC

và

IA BC

.

 

P

có vectơ pháp tuyến

 

1;1;1



P

n

có giá vuông góc với



.

Vậy



nhận

 

,

 



 

  

P

u n AI

 

1; 1;0 

làm vectơ chỉ phương và đi qua

 

0;1; 2A

: 1

2







   





 



x t

y t

z

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9

Câu 15. Trong không gian với hệ tọa độ

Oxyz

cho mặt phẳng

 

: 2 0P z  

,

 

0;0; 2K 

, đường thẳng

:

1 1 1

x y z

d  

. Phương trình mặt cầu tâm thuộc đường thẳng

d

và cắt mặt phẳng

 

P

theo thiết

diện là đường tròn tâm

K

, bán kính

5r 

là

A.

 

2

2 2

2 16x y z   

. B.

2 2 2

16x y z  

.

C.

 

2

2 2

2 9x y z   

. D.

2 2 2

9x y z   .

Lời giải

Chọn D

 

P

có vectơ pháp tuyến

 

0;0;1n 



.

Viết lại phương trình của đường thẳng

d

dưới dạng tham số:

x t

y t

z t

















.

Gọi

I

là tâm của mặt cầu cần lập. Vì

I d

nên giả sử

 

; ;I t t t

. Có

 

; ; 2IK t t t    



.

Thiết diện của mặt cầu và mặt phẳng

 

P

là đường tròn tâm

K

nên ta có

 

IK P

. Suy ra

IK



và

 

0;0;1n 



cùng phương. Do đó tồn tại số thực

k

để

.0

0

.0

2

2 .1

t k

t

IK k n t k

k

t k

 









    

 

 





  



 

.

Suy ra

 

0;0;0I

. Tính được

 

, 2d I P 

.

Gọi

R

là bán kính mặt cầu. Ta có:

 

2

, 3R r d I P

 

  

 

.

Vậy mặt cầu cần tìm có phương trình:

2 2 2

9x y z  

.

Câu 16. Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

 

: 3 0P x y z   

và hai điểm

 

1;1;1M

,

 

3; 3; 3N   

. Mặt cầu

 

S

đi qua M, N và tiếp xúc với mặt phẳng

 

P

tại điểm

Q

.

Biết rằng

Q

luôn thuộc một đường tròn cố định. Tìm bán kính của đường tròn đó.

A.

2 11

3

R 

. B.

6R 

. C.

2 33

3

R 

. D.

4R 

.

Lời giải

Chọn B

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 10 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

* Đường thẳng

MN

có phương trình là:

1

: 1

1

x t

MN y t

z t

 





 





 



.

* Gọi

 

I MN P

 

khi đó tọa độ điểm

I

ứng với

t

thỏa mãn:

1 1 1 3 0 2 0 2t t t t t           

 

3;3;3 2 3, 6 3

I IM IN   

.

* Do mặt cầu

 

S

đi qua M, N và tiếp xúc với đường thẳng

IQ

tại điểm

Q

nên ta có:

2 2 2 2

. . 36 6

IQ IM IN KI R IQ IM IN IQ

       

Vậy

Q

luôn thuộc đường tròn tâm

I

bán kính

6

R



.

Câu 17. (Nguyễn Huệ- Ninh Bình- 2019)Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

 

: 2 2 3 0

P x y z

   

và mặt cầu

     

2 2

2

: 1 3 9

S x y z

    

và đường thẳng

2 1

:

2 1 2

x y z

d

 

 



. Cho các phát biểu sau đây:

I. Đường thẳng

d

cắt mặt cầu

 

S

tại 2 điểm phân biệt.

II. Mặt phẳng

 

P

tiếp xúc với mặt cầu

 

S

.

III. Mặt phẳng

 

P

và mặt cầu

 

S

không có điểm chung.

IV. Đường thẳng

d

cắt mặt phẳng

 

P

tại một điểm.

Số phát biểu đúng là:

A.

4

. B.

1

. C.

2

. D.

3

.

Lời giải

Chọn D

Mặt cầu

 

S

có tâm

 

1; 3;0

I 

, bán kính

3

R



.

Phương trình tham số của đường thẳng

2

: 2

1 2

x t

d y t

z t

 





  





  



.

Xét hệ phương trình

   

 

2

2 2

2

9 2 6 0 1

1 2

1 3 9

x t

y t

t t

z t

x y z

 





  



   



  



    



.

Phương trình (1) có 2 nghiệm phân biệt nên

d

cắt

 

S

tại 2 điểm phân biệt.

 

2.1 2. 3 0 3

11

,

3 3

d I P R

   

   

 

P

và

 

S

không có điểm chung.

Xét hệ phương trình

2

3

1 2

2

2 2 3 0

x t

y t

t

z t

x y z

 





  



 



  



   



.

d

cắt

 

P

tại một điểm.

Vậy có 3 phát biểu đúng.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11

Câu 18. (Chuyên Hoàng Văn Thụ-Hòa Bình-2019)Trong không gian Oxyz, cho mặt cầu

       

2 2 2

2

: 1 2 1 3S x y z     

, mặt phẳng

 

: 3 0P x y z   

và điểm

 

1;0; 4N 

thuộc

 

P

. Một đường thẳng



đi qua N nằm trong

 

P

cắt

 

S

tại hai điểm A, B thỏa mãn

4AB 

.

Gọi

 

1; ;u b c



,

 

0c 

là một vecto chỉ phương của



, tổng

b c

bằng

A.

1

. B.

3

. C.

1

. D.

45

.

Lời giải

Chọn D

Ta có mặt cầu (S) có tâm

 

1;2;1I

bán kính

3R 

.

Gọi H và K lần lượt là hình chiếu vuông góc của I lên đường thẳng



và mặt phẳng (P).

Suy ra H là trung điểm của đoạn AB nên AH = 2

 

2 2

, 5d I IH IA AH     

và

 

1 2 1 3

, 3

3

IK d I P

  

  

.

Ta có

 

IK P

IK

P

 



  



 





mà

IH  

KH  

hay

 

,KH d K 

và

2 2

2KH IH IK  

.

Do

 

IK P

nên phương trình tham số đường thẳng

1

: 2

1

x t

IK y t

z t

 





 





 



 

1 ;2 ;1K t t t   

.

Mà

   

1 2 1 3 0 1 0;3;0K P t t t t K            

Từ đây ta có

 

     

2 2 3

2 2

,

4 3 4 3

, 2

1

KN u

b c c b

KH d K

u

b c

 

     

 

    

 

 



(*).

Mặt khác ta có

 

. 0 1 0 1

P P

P u n u n b c b c            

   

.

Thay vào (*) ta được

N

I

K

H

B

A

P

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 12 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

       

2 2 3 2

2

2 2

2

4 4 4 2 1 1

3 24 48 4 4 4

20 44 0

22( )

2( )

c c c c c

c c c c

c c

c N

c L

         

     

   









 



Suy ra

23 45

b b c

   

.

Câu 19. (Chuyên Hạ Long 2019) Trong không gian với hệ trục

Oxyz

cho hai đường thẳng

1

1 1 1

:

2 1 2

x y z  

  

và

2

1 1 1

:

2 2 1

x y z  

  

. Tính diện tích mặt cầu có bán kính nhỏ

nhất, đồng thời tiếp xúc với cả hai đường thẳng

1



và

2



.

A.

16

17



(đvdt). B.

4

17



(đvdt). C.

16

17



(đvdt). D.

4

17



(đvdt).

Lời giải

Gọi

;A B

là hai điểm thuộc lần lượt

1



và

2



sao cho

AB

là đoạn thẳng vuông góc chung giữa 2

đường. Gọi

M

là trung điểm

AB

. Dễ có mặt cầu tâm

M

bán kính

2

AB

R 

tiếp xúc với hai đường

thẳng

1



và

2



là mặt cầu có bán kính bé nhất.

Ta có tọa độ theo tham số của

;A B

lần lượt là:

1 1 1

(2 1; 1;2 1)

A t t t

  

và

2 2 2

(2 1;2 1; 1)

B t t t

  

2 1 2 1 2 1

(2 2 2;2 2; 2 2)

AB t t t t t t

      



.

Có

1

(2;1;2)

u



và

2

(2;2;1)

u



lần lươt là 2 vectơ chỉ phương của

1



và

2



nên

1

2

AB u















 

 

2 1 2 1 2 1

(2 2 2).2 (2 2).1 ( 2 2).2 0

(2 2 2).2 (2 2).2 ( 2 2).1 0

t t t t t t

        







        



.

1

2 1

2

10

8 9 10 0

17

9 8 10 0 10

17

t

t t

t







  





 

 

   











3 7 3

( ; ; )

17 17 17

A





;

3 3 7

B( ; ; )

17 17 17

 

6 4 4

( ; ; )

17 17 17

AB





.

2 2 2

( 6) 4 4

1 17

.

2 2 17 17

AB

R

  

   .

Diện tích mặt cầu cần tính là

2

1 4

4 . 4. .

17

S R



 

  

(đvdt).

Câu 20. (THPT Quang Trung Đống Đa Hà Nội 2019) Trong không gian với hệ tọa độ

Oxyz

, cho hai

đường thẳng

1

2

:

4

x t

d y t

z

















và

2

3 '

: '

0

x t

d y t

z

 















. Viết phương trình mặt cầu

 

S

có bán kính nhỏ nhất

tiếp xúc với cả hai đường thẳng

1

d

và

2

.d

A.

       

2 2 2

: 2 1 2 4.

S x y z

     

B.

       

2 2 2

: 2 1 2 16.

S x y z     

C.

     

2 2

2

: 2 1 ( 2) 4.

S x y z

     

D.

   

2

2 2

: 2 ( 1) ( 2) 16.

S x y z     

Lời giải

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13

Đường thẳng

1

d có vectơ chỉ phương

1

(2;1;0)u 



.

Đường thẳng

2

d có vectơ chỉ phương

2

( 1;1;0)u  



.

Để phương trình mặt cầu

 

S

có bán kính nhỏ nhất và đồng thời tiếp xúc với cả hai đường thẳng

1

d và

2

d khi và chỉ khi:

Tâm mặt cầu

 

S

nằm trên đoạn thẳng vuông góc chung của 2 đường thẳng

1

d và

2

d , đồng thời

là trung điểm của đoạn thẳng vuông góc chung.

Gọi điểm

 

2 ; ;4M t t

thuộc

1

d ; gọi điểm

(3 '; ';0)N t t

thuộc

2

d với

MN

là đoạn vuông góc

chung của

1

d và

2

d .

Ta có

 

3 ' 2 ; ' ; 4MN t t t t    



.

MN

là đoạn thẳng vuông góc chung

1

2

. 0

MN u

















 

 

   

2. 3 2 0

1 . 3 2 0

t t t t

 

    







 

     





5 6 1

2 3 1

t t t



  

 

 

 

 

  

 

(2;1;4)

(2;1;0)

M

N









.

Gọi điểm

I

là tâm mặt cầu

 

S

, do đó điểm

I

là trung điểm

MN

.

 

2;1;2I

2R IM IN   

.

Suy ra mặt cầu

 

S

:

     

2 2 2

2 1 2 4x y z     

.

Câu 21. (KTNL GV Thuận Thành 2 Bắc Ninh 2019) Trong không gian với hệ trục

,Oxyz

cho mặt cầu

 

2 2 2

: 2 4 6 13 0S x y z x y z      

và đường thẳng

1 2 1

:

1 1 1

x y z

d

  

 

. Điểm

   

; ; , 0M a b c a 

nằm trên đường thẳng

d

sao cho từ

M

kẻ được ba tiếp tuyến

, ,MA MB MC

đến mặt cầu

 

S

(

, ,A B C

là các tiếp điểm) và



0

60AMB 

,



0

60BMC 

,



0

120CMA 

. Tính

3 3 3

a b c 

.

A.

3 3 3

173

9

a b c  

. B.

3 3 3

112

9

a b c  

. C.

3 3 3

8a b c   

. D.

3 3 3

23

9

a b c  

.

Lời giải

Chọn B

Mặt cầu

 

S

có tâm

 

1;2; 3I 

và bán kính

 

2

2 2

1 2 3 13 3 3R      

Gọi

 

C

là đường tròn giao tuyến của mặt phẳng

 

ABC

và mặt cầu

 

S

.

Đặt

MA MB MC x  

khi đó

; 2; 3AB x BC x CA x  

do đó tam giác

ABC

vuông tại

B

nên trung điểm

H

của

AC

là tâm đường tròn

 

C

và

, ,H I M

thẳng hàng.

Vì



0

120AMC 

nên tam giác

AIC

đều do đó

3x R

3x 

suy ra

2 2 6IM AM x  

.

H

M

A

I

C

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 14 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Lại có

M d

nên

   

1 ; 2 ;1 , 1

M t t t t

     

mà

6

IM



nên

     

2 2 2

2 4 4 36

t t t

     

2

3 4 0t t  

0

4

3

t















.

Mà a > 0 nên

4

3

t



suy ra

1 2 7

; ;

3 3 3

H

 



 

 

nên

3 3 3

112

9

a b c  

.

Câu 22. (Chuyên Nguyễn Tất Thành Yên Bái 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho

điểm

 

3;3; 3

M

 

thuộc mặt phẳng

 

: 2 2 15 0

x y z



   

và mặt cầu

       

2 2 2

: 2 3 5 100

S x y z     

. Đường thẳng



qua

M

, nằm trên mặt phẳng

 



cắt

 

S

tại

,A B

sao cho độ dài

AB

lớn nhất. Viết phương trình đường thẳng



.

A.

3 3 3

1 1 3

x y z

  

 

. B.

3 3 3

1 4 6

x y z

  

 

.

C.

3 3 3

16 11 10

x y z

  

 



. D.

3 3 3

5 1 8

x y z

  

 

.

Lời giải

Ta có: Mặt cầu

 

S

có tâm

 

2;3;5

I

, bán kính

10

R



.

 

2

2 2

2.2 2.3 5 15

, 6

2 2 1

d I R



  

  

  

     

;S C H r



  

,

H

là hình chiếu của

I

lên

 



.

Gọi

1



là đường thẳng qua

I

và vuông góc với

 



1

 

có VTCP là

 

1

2; 2;1

u



 



.



PTTS

1

2 2

: 3 2

5

x t

y t

z t

 





  





 



. Tọa độ

H

là nghiệm của hệ:

2 2

3 2

5

2 2 15 0

x t

y t

z t

x y z

 





 





 



   



2

7

3

x

y

z

 





 









 

2;7;3

H 

.

Ta có

AB

có độ dài lớn nhất

AB

là đường kính của

 

C

MH  

.

Đường thẳng

MH

đi qua

 

3;3; 3

M

 

và có VTCP

 

1; 4;6

MH 



.

Suy ra phương trình

3 3 3

: .

1 4 6

x y z

  

  

Câu 23. (Mã 104 2017) Trong không gian với hệ tọa độ

Oxyz

, cho ba điểm

 

2;0;0

A 

,

 

0; 2;0

B 

,

 

0;0; 2

C



. Gọi

D

là điểm khác

O

sao cho

DA

,

DB

,

DC

đôi một vuông góc nhau và

 

; ;I a b c

là tâm mặt cầu ngoại tiếp tứ diện

ABCD

. Tính

S a b c  

.

A.

4

S

 

B.

1

S

 

C.

2

S

 

D.

3

S

 

Lời giải

Chọn B

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15

Gọi

d

là trục của

ABC

, ta có

 

: 2 0ABC x y z   

.

Do

ABC

đều nên

d

đi qua trọng tâm

2 2 2

; ;

3 3 3

G

 

  

 

 

và có VTCP

(1;1;1)u 



, suy ra

2

3

2

:

3

2

3

x t

d y t

z t



  



  





  





.

Ta thấy

DAB DBC DCA    

, suy ra

DA DB DC D d   

nên giả sử

2 2 2

; ;

3 3 3

D t t t

 

     

 

 

.

Ta có

4 2 2 2 4 2 2 2 4

; ; ; ; ; ; ; ;

3 3 3 3 3 3 3 3 3

AD t t t BD t t t CD t t t

     

                 

     

     

  

Có

 

2 4 4 4

; ;

. 0

3 3 3 3

2

. 0

0;0;0 ( )

3

t D

AD BD

AD CD

t D loai



 

     

 









 















 





 

.

Ta có

2 2 2

; ;

3 3 3

I d I t t t

 

       

 

 

, do tứ diện

ABCD

nội tiếp mặt cầu tâm

I

nên

1 1 1 1

; ; 1

3 3 3 3

IA ID t I S

 

         

 

 

.

Câu 24. (Chuyên Hạ Long 2019) Trong không gian

Oxyz

, cho

 

:2 2 1 0P x y z   

,

   

0;0;4 , 3;1;2A B

. Một mặt cầu

 

S

luôn đi qua

,A B

và tiếp xúc với

 

P

tại

C

. Biết rằng,

C

luôn thuộc một đường tròn cố định bán kính

r

. Tính bán kính

r

của đường tròn đó.

A. Đáp án khác. B.

4

2 244651

3

r 

. C.

2 244651

9

r 

. D.

2024

3

r 

.

Lời giải

Cách 1:

d

A

D

C

M

B

I

G

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 16 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Ta có

 

3;1; 2AB 



là véc tơ chỉ phương của đường thẳng

AB

.

Phương trình tham số của đường thẳng AB là

3

4 2

x t

y t

z t













 



.

Giả sử

AB

cắt

 

P

tại

 

3 ; ;4 2T t t t

. Do

T 

 

7

:2 2 1 0

3

P x y z t



     

.

Khi đó

7 26 7 14 7 14 10 20 10 14

7; ; ; 7; ; ; 10; ;

3 3 3 3 3 3 3 3

T TA TA TB TB

  

     

    

     

     

 

.

Ta có

2

980 14 5

.

9 3

TC TA TB TC   

.

Điểm

C

thuộc mặt phẳng

 

P

và cách điểm

T

cố định một khoảng

14 5

3

.

Vậy

C

luôn thuộc một đường tròn cố định bán kính

r 

14 5

3

.

Cách 2:

Ta có

 

,

7

; 14

, 10

d A P

TA

AB

TB d B P

  

.

Giả sử

AB

cắt

 

P

tại T . Suy ra A nằm giữa B và T ( vì

,A B

cùng phía so với

 

P

).

Khi đó ta có

7

14

3

10 14

3

7

10

T

TB TA

TA TB

A

TB



 



 



 













2

980 14 5

.

9 3

TC TA TB TC    

Câu 25. (KTNL GV Thuận Thành 2 Bắc Ninh 2019) Trong không gian với hệ tọa độ

Oxyz

, cho hình

chóp

.S ABCD

với

 

1; 1;6S 

,

 

1;2;3A

,

 

3;1;2B

,

 

4;2;3C

,

 

2;3;4D

. Gọi

I

là tâm mặt

cầu

 

S

ngoại tiếp hình chóp. Tính khoảng cách

d

từ

I

đến mặt phẳng

 

SAD

.

A.

3 3

2

d 

. B.

6

2

d 

. C.

21

2

d 

. D.

3

2

d 

.

Lời giải

Chọn B

Ta có:

 

2; 1; 1AB   



,

 

1;1;1AD 



và

 

2; 1; 1DC   



.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17

Ta thấy:

. 2.1 1.1 1.1 0

AB AD

   

 

và

AB DC



 

nên tứ giác

ABCD

là hình chữ nhật.

Gọi

M

là trung điểm của

AC

. Ta có:

5

;2;3

2

M

 

 

 

.

Gọi

d

là đường thẳng đi qua

M

và vuông góc với mặt phẳng

 

ABCD

.

Ta có:

 

, 0; 3;3

AB AD

 

 

 

 

.

Vectơ chỉ phương của đường thẳng

d

là:

 

0; 1;1

u  



.

Phương trình tham số của đường thẳng

d

là:

5

2

3

x

y t

z t







 





 





.

Ta có:

 

0;3; 3

SA

 



. Ta thấy

SA



cùng phương với

u



nên suy ra

 

SA ABCD



.

Gọi

N

là trung điểm của

SA

, ta có:

1 9

1; ;

2 2

N

 

 

 

.

Do

 

; ;I x y z

là tâm mặt cầu ngoại tiếp hình chóp

.

S ABCD

nên

5

;2 ;3

2

.

I t t

I d

NI d

NI u



 

 





 





 

 











 

Mà:

3 3 3

; ;

2 2 2

NI t t

 

   

 

 



. Suy ra:

3 3 3 5 1 9

. 0 0 ; ;

2 2 2 2 2 2

NI u t t t I

 

        

 

 





.

Ta có:

 

, 6; 3; 3

SA AD

 

  

 

 

.

Một vectơ pháp tuyến của

 

SAD

là:

 

1

, 2; 1; 1

6

n SA AD

 

   

 

 



.

Phương trình tổng quát của mặt phẳng

 

SAD

là:

     

2 1 2 3 0

x y z

     

2 3 0

x y z

    

.

Vậy

 

5 1 9

2. 3

6

2 2 2

,

2

4 1 1

d I SAD

  

 

 

.

Câu 26. Trong không gian

Oxyz

, xét số thực

 

0;1

m 

và hai mặt phẳng

 

: 2 2 10 0

x y z

    

và

 

: 1

1 1

x y z

m m

   



. Biết rằng, khi

m

thay đổi có hai mặt cầu cố định tiếp xúc đồng thời với cả

hai mặt phẳng

   

, 

. Tổng bán kính của hai mặt cầu đó bằng

A.

6

B.

3

C.

9

D.

12

Lời giải

Chọn C

Gọi

 

; ;I a b c

là tâm mặt cầu.

Theo giả thiết ta có

 

, ,R d I d I

   

.

Mà

 

2

1

,

1 1

1

a b

c

m m

d I

m

  



 

 



NGUYỄN BẢO VƯƠNG - 0946798489

Trang 18 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Ta có

 

   

 

2

1 1 1 1 1 1

1 2 . 1

1 1

1

1 1 1 1

2 . 1 1(do 0;1

1 1 1

m m m m m

m

m m m m m m

 

     

 

 

 



 

     

 

  

 

Nên

     

 

     

2 2

2

2 2 2

2

1 1 1

1

1 1 0 1

1 1 0 2

a m bm cm m m m

m m

R

m m

a am bm cm cm m m

R

m m

R Rm Rm a am bm cm cm m m

m R c m a b c R R a

m R c m b c a R R a

     







     

 

 



        





         





         





         





Xét (1) do mặt cầu tiếp xúc với tiếp xúc đồng thời với cả hai mặt phẳng

   

, 

với mọi

 

0;1

m

nên pt (1) nghiệm đúng với mọi

 

0;1

m

.

 

1 0

1 0 ; ;1

0 1

R c a R

a b c R b R I R R R

R a c R

   

 

 

         

 

 

   

 

.

Mà

 

2 2 1 10

3

, 3 12

6( )

3

R R R

R

R d I R R R

R l

   





       



 



Xét (2) tương tự ta được

 

1 0

1 0 ; ; 1

0 1

R c a R

b c a R b R I R R R

R a c R

    

 

 

            

 

 

   

 

Mà

 

2 2 1 10

6

, 3 12

3( )

3

R R R

R

R d I R R R

R l

    





       



 



.

Vậy

1 2

9

R R

 

.

Câu 27. (Chuyên Lê Hồng Phong Nam Định 2019) Trong không gian với hệ tọa độ

Oxyz

, cho mặt

phẳng

 

: 2 2 3 0

P x y z

   

và mặt cầu

 

S

tâm

 

5; 3;5

I 

, bán kính

2 5

R  . Từ một điểm

A

thuộc mặt phẳng

 

P

kẻ một đường thẳng tiếp xúc với mặt cầu

 

S

tại

B

. Tính

OA

biết

4AB 

.

A.

11

OA 

. B.

5

OA



. C.

3

OA



. D.

6

OA  .

Lời giải

Chọn A

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19

Khoảng cách từ điểm I đến mp(P) là:

 

2 2 2

5 2.( 3) 2.5 3

;( ) 6

1 ( 2) 2

d I P

   

 

  

.

AB

tiếp xúc với

( )S

tại

B

nên tam giác

AIB

vuông tại B, do đó ta có:

 

2

2 2 2 2 2

2 5 4 6 ;( )IA IB AB R AB d I P       

A

là hình chiếu của I lên (P)

Đường thẳng IA đi qua

 

5; 3;5I 

có VTCP

 

( )

1; 2;2

P

u n  

 

có phương trình

5

3 2

5 2

x t

y t

z t

 





  





 



Có

( )A IA P 

5 2( 3 2 ) 2(5 2 ) 3 0 2 (3;1;1)t t t t A            

11OA 

.

Câu 28. Trong không gian cho mặt cầu

2 2 2

9x y z   và điểm

 

0 0 0

; ;M x y z

thuộc

1

: 1 2

2 3

x t

d y t

z t

 





 





 



. Ba điểm

A

,

B

,

C

phân biệt cùng thuộc mặt cầu sao cho

MA

,

MB

,

MC

là tiếp

tuyến của mặt cầu. Biết rằng mặt phẳng

 

ABC

đi qua

 

1;1;2D

. Tổng

2 2 2

0 0 0

T x y z  

bằng

A.

30

B.

26

C.

20

D. 21

Lời giải

Chọn B

Mặt cầu

 

S

có tâm

 

0;0;0O

và bán kính

R

. Gọi

 

0 0 0

1 ;1 2 ;2 3M t t t d   

.

Gỉa sử

   

; ;T x y z S

là một tiếp điểm của tiếp tuyến

MT

với mặt cầu

 

S

. Khi đó

2 2 2

OT MT OM 

     

 

     

2 2 2

0 0 0 0 0 0

9 1 1 2 2 3 1 1 2 2 3x t y t z t t t t               

   

   

     

0 0 0

1 1 2 2 3 9 0t x t t z       

.

Suy ra phương trình mặt phẳng

 

ABC

có dạng

     

0 0 0

1 1 2 2 3 9 0t x t y t z      

Do

   

1;1;2D ABC

nên

 

0 0

1 1 2 2. 2 3 9 0t t t      

0

1t  

 

0; 1;5M 

.

Vậy

 

2

2 2

0 1 5 26T     

.

Câu 29. (Chuyên KHTN 2019) Trong không gian với hệ tọa độ

Oxyz

cho hai điểm

   

0;0;3 , 2;0;1A B 

và mặt phẳng

 

: 2 2 8 0x y z



   

. Hỏi có bao nhiêu điểm

C

trên mặt

phẳng

 



sao cho tam giác

ABC

đều?

A.

2

. B.

1

. C.

0

. D. Vô số.

Lời giải

Gọi

 

P

mặt phẳng trung trực của

AB

, khi đó phương trình của

 

P

là:

1 0x z  

.

Ta có

   

1;0;1 , 2; 1; 2

P

n n



  

 

nên

 

, 1;0; 1

P

n n



 

 

 

 

.

Gọi

d

là giao tuyến của mặt phẳng

 

P

với mặt phẳng

 



. Chọn

 

1;0; 1

d

u  



và điểm

 

1;10;0M d

nên phương trình tham số của

d

là:

1

10

x t

y

z t

 











 



.

Do tam giác ABC đều nên

CA CB

hay

C

thuộc mặt phẳng trung trực của

AB

mà

 

C





nên

   

C P d



  

suy ra tọa độ

C

có dạng

 

1 ;10;C t t 

.

,Oxyz

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 20 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Do

ABC

đều nên

AC AB

, thay tọa độ các điểm ta có:

           

2 2 2 2 2 2

1 0 10 0 3 2 0 0 0 1 3

t t             

 

2

4 51 0 *

t t   

Do phương trình

 

*

vô nghiệm nên không tồn tại điểm

C

thỏa mãn yêu cầu bài toán.

Câu 30. (Chuyên Nguyễn Trãi Hải Dương 2019) Trong không gian

Oxyz

, cho mặt cầu

2 2 2

9

x y z

  

và điểm

 

0 0 0

; ; M x y z

thuộc đường thẳng

1

: 1 2 .

2 3

x t

d y t

z t

 





 





 



Ba điểm

,A

,B

C

phân biệt cùng

thuộc mặt cầu sao cho

,MA

,MB

MC

là tiếp tuyến của mặt cầu. Biết rằng mặt phẳng

 

ABC

đi

qua

 

1; 1; 2

D

. Tổng

2 2 2

0 0 0

T x y z  

bằng

A.

30

. B.

26

. C.

20

. D.

21

.

Lời giải

Mặt cầu

 

1

:S

2 2 2

9

x y z

  

có tâm

 

0; 0; 0

O

, bán kính

1

3

R



.

M d

 

1 ; 1 2 ; 2 3M a a a

   

.

Do

,MA

,MB

MC

là những tiếp tuyến tại

,A

,B

C

với mặt cầu

 

1

S

.

Suy ra

2 2 2 2

9

MA MB MC OM

   

.

Khi đó

,A

,B

C

 

2

S



có tâm là

M

, bán kính

2

9

R OM

 

.

Ta có phương trình

 

2

:S

 

2 2 2

2

1 2 1 2 3 9

x a y a z a OM

         

.



 

2

:S

     

2 2 2

2 1 2 2 1 2 2 3 9 0

x y z a x a y a z

         

.

Mặt khác theo giả thiết

,A

,B

C

cùng thuộc mặt cầu

 

1

S

.

Suy ra tọa độ

,A

,B

C

thỏa mãn hệ:

     

2 2 2

9 0

2 1 2 2 1 2 2 3 9 0

x y z

x y z a x a y a z



   





         





.

Do đó phương trình mặt phẳng

 

ABC

là:

     

2 1 2 2 1 2 2 3 18 0

a x a y a z

      

.

 

D ABC



     

2 1 2 2 1 4 2 3 18 0

a a a

       

1

a

  

.

Với

1

a

 

, ta có

 

0; 1;5

M 

. Khi đó

2 2 2

0 0 0

26

T x y z

   

.

Câu 31. (Tỉnh Bắc Ninh 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho mặt cầu

( ) :S

2 2 2

2 2 1 0

x y z x z

     

và đường thẳng

2

:

1 1 1

x y z

d



 



. Hai mặt phẳng

( )P

,

( )P



chứa

d

và tiếp xúc với

( )S

tại

T

,

T



. Tìm tọa độ trung điểm

H

của

TT



.

A.

7 1 7

; ;

6 3 6

H

 



 

 

. B.

5 2 7

; ;

6 3 6

H

 



 

 

. C.

5 1 5

; ;

6 3 6

H

 



 

 

. D.

5 1 5

; ;

6 3 6

H

 



 

 

.

Lời giải

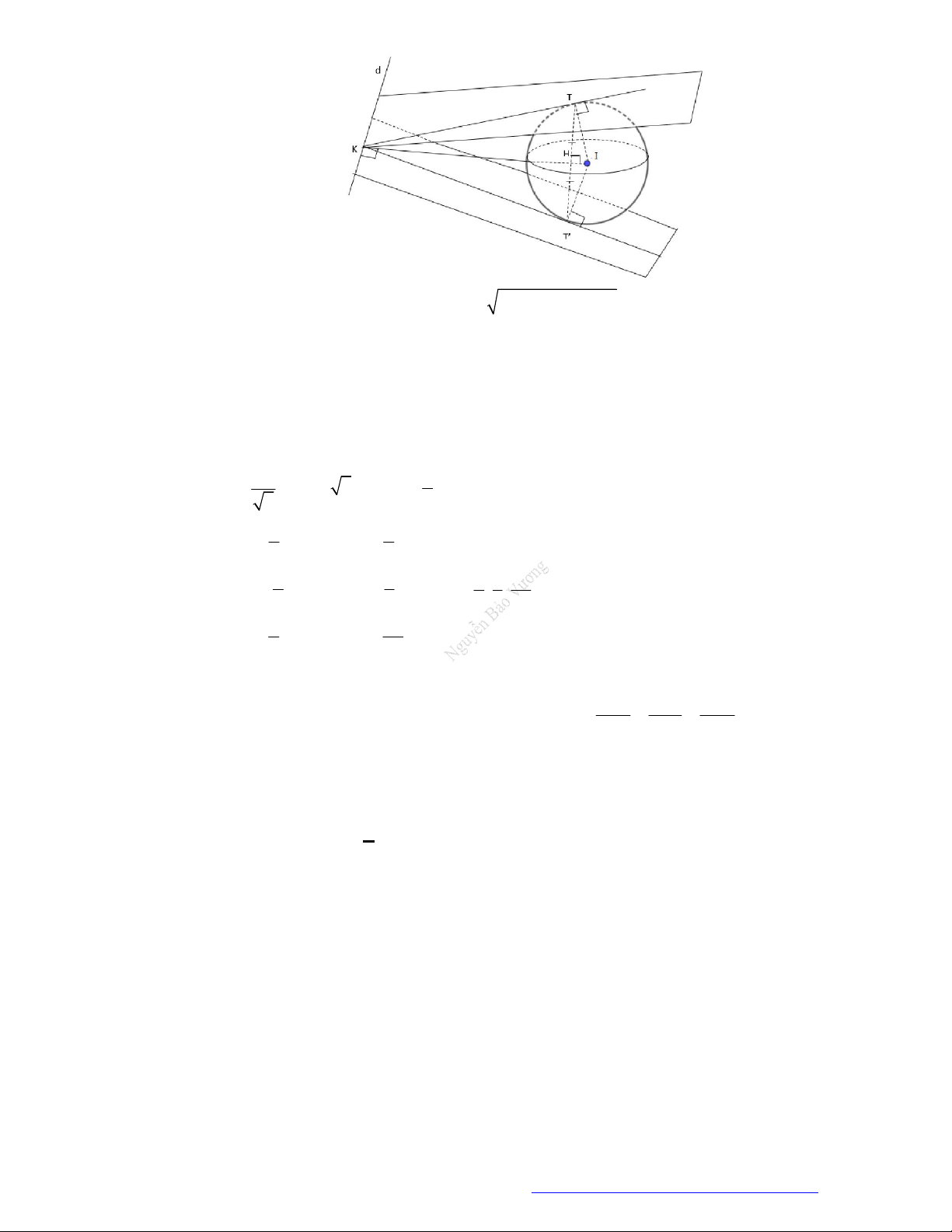
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21

Mặt cầu

( )S

tâm

(1;0; 1)I 

, bán kính

2 2 2

1 0 ( 1) 1 1R      

.

Gọi

K

là hình chiếu vuông góc của

I

lên

d

.

K d

nên ta có thể giả sử

( ; 2 ; )K t t t 

( 1;2 ; 1)IK t t t    



,

(1;1; 1)

d

u  



là một véctơ chỉ phương của đường thẳng

d

IK d

. 0 1 2 1 0

d

IK u t t t        

 

0t 

.

(0; 2;0)K

ITK

vuông tại

T

có

TH

là đường cao nên

2

.IT IH IK

.

1

6

IH 

 

6IK 

1

6

IH IK 

 

. Giả sử

( ; ; )H x y z

1

1 .( 1)

6

1

0 .2

6

1

1 .1

6

x

y

z



  



  





 





5

6

1

3

5

6

x

y

z







 















Vậy

5 1 5

; ;

6 3 6

H



 

 

 

Câu 32. Cho hai đường thẳng

2

:

2 2

x

d y t

z t

 











 



 

t 

,

3 1 4

:

1 1 1

x y z  

  



và mặt phẳng

 

: 2 0P x y z   

. Gọi

d



,





lần lượt là hình chiếu của

d

và



lên mặt phẳng

 

P

. Gọi

 

; ;M a b c

là giao điểm của hai đường thẳng

d



và





. Biểu thức

.a b c

bằng

A.

4

. B.

5

. C.

3

. D.

6

.

Lời giải

Do

d



là hình chiếu của

d

lên mặt phẳng

 

P

khi đó

d



là giao tuyến của mặt phẳng

 

P

và mặt

phẳng

 



chứa

d

và vuông góc với mặt phẳng

 

P

.

 một vec tơ pháp tuyến của mặt phẳng

 



là

 

, 3;2; 1

d P

n u n



 

   

 

  

.

Phương trình mặt phẳng

 



đi qua

 

2;0;2A 

và có một vec tơ pháp tuyến

 

3;2; 1n



  



là

3 2 4 0x y z   

.

Do





là hình chiếu của



lên mặt phẳng

 

P

khi đó





là giao tuyến của mặt phẳng

 

P

và mặt

phẳng

 



chứa



và vuông góc với mặt phẳng

 

P

.

 một vec tơ pháp tuyến của mặt phẳng

 



là

 

, 0; 2; 2

P

n u n





 

   

 

  

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 22 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Phương trình mặt phẳng

 



đi qua

 

3;1;4

B

và có một vec tơ pháp tuyến

 

0; 2; 2

n



  



là

5 0

y z

  

.

Tọa độ điểm

M

là nghiệm của hệ phương trình

2 0 1

3 2 4 0 2

5 0 3

x y z x

x y z y

y z z

     

 

 

     

 

 

   

 

.

Vậy

 

1;2;3

M 

. 1 2.3 5

a b c

     

.

Câu 33. (Thpt Vĩnh Lộc - Thanh Hóa 2019) Trong không gian với hệ tọa độ

Oxyz

, cho đường thẳng

d

là giao tuyến của hai mặt phẳng

 

: 2 1 0

x my z m



    

và

 

: 2 0

mx y mz m



    

. Gọi



là hình chiếu vuông góc của

d

lên mặt phẳng

 

Oxy

. Biết rằng với mọi số thực

m

thay đổi thì

đường thẳng



luôn tiếp xúc với một đường tròn cố định. Tính bán kính

R

của đường tròn đó.

A.

2

. B.

1

. C.

4

. D.

3

.

Lời giải

Chọn A

Mặt phẳng

 

: 2 1 0

x my z m



    

có một vectơ pháp tuyến là

 

1

1; ;1n m

 



.

Mặt phẳng

 

: 2 0

mx y mz m



    

có một vectơ pháp tuyến là

 

2

;1;

n m m 



.

Ta có

   

1 1

;0; 1M m m d

m m

 

 

       

 

 

.

Đường thẳng

d

có một vectơ chỉ phương là

 

2 2

1 2

; 1;2 ; 1

u n n m m m

 

   

 

  

.

Gọi

 

P

là mặt phẳng chứa đường thẳng

d

và vuông góc với mặt phẳng

 

Oxy

. Khi đó

 

P

có

một vectơ pháp tuyến là

 

2

; 2 ;1 ;0

n u k m m

 

  

 

  

(với

 

0;0;1

k 



).

Phương trình mặt phẳng

 

P

là

 

2 2

2 1 2 2 0

mx m y m

    

.

Trong mặt phẳng

 

Oxy

, gọi

 

; ;0I a b

là tâm đường tròn.

Theo giả thiết



là tiếp tuyễn của đường tròn



   

 

; ;

d I d d I P R 

(cố định)



 

2 2

2

2 2

2 1 2 2

0

4 1

ma m b m

R

m m

   

 

 



 

2

2 2 2

0

1

am b m b

R

m

   

 





 

2 2

2 2 2 1

am b m b R m



     



      





2 0

2

2 0

2

a

b R

a

b R

 







 









 















  









  





0

2 0

0

2 0

a

b

R

a

b

R

 

















 



























  





.

Vậy

2R 

.

Câu 34. Trong không gian với hệ tọa độ

Oxyz

, cho ba điểm

 

6; 0; 0

M

,

 

0; 6; 0

N

,

 

0; 0; 6

P

. Hai

mặt cầu có phương trình

 

2 2 2

1

: 2 2 1 0

S x y z x y

     

và

 

2 2 2

2

: 8 2 2 1 0

S x y z x y z

      

cắt nhau theo đường tròn

 

C

. Hỏi có bao nhiêu mặt cầu

có tâm thuộc mặt phẳng chứa

 

C

và tiếp xúc với ba đường thẳng

MN

,

NP

,

PM

?

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23

A.

1

. B.

3

. C. Vô số. D.

4

.

Lời giải

Chọn C

Nếu điểm

 

; ;A x y z

thuộc

 

C

thì

2 2 2

2 2 1 0

3 2 0

8 2 2 1 0

x y z x y

x y z

x y z x y z



     



   



      





.

Suy ra phương trình mặt phẳng

 



chứa đường tròn

 

C

là

3 2 0

x y z

  

.

Phương trình mặt phẳng

 

MNP

là

6 0

x y z

   

.

Gọi

I

là tâm mặt cầu thỏa bài toán,

H

là hình chiếu vuông góc của

I

trên mặt phẳng

 

MNP

,

J

,

K

,

L

lần lượt là hình chiếu vuông góc của

H

trên các đường thẳng

MN

,

NP

,

PM

. Ta có

IJ IK IL HJ HK HL    

.

Suy ra

I

thuộc đường thẳng đi qua tâm đường tròn nội tiếp hoặc tâm đường tròn bàng tiếp của

tam giác

MNP

và vuông góc với mặt phẳng

 

MNP

.

Hình chóp

.

O MNP

là hình chóp đều nên đường thẳng đi qua tâm đường tròn nội tiếp của tam giác

MNP

và vuông góc với mặt phẳng

 

MNP

cũng chính là đường thẳng

d

đi qua

O

và vuông góc

với mặt phẳng

 

MNP

.

Phương trình đường thẳng

d

là

x y z 

.

Dễ thấy

 

d





suy ra mọi điểm thuộc

d

đều là tâm của một mặt cầu thỏa bài toán. Vậy có vô

số mặt cầu có tâm thuộc mặt phẳng chứa

 

C

và tiếp xúc với ba đường thẳng

MN

,

NP

,

PM

.

Câu 35. Trong không gian cho mặt phẳng

 

: 6 0

P x z

  

và hai mặt cầu

 

2 2 2

1

: 25

S x y z

  

,

 

2

:S

2 2 2

4 4 7 0

x y z x z

     

. Biết rằng tập hợp tâm

I

các mặt cầu tiếp xúc với cả hai mặt

cầu

 

1

S

,

 

2

S

và tâm

I

nằm trên

 

P

là một đường cong. Tính diện tích hình phẳng giới hạn

bởi đường cong đó.

A.

7

3



. B.

7

9



. C.

9

7



. D.

7

6



.

Lời giải

Chọn B

Mặt cầu

 

1

S

có tâm

 

0;0;0

O

và bán kính

1

5

R



. Mặt cầu

 

S

có tâm

 

2;0;2

E 

bán kính

2

1

R



. Ta có

 

1

6

,

2

d O P R 

và

 

2

E, 2

d P R 

,

2 2

OE 

,

2 1

OE R R 

nên mặt

cầu

 

2

S

nằm trong mặt cầu

 

1

S

. Như vậy mặt cầu

 

S

tâm

I

tiếp xúc với cả

 

1

S

và

 

2

S

thì

I

M

N

P

H

J

K

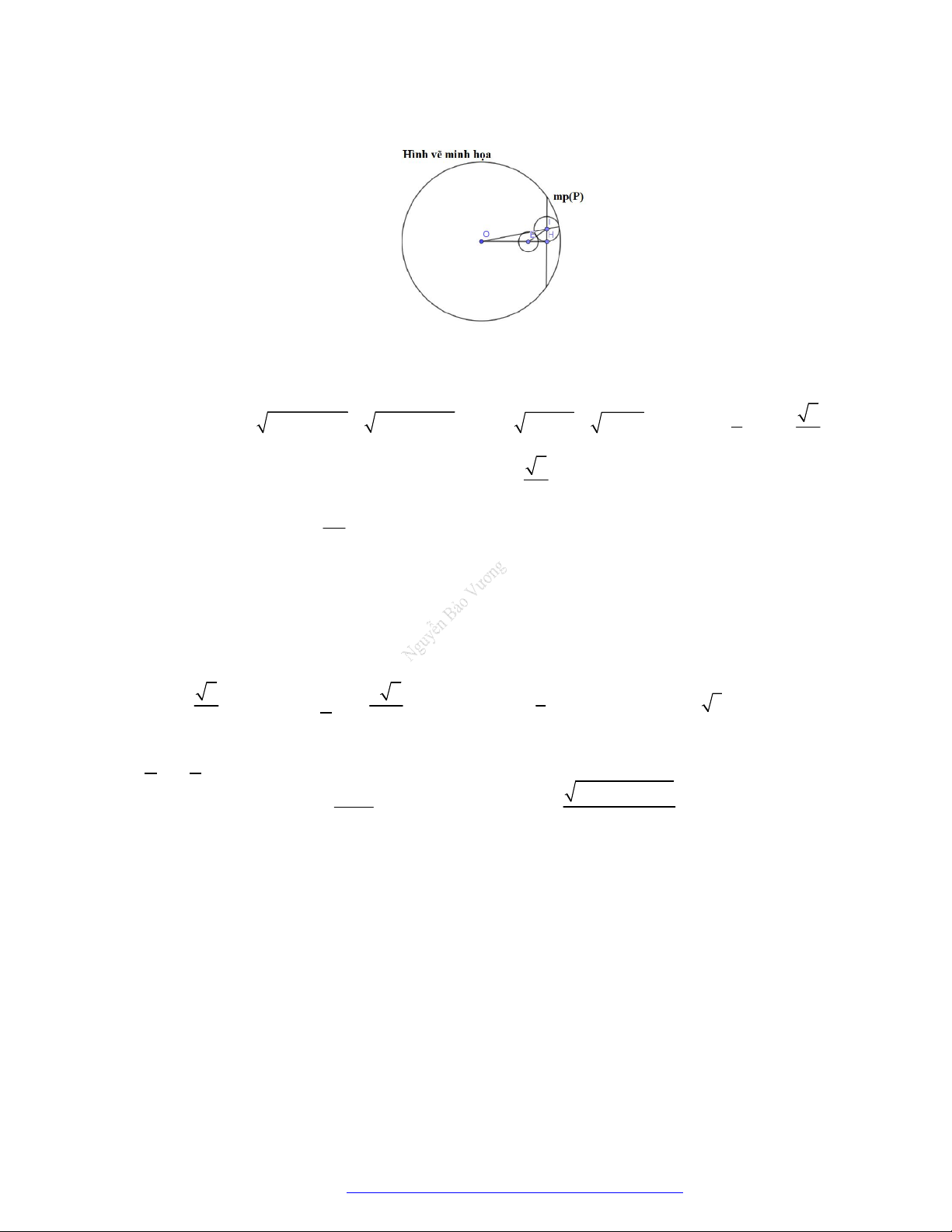
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 24 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

 

S

tiếp xúc trong mặt cầu

 

1

S

và tiếp xúc ngoài với

 

2

S

. Gọi

R

là bán kính của

 

S

khi đó

ta có hệ

1

1 2

2

6

OI R R

OI EI R R OI EI

EI R R



 



      



 





.

Nhận xét:

 

2;0;2OE  



nên

OE

vuông góc với

 

: 6 0P x z  

.

Gọi

H

là hình chiếu vuông góc của

O

lên

 

P

, đặt

IH x

, điều kiện

0x 

. Khi đó ta có

6OI EI 

2 2 2 2

6OH HI EH HI    

2 2 2

7 7

18 2 6

9 3

x x x x        

.

Vậy điểm

I

thuộc đường tròn tâm

H

bán kính

7

3

r 

. Nên diện tích hình phẳng giới hạn bởi

đường tròn là:

2

7

9

S r



 

.

Câu 36. Trong không gian với hệ tọa độ

,Oxyz

cho phương trình mặt

cầu:

   

2 2 2

: 2 2 2 3 0

m

S x y z m x my mz m        

.

Biết rằng với mọi số thực

m

thì

 

m

S

luôn chứa một đường tròn cố định. Tính bán kính

r

của

đường tròn đó.

A.

2

3

r 

. B.

4 2

3

r 

. C.

1

3

r 

. D.

3r 

.

Lời giải

Chọn B

Mặt cầu

 

m

S

có tâm

2

; ;

2

m

I m m



 

 

 

 

và bán kính

2

9 8 16

2

m m

R

 



.

Với

1

m ,

2

m tùy ý và khác nhau, ta được hai phương trình mặt cầu tương ứng:

   

2 2 2

1 1 1 1

2 2 2

2 2 2 2

2 2 2 3 0 1

2 2 2 3 0 2

x y z m x m y m z m



        





        





.

Lấy

 

1

trừ

 

2

theo vế, ta được:

       

1 2 1 2 1 2 1 2

2 2 0m m x m m y m m z m m       

   

1 2

. 2 2 1 0m m x y z     

 

2 2 1 0 3x y z    

.

Dễ thấy

 

3

là phương trình tổng quát của mặt phẳng.

 Họ mặt cầu

 

m

S

có giao tuyến là đường tròn nằm trên mặt phẳng

 

P

cố định có phương

trình:

2 2 1 0x y z   

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25

Mặt khác, đặt

 

2

2 2

2

2 2 1

9 4

2

,

6

1 2 2

m

m m

m

d d I P



   

 

   

 

  

.

 

2

2 2 2

9 4

9 8 16 32

4 36 9

m

m m

r R d m

 

 

        . Vậy

4 2

3

r 

.

Câu 37. Trong không gian với hệ trục tọa độ

Oxyz

, cho mặt câu

 

2 2

: 2 4 6 13 0S x y x y z     

và

đường thẳng

1 2 1

:

1 1 1

x y z

d

  

 

. Điểm

  

; ; 0M a b c a 

nằm trên đường thẳng

d

sao cho

từ

M

kẻ được ba tiếp tuyến

, ,MA MB MC

đến mặt cầu

 

S

(

, ,A B C

là các tiếp điểm) thỏa mãn



60AMB   ,



90BMC  ,



120CMA   .Tính

Q a b c  

.

A.

3Q 

. B.

10

3

Q 

. C.

2Q 

. D.

1Q 

.

Lời giải

Chọn C

Mặt cầu

 

S

có tâm

 

1;2; 3I 

và bán kính

 

2

2 2

1 2 3 13 3 3R      

.

Gọi đường tròn

 

C

là giao tuyến của mặt phẳng

 

ABC

với mặt câu

 

S

.

Đặt

 

0MA MB MC x x   

.

Áp dụng định lý cosin trong

AMB

và

CMA

, ta có:



2 2 2 2 2 2

2 . .cos 2 2 cos60AB MA MB MA MB AMB x x x AB x         .



2 2 2 2 2 2

2 . .cos 2 2 cos120 3 3AC MA MC MA MC AMC x x x AC x        

.

Vì

BMC

vuông tại

M

nên:

2 2

2BC MB MC x  

.

Mặt khác

   

2 2

2 2 2 2 2

2 3 3AB BC x x x x AC     

nên

ABC

vuông tại

B

.

Gọi

H

là trung điểm của

AC

thì

H

là tâm của đường tròn

 

C

và ba điểm

, ,H I M

thẳng hàng.

Do



120AMC   nên



60AIC  , suy ra

AIC

đều và 3 3AC IA IC R    .

Suy ra 3 3 3 3x x   và

2 2.3 3

cos30 6

3 3

IA

IA IM IM      .

Điểm

M d

nên

       

2 2 2

2 2

1; 2; 1 2 4 4 3 4 36M t t t IM t t t t t            

.

H

M

C

A

I

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 26 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Mà

 

2 2 2

0 1; 2;1

36

3 4 36 36 3 4 0

4

1 2 7

; ;

3 3 3 3

t M

IM t t t t

t M

   



        









 







 



Vì

0

M

x



nên điểm cần tìm là

1

2 7

; ;

3 3 3

M

 







 

, suy ra

2

Q



.

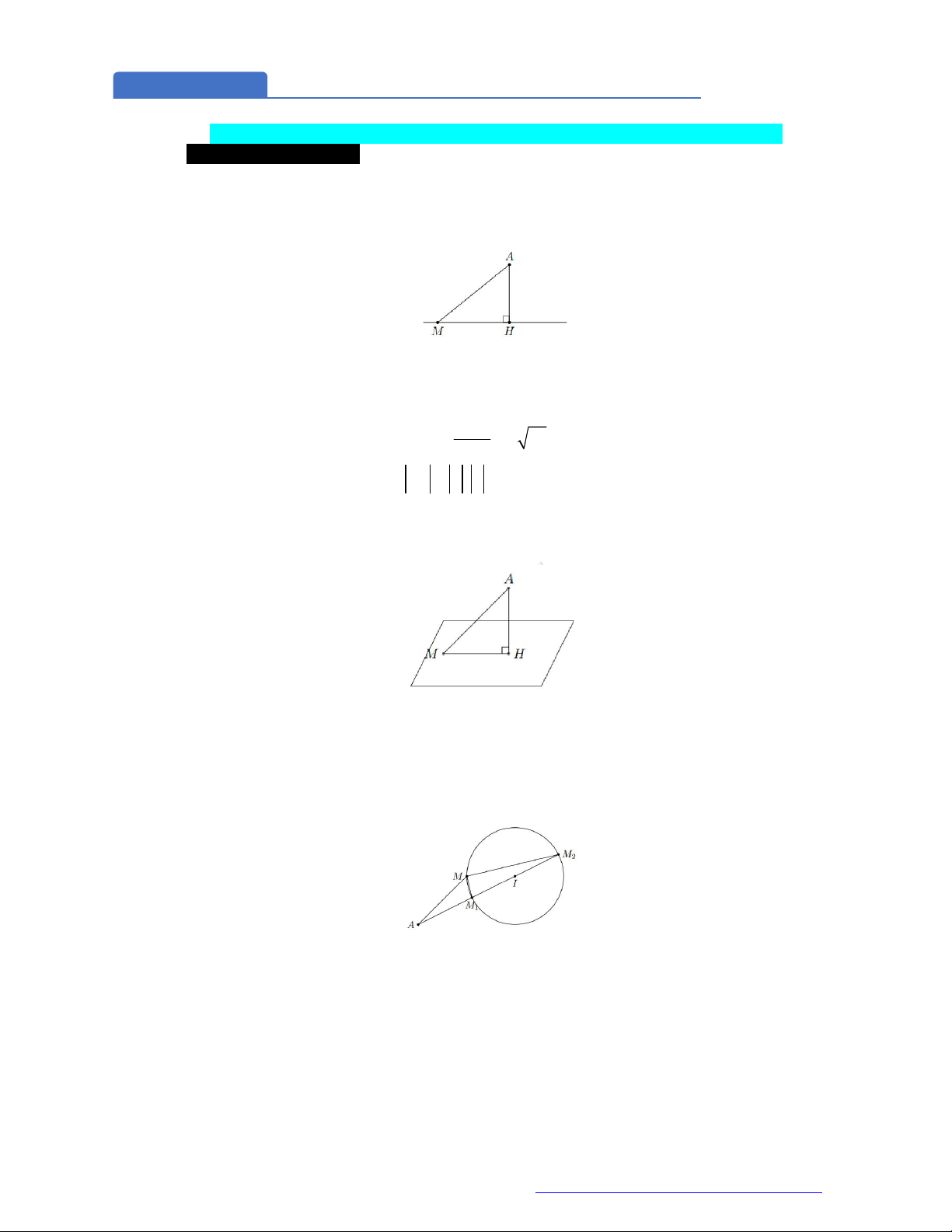
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương  https://www.facebook.com/phong.baovuong Trang 1

TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH GIỎI – MỨC 9-10 ĐIỂM

Dạng 2 Bài toán cực trị

1. Một số bất đẳng thức cơ bản

Kết quả 1. Trong một tam giác, cạnh đối diện với góc lớn thì lớn hơn

Kết quả 2. Trong các đường xiên và đường vuông góc kẻ từ một điểm nằm ngoài đường thẳng đến đường

thẳng đó thì đường vuông góc là đường ngắn nhất. Như trong hình vẽ ta luôn có

AM AH

Kết quả 3. Với ba điểm

, ,A B C

bất kì ta luôn có bất đẳng thức

.AB BC AC 

Tổng quát hơn ta có bất đẳng thức của đường gấp khúc: Với

n

điểm

1 2

, ,....

n

A A A ta luôn có

1 2 2 3 1 1

...

n n n

A A A A A A A A



   

Kết quả 4. Với hai số không âm

,x y

ta luôn có

2

x y

xy





. Đẳng thức xảy ra khi và chỉ khi

x y

Kết quả 5. Với hai véc tơ

,a b

 

ta luôn có . .a b a b

   

. Đẳng thức xảy ra khi

,a kb k 

 



2. Một số bài toán thường gặp

Bài toán 1. Cho điểm

A

cố định và điểm

M

di động trên hình

 

H

(

 

H

là đường thẳng, mặt phẳng). Tìm

giá trị nhỏ nhất của

AM

Lời giải: Gọi

H

là hình chiếu vuông góc của

A

lên hình

 

H

. Khi đó, trong tam giác

AHM

Vuông tại .

M

ta có

.AM AH

Đẳng thức xảy ra khi

M H

. Do đó

AM

nhỏ nhất khi

M

là hình chiếu của

A

lên

 

H

Bài toán 2. Cho điểm

A

và mặt cầu

 

S

có tâm

,I

bán kính

,R

M

là điểm di động trên

 

S

. Tìm giá trị

nhỏ nhất và giá trị lớn nhất của

AM

.

Lời giải. Xét

A

nằm ngoài mặt cầu

( ).S

Gọi

1 2

,M M lần lượt là giao điểm của đường thẳng

AI

với mặt

cầu

 

1 2

( )S AM AM

và

( )



là mặt phẳng đi qua

M

và đường thẳng

.AI

Khi đó

( )



cắt

( )S

theo một

đường tròn lớn

( ).C

Ta có



1 2

90 ,M MM



 nên



2

AMM và



1

AM M là các góc tù, nên trong các tam giác

1

AMM và

2

AMM ta có

1 2

AI R AM AM AM AI R     

Tương tự với

A

nằm trong mặt cầu ta có

R AI AM R AI   

Vậy

min | |,maxAM AI R AM R AI   

Bài toán 3. Cho măt phẳng

( )P

và hai điểm phân biệt

, .A B

Tìm điể

M

thuộc

( )P

sao cho

PHƯƠNG TRÌNH ĐƯỜNG THẲNG

Chuyên đề 31

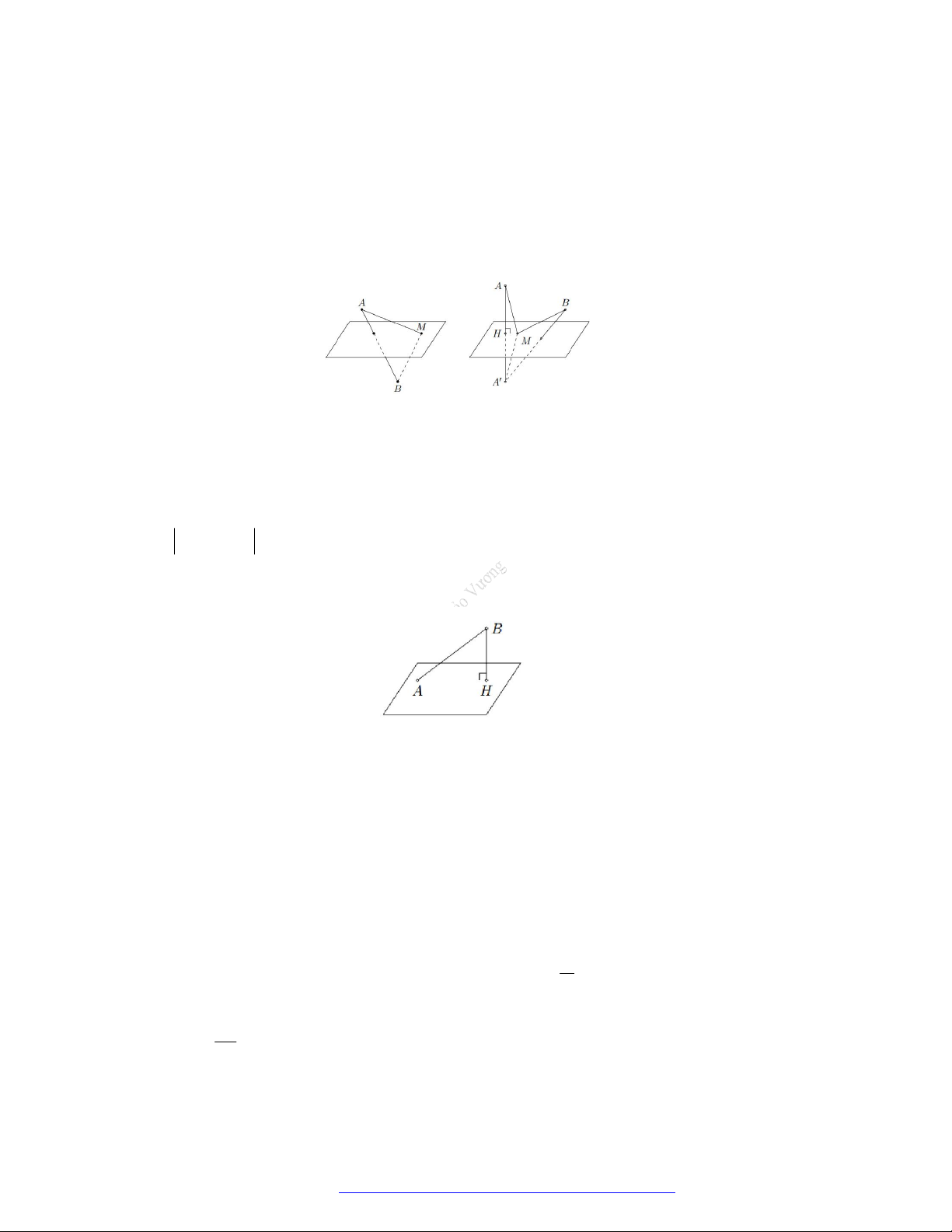
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

1.

MA MB

nhỏ nhất.

2.

| |MA MB

lớn nhất.

Lời giải.

1. Ta xét các trường hợp sau

- TH 1: Nếu

A

và

B

nằm về hai phía so với

( )P

. Khi đó

AM BM AB 

Đẳng thức xảy ra khi

M

là giao điểm của

AB

với

( )P

.

- TH 2: Nếu

A

và

B

nằm cùng một phía so với

( )P

. Gọi

A



đối xứng với

A

qua

( )P

. Khi đó

AM BM A M BM A B

 

   

Đẳng thức xảy ra khi

M

là giao điểm của A B



với

( )P

.

2. Ta xét các trường hợp sau

- TH 1: Nếu

A

và

B

nằm cùng một phía so với

( )P

. Khi đó

| |AM BM AB 

Đẳng thức xảy ra khi

M

là giao điểm của

AB

với

( )P

.

- TH 2: Nếu

A

và

B

nằm khác phía so với

( )P

. Gọi

'A

đối xứng với

A

qua

 

P

, Khi đó

| |AM BM A M BM A B

 

   

Đẳng thức xảy ra khi

M

là giao điểm của

A B



với

( )P

.

Bài toán 4. Viết phương trinh măt phẳng

( )P

di qua

A

và cách

B

một khoảng lớn nhất.

Lời giải. Gọi

H

là hình chiếu của

B

lên mặt phẳng

( ),P

khi đó

d( ,( ))B P BH BA 

Do đó

 

P

là mặt phẳng đi qua

A

vuông góc với

AB

Bài toán 5. Cho các số thực dương

,

 

và ba điểm

, ,A B

C. Viết phương trình măt phẳng

( )P

đi qua

C

và

d( ,( )) d( ,( ))T A P B P

 

 

nhỏ nhất.

Lời giải.

1. Xét

,A B

nằm về cùng phía so với

( )P

.

- Nếu ( )AB P‖ thì

( )d( ,( )) ( )P A P AC

   

   

- Nếu đường thẳng

AB

cắt

( )P

tại

.I

Gọi

D

là điểm thỏa mãn IB ID







 

và

E

là trung điểm

.BD

Khi đó

d( ,( )) d( ,( )) 2 d( ,( )) 2( )

IB

P A P D P E P EC

ID

    

      

2. Xét

,A B

nằm về hai phía so với

( )P

. Gọi

I

là giao điểm của

AB

và ( ),P B



là điểm đối xứng với

B

qua

I

. Khi đó

 

d( ,( )) d ,( )P A P B P

 



 

Đến đây ta chuyển về trường hợp trên.

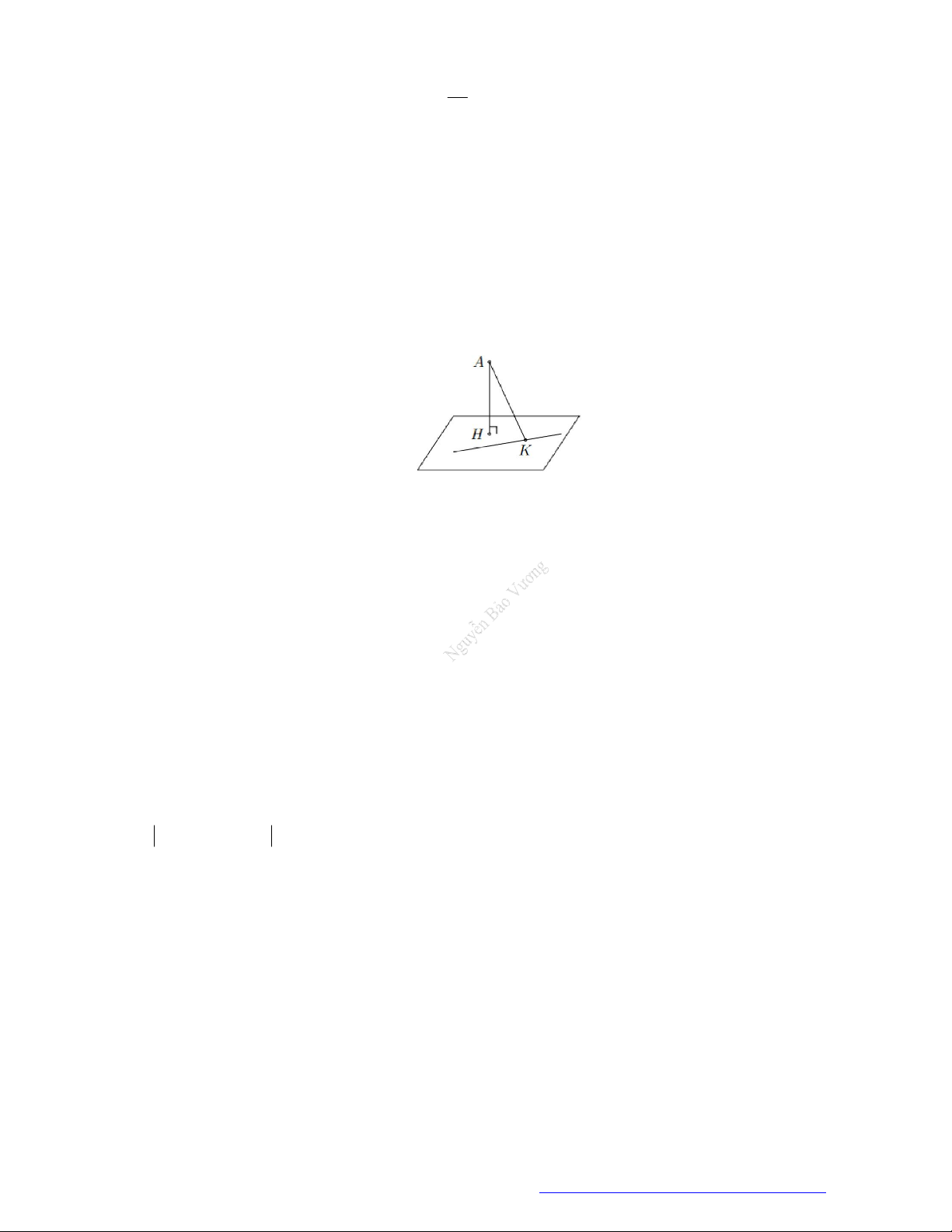
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3

So sánh các kết quả ở trên ta chọn kết quả lớn nhất.

Bài toán 6. Trong không gian cho

n

điểm

1 2

, , ,

n

A A A và diểm

.A

Viết phương trình mặt phẳng

( )P

đi

qua

A

và tổng khoảng cách từ các điểm

( 1,

i

A i n

) lớn nhất.

Lời giải.

- Xét

n

điểm

1 2

, , ,

n

A A A nằm cùng phía so với

( ).P

Gọi

G

là trọng tâm của

n

điểm đã cho. Khi đó

 

1

d ,( ) d( ,( ))

n

i

A P n G P nGA



 



- Trong

n

điểm trên có

m

điểm nằm về một phía và

k

điểm nằm về phía khác

(m k n 

). Khi đó, gọi

1

G là trọng tâm của

m

điểm,

2

G là trọng tâm của

k

điểm

3

G đối xứng với

1

G qua

.A

Khi dó

   

3 2

md ,( ) d ,( )P G P k G P 

Đến đây ta chuyển về bài toán trên.

Bài toán 7.Viết phương trình mặt phẳng

 

P

đi qua đường thẳng



và cách

A

một khoảng lớn nhất

Lời giải. Gọi

,H K

lần lượt là hình chiếu của

A

lên mặt phẳng

( )P

và đường thẳng

.

Khi đó

d( ,( ))A P AH AK 

Do đó

( )P

là mặt phẳng đi qua

K

và vuông góc vói

.AK

Bài toán 8. Trong không gian

Oxyz,

cho các điểm

1 2

, , , .

n

A A A

Xét véc tơ

1 1 2 2 n n

w MA M A M A

  

   

  





Trong đó

1 2

; ...

n

  

là các số thực cho trước thỏa mãn

1 2

... 0

n

  

    . Tìm điểm

M

thuôc măt phẳng

( )P

sao cho

| |w



có đô dài nhỏ nhất.

Lời giải. Gọi

G

là điểm thỏa mãn

1 1 2 2

0

n n

GA GA GA

  

   

   



(điểm

G

hoàn toàn xác định).

Ta có

k

MA MG GA 





vói

1;2; ; ,k n 

nên

   

1 2 1 1 2 2 1 2

w

n n n n

MG GA GA GA MG

        

         

 

  





Do đó

1 2

| | | |

n

w MG

  

    





Vi

1 2 n

  

   là hằng số khác không nên

| |w



có giá trị nhỏ nhất khi và chỉ khi

MG

nhỏ nhất, mà

( )M P

nên điểm

M

cần tìm là hình chiếu của

G

trên mặt phẳng

( )P

.

Bài toán 9. Trong không gian Oxy

,z

cho các diểm

1 2

, , , .

n

A A A Xét biểu thức:

2 2 2

1 1 2 2 n n

T MA MA MA

  

   

Trong đó

1 2

, , ,

n

  

 là các số thực cho trước. Tìm điểm M thuộc măt phẳng

( )P

sao cho

1.

T

giá trị nhỏ nhất biết

1 2

0

n

  

   .

2. T có giá trị lớn nhất biết

1 2

0

n

  

   .

Lời giải. Gọi

G

là điểm thỏa mãn

1 1 2 2

0

n n

GA GA GA

  

   

   



Ta có

k

MA MG GA 





với

1;2; ; ,k n 

nên

 

2

2 2 2

2

k k k k

MA MG GA MG MG GA GA     

 

 

Do đó

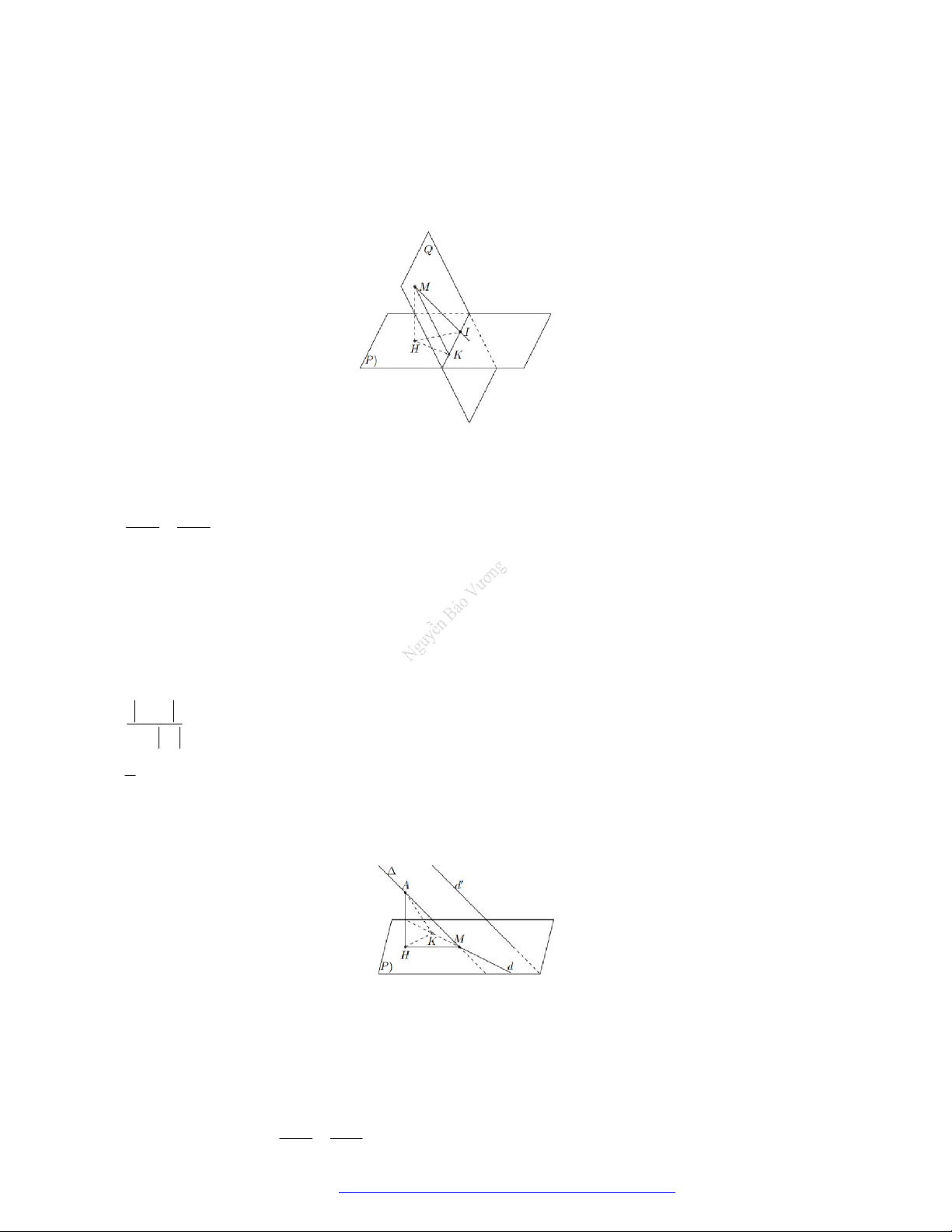
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

 

2 2 2 2

1 2 1 1 2 2n n n

T MG GA GA GA

     

      

Vì

2 2 2

1 1 2 2 n n

GA GA GA

  

  

không đổi nên

•

với

1 2

0

n

  

   thì

T

đạt giá trị nhỏ nhất khi và chỉ khi

MG

nhỏ nhất.

•

với

1 2

0

n

  

   thì

T

đạt giá trị lớn nhất khi và chỉ khi

MG

nhỏ nhất.

Mà

( )M P

nên

MG

nhỏ nhất khi điểm

M

là hình chiếu của

G

trên mặt phẳng

( )P

.

Bài toán 10. Trong không gian Oxyz, cho đường thẳng d và mặt phẳng

( )P

cắt nhau. Viết phương trình của

mặt phẳng

( )Q

chứa

d

và tạo với mặt phẳng

( )P

một góc nhỏ nhất.

Lời giải. Gọi

I

là giao điểm của đường thẳng

d

với mặt phẳng

( )P

và lấy điểm

,M d M I 

. Gọi

,H K

lầ lượt là hình chiếu của

M

lên

( )P

và giao tuyến



của

( )P

và

( )Q

.

Đặt



là góc giữa

( )P

và

( ),Q

ta có



,MKH





do đó

tan

HM HM

HK HI



 

Do đó

( )Q

là mặt phẳng đi qua

d

và vuông góc với mặt phẳng

( ),MHI

nên

( )Q

đi qua

M

và nhận

 

P d d

n u u 

  

làm VTPT.

Chú ý. Ta có thể giải bài toán trên bằng phương pháp đai số như sau:

- Goi

2 2 2

( ; ; ), 0n a b c a b c   



là một VTPT của mặt phẳng

( ).Q

Khi đó 0

d

n u 

 

từ đây ta rút được

a

theo

,b c

(hoặc

b

theo

,a c

hoặc

c

theo

,a b

).

- Gọi



là góc giữa

( )P

và

( ),Q

ta có

cos ( )

| |

P

n n

f t

n n





 



 

với

, 0.

b

t c

c

 

Khảo sát

( )f t

ta tìm được max của

( )f t

Bài toán 11. Trong không gian Oxyz, cho hai đường thẳng

d

và

d



chéo nhau. Viết phương trinh mặt

phẳng

( )P

chứa

d

và tạo với

d



một góc lớn nhất.

Lời giải. Trên đường thẳng

d

, lấy điểm

M

và dựng đường thẳng



đi qua

M

song song với

d



. Khi đó

góc giữa



và

( )P

chính là góc giữa

d



và

( )P

.

Trên đường thẳng



, lấy điểm

A

. Gọi

H

và

K

lần lượt là hình chiếu của

A

lên

( )P

và

,d



là góc giữa



và

( )P

.

Khi đó



AMH





và

cos

HM KM

AM AM



 

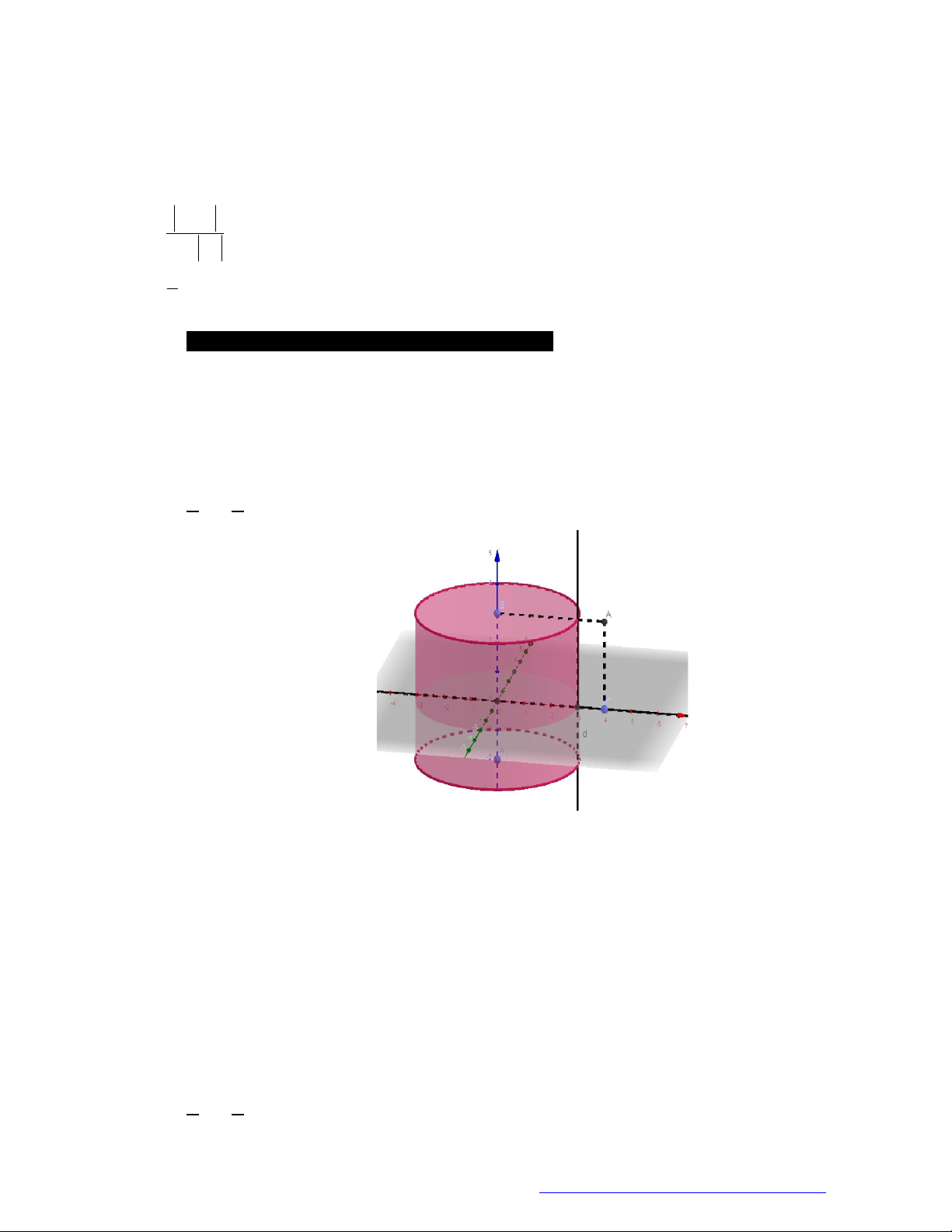
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5

Suy ra

( )P

là mặt phẳng chứa

d

và vuông góc với mặt phẳng

( ).AMK

Do dó

( )P

đi qua

M

và nhận

 

d d

d

u u u



 

  

làm VTPT.

Chú ý. Ta có thể giải bài toán trên bằng phương pháp đại số như sau:

- Goi

2 2 2

( ; ; ), 0n a b c a b c   



là một VTPT của măt phẳng

( ).P

Khi đó 0

d

n u 

 

từ đây ta rút được

a

theo

,b c

(hoặc

b

theo

,a c

hoặc

c

theo

,a b

).

- Gọi



là góc giữa

( )P

và

,d



ta có

sin ( )

| |

d

n u

f t

n u







 



 

với

, 0.

b

t c

c

 

Khảo sát

( )f t

ta tìm được max của

( )f t

Dạng 2.1. Cực trị liên quan đến khoảng cách, góc

Câu 1. (Mã 101 - 2019) Trong không gian

Oxyz

, cho điểm

 

0;4; 3A 

. Xét đường thẳng

d

thay đổi,

song song với trục

Oz

và cách trục

Oz

một khoảng bằng

3

. Khi khoảng cách từ

A

đến

d

nhỏ

nhất,

d

đi qua điểm nào dưới đây?

A.

 

0;5; 3 .Q 

B.

 

3;0; 3 .P  

C.

 

0; 3; 5 .M  

D.

 

0;3; 5 .N 

Lời giải

Chọn D

Đường thẳng

d

thay đổi, song song với trục

Oz

và cách trục

Oz

một khoảng bằng

3

nên

d

nằm

trên mặt trụ tròn xoay có trục là

Oz

và bán kính bằng

3

.

Gọi

I

là hình chiếu của

A

lên

Oy

, khoảng cách từ

A

đến

d

nhỏ nhất khi

d

đi qua giao điểm

của

Oy

với mặt trụ là điểm

 

0;3;0I

nên

d

đi qua điểm

 

0;3; 5N 

.

Câu 2. (Mã 103 2019) Trong không gian Oxyz, cho điểm

 

0;3; 2A 

. Xét đường thẳng

d

thay đổi

song song với Oz và cách Oz một khoảng bằng 2. Khi khoảng cách từ

A

đến

d

nhỏ nhất.

d

đi

qua điểm nào dưới đây?

A.

 

0;2; 5Q 

. B.

 

0;4; 2M 

. C.

 

2;0; 2P  

. D.

 

0; 2; 5N  

.

Lời giải

Chọn A

Vì

d

song song với Oz và cách Oz một khoảng bằng 2 nên

d

thuộc mặt trụ trục Oz và bán kính

bằng 2. Có

 

0;0; 2H 

là hình chiếu vuông góc của

 

0;3; 2A 

trên Oz.

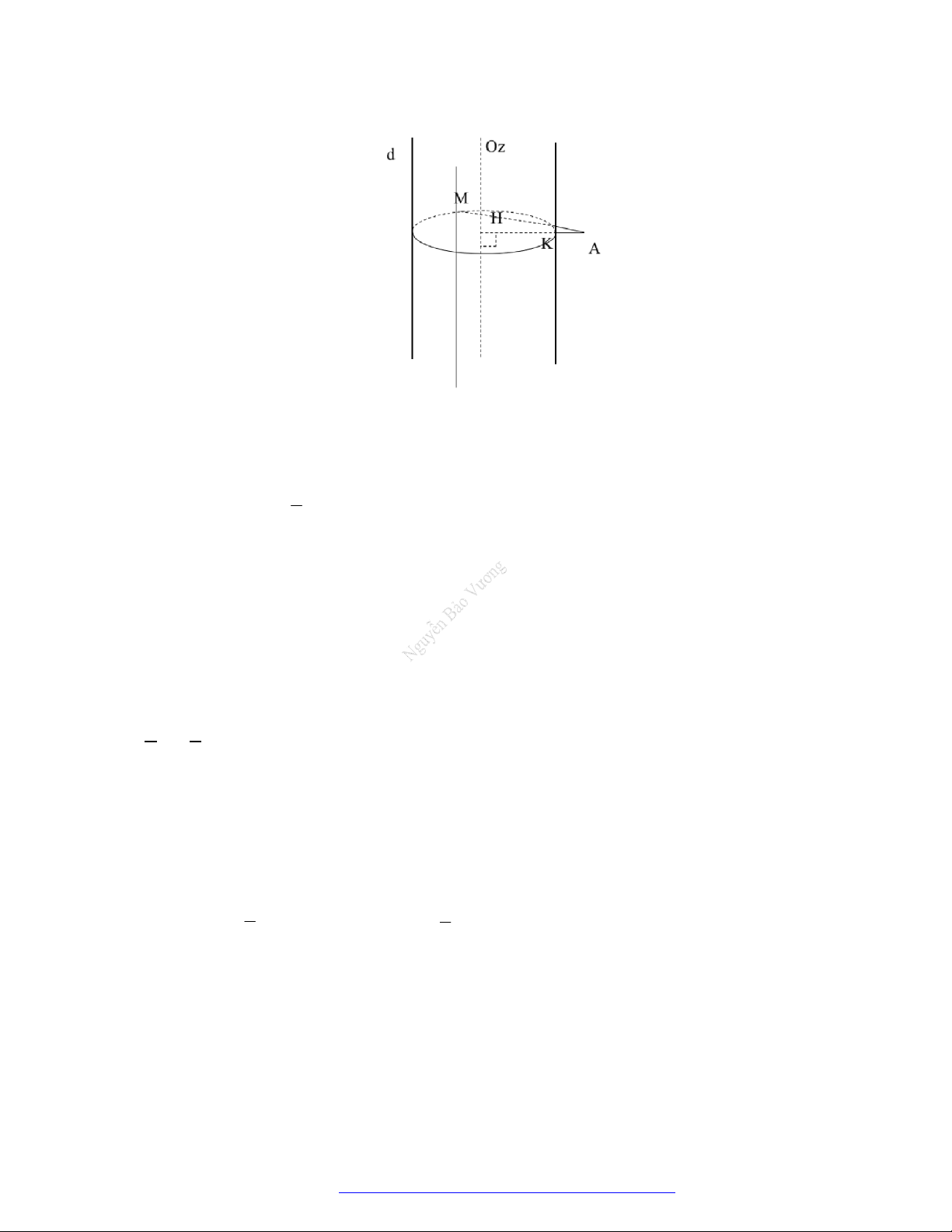
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Có

 

0;3;0 3HA HA 



nên A nằm ngoài mặt trụ.

Gọi (P) là mặt phẳng qua A và vuông góc với Oz. M là hình chiếu vuông góc của A trên

d

Gọi K là giao điểm của AH và mặt trụ (

K

nằm giữa A và H).

Dễ thấy

   

; ; ; 1d A d AM AK AK AH d A d    

Dấu bằng xảy ra khi và chỉ khi

M K

.

Khi đó ta có:

 

0

2

0;2; 2 : 2 ( )

3

2

x

HK HA K d y t R

z t







     





  





 

Với

3t 

ta thấy

d

đi qua điểm

Q

.

Câu 3. (Mã 102 - 2019) Trong không gian

Oxyz

, cho điểm

 

0;4; 3A 

. Xét đường thẳng

d

thay đổi,

song song với trục

Oz

và cách trục

Oz

một khoảng bằng 3. Khi khoảng cách từ

A

đến

d

lớn

nhất,

d

đi qua điểm nào dưới đây?

A.

 

0;3; 5N 

. B.

 

0; 3; 5M  

. C.

 

3;0; 3P  

. D.

 

0;11; 3Q 

.

Lời giải

Chọn B

Vì

d

thay đổi, song song với trục

Oz

và cách trục

Oz

một khoảng bằng 3 nên

d

là đường sinh

của hình trụ có trục là

Oz

và có bán kính đáy

3r 

.

Gọi

A



là hình chiếu của

A

lên trục

Oz

 

0;0; 3A



 

và

4AA





.

Gọi

 

; ;H x y z

là hình chiếu của

A

lên

d

.

AH

lớn nhất khi

A

,

A



,

H

thẳng hàng và

4 3 7AH AA A H AA r

  

      

.

Khi đó

7

4

AH AA





 

   

7

; 4; 3 0; 4;0

4

x y z    

0

3

x

y

z







  





 



 

0; 3; 3H  

.

Vậy

d

qua

 

0; 3; 3H  

có vectơ chỉ phương

 

0;0;1k 



nên có phương trình

0

3

x

y

z t







 





  



suy

ra

d

đi qua điểm

 

0; 3; 5M  

.

Câu 4. (Mã 104 2019) Trong không gian

,Oxyz

cho điểm

 

0;3; 2 .A 

Xét đường thẳng

d

thay đổi,

song song với trục

Oz

và cách trục

Oz

một khoảng bằng

2.

Khi khoảng cách từ

A

đến

d

lớn

nhất,

d

đi qua điểm nào dưới đây?

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7

A.

 

0;8; 5M 

. B.

 

0;2; 5N 

. C.

 

0; 2; 5P  

. D.

 

2;0; 3Q  

.

Lời giải

Chọn C

Do đường thẳng

/ /d Oz

nên

d

nằm trên mặt trụ có trục là

Oz

và bán kính trụ là

2.R 

Gọi

H

là hình chiếu của

A

trên trục

Oz

, suy ra tọa độ

 

0;0; 2 .H 

Do đó

 

,

3.

A Oz

d AH 

Gọi

B

là điểm thuộc đường thẳng

AH

sao cho

3

5

AH AB

 

 

0; 2; 2 .B  

Vậy

 

max

, 5d A d d 

là đường thẳng đi qua

B

và song song với

.Oz

Phương trình tham số của

0

: 2 .

2

x

d y

z t







 





  



Kết luận:

d

đi qua điểm

 

0; 2; 5 .P  

Câu 5. (THCS - THPT Nguyễn Khuyến 2019) Trong không gian

Oxyz

, cho đường thẳng

:

2 2 1

x y z

  

và mặt phẳng

 

: 2 2 0P x y z  

. Gọi

 

Q

là mặt phẳng chứa



sao cho góc

giữa hai mặt phẳng

 

P

và

 

Q

là nhỏ nhất. Phương trình mặt phẳng

 

Q

là

A.

2 0x y z  

. B.

22 10 0x y z  

. C.

2 0x y z  

. D.

10 22 0x y z  

.

Lời giải

Đường thẳng

:

2 2 1

x y z

  

được viết lại dưới dạng tham số

2

: 2

x t

y t

z t







 









d

Q

P

Δ

A

H

B

K

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 8 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Xét hệ phương trình

2 0

0

2 2 0 0

x t t

y t x

z t y

x y z z

 

 

 

 

 



 

 

 

   

 

. Do đó



cắt

 

P

tại điểm

 

0;0;0 O

A



.

Lại có



và

 

P

không vuông góc nhau nên ta đi chứng minh góc nhỏ nhất giữa

 

P

và

 

Q

là

góc giữa



và

 

P

. Thật vậy trên



lấy

B

khác

A

, kẻ

BH

vuông góc với

 

P

tại

H

và

BK

vuông góc

d

tại

K

(

d

là giao tuyến của

 

P

và

 

Q

) tại

K

. Khi đó góc giữa

 

Q

và

 

P

là

góc



BKH

.

HA HK

 



tan tan

BH BH

BKH BAH

HK HA

  



 



, 90

4

, arcsin

9

tan tan

BKH BAH

BKH BAH P

BKH BAH







 

    



 

 









Đẳng thức xảy ra

.K A d    

Do đó, góc giữa hai mặt phẳng

 

P

và

 

Q

là nhỏ nhất khi và chỉ khi

 

Q

chứa

 



và cắt

 

P

theo một giao tuyến vuông góc



.

*)Viết phương trình của

 

Q

Đường thẳng



có vectơ chỉ phương

 

1

2;2;1



u 

,

 

P

có vectơ pháp tuyến

 

1

1;2; 2



n

 

nên

d

có vectơ chỉ phương

 

2 1 1

, 6;5;2

  

u u n

 

  

 

.

 

Q

chứa



và d nên nhận

 

2 2 1

; 1;10; 22

  

n u u

 

  

 

làm vectơ pháp tuyến.

Vậy mặt phẳng

 

Q

đi qua

 

0;0;0

A

và nhận

 

2

1;10; 22

n  



làm vectơ pháp tuyến nên có

phương trình

10 22 0

x y z

  

.

Câu 6. Trong không gian

Oxyz

, cho điểm

 

1;1;2

A

và mặt phẳng

   

: 1 1 0

P m x y mz

    

, với

m

là tham số. Biết khoảng cách từ điểm

A

đến mặt phẳng

 

P

lớn nhất. Khẳng định đúng trong bốn

khẳng định dưới đây là

A.

2 6

m

 

. B.

6

m



. C.

2 2

m

  

. D.

6 2

m

  

.

Lời giải

Cách 1:

Ta có

 

2

1 1 2 1 3 1

;

2 1

1 1

m m m

d A P

m m

    

 

 

  

.

Xét

 

  

 

2

1

3 1 5 3 1

0

3

2 1

5

m m m

m

f m f m

m m

m



  







    



 





.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9

Vậy

 

14

max ;

3

d A P 

khi

 

5 2;6m  

.

Cách 2:

Ta đi tìm đối tượng cố định của mặt phẳng

 

P

:

     

: 1 1 0 1 0P m x y mz x z m x y          

.

Với mọi

m

mặt phẳng

 

P

luôn đi qua giao tuyến của hai mặt phẳng

0

1 0

x z

x y

 





   



tức

luôn đi qua đường thẳng

 

: 1

x t

d y t

z t







 





 



.

Gọi

     

;1 ; 1; ; 2H t t t d AH t t t       



. Để khoảng cách từ

A

đến

 

P

lớn nhất thì

 

AH P AH 



cùng phương với VTPT của

 

P

là

 

1;1;

P

n m m 



, suy ra:

 

1

1 2

3

2

1 1

5 2;6

t

mt t t

t t t

mt t

m m

m



 

  



  



   

 

  







 



.

Câu 7. (THPT Quang Trung Đống Đa Hà Nội 2019) Trong không gian với hệ tọa độ

Oxyz

, cho hai

điểm

(1;1;1)A

,

(2;0;1)B

và mặt phẳng

( ) : 2 2 0.P x y z    

Viết phương trình chính tắc của

đường thẳng

d

đi qua

A

, song song với mặt phẳng

( )P

sao cho khoảng cách từ

B

đến

d

lớn

nhất.

A.

1 1 1

:

3 1 2

x y z

d

  

  



. B.

2

:

2 2 2

x y z

d



  



.

C.

2 2

:

1 1 1

x y z

d

 

  



. D.

1 1 1

:

3 1 1

x y z

d

  

  

 

.

Lời giải

Gọi

( ')P

chứa

A

và song song

( )P

suy ra

( ') : 2 4 0P x y z    

.

Ta thấy

( ')B P

do đó

( , )d B d

đạt giá trị lớn nhất là

.AB

Khi đó

d

vuông góc với

AB

và

d

vuông góc với giá của

n



là VTPT của

( )P

.

Suy ra một VTCP của

d

là , (2;2; 2)u n AB

 

  

 



 

.

d

P'

B

A

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 10 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Kết hợp với điểm

A

thuộc

d

nên ta chọn đáp án C.

Câu 8. (KTNL GV THPT Lý Thái Tổ 2019) Trong không gian với hệ tọa độ

Oxyz

, cho đường thẳng

1 2

:

1 2 1

x y z

d

 

 



. Gọi

 

P

là mặt phẳng chứa đường thẳng

d

và tạo với mặt phẳng

 

: 2 2 2 0Q x y z   

một góc có số đo nhỏ nhất. Điểm

 

1;2;3A

cách mặt phẳng

 

P

một

khoảng bằng:

A.

3

. B.

5 3

3

. C.

7 11

11

. D.

4 3

3

.

Lời giải

Chọn A

1 2

:

1 2 1

x y z

d

 

 



có VTCP

 

1; 2; 1u   



.

 

: 2 2 2 0Q x y z   

có VTPT

 

2; 1; 2n   



.

Gọi



là góc tạo bởi

d

và

 

Q

, ta có

 

6

sin cos ,

3

u n



 

 

.

Từ hình vẽ, ta có

 



,d P MBH

và

   

 



,P Q MCH

.

Ta thấy



6

sin

3

MH MH

MCH

MC MB

  

.

Vậy góc

   

 



,P Q MCH

nhỏ nhất khi



6

sin

3

MCH 

hay



3

cos

3

MCH 

*Viết phương trình mặt phẳng (P)

-CÁCH 1:

Mặt phẳng

 

: 0P Ax By Cz D   

Ta có

 

2 2 2

2 0

. 0

2 2

3

cos ,

3

Q

A B C

n u

A B C

n n

A B C



  









 

 



 



 



 

 

 

2

2 2

2

6 6 12 0 1

3 3 2

A B C

B C BC

B B C B C

 



 



 

 

 

  

   









Nếu

0B 

suy ra

0A C 

loại.

Nếu

0B 

từ

 

1

suy ra

2

2 1 0 1

C C C

C B

B B B

 

        

 

 

suy ra

A B

.

Mặt phẳng

 

: 0P Bx By Bz D   

đi qua điểm

 

0; 1;2N d 

suy ra

3D B

.

Vậy phương trình mặt phẳng

 

: 3 0P x y z   

. Suy ra

 

; 3d A P  .

M

H

B

C

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11

-CÁCH 2

Gọi

( ) ( )P Q  

thì góc giữa

( )P

và

( )Q

nhỏ nhất khi và chỉ khi

d 

. Do đó, mặt phẳng (P)

thỏa đề bài là mặt phẳng chứa

d

và cắt (Q) theo giao tuyến



sao cho

d 

.



 



 



 







(Q)

d

nhận



 



 



 

u

d Q

u ,n

làm vec tơ chỉ phương.

(Q)

chứa

d

và



 (P)

qua

0 1 2 M( ;- ; ) d

và nhận

6 6 6



 

  

 

  

d

n u ,u ( ; ; )

làm vectơ

pháp tuyến

3 0    (P) : x y z .

Vậy

 

; 3d A P 

.

Câu 9. (Chuyên Bắc Giang 2019) Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm

 

1;2; 3A 

,

 

2; 2;1B  

và mặt phẳng

 



:

2 2 9 0x y z   

. Gọi

M

là điểm thay đổi trên mặt phẳng

 



sao cho

M

luôn nhìn đoạn

AB

dưới một góc vuông. Xác định phương trình đường thẳng

MB

khi

MB

đạt giá trị lớn nhất.

A.

2

2 2

1 2

x t

y t

z t

  





  





 



B.

2 2

2

1 2

x t

y t

z t

  





  





 



C.

2

1 2

x t

y

z t

  





 





 



D.

2

1

x t

y t

z

  





  









Lời giải

Chọn C

Ta có:

   

2. 2 2. 2 1 9 0     

 

B  

.

Gọi

H

là hình chiếu của

A

trên

 



thì

AH MB

,

AM MB

MH MB 

MB BH 

. Dấu bằng xảy ra khi

M H

, lúc đó

M

là hình chiếu của

A

trên

 



.

Gọi

 

; ;H x y z

,

 

1; 2; 3AH x y z   



.

Ta có hệ phương trình

2 2 9 0

1 2 3

2 2 1

x y z

   







  

 



 

2 2 9

1

2 5

x y z

x y

x z

   





   





  



3

2

1

x

y

z

 





  





 



 

3; 2; 1M   

 

1;0;2MB 



2

: 2

1 2

x t

MB y

z t

  





  





 



.

Câu 10. -(Chuyên Nguyễn Tất Thành Yên Bái 2019) Viết phương trình đường thẳng

a

đi qua

 

4; 2; 1M 

, song song với mặt phẳng

( ) : 3 4 12 0x y z   



và cách

 

2; 5; 0A 

một

khoảng lớn nhất.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 12 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

A.

4

2

1

x t

y t

z t

 





  





 



. B.

4

2

1

x t

y t

z t

 





  





  



. C.

1 4

1 2

1

x t

y t

z t

 





 





  



. D.

4

2

1

x t

y t

z t

 





  





 



.

Lời giải

 

6; 7;1AM  



, vectơ pháp tuyến của

 



là

(3; 4;1)n  



.

Gọi

H

là hình chiếu vuông góc của

A

trên

a

.

 

; 86d A a AH AM  



 

;d A a

lớn nhất khi

H M

.

Khi đó

a

là đường thẳng đi qua

M

, song song với

 



và vuông góc với

AM

.

Gọi

u



là vectơ chỉ phương của

a

u n

u AM

















 

 

;

   

, 3; 3; 3 3 1;1;1AM n

 

     

 

 

.

Chọn

 

1;1;1u 



. Đáp án D thỏa mãn.

----------------------------------------

Câu 11. (Chuyên Nguyễn Trãi Hải Dương 2019) Đường thẳng



đi qua điểm

 

3;1;1M

, nằm trong mặt

phẳng

 

: 3 0x y z



   

và tạo với đường thẳng

1

: 4 3

3 2

x

d y t

z t







 





  



một góc nhỏ nhất thì phương trình

của



là

A.

1

2

x

y t

z t









 











. B.

8 5

3 4

2

x t

y t

z t



 







  







 



. C.

1 2

1

3 2

x t

y t

z t



 







 







 



. D.

1 5

1 4

3 2

x t

y t

z t



 







 







 



.

Lời giải

Đường thẳng

d

có vectơ chỉ phương là

 

0;3; 2u  



.

Mặt phẳng

 



có vectơ pháp tuyến là

 

1;1; 1n  



.

Vì

   

. 0.1 3.1 2 . 1 5 0u n       

 

nên

d

cắt

 



.

Gọi

1

d là đường thẳng đi qua

M

và

1

d //

d

, suy ra

1

d có phương trình:

3

1 3

1 2

x

y t

z t







 





 



.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13

Lấy

 

1

3;4; 1

N d 

. Gọi

K

,

H

lần lượt là hình chiếu vuông góc của

N

trên mặt phẳng

 



và

đường thẳng



.

Ta có:

 



,

d NMH

 

và



sin .

NH NK

NMH

MN MN

 

Do vậy

 



,

d



nhỏ nhất khi

K H

hay



là đường thẳng

MK

.

Đường thẳng

NK

có phương trình:

3

4

1

x t

y t

z t

 





 





  



.

Tọa độ điểm

K

ứng với

t

là nghiệm của phương trình:

     

5

3 4 1 3 0

3

t t t t

          

. Suy ra

4 7 2

; ;

3 3 3

K

 

 

 

.

Câu 12. (Chuyên Thái Bình 2019) Trong không gian

Oxyz

, cho điểm

 

1;1;1

A

và mặt phẳng

( ) : 2 0

P x y

 

. Gọi



là đường thẳng đi qua

A

, song song với

( )P

và cách điểm

 

1;0;2

B 

một khoảng ngắn nhất. Hỏi



nhận vecto nào dưới đây là vecto chỉ phương ?

A.

 

6;3; 5

u

 



. B.

 

6; 3;5

u  



. C.

 

6;3;5

u 



. D.

 

6; 3; 5

u

  



.

Lời giải

Gọi

( )Q

chứa



và song song với

( )P

. Suy ra

( )Q

có phương trình:

1 2( 1) 0 2 3 0

x y x y

       

.

Khi đó

 

min

;

d B BH

 

với

H

là hình chiếu của

B

lên mặt phẳng

( )Q

.

Đường thẳng

BH

đi qua

B

, vuông góc với mặt phẳng

( )Q

có phương trình

1

2 ,

2

x t

y t t

z

  





 











.

Tọa độ giao điểm

H

của đường thẳng

BH

và mặt phẳng

( )Q

là nghiệm của hệ:

1

2

2 3 0

x t

y t

z

x y

  



















  



. Giải hệ trên ta được

1 8

; ;2

5 5

H

 



 

 

.

Do đó



là đường thẳng

AH

có

6 3

; ; 1

5 5

AH

 

  

 

 



.

Suy ra

 

6; 3; 5

u

  



cũng là một vecto chỉ phương của



.

Câu 13. Trong không gian với hệ tọa độ

Oxyz

cho điểm

 

2; 1; 2

A

 

và đường thẳng

 

d

có phương

trình

1 1 1

x y z  

 



. Gọi

 

P

là mặt phẳng đi qua điểm

A

, song song với đường thẳng

 

d

và khoảng cách từ

d

tới mặt phẳng

 

P

là lớn nhất. Khi đó mặt phẳng

 

P

vuông góc với mặt

phẳng nào sau đây?

A.

6 0

x y

  

. B.

3 2 10 0

x y z

   

.

C.

2 3 1 0

x y z

   

. D.

3 2 0

x z

  

.

Lời giải

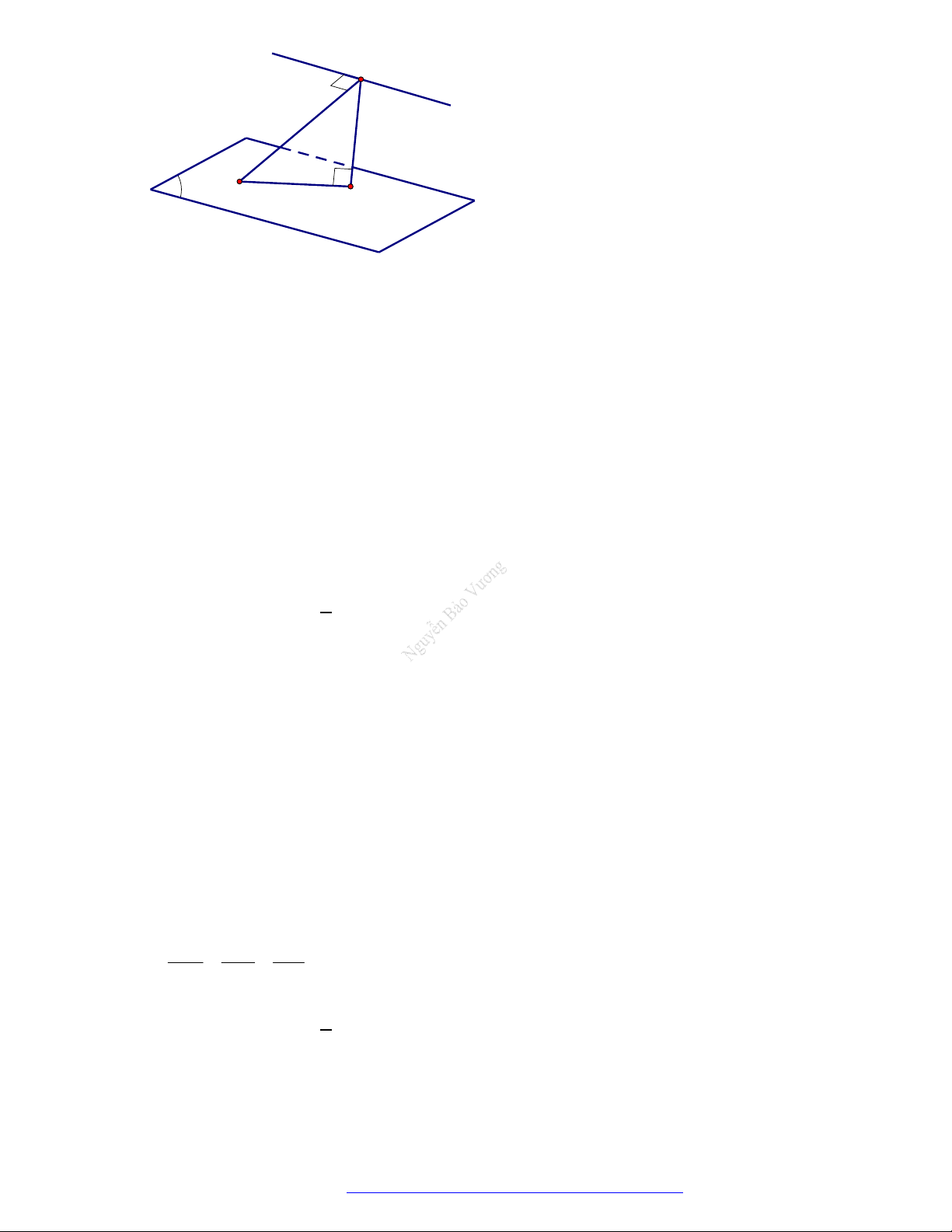
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 14 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Gọi

H

là hình chiếu của

A

lên đường thẳng

d

. Ta suy ra

 

1;1;1H

.

Gọi

 

P

là mặt phẳng đi qua điểm

A

và

 

P

song song với đường thẳng

d

. Gọi

K

là hình chiếu

của

H

lên mặt phẳng

 

P

. Do

 

// d P

nên ta có

 

, ,d d P d H P HK 

.

Ta luôn có bất đẳng thức

HK HA

. Như vậy khoảng cách từ

 

d

đến

 

P

lớn nhất bằng

AH

.

Và khi đó

 

P

nhận

 

1;2;3AH  



làm vectơ pháp tuyến.

Do

 

P

đi qua

 

2; 1; 2A  

nên ta có phương trình của

 

P

là:

2 3 10 0x y z   

.

Do đó

 

P

vuông góc với mặt phẳng có phương trình:

3 2 0x z  

.

Câu 14. Trong không gian với hệ toạ độ

Oxyz

, gọi

 

P

là mặt phẳng đi qua hai điểm

 

1; 7; 8A  

,

 

2; 5; 9B  

sao cho khoảng cách từ điểm

 

7; 1; 2M  

đến

 

P

đạt giá trị lớn nhất. Biết

 

P

có

một véctơ pháp tuyến là

 

; ;4n a b



, khi đó giá trị của tổng

a b

là

A.

1

. B.

3

. C.

6

. D.

2

.

Lời giải

Phương trình tham số của đường thẳng

AB

là

1

7 2

8

x t

y t

z t

 





  





  



.

Gọi

H

,

K

lần lượt là hình chiếu của

M

trên

 

P

và đường thẳng

AB

.

Ta tìm được điểm

 

3; 3; 10K  

. Ta luôn có bất đẳng thức

 

,d M P MH MK 

.

Dấu bằng xảy ra khi và chỉ khi

H K

. Khi đó

   

4; 2; 8 2 2;1;4MH      



.

Mặt phẳng

 

P

có một vectơ pháp tuyến là

 

2;1;4n 



. Vậy ta có

3a b 

.

Câu 15. Trong không gian với hệ tọa độ

Oxyz

, cho điểm

 

3; 1;0A 

và đường thẳng

2 1 1

:

1 2 1

x y z

d

  

 



. Mặt phẳng

 



chứa

d

sao cho khoảng cách từ

A

đến

 



lớn nhất có

phương trình là

A.

2 0x y z   

. B.

0x y z  

.

C.

1 0x y z   

. D.

2 5 0x y z    

.

Lời giải

Gọi

,H K

lần lượt là hình chiếu của

A

lên

 



và

d

. Khi đó ta có

AH AK

.

Vì

H d

nên

 

2 ; 1 2 ;1H t t t   

 

1 ;2 ;1AH t t t    



.

d

P

A

K

H

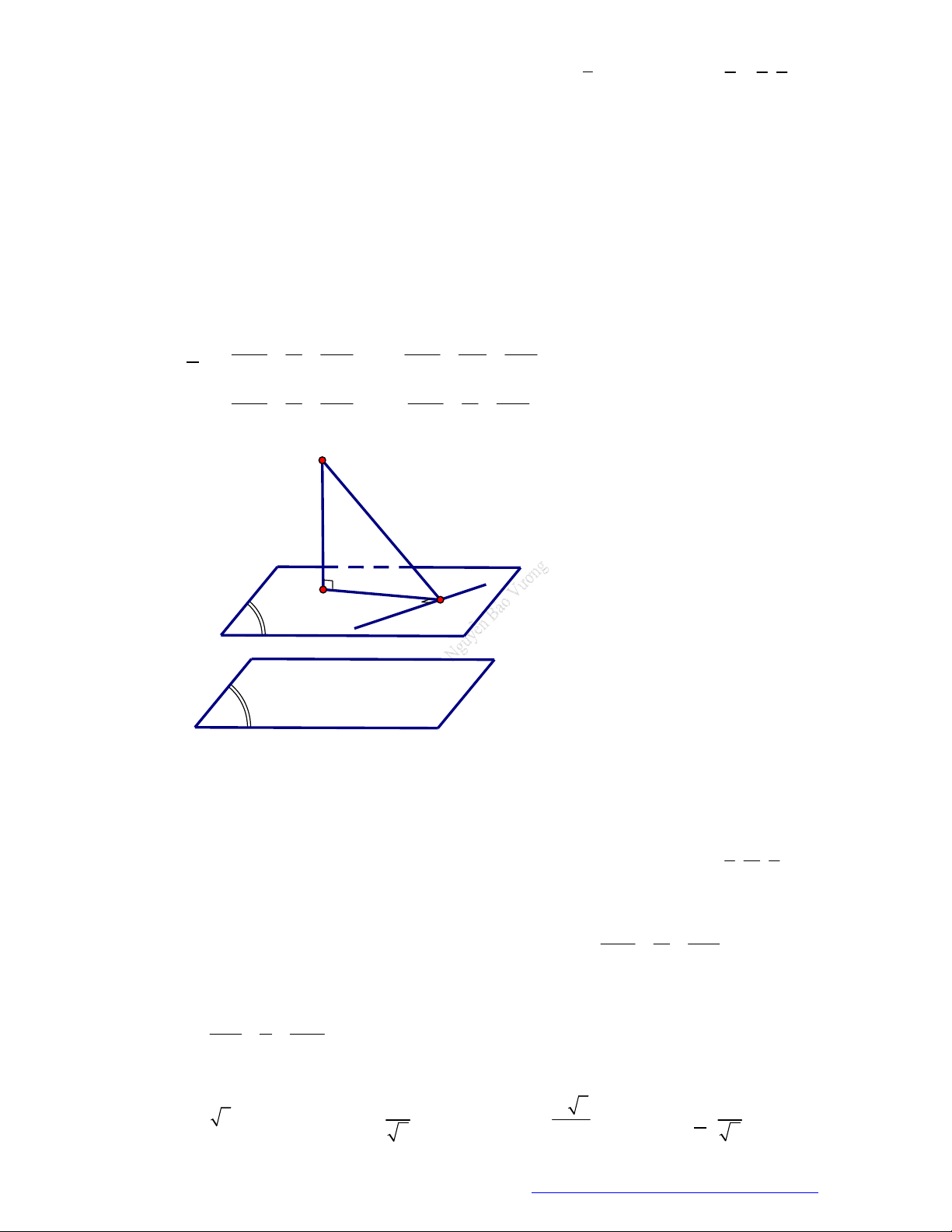
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15

Do

AH d

nên ta có

 

1 2.2 1 0t t t      

1

3

t  

. Khi đó

2 2 2

; ;

3 3 3

AH

 

  

 

 



.

Khoảng cách từ

A

đến

 



lớn nhất khi và chỉ khi

AH AK

. Do đó

 



có vectơ pháp tuyến là

 

1;1; 1n  



. Vậy

 

:



     

1 2 1 1 1 1 0x y z     

0x y z   

.

Vẫn là đánh giá bất đẳng thức

AH AK

nói trên, nhưng bài toán sau đây lại phát biểu hơi khác

một chút.

Câu 16. Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm

 

3;0;1A 

,

 

1; 1;3B 

và mặt phẳng

 

: 2 2 5 0P x y z   

. Viết phương trình chính tắc của đường thẳng

d

đi qua

A

, song song với

mặt phẳng

 

P

sao cho khoảng cách từ

B

đến

d

nhỏ nhất.

A.

3 1

:

26 11 2

x y z

d

 

 



. B.

3 1

:

26 11 2

x y z

d

 

 



.

C.

3 1

:

26 11 2

x y z

d

 

 

. D.

3 1

:

26 11 2

x y z

d

 

 

 

.

Lời giải

Ta thấy rằng

d

đi qua

A

và

d

song song với

 

P

nên

d

luôn nằm trong mặt phẳng

 

Q

qua

A

và

   

// Q P

. Như vậy bây giờ ta chuyển về xét trong mặt phẳng

 

Q

để thay thế cho

 

P

. Ta

lập được phương trình mặt phẳng

 

: 2 2 1 0Q x y z   

.

Gọi

,H K

lần lượt là hình chiếu của

B

lên

 

Q

và

d

. Ta tìm được

1 11 7

; ;

9 9 9

H

 



 

 

. Ta luôn có

được bất đẳng thức

 

;d B d BK BH 

nên khoảng cách từ

B

đến

d

bé nhất bằng

BH

.

Đường thẳng

d

bây giờ đi qua

,A H

nên có phương trình

3 1

26 11 2

x y z 

 



.

Câu 17. (Sở Thanh Hóa 2019) Trong không gian

Oxyz

, cho điểm

 

2;5;3A

và đường thẳng

1 2

:

2 1 2

x y z

d

 

 

. Gọi

 

P

là mặt phẳng chứa

d

sao cho khoảng cách từ

A

đến

 

P

là lớn

nhất. Khoảng cách từ gốc tọa độ

O

đến

 

P

bằng

A.

2

. B.

3

6

. C.

11 2

6

. D.

1

2

.

Lời giải

d

Q

P

B

H

K

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 16 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Gọi

 

; ;n a b c





là một vectơ pháp tuyến của

 

P

, với

2 2 2

0

a b c

  

.

Điểm

   

1;0;2

M d M P

  

.

Phương trình của

   

: 2 0

P ax by cz a c

    

.

Một vectơ chỉ phương của

d

là

 

2;1;2 . 0 2 2 0

u n u n u a b c

        

    

.

   

 

2 2 2 2

2 2

| 5 | 9 | |

2 2 ,

4

a b c a c

b a c d A P

a b c

a c a c

  

      

 

  

.

Ta có

 

2

2 2 2 2

2

a c

a c a c a c



     

với

, .

a c

 

Suy ra:

 

   

2

2 2 2

2 2

9

4 4 .

2 2

a c

a c a c a c a c



       

Do đó

 

2

2 2

2

9 | | 9 | | 9 | | 2

, 3 2.

3| |

9

4

2

a c a c a c

d A P

a c

a c a c

a c

  

   



  



 

, 3 2

4

a c

Max d A P

b a





  



 



. Chọn

1 4.

a c b

    

Phương trình

   

 

1

: 4 3 0 , .

2

P x y z d O P     

Câu 18. (Chuyên Phan Bội Châu 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho hai điểm

   

1;2;3 , 5; 4; 1

A B

 

và mặt phẳng

 

P

qua

Ox

sao cho

 

, ,

2 ,

B P A P

d d P



cắt

AB

tại

 

; ;I a b c

nằm giữa

AB

. Tính

a b c 

A.

8

B.

6

C.

12

D.

4

Lời giải

Do mặt phẳng

 

P

qua

Ox

nên phương trình mặt phẳng

 

P

có dạng

0

by cz

 

 

2 2

0

b c

 

 

, ,

2 2 2 2

4 4 6

4 2 3

2 2.

4 4 6

8 7 0

0

B P A P

b c b c

d d

b c b c

b c

c

   

  



   



    

 



 











Trường hợp 1:

8 7 0

b c

 

chọn

7; 8

b c

  

khi đó

 

: 7 8 0

P y z

 

Xét

 

, 7 8f y z y z 

Thay tọa độ

,A B

vào ta được

     

 

7.2 8.3 7. 4 8. 1 0    

suy ra

,A B

nằm cùng phía so với

 

P

(loại)

Trường hợp 2:

0

c



suy ra phương trình

 

: 0

P y



Thay tọa độ

,A B

vào ta được

 

2. 4 0 

suy ra

,A B

nằm khác phía so với

 

P

. Do đó đường

thẳng

AB

cắt

 

P

tại

I

nằm giữa

AB

Phương trình tham số của đường thẳng

AB

:

 

1 4

2 6

3 4

x t

y t t

z t

 





  





 





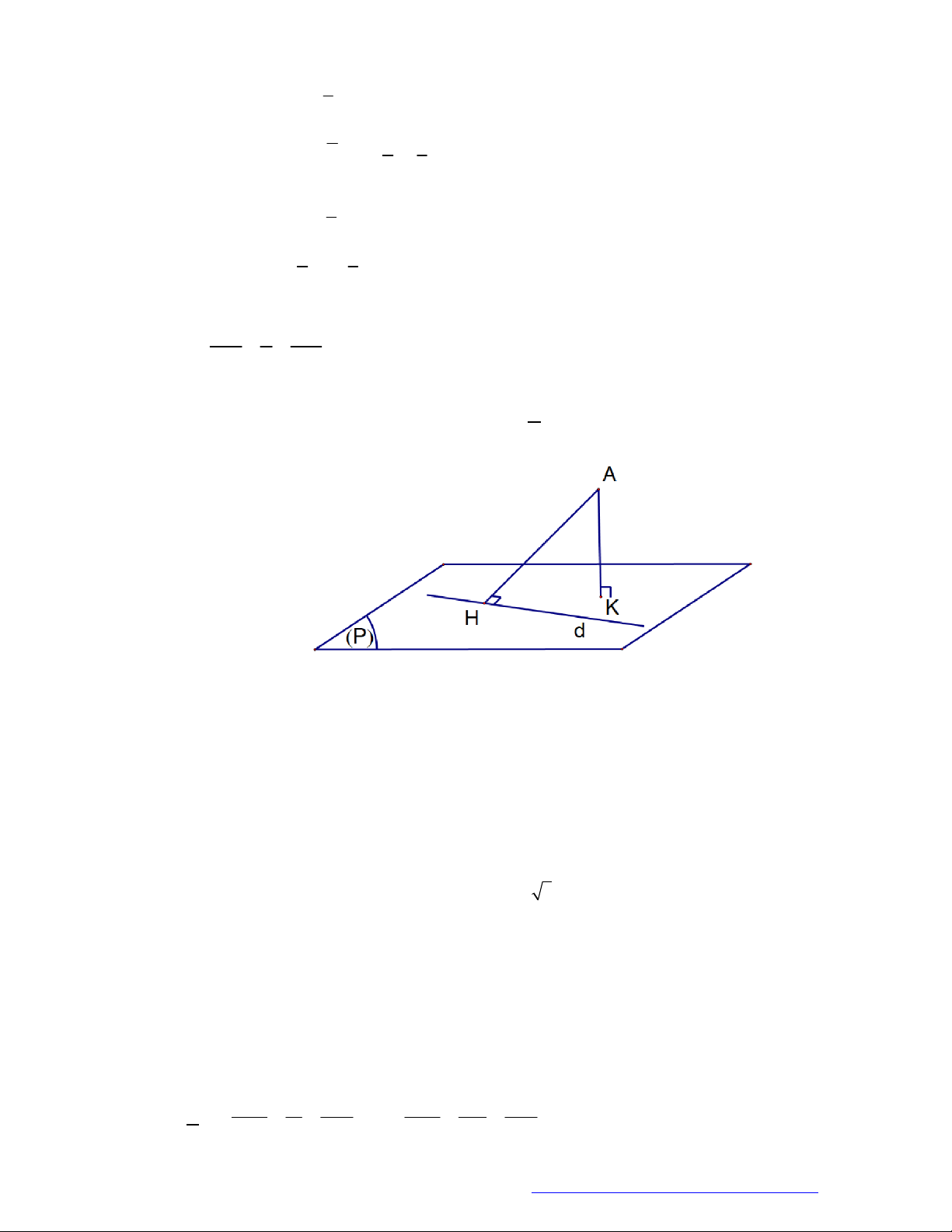
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17

Tọa độ điểm

I

là nghiệm hệ phương trình

1

3

1 4

7

2 6

7 5

;0;

3

3 4

3 3

0

5

3

t

x t

y t

x

I

z t

y

z







 





 



 

 

 

 

 

 

 

 



 













Vậy

7 5

0 4

3 3

a b c     

Câu 19. (Đề Thi Công Bằng KHTN -2019) Trong không gian Oxyz, cho đường thẳng

1 1

:

2 1 1

x y z

d

 

 



và điểm

(1;2;3)A

. Gọi

( )P

là mặt phẳng chứa d và cách điểm A một khoảng

cách lớn nhất. Vectơ nào dưới đây là một vectơ pháp tuyến của

( )P

.

A.

(1;0;2)n 



. B.

(1;0; 2)n  



. C.

(1;1;1)n 



. D.

(1;1; 1)n  



.

Lời giải

Gọi H là hình chiếu vuông góc của A lên đường thẳng d, gọi K là hình chiếu vuông góc của A lên

( )P

. Do đó khoảng cách từ A đến

( )P

là:

 

;( ) .d A P AK

Ta có

2 1

:

1

x t

d y t

z t

  











 



. Vì

H d

nên

 

2 1; ; 1H t t t  

.

 

2 2; 2; 2AH t t t   



, VTCP của đường thẳng d là

 

2;1;1

d

u 



.

. 0 2( 2 t 2) t 2 t 2 0 0

d d

AH u AH u t             

   

.

Do đó

 

1;0;1H 

và

 

2; 2; 2 2 3AH AH    



(không đổi).

Vì

AK AH

( đường vuông góc luôn ngắn hơn đường xiên) nên

AK

lớn nhất khi

AK AH

hay

K H

.

Ta có

( 2; 2; 2) 2(1;1;1)AK AH      

 

. Vậy, một vec tơ pháp tuyến của

( )P

là

(1;1;1)n 



.

Câu 20. (Chuyên Thái Bình - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm

 

3;0;1A 

,

 

1; 1;3B 

và mặt phẳng

 

: 2 2 5 0P x y z   

. Viết phương trình chính tắc của đường thẳng

d

đi qua

A

, song song với mặt phẳng

 

P

sao cho khoảng cách từ

B

đến

d

nhỏ nhất.

A.

3 1

:

26 11 2

x y z

d

 

 



. B.

3 1

:

26 11 2

x y z

d

 

 



.

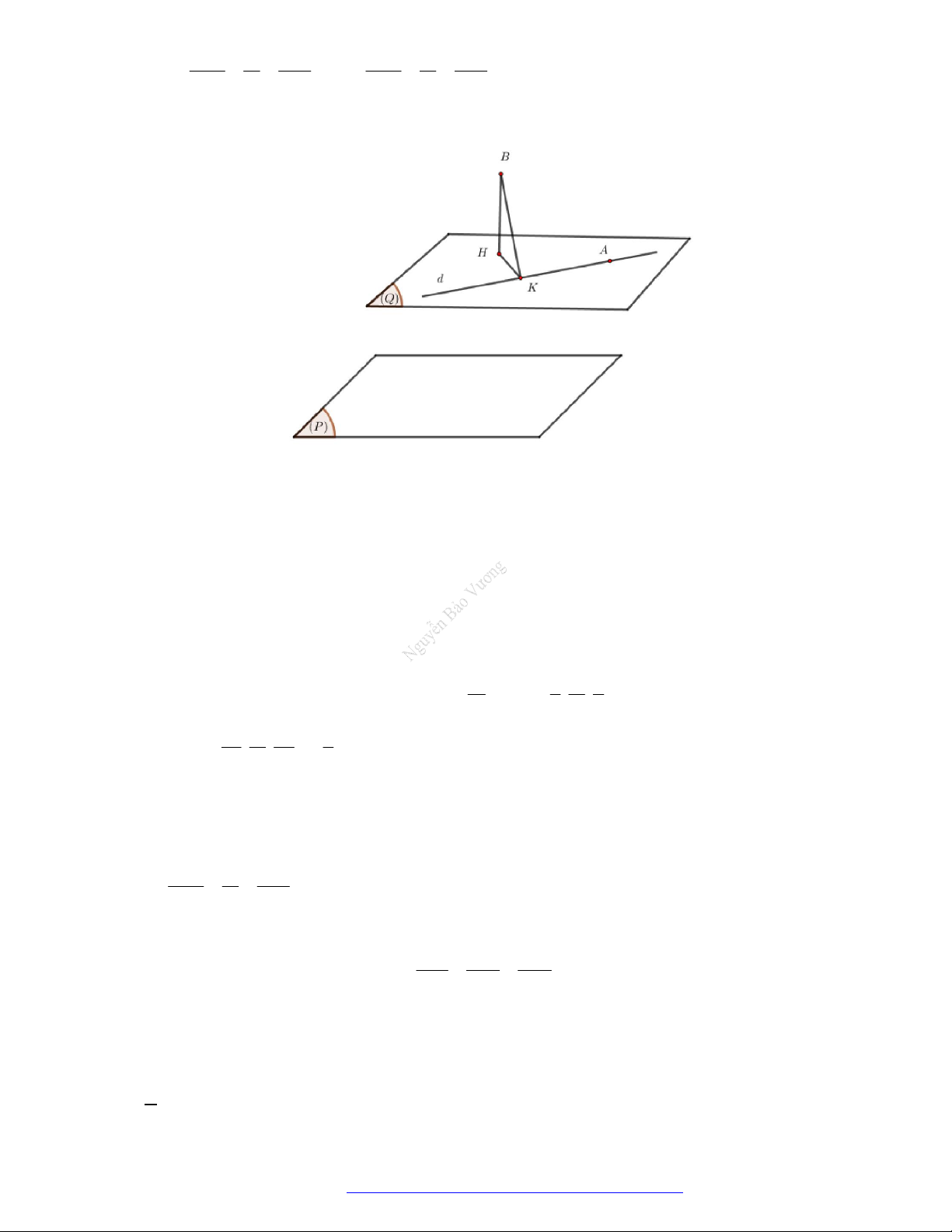
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 18 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

C.

3 1

:

26 11 2

x y z

d

 

 

. D.

3 1

:

26 11 2

x y z

d

 

 

 

.

Lời giải

Gọi mặt phẳng

 

Q

là mặt phẳng đi qua

A

và song song với mặt phẳng

 

P

. Khi đó phương

trình của mặt phẳng

 

Q

là

     

1 3 2 0 2 1 0x y z     

2 2 1 0x y z    

.

Gọi

H

là hình chiếu của điểm

B

lên mặt phẳng

 

Q

, khi đó đường thẳng

BH

đi qua

 

1; 1;3B 

và nhận

 

1; 2;2

Q

n  



làm vectơ chỉ phương có phương trình tham số là

1

1 2

3 2

x t

y t

z t

 





  





 



.

Vì

 

H BH Q 

H BH 

 

1 ; 1 2 ;3 2H t t t    

và

 

H Q

nên ta có

     

1 2 1 2 2 3 2 1 0t t t       

10

9

t  

1 11 7

; ;

9 9 9

H

 

 

 

 

.

26 11 2

; ;

9 9 9

AH



 

 

 

 



 

1

26;11; 2

9

 

.

Gọi

K

là hình chiếu của

B

lên đường thẳng

d

, khi đó

Ta có

 

;d B d BK BH 

nên khoảng cách từ

B

đến

d

nhỏ nhất khi

BK BH

, do đó đường

thẳng

d

đi qua

A

và có vectơ chỉ phương

 

26;11; 2u  



có phương trình chính tắc:

3 1

:

26 11 2

x y z

d

 

 



.

Câu 21. (Sở Quảng Nam - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

 

: 4 0P x y z  

, đường thẳng

1 1 3

:

2 1 1

x y z

d

  

 



và điểm

 

1; 3; 1A

thuộc mặt phẳng

 

P

. Gọi



là đường thẳng đi qua

A

, nằm trong mặt phẳng

 

P

và cách đường thẳng

d

một

khoảng cách lớn nhất. Gọi

 

; ; 1u a b



là một véc tơ chỉ phương của đường thẳng



. Tính

2a b

.

A.

2 3a b  

. B.

2 0a b 

. C.

2 4a b 

. D.

2 7a b 

.

Lời giải

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19

Đường thẳng

d

đi qua

 

1; 1; 3M 

và có véc tơ chỉ phương

 

1

2; 1; 1u  



.

Nhận xét rằng,

A d

và

   

7; 3; 1d P I   

.

Gọi

 

Q

là mặt phẳng chứa

d

và song song với



. Khi đó

   

 

, , ,d d d Q d A Q   

.

Gọi

H

,

K

lần lượt là hình chiếu vuông góc của

A

lên

 

Q

và

d

. Ta có

AH AK

.

Do đó,

 

,d d

lớn nhất 

 

,d A Q

lớn nhất

max

AH

H K 

. Suy ra

AH

chính là đoạn

vuông góc chung của

d

và

.

Mặt phẳng

 

R

chứa

A

và

d

có véc tơ pháp tuyến là

 

1

,

R

n AM u

 



 

  

 

2; 4; 8 

.

Mặt phẳng

 

Q

chứa

d

và vuông góc với

 

R

nên có véc tơ pháp tuyến là

   

1

,

Q R

n n u

 



 

  

 

12; 18; 6 

.

Đường thẳng



chứa trong mặt phẳng

 

P

và song song với mặt phẳng

 

Q

nên có véc tơ chỉ

phương là

   

,

P R

u n n

 



 

  

 

66; 42; 6 

 

6 11; 7; 1 

.

Suy ra,

11; 7a b  

. Vậy

2 3a b  

.

Câu 22. ( Bắc Giang 2018) Trong không gian với hệ tọa độ

Oxyz

cho điểm

 

2;1;3A

và mặt phẳng

   

: 2 1 2 0P x my m z m     

,

m

là tham số. Gọi

 

; ;H a b c

là hình chiếu vuông góc của

điểm

A

trên

 

P

. Tính

a b

khi khoảng cách từ điểm

A

đến

 

P

lớn nhất ?

A.

1

2

a b  

. B.

2a b 

. C.

0a b 

. D.

3

2

a b 

.

Lời giải

   

2 1 2 0 2 1 2 0x my m z m m y z x z            

(*)

Phương trình (*) có nghiệm với

m

2 1 0

2 0

y z

x z

  







  



.

Suy ra

 

P

luôn đi qua đường thẳng

2

: 1 2

x t

d y t

z t

 





 









.

 

2 ;1 2 ;K d K t t t   

,

 

; 2 ; 3AK t t t  



Đường thẳng

d

có VTCP

 

1; 2;1u  



1 3 1

. 0 4 3 0 ;0;

2 2 2

AK u t t t t K

 

        

 

 

 

Ta có

AH AK

max

AH AK 

H K 

.

Vậy

3

2

a b 

.

d

(Q)

(P)

A

I

A

K

H

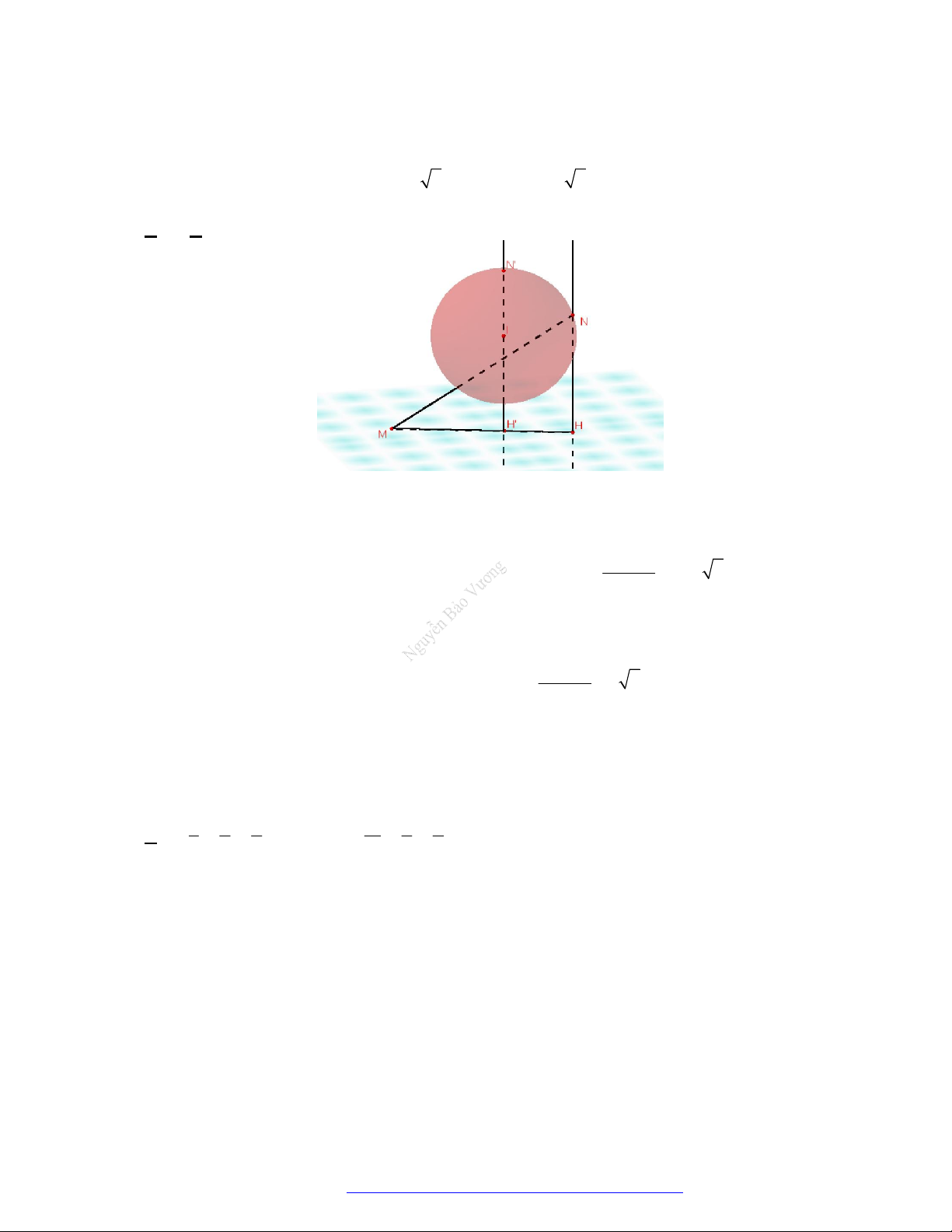
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 20 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 23. (Đề Tham Khảo 2017) Trong không gian với hệ tọa độ

,Oxyz

cho mặt phẳng

 

: 2 2 3 0P x y z   

và mặt cầu

 

2 2 2

: 2 4 2 5 0.S x y z x y z      

Giả sử

 

M P

và

 

N S

sao cho



MN

cùng phương với vectơ

 

1;0;1u



và khoảng cách giữa

M

và

N

lớn nhất.

Tính

.MN

A.

3MN

B.

1 2 2 MN

C.

3 2MN

D.

14MN

Lời giải

Chọn C

Mặt phẳng có vtpt

 

1; 2; 2n  



. Mặt cầu

 

S

có tâm

 

1; 2; 1I 

và bán kính

1r 

. Nhận

thấy rằng góc giữa

u



và

n



bằng

ο

45

. Vì

 

; 2 1d I P r   nên

 

P

không cắt

 

S

.

Gọi

H

là hình chiếu của

N

lên

 

P

thì



ο

45NMH 

và

ο

2

sin 45

NH

MN NH 

nên

MN

lớn

nhất khi và chỉ khi

NH

lớn nhất. Điều này xảy ra khi

N N





và

H H





với

N



là giao điểm

của đường thẳng

d

qua

I

, vuông góc

 

P

và

H



là hình chiếu của

I

lên

 

.P

Lúc đó

 

max

; 3NH N H r d I P

 

    và

max

ο

3 2

sin 45

NH

MN   .

Câu 24. (SGD&ĐT Đồng Tháp - 2018) Trong không gian với hệ trục tọa độ

Oxyz

, cho mặt cầu

     

2 2

2

: 1 2 4S x y z    

có tâm

I

và mặt phẳng

 

: 2 2 2 0P x y z   

. Tìm tọa độ điểm

M

thuộc

 

P

sao cho đoạn

IM

ngắn nhất.

A.

1 4 4

; ;

3 3 3

 

  

 

 

. B.

11 8 2

; ;

9 9 9

 

  

 

 

C.

 

1; 2;2

. D.

 

1; 2; 3 

.

Lời giải

Ta có tâm

 

1; 2;0I 

và bán kính

R 2

.

Khoảng cách từ

I

đến mặt phẳng

 

P

ngắn nhất khi

M

là hình chiếu của

I

lên mặt phẳng

 

P

.

Đường thẳng đi qua

I

và vuông góc với mặt phẳng

 

P

có phương trình tham số là

1 2

2

x t

y t

z t

 





  









.

Khi đó tọa độ của

M

là nghiệm của hệ phương trình

 

P

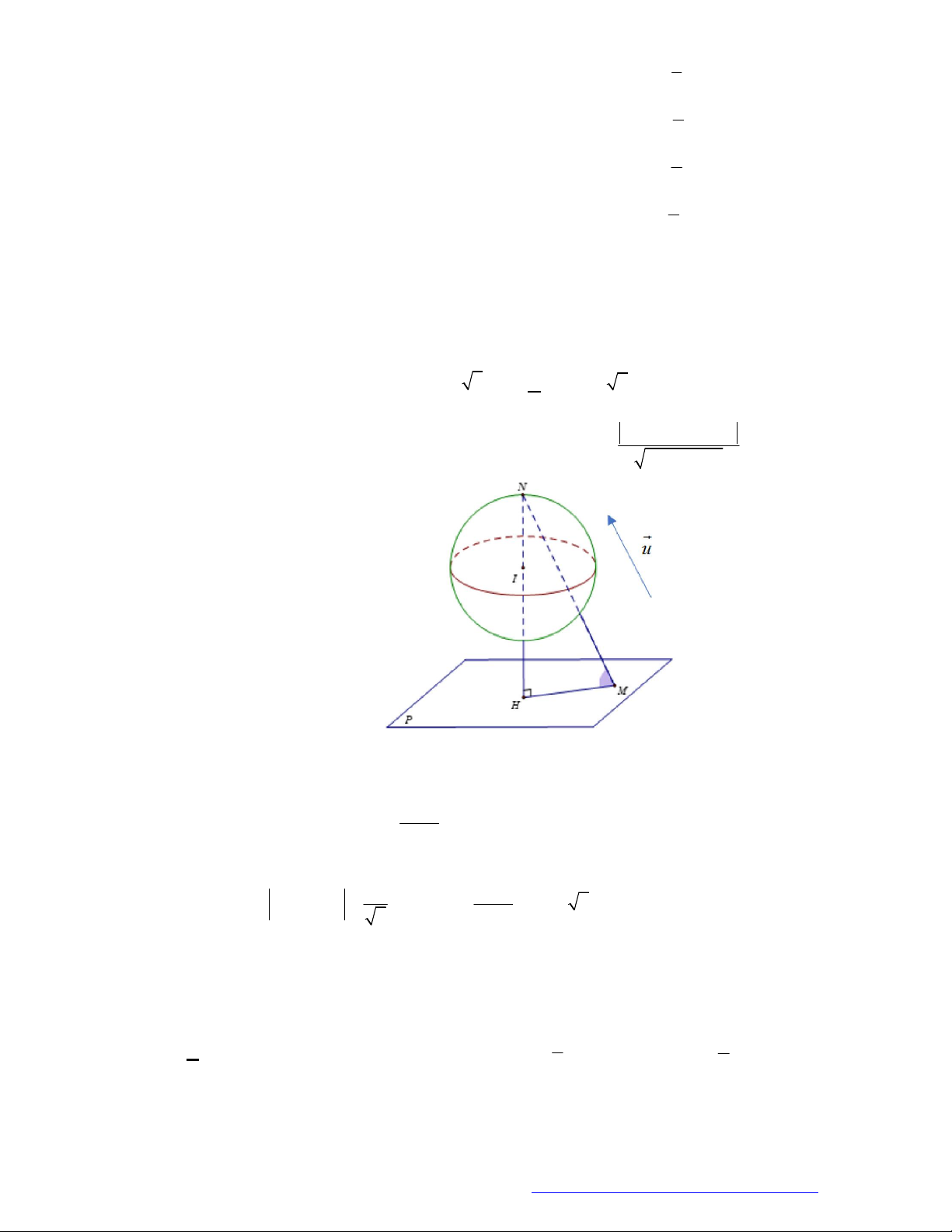
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21

1 2

2

2 2 2 0

x t

y t

z t

x y z

 





  









   



     

1 2

2

2 1 2 2 2 2 2 0

x t

y t

z t

t t t

 





  











      



1

3

4

3

4

3

2

3

x

y

z

t



 



 









 



 



.

Câu 25. (THPT Ba Đình 2019) Trong không gian với hệ tọa độ

,Oxyz

cho mặt phẳng

 

: 2 2 3 0P x y z   

và mặt cầu

 

2 2 2

: 2 4 2 5 0S x y z x y z      

. Giả sử

 

M P

và

 

N S

sao cho

MN



cùng phương với vectơ

 

1;0;1u 



và khoảng cách giữa

M

và

N

lớn

nhất. Tính

.MN

A.

3MN 

. B.

1 2 2MN  

. C.

3 2MN 

. D.

14MN 

.

Lời giải.

 

S

có tâm

 

1;2;1I 

và bán kính

1R 

. Ta có:

 

2 2 2

1 2.2 2.1 3

d , 2

1 2 2

I P R

   

  

 

.

Gọi

H

là hình chiếu vuông góc của

N

trên mặt phẳng

 

P

và



là góc giữa

MN

và

NH

.

Vì

MN



cùng phương với

u



nên góc



có số đo không đổi,



HNM





.

Có

1

.cos .

cos

HN MN MN HN



  

nên

MN

lớn nhất



HN

lớn nhất



 

, 3HN d I P R  

.

Có

 

1

cos cos ,

2

P

u n



 

 

nên

1

3 2

cos

MN HN



 

.

Câu 26. (HSG Bắc Ninh 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho mặt cầu

2 2 2

( ) : 2 4 2 3 0S x y z x y z       và mặt phẳng

( ) : 2 2 14 0P x y z   

. Điểm

M

thay đổi

trên

 

S

, điểm

N

thay đổi trên

( )P

. Độ dài nhỏ nhất của

MN

bằng

A.

1

B.

2

C.

1

2

D.

3

2

Lời giải

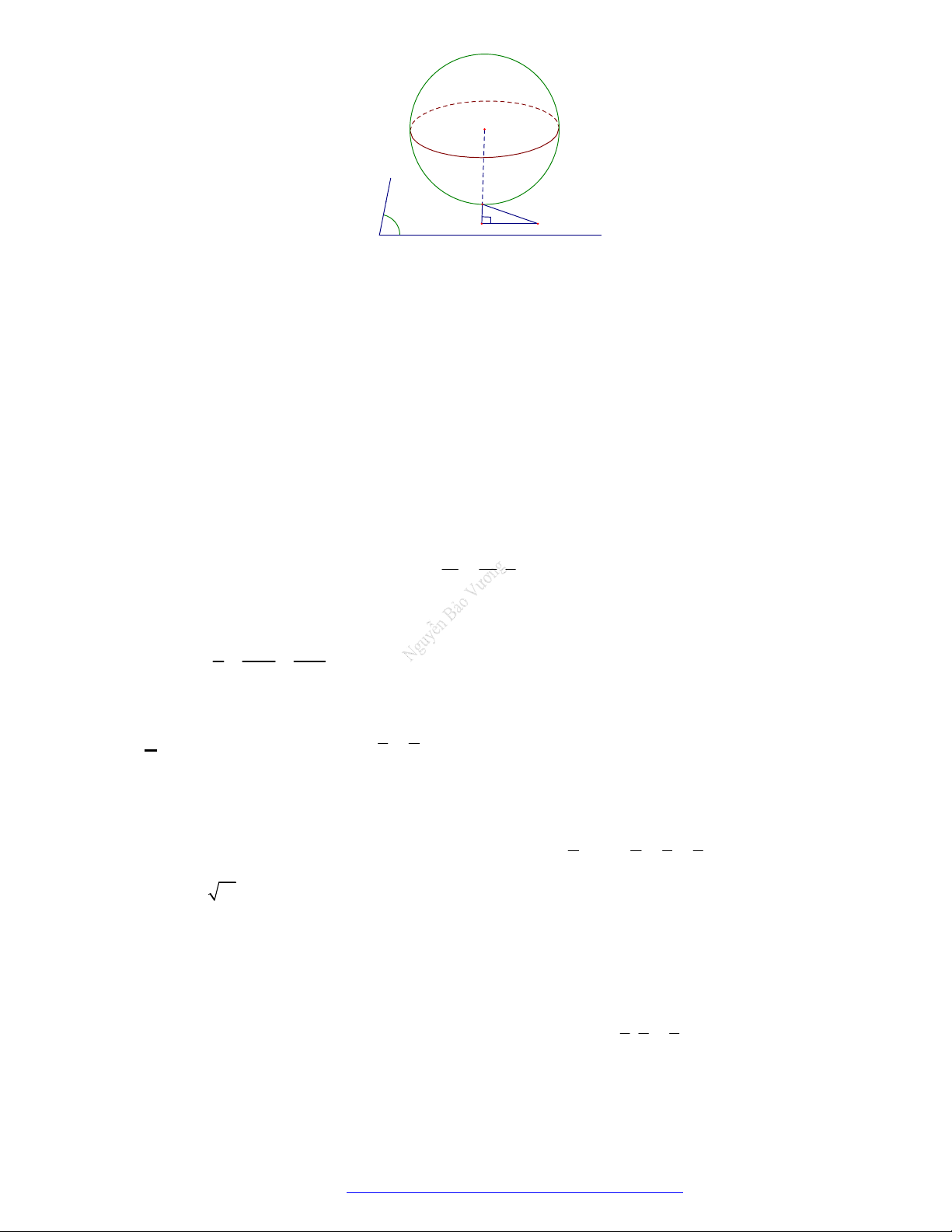
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 22 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Mặt cầu

( )S

có tâm

(1; 2; 1)I  

, bán kính

3R 

;

 

;( ) 4d I P R 

mặt cầu

( )S

và mặt phẳng

( )P

không có điểm chung.

Dựng

( ), ( ( ))IH P H P 

. Ta có:

MN

nhỏ nhất khi

M

là giao điểm của đoạn

IH

với

( )S

và

N H

.

Phương trình đường thẳng

IH

:

 

1 2

2 ;

1 2

x t

y t t

z t

 





   





  





Điểm

 

1 2 ; 2 ; 1 2 ( )M t t t S     

nên

     

2 2 2

1 2 1 9x y z     

     

2 2 2

2 2 9 1t t t t       

. Khi đó

   

1 2

3; 3;1 , 1; 1; 3M M   

.

Thử lại:

 

1

;( ) 1d M P 

;

 

2

;( ) 7 4d M P IH  

(loại).

Vậy

min

1MN MH 

khi

 

11 10 5

3; 3;1 ; N ; ;

3 3 3

M

 

 

 

 

.

Câu 27. Trong không gian với hệ tọa độ

Oxyz

, cho mặt cầu

 

S

tâm

 

1; 2;1I 

; bán kính

4R 

và đường

thẳng

1 1

:

2 2 1

x y z

d

 

 

 

. Mặt phẳng

 

P

chứa

d

và cắt mặt cầu

 

S

theo một đường tròn có

diện tích nhỏ nhất. Hỏi trong các điểm sau điểm nào có khoảng cách đến mặt phẳng

 

P

lớn nhất.

A.

 

0;0;0O

. B.

3 1

1; ;

5 4

A

 



 

 

. C.

 

1; 2; 3B   

. D.

 

2;1;0C

.

Lời giải

Gọi

 

2 ;1 2 ; 1H t t t  

là hình chiếu của

I

lên đường thẳng

d

.

Ta có:

     

2 4 1 5

. 0 2 2 1 2 3 2 2 0 ; ;

3 3 3 3

d

IH u t t t t H

 

             

 

 

 

.

Vì 10 4IH R   

d

cắt mặt cầu

 

S

tại

2

điểm phân biệt.

Mặt phẳng

 

Q

bất kì chứa

d

luôn cắt

 

S

theo một đường tròn bán kính

r

.

Khi đó

 

2 2 2 2 2

, , 16 10 6r R d I Q R d I d      

.

Do vậy mặt phẳng

 

P

chứa

d

cắt mặt cầu theo một đường tròn có diện tích nhỏ nhất khi và chỉ

khi

 

, ,d I P d I d

hay mặt phẳng

 

P

đi qua

H

nhận

1 5 8

; ;

3 3 3

IH

 

 

 

 



làm vectơ pháp

tuyến, do đó

 

P

có phương trình

5 8 13 0x y z   

.

Khi đó điểm

 

0;0;0O

có khoảng cách đến

 

P

lớn nhất.

P

M

I

H

N

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23

Câu 28. (Sở Thanh Hóa 2019) Trong không gian

Oxyz

cho mặt phẳng

 

: 1 0

P y

 

, đường thẳng

1

: 2

1

x

d y t

z







 









và hai điểm

 

1; 3;11

A  

,

1

;0;8

2

B

 

 

 

. Hai điểm

M

,

N

thuộc mặt phẳng

 

P

sao

cho

 

, 2

d M d



và

2

NA NB

. Tìm giá trị nhỏ nhất của đoạn

MN

.

A.

min

1

MN



. B.

min

2

MN 

. C.

min

2

MN 

. D.

min

2

.

3

MN



Lời giải

Gọi

   

1;2 ;1I d P I t

   

   

2 1 0 1 1;1;1

I P t t I       

Ta có

 

d P M

 

thuộc đường tròn tâm

 

1

1;1;1 , 2

I R



.

   

       

2

2 2 2 2

2

2 2 2

1

; ; 1 ; 3 y;11 ; ; ;8

2

1

2 1 3 11 4 8

2

3 3 3 6 6 42 126 0

2 2 14 42 0

N x y z NA x z NB x y z

NA NB x y z x y z

x y z x y z

 

        

 

 

 

 

           

 

 

 

 

 

       

 

Vậy

 

2

1;1;7 ; 3

N S J R

 

và

 

: 1

J P y

 

Nên

N

thuộc đường tròn tâm

 

2

1;1;7 ; 3

J R



Ta có

1 2 min 1 2

IJ 6 IJ 1

R R MN R R

       

Câu 29. (THPT Yên Phong Số 1 Bắc Ninh 2019) Trong không gian với hệ tọa độ

Oxyz

, cho các điểm

 

1;0; 0

A

,

 

3;2;0

B

,

 

1;2; 4

C



. Gọi

M

là điểm thay đổi sao cho đường thẳng

MA

,

MB

,

MC

hợp với mặt phẳng

 

ABC

các góc bằng nhau;

N

là điểm thay đổi nằm trên mặt cầu

       

2 2 2

1

: 3 2 3

2

S x y z

     

. Tính giá trị nhỏ nhất của độ dài đoạn

MN

.

A.

3 2

2

. B.

2

. C.

2

. D.

5

.

Lời giải

Chọn C

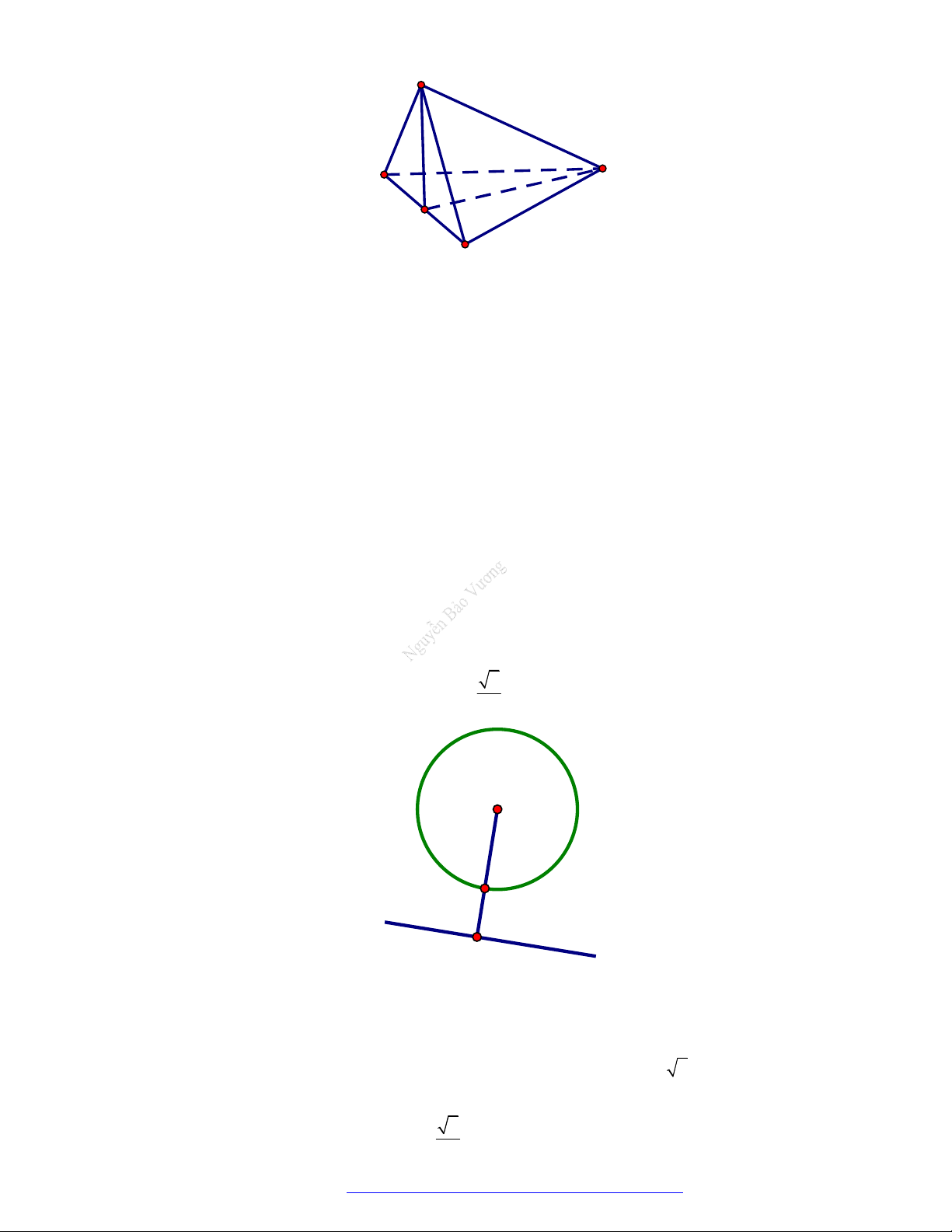
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 24 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Ta có:

(2;2;0), (-2;2;4) . 0 ABCAB AC AB AC     

   

suy ra vuông tại .

Gọi là hình chiếu vuông góc của điểm trên mặt phẳng . Ta có:

Theo giả thiết

Do đó: nên là tâm đường tròn ngoại tiếp .

Suy ra: là trung điểm của  .

Ta có: , Chọn vecto chỉ phương của đường thẳng là .

Phương trình đường thẳng có dạng:

Mặt cầu có tâm và bán kính .

Gọi là hình chiếu vuông góc của điểm trên đường thẳng .

Ta có:

Do nên , ta được: . Khi đó: và

Do IK > R nên đường thẳng MH không cắt mặt cầu.

Ta có:

H

B

A

C

M

ABC

A

H

M

 

ABC

 



 



 



, ,

MA ABC MA HA MAH

MB ABC MB HB MBH

MC ABC MC HC MCH

 

 



 

. .MAH MBH MCH MAH MBH MCH g c g

       

HA HB HC 

H

ABC

H

BC

 

1;2;2

H

 

, 8; 8;8

AB AC

 

 

 

 

MH

 

1; 1;1

MH

u  



MH

1

2 ,

2

x t

y t t

z t

 





  





 





( )S

 

3;2;3

I

2

R 

N

M

I

 

1 ;2 ;2

K t t t  

I

MH

   

2; ; 1 , 1; 1;1

MH

IK t t t u     

 

IK MH

. 0

MH

IK u



 

1t 

 

2;1;3

K

2

IK 

 

2

,

2

MN d I MH IN IK IN    

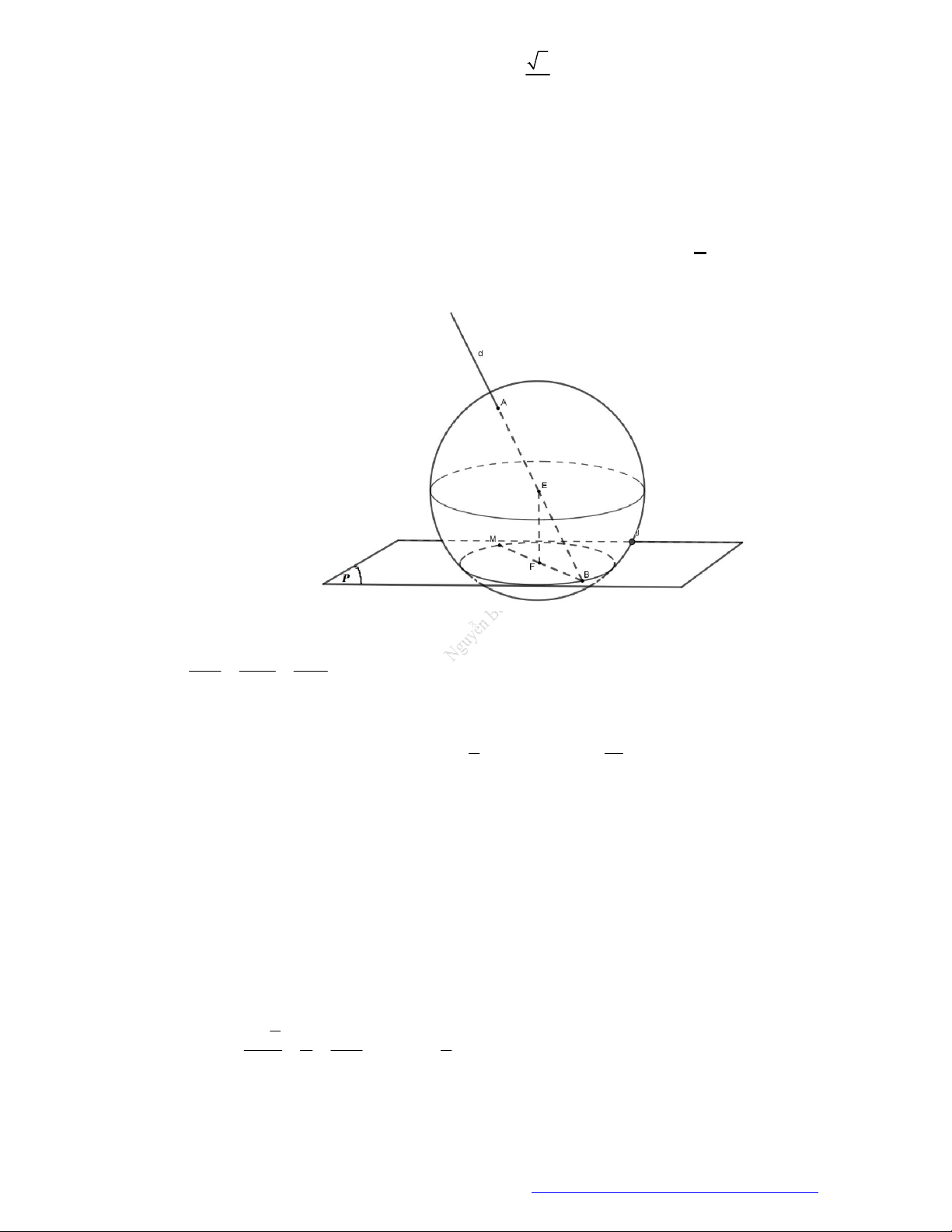
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25

Vậy giá trị nhỏ nhất của độ dài đoạn bằng

Câu 30. (Sở Bình Phước - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho điểm

 

1; 2; 3A 

và mặt

phẳng

 

: 2 2 9 0P x y z   

. Đường thẳng

d

đi qua

A

và có vectơ chỉ phương

 

3; 4; 4u  



cắt

 

P

tại điểm

B

. Điểm

M

thay đổi trong

 

P

sao cho

M

luôn nhìn đoạn

AB

dưới góc

90

.

Khi độ dài

MB

lớn nhất, đường thẳng

MB

đi qua điểm nào trong các điểm sau?

A.

 

3;2;7J 

. B.

 

3;0;15K

. C.

 

2; 1;3H  

. D.

 

1; 2;3I  

.

Lời giải

- Đường thẳng

d

đi qua

A

và có vectơ chỉ phương

 

3; 4; 4u  



có phương trình là:

1 2 3

3 4 4

x y z  

 



giao điểm của

d

và

 

P

là

 

2; 2;1B   

.

- Do

M

luôn nhìn đoạn

AB

dưới góc

90

nên

M

nằm trên mặt cầu

 

S

đường kính

AB

.

Gọi

E

là trung điểm của

AB

1

;0; 1

2

E

 

   

 

 

2

41

4

AE 

 

2 2 2

: 2 9 0S x y z x z      

.

- Lại do

 

M P

nên

M

nằm trên đường tròn giao tuyến của mặt phẳng

 

P

và mặt cầu

 

S

,

gọi là đường tròn

 

C

.

- Mặt khác

B

là điểm cố định trên đường tròn

 

C

nên độ dài

MB

lớn nhất khi

MB

là đường

kính của đường tròn

 

C

.

- Gọi

F

là tâm của

 

C

F

là hình chiếu vuông góc của

E

trên

 

P

.

Đường thẳng

EF

nhận vectơ pháp tuyến

 

2;2; 1n  



của

 

P

làm vectơ pháp tuyến

1

2

:

2 2 1

x

y z

EF



  



5

; 2;0

2

F

 

   

 

 

(là giao điểm của

 

P

và

EF

).

- Vì

MB

là đường kính của

 

C

nên

 

3; 2; 1M    

 

1;0;2MB 



là vectơ chỉ phương của

đường thẳng

MB

 phương trình đường thẳng

MB

là:

MN

2

.

2

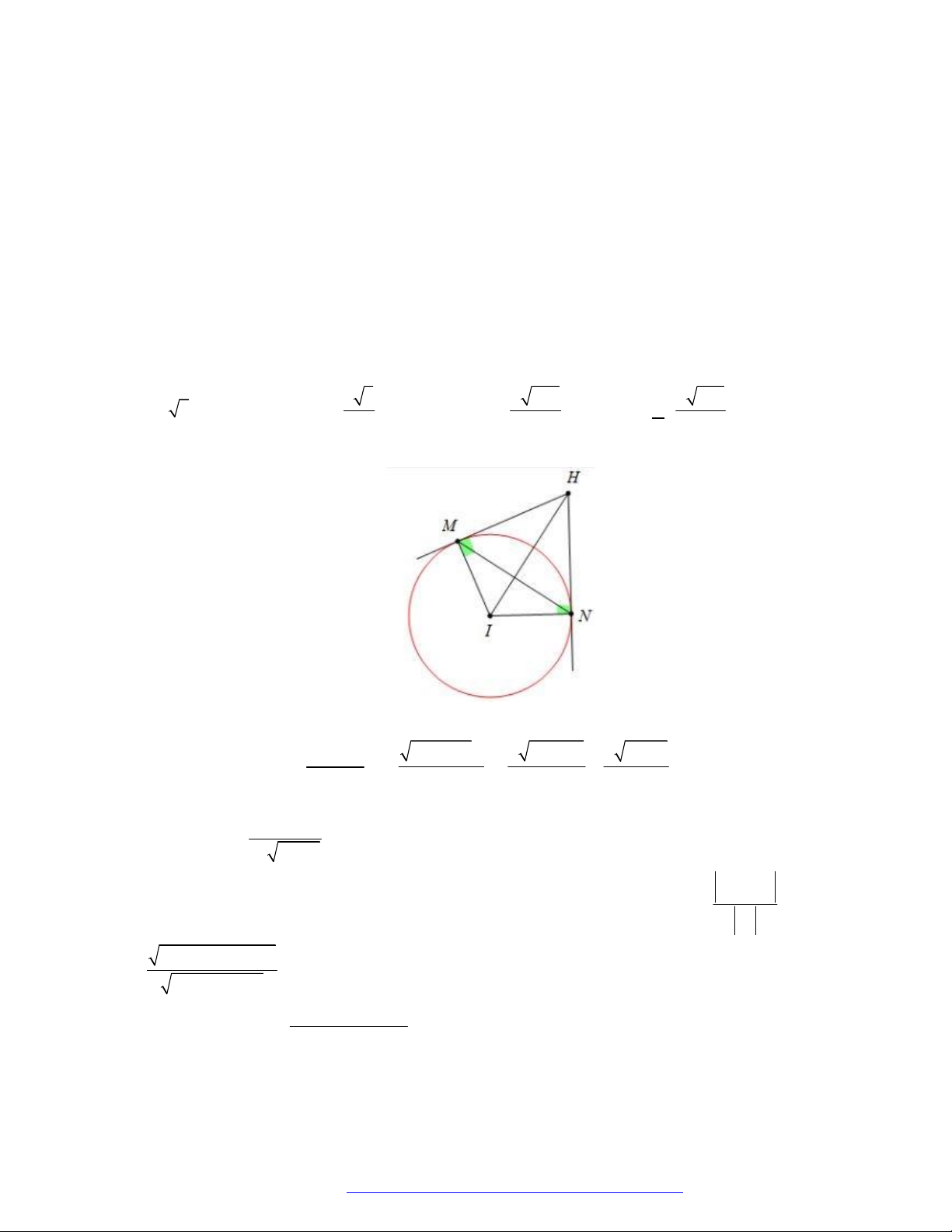
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 26 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

2

1 2

x t

y

z t

  





 





 



 

t  

- Trong các điểm đã cho ở các đáp án A, B, C, D chỉ có điểm

 

1; 2;3I  

(đáp án D) thuộc đường

thẳng

MB

.

Câu 31. (Sở Bạc Liêu - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho mặt cầu

 

S

có tâm

 

1;2;3I

và có bán kính

2r 

. Xét đường thẳng

 

1

:

1

x t

d y mt t

z m t



 



  





 





,

m

là tham số thực. Giả sử

   

,P Q

là mặt phẳng chứa

d

và tiếp xúc với

 

S

lần lượt tại

,M N

. Khi đó đoạn

MN

ngắn

nhất hãy tính khoảng cách từ điểm

 

1;0;4B

đến đường thẳng

d

.

A.

5

. B.

5 3

3

. C.

4 237

21

. D.

4 273

21

.

Lời giải

Mặt phẳng thiết diện đi qua tâm

, ,I M N

cắt đường thẳng

d

tại

 

, ,H IH d d I d IH  

.

Ta có

.

2 2.

MH MI

MN MK

IH

 

2 2

.

2.

IH r r

IH





 

2 2

4 4 4 4IH x

f x

IH x

 

  

với

2x IH 

.

Ta có

 

2 2

4

0, 2

4

f x x

x x



   



, suy ra hàm số đồng biến trên

 

2;

.

Do đó

min min

MN IH . Ta có

   

1; ; 1 , 1;0;0

d

u m m A d   



, suy ra

 

,

d

u IA

d I d

u

 

 



 



2

25 20 17

2 2 2

m m

 

.

Xét hàm số

 

2

25 20 17

2 2 2

m m

f m

m m

 



 

có bảng biến thiên là

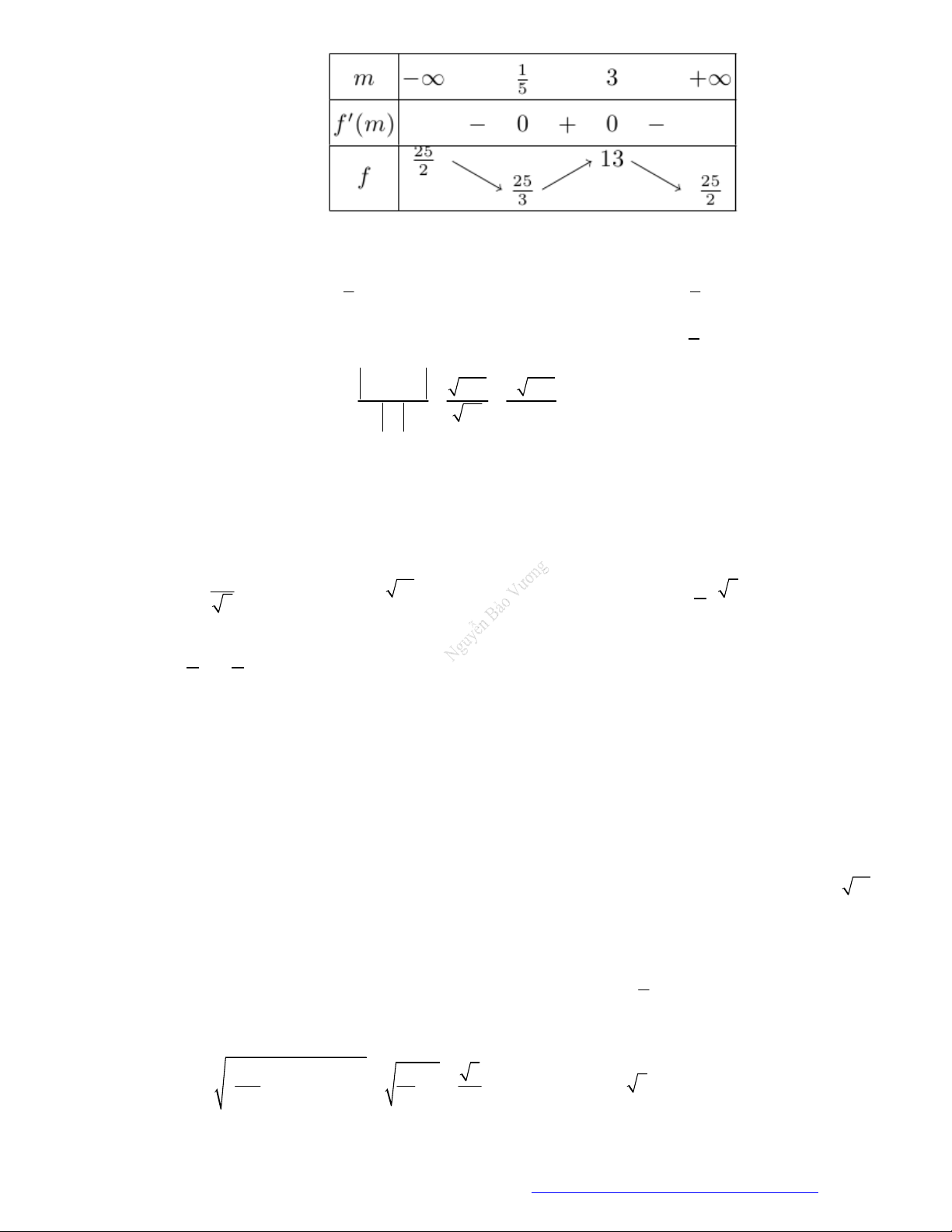
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27

Suy ra

min

IH

khi

1

5

m 

. Đường thẳng

d

có phương trình là

 

1

:

5

4

5

x t

d y t t

z t





 



  





 







.

Khoảng cách

 

,

416 4 273

,

21

42

d

AB u

d B d

u

 

 

  

 



.

Câu 32. (Hậu Lộc 2-Thanh Hóa 2019) Trong không gian

Oxyz

, cho mặt phẳng

 

: 2 2 9 0P x y z   

và điểm

 

1;2; 3A 

. Đường thẳng

d

đi qua

A

và có véc tơ chỉ phương

 

3;4; 4u  



cắt

 

P

tại

B

. Điểm

M

thay đổi trên

 

P

sao cho

M

luôn nhìn đoạn

AB

dưới một góc

90

. Độ dài đoạn

MB

lớn nhất bằng

A.

36

5

. B.

41

. C.

6

. D.

5

.

Lời giải

Chọn D

Phương trình đường thẳng

1 3

: 2 4

3 4

x t

d y t

z t

 





 





  



nên tọa độ điểm

B

thỏa mãn hệ:

1 3

2 4

3 4

2 2 9 0

x t

y t

z t

x y z

 





 





  



   



       

2 1 3 2 2 4 3 4 9 0 1 2; 2;1t t t t B              

.

Do

M

nhìn đoạn

AB

dưới một góc

90

nên

M

thuộc mặt cầu

 

S

có đường kính

41AB 

.

Lại do

 

M P

nên

M

thuộc đường tròn giao tuyến giữa mặt cầu

 

S

và mặt phẳng

 

P

.

Do

MB

là một dây cung của đường tròn này nên

MB

lớn nhất khi nó là đường kính của đường

tròn giao tuyến giữa mặt cầu

 

S

và mặt phẳng

 

P

. Gọi

1

;0; 1

2

I

 

 

 

 

là trung điểm

AB

thì

I

là tâm mặt cầu

 

S

và

 

; 3d I P 

. Khi đó bán kính đường tròn giao tuyến là

 

2

41 5

; 9

2 4 2

AB

r d I P

 

    

 

 

. Vậy

max

2 5.MB r 

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 28 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 33. (Chuyên Nguyễn Trãi Hải Dương 2019) Đường thẳng



đi qua điểm

 

3;1;1

M

, nằm trong mặt

phẳng

 

: 3 0

x y z



   

và tạo với đường thẳng

1

: 4 3

3 2

x

d y t

z t







 





  



một góc nhỏ nhất thì phương

trình của



là:

A.

1

2

x

y t

z t









 











. B.

8 5

3 4

2

x t

y t

z t



 







  







 



. C.

1 2

1

3 2

x t

y t

z t



 







 







 



. D.

1 5

1 4

3 2

x t

y t

z t



 







 







 



.

Lời giải

Chọn B

Cách 1.

Hình.

Gọi

d



là hình chiếu vuông góc của

d

lên

 



, khi đó góc

 



,d d



là góc nhỏ nhất trong các góc

tạo bởi

d

với đường thẳng bất kỳ trong

 



.

d

có véc tơ chỉ phương

 

0;3; 2

d

u

 



,

 



có véc tơ pháp tuyến

 

1;1; 1

n



 



, gọi

n





là véc tơ

pháp tuyến của mặt phẳng

 



tạo bởi

d

và

d



thì

,

d

n u n n

  

 

   

ta chọn

 

 

, 1;2;3

d

n n u

 

 

  

Gọi

d

u





là véc tơ chỉ phương của

d



thì

,

d d

u n u n

 

 

 

   

, ta chọn

 

, 5; 4;1

d

u n n

 



 

  

 

  

.

Đường thẳng



song song hoặc trùng với

d



nên có véc tơ chỉ phương

 

5; 4;1

d

u u





  

 

.

Trong các đáp án A, B, C, D cho ở đề bài thì chỉ có đáp án B có véc tơ chỉ phương thỏa điều kiện.

Thay tọa độ của

M

vào phương trình của



trong đáp án B ta được:

3 8 5

1 3 4 1

1 3 2

t

t t

t



 





 

     







  



(thỏa mãn).

Vậy đáp án B thỏa yêu cầu bài toán.

Cách 2.

d

có véc tơ chỉ phương

 

0;3; 2

d

u

 



,

 



có véc tơ pháp tuyến

 

1;1; 1

n



 



,

Giả sử



có véc tơ chỉ phương

 

2 2 2

; ; , 0

u a b c a b c



   



Do

 



 

ta có: . 0 0

n u a b c c a b





       

 

.

Gọi



là góc giữa



và

d

,

0;

2





 



 

 

, khi đó:

 

2 2 2 2 2

3 2 2

cos cos ,

13. 13. 2 2 2

d

b c b a

u u

a b c a b ab





 

  

   

 

Góc



nhỏ nhất khi và chỉ khi

cos



lớn nhất, ta xét các trường hợp:

Trường hợp 1. Nếu

0

a



ta được

1

cos

26





.

Trường hợp 2. Nếu

0

a



ta được:

 

2

cos ,

26 1

t

b

t

a

t t





 

 

 

 

 

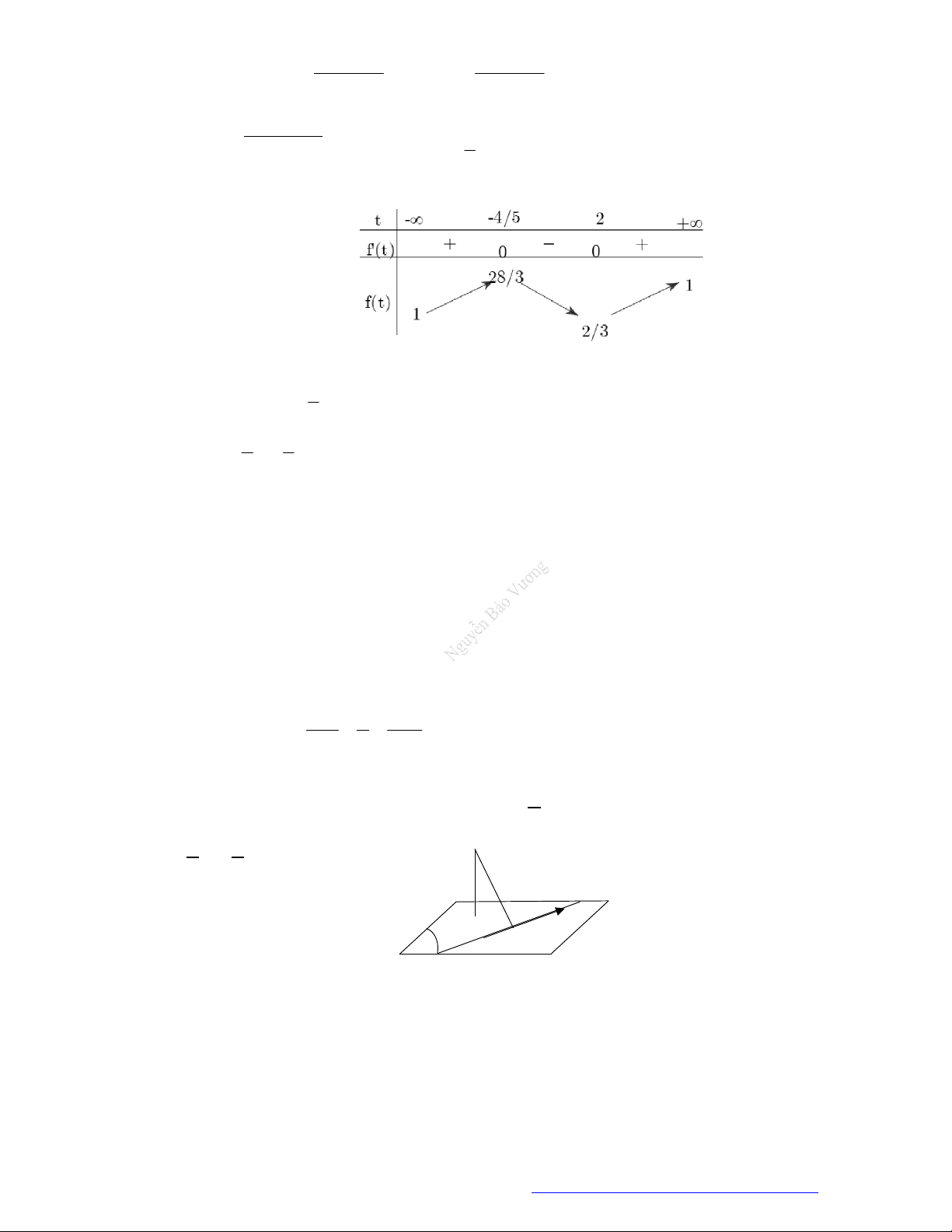
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 29

Ta có

2

4 4

26cos

1

t t



 



 

, đặt

 

2

4 4

,

1

t t

f t t

t t

 

 

 

 , có:

 

2

5 6 8

, 0

4

1

5

t

t t

f t f t

t

t t





 



 

  



 

 



.

Bảng biến thiên của hàm số

 

f t

:

Do

cos 0





nên

cos



lớn nhất khi

 

f t

lớn nhất, từ bảng biến thiên ta được

 

4

max

5

f t f

 

 

 

 



.

Khi đó

4

5 4

5

b

b a

a

    

, chọn

5 4a b   

và ta được và ta được

1c 

.

Đường thẳng



có véc tơ chỉ phương

 

5; 4;1u



 



.

Trong các đáp án A, B, C, D cho ở đề bài thì chỉ có đáp án B có véc tơ chỉ phương thỏa điều kiện.

Thay tọa độ của

M

vào phương trình của



trong đáp án B ta được:

3 8 5

1 3 4 1

1 3 2

t

t t

t



 





 

     







  



(thỏa mãn).

Vậy đáp án B thỏa yêu cầu bài toán.

Câu 34. (THPT Ngô Quyền - Ba Vì - Hải Phòng 2019) Trong không gian

Oxyz

, cho điểm

 

2; 5; 3A

và

đường thẳng

d

:

1 2

2 1 2

x y z 

 

. Biết rằng

 

P

:

3 0ax by cz   

 

, ,a b c 

là mặt phẳng

chứa

d

và khoảng cách từ

A

đến

 

P

lớn nhất. Khi đó tổng

T a b c  

bằng

A.

3

. B.

3

. C.

2

. D.

5

.

Lời giải

Chọn C

Đường thẳng

d

đi qua

 

1; 0; 2M

, có 1VTCP

 

2; 1; 2u 



.

Gọi

H

,

K

lần lượt là hình chiếu của

A

trên

 

P

và trên

d

thì

AH AK

(cố định).

Do đó, khoảng cách từ

A

đến

 

P

lớn nhất khi

H K

hay

 

P AK

.

 

2 1; ;2 2K t t t d  

là hình chiếu của

A

trên

d

khi

AK u





, với

 

2 1; 5;2 1AK t t t   



.

. 0AK u 





     

2 2 1 5 2 2 1 0t t t      

1t 

.



A

P

K

H

d

u



NGUYỄN BẢO VƯƠNG - 0946798489

Trang 30 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

 

P

qua

 

1; 0; 2

M

, có một VTPT

 

1; 4; 1

AK  



nên

 

P

:

4 3 0

x y z

   

.

Suy ra

T a b c  

 

1 4 1 2     

.

Câu 35. (ĐH - Quốc Tế - 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho hai điểm

 

2;1; 3

A



,

 

3;2;1

B 

. Gọi

 

d

là đường thẳng đi qua

 

1;2;3

M

sao cho tổng khoảng cách từ

A

đến

 

d

và

từ

B

đến

 

d

là lớn nhất. Khi đó phương trình đường thẳng

 

d

là

A.

1

2

5 4

x z

y



  



. B.

1 2 3

3 2 1

x y z

  

 



.

C.

1 2 3

1 13 2

x y z

  

 



. D.

1 2 3

3 2 2

x y z

  

 



.

Lời giải

Chọn C

Ta có

 

,

d A d AM



,

 

,

d B d BM



.

 

, ,

d A d d B d



đạt giá trị lớn nhất khi và chỉ khi

 

AM d

BM d













.

 

1; 1; 6

MA

  



và

 

4;0; 2

MB

  



.

Khi đó

 

d

có vecto chỉ phương

   

1

, 2;26; 4 1;13; 2

u MA MB u

 

     

 

   

.

Phương trình

 

1 2 3

:

1 13 2

x y z

d

  

 



.

Câu 36. (Chuyên Ngữ Hà Nội 2019) Trong không gian với hệ tọa độ

,Oxyz

cho đường thẳng

:

x y z

d

 

 



1 2

1 2 1

và mặt phẳng

 

:P x y z

   2 2 2 0

.

 

Q

là mặt phẳng chứa

d

và tạo

với mp

 

P

một góc nhỏ nhất. Gọi

 

; ;

Q

n a b



1



là một vectơ pháp tuyến của

 

Q

. Đẳng thức nào

đúng?

A.

.

a b

  1

B.

.

a b

  2

C.

.

a b

  1

D.

.

a b

  0

Lời giải

Chọn B

Đường thẳng

d

đi qua điểm

 

; ;

M

0 1 2

và có vectơ chỉ phương

 

; ; .

d

u  

1 2 1



Theo giả thiết,

 

d Q

và

 

; ;

Q

n a b



1



là một vectơ pháp tuyến của

 

Q

nên ta có

.

d Q

u n

 0

 

 

.a b a b

       2 1 0 2 1 1

Mặt phẳng

 

P

có vectơ pháp tuyến

 

; ;

P

n

  2 1 2



.

Ta có

   



 



 

cos , cos ,

.

P Q

a b

P Q n n

a b

 

 





 









 

 

2 2

2

3 1

 

Thế

 

1

vào

 

2

ta được

   



 

cos ,

b

P Q

b b



 

2

5 4 2

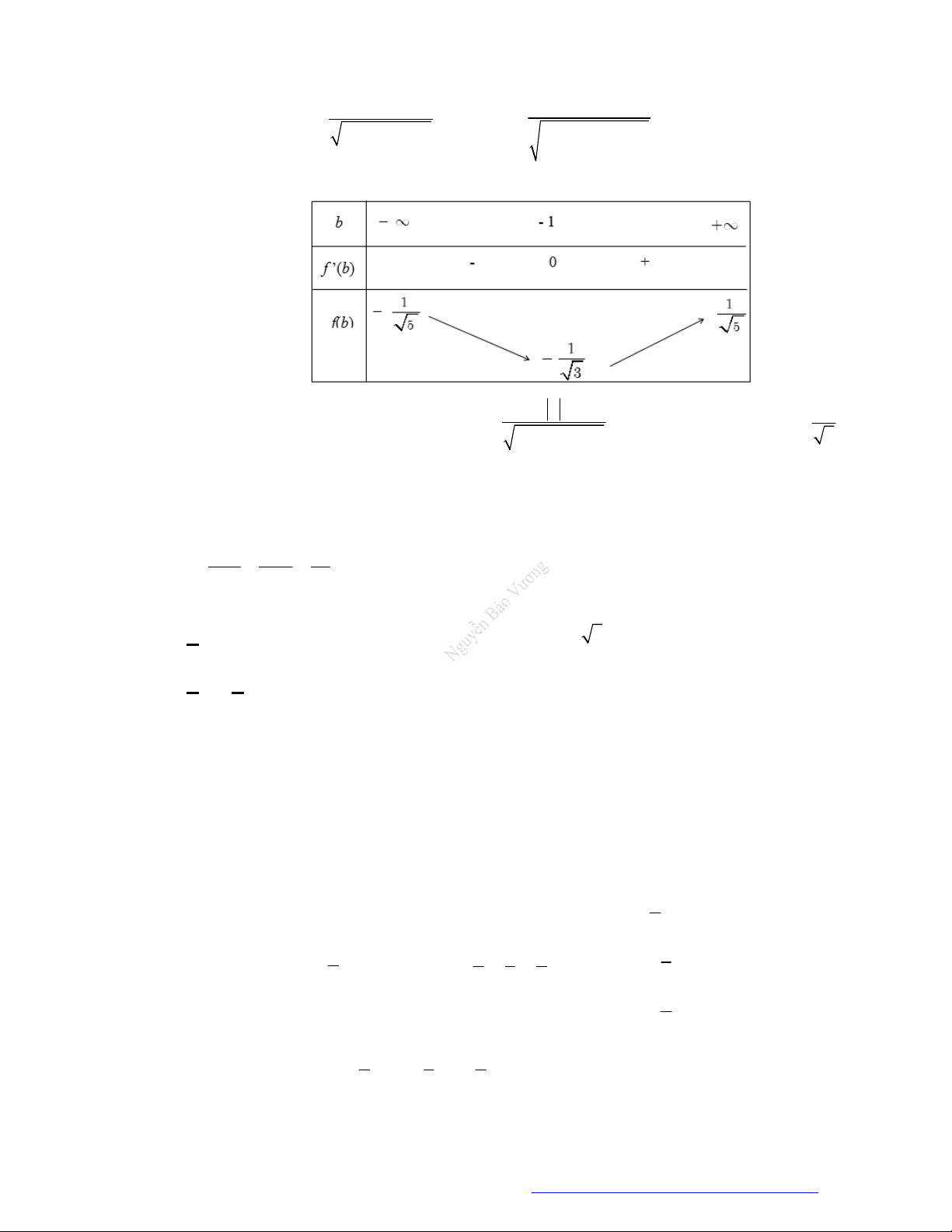
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 31

Khi góc giữa

 

P

và

 

Q

nhỏ nhất thì

   



 

cos ,P Q

đạt giá trị lớn nhất.

Xét hàm số

 

b

f b

b b



 

2

5 4 2

, có

 

'

b

f b b

b b



   

 

3

2

1

0 1

5 4 2

.

Bảng biến thiên

Từ đó suy ra với hàm số

 

b

g b

b b



 

2

5 4 2

có

   

max g b g  

1

3



khi

b a    1 1

Vậy:

.a b  2

Câu 37. (Chuyên Bắc Giang 2019)Trong không gian với hệ tọa độ

Oxyz

, cho đường thẳng

1 1

:

2 1 1

x y z

d

 

 



,

 

2;1;0M

. Gọi

 

; ;H a b c

là điểm thuộc

d

sao cho

MH

có độ dài nhỏ

nhất. Tính

2 2 2

T a b c  

.

A.

6T 

. B.

12T 

. C.

5T 

. D.

21T 

.

Lời giải

Chọn A

Phương trình tham số của đường thẳng

1 2

1

x t

d y t

z t

 





  





 



. Vì

H d

nên tọa độ điểm

H

có dạng

 

1 2 ; 1 ;H t t t   

. Độ dài

MH

nhỏ nhất khi và chỉ khi

H

là hình chiếu của

M

lên

d

.

Ta có

 

2;1; 1u 



là vectơ chỉ phương của

d

,

 

1 2 ; 2 ;MH t t t    



.

H

là hình chiếu của

M

lên

d

. 0MH u 

 

   

2 1 2 2 0t t t       

6 4 0t  

2

3

t 

. Tọa độ điểm

7 1 2

; ;

3 3 3

H

 

 

 

 

suy ra

7

3

1

3

2

3

a

b

c







 





 





.

Vậy

2 2 2

7 1 2

6

3 3 3

T a b c

     

       

     

     

.

Câu 38. (SGD Điện Biên - 2019) Trong không gian

Oxyz

, cho điểm

 

1;2; 3A 

và mp

 

:P

2 2 9 0x y z   

. Đường thẳng

d

qua

A

và vuông góc với mp

 

:Q

3 4 4 5 0x y z   

, cắt

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 32 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

mp

 

P

tại

B

. Điểm

M

nằm trong mp

 

P

sao cho

M

luôn nhìn

AB

dưới góc vuông. Tính độ

dài lớn nhất của

MB

.

A.

41

2

M 

. B.

5

2

MB 

. C.

5

MB 

. D.

41

MB 

.

Lời giải

Chọn C.

Đường thẳng

d

qua

A

và vuông góc với mp

 

:Q

3 4 4 5 0

x y z

   



1 3

: 2 4

3 4

x t

d y t

z t

 





 





  



B

là giao điểm của

d

và mặt phẳng

 

P

 

2; 2;1

B  

.



90

AMB

 



M

thuộc mặt cầu

 

S

có đường kính

AB

.



M

thuộc đường tròn

 

C

giao tuyến của mặt cầu

 

S

và mặt phẳng

 

P

.

BM

lớn nhất bằng đường kính của đường tròn

 

C

.

Ta có

 

S

có tâm

1

;0; 1

2

I

 

 

 

 

, bán kính

41

2

R 

.

 

, 3

d I P



.

Bán kính của đường tròn

 

C

là:

 

2 2

41 5

, 9

4 2

r R d I P    

.

Vậy

BM

lớn nhất bằng

2 5

r  .

Câu 39. (SP Đồng Nai - 2019) Trong không gian

Oxyz

, cho bốn điểm

     

3;0;0 , 0;2;0 , 0;0;6

A B C

và

 

1;1;1

D

. Gọi



là đường thẳng đi qua

D

và thỏa mãn tổng khoảng cách từ các điểm

, ,A B C

đến



là lớn nhất. Hỏi



đi qua điểm nào trong các điểm dưới đây?

A.

 

5;7;3

M

. B.

 

1; 2;1

M  

. C.

 

3;4;3

M

. D.

 

7;13;5

M

.

Lời giải

Chọn A

Gọi

 

P

là mặt phẳng đi qua 3 điểm

, ,A B C



B

C

A

D

K

H

J

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 33

Ta có phương trình của

 

P

:

1

3 2 6

x y z

  

2 3 6 0x y z    

Ta thấy

   

1;1;1D P

Gọi

, ,H J K

lần lượt là hình chiếu của

, ,A B C

lên



Khi đó:

, ,AH AD BJ BD CK CD  

Suy ra tổng khoảng cách từ các điểm

, ,A B C

đến



là

lớn nhất bằng

AD BD CD 

hay



là đường thẳng đi qua

D

và vuông góc với

 

P

Suy ra phương trình

1 2

: 1 3

1

x t

y t

z t

 





  





 



khi đó



đi qua

 

5;7;3M

Câu 40. (Chuyên - KHTN - Hà Nội - 2019) Trong không gian

Oxyz

, cho đường thẳng

d

:

1 1

2 1 1

x y z 

 



và điểm

 

1;2;3A

. Gọi

 

P

là mặt phẳng chứa

d

và cách điểm

A

một khoảng

cách lớn nhất. Véc-tơ nào dưới đây là một véc-tơ pháp tuyến của

 

P

?

A.

 

1;0;2n 



. B.

 

1;0; 2n  



. C.

 

1;1;1n 



. D.

 

1;1; 1n  



.

Lời giải

Chọn C

Gọi

H

là hình chiếu của

A

xuống mặt phẳng

 

P

. Từ

H

kẻ

HM d

. Dễ thấy

AM d

.

Ta có

AH AM

. Suy ra khoảng cách từ

A

đến

 

P

lớn nhất khi

M H

, hay

 

IM P

.

Phương trình tham số của

d

:

1 2

1

x t

y t

z t

  











 



 

t 

, véc-tơ chỉ phương là

 

2;1;1u  



.

M d

 

1 2 ; ;1M t t t   

 

2 2 ;2 ;2MA t t t    



.

MA u

 

. 0MAu 

 

       

2 . 2 2 1. 2 1. 2 0t t t       

0t 

.

Suy ra

 

1;0;1M 

 

2;2;2MA 



.

Do

 

1;1;1n 



cùng hướng với

MA



nên

 

1;1;1n 



là một véc-tơ pháp tuyến của

 

P

.

Câu 41. (Chuyên Quang Trung- Bình Phước2019) Trong không gian

Oxyz

cho hai đường thẳng

1

:

1 1 1

x y z 

  

và

1

'

1 2 1

x y z

   

. Xét điểm

M

thay đổi. Gọi

,a b

lần lượt là khoảng

cách từ M đến



và

'

. Biểu thức

2 2

2a b

đạt giá trị nhỏ nhất khi và chỉ

khi

 

0 0 0 0

, ,M M x y z

. Khi đó giá trị

0 0

x y bằng

A.

4

3

. B.

0

. C.

2

3

. D.

2

.

Lời giải

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 34 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Chọn C

Giả sử

PQ

là đoạn vuông góc chung của hai đường thẳng



và

'

Với

P

 

và

'

Q

 

có

 

0,0,1

P

và

 

1,0,0

Q

. Gọi E, F lần lượt là hình chiếu của M trên đường

thẳng



và

'

Khi đó ta có

a b ME MF EF PQ    

hay

2

a b

 

.

Nhận thấy

 

   

 

2 2

2 2 2 2 2 2

1 2 4 2 2

2 2 2

3 3 3 3 3

a b a b a ab b a b a b

 





         









 

Do đó ta có

   

2 2

1 2

2 0 2

3 3

a b a b a b

     

hay

2 2

4

2

3

a b

 

.

Vậy giá trị nhỏ nhất của

2 2

2a b

bằng

4

3

đạt được khi dấu bằng xảy ra khi

2

M EF

EF PQ

a b



















hay

2

MP MQ 

 

hay

2 1

,0,

3 3

M

 













 

.

Câu 42. (Chuyên Thái Bình - 2019) Trong không gian với hệ tọa độ

Oxyz

, cho điểm

 

1;1;1

A

và mặt

phẳng

 

: 2 0

P x y

 

. Gọi



là đường thẳng đi qua

A

song song với

 

P

và cách

 

1;0;2

B



một khoảng nhỏ nhất. Hỏi



nhận vectơ nào dưới đây làm vecto chỉ phương?

A.

 

6;3; 5

u

 



. B.

 

6; 3;5

u  



. C.

 

6;3;5

u 



. D.

 

6; 3; 5

u

  



.

Lời giải

Chọn D

Gọi

 

2 2 2

; ; , 0

u a b c a b c

   



là một vecto chỉ phương của



.

Mặt phẳng

 

: 2 0

P x y

 

có một vecto pháp tuyến là

 

1; 2;0

n 



.



song song với

 

P

nên

. 0 2 0 2 .n u a b a b      

 

 

2 ; ;u b b c

  



.

Ta có

 

2; 1;1 ,

AB   



 

, ;2 2 ;4u AB b c b c b

 

  

 

 

 

.

Khoảng cách từ

 

1;0;2

B



đến



là

 

2 2

,

21 6 5

,

5

u AB

b bc c

d B

b c

u

 

 

 

 

  



 



.

Nếu

 

21

0 0 , .

5

c b d B     

Nếu

0

c



 

2

21 6 5

,

5 1

b b

c c

d B

b

c

 





 









 

 

 















 

, đặt

b

t

c

 

 

2

21 6 5

,

5 1

t t

d B

t

 

 



.

Xét

   

 

2 2

2

21 6 5 30 8 6

,

5 1

t t t t

f t f t

t

   



 



.

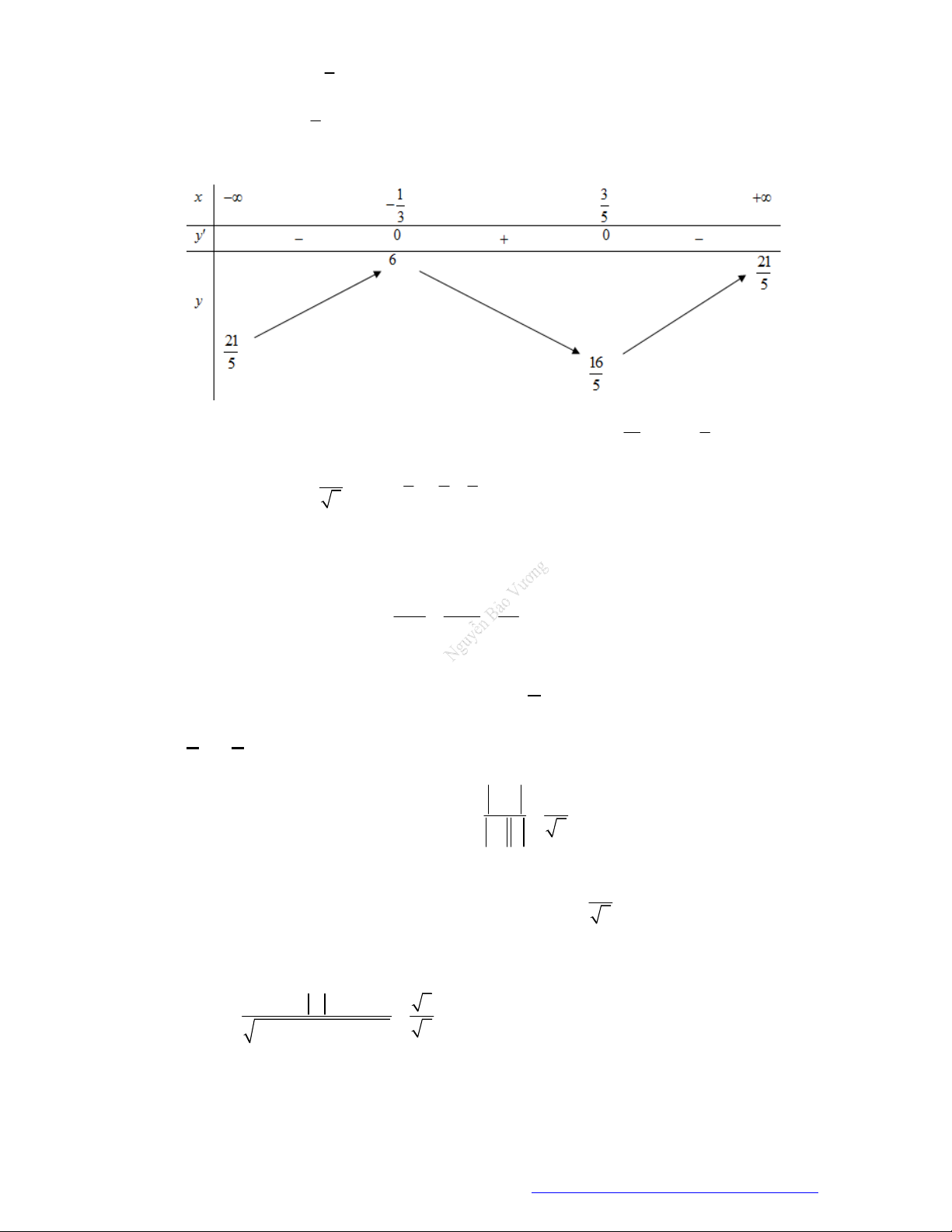
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 35

 

1

3

0

3

5

t

f t

t





 





 









.

Bảng biến thiên

Dựa vào bảng biến thiên ta có giá trị nhỏ nhất của

 

f t

bằng

16

5

khi

3

.

5

t 

 

min

4

,

5

d B  

khi

3 3

.

5 5

b

t

c

  

Chọn

3, 5 6.b c a     

Vậy



nhận vecto

 

6; 3; 5u   



làm vecto chỉ phương

Câu 43. (Chuyên Nguyễn Huệ-HN-2019) Trong không gian với hệ trục toạ độ

,Oxyz

gọi

 

P

là mặt

phẳng chứa đường thẳng

1 2

:

1 1 2

x y z

d

 

 

 

và tạo với trục

Oy

góc có số đo lớn nhất. Điểm

nào sau đây thuộc mặt phẳng

 

P

?

A.

 

3;0;4 .E 

B.

 

3;0;2 .M

C.

 

1; 2; 1 .N   

D.

 

1;2;1 .F

Lời giải

Chọn C

Ta có VTCP của đường thẳng

d

là

(1; 1; 2)

d

u   



và VTCP của trục

Oy

là

(0;1;0)j 



.

Gọi



là góc giữa

d

và

Oy

, ta có

.

1

cos 0

6

d

u j



  

 

với

Gọi



là góc giữa mặt phẳng

( )P

và

Oy

, do

( )P

chứa

d

nên ta có

 



. Dấu bằng xảy ra khi

mặt phẳng

( )P

tạo với

Oy

một góc



thỏa mãn

1

cos

6





.

( )P

chứa

d

nên

( )P

có dạng

2 2

( 1) (2 2) 0, 0m x y n x z m n       

2 2

( 2 ) 2 0, 0m n x my nz m n m n        

2 2

2 2 2

5

sin 4 20 25 0 2 5 0

6

( 2 )

m

m mn n m n

m n m n



        

  

.

Chọn

5, 2m n  

suy ra phương trình mặt phẳng

( )P

:

5 2 9 0.x y z   

Vậy điểm

( 1; 2; 1) ( )N P   

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 36 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 44. (Chuyên Lê Quý Đôn Quảng Trị 2019) Trong không gian

,Oxyz

cho mặt cầu

2 2 2

5

( ) : ( 1) ( 1)

6

    

S x y z

, mặt phẳng

( ) : 1 0   

P x y z

và đường thẳng

:

1 1 1

  

x y z

. Điểm

M

thay đổi trên đường tròn giao tuyến của

( )P

và

( )S

. Giá trị lớn nhất của

( ; )

d M

là

A.

3 2

.

2

B.

2 2.

C.

2.

D.

2

.

2

Lời giải

Chọn A

Mặt cầu

( )S

có tâm là

(1; 1;0)

I

và bán kính

30

6

R

.

Ta có:

1

( ;( ))

3

 d I P R

. Khi đó bán kính đường tròn giao tuyến là:

2 2

5 1 2

.

6 3 2

    r R d



qua

O

và có vectơ chỉ phương

(1;1;1)





a

(1; 1;0), , ( 1; 1;2).

 

     

 

  

OI OI a

Ta có:

 

,

1 1 4

; 2.

1 1 1

 

 

 

   

 

 



OI a

d I

a

Mặt khác

( )P 

, gọi

H

là tâm của đường tròn

( )C

giao tuyến của

( )P

và

( )S

.

Ta có:

// .IH 

Do đó

( ; )d M 

lớn nhất

 

( ; ) ; ( ; )       d M r d IH r d I

Khoảng cách lớn nhất của

2 3 2

(M; ) 2 .

2 2

   d

Vậy đáp án cần chọn là A.

Câu 45. (SP Đồng Nai - 2019) Trong không gian với hệ tọa độ

Oxyz

, cho hình lăng trụ đứng

.

ABC A B C

  

có

 

0

;0;0

A x

 

0

;0;0

B x

,

 

0;1;0

C

và

 

0 0

;0;B x y





trong đó

0 0

;x y

là các số

thực dương và thỏa mãn

0 0

4

x y

 

. Khi khoảng cách giữa hai đường thẳng

AC



và

B C



lớn

nhất thì bán kính

R

của mặt cầu ngoại tiếp hình lăng trụ

.

ABC A B C

  

bằng bao nhiêu?

A.

29

2

R 

. B.

29

4

R 

. C.

41

4

R 

. D.

3 6

2

R 

.

Lời giải

Chọn A

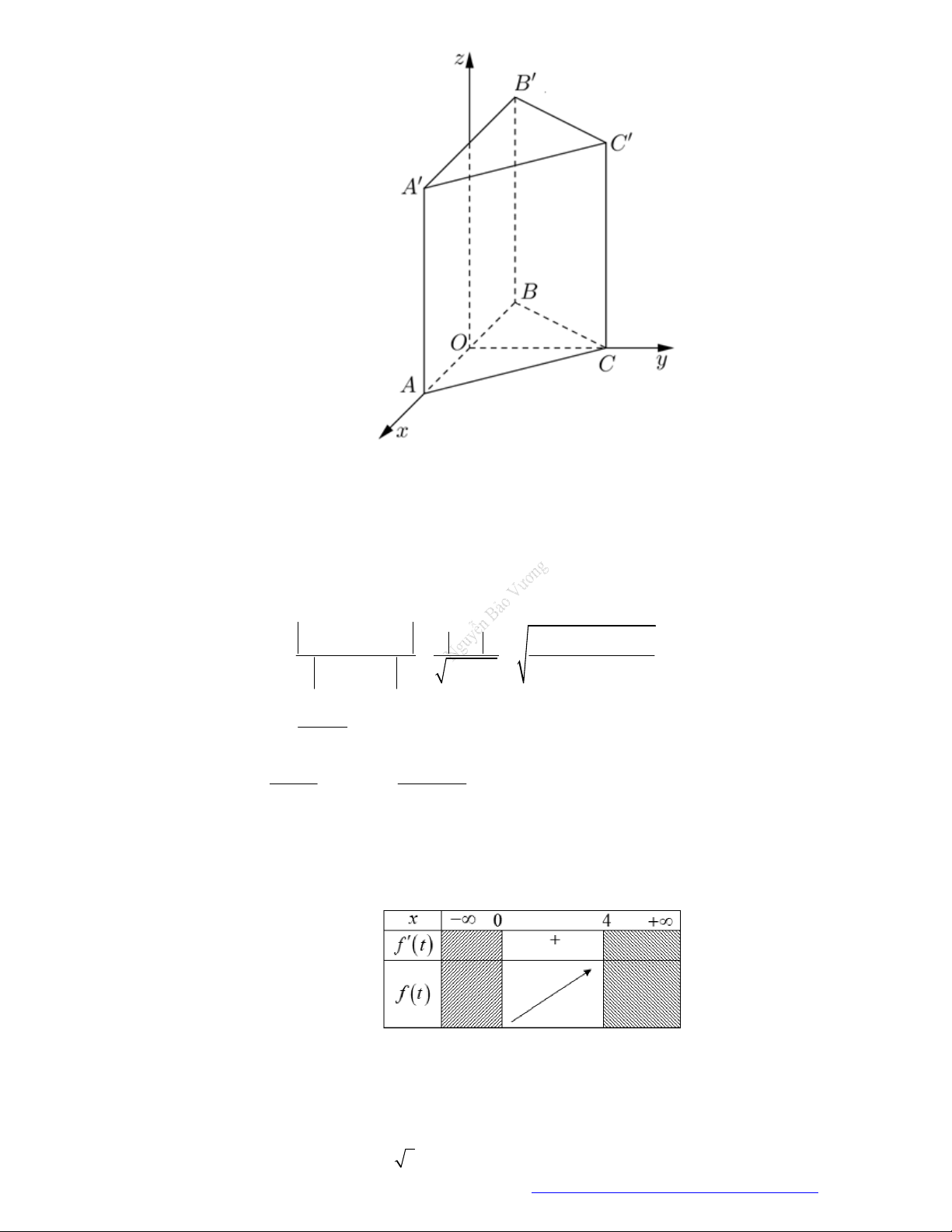
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 37

+ Xác định tọa độ các đỉnh hình lăng trụ

.ABC A B C

  

.

 

0

;0;0A x

,

 

0

;0;0B x

,

 

0;1;0C

 

0 0

;0;A x y



,

 

0 0

;0;B x y





,

 

0

0;1;C y



+ Tính khoảng cách giữa hai đường thẳng

AC



và

B C



.

 

0 0

;1;AC x y



 



,

 

0 0

;1;B C x y



 



và

 

0

0;0;CC y







 

0

2

2 2

0 0 0 0

0

2

0

,

2

.

,

AC B C CC

d AC B C

AC

x y x y

x y

B C

 

  

 

 

 

 

 





 





  

 

Đặt

2

0 0

4

2

x y

t x y



 

  

 

 





0;4t 

Xét

   

 

2 2

2

32 2

16 2

t t t

f t f t

t





  



.

Cho

 

0

16

t

f t

t







 







Bảng biến thiên

Giá trị lớn nhất của

 

,d AC B C

 

bằng

 

4f

nên

0 0

4x y 

 

1

Mặt khác

0 0

4x y 

 

2

Từ

 

1

và

 

2

ta có

0 0

2x y  .

Khi đó,

4AB 

, 5AC BC  và chiều cao hình lăng trụ là

2h CC



 

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 38 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Ta có

. . 5

4 2

ABC

AB AC BC

r

S



 

là bán kính đường tròn ngoại tiếp đáy

ABC

.

Vậy

2 22

2

5 2 2

2 2

9

2 2

h

R r

   

  



 

  

   

 

 

 

.

Câu 46. (Chu Văn An - Hà Nội - 2019) Trong không gian

Oxyz

, cho hai điểm

 

2;1; 2

A



,

 

5;1;1

B

và

mặt cầu

 

2 2 2

: 6 12 9 0

S x y z y z

     

. Xét đường thẳng

d

đi qua

A

và tiếp xúc với

 

S

sao cho khoảng cách từ

B

đến

d

nhỏ nhất. Phương trình của đường thẳng

d

là

A.

2

1

2 2

x

y t

z t







 





  



. B.

2

1 4

2

x

y t

z t







 





  



. C.

2 2

1 2

2

x t

y t

z t

 





 





  



. D.

2

1 4

2

x t

y t

z t

 





 





  



.

Lời giải

Chọn C

Mặt cầu

 

S

có tâm

 

0; 3; 6

I

 

và bán kính

2 2

3 6 9 6

R

   

.

Vì

IA R

nên

 

A S d 

đi qua

A

và vuông góc với

IA d

nằm trong

 

P

là mặt phẳng đi

qua

A

và vuông góc với

IA

. Ta có

 

: 2 2 0

P x y z

  

.

Mặt khác, ta luôn có:

   

 

d , d , 3

B d B P

 

. Đẳng thức xảy ra

d

là hình chiếu của đường

thẳng

AB

trên

 

P

.

Ta tìm hình chiếu

H

của

B

trên

 

P

:

Gọi



là đường thẳng qua

B

và vuông góc với

 

5 1 1

:

1 2 2

x y z

P

  

   

.

Vì

H

là giao điểm của



và

 

P

nên tọa độ

H

là nghiệm của hệ:

5 1 1

1 2 2

2 2 0

x y z

  



 







  



 

4

1 4; 1; 1

1

x

y H

z







     





 



.

 

2; 2;1

AH  



.

Do đó,

d

là đường thẳng đi qua hai điểm

A

và

H

nên có phương trình:

2 2

1 2

2

x t

y t

z t

 





 





  



.

Dạng 2.2. Cực trị lên quan đến giá trị biểu thức

Câu 47. (THPT - Yên Định Thanh Hóa 2019) Trong không gian

Oxyz

, cho đường thẳng

d

có phương

trình

1

2

x t

y t

z t

 





 





 



và ba điểm

 

6;0;0

A

,

 

0;3;0

B

,

 

0;0;4

C

. Gọi

 

; ;M a b c

là điểm thuộc

d

sao

cho biểu thức

2 2 2

2 3

P MA MB MC

  

đạt giá trị nhỏ nhất, khi đó

a b c 

bằng

A.

3

. B.

4

. C.

1

. D.

2

.

Lời giải

Vì

M d

nên giả sử

 

1 ;2 ;M t t t  

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 39

Ta có:

2 2 2 2 2 2

3 14 29; 3 4 2; 3 10 21

MA t t MB t t MC t t

        

 

2

2 2 2 2

2 3 18 36 96 18 1 78 78

P MA MB MC t t t

          

Do đó

2 2 2

2 3

P MA MB MC

  

đạt giá trị nhỏ nhất khi và chỉ khi

1

t

 

, khi đó:

 

2;1;1 4

M a b c

   

.

Câu 48. (Lê Quý Đôn - Quảng Trị - 2018) Trong không gian

Oxyz

, cho

2

điểm

 

3; 2;3

A 

,

 

1;0;5

B

và đường thẳng

1 2 3

:

1 2 2

x y z

d

  

 



. Tìm tọa độ điểm

M

trên đường thẳng

d

để

2 2

MA MB

đạt giá trị nhỏ nhất.

A.

 

1;2;3

M

. B.

 

2;0;5

M

. C.

 

3; 2;7

M 

. D.

 

3;0;4

M

.

Lời giải

Gọi

I

là trung điểm của

AB

, ta có

 

2; 1; 4

I  

.

Khi đó:

2 2

MA MB MA MB  

 

   

2 2

MI IA MI IB

   

   

 

2 2 2

2 2 .

MI IA IB MI IA IB

    

     

2 2 2

2MI IA IB  

2

6

MI

 

.

Do đó

2 2

MA MB

đạt giá trị nhỏ nhất khi và chỉ khi

MI

có độ dài ngắn nhất, điều này xảy ra khi

và chỉ khi

M

là hình chiếu vuông góc của

I

trên đường thẳng

d

.

Phương trình mặt phẳng

 

P

đi qua

I

và vuông góc với đường thẳng

d

là

     

1. 2 2. 1 2. 4 0

x y y

     

hay

 

: 2 2 12 0

P x y z

   

.

Phương trình tham số của đường thẳng

d

là:

1

2 2

3 2

x t

y t

z t

 





 





 



.

Tọa độ điểm

M

cần tìm là nghiệm

 

; ;x y z

của hệ phương trình:

1

2 2

3 2

2 2 12 0

x t

y t

z t

x y z

 





 





 



   



2

0

5

1

x

y

z

t























. Vậy

 

2;0;5

M

.

Câu 49. (THPT Chu Văn An - Hà Nội - 2018) Trong không gian

Oxyz

, cho đường thẳng

1

:

1 1 1

x y z

  

và hai điểm

 

1;2; 5

A



,

 

1;0;2

B 

. Biết điểm

M

thuộc



sao cho biểu thức

MA MB



đạt giá trị lớn nhất

max

T

. Khi đó,

max

T

bằng bao nhiêu?

A.

max

57

T 

. B.

max

3

T



. C.

max

2 6 3

T

 

. D.

max

3 6

T 

.

Lời giải

Do

M

thuộc



nên

 

;1 ;M t t t



.

Khi đó

 

2

3 6 27 3 1 24

MA t t t

     

,

2

3 6

MB t

 

.

Do đó

 

2

3 1 24 3 6

MA MB t t

     

.

Xét hai véc tơ

 

3 1 ; 24

u t 



và

 

3 ; 6

v t 



.

Ta có

3

u v u v

   

   

nên

max

3

T



.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 40 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Dấu bằng xảy ra khi

 

3 1 ; 24

u t 



và

 

3 ; 6

v t 



ngược hướng hay

1t 

.

Câu 50. Trong không gian với hệ tọa độ

Oxyz

, cho đường thẳng

2 1

:

1 2 3

x y z

d

 

 

và hai điểm

 

2;0;3

A

,

 

2; 2; 3

B

 

. Biết điểm

 

0 0 0

; ;M x y z

thuộc

d

thỏa mãn

4 4

MA MB

nhỏ nhất. Tìm

0

x

.

A.

0

1

x



. B.

0

3

x



. C.

0

x



. D.

0

2

x



.

Lời giải

Gọi

I

là trung điểm của

AB

. Khi đó ta có

 

2 2

2

4 4 2 2 2 2 2 2

4 4

4 2 2 4 2 2

2

4 2

4 2 2 2 4

2 . 2 2

2 4

4 2 2

4 8

3 7

2 3 2

4 4 10

AB AB

MA MB MA MB MA MB MI MI

AB AB

MI MI AB MI MI AB

AB AB

MI MI AB MI AB

   

       

   

   

     

 

     

 

 

Do đó,

4 4

MA MB

đạt GTNN khi

MI

nhỏ nhất



M

là hình chiếu vuông góc của

I

lên

d

.

Điểm

 

2; 1;0

I 

. Lấy

 

2 ; 1 2 ;3 d

M t t t

   

.

 

;2 ;3IM t t t





. 0 4 9 0 0

d d

IM u IM u t t t t

        

   

Suy ra

M I

.

Vậy

0

2

x



Câu 51. (Chuyên Hà Tĩnh - 2018) Trong không gian

Oxyz

, cho ba điểm

 

1;0;1

A 

,

 

3;2;1

B

,

 

5;3;7

C

. Gọi

 

; ;M a b c

là điểm thỏa mãn

MA MB

và

MB MC

đạt giá trị nhỏ nhất. Tính

P a b c  

A.

4P 

. B.

0

P



. C.

2P 

. D.

5

P



.

Lời giải

Gọi

I

là trung điểm của

AB

, suy ra

 

1;1;1

I

;

 

4;2;0

AB 



.

Phương trình mặt phẳng trung trực của

AB

:

 

: 2 3 0

x y



  

.

Vì

   

2.3 1.2 3 . 2.5 1.3 3 50 0     

nên

B

,

C

nằm về một phía so với

 



, suy ra

A

,

C

nằm về hai phía so với

 



.

Điểm

M

thỏa mãn

MA MB

khi

 

M





. Khi đó

MB MC MA MC AC   

.

MB MC

nhỏ nhất bằng

AC

khi

 

M AC



 

.

Phương trình đường thẳng

AC

:

1 2

x t

y t

z t

  











 



, do đó tọa độ điểm

M

là nghiệm của hệ phương

Câu 52. (THPT An Lão Hải Phòng 2019) Trong không gian với hệ tọa độ Oxyz, cho 3 điểm

     

1;2;3 , 0;1;1 , 1;0; 2

A B C



và mặt phẳng

 

: 2 0

P x y z

   

. Gọi M là điểm thuộc mặt

phẳng (P) sao cho giá trị của biểu thức

2 2 2

2 3

T MA MB MC

   nhỏ nhất. Tính khoảng cách từ M

đến mặt phẳng

 

:2 2 3 0

Q x y z

   

?

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 41

A.

2 5

3

B.

121

54

C.

24

D.

91

54

Lời giải

Chọn D

Gọi

 

; ;I a b c

là điểm thỏa mãn

2 3 0

IA IB IC

  

   

.

Ta có

     

1 ;2 ;3 , ;1 ;1 , 1 ; ; 2

IA a b c IB a b c IC a b c         

  

2

3

1 2 3 3 0 6 4

2

2 3 0 2 2 2 3 0 6 4

3

3 2 2 6 3 0 6 1

1

6

a

a a a a

IA IB IC b b b b b

c c c c

c







     

 



  

            

  

  

       

 









   

2 2 1

; ;

3 3 6

I

 



 

 

.

Ta chứng minh được

2 2 2 2

6 2 3

T MI IA IB IC

   

. Do đó T đạt GTNN khi

MI

đạt GTNN



M

là hình chiếu vuông góc của I trên mặt phẳng (P).

Ta có

2

3

2

:

3

1

6

x t

MI y t

z t



 



 





 





,

 

2 2 1 19 19

; ; , 3 0

3 3 6 6 18

M MI M t t t M P t t

 

           

 

 

 

7 7 22

3

7 7 11 91

9 18 9

; ; ;

18 18 9 3 54

M d M Q

   

 

      

 

 

.

Câu 53. (THPT Cẩm Giàng 2 2019) Trong không gian

Oxyz

, cho ba điểm

 

10; 5;8

A  

,

 

2;1; 1

B



,

 

2;3;0

C

và mặt phẳng

 

: 2 2 9 0

P x y z

   

. Xét

M

là điểm thay đổi trên

 

P

sao cho

2 2 2

2 3

MA MB MC

 

đạt giá trị nhỏ nhất. Tính

2 2 2

2 3

MA MB MC

 

.

A.

54

.

B.

282

.

C.

256

.

D.

328

.

Lời giải

Gọi

 

; ;I x y z

là điểm thỏa mãn

2 3 0

IA IB IC

  

   

.

Ta có

 

10 ; 5 ;8

IA x y z     



,

 

2 ;1 ; 1

IB x y z    



,

 

2 ;3 ;

IC x y z   



.

Khi đó,

     

10 2 2 3 2 0

5 2 1 3 3 0

8 2 1 3 0

x x x

y y y

z z z

      





      





      



0

1

x

y

z







 











 

0;1;1

I

.

Với điểm

M

thay đổi trên

 

P

, ta có

2 2 2

2 3

MA MB MC

 

     

2 2 2

2 3

MI IA MI IB MI IC

     

     

 

2 2 2 2

6 2 3 2 2 3

MI IA IB IC MI IA IB IC

      

   

2 2 2 2

6 2 3

MI IA IB IC

   

(Vì

2 3 0

IA IB IC

  

   

).

Ta lại có

2 2 2

2 3

IA IB IC

 

185 2.8 3.9  

228

.

Do đó,

2 2 2

2 3

MA MB MC

 

đạt giá trị nhỏ nhất



MI

đạt giá trị nhỏ nhất



M

là hình chiếu vuông góc của

I

trên

 

P

.

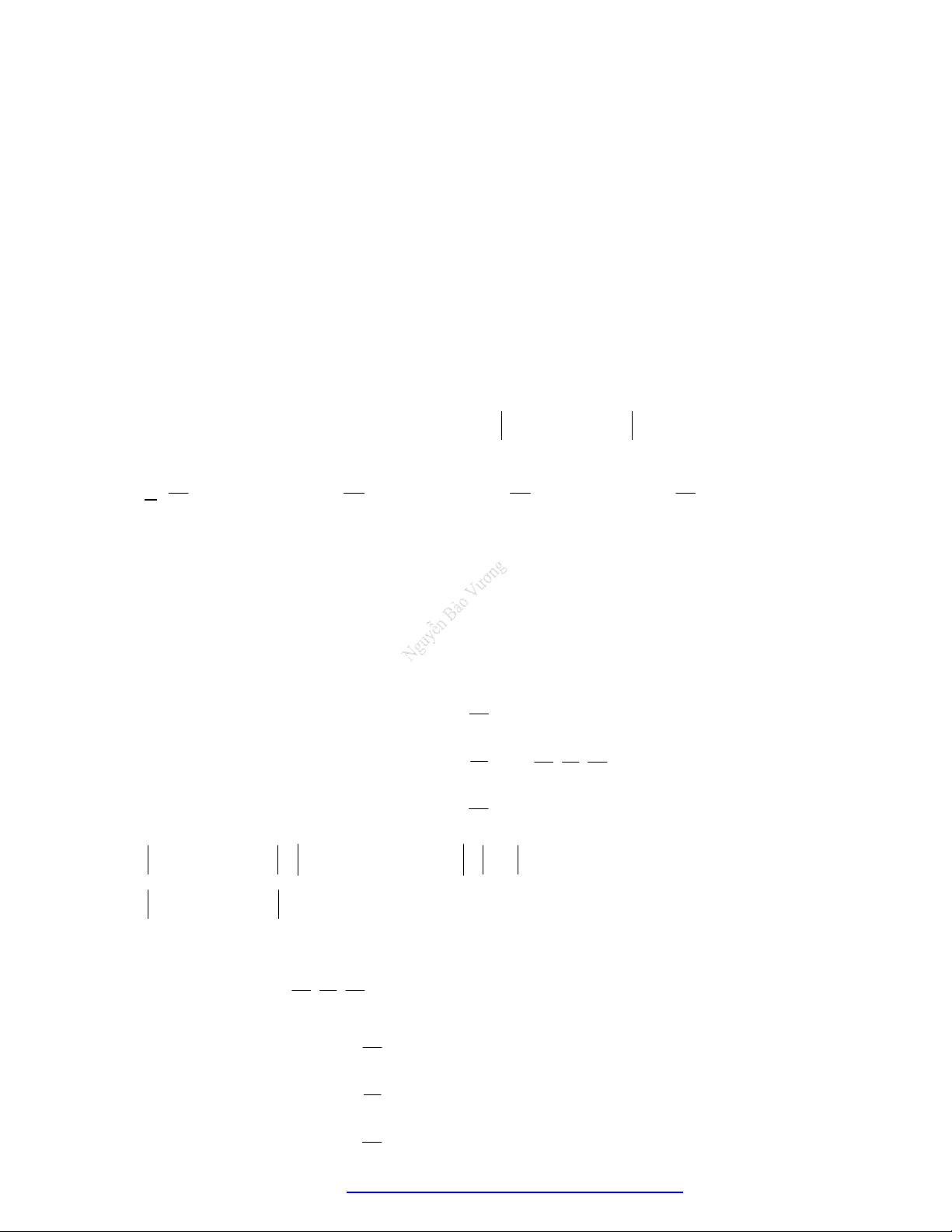
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 42 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Khi đó,

 

, 3

MI d I P

 

.

Vậy giá trị nhỏ nhất của

2 2 2

2 3

MA MB MC

 

bằng

2

6 228

MI 

6.9 228 

282

.

Giá trị nhỏ nhất của

2 2 2

2 3

MA MB MC

 

đạt được khi và chỉ khi

M

là hình chiếu vuông góc

của

I

trên

 

P

.

Lưu ý thêm cách tìm điểm

M

như sau:

Gọi



là đường thẳng qua

I

và vuông góc với

 

P

. Phương trình của



:

1 2

x t

y t

z t







 





 



.

Ta có

 

M P

  

. Xét phương trình

   

2 1 2 2 1 2 9 0

t t t

     

9 9 0

t

  

1t 



 

1;3; 1

M



.

Câu 54. Trong không gian

Oxyz

cho mặt phẳng

 

: 3 0

P x y z

   

và ba điểm

 

3;1;1

A

,

 

7;3;9

B

và

 

2;2;2

C

. Điểm

 

; ;M a b c

trên

 

P

sao cho

2 3

MA MB MC

 

  

đạt giá trị nhỏ nhất. Tính

2 10

a b c 

.

A.

62

9

. B.

27

9

. C.

46

9

. D.

43

9

.

Lời giải

+ Gọi

 

; ;I x y z

là điểm thỏa mãn

2 3 0

IA IB IC

  

   

.

Ta có

 

3 ;1 ;1

7 ;3 ;9

2 ;2 ;2

IA x y z

IB x y z

IC x y z



   



   





   







.

+

23 6 0

2 3 0 13 6 0

25 6 0

x

IA IB IC y

z

 





     





 



   

23

6

13

6

25

6

x

y

z







 











23 13 25

; ;

6 6 6

I

 



 

 

.

 

2 3 6 2 3 6 6MA MB MC MI IA IB IC MI MI

       

       

.

2 3

MA MB MC

 

  

đạt giá trị nhỏ nhất



M

là hình chiếu của

I

lên mặt phẳng

 

P

.

+ Gọi đường thẳng

 

d

đi qua

I

và vuông góc

 

P

.

Ta có

 

d

đi qua

23 13 25

; ;

6 6 6

I

 

 

 

và nhận

 

1;1;1

p

n 



làm véc tơ chỉ phương.

Suy ra phương trình

 

23

6

13

:

6

25

6

x t

d y t

z t



 



 





 





.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 43

 

23 13 25

; ;

6 6 6

M d M t t t

 

    

 

 

 

M P



23 13 25

3 0

6 6 6

t t t

       

43

18

t



 

13 2 16

; ;

9 9 9

M



 



 

 

.

Do đó

13

9

2

9

16

9

a

b

c

























62

2 10

9

a b c  

.

Câu 55. (THPT Lê Quý Dôn Dà Nẵng 2019) Trong không gian

Oxyz

, cho 3 điểm

( 8;1;1)

A



,

(2;1;3)

B

và

(6;4;0)

C

. Một điểm

M

di động trong không gian sao cho

. . 34

MA MC MA MB

 

   

. Cho biết

MA MB



đạt giá trị lớn nhất khi điểm

M

trùng với điểm

0 0 0 0

( ; ; )M x y z

. Tính tích số

0 0 0

x y z

.

A.

16.

B.

18.

C.

14.

D.

12.

Lời giải

Gọi

( ; ; )M a b c

.

Ta có

 

. . 34 34 . 34

MA MC MAMB MA MC MB MA BC

      

        

Mặt khác

( 8 ;1 ;1 )MA a b c    



,

(4;3; 3)

BC

 



Suy ra

4( 8 ) 3(1 ) 3(1 ) 34 4 3 3 66 0

a b c a b c

            

.

Vậy

( )M P

có phương trình

4 3 3 66 0

x y z

    

.

Ký hiệu

( ) ( ; ; ) 4 3 3 66

f M f x y z x y z

     

, với

( ; ; )M x y z

Ta có

( ). ( ) ( 4( 8) 3.1 3.1 66)(( 4.2 3.1 3.3 66) ( 34).( 6

8) 2312 0

f A f B

              

Suy ra điểm

( 8;1;1)

A



và điểm

(2;1;3)

B

nằm về cùng 1 phía so với mặt phẳng

( )P

.

Khi đó

MA MB AB

 

(tính chất 3 cạnh của tam giác) suy ra

MA MB



đạt giá trị lớn nhất khi

, ,M A B

thẳng hàng và

M

nằm ngoài đoạn thẳng

AB

hay

M

là giao điểm của đường thẳng

AB

với

( )P

.

Đường thẳng

AB

có véc tơ chỉ phương

(10;0;2)

AB 



và qua điểm

(2;1;3)

B

nên có phương trình

2 5

1

3

x t

y

z t

 











 



.

Suy ra

4(2 5 ) 3.1 3(3 ) 66 0 17 68 4

t t t t

            

.

Vậy

( 18;1; 1)

M

 

hay

0 0 0

18.

x y z 

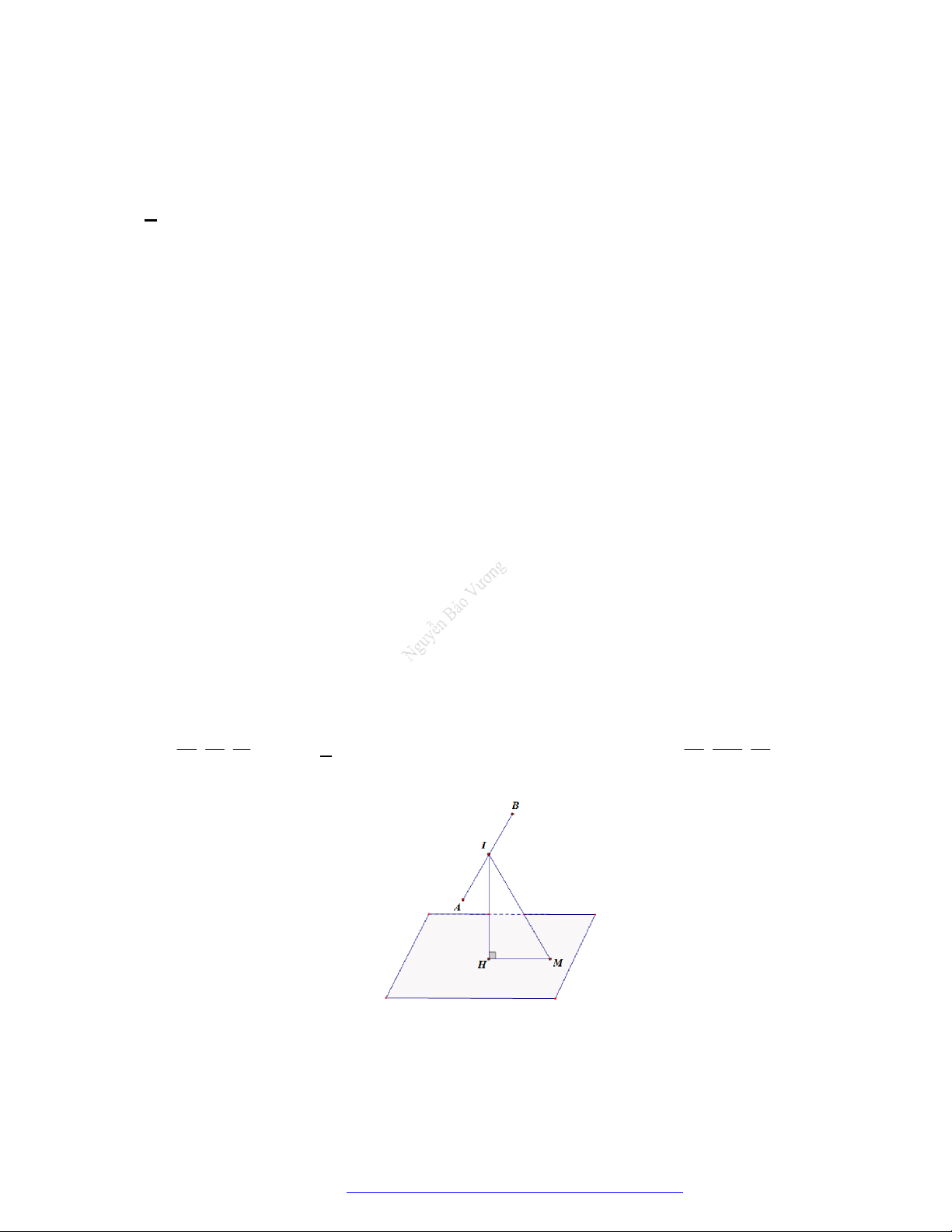
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 44 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 56. Trong không gian với hệ tọa độ

Oxyz

, cho tam giác

ABC

với

 

2;1;3 ,A

 

1; 1;2 ,B 

 

3; 6;0 ,C 

 

2; 2; 1 .D  

Điểm

 

; ;M x y z

thuộc mặt phẳng

 

: 2 0P x y z   

sao cho

2 2 2 2

S MA MB MC MD   

đạt giá trị nhỏ nhất. Tính giá trị của biểu thức

  

2 2 2

P x y z

.

A.

 6P

. B.

2P 

. C.

 0P

. D.

2P  

.

Lời giải

Với mọi điểm

I

ta có

     

2 2 2

2 2S NA NB NC NI IA NI IB NI IC        

     

 

2 2 2 2

4 2 2 2NI NI IA IB IC IA IB IC      

   

Chọn điểm

I

sao cho

2 0IA IB IC  

   

2 0 4 0IA IB IC IA AB AC      

       

Suy ra tọa độ điểm

I

là

 

0;1;2I

.

Khi đó

2 2 2 2

4 2S NI IA IB IC   

, do đó

S

nhỏ nhất khi

N

là hình chiếu của

I

lên mặt

phẳng

 

P

.

Phương trình đường thẳng đi qua

I

và vuông góc với mặt phẳng

 

P

là

0

1

2

x t

y t

z t





 



 





 





Tọa độ điểm

   

;1 ;2N t t t P  

1 2 2 0 1t t t t         

 

1;2;1N 

.

Câu 57. (Chuyên Nguyễn Trãi Hải Dương 2019) Trong không gian

Oxyz

cho

 

4; 2;6A 

,

 

2;4;2B

,

 

: 2 3 7 0M x y z



    

sao cho

.MA MB

 

nhỏ nhất. Tọa độ của

M

bằng

A.

29 58 5

; ;

13 13 13

 

 

 

. B.

 

4;3;1

. C.

 

1;3;4

. D.

37 56 68

; ;

3 3 3



 

 

 

.

Lời giải

Gọi

I

là trung điểm

 

3;1;4AB I

. Gọi

H

là hình chiếu của

I

xuống mặt phẳng

 



.

Ta có

     

2 2 2 2

. . .MA MB MI IA MI IB MI MI IA IB IA MI IA        

        

.

Do

IA

không đổi nên

.MA MB

 

nhỏ nhất khi

MI

nhỏ nhất

MI IH M H   

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 45

Gọi



là đường thẳng đi qua

I

và vuông góc với mặt phẳng

 



. Khi đó



nhận

 

1;2; 3

n



 



làm vectơ chỉ phương. Do đó



có phương trình

3

1 2

4 3

x t

y t

z t

 





 





 



.

 

3 ;1 2 ;4 3H H t t t    

.

       

3 2 1 2 3 4 3 7 0

H t t t



        

 

1 4;3;1

t H  

.

Vậy

 

4;3;1

M

.

Câu 58. Trong không gian với hệ tọa độ

Oxyz

,cho hai điểm

(1;0;2), (3;1; 1).

A B



và mặt phẳng

( ) : 1 0.

P x y z

   

Gọi

( ; ; ) ( )M a b c P

sao cho

3 2

MA MB



 

đạt giá trị nhỏ nhất. Tính

9a 3 6 .S b c  

A.

4.

B.

3.

C.

2.

D.

1.

Lời giải

Gọi

( ; ; )I m n p

là điểm thỏa mãn:

3 2 0.

IA IB

 

  

Ta có

(1 ; ;2 ); (3 ;1 ; 1 ).IA m n p IB m n p

        

 

3(1 ) 2(3 ) 0 3

3 2 0 3( ) 2(1 ) 0 2 ( 3; 2;8).

3(2 ) 2( 1 ) 0 8

m m m

IA IB n n n I

p p p

     

 

 

            

 

 

     

 

  

Ta có

3 2 3( ) 2( ) .MA MB MI IA MI IB MI MI

      

      

Khi đó,

3 2

MA MB



 

đạt giá trị nhỏ nhất,

( )M P

MI

nhỏ nhất,

( )M P

M

là hình chiếu vuông góc của

I

trên

( ).P

Gọi



là đường thẳng qua

I

và vuông góc với

( ).P

Khi đó



nhận vectơ pháp tuyến của

( )P

là

(1;1;1)

n 



làm vecto chỉ phương

3

: 2 .

8

x t

y t

z t

  





    





 



Tọa độ

M

là nghiệm của hệ

11

3

11

3

2

8

3

9a 3 6 3.

8 8

3

22

3

1 0

22

2

3

a

x t

x

y t

b S b c

z t

y

x y z

c

z

t







 



  





 



  



 

        

  

 

  

 

  

   





 









 

Câu 59. (KTNL GV THPT Lý Thái Tổ 2019) Trong không gian với hệ trục tọa độ

Oxyz

, cho ba điểm

     

1;4;5 , 3;4;0 , 2; 1;0

A B C

và mặt phẳng

 

:3 3 2 12 0.   

x y z



Gọi

 

; ;M a b c

thuộc

 



sao cho

2 2 2

3 

MA MB MC

đạt giá trị nhỏ nhất. Tính tổng

.  S a b c

A.

3

. B.

2

. C.

2

. D.

1

.

Lời giải

Chọn A

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 46 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Gọi điểm

 

; ;I x y z

thỏa mãn

3 0.  

   

IA IB IC

Mà

 

1 ;4 ;5 1 ;4 ;5

3 ;4 ; 3 ;4 ;

2 ; 1 ; 3 6 3 ; 3 3 ; 3

 

       

 

        

 

 

         

 

 

 

IA x y z IA x y z

IB x y z IB x y z

IC x y z IC x y z

 

3 10 5 ;5 5 ;5 5

      

  

IA IB IC x y z

Do đó:

 

2

3 0 1 2;1;1 .

1







     









   

x

IA IB IC y I

z

Mặt khác:

     

2 2 2

3 3       

     

MA MB MC MI IA MI IB MI IC

2 2 2 2

0

5 2. . 3 3

 

      

 

 



  



MI MI IA IB IC IA IB IC

Vì

, , ,I A B C

cố định nên

2 2 2

3 

IA IB IC

không đổi

Do đó:

2 2 2

3

MA MB MC

 

nhỏ nhất

2

MI



nhỏ nhất

MI

nhỏ nhất



M

là hình chiếu của

I

trên mặt phẳng

 



.

Phương trình đường thẳng

d

qua

I

và vuông góc với mặt phẳng

 



là:

2 1 1

.

3 3 2

x y z

  

 

 

Gọi

   

.

M d



 

Tọa độ của

M

là nghiệm của hệ phương trình:

7

2

3 6 3 3

2 1 1

1 7 1

2 4 3 3 ; ;0 .

3 3 2

2 2 2

3 3 2 12 0

0

x

x y

x y z

x z y M

x y z

z







   



  





 

  

 

         

 

  

 

 

  

   









Vậy

7 1

, , 0 3.

2 2

a b c S a b c

        

Câu 60.

(

Dề Thi Công Bằng

KHTN 2019) Trong không gian

Oxyz

cho các điểm

(1;2;0), (1; 1;3), (1; 1; 1)

A B C

  

và mặt phẳng

( ) :3 3 2 15 0

P x y z

   

. Xét

( ; ; )M a b c

thuộc mặt

phẳng

( )P

sao cho

2 2 2

2

MA MB MC

 

nhỏ nhất. Giá trị của

a b c 

bằng

A.

3

. B.

7

. C.

2

. D.

1

.

Lời giải

Gọi

I

là điểm thỏa mãn:

2 0 2(

0

) ( ) ( )IA IC IB OA OI OC OI OB OI

         

         



 

2

1;2; 2

2

OA OC OB

OI I

 

   

  



Ta có

 

2

2 2 2

2

2 2 2 2 2 4 .MA MA MI IA MI IA MI IA

     

      

 

2

2 2 2

2

2 .MB MB MI IB MI IB MI IB

     

      

 

2

2 2 2

2

2 .MC MC MI IC MI IC MI IC

     

      

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 47

Suy ra

 

2 2 2 2 2 2 2

2 2 2 2 2

MA MB MC MI IA IC IB MI IA IC IB

        

   

Suy ra

2 2 2 2 2 2 2

2 2 2

MA MB MC MI IA IC IB

     

. Do I cố định nên

2 2 2

2

IA IC IB

 

không

đổi. Vậy

2 2 2

2

MA MB MC

 

nhỏ nhất

MI

nhỏ nhất

MI

nhỏ nhất

M

là hình chiếu của

I trên (P).

 Đường thẳng



qua

 

1;2; 2

I



và vuông góc với

 

P

là:

1 3

2 3

2 2

x t

y t

z t

 





 





  



Suy ra tọa độ điểm

M

là nghiệm của hệ

 

1 3 4

2 3 1

4; 1;0

2 2 0

3 3 2 15 0 1

x t x

y t y

M

z t z

x y z t

  

 

 

   

 

  

 

   

 

    

 

Suy ra

3

a b c

  

Câu 61. (Trần Phú - Hà Tĩnh - 2018) Trong không gian

Oxyz

, cho ba điểm

 

1; 2;1

A 

,

 

5; 0; 1

B



,

 

3;1; 2

C

và mặt phẳng

 

:3 3 0

Q x y z

   

. Gọi

 

; ;M a b c

là điểm thuộc

 

Q

thỏa mãn

2 2 2

2

MA MB MC

 

nhỏ nhất. Tính tổng

5a b c 

.

A.

11

. B.

9

. C.

15

. D.

14

.

Lời giải

Gọi

E

là điểm thỏa mãn

2 0

EA EB EC

  

   

 

3;0;1

E

.

Ta có:

2 2 2

2

S MA MB MC

  

2 2 2

2

MA MB MC

  

  

     

2 2 2

2

ME EA ME EB ME EC

     

     

2 2 2 2

4 2

ME EA EB EC

   

.

Vì

2 2 2

2

EA EB EC

 

không đổi nên

S

nhỏ nhất khi và chỉ khi

ME

nhỏ nhất.

M

là hình chiếu vuông góc của

E

lên

 

Q

.

Phương trình đường thẳng

:ME

3 3

1

x t

y t

z t

 











 



.

Tọa độ điểm

M

là nghiệm của hệ phương trình:

3 3

1

3 3 0

x t

y t

z t

x y z

 











 



   



0

1

2

1

x

y

z

t







 











 



.

 

0; 1; 2

M 

0

a

 

,

1

b

 

,

2

c



.

5 0 1 5.2

a b c

     

9

.

Câu 62. (Lê Quý Đôn - Quảng Trị - 2018) Trong không gian với hệ trục tọa độ

Oxyz

cho 3 điểm

 

1;1;1

A

,

 

0;1;2

B

,

 

2;1;4

C 

và mặt phẳng

 

: 2 0   

P x y z

. Tìm điểm

 

N P



sao cho

2 2 2

2

S NA NB NC

  

đạt giá trị nhỏ nhất.

A.

4 4

;2;

3 3

N

 



 

 

. B.

 

2;0;1

N 

. C.

1 5 3

; ;

2 4 4

N

 



 

 

. D.

 

1;2;1

N 

.

Lời giải

Với mọi điểm

I

ta có

     

2 2 2

2 2        

     

S NA NB NC NI IA NI IB NI IC

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 48 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

 

2 2 2 2

4 2 2 2      

   

NI NI IA IB IC IA IB IC

Chọn điểm

I

sao cho

2 0

IA IB IC

  

   

2 0 4 0

IA IB IC IA AB AC

      

       

Suy ra tọa độ điểm

I

là:

 

0;1;2

I

.

Khi đó

2 2 2 2

4 2

S NI IA IB IC

   

, do đó

S

nhỏ nhất khi

N

là hình chiếu của

I

lên mặt phẳng

 

P

.

Phương trình đường thẳng đi qua

I

và vuông góc với mặt phẳng

 

P

là:

0

1

2

 





 





 



x t

y t

z t

Tọa độ điểm

   

;1 ;2

N t t t P

  

1 2 2 0 1

t t t t

         

 

1;2;1

 N

.

Câu 63. (Chuyên Phan Bội Châu 2019) Trong không gian với hệ trục tọa độ

Ox ,yz

cho mặt cầu

       

2 2 2

: 1 2 1 9

S x y z

     

và hai điểm

 

4;3;1

A

,

 

3;1;3

B

; M là điểm thay đổi trên

 

S

. Gọi

,m n

là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức

2 2

2P MA MB 

. Xác định

 

.m n



A.

64

. B.

68

. C.

60

. D.

48

.

Lời giải

Xét điểm I sao cho:

2 0.

IA IB

 

  

Giả sử

 

; ; ,I x y z

ta có:

   

4 ;3 ;1 , 3 ;1 ;3 .IA x y z IB x y z

     

 

Do đó:

 

2 4 3

2 0 2 3 1 5;5; 1 .

2 1 3

x x

IA IB y y I

z z

  



       





  



  

Do đó:

2 2

2P MA MB 

   

2 2

2

MI IA MI IB

   

   





2 2 2 2

2 2 4 . 2 .MI IA MI IA MI IB MI IB

     

       

 

2 2 2

MI IA IB MI IA IB

    

     

 

2 2 2

MI IA IB MI IA IB

    

  

2 2 2

2 .MI IA IB

  

Do I cố định nên

2 2

,IA IB

không đổi. Vậy

P

lớn nhất (nhỏ nhất)

2

MI



lớn nhất (nhỏ nhất).

MI

lớn nhất (nhỏ nhất)

M

là giao điểm của đường thẳng IK (với

 

1;2; 1

K



là tâm của

mặt cầu (S)) với mặt cầu (S).

Ta có: MI đi qua

 

5;5; 1

I



và có vectơ chỉ phương là

 

4;3;0 .

KI



Phương trình của MI là:

1 4

2 3

1.

x t

y t

z

 





 





 



Tọa độ điểm M cần tìm ứng với giá trị t là nghiệm của phương trình:

     

2 2 2

2

3

5

1 4 1 2 3 2 1 1 9 25 9

3

.

5

t

t t t

t







           



 





TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 49

Với

1 1

3 17 19

; ; 1 2 (min).

5 5 5

t M M I

 

    

 

 

Với

1 2

3 7 1

; ; 1 8 (max).

5 5 5

t M M I

 

      

 

 

Vậy

max

min

48

60.

12

m P

m n

n P

 



  



  



Câu 64. (Chuyên KHTN 2019) Trong không gian với hệ tọa độ

Oxyz

cho ba điểm

     

8;5; 11 , 5;3; 4 , 1;2; 6A B C  

và mặt cầu

       

2 2 2

: 2 4 1 9S x y z     

. Gọi điểm

 

; ;M a b c

là điểm trên

 

S

sao cho MA MB MC 

  

đạt giá trị nhỏ nhất. Hãy tìm

a b

.

A.

6

. B.

2

. C.

4

. D. 9.

Lời giải

Gọi

N

là điểm thỏa mãn

0NA NB NC  

   

, suy ra

 

2;0;1N 

.

Khi đó:

       

MA MB MC MN NA MN NB MN NC NA NB NC MN MN            

            

.

Suy ra MA MB MC 

  

nhỏ nhất khi

MN

nhỏ nhất. Mặt cầu

 

S

có tâm

 

2;4; 1I 

, suy ra:

   

4;4; 2 2;2; 1NI    



. Phương trình

2 2

4 2

1

x t

NI y t

z t

 





  





  



. Thay phương trình NI vào phương

trình

 

S

ta được:

     

2 2 2

2

1

2 2 9 1

1

t

t t t t

t





      



 



.

Suy ra

NI

cắt

 

S

tại hai điểm phân biệt

   

1 2

3;6; 2 , 0;2;0N N

.

Vì

1 2

NN NN nên MN nhỏ nhất khi và chỉ khi

2

M N . Vậy

 

0;2;0M

là điểm cần tìm.

Suy ra:

2.a b 

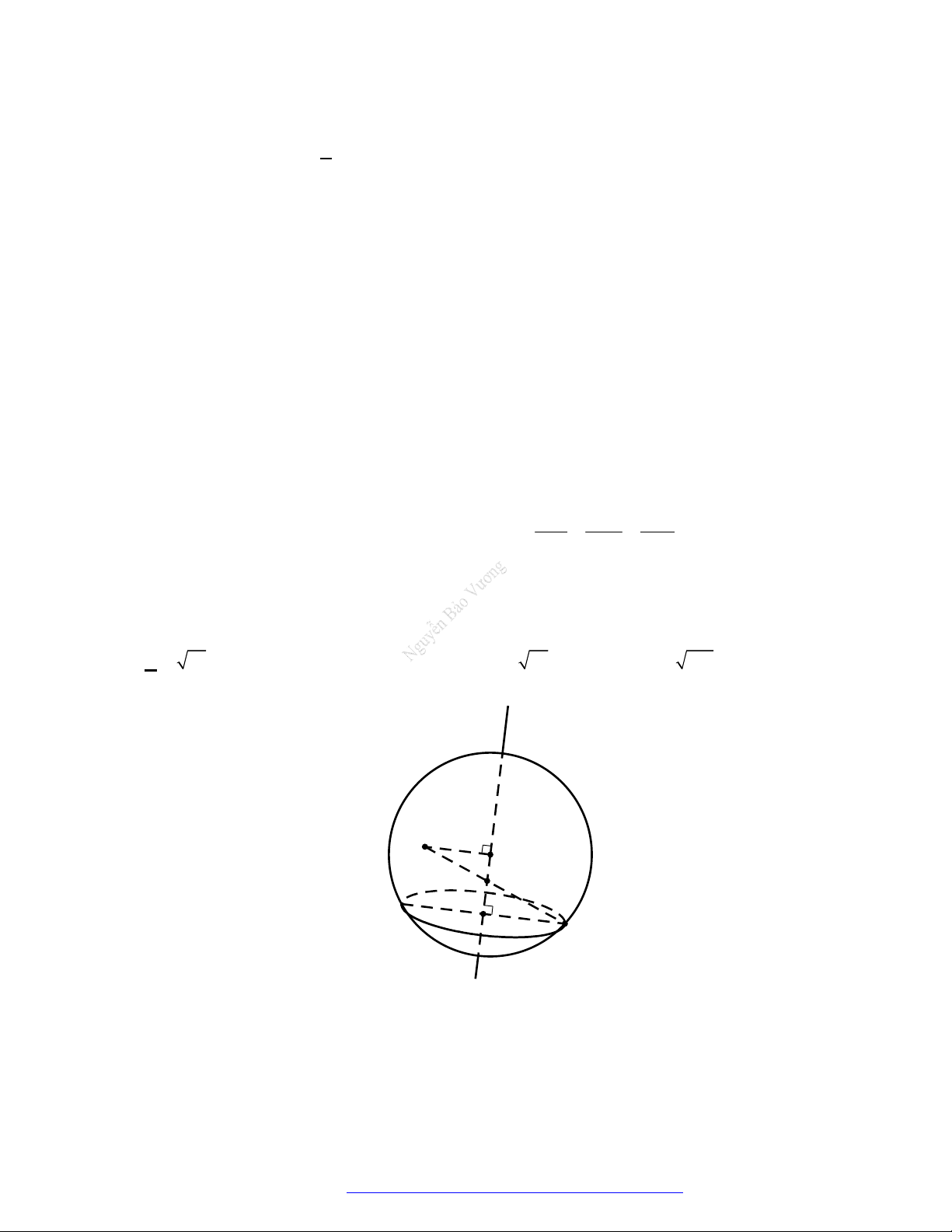
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 50 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 65. Cho mặt cầu

       

2 2 2

: 2 1 3 9S x y z     

và hai điểm

 

1 ; 1 ; 3A

,

 

21 ; 9 ; 13B 

.

Điểm

 

; ; M a b c

thuộc mặt cầu

 

S

sao cho

2 2

3MA MB

đạt giá trị nhỏ nhất. Khi đó giá trị

của biểu thức

. .T a b c

bằng

A.

3

. B.

8

. C.

6

. D.

18

.

Lời giải

Gọi điểm

I

thỏa mãn

 

3 0 6 ; 3 ; 1IA IB I   

  

.

Khi đó

     

2 2

2 2 2 2 2

3 3 4 3 2 . 3MA MB MI IA MI IB MI IA IB MI IA IB         

      

2 2 2

4 3MI IA IB  

.

Do

2 2

3IA IB

không đổi vì ba điểm

; ;A B I

cố định nên

2 2

3MA MB

đạt giá trị nhỏ nhất khi

MI

nhỏ nhất. Khi đó

M

là giao điểm của đường thẳng

IJ

với mặt cầu

 

S

, (

 

2 ; 1 ; 3J

là tâm của

mặt cầu

 

S

).

Ta có phương trình đường thẳng

IJ

là

2 2

1

3 2

x t

y t

z t

 





 





 



 

1

2

4; 2 ; 1

0 ; 0 ; 5

M

IJ S

M



  





.

Kiểm tra

 

1 2

3 9IM IM 

nên

 

1

4;2;1M

là điểm cần tìm. Vậy

. . 8T a b c 

.

Câu 66. Trong không gian

Oxyz

cho đường thẳng

1 2 3

:

2 3 4

x y z

d

  

 

và mặt cầu

 

S

:

     

2 2 2

3 4 5 729x y z     

. Cho biết điểm

 

2; 2; 7A   

, điểm

B

thuộc giao tuyến của

mặt cầu

 

S

và mặt phẳng

 

: 2 3 4 107 0P x y z   

. Khi điểm

M

di động trên đường thẳng

d

giá trị nhỏ nhất của biểu thức

MA MB

bằng

A. 5 30 . B.

27

. C. 5 29 . D. 742 .

Lời giải

Mặt cầu

 

S

có tâm

 

3; 4; 5I   

và bán kính

27R 

.

Đường thẳng

d

có 1 véc-tơ chỉ phương là

   

2;3;4u d P  



.

Gọi

K

là giao điểm của mặt phẳng

 

P

và đường thẳng

d

. Vì

I d

nên

K

là tâm của đường

tròn giao tuyến và

KB d

.

Ta có

 

1;2; 2 3IA IA   



và

. 0IAu IA d  

 

.

d

M

K

I

B

A

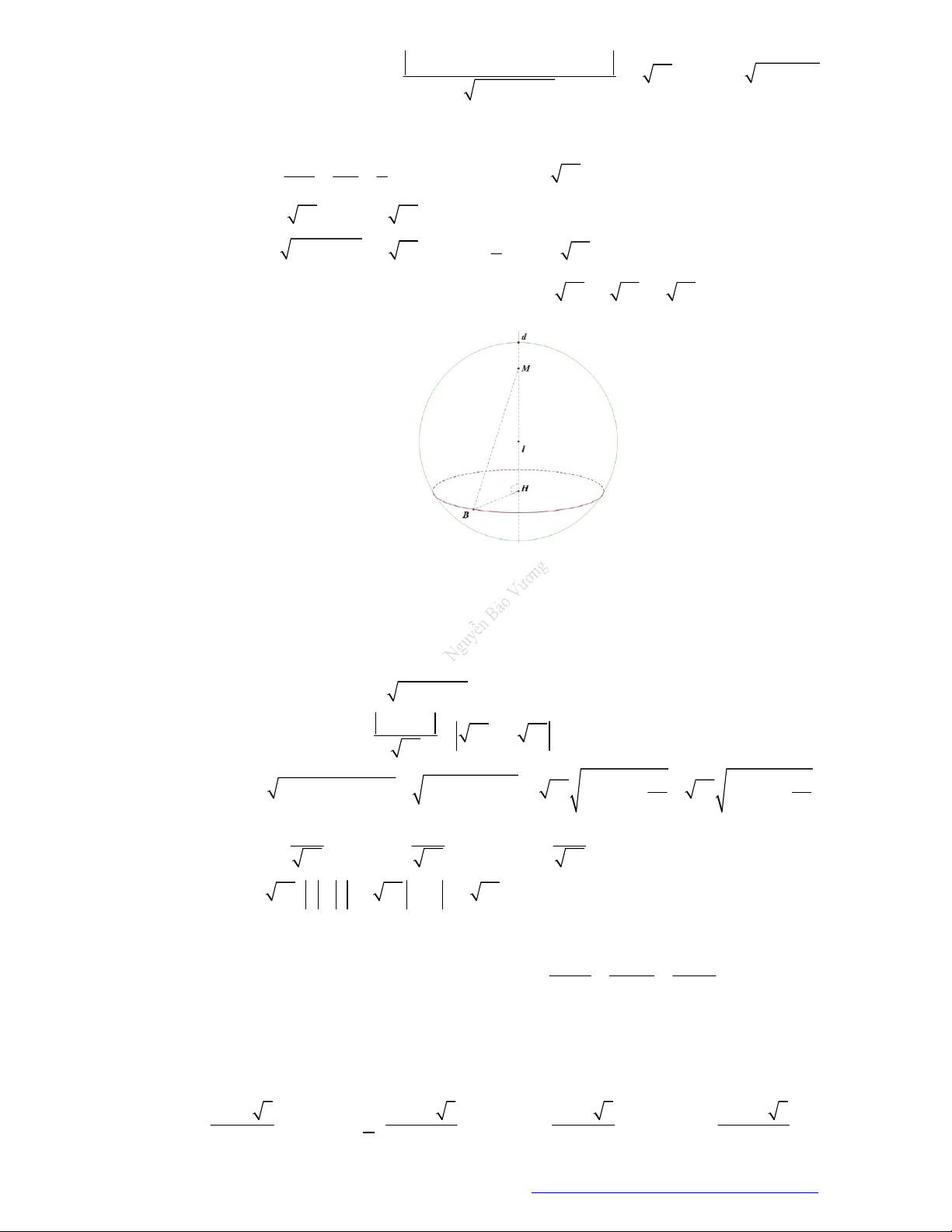
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 51

Ta tính được

 

     

2 2 2

2. 3 3. 4 4 5 107

d , 5 29

2 3 4

IK I P

     

  

 

và

2 2

2KB R IK  

.

Do

M

di động trên đường thẳng

d

(trục của đường tròn giao tuyến) và

B

thuộc đường tròn giao

tuyến nên biểu thức

MA MB

nhỏ nhất khi và chỉ khi

M AB d 

.

Khi đó, ta có

3

2

MI IA

MK KB

 

và 5 29MI MK IK   .

Suy ra

3 29MI 

,

2 29MK 

.

Ta có

2 2

3 30AM IA MI  

2

2 30

3

BM AM  

.

Vậy giá trị nhỏ nhất của

MA MB

là 3 30 2 30 5 30AM BM    .

Cách 2:

Ta có

 

S

có tâm

 

3; 4; 5I   

,

bán kính

27R 

.

Dễ thấy

d

đi qua

 

3; 4; 5I   

và vuông góc với

 

P

.

 

P

cắt

 

S

theo đường tròn có bán kính

2r 

.

 

1 2 ;2 3 ;3 4M d M t t t    

.

Ta có

2 2

.T MA MB MA MH r    

Lại có

29 87

( ;( )) 29 3 29

29

t

MH d M P t



   

.

Suy ra

 

2

29 116 125 29 3 4T t t t     

   

2 2

9 4

29 2 29 3 .

29 29

t t     

Xét

3

2;

29

u t

 

 

 

 



,

2

3 ;

29

v t

 

 

 

 



5

5;

29

u v

 

  

 

 

 

.

Do đó

 

29 29 5 50T u v u v    

   

.

Câu 67. (THPT Chuyên Thái Bình - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho mặt phẳng

 

: 1 0P x y z   

, đường thẳng

 

15 22 37

:

1 2 2

x y z

d

  

 

và mặt cầu

 

2 2 2

: 8 6 4 4 0S x y z x y z      

. Một đường thẳng

 



thay đổi cắt mặt cầu

 

S

tại hai

điểm

,A B

sao cho

8AB 

. Gọi

A



,

B



là hai điểm lần lượt thuộc mặt phẳng

 

P

sao cho

AA



,

BB



cùng song song với

 

d

. Giá trị lớn nhất của biểu thức

AA BB

 



là

A.

8 30 3

9



. B.

24 18 3

5



. C.

12 9 3

5



. D.

16 60 3

9



.

Lời giải

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 52 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Mặt cầu

 

S

có tâm

 

4;3; 2I 

và bán kính

5R 

.

Gọi

H

là trung điểm của

AB

thì

IH AB

và

3IH 

nên

H

thuộc mặt cầu

 

S



tâm

I

bán

kính

3R





.

Gọi

M

là trung điểm của

A B

 

thì

2AA BB HM

 

 

,

M

nằm trên mặt phẳng

 

P

.

Mặt khác ta có

 

4

;

3

d I P R 

nên

 

P

cắt mặt cầu

 

S

và

 

5

sin ; sin

3 3

d P



 

. Gọi

K

là hình chiếu của

H

lên

 

P

thì

.sinHK HM





.

Vậy để

AA BB

 



lớn nhất thì

HK

lớn nhất

HK

đi qua

I

nên

 

max

4 4 3 3

; 3

3 3

HK R d I P





    

.

Vậy

AA BB

 



lớn nhất bằng

4 3 3 3 3 24 18 3

2 .

5 5

3

 

 



 

 

.

Câu 68. (Đại học Hồng Đức –Thanh Hóa 2019) Trong không gian với hệ tọa độ

Oxyz

, cho

 

3;1;1A 

,

 

5;1;1B

và hai mặt phẳng

 

: 2 4 0P x y z   

,

 

: 1 0Q x y z    

. Gọi

 

; ;M a b c

là

điểm nằm trên hai mặt phẳng

 

P

và

 

Q

sao cho

MA MB

đạt giá trị nhỏ nhất. Tính

2 2 2

T a b c  

.

A.

5

. B.

29

. C.

13

. D.

3

.

Lời giải

Chọn D

Từ giả thiết ta có

M

thuộc giao tuyến

d

của hai mặt phẳng

 

P

và

 

Q

.

Mặt phẳng

 

P

có một vectơ pháp tuyến là

 

1;2;1

P

n 



. Mặt phẳng

 

Q

có một vectơ pháp

tuyến là

 

1;1;1

Q

n  



. Khi đó đường thẳng

d

đi qua

 

1;1;1N

và có một vectơ chỉ phương là

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 53

 

, 1; 2;3

d P Q

u n n

 

  

 

  

nên có phương trình tham số là

1

: 1 2

1 3

x t

d y t

z t

 





 





 



suy ra

 

1 ;1 2 ;1 3M t t t

  

.

   

2 2

2 2 2 2 2 2

4 4 9 4 4 9 14 8 16 14 8 16

MA MB t t t t t t t t t t

              

Bài toán trở thành tìm giá trị nhỏ nhất của hàm số

 

2 2 2 2

4 8 4 8

14 8 16 14 8 16 14

7 7 7 7

f t t t t t t t t t

 

           

 

 

2 2

2 2 2 2

14

7 7

t t

 

   

 

     

   

 

   

 

.

Đặt

2 2

;

7

u t

 

 

 

 



,

2 2

;

7

v t

 

 

 

 



.

Khi đó

 

14 14

f t u v u v

 

   

 

   

. Suy ra

 

2

4 4 8 7

14.

7 49

7

f t

 

  

 

 

.

Dấu bằng xảy ra khi và chỉ khi hai vectơ

u



và

v



cùng hướng hay

2

7

0 0

2 2

7

t



   



.

Do đó

 

1;1;1

M

. Vậy

2 2 2

3

T a b c

   

.

Dạng 2.3. Cực trị liên quan đến chu vi, diện tích, bán kính, thể tích

Câu 69. (Chuyên Hùng Vương Gia Lai 2019) Trong không gian

Oxyz

, cho hình hộp chữ nhật

.

ABCD A B C D

   

có

A

trùng với gốc tọa độ

O

, các đỉnh

( ;0;0)

B a

,

(0; ;0)D a

,

(0;0; )A b



với

, 0

a b



và

2

a b

 

. Gọi

M

là trung điểm của cạnh

CC



. Thể tích của khối tứ diện

BDA M



có

giá trị lớn nhất bằng

A.

64

27

. B.

32

27

. C.

8

27

. D.

4

27

.

Lời giải

Chọn C

A

D

y

'C

'D

'A

z

x

B

'B

C

M

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 54 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Tọa độ điểm

( ; ;0), '( ; ; ), ( ; ; )

2

b

C a a C a a b M a a

.

' (- ;0; ), (- ; ;0), (0; ; )

2

b

BA a b BD a a BM a  

  

.

2

', ( ; ; )BA BD ab ab b

 

   

 



nên

2

'

1

', .

6 4

BDA M

a b

V BA BD BM

 

 

 

  

.

Ta có:

3

2

'

2 64 32 8

. .(2 )

3 27 27 27

BDA M

a a b

a a b a b V

 

 

     

 

 

.

Câu 70. (THPT Nguyễn Huệ - Huế - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho đường thẳng

 

1 2

: 1

2

x t

d y t

z t

  





 









và hai điểm

 

1;5;0

A

,

 

3;3;6

B

. Gọi

 

; ;M a b c

là điểm trên

 

d

sao cho chu

vi tam giác

MAB

đạt giá trị nhỏ nhất. Tính

P a b c  

.

A.

1P 

. B.

3

P

 

. C.

3

P



. D.

1P  

.

Lời giải

 

1 2 ;1 ;2M d M t t t

    

.

Chu vi tam giác

MAB

là:

AM BM AB 

. Vì

AB const

nên chu vi nhỏ nhất khi

 

AM BM



nhỏ nhất.

 

2 2; 4;2AM t t t

  



,

 

2 4; 2;2 6

BM t t t

   



.

 

2 2

9 20 9 36 56 3 2 5 6 3 2 5

AM BM t t t t t          

Đặt

     

3 ;2 5 , 6 3 ;2 5 6;4 5

u t v t u v     

   

.

Áp dụng bất đẳng thức vectơ:

u v u v  

   

. Dấu bằng xảy ra khi

u



,

v



cùng hướng.

Ta có:

 

2

6 4 5 2 29

AM BM u v u v        

   

. Do đó

 

AM BM



nhỏ nhất khi

tồn tại số

k

dương sao cho

u kv

 

 

3 6 3

2 5 2 5

t k t

k

 













1

t

k













. Khi đó

 

1;0;2

M

.

Vậy

1 0 2 3

P a b c

      

.

Câu 71. (Hoàng Hoa Thám Hưng Yên 2019) Trong không gian với hệ tọa độ

Oxyz

, cho tứ diện

ABCD

có

 

1;1;6

A 

,

 

3; 2; 4

B

  

,

 

1;2; 1

C



,

 

2; 2;0

D 

. Điểm

 

; ;M a b c

thuộc đường thẳng

CD

sao cho tam giác

ABM

có chu vi nhỏ nhất. Tính

a b c 

.

A.

1

. B.

2

. C.

3

. D.

0

.

Lời giải

Gọi

ABM

C

là chu vi của tam giác

ABM

.

A

B

H

D

C

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 55

 

2; 3; 10

AB    



113

AB 

 

2; 3; 10

AB    



,

 

1; 4;1

CD  



. 2 12 10 0

AB CD

     

 

AB CD 

.

Gọi

 

P

là mặt phẳng chứa đường thẳng

AB

và vuông góc với đường thẳng

CD

.

H

là giao điểm của

 

P

và đường thẳng

CD

.

Phương trình mặt phẳng

 

P

qua

 

1;1;6

A 

có véc tơ pháp tuyến

 

1; 4;1

CD  



là:

4 1 0

x y z

   

.

Phương trình đường thẳng

CD

:

1

2 4

1

x t

y t

z t

 





 





  



.

 

1 ;2 4 ; 1

H CD H t t t     

.

   

1 4 2 4 1 1 0

H P t t t

        

1

2

t

 

3 1

;0;

2 2

H

 

 

 

 

.

Với

M CD 

, ta có

AM AH

BM BH











AM BM AH BH   

.

113

ABM

C AB AM BM AH BH

     

,

M CD 

.

Suy ra

113

ABM

minC AH BH

  

, đạt được

M H

3 1

;0;

2 2

M

 

 

 

 

.

Vậy

1a b c  

.

Câu 72. Trong không gian với hệ tọa độ

Oxyz

cho tứ diện

ABCD

có

 

1;1;6

A 

,

 

3; 2; 4

B

  

,

 

1;2; 1

C



,

 

2; 2;0

D 

. Điểm

 

; ;M a b c

thuộc đường thẳng

CD

sao cho tam giác

ABM

có chu

vi nhỏ nhất. Tính

.a b c 

A.

1

. B.

2

. C.

3

. D.

0

.

Lời giải

Ta có

ABM

C AM BM AB



  

mà

AB

không đổi suy ra

ABM

C



nhỏ nhất khi

AM BM

nhỏ

nhất.

Ta có

 

2; 3; 10 ,

AB    



 

1; 4;1

CD  



.

Xét

. 0

AB CD AB CD

  

 

. Gọi

 



qua

AB

và vuông góc với

CD

.

 



đi qua

 

1;1;6

A 

và nhận

 

1; 4;1

CD  



làm véc tơ pháp tuyến.

Suy ra

 



có phương trình là:

4 1 0.

x y z

   

Vì điểm

M

thuộc

CD

sao cho

AM BM

nhỏ nhất nên

 

M CD



 

.

 



:

4 1 0

x y z

   

,

CD

có phương trình:

1

2 4

1

x t

y t

z t

 





 





  



 

M CD



 

3 1

;0;

2 2

M



 



 

 

3 1

0 1

2 2

a b c



      

.

Câu 73. (Chuyên Lê Hồng Phong Nam Định 2019) Trong không gian với hệ tọa độ

Oxyz

, cho mặt

phẳng

 

: 2 0

P x y z

   

và hai điểm

   

3;4;1 ; 7; 4; 3

A B

 

. Điểm

  

; ; 2

M a b c a



thuộc

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 56 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

 

P

sao cho tam giác

ABM

vuông tại

M

và có diện tích nhỏ nhất. Khi đó giá trị biểu thức

T a b c  

bằng:

A.

6

T



. B.

8

T



. C.

4T 

. D.

0

T



.

Lời giải

Chọn D

Ta có:

1

.

2

ABM

S AB MH



với

H

là hình chiếu vuông góc của

M

lên AB.

Do

AB

không đổi nên

ABM

S

nhỏ nhất khi

MH

nhỏ nhất.

 

4; 8; 4

. 0 //( )

1;1; 1

P

AB

AB n AB P

n



  



  



 







 



MH

nhỏ nhất khi

M

nằm trên giao tuyến của mặt phẳng

 

Q

và

 

P

;

với

 

Q

là mặt phẳng chứa

AB

và vuông góc với mp

 

P

.

 

4; 8; 4

3;0;3

1;1; 1

Q

P

AB

n



  



  



 









phương trình mp

 

Q

là

4 0

x z

  

.

M

nằm trên giao tuyến của mặt phẳng

 

Q

và

 

P

nên tọa độ

M

là nghiệm của hệ phương trình

 

4 0

2 2 ;2 2 ;4

2 0

4

x t

x z

y t M t t t

x y z

z t





  





     

 

   





 



với

2t 

.

Ta có

   

3; 2 2 ;3 ; 7;6 2 ;7

AM t t t BM t t t        

 

.

Tam giác

ABM

vuông tại

M

nên

        

. 0 3 7 2 2 6 2 3 7 0

AM BM t t t t t t

           

 

        

 

3

3 7 2 3 1 0 3 3 5 0

5

3

t n

t t t t t t

t l







           









.

+

 

3 3; 4;1 3 4 1 0

t M a b c

         

.

Câu 74. (Chuyên Lê Quý Đôn Điện Biên 2019) Trong không gian

Oxyz

, cho mặt cầu

   

2 2

2

( ) : 3 1 4

S x y z

    

và đường thẳng

1 2

: 1 ,( )

x t

d y t t

z t

 





   





 





. Mặt phẳng chứa

d

và cắt

( )S

theo một đường tròn có bán kính nhỏ nhất có phương trình là

A.

1 0

y z

  

. B.

3 5 2 0

x y z

   

.

C.

2 3 0

x y

  

. D.

3 2 4 8 0

x y z

   

.

Lời giải

Mặt cầu

 

S

có tâm

 

3;1;0

I

và bán kính

2R 

.

Gọi

H

là hình chiếu của

I

trên

d

.

 

1 2 ; 1 ;H d H t t t     

;

 

2 2 ; 2 ;IH t t t     



.

Véctơ chỉ phương của

d

là

 

2;1; 1

d

u

 



.

. 0

d

IH u



 

   

2 2 2 1 2 0

t t t

       

1t 

. Suy ra

 

3;0; 1

H



2

IH 

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 57

Gọi

 

P

là mặt phẳng chứa đường thẳng

d

và cắt mặt cầu

 

S

theo đường tròn có bán kính

r

.

Ta có

 

2 2

2

, 4 ,r R d I P d I P

   

   

   

.

Mà

 

, 2d I P IH 

nên

 

2

4 , 4 4 2 2r d I P IH

 

      

 

.

Suy ra

2min r 

, đạt được khi

 

IH P

.

Khi đó mặt phẳng

 

P

đi qua

 

3;0; 1H 

nhận

 

0; 1; 1IH   



làm một véctơ pháp tuyến.

Phương trình mặt phẳng

 

P

là:

     

0 3 1 0 1 1 0x y z     

1 0y z   

.

Câu 75. Trong không gian với hệ tọa độ Oxyz, cho hai điểm

(3; 2;6), (0;1;0)A B

và mặt cầu

2 2 2

( ) : ( 1) ( 2) ( 3) 25S x y z      . Mặt phẳng

( ) : 2 0P ax by cz   

đi qua A, B và cắt theo

giao tuyến là đường tròn có bán kính nhỏ nhất. Tính

T a b c  

.

A.

3T 

B.

5T 

C.

2T 

D.

4T 

Lời giải

Mặt cầu

 

S

có tâm

 

1; 2;3 ,I

bán kính

5.R 

Mặt phẳng

 

P

có vec-tơ pháp tuyến

 

; ;

P

n a b c



Theo giả thiết

   

0;1;0 : 2 0 2.B P b b    

Ta có:

 

3;3; 6AB   



cùng phương với

 

1; 1;2u  



.

Phương trình đường thẳng

: 1

2

x t

AB y t

z t







 









Gọi

r

là bán kính đường tròn giao tuyến.

K

là hình chiếu vuông góc của

I

lên đường thẳng

,AB

H

là hình chiếu vuông góc của

I

lên

 

P

Ta có:

   

;1 ;2 1; 1;2 3K AB K t t t IK t t t        



 

. 0 1 0; 2; 1IK AB AB IK t IK        

  

.

 

2 2 2 2

, 25 , 25r R d I P d I P IH      .

Ta có:

min max

r IH .

Mà

 

max

IH IK IH IK H K P IK      

P

n



và

IK



cùng phương.

0 0

0

. 2 1

1

P

a a

a

n k IK b k k

c

c k c

 

 





 

        

  





 

  

 





0 2 1 3.t a b c       

H

I

K

A

B

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 58 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 76. Trong không gian

,Oxyz

cho mặt cầu

       

2 2 2

: 1 2 3 48

S x y z

     

Gọi

 



là mặt

phẳng đi qua hai điểm

   

0;0; 4 , 2;0;0

A B

và cắt mặt cầu

 

S

theo giao tuyến là đường tròn

 

C

. Khối nón

 

N

có đỉnh là tâm của

 

S

, đường tròn đáy là

 

C

có thể tích lớn nhất bằng

A.

128

3



B.

39



C.

88

3



C.

215

3



Lời giải

Chọn B

Ta có tâm cầu

 

1; 2;3 ;R 4 3

I  

Gọi

H

là hình chiếu vuông góc của tâm cầu

I

lên mặt phẳng

 



Vậy chiều cao của khối nón

 

N

là

 

,

h d I P IH IK

  

, trong đó

K

là hình chiếu vuông góc

của

I

lên

AB

Gọi

 

Q

là mặt phẳng đi qua

I

và vuông góc với ta có

 

: 2z 7 0

Q x

  

Phương trình

: 0

4 2

x t

AB y

z t













  



thế vào

 

Q

ta được

8 4 7 0 3t t t     

Tọa độ

 

3;0;2 3

K IK

 

Bán kính của khối nón

2

48

r h 

Vậy thể tích của khối nón

   

 

2 2 2

1 1 1

. 48 . 48 . 0;3

3 3 3

V r h h h h h h

  

      

Khảo sát

V

ta tìm được

max

39

V





Câu 77. (Chuyên Hùng Vương Gia Lai 2019) Trong không gian

Oxyz

, cho hình hộp chữ nhật

.

ABCD A B C D

   

có

A

trùng với gốc tọa độ

O

, các đỉnh

( ;0;0)

B a

,

(0; ;0)D a

,

(0;0; )A b



với

, 0

a b



và

2

a b

 

. Gọi

M

là trung điểm của cạnh

CC



. Thể tích của khối tứ diện

BDA M



có

giá trị lớn nhất bằng

A.

64

27

. B.

32

27

. C.

8

27

. D.

4

27

.

Lời giải

Chọn C

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 59

Tọa độ điểm

( ; ;0), '( ; ; ), ( ; ; )

2

b

C a a C a a b M a a

.

' (- ;0; ), (- ; ;0), (0; ; )

2

b

BA a b BD a a BM a  

  

.

2

', ( ; ; )BA BD ab ab b

 

   

 



nên

2

'

1

', .

6 4

BDA M

a b

V BA BD BM

 

 

 

  

.

Ta có:

3

2

'

2 64 32 8

. .(2 )

3 27 27 27

BDA M

a a b

a a b a b V

 

 

     

 

 

.

Câu 78. Trong không gian

Oxyz

, cho đường thẳng

4 3

: 3 4

0

x t

d y t

z

 





 









. Gọi

A

là hình chiếu vuông góc của

O

trên

d

. Điểm

M

di động trên tia

Oz

, điểm

N

di động trên đường thẳng

d

sao cho

MN OM AN 

. Gọi

I

là trung điểm đoạn thẳng

OA

. Trong trường hợp diện tích tam giác

IMN

đạt giá trị nhỏ nhất, một vectơ pháp tuyến của mặt phẳng

 

,M d

có tọa độ là

A.

 

4;3;5 2

. B.

 

4;3;10 2

. C.

 

4;3;5 10

. D.

 

4;3;10 10

.

Lời giải

Chọn A

Gọi

 

4 3 ;3 4t;0A t 

là hình chiếu vuông góc của

O

trên

d

A

D

y

'C

'D

'A

z

x

B

'B

C

M

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 60 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

 

. 0 0 4;3;0

d

OA d OAu t A      

 

.

Trên

Oz

lấy điểm

P

sao cho

OP AN MP OM OP MN    

và

AIN OIP IN IP    

Ta có

IMP IMN  

, kẻ

IH MN IH IO  

min

1

. min

2

IMN IMN

S IH MN S MN

 

   

Ta có

2

2 2 2 2

2 25 5 2

2

MO AN

MN MO OA AN MN



 

      

 

 

Vậy

min

5 2 5 2

5 2 0;0;

2 2

MN OM AN M

 

    

 

 

Một vectơ pháp tuyến của mặt phẳng

 

,dM

là

15

, 10 2; ;25

2

d

MA u

 

 



 

 

 

 

Chọn

 

4;3;5 2n 



Câu 79. Trong không gian

Oxyz

, cho điểm

1 3

; ;0

2 2

M

 

 

 

và mặt cầu

 

2 2 2

: 8S x y z  

. Đường thẳng

d

thay đổi, đi qua điểm

,M

cắt mặt cầu

 

S

tại hai điểm phân biệt

,A B

. Tính diện tích lớn nhất

S

của tam giác

OAB

.

A.

7S 

. B.

4S 

. C.

2 7S 

. D.

2 2S 

.

Lời giải

Chọn A

Mặt cầu

 

S

có tâm

 

0;0;0O 

, bán kính

2 2R 

.

Ta có

1OM M 

nằm trong mặt cầu. Gọi

I

là trung điểm

AB OI AB 

.

Đặt

0 1.x OI OM x    

Khi đó

 

2 2 2

1

. 8

2

OAB

S OI AB OI R OI x x f x



     

.

 

2

2 4

8

0 1

x

f x x



  





 , ta có bảng biến thiên

Vậy

max 7

OAB

S





khi

1OI 

hay

.I M

Câu 80. Trong không gian

Oxyz

, cho điểm

 

1;4;3A

và mặt phẳng

 

: 2 0P y z 

. Biết điểm

B

thuộc

 

P

, điểm

C

thuộc

 

Oxy

sao cho chu vi tam giác

ABC

nhỏ nhất. Hỏi giá trị nhỏ nhất đó là

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 61

A.

6

5

. B.

2

5

. C.

4

5

. D.

5

.

Lời giải

Chọn C

Gọi

H

là hình chiếu vuông góc của

 

1

;4;3

A

lên mặt phẳng

 

O

xy

 

1

;4;0

H

Gọi

1

A

là

điểm đôi xứng của

A

qua mặt

phẳng

 

O

xy

, ta t

ìm được

 

1

;4; 3

A



Gọi

K

là

hình chiếu vuông góc của

 

1

;4;3

A

l

ên mặt phẳng

 

P

Ta

có phương trình đường thẳng

1

: 4 2

3

x

AK y t

z t







 











,

Gọi

 

1

;4 2 ;3

K

t t AK



 

Mặ

t khác,

 

5

5 0 1

K

P t t



     

 

1

;2;4

K

Gọi

2

A

là

điểm đôi xứng của

A

qua

mặt phẳng

 

P

thì

K

l

à trung điểm của

2

AA

.

Ta

có

2

1

2 0

5

A K A

x

x x

y y y

z zx z





 





 







 



 

2

1

;0;5

A

Ta

có chu vi tam giác

A

BC

l

à

1

2 1 2

ABC

P

AC AB BC A C A B BC A A





     

.

Dấ

u bằng xảy ra khi

1

2

, , ,A A B C

t

hẳng hàng

Suy ra

 

1

2

min

4

5

ABC

P

A A





.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương  https://www.facebook.com/phong.baovuong Trang 1

TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH KHÁ GIỎI MỨC ĐỘ 8-9-10 ĐIỂM

Phương pháp giải một số bài toán

1. Gắn tọa độ đối với hình chóp

1.1. Hình chóp có cạnh bên (SA) vuông góc với mặt đáy:

Đáy là tam giác đều

Gọi O là trung điểm BC. Chọn hệ

trục như hình vẽ,

1AB a 

.

Tọa độ các điểm là:

3 1

(0;0;0), 0; ;0 , ;0;0 ,

2 2

O A B

 



 

 



1 3

;0;0 , 0; ;

2 2

SA

C S OH



 

 

 

.

Đáy là tam giác cân tại A

Gọi O là trung điểm BC. Chọn hệ

trục như hình vẽ,

1a 

.

Tọa độ các điểm là:

   

(0;0;0), 0; ;0 , ;0;0 ,

O A OA B OB

 



;0;0 , 0; ;

SA

C OC S OA OH



 

 

 

.

Đáy là tam giác cân tại B

Gọi O là trung điểm AC. Chọn hệ

trục như hình vẽ,

1a 

.

Tọa độ các điểm:

 

0;0;0O

,

   

;0;0 , 0, ;0 ,A OA B OB

 



;0;0 , ;0;

SA

C OC S OA OH



 



 

 

.

Đáy là tam giác vuông tại B

Chọn hệ trục như hình vẽ,

1a 

.

Tọa độ các điểm:

 

0;0;0B O

,

   

0; ;0 , ,0;0 ,A AB C BC



0; ;

SA

S AB BH



 

 

 

.

Đáy là tam giác vuông tại A

Chọn hệ trục như hình vẽ,

1

a 

.

Tọa độ các điểm:

 

0;0;0A O

,

   

0; ;0 , ;0;0 ,B OB C AC

 

0;0;S SA

.

Đáy là tam giác thường

Dựng đường cao BO của

.ABC

Chọn hệ trục như hình vẽ,

1a 

.

Tọa độ các điểm:

 

0;0;0O

,

   

;0;0 , 0, ;0 ,A OA B OB

 



;0;0 , ;0;

SA

C OC S OA OH



 



 

 

.

Đáy là hình vuông, hình chữ nhật

Chọn hệ trục như hình vẽ,

1.

a 

Tọa độ

 

0;0;0A O

,

 

0; ;0 ,

B AB

     

; ;0 , ;0;0 , 0;0;C AD AB D AD S SA

.

Đáy là hình thoi

Chọn hệ trục như hình vẽ,

1.

a 

Tọa độ

 

0;0;0O

,

 

;0;0 ,A OA

   

0; ;0 , ;0;0B OB C OC

 



0; ;0 , ;0;

SA

D OD S OA OH



 



 

 

.

Đáy là hình thang vuông

Chọn hệ trục như hình vẽ,

1.

a 

Tọa độ

 

0;0;0A O

,

   

0; ;0 , ; ;0 ,B AB C AH AB

   

;0;0 , 0;0; .D AD S SA

ỨNG DỤNG HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN

Chuyên đề 32

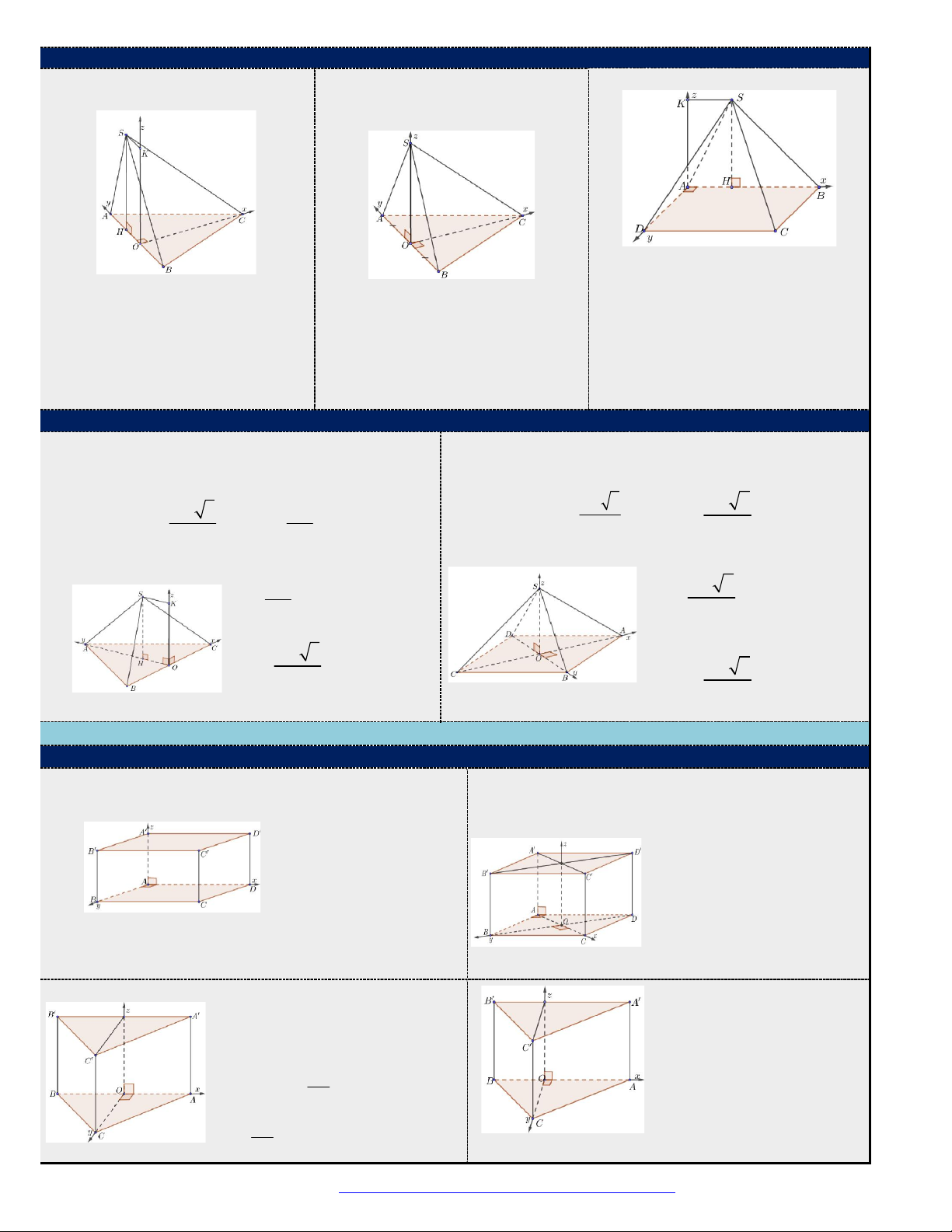
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

1.2. Hình chóp có mặt bên (SAB) vuông góc với mặt đáy

Đáy là tam giác, mặt bên là tam

giác thường

Vẽ đường cao CO trong

ABC

.

Chọn hệ trục như hình, a = 1.

Ta có:

   

0;0;0 , 0; ;0 ,O A OA

   



0; ;0 , ;0;0 , 0; ;

SH

B OB C OC S OH OK



 



 

 

Đáy là tam giác cân tại C (hoặc

đều), mặt bên là tam giác cân tại S

(hoặc đều)

Gọi O là trung điểm BC, chọn hệ

trục như hình, a = 1.

Ta có:

   

0;0;0 , 0; ;0 ,O A OA

     

0; ;0 , ;0;0 , 0;0;

B OB C OC S SO



Đáy là hình vuông-hình chữ nhật

Dựng hệ trục như hình, chọn a = 1.

Ta có:

   

0;0;0 , ;0;0A O B AB

   



; ;0 , 0; ;0 , ;0;

SH

C AB AD D AD S AH AK



 

 

 

1.3. Hình chóp đều

Hình chóp tam giác đều

Gọi O là trung điểm một cạnh đáy. Dựng hệ trục như

hình vẽ và a = 1. Tọa độ điểm:

 

0;0;0 ,O

3

0; ;0

2

AB

A

 

 

 

,

;0;0

2

BC

B

 



 

 

,

;0;0

2

BC

C

 

 

 

,



3

0; ;

6

SH

OH

AB

S OK





 

 

 

.

Hình chóp tứ giác đều

Chọn hệ trục như hình với a = 1. Tọa độ

điểm:

 

0;0;0 ,O

2

;0;0 ,

2

OA

AB

A





 

 

 

2

0; ;0

2

OB

AB

B





 

 

 

,

2

;0;0 ,

2

OA

AB

C





 

 



 

 

2

0; ;0

2

OB

AB

D



 

 



 

 



 

0;0;S SO

.

2. Gắn tọa độ đối với hình lăng trụ

2.1. Lăng trụ đứng

Hình lập phương, hình hộp chữ nhật

Dựng hệ trục như hình vẽ với a = 1. Tọa độ điểm:

 

0;0;0 ,A O

 

0; ;0 ,B AB

 

; ;0

C AD AB

,

 

;0;0D AD

,

 

0;0; ,A AA

 

 

0; ; ,B AB AA

 

 

; ;C AD AB AA

 

,

 

;0; .D AD AA

 

Lăng trụ đứng đáy là hình thoi

Gọi O là tâm hình thoi đáy, ta dựng hệ trục như hình

với

 

0;0;0 ,O

 

;0;0 ,A OA

 

0; ;0 ,B OB

 

;0;0 ,

C OC

 

0; ;0 ,D OD

 

;0; ,A OA AA

 



 

0; ; ,B OB AA

 

 

;0; ,C OC CC

 

 

0; ;D OD DD

 



Lăng trụ tam giác đều

Gọi O là trung điểm một cạnh

đáy, chọn hệ trục như hình vẽ với

a = 1. Ta có:

 

0;0;0 ,O

;0;0 ,

2

AB

A

 

 

 

;0;0 ,

2

AB

B

 



 

 

 

0; ;0 ,C OC

Lăng trụ đứng có đáy tam

giác thường

Vẽ đường cao CO trong tam

giác ABC và chọn hệ trục

như hình vẽ với a = 1.

Tọa độ điểm là:

 

0;0;0 ,O

 

;0;0 ,A OA

 

;0;0 ,B OB

 

0; ;0 ,C OC

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3

 

;0; ,A OA AA

 

;0; ,

2

AB

B BB

 

 



 

 

 

0; ; .C OC CC

 

 

;0; ,A OA AA

 

 

;0; ,B OB BB

 



 

0; ; .C OC CC

 

2.2. Lăng trụ nghiêng:

Lăng trụ nghiêng có đáy là tam giác đều, hình chiếu

của đỉnh trên mặt phẳng đối diện là trung điểm một

cạnh tam giác đáy

Dựng hệ trục như hình vẽ, ta dễ dàng xác định được các

điểm

, , , ,O A B C A

  

.

Tìm tọa độ các điểm còn lại thông qua hệ thức vectơ

bằng nhau:

AA BB CC

  

 

  

.

Lăng trụ nghiêng có đáy là hình vuông hoặc hình

chữ nhật, hình chiếu của một đỉnh là một điểm

thuộc cạnh đáy không chứa đỉnh đó

Dựng hệ trục như hình vẽ, ta dễ dàng xác định được

các điểm

, , , , ,O A B C D A

   

.

Tìm tọa độ các điểm còn lại thông qua hệ thức vectơ

bằng nhau:

AA BB CC DD

   

  

   

.

Dạng 1. Ứng dụng hình học giải tích OXYZ để giải quyết bài toán tìm GÓC

Câu 1. (Mã 103 2018) Cho hình lập phương

.ABCD A B C D

   

có tâm

O

. Gọi

I

là tâm của hình vuông

A B C D

   

và điểm

M

thuộc đoạn

OI

sao cho

2MO MI

(tham khảo hình vẽ). Khi đó sin của

góc tạo bởi hai mặt phẳng

 

MC D

 

và

 

MAB

bằng

A.

7 85

85

B.

17 13

65

C.

6 85

85

D.

6 13

65

Câu 2. (Mã 102 2018) Cho hình lập phương

.ABCD A B C D

   

có tâm

.O

Gọi

I

là tâm của hình vuông

A B C D

   

và

M

là điểm thuộc đoạn thẳng

OI

sao cho

1

2

MO MI

(tham khảo hình vẽ). Khi đó

cosin của góc tạo bởi hai mặt phẳng

( )MC D

 

và

( )MAB

bằng

A.

6 13

.

65

B.

7 85

.

85

C.

6 85

.

85

D.

17 13

.

65

Câu 3. (THPT Hùng Vương Bình Phước 2019) Cho hình hộp chữ nhật

.ABCD A B C D

   

, có

, 2,AB a AD a 

góc giữa

A C



và mặt phẳng

 

ABCD

bằng

30

. Gọi

H

là hình chiếu vuông

góc của

A

trên

A B



và

K

là hình chiếu vuông góc của

A

trên

.A D



Tính góc giữa hai mặt

phẳng

 

AHK

và

 

ABB A

 

.

A.

60

. B.

45

. C.

90

. D.

30

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 4. (THPT Lương Thế Vinh Hà Nội 2019) Cho hình chóp

.

S ABCD

có đáy

ABCD

là hình vuông

cạnh

a

,

SAB

là tam giác đều và

 

SAB

vuông góc với

 

ABCD

. Tính

cos



với



là góc tạp

bởi

 

SAC

và

 

SCD

.

A.

3

7

. B.

6

7

. C.

5

7

. D.

2

7

.

Câu 5. (Chuyên Sơn La 2019) Cho hình chóp tứ giác đều

.

S ABCD

có đáy

ABCD

là hình vuông cạnh

a

, tâm

O

. Gọi

M

và

N

lần lượt là trung điểm của hai cạnh

SA

và

BC

, biết

6

2



a

MN

. Khi

đó giá trị sin của góc giữa đường thẳng

MN

và mặt phẳng

 

SBD

bằng

A.

2

5

. B.

3

. C.

5

. D.

3

.

Câu 6. (THPT Lê Quý Đôn Đà Nẵng -2019) Cho hình lập phương

D. ' ' ' 'ABC A B C D

có cạnh a. Góc

giữa hai mặt phẳng

 

' '

A B CD

và

 

' 'ACC A

bằng

A.

60 .

B.

30 .

C.

45 .

D.

75 .

Câu 7. (Sở Bắc Ninh -2019) Cho hình chóp

.

O ABC

có ba cạnh

OA

,

OB

,

OC

đôi một vuông góc và

  OA OB OC a

. Gọi

M

là trung điểm cạnh

AB

. Góc tạo bởi hai vectơ



BC

và



OM

bằng

A.

135

. B.

150

. C.

120

. D.

60

.

Câu 8. (THPT Trần Phú - Đà Nẵng - 2018) Cho hình chóp

.

S ABCD

có đáy

ABCD

là hình vuông có

độ dài đường chéo bằng

2a

và

SA

vuông góc với mặt phẳng

 

ABCD

. Gọi



là góc giữa hai

mặt phẳng

 

SBD

và

 

ABCD

. Nếu

tan 2





thì góc giữa hai mặt phẳng

 

SAC

và

 

SBC

bằng

A.

30

. B.

60

. C.

45

. D.

90

.

Câu 9. (THPT Nam Trực - Nam Định - 2018) Cho hình chóp tứ giác đều

.

S ABCD

có

AB a

,

2SA a



. Gọi

G

là trọng tâm tam giác

SCD

. Góc giữa đường thẳng

BG

với đường thẳng

SA

bằng:

A.

3

arccos

5

. B.

5

arccos

5

. C.

5

arccos

3

. D.

15

arccos

5

.

Câu 10. (Chuyên Hà Tĩnh - 2018) Cho hình lăng trụ

.

ABC A B C

  

có

.

A ABC



là tứ diện đều cạnh

a

. Gọi

M

,

N

lần lượt là trung điểm của

AA



và

BB



. Tính tan của góc giữa hai mặt phẳng

 

ABC

và

 

CMN

.

A.

2

5

. B.

3 2

4

. C.

2 2

5

. D.

4 2

13

.

Câu 11. (Chuyên Lam Sơn - Thanh Hóa - 2018 ) Xét tứ diện

OABC

có

OA

,

OB

,

OC

đôi một vuông

góc. Gọi



,



,



lần lượt là góc giữa các đường thẳng

OA

,

OB

,

OC

với mặt phẳng

 

ABC

(hình vẽ).

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5

Khi đó giá trị nhỏ nhất của biểu thức

     

2 2 2

3 cot . 3 cot . 3 cotM

  

   

là

A.

48

. B.

125

. C. Số khác. D.

48 3

.

Câu 12. (Kinh Môn - Hải Dương 2019) Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

2a

, cạnh bên

SA a

và vuông góc với mặt phẳng đáy. Gọi

M

là trung điểm cạnh

SD

. Tan của

góc tạo bởi hai mặt phẳng

 

AMC

và

 

SBC

bằng

A.

5

. B.

2 5

5

. C.

3

2

. D.

2 3

3

.

Câu 13. Cho hình chóp

.S ABCD

đáy là hình thang vuông tại

A

và

B

,

, 2AB BC a AD a  

. Biết

( ), SA ABCD SA a 

. Gọi

M

và

N

lần lượt là trung điểm của

SB

và

CD

. Tính sin góc giữa

đường thẳng

MN

và mặt phẳng

( )SAC

.

A.

3 5

.

10

B.

2 5

.

5

C.

5

.

5

D.

55

.

10

Câu 14. (Chuyên Lê Quý Đôn – Điện Biên 2019) Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông

cạnh

a

, cạnh bên

2SA a

và vuông góc với mặt phẳng đáy. Gọi

M

là trung điểm cạnh

.SD

Tính tang của góc tạo bởi hai mặt phẳng

 

AMC

và

 

SBC

bằng

A.

3

.

2

B.

2 3

.

3

C.

5

.

5

D.

2 5

.

5

O

C

B

A

S

M

A

C

B

D

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 15. Cho khối tứ diện

ABCD

có

3BC 

,

4CD 

,



0

90ABC ADC BCD   . Góc giữa đường

thẳng

AD

và

BC

bằng

0

60

. Côsin góc giữa hai phẳng

 

ABC

và

 

ACD

bằng

A.

43

86

. B.

4 43

43

. C.

2 43

43

. D.

43

.

Câu 16. Cho hình chóp

.S ABCD

có

ABCD

là hình vuông cạnh

a

,

 

SA ABCD

và

SA a

. Gọi

E

và

F

lần lượt là trung điểm của

SB

,

SD

. Côsin của góc hợp bới hai mặt phẳng

 

AEF

và

 

ABCD

là.

A.

1

2

. B.

3

. C.

3

. D.

3

2

.

Câu 17. Cho hình lập phương

. ' ' ' 'ABCD A B C D

có cạnh bằng

,a

gọi



là góc giữa đường thẳng

'A B

và mặt phẳng

 

' ' .BB D D

Tính

sin



.

A.

3

.

5

B.

3

.

2

C.

1

.

2

D.

3

.

4

Câu 18. Cho hình lăng trụ

.ABC A B C

  

có đáy

ABC

là tam giác vuông tại

A

,

AB a

, 3AC a . Hình

chiếu vuông góc của

A



lên mặt phẳng

 

ABC

là trung điểm

H

của

BC

, 5A H a



 . Gọi



là

góc giữa hai đường thẳng

A B



và

B C



. Tính

cos



.

A.

7 3

cos

48





. B.

3

cos

2





. C.

1

cos

2





. D.

7 3

cos

24





.

Câu 19. Cho hình hộp đứng

. ' ' ' 'ABCD A B C D

có đáy là hình thoi, tam giác

ABD

đều. Gọi

, M N

lần

lượt là trung điểm của

BC

và

' 'C D

, biết rằng

'MN B D

. Gọi



là góc tạo bởi đường thẳng

MN

và mặt đáy

 

ABCD

, khi đó

cos



bằng:

A.

1

cos

3





. B.

3

cos

2





. C.

1

cos

10





. D.

1

cos

2





.

Dạng 2. Ứng dụng hình học giải tích OXYZ để giải quyết bài toán tìm KHOẢNG CÁCH

Câu 20. (Chuyên Lê Quý Đôn Quảng Trị 2019) Cho hình hộp chữ nhật

.ABCD A B C D

   

có các kích

thước

4, 3, 5AB AD AA



  

. Khoảng cách giữa hai đường thẳng

'AC

và

'B C

bằng

A.

3

2

. B.

2

. C.

5 2

3

. D.

30

19

.

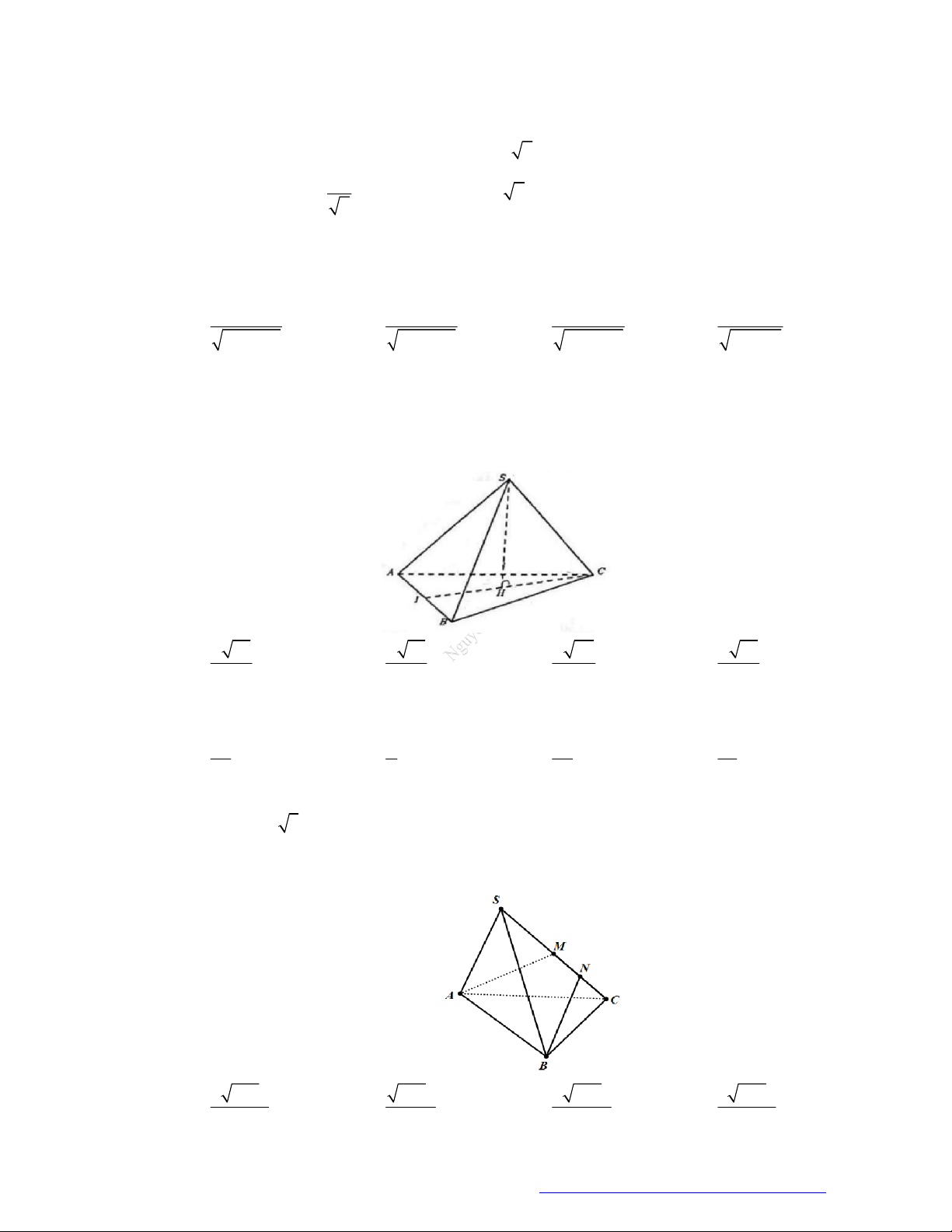
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7

Câu 21. (Việt Đức Hà Nội 2019) Trong không gian với hệ tọa độ

Oxyz

, cho hình chóp

.S ABCD

, đáy

ABCD

là hình chữ nhật. Biết

 

0;0;0A

,

 

2;0;0D

,

 

0;4;0B

,

 

0;0;4S

. Gọi

M

là trung điểm

của

SB

. Tính khoảng cách từ

B

đến mặt phẳng

 

CDM

.

A.

 

, 2d B CDM 

. B.

 

, 2 2d B CDM 

.

C.

 

1

,

2

d B CDM  . D.

 

, 2d B CDM 

.

Câu 22. (HSG Bắc Ninh 2019) Cho hình lăng trụ đứng

.ABC A B C

  

có đáy

ABC

là tam giác vuông cân,

AB AC a 

,

AA h





 

, 0a h 

. Tính khoảng cách giữa hai đường thẳng chéo nhau

AB



và

BC



theo

a

,

h

.

A.

2 2

5

ah

a h

. B.

2 2

5

ah

a h

. C.

2 2

2

ah

a h

. D.

2 2

ah

a h

.

Câu 23. (Cụm Liên Trường Hải Phòng 2019) Cho hình chóp

.S ABC

có đáy là tam giác đều cạnh bằng

a

. Gọi

I

là trung điểm của

AB

, hình chiếu của

S

lên mặt phẳng

 

ABC

là trung điểm của

CI

,

góc giữa

SA

và mặt đáy bằng

0

45

(hình vẽ bên). Gọi

G

là trọng tâm tam giác

SBC

. Khoảng

cách giữa hai đường thẳng

SA

và

CG

bằng

A.

21

14

a

B.

14

8

a

C.

77

22

a

D.

21

7

a

Câu 24. (Chuyên Lê Quý Đôn - Đà Nẵng 2018) Cho hình lập phương

.ABCD A B C D

   

cạnh bằng

a

.

Gọi

K

là trung điểm

DD



. Tính khoảng cách giữa hai đường thẳng

CK

và

A D



.

A.

4

3

a

. B.

3

a

. C.

2

3

a

. D.

3

4

a

.

Câu 25. (THPT Hoàng Hoa Thám - Hưng Yên 2019) Cho hình chóp

S.ABC

có đáy

ABC

là tam giác

đều cạnh

2 3a

, mặt bên

SAB

là tam giác cân với



0

120ASB 

và nằm trong mặt phẳng vuông

góc với đáy. Gọi

M

là trung điểm của

SC

và

N

là trung điểm của

MC

. Tính khoảng cách giữa

hai đường thẳng

AM

,

BN

.

A.

2 327

79

a

. B.

237

79

a

. C.

2 237

79

a

. D.

5 237

316

a

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 8 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 26. (Chuyên - Vĩnh Phúc - 2019) Cho hình chóp

.S ABC

có đáy

ABC

là tam giác vuông

tại

A

,

1cmAB 

, 3cmAC  . Tam giác

SAB

,

SAC

lần lượt vuông tại

B

và

C

. Khối cầu ngoại

tiếp hình chóp

.S ABC

có thể tích bằng

3

5 5

cm

6



. Tính khoảng cách từ

C

tới

 

SAB

.

A.

3

cm

2

. B.

5

cm

4

. C.

3

4

cm

. D.

5

cm

2

.

Câu 27. (Chuyên Lam Sơn 2019) Một phần sân trường được định vị bởi các điểm

A

,

B

,

C

,

D

như

hình vẽ.

Bước đầu chúng được lấy “ thăng bằng” để có cùng độ cao, biết

ABCD

là hình thang vuông ở

A

và

B

với độ dài

25mAB 

,

15mAD 

,

18mBC 

. Do yêu cầu kĩ thuật, khi lát phẳng phần sân

trường phải thoát nước về góc sân ở

C

nên người ta lấy độ cao ở các điểm

B

,

C

,

D

xuống thấp

hơn so với độ cao ở

A

là

10cm

,

cma

,

6cm

tương ứng. Giá trị của

a

là số nào sau đây?

A.

15,7cm

. B.

17,2cm

. C.

18,1cm

. D.

17,5cm

.

Câu 28. (Chuyên Bắc Giang 2019) Cho tứ diện

OABC

, có

, ,OA OB OC

đôi một vuông góc và

5, 2, 4OA OB OC  

. Gọi

,M N

lần lượt là trung điểm của

OB

và

OC

. Gọi

G

là trọng tâm

của tam giác

ABC

. Khoảng cách từ

G

đến mặt phẳng

 

AMN

là:

A.

20

.

3 129

B.

20

.

129

C.

1

.

4

D.

1

.

2

Câu 29. Cho hình lăng trụ

. ' ' 'ABC A B C

có đáy là tam giác đều cạnh

a

, gọi

M

là trung điểm của

AB

,

'A CM

cân tại

'A

và nằm trong mặt phẳng vuông góc với đáy. Biết thể tích khối lăng trụ bằng

3

4

a

. Khoảng cách giữa hai đường thẳng

AB

và

'CC

A.

57

19

a

. B.

2 57

19

a

. C.

2 39

13

a

. D.

2 39

3

a

.

Câu 30. (Sở Nam Định 2019) Cho hình chóp

.S ABCD

đáy là hình thang vuông tại

A

và

D

,

 

SA ABCD

. Góc giữa

SB

và mặt phẳng đáy bằng

o

45

,

E

là trung điểm của

SD

,

2AB a

,

AD DC a 

. Tính khoảng cách từ điểm

B

đến mặt phẳng

 

ACE

.

A.

2

3

a

. B.

4

3

a

. C.

a

. D.

3

4

a

.

Dạng 3. Ứng dụng hình học giải tích OXYZ để giải quyết bài toán tìm THỂ TÍCH, BÁN

KÍNH

Câu 31. (Mã 102 2018) Trong không gian

,Oxyz

cho mặt cầu

 

S

có tâm

 

1;2;1I 

và đi qua điểm

 

1;0; 1 .A 

Xét các điểm

, ,B C D

thuộc

 

S

sao cho

, ,AB AC AD

đôi một vuông góc với nhau.

Thể tích của khối tứ diện

ABCD

có giá trị lớn nhất bằng

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9

A.

64

B.

32

3

C.

64

3

D.

32

Câu 32. (Mã 104 2018) Trong không gian

Oxyz

, cho mặt cầu

 

S

có tâm

 

1;0;2

I 

và đi qua điểm

 

0;1;1

A

. Xét các điểm

B

,

C

,

D

thuộc

 

S

sao cho

AB

,

AC

,

AD

đôi một vuông góc với

nhau. Thể tích của khối tứ diện

ABCD

có giá trị lớn nhất bằng

A.

8

3

B.

4

C.

4

3

D.

8

Câu 33. (Chuyên Hùng Vương Gia Lai 2019) Trong không gian

Oxyz

, cho hình hộp chữ nhật

.

ABCD A B C D

   

có

A

trùng với gốc tọa độ

O

, các đỉnh

( ;0;0)

B a

,

(0; ;0)D a

,

(0;0; )A b



với

, 0

a b



và

2

a b

 

. Gọi

M

là trung điểm của cạnh

CC



. Thể tích của khối tứ diện

BDA M



có

giá trị lớn nhất bằng

A.

64

27

. B.

32

27

. C.

8

27

. D.

4

27

.

Câu 34. (THPT-Thang-Long-Ha-Noi- 2019) Cho hình lập phương

.

ABCD A B C D

   

cạnh

a

. Gọi

,M N

lần lượt là trung điểm của

BC

và

A B

 

. Mặt phẳng

 

'MND

chia khối lập phương thành hai khối

đa diện, trong đó khối chứa điểm

C

gọi là

 

H

. Tính thể tích khối

 

H

.

A.

3

55

72

a

. B.

3

55

144

a

. C.

3

181

486

a

. D.

3

55

48

a

.

Câu 35. (Chuyên Thăng Long - Đà Lạt - 2018) Trong không gian với hệ trục tọa độ

,Oxyz

cho hình hộp

chữ nhật

.

ABCD A B C D

   

có

A

trùng với gốc tọa độ

O

các đỉnh

     

;0;0 , 0; ;0 , 0;0;B m D m A n



với

, 0

m n



và

4.

m n

 

Gọi

M

là trung điểm của cạnh

.CC



Khi đó thể tích tứ diện

BDA M



đạt giá trị lớn nhất bằng

A.

9

4

. B.

64

27

. C.

75

32

. D.

245

108

.

Câu 36. (Nho Quan A - Ninh Bình - 2019) Cho hình lập phương

.

ABCD A B C D

   

có độ dài cạnh bằng

1

. Gọi

, , ,M N P Q

lần lượt là trung điểm của

, , ,

AB BC C D DD

  

. Gọi thể tích khối tứ diện

MNPQ

là phân số tối giản

a

b

, với

*

,a b 



. Tính

a b

.

A.

9

. B.

25

. C.

13

. D.

11

.

Câu 37. Trong không gian

Oxyz

,tập hợp tất cả các điểm thỏa mãn

2

x y z

  

và

2 2

x y z

   

là một khối đa diện có thể tích bằng

A.

3

. B.

2

. C.

8

3

. D.

4

3

.

Câu 38. (Thi thử cụm Vũng Tàu - 2019) Cho hình hộp chữ nhật

. '

  

ABCD A B C D

có

1; 2; 3



  

AB AD AA

. Mặt phẳng

( )P

đi qua

C



và cắt các tia

; ;

AB AD AA



lần lượt tại

; ;E F G

(khác

A

) sao cho thể tích khối tứ diện

AEFG

nhỏ nhất. Tổng của

AE AF AG 

bằng.

A.

18

. B.

17

. C.

15

. D.

16

.

Câu 39. (Chuyên Nguyễn Du-ĐăkLăk 2019) Cho tứ diện đều

ABCD

cạnh

a

. Gọi

K

là trung điểm

AB

, gọi

,M N

lần lượt là hình chiếu vuông góc của

K

lên

,AD AC

. Tính theo

a

bán kính mặt

cầu ngoại tiếp hình chóp

.

K CDMN

.

A.

3

4

a

. B.

2

4

a

. C.

3 3

8

a

. D.

3 2

8

a

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 10 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 40. (Chuyên Thái Bình -2019) Cho hình chóp

.

S

ABCD

có đáy

AB

CD

là hình vuông cạnh

a

,

SAD

là tam giác đều và nằm trong mặt phẳng với đáy. Gọi

M

và

N

lần

lượt là trung điểm của

BC

và

C

D

. B

án kính của mặt cầu ngoại tiếp hình chóp

.

S

CMN

bằng

A.

9

3

12

a

. B.

2

9

8

a

. C

.

5

3

12

a

. D

.

3

7

6

a

.

Câu

41. (Chuyên KHTN - 2018) Trong không gian với hệ tọa độ

Oxyz

,

cho hai điểm

 

5

;0;0

A

và

 

3

;4;0

B

.

Với

C

là

điểm nằm trên trục

Oz

,

gọi

H

l

à trực tâm của tam giác

AB

C

.

Khi

C

di

động trên trục

Oz

t

hì

H

luôn t

huộc một đường tròn cố định. Bán kính của đường tròn đó bằng

A.

5

4

. B.

3

2

. C

.

5

2

. D

.

3

.

Câu

42. (Chuyên Vinh - 2018) Trong không gian

,Ox

yz

cho

các điểm

A

,

B

,

C

(không

trùng

O

)

lần

lượt thay đổi trên các trục

O

x

,

Oy

,

Oz

và luôn thỏa mãn điều kiện: tỉ số giữa diện tích của tam

giác

AB

C

và

thể tích khối tứ diện

OA

BC

bằng

3

.

2

Biết rằng mặt phẳng

 

ABC

l

uôn tiếp xúc với

một mặt cầu cố định, bán kính của mặt cầu đó bằng

A.

3

.

B.

2

.

C

.

4

.

D

.

1.

Câu

43. (Chuyên Lê Hồng Phong - TPHCM - 2018) Trong không gian với hệ tọa độ

Oxyz

,

cho

3

đường

thẳng

 

1

1 1 1

:

2

1 2

x y z

d

  

 



,

 

2

3 1 2

:

1

2 2

x y z

d

  

 

,

 

3

4 4 1

:

2

2 1

x y z

d

  

 



.

Mặt cầu bán kính nhỏ nhất tâm

 

;

;I a b c

, tiếp xúc với

3

đường thẳng

 

1

d

,

 

2

d

,

 

3

d

. Tính

2 3S a b c  

.

A.

1

0

S



. B.

1

S



. C

.

1

2

S



. D

.

1

3

S



.

Câu

44. Cho hình chóp

.

S

ABCD

c

s đáy là hình thang vuông tại

A

v

à

B

,

2

2 2AD AB BC a  

,

cạnh

bên

S

A

vuông

góc với mặt phẳng đáy,

2S

A a

.

Gọi

E

là

trung điểm cạnh

A

D

.

Tính bán kính

mặt cầu ngoại tiếp hình chóp

.

S

CDE

.

A.

3

2

a

. B.

1

2

a

. C

.

6

2

a

. D.

3

4

a

.

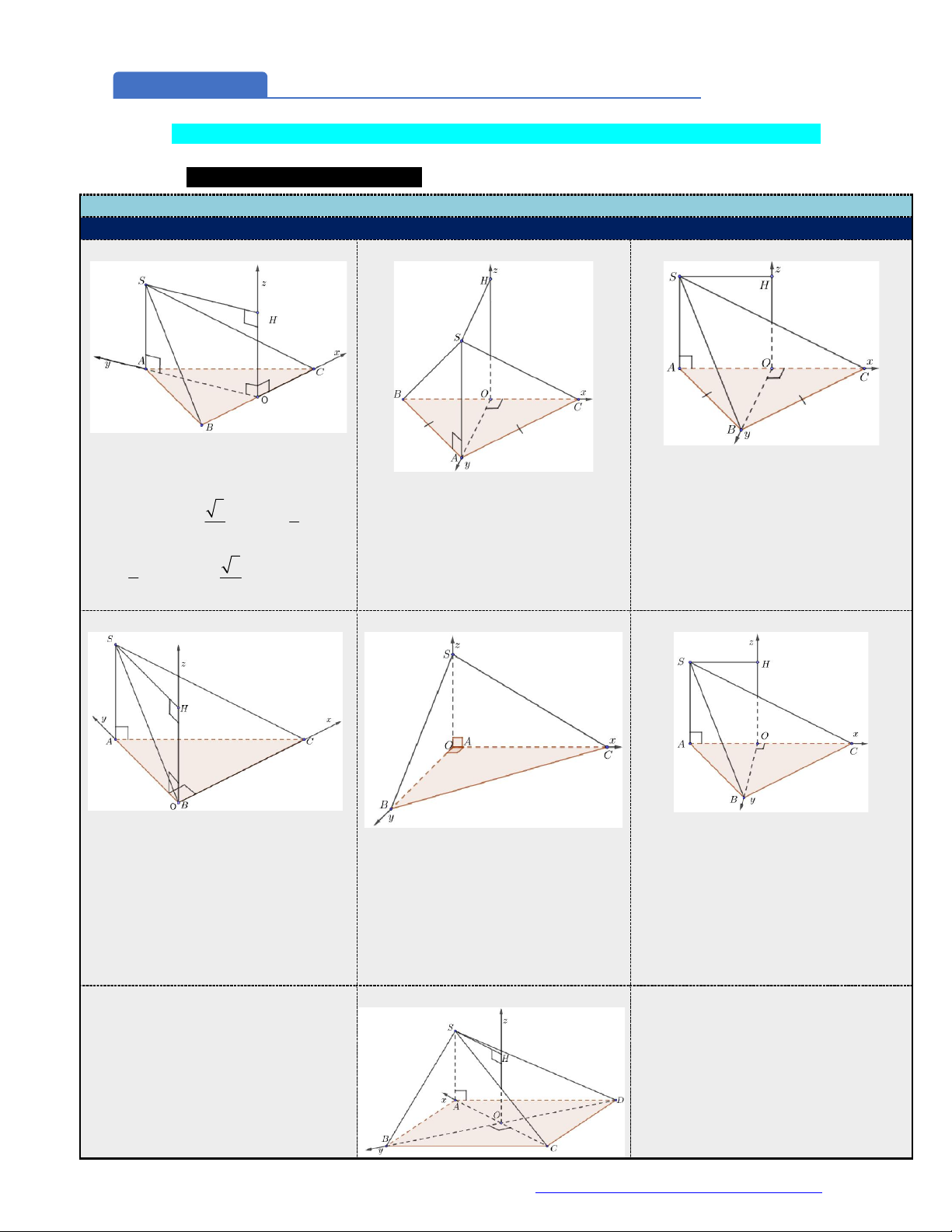
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương  https://www.facebook.com/phong.baovuong Trang 1

TÀI LIỆU DÀNH CHO ĐỐI TƯỢNG HỌC SINH KHÁ GIỎI MỨC ĐỘ 8-9-10 ĐIỂM

Phương pháp giải một số bài toán

1. Gắn tọa độ đối với hình chóp

1.1. Hình chóp có cạnh bên (SA) vuông góc với mặt đáy:

Đáy là tam giác đều

 Gọi O là trung điểm BC. Chọn hệ

trục như hình vẽ,

1AB a 

.

 Tọa độ các điểm là:

3 1

(0;0;0), 0; ;0 , ;0;0 ,

2 2

O A B

 



 

 



1 3

;0;0 , 0; ;

2 2

SA

C S OH



 

 

 

.

Đáy là tam giác cân tại A

 Gọi O là trung điểm BC. Chọn hệ

trục như hình vẽ,

1a 

.

 Tọa độ các điểm là:

   

(0;0;0), 0; ;0 , ;0;0 ,

O A OA B OB

 



;0;0 , 0; ;

SA

C OC S OA OH



 

 

 

.

Đáy là tam giác cân tại B

 Gọi O là trung điểm AC. Chọn hệ

trục như hình vẽ,

1a 

.

 Tọa độ các điểm:

 

0;0;0O

,

   

;0;0 , 0, ;0 ,A OA B OB

 



;0;0 , ;0;

SA

C OC S OA OH



 



 

 

.

Đáy là tam giác vuông tại B

 Chọn hệ trục như hình vẽ,

1a 

.

 Tọa độ các điểm:

 

0;0;0B O

,

   

0; ;0 , ,0;0 ,A AB C BC



0; ;

SA

S AB BH



 

 

 

.

Đáy là tam giác vuông tại A

 Chọn hệ trục như hình vẽ,

1

a 

.

 Tọa độ các điểm:

 

0;0;0A O

,

   

0; ;0 , ;0;0 ,B OB C AC

 

0;0;S SA

.

Đáy là tam giác thường

 Dựng đường cao BO của

.ABC

Chọn hệ trục như hình vẽ,

1a 

.

 Tọa độ các điểm:

 

0;0;0O

,

   

;0;0 , 0, ;0 ,A OA B OB

 



;0;0 , ;0;

SA

C OC S OA OH



 



 

 

.

Đáy là hình vuông, hình chữ nhật Đáy là hình thoi

Đáy là hình thang vuông

ỨNG DỤNG HÌNH HỌC GIẢI TÍCH TRONG KHÔNG GIAN

Chuyên đề 32

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

 Chọn hệ trục như hình vẽ,

1.

a 

 Tọa độ

 

0;0;0A O

,

 

0; ;0 ,

B AB

     

; ;0 , ;0;0 , 0;0;C AD AB D AD S SA

.

 Chọn hệ trục như hình vẽ,

1.

a



 Tọa độ

 

0;0;0O

,

 

;0;0 ,A OA

   

0; ;0 , ;0;0B OB C OC

 



0; ;0 , ;0;

SA

D OD S OA OH



 



 

 

.

 Chọn hệ trục như hình vẽ,

1.

a 

 Tọa độ

 

0;0;0A O

,

   

0; ;0 , ; ;0 ,B AB C AH AB

   

;0;0 , 0;0; .D AD S SA

1.2. Hình chóp có mặt bên (SAB) vuông góc với mặt đáy

Đáy là tam giác, mặt bên là tam

giác thường

 Vẽ đường cao CO trong

ABC

.

Chọn hệ trục như hình, a = 1.

 Ta có:

   

0;0;0 , 0; ;0 ,O A OA

   



0; ;0 , ;0;0 , 0; ;

SH

B OB C OC S OH OK



 



 

 

Đáy là tam giác cân tại C (hoặc

đều), mặt bên là tam giác cân tại S

(hoặc đều)

 Gọi O là trung điểm BC, chọn hệ

trục như hình, a = 1.

 Ta có:

   

0;0;0 , 0; ;0 ,O A OA

     

0; ;0 , ;0;0 , 0;0;

B OB C OC S SO



Đáy là hình vuông-hình chữ nhật

 Dựng hệ trục như hình, chọn a = 1.

 Ta có:

   

0;0;0 , ;0;0A O B AB

   



; ;0 , 0; ;0 , ;0;

SH

C AB AD D AD S AH AK



 

 

 

1.3. Hình chóp đều

Hình chóp tam giác đều

Gọi O là trung điểm một cạnh đáy. Dựng hệ trục như

hình vẽ và a = 1. Tọa độ điểm:

 

0;0;0 ,O

3

0; ;0

2

AB

A

 

 

 

,

;0;0

2

BC

B

 



 

 

,

;0;0

2

BC

C

 

 

 

,



3

0; ;

6

SH

OH

AB

S OK





 

 

 

.

Hình chóp tứ giác đều

Chọn hệ trục như hình với a = 1. Tọa độ

điểm:

 

0;0;0 ,O

2

;0;0 ,

2

OA

AB

A





 

 

 

2

0; ;0

2

OB

AB

B





 

 

 

,

2

;0;0 ,

2

OA

AB

C





 

 



 

 

2

0; ;0

2

OB

AB

D



 

 



 

 



 

0;0;S SO

.

2.

Gắn tọa độ đối với hình lăng trụ

2.1.

Lăng trụ đứng

Hình lập phương, hình hộp chữ nhật

Dựng hệ trục như hình vẽ với a = 1. Tọa độ điểm:

Lăng trụ đứng đáy là hình thoi

Gọi O là tâm hình thoi đáy, ta dựng hệ trục như hình

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3

 

0;0;0 ,A O

 

0; ;0 ,B AB

 

; ;0

C AD AB

,

 

;0;0D AD

,

 

0;0; ,

A AA

 

 

0; ; ,

B AB AA

 

 

; ;C AD AB AA

 

,

 

;0; .D AD AA

 

với

 

0;0;0 ,O

 

;0;0 ,A OA

 

0; ;0 ,B OB

 

;0;0 ,C OC

 

0; ;0 ,

D OD

 

;0; ,

A OA AA

 



 

0; ; ,B OB AA

 

 

;0; ,C OC CC

 

 

0; ;D OD DD

 



Lăng trụ tam giác đều

Gọi O là trung điểm một

cạnh đáy, chọn hệ trục

như hình vẽ với a = 1. Ta

có:

 

0;0;0 ,O

;0;0 ,

2

AB

A

 

 

 

;0;0 ,

2

AB

B

 



 

 

 

0; ;0 ,

C OC

 

;0; ,A OA AA

 

;0; ,

2

AB

B BB

 

 



 

 

 

0; ; .C OC CC

 

Lăng trụ đứng có đáy tam giác thường

Vẽ đường cao CO

trong tam giác ABC

và chọn hệ trục như

hình vẽ với a = 1.

Tọa độ điểm là:

 

0;0;0 ,O

 

;0;0 ,

A OA

 

;0;0 ,B OB

 

0; ;0 ,C OC

 

;0; ,A OA AA

 

 

;0; ,B OB BB

 



 

0; ; .C OC CC

 

2.2. Lăng trụ nghiêng:

Lăng trụ nghiêng có đáy là tam giác đều, hình chiếu

của đỉnh trên mặt phẳng đối diện là trung điểm một

cạnh tam giác đáy

 Dựng hệ trục như hình vẽ, ta dễ dàng xác định được các

điểm

, , , ,O A B C A

  

.

 Tìm tọa độ các điểm còn lại thông qua hệ thức vectơ

bằng nhau:

AA BB CC

  

 

  

.

Lăng trụ nghiêng có đáy là hình vuông hoặc hình

chữ nhật, hình chiếu của một đỉnh là một điểm

thuộc cạnh đáy không chứa đỉnh đó

 Dựng hệ trục như hình vẽ, ta dễ dàng xác định được

các điểm

, , , , ,O A B C D A

   

.

 Tìm tọa độ các điểm còn lại thông qua hệ thức vectơ

bằng nhau:

AA BB CC DD

   

  

   

.

Dạng 1. Ứng dụng hình học giải tích OXYZ để giải quyết bài toán tìm GÓC

Câu 1. (Mã 103 2018) Cho hình lập phương

.ABCD A B C D

   

có tâm

O

. Gọi

I

là tâm của hình vuông

A B C D

   

và điểm

M

thuộc đoạn

OI

sao cho

2MO MI

(tham khảo hình vẽ). Khi đó sin của góc tạo

bởi hai mặt phẳng

 

MC D

 

và

 

MAB

bằng

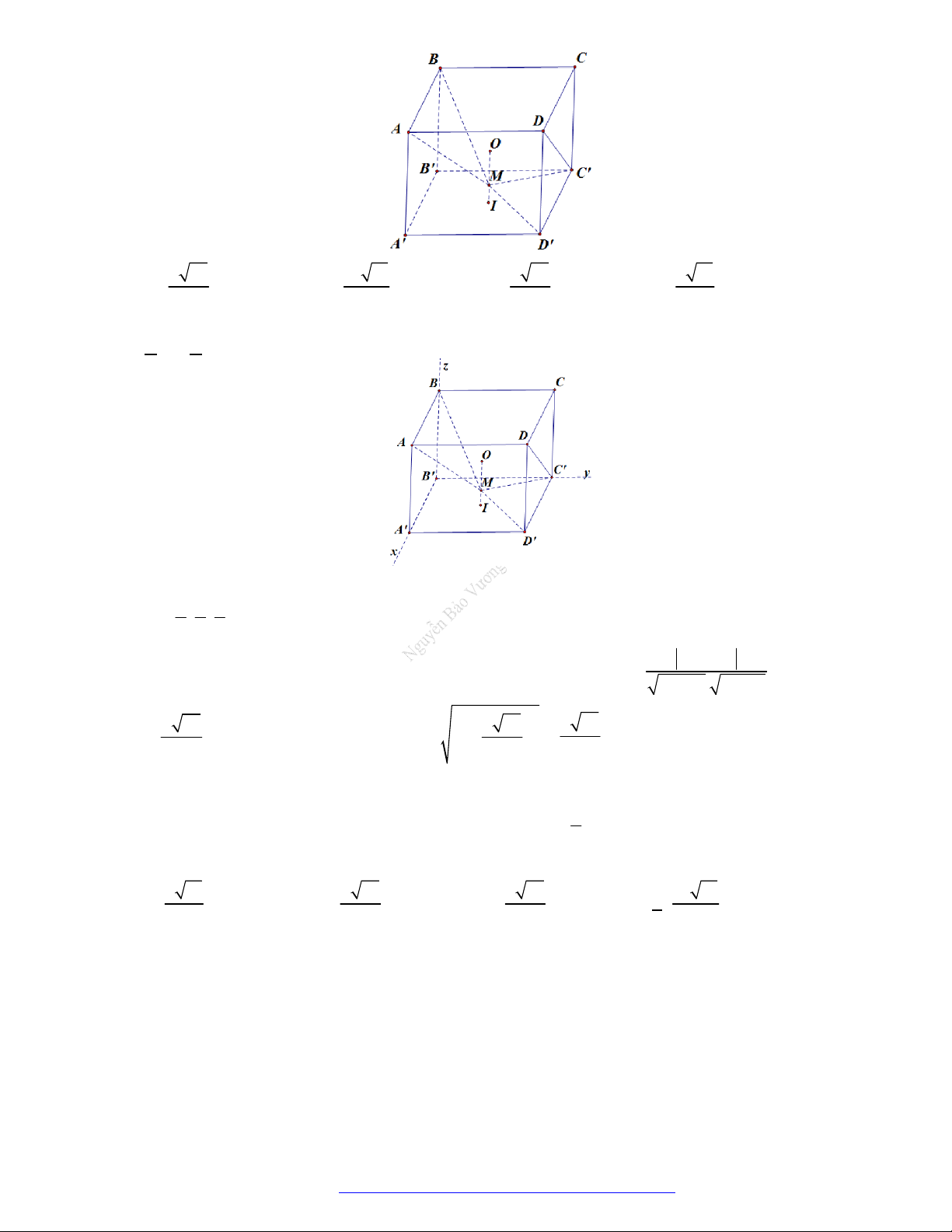
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

A.

7 85

85

B.

17 13

65

C.

6 85

85

D.

6 13

65

Lời giải

Chọn C

Gắn hệ trục tọa độ như hình vẽ, cạnh hình lập phương là

1

, ta được tọa độ các điểm như sau :

1 1 1

; ;

2 2 6

M

 

 

 

 

, 0;1;0C



 

, 1;1;0D



và

 

1;0;1A

 

, 0;0;1B

.

Khi đó

 

0;1;3

MC D

n

 





 

; 0;5;3

MAB

n 



nên

   

 



cos ,MAB MC D

 

2 2 2 2

5.1 3.3

5 3 . 1 3





 

7 85

85



. Suy ra

   

 



sin ,MAB MC D

 

2

7 85

1

85

 

 

 

 

6 85

85



.

Câu 2. (Mã 102 2018) Cho hình lập phương

.ABCD A B C D

   

có tâm

.O

Gọi

I

là tâm của hình vuông

A B C D

   

và

M

là điểm thuộc đoạn thẳng

OI

sao cho

1

2

MO MI

(tham khảo hình vẽ). Khi đó cosin

của góc tạo bởi hai mặt phẳng

( )MC D

 

và

( )MAB

bằng

A.

6 13

.

65

B.

7 85

.

85

C.

6 85

.

85

D.

17 13

.

65

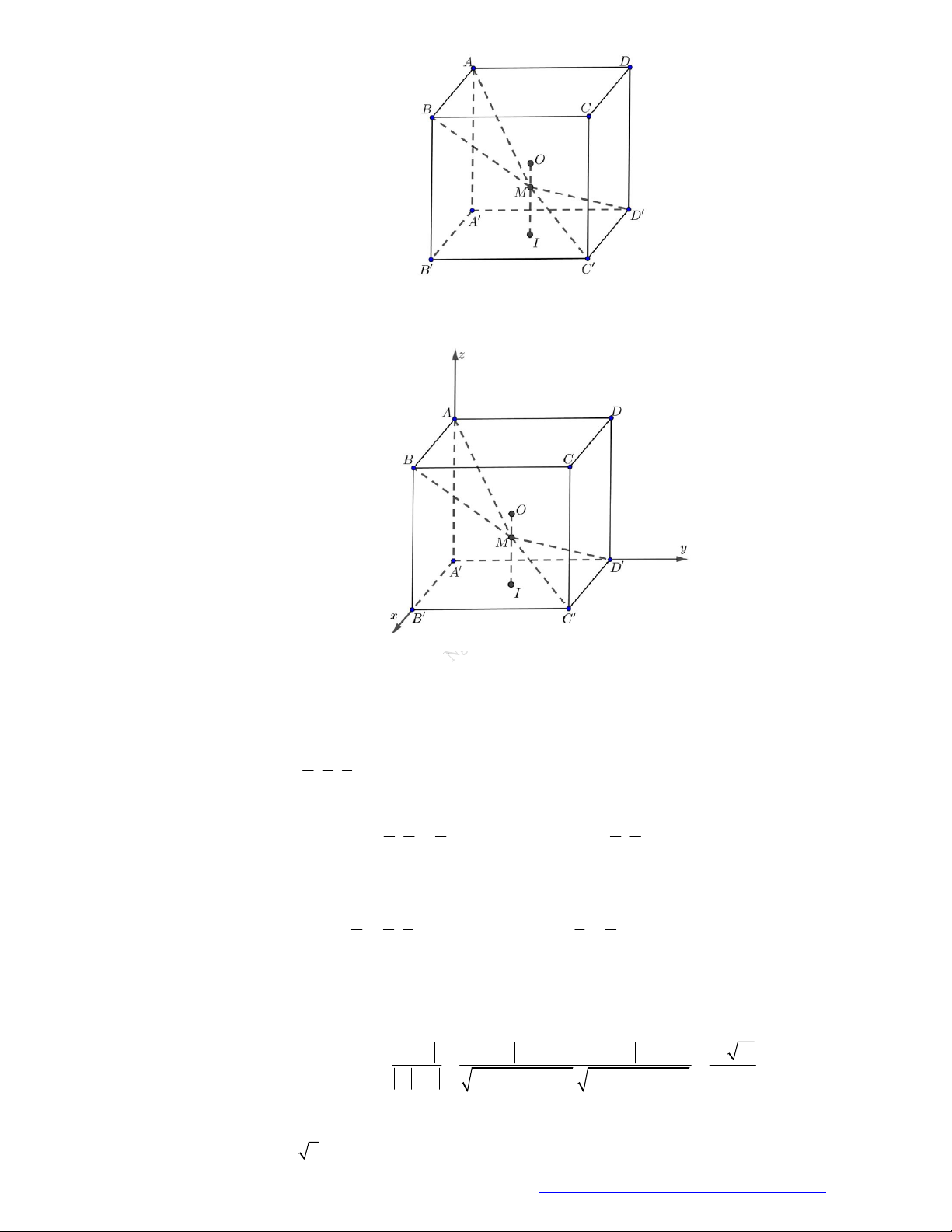
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5

Lời giải

Không mất tính tổng quát ta đặt cạnh của khối lập phương là 1.

Chọn hệ trục tọa độ sao cho

(0;0;0),A



(1;0;0),B



(0;1;0)D



và

(0;0;1)A

(như hình vẽ).

Khi đó ta có:

1 1 1

; ; .

2 2 3

M

 

 

 

Suy ra:

1 1 2

(1;0;0), ; ;

2 2 3

AB MA

 

   

 

 

 

1

2 1

, 0; ; (0; 4;3)

3 2

AB MA n

 

 

    

 

 

 

 



là VTPT của mặt

phẳng

( ).MAB

2

1 1 1 1 1

(1;0;0), ; ; , 0; ; (0;2; 3)

2 2 3 3 2

D C MD D C MD n

   

 

     

        

   

 

   

   



là VTPT của mặt

phẳng

( )MC D

 

.

cosin của góc giữa hai mặt phẳng

( )MAB

và

( )MC D

 

bằng:

1 2

2 2 2 2 2 2

1 2

. 0.0 4.2 3.( 3)

17 13

cos( , ) .

. 65

0 ( 4) 3 . 0 2 ( 3)

n n

  

  

     

 

Câu 3. (THPT Hùng Vương Bình Phước 2019) Cho hình hộp chữ nhật

.ABCD A B C D

   

, có

, 2,AB a AD a 

góc giữa

A C



và mặt phẳng

 

ABCD

bằng

30

. Gọi

H

là hình chiếu vuông góc

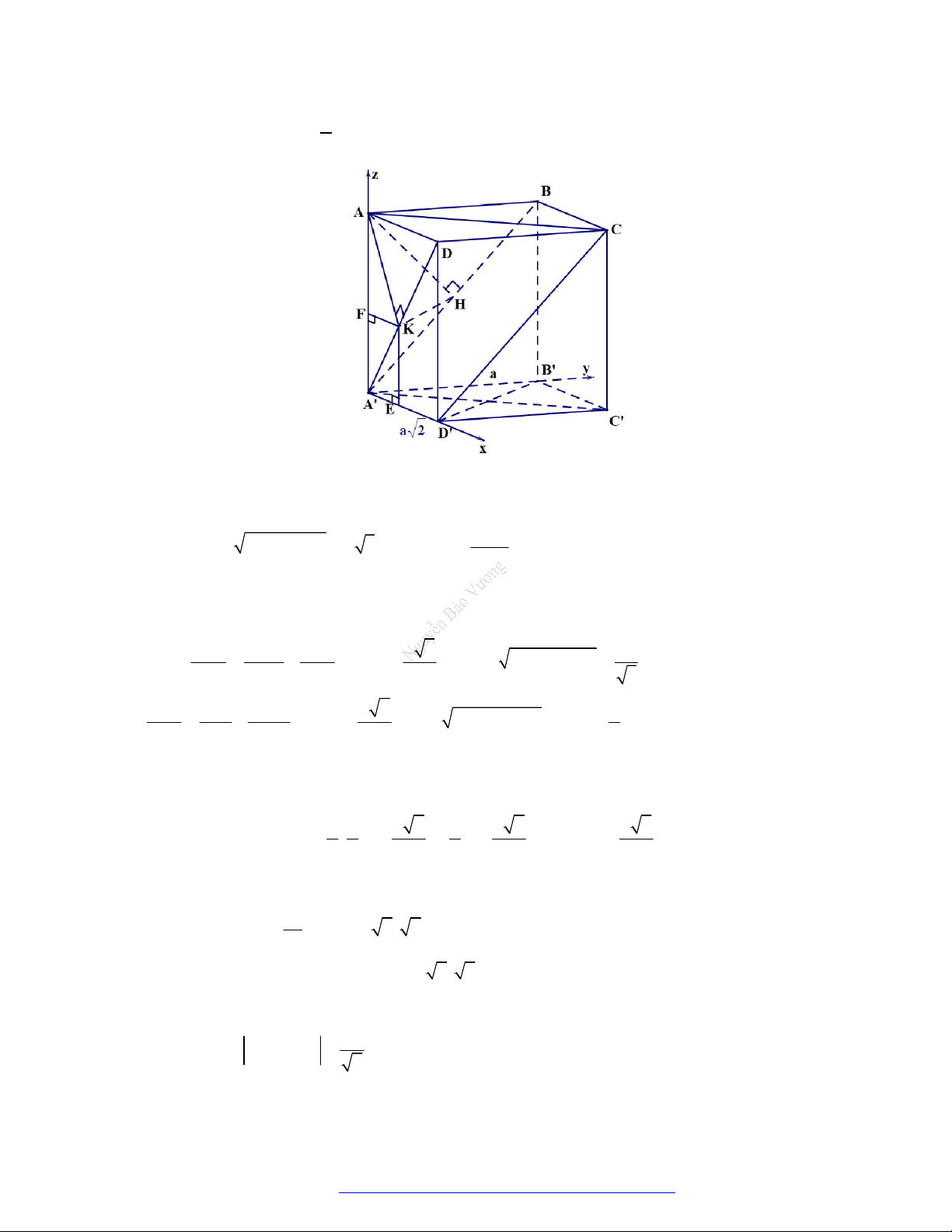
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

của

A

trên

A B



và

K

là hình chiếu vuông góc của

A

trên

.A D



Tính góc giữa hai mặt phẳng

 

AHK

và

 

ABB A

 

.

A.

60

. B.

45

. C.

90

. D.

30

.

Lời giải

Do

.ABCD A B C D

   

là hình hộp chữ nhật nên

' 'A C

là hình chiếu vuông góc của

'A C

trên



0

( ) ( ' ,( )) ( ' , ' ') ' ' 30 .ABCD A C ABCD A C A C CA C   

Ta có



2 2

'

3;tan ' ' ' .

' '

CC

AC AB AD a CA C CC a

A C

     

Kết hợp với giả thiết ta được

' 'ABB A

là hình vuông và có

H

là tâm.

Gọi

,E F

lần lượt là hình chiếu vuông góc của

K

trên

' '& ' .A D A A

Ta có

2 2 2

1 1 1 6

;

' 3

a

AK

AK A A AD

   

2 2

' ' ;

3

a

A K A A AK  

2 2

2 2 2

1 1 1 2

; ' .

' 3 3

a a

KF KE A K KF KE

KF KA A K

       

Ta chọn hệ trục tọa độ

Oxyz

thỏa mãn

'O A

còn

, , D B A

 

theo thứ tự thuộc các tia

, , .Ox Oy Oz

Khi đó ta có tọa độ các điểm lần lượt là:

2 2 2

(0;0; ), '(0; ;0), (0; ; ), ( ;0; ), ( ;0;0), (0;0; ).

2 2 3 3 3 3

a a a a a a

A a B a H K E F

Mặt phẳng

 

' 'ABB A

là mặt phẳng

( )yOz

nên có VTPT là

1

(1;0;0);n 



Ta có

2

2 2

, , (2; 2; 2).

6

a

AK AH n n

 



 

   

Mặt phẳng

( )AKH

có VTPT là

2

(2; 2; 2);n 



Gọi



là góc giữa hai mặt phẳng

 

AHK

và

 

ABB A

 

.

Ta có

0

1 2

1

( , ) 45 .

2

cos cos n n

 

   

 

Câu 4. (THPT Lương Thế Vinh Hà Nội 2019) Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

a

,

SAB

là tam giác đều và

 

SAB

vuông góc với

 

ABCD

. Tính

cos



với



là góc tạp bởi

 

SAC

và

 

SCD

.

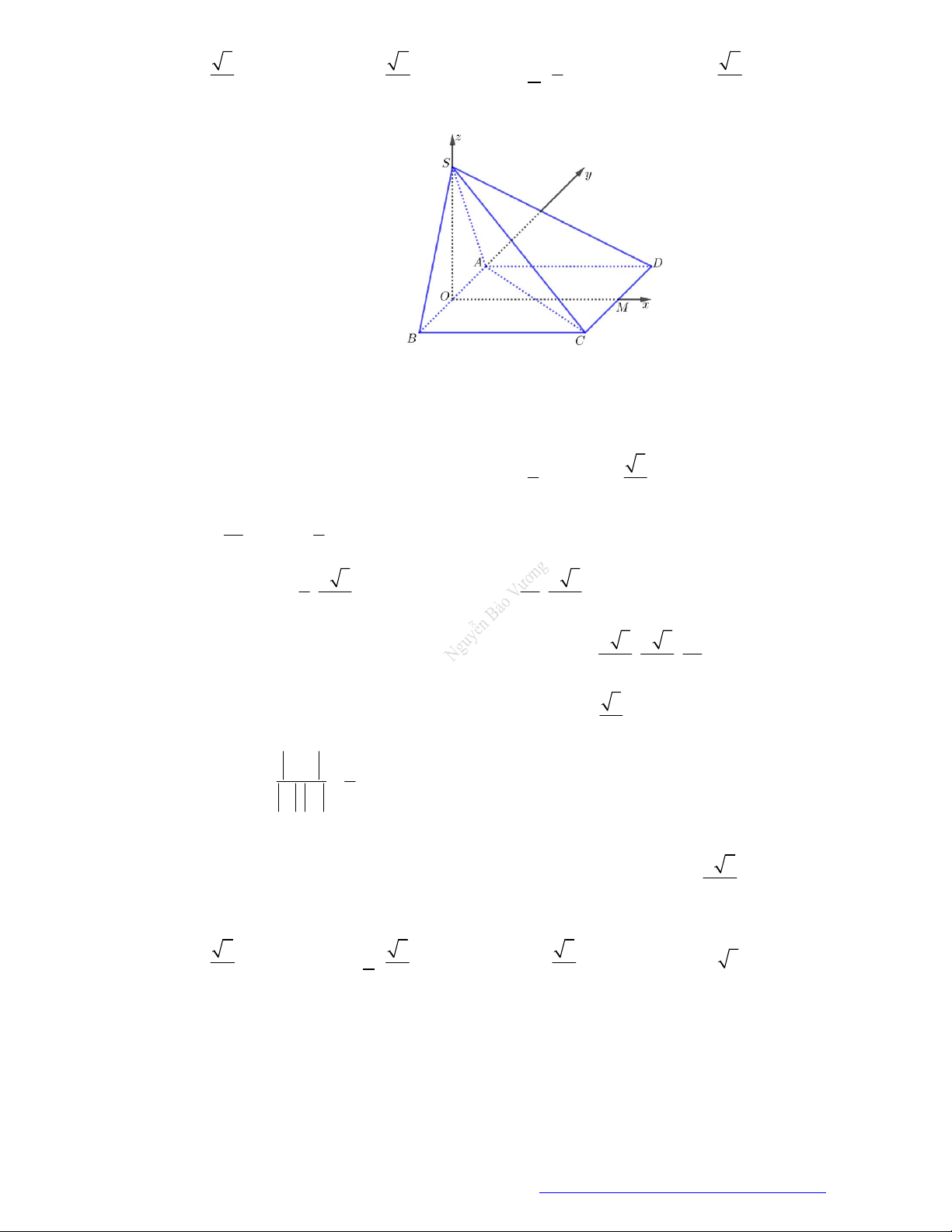
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7

A.

3

7

. B.

6

7

. C.

5

7

. D.

2

7

.

Lời giải

Chú ý: Ta có thể giải bài toán với cạnh hình vuông

1a 

.

Gọi

,O M

lần lượt là trung điểm của

,AB CD

. Vì

SAB

là tam giác đều và

 

SAB

vuông góc với

 

ABCD

nên

 

SO ABCD

.

Xét hệ trục

Oxyz

có

   

1 3

0;0;0 , 1;0;0 , 0; ;0 , 0;0;

2 2

O M A S

 

 

 

. Khi đó

1 1

1; ;0 , 1; ;0

2 2

C D



   

   

   

.

Suy ra

   

1 3 1 3

0; ; , 1; 1;0 , 1; ; , 0;1;0

2 2 2 2

SA AC SC CD

   

  

   

   

   

   

.

Mặt phẳng

 

SAC

có véc tơ pháp tuyến

1

3 3 1

, ; ;

2 2 2

n SA AC

 

  

 

 

 

 

 

 

  

.

Mặt phẳng

 

SAD

có véc tơ pháp tuyến

1

3

, ;0;1

2

n SC CD

 

 

 

 

 

 

 

  

.

Vậy

1 2

.

5

cos

7

.

n n



 

 

.

Câu 5. (Chuyên Sơn La 2019) Cho hình chóp tứ giác đều

.S ABCD

có đáy

ABCD

là hình vuông cạnh

a

, tâm

O

. Gọi

M

và

N

lần lượt là trung điểm của hai cạnh

SA

và

BC

, biết

6

2



a

MN

. Khi đó giá trị sin của

góc giữa đường thẳng

MN

và mặt phẳng

 

SBD

bằng

A.

2

5

. B.

3

. C.

5

. D.

3

.

Lời giải

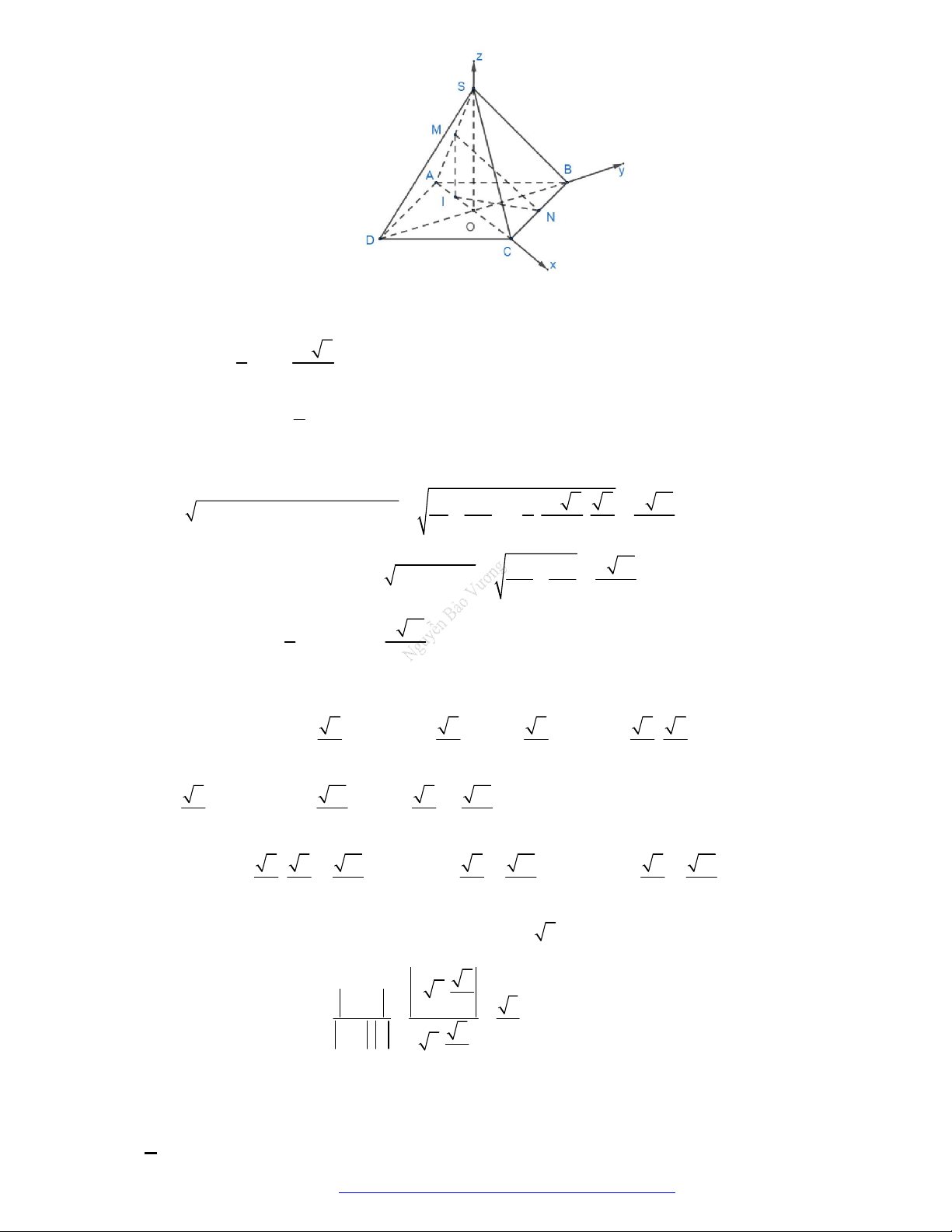
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 8 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Gọi

I

hình chiếu của

M

lên

 

ABCD

, suy ra

I

là trung điểm của

AO

.

Khi đó

3 3 2

4 4

a

CI AC 

.

Xét

CNI

có:

2

a

CN 

,



45

o

NCI 

.

Áp dụng định lý cosin ta có:

2 2

9 3 2 2 10

2 . .cos 45 2. . .

4 8 2 4 2 4

o

a a a a a

NI CN CI CN CI      

.

Xét

MIN

vuông tại

I

nên

2 2

3 5 14

2 8 4

a a a

MI MN NI     .

Mà

1 14

/ / ,

2 2

a

MI SO MI SO SO  

.

Chọn hệ trục tọa độ

Oxyz

như hình vẽ:

Ta có:

 

0;0;0O

,

2

0; ;0

2

B

 

 

 

,

2

0; ;0

2

D

 



 

 

,

2

;0;0

2

C

 

 

 

,

2 2

; ;0

4 4

N

 

 

 

,

2

;0;0

2

A

 



 

 

,

14

0;0;

4

S

 

 

 

,

2 14

;0;

4 4

M

 



 

 

.

Khi đó

2 2 14

; ;

2 4 4

MN

 

 

 

 



,

2 14

0; ;

2 2

SB

 

 

 

 



,

2 14

0; ;

2 2

SD

 

  

 

 



.

Vectơ pháp tuyến mặt phẳng

 

SBD

:

 

7 ;0;0n SB SD   

  

.

Suy ra

 

2

7.

.

2

3

sin ,

3

6

.

7.

2

MN n

MN SBD

MN n



  

 

.

Câu 6. (THPT Lê Quý Đôn Đà Nẵng -2019) Cho hình lập phương

D. ' ' ' 'ABC A B C D

có cạnh a. Góc giữa hai mặt

phẳng

 

' 'A B CD

và

 

' 'ACC A

bằng

A.

60 .

B.

30 .

C.

45 .

D.

75 .

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9

Lời giải

Chọn hệ trục tọa độ Oxyz sao cho gốc tọa độ

', ' ', ' ', ' .O A Ox A D Oy A B Oz A A   

Khi đó:

'(0; 0;0)A

,

'( ;0;0)D a

,

'(0; ;0)B a

,

'( ; ;0)C a a

,

(0;0; )A a

,

( ; 0; )D a a

,

(0; ; )B a a

,

( ; ; )C a a a

.

' ' (0; ;0), ' ( ;0; ), ' (0;0; ), ' ' ( ; ;0).A B a A D a a A A a A C a a    

   

2 2

' ', ' ( ;0; ).A B A D a a

 

 

 

 

Chọn

1

(1;0; 1)n  



là vectơ pháp tuyến của mặt phẳng

 

' 'A B CD

.

2 2

' , ' ( ; ;0).A A A C a a

 

 

 

 

Chọn

2

( 1;1;0)n  



là vectơ pháp tuyến của mặt phẳng

 

' 'ACC A

.

Góc giữa hai mặt phẳng

 

' 'A B CD

và

 

' 'ACC A

là:

 

1 2

1

cos = cos , 60 .

2

2. 2

n n

 



    

 

Câu 7. (Sở Bắc Ninh -2019) Cho hình chóp

.O ABC

có ba cạnh

OA

,

OB

,

OC

đôi một vuông góc và

  OA OB OC a

. Gọi

M

là trung điểm cạnh

AB

. Góc tạo bởi hai vectơ



BC

và



OM

bằng

A.

135

. B.

150

. C.

120

. D.

60

.

Lời giải

Cách 1:

Ta có

 

2

1

2

.

2 2



 



    





 



  

 

  

OM OA OB

a

OM BC OB

BC OC OB

.

2 2

2  BC OB OC a

và

2 2

1 1 2

2 2 2

   

a

OM AB OA OB

.

Do đó:

   

2

. 1

2

cos , . 120

. 2

2

. 2

2



      

 

   

a

OM BC

OM BC OM BC

OM BC

a

.

Cách 2:

M

C

B

O

A

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 10 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Chọn hệ trục tọa độ

Oxyz

như hình vẽ.

Ta có:

 

0;0;0O

,

 

0; ;0A a

,

 

;0;0B a

,

 

0;0;C a

,

; ;0

2 2

 

 

 

a a

M

.

Khi đó ta có:

 

;0; 



BC a a

,

; ;0

2 2

 



 

 



a a

OM



 



cos ;

 

BC OM

.



 

BC OM

2

. 2.

2





a

1

2

 



 



; 120 

 

BC OM

.

Câu 8. (THPT Trần Phú - Đà Nẵng - 2018) Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông có độ dài

đường chéo bằng

2a

và

SA

vuông góc với mặt phẳng

 

ABCD

. Gọi



là góc giữa hai mặt phẳng

 

SBD

và

 

ABCD

. Nếu

tan 2





thì góc giữa hai mặt phẳng

 

SAC

và

 

SBC

bằng

A.

30

. B.

60

. C.

45

. D.

90

.

Lời giải

Gọi

I AC BD 

.

Hình vuông

ABCD

có độ dài đường chéo bằng

2a

suy ra hình vuông đó có cạnh bằng

a

.

Ta có

   

SBD ABCD BD

SI BD

AI BD

 













   

 



 





; ;SBD ABCD SI AI SIA  

.

Ta có



tan tan

SA

SIA SA a

AI



   

.

Chọn hệ trục tọa độ

Oxyz

như hình vẽ. Ta có

 

0;0;0A

,

 

;0;0B a

,

 

; ;0C a a

,

 

0;0;S a

.

Khi đó

 

0;0;SA a 



;

 

; ;SC a a a 



;

 

;0;SB a a 



.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11

Mặt phẳng

 

SAC

có vectơ pháp tuyến

 

1

1;1;0n  



.

Mặt phẳng

 

SBC

có vectơ pháp tuyến

 

2

1;0;1n 



.

Suy ra

   







1 2

.

cos ;

.

n n

SAC SBC

n n



 

1 1

2

2. 2

 

   







; 60SAC SBC  

.

Câu 9. (THPT Nam Trực - Nam Định - 2018) Cho hình chóp tứ giác đều

.S ABCD

có

AB a

,

2SA a

. Gọi

G

là trọng tâm tam giác

SCD

. Góc giữa đường thẳng

BG

với đường thẳng

SA

bằng:

A.

3

arccos

5

. B.

5

arccos

5

. C.

5

arccos

3

. D.

15

arccos

5

.

Lời giải

Gọi

O AC BD 

.

Tam giác

SAO

vuông :

2 2

6

2

a

SO SA AO  

Gắn tọa độ như hình vẽ

 

0;0;0A

,

 

;0;0B a

,

 

; ;0C a a

,

 

0; ;0D a

,

; ;0

2 2

a a

O

 

 

 

,

6

; ;

2 2 2

a a a

S

 

 

 

.

Vì

G

là trọng tâm tam giác

SCD

nên

5 6

; ;

2 6 6

a a a

G

 

 

 

.

Ta có :

6

; ;

2 2 2

a a a

AS

 



 

 



 

1;1; 6

2

a



,

 

5 6

; ; 3;5; 6

2 6 6 6

a a a a

BG

 



  

 

 



.

Góc giữa đường thẳng

BG

với đường thẳng

SA

bằng:

 

.

cos ;

.

BG AS

BG SA

BG AS



 

3 5 6

5

40. 8

  

 

.

Câu 10. (Chuyên Hà Tĩnh - 2018) Cho hình lăng trụ

.ABC A B C

  

có

.A ABC



là tứ diện đều cạnh

a

. Gọi

M

,

N

lần lượt là trung điểm của

AA



và

BB



. Tính tan của góc giữa hai mặt phẳng

 

ABC

và

 

CMN

.

A.

2

5

. B.

3 2

4

. C.

2 2

5

. D.

4 2

13

.

Lời giải

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 12 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Gọi

O

là trung điểm của

AB

. Chuẩn hóa và chọn hệ trục tọa độ sao cho

 

0;0;0O

,

1

;0;0

2

A

 

 

 

,

1

;0;0

2

B

 



 

 

,

3

0; ;0

2

C

 

 

 

,

3

0; ;0

6

H

 

 

 

,

6

3

a

A H





3 6

0; ;

6 3

A

 





 

 

Ta có

AB A B

 



 

3 6

1; ;

6 3

B

 



 

 

 

. Dễ thấy

 

ABC

có vtpt

 

1

0;0;1n 



.

M

là trung điểm

AA



1 3 6

; ;

4 12 6

M

 



 

 

,

N

là trung điểm

BB



3 3 6

; ;

4 12 6

N

 





 

 

 

1;0;0MN  



,

1 5 3 6

; ;

4 12 6

CM

 





 

 





 

CMN

có vtpt

2

6 5 3

0; ;

6 12

n

 



 

 



 

3

0;2 2;5

12



cos





5

33

2

1

tan 1

cos



  

2 2

5



Câu 11. (Chuyên Lam Sơn - Thanh Hóa - 2018 ) Xét tứ diện

OABC

có

OA

,

OB

,

OC

đôi một vuông góc. Gọi



,



,



lần lượt là góc giữa các đường thẳng

OA

,

OB

,

OC

với mặt phẳng

 

ABC

(hình vẽ).

Khi đó giá trị nhỏ nhất của biểu thức

     

2 2 2

3 cot . 3 cot . 3 cotM

  

   

là

O

C

B

A

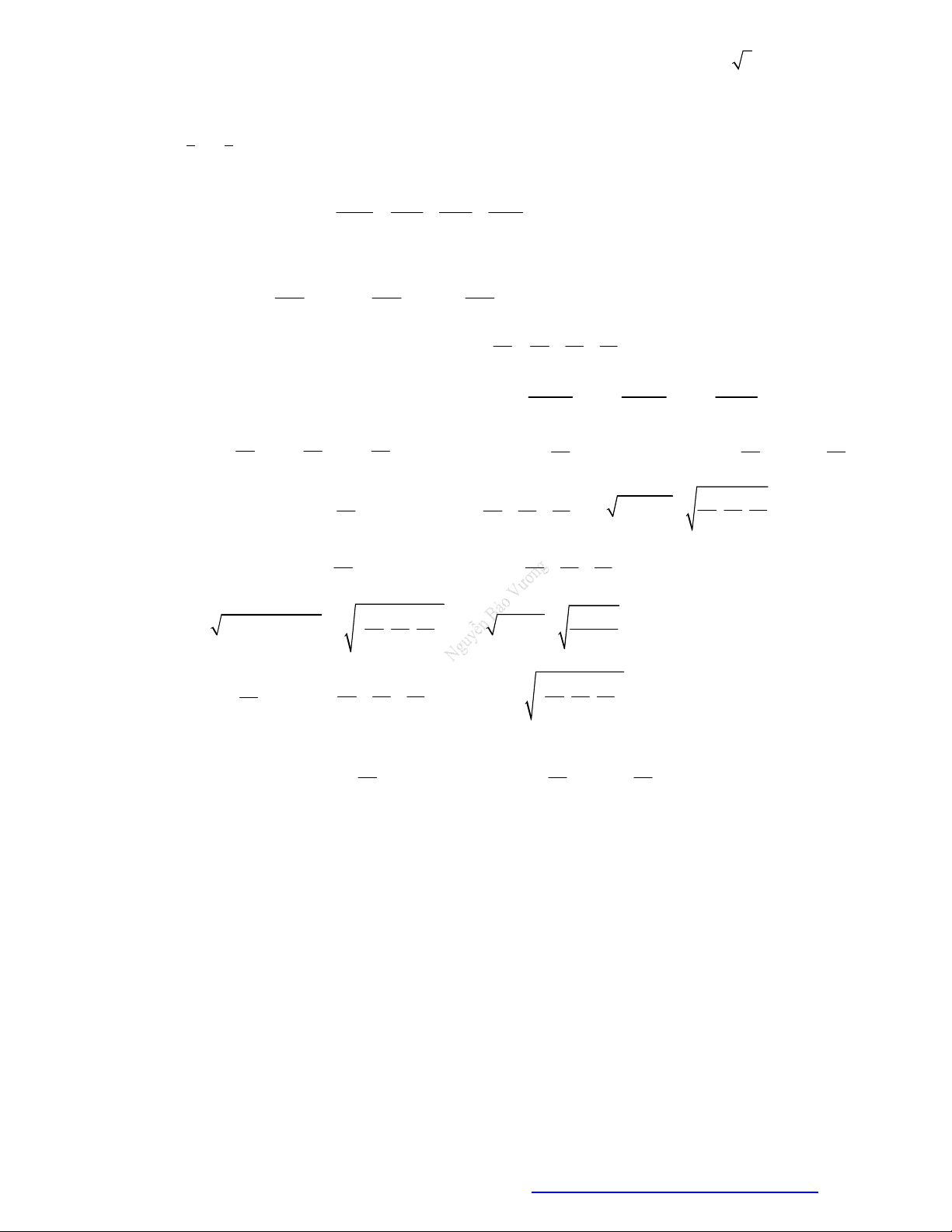
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13

A.

48

. B.

125

. C. Số khác. D.

48 3

.

Lời giải

Chọn B

Gọi

H

là trực tâm tam giác

ABC

, vì tứ diện

OABC

có

OA

,

OB

,

OC

đôi một vuông góc nên ta

có

 

OH ABC



và

2 2 2 2

1 1 1 1

OH OA OB OC

  

.

Ta có

 



;

OA ABC OAH



  ,

 



;

OB ABC OBH



  ,

 



;

OC ABC OCH



  .

Nên

sin

OH

OA





,

sin

OH

OB





,

sin

OH

OC





.

Đặt

a OA

,

b OB

,

c OC

,

h OH

thì

2 2 2 2

1 1 1 1

h a b c

  

và

     

2 2 2

3 cot . 3 cot . 3 cot

M

  

   

2 2 2

1 1 1

2 . 2 . 2

sin sin sin

  

   

 

   

 

   

 

   

2 2 2

2 . 2 . 2

a b c

h h h

     

   

     

     

   

2 2 2 2 2 2 2 2 2 2 2 2

2 4 6

1 1 1

8 4 . 2 . .

a b c a b b c c a a b c

h h h

       

.

Ta có:

 

2 2 2

2

1

.

a b c

h

 

 

2 2 2

1 1 1

.a b c

a b c

 

    

 

 

3 2 2 2

3

2 2 2

1 1 1

3 . . .3 . . 9

a b c

 

.

 

2 2 2 2 2 2

4

1

.

a b b c c a

h

 

 

2

2 2 2 2 2 2

2 2 2

1 1 1

.a b b c c a

a b c

 

    

 

 

2

3

2 2 2 2 2 2

3

2 2 2

1 1 1

3 . . . 3 . .a b b c c a

a b c

 



 

 

3

4 4 4

3

4 4 4

1

3 .9 27 

a b c

.

2 2 2

6

1

.

a b c

h

3

2 2 2 2 2 2

3

2 2 2 2 2 2

1 1 1 1 1 1

. . 3 . . 27

a b c a b c

 

   

    

 

   

 

   

 

.

Do đó:

   

2 2 2 2 2 2 2 2 2 2 2 2

2 4 6

1 1 1

8 4 . 2 . .

M a b c a b b c c a a b c

h h h

       

8 4.9 2.27 27 125    

.

Dấu đẳng thức xảy ra khi và chỉ khi

a b c 

, hay

OA OB OC 

.

Vậy

min 125

M



.

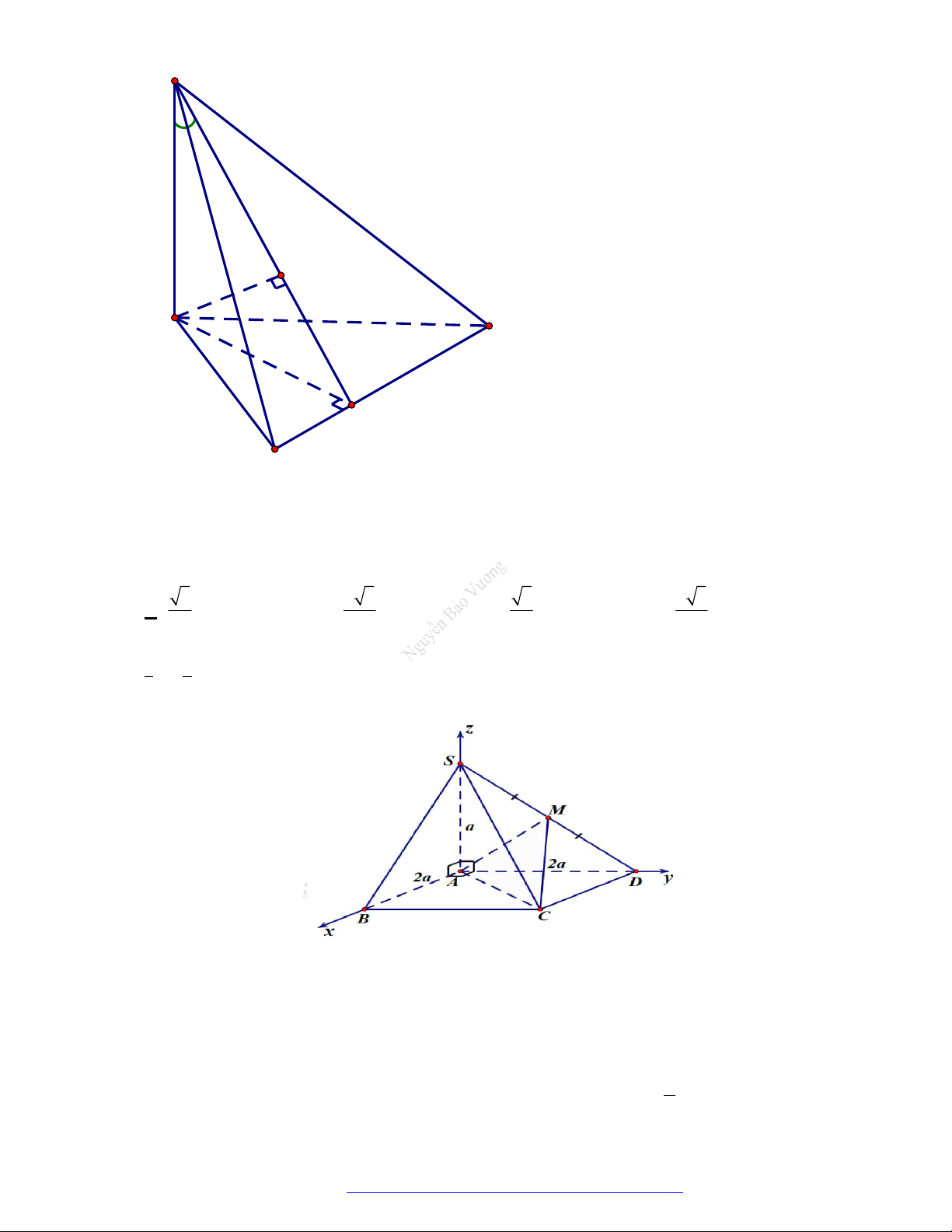
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 14 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 12. (Kinh Môn - Hải Dương 2019) Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

2a

, cạnh

bên

SA a

và vuông góc với mặt phẳng đáy. Gọi

M

là trung điểm cạnh

SD

. Tan của góc tạo bởi hai

mặt phẳng

 

AMC

và

 

SBC

bằng

A.

5

. B.

2 5

5

. C.

3

2

. D.

2 3

3

.

Lời giải

Chọn A

Chọn hệ trục tọa độ sao cho

A O

, như hình vẽ:

Khi đó ta có:

 

0;0;0A

,

 

2 ;0;0B a

,

 

0;2 ;0D a

,

 

2 ;2 ;0C a a

,

 

0;0;S a

,

0; ;

2

a

M a

 

 

 

.

h

c

b

a

α

A

O

B

C

H

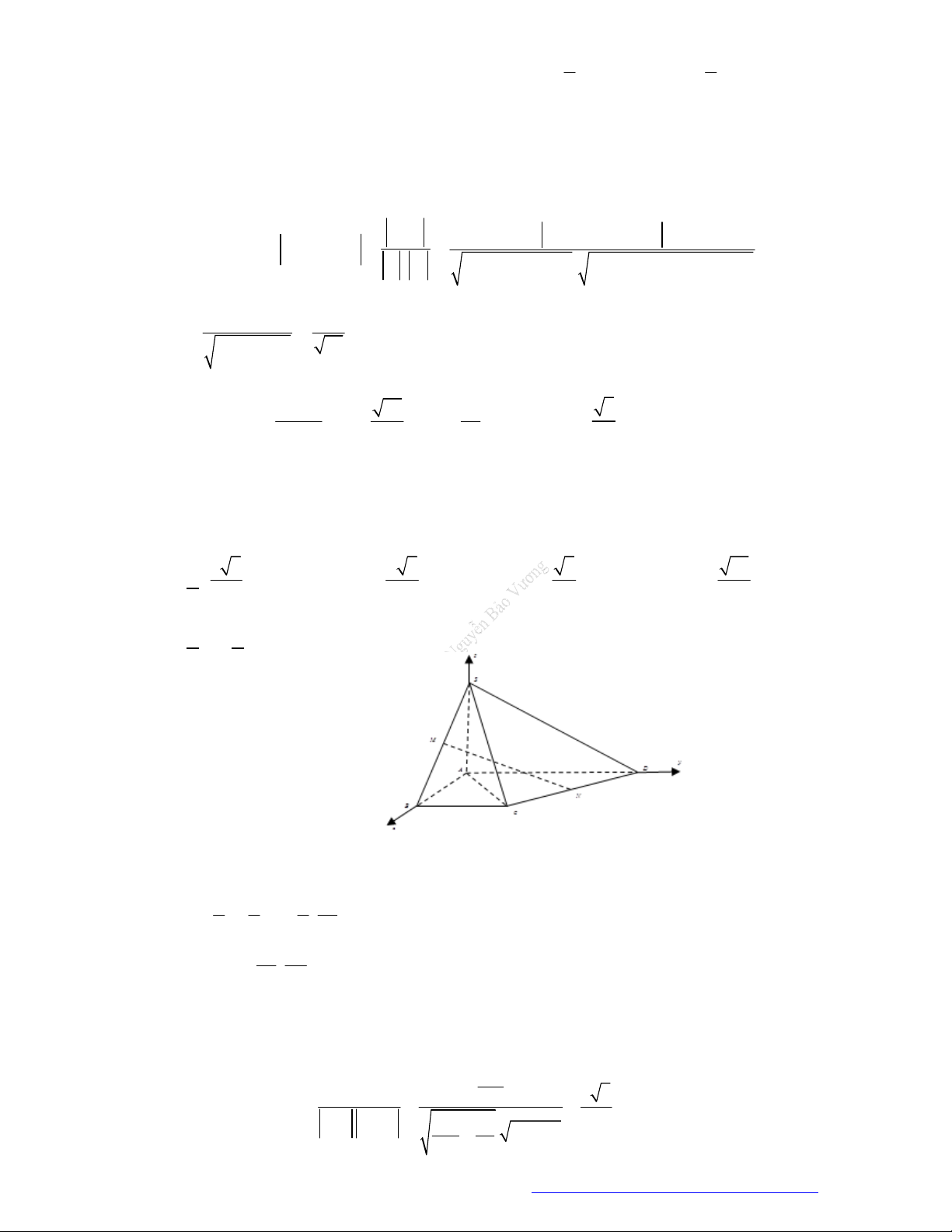
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15

 

2 ;0;SB a a 



,

 

2 ;2 ;SC a a a 



,

0; ;

2

a

MA a

 

  

 

 



,

2 ; ;

2

a

MC a a

 

 

 

 



.

1

,n SB SC

 



 

  

 

2 2

2 ;0;4a a

và

2

,n MA MC

 



 

  

 

2 2 2

; ;2a a a 

.

Gọi



(

0 90



   

) là góc tạo bởi hai mặt phẳng

 

AMC

và

 

SBC

.

ta có

 

1 2

cos cos ,n n





 

1 2

.

n n



 

 

4

2

4

10

20.6.

a



5

30



.

Mà

2

1

tan 1

cos



 

2

30

1

5

 

 

 

 

5

25



. Suy ra

5

tan

5





.

Câu 13. Cho hình chóp

.S ABCD

đáy là hình thang vuông tại

A

và

B

,

, 2AB BC a AD a  

. Biết

( ), SA ABCD SA a 

. Gọi

M

và

N

lần lượt là trung điểm của

SB

và

CD

. Tính sin góc giữa đường

thẳng

MN

và mặt phẳng

( )SAC

.

A.

3 5

.

10

B.

2 5

.

5

C.

5

.

5

D.

55

.

10

Lời giải

Chọn A

Đặt không gian

Oxyz

với

(0;0;0), , , A O AB Ox AD Oy AS Oz   

.

Ta có:

(0;0; ), ( ;0;0), (0;2 ;0), ( ; ;0)S a B a D a C a a

.

3

( ;0; ), ( ; ;0)

2 2 2 2

a a a a

M N

3

(0; ; )

2 2

a a

MN







(0;0; ), ( ; ;0)AS a AC a a 

 

2 2

, ( ; ;0)AS AC a a

 

  

 

 

là vtpt của mặt phẳng

( )SAC

.

3

( )

2 2

( )

4 4

3

. 3 5

2

sin( ;( ))

10

9

.

4 4

SAC

a

MN n

MN SAC

MN n

a a

  

 

 

.

         

2 2 2 2

2 2 2 2 2

2 . 4 .2

2 4 . 2

a a a a

a a a a a





   

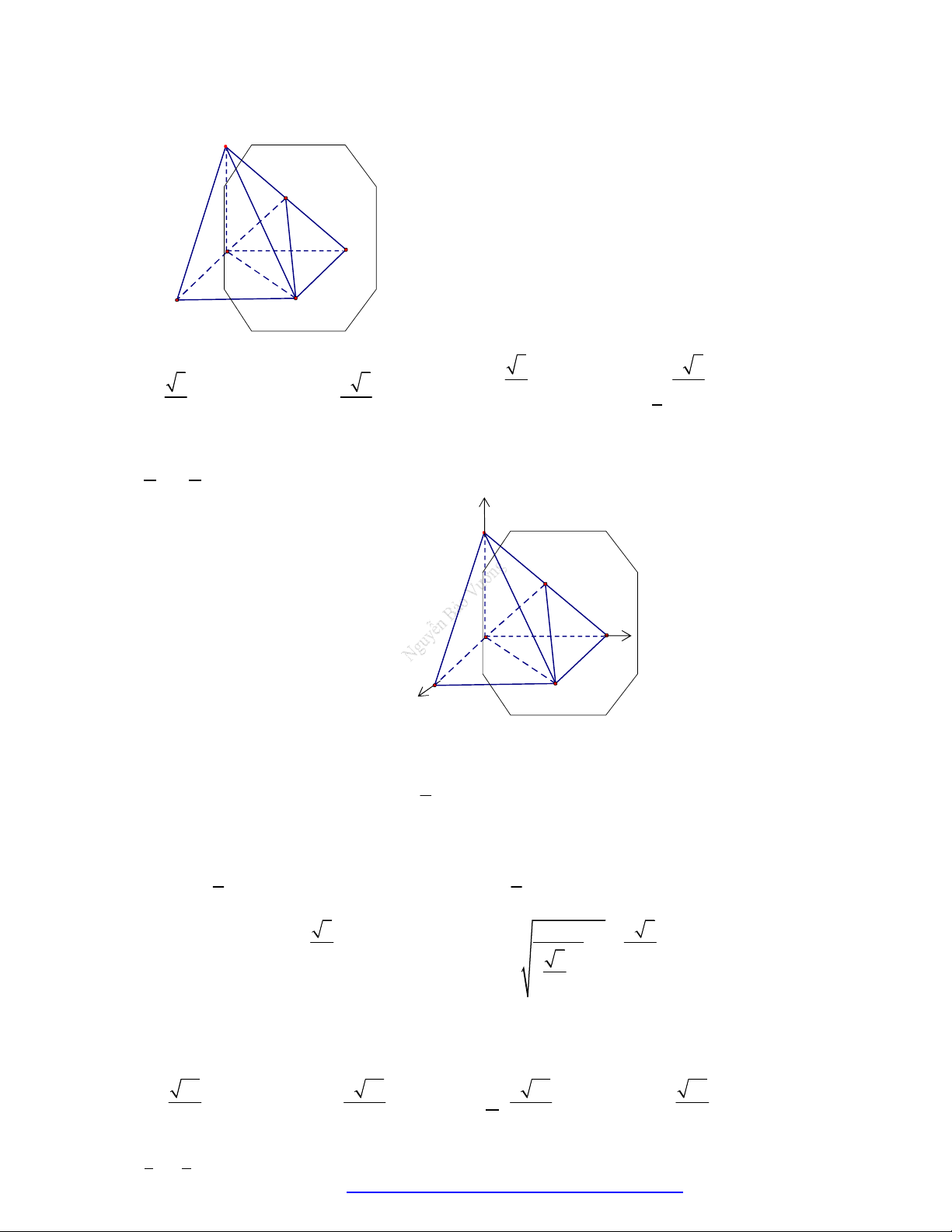
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 16 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Câu 14. (Chuyên Lê Quý Đôn – Điện Biên 2019) Cho hình chóp

.

S ABCD

có đáy

ABCD

là hình vuông cạnh

a

,

cạnh bên

2SA a

và vuông góc với mặt phẳng đáy. Gọi

M

là trung điểm cạnh

.SD

Tính tang của góc

tạo bởi hai mặt phẳng

 

AMC

và

 

SBC

bằng

A.

3

.

2

B.

2 3

.

3

C.

5

.

5

D.

2 5

.

5

Lời giải

Chọn D

Sử dụng phương pháp tọa độ trong không gian

Gắn hình chóp vào hệ trục tọa độ Oxyz.

(0;0;0)

O A



;

(1; 0;0); D(0;1; 0); (1;1;0); (0;0; 2)

B C S

Do M là trung điểm của SD nên

1

0; ;1

2

M

 

 

 

 

(0;1;0); (1;0; 2) ; 2;0;1

BC SB BC SB

 

    

 

   

1 1

0; ;1 ; (1;1;0) ; 1;1;

2 2

MA AC MA AC

   

 

     

   

 

   

   

. VTPT của (AMC) là:

 

2; 2;1

n  



   

 

   

 

2

5 1 2 5

cos ; tan ; 1

3 5

5

3

SBC AMC SBC AMC    

 

 

 

Câu 15. Cho khối tứ diện

ABCD

có

3

BC



,

4

CD



,



0

90

ABC ADC BCD

  

. Góc giữa đường thẳng

AD

và

BC

bằng

0

60

. Côsin góc giữa hai phẳng

 

ABC

và

 

ACD

bằng

A.

43

86

. B.

4 43

43

. C.

2 43

43

. D.

43

.

Lời giải

Chọn C

S

M

A

C

B

D

x

z

y

1

2

S

M

A

C

B

D

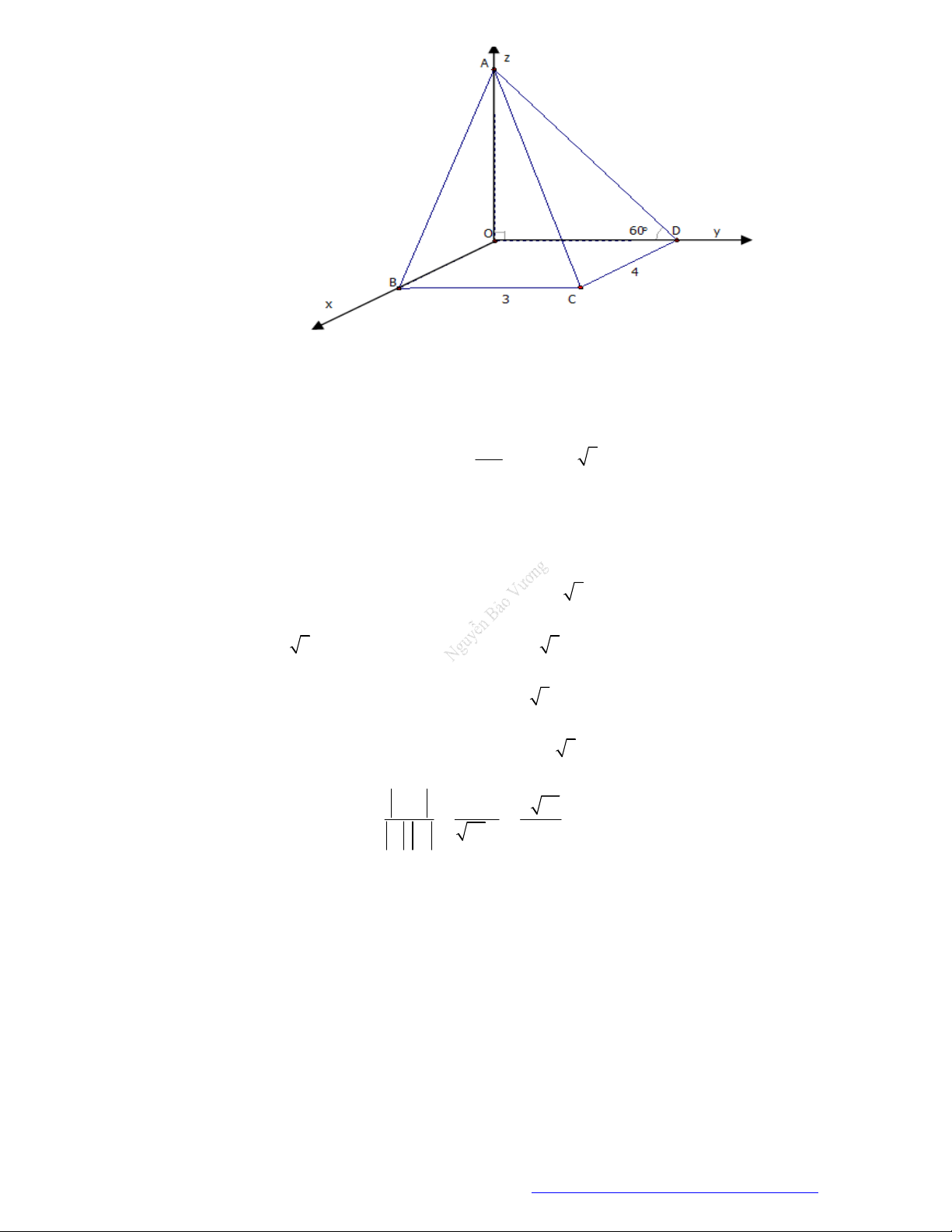
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17

Dựng

 

AO BCD

khi đó

O

là đỉnh thứ tư của hình chữ nhật

BCDO

.

Góc giữa đường thẳng

AD

và

BC

là góc giữa đường thẳng

AD

và

OD

và bằng



0

60ADO 

Xét tam giác

ADO

vuông tại

O

:

0

tan60 3 3.

OA

OD

  

Gắn hệ tọa độ

Oxyz

vào hình chóp như hình vẽ.

Ta có:

 

0;0;0O

;

 

4;0;0B

;

 

0;3;0D

;

 

4;3;0C

;

 

0;0;3 3A

.

 

4;0; 3 3AB  



;

 

0;3;0BC 



;

 

0;3; 3 3AD  



;

 

4;0;0CD  



.

Mặt phẳng

 

ABC

nhận véctơ

 

1

, 9 3;0;12n AB BC

 

 

 

 

  

làm véctơ pháp tuyến.

Mặt phẳng

 

ADC

nhận véctơ

 

2

, 0;12 3;12n AD CD

 

 

 

 

  

làm véctơ pháp tuyến.

Nên

   

 

1 2

.

4 2 43

cos ;

43

43.2

.

n n

ABC ADC

n n

   

 

Câu 16. Cho hình chóp

.S ABCD

có

ABCD

là hình vuông cạnh

a

,

 

SA ABCD

và

SA a

. Gọi

E

và

F

lần lượt là trung điểm của

SB

,

SD

. Côsin của góc hợp bới hai mặt phẳng

 

AEF

và

 

ABCD

là.

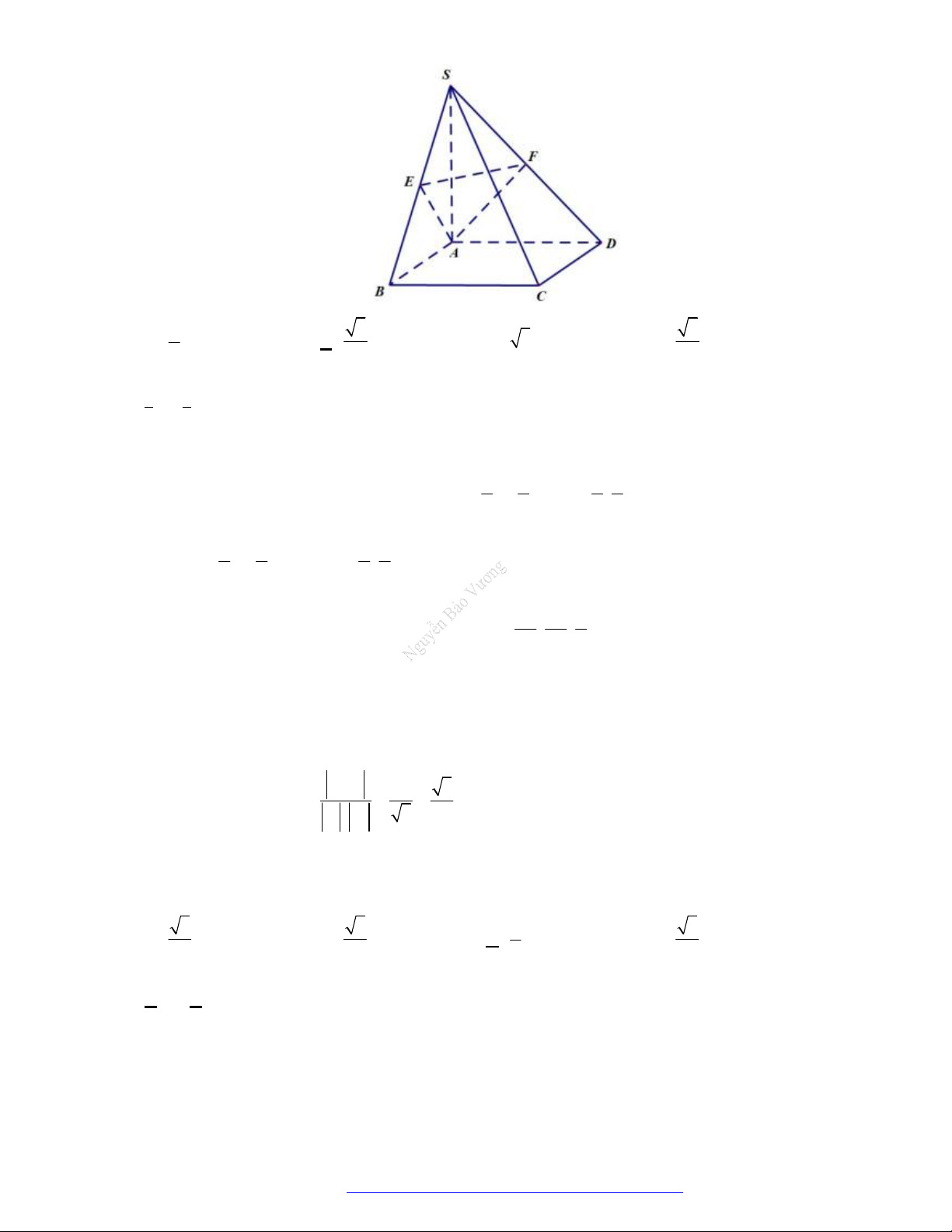
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 18 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

A.

1

2

. B.

3

. C.

3

. D.

3

2

.

Lời giải

Chọn B

Chọn hệ trục tọa độ

yzOx

sao cho

A O

,

B Ox

,

D Oy

,

S Oz

.

 

;0;0B a

,

 

0; ;0D a

,

 

0;0;aS

. Khi đó

;0;

2 2

a a

E

 

 

 

,

0; ;

2 2

a a

F

 

 

 

.

;0;

2 2

a a

AE

 

 

 

 



,

0; ;

2 2

a a

AF

 



 

 



.

Vectơ pháp tuyến của mp

 

AEF

là

1

, ; ;

4 4 4

a a a

n AB AF

 

 

 

 

 

 

 

  

 

1

1;1; 1 .n  



.

Vectơ pháp tuyến của mp

 

ABCD

là

2

(0;0; )n AS a 

 

 

2

0;0;1 .n 



.

Vậy côsin góc giữa 2 mặt phẳng

 

AEF

và

 

ABCD

là.

   

 

1 2

.

1 3

cos ,

3

.

n n

AEF ABCD

n n

   

 

.

Câu 17. Cho hình lập phương

. ' ' ' 'ABCD A B C D

có cạnh bằng

,a

gọi



là góc giữa đường thẳng

'A B

và mặt

phẳng

 

' ' .BB D D

Tính

sin



.

A.

3

.

5

B.

3

.

2

C.

1

.

2

D.

3

.

4

Lời giải

Chọn C

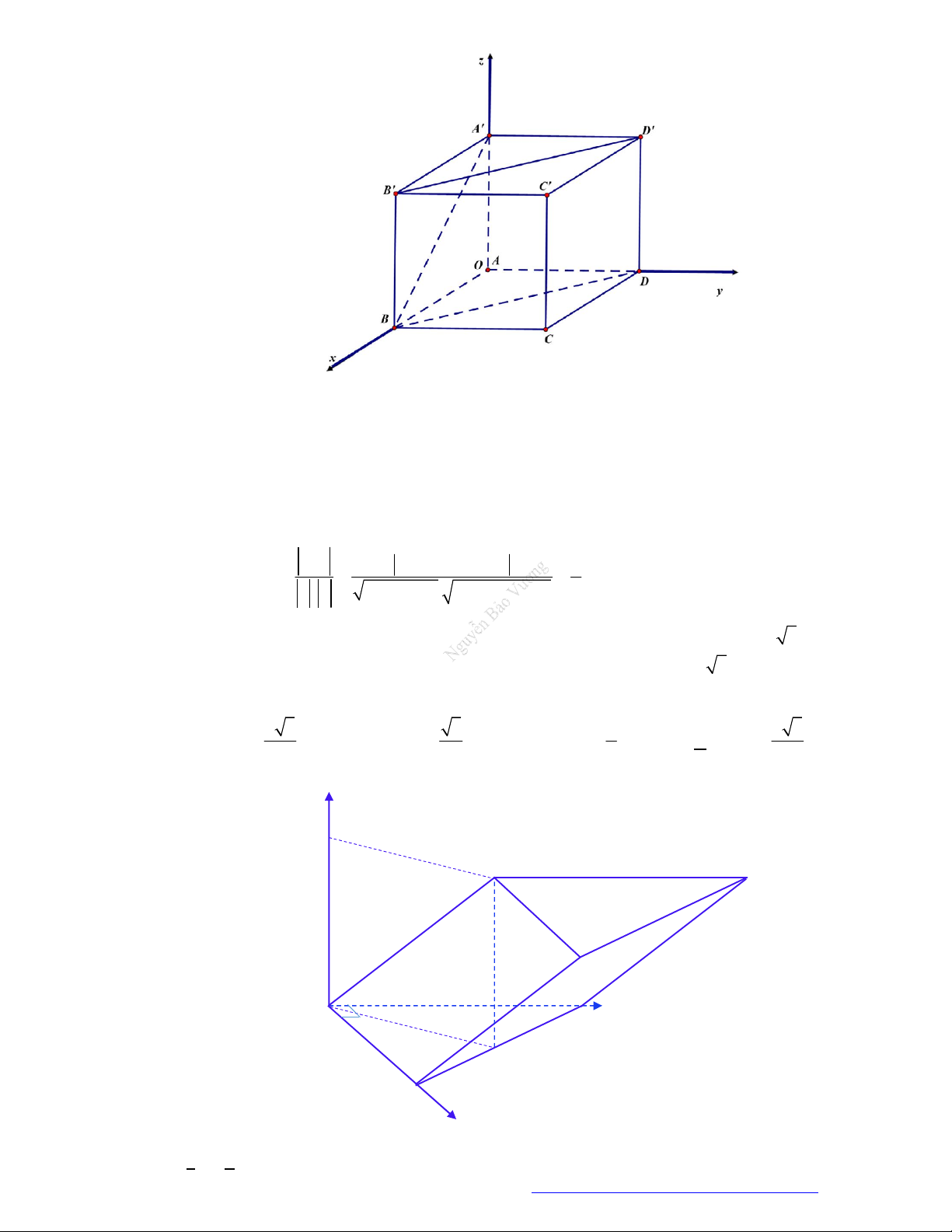
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19

+Chọn hệ trục tọa độ

Oxyz

với

       

0;0;0 , ;0;0 , ; ;0 , 0; ;0A O B a C a a D a

,

 

' 0;0; ,A a

 

' ;0; ,B a a

   

' ; ; , ' 0; ; .C a a a D a a

+Ta thấy

 

' 'OC BB D D

và

 

; ;0OC a a



nên suy ra mặt phẳng

 

' 'BB D D

có một vec tơ

pháp tuyến là

 

1;1;0.n 



.

+Đường thẳng

'A B

có vectơ chỉ phương là

 

' ;0;A B a a 



ta chọn

 

1;0; 1 .u  



+Ta có

2 2 2 2 2 2

.

1.1 1.0 0.( 1)

1

sin .

2

.

1 1 0 . 1 0 ( 1)

n u



  

  

    

 

 

Câu 18. Cho hình lăng trụ

.ABC A B C

  

có đáy

ABC

là tam giác vuông tại

A

,

AB a

,

3AC a

. Hình chiếu

vuông góc của

A



lên mặt phẳng

 

ABC

là trung điểm

H

của

BC

,

5A H a





. Gọi



là góc giữa hai

đường thẳng

A B



và

B C



. Tính

cos



.

A.

7 3

cos

48





. B.

3

cos

2





. C.

1

cos

2





. D.

7 3

cos

24





.

Lời giải

Chọn D

H

A



C



B



A

B

C

x

y

z

O

D

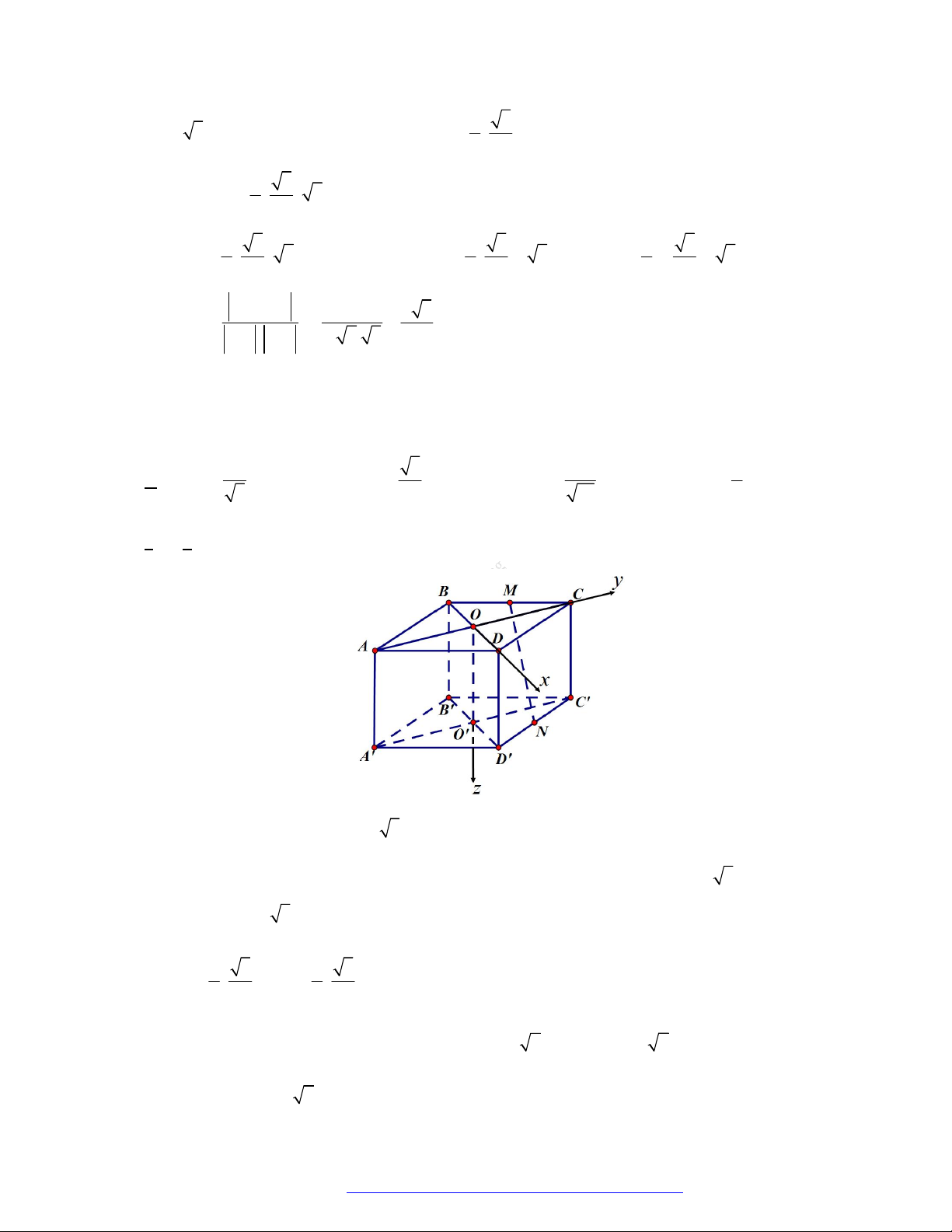
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 20 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Ta chọn hệ trục tọa độ

Oxyz

với

O A

như hình vẽ, chọn

1a 

đơn vị, khi đó ta có tọa độ điểm

 

1;0;0B

,

 

0; 3;0C suy ra trung điểm của

BC

là

1 3

; ;0

2 2

H

 

 

 

, vì

H

là hình chiếu của

A



nên suy ra

tọa độ của

1 3

; ; 5

2 2

A

 



 

 

. Ta tìm tọa độ

B



, gọi tọa độ

 

; ;B x y z



khi đó ta có

A B OB

 



 

nên

tọa độ

3 3

; ; 5

2 2

B

 



 

 

. Ta cũng có

3 3

; ; 5

2 2

B C

 



  

 

 



và

1 3

; ; 5

2 2

A B

 



  

 

 



. Từ đó ta

có

.

cos

.

A B B C



 



 

 

7 7 3

24

2. 6. 8

  .

Câu 19. Cho hình hộp đứng

. ' ' ' 'ABCD A B C D

có đáy là hình thoi, tam giác

ABD

đều. Gọi

, M N

lần lượt là

trung điểm của

BC

và

' 'C D

, biết rằng

'MN B D

. Gọi



là góc tạo bởi đường thẳng

MN

và mặt

đáy

 

ABCD

, khi đó

cos



bằng:

A.

1

cos

3



 . B.

3

cos

2





. C.

1

cos

10



 . D.

1

cos

2





.

Lời giải

Chọn A

* Chọn

2 2; 2 3AB BD AC   

, đặt

'AA h

, chọn hệ trục tọa độ

Oxyz

như hình vẽ ta có:

 

1;0;0D

,

 

1;0;0B 

,

 

0; 3;0C

,

 

' 1;0;D h

,

 

' 0; 3;C h

,

 

' 1;0;B h

.

1 3 1 3

; ;0 , ; ;

2 2 2 2

M N h

   

 

   

   

,

 

1;0;MN h



,

 

' 2;0;B D h 



.

* Do

2

' . ' 0 2 0 2MN B D MN B D h h       

 

 

1;0; 2MN 



. Ta có:

 

// 1;0; 2MN u MN 

 

,

   

0;0;1ABCD n j  

 

.

* Do



là góc tạo bởi đường thẳng

MN

và mặt đáy

 

ABCD

nên ta có:

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 21

 

2

.

2 1

sin cos ; cos 1 sin

3 3

.

u n

  

      

 

.

Dạng 2. Ứng dụng hình học giải tích OXYZ để giải quyết bài toán tìm KHOẢNG CÁCH

Câu 20. (Chuyên Lê Quý Đôn Quảng Trị 2019) Cho hình hộp chữ nhật

.ABCD A B C D

   

có các kích thước

4, 3, 5AB AD AA



  

. Khoảng cách giữa hai đường thẳng

'AC

và

'B C

bằng

A.

3

2

. B.

2

. C.

5 2

3

. D.

30

19

.

Lời giải

Chọn D

Chọn hệ trục tọa độ như hình vẽ.

Có

       

00;0 , ' 4;3;5 , 4;3;0 , ' 4;0;5A C C B

,

       

' 4;3;5 , ' 0;3; 5 , ', ' 30; 20;12 , 0;0;5

 



      

 

    

AC B C AC B C CC

,

Vậy khoảng cách giữa hai đường thẳng cần tìm là:

 

', ' .

60 30

', '

19

1444

', '

 



 

  

 

 

  

 

AC B C CC

d AC B C

AC B C

.

Câu 21. (Việt Đức Hà Nội 2019) Trong không gian với hệ tọa độ

Oxyz

, cho hình chóp

.S ABCD

, đáy

ABCD

là

hình chữ nhật. Biết

 

0;0;0A

,

 

2;0;0D

,

 

0;4;0B

,

 

0;0;4S

. Gọi

M

là trung điểm của

SB

. Tính

khoảng cách từ

B

đến mặt phẳng

 

CDM

.

A.

 

, 2d B CDM 

. B.

 

, 2 2d B CDM 

.

C.

 

1

,

2

d B CDM 

. D.

 

, 2d B CDM 

.

Lời giải

3

5

4

C'

A'

A

D

C

B

B'

D'

x

y

z

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 22 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Tứ giác

ABCD

là hình chữ nhật nên

A C B D

x x x x

y y y y

z z z z

  





  





  



2

4

0

C

x

y

z







 









 

2;4;0C

.

M

là trung điểm của

SB

 

0;2;2M

.

Viết phương trình mặt phẳng

 

CDM

:

 

0; 4;0CD  



,

 

2; 2;2CM   



 

8;0; 8CD CM    

 

.

 

CDM

có một véc tơ pháp tuyến

 

1;0;1n 



.

Suy ra

 

CDM

có phương trình:

2 0x z  

.

Vậy

 

2 2 2

0 0 2

; 2

1 0 1

d B CDM

 

 

 

.

Câu 22. (HSG Bắc Ninh 2019) Cho hình lăng trụ đứng

.ABC A B C

  

có đáy

ABC

là tam giác vuông cân,

AB AC a 

,

AA h





 

, 0a h 

. Tính khoảng cách giữa hai đường thẳng chéo nhau

AB



và

BC



theo

a

,

h

.

A.

2 2

5

ah

a h

. B.

2 2

5

ah

a h

. C.

2 2

2

ah

a h

. D.

2 2

ah

a h

.

Lời giải

Chọn hệ trục tọa độ như hình vẽ.

 

0;0;0A

;

 

0;0;A h



;

 

0; ;0C a

;

 

;0;0B a

;

 

;0;B a h



;

 

0; ;C a h



.

 

;0;AB a h







;

 

; ;BC a a h



 



;

 

2

; ; 2 ;AB BC ah ah a

 

 

  

 

 

;

 

;0;0AB a



.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 23

 

2 2

; .

;

5

;

d

AB BC AB

ah

AB BC

a h

AB BC

 

 

 

 

 

 

 



 

  

 

.

Câu 23. (Cụm Liên Trường Hải Phòng 2019) Cho hình chóp

.S ABC

có đáy là tam giác đều cạnh bằng

a

. Gọi

I

là

trung điểm của

AB

, hình chiếu của

S

lên mặt phẳng

 

ABC

là trung điểm của

CI

, góc giữa

SA

và

mặt đáy bằng

0

45

(hình vẽ bên). Gọi

G

là trọng tâm tam giác

SBC

. Khoảng cách giữa hai đường thẳng

SA

và

CG

bằng

A.

21

14

a

B.

14

8

a

C.

77

22

a

D.

21

7

a

Lời giải

Chọn B

Đặt hệ trục tọa độ

Oxyz

sao cho

 

0;0;0I

,

;0;0

2

 

 

 

a

A

,

;0;0

2

 



 

 

a

B

,

3

0; ;0

2

 

 

 

a

C

.

Ta có

3

2



a

CI

,

3

4



a

IH

,

7

4



a

AH

H

là trung điểm

CI

suy ra

3

0; ;0

4

 

 

 

a

H

.

 



0

45 , ,  SA ABC SA AH SAH

7

4

 

a

SH

3 7

0; ;

4 4

 



 

 

a a

S

.

Ta có:

3 7

; ;

2 4 4

 

  

 

 



a a a

SA

,

3 7

; ;

6 4 12

 

  

 

 



a a a

CG

,

3

; ;0

2 2

 

 

 

 



a a

CA

21 3

, ;0;

12 12

 

 



 

 

 

 

 

a a

SA CG

6

,

6

 

 

 

 

a

SA CG

.

Khoảng cách giữa

SA

và

CG

:

, .

14

8

,

 

 



 

 

  

 

SA CG CA

a

SA CG

.

Câu 24. (Chuyên Lê Quý Đôn - Đà Nẵng 2018) Cho hình lập phương

.ABCD A B C D

   

cạnh bằng

a

. Gọi

K

là

trung điểm

DD



. Tính khoảng cách giữa hai đường thẳng

CK

và

A D



.

A.

4

3

a

. B.

3

a

. C.

2

3

a

. D.

3

4

a

.

Lời giải

Gọi

M

là trung điểm

BB



. Ta có:

//CK A M



 

//CK A MD





.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 24 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Khi đó:

   

 

, , ,d CK A D d CK A MD d C A MD

  

 

.

Gắn hệ trục tọa độ như hình vẽ:

Ta có:

 

0;0;0A

,

 

;0;0B a

,

 

0; ;0D a

,

 

0;0;A a



,

 

;0;B a a



,

 

; ;0C a a

,

;0;

2

a

M a

 

 

 

.

;0;

2

a

A M a

 



 

 

 



,

 

0; ;A D a a



 



,

2

2 2

, ; ;

2

a

A M A D a a

 

 

 



 

 

 

 

.

Vậy mặt phẳng

 

A MD



nhận

 

1;2;2n 



làm vectơ pháp tuyến.

Phương trình mp

 

: 2 2 2 0A MD x y z a



   

.

Do đó:

 

2 2

,

3 3

a a a

a

d C A DM

 



  .

Câu 25. (THPT Hoàng Hoa Thám - Hưng Yên 2019) Cho hình chóp

S.ABC

có đáy

ABC

là tam giác đều cạnh

2 3a

, mặt bên

SAB

là tam giác cân với



0

120ASB 

và nằm trong mặt phẳng vuông góc với đáy. Gọi

M

là trung điểm của

SC

và

N

là trung điểm của

MC

. Tính khoảng cách giữa hai đường thẳng

AM

,

BN

.

A.

2 327

79

a

. B.

237

79

a

. C.

2 237

79

a

. D.

5 237

316

a

Lời giải

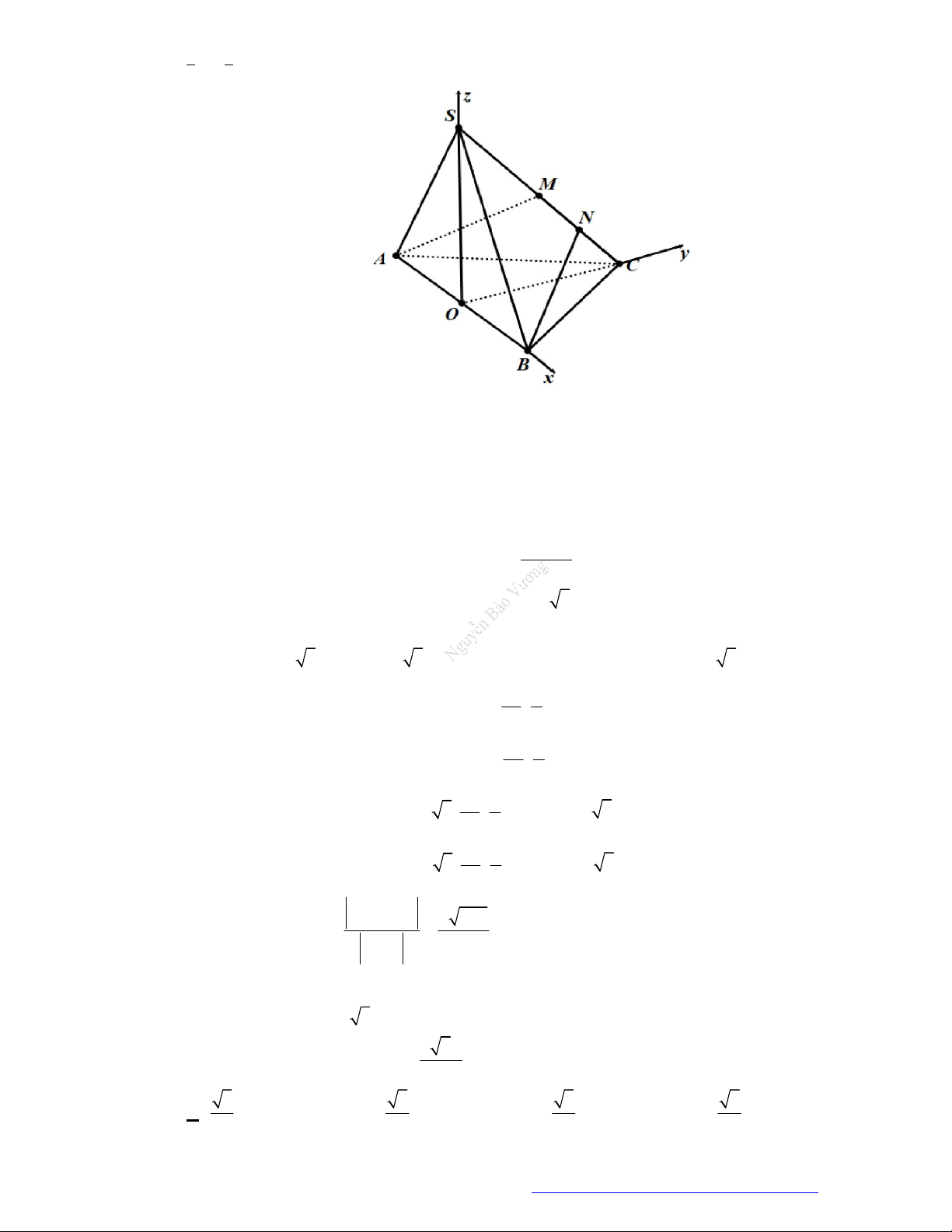
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 25

Chọn C

Gọi

O

là trung điểm

AB

,

SAB

cân tại

S SO AB 

.

Ta có:

    

   

 

SAB ABC gt

SAB ABC AB SO ABC

SO AB cmt





   









.

Xét

SOB

vuông tại

O

có



0

60

OB

OSB SO a

tan

   

Ta có:

OC

là đường cao của tam giác đều cạnh

2 3a

nên:

3OC a

Gắn hình chóp

S.ABC

lên hệ trục tọa độ

Oxyz

như hình vẽ. Khi đó ta có:

 

   

 

0 0 0 3 0 0 3 0 0 0 3 0 0 0 2 3 0 0O ; ; ,B a ; ; , A a ; ; ;C ; a; ;S ; ;a AB a ; ;  



M

là trung điểm

SC

nên

M

có tọa độ:

3

0

2 2

a a

; ;

 

 

 

.

N

là trung điểm

MC

nên

N

có tọa độ:

9

0

4 4

a a

; ;

 

 

 

.

AM

có véc tơ chỉ phương

3

2 2

a a

AM a ; ;

 

 

 



hoặc

 

2 3 3 1a ; ;



BN

có véc tơ chỉ phương

9

3

4 4

a a

BN a ; ;

 



 

 



hoặc

 

4 3 9 1b ; ;



Ta có:

 

2 237

79

a,b .AB

d AM ; BN a

a,b

 

 

 

 

 

  

 

Câu 26. (Chuyên - Vĩnh Phúc - 2019) Cho hình chóp

.S ABC

có đáy

ABC

là tam giác vuông

tại

A

,

1cmAB 

,

3cmAC 

. Tam giác

SAB

,

SAC

lần lượt vuông tại

B

và

C

. Khối cầu ngoại tiếp

hình chóp

.S ABC

có thể tích bằng

3

5 5

cm

6



. Tính khoảng cách từ

C

tới

 

SAB

.

A.

3

cm

2

. B.

5

cm

4

. C.

3

4

cm

. D.

5

cm

2

.

Lời giải

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 26 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Chọn A

Gọi

I

là trung điểm

SA

. Do tam giác

SAB

,

SAC

lần lượt vuông tại

B

và

C

nên

IA IS IB IC  

. Vậy

I

là tâm cầu ngoại tiếp chóp

.S ABC

.

Vì cầu ngoại tiếp hình chóp

.S ABC

có thể tích bằng

3

5 5

cm

6





5

2

R IA IS IB IC    

Suy ra

5; 2, 2SA SB SC  

.

Gán hệ trục tọa độ gốc

A

. ta có

   

 

0,0,0 ;B 1,0,0 ;C 0, 3,0A

Giả sử

 

, , , 0S a b c c 

. Ta có hệ phương trình

 

2 2 2

2

2 2 2 2 2

2

2 2 2

2 2

5

1

5 5

2 1 4 2 3 3 1, 3,1

1

2 2 3 1

3 2

a b c

a

SA a b c

SB a b c a b c a b S

c

SC a b c b

a b c



  



 



   



 



             

   

   



     



 

   





Mặt phẳng

 

SAB

qua

 

0,0,0A

có vecto pháp tuyến

 

0,1, 3n 



Phương trình mặt phẳng

 

SAB

là:

3 0y z 

Vậy

 

3

,

2

d C SAB 

.

Câu 27. (Chuyên Lam Sơn 2019) Một phần sân trường được định vị bởi các điểm

A

,

B

,

C

,

D

như hình vẽ.

Bước đầu chúng được lấy “ thăng bằng” để có cùng độ cao, biết

ABCD

là hình thang vuông ở

A

và

B

với độ dài

25mAB 

,

15mAD 

,

18mBC 

. Do yêu cầu kĩ thuật, khi lát phẳng phần sân trường

phải thoát nước về góc sân ở

C

nên người ta lấy độ cao ở các điểm

B

,

C

,

D

xuống thấp hơn so với độ

cao ở

A

là

10cm

,

cma

,

6cm

tương ứng. Giá trị của

a

là số nào sau đây?

A.

15,7cm

. B.

17,2cm

. C.

18,1cm

. D.

17,5cm

.

Lời giải

Chọn B

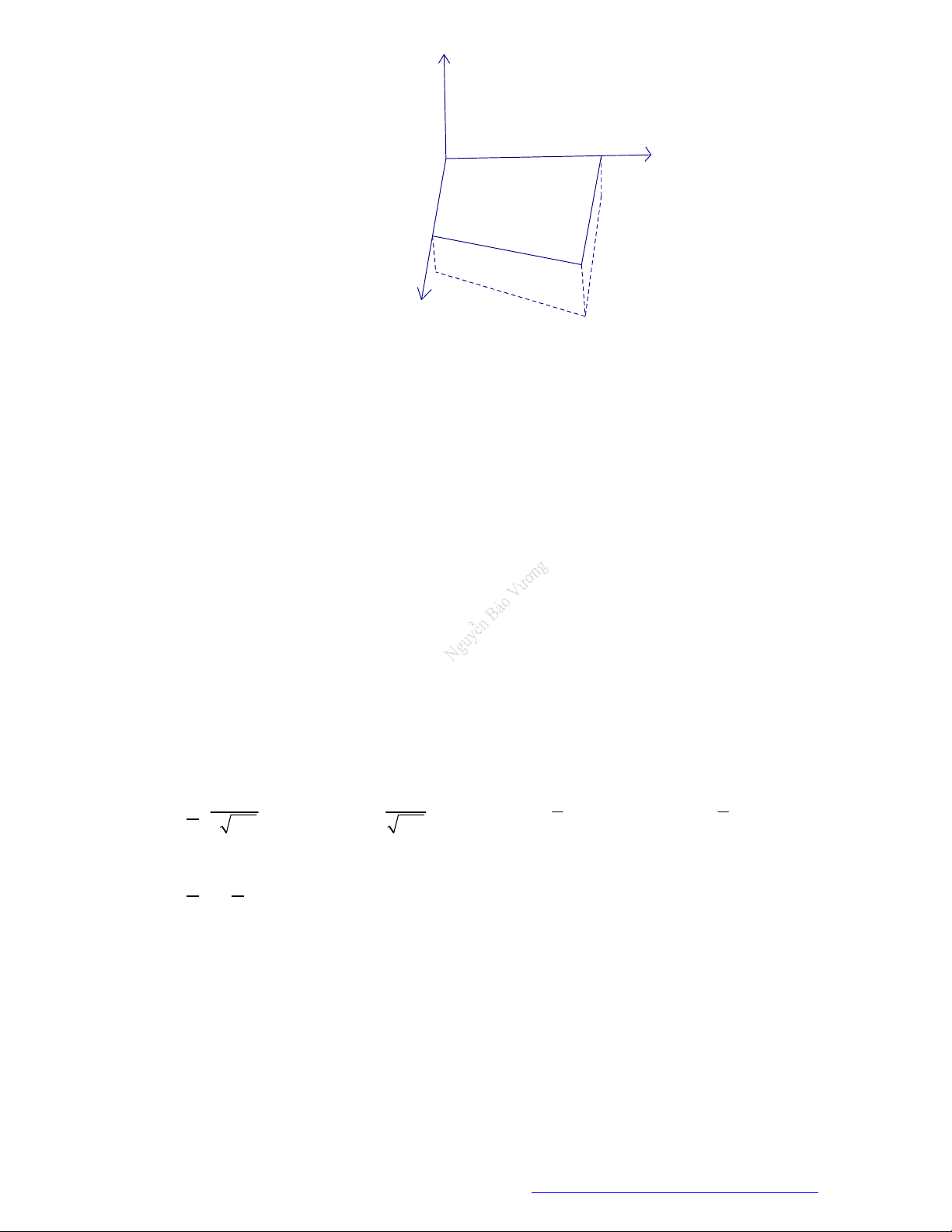
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 27

Chọn hệ trục tọa độ

Oxyz

sao cho:

O A

, tia

Ox AD

; tia

Oy AB

.

Khi đó,

 

0;0;0A

;

 

0;2500;0B

;

 

1800;2500;0C

;

 

1500;0;0D

.

Khi hạ độ cao các điểm ở các điểm

B

,

C

,

D

xuống thấp hơn so với độ cao ở

A

là

10cm

,

cma

,

6cm

tương ứng ta có các điểm mới

 

0;2500; 10B





;

 

1800;2500;C a





;

 

1500;0; 6D





.

Theo bài ra có bốn điểm

A

;

B



;

C



;

D



đồng phẳng.

Phương trình mặt phẳng

 

: 250 0AB D x y z

 

  

.

Do

   

1800; 2500;C a AB D

  

 

nên có:

1800 2500 250 0 17,2a a    

.

Vậy

17,2cma 

.

Câu 28. (Chuyên Bắc Giang 2019) Cho tứ diện

OABC

, có

, ,OA OB OC

đôi một vuông góc và

5, 2, 4OA OB OC  

. Gọi

,M N

lần lượt là trung điểm của

OB

và

OC

. Gọi

G

là trọng tâm của

tam giác

ABC

. Khoảng cách từ

G

đến mặt phẳng

 

AMN

là:

A.

20

.

3 129

B.

20

.

129

C.

1

.

4

D.

1

.

2

Lời giải

Chọn A

Chọn hệ trục tọa độ

Oxyz

như hình vẽ.

z

y

x

B'

C'

D'

D

C

B

A

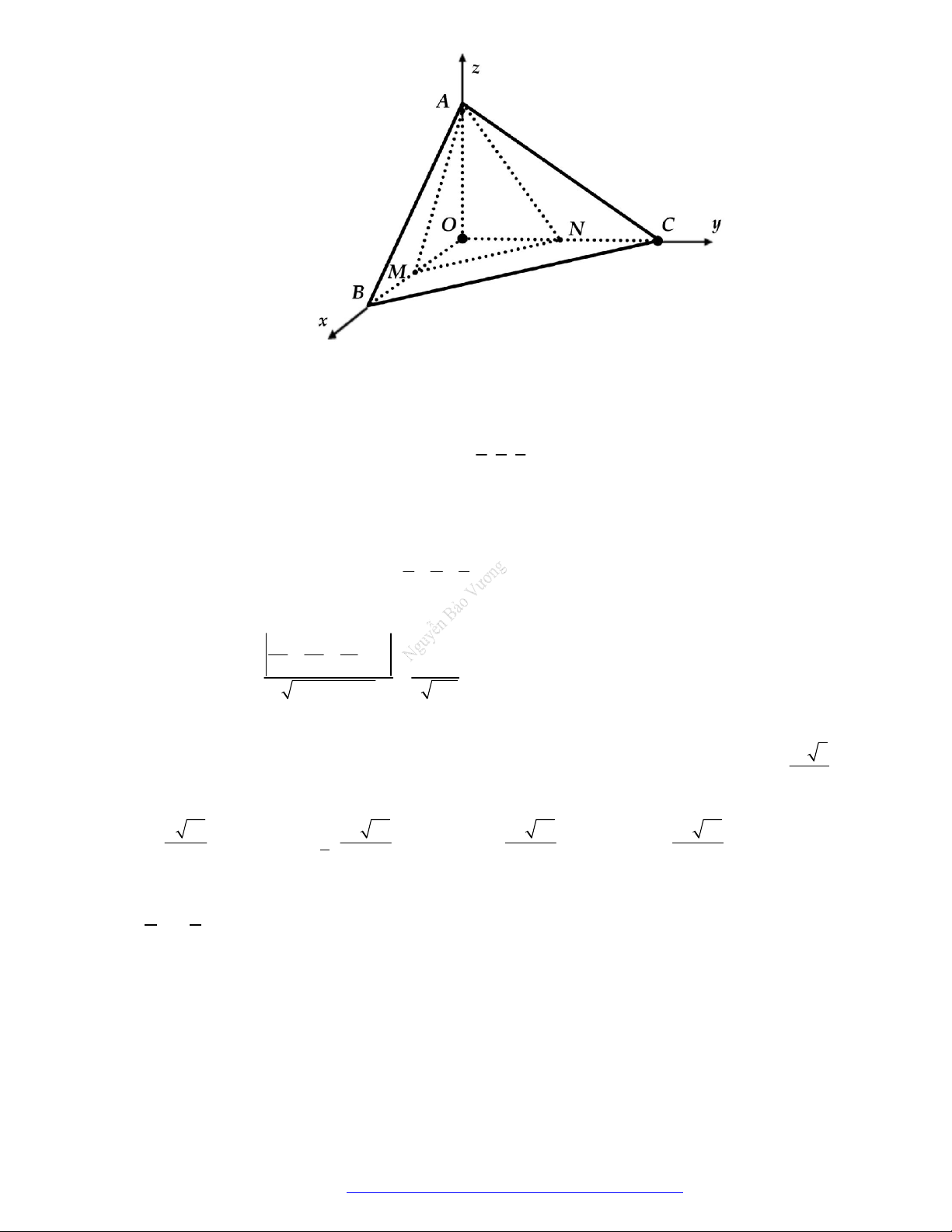
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 28 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Ta có

 

0;0;0O

,

Oz, ,A B Ox C Oy  

sao cho

5, 2, 4AO OB OC  

     

0;0;5 , 2;0;0 , 0;4;0A B C

.

Khi đó:

G

là trọng tâm tam giác

ABC

nên

2 4 5

; ;

3 3 3

G

 

 

 

M

là trung điểm

OB

nên

 

1;0;0M

N

là trung điểm

OC

nên

 

0;2;0N

.

Phương trình mặt phẳng

 

AMN

là:

1

1 2 5

x y z

  

hay

10 5 2 10 0x y z   

Vậy khoảng cách từ

G

đến mặt phẳng

 

AMN

là:

 

20 20 10

10

20

3 3 3

,

100 25 4 3 129

d G AMN

  

 

 

.

Câu 29. Cho hình lăng trụ

. ' ' 'ABC A B C

có đáy là tam giác đều cạnh

a

, gọi

M

là trung điểm của

AB

,

'A CM

cân tại

'A

và nằm trong mặt phẳng vuông góc với đáy. Biết thể tích khối lăng trụ bằng

3

4

a

.

Khoảng cách giữa hai đường thẳng

AB

và

'CC

A.

57

19

a

. B.

2 57

19

a

. C.

2 39

13

a

. D.

2 39

3

a

.

Lời giải

Chọn B

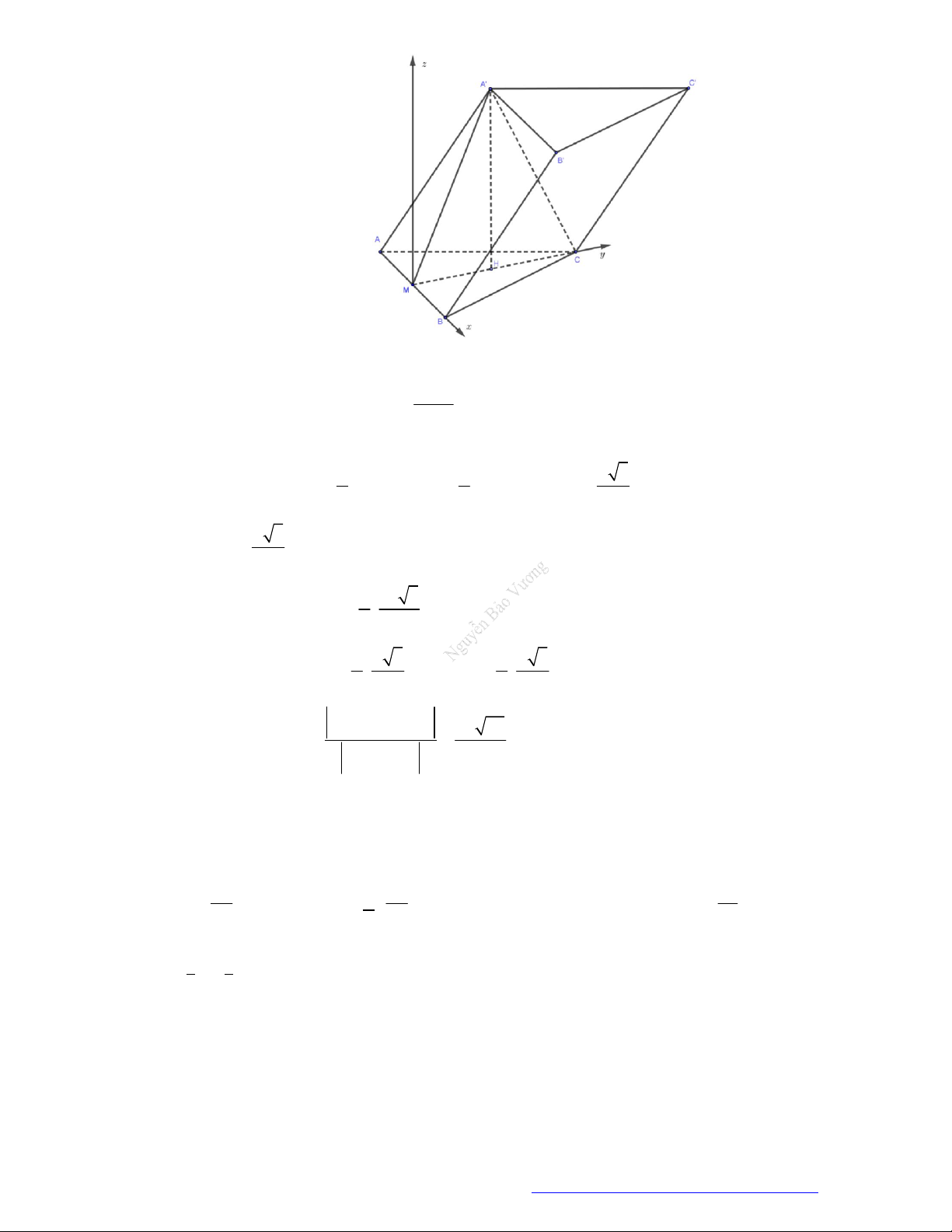
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 29

Gọi

H

là trung điểm

 

' 'MC A H MC A H ABC   

.

Ta có

. ' '

ABC

S

V S A H A H a

V



   

.

Chọn hệ trục toạ độ

Oxyz

sao cho:

 

3

0;0;0 , ;0;0 , ;0;0 , 0; ;0

2 2 2

a a a

O M A Ox B Ox C Oy

 

   

    

 

   

 

   

 

và

/ / 'Mz A H

.

3

' 0; ;

4

a

A a

 



 

 

.

Ta có.

3 3

' ' ' ; ;

2 4

a a

CC AA C a

 

 

 

 

 

.

 

3 3

;0;0 , ' ; ; , ; ;0

2 4 2 2

a a a a

AB a CC a AC

   

  

   

   

  

.

Vậy

 

, ' .

2 57

, '

19

, '

AB CC AC

a

d AB CC

AB CC

 

 

 

 

 

  

 

.

Câu 30. (Sở Nam Định 2019) Cho hình chóp

.S ABCD

đáy là hình thang vuông tại

A

và

D

,

 

SA ABCD

.

Góc giữa

SB

và mặt phẳng đáy bằng

o

45

,

E

là trung điểm của

SD

,

2AB a

,

AD DC a 

. Tính

khoảng cách từ điểm

B

đến mặt phẳng

 

ACE

.

A.

2

3

a

. B.

4

3

a

. C.

a

. D.

3

4

a

.

Lời giải

Chọn B

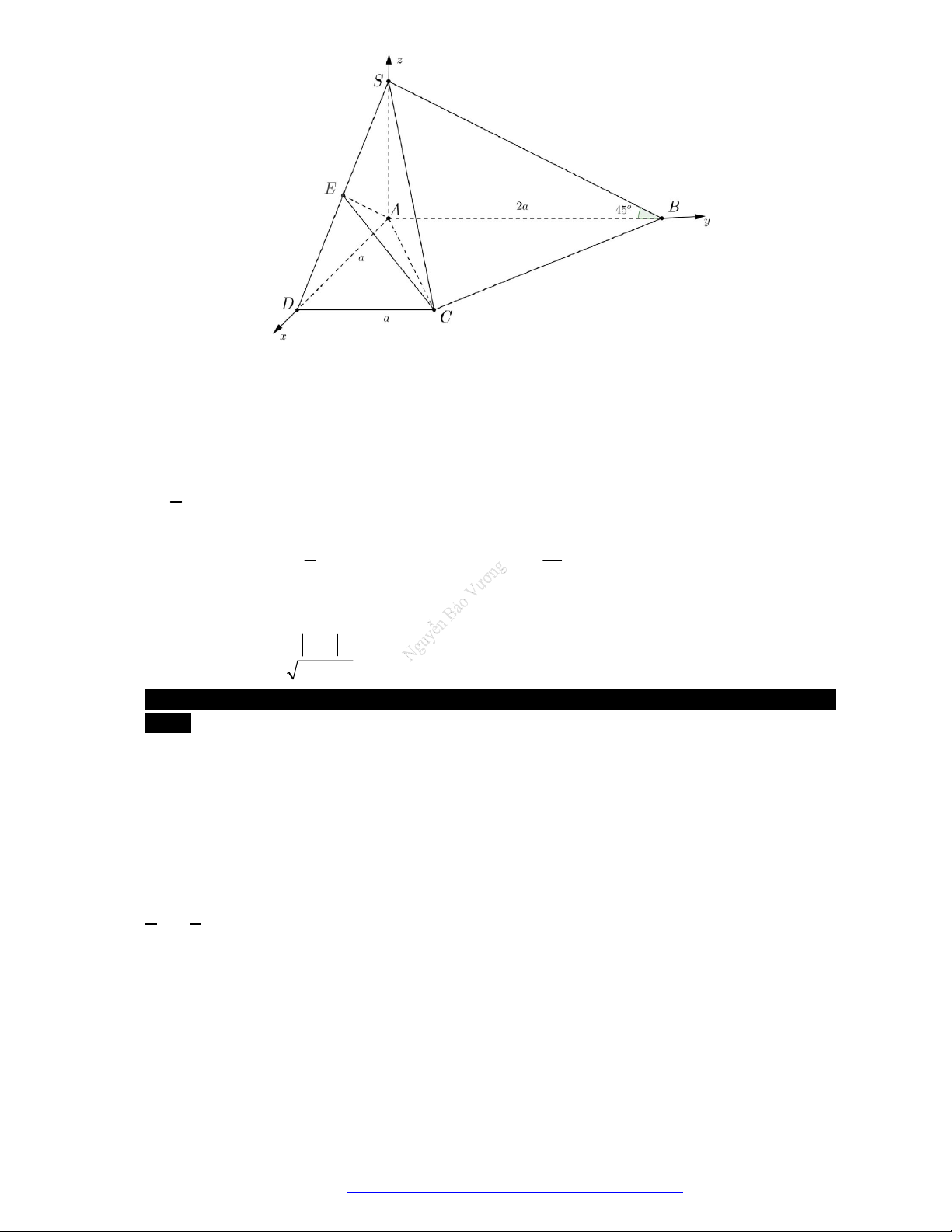
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 30 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Hình chiếu của

SB

trên mặt phẳng

 

ABCD

là

AB



Góc giữa

SB

và mặt đáy là góc giữa

SB

và

AB

và bằng góc



o

45SBA 

.

Tam giác

SAB

vuông cân tại

A

2SA a 

.

Chọn hệ trục tọa độ như hình vẽ ta có:

 

0;0;0A

,

 

0;2 ;0B a

,

 

; ;0C a a

,

 

;0;0D a

,

 

0;0;2S a

,

;0;

2

a

E a

 

 

 

.

 

; ;0AC a a



,

;0;

2

a

AE a

 



 

 



2

2 2

E ; ;

2

a

AC A a a

 

    

 

 

 



mặt phẳng

 

ACE

có véctơ pháp tuyến

 

2; 2; 1n   



 

: 2 2 0ACE x y z   

.

Vậy

 

2.2

4

,

3

4 4 1

a

d B ACE  

 

.

Dạng 3. Ứng dụng hình học giải tích OXYZ để giải quyết bài toán tìm THỂ TÍCH, BÁN

KÍNH

Câu 31. (Mã 102 2018) Trong không gian

,Oxyz

cho mặt cầu

 

S

có tâm

 

1;2;1I 

và đi qua điểm

 

1;0; 1 .A 

Xét các điểm

, ,B C D

thuộc

 

S

sao cho

, ,AB AC AD

đôi một vuông góc với nhau. Thể tích của khối tứ

diện

ABCD

có giá trị lớn nhất bằng

A.

64

B.

32

3

C.

64

3

D.

32

Lời giải

Chọn B

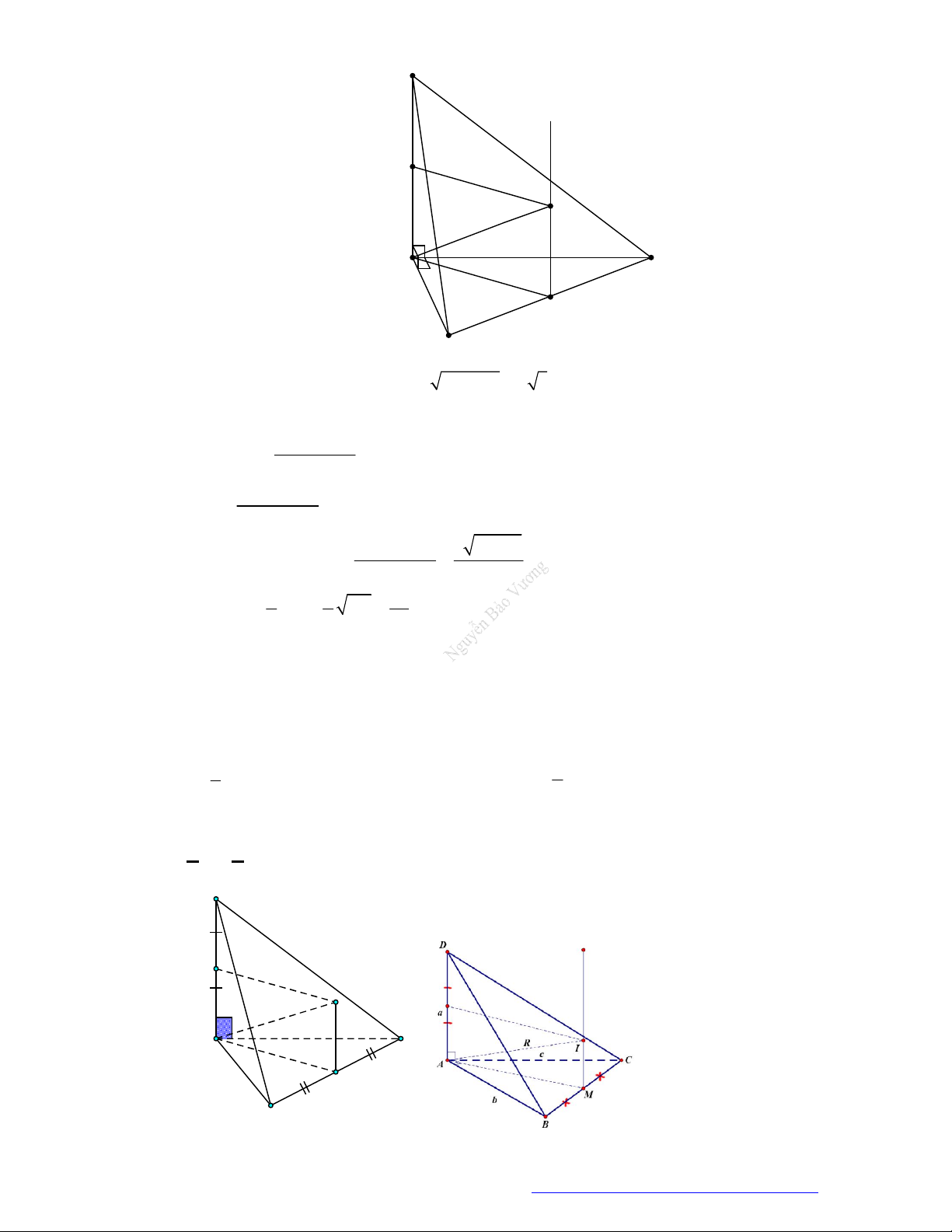
TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 31

Mặt cầu

 

S

có bán kính 4 4 4 2 3.r IA    

Đặt

; ;AB a AC b AD c  

Ta có

2 2 2

2

4

a b c

IA

 



Do đó

2 2 2

12

4

a b c 



Theo BĐT Cô-si ta có:

32 2 2 2 2 2

3

4 4

a b c a b c 



Do đó

3

1 1 32

16 .

6 6 3

V abc  

Dấu bằng xảy ra khi và chỉ khi

.a b c 

.

Câu 32. (Mã 104 2018) Trong không gian

Oxyz

, cho mặt cầu

 

S

có tâm

 

1;0;2I 

và đi qua điểm

 

0;1;1A

.

Xét các điểm

B

,

C

,

D

thuộc

 

S

sao cho

AB

,

AC

,

AD

đôi một vuông góc với nhau. Thể tích của

khối tứ diện

ABCD

có giá trị lớn nhất bằng

A.

8

3

B.

4

C.

4

3

D.

8

Lời giải

Chọn C

Đặt:

AD a

,

AB b

,

AC c

.

I

N

M

A

C

B

D

R

c

b

a

I

M

B

A

C

D

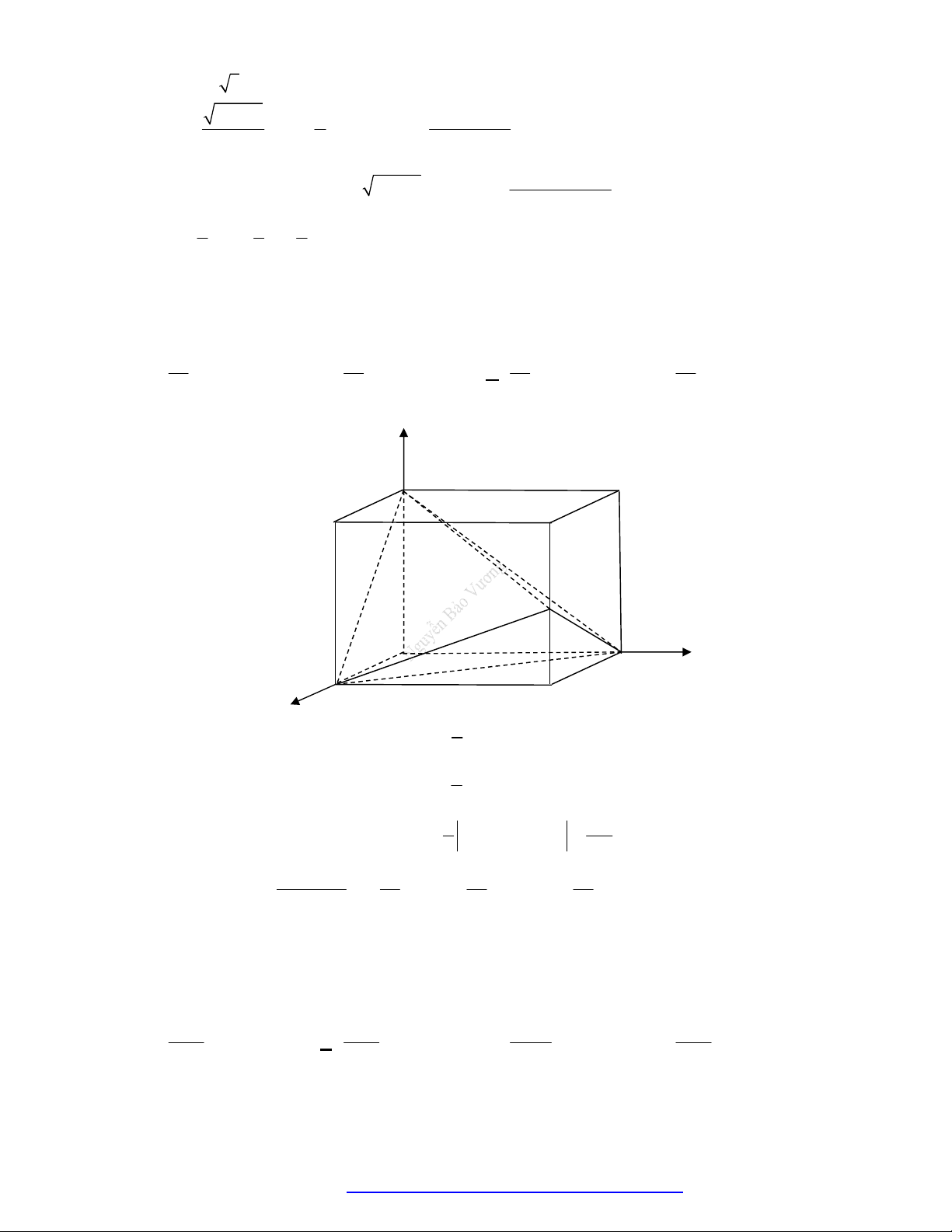
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 32 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Ta có:



3

R IA  .



2 2 2 2 2

2 2

; 3

2 2 4

b c a b a c

AM IM R IA

  

     

.

AD BĐT Cosi:

 

3

2 2 2

3

2 2 2 2 2 2 2 2 2

3 8

27

b a c

b a c b a c b a c abc

 

      

.

1 1 4

.8

6 6 3

V abc

   

.

Câu 33. (Chuyên Hùng Vương Gia Lai 2019) Trong không gian

Oxyz

, cho hình hộp chữ nhật

.

ABCD A B C D

   

có

A

trùng với gốc tọa độ

O

, các đỉnh

( ;0;0)

B a

,

(0; ;0)D a

,

(0;0; )A b



với

, 0

a b



và

2

a b

 

. Gọi

M

là trung điểm của cạnh

CC



. Thể tích của khối tứ diện

BDA M



có giá trị lớn nhất bằng

A.

64

27

. B.

32

27

. C.

8

27

. D.

4

27

.

Lời giải

Tọa độ điểm

( ; ;0), '( ; ; ), ( ; ; )

2

b

C a a C a a b M a a

.

' (- ;0; ), (- ; ;0), (0; ; )

2

b

BA a b BD a a BM a  

  

.

2

', ( ; ; )BA BD ab ab b

 

   

 



nên

2

'

1

', .

6 4

BDA M

a b

V BA BD BM

 

 

 

  

.

Ta có:

3

2

'

2 64 32 8

. .(2 )

3 27 27 27

BDA M

a a b

a a b a b V

 

 

     

 

 

.

Câu 34. (THPT-Thang-Long-Ha-Noi- 2019) Cho hình lập phương

.

ABCD A B C D

   

cạnh

a

. Gọi

,M N

lần lượt là

trung điểm của

BC

và

A B

 

. Mặt phẳng

 

'MND

chia khối lập phương thành hai khối đa diện, trong đó

khối chứa điểm

C

gọi là

 

H

. Tính thể tích khối

 

H

.

A.

3

55

72

a

. B.

3

55

144

a

. C.

3

181

486

a

. D.

3

55

48

a

.

Lời giải

A

D

y

'C

'D

'A

z

x

B

'B

C

M

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 33

Thể tích khối lập phương bằng

3

a

.

Mặt phẳng

 

MND



cắt cạnh

DC

tại

E

thỏa

1

4

EC DC

; cắt

BB



tại

P

sao cho

1

3

BP BB





.

Khi đó

 

. . .C D NPME C CEM C B PN

H

V V V V

    

  

.

Có

3

.

1 2

. .

6 2 3 18

B C NP

a a a

V a

 

 

3

.

1

. .

6 4 2 48

C C ME

a a a

V a



  .

Gắn hệ trục tọa độ như hình vẽ; lấy đơn vị trên trục 1 đơn vị bằng

a

.

Ta có

 

0;0;0C

,

 

0;0;1C



,

1

;0;0

4

E

 

 

 

,

1

0; ;0

2

M

 

 

 

,

1

0;0;

3

R

 



 

 

,

1

;1;0

4

Q

 



 

 

,

 

1;0;1D



.

Mặt phẳng

 

: 1 4 2 3 1 0

1 1 1

4 2 3

x y z

MND x y z



       



 

4 29

,

29

d C MND

 

 

29 1 29 11 29

4 12 4 48

MPND E EQND PMQ

S S S

 

    

 

3

.

1 11

, .

3 36

C D NPME D NPME

V d C MND S a

  

 

 

.

Vậy

 

3

55

144

H

V a

.

Câu 35. (Chuyên Thăng Long - Đà Lạt - 2018) Trong không gian với hệ trục tọa độ

,Oxyz

cho hình hộp chữ nhật

.ABCD A B C D

   

có

A

trùng với gốc tọa độ

O

các đỉnh

     

;0;0 , 0; ;0 , 0;0;B m D m A n



với

, 0m n 

và

4.m n 

Gọi

M

là trung điểm của cạnh

.CC



Khi đó thể tích tứ diện

BDA M



đạt giá trị

lớn nhất bằng

A.

9

4

. B.

64

27

. C.

75

32

. D.

245

108

.

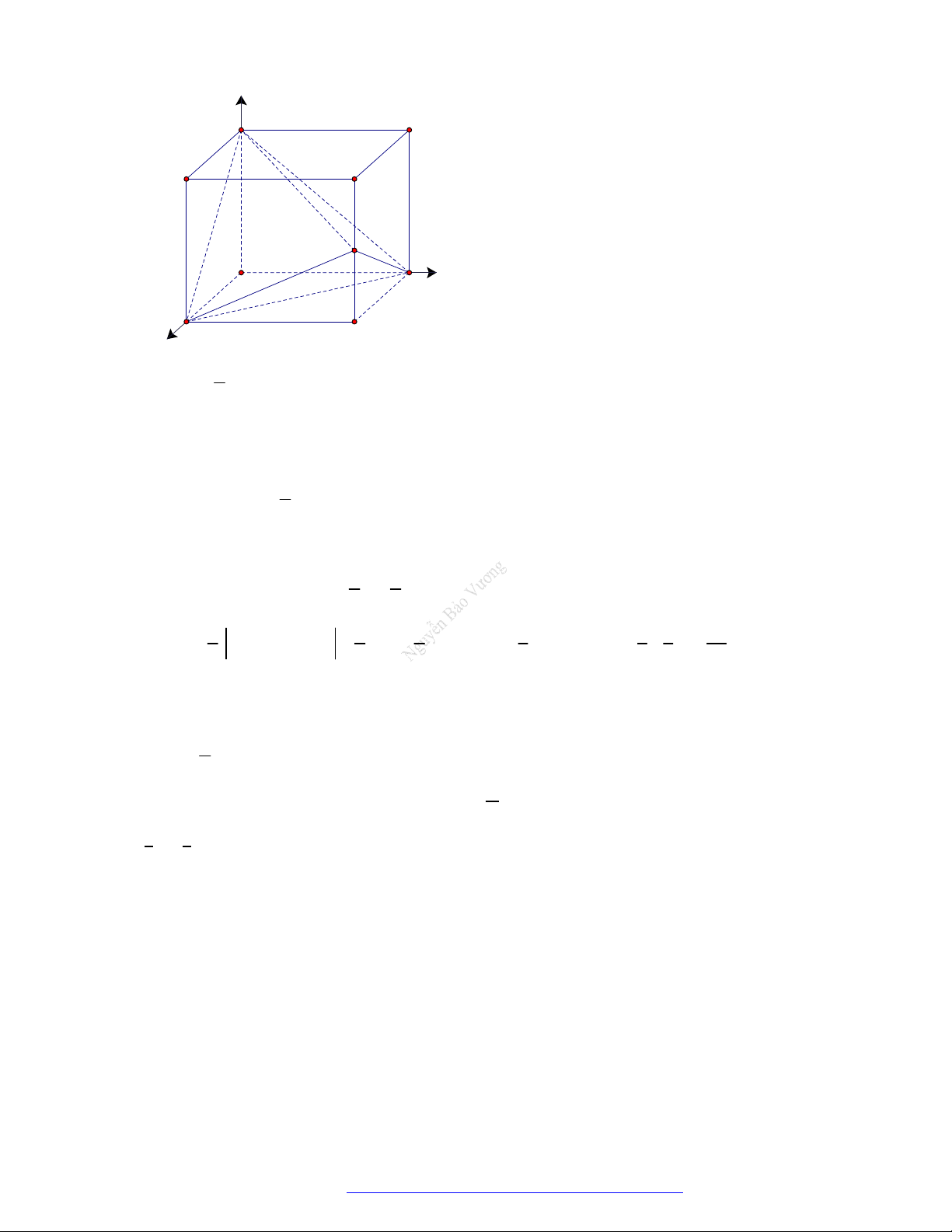
NGUYỄN BẢO VƯƠNG - 0946798489

Trang 34 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Lời giải

; ;

2

n

M m m

 

 

 

Ta có

 

;0;

; ;0

0; ;

2

BA m n

BD m m

n

BM m



 

 



 

 





 

2

; ; ;BA BD mn mn m

 



   

 

 

2 2 2

3

; . .

2 2

n

BA BD BM m n m m n

 



    

 

  

   

3

2 2

1 1 1 1 1 8 64

. ; . 4 . 8 2 . .

6 4 4 8 8 3 27

BA DM

V BA BD BM m n m m m m m



 

 



       

 

 

 

  

Câu 36. (Nho Quan A - Ninh Bình - 2019) Cho hình lập phương

.ABCD A B C D

   

có độ dài cạnh bằng

1

. Gọi

, , ,M N P Q

lần lượt là trung điểm của

, , ,AB BC C D DD

  

. Gọi thể tích khối tứ diện

MNPQ

là phân số

tối giản

a

b

, với

*

,a b 

. Tính

a b

.

A.

9

. B.

25

. C.

13

. D.

11

.

Lời giải

Chọn C

a

n

m

x

y

z

M

C

D

A

C'

B

D'

A'

B'

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 35

Thiết lập hệ tọa độ

Oxyz

như hình vẽ, gốc

O B





. Khi đó:

1

0; ;1

2

M

 

 

 

,

1

;0;1

2

N

 

 

 

,

1

1; ;0

2

P

 

 

 

,

1

1;1;

2

Q

 

 

 

.

1 1

; ; 0

2 2

MN

 

 

 

 



,

 

1;0; 1MP  



,

1 1

1; ;

2 2

MQ

 

 

 

 



.

Suy ra

1

, .

6

MNPQ

V MN MP MQ

 



 

  

1

12



1; 12a b  

13a b  

.

Câu 37. Trong không gian

Oxyz

,tập hợp tất cả các điểm thỏa mãn

2x y z  

và

2 2x y z   

là

một khối đa diện có thể tích bằng

A.

3

. B.

2

. C.

8

3

. D.

4

3

.

Lời giải

Chọn D

Tập các điểm

 

; ;M x y z

có tọa độ thỏa

2x y z  

là bát diện đều tâm

O

, các đỉnh có tọa

độ

           

2;0;0 , 2;0;0 , 0;2;0 , 0; 2;0 , 0;0;2 , 0;0; 2  

.

Tập các điểm

 

; ;M x y z

có tọa độ thỏa

2 2x y z   

là bát diện đều tâm

 

2;0;0A

, các

đỉnh có tọa độ

           

0;0;0 , 4;0;0 , 2;2;0 , 2; 2;0 , 2;0;2 , 2;0; 2 

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 36 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Giao của hai bát diện đều trên là một bát diện đều có tâm

 

1;0;0H

, các đỉnh là:

 

0;0;0O

,

 

2;0;0A

,

 

1;0;1B

,

 

1; 1;0C 

,

 

1;1;0D

,

 

1;0; 1E 

.

Ta có

2, 1AD BH 

.

Thể tích khối đa diện:

2

1 4

2. . .

3 3

V BH AD 

.

Câu 38. (Thi thử cụm Vũng Tàu - 2019) Cho hình hộp chữ nhật

. '

  

ABCD A B C D

có

1; 2; 3



  AB AD AA

.

Mặt phẳng

( )P

đi qua

C



và cắt các tia

; ;AB AD AA



lần lượt tại

; ;E F G

(khác

A

) sao cho thể tích

khối tứ diện

AEFG

nhỏ nhất. Tổng của

AE AF AG 

bằng.

A.

18

. B.

17

. C.

15

. D.

16

.

Lời giải

Chọn A

Trong không gian xây dựng hệ toạ độ

Oxyz

sao cho

; (1;0;0); (0;2;0);A (0;0;3)A O B D





Khi đó ta có

(1;2;3)C



Giả sử mặt phẳng

( )P

cắt các trục

; ;Ox Oy Oz

lần lươt tại

( ;0;0); (0; ;0); (0;0; )E a F b G c

, với

0; 0; 0a b c  

.

Khi đó phương trình mặt phẳng

( )P

là

1

x y z

a b c

  

,

Do mặt phẳng

( )P

đi qua

(1;2;3)C



.

Nên ta có

1 2 3

1

a b c

  

hay

3

1 2 3 6

1 3 162abc

a b c abc

     

.

Mặt khác thể tích khối tứ diện

AEFG

là

1

27

6

V abc 

, dấu

" "

xảy ra khi

1 2 3

1

a b c



 







  





.

Tức là

3; 6; 9a b c  

.

Vậy tổng

18AE AF AG  

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 37

Câu 39. (Chuyên Nguyễn Du-ĐăkLăk 2019) Cho tứ diện đều

ABCD

cạnh

a

. Gọi

K

là trung điểm

AB

, gọi

,M N

lần lượt là hình chiếu vuông góc của

K

lên

,AD AC

. Tính theo

a

bán kính mặt cầu ngoại tiếp

hình chóp

.K CDMN

.

A.

3

4

a

. B.

2

4

a

. C.

3 3

8

a

. D.

3 2

8

a

.

Lời giải

Chọn D

Coi

1a 

, ta có:

3 6 1 3

, ; ;

2 3 4 6

KC DH AN AC HK   

.

Chọn hệ trục

Oxyz

sao cho

 

1 3 3 6

0;0;0 , 0; ;0 , ;0;0 , ;0;

2 2 6 3

K O A C D

   

 



   

 

   

 

   

.

Ta có:

1 3 3

; ;0

4 8 8

AN AC N

 

 

 

 

 

.

Ta có: Tứ giác

CDMN

là hình thang cân. Do đó mặt cầu ngoại tiếp hình chóp

.K CDMN

cũng

chính là mặt cầu ngoại tiếp tứ diện

KCDN

.

Giả sử mặt cầu

 

S

ngoại tiếp tứ diện

KCDN

có phương trình:

 

2 2 2 2 2 2

2 2 2 0 0x y z ax by cz d a b c d          

.(1)

Vì

 

2 2 2

0

3

4

0

3 2

, , ,

3 2 6 3

8

6

3 3 4

8

3 3 3

0

4 4 16

d

a

b

K C D N S R a b c d

a c

c

d

a b







 



 







        

 

  

 

 

 



  







.

Vậy

3 2

.

8

a

R 

Câu 40. (Chuyên Thái Bình -2019) Cho hình chóp

.S ABCD

có đáy

ABCD

là hình vuông cạnh

a

,

SAD

là tam

giác đều và nằm trong mặt phẳng với đáy. Gọi

M

và

N

lần lượt là trung điểm của

BC

và

CD

. Bán kính

của mặt cầu ngoại tiếp hình chóp

.S CMN

bằng

A.

93

12

a

. B.

29

8

a

. C.

5 3

12

a

. D.

37

6

a

.

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 38 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

Lời giải

Chọn hệ tọa độ

Oxyz

như hình vẽ.

 

1 1 1 3

1;0;0 , ; ;0 , 1; ;0 , 0;0;

2 2 2 2

M N C S

 

   

 

   

   

 

.

Gọi

 

; ;I x y z

là tâm mặt cầu ngoại tiếp hình chóp

.S CMN MI NI CI SI   

.

Ta có:

 

1 1 1 3

1; ; , ; ; , 1; ; , ; ;

2 2 2 2

MI x y z NI x y z CI x y z SI x y z

 

   

         

 

   

   

 

   

.

Từ

MI NI CI SI  

ta có hệ:

 

2 2

2

2 2 2

2

2 2

2

2 2 2

1 1

3

1

2 2

4

1 1 1 1

1

2 2 2 4

5 3

1 3

1

12

2 2

x y z x y z

x

x y z x y z y

z

x y z x y z



   





       

   





   



 

     

          

 

     

     

 

 



 

       

 





 



.

3 1 5 3 1 1 5 3

; ; ; ;

4 4 12 4 4 12

I IM

   

    

   

   



.

 Bán kính mặt cầu ngoại tiếp hình chóp

.S CMN

là:

93

12

R IM 

.

Câu 41. (Chuyên KHTN - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho hai điểm

 

5;0;0A

và

 

3;4;0B

. Với

C

là điểm nằm trên trục

Oz

, gọi

H

là trực tâm của tam giác

ABC

. Khi

C

di động trên trục

Oz

thì

H

luôn thuộc một đường tròn cố định. Bán kính của đường tròn đó bằng

A.

5

4

. B.

3

2

. C.

5

2

. D. 3 .

Lời giải

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 39

Ta có

 

0;0;C c

. Dễ thấy tam giác

ABC

cân tại

C

. Gọi

 

4;2;0E 

là trung điểm của

AB

. Ta

có mặt phẳng

 

OCE

vuông góc với

AB

(do

AB OC

AB CE











) và là mặt phẳng cố định.

Gọi

K

là trực tâm tam giác

OAB

, do

A

,

B

và

K

cùng nằm trong mặt phẳng

 

Oxy

nên

. 0

OK AB

BK OA















 

 

. 2 .4 0

3 0

x y

x

  







 





3

2

x

y

















. Tìm được

3

3; ;0

2

K

 



 

 

.

Ta chứng minh được

 

KH CAB

do

 

AB OEC

HK AB

HK CA

CA BHK











 









.

Suy ra



90KHE   . Suy ra

H

thuộc mặt cầu đường kính

1 5

1

4 2

KE   

và

 

3

, ,

2

d B SCD d H SCD 

thuộc mặt phẳng

 

OCE

cố định. Vậy

H

luôn thuộc một

đường tròn cố định có bán kính

5

4

R 

.

Câu 42. (Chuyên Vinh - 2018) Trong không gian

,Oxyz

cho các điểm

A

,

B

,

C

(không trùng

O

) lần lượt thay

đổi trên các trục

Ox

,

Oy

,

Oz

và luôn thỏa mãn điều kiện: tỉ số giữa diện tích của tam giác

ABC

và thể

tích khối tứ diện

OABC

bằng

3

.

2

Biết rằng mặt phẳng

 

ABC

luôn tiếp xúc với một mặt cầu cố định,

bán kính của mặt cầu đó bằng

A.

3.

B.

2.

C.

4.

D.

1.

Lời giải

x

z

H

E

y

A

O

B

C

K

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 40 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

B

A

C

1

d

3

d

2

d

I

Ta có

 

1

. ,

3

ABC ABC

OABC

ABC

S S

V

S d O ABC



 

3

,d O ABC



Mà

3

2

ABC

OABC

S

V



nên

 

, 2d O ABC 

.

Vậy mặt phẳng

 

ABC

luôn tiếp xúc mặt cầu tâm

O

, bán kính

2R 

.

Câu 43. (Chuyên Lê Hồng Phong - TPHCM - 2018) Trong không gian với hệ tọa độ

Oxyz

, cho

3

đường thẳng

 

1

1 1 1

:

2 1 2

x y z

d

  

 



,

 

2

3 1 2

:

1 2 2

x y z

d

  

 

,

 

3

4 4 1

:

2 2 1

x y z

d

  

 



. Mặt cầu bán kính

nhỏ nhất tâm

 

; ;I a b c

, tiếp xúc với

3

đường thẳng

 

1

d

,

 

2

d

,

 

3

d

. Tính

2 3S a b c  

.

A.

10S 

. B.

11S 

. C.

12S 

. D.

13S 

.

Lời giải

 

1

d

đi qua điểm

 

1;1;1A

có VTCP

 

1

2;1; 2u  



.

 

2

d

đi qua điểm

 

3; 1;2B 

có VTCP

 

2

1;2;2u 



.

 

3

d

đi qua điểm

 

4;4;1C

có VTCP

 

3

2; 2;1u  



.

Ta có

1 2

. 0u u 

 

,

2 3

. 0u u 

 

,

3 1

. 0u u 

 

 

1

d

,

 

2

d

,

 

3

d

đôi một vuông góc với nhau.

1 2

, . 0u u AB

 



 

  

,

2 3

, . 0u u BC

 



 

  

,

3 1

, . 0u u CA

 



 

  

 

1

d

,

 

2

d

,

 

3

d

đôi một chéo nhau.

Lại có:

 

2; 2;1AB  



;

1

. 0AB u 

 

và

2

. 0AB u 

 

nên

 

1

d

,

 

2

d

,

 

3

d

chứa

3

cạnh của hình hộp

chữ nhật như hình vẽ.

Vì mặt cầu tâm

 

; ;I a b c

tiếp xúc với

3

đường thẳng

 

1

d

,

 

2

d

,

 

3

d

nên bán kính

     

1 2 3

, , ,R d I d d I d d I d  

     

2 2 2 2

1 2 3

, , ,R d I d d I d d I d   

2

1

2

1

,AI u

R

u

 

 

 

 

 

 

 

 



2

,BI u

u

 

 

 

 



 

 

 



2

3

,CI u

u

 

 

 

 



 

 

 



, với

2 2 2

1 2 3

9u u u  

  

,

 

1; 1; 1AI a b c   



,

 

1

, 2 1;2 2 4; 2 1AI u b c a c a b

 

       

 

 

.

 

3; 1; 2BI a b c   



,

 

2

, 2 2 6; 2 4;2 7BI u b c a c a b

 

       

 

 

.

TÀI LIỆU ÔN THI THPTQG 2021

Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 41

 

4; 4; 1CI a b c   



,

 

3

, 2 6; 2 2; 2 2 16CI u b c a c a b

 

        

 

 

.

2

1

2

3

9 ,

R AI u

R BI u

R CI u



 



 



 





 



 



 





 

 

2 2 2

2

1 2 3

27 , , ,R AI u BI u CI u

     

   

     

     

 

2 2 2 2

27 18 126 54 54 423R a b c a b c       

2 2 2

2

7 3 3 243 243

27 18 18 18

2 2 2 2 2

R a b c

     

        

     

     

min

3

2

R  khi

7

2

a 

,

3

2

b c 

7 3 3

; ;

2 2 2

I

 



 

 

.

Khi đó

2 3 11S a b c   

.

Câu 44. Cho hình chóp

.S ABCD

cs đáy là hình thang vuông tại

A

và

B

,

2 2 2AD AB BC a  

, cạnh bên

SA

vuông góc với mặt phẳng đáy,

2SA a

. Gọi

E

là trung điểm cạnh

AD

. Tính bán kính mặt cầu

ngoại tiếp hình chóp

.S CDE

.

A.

3

2

a

. B.

11

2

a

. C.

6

2

a

. D.

3

4

a

.

Lời giải

Chọn B

Dễ tính được

AB BC AE a  

Gắn hình chóp vào hệ trục tọa độ

Oxyz

với

O A

,

, , 2AB i AE j AS k  

  



 

Khi đó ta có

       

0;1;0 , 1;1;0 , 0;2;0 , 0;0;2E C D S

Gọi

 

; ;I a b c

là tâm mặt cầu ngoại tiếp hình chóp ta có:

     

2 2 2

1

1 1 1 2 1 0

2

IE IC a b c a b c a a              

C

E

A

D

S

B

NGUYỄN BẢO VƯƠNG - 0946798489

Trang 42 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/

   

2 2

2 2 2 2

3

1

2 2 3 0

2

I

E ID a b c a b c b b



            

   

2

2 2 2 2

2

3 3

1

2 4 2 3 0

4

2

b

I

E IS a b c a b c c b c





              

Vậy

1

3 3

; ;

2 2 2

I





 

 

suy

ra bán kính mặt cầu cần tìm là

11

2

R

IE 

Chuyên đề phương pháp toạ độ trong không gian ôn thi THPT 2021 – Nguyễn Bảo Vương

Chương 3: Phương pháp tọa độ trong không gian 143 tài liệu

Toán 12 3.8 K tài liệu

Bình luận

Chuyên đề phương pháp toạ độ trong không gian ôn thi THPT 2021 – Nguyễn Bảo Vương