Chuyên Đề Phương Trình Bậc Nhất Hai Ẩn Ôn Thi Vào 10 Giải Chi Tiết
Nhận dạng phương trình bậc nhất hai ẩn, nghiệm của phương trình bậc nhất hai ẩn và biểu diễn tập nghiệm trên mặt phẳng tọa độ. Phương trình nào sau đây không phải là phương trình bậc nhất hai ẩn. Phương trình nào là phương trình bậc nhất Khẳng định nào sau đây là đúng? Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Chủ đề: Tài liệu ôn thi vào 10 môn Toán 114 tài liệu
Môn: Môn Toán 1.3 K tài liệu
Tác giả:
Preview text:
CHUYÊN ĐỀ 14. PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
DẠNG 1: Nhận dạng phương trình bậc nhất hai ẩn, nghiệm của phương trình bậc nhất hai
ẩn và biểu diễn tập nghiệm trên mặt phẳng tọa độ.
PHẦN I. BÀI TẬP TRẮC NGHIỆM
1. TRẮC NGHIỆM CHỌN ĐÁP ÁN
Câu 1. [NB] Phương trình bậc nhất hai ẩn là
A. y 3x 5 .
B. x 3y 2 .
C. 2x 4 y 6 0 .
D. Cả 3 đáp án trên. Lời giải Chọn D
Vì phương trình bậc nhất hai ẩn x và y là hệ thức dạng
ax by c 1
Trong đó a,b và c là các số đã biết ( a 0 hoặc b 0 ).
Câu 2. [NB] Phương trình bậc nhất hai ẩn là A.
y 2x 7 0 .
B. x 3y 2 .
C. x 5y 8 0 . D. 2
x y 7 0 . Lời giải Chọn C
Vì phương trình bậc nhất hai ẩn x và y là hệ thức dạng
ax by c 1
Trong đó a,b và c là các số đã biết ( a 0 hoặc b 0 ).
Câu 3. [NB] Phương trình nào sau đây không phải là phương trình bậc nhất hai ẩn
A. x y 3 .
B. 2x 5 y 0 .
C. 7x 3y 11 0 . D. 2 x y 3 . Lời giải Chọn D Vì phương trình 2
x y 3 có bậc là 2
Câu 4. [NB] Cặp số nào sau đây là một nghiệm của phương trình x 3y 1? A. 4; 1 . B. 2;0 . C. 1;2 . D. 2; 1 . Lời giải Chọn A
Xét x 4 và y 1 x 3.11 4 TM Do đó cặp số 4;
1 là nghiệm của phương trình
Câu 5. [TH] Cặp số nào sau đây là một nghiệm của phương trình 3x 4 y 5 0 ? 5 A. 1;2 . B. 5;5. C. 0; .
D. Cả 3 đáp án trên. 4 Lời giải Chọn C 5 5
Xét x 0 và y
x 4. 5 : 3 0 TM 4 4 Trang 1 Do đó cặ 5 p số 0;
là nghiệm của phương trình 4
Câu 6. [TH] Phương trình 5
x y 0 có bao nhiêu nghiệm?
A. Phương trình vô nghiệm..
B. Phương trình có một nghiệm.
C. Phương trình có hai nghiệm.
D. Phương trình có vô số nghiệm. Lời giải Chọn D
Phương trình có vô số nghiệm vì với mỗi giá trị của x cho ta một giá trị của y
Câu 7. [TH] Công thức nghiệm tổng quát của phương trình 3x 0 y 12 là x x A. B. y 4 y 4 y y C. D. x 4 x 4 Lời giải Chọn D x 4
3x 0 y 12 y
Câu 8. [TH] Giá trị của a để phương trình ax 3y 6 có nghiệm 1; 2 là
A. a 3
B. a 2
C. a 0 D. a 3 Lời giải Chọn D
Thay x 1; y 2
vào phương trình ax 3y 6 ta được: . a 1 3.( 2
) 6 a 0 2
Câu 9. [VD] Giá trị của a để phương trình 3y 2ax 0 có nghiệm 1; là 3 A. a 3
B. a 2
C. a 0 D. a 1 Lời giải Chọn D 2
Thay x 1; y
vào phương trình 3y 2ax 0 ta được: 3 2 3. 2. .
a 1 0 a 1 3
Câu 10. [VD] Giá trị của m để phương trình 4mx 3y 8
có nghiệm 2;0 là
A. m 1 B. m 1 C. m 2 D. m 2 Lời giải Chọn B Trang 2
Thay x 2; y 0 vào phương trình 4mx 3y 8 ta được: 4. . m 2 3.0 8 m 1
Câu 11. [VD] Giá trị của mđể phương trình 2x 8 y 3
m có nghiệm 5 ; 1 là A. m 6 B. m 6
C. m 6 D. m 6 Lời giải Chọn D Thay x 5
; y 1 vào phương trình 2x 8y 3 m ta được: 2. 5 8. 1 3
.m m 6
Câu 12. [VD] Tập nghiệm của phương trình x y 3 là A. S
x;x 3| x . B. S
x;x 3| x . C. S
x;x 3| x . D. S
x 3;x| x . Lời giải Chọn D x
x y 3
y 3 x
2. TRẮC NGHIỆM ĐÚNG SAI
Trong mỗi ý a), b), c), d) ở mỗi câu, em chọn đúng hoặc sai
Câu 1. Phương trình nào là phương trình bậc nhất Khẳng định nào sau đây là đúng?
a) 2x 3 2x y .
b) 2x 3 y c) 2 x y 1.
d) 2x 4 y . Lời giải
a) Sai b) Đúng c) Sai d) Đúng
a) Sai vì hệ số a 0
b) Đúng vì Phương trình bậc nhất hai ẩn x và y là hệ thức dạng: ax by c 1
Trong đó a,b và c là các số đã biết ( a 0 hoặc b 0 ).
c) Sai vì bậc của phương trình là bậc 2
d) Đúng Phương trình bậc nhất hai ẩn x và y là hệ thức dạng: ax by c 1
Trong đó a,b và c là các số đã biết ( a 0 hoặc b 0 ).
Câu 2. Phương trình nào sau đây là phương trình bậc nhất hai ẩn? Khẳng định nào sau đây là đúng? a) 2 2x 3y 0 b) 3 x y 5
c) xy x 1
d) 2x 3y 4 Lời giải Trang 3
a) Sai b) Sai c) Sai d) Đúng
Câu a, b, c Sai vì phương trình đó không phải phương trình bậc nhất
d) Đúng vì Phương trình bậc nhất hai ẩn x và y là hệ thức dạng: ax by c 1
Trong đó a,b và c là các số đã biết ( a 0 hoặc b 0 ).
Câu 3. Cho phương trình 2x y 4 . Khẳng định nào sau đây là đúng? x
a) Công thức nghiệm tổng quát của phương trình là
y 2x 4
b) Phương trình luôn vô nghiệm.
c) Phương trình có vô số nghiệm.
d) Phương trình có cùng tập nghiệm với phương trình 2x 4 y . Lời giải
a) Đúng b) Sai c) Đúng d) Sai x
Phương trình 2x y 4 luôn có vô số nghiệm theo công thức
y 2x 4
Câu 4. Cho phương trình mx 4 y 2 có một nghiệm là 1; 2 . Khẳng định nào sau đây là đúng?
a) Khi m 2 phương trình có một nghiệm 1; 2 .
b) Khi m 10 phương trình có một nghiệm 1; 2 . c) Khi m 2
phương trình vô nghiệm. d) Khi m 1
phương trình có hai nghiệm. Lời giải
a) Sai b) Đúng c) Sai d) Sai
Thay x 1, y 2 vào phương trình ta được: .
m 1 4.2 2 m 10.
Câu 5. Công thức nghiệm tổng quát của phương trình 4x 0 y 4 . Khẳng định nào sau đây đúng? a) x 1 x 1 b) y R y c) x 1
d) y R Lời giải
a) Sai b) Đúng c) Đúng d) Sai
Phương trình 4x 0 y 4 4x 4 x 1 x 1
Vậy công thức nghiệm tổng quát là . y R
Câu 6. Nghiệm nguyên của phương trình x 3y 4 . Khẳng định nào sau đây đúng? a) 4 3 ;
y y với ( y Z ). Trang 4 b) 1; 3 c) 1;4 d) 3 ;4 Lời giải
a) Đúng b) Sai c) Sai d) Sai
x 3y 4 x 4 3y
Nghiệm nguyên tổng quát của phương trình là 4 3 ; y y Z .
3. TRẮC NGHIỆM TRẢ LỜI NGẮN
Câu 1. [NB] Với giá trị nào của a thì phương trình sau vô nghiệm ax 0 y 5 ? Lời giải
Phương trình ax 0y 5 có b 0 nên vô nghiệm khi a 0 .
Câu 2. [NB] Nghiệm tổng quát của phương trình 2
x y 4 là gì? Lời giải Ta có: 2
x y 4 y 2 x 4 .
Câu 3. [TH] Nghiệm tổng quát của phương trình 1 x 2 y 1 là bao nhiêu? 2 Lời giải 1 Ta có: x 2 y 1
x 4 y 2 2
x 4 y 2 Do đó
là nghiệm của phương trình y
Câu 4. [VD] Cho phương trình m 2 x my 1
( m là tham số). Hỏi phương trình luôn có
nghiệm là bao nhiêu với mọi m ? Lời giải
Giả sử phương trình luôn có nghiệm x ; y với mọi m 0 0
Khi đó: m 2 x my 1 mọi m 0 0
m 2x my 1 0 m 0 0
x y m 2x 1 0 m 0 0 0 x y 0 0 0 m 2x 1 0 0 1 y 0 2 m 1 x 0 2
Câu 5. [VDC] Tìm nghiệm nguyên âm lớn nhất của phương trình 5
x 2y 7 . Lời giải Trang 5 5x 7 x 7 5
x 2y 7 2y 5x 7 y y 2x 2 2 Đặt x 7 t
x 2t 7 y 2.2t 7 t y 5t 14t 2
x 2t 7
Nên nghiệm nguyên của phương trình là t
y 5t 14 7 t x 0 t 2 14
Vì x, y nguyên âm nên : 2 7 0 t y 0 5t 14 0 14 5 t 5
Vì nghiệm nguyên âm lớn nhất, mà t nguyên nên t 2 Vậy x 3 ; y 4 .
PHẦN II. BÀI TẬP TỰ LUẬN Phương pháp giải:
1. Phương trình bậc nhất hai ẩn x và y là hệ thức dạng: ax by c 1
Trong đó a,b và c là các số đã biết ( a 0 hoặc b 0 ).
2. Nếu tại x x và y y ta có ax by c là một khẳng định đúng thì cặp số x ; y được o o 0 0 o o
gọi là một nghiệm của phương trình 1
Xét phương trình bậc nhất hai ẩn .
3. Để viết công thức nghiệm tổng quát của phương trình, trước tiên, ta biểu diễn x theo y (hoặc
y theo x ) rồi đưa ra kết luận về công thức nghiệm tổng quát.
4. Để biểu diễn tập nghiệm của phương trình trên mặt phẳng tọa độ, ta vẽ đường thẳng d có
phương trình ax by c .
Ví dụ 1 [NB]: Trong các hệ thức sau, hệ thức nào là phương trình bậc nhất hai ẩn? 2x 3y 5
4x 7 y 10 3
x 5y 2
0x 2 y 4
2x 0 y 3
0x 0 y 6 Lời giải
Hệ thức 0x 0 y 6 có a b 0 nên không phải là phương trình bậc nhất hai ẩn. Các hệ thức
còn lại đều là phương trình bậc nhất hai ẩn.
Ví dụ 2 [TH]: Tìm nghiệm tổng quát của các phương trình sau:
a) 3x y 2 ; b) x 5y 3 0
c) 4x 0 y 2 d) 0x 2 y 5 Lời giải
a) 3x y 2 Suy ra y 3x 2 . Vậy phương trình có nghiệm tổng quát ;
x 3x 2 với x tuỳ ý
b) x 5y 3 0 Suy ra x 5 y 3. Vậy phương trình có nghiệm tổng quát 5
y 3; y với y Trang 6
c) 4x 0 y 2
. Phương trình có nghiệm tổng quát 1 ; y
với y tuỳ ý. 2 5
d) 0x 2 y 5 . Phương trình có nghiệm tổng quát x;
với x tuỳ ý. 2
Ví dụ 3 [TH]: Tìm m trong mỗi trường hợp sau:
a) 1;2 là nghiệm của phương trình mx y 5 0 ; b) Điểm (
A 0;3) thuộc đường thẳng 4x my 6 0 . Lời giải
a) Thay x 1, y 2 vào phương trình ta có .
m 1 2 5 0 m 3.
b) Thay x 0, y 3 vào phương trình đường thẳng, ta có 4.0 .
m 3 6 m 2 .
Ví dụ 4 [TH]: Viết công thức nghiệm tổng quát và biểu diễn tập nghiệm của phương trình
x 5y 3 trên mặt phẳng tọa độ. Lời giải
Ta có : x 5y 3 x 3 5 y
x 3 5y
Vậy phương trình có nghiệm tổng quát là y
Đường thẳng biểu diễn tập nghiệm của phương trình là đường thẳng x 5y 3 .
+ Tại y 0 thì x 3 ⇒ Đường thẳng đi qua điểm 3; 0. + Tại thì 3
y ⇒ Đường thẳng đi qua điểm ( 3 0; ). 5 5 Vậy đường thẳng 3
x 5 y 3 là đường thẳng đi qua hai điểm 3; 0 và ( 0; ). 5
Ví dụ 5 [TH]: Xét phương trình x 10 y 4
a) Hãy chỉ ra ba nghiệm của phương trình.
b) Viết tập nghiệm của phương trình. Lời giải
a) Ba cặp số 6;1 ; 4 ; 0 và 1 4; 1
là ba nghiệm của phương trình.
b) Ta có: x 10 y 4
⇔ x 10y 4 .
Vậy nghiệm tổng quát của phương trình là 10y 4; y y R .
Ví dụ 6 [VD]: Giả sử ;
x y là nghiệm của phương trình bậc nhất hai ẩn x 2 y 5 Trang 7
a) Hoàn thành bảng sau đây: x 2 1 0 ? ? y ? ? ? 1 2
Từ đó suy ra 5 nghiệm của phương trình đã cho.
b) Tính y theo x . Từ đó cho biết phương trình đã cho có bao nhiêu nghiệm. Lời giải a) Ta có: x 2 1 0 3 1 7 5 y 3 1 2 2 2 7 5
Vậy 5 nghiệm của phương trình đã cho là: 2; ; 1 ; 3 ; 0; ; 3; 1 ;1;2 2 2 5 x b) Ta có: y
. Với mỗi giá trị x tùy ý cho trước, ta luôn tìm được một giá trị y tương ứng. 2
Do đó phương trình đã cho vô số nghiệm.
Ví dụ 7 [VD]: Xác định a để phương trình ax y 1 có nghiệm: 2; 5
Viết công thức nghiệm và biểu diễn tập nghiệm với a tìm được trên mặt phẳng tọa độ. Lời giải
Phương trình ax y 1 có nghiệm 2;5
2a 6 a 3
Vậy khi a 3 thì phương trình ax y 1 có nghiệm 2;5.
Với a 3 có 3x y 1 => y 3x 1 x R
Công thức nghiệm của phương trình
y 3x 1
Tập nghiệm của phương trình được biểu diễn bởi đường thẳng trên mặt phẳng tọa độ. 1 1
+ Tại y 0 thì x
⇒ Đường thẳng đi qua điểm ;0 . 3 3
+ Tại x 0 thì y 1 ⇒ Đường thẳng đi qua điểm 0; 1 . 1
Vậy đường thẳng y 3x 1 là đường thẳng đi qua hai điểm ;0 và 0; 1 . 3 Trang 8 BÀI TẬP TỰ LUYỆN
Bài 1. [NB] Kiểm tra cặp số sau có phải là nghiệm của phương trình 2x y 1 0 hay không?
a) (1;1) ; b) (0,5;3) . c) 0;0 Lời giải
a) Thay x 1 và y 1 vào phương trình, ta có 2.111 0 . Vậy cặp số (1;1) là nghiệm của phương trình.
b) Thay x 0,5 và y 3 vào phương trình, ta có 2.0,5 3 1 3
0 . Vậy cặp số (0,5;3)
không là nghiệm của phương trình.
c) Thay x 0, y 0 vào phương trình ta có 1
0. Vậy cặp số 0;0 không phải là nghiệm của phương trình.
Bài 2. [NB] Trong các cặp số (2;1) , (3; 1
) ,(0;5) cặp số nào là nghiệm của phương trình
x 2 y 4 0 . Lời giải
Với (2;1) , ta có 2 21 4 0 ( 2;1) là nghiệm. Với (3; 1 ), ta có 3 2( 1 ) 4 3 0 (3; 1 ) không là nghiệm.
Với (0;5) , ta có 0 25 4 6 0 (0;5) không là nghiệm.
Bài 3. [TH] Viết công thức nghiệm tổng quát và biểu diễn tập nghiệm của các phương trình sau
trên mặt phẳng tọa độ:
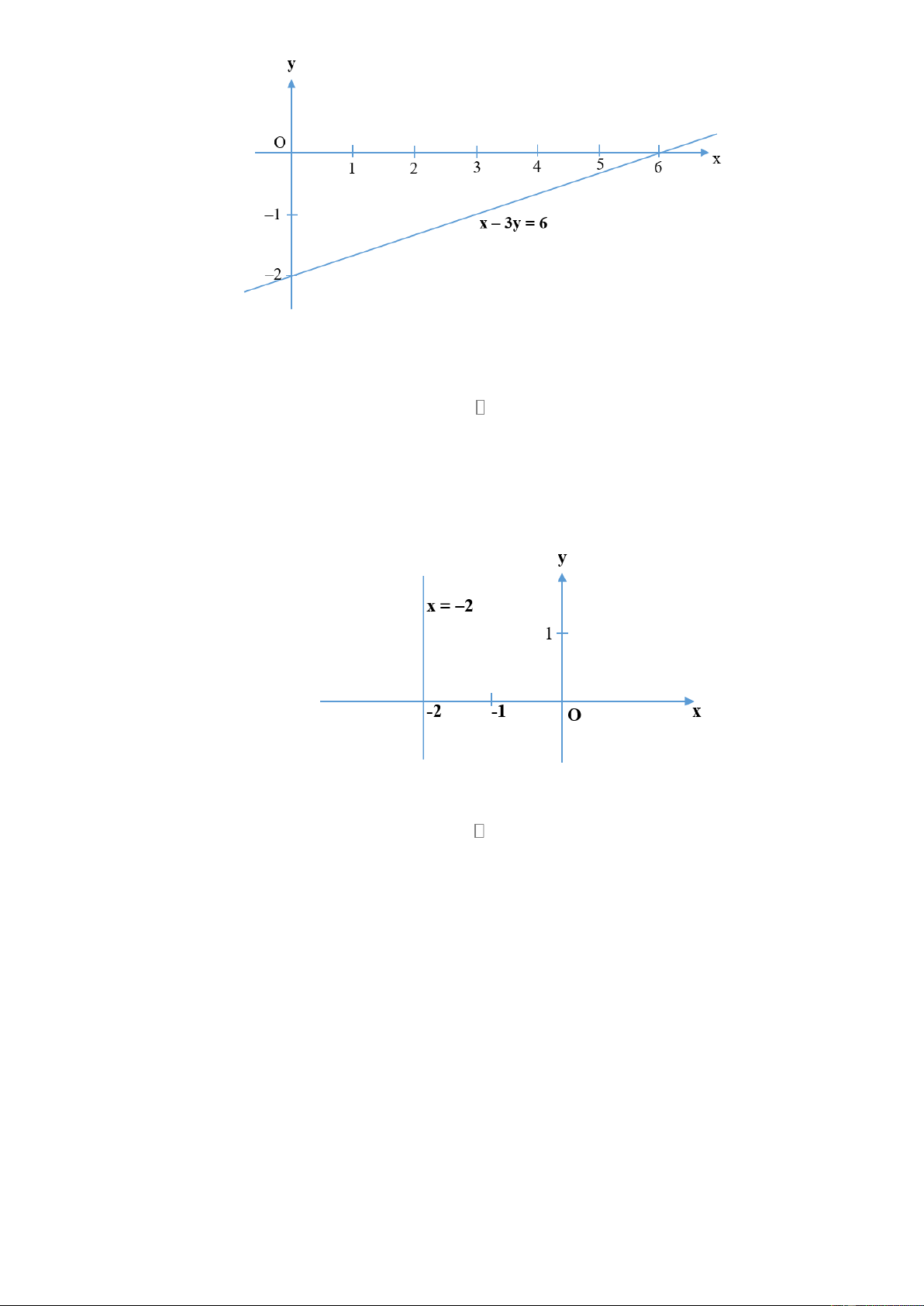
a) x 3y 6 b) 7x 0 y 14
c) 0x 4 y 8 Lời giải
a) Ta có : x 3y 6 x 6 3y
x 6 3y
Vậy phương trình có nghiệm tổng quát là y
Đường thẳng biểu diễn tập nghiệm của phương trình là đường thẳng x 3y 6 .
+ Tại y 0 thì x 6 ⇒ Đường thẳng đi qua điểm 6; 0.
+ Tại x 0 thì y 2 ⇒ Đường thẳng đi qua điểm 0; 2 .
Vậy đường thẳng x 3y 6 là đường thẳng đi qua hai điểm 6; 0và (0; 2 ) . Hình vẽ: Trang 9
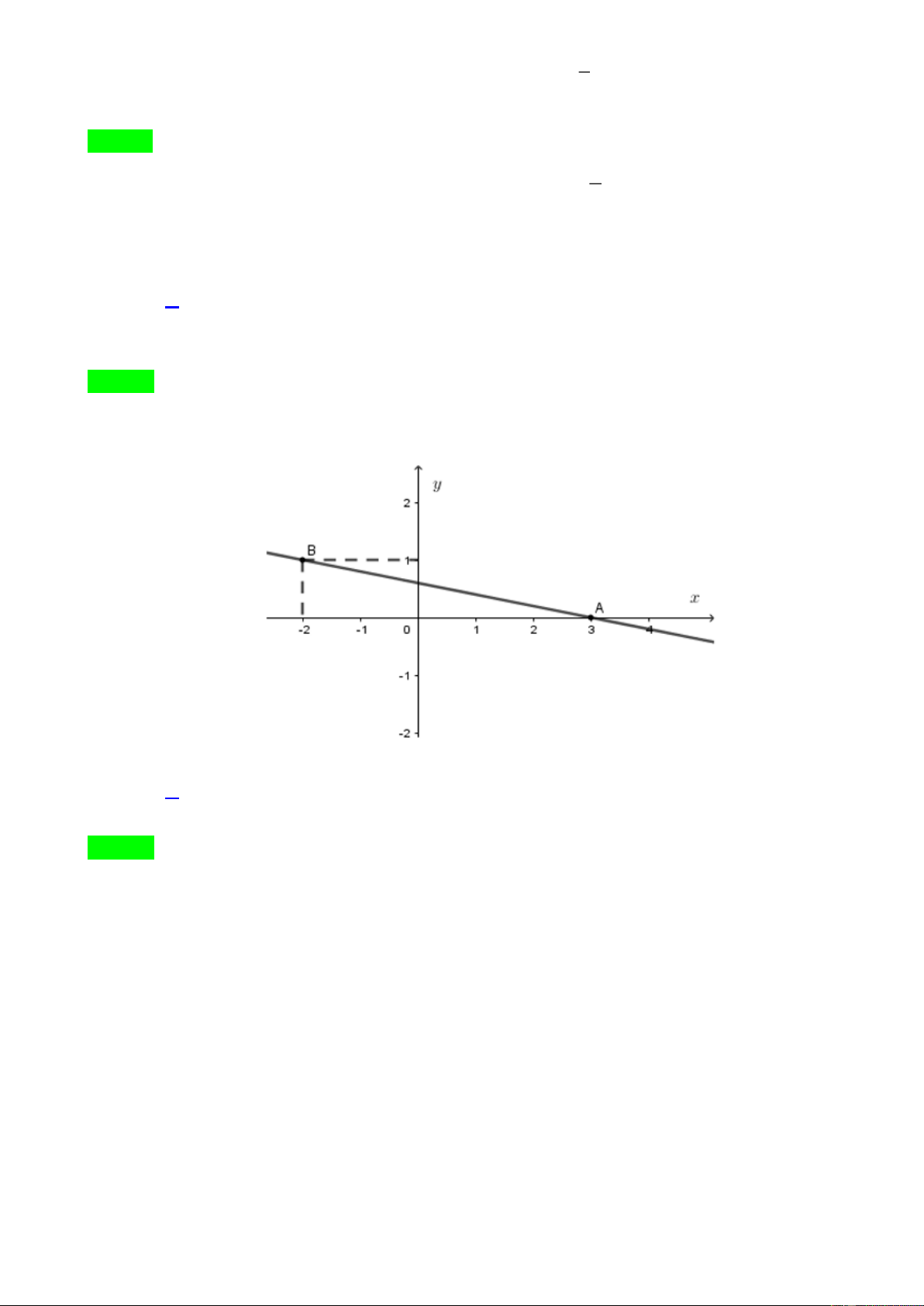
b) Ta có : 7x 0 y 1 4 7x 1 4 x 2 x 2
Vậy phương trình có nghiệm tổng quát là y
Đường thẳng biểu diễn tập nghiệm của phương trình là đường thẳng x 2 .
Vậy đường thẳng là đường thẳng song song với trục tung, cắt trục hoành tại điểm có hoành độ bằng 2 . Hình vẽ:
c) Ta có : 0x 4 y 20 4
y 20 y 5 x
Vậy phương trình có nghiệm tổng quát là y 5
Đường thẳng biểu diễn tập nghiệm của phương trình là đường thẳng y 5 .
Vậy đường thẳng y 5 là đường thẳng song song với trục hoành, cắt trục tung tại điểm có tung độ bằng 5 . Hình vẽ: Trang 10
Bài 4. [VD] Tìm 3 nghiệm của phương trình 2x 3y 5 . Lời giải 5 5
+ Cho y 0 x ;0
là một nghiệm của phương trình. 2 2
+ Cho y 1 x 4 4;
1 là một nghiệm của phương trình. + Cho y 1
x 1 1;
1 là một nghiệm của phương trình. 5 ;0 ,4; 1 ,1;
1 là 3 nghiệm cần tìm của phương trình 2x 3y 5 . 2
Bài 5. [VD] Tìm 4 nghiệm của phương trình x 6 y 2 . Lời giải
+ Cho y 0 x 2 2
;0 là một nghiệm của phương trình.
+ Cho y 1 x 4 4;
1 là một nghiệm của phương trình. + Cho y 1 x 8 8 ;
1 là một nghiệm của phương trình. 1 1 + Cho y x 1 1;
là một nghiệm của phương trình. 2 2
1 2;0 , 4;1 , 8; 1 , 1;
là 4 nghiệm cần tìm của phương trình x 6y 2 . 2
Bài 6. [VD] Xác định a để phương trình ax y 3 có nghiệm 1 ; 3 . Lời giải
Phương trình ax y 3 có nghiệm 1 ; 3 3 . a 3 ( 1 ) 3a 2 2 a 3 Vậy khi 2 a
thì phương trình ax y 3 có nghiệm 1 ; 3 3
Dạng 2. Tìm điều kiện của tham số để đường thẳng ax by c thỏa mãn điều kiện cho trước
PHẦN I. BÀI TẬP TRẮC NGHIỆM
Bài 1. Cho đường thẳng d có phương trình mx 2 y m 3 . Tìm các giá trị của tham số m để
song song với trục hoành. Trang 11 A. m 3 . B. m 2 . C. m 1 . D. m 0 . Lời giải Chọn D
Để đường thẳng d song song với trục hoành khi m 0
Bài 2. Cho đường thẳng d có phương trình (m 2)x (3m 1) y 6m 2 . Tìm các giá trị của
tham số m để d song song với trục hoành.
A. m 1.
B. m 2 .
C. m 3. D. m 4 . Lời giải Chọn B
Để đường thẳng d song song với trục hoành khi m 2 0 suy ra m 2
Bài 3. Cho đường thẳng d có phương trình (5m 15)x 2my m 2. Tìm các giá trị của tham
số m để d song song với trục hoành.
A. m 1.
B. m 2 .
C. m 3. D. m 4 . Lời giải Chọn C
Để đường thẳng d song song với trục hoành khi 5m 15 0 suy ra m 3
Bài 4. Cho đường thẳng d có phương trình m
1 x (2m 1) y m 1. Tìm các giá trị của
tham số m để d trùng với trục hoành.
A. m 1. B. m 1 . 1 1 C. m . D. m . 2 2 Lời giải Chọn A
Để đường thẳng d song song với trục hoành khi m 1 0 suy ra m 1
Bài 5. Cho đường thẳng d có phương trình m 4 x (m 1) y 3 . Tìm các giá trị của tham
số m để d song song với trục tung. A. m 2 .
B. m 2 .
C. m 1. D. m 1 . Lời giải Chọn D
Để đường thẳng d song song với trục tung khi m 1 0 suy ra m 1
Bài 6. Cho đường thẳng d có phương trình (m 2)x (3m 1) y 6m 2 . Tìm các giá trị của
tham số m để song song với trục tung. Trang 12 1 2 A. m . B. m . 3 3 1
C. m 2 . D. m . 3 Lời giải Chọn A Để đường thẳng 1
d song song với trục tung khi 3m 1 0 suy ra m 3 m
Bài 7. Cho đường thẳng d có phương trình
1.x (1 2m)y 2 . Tìm các giá trị của tham 2
số m để d song song với trục tung. 1
A. m 1. B. m . 2 1
C. m 2 . D. m . 2 Lời giải Chọn D Để đường thẳng 1
d song song với trục tung khi 1 2m 0 suy ra m 2
Bài 8. Cho đường thẳng d có phương trình (2m 4)x (m 1) y m 5. Tìm các giá trị của
tham số m để d đi qua gốc tọa độ.
A. m 2 .
B. m 1. C. m 5 . D. m 5. Lời giải Chọn C
Để đường thẳng d đi qua gốc tọa độ khi x 0; y 0 suy ra m 5
Bài 9. Cho đường thẳng d có phương trình 3x (m 1) y m 3. Tìm các giá trị của tham số
m để d đi qua điểm M ( 1 ;0) .
A. m 0 . B. m 1 . C. m 3 . D. m 6 . Lời giải Chọn D
Để đường thẳng d đi M ( 1 ;0) khi x 1
; y 0 suy ra m 6
Bài 10. Cho đường thẳng d có phương trình (5m 15)x 2my m 2. Tìm các giá trị của
tham số m để d đi qua điểm N(0;3). 2
A. m 2 . B. m . 5 Trang 13 1
C. m 3. D. m . 3 Lời giải Chọn B Để đường thẳng 2
d đi N (0;3) khi x 0; y 3 suy ra m 5
Bài 11. Cho đường thẳng d có phương trình (2m 4)x (m 1) y m 5. Tìm các giá trị của
tham số m để d đi qua điểm P(2; 5) . A. m 4 .
B. m 4 . C. m 5 .
D. m 5 . Lời giải Chọn A
Để đường thẳng d đi P(2; 5) khi x 2; y 5 suy ra m 4
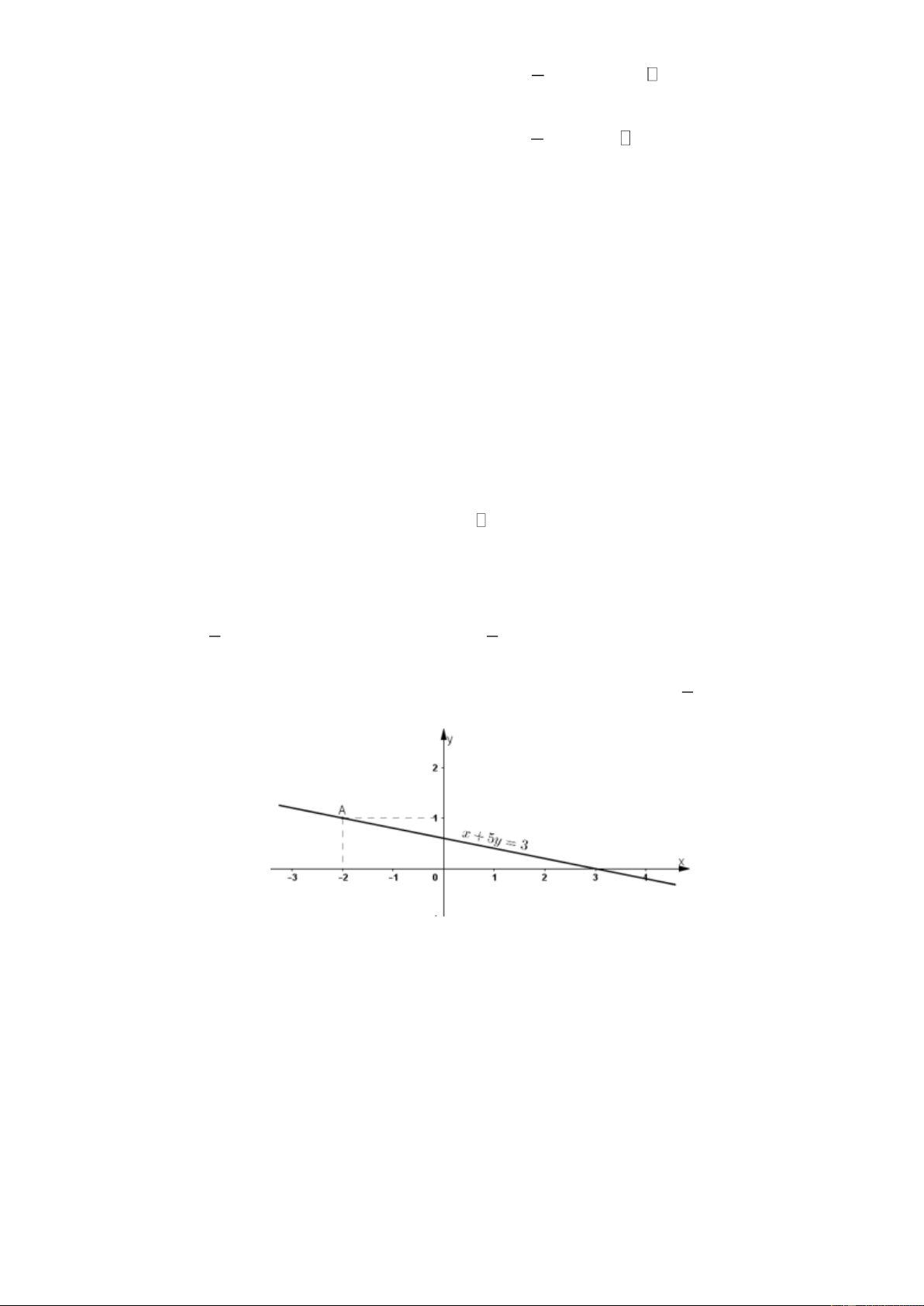
Bài 12. Chọn khẳng định đúng. Hình vẽ dưới đây biểu diễn tập nghiệm của phương trình nào?
A. 3x y 2 .
B. x 2 y 4 .
C. x 5y 3 .
D. 0x 2 y 5 . Lời giải Chọn C
Đường thẳng AB đi qua điểm B( 2 ;1) và (
A 3;0) nên có phương trình x 5y 3
2. TRẮC NGHIỆM ĐÚNG SAI
Trong mỗi ý a), b), c), d) ở mỗi câu, em chọn đúng hoặc sai
Câu 1. Cho đường thẳng d có phương trình 2 .
m x m
3 y 2. Khẳng định nào sau đây là đúng?
a) m 0 khi đường thẳng d song song với trục hoành..
b) m 0 khi đường thẳng d song song với trục tung.
c) m 3 khi đường thẳng d song song với trục tung..
d) m 3 khi đường thẳng d song song với trục hoành.. Lời giải
a) Đúng b) Sai c) Đúng d) Sai
Để đường thẳng d song song với trục tung khi m 3 0 suy ra m 3 Trang 14
Để đường thẳng d song song với trục hoành khi m 0 2m 4
Câu 2. Cho đường thẳng d có phương trình
x m 5 y 0 . Khẳng định nào sau đây là m 3 đúng? a) m 2
khi đường thẳng d song song với trục hoành.. b) m 2
khi đường thẳng d song song với trục tung.
c) m 5 khi đường thẳng d song song với trục tung..
d) m 5 khi đường thẳng d song song với trục hoành.. Lời giải
a) Đúng b) Sai c) Đúng d) Sai Để đường thẳng m
d song song với trục tung khi 2 4 0 m m suy ra 2 3
Để đường thẳng d song song với trục hoành khi m 5
Câu 3. Cho đường thẳng d có phương trình x 2m
3 y m 6 . Khẳng định nào sau đây là đúng? a) m 6
khi đường thẳng d đi qua gốc tọa độ.
b) m 0 khi đường thẳng d đi qua gốc tọa độ.
c) m 5 khi đường thẳng d đi qua gốc tọa độ. d) m 5
khi đường thẳng d đi qua gốc tọa độ. Lời giải
a) Đúng b) Sai c) Sai d) Sai
Để đường thẳng d đi O(0;0) khi x 0; y 0 suy ra m 6
Câu 4. Khẳng định nào sau đây là đúng? Đường thẳng d biểu diễn tập nghiệm của phương trình
3x y 3 là:
a) Đường thẳng song song với trục hoành.
b) Đường thẳng song song với trục tung.
c) Đường thẳng đi qua gốc tọa độ.
d) Đường thẳng song song với trục hoành đi qua điểm A1;0 . Lời giải
a) Sai b) Sai c) Sai d) Đúng
Ta có: 3x y 3 suy ra y 3x 3.
Nghiệm tổng quát của phương trình x
y 3x 3
Biểu diễn hình học tập nghiệm của đường thẳng y 3x 3 đi qua điểm A1;0 và B0; 3
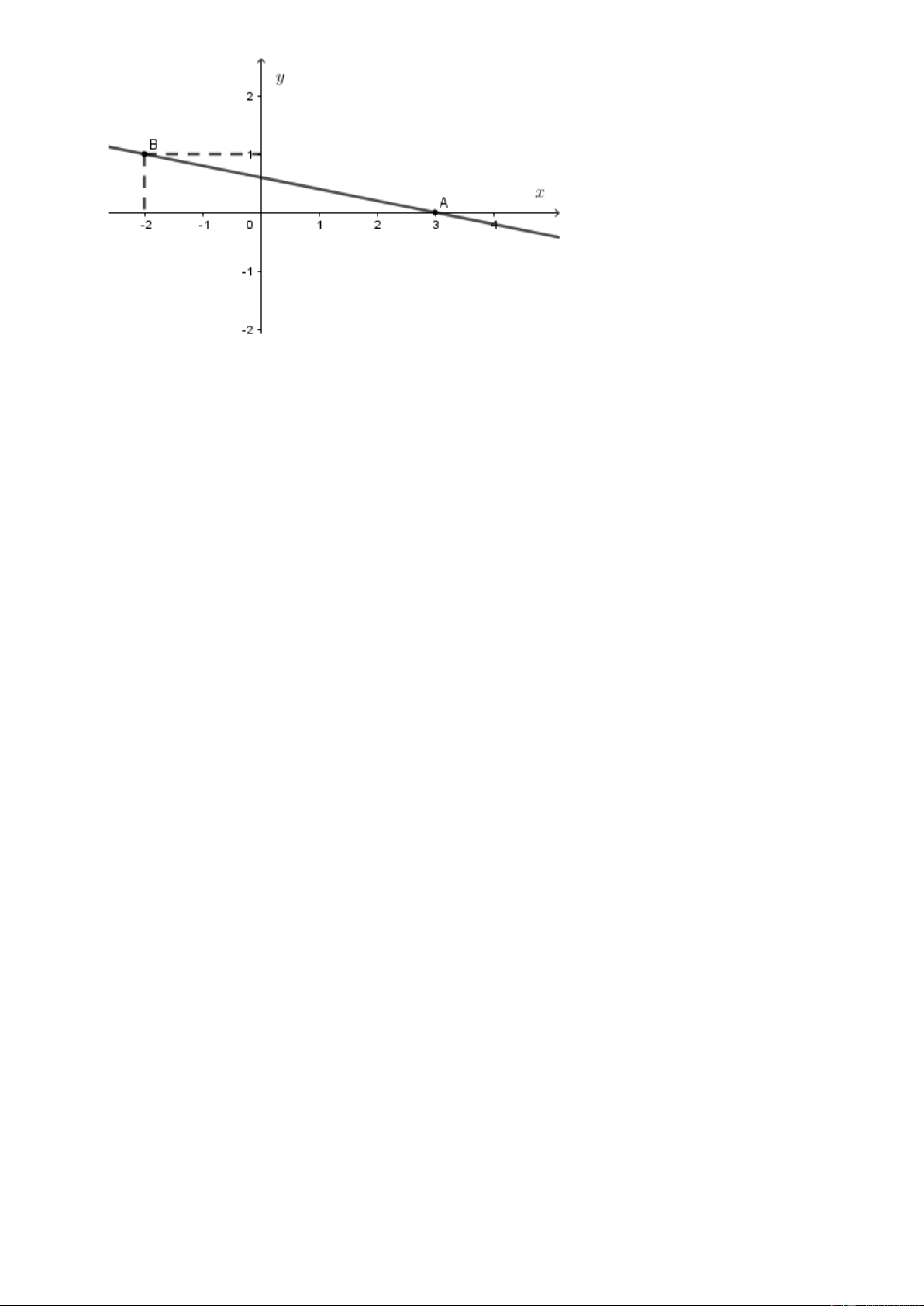
Câu 5. Hình vẽ dưới đây biểu diễn tập nghiệm của phương trình nào?. Khẳng định nào sau đây đúng? Trang 15 x
a) 3x y 2
b) x 2 y 4
c) x 5y 3
d) 0x 2 y 5 Lời giải
a) Sai b) Sai c) Đúng d) Sai
Nhận thấy điểm 3;0 ; 2 ;
1 thuộc đồ thị hay thuộc tập nghiệm của phương trình
Xét đường thẳng 3x y 2
Thay x 3; y 0 ta được 3.3 0 9 2 nên Sai
Xét đường thẳng x 2 y 4
Thay x 3; y 0 ta được 3 2.0 5 4 nên Sai
Xét đường thẳng x 5y 3
Thay x 3; y 0 ta được 3 5.0 3 nên Đúng
Xét đường thẳng 0x 2 y 5
Thay x 3; y 0 ta được 0.3 2.0 0 5 nên Sai
Câu 6. Đường thẳng 2mx m 4 y m cắt trục Ox, Oy tại hai điểm phân biệt khi nào? Khẳng
định nào sau đây đúng?
a) m 0;m 4
b) m 0;m 4
c) m 0;m 4
d) m 0;m 4 Lời giải
a) Sai b) Đúng c) Sai d) Sai
Đường thẳng 2mx m 4 y m cắt hai trục Ox, Oy khi và chỉ khi a 0 m 0 m b 0 0 m 4 0 m 4 c 0
3. TRẮC NGHIỆM TRẢ LỜI NGẮN Trang 16
Câu 1. [NB] Phương trình đường thẳng d : mx 2 y 4 đi qua điểm cố định M có tọa độ là bao nhiêu? Lời giải
Giả sử M x ; y là điểm cố định mà đường thẳng mx 2 y 4 đi qua 0 0
mx 2 y 4 với m 0 0
mx 2 y 4 0 m 0 0 mx 0 0 m 2 y 4 0 0 x 0 0 m y 2 0
Vậy điểm M 0;2 là điểm cố định mà đt mx 2 y 4 đi qua.
Câu 2. [TH] Đường thẳng 2x y 4 đi qua điểm nào trong các điểm sau: 1 1 M 2;4 , N ;4 2 , P1; 2 , Q ; 2 3 ? 2 3 2 Lời giải
*Thay tọa độ điểm M 2;4 vào phương trình đường thẳng, ta được: 2.2 4 0 4
Vậy đường thẳng không đi qua điểm M 1
*Thay tọa độ điểm N (
;4 2) vào phương trình đường thẳng, ta được: 2 1 2. 4 2 4 (đúng) 2
Vậy đường thẳng đi qua điểm N
Thay tọa độ điểm P1; 2
vào phương trình đường thẳng, ta được: 2.1 2 4 4
Vậy đường thẳng không đi qua P1; 2 1
*Thay tọa độ điểm Q ; 2 3
vào phương trình đường thẳng, ta được: 3 2 1 2. 2 3 4 (đúng) 3 2
Vậy đường thẳng đi qua điểm Q
Do đó đường thẳng 2x y 4 đi qua hai điểm N, Q .
Câu 3. [VD] Cho đường thẳng d : mx y 3 và '
d : 3x y 5 . Tìm m để ∥ ' d d . Lời giải
Ta biến đổi phương trình đường thẳng d và ' d về dạng
d: y mx 3 và 'd : y 3x 5 Trang 17
Điều kiện để ∥ ' d d là m 3 .
Câu 4. [VDC] Tìm m để đường thẳng mx m 4 y m cắt trục Ox, Oy tại hai điểm phân biệt. Lời giải
Đường thẳng mx m 4 y m cắt hai trục Ox, Oy khi và chỉ khi a 0 m 0 m b 0 0 m 4 0 m 4 c 0
PHẦN II. BÀI TẬP TỰ LUẬN Phương pháp giải:
Ta có thể sử dụng một số lưu ý sau đây khi giải dạng toán này: 1. Nếu c
a 0 và b 0 thì phương trình đường thẳng d : ax by c có dạng d : x a
Khi đó d song song hoặc trùng với Oy . 2. Nếu c
a 0 và b 0 thì phương trình đường thẳng có dạng d : y b
Khi đó d song song hoặc trùng với Ox
3. Đường thẳng d : ax by c đi qua điểm M x ; y khi và chỉ khi ax by . c o o o o
Ví dụ 1 [NB]: Cho phương trình x 2 y a 1. Hãy chọn hệ số a để đường thẳng
x 2 y a 1 đi qua điểm ( O 0; 0) ). Lời giải
Đường thẳng x 2 y a 1 đi qua điểm
0 2.0 a 1 a 1
Vậy a 1 thì đường thẳng x 2 y a 1 đi qua điểm ( O 0; 0) .
Ví dụ 2 [TH]: Cho đường thẳng d có phương trình m – 2 x 3m –
1 y 6m – 2
Tìm các giá trị của tham số m để:
a) d song song với trục hoành;
b) d song song với trục tung. Lời giải
a) Đường thẳng d có phương trình m – 2 x 3m –
1 y 6m – 2 song song với trục hoành m – 2 0 3m –1 0 6m – 2 0 m 2 1 Suy ra m m 2 3 1 m 3 Trang 18
Vậy m 2 thì đường thẳng d song song với trục hoành
b) Đường thẳng d có phương trình song song với trục tung m 2 m – 2 0 1
3m – 1 0 Suy ra m Suy ra m 3 6 m – 2 0 1 m 3
Vậy không có giá trị nào của m để đường thẳng d song song với trục tung.
Ví dụ 3 [TH]: Cho đường thẳng d có phương trình: 2m –
1 x 3m –
1 y 4m – 2.
Tìm các giá trị của tham số m để:
a) d song song với trục hoành;
b) song song với trục tung. Lời giải
a) Đường thẳng d có phương trình 2m –
1 x 3m –
1 y 4m – 2 song song với trục hoành 2m – 1 0 3(m –1) 0 4m – 2 0 1 m 2 1 m 2 m
Vậy không có giá trị nào của m để đường thẳng d song song với trục hoành.
b) Đường thẳng d có phương trình 2m –
1 x 3m –
1 y 4m – 2 song song với trục tung 2m – 1 0 3(m –1) 0 4m – 2 0 1 m 2 m 1 1 m 2 m 1
Vậy m 1 thì đường thẳng d song song với trục tung.
Ví dụ 4 [VD]: Xác định a và b để đồ thị hàm số y ax b đi qua hai điểm A2; 2 và B 1 ; 3 . Lời giải
Đồ thị hàm số y ax b đi qua điểm A2; 2 Suy ra 2 .
a 2 b suy ra b 2 – 2a (1) Trang 19
Đồ thị hàm số đi qua điểm B 1 ; 3 Suy ra 3 . a 1 b (2) Thay
1 vào 2 ta có: 3 a
– 2 – 2a 3a 5 5 a 3 5 4 b 2 2. 3 3 5 4 Vậy a và b
thì đồ thị hàm số đi qua 2 điểm A2; 2
và B 1 ; 3 . 3 3 BÀI TẬP TỰ LUYỆN
Bài 1. [NB] Cho phương trình 2
x y b. Hãy chọn hệ số b để đường thẳng 2
x y b đi qua điểm O( 0; 0) . Lời giải Đường thẳng 2
x y b đi qua điểm O( 0; 0) b 0
Vậy b 0 thì đường thẳng 2
x y b đi qua điểm O( 0; 0) .
Bài 2. [NB] Cho phương trình b
x y 2
. Hãy chọn hệ số b để đường thẳng b
x y 2 đi qua điểm I ( 2 ; 0) . Lời giải Đường thẳng b
x y 2
đi qua điểm I( 2 ; 0) 2b 2 b 1 Vậy b 1
thì đường thẳng b
x y 2
đi qua điểm I( 2 ; 0) .
Bài 3. [NB] Cho phương trình x by 5
. Hãy chọn hệ số b để đường thẳng x by 5 đi qua điểm P(1 ; 2 ) . Lời giải
Đường thẳng x by 5
đi qua điểm P(1 ; 2 ) 2 b 6 b 3
Vậy b 3 thì đường thẳng x by 5
đi qua điểm P(1 ; 2 ) .
Bài 4. [TH] Cho đường thẳng d có phương trình 2m
3 x 3m 1 y m 2
Tìm các giá trị của tham số m để:
a) d song song với trục hoành;
b) d song song với trục tung. Lời giải
a) Đường thẳng d có phương trình song song với trục hoành Trang 20