
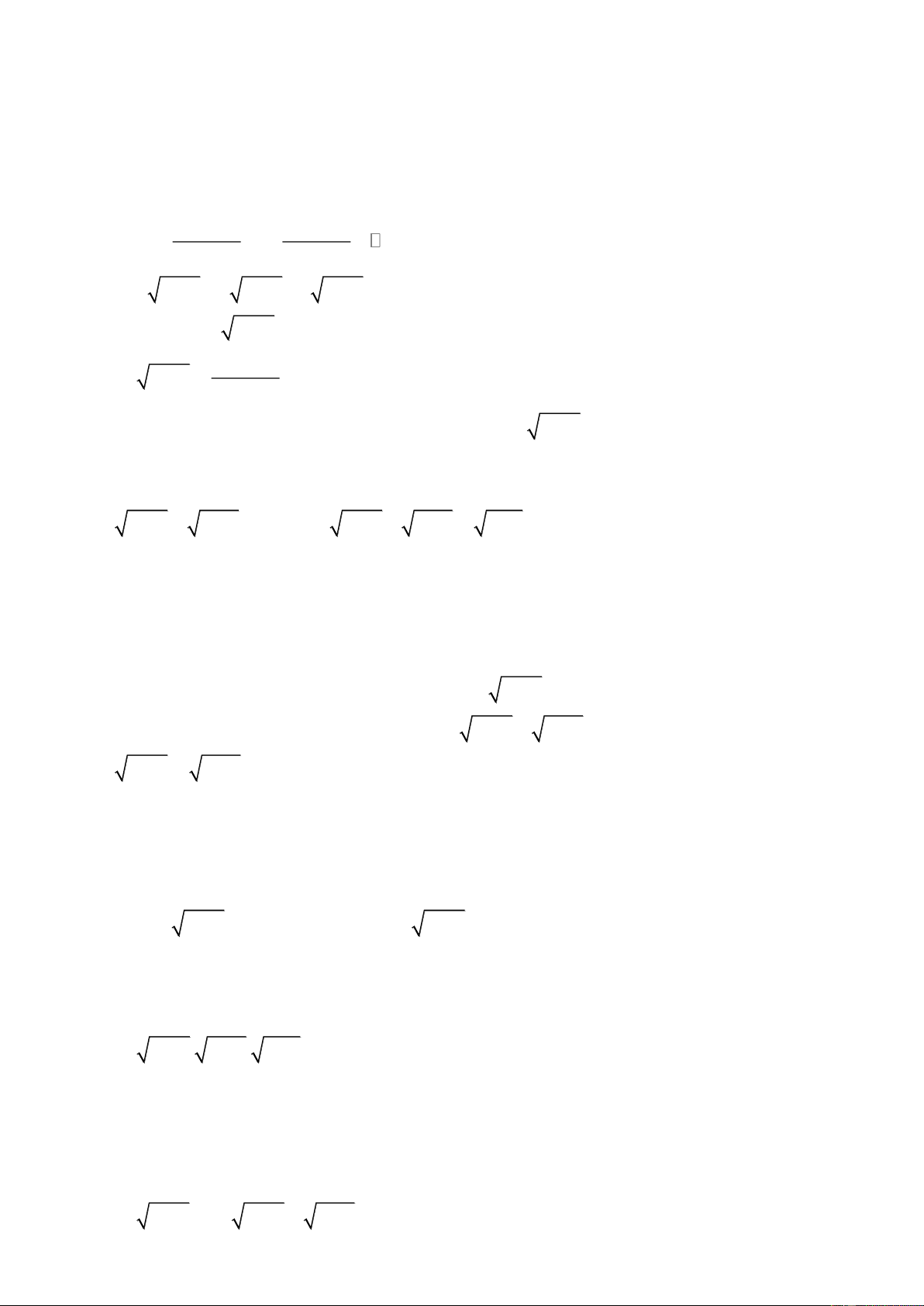






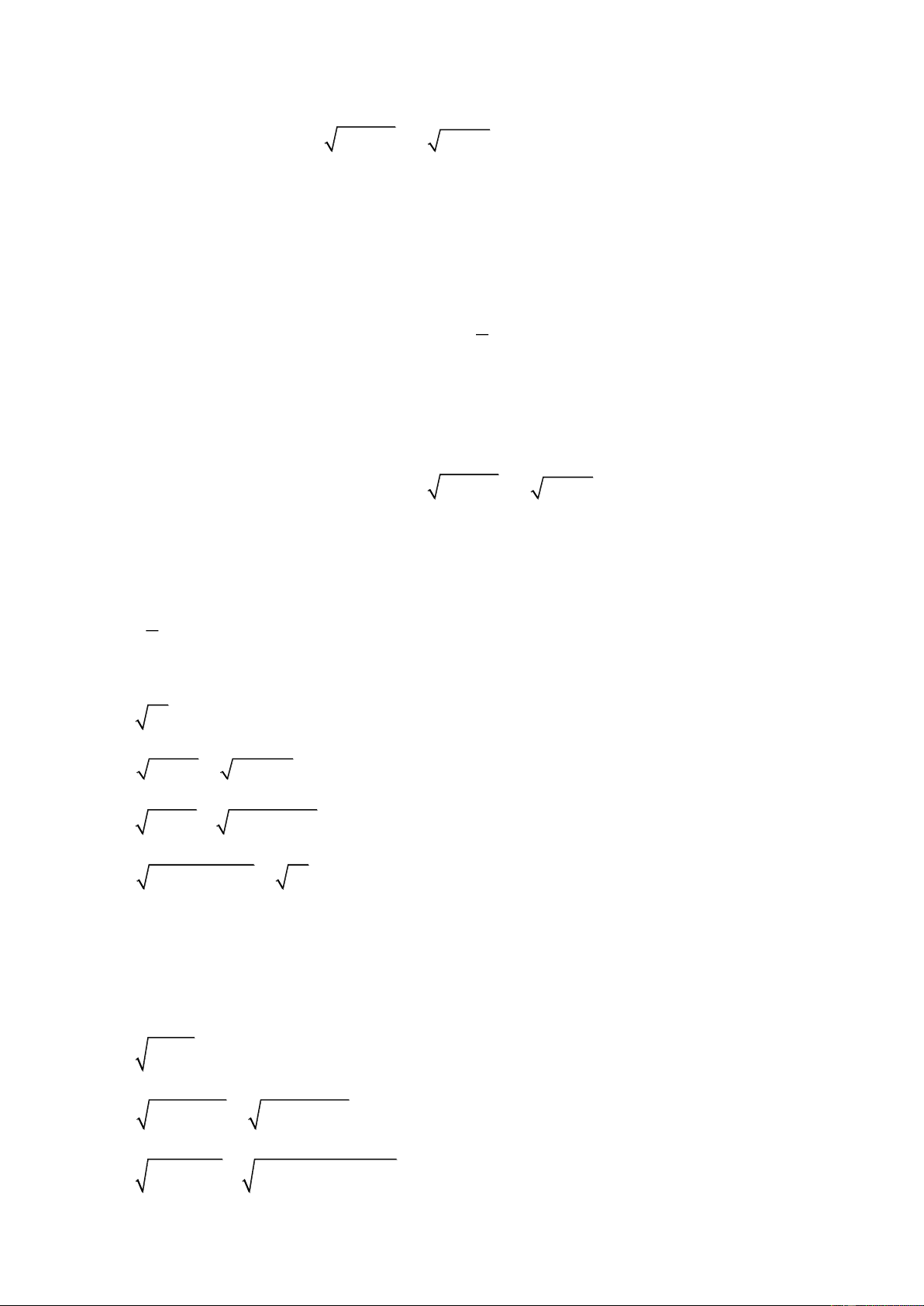






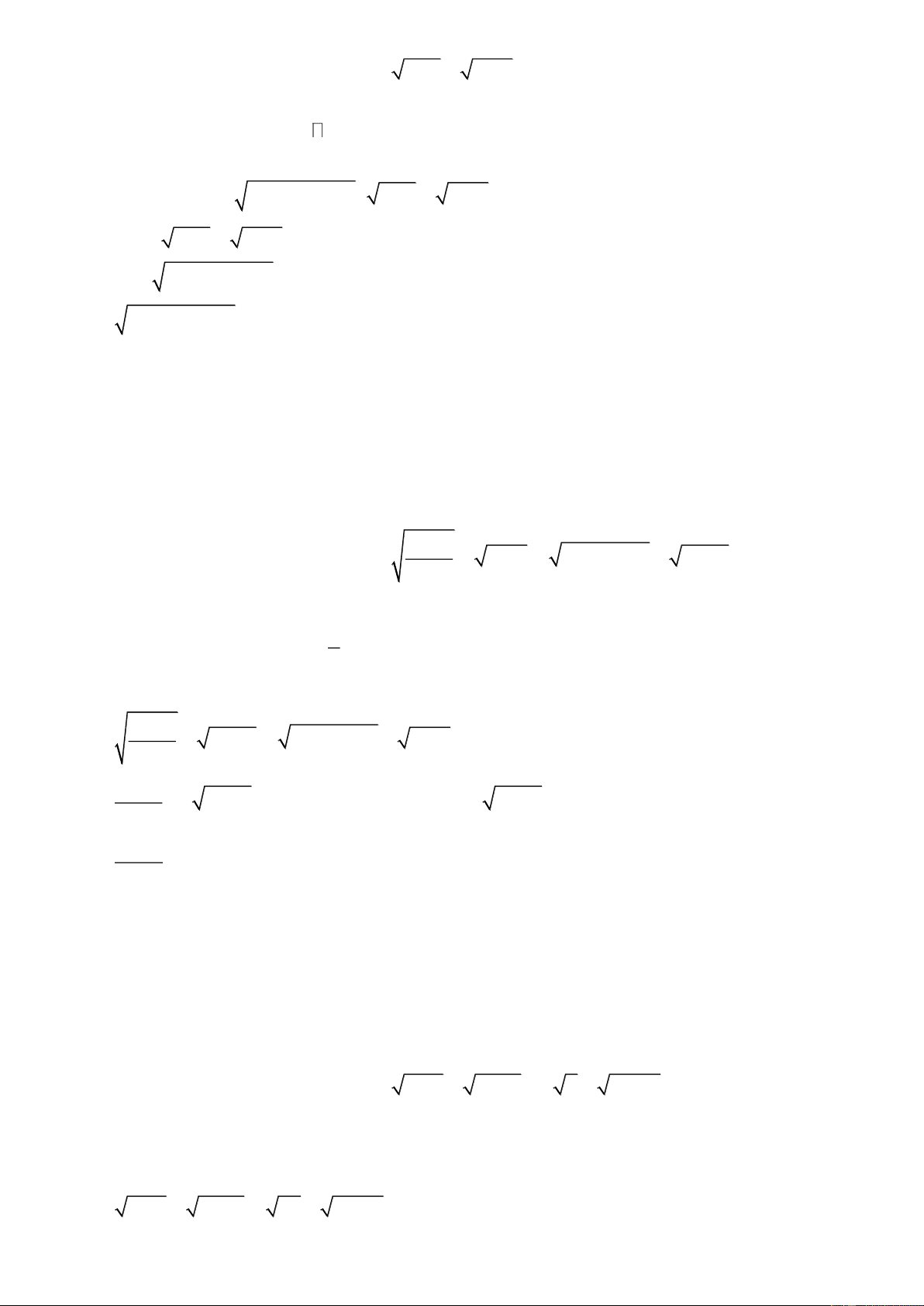
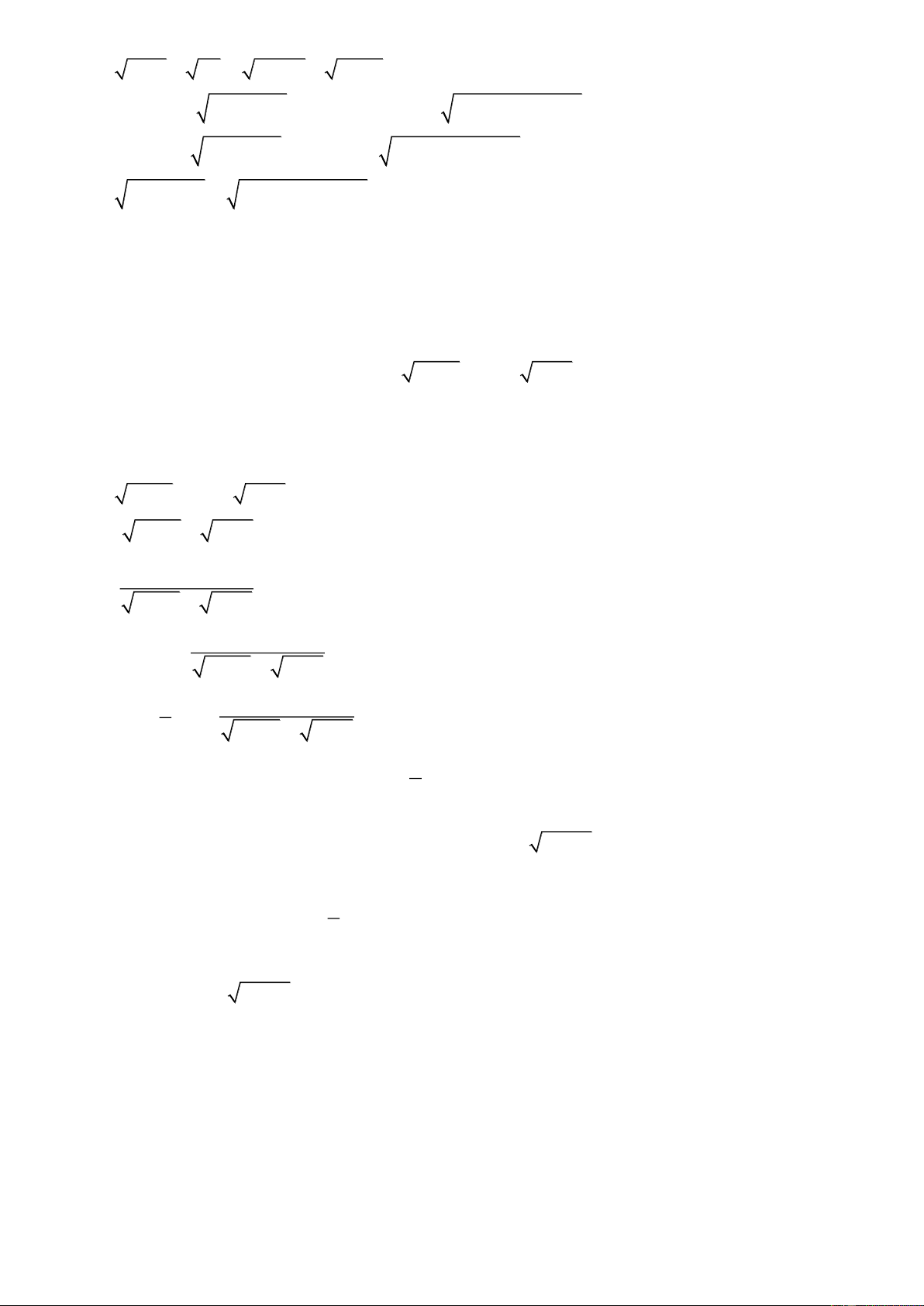



Preview text:
CHUYÊN ĐỀ 10: PHƯƠNG TRÌNH CHỨA CĂN THỨC
A. KIẾN THỨC CẦN NHỚ
Phương trình chứa căn thức có thể được phân loại như sau:
1. Loại 1: Phương trình trong căn có thể viết dưới dạng bình phương của một biểu thức.
Cách 1: Với a 0; a . 2
f (x) a . f ( ) x a .
f (x) a .
f (x) a
Cách 2: Với a 0; a . 2
f (x) a . 2 2
f (x) a
Phương pháp: Để giải dạng phương trình này điều cơ bản là phải viết được biểu
thức dưới dấu căn ở dạng bình phương rồi đưa ra ngoài dấu căn để trở thành phương
trình chứa dấu giá trị tuyệt đối hoặc sử dụng phương pháp bình phương 2 vế của phương trình.
Lưu ý: Nếu a 0 thì phương trình 2
f (x) a vô nghiệm.
2. Loại 2: Phương trình dạng f (x) g(x) . Phương pháp giải: f (x) g(x) .
f (x) 0
f (x) g(x) . g(x) 0
f (x) g(x)
3. Loại 3: Phương trình chứa biểu thức dưới dấu căn không viết được dưới dạng
bình phương (trong phương trình chỉ chứa một căn thức).
f (x) g(x) (1) (hoặc dạng
f (x) a , lúc này g(x) a ).
Cách giải 1: (Sử dụng phương trình hệ quả). ĐK: f ( ) x 0 .
Bình phương hai vế phương trình (1) ta có pt hệ quả: 2
f (x) g (x) , giải tìm x ?
Thế vào phương trình (1) xem có thỏa mãn hay không.
Kết luận nghiệm của phương trình (1).
Cách giải 2: (Sử dụng phép biến đổi tương đương).
f (x) g(x) . Trang 1 g(x) 0 . 2
f (x) g (x) Lưu ý: Khi g( )
x 0 phương trình (1) vô nghiệm.
4. Loại 4: Phương trình chứa nhiều căn thức, các căn thức có thể đưa về dạng giống nhau. Với d d 0; .
a b c
a b c
a f (x) b f (x) c f (x) d .
a b c f (x) d . d f (x) .
a b c
Sau khi rút gọn đưa về giải phương trình Loại 3 f (x) g(x) .
5. Loại 5: Phương trình chứa các căn khác nhau, biểu thức trong căn không viết
được dưới dạng bình phương.
f (x) g(x) k hoặc
f (x) g(x) h(x) . Phương pháp: f (x) 0 f (x) 0 Với điều kiện
hoặc g(x) 0 . g(x) 0 h(x) 0
Ta thường bình phương 2 vế đưa về Loại 3 f (x) g(x) để giải.
Đối với các phương trình có dạng
f (x) g(x) k cần biến đổi về dạng f (x)
g(x) k .
(Lí do: Để đảm bảo 2 vế của phương trình đều không âm rồi mới đem bình phương).
6. Loại 6: Quy về phương trình bậc hai bằng phương pháp đặt ẩn phụ.
Phương pháp: Sử dụng các phương pháp biến đổi đưa phương trình về dạng f (x)
f (x) c 0 rồi đặt ẩn phụ
f (x) t; t 0 đưa về giải phương trình bậc hai ẩn t .
7. Loại 7: Phương trình chứa căn mà biểu thức trong căn ở dạng thương hoặc dạng tích
f (x). g(x). ( h x) 0 . f (x) 0 g(x) 0 . h(x) 0
8. Loại 8: Giải các phương trình căn bậc ba 3 3 3 f (x) ; a
f (x) g(x) a . Trang 2
+ Ở căn bậc lẻ: 2k 1 2k 1 f (x);
g(x) có nghĩa với mọi x nên không cần đặt điều kiện.
+ Ở luỹ thừa bậc lẻ: a b 2n 1 2n 1 a b (n )
Nên không cần xét đến dấu của hai vế.
Phương pháp: Lập phương hai vế theo công thức a b3 3 2 2 3 3
a a b ab b a aba b 3 3 3 3
b và biến đổi linh hoạt đưa về dạng .
A B 0 để giải. B. BÀI TẬP
DẠNG 1: PHƯƠNG TRÌNH CHỨA CĂN THỨC
PHẦN I. BÀI TẬP TRẮC NGHIỆM
1. TRẮC NGHIỆM CHỌN ĐÁP ÁN
Câu 1. [NB] Điều kiện xác định của phương trình x 10 3 là:
A. x 10 0 .
B. x 10 0 .
C. x 10 . D. x 10 . Lời giải Chọn C
Điều kiện xác định của phương trình x 10 3 là x 10 0 hay x 10.
Câu 2. [NB] Điều kiện có nghiệm của phương trình x x 2 là:
A. x 2 0 .
B. x 2 .
C. x 0 . D. x 2 . Lời giải Chọn D
Điều kiện có nghiệm của phương trình x x 2 là x 2 0 hay x 2.
Câu 3. [NB] Tìm m để phương trình x m 1 có nghiệm là x 1?
A. m 1.
B. m 0 . C. m 1 . D. m 2 . Lời giải Chọn B
Vì phương trình x m 1 có nghiệm x 1 nên ta có: 1 m 1 1 m 1 Trang 3 m 0
Câu 4. [NB] Phương trình 2 x 4 có nghiệm là:
A. x 1.
B. x 2 . C. x 1 . D. x 4 . Lời giải Chọn A
Điều kiện: x 0 . Ta có: 2 x 4 . 2 x 2 . x 1. x 1.
Câu 5. [TH] Tìm nghiệm của phương trình 2
x x 6 x 3 .
A. x 3. B. x 3 .
C. x 3 . D. Vô nghiệm. Lời giải Chọn A Ta có: 2
x x 6 x 3 . x 3 . 2
x 2x 3 0 x 3.
Câu 6. [TH] x 3 là nghiệm của phương trình nào trong các phương trình sau: A. 2
2x 3 4x 3 . B. 2x 1 x 1 .
C. 2x 5 1 x . D. 2
x x 3 x . Lời giải Chọn D
Thay x 3 vào mỗi phương trình: Trang 4 2 2 3
3 4 3 3 (Sai).
2 3 1 3 1 (Sai).
2 3 5 1 3 (Sai). 2 3
3 3 3 (Đúng).
Câu 7. [TH] Phương trình nào sau đây vô nghiệm?
A. x 2 x 1 x 1 1. B. 2
x x 3x 5 . C. 2
2x 3 4x 3 . D. 2
1 x x 1. Lời giải Chọn B Ta thấy:
Phương trình x 2 x 1 x 1 1 có 1 nghiệm x 5. Phương trình 2
2x 3 4x 3 có 1 nghiệm x 2. Phương trình 2
1 x x 1 có 1 nghiệm x 1.
Câu 8. [TH] Tìm nghiệm của phương trình 2 2
x 1 x 1 0 .
A. x 1; x 2 . B. x 1 . C. x 1
; x 2 . D. x 1; x 2 . Lời giải Chọn C x 1 Điều kiện: 2 x 1 0 hay . x 1 Ta có: 2 2
x 1 x 1 0 . 2 x 2
1 1 x 1 0. 2 x 1 0 . 2 1 x 1 0 Trang 5 x 1 . x 2
Câu 9. [VD] Tập nghiệm của phương trình 2 2
4x 12x 3 4x 12x 11 13 0 là: 3 2 3 A. S .
B. S 1; 2 .
C. S . D. S . 2 2 Lời giải Chọn A Điều kiện: 2
4x 12x 11 0 hay x . Đặt 2
4x 12x 11 t 3 ta có: 2 t 3t 2 0 . t 1(ktm) . t 2(tm) Do đó: 2
4x 12x 11 2 2
4x 12x 7 0 . 3 2 ' 8; x . 1,2 2
Câu 10. [VD] Tìm nghiệm của phương trình 2
9x 6x 1 11 6 2 . 2 2 2 4
A. x 1; x 2 . B. x ; x . 3 3
C. x 2; x 3
. D. x 1; x 2 . Lời giải Chọn B Điều kiện: 2
9x 6x 1 0 hay x . Ta có: 2
9x 6x 1 11 6 2 . 2
9x 6x 1 11 6 2 .
x 2 2 3 1 3 2 . Trang 6 3x 1 3 2 .
3x 1 2 3 2 2 x (tm) 3 . 2 4 x (tm) 3 2x 3
Câu 11. [VD] Tìm nghiệm của phương trình 2 x . 1 1 1 A. x 2
. B. x . C. x . D. x 1. 2 3 Lời giải Chọn B Điều kiện 2x 3 : 0 . x 1 2x 3 Ta có: 2 x . 1 2x 3 4. x 1 2x 3 4 0. x 1 1 2x 0. x 1 1 x (tm) . 2
Câu 12. [VDC] Tổng bình phương các nghiệm của phương trình 3x 1
x 3 x 1 là: A. 106 . B. 107 . C. 108 . D. 109 . Lời giải Chọn B Điều kiện 1 : x . 3 Trang 7
Đặt a 3x 1;b x 3 (a 0;b 0) suy ra 2 2
a b 2x 2 .
Mặt khác phương trình đã cho trở thành a b x 1. Ta có hệ phương trình 2 2
a b 2x 2
a b x 1 x
1 a b 2 x 1
a b x 1 x
1 a b 2 0
a b x 1 x 1
a b 0 a b 2
a b x 1
• Xét x =1 là một nghiệm của phương trình đã cho. a b 2 • Với suy ra:
a b x 1 2a x 1.
2 3x 1 x 1 . 1 x 3 . 2 12
x 4 x 2x 1 1 x 3 . 2
x 10x 3 0 x 5 2 7 . x 5 2 7
Vậy: Tổng bình phương các nghiệm của phương trình 3x 1 x 3 x 1 là: 2 2 2 1 5 2 7 5 2 7
1 2.25 28 107 . Trang 8
2. TRẮC NGHIỆM ĐÚNG SAI
Trong mỗi ý a), b), c), d) ở mỗi câu, em chọn đúng hoặc sai
Câu 1. Cho phương trình 2
4x 9 2 2x 3 .
a) Phương trình có điều kiện xác định là 2x 3 0.
b) Phương trình có điều kiện xác định là 2
4x 9 0; 2x 3 0 .
c) Phương trình có điều kiện xác định là 2 4x 9 0 .
d) Phương trình có điều kiện xác định là 3 x . 2 Lời giải a) S b) Đ c) S d) Đ
- Điều kiện xác định của phương trình 2
4x 9 2 2x 3 là: 2
4x 9 0; 2x 3 0 . 2x 3 0 . 3 x . 2
Câu 2. Số x 2
là nghiệm của phương trình nào? a) 4 x 4 . b) 3 2x 4 x 3 . c) 2 2
x 4 x 4x 4 0 . d) 2 2
9x 12x 4 x . Lời giải a) Đ b) S c) Đ d) S - Thay x 2
vào mỗi phương trình: a) 4 2 4 . (Đúng) b) 3 2 2 4 2 3 . (Sai) 2 2 c) 2 4 2 4 2
4 0 . (Đúng) Trang 9 2 2 d) 9 2 12 2 4 2 . (Sai) 1 3 x 1
Câu 3. Cho phương trình x 1 9x 9 24 2m 3 . 2 2 64
a) Phương trình có nghiệm với m 3.
b) Phương trình có nhiều nhất 1 nghiệm với mọi m.
c) Phương trình có nghiệm với 3 m . 2
d) Phương trình có nghiệm với 3 m . 2 Lời giải a) S b) Đ c) Đ d) Đ - Ta có: 1 3 x 1 x 1 9x 9 24 2m 3 . 2 2 64 1 9 x 1
x 1 3. x 1 2m 3 . 2 2
x 1 3 2m .
Điều kiện có nghiệm của phương trình x 1 3 2m là: 3 2m 0 . 3 m . 2
Khi đó: x 1 3 2m .
x m2 3 2 1.
Câu 4. Cho phương trình 3 2 3 2 3 2
8x 16 x 2 27x 54 m 1 .
a) Với m 0 phương trình vô nghiệm.
b) Với m 1 phương trình có 1 nghiệm là 9 x . 8
c) Với m 1 phương trình luôn có nghiệm.
d) Với mọi m phương trình vô nghiệm. Trang 10 Lời giải a) Đ b) S c) S d) Đ - Ta có: 3 2 3 2 3 2
8x 16 x 2 27x 54 m 1 . 3 2 3 2 3 2
2. x 2 x 2 3. x 2 m 1 . 3 2 2
x 2 m 1. (Vô lý vì 3 2 2 x 2 0; m 1 0)
Vậy: Với mọi m phương trình vô nghiệm.
3. TRẮC NGHIỆM TRẢ LỜI NGẮN
Câu 1. [NB] Tìm điều kiện xác định của phương trình 3 x 1 x 3 x 2 4 . Lời giải
Đáp án: x 2 .
Điều kiện xác định của phương trình 3 x 1 x 3 x 2 4 là:
x 1 0; x 2 0 . x 2 .
Câu 2. [NB] Tìm điều kiện có nghiệm của phương trình x 1 x 3 . Lời giải
Đáp án: x 3.
Điều kiện có nghiệm của phương trình x 1 x 3 là: x 3 0. x 3.
Câu 3. [TH] Các giá trị của m để phương trình 2
x 2 m có nghiệm là bao nhiêu? Lời giải
Đáp án: m . Vì 2
m 0 nên phương trình 2
x 2 m có nghiệm với mọi m. Ta có: 2 x 2 m . 4 x 2 m . 4 x m 2 . Vậy: PT luôn có nghiệm 4
x m 2 với m .
Câu 4. [TH] Giải phương trình: x x 0 . Trang 11 Lời giải
Đáp án: x 0; 1 .
Điều kiện: x 0 .
Ta có: x x 0 .
x 1 x 0. x 0 . 1 x 0 x 0 . x 1
Vậy: Nghiệm của phương trình là: x 0; 1 .
Câu 5. [VD] Các giá trị của m để phương trình 2 2
8x x m có 1 nghiệm là bao nhiêu? Lời giải
Đáp án: m 2 ; 2 . Ta có: 2 2
8x x m . 2 4
8x x m . 2 4
x 8x m 0 . 4 ' 16 m . ĐK để phương trình 2 2
8x x m có 1 nghiệm là: 4 ' 16 m 0 m 2 . Vậy: m 2 ; 2 .
Câu 6. [VDC] Các giá trị của m để tổng 2 nghiệm của phương trình 2 2mx x 3
bằng 10 là bao nhiêu? Lời giải
Đáp án: m 5. Ta có: 2
2mx x 3. 2
2mx x 9 . 2
x 2mx 9 0. Trang 12 2 ' m 9. ĐK để phương trình 2 2
8x x m có nghiệm là: 2 ' m 3 0.
Theo hệ thức Vi-et ta có: x x 2m. 1 2
Do đó, để x x 10 thì 2m 10 hay m 5 (t ) m . 1 2 Vậy: m 5.
PHẦN II. BÀI TẬP TỰ LUẬN Phương pháp giải:
Trong việc giải phương trình vô tỷ nếu việc tìm những giá trị của x thỏa mãn điều
kiện xác định, điều kiện có nghiệm (hay g(x) 0) là phức tạp thì ta nên triển khai
việc tìm nghiệm của phương trình sau đó thử vào điều kiện để xét xem nghiệm vừa
tìm được có thỏa mãn điều kiện bài toán hay không. Các phương pháp sau thường
được dùng để giải phương trình chứa căn thức:
☑️Phương pháp nâng lên lũy thừa.
☑️Phương pháp sử dụng lượng liên hợp.
☑️Phương pháp sử dụng ẩn phụ. BÀI TẬP MẪU
Ví dụ 1 [NB]: Giải phương trình x 2 9 2 6 . Lời giải Ta có: x 2 9 2 6 . 3 x 2 6 . x 2 2 . x 2 2 . x 2 2 x 4 . x 0
Vậy: x 4 hoặc x 0 là nghiệm của phương trình.
Ví dụ 2 [TH]: Giải phương trình 2
2x 1 x 1. Lời giải Ta có: 2
2x 1 x 1. Trang 13 x 1 0 . 2x 1 x 2 2 1 x 1 . 2 2
2x 1 x 2x 1 x 1 . 2
x 2x 0 x 1 x 0 . x 2 x 0 .
Vậy: x 0 là nghiệm của phương trình.
Ví dụ 3 [TH]: Giải phương trình 3 2x 5 8x 7 18x 28 . Lời giải
Điều kiện: x 0 . Ta có:
3 2x 5 8x 7 18x 28 .
3 2x 10 2x 21 2x 28 . 14 2x 28 . 2x 2 . 2x 4 . x 2(t ) m .
Vậy: x 2 là nghiệm của phương trình.
Ví dụ 4 [VD]: Giải phương trình 5 x 31 x 6 . Lời giải Ta có:
5 x 31 x 6 . 5 x 31 .
5 x 31 x 2
5 x31 x 36 5 x 31 .
5 x31 x 0 5 x 31 . 5 x 31 x 0 Trang 14 5 x 31 x 5 . x 31 x 5 . x 31
Vậy: Phương trình có 2 nghiệm là: x 5
và x 31.
Ví dụ 5 [VD]: Giải phương trình 2x 5 5 2x 1 0. Lời giải Ta có:
2x 5 5 2x 1 0 .
2x 1 5 2x 1 4 0 .
Đặt 2x 1 t 0 . Phương trình trở thành: 2
t 5t 4 0 . t 1(tm) . t 4(tm) Với t 1 ta có: 2x 1 1. 2x 1 1. x 0 . Với t 4 ta có: 2x 1 4 . 2x 1 16 . 15 x . 2 Vậy 15
: Phương trình có 2 nghiệm là: x 0 và x . 2
Ví dụ 6 [VD]: Giải phương trình 2x 84 x 2 2x 8 0. Lời giải Ta có:
2x 84 x 2 2x 8 0.
2x 8 4 x 2 0. 2x 8 0 .
4 x 2 0(VN) x 4 .
Vậy: Phương trình có nghiệm x 4. Trang 15
Ví dụ 7 [VD]: Giải phương trình 3 3
x 1 7 x 2 . Lời giải
Điều kiện xác định: x . Lập phương 2 vế ta có:
x x
x x3 3 3 1 7 3 1 7
x 1 7 x 8. Thay 3 3
x 1 7 x 2 vào phương trình trên, ta được: 3 8 6 x
1 7 x 8 . 3 x
1 7 x 0 .
x 17 x 0. x 1 . x 7
Thay lại vào phương trình ban đầu ta thấy nghiệm đúng.
Vậy: Phương trình có 2 nghiệm x 1
và x 7. 3 Ví dụ 8 [VD] x 8
: Giải phương trình 2
x 2 x 2x 4 2x 1 . 2x 1 Lời giải Điều kiện xác định 1 : x . 2 Ta có: 3 x 8 2
2x 1 x 2x 4 x 2 . Bình phương 2 vế ta suy ra: 2x 1 3 x 8 3
2 x 8 2x 1 2
x 2x 4 3
2 x 8 x 2 . 2x 1 3 x 8 2
x 3x 5 . 2x 1 3 2
x 5x 7x 3 0. x 1 . x 3
Thay lại vào phương trình ban đầu ta thấy chỉ có giá trị x 1 thỏa mãn.
Vậy: Phương trình có nghiệm x 1.
Ví dụ 9 [VD]: Giải phương trình x 3 3x 1 2 x 2x 2 . Lời giải
Điều kiện xác định: x 0 . Ta có:
x 3 3x 1 4x 2x 2 . Trang 16
x 3 4x
2x 2 3x 1 . Bình phương 2 vế ta suy ra:
x 3 2 x 34x 4x 2x 2 2 2x 23x 1 3x 1 .
5x 3 2 4x x 3 5x 3 2 2x 23x 1 .
4x x 3 2x 23x 1 . 2
x 2x 1 0. x 1.
Thử lại ta thấy x 1 thỏa mãn phương trình ban đầu.
Vậy: Phương trình có nghiệm x 1.
Ví dụ 10 [VD]: Giải phương trình 3x 1 2x x 4 5 . Lời giải
Điều kiện xác định: x 4 . Ta có:
3x 1 2x x 4 5 .
3x1 x42x50. 2x 5
2x 5 0.
3x 1 x 4 x 1 2 5 1 0 .
3x 1 x 4 5 1 x (Do
1 0 với mọi x 4). 2 3x 1 x 4
Vậy: Phương trình có nghiệm 5 x . 2
Ví dụ 11 [VDC]: Giải phương trình 2
2x 6x 1 4x 5 . Lời giải Điều kiện xác định 5 : x . 4 Ta có: 2
2x 6x 1 4x 5 . 2
2x 6x 1 0 .
2x 6x 2 2 1 4x 5 2
2x 6x 1 0 . 4 3 2
x 6x 8x 2x 1 0 Trang 17 2
2x 6x 1 0 . 2 x 2x
1 2x 4x 1 0 3 11 x 2 3 11 x . 2 x 1 2 x 2 3 x 1 2 . x 2 3
Vậy: Tập nghiệm của phương trình đã cho là: T 1 2;2 3 . 1 1
Ví dụ 12 [VDC]: Giải phương trình 2 . 2 x 2 x Lời giải 2 x 2
Điều kiện xác định: . x 0 x a Đặt: . Suy ra: 2 2
a b 2 (b 0) . 2
2 x b Ta có: 1 1 2 a b . 2 2
a b 2
a b 2ab . a b 2 2ab 2
a b 2ab . 2
ab2 ab 1 0
a b 2ab ab 1 . 1 ab 2 Trang 18
a b 2 ab 1
a b 1 . 1 ab 2 a b 2 + Với
, suy ra a,b là nghiệm của phương trình: ab 1 2
X 2X 1 0. X 1.
Từ đó cho ta a 1 hay x 1. a b 1 + Với
1 , suy ra a,b là nghiệm của phương trình: ab 2 1 2 X X 0 . 2 1 3 X . 2 1 3 1 3 Từ đó cho ta a hay x . 2 2 Vậy 1 3
: Tập nghiệm của phương trình đã cho là: T 1 ; . 2
☑️BÀI TẬP TỰ LUYỆN
Bài 1. [NB] Giải phương trình 2
x 4x 9 3 . Hướng dẫn Ta có: 2
x 4x 9 3 . 2
x 4x 9 9. 2 x 4x 0.
x x 4 0. x 4 . x 0
Vậy: x 4 hoặc x 0 là nghiệm của phương trình.
Bài 2. [NB] Giải phương trình 2
x 6x 4 4 x . Hướng dẫn Ta có: Trang 19 2
x 6x 4 4 x . x 4 . 2
x 6x 4 4 x x 4 . 2
x 5x 0 x 4 x 0. x 5 x 0 .
Vậy: x 0 là nghiệm của phương trình.
Bài 3. [TH] Giải phương trình 3 3x 12x 3 27x 1 6 . Hướng dẫn
Điều kiện: x 0 . Ta có:
3 3x 12x 3 27x 1 6 .
3 3x 2 3x 9 3x 16 . 4 3x 1 6 . 3x 4 . 3x 16. 16 x (tm) . 3 Vậy 16 : x
là nghiệm của phương trình. 3
Bài 4. [VD] Giải phương trình 3 x 2 x 1. Hướng dẫn Ta có:
3 x 2 x 1. 3 x 2 .
3 x 1 2 x 3 x 2 . 3
x 1 2 x 2 2 x 3 x 2 .
2 x x Trang 20




