Chuyên đề phương trình đại số – Trịnh Bình

Tài liệu chuyên đề phương trình đại số gồm 56 trang được tổng hợp bởi tác giả Trịnh Bình, hướng dẫn phương pháp giải các bài toán phương trình đại số, giúp học sinh học tốt chương trình Đại số lớp 9 và ôn tập chuẩn bị cho kỳ thi tuyển sinh vào lớp 10 môn Toán.

82 41 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu ôn thi vào 10 môn Toán

Môn: Môn Toán

Thông tin:

54 trang 7 tháng trước

Tác giả:

Profile Nguyễn Vân
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
2
CHỦ ĐỀ 1. PHƢƠNG TRÌNH ĐA THỨC BẬC CAO
A. Kiến thức cần nhớ
 gic bng chuy
dtrình tích.
Phƣơng trình tích
- c ca bin x.
- n gi
A(x) = 0 và B(x) = 0 , ri ly tt c các nghic.
A(x). B(x) = 0 A(x) = 0 hoặc B(x) = 0.
- M rng:
B. Một số ví dụ minh họa
I. Phƣơng trình bậc 3.
1) Lý thuyết.
ng:
32
ax 0 0bx cx d a
(1)
Phƣơng pháp giải. ng  gichúng ta phc
mt nghim
0
x
c tích thành nhân t và chuyn v gii
c 2.
3 2 2
0
ax 0 0bx cx d x x mx nx p
0
2
0 (*)
xx
mx nx p
t cách gii tng quát theo
.
Mu cht ca vic gic mt nghim
0
x
c
t s chú ý v cách nhm nghim c
- Nu tng các h s cng 0 tc là a + b + c 
(1) nghim
0
1x
. Chng hn:
ta có: 4 1 + 2 5 = 0
- Nu tng các h s bc chn bng tng các h s bc l cng 0 tc là
a - b + c - m
0
1x 
. Chng hn:
32
5 3 9 0x x x
ta có 1 + 5 + 3 9 = 0.
A(x) 0
B(x) 0
A(x).B(x).....M(x) 0
...
M(x) 0

THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
3
- Nu a, b, c, d là các s nguyên và
0
m
x
n
là nghim hu t cc ca d và n
c cc bing hm
0
x
c ca d.
Thí dụ 1. Gi
3 3 2 3 2
) 3 2 0 ) 3 – 7 – 7 3 0 ) 3 10 0.a x x b y y y c x x x
Hƣớng dẫn giải
a) Ta thy a + b + c + d = 1 + 0 t nghim x = 1.
PT x
3
x
2
+ x
2
x 2x + 2 = 0
x
2
(x 1) + x(x 1) 2(x 1) = 0
(x 1)(x
2
+ x 2) = 0




2
1 0 1
2 0 2
xx
x x x
Vy tp nghim c
1;
2S
b) Ta thy a - b + c - d = 3 + 7 7 m y = - 1.
PT 3y
3
+ 3y
2
10y
2
10y + 3y + 3 = 0
3y
2
(y + 1) 10y(y + 1) + 3(y + 1) = 0
(y + 1)( 3y
2
10y + 3) = 0 (y + 1)( 3y
1)(y 3) = 0.
.
Vy tp nghim ca  là
c) Ta có d = - 10 ta nhm các s c ca 10 thì thy x = 2 là nghim c
32
3 2 2
2
2
3 10 0
2 2 5 10 0
. 2 . 2 5. 2 0
2 5 0
2
x x x
x x x x x
x x x x x
x x x
x

Do
2
50x x x
Vm x = 2.
y1
y 1 0
1
3y 1 0 y
3
y 3 0
y3



1
S 1; ; 3
3




THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
4
Thí dụ 2. Gi
3 2 3 2 3 2
) 8 4 1 0 ) 3 7 17 5 0 ) 2 5 2 0.a x x b x x x c x x x
Hƣớng dẫn giải
b) u có nghim hu t s có dng
0
1
x
n

vc 8. Ta th các giá tr
1 1 1
;;
2 4 8

nhn thy
1
2
x
là nghim c
 (2x 1).
4
3
2
2
8 4 1 0
8 1 4 2 0
2 1 4 2 1 2 2 1 0
2 1 4 2 1 0
xx
xx
x x x x
x x x
1
2
15
4
x
x

Vy tp nghim c
1 1 5
;
24
S






b) Ta có a = 3, d = -5 u có nghim hu t s có dng
0
m
x
n
vc -c ca 3. Ta th các giá tr
15
;
33

nhn thy
1
3
x
là nghim ca
 (3x 1).
3
3 2 2
2
2
2
3 7 17 5 0
3 6 2 15 5
3 1 2 3 1 5 3 1 0
3 1 2 5 0
3 1 1 4 0
x x x
x x x x x
x x x x x
x x x
xx


3 1 0
1
3
x
x

Vm
1
3
x
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
5
 a h s
2
m dng
0
2xa
t
2xa
nhm trit tiêu h s
2
ng:
32
32
2
2
2 2 2 2 5 2 2 0
2 2 5 1 0
1 2 4 1 0
1
2 4 1 0
1
6
1
2
2
23
a a a
a a a
a a a
a
aa
a
a
x
x
Vy tp nghim c
2;
2 3S
Thí dụ 3. Gi
a) (z + 3)
3
(z + 1)
3
= 98. b) (4x + 3)
3
(2x 5)
3
= ( 2x + 8)
3
;
c) (3x + 2016)
3
+ (3x 2019)
3
= (6x 3)
3
; d) (2x 7)
3
+
(9 2x)
3
= 152.
Hƣớng dẫn giải
a)  z
3
+ 9z
2
+ 27z + 27 z
3
3z
2
3z 1 = 98
6z
2
+ 24z 72 = 0
z
2
+ 4z 12 = 0
z
2
+ 6z 2z 12 = 0
(z + 6)(z 2) = 0
Tp nghim c .
* Nhận xét : Ta có cách gii khác:
Do z + 2 là trung bình cng c
thành (y + 1)
3
(y 1)
3
= 98
y
3
+ 3y
2
+ 3y + 1 y
3
+ 3y
2
3y + 1 = 98 6y
2
= 96
z 6 0
z 2 0


z6
z2

S 6
; 2
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
6
y
2
= 16
Tp nghim c .
t y = 4x + 3 ; z = 2x 5 ; thì y z = 2x + 8 . Ta có :
y
3
z
3
= (y z)
3
y
3
z
3
= y
3
z
3
3yz(y z) 3yz(y z) = 0
hay
Tp nghim c
 t u = 3x + 2016 ; v = 3x 2019 thì u + v = 6x 3 .
 thành u
3
+ v
3
(u + v)
3
= 0 hay
u
3
+ v
3
[u
3
+ v
3
+ 3uv(u + v) ] = 0 3uv(u + v) = 0
Tp nghim c
d) (2x 7)
3
+
(9 2x)
3
= 152.
t 2x 8 = y thì 2x 7 = y + 1 ; 9 2x = 1 y .
 thành (y + 1)
3
+ (1 y)
3
= 152
Khai trin, rút gn (hoc dùng hng thc a
3
+ b
3
c
6y
2
+ 2 = 152 6y
2
150 = 0 6(y + 5)(y 5) = 0.
- Vi y + 5 = 0 thì 2x 8 + 5 = 0 x = 1,5
- Vi y 5 = 0 thì 2x 8 5 = 0 x = 6,5
Tp nghim c
Lƣu ý: Trong các bài toán xut hin các dng (a + b)
3
; và a
3
b
3
.
Ta có: và
Thí dụ 4. Gi
a) x
3
3x
2
+ 3x 4 = 0. b) 2x
3
+ 3x
2
6x + 4 = 0
y4
y4

z 2 4
z 2 4

z2
z6

S 6
; 2
y0
z0
y z 0

4 3 0
2 5 0
2 8 0



x
x
x
0,75
2,5
4


x
x
x
S 4
; 0,75; 2,5
u0
v0
u v 0

3 2016 0
3 2019 0
6 3 0



x
x
x
x 672
x 673
x 0,5

S 6
72; 0,5;673
S 1
,5; 6,5
3
ab
3
33
a b a b 3ab(a b)
3 3 2 2
a b a b a ab b
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
7
Hƣớng dẫn giải
 m hu t c ca 4, ta th các giá tr
1; 2; 4
u
không là nghim. Mt khác li thy các h s 1; - 3; 3 ging hng thc
a
3
- 3a
2
+ 3a 1 = (a - 1)
3
nên ta bi
x
3
3x
2
+ 3x 4 = 0
32
3
3
3
3 3 1 3
13
13
13
x x x
x
x
x
Vy nghim c
3
13x 
b) Bm nghim d thm hu t. Ta
bi
32
32
3 3 2
3
3
3
3
3
2 3 6 4 0
4 6 12 8 0
5 6 12 8
5. 2
5. 2
2
51
x x x
x x x
x x x x
xx
xx
x


3
2
51
x
II. Phƣơng trình bậc bốn.
1) Lý thuyết.
ng:
4 3 2
ax 0 0bx cx dx e a
Phƣơng pháp giải.  gi      ng nhm mt nghim và
phân c 4 thành tích ca mc bc bc nh
 gic 3 hoc phân tích thành tích hai tam thc
bc 2, hot n ph chuyn v gic 2. Ta xét các dc bit
 
Dạng 1. 
42
0 0 2.1 ax bx c a
Phƣơng pháp giải. t
2
( 0)y x y

2
0 2.2 ay by c
c 2 d c nghim t suy ra x.
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
8
Chú ý: S nghim c thuc s nghi
(2.2)
Thí dụ 5. Gi
x
4
5x
2
+ 4 = 0.
Hƣớng dẫn giải
t
2
( 0)y x y
 thành:
2
2
2
1
5 4 0 1 4 0
4
1
1
2
4
y
y y y y
y
x
x
x
x



Vy tp nghim c
1;
2 S
Dạng 2. ng:
44
x m x n p
(p > 0)
Phƣơng pháp giải: t
2
ab
yx

Chuyn v n y
n y s c.
Thí dụ 6. Gi
44
2004 2006 2 xx
Hƣớng dẫn giải
t
2004 2006
2005
2
y x x
 thành:
2
4 4 2 2 2 2
2
2
2 2 4 2 4 2
4 2 2 2
2
1 1 2 1 1 2 1 . 1 2
2 2 2 1 2 4 8 4 2 4 2 2
2 12 0 2 6 0
00
2005 0
2005
y y y y y y
y y y y y y
y y y y
yy
x
x





Vm x = 2005
Dạng 3. ng:
x a x b x c x d e

Phƣơng pháp giải:
22
PT x a b x ab x c d x cd e
t
2
t x a b x

t ab t cd e
c 2 d
ging gic nghim ca bài toán.
Thí dụ 6. Gi
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
9
) 1
2 4 5 10 ) 4 7 4 5 1 2 1 9. a x x x x b x x x x
Hƣớng dẫn giải
a) Ta có:
22
1 2 4 5 10
1 5 2 4 10
6 5 6 8 10
x x x x
x x x x
x x x x
t t = x
2
 thành:
2
5 8 10
13 30 0
3 10 0
tt
tt
tt
3
10


t
t
2
2
2
22
2
6 3 0
6 10 0
6 3 0 6 10 3 1 0
36
36
36
xx
xx
x x dox x x
x
x
x
Vy tp nghim c
3 6
; 3 6 S
b) * Tìm cách giải : Ta thy nu v trái nhân 4 vào nhân t th ba, nhân 2 vào nhân t th
 bn nhân t c mà h s cu là 4. V phi nhân v
u nhân (4x + 7) vi (4x + 2) ; (4x + 5) vi
(4x + 4) ta thy kt qu xut hin các hng t ging nhau 16x
2
+ 36x nên có th t n ph
 gii.
Ta có (4x + 7)(4x + 5)(x + 1)(2x + 1) = 9
(4x + 7)(4x + 5)(4x + 4)(4x + 2) = 72
(16x
2
+ 36x + 14)(16x
2
+ 36x + 20) = 72.
t 16x
2
+ 36x + 17 = y ta có :
(y 3)(y + 3) = 72 y
2
9 = 72 y
2
= 81 y = 9 .
- Vi 16x
2
+ 36x + 17 = 9 4x
2
+ 9x + 2 = 0 4x
2
+ 8x + x + 2 = 0
4x
2
+ 8x + x + 2 = 0 4x(x + 2) + (x + 2) = 0
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
10
(x + 2)(4x + 1) = 0
- Vi 16x
2
+ 36x + 17 = 9 16x
2
+ 36x + 26 = 0 vô nghim vì
16x
2
+ 36x + 26 = .
Vy tp nghim ctrình là .
Thí dụ 7. Gi (x 2)(x 3)(x 5)(x 6) = 31(x
2
8x + 12) + 128. (1)
* Tìm cách giải : Xét v trái nu nhân nhân t th nht vi nhân t th  th
hai nhân nhân t th 3 ta có ( x
2
8x + 12)( x
2
8x + 15). Mi nhân t là mc có
cùng h s ca x
2
và ca x.
 thành ( x
2
8x + 12)( x
2
8x + 15) = 31(x
2
8x + 12) + 128 .
t n ph.
Hƣớng dẫn giải
(x 2)(x 3)(x 5)(x 6) = 31(x
2
8x + 12) + 128
( x
2
8x + 12)( x
2
8x + 15) = 31(x
2
8x + 12) + 128. (2)
t x
2
8x + 12 = y thì x
2
8x + 15 = y + 3
Khi  thành y(y + 3) = 31y + 128
y
2
+ 3y 31y 128 = 0 ; y
2
+ 4y 32y 128 = 0
y(y + 4) 32(y + 4) = 0 ; (y + 4)(y 32) = 0
Vi y + 4 = 0 x
2
8x + 16 = 0 (x 4)
2
= 0 x = 4
Vi y 32 = 0 x
2
8x 20 = 0 x
2
10x + 2x 20 = 0
(x 10)(x + 2) = 0 x = 10 hoc x = 2
Vy tp nghim c
Dạng 4. ng:
2 2 2
12
(ax )(ax ) .b x c b x c mx
Phƣơng pháp giải:
– Bƣớc 1: nhn xét x = 0 không là nghim c
- Bƣớc 2: Chia hai v c
2
x
.
 thành:
12
ax
cc
ax b b m
xx
Bƣớc 3: t
c
t ax
x

chuyn v gin.
x 2 0 x 2
4x 1 0 x 0,25



2
9 23
4x 0 , x
24



S 2
; 0,25
y 4 0
y 32 0


S 2
; 4;10
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
11
Thí dụ 8. Gi
2 2 2
(2 3 1)(2 5 1) 9 (1) x x x x x
Hƣớng dẫn giải
Nhn thy x = 0 không phi là nghim c
- Chia hai v c
2
x
c:
11
2x 3 2x 5 9 (*)
xx
t
1
2tx
x

 thành: (t 3)(t + 5) = 9
2
6
2 24 0 ( 6)( 4) 0
4
t
t t t t
t

Vi t = - 6 ta có:
2
1 3 7
2 6 2 6 1 0 .
2
x x x x
x

Vi t = 4 ta có:
2
1 2 2
2 4 2 4 1 0 .
2
x x x x
x
Vm:
37
2
x

,
22
2
x
.
Thí dụ 9. Gi
2 2 2
( 5 1)( 4) 6( 1) (2) x x x x
Hƣớng dẫn giải
t
1ax
thay x = a + 1 và rút gc:
2 2 2
(u 7 3)( 2 3) 6 (*)u u u u
 gii ti trên.
Gic 4 nghim là:
1 21
3 7; .
2
xx

Dạng 5. ng:
2
,x a x b x c x d ex

ab cd
.
Phƣơng pháp giải:
– Bƣớc 1: nhn xét x = 0 không là nghim c
- Bƣớc 2:
2 2 2
PT x a b x ab x c d x cd ex
Chia hai v c
2
0x
.
 thành:
ab cd
x a b x c d e
xx
Bƣớc 3: t
ab cd
t x x
xx

t a
b t c d e
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
12
c 2 d c t t c x.
Thí dụ 10. Gi
2 2 2 2
) 2 1 8 4 4 ) 3 2 9 18 168a x x x x x b x x x x x
Hƣớng dẫn giải
a)
2 2 2 2
2 4 1 8 4 6 8 9 8 4PT x x x x x x x x x x
.
Do
0x
không là nghim nên chia hai v c
2
x
c:
88
6 9 4xx
xx
.
t
8
yx
x

 thành
2
5
6 9 4 15 50 0
10
y
y y y y
y
.
Vi
5y
thì
2
8
5 5 8 0x x x
x
(vô nghim).
Vi
10y
thì
2
5 17
8
10 10 8 0
5 17
x
x x x
x
x


.
Vy tp nghim c
5 1
7;5 17S
.
b) Ta có:
2 2 2
22
3 2 9 18 168
1 2 3 6 168
1 6 2 4 168
7 6 5 6 168
x x x x x
x x x x
x x x x
x x x x
Chia hai – Nhn thy x = 0 không là nghim c
v c
2
x
c:
66
7 5 168xx
xx
t
6
yx
x

 thành:
7 5
168yy
2
7
12 133 0
19
y
yx
y

THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
13

2
2
1
6
6
7
7 6 0
19 337
6
19 6 0
2
19
19 337
2
x
x
x
xx
x
x
xx
x
x
x




Vm
19 337 19 337
1, 6, ,
22
x x x x
Dạng 6. ng:
2
2 2 2
1 1 2 2
a bx c x d a bx c x d Ax
Phƣơng pháp giải:
– Bƣớc 1: nhn xét x = 0 không là nghim c
- Bƣớc 2: Chia hai v c
2
0x
.
 thành:
22
1 1 2 2
dd
a bx c a bx c A
xx
Bƣớc 3: t
d
t bx
x


22
1 1 2 2
a t c a t c A
c 2 d c t t c x.
Thí dụ 11. Gi
22
2 2 2
3 2 1 2 3 1 5 0x x x x x
Hƣớng dẫn giải
D thy
0x
không là nghim c
Chia hai v c
2
x
c
22
11
3 2 2 3 5 0xx
xx
.
t
1
yx
x

 thành:
22
2
1
3 2 2 3 5 0 1 0
1
y
y y y
y

.
Suy ra
1
15
1
2
1
15
1
2
x
x
x
x
x
x


.
Vy tp nghim c
1 5 1 5
;
22
S





.
Dạng 7. ng:
4 3 2
ax 0.bx cx bx a
Phƣơng pháp giải:
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
14
– Bƣớc 1: Nhn xét x = 0 có phi là nghim nghim c
- Bƣớc 2: Chia hai v c
2
0x
c:
2
2
ax 0.
ba
bx c
xx
- Bƣớc 3: t
22
2
11
2y x y x
xx
 thành:
2
20a y by c
c 2 d c y và suy ra x.
Thí dụ 12. Gi
4 3 2
6x 5x 38x 5x 6 0
Hƣớng dẫn giải

Chia 
2

2
2
56
6x 5x 38 0
xx
2
2
11
6 x 5 x 38 0
xx

1
yx
x

thì:
22
2
1
x y 2
x

2
5y 50 = 0 <=> (3y 10)(2y + 5) = 0

10 5
y và y
32

10
y
3
thì:
2
1 10
x 3x 10x 3 0
x3
<=> (3x 1)(x 3) = 0 <=>
1
2
1
x
3
x3

5
y
2

thì:
2
15
x 2x 5x 2 0
x2
<=> (2x + 1)(x + 3) = 0 <=>
3
4
1
x
2
x2


Vn nghim:
11
, , 2, 3
32
x x x x
Dạng 8. ng:
4 3 2 2
00ax bx cx kbx k a k
Phƣơng pháp giải:
– Bƣớc 1: Nhn xét x = 0 có phi là nghim nghim c
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
15
- Bƣớc 2: Chia hai v c
2
0x
c:
2
2
2
0
kk
a x b x c
xx






- Bƣớc 3: t
k
tx
x

vi
2tk
ta có
2
2
22
2
22
kk
x x k t k
xx



.
 thành:
2
20a t k bt c
c 2 d c y và suy ra x.
4 3 2
2 21 34 105 50 0x x x x
Thí dụ 13. Gi
4 3 2
2 21 34 105 50 0x x x x
Hƣớng dẫn giải
Ta thy
105
5
21
k
và
2
50
25
2
k 
c bn có h
s i xng t l.
2
2
25 5
8 2 21 34 0xx
xx
.
t
5
tx
x

suy ra
22
2
25
10tx
x
.
 thành
2
2 21 54 0 6t t t
hoc
9
2
t
.
Vi
6t
thì
22
12
5
6 6 5 6 5 0 3 14; 3 14x x x x x x x
x
.
Vi
9
2
x
thì
2
34
5 9 9 161 9 161
2 9 10 0 ;
2 4 4
x x x x x
x

.
Vy PT (8) có tp nghim
9 161 9 161
3 14;3 14; ;
44
S






.
Có nhiu bài toán bc bn không mu mc vit n ph  gii phi thc s linh hot
không th phân thành dng c thn mt s bài toán sau:
Thí dụ 14. Gi
2
2
23
3 1 2 1 5 1x x x x
Hƣớng dẫn giải
Vì
1x 
không là nghim c hai v cho
3
1x
c:
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
16
2
2
11
32
11
x x x
x x x
t
2
2
1 2 1
3 5 3 5 2 0 2,
13
xx
t t t t t t
xt

*
2
3 13
2 3 1 0
2
t x x x
*
2
1
3 2 4 0
3
t x x
m
Vm
3 13
2
x
Thí dụ 15. Gi(4x 19)
4
+ (4x 20)
4
= (39 8x)
4
Hƣớng dẫn giải
t 4x 19 = y; 4x 20 = z thì y + z = 8x 39 ta có y
4
+ z
4
(y + z)
4
= 0
y
4
+ z
4
= 0
= 0
4yz
Tp nghim c
Nhận xét:  i vi hu hc bn có h s không quá cao
u có th chuyn v c 4 tng quát ax
4
+ bx
3
+ cx
2
+ dx + e = 0 vi
i gii b s bnh cho dù dng ý c là
ng tt n ph  n bài toán.
Tôi s minh hng bài toán sau:
Thí dụ 16. Gi
4 3 2
4 10 37 14 0 (1)x x x x
Hƣớng dẫn giải
Phân tích: n vic phân tích:
4 3 2 2 3 4
y 4y z 6y z 4yz z
3 2 2 3
4y z 6y z 4yz
22
6
4yz y yz z 0
4



2
2
37
y z z 0
4 16







y0
z0
4 19 0 4,75
4 20 0 5



xx
xx
S 4
,75;5
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
17
4 3 2 2 2 4 3 2
4 10 37 14 0x x x x x px q x rx s x p r x s pr q x ps qr x qs
ng nht h s:
4
10
37
14
pr
s pr q
ps qr
qs


.
Xut phát t qs = -a h ta thy nhc : p = -5, q = 2,
r = 1, s = -7 tha mãn h 
Từ đó có lời giải:
4 3 2 2 2
4 10 37 14 5 2 7x x x x x x x x
Suy ra:
2
4 3 2 2 2
2
5 2 0
4 10 37 14 0 5 2 7 0
70
xx
x x x x x x x x
xx
Gic nghim:
12
5 17 1 29
;
22
xx

Ho s bng sau:
Dạng 1. ng:
42
x ax bx c
Phƣơng pháp giải:
Ta thêm bt vào 2 v mng:
22
2mx m
 thành:
2 2 2 2
( ) (2 )x m m a x bx c m
Ta mong mun v phi có dng:
2
()Ax B
22
20
4(2 )( ) 0
ma
m
b m a c m


Thí dụ 17. Gi
42
10 20 0x x x
Hƣớng dẫn giải
4 2 4 2
10 20 0 10 20x x x x x x
Ta thêm vào 2 v ng:
22
2mx m
 thành:
4 2 2 2 2
2 (10 2 ) 20x mx m m x x m
Ta có
2
9
1 4( 20)(10 2 ) 0
2
VP
m m m
. Ta vit l
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
18
2 2 2
4 2 2 2
9 1 9 1
90
2 4 2 2
x x x x x x
22
1 17
( 5)( 4) 0
2
x x x x x

và
1 21
2
x
.
Vm
1 17 1 21
,
22
xx

Dạng 2. ng:
4 3 2
x ax bx cx d
Phƣơng pháp giải:
Ta s to ra v phi mt biu thng:
2
2
2
a
x x m




Bng cách khai trin biu thc:
2
2
2 4 3 2 2
2
24
aa
x x m x ax m x amx m






.
Ta thy cn thêm vào hai v mng:
2
22
2
4
a
m x amx m




thành:
2
2
2 2 2
2 ( )
24
aa
x x m m b x am c x m d






Bây gi ta cn:
2
2
22
20
4
?
( ) 4 2 0
4
VP
a
mb
m
a
am c m b m d




Thí dụ 18. Gi
4 3 2
6 8 2 1 0x x x x
Hƣớng dẫn giải
ng:
4 3 2 4 3 2
6 8 2 1 0 6 8 2 1x x x x x x x x
Ta to ra v trái dng:
2 2 4 3 2 2
( 3 ) 6 (9 2 ) 6x x m x x m x mx m
Tc là thêm vào hai v mng là:
22
(9 2 ) 6m x mx m
 thành:
2 2 2 2
( 3 ) (2 1) (6 2) 1x x m m x m x m
. Ta cn
2
' (3 1) (2 1)( 1) 0 0
VP
m m m m
.
 thành:
2 2 2
( 3 ) ( 1)x x x
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
19
22
23
23
( 4 1)( 2 1) 0
12
12
x
x
x x x x
x
x




Vm
2 3;
2 3;1 2;1 2S
II. Phƣơng trình cao hơn bậc bốn.
i v dng
 trình tích ho t n ph   gi    c thp hoc vi
nhii vic có th s d gii
toán. Chúng ta minh ha qua các ví d sau:
Thí dụ 19. Giy
2
(y
4
29y
2
+ 244)
= 576. (1)
Hƣớng dẫn giải
(1) y
6
29y
4
+ 244y
2
576 = 0 .
y
6
4y
4
25y
4
+ 100y
2
+ 144y
2
576 = 0
y
4
(y
2
4) 25y
2
(y
2
4) + 144(y
2
4) = 0
(y
2
4)(y
4
25y
2
+ 144) = 0
(y
2
4)(y
4
9y
2
16y
2
+ 144) = 0
(y
2
4)[y
2
(y
2
9) 16(y
2
9)] = 0
(y
2
4)(y
2
9)(y
2
16) = 0
(y 4)(y 3)(y 2)(y + 2)( y+ 3)(y + 4) = 0 .
Vm là : y = 2; y = 3; y = 4.
Tp nghim c .
Thí dụ 20. Gi6x
5
29x
4
+ 27x
3
+ 27x
2
29x + 6 = 0
(Thi học sinh giỏi lớp 9 tỉnh Thanh Hóa năm học 2005 – 2006)
Hƣớng dẫn giải
Bii thành (x + 1)(6x
4
35x
3
+ 62x
2
35x + 6) = 0.
c x = 1 là 1 nghim.
Vi 6x
4
35x
3
+ 62x
2
35x + 6 = 0 do x = 0 không là nghim nên chia hai v cho x
2
c :
S 4
; 3; 2; 2; 3; 4
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
20
t thì
 thành 6(y
2
2) 35y + 62 = 0 (2y 5)(3y 10) = 0
Thay vào 2y 5 = 0 gic x = 2 hoc x = .
Thay vào 3y 10 = 0 gic x = 3 hoc x =
Tp nghim c .
Thí dụ 21. Gi (x
2
4x + 11)(x
4
- 8x
2
+ 21) = 35.
(Đề thi vào lớp 10 trường THPT chuyên Nguyễn Trãi, Hải Dương năm học 2012 – 2013)
Hƣớng dẫn giải
và nên v trái không nh 
Ta suy ra . Vy nghim c
Thí dụ 22. Gi
3
33
5 5 5 24 30 0x x x x
Hƣớng dẫn giải
Ta có:
33
5 30 5 5 5 5x x x x x
nên 
3
3 3 3
5 5 5 24 24 30 0x x x x x x
.
t
3
55u x x
c h:
3
22
3
55
60
55
u u x
u x u ux x u x
x x u
.
32
4 5 0 1 5 0 1x x x x x x
.
Vy
1x 
là nghim duy nht c
2
2
11
6 x 35 x 62 0
xx
1
xy
x

22
2
1
x y 2
x
1
yx
x

1
2
1
yx
x

1
3
11
1; ; ;2; 3
32



2 4 2
x 4x+11 x 8x 21 35
2
2
2
x 2 7 x 4 5 35





2
x
2 0, x
2
2
x 4 0, x
2
2
2
(x 2) 0
x2
x 4 0



THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
21
CHỦ ĐỀ 2. PHƢƠNG TRÌNH CHỨA ẨN Ở MẪU THỨC
A. Kiến thức cần nhớ
Bước 1u kinh cc là tìm giá tr ca n làm tt c
các mu thc ct t
Bước 2 ng mu hai v ci kh mu.
Bước 3 : Gia nhc.
Bước 4 : (Kt lun) . Trong các giá tr c c 3, các giá trị thỏa mãn điều kiện
xác định chính là nghim c
* Chú ý : Nu A(x) = 0 ti x = x1 hoc x = x2 thì
A(x) 0 khi x x1 và x x2
B. Một số ví dụ minh họa
Một số bài tập cơ bản:
Thí dụ 23. Gi
2
1 1 3 1 25 4 4 6
) ) .
1 2 2 6 2 4 25 1 5 1 1 5
x
ab
x x x x x x x
Hƣớng dẫn giải
  1 ; x 2 và x 3.
(1) 2(x 2)(x 3) + 2(x 1)(x 3) = 3(x 1)(x 2) (x 1)(x 3)
2x
2
10x + 12 + 2x
2
8x + 6 = 3x
2
9x + 6 x
2
+ 4x 3
2x
2
13x + 15 = 0 (2x 3)(x 5) = 0
Hai giá tr x = 1,5 và x = 5 th
 0,2.
(2) 25 + 4x = 4(5x 1) + 6(5x + 1)
25 + 4x = 20x 4 + 30x + 6
46 x = 23 x = 0,5.
Giá tr này thm là x = 0,5.
2x 3 0 x 1,5
x 5 0 x 5





THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
22
Thí dụ 24. Gi
2
2
2 5 5 41 3 8
1 3 4 4
x x x x
x x x x

Hƣớng dẫn giải
Ta có (1)
 4 và x 1.
ng mu s hai v và kh m
(2x 5)(x 4) + x
2
5x 41 = (3x 8)(x + 1)
2x
2
13x + 20 + x
2
5x 41 = 3x
2
5x 8
13x = 13 x = 1 .
Giá tr này không thm.
Một số dạng phƣơng trình phân thức thƣờng gặp:
Dạng 1. ng:
12
12
....
n
n
a
aa
A
x b x b x b
Phƣơng pháp giải: Nhóm tng cm phân thc làm xut hin nhân t chung.
Thí dụ 25. Gi
1 1 1 1 1
0
1 2 3 4x x x x x
Hƣớng dẫn giải
u kin
1;
2; 3; 4;0x
. Ta bi
22
1 1 1 1 1
0
4 1 3 2
2 2 2 2
1
0
4 4 3 2
x x x x x
xx
x x x x x

2 2 2
1 1 1
0
4 4 3 2( 4 4)x x x x x x
.
2
2 5 5 41 3 8
1 ( 1)( 4) 4

x x x x
x x x x
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
23
t
2
4u x x
 thành
1 1 1
0
3 2 4u u u

2
25 145
5 25 24
10
0
2 3 4
25 145
10
u
uu
u u u
u




.

2
2
25 145
4
10
25 145
4
10
xx
xx




.
c tp nghim c
15 145 15 145 15 145 15 145
2 ; 2 ; 2 ; 2
10 10 10 10
S





.
Dạng 2. ng:
1 1 2 2
12
....
nn
n
a x b
a x b a x b
A
x c x c x c

Phƣơng pháp giải: Ta bi
12
12
12
....
n
n
n
d
dd
a a a A
x c x c x c
Thí dụ 26. Gi
4 4 8 8 8
1 1 2 2 3
x x x x
x x x x
Hƣớng dẫn giải
Bi
22
5 5 10 10 8
1 1 2 2 3
10 40 8
1 4 3
x x x x
xx

.
t
2
1, 4; 0u x u u u
d
2
16
4 65 16 0
1
4
u
uu
u
.
c tp nghim c
11
; 4; ;4
22
S



.
Dạng 3. ng:
i)
22
12
mx nx
p
ax b x c ax b x c

THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
24
ii)
22
11
22
22
0;
ax b x c ax d x c
ax b x c ax d x c

iii)
2
1
22
2
0.
ax b x c
px
ax b x c ax dx c



0
Phƣơng pháp giải dạng i:
Nhn xét
0x
không phi là nghim c
Vi
0x
, ta chia c t s và mu s cho
x
c:
ab
c
pp
x m x n
xx

.
t
2
22
2
2 2 2
kk
t x t x k k k
xx
.
 quy v c 2 theo
t
.
Các dng ii) và iii) gi.
Thí dụ 27. Gi
22
2 13
6
3 4 1 3 2 1
xx
x x x x

.
(Thi vào lớp 10 chuyên Quốc học Huế năm học 1996 - 1997)
Hƣớng dẫn giải
u kin:
2
2
1
3 4 1 0
1
3 2 1 0
3
x
xx
x
xx



D thy x = 0 không phi là nghim c và mu ca mi
phân thc:
t
1
34xt
x
 thành:
2
1
2 13
6 2 7 4 0
2
6
4.
t
tt
tt
t

Vi
1
2
t
thì
2
4
11
3
3 4 6 11 4 0
1
2
2
x
x x x
x
x
2 13
6.
11
3 4 3 2xx
xx

THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
25
Vi
4t 
thì
2
1
3 4 4 6 1 0xx
x
(loi)
Vm:
41
,
32
xx
Dạng 4. ng:
2
2
ax
xb
xa




vi
0,a x a
.
Phƣơng pháp giải:
Da vào hng thc
2
22
2a b a b ab
.
Ta vit l
2
2
2 2 2
2 . 2 0
ax x x x
x a b a b
x a x a x a x a






.
t
2
x
t
xa
quy v c 2.
Thí dụ 28. Gi

2
2
2
x
x3
x1
.
(Thi học sinh giỏi huyện Phù Ninh 2013-2014)
Hƣớng dẫn giải
iu kin:
1x
2
2
2 2 2
2
22
2
x x x x
PT x 3 2. 2 3 0
x 1 x 1 x 1 x 1
x
30
xx
x1
3 1 0
x 1 x 1
x
10
x1







=>
2
2
x
) 3 0 x 3x 3 0
x1
(vô lý)
2
1
2
2
15
x
x
2
) 1 0 x x 1 0
x1
15
x
2
Vm
12
1 5 1 5
x ,x
22


THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
26
Có nhiu bài toán bc bn không mu mc vic bit n ph  gii phi
thc s linh hot không th phân thành dng c thn mt s bài toán sau:
Thí dụ 29. Gi
2 2 2
1 1 1 3
.
5 4 11 28 17 70 4 2x x x x x x x
.
Hƣớng dẫn giải
Ta có:
2 2 2
1 1 1 3
5 4 11 28 17 70 4 2
1 1 1 3
(*)
( 1)(x 4) ( 4)( 7) ( 7)( 10) 4 2
x x x x x x x
x x x x x x
T u ki 
1
1; 4; 7; 10;
2
x

2
1 1 1 1 1 1 1 1 1 3
(*)
3 1 4 3 4 7 3 7 10 4 2
1 1 9
7 12 0
1 10 4 2
3
4.
x x x x x x x
xx
x x x
x
x


Kt hp vu kin ta có nghim duy nht x = -3.
Thí dụ 30. Gi
22
11
15.
( 1)xx

.
Hƣớng dẫn giải

0
1
x
x

.
i:
22
2 2 2 2
2
22
1 1 ( 1)
15 15
( 1) ( 1)
1 2 ( 1) 1 2
15 15
( 1) ( 1) ( 1)
xx
x x x x
xx
x x x x x x






t
1
( 1)
t
xx
 thành:
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
27
2
3
2 15 0
5
t
tt
t

Vi t = 3 ta có:
2
1 3 21
3 3 3 1 0 .
( 1) 6
x x x
xx

Vi t = - 5 suy ra:
2
1 5 5
5 5 5 1 0 .
( 1) 10
x x x
xx

n nghim
3 21
6
x

,
55
10
x

Thí dụ 31. Gi
42
32
31
3
xx
x x x


.
Hƣớng dẫn giải
u kiên:
32
0
0
15
2
x
x x x
x

Chia chia t và mu ca phân thc cho
2
0x

2
2
1
3
3
1
1
x
x
x
x


t
2 2 2 2
22
1 1 1
2 5 3t x t x t x
x x x
 thành:
2
2
5
3 3 2 0 1
1
t
t t t
t
hoc
2t
Vi t = 1 thì
2
1 1 5
1 1 0 .
2
x x x x
x
Vi t = 2 thì
2
1
2 2 1 0 1 2.x x x x
x
Vn nghim là:
15
2
x
và
12x 
Thí dụ 32. Gi
22
1 1 2
12 .
2 3 3
x x x
x x x

.
Hƣớng dẫn giải
u kin:
2
3
x
x
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
28
t
1
1
2
2
3
3
x
u
x
x
uv
x
x
v
x

.
  thành:
2 2 2 2
12 12 0
3
( 3 )( 4 ) 0
4
u uv v u uv v
uv
u v u v
uv

Vi u = 3v ta có:
2
1 2 8 46
3. 2 16 9 0 .
2 3 2
xx
x x x
xx

Vi u = -4v ta có:
2
12
4. 5 12 19 0 ( )
23
xx
x x VN
xx


Vm
8 46
2
x
Dạng 5. S d     gi a phân thc
Thí dụ 32. Gi
2 2 2
3 4 1
3 3 9 2x x x x x

.
Hƣớng dẫn giải
u kin:
2
2
2
30
3 9 0 0.
20
xx
x x x
x
Vu kin x
i:
2 2 2
1 4 3
2 3 9 3x x x x x

c ht ta chng minh bng thc:
2 2 2
()
(*)
a b a b
x y x y

.
Tht vy, áp dng bng thc bu-nhi-a-cp-xki cho hai b s
;xy
và
;
ab
xy




ta có:
2
2
2 2 2
22
2
()a b a b a b
x y a b
x y x y
xy














Dy ra khi
ab
xy
Vc chng minh.
Áp d
22
2 2 2 2 2 2 2
1 4 1 (2) (1 2) 3
2 3 9 2 3 9 2 3 9 3x x x x x x x x x x x
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
29
m khi và ch khi
22
22
1 2 1 13
3 9 4
2 3 9 2
x x x x
x x x

Vm
1 13
2
x
.
CHỦ ĐỀ 3. PHƢƠNG TRÌNH CHỨA ẨN TRONG DẤU
GIÁ TRỊ TUYỆT ĐỐI
A. Kiến thức cần nhớ
 giá tr tuyi :
 gia n trong du giá tr tuyi cn kh du giá tr tuyt
i. Ta cn nh giá tr tuyi ca mt biu thc bng chính nó nu nó có giá tr không
âm, bng s i ca nó nu nó có giá tr  b du giá tr tuyi ta phi xét
các giá tr làm biu thc âm hoc không âm.
B. Một số ví dụ minh họa
Thí dụ 33. Gi
2 2 2 2
) 3 2 0 ) 4 1 31 ) 2 4 8 8a x x b x x c x x x x
.
Hƣớng dẫn giải
a) 
2
3 2 0xx
1
1 2 0
2
x
xx
x
.

2; 1; 1; 2x
b) Ta có:
ˆ
A neu A 0
A
ˆ
A neu A 0

THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
30

2
4x 32 = 0 (x 8)(x + 4) = 0

2
4x + 30 = 0 vô nghim
vì x
2
4x + 30 = (x 2)
2
+ 26 > 0 , x .
Vy nghim c 4 .
c) Do x
2
2x + 4 = (x 1)
2
+ 3 > 0 , x nên
 x
2
2x + 4 = 8x x
2
8
x
2
5x + 6 = 0 (x 3)(x 2) = 0
Vm x = 2 và x = 3.
Thí dụ 34. Gi
) 2 5 7 9 21 ) 2 1 4 8 10 15.a x b x
.
Hƣớng dẫn giải
a) PT
.
b) PT
Thí dụ 35. Gi
. a)
3 3 6 5 2 8x x x
; b)
22
9 25 26xx
;
2
2
2
4 1 31
4 1 31
4 1 31
xx
xx
xx
2
2
4 32 0
4 30 0

xx
xx
x8
x4

22
x 2x 4 x 2x 4
x3
x2
2x 5 7 9 21
2x 5 7 12
2x 5 7 12
2x 5 5 (loai)
2x 5 19

2x 5 19 x 7
2x 5 19 x 12



2x 1 4 8 25
2 1 4 8 25
2 1 4 8 25
x
x
2x 1 4 33 (loai)
2x 1 4 17
2x 1 4 17
2x 1 4 17
2x 1 13 (loai)
2x 1 21

2x 1 21
2x 1 21

x 10
x 11

THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
31
c)
5 3 1
1 2 2 5 10 . d) 4
3 3 2
xx
x x x x
xx
Hƣớng dẫn giải
a) Lp bng xét giá tr tuyi (hay bng phá d
x
2 2,5 3
3 x | 3 x | 3 x 0 x 3
6 3x 0 3x 6 | 3x 6 | 3x 6
2x 5 | 2x 5 0 5 2x | 5 2x
V trái
14 6x | 0x + 2 | 4x 8 | 6x 14
Vy : + Vi x < 2 thì 14 6x = 8 x = 1 (tha mãn)
+ Vi thì 0x + 2 = 8 Vô nghim
+ Vi 2< thì 4x 8 = 8 x = 4 ( loi )
+ Vi x > 3 thì 6x 14 = 8 x = (tha mãn)
Nghim c 
b) Lp b
x
2
9 25
9 x
2
0 x
2
9 | x
2
9
25 x
2
| 25 x
2
0 x
2
25
V trái
34 2x
2
| 0x
2
16 | 2x
2
34
Vi x
2
9 ; 34 2x
2
= 26 x
2
= 4 x = 2 .
Vi 9 < x
2
< 25 ; 0x
2
16 = 26 Vô nghim
Vi x
2
25 ; 2x
2
34 = 26 x
2
= 30 x = .
Vy nghim c 2 và x = .
c)  có v trái không âm nên
10x  x = 2.
Vm x = 2.
x3
3x 6
5 2x
2 x 2,5
x3
11
3
2
3
3
9
2
x
2
x 25
30
30
x 1 2x 5 3x 2 10x
0 x 0
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
32
d) u kin x 3 +
x23
0 .
Bc t lp bng xét du.

53 x
-
1x
- 4
32 x
- 4x + 12 = 0 (*)
Xét x < -
2
3
Thì (*)
- 3x + 5 + ( x 1) + 4(2x + 3) 4x + 12 = 0
2x = -28
x = - 14 (Th
Xét -
2
3
 Thì (*)
- 3x + 5 + x 1 4(2x + 3) 4x + 12 = 0
x =
7
2
(Th
Xét 1 
3
5
Thì (*)
- 3x + 5 (x -1) 4(2x + 3) 4x + 12 = 0
x =
8
3
(loi)

3
5
Thì (*)
3x 5 (x 1) 4(2x + 3) 4x + 12 = 0
x = -
5
2
(Loi)
Vm x
7
2
;14
Thí dụ 36. Gi
3 4 5 2 1.xx
Hƣớng dẫn giải
(1)
a) Vi ta lp bng xét giá tr tuyi :
3x 4 5 1 x 2
3x 4 5 1 x 2
3x 4 5 1 x 2
3x 4 x 2 6
3x 4 x 2 4
3x 4 x 2 6
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
33
x
2
4 3x | 4 3x 0 3x 4
2 x 0 x + 2 | x + 2
V trái
6 2x | 4x + 2 | 2x 6
Vi x 2 ; 6 2x = 6 x = 0 (tha mãn).
Vi 2 < x < ; 4x + 2 = 6 x = 1 (tha mãn)
Vi x ; 2x 6 = 6 x = 6 (tha mãn)
b) Vi lp bng xét giá tr tuyi :
x
2
4 3x | 4 3x 0 3x 4
2 x 0 x + 2 | x + 2
V trái
2 4x | 2x + 6 | 4x 2
Vi x 2 ; 2 4x = 6 x = 1 ( không tha mãn).
Vi 2 < x < ; 2x + 6 = 4 x = 1 (tha mãn)
Vi x ; 4x 2 = 4 x = (tha mãn)
Vy tp nghim c
Thí dụ 36. Gi: | x + 1|
2016
+ |x + 2|
2017
= 1
(Trích đề thi học sinh giỏi huyện Ba Vì năm học 2017-2018)
Hƣớng dẫn giải
- 2 và x = - 
* Xét x < - 2:
Ta có: x + 1< -1 và x + 2< 0. Suy ra: |x+1| >1;|x + 2| >0

2016
>1;|x + 2|
2017
>0

2016
+ |x + 2|
2017
> 1
- 
* Xét -2 < x < -1:
4
3
3x 4
x2
4
3
4
3
3x 4 x 2 4
4
3
3x 4
x2
4
3
4
3
3
2
3
S 1; 0;1; ; 6
2




THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
34
Ta có: -1< x + 1< 0 và 0< x + 2 <1 . Suy ra: 0< |x + 1| < 1 ; 0 < |x + 2| <1
Và |x+1| = -x - 1; |x + 2| = x + 2

2016
< |x+1| ; |x + 2|
2017
< |x+2|

2016
+ |x + 2|
2017
< |x+1| + |x +2|= -x 1 + x + 2= 1
-2 < x < -
* Xét: x > -1:
Ta có: x + 1 > 0 và x + 2 > 1.Suy ra: |x+1| > 0 và |x + 2| > 1.

2016
+ |x + 2|
2017
> 1
-
Kết luận: 
󰇝
 
󰇞
BÀI TẬP TỔNG HỢP
Chủ đề 1. Phƣơng trình đa thức bậc cao
Câu 1. (Đề HSG huyện Cẩm Giàng 2015-2016)
Gi
2
22
x 2x 2x 4x 3
Câu 2. (Đề HSG huyện Gia Lộc 2015-2016)
Gi
4 3 2
2x 7x 9x 7x 2 0
Câu 3. (Đề HSG huyện Vũ Quang 2018-2019)
Tìm các s nguyên
x
th
3 1
4 1 6 1 12 1 330x x x x
Câu 4. (Đề HSG huyên Thanh Oai 2013-2014)
Gi
x 3
x 4 x 5 x 6 24
Câu 5. (Trích đề chuyên Đăk Nông 2019-2020)
Gi .
Câu 6. (Trích đề chuyên Tây Ninh 2019-2020)

Câu 7. (Trích đề chuyên Quảng Trị 2019-2020)
Gi
Câu 8. (Trích đề chuyên Đồng Nai 2018-2019)
Gi
2
2 1 3 12x x x
42
20 0xx
3
6 3 5 2
3 3 9 1x x x x
4 3 2
x 9x 24x 27x 9 0 (x R)
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
35
Câu 9. Gi
2 4 2
1 2 1 0x x x
Câu 10. Gi 8x = 0
(Tuyển sinh lớp 10 khối THPT chuyên Toán – Tin ĐHSP Vinh năm học 2002 – 2003)
Câu 11. Gi
4
4x
3
19x
2
+ 106x 120 = 0.
(Thi vào lớp 10 THPT chuyên Trần Đại Nghĩa TP Hồ Chí Minh năm học 2003 – 2004)
Câu 12. Gi(x
2
+ 3x + 2)( x
2
+ 7x + 12) = 24.
(Đề thi tuyển vào lớp 10 chuyên ĐHSPNN Hà Nội năm học 2004 – 2005)
Câu 13. Gi
5
29x
4
+ 27x
3
+ 27x
2
29x + 6 = 0
(Thi học sinh giỏi lớp 9 tỉnh Thanh Hóa năm học 2005 – 2006)
Câu 14. Gitrình (3x + 4)(x + 1)(6x + 7)
2
= 6.
(Tuyển sinh lớp 10 THPT chuyên ĐHSP Hà Nội năm học 2006 – 2007)
Câu 15. Gi
2
2x)
2
+ 3x
2
6x = 2 .
(Thi học sinh giỏi lớp 9 huyện Thường Tín Hà Tây năm học 2006 – 2007)
Câu 16. Gi + 3)
2
(2x + 1)(x + 1) = 810.
(Tuyển sinh lớp 10 chuyên Tin Quốc học Huế năm học 2019 – 2010)
Câu 17. Gi
3
+ 3x 140 = 0.
(Đề thi tuyển vào lớp 10 THPT chuyên Lam Sơn, Thanh Hóa năm học 2010 – 2011)
Câu 18. Gi .
(Đề thi tuyển vào lớp 10 THPT chuyên Quang Trung, Bình Phước năm học 2010 – 2011)
Câu 19. Gi .
( Thi tuyển sinh lớp 10 chuyên TP Hồ Chí Minh năm học 2010 – 2011)
Câu 20. Gi .
(Đề thi vào lớp 10 trường THPT chuyên Nguyễn Trãi, Hải Dương năm học 2012 – 2013)
Câu 21. (Đề thi HSG huyện Thanh Thủy 2016-2017)



Câu 22. (Trích đề chuyên Phú Yên năm 2012-2013)
Gi
3 3 3
1005 1007 2 -2012 0x x x
Chủ đề 2. Phƣơng trình phân thức
Câu 23. Gi
1 1 1 1
2008 1 2009 2 2010 4 2011 5x x x x

Câu 24. (Đề HSG quận Bắc Từ Lim 2018-2019)
2
2
x 2x 3 x 1 x(2x 1)
2
22
2x x 2x x 12 0
2 4 2
x 4x+11 x 8x 21 35
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
36
Gi
5 x 5 x
x x 6
x 1 x 1


Câu 25. (Chuyên Bà Rịa Vũng Tàu năm 2019-2020)
Gi
Câu 26. (Trích đề chuyên Đắc Lắc năm 2018-2019)

2
22
15 ( 1) 15 3
6 4 ( 2 4)
xx
x x x x x
.
Câu 27. (Trích đề chuyên Quản Nam năm 2015-2016)
Gi
2 2 2 2
6 4 7 3
0
x 9 x 11 x 8 x 12
Câu 28. (Trích Chuyên Hòa Bình năm 2015-2016)
Gi
1 1 1 1
3 1 2 4 9 2 5 4x x x x
Câu 29. Gi
a) ;
b) ;
c) .
Câu 30. Gi .
Câu 31. Gi .
(Thi vào lớp 10 chuyên Quốc học Huế năm học 1996 - 1997)
Câu 32. Gi .
(Đề thi vào lớp 10 THPT chuyên ĐHSP Hà Nội năm học 2000 – 2001)
Câu 33. Gi .
(Đề thi tuyển sinh vào lớp 10 Quốc học Huế năm học 2002 – 2003)
Câu 34. Gi
.
2
2
2
9
40
3
x
x
x
2 2 2 3 2
3 4 5 14
x 5x 6 x 7x 12 x 6x 8 x 9x 26x 24
2 2 2
1 1 1 19
...
x 3x 2 x 5x 6 x 39x 380 42
2 2 2
2 2 2 5
...
x 2x x 6x 8 x 18x 80 12
2 2 2
2
x 4x 6 x 6x 12 x 24
(2x 5)
x 2 x 3 x 5x 6
6
32
13
352
2
22
xx
x
xx
x
32
3
3
x 3x
x 2 0
(x 1) x 1

2
2
5
x 4x 1 0
x 4x 5

2 2 2 2
1 1 1 1 1
x 5x 6 x 7x 12 x 9x 20 x 11x 30 8
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
37
(Khảo sát chất lượng học sinh giỏi Toán 8 huyện Thường Tín Hà Nội năm học 2012 – 2013).
Câu 35. Gi .
(Đề thi tuyển sinh vào lớp 10 THPT chuyên ĐHSP Hà Nội năm học 2014 – 2015)
Câu 36. Gi .
(Đề thi học sinh giỏi Toán 9 Huyện Thường Tín Hà Nội năm học 2014 – 2015)
Câu 37. Gi
(Đề thi chọn đội tuyển Toán 9 quận Gò Vấp TP Hồ Chí Minh năm học 2014 – 2015)
Câu 38. Gi
(Khảo sát chất lượng học sinh giỏi Toán 8 huyện Thường Tín Hà Nội năm học 2014 – 2015).
Câu 39. Giảicácphươngtrình:
a)
2
2
2
25
11
5
x
x
x

. (Trích đề thi vào lớp 10 chuyên Lam Sơn Thanh Hóa 2013).
b)
22
12 3
1
4 2 2 2
xx
x x x x

. (Trích đề thi vào lớp 10 chuyên Đại học Vinh 2010).
c)
2
2
2
3 6 3
2
x
xx
x
(Trích đề thi vào lớp 10 chuyên ĐHSP Hà Nội 2008).
d)
32
3
3
3
20
1
1
xx
x
x
x
Câu 40. Giảicácphươngtrình:
1 1 1 1 1
0
1 2 3 4x x x x x
.
Câu 41. Giảicácphươngtrình:
4 4 8 8 8
1 1 2 2 3
x x x x
x x x x
.
Câu 42. Giảicácphươngtrình:
2 2 2
1 6 2 5
2 12 35 4 3 10 24
x x x x
x x x x x x x x
.
Câu 43. Giảicácphươngtrình:
22
43
1
4 8 7 4 10 7
xx
x x x x

Câu 44. Giảicácphươngtrình:.
2 2 2 2
1 2 2 3 3 4 4
0
1 2 3 4
x x x x x x x x
x x x x
.
Câu 45. Giảicácphươngtrình:
2
2
2
12
3 6 3
2
x
xx
x
.
Câu 46. Giảicácphươngtrình:
22
2 13
6
3 5 2 3 2
xx
x x x x

.
2
3
x x 56
21x 22
4
4 7x x 2


22
2
x x 2x
x 1 x 1 x 1

22
1 3 2
2
x x 1 (x 1)

22
22
x 2x 1 x 2x 2 7
x 2x 2 x 2x 3 6

THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
38
Câu 47. Giảicácphươngtrình:
22
2
2
2 2 4
20 5 20 0
1 1 1
x x x
x x x
.
Chủ đề 3. Phƣơng trình có dấu giá trị tuyệt đối
Câu 48. Gi
2 1
1 2 4x x x x
(Đề HSG huyện Vũ Quang 2018-2019)
Câu 49. Gi .
((Đề thi vào lớp 10 chuyên, Quốc học Huế năm học 1994 – 1995)
Câu 50. Gi .
(Thi học sinh giỏi lớp 9 TP Hồ Chí Minh năm học 1994 – 1995)
Câu 51. Gi .
(Thi vào lớp 10 chuyên Lê Hồng Phong TP Hồ Chí Minh năm học 1995- 1996)
Câu 52. Gi .
(Thi học sinh giỏi lớp 9 PT TP Hồ Chí Minh năm học 2001- 2002)
Câu 53. Gi .
(Thi vào lớp 10 PT năng khiếu ĐHQG TP Hồ Chí Minh năm học 2003- 2004)
Câu 54. Gi .
(Đề thi tuyển sinh THPT chuyên ĐHQG Hà Nội năm 2004).
Câu 55. Gi
(Đề thi học sinh giỏi lớp 9 tỉnh Thanh Hóa năm học 2004 – 2005)
Câu 56. Tìm x tha
(Chuyên Đà Nẵng năm 2019-2020)
HƢỚNG DẪN GIẢI
Câu 1.
22
2 2 2 2
2 2 4 3 2 2 2 3 0x x x x x x x x
(1)
t
2
2x x a
  thành
2
2 3 0aa
1 3
0aa
a = 1 hoc a = 3
+ Vi a = 1, ta có x
2
+ 2x = 1
(x + 1)
2
= 0
x = 1
x x 1 x 2 7
22
x 1 x 1 3
x x 2 2
2
(x 1) 2 x 1 8 0
2
2x 5 x 3x 1
2
x 1 x 1 1 x 1
2006 2006
x 2005 x 2006 1
9x 8 7x 6 5x 4 3x 2 x 0.
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
39
+ Vi a = 3, ta có x
2
+ 2x = 3
x + 2x 3 = 0
(x 1)(x + 3) = 0
x = 1 hoc x = 3
Vp nghim là S =
1;
1; 3
Câu 2.
Vì x = 0 không là nghim c
0.
Chia hai v c
2
x
c:
2
2
11
2 7 9 0xx
xx
t
1
yx
x

thì
22
2
1
2yx
x
.

2
2( 2) 7 9 0yy
2y
2
- 7y + 5=0
(y - 1)(2y - 5) = 0
10
2 5 0
y
y


*Vi y-1 = 0 ta có
1
x
x
-1 = 0
x
2
-x+1 = 0 vô nghim vì
x
2
- x + 1=
2
13
0,
24
xx



*Vi 2y - 5 = 0 ta có 2.
1



x
x
- 5 = 0
2x
2
- 5x + 2 = 0
(2x - 1).(x - 2) = 0
2
1
2
x
x
Vy x = 2 và x =
1
2
là nghim c
Câu 3.
Ta có:
22
3 1 4 1 6 1 12 1 330 36 15 1 24 10 1 330x x x x x x x x
22
3 12 5 1 2 12 5 1 330x x x x
t:
2
12 5y x x
.
Ta có:
22
3 1 2 1 330 6 5 1 330 6 5 329 0y y y y y y
2
6 42 47 329 0 6 7 47 7 0y y y y y y
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
40
7
7 6 47 0
47
6
y
yy
y
Vì
x Z y Z

7y
.
Ta có:
2 2 2
12 5 7 12 5 7 0 12 12 7 7 0 12 1 7 1 0x x x x x x x x x x
1
1 12 7 0
7
12
x
xx
x
Do
1x Z x
tha mãn bài toán.
Câu 4.
3 6
4 5 24x x x x
22
9 18 9 20 24x x x x
(1)
t
yxx 199
2
 thành :
2
1 1 24 0 25 0 5 5 0y y y y y
22
9 24 9 14 0x x x x
2
2 7 9 24 0x x x x
2
2 7 9 24 0x x x x
Chng t
0249
2
xx
Vy nghim c
2; 7.xx
Câu 5.
PT bii thành .
t  thành
.
Vi c .
Vm .
Câu 6.
t  thành
 có hai nghim phân bit (nhn); (loi)
22
4 4 4 3 12x x x x
2
2
4 4 2 0t x x x
2
4
12 0
3
tn
tt
tl

4t
22
0
4 4 4 4 0
4
x
x x x x
x
0, 4xx
2
,0t x t
2
20 0 1tt
2
4 81b ac
1
4t
5t 
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
41
Vi c . V nghim là
Câu 7.
3
6 3 5 2
3 3 9 1x x x x
t:

(VN)
+)
Vm
Câu 8.
Vi x = 0, m.
Vi x 0, chia 2 v c
Câu 9. PT
2 2 2 2
1 1 2 1 0x x x x
4 2 4 2
2 1 0x x x x
2
4 2 4 2
2 1 0x x x x
2
4 2 4 2
1 0 1 0x x x x
.
Gic tp nghim ca PT là
5 1 5 1
;
22






.
Câu 10. t y = x + 15 ta có (y 6)(y 5)(y 4) 8(y 15) = 0
4t
2x 
2
2x 
33
2 3 2 3
3 1 3 3x x x x
23
,3x a x b
3
33
1 3 1 3 3 0a b ab a b ab a b ab
2
1 1 3 1 0a b a b a b ab a b




22
1 1 0a b a b ab a b
2 2 2
22
) 1 0 1 1 0 1a b ab a b a b a b a b
23
11xx
2 3 2
1 0 3 1 0 1 2 2 0 1.a b x x x x x x
1.x
(*) 0x + 9 = 0
2
x
2
2
2
2
2
27 9 3 3
(*) x - 9x + 24 - + = 0 x 9 x 18 0
x x x
x
3
x 3 0
33
x
x 3 x 6 0
3
xx
x 6 0
x
x 3x 3 0 (VN) x 3 6
x 6x 3 0
x 3 6

THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
42
y(y
2
15y + 66) = 0 . Do y
2
15y + 66 =
y = 0 x = 15. (Cách khác: t x + 10 = y. Bc t gii)
Câu 11. Bi 2)(x 3)(x 4)(x + 5) = 0
Tp nghim : S = .
Câu 12. Bi
(x
2
+ 5x + 4)(x
2
+ 5x + 6) = 24 .
t x
2
+ 5x + 5 = t ta có (t 1)(t + 1) = 24 t
2
= 5 t = 5.
Xét vi t = 5 và t = c hai nghim là x = 0 và x = 5 .
Câu 13. Bii thành (x + 1)(6x
4
35x
3
+ 62x
2
35x + 6) = 0.
c x = 1 là 1 nghim. Vi 6x
4
35x
3
+ 62x
2
35x + 6 = 0 do x = 0 không là
nghim nên chia hai v cho x
2
c :
t thì
 thành 6(y
2
2) 35y + 62 = 0 (2y 5)(3y 10) = 0
Thay vào 2y 5 = 0 gic x = 2 hoc x = .
Thay vào 3y 10 = 0 gic x = 3 hoc x =
Tp nghim c .
Câu 14. Nhân (3x + 4) vi 2 ; (x + 1) vi 6 và v phi vc
(6x + 8)(6x + 6)(6x + 7)
2
t 6x
 tr thành
(y + 1)(y 1)y
2
= 72 y
4
y
2
72 = 0 (y
2
9)(y
2
+ 8) = 0 y = 3 (do y
2
+ 8 > 0, y) . Gii
tic nghim x = và x = .
Câu 15. (x
2
2x)
2
+ 3x
2
6x = 2 (x
2
2x)
2
+ 3(x
2
2x) + 2 = 0 .
t x
2
2x = y ta có y
2
+ 3y + 2 = 0 (y + 1)(y + 2) = 0 y = 1 hoc y = 2. Vi x
2
2x
= 1 (x 1)
2
= 0 x = 1.
Vi x
2
2x = 2 (x 1)
2
+ 1 = 0 vô nghim.
Câu 16. (4x + 3)
2
(2x + 1)(x + 1) = 810
t 2x
2
 thành
(8y + 9)(y + 1) 810 = 0 8y
2
+ 17y 801= 0 (y 9)(8y + 89) = 0
2
15 39
y 0; y
24



5;
2;3; 4
2
2
11
6 x 35 x 62 0
xx
1
xy
x

22
2
1
x y 2
x
1
yx
x

1
2
1
yx
x

1
3
11
1; ; ;2; 3
32



2
3
5
3
22
8 2x 3x 9 2x 3x+1 810


THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
43
* y 9 = 0 tc là 2x
2
+ 3x 9 = 0 (x + 3)(2x 3) = 0 x = 3 hoc x = 1,5.
* 8y + 89 = 0 tc là 16x
2
+ 24x + 89 = 0 vô nghim vì 16x
2
+ 24x + 89 = (4x + 3)
2
+ 80 > 0 , x.
Vm x = 3 và x = 1,5.
Cách khác: Bi(4x + 3)
2
t
4x + 3 = y . (Bc t gii tip)
Câu 17. x
3
+ 3x 140 = 0 x
3
5x
2
+ 5x
2
25x + 28x 140 = 0
(x 5)( x
2
+ 5x + 28) = 0 x = 5 do x
2
+ 5x + 28 =
Câu 18.
t x
2

2
2y 3 = 0 (y 3)(y + 1) = 0
Thay y = x
2
2x vào ta có tp nghim c .
Câu 19. t 2x
2
 thành :
u
2
+ u 12 = 0 (u 3)(u + 4) = 0 u 3 = 0 hoc u + 4 = 0.
* u 3 = 0 ta có 2x
2
x 3 = 0 (x + 1)(2x 3) = 0 x = 1 hoc x = 1,5.
* u + 4 = 0 ta có 2x
2
x + 4 = 0 vô nghim vì 2x
2
x + 4 = > 0 , x. V
hai nghim x = 1 và x = 1,5.
Câu 20.
và nên v trái không nh 
Ta suy ra . Vy nghim c
Câu 21. 









-
-
3
4


3
4
-

3
2
14

3
2
14
Câu 22. 
1005 ; 1007 ; 2 -2012X x Y x Z x
 X + Y + Z = 0 thì:
3 3 3
3X Y Z XYZ

2
5 87
x 0, x
24



2
2
x 2x 3 x 1 x(2x 1)
2
22
x 2x 2 x 2x 3 0
1;
1; 3
2
1 31
2x
48




2 4 2
x 4x+11 x 8x 21 35
2
2
2
x 2 7 x 4 5 35





2
x
2 0, x
2
2
x 4 0, x
2
2
2
(x 2) 0
x2
x 4 0



THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
44
1005
3(1005 )(1007 )(2 -2012)=0 1006
1007
x
x x x x
x
.
x = 1005, x = 1006, x = 1007.
Chủ đề 2. Phƣơng trình phân thức
Câu 23. 
1 2 4 5
; ; ; .
2008 2009 2010 2011
x

1 1 1 1
2008 1 2011 5 2010 4 2009 2
4019 6 4019 6
(2008 1)(2011 5) (2009 2)(2010 4)
4019 6 0
11
(2008 1)(2011 5) (2009 2)(2010 4)
6
4019
(2009 2)(2010 4) (2008 1)(2011 5) 0
6
40
x x x x
xx
x x x x
x
x x x x
x
x x x x
x





2
6
19 4019
4019 6 0 1
2 5 3 0 3
2
x
xx
xx
x









Vm:
63
; 1; .
4019 2
x x x
Câu 24.  :
1x 
t
5
1
x
xa
x



;
5
1
x
xb
x

Ta có :
22
5 5 5 5
5
1 1 1
x x x x x x x
a b x x
x x x
Mà
. 6ab

2
3
6
5
3
2
a
b
ab
ab
a
b


Vi
2; 3ab
thì
2
3 2 0 1x x x
hoc
2x
Vi
3; 2ab
thì
2
2 3 0xx
(PT vô nghim)
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
45
Câu 25.
Ta có:
t 
2
6t -40 =0
vô nghim
Vy tp nghim c
Câu 26.

0;
3 5; 3 5 *x x x
.

22
1 1 1
6 4 2 4 15x x x x x

1 1 1
(1)
44
15
62xx
xx

.

4
xt
x

2;
6tt
.

4
1 1 1
12
6 2 15
t
t
tt


.

4t
ta có
4
42xx
x


12t
ta có
6 4 2
4
12
6 4 2
x
x
x
x


mãn (*).
Câu 27.
u kin:
x 3;x 11;x 2 2;x 3 2
2 2 2 2
6 4 7 3
pt 1 1 1 1 0
x 9 x 11 x 8 x 12
2 2 2 2
2 2 2 2
15 x 15 x 15 x 15 x
0
x 9 x 11 x 8 x 12
2
2 2 2 2
1 1 1 1
(15 x )( ) 0
x 9 x 11 x 8 x 12
2
15 x 0
(1) hoc
2 2 2 2
1 1 1 1
0 (2)
x 9 x 11 x 8 x 12
Gic
x 15
2
4 2 4 2
11
(2) (2x 20)( ) 0
x 20x 99 x 20x 96
x 10
Kt lum:
x 15;x 15
;
x 10;x 10
2
2
2
9
40
3
x
x
x
2
2
2 2 2
36
40 0 6. 40 0
3 3 3 3
x x x x
x
x x x x
2
3
x
t
x
10
4
t
t
10t
2
2
10 10 30 0
3
x
xx
x
4t
2
2
2
4 4 12 0
6
3
x
x
xx
x
x
2;6S
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
46
Câu 28. 
1 2 5
, 2, ,
3 9 4
x x x x
Ta có pt:
5 3 5 3
(3 1)(2 4) (9 2)(5 4 )
xx
x x x x

22
3
3
5
5
(3 1)(2 4) (9x 2)(5 4x)
6 12 2 4 36 45 8 10
3
()
5
6
()
7
1
()
6
x
x
xx
x x x x x x
x TM
x TM
x TM

 


Vm phân bi
Câu 29. u kin : x 2; x 3; x 4; Phân tích các mu thành nhân t ta có
ng và kh m
3(x 4) 4(x 2) = 5(x 3) + 14
3x 12 4x + 8 = 5x 15 + 14 x = 0,5 th
  .
Nhn xét: vi n N thì
Bi
ng và kh m
x
2
+ 21x 22 = 0 (x 1)(x + 22) = 0 th
 
Nhn xét : vi n N ta có
Bi
3 4 5 14
( 2)( 3) ( 3)( 4) ( 2)( 4) ( 2)( 3)( 4)
x x x x x x x x x
1;
2; 3;...; 19; 20
1 (x n 1) (x n) 1 1
(x n)(x n 1) (x n)(x n 1) x n x n 1
1 1 1 19
...
(x 1)(x 2) (x 2)(x 3) (x 19)(x 20) 42
1 1 1 1 1 1 19
...
x 1 x 2 x 2 x 3 x 19 x 20 42
1 1 19
1 20 42

xx
x1
x 22

0;
2;4;6;8;10
2 (x n) (x n 2) 1 1
(x n)(x n 2) (x n)(x n 2) x n 2 x n
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
47
ng và kh m
2
10x 24 = 0
(x 12)(x + 2) = 0 th
Câu 30. Ta có th vn d gii. Nng mu ngay s xut hi
thc bc ba, vic thc hin s o và ngn gn

*  2; x 3. Bi
ng và kh m
2
+ 5x 36 = 0
(x + 9)(x 4) = 0 x = 9 hoc x = 4 th
Câu 31. 
2
5x + 3 = (x 1)(2x 3) 0 khi x 1 và x 1,5
2x
2
+ x + 3 = . Do x = 0 không là nghim ct 2x +
= t : PT  5 và t 1.
Ta có
(1) vô nghim vì 2x
2
x + 3 =
(2) (x 2)(4x 3) = 0 x = 2 hoc x = th
2 2 2 5
...
x(x 2) (x 2)(x 4) (x 8)(x 10) 12
1 1 1 1 1 1 5
...
x 2 x x 4 x 2 x 10 x 8 12
1 1 5
10 12

xx
x 12
x2

2 2 2
(x 4x 4) 2 (x 6x 9) 3 x 24
(2x 5)
x 2 x 3 (x 2)(x 3)
2
2 3 x 24
(x 2) (x 3) (2x 5)
x 2 x 3 (x 2)(x 3)
2
2 3 x 24
0
x 2 x 3 (x 2)(x 3)
2
1 23
2 x 0 , x
48



x
3
2 13
6
33
2x 5 2x 1
xx

2 13
6
t 5 t 1


2
t1
6t 39t 33 0 (t 1)(6t 33) 0
t 5,5
2
2
3
2x 1
2x x 3 0. (1)
x
3 11
4x 11x 6 0. (2)
2x
x2


2
1 23
2 x 0 , x
48



4
3
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
48
Vm là x = 2 ; x = .
Câu 32. T (a + b)
3
= a
3
+ b
3
+ 3ab(a + b) a
3
+ b
3
= (a + b)
3
3ab(a + b)
Áp d gi 1
PT
t y = ta có
y
3
3y
2
+ 3y 1 1 = 0 (y 1)
3
= 1 y = 2.
Hay là = 2 x
2
= 2x 2 x
2
2x + 2 = 0
m vì x
2
2x + 2 = (x 1)
2
+ 1 > 0
Câu 33.  R do x
2
4x + 5 = (x 2)
2
+ 1
t x
2
4x + 5 = y thì y 1 và x
2
+ 4x 1 = 
5 y
2
+ 4y = 0 (y 5)(y + 1) = 0
* x
2
4x + 5 = 5 x(x 4) = 0 x = 0 hoc x = 4. Tp nghim S = .
Câu 34. 
PT
x
2
8x 20 = 0 (x + 2)(x 10) = 0
x = 2 hoc x = 10. Tp nghim S = .
Câu 35.  và x
3
2.
* Xét x
3
21x 20 = 0 (x + 1)(x c :
x = 4; x = 1 ; x = 5 th
* Xét bii thành x
3
7x + 6 = 0
4
3
3
2
x x x 3x
x 3x. x 2 0
x 1 x 1 x 1 x 1
32
2 2 2
x x x
3 3 1 1 0
x 1 x 1 x 1
2
x
x1
2
x
x1
x.
0; x.
5
y 4 0
y
y5
y 1(loai)

0;
4
2;
3;4;5;6
1 1 1 1 1
(x 2)(x 3) (x 3)(x 4) (x 4)(x 5) (x 5)(x 6) 8
1 1 1 1 1 1 1 1 1
x 3 x 2 x 4 x 3 x 5 x 4 x 6 x 5 8
1 1 1
x 6 x 2 8

2;
10
4
x
7
2
3
x x 56
21x 22
4
4 7x x 2


2
3
x x 56
21x 22
5 1 0
4 7x x 2

33
3
x 56x 20 35x x 2 21x 22
0
4 7x x 2


3
3
11
x 21x 20 0
4 7x x 2




3
11
0
4 7x x 2


THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
49
(x 1)(x c x = 3; x = 1 ; x = 2 th
Vy tp nghim c .
Câu 36.  1.
x
2
(x + 1) x
2
(x 1) = 2x 2x
2
2x = 0
2x(x 1) = 0 x = 0 hoc x = 1. Loi x = 1.
Tp nghim S = ..
Câu 37.  và x 1.
Vi và x 1 thì
*Vi x 1 = 0 x = 1 th
*Vi (1 + x)
3
+ x
3
= 0 (1 + x)
3
= x
3
1 + x = x x = th
Tp nghim là S = .
Câu 38. 
t x
2
 thành
5t
2
7t 6 = 0 (t 2)(5t + 3) = 0 t = 2 ( do t > 0)
Hay x
2
2x + 2 = 2 x
2
2x = 0 x(x 2) = 0 x = 0 hc x = 2.
Tp nghim là S = .
Câu 39. a)Điều kiện
5x 
Ta viết lạiphươngtrìnhthành
2
2
2 2 2
5 10 10
11 0 11 0
5 5 5 5
x x x x
x
x x x x






.Đặt
2
5
x
t
x
thìphươngtrìnhcódạng
2
1
10 11 0
11
t
tt
t

4;
3; 1;1; 2;5
22
2
x x 2x
x 1 x 1 x 1

0
x0
22
1 3 2
2
x x 1 (x 1)

22
1 3 2
11
x x 1 (x 1)

22
22
1 x x x
x (x 1)

33
22
(1 x) (1 x) x
0
x (x 1)


x0
33
(1 x) (1 x) x 0


33
1 x 0
(1 x) x 0

1
2
1
;1
2



xR
t 1 t 7
t t 1 6

0;
2
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
50
Nếu
1t
ta có:
2
2
1 21
1 5 0
52
x
x x x
x
. Nếu
2
11 11
5
x
t
x
2
11 55 0xx
phươngtrìnhvônghiệm.
b) Để ý rằng nếu
x
là nghiệm thì
0x
nên ta chia cả tử số và mẫu số vế trái cho
x
thì thu
được:
12 3
1
22
42xx
xx

.Đặt
2
2tx
x
thìphươngtrìnhtrở thành:
22
1
12 3
1 12 3 6 2 7 6 0
6
2
t
t t t t t t
t
tt
.
Với
1t
ta có:
2
2
2 1 2 0x t t
x
vô nghiệm. Với
6t
ta có:
2
2
2 6 4 2 0 2 2x x x x
x
.
c)
2
2
2 2 1 0 3 3 1 0
2 2 2
x x x
x x x x
x x x
.
Giải2phươngtrìnhtathuđược các nghiệm là
33
6;
3
xx

.
d) Sử dụngHĐT
3
33
3a b a b ab a b
ta viết lạiphươngtrìnhthành:
3
3 2 2 2
3
3
33
2 0 3 2 0
1 1 1 1 1
1
x x x x x x
x x x
x x x x x
x


hay
3 2 3
2 2 2 2 2
2
3
3 2 0 1 1 1 1 2 2 0
1 1 1 1 1
x x x x x
xx
x x x x x
. Suy ra
phươngtrìnhđãchovônghiệm.
Câu 40. Điều kiện
1;
2; 3; 4;0x
. Ta biếnđổiphươngtrìnhthành
22
2 2 2 2
1 1 1 1 1 1
00
4 1 3 2 4 4 3 2
xx
x x x x x x x x x x

2 2 2
1 1 1
0
4 4 3 2( 4 4)x x x x x x
.Đặt
2
4u x x
,phươngtrìnhtrở thành
1 1 1
0
3 2 4u u u

2
25 145
5 25 24
10
0
2 3 4
25 145
10
u
uu
u u u
u




.
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
51
Dođó
2
2
25 145
4
10
25 145
4
10
xx
xx




.Tìmđược tập nghiệm củaphươngtrìnhlà
15 145 15 145 15 145 15 145
2 ; 2 ; 2 ; 2
10 10 10 10
S





.
Câu 41. Biếnđổiphươngtrìnhthành
22
5 5 10 10 8 10 40 8
1 1 2 2 3 1 4 3x x x x x x
.
Đặt
2
1, 4; 0u x u u u
dẫnđếnphươngtrình
2
16
4 65 16 0
1
4
u
uu
u
.bTìmđược tập nghiệm củaphươngtrìnhlà
11
; 4; ;4
22
S



.
Câu 42. Điều kiện
7;
6; 5; 4; 3; 2; 1;0x
. Biếnđổiphươngtrìnhthành
1 6 2 5
2 5 7 1 3 4 6
x x x x
x x x x x x x x
1 1 1 6 1 1
2 2 2 5 7
xx
x x x x

2 1 1 5 1 1
2 1 3 4 6
xx
x x x x x

1 1 1 1 1 1 1 1
2 5 7 1 3 4 6x x x x x x x x
1 1 1 1 1 1 1 1
7 2 5 1 6 3 4x x x x x x x x x
2 2 2 2
1 1 1 1
2 7 0
7 7 10 7 6 7 12
x
x x x x x x x



2 2 2 2
7
2
1 1 1 1
0(*)
7 7 10 7 6 7 12
x
x x x x x x x x

.
Đặt
2
7u x x
thìphươngtrình(*)códạng
1 1 1 1 1 1 1 1
00
10 6 12 6 10 12u u u u u u u u
2
18 90 0uu
.
Mặt khác
2
2
18 90 9 9 0u u u
với mọi
u
.Dođóphươngtrình(*)vônghiệm.
Vậyphươngtrìnhđãchocónghiệm duy nhất
7
2
x 
.
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
52
Câu 43. Điều kiện
4;
3; 2; 1x
. Biếnđổiphươngtrìnhthành
1 2 3 4 1 4 2 3
00
1 2 3 4 1 4 2 3x x x x x x x x
22
31
0
5 4 5 6
x
x x x x



22
0
31
0(*)
5 4 5 6
x
x x x x

.
Đặt
2
5u x x
thìphươngtrình(*)trở thành
3 1 11
0
4 6 2
u
uu

. Từ đótacó
2
53
2 10 11 0
2
x x x

.
Vậy tập nghiệm củaphươngtrìnhđãcholà
5 3 5 3
0; ;
22
S





.
Câu 44. Do
0x
không là nghiệm củaphươngtrìnhnênchiacả tử và mẫu của mỗi phân thức ở vế
trái củaphươngtrìnhcho
x
, rồiđặt
7
4yx
x

tađược
43
1
8 10yy


.
Phươngtrìnhtrêncó2nghiệm
16, 9yy
.
Với
9y
thì
2
7
4 9 4 9 7 0x x x
x
.Phươngtrìnhnàyvônghiệm.
Với
16y
thì
2
7
4 16 4 16 7 0x x x
x
.Phươngtrìnhnàycóhainghiệm
12
17
;
22
xx
.
Vậyphươngtrìnhđãchocótập nghiệm là
17
;
22
S



.
Câu 45. Điều kiện
2x 
. Khử mẫu thứctađượcphươngtrìnhtươngđương:
4 3 2 4 2 2
3 6 16 36 12 0 3 6 6 16 12 0x x x x x x x x
.
đặt
2
6tx
thì
2 4 2
12 36t x x
, suy ra
4 2 2
3 3 36 108x t x
, PT trên thành
2
3 6 20 0 3 6 20 0 0t xt t t t x t
hoặc
3 6 20tx
. Với
0t
thì
2
60x 
, suy
ra
6x 
(thỏamãnđk).Với
3 6 20tx
ta có
2
3 18 6 20xx
hay
2
3 6 2 0xx
suy ra
33
3
x

(thỏamãnđk).Vậy tập nghiệm của PT(4) là
3 3 3 3
; 6; ; 6
33
S






.
Câu 46. Đặt
2
32tx
PT(5) trở thành
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
53
2 13
6
5
xx
t x t x


.ĐK:
5,t x t x
.
Khử mẫu thứctađượcPTtươngđương
22
2 13 11 0 2 11 0t tx x t x t x
tx
hoặc
11
2
tx
(thỏamãnĐK)
Với
tx
thì
22
3 2 3 2 0x x x x
phươngtrìnhvônghiệm.
Với
11
2
tx
thì
2
11 1
3 2 6 11 2 0
22
x x x x x
hoặc
4
3
x
.
Vậy tập nghiệm của PT(5) là
14
;
23



.
Câu 47. Điều kiện
1x 
.
Đặt
22
;
11
xx
yz
xx



, PT có dạng:
2
22
20 5 20 0 5 2 0 2y z yz y z y z
Dẫnđến
22
2. 2 2 1 2 1
11
xx
x x x x
xx


2 2 2
2 6 4 3 2 9 2 0x x x x x x
9 73
2
x

hoặc
9 73
2
x
(thỏamãnđiều
kiện).
Vậy tập nghiệm của PT(2) là
9 73 9 73
;
22






Chủ đề 3. Phƣơng trình có dấu giá trị tuyệt đối
Câu 48.
Xét
2x

22
2 1 1 2 4 4 1 4x x x x x x
2
4 2 2
57
5 8 0 0
24
x x x



, (vô nghim).
- Xét
2x

22
2 1 1 2 4 4 1 4x x x x x x
2
4 2 2 2
2
0
0
5 0 5 0
5
5
x
x
x x x x
x
x

.
Kt hp vu kin
2x
c nghim c
5x
.
Câu 49. Lập bảngxétGTTĐrồi xét các khoảng :
*Nếu x <– 2 thì PT – x – x – 1– x – 2 = 7 x =
*Nếu – 2 x < – 1 thì PT – x – x – 1+ x + 2 = 7 x = – 6 (loại)
10
3
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
54
*Nếu – 1 x 0 thì PT – x + x + 1+ x + 2 = 7 x = 4 (loại)
*Nếu x > 0 thì PT x + x + 1+ x + 2 = 7 x = .
Phươngtrìnhcóhainghiệm là x = và x = .
Câu 50. x
2
– 1 + 4 – x
2
= 3
Dấu“=”xảy ra
. Nghiệmphươngtrìnhlà ;
Câu 51. Lập bảngxétGTTĐrồi xét các khoảng :
* Với phươngtrìnhthành– x – 2 + x = 2 0x = 4 vô nghiệm.
* Với phươngtrìnhthànhx– 2 + x = 2 x = 2 (nhận)
* Vớix>2phươngtrìnhthànhx– x + 2 = 2 0x + 2 = 2 vô số nghiệm.
Vậy nghiệm củaphươngtrìnhlàx 2
Câu 52. Đặt y = thì y 0.Phươngtrìnhtrở thành :
y
2
+ 2y – 8 = 0 (y – 2)(y + 4) = 0 y = 2 hoặc y = – 4 (loại) .
Vậy y = 2 = 2
Nghiệm củaphươngtrìnhlàx=3vàx=–1.
Câu 53. * Nếu x thì khi ấy
x
2
+ x – 6 = 0 (x + 3)(x – 2) = 0 x = – 3 hoặc x = 2 . Loại x = – 3
* Nếu x thì khi ấy
x
2
+ 5x + 4 = 0 (x + 4)(x + 1) = 0 x = – 4 hoặc x = – 1. Loại x = – 1.
Nghiệm củaphươngtrìnhlàx=2vàx=– 4.
Câu 54. Ta có nên
* (1) x + 1 = 1 ; (2) x – 1 = 1
Tập nghiệm củaphươngtrìnhlàS=
Câu 55. * Khi x = 2005 ; x = 2006 thì vế trái và vế phảiđều cùng số trị là1.Dođóx=2005
và x = 2006 là nghiệm củaphươngtrình.
4
3
10
3
4
3
22
x 1 x 4
22
x 1 4 x
2 2 2
(x 1)(4 x ) 0 1 x 4 1 x 2
2 x 2
x1
x1

1 x 2
2 x 1

1 x 2
2 x 1
x0
0 x 2
x1
x1
x 1 2 x 3
x 1 2 x 1



2,5
2x 5 2x+5
2
2x+5 x 3x 1
2,5
2x 5 2x 5
2
2x 5 x 3x 1
ab a . b
2
x 1 x 1 1 x 1
x 1. x 1 x 1 x 1 1 0
x 1 1 0 (1)
x 1 1 . x 1 1 0
x 1 1 0 (2)
x0
x2

x0
x2
2;
0;2
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
55
*Với x < 2005 thì và
Dođó phươngtrìnhvônghiệm.
*Với x > 2006 thì và
Dođó phươngtrìnhvônghiệm.
* Với 2005 < x < 2006 thì 0 < x – 2005 < 1 và – 1 < x – 2006 < 0
và
phươngtrìnhvônghiệm.
Vậy nghiệm củaphươngtrìnhlàx=2005vàx=2006.
Câu 56.
T  bài suy ra x < 0
Suy ra 9x 8 < 0; 7x 6 < 0; 5x 4 < 0; 3x 2 < 0
 thành
-23x + 20 = 0. Kt lun pt vô nghim
x 2005 0
x 2006 1
2006 2006
x 2005 x 2006 1
x 2005 1
x 2006 0
2006 2006
x 2005 x 2006 1
2006
x 2005 x 2005 x 2005
2006
x 2006 x 2006 2006 x
2006 2006
x 2005 x 2006 x 2005 2006 x 1
9 8 7 6 5 4 3 2 0x x x x x
| 1/54
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

2
CHỦ ĐỀ 1. PHƢƠNG TRÌNH ĐA THỨC BẬC CAO A. Kiến thức cần nhớ
Để giải phương trình đa thức bậc cao chúng ta thường chuyển phương trình đó về dạng phương trình tích.
Phƣơng trình tích
- Phương trình có dạng: A(x). B(x) = 0 ; trong đó A(x), B(x) l| c{c đa thức của biến x.
- Phương ph{p chung : Muốn giải phương trình A(x).B(x) = 0 ta giải hai phương trình
A(x) = 0 và B(x) = 0 , rồi lấy tất cả các nghiệm thu được.
A(x). B(x) = 0 A(x) = 0 hoặc B(x) = 0. A(x)  0 B(x)  0 - Mở rộng:
A(x).B(x).....M(x)  0  ...   M(x)  0
B. Một số ví dụ minh họa
I. Phƣơng trình bậc 3. 1) Lý thuyết.
Phương trình bậc 3 l| phương trình có dạng: 3  2 ax
bx cx d  0 a  0 (1)
Phƣơng pháp giải. Thông thường để giải được phương trình (1) chúng ta phải tìm được
một nghiệm x của phương trình, sau đó ph}n tích thành nhân tử và chuyển về giải 0 phương trình bậc 2.  x x 3 ax  2
bx cx d  0  x x mx nx p 0   0 0   2     2
mx nx p   0 (*)
Phương trình (*) l| phương trình bậc 2 chúng ta đã biết cách giải tổng quát theo  .
Mấu chốt của việc giải phương trình bậc (3) l| tìm được một nghiệm x của phương trình 0
đó, chúng ta có một số chú ý về cách nhẩm nghiệm của phương trình bậc 3 như sau:
- Nếu tổng các hệ số của phương trình (1) bằng 0 tức là a + b + c + d = 0 thì phương trình
(1) nghiệm x  1 . Chẳng hạn: 3 2
4x x  2x  5  0 ta có: 4 – 1 + 2 – 5 = 0 0
- Nếu tổng các hệ số bậc chẵn bằng tổng các hệ số bậc lẻ của phương trình (1) bằng 0 tức là
a - b + c - d = 0 thì phương trình (1) có nghiệm x  1  . Chẳng hạn: 3 2
x  5x  3x  9  0 0 ta có 1 + 5 + 3 – 9 = 0. THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 3 m
- Nếu a, b, c, d là các số nguyên và x
là nghiệm hữu tỷ của (1) thì m l| ước của d và n 0 n
l| ước của a. Đặc biệt trường hợp a = 1 thì phương trình (1) có nghiệm x l| ước của d. 0
Thí dụ 1. Giải phương trình: 3 3 2 3 2
a) x  3x  2  0 )
b 3y – 7 y – 7 y  3  0 ) c
x x  3x 10  0. Hƣớng dẫn giải
a) Ta thấy a + b + c + d = 1 + 0 – 3 + 2 = 0 nên phương trình có một nghiệm x = 1.
PT  x3 – x2 + x2 – x – 2x + 2 = 0
 x2(x – 1) + x(x – 1) – 2(x – 1) = 0
 (x – 1)(x2 + x – 2) = 0  x 1  0 x   1   2 
x x  2  0 x    2
Vậy tập nghiệm của phư
ơng trình l| S  1;  2
b) Ta thấy a - b + c - d = 3 + 7 – 7 – 3 = 0 nên phương trình có nghiệm y = - 1.
PT  3y3 + 3y2 – 10y2 – 10y + 3y + 3 = 0
 3y2(y + 1) – 10y(y + 1) + 3(y + 1) = 0
 (y + 1)( 3y2 – 10y + 3) = 0  (y + 1)( 3y – 1)(y – 3) = 0. y  1  y 1  0   1  3y 1  0  y  .   3 y  3  0  y  3   1 
Vậy tập nghiệm của phương trình là S   1  ; ; 3  3 
c) Ta có d = - 10 ta nhẩm các số l| ước của 10 thì thấy x = 2 là nghiệm của phương trình. 3 2
x x  3x 10  0 3 2 2
x  2x x  2x  5x 10  0 2
x .x  2  .xx  2  5.x  2  0  x  2 2
x x  5  0  x  2 Do 2
x x  5  0 x
Vậy phương trình có nghiệm x = 2. THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 4
Thí dụ 2. Giải phương trình: 3 2 3 2 3 2
a) 8x  4x 1  0 )
b 3x  7x 17x  5  0
c) x  2x  5x  2  0. Hƣớng dẫn giải 1
b) Ta có a = 8, d = 1 nên phương trình nếu có nghiệm hữu tỷ sẽ có dạng x   0 n 1 1 1 1
với n l| ước 8. Ta thử các giá trị  ;  ;  nhận thấy x
là nghiệm của phương trình 2 4 8 2
do đó ta t{ch phương trình theo nh}n tử (2x – 1). 4
8x  4x 1  0   3 8x  
1  4x  2  0  2x   1  2
4x  2x   1  2 2x   1  0  2x   1  2
4x  2x   1  0  1 x   2   1   5 x   4 1 1   5 
Vậy tập nghiệm của phương trình l| S   ;  2 4   m
b) Ta có a = 3, d = -5 nên phương trình nếu có nghiệm hữu tỷ sẽ có dạng x  0 n 1 5 1
với m l| ước -5 v| n l| ước của 3. Ta thử các giá trị  ;  nhận thấy x  là nghiệm của 3 3 3
phương trình do đó ta t{ch phương trình theo nh}n tử (3x – 1). 3
3x  7x 17x  5  0 3 2 2
 3x x  6x  2x 15x  5 2
x 3x  
1  2x 3x   1  53x   1  0  3x   1  2
x  2x  5  0  3x   1  x  2 1  4  0    3x 1  0 1  x  3 1
Vậy phương trình có nghiệm x  3 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 5
b) Phương trình chứa hệ số 2 nên ta đo{n có nghiệm dạng x a 2 nên ta đặt x a 2 0
nhằm triệt tiêu hệ số 2 khi đó phương trình có dạng: 3 2
2 2a  2 2a  5 2a  2  0 3 2
 2a  2a  5a 1  0  a   1  2
2a  4a   1  0  a  1   2
2a  4a 1  0  a  1   6 a  1    2  x  2
 x 2 3
Vậy tập nghiệm của phương trình l| S   2; 2  3
Thí dụ 3. Giải phương trình: a) (z + 3)3 – (z + 1)3 = 98.
b) (4x + 3)3 – (2x – 5)3 = ( 2x + 8)3 ;
c) (3x + 2016)3 + (3x – 2019)3 = (6x – 3)3;
d) (2x – 7)3 + (9 – 2x)3 = 152. Hƣớng dẫn giải
a) Phương trình  z3 + 9z2 + 27z + 27 – z3 – 3z2 – 3z – 1 = 98  6z2 + 24z – 72 = 0  z2 + 4z – 12 = 0  z2 + 6z – 2z – 12 = 0  (z + 6)(z – 2) = 0     z 6 0  z  2  0     z 6  z  2
Tập nghiệm của phương trình (1) l| S   6  ;  2 .
* Nhận xét : Ta có cách giải khác:
Do z + 2 là trung bình cộng của z +1 v| z + 3 nên ta đặt z + 2 = y phương trình trở
thành (y + 1)3 – (y – 1)3 = 98
 y3 + 3y2 + 3y + 1 – y3 + 3y2 – 3y + 1 = 98  6y2 = 96 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 6    y2 = 16  y 4  y  4        z 2 4   z 2  z  2  4  z  6 
Tập nghiệm của phương trình (1) l| S   6  ;  2 .
b) Đặt y = 4x + 3 ; z = 2x – 5 ; thì y – z = 2x + 8 . Ta có :
y3 – z3 = (y – z)3  y3 – z3 = y3 – z3 – 3yz(y – z)  3yz(y – z) = 0 y  0 4x  3  0 x   0,75     z  0 hay  2x  5  0   x  2, 5  y  z  0  2x  8  0  x   4 
Tập nghiệm của phương trình l| S   4  ;  0,75 ; 2,  5
c) Đặt u = 3x + 2016 ; v = 3x – 2019 thì u + v = 6x – 3 .
Phương trình trên trở thành u3 + v3 – (u + v)3 = 0 hay
u3 + v3 – [u3 + v3 + 3uv(u + v) ] = 0  –3uv(u + v) = 0 u  0 3x  2016  0 x  672      v  0  3x  2019  0    x  673  u  v  0  6x  3  0  x  0,5 
Tập nghiệm của phương trình l| S   6  72 ; 0,5 ; 67  3
d) (2x – 7)3 + (9 – 2x)3 = 152.
Đặt 2x – 8 = y thì 2x – 7 = y + 1 ; 9 – 2x = 1 – y .
Do đó phương trình trở thành (y + 1)3 + (1 – y)3 = 152
Khai triển, rút gọn (hoặc dùng hằng đẳng thức a3 + b3 ta được
6y2 + 2 = 152  6y2 – 150 = 0  6(y + 5)(y – 5) = 0.
- Với y + 5 = 0 thì 2x – 8 + 5 = 0  x = 1,5
- Với y – 5 = 0 thì 2x – 8 – 5 = 0  x = 6,5
Tập nghiệm của phương trình l| S   1,5 ; 6,  5
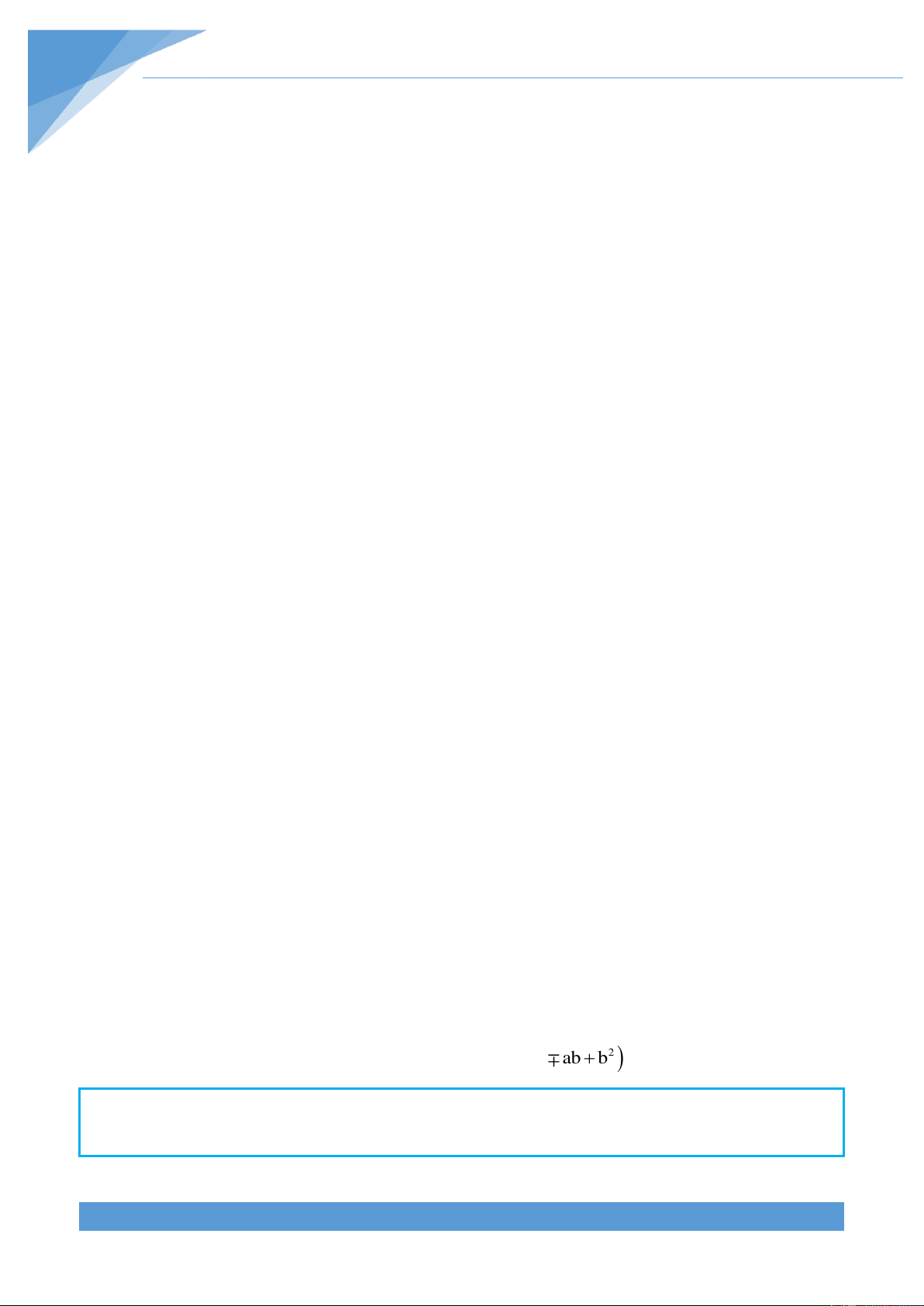
Lƣu ý: Trong các bài toán xuất hiện các dạng (a + b)3 ;   3 a b và a3  b3 . Ta có:   3 3 3 a b
 a  b  3ab(a  b) và 3 3      2 2 a b a b a ab  b 
Thí dụ 4. Giải phương trình: a) x3 – 3x2 + 3x – 4 = 0. b) 2x3 + 3x2 – 6x + 4 = 0 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 7 Hƣớng dẫn giải
a) Phương trình có nghiệm hữu tỷ x = a thì a l| ước của 4, ta thử các giá trị 1  ; 2  ; 4  đều
không là nghiệm. Mặt khác lại thấy các hệ số 1; - 3; 3 giống hằng đẳng thức
a3 - 3a2 + 3a – 1 = (a - 1)3 nên ta biến đổi như sau: x3 – 3x2 + 3x – 4 = 0 3 2
x  3x  3x 1  3  x  3 1  3 3  x 1  3 3  x  1 3
Vậy nghiệm của phương trình l| 3 x  1 3
b) Bằng phương ph{p nhẩm nghiệm dễ thấy phương trình không có nghiệm hữu tỷ. Ta biến đổi như sau: 3 2
2x  3x  6x  4  0 3 2
 4x  6x 12x  8  0 3 3 2
 5x x  6x 12x  8
  5.x3  x  23 3 3
 5.x x  2 2   x  3 5 1 2 
Vậy nghiệm của phương trình l|: x  3 5 1
II. Phƣơng trình bậc bốn. 1) Lý thuyết. 4 3 2
ax  bx cx dx e  0 a0
Phương trình bậc 4 l| phương trình có dạng:
Phƣơng pháp giải. Để giải phương trình bậc 4 chúng ta thường nhẩm một nghiệm và
phân tích phương trình bậc 4 thành tích của một đa thức bậc 3 v| đa thức bậc nhất sau đó
dùng c{c phương ph{p để giải phương trình bậc 3 hoặc phân tích thành tích hai tam thức
bậc 2, hoặc đặt ẩn phụ chuyển về giải phương trình bậc 2. Ta xét các dạng to{n đặc biệt
thường giao trong c{c đề thi như sau:
Dạng 1. Phương trình trùng phương: 4 2
ax bx c  0 a  0 2.  1
Phƣơng pháp giải. – Đặt 2 y x
( y  0) khi đó phương: 2
ay by c  0 2.2
Đ}y l| phương trình bậc 2 dễ d|ng tính được nghiệm từ đó suy ra x. THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 8
Chú ý: Số nghiệm của phương trình (2.1) phụ thuộc số nghiệm dương của phương trình (2.2)
Thí dụ 5. Giải phương trình: x4 – 5x2 + 4 = 0. Hƣớng dẫn giải Đặt 2
y x ( y  0) khi đó phương trình trở thành:  y 1 2
y  5y  4  0   y  
1  y  4  0  y  4 2  x 1  x  1      2 x  4 x  2 
Vậy tập nghiệm của phương trình l| S   1  ;  2
Dạng 2. Phương trình có dạng:  x m4  x n4     p (p > 0) a b
Phƣơng pháp giải: Đặt y x
Chuyển về phương trình ẩn y 2
Phương trình ẩn y sẽ l| phương trình trung phương quen thuộc.
Thí dụ 6. Giải phương trình: 4 4
x  2004   x  2006  2 Hƣớng dẫn giải 2004  2006
Đặt y x
x  2005 . Khi đó phương trình trở thành: 2  y   1   y   1
 2   y   1   y   2 4 4 2 2
1   2  y  2 1 . y  2 1  2   2 2
 2y  2  2    2y  2 4 2 4 2 1
 2  4y  8y  4  2y  4y  2  2 4 2 2
 2y 12y  0  2y  2 y  6  0 2
y  0  y  0  x  2005  0  x  2005
Vậy phương trình có nghiệm x = 2005
Dạng 3. Phương trình có dạng:  x a x b x c x d   e trong đó a + b = c + d. Phƣơng pháp giải: 2
PT x  a b 2 
x ab x  c d x cd       e 2
Đặt t x  a bx ta được phương trình t abt cd   e đ}y l| phương trình bậc 2 dễ
giảng giải v| suy ra được nghiệm của bài toán.
Thí dụ 6. Giải phương trình: THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 9 a)  x  
1  x  2 x  4 x  5  10 ) b
4x 74x 5x   1 2x   1  9. Hƣớng dẫn giải a) Ta có:
x  1x  2x  4x 5 10  x   1  x  5 
  x  2 x  4 10    2
x  6x  5 2
x  6x  8  10
Đặt t = x2 + 6x khi đó phương trình trở thành:
t 5t 8 10 2
t 13t  30  0
 t  3t 10  0  t  3   t  10  2
x  6x  3  0   2
x  6x 10  0
x  6x  3  0 dox  6x 10  x 32 2 2 1  0 
 x  32  6  x  3   6  x  3   6
Vậy tập nghiệm của phương trình l| S   3   6; 3   6
b) * Tìm cách giải : Ta thấy nếu vế trái nhân 4 vào nhân tử thứ ba, nhân 2 vào nhân tử thứ
tư thì cả bốn nhân tử đều l| c{c đa thức mà hệ số của x đều là 4. Vế phải nhân với 8 để
được phương trình mới tương đương. Sau đó nếu nhân (4x + 7) với (4x + 2) ; (4x + 5) với
(4x + 4) ta thấy kết quả xuất hiện các hạng tử giống nhau 16x2 + 36x nên có thể đặt ẩn phụ để giải.
Ta có (4x + 7)(4x + 5)(x + 1)(2x + 1) = 9
 (4x + 7)(4x + 5)(4x + 4)(4x + 2) = 72
 (16x2 + 36x + 14)(16x2 + 36x + 20) = 72.
Đặt 16x2 + 36x + 17 = y ta có :
(y – 3)(y + 3) = 72  y2 – 9 = 72  y2 = 81  y =  9 .
- Với 16x2 + 36x + 17 = 9  4x2 + 9x + 2 = 0  4x2 + 8x + x + 2 = 0
 4x2 + 8x + x + 2 = 0  4x(x + 2) + (x + 2) = 0 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 10        (x + 2)(4x + 1) = 0  x 2 0 x 2    4x 1  0 x  0  ,25
- Với 16x2 + 36x + 17 = – 9  16x2 + 36x + 26 = 0 vô nghiệm vì 2  9  23 16x2 + 36x + 26 = 4x    0 , x    .  2  4
Vậy tập nghiệm của phương trình là S   2  ;  0,2  5 .
Thí dụ 7. Giải phương trình: (x – 2)(x – 3)(x – 5)(x – 6) = 31(x2 – 8x + 12) + 128. (1)
* Tìm cách giải : Xét vế trái nếu nhân nhân tử thứ nhất với nhân tử thứ tư v| nh}n tử thứ
hai nhân nhân tử thứ 3 ta có ( x2 – 8x + 12)( x2 – 8x + 15). Mỗi nhân tử là một đa thức có
cùng hệ số của x2 và của x.
Phương trình trở thành ( x2 – 8x + 12)( x2 – 8x + 15) = 31(x2 – 8x + 12) + 128 .
Do đó ta dùng phương ph{p đặt ẩn phụ. Hƣớng dẫn giải
(x – 2)(x – 3)(x – 5)(x – 6) = 31(x2 – 8x + 12) + 128
 ( x2 – 8x + 12)( x2 – 8x + 15) = 31(x2 – 8x + 12) + 128. (2)
Đặt x2 – 8x + 12 = y thì x2 – 8x + 15 = y + 3
Khi ấy phương trình (2) trở thành y(y + 3) = 31y + 128
 y2 + 3y – 31y – 128 = 0 ;  y2 + 4y – 32y – 128 = 0   
 y(y + 4) – 32(y + 4) = 0 ;  y 4 0
(y + 4)(y – 32) = 0  y32  0
Với y + 4 = 0  x2 – 8x + 16 = 0  (x – 4)2 = 0  x = 4
Với y – 32 = 0  x2 – 8x – 20 = 0  x2 – 10x + 2x – 20 = 0
 (x – 10)(x + 2) = 0  x = 10 hoặc x = – 2
Vậy tập nghiệm của phương trình l| S   2  ; 4 ;1  0
Dạng 4. Phương trình có dạng: 2 2 2
(ax  b x c)(ax  b x c)  mx . 1 2 Phƣơng pháp giải:
– Bƣớc 1: nhận xét x = 0 không là nghiệm của phương trình.
- Bƣớc 2: Chia hai vế của phương trình cho 2 x .  c  c
Phương trình trở thành: ax b  ax  b   m  1  2   x  x c
Bƣớc 3: Đặt t ax
chuyển về giải phương trình bậc 2 cơ bản. x THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 11
Thí dụ 8. Giải phương trình: 2 2 2
(2x  3x 1)(2x  5x 1)  9x (1) Hƣớng dẫn giải
– Nhận thấy x = 0 không phải là nghiệm của Phương trình.
- Chia hai vế của Phương trình (1) cho 2 x  0 ta được:  1  1  2 x 3  2 x 5   9 (*)     x  x  1
Đặt t  2x
. Khi đó phương trình (*) trở thành: (t – 3)(t + 5) = 9 xt  6  2
t  2t  24  0  (t  6)(t  4)  0   t 4 1 3   7 Với t = - 6 ta có: 2 2x   6
  2x  6x 1  0  x  . x 2 1 2  2 Với t = 4 ta có: 2 2x
 4  2x  4x 1  0  x  . x 2 3   7 2  2
Vậy phương trình đã cho có 4 nghiệm: x  , x  . 2 2
Thí dụ 9. Giải phương trình: 2 2 2
(x  5x 1)(x  4)  6(x 1) (2) Hƣớng dẫn giải
Đặt a x 1 thay x = a + 1 và rút gọn ta được: 2 2 2
(u  7u  3)(u  2u  3)  6u (*)
Đến đ}y có thể giải tiếp như ví dụ trên. 1   21
Giải ra ta được 4 nghiệm là: x  3  7; x  . 2
Dạng 5. Phương trình có dạng:  x a x b x c x d  2
ex , trong đó ab cd . Phƣơng pháp giải:
– Bƣớc 1: nhận xét x = 0 không là nghiệm của phương trình. - Bƣớc 2: 2       2        2 PT x a b x ab x c
d x cd   ex    
Chia hai vế của phương trình cho 2 x  0 .  ab   cd
Phương trình trở thành: x
a b x
c d e      x   xab cd
Bƣớc 3: Đặt t x   x
. Ta có phương trình: t a bt c d   e x x THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 12
Đ}y l| phương trình bậc 2 dễ d|ng tính được t từ đó tính được x.
Thí dụ 10. Giải phương trình:
a x   x   x   x   2  x b
 2x x  2x x  2 ) 2 1 8 4 4 ) 3 2 9 18  168x Hƣớng dẫn giải a) PT    x  
x   x  x   2   x  
 2x x  2x x  2 2 4 1 8 4 6 8 9 8  4x .
Do x  0 không là nghiệm nên chia hai vế của phương trình cho 2 x ta được:  8  8  x   6 x   9  4    .  x  x  8  y  5
Đặt y x
thì phương trình trở thành  y  6 y  9 2
 4  y 15y  50  0   . xy 10 8 Với y  5 thì 2 x
 5  x  5x  8  0 (vô nghiệm). x 8 x  5 17 Với y  10 thì 2 x
10  x 10x  8  0   . x x  5 17
Vậy tập nghiệm của phương trình l| S  5 17;5 17 . b) Ta có:
 2x 3x2 2x 9x18 2 168x  x  
1  x  2 x  3 x  6  168  x   1  x  6 
  x  2 x  4 168    2
x  7x  6 2
x  5x  6  168
Chia hai – Nhận thấy x = 0 không là nghiệm của phương trình:  6  6 
vế của phương trình cho 2
x ta được: x
 7 x   5 168     x  x  6
Đặt y x
phương trình trở thành:  y  7 y  5 168 xy  7 2
y 12x 133  0  y  19  THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 13   x  1   x  6  6   x   7 2  x
x  7x  6  0    Do đó: 19 337       2 x 6 
x 19x  6  0      2 x 19  x   1  9  337  x    2 1  9  337 1  9  337
Vậy phương trình có 4 nghiệm x  1, x  6, x  , x  2 2 2
Dạng 6. Phương trình có dạng: a bx c x d
a bx c x d Ax 1  2 1  2 2 2  2 Phƣơng pháp giải:
– Bƣớc 1: nhận xét x = 0 không là nghiệm của phương trình.
- Bƣớc 2: Chia hai vế của phương trình cho 2 x  0 . 2 2  d   d
Phương trình trở thành: a bx   c
a bx   cA 1  1  2  2   x   xd 2 2
Bƣớc 3: Đặt t bx
. Ta có phương trình: a t ca t cA 1  1  2  2  x
Đ}y l| phương trình bậc 2 dễ d|ng tính được t từ đó tính được x.  2 2
Thí dụ 11. Giải phương trình:  2
x x     2 x x   2 3 2 1 2 3 1  5x  0 Hƣớng dẫn giải
Dễ thấy x  0 không là nghiệm của phương trình. 2 2  1   1 
Chia hai vế của phương trình cho 2
x ta được 3 x
 2  2 x   3  5  0     .  x   x  1   2 2 y 1
Đặt y x  , phương trình trở thành: 3 y  2  2 y  3 2
 5  0  y 1  0   . xy  1   1  1   5 x  1  x  Suy ra x 2    . 1   1 5 x   1   x   x  2  1   5 1 5 
Vậy tập nghiệm của phương trình l| S   ;  .  2 2  
Dạng 7. Phương trình có dạng: 4 3 2
ax  bx cx bx a  0. Phƣơng pháp giải: THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 14
– Bƣớc 1: Nhận xét x = 0 có phải là nghiệm nghiệm của phương trình hay không.
- Bƣớc 2: Chia hai vế của phương trình cho 2 x  0 ta được: b a 2
ax  bx c    0. 2 x x 1 1 - Bƣớc 3: Đặt 2 2 y x   y x
 2 . Khi đó phương trình trở thành: 2 x x a  2 y
2  by c  0
Đ}y l| phương trình bậc 2 dễ gi|ng tính được y và suy ra x.
Thí dụ 12. Giải phương trình: 4 3 2
6x  5x  38x  5x  6  0 Hƣớng dẫn giải
Ta thấy x = 0 không phải l| nghiệm của phương trình
Chia cả 2 vế của phương trình cho x2 ta được: 5 6 2 6x  5x  38    0 2 x x  1   1  2  6 x   5 x   38  0     2  x   x  1 1 Đặt y  x  thì: 2 2 x   y  2 x 2 x
Ta được pt: 6y2 – 5y – 50 = 0 <=> (3y – 10)(2y + 5) = 0 10 5 Do đó: y  và y   3 2 10 1 10 * Với y  thì: 2 x    3x 10x  3  0 3 x 3  1 x  
<=> (3x – 1)(x – 3) = 0 <=> 1 3 x  3  2 5 1 5 * Với y   thì: 2 x 
   2x  5x  2  0 2 x 2  1 x   
<=> (2x + 1)(x + 3) = 0 <=> 3 2 x  2   4 1 1 
Vậy phương trình có bốn nghiệm: x  , x  , x  2  , x  3 3 2
Dạng 8. Phương trình có dạng: 4 3 2 2
ax bx cx kbx k a  0k  0 Phƣơng pháp giải:
– Bƣớc 1: Nhận xét x = 0 có phải là nghiệm nghiệm của phương trình hay không. THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 15
- Bƣớc 2: Chia hai vế của phương trình cho 2 x  0 ta được: 2  k   k  2 a x    b x   c  0   2 x    x  2 k 2 kk
- Bƣớc 3: Đặt t x
với t  2 k ta có 2 2 x   x
 2k t  2k   . x 2 xx
Khi đó phương trình trở thành: a  2
t  2k   bt c  0
Đ}y l| phương trình bậc 2 dễ gi|ng tính được y và suy ra x. 4 3 2
2x  21x  34x 105x  50  0
Thí dụ 13. Giải phương trình: 4 3 2
2x  21x  34x 105x  50  0 Hƣớng dẫn giải 105 50 Ta thấy k   5  và 2 k
 25 nên phương trình (8) l| phương trình bậc bốn có hệ 21  2  25   5 
số đối xứng tỉ lệ. 8 2  2 x   21 x   34  0     . 2  x   x  5 25
Đặt t x  suy ra 2 2 t x  10. x 2 x 9
Phương trình (9) trở thành 2
2t  21t  54  0  t  6 hoặc t  . 2 5 Với t  6 thì 2 2 x
 6  x  6x  5  x  6x  5  0  x  3 14; x  3 14 . 1 2 x 9 5 9 9  161 9  161 Với x  thì 2 x
  2x  9x 10  0  x  ; x  . 2 3 4 x 2 4 4  9  161 9  161  
Vậy PT (8) có tập nghiệm S  3   14;3  14; ;  .  4 4  
Có nhiều bài toán bậc bốn không mẫu mực việc đặt ẩn phụ để giải phải thực sự linh hoạt
không thể phân thành dạng cụ thể, chúng ta đi đến một số bài toán sau:  2
Thí dụ 14. Giải phương trình: x x    x  2 2   3 3 1 2 1 5 x   1 Hƣớng dẫn giải Vì x  1
 không là nghiệm của phương trình nên chia cả hai vế cho 3 x 1 ta được: THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 16 2 x x 1 x 1 2 x x 1 2 1 3  2 2 t
 3t   5  3t  5t  2  0  t  2,t   2 x 1
x x  . Đặt 1 x 1 t 3 3  13 * 2
t  2  x  3x 1  0  x  2 1 * 2 t  
 3x  2x  4  0 phương trình vô nghiệm 3 3  13
Vậy phương trình có nghiệm x  2
Thí dụ 15. Giải phương trình: (4x – 19)4 + (4x – 20)4 = (39 – 8x)4 Hƣớng dẫn giải
Đặt 4x – 19 = y; 4x – 20 = z thì y + z = 8x – 39 ta có y4 + z4 – (y + z)4 = 0  y4 + z4 – 4 3 2 2 3 4
y  4y z  6y z  4yz  z = 0    3 2 2 3 6 4
 y z  6y z  4yz = 0  2 2 4yz y  yz  z  0    4  2      x   x    3  7 4yz 2  y  z  z     0  y 0   4 19 0 4, 75     4  16   z  0 4x  20  0 x  5
Tập nghiệm của phương trình l| S  4,75 ;  5
Nhận xét: Trong c{c đề thi đối với hầu hết phương trình bậc bốn có hệ số không quá cao
chúng ta đều có thể chuyển về phương trình bậc 4 tổng quát ax4 + bx3 + cx2 + dx + e = 0 với
a ≠ 0 v| giải giải bằng phương ph{p hệ số bất định cho dù dụng ý của người ra đề là
hướng tới c{ch đặt ẩn phụ để đơn giản bài toán.
Tôi sẽ minh họa phương ph{p n|y bằng bài toán sau:
Thí dụ 16. Giải phương trình: 4 3 2
x  4x 10x  37x 14  0 (1) Hƣớng dẫn giải
Phân tích: Ta nghĩ đến việc phân tích: THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 17 4 3 2 x x x x    2
x px q 2
x rx s 4
x   p r 3
x  s pr q 2 4 10 37 14
x   ps qr x qs  0  p r  4  
s pr q  10 Đồng nhất hệ số:  . ps qr  37   qs  14 
Xuất phát từ qs = -14 v| c{c phương trình trên của hệ ta thấy nhẩm được : p = -5, q = 2,
r = 1, s = -7 thỏa mãn hệ phương trình.
Từ đó có lời giải: 4 3 2 x x x x    2
x x   2 4 10 37 14 5 2 x x  7 Suy ra:
x x  
x  4x 10x  37x 14  0
 x 5x  2x x 7 2 5 2 0 4 3 2 2 2  0   2
x x  7  0 5  17 1   29
Giải hai phương trình bậc 2 n|y ta được nghiệm: x  ; x  1 2 2 2
Hoặc cũng l| hệ số bất định nhưng ta chia th|nh 2 dạng sau:
Dạng 1. Phương trình có dạng: 4 2
x ax bx c Phƣơng pháp giải:
Ta thêm bớt vào 2 vế một lượng: 2 2
2mx m khi đó phương trình trở thành: 2 2 2 2 (x  ) m
 (2m a)x bx c m
2m a  0
Ta mong muốn vế phải có dạng: 2 ( Ax B)    m 2 2
  b  4(2m a)(c m )  0
Thí dụ 17. Giải phương trình: 4 2
x 10x x  20  0 Hƣớng dẫn giải 4 2 4 2
x 10x x  20  0  x  10x x  20
Ta thêm vào 2 vế phương trình một lượng: 2 2 2mx m
Khi đó phương trình trở thành: 4 2 2 2 2
x  2mx m  (10  2 )
m x x m  20 9 Ta có 2
 1 4(m  20)(10  2 )
m  0  m  
. Ta viết lại phương trình th|nh: VP 2 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 18 2 2 2  9  1  9   1  4 2 2 2 x  9x
x x   x   x   0        2  4  2   2  1   17 1 21 2 2
 (x x  5)(x x  4)  0  x  và x  . 2 2 1   17 1 21
Vậy phương trình có 4 nghiệm x  , x  2 2
Dạng 2. Phương trình có dạng: 4 3 2
x ax bx cx d Phƣơng pháp giải: 2  a
Ta sẽ tạo ra ở vế phải một biểu thức bình phương dạng: 2 x x m    2 
Bằng cách khai triển biểu thức: 2 2  a   a  2 4 3 2 2 x x mx ax     2m
x amx m .  2   4  2  a
Ta thấy cần thêm vào hai vế một lượng: 2 2  2m
x amx m khi đó phương trình trở  4  thành: 2 2  a   a  2 2 2 x x m     2m
bx  (am c)x m d  2   4  2  a 2m   b  0   4 Bây giờ ta cần:   m  ? 2  a  2
  (am c)  42m bm d VP  2  0   4 
Thí dụ 18. Giải phương trình: 4 3 2
x  6x  8x  2x 1  0 Hƣớng dẫn giải Phương trình có dạng: 4 3 2 4 3 2
x  6x  8x  2x 1  0  x  6x  8
x  2x 1
Ta tạo ra vế trái dạng: 2 2 4 3 2 2 (x  3x  ) m
x  6x  (9  2 )
m x  6mx m
Tức là thêm vào hai vế một lượng là: 2 2 (9  2 )
m x  6mx m phương trình trở thành: 2 2 2 2 (x  3x  ) m
 (2m 1)x  (6m  2)x m 1. Ta cần 2
'  (3m 1)  (2m 1)(m 1)  0  m  0 . VP Phương trình trở thành: 2 2 2
(x  3x)  (x 1) THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 19 x  2  3  x  2  3 2 2
 (x  4x 1)(x  2x 1)  0  x 1 2   x 1 2
Vậy phương trình có 4 nghiệm S  2  3;2  3;1 2;1 2
II. Phƣơng trình cao hơn bậc bốn.
Đối với c{c phương trình bậc cao hơn 4 phương ph{p chung l| dùng c{ch đưa về dạng
phương trình tích hoặc đặt ẩn phụ để đưa về giải c{c phương trình bậc thấp hoặc với
nhiều b|i to{n chúng ta nên lưu t}m tới việc có thể sử dụng phương ph{p đ{nh gi{ để giải
toán. Chúng ta minh họa qua các ví dụ sau:
Thí dụ 19. Giải phương trình: y2 (y4 – 29y2 + 244) = 576. (1) Hƣớng dẫn giải
(1)  y6 – 29y4 + 244y2 – 576 = 0 .
 y6 – 4y4 – 25y4 + 100y2 + 144y2 –576 = 0
 y4 (y2– 4) – 25y2(y2 – 4) + 144(y2 – 4) = 0
 (y2– 4)(y4– 25y2 + 144) = 0
 (y2– 4)(y4– 9y2 – 16y2 + 144) = 0
 (y2– 4)[y2(y2– 9) – 16(y2 – 9)] = 0
 (y2– 4)(y2– 9)(y2 –16) = 0
 (y – 4)(y – 3)(y – 2)(y + 2)( y+ 3)(y + 4) = 0 .
Vậy phương trình (1) có 6 nghiệm là : y =  2; y =  3; y =  4.
Tập nghiệm của phương trình l| S   4
 ; 3;  2 ; 2 ; 3; 4 .
Thí dụ 20. Giải phương trình: 6x5 – 29x4 + 27x3 + 27x2 – 29x + 6 = 0
(Thi học sinh giỏi lớp 9 tỉnh Thanh Hóa năm học 2005 – 2006) Hƣớng dẫn giải
Biến đổi thành (x + 1)(6x4 – 35x3 + 62x2 – 35x + 6) = 0.
Ta tìm được x = –1 là 1 nghiệm.
Với 6x4 – 35x3 + 62x2 – 35x + 6 = 0 do x = 0 không là nghiệm nên chia hai vế cho x2 ta được : THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 20  1   1  1 1 2 6 x   35 x   62  0     . Đặt x   y thì 2 2 x   y  2 2  x   x  x 2 x
Phương trình trở thành 6(y2 – 2) – 35y + 62 = 0  (2y – 5)(3y – 10) = 0 1 Thay y  x  1
vào 2y – 5 = 0 giải ra ta tìm được x = 2 hoặc x = . x 2 1 Thay y  x  1
vào 3y – 10 = 0 giải ra ta tìm được x = 3 hoặc x = x 3  1 1 
Tập nghiệm của phương trình l| S =  1  ; ; ;2 ; 3.  3 2 
Thí dụ 21. Giải phương trình: (x2 – 4x + 11)(x4 - 8x2 + 21) = 35.
(Đề thi vào lớp 10 trường THPT chuyên Nguyễn Trãi, Hải Dương năm học 2012 – 2013) Hƣớng dẫn giải  2   4 2       x 4x+11 x  8x  2  1  35      2 2 2 x 2 7 x 4  5  35       2 x 2  0, x  và   2 2 x 4  0, x
 nên vế trái không nhỏ hơn 35. 2 (x 2)  0  Ta suy ra   x  2 2
. Vậy nghiệm của phương trình l| x = 2.  2  x 4   0
Thí dụ 22. Giải phương trình: x x  3 3 3 5
5  5x  24x  30  0 Hƣớng dẫn giải Ta có: 3 x x    3 5 30
5 x  5x  5  x  5 nên phương trình tương đương
x x 3 3   3 x x  3 5 5 5 24
x  24x  30  0 . Đặt 3
u x  5x  5. Ta được hệ: 3 u
  5u  5  x
 u x 2 2
u ux x  6  0  u x . 3 
x  5x  5  u 3
x x    x   2 4 5 0
1 x x  5  0  x  1  . Vậy x  1
 là nghiệm duy nhất của phương trình. THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 21
CHỦ ĐỀ 2. PHƢƠNG TRÌNH CHỨA ẨN Ở MẪU THỨC
A. Kiến thức cần nhớ
Bước 1: Tìm điều kiện x{c định của phương trình. (tức là tìm giá trị của ẩn làm tất cả
các mẫu thức của phương trình kh{c 0). Viết tắt: ĐKXĐ.
Bước 2 : Quy đồng mẫu hai vế của phương trình rồi khử mẫu.
Bước 3 : Giải phương trình vừa nhận được.
Bước 4 : (Kết luận) . Trong các giá trị tìm được ở bước 3, các giá trị thỏa mãn điều kiện
xác định chính là nghiệm của phương trình đã cho.
* Chú ý : Nếu A(x) = 0 tại x = x1 hoặc x = x2 thì
A(x)  0 khi x  x1 và x  x2 B.
Một số ví dụ minh họa
Một số bài tập cơ bản:
Thí dụ 23. Giải phương trình: 1 1 3 1 25  4x 4 6 a)    ) b   . 2 x 1 x  2 2x  6 2x  4 25x 1 5x 1 1 5x Hƣớng dẫn giải
a) ĐKXĐ : x  1 ; x  2 và x  3.
(1)  2(x – 2)(x – 3) + 2(x – 1)(x – 3) = 3(x – 1)(x – 2) – (x – 1)(x – 3)
 2x2 – 10x + 12 + 2x2 – 8x + 6 = 3x2 – 9x + 6 – x2 + 4x – 3
 2x2 – 13x + 15 = 0  (2x – 3)(x – 5) = 0 2x  3  0 x 1,5     x  5  0 x  5
Hai giá trị x = 1,5 và x = 5 thỏa mãn ĐKXĐ nên l| nghiệm phương trình (1). b) ĐKXĐ : x   0,2.
(2)  25 + 4x = 4(5x – 1) + 6(5x + 1)  25 + 4x = 20x – 4 + 30x + 6
 – 46 x = – 23  x = 0,5.
Giá trị này thỏa mãn ĐKXĐ. Vậy phương trình có nghiệm là x = 0,5. THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 22 2 2x  5 x  5x  41 3x  8
Thí dụ 24. Giải phương trình:   2 x 1 x  3x  4 x  4 Hƣớng dẫn giải 2 2x  5 x  5x  41 3x  8 Ta có (1)    x 1
(x 1)(x  4) x  4
ĐKXĐ : x  4 và x  –1.
Quy đồng mẫu số hai vế và khử mẫu ta có phương trình :
(2x – 5)(x – 4) + x2 – 5x – 41 = (3x – 8)(x + 1)
 2x2 – 13x + 20 + x2 – 5x – 41 = 3x2 – 5x – 8
 – 13x = 13  x = –1 .
Giá trị này không thỏa mãn ĐKXĐ . Vậy phương trình (1) vô nghiệm.
Một số dạng phƣơng trình phân thức thƣờng gặp: a a a
Dạng 1. Phương trình có dạng: 1 2  .... n   A x b x b x b 1 2 n
Phƣơng pháp giải: Nhóm từng cụm phân thức làm xuất hiện nhân tử chung.  1 1 1 1 1
Thí dụ 25. Giải phương trình:      0 x x 1 x  2 x  3 x  4 Hƣớng dẫn giải
Điều kiện x  1  ; 2  ; 3  ; 4  ; 
0 . Ta biến đổi phương trình th|nh  1 1   1 1  1      0    
x x  4   x 1 x  3  x  2 2 x  2 2 x  2 1     0 2 2 x  4x x  4x  3 x  2 1 1 1     0 2 2 2 x  4x x  4x  3 2(x  4x  . 4) THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 23 1 1 1 Đặt 2
u x  4x , phương trình trở thành    u u  u   0 3 2 4  2  5  145 u  2
5u  25u  24 10     .
u u  u   0 2 3 4  2  5  145 u   10  2  5  145 2 x  4x  Do đó 10  .  2  5  145 2 x  4x   10
Tìm được tập nghiệm của phương trình l|    15  145 15  145 15  145 15  145  S   2   ; 2   ; 2   ; 2   . 10 10 10 10   a x b a x b a x b
Dạng 2. Phương trình có dạng: 1 1 2 2  .... n n   A x c x c x c 1 2 n
Phƣơng pháp giải: Ta biến đổi phương trình th|nh: d d d 1 2 a   a  .... na   A 1 2 n x c x c x c 1 2 n      x 4 x 4 x 8 x 8 8
Thí dụ 26. Giải phương trình:      x 1 x 1 x  2 x  2 3 Hƣớng dẫn giải
Biến đổi phương trình th|nh: 5 5  10 10 8      x 1 x 1 x  2 x  2 3 . 10 40 8     2 2 x 1 x  4 3 u 16 Đặt 2
u x u  1,u  4;u  0 dẫn đến phương trình: 2 4u 65u 16 0      1  . u   4  1 1 
Tìm được tập nghiệm của phương trình l| S   ; 4  ; ;4 .  2 2 
Dạng 3. Phương trình có dạng: mx nx i)   p 2 2
ax b x c
ax b x c 1 2 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 24 2 2
ax b x c
ax d x c ii) 1 1   0; 2 2
ax b x c
ax d x c 2 2 2
ax b x c px iii) 1   0. 2 2
ax b x c
ax dx c 2 Trong đó: a, p, m, n  0
Phƣơng pháp giải dạng i:
Nhận xét x  0 không phải là nghiệm của phương trình.
Với x  0 , ta chia cả tử số và mẫu số cho x thì thu được: a b   c . p p x m x n x x 2 k k Đặt 2 2 t x   t x
 2k  2 k  2k . 2 x x
Thay v|o phương trình để quy về phương trình bậc 2 theo t .
Các dạng ii) và iii) giải ho|n to|n tương tự.  2x 13x
Thí dụ 27. Giải phương trình:   6 . 2 2 3x  4x 1 3x  2x 1
(Thi vào lớp 10 chuyên Quốc học Huế năm học 1996 - 1997) Hƣớng dẫn giải   x  1 2 3
x  4x 1  0  Điều kiện:    1 2
3x  2x 1  0 x      3
Dễ thấy x = 0 không phải là nghiệm của phương trình, do đó chia chia tử và mẫu của mỗi
phân thức cho x ta được: 2 13   6. 1 1 3x  4  3x  2  x x  1 1 2 13 t  Đặt  3x
 4  t khi đó phương trình trở thành: 2 
 6  2t  7t  4  0  2 x t t  6  t  4.   4 x  1 1 1  Với 3 t  thì 2 3x
 4   6x 11x  4  0   2 x 2 1 x   2 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 25 1 Với t  4  thì 2 3x   4  4
  6x 1  0 (loại) x 4 1
Vậy phương trình có nghiệm: x  , x  3 2 2  ax
Dạng 4. Phương trình có dạng: 2 x   b  
với a  0, x  a .  x a Phƣơng pháp giải:
Dựa vào hằng đẳng thức a b  a b2 2 2  2ab .
Ta viết lại phương trình th|nh: 2 2 2 2 2  ax xx x x   2 . ab       2ab  0 .  x a x ax a x a 2 x
Đặt t x  quy về phương trình bậc 2. a 2  x
Thí dụ 28. Giải phương trình: 2 x    3 . x  12
(Thi học sinh giỏi huyện Phù Ninh 2013-2014) Hƣớng dẫn giải Điều kiện: x  1  2 2 2 2 2  x  x  x   x  PT   x    3  2.     2   3  0  x  1  x  1  x  1   x  1  2  x    => 2 2 3 0  x  x  x  1    3 1  0   2  x  1  x  1   x 1 0  x 1 2 x 2 )
 3  0  x  3x  3  0 x  (vô lý) 1  1  5   2 x1 x 2          2 ) 1 0 x x 1 0 x  1  1  5 x  2  2 1 5 1 5
Vậy phương trình có 2 nghiệm x  , x  1 2 2 2 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 26
Có nhiều bài toán bậc bốn không mẫu mực việc biến đổi v| đặt ẩn phụ để giải phải
thực sự linh hoạt không thể phân thành dạng cụ thể, chúng ta đi đến một số bài toán sau:  1 1 1 3
Thí dụ 29. Giải phương trình:    . . 2 2 2 x  5x  4 x 11x  28 x 17x  70 4x  2 Hƣớng dẫn giải Ta có: 1 1 1 3    2 2 2 x  5x  4 x 11x  28 x 17x  70 4x  2 1 1 1 3     (*) (x 1)(x 4)
(x  4)(x  7)
(x  7)(x 10) 4x  2 1
Từ suy ra điều kiện để phương trình có nghĩa l|: x  1  ; 4  ; 7  ; 1  0; 2 Khi đó: 1  1 1  1  1 1  1  1 1  3 (*)             
3  x 1 x  4  3  x  4
x  7  3  x  7 x 10  4x  2 1 1 9 2   
x  7x 12  0 x 1 x 10 4x  2  x  3   x  4. 
Kết hợp với điều kiện ta có nghiệm duy nhất x = -3.  1 1
Thí dụ 30. Giải phương trình:  15. . 2 2 x (x 1) Hƣớng dẫn giải x  0 ĐK:  . x  1 
Khi đó phương trình đã cho tương đương với: 2 2 1 1 (x 1)  x  15  15 2 2 2 2 x (x 1) x (x 1) 2 1 2x(x 1)  1  2  15   15   2 2 x (x 1)
x(x 1)  x(x 1) 1 Đặt  t x(x
khi đó phương trình trở thành: 1) THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 27  t  3 2
t  2t 15  0  t  5  1 3   21 Với t = 3 ta có: 2
 3  3x  3x 1  0  x  . x(x 1) 6 1 5   5 Với t = - 5 suy ra: 2  5
  5x  5x 1  0  x  . x(x 1) 10 3   21 5   5
Phương trình đã cho có bốn nghiệm x  , x  6 10 4 2    x 3x 1
Thí dụ 31. Giải phương trình:  3 . 3 2
x x x Hƣớng dẫn giải x  0  Điều kiên: 3 2
x x x  0   1   5 x   2
Chia chia tử và mẫu của phân thức cho 2
x  0 ta được phương trình tương đương: 1 2 x  3  2 x  1 1 1 3 . Đặt 2 2 2 2 t x   t x
 2  t  5  x   3 1 2 2 x x x x 1 x 2 t  5
Khi đó, phương trình trở thành: 2
 3  t  3t  2  0  t 1 t t  hoặc 2 1 1 1 5 Với t = 1 thì 2 x
1  x x 1 0  x  . x 2 1 Với t = 2 thì 2 x
 2  x  2x 1  0  x 1 2. x 1 5
Vậy phương trình có bốn nghiệm là: x  và x 1 2 2 2 2         x 1 x 1 x 2
Thí dụ 32. Giải phương trình:  12 .     .  x  2  x  3  x  3  Hƣớng dẫn giải x  2
Điều kiện: x  3 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 28  x 1 u   x  2 x 1   uv  Đặt x  2 x  3 v  .  x  3
Khi đó, phương trình đã cho trở thành: 2 2 2 2
u uv  12v u uv 12v  0  u  3v
 (u  3v)(u  4v)  0  u  4v x 1 x  2 8  46 Với u = 3v ta có: 2  3.
 2x 16x  9  0  x  . x  2 x  3 2 x 1 x  2 Với u = -4v ta có: 2  4  .
 5x 12x 19  0 (VN) x  2 x  3 8  46
Vậy phương trình đã cho có nghiệm x  2
Dạng 5. Sử dụng phương ph{p đ{nh gi{ để giải phương trình chứa phân thức  3 4 1
Thí dụ 32. Giải phương trình:   . 2 2 2 x x  3 x  3x  9 2x Hƣớng dẫn giải 2
x x  3  0  Điều kiện: 2
x  3x  9  0  x  0.  2 2x  0  1 4 3
Với điều kiện x  0 phương trình đã cho tương đương với:   2 2 2 2x x  3x  9 x x  3 2 2 2 a b (a b)
Trước hết ta chứng minh bất đẳng thức:   (*) . x y x ya b
Thật vậy, áp dụng bất đẳng thức bu-nhi-a-cốp-xki cho hai bộ số  x; y  và  ;    ta có: x y   2         
x    y  2 a b       
  a b 2 2 2 2 2 2 a b (a b)         x yx y x y     a b Dấu “=” xảy ra khi  x y
Vậy BĐT (*) được chứng minh. 2 2 1 4 1 (2) (1 2) 3 Áp dụng BĐT (*) ta có:      2 2 2 2 2 2 2 2x x  3x  9 2x x  3x  9
2x x  3x  9 x x  3 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 29
Do đó phương trình n|y có nghiệm khi và chỉ khi 1 2 1 13 2 2 
x  3x  9  4x x  2 2 2x x  3x  9 2 1 13
Vậy phương trình đã cho có hai nghiệm x  . 2
CHỦ ĐỀ 3. PHƢƠNG TRÌNH CHỨA ẨN TRONG DẤU
GIÁ TRỊ TUYỆT ĐỐI
A. Kiến thức cần nhớ A nˆeu A  0
Định nghĩa về giá trị tuyệt đối : A  A nˆeu A  0
Để giải phương trình có chứa ẩn trong dấu giá trị tuyệt đối cần khử dấu giá trị tuyệt
đối. Ta cần nhớ giá trị tuyệt đối của một biểu thức bằng chính nó nếu nó có giá trị không
âm, bằng số đối của nó nếu nó có giá trị }m. Do đó để bỏ dấu giá trị tuyệt đối ta phải xét
các giá trị làm biểu thức âm hoặc không âm.
B. Một số ví dụ minh họa
Thí dụ 33. Giải phương trình: 2 2 2 2
a) x  3 x  2  0 )
b x  4x 1  31
c) x  2x  4  8x x  8 . Hƣớng dẫn giải 2
a) Phương trình đã cho tương đương với phương trình x 3 x 2 0 x 1 x 1 x 2 0 . x 2
Phương trình có nghiệm x 2; 1; 1; 2 b) Ta có: THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 30 2
x  4x 1  31 2
x  4x 32  0 2
x  4x 1  31     2
x  4x 1  3  1 2
x  4x  30  0  
Phương trình x2 – 4x – 32 = 0  (x – 8)(x + 4) = 0  x 8  x  4 
Phương trình x2 – 4x + 30 = 0 vô nghiệm
vì x2 – 4x + 30 = (x – 2)2 + 26 > 0 ,  x .
Vậy nghiệm của phương trình l| x = 8 v| x = – 4 .
c) Do x2 – 2x + 4 = (x – 1)2 + 3 > 0 ,  x nên 2 2
x  2x  4  x  2x  4 . Do đó PT  x2 – 2x + 4 = 8x – x2 – 8  
 x2 – 5x + 6 = 0  (x – 3)(x – 2) = 0  x 3  x  2
Vậy phương trình có 2 nghiệm x = 2 và x = 3.
Thí dụ 34. Giải phương trình:
a) 2x  5  7  9  21 ) b
2x 1  4  8 10  15. . Hƣớng dẫn giải  2x  5  7  1  2  2x  5  5  (loai)
a) PT  2x  5  7  9  21      2x  5  7 12   2x  5 19          2x 5 19 x 7    . 2x  5  19 x  12
 2x 1  4  8  2  5 b) PT 
2x 1  4  8  25   2x 1 4 8  25   2x 1  4  3  3 (loai)  2x 1  4  1  7  2x 1  1  3 (loai)        2x 1  4  17   2x 1  4 17   2x 1  21          2x 1 21   x 10  2x 1  21 x 11
Thí dụ 35. Giải phương trình:
. a) x  3  3x  6  5  2x  8 ; b) 2 2
x  9  x  25  26 ; THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 31
5  3x x 1
c) x 1  x  2  2x  5  10 . x d)  4
x  3  3  2x Hƣớng dẫn giải
a) Lập bảng xét giá trị tuyệt đối (hay bảng phá dấu GTTĐ): x 2 2,5 3 x  3 3 – x | 3 – x | 3 – x 0 x – 3 3x  6 6 – 3x 0 3x – 6 | 3x – 6 | 3x – 6 5  2x 2x – 5 | 2x – 5 0 5 – 2x | 5 – 2x Vế trái 14 – 6x | 0x + 2 | 4x – 8 | 6x – 14 Vậy : + Với x < 2
thì 14 – 6x = 8  x = 1 (thỏa mãn)
+ Với 2  x  2,5 thì 0x + 2 = 8 Vô nghiệm
+ Với 2< x  3 thì 4x – 8 = 8  x = 4 ( loại )
+ Với x > 3 thì 6x – 14 = 8  11 x = (thỏa mãn) 3 2
Nghiệm của phương trình : x = 1 v| x = 3 3 b) Lập bảng xét GTTĐ : x2 9 25 2 x  9 9 – x2 0 x2 – 9 | x2 – 9 2 x  25 25 – x2 | 25 – x2 0 x2 – 25 Vế trái 34 – 2x2 | 0x2 – 16 | 2x2 – 34
Với x2  9 ; 34 – 2x2 = 26  x2 = 4  x =  2 .
Với 9 < x2 < 25 ; 0x2 – 16 = 26 Vô nghiệm
Với x2  25 ; 2x2 – 34 = 26  x2 = 30  x =  30 .
Vậy nghiệm của phương trình l| x =  2 và x =  30 .
c) Phương trình x 1  2x  5  3x  2  10x có vế trái không âm nên
10x  0  x  0 do đó x + 1 + 2x + 5 + 3x + 2 = 10x  x = 2.
Vậy phương trình có nghiệm x = 2. THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 32
d) Điều kiện x – 3 + 3  2x  0 .
Bạn đọc tự lập bảng xét dấu.
Phương trình tương đương
3x  5 - x 1 - 4 2x  3 - 4x + 12 = 0 (*) 3 Xét x < -
Thì (*)  - 3x + 5 + ( x – 1) + 4(2x + 3) – 4x + 12 = 0 2  2x = -28  x = - 14 (Thỏa mãn đk) 3 Xét - ≤ x < 1 Thì (*) 2
 - 3x + 5 + x – 1 – 4(2x + 3) – 4x + 12 = 0  2 x = (Thỏa mãn đk) 7 5 Xét 1 ≤ x < Thì (*) 3
 - 3x + 5 – (x -1) – 4(2x + 3) – 4x + 12 = 0  3 x = (loại) 8 5 Xét x ≥
Thì (*)  3x – 5 – (x – 1) – 4(2x + 3) – 4x + 12 = 0 3  2 x = - (Loại) 5  2 
Vậy phương trình có nghiệm x  ; 14   7 
Thí dụ 36. Giải phương trình:
3x  4  5  x  2  1. Hƣớng dẫn giải
 3x  4  5 1 x  2 (1) 
3x  4  5  1 x  2     3x  4  5  1   x  2   3x  4  x  2  6   3x  4  x  2  4 
a) Với 3x  4  x  2  6 ta lập bảng xét giá trị tuyệt đối : THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 33 x 4 – 2 3 3x  4 4 – 3x | 4 – 3x 0 3x – 4 x  2 – 2 – x 0 x + 2 | x + 2 Vế trái 6 – 2x | – 4x + 2 | 2x – 6
Với x  – 2 ; 6 – 2x = 6  x = 0 (thỏa mãn). 4
Với – 2 < x < ; – 4x + 2 = 6  x = – 1 (thỏa mãn) 3 Với x  4
; 2x – 6 = 6  x = 6 (thỏa mãn) 3
b) Với 3x  4  x  2  4 lập bảng xét giá trị tuyệt đối : x 4 – 2 3 3x  4 4 – 3x | 4 – 3x 0 3x – 4 x  2 – 2 – x 0 x + 2 | x + 2 Vế trái 2 – 4x | – 2x + 6 | 4x – 2
Với x  – 2 ; 2 – 4x = 6  x = – 1 ( không thỏa mãn). 4
Với – 2 < x < ; – 2x + 6 = 4  x = 1 (thỏa mãn) 3 Với x  4 ; 4x – 2 = 4  3 x = (thỏa mãn) 3 2  3 
Vậy tập nghiệm của phương trình l| S   1  ; 0;1; ; 6  2 
Thí dụ 36. Giải phương trình:
| x + 1|2016 + |x + 2|2017 = 1
(Trích đề thi học sinh giỏi huyện Ba Vì năm học 2017-2018) Hƣớng dẫn giải
Dễ thấy x = - 2 và x = - 1 l| nghiệm của phương trình. * Xét x < - 2:
Ta có: x + 1< -1 và x + 2< 0. Suy ra: |x+1| >1;|x + 2| >0
Do đó: |x+1|2016 >1;|x + 2|2017 >0
Vì thế: | x + 1|2016 + |x + 2|2017 > 1
Vậy với x < - 2 phương trình vô nghiệm. * Xét -2 < x < -1: THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 34
Ta có: -1< x + 1< 0 và 0< x + 2 <1 . Suy ra: 0< |x + 1| < 1 ; 0 < |x + 2| <1
Và |x+1| = -x - 1; |x + 2| = x + 2
Vì thế: |x + 1|2016 < |x+1| ; |x + 2|2017 < |x+2|
Vậy: |x + 1|2016 + |x + 2|2017 < |x+1| + |x +2|= -x – 1 + x + 2= 1
Do đó với -2 < x < -1 phương trình vô nghiệm. * Xét: x > -1:
Ta có: x + 1 > 0 và x + 2 > 1.Suy ra: |x+1| > 0 và |x + 2| > 1.
Vậy: | x + 1|2016 + |x + 2|2017 > 1
Do đó với x > -1 phương trình vô nghiệm.
Kết luận: Tập nghiệm của phương trình l|: S= { }
BÀI TẬP TỔNG HỢP
Chủ đề 1. Phƣơng trình đa thức bậc cao
Câu 1. (Đề HSG huyện Cẩm Giàng 2015-2016)
Giải phương trình:   2 2 2 x 2x  2x  4x  3
Câu 2. (Đề HSG huyện Gia Lộc 2015-2016) Giải phương trình: 4 3 2
2x 7x  9x 7x  2  0
Câu 3. (Đề HSG huyện Vũ Quang 2018-2019)
Tìm các số nguyên x thỏa mãn phương trình: 3x   1 4x   1 6x   1 12x   1  330
Câu 4. (Đề HSG huyên Thanh Oai 2013-2014)
Giải phương trình: x  3x  4x  5x  6  24
Câu 5. (Trích đề chuyên Đăk Nông 2019-2020) 2
Giải phương trình  x  2  x  
1  x  3 12 .
Câu 6. (Trích đề chuyên Tây Ninh 2019-2020) Giải phương trình 4 2
x x  20  0
Câu 7. (Trích đề chuyên Quảng Trị 2019-2020)
Giải phương trình: x   x  3 6 3 5 2 3
 3x  9x 1
Câu 8. (Trích đề chuyên Đồng Nai 2018-2019) Giải phương trình 4 3 2
x  9x  24x  27x  9  0 (x R) THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 35
Câu 9. Giải c{c phương trình: 2 x  4 x   2
1 x  2 1  0
Câu 10. Giải phương trình (x + 9)(x + 10)((x + 11) – 8x = 0
(Tuyển sinh lớp 10 khối THPT chuyên Toán – Tin ĐHSP Vinh năm học 2002 – 2003)
Câu 11. Giải phương trình x4 – 4x3 – 19x2 + 106x – 120 = 0.
(Thi vào lớp 10 THPT chuyên Trần Đại Nghĩa TP Hồ Chí Minh năm học 2003 – 2004)
Câu 12. Giải phương trình (x2 + 3x + 2)( x2 + 7x + 12) = 24.
(Đề thi tuyển vào lớp 10 chuyên ĐHSPNN Hà Nội năm học 2004 – 2005)
Câu 13. Giải phương trình 6x5 – 29x4 + 27x3 + 27x2 – 29x + 6 = 0
(Thi học sinh giỏi lớp 9 tỉnh Thanh Hóa năm học 2005 – 2006)
Câu 14. Giải phương trình (3x + 4)(x + 1)(6x + 7)2 = 6.
(Tuyển sinh lớp 10 THPT chuyên ĐHSP Hà Nội năm học 2006 – 2007)
Câu 15. Giải phương trình (x2 – 2x)2 + 3x2 – 6x = – 2 .
(Thi học sinh giỏi lớp 9 huyện Thường Tín Hà Tây năm học 2006 – 2007)
Câu 16. Giải phương trình (4x + 3)2(2x + 1)(x + 1) = 810.
(Tuyển sinh lớp 10 chuyên Tin Quốc học Huế năm học 2019 – 2010)
Câu 17. Giải phương trình x3 + 3x – 140 = 0.
(Đề thi tuyển vào lớp 10 THPT chuyên Lam Sơn, Thanh Hóa năm học 2010 – 2011) 2
Câu 18. Giải phương trình  2 x  2x  3x   1  x(2x 1) .
(Đề thi tuyển vào lớp 10 THPT chuyên Quang Trung, Bình Phước năm học 2010 – 2011)
Câu 19. Giải phương trình   2 2 2 2x x  2x  x 12  0 .
( Thi tuyển sinh lớp 10 chuyên TP Hồ Chí Minh năm học 2010 – 2011)
Câu 20. Giải phương trình  2   4 2 x 4x+11 x  8x  2  1  35 .
(Đề thi vào lớp 10 trường THPT chuyên Nguyễn Trãi, Hải Dương năm học 2012 – 2013)
Câu 21. (Đề thi HSG huyện Thanh Thủy 2016-2017)
Giải phương trình: 5x3 + 6x2 + 12x + 8 = 0
Câu 22. (Trích đề chuyên Phú Yên năm 2012-2013) Giải phương trình: 3 3 3 1005 x 1007 x 2x - 2012 0
Chủ đề 2. Phƣơng trình phân thức 1 1 1 1
Câu 23. Giải phương trình:    2008x 1 2009x  2 2010x  4 2011x  5
Câu 24. (Đề HSG quận Bắc Từ Lim 2018-2019) THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 36  5  x  5  x 
Giải phương trình: x x      6  x  1  x  1 
Câu 25. (Chuyên Bà Rịa Vũng Tàu năm 2019-2020) 2 9x Giải phương trình 2 x 40 2 x 3
Câu 26. (Trích đề chuyên Đắc Lắc năm 2018-2019) 2 15
(x 1) 15x  3 Giải phương trình:  . 2 2 x  6x  4
x(x  2x  4)
Câu 27. (Trích đề chuyên Quản Nam năm 2015-2016) 6 4 7 3 Giải phương trình sau:     0 2 2 2 2 x  9 x 11 x  8 x 12
Câu 28. (Trích Chuyên Hòa Bình năm 2015-2016) 1 1 1 1 Giải phương trình:    3x 1 2x  4 9x  2 5  4x
Câu 29. Giải c{c phương trình : 3 4 5 14 a)    ; 2 2 2 3 2 x  5x  6 x  7x 12 x  6x  8 x  9x  26x  24 1 1 1 19 b)  ...  ; 2 2 2 x  3x  2 x  5x  6 x  39x  380 42 2 2 2 5 c)  ...  . 2 2 2 x  2x x  6x  8 x 18x  80 12 2 2 2 x  4x  6 x  6x 12 x  24
Câu 30. Giải phương trình:   (2x 5)  . 2 x  2 x  3 x  5x  6 2x 13x
Câu 31. Giải phương trình   6 . 2 2 x  5x  3 2 2 x x  3
(Thi vào lớp 10 chuyên Quốc học Huế năm học 1996 - 1997) 3 2 x 3x
Câu 32. Giải phương trình 3 x    2  0. 3 (x 1) x 1
(Đề thi vào lớp 10 THPT chuyên ĐHSP Hà Nội năm học 2000 – 2001) 5
Câu 33. Giải phương trình 2  x  4x 1  0 . 2 x  4x  5
(Đề thi tuyển sinh vào lớp 10 Quốc học Huế năm học 2002 – 2003)
Câu 34. Giải phương trình 1 1 1 1 1     . 2 2 2 2 x  5x  6 x  7x 12 x  9x  20 x 11x  30 8 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 37
(Khảo sát chất lượng học sinh giỏi Toán 8 huyện Thường Tín Hà Nội năm học 2012 – 2013). x  2 x  56 21x  22
Câu 35. Giải phương trình   4 . 3 4  7x x  2
(Đề thi tuyển sinh vào lớp 10 THPT chuyên ĐHSP Hà Nội năm học 2014 – 2015) 2 2 x x 2x
Câu 36. Giải phương trình   . 2 x 1 x 1 x 1
(Đề thi học sinh giỏi Toán 9 Huyện Thường Tín Hà Nội năm học 2014 – 2015) 1 3 2
Câu 37. Giải phương trình    2 2 2 x x 1 (x 1)
(Đề thi chọn đội tuyển Toán 9 quận Gò Vấp TP Hồ Chí Minh năm học 2014 – 2015) 2 2 x  2x 1 x  2x  2 7
Câu 38. Giải phương trình   2 2 x  2x  2 x  2x  3 6
(Khảo sát chất lượng học sinh giỏi Toán 8 huyện Thường Tín Hà Nội năm học 2014 – 2015).
Câu 39. Giải các phương trình: 2 25x a) 2 x   
. (Trích đề thi vào lớp 10 chuyên Lam Sơn Thanh Hóa 2013). x  5 11 2 12x 3x b)
1. (Trích đề thi vào lớp 10 chuyên Đại học Vinh 2010). 2 2 x  4x  2 x  2x  2 2 x c) 2    (Trích đềx x
thi vào lớp 10 chuyên ĐHSP Hà Nội 2008). x  2 3 6 3 2 3 2 x 3x d) 3 x     x   2 0 3 1 x 1
Câu 40. Giải các phương trình: 1 1 1 1 1      0. x x 1 x  2 x  3 x  4 x x x x
Câu 41. Giải các phương trình: 4 4 8 8 8      . x 1 x 1 x  2 x  2 3 x 1 x  6 x  2 x  5
Câu 42. Giải các phương trình:    . x x  2 2 2 2 x 12x  35 x  4x  3 x 10x  24 4x 3x
Câu 43. Giải các phương trình:  1 2 2 4x  8x  7 4x 10x  7 2 2 2 2 x x 1 x  2x  2 x  3x  3 x  4x  4
Câu 44. Giải các phương trình: .     0 x 1 x  2 x  3 x  . 4 2 x 12
Câu 45. Giải các phương trình: 2     x x . x  2 3 6 3 2 2x 13x
Câu 46. Giải các phương trình:   6 . 2 2 3x  5x  2 3x x  2 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 38 2 2 2  x  2   x  2  x  4
Câu 47. Giải các phương trình: 20  5  20  0     . 2  x 1   x 1  x 1
Chủ đề 3. Phƣơng trình có dấu giá trị tuyệt đối
x  2  x   1  x   1  x  2  4
Câu 48. Giải phương trình
(Đề HSG huyện Vũ Quang 2018-2019)
Câu 49. Giải phương trình x  x 1  x  2  7 .
((Đề thi vào lớp 10 chuyên, Quốc học Huế năm học 1994 – 1995)
Câu 50. Giải phương trình 2 2 x 1  x 1  3 .
(Thi học sinh giỏi lớp 9 TP Hồ Chí Minh năm học 1994 – 1995)
Câu 51. Giải phương trình x  x  2  2 .
(Thi vào lớp 10 chuyên Lê Hồng Phong TP Hồ Chí Minh năm học 1995- 1996)
Câu 52. Giải phương trình 2
(x 1)  2 x 1  8  0 .
(Thi học sinh giỏi lớp 9 PT TP Hồ Chí Minh năm học 2001- 2002)
Câu 53. Giải phương trình 2 2x  5  x  3x 1 .
(Thi vào lớp 10 PT năng khiếu ĐHQG TP Hồ Chí Minh năm học 2003- 2004)
Câu 54. Giải phương trình 2
x 1  x 1  1 x 1 .
(Đề thi tuyển sinh THPT chuyên ĐHQG Hà Nội năm 2004). 2006 2006
Câu 55. Giải phương trình x  2005  x  2006 1
(Đề thi học sinh giỏi lớp 9 tỉnh Thanh Hóa năm học 2004 – 2005)
Câu 56. Tìm x thỏa 9x  8  7x  6  5x  4  3x  2  x  0.
(Chuyên Đà Nẵng năm 2019-2020) HƢỚNG DẪN GIẢI Câu 1.
x x2  x x  x x2 2 2 2   2 2 2 4 3 2
2 x  2x  3  0 (1) Đặt 2
x  2x a , phương trình (1) trở thành 2
a  2a  3  0  a   1 a  3  0  a = –1 hoặc a = 3
+ Với a = –1, ta có x2 + 2x = –1  (x + 1)2 = 0  x = –1 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 39
+ Với a = 3, ta có x2 + 2x = 3  x + 2x – 3 = 0  (x – 1)(x + 3) = 0  x = 1 hoặc x = –3
Vậy phương trình có tập nghiệm là S =  1  ;1;  3 Câu 2.
Vì x = 0 không là nghiệm của phương trình nên x  0.
Chia hai vế của phương trình cho 2 x ta được:  1   1  2 2 x   7 x   9  0     2  x   x  1 1
Đặt y x  thì 2 2
y  2  x  . x 2 x
Do đó ta có phương trình: 2
2( y  2)  7 y  9  0     y 1 0
2y2 - 7y + 5=0  (y - 1)(2y - 5) = 0  2y5  0 1
*Với y-1 = 0 ta có x
-1 = 0  x2-x+1 = 0 vô nghiệm vì x 2  1  3 x2 - x + 1= x    0, x     2  4  1 
*Với 2y - 5 = 0 ta có 2. x  
 - 5 = 0  2x2 - 5x + 2 = 0  x  x  2  (2x - 1).(x - 2) = 0   1 x   2 1 Vậy x = 2 và x =
là nghiệm của phương trình 2 Câu 3.
Ta có:  x   x   x   x      2 x x   2 3 1 4 1 6 1 12 1 330 36 15
1 24x 10x   1  330
   2x x     2 3 12 5 1
2 12x  5x 1  330  Đặt: 2
y  12x  5x .
Ta có:  y   y   2 2 3 1 2
1  330  6y  5y 1  330  6y  5y  329  0 2
 6y  42y  47y 329  0  6yy 7 47 y 7  0 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 40  y  7  
y  76y  47  0  47   y   6
Vì x Z y Z , do đó y  7 . Ta có: 2 2 2
12x  5x  7  12x  5x  7  0 12x 12x  7x  7  0 12x x   1  7  x   1  0 x 1 x  1 12x 7 0       7  x   12
Do x Z x 1 thỏa mãn bài toán. Câu 4. x  
3  x  6 x  4 x  5  24   2 x x   2 9
18 x  9x  20  24 (1)
Đặt x2  9x 19  y phương trình (1) trở thành :
y   y   2 1
1  24  0  y  25  0   y  5 y  5  0   2 x x   2 9 24
x  9x 14  0
 x  x   2 2 7
x  9x  24  0
 x  x   2 2 7
x  9x  24  0 Chứng tỏ 2
x  9x  24  0
Vậy nghiệm của phương trình : x  2  ; x  7  . Câu 5. PT biến đổi thành  2
x x   2 4 4
x  4x  3 12 .
Đặt t x x    x  2 2 4 4 2
 0 , phương trình trở thành
t  4n 2
t t 12  0   . t  3   l x  0
Với t  4, ta được 2 2
x  4x  4  4  x  4x  0   . x  4
Vậy phương trình đã cho có hai nghiệm x  0, x  4. Câu 6. Đặt 2
t x ,t  0 , phương trình đã cho trở thành 2t t  20  0   1 2
  b  4ac  81 Phương trình  
1 có hai nghiệm phân biệt t  4 (nhận); t  5  (loại) THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 41
Với t  4 tìm được x  2
 . Vậy phương trình đã cho có 2 nghiệm là x  2  Câu 7. 3 3
x   x  3 6 3 5 2 3
 3x  9x 1   2 x    3 x   2   x  3 3 1 3 x  3 Đặt: 2 3 x  ,
a x  3  b 3 Ta có phương trình: 3 3
a b 1  3ab  a b 1 3aba b  3ab  0
 a b     a b2 1
 a b 1 3ab   a b    1  0 
 a b   2 2
1 a b ab a b   1  0
a b ab a b    a b2 a  2  b  2 2 2 ) 1 0 1
1  0  a b  1 2 3
x x 11 (VN) +) 2 3
a b    x x      x   2 1 0 3 1 0
1 x  2x  2  0  x 1.
Vậy phương trình có nghiệm x  1. Câu 8.
Với x = 0, (*)  0x + 9 = 0 (phương trình vô nghiệm.
Với x  0, chia 2 vế của phương trình (*) cho 2 x 2     2 27 9 3 3 (*)  x - 9x + 24 - + = 0  x   9 x   18      0 2 x x  x   x   3 x   3  0 3 3     x
 x   3x   6   0    x  x   3 x   6  0  x 2 x  3x  3  0 (VN) x  3  6     2 x  6x  3  0 x  3  6 Câu 9. PT 2  x  2 x   2 x   2 1 1 x  2 1 0   4 2 x x  4 2
x x  2 1  0
 x x 2 4 2   4 2
2 x x  1  0
 x x  2 4 2 4 2 1
 0  x x 1 0.    5 1 5 1 
Giải phương trình trùng phương trên ta được tập nghiệm của PT là  ;  . 2 2  
Câu 10. Đặt y = x + 15 ta có (y – 6)(y – 5)(y – 4) – 8(y – 15) = 0 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 42 2   15  39
y(y2 – 15y + 66) = 0 . Do y2 – 15y + 66 = y    0 ; y     2  4
 y = 0  x = – 15. (Cách khác: Đặt x + 10 = y. Bạn đọc tự giải)
Câu 11. Biến đổi phương trình th|nh (x – 2)(x – 3)(x – 4)(x + 5) = 0 Tập nghiệm : S =  5  ; 2; 3;  4 .
Câu 12. Biến đổi phương trình th|nh (x + 1)(x + 2)(x + 3)(x + 4) = 24
 (x2 + 5x + 4)(x2 + 5x + 6) = 24 .
Đặt x2 + 5x + 5 = t ta có (t – 1)(t + 1) = 24  t2 = 5  t =  5.
Xét với t = 5 và t = – 5 ta tìm được hai nghiệm là x = 0 và x = – 5 .
Câu 13. Biến đổi thành (x + 1)(6x4 – 35x3 + 62x2 – 35x + 6) = 0.
Ta tìm được x = –1 là 1 nghiệm. Với 6x4 – 35x3 + 62x2 – 35x + 6 = 0 do x = 0 không là
nghiệm nên chia hai vế cho x2 ta được :  1   1  1 1 2 6 x   35 x   62  0     . Đặt x   y thì 2 2 x   y  2 2  x   x  x 2 x
Phương trình trở thành 6(y2 – 2) – 35y + 62 = 0  (2y – 5)(3y – 10) = 0 1 Thay y  x  1
vào 2y – 5 = 0 giải ra ta tìm được x = 2 hoặc x = . x 2 1 Thay y  x  1
vào 3y – 10 = 0 giải ra ta tìm được x = 3 hoặc x = x 3  1 1 
Tập nghiệm của phương trình l| S =  1  ; ; ;2 ; 3.  3 2 
Câu 14. Nhân (3x + 4) với 2 ; (x + 1) với 6 và vế phải với 12 ta được
(6x + 8)(6x + 6)(6x + 7)2 = 72 . Đặt 6x + 7 = y phương trình trở thành
(y + 1)(y – 1)y2 = 72  y4 – y2 – 72 = 0  (y2 – 9)(y2 + 8) = 0  y =  3 (do y2 + 8 > 0,  y) . Giải 2
tiếp ta tìm được nghiệm x =  5 và x =  . 3 3
Câu 15. (x2 – 2x)2 + 3x2 – 6x = – 2  (x2 – 2x)2 + 3(x2 – 2x) + 2 = 0 .
Đặt x2 – 2x = y ta có y2 + 3y + 2 = 0  (y + 1)(y + 2) = 0  y = – 1 hoặc y = – 2. Với x2 – 2x
= – 1  (x – 1)2 = 0  x = 1.
Với x2 – 2x = – 2  (x – 1)2 + 1 = 0 vô nghiệm.
Câu 16. (4x + 3)2(2x + 1)(x + 1) = 810    2    2 8 2x 3x 9 2x  3x+  1  810
Đặt 2x2 + 3x = y phương trình trở thành
(8y + 9)(y + 1) – 810 = 0  8y2 + 17y – 801= 0  (y – 9)(8y + 89) = 0 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 43
* y – 9 = 0 tức là 2x2 + 3x – 9 = 0  (x + 3)(2x – 3) = 0  x = –3 hoặc x = 1,5.
* 8y + 89 = 0 tức là 16x2 + 24x + 89 = 0 vô nghiệm vì 16x2 + 24x + 89 = (4x + 3)2 + 80 > 0 ,  x.
Vậy phương trình có hai nghiệm x = –3 và x = 1,5.
Cách khác: Biến đổi phương trình th|nh (4x + 3)2(4x + 2)(4x + 4) = 6480. Đặt
4x + 3 = y . (Bạn đọc tự giải tiếp)
Câu 17. x3 + 3x – 140 = 0  x3 – 5x2 + 5x2 – 25x + 28x – 140 = 0 2   5  87
(x – 5)( x2 + 5x + 28) = 0  x = 5 do x2 + 5x + 28 = x    0, x     2  4 2 2 Câu 18.  2 x  2x  3x   1  x(2x 1)   2     2 x 2x 2 x  2x 3  0
Đặt x2 – 2x = y phương trình th|nh y2 – 2y – 3 = 0  (y – 3)(y + 1) = 0
Thay y = x2 – 2x vào ta có tập nghiệm của phương trình l| S =  1  ;1;  3 .
Câu 19. Đặt 2x2 – x = u phương trình trở thành :
u2 + u – 12 = 0  (u – 3)(u + 4) = 0  u – 3 = 0 hoặc u + 4 = 0.
* u – 3 = 0 ta có 2x2 – x – 3 = 0  (x + 1)(2x – 3) = 0  x = – 1 hoặc x = 1,5. 2  1  31
* u + 4 = 0 ta có 2x2 – x + 4 = 0 vô nghiệm vì 2x2 – x + 4 = 2 x    
> 0 , x. Vậy phương trình có  4  8
hai nghiệm x = –1 và x = 1,5.      
Câu 20.  2   4 2 x 4x+11 x  8x  2  1  35      2 2 2 x 2 7 x 4  5  35       2 x 2  0, x  và   2 2 x 4  0, x
 nên vế trái không nhỏ hơn 35. 2 (x 2)  0  Ta suy ra   x  2 2
. Vậy nghiệm của phương trình l| x = 2.  2  x 4   0
Câu 21. Ta có: 5x3 + 6x2 + 12x + 8 = 0
<=> 4x3 + (x3 + 3.x2.2 + 3.22.x + 23) = 0 <=> (x + 2)3 = - 4x3 <=> x + 2 = - 3 4 .x <=> (1 + 3 4 ).x = - 2 2  2  <=> x =
Vậy pt đã cho có nghiệm duy nhất x = 3 1  4 3 1  4
Câu 22. Đặt X 1005 ; x Y 1007 ; x Z 2x - 2012
Dễ chứng mình với: X + Y + Z = 0 thì: 3 3 3 X Y Z 3XYZ
Phương trình đã cho trở th|nh: THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 44 x 1005 3(1005 x)(1007 x)(2x - 2012)=0 x 1006 . x 1007
Vậy phương trình đã cho có 3 nghiệm x = 1005, x = 1006, x = 1007.
Chủ đề 2. Phƣơng trình phân thức 1 2 4 5
Câu 23. ĐK: x   ;  ;  ;  . 2008 2009 2010 2011
Khi đó phương trình đã cho tương đương. 1 1 1 1    2008x 1 2011x  5 2010x  4 2009x  2 4019x  6 4019x  6  
(2008x 1)(2011x  5)
(2009x  2)(2010x  4)  4019x  6  0   1 1  
(2008x 1)(2011x  5) (2009x  2)(2010x  4)  6 x     4019 
(2009x  2)(2010x  4)  (2008x 1)(2011x  5)  0  6  6 x   x     4019 4019  
 4019x  6  0  x  1    2 2x 5x 3 0     3   x     2 6 3
Vậy phương trình có ba nghiệm: x   ; x  1  ; x   . 4019 2  5  x  5  x
Câu 24. ĐKXĐ : x  1  . Đặt xa   ; x   bx 1  x 1 2 2  5  x   5  x
5x x x x  5  x
Ta có : a b xx    5      x 1   x 1  x 1 a  2  ab  6 b   3 Mà . a b  6 Do đó   a b  5 a  3   b   2
Với a  2; b  3 thì 2
x  3x  2  0  x  1 hoặc x  2
Với a  3; b  2 thì 2
x  2x  3  0 (PT vô nghiệm) THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 45 Câu 25.Ta có: 2 2 2 9x 2 2 2 3x 6x x x 2 x 40 x 40 0 6. 40 0 2 x 3 x 3 x 3 x 3 x 3 2 x t 10 Đặt t
ta có phương trình t2 – 6t -40 =0 x 3 t 4 2 x t 10 2 10 x 10x 30 0 vô nghiệm x 3 2 x x 2 t 4 2 4 x 4x 12 0 x 3 x 6
Vậy tập nghiệm của phương trình l| S 2; 6 Câu 26.
Điều kiện: x  0; x  3 5; x  3  5   * . 1 1 1
Phương trình biến đổi th|nh:   2 2 x  6x  4 x  2x  4 15x 1 1 1    (1) . 4 4 15 x   6 x   2 x x 4 Đặt x
t t  2;t  6 . x 1 1 1 t  4  PT (1) trở th|nh:     . t  6 t  2 15 t 12 4 Với t  4  ta có x   4   x  2  thỏa mãn (*). x 4 x  6  4 2
Với t  12 ta có x  12   thỏa mãn (*). x x  6  4 2 Câu 27. Điều kiện: x  3  ;x   11;x  2  2;x  3  2 6 4 7 3 pt  1 11 1  0 2 2 2 2 x  9 x 11 x  8 x 12 2 2 2 2 15  x 15  x 15  x 15  x      1 1 1 1 0 2  (15  x )(    )  0 2 2 2 2 x  9 x 11 x  8 x 12 2 2 2 2 x  9 x 11 x  8 x 12 2  1 1 1 1 15  x  0 (1) hoặc     0 (2) 2 2 2 2 x  9 x 11 x 8 x 12
Giải (1) ta được x   15 2 1 1 (2)  (2x  20)(  )  0  x   10 4 2 4 2 x  20x  99 x  20x  96
Kết luận phương trình có nghiệm: x  15; x   15 ; x  10; x   10 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 46 1 2 5
Câu 28. ĐK: x  , x  2
 , x  , x  3 9 4 5x  3 5x  3 Ta có pt: 
(3x 1)(2x  4)
(9x  2)(5  4x)  3   3 x x      5  5   2 2
(3x 1)(2x  4)  (9 x 2)(5  4 x)
6x 12x  2x  4  36
x  45x  8x 10  3 x   (TM )  5  6 
 x  (TM )  7  1 x  (TM )  6
Vậy phương trình đã có có 3 nghiệm phân biệt như trên.
Câu 29. a) Điều kiện : x  2; x  3; x  4; Phân tích các mẫu thành nhân tử ta có 3 4 5 14   
(x  2)(x  3)
(x  3)(x  4)
(x  2)(x  4)
(x  2)(x  3)(x  4)
Quy đồng và khử mẫu được phương trình
3(x – 4) – 4(x – 2) = 5(x – 3) + 14
 3x – 12 – 4x + 8 = 5x – 15 + 14  x = – 0,5 thỏa mãn ĐKXĐ. b) ĐKXĐ : x  1  ; 2  ; 3  ;...; 1  9; 2   0 .     Nhận xét: với n  1 (x n 1) (x n) 1 1 N thì    (x  n)(x  n 1) (x  n)(x  n 1) x  n x  n 1 1 1 1 19
Biến đổi phương trình đã cho th|nh :  ...  (x 1)(x  2) (x  2)(x  3) (x 19)(x  20) 42  1 1 1 1 1 1 19    ...   x 1 x  2 x  2 x  3 x 19 x  20 42  1 1 19  
. Quy đồng và khử mẫu được phương trình x 1 x  20 42  
x2 + 21x – 22 = 0  (x – 1)(x + 22) = 0  x 1  thỏa mãn ĐKXĐ x  22 
c) ĐKXĐ : x 0; 2; 4; 6;8;1  0
Nhận xét : với n  N ta có 2 (x  n)  (x  n  2) 1 1    (x  n)(x  n  2) (x  n)(x  n  2) x  n  2 x  n
Biến đổi phương trình đã cho th|nh : THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 47 2 2 2 5  ...  x(x  2) (x  2)(x  4) (x  8)(x 10) 12  1 1 1 1 1 1 5    ...    1 1 5   x  2 x x  4 x  2 x 10 x  8 12 x 10 x 12
Quy đồng và khử mẫu được phương trình x2 – 10x – 24 = 0  
 (x – 12)(x + 2) = 0  x 12  thỏa mãn ĐKXĐ. x  2 
Câu 30. Ta có thể vận dụng c{c bước để giải. Nếu quy đồng mẫu ngay sẽ xuất hiện c{c đa
thức bậc ba, việc thực hiện sẽ d|i .Tuy nhiên có phương ph{p kh{ s{ng tạo và ngắn gọn như sau :
* ĐKXĐ : x  2; x  3. Biến đổi phương trình th|nh : 2 2 2
(x  4x  4)  2 (x  6x  9)  3 x  24   (2x 5)  x  2 x  3 (x  2)(x  3) 2   2 3 x 24 (x  2)   (x 3)   (2x 5)  x  2 x  3 (x  2)(x  3) 2   2 3 x 24    0 x  2 x  3 (x  2)(x  3)
Quy đồng và khử mẫu được phương trình x2 + 5x – 36 = 0
 (x + 9)(x – 4) = 0  x = – 9 hoặc x = 4 thỏa mãn ĐKXĐ.
Câu 31. ĐKXĐ : 2x2 – 5x + 3 = (x – 1)(2x – 3)  0 khi x  1 và x  1,5 2  1  23 3 2x2 + x + 3 = 2 x    0 , x  
. Do x = 0 không là nghiệm của phương trình , đặt 2x +  4  8 x 2 13 = t : PT    6  2 13 
 6 . ĐKXĐ t  5 và t  – 1. 3 3 2x  5  2x 1 t  5 t 1 x x t 1 2
 6t  39t  33  0  (t 1)(6t  33)  0  t 5,5  3 2x   1 2  2x  x  3  0. (1) x Ta có    2 3 11  4x 11x  6  0. (2) 2x    x 2 2  1  23
(1) vô nghiệm vì 2x2 – x + 3 = 2 x    0 , x    4  8 3
(2)  (x – 2)(4x – 3) = 0  x = 2 hoặc x = thỏa mãn ĐKXĐ. 4 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 48 3
Vậy phương trình có hai nghiệm là x = 2 ; x = . 4
Câu 32. Từ (a + b)3 = a3 + b3 + 3ab(a + b)  a3 + b3 = (a + b)3 – 3ab(a + b)
Áp dụng để giải phương trình. Ta có ĐKXĐ : x  1 3 2  x  x  x  3x PT  x   3x. x    2  0      x 1 x 1 x 1 x 1 3 2 2 2 2  x   x   x  2 x     3   3
 11  0 . Đặt y = ta có  x 1  x 1  x 1 x 1
y3 – 3y2 + 3y – 1 – 1 = 0  (y – 1)3 = 1  y = 2. 2 x Hay là
= 2  x2 = 2x – 2  x2 – 2x + 2 = 0 x 1
Phương trình đã cho vô nghiệm vì x2 – 2x + 2 = (x – 1)2 + 1 > 0 x. 
Câu 33. ĐKXĐ: x  R do x2 – 4x + 5 = (x – 2)2 + 1  0 ; x  .
Đặt x2 – 4x + 5 = y thì y  1 và – x2 + 4x – 1 = – y + 4 . Phương trình th|nh 5  
 y  4  0  5 – y2 + 4y = 0  (y – 5)(y + 1) = 0  y 5  y y  1  (loai)
* x2 – 4x + 5 = 5  x(x – 4) = 0  x = 0 hoặc x = 4. Tập nghiệm S = 0;  4 .
Câu 34. ĐKXĐ x 2;3; 4;5;  6 1 1 1 1 1 PT      (x  2)(x  3) (x  3)(x  4) (x  4)(x  5) (x  5)(x  6) 8 1 1 1 1 1 1 1 1 1          x  3 x  2 x  4 x  3 x  5 x  4 x  6 x  5 8 1 1 1  
  x2 – 8x – 20 = 0  (x + 2)(x – 10) = 0 x  6 x  2 8
 x = – 2 hoặc x = 10. Tập nghiệm S =  2  ;1  0 . 4 Câu 35. ĐKXĐ : x  và x3  – 2. 7 x  2 x  56 x  2 x  56 21x  22    21x 22 4   5 1  0 3 4  7x x  2 3 4  7x x  2 3 3        x 56x 20 35x x 2 21x 22   0 3 4  7x x  2    1 1  3 x  21x  20   0   3  4  7x x  2 
* Xét x3 – 21x – 20 = 0  (x + 1)(x – 5)(x + 4) = 0 ta tìm được :
x = – 4; x = –1 ; x = 5 thỏa mãn ĐKXĐ. 1 1 * Xét 
 0 biến đổi thành x3 – 7x + 6 = 0 3 4  7x x  2 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 49
 (x –1)(x – 2)(x + 3) = 0 ta tìm được x = – 3; x = 1 ; x = 2 thỏa mãn ĐKXĐ.
Vậy tập nghiệm của phương trình l| S =  4  ;  3; 1;1; 2;  5 .
Câu 36. ĐKXĐ : x   1. 2 2 x x 2x     2
x2(x + 1) – x2(x – 1) = 2x 2x2 – 2x = 0 x 1 x 1 x 1
 2x(x – 1) = 0  x = 0 hoặc x = 1. Loại x = 1.  Tập nghiệm S =   0 ..
Câu 37. ĐKXĐ : x  0 và x  – 1. 1 3 2    1 3 2 2  11  2 2 x x 1 (x 1) 2 2 x x 1 (x 1) 2 2   3 3 (1 x) (1 x)  x   1 x x x      0 2 2 x (x 1) 2 2 x (x 1) 1   x  0
Với x  0 và x  – 1 thì 3 3
(1 x) (1 x)  x   0     3 3 (1 x)  x  0
*Với x – 1 = 0  x = 1 thỏa mãn ĐKXĐ.
*Với (1 + x)3 + x3 = 0  (1 + x)3 = – x3  1 + x = – x  1 x =  thỏa mãn ĐKXĐ. 2  1 
Tập nghiệm là S =  ;1 .  2  Câu 38. ĐKXĐ : x  R t 1 t 7
Đặt x2 – 2x + 2 = t > 0 phương trình trở thành   t t 1 6
 5t2 – 7t – 6 = 0  (t – 2)(5t + 3) = 0  t = 2 ( do t > 0)
Hay x2 – 2x + 2 = 2  x2 – 2x = 0  x(x – 2) = 0  x = 0 hặc x = 2.
Tập nghiệm là S = 0;  2 .
Câu 39. a) Điều kiện x  5  2 2 2 2 2  5x  10xx  10x
Ta viết lại phương trình thành x   11  0       11  0 . Đặt  x  5  x  5  x  5  x  5 2 xt 1 t
t 10t 11  0   x
thì phương trình có dạng 2 5 t  11  THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 50 2 x 1 21 2 x Nếu t  1 ta có: 2
1  x x  5  0  x  . Nếu t  1  1   1  1 x  5 2 x  5 2
x 11x  55  0 phương trình vô nghiệm.
b) Để ý rằng nếu x là nghiệm thì x  0 nên ta chia cả tử số và mẫu số vế trái cho x thì thu đượ 12 3 2 c: 
1. Đặt t x   2 thì phương trình trở thành: 2 2 x x  4  x  2  x x 12 3 t 1 2 2
 1 12t  3t  6  t  2t t  7t  6  0   . t  2 tt  6 2 Với t  1 ta có: 2 x
 2 1  t t  2  0 vô nghiệm. Với t  6 ta có: x 2 2 x
 2  6  x  4x  2  0  x  2  2 . x 2  x  2  x  x  c)   x  2   2x   1  0   x  3  3x 1  0    .  x  2   x  2  x  2  3   3
Giải 2 phương trình ta thu được các nghiệm là x   6; x  . 3 3 d) Sử dụng HĐT 3 3
a b  a b  3aba b ta viết lại phương trình thành: 3 3 2 2 2 x 3xx xx  3x 3 x                 hay x   2 0 x 3 x 2 0 3 1 x 1  x 1 x 1 x 1 x 1 3 2 3 2 2 2 2 2  x   x  3xxx 2    3    2  0   1 1
1 1  x  2x  2  0. Suy ra  x 1  x 1 x 1  x 1  x 1
phương trình đã cho vô nghiệm.
Câu 40. Điều kiện x  1  ; 2  ; 3  ; 4  ; 
0 . Ta biến đổi phương trình thành  1 1   1 1  1 2 x  2 2 x  2 1      0     0     2 2
x x  4   x 1 x  3  x  2 x  4x x  4x  3 x  2 1 1 1     0 . Đặt 2
u x  4x , phương trình trở thành 2 2 2 x  4x x  4x  3
2(x  4x  4)  2  5  145 u  1 1 1 2   
5u  25u  24 10   0   . u u  u   0 3 2 4
2u u  3u  4  2  5  145 u   10 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 51  2  5  145 2 x  4x  Do đó 10 
. Tìm được tập nghiệm của phương trình là  2  5  145 2 x  4x   10    15  145 15  145 15  145 15  145  S   2   ; 2   ; 2   ; 2   . 10 10 10 10   5 5  10 10 8 10 40 8
Câu 41. Biến đổi phương trình thành          . 2 2 x 1 x 1 x  2 x  2 3 x 1 x  4 3 Đặt 2
u x u  1,u  4;u  0 dẫn đến phương trình u 16   2 4u 65u 16 0      1 . bTìm đượ    
c tập nghiệm của phương trình là 1 1 S ; 4; ; 4 . u   2 2   4
Câu 42. Điều kiện x  7  ; 6  ; 5  ; 4  ; 3  ; 2  ; 1  ; 
0 . Biến đổi phương trình thành x 1 x  6 x  2 x  5   
x x  2  x  5 x  7 x  
1  x  3  x  4 x  6 x 1 1 1  x  6  1 1          x 2 1 1 x 5  1 1              2  x x  2  2  x  5 x  7 
2  x 1 x  3  x x  4 x  6  1 1 1 1 1 1 1 1         x x  2 x  5 x  7 x 1 x  3 x  4 x  6  1 1   1 1   1 1   1 1                 
x x  7   x  2 x  5   x 1 x  6x   x  3 x  4      x   1 1 1 1 2 7     0   2 2 2 2
x  7 x  7x 10 x  7x  6 x  7x 12   7 x    2   . 1 1 1 1      0(*) 2 2 2 2
 x  7x x  7x 10 x  7x  6 x  7x 12 Đặt 2
u x  7x thì phương trình (*) có dạng 1 1 1 1  1 1   1 1      0      0     2
u 18u  90  0. u u 10 u  6 u 12
u u  6   u 10 u 12  Mặt khác u u   u  2 2 18 90 9
 9  0 với mọi u . Do đó phương trình (*) vô nghiệm. 7
Vậy phương trình đã cho có nghiệm duy nhất x   . 2 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 52
Câu 43. Điều kiện x  4  ; 3  ; 2  ; 
1 . Biến đổi phương trình thành 1 2 3 4  1 4   2 3      0      0     x 1 x  2 x  3 x  4
x 1 x  4   x  2 x  3  x  0  3 1    x   0    3 1 . 2 2
x  5x  4 x  5x  6     0(*) 2 2
x  5x  4 x  5x  6 Đặ 3 1 11 t 2
u x  5x thì phương trình (*) trở thành   0  u   . Từ đó ta có u  4 u  6 2 5   3 2
2x 10x 11  0  x  . 2      
Vậy tập nghiệm của phương trình đã cho là 5 3 5 3 S  0; ;  .  2 2  
Câu 44. Do x  0 không là nghiệm của phương trình nên chia cả tử và mẫu của mỗi phân thức ở vế 7
trái của phương trình cho x , rồi đặt y  4x  ta được x 4 3  1. y  8 y 10
Phương trình trên có 2 nghiệm y 16, y  9. 7 Với y  9 thì 2 4x
 9  4x  9x  7  0 . Phương trình này vô nghiệm. x 7 1 7 Với y  16 thì 2 4x
16  4x 16x  7  0 . Phương trình này có hai nghiệm x  ; x  . x 1 2 2 2 1 7 
Vậy phương trình đã cho có tập nghiệm là S   ;  . 2 2
Câu 45. Điều kiện x  2
 . Khử mẫu thức ta được phương trình tương đương: 4 3 2 4 x x x x
  x x 2 x   2 3 6 16 36 12 0 3 6 6 16x 12  0 . đặt 2
t x  6 thì 2 4 2
t x 12x  36 , suy ra 4 2 2
3x  3t  36x 108 , PT trên thành 2
3t  6xt  20t  0  t 3t  6x  20  0  t  0 hoặc 3t  6
x  20. Với t  0 thì 2 x  6  0 , suy
ra x   6 (thỏa mãn đk). Với 3t  6  x  20 ta có 2 3x 18  6  x  20 hay 2
3x  6x  2  0 suy ra 3   3  3   3 3   3  x
(thỏa mãn đk). Vậy tập nghiệm của PT(4) là S   ;  6; ; 6  . 3  3 3   Câu 46. Đặt 2
t  3x  2 PT(5) trở thành THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 53 2x 13x   6 . ĐK: t  5 , x t  x . t  5x t x
Khử mẫu thức ta được PT tương đương 2 2
2t 13tx 11x  0  t x2t 11x  0  11
t x hoặc t x (thỏa mãn ĐK) 2
Với t x thì 2 2
3x  2  x  3x x  2  0 phương trình vô nghiệm. 11 11 1 4 Với t x thì 2 3x  2 
x  6x 11x  2  0  x  hoặc x  . 2 2 2 3 1 4
Vậy tập nghiệm của PT(5) là  ;  . 2 3
Câu 47. Điều kiện x  1  .   Đặ x 2 x 2 t  y;  z , PT có dạng: y z yz
  y z2 2 2 20 5 20 0 5 2
 0  2y z x 1 x 1 x  2 x  2 Dẫn đến 2. 
 2x  2x  
1   x  2 x   1 x 1 x 1  9  73 2 2 2
 2x  6x  4  x  3x  2  x 9x  2  9 73 0  x  hoặc x  (thỏa mãn điều 2 2 kiện). 9  73 9  73 
Vậy tập nghiệm của PT(2) là  ;   2 2  
Chủ đề 3. Phƣơng trình có dấu giá trị tuyệt đối Câu 48.
– Xét x  2 ta có phương trình:  x   x   x   x      2 x   2 2 1 1 2 4 4 x   1  4 2  5  7 4 2 2
x  5x  8  0  x    0   , (vô nghiệm).  2  4
- Xét x  2 ta có phương trình:  x   x   x   x      2 x   2 2 1 1 2 4 4 x   1  4 x  x
x  5x  0  x x 5 2 0 0 4 2 2 2  0     . 2 x  5 x   5
Kết hợp với điều kiện x  2 ta được nghiệm của phương trình l| x  5 .
Câu 49. Lập bảng xét GTTĐ rồi xét các khoảng :
*Nếu x <– 2 thì PT  – x – x – 1– x – 2 = 7  10 x =  3
*Nếu – 2  x < – 1 thì PT  – x – x – 1+ x + 2 = 7  x = – 6 (loại) THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 54
*Nếu – 1  x  0 thì PT  – x + x + 1+ x + 2 = 7  x = 4 (loại)
*Nếu x > 0 thì PT  x + x + 1+ x + 2 = 7  4 x = . 3 10
Phương trình có hai nghiệm là x =  4 và x = . 3 3 Câu 50. 2 2 x 1  x  4  2 2 x 1  4  x  x2 – 1 + 4 – x2 = 3  2   x  2  Dấu “=” xảy ra  2 2 2
(x 1)(4  x )  0  1  x  4  1  x  2  x  1  x  1  1   x  2 
. Nghiệm phương trình là 1  x  2 ;  2   x  1   2   x  1 
Câu 51. Lập bảng xét GTTĐ rồi xét các khoảng :
* Với x  0 phương trình thành – x – 2 + x = 2  0x = 4 vô nghiệm.
* Với 0  x  2 phương trình thành x – 2 + x = 2  x = 2 (nhận)
* Với x > 2 phương trình thành x – x + 2 = 2  0x + 2 = 2 vô số nghiệm.
Vậy nghiệm của phương trình là x  2
Câu 52. Đặt y = x 1 thì y  0. Phương trình trở thành :
y2 + 2y – 8 = 0  (y – 2)(y + 4) = 0  y = 2 hoặc y = – 4 (loại) .      Vậy y = 2  x 1 = 2  x 1 2 x 3    x 1  2  x  1 
Nghiệm của phương trình là x = 3 và x = –1.
Câu 53. * Nếu x  2
 ,5 thì 2x  5  2x+5 khi ấy 2 2x+5  x  3x 1
 x2 + x – 6 = 0  (x + 3)(x – 2) = 0  x = – 3 hoặc x = 2 . Loại x = – 3 * Nếu x  2  ,5 thì 2x  5  2  x 5 khi ấy 2 2  x 5  x 3x 1
 x2 + 5x + 4 = 0  (x + 4)(x + 1) = 0  x = – 4 hoặc x = – 1. Loại x = – 1.
Nghiệm của phương trình là x = 2 và x = – 4.
Câu 54. Ta có ab  a . b nên 2
x 1  x 1  1 x 1  x 1 . x 1  x 1  x 1 1  0    
         x 1 1 0 (1)
x 1 1 . x 1 1  0   x 1 1 0 (2)      * (1)  x + 1 =  1  x
0 ; (2)  x – 1 =  1  x 0   x  2  x  2
Tập nghiệm của phương trình là S =  2  ; 0;  2
Câu 55. * Khi x = 2005 ; x = 2006 thì vế trái và vế phải đều cùng số trị là1. Do đó x = 2005
và x = 2006 là nghiệm của phương trình. THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 55
*Với x < 2005 thì x  2005  0 và x  2006  1 Do đó 2006 2006 x  2005  x  2006
1  phương trình vô nghiệm.
*Với x > 2006 thì x  2005  1 và x  2006  0 Do đó 2006 2006 x  2005  x  2006
1  phương trình vô nghiệm.
* Với 2005 < x < 2006 thì 0 < x – 2005 < 1 và – 1 < x – 2006 < 0  2006 x  2005  x  2005  x  2006 2005 và x  2006  x  2006  2006  x  2006 2006 x  2005  x 2006
 x  2005 2006 x 1  phương trình vô nghiệm.
Vậy nghiệm của phương trình là x = 2005 và x = 2006. Câu 56.
Từ đề bài suy ra x < 0
Suy ra 9x – 8 < 0; 7x – 6 < 0; 5x – 4 < 0; 3x – 2 < 0
Phương trình đã cho trở thành 9
x  8  7x  6  5x  4  3x  2  x  0
 -23x + 20 = 0. Kết luận pt vô nghiệm THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC