Chuyên đề phương trình vô tỷ ôn thi vào lớp 10

Tài liệu gồm 100 trang, hướng dẫn phương pháp giải và tuyển chọn các bài tập chuyên đề phương trình vô tỷ, có đáp án và lời giải chi tiết, giúp học sinh lớp 9 ôn tập chuẩn bị cho kì thi tuyển sinh vào lớp 10 môn Toán

Chủ đề:

Tài liệu ôn thi vào 10 môn Toán 110 tài liệu

Môn:

Môn Toán 1.3 K tài liệu

Thông tin:
100 trang 1 năm trước
Tác giả:
N
Nguyễn Vân
docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Chuyên đề phương trình vô tỷ ôn thi vào lớp 10

Tài liệu gồm 100 trang, hướng dẫn phương pháp giải và tuyển chọn các bài tập chuyên đề phương trình vô tỷ, có đáp án và lời giải chi tiết, giúp học sinh lớp 9 ôn tập chuẩn bị cho kì thi tuyển sinh vào lớp 10 môn Toán

107 54 lượt tải Tải xuống

Chủ đề: Tài liệu ôn thi vào 10 môn Toán 110 tài liệu

Môn: Môn Toán 1.3 K tài liệu

Thông tin:

100 trang 1 năm trước

Tác giả:

Profile Nguyễn Vân
THCS.TOANMATH.com
MỘT SỐ PHƯƠNG PHÁP GIẢI
PHƯƠNG TRÌNH VÔ TỶ
1. Phương trình vô tỷ cơ bản:
2
() 0
() ()
() ()
gx
f x gx
fx g x
≥
= ⇔
=
Ví dụ 1: Giải các phương trình:
a)
2
2 62 1
xx x+ += +
b)
21 49x xx++ = +
Lời giải:
a). Phương trình tương đương với:
22x = +
b). Điều kiện:
0x ≥
. Bình phương 2 vế ta được:
22
22
8
3 122 4 9 22 8
4(2 ) ( 8)
x
x xx x xxx
xx x
≥−
++ += +⇔ +=+⇔
+=+
2
4
8
16
7 12 64 0
7
x
x
x
xx
=
≥−
⇔⇔
= −
− −=
. Đối chiếu với điều kiện ta thấy chỉ có
4x =
là nghiệm của phương trình.
Ví dụ 2: Giải các phương trình:
II. MỘT SỐ DẠNG PHƯƠNG TRÌNH VÔ TỶ THƯỜNG GẶP
1. Giải phương trình vô tỷ bằng phương pháp sử dụng biểu thức liên hợp:
THCS.TOANMATH.com
Dấu hiệu:
+ Khi ta gặp các bài toán giải phương trình dạng:
Mà không thể đưa về một ẩn, hoặc khi đưa về một ẩn thì tạo ra những
phương trình bậc cao dẫn đến việc phân tích hoặc giải trực tiếp khó khăn.
+ Nhẩm được nghiệm của phương trình đó: bằng thủ công ( hoặc sử dụng
máy tính cầm tay)
Phương pháp:
• Đặt điều kiện chặt của phương trình ( nếu có)
Ví dụ: Đối phương trình:
22
33 2 72x xx++= ++
.
+ Nếu bình thường nhìn vào phương trình ta thấy:
Phương trình xác định với mọi
xR∈
. Nhưng đó chưa phải là điều kiện
chặt. Để giải quyết triệt để phương trình này ta cần đến điều kiện chặt đó là:
+ Ta viết lại phương trình thành:
22
3 2 72 3x xx+− += −
Để ý rằng:
22
3 2 70xx+− +<
do đó phương trình có nghiệm khi
3
2 30
2
xx−<⇔ <
• Nếu phương trình chỉ có một nghiệm
0
x
:
Ta sẽ phân tích phương trình như sau: Viết lại phương trình thành:
0 00
() ( ) () ( ) () ( ) 0
nm
nm
f x f x gx gx hx hx− + − +− =
Sau đó nhân liên hợp cho từng cặp số hạng với chú ý:
+
( )
(
)
33
2 23
33
a b a ab b a b− ++ =−
+
( )( )
2
ab ab ab− +=−
THCS.TOANMATH.com
+ Nếu
() 0hx
=
có nghiệm
0
xx
=
thì ta luôn phân tích được
0
() ( )()hx x x gx= −
Như vậy sau bước phân tích và rút nhân tử chung
0
xx−
thì phương trình
ban đầu trở thành:
0
0
0
( ) () 0
() 0
xx
x x Ax
Ax
−=
−=⇔
=
Việc còn lại là dùng hàm số , bất đẳng thức hoặc những đánh giá cơ bản để
kết luận
() 0
Ax =
vô nghiệm.
• Nếu phương trình có 2 nghiệm
12
,xx
theo định lý viet đảo ta có nhân
tử chung sẽ là:
2
1 2 12
( ).x x x x xx−+ +
Ta thường làm như sau:
+ Muốn làm xuất hiện nhân tử chung trong
()
n
fx
ta trừ đi một lượng
ax b+
. Khi đó nhân tử chung sẽ là kết quả sau khi nhân liên hợp của
() ( )
n
f x ax b−+
+ Để tìm
,ab
ta xét phương trình:
() ( ) 0
n
f x ax b− +=
. Để phương trình có
hai nghiệm
12
,xx
ta cần tìm
,ab
sao cho
11
22
()
()
n
n
ax b f x
ax b f x
+=
+=
+ Hoàn toàn tương tự cho các biểu thức còn lại:
Ta xét các ví dụ sau:
Ví dụ 1: Giải các phương trình:
a)
3
3
5 1 2 1 40x xx−+ −+− =
b)
2
2 4 2 53x xx x−+ −= − −
Giải:
THCS.TOANMATH.com
a).
Phân tích: Phương trình trong đề bài gồm nhiều biểu thức chứa căn nhưng
không thể quy về 1 ẩn. Nếu ta lũy thừa để triệt tiêu dấu
3
,
thì sẽ tạo ra
phương trình tối thiểu là bậc 6. Từ đó ta nghỉ đến hướng giải : Sử dụng biểu
thức liên hợp để tách nhân tử chung.
Điều kiện
3
1
5
x ≥
Ta nhẩm được nghiệm của phương trình là:
1x =
. Khi đó
3
3
5 1 5 1 2; 2 1 2 1 1xx−= −= −= −=
Ta viết lại phương trình thành:
3
3
5 12 2 11 10x xx
−−+ −−+−=
( )
3
32
3
3
5 5 22
10
5 120
21 211
xx
x
x
xx
−−
⇔ + + −=
−+ =
− + −+
( )
2
32
3
3
5( 1) 2
( 1) 1 0
5 12
21 211
xx
x
x
xx

++

⇔− + +=

−+
− + −+

Dễ thấy :
Với điều kiện
3
1
5
x ≥
thì
( )
2
32
3
3
5( 1) 2
10
5 12
21 211
xx
x
xx
++
+ +>
−+
− + −+
Nên phương trình đã cho có nghiệm duy nhất
2x =
b). Điều kiện:
[ ]
2; 4x ∈
Ta nhẩm được nghiệm của phương trình là:
3x =
. Khi đó
2 321;4 431xx−= −= −= −=
Từ đó ta có lời giải như sau:
THCS.TOANMATH.com
Phương trình đã cho tương đương với:
2
2 11 4 2 5 3x xx x− −+− − = − −
33
( 3)(2 1)
211 4
xx
xx
xx
−−
⇔ + =−+
−− + −
( )
11
3 (2 1) 0
211 4
xx
xx

⇔− + − + =

−− + −

3
11
(2 1) 0
211 4
x
x
xx
=
+ − +=
−+ + −
Để ý rằng: Với điều kiện
[ ]
2; 4x
∈
thì
11
1; 1; 2 1 5
21 1 4
x
xx
≤ ≤ +≥
−+ + −
nên
11
(2 1) 0
211 4
x
xx
+ − +<
−+ + −
Từ đó suy ra:
3
x =
là nghiệm duy nhất của phương trình.
Nhận xét: Để đánh giá phương trình cuối cùng vô nghiệm ta thường dùng
các ước lượng cơ bản:
AB A+≥
với
0B ≥
từ đó suy ra
1
A
AB
≤
+
với mọi
số
,AB
thỏa mãn
0
0
AB
B
+>
≥
Ví dụ 2: Giải các phương trình:
a)
3
23
12x xx−+ = −
b)
( )
3
2
3
2 4 7 3 28 0x xx x x− − − −− + =
Giải:
a). Điều kiện:
3
2x ≥
.
THCS.TOANMATH.com
Ta nhẩm được nghiệm
3
x =
. Nên phương trình được viết lại như sau:
3
23
12 3 25x xx−−+−= −−
23
33
22 3
9 27
3
12 14 25
xx
x
xx x
−−
⇔ +−=
−+ −+ − +
2
33
22 3
3 39
( 3) 1 0
12 14 25
x xx
x
xx x

+ ++
⇔ − +− =

−+ −+ − +

2
33
22 3
3
3 39
10
12 14 25
x
x xx
xx x
=
⇔
+ ++
+− =
−+ −+ − +
Ta dự đoán:
2
33
22 3
3 39
10
12 14 25
x xx
xx x
+ ++
+− <
−+ −+ − +
( Bằng cách thay
một giá trị
3
2x ≥
ta sẽ thấy
2
33
22 3
3 39
10
12 14 25
x xx
xx x
+ ++
+− <
−+ −+ − +
)
Ta sẽ chứng minh:
33
22
3
1
12 14
x
xx
+
<
−+ −+
và
2
3
39
2
25
xx
x
++
>
−+
Thật vậy:
+ Ta xét
( )
( )
2
3
22
3
2
3
22
3
3
1 12 1 1
1 2 14
x
x xx
xx
+
<⇔ − + −>−
− + −+
Đặt
3
23
10 1x t xt−=>⇒ = +
. Bất phương trình tương đương với
2 3 432
21 1 3 6 4 0tt t tttt+ +> +⇔ + + + >
. Điều này là hiển nhiên đúng.
THCS.TOANMATH.com
+ Ta xét:
2
2 3 432
3
39
2 3 12 2 2 7 6 90
25
xx
xx x xxxx
x
++
>⇔+−> −⇔+ + −+>
−+
0(*)
x∀≥
. Điều này luôn đúng.
Từ đó suy ra phương trình có nghiệm duy nhất:
3x =
b.) Điều kiện:
7x ≥
.
Để đơn giản ta đặt
3
33
7xt xt=≥ ⇒=
Phương trình đã cho trở thành:
2 33 3 32 33
2 ( 4) 7 3 28 0 3 2 28 ( 4) 7 0tttt t ttt tt−−−−−+=⇔−+−+−−=
Nhẩm được
2
t
=
. Nên ta phân tích phương trình thành:
(
)
32 3 3
4 2 32 ( 4) 7 1 0tt t t t
⇔ − + − + − −− =
( )
2
23
3
24
( 2) 4 7 16 ( 4) 0
71
tt
t tt t
t


++
⇔− ++ + − =


−+



Để ý rằng
2
4 7 16 0tt++>
và
3
7t ≥
nên ta có
( )
2
23
3
24
4 7 16 ( 4) 0
71
tt
tt t
t

++
++ + − >

−+

. Vì vậy phương trình có nghiệm
duy nhất
28tx=⇔=
.
Nhận xét: Việc đặt
3
xt=
trong bài toán để giảm số lượng dấu căn đã giúp
đơn giản hình thức bài toán .
Ngoài ra khi tạo liên hợp do
3
( 4) 0t −>
nên ta tách nó ra khỏi biểu thức để
các thao tác tính toán được đơn giản hơn.
Ví dụ 3: Giải các phương trình:
a)
2
4 3 19 3 2 9x xx x++ − = + +
THCS.TOANMATH.com
b)
c)
( )
2
37
21
x
x
xx
+
+=
+
(Tuyển sinh vòng 1 lớp 10 Trường THPT
chuyên Tự nhiên- ĐHQG Hà Nội 2012)
d)
32
2
2
5 42
2
23
xxx
xx
xx
+ ++
= ++
++
a). Điều kiện:
19
3
3
x−≤ ≤
Ta nhẩm được 2 nghiệm là
1, 2xx= = −
nên ta phân tích để tạo ra nhân tử
chung là:
2
2
xx+−
. Để làm được điều này ta thực hiện thêm bớt nhân tử
như sau:
+ Ta tạo ra
4 3( )0
x ax b+− + =
sao cho phương trình này nhận
1, 2xx
= = −
là nghiệm.
Để có điều này ta cần:
4
8
3
2 4 20
3
a
ab
ab
b
=
+=
⇔

− +=
=
+ Tương tự
19 3 ( ) 0x mx n−− +=
nhận
1, 2xx= = −
là nghiệm.
Tức là
1
5
3
2 5 13
3
a
mn
mn
b
= −
+=
⇔

− +=
=
Từ đó ta phân tích phương trình thành:
THCS.TOANMATH.com
( )
2
4 20 13
4 3 x 19 3 2 0
3 3 33
x
x x xx

+− + + − − − − +− =


( )
(
)
2
4 3 19 3 (13 )
3 3 5 20
33
xx
x x xx
−− −

⇔ +− + + − −− =

( )
( )
22
2
42 2
20
3
33 5
3 3 19 3 (13 )
xx xx
xx
xx
xx

− −+ − −+
⇔ + − +− =


++ +
−+ −



( )
( )
2
41 1
2 . 10
3
33 5
3 3 19 3 (13 )
xx
xx
xx


⇔− − − + + =


++ +
−+ −


Dễ thấy với
19
3
3
x−≤ ≤
thì
( )
1
0,
33 5xx
>
++ +
1
0
3 3 19 3 (13 )xx
>

−+ −

Nên
( )
41 1
. 10
3
33 5
3 3 19 3 (13 )
xx
xx
+ +>

++ +
−+ −

.
Phương trình đã cho tương đương với
2
1
20
2
x
xx
x
=
+−=⇔
= −
Vậy phương trình có 2 nghiệm là:
3, 8
xx= =
.
b). Điều kiện:
8
3
x ≥
.
Phương trình được viết lại như sau:
5 3 8 5 1 2 11x xx−− += −
THCS.TOANMATH.com
Ta nhẩm được 2 nghiệm
3, 8xx= =
nên suy ra nhân tử chung là:
2
11 24xx
−+
Ta phân tích với nhân tử
53 8
x −
như sau:
+ Tạo ra
( )
53 8 0x ax b−− + =
sao cho phương trình này nhận
3, 8xx= =
là nghiệm. Tức là
,
ab
cần thỏa mãn hệ:
35 3
8 20 4
ab a
ab b
+= =

⇔

+= =−

+ Tương tự với
5 1( )0x mx n
+− + =
ta thu được:
3 10 1
8 15 7
mn m
mn n
+= =

⇔

+= =

Phương trình đã cho trở thành:
22
9( 11 24) 11 24
5 3 8 (3 4) ( 7) 5 1 0 0
5 3 8 (3 4) ( 7) 5 1
xx xx
xxx x
xxx x
− −+ −+
−− − + + − += ⇔ + =
−+ − + + +
( )
2
91
11 24 0
5 3 8 (3 4) ( 7) 5 1
xx
xxx x

−
⇔−+ + =

−+ − + + +

2
11 24 0
91
0
5 3 8 (3 4) ( 7) 5 1
xx
xxx x
− +=
⇔
−
+=
−+ − + + +
Ta xét
91
()
5 3 8 (3 4) ( 7) 5 1
Ax
xxx x
−
= +
−+ − + + +
Ta chứng minh:
() 0Ax <
tức là:
91
0
5 3 8 (3 4) ( 7) 5 1xxx x
−
+<
−+ − + + +
5 3 8 3 4 9( 7 5 1) 0xx x x⇔ −+ −− ++ + <
THCS.TOANMATH.com
25 275
38538 45 10
44
x x xx⇔ −− −+ + ++ +>
2
5 275
3 8 45 1 0
24
x xx

⇔ −− + ++ +>


. Điều này là hiển nhiên đúng.
Vậy phương trình có 2 nghiệm là:
3, 8xx
= =
.
Chú ý:
Những đánh giá để kết luận
() 0Ax <
thường là những bất đẳng thức không
chặt nên ta luôn đưa về được tổng các biểu thức bình phương.
Ngoài ra nếu tinh ý ta có thể thấy:
5 3 8 3 4 9( 7 5 1) 0xx x x−+ −− ++ + <
5 3 8 3 4 9 63 5 81 81xxx x−+ −≤ + + +
Nhưng điều này là hiển nhiên đúng
do:
5 3 8 5 81 81;3 4 9 63x xx x−< + −< +
với mọi
8
3
x ≥
c). Điều kiện:
0x >
Ta nhẩm được
1; 3xx= =
nên biến đổi phương trình như sau:
Ta có: khi
1x = ⇒
( )
2
7
2
21
x
x
+
=
+
, khi
( )
2
7
32
21
x
x
x
+
=⇒=
+
nên ta trừ 2 vào 2
vế thì thu được:
( )
2 22
3 7 32 4 3
22
2 1 2( 1)
x x xx x
x
xx x
x
+ +− − +
+ −= −⇔ =
++
2
22
3
3
4 30
43 43
2( 1)
32
3 2 2( 1)
xx
xx xx
x
x xx
x xx x
− +=
−+ −+
= ⇔
+
++
++= +
(1)
(2)
Giải (1) suy ra
1, 3xx= =
Giải (2) ta có:
3
3 2 2( 1)x xx x++= +
33
3 2 3 40 1xx xx x⇔ + =⇔ + −=⇔=
Kết luận: Phương trình có nghiệm là
1; 3xx= =
THCS.TOANMATH.com
Nhận xét: Ta cũng có thể phân tích phương trình như câu a,b .
d). Ta có:
32 2
5 4 2 ( 3)( 2 3) 5 7
xxx x xx x+ ++=+ ++−−
nên phương trình
tương đương với
32
22
22
5 42 57
2 3 23 0
23 23
xxx x
xx x x x
xx xx
+ ++ +
= ++⇔+− + +− =
++ ++
(
)
2
2
11
57 0
23
( 3) 2
x
xx
x xx

⇔+ − =


++
+ + ++

( )
2
2
570
11
0 (1)
23
( 3) 2
x
xx
x xx
+=

⇔
−=


++
+ + ++

Giải
(1)
:
22
2
2
11
20
23
( 3) 2
xx xx
xx
x xx
− ⇔ +− ++=
++
+ + ++
.
Đặt
2
20xxt ++>=
. Phương trình trở thành:
22
2
20
1( )
1
20
2
x
xx
x
t
tt
tL
=
−− = ⇔ ⇔
= −
=
+−=⇔
= −
Kết luận: Phương trình có 3 nghiệm:
7
; 1; 2
5
x xx=−==−
Ví dụ 5: Giải các phương trình sau:
a)
33
15 2 8 3x xx+ += ++
b)
3 1 31 0xx x
+− + +− =
a). Phương trình được viết lại như sau:
THCS.TOANMATH.com
3 3 33
15 2 8 3 15 8 3 2x x xx x x++= ++⇔ +− +=−
.Để phương trình
có nghiệm ta cần:
2
3 20
3
xx
−≥⇔≥
. Nhẩm được
1x =
nên ta viết lại
phương trình thành:
33
15 4 8 3 3 3x xx+ −= +−+ −
( )
( )
22
33
11
( 1) 3 0
15 4 8 3
xx xx
x
xx

++ ++

⇔− − −=

+ + ++

Để ý rằng:
( ) ( )
22
33
11
30
15 4 8 3
xx xx
xx
++ ++
− −<
+ + ++
nên phương trình có nghiệm
duy nhất
1x =
b). Điều kiện
1
3;
3
x

∈− −


Ta viết lại phương trình như sau:
3 1 31 0xx x+− + +− =
(
)
22 1 1
1 0 22 0
2
31 3 31 3
x
xx
xx xx
−

⇔ +− = ⇔ − − =

++ + ++ +

1
3 1 32
x
xx
=
⇔
++ + =
Xét phương trình:
3 1 32xx++ + =
. Bình phương 2 vế ta thu được:
2
0
4 4 2 (3 1)( 3) 4 (3 1)( 3) 2
10 3 0
x
x xx xx x
xx
≤
++ + +=⇔ + +=−⇔
− −=
5 27x⇔=−
Kết luận: Phương trình có 2 nghiệm là
1, 5 2 7xx
= = −
THCS.TOANMATH.com
Nhận xét:
+ Ta thấy phương trình có nghiệm
1x =
. Nếu ta phân tích phương trình
thành
3 122 344 0x xx+−+− ++− =
thì sau khi liên hợp phương trình
mới thu được sẽ là:
33 1
44 0
3 12 2 3
xx
x
xx
−−
+ +− =
++ + +
( )
31
1 40
3 12 2 3
x
xx

⇔− + −=

++ + +

.Rõ ràng phương trình hệ quả
31
40
3 12 2 3xx
+ −=
++ + +
phức tạp hơn phương trình ban đấu rất
nhiều.
+ Để ý rằng khi
1x =
thì
31 3xx+= +
nên ta sẽ liên hợp trực tiếp biểu
thức
31 3xx+− +
.
2. Đặt ẩn phụ dựa vào tính đẳng cấp của phương trình:
Ta thường gặp phương trình dạng này ở các dạng biến thể như:
+
2 32
ax bx c d px qx rx t+ += + + +
(1)
+
2 4 32
ax bx c d px qx rx ex h+ += + + + +
(2)
+
22 2
A ax bx c B ex gx h C rx px q+ ++ + += + +
(*)
Thực chất phương trình
(*)
khi bình phương 2 vế thì xuất hiện theo dạng
(1)
hoặc (2).
Để giải các phương trình (1), (2).
Phương pháp chung là:
+ Phân tích biểu thức trong dấu thành tích của
2
đa thức
(), ()Px Qx
THCS.TOANMATH.com
+ Ta biến đổi
2
() ()ax bx c mP x nQ x+ += +
bằng cách đồng nhất hai vế.
Khi đó phương trình trở thành:
() () (). ()mPx nQx d PxQx+=
Chia hai vế cho biểu thức
() 0Qx
>
ta thu được phương trình:
() ()
() ()
Px Px
m nd
Qx Qx
+=
. Đặt
()
0
()
Px
t
Qx
= ≥
thì thu được phương trình:
2
0mt dt n− +=
.
Một cách tổng quát: Với mọi phương trình có dạng:
2
() () () () (). () 0
n n nk k
n
aP x bQ x cP x Q x d P x Q x
−
++ + =
thì ta luôn giải được
theo cách trên.
Một số ví dụ:
Ví dụ 1: Giải các phương trình:
a)
23
2( 3 2) 3 8
xx x−+= +
b)
2
1 4 13x xx x++ − +=
c)
(
) ( )
22 3
4 3 12 1x x xx x+ − += +
Lời giải:
a). Điều kiện:
2x ≥−
.
Ta viết lại phương trình thành:
22
2( 3 2) 3 ( 2)( 2 4)xx x xx−+= + −+
Giả sử
22
3 2 ( 2) ( 2 4)x x mx nx x− += + + − +
. Suy ra
,mn
phải thỏa mãn
THCS.TOANMATH.com
1
1
23
1
242
n
m
mn
n
mn
=
= −
− =−⇔

=
+=
Phương trình đã cho có dạng:
22
2( 2) 2( 2 4) 3 ( 2)( 2 4) 0x xx x xx− ++ − +− + − +=
.
Chia phương trình cho
2
2 40
xx− +>
ta thu được:
22
2 ( 2)
2 3 20
24 ( 24)
xx
xx xx
++

− − +=

−+ −+

Đặt
2
( 2)
0
( 2 4)
x
t
xx
+
= ≥
−+
ta thu được phương trình:
2
2 3 20
tt− − +=
2
1
2
t
t
= −
⇔
=
do
2
2
1 ( 2) 1
0 2 4 4( 2)
2 ( 2 4) 2
x
t t xx x
xx
+
≥⇒= ⇔ = ⇔ − += +
−+
.
2
3 13
6 40
3 13
x
xx
x
= +
− −=⇔
= −
b). Điều kiện:
2
0
4 10
x
xx
≥
− +≥
Bình phương 2 vế của phương trình ta thu được:
2 22
212(1) 41 419xx x xx xx x+++ + −++−+=
2 22
2 11 2 2 ( 2 1)( 4 1) 0x x xxxx⇔ − ++ + + − + =
Giả sử
THCS.TOANMATH.com
2 22
1
2
2
2 11 2 ( 2 1) ( 4 1) 2 4 11
5
2
2
mn
m
x x mx x nx x m n
n
mn
+=
= −

− += + ++ − +⇒ − =− ⇔


=
+=
Phương trình trở thành:
2 2 22
15
( 2 1) ( 4 1) 2 ( 2 1)( 4 1) 0
22
xx xx xxxx− + ++ − ++ + + − +=
Chia phương trình cho
2
2 10
xx+ +>
ta thu được:
22
22
41 41
15 4 0
21 21
xx xx
xx xx

−+ −+
−+ + =

++ ++

. Đặt
2
2
41
0
21
xx
t
xx

−+
= ≥

++

ta có
Phương trình
2
2
2
1
1 41 1
5 4 10
1
5 2 1 25
5
t
xx
tt t
xx
t
= −

−+
+ −= ⇔ ⇔= ⇔ =

++
=

2
1
24 102 24 0
4
4
x
xx
x
=
⇔ − +=⇔
=
Kết luận: Phương trình có 2 nghiệm
1
,4
4
xx= =
Nhận xét: Trong lời giải ta đã biến đổi:
2 22
( 1) 4 1 ( 2 1)( 4 1)
x xx xxxx+ −+= ++ −+
là vì
10x +>
c). Điều kiện:
1x ≥−
Ta viết lại phương trình thành:
( )
2
12 2 23 1 0x x x xx

− − −− + =

2
1
2 2 23 1 0
x
x x xx
=
⇔
− −− +=
THCS.TOANMATH.com
Xét phương trình:
22
2223102312(1)0
x x xx x xx x−−−+=⇔−+−+=
.
Dễ thấy
1x = −
không phải là nghiệm.
Xét
1
x
>−
ta chia cho
1x +
thì thu được phương trình:
2
2
1
2 3 20
1
1
1
1
x
xx
x
x
x
x
x
=
+
− −=⇔
+
+
= −
+
(1)
(2)
Giải (1):
2
0
2 2 22
4 40
1
x
x
x
xx
x
≥
=⇔ ⇔=+
− −=
+
Giải (2):
2
0
1 2 22
4 40
1
x
x
x
xx
x
≤
=−⇔ ⇔ = −
− −=
+
Kết hợp điều kiện ta suy ra các nghiệm của phương trình là:
1; 2 2 2xx= = ±
Ví dụ 2: Giải các phương trình:
a)
22 3
4(2 1) 3( 2 ) 2 1 2( 5 )
x x xx x x+ + − −= +
b)
22
5 4 3 18 5x xx x x+ − −−=
c)
22
5 14 9 20 5 1x x xx x− +− −− = +
Lời giải:
a). Điều kiện
1
2
x ≥
Phương trình đã cho được viết lại như sau:
THCS.TOANMATH.com
32
2 8 10 4 3 ( 2) 2 1 0x x x xx x− + −− − −=
2
( 2)(2 4 2) 3 ( 2) 2 1 0x x x xx x⇔ − − + − − −=
2
( 2) (2 4 2) 3 2 1 0
x x x xx

⇔− − +− −=

2
20
(2 4 2) 3 2 1 0
x
x x xx
−=
⇔
− + − −=
Xét phương trình:
2 22
2 4 23 2 1 0 2 4 23 (2 1) 0xx xx xx xx
− +− −=⇔ − +− − =
Ta giả sử:
22
2
2 4 2 (2 1)
2
m
x x mx n x
n
=
− += + −⇒
= −
Phương trình trở thành:
22
2 2(2 1) 3 (2 1) 0x x xx
− −− − =
. Chia cho
2
0x >
Ta có:
22
21 21
2 2. 3 0
xx
xx
−−

− −=


. Đặt
2
21
0
x
t
x
−
= ≥
phương trình mới
là:
2
2
2 3 20
1
2
t
tt
t
= −
− − +=⇔
=
Với
1
2
t
=
ta có:
2
2
4 23
2 11
8 40
2
4 23
x
x
xx
x
x
= +
−
= ⇔ − +=⇔
= −
Nhận xét:
+ Đối với phương trình
2
2 4 23 2 1 0x x xx
− +− −=
ta có thể không cần
đưa
x
vào trong dấu khi đó ta phân tích:
22
2 4 2 (2 1)x x mx n x− += + −
và chia như trên thì bài toán vẫn được giải quyết. Việc đưa vào là giúp
các em học sinh nhìn rõ hơn bản chất bài toán.
THCS.TOANMATH.com
+ Ngoài ra cần lưu ý rằng: Khi đưa một biểu thức
()Px
vào trong dấu
2n
thì điều kiện là
() 0Px ≥
. Đây là một sai lầm học sinh thường mắc phải khi
giải toán.
b). Điều kiện:
2
2
3 18 0
06
5 40
xx
xx
xx
−−≥
≥ ⇔≥
+≥
.
Phương trình đã cho được viết lại thành:
22
5 4 3 18 5xxxx x+ = −−+
Bình phương 2 vế và thu gọn ta được:
22
2 9 9 5 ( 3 18) 0x x xx x− +− − − =
Nếu ta giả sử
22
2 9 9 ( 3 18)x x mx n x x− += + − −
thì
,mn
phải thỏa mãn
2
39
18 9
n
mn
n
=
−=−
−=
điều này là hoàn toàn vô lý.
Để khắc phục vấn đề này ta có chú ý sau :
2
3 18 ( 6)( 3)xx x x
−−=− +
khi
đó
22
( 318) (6)(3) ( 6)(3)xx x xx x x x x−− = − += − +
Bây giờ ta viết lại phương trình thành:
22
2 9 9 5 ( 6 )( 3) 0x x x xx− +− − + =
Giả sử:
22
2
2
2 9 9 ( 6 ) ( 3) 6 9
3
3
m
m
x x mx x nx m n
n
n
=
=
− + = − + + ⇒− + =−⇔

=
=
Như vậy phương trình trở thành:
22
2( 6 ) 3( 3) 5 ( 6 )( 3) 0xx x xxx− + +− − + =
Chia cho
30x +>
ta thu được:
22
66
2 5 30
33
xx xx
xx

−−
− +=

++

THCS.TOANMATH.com
Đặt
2
2
1
6
0 2 5 30
3
3
2
t
xx
t tt
x
t
=

−
= ≥⇒ − +=⇔

+
=

Trường hợp 1:
2
2
7 61
6
2
1 1 7 30
3
7 61
2
x
xx
t xx
x
x
+
=

−
=⇔ =⇔ − −=⇔

+
−

=
Suy ra
7 61
2
x
+
=
thỏa mãn điều kiện.
Trường hợp 2:
2
2
9
3 63
4 33 27 0 9
3
2 32
4
x
xx
t xx x
x
x
=

−
=⇔ = ⇔ − − =⇔ ⇒=

+
= −

Tóm lại: Phương trình có 2 nghiệm là:
7 61
2
x
+
=
và
9x =
c). Điều kiện
5
x ≥
.
Chuyển vế bình phương ta được:
( )
( )
22
2 5 2 5 20 1x x xx x− += −− +
Giả sử:
(
)
( )
22
2 5 2 20 1x x mx x nx− += −− + +
Khi đó ta có :
2
5
20 2
m
mn
mn
=
−+=−
− +=
không tồn tại
,mn
thỏa mãn hệ.
Nhưng ta có :
( )
(
) ( )( )( ) ( )
( )
22
201451445xxxxxxxxx−− += + − += + − −
THCS.TOANMATH.com
Giả sử:
( )
( )
22
2 52 45 4
xx xx x
αβ
− += − − + +
. Suy ra
2
2
45
3
542
m
m
mn
n
mn
=
=
− + =−⇒

=
−+=
Ta viết lại phương trình:
( )
( )
22
2 453 45( 45)(4)xx x xx x−−+ += −− +
.
Chia hai vế cho
40x +>
ta thu được:
22
45 45
2 5 30
44
xx xx
xx

−− −−
− +=

++

Đặt
2
45
0
4
xx
t
x

−−
= ≥

+

ta thu được phương trình:
2
1
2 5 30
3
2
t
tt
t
=
− +=⇔
=
Trường hợp 1:
2
2
5 61
45
2
1 1 5 90
4
5 61
2
x
xx
t xx
x
x
+
=
−−
=⇔ =⇔ − −=⇔
+
−
=
Trường hợp 2:
2
2
8
3 4 59
4 25 56 0
7
2 44
4
x
xx
t xx
x
x
=
−−
=⇔ =⇔ − −=⇔
+
= −
Kết hợp điều kiện ta suy ra các nghiệm của phương trình là:
5 61
8;
2
xx
+
= =
Ví dụ 3: Giải các phương trình:
a)
22
2 21 3 41xx x xx+ + −= + +
THCS.TOANMATH.com
b)
32 3
3 2 ( 2) 6 0xx x x
− + + −=
Lời giải: a). Điều kiện:
1
2
x
≥
.
Bình phương 2 vế phương trình ta thu được:
2 2 2 22
412( 2)(21)3 41 1 ( 2)(21)0
xx xxx xx x xxx+ −+ + −= + +⇔ +− + −=
Ta giả sử:
22
1
1
1 ( 2 ) (2 1) 1
1
220
m
m
x mx x n x n
n
mn
=
=
+= + + − ⇔ =− ⇔

= −
+=
Phương trình trở thành:
22
22
21 21
( 2 ) (2 1) ( 2 )(2 1) 0 1 0
22
xx
xx x xxx
xx xx
−−

+ − − − + − = ⇔− − + =

++

Đặt
2
2
21 1 5
0 10
22
x
t tt t
xx
− −±

= ≥ ⇒− − + = ⇔ =

+

Về cơ bản đến đây ta hoàn toàn tìm được
x
. Nhưng với giá trị
( )
2
3
1
0
31x
>
+
như vậy việc tính toán sẽ gặp khó khăn.
Để khắc phục ta có thể xử lý theo hướng khác như sau:
Ta viết lại:
22
( 2 )(2 1) ( 2)(2 )x xx x xx+ −= + −
lúc này bằng cách phân
tích như trên ta thu được phương trình:
22
22
11 22
(2 ) ( 2) ( 2)(2 ) 0 2 1 0
22 22
xx xx
xx x x xx
xx
−−
−+ +− + −=⇔ − +=
++
THCS.TOANMATH.com
Đặt
2
2 22
2
0 2 10 1 2 2 10
2
xx
t t t t xxx xx
x
−
= ≥⇒ − +=⇔=⇔ −=+⇔ −−=
+
15
2
x
±
⇔=
. Kiểm tra điều kiện ta thấy chỉ có giá trị
15
2
x
+
=
là thỏa
mãn điều kiện.
b). Điều kiện:
2
x ≥−
.
Ta viết lại phương trình thành:
33
3 ( 2) 2 ( 2) 0x xx x− ++ + =
Để ý rằng:
Nếu ta đặt
2
yx= +
thì phương trình trở thành:
3 23
3 20x xy y
− +=
. Đây
là một phương trình đẳng cấp bậc
3
. Từ định hướng trên ta có lời giải cho
bài toán như sau:
+ Xét trường hợp:
0x =
không thỏa mãn phương trình:
+ Xét
0x ≠
. Ta chia phương trình cho
3
x
thì thu được:
3
23
( 2)
( 2)
13 2 0
x
x
xx
+
+
−+ =
.
Đặt
2x
t
x
+
=
ta có phương trình:
32
1
2 3 10
2
1
t
tt
t
= −
− += ⇔
=
Trường hợp 1:
1
2
t
= −
2
0
21
2 2 2 23
2
4 80
x
x
xx x
x
xx
≤
+
⇔ =− ⇔ + =−⇔ ⇔ =−
− −=
Trường hợp 1:
1t =
THCS.TOANMATH.com
2
0
2
12 2
20
x
x
xx x
x
xx
≥
+
⇔ =⇔ +=⇔ ⇔=
−−=
Kết luận: Phương trình có 2 nghiệm:
2; 2 2 3xx= = −
Ví dụ 4: Giải các phương trình:
a)
32 54
2 31 1
xx x xx− − += + +
b)
42
5 84 8x xx
+= +
Lời giải:
a). Hình thức bài toán dễ làm cho người giải bối rối nhưng để ý thật kỹ ta
thấy:
Chìa khóa bài toán nằm ở vấn đề phân tích biểu thức:
54
1xx++
Ta thấy do vế trái là biểu thức bậc
3
nên ta nghỉ đến hướng phân tích:
54 2 3 2
1 ( 1)( 1)x x x ax x bx cx+ += + + + + +
. Đồng nhất hai vế ta thu được:
1; 0; 1ab c= = = −
. Nên ta viết lại phương trình đã cho thành:
3 2 32
2( 1) ( 1) ( 1).( 1) 0xx xx xx xx−+ − ++ − −+ ++ =
Chia cho
2
10xx+ +>
ta thu được:
33
22
11
2. 1 0
11
xx xx
xx xx

−+ −+
− −=

++ ++

. Đặt
3
2
1
0
1
xx
t
xx

−+
= ≥

++

ta có
phương trình:
2
1
2 10
1
()
2
t
tt
tL
=
−−= ⇔
= −
THCS.TOANMATH.com
Giải
3
32
2
0
1
1 1 20 1
1
2
x
xx
t xx x x
xx
x
=
−+
=⇔ =⇔−− =⇔ =−
++
=
Kết luận: Thử lại ta thấy
3
nghiệm:
0, 1; 2xx x= =−=
đều thỏa mãn.
b). Điều kiện:
4
0
80
2
x
xx
x
≥
+ ≥⇔
≤−
Ta thấy chìa khóa bài toán nằm ở việc phân tích biểu thức:
( )
( )
( ) ( )( )
4 3 2 22
8 8 2 24 2 24xxxx xx xx xxxx+= += + −+= + −+
Giả sử
22 2
4
4 8 ( 2 4) ( 2 ) 2 2 0 2
48
mn
x mx x nx x m n m n
m
+=
+= − + + + ⇒− + = ⇔ = =
=
Phương trình trở thành:
2 2 22
2( 2 4) 2( 2 ) 5 ( 2 4)( 2 ) 0xx xx xx xx−++ + − −+ + =
. Chia hai vế cho
2
2 40xx
− +>
ta thu được:
22
22
22
2 5 20
24 24
xx xx
xx xx
++
− +=
−+ −+
. Đặt
2
2
2
0
24
xx
t
xx
+
= ≥
−+
ta có phương trình:
2
2
2 5 20
1
2
t
tt
t
=
− +=⇔
=
Trường hợp 1:
2
2
2
2
2 4 3 10 16 0
24
xx
t xx
xx
+
=⇔ =⇔ − +=
−+
vô nghiệm
Trường hợp 2:
2
2
2
5 37
1 21
3
3 10 4 0
2 2 44
5 37
3
x
xx
t xx
xx
x
−−
=
+
= ⇔ = ⇔ + −=⇔
−+
−+
=
THCS.TOANMATH.com
Kết luận: Phương trình có hai nghiệm là:
5 37
3
5 37
3
x
x
−−
=
−+
=
Nhận xét: Ta có thể phân tích:
( )
4 3 2 22
8 8 ( 2)( 2 4) ( 2 )( 2 4)xxxx xx xx xxxx+= += + −+= + −+
Chú ý rằng: Trong một số phương trình: Ta cần dựa vào tính đẳng cấp của
từng nhóm số hạng để từ đó phân tích tạo thành nhân tử chung.
Ví dụ 5: Giải các phương trình:
a)
2
( 2)( 2 3 2 1) 2 5 3 1 0x x x xx
+ +− + + + +−=
b)
22
( 4) 2 4 3 6 4x x xx
+ += + −
c)
2 22
( 6 11) 1 2( 4 7) 2
x x xx x x x
− + −+= − + −
Giải:
a). Đặt
23 , 1 , 0x a x b ab+= +=⇒ ≥
Phương trình đã cho trở thành:
22 2 2
( )( 2 ) ( 2 ) 0a b a b a ab b− − − −− =
( 2 )( )( ) ( )( 2 ) 0 ( 2 )( )( 1) 0a ba ba b a ba b a ba ba b⇔− −+−−−=⇔− −+−=
Ta quy bài toán về giải 3 phương trình cơ bản là:
2 3 10
22 3 1 0
2 3 110
xx
xx
xx
+− +=
+− +=
+ + +−=
Với điều kiện:
1 1, 0x ab≥− ⇒ ≥ ≥
THCS.TOANMATH.com
Trường hợp 1:
23 1023 1 2()
x x xx xL+− += ⇔ += +⇔ =−
Trường hợp 2:
11
2 2 3 1 0 8 12 1 ( )
7
x x xxx L+− += ⇔ + = +⇔ =−
Trường hợp 3:
2 3 110xx
+ + +−= . Vì
2 3 1, 1 0 0x x VT+≥ +≥⇒ ≥
Dấu bằng xảy ra khi và chỉ khi
1x = −
.
Tóm lại phương trình có nghiệm duy nhất
1x = −
b). Điều kiện
2x ≥−
Ta thấy rằng nếu bình phương trực tiếp sẽ dẫn đến phương trình bậc
5
Để khắc phục ta sẽ tìm cách tách
2
4x +
ra khỏi
24x
+
Từ đó ta viết lại phương trình như sau:
2 22
( 4) 2 4 4 4 6x x x xx
+ ++ += +
2 22
( 4)( 2 4 1) 2 (2 3) ( 4)( 2 4 1) 2 ( (2 4) 1)xx xxxx xx⇔ + ++= + ⇔ + ++= + −
2
( 4)( 2 4 1) 2 ( 2 4 1)( 2 4 1)x x xx x⇔ + ++= ++ +−
Do
2 410
x + +>
. Phương trình đã cho tương đương với
( )
2
22
42(241) 242240 24 0x x x x x xx x x⇔+= +−⇔++− +=⇔− + =
2
2 40 2 40 1 5x x xx x− +=⇔ − −=⇒=+
Kết luận: Phương trình có nghiệm duy nhất
15x = +
c). Điều kiện:
2x ≥
THCS.TOANMATH.com
Giả sử
22
1
6 11 ( 1) ( 2) 6 1, 5
2 11
m
x x mx x nx m n m n
mn
=
− + = −++ − ⇒−+=−⇔ = =−
−=
22
1
4 7 ( 1) ( 2) 4 1, 3
27
p
x x px x qx p q p q
pq
=
− += −+ + − ⇒−+=−⇔ = =−
−=
Phương trình đã cho trở thành:
2 22
( 1) 5( 2) 1 2 ( 1) 3( 2) 2 0xx x xx xx x x

−+ − − −+− −+ − − −=

Chia phương trình cho
23
( 1)xx−+
ta thu được:
3
22 2
22 2
1 5. 2 6 0
11 1
xx x
xx xx xx
−− −

−− + =

−+ −+ −+

Đặt
2
2
0
1
x
t
xx
−
= ≥
−+
Ta thu được phương trình:
32
1
1
6 5 2 10
3
1
()
2
t
ttt t
tL
=
− − += ⇔ =
= −
+ Nếu
2
1 2 3 0( )t a b x x VN=⇔ =⇔ − +=
+ Nếu
2
1
10 19 0 5 6
3
t xx x=⇔ − + =⇔=±
Kết luận:
56x = ±
THCS.TOANMATH.com
2. Giải phương trình vô tỷ bằng phương pháp đặt ẩn phụ không hoàn
toàn.
+ Đặt ẩn phụ không hoàn toàn là phương pháp chọn một số hạng trong
phương trình để đặt làm ẩn sau đó ta quy phương trình ban đầu về dạng một
phương trình bậc 2:
2
() () 0mt g x t h x
+ +=
( phương trình này vẫn còn ẩn
x
)
+ Vấn đề của bài toán là phải chọn giá trị
m
bằng bao nhiêu để phương
trình bậc 2 theo ẩn
t
có giá trị
∆
chẵn
[
]
(
)
2
()
Ax∆=
như thế viêc tính
t
theo
x
sẽ được dễ dàng.
+ Thông thường khi gặp các phương trình dạng:
22
() 0ax bx c dx e px qx r+ ++ + + +=
thì phương pháp đặt ẩn phụ không
hoàn toàn tỏ ra rất hiệu quả:
+ Để giải các phương trình dạng này ta thường làm theo cách:
- Đặt
2
() ()fx t t fx=⇒=
- Ta tạo ra phương trình:
2
() () 0mt g x t h x+ +=
Ta có
[ ]
2
2
1 11
() 4.() () () ()gx mhx f mx g mx h m∆= − = + +
. Để
∆
có dạng
[ ]
2
()Ax
thì điều kiện cần và đủ là
[ ]
2
1 11
() 4().() 0
m
gm fmgm m∆= − =⇒
Ta xét các ví dụ sau:
Ta xét các ví dụ sau:
Ví dụ 1: Giải các phương trình:
a)
22
1 ( 1) 2 3 0x x xx+− + − + =
THCS.TOANMATH.com
b)
2
22 4 42 9 16x xx++ −= +
c)
2
(27)27 97
x x xx+ += + +
(Trích đề TS lớp 10 Chuyên Tự nhiên –
ĐHQG Hà Nội 2009)
Giải:
a) Đặt
2 22
230 23txx txx= −+>⇒=−+
Phương trình đã cho trở thành:
2
1(1)0x xt+− + =
Ta sẽ tạo ra phương trình:
2 22
( 1) 1 ( 2 3) 0mt x t x m x x−+++− − +=
(Ta đã thêm vào
2
mt
nên phải bớt đi một lượng
22
( 2 3)mt m x x= −+
)
Phương trình được viết lại như sau:
22
( 1) (1 ) 2 1 3 0mt x t m x mx m− + + − + +− =
22
( 1) 4 (1 ) 2 1 3x m m x mx m

⇒∆= + − − + + −

2 2 22
(4 4 1) (2 8 ) 12 4 1
mmx mxmm= −+ +− + −+
Ta mong muốn
2 22 2 2
(Ax ) (1 4 ) (12 4 1)(4 4 1) 0 1
m
B m mm mm m∆= + ⇔∆=− − −+ −+=⇔=
Phương trình mới được tạo ra là:
2
( 1) 2 2 0t xtx− + + −=
Ta có
22
6 9 ( 3)xx x∆= − + = −
Từ đó ta có:
1 ( 3)
2
2
1 ( 3)
1
2
xx
t
xx
tx
+− −
= =
++ −
= = −
THCS.TOANMATH.com
+ Trường hợp 1:
22
1 2 3 2 2 10 1 2t xx xx x=⇔ −+=⇔−−=⇔=±
+ Trường hợp 2:
2
22
1
1 23 1
23 21
x
tx x x x
xx xx
≥
= −⇔ − + = −⇔
−+=−+
Phương trình vô nghiệm.
Tóm lại: Phương trình có 2 nghiệm là:
12x = ±
b) Điều kiện:
22x−≤ ≤
Bình phương 2 vế phương trình và thu gọn ta được:
22
9 16 8 2 8 32 0x xx− − +−=
.
Đặt
2
82tx= −
ta tạo ra phương trình là:
2 22
22
16 (8 2 ) 9 8 32 0
16 (9 2 ) 8 8 32 0
mt t m x x x
mt t m x x m
− − − + +−=
⇔ − ++ + − − =
2
22 2
64 (9 2 ) 8 8 32
( 2 9 ) 8 8 32 64
m mx x m
m m x mx m m
′

∆= − + + − −

=−− + ++ +
Ta mong muốn
2
'( )
Ax B∆= + ⇔
0∆=
phải có nghiệm kép . Tức là:
22 2
16 ( 2 9 )(8 32 64) 0 4
m
m m mm m m
′
∆ = −− − + + = ⇔ =−
Từ đó suy ra phương trình mới là:
22
4 16 8 0t tx x−− ++=
Tính được:
22
8 (2 8)
42
' 4 32 64 (2 8)
8 (2 8)
4
42
xx
t
xx x
xx
t
−+
= =
−
∆= + + = + ⇒
++
= =−−
−
+ Trường hợp 1:
2
22
0
42
82
22 3
4(8 2 )
x
xx
tx x
xx
≥
=⇔ − =⇔ ⇔=
−=
THCS.TOANMATH.com
+ Trường hợp 2:
2
22
8
4 82 4
22
4(8 2 ) ( 8)
x
xx
t x VN
xx
≤−
=−−⇔ − =−−⇔
−=+
Tóm lại phương trình có nghiệm duy nhất
42
3
x =
c). Đặt
27xt+=
ta tạo ra phương trình:
( ) (
)
22
2 7 92 77 0mt x t x m x m− + + + − +− =
Làm tương tự như trên ta tìm được
1m =
. Nên phương trình có dạng
( ) ( )
( )
2
22 2
7
27 70 27 4 7 49
tx
t xtxx x xx
tx
= +
− + + + = ⇒∆= + − + = ⇒
=
giải theo các trường hợp của
t
ta tìm được
122x = +
là nghiệm của
phương trình.
Ví dụ 3: Giải các phương trình:
a)
22
109823130x xxx x− − − ++=
b)
32 3
6 2 3 (5 1) 3 0xxx x x+ − +− − + =
c)
2
4 1 1 3 21 1x x xx+−= + − + −
Lời Giải:
a) Điều kiện:
1
1
2
x
x
≥
≤
Đặt
2
2 31t xx= −+
ta tạo ra phương trình:
22
8 (10 2 ) (3 9) 3 0mt xt m x m x m− + − + − +− =
THCS.TOANMATH.com
Ta có
22
16 (10 2 ) (3 9) 3x m mx m x m

∆= − − + − + −

22
16 (10 2 ) (3 9) 3
x m mx m x m

= − − + − +−

2 2 22
(2 10 16) (9 3 ) 3m m x m mxm m= − + + − +−
Ta cần :
22 2 2
(9 3 ) 4(2 10 16)( 3 ) 0 3
m
mm m m m m m∆= − − − + − =⇒ =
Phương trình đã cho trở thành:
22
2
38 4 0
3
2
tx
t xt x
tx
=
−+ =⇔
=
Trường hợp
1
2
2 22
00
22
2 31
33
9(2 3 1) 4 14 27 9 0
xx
tx xx x
xx x x x
≥≥

= ⇔ − += ⇔ ⇔

− + = − +=

⇔
3
2
3
7
x
x
=
=
Trường hợp 2:
2
0
1
2 2 3 12
3 10
3
x
tx x x x x
x
≥
= ⇔ − += ⇔ ⇔ =
− +=
Kết luận: Phương trình có 3 nghiệm:
331
,,
273
xxx= = =
b) Điều kiện:
1x ≥
. Đặt
3 32
30 3t x xt= +≥⇔ = −
. Do hệ số của
3
x
trong phương trình là:
1
. Phương trình đã cho trở thành:
22
(5 1) 6 2 0t xtx x− −+ −=
22 2 2
(5 1) 4(6 2 ) 2 1 ( 1)x xxxx x∆= − − − = − + = −
.
THCS.TOANMATH.com
Suy ra:
(5 1) ( 1)
2
2
(5 1) ( 1)
31
2
xx
tx
xx
tx
−− −
= =
−+ −
= = −
Trường hợp 1:
3
32
1
0
3 21
32
2
4 30
3 21
()
2
x
x
xx x
xx
xL
=
≥
+
+= ⇔ ⇔ =
− +=
−
=
Trường hợp 2:
3
32
1
1
3 3 1 4 23
3
9 6 20
4 2 3( )
x
x
xx x
xxx
xL
=
≥
+ = −⇔ ⇔ = +
− + +=
= −
Tóm lại phương trình có 3 nghiệm:
3 21
1, , 4 3 2
2
xx x
+
= = = +
a) Điều kiện:
11
x−≤ ≤
. Ta viết phương trình thành:
2
4 1 21 3 1 1x xx x+− − = ++ −
.
Bình phương 2 vế ta thu được phương trình mới:
22 2 2
16( 1) 4(1 ) 16 1 9 6 1 2(3 1) 1 1x x x xx x x x+ + − − − = + ++ + − +−
22
8 6 18 (6 18) 1 0xx x x⇔ − −+ + − =
Đặt
2
1tx= −
ta tạo ra phương trình:
22
(6 18) (8 ) 6 18 0mt x t m x x m+ + ++ − −−=
Có
22
' (3 9) (8 ) 6 18x m mx x m

∆= + − + − − −

THCS.TOANMATH.com
22 2
(9 8 ) (54 6 ) 18 81m m x mx m m=−− + + ++ +
Ta mong muốn
2 2 22
( ) ' (3 27) (9 8 )( 18 81) 0
m
Ax B m m m m m∆= + ⇔∆ = + − − − + + =
Từ đó tính được
8
m = −
Phương trình đã cho trở thành:
2
8 (6 18) 6 10 0t x tx
−+ + −−=
Ta có
22
' (3 9) 8(6 10) (3 1)x xx∆= + − + = +
Suy ra
3 9 (3 1) 3 5
84
3 9 (3 1)
1
8
xx x
t
xx
t
− −− + +
= =
−
− −+ +
= =
−
Trường hợp 1:
2
11 1 0t xx=⇔ − =⇔=
thỏa mãn điều kiện
Trường hợp 2:
2 22
35
4 1 3 5 16(1 ) 9 30 25
4
x
t xx x x x
+
= ⇔ − = +⇔ − = + +
22 2
3
16(1 ) 9 30 25 25 30 9 0
5
xxx xx x−=++⇔ ++=⇔=−
Thử lại ta thấy:
3
5
x = −
thỏa mãn phương trình:
Kết luận: Phương trình có 2 nghiệm
3
0,
5
xx= = −
Chú ý: Ở bước cuối cùng khi giải ra nghiệm ta phải thử lại vì phép bình
phương lúc đầu khi ta giải là không tương đương.
Ví dụ 4) Giải các phương trình:
a)
2
55xx−= −
THCS.TOANMATH.com
b)
42
23 3 3 0x xx
− ++− =
( )
22
8 3 4 2 44
x x xx x+ + +− +=
Giải:
a) Điều kiện:
2
5
5
x
x
≤
≥
Bình phương 2 vế ta thu được:
22 4
5 (2 1).5 0x xx− + ++ =
Ta coi đây là phương trình bậc 2 của
5
ta có:
22 4 2 2
(2 1) 4( ) 4 4 1 (2 1)x xx x x x∆= + − + = − + = +
Từ đó suy ra
22
22
1
5 (2 1 2 1)
2
1
5 (2 1 2 1) 1
2
x x xx
x x xx
= ++ − = +
= +− + = − +
Trường hợp 1:
2
1 21
2
50
1 21
2
x
xx
x
−−
=
+−=⇔
−+
=
Trường hợp 2:
2
1 17
2
40
1 17
2
x
xx
x
−
=
−−=⇔
+
=
Đối chiếu với điều kiện ta có 4 nghiệm đều thỏa mãn phương trình.
b) Ta viết lại phương trình thành:
24
3 (2 1) 3 0x xx− + ++ =
Ta coi đây là phương trình bậc 2 của
3
ta có:
THCS.TOANMATH.com
22 4 2 2
(2 1) 4( ) 4 4 1 (2 1)
x xx x x x∆= + − + = − + = +
Từ đó suy ra
22
2
2
22
1
3 (2 1 2 1)
30
2
1
1 30
3 (2 1 2 1) 1
2
x x xx
xx
xx
x x xx
= ++ − = +

+− =
⇔

− +− =

= +− + = − +
Giải 2 phương trình trên ta thu được các nghiệm của phương trình đã cho
là:
1 1 43
2
x
−± +
=
hoặc
1 43 3
2
x
−± −
=
c) Điều kiện
4x
≥−
Ta viết lại phương trình thành:
(
)
22
4 4 2 48 2 80x xx x x x++ +− ++ + −=
. Coi đây là phương trình
bậc 2 ẩn
4x +
thì
( ) ( ) ( )
22
2 22
4 2 48 2 8 4 6xx x x xx∆= +− − + − = +−
.
Từ đó suy ra
42
42 1
xx
xx
+=−
+= +
Giải 2 trường hợp ta thu được các nghiệm của phương trình là:
1 65
8
3 57
8
x
x
−
=
−+
=
Ví dụ 5: Giải các phương trình:
a)
22
3(211)(13821)x xx x+− = + + +
b)
22
3 6 2 13 1xx x x+ ++ −= +
Lời Giải:
THCS.TOANMATH.com
a) Ta viết lại phương trình thành:
22
3 3 (8 3) 2 1 0xx x x+++ − +=
.
Đặt
2
2 10tx
= +≥
suy ra
22
21tx= +
.
Ta tạo ra phương trình:
22
(8 3) (3 2 ) 3 0
mt x t m x x m
+ − +− ++−=
.
Ta có
22
(8 3) 4 (3 2 ) 3x m mx x m

∆= − − − + + − =

22 2
(8 12 64) (48 4 ) 4 12 9mmx mxmm= −+ −+ +−+
.
Ta cần
22 2
' (24 2 ) (8 12 64)(4 12 9) 0 3
m
m mm mm m∆=+ − −+ −+=⇒=
.
Phương trình trở thành:
22
3 (8 3) 3 0t x txx+ − − +=
.
Ta có:
22 2 2
(8 3) 12.( 3 ) 100 60 9 (10 3)x xx x x x∆= − − − + = − + = −
.
Từ đó tính được :
38(103)
31
6
3 8 (10 3)
63
xx
tx
xx x
t
−− −
= =−+
−+ −
= = −
Trường hợp 1:
2
2
1
2 1 31 0
3
9 60
x
xx x
xx
≤
+=− +⇔ ⇔ =
−=
Trường hợp 2:
2
2
0
21
3
17 9 0
x
x
x VN
x
≤
+=− ⇔
+=
Vậy phương trình có nghiệm duy nhất:
0x =
b) Điều kiện:
1
2
x ≥
.
Ta viết lại phương trình thành:
22
3 63 1 2 1xx x x+ + = +− −
.
Bình phương 2 vế và thu gọn ta được phương trình mới:
THCS.TOANMATH.com
22
10 3 6 2(3 1) 2 1 0xx x x+ −− + −=
Đặt
2
2 10tx
= −≥
suy ra
22
21tx= −
.
Ta tạo ra phương trình:
22
2(3 1) (10 2 ) 3 6 0
mt x t m x x m− + + − + −+ =
. Ta
có
22
' (3 1) (10 2 ) 3 6x m mx x m

∆= + − − + − +

22 2
(2 10 9) (6 3 ) 6 1m m x mx m m= − + +− − + +
.
Ta cần
22 2
(6 3 ) 4(2 10 9)( 6 1) 0 4
m
m m m mm m
∆= − − − + − + + =⇒ =
.
Phương trình trở thành:
22
4 2(3 1) 2 3 2 0t xtx x− + + + −=
.
Ta có:
22 2 2
' (3 1) 4.(2 3 2) 6 9 ( 3)
x xx xx x∆= + − + − = − + = −
.
Từ đó tính được:
3 1 ( 3) 2
42
3 1 ( 3) 2 1
42
xx x
t
xx x
t
+− − +
= =
++ − −
= =
Trường hợp 1:
2
2
2 2 15
2
2
7
21
2
7 4 80
2 2 15
7
x
x
x
x
xx
x
+
=
≥−
+
−= ⇔ ⇔
− −=
−
=
.
Đối chiếu với điều kiện ban đầu ta thấy chỉ có
2 2 15
7
x
+
=
là thỏa mãn
điều kiện .
Trường hợp 2:
2
2
16
1
21
2
21
2
2
16
4 4 50
2
x
x
x
x
xx
x
−−
=
≥
−
−= ⇔ ⇔
−+
+ −=
=
.
THCS.TOANMATH.com
Đối chiếu với điều kiện ban đầu ta thấy chỉ có
16
2
x
−+
=
là thỏa mãn
điều kiện .
Vậy phương trình có 2 nghiệm là:
2 2 15
7
x
+
=
và
16
2
x
−+
=
SỬ DỤNG HẰNG ĐẲNG THỨC ĐỂ GIẢI PHƯƠNG TRÌNH
Dấu hiệu:
Các bài toán giải được bằng hằng đẳng thức thường có dạng:
( )
32
ax bx cx d e fx h px q+ + += + +
hoặc
32 32
3
ax bx cx d e px qx rx s+ + += + + +
Phương pháp chung để giải các bài toán này là: Đặt
( )
n
fx y=
với
2n =
hoặc
3n =
.
Đưa phương trình ban đầu về dạng
( ) ( )
3
3
m Ax B n Ax B my ny+ + += +
Ví dụ 1:
a)
32
3
8 36 53 25 3 5xxx x− + −= −
b)
3
32 2
8 13 7 2 3 3x xx xx− += +−
c)
3
24 11 16 2 1 1 0x xx
− − −−=
.
d)
3
3
66 4 4xx= ++
e)
3
3
1 22 1xx+= −
f)
( )
( )
2
4 1 3 52xx x x+=− −
THCS.TOANMATH.com
Giải:
Những phương trình có dạng:
( )
32
ax bx cx d ex h px q+ + += + +
(1)
Hoặc:
32 32
3
ax bx cx d e px qx rx h
+ + += + + +
(2)
ta thường giải theo cách:
Đối với (1): Đặt
px q y+=
khi đó
2
yp
x
q
−
=
thay vào phương trình ta
đưa về dạng:
32 3
ax bx cx d Ay By+ + += +
. Sau đó biến đổi phương trình
thành:
[ ]
3
3
. () .()A u x B u x Ay By+=+
Đối với (2): Đặt
32
3
g px qx rx h y+ + +=
sau đó tạo ra hệ tạm:
( )
32
33 2 3
.ax bx cx d s y
g px qx rx h y
+ + +=
+ ++=
cộng hai phương trình ta thu được:
32 3
.Ax Bx Cx D s y y+ + += +
sau đó đưa phương trình về dạng:
[ ] [ ]
3
3
() . () .ux s ux y sy+=+
Ta xét các ví dụ sau:
a) Đặt
3
35xy−=
ta có hệ sau:
32
3
8 36 53 25
35
xxx y
xy
− + −=
−=
(I)
Cộng hai phương trình của hệ với nhau ta thu được:
32 3
8 36 56 30
x x x yy− + −=+
(*). Ta nghỉ đến việc biến đổi vế trái
thành:
[ ]
3
() ()Ax Ax+
để phương trình có dạng:
[ ]
3
3
() ()Ax Ax y y+=+
Giả sử:
32 3
8 36 56 30 (2 ) (2 )x x x xa xa− + −= + + +
.
THCS.TOANMATH.com
Đồng nhất hệ số của
2
3xa
⇒=−
Như vậy phương trình
(*)
có dạng:
33
(2 3) (2 3)x x yy− + −= +
(1)
Đặt
(2 3)zx= −
. Từ phương trình ta suy ra
33
z zy y
+= +
(
)
(
)
33 2 2
10
z z y y z y z zy y+= +⇔ − + + + =
. Do
2
22 2
3
1 1 0, ,
24
y
z zy y z y y z PT y z

+ + += + + +> ∀ ⇒ ⇔ =


32
2 3 8 36 53 25 2 3yx x x x x⇔ = −⇔ − + − = −
32
53
8 36 51 22 0
4
2
x
xxx
x
±
=
⇔ − + −=⇔
=
Qua ví dụ trên ta thấy việc chuyển qua hệ tạm (I) giúp ta hình dung bài
toán được dễ dàng hơn.
b) Đặt
3
2
33xx y+ −=
ta thu được hệ phương trình sau:
32
23
8 13 7 2
33
x x xy
xx y
− +=
+ −=
. Cộng hai phương trình của hệ ta thu được:
32 3 3 3
8 12 10 3 2 (2 1) 2(2 1) 2
x x x yy x x yy− + −= + ⇔ − + − = +
(*)
Đặt
21zx= −
ta thu được phương trình:
33
22z zy y+=+
( )
( )
2 2 32
2 0 2 1 8 13 7 4 2z y z zy y z y y x x x x x⇔ − + + + = ⇔ = ⇔ = −⇔ − + = −
32
1
8 13 3 2 0
5 89
16
x
x xx
x
=
⇔ − + +=⇔
±
=
c) Điều kiện:
1
2
x ≥
. Ta đặt
21 0xa−= ≥
thì phương trình đã cho trở
thành:
33
23 3 2
12 1 8 8 1 0 8 8 1 12 1a aa aa a+− − −= ⇔ + += +
THCS.TOANMATH.com
Đặt
3
2
12a 1
y+=
ta thu được hệ sau:
3
23
8 81
12 1
aa y
ay
+ +=
+=
. Cộng hai phương
trình của hệ với nhau ta thu được:
33
(2 1) (2 1)
a a yy+ + += +
(*)
Đặt
21az+=
ta có:
33
z zy y+= +
.
Tương tự như các bài toán trên ta suy ra
zy=
.
Theo (*) ta có
3
1
218 8121 0
2
ya aaaa x⇔ = +⇒ + += +⇔ = ⇒ =
Kết luận:
1
2
x
=
là nghiệm duy nhất của phương trình:
d) Đặt
3
64yx= +
ta có hệ sau:
( )
( )
3
3 3 22
3
46
6 6 60
64
xy
x xy y xyx xyy xy
xy
−=
⇔ + = + ⇔ − + + + =⇔=
+=
Thay vào phương trình ta có:
( )
( )
32
2
640 2 220 13
13
x
xx x xx x
x
= −
− −=⇔ + − − =⇔ =+
= −
e) Đặt
3
21yx= −
ta có hệ:
( )
( )
3
3 3 22
3
12
2 2 20
21
xy
x xy y xyx xyy xy
xy
+=
⇔ + = + ⇔ − + + + =⇔=
= +
Suy ra
( )
( )
32
1
15
2 10 1 1 0
2
15
2
x
x x x xx x
x
=
−−
− += ⇔ − + − = ⇔ =
−+
=
THCS.TOANMATH.com
f)
(
)
(
)
2
4 1 3 52
xx x x+=− −
Đặt
2
5
52 0
2
y
xy x
−
− =≥⇒=
thay vào ta có:
( )
( )
( )
2
2 33 2 2
5
4 1 3 8 2 2 2 4 2. 2 0
2
y
x x y x x y y x y x xy y

−
+ =− ⇔ + =+ ⇔ − + ++=


2
1 21
2
2 4 2 50
1 21
2
x
yx x x
x
−+
=
= ⇔ + −=⇔
−−
=
Thử lại ta thấy chỉ có
1 21
2
x
−+
=
thỏa mãn điều kiện bài toán.
Ví dụ 2: Giải các phương trình sau:
a)
222
3
7 1382 (133)x x xx x x
− += + −
b)
3
32 632
341 2x x x xx
+ −= + +
c)
3
33
3
3
2
22
xx x x
x

−+
= +


Giải:
a) Nhận thấy
0x =
không phải là nghiệm của phương trình:
Chia hai vế phương trình cho
3
x
ta thu được:
3
23 2
7 13 8 1 3
23
xxx xx
− + = +−
.
Đặt
3
2
13
3y
xx
= +−
ta thu được hệ sau:
23
3
2
7 13 8
2
13
3
y
xx x
y
xx
−+=
+ −=
.
THCS.TOANMATH.com
Cộng hai phương trình của hệ ta có:
3
33
32
8 12 10 2 2
3 2 12 1 2yy yy
xx x x x

− + −= + ⇔ − + − = +


(*)
Đặt
2
1z
x
= −
ta thu được:
(
)
(
)
3 3 22
2 2 20
z zy y zyz yzy zy+ = + ⇒ − + + + =⇔=
23 32
2 7 13 8 4 8 13 3
1 2 20
y
x xxxx xxx
⇔=−⇔−+=−⇔−++=
.
Suy ra
5 89
1,
4
xx
−±
= =
b) Nhận thấy
0x =
không phải là nghiệm của phương trình nên ta chia hai
vế phương trình cho x thì thu được phương trình tương đương
là:
23
3
11
34 2xx x
xx
+ − = ++
.
Đặt
3
3
1
2yx
x
= ++
ta có hệ sau:
2
33
1
34
1
2
xx y
x
xy
x
+ −=
++ =
. Cộng hai phương
trình của hệ ta có:
33
( 1) ( 1)x x yy+ + += +
.
Từ phương trình ta suy ra
2
1
13 4 1yx x x x
x
= +⇔ + − = +
2 32
1
1
3 4 1 3 3 10
3
3
x
x x x x xx
x
x
= −
+ − = +⇔ + − −= ⇔
= ±
.
c) Ta viết lại phương trình thành:
( )
3
3
33
16 4 4 12xx x x x−− = +
THCS.TOANMATH.com
Đặt
3
3
4 12yxx= +
ta có hệ tạm sau:
(
)
3
3
33
16 4
4 12
xx x y
x xy
−− =
+=
Cộng hai vế hệ phương trình ta thu được:
( ) ( )
3
3 33
44xx xx y y− + −=+
Đặt
3
zx x= −
ta có:
( )
( )
3 3 22
4 4 40z z y y z y z yz y+=+ ⇔− +++=
( )
3
33
4 12xx x x⇔−=+
( )
3
22 2
1 4 12 0
xx x x

⇔ −− − =


2
0
3
x
x
=
⇔
=
Vậy phương trình đã cho có 3 nghiệm là:
0; 3xx= = ±
PHƯƠNG PHÁP ĐÁNH GIÁ
Những kỹ thuật qua trọng để giải phương trình giải bằng phương pháp
đánh giá ta thường sử dụng là:
+ Dùng hằng đẳng thức:
22 2
1 2 12
.. 0 .. 0
nn
A A A AA A
+ + =⇔====
+ Dùng các bất đẳng thức cổ điển Cô si, Bunhiacopxki, Bất đẳng thức hình
học
+ Dùng phương pháp khảo sát hàm số để tìm
,GTLN GTNN
:
Ví dụ 1: Giải các phương trình sau:
a)
2
4 3 3 4 3 22 1x x xx x+ += ++ −
.
b)
13 1 9 1 0xx−+ +=
.
c)
( )
( )
3
5 2 2 2 11 0xx x+ − +− =
(Trích đề tuyển sinh lớp 10 chuyên
Toán Trường chuyên Amsterdam 2014).
THCS.TOANMATH.com
d)
( )
1
12 43 9
2
x y z xyz−+ − + − = + +
Lời giải:
a) Điều kiện
1
2
x ≥
. Ta viết lại phương trình thành:
( )
2
4 4 3 32122110x xx x x x− + + + + −− −+=
( )
(
)
22
2 30
2 3 2 11 0 1
2 11 0
xx
xx x x
x
− +=
⇔ − + + −− = ⇔ ⇔ =
−−=
.
b) Điều kiện:
1x ≥
. Ta viết lại phương trình thành:
19
13 1 1 9 1 3 1 0
44
xx x x

−− −+ + +− ++ =


22
1
10
13 5
2
13 1 9 1 0
3
22 4
10
2
x
xx x
x
−− =

⇔ −− + +− = ⇔ ⇔ =


+− =
.
c) Điều kiện
1
2
x ≥−
.Ta viết lại phương trình thành:
( )
(
)
2
44
0
5 2122110 5 211 0
2 11 0
x
xx x x x
x
=
+ +− ++ = ⇔ + +− = ⇔
+−=
Suy ra
0x =
là nghiệm duy nhất của phương trình.
d) Điều kiện
1; 4; 9xy z≥≥≥
ta viết lại phương trình thành:
2 14 46 9x y z xyz−+ − + − = + +
12 11 44 4 4 96 9 9 0xx y y z z
⇔−− −++−− −++−− −+=
( )
( ) ( )
2 22
11 0
2
11 42 93 0 420 8
18
930
x
x
xy z y y
z
z
−−=
=

−− + −− + −− =⇔ −−=⇔ =


=
−−=
THCS.TOANMATH.com
Ví dụ 2: Giải các phương trình sau:
a)
3
43
16 5 6 4x xx
+= +
b)
3
42 3
4 3 4 3 16 12
xx x x x
+ + += +
c)
2
3
96 20 2 8 1 4 (8 1) 0
x x x x xx
− ++ −− + =
Giải:
a) Vì
4
16 5 0
x +>
nên phương trình đã cho có nghiệm khi
32
4 0 (4 1) 0 0x x xx x
+≥⇔ +≥⇔≥
. Để ý rằng khi
1
2
x =
thì
VT VP=
nên ta nghỉ đến sử dụng bất đẳng thức Cô si sao cho dấu bằng xảy ra khi
1
2
x
=
. Mặt khác khi
1
2
x =
3
11
4 4. 1
82
xx⇒ += + =
thì Từ những cơ sở
trên ta có lời giải như sau: Theo bất đẳng thức Cô si dạng
3
3 abc a b c≤++
ta có
Ta có
( )
( )
3
33 3 3
3
6 4 2.3. 4 .1.1 2 4 1 1 8 2 4xx xx xx x x+ = + ≤ + ++ = + +
Mặt khác ta có:
(
)
( )
2
4 3 43 2
16 5 (8 2 4) 16 8 2 1 2 1 4 2 1 0x xx xxx x xx+− ++= − −+= − ++≥
Suy ra
VT VP≥
. Dấu bằng xảy ra khi và chỉ khi
22
2
2(2 1) (2 2 1) 0
1
2
4 (4 1) 2
x xx
x
xx
− + +=
⇔=
= +=
Tóm lại: Phương trình có nghiệm duy nhất
1
2
x =
b) Vì
42
4 3 40xx x+ + +>
nên phương trình đã cho có nghiệm khi
32
16 12 0 4 (4 3) 0 0x x xx x+ ≥⇔ + ≥⇔≥
. Để ý rằng khi
1
2
x =
thì
VT VP=
nên ta nghỉ đến sử dụng bất đẳng thức Cô si sao cho dấu bằng
THCS.TOANMATH.com
xảy ra khi
1
2
x
=
. Khi
1
2
x
=
thì
3
11
16 12 16. 12. 8
82
xx+= + =
. Từ những
cơ sở trên ta có lời giải như sau:
Theo bất đẳng thức Cô si dạng
3
3 abc a b c≤++
ta có
( )
( )
( )
33 3 3
33
31
3 16 12 16 12 .8.8 16 12 8 8 4 3 4
44
xx xx xx xx+ = + ≤ + ++ = + +
Mặt khác ta có:
42 3 4 32 2 2
4 3 4 (4 3 4) 4 4 (2 1) 0
xx x x x x xx xx+++− ++= − += − ≥
.
Dấu bằng xảy ra khi và chỉ khi
22
2
(2 1) 0
1
2
2 (4 3)
xx
x
xx
−=
⇔=
= +
c) Điều kiện:
1
8
x ≥
. Để ý rằng
1
8
x
=
là nghiệm của phương trình nên ta có
lời giải như sau:
2
33
1 1 4 (8 1) 32 4 2
4 (8 1) 1.1.4 (8 1)
33
xx x x
xx xx
++ + + +
+= +≤ =
.
Mặt khác ta có
22 2
2
32 4 2 256 64 4 4(8 1)
96 20 2 0
3 33
xx x x x
xx
++ − + −
− +− = = ≥
.
Suy ra
2
3
96 20 2 8 1 4 (8 1) 0x x x x xx− ++ −− + ≥
.
Dấu bằng xảy ra khi và chỉ khi
1
8
x =
Ví dụ 2: Giải các phương trình sau:
a)
4
1 12
21 43
x
xx
+=
−−
THCS.TOANMATH.com
b)
11 1 1
3
21 41 52xx x x

+= +

− −−

c)
44
44
41 52
21
33
xx
xx
−−
+ −= +
d)
22
4 21 3 10 2xx xx−+ + −−+ + =
Giải:
a) Điều kiện:
1
2
x >
.
Phương trình đã cho có thể viết lại như sau:
4
2
21 43
xx
xx
+=
−−
.
+ Ta chứng minh:
1
21
x
x
≥
−
. Thật vậy bất đẳng thức tương đương với
22
2 1 ( 1) 0xx x≥ −⇔ − ≥
. Điều này là hiển nhiên đúng.
Dấu bằng xảy ra khi và chỉ khi
1x =
Ta chứng minh:
4
1
43
x
x
≥
−
. Thật vậy bất đẳng thức tương đương với
4 4 22
22
43 430( 21)( 23)0
( 1) ( 2 3) 0
xx xx xxxx
x xx
≥ −⇔ − +≥⇔ − + + + ≥
⇔− + +≥
Điều này là hiển nhiên đúng. Dấu bằng xảy ra khi và chỉ khi
1x =
Từ đó suy ra
2VT ≥
. Dấu bằng xảy ra khi và chỉ khi
1x =
b)
11 1 1
3
21 41 52xx x x

+= +

− −−

Ta thấy rằng:
41 21;52 2121x xxx x xx x−=++− −=+−+−
Theo bất đẳng thức cô si ta có
THCS.TOANMATH.com
( )
11 1
219
21
11 1 9
21 21
xx x
xx x
x x x xx x

+ + + + −≥

−

⇒++ ≥
− ++ −
Mặt khác ta có
2
( 21)3(41) 21 3(41)xx x x xx x x++ −≤ −⇒++ −≤ −
(Theo
bất đẳng thức Bunhiacopxki cho 3 số)
Từ đó suy ra:
2 1 33
21 41
xx x
+≥
−−
Tương tự ta cũng có:
1 2 33
21 52xx x
+≥
−−
Cộng hai bất đẳng thức cùng chiều ta có:
3 3 33 33
21 41 52xx x x
+≥+
−−−
11 1 1
3
21 41 52
xx x x

⇔+ ≥ +

− −−

.
Dấu bằng xảy ra khi và chỉ khi
1x =
c) Áp dụng bất đẳng thức Bunhiacopxki dạng:
2 2222 22
(ax ) ( )( )bycz abcx yz++ ≤ ++ ++
ta có:
( )
( )
( )
2
444
2 1 111 2 1xx x xx x++ −≤++ ++ −
.
(
)
444
21 3 21xx x xx x⇔++ −≤ ++ −
Lại có
21 3(41)xx x x+ + −≤ −
suy ra
THCS.TOANMATH.com
444
4
21 33(41) 27(41)xx x x x+ + −≤ − = −
(1)
Tương tự:
44 4
4
2 1 2 1 3 3(5 2) 27(5 2)xx x x x+−+−≤ −= −
(2)
Cộng hai bất đẳng thức cùng chiều (1), (2) ta có:
( )
44
44
44
44
3 2 1 27(4 1) 27(5 2)
41 52
21
33
xx x x
xx
xx
+ −≤ −+ −
−−
⇔ + −≤ +
Dấu bằng xảy ra khi và chỉ khi
1x =
.
c) Ta có
11
( 3)(7 ) ( 2)(5 )
( 3)(7 ) ( 2)(5 )
x
VT x x x x
x xx x
+
= + −− + −=
+ −+ + −
Điều kiện xác định là
25x
−≤ ≤
Theo bất đẳng thức Cauchy ta có:
[ ]
1 1 13
(3)(7) (26)(7) (26)(7)
2 22 22
x
xx xx x x
+
+ − = + −≤ ++− =
và
[ ]
11 9
( 2)(5 ) (2 4)(5 ) (2 4) (5 )
2 22 22
x
xx xx x x
+
+−= +−≤ ++−=
Như vậy:
1
( 3)(7 ) ( 2)(5 ) ( 11)
2
x xx x x+ −+ + −≤ +
Từ đó ta suy ra:
11
2
( 3)(7 ) ( 2)(5 )
x
VT
x xx x
+
= ≥
+ −+ + −
. Dấu bằng
xảy ra khi và chỉ khi:
(26)(7)
1
(2 4) (5 )
3
xx
x
xx
+=−
⇔=
+=−
THCS.TOANMATH.com
Vậy
1
3
x =
là nghiệm duy nhất của phương trình:
Ví dụ 4: Giải các phương trình sau:
a)
(
)
22 2 2
1
31 1 7 4
22
x xxxx xx−+ − − += −+
b)
( )
22 2 2
17 1
13 6 10 5 13 17 48 36 36 8 21
22
x x x x x x xx−++ − + + − += − −
c)
2 22
1 12
xx xx xx+−+− ++= −+
Giải:
Điều kiện:
1
1
3
xx≥ ∨ ≤−
Áp dụng BĐT Bunhiacopski cho hai bộ số
( )
1;1; x−
và
(
)
22 2
3 1; ; 1x x xx−− +
ta có:
( )( )
22
(*) 2 5VT x x x≤+ −
. Dấu “=”
xảy ra khi và chỉ khi
1x =
. Do
1
1
3
xx≥ ∨ ≤−
nên
2
50xx
−>
Áp dụng BĐT Cauchy ta có:
( ) ( ) ( )
( )( )
2 2 22
22
11
(*) 5 2 1 .2 5 2 2
22 22
52
VP xx x xx x
x xx

= −+ + ≥ − +

= −+
Dấu “=” xảy ra khi
1x = −
và
4
3
x =
. Từ đó ta có nghiệm của PT(*) là:
1x = −
b) Ta có:
THCS.TOANMATH.com
( ) ( )
( )
22
22 2
2
53
31 23 2 46
22
VT x x x x x x

= ++−+ − +− + +−


5
3 12
2
x xx≥ ++ − +
5 33
3 12 6 6
2 22
VT x x x x x
⇒ ≥ ++ − + = − ≥ −
.
Dấu “=” xảy ra khi và chỉ khi
3
2
x =
. Mặt khác ta cũng có:
(
)
(
)
(
)
2
2
1 1 13
12 3 2 4 12 9 12 3 2 2 3 12 3 6
2 2 22
VP x x x x x x x


= −− − + = −− − ≤ − = −


Dấu “=” xảy ra khi và chỉ khi
3
2
x =
. Từ đó ta có nghiệm của phương
trình là
3
2
x =
c) Theo bất đẳng thức Cô si ta có:
2
22 2
1
1 1( 1) 1 ( 1)
22
xx
xx xx xx
+

+−= +− ≤ + +− =

Dấu bằng xảy ra khi và chỉ khi
2
1
1 ( 1)
2
x
xx
x
=
= +− ⇔
= −
2
22 2
12
1 1( 1) 1 ( 1)
22
xx
xx xx xx
− ++

− ++= − ++ ≤ +− ++ =

.
Dấu bằng xảy ra khi và chỉ khi
2
1
1 ( 1)
0
x
xx
x
=
=− ++ ⇔
=
Từ đó suy ra
22
2
( 1)
22
xx xx
VT x
+ − ++
≤+ =+
.
Mặt khác ta có
22
2 ( 1) ( 1) 0xx x x−+− + = − ≥
.
Dấu bằng xảy ra khi và chỉ khi
1x =
THCS.TOANMATH.com
Từ đó suy ra phương trình có nghiệm duy nhất
1x =
.
Ví dụ 5: Giải các phương trình sau:
a)
3
32
14 2(1 2 1)
xx x x
− += + − −
b)
12 12( 5 4 )xx x x x+ + = −+ −
Giải:
a) Điều kiện:
2
2 10xx− −≥
Phương trình đã cho tương đương với:
3
32
14 2 2 1 2x xx x
− = − −+−
Do
2
2 2 10xx− −≥
nên từ phương trình ta cũng suy ra:
3
3
14 2xx− ≥−
Lập phương 2 vế ta thu được:
3 32
14 (2 ) 6( 2 1) 0xxxx− ≥ − ⇔ − −≤
Như vậy phương trình có nghiệm khi và chỉ khi
2
12
2 10
12
x
xx
x
= +
− −= ⇔
= −
Kết luận: Phương trình có 2 nghiệm là:
12x = +
và
12x = −
b) Điều kiện:
04
x≤≤
.
Xét
( ) 12
fx x x x= ++
trên
[ ]
0; 4
Dễ thấy
12 (0) ( ) (4) 12 12f f x f VT
=≤≤=⇒≤
(1)
Xét
() 5 4gx x x= −+ −
trên
[ ]
0; 4
ta có
Dễ thấy
1 (4) ( ) (0) 5g gx g=≤≤=
. Suy ra
12VP ≥
(2)
Từ (1), (2) suy ra phương trình có nghiệm khi
12 4VT VP x= = ⇔=
.
THCS.TOANMATH.com
MỘT SỐ CÁCH ĐẶT ẨN PHỤ KHÁC
1) Đặt ẩn phụ hoàn toàn để quy về phương trình một ẩn.
+ Điểm mấu chốt của phương pháp này là phải chọn một biểu thức
()fx
để đặt
()fx t=
sao cho phần còn lại phải biểu diễn được theo ẩn
t
.
Những bài toán dạng này nói chung là dễ.
+ Trong nhiều trường hợp ta cần thực hiện phép chia cho một biểu thức có
sẵn ở phương trình từ đó mới phát hiện ẩn phụ. Tùy thuộc vào cấu trúc
phương trình ta có thể chia cho
()gx
phù hợp (thông thường ta chia cho
k
x
với k là số hữu tỷ)
+ Đối với những bài toán mà việc đưa về một ẩn dẫn đến phương trình mới
phức tạp như: Số mũ cao, căn bậc cao .. thì ta có thể nghỉ đến hướng đặt
nhiều ẩn phụ để quy về hệ phương trình hoặc dựa vào các hằng đẳng thức
để giải toán.
Ta xét các ví dụ sau:
Ví dụ 1: Giải các phương trình sau:
a)
2
(1 )(2 3 3)x xx x=− −+
b)
3
2 42
21x xx x+ −=+
c)
2
1 4 13x xx x++ − + =
d)
2
1
2 31
x xx x
x
+ −= +
.
Giải:
a) Điều kiện:
0x ≥
. Phương trình đã cho có thể viết lại như sau:
2 22
(1 ) 2 3(1 ) 2 (1 ) 3(1 )x xx x x x x x

=− +− ⇔= − +−

. Ta thấy
0x =
không phải là nghiệm của phương trình. Ta chia hai vế cho
2
x
thì
THCS.TOANMATH.com
thu được:
2
11
12 3
xx
xx

−−
= +



. Đặt
1 x
t
x
−
=
ta có phương trình
theo
t
:
2
1
3 2 10
1
3
t
tt
t
= −
+ −= ⇔
=
Trường hợp 1:
1t = −
ta có:
1
1 1 0( )
x
x x VN
x
−
=−⇔ − +=
Trường hợp 2:
1
3
t =
ta có:
3 21
()
1 1 15 3 21
2
3 30
32
3 21
2
xL
x
xx x
x
x
−
=
−+
= ⇔− −=⇔ ⇒ =
+
=
Kết luận: Phương trình có nghiệm duy nhất:
15 3 21
2
x
+
=
b) Ta thấy
0x =
không phải là nghiệm của phương trình. Vì vậy ta chia hai
vế cho
x
thì thu được:
33
11 1 1
2 20xx x x
xx x x
+ −=+⇔−+ −−=
Đặt
3
1
tx
x
= −
ta thu được phương trình:
32
1 15
20 1 1 10
2
tt t x xx x
x
±
+− = ⇔=⇒ − =⇔ − −= ⇔ =
⇔
Kết luận: Phương trình có nghiệm
15
2
x
±
=
c) Điều kiện:
2
0
0 23
4 10
23
x
x
xx
x
≥
≤≤−
⇔
− +≥
≥+
.
THCS.TOANMATH.com
Ta thấy
0x =
không phải là nghiệm của phương trình. Chia hai vế cho
x
ta thu được:
11
43xx
x
x
+ + −+ =
. Đặt
2
11
2
t x tx
x
x
= + ⇒ =++
theo bất đẳng thức Cô si ta có
2t ≥
. Thay
vào phương trình ta có:
2
22
3
5
63
2
6 69
t
tt t
t tt
≤
− = −⇔ ⇔=
−= − +
2
4
25 1
2 4 17 4 0
1
4
4
x
x xx
x
x
=
⇔ =++⇔ − +=⇔
=
Kết luận: Phương trình có 2 nghiệm:
1
4,
4
xx= =
d). Nhận xét:
0x =
không phải là nghiệm của phương trình:
Ta chia hai vế cho
x
khi đó phương trình trở thành:
11
2 30xx
xx
− + − −=
. Đặt
1
0tx
x
= −≥
phương trình trở thành:
22
1 15
2 30 1 1 10
2
t t t x xx x
x
±
+ −= ⇒=⇔ − =⇔ − −= ⇔ =
Ví dụ 2: Giải các phương trình sau:
a)
2
(13 4 ) 2 3 (4 3) 5 2 2 8 16 4 15x x x x xx− −+ − − =+ − −
b)
7 3 7 (4 7) 7 32xx x
−+ − −=
.
Giải:
a) Điều kiện
35
22
x≤≤
.
THCS.TOANMATH.com
Phương trình được viết lại như sau:
(
)
7 2 3 52 2(2 3)2 3(52)52
2 8 (5 2 )(2 3)
x x xx xx
xx

−+ − − − −+ − −

=+− −
Đặt
2
2
2 3 5 2 (5 2 )(2 3)
2
t
t x x xx
−
= −+ − ⇒ − − =
. Điều kiện
( )
22t≤≤
.
Phương trình đã cho có dạng:
32
4 60 2 2t tt t x− ++ = ⇒= ⇒ =
Ngoài ra ta cũng có thể giải phương trình trên bằng cách đưa về hệ.
b) Điều kiện:
7
7
3
x≤≤
.Phương trình đã cho được viết lại như sau:
1 3 13
(37) (7)37 (7) (37)7 32
2 2 22
x xx x x x

− + − −+ − + − −=


⇔
[ ] [ ]
(37)(7)37(7)(37)7 64x xx x x x−+− −+ −+ − −=
Đặt
37 7tx x= −+ −
( )
3
(37)37(7)7 3(37)(7)37 7
t x x x x x xx x⇒ = − −+ − −+ − − −+ −
Từ phương trình suy ra
3
64 4tt
= ⇔=
. Hay
37 7 4xx−+ −=
Bình phương 2 vế ta thu được:
2
11 2 2
(3 7)(7 ) 8 4 44 113 0
2
x x xx x x
±
− − =−⇔ − + =⇔=
Tại sao ta phân tích được hai phương trình như trên:
Ta thấy với những phương trình:
THCS.TOANMATH.com
( ) ( ) ( )( ) 0axb cxd exh gxk r cxdgxk s+ + + + ++ + + +=
thì một
trong những cách xử lý khá hiệu quả là:
Phân tích:
( )( )ax b m cx d n gx k+= + + +
và
'( ) '( )exhmcxd ngxk+= + + +
sau đó ta có thể đặt ẩn phụ trực tiếp ,
hoặc đặt hai ẩn phụ để quy về hệ.
Ví dụ:
Khi giải phương trình:
2
(13 4 ) 2 3 (4 3) 5 2 2 8 16 4 15x x x x xx− −+ − − =+ − −
ta thực hiện
các phân tích :
+ Giả sử:
13 4 (2 3) (5 2 )xmx n x
− = −+ −
.
Đồng nhất hai vế ta suy ra:
22 4
37
,
3 5 13
22
mn
mn
mn
−=−
⇔= =
−+=
+ Tương tự ta giả sử:
73
(4 3) (2 3) (5 2 ) ,
22
x mx n x m n
′ ′ ′′
−= −+ − ⇒ = =
Khi giải phương trình:
7 3 7 (4 7) 7 32xx x−+ − −=
.
Ta thực hiện phân tích:
(3 7) (7 ) 7mx n x
−+ −=
và
(3 7) (7 ) 4 7
px q x x−+ −= −
Sau đó đồng nhất 2 vế để tìm m, n, p, q ta
có:
13 31
;; ;
22 22
mn pq= = = =
Như vậy ngoài cách đặt ẩn phụ như trên ta có thể giải các bài toán theo
cách khác như sau:
a) Điều kiện
35
22
x≤≤
.
Đặt
2 3, 5 2a xb x= −=−
thì
22
2ab+=
.
Từ cách phân tích trên ta có hệ sau:
THCS.TOANMATH.com
22 2
22 22 3
2 ( )2 2
(3 7 ) (3 7 ) 4 16 3( ) 2 ( ) 16 4 0
a b a b ab
a b a b a b ab a b ab a b ab

+= + − =

⇔

+ + + =+ + − + − −=


2
32 2
( )2 2
3()2()()82()40
a b ab
ab ab ab ab
+− =
⇔

+ +−+ ++ −+ −=

.
Đặt
,
a b S ab P+= =
điều kiện
2
, 0; 4SP S P≥≥
.
Ta có hệ mới sau:
2
32
22 2
12
2
2 8 2 12 0
SP S
ab x
P
SSS
−= =
⇒ ⇔==⇔=

=
− + +=
b) Đặt
3 7, 7a xb x
= −=−
ta có hệ phương trình
( )
22
22
3
4
64
3 14.
3 14.
a
b
b
b
a
ab
a
+
+
⇔

=
=
+=
+=
Giải hệ phương trình ta thu được:
,ab x⇒
.
2) Đặt ẩn phụ hoàn để quy về hệ đối xứng loại 2:
Phương pháp này đặc biệt hiệu quả với các phương trình dạng:
2
ax bx c d ex h+ += +
hoặc
32
3
ax bx cx d e gx h+ + += +
Với mục đích tạo ra các hệ đối xứng hoặc gần đối xứng ta thường làm
theo cách:
Đối với những phương trình dạng:
2
ax bx c d ex h+ += +
.
Ta đặt
my n ex h+= +
thì thu được quan hệ:
22
22 2 22 2
( ) ax 0
2 20
ax bx c d my n bx dmy c dn
m y mny n ex h m y mny ex n h

++= + +− +− =

⇔

++=+ +−+−=


THCS.TOANMATH.com
Ta mong muốn có quan hệ
xy=
. Nếu điều này xảy ra thì từ hệ trên ta sẽ
có:
22
a
(*)
2
b dm c dn
m mn n h
−−
= =
−
.
Công việc còn lại là chọn
,
mn
chẵn thỏa mãn
(*)
Đối với những phương trình dạng:
32
3
ax bx cx d e gx h+ + += +
Ta đặt:
3
my n gx h
+= +
thì thu được hệ:
32
33 2 2 22 3
32
33 2 2 22 3
()
33
0
33 0
ax bx cx d e my n
m y m ny mn y n gx h
ax bx cx emy d en
m y m ny mn y gx n h
+ + += +
+ + +=+
+ + − +− =
⇔
+ + − + −=
Để thu được quan hệ
xy
=
ta cần:
32 2 3
33
a b c em d en
m m n mn g n h
−−
= = =
+ −−
Ví dụ 1: Giải các phương trình sau:
a)
2
2 61 45xx x− −= +
b)
2
2 37
4 1 9 26 0
33
x xx+− + − =
c)
32
3
3 5 8 36 53 25x xxx−= − + −
d)
32
3
27 81 8 27 54 36 54x xxx
−= − + −
Giải:
a) Điều kiện:
5
4
x ≥−
. Đặt
45my n x
+= +
khi đó ta có hệ:
22
22 2 22 2
2 6 1 4 12 2 2 2 0
2 4 5 2 4 50
x x my n x x my n
m y mny n x m y mny x n

− −= + − − −− =

⇔

++=+ +−+−=


Ta cần tìm
,mn
để tạo ra quan hệ
xy=
22
4 122 22
24 5
mn
m mn n
− − −−
⇔= =
−−
THCS.TOANMATH.com
Chọn
2
2
22
1
2 30
5
23
16
4 12
1
44
n
nn
n
mn
n
n
−−
=
+ −=
−
=⇒ ⇔ ⇒=−

−
= −
=
−
Chú ý:
Việc nhân số
2
vào phương trình (1) của hệ để tạo ra
2
4 12 1xx−−
là rất
cần thiết để chọn
m
được chẵn và nhóm
2
4 12 2xx−−
thành bình
phương biểu thức bậc 2 được dễ hơn.
Từ đó ta có lời giải cho bài toán như sau:
Đặt
23 45yx−= +
thì thu được hệ:
22
22
4 12 2 2(2 3) (2 3) 4 5
(2 3) 4 5 (2 3) 4 5
xx y x y
yx yx

− −= − − = +

⇔

−=+ −=+


.
Trừ hai phương trình của hệ cho nhau ta có:
22
(2 3) (2 3) 4( ) 2( )(4 4 4) 0x y yx xy x y− − − = −⇔ − + −=
2
xy
xy
=
⇔
+=
Trường hợp 1:
2
(2 3) 4 5
23 45 2 3
3
2
xx
xy x x x
x
−=+
= ⇔ −= + ⇔ =+
≥
Trường hợp:
2
(1 2 ) 4 5
2 2(2)3 45 12
1
2
xx
yx x x x
x
−=+
=−⇔ − −= +⇔ ⇔ =−
≤
Kết luận: Phương trình có 2 nghiệm là:
2 3, 1 2
xx=+=−
b) Điều kiện:
1
4
x ≥−
.
THCS.TOANMATH.com
Phương trình đã cho được viết lại như sau:
2
47 2
9 26 4 1
33
xx x
− += +
Đặt
41my n x+= +
22
22 2 22 2
37 2 2 37 2
9 26 ( ) 9 26 0
33 3 33
2 4 1 2 4 10
x x my n x x my n
m y mny n x m y mny x n

−+= + −− +−=

⇒⇔


++=+ +−+−=

Ta cần:
22
2 37 2
26
9
3 33
24 1
mn
m mn n
−− −
= =
−−
. Chọn
2
28
1
64
34
37 2
33
1
1
n
mn
n
n
−
=
−
=⇒ ⇒=−
−−
=
−
Đặt
34 41yx
−= +⇒
Hệ phương trình sau:
( )
( )
( )
( )( )
−
−

⇔

−−
−

2
2
2
3x 4 = 2x + 2y + 1
3y 4 = 4x + 1
x y 9x + 9y 22 = 0
3y 4 = 4x + 1
( )
−
⇔
−
2
3y 4 = 4x + 1
x=y
9x + 9y 22 = 0
Giải phương trình ứng với 2 trường hợp trên ta thu được các nghiệm là
14 61
9
x
+
=
và
12 53
9
x
−
=
Chú ý: Ta có thể tìm
,mn
nhanh hơn bằng cách:
THCS.TOANMATH.com
c) Đặt
45my n x+= +
khi đó ta có hệ:
2
2
(2 3) 2( ) 11
( )45
x my n
my n x
− = ++
+=+
Trừ hai phương trình cho nhau:
22
(2 3) ( ) 2 4 2 6x my n my x n− − + = −++
Để có quan hệ:
xy=
ta cần:
24
2; 3
2 60
my x
mn
n
=
⇒= =−
+=
.
Tương tự khi giải quyết câu b).
d) Đặt
3
35my n x+= −
ta có hệ sau:
32
32
3
33 2 2 2 3
8 36 53 25 0
3 5 8 36 53 25
3 3 3 50
x x x my n
x xxx
m y m ny mn y x n
− + − −− =
−= − + − ⇔
+ + − + +=
Ta chọn
,mn
sao cho
32 2 3
8 -36 53- - - 25
2, 3
3 3 -3 5
mn
mn
m m n mn n
= = = ⇒= =−
+
Đặt
3
23 35yx−= −
. Ta có hệ phương trình sau:
3
3
(2 3) 2 3 2
(2 3) 3 5
x yx
yx
− = −+−
−=−
Trừ hai phương trình cho nhau ta thu được:
33
(2 3) (2 3) 2 2
x y yx−− −=−
22
2( ) (2 3) (2 3)(2 3) (2 3) 1 0xy x x y y x y

⇔ − −+ − −+ −+=⇔=

Do
22
(2 3) (2 3)(2 3) (2 3) 1x xy y−+ − −+ −+
( )
2
2
23 3
(2 3) 2 3 1 0
24
y
xy
−

= − + + − +>




Giải
xy=
ta có:
( )
2
32
2 3 3 5 8 36 54 27 3 5x x xxx x− = −⇔ − + − = −
THCS.TOANMATH.com
( )
( )
2
2
2 8 20 11 0
53
4
x
x xx
x
=
⇔− − + =⇔
±
=
Kết luận: Phương trình đã cho có 3 nghiệm:
2x =
,
53
4
x
±
=
d) Ta viết lại phương trình thành:
3
3
27 81 8 (3 2) 46xx
−= − −
Đặt
3
3 2 81 8
yx−= −
ta có hệ phương trình:
( )
( )
3
3
3 2 81 8
3 2 27(3 2) 46
yx
xy
−=−
− = −+
⇔
(
)
(
)
3
3
3 2 81 8
3 2 81 8
yx
xx
−=−
−=−
.
Trừ hai phương trình của hệ ta thu được:
( ) ( )
33
3 2 3 2 81( )x y yx−− −= −
( ) ( )( ) ( )
22
3( )32 3232 32 270xy x x y y x y

⇔− −+− −+−+ =⇔=

.
Thay vào ta được:
(
)
3
32
0
3 2 27(3 2) 46 27 54 33 0
3 25
3
x
x x xxx
x
=
− = −+ ⇔ − − =⇔
±
=
Kết luận: Phương trình có 3 nghiệm là:
0x =
,
3 25
3
x
±
=
Chú ý:
+ Với những phương trình dạng:
[ ]
() ()
n
n
fx b aafx b+= −
(*)
Bằng phép đặt
(); ()
n
t fx y afx b= = −
ta có hệ đối xứng loại 2 là:
n
n
t b ay
y b at
+=
+=
THCS.TOANMATH.com
+ Trong phương trình (*) nếu ta thay a, b bởi các biểu thức chứa
x
thì
cách giải phương trình vẫn như trên. Những phương trình dạng này
thường có hình thức và lời giải khá đẹp.
* Ta xét ví dụ sau:
Ví dụ 2: Giải các phương trình sau:
a)
22
4 11 6 ( 1) 2 6 6
x x x xx− += − − +
b)
3
32
8 13 7 ( 1) 3 2xx x x− += + −
.
Giải:
a) Ta viết lại phương trình thành:
2
(2 3) 3 ( 1) ( 1)(2 3) ( 3)x x x xx x− +−= − − − − −
Đặt
2 3, ( 1)(2 3) ( 3)axb x x x= − = − −−−
ta thu được hệ sau:
2
2
3 ( 1)
3 ( 1)
ax x b
bx x a
+−= −
+−= −
. Trừ hai phương trình của hệ ta được:
22
( 1)( ) ( )( 1) 0
a b x ba ababx− = − − ⇔ − ++− =
Trường hợp 1:
2
2
33
3
()
2
23 2 66
2
33
2 6 30
()
2
xL
x
ab x x x
xx
x TM
−
=
≥
=⇔ −= − + ⇔ ⇔
+
− +=
=
Trường hợp 2:
22
2
23266 30 2663
2
()
7 30 36 0
x xx x xx x
x
VN
xx
−+ − + +−= ⇔ − =−
≤
⇔
− +=
THCS.TOANMATH.com
Vậy phương trình có nghiệm duy nhất:
33
2
x
+
=
b) Ta viết lại phương trình thành:
32 2
3
(2 1) ( 1) ( 1) ( 1)(2 1) 1
x xx x x x xx− − −− = + + − + −−
Đặt
3
22
3
2 1, ( 1)(2 1) 1 3 2a x b x x xx x
= − = + − + −−= −
ta thu được hệ
phương trình:
32
32
( 1) ( 1)
( 1) ( 1)
a xx x b
b xx x a
− −+ = +
− −+ = +
. Trừ hai phương trình của hệ
cho nhau ta thu được:
22
( )( 1) 0aba abb x− + + ++ =
Trường hợp 1:
ab=
ta có:
3
2 32
1
2 1 3 2 8 15 6 1 0
1
8
x
x x x xx
x
=
−= − ⇔ − + += ⇔
= −
Trường hợp 2:
2
22 2
3
10 (2 1) 10
24
b
a ab b x a x x

+ + + += ⇔ + + − + +=


2
22
4 4 2(2 1) 5 0( )
2
b
a x x VN

⇔ + + + − +=


Tóm lại phương trình có 2 nghiệm là
1
1,
8
xx= = −
.
3) Một số cách đặt ẩn phụ khác:
Ví dụ 1: Giải các phương trình sau:
a)
3
3
3
6 66xx− + +=
b)
2 22
2( 1) 2 2 3 4 5 0xx x x x++ + + −− + =
.
THCS.TOANMATH.com
Giải:
a) Đặt
3
3
3
3
66
6
6
x z zx
yz
zy
+= −=

⇒

−=
+=
Mặt khác với các phép đặt ẩn phụ trên, từ phương trình trong đầu bài, ta
có
3
60
xy−−=
.
Như vậy ta được hệ phương trình:
3
3
3
6
6
6
xy
yz
zx
= +
= +
= +
(1)
(2)
(3)
Nhìn thấy hệ trên không thay đổi khi hoán vị vòng quanh đối với
,,xyz
nên không mất tính tổng quát, ta có thể giả thiết
(
)
max , ,x xyz
=
(
x
là
số lớn nhất trong 3 số
,,xyz
hay
,x yx z≥≥
)
Nếu
xy>
, từ (1) và (2) suy ra
33
66y x y z yz+= > =+⇒ >
Khi đó từ (2), (3) suy ra
33
66y x y x zx+= > =+⇒>
. Mâu thuẫn với
giả thiết
xz≥
ở trên. Do đó phải có
xy=
.
Với
xy=
, từ (1) và (2) suy ra
yz=
Vậy
xyz= =
Phương trình (1) trở thành:
3
60xx
−−=
hay
( )
( )
2
2 230x xx− + +=
(4)
Vì
( )
2
2
2 3 1 20xx x+ += + +>
nên PT (4) có nghiệm duy nhất
2x =
.
b) Đặt
2
1yx x= +−
khi đó phương trình đưa về
( )
22
1 54
2 2 1 3 54 1
2
x
y y x yy
−+ +
+ + =+ + ⇔ + −=
THCS.TOANMATH.com
Đặt
1 54
2
x
z
−+ +
=
điều kiện
1
2
z
−
≥
.
Ta có
22
2 1 54 4 4 154 1z x z z xzz x
+= + ⇒ + +=+ ⇒ +−=
.
Do đó ta có hệ phương trình:
2
2
2
1
1
1
xx y
yy z
zz x
+ −=
+ −=
+−=
(*)
( )
( )
(
)
11
11
11
xx y
yy z
zz x
+=+
⇔ +=+
+=+
.
Do điều kiện
1
11
2
z yz
−
≥ ⇒ ≠− ⇒ ≠−
.
Nhân các phương trình theo vế rồi rút gọn được
1xyz =
.
Mặt khác từ hệ phương trình (*), cộng các phương trình vế theo vế ta có:
2 22
3
31x y z xyz xyz++=≥ ⇒ ≤
.
Do đẳng thức xảy ra nên phải có
2 22
11x y z xyz= = =⇔===
(vì
,, 1xyz≠−
).
Vậy phương trình đã cho có nghiệm duy nhất
1x =
.
Ví dụ 2: Giải các phương trình sau:
a)
2 432
2 47 4 3 27xx xxxx+ += + + − −
b)
41 5
2x xx
xx x
+ −=+ −
c)
62 62 8
3
55
xx
xx
−+
+=
−+
b)
2(5 3) 1 5( 1) 3 3(5 1)xx x xx
− ++ + − = +
Giải:
THCS.TOANMATH.com
Cách 1: Biến đổi pt như sau:
( ) (
)
2
22 2
42 472 47 162 4735
xx xx xx++= ++ − +++
(1)
Đặt
2
2 47
xx a
+ +=
(với
5a ≥
), ta có:
( )
( )
(
)( )
2
2
42 2 2 2
4 16 35 6 2 1 2 7 2 5 0(*)aa a a a a a a a
=− +⇔−=+⇔−− +−=
Với
5a ≥
thì
2
2 50aa+ −>
, nên từ (*) suy ra
2
2 70aa− −=
, phương
trình này có 2 nghiệm là
122a
= ±
. Đối chiếu với điều kiện
5a ≥
chỉ chọn được
122a = +
.
Khi đó
( )
22
2 4 7 1 22 2 1 22 0xx xx++=+ ⇔+−+ =
(**)
Phương trình (**) có 2 nghiệm là
1 2 22−± +
. Vậy tập nghiệm của
PT đã cho là
{ }
1 2 22−± +
.
Cách 2: Biến đổi PT về dạng:
( ) (
) ( )
2 42
2 15 13 15
x xx++=+− +−
Đặt
( ) ( )
( )
22
1 ; 2 1 5 , 0; 5x u x vu v+ = + += ≥ ≥
. Ta có hệ:
2 22
22
10
35
25
25 25
uv
u u v u uv v
vu
uv uv
−−=

− −= −= +

⇔⇔

= +
+= +=


Dẫn đến
2
4 40uu− −=
, PT này có 2 nghiệm
2 22±
. Do
0u ≥
nên
chọn
2 22u = +
. Từ đó suy ra kết quả như cách 1.
b) Điều kiện trên ta được:
5
2
x ≥
hoặc
10x−≤ <
(*).
THCS.TOANMATH.com
Phương trình (1) tương đương:
1 54
2
x xx
x xx
−− −=−
Đặt
15
;2ux v x
xx
=−= −
với
0; 0uv≥≥
. Ta được:
4
uv x
x
−=−
(1)
Lại có
22
5 14
2vu x x x
x xx

−= − −− =−


(2)
Từ (1) và (2) suy ra:
( )( )
22
10v u uv uvuv− =−⇔ − ++ =
. Vì
10uv++>
nên
0uv
−=
2
2
4
04
2
x
xx
x
x
=
⇔−=⇔ =⇔
= −
Thử lại thấy nghiệm
2x = −
không thỏa mãn điều kiện , nghiệm
2x =
thỏa mãn phương trình.
c) Điều kiện:
5 x 5.−<<
Đặt:
a = 5 + x; b = 5 - x (a,b > 0).
Khi đó ta có:
22
622 4;622 4xb xa−= − += −
Khi đó ta có:
−−
⇔− −
⇔−
22
22
2b 4 2a 4 8 8
+ = (2b 4)a + (2a 4)b = ab
a b3 3
8
2ab(a + b) 4(a + b) = ab
3
Từ đó ta có hệ phương trình:

−−

⇔


−

22 2
88
2ab(a + b) 4(a + b) = ab 2ab(a + b) 4(a + b) = ab
33
a + b = 10 (a + b) 2ab = 10
Đặt:
≥S = a + b; P = ab,S 10.
THCS.TOANMATH.com
Hệ phương trình trên trở thành:
−
−
2
8
2SP 4S = P
3
S 2P = 10
Từ phương trình (2) ta có:
−
2
S 10
P=
2
thế lên phương trình trên và rút
gọn ta được:
32 2
6 8 84 80 0 ( 4)(3 8 10) 0SS S S SS
− − +=⇔− +− =⇔
) 4 (TMS
=
2
(3 8 1 10
)0 ì
0 .V
SS SNv+−= >
4S =
22
4
3 5 . 5 3 25 9 16 (TM)
4
x
P xb x x
x
=
⇒ =⇔ + −=⇔ − =⇔ = ⇔
= −
Vậy phương trình đã cho có 2 nghiệm là:
4; 4xx= = −
d) Điều kiện
13x−≤ ≤
Đặt
1
3
ux
vx
= +
= −
ta suy ra
2
22
22
22
1
3 2 53
4 51
4
ux
uv x
uv x
uv
= +
−=−
−=+
+=
Phương trình đã cho trở thành:
( ) ( )
2 2 2 22 2 2
23 2 5 34 6 (2 ) ( 3)u v uv u v u u v u− + = − ⇔ −= +
.
Thay
2
4vu= −
ta thu được phương trình:
( ) ( )
( )
( )
( )
2 2 2 22
22
23 2 5 34
2
62 4 3
5 145
10
u v uv u v
u
u u uu
u
−+= −
=
⇔ −=− +⇔
+
=
THCS.TOANMATH.com
Từ đó tìm được các nghiệm của phương trình là:
3
7 145
10
x
x
=
+
=
Khi gặp các phương trình dạng:
.() . ()
nm
ab cfx d e hfx g+ ++ =
ta
có thể đặt ẩn phụ theo cách:
Đặt
.() ()
n
n
ub
b cfx u fx
c
−
+ =⇒=
,
.() ()
m
m
ve
e hfx v fx
h
−
+ =⇒=
Từ đó ta có hệ phương trình:
0
nm
au dv g
u bv e
ch
+=
−−
−=
Ví dụ 1: Giải các phương trình sau:
a)
3
24 12 6xx++ −=
b)
22
4
6
1 11 1x xx x− + + −+ − =
c)
2
2
11
3
xx x x+ −= +−
d)
33 3
1 2 23xx x−+ − = −
Giải:
a) Điều kiện:
12x ≤
Đặt
33
24 ; 12 36, 0u xv x u v
= + = −⇒≤ ≥
, ta có hệ phương trình:
( )
( )
2
2
32
3
6
6
6
12 0(*)
36
6 36
vu
vu
uv
uu u
uv
uu
= −
= −
+=

⇔⇔

+− =
+=
+− =
Phương trình (*) có 3 nghiệm
0; 4; 3uu u= =−=
thỏa mãn
3
36u ≤
.
Từ đây ta tìm được:
24; 88; 3xxx=−=−=
Vậy phương trình đã cho có 3 nghiệm
24; 88; 3xxx
=−=−=
.
THCS.TOANMATH.com
b) Điều kiện:
15
1
2
x
−+
≤≤
.
Ta thấy tổng của biểu thức trong căn bằng 1 nên ta đặt:
− −− ≥
4
22
6
a=1x,b=x+x 1,c=1x;a,b,c 0
.
Khi đó ta có hệ:
246
1
1
,, 0
abc
abc
abc
++=
++=
≥
Vì
2
4 246
6
,, 0
0 ,, 1 1
1
aa
abc
abc b b a b c
abc
cc
≤
≥
⇒ ≤ ≤⇒ ≤ ⇒ + + ≤

++=
≤
.
Hệ phương trình có nghiệm khi
2
4
6
1
aa
bb x
cc
=
= ⇔=
=
là nghiệm của phương
trình đã cho.
c) Đặt
1tx x= +−
thì
2
2
1
2
t
xx
−
−=
Khi đó phương trình đã cho trở thành phương trình bậc hai với ẩn là t:
2
2
1
1 3 2 0 1; 2
3
t
tt t t t
−
+ =⇔ − += ⇔= =
Vậy ta có:
( )
2
11
20
0; 1
2
12
xx
xx
xx
VN VT
xx
+ −=
−=
⇔ ⇔= =
<
+ −=
d) Sử dụng đẳng thức:
( ) ( )
3
33
a+b =a +b +3ab a+b
.
Lập phương 2 vế ta thu được:
THCS.TOANMATH.com
( )
( )
(
)
⇔− − − − − −
33
3
2x3+3 x1x2 x1+x2=2x3
Thay
33 3
1 2 23xx x−+ − = −
thì phương trình trở thành:
( )(
)(
)
−− − ⇔
3
3
x 1 x 2 2x 3 =0 x=1,x=2,x=
2
Ví dụ 2: Giải các phương trình sau:
a)
2
7 7 7 6 2 49 7 42 181 14x x xx x++ −+ + − = −
b)
51
5 24
2
2
xx
x
x
+ =++
c)
( )
( )
3
32 2
1 21x xx x+− = −
d)
( )( ) (
)
3
1 32 1 8
1
x
xx x
x
+
− ++ − =
−
Giải:
a) Điều kiện:
6
7
x ≥
.
Đặt
( )
22
7 7 7 6, 0 14 2 49 7 42 1t x x t x xx t= ++ − ≥ ⇒ + + − = −
BPT đã cho trở thành:
22
13
1 181 182 0 13
14
t
tt t t t
t
=
+ −= ⇔ +− = ⇔ ⇔ =
= −
7 7 7 6 13xx⇔ ++ −=
(*)
Vì hàm số
( ) 7 7 7 6 13fx x x= ++ −−
là hàm đồng biến và
(6) 0f =
Kết hợp với điều kiện suy ra nghiệm của phương trình là
6x =
.
THCS.TOANMATH.com
b) Điều kiện:
0x >
. Phương trình
11
5 24
4
2
xx
x
x


⇔ + =++




Đặt
( )
2
11
,2 1
4
2
tx t x t
x
x
= + ≥ ⇒+ = −
.
Phương trình trở thành:
(
)
22
5 2 1 4 2 5 20 2
t t tt t= −+⇔ − +=⇔=
1
3
4
x
x
⇔+ =
2
3 22
2
4 12 1 0
3 22
2
x
xx
x
−
=
⇔ − += ⇔
+
=
là nghiệm của pương trình.
c) Điều kiện:
11
x−≤ ≤
. Phương trình đã cho tương đương với
(
)
(
)
22 2 2 2
1 1 1 2(1 )x xxx x x x x+ − − − +− = −
Đặt
2
22
1
11
2
t
tx x x x
−
=+−⇒ = −
. Ta có phương trình:
( )
( )
22
32 2
11
1 2 2 3 2 0 2 22 1 0
22
tt
t t tt t t t

−−
− = ⇔+ −− =⇔− + +=


2
22
22 1 0 2 1
tt
tt t

= =
⇔⇔

+ += =− ±


+ Nếu:
2t =
( )
( )
2
2 22
1 22 1 2 1 1x x x x x x do x⇔+−= ⇔ −=−⇔ − =− ≤
THCS.TOANMATH.com
2
1
2 22 1 0
2
xx x⇔ − += ⇔ =
+ Nếu
2
21 1 1 2t xx=− −⇔ + − =−−
vô nghiệm ,do
1
VT VP≥− >
+ Nếu
2
21 1 1 2t xx=− +⇔ − =− −
(
)
2
1 12
1 2 210
x
xx
−≤ ≤−
⇔
− − − +=
1 2 22 1
2
x
−− −
⇔=
Vậy phương trình có 2 nghiệm
2
;
2
x =
1 2 22 1
2
x
−− −
=
.
d). Điều kiện:
3
03
1
x
x
x
+
≥ ⇔ ≤−
−
hoặc
1x >
. Đặt
( )
3
1
1
x
tx
x
+
= −
−
thì
(
)( )
2
13tx x=−+
ta có phương trình:
2
2
2 80
4
t
tt
t
=
+ −=⇔
= −
Nếu
( )( )
2
122
2 1 3 4 2 70
122
x
t x x xx
x
=−+
=⇒ − + =⇔ + −=⇔
=−−
Nết
4
t = −
thì
( )( )
2
1 25
1 3 16 2 19 0
125
x
x x xx
x
=−+
− +=⇔ + −=⇔
=−−
Tóm lại phương trình có 4 nghiệm là:
{ }
1 22;1 22;1 25;1 25x =−+ −− −− −+
.
MỘT SỐ BÀI TẬP RÈN LUYỆN.
Giải các phương trình sau:
1)
( )
2
62 3 4 3x x xx x x+++ += + +
(1).
THCS.TOANMATH.com
2)
2
22
2
21
xx
x
x
++
+=
+
.
3)
( )
2
1 2 1 1 1 31x xx x x++ + = −+ − + −
.
4)
( )
( )
( )
12 3xx xx xx++ + = −
.
5) Tìm tất cả các số nguyên dương
1p >
sao cho phương trình sau có
nghiệm duy nhất
32
1
1 10
1
x px p x
p

+ + −+ +=

−

6)
3
22
4 31 4 1xx x x
−++=−
.
7)
42
2016 2016xx++ =
.
8) Tìm
k
để phương trình sau có nghiệm:
( )
( )
22 2
2 22 15 6 3 2 1
x xxk kk x

+ − −+ − + = =

. Trích đề thi vào
lớp 10 Chuyên Amsterdam 2002).
9) Cho phương trình
( )
64
13 2mx x
+= +
a) Giải phương trình với
10
m =
.
b) Tìm
m
để phương trình có đúng hai nghiệm.
10)
( )
2 22
2 1 13 6 10x x x xx− + −− + −=
.
11)
( ) ( ) (
)
121221241xxxx+= ++ ++ +
.
12)
41 5
2x xx
xx x
+ −=+ −
(*).
13)
22
9
1
xx
x
+= +
+
.
14)
(
) ( )
2
31 12x x xx x+− −=
(1).
15)
2
4 1 5 14x xx+= − +
.
16)
( )
(
)
2
2 2 1 7 10 3
x x xx+− − + + + =
(1).
THCS.TOANMATH.com
17)
22
22
33
12 4 4xx
xx
−+ −=
(*).
18)
( )( )
3 1 11x xx+− −+ =
(THPT chuyên KHTN-ĐHQG Hà Nội
2011-2012).
19) Giải bất phương trình:
( )
2
3
3
25 2 9 4
xx x
x
+≥+
. Trích đề thi vòng 2,
THPT chuyên Hà Nội Amsterdam 2004-2005
20)
( )
( )
3
2
42 2
1
11
x
x x xx x
x
+
+ ++ −+ ≤
21)
( )( )
3
44
4
2 4 2 4 6 3 30x x x x xxx− − + −+ −+ ≤ +
22)
( )
22
12 2 2 3 2x x xx x+ − = −−
(Trích đề tuyển sinh lớp 10 Chuyên
Lam Sơn Thanh Hóa 2014)
23)
22
2 1 12 2x x xx−+ − = −
. (Trích đề tuyển sinh lớp 10 PTNK-
ĐHQG Tp Hồ Chí Minh 2015).
24)
+ −− +=
2
8x 16x 20 x 15 0
25)
− +=− −+
22
4x 11x 10 (x 1) 2x 6x 2
26)
− +=− + +
2 42
3
x 3x 1 x x 1
3
27)
−+ −+ − + =
2
2 x 1 3 5 x 3x 30x 71 0
28)
(
)
− + −= − +
22
2x 4x 1 2x 1 4x 7x 3
29)
−+ − = −
33
3
x1 x2 2x3
30)

−

+ + + +=

−
−

22
22
2
1 x 5 1x x
20
2x
x 1x
1x
31)
(
)
+= +
32
5 x 1 2x 2
32)
++ += + +
33
22
33
2x 2 2x 1 2x 2x 1
33)
( )
+ − += − +
32 3
x 6x 2x 3 5x 1 x 3
34)
++
+ −=
+
+
2
2
2
x x1 2
x4
x4
x1
THCS.TOANMATH.com
35)
+ −=+
+
2
2
2 18x
25x 9 9 x 4
x
x1
36)
+ + +≤ + + +
2
20x 80x 125 2x 1 4 3x 6
37)
−+ +=
24 24
13 x x 9 x x 16
LỜI GIẢI BÀI TẬP RÈN LUYỆN
1) Giải:
Điều kiện:
3
x ≥−
Ta có: (1)
2
3 2 34 360x x xx x⇔ − + +− ++=
(2)
Đặt
3
tx x=++
Do đó (2)
( )
(
)
2
4 3 0 1 3 0 1; 3
t t t t tt⇒ − += ⇔ − − = ⇔= =
Với
1t =
, ta giải phương trình
31 31xx x x+ +=⇔ +=−
( )
2
22
10
11
312 3 2 0
31
x
xx
x xx x x
xx
−≥
≤≤

⇔⇔ ⇔

+=− + − −=
+= −

1
3 17 3 17
22
3 17
2
x
xx
x
≤
+−
= ⇔=
⇔
−
=
Với
3
t =
, ta giải phương trình
33 33xx x x+ +=⇔ +=−
3
11
6
x
xx
x
≤
⇔
=⇔=
=
THCS.TOANMATH.com
Vậy phương trình đã cho có hai nghiệm
3 17
,1
2
xx
−
= =
.
2)
Điều kiện
1
2;
2
xx≥− ≠−
.
Ta có (1)
( )
2
21 2 22x x xx⇔ + += + +
( )
( ) ( )
12 1 2x x x xx x⇔ ++ += + + +
( ) ( ) ( )
2 21 2 10x x x xx⇔ + − + ++ + =
( )
( )
2 2 10x xx x

⇔ +− +− + =

Trường hợp 1:
2xx+=
với
0x ≥
( )( )
2
20 2 1 0xx x x⇒ −−=⇔ − + =
2x
⇔=
(thỏa mãn) hoặc
1x = −
(loại)
Trường hợp 2:
21xx+=+
với
2
1 10x xx≥− ⇒ + − =
15
2
x
−+
⇔=
( thỏa mãn) hoặc
15
2
x
−−
=
(loại)
Vậy phương trình có hai nghiệm
15
2,
2
xx
−+
= =
.
3)
Đặt
1, 1u xv x=+=−
( , 0)uv
≥
Phương trình đã cho trở thành:
( )
22 2 2
2 3 31 2 0u u v v uv v u v u u+ =− ++ ⇔ − + + +=
(1)
THCS.TOANMATH.com
Xem (1) như là phương trình bậc hai đối với biến
v
, giải ra được
uv=
hoặc
21vu= +
.
Xét
21vu= +
, vì
(
)
2
2 22
1 2 2 21
v xu uu
=−=− ⇒− = +
2
1
()
5 4 10
5
1( )
u tm
uu
ul
=
⇔ + −= ⇔
= −
. Với
1 24
5 25
ux=⇒=−
Vậy phương trình có hai nghiệm
24
0;
25
xx
= = −
.
4) Giải:
Điều kiện:
2
0
3
x
x
x
≤−
=
≥
Dễ thấy
0x =
là 1 nghiệm và
3x =
không là nghiệm của phương trình đã
cho
Xét
0, 3
xx≠≠
khi đó phương trình đã cho tương đương với
12 4 5
11 1 1
33 3 3
xx
xx x x
++
+ =⇔+ ++ =
−− − −
Đặt
4
1
3
a
x
= +
−
( 0)a
>
;
5
1
3
b
x
= +
−
( 0)b >
Ta có hệ
22
1
4 21( )
541
4 21
ab
al
ab
a
+=
=−−
⇔

−=
=−+
4 2 21
1 4 21
33
x
x
−
⇒+ =−+ ⇔ =
−
THCS.TOANMATH.com
Vậy phương trình có hai nghiệm
2 21
0;
3
xx
−
= =
.
5) Phương trình đã cho tương đương với
( )
2
1
10
1
xp x x
p

+− ++ =

−

2
1
1
0
1
xp
xx
p
=−+
⇔
++ =
−
(1)
(2)
Yêu cầu bài toán tương đương (2) vô nghiệm
hoặc có nghiệm kép
( )
1xp=−−
Vậy
{ }
2; 3; 4p ∈
.
6)
Phương trình đã cho tương đương với
(
)
( )
22
3
2 27 2 3
xx− + +− =
.
Do
( ) (
)
22
3
2 27 2 3,x xx− + + − ≥∀
và đẳng thức xảy ra khi và chỉ khi
2x =
nên phương trình có nghiệm duy nhất
2x =
.
7)
Phương trình đã cho tương đương với:
( )
42 2 2
11
2016 2016
44
xx x x+ += + − + +
22
22
11
2016
22
xx

⇔+= + −


2 2 2 2 42
11
2016 1 2016 2015 0
22
x x x x xx⇔+= + −⇔+= + ⇔+− =
.
Vậy phương trình có hai nghiệm
1 8061 1 8061
;
22
xx
−+ −+
= =
.
THCS.TOANMATH.com
8) Giải:
Phương trình đã cho tương đương với:
(
)
( )
(
) ( )
22 2 2
2 2.21 4 41 21121
x xxk kk kk x

+ − −+ − ++ − ++ = +

( )
( )
( )
( ) ( )
2 22
22
2 21 2 1 1 0 1x x k x k x xk⇔ + − + + + − + − =⇔==
.
Vậy phương trình có nghiệm khi
1k =
.
9) Phương trình đã cho tương đường với:
( )( )
( ) ( )
2 42 2 42
1 13 1 1mx xx x xx

+ −+= ++ −+

2 42
42 2
11
3 11
m x xx
xx x
+ −+
⇔= +
−+ +
Đặt
42
2
1
1
xx
t
x
−+
=
+
,
( 0)t >
ta được:
2
1
. 10
3
mm
t tt
tt
=+⇔ − +=
a) Với
10m
=
ta có phương trình:
2
3 10 3 0tt− +=
ta suy ra
3t =
hoặc
1
3
t
=
b) Tự giải
10) .Giải:
Điều kiện:
1x ≥
. Phương trình tương đương với
(
)
2 22 2
12 1 1 2 14 4 10x x x xx xx−− + −+++− +−=
(
)
(
)
2
22
2
31
3 12 1 0
21
xx
xx xx
xx
= −
⇔−− −−−=⇔
−= −
Trường hợp
2
22 2
0 1 011
31
9 18 1
x
xx
xx x
≤ ≤ ≤≤

= −⇔ ⇔

=−=−

(vô nghiệm).
THCS.TOANMATH.com
Trường hợp
2
22
12
12
12
5
21
5
45
4
44 1
4
x
x
x
xx x
x
x
xx x
≤≤
≤≤
≤≤
−=−⇔ ⇔⇔⇔=

=
=
− += −
.
11) .Giải:
Điều kiện
1x ≥−
.Ta có
3x
=
là một nghiệm của phương trình.
Với
3x >
. Đặt
( )
1, 4x yy+= >
, phương trình đã cho
thành:
2 22 24
yyyy=++
.
Ta có
2
4 24 2
y yy yy<=⇒ <
22224 224 22 4yyyyyyyyy⇒+ + <+ <+=<
Phương trình vô nghiệm.
Với
03
x<<
. Chứng minh tương tự, ta có phương trình vô nghiệm.
Vậy
3x =
là nghiệm duy nhất của phương trình.
12) Giải:
Ta có (*)
4 15
20xx x
x xx
⇔ −+ − − − =
(1)
Đặt
15
;2
ux v x
xx
=−= −
thì
,0uv≥
và
22
4
uv x
x
−=−
Do đó (1) thành:
( )( )
22
0 10u v uv uvuv u v− +−= ⇔ − ++ =⇔ =
(vì
,0uv≥
)
Từ đó ta có:
1 515
2 20x xxx
x xxx
−= −⇔−= −≥
(2)
THCS.TOANMATH.com
Phương trình
15
2
xx
xx
−= −
có nghiệm là
2x = ±
Từ (2) suy ra chỉ có
2
x =
là nghiệm của phương trình đã cho.
13)
Giải:Điều kiện
0x ≥
.
Phương trình tương đương với:
8 42 9 1 42
90
11
11
xx x
xx
xx
xx
+
+=+ + ⇔ − =
++
++
2
8 42 22
10 1 0
1
11
xx x
x
xx

⇔ − += ⇔ − =


+
++

22 1
18 1
7
1
x
xx x
x
⇔ =⇔ = +⇔ =
+
(thỏa mãn
14) Giải:
Điều kiện:
1
x ≥
. Dễ thấy
0x =
là nghiệm của (1)
Với
0x ≠
, chia hai vế của (1) cho
2
0x ≠
, ta được:
(1)
11
3 12
xx
⇔ +− −=
Đặt
11
3 0, 1 0uv
xx
= +≥ = −≥
Ta có hệ phương trình:
( )
2
22
2
2
2
4
24
uv
uv
uv
vv
= +
−=
⇔

+=
+ +=
(2)
(3)
Giải hệ ta được
0, 2vu= =
từ đó ta có
1x =
.
THCS.TOANMATH.com
15) .Giải:
( )
( )
2
6 9 14 14 0
xx x x
⇔ − + + +− ++ =
( )
(
)
2
2
3 12 0xx
⇔ − + +− =
30
3
120
x
x
x
−=
⇔ ⇔=
+− =
Vậy phương trình có nghiệm duy nhất là
3x =
.
16) Giải:
Điều kiện:
2x ≥−
Nhân hai vế của phương trình (1) với
5 20xx++ +>
, ta được phương
trình tương đương:
2
1 7 10 5 2xx x x+ ++= ++ +
()
()
l
tm
.
17) Giải:
Đặt
2
,0y xy
= ≥
, ta có (*) thành:
33
12 4 4yy
yy
−= − −
Bình phương rồi biến đổi thành:
(
)
2
22
4 3 0 4 30y y yy−− =⇔ −−=
Do đó các nghiệm của phương trình là
1, 1xx= = −
.
18) Điều kiện:
01x≤≤
THCS.TOANMATH.com
Nhân cả tử và mẫu vế trái với biểu thức
3xx
++
ta thu được:
(
)
( )
( )
3
3 1 11 1 11
3
x xx x
xx
+− −+ =⇔ −+ =
++
31 1 3
xxx⇔ − += + +
(*)
Nếu
1x =
thì
(*) 3 (*)VT VP= =
nên
1x =
là nghiệm của phương trình.
Nếu
01x
≤<
thì
1 0 31 3 3xx− >⇒ −+>
hay VT(*)
3>
với
01
x≤<
Vì
01x≤<
nên
3 1 3 2, 1 1 (*) 3
x x VP
+< += < =⇒ <
Do đó phương trình đã cho không có nghiệm trong nửa khoảng
[
)
0;1
.
Vậy phương tình đã cho có nghiệm duy nhất
1x =
.
19) Giải:
Điều kiện:
0x ≠
Trường hợp
0x >
: áp dụng bất đẳng thức Cô si ta có:
( )
22
2
3
3
3529 5529
4 3 . . 25 2 9
3 3 33 3
xx
x x xx xx
xx x
++
+= + ≥ = +
Dấu bằng xảy ra khi và chỉ khi
2
529
3
33
x
xx
x
+
= ⇔=
Trường hợp
0x <
: từ phần trên ta thấy, với mọi
0
x <
đều thỏa mãn bất
phương trình
Đáp số
3
0
x
x
=
<
.
20) .Giải:
THCS.TOANMATH.com
Điều kiện
0x >
Chia cả hai vế bất phương trình cho
( )
2
1
xx+
và đặt
1
,2tx t
x
=+≥
, ta
đưa về bất phương trình
11
1 tt
tt
− ≤− −
Với điều kiện
2t ≥
thì cả hai vế của (1) đều dương. Bình phương hai vế ta
đưa về bất phương trình tương đương
2
1
10t
t

−− ≥



Bất phương trình này nghiệm đúng với mọi
2t ≥
.
Vậy nghiệm của bất phương tình đã cho là
0x
>
.
21) .Giải:
Điều kiện:
24x≤≤
Áp dụng bất đẳng thức Cô si ta có:
( )
(
)
4
24
24 1
2
xx
xx
−+−
− −≤ =
;
21
1
21 1
2
2 2.1
2 24
x
xx
xx
−+
+
−+ +
−= − ≤ ≤ =
;
4
7
4
2
x
x
−+
−≤
;
33
6 3 2 .27 27xx x x= ≤+
Do đó
VT VP≤
với mọi
x
thỏa mãn
24x≤≤
Vậy nghiệm của bất phương trình là
24x≤≤
.
22) Đặt
2 22
22022t xx xxt= − ≥⇒ − =
. Phương trình trở thành :
( )
2
1 20t x tx− + −−=
. Ta có
THCS.TOANMATH.com
(
)
(
)
2
2
13
1
2
2 14 8 3
13
2
2
xx
t
xx x x
xx
tx
+− +
= = −
∆=++++=+ ⇒
++ +
= = +
. Do
0t ≥
ta chỉ
cần giải:
2
2
0
2 2 2 3 13
6 40
x
x xx x
xx
≥
− =+⇔ ⇒=+
− −=
.
23) Điều kiện:
2
2
2 10
12 0
0
x
x
xx
−≥
−≥
−≥
. Bình phương 2 vế ta thu được:
(
)
( )
(
)
2 22
2 112 2 2 112 4
x x x x xx−+− + − − = −
(
)
( )
22
2 2 2 2 112 0xx x x⇔− + − − − =
(
)
2
2 22
15
2
12 2 1 0 12 2 1 10
15
2
x
x x x x xx
x
−−
=
⇔ − − − = ⇔− = −⇔ + −= ⇔
−+
=
Đối chiếu với điều kiện nài toán chỉ có nghiệm
15
2
x
−+
=
thỏa mãn điều
kiện.
24) Ta viết lại phương trình thành:
( )
+ −− +=⇔ + −= +
2
2
16x 32x 40 2 x 15 0 4x 4 56 4x 60
Đặt
+=+4x 60 4y 4
ta có hệ sau:
( )
( )
( )
( )

+=+ +=+

⇔


+ −=+ + =+

22
22
4y 4 4x 60 4y 4 4x 60
4x 4 56 4y 4 4x 4 4y 60
.
Trừ từng vế 2 phương trình của hệ ta có:
THCS.TOANMATH.com
( ) ( ) ( )
( )( ) ( )
+ − + = − ⇔ − ++ = −
22
4x4 4y4 4yx 16xyxy8 4yx
(
)
=
⇔
++ =
xy
4x y 8 1
Giải phương trình ứng với 2 trường hợp ta thu được:
−+
= =
9 221
x 1; x
9
25) Điều kiện:
−
≤
+
≥
35
x
2
35
x
2
Ta viết lại phương trình thành:
( )
− ++=− − −−+
2
2x 3 (x 1) (x 1) (x 1)(2x 3) (x 1)
Đặt
= −
= − −−+
u 2x 3
v (x 1)(2x 3) (x 1)
ta có hệ phương trình:
++= −
++= −
2
2
u x 1 (x 1)v
v x 1 (x 1)u
Trừ từng vế hai phương trình ta có:
( )(
)
=
− ++− =⇔
=−−+
uv
uvuvx1 0
u vx1
Giải theo hai trường hợp ta thu được phương trình vô nghiệm.
26) Cách 1: Ta viết lại phương trình thành:
(
)
(
)
− +=− ++ −+
2 22
3
x 3x1 x x1x x1
3
(
)
(
)
(
)
(
)
⇔ −+ − ++ =− ++ −+
2 2 22
3
2x x1 x x1 x x1x x1
3
THCS.TOANMATH.com
Chia phương trình cho
(
)
++ >
2
x x1 0
ta thu được:
 
−+ −+
⇔ −=−
 
 
++ ++
 
22
22
x x1 3 x x1
21
3
x x1 x x1
. Đặt

−+
= >


++

2
2
x x1
t0
x x1
Ta có phương trình:
+ −=⇒=
2
31
2t t 1 0 t
3
3
Giải
* Cách 2:
Xét
>x0
chia hai vế phương trình ta có:
−+ =− ++
2
2
13 1
x3 x 1
x3
x
Đặt
=+≥
1
tx 2
x
ta có phương trình:
−=− −
2
3
t3 t 1
3
Xét
<x0
chia hai vế phương trình ta có:
−+ = ++
2
2
13 1
x3 x 1
x3
x
Đặt
= +
1
tx
x
ta có phương trình:
−= −
2
3
t3 t 1
3
27) Điều kiện:
≤≤1x5
. Phương trình được viết lại:
Ta viết lại phương trình thành:
−−+ −+ − + =
2
2 x 1 4 3 5 x 3x 30x 75 0
THCS.TOANMATH.com
(
)
−
⇔ + −+ − − =
−+
x5
2 3 5 x (x 5)(3x 15) 0
x12
( )
=
−
⇔ + −+ − − =
−−
+− − − =
−+
−+
x5
x5
2 3 5 x (x 5)(3x 15) 0
25 x
3 5 x(3x 15) 0
x12
x12
Ta thấy

− − − ≥∀∈

5 x(3x 15) 0 x 1; 5
Ta chứng minh:
−−
+≥⇔ −+− − ≥
−+
25 x
3 0 3x 1 6 25 x 0
x12
nhưng điều
này là hiển nhiên đúng do:
−≤ −=25 x 25 1 4
nên
− −>6 25 x 0
Vậy phương trình có nghiệm duy nhất
=x5
28) Điều kiện
≥
1
x
2
. Đặt
=−= −u x1;v 2x1
phương trình đã cho trở
thành
(
)
(
)
( )(
)
− = − ⇔ − +=
22
2u 1 v 2v 1 u u v 2uv 1 0
+ Nếu
≥
= ⇒−= −⇔ ⇔ =+
− +=
2
x1
u v x1 2x1 x 2 2
x 4x 2 0
+ Nếu
( )

+=⇔ − −=⇒∈


1
2uv 1 0 2 1 x 2x 1 1 x ;1
2
Mặt khác ta có:
( )

−< − =


1
21 x 21 1
2
;
−≤ −=2x 1 2 1 1
nên phương
trình đã cho vô nghiệm
Kết luận:
= +x2 2
29) Sử dụng đẳng thức:
( ) ( )
+ =++ +
3
33
ab a b 3abab
.
THCS.TOANMATH.com
Phương trình
( )( )
( )
⇔ −+ − − −+ − = −
33
3
2x33 x1x2 x1 x2 2x3
( )
( )
(
)
−+ − = −
⇔ ⇔= = =
− − −=
33
3
3
x1 x2 2x3
3
(*) x 1;x 2;x
2
x1x22x3 0
30)
Điều kiện:
11x−< <
. Đặt
−
= + ⇒= + +
−
−
22
2
22
2
1x x 1 x
t t1
x
x 1x
1x
.
PT đã cho thành:
+ +=⇔=−
2
2t 5t 2 0 t 2;
*
=−⇔
t2
−< <
−
=− + =−⇔ ⇔ =−
+=
−
−
2
2
2
22
1x0
11x x 1
t 2x
1x
2x
3
2
1x
x 1x
*
=−⇔
1
t
2
−< <
−
+ =−⇔
+=−
−
−
2
2
2
22
1x0
1x x 1
1x 3
x2
1x
4
x 1x
hệ vô nghiệm.
Vậy phương trình đã cho có nghiệm duy nhất
= −
1
x
2
.
31)
Điều kiện.
≥−x1
( )
(
)
(
)
( )
⇔ + −+ = −+ + +
++
⇔ − + = − +>∀
−+ −+
22
2
22
PT 5 x1x x1 2x x1 2x1
x1 x1
2 5 2 0(Do : x x 1 0 x)
x x1 x x1
Đặt
+
= ≥
−+
2
x1
t ,t 0
x x1
, ta có:
=
− +=⇔
=
2
t2
2t 5t 2 0
1
t
2
*
+
=⇔ =⇔ − +=
−+
2
2
x1
t 2 4 4x 5x 3 0
x x1
PT vô nghiệm
THCS.TOANMATH.com
*
+±
= ⇔ = ⇔ − −=⇔=
−+
2
2
1 x 1 1 5 37
t x 5x 3 0 x
24 2
x x1
32) Do
≥VT 1
nên
⇒ ≥ ⇔ ≥−VP 1 x 1
.
Ta có PT

⇔ +−++ −+=


3 3 33
2 2 22
2x 1 2x 2 2x 2x 1 0
(
)
(
)
(
)
(
)
(
)
(
)
−− −−
⇔ +=
++++++ + +++
22
22 2
3
2 2 2 42 2
33 3
3
3
2x 2x 1 2x 2x 1
0
2x 1 2x 1 2x 2 2x 2 x 2x 2x 1 2x 1
±
⇔ − −= ⇔ =
2
13
2x 2x 1 0 x
2
là nghiệm của phương trình đã cho.
33) Điều kiện:
≥−
3
x3
.
Ta thấy
=
1
x
5
không là nghiệm của phương trình nên ta có:
Phương trình
+ −+
⇔=+
−
32
3
x 6x 2x 3
x3
5x 1
.
+−+ −+
⇔ − = +− ⇔ = +−
−−
32 32
33
x 6x 2x 3 x 4x 3
2x x 3 2x x 3 2x
5x 1 5x 1
(1)
* Nếu
( )
(
)
≤
≤
−

+− =⇔ ⇔ ⇔=

− −−=
− +=
3
2
32
x0
x0
3 21
x 3 2x 0 x
x 1 x 3x 3 0
2
x 4x 3 0
Khi đó (1) đúng
⇒
−
=
3 21
x
2
là một nghiệm của phương trình.
* Nếu
( )
− +=
− −+ −+
≠ ⇒⇔ = ⇔
−
++ = −
++
32
32 32
3
3
x 4x 3 0
3 21 x 4x 3 x 4x 3
x1
2 5x 1
x 3 2x 5x 1
x 3 2x
(1)
(2)
Ta thấy: (1) có 2 nghiệm
+
= =
3 21
x 1; x
2
THCS.TOANMATH.com
( )
(
)
≥
≥
⇔ + = −⇔ ⇔


− −−=
− + +=
3
2
32
1
1
x
x
3
(2) x 3 3x 1 3
x 1 x 8x 2 0
x 9x 6x 2 0
=
⇔
= +
x1
x 4 32
Vậy phương trình có 4 nghiệm:
±
= = = +
3 21
x 1;x ;x 4 3 22
2
.
34) Điều kiện:
4x >−

++

⇔ − + −= −

+
+

2
2
2
x x1 2
PT 2 1 x 3 1
x4
x1
(
)
++
−+
+
⇔ + −+ =

++
++ +

+

+
2
2
2
2
22
x x1
4x1
x4
x3 0
x x1
2 x1x1
1
x4
(
)
( )
(
)
−
−
⇔ + −+ =

++ +
+ ++ ++


2
2
2
22
2
2x 3
x3
x3 0
2 x1x1
x4x x1 x4
(
)
( )
(
)


⇔ − ++ =



+ ++ ++
++ +




2
2
22
21
x3 1 0
x4x x1 x4
2 x1x1
⇔ −=⇔=±
2
x 30 x 3
35) Điều kiện:
≥
2
x
3
* Với
≥
2
x
3
, phương trình đã cho tương đương với:
THCS.TOANMATH.com
−
+=+
+
2
22
9 9x 4 2 18
25
x
x x1
(1)
Dễ thấy phương trình (1) có
>VT 25
và do
≥
2
x
3
ta có
≤+ <
9 162
VP 25
2 13
nên phương trình đã cho vô nghiệm
* Với
≤−
2
x
3
phương trình đã cho tương đương với
(2)
Đặt

= <≤


2
19
t0 t
4
x
, phương trình (2) thành:
18t 18t
25 9 9 4t 2t 9 9 9 4t 2t 16
1t 1t
− −=+ ⇔− −=+ −
++
⇔
( ) ( )( )
( )
36t 2 2t 2 t 4
18 t 4
t2 0
t1 t1
9 4t 1 9 4t 1
− −+

+
= ⇔− − =

++
−+ −+

(1)
Lưu ý rằng với
<≤
9
0t
4
có
≥
−+
18 18
4
9 4t 1
và
+
=+ <<
++
t 4 3 18
14
t1 t1 4
nên
+
−>
+
−+
18 t 4
0
t1
9 4t 1
.
Vậy (3)
⇔=⇒ =−
2
t2 x
2
KL: Phương trình có 1 nghiệm
= −
2
x
2
36) Điều kiện:
≥−x2
BPT được viết lại:
( ) ( )
2
5 2x 1 20 3x 6 2x 1 4 3x 6+ + + ≤ ++ +
Đặt a = 2x + 1; b
22
3x 6 ; BPT 5a 20b a 4b+ ⇔ + ≤+
THCS.TOANMATH.com
( )
+≥
⇔ ⇔=
+ ≤+
2
22
a 4b 0
ab
5a 20b a 4b
≥−
+= + ⇔ ⇔ =
+−=
2
1
x
2x 1 3x 6 x 1
2
4x x 5 0
Kết luận: Nghiệm của bất phương trình là:
=x1
37) Điều kiện: −1 ≤ x ≤ 1
Bình phương 2 vế ta có :

−+ + =


2
222
x 13 1 x 9 1 x 256
Áp dụng bất đẳng thức Bunhiacopxki:
(
)
(
)
(
)

− + + ≤ + − ++ = −


2
2 2 22 2
13. 13. 1 x 3. 3. 3 1 x 13 27 13 13 x 3 3x 40 16 10x
Áp dụng bất đẳng thức Côsi:
(
)

−≤ =


2
22
16
10x 16 10x 64
2
Dấu bằng
=
+
−=
⇔⇔
= −
= −
2
2
22
2
x
1x
1x
5
3
2
x
10x 16 10x
5
| 1/100

Tài liệu khác của Môn Toán

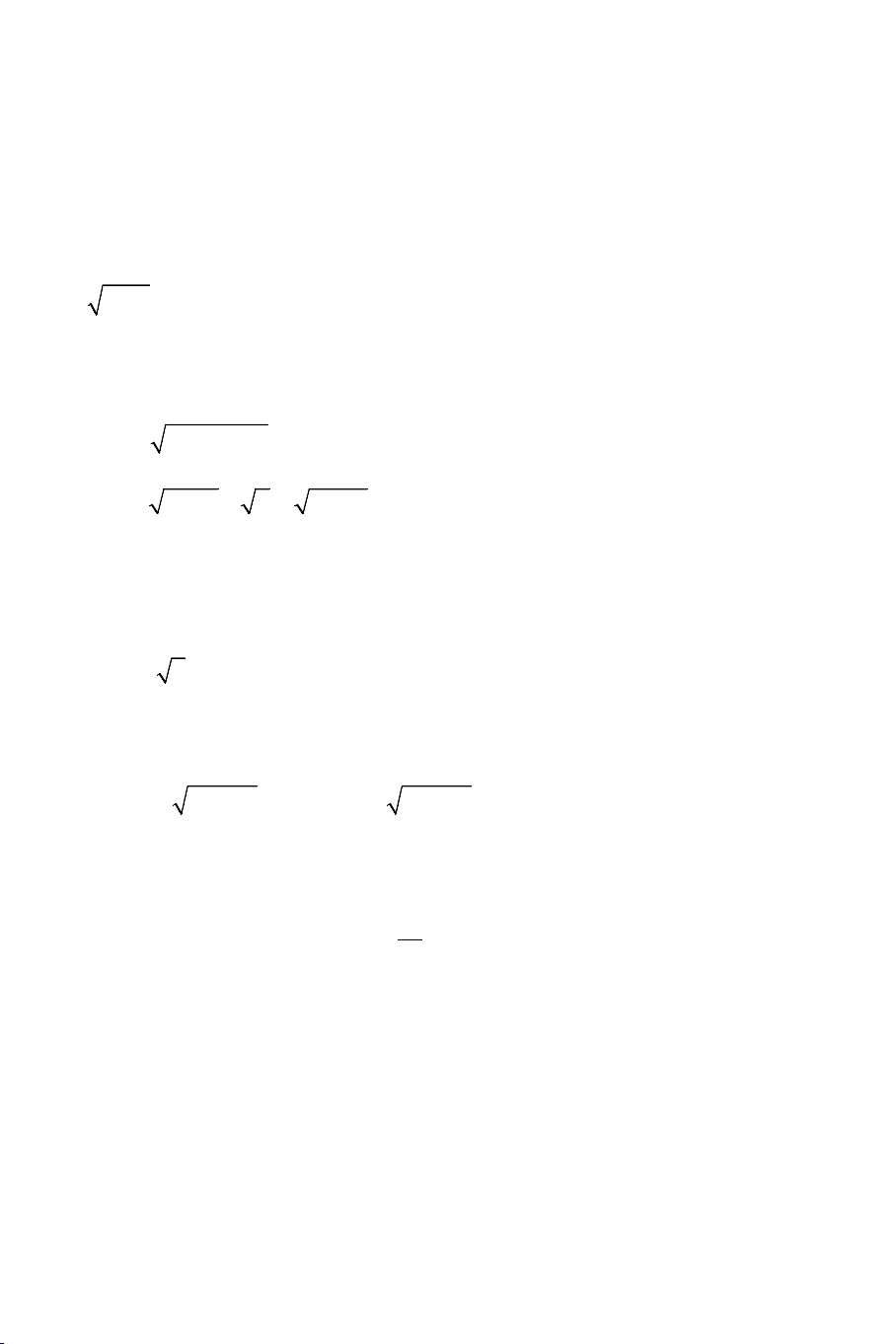
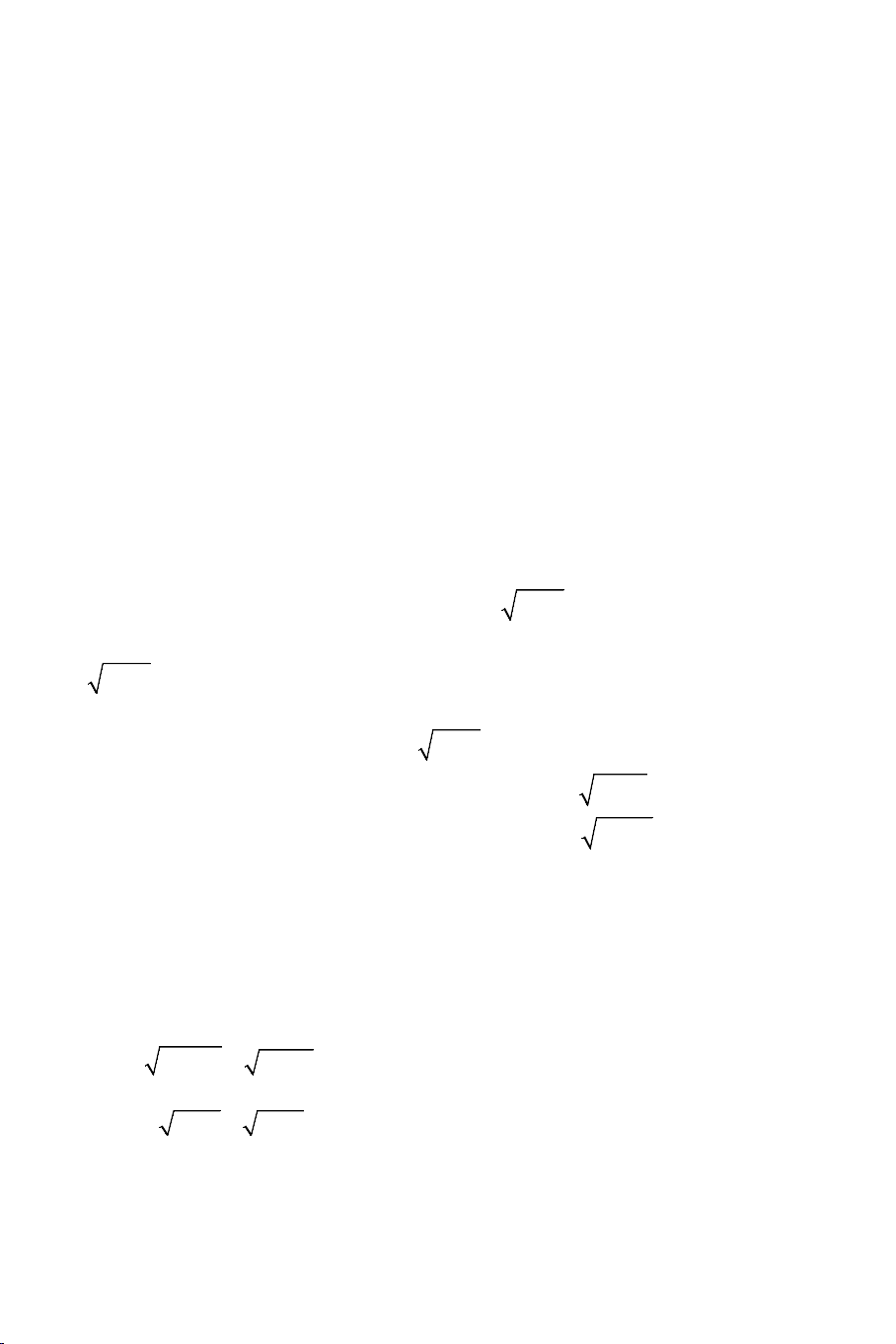
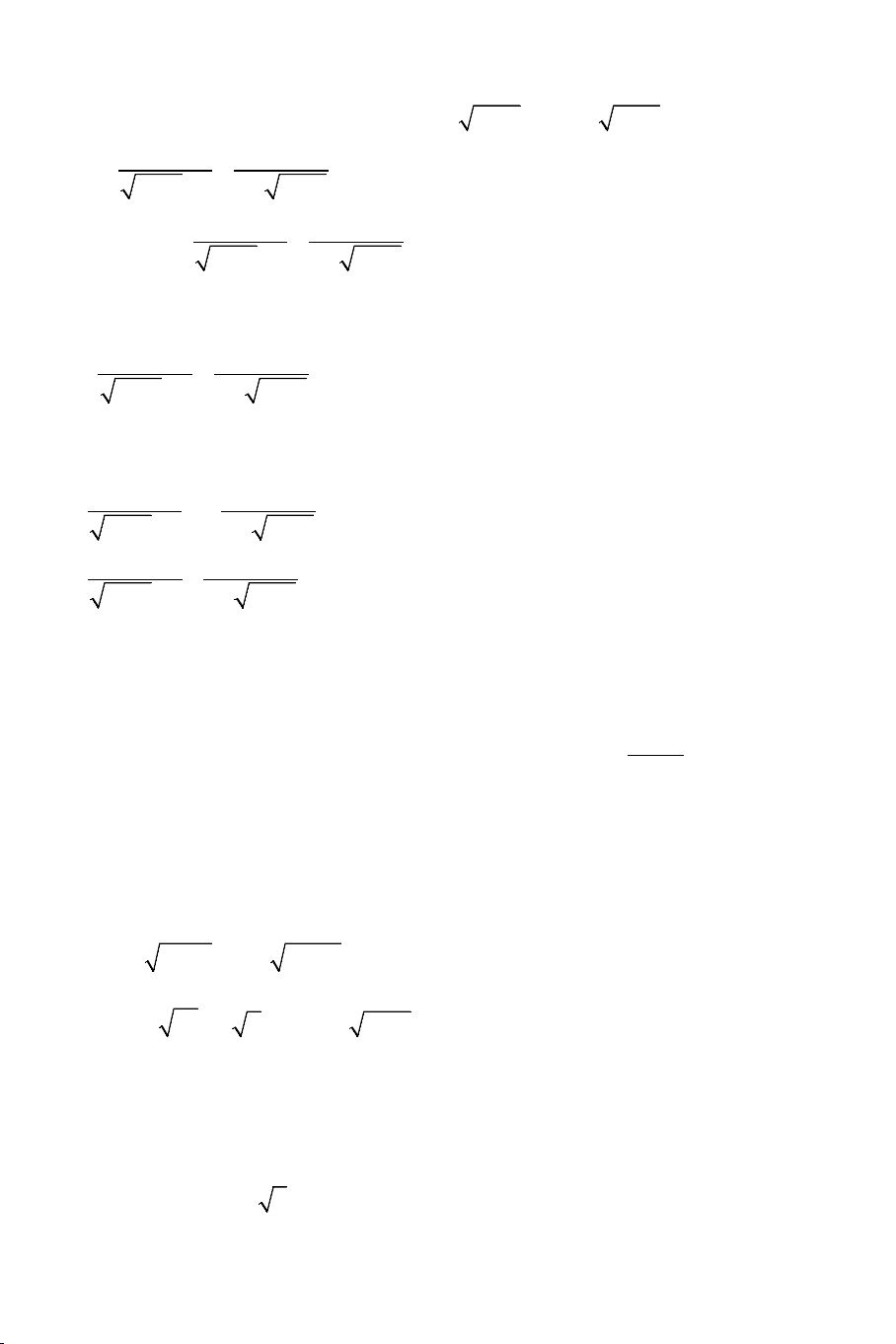
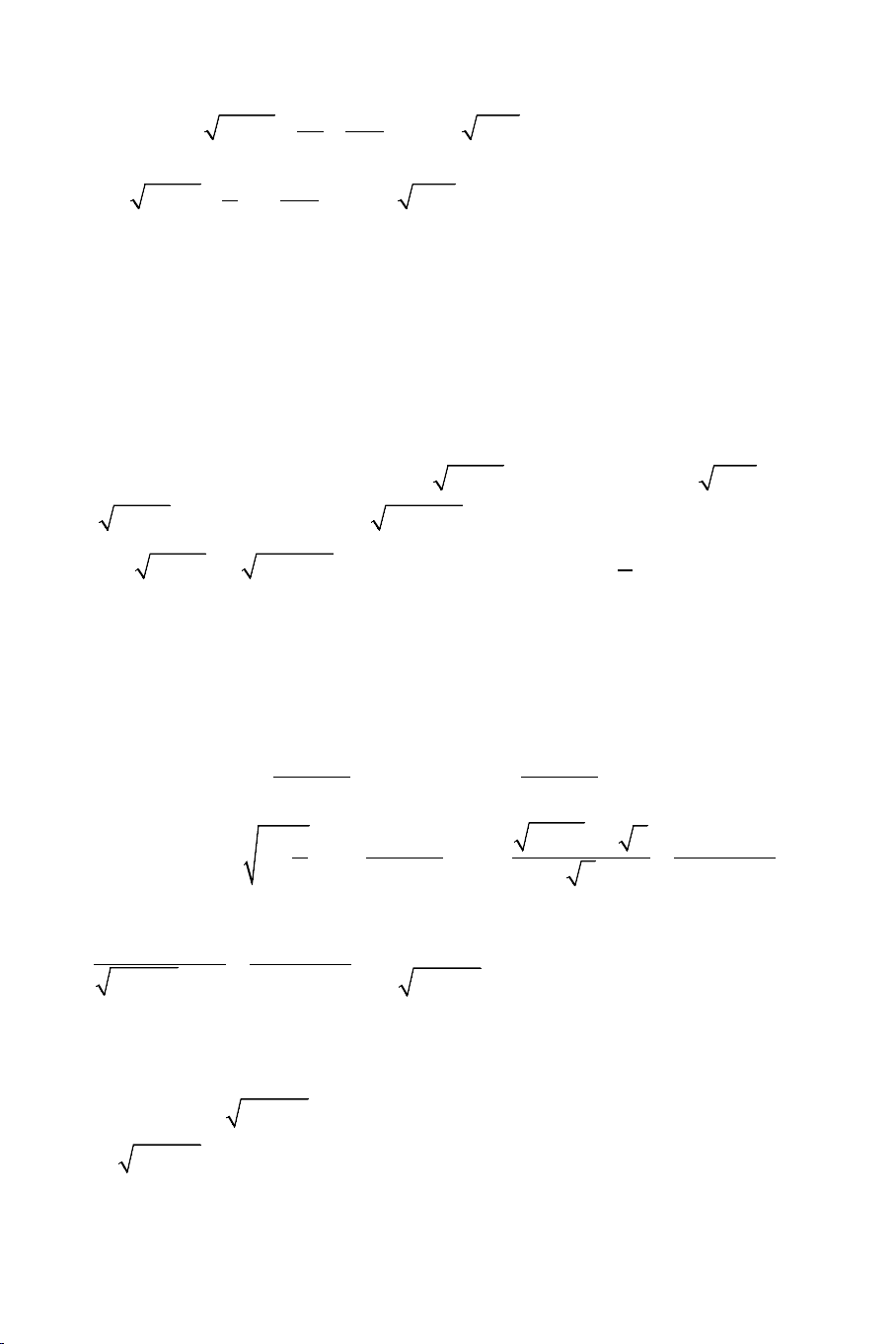
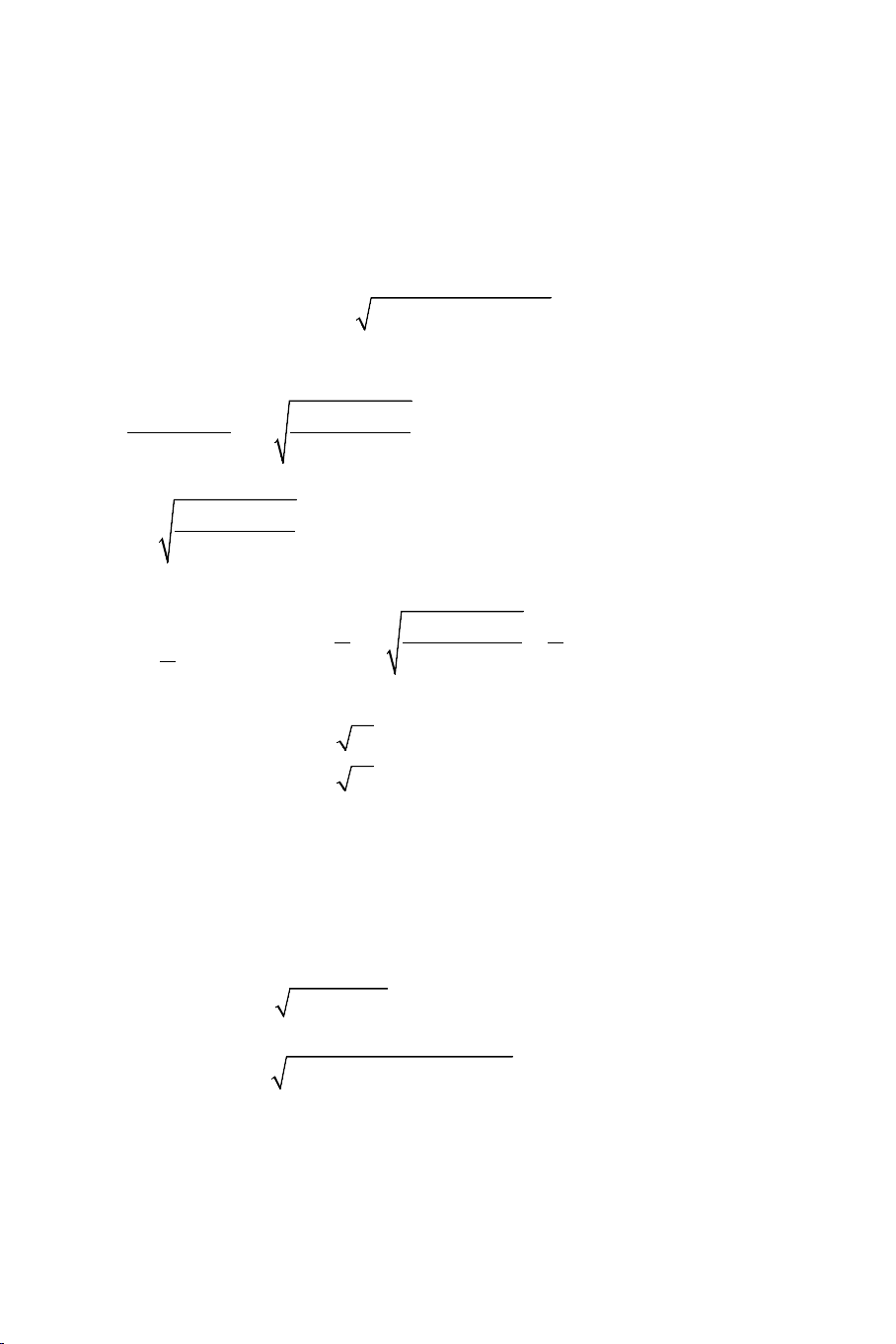
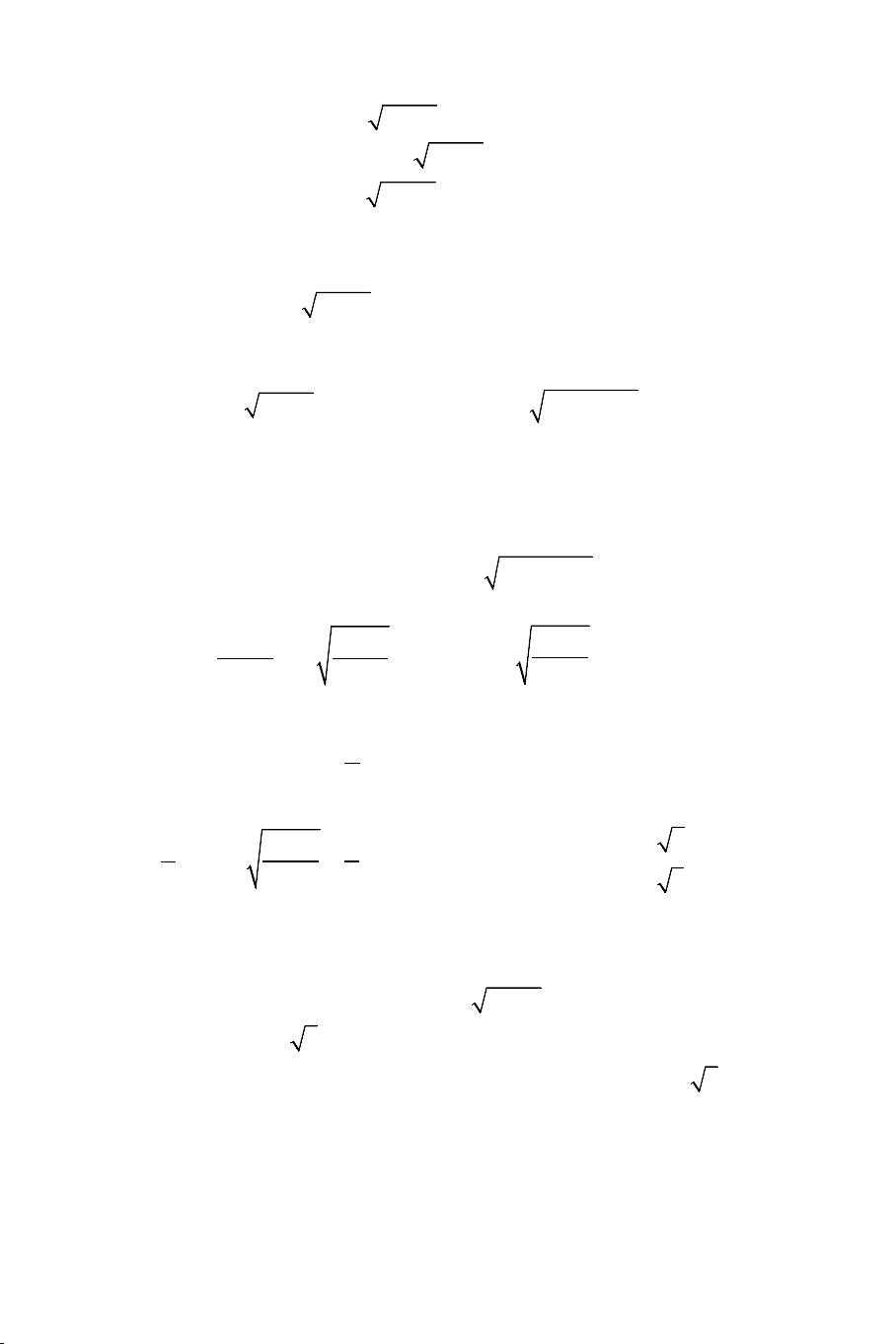
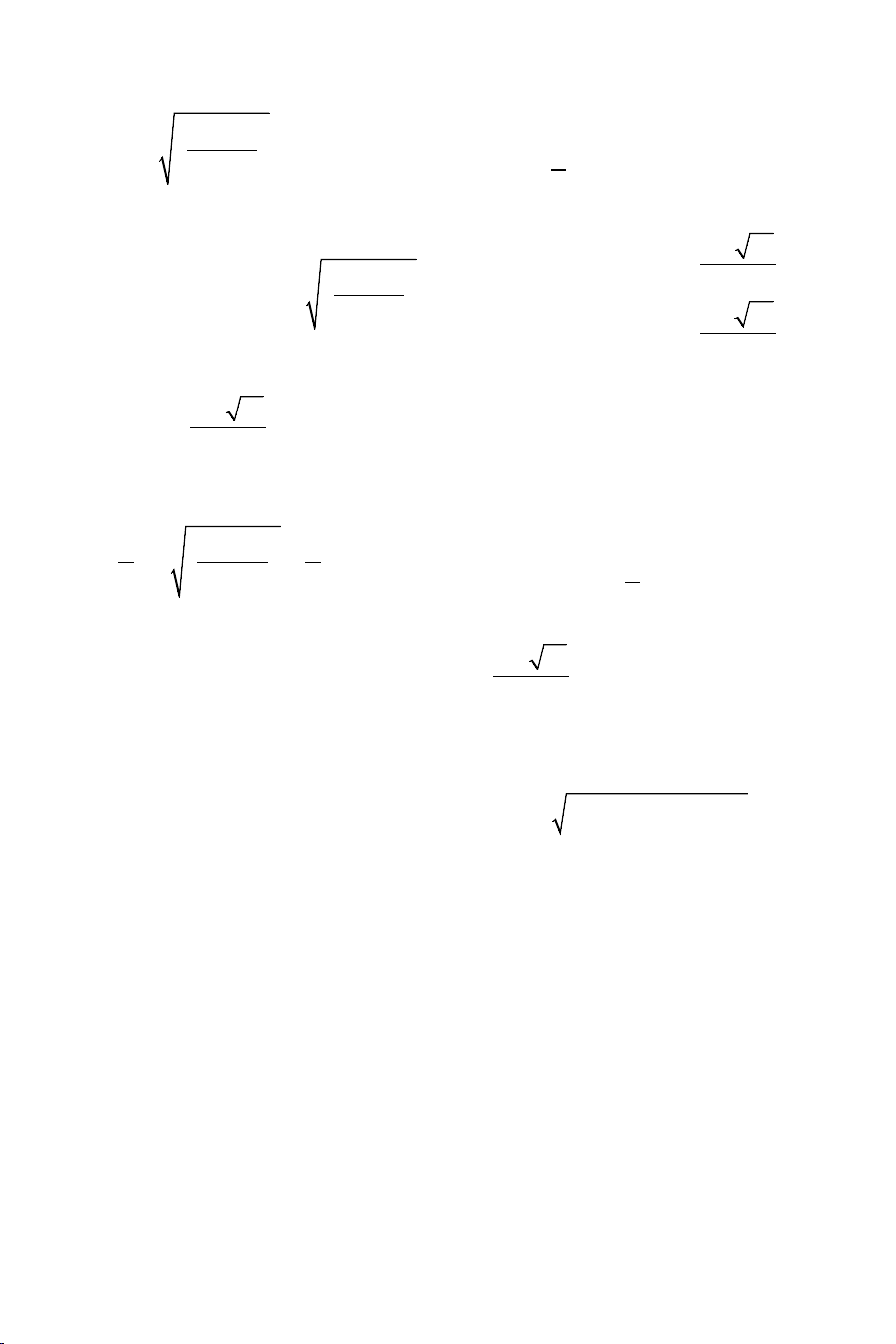
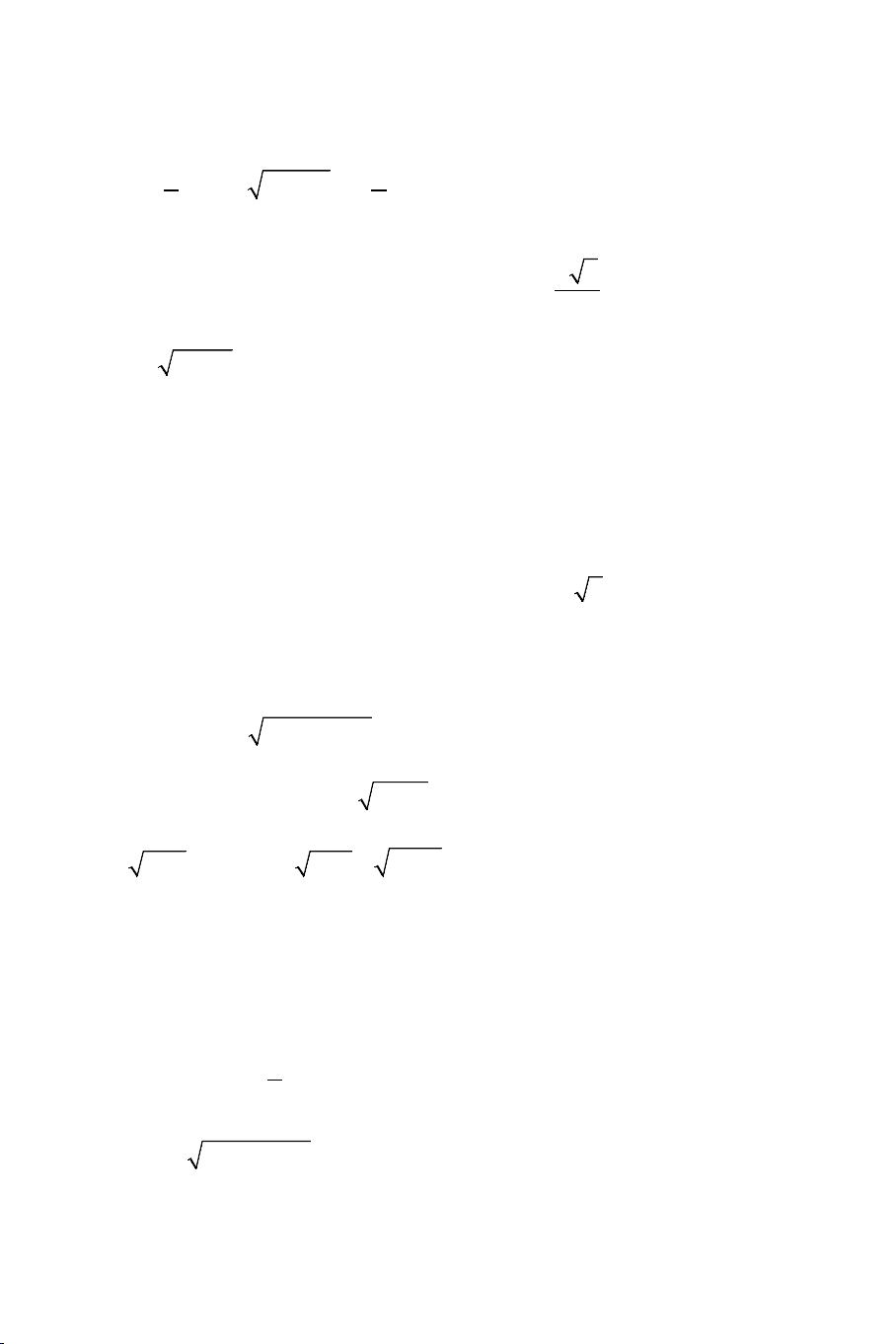
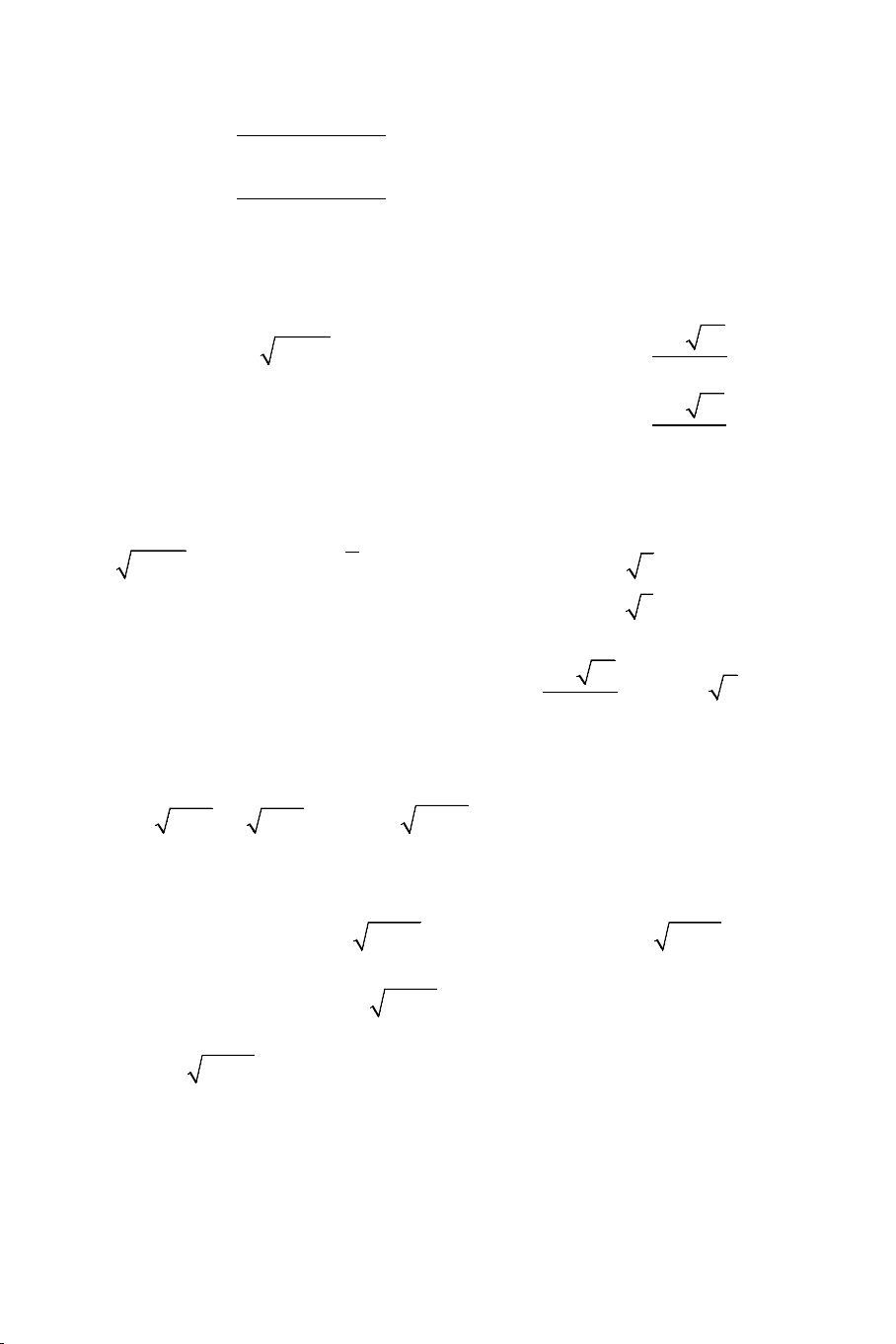
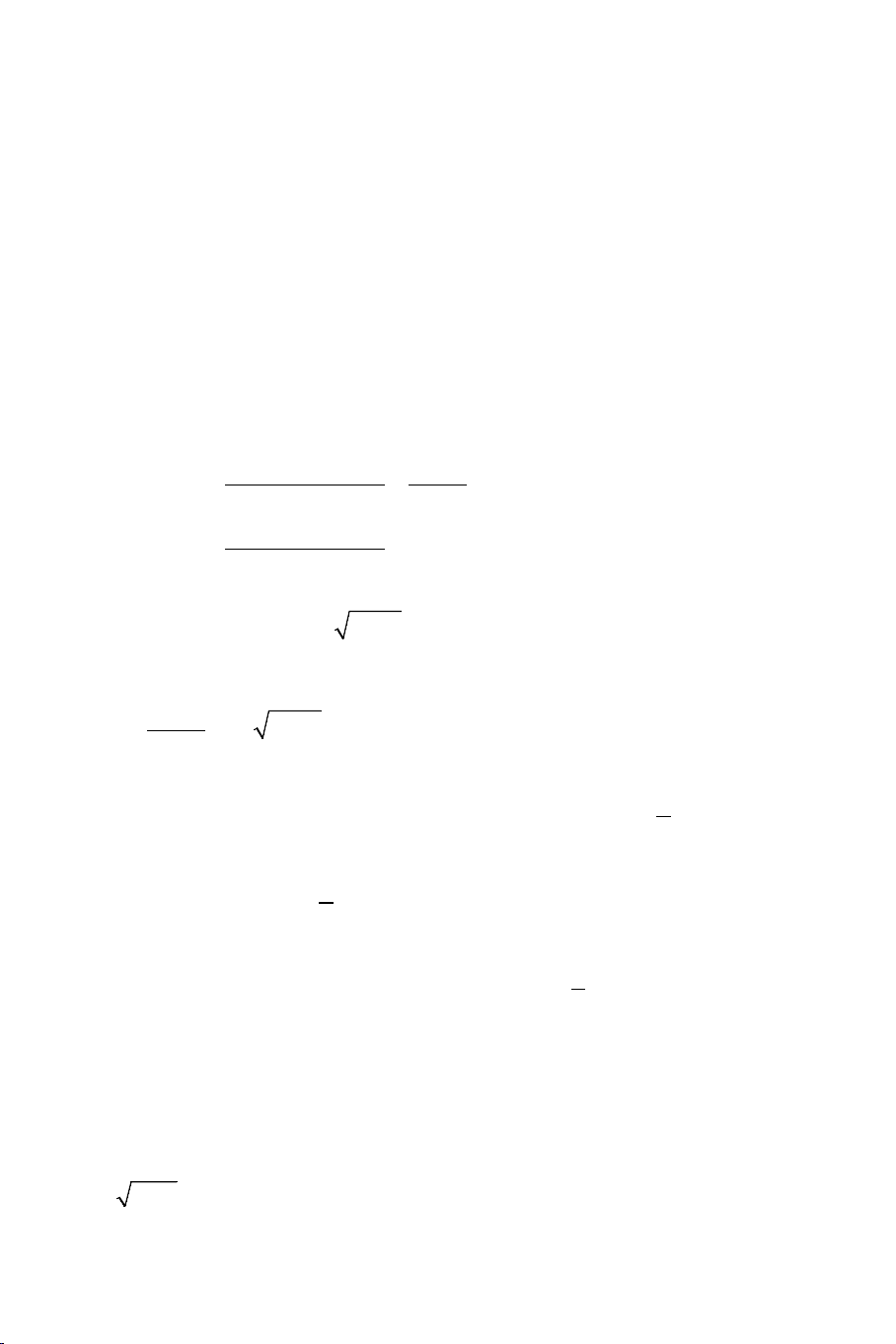
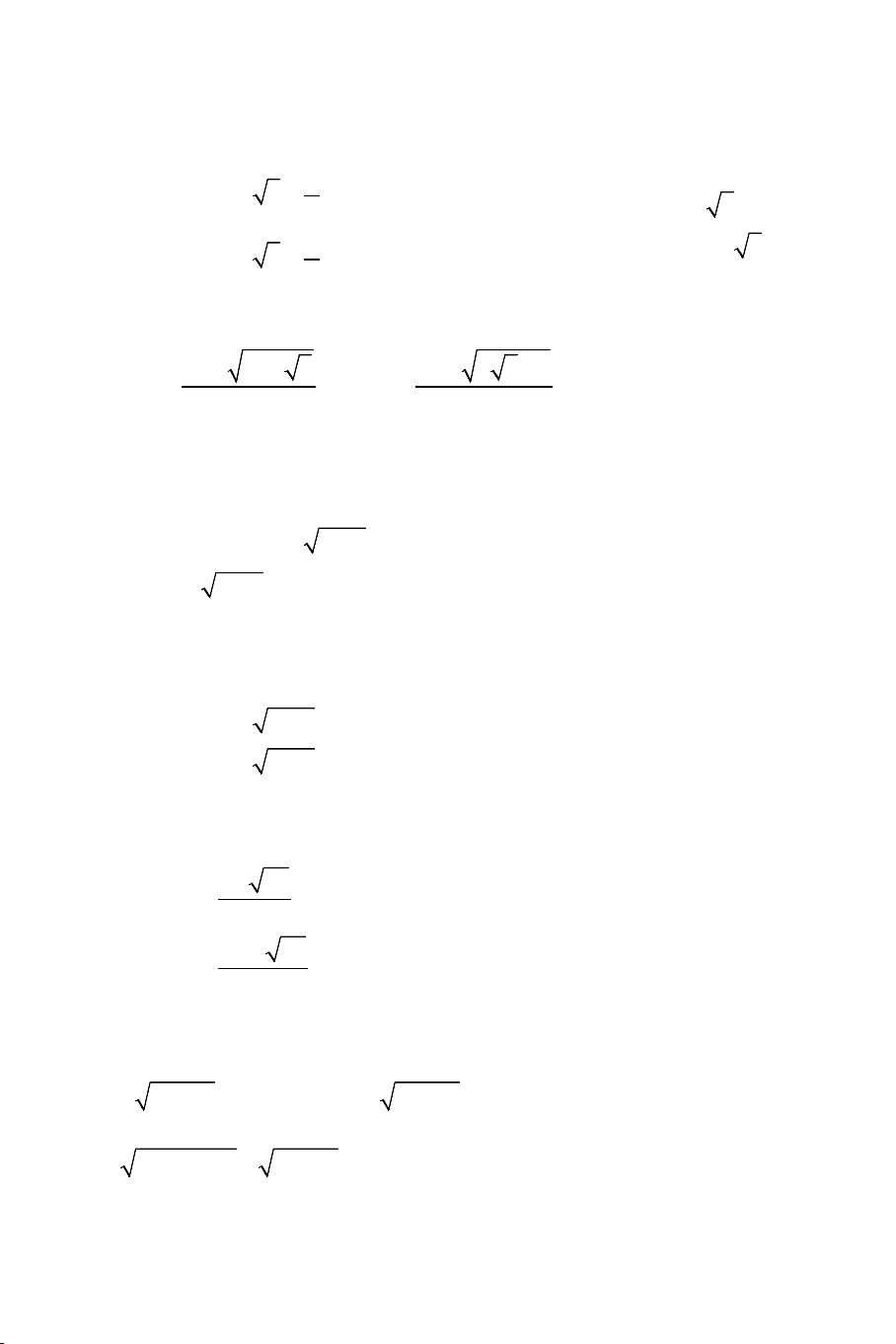
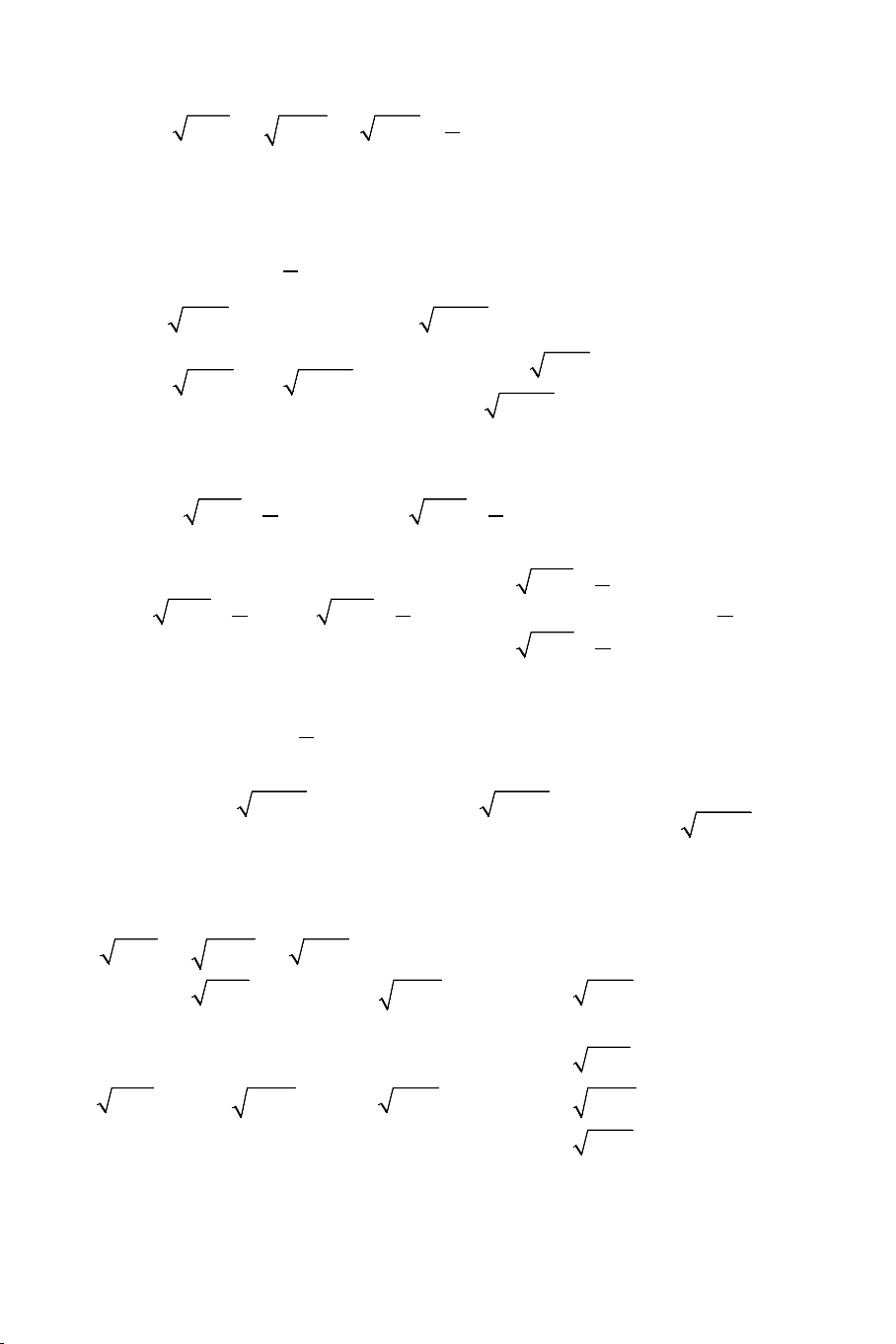
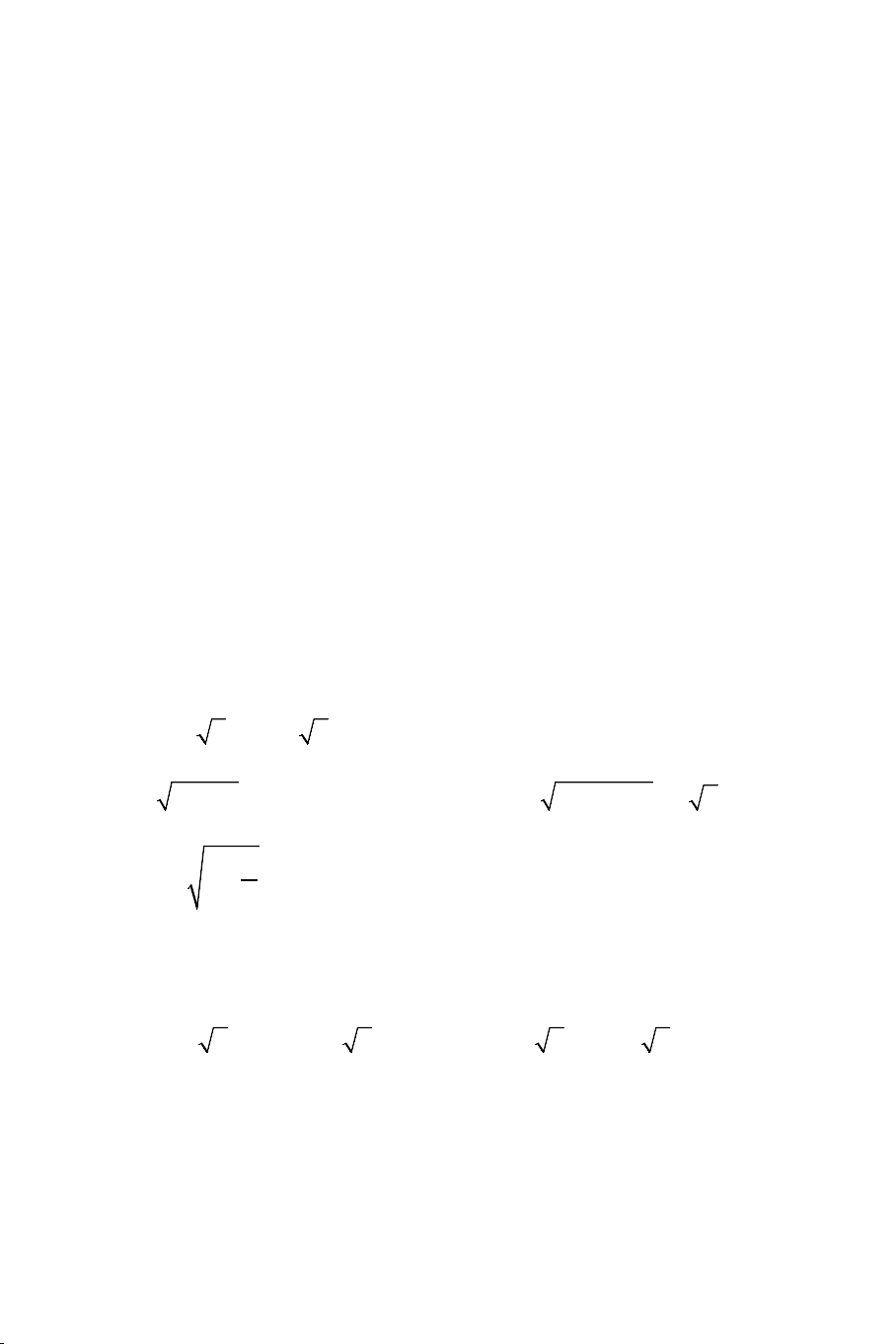
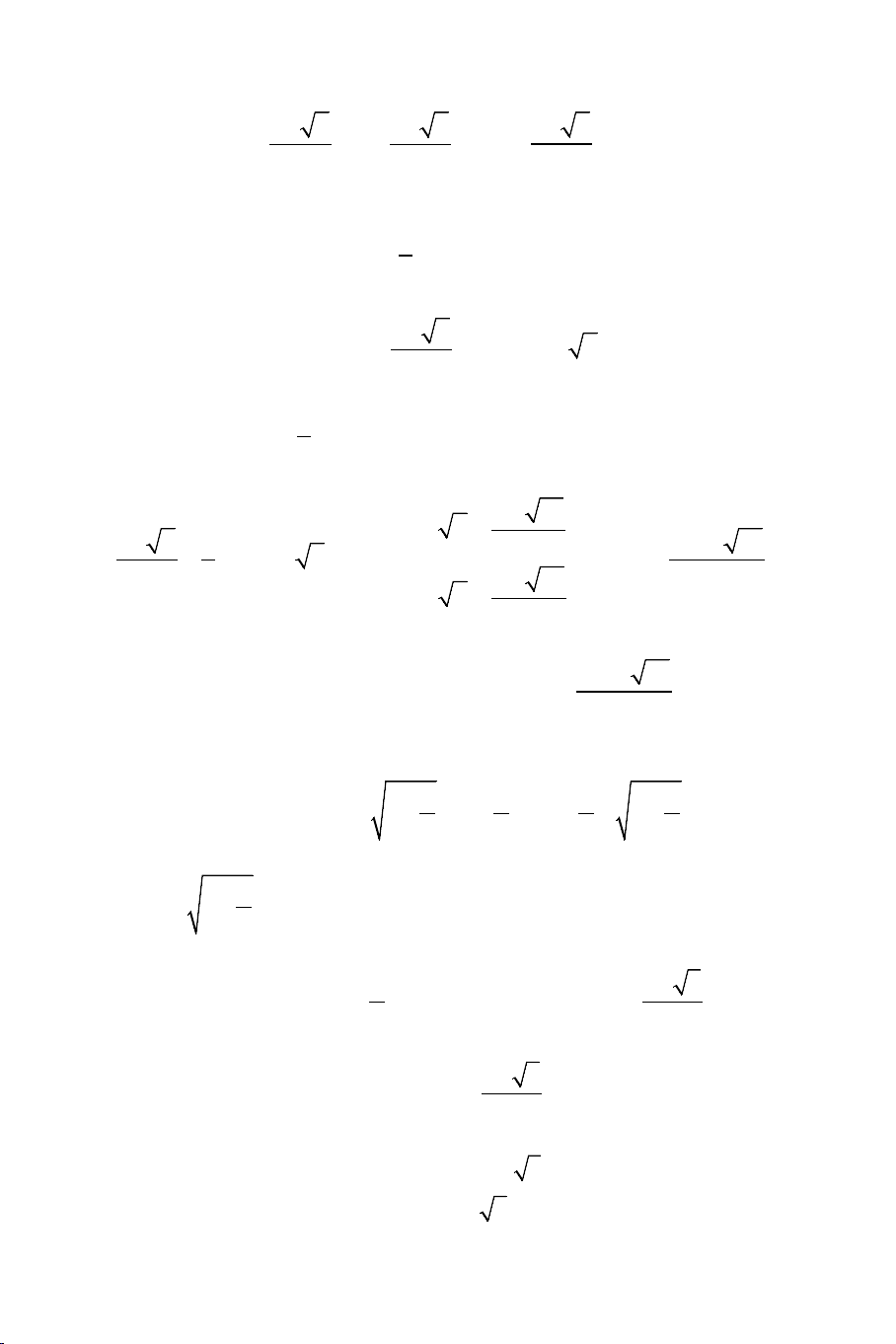
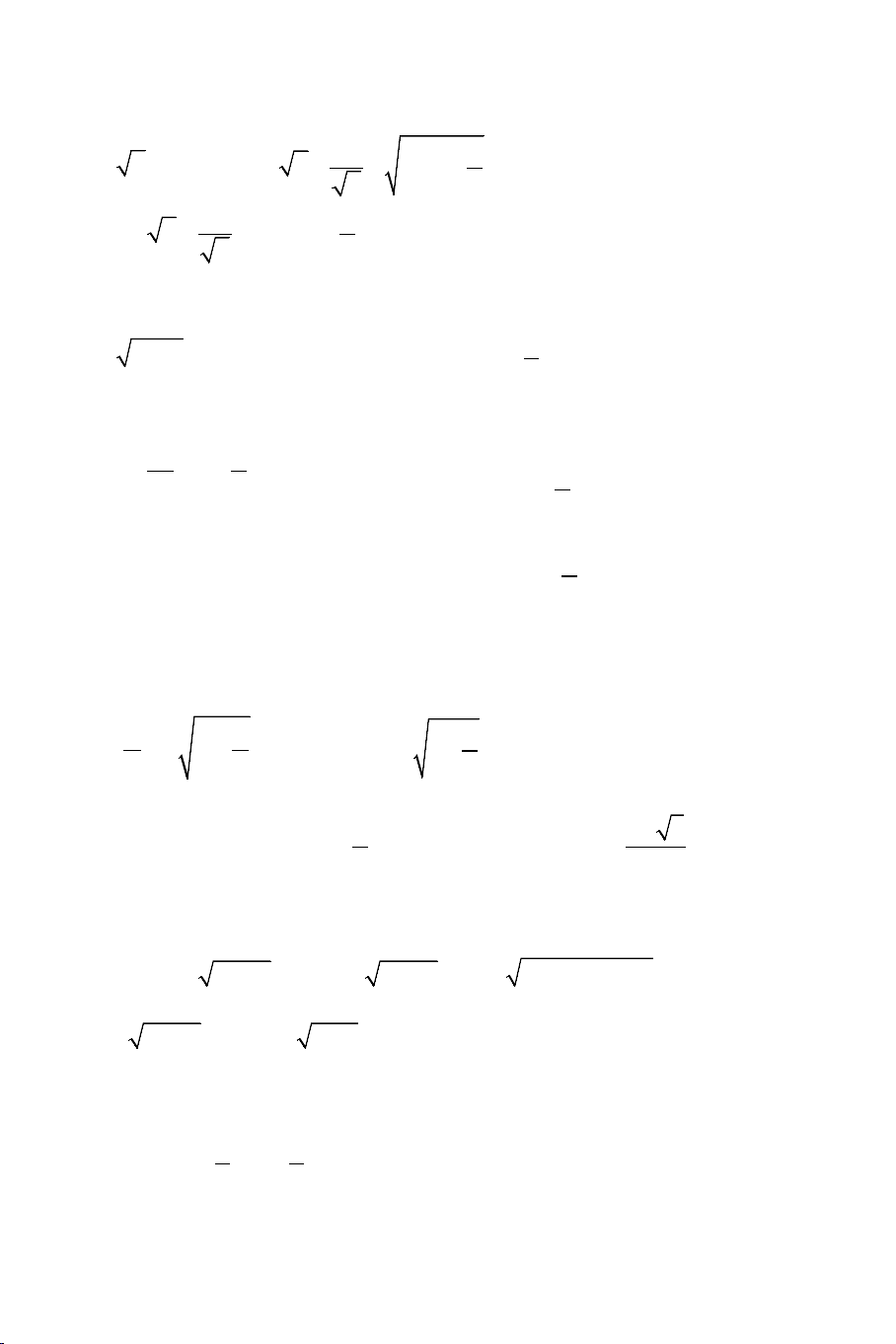
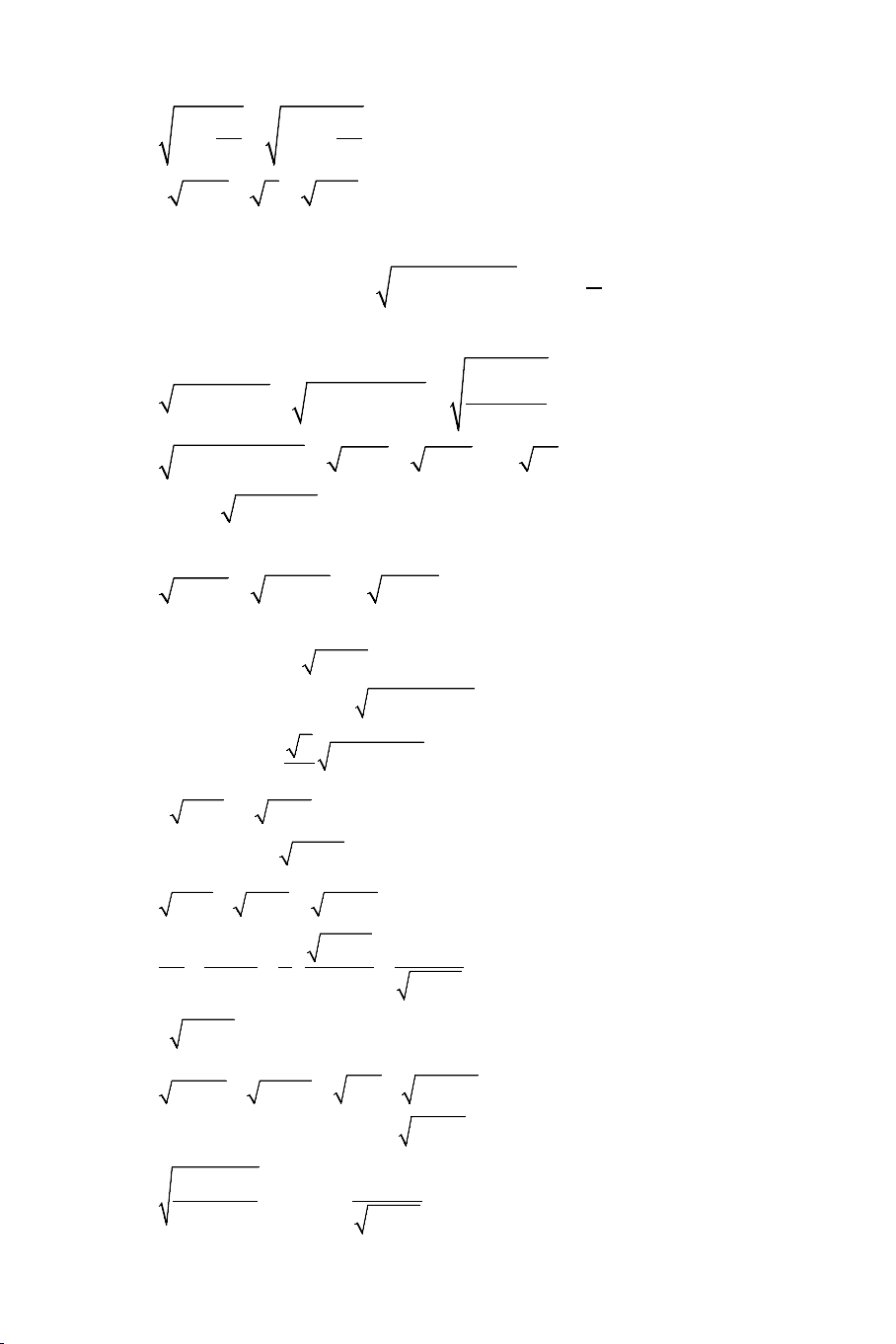
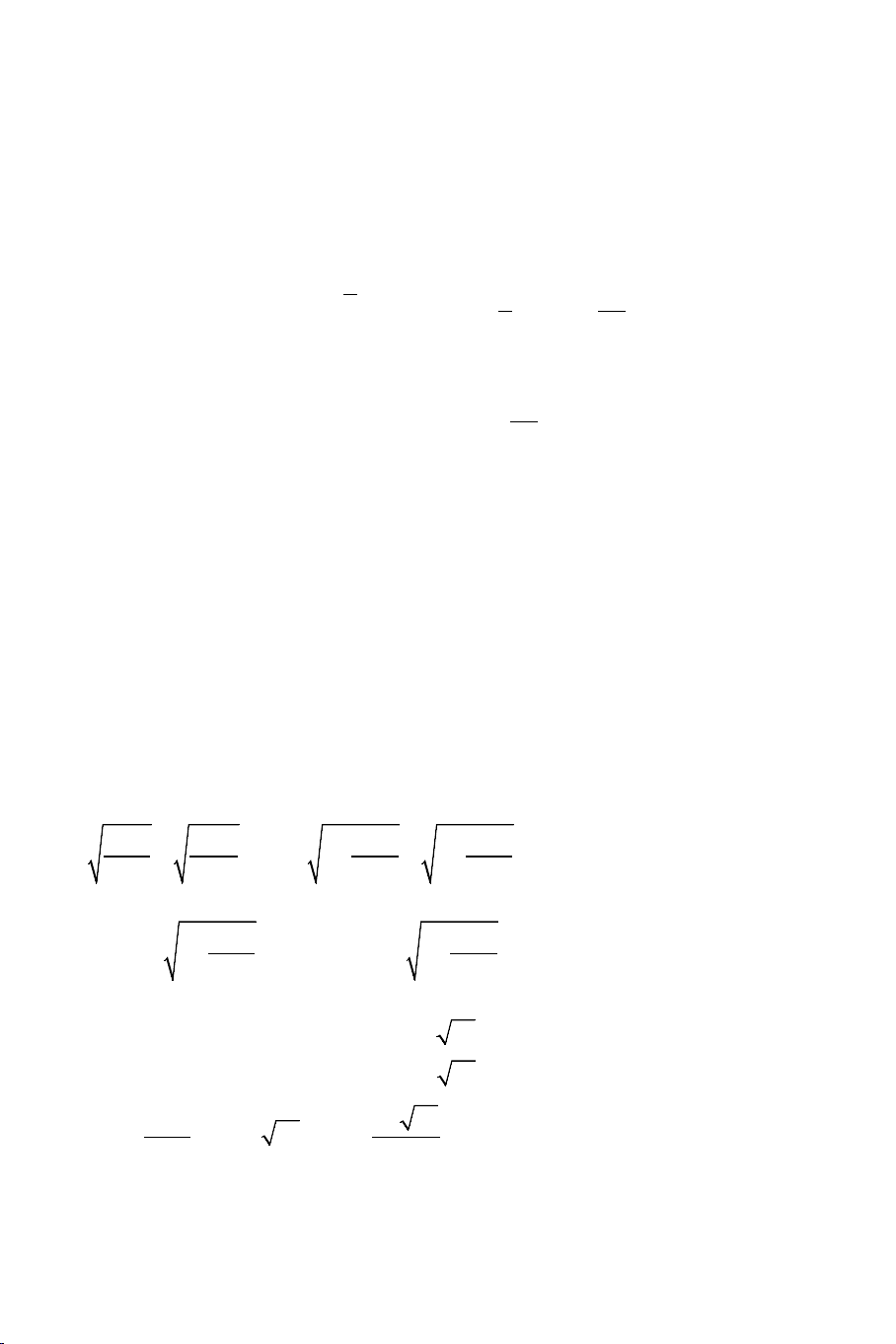
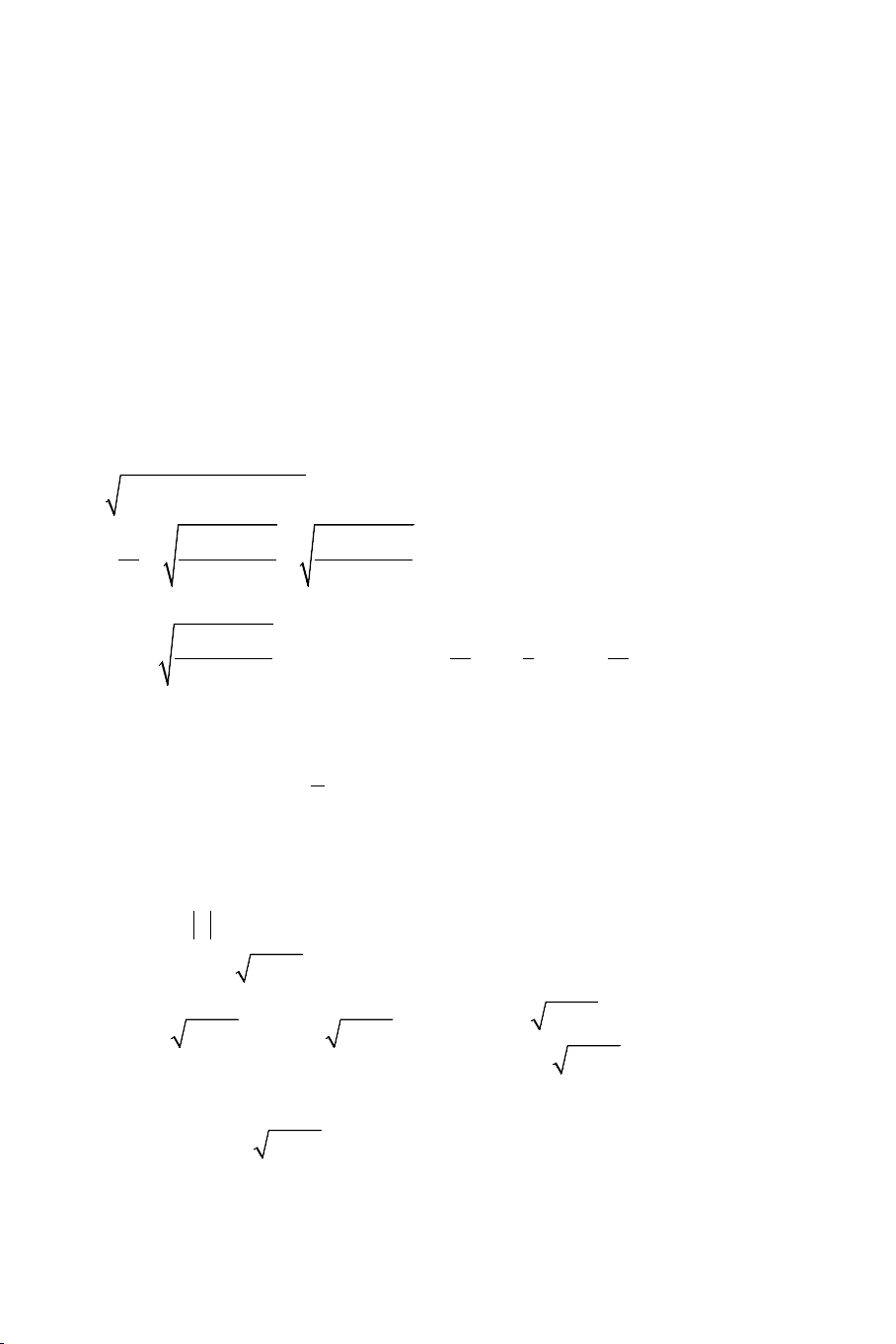
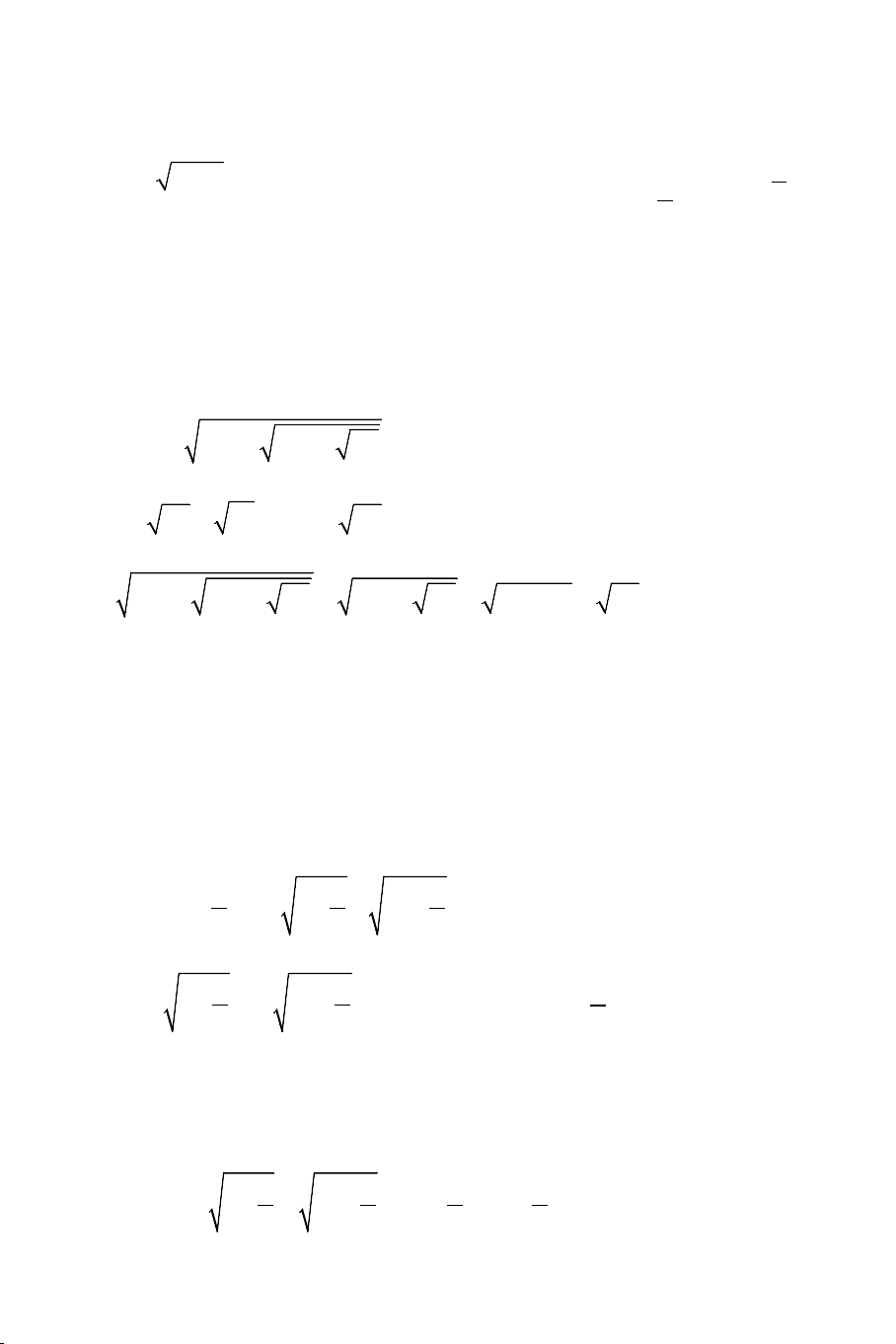
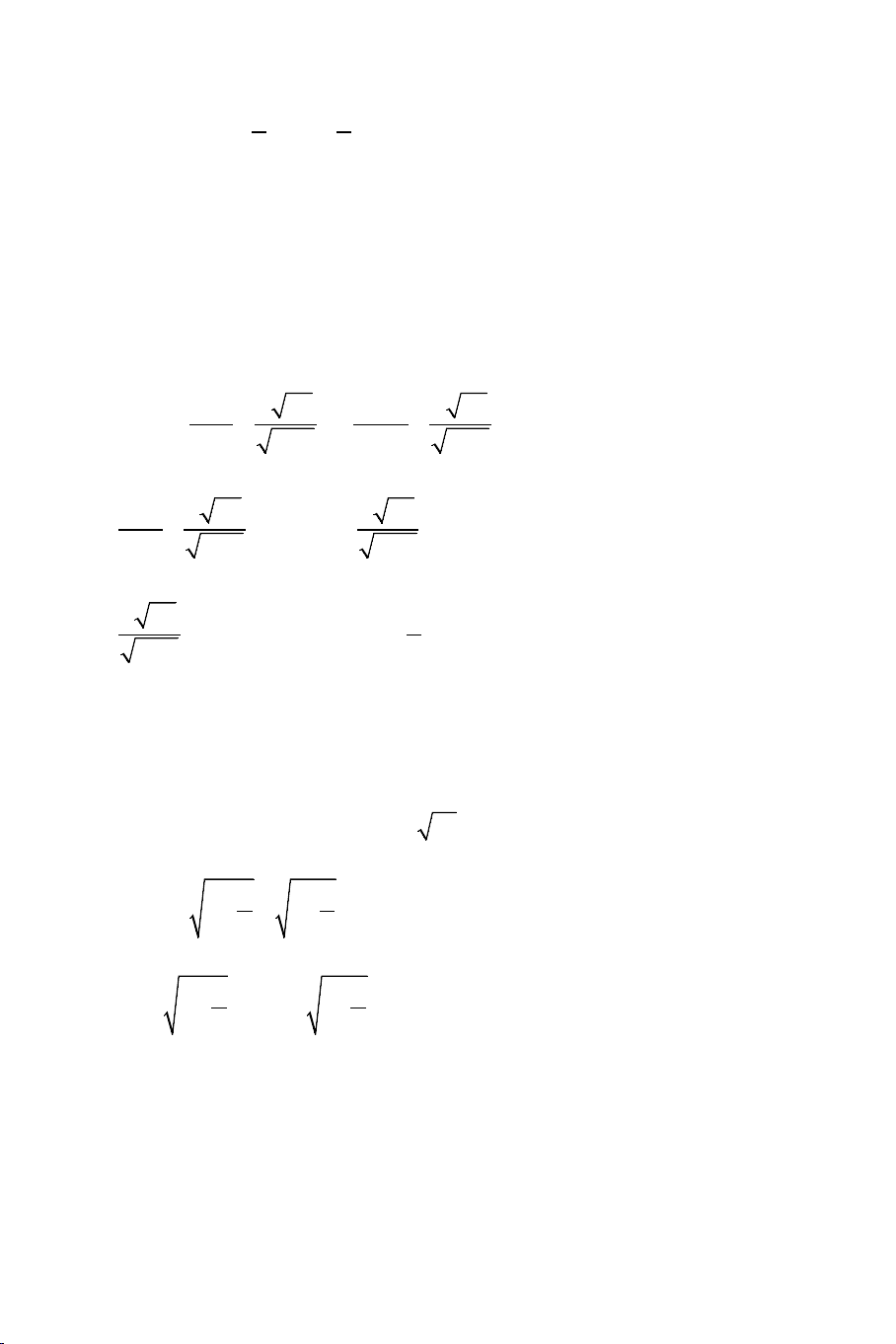
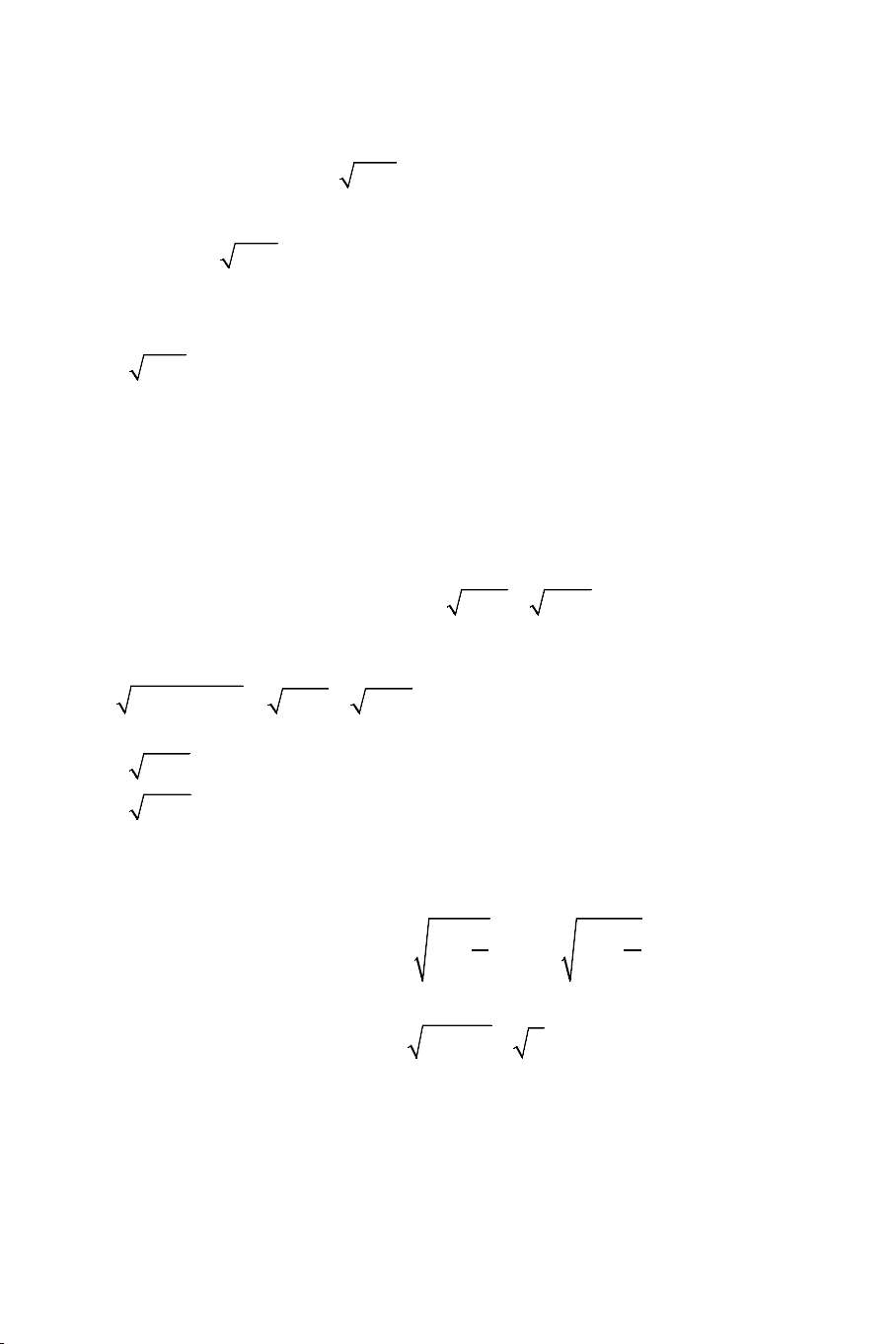
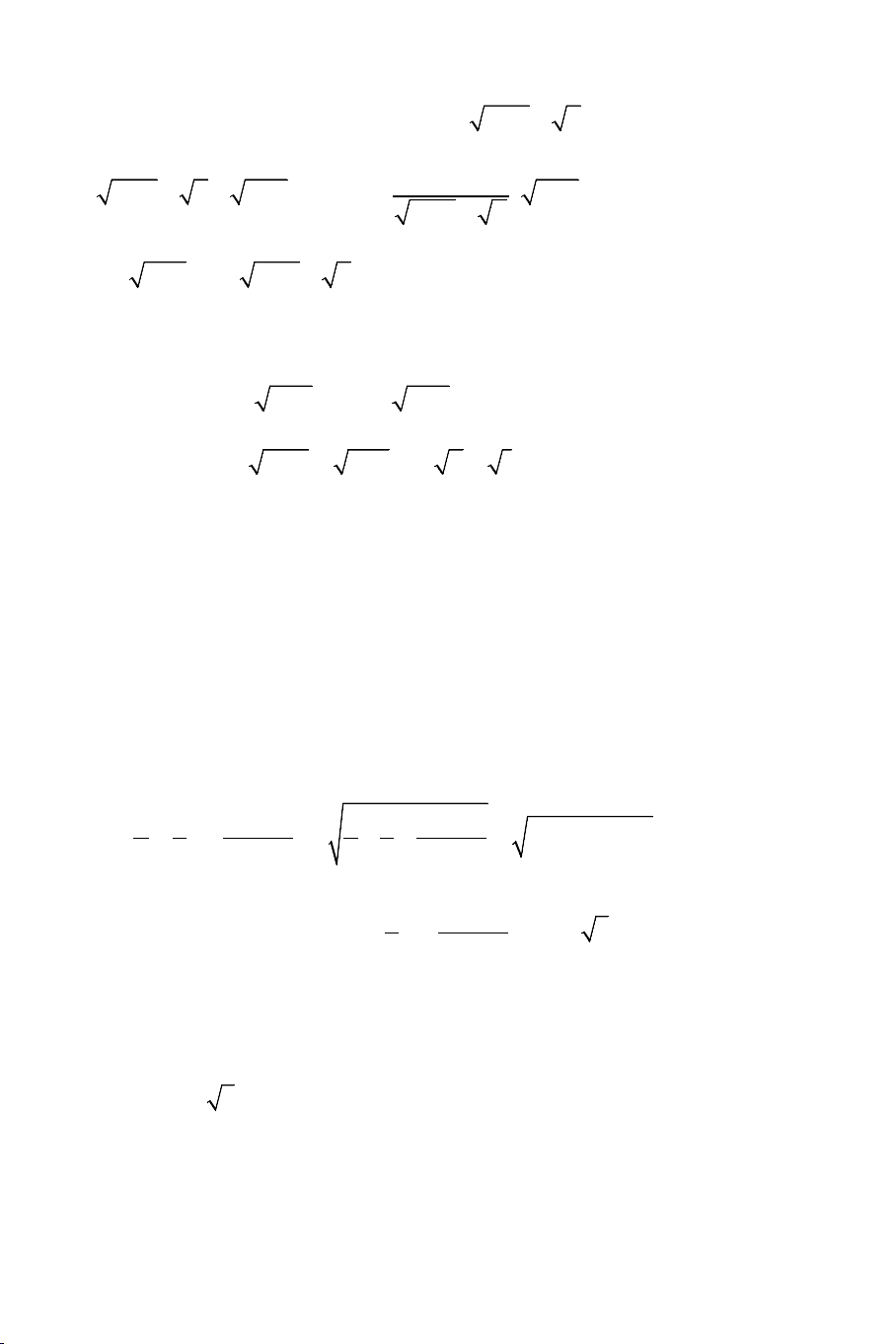
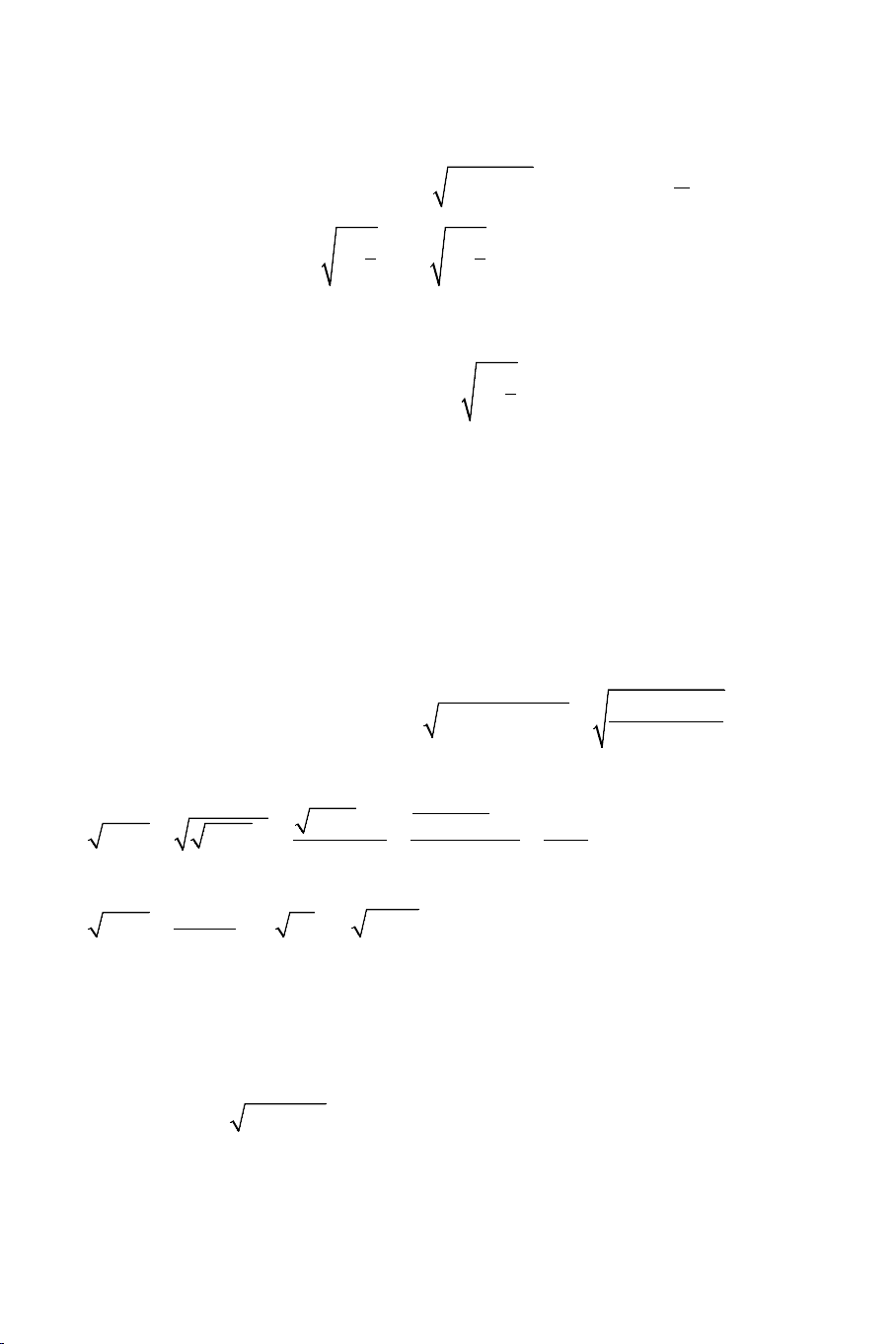
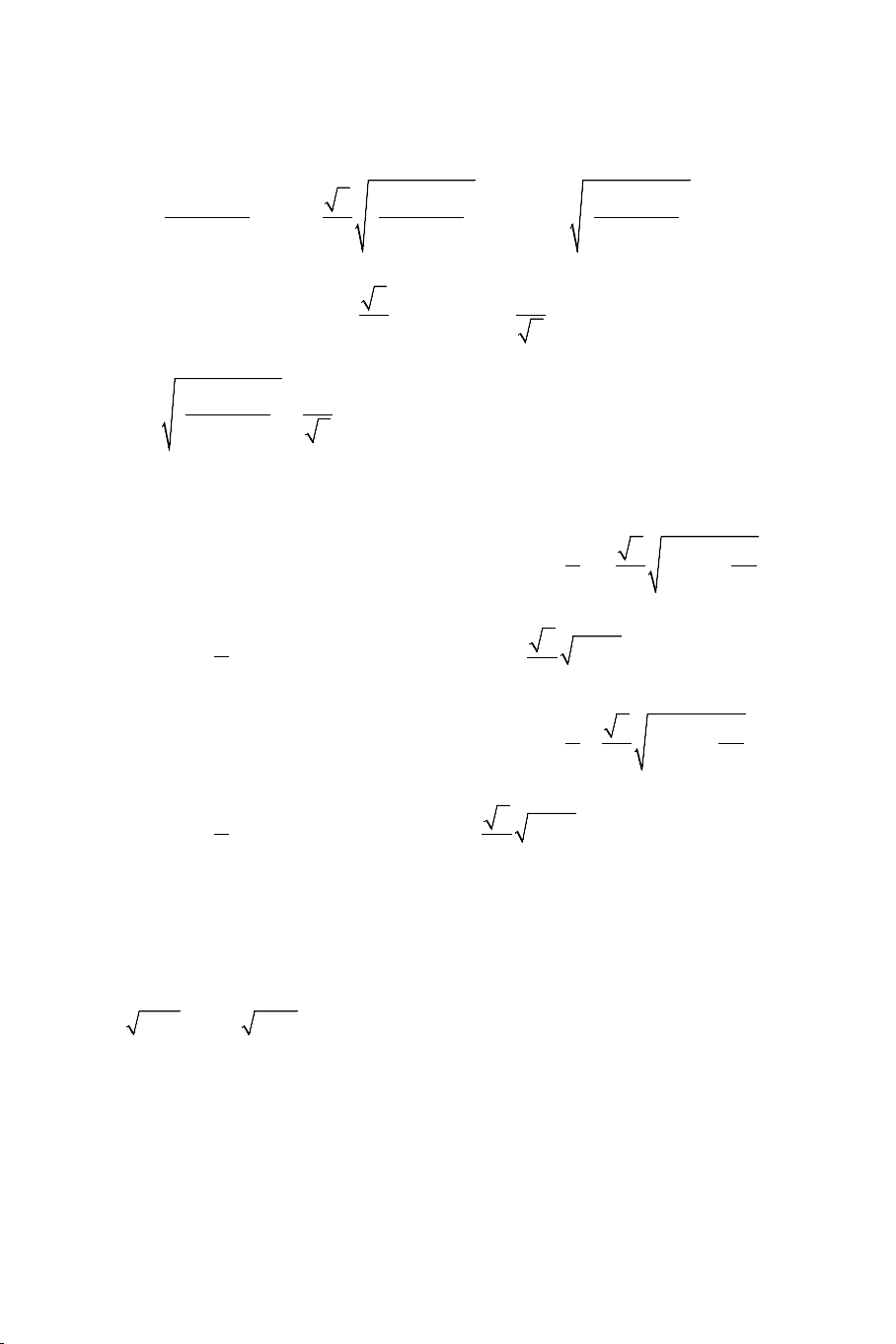
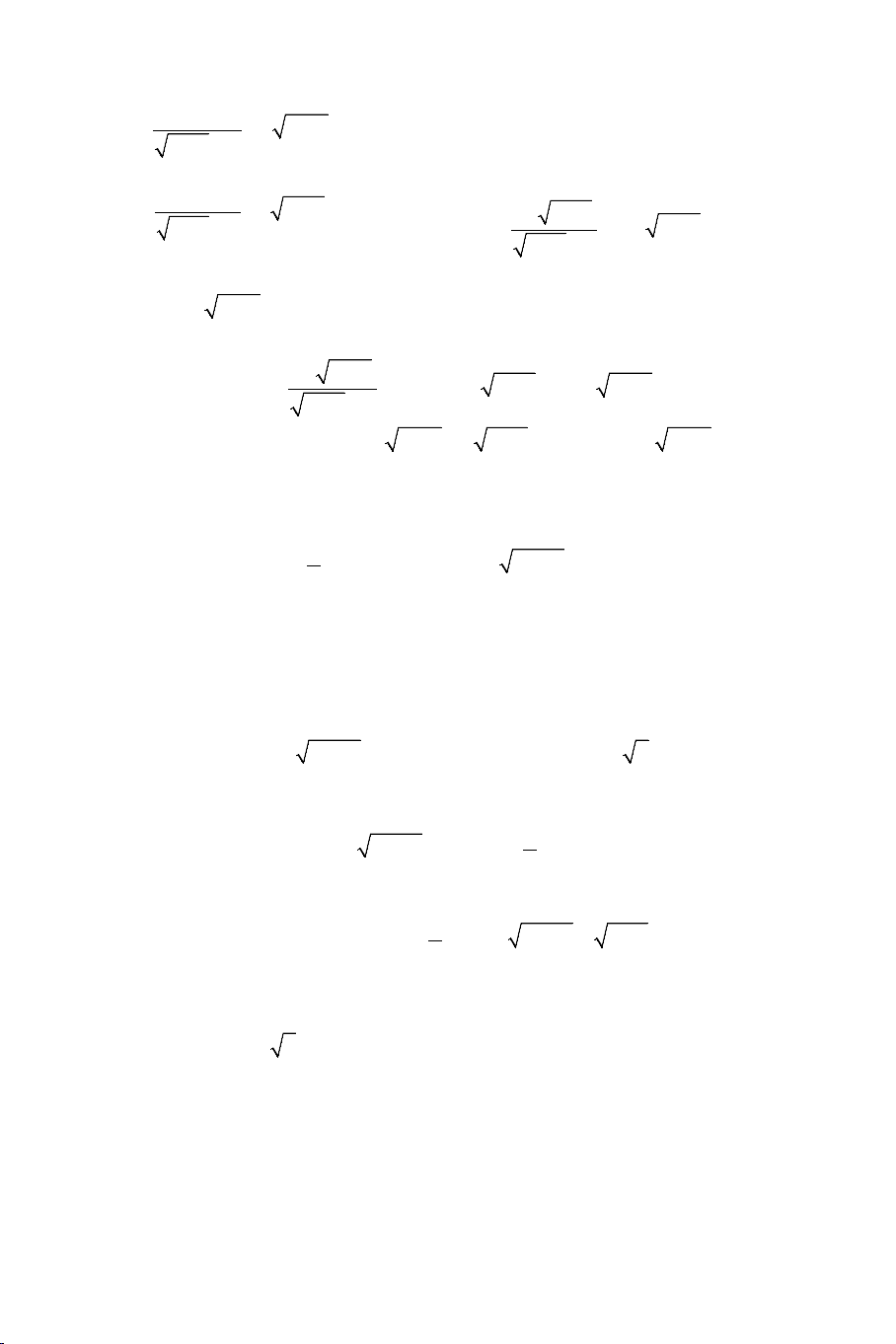
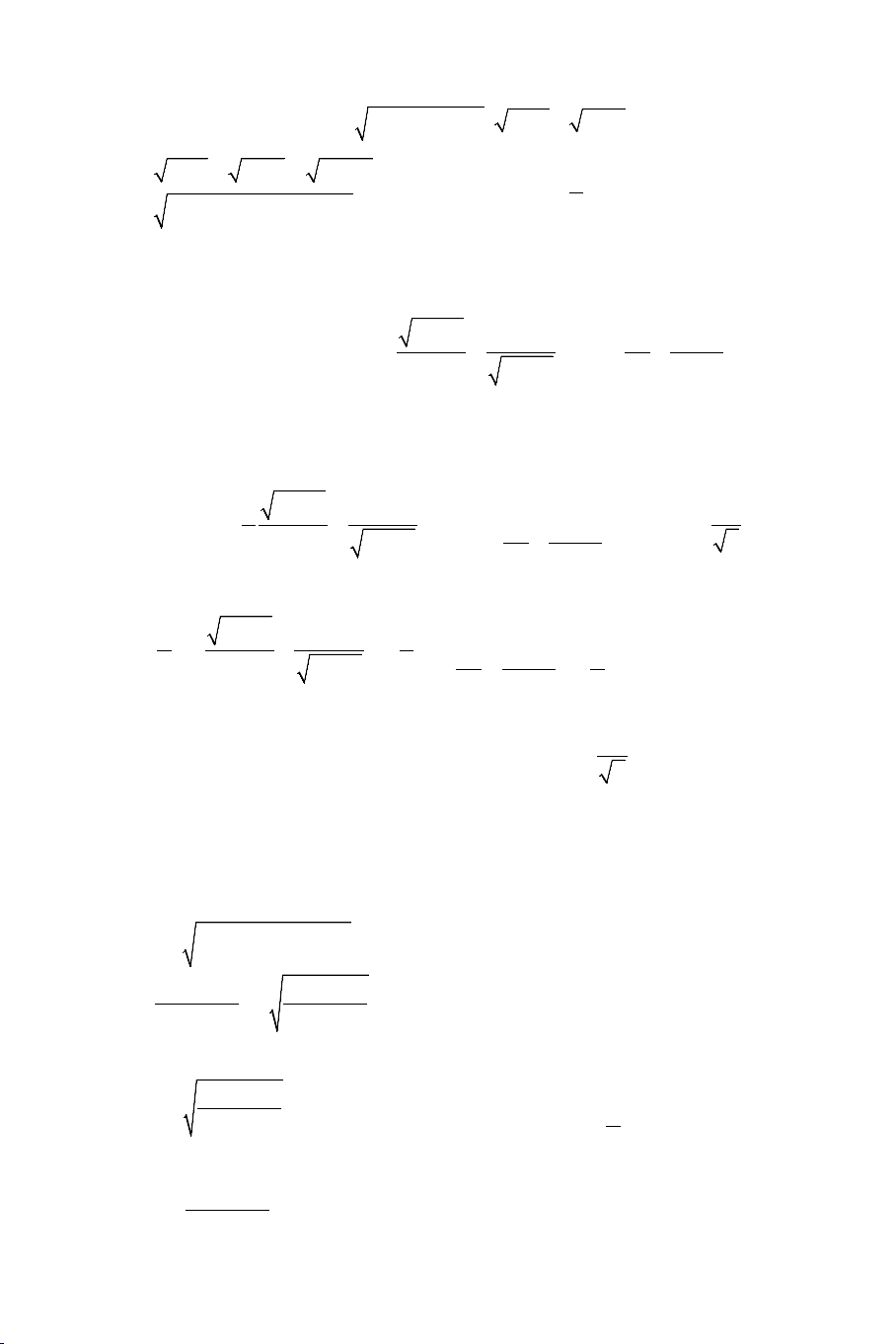
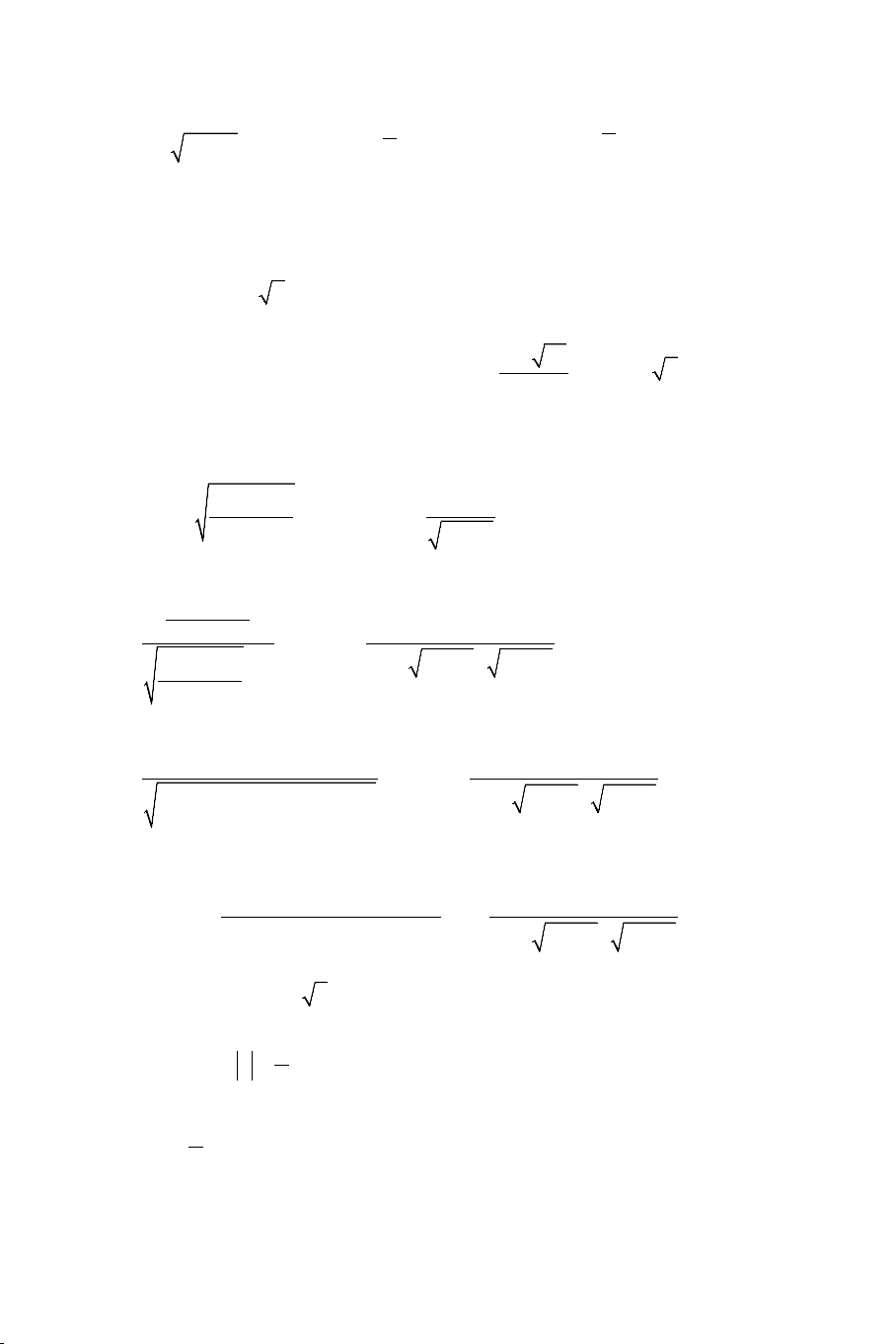
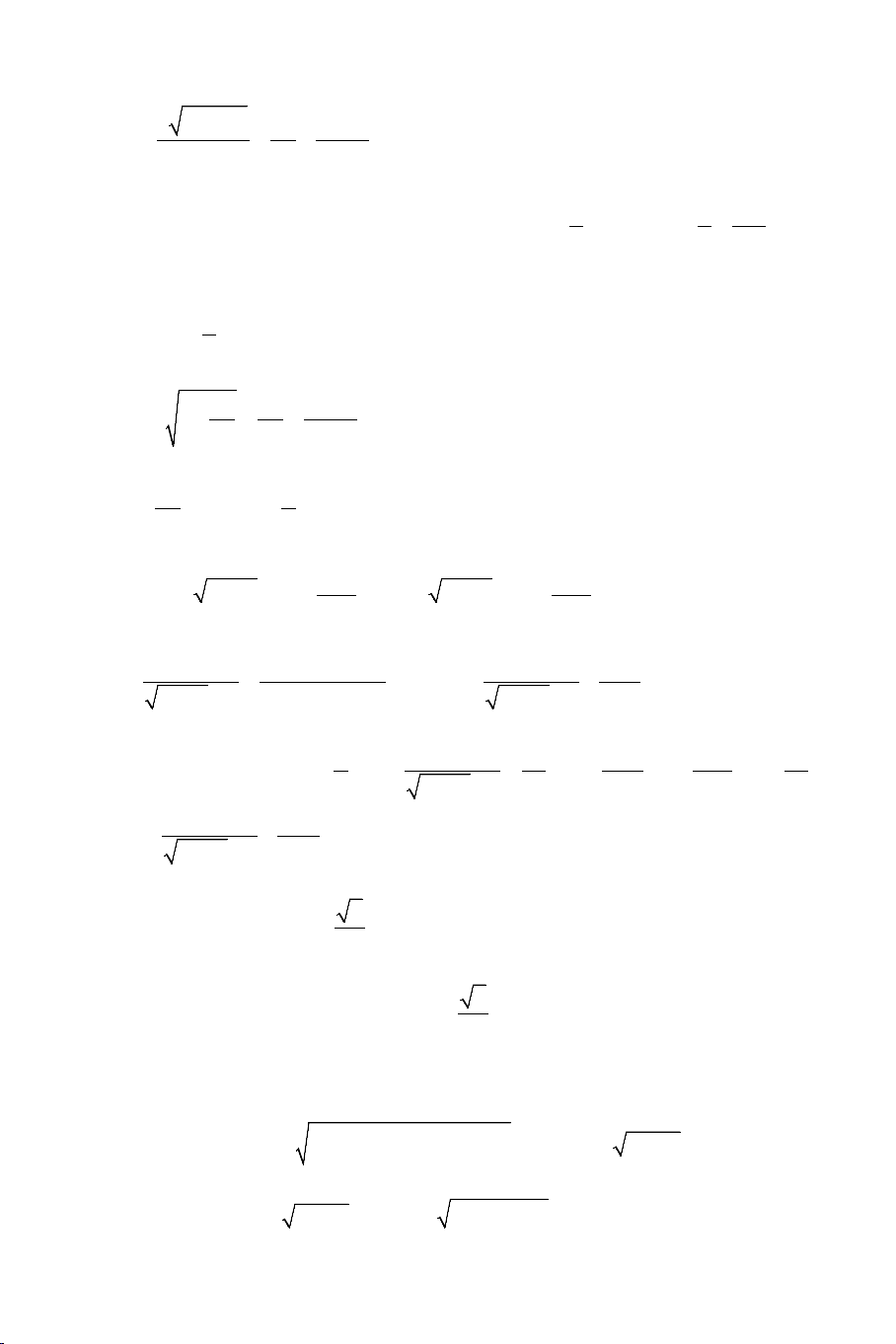
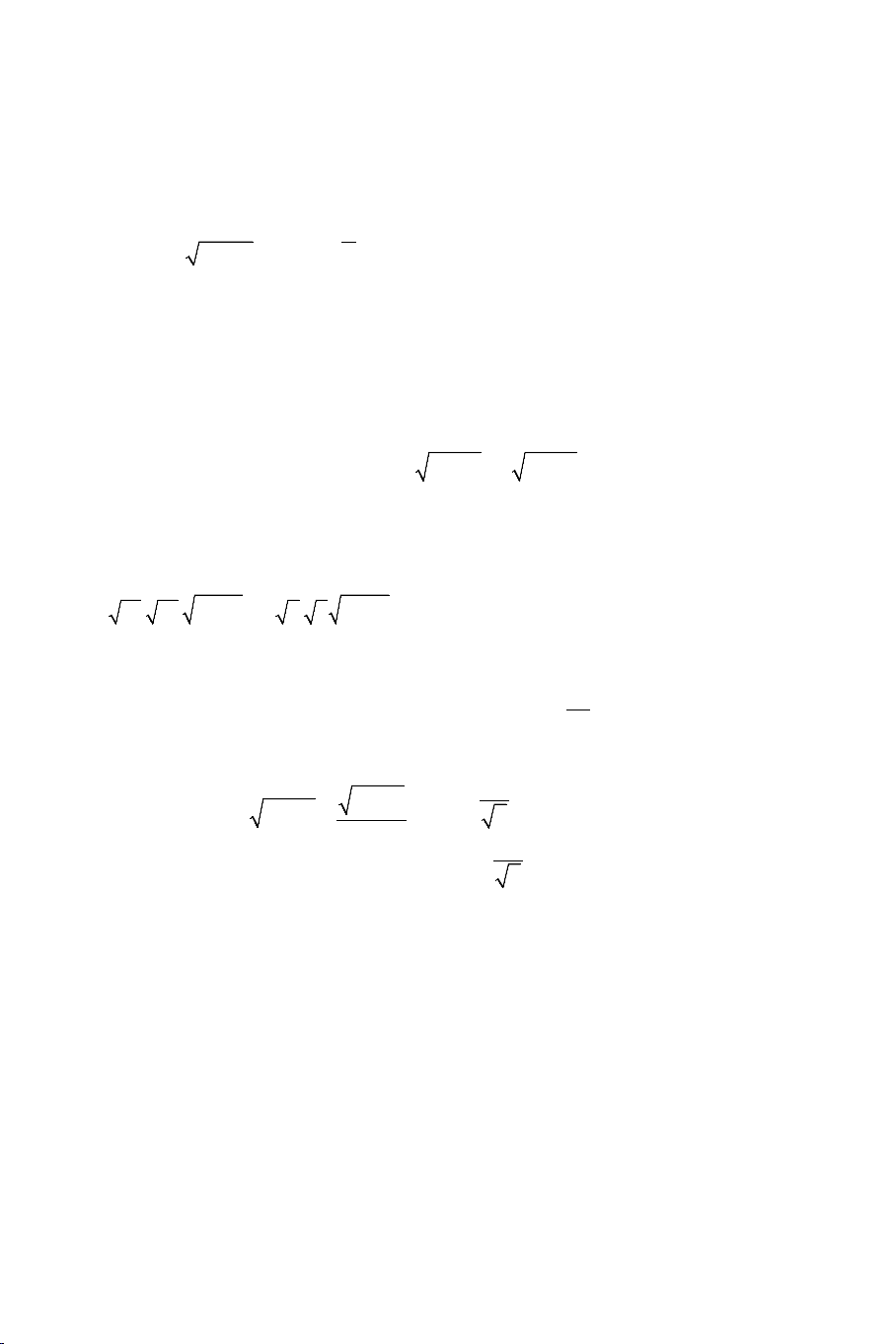
Preview text:

MỘT SỐ PHƯƠNG PHÁP GIẢI
PHƯƠNG TRÌNH VÔ TỶ
1. Phương trình vô tỷ cơ bản: g(x) ≥ 0
f (x) = g(x) ⇔  2
f (x) = g (x)
Ví dụ 1: Giải các phương trình: a) 2
x + 2x + 6 = 2x +1
b) 2x +1 + x = 4x + 9 Lời giải:
a). Phương trình tương đương với: x = 2 + 2
b). Điều kiện: x ≥ 0 . Bình phương 2 vế ta được: x ≥ 8 − 2 2
3x +1+ 2 2x + x = 4x + 9 ⇔ 2 2x + x = x + 8 ⇔  2 2
4(2x + x) = (x + 8) x = 4 x ≥ 8 −  ⇔  ⇔
. Đối chiếu với điều kiện ta thấy chỉ có 2 16
7x −12x − 64 = 0 x = −  7
x = 4 là nghiệm của phương trình.
Ví dụ 2: Giải các phương trình:
II. MỘT SỐ DẠNG PHƯƠNG TRÌNH VÔ TỶ THƯỜNG GẶP
1. Giải phương trình vô tỷ bằng phương pháp sử dụng biểu thức liên hợp: THCS.TOANMATH.com Dấu hiệu:
+ Khi ta gặp các bài toán giải phương trình dạng: n ( ) m
f x + g(x) + h(x) = 0
Mà không thể đưa về một ẩn, hoặc khi đưa về một ẩn thì tạo ra những
phương trình bậc cao dẫn đến việc phân tích hoặc giải trực tiếp khó khăn.
+ Nhẩm được nghiệm của phương trình đó: bằng thủ công ( hoặc sử dụng máy tính cầm tay) Phương pháp:
• Đặt điều kiện chặt của phương trình ( nếu có)
Ví dụ: Đối phương trình: 2 2
x + 3 + 3 = 2x + 7 + 2x .
+ Nếu bình thường nhìn vào phương trình ta thấy:
Phương trình xác định với mọi x ∈ R . Nhưng đó chưa phải là điều kiện
chặt. Để giải quyết triệt để phương trình này ta cần đến điều kiện chặt đó là:
+ Ta viết lại phương trình thành: 2 2
x + 3 − 2x + 7 = 2x − 3 Để ý rằng: 2 2
x + 3 − 2x + 7 < 0 do đó phương trình có nghiệm khi 3
2x − 3 < 0 ⇔ x < 2
• Nếu phương trình chỉ có một nghiệm x : 0
Ta sẽ phân tích phương trình như sau: Viết lại phương trình thành: n ( ) n − ( ) m + ( ) m f x f x
g x − g(x ) + h(x) − h(x ) = 0 0 0 0
Sau đó nhân liên hợp cho từng cặp số hạng với chú ý:
+ ( 3 a −b)(3 2 3 3 2
a + ab + b ) 3
= a − b + ( − )( + ) 2 a b
a b = a − b THCS.TOANMATH.com
+ Nếu h(x) = 0 có nghiệm x = x thì ta luôn phân tích được 0
h(x) = (x − x )g(x) 0
Như vậy sau bước phân tích và rút nhân tử chung x − x thì phương trình 0 x − x = 0 ban đầu trở thành: 0 (x − x ) ( A x) = 0 ⇔ 0   ( A x) = 0
Việc còn lại là dùng hàm số , bất đẳng thức hoặc những đánh giá cơ bản để kết luận (
A x) = 0 vô nghiệm.
• Nếu phương trình có 2 nghiệm x , x theo định lý viet đảo ta có nhân 1 2 tử chung sẽ là: 2
x − (x + x )x + x .x 1 2 1 2
Ta thường làm như sau:
+ Muốn làm xuất hiện nhân tử chung trong n f (x) ta trừ đi một lượng
ax + b . Khi đó nhân tử chung sẽ là kết quả sau khi nhân liên hợp của
n f (x) − (ax + b)
+ Để tìm a,b ta xét phương trình: n f (x) − (ax + b) = 0 . Để phương trình có  n ax + b =  f (x )
hai nghiệm x , x ta cần tìm a,b sao cho 1 1 1 2  n
ax + b = f (x )  2 2
+ Hoàn toàn tương tự cho các biểu thức còn lại: Ta xét các ví dụ sau:
Ví dụ 1: Giải các phương trình: a) 3 3
5x −1 + 2x −1 + x − 4 = 0 b) 2
x − 2 + 4 − x = 2x − 5x − 3 Giải: THCS.TOANMATH.com a).
Phân tích: Phương trình trong đề bài gồm nhiều biểu thức chứa căn nhưng
không thể quy về 1 ẩn. Nếu ta lũy thừa để triệt tiêu dấu 3 , thì sẽ tạo ra
phương trình tối thiểu là bậc 6. Từ đó ta nghỉ đến hướng giải : Sử dụng biểu
thức liên hợp để tách nhân tử chung. Điều kiện 1 3 x ≥ 5
Ta nhẩm được nghiệm của phương trình là: x =1. Khi đó 3 3
5x −1 = 5 −1 = 2; 2x −1 = 2 −1 =1
Ta viết lại phương trình thành: 3 3
5x −1 − 2 + 2x −1 −1+ x −1 = 0 3 5x − 5 2x − 2 ⇔ + + x −1 = 0 3 − + = 3 5x 1 2 0 (2x − )2 3 1 + 2x −1 +1  2 5(x x 1) 2  + + (x 1)  1 ⇔ − + + = 0  3 3 5x 1 2 (2x )2 3 1 2x 1 1  − + − + − +   Dễ thấy : 2 + + Với điều kiện 1 5(x x 1) 2 3 x ≥ thì + +1 > 0 5 3 − + 3 5x 1 2 (2x − )2 3 1 + 2x −1 +1
Nên phương trình đã cho có nghiệm duy nhất x = 2
b). Điều kiện: x ∈[2;4]
Ta nhẩm được nghiệm của phương trình là: x = 3. Khi đó
x − 2 = 3− 2 =1; 4 − x = 4 − 3 =1
Từ đó ta có lời giải như sau: THCS.TOANMATH.com
Phương trình đã cho tương đương với: 2
x − 2 −1+1− 4 − x = 2x − 5x − 3 x − 3 x − 3 ⇔ +
= (x − 3)(2x +1)
x − 2 −1 1+ 4 − x (x ) 1 1 3 (2x 1) ⇔ − + − + = 0  x 2 1 1 4 x  − − + −  x = 3  1 1  + − (2x +1) = 0
 x − 2 +1 1+ 4 − x
Để ý rằng: Với điều kiện x ∈[2;4] thì 1 1 ≤ 1; ≤1;2x +1≥ 5 nên x − 2 +1 1+ 4 − x 1 1 +
− (2x +1) < 0
x − 2 +1 1+ 4 − x
Từ đó suy ra: x = 3 là nghiệm duy nhất của phương trình.
Nhận xét: Để đánh giá phương trình cuối cùng vô nghiệm ta thường dùng
các ước lượng cơ bản: A + B ≥ A với B ≥ 0 từ đó suy ra A ≤1 với mọi A + BA + B > 0 số , A B thỏa mãn  B ≥ 0
Ví dụ 2: Giải các phương trình: a) 3 2 3
x −1 + x = x − 2 b) 3 2 3
x − 2 x − (x − 4) x − 7 −3x + 28 = 0 Giải: a). Điều kiện: 3 x ≥ 2 . THCS.TOANMATH.com
Ta nhẩm được nghiệm x = 3. Nên phương trình được viết lại như sau: 3 2 3
x −1 − 2 + x − 3 = x − 2 − 5 2 3 x − 9 x − 27 ⇔ + x − 3 = 3 2 3 2 3
x −1 + 2 x −1 + 4 x − 2 + 5 2  x + 3 x + 3x + 9  ⇔ (x − 3)  +1−  = 0 3 2 3 2 3
x −1 + 2 x −1 + 4 x − 2 + 5 x = 3  2 ⇔ x + 3 x + 3x + 9  +1− = 0  3 2 3 2 3
x −1 + 2 x −1 + 4 x − 2 + 5 2 + + + Ta dự đoán: x 3 x 3x 9 +1− < 0 ( Bằng cách thay 3 2 3 2 3
x −1 + 2 x −1 + 4 x − 2 + 5 2 + + + một giá trị 3 x ≥ 2 ta sẽ thấy x 3 x 3x 9 +1− < 0) 3 2 3 2 3
x −1 + 2 x −1 + 4 x − 2 + 5 2 + + Ta sẽ chứng minh: x + 3 x x < 1 và 3 9 > 2 3 2 3 2
x −1 + 2 x −1 + 4 3 x − 2 + 5 Thật vậy: + Ta xét x + 3 < 1 ⇔ ( 2 x − )2 3 2 3
1 + 2 x −1 > x −1 ( 2x − )2 3 2 3 1 + 2 x −1 + 4 Đặt 3 2 3
x −1 = t > 0 ⇒ x = t +1 . Bất phương trình tương đương với 2 3 4 3 2
t + 2t +1 > t +1 ⇔ t + 3t + 6t + 4t > 0 . Điều này là hiển nhiên đúng. THCS.TOANMATH.com + Ta xét: 2 x + 3x + 9 2 3 4 3 2
> 2 ⇔ x + 3x −1 > 2 x − 2 ⇔ x + 2x + 7x − 6x + 9 > 0 3 x − 2 + 5 x
∀ ≥ 0(*) . Điều này luôn đúng.
Từ đó suy ra phương trình có nghiệm duy nhất: x = 3
b.) Điều kiện: x ≥ 7 . Để đơn giản ta đặt 3 3 3
x = t ≥ 7 ⇒ x = t
Phương trình đã cho trở thành: 2 3 3 3 3 2 3 3
t − 2t − (t − 4) t − 7 − 3t + 28 = 0 ⇔ 3t − t + 2t − 28 + (t − 4) t − 7 = 0
Nhẩm được t = 2. Nên ta phân tích phương trình thành: 3 2 3
⇔ t − t + t − + t − ( 3 4 2 32 (
4) t − 7 − )1 = 0   + + 
⇔ t − ( t + t + ) 2 2 3 t 2t 4 ( 2) 4 7 16 + (t − 4)  = 0 3   t − 7 +1 Để ý rằng 2
4t + 7t +16 > 0 và 3t ≥ 7 nên ta có (  + +  t + t + ) 2 2 3 t 2t 4 4 7 16 + (t − 4)
 > 0 . Vì vậy phương trình có nghiệm 3  t − 7 +1
duy nhất t = 2 ⇔ x = 8.
Nhận xét: Việc đặt 3 x = t trong bài toán để giảm số lượng dấu căn đã giúp
đơn giản hình thức bài toán .
Ngoài ra khi tạo liên hợp do 3
(t − 4) > 0 nên ta tách nó ra khỏi biểu thức để
các thao tác tính toán được đơn giản hơn.
Ví dụ 3: Giải các phương trình: a) 2
4 x + 3 + 19 − 3x = x + 2x + 9 THCS.TOANMATH.com b) 2x 11 3x 8 x − − − +1 = 5 2 c) + 3 x 7 x + =
(Tuyển sinh vòng 1 lớp 10 Trường THPT x 2(x + ) 1
chuyên Tự nhiên- ĐHQG Hà Nội 2012) 3 2 d) + + +
x 5x 4x 2 2
= x + x + 2 2 x + 2x + 3 a). Điều kiện: 19 3 − ≤ x ≤ 3
Ta nhẩm được 2 nghiệm là x =1, x = 2
− nên ta phân tích để tạo ra nhân tử chung là: 2
x + x − 2. Để làm được điều này ta thực hiện thêm bớt nhân tử như sau:
+ Ta tạo ra 4 x + 3 − (ax + b) = 0 sao cho phương trình này nhận x =1, x = 2 − là nghiệm.  4  + = 8 a a b = 
Để có điều này ta cần:  3  ⇔  2a b 4  − + = 20 b  =  3
+ Tương tự 19 − 3x − (mx + n) = 0 nhận x =1, x = 2 − là nghiệm.  1  + = 5 a m n = −  Tức là  3  ⇔  2m n 5  − + = 13 b  =  3
Từ đó ta phân tích phương trình thành: THCS.TOANMATH.com  4 20  13 4 3 x 19 3 x x x  + − + + − − − − ( 2 x + x − 2) =     0  3 3   3 3  4 ⇔  x + − (x + )
3 19 − 3x − (13− x) 3 3 5  + −  
( 2x − x−2) = 0 3 3 2 2
4  −x − x + 2  −x − x + 2 ⇔   + − ( 2
x + x − 2) = x + +  (x + ) 0 3 3 3
5  33 19−3x + (13− x)     ⇔ −( 2 x − x − ) 4 1 1 2  . + +  = x + + (x + ) 1 0 3 3 3 5
33 19 − 3x + (13− x)      Dễ thấy với 19 3 − ≤ x ≤ thì 1 > 0, 3
3 x + 3 + (x + 5) 1 > 0
33 19 − 3x + (13− x)   Nên 4 1 1 . + + > . x + + (x + ) 1 0 3 3 3 5
33 19 − 3x + (13− x)   x =1
Phương trình đã cho tương đương với 2
x + x − 2 = 0 ⇔  x = 2 −
Vậy phương trình có 2 nghiệm là: x = 3, x = 8 . b). Điều kiện: 8 x ≥ . 3
Phương trình được viết lại như sau: 5 3x −8 − 5 x +1 = 2x −11 THCS.TOANMATH.com
Ta nhẩm được 2 nghiệm x = 3, x = 8 nên suy ra nhân tử chung là: 2
x −11x + 24
Ta phân tích với nhân tử 5 3x −8 như sau:
+ Tạo ra 5 3x −8 − (ax + b) = 0 sao cho phương trình này nhận x = 3, x = 8 3  a + b = 5 a = 3
là nghiệm. Tức là a,b cần thỏa mãn hệ:  ⇔ 8  a b 20 b  + =  = 4 − 3  m + n =10 m =1
+ Tương tự với 5 x +1 − (mx + n) = 0 ta thu được:  ⇔ 8  m n 15  + = n = 7
Phương trình đã cho trở thành: 2 2 9(
− x −11x + 24) x −11x + 24
5 3x −8 − (3x − 4) + (x + 7) − 5 x +1 = 0 ⇔ + = 0
5 3x −8 + (3x − 4) (x + 7) + 5 x +1 ⇔ (  −  2 x − x + ) 9 1 11 24  +  = 0
5 3x −8 + (3x − 4) (x + 7) + 5 x +1 2
x −11x + 24 = 0  ⇔ 9 − 1  + = 0
5 3x −8 + (3x − 4) (x + 7) +5 x +1 Ta xét 9 − 1 ( A x) = +
5 3x −8 + (3x − 4) (x + 7) + 5 x +1 Ta chứng minh: − ( A x) < 0 tức là: 9 1 + < 0
5 3x −8 + (3x − 4) (x + 7) + 5 x +1
⇔ 5 3x −8 + 3x − 4 − 9(x + 7 + 5 x +1) < 0 THCS.TOANMATH.com 25 275
⇔ 3x −8 − 5 3x −8 + +
+ x + 45 x +1 > 0 4 4 2  5  275 ⇔ 3x −8 − +
+ x + 45 x +1 >  
0. Điều này là hiển nhiên đúng.  2  4
Vậy phương trình có 2 nghiệm là: x = 3, x = 8 . Chú ý:
Những đánh giá để kết luận (
A x) < 0 thường là những bất đẳng thức không
chặt nên ta luôn đưa về được tổng các biểu thức bình phương.
Ngoài ra nếu tinh ý ta có thể thấy: 5 3x −8 + 3x − 4 − 9(x + 7 + 5 x +1) < 0
5 3x −8 + 3x − 4 ≤ 9x + 63+ 5 81x + 81 Nhưng điều này là hiển nhiên đúng
do: 5 3x −8 < 5 81x + 81;3x − 4 < 9x + 63 với mọi 8 x ≥ 3
c). Điều kiện: x > 0
Ta nhẩm được x =1; x = 3 nên biến đổi phương trình như sau: 2 2
Ta có: khi x =1⇒ x + 7 x + 7 ( = , khi x = 3 ⇒ = 2 nên ta trừ 2 vào 2 x + ) 2 2 1 2(x + ) 1 2 2 2 + + − − + vế thì thu được: 3 x 7
x 3 2 x x 4x 3 x + − 2 = − ⇔ = x (x + ) 2 2 1 x 2(x +1) 2 2 2 x − 4x + 3 x − 4x + 3
x − 4x + 3 = 0 (1) = ⇔  3 3
x + 3x + 2x 2(x +1)
 x + 3x + 2x = 2(x +1) (2)
Giải (1) suy ra x =1, x = 3 Giải (2) ta có: 3
x + 3x + 2x = 2(x +1) 3 3
⇔ x + 3x = 2 ⇔ x + 3x − 4 = 0 ⇔ x =1
Kết luận: Phương trình có nghiệm là x =1; x = 3 THCS.TOANMATH.com
Nhận xét: Ta cũng có thể phân tích phương trình như câu a,b . d). Ta có: 3 2 2
x + 5x + 4x + 2 = (x + 3)(x + 2x + 3) − 5x − 7 nên phương trình tương đương với 3 2
x + 5x + 4x + 2 2 2 5x + 7
= x + x + 2 ⇔ x + 3− x + 2x + 3 − = 0 2 2 x + 2x + 3 x + 2x + 3   ⇔ ( x + ) 1 1 5 7  −  = 0 2  2
 (x + 3) + x + x + 2 x + 2x + 3  (5x + 7) = 0  ⇔   1 1   −  = 0 (1)  2  2
 (x + 3) + x + x + 2 x + 2x + 3  Giải (1) : 1 1 2 2 −
⇔ x + x − x + x + 2 = 0 . 2 2
(x + 3) + x + x + 2 x + 2x + 3 Đặt 2
t = x + x + 2 > 0 . Phương trình trở thành: t = 2 x =1 2 2
t − t − 2 = 0 ⇔ ⇔ 
x + x − 2 = 0 ⇔ t = 1( − L)  x = 2 −
Kết luận: Phương trình có 3 nghiệm: 7
x = − ; x =1; x = 2 − 5
Ví dụ 5: Giải các phương trình sau: a) 3 3
x +15 + 2 = x + 8 + 3x
b) 3x +1 − x + 3 +1− x = 0
a). Phương trình được viết lại như sau: THCS.TOANMATH.com 3 3 3 3
x +15 + 2 = x + 8 + 3x ⇔ x +15 − x + 8 = 3x − 2.Để phương trình có nghiệm ta cần: 2
3x − 2 ≥ 0 ⇔ x ≥ . Nhẩm được x =1 nên ta viết lại 3 phương trình thành: 3 3
x +15 − 4 = x + 8 − 3+ 3x − 3
 ( 2x + x + )1 ( 2x + x + )1  ⇔ (x −1)  − − 3 = 0 3 3  x +15 + 4 x + 8 +  3 
( 2x + x+ )1 ( 2x + x+ )1 Để ý rằng: −
− 3 < 0 nên phương trình có nghiệm 3 3 x +15 + 4 x + 8 + 3 duy nhất x =1 b). Điều kiện 1 x  3;  ∈ − −  3  
Ta viết lại phương trình như sau: 3x +1 − x + 3 +1− x = 0 2x − 2 x ( x ) 1 1 1 0 2 2  ⇔ + − = ⇔ − − =   0 3x +1 + x + 3
 3x +1 + x + 3 2  x = 1 ⇔ 
 3x +1 + x + 3 = 2
Xét phương trình: 3x +1 + x + 3 = 2 . Bình phương 2 vế ta thu được: x ≤ 0
4x + 4 + 2 (3x +1)(x + 3) = 4 ⇔ (3x +1)(x + 3) = 2 − x ⇔  2
x −10x − 3 = 0
⇔ x = 5 − 2 7
Kết luận: Phương trình có 2 nghiệm là x =1, x = 5 − 2 7 THCS.TOANMATH.com Nhận xét:
+ Ta thấy phương trình có nghiệm x =1. Nếu ta phân tích phương trình
thành 3x +1 − 2 + 2 − x + 3 + 4 − 4x = 0 thì sau khi liên hợp phương trình − −
mới thu được sẽ là: 3x 3 1 x + + 4 − 4x = 0
3x +1 + 2 2 + x + 3 (x ) 3 1 1 4 ⇔ − + − = 
 0 .Rõ ràng phương trình hệ quả
 3x +1 + 2 2 + x + 3  3 1 +
− 4 = 0 phức tạp hơn phương trình ban đấu rất
3x +1 + 2 2 + x + 3 nhiều.
+ Để ý rằng khi x =1 thì 3x +1 = x + 3 nên ta sẽ liên hợp trực tiếp biểu
thức 3x +1 − x + 3 .
2. Đặt ẩn phụ dựa vào tính đẳng cấp của phương trình:
Ta thường gặp phương trình dạng này ở các dạng biến thể như: + 2 3 2
ax + bx + c = d px + qx + rx + t (1) + 2 4 3 2
ax + bx + c = d px + qx + rx + ex + h (2) + 2 2 2
A ax + bx + c + B ex + gx + h = C rx + px + q (*)
Thực chất phương trình (*) khi bình phương 2 vế thì xuất hiện theo dạng (1) hoặc (2).
Để giải các phương trình (1), (2). Phương pháp chung là:
+ Phân tích biểu thức trong dấu
thành tích của 2 đa thức P(x),Q(x) THCS.TOANMATH.com + Ta biến đổi 2
ax + bx + c = mP(x) + nQ(x) bằng cách đồng nhất hai vế.
Khi đó phương trình trở thành: mP(x) + nQ(x) = d P(x).Q(x)
Chia hai vế cho biểu thức Q(x) > 0 ta thu được phương trình: P(x) P(x) m + n = d . Đặt P(x) t =
≥ 0 thì thu được phương trình: Q(x) Q(x) Q(x) 2
mt − dt + n = 0 .
Một cách tổng quát: Với mọi phương trình có dạng: n n n−k k 2 ( ) + ( ) + ( ) ( ) n aP x bQ x cP
x Q x + d P(x).Q(x) = 0 thì ta luôn giải được theo cách trên. Một số ví dụ:
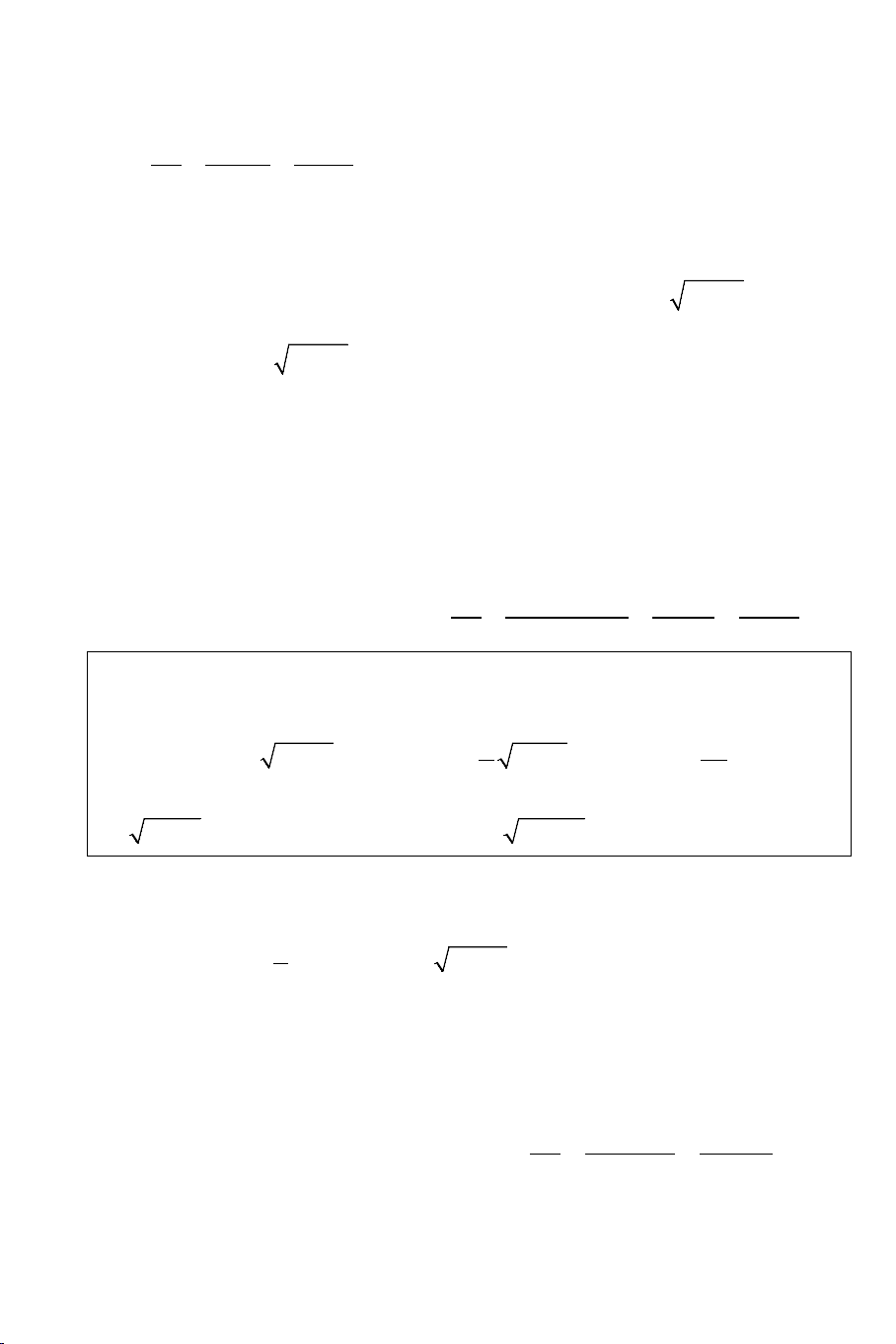
Ví dụ 1: Giải các phương trình: a) 2 3
2(x − 3x + 2) = 3 x + 8 b) 2
x +1+ x − 4x +1 = 3 x c) 2 x + ( 2
x − x) x + = ( 3 4 3 1 2 x + ) 1 Lời giải:
a). Điều kiện: x ≥ 2 − .
Ta viết lại phương trình thành: 2 2
2(x − 3x + 2) = 3 (x + 2)(x − 2x + 4) Giả sử 2 2
x − 3x + 2 = m(x + 2) + n(x − 2x + 4) . Suy ra ,
m n phải thỏa mãn THCS.TOANMATH.com n =1  m = 1 − m − 2n = 3 − ⇔   n =1 2m + 4n =  2
Phương trình đã cho có dạng: 2 2 2(
− x + 2) + 2(x − 2x + 4) − 3 (x + 2)(x − 2x + 4) = 0 .
Chia phương trình cho 2
x − 2x + 4 > 0 ta thu được:  x + 2  (x + 2) 2 − − 3 + 2 =   0 2 2
x − 2x + 4  (x − 2x + 4) Đặt (x + 2) t =
≥ 0 ta thu được phương trình: 2 2
− t − 3t + 2 = 0 2 (x − 2x + 4) t = 2 −  ⇔ 1 (x + 2) 1 1 do 2 ≥ ⇒ = ⇔ = ⇔ − + = + . t 0 t x 2x 4 4(x 2) t = 2 2 (x − 2x + 4) 2  2 x = 3+ 13 2
x − 6x − 4 = 0 ⇔  x = 3− 13 x ≥ 0 b). Điều kiện:  2
x − 4x +1 ≥ 0
Bình phương 2 vế của phương trình ta thu được: 2 2 2
x + 2x +1+ 2(x +1) x − 4x +1 + x − 4x +1 = 9x 2 2 2
⇔ 2x −11x + 2 + 2 (x + 2x +1)(x − 4x +1) = 0 Giả sử THCS.TOANMATH.com  1 m + n = 2 m = −  2 2 2   2
2x −11x + 2 = m(x + 2x +1) + n(x − 4x +1) ⇒ 2m − 4n = 1 − 1 ⇔  5 m + n =  2 n =  2 Phương trình trở thành: 1 2 5 2 2 2
− (x + 2x +1) + (x − 4x +1) + 2 (x + 2x +1)(x − 4x +1) = 0 2 2 Chia phương trình cho 2
x + 2x +1 > 0 ta thu được: 2 2
x − 4x +1
x − 4x +1 2  − +  1 − + 5 x 4x 1   + 4 
 = 0 . Đặt t =   ≥ 0 ta có 2 2  x + 2x +1  x + 2x +1 2  x + 2x +1 t = 1 − 2  − +  Phương trình 2 1 x 4x 1 1 5t 4t 1 0  + − = ⇔ 1 ⇔ t = ⇔   = 2 t = 5
x + 2x +1 25  5  1 x = 2 24x 102x 24 0  ⇔ − + = ⇔ 4  x = 4
Kết luận: Phương trình có 2 nghiệm 1
x = , x = 4 4
Nhận xét: Trong lời giải ta đã biến đổi: 2 2 2
(x +1) x − 4x +1 = (x + 2x +1)(x − 4x +1) là vì x +1 > 0
c). Điều kiện: x ≥ 1 −
Ta viết lại phương trình thành: (x − ) 2
1 2x − 2x − 2 − 3x x +1 = 0   x = 1 ⇔  2
2x − 2x − 2 − 3x x +1 = 0 THCS.TOANMATH.com Xét phương trình: 2 2
2x − 2x − 2 − 3x x +1 = 0 ⇔ 2x − 3x x +1 − 2(x +1) = 0. Dễ thấy x = 1
− không phải là nghiệm. Xét x > 1
− ta chia cho x +1 thì thu được phương trình:  x = 2 (1) 2 x xx +1 2 − 3 − 2 = 0 ⇔  x +1 x +1  x = 1 −  (2)  x +1 xx ≥ 0 Giải (1): = 2 ⇔ 
⇔ x = 2 + 2 2 2 x +1
x − 4x − 4 = 0 xx ≤ 0 Giải (2): = 1 − ⇔ 
⇔ x = 2 − 2 2 2 x +1
x − 4x − 4 = 0
Kết hợp điều kiện ta suy ra các nghiệm của phương trình là:
x =1; x = 2 ± 2 2
Ví dụ 2: Giải các phương trình: a) 2 2 3
4(2x +1) + 3(x − 2x) 2x −1 = 2(x + 5x) b) 2 2
5x + 4x − x − 3x −18 = 5 x c) 2 2
5x −14x + 9 − x − x − 20 = 5 x +1 Lời giải: a). Điều kiện 1 x ≥ 2
Phương trình đã cho được viết lại như sau: THCS.TOANMATH.com 3 2
2x −8x +10x − 4 − 3x(x − 2) 2x −1 = 0 2
⇔ (x − 2)(2x − 4x + 2) − 3x(x − 2) 2x −1 = 0 2
⇔ (x − 2) (2x − 4x + 2) − 3x 2x −1 = 0   x − 2 = 0 ⇔  2
(2x − 4x + 2) − 3x 2x −1 = 0 Xét phương trình: 2 2 2
2x − 4x + 2 − 3x 2x −1 = 0 ⇔ 2x − 4x + 2 − 3 x (2x −1) = 0 m = 2 Ta giả sử: 2 2
2x − 4x + 2 = mx + n(2x −1) ⇒  n = 2 −
Phương trình trở thành: 2 2
2x − 2(2x −1) − 3 x (2x −1) = 0 . Chia cho 2 x > 0  −  − − Ta có: 2x 1 2x 1 x 2 − 2. − 3 = 2 1   0 . Đặt t = ≥ 0 phương trình mới 2 2  xx 2 xt = 2 − là: 2 2t 3t 2 0  − − + = ⇔ 1 t =  2 2x −1 1 x = 4 + 2 3 Với 1 t = ta có: 2
= ⇔ x −8x + 4 = 0 ⇔  2 2 x 2 x = 4 − 2 3 Nhận xét:
+ Đối với phương trình 2
2x − 4x + 2 − 3x 2x −1 = 0 ta có thể không cần
đưa x vào trong dấu khi đó ta phân tích: 2 2
2x − 4x + 2 = mx + n(2x −1)
và chia như trên thì bài toán vẫn được giải quyết. Việc đưa vào là giúp
các em học sinh nhìn rõ hơn bản chất bài toán. THCS.TOANMATH.com
+ Ngoài ra cần lưu ý rằng: Khi đưa một biểu thức P(x) vào trong dấu 2n
thì điều kiện là P(x) ≥ 0 . Đây là một sai lầm học sinh thường mắc phải khi giải toán. 2
x − 3x −18 ≥ 0
b). Điều kiện: x ≥ 0 ⇔ x ≥ 6 .  2 5x + 4x ≥  0
Phương trình đã cho được viết lại thành: 2 2
5x + 4x = x − 3x −18 + 5 x
Bình phương 2 vế và thu gọn ta được: 2 2
2x − 9x + 9 − 5 x(x − 3x −18) = 0 Nếu ta giả sử 2 2
2x − 9x + 9 = mx + n(x − 3x −18) thì ,
m n phải thỏa mãn n = 2  m − 3n = 9
− điều này là hoàn toàn vô lý.  18 − n =  9
Để khắc phục vấn đề này ta có chú ý sau : 2
x − 3x −18 = (x − 6)(x + 3) khi đó 2 2
x(x − 3x −18) = x(x − 6)(x + 3) = (x − 6x)(x + 3)
Bây giờ ta viết lại phương trình thành: 2 2
2x − 9x + 9 − 5 (x − 6x)(x + 3) = 0 m = 2  m = 2 Giả sử: 2 2
2x − 9x + 9 = m(x − 6x) + n(x + 3) ⇒  6 − m + n = 9 − ⇔   n = 3 n =  3
Như vậy phương trình trở thành: 2 2
2(x − 6x) + 3(x + 3) − 5 (x − 6x)(x + 3) = 0 2 2  −   − 
Chia cho x + 3 > 0 ta thu được: x 6x x 6 2  − 5 x   + 3 = 0 x + 3   x + 3  THCS.TOANMATH.com t =1 2  −  Đặt x 6x 2 t   0 2t 5t 3 0  = ≥ ⇒ − + = ⇔ 3 x + 3   t =  2  7 + 61  = 2 x  −  Trường hợp 1: x 6x 2 2 t =1 ⇔ 
 = 1 ⇔ x − 7x − 3 = 0 ⇔  x + 3   7 − 61 x =  2 Suy ra 7 61 x + =
thỏa mãn điều kiện. 2 Trường hợp 2: x = 9 2 3
x − 6x  3 2 t   4x 33x 27 0  = ⇔ = ⇔ − − = ⇔ 3 ⇒ x = 9 2  x + 3  2 x = −  4
Tóm lại: Phương trình có 2 nghiệm là: 7 61 x + = và x = 9 2
c). Điều kiện x ≥ 5.
Chuyển vế bình phương ta được: 2 x − x + = ( 2 2 5
2 5 x − x − 20)(x + ) 1 Giả sử: 2
x − x + = m( 2 2 5 2
x − x − 20) + n(x + ) 1 m = 2
Khi đó ta có : −m + n = 5 − không tồn tại ,
m n thỏa mãn hệ.  20 − m + n =  2 Nhưng ta có :
( 2x − x− )(x+ ) = (x+ )(x− )(x+ ) = (x+ )( 2 20 1 4 5 1
4 x − 4x − 5) THCS.TOANMATH.com Giả sử: 2
x − x + = α ( 2 2 5 2
x − 4x − 5) + β (x + 4) . Suy ra m = 2  m = 2  4 − m + n = 5 − ⇒   n = 3 5 − m + 4n =  2
Ta viết lại phương trình: ( 2
x − x − ) + (x + ) 2 2 4 5 3
4 = 5 (x − 4x − 5)(x + 4) .
Chia hai vế cho x + 4 > 0 ta thu được: 2 2
x − 4x − 5 
x − 4x − 5  2  − 5   + 3 = 0 x + 4   x + 4  2  − −  Đặt x 4x 5 t = 
 ≥ 0 ta thu được phương trình:  x + 4  t =1 2 2t 5t 3 0  − + = ⇔ 3 t =  2  5 + 61  = 2 x Trường hợp 1: x − 4x − 5 2 2 t =1 ⇔
= 1 ⇔ x − 5x − 9 = 0 ⇔  x + 4  5 − 61 x =  2 x = 8 2 − − Trường hợp 2: 3 x 4x 5 9 2 t 4x 25x 56 0  = ⇔ = ⇔ − − = ⇔ 7 2 x + 4 4 x = −  4
Kết hợp điều kiện ta suy ra các nghiệm của phương trình là: 5 61 x 8; x + = = 2
Ví dụ 3: Giải các phương trình: a) 2 2
x + 2x + 2x −1 = 3x + 4x +1 THCS.TOANMATH.com b) 3 2 3
x − 3x + 2 (x + 2) − 6x = 0
Lời giải: a). Điều kiện: 1 x ≥ . 2
Bình phương 2 vế phương trình ta thu được: 2 2 2 2 2
x + 4x −1+ 2 (x + 2x)(2x −1) = 3x + 4x +1 ⇔ x +1− (x + 2x)(2x −1) = 0 m =1  m =1 Ta giả sử: 2 2
x +1 = m(x + 2x) + n(2x −1) ⇔ n = 1 − ⇔   n = 1 − 2m + 2n =  0 Phương trình trở thành: 2 2  2x −1   2x −1 (x 2x) (2x 1) (x 2x)(2x 1) 0  + − − − + − = ⇔ − − +1 =     0 2 2  x + 2x   x + 2x  −  − ± Đặt 2x 1 2 1 5 t = ≥  0 ⇒ t
− − t +1 = 0 ⇔ t =  2  x + 2x  2
Về cơ bản đến đây ta hoàn toàn tìm được x . Nhưng với giá trị 1
> 0 như vậy việc tính toán sẽ gặp khó khăn. (3x + )2 3 1
Để khắc phục ta có thể xử lý theo hướng khác như sau: Ta viết lại: 2 2
(x + 2x)(2x −1) = (x + 2)(2x − x) lúc này bằng cách phân
tích như trên ta thu được phương trình: 2 2 1 2 1 2 2x − x 2 −
(2 − ) + ( + 2) − ( + 2)(2 − ) = 0 ⇔ − 2 x x x x x x x x +1 = 0 2 2 x + 2 x + 2 THCS.TOANMATH.com Đặt 2 2x − x 2 2 2 t =
≥ 0 ⇒ t − 2t +1 = 0 ⇔ t =1 ⇔ 2x − x = x + 2 ⇔ x − x −1 = 0 x + 2 1 5 x ± ⇔ =
. Kiểm tra điều kiện ta thấy chỉ có giá trị 1 5 x + = là thỏa 2 2 mãn điều kiện.
b). Điều kiện: x ≥ 2 − .
Ta viết lại phương trình thành: 3 3
x − 3x(x + 2) + 2 (x + 2) = 0 Để ý rằng:
Nếu ta đặt y = x + 2 thì phương trình trở thành: 3 2 3
x − 3xy + 2y = 0 . Đây
là một phương trình đẳng cấp bậc 3. Từ định hướng trên ta có lời giải cho bài toán như sau:
+ Xét trường hợp: x = 0 không thỏa mãn phương trình:
+ Xét x ≠ 0 . Ta chia phương trình cho 3
x thì thu được: 3 (x + 2) (x + 2) 1− 3 + 2 = 0. 2 3 x x  1 t = − Đặt x + 2 t = ta có phương trình: 3 2 2t 3t 1 0  − + = ⇔ 2 x  t =1 Trường hợp 1: 1 t = − 2 x + 2 1 x ≤ 0 ⇔
= − ⇔ 2 x + 2 = −x ⇔ 
⇔ x = 2 − 2 3 2 x 2
x − 4x −8 = 0
Trường hợp 1: t =1 THCS.TOANMATH.com x + 2 x ≥ 0 ⇔
=1 ⇔ x + 2 = x ⇔  ⇔ x = 2 2 x
x − x − 2 = 0
Kết luận: Phương trình có 2 nghiệm: x = 2; x = 2 − 2 3
Ví dụ 4: Giải các phương trình: a) 3 2 5 4
2x − x − 3x +1 = x + x +1 b) 4 2
5 x + 8x = 4x + 8 Lời giải:
a). Hình thức bài toán dễ làm cho người giải bối rối nhưng để ý thật kỹ ta thấy:
Chìa khóa bài toán nằm ở vấn đề phân tích biểu thức: 5 4 x + x +1
Ta thấy do vế trái là biểu thức bậc 3 nên ta nghỉ đến hướng phân tích: 5 4 2 3 2
x + x +1 = (x + ax +1)(x + bx + cx +1) . Đồng nhất hai vế ta thu được:
a =1;b = 0;c = 1
− . Nên ta viết lại phương trình đã cho thành: 3 2 3 2
2(x − x +1) − (x + x +1) − (x − x +1).(x + x +1) = 0 Chia cho 2
x + x +1 > 0 ta thu được: 3 3
x − x +1
x − x +1 3  − +  2. x x 1   − 
 −1 = 0 . Đặt t =   ≥ 0 ta có 2 2  x + x +1  x + x +1 2  x + x +1 t =1 phương trình: 2 2t t 1 0  − − = ⇔ 1 t = − (L)  2 THCS.TOANMATH.com x = 0 3 − + Giải x x 1 3 2 t 1 1 x x 2x 0  = ⇔ = ⇔ − − = ⇔ x = 1 − 2 x x 1  + + x =  2
Kết luận: Thử lại ta thấy 3 nghiệm: x = 0, x = 1;
− x = 2 đều thỏa mãn. x ≥ 0 b). Điều kiện: 4
x + 8x ≥ 0 ⇔  x ≤ 2 −
Ta thấy chìa khóa bài toán nằm ở việc phân tích biểu thức: 4
x + x = x( 3
x + ) = x(x + )( 2
x − x + ) = ( 2 x + x)( 2 8 8 2 2 4 2
x − 2x + 4)Giả sử m + n = 4 2 2 2 4x 8 m(x 2x 4) n(x 2x)  + = − + + + ⇒  2
− m + 2n = 0 ⇔ m = n = 2 4m =  8 Phương trình trở thành: 2 2 2 2
2(x − 2x + 4) + 2(x + 2x) − 5 (x − 2x + 4)(x + 2x) = 0 . Chia hai vế cho 2 2 + + 2 x x x x x
− 2x + 4 > 0 ta thu được: 2 2 2 − 5 + 2 = 0. Đặt 2 2 x − 2x + 4 x − 2x + 4 t = 2 2 x + 2x t =
≥ 0 ta có phương trình: 2 2t 5t 2 0  − + = ⇔ 2 x − 2x + 4 1 t =  2 2 + Trường hợp 1: x 2x 2 t = 2 ⇔
= 4 ⇔ 3x −10x +16 = 0 vô nghiệm 2 x − 2x + 4 Trường hợp 2:  5 − − 37  = 2 x 1 x + 2x 1 2 3 t = ⇔
= ⇔ 3x +10x − 4 = 0 ⇔  2 2 x − 2x + 4 4  5 − + 37 x =  3 THCS.TOANMATH.com  5 − − 37 x =
Kết luận: Phương trình có hai nghiệm là: 3   5 − + 37 x =  3
Nhận xét: Ta có thể phân tích: 4
x + x = x( 3 x + ) 2 2 2 8
8 = x(x + 2)(x − 2x + 4) = (x + 2x)(x − 2x + 4)
Chú ý rằng: Trong một số phương trình: Ta cần dựa vào tính đẳng cấp của
từng nhóm số hạng để từ đó phân tích tạo thành nhân tử chung.
Ví dụ 5: Giải các phương trình: a) 2
(x + 2)( 2x + 3 − 2 x +1) + 2x + 5x + 3 −1 = 0 b) 2 2
(x + 4) 2x + 4 = 3x + 6x − 4 c) 2 2 2
(x − 6x +11) x − x +1 = 2(x − 4x + 7) x − 2 Giải:
a). Đặt 2x + 3 = a, x +1 = b ⇒ a,b ≥ 0
Phương trình đã cho trở thành: 2 2 2 2
(a − b )(a − 2b) − (a − ab − 2b ) = 0
⇔ (a − 2b)(a − b)(a + b) − (a − b)(a − 2b) = 0 ⇔ (a − 2b)(a − b)(a + b −1) = 0
 2x + 3 − x +1 = 0 
Ta quy bài toán về giải 3 phương trình cơ bản là: 2 2x + 3 − x +1 = 0
 2x+3 + x+1−1=  0 
Với điều kiện: x ≥ 1
− ⇒ a ≥1,b ≥ 0 THCS.TOANMATH.com
Trường hợp 1: 2x + 3 − x +1 = 0 ⇔ 2x + 3 = x +1 ⇔ x = 2 − (L) Trường hợp 2: 11
2 2x + 3 − x +1 = 0 ⇔ 8x +12 = x +1 ⇔ x = − (L) 7
Trường hợp 3: 2x + 3 + x +1 −1 = 0 . Vì 2x + 3 ≥1, x +1 ≥ 0 ⇒ VT ≥ 0
Dấu bằng xảy ra khi và chỉ khi x = 1 − .
Tóm lại phương trình có nghiệm duy nhất x = 1 −
b). Điều kiện x ≥ 2 −
Ta thấy rằng nếu bình phương trực tiếp sẽ dẫn đến phương trình bậc 5
Để khắc phục ta sẽ tìm cách tách 2
x + 4 ra khỏi 2x + 4
Từ đó ta viết lại phương trình như sau: 2 2 2
(x + 4) 2x + 4 + x + 4 = 4x + 6x 2 2 2
⇔ (x + 4)( 2x + 4 +1) = 2x(2x + 3) ⇔ (x + 4)( 2x + 4 +1) = 2x( (2x + 4) −1) 2
⇔ (x + 4)( 2x + 4 +1) = 2x( 2x + 4 +1)( 2x + 4 −1)
Do 2x + 4 +1 > 0 . Phương trình đã cho tương đương với ⇔ x + = x
x + − ⇔ x + x + − x x + = ⇔ (x − x + )2 2 2 4 2 ( 2 4 1) 2 4 2 2 4 0 2 4 = 0 2
x − 2x + 4 = 0 ⇔ x − 2x − 4 = 0 ⇒ x =1+ 5
Kết luận: Phương trình có nghiệm duy nhất x =1+ 5
c). Điều kiện: x ≥ 2 THCS.TOANMATH.com Giả sử m =1 2 2
x 6x 11 m(x
x 1) n(x 2)  − + = − + +
− ⇒ −m + n = 6
− ⇔ m =1,n = 5 − m− 2n =  11  p =1 2 2
x 4x 7 p(x
x 1) q(x 2)  − + = − + +
− ⇒ − p + q = 4
− ⇔ p =1,q = 3 − p − 2q =  7
Phương trình đã cho trở thành: 2 2 2
(x − x +1) − 5(x − 2) x − x +1 − 2 (x − x +1) − 3(x − 2) x − 2 = 0     Chia phương trình cho 2 3
(x − x +1) ta thu được: 3 x − 2 x − 2  x − 2 1 5. 2 6  − − + =   0 2 2 2 x − x +1 x − x +1
x − x +1 − Đặt x 2 t = ≥ 0 2 x − x +1  t =1 
Ta thu được phương trình: 3 2 1 6t 5t 2t 1 0  − − + = ⇔ t =  3  1 t = − (L)  2 + Nếu 2
t =1 ⇔ a = b ⇔ x − 2x + 3 = 0(VN) + Nếu 1 2
t = ⇔ x −10x +19 = 0 ⇔ x = 5 ± 6 3
Kết luận: x = 5 ± 6 THCS.TOANMATH.com
2. Giải phương trình vô tỷ bằng phương pháp đặt ẩn phụ không hoàn toàn.
+ Đặt ẩn phụ không hoàn toàn là phương pháp chọn một số hạng trong
phương trình để đặt làm ẩn sau đó ta quy phương trình ban đầu về dạng một phương trình bậc 2: 2
mt + g(x)t + h(x) = 0 ( phương trình này vẫn còn ẩn x )
+ Vấn đề của bài toán là phải chọn giá trị m bằng bao nhiêu để phương
trình bậc 2 theo ẩn t có giá trị ∆ chẵn (∆ = [A x ]2
( ) ) như thế viêc tính t
theo x sẽ được dễ dàng.
+ Thông thường khi gặp các phương trình dạng: 2 2
ax + bx + c + (dx + e) px + qx + r = 0 thì phương pháp đặt ẩn phụ không
hoàn toàn tỏ ra rất hiệu quả:
+ Để giải các phương trình dạng này ta thường làm theo cách: - Đặt 2
f (x) = t ⇒ t = f (x)
- Ta tạo ra phương trình: 2
mt + g(x)t + h(x) = 0
Ta có ∆ = [g(x)]2 2 − 4 .
m h(x) = f (m)x + g (m)x + h (m) . Để ∆ có dạng 1 1 1 [A x ]2
( ) thì điều kiện cần và đủ là
∆ = g m − f m g m = ⇒ m m [ ( )]2 4 ( ). ( ) 0 1 1 1 Ta xét các ví dụ sau:
Ta xét các ví dụ sau:
Ví dụ 1: Giải các phương trình: a) 2 2
x +1− (x +1) x − 2x + 3 = 0 THCS.TOANMATH.com b) 2
2 2x + 4 + 4 2 − x = 9x +16 c) 2
(2x + 7) 2x + 7 = x + 9x + 7 (Trích đề TS lớp 10 Chuyên Tự nhiên – ĐHQG Hà Nội 2009) Giải: a) Đặt 2 2 2
t = x − 2x + 3 > 0 ⇒ t = x − 2x + 3
Phương trình đã cho trở thành: 2
x +1− (x +1)t = 0
Ta sẽ tạo ra phương trình: 2 2 2
mt − (x +1)t + x +1− m(x − 2x + 3) = 0 (Ta đã thêm vào 2
mt nên phải bớt đi một lượng 2 2
mt = m(x − 2x + 3) )
Phương trình được viết lại như sau: 2 2
mt − (x +1)t + (1− m)x + 2mx +1− 3m = 0 2 2
⇒ ∆ = (x +1) − 4m (1− m)x + 2mx +1− 3m   2 2 2 2
= (4m − 4m +1)x + (2 −8m )x +12m − 4m +1 Ta mong muốn 2 2 2 2 2
∆ = (Ax + B) ⇔ ∆ = − m − m − m +
m − m + = ⇔ m = m (1 4 ) (12 4 1)(4 4 1) 0 1
Phương trình mới được tạo ra là: 2t − (x +1)t + 2x − 2 = 0 Ta có 2 2
∆ = x − 6x + 9 = (x − 3) 
x +1− (x − 3) t = = 2  Từ đó ta có: 2  x +1+ (x −  3) t = = x −1  2 THCS.TOANMATH.com + Trường hợp 1: 2 2
t =1 ⇔ x − 2x + 3 = 2 ⇔ x − 2x −1 = 0 ⇔ x =1± 2 + Trường hợp 2: x ≥1 2
t = x −1 ⇔ x − 2x + 3 = x −1 ⇔  2 2
x − 2x + 3 = x − 2x +1
Phương trình vô nghiệm.
Tóm lại: Phương trình có 2 nghiệm là: x =1± 2 b) Điều kiện: 2 − ≤ x ≤ 2
Bình phương 2 vế phương trình và thu gọn ta được: 2 2
9x −16 8 − 2x + 8x − 32 = 0 . Đặt 2
t = 8 − 2x ta tạo ra phương trình là: 2 2 2
mt −16t − m(8 − 2x ) + 9x + 8x − 32 = 0 2 2
⇔ mt −16t + (9 + 2m)x + 8x −8m − 32 = 0 2
∆′ = 64 − m (9 + 2m)x + 8x −8m − 32   2 2 2 = ( 2
− m − 9m)x + 8mx + 8m + 32m + 64 Ta mong muốn 2
∆ ' = (Ax + B) ⇔ ∆ = 0 phải có nghiệm kép . Tức là: 2 2 2
∆′ = m − − m − m m + m + = ⇔ m = − m 16 ( 2 9 )(8 32 64) 0 4
Từ đó suy ra phương trình mới là: 2 2 4
− t −16t + x + 8x = 0  8 − (2x + 8) x t = =  Tính được: 2 2 4 − 2
∆ ' = 4x + 32x + 64 = (2x + 8) ⇒  8 + (2x +  8) x t = = − − 4  4 − 2 x xx ≥ 0 + Trường hợp 1: 2 4 2
t = ⇔ 8 − 2x = ⇔  ⇔ x = 2 2 2 2
4(8 − 2x ) = x 3 THCS.TOANMATH.com + Trường hợp 2: x xx ≤ 8 − 2
t = − − 4 ⇔ 8 − 2x = − − 4 ⇔  VN 2 2 2 2
4(8 − 2x ) = (x + 8)
Tóm lại phương trình có nghiệm duy nhất 4 2 x = 3
c). Đặt 2x + 7 = t ta tạo ra phương trình: 2 mt − ( x + ) 2 2
7 t + x + (9 − 2m) x + 7 − 7m = 0
Làm tương tự như trên ta tìm được m =1. Nên phương trình có dạng t = x + 7 2 t − (2x + 7) 2
t + x + 7x = 0 ⇒ ∆ = (2x + 7)2 − 4( 2
x + 7x) = 49 ⇒  t = x
giải theo các trường hợp của t ta tìm được x =1+ 2 2 là nghiệm của phương trình.
Ví dụ 3: Giải các phương trình: a) 2 2
10x − 9x −8x 2x − 3x +1 + 3 = 0 b) 3 2 3
x + 6x − 2x + 3− (5x −1) x + 3 = 0 c) 2
4 x +1 −1 = 3x + 2 1− x + 1− x Lời Giải: x ≥1 a) Điều kiện:  1 x ≤  2 Đặt 2
t = 2x − 3x +1 ta tạo ra phương trình: 2 2
mt −8xt + (10 − 2m)x + (3m − 9)x + 3− m = 0 THCS.TOANMATH.com Ta có 2 2
∆ = 16x − m (10 − 2m)x + (3m − 9)x + 3− m   2 2
= 16x − m (10 − 2m)x + (3m − 9)x + 3− m   2 2 2 2
= (2m −10m +16)x + (9m − 3m )x + m − 3m Ta cần : 2 2 2 2 ∆ = m − m − m − m +
m − m = ⇒ m = m (9 3 ) 4(2 10 16)( 3 ) 0 3  2 t = x
Phương trình đã cho trở thành: 2 2 3t 8xt 4x 0  − + = ⇔ 3  t = 2x Trường hợp 1 2 2 x ≥ 0 x ≥ 0 2
t = x ⇔ 2x − 3x +1 = x ⇔  ⇔  2 2 2 3 3 9(
 2x − 3x +1) = 4x 14
x − 27x + 9 = 0  3 x =  ⇔ 2   3 x =  7 x ≥ 0 Trường hợp 2: 2 1
t = 2x ⇔ 2x − 3x +1 = 2x ⇔  ⇔ x =  3 − x +1 = 0 3
Kết luận: Phương trình có 3 nghiệm: 3 3 1
x = , x = , x = 2 7 3
b) Điều kiện: x ≥1. Đặt 3 3 2
t = x + 3 ≥ 0 ⇔ x = t − 3 . Do hệ số của 3 x
trong phương trình là: 1. Phương trình đã cho trở thành: 2 2
t − (5x −1)t + 6x − 2x = 0 2 2 2 2
∆ = (5x −1) − 4(6x − 2x) = x − 2x +1 = (x −1) . THCS.TOANMATH.com
(5x −1) − (x −1) t = = 2x  Suy ra: 2 
(5x −1) + (x −  1) t = = 3x −1  2  x =1 x  ≥ 0  + Trường hợp 1: 3 3 21
x + 3 = 2x ⇔  ⇔ x = 3 2 x 4x 3 0  − + = 2   3− 21 x = (L)  2 Trường hợp 2: x =1  1 x ≥  3
x + 3 = 3x −1 ⇔  3 ⇔ x = 4 + 2 3  3 2
x − 9x + 6x + 2 = 0 x = 4−  2 3(L) +
Tóm lại phương trình có 3 nghiệm: 3 21 x =1, x = , x = 4 + 3 2 2 a) Điều kiện: 1
− ≤ x ≤1. Ta viết phương trình thành: 2
4 x +1 − 2 1− x = 3x +1+ 1− x .
Bình phương 2 vế ta thu được phương trình mới: 2 2 2 2
16(x +1) + 4(1− x) −16 1− x = 9x + 6x +1+ 2(3x +1) 1− x +1− x 2 2
⇔ 8x − 6x −18 + (6x +18) 1− x = 0 Đặt 2
t = 1− x ta tạo ra phương trình: 2 2
mt + (6x +18)t + (8 + m)x − 6x −18 − m = 0 Có 2 2
∆ ' = (3x + 9) − m (8 + m)x − 6x −18 − m   THCS.TOANMATH.com 2 2 2
= (9 −8m − m )x + (54 + 6m)x + m +18m + 81 Ta mong muốn 2 2 2 2
∆ = (Ax + B) ⇔ ∆ ' = m +
− − m − m m + m + = m (3 27) (9 8 )( 18 81) 0
Từ đó tính được m = 8 −
Phương trình đã cho trở thành: 2 8
− t + (6x +18)t − 6x −10 = 0 Ta có 2 2
∆ ' = (3x + 9) −8(6x +10) = (3x +1)  3
− x − 9 − (3x +1) 3x + 5 t = =  Suy ra 8 − 4  3
− x − 9 + (3x +  1) t = = 1  8 − Trường hợp 1: 2
t =1 ⇔ 1− x =1 ⇔ x = 0 thỏa mãn điều kiện Trường hợp 2: 3x + 5 2 2 2 t =
⇔ 4 1− x = 3x + 5 ⇔ 16(1− x ) = 9x + 30x + 25 4 2 2 2 3
16(1− x ) = 9x + 30x + 25 ⇔ 25x + 30x + 9 = 0 ⇔ x = − 5 Thử lại ta thấy: 3
x = − thỏa mãn phương trình: 5
Kết luận: Phương trình có 2 nghiệm 3 x = 0, x = − 5
Chú ý: Ở bước cuối cùng khi giải ra nghiệm ta phải thử lại vì phép bình
phương lúc đầu khi ta giải là không tương đương.
Ví dụ 4) Giải các phương trình: a) 2
5 − x = x − 5 THCS.TOANMATH.com b) 4 2
x − 2 3x + x + 3− 3 = 0 2 x + x + ( 2 8 3
4x + x − 2) x + 4 = 4 Giải: x ≤ 5 a) Điều kiện:  2 x ≥ 5
Bình phương 2 vế ta thu được: 2 2 4
5 − (2x +1).5 + x + x = 0
Ta coi đây là phương trình bậc 2 của 5 ta có: 2 2 4 2 2
∆ = (2x +1) − 4(x + x ) = 4x − 4x +1 = (2x +1)  1 2 2
5 = (2x +1+ 2x −1) = x + x  Từ đó suy ra 2   1 2 2
5 = (2x +1− 2x +1) = x − x +1  2  1 − − 21 x = Trường hợp 1: 2 2
x + x − 5 = 0 ⇔   1 − + 21 x =  2  1− 17 x = Trường hợp 2: 2 2
x − x − 4 = 0 ⇔   1+ 17 x =  2
Đối chiếu với điều kiện ta có 4 nghiệm đều thỏa mãn phương trình.
b) Ta viết lại phương trình thành: 2 4
3− (2x +1) 3 + x + x = 0
Ta coi đây là phương trình bậc 2 của 3 ta có: THCS.TOANMATH.com 2 2 4 2 2
∆ = (2x +1) − 4(x + x ) = 4x − 4x +1 = (2x +1)  1 2 2
3 = (2x +1+ 2x −1) = x + x 2  2
x + x − 3 = 0 Từ đó suy ra  ⇔  2  1 2 2  = + − + = − +
x − x +1− 3 = 0 3
(2x 1 2x 1) x x 1  2
Giải 2 phương trình trên ta thu được các nghiệm của phương trình đã cho là: 1 1 4 3 x − ± + = hoặc 1 4 3 3 x − ± − = 2 2
c) Điều kiện x ≥ 4 −
Ta viết lại phương trình thành: x + + ( 2 x + x − ) 2 4 4
2 x + 4 + 8x + 2x −8 = 0 . Coi đây là phương trình
bậc 2 ẩn x + 4 thì
∆ = ( x + x − )2 − ( x + x − ) = ( x + x − )2 2 2 2 4 2 4 8 2 8 4 6 .  x + 4 = 2 − x Từ đó suy ra 
 x + 4 = 2x +1
Giải 2 trường hợp ta thu được các nghiệm của phương trình là:  1− 65 x = 8   3 − + 57 x =  8
Ví dụ 5: Giải các phương trình: a) 2 2
3( 2x +1 −1) = x(1+ 3x + 8 2x +1) b) 2 2
x + 3x + 6 + 2x −1 = 3x +1 Lời Giải: THCS.TOANMATH.com
a) Ta viết lại phương trình thành: 2 2
3x + x + 3+ (8x − 3) 2x +1 = 0 . Đặt 2
t = 2x +1 ≥ 0 suy ra 2 2 t = 2x +1.
Ta tạo ra phương trình: 2 2
mt + (8x − 3)t + (3− 2m)x + x + 3− m = 0 . Ta có 2 2
∆ = (8x − 3) − 4m (3− 2m)x + x + 3− m =   2 2 2
= (8m −12m + 64)x − (48 + 4m)x + 4m −12m + 9 . Ta cần 2 2 2 ∆ ' =
+ m − m − m +
m − m + = ⇒ m = . m (24 2 ) (8 12 64)(4 12 9) 0 3
Phương trình trở thành: 2 2
3t + (8x − 3)t − 3x + x = 0 . Ta có: 2 2 2 2
∆ = (8x − 3) −12.( 3
− x + x) =100x − 60x + 9 = (10x − 3) . 
3−8x − (10x − 3) t = = 3 − x +1  Từ đó tính được : 6 
3−8x + (10x −  3) x t = = −  6 3  1 x ≤ Trường hợp 1: 2 2x +1 = 3 − x +1 ⇔  3 ⇔ x = 0  2 9  x − 6x = 0 xx ≤ 0 Trường hợp 2: 2 2x +1 = − ⇔  VN 2 3 17  x + 9 = 0
Vậy phương trình có nghiệm duy nhất: x = 0 b) Điều kiện: 1 x ≥ . 2
Ta viết lại phương trình thành: 2 2
x + 3x + 6 = 3x +1− 2x −1 .
Bình phương 2 vế và thu gọn ta được phương trình mới: THCS.TOANMATH.com 2 2
10x + 3x − 6 − 2(3x +1) 2x −1 = 0 Đặt 2
t = 2x −1 ≥ 0 suy ra 2 2 t = 2x −1.
Ta tạo ra phương trình: 2 2
mt − 2(3x +1)t + (10 − 2m)x + 3x − 6 + m = 0 . Ta có 2 2
∆ ' = (3x +1) − m (10 − 2m)x + 3x − 6 + m   2 2 2
= (2m −10m + 9)x + (6 − 3m)x − m + 6m +1. Ta cần 2 2 2 ∆ = − m − m − m +
−m + m + = ⇒ m = . m (6 3 ) 4(2 10 9)( 6 1) 0 4
Phương trình trở thành: 2 2
4t − 2(3x +1)t + 2x + 3x − 2 = 0 . Ta có: 2 2 2 2
∆ ' = (3x +1) − 4.(2x + 3x − 2) = x − 6x + 9 = (x − 3) . 
3x +1− (x − 3) x + 2 t = =  Từ đó tính được: 4 2 
3x +1+ (x − 3) 2x −  1 t = =  4 2  2 + 2 15 x = x + 2 x ≥ 2 − Trường hợp 1: 2 7 2x −1 = ⇔  ⇔  . 2 2
7x − 4x − 8 = 0  2 − 2 15 x =  7
Đối chiếu với điều kiện ban đầu ta thấy chỉ có 2 2 15 x + = là thỏa mãn 7 điều kiện .  1 − − 6  1 x = x − x ≥ Trường hợp 2: 2 2 1 2 2x −1 = ⇔  2 ⇔  . 2  2  1 − + 6
4x + 4x − 5 = 0 x =  2 THCS.TOANMATH.com
Đối chiếu với điều kiện ban đầu ta thấy chỉ có 1 6 x − + = là thỏa mãn 2 điều kiện .
Vậy phương trình có 2 nghiệm là: 2 2 15 x + = và 1 6 x − + = 7 2
SỬ DỤNG HẰNG ĐẲNG THỨC ĐỂ GIẢI PHƯƠNG TRÌNH Dấu hiệu:
Các bài toán giải được bằng hằng đẳng thức thường có dạng: 3 2
ax + bx + cx + d = e( fx + h) px + q hoặc 3 2 3 3 2
ax + bx + cx + d = e px + qx + rx + s
Phương pháp chung để giải các bài toán này là: Đặt n f (x) = y với n = 2 hoặc n = 3.
Đưa phương trình ban đầu về dạng ( + )3 + ( + ) 3 m Ax B
n Ax B = my + ny Ví dụ 1: a) 3 2 3
8x − 36x + 53x − 25 = 3x − 5 b) 3 2 3 2
8x −13x + 7x = 2 x + 3x − 3
c) 3 24x −11 −16x 2x −1 −1 = 0 . d) 3 3
x = 6 6x + 4 + 4 e) 3 3
x +1 = 2 2x −1 f) ( 2 4x + )
1 x = (3− x) 5 − 2x THCS.TOANMATH.com Giải:
Những phương trình có dạng: 3 2
ax + bx + cx + d = (ex + h) px + q (1) Hoặc: 3 2 3 3 2
ax + bx + cx + d = e px + qx + rx + h (2)
ta thường giải theo cách: 2 −
Đối với (1): Đặt px + q = y khi đó y p x = thay vào phương trình ta q đưa về dạng: 3 2 3
ax + bx + cx + d = Ay + By . Sau đó biến đổi phương trình
thành: A [u x ]3 3 . ( ) + .
B u(x) = Ay + By Đối với (2): Đặt 3 3 2
g px + qx + rx + h = y sau đó tạo ra hệ tạm: 3 2
ax + bx + cx + d =  .sy
cộng hai phương trình ta thu được: 3 g  ( 3 2
px + qx + rx + h) 3 =  y 3 2 3
Ax + Bx + Cx + D = .sy + y sau đó đưa phương trình về dạng:
[u x ]3 + s [u x ] 3 ( )
. ( ) = y + .sy
Ta xét các ví dụ sau: 3 2 8
 x −36x + 53x − 25 = y
a) Đặt 3 3x − 5 = y ta có hệ sau:  (I) 3 3
 x − 5 = y
Cộng hai phương trình của hệ với nhau ta thu được: 3 2 3
8x − 36x + 56x − 30 = y + y (*). Ta nghỉ đến việc biến đổi vế trái thành: [ ( A x)]3 + (
A x) để phương trình có dạng: [A x ]3 3 ( ) + (
A x) = y + y Giả sử: 3 2 3
8x − 36x + 56x − 30 = (2x + a) + (2x + a) . THCS.TOANMATH.com
Đồng nhất hệ số của 2 x ⇒ a = 3 −
Như vậy phương trình (*) có dạng: 3 3
(2x − 3) + (2x − 3) = y + y (1)
Đặt z = (2x − 3) . Từ phương trình ta suy ra 3 3
z + z = y + y 3 3
z + z = y + y ⇔ (z − y)( 2 2
z + zy + y + ) 1 = 0 . Do 2 2 2  y  3 2
z + zy + y +1 = z + + y +1 > 0, y
∀ , z ⇒ PT ⇔ y =   z  2  4 3 2
⇔ y = 2x − 3 ⇔ 8x − 36x + 53x − 25 = 2x − 3  5 ± 3 3 2 ⇔ 8 − 36 + 51 − 22 = 0 x x x x = ⇔ 4  x = 2
Qua ví dụ trên ta thấy việc chuyển qua hệ tạm (I) giúp ta hình dung bài
toán được dễ dàng hơn. b) Đặt 3 2
x + 3x − 3 = y ta thu được hệ phương trình sau: 3 2 8
 x −13x + 7x = 2y
. Cộng hai phương trình của hệ ta thu được: 2 3
x + 3x − 3 = y 3 2 3 3 3
8x −12x +10x − 3 = y + 2y ⇔ (2x −1) + 2(2x −1) = y + 2y (*)
Đặt z = 2x −1 ta thu được phương trình: 3 3
z + 2z = y + 2y ⇔ (z − y)( 2 2
z + zy + y + ) 3 2
2 = 0 ⇔ z = y ⇔ y = 2x −1 ⇔ 8x −13x + 7x = 4x − 2 x =1 3 2
8x 13x 3x 2 0  ⇔ − + + = ⇔ 5 ±  89 x =  16 c) Điều kiện: 1
x ≥ . Ta đặt 2x −1 = a ≥ 0 thì phương trình đã cho trở 2 thành: 3 2 3 3 3 2
12a +1 −8a −8a −1 = 0 ⇔ 8a + 8a +1 = 12a +1 THCS.TOANMATH.com 3 8
 a +8a +1= y Đặt 3 2
12a +1 = y ta thu được hệ sau:  . Cộng hai phương 2 3 12  a +1 = y
trình của hệ với nhau ta thu được: 3 3
(2a +1) + (2a +1) = y + y (*)
Đặt 2a +1 = z ta có: 3 3
z + z = y + y .
Tương tự như các bài toán trên ta suy ra z = y . Theo (*) ta có 3 1
⇔ y = 2a +1⇒ 8a + 8a +1 = 2a +1 ⇔ a = 0 ⇒ x = 2 Kết luận: 1
x = là nghiệm duy nhất của phương trình: 2 d) Đặt 3
y = 6x + 4 ta có hệ sau: 3
x − 4 = 6y 3 3 
⇔ x + 6x = y + 6y ⇔ (x − y)( 2 2
x + xy + y + 6 = 0 ⇔ x = y 3 ) 6x + 4 = y
Thay vào phương trình ta có: x = 2 −  3
x − 6x − 4 = 0 ⇔ (x + 2)( 2
x − 2x − 2) = 0 ⇔ x =1+  3 x =1−  3 e) Đặt 3
y = 2x −1 ta có hệ: 3 x +1= 2y 3 3 
⇔ x + 2x = y + 2y ⇔ (x − y)( 2 2
x + xy + y + 2 = 0 ⇔ x = y 3 ) 2x = y +1  x =1   − − Suy ra 3
x − x + = ⇔ (x − )( 2 x + x − ) 1 5 2 1 0 1 1 = 0 ⇔ x =  2   1 − + 5 x =  2 THCS.TOANMATH.com f) ( 2 4x + )
1 x = (3− x) 5 − 2x 2 Đặt 5 5 2 0 y x y x − − = ≥ ⇒ = thay vào ta có: 2 (  −  4x + ) 2 2 5 y 3 3 1 x = 3−
y ⇔ 8x + 2x = y + 2y ⇔ (2x − y)( 2 2 4x + 2 . x y + y + 2) = 0  2   1 − + 21 x = 2 2
y = 2x ⇔ 4x + 2x − 5 = 0 ⇔ 
Thử lại ta thấy chỉ có 1 − − 21 x =  2 1 21 x − + = 2
thỏa mãn điều kiện bài toán.
Ví dụ 2: Giải các phương trình sau: a) 2 2 3 2
7x −13x + 8 = 2x x(1+ 3x − 3x ) b) 3 2 3 6 3 2
3x + 4x −1 = x + 2x + x 3 3 3  −  + c) x x x 3x 3   = 2x +  2  2 Giải:
a) Nhận thấy x = 0 không phải là nghiệm của phương trình:
Chia hai vế phương trình cho 3 x ta thu được: 7 13 8 1 3 − + = 3 2 + − 3 . 2 3 2 x x x x x 7 13 8 − + = 2y  2 3 Đặt 1 3 =  x x x 3 y
+ − 3 ta thu được hệ sau: . 2 x x  1 3  3 + − 3 = y 2  x x THCS.TOANMATH.com
Cộng hai phương trình của hệ ta có: 3 8 12 10 3  2   2  3 − +
− 3 = y + 2y ⇔ −1 + 2 −1 = y +     2y (*) 3 2 x x xx   x  Đặt 2
z = −1 ta thu được: x 3 3
z + z = y + y ⇒ (z − y)( 2 2 2 2
z + yz + y + 2) = 0 ⇔ z = y 2 7 13 8 4 8 13 3 ⇔ y = −1 ⇔ − + = − 2 ⇔ − + + 2 = 0 . 2 3 3 2 x x x x x x x x Suy ra 5 89 x 1, x − ± = = 4
b) Nhận thấy x = 0 không phải là nghiệm của phương trình nên ta chia hai
vế phương trình cho x thì thu được phương trình tương đương là: 2 1 3 1 + − = 3 3x 4x x + 2 + . x x  2 1
3x + 4x − = y  Đặt 3 1 =  x 3 y
x + 2 + ta có hệ sau: . Cộng hai phương x   3 1 3 x + 2 + = y  x trình của hệ ta có: 3 3
(x +1) + (x +1) = y + y .
Từ phương trình ta suy ra 2 1
y = x +1 ⇔ 3x + 4x − = x +1 xx = 1 − 2 1 3 2 3x 4x x 1 3x 3x x 1 0  + − = + ⇔ + − − = ⇔ .  3 x x = ±  3
c) Ta viết lại phương trình thành: ( 3 x − x)3 3 3
−16x = 4 4x +12x THCS.TOANMATH.com (x − x)3 3 −16x = 4y Đặt 3 3
y = 4x +12x ta có hệ tạm sau:  3 3
4x +12x = y
Cộng hai vế hệ phương trình ta thu được: (x − x)3 3 + ( 3 x − x) 3 4 = y + 4y Đặt 3
z = x − x ta có: 3 3
z + z = y + y ⇔ (z − y)( 2 2 4 4
z + yz + y + 4) = 0 ⇔ (x − x)3 3 3 = 4x +12x x = 0 x x (x )3 2 2 2 1 4x 12 ⇔ − − − = 0  ⇔     2 x = 3
Vậy phương trình đã cho có 3 nghiệm là: x = 0; x = ± 3
PHƯƠNG PHÁP ĐÁNH GIÁ
Những kỹ thuật qua trọng để giải phương trình giải bằng phương pháp
đánh giá ta thường sử dụng là:
+ Dùng hằng đẳng thức: 2 2 2
A + A +..A = ⇔ A = A = = A = n 0 .. n 0 1 2 1 2
+ Dùng các bất đẳng thức cổ điển Cô si, Bunhiacopxki, Bất đẳng thức hình học
+ Dùng phương pháp khảo sát hàm số để tìm GTLN,GTNN :
Ví dụ 1: Giải các phương trình sau: a) 2
4x + 3x + 3 = 4x x + 3 + 2 2x −1 .
b) 13 x −1 + 9 x +1 = 0 . c) x( 3
5x + 2) − 2( 2x +1− )
1 = 0 (Trích đề tuyển sinh lớp 10 chuyên
Toán Trường chuyên Amsterdam 2014). THCS.TOANMATH.com d) 1
x −1 + 2 y − 4 + 3 z − 9 = (x + y + z) 2 Lời giải: a) Điều kiện 1
x ≥ . Ta viết lại phương trình thành: 2 2
4x − 4x x + 3 + (x + 3) + 2x −1− 2 2x −1 +1 = 0 ⇔ (  − + =
x − x + )2 +( x − − )2 2x x 3 0 2 3 2 1 1 = 0 ⇔  ⇔ x =1.  2x −1 −1 = 0
b) Điều kiện: x ≥1. Ta viết lại phương trình thành:  1   9 13 x 1 x 1 9 x 1 3 x 1  − − − + + + − + + =     0  4   4   1 2 2 x −1 − = 0  1   3    2 5 ⇔ 13 x −1 − +  9 x +1 − =  0 ⇔  ⇔ x = .  2   2  3 4  x +1− = 0  2 c) Điều kiện 1
x ≥ − .Ta viết lại phương trình thành: 2 x =
5x + (2x +1− 2 2x +1+ )
1 = 0 ⇔ 5x + ( 2x +1− )2 0 4 4
1 = 0 ⇔  2x+1−1=0
Suy ra x = 0 là nghiệm duy nhất của phương trình.
d) Điều kiện x ≥1; y ≥ 4; z ≥ 9 ta viết lại phương trình thành:
2 x −1 + 4 y − 4 + 6 z − 9 = x + y + z
⇔ x −1− 2 x −1 +1+ y − 4 − 4 y − 4 + 4 + z − 9 − 6 z − 9 + 9 = 0  x −1 −1= 0 x = 2 (  x 1 )2 1
( y 4 2)2 ( z 9 3)2 0  y 4 2 0  − − + − − + − − = ⇔ − − = ⇔ y = 8   − − = z =  18  z 9 3 0  THCS.TOANMATH.com
Ví dụ 2: Giải các phương trình sau: a) 4 3 3
16x + 5 = 6 4x + x b) 4 2 3 3
4x + x + 3x + 4 = 3 16x +12x c) 2 3
96x − 20x + 2 + x 8x −1 − 4x(8x +1) = 0 Giải: a) Vì 4
16x + 5 > 0 nên phương trình đã cho có nghiệm khi 3 2
4x + x ≥ 0 ⇔ x(4x +1) ≥ 0 ⇔ x ≥ 0 . Để ý rằng khi 1
x = thì VT = VP 2
nên ta nghỉ đến sử dụng bất đẳng thức Cô si sao cho dấu bằng xảy ra khi 1 x = . Mặt khác khi 1 x = 3 1 1
⇒ 4x + x = 4. + =1 thì Từ những cơ sở 2 2 8 2
trên ta có lời giải như sau: Theo bất đẳng thức Cô si dạng 3
3 abc ≤ a + b + c ta có Ta có 3 3 x + x =
( 3x + x) ≤ ( 3x + x+ + ) 3 3 6 4 2.3. 4 .1.1 2 4
1 1 = 8x + 2x + 4 Mặt khác ta có: 4 3 4 3
x + − x + x + = x − x − x + = ( x − )2 ( 2 16 5 (8 2 4) 16 8
2 1 2 1 4x + 2x + ) 1 ≥ 0
Suy ra VT ≥ VP . Dấu bằng xảy ra khi và chỉ khi 2 2
2(2x −1) (2x + 2x +1) = 0 1  ⇔ x = 2
4x = (4x +1) = 2 2
Tóm lại: Phương trình có nghiệm duy nhất 1 x = 2 b) Vì 4 2
4x + x + 3x + 4 > 0 nên phương trình đã cho có nghiệm khi 3 2
16x +12x ≥ 0 ⇔ 4x(4x + 3) ≥ 0 ⇔ x ≥ 0 . Để ý rằng khi 1 x = thì 2
VT = VP nên ta nghỉ đến sử dụng bất đẳng thức Cô si sao cho dấu bằng THCS.TOANMATH.com xảy ra khi 1 x = . Khi 1 x = thì 3 1 1
16x +12x =16. +12. = 8. Từ những 2 2 8 2
cơ sở trên ta có lời giải như sau:
Theo bất đẳng thức Cô si dạng 3
3 abc ≤ a + b + c ta có ( 3x + x) 3 = ( 3x + x) 1 3 16 12 16 12 .8.8 ≤ ( 3
16x +12x + 8 + 8) 3 3 3 = 4x + 3x + 4 4 4 Mặt khác ta có: 4 2 3 4 3 2 2 2
4x + x + 3x + 4 − (4x + 3x + 4) = 4x − 4x + x = x (2x −1) ≥ 0 . 2 2
x (2x −1) = 0
Dấu bằng xảy ra khi và chỉ khi 1  ⇔ x = 2
2 = x(4x + 3) 2 c) Điều kiện: 1
x ≥ . Để ý rằng 1
x = là nghiệm của phương trình nên ta có 8 8 lời giải như sau: 2
1 1 4x(8x 1) 32x 4x 2 3 3 4x(8x 1) 1.1.4x(8x + + + + + + = +1) ≤ = . 3 3 Mặt khác ta có 2 2 2 2 32x
4x 2 256x 64x 4 4(8x 1) 96x 20x + + − + − − + 2 − = = ≥ 0 . 3 3 3 Suy ra 2 3
96x − 20x + 2 + x 8x −1 − 4x(8x +1) ≥ 0.
Dấu bằng xảy ra khi và chỉ khi 1 x = 8
Ví dụ 2: Giải các phương trình sau: a) 1 1 2 + = 4 2x −1 4x − 3 x THCS.TOANMATH.com b) 1 1  1 1 3  + = + x 2x 1   4x 1 5x 2  − − −  c) 4x 1 5x 2 4 4 = 4 + 4 x 2x − − + −1 3 3 d) 2 2
−x + 4x + 21 − −x + 3x +10 = 2 Giải: a) Điều kiện: 1 x > . 2
Phương trình đã cho có thể viết lại như sau: x x + = 2 . 4 2x −1 4x − 3 + Ta chứng minh: x
≥1. Thật vậy bất đẳng thức tương đương với 2x −1 2 2
x ≥ 2x −1 ⇔ (x −1) ≥ 0 . Điều này là hiển nhiên đúng.
Dấu bằng xảy ra khi và chỉ khi x =1 Ta chứng minh: x
≥ 1. Thật vậy bất đẳng thức tương đương với 4 4x − 3 4 4 2 2
x ≥ 4x − 3 ⇔ x − 4x + 3 ≥ 0 ⇔ (x − 2x +1)(x + 2x + 3) ≥ 0 2 2
⇔ (x −1) (x + 2x + 3) ≥ 0
Điều này là hiển nhiên đúng. Dấu bằng xảy ra khi và chỉ khi x =1
Từ đó suy ra VT ≥ 2 . Dấu bằng xảy ra khi và chỉ khi x =1 b) 1 1  1 1 3  + = + x 2x 1   4x 1 5x 2  − − − 
Ta thấy rằng: 4x −1 = x + x + 2x −1;5x − 2 = x + 2x −1+ 2x −1
Theo bất đẳng thức cô si ta có THCS.TOANMATH.com  1 1 1  + +
( x + x + 2x−1)≥   9  x x 2x −1  1 1 1 9 ⇒ + + ≥ x x 2x −1
x + x + 2x −1 Mặt khác ta có 2
( x + x + 2x −1) ≤ 3(4x −1) ⇒ x + x + 2x −1 ≤ 3(4x −1) (Theo
bất đẳng thức Bunhiacopxki cho 3 số) Từ đó suy ra: 2 1 3 3 + ≥ x 2x −1 4x −1 Tương tự ta cũng có: 1 2 3 3 + ≥ x 2x −1 5x − 2
Cộng hai bất đẳng thức cùng chiều ta có: 3 3 3 3 3 3 + ≥ + x 2x −1 4x −1 5x − 2 1 1  1 1 3  ⇔ + ≥ +   . x 2x −1  4x −1 5x − 2 
Dấu bằng xảy ra khi và chỉ khi x =1
c) Áp dụng bất đẳng thức Bunhiacopxki dạng: 2 2 2 2 2 2 2
(ax + by + cz) ≤ (a + b + c )(x + y + z ) ta có:
( x + x + x− )2 4 4 4 2 1 ≤ (1+1+ )
1 ( x + x + 2x −1). 4 4 4
⇔ x + x + 2x −1 ≤ 3( x + x + 2x −1)
Lại có x + x + 2x −1 ≤ 3(4x −1) suy ra THCS.TOANMATH.com 4 4 4 4
x + x + 2x −1 ≤ 3 3(4x −1) = 27(4x −1) (1) Tương tự: 4 4 4 4
x + 2x −1 + 2x −1 ≤ 3 3(5x − 2) = 27(5x − 2) (2)
Cộng hai bất đẳng thức cùng chiều (1), (2) ta có: 3( 4 4 x + 2x −1) 4 4
≤ 27(4x −1) + 27(5x − 2) 4x −1 5x − 2 4 4 ⇔ + − ≤ 4 + 4 x 2x 1 3 3
Dấu bằng xảy ra khi và chỉ khi x =1. c) Ta có x +11
VT = (x + 3)(7 − x) − (x + 2)(5 − x) =
(x + 3)(7 − x) + (x + 2)(5 − x)
Điều kiện xác định là 2 − ≤ x ≤ 5
Theo bất đẳng thức Cauchy ta có: 1 1 x + − x = x + − x ≤
[ x + + − x ] x +13 ( 3)(7 ) (2 6)(7 ) (2 6) (7 ) = 2 2 2 2 2 và 1 1 x + − x = x + − x ≤
[ x + + − x ] x +9 ( 2)(5 ) (2 4)(5 ) (2 4) (5 ) = 2 2 2 2 2 Như vậy: 1
(x + 3)(7 − x) + (x + 2)(5 − x) ≤ (x +11) 2 + Từ đó ta suy ra: x 11 VT = ≥ 2 . Dấu bằng
(x + 3)(7 − x) + (x + 2)(5 − x)
(2x + 6) = (7 − x) xảy ra khi và chỉ khi: 1  ⇔ x =
(2x + 4) = (5 − x) 3 THCS.TOANMATH.com Vậy 1
x = là nghiệm duy nhất của phương trình: 3
Ví dụ 4: Giải các phương trình sau: a) 2 2 2 1
3x −1 + x − x − x x +1 = ( 2 7x − x + 4) 2 2 b) 2 2 17 2 1
13x − 6x +10 + 5x −13x +
+ 17x − 48x + 36 = ( 2 36x −8x − ) 21 2 2 c) 2 2 2
x + x −1 + −x + x +1 = x − x + 2 Giải: Điều kiện: 1
x ≥1∨ x ≤ − 3
Áp dụng BĐT Bunhiacopski cho hai bộ số (1;1;−x) và ( 2 2 2
3x −1; x − x; x +1) ta có: VT ≤ ( 2x + )( 2 (*)
2 5x − x) . Dấu “=”
xảy ra khi và chỉ khi x =1. Do 1
x ≥1∨ x ≤ − nên 2 5x − x > 0 3
Áp dụng BĐT Cauchy ta có: 1 2 VP =  x − x +  ( 2x + ) 1 (*) 5 2 1  ≥ .2  ( 2 5x − x)2( 2 x + 2) 2 2 2 2 = ( 2 5x − x)( 2 x + 2)
Dấu “=” xảy ra khi x = 1 − và 4
x = . Từ đó ta có nghiệm của PT(*) là: 3 x = 1 − b) Ta có: THCS.TOANMATH.com 2 2 VT = (3x + )2 1 + (2x − 3)2  5   3  2 + 2x − + x − + x + (4x −     6)2  2   2  5
≥ 3x +1 + 2x − + x 5 3 3
⇒ VT ≥ 3x +1+ 2x − + x = 6x − ≥ 6x − . 2 2 2 2
Dấu “=” xảy ra khi và chỉ khi 3
x = . Mặt khác ta cũng có: 2 1
VP =  x − −  ( 2x − x+ ) 1
 =  x − − ( x − )2 1  ≤ ( x − ) 3 12 3 2 4 12 9 12 3 2 2 3 12 3 = 6x − 2  2   2 2
Dấu “=” xảy ra khi và chỉ khi 3
x = . Từ đó ta có nghiệm của phương 2 trình là 3 x = 2
c) Theo bất đẳng thức Cô si ta có: 2 2 2 1 2 + −1 = 1( + −1) ≤ 1+ ( + −1) x x x x x x x x +   = 2   2 x =1
Dấu bằng xảy ra khi và chỉ khi 2
1 = (x + x −1) ⇔  x = 2 − 2 2 2 1 2 x x 2
−x + x +1 = 1(−x + x +1) ≤ 1+ (−x + x − + +  +1) = 2   . 2 x =1
Dấu bằng xảy ra khi và chỉ khi 2
1 = (−x + x +1) ⇔  x = 0 2 2 + − + + Từ đó suy ra x x x x 2 VT ≤ + = (x +1) . 2 2 Mặt khác ta có 2 2
x − x + 2 − (x +1) = (x −1) ≥ 0 .
Dấu bằng xảy ra khi và chỉ khi x =1 THCS.TOANMATH.com
Từ đó suy ra phương trình có nghiệm duy nhất x =1.
Ví dụ 5: Giải các phương trình sau: a) 3 3 2
14 − x + x = 2(1+ x − 2x −1)
b) x x + x +12 =12( 5 − x + 4 − x) Giải: a) Điều kiện: 2
x − 2x −1≥ 0
Phương trình đã cho tương đương với: 3 3 2
14 − x = 2 x − 2x −1 + 2 − x Do 2
2 x − 2x −1 ≥ 0 nên từ phương trình ta cũng suy ra: 3 3
14 − x ≥ 2 − x
Lập phương 2 vế ta thu được: 3 3 2
14 − x ≥ (2 − x) ⇔ 6(x − 2x −1) ≤ 0
Như vậy phương trình có nghiệm khi và chỉ khi x =1+ 2 2
x − 2x −1 = 0 ⇔  x =1− 2
Kết luận: Phương trình có 2 nghiệm là: x =1+ 2 và x =1− 2
b) Điều kiện: 0 ≤ x ≤ 4.
Xét f (x) = x x + x +12 trên [0;4] Dễ thấy
12 = f (0) ≤ f (x) ≤ f (4) =12 ⇒ VT ≤12 (1)
Xét g(x) = 5 − x + 4 − x trên [0;4] ta có
Dễ thấy 1 = g(4) ≤ g(x) ≤ g(0) = 5 . Suy ra VP ≥12 (2)
Từ (1), (2) suy ra phương trình có nghiệm khi VT = VP =12 ⇔ x = 4 . THCS.TOANMATH.com
MỘT SỐ CÁCH ĐẶT ẨN PHỤ KHÁC
1) Đặt ẩn phụ hoàn toàn để quy về phương trình một ẩn.
+ Điểm mấu chốt của phương pháp này là phải chọn một biểu thức f (x)
để đặt f (x) = t sao cho phần còn lại phải biểu diễn được theo ẩn t .
Những bài toán dạng này nói chung là dễ.
+ Trong nhiều trường hợp ta cần thực hiện phép chia cho một biểu thức có
sẵn ở phương trình từ đó mới phát hiện ẩn phụ. Tùy thuộc vào cấu trúc
phương trình ta có thể chia cho g(x) phù hợp (thông thường ta chia cho k
x với k là số hữu tỷ)
+ Đối với những bài toán mà việc đưa về một ẩn dẫn đến phương trình mới
phức tạp như: Số mũ cao, căn bậc cao .. thì ta có thể nghỉ đến hướng đặt
nhiều ẩn phụ để quy về hệ phương trình hoặc dựa vào các hằng đẳng thức để giải toán. Ta xét các ví dụ sau:
Ví dụ 1: Giải các phương trình sau: a) 2
x = (1− x)(2x − 3 x + 3) b) 2 3 4 2
x + x − x = 2x +1 c) 2
x +1+ x − 4x +1 = 3 x d) 2 1
x + 2x x − = 3x +1. x Giải:
a) Điều kiện: x ≥ 0 . Phương trình đã cho có thể viết lại như sau: 2 2 2
x = (1− x) 2x + 3(1− x) ⇔ x = 2x(1− x) + 3(1− x)   . Ta thấy
x = 0 không phải là nghiệm của phương trình. Ta chia hai vế cho 2 x thì THCS.TOANMATH.com 2  −   −  − thu được: 1 x 1 1 = 2  + 3 x    . Đặt 1
x = t ta có phương trình x   x      xt = 1 − theo t : 2 3t 2t 1 0  + − = ⇔ 1 t =  3 −
Trường hợp 1: t = 1 − ta có: 1 x = 1
− ⇔ x − x +1 = 0(VN) x Trường hợp 2: 1 t = ta có: 3  3− 21  x = (L) − + 1 x 1 2 15 3 21
= ⇔ x − 3 x − 3 = 0 ⇔  ⇒ x = x 3  3+ 21 2  x =  2
Kết luận: Phương trình có nghiệm duy nhất: 15 3 21 x + = 2
b) Ta thấy x = 0 không phải là nghiệm của phương trình. Vì vậy ta chia hai
vế cho x thì thu được: 1 1 1 1 + 3 − = + ⇔ − + 3 x x 2 x x − − 2 = 0 x x x x Đặt 1 = 3 t
x − ta thu được phương trình: x ± 3 1 2 1 5
t + t − 2 = 0 ⇔ t =1⇒ x − =1 ⇔ x − x −1 = 0 ⇔ x = ⇔ x 2
Kết luận: Phương trình có nghiệm 1 5 x ± = 2 x ≥ 0 0 ≤ x ≤ 2 − 3 c) Điều kiện:  ⇔  . 2
x − 4x +1 ≥ 0 x ≥ 2 + 3 THCS.TOANMATH.com
Ta thấy x = 0 không phải là nghiệm của phương trình. Chia hai vế cho x ta thu được: 1 1 x +
+ x − 4 + = 3. Đặt x x 1 2 1 t = x +
⇒ t = x + + 2 theo bất đẳng thức Cô si ta có t ≥ 2 . Thay x x vào phương trình ta có: t  ≤ 3 2 5
t − 6 = 3− t ⇔  ⇔ t = 2 2 t
 − 6 = t − 6t + 9 2 x = 4 25 1 2 x 2 4x 17x 4 0  ⇔ = + + ⇔ − + = ⇔ 1  4 x x =  4
Kết luận: Phương trình có 2 nghiệm: 1 x = 4, x = 4
d). Nhận xét: x = 0 không phải là nghiệm của phương trình:
Ta chia hai vế cho x khi đó phương trình trở thành: 1 1
x − + 2 x − − 3 = 0. Đặt 1
t = x − ≥ 0 phương trình trở thành: x x x 2 1 2 1± 5
t + 2t − 3 = 0 ⇒ t =1 ⇔ x − =1 ⇔ x − x −1 = 0 ⇔ x = x 2
Ví dụ 2: Giải các phương trình sau: a) 2
(13− 4x) 2x − 3 + (4x − 3) 5 − 2x = 2 + 8 16x − 4x −15
b) 7 3x − 7 + (4x − 7) 7 − x = 32. Giải: a) Điều kiện 3 5 ≤ x ≤ . 2 2 THCS.TOANMATH.com
Phương trình được viết lại như sau:
7( 2x −3 + 5− 2x)− 2(2x −3) 2x −3 + (5− 2x) 5− 2x   Đặt
= 2+8 (5−2x)(2x −3) 2 t 2 t 2x 3 5 2x (5 2x)(2x − = − + − ⇒ − − 3) = . Điều kiện 2 ( 2 ≤t ≤ 2).
Phương trình đã cho có dạng: 3 2
t − 4t + t + 6 = 0 ⇒ t = 2 ⇒ x = 2
Ngoài ra ta cũng có thể giải phương trình trên bằng cách đưa về hệ.
b) Điều kiện: 7 ≤ x ≤ 7 .Phương trình đã cho được viết lại như sau: 3 1 3  1 3 (3x 7) (7 x) 3x 7 (7 x) (3x 7) − + − − + − + − 7 − x = 32  2 2  2 2     
⇔ [(3x − 7) + (7 − x)] 3x − 7 +[(7 − x) + (3x − 7)] 7 − x = 64
Đặtt = 3x − 7 + 7 − x 3
⇒ t = (3x − 7) 3x − 7 + (7 − x) 7 − x + 3 (3x − 7)(7 − x) ( 3x −7 + 7 − x)
Từ phương trình suy ra 3t = 64 ⇔ t = 4 . Hay 3x − 7 + 7 − x = 4
Bình phương 2 vế ta thu được: 2 11 2 2
(3x 7)(7 x) 8 x 4x 44x 113 0 x ± − − = − ⇔ − + = ⇔ = 2
Tại sao ta phân tích được hai phương trình như trên:
Ta thấy với những phương trình: THCS.TOANMATH.com
(ax + b) cx + d + (ex + h) gx + k + r (cx + d)(gx + k) + s = 0 thì một
trong những cách xử lý khá hiệu quả là:
Phân tích: ax + b = m(cx + d) + n(gx + k) và
ex + h = m'(cx + d) + n'(gx + k) sau đó ta có thể đặt ẩn phụ trực tiếp ,
hoặc đặt hai ẩn phụ để quy về hệ. Ví dụ:
Khi giải phương trình: 2
(13− 4x) 2x − 3 + (4x − 3) 5 − 2x = 2 + 8 16x − 4x −15 ta thực hiện các phân tích :
+ Giả sử:13− 4x = m(2x − 3) + n(5 − 2x) . 2m − 2n = 4 −
Đồng nhất hai vế ta suy ra: 3 7  ⇔ m = ,n =  3 − m + 5n =13 2 2 + Tương tự ta giả sử: 7 3
(4x − 3) = m (′2x − 3) + n (′5 − 2x) ⇒ m′ = ,n′ = 2 2
Khi giải phương trình:7 3x − 7 + (4x − 7) 7 − x = 32.
Ta thực hiện phân tích: m(3x − 7) + n(7 − x) = 7 và
p(3x − 7) + q(7 − x) = 4x − 7 Sau đó đồng nhất 2 vế để tìm m, n, p, q ta có: 1 3 3 1
m = ;n = ; p = ;q = 2 2 2 2
Như vậy ngoài cách đặt ẩn phụ như trên ta có thể giải các bài toán theo cách khác như sau: a) Điều kiện 3 5 ≤ x ≤ . 2 2
Đặt a = 2x − 3,b = 5 − 2x thì 2 2 a + b = 2 .
Từ cách phân tích trên ta có hệ sau: THCS.TOANMATH.com 2 2 2 a + b = 2
(a + b) − 2ab = 2  ⇔  2 2 2 2 3
(3a + 7b )a + (3b + 7a )b = 4 +16ab 3
 (a + b) − 2ab(a + b) −16ab − 4 = 0 2
(a + b) − 2ab =  2 ⇔  . 3 2 2
3(a + b) + 2 − (a + b)  (a + b) + 82 − (a + b)  − 4 =  0     
Đặt a + b = S,ab = P điều kiện 2
S, P ≥ 0;S ≥ 4P . Ta có hệ mới sau: 2
S − 2P = 2 S = 2  ⇒ 
⇔ a = b =1 ⇔ x = 2 3 2
2S −8S + 2S +12 = 0 P = 2
b) Đặt a = 3x − 7,b = 7 − x ta có hệ phương trình (
 a +b)3 = 64 a + b = 4  ⇔  2 2 2 2
a + 3b =14. a + 3b = 14.
Giải hệ phương trình ta thu được: a,b ⇒ x .
2) Đặt ẩn phụ hoàn để quy về hệ đối xứng loại 2:
Phương pháp này đặc biệt hiệu quả với các phương trình dạng: 2
ax + bx + c = d ex + h hoặc 3 2 3
ax + bx + cx + d = e gx + h
Với mục đích tạo ra các hệ đối xứng hoặc gần đối xứng ta thường làm theo cách:
Đối với những phương trình dạng: 2
ax + bx + c = d ex + h .
Ta đặt my + n = ex + h thì thu được quan hệ: 2 2
ax + bx + c = d(my + n)
ax + bx − dmy + c − dn = 0  ⇔  2 2 2 2 2 2
m y + 2mny + n = ex + h
m y + 2mny − ex + n − h = 0 THCS.TOANMATH.com
Ta mong muốn có quan hệ x = y . Nếu điều này xảy ra thì từ hệ trên ta sẽ − − có: a b dm c dn = = (*) . 2 2 m 2mn n − h
Công việc còn lại là chọn ,
m n chẵn thỏa mãn (*)
Đối với những phương trình dạng: 3 2 3
ax + bx + cx + d = e gx + h Ta đặt: 3
my + n = gx + h thì thu được hệ: 3 2
ax + bx + cx + d = e(my + n)  3 3 2 2 2 2 3
m y + 3m ny + 3mn y + n = gx + h 3 2
ax + bx + cx − emy + d − en = 0 ⇔  3 3 2 2 2 2 3
m y + 3m ny + 3mn y − gx + n − h = 0 − −
Để thu được quan hệ x = y ta cần: a b c em d en = = = 3 2 2 3 m 3m n + 3mn −g n − h
Ví dụ 1: Giải các phương trình sau: a) 2
2x − 6x −1 = 4x + 5 2 37 b) 2
4x +1 − 9x + 26x − = 0 3 3 c) 3 3 2
3x − 5 = 8x − 36x + 53x − 25 d) 3 3 2
27 81x −8 = 27x − 54x + 36x − 54 Giải: a) Điều kiện: 5
x ≥ − . Đặt my + n = 4x + 5 khi đó ta có hệ: 4 2 2
2x − 6x −1= my + n
4x −12x − 2my − 2 − 2n = 0  ⇔  2 2 2 2 2 2
m y + 2mny + n = 4x + 5
m y + 2mny − 4x + n − 5 = 0 − − − − Ta cần tìm ,
m n để tạo ra quan hệ x = y 4 12 2m 2 2n ⇔ = = 2 2 m 2mn − 4 n − 5 THCS.TOANMATH.com  2 − − 2n =1 2  2  n − 5
n + 2n − 3 = 0 Chọn m = 2 ⇒  ⇔  ⇒ n = 3 − 16 −  4n = 12 = 1 − 4n − 4 Chú ý:
Việc nhân số 2 vào phương trình (1) của hệ để tạo ra 2
4x −12x −1 là rất
cần thiết để chọn m được chẵn và nhóm 2
4x −12x − 2 thành bình
phương biểu thức bậc 2 được dễ hơn.
Từ đó ta có lời giải cho bài toán như sau:
Đặt 2y − 3 = 4x + 5 thì thu được hệ: 2 2
4x −12x − 2 = 2(2y −3)
(2x −3) = 4y + 5  ⇔  . 2 2
(2y − 3) = 4x + 5
(2y − 3) = 4x + 5
Trừ hai phương trình của hệ cho nhau ta có: x = y 2 2
(2x − 3) − (2y − 3) = 4(y − x) ⇔ 2(x − y)(4x + 4y − 4) = 0 ⇔  x + y = 2 Trường hợp 1: 2
(2x − 3) = 4x + 5 x y 2x 3 4x 5  = ⇔ − = +  3 ⇔ x = 2 + 3 x ≥  2 Trường hợp: 2
(1− 2x) = 4x + 5 y 2 x 2(2 x) 3 4x 5  = − ⇔ − − = + ⇔  1 ⇔ x =1− 2 x ≤  2
Kết luận: Phương trình có 2 nghiệm là: x = 2 + 3, x =1− 2 b) Điều kiện: 1 x ≥ − . 4 THCS.TOANMATH.com
Phương trình đã cho được viết lại như sau: 2 47 2 9x − 26x + = 4x +1 3 3
Đặt my + n = 4x +1  2 37 2  2 2 37 2 9  x − 26x + = (my + n) 9
x − 26x − my + − n = 0 ⇒  3 3 ⇔  3 3 3  2 2 2  2 2 2
m y + 2mny + n = 4x +1
m y + 2mny − 4x + n −1 = 0 2 37 2 26 − − m − n Ta cần: 9 3 3 3 = = . Chọn 2 2 m 2mn − 4 n −1  28 − = 1 6n − 4 m 3  = ⇒  37 2 ⇒ n = 4 − − −  n 3 3  = 1 2  n −1
Đặt 3y − 4 = 4x +1 ⇒ Hệ phương trình sau: (  3x − 2 2  4) = 2x + 2y +1 (3y − 4) = 4x +1  ⇔ (3y − 2  4) = 4x +1 (x −  y)(9x + 9y − 22) = 0 ( − )2 3y 4 = 4x + 1  ⇔ x = y 9x+9y−  22 = 0
Giải phương trình ứng với 2 trường hợp trên ta thu được các nghiệm là 14 61 x + = và 12 53 x − = 9 9 Chú ý: Ta có thể tìm ,
m n nhanh hơn bằng cách: THCS.TOANMATH.com 2
(2x −3) = 2(my + n) +11
c) Đặt my + n = 4x + 5 khi đó ta có hệ:  2
(my + n) = 4x + 5
Trừ hai phương trình cho nhau: 2 2
(2x − 3) − (my + n) = 2my − 4x + 2n + 6 2my = 4x
Để có quan hệ: x = y ta cần:  ⇒ m = 2;n = 3 − . 2n + 6 = 0
Tương tự khi giải quyết câu b). d) Đặt 3
my + n = 3x − 5 ta có hệ sau: 3 2 8
 x −36x + 53x − my − n − 25 = 0 3 3 2
3x − 5 = 8x − 36x + 53x − 25 ⇔  3 3 2 2 2 3
m y + 3m ny + 3mn y − 3x + n + 5 = 0 Ta chọn , m n sao cho 8 -36 53- m -n - 25 = = = ⇒ m = 2,n = 3 − 3 2 2 3 m
3m n 3mn -3 n + 5 Đặt 3
2y − 3 = 3x − 5 . Ta có hệ phương trình sau: 3
(2x −3) = 2y −3+ x − 2  3
(2y − 3) = 3x − 5
Trừ hai phương trình cho nhau ta thu được: 3 3
(2x − 3) − (2y − 3) = 2y − 2x 2 2
⇔ 2(x − y) (2x − 3) + (2x − 3)(2y − 3) + (2y − 3) +1 = 0 ⇔ x = y   Do 2 2
(2x − 3) + (2x − 3)(2y − 3) + (2y − 3) +1 2   2y − 3  3 = (2x −3) + +  (2y −3)2 +1>   0   2  4
Giải x = y ta có: ( x − )2 3 2 2
3 = 3x − 5 ⇔ 8x − 36x + 54x − 27 = 3x − 5 THCS.TOANMATH.com x = 2 (x 2)( 2 8x 20x ) 11 0  ⇔ − − + = ⇔ 5 ±  3 x =  4
Kết luận: Phương trình đã cho có 3 nghiệm: x = 2 , 5 3 x ± = 4
d) Ta viết lại phương trình thành: 3 3
27 81x −8 = (3x − 2) − 46 Đặt 3
3y − 2 = 81x −8 ta có hệ phương trình: (
 3y − 2)3 = 81x − 3  8 (
 3y − 2) = 81x −  8  ⇔  . (  3x − 2 3  )3 = 27(3y − 2) + 46 (  3x − 2  ) = 81x −8
Trừ hai phương trình của hệ ta thu được: ( x − )3 − ( y − )3 3 2 3 2 = 81(y − x)
⇔ x − y ( x − )2 + ( x − )( y − ) + ( y − )2 3( ) 3 2 3 2 3 2 3
2 + 27 = 0 ⇔ x = y   . Thay vào ta được: x = 0 (3x 2)3 3 2 27(3x 2) 46
27x 54x 33x 0  − = − + ⇔ − − = ⇔ 3±  2 5 x =  3
Kết luận: Phương trình có 3 nghiệm là: x = 0 , 3 2 5 x ± = 3 Chú ý:
+ Với những phương trình dạng: [ ( )]n n
f x + b = a af (x) − b (*) Bằng phép đặt = ( ); n
t f x y = af (x) − b ta có hệ đối xứng loại 2 là: n t  + b = ay n
y + b = at THCS.TOANMATH.com
+ Trong phương trình (*) nếu ta thay a, b bởi các biểu thức chứa x thì
cách giải phương trình vẫn như trên. Những phương trình dạng này
thường có hình thức và lời giải khá đẹp.
* Ta xét ví dụ sau:
Ví dụ 2: Giải các phương trình sau: a) 2 2
4x −11x + 6 = (x −1) 2x − 6x + 6 b) 3 3 2
8x −13x + 7 = (x +1) 3x − 2 . Giải:
a) Ta viết lại phương trình thành: 2
(2x − 3) + x − 3 = (x −1) (x −1)(2x − 3) − (x − 3)
Đặt a = 2x − 3,b = (x −1)(2x − 3) − (x − 3) ta thu được hệ sau: 2
a + x −3 = (x −1)b
. Trừ hai phương trình của hệ ta được: 2 b
 + x − 3 = (x −1)a 2 2
a − b = (x −1)(b − a) ⇔ (a − b)(a + b + x −1) = 0 Trường hợp 1:  3− 3  3 x = (L) x ≥ 2 2
a = b ⇔ 2x − 3 = 2x − 6x + 6 ⇔  2 ⇔   2  3+ 3
2x − 6x + 3 = 0 x = (TM )  2 Trường hợp 2: 2 2
2x − 3+ 2x − 6x + 6 + x − 3 = 0 ⇔ 2x − 6x = 6 − 3xx ≤ 2 ⇔  (VN) 2
7x − 30x + 36 = 0 THCS.TOANMATH.com
Vậy phương trình có nghiệm duy nhất: 3 3 x + = 2
b) Ta viết lại phương trình thành: 3 2 3 2
(2x −1) − (x − x −1) = (x +1) (x +1)(2x −1) + x − x −1 Đặt 3 2 3 2
a = 2x −1,b = (x +1)(2x −1) + x − x −1 = 3x − 2 ta thu được hệ 3 2
a − (x − x +1) = (x +1)b phương trình: 
. Trừ hai phương trình của hệ 3 2 b
 − (x − x +1) = (x +1)a cho nhau ta thu được: 2 2
(a − b)(a + ab + b + x +1) = 0
Trường hợp 1: a = b ta có: x =1 3 2 3 2 2x 1 3x 2 8x 15x 6x 1 0  − = − ⇔ − + + = ⇔ 1 x = −  8 2 Trường hợp 2: 2 2  b  3 2
a + ab + b + x +1 = 0 ⇔ a +
+ (2x −1) + x +1 =   0  2  4 2  b  2 2 ⇔ 4 a +
+ 4x + 2(2x −1) + 5 =   0(VN)  2 
Tóm lại phương trình có 2 nghiệm là 1 x =1, x = − . 8
3) Một số cách đặt ẩn phụ khác:
Ví dụ 1: Giải các phương trình sau: a) 3 3 3
x − 6 + x + 6 = 6 b) 2 2 2
2(x + x +1) + 2x + 2x − 3− 4x + 5 = 0 . THCS.TOANMATH.com Giải: 3 3
 x + 6 = z z − x = 6 a) Đặt  ⇒  3 3  z + 6 = y
y − z = 6
Mặt khác với các phép đặt ẩn phụ trên, từ phương trình trong đầu bài, ta có 3
x − y − 6 = 0 . 3 x = y + 6 (1) 
Như vậy ta được hệ phương trình: 3
y = z + 6 (2)  3 z = x + 6  (3)
Nhìn thấy hệ trên không thay đổi khi hoán vị vòng quanh đối với x, y, z
nên không mất tính tổng quát, ta có thể giả thiết x = max (x, y, z) ( x là
số lớn nhất trong 3 số x, y, z hay x ≥ y, x ≥ z )
Nếu x > y , từ (1) và (2) suy ra 3 3
y + 6 = x > y = z + 6 ⇒ y > z
Khi đó từ (2), (3) suy ra 3 3
y + 6 = x > y = x + 6 ⇒ z > x . Mâu thuẫn với
giả thiết x ≥ z ở trên. Do đó phải có x = y .
Với x = y , từ (1) và (2) suy ra y = z
Vậy x = y = z
Phương trình (1) trở thành: 3
x − x − 6 = 0 hay (x − )( 2
2 x + 2x + 3) = 0 (4) Vì 2
x + 2x + 3 = (x + )2
1 + 2 > 0 nên PT (4) có nghiệm duy nhất x = 2 . b) Đặt 2
y = x + x −1 khi đó phương trình đưa về 2 ( ) 2 1 5 4 2 2 1 3 5 4 1 x y y x y y − + + + + = + + ⇔ + − = 2 THCS.TOANMATH.com Đặt 1 5 4x z − + + = điều kiện 1 z − ≥ . 2 2 Ta có 2 2
2z +1 = 5 + 4x ⇒ 4z + 4z +1 = 5 + 4x ⇒ z + z −1 = x . 2
x + x −1 = yx(x + ) 1 = y +1  
Do đó ta có hệ phương trình: 2
y + y −1 = z (*) ⇔ y ( y + ) 1 = z +1.  2
z + z −1 = x   z  ( z + ) 1 = x +1 − Do điều kiện 1 z ≥ ⇒ y ≠ 1 − ⇒ z ≠ 1 − . 2
Nhân các phương trình theo vế rồi rút gọn được xyz =1.
Mặt khác từ hệ phương trình (*), cộng các phương trình vế theo vế ta có: 2 2 2 3
x + y + z = 3 ≥ xyz ⇒ xyz ≤1.
Do đẳng thức xảy ra nên phải có 2 2 2
x = y = z =1 ⇔ x = y = z =1 (vì
x, y, z ≠ 1 − ).
Vậy phương trình đã cho có nghiệm duy nhất x =1.
Ví dụ 2: Giải các phương trình sau: a) 2 4 3 2
2x + 4x + 7 = x + 4x + 3x − 2x − 7 b) 4 1 5
+ x − = x + 2x − x x x − + c) 6 2x 6 2x 8 + = 5 − x 5 + x 3
b) 2(5x − 3) x +1 + 5(x +1) 3− x = 3(5x +1) Giải: THCS.TOANMATH.com
Cách 1: Biến đổi pt như sau:
x + x + = ( x + x + )2 2 2 − ( 2 4 2 4 7 2 4 7
16 2x + 4x + 7) + 35 (1) Đặt 2
2x + 4x + 7 = a (với a ≥ 5 ), ta có: 4 2
a = a − a + ⇔ ( 2
a − )2 = ( a + )2 ⇔ ( 2 a − a − )( 2 4 16 35 6 2 1 2
7 a + 2a − 5) = 0(*) Với a ≥ 5 thì 2
a + 2a − 5 > 0 , nên từ (*) suy ra 2
a − 2a − 7 = 0 , phương
trình này có 2 nghiệm là a =1± 2 2 . Đối chiếu với điều kiện a ≥ 5
chỉ chọn được a =1+ 2 2 . Khi đó 2 2
2x + 4x + 7 =1+ 2 2 ⇔ x + 2x − (1+ 2 2) = 0 (**)
Phương trình (**) có 2 nghiệm là 1
− ± 2 + 2 2 . Vậy tập nghiệm của PT đã cho là { 1 − ± 2 + 2 2}.
Cách 2: Biến đổi PT về dạng:
(x + )2 + = (x + )4 − (x + )2 2 1 5 1 3 1 − 5
Đặt (x + )2 = u (x + )2 1 ; 2
1 + 5 = v,(u ≥ 0;v ≥ 5). Ta có hệ: 2 2 2 u
 −3u −5 = v u
 −u = v + v u  −  v −1 = 0  ⇔  ⇔  2 2
2u + 5 = v 2u + 5 = v v = 2u + 5 Dẫn đến 2
u − 4u − 4 = 0 , PT này có 2 nghiệm 2 ± 2 2 . Do u ≥ 0 nên
chọn u = 2 + 2 2 . Từ đó suy ra kết quả như cách 1.
b) Điều kiện trên ta được: 5 x ≥ hoặc 1 − ≤ x < 0 (*). 2 THCS.TOANMATH.com
Phương trình (1) tương đương: 1 5 4
x − − 2x − = x − x x x Đặt 1 5
u = x − ;v = 2x − với u ≥ 0;v ≥ 0 . Ta được: 4
u − v = x − x x x (1) Lại có 2 2  5   1  4
v − u = 2x − −   x − =  x −  (2)  x   x x Từ (1) và (2) suy ra: 2 2
v − u = u − v ⇔ (u − v)(u + v + ) 1 = 0 . Vì 4 x = 2
u + v +1 > 0 nên u − v = 0 2
⇔ x − = 0 ⇔ x = 4 ⇔ x  x = 2 −
Thử lại thấy nghiệm x = 2
− không thỏa mãn điều kiện , nghiệm x = 2 thỏa mãn phương trình. c) Điều kiện: 5 − < x < 5.
Đặt: a = 5 + x; b = 5 - x (a,b > 0). Khi đó ta có: 2 2
6 − 2x = 2b − 4; 6 + 2x = 2a − 4 Khi đó ta có: 2 2b − 2 4 2a − 4 8 8 + = ⇔ 2 (2b − 2 4)a + (2a − 4)b = ab a b 3 3 8
⇔ 2ab(a + b) − 4(a + b) = ab 3
Từ đó ta có hệ phương trình:  8  8
2ab(a + b) − 4(a + b) = ab
2ab(a + b) − 4(a + b) = ab  3 ⇔  3  2 2   a + b = 10  2 (a + b) − 2ab = 10
Đặt: S = a + b;P = ab,S ≥ 10. THCS.TOANMATH.com  8 2SP − 4S = P
Hệ phương trình trên trở thành:  3  2 S − 2P = 10 2 S −
Từ phương trình (2) ta có: 10 P =
thế lên phương trình trên và rút 2 gọn ta được: 3 2 2
6S −8S −84S + 80 = 0 ⇔ (S − 4)(3S + 8S −10) = 0 ⇔ S = 4 (TM) 2
3S + 8S −10 = 0(VN) ì v S > 10. S = 4  x = 4 2 2
⇒ P = 3 ⇔ 5 + x. 5 − b = 3 ⇔ 25 − x = 9 ⇔ x =16 ⇔  (TM)  x = 4 −
Vậy phương trình đã cho có 2 nghiệm là: x = 4; x = 4 − d) Điều kiện 1 − ≤ x ≤ 3 2 u  = x +1  u  = x +1 2 2 3
u − 2v = 5x − 3 Đặt  ta suy ra  v = 3− x 2 2
4u − v = 5x +1  2 2 u  + v = 4
Phương trình đã cho trở thành: ( 2 2 u − v ) 2 + uv = ( 2 2 u − v ) 2 2 2 3 2 5 3 4
⇔ 6u (2 − u) = v (u + 3) . Thay 2
v = 4 − u ta thu được phương trình: 2( 2 2 3u − 2v ) 2 + 5uv = 3( 2 2 4u − v ) u = 2 2 6u (2 u) ( 2 4 u )(u 3)  ⇔ − = − + ⇔ 5 +  145 u =  10 THCS.TOANMATH.com x = 3
Từ đó tìm được các nghiệm của phương trình là:  7 +  145 x =  10
Khi gặp các phương trình dạng: n + . ( ) m
a b c f x + d e + .
h f (x) = g ta
có thể đặt ẩn phụ theo cách: n − m − Đặt u b v e n b + .
c f (x) = u ⇒ f (x) = , m e + .
h f (x) = v ⇒ f (x) = c h
au + dv = g
Từ đó ta có hệ phương trình:  n m
u − b v − e − =  0  c h
Ví dụ 1: Giải các phương trình sau:
a) 3 24 + x + 12 − x = 6 b) 2 4 2 6
1− x + x + x −1 + 1− x =1 c) 2 2 1+
x − x = x + 1− x d) 3 3 3
x −1 + x − 2 = 2x − 3 3 Giải:
a) Điều kiện: x ≤12 Đặt 3 3
u = 24 + x;v = 12 − x ⇒ u ≤ 36,v ≥ 0 , ta có hệ phương trình: u  + v = 6 v = 6 − uv = 6 − u    ⇔  ⇔  3 2 3 u  + v = 36 u  +  (6−u)2 = 36 u  ( 2
u + u −12) = 0(*)
Phương trình (*) có 3 nghiệm u = 0;u = 4; − u = 3 thỏa mãn 3 u ≤ 36 .
Từ đây ta tìm được: x = 24 − ; x = 88 − ; x = 3
Vậy phương trình đã cho có 3 nghiệm x = 24 − ; x = 88 − ; x = 3. THCS.TOANMATH.com − + b) Điều kiện: 1 5 ≤ x ≤1 . 2
Ta thấy tổng của biểu thức trong căn bằng 1 nên ta đặt: − 2 4 2 − 6
a = 1 x ,b = x + x 1,c = 1− x; a, b, c ≥ 0 .
a + b + c =1 Khi đó ta có hệ:  2 4 6
a + b + c = 1
a,b,c ≥ 0  2 a ≤ a
a,b,c ≥ 0  Vì 4 2 4 6 
⇒ 0 ≤ a,b,c ≤1⇒ b
 ≤ b ⇒ a + b + c ≤ 1.
a + b + c = 1  6 c ≤ c  2 a = a
Hệ phương trình có nghiệm khi 4 b
 = b ⇔ x =1 là nghiệm của phương  6 c = c  trình đã cho. 2
c) Đặt t = x + 1− x thì 2 t 1 x x − − = 2
Khi đó phương trình đã cho trở thành phương trình bậc hai với ẩn là t: 2 − t 1 2 1+
= t ⇔ t − 3t + 2 = 0 ⇔ t =1; t = 2 3  + − =  2 x 1 x 1 x − x = Vậy ta có: 2 0  ⇔  ⇔ x = 0; x =1
 x + 1− x = 2 VN  (VT < 2)
d) Sử dụng đẳng thức: ( )3 3 3 a + b = a + b + 3ab(a + b) .
Lập phương 2 vế ta thu được: THCS.TOANMATH.com ⇔ − ( − )( − ) (3 − 3 3 2x 3 + 3 x 1 x 2 x 1 + x − 2 ) = 2x − 3 Thay 3 3 3
x −1 + x − 2 = 2x − 3 thì phương trình trở thành: 3
3 (x − 1)(x − 2)(2x − 3) = 0 ⇔ x = 1,x = 2,x = 2
Ví dụ 2: Giải các phương trình sau: a) 2
7x + 7 + 7x − 6 + 2 49x + 7x − 42 =181−14x b) 5 1 5 x + = 2x + + 4 2 x 2x
c) x + ( − x )3 3 2 = x ( 2 1 2 1− x ) +
d) (x − )(x + ) + (x − ) x 3 1 3 2 1 = 8 x −1 Giải: a) Điều kiện: 6 x ≥ . 7 Đặt t = x + + x − (t ≥ ) 2 2 7 7 7 6,
0 ⇒14x + 2 49x + 7x − 42 = t −1 BPT đã cho trở thành: t = 13 2 2
t + t −1 =181 ⇔ t + t −182 = 0 ⇔ ⇔ t =  13 t = 14 −
⇔ 7x + 7 + 7x − 6 =13 (*)
Vì hàm số f (x) = 7x + 7 + 7x − 6 −13 là hàm đồng biến và f (6) = 0
Kết hợp với điều kiện suy ra nghiệm của phương trình là x = 6 . THCS.TOANMATH.com b) Điều kiện: x   > 0 . Phương trình 1  1 5 x  2 x  ⇔ + = + +   4  2 x   4x  Đặt 1 t = x + ,(t ≥ 2) 1 2 ⇒ x + = t −1. 2 x 4x
Phương trình trở thành: t = ( 2t − ) 2 5 2
1 + 4 ⇔ 2t − 5t + 2 = 0 ⇔ t = 2 1 ⇔ x + = 3 4x  3− 2 2 x = 2 2
⇔ 4x −12x +1 = 0 ⇔ 
là nghiệm của pương trình.  3+ 2 2 x =  2 c) Điều kiện: 1
− ≤ x ≤1. Phương trình đã cho tương đương với ( 2 x + − x )( 2 2 2
x − x − x + − x ) 2 1 1 1 = x 2(1− x ) 2 − Đặt 2 t 1 2
t = x + 1− x ⇒
= x 1− x . Ta có phương trình: 2 2 2  t −1 t −1 3 2 t 1−  = 2
⇔ t + 2t − 3t − 2 = 0 ⇔ (t − 2)( 2t + 2 2t + ) 1 = 0  2  2 t = 2 t = 2 ⇔  ⇔  2
t + 2 2t +1= 0 t = − 2 ±1 + Nếu: t = 2 2 2 2 ⇔ x + − x = ⇔ − x =
− x ⇔ ( − x) 2 1 2 2 1 2
= 1− x (do x ≤ ) 1 THCS.TOANMATH.com 2 1
⇔ 2x − 2 2x +1 = 0 ⇔ x = 2 + Nếu 2
t = − 2 −1 ⇔ x + 1− x = 1
− − 2 vô nghiệm ,do VT ≥ 1 − > VP + Nếu 2
t = − 2 +1 ⇔ 1− x =1− 2 − x  1 − ≤ x ≤1− 2  ⇔ 1 2 2 2 1  x − − − ⇔ = 2 x −  (1− 2)x− 2 +1=  0 2
Vậy phương trình có 2 nghiệm 2 x = ; 1 2 2 2 1 x − − − = . 2 2 + +
d). Điều kiện: x 3 ≥ 0 ⇔ x ≤ 3
− hoặc x >1. Đặt t = (x − ) x 3 1 thì x −1 x −1 t = 2 2 t = (x − )
1 (x + 3) ta có phương trình: 2t + 2t −8 = 0 ⇔  t = 4 − x = 1 − + 2 2
Nếu t = 2 ⇒ (x − ) 1 (x + 3) 2
= 4 ⇔ x + 2x − 7 = 0 ⇔  x = 1 − − 2 2 x = 1 − + 2 5 Nết t = 4 − thì (x − ) 1 (x + 3) 2
= 16 ⇔ x + 2x −19 = 0 ⇔  x = 1 − − 2 5
Tóm lại phương trình có 4 nghiệm là: x = { 1 − + 2 2; 1 − − 2 2; 1 − − 2 5; 1 − + 2 5}.
MỘT SỐ BÀI TẬP RÈN LUYỆN.
Giải các phương trình sau: 1) 2
x + x + 6 + 2x x + 3 = 4(x + x +3) (1). THCS.TOANMATH.com 2 2) + + x 2x 2 x + 2 = . 2x +1
3) x + + (x + ) 2 1 2
1 = x −1+ 1− x + 3 1− x .
4) x(x + )
1 + x(x + 2) = x(x − 3) .
5) Tìm tất cả các số nguyên dương p >1 sao cho phương trình sau có nghiệm duy nhất   3 2 1
x + px + p −1+ x +1 =   0 p −1 6) 3 2 2
x − 4x + 31 + x = 4x −1. 7) 4 2
x + x + 2016 = 2016 .
8) Tìm k để phương trình sau có nghiệm: ( 2x + ) 2
x − x( k − ) 2 2 2 2
1 + 5k − 6k + 3 = 2x =1   . Trích đề thi vào
lớp 10 Chuyên Amsterdam 2002). 9) Cho phương trình 6 m x + = ( 4 1 3 x + 2)
a) Giải phương trình với m =10 .
b) Tìm m để phương trình có đúng hai nghiệm. 10) 2 x − (x + ) 2 2 2
1 x −1 − 3x + 6x −1 = 0 .
11) x +1 = 2(x + ) 1 + 2 2(x + ) 1 + 2 4(x + ) 1 . 12) 4 1 5
+ x − = x + 2x − (*). x x x 13) 2 2 x + 9 = x + . x +1
14) x( x + ) − x(x − ) 2 3 1 1 = 2 x (1). 15) 2
4 x +1 = x − 5x +14 .
16) ( x + − x − )( 2 2
2 1+ x + 7x +10) = 3 (1). THCS.TOANMATH.com 17) 3 2 3 2 12 − + 4x − = 4x (*). 2 2 x x
18) ( x +3 − x)( 1− x + )1 =1(THPT chuyên KHTN-ĐHQG Hà Nội 2011-2012).
19) Giải bất phương trình: 25x( 2 3 3
2x + 9) ≥ 4x + . Trích đề thi vòng 2, x
THPT chuyên Hà Nội Amsterdam 2004-2005 x +1
20) x + x +1 + x(x − x + ) ( )3 2 4 2 2 1 ≤ x
21) 4 (x − 2)(4 − x) 4 4 3
+ x − 2 + 4 − x + 6x 3x ≤ x + 30 22) (x + ) 2 2
1 2x − 2x = 2x − 3x − 2 (Trích đề tuyển sinh lớp 10 Chuyên Lam Sơn Thanh Hóa 2014) 23) 2 2
2x −1 + 1− 2x = 2 x − x . (Trích đề tuyển sinh lớp 10 PTNK-
ĐHQG Tp Hồ Chí Minh 2015). 24) 2
8x + 16x − 20 − x + 15 = 0 25) 2 − + = − 2 4x 11x 10 (x 1) 2x − 6x + 2 26) 2 3 x − 3x + 1 = − 4 x + 2 x + 1 3 27) − + − + 2
2 x 1 3 5 x 3x − 30x + 71 = 0 28) ( 2 − + ) − = 2 2x 4x 1 2x 1 4x − 7x + 3 29) 3 − + 3 − = 3 x 1 x 2 2x − 3 2  2  30) 1 x 5 1 − x x + +  +  + 2 = 0 2 2 x 1 x 2  x 2  − 1 −  x  31) 3 + = ( 2 5 x 1 2 x + 2) 32) 3 + + 3 2x 2 2x + 1 = 3 2 2x + 3 2 2x + 1
33) 3 + 2 − + = ( − ) 3 x 6x 2x 3 5x 1 x + 3 2 34) x + x + 1 2 + 2 x − 4 = x + 4 2 x + 1 THCS.TOANMATH.com 35) 2 18x 25x + 2 9 9x − 4 = + 2 x x + 1 36) 2
20x + 80x + 125+ ≤ 2x + 1 + 4 3x + 6 37) 2 − 4 + 2 + 4 13 x x 9 x x = 16
LỜI GIẢI BÀI TẬP RÈN LUYỆN 1) Giải: Điều kiện: x ≥ 3 − Ta có: (1) 2
⇔ x − 3x + 2x x + 3 − 4 x + 3 + 6 = 0 (2)
Đặt t = x + x + 3 Do đó (2) 2
⇒ t − 4t + 3 = 0 ⇔ (t − )
1 (t − 3) = 0 ⇔ t =1;t = 3
Với t =1, ta giải phương trình x + x + 3 =1 ⇔ x + 3 =1− x 1  − x ≥ 0  x ≤1 x ≤1 ⇔  ⇔  ⇔  x + 3 =  (1− x)2 2 2
x + 3 =1− 2x + x
x − 3x − 2 = 0 x ≤1  3+ 17 3− 17 x = ⇔ x = ⇔  2 2   3− 17 x =  2
Với t = 3 , ta giải phương trình x + x + 3 = 3 ⇔ x + 3 = 3− x x ≤ 3 
⇔ x =1 ⇔ x =1  x = 6 THCS.TOANMATH.com −
Vậy phương trình đã cho có hai nghiệm 3 17 x = , x =1. 2 2) Điều kiện 1 x ≥ 2; − x ≠ − . 2 Ta có (1) ⇔ ( x + ) 2 2
1 x + 2 = x + 2x + 2 ⇔ (x + x + )
1 x + 2 = x(x + ) 1 + (x + 2)
⇔ (x + 2) − (2x + )
1 x + 2 + x(x + ) 1 = 0
⇔ ( x + 2 − x) x + 2 −(x + ) 1  = 0  
Trường hợp 1: x + 2 = x với x ≥ 0 2
⇒ x − x − 2 = 0 ⇔ (x − 2)(x + ) 1 = 0
⇔ x = 2 (thỏa mãn) hoặc x = 1 − (loại)
Trường hợp 2: x + 2 = x +1 với 2 x ≥ 1
− ⇒ x + x −1 = 0 1 5 x − + ⇔ = ( thỏa mãn) hoặc 1 5 x − − = (loại) 2 2
Vậy phương trình có hai nghiệm 1 5 x 2, x − + = = . 2 3)
Đặt u = x +1,v = 1− x (u,v ≥ 0)
Phương trình đã cho trở thành: 2 2 2
u + u = −v + v + uv ⇔ v − ( u + ) 2 2 3
3 1 v + 2u + u = 0 (1) THCS.TOANMATH.com
Xem (1) như là phương trình bậc hai đối với biến v , giải ra được u = v hoặc
v = 2u +1.
Xét v = 2u +1, vì 2 2 2
v =1− x = 2 − u ⇒ 2 − u = (2u + )2 1  1 u = (tm) 2 5u 4u 1 0  ⇔ + − = ⇔ 5 . Với 1 24 u = ⇒ x = −  5 25 u = 1( − l)
Vậy phương trình có hai nghiệm 24 x = 0; x = − . 25 4) Giải: x ≤ 2 −
Điều kiện: x = 0  x ≥  3
Dễ thấy x = 0 là 1 nghiệm và x = 3 không là nghiệm của phương trình đã cho
Xét x ≠ 0, x ≠ 3 khi đó phương trình đã cho tương đương với x +1 x + 2 4 5 + = 1 ⇔ 1+ + 1+ = 1 x − 3 x − 3 x − 3 x − 3 Đặt 4 a = 1+ (a > 0) ; 5 b = 1+ (b > 0) x − 3 x − 3 a + b =1 a = 4 − − 21(l) Ta có hệ  ⇔  2 2 5  a − 4b =1 a = 4 − + 21 4 2 − 21 ⇒ 1+ = 4 − + 21 ⇔ x = x − 3 3 THCS.TOANMATH.com
Vậy phương trình có hai nghiệm 2 21 x 0; x − = = . 3  
5) Phương trình đã cho tương đương với (x + p − ) 2 1 1 x + x + =   0  p −1 x = − p +1  (1) ⇔
Yêu cầu bài toán tương đương (2) vô nghiệm 2 1 x + x + = 0 (2)  p −1
hoặc có nghiệm kép x = −( p − ) 1 Vậy p ∈{2;3; } 4 . 6)
Phương trình đã cho tương đương với (x − )2 + + (x − )2 3 2 27 2 = 3 . Do (x − )2 + + (x − )2 3 2 27 2 ≥ 3, x
∀ và đẳng thức xảy ra khi và chỉ khi
x = 2 nên phương trình có nghiệm duy nhất x = 2 . 7)
Phương trình đã cho tương đương với: 4 2 1 x + x + = ( 2 x + ) 2 1
2016 − x + 2016 + 4 4 2 2  2 1   2 1 x   x 2016  ⇔ + = + −  2 2      2 1 2 1 2 2 4 2
⇔ x + = x + 2016 − ⇔ x +1 = x + 2016 ⇔ x + x − 2015 = 0 . 2 2 − + − +
Vậy phương trình có hai nghiệm 1 8061 1 8061 x = ; x = . 2 2 THCS.TOANMATH.com 8) Giải:
Phương trình đã cho tương đương với: ( 2x + ) 2
x − x ( k − ) + 
( 2k − k + )+( 2 2 2 . 2 1 4 4 1 k − 2k + ) 1 +1 = 2x +1  ⇔ ( 2
x + )(x − k + )2 + ( 2 2 2 1 x + 2)(k − )2 1 + (x − )2
1 = 0 ⇔ x = k =1.
Vậy phương trình có nghiệm khi k =1.
9) Phương trình đã cho tương đường với: m ( 2 x + )( 4 2
x − x + ) = ( 2 x + ) + ( 4 2 1 1 3 1 x − x +  )1 2 4 2 m x +1 x − x +1 ⇔ = + 4 2 2 3 x − x +1 x +1 4 2 − + Đặt x x 1 t =
, (t > 0) ta được: m 1 2 m
= t + ⇔ t − .t +1 = 0 2 x +1 3 t t
a) Với m =10 ta có phương trình: 2
3t −10t + 3 = 0 ta suy ra t = 3 hoặc 1 t = 3 b) Tự giải 10) .Giải:
Điều kiện: x ≥1. Phương trình tương đương với 2
x − − (x + ) 2 2 2 1 2
1 x −1 + x + 2x +1− 4x + 4x −1 = 0 ⇔ (  x = x −
3x − x −1)(2− x − x −1) 2 3 1 2 2 = 0 ⇔  2
2− x = x −1 0 ≤ x ≤1 0 ≤1 ≤1 Trường hợp 2
3x = x −1 ⇔  ⇔  (vô nghiệm). 2 2 2 9  x = x −1 8  x = 1 − THCS.TOANMATH.com Trường hợp 1  ≤ x ≤ 2 1  ≤ x ≤ 2 1  ≤ x ≤ 2 2  5
2 − x = x −1 ⇔  ⇔  ⇔  ⇔ x = . 2 2 5
x − 4x + 4 = x −1 4x = 5 x = 4  4 11) .Giải: Điều kiện x ≥ 1
− .Ta có x = 3 là một nghiệm của phương trình.
Với x > 3. Đặt x +1 = y,( y > 4) , phương trình đã cho
thành: y = 2y + 2 2y + 2 4y . Ta có 2
4y < y = y ⇒ 2 4y < 2y
⇒ 2y + 2 2y + 2 4y < 2y + 2 4y < 2y + 2y = 4y < y
Phương trình vô nghiệm.
Với 0 < x < 3 . Chứng minh tương tự, ta có phương trình vô nghiệm.
Vậy x = 3 là nghiệm duy nhất của phương trình. 12) Giải: Ta có (*) 4 1 5
⇔ − x + x − − 2x − = 0 (1) x x x Đặt 1 5
u = x − ;v = 2x − thì u,v ≥ 0 và 2 2 4
u − v = − x x x x Do đó (1) thành: 2 2
u − v + u − v = 0 ⇔ (u − v)(u + v + )
1 = 0 ⇔ u = v (vì
u,v ≥ 0) Từ đó ta có: 1 5 1 5
x − = 2x − ⇔ x − = 2x − ≥ 0 (2) x x x x THCS.TOANMATH.com Phương trình 1 5
x − = 2x − có nghiệm là x = 2 ± x x
Từ (2) suy ra chỉ có x = 2 là nghiệm của phương trình đã cho. 13)
Giải:Điều kiện x ≥ 0 .
Phương trình tương đương với: 8 4 2x 9x +1 4 2 + 9 x x = x + + ⇔ − = 0 x +1 x +1 x +1 x +1 2 8x 4 2x  2 2  ⇔ − +1 = 0 x ⇔  −1 = 0 x 1 x 1  x 1  + + +   2 2x 1 ⇔
= 1 ⇔ 8x = x +1 ⇔ x = (thỏa mãn x +1 7 14) Giải:
Điều kiện: x ≥1. Dễ thấy x = 0 là nghiệm của (1)
Với x ≠ 0 , chia hai vế của (1) cho 2
x ≠ 0 , ta được: (1) 1 1 ⇔ 3+ − 1− = 2 x x Đặt 1 1
u = 3+ ≥ 0,v = 1− ≥ 0 x x u  − v = 2 u  = v + 2 (2) Ta có hệ phương trình:   ⇔  2 2 u  + v = 4 (  2 + v  )2 2 + v = 4 (3)
Giải hệ ta được v = 0,u = 2 từ đó ta có x =1. THCS.TOANMATH.com 15) .Giải: ⇔ ( 2
x − 6x + 9) + (x +1− 4 x +1+ 4) = 0
⇔ (x − ) + ( x + − )2 2 3 1 2 = 0 x − 3 = 0 ⇔  ⇔ x = 3 x +1 − 2 = 0
Vậy phương trình có nghiệm duy nhất là x = 3. 16) Giải: Điều kiện: x ≥ 2 −
Nhân hai vế của phương trình (1) với x + 5 + x + 2 > 0 , ta được phương
trình tương đương: 2
1+ x + 7x +10 = x + 5 + x + 2 x + 5 =1 x = 4 − (l) ⇔  ⇔  .  x + 2 =1 x = 1 − (tm) 17) Giải: Đặt 2
y = x , y ≥ 0 , ta có (*) thành: 3 3
12 − = 4y − 4y − y y
Bình phương rồi biến đổi thành: ( y − − y)2 2 2 4 3
= 0 ⇔ 4y − y − 3 = 0
Do đó các nghiệm của phương trình là x =1, x = 1 − .
18) Điều kiện: 0 ≤ x ≤1 THCS.TOANMATH.com
Nhân cả tử và mẫu vế trái với biểu thức x + 3 + x ta thu được:
( x+ − x)( −x + ) 3 3 1 1 =1 ⇔ ( 1−x + )1 =1 x + 3 + x
⇔ 3 1− x +1 = x + 3 + x (*)
Nếu x =1 thì VT(*) = 3 = VP(*) nên x =1 là nghiệm của phương trình.
Nếu 0 ≤ x <1 thì 1− x > 0 ⇒ 3 1− x + 3 > 3 hay VT(*) > 3 với 0 ≤ x <1
Vì 0 ≤ x <1 nên x + 3 < 1+ 3 = 2, x < 1 =1⇒ VP(*) < 3
Do đó phương trình đã cho không có nghiệm trong nửa khoảng [0; ) 1 .
Vậy phương tình đã cho có nghiệm duy nhất x =1. 19) Giải:
Điều kiện: x ≠ 0
Trường hợp x > 0 : áp dụng bất đẳng thức Cô si ta có: 2 2 3 5 2x + 9 5 5 2x + 9 4x + = x + ≥ 3 . x . x = 25x( 2 3 3 2x + 9) x 3 3x 3 3 3x 2 +
Dấu bằng xảy ra khi và chỉ khi 5 2x 9 x = ⇔ x = 3 3 3x
Trường hợp x < 0 : từ phần trên ta thấy, với mọi x < 0 đều thỏa mãn bất phương trình  = Đáp số x 3  . x < 0 20) .Giải: THCS.TOANMATH.com
Điều kiện x > 0
Chia cả hai vế bất phương trình cho x( 2 x + ) 1 và đặt 1
t = x + ,t ≥ 2 , ta x
đưa về bất phương trình 1 1
1− ≤ t − t − t t
Với điều kiện t ≥ 2 thì cả hai vế của (1) đều dương. Bình phương hai vế ta 2  
đưa về bất phương trình tương đương 1  t − −1 ≥ 0  t   
Bất phương trình này nghiệm đúng với mọi t ≥ 2.
Vậy nghiệm của bất phương tình đã cho là x > 0 . 21) .Giải:
Điều kiện: 2 ≤ x ≤ 4 − + −
Áp dụng bất đẳng thức Cô si ta có: x 2 4 x
4 ( x − 2)(4 − x) ≤ = 1; 2 x − 2 +1 +1 x − 2 +1 2 x +1 x − 2 = x − 2.1 ≤ ≤ = ; 2 2 4 x 7 4 4 x − + − ≤ ; 3 3
6x 3x = 2 x .27 ≤ x + 27 2
Do đó VT ≤ VP với mọi x thỏa mãn 2 ≤ x ≤ 4
Vậy nghiệm của bất phương trình là 2 ≤ x ≤ 4 . 22) Đặt 2 2 2
t = 2x − 2x ≥ 0 ⇒ 2x − 2x = t . Phương trình trở thành : 2 t − (x + )
1 t − x − 2 = 0 . Ta có THCS.TOANMATH.com x +1− (x + 3) t = = 1 − 2
∆ = x + x + + x + = (x + )2 2 2 1 4 8 3 ⇒  . Do t ≥ 0 ta chỉ  x +1+ x + 3 t = = x + 2  2 x ≥ 0 cần giải: 2
2x − 2x = x + 2 ⇔  ⇒ x = 3+ 13 . 2
x − 6x − 4 = 0 2x −1 ≥ 0 23) Điều kiện:  2 1
 − 2x ≥ 0 . Bình phương 2 vế ta thu được:  2 x − x ≥  0 2 x − + − x + ( x − )( 2 − x ) = ( 2 2 1 1 2 2 2 1 1 2 4 x − x ) 2
⇔ − x + x − ( x − )( 2 2 2 2 2 1 1− 2x ) = 0  1 − − 5 ⇔ (  = − x − x − ) x 2 2 2 2 2 1 2
2 1 = 0 ⇔ 1− 2x = 2x −1 ⇔ x + x −1 = 0 ⇔  1 − + 5 x =  2
Đối chiếu với điều kiện nài toán chỉ có nghiệm 1 5 x − + = thỏa mãn điều 2 kiện.
24) Ta viết lại phương trình thành: 2 2
16x + 32x − 40 − 2 x + 15 = 0 ⇔ (4x + 4) − 56 = 4x + 60
Đặt 4x + 60 = 4y + 4 ta có hệ sau: ( 2 2  4y 4) 4x 60 ( + = + 4y +  4) = 4x + 60  ⇔  . (4x + 4)2 − 56 = 4y + 4 (4x + 4)2 = 4y +   60
Trừ từng vế 2 phương trình của hệ ta có: THCS.TOANMATH.com ( + )2 − ( + )2 4x 4
4y 4 = 4(y − x) ⇔ 16(x − y)(x + y + 8) = 4(y − x) x = y ⇔  4(x + y + 8) =  1
Giải phương trình ứng với 2 trường hợp ta thu được: −9 + 221 x = 1;x = 9  3 − 5 x ≤ 25) Điều kiện:  2  3 + 5 x ≥  2
Ta viết lại phương trình thành: ( − )2
2x 3 + (x + 1) = (x − 1) (x − 1)(2x − 3) − (x + 1) u = 2x − 3 Đặt   ta có hệ phương trình:
v = (x − 1)(2x − 3) − (x +  1)  2 u + x + 1 = (x − 1)v   2 v + x + 1 = (x −  1)u
Trừ từng vế hai phương trình ta có: ( v)(u v x 1) u = v u − + + − = 0 ⇔  u = −v − x +  1
Giải theo hai trường hợp ta thu được phương trình vô nghiệm.
26) Cách 1: Ta viết lại phương trình thành: 2 3 x − 3x + 1 = − ( 2x +x+1)( 2x −x+1) 3 3 ⇔ 2( 2 x − x + 1) −( 2 x + x + 1) = − ( 2x +x+1)( 2x −x+1) 3 THCS.TOANMATH.com
Chia phương trình cho ( 2x + x +1) > 0 ta thu được:  2   2  x − x + 1 3 x − x + 1  2  x − x + 1 ⇔ 2  − 1 = −   . Đặt t =   >  0 2  x x 1 3  2   2  + + x + x +    1  x + x +  1  Ta có phương trình: 2 3 1 2t + t − 1 = 0 ⇒ t = 3 3  2  Giải x − x + 1 1   = ⇔ x =  1 2  x + x +  1  3 * Cách 2: Xét x 1 3 1
> 0 chia hai vế phương trình ta có: x − 3 + = − 2 x + 1 + 2 x 3 x Đặt 1
t = x + ≥ 2 ta có phương trình: 3 t − 3 = − 2 t − 1 x 3 Xét x 1 3 1
< 0 chia hai vế phương trình ta có: x − 3 + = 2 x + 1 + 2 x 3 x Đặt 1
t = x + ta có phương trình: 3 t − 3 = 2 t − 1 x 3
27) Điều kiện:1≤ x ≤ 5 . Phương trình được viết lại:
Ta viết lại phương trình thành: − − + − + 2
2 x 1 4 3 5 x 3x − 30x + 75 = 0 THCS.TOANMATH.com (x − 5) ⇔ 2
+ 3 5 − x + (x − 5)(3x − 15) = 0 x − 1 + 2 ( 5) x = 5 x −  ⇔ 2
+ 3 5 − x + (x − 5)(3x − 15) = 0  −2 5 − x x − 1 + 2 + 3 − 5 − x(3x − 15) =  0  x − 1 + 2
Ta thấy − 5 − x(3x − 15) ≥ ∀ 0 x∈ 1;5  
Ta chứng minh: −2 5 − x + 3 ≥ 0 ⇔ 3 x − 1 + 6 − 2 5 − x ≥ 0 nhưng điều x − 1 + 2
này là hiển nhiên đúng do: 2 5 − x ≤ 2 5 − 1 = 4 nên 6 − 2 5 − x > 0
Vậy phương trình có nghiệm duy nhất x = 5 28) Điều kiện 1
x ≥ . Đặt u = x − 1;v = 2x − 1 phương trình đã cho trở 2 thành ( 2 − ) =( 2 2u 1 v
2v − 1)u ⇔ (u − v)(2uv +1) = 0 x ≥ 1 + Nếu 
u = v ⇒ x − 1 = 2x − 1 ⇔  ⇔ x = 2 + 2  2 x − 4x + 2 =  0 + Nếu 2uv 1 0 2(1 x)  1  + = ⇔ −
2x − 1 = 1 ⇒ x∈ ;1  2 
Mặt khác ta có: 2(1 x)  1  − < 2 1 − = 
 1 ; 2x − 1 ≤ 2 − 1 = 1 nên phương  2  trình đã cho vô nghiệm Kết luận: x = 2 + 2
29) Sử dụng đẳng thức:( + )3 = 3 + 3 a b a b + 3ab(a + b) . THCS.TOANMATH.com Phương trình ⇔ − + ( − )( − )(3 − + 3 3 2x 3 3 x 1 x 2 x 1 x − 2 ) = 2x − 3
3 x −1 + 3 x − 2 = 3 2x −  3 3 ⇔  (*) x 1;x 2;x
3 (x − 1)(x − 2)(2x − 3) ⇔ = = = = 0 2  30) 2 2 Điều kiện: 1
− < x <1 . Đặt 1 − x x 1 x t = + ⇒ 2 t = + + 1. x 1 − 2 x x 1 − 2 2 x PT đã cho thành: 2 2t + 5t + 2 = 0 ⇔ t = −2; −1 < x < 0 2 * 1 1 − t x x 1 = −2 ⇔  t = − + = −2 ⇔  2 ⇔ 1 x x = − 2 x 2 + = 1 − x  3 2  2 x 1 − 2 x −1 < x < 0 2 * 1 t 1 − = − ⇔ x x 1  + = − ⇔ 2 hệ vô nghiệm. 2  1 x 3 x 2 2 + = − 1 − x   2 x 1 − 2 x 4
Vậy phương trình đã cho có nghiệm duy nhất 1 x = − . 2 31) Điều kiện. x ≥ −1 PT ⇔ 5 (x + 1)( 2 x − x + 1) = 2( 2 x − x + 1) + 2(x +1) x + 1 x + 1 ⇔ 2 − 5 + 2 = 2 0(Do : x − x + 1 > 0∀x) 2 x − x + 2 1 x − x + 1 t = 2 Đặt x + 1 t = ,t ≥ 0 , ta có: 2  2t − 5t + 2 = 0 ⇔ 2 1 x − x + 1 t =  2 * x + 1 t = 2 ⇔ = 4 ⇔ 2
4x − 5x + 3 = 0 PT vô nghiệm 2 x − x + 1 THCS.TOANMATH.com * 1 x + 1 1 2 5 ± 37 t = ⇔
= ⇔ x − 5x − 3 = 0 ⇔ x = 2 2 x − x + 1 4 2
32) Do VT ≥ 1 nên ⇒ VP ≥ 1 ⇔ x ≥ −1 . Ta có PT  3 2 3 2   3 2 3 2 
⇔  2x + 1 − 2x + 2  +  2x − 2x + 1 = 0     2 2x − 2x − 2 1 2x − 2x − 1 ⇔ + = 0 3 ( 2 2 2 2 2x + 1) +3 ( 2 2x + 1)(2x+ 2) + 3 ( 2 2x + 2) 3 4x + 3 2 2x (2x +1) + 3 ( 2 2x + 1) 2 1 ± 3
⇔ 2x − 2x − 1 = 0 ⇔ x =
là nghiệm của phương trình đã cho. 2
33) Điều kiện: ≥ −3 x 3 . Ta thấy 1
x = không là nghiệm của phương trình nên ta có: 5 3 2 Phương trình x + 6x − 2x + 3 ⇔ = 3 x + 3 . 5x − 1 3 x + 2 6x − 2x + 3 3 x − 2 3 4x + 3 ⇔ − 2x = x + 3 − 2x ⇔ = 3 x + 3 − 2x (1) 5x − 1 5x − 1   x 0 x ≤ ≤ 0 * Nếu 3   3 − 21 x + 3 − 2x = 0 ⇔  ⇔ x 3 2 2 x − 4x + 3 =  0 (x −  1) x 3x 3 0 2  ( − − ) ⇔ = = Khi đó (1) đúng ⇒ 3 − 21 x =
là một nghiệm của phương trình. 2 3 2 3 2  3 − 21 x − 4x + 3 x − 4x + 3 3 x − 2 4x + 3 = 0 * Nếu (1) x ≠ ⇒ (1) ⇔ = ⇔  2 5x − 1 3  x + 3 + 3 2x x + 3 + 2x = 5x − (2)  1
Ta thấy: (1) có 2 nghiệm 3 + 21 x = 1;x = 2 THCS.TOANMATH.com   1 1 x x 3  ≥ ≥ 
(2) ⇔ x + 3 = 3x − 1 ⇔  3 ⇔  3  3 x − 2 9x + 6x + 2 = 2  0 (x −1) x 8x 2 0  ( − − )= x = 1 ⇔  x = 4 +  3 2
Vậy phương trình có 4 nghiệm: 3 ± 21 x = 1;x = ;x = 4 + 3 22 . 2
34) Điều kiện: x > 4 −  2  x + x + 1 2 PT ⇔  2 −  1 + 2 x − 3 = − 1  x + 4  2 x +   1 2 x + x + 1 4 − x 1 x 4 2 ( 2 + + ) ⇔ + x − 3 + = 0 2  2  x + x + 1  2 + x + 1  2 x + + 1 1   x + 4 2( 2 x − 3) 2 2 x − 3 ⇔ + x − 3 + = 0 (x + 4)( 2x + x+1)  2  + x + 4  2 + x + 1  2 x + 1     ( 2x 3)  2 1 ⇔ −  + 1 +  = 0 (x + 4)( 2 x + x + 1)  2  + x + 2 4   2 + x + 1  x + 1     ⇔ 2 x − 3 = 0 ⇔ x = ± 3 35) Điều kiện: 2 x ≥ 3 * Với 2
x ≥ , phương trình đã cho tương đương với: 3 THCS.TOANMATH.com 2 9 9x − 4 2 18 25 + = + (1) 2 2 x x x + 1
Dễ thấy phương trình (1) có 2 9 162
VT > 25 và do x ≥ ta có VP ≤ + < 25 3 2 13
nên phương trình đã cho vô nghiệm * Với 2
x ≤ − phương trình đã cho tương đương với 3 4 2 18 25 − 9 9 − = + (2) 2 2 2 x x x + 1 Đặt 1  9  = t 0 < t ≤ 
 , phương trình (2) thành: 2 x  4  18t 18t 25 − 9 9 − 4t = 2t + ⇔ 9 − 9 9 − 4t = 2t + − 16 1 + t 1 + t 36(t − 2) 2(t − 2)(t + 4) ⇔ = ⇔ ( − ) 18 t + 4  t 2  −  = 0 (1) 9 − 4t + 1 t + 1  9 − 4t + 1 t + 1  Lưu ý rằng với 9 0 18 18 t 4 3 18 < t ≤ có ≥ và + = 1+ < 4 < 4 9 − 4t + 1 4 t + 1 t + 1 4 nên 18 t + 4 − > 0 . 9 − 4t + 1 t + 1 Vậy (3) 2 ⇔ t = 2 ⇒ x = − 2
KL: Phương trình có 1 nghiệm 2 x = − 2
36) Điều kiện: x ≥ −2
BPT được viết lại: ( + )2
5 2x 1 + 20(3x + 6) ≤ 2x + 1+ 4 3x + 6 Đặt a = 2x + 1; b 2 2
3x + 6 ; BPT ⇔ 5a + 20b ≤ a + 4b THCS.TOANMATH.com a + 4b ≥  0 ⇔  a b 2 2 2 5a + 20b ≤  (a + 4b) ⇔ =  1 x ≥ − 2x + 1 = 3x + 6 ⇔  2 ⇔ x = 1  2 4x + x − 5 =  0
Kết luận: Nghiệm của bất phương trình là: x = 1
37) Điều kiện: −1 ≤ x ≤ 1 2
Bình phương 2 vế ta có : 2  2 2 
x 13 1− x + 9 1+ x  = 256  
Áp dụng bất đẳng thức Bunhiacopxki:  2 2 2  − + +  ≤ ( + )( − 2 + + 2 ) = ( − 2 13. 13. 1 x 3. 3. 3 1 x 13 27 13 13x 3 3x 40 16 10x )   2
Áp dụng bất đẳng thức Côsi: 2 10x ( 2 16 10x )  16  − ≤ =   64  2    2 2 x = 2 1 + x  Dấu bằng  1− x =  ⇔ 5  ⇔ 3   2 2 10x = 16 − 2 10x x = −   5 THCS.TOANMATH.com