Chuyên đề rút gọn biểu thức chứa căn và bài toán liên quan

Tài liệu gồm 91 trang được sưu tầm và tổng hợp bởi tác giả Trịnh Bình, phân dạng và hướng dẫn giải các dạng toán chủ đề rút gọn biểu thức chứa căn và các bài toán liên quan, đây là dạng toán được bắt gặp thường xuyên trong chương trình Toán 9 và trong đề thi tuyển sinh vào lớp 10 môn Toán. Mời bạn đọc đón xem.

41 21 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung Toán 9

Môn: Toán 9

Thông tin:

88 trang 8 tháng trước

Tác giả:

Profile Hà Việt Anh
3
CHUYÊN ĐỀ: RÚT GỌN BIỂU THỨC CHỨA CĂN
VÀ BÀI TOÁN LIÊN QUAN
Các công thức biến đổi căn thức
1.
≥
= =
−
2
nÕu A 0
nÕu A < 0
A
AA
A
2.
.AB A B=
(Với
0; 0≥≥AB
)
3.
=
AA
B
B
(Với
0; 0≥>AB
)
4.
2
AB A B=
(Với
0≥B
)
5.
(Với
0; 0≥≥AB
)
6.
2
A B AB= −
(Với
0; 0<≥AB
)
7.
(Với
0; 0≥>AB
)
8.
=
A AB
B
B
(Với
0>B
)
9
( )
2
±
=
−
±
C AB
C
AB
AB
(Với
2
0;A B≥≠A
)
10
( )
±
=
−
±
CA B
C
AB
AB
(Với
0; 0;A B≥≥≠AB
)
11
( )
3
3
3
3
= =A AA
Cách tìm điều kiện trong bài toán chứa căn thức
BIỂU THỨC - ĐKXĐ: VÍ DỤ
1.
A
ĐKXĐ:
0≥A
Ví dụ:
2018−x
ĐKXĐ:
2018≥x
2.
A
B
ĐKXĐ:
0≠B
Ví dụ:
4
7
+
−
x
x
ĐKXĐ:
7≠x
3.
A
B
ĐKXĐ:
0>B
Ví dụ:
1
3
+
−
x
x
ĐKXĐ:
3>x
4.
A
B
ĐKXĐ:
0; 0≥>AB
Ví dụ:
3−
x
x
ĐKXĐ:
0
3
3
≥
⇔>
>
x
x
x
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
4
5.
A
B
ĐKXĐ:
0
0
0
0
≤
<
≥
>
A
B
A
B
Ví dụ:
1
2
+
+
x
x
ĐKXĐ:
10
20
2
1
10
20
+≤
+<
<−
⇔
≥
+≥
+>
x
x
x
x
x
x
6.
Cho a > 0 ta có:
2
>
>⇔
<−
xa
xa
xa
Ví dụ:
2
1>x
>
⇔
<−
xa
xa
7.
Cho a > 0 ta có:
2
< ⇔− < <x a ax a
Ví dụ:
2
42 2<⇔−<<xx
Dạng 1: Các bài toán biến đổi căn thức thường gặp
Thí dụ 1. (Trích đề thi HSG huyện Nghi Xuân Hà Tĩnh)
Tính giá trị của biểu thức:
A 6 25 14 65=− +−
Lời giải
Ta có:
( ) ( )
22
A 6 25 14 65 5 1 3 5 5 13 5 2= − + − = − + − = −+− =
Thí dụ 2. (Trích đề thi HSG tỉnh Lâm Đồng năm 2010-2011)
Cho
( )
3
3
3
21
E 21
3
−
= +
. Chứng minh rằng E là số nguyên
Lời giải
Ta có:
( )
( )
( )
( )
( )
3
3
3
3
33
2
3
333 3
3
21
21
E 21. 2132 21
33
1 2 4 21 211
−
−

= + = ++ +


= + + − = −=
=
22
(8 3 7) (8 3 7)− −+
Vậy E là số nguyên
Thí dụ 3. (Trích đề thi chọn HSG tỉnh Hòa Bình Năm 2010-2011)
Rút gọn:
44
4
8 21 8 21
A
8 21
+ −− − −
=
−+
.
Lời giải
Đặt
T
A
M
=
. Ta có T > 0 nên
2
TT=
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
5
Xét
2
4 44 4
T 8 21 2. 8 21. 8 21 8 21

=+−− +− −−+−−


( )
4
4
4
4
28 2 8 2 1
28 2 2 1
2 8 21
T 2 8 21
A2
= − −−
=−+

= −+



⇒= − +


⇒=
Thí dụ 4. (Trích đề thi HSG Phú Thọ năm 2012-2013)
Rút gọn biểu thức: A=
2 10 30 2 2 6 2
:
2 10 2 2 3 1
+−−
−−
Lời giải
Ta có:
2 10 30 2 2 6 2
:
2 10 2 2 3 1
+−−
−−
=
22(51) 6(51) 31 2 3 31 423 31 31 31 1
. . ..
2 2 2 4 2 2 22
2 2( 5 1)
−+−−+ −+ −+−
= = = =
−
Thí dụ 5. (Trích đề thi HSG T.P Bắc Giang năm 2016-2017)
Tính giá trị của biểu thức N =
43 43
27 10 2
4 13
++−
+−
+
Lời giải
Ta có: N=
2( 4 3 4 3)
25 10 2 2
8 2 13
++−
+− +
+
=
2
2( 4 3 4 3)
(5 2)
(43)24343(43)
++−
+−
+ + + − ++
2
2
2( 4 3 4 3) 2( 4 3 4 3)
(52) 52
43 43
( 4 3 4 3)
25 25
++− +
+−
= +
− = +−
++−
++−
= +− =
Thí dụ 6. (Trích đề thi Chọn HSG tỉnh Long An năm 2012)
Không sử dụng máy tính, hãy thực hiện phép tính:A =
2 3 4 15 10
23 3 5
−+− +
−
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
6
Lời giải
Ta có: A =
2 3 4 15 10
23 3 5
−+− +
−
2 2 3 4 15 10
2 23 3 5

−+− +


=

−


4 23 8 215 25
46 6 5
− +− +
=
−
( ) ( )
( )
22
2
3 1 5 3 25
35 1
−+ − +
=
−
3 1 5 3 25
35 1
−+ − +
=
−
35 1
1
35 1
−
= =
−
Thí dụ 7. (Trích đề thi HSG huyện Nga Sơn-Thanh Hóa năm 2016-2017)
Rút gọn biểu thức: B =
322
32
322
32
−−
−
+
++
+
Lời giải
Ta có:
B 23 23 2323
2 3
33 3
2 4 23 2 4 23
B (2 3)(3 3) (3 3)(2 3) 3 3 3 3
6
2 (3
3)(3 3)
B
1B 2
2
+ − +−
= +=+
+−
++ −−
+ − + + − + +−
= =
+−
=⇒=
Thí dụ 8. (Trích đề thi HSG huyện Thạch Hà năm 2016-2017)
So sánh
22
2017 1 2016 1−− −
và
Lời giải
Ta có:
2 22 2
22
22
( 2017 1 2016 1)( 2017 1 2016 1)
2015 1 2014 1
2017 1 2016 1
−− − −+ −
−− −=
−+ −
2 2 22
22 22 22
(2015 1) (2014 1) 2017 2016 (2017 2016)(2017 2016)
2017 1 2016 1 2017 1 2016 1 2017 1 2016 1
−− − − − +
= = =
−+ − −+ − −+ −
22 22
2017 2016 2.2016
2017 1 2016 1 2017 1 2016 1
+
= >
−+ − −+ −
Vậy
22
2017 1 2016 1−− −
>
22
2.2016
2017 1 2016 1−+ −
Thí dụ 9. Rút gọn các biểu thức:
22
2.2016
2017 1 2016 1−+ −
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
7
a)
33
A 5 3 29 12 5 b) B 70 4901 70 4901= −− − = − + +
Lời giải
( )
( )
2
a) A 5 3 29 12 5 5 3 2 5 3
5 51 1
= −− − = −− −
= − −=
b) Đặt
33
0
x 70 4901 70 4901=− ++
3
33
3
0
33 3 3
x 70 4901 70 4901
70 4901 70 4901 3 70 4901. 70 4901 70 4901 70 4901
140 3x

⇒= − + +



=− ++ + − + − + +


= +
Khi đó ta có:
( )
( )
32
00 0
x 3x 140 0 x 5 x 5x 28 0+ − =⇔ − ++ =
Mà
( )
2
00 0
x 5x 28 0 do 0 x 5+ + > ∆< ⇒ =
Vậy B = 5.
Thí dụ 10. Rút gọn biểu thức:
2 3 6 84
P
234
++++
=
++
Lời giải
Ta có:
( )
( )
( ) ( ) ( )
( )
232 468
2 3 6 84
P
234 2
34
234 468 234 2234
234 2
34
+++ ++
++++
= =
++ ++
++ + ++ ++ + ++
= =
++ ++
12= +
Dạng 2: Dùng ẩn phụ đơn giản hóa bài toán
Thí dụ 1. Rút gọn biểu thức:
4
4
4
4
4
1
7
2 67
7
A7 .
7 1 343
1
7
77
7
7
−
= −− + +

−
+



Lời giải
Đặt
4
4
a 7a7= ⇒=
và
2
a7=
ta có:
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
8
( )
2
22
2
3 32
2
42 6 4 24 2 4
4
32 32
1
a
2 6 7 1 2a 13a 7
a
Aa
1
aa
1
a a (a 1)
a
aa
a
a
a a 2a 2a 13a a 2a (7 a )
0 Do a 7
a (a 1) a (a 1)
−
−+
= −− + + = +

+
−
+


+− − + + −
= = = =
++
Thí dụ 2. Rút gọn biểu thức:
444
2
B.
4 3 5 2 25 125
=
−− −
Lời giải
Đặt
2 3 4 6 25
4 44
b 5 b 25,b 125,b 5,b 5b ,b 5b.= ⇒= = = = =
Ta có:
23
2
B
4 3b 2b 3b
=
−+ −
Mặt khác:
32
3 2 3 2 3 2 22
1 1 (b 3b) (2b 4)
b 2b 3b 4 (b 3b) (2b 4) (b 3b) (2b 4)
++ +
= =
−+− +−+ +−+
3 2 32 2 542
24
b 3b 2b 4 (b 2b 3b 4)(b 3) b 2b 2b 9b 12
8
2b6 2
(b9)
+++ +++ − +−−−
==−=
−− −
2
2
b 2b 1 b 1
.
42
− − − +
= =
−


Vậy
2
4
2 44
B2 .
b1 b1
51

= =
=

++
+

Thí dụ 3. Rút gọn biểu thức:
2
44
44
21
1
2
4 21 2
2
E.
12 2 12
++

−+
= +−


−+

Lời giải
Đặt
42
44
2a a 2,4a 2=⇒= ==
Ta có:
( )
2
22 2
2
24
2 22
22
21
1
a a 1a 1
a 1a 1 1
aa
E a0
1a a a
1a a
a
a1a
++

−+ +
+
= + − =−+ − = − =

−
+
+

Vậy E = 0
Dạng 3: Các bài toán về tính tổng dãy có quy luật
Thí dụ 1. Rút gọn:
11 1 1
S ....
2 1 1 2 3 2 2 3 1999 1998 1998 1999 2000 1999 1999 2000
= + ++ +
++ + +
Lời giải
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
9
Với
k N,k 1:∈≥
( )
( )
( ) ( )
( )
( )
( )
2
2
k1 kkk1 k1 kkk1
1 11
.1
kk 1
k1 kkk1 k
k1
k1.kkk1
+ −+ + −+
= = =
−
+
+ ++ +
+−+
Áp dụng (1) với k = 1, 2, 3,....., 1999 ta được
1 11
;
21 12 1 2
1 11
;
32 23 2 3
1 11
.
2000 1999 1999 2000 1999 2000
= −
+
= −
+
−−−−−−−−−−−−−
= −
+
Cộng các đẳng thức trên theo vế ta được:
11 1 1
S ....
2 1 1 2 3 2 2 3 1999 1998 1998 1999 2000 1999 1999 2000
1111 1 1
.....
1 2 2 3 1999 2000
= + ++ +
++ + +
= − + − ++ −
Thí dụ 2. Rút gọn:
222222 222222
111 111 1 1 1 1 1 1
A .... .
1 2 3 1 3 4 1 1998 1999 1 1999 2000
=++++++++ + ++ +
Lời giải
Với
k N,k 2:∈≥
( )
( )
2
22
11 1 1 2 2 2
11
k1k k1
k
k 1k
k
k1

+−=+ ++− −

−−
−

−
( )
( )
( )
( )
22
2
22
22
1 1 2 2 22
1
k1k1 k k
k
k1
1 1 11
11
k1k
k
k1
1 1 11
1 11
k1k
k
k1
=+ + + − +−
−−
−

⇒+ + = + −

−

−
⇒+ + =+ −
−
−
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
10
Áp dụng (1) với k = 1, 2, 3,....., 2000 ta được
11 11 1 1 1 1
A 1 1 ... 1 1 .
2 3 3 4 1998 1999 1999 2000
11
1998
2 2000
 
=+− ++− +++ − ++ −
 
 
= +−
Thí dụ 3. Rút gọn các biểu thức
111 1
...
12 23 34 1
A
nn


;
Lời giải
Ta có:
1 21
21
12
2 1 21
1 32
32
23
2 33 2
11
1
1
11
nn
nn
nn
nn nn









Do đó:
111 1
... 2 1 3 2 .... 1 1
12 23 34 1
A nn n
nn


Thí dụ 4.
a) Chứng minh rằng:
11 1
.... 4
1 2 3 4 79 80
+ ++ >
++ +
.
b) Chứng minh rằng:
111 1 1
... 2 1
12 23 34 1 1nn n

++++ >−

++

.
c) Chứng minh:
1111 1
2 2 ...
2 1
1234
nn
n
−<+++++< −
với mọi số nguyên
dương
2n ≥
.
Lời giải
a) Xét
11 1
....
1 2 3 4 79 80
A = + ++
++ +
,
11 1
..
2 3 4 5 80 81
B = + ++
++ +
Dễ thấy
AB>
.
Ta có
111 1 1
....
1 2 2 3 3 4 79 80 80 81
AB+=++++ +
+++ + +
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
11
Mặt khác ta có:
( )
( )( )
1
1
1
1
11
kk
kk
kk
k kk k
+−
= = +−
++
++ +−
Suy ra
( ) ( )
( )
2 1 3 2 ... 81 80 81 1 8AB+ = − + − + + − = −=
. Do
AB>
suy ra
2 84AAB A>+=⇔>
.
b) Để ý rằng:
( )
11 1 1
1 21
( 1) 1
k k kk
kk k k
−= <
++
+ ++
với mọi
k
nguyên dương.
Suy ra
1 11 1 1 1
21 2 .. 2 21
2 23 1 1
VT
nn n


> − + − ++ − = −


++


.
c) Đặt
1111 1
...
1234
P
n
=+++++
Ta có:
2 12 2
12 1nn n n nn
<= <
++ +
−
với mọi số tự nhiên
2n ≥
.
Từ đó suy ra
( ) ( )
222
21 2 1
12 1
n n nn
n n n nn
+− = < < = − −
++ + −
hay
( )
( )
2
21 2 1n n nn
n
+− < < − −
Do đó:
( )
( )
( )
2 2 1 3 2 ... 1n nT

−+−+++− <

và
( ) ( ) ( )
1 2 2 1 3 2 .... 1T nn

<+ − + − + − −

.
Hay
22 21nTn−< < −
.
Thí dụ 5. Chứng minh rằng với mọi số nguyên dương
2n >
, ta có:
14710 3 23 1 1
. . . .... .
3 6 9 12 3 3 3
31
nn
nn
n
−+
<
+
+
.
Lời giải
Để ý rằng các phân số có tử và mẫu hơn kém nhau 2 đơn vị, nên ta nghĩ đến đẳng thức
( )
22
1
22
2
nn
nnn n
nn
−
< ⇔ < +−⇔>
+
. Kí hiệu
14710 3 23 1
. . . .... .
3 6 9 12 3 3 3
nn
P
nn
−+
=
+
. Ta có:
2
14710 3 23 1 14710 3 23 1
. . . ... . . . . ... .
3691233336912333
nn nn
P
nn nn
−+ −+

=

++

THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
12
136 9 3 3 3 14710 3 23 1
. . . ... . . . . ... .
3 4 7 10 3 2 3 1 3 6 9 12 3 3 3
n n nn
n n nn
− −+
<
−+ +
11367 9 3 33 2 3 3 1
..... ... . . .
3 3 4 7 9 10 3 2 3 3 1 3 3
n n nn
n nn n
−− +
<
− ++
( ) ( )
11
33 3 9 1nn
= =
++
.
Từ đây suy ra
1
31
P
n
<
+
. Bất đẳng thức được chứng minh.
Dạng 4: Bài toán rút gọn biểu thức chứa một hay nhiều ẩn
Thí dụ 1. Rút gọn:
( )
2
4
44
21
1
a
a a1 a
a
B a 0,a 1 .
1a a 1a
++

−+
= + − >≠


−+

Lời giải
Đặt
( )
24
4
t a t 0 a t ,a t= >⇒ = =
Khi đó:
2
22
24
2
21
1
t t 1t
tt
B
1t t
1t
++

−+
=+−

−
+

( )
( )
2
2
2
2
2
22
2
2 22
22
1
1
1
1
tt 1
t
11
t
t tt
1t t t
1t 1t
1 t1 11
t tt
tt 1
0

+

+

−


= ++ − =−++ −


−
++



+
=−=−
+
=
Thí dụ 2. (Trích đề thi HSG tỉnh Hải Dương năm 2012-2013)
Rút gọn biểu thức:
2
A = x 50 x + 50 x + x 50

−− −


với
x 50≥
Lời giải
Ta có :
(
)
(
)
(
)
(
)
(
)
( )
2
2 22 2 2
2 2 2 2 22
A = x - 50 - x + 50 x + x -50 A = x - 50 + x + 50 - 2 x -50 x + x -50
A = 2x -2 x -50 x + x -50 A = 2 x - x +50

⇒


⇒⇒
Vậy:
2
A =100
Nhưng do theo giả thiết ta thấy
2
A = x - 50 - x + 50 x + x -50



< 0
A= -10⇒
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
13
Thí dụ 3. (Trích đề thi HSG Hải Dương năm 2013-2014)
Rút gọn biểu thức
(
)
23 3
2
1 1 x . (1 x) (1 x)
A
2 1x
−− + + −
=
−−
với
1x1−≤ ≤
.
Lời giải
Ta có:
( )
(
)
22
2
1 1x. 1x 1x 2 1x
A
2 1x
−− ++− −−
=
−−
( )
2
1 1x. 1x 1x= − − ++ −
(
)
( )
(
)
(
)
2
2 22
1 1x 1x 1x 1 1x 221x= −− ++− = −− + −
2
2x=
=
x2
Thí dụ 4. (Trích đề thi HSG T.P Bắc Giang năm 2016-2017)
Cho a, b là số hữu tỉ thỏa mãn
(
)
( )
2
22
a b 2ab+− +
+
2
(1 ab) 4ab−=−
Chứng minh
1 ab+
là số hữu tỉ
Lời giải
Ta có:
( ) ( )
( )
( )

⇒ + − + + ++ =


⇔+−+ +++ =

⇔ + −+ =⇒+ +


⇔ + =+ ⇔+= + ∈ ∈
22
2
4
22
2
2
2
2
(GT) a b 2(ab 1) (a b) 1 ab 0
a b 2(a b) (1 ab) (1 ab) 0
a b (1 ab) 0 (a b) -(1 ab)=0
(a b) 1 ab a b 1 ab Q; do: a;b Q
Thí dụ 5. (Trích đề thi HSG T.P Bắc Giang năm 2016-2017)
Cho biểu thức M=
aa bb a b
ab
ab ba
−
−−
−
+−
với a, b > 0 và a
≠
b
Rút gọi M và tính giá trị biểu thức M biết
( )( )
1 a 1 b 2 ab 1− −+ =
Lời giải
Rút gọn M=
ab
ab−
với a, b > 0 và a
≠
b
Ta có
( )( )
( )
−−+=⇔−−++=

⇔= − ⇔ =⇔ =


−−

2
2
1 a 1 b 2 ab 1 ab a b 1 2 ab 1
ab ab
ab a b 1 1
ab ab
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
14
+ Nếu a > b > 0
ab
a b a b0;ab0 0
ab
ab ab ab
1 M1
ab ab ab
⇒ > ⇒ − > >⇒ >
−
⇒ = ⇒ =⇒=
−− −
+ nếu 0 < a < b
ab
a b a b 0; ab 0 0
ab
ab ab ab
1M 1
ab ab ab
⇒ < ⇒ − < >⇒ <
−
−−
⇒ = ⇒ =⇒=−
−− −
Dạng 4: Bài toán rút gọn biểu thức và bài toán liên quan
Bước 1:
Tìm điều kiện xác định.
Bước 2:
Tìm mẫu thức chung, quy đồng mẫu thức, rút gọn tử, phân tích
tử thành nhân tử.
Bước 3:
Chia cả tử và mẫu cho nhân tử chung của tử và mẫu.
Bước 4:
Khi nào phân thức tối giản thì ta hoàn thành việc rút gọn.
Dạng 1. Tính giá trị biểu thức P khi cho x = k (k là hằng số)
Phương pháp:
- Bước 1: - Đặt điều kiện của x để biểu thức P có nghĩa.
- Bước 2: - Rút gọn biểu thức P và rút gọn k nếu cũng là một biểu thức chứa căn phức tạp
- Bước 3: Thay giá trị x = k vào biểu thức đã rút gọn rồi tính ra kết quả.
Ví dụ minh họa:
Thí dụ 1. Cho biểu thức:
1x x
P:
x x1 x x

= +


++

, với x > 0.
a) Rút gọn biểu thức P.
b) Tìm giá trị của P khi x
= 4.
Lời giải
a) Điều kiện:
>x0
( )
( )
x1 x
1 x x xx
xx1
P: .
x x1 x x x
x
x x1
++

+ ++
=+= =


++
+

b) Ta có khi x = 4 thì:
x x14 414217
P
22
x4
++++++
= = = =
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
15
Thí dụ 2. (Trích đề thi HSG huyện lớp 9 năm 2013-2014)
Cho biểu thức:
xy xy
x y 2xy
P :1
1 xy
1 xy 1 xy

+−

++

=++


−
−+


.
a) Rút gọn biểu thức P.
b) Tính giá trị của P với
2
x
23
=
+
.
Lời giải
a) ĐKXĐ:
x 0;y 0;xy 1≥≥ ≠
.
Mẫu thức chung là 1 – xy
( x y)(1 xy) ( x y)(1 xy)
1 xy x y 2xy
P:
1 xy 1 xy
+ + +− −
− +++
=
−−
x xy y yx x xy y yx
1 xy
.
1 xy 1
x y xy
++++−−+
−
=
− ++
+
2( x y x)
2 x(1 y)
2x
(1 x)(1 y) (1 x)(1 y) 1 x
+
+
= = =
++ ++ +
b) Ta có:
2
2 2(2 3)
x 3231(31)
43
23
−
= = =− += −
−
+
2
x (31) 31 31= − = −= −
2
2( 3 1) 2 3 2
P
1 ( 3 1) 1 3 2 3 1
2( 3 1) 6 3 2
P
13
5 23
−−
= = =
+ − +− +
−+
= =
−
Thí dụ 3. (Trích đề thi HSG tỉnh Thanh Hóa năm học 2011-2012)
Cho biểu thức P =
x1 x8 3x11 1
:
10 x
3 x1 x3x11 x1

− + −+
+−


−
+ − −
−− −

1) Rút gọn P
2) Tính giá trị của P khi x =
44
3 22 3 22
3 22 3 22
+−
−
−+
Lời giải
Điều kiện:
1 x 10<≠
1)
3x19 1 2x14
P :.
10 x
x1 x13

−+ −
+
=

−
− −−


THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
16
( )
x1. x13
3( x 1 3)
P.
10 x
2x1 4
− −−
−+
=
−
−+
3 x 1(x 10)( x 1 2) 3(x 2)
P
2(10 x)(x 1 4) 2(x 5)
− − −− −
= =
−
− −− −
2)
22
44
44
3 22 3 22
x (
3 22) (3 22) 3 22 3 22
3 22 3 22
+−
= − = + − − =+ −−
−+
=> x =
1 2(21)2+ − −=
vì x>1
Vậy P = 0
Dạng 2. Tìm giá trị của biến x để biểu thức P = k (k là hằng số)
Phương pháp:
- Bước 1: - Đặt điều kiện của x để biểu thức P có nghĩa.
- Bước 2: - Rút gọn biểu thức P.
- Bước 3: - Giải phương trình P – k = 0.
- Bước 4: Đối chiếu điều kiện của x và kết luận.
Ví dụ minh họa:
Thí dụ 1. Cho
2 39
9
33
x xx
P
x
xx
+
=+−
−
+−
, với
0, 9xx≥≠
.
1) Rút gọn
P
.
2) Tìm giá trị của
x
để
1
3
P =
.
Lời giải
1)
( ) ( )
( )( )
32 339
3
3
33
xx xx x
P
x
xx
−+ +− −
= =
+
−+
2)
1 31
3 9 36
33
3
P xx
x
= ⇔ = ⇒ +=⇔ =
+
(thỏa mãn ĐKXĐ)
Thí dụ 2. (Trích đề thi HSG Ninh Bình năm học 2012-2013)
Cho biểu thức: P =
2
x - x 2x + x 2(x - 1)
- + (x > 0, x 1).
x + x + 1 x x - 1
≠
1. Rút gọn P.
2. Tìm giá trị của x để P = 3.
Lời giải
1/Ta có:
3
x( x 1) x(2 x 1) 2( x 1)( x 1)
P
x x1 x x1
− + −+
=−+
++ −
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
17
x( x 1)(x x 1)
2 x 1 2( x 1)
x x1
− ++
= − −+ +
++
x x1=−+
2/ Ta có: P = 3
⇔
x x1−+
= 3
⇔
x x20− −=
Đặt
x
= t,
t0≥
ta được pt
2
t 1 (L)
t t20
t 2 (TM)
=−
−− = ⇔
=
Ta có t = 2 ta được
x
= 2
⇔
x = 4 (thỏa mãn ĐK).
Vậy x = 4 thì P = 3.
Thí dụ 3. (Trích đề thi HSG tỉnh Hà Nam năm 2012-2013)
Cho biểu thức:
y xy
x
P
( x y)(1 y) ( x y)( x 1) ( x 1)(1 y)
=−−
+ − + + +−
1. Rút gọn biểu thức P.
2. Tìm các giá trị x, y nguyên thỏa mãn P = 2.
Lời giải
1) Điều kiện :
x 0;y 0;y 1;x y 0≥ ≥ ≠ +≠
.
( )
( )( )
( )
x(1 x) y(1 y ) xy x y
P
x y1x1y
+ −− − +
=
+ +−
( ) ( )
( )
( )( )
(x y) x x y y xy x y
x y1x1y
−+ + − +
=
++−
( )
( )
( )
( )
( )
x y x y x xy y xy
x y1x1y
+ − +− +−
=
++−
( )
( )
( )
( )
( )
( )
xx1 yx1 y1 x1 x
1x1y
+− ++ + −
=
+−
( )
x y y yx
1y
− +−
=
−
( )( ) ( )
( )
x1y1y y1y
1y
− +− −
=
−
x xy y=+−
2) P = 2
⇔
x xy y+−
= 2 với
x 0;y 0;y 1;x y 0≥ ≥ ≠ +≠
( )
( )
( )
( )
x1y y11 x11y1⇔ +−+=⇔−+=
Ta có: 1 +
y1≥
⇒
x11−≤
0x4⇔≤≤
⇒ x = 0; 1; 2; 3 ; 4
Thay vào P ta được các cặp giá trị (4;0) và (2;2) thỏa mãn.
Dạng 3. Tìm giá trị của biến x để biểu thức P = A (A là biểu thức chứa ẩn)
Phương pháp:
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
18
- Bước 1: - Đặt điều kiện của x để biểu thức P có nghĩa.
- Bước 2: - Rút gọn biểu thức P.
- Bước 3: - Giải phương trình P – A = 0.
- Bước 4: Đối chiếu điều kiện của x và kết luận.
Ví dụ minh họa:
Thí dụ 1. Cho biểu thức
21 1
.
2 21
xx
P
x xx x
−+

= +

+ +−

với
0x >
và
1x ≠
.
a) Chứng minh rằng
1x
P
x
+
=
.
b) Tìm các giá trị của
x
để
22 5Px= +
.
Lời giải
a) Ta có:
( )
( ) ( )
( )
1. 2
2 1 11
..
11
22
xx
x xx x x
P
x xx
xx xx

−+
−+ + + +

= = =

−−
++

.
b) Theo câu a)
1x
P
x
+
=
22
225 25
x
Px x
x
+
⇒ = +⇔ = +
2 225 23 20x xxxx+= + ⇔ + −=
và
0x >
( )
1 11
20
2 24
xx xx

⇔ + − =⇔ =⇔=


.
Dạng 4. Tìm giá trị của ẩn đê biểu thức thỏa mãn một bất đẳng thức A > k
≥≤<( ; ; k)
với k là hằng số.
Phương pháp:
- Bước 1: - Đặt điều kiện của x để biểu thức A có nghĩa.
- Bước 2: - Rút gọn biểu thức A.
- Bước 3: - Giải bất phương trình A– k > 0.
- Bước 4: Đối chiếu điều kiện của x và kết luận.
Ví dụ minh họa:
Thí dụ 1. Cho biểu thức
11
1 21
x
A
xx x x x

= −÷

+ + ++

, với
0x >
.
a) Rút gọn biểu thức
A
.
b) Tìm các giá trị của
x
để
1
2
A >
.
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
19
Lời giải
a) Với
0x >
, ta có
( )
( ) ( )
22
21 1
11 1
1 ( 1)
1
xx x
x
x x xx x
A
xx

++ +
−

−⋅ = ⋅

++

=
+
(1 )( 1) 1
.
xx x
xx
− +−
= =
b) Với
0x >
, ta có
11 1 2
22 3 2 .
22 3
x
A xx x x
x
−
>⇔ >⇔− >⇔ <⇔<
Vậy các giá trị
x
cần tìm là
2
0
3
x<<
.
Thí dụ 2. Cho biểu thức
2
4 21
1 32
xx x
M
x
x xx

−−
=−⋅


−−+

, với
0x >
,
1x ≠
,
4x ≠
.
a) Rút gọn
M
.
b) Tìm
x
để
4M <
.
Lời giải
Điều kiện
0x >
,
1x ≠
,
4x ≠
. Ta có
( )
( )
2 22
4 2 141 141
.
11
12
x x x xx x
x xx
xx
xx
M

− − −− −

− ⋅=⋅=

−−
−−

=
Ta có
0x >
nên
2
0x >
khi đó
22
2
41 1
4 4 4 4 1 0 (2 1) 0 .
2
x
M x
x x x
x
−
<⇔ <⇔ − +>⇔ − >⇔≠
Vậy với
0x >
,
1
2
x ≠
,
1x ≠
,
4x ≠
thì
4M <
.
Thí dụ 2. Cho biểu thức
( )
3 3 3 12 2 27 ,A = −+
11
11
xx xx
B
xx

+−
=+ ⋅−


+−

0, 1.vôùi xx>≠
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
20
a) Rút gọn biểu thức
A
và
B
.
b) Tìm các giá trị của
x
sao cho
0AB⋅≤
.
Lời giải
a) Ta có
( ) ( )
3 3 3 12 2 27 3 3 6 3 6 3 3.A = − + = −+ =
Với
0x >
và
1x ≠
, ta có
21 21
11
1 111
xx xxxx xx
x xx x
B

+ − ++−+−
=+ ⋅− = ⋅


+ −+ −

(
) ( )
( ) ( )
22
11
1 11
11
xx
xx x
xx
+−−
= ⋅ =− +⋅ −=−
+−
( )
0 31 0 1AB x x⋅≤⇔ − ≤⇔≥
.
Vậy
1x ≥
thỏa yêu cầu bài toán.
Dạng 5. So sánh biểu thức A với k (hằng số) hoặc với biểu thức B (chứa ẩn)
Phương pháp:
- Bước 1: - Đặt điều kiện của x để biểu thức A có nghĩa.
- Bước 2: - Rút gọn biểu thức A.
- Bước 3: - Xét dấu của hiệu A – k hoặc A – B và đưa ra kết luận.
Ví dụ minh họa:
Thí dụ 1. Cho biểu thức
( )
2
1
6 10 2
1
14
a
a
B
a
aa a a a
−

−
=+⋅


−
−− +

(với
0, 1aa>≠
).
a) Rút gọn biểu thức
B
.
b) Đặt
( )
1C Ba a= −+
. So sánh
C
và
1
.
Lời giải
a) Ta có
( ) ( ) ( )
( )
1 1 1 11aa a a a a a a a−− += − − − = − −
.
Do đó
( )
( )
( )
2
1
6 10 2
1
4
11
a
a
a
a
aa
B

−
−

=+⋅

−
−−

( )
( )
( )
( )
2
2
6 1 10 2 1
4
11
a aa
a
aa
−+ − −
= ⋅
+⋅ −
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
21
44 1
.
4 ( 1)
a
aa a
+
= =
+
b) Ta có
11
1 2 1 1.
aa
Ca
aa
−+

= = + −≥ −=


Đẳng thức xảy ra khi
1a =
(loại). Vậy
1.C >
Ví dụ 2: Cho biểu thức
11 1
:
1 21
a
M
aa a a a
+

= +

− − −+

với
0a >
và a
1≠
.
a) Rút gọn biểu thức
M
.
b) So sánh
M
với 1.
Lời giải
a) Điều kiện:
0a >
và
1a ≠
11 1
:
1 21
a
M
aa a a a
+

= +

− − −+

( )
( )
2
11 1
:
1
1
1
a
a
aa
a

+

= +

−
−
−

( )
( ) ( )( )
( )( )
22
11 1
1
.
1
1 11
1
a aa
a
a
aa aa a
a
a
−+−
+
= =
+
− −+
−
=
b) Xét hiệu:
11
1 10
a
M
aa
−−
−= −= <
với
0a >
và
1a ≠
Vậy
1M <
.
Ví dụ 3: Cho biểu thức
2
1 11
.
2
1 12
xx x
P
xx x

−+
=−−


+−

.
a) Rút gọn biểu thức
.P
b) So sánh
P
với
2 x−
.
Lời giải
a) Điều kiện:
0 ; 1.xx>≠
( )
( )
( )
( )
22
2
2
2
11
1 11 1
..
2
1 12 2
11
4 11
.
1
2
xx
xx x x
P
xx x x
xx
xx x
x
xx
−− +

−+ −

= − −=



+−
+−


− −−

= =

−

Vậy
1 x
P
x
−
=
với
0 ; 1.xx>≠
b) Xét hiệu
( )
11
22
xx
Px x
xx
−+
−− = + =
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
22
Với
( )
1
0; 1 0 2 0
x
xx P
x
x
+
> ≠ ⇒ > ⇒ −− >
2Px⇒ >−
.
Dạng 6. So sánh biểu thức rút gọn
A
với
A
hoặc
2
A
với
A
.
Phương pháp:
Bước 1: + Xác định điều kiện của
x
để
0A >
(nếu
A
chưa phải biểu thức dương)
Bước 2: + So sánh
A
với 1 bằng cách xét hiệu
1A−
theo điều kiện
x
đã có:
Bước 3: - Nếu
01A<<
thì
AA>
.
Bước 4: - Nếu
1A >
thì
AA<
.
+ Chú ý: Dạng này còn có biến thể là so sánh biểu thức rút gọn
A
với
2
A
(chỉ xét với biểu
thức
A
dương).
Ví dụ 1: Cho biểu thức
1 1 2 12
:
1
11
x x xx x x
A
x
x x x
x

+ − +−

=−+



−
−+


với
1
0; ; 1
4
xx x>≠ ≠
.
a) Rút gọn biểu thức
A
.
b) So sánh
A
với
A
.
Lời giải
a) Điều kiện:
1
0; ; 1.
4
xx x>≠ ≠
1 1 2 12
:
1
11
x x xx x x
A
x
x x xx

+ − +−

=−+



−
−+


( )
( )( )
( )( )
( )( )
( )
( )
12 1 12 1
21
:
11 1 1 1
xxxxx
x
x x x x x xx

+− +−
−

= +

− − + + −+

( )
( )
21 1
:2 1
11
1
xx
x
x xx
xx


−
= −+



− −+
−



( )
( )
( )
( )
( )
11
21
:2 1:
1 11
xx x x
x
x
x x x xx
− ++ −
−
= −
− − −+
( )
( )
( )
11
:
11 1
1
x x x xx
xx
x
=
− − −+
−+
=
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
23
b) Biến đổi
11
1
xx
Ax
xx
−+
= =+−
.
Áp dụng BĐT cosi có:
1
2x
x
+>
với mọi
1
0; ; 1
4
xx x>≠ ≠
( )
1
11 1 10 1 0A x A A AA
x
⇒ = + −>⇒ >⇒ −> ⇒ − >
0AA AA⇒ − >⇒ >
.
Ví dụ 2: Cho biểu thức
12
:.
4
22
x
A
x
xx

= −


−
−−

a) Rút gọn biểu thức
.A
b) So sánh
A
với
2
A
.
Lời giải
a) Điều kiện:
0 ; 4.xx>≠
( )
( )
( )
( )
12 2 2
:.
42
22
22
22 2 1
.
2
2
22
x x
x x
A
x
xx
xx
x xx
x
xx

++ −
=−=


−
−−
−+

+ −+
= =
+
−+
b) Với mọi
0; 4xx>≠
thì
.
Mà
1
12 1
2
x
xxA
x
+
+< + ⇒ = <
+
Vậy
01A<<
với mọi
0; 4xx>≠
2
AA⇒<
với mọi
0; 4xx>≠
.
Dạng 7. Chứng minh với mọi giá trị của x và thì A > k
≥≤<( ; ; k)
với k là hằng số
Phương pháp:
- Bước 1: - Đặt điều kiện của x để biểu thức A có nghĩa.
- Bước 2: - Rút gọn biểu thức A.
- Bước 3: - Chứng minh hiệu A– k > 0
∀x
Thí dụ 1. (Trích đề Thi HSG huyện Bình Giang năm 2012-2013)
Cho biểu thức:
x2 x1 1
A
xx 1 x x 1 1 x
++
=++
− ++ −
với
x0,x1≥≠
1) Rút gọn A
2) Chứng tỏ rằng:
1
A
3
<
Lời giải
Ta có:
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
24
1)
( )
( )
x2 x1 1
A
x x1 x1
x1x x1
++
= +−
++ −
− ++
( )( )
( )( )
x2x1x x1
A
x1x x1
xx
A
x1x x1
++−−− −
=
− ++
−
=
− ++
( )
( )( )
x x1
x
A
x x1
x1x x1
−
= =
++
− ++
, với
x0,x1≥≠
2) Xét
( )
2
x1
11 x
A
33
x x1 3(x x1)
−
−=− =
++ ++
Do
x0,x1≥≠
( )
2
2
13
x 1 0 và x x 1 x 0
24

⇒ − > + += + + >


1
A0
3
⇒− >⇔
1
A
3
<
Thí dụ 2. (Trích đề thi HSG huyện Cam Lộ)
Cho biểu thức: P =
1
x +1 x x +1 x- x +1
32
−+
a) Rút gọn P.
b) Chứng minh P
≥
0.
Lời giải
a)
ĐKXĐ:
x0≥
P =
1
x +1 x x +1 x- x +1
32
−+
=
( )
( )
1
x +1 x
- x +1
x +1 x- x +1
32
−+
=
( )
( )
( )
( )
( )
x- x +1 x +1
x+ x
x +1 x- x +1 x +1 x- x +1
32−+
=
=
x
x- x +1
b)
x
0≥
x- x
1+
= x
2
1 33
2 44

− +≥


THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
25
Do đó: P=
x
x- x +1
0≥
Thí dụ 3. (Trích đề thi HSG T.P Đà Nẵng năm học 2013-2014)
Cho biểu thức:
2
a 1 aa 1 a aa a 1
M
a a a a aa
+ − − +−
=++
−−
với a > 0, a ≠ 1.
Chứng minh rằng
M 4.>
Lời giải
Do a > 0, a ≠ 1 nên:
a a 1 ( a 1)(a a 1) a a 1
a a a( a 1) a
− − ++ ++
= =
−−
và
2
a a a a 1 (a 1)(a 1) a(a 1) (a 1)(a a 1) a a 1
a a a a(1 a) a(1 a) a
− +− + −− − − −+ −+−
= = =
− −−
⇒
a1
M2
a
+
= +
Do
a 0; a 1>≠
nên:
2
( a 1) 0 a 1 2 a− > ⇔ +>
⇒
2a
M 24
a
> +=
Dạng 8. Tìm giá trị của x để biểu thức thỏa mãn một bất đẳng thức A > B
≥≤<( ; ; B)
với B là biểu thức chứa ẩn.
Phương pháp:
- Bước 1: - Đặt điều kiện của x để biểu thức A có nghĩa.
- Bước 2: - Rút gọn biểu thức A.
- Bước 3: - Giải bất phương trình A– B > 0.
- Bước 4: Đối chiếu điều kiện của x và kết luận.
Ví dụ minh họa:
Thí dụ 1. Cho biểu thức
1
:
44 2 2
x xx
A
xx xxx
+

= +

++ + +

, với
0x >
.
a) Rút gọn biểu thức
A
.
b) Tìm tất cả các giá trị của
x
để
1
3
A
x
≥
.
Lời giải
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
26
Ta có
2
11
::
4 4 2 2 ( 2) ( 2) 2
x xx x x x
A
xx xxx x xx x

++

= += +


++ + + + + +


2
1
:
( 2) 2 2
x xx
x xx

+
= +


+ ++

22
2
1 1 (1 )
::
( 2) 2 ( 2) 2
1 21
.
( 2) (1 ) ( 2)
xxxxxx
xxx x
xx
x x x xx
++ + +
= =
+++ +
++
=⋅=
++ +
Ta có
1 1 1 11
( 0)
3
3 ( 2) 3 2
A do
x
xxx xx
≥⇔ ≥⇔ ≥ >
++
2 3 0 1 0 1.x xx⇔ +≤⇔< ≤⇔<≤
Vậy để
1
3
A
x
≥
thì
01x<≤
.
Thí dụ 2. Cho hai biểu thức
4
1
x
A
x
+
=
−
và
31 2
23 3
x
B
xx x
+
= −
+− +
với
0x
,
1x ≠
.
a) Tính giá trị của biểu thức
A
khi
9x =
.
b) Chứng minh
1
1
B
x
=
−
.
c) Tìm tất cả giá trị của
x
để
5.
4
Ax
B
+
Lời giải
a) Với
9x =
ta có
7
2
A =
.
b) Với
0x
,
1x ≠
ta có
31 2 31 2312(1)1
.
2 3 3 ( 3)( 1) 3 ( 3)( 1) 1
x x x
x
xx x xx x xx x
B
+ + +−
−
−= −= =
+− + +− + +− −
=
c) Ta có
41
:4
11
Ax
x
B
xx
+
= =
+
−−
.
( )
2
5 4 4 0 2 0 4.
4
Ax
xx x x
B
+⇔− + ⇔ − ⇔= 
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
27
Dạng 9.
Tìm giá trị của ẩn để biểu thức nhận giá trị nguyên
Phương pháp 1: Đưa về biểu thức về dạng chứa phân thức mà tử nguyên, tìm giá trị ẩn để
mẫu là ước của tử.
- Bước 1: - Đặt điều kiện của x để biểu thức A có nghĩa.
- Bước 2: - Rút gọn biểu thức A và đưa về dạng phân thức có tử là số nguyên.
- Bước 3: - Lý luận để biểu thức là số nguyên thì mẫu số phải là ước của tử, từ đó tìm giá
trị ẩn.
- Bước 4: Đối chiếu điều kiện của x và kết luận.
Ví dụ minh họa:
Thí dụ 1. Cho biểu thức
32
9
33
−
=−−
−
−+
aa
A
a
aa
với
0, 9aa≥≠
.
a) Rút gọn
A
.
b) Tìm các số nguyên
a
để
A
nhận giá trị nguyên.
Lời giải
a) Với
0, 9aa≥≠
, ta có
( )
( )
33 3
3 2 2 11
9 9 9 99
33
+−
−−
− −= − −=
− − − −−
−+
=
aa a
aa a
a a aa
A
a
aa
b)
11
9
∈=
−
a
A
khi và chỉ khi 11 chia hết cho
9a −
. Do đó
9 1 10
91 8
9 11 20
9 11 2 (l).
aa
aa
aa
aa
−= =


−=− =

⇔

−= =

−=− =−

Vậy
{8;10;20}a∈
thì
A
nhận giá trị nguyên.
Thí dụ 2. (Trích đề thi HSG huyện Thanh Oai 2014-2015)
Cho biểu thức A =
x 5 x 25 x x 3 x 5
1:
x 25
x 2 x 15 x 5 x 3

− − +−
− −+


−
+− + −

1. Rút gọn A
2. Tìm số nguyên x để A nguyên
Lời giải
1)
Điều kiện
x 0,x 25,x 9≥≠ ≠
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
28
Rút gọn
5
A
x3
=
+
2) x
∈
z =>
x3+
là Ư(5)
=>
x 3 1 (loai)
x35 x4
+=
+==>=
Thí dụ 3. (Trích đề thi HSG huyện Thanh Oai năm 2015-2016)
Cho
x x3 x2 x2
M1 :
x1 x23 x x5x6

++ +
=− ++


+ − − −+

1) Rút gọn M
2) Tìm giá trị nguyên của x để biểu thức M nhận giá trị là số nguyên
Lời giải
ĐKXĐ:
( )
x 0;x 4,x 9 *≥≠≠
1) Rút gọn M: Với
( )
x 0;x 4,x 9 *≥≠≠
Rút gọn ta được:
x2
M
x1
−
=
+
2)
x2 x13 x1 3 3
M1
x1 x1 x1 x1 x1
− +− +
= = =−=−
+ + ++ +
Biểu thức M có giá trị nguyên khi và chỉ khi:
( ) ( )
( )
3 x1 x1 U3+⇒ +∈
Ư(3)
{ }
1; 3∈± ±
Vì
≥⇒ ≥⇒ +≥x0x0x11
Nên
{ }
x 1 1; 3+∈
Xảy ra các trường hợp sau:
)x11 x 0 x0+ +=⇔ = ⇔ =
(TMĐK (*))
)x13 x 2 x4+ += ⇔ = ⇔ =
. (không TMĐK (*) loại )
Vậy x = 0 thì M nhận giá trị nguyên.
Phương pháp 2: Đánh giá khoảng giá trị cùa biểu thức, từ khoảng giá trị đó ta có các giá
trị nguyên mà biểu thức có thể đạt được.
- Bước 1: - Đặt điều kiện của x để biểu thức A có nghĩa.
- Bước 2: - Rút gọn biểu thức A.
- Bước 3: - Đánh giá khoảng giá trị mà biểu thức A có thể đạt được, từ khoảng giá trị đó ta
có các giá trị nguyên mà biểu thức A có thể đạt được.
1
2
+
−
=
x
x
M
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
29
- Bước 4: Giải phương trình vế trái là biểu thức A đã rút gọn, vế phải là các giá trị nguyên
nằm trong miền giá trị của A, đối chiếu điều kiện và kết luận.
Thí dụ 1. Cho biểu thức
2 24
9
3
= +
−
−
−xx
x
A
x
và
7
8
=
+
B
x
với
0,x 9≥≠x
.
a) Rút gọn
A
.
b) Tìm các số nguyên
x
để
.=P AB
nhận giá trị nguyên.
Lời giải
a) ta có:
( )
( )( ) ( )( )
( )( )
( )
( )
. 3 2 24
5 24
3
33 33
38
8
3
33
2 24
9
++ −
+−
=+= =
−
+− +−
−+
−
+
= =
+
+−
−
xx x
xx
A
xx xx
xx
x
x
x
x
x
x
xx
b) ta có:
87 7 7
.. 0
3
38 3
+
= = = ⇒< ≤
++ +
x
P AB P
xx x
Vậy các giá trị nguyên mà P có thể đạt được là 1 và 2.
Với P = 1 ta có:
( )
7
1 3 7 4 16
3
=⇒ +=⇒=⇒=
+
x x x TM
x
Với P = 2 ta có:
( )
7 11
2 2 67
24
3
=⇒ +=⇒ = ⇒=
+
x x x TM
x
Thí dụ 2. (Trích đề thi HSG tỉnh Hải Phòng năm 2016-2017)
Cho biểu thức
+ − − +−
=++
−−
2
a 1 aa 1 a aa a 1
B
a a a a aa
với a > 0, a ≠ 1.
Với những giá trị nào của a thì biểu thức
=
6
A
B
nhận giá trị nguyên?
Lời giải.
Với điều kiện
a 0; a 1>≠
thì:
( )
( )
( )
( )
( )
( )
( )
( )
− ++ − + −+
+
=+−
− −+
a1a a1 a1 a1a a1
a1
B
a
a a1 a a1 a1
( )
+
+ ++ −+
=+−=
2
a1
a1a a1a a1
B
aa a a
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
30
Khi đó
( )
= = >
+
2
6 6a
A0
B
a1
. Ta thấy với
0a1 a a10<≠⇒− +>
( )
( )
2
2
6a
a 1 3a 2
a1
⇔ +> ⇔ <
+
Do
0N2<<
Để N có giá trị nguyên thì N = 1.
⇔
6a
1
a 2a 1
=
++
⇔
⇔
( )
2
a 3 2 a 7 4 3( )
a2 3
a 3 2 a 7 4 3( )

=+=+
−=⇔ ⇔


=−+ =−

tháa m·n
tháa m·n
Vậy
a 7 4 3.= ±
Thí dụ 3. (Trích đề thi HSG tỉnh Vĩnh Phúc năm 2011-2012)
Cho biểu thức
2
x 2x x 1 1 2x 2x
P
xx 1 xx x x x x
− + +−
=++
− ++ −
Tìm tất cả các giá trị của
x
sao cho giá trị của P là một số nguyên.
Lời giải
Điều kiện:
x 0, x 1>≠
. Khi đó ta có
Rút gọn biểu thức ta được
x2
P
x x1
+
=
++
Ta có
( )
Px P 1 x P 2 0+ − +−=
, ta coi đây là phương trình bậc hai của
x
. Nếu
P0 x20= ⇒− − =
vô lí, suy ra
P0≠
nên để tồn tại
x
thì phương trình trên có
( ) ( )
2
P 1 4P P 2 0∆= − − − ≥
( )
2
22
44
3P 6P 1 0 P 2P 1 P 1
33
⇔− + +≥ ⇔ − +≤ ⇔ − ≤
Do P nguyên nên
( )
2
P1−
bằng 0 hoặc 1
+) Nếu
( )
2
P1 0 P1 x1− =⇔=⇔=
không thỏa mãn.
+) Nếu
( )
2
P2
P1 1 P22xx0x0
P0
=
− =⇔ ⇒=⇔ + =⇔=
=
không thỏa mãn
Vậy không có giá trị nào của x thỏa mãn.
Phương pháp 3: Đặt biểu thức bằng một tham số nguyên, tìm khoảng giá trị của tham số,
từ khoảng giá trị đó ta xét các giá trị nguyên của tham số, giải ra tìm ẩn.
- Bước 1: - Đặt điều kiện của x để biểu thức A có nghĩa.
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
31
- Bước 2: - Rút gọn biểu thức A.
- Bước 3: - Đánh giá khoảng giá trị mà biểu thức A có thể đạt được, từ khoảng giá trị đó ta
có các giá trị nguyên mà biểu thức A có thể đạt được.
- Bước 4: Giải phương trình vế trái là biểu thức A đã rút gọn, vế phải là các giá trị nguyên
nằm trong miền giá trị của A, đối chiếu điều kiện và kết luận.
Thí dụ 1. Cho biểu thức
2 24
9
3
= +
−
−
−xx
x
A
x
và
7
8
=
+
B
x
với
0,x 9≥≠x
.
a) Rút gọn
A
.
b) Tìm các số nguyên
x
để
.=P AB
nhận giá trị nguyên.
Lời giải
a) ta có:
( )
( )( )
( )( )
( )
( )
( )
( )
. 3 2 24
5 24
3
33 33
38
8
3
33
2 24
9
++ −
+−
=+= =
−
+− +−
−+
−
+
= =
+
+−
−
xx x
xx
A
xx xx
xx
x
x
x
x
x
x
xx
b) ta có:
87 7
..
38 3
+
= = =
++ +
x
P AB
xx x
Vậy các giá trị nguyên mà P có thể đạt được là 1 cà 2.
Đặt
( ) { }
7 7 73 7
0 3 07300 1;2
3
3
−
= > ⇒ = −= ≥⇒− ≥⇒<≤ ⇒=
+
n
nn x n
n n
nn
x
Với n = 1 ta có:
( )
7
1 3 7 4 16
3
=⇒ +=⇒=⇒=
+
x x x TM
x
Với n = 2 ta có:
( )
7 11
2 2 67
24
3
=⇒ +=⇒ = ⇒=
+
x x
x TM
x
Thí dụ 2. (Trích đề thi HSG huyện Thanh Oai năm 2015-2016)
Cho
x x3 x2 x2
M1 :
x1 x23 x x5x6

++ +
=− ++


+ − − −+

1) Rút gọn M
2) Tìm giá trị nguyên của x để biểu thức M nhận giá trị là số nguyên
Lời giải
ĐKXĐ:
( )
x 0;x 4,x 9 *≥≠≠
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
32
1) Rút gọn M: Với
( )
x 0;x 4,x 9 *≥≠≠
Rút gọn ta được:
x2
M
x1
−
=
+
2)
x2 x13 x1 3 3
M1
x1 x1 x1 x1 x1
− +− +
= = =−=−
+ + ++ +
Đặt
( )
−
= > ⇒ = −=
+
3 3
3n
nn 0 x 1
nn
x1
Do
≥x0
nên
{ }
−
≥⇔−≥⇒<≤⇒ =
3n
0 3 n 0 0 n 3 n 1;2;3
n
Xảy ra các trường hợp sau:
+ =⇔ += ⇔ = ⇔ =
+
3
) 1 x13 x 2 x4
x1
(không TMĐK (*) loại)
+ = ⇔ += ⇔ = ⇔ =
+
3 3 11
) 2 x1 x x
2 24
x1
. ( loại do x không nguyên (*) )
+ = ⇔ +=⇔ =
+
3
) 3 x11 x0
x1
. ( TMĐK (*) )
Vậy x = 0 thì M nhận giá trị nguyên.
Dạng 10. Tìm giá trị của ẩn để biểu thức đạt GTNN hoặc GTLN
Phương pháp 1: Thêm bớt rồi dùng bất đẳng thức Cauchy hoặc đánh giá dựa vào điều
kiện
Thí dụ 37. (Trích đề thi HSG huyện Thanh Oai 2014-2015)
Cho biểu thức A =
x 5 x 25 x x 3 x 5
1:
x 25
x 2 x 15 x 5 x 3

− − +−
− −+


−
+− + −

1. Rút gọn A
2. Với x
0≥
, x
≠
25, x
≠
9 tìm giá trị nhỏ nhất của biểu thức: B =
A(x 16)
5
+
Lời giải
b) Điều kiện
x 0,x 25,x 9≥≠ ≠
Rút gọn
5
A
x3
=
+
b) Ta có :
1
2
+
−
=
x
x
M
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
33
A(x 16) 5(x 16) x 16
B
5
5(x3 x3
+ ++
= = =
++
=
25 25
x3 x3 6
x3 x3
−+ = ++ −
++
Theo bất đẳng thức Cauchy:
( )
= ++ −≥ + −= −=
++
25 25
B x 3 6 2 x 3 . 6 2.5 6 4
x3 x3
=>
B4≥
=> min B = 4
+= ⇔ +=⇔=
+
25
x3 x35 x4
x3
Thí dụ 2. (Trích đề thi HSG huyện Tư Nghĩa năm 2016-2017)
Cho biểu thức
2
21 1 1
.( )
3
2
1 21 2
1
xx
A
xx
x
−
=++
++ −+
+
a) Tìm điều kiện của x để biểu thức A có nghĩa
b) Rút gọn biểu thức A
c) Tìm giá trị nhỏ nhất của A.
Lời giải
a) Điều kiện của x để biểu thức A có nghĩa :
3
20
2
10
1
21
x
x
x
x
x
+≥
≥−
+≠ ⇔

≠−
+≠
b) Rút gọn biểu thức A
2
32
2
22
22
2 1 1 1 ( 2) 1 2
.( ) .
1 2 (
1)( 1) 2 1 ( 2)
1 21 2
( 2) 1 ( 2) ( 1)
( 1)( 1) 1 ( 1)( 1)
( 1) 1
( 1)( 1) 1
x x xx
A
x x
xx x
xx
xx xx
x x
x xx x x xx
x
x xx xx
−−
=+ += +
+ +
−+ − +
++ −+
− −
− −+
= −=
+ −+ + + −+
−+ −
= =
+ −+ −+
c) Tìm giá trị nhỏ nhất của A.
Ta có
2
2
11
13
1
()
24
A
xx
x
−−
= =
−+
−+
Ta có A nhỏ nhất khi
2
13
()
24
x −+
đạt giá trị nhỏ nhất
Vậy: Giá trị nhỏ nhất của là A là
4
3
−
khi
1
2
x −
= 0
⇔
1
2
x =
Thí dụ 3. Cho biểu thức
( )
2
11 1
:,
1
1
x
A
xx x
x
+

= +

−−

−
với
0, 1.xx>≠
a) Rút gọn biểu thức
A
.
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
34
b) Tìm giá trị lớn nhất của biểu thức
9PA x= −
.
Lời giải
a) Với điều kiện
0x >
,
1x ≠
ta có
( )
( )
( )
2
2
1
11 1 1 1
:.
11
1
1
x
xx x
A
xx x x
x
xx
x
−
++ −

=+ = ⋅=

−− +
−

−
b) Với điều kiện
0x >
,
1x ≠
ta có
11 1
9 91 919 .
x
PAxxxx
xx x
−

=−= −=−−=− +


Theo bất đẳng thức Cô-si ta có
1 11
9 2 9 9 6.x xx
x xx
+≥ ⋅⇔ +≥
Như vậy
5P ≤−
.
Đẳng thức xảy ra khi
1
9 x
x
=
hay
1
9
x =
.
Vậy giá trị lớn nhất của
P
là
5−
khi
1
9
x =
.
Phương pháp 2: Dùng miền giá trị
Thí dụ 1. Cho biểu thức
( )
2
11 1
:,
1
1
x
A
xx x
x
+

= +

−−

−
với
0, 1.xx>≠
a) Rút gọn biểu thức
A
.
b) Tìm giá trị lớn nhất của biểu thức
9PA x= −
.
Lời giải
a) Với điều kiện
0x >
,
1x ≠
ta có
( )
( )
( )
2
2
1
11 1 1 1
:.
11
1
1
x
xx x
A
xx x x x
xx
x
−
++ −

=+ = ⋅=

−− +
−

−
b) Với điều kiện
0x >
,
1x ≠
ta có
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
35
( )
( )
( )
( ) ( )
2
11
9 91 9 1
. 19
9 1 10
9 1 10 *
−
=−= −=−− <
⇔ = −−
⇔ + − +=
⇔ + − +=
x
PAxxxP
xx
Px x x
xP x
xP x
Để tồn tại P thì phương trình (*) phải có nghiệm, tức là:
( ) ( ) ( )
22
1 36 0 1 36 1 6 1 5∆= − − ≥ ⇔ − ≥ ⇔ − ≤− < ⇔ ≤−P P P do P P
Như vậy
5P ≤−
khi
( )
( )
1 51
11
2.9 2.9 3 9
− − −−−
= = =⇒=
P
xx
Vậy giá trị lớn nhất của
P
là
5−
khi
1
9
x =
.
Dạng 11. Chứng minh biểu thức luôn âm hoặc luôn dương
Phương pháp:
- Để chứng minh biểu thức A luôn dương ta chỉ ra
( )
2
1
0=+>A A kk
-
- Để chứng minh biểu thức A luôn âm ta chỉ ra
( )
2
1
0=−− >A A kk
Ví dụ minh họa:
Thí dụ 1. Cho biểu thức
2
1
12
:.
1

= −

+
+
+
A
x
x
xxx
với
0, 1.xx>≠
a) Rút gọn biểu thức
A
.
b) Chứng minh A luôn âm với với mọi giá trị x làm A xác định.
Lời giải
a) Điều kiện: x > 0
Khi đó:
2
1
12
:.
1

= −

+
+
+
A
x
x
xxx
( )( )
( )
( )
( )
( )
1
12
..
22
11 11
21
−+
− +− −
= =
+ −+ + −+
−
=
−+
x
xx x x x
x xx x xx
x
xx
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
36
Do
( )
2
13
0; 1 0 0
24
21
−

− < − += − + > ⇒ <
∀


−+
x
x xx x x
xx
Vậy A luôn âm với với mọi giá trị x làm A xác định.
Thí dụ 2. Cho biểu thức
11
.
1 11
+
=++
−+ − − +
xx x
A
x x xx x
a) Rút gọn biểu thức
A
.
b) Chứng minh A không âm với mọi giá trị x làm A xác định.
Lời giải
a) Điều kiện:
1≥x
( )( )
( )
11
11 1
1
11
1
11
21
+
=++
−+ −− +
+
−− + + −
= +
+
−+ −−
=−−
xx x
A
x xx x x
xx
x xxx
x
x xx x
xx
b) Ta có:
( )
( )
2
21 1211 110 1= − −= − − −+= −− ≥ ∀≥Ax x x x x x
A không âm với mọi giá trị
1≥x
.
Dạng 12. Tìm
x
biết biểu thức
P
thỏa mãn phương trình, bất phương trình chứa
dấu giá trị tuyệt đối.
Phương pháp:
Tìm x để |A| = A.
Phương pháp:
|| 0AA A=⇔≥
Cần tìm
x
thỏa mãn ĐK để
0A ≥
.
Tìm x để |A| = - A.
Phương pháp:
|| 0A AA=−⇔ ≤
Cần tìm
x
thỏa mãn ĐK để
0A ≤
.
Tìm x để
2
.AA=
Phương pháp:
2
0.AAA=⇔≥
Cần tìm
x
thỏa mãn ĐK để
0A ≥
.
Tìm x để |A| > - A.
Phương pháp:
|| 0A AA>− ⇔ >
Cần tìm
x
thỏa mãn ĐK để
0A >
.
Tìm x để
AA>
.
Phương pháp:
01AA A> ⇔< <
Cần tìm
x
thỏa mãn ĐK để
01A<<
.
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
37
Tìm x để
AA<
.
Phương pháp:
1AA A<⇔>
Cần tìm
x
thỏa mãn ĐK để
1A >
.
Tìm x để
;;;.AbAbAbAb>≥<≤
Phương pháp:
Cần tìm
x
thỏa mãn ĐK để:
0; ; 0; 0.Ab Ab Ab Ab−> −≥ −< −≤
Ví dụ minh họa:
Ví dụ 1: Cho biểu thức:
1
1
x
A
x

= +


+

:
12
11
x
x xx x x

−


− + −−

a) Rút gọn biểu thức
A
.
b) Tìm
x
để
1A >
.
Lời giải
a) Điều kiện:
0; 1xx≥≠
. Kết quả rút gọn
1
1
xx
A
x
++
=
−
1 2 11 2
1: :
11
1 1 1
( 1)( 1)
x x
xx x
A
xx
x xx x x x
x x


++
=+
− = −




++
− + −− −
+ +


2
1 2 1 1 ( 1)( 1) 1
:.
11
( 1)( 1) ( 1) 1
xx x x xx x x xx
xx
xx x x

++ + + ++ + + ++
= = =


++
++ + +

.
b) Ta có:
1A >⇔
1
1
xx
x
++
−
> 1
⇔
1
10
1
xx
x
++
−>
−
⇔
11
0
1
xx x
x
+ +− +
>
−
2
0
1
x
x
+
⇔>
−
10 1xx⇒ −> ⇔ >
( do
20x +>
) .
Kết hợp với ĐKXĐ
01x≤<
thì
1A >
.
Ví dụ 2: Cho biểu thức
( )
21
1
1
xx
A
x
xx
−
= −
−
−
a) Tìm ĐKXĐ, rút gọn biểu thức A .
b) Với giá trị nào của x thì
AA>
.
Lời giải
a) Điều kiện:
0 ; 1.xx>≠
Kết quả rút gọn
1x
A
x
−
=
.
b) Ta có:
0AA A>⇔<
1
0 10
x
x
x
−
⇔ < ⇔ −<
(vì
0x >
với mọi
0; 1 . )xx>≠
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
38
11xx⇔ <⇔ <
Kết hợp với điều kiện xác định
01x<<
thì
AA>
.
Dạng 13. Tìm giá trị tham số m để x thỏa mãn phương trình, bất phương trình.
Phương pháp:
- Đối với phương trình ta đưa phương trình về dạng f(m).x = k
- Xét các trường hợp:
Trường hợp 1:
() 0fm=
, kết luận về bất phương trình nhận được.
Trường hợp 2:
() 0≠fm
, tìm được tập nghiệm x, rồi lập luận theo điều kiện nghiệm x thỏa mãn.
- Đối với bất phương trình biến đổi bất phương trình về một trong các dạng sau:
( ).fmx k>
hoặc
( ).fmx k≥
hoặc
( ).fmx k<
hoặc
( ).fmx k≤
( ).fm x k>
hoặc
( ).fm x k≥
hoặc
( ).fm x k<
hoặc
( ).fm x k≤
- Xét các trường hợp:
Trường hợp 1:
() 0fm=
, kết luận về bất phương trình nhận được.
Trường hợp 2:
() 0fm>
, tìm được tập nghiệm x, rồi lập luận theo điều kiện nghiệm x thỏa mãn.
Trường hợp 3:
() 0fm<
, tìm được tập nghiệm x, rồi lập luận theo điều kiện nghiệm x thỏa mãn.
Ví dụ 1: Cho biểu thức:
2−
=
x
A
x
và
17 9
9
3
−−
= −
−
−
xx
B
x
x
với
0, 9>≠xx
a) Rút gọn
B
.
b) Cho biểu thức
=
A
P
B
, tìm giá trị của m để x thỏa mãn
2= −Pm
Lời giải
a) Ta có:
( )( )
( )
( ) ( )( )
( )( )
( )
( )
1 37 9 3 2
179 56 2
9
33
33 33 33
− +− + −
−
− − −+ −
=−= =
= =
−
−+
−+ −+ −+
xx x x
x
x x x
x x
B
x
xx
xx xx xx
b) Ta có:
2 2 23 3
:.
32
− − −+ +
= = = =
+−
Ax x x x x
P
B
xxxxx
với điều kiện:
0, 9, 4>≠≠xxx
( )
33
2 2 3 2 33
3
+
= −⇔ = −⇔ += − ⇔ − =⇔ =
−
x
P m m
x mx x m x x
m
x
Ta có:
0, 9, 4 0, 2, 3>≠≠⇒> ≠ ≠xxx x x x
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
39
Để x thỏa mãn P = m - 2 thì:
3
0
3
3
39
2
32
15
3
4
4
3
>
>
−

≠⇔ ≠

−


≠
≠

−
m
m
m
m
m
m
Ví dụ 2. Cho biểu thức:
4 8 41
:
4
22
xx x
P
x
x x xx
−
=−+
−
−+
với
0, 1, 4xxx> ≠≠
a) Rút gọn
P
.
b) Tìm m để với mọi giá trị
4x >
thì
( )
1. 1m x Px− <−
Lời giải
a) Ta có: với
0, 1, 4xxx> ≠≠
4 8 41
:
4
22
xx x
P
x
x x xx
−
=−+
−
−+
4 .(2 ) 8 4 ( 2)
:
(2 )(2 ) ( 2)
x x xx x
x x xx
+− −++
=
−+ +
48 2 2
:
(2 )(2 ) ( 2)
xx x
x x xx
−+ −
=
−+ +
4 ( 2)
.
2 22
x xx
xx
+
=
+−
2
1
x
x
=
−
.
Vậy
2
1
x
P
x
=
−
b) Với
0, 1, 4xxx> ≠≠
ta có
2
1
x
P
x
=
−
( )
1. 1m x Px− <−
( )
2
1. 1
1
x
mx x
x
⇔ − <−
−
.2 1mx x⇔ <−
( )
21 1mx⇔ − <−
Trường hợp 1: Khi
1
2 10 0 1
2
mm− = ⇔ = ⇒ <−
(vô lý).
Trường hợp 2: Khi
1
2 10
2
mm−< ⇔ <
1
12
x
m
⇒>
−
, khi đó để bất phương trình
thỏa mãn với mọi
4x >
thì:
1 1 148 8 3
4 40 0
0
12 12 12
12
mm
mm m m
−+ −
≤⇔ −≤⇔ ≤⇔ ≤
−− − −
Mà
3
12 0 8 30 .
8
mm m− >⇒ −≤⇔ ≤
Trường hợp 3: Khi
1
2 10
2
mm−> ⇔ >
1
0
12
x
m
⇒< <
−
, khi đó mọi giá trị
x
là âm
nên không thỏa mãn điều kiện và yêu cầu bài toán.
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
40
Vậy với
3
8
m ≤
thì bất phương trình thỏa mãn với mọi
4.x >
Ví dụ 3. Cho biểu thức
21
1
xx x x xx x x
P
xx x x xx
+− −− +
= −
++ −
a) Rút gọn biểu thức
P
.
b) Tìm giá trị của
m
để mọi
2x >
ta có:
( )
( )
. 13 1 .P x x mx x+ + −> − +
Lời giải
a) Điều kiện:
0; 1xx≥≠
.
21
1
xx x x xx x x
P
xx x x xx
+− −− +
= −
++ −
( )
( )
( ) ( )
21 11
1
1
xx x xx x
P
xx
xx x
+ − −− −
= −
−
++
( )
( )
( )( )
11
21
1
11
xx
xx
P
xx
x xx
−−
+−
= −
++
− ++
2 11
1
xx x
P
xx
+ −− +
=
++
1
xx
P
xx
+
=
++
b) Ta có:
1
xx
P
xx
+
=
++
với
0; 1xx≥≠
.
( )
( )
( )
( )
( )
( )
( )
( )
. 13 1
. 13 1
1
31
3 10
1 30
1 3 (*)
P x x mx x
xx
x x mx x
xx
x x mx x
x mx
mx m
mx m
+ + −> − +
+
⇔ + + −> − +
++
⇔+ −> − +
⇔ −− − >
⇔ − + −>
⇔ − >−
Trường hợp 1: Khi
1 0 1 02mm− =⇔ =⇒>
(vô lý).
Trường hợp 2: Khi
10 1mm− <⇔ >
3
1
m
x
m
−
⇒<
−
, khi đó:
+ Nếu
3
2
1
m
m
−
<
−
tức là
2x <
thì mọi giá trị
2x >
sẽ không thỏa mãn bất phương
trình.
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
41
+ Nếu
3
2
1
m
m
−
>
−
tức là
3
2
1
m
x
m
−
<<
−
thì chỉ có một số giá trị
2x >
thỏa mãn bất
phương trình (Tập nghiệm của bất phương trình (∗) không chứa hết các giá
trị
2x >
)
⇒
Trường hợp 2 không thỏa mãn với mọi giá trị
2.x >
Trường hợp 3: Khi
10 1mm− >⇔ <
3
1
m
x
m
−
⇒>
−
, khi đó để bất phương trình thỏa
mãn với mọi
2x >
thì:
33 1
2 20 0
11 1
mmm
mm m
−− +
≤⇔ −≤⇔ ≤
−− −
Mà
1 0 10 1mm m− >⇒ +≤⇒ ≤−
kết hợp với
1m <
ta được
1m ≤−
Vậy với
1m ≤−
thì bất phương trình thỏa mãn với mọi
2.x >
Ví dụ 4. Cho biểu thức:
43 2
:.
22 2
x xx
P
xx x x x
−+
=−+
−− −
a) Rút gọn biểu thức
.P
b) Tìm các giá trị của a để có
x
thỏa mãn:
( )
1.P x xa+> +
Lời giải
a) Điều kiện:
0 ; 4.xx>≠
43 2
:.
22 2
x xx
P
xx x x x

−+
=−+


−− −

( )
( )
2
43
P.
4
2
xx
xx
xx
xx
−
−+
=
−−
−
( )
( )
( )
41 2
.
4
2
x xx
P
xx
−−
=
−
−
1Px= −
b) Ta có:
1Px= −
với
0 ; 4.xx>≠
( )
1P x xa+> +
( )
( )
11x x xa⇔− +> +
1 x xa⇔− > +
1 (*)xx a⇔ + − <−
11
1
44
xx a

⇔ + + − − <−


2
15
24
xa

⇔ + <−


Với
2
11
0
24
xx

>⇒ + >


THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
42
2
1 15
1
4 24
x aa

⇒ < + < −⇒<


Vậy với
1a <
thì có
x
thỏa mãn:
( )
1P x xa+> +
.
BÀI TẬP VẬN DỤNG
Câu 1. (Trường chuyên tỉnh Bình Thuận năm 2019-2020)
Cho biểu thức:
159
25
55
+−
=−−
−
+−
xx x
P
x
xx
với
0, 25≥≠xx
.
a) Rút gọn biểu thức P.
b) Tìm tất cả các giá trị của
x
để P < 1.
Câu 2. (Trường chuyên tỉnh Bình Định vòng 2 năm 2019-2020)
Rút gọn biểu thức:



23 5 23 5
.
22 3 5 22 3 5
A
Câu 3. (Trường chuyên tỉnh Bạc Liêu năm 2019-2020)
Rút gọn biểu thức:
( )
( )
13 4 3 7 4 3 8 20 2 43 24 3B =− +−++
.
Câu 4. (Trường chuyên tỉnh Bắc Giang chuyên toán năm 2019-2020)
Cho
,xy
là các số thực dương và
3
22 22
3
3 33
3
1.P x x xy y y yx x y=++++++++
Chứng minh rằng
3
2
3
3
1.xy P+ +=
Câu 5. (Trường chuyên tỉnh Bắc Ninh vòng 2 năm 2019-2020)
Tính giá trị của biểu thức:


432
2
2 3 38 5
45
xxx x
A
xx
khi
= +23x
.
Câu 6. (Trường chuyên tỉnh Bến Tre vòng 2 năm 2019-2020)
Tính giá trị của biểu thức:
1 51 5
1 51 5
.
5
A
−+
−
+−
=
Câu 7. (Trường chuyên tỉnh Cao Bằng vòng 2 năm 2019-2020)
Cho biểu thức
12 2
:1
1
11
xx
P
x
x xx x x

=−−

+
− + −−

với
0, 1xx≥≠
.
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
43
a) Rút gọn biểu thức
P
.
b) Tìm tất các giá trị của
x
để
1P ≥
.
Câu 8. (Trường chuyên tỉnh Cần thơ chuyên toán năm 2019-2020)
Cho biểu thức
( ) ( )
( )
2
41 41
1
.1
1
41
xx xx
A
x
xx
− −+ + −

= −

−

−−
trong đó
1, 2xx>≠
.
a) Rút gọn biểu thức
A
b) Tìm các giá trị nguyên của
x
để giá trị biểu thức
A
là số nguyên.
Câu 9. (Trường chuyên tỉnh DAK NONG vòng 2 năm 2019-2020)
Cho biểu thức:


++
=+−




−
−− +


aa
P
a
aa a a a
2
1 3 5 ( 1)
.1
1
14
.
Tìm điều kiện xác định và rút gọn biểu thức
P
.
Câu 10. (Trường chuyên tỉnh Gia lai chuyên tin năm 2019-2020)
Rút gọn biểu thức:
3 16 7 1 3
23 3 1
xx x x
P
xx x x
+− + −
= −−
+− + −
(
0, 1xx≥≠
).
Câu 11. (Trường chuyên tỉnh Gia Lai không chuyên năm 2019-2020)
Rút gọn biểu thức
4 44
:
22 4
a aa
P
aa
− −+
=
+−
, với
0, 4aa≥≠
.
Câu 12. (Trường chuyên tỉnh Gia lai vòng 2 năm 2019-2020)
Rút gọn biểu thức:
2
4 23 6 25
53
A =++−+
+
.
Câu 13. (Trường chuyên tỉnh Hà Giang vòng 1 năm 2019-2020)
Cho biểu thức:
( )
1( )
3 31
:
22 2
x xy
xx
M
x xy y x x y y x y x xy y

−−
= −+


++ − − + +

a) Rút gọn biểu thức M.
b) Tìm các số nguyên x sao cho biểu thức M có giá trị nguyên.
Câu 14. (Trường chuyên tỉnh Hà Nam chuyên toán năm 2019-2020)
Cho biểu thức::








24 3 2 2
:
2 23 5 6
x xx x
A
x x x xx x
,
(với
0,x
4, 9xx
).
1. Rút gọn biểu thức
A
.
2. Tìm
x
để biểu thức
A
đạt giá trị nhỏ nhất.
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
44
Câu 15. (Trường chuyên tỉnh Hà Nam thi chung năm 2019-2020)
Rút gọn các biểu thức sau:
1.
4 3 2 27 12A 
.
2.
12 1
:
1
1
aa
B
a
a aa




, (với
0, 1aa
).
Câu 16. (Trường chuyên tỉnh Hòa Bình Chuyên Tin năm 2019-2020)
1) Tìm điều kiện xác định:
12
2
1
A
x
x
= −
−
−
2) Rút gọn:
5 12 27B = −
3) Rút gọn:
1
1
1
a
C
a
−
= −
−
Câu 17. (Trường chuyên tỉnh Hòa Bình Chuyên Toán năm 2019-2020)
Cho biểu thức:
3 93 2 1
1
2 12
aa a
A
aa a a
+− −
= −+−
+− − +
1)Rút gọn biểu thức A.
2)Tìm giá trị của a để
2A =
.
Câu 18. (Trường chuyên tỉnh Hòa Bình dành cho tất cả các thí sinh năm 2019-2020) Rút gọn:
( 5 3)( 5 3) 6A = − ++
Câu 19. (Trường chuyên tỉnh Hưng Yên Vòng 2 năm 2019-2020)
a) Cho
a
là số thực khác
1
và
1−
. Rút gọn biểu thức
2
3
2
3
1
3
12
1
11
1
3
1
a
aa
a
P
aa
a
a
+

+

+
−

= ÷−
−−
−

+

+

.
b) Cho các số thực
,,xya
thoản mãn
2 42 2 42
33
x xy y yx a+ ++ =
.
Chứng minh rằng:
33
222
3
xya+=
.
Câu 20. (Trường chuyên tỉnh Hải Dương chuyên toán năm 2019-2020)
Cho
2 12
1.
1
1 21
x x xx x x x x
P
x
xx x

+− −+ −
=+−

−
−−

với
1
0, 1,
4
xxx≥ ≠≠
.
a) Rút gọn P.
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
45
b)Tìm các giá trị của x sao cho
4
5
P =
.
Câu 21. (Trường chuyên tỉnh Hải phòng vòng 2 năm 2019-2020)
Cho biểu thức:
3 13
:
1 11 1


 

xx x
P
xx xx x xx
(với
0x
).
Rút gọn biểu thức
.P
Tìm các giá trị của
x
để
1
.
5
P
Câu 22. (Trường chuyên tỉnh Hậu Giang chuyên toán năm 2019-2020)
Cho biểu thức
 2 15 8 2 1.Ax x
a) Tìm điều kiện của
x
để biểu thức A có nghĩa.
b) Tìm
x
để
3.A
Câu 23. (Trường chuyên tỉnh Hậu Giang chuyên toán năm 2019-2020)
Cho

33
1 2 4.x
Tính giá trị đúng của biểu thức

5 4 32
4 2 2019.Ax x x x x
Câu 24. (Trường chuyên tỉnh Kon Tum cho tất cả các thí sinh năm 2019-2020)
a) Tìm điều kiện của
x
để biểu thức
1
3
x
x
có nghĩa.
b) Chứng minh đẳng thức
11 1
11
aa aa
a
aa














0, 1 .aa
Câu 25. (Trường chuyên tỉnh Kon Tum vòng 2 năm 2019-2020)
1) Không dùng máy tính cầm tay, hãy tính giá trị biểu thức
3 5. 3 5
10 2
P

2) Rút gọn rồi tính giá trị của biểu thức
23 2
2
xx
Q
x

tại
2020 2 2019x 
Câu 26. (Trường chuyên tỉnh Lào Cai Vòng 1 năm 2019-2020)
Tính giá trị các biểu thức sau:
)43+a
2
b) 5 (6 5)+−
Câu 27. (Trường chuyên tỉnh Lào Cai Vòng 1 năm 2019-2020)
Cho biểu thức:
2
2
22 1 1
1
11
+
= +−
−
+−
xx
H
x
xx
(với
0; 1≥≠xx
)
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
46
a) Rút gọn biểu thức
H
.
b)Tìm tất cả các giá trị của x để
0−<xH
Câu 28. (Trường chuyên tỉnh Lâm Đồng vòng 2 năm 2019-2020)
Tính giá trị biểu thức:
( )( )
23 132 1 13 4319 62T =+ −− +
.
Câu 29.
(
Trường chuyên tỉnh Nam Định cho lớp chuyên KHTN năm 2019-2020)
Tìm điều kiện xác định của biểu thức
2019 3
.
9
3
P
x
x
= −
−
−
Câu 30.
(Trường chuyên tỉnh Nam Định cho lớp chuyên KHTN năm 2019-2020)
Cho biểu thức
2
11
4:
11 1
a a a aa
Pa
aa a
+− +
= −+
−+ +
với
0, 1.aa>≠
1) Rút gọn biểu thức
.P
2) Tìm các giá trị nguyên của
a
để
P
nhận giá trị là số nguyên.
Câu 31. (Trường chuyên tỉnh Nam Định chuyên toán năm 2019-2020)
Cho
3 5 23 3 5 23x =++ +−+
. Tính giá trị của biểu thức
( )
2Px x= −
.
Câu 32.
(Trường chuyên tỉnh Nam Định lớp chuyên KHXH năm 2019-2020)
Tìm điều kiện xác định của biểu thức:
2019 3
.
9
3
P
x
x
= −
−
−
Câu 33.
(Trường chuyên tỉnh Nam Định lớp chuyên KHXH năm 2019-2020)
Cho biểu thức:
11 1
4.
11
aa
Pa
a a aa

+−
= −+


−+

với
0, 1.aa>≠
1) Rút gọn biểu thức
.P
2) Tính giá trị của
P
khi
9 4 2.a = +
Câu 34. (Trường chuyên tỉnh Ninh Bình chuyên toán năm 2019-2020)
Với
x0>
, xét hai biểu thức:
2x
A
x
+
=
và
x 3 2x 9
B
x x 3x
−+
= +
+
.
Tìm tất cả các giá trị của
x
để
A5
.
B3
>
Câu 35. (Trường chuyên tỉnh Ninh Bình chuyên toán năm 2019-2020)
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
47
Rút gọn biểu thức :
5 6 7 33 128 1
C
32
−+ −
=
−
.
Câu 36. (Trường chuyên tỉnh Phú Yên Vòng 2 năm 2019-2020)
Cho biểu thức:
32 2 2
:1
23 5 6 2
xx x x
A
x xx x x x

++ + −

= ++ −


− − − + −−


.
a)Rút gọn biểu thức
A
.
b)Tìm
x
để
1
2PA
x
= −
đạt giá trị lớn nhất.
Câu 37. (Trường chuyên tỉnh PTNK ( VÒNG 1 ) năm 2019-2020)
Tìm
a
, biết:
( )
( )
( )
( )
( )
( )
22
1 1 21 1 21 1
1
41 1
+ − − ++ + +− +
−=
−+
a a aa aa
aa a
a
.
Câu 38. (Trường chuyên tỉnh Quảng Nam Vòng 2 năm 2019-2020)
Cho biểu thức
2
22 8 1
11 3

+ + − +−
= −⋅

−+ + +

x x x xx x
A
x x xx x
với
0≥x
.
Rút gọn biểu thức A và tìm x để
6=A
.
Câu 39. (Trường chuyên tỉnh Quảng Ngãi chuyên toán năm 2019-2020)
Cho biểu thức:
x xx x x
P
x x x xx x
+ −+
=+−
−+
2
23 1
với
,xx>≠01
.
Rút gọn và tìm giá trị nhỏ nhất của biểu thức
P
Câu 40. (Trường chuyên tỉnh Quảng Ninh Vòng 2 năm 2019-2020)
Cho biểu thức :
4 9 3 12 1
32 1 2
xx x x
A
xx x x
−− + − −
= +−
++ + +
(với
0x ≥
).
a) Rút gọn biểu thức
A
;
b) Tìm giá trị lớn nhất của
A
.
Câu 41. (Trường chuyên tỉnh Sơn La Vòng 2 năm 2019-2020)
a) Rút gọn biểu thức:
A =
1
1
x
x

−

+

:
32 2
2 3 56
xx x
x x xx

++ +
−+

− − −+

(với
0; 4; 9xxx≥≠≠
)
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
48
b) Cho
3
( 3 1) 10 6 3
21 4 5 3
x
−+
=
++
hãy tính
2 2019
( 4 2)Bx x= +−
Câu 42. (Trường chuyên tỉnh Thái Bình vòng 1 năm 2019-2020)
Cho biểu thức:
( )
2 11

+−
= ++ ⋅


+

xy x y xy
P
xy
xy x
x y y
(với
0; 0>>xy
).
1. Rút gọn biểu thức P.
2. Biết
16=xy
. Tìm giá trị nhỏ nhất của P.
Câu 43. (Trường chuyên tỉnh Thái Nguyên chuyên tin năm 2019-2020)
Cho:
33
70 4901 70 4901.=+ +−x
Không sử dụng máy tính cầm tay, hãy chứng minh
x
là số nguyên tố.
Câu 44. (Trường chuyên tỉnh Tiền Giang chuyên tin năm 2019-2020)
Rút gọn biểu thức:
4 10 2 5 4 10 2 5A =+ + +− +
.
Câu 45. (Trường chuyên tỉnh Tiền Giang Vòng 2 năm 2019-2020)
Cho
33
2 23 2 23 1x =+ +− −
.
Tính giá trị biểu thức
( )
3
32
39Pxx x= ++
Câu 46. (Trường chuyên tỉnh Tuyên Quang chuyên toán năm 2019-2020)
Tính tổng:
22
11 1 1
...
31 5 3 7 5
2019 2019 2
= + + ++
++ +
+−
S
Câu 47. (Trường chuyên tỉnh Tây Ninh Vòng 2 năm 2019-2020)
Rút gọn biểu thức:
( )
( )
2 22 1
2
aa
T
aa
−−
=
−−
với
0, 4aa>≠
.
Câu 48. (Trường chuyên tỉnh Vĩnh Long vòng 2 năm 2019-2020)
a) Cho biểu thức:
( )
2
11 1
:
1
1
+

= +

−−

−
x
P
x xx
x
.
Tìm điều kiện xác định của
P
và giá trị của
x
để
1
2
=P
.
b) Rút gọn biểu thức
3
46 5 61 69 28 5.= −+ −A
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
49
Câu 49. (Trường chuyên tỉnh An Giang Vòng 2 năm 2019-2020)
Rút gọn:
22
13 2 13 2
.
22
13 13
A
+−
=− −−
+−
Câu 50. (Trường chuyên tỉnh Bà Rịa Vũng Tàu thi chung năm 2019-2020)
Rút gọn biểu thức:
( )
3 5 27 20 5 3 15A = −− +
.
Câu 51. (Trường chuyên tỉnh Bình Phước chuyên toán năm 2019-2020)
Cho biểu thức:
( )
23
33
2 3 13
−
−+
= −+
−− + −
x
xx x
A
xx x x
a) Rút gọn biểu thức 𝐴.
b) Tính giá trị của biểu thức 𝐴 khi
4 23= −x
Câu 52. (Trường chuyên tỉnh Long An chuyên toán dự bị năm 2019-2020)
Cho biểu thức
( )
23 8 1 1
1
1 2 11
x x xx x x
Px
x x xx

−− + − +
= + −− −

+ + +−

với
0, 1xx≥≠
.
a) Rút gọn biểu thức
P
.
b) Tìm tất cả số nguyên tố
x
để
1P ≤
.
Câu 53. (Trường chuyên tỉnh Long An chuyên toán năm 2019-2020)
Cho biểu thức với
0.x >
a) Rút gọn biểu thức
.P
b) Chứng minh:
3.P ≤
Câu 54. (Trường chuyên tỉnh Quảng Trị Vòng 2 năm 2019-2020)
Cho biểu thức:
( )
2
21
22
1 11
x
xxxx
A
x xx x
−
+−
=+−
+ −+ −
với
0, 1.xx≥≠
Tìm tất cả các giá trị của
x
để
0.A ≤
Câu 55. (Trường chuyên tỉnh Thừa Thiên Huế vòng 2 năm 2019-2020)
Rút gọn biểu thức:
3x 9x 3 x 1 x 2
P.
x x 2 x 2 x 1
+− + −
= −−
+− + −
Tìm x để
P 3.=
Câu 56. (Trường chuyên tỉnh Yên Bái vòng 2 năm 2019-2020)
2
2 22 1
1 11
x x xxx
P
xx x x xx

+ −−
= + −⋅

−+ + −+

THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
50
Cho biểu thức:
1 11
.
11
x
Ax
xxx x

−

=+−



−+ +


.
1. Tìm điều kiện của
x
để biểu thức
A
có nghĩa. Rút gọn biểu thức
A
.
2. Tìm các giá trị nguyên của
x
để
A
có giá trị nguyên.
Câu 57. (Trường chuyên tỉnh Chuyên ĐHSP vòng 1 năm 2019-2020)
Cho các số thực
,,xya
thoản mãn
2 42 2 42
33
x xy y yx a+ ++ =
.
Chứng minh rằng
33
222
3
xya+=
.
Câu 58. (Chuyên Nam Định 2018)
a) Rút gọn biểu thức
2 22
2
y xy
x
P.
(x y)(1 y) (x y)(1 x) (1 x)(1 y)
=−−
+− ++ +−
b) Chứng minh rằng
22 22 2 2
11 11 1 1
1 1
... 1 2018.
1 2 2 3 2017
2018
++++++++ + <
Câu 59. (Chuyên Hà Tĩnh 2018)
Cho
,,xyz
là các số hữu tỉ thỏa mãn
111
xyz
+=
. Chứng minh rằng
222
xyz++
là số
hữu tỉ
Câu 60. (Chuyên Bình Định 2018)
Cho biếu thức :
( )
2
33
a b ab
ab a b
T:
ab
ab ab
−+

−−
= −


−
+−

, với
a b,a 0,b 0≠>>
a) Rút gọn biểu thức T
b) Chứng tỏ T > 1
Câu 61. (Chuyên Cà Mau 2018)
Rút gọn các biểu thức sau
a) A 4 20 45 3 125 2 405 b) B 9 4 2 9 4 2= − + − =
− ++
Câu 62. (Chuyên Lam Sơn 2018)
Tính giá trị biểu thức
11 1
P 1 1 ........ 1
1 2 1 2 3 1 2 3 .... 2018

=−− −

+ ++ +++ +

Câu 63. (Chuyên Hưng Yên 2018)
Cho các biểu thức
2
x1 1
A:
xx x x x x
+−
=
++ − +
và
42
B x 5x 8x 2025=− −+
với
x 0,x 1>≠
a) Rút gọn biểu thức A
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
51
b) Tìm các giá trị của
x
để biểu thức
2
T B 2A= −
đạt giá trị nhỏ nhất
Câu 64. (Chuyên Bến Tre 2018)
Cho biểu thức
1
ab a ba b
P
ab
+− −
=
+
với
,ab
là hai số thực dương
a) Rút gọn biểu thức
( )
( )
1
:P
a bab++
b) Tính giá trị của biểu thức
P
khi
2019 2 2018a = +
và
2020 2 2019b = +
Câu 65. (Chuyên Hà Nam 2018)
Cho biểu thức
( )
2
2
2
1 1 11
1 2 10 1
11
11
aa
Q aa
a
aa
aa
aa
+−
= + −−
− + < <
+− −
− −+
1) Rút gọn
Q
2) So sánh
3
,QQ
Câu 66. (Chuyên Lâm Đồng 2018)
Tính giá trị biểu thức
( )( )
A 4 15 10 6 4 15=+ −−
Câu 67. (Chuyên Đồng Nai 2018)
Cho biểu thức
a a a 4a
P.
a2a3a2 a

+−
= +


+ ++

a) Rút gọn biểu thức P
b) Tìm các số thực dương a sao cho
P
đạt giá trị lớn nhất
Câu 68. (Chuyên Nguyễn Trãi 2018)
Cho
( )
( )
2
2
2
a
x a 1 1 a ,a 0
a1
=+− + + >
+
;
2
x x 2x 1 1
P
x 2x 1
+ − ++
=
−+
Rút gọn P theo a
Câu 69. (Chuyên Năng Khiếu TP. Hồ Chí Minh 2018)
Biết
0xy<≤
và
( ) ( )
( )
( )
( ) ( )
22
xy xy
y
x5
3
xy2x2y) xxy yxy


+ +−


++=


+ ++ + +




. Tính
x
y
Câu 70. (Chuyên Bắc Ninh 2018)
Rút gọn biểu thức :
22 22 422
2
22 22
a ab a ab 4aab
P : ,a b 0
b
a ab a ab

++ −+ −

= − >>

−+ ++

Câu 71. (Chuyên Hải Dương 2016)
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
52
Rút gọn biểu thức:
22
ax ax
A 2a 2a
xx
++
= −+ +
với
a 0, x 0>>
.
Câu 72. (Chuyên Vĩnh Long 2018)
a) Cho biểu thức
x 3x 2 1 1
A:
xx 8 x 2 x

++
= −


−−

với
x0>
và
x4≠
. Tìm giá trị của
A
tại
x 14 6 5= +
.
b) Tính giá trị biểu thức
A 12 80 32 3 12 80 32 3=−− −+−
.
Câu 73. (Chuyên Bắc Giang 2018)
Cho biểu thức
x 4x 4 x x 1 1
A:
1x
x x2 x11 x


++ +
=+−



−
+− + −


(với
x 0; x 1>≠
).
a) Rút gọn biểu thức
A
.
b) Có bao nhiêu giá trị nguyên của
x
để
1 2018
A.
2018
+
≥
Câu 74. (Chuyên Quảng Nam 2018)
Cho biểu thức
a 1 ab a 2a b 2 ab
A 1:
1 ab
ab 1 1 ab

++ +
=++


−
+−

.
với
a 0; b 0>>
và
ab 1≠
.
Rút gọn biểu thức
A
và tìm giá trị lớn nhất của
A
khi
a + b = ab
.
Câu 75. (Chuyên Bà Rịa Vũng Tàu 2018)
Rút gọn biểu thức:
3
1 a a 2a 1
P 1 a (a 1)
a1 a

+ −+

= +− >

−

Câu 76. (Chuyên Điện Biên 2018)
Cho biểu thức
,(x 0;x 25)
x2 x33x4x5
P
x 1 5 x x 4x 5
≥≠
+ + +−
=−−
+ − −−
.
a) Rút gọn
.P
Tìm các số thực
x
để
P2>−
.
b) Tìm các số tự nhiên
x
là số chính phương sao cho
P
là số nguyên.
Câu 77. (Chuyên Đà Nẵng 2018)
Cho biểu thức
( )
2
2x 1
x x 2x x
A
x1 x x1 x
−
−+
=+−
− ++
với
0, 1xx>≠
Chứng minh rằng:
3
A
4
≥
Câu 78. (Chuyên Đà Nẵng 2018)
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
53
Cho biểu thức:
22 22 22
y
xx
Q 1:
xy xy x xy


= −+

− − −−

với
xy0>>
.
1. Rút gọn Q.
2. Xác định giá trị của Q khi
3=xy
.
Câu 79. (HSG TP. Hải Phòng 2018)
Cho biểu thức
( )
3
x y 2x x y y
3 xy 3y
A
xy
xx yy
−+ +
−
= +
−
+
với
x,y 0≥
và
xy≠
.
Chứng minh rằng giá trị của biểu thức
A
không phụ thuộc giá trị của biến.
Câu 80. (HSG Quận Hồng Bàng 2018)
Cho biểu thức
( )
( )
( )
( )
( )
( )
y xy
x
P.
x y1 y x y x1 x11 y
=−−
+ − + + +−
a) Tìm điều kiện của x, y để biểu thức
P
xác định và rút gọn
;P
b) Tìm x, y nguyên thỏa mãn phương trình
P 2.=
Câu 81. (HSG Quận Lê Chân 2018)
Cho biểu thức
( )
22
22 22
ab a b
ab ab
abab ab
ab
P ab0

−+
⋅


++ −
− −+ −

−
= + >>
Chứng minh rằng khi
ab1−=
thì
P 2 2 2.≥+
Câu 82. (HSG Quận Ngô Quyền 2018)
Cho biểu thức
xy xy
x y 2xy
P :1 .
1 xy
1 xy 1 xy

+−

++

=++


−
−+


a) Rút gọn biểu thức
;P
b) Tính giá trị của
P
với
2
x.
23
=
+
Câu 83. (HSG Quận Thủy Nguyên 2018)
Cho biểu thức
x 3x 2 x x 1 1
P :.
x1
x x2 x1 x1


++ +
=−+



−
+− + −


(với
0; 1xx>≠
)
a) Rút gọn biểu thức
;P
b) Với giá trị của
x
ta có
1 x1
1.
P8
+
−≥
Câu 84. (HSG Thanh Hóa 2017)
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
54
Cho biểu thức
2
x 2x x 1 12x 2x
P
xx 1 xx x x x x
− + +−
=++
− ++ −
, với
0, 1.xx>≠
Rút gọn
P
và tìm tất cả các giá trị của
x
sao cho giá trị của P là một số nguyên.
Câu 85. (HSG Hải Dương 2017)
Cho biểu thức
22
xxxx
A.
x x1x x1
−+
= +
++ −+
Rút gọn
B 1 2A 4 x 1=− −+
(
1
0x )
4
≤≤
Câu 86. (HSG Hải Phòng 2017)
Cho
a 3 5 23 3 5 23=++ +−+
. Chứng minh
Câu 87. (HSG Hải Dương 2016)
Cho biểu thức:
( ) ( )
22
P 1x 1x 1x 1x 1x 1x= −+ − − + −− − −
(với
1 1).x−≤ ≤
Tính giá trị của biểu thức P khi
1
x
2019
= −
Câu 88. (HSG Thái Bình 2011)
Chứng minh rằng:
87 1 1 1 88
...
89 45
2 1 3 2 2011 2010
< + ++ <
Câu 89. (HSG Chuyên Hưng Yên 2019-2020)
Rút gọn biểu thức
( )
2
1
A 2 2 5 20 20
5
= − +−
.
HƯỚNG DẪN GIẢI
Câu 1.
a)
( ) ( )( )
( )
( )
( )
5 15 59
159
25
55
55
−−+++−
+−
=−− =
−
+−
+−
x xx x x
xx x
P
x
xx
xx
( ) ( ) ( )
( )( ) ( )( )
( )
( )( )
5 6 5 59 2 5
2 10
55 55 55
−−+ ++− − +
−−
= = =
+− +−
+−
xx x x x x
x
xx
xx xxxx
2
5
=
−
x
x
b)
( )
25
22 5
1 1 10 0
0
55 5 5
−−
+
<⇔ <⇔ −< ⇔ <
⇔ <
−− − −
xx
xx x
P
xx x x
5 0 5 0 25⇔ −<⇔ <⇔≤<x xx
Vậy
0 25≤<x
Câu 2.
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
55
22 3 5 22 3 5 8 26 25 26 25 9 5 
22
8 2 5 1 2 5 1 2 6 25 2 25 2 10. 
2352235435356254353551  
12 4 5 2 5 2 10 2 5 . 

23522 35435 35625435 3551  
12 4 5 2 5 2 10 2 5 . 
Do đó:

23 5 2 2 3 5 23 5 2 2 3 5
10 2 5 10 2 5 20
2.
10 10
22 3 5 22 3 5
A




Vậy
2.A
Cách khác:
Ta có:
2
23 5
6 25 6 25 6 25 4
2
55 55
22 3 5 4 6 25
4 51





2
23 5
6 25 6 25 6 25 4
2
55 55
22 3 5 4 6 25
4 51





Do đó:
4 4 20 4 5 20 4 5 40
4 4 4 2.
25 5 20
5 55 5
A


  


Vậy
2.A
Câu 3.
( )( )
13 4 3 7 4 3 8 20 2 43 24 3B =− +−++
=
(
)
2
91 52 3 28 3 48 8 13 4 3 7 4 3+−−− −++
=
(
)
43 24 3 8 13 4 3 7 4 3+ − − ++
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
56
=
( ) ( )
22
43 24 3 8 2 3 1 2 3

+ − −+ +


=
( )
43 24 3 8 2 3 1 2 3+ − −+ +
= 35
Câu 4.
Đặt
( )
3
3
; ,0a x b y ab= = >
, ta có
( )
322 32 2
1
11
P a a a b b b ab a b
ab ab
= + + + + + + ++
= ++ ++
.
3
2
3
3
1 1.P ab x y=++= + +
.
Câu 5.
Ta có
( )
2
2
x2 3 x2 3 x 4x10− = ⇒ − =⇒ − +=
.
22
x 4x 5 x 4x 1 4 2−+= −++=
..
432
x 2x 3x 38x 5−+−+
( ) ( ) ( )
4 32 3 2 2
x 4x x 2x 8x 2x 10x 40x 10 5 5= − + + − + + − + −=−
5
2
A

.
.
Câu 6.
( ) ( )
( )
( )
22
15 15
1 51 5
125 5125 5
1 51 5
45
1 51 5
15
1
5 5 5 4
5
− −+
−+
−+−−−
−
+−
−
+−
−
= = = =
=
−
A
Câu 7.
a) Biến đổi được
( )
( )
1 2 12
1 11
11
xx
x xx x x x
xx
−=−
− + −− −
−+
Biến đổi được
( )
( )
( )
( )
1 2 12
1
11 11
x xx
x
xx xx
+−
−=
−
−+ −+
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
57
2 12
1
11
xx x
xx
+−
−=
++
1
1
P
x
=
−
b)
12
11 0
11
x
P
xx
−
≥⇔ ≥⇔ ≥
−−
TH1:
20 2 4
14
1
10 1
x xx
x
x
xx

−≥ ≤ ≤

⇔ ⇔ ⇔< ≤

>
−> >


TH2:
20 2 4
1
10 1
x xx
x
xx

−≤ ≥ ≥

⇔⇔

<
−< <


(không xảy ra).
Vậy các giá trị
x
cần tìm là
14x<≤
.
Câu 8.
a)
( )
( )
( )
2
41 41
1
.1
1
41
xx xx
A
x
xx
− −+ + −

= −

−

−−
2
21 21 2
.
1
44
xx xx x
A
x
xx
− −+ + − −

=

−

−+
111 1
2
.
21
xx
x
A
xx
−− ++ −
−

=

−−

Nếu
12x<<
thì
2
1
A
x
=
−
Nếu
2x >
thì
2
1
A
x
=
−
b) - Nếu
12x<<
thì không có giá trị nguyên.
- Nếu
2x >
thì
2
1
A
x
=
−
+
( )
11 2x xl−=⇔ =
+
( )
12 5x xn−= ⇔ =
Câu 9.
Điều kiện:
aa0, 1.>≠
( )
( )
( )
( )
( )
( )
( )
22
1 41 1
1 35
..
1
44
11 11

− +−
+

=+
=

−
−− −−

a aa
a
P
a
aa
aa aa
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
58
1
a
=
.
Câu 10.
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
+− + −
= −−
+− + −
+ −+ − +
+−
= −
+−
+−
+ − −+ −
= −
−+ +−
3 16 7 1 3
23 3 1
11 3 3
34 7
23
31
34 7 1 9
13 31
xx x x
P
xx x x
xx x x
xx
xx
xx
xx x x
xx x x
(
)
(
)
(
)
(
)
(
)
(
)
+− −
= −
−+ +−
++
=
+−
3 4 7 2 10
13 31
43
31
xx x
xx x x
xx
xx
(
)
(
)
(
)
(
)
++
=
+−
+
=
−
31
31
1
1
xx
xx
x
x
Câu 11.
( )
( )
( )
( )
( )
( )
2
22 2
4 44 2
2
: : 2
: 2. 2
2
22 4 2 2
22
−+ −
− −+ −
= = =
− =−=
+− + −
−
aa a
a aa a
P aa
aa a a
a
Câu 12.
22
2
( 3 1) ( 5 1)
53
A = ++ −+
+
2
31 51
53
= ++ −+
+
2( 5 3)
35
2
−
=++
25=
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
59
Câu 13.
a).Điều kiện:
0; 0; ; 1x y x yx≥≥≠ ≠
( ) ( )
( )
( )
33 2
.
1
x x y x x xy y x xy y
M
xx yy
x xy
−−+++ ++
=
−
−−
;
( )
( )
( )
( )
( )
2
2
.
1
x xy y
x xy y
M
xyxxyyx xy
++
−+
=
− ++ − −
2
1
M
x
=
−
b).Để M có giá trị nguyên khi x-1 là ước của 2.
Các ước nguyên của 2 là
1; 2±±
.
Do đó ta có
11 2
11 0
12 3
12 1
xx
xx
xx
xx
−= =


−=− =

⇔

−= =

−=− =−

Vì
0; 1xx≥≠
nên có x = 0; x = 2; x = 3 thỏa mãn bài ra.
Câu 14.
1. Rút gọn biểu thức
A
.
( )
( )
( )
( )
( )
( )

+ −− + −+ +
+

=

−−
−−


xx xx x
x
A
xx
xx
33 22 2
24
:
2
23
( )( )
( ) ( )
( )( )

−−−+ +
+

=

+− − −


xx x
x
A
xx x x
94 2
24
:
12 23
( )( ) ( )( )

+−

=

+− − −


xx
A
xx x x
24 3
:
12 23
+
=
+
x
A
x
24
1
2) Tìm x để A đạt giá trị nhỏ nhất.
24 1 25 25 25
1 12
11 1 1
+ −+
= = = −+ = ++ −
++ + +
xx
M xx
xx x x
Áp dụng bất đẳng thức Cauchy cho 2 số ta có
25
1 10
1
++ ≥
+
x
x
Do đó
8≥M
.
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
60
Đẳng thức xảy ra khi
( )
2
1 25 1 5 16+ = ⇔ += ⇔ =x xx
.
Vậy giá trị nhỏ nhất của M bằng 8, đạt được khi x = 16.
Câu 15.
1.
4 3 2 27 12A 
43 63 23
0
2.
12 1
:
1
1
aa
B
a
a aa





với
0, 1aa
12
.1
1 ( 1)
aa
a
a aa




2
( 1) 2 ( 1)
.1
( 1)( 1)
a aa
a
aa



31a
Câu 16.
1..ĐK:
1
2
x
x
>
≠
2..
10 3 3 3 7 3B = −=
3..ĐK:
0
1
a
a
≥
≠
;
11Ca a= +−=
Câu 17.
1).Điều kiện
a0
và
a1
( )
3( 1) 2 1
1
( 2)( 1) 1 2
3( 1) 2 ( 2) 1 ( 2)( 1)
( 2)( 1)
1
1
aa a
A
aa a a
aa a a a a a
A
aa
a
A
a
+− −
= −+−
+− − +
+−− − ++−− + −
=
+−
+
=
−
2).
1
1
a
A
a
+
=
−
để
1
22
1
a
A
a
+
=⇔=
−
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
61
Học sinh giải phương trình và tìm ra giá trị của
3
1
9
a
a
=
=
Câu 18.
( 5 3)( 5 3) 6 5 9 6 2= − + +=−+=A
Câu 19.
a) Ta có
( ) ( )
( )
( ) ( )
( )
( )
( )
( )
( )
22
2
2
2
3
2 22
3
2
2
131
1
3
11
1
12 2
1
11 1
11
13 1
1
3
1
1
aa
a
a aa
a
aa a
a
P
aa a
a aa
aa
a
a
a
++ −
+

+

+ −+
−
+
−

= ÷ −= ÷ −
−− −
− ++
−+ +
−

+

+

+
( )
( )
( )
( )
( )
( )
( )
( )
2
22
2
22
41 1 1
1
2
..
1
41 1 1
1
aa a aa
a
a
a
aa a aa
a
−+ −
++
+
= −
−
++ +
−+
−
12 1
1
111
a aa
aaa
+−
=−==−
−−−
.
Vậy
1P = −
.
b) Đặt
3
2
sx=
và
2
3
ty=
thì đẳng thức đề bài có thể viết lại thành
3 2 32
s st t ts a++ +=
.
Do
,0st≥
nên
3 2 32
,s st sst t tstst+= + += +
.
Từ đó ta có
hay
( )
3
2
st a+=
.
Suy ra
3
2
st a+=
. Đây là kết quả cần chứng minh.
Câu 20.
( 1)(2 1) (2 1)( 1) ( 1)
)1 .
(1 )(1 ) (1 )( 1) 2 1

+ − −+ −
=+−

− + − ++ −

x x x x x xx
aP
x x xx x x
( 1)
1
1
xx
Px
xx

+
=+− +

++

(1 )( 1) ( 1)
1
(1 ) 1 1
11
xx x x x
P
xx
xx x x x x x
xx xx
− + ++ +
=
++
− +− + + +
= =
++ ++
4 14
)
55
1
7 4 3
4 10
7 4 3
+
=⇒=
++
= −
⇒ − += ⇔
= +
x
bP
xx
x
xx
x
(tháa m·n)
(tháa m·n)
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
62
Vậy để
4
5
P =
thì
7 43x = ±
Câu 21.
13
:
11
x
P
xx xx
 
.
1
3x
..
1 11
2
55
3
Px
x
 
4x
..
Vậy
04x
thỏa mãn bài toán..
Câu 22.
a) Ta có
 2 15 8 2 1 2 1 2.4. 2 1 16Ax x x x
 
2
(2 14) 2 14.xx
Biểu thức
A
có nghĩa khi và chỉ khi

1
2 10 .
2
xx
2143 217
) 3 2 14 3
214 3 211
xx
bA x
xx



 




25
.
1
x
x
Câu 23.
Ta có
 
33 3 3 33
1 2 4 ( 2 1) ( 2 1)(1 2 4 )xx

33
32
( 2 1) 1 2 1 3 3 1 0.x xx x x x
Khi đó

5 4 32
4 2 1 2020Ax x x x x

2 32
( 1)( 3 3 1) 2020 2020.xx x x x
Câu 24.
a) Điều kiện của
x
để biểu thức
1
3
x
x
có nghĩa là
30x
.
3x
.
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
63
b).Chứng minh đẳng thức
11 1
11
aa aa
a
aa














0, 1 .aa
.
Ta có
11
11 1 1
11 1 1
aa aa
aa aa
aa a a































.
11aa
.
1 a
.
Câu 25.
1) Không dùng máy tính cầm tay, hãy tính giá trị biểu thức
3 5. 3 5
10 2
P

3 5. 3 5 . 2 5 1
8
P

2
5 1 .2 5 2
6 2 5. 3 5 5 3 5
88



5 1 .2. 5 1
8

2. 5 1
1
8

2) Rút gọn rồi tính giá trị của biểu thức
23 2
2
xx
Q
x

tại
2020 2 2019x 
Ta có
2
2020 2 2019 2019 2 2019 1 2019 1x  
2019 1x
21 2
23 2
22
xx
xx
Q
xx




21Qx
2 2019 1 1 2 2019 1Q 
Câu 26.
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
64
a).
43235+=+=
b).
2
5(65) 565+ − = +−
56 56= +− =
Câu 27.
a).
2
2
22112(1)11211
1 (x
1)(1 ) 1
11 11
11
++
= +−= +−=+−
− −
+ −
+− +−
+−
x x xx x
H
x xx
xx xx
xx
2 1 ( 1)
1
+ −− +
=
−
xx x
x
22
1
−
=
−
x
x
2(x 1)
2
1
−
= =
−x
b).Ta có
0 20 2 4− <⇔ −<⇔ <⇔<xH x x x
Mà
0; 1≥≠xx
, suy ra:
0 4; 1≤< ≠xx
Vậy: Với
0 4; 1≤< ≠xx
thì
0+<xH
Câu 28.
Tính được
13 43 23 1−=−
và
19 6 2 3 2 1+=−
Đưa được về dạng
( )
( )
22
22
23 1 32 1T

=−−


Tính đúng kết quả T = 187
Câu 29.
Biểu thức xác định khi
0
30
9
x
x
x
≥
−≠
≠
.
0
9.
x
x
≥
⇔
≠
.
Câu 30.
1).Với
0, 1aa>≠
ta có
2
.
1
a aa
aa
a
+
=
+
.
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
65
Và
( ) ( ) ( )( )
( )( )
22
1 14 1 1
11
4
11
11
a a aa a
aa
a
aa
aa
+− −+ − +
+−
− +=
−+
−+
.
4
.
1
aa
a
=
−
.
Do đó
4 14
..
11
aa
P
aa
aa
= =
−−
.
2).Với
a
nguyên thì P nhận giá trị là số nguyên khi và chỉ khi
14
12
11
11
12
14
a
a
a
a
a
a
−=−
−=−
−=−
−=
−=
−=
.
3
1
0
2
3
5
a
a
a
a
a
a
= −
= −
=
⇔
=
=
=
Đối chiếu với điều kiện ta có
2,3,5aaa= = =
(thỏa mãn)..
Câu 31.
+ Có
.
+ Do nên .
+ Suy ra hay , do đó .
Câu 32.
Biểu thức xác định khi
30
9
x
x
−>
≠
.
3
9.
x
x
>
⇔
≠
.
Câu 33.
( )
2
22
3 5 23 3 5 23 6 23 5 23 6 24 23x

= ++ +−+ =+ −+ =+ −


( )
( )
2
62 31 423 31=+ −=+ = +
0x >
31x = +
( )
2
13x −=
2
22xx−=
2P = −
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
66
1).Với
0, 1aa>≠
ta có
( ) ( ) ( )( )
( )( )
22
1 14 1 1
11
4
11
11
a a aa a
aa
a
aa
aa
+− −+ − +
+−
− +=
−+
−+
.
( )
2 1 2 14 1
1
aaaa aa
a
++−+−+ −
=
−
.
4
1
aa
a
=
−
.
Do đó
4 14
..
11
aa
P
aa
aa
= =
−−
.
2).Ta có
( )
2
9 42 22 1 22 1.a =+ = += +
.
Do đó
2.P =
.
Câu 34.
.
..
Với ta có: .
(vì )
Câu 35.
Ta có: .
.
.
( )
( )
( )
( )
( )
x3 x3 2x9
x92x9
B
x x3 x
x3
− ++ +
−+ +
= =
++
( )
( )
x x2
x 2x x
2
x(x3) x3
x x3
+
++
= = =
++
+
x0>
A52x2x5
:
B3 3
x x3
++
>⇔ >
+
x35
3
x
+
⇔>
3x 9 5x⇔ +>
3x 0>
x0∀>
81
2x 9 0 x .
4
⇔ <⇔<<
2
5 6 7 (4 2 1) 1
5 6 7 33 128 1
C
32 32
− +−
−+ −
= =
−−
2
5 6 (2 2) 1
566 42 1
32 32
−−
−−
= =
−−
5 11 6 2
32
−
=
−
2
5 (3 2)
32
−
=
−
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
67
.
Câu 36.
a) Rút gọn biểu thức A.
Điều kiện:
0, 4, 9xxx> ≠ ≠⋅
Ta có:
( )
( )
32 2 32 2
23 5 6 23
23
xx x xx x
xxxxxx
xx
++ + ++ +
++ =++
−− −+ −−
−−
( )( ) ( )( ) ( )
( )( )
33 22 2
23
xx xx x
xx
+ −− + −+ +
=
−−
( )
( )
( )
( )
94 2
1
2
23
xx x
x
xx
−− − + +
= =
⋅
−
−−
( )
( )
( )
22
2
1
2 22
12
x xx
x xx
xx xx xx
xx
−− − −
−
−= = = ⋅
−− −− −−
+−
Do đó
( )( )
11
:
2
12
xx
A
xx
xx
+
= = ⋅
−
+−
b) Tìm
x
để
1
2PA
x
= −
đạt giá trị lớn nhất.
Ta có
2 21 2 1
2
x
P
xx
xx
+
= −=+ −
2
1
1 3 3.
x

=− − +≤


Dấu “=” xảy ra khi
1
1 1.x
x
=⇔=
Vậy
max 3 1.Px=⇔=
Câu 37.
Điều kiện:
0>a
và
1≠a
. Ta có:
( ) ( ) ( )
( )
22
1 1 12 12 4+ − − = ++ − +− =a a a aa a a
5(3 2)
5.
32
−
= =
−
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
68
và
( )
( )
( ) ( )
21 1 21 1 21 1++ + +− + = + − + =a a a a a aa
.
Do đó, phương trình đã cho có thể được viết lại thành
11
1
11
−=
−+aa
.
Phương trình này tương đương với
( )
( )
( )
( )
11
1
11
+− −
=
+−
aa
aa
hay
2
1
1
=
−a
.
Như thế, ta có
12−=a
hay
3=a
(thỏa mãn).
Vậy có duy nhất một giá trị
a
thỏa mãn yêu cầu đề bài là
3=a
.
Câu 38.
Với
0≥x
, ta có:
( )( )
( )( )
( ) ( )
( )
( )
( )
( )( )
( )( )
2
22 8 1
11 3
2 12 8 1 1
3
11
11
3 22 8
13
1
326
3
1
23
3
21
32

+ + − +−
= −⋅

−+ + +

+ +− − −+ −
= ⋅
+
+ −+
+−
+ +− −
= ⋅
++
−
=+ − −⋅
+
−
= − +⋅
+
=−−
=−+
x x x xx x
A
x x xx x
x x x xx x x
x
x xx
xx x
xx x
xx x
x
xxx
x
x
xx
x
xx
xx
( )
( )
( )
6 3 26 3 40
4 40 4 1 0
4 0 vì 1 0 0
=⇔− +=⇔− −=
⇔+ − −=⇔ − + =
⇔ − = +> ∀≥
A xx xx
xx x x x
x xx
16⇔=x
(TMĐK)
Vậy với
16=x
thì
6=A
.
Câu 39.
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
69
( )
( )
( )
( )
( )
x x x xxx
x xx x x x
P
x x x xx x x
xx xx
− ++ +
+ −+ +
=+− =+ −
−+
−+
2
11 1
23 1 23
11
( )
( )
( )( )
( )
xx x x x
x xx x
xx
xx xx
xx xx
+ +
−+
+ ++ +
++
=+− =+−
++
1 11
23 1 23 1
11
( )
( )
( )( )
( )
xx x x x
x xx x
xx
xx xx
xx xx
+ +
−+
+ ++ +
++
=+− =+−
++
1 11
23 1 23 1
11
x xx xx x x
x
xx x x x
+ ++ −+ + +
= + − = = ++
2 3 1 12 2 3 3
22
Áp dụng bất đẳng thức Cauchy, ta có
xP
x
+ ≥ ⇒ ≥+
3
2 26 2 26
Dấu bằng xảy ra khi
( )
x tmdk=
3
2
Câu 40.
a).
( )
( )
( )( )
( )( )
( )( )
( )
( )
1 22 1 1
49 3
12 12 12
xx xx
xx
A
xx xx xx
−+ −+
−− +
=+−
++ ++ ++
( )
( )
( )
( )
15 2
15
1
12
xx
x
x
xx
−+
−
= =
+
++
.
b).
15 6
5
11
x
A
xx
−
= =−+
++
. Với mọi
0x ≥
ta có:
11x +≥
nên
6
6
1x
≤
+
Do đó
6
51
1
A
x
=−+ ≤
+
. Giá trị lớn nhất của
A
là
1
đạt được khi
0x =
.
Câu 41.
a)
32 2
1:
1 2 3 56
xxx x
A
x x x xx

++ +
=− −+

+ − − −+

Với
0; 4; 9.xxx≥≠≠
( )
( )
( )
( )
( )
( )
33 22 2
1
:
1
23
xx xx x
A
x
xx
+ −− + −+ +
=
+
−−
1
:
1
A
x
=
+
( )( )
94 2
23
xx x
xx
−−++ +
−−
( )( )
13
:
1
23
x
x
xx
−
=
+
−−
11 2
:
12 1
x
A
xx x
−
= =
+− +
.
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
70
b) Ta có
3
3
3
1063 (13)13+=+ =+
2
21 45 (25 1) 25 1+ = += +
Nên
( 3 1)( 3 1) 2
52
25 4 25 4
x
−+
= = = −
++
Vậy
2 2019 2019
( 4 2) ( 1) 1Bx x= +− =− =−
Câu 42.
1. Ta có:
( )
( )
( )
( )
( )
2
2 11
2

+−
= ++ ⋅


+

+−
++
= ⋅
+ +−
+
= ⋅
+
+
=
xy x y xy
P
xy
xy x x y y
xy x y xy
xy y x
xy
x y x y xy
xy
xy
xy
xy
xy
xy
Vậy
+
=
xy
P
xy
với
0; 0>>xy
.
2.Áp dụng bất đẳng thức Cô-si, ta có:
2 2 16 4
4
1
16
+≥ = =
⇒≥ =
x y xy
P
Dấu “=” xảy ra
4⇔==xy
Vậy
min 1=P
tại
4= =xy
.
Câu 43.
Ta có:
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
71
( )
( )
(
)
( )
( )
33
33
3
3
3
3
2
2
2
70 4901 70 4901
140 3 70 4901 70 4901 70 4901 70 4901
140 3
3 140 0
5 5 28 0
5 87
5 do 5 28 0
24
=+ +−
⇒= + + − + + −
⇔= −
⇔+− =
⇔− ++ =


⇔ = + + = + + > ∀∈





x
x
xx
xx
x xx
x xx x x
Vì vậy
x
là số nguyên tố..
Câu 44.
Ta có
(
)
(
)
2
0 8 2 4 10 2 5 4 10 2 5AA>⇒ =+ + + − +
.
( ) ( )
2
2
8216 1025 82625 82 51A =+ −+ =+ − =+ −
.
( )
( )
2
2
8 2 5 1 6 25 5 1A =+ −=+ = +
.
51A⇒= +
..
Câu 45.
33
2 23 2 23 1x =+ +− −
33
1 2 23 2 23x⇔ += + + −
( ) ( )
3
32
1 46 1 3 9 3x x xxx⇒ + =− +⇒ + + =−
( ) ( )
33
32 3
2
39 3 9Pxx x x x x= ++ = + +
27P = −
Câu 46.
Ta có:
22
11 1 1
...
13 35 5 7
2019 2 2019
= + + ++
+++
−+
S
22
22
1 3 3 5 5 7 2019 2 2019
...
1 3 3 5 5 7 2019 2 2019
− − − −−
⇒= + + ++
− − − −
−
S
22
1 3 3 5 5 7 ... 2019 2 2019
2
−+−+−++ −−
⇒=
−
S
2
1 2019 1 2019
1009
22
−−
⇒= = =
−−
S
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
72
Vậy
1009=S
Câu 47.
Rút gọn biểu thức
( )
( )
2 22 1
2
aa
T
aa
−−
=
−−
với
0, 4aa>≠
.
( )
( )
( )
( )
2 22 1 2 2 1a a aa− −= − −
( )
( )
( )
22 1 1a aa= − −+
( )( )
2 12aa a a− −= + −
Vậy
( )
21Ta= −
.
Câu 48.
a) Điều kiện:
0>x
;
1≠x
.
( )
( )
( )
2
2
1
11 11 1
:.
1 11
1
1

−
+


=+=+


−− − +
−

−

x
x
P
x xx x x
xx
x
.
( )
( )
2
1
11
.
1
1
−
+−
= =
+
−
x
xx
xx
xx
.
( )
1 11
2. 1 2
4
22
−
=⇔ =⇔ −= ⇔ =⇔=
x
P x xx x
x
(thỏa điều kiện).
Vậy giá trị cần tìm là
4=x
.
b)
( ) ( ) ( )
32 3
23
3
33
46 5 61 2 5 3. 2 5 .1 3.2 5.1 1 2 5 1 2 5 1.− = − + −= − = −
( ) ( )
22
69 28 5 49 2.7.2 5 2 5 7 2 5 7 2 5.−=− + =− =−
3
46 5 61 69 28 5 2 5 1 7 2 5 6.= − + − = −+ − =A
Câu 49.
22
13 2 13 2
22
13 13
A
+−
=− −−
+−
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
73
( )
( )
( )
( )
22
22
134 134
21 3 21 3

+− −−

= −

+−


.
( ) ( )
22
23 23
21 3 21 3

−

= −

+−

( )
( )
22
3 3 33
4 23 4 23
13 13
=−=−
+−
+−
12 6 3 12 6 3 12 3
33
16 12 4
− −−
= =
−=−
−
Vậy
33A = −
.
Cách khác:
( )
( )
( )
2
13 4
1 3 2 2
3 3
2
13 13
21 3 21 3
+−

+
−= = =

++
++

( )
( )
( )
2
13 4
1 3 2 2
3 3
2
13 13
21 3 21 3
−−

−−
−= = =−

−−
−−

.
( ) ( )
22
22
3 333
13 13
13 13
A

= −− = −

+−

+−
3 3 12 6 3 12 6 3 12 3
16 12 4
4 23 4 23
− −−
=−= =−
−
+−
Vậy
33A = −
.
Câu 50.
( )
3 5 27 20 5 3 15A = −− +
.
( )
35 33 25 5 315= −− +
.
( )
5 3 3 5 3 15=−+
.
5 3 15 3 15 5=−+=
.
Câu 51.
a) Rút gọn biểu thức 𝐴 .
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
74
Điều kiện:
0
9
≥
≠
x
x
Ta có:
( )( ) ( )( )
3 2 12 18 4 3 3 8 24
13 13
−− + − −− − − + −
= =
+− +−
xx x x x x xx x x
A
xx xx
( ) ( )
( )( )
( )
( )
( )( )
38 3 3 8
8
1
13 13
−+ − − +
+
= = =
+
+− +−
xx x x x
x
x
xx xx
b)Tính giá trị của biểu thức 𝐴 khi
4 2 3.= −x
Ta có :
( )
2
423 3231 31 31 31= − =− += − ⇒ = − = −xx
4 23 8 12 23
43 2
311 3
−+ −
= =
= −
−+
A
Câu 52.
a) Ta có:
23
3
1
xx
x
x
−−
= −
+
8
24
2
xx
xx
x
+
=−+
+
1 14
1
11
xx x
x
xx
− +−
−=
−
+−
51Px x=−+
b) Tìm tất cả số nguyên tố
x
để
1P ≤
10 5Px≤⇔ ≤ ≤
2, 3, 5, 7, 11, 13, 17, 19, 23.xxxxx x x x x= = = = = = = = =
Câu 53
a).
( )
2
1
1
xx
xx
xx
+
= +
−+
( ) ( )
2 22
2 12 1
1
xxx
xx
xx
−−
− = −− −
+
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
75
b).
.
Câu 54.
2( 1) 2A x xx x= −++ −
2 ( 1)( 2)xx x x=+ −= − +
( 1)( 2) 0 1 0 0 1.xx x x− + ≤⇔ −≤⇔≤≤
Đối chiếu điều kiện giá trị cần tìm
0 1.x≤<
Câu 55.
Điều kiện:
x 0, x 1.≥≠
Ta có
3x3x3 x1 x1 x2 x2
P
x1 x2
( )( ) ( )( )
( )( )
+−−+ −−+ −
=
−+
x3x2 x1 x2 x1
x1 x2 x1 x 2 x1
( )( )
( )( ) ( )( )
++ + + +
= = = ⋅
−+ −+ −
x1
P3 3 x2 x4
x1
+
=⇔ =⇔ =⇔=
−
(thỏa mãn điều kiện).
Câu 56.
Điều kiện:
0x >
.
1 11
.
11
x
Ax
xxx x

−

=+−


−+ +


( )( ) ( )
( )( )
11 1
1
.
11
x x xx
xx
x
xx x

− +− − +

+

=


−+ +


12
.
1
xx x
x xx

+−
=

+

2x
x
−
=
2
2 22
1
11
x x xxx
xx
xx x x
+ −−
+ − =++
−+ +
1
1
xx
P
xx
++
=
−+
( )
3 13 1P xx xx≤ ⇔ + +≤ − +
( )
2
2 10x⇔ −≥
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
76
2. Ta có
22
1
x
A
xx
−
= = −
Suy ra
A
nhận giá trị nguyên khi và chỉ khi
x
là ước nguyên của
2
.
Hay
{ }
1;1; 2; 2x ∈− −
.
Ta có:
1x = −
(Vô nghiệm).
11xx=⇔=
(thỏa mãn).
24xx=⇔=
(thỏa mãn)
2x = −
(Vô nghiệm).
Vậy để
A
nguyên thì
{ }
1; 4x∈
.
Câu 57.
Đặt
3
2
sx=
và
2
3
ty=
thì đẳng thức đề bài có thể viết lại thành
3 2 32
s st t ts a++ +=
.
Do
,0st≥
nên
3 2 32
,s st sst t tstst+= + += +
.
Từ đó ta có
hay
( )
3
2
st a+=
.
Suy ra
3
2
st a+=
. Đây là kết quả cần chứng minh.
Câu 58. a) Điều kiện:
x y; x 1; y 1.≠− ≠− ≠
3 2 2 3 32 23 2 2 22
x x y y xy xy x xy y x y xy
P
(x y)(1 y)(1 x) (1
y)(1 x)
+ − + − − − + +−−
= =
+−+ −+
22
x xy x y
1x
+ +−
=
+
x xy y.=+−
b) Đặt
22 22 2 2
11 11 1 1
S 1 1
... 1 .
1 2 2 3 2017
2018
=++++++++ +
Ta có
2
22
1 1 11 2
11
n n1 n(n1)
n (n 1)

++ =+− +

++
+

*
(n )∈
2
11 11
1 1.
n n1 n n1

= +− =+−

++

Áp dụng đẳng thức trên ta được
11 11 1 1
S 1 1 ... 1
1 2 2 3 2017 2018

= +− + +− ++ + −


THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
77
=
1
2018 2018.
2018
−<
(điều phải chứng minh)
Câu 59.
Từ giả thiết đã cho ta có:
111
xz yz xy 2xy 2xz 2yz 0
xyz
+=⇔ + = ⇔ − − =
( )
2
222 222
x y z x y z 2xy2xz2yz xyz xyz⇒ + + = + + + − − = +− =+−
222
xyz⇒ ++
là một số hữu tỉ
Vậy ta có điều phải chứng minh
Câu 60.
a) Rút gọn T:
Với
a b,a 0,b 0≠>>
, ta có:
( )
( )
( )( )
( )
3 33 3
abab
a b ab a a b b a b a b a b ab a
b ab
T:
ab ab a
b
abab a
bab
−+
+− + − − − + +− +−
= =
⋅=
++
−+ −
Vậy :
a b ab
T
ab
+−
=
, với
a b,a 0,b 0≠>>
.
b) Chứng tỏ T > 1
Ta có:
a b ab
T
ab
+−
=
, với
a b,a 0,b 0≠>>
. (kết quả câu 1.a)
( ) ( )
22
ab ab ab
T 11
ab ab
−+ −
⇔ = = +>
(vì
ab 0, a b 0> −≠
với
a b,a 0,b 0≠>>
)
Vậy T > 1
Câu 61.
Ta có ngay:
A 4 20 45 3 125 2 405
85 35 155 185 25
B 9 42 9 42
= −+ −
=−+ − =
=− ++
( ) ( )
22
2 2 2.2 2.1 1 2 2 2.2 2.1 1= − ++ + +
( )
( )
22
22 1 22 1
22 1 22 1 22 122 1 42 (do22 1 0)
= −+ +
= − + + = −+ += −
>
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
78
Câu 62. Ta có:
2.3 1 2
12 3
2 1 2 2.3
+== ⇒ =
+
3.4 1 2
123 6
2 1 2 3 3.4
.................
2018.2019 1 2
1 2 3 ..... 2018
2 1 2 3 ...... 2018 2018.2019
22 2
P 1 1 ...... 1
2.3 3.4 2018.2019
2.3 2 3.4 2 2018.2019 2
. .......
2.3 3.4 2018.2019
++== ⇒ =
++
+++ + = ⇒ =
+++ +

=−− −


−− −
=
( ) ( )
( ) ( )
4 10 4074340
. ...........
2.3 3.4 2018.2019
1.4 2.5 3.6 2016.2019 2017.2020
. . ........ .
2.3 3.4 4.5 2017.2018 2018.2019
1.2.......2017 . 4.5.......2020
1.2020 2020 1010
2018.3 6054 3027
2.3.......2018 . 3.4.5.......2019
=
=
= = = =
Câu 63.
a) Điều kiện
x 0;x 1>≠
( )
( )
( )
( )
( )
( )
( )
( )
2
2
x1 1 x1
A : .x
x
xx x x x x
xx x 1
x1
.xxx 1
x. x x 1
x1
. x1x x1 x1 x1 x1
x x1
+− +
= = −
++ − +
++
+
= −
++
+
= −
+ += + −=−
++
b) Ta có:
2
T B 2A= −
( )
( )
( )
2
42
42 2
42
42 2
2
2
2
x 5x 8x 2025 2 x 1
x 5x 8x 2025 2x 4x 2
x 7x 4x 2023
x 8x 16 x 4x 4 2003
x 4 x 2 2023
=− −+ − −
=− −+ − +−
=− −+
= − + + − ++
=−+−+
Vì
( )
( )
2
2
2
x 4 0, x 2 0 T 2003−≥ −≥⇒≥
Dấu “=” xảy ra
2
x2
x 40
x2
x2
x20
x2
=
−=
⇔ ⇔ ⇔=
= −

−=
=
Vậy với
min
T 2003 x 2= ⇔=
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
79
Câu 64.
a) Rút gọn biểu thức
( )
( )
1
P:
a bab++
Điều kiện :
a 0,b 0>>
( )
( )
( )( )
( )
( )
( )
( )
( )
( )
( ) ( )( )
22
.1
11
1
:.
abab ab ab ab
P ab
ab ab
P P
a bab
a bab
a b a bab abab a b
−+− − +
= = =
−
++
⇒ =
++
++
= − + +=− +=−
b) Ta có:
( )
( )
( )
2
2
2018 1
2019 2 2018 2018 1
2020 2 2019 2019 1
2019 1
2018 1 2019 1 2018 2019
a
aa
bb
b
Pab
= +

=+=+

⇔⇒

=+=+


= +
⇒ = − = +− + = −
Câu 65. 1) Điều kiện
01a<<
( )
( )
( )
2
2
2
2
2
2
2
2
2
1 1 11
1 21
11
11
1
1 11
21
11
11 1
1 1 11
1
1111

+−
= + −−
− +

+− −
− −+



−
+−

= + −
−+



+− −
− −− +




+ −−
= + −−



+− − +− −


aa
Q aa
aa
aa
aa
a
aa
aa
aa
aa
aa a
a aa
a
aa
aa aa
2
1111
. 1 ( 0)
11

++ − −
= −− >


+− −

aaa
a do a
aa
aa
( )
2
1 111
. 1 ( 0 1)
11
++ − − −
= − <<
+− −
a aa
a do a
a
aa
( )
( )
( )
( )
2
1111
11
.1
11
++ − +− −
−−
= −
+− −
aaaa
a
a
a
aa
2
2
11 1 1
. .(1 )
1 1 21
+ −+ − −
= −
+ +− − −
aa a
a
a
aa a
2
2
2 11
. (1 )
2 21
−−
= −
−−
aa
a
a
a
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
80
(1 ) 1=−− =−aa
2) Điều kiện
0a1<<
Ta có:
( )
3
3
Q a1= −
Xét hiệu :
( ) ( )
( ) ( ) ( )( )( )
3
3
2
Q Q a1 a1
a1 a1 1 a1a11a11 a(a1)(a2)
−=− −−

= − − − = − −− −+ = − −


Mà
( )( )
33
a0
0a1 a10 aa1a2 0
a20
Q Q0 Q Q
>
< <⇒ −< ⇒ − − >
−<
⇒ − >⇔ >
Vậy
3
QQ>
Câu 66.
( )
( )
( ) ( )
( )
( ) ( )
( )
( ) ( )
2
A 4 15 10 6 4 15 4 15. 2. 5 3 4 15 4 15
8 2 15. 5 3 . 16 15 5 3 . 5 3 .1
5 3. 5 3 5 3 2
=+ − −=+ − + −
= + − −= + −
= + − =−=
Câu 67.
a) Điều kiện
a0>
a a a 4a
P.
a2a3a2 a

+−
= +


+ ++

( )
( )( )
( )( ) ( )( )
( )( )
a. a 1
a 4a
.
a2 a
a1 a2
a a 4a
.
a2 a2 a
2a2a a.a12a
aa
.
a2 a a
a12 a a a 2

+
−

= +

+
++



−
= +


++

− + +−
+
= =
+
= + − =−+ +
b) Điều kiện
0a >
. Ta có:
2
1 99
Paa2 a
2 44

=−+ + =− − + ≤


Dấu “=” xảy ra
1 11
a 0 a a (tm)
2 24
⇔ −=⇔ = ⇔=
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
81
Vậy
9
MaxP
4
=
khi
1
a
4
=
Câu 68.
Điều kiện
a 0;x 1>≠
( )
( )
( )
( )
2
2
2
2 432
2
4 32 2
2
2
2
2
2 22
22
2
a
x a1 1a
a1
a 2a 1 a 2a 2a
a1
(a 1)
a 2a a 2a 1 2a
a1
a1
a a1
a1
a1
a a1 a a1 a a1
a1 a1
do 0
a1 a1 a1
a 2a 1 a a 1 a
1a 0
a1 a1
0x1 a0
xx
x x 2x 11
P
x 2x 1
=+− + +
+
+ ++ + +
=+−
+
+ + + ++
=+−
+
++
=+−
+

++ ++ ++
=+− = +− >

+++

+ +− −−
= =
<∀>
++
⇒ < < ∀>
+−
+ − ++
⇒= =
−+
( )
( )
( )
2
2
11
x1
x x11
2a 1
x1 x1 2
2a 2
a
1x a
1a
x1
1
a1
+
−
+ −+
+
+− +
= = =
= = +
− +−
−
−
+
Vậy
P 2a 2= +
Câu 69.
( ) ( )
( ) ( )
( )
( ) ( )
( )
22
xy xy
y
x5
3
x y.x y 2x2y x.x y y.x y
x y 2xy x y 2xy yy xx
5
xy2x4y 3
xy. x y


+ +−


++=


+ − ++ +
+




++ ++− +
⇔ +
=
−+ +
+
( )( )
( )
x y x y xy
2(x y)
5
3(x y) 3
xy. x y
+ +−
+
⇔+ =
+
+
x y xy
1
xy
+−
⇔=
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
82
x y xy xy⇔+− =
( )
2
x y 2 xy 0
xy 0
⇔+− =
⇔− =
x
xy 1
y
⇔=⇒ =
Vậy
x
1
y
=
Câu 70.
22 22 422
2
22 22
4
:, 0

++ −+ −
= − >>


−+ ++

a ab a ab aab
P ab
b
a ab a ab
(
)
(
)
(
)
(
)
( )
22
22 22
2
22 22 222
.
4
+ + −− +
=
++ −+ −
a ab a ab
b
a aba ab aab
(
)
( )
222 22 222 22
2
2 22
22
22 2 22
2
22 22
22
.
4. .
4
.
4. .
+++ +− ++− +
=
−−
−
++
= =
−−
aab aab aab aab
b
a ab
aa b
aa b b aa b
b
aab aab
22
22
22
22
0
0
+
>
−
=
+
−<
−
ab
khi a
ab
ab
khi a
ab
Câu 71.
( ) (
)
22
22
xa xa
a x 2x a a x 2x a
A =
x x xx
−+
+− ++
=++
x ax a
x
− ++
=
.
+) Với
xa≥
thì
xaxa−=−
nên A =
x a x a 2x
2x
xx
− ++
= =
.
+) Với
0x a<<
thì
( )
xa xa ax− =−− = −
nên A =
a x x a 2a
xx
−++
=
.
Câu 72.
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
83
a) Với
x 0;x 4>≠
, ta có:
x 3x 2 1 1
A:
xx 8 x 2 x

++
= −


−−

( )
( )
( )
( )
x3x2 x2x4
x
x 2 x 2x 4 x 2 x 2x 4

++ ++

= −

−++ −++


.
( )
( )
x2 x
x.
x 2x 4
x 2 x 2x 4
−
= =
++
−++
Ta có
( )
( )
22
x 14 6 5 9 2.3. 5 5 3 5 x 3 5 3 5 3 5.= + =+ += + ⇒ = + = + =+
Khi đó, ta có:
( )
( )
35 35 35 1
A.
8
24 8 5
14 6 5 2. 3 5 4 8 3 5
+ ++
= = = =
+
++++ +
b) Ta có
( )
2
2
A 24 84 23 23 2=−+ = −
( )
A 23 2⇒=± −
Do
A0<
nên
A 2 23= −
.
Câu 73.
a) + Biến đổi
( )
( )
( )
( )
( )
( )
2
x2 x x1
x 4x 4 x x
1x
x x2
x1 x2 x1 x1
++
++ +
+= −
−
+−
−+ −+
=
x2 x 2
x1 x1 x1
+
−=
−−−
+ Biến đổi
( )
( )
1 1 2x
x11 x
x1 x1
−=
+−
+−
+ Ta có
( )
( )
( )
( )
x1 x1
2 2x 2
A: .
x1 x1
2x
x1 x1
+−
= =
−−
+−
+ Vậy
x1
A
x
+
=
, với điều kiện
x 0, x 1>≠
.
b) Ta có:
1 2018 1 1 1 1
A 11
2018 x 2018 x 2018
+
≥ ⇔+ ≥+ ⇔ ≥
x 2018 0 x 2018≤ ⇒<≤
Vì
x 0, x 1>≠
và
x
nguyên nên
{ }
x 2;3;4;...; 2018∈
. Suy ra có 2017 giá trị nguyên của
x
thỏa mãn bài toán.
Câu 74. Ta có:
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
84
2 2 a 2a b 2 ab
A:
1 ab 1 ab
++
=
−−
2(1 a) 1
2 ab(1 a) ab
+
= =
+
Khi
a 0; b 0>>
,
11 1 1
1 11
ab a b
⇔ =⇔+=⇔=−
a+ b
a + b = ab
ab
Do đó
2
1 1 1 11 1
A (1 )
4 24
bb b

= − =− −≤


. Dấu “ = “ xảy ra
b 4; a 4⇔= =
. Vậy giá
trị lớn nhất của A là
1
4
khi
ab4= =
Câu 75.
Ta có:
( )
( )( )
( )( )
( )
3
2
1 a a 2a 1
P 1 a a1
a1 a
1 a1 aa a
1
P 1
a.
a
a1 a1
1 aa a1
P 1
a. (Do a1 a1 a10)
a1 a

+ −
+

= +− >

−


+ −+ −

= +−

−+



−+ −
= +− >⇒
>⇒ −>


−

1 aa a1a a a1
P.
a1 a
a a1
P.1
a1 a
− ++ −−+ −
=
−
−
= =
−
Câu 76.
( )( )
x2 x33x4x5 x2 x3 3x4x5
a) P
x15 x x4x5 x15 x
x1 x5
+ + +− + + +−
=−− =−−
+− −− +−
+−
(x 2)(x 5)(x 3)(x 1)(3x 4x 5)
(x 1)(x 5)
+ −+ + +− + −
=
+−
x 3x 2
(x 1)(x 5)
−− −
=
+−
(x 1)(x 2) x 2
(x 1)(x 5) x 5
++ +
=−=−
+− −
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
85
Ta có
x5
x2 x2
P2 22 0
x5 x5
x 12
<
++
>− ⇔− >− ⇔ − > ⇔
−−
>
.
+ Với
x5 0x25<⇔≤<
.
+ Với
x 12 x 144> ⇔>
.
Câu 77.
Điều kiện :
0, 1xx>≠
( )
( )
( )
( )
2
2
2x 1
x x 2x x
A
x1 x x1 x
xxx 1
2 x1 2
x1
x x1
13 1 33
1 x. x 1 x x x
44 2 44
−
−+
=+−
− ++
−
= −+ − −
++

=+ − =− ++= − +≥


Vậy
3
A.
4
≥
Dấu
""=
xảy ra
11
x 0 x (tm)
24
⇔ −=⇔=
Câu 78.
a) Ta có:
22 22 22
y
xx
Q 1:
xy xy x xy


= −+

− − −−

22 22
22 22
x xyx xy
x
y
xy xy
+− −−
=−⋅
−−
222
22 22
xxy
x
xy yxy
−+
= −
−−
22 22
y
x
xy xy
= −
−−
( )
2
xy
xy
xy.xy xy
−
−
= =
+− +
Vậy
xy
Q
xy
−
=
+
với
xy0>>
.
b) Ta có:
Thay
x 3y=
(thỏa mãn ĐK) vào biểu thức Q, ta được:
3y y 2y
2
Q
2
3y y 4y
−
= = =
+
Vậy
2
Q
2
=
khi
x 3y=
.
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
86
Câu 79.
( )
3
x y 2x x y y
3 xy 3y
A
xy
xx yy
−+ +
−
= +
−
+
với
x,y 0≥
và
xy≠
( )( )
( )
( )( )
3y x y
x x 3x y 3y x y y 2x x y y
xyxxyy xyxy
−
− + −+ +
= +
+ −+ − +
( )
( )
( )
3 x x xy y
3y
xy
x y x xy y
−+
= +
+
+ −+
3y
3x
xyxy
= +
++
3x 3y
3
xy
+
= =
+
Vậy giá trị của biểu thức
A
không phụ thuộc vào giá trị của biến với
x,y 0≥
và
x y.≠
Câu 80.
a) ĐKXĐ:
x0;y0,y1,xy0.≥ ≥ ≠ +≠
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
x x 1 y 1 y xy x y
P
x y1 y x1
x y x y x xy y xy
x xy y.
x y1 y x1
+− − − +
=
+− +
+ − +− +−
= =
+−
+− +
( )
( )
( )( )
) 2 2 1 1 1 11 1=⇔ + − =⇔ + − +=⇔ − + =b P x xy y x y y x y
Ta có:
1y1x11x2x4.+ ≥⇒ −≤⇒ ≤ ⇔ ≤
Kết hợp với điều kiện
{ }
x 0 0 x 4 x 0;1;2;3;4≥⇒≤≤⇔∈
Thay vào phương trình trên
P2=
Ta được
( ) ( ) ( )
{ }
x;y 4;0 ; 2;2∈
Câu 81.
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
87
( )
( )
( )
( )
( )
( )
( ) ( )
( )
22
22 22
22
22
22
22
22
ab a b
ab ab
abab ab
ab a b
ab ab
ab ab ab
ab
ab. ab ab ab. ab ab
ab
ab ab ab. ab ab
ab
2a b. a b
ab
2bab ab.
ab
P ab0
ab

−+
⋅


++ −
− −+ −


−+

= ⋅

++ −
− +− −
−


− +− − + − ++ −
+
= ⋅
− ++ − +− −
−
−+
+
= ⋅
−−
−
= + >>
−
+
22
ab
b
ab
+
=
+
Vì a – b = 1 a = b + 1 khi đó theo BĐT AM – GM:
( )
2
2
22 2
b1 b
a b 2b 2b 1 1 1
= 2b + 2 2 2b 2 2 2 2
bb b b b
P
++
+ ++
= = = +≥ ⋅ += +
Câu 82.
a) ĐKXĐ:
0; 0, 1.x y xy≥≥ ≠
( )
( )
( )
( )
11
12
:
11
1
.
11
+ + +− −

− +++
=

−−

++++−−+
−
=
− ++
+
x y xy x y xy
xy x y xy
P
xy x
y
x xy y yx x xy y yx
xy
xy x
y xy
( )
( )( )
( )
( )( )
2
21
2
11 11 1
+
+
= = =
++ ++ +
x yx
xy
x
xy xy x
b) Với
( )
( )
( )
( )
2
22 3
2
x 4 23 3 1.
23
2 32 3
−
= = =−=−
+
+−
( )
2
x 31 31 31= − = −= −
( )
( )
2
2 31
23 2 63 2
P.
13
5 23
1 31
−
−+
= = =
−
+−
Câu 83.
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
88
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
x 3x 2 x x 1 1
a) P :
x1
x x2 x
1 x1
x 3x 2 x x 1 x 1
:
x1
x2 x1 x
1 x1
x1 x1
x 3x 2 x 2x
.
2x
x2 x1
x1 x1
x2 x1
..
2x 2x
x2 x1


++ +
=−+



−
+− +
−



+ + −+
+

= −

−
+− +−


+−
+ +−−
=
+−
+−
++
= =
+−
( )
x 0;x 1
1 x1
b) 1
2x x 1
P8
1*
8
x1
> ≠
+
− ≥⇔
+
−≥
+
( )
( )
( )
( )
( )
2
2
16 x x 1
* 1 x 3 0 x 9 tm
8 x1
−+
⇔ ≥ ⇔ − ≤⇔ =
+
Vậy
x9=
thì
1 x1
1
P8
+
−≥
Câu 84.
Với điều kiện
x 0,x 1>≠
, ta có:
( )
( )
( )
( )
( )
x 2x x 1 2x 2x 1
P
x1x x1 xx x1 x x1x x1
− + −+
= ++
− ++ ++ − ++
( )
( )
( )
( )
( )
xx 2x x 1 x 1 2x 2x 1
x x1x x1
− + + −+ − +
=
− ++
( )
( )
( )
xx x 2
x x1x x1
+−
=
− ++
( )
( )
( )
( )
x1 x2
x2
.
x x1
x1x x1
−+
+
= =
++
− ++
Ta có với điều kiện
x0,x1 x x1 x11> ≠⇒+ +> +>
x2 x2 1
0P 1 2
x x1 x1 x1
++
⇒<= < =+ <
++ + +
Do
P
nguyên nên suy ra
x2
P1 1 x1
x x1
+
=⇔ =⇔=
++
(loại).
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
89
Vậy không có giá trị của
x
để
P
nhận giá trị nguyên.
Câu 85.
Ta có
( ) ( )
22
xxxx
A xx1 xx12x.
x x1x x1
−+
= + = −+ +=
++ −+
Do đó
( )
B 1 2A 4x 1 1 2x 1 1 12x 2x.=− − +=− −=− − =
Câu 86.
Ta có:
( )
2
a 3 5 23 3 5 23 29 5 23=+++−++−+
6 24 23=+−
( ) ( ) ( )
22
62 31 62 31423 1 3=+ −=+ −+ =+
Vì
a0>
nên
a 31= +
. Do đó
( )
2
a1 3−=
hay
Câu 87.
( )
( )
( )
( )
( )
22
22
P 1x 1 1x 1 1x
P 1x221 1x 21x1 x

=− +−+−−


⇒ =− + −− = − +
Mà
( )
( )
( )
22
P 1x 1x 1x 1x 1x 1x 0 P 21x= −+ − − + −− − − ≥⇒ = −
Với
1 2019
x P
2.
2019 2018
=− ⇒=
Câu 88.
Với n là số nguyên dương ta có:
( )
( )
1 n 11 1 n 1 1
n
n n1 n1
n 1n
n1 n n
n n1

= = − =− >−

++
+
++

Suy ra:
1 1 1 111 1 1
A ... 1 ...
2 1 3 2 2011 2010 2 2 3 2010 2011
= + ++ >− + − ++ −
1 2 87
1 1.
89 89
2011
=− >− =
Lại có:
( )
( )
1 2 22
n1 n n n1
n1 n1 n n
<=−
++
+ ++
2 2 2 2 2 1 1 88
A 2 ... 2
1 2 1
45 45
2 2 3 2010 2011 2011


⇒ <− + − ++ − = − < − =




THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
90
Câu 89.
Ta có
( )
( )
2
15
A 2 2 5 20 20. 2 2 5 2 5 20.
55
2 5 2 25 45 25 4 25 45 4
= − + − =−+ −
= −+−=−+−=−
THCS.TOANMATH.com
TÀI LIỆU TOÁN HỌC
| 1/88
| | Tải xuống

Có thể bạn quan tâm:

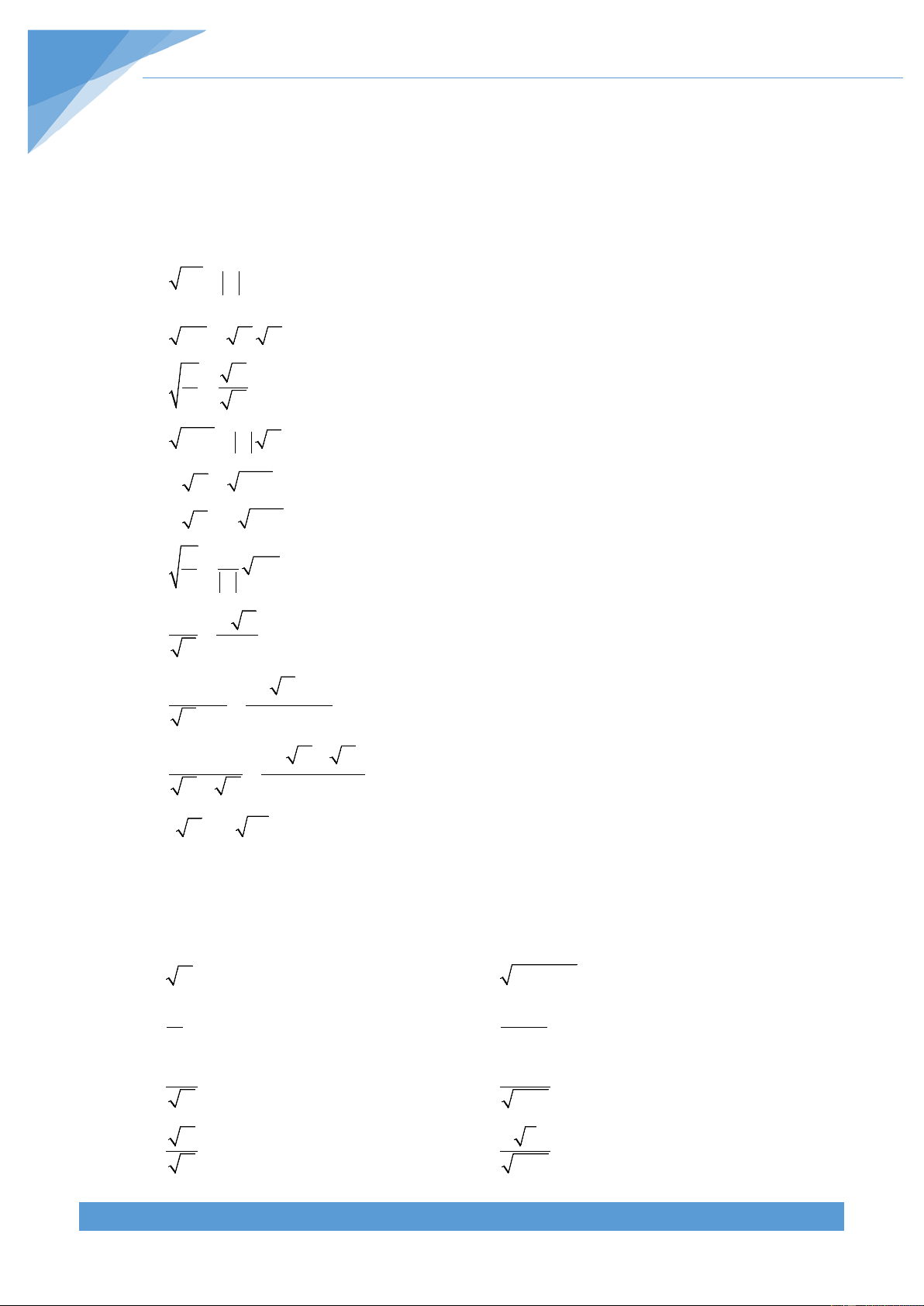
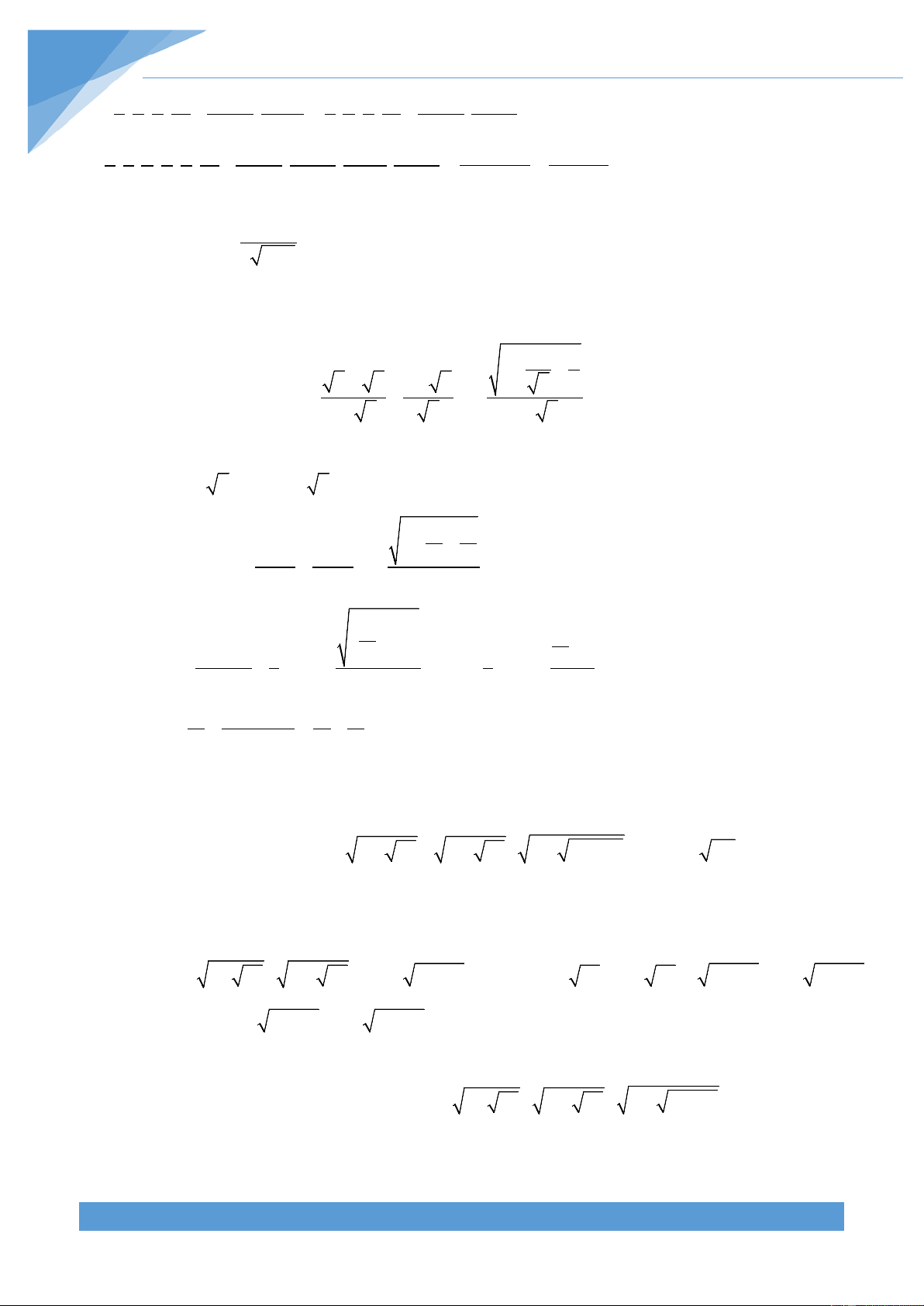
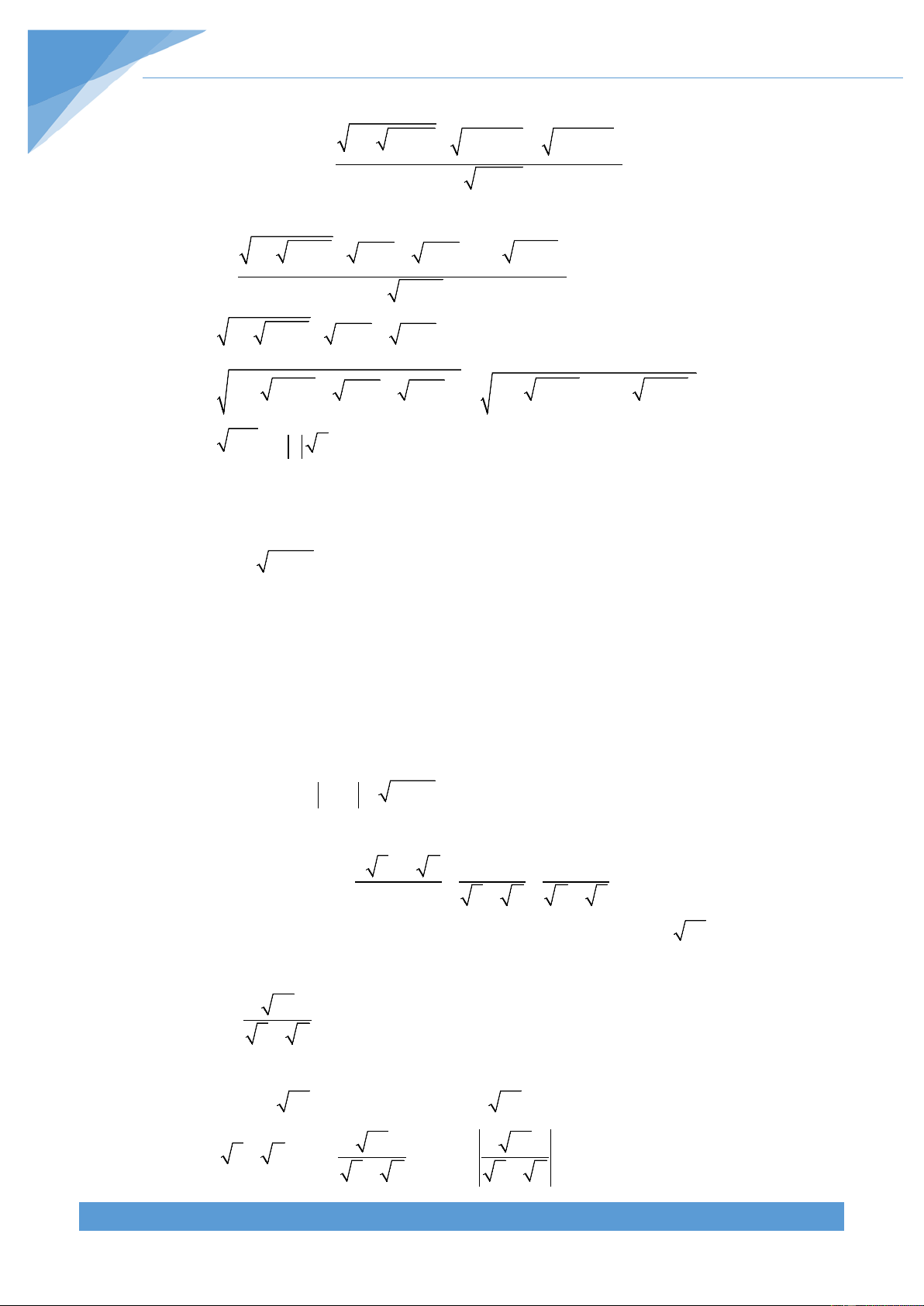
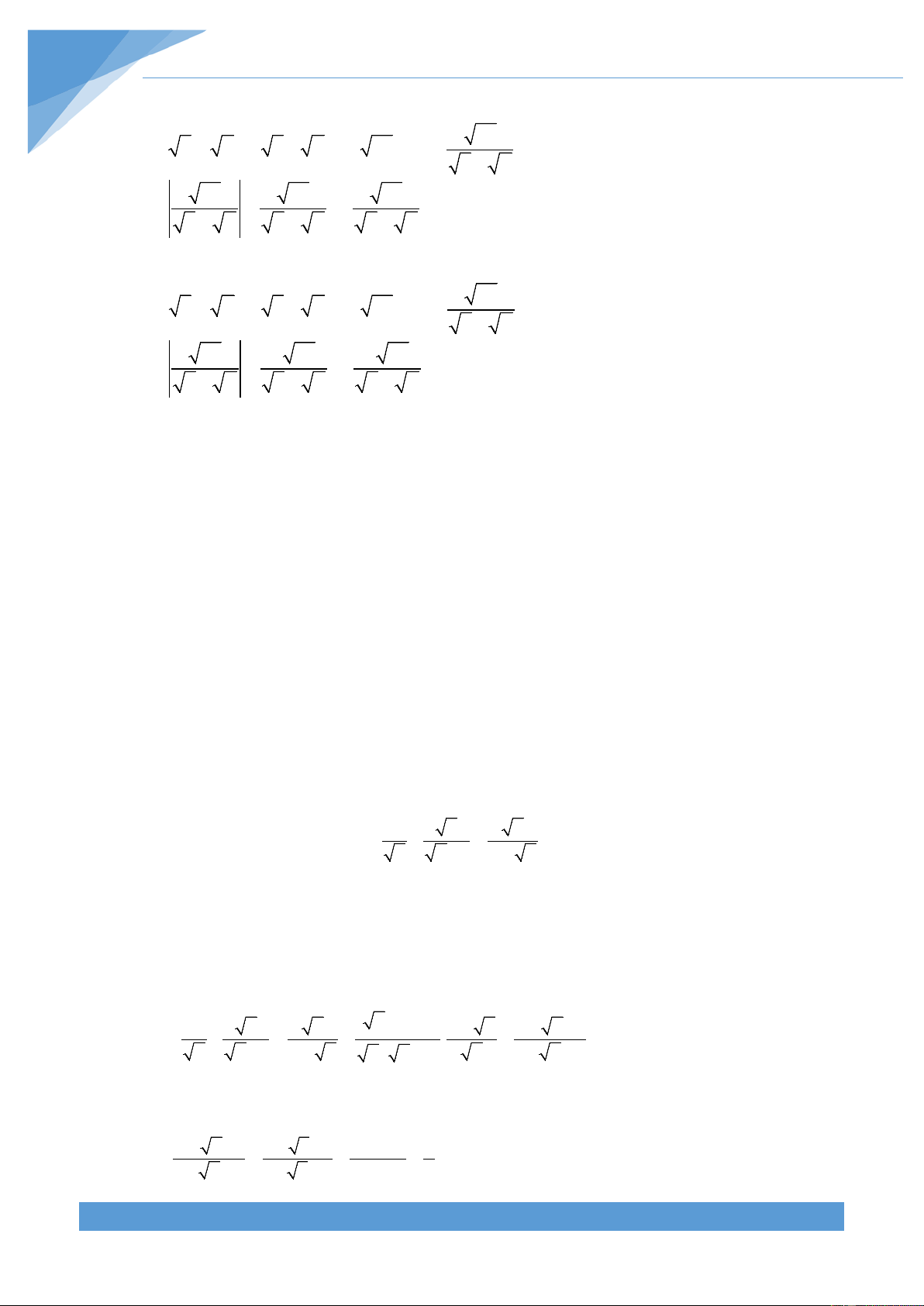
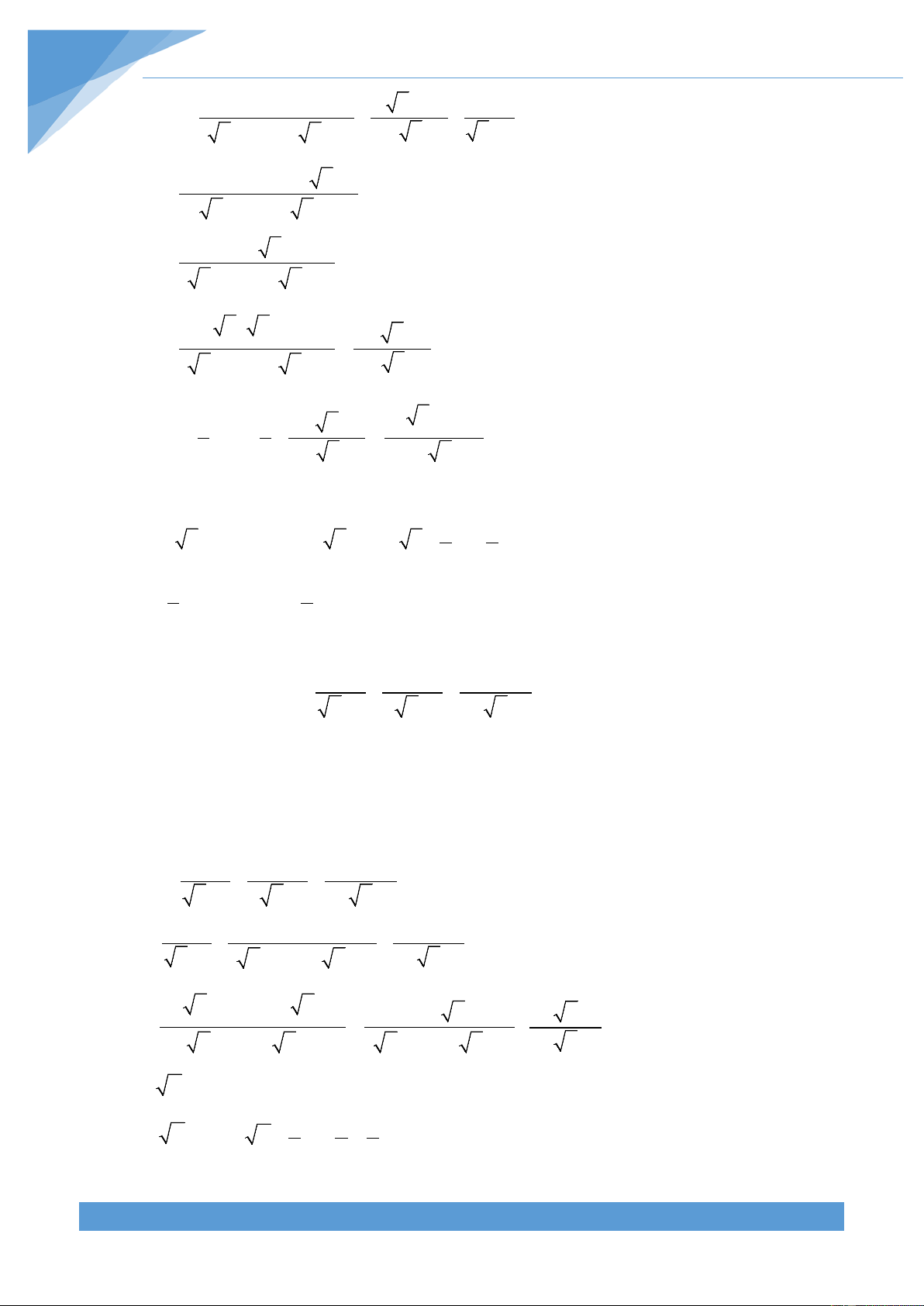
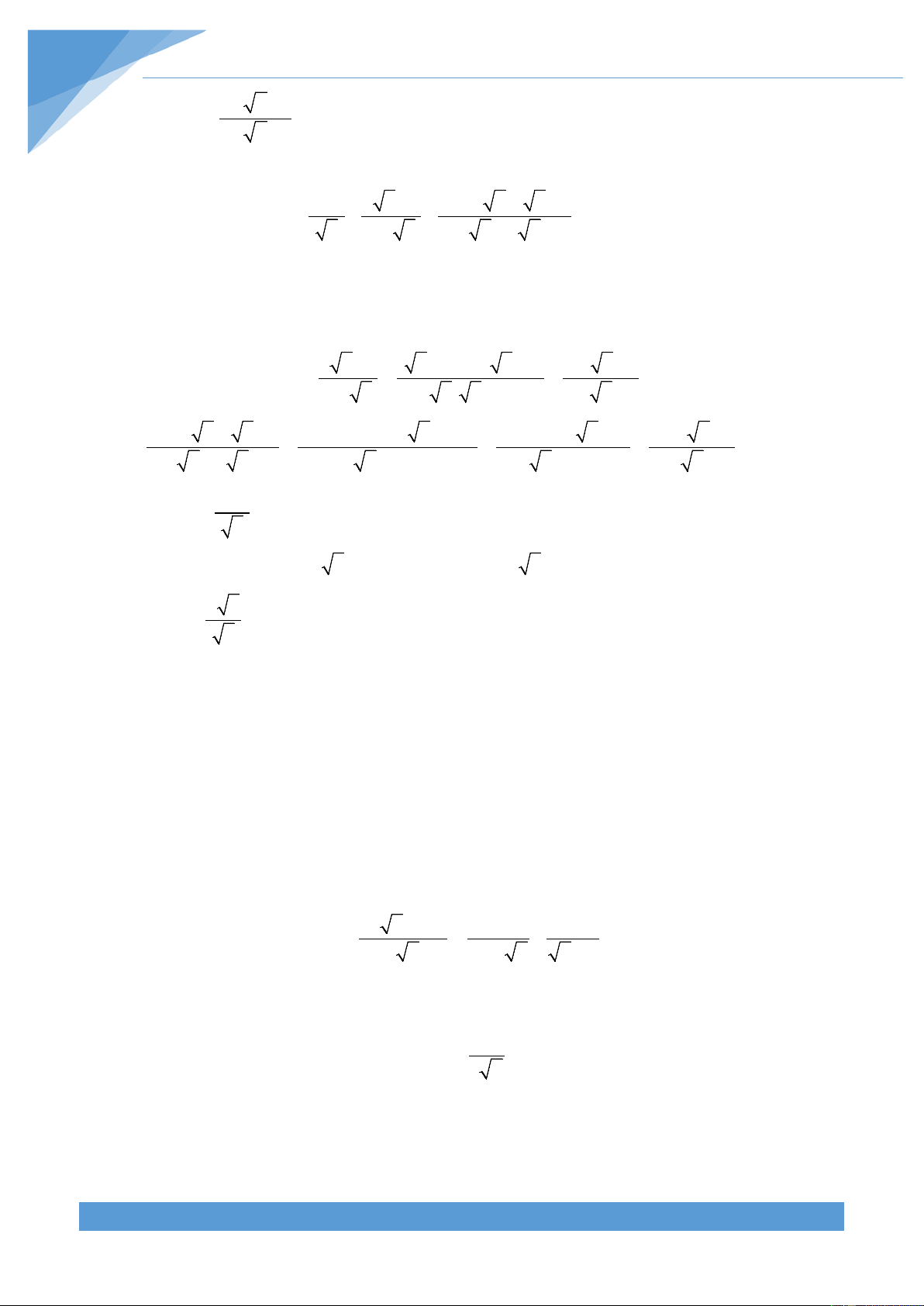
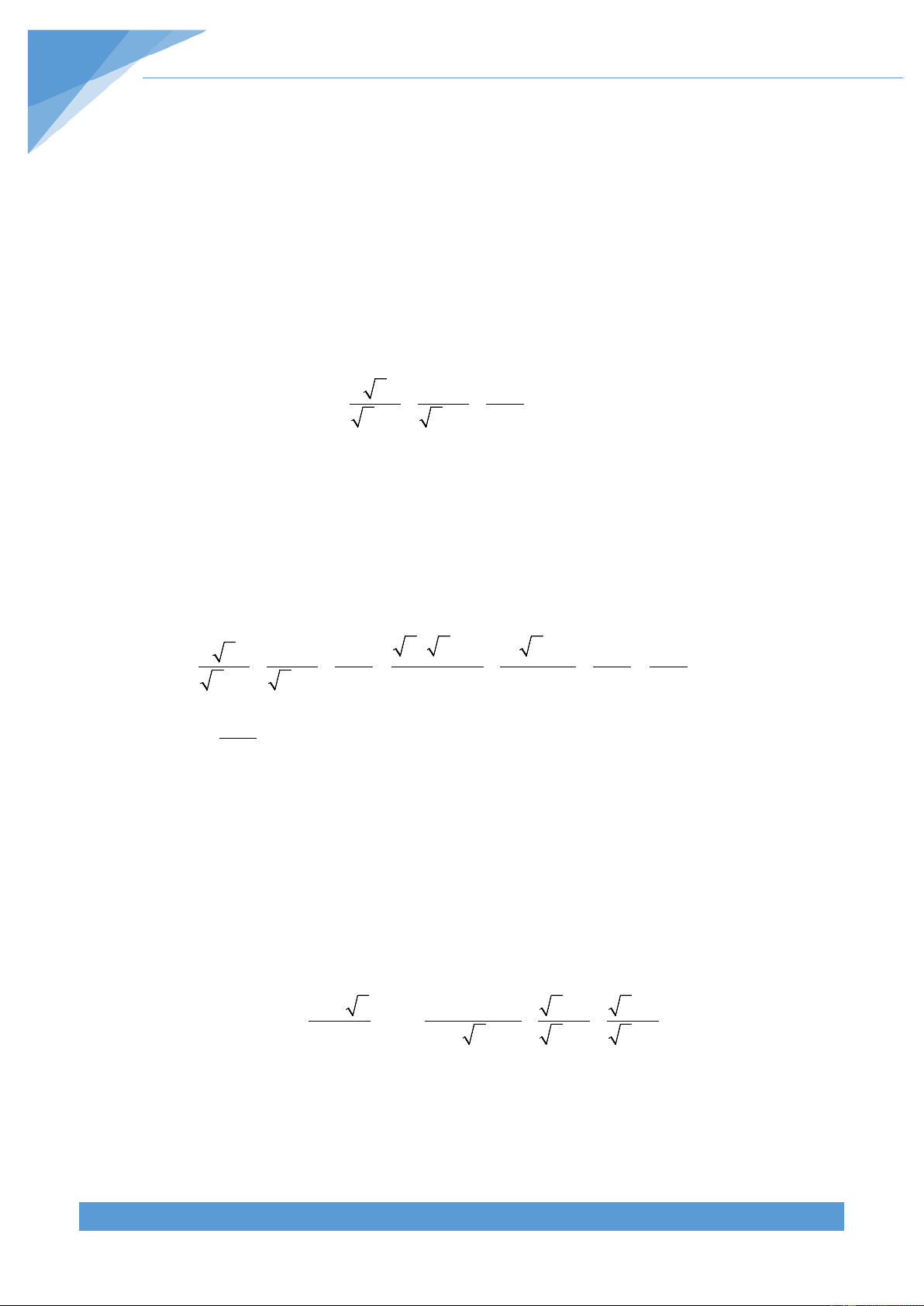
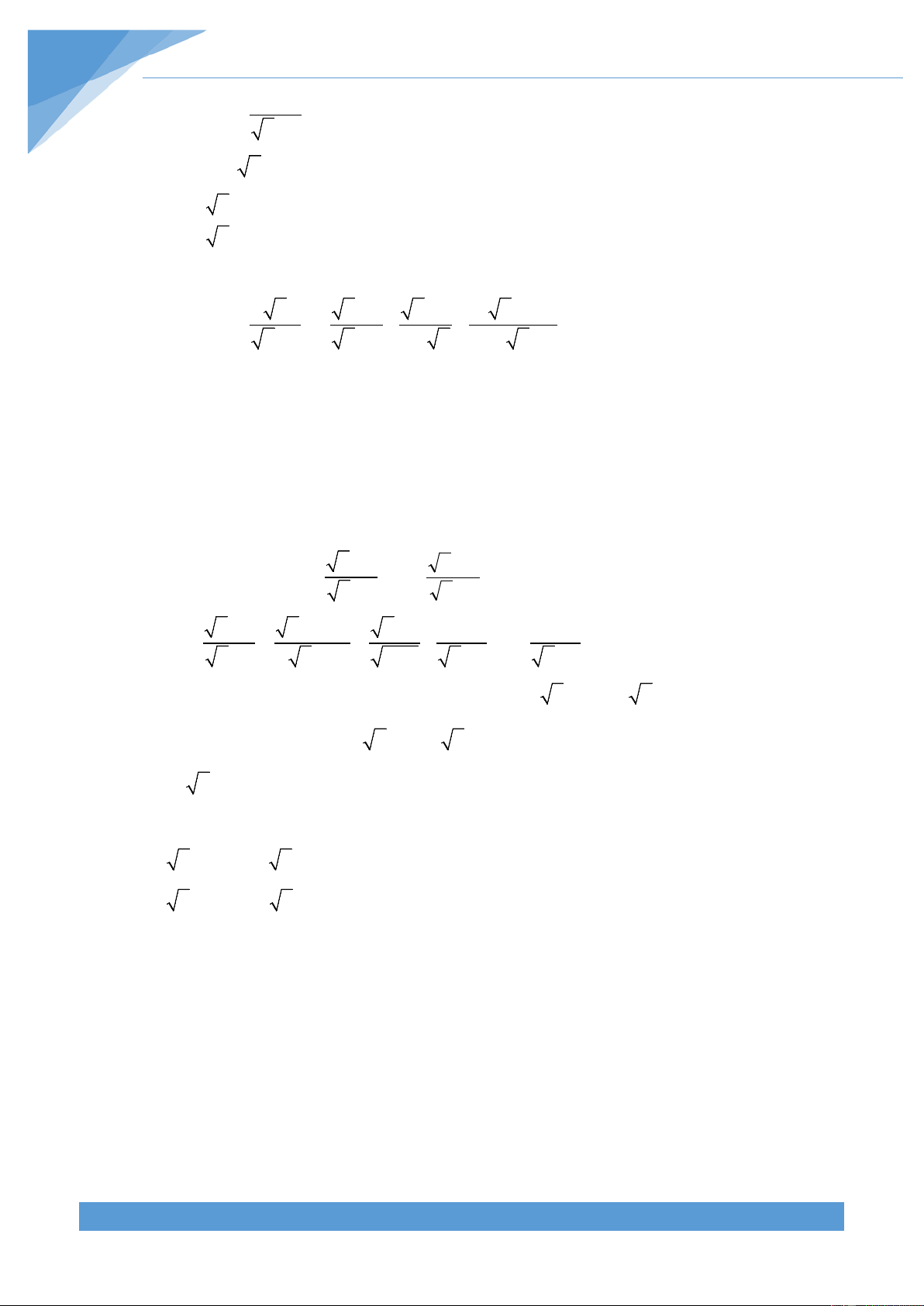
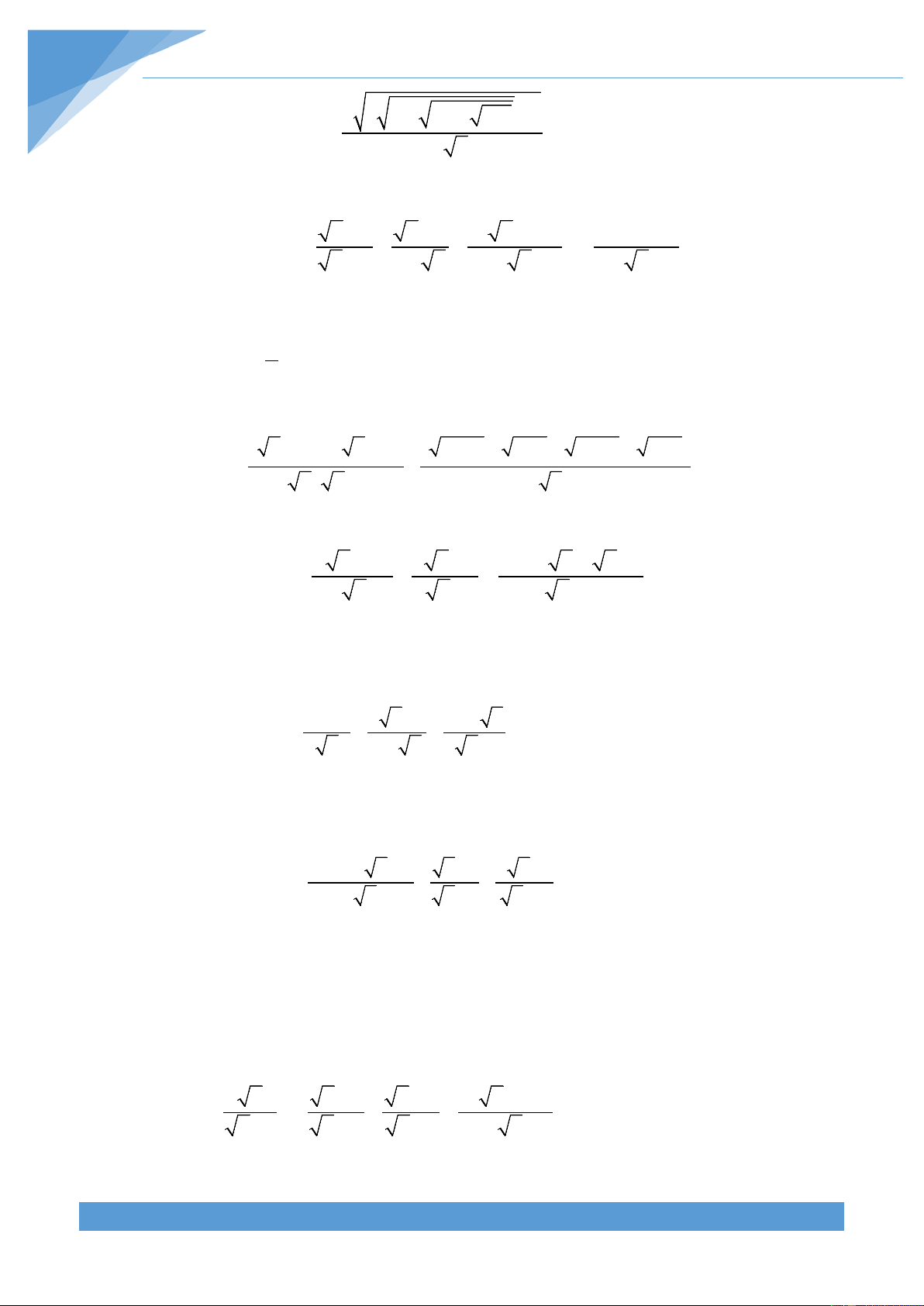
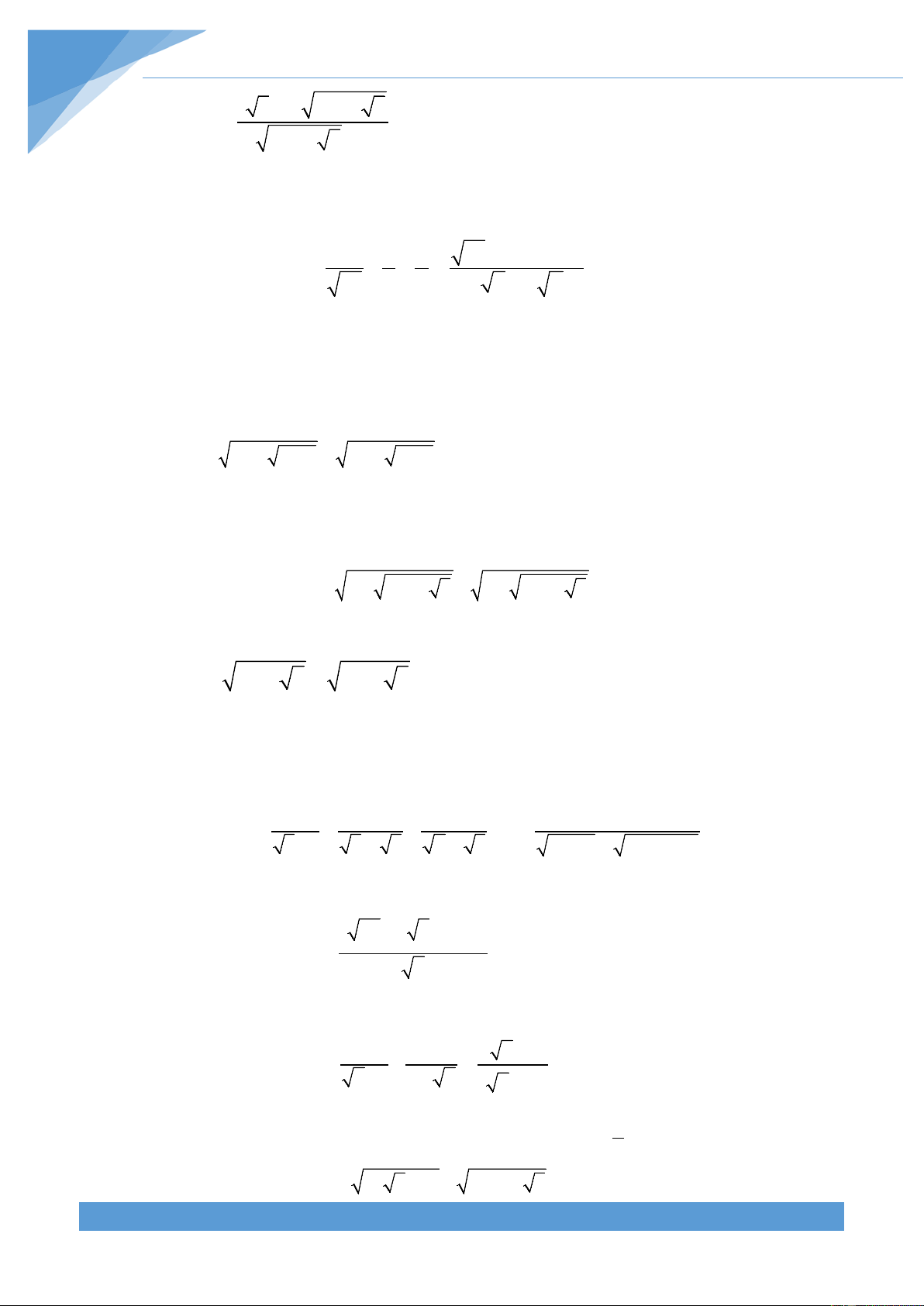
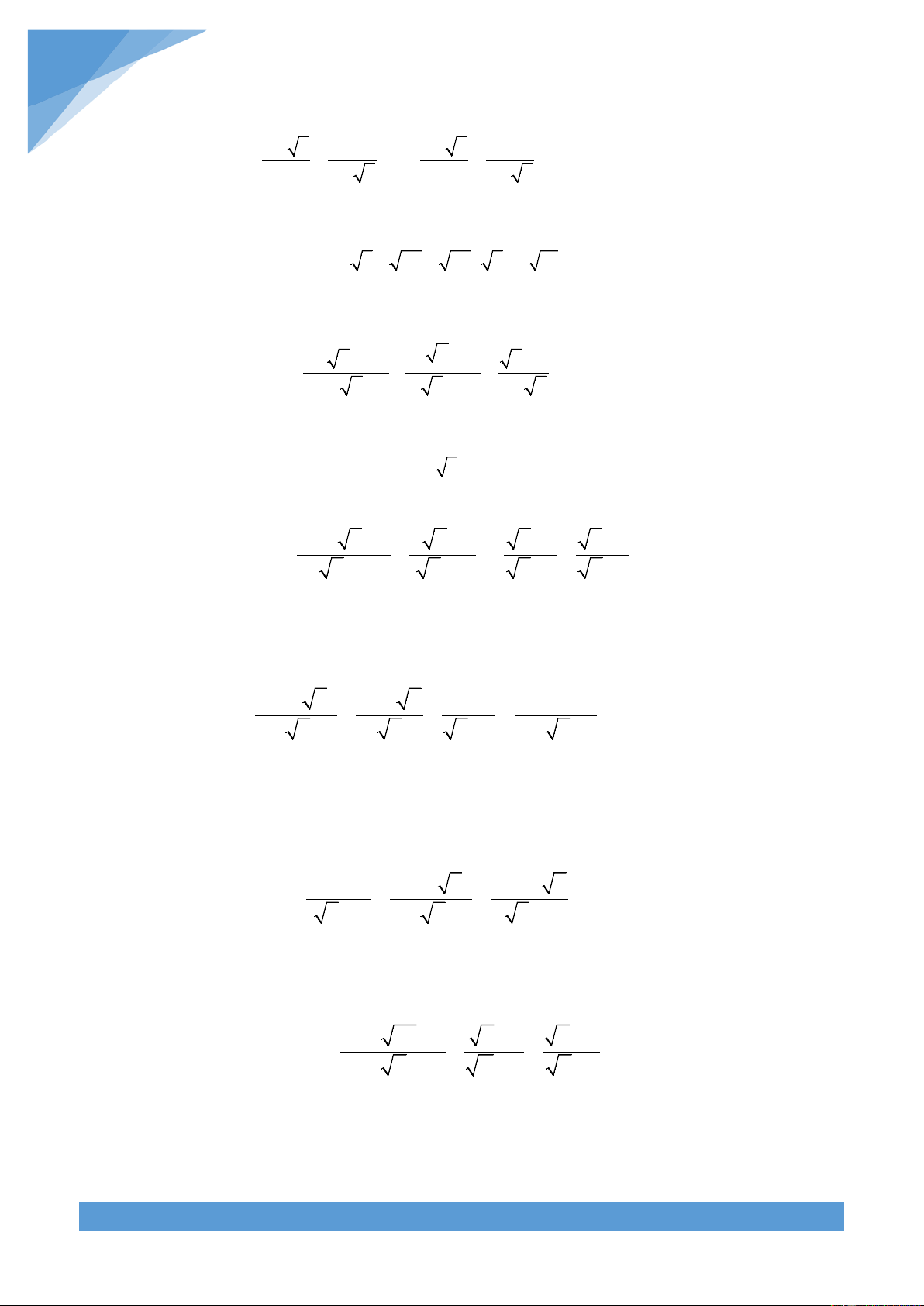
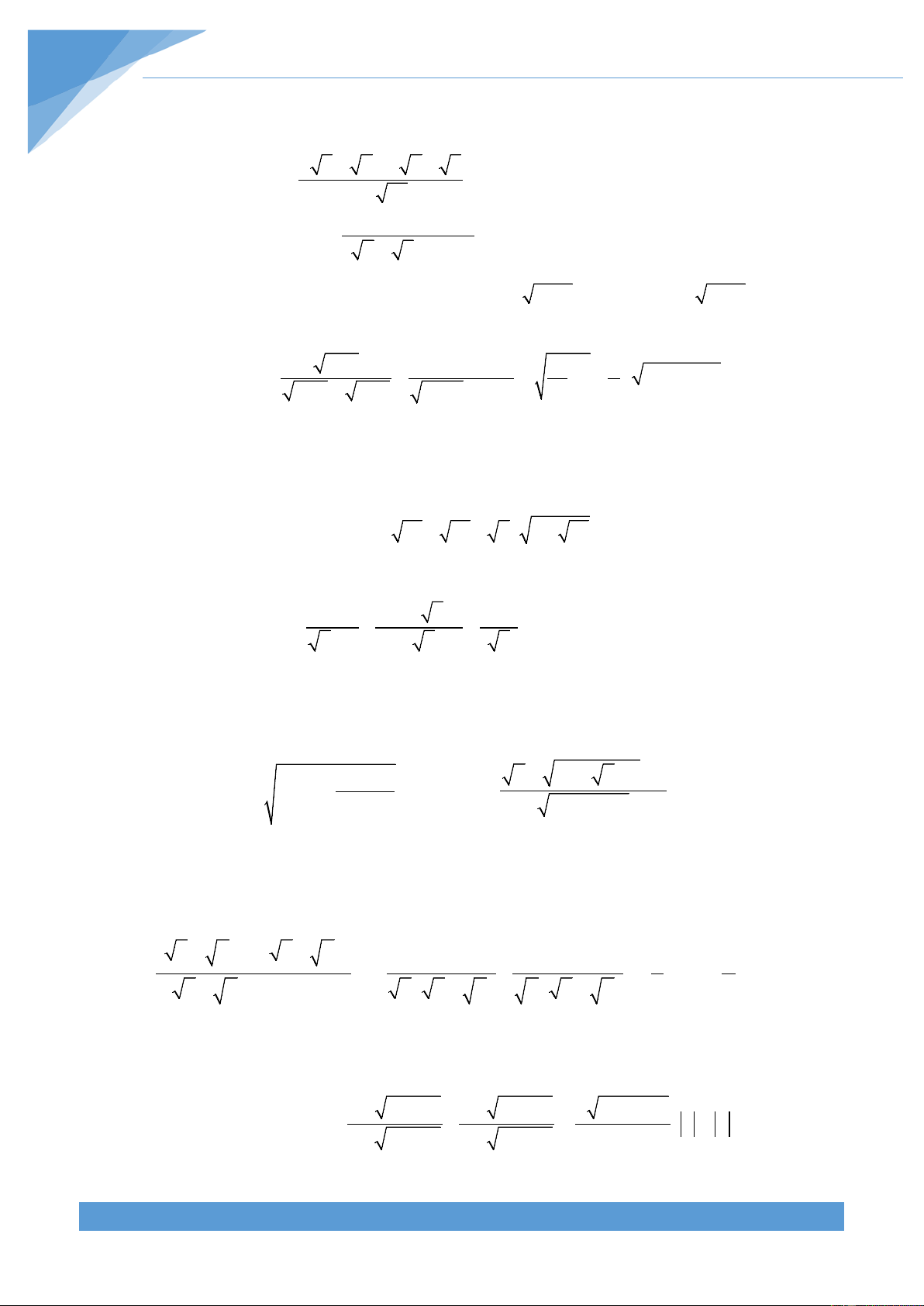
Preview text:

3
CHUYÊN ĐỀ: RÚT GỌN BIỂU THỨC CHỨA CĂN
VÀ BÀI TOÁN LIÊN QUAN
Các công thức biến đổi căn thức A nÕu A 0 2  ≥ 1.
A = A = −A nÕu A < 0 2. AB = A. B
(Với A ≥ 0; B ≥ 0) 3. A = A
(Với A ≥ 0; B > 0 ) B B 4. 2 A B = A B (Với B ≥ 0) 5. 2 A B = A B
(Với A ≥ 0; B ≥ 0) 6. 2 A B = − A B
(Với A < 0; B ≥ 0) 7. A 1 = AB
(Với A ≥ 0; B > 0 ) B B 8. A = A B (Với B > 0 ) B B
C ( A ± B C ) 9 = (Với 2 A ≥ 0; A ≠ B ) 2 A ± B A − B
C ( A ± B C ) 10 =
(Với A ≥ 0; B ≥ 0;A ≠ B ) A ± B A − B 11 ( 3 A)3 3 3 = A = A
Cách tìm điều kiện trong bài toán chứa căn thức BIỂU THỨC - ĐKXĐ: VÍ DỤ 1. A ĐKXĐ: A ≥ 0
Ví dụ: x − 2018 ĐKXĐ: x ≥ 2018 x + 2. A ĐKXĐ: 4 B ≠ 0 Ví dụ: ĐKXĐ: x ≠ 7 B x − 7 x + 3. A ĐKXĐ: B > 0 Ví dụ: 1 ĐKXĐ: x > 3 B x − 3 x ≥ 0 4. A ĐKXĐ: x
A ≥ 0; B > 0 Ví dụ: ĐKXĐ:  ⇔ x > 3 B x − 3 x > 3 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 4 A ≤ 0 x +1≤ 0   B < 0 x + 2 < 0 x < 2 − 5. A ĐKXĐ: x +  Ví dụ: 1 ĐKXĐ: ⇔   BA ≥ 0 x + x + ≥ x ≥  2 1 0 1   B > 0 x + 2 > 0 Cho a > 0 ta có: x > a 6. x > a Ví dụ: 2 x > 1 ⇔  2 x > a ⇔ 
x < − a
x < − a Cho a > 0 ta có: 7. Ví dụ: 2 x < 4 ⇔ 2 − < x < 2 2
x < a ⇔ − a < x < a
Dạng 1: Các bài toán biến đổi căn thức thường gặp
Thí dụ 1. (Trích đề thi HSG huyện Nghi Xuân Hà Tĩnh)
Tính giá trị của biểu thức: A = 6 − 2 5 + 14 − 6 5 Lời giải Ta có: = − + − = ( − )2 + ( − )2 A 6 2 5 14 6 5 5 1 3 5 = 5 −1+ 3 − 5 = 2
Thí dụ 2. (Trích đề thi HSG tỉnh Lâm Đồng năm 2010-2011) Cho E = ( 2 +1) 3 3 2 −1 3
. Chứng minh rằng E là số nguyên 3 Lời giải Ta có: − E ( 2 1) (3 2 1) 2 −1 3  2 . 2 1 3 2  ( 2 1) 3 3 3 3 3  = + = + + + 3  3 = 2 2 (8 − 3 7) − (8 + 3 7) = ( 3 3 1+ 2 + 4 )(3 2 −1) 3 3 = 2 −1 = 1 Vậy E là số nguyên
Thí dụ 3. (Trích đề thi chọn HSG tỉnh Hòa Bình Năm 2010-2011) 4 4 Rút gọn: 8 + 2 −1 − 8 − 2 −1 A = . 4 8 − 2 + 1 Lời giải Đặt T A = . Ta có T > 0 nên 2 T = T M THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 5 Xét 2  4  4 4  4 T  8 2 1 2. 8 2 1. 8 2 1  8 2 1 = + − − + − − − + − −      4 = 2 8 − 2 8 − ( 2 −1) 4 = 2 8 − 2 2 + 1  4 2 8 2 1 = − +     4 T 2 8 2 1 ⇒ = − +    ⇒ A = 2
Thí dụ 4. (Trích đề thi HSG Phú Thọ năm 2012-2013)
Rút gọn biểu thức: A= 2 10 + 30 − 2 2 − 6 2 : 2 10 − 2 2 3 −1 Lời giải
Ta có: 2 10 + 30 − 2 2 − 6 2 : = 2 10 − 2 2 3 −1
2 2( 5 −1) + 6( 5 −1) 3 −1 2 + 3 3 −1 4 + 2 3 3 −1 3 + 1 3 −1 1 . = . = . = . = 2 2( 5 −1) 2 2 2 4 2 2 2 2
Thí dụ 5. (Trích đề thi HSG T.P Bắc Giang năm 2016-2017)
Tính giá trị của biểu thức N = 4 + 3 + 4 − 3 + 27 −10 2 4 + 13 Lời giải
Ta có: N= 2( 4 + 3 + 4 − 3 ) + 25 −10 2 + 2 8 + 2 13 = 2( 4 + 3 + 4 − 3 ) 2 + (5 − 2)
(4 + 3) + 2 4 + 3 4 − 3 + (4 + 3) 2( 4 + 3 + 4 − 3 ) 2 2( 4 + 3 + 4 − 3 ) = + (5 − 2) = + 5 − 2 2 ( 4 + 3 + 4 − 3 ) 4 + 3 + 4 − 3 = 2 + 5 − 2 = 5
Thí dụ 6. (Trích đề thi Chọn HSG tỉnh Long An năm 2012)
Không sử dụng máy tính, hãy thực hiện phép tính:A = 2 − 3 + 4 − 15 + 10 23 − 3 5 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 6 Lời giải 2  2 3 4 15 10  − + − + 
Ta có: A = 2 − 3 + 4 − 15 + 10   = 23 − 3 5 2  23 3 5  −    ( 3−1)2 + ( 5− 3)2 4 − 2 3 + 8 − 2 15 + 2 5 + 2 5 = = 46 − 6 5 (3 5−1)2 3 −1+ 5 − 3 + 2 5 3 5 −1 = = = 1 3 5 −1 3 5 −1
Thí dụ 7. (Trích đề thi HSG huyện Nga Sơn-Thanh Hóa năm 2016-2017) + − Rút gọn biểu thức: B = 2 3 2 3 + 2 + 2 + 3 2 − 2 − 3 Lời giải Ta có: B 2 + 3 2 − 3 2 + 3 2 − 3 = + = + 2 + + − − 3 + 3 3 − 3 2 4 2 3 2 4 2 3 B
(2 + 3)(3 − 3) + (3 + 3)(2 − 3) 3 + 3 + 3 − 3 = = 2 (3 + 3)(3 − 3) 6 B =1 ⇒ B = 2 2
Thí dụ 8. (Trích đề thi HSG huyện Thạch Hà năm 2016-2017) So sánh 2.2016 2 2 2017 −1 − 2016 −1 và 2 2 2017 −1 + 2016 −1 Lời giải 2 2 2 2 Ta có:
( 2017 −1 − 2016 −1)( 2017 −1 + 2016 −1) 2 2 2015 −1 − 2014 −1 = 2 2 2017 −1 + 2016 −1 2 2 2 2 (2015 −1) − (2014 −1) 2017 − 2016 (2017 − 2016)(2017 + 2016) = = = 2 2 2 2 2 2 2017 −1 + 2016 −1 2017 −1 + 2016 −1 2017 −1 + 2016 −1 2017 + 2016 2.2016 = > 2 2 2 2 2017 −1 + 2016 −1 2017 −1 + 2016 −1 Vậy 2.2016 2 2 2017 −1 − 2016 −1 > 2 2 2017 −1 + 2016 −1
Thí dụ 9. Rút gọn các biểu thức: THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 7 a) 3 3 A = 5 − 3 − 29 −12 5 b) B = 70 − 4901 + 70 + 4901 Lời giải = − − − = − − ( − )2 a) A 5 3 29 12 5 5 3 2 5 3 = 5 − ( 5 −1) = 1 b) Đặt 3 3 x = 70 − 4901 + 70 + 4901 0 3 3  3 3 x  70 4901 70 4901  ⇒ = − + + 0    3 3  3 3 70 4901 70 4901 3 70 4901. 70 4901  70 4901 70 4901  = − + + + − + − + +    = 140 + 3x Khi đó ta có: 3
x + 3x −140 = 0 ⇔ (x − 5)( 2 x + 5x + 28 = 0 0 0 0 ) Mà 2
x + 5x + 28 > 0 do ∆ < 0 ⇒ x = 5 0 0 ( ) 0 Vậy B = 5. + + + +
Thí dụ 10. Rút gọn biểu thức: 2 3 6 8 4 P = 2 + 3 + 4 Lời giải Ta có: + + + + ( 2 + 3+2)+( 4 + 6 + 8 2 3 6 8 4 ) P = = 2 + 3 + 4 2 + 3 + 4
( 2 + 3+ 4)+( 4 + 6 + 8) ( 2 + 3+ 4)+ 2( 2 + 3+ 4) = = 2 + 3 + 4 2 + 3 + 4 = 1+ 2
Dạng 2: Dùng ẩn phụ đơn giản hóa bài toán 1 7 − 2 7 6 7
Thí dụ 1. Rút gọn biểu thức: 4 A = − 7 − + + . 4 4 7   4 1 1 343 4 7 − 7  7 +  7  7    Lời giải Đặt 4 4 a = 7 ⇒ a = 7 và 2 a = 7 ta có: THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 8 2 1 a − 2 2 2 2 a 6 7 1− 2a 13a + 7 A = − a − + + = + 3 3 2 a 1 2  1  a a a (a + 1) a − a a + a a    4 2 6 4 2 4 2 4 a + a − 2a − 2a + 13a + a 2a (7 − a ) = = = 0 ( 4 Do a = 7 3 2 3 2 ) a (a + 1) a (a + 1) 2
Thí dụ 2. Rút gọn biểu thức: B = . 4 4 4 4 − 3 5 − 2 25 − 125 Lời giải Đặt 4 2 4 3 4 4 6 2 5
b = 5 ⇒ b = 25,b = 125,b = 5,b = 5b ,b = 5b. 2 Ta có: B = 2 3 4 − 3b + 2b − 3b 3 2 + + + Mặt khác: 1 1 (b 3b) (2b 4) = = 3 2 3 2 3 2 2 2
b − 2b + 3b − 4 (b + 3b) −(2b + 4) (b + 3b) −(2b + 4) 3 2 3 2 2 5 4 2 b + 3b + 2b + 4
(b + 2b + 3b + 4)(b − 3) b + 2b − 2b − 9b −12 = = − = 2 4 2 − b − 6 2(b − 9) 8 2 2 −b − 2b −1  b + 1  = = −  . 4  2  2 Vậy  2  4 4 B = 2 = =   . 4  b + 1  b + 1 5 + 1 2 1 2 1+ + 4 4  4 − 2 1+ 2  2 2
Thí dụ 3. Rút gọn biểu thức: E =  +  − .  4 4 1 2 2  − 1+   2 Lời giải Đặt 4 4 4 2 2 = a ⇒ a = 2, 4 = a = 2 Ta có: 2 1 1+ + 2 2 2 2 2 2 4  a − a 1+ a  a a  1+ a  1+ a 1 1 E =  +  − =  a − +  − = − = 0 2 2  1− a a  1+ a  a  a ( 2 1+ a ) 2 2 a a Vậy E = 0
Dạng 3: Các bài toán về tính tổng dãy có quy luật
Thí dụ 1. Rút gọn: 1 1 1 1 S = + + ....+ + 2 1 + 1 2 3 2 + 2 3
1999 1998 + 1998 1999 2000 1999 + 1999 2000 Lời giải THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 9 Với k∈N,k ≥ 1: 1
(k+1) k −k k+1 (k+1) k −k k+1 1 1 ( = = = − k + 1) . 1 k + k k +1 (k +1)2 2 .k − k (k +1) k(k +1) ( ) k k + 1
Áp dụng (1) với k = 1, 2, 3,....., 1999 ta được 1 1 1 = − ; 2 1 + 1 2 1 2 1 1 1 = − ; 3 2 + 2 3 2 3
− − − − − − − − − − − − − 1 1 1 = − . 2000 1999 + 1999 2000 1999 2000
Cộng các đẳng thức trên theo vế ta được: 1 1 1 1 S = + + ....+ + 2 1 + 1 2 3 2 + 2 3
1999 1998 + 1998 1999 2000 1999 + 1999 2000 1 1 1 1 1 1 = − + − + .....+ − 1 2 2 3 1999 2000 1 1 = − 1 2000 2000 −1 = 2000 20 5 −1 = 20 5
Thí dụ 2. Rút gọn: 1 1 1 1 1 1 1 1 1 1 1 1 A = + + + + + + ....+ + + + + + . 2 2 2 2 2 2 2 2 2 2 2 2 1 2 3 1 3 4 1 1998 1999 1 1999 2000 Lời giải Với k∈N,k ≥ 2 : 2  1 1  1 1 2 2 2 1+ − =  1+ + + − −   k −1 k  (k−1)2 2k k−1 (k−1)k k 1 1 2 2 2 2 = 1+ + + − + − (k 1)2 2k k−1 k− − 1 k k 2 1 1  1 1 1 1  ⇒ + + = + − (  k −1)2 2 k  k −1 k  1 1 1 1 ⇒ 1+ + = 1+ − 1 2 2 ( ) (k 1) k k − − 1 k THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 10
Áp dụng (1) với k = 1, 2, 3,....., 2000 ta được  1 1   1 1   1 1   1 1 A 1 1 ... 1 1  = + − + + − + + + − + + −        .  2 3   3 4   1998 1999   1999 2000  1 1 = 1998 + − 2 2000
Thí dụ 3. Rút gọn các biểu thức 1 1 1 1 A     ...  ; 1  2 2  3 3  4 n  1  n Lời giải Ta có: 1 2  1  
      2 1 1 2 2 1 2 1 1 3  2  
      3  2 2 3 2 3 3 2
                         1 n n  1     n   n
n n   n n   n n 1 1 1 1 Do đó: 1 1 1 1 A     ... 
 2  1  3  2  ....  n n  1  n  1 1  2 2  3 3  4 n  1  nThí dụ 4. a) Chứng minh rằng: 1 1 1 + +....+ > 4 . 1 + 2 3 + 4 79 + 80 b) Chứng minh rằng: 1 1 1 1  1  + + + ...+ > 2 1−   . 1 2 2 3 3 4 n n +1  n +1  c) Chứng minh: 1 1 1 1 1 2 n − 2 < + + + + ...+
< 2 n −1 với mọi số nguyên 1 2 3 4 n dương n ≥ 2 . Lời giải a) Xét 1 1 1 A = + +....+ , 1 1 1 B = + + ..+ 1 + 2 3 + 4 79 + 80 2 + 3 4 + 5 80 + 81
Dễ thấy A > B . Ta có 1 1 1 1 1 A + B = + + +....+ + 1 + 2 2 + 3 3 + 4 79 + 80 80 + 81 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 11 ( k +1− 1 k ) Mặt khác ta có: = ( = + − + +
k + + k )( k + − k ) k 1 k k k 1 1 1
Suy ra A + B = ( 2 − 1)+( 3 − 2)+...+( 81− 80) = 81−1= 8 . Do A > B suy ra
2 A > A + B = 8 ⇔ A > 4 . b) Để ý rằng: 1 1 1 1 − = <
với mọi k nguyên dương. k k +1
k(k +1) ( k +1 + k ) 2k k +1 Suy ra  1   1 1   1 1   1  VT > 2 1− + 2 − + ..+ 2 − = 2 1−         .  2   2 3   n n +1   n +1  c) Đặt 1 1 1 1 1 P = + + + +...+ 1 2 3 4 n Ta có: 2 1 2 2 < = <
với mọi số tự nhiên n ≥ 2 . n + n +1 n 2 n n + n −1
Từ đó suy ra ( n + − n) 2 2 2 2 1 = < <
= 2( n − n −1) hay n +1 + n 2 n n + n −1 ( n+ − n) 2 2 1 <
< 2( n − n −1) n
Do đó: 2 ( 2 − 1)+( 3 − 2)+...+( n+1− n) <T  và
T < 1+ 2 ( 2 − )
1 + ( 3 − 2 ) +....( n − n −1) .
Hay 2 n − 2 < T < 2 n −1.
Thí dụ 5. Chứng minh rằng với mọi số nguyên dương n > 2 , ta có: 1 4 7 10 3n − 2 3n +1 1 . . . .... . < . 3 6 9 12 3n 3n + 3 3 n +1 Lời giải
Để ý rằng các phân số có tử và mẫu hơn kém nhau 2 đơn vị, nên ta nghĩ đến đẳng thức n n −1 − + < ( n n 2 2
⇔ n < n + n − 2 ⇔ n > 2) . Kí hiệu 1 4 7 10 3 2 3 1 P = . . . .... . . Ta có: n + 2 n 3 6 9 12 3n 3n + 3
 1 4 7 10 3n − 2 3n +1  1 4 7 10 3n − 2 3n +1  2 P = . . . ... . . . . ... .     3 6 9 12 3n 3n + 3  3 6 9 12 3n 3n + 3  THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 12  1 3 6 9 3n − 3 3n   1 4 7 10
3n − 2 3n +1  < . . . ... . . . . ... .   
 3 4 7 10 3n − 2 3n +1 3 6 9 12 3n 3n + 3  1 1 3 6 7 9
3n − 3 3n − 2 3n 3n +1 < 1 1 . . . . . ... . . . = = . 3 3 4 7 9 10 3n − 2 3n 3n +1 3n + 3 3(3n + 3) 9 (n + ) 1 Từ đây suy ra 1 P <
. Bất đẳng thức được chứng minh. 3 n +1
Dạng 4: Bài toán rút gọn biểu thức chứa một hay nhiều ẩn 2 1 2 1+ + 4  a − a 1+ a  a a
Thí dụ 1. Rút gọn: B =  +  − (a > 0,a ≠ 1).  4 4 1 a a  − 1+   a Lời giải Đặt 4 t = a (t > 0) 2 4 ⇒ a = t ,a = t 2 1 2 2 2 1+ + 2 4  t − t 1+ t  Khi đó: t t B =  +  − 2 1− t t 1+   t 2  1  ( − ) + 1 2  1 2 2 +   1 t t 1 1  t 2   1  t =  + + t − = −  t + + t − 2  2  1− t t   1+ t   t  1+ t 2 1 t + 1 1 1 = − = − 2 2 t t ( 2t +1) 2 2 t t = 0
Thí dụ 2. (Trích đề thi HSG tỉnh Hải Dương năm 2012-2013) Rút gọn biểu thức:   2
A =  x − 50 − x + 50  x + x − 50 với x ≥ 50   Lời giải Ta có : 2 2   A =  x - 50 - x + 50    ( 2 x + x - 50 ) 2 ⇒ A = ( 2 x - 50 + x + 50 - 2 x - 50 )( 2 x + x - 50 ) 2 ⇒ A = ( 2 2x - 2 x - 50 )( 2 x + x - 50 ) 2 ⇒ A = 2( 2 2 x - x + 50) Vậy: 2 A = 100
Nhưng do theo giả thiết ta thấy   2
A =  x - 50 - x + 50  x + x - 50 < 0   ⇒ A= -10 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 13
Thí dụ 3. (Trích đề thi HSG Hải Dương năm 2013-2014) 2 1− 1− x .( 3 3 (1+ x) + (1− x) ) Rút gọn biểu thức A = với 1 − ≤ x ≤ 1. 2 2 − 1− x Lời giải 2 1− 1− x .( 1+ x + 1− x)( 2 2 − 1− x ) Ta có: A = 2 2 − 1− x 2
= 1− 1− x .( 1+ x + 1− x) = ( − − )( + + − )2 2 = ( 2 − − )( 2 1 1 x 1 x 1 x 1 1 x 2 + 2 1− x ) 2 = 2x = x 2
Thí dụ 4. (Trích đề thi HSG T.P Bắc Giang năm 2016-2017)
Cho a, b là số hữu tỉ thỏa mãn ( + − )( + )2 2 2 a b 2 a b + 2 (1−ab) = 4ab −
Chứng minh 1+ ab là số hữu tỉ Lời giải Ta có:  (GT) (a b)2  ⇒ +
− 2(ab + 1) (a + b) + (1+ ab)2 2 =  0   ⇔ (a + b)4 − 2(a + 2 b) (1+ ab) + (1+ 2 ab) = 0 (a b)2 2 ⇔ + − (1+ ab) = 0 ⇒ (a + 2 b) -(1+  ab)=0   ⇔ (a + 2
b) = 1+ ab ⇔ a + b = 1+ ab ∈Q; do: a;b∈Q
Thí dụ 5. (Trích đề thi HSG T.P Bắc Giang năm 2016-2017)
Cho biểu thức M= a a − b b a b − −
với a, b > 0 và a ≠ b a − b a + b b − a
Rút gọi M và tính giá trị biểu thức M biết (1−a)(1− b) + 2 ab = 1 Lời giải Rút gọn M=
ab với a, b > 0 và a≠ b a − b Ta có
(1−a)(1− b)+ 2 ab = 1⇔ ab−a − b+1+ 2 ab = 1 ab ( a b)  2 2 ab ab ⇔ = − ⇔   = 1 ⇔ =   1 a − b a −   b THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 14 + Nếu a > b > 0 ab
⇒ a > b ⇒ a − b > 0; ab > 0 ⇒ > 0 a − b ab ab ab ⇒ = ⇒ = 1 ⇒ M = 1 a − b a − b a − b + nếu 0 < a < b ab
⇒ a < b ⇒ a − b < 0; ab > 0 ⇒ < 0 a − b ab − ab − ab ⇒ = ⇒ = 1 ⇒ M = 1 − a − b a − b a − b
Dạng 4: Bài toán rút gọn biểu thức và bài toán liên quan
Bước 1: Tìm điều kiện xác định.
Bước 2: Tìm mẫu thức chung, quy đồng mẫu thức, rút gọn tử, phân tích tử thành nhân tử.
Bước 3: Chia cả tử và mẫu cho nhân tử chung của tử và mẫu.
Bước 4: Khi nào phân thức tối giản thì ta hoàn thành việc rút gọn.
Dạng 1. Tính giá trị biểu thức P khi cho x = k (k là hằng số) Phương pháp:
- Bước 1: - Đặt điều kiện của x để biểu thức P có nghĩa.
- Bước 2: - Rút gọn biểu thức P và rút gọn k nếu cũng là một biểu thức chứa căn phức tạp
- Bước 3: Thay giá trị x = k vào biểu thức đã rút gọn rồi tính ra kết quả. Ví dụ minh họa:  
Thí dụ 1. Cho biểu thức: 1 x x P =  +  :   , với x > 0. x x + 1 x + x   a) Rút gọn biểu thức P.
b) Tìm giá trị của P khi x = 4. Lời giải a) Điều kiện: x > 0   ( x + )1+ x 1 x x x + x x + x + 1 P =  +  : = =   + +   x ( x + ) . x x 1 x x 1 x x b) Ta có khi x = 4 thì: x + x + 1 4 + 4 + 1 4 + 2 + 1 7 P = = = = x 4 2 2 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 15
Thí dụ 2. (Trích đề thi HSG huyện lớp 9 năm 2013-2014)  x + y x − y   + +  Cho biểu thức: x y 2xy P =  +  : 1+  .  1− xy 1+ xy     1− xy  a) Rút gọn biểu thức P. 2
b) Tính giá trị của P với x = . 2 + 3 Lời giải
a) ĐKXĐ: x ≥ 0; y ≥ 0; xy ≠ 1.
Mẫu thức chung là 1 – xy
( x + y)(1+ xy) + ( x − y)(1− xy) 1− xy + x + y + 2xy P = : 1− xy 1− xy
x + x y + y + y x + x − x y − y + y x 1− xy = . 1− xy 1+ x + y + xy 2( x + y x) 2 x(1+ y) 2 x = = = (1+ x)(1+ y) (1+ x)(1+ y) 1+ x b) 2 2(2 − 3) Ta có: 2 x = = = 3 − 2 3 + 1 = ( 3 −1) 2 + 3 4 − 3 2
x = ( 3 −1) = 3 −1 = 3 −1 2( 3 −1) 2 3 − 2 P = = = 2 1+ ( 3 −1) 1+ 3 − 2 3 + 1 2( 3 −1) 6 3 + 2 P = = 5 − 2 3 13
Thí dụ 3. (Trích đề thi HSG tỉnh Thanh Hóa năm học 2011-2012)  − +   − +  Cho biểu thức P = x 1 x 8 3 x 1 1 1  +  :  − 
 3+ x −1 10 − x   x − 3 x −1 −1 x −    1  1) Rút gọn P
2) Tính giá trị của P khi x = 3 + 2 2 3 − 2 2 4 − 4 3 − 2 2 3 + 2 2 Lời giải
Điều kiện: 1 < x ≠ 10 − +  − +  1) 3 x 1 9 1 2 x 1 4 P = :  .  10 − x  x −1 x −1 − 3  THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 16 x −1. − + ( x−1−3 3( x 1 3) ) P = . 10 − x 2 x −1 + 4
3 x −1(x −10)( x −1 − 2) 3(x − 2) P = = − 2(10 − x)(x −1− 4) 2(x − 5) 2) 3 + 2 2 3 − 2 2 4 2 4 2 = 4 − 4 x
= (3 + 2 2) − (3 − 2 2) = 3 + 2 2 − 3 − 2 2 3 − 2 2 3 + 2 2
=> x =1+ 2 −( 2 −1) = 2 vì x>1 Vậy P = 0
Dạng 2. Tìm giá trị của biến x để biểu thức P = k (k là hằng số) Phương pháp:
- Bước 1: - Đặt điều kiện của x để biểu thức P có nghĩa.
- Bước 2: - Rút gọn biểu thức P.
- Bước 3: - Giải phương trình P – k = 0.
- Bước 4: Đối chiếu điều kiện của x và kết luận. Ví dụ minh họa: + Thí dụ 1. Cho x 2 x 3x 9 P = + −
, với x ≥ 0, x ≠ 9 . x + 3 x − 3 x − 9 1) Rút gọn P .
2) Tìm giá trị của x để 1 P = . 3 Lời giải
x ( x − 3) + 2 x ( x + 3) − 3x − 9 1) 3 P = ( = x − 3)( x + 3) x + 3 2) 1 3 1 P = ⇔
= ⇒ x + 3 = 9 ⇔ x = 36 (thỏa mãn ĐKXĐ) 3 x + 3 3
Thí dụ 2. (Trích đề thi HSG Ninh Bình năm học 2012-2013) 2 Cho biểu thức: P = x - x 2x + x 2(x - 1) - + (x > 0, x ≠ 1). x + x + 1 x x - 1 1. Rút gọn P.
2. Tìm giá trị của x để P = 3. Lời giải 3 1/Ta có: x( x −1) x(2 x + 1) 2( x −1)( x + 1) P = − + x + x + 1 x x −1 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 17 x( x −1)(x + x + 1) = − 2 x −1+ 2( x + 1) x + x + 1 = x − x + 1
2/ Ta có: P = 3 ⇔ x − x + 1 = 3 ⇔ x − x − 2 = 0 t = 1 ( − L)
Đặt x = t, t ≥ 0 ta được pt 2t − t − 2 = 0 ⇔ t =  2 (TM)
Ta có t = 2 ta được x = 2 ⇔ x = 4 (thỏa mãn ĐK). Vậy x = 4 thì P = 3.
Thí dụ 3. (Trích đề thi HSG tỉnh Hà Nam năm 2012-2013) Cho biểu thức: x y xy P = − −
( x + y)(1− y) ( x + y)( x + 1) ( x + 1)(1− y)
1. Rút gọn biểu thức P.
2. Tìm các giá trị x, y nguyên thỏa mãn P = 2. Lời giải
1) Điều kiện : x ≥ 0 ; y ≥ 0 ; y ≠ 1 ; x + y ≠ 0 .
x(1 + x) − y(1 − y ) − xy( x + y) (x − y) + (x x + y y) − xy( x + y) P = ( = x + y )(1 + x )(1 − y) ( x + y)(1 + x)(1 − y)
( x + y)( x − y + x − xy + y −xy) = ( x + y)(1 + x)(1 − y)
x ( x + 1) − y ( x + 1) + y(1 + x)(1 − x) = (1 + x)(1 − y) x − y + y − y x
x (1 − y)(1 + y) − y (1 − y) = ( = 1 − y ) (1 − y) = x + xy − y 2) P = 2 ⇔
x + xy − y = 2 với x ≥ 0 ; y ≥ 0 ; y ≠ 1 ; x + y ≠ 0
⇔ x (1 + y) − ( y + 1) = 1 ⇔ ( x − 1)(1 + y) = 1
Ta có: 1 + y ≥ 1 ⇒ x −1 ≤ 1 ⇔ 0 ≤ x ≤ 4 ⇒ x = 0; 1; 2; 3 ; 4
Thay vào P ta được các cặp giá trị (4;0) và (2;2) thỏa mãn.
Dạng 3. Tìm giá trị của biến x để biểu thức P = A (A là biểu thức chứa ẩn) Phương pháp: THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 18
- Bước 1: - Đặt điều kiện của x để biểu thức P có nghĩa.
- Bước 2: - Rút gọn biểu thức P.
- Bước 3: - Giải phương trình P – A = 0.
- Bước 4: Đối chiếu điều kiện của x và kết luận. Ví dụ minh họa:  −  +
Thí dụ 1. Cho biểu thức x 2 1 x 1 P = + .  
với x > 0 và x ≠ 1.  x + 2 x x + 2  x −1 + a) Chứng minh rằng x 1 P = . x
b) Tìm các giá trị của x để 2P = 2 x + 5 . Lời giải a) Ta có:    − +  x − + x x + ( x )1.( x 2 2 1 ) x +1 x +1 P     = = = .  x
( x +2) . x −  x   ( x +2) . 1  x −1 x  + b) Theo câu a) x 1 P = x 2 x + 2
⇒ 2P = 2 x + 5 ⇔
= 2 x + 5 2 x + 2 = 2x + 5 x ⇔ 2x + 3 x − 2 = 0 và x > 0 x (   ⇔ x + ) 1 1 1 2 x −
= 0 ⇔ x = ⇔ x =   .  2  2 4
Dạng 4. Tìm giá trị của ẩn đê biểu thức thỏa mãn một bất đẳng thức A > k (≥; ≤; < k) với k là hằng số. Phương pháp:
- Bước 1: - Đặt điều kiện của x để biểu thức A có nghĩa.
- Bước 2: - Rút gọn biểu thức A.
- Bước 3: - Giải bất phương trình A– k > 0.
- Bước 4: Đối chiếu điều kiện của x và kết luận. Ví dụ minh họa:  
Thí dụ 1. Cho biểu thức 1 1 x A = − ÷  
, với x > 0 . x + x x +1  x + 2 x +1
a) Rút gọn biểu thức A .
b) Tìm các giá trị của x để 1 A > . 2 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 19 Lời giải
a) Với x > 0 , ta có   ( x)2 + x + ( x + − x )2 2 1 1 1 1 1 A   = − ⋅ = ⋅  x  ( x + )1 x +1 x x ( x +1) x  (1− x )( x +1) 1− x = = . x x
b) Với x > 0 , ta có 1 1− x 1 2 A > ⇔
> ⇔ 2 − 2x > x ⇔ 3x < 2 ⇔ x < . 2 x 2 3
Vậy các giá trị x cần tìm là 2 0 < x < . 3  −  −
Thí dụ 2. Cho biểu thức 4x x 2 x 1 M =  − ⋅
, với x > 0 , x ≠ 1, x ≠ 4 . 2   x −1 x − 3 x + 2 x   a) Rút gọn M .
b) Tìm x để M < 4 . Lời giải
Điều kiện x > 0 , x ≠ 1, x ≠ 4 . Ta có   4x x − 2 x −1 4x −1 x −1 4x −1 M   = − ⋅ = ⋅ =  x −1 
( x − )1( x −2) . 2 2 2  x x −1 x x  Ta có x > 0 nên 2 x > 0 khi đó 4x −1 1 2 2 M < 4 ⇔
< 4 ⇔ 4x − 4x +1 > 0 ⇔ (2x −1) > 0 ⇔ x ≠ . 2 x 2 Vậy với x > 0 , 1 x ≠
, x ≠ 1, x ≠ 4 thì M < 4 . 2
Thí dụ 2. Cho biểu thức
A = 3 ( 3 − 3 12 + 2 27 ),  x + x   x − x B = 1+ ⋅1−    
 vôùi x > 0, x ≠ 1. x +1 x −1     THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 20
a) Rút gọn biểu thức A và B .
b) Tìm các giá trị của x sao cho A⋅ B ≤ 0. Lời giải
a) Ta có A = 3 ( 3 −3 12 + 2 27) = 3( 3 −6 3 + 6 3) = 3.
Với x > 0 và x ≠ 1, ta có  x + x   x − x
x + 2 x +1 −x + 2 x −1 B = 1+ ⋅1−  = ⋅     x +1 x −1 x +1 x −1    
( x + )2 −( x − )2 1 1 = ⋅ = −( x + ) 1 ⋅ ( x − ) 1 = 1− x x +1 x −1
A ⋅ B ≤ 0 ⇔ 3(1− x) ≤ 0 ⇔ x ≥ 1.
Vậy x ≥1 thỏa yêu cầu bài toán.
Dạng 5. So sánh biểu thức A với k (hằng số) hoặc với biểu thức B (chứa ẩn) Phương pháp:
- Bước 1: - Đặt điều kiện của x để biểu thức A có nghĩa.
- Bước 2: - Rút gọn biểu thức A.
- Bước 3: - Xét dấu của hiệu A – k hoặc A – B và đưa ra kết luận. Ví dụ minh họa:  −  − 6 10 2 ( a a )2 1
Thí dụ 1. Cho biểu thức B =  + ⋅ 
(với a > 0, a ≠ 1). a 1  −
a a − a − a +1 4 a  
a) Rút gọn biểu thức B .
b) Đặt C = B(a − a + )1 . So sánh C và 1. Lời giải
a) Ta có a a − a − a +1 = a( a − )1−( a − )1 = ( a − )1(a − )1.   − 6 ( a − )
1 +10 − 2 a ( a − )2 6 10 − 2 ( a a )21 1 Do đó B   = + ⋅ = ⋅  a −1 ( 2 a − ) 1 ( a −  )1 4 a  ( + )⋅( − ) 4 1 1 a a a THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 21 4 + 4 a 1 = = . 4 a ( a +1) a b) Ta có a − a +1  1  C = = a + −1 ≥ 2 −1 = 1.   aa
Đẳng thức xảy ra khi a =1 (loại). Vậy C >1.
Ví dụ 2: Cho biểu thức  1 1  a +1 M = + :  
với a > 0 và a ≠ 1.  a − a
a −1  a − 2 a +1
a) Rút gọn biểu thức M . b) So sánh M với 1. Lời giải
a) Điều kiện: a > 0 và a ≠ 1    1 1  a +1 1 1 a +1 M = + :     = + :  a − a
a −1  a − 2 a +1
a ( a − )1 a −1 ( a −   )2 1
( a − )2 ( + a)( a − + a )2 1 1 1 1 = = a ( a − ) . 1 a +1 a ( a − ) 1 ( a + ) 1 a −1 = a − − b) Xét hiệu: a 1 1 M −1 = −1 =
< 0 với a > 0 và a ≠ 1 a a Vậy M <1. 2  − +   
Ví dụ 3: Cho biểu thức x 1 x 1 1 x P =  − . −      . x +1 x −1 2 x 2     a) Rút gọn biểu thức . P
b) So sánh P với − 2 x . Lời giải
a) Điều kiện: x > 0 ; x ≠ 1.  − +    ( x − )2 1 − ( x + x x x )2 2 2 1 1 1 1  1− x P =  − . −  =       x +1 x −1 2 x    
( x + )1( x − ) . 2 1  2 x  2 4
− x x −1  1− x = . =  
x −1  2 x x − Vậy 1 x P =
với x > 0 ; x ≠ 1. x − +
b) Xét hiệu P − (− x) 1 x x 1 2 = + 2 x = x x THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 22 + Với x 1
x > 0 ; x ≠ 1 ⇒
> 0 ⇒ P − (− 2 x) > 0 x ⇒ P > 2 − x .
Dạng 6. So sánh biểu thức rút gọn A với A hoặc 2
A với A . Phương pháp:
Bước 1: + Xác định điều kiện của x để A > 0 (nếu A chưa phải biểu thức dương)
Bước 2: + So sánh A với 1 bằng cách xét hiệu A −1 theo điều kiện x đã có:
Bước 3: - Nếu 0 < A <1 thì A > A .
Bước 4: - Nếu A >1 thì A < A .
+ Chú ý: Dạng này còn có biến thể là so sánh biểu thức rút gọn A với 2
A (chỉ xét với biểu
thức A dương).    + − + − 
Ví dụ 1: Cho biểu thức 1 1 2x x 1 2x x x x A = − :    +    với 1− x x  1− x 1+ x x   1 x > 0; x ≠ ; x ≠ 1. 4
a) Rút gọn biểu thức A .
b) So sánh A với A . Lời giải a) Điều kiện: 1 x > 0; x ≠ ; x ≠ 1. 4  1
1   2x + x −1
2x x + x − x A = − :    +    1− x x  1− x 1+ x x    −
( x + )1(2 x − )1 x( x + )1(2 x −  x )1 2 1 =  +  x ( x − ) : 1 
 (1− x )(1+ x )
(1+ x)(1− x + x)  2 x −1   1 x  =  −  +   
x ( x − ) : (2 x )1 1  1− x 1− x + x    1− x + x + x 1− 2 −1 x x = −
x ( x − ) : (2 x ) ( ) 1 : 1
(1− x)(1− x + x) 1 1 = x ( x − ) : 1
(1− x)(1− x + x) 1− x + x = x THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 23 − + b) Biến đổi 1 x x 1 A = = x + −1. x x Áp dụng BĐT cosi có: 1 x + > 2 với mọi 1 x > 0; x ≠ ; x ≠ 1 x 4 1 ⇒ A = x +
−1 >1⇒ A >1⇒ A −1 > 0 ⇒ A ( A − )1 > 0 x
⇒ A − A > 0 ⇒ A > A .  
Ví dụ 2: Cho biểu thức x 1 2 A =  −  : .   x − 4 2 − x x − 2   a) Rút gọn biểu thức . A b) So sánh A với 2 A . Lời giải
a) Điều kiện: x > 0 ; x ≠ 4.  x 1  2 x + x + 2 x − 2 A =  −  : =   x − 2 − x x − 2  
( x −2)( x +2). 4 2 2 x + 2 x − 2 x +1 = ( =
x − 2)( x + 2) . 2 x + 2 + b) Với mọi x
x > 0 ; x ≠ 4 thì 1 A = > 0. x + 2 + Mà x 1 x +1 < x + 2 ⇒ A = <1 x + 2
Vậy 0 < A <1 với mọi x > 0 ; x ≠ 4 2
⇒ A < A với mọi x > 0 ; x ≠ 4.
Dạng 7. Chứng minh với mọi giá trị của x và thì A > k (≥; ≤; < k) với k là hằng số Phương pháp:
- Bước 1: - Đặt điều kiện của x để biểu thức A có nghĩa.
- Bước 2: - Rút gọn biểu thức A.
- Bước 3: - Chứng minh hiệu A– k > 0 ∀x
Thí dụ 1. (Trích đề Thi HSG huyện Bình Giang năm 2012-2013) Cho biểu thức: x + 2 x + 1 1 A = + + với x ≥ 0, x ≠ 1 x x −1 x + x + 1 1− x 1) Rút gọn A 2) Chứng tỏ rằng: 1 A < 3 Lời giải Ta có: THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 24 1) x + 2 x + 1 1 A = ( + −
x −1)(x + x +1) x + x +1 x −1 x + 2 + x −1− x − x −1 A = ( x−1)(x+ x+1) x − x A = ( x−1)(x+ x+1) x ( x −1) x A = ( = , với x ≥ 0, x ≠ 1 x −1)(x + x +1) x + x +1 1 1 x ( − )2 x 1 2) Xét − A = − = 3 3 x + x +1 3(x + x +1) Do x ≥ 0, x ≠ 1 ⇒ ( − ) 2 2  1  3 x 1 > 0 và x + x + 1 = x + + >   0  2  4 1 1 ⇒ − A > 0 ⇔ A < 3 3
Thí dụ 2. (Trích đề thi HSG huyện Cam Lộ) 3 2 Cho biểu thức: P = 1 − + x +1 x x +1 x - x +1 a) Rút gọn P. b) Chứng minh P ≥ 0. Lời giải a) ĐKXĐ: x ≥ 03 2 P = 1 − + x +1 x x +1 x - x +1 = 1 3 2 − + x +1 ( x ) +1 (x - x ) +1 x - x +1 x - x +1− 3 + 2 ( x ) +1 = x + x ( = = x x ) +1 (x - x ) +1 ( x ) +1 (x - x ) +1 x - x +1 b) x ≥ 0 2  1  3 3 x - x + 1 = x − + ≥  2    4 4 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 25 Do đó: P= x ≥ 0 x - x +1
Thí dụ 3. (Trích đề thi HSG T.P Đà Nẵng năm học 2013-2014) 2 Cho biểu thức:
a + 1 a a −1 a − a a + a −1 M = + + với a > 0, a ≠ 1. a a − a a − a a Chứng minh rằng M > 4. Lời giải Do a > 0, a − − + + + + ≠ 1 nên: a a 1 ( a 1)(a a 1) a a 1 = = và a − a a( a −1) a 2
a − a a + a −1 (a + 1)(a −1) − a(a −1) (a −1)(a − a + 1) a − + a −1 = = = a − a a a(1− a) a(1− a) a a +1 ⇒ M = + 2 a Do a > 0; a ≠ 1 nên: 2
( a −1) > 0 ⇔ a +1 > 2 a 2 a ⇒ M > + 2 = 4 a
Dạng 8. Tìm giá trị của x để biểu thức thỏa mãn một bất đẳng thức A > B(≥; ≤; < B)
với B là biểu thức chứa ẩn. Phương pháp:
- Bước 1: - Đặt điều kiện của x để biểu thức A có nghĩa.
- Bước 2: - Rút gọn biểu thức A.
- Bước 3: - Giải bất phương trình A– B > 0.
- Bước 4: Đối chiếu điều kiện của x và kết luận. Ví dụ minh họa: +  
Thí dụ 1. Cho biểu thức x 1 x x A = : +   , với x > 0 .
x + 4 x + 4  x + 2 x x + 2 
a) Rút gọn biểu thức A .
b) Tìm tất cả các giá trị của x để 1 A ≥ . 3 x Lời giải THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 26 +   +   Ta có x 1 x x x 1 x x A = : + = :    +  2
x + 4 x + 4  x + 2 x x + 2  ( x + 2)  x( x + 2) x + 2  x +1  x x  = :  +  2   ( x + 2) x + 2 x + 2   x +1 x + x x +1 x (1+ x ) = : = : 2 2 ( x + 2) x + 2 ( x + 2) x + 2 x +1 x + 2 1 = ⋅ = . 2 ( x + 2) x (1+ x ) x ( x + 2) Ta có 1 1 1 1 1 A ≥ ⇔ ≥ ⇔ ≥ (do 0) x > 3 x x ( x + 2) 3 x x + 2 3
⇔ x + 2 ≤ 3 ⇔ 0 < x ≤1 ⇔ 0 < x ≤1. Vậy để 1 A ≥ thì 0 < x ≤1. 3 x + +
Thí dụ 2. Cho hai biểu thức x 4 x A = và 3 1 2 B = − với x 0  , x ≠1. x −1 x + 2 x − 3 x + 3
a) Tính giá trị của biểu thức A khi x = 9 . b) Chứng minh 1 B = . x −1
c) Tìm tất cả giá trị của A x x để  + 5. B 4 Lời giải a) Với x = 9 ta có 7 A = . 2 b) Với x 0  , x ≠1 ta có 3 x +1 2 3 x +1 2
3 x +1− 2( x −1) 1 B = − = − = = . x + 2 x − 3 x + 3
( x + 3)( x −1) x + 3
( x + 3)( x −1) x −1 + c) Ta có A x 4 1 = : = x + 4 . B x −1 x −1 A x
 + ⇔ x − x +  ⇔ ( x − )2 5 4 4 0 2 0  ⇔ x = 4. B 4 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 27
Dạng 9. Tìm giá trị của ẩn để biểu thức nhận giá trị nguyên
Phương pháp 1: Đưa về biểu thức về dạng chứa phân thức mà tử nguyên, tìm giá trị ẩn để mẫu là ước của tử.
- Bước 1: - Đặt điều kiện của x để biểu thức A có nghĩa.
- Bước 2: - Rút gọn biểu thức A và đưa về dạng phân thức có tử là số nguyên.
- Bước 3: - Lý luận để biểu thức là số nguyên thì mẫu số phải là ước của tử, từ đó tìm giá trị ẩn.
- Bước 4: Đối chiếu điều kiện của x và kết luận. Ví dụ minh họa: a a −
Thí dụ 1. Cho biểu thức 3 2 A = − −
với a ≥ 0,a ≠ 9. a − 3 a + 3 a − 9 a) Rút gọn A .
b) Tìm các số nguyên a để A nhận giá trị nguyên. Lời giải
a) Với a ≥ 0,a ≠ 9, ta có a a −
a ( a + 3) 3( a − 3 3 2 ) a−2 11 A = − − = − − = a − 3 a + 3 a − 9 a − 9 a − 9 a − 9 a − 9 b) 11 A =
∈ khi và chỉ khi 11 chia hết cho a − 9 . Do đó a − 9 a − 9 = 1 a = 10   a − 9 = 1 − a = 8   ⇔ a − 9 =11 a = 20   a − 9 = 1 − 1 a = 2 − (l).
Vậy a ∈{8;10;20} thì A nhận giá trị nguyên.
Thí dụ 2. (Trích đề thi HSG huyện Thanh Oai 2014-2015)  −   − + −  Cho biểu thức A = x 5 x 25 x x 3 x 5  − 1 :  − +   x − 25   x + 2 x −15 x + 5 x −    3  1. Rút gọn A
2. Tìm số nguyên x để A nguyên Lời giải ≥ ≠ ≠ 1) Điều kiện x 0,x 25,x 9 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 28 5 Rút gọn A = x +3
2) x ∈ z => x + 3 là Ư(5)  x + 3 = 1 (loai) =>   x + 3 = 5 => x =  4
Thí dụ 3. (Trích đề thi HSG huyện Thanh Oai năm 2015-2016)  x   x + 3 x + 2 x + 2  Cho M = 1−  :  + +   x 1  x 2 3 x x 5 x 6  + − − − +     1) Rút gọn M
2) Tìm giá trị nguyên của x để biểu thức M nhận giá trị là số nguyên Lời giải
ĐKXĐ: x ≥ 0;x ≠ 4,x ≠ 9 (*)
1) Rút gọn M: Với x ≥ 0; x ≠ 4,x ≠ 9 (*) Rút gọn ta được: x − 2 x − 2 M = M = x + 1 x + 1 2) x − 2 x + 1− 3 x + 1 3 3 M = = = − = 1− x + 1 x + 1 x + 1 x + 1 x + 1
Biểu thức M có giá trị nguyên khi và chỉ khi: 3( x +1) ⇒ ( x +1)∈U(3) Ư(3) ∈{ 1; ± ± }
3 Vì x ≥ 0 ⇒ x ≥ 0 ⇒ x +1 ≥ 1 Nên x + 1∈{1; } 3
Xảy ra các trường hợp sau:
+) x + 1 = 1 ⇔ x = 0 ⇔ x = 0 (TMĐK (*))
+) x + 1 = 3 ⇔ x = 2 ⇔ x = 4 . (không TMĐK (*) loại )
Vậy x = 0 thì M nhận giá trị nguyên.
Phương pháp 2: Đánh giá khoảng giá trị cùa biểu thức, từ khoảng giá trị đó ta có các giá
trị nguyên mà biểu thức có thể đạt được.
- Bước 1: - Đặt điều kiện của x để biểu thức A có nghĩa.
- Bước 2: - Rút gọn biểu thức A.
- Bước 3: - Đánh giá khoảng giá trị mà biểu thức A có thể đạt được, từ khoảng giá trị đó ta
có các giá trị nguyên mà biểu thức A có thể đạt được. THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 29
- Bước 4: Giải phương trình vế trái là biểu thức A đã rút gọn, vế phải là các giá trị nguyên
nằm trong miền giá trị của A, đối chiếu điều kiện và kết luận. x x −
Thí dụ 1. Cho biểu thức 2 24 A = + và 7 B =
với x ≥ 0, x ≠ 9. x − 3 x − 9 x + 8 a) Rút gọn A .
b) Tìm các số nguyên x để P = .
A B nhận giá trị nguyên. Lời giải a) ta có: x. x + + x − x 2 x − 24
( 3) 2 24 x+5 x −24 A = + = = x − 3 x − 9 ( x +3)( x −3) ( x +3)( x −3)
( x −3)( x +8) x +8 = ( = x + 3)( x − 3) x + 3 b) ta có: x + 8 7 7 7 P = . A B = . = ⇒ 0 < P ≤ x + 3 x + 8 x + 3 3
Vậy các giá trị nguyên mà P có thể đạt được là 1 và 2. 7 Với P = 1 ta có:
=1⇒ x + 3 = 7 ⇒ x = 4 ⇒ x =16 (TM ) x + 3 7 1 1 Với P = 2 ta có:
= 2 ⇒ 2 x + 6 = 7 ⇒ x = ⇒ x = (TM ) x + 3 2 4
Thí dụ 2. (Trích đề thi HSG tỉnh Hải Phòng năm 2016-2017) 2 Cho biểu thức
a + 1 a a −1 a − a a + a −1 B = + + với a > 0, a ≠ 1. a a − a a − a a
Với những giá trị nào của a thì biểu thức 6
A = nhận giá trị nguyên? B Lời giải.
Với điều kiện a > 0; a ≠ 1thì:
( a −1)(a+ a +1) ( a −1)( a +1)(a− a + + 1 a 1 ) B = + a a ( a 1) − − a ( a −1)( a +1) ( 2 a + + + + − + 1 a 1 a a 1 a a 1 ) B = + − = a a a a THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 30 Khi đó 6 6 a A = =
. Ta thấy với 0 < a ≠ 1 ⇒ a − a + 1 > 0 B ( a 1) > 0 2 + ⇔ ( + )2 6 a a 1 > 3 a ⇔ ( < a + 1) 2 2 Do 0 < N < 2
Để N có giá t rị nguyên thì N = 1. ⇔ 6 a = 1 ⇔ a − 4 a + 1 = 0 a + 2 a + 1  = +  = + tháa m·n ⇔ ( − )2 a 3 2 a 7 4 3 ( ) a 2 = 3 ⇔  ⇔   a = − 3 + 2 a = 7 −   4 3 (tháa m·n) Vậy a = 7 ± 4 3.
Thí dụ 3. (Trích đề thi HSG tỉnh Vĩnh Phúc năm 2011-2012) Cho biểu thức x − 2 x x + 1 1+ 2x − 2 x P = + + 2 x x −1 x x + x + x x − x
Tìm tất cả các giá trị của x sao cho giá trị của P là một số nguyên. Lời giải
Điều kiện: x > 0, x ≠ 1. Khi đó ta có
Rút gọn biểu thức ta được x + 2 P = x+ x +1
Ta có Px + (P −1) x + P − 2 = 0, ta coi đây là phương trình bậc hai của x . Nếu
P = 0 ⇒ − x − 2 = 0 vô lí, suy ra P ≠ 0 nên để tồn tại x thì phương trình trên có ∆ = ( − )2 P 1 − 4P(P − 2) ≥ 0 ⇔ − + + ≥ ⇔ − + ≤ ⇔ ( − )2 2 2 4 4 3P 6P 1 0 P 2P 1 P 1 ≤ 3 3
Do P nguyên nên ( − )2 P 1 bằng 0 hoặc 1 +) Nếu ( − )2
P 1 = 0 ⇔ P = 1 ⇔ x = 1 không thỏa mãn.  = +) Nếu ( − )2 P 2 P 1 = 1 ⇔ 
⇒ P = 2 ⇔ 2x + x = 0 ⇔ x = 0 không thỏa mãn P =  0
Vậy không có giá trị nào của x thỏa mãn.
Phương pháp 3: Đặt biểu thức bằng một tham số nguyên, tìm khoảng giá trị của tham số,
từ khoảng giá trị đó ta xét các giá trị nguyên của tham số, giải ra tìm ẩn.
- Bước 1: - Đặt điều kiện của x để biểu thức A có nghĩa. THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 31
- Bước 2: - Rút gọn biểu thức A.
- Bước 3: - Đánh giá khoảng giá trị mà biểu thức A có thể đạt được, từ khoảng giá trị đó ta
có các giá trị nguyên mà biểu thức A có thể đạt được.
- Bước 4: Giải phương trình vế trái là biểu thức A đã rút gọn, vế phải là các giá trị nguyên
nằm trong miền giá trị của A, đối chiếu điều kiện và kết luận. x x −
Thí dụ 1. Cho biểu thức 2 24 A = + và 7 B =
với x ≥ 0, x ≠ 9. x − 3 x − 9 x + 8 a) Rút gọn A .
b) Tìm các số nguyên x để P = .
A B nhận giá trị nguyên. Lời giải a) ta có: x. x + + x − x 2 x − 24
( 3) 2 24 x+5 x −24 A = + = = x − 3 x − 9 ( x +3)( x −3) ( x +3)( x −3)
( x −3)( x +8) x +8 = ( = x + 3)( x − 3) x + 3 b) ta có: x + 8 7 7 P = . A B = . = x + 3 x + 8 x + 3
Vậy các giá trị nguyên mà P có thể đạt được là 1 cà 2. 7 7 7 − 3n 7 Đặt
= n (n > 0) ⇒ x = −3 =
≥ 0 ⇒ 7 − 3n ≥ 0 ⇒ 0 < n ≤ ⇒ n = {1; } 2 x + 3 n n 3 7 Với n = 1 ta có:
=1⇒ x + 3 = 7 ⇒ x = 4 ⇒ x =16 (TM ) x + 3 7 1 1 Với n = 2 ta có:
= 2 ⇒ 2 x + 6 = 7 ⇒ x = ⇒ x = (TM ) x + 3 2 4
Thí dụ 2. (Trích đề thi HSG huyện Thanh Oai năm 2015-2016)  x   x + 3 x + 2 x + 2  Cho M = 1−  :  + +   x 1  x 2 3 x x 5 x 6  + − − − +     1) Rút gọn M
2) Tìm giá trị nguyên của x để biểu thức M nhận giá trị là số nguyên Lời giải
ĐKXĐ: x ≥ 0;x ≠ 4,x ≠ 9 (*) THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 32
1) Rút gọn M: Với x ≥ 0; x ≠ 4,x ≠ 9 (*) Rút gọn ta được: x − 2 x − 2 M = M = x + 1 x + 1 2) x − 2 x + 1− 3 x + 1 3 3 M = = = − = 1− x + 1 x + 1 x + 1 x + 1 x + 1 Đặt 3 n (n 0) 3 3 − n = > ⇒ x = −1 = x + 1 n n
Do x ≥ 0 nên 3 − n ≥ 0 ⇔ 3 − n ≥ 0 ⇒ 0 < n ≤ 3 ⇒ n = {1;2; } 3 n
Xảy ra các trường hợp sau: 3 +)
= 1 ⇔ x + 1 = 3 ⇔ x = 2 ⇔ x =4 (không TMĐK (*) loại) x +1 3 3 1 1 +)
= 2 ⇔ x + 1 = ⇔ x = ⇔ x = . ( loại do x không nguyên (*) ) x +1 2 2 4 3 +)
= 3 ⇔ x + 1 = 1 ⇔ x = 0 . ( TMĐK (*) ) x +1
Vậy x = 0 thì M nhận giá trị nguyên.
Dạng 10. Tìm giá trị của ẩn để biểu thức đạt GTNN hoặc GTLN
Phương pháp 1: Thêm bớt rồi dùng bất đẳng thức Cauchy hoặc đánh giá dựa vào điều kiện
Thí dụ 37. (Trích đề thi HSG huyện Thanh Oai 2014-2015)  −   − + −  Cho biểu thức A = x 5 x 25 x x 3 x 5  − 1 :  − +   x − 25   x + 2 x −15 x + 5 x −    3  1. Rút gọn A 2. Với x +
≥ 0 , x ≠ 25, x ≠ 9 tìm giá trị nhỏ nhất của biểu thức: B = A(x 16) 5 Lời giải
b) Điều kiện x ≥ 0,x ≠ 25,x ≠ 9 5 Rút gọn A = x +3 b) Ta có : THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 33 A(x + 16) 5(x + 16) x + 16 25 25 B = = = = x − 3 + = x + 3 + − 6 5 5( x + 3 x + 3 x + 3 x + 3
Theo bất đẳng thức Cauchy: 25 25 B = x + 3 + − 6 ≥ 2 ( x + 3). − 6 = 2.5 − 6 = 4 x + 3 x + 3 25
=> B ≥ 4 => min B = 4 x + 3 = ⇔ x + 3 = 5 ⇔ x = 4 x + 3
Thí dụ 2. (Trích đề thi HSG huyện Tư Nghĩa năm 2016-2017) 2 Cho biểu thức x − 2x 1 1 1 A = + .( + ) 3 + 2 x 1 1+ x + 2 1− x + 2
a) Tìm điều kiện của x để biểu thức A có nghĩa b) Rút gọn biểu thức A
c) Tìm giá trị nhỏ nhất của A. Lời giải x + 2 ≥ 0
a) Điều kiện của x để biểu thức A có nghĩa :  x ≥ 2 − 3 x +1 ≠ 0 ⇔   x ≠ 1 −  x + 2 ≠ 1 b) Rút gọn biểu thức A 2 x − 2x 1 1 1 x(x − 2) 1 2 A = + .( + ) = + . 3 2 x +1 2 1+ x + 2 1− x + 2
(x +1)(x − x +1) 2 1− (x + 2) 2 x(x − 2) 1
x(x − 2) − (x − x +1) = − = 2 2
(x +1)(x − x +1) x +1
(x +1)(x − x +1) −(x +1) 1 − = = 2 2
(x +1)(x − x +1) x − x +1
c) Tìm giá trị nhỏ nhất của A. Ta có 1 − 1 − A = = 2 x − x +1 1 3 2 (x − ) + 2 4 Ta có A nhỏ nhất khi 1 3 2 (x − ) +
đạt giá trị nhỏ nhất 2 4
Vậy: Giá trị nhỏ nhất của là A là 4 − khi 1 x − = 0 ⇔ 1 x = 3 2 2   +
Thí dụ 3. Cho biểu thức 1 1 x 1 A = + :  
với x > 0, x ≠ 1.  x − x
x −1  ( x − ) , 2 1
a) Rút gọn biểu thức A . THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 34
b) Tìm giá trị lớn nhất của biểu thức P = A − 9 x . Lời giải
a) Với điều kiện x > 0 , x ≠ 1 ta có   + + ( x − x x )2 1 1 1 1 1 x −1 A = + : = ⋅ =    x − x x −1  ( − ) . 2 1 x ( x x − ) 1 x +1 x
b) Với điều kiện x > 0 , x ≠ 1 ta có x −1 1  1 
P = A − 9 x = − 9 x = 1−
− 9 x =1− 9 x + .   x xx
Theo bất đẳng thức Cô-si ta có 1 1 1 9 x + ≥ 2 9 x ⋅ ⇔ 9 x + ≥ 6. x x x Như vậy P ≤ 5 − . Đẳng thức xảy ra khi 1 9 x = hay 1 x = . x 9
Vậy giá trị lớn nhất của P là 5 − khi 1 x = . 9
Phương pháp 2: Dùng miền giá trị   +
Thí dụ 1. Cho biểu thức 1 1 x 1 A = + :  
với x > 0, x ≠ 1.  x − x
x −1  ( x − ) , 2 1
a) Rút gọn biểu thức A .
b) Tìm giá trị lớn nhất của biểu thức P = A − 9 x . Lời giải
a) Với điều kiện x > 0 , x ≠ 1 ta có   + + ( x − x x )2 1 1 1 1 1 x −1 A = + : = ⋅ =    x − x x −1  ( − ) . 2 1 x ( x x − ) 1 x +1 x
b) Với điều kiện x > 0 , x ≠ 1 ta có THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 35 x −1 1
P = A − 9 x = − 9 x = 1−
− 9 x (P < ) 1 x x ⇔ . P x = x −1− 9x
⇔ 9x + (P − ) 1 x +1 = 0
⇔ 9( x )2 +(P − ) 1 x +1 = 0 (*)
Để tồn tại P thì phương trình (*) phải có nghiệm, tức là:
∆ = (P − )2 − ≥ ⇔ (P − )2 1 36 0 1 ≥ 36 ⇔ P −1 ≤ 6 − (do P < ) 1 ⇔ P ≤ 5 − −(P − ) 1 −( 5 − − ) Như vậy 1 1 1 P ≤ 5 − khi x = = = ⇒ x = 2.9 2.9 3 9
Vậy giá trị lớn nhất của P là 5 − khi 1 x = . 9
Dạng 11. Chứng minh biểu thức luôn âm hoặc luôn dương Phương pháp:
- Để chứng minh biểu thức A luôn dương ta chỉ ra 2
A = A + k k > 0 - 1 ( )
- Để chứng minh biểu thức A luôn âm ta chỉ ra 2
A = − A − k k > 0 1 ( ) Ví dụ minh họa:  1 x +  2
Thí dụ 1. Cho biểu thức 2 A = − : .  
với x > 0, x ≠ 1.
x +1 x x +1 x
a) Rút gọn biểu thức A .
b) Chứng minh A luôn âm với với mọi giá trị x làm A xác định. Lời giải a) Điều kiện: x > 0  x +  Khi đó: 1 2 2 A = − : .  
x +1 x x +1 x − x x x x ( x + − + − − )1 1 2 = x ( x ) = +1 (x − x + ). 1
( x + )1(x− x + ). 2 1 2 − = x 2 ( x − x + ) 1 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 36 2 Do  1  3 − − < x x 0; x − x +1 = x − + > 0 ⇒ x
(x− x + ) <0 ∀    2 4 2 1
Vậy A luôn âm với với mọi giá trị x làm A xác định. x x +
Thí dụ 2. Cho biểu thức 1 1 = + + x A . x −1 + x x − x −1 x +1
a) Rút gọn biểu thức A .
b) Chứng minh A không âm với mọi giá trị x làm A xác định. Lời giải
a) Điều kiện: x ≥1 1 1 x x + = + + x A x −1 + x x −1 − x x +1 x x x x x ( x + − − + + − )1 1 1 = ( +
x −1 + x )( x −1 − x ) x +1 = x − 2 x −1
b) Ta có: A = x −
x − = ( x − ) −
x − + = ( x − − )2 2 1 1 2 1 1 1 1 ≥ 0 ∀x ≥1
A không âm với mọi giá trị x ≥1.
Dạng 12. Tìm x biết biểu thức P thỏa mãn phương trình, bất phương trình chứa
dấu giá trị tuyệt đối. Phương pháp:
Tìm x để |A| = A.
Phương pháp: | A |= A ⇔ A ≥ 0
Cần tìm x thỏa mãn ĐK để A ≥ 0.
Tìm x để |A| = - A.
Phương pháp: | A |= −A ⇔ A ≤ 0
Cần tìm x thỏa mãn ĐK để A ≤ 0. Tìm x để 2 A = . A Phương pháp: 2
A = A ⇔ A ≥ 0.
Cần tìm x thỏa mãn ĐK để A ≥ 0.
Tìm x để |A| > - A.
Phương pháp: | A |> −A ⇔ A > 0
Cần tìm x thỏa mãn ĐK để A > 0 . Tìm x để
A > A .
Phương pháp: A > A ⇔ 0 < A <1
Cần tìm x thỏa mãn ĐK để 0 < A <1. THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 37
Tìm x để A < A .
Phương pháp: A < A ⇔ A >1
Cần tìm x thỏa mãn ĐK để A >1.
Tìm x để A > b ; A ≥ b ; A < b ; A ≤ . b Phương pháp:
Cần tìm x thỏa mãn ĐK để: A − b > 0 ; A − b ≥ ; A − b < 0 ; A − b ≤ 0. Ví dụ minh họa:    
Ví dụ 1: Cho biểu thức: x x A = 1+    : 1 2  −    x +1   x −1
x x + x − x −1  
a) Rút gọn biểu thức A .
b) Tìm x để A >1. Lời giải + + a) Điều kiện: x x
x ≥ 0; x ≠ 1 . Kết quả rút gọn 1 A = x −1  x   1 2 x
  x + x +1  1 2 xA = 1+  :  −  =   :  −          x +1 x −1
x x + x − x −1 x +1 x −1 ( x +1)(x +1)        
x + x +1  x + 2 x +1  x + x +1 ( x +1)(x +1) x + x +1 =   :   = . =     . 2 x +1 ( x +1)(x +1) x +1 ( x +1) x +1     + + b) Ta có: x x A > 1 ⇔ 1 > 1 x −1 + + + + − + + ⇔ x x 1 − x x x x 2 1 > 0 ⇔ 1 1 > 0 ⇔ > 0 x −1 x −1 x −1
⇒ x −1 > 0 ⇔ x >1 ( do x + 2 > 0 ) .
Kết hợp với ĐKXĐ 0 ≤ x <1 thì A >1.
Ví dụ 2: Cho biểu thức x 2 x −1 A = − x −1 x ( x − ) 1
a) Tìm ĐKXĐ, rút gọn biểu thức A .
b) Với giá trị nào của x thì A > A . Lời giải − a) Điều kiện: x
x > 0 ; x ≠ 1. Kết quả rút gọn 1 A = . x
b) Ta có: A > A ⇔ A < 0 x −1 ⇔
< 0 ⇔ x −1< 0 (vì x > 0 với mọi x > 0; 1 x ≠ . ) x THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 38
⇔ x <1 ⇔ x <1
Kết hợp với điều kiện xác định 0 < x <1 thì A > A .
Dạng 13. Tìm giá trị tham số m để x thỏa mãn phương trình, bất phương trình. Phương pháp:
- Đối với phương trình ta đưa phương trình về dạng f(m).x = k
- Xét các trường hợp:
Trường hợp 1: f (m) = 0 , kết luận về bất phương trình nhận được.
Trường hợp 2: f (m) ≠ 0, tìm được tập nghiệm x, rồi lập luận theo điều kiện nghiệm x thỏa mãn.
- Đối với bất phương trình biến đổi bất phương trình về một trong các dạng sau:
f (m).x > k hoặc f (m).x ≥ k hoặc f (m).x < k hoặc f (m).x ≤ k
f (m). x > k hoặc f (m). x ≥ k hoặc f (m). x < k hoặc f (m). x ≤ k
- Xét các trường hợp:
Trường hợp 1: f (m) = 0 , kết luận về bất phương trình nhận được.
Trường hợp 2: f (m) > 0 , tìm được tập nghiệm x, rồi lập luận theo điều kiện nghiệm x thỏa mãn.
Trường hợp 3: f (m) < 0 , tìm được tập nghiệm x, rồi lập luận theo điều kiện nghiệm x thỏa mãn. − x − x −
Ví dụ 1: Cho biểu thức: 2 = x A và 1 7 9 B = −
với x > 0, x ≠ 9 x x − 3 x − 9 a) Rút gọn B .
b) Cho biểu thức = A P
, tìm giá trị của m để x thỏa mãn P = m − 2 B Lời giải a) Ta có: x − x −
( x − )1( x +3)−7 x +9 x − x +
( x −3)( x −2 1 7 9 5 6 ) x −2 B = − = = = = x − 3 x − 9 ( x −3)( x +3)
( x −3)( x +3) ( x −3)( x +3) x +3 b) Ta có: A x − 2 x − 2 x − 2 x + 3 x + 3 P = = : = . =
với điều kiện: x > 0, x ≠ 9, x ≠ 4 B x x + 3 x x − 2 x x + 3 P = m − ⇔
= m − ⇔ x + = m x − x ⇔ (m − ) 3 2 2 3 2 3 x = 3 ⇔ x = x m − 3
Ta có: x > 0, x ≠ 9, x ≠ 4 ⇒ x > 0, x ≠ 2, x ≠ 3 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 39  3  > 0  m −  m > 3 3    3  9
Để x thỏa mãn P = m - 2 thì:  ≠ 2 ⇔  m ≠ m − 3 2    3  15 ≠ 4 m ≠   m − 3  4    − 
Ví dụ 2. Cho biểu thức: 4 x 8x x 4 1 P =  −  :  +    
 với x > 0, x ≠ 1, x ≠ 4 2 − x 4 − x x + 2 x x     a) Rút gọn P .
b) Tìm m để với mọi giá trị x > 4 thì m( x − )1.P < x −1 Lời giải
a) Ta có: với x > 0, x ≠ 1, x ≠ 4  4 x 8x   x − 4 1  P =  −  :  +      2 − x 4 − x x + 2 x x     4 x.(2 + x ) − 8x
x − 4 + ( x + 2) = : (2 − x )(2 + x ) x ( x + 2) 4 − x + 8 x 2 x − 2 = : (2 − x )(2 + x ) x ( x + 2) 4 x x ( x + 2) = . 2 + x 2 x − 2 2x = . x −1 Vậy 2x P = x −1 b) Với x
x > 0, x ≠ 1, x ≠ 4 ta có 2 P = x −1 x m ( x − )
1 .P < x −1 ⇔ m ( x − ) 2 1 . < x −1 ⇔ .2
m x < x −1 ⇔ (2m − ) 1 x < 1 − x −1 Trường hợp 1: Khi 1
2m −1 = 0 ⇔ m = ⇒ 0 < 1 − (vô lý). 2 Trường hợp 2: Khi 1
2m −1 < 0 ⇔ m < 1 ⇒ x >
, khi đó để bất phương trình 2 1− 2m
thỏa mãn với mọi x > 4 thì: 1 1 1− 4 + 8m 8m − 3 ≤ 4 ⇔ − 4 ≤ 0 ⇔ ≤ 0 ⇔ ≤ 0 1− 2m 1− 2m 1− 2m 1− 2m Mà 3
1− 2m > 0 ⇒ 8m − 3 ≤ 0 ⇔ m ≤ . 8 Trường hợp 3: Khi 1
2m −1 > 0 ⇔ m > 1 ⇒ x <
< 0 , khi đó mọi giá trị x là âm 2 1− 2m
nên không thỏa mãn điều kiện và yêu cầu bài toán. THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 40 Vậy với 3 m ≤
thì bất phương trình thỏa mãn với mọi x > 4. 8 + − − − +
Ví dụ 3. Cho biểu thức 2x x x x x x x x 1 P = −
x x + x + x x x −1
a) Rút gọn biểu thức P .
b) Tìm giá trị của m để mọi x > 2 ta có: .
P ( x + x + )
1 − 3 > m ( x − ) 1 + x. Lời giải
a) Điều kiện: x ≥ 0 ; x ≠ 1.
2x x + x − x
x x − x − x +1 P = −
x x + x + x x x −1
x (2x + x − ) 1 x ( x − ) 1 − ( x − ) 1 P = −
x ( x + x + ) 1 x x −1 + − ( x − )1(x− x x ) 1 2 1 P = − x + x +1
( x − )1(x+ x + )1
2x + x −1− x +1 P = x + x +1 x + x
P = x + x +1 + b) Ta có: x x P =
với x ≥ 0 ; x ≠ 1. x + x +1 .
P ( x + x + )
1 − 3 > m ( x − ) 1 + x x + x ⇔ .( x + x + )
1 − 3 > m ( x − ) 1 + x x + x +1
⇔ x + x − 3 > m(x − ) 1 + x
⇔ x − 3 − m(x − ) 1 > 0
⇔ (1− m) x + m − 3 > 0
⇔ (1− m) x > 3− m (*)
Trường hợp 1: Khi 1− m = 0 ⇔ m =1⇒ 0 > 2 (vô lý). Trường hợp 2: Khi − m
1− m < 0 ⇔ m > 3 1 ⇒ x < , khi đó: 1− m
+ Nếu 3− m < 2 tức là x < 2 thì mọi giá trị x > 2 sẽ không thỏa mãn bất phương 1− m trình. THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 41 + Nếu 3− m − > m 2 tức là 3 2 < x <
thì chỉ có một số giá trị x > 2 thỏa mãn bất 1− m 1− m
phương trình (Tập nghiệm của bất phương trình (∗) không chứa hết các giá trị x > 2 )
⇒ Trường hợp 2 không thỏa mãn với mọi giá trị x > 2. Trường hợp 3: Khi − m
1− m > 0 ⇔ m < 3 1 ⇒ x >
, khi đó để bất phương trình thỏa 1− m
mãn với mọi x > 2 thì: 3 − m 3 − m m +1 ≤ 2 ⇔ − 2 ≤ 0 ⇔ ≤ 0 1− m 1− m 1− m
Mà 1− m > 0 ⇒ m +1≤ 0 ⇒ m ≤ 1
− kết hợp với m < 1ta được m ≤ 1 − Vậy với m ≤ 1
− thì bất phương trình thỏa mãn với mọi x > 2.  −   + 
Ví dụ 4. Cho biểu thức: x 4 3 x 2 x P =  −  :  + .     x − 2 x 2 − x x 2 − x     a) Rút gọn biểu thức . P
b) Tìm các giá trị của a để có x thỏa mãn: P( x + )1 > x + .a Lời giải
a) Điều kiện: x > 0 ; x ≠ 4.  x − 4 3   x + 2 xP =  −  :  + .     x − 2 x 2 − x x 2 − x     x − x − + x ( x 2 4 3 ) P =
x ( x − 2) . x − 4 − x 4 ( x − ) 1 x ( x − 2) P = x ( x − 2) . 4 − P = 1− x
b) Ta có: P =1− x với x > 0 ; x ≠ 4. P ( x + ) 1 > x + a
⇔ (1− x)( x + )1 > x + a
⇔ 1− x > x + a
⇔ x + x −1 < −a (*)  1  1 ⇔ x + x + − −1 < −a    4  4 2  1  5 ⇔ x + < − a    2  4 2 Với  1  1 x > 0 ⇒ x + >    2  4 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 42 2 1  1  5 ⇒ < x +
< − a ⇒ a < 1   4  2  4
Vậy với a <1 thì có x thỏa mãn: P( x + )1 > x + a.
BÀI TẬP VẬN DỤNG
Câu 1. (Trường chuyên tỉnh Bình Thuận năm 2019-2020) x x + − Cho biểu thức: 1 5 9 = − − x P
với x ≥ 0, x ≠ 25. x + 5 5 − x x − 25
a) Rút gọn biểu thức P.
b) Tìm tất cả các giá trị của x để P < 1.
Câu 2. (Trường chuyên tỉnh Bình Định vòng 2 năm 2019-2020) 2 3 5 2 3 5
Rút gọn biểu thức: A   . 2 2  3  5 2 2  3 5
Câu 3. (Trường chuyên tỉnh Bạc Liêu năm 2019-2020)
Rút gọn biểu thức: B = (13− 4 3)(7 + 4 3) −8 20 + 2 43+ 24 3 .
Câu 4. (Trường chuyên tỉnh Bắc Giang chuyên toán năm 2019-2020)
Cho x, y là các số thực dương và 3 2 2 2 2 3 3 3 3 3 P = x + x + x y + y + y + y x + x + y +1. Chứng minh rằng 3 3 2 3 x + y +1 = P .
Câu 5. (Trường chuyên tỉnh Bắc Ninh vòng 2 năm 2019-2020) 4 3 2
Tính giá trị của biểu thức:
x  2x  3x  38x  5 A  khi x =2 + 3 . 2 x  4x  5
Câu 6. (Trường chuyên tỉnh Bến Tre vòng 2 năm 2019-2020) 1 − 5 1 + 5 −
Tính giá trị của biểu thức: 1 + 5 1 − 5 A = . 5
Câu 7. (Trường chuyên tỉnh Cao Bằng vòng 2 năm 2019-2020)     Cho biểu thức 1 2 x 2 x P =  −  : 1−
 với x ≥ 0, x ≠ 1. x −1 x x + x − x −1 x +1     THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 43
a) Rút gọn biểu thức P .
b) Tìm tất các giá trị của x để P ≥ 1.
Câu 8. (Trường chuyên tỉnh Cần thơ chuyên toán năm 2019-2020)
x − 4 ( x − )
1 + x + 4 ( x − ) 1 Cho biểu thức  1  A = . 1− 
 trong đó x > 1, x ≠ 2 . 2 x − ( x − )  x −1 4 1 
a) Rút gọn biểu thức A
b) Tìm các giá trị nguyên của x để giá trị biểu thức A là số nguyên.
Câu 9. (Trường chuyên tỉnh DAK NONG vòng 2 năm 2019-2020)  1 3 a   2  Cho biểu thức: + 5 ( a + P 1) =  + . −1 .  a −1   
a a − a − a +  1  4 a
Tìm điều kiện xác định và rút gọn biểu thức P .
Câu 10. (Trường chuyên tỉnh Gia lai chuyên tin năm 2019-2020) 3x + 16x − 7 x + 1 x − 3
Rút gọn biểu thức: P = − −
(x ≥ 0,x ≠ 1). x + 2 x − 3 x + 3 x − 1
Câu 11. (Trường chuyên tỉnh Gia Lai không chuyên năm 2019-2020) − − + Rút gọn biểu thức a 4 a 4 a 4 P = :
, với a ≥ 0,a ≠ 4 . a + 2 2 a − 4
Câu 12. (Trường chuyên tỉnh Gia lai vòng 2 năm 2019-2020) Rút gọn biểu thức: 2
A = 4 + 2 3 + 6 − 2 5 + . 5 + 3
Câu 13. (Trường chuyên tỉnh Hà Giang vòng 1 năm 2019-2020)  3 x 3x 1  (x − ) − Cho biểu thức: 1 ( x y ) M =  − + :   x + xy + y x x − y y x − y
2x + 2 xy + 2 y  
a) Rút gọn biểu thức M.
b) Tìm các số nguyên x sao cho biểu thức M có giá trị nguyên.
Câu 14. (Trường chuyên tỉnh Hà Nam chuyên toán năm 2019-2020)   Cho biểu thức:: x  24 x  3 x  2 x   2  A  :     ,
x x  2  x  2 3  x
x  5 x  6  
(với x  0, x  4,x  9 ).
1. Rút gọn biểu thức A.
2. Tìm x để biểu thức A đạt giá trị nhỏ nhất. THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 44
Câu 15. (Trường chuyên tỉnh Hà Nam thi chung năm 2019-2020)
Rút gọn các biểu thức sau:
1. A  4 3  2 27  12 .      2. a 1 2a 1 B       :
, (với a  0,a  1).
 a 1 a a  a 1 
Câu 16. (Trường chuyên tỉnh Hòa Bình Chuyên Tin năm 2019-2020)
1) Tìm điều kiện xác định: 1 2 A = − x −1 x − 2
2) Rút gọn: B = 5 12 − 27 3) Rút gọn: a −1 C = −1 a −1
Câu 17. (Trường chuyên tỉnh Hòa Bình Chuyên Toán năm 2019-2020) Cho biểu thức: 3a + 9a − 3 a − 2 1 A = − + −1 a + a − 2 a − 1 a + 2 1)Rút gọn biểu thức A.
2)Tìm giá trị của a để A = 2 .
Câu 18. (Trường chuyên tỉnh Hòa Bình dành cho tất cả các thí sinh năm 2019-2020) Rút gọn:
A = ( 5 − 3)( 5 + 3) + 6
Câu 19. (Trường chuyên tỉnh Hưng Yên Vòng 2 năm 2019-2020) 2  a +1 + 3   3 a) Cho  a −1 a + 1 2a
a là số thực khác 1 và 1
− . Rút gọn biểu thức P = ÷ − . 2 3  a −1 a −1 a −1 + 3    a +1
b) Cho các số thực x, y, a thoản mãn 2 4 2 2 4 2 3 3 x + x y + y + y x = a . Chứng minh rằng: 3 2 2 3 2 3 x + y = a .
Câu 20. (Trường chuyên tỉnh Hải Dương chuyên toán năm 2019-2020)  + − − +  − Cho 2x x 1 2x x x x x x P = 1 +  − . với 1
x ≥ 0, x ≠ 1, x ≠ . 1 − x 1 − x x 2 x −1   4 a) Rút gọn P. THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 45
b)Tìm các giá trị của x sao cho 4 P = . 5
Câu 21. (Trường chuyên tỉnh Hải phòng vòng 2 năm 2019-2020)   Cho biểu thức: 3 x x 1   x  3 P     :   (với x  0).
 x x 1 x x 1
x 1 x x 1 Rút gọn biểu thức .
P Tìm các giá trị của x để 1 P  . 5
Câu 22. (Trường chuyên tỉnh Hậu Giang chuyên toán năm 2019-2020)
Cho biểu thức A  2x  15  8 2x 1.
a) Tìm điều kiện của x để biểu thức A có nghĩa.
b) Tìm x để A  3.
Câu 23. (Trường chuyên tỉnh Hậu Giang chuyên toán năm 2019-2020) Cho x   3  3 1 2
4. Tính giá trị đúng của biểu thức A  5 x  4 x  3 x  2 4
x  2x  2019.
Câu 24. (Trường chuyên tỉnh Kon Tum cho tất cả các thí sinh năm 2019-2020)
a) Tìm điều kiện của x để biểu thức x 1 có nghĩa. x3   
b) Chứng minh đẳng thức 1  a a       1  aa    
a0,a  1.     1aa 1  a 1
Câu 25. (Trường chuyên tỉnh Kon Tum vòng 2 năm 2019-2020) 3 5 .3 5
1) Không dùng máy tính cầm tay, hãy tính giá trị biểu thức P  10  2
2) Rút gọn rồi tính giá trị của biểu thức 2x3 x 2 Q
tại x  20202 2019 x 2
Câu 26. (Trường chuyên tỉnh Lào Cai Vòng 1 năm 2019-2020)
Tính giá trị các biểu thức sau: a) 4 + 3 2 b) 5 + (6 − 5)
Câu 27. (Trường chuyên tỉnh Lào Cai Vòng 1 năm 2019-2020) 2 Cho biểu thức: 2x + 2x 1 1 H = + −
(với x ≥ 0; x ≠ 1) 2 x −1 x +1 x −1 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 46
a) Rút gọn biểu thức H .
b)Tìm tất cả các giá trị của x để x − H < 0
Câu 28. (Trường chuyên tỉnh Lâm Đồng vòng 2 năm 2019-2020)
Tính giá trị biểu thức: T = (2 3 + )1(3 2 − )1 13− 4 3 19+ 6 2 .
Câu 29. (Trường chuyên tỉnh Nam Định cho lớp chuyên KHTN năm 2019-2020)
Tìm điều kiện xác định của biểu thức 2019 3 P = − . x − 3 x − 9
Câu 30. (Trường chuyên tỉnh Nam Định cho lớp chuyên KHTN năm 2019-2020) 2  + −   +  Cho biểu thức a 1 a 1 a a a P =  − + 4 a  :    
 với a > 0, a ≠ 1. a −1 a +1 a +1     1) Rút gọn biểu thức . P
2) Tìm các giá trị nguyên của a để P nhận giá trị là số nguyên.
Câu 31. (Trường chuyên tỉnh Nam Định chuyên toán năm 2019-2020)
Cho x = 3 + 5 + 2 3 + 3 − 5 + 2 3 . Tính giá trị của biểu thức P = x(2 − x) .
Câu 32. (Trường chuyên tỉnh Nam Định lớp chuyên KHXH năm 2019-2020)
Tìm điều kiện xác định của biểu thức: 2019 3 P = − . x − 3 x − 9
Câu 33. (Trường chuyên tỉnh Nam Định lớp chuyên KHXH năm 2019-2020)  + −  Cho biểu thức: a 1 a 1 1 P =  − + 4 a .  
với a > 0, a ≠ 1. a −1 a +1 a a   1) Rút gọn biểu thức . P
2) Tính giá trị của P khi a = 9 + 4 2.
Câu 34. (Trường chuyên tỉnh Ninh Bình chuyên toán năm 2019-2020) + − +
Với x > 0, xét hai biểu thức: 2 x A = và x 3 2 x 9 B = + . x x x + 3 x
Tìm tất cả các giá trị của x để A 5 > . B 3
Câu 35. (Trường chuyên tỉnh Ninh Bình chuyên toán năm 2019-2020) THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 47 − + − Rút gọn biểu thức : 5 6 7 33 128 1 C = . 3 − 2
Câu 36. (Trường chuyên tỉnh Phú Yên Vòng 2 năm 2019-2020)  + + +   − Cho biểu thức: x 3 x 2 x 2 x 2  A =  + +  : −1  . x − 2 3 − x x − 5 x + 6 
  x − x − 2 
a)Rút gọn biểu thức A. b)Tìm x để 1 P = 2 A −
đạt giá trị lớn nhất. x
Câu 37. (Trường chuyên tỉnh PTNK ( VÒNG 1 ) năm 2019-2020)
( a + )2 −( a − )2 1 1
( 2a+1+ a+1)( 2a+1− a+1) Tìm a , biết: . a ( a − ) − a ( a + ) = 1 4 1 1
Câu 38. (Trường chuyên tỉnh Quảng Nam Vòng 2 năm 2019-2020) 2  x +
x +  x − x x + x − Cho biểu thức 2 2 8 1 A =  −  ⋅ với x ≥ 0 . x − x +1 x x +1 x + 3  
Rút gọn biểu thức A và tìm x để A = 6 .
Câu 39. (Trường chuyên tỉnh Quảng Ngãi chuyên toán năm 2019-2020) + − 2 2 3 1 + Cho biểu thức: x x x x x P = + − với x > , 0 x ≠ 1. x x − x x x + x
Rút gọn và tìm giá trị nhỏ nhất của biểu thức P
Câu 40. (Trường chuyên tỉnh Quảng Ninh Vòng 2 năm 2019-2020) − − + − − Cho biểu thức : 4x 9 x 3 x 1 2 x 1 A = + − (với x ≥ 0 ). x + 3 x + 2 x +1 x + 2
a) Rút gọn biểu thức A ;
b) Tìm giá trị lớn nhất của A .
Câu 41. (Trường chuyên tỉnh Sơn La Vòng 2 năm 2019-2020) a) Rút gọn biểu thức:    + + +  A = x x x x 1−  : 3 2 2  − +
(với x ≥ 0; x ≠ 4; x ≠ 9 ) x +1   x − 2 x − 3 x − 5 x + 6   THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 48 3 − + b) Cho ( 3 1) 10 6 3 x = hãy tính 2 2019
B = (x + 4x − 2) 21 + 4 5 + 3
Câu 42. (Trường chuyên tỉnh Thái Bình vòng 1 năm 2019-2020)  2 1 1 
xy ( x + y) − Cho biểu thức: = xy P  + + ⋅  
(với x > 0; y > 0). xy x y x x +   y y
1. Rút gọn biểu thức P.
2. Biết xy = 16 . Tìm giá trị nhỏ nhất của P.
Câu 43. (Trường chuyên tỉnh Thái Nguyên chuyên tin năm 2019-2020) Cho: 3 3
x = 70 + 4901 + 70 − 4901.
Không sử dụng máy tính cầm tay, hãy chứng minh x là số nguyên tố.
Câu 44. (Trường chuyên tỉnh Tiền Giang chuyên tin năm 2019-2020)
Rút gọn biểu thức: A = 4 + 10 + 2 5 + 4 − 10 + 2 5 .
Câu 45. (Trường chuyên tỉnh Tiền Giang Vòng 2 năm 2019-2020) Cho 3 3
x = 2 + 2 3 + 2 − 2 3 −1.
Tính giá trị biểu thức P = x (x + x + )3 3 2 3 9
Câu 46. (Trường chuyên tỉnh Tuyên Quang chuyên toán năm 2019-2020) Tính tổng: 1 1 1 1 S = + + + ... + 2 2 3 + 1 5 + 3 7 + 5 2019 + 2019 − 2
Câu 47. (Trường chuyên tỉnh Tây Ninh Vòng 2 năm 2019-2020)
( 2a−2 2)(a− )1
Rút gọn biểu thức: T =
với a > 0,a ≠ 4 . a − a − 2
Câu 48. (Trường chuyên tỉnh Vĩnh Long vòng 2 năm 2019-2020)  1 1  x +1 P = + :  
x −1 x − x  ( x − )2 a) Cho biểu thức: 1 .
Tìm điều kiện xác định của P và giá trị của x để 1 P = . 2 b) Rút gọn biểu thức 3 A = 46 5 − 61 + 69 − 28 5 . THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 49
Câu 49. (Trường chuyên tỉnh An Giang Vòng 2 năm 2019-2020) 2 2  +   −  Rút gọn: 1 3 2 1 3 2 A =  −  −  −  . 2 1 + 3 2 1 − 3    
Câu 50. (Trường chuyên tỉnh Bà Rịa Vũng Tàu thi chung năm 2019-2020)
Rút gọn biểu thức: A = (3 5 − 27 − 20) 5 +3 15 .
Câu 51. (Trường chuyên tỉnh Bình Phước chuyên toán năm 2019-2020) 2 x x − ( x −3 3 ) Cho biểu thức: x + 3 A = − + x − 2 x − 3 x +1 3 − x
a) Rút gọn biểu thức 𝐴.
b) Tính giá trị của biểu thức 𝐴 khi x = 4 − 2 3
Câu 52. (Trường chuyên tỉnh Long An chuyên toán dự bị năm 2019-2020) − − +  − +  Cho biểu thức x 2 x 3 x x 8 x 1 x 1 P = + −  − ( x − )
1 với x ≥ 0, x ≠ 1. x +1 x + 2 x +1 x −1  
a) Rút gọn biểu thức P .
b) Tìm tất cả số nguyên tố x để P ≤1.
Câu 53. (Trường chuyên tỉnh Long An chuyên toán năm 2019-2020) 2  + − −  Cho biểu thức x x 2x x 2x 2 1 P =  + −  ⋅ với x > 0. x − x +1 x x +1 x − x +1   a) Rút gọn biểu thức . P
b) Chứng minh: P ≤ 3.
Câu 54. (Trường chuyên tỉnh Quảng Trị Vòng 2 năm 2019-2020) 2( x − ) 2 + − Cho biểu thức: 1 x x 2x 2 x A = + −
với x ≥ 0, x ≠ 1. x +1 x − x +1 x −1
Tìm tất cả các giá trị của x để A ≤ 0.
Câu 55. (Trường chuyên tỉnh Thừa Thiên Huế vòng 2 năm 2019-2020) + − + − Rút gọn biểu thức: 3x 9x 3 x 1 x 2 P = − − . x + x − 2 x + 2 x −1 Tìm x để P = 3.
Câu 56. (Trường chuyên tỉnh Yên Bái vòng 2 năm 2019-2020) THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 50    −  Cho biểu thức: 1 x 1 1 A = x + .    − .  x    x x 1 x 1 − + + 
1. Tìm điều kiện của x để biểu thức A có nghĩa. Rút gọn biểu thức A.
2. Tìm các giá trị nguyên của x để A có giá trị nguyên.
Câu 57. (Trường chuyên tỉnh Chuyên ĐHSP vòng 1 năm 2019-2020)
Cho các số thực x, y, a thoản mãn 2 4 2 2 4 2 3 3 x + x y + y + y x = a . Chứng minh rằng 3 2 2 3 2 3 x + y = a .
Câu 58. (Chuyên Nam Định 2018) 2 2 2 2 a) Rút gọn biểu thức x y x y P = − − .
(x + y)(1− y) (x + y)(1+ x) (1+ x)(1− y) b) Chứng minh rằng 1 1 1 1 1 1 1+ + + 1+ + + ...+ 1+ + < 2018. 2 2 2 2 2 2 1 2 2 3 2017 2018
Câu 59. (Chuyên Hà Tĩnh 2018)
Cho x, y, z là các số hữu tỉ thỏa mãn 1 1 1 + = . Chứng minh rằng 2 2 2 x + y + z là số x y z hữu tỉ
Câu 60. (Chuyên Bình Định 2018) ( − )2 + 3 3 a b ab   Cho biếu thức : a − b a − b T = :  −
, với a ≠ b,a > 0,b > 0 a + b  a − b a − b    a) Rút gọn biểu thức T b) Chứng tỏ T > 1
Câu 61. (Chuyên Cà Mau 2018)
Rút gọn các biểu thức sau a)
A = 4 20 − 45 + 3 125 − 2 405 b) B = 9 − 4 2 + 9 + 4 2
Câu 62. (Chuyên Lam Sơn 2018)     
Tính giá trị biểu thức 1 1 1 P = 1− 1− ........1−   1 2  1 2 3   1 2 3 .... 2018  + + + + + + + 
Câu 63. (Chuyên Hưng Yên 2018) Cho các biểu thức x + 1 1 A : − = và 4 2
B = x − 5x − 8x + 2025 với 2 x x + x + x −x + x x > 0,x ≠ 1 a) Rút gọn biểu thức A THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 51
b) Tìm các giá trị của x để biểu thức 2
T = B − 2A đạt giá trị nhỏ nhất
Câu 64. (Chuyên Bến Tre 2018) + − − Cho biểu thức a b a b a b P =
với a,b là hai số thực dương 1+ ab a) Rút gọn biểu thức 1
P : ( a + b)(a+b)
b) Tính giá trị của biểu thức P khi a = 2019 + 2 2018 và b = 2020 + 2 2019
Câu 65. (Chuyên Hà Nam 2018)  + −   Cho biểu thức 1 a 1 a 1 1 2 Q =  + 
−1 −  a − 2a +1 0 < a <1 2 ( )    2 1+ a − 1− a  1− a −1+ a a a   1) Rút gọn Q 2) So sánh 3 Q, Q
Câu 66. (Chuyên Lâm Đồng 2018)
Tính giá trị biểu thức A = (4 + 15)( 10 − 6) 4 − 15
Câu 67. (Chuyên Đồng Nai 2018)  +  Cho biểu thức a a a 4 − a P =  + .  a 2 a 3 a 2  + + +   a a) Rút gọn biểu thức P
b) Tìm các số thực dương a sao cho P đạt giá trị lớn nhất
Câu 68. (Chuyên Nguyễn Trãi 2018) 2 Cho x + x − 2 x + 1 + 1 2 a x = a + 1− 1+ a + , a > 0 ; P = 2 ( ) (a +1) 2 x − 2x + 1 Rút gọn P theo a
Câu 69. (Chuyên Năng Khiếu TP. Hồ Chí Minh 2018) Biết 0 < x ≤ y và  ( )2 ( )2 x y x y    + + −    y x  5 . Tính x  ( + + =   x y ) 2(x 2y))    x y  ( x y) y( x y) + + + + +  3   
Câu 70. (Chuyên Bắc Ninh 2018)  2 2 2 2  4 2 2 Rút gọn biểu thức : a + a + b a − a + b 4 a − a b P =  −  : , a > b > 0 2  2 2 2 2  a a b a a b  − + + + b 
Câu 71. (Chuyên Hải Dương 2016) THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 52 2 2 Rút gọn biểu thức: a + x a + x A = − 2 a +
+ 2 a với a > 0, x > 0 . x x
Câu 72. (Chuyên Vĩnh Long 2018)  + +  a) Cho biểu thức x 3 x 2 1 1 A =  −  : ≠ 
với x > 0 và x 4. Tìm giá trị của x x 8 x 2  − −   x
A tại x = 14 + 6 5 .
b) Tính giá trị biểu thức A = 12 − 80 − 32 3 − 12 + 80 − 32 3 .
Câu 73. (Chuyên Bắc Giang 2018)  + + +  Cho biểu thức x 4 x 4 x x  1 1  A =  +  : −    (với x > 0; x ≠ 1).  x + x − 2
1− x   x +1 1− x 
a) Rút gọn biểu thức A .
b) Có bao nhiêu giá trị nguyên của + x để 1 2018 A ≥ . 2018
Câu 74. (Chuyên Quảng Nam 2018)  + +   +  Cho biểu thức a 1 ab a 2a b 2 ab A =  + + 1 :    . ab + 1 1−  ab   1− ab    
với a > 0; b > 0 và ab ≠ 1.
Rút gọn biểu thức A và tìm giá trị lớn nhất của A khi a + b = ab .
Câu 75. (Chuyên Bà Rịa Vũng Tàu 2018)  3  Rút gọn biểu thức: 1+ a a − 2 a + 1 P =  + 1− a  (a > 1)  a −1  a  
Câu 76. (Chuyên Điện Biên 2018) + + + − Cho biểu thức x 2 x 3 3x 4 x 5 P = − − ,(x ≥ 0; x ≠ 25). x +1 5 − x x − 4 x − 5 a) Rút gọn .
P Tìm các số thực x để P > 2 − .
b) Tìm các số tự nhiên x là số chính phương sao cho P là số nguyên.
Câu 77. (Chuyên Đà Nẵng 2018) ( − ) 2 2 x 1 Cho biểu thức x − x 2x + x A = + −
với x > 0, x ≠ 1 x −1 x + x + 1 x Chứng minh rằng: 3 A ≥ 4
Câu 78. (Chuyên Đà Nẵng 2018) THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 53   Cho biểu thức: x x y Q = − 1+  : với x > y > 0 . 2 2  2 2  2 2 x − y x − y x − x − y   1. Rút gọn Q.
2. Xác định giá trị của Q khi x = 3y .
Câu 79. (HSG TP. Hải Phòng 2018) ( − )3 x y + 2x x + y y 3 xy − 3y Cho biểu thức A = + với x,y ≥ 0 và x ≠ y . x x + y y x − y
Chứng minh rằng giá trị của biểu thức A không phụ thuộc giá trị của biến.
Câu 80. (HSG Quận Hồng Bàng 2018) Cho biểu thức x y xy P = ( )( )−( )( )− + − + + ( + )( − ). x y 1 y x y x 1 x 1 1 y
a) Tìm điều kiện của x, y để biểu thức P xác định và rút gọn ; P
b) Tìm x, y nguyên thỏa mãn phương trình P = 2.
Câu 81. (HSG Quận Lê Chân 2018) 2 2  a − b a − b  a + b Cho biểu thức P =  + ⋅ (a > b > 0)  2 2  2 2  a + b + a − b a − b − a + b  a − b
Chứng minh rằng khi a − b = 1thì P ≥ 2 2 + 2.
Câu 82. (HSG Quận Ngô Quyền 2018)  + −  Cho biểu thức x y x y  x + y + 2xy  P =  +  : 1+ .  1− xy 1+ xy     1− xy  a) Rút gọn biểu thức ; P
b) Tính giá trị của P với 2 x = . 2 + 3
Câu 83. (HSG Quận Thủy Nguyên 2018)  + + +  Cho biểu thức x 3 x 2 x x  1 1  P =  −  : +  . > ≠ 
(với x 0; x 1 )  x + x − 2 x −1   x +1 x −1 a) Rút gọn biểu thức ; P b) Với giá trị của + x ta có 1 x 1 − ≥ 1. P 8
Câu 84. (HSG Thanh Hóa 2017) THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 54 Cho biểu thức x − 2 x x + 1 1+ 2x − 2 x P = + +
, với x > 0, x ≠ 1. Rút gọn P 2 x x −1 x x + x + x x − x
và tìm tất cả các giá trị của x sao cho giá trị của P là một số nguyên.
Câu 85. (HSG Hải Dương 2017) 2 2 Cho biểu thức x − x x + x A = +
. Rút gọn B = 1− 2A − 4 x + 1 ( 1 0 ≤ x ≤ ) x + x + 1 x − x + 1 4
Câu 86. (HSG Hải Phòng 2017)
Cho a = 3 + 5 + 2 3 + 3 − 5 + 2 3 . Chứng minh 2 a − 2a − 2 = 0.
Câu 87. (HSG Hải Dương 2016) Cho biểu thức: = − + ( − ) 2 − + − − ( − ) 2 P 1 x 1 x 1 x 1 x 1 x 1− x (với 1 − ≤ x ≤ 1).
Tính giá trị của biểu thức P khi 1 x = − 2019
Câu 88. (HSG Thái Bình 2011) Chứng minh rằng: 87 1 1 1 88 < + + ...+ < 89 2 1 3 2 2011 2010 45
Câu 89. (HSG Chuyên Hưng Yên 2019-2020) Rút gọn biểu thức = ( − )2 1 A 2 2 5 + 20 − 20 . 5 HƯỚNG DẪN GIẢI Câu 1. + −
x (5 − x ) − ( x + ) 1 (5 + x ) + (5 − 9 1 5 9 x x x x ) a) P = − − = x + 5 5 − x x − 25 ( x +5)(5− x)
(5 x − x)−(x+6 x +5)+(5−9 x) 2 − − x − x x ( x +5 2 10 ) = 2 x ( = = = x + 5)(5 − x )
( x +5)(5− x) ( x +5)(5− x) x −5 2 x − x x ( x −5 2 2 ) b) x + 5 P < 1 ⇔ < 1 ⇔ −1 < 0 ⇔ < 0 ⇔ < 0 x − 5 x − 5 x − 5 x − 5
⇔ x − 5 < 0 ⇔ x < 5 ⇔ 0 ≤ x < 25 Vậy 0 ≤ x < 25 Câu 2. THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 55
2 2 3 52 2 3 582 62 5 2 62 5 95     2    2 8 2 5 1 2
5 1 2  62 5  2  2 5  2 10.
2 3 52 2  3 5 43 53 5 62 5  43 53 5 5 1
12  4 5 2 5 2 10  2 5.
2 3 52 2  3 5 43 53 5 62 5  43 53 5 5  1
124 5  2 5 2 102 5. Do đó:
2 3 52 2  3 5 23 52 2  3 5 102 5 102 5 20 A            2. 10 10 2 2 3 5 2 2 3 5 Vậy A  2. Cách khác: 2 3 5 Ta có: 6  2 5 6  2 5 6  2 5 4     2 2 2  3 5 4  6  2 5 4   5  2 5  5 5 5 1 2 3 5 6 2 5 6 2 5 6 2 5 4     2 2 2  3 5 4  62 5 4   5  2 5 5 5 5 1   Do đó: 4 4 20 4 5  20  4 5 40 A  4       4   4   2. 5 5 5 5 255 20 Vậy A  2. Câu 3.
B = (13 − 4 3)(7 + 4 3) − 8 20 + 2 43 + 24 3 = + − − − ( − + + )2 91 52 3 28 3 48 8 13 4 3 7 4 3
= 43 + 24 3 − 8( 13− 4 3 + 7 + 4 3) THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 56   = + − ( − )2 + ( +  )2 43 24 3 8 2 3 1 2 3   
= 43 + 24 3 − 8(2 3 −1+ 2 + 3) = 35 Câu 4. Đặt 3 3 a = x; b =
y (a,b > 0) , ta có 3 2 2 3 2 2
P = a + a + a b + b + b + ab + a + b +1 . =(a + b + ) 1 a + b +1 3 2 3 3
P = a + b +1 = x + y +1. . Câu 5. Ta có − = ⇒ ( − )2 2 x 2 3 x 2 = 3 ⇒ x − 4x +1 = 0. 2 2 x − 4x + 5 = x − 4x +1+ 4 = 2 .. 4 3 2 x − 2x + 3x − 38x + 5 5 = ( 4 3 2 − + )+( 3 2 − + )+( 2 x 4x x 2x 8x 2x 10x − 40x +10) − 5 = 5 −  A  . 2 . Câu 6. ( − )2 −( + )2 1 5 1 5 1− 5 1+ 5 − + − − − − + − 1+ 5 1− 5 ( )( ) 1 2 5 5 1 2 5 5 1 5 1 5 − 4 − 5 1 5 A = = = = = 1 5 5 5 4 − 5 Câu 7.
a) Biến đổi được 1 2 x 1 2 x − = − x −1 x x + x − x −1 x −1 ( x − )1(x+ )1 Biến đổi được 1 2 x x +1 − 2 x − = x −1
( x − )1(x+ )1 ( x − )1(x+ )1 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 57 2 x x +1 − 2 x 1 − = x +1 x +1 1 P = x −1 − b) 1 2 x P ≥ 1 ⇔ ≥ 1 ⇔ ≥ 0 x −1 x −1  − ≥  ≤  ≤ TH1: 2 x 0 x 2 x 4  ⇔  ⇔  ⇔ 1 < x ≤ 4  − >  > x > 1 x 1 0 x 1  − ≤  ≥  ≥ TH2: 2 x 0 x 2 x 4  ⇔  ⇔  (không xảy ra).  − <  < x < 1 x 1 0 x 1
Vậy các giá trị x cần tìm là 1 < x ≤ 4 . Câu 8. a)
x − 4 ( x − )
1 + x + 4 ( x − ) 1  1  A = . 1−   2 x − ( x − )  x −1 4 1  x − 2 x −1 +
x + 2 x −1  x − 2  A = .  2 − +  x −1 x 4x 4  x −1 −1 +1+
x −1  x − 2  A = .  x − 2  x −1 
Nếu 1< x < 2 thì 2 A = 1− x Nếu x > 2 thì 2 A = x −1
b) - Nếu 1< x < 2thì không có giá trị nguyên.
- Nếu x > 2 thì 2 A = x −1
+ x −1 =1 ⇔ x = 2 (l)
+ x −1 = 2 ⇔ x = 5 (n) Câu 9.
Điều kiện: a > 0,a ≠ 1.   a ( a − )2 ( a + ) ( a − + )2 1 4 1 1 1 3 5   P = + =  a − (a − ) 1 ( a − ) . 1  a (a − ) 1 ( a −   ). 1 4 1 4 a THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 58 1 = . a Câu 10. 3x + 16x − 7 x + 1 x − P = − − 3 x + 2 x − 3 x x ( x + x x 1)3( − 1 +
x − 1) + ( x − 3)( x + + − 3 3 4 7 ) = − x + 2 x − 3 ( x +3)( x −1) 3x + 4 x − 7 x − 1 + x − = 9 ( x 1)( x 3) − − + ( x +3)( x −1) 3x + 4 x − 7 2x − = 10 ( x 1)( x 3) − − + ( x +3)( x −1) x + 4 x + = 3 ( x +3)( x −1) ( x +3)( x +1)
= ( x +3)( x −1) x + = 1 x − 1 Câu 11. a a a
( a − )( a + ) ( a − − − + )2 2 2 2 4 4 4 a − 2 2 P = : = : = a − = a − = a + 2 2 a − 4 a + 2 2( a − 2) ( 2) : ( 2). 2 2 a − 2 Câu 12. 2 2 2
A = ( 3 +1) + ( 5 −1) + 5 + 3 2 = 3 +1+ 5 −1+ 5 + 3 2( 5 − 3) = 3 + 5 + 2 = 2 5 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 59 Câu 13.
a).Điều kiện: x≥ 0; y ≥ 0; x ≠ y; x ≠ 1
3 x ( x − y ) − 3x + x + xy + y 2( x + xy + y) M = . ; x x − y y
(x − )1( x − y) 2 − 2 +
(x+ xy + y x xy y )
M = ( x − y)(x+ xy + y).(x− )1( x − y) 2 M = x −1
b).Để M có giá trị nguyên khi x-1 là ước của 2.
Các ước nguyên của 2 là 1 ± ;± 2.  x −1 = 1  x = 2   − = − = Do đó ta có x 1 1 x 0   ⇔  x −1 = 2  x = 3   x −1 = 2 − x = 1 −
Vì x ≥ 0; x ≠ 1 nên có x = 0; x = 2; x = 3 thỏa mãn bài ra. Câu 14.
1. Rút gọn biểu thức A.  x
( x 3)( x 3) ( x 2)( x 2)  + − − + − + x + + 2 24   A = :  x x 2 x 2 x 3  ( )( )  − − − −    x + 24 ( x 9) ( x 4)  − − − + x + 2 A = ( : x )1( x 2)  x 2 x 3  ( )( )  + − − −     x + 24  x − 3  A = ( : x
)1( x 2)  x 2 x 3 ( )( ) + − − −   x + A 24 = x +1
2) Tìm x để A đạt giá trị nhỏ nhất. x + 24 x −1+ 25 25 25 M = = = x −1+ = x +1+ − 2 x +1 x +1 x +1 x +1
Áp dụng bất đẳng thức Cauchy cho 2 số ta có 25 x +1+ ≥10 x +1 Do đó M ≥ 8 . THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 60
Đẳng thức xảy ra khi ( x + )2 1
= 25 ⇔ x +1 = 5 ⇔ x =16 .
Vậy giá trị nhỏ nhất của M bằng 8, đạt được khi x = 16. Câu 15.
1. A  4 3  2 27  12  4 3  6 3  2 3  0   2. a  1 2a  1 B       :
với a  0,a  1  
 a 1 a a a 1   a 1 2a       .   a   1  a 1
a( a  1) 2
( a  1)  2 a( a  1)  .a   1
( a  1)( a  1)  3a  1 Câu 16.  > 1..ĐK: x 1  x ≠ 2
2.. B =10 3 − 3 3 = 7 3  ≥ 3..ĐK: a 0 
; C = a +1−1 = aa ≠ 1 Câu 17.
1).Điều kiện a  0 và a 1 3(a + a − 1) a − 2 1 A = − + −1
( a + 2)( a − 1) a − 1 a + 2 3(a +
a − 1) − ( a − 2)( a + 2) + a −1 − ( a + 2)( a −1) A =
( a + 2)( a − 1) a + 1 A = a − 1 2). a +1 a + A = để 1 A = 2 ⇔ = 2 a −1 a − 1 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 61 a = 3
Học sinh giải phương trình và tìm ra giá trị của  1 a =  9 Câu 18.
A = ( 5 − 3)( 5 + 3) + 6 = 5 − 9 + 6 = 2 Câu 19. (a + )2 1 + 3(a −  + )2 2 1 a 1  + 3 2    a −1 a + 1 2a a −1 (a + ) 1 ( 2 3 a − a + ) a) Ta có ( ) 1 2a P = ÷ − = ÷ − 2 3  a −1 a −1 a −1 (a − )2 1 + 3(a + )2 1 (a − ) 1 ( 2 a + a + ) 1 a −1 + 3    a +1 (a + )2 1 4( 2 a − a + ) 1 (a + )2 1
(a − )1( 2a + a + )1 2a + − = − a 1 2a 1 a = − = = 1 − . 4( . . 2 a + a + ) 1 (a − )2 1
(a + )1( 2a − a + )1 a −1 a −1 a −1 a −1 Vậy P = 1 − . b) Đặt 3 2 s = x và 2 3 t =
y thì đẳng thức đề bài có thể viết lại thành 3 2 3 2
s + s t + t + t s = a .
Do s, t ≥ 0 nên 3 2 3 2
s + s t = s s + t ,
t + t s = t s + t .
Từ đó ta có (s + t) s + t = a hay ( + )3 2 s t = a . Suy ra 3 2 s + t =
a . Đây là kết quả cần chứng minh. Câu 20.
 ( x +1)(2 x −1)
x (2 x −1)( x +1)  x ( x −1) a) P = 1 +  − . (1 − x )(1 + x ) (1 − x )(x + x +1) 2 x −1    x( x + 1) 
P = 1 +  − x +  x + x + 1  
(1 − x )(x + x +1) + x( x +1) P = x + x +1
(1 − x )x +1 − x + x x + x x +1 = = x + x +1 x + x +1 4 x +1 4 b) P = ⇒ = 5 x + x +1 5
x = 7 − 4 3 (tháa m·n)
⇒ x − 4 x +1 = 0 ⇔ x =7+4 3 (tháa m·n) THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 62 Vậy để 4 P = thì x = 7 ± 4 3 5 Câu 21. 1 x  3 P  : .
x x 1 x x 1 1  .. x  3 1 1 1 P  
  x  2  x  4 . 5 x  3 5
Vậy 0  x  4 thỏa mãn bài toán.. Câu 22.
a) Ta có A  2x  15  8 2x 1  2x 1  2.4. 2x 1  16  x   2 ( 2 1
4)  2x  1  4 . Biểu thức 1
A có nghĩa khi và chỉ khi 2x  1  0  x  . 2   2x 1 4 3      2x  1  7
b)A  3  2x  1  4  3    
 2x  1  4  3  2x  1  1   x   25   . x   1 Câu 23.
Ta có x   3  3  3  x  3   3  3 1 2 4 ( 2 1) ( 2 1)(1 2 4)
 3  x   3 x x   3 x  2 ( 2 1) 1 2 1
3x  3x  1  0. Khi đó A  5 x  4 x  3 x  2 4
x  2x  1  2020  2 x x  3 x  2 ( 1)(
3x  3x  1)  2020  2020. Câu 24.
a) Điều kiện của x để biểu thức x 1 có nghĩa là x3  0 . x3  x  3 . THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 63   
b).Chứng minh đẳng thức 1  a a       1  aa    
a  0,a   1 ..     1aa 1  a 1      a      
a 1 a         .        a a a a a   1  Ta có 1 1 1   1          a 1 a 1    a 1      a 1     
 1 a1 a.  1a . Câu 25. 3 5 .3 5
1) Không dùng máy tính cầm tay, hãy tính giá trị biểu thức P  10  2
3 5 .3 5. 2 5  1 P  8
62 5 .3 5 53 5   2 5 1 .2 5 2   8 8  5 1.2. 5 1  8 2.5  1   1 8
2) Rút gọn rồi tính giá trị của biểu thức 2x3 x 2 Q
tại x  20202 2019 x 2 Ta có x         2 2020 2 2019 2019 2 2019 1 2019 1  x  2019 1 xx
2 x  1 x2 2 3 2  Q   x 2 x 2 Q  2 x 1
Q  2 2019   1 1 2 2019 1 Câu 26. THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 64 a). 4 + 3 = 2 + 3 = 5 b). 2 5 + (6 − 5) = 5 + 6 − 5 = 5 + 6 − 5 = 6 Câu 27. 2 a). 2x + 2x 1 1 2x(x +1) 1 1 2x 1 1 H = + − = + − = + − 2 x −1 x +1 x −1 (x−1)(1+ x) x +1 x −1 x −1 x +1 x −1
2x + x −1− ( x +1) = 2x − 2 = x −1 x −1 2(x−1) = = 2 x −1
b).Ta có x − H < 0 ⇔ x − 2 < 0 ⇔ x < 2 ⇔ x < 4
Mà x ≥ 0; x ≠ 1, suy ra: 0 ≤ x < 4; x ≠ 1
Vậy: Với 0 ≤ x < 4; x ≠ 1 thì x + H < 0 Câu 28.
Tính được 13− 4 3 = 2 3 −1 và 19 + 6 2 = 3 2 −1 Đưa được về dạng     T = ( )2 − ( )2 2 2 2 3 1 3 2 −1     
Tính đúng kết quả T = 187 Câu 29. x ≥ 0 
Biểu thức xác định khi  x −3 ≠ 0 . x ≠ 9  x ≥ 0 ⇔  . x ≠ 9. Câu 30. 2 + 1).Với a a a
a > 0, a ≠ 1 ta có = a a. . a +1 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 65 + − − + − + +1 −1 ( a )2 ( a )2 1 1 4 a ( a )1( a a a )1 Và − + 4 a = . a −1 a +1
( a − )1( a + )1 4a a = . . a −1 Do đó 4a a 1 4 P = . = . . a −1 a a a −1 a −1 = 4 − a −1= 2 −   − = − 2).Với a 1 1
a nguyên thì P nhận giá trị là số nguyên khi và chỉ khi  . a −1 = 1  a −1 = 2  a −1 = 4 a = 3 − a = 1 −  a = 0 ⇔ 
Đối chiếu với điều kiện ta có a = 2,a = 3,a = 5 (thỏa mãn).. a = 2  a = 3  a = 5 Câu 31. 2   + Có 2 2 x = 3 + 5 + 2 3 + 3 − 5 + 2 3 = 6 + 2 3 −   (5+2 3) =6+2 4−2 3   = + ( − ) = + = ( + )2 6 2 3 1 4 2 3 3 1 .
+ Do x > 0 nên x = 3 +1. + Suy ra (x − )2 1 = 3 hay 2
x − 2x = 2 , do đó P = 2 − . Câu 32.  − >
Biểu thức xác định khi x 3 0  . x ≠ 9 x > 3 ⇔  . x ≠ 9. Câu 33. THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 66 + − − + − + +1 −1 ( a )2 ( a )2 1 1 4 a ( a )1( a a a )1
1).Với a > 0,a ≠ 1 ta có − + 4 a = . a −1 a +1
( a − )1( a + )1
a + 2 a +1− a + 2 a −1+ 4 a (a − ) 1 = . a −1 4a a = . a −1 Do đó 4a a 1 4 P = . = . . a −1 a a a −1 2).Ta có a = + = ( + )2 9 4 2 2 2 1 = 2 2 +1. . Do đó P = 2. . Câu 34.
( x −3)( x +3)+(2 x +9) x−9+2 x +9 B = = . x ( x + 3) x ( x + 3) x + ( x +2 x 2 x ) x +2 = = = .. x ( x + 3) x ( x + 3) x + 3 + + + Với A 5 2 x 2 x 5 x 3 5 x > 0 ta có: > ⇔ : > ⇔ > . B 3 x x + 3 3 x 3
⇔ 3 x + 9 > 5 x (vì 3 x > 0 x ∀ > 81
0 ) ⇔ 2 x < 9 ⇔ 0 < x < . 4 Câu 35. 2 5 6 7 − 33 + 128 −1 5 6 7 − (4 2 +1) −1 Ta có: C = = . 3 − 2 3 − 2 2 5 6 6 − 4 2 −1 5 6 (2 − 2) −1 = = . 3 − 2 3 − 2 5 11− 6 2 2 = 5 (3 − 2) = . 3 − 2 3 − 2 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 67 5(3 − 2) = = 5. . 3 − 2 Câu 36.
a) Rút gọn biểu thức A.
Điều kiện: x > 0, x ≠ 4, x ≠ 9⋅ Ta có: x + 3 x + 2 x + 2 x + 3 x + 2 x + 2 + + = + + x − 2 3 − x x − 5 x + 6 x − 2 3 − x
( x −2)( x −3)
( x +3)( x −3)−( x +2)( x −2)+( x +2) =
( x −2)( x −3)
x − 9 − ( x − 4) + ( x + 2) 1 = ( = ⋅
x − 2)( x − 3) x − 2 x − 2 − − − x − (x x 2 2 ) x x −1 = = = ⋅ x − x − 2 x − x − 2 x − x − 2
( x + )1( x −2) + Do đó 1 x x 1 A = : = ⋅ x − 2 ( x + ) 1 ( x − 2) x
b) Tìm x để 1 P = 2 A −
đạt giá trị lớn nhất. x + Ta có 2 x 2 1 2 1 P = − = 2 + − x x x x 2  1  = − −1 + 3 ≤ 3.    x
Dấu “=” xảy ra khi 1 = 1 ⇔ x = 1. x
Vậy maxP = 3 ⇔ x = 1. Câu 37.
Điều kiện: a > 0 và a ≠ 1. Ta có:
( a + )2 −( a − )2 1 1
= (a +1+ 2 a)−(a +1− 2 a) = 4 a THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 68 và
( 2a+1+ a+1)( 2a+1− a+1)=(2a+ )1−(a+ )1= a.
Do đó, phương trình đã cho có thể được viết lại thành 1 1 − =1. a −1 a +1
( a + )1−( a − )1
Phương trình này tương đương với ( hay 2 =1.
a + )( a − ) =1 1 1 a −1
Như thế, ta có a −1 = 2 hay a = 3 (thỏa mãn).
Vậy có duy nhất một giá trị a thỏa mãn yêu cầu đề bài là a = 3. Câu 38.
Với x ≥ 0 , ta có: 2  x + 2
2 x + 8  x − x x + x −1 A =  −  ⋅ x − x +1 x x +1 x + 3  
( x +2)( x + )1−2 x −8 x x( x − )1+( x − )1 = ( x + ) ⋅ 1 ( x − x + ) 1 x + 3 x x x (x x + )1( x − + + − − )1 3 2 2 8 = ⋅ x x +1 x + 3
= (x + x − x − ) x −1 3 2 6 ⋅ x + 3
= ( x − )( x + ) x −1 2 3 ⋅ x + 3
= ( x − 2)( x − ) 1 = x − 3 x + 2
A = 6 ⇔ x − 3 x + 2 = 6 ⇔ x − 3 x − 4 = 0
⇔ x + x − 4 x − 4 = 0 ⇔ ( x − 4)( x + ) 1 = 0 ⇔ x − 4 = ( 0 vì x +1 > 0 ∀x ≥ 0) ⇔ x = 16 (TMĐK)
Vậy với x = 16 thì A = 6 . Câu 39. THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 69 + − 2 + +
( x − )1(x+ x + )1 x(x x + x x x x x x )1 2 3 1 2 3 P = + − = + − x x − x x x + x x x ( x − ) 1 x ( x + ) 1 2 + 3 + +1
(x x + )1 2 +3 + +1 ( x + )1(x− x + x x x x x x )1 = + − = + − x x x ( x + ) 1 x x x ( x + ) 1 2 + 3 + +1
(x x + )1 2 +3 + +1 ( x + )1(x− x + x x x x x x )1 = + − = + − x x x ( x + ) 1 x x x ( x + ) 1
2x + 3 x + x +1 x − x +1 2x + 2 x + = + − = 3 = 3 2 x + + 2 x x x x x
Áp dụng bất đẳng thức Cauchy, ta có 3 2 x +
≥ 2 6 ⇒ P ≥ 2 + 2 6 x
Dấu bằng xảy ra khi x = 3 (tmdk) 2 Câu 40. − + − + 4 − − 9 + 3
( x )1( x 2) (2 x )1( x x x )1 a). A = ( + − x + )
1 ( x + 2) ( x + )
1 ( x + 2) ( x + ) 1 ( x + 2)
(1−5 x)( x +2) 1−5 x = ( = . x + ) 1 ( x + 2) x +1 − b). 1 5 x 6 A = = 5 − +
. Với mọi x ≥ 0 ta có: x +1≥1 nên 6 ≤ 6 x +1 x +1 x +1 Do đó 6 A = 5 − +
≤ 1. Giá trị lớn nhất của A là 1 đạt được khi x = 0 . x +1 Câu 41.    + + +  a) x x 3 x 2 x 2 A = 1−  :  − +
 Với x ≥ 0; x ≠ 4; x ≠ 9. x + 1 x − 2 x − 3 x − 5 x + 6    
( x +3)( x −3)−( x +2)( x −2)+ x +2 1 A = : x +1
( x −2)( x −3) 1
x − 9 − x + 4 + x + 2 1 x − 3 A = : = : x +1
( x −2)( x −3)
x +1 ( x − 2)( x − 3) 1 1 x − 2 A = : = . x +1 x − 2 x +1 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 70 b) Ta có 3 3 3 10 + 6 3 = (1+ 3) = 1+ 3 2 21+ 4 5 = (2 5 +1) = 2 5 +1 − + Nên ( 3 1)( 3 1) 2 x = = = 5 − 2 2 5 + 4 2 5 + 4 Vậy 2 2019 2019
B = (x + 4x − 2) = ( 1) − = 1 − Câu 42. 1. Ta có:  2 1 1 
xy ( x + y) − = xy P  + + ⋅   xy x y x x +   y y 2
xy (x + y − + + xy xy y x ) = ⋅ xy
( x + y)(x+ y− xy) ( x + y)2 = ⋅ xy xy x + y x + = y xy + Vậy = x y P
với x > 0; y > 0. xy
2.Áp dụng bất đẳng thức Cô-si, ta có: x + y ≥ 2 xy = 2 16 = 4 4 ⇒ P ≥ = 1 16
Dấu “=” xảy ra ⇔ x = y = 4
Vậy min P = 1 tại x = y = 4 . Câu 43. Ta có: THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 71 3 3 x = 70 + 4901 + 70 − 4901 3 3
⇒ x = 140 + 3 (70 + 4901)(70 − 4901)(3 3 70 + 4901 + 70 − 4901 ) 3
⇔ x = 140 − 3x 3
⇔ x + 3x −140 = 0 ⇔ (x − 5)( 2 x + 5x + 28) = 0 2  5 87    2 ⇔ x = 5
do x + 5x + 28 = x + + > 0∀x ∈     2 4     
Vì vậy x là số nguyên tố.. Câu 44. Ta có 2
A > 0 ⇒ A = 8 + 2 (4 + 10 + 2 5 )(4 − 10 + 2 5 ) . A = + − ( + ) = + − = + ( − )2 2 8 2 16 10 2 5 8 2 6 2 5 8 2 5 1 . A = + ( − ) = + = ( + )2 2 8 2 5 1 6 2 5 5 1 . ⇒ A = 5 +1.. Câu 45. 3 3
x = 2 + 2 3 + 2 − 2 3 −1 3 3
⇔ x +1 = 2 + 2 3 + 2 − 2 3
⇒ (x + )3 = − (x + ) 3 2 1 4 6
1 ⇒ x + 3x + 9x = 3 −
P = x ( x + x + )3 = ( x + x + x)3 3 2 3 2 3 9 3 9 P = 27 − Câu 46. Ta có: 1 1 1 1 S = + + + ... + 2 2 1 + 3 3 + 5 5 + 7 2019 − 2 + 2019 2 2 1 − 3 3 − 5 5 − 7 2019 − 2 − 2019 ⇒ S = + + + ... + 2 2 1 − 3 3 − 5 5 − 7 2019 − 2 − 2019 2 2
1 − 3 + 3 − 5 + 5 − 7 + ... + 2019 − 2 − 2019 ⇒ S = 2 − 2 1 − 2019 1 − 2019 ⇒ S = = = 1009 2 − 2 − THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 72 Vậy S =1009 Câu 47.
( 2a−2 2)(a− )1
Rút gọn biểu thức T =
với a > 0,a ≠ 4 . a − a − 2
( 2a −2 2)(a− )1= 2( a −2)(a− )1
= 2 ( a −2)( a − )1( a + )1
a − a − 2 = ( a + )1( a −2)
Vậy T = 2 ( a − )1. Câu 48.
a) Điều kiện: x > 0 ; x ≠ 1.     x ( x − + )2 1 1 1 1 1 1 P :   = + = +   .
x −1 x − x  ( x − ) . 2  x −1  1  x ( x − ) 1 x +1  x ( x − + )2 1 1 x −1 = . x ( x − ) . = 1 x +1 x 1 x −1 1 P = ⇔
= ⇔ 2.( x − )1 = x ⇔ x = 2 ⇔ x = 4 (thỏa điều kiện). 2 x 2
Vậy giá trị cần tìm là x = 4 . b) 3 3 − = ( )3 − ( )2 3 46 5 61 2 5 3. 2 5 .1+ 3.2 5.1 −1 = (2 5 − )3 2 3 1 = 2 5 −1. − = − + ( )2 = ( − )2 69 28 5 49 2.7.2 5 2 5 7 2 5 = 7 − 2 5. 3 A =
46 5 − 61 + 69 − 28 5 = 2 5 −1+ 7 − 2 5 = 6. Câu 49. 2 2 1+ 3 2  1− 3 2  A =  −  −  −  2 1 + 3 2 1 − 3     THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 73   ( + ) 2   −   ( − ) 2 2 2  1 3 4 1 3 − 4  = −     .
 2(1+ 3)   2(1− 3)      2 2     2 3 2 − 3 =   −    2  (1+ 3)   2   (1− 3)  3 3 3 3 = ( + ) − = − 2 ( − )2 4+2 3 4−2 3 1 3 1 3 12 − 6 3 − 12 − 6 3 12 3 = = − = 3 − 3 16 − 12 4 Vậy A = 3 − 3 . Cách khác:  +  ( + )2 1 3 − 4 1 3 2 2 3 3  −  = = = 2 1 + 3   2(1+ 3) 2(1+ 3) 1+ 3  −  ( − )2 1 3 − 4 1 3 2 2 − 3 3  −  = = = − . 2 1 − 3   2(1− 3) 2(1− 3) 1 − 3 2 2  3   3  3 3 A =   −  −  = − 1 + 3 1 − 3     (1+ 3)2 (1− 3)2 3 3 12 − 6 3 −12 − 6 3 12 3 = − = = − 4 + 2 3 4 − 2 3 16 −12 4 Vậy A = 3 − 3 . Câu 50.
A = (3 5 − 27 − 20 ) 5 + 3 15 .
= (3 5 −3 3 − 2 5) 5 +3 15 . = ( 5 −3 3) 5 +3 15 . = 5 − 3 15 + 3 15 = 5 . Câu 51.
a) Rút gọn biểu thức 𝐴 . THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 74
Điều kiện: x ≥ 0  x ≠ 9 Ta có:
x x − 3 − 2x +12 x −18 − x − 4 x − 3
x x − 3x + 8 x − 24 A = ( x ) = +1 ( x −3)
( x + )1( x −3)
x ( x − 3) + 8( x − 3)
( x −3)(x+8) x+8 = ( x + ) = = 1 ( x − 3)
( x + )1( x −3) x +1
b)Tính giá trị của biểu thức 𝐴 khi x = 4 − 2 3. Ta có : x = − = − + = ( − )2 4 2 3 3 2 3 1 3 1
⇒ x = 3 −1 = 3 −1 4 − 2 3 + 8 12 − 2 3 A = = = 4 3 − 2 3 −1+1 3 Câu 52. a) Ta có:
x − 2 x − 3 = x −3 x +1
x x + 8 = x − 2 x + 4 x + 2 x −1 x +1 4 − x − = x +1 x −1 x −1
P = x − 5 x +1
b) Tìm tất cả số nguyên tố x để P ≤1 P ≤ 1 ⇔ 0 ≤ x ≤ 5
x = 2, x = 3, x = 5, x = 7, x = 11, x = 13, x = 17, x = 19, x = 23. Câu 53 2 + a). x
x = x ( x + )1 x − x +1 2x − x 2x − 2 − = (2 x − ) 1 − 2( x − ) 1 x x +1 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 75 2 x + x 2x − x 2x − 2 + − = x + x +1 x − x +1 x x +1 x + x +1
P = x − x +1
b). P ≤ 3 ⇔ x + x +1 ≤ 3(x − x + ) 1 ⇔ ( x − )2 2 1 ≥ 0. Câu 54. A =
2( x −1) + x + x − 2 x
= x + x − 2 = ( x −1)( x + 2)
( x −1)( x + 2) ≤ 0 ⇔
x −1 ≤ 0 ⇔ 0 ≤ x ≤ 1.
Đối chiếu điều kiện giá trị cần tìm 0 ≤ x <1. Câu 55.
Điều kiện: x ≥ 0, x ≠ 1.Ta có
3x + 3 x − 3 − ( x +1)( x −1) − ( x + 2)( x − 2) P = ( x −1)( x + 2) x + 3 x + 2 ( x +1)( x + 2) x +1 = = = ⋅ ( x −1)( x + 2) ( x −1)( x + 2) x −1 x +1 P = 3 ⇔
= 3 ⇔ x = 2 ⇔ x = 4 (thỏa mãn điều kiện). x −1 Câu 56.
Điều kiện: x > 0 .  1   x −1 1  A = x + .    −  
x x − x +1 x +1     +  ( x − ) 1 ( x + )
1 − ( x − x +  x x )1 1 =  .  x    
(x− x + )1( x + )1  
x x +1  x − 2  − = x 2  .  = x x x +1     x THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 76 − 2. Ta có x 2 2 A = = 1− x x
Suy ra A nhận giá trị nguyên khi và chỉ khi x là ước nguyên của 2. Hay x ∈{ 1 − ;1; 2 − ; } 2 . Ta có: x = 1 − (Vô nghiệm).
x = 1 ⇔ x = 1 (thỏa mãn).
x = 2 ⇔ x = 4 (thỏa mãn) x = 2 − (Vô nghiệm).
Vậy để A nguyên thì x ∈{1; } 4 . Câu 57. Đặt 3 2 s = x và 2 3 t =
y thì đẳng thức đề bài có thể viết lại thành 3 2 3 2
s + s t + t + t s = a .
Do s, t ≥ 0 nên 3 2 3 2
s + s t = s s + t ,
t + t s = t s + t .
Từ đó ta có (s + t) s + t = a hay ( + )3 2 s t = a . Suy ra 3 2
s + t = a . Đây là kết quả cần chứng minh.
Câu 58. a) Điều kiện: x ≠ −y; x ≠ 1; − y ≠ 1. 3 2 2 3 3 2 2 3 2 2 2 2
x + x − y + y − x y − x y x − xy + y + x − y − x y P = = (x + y)(1− y)(1+ x) (1− y)(1+ x) 2 2 x + x y + x − y = 1+ x = x + xy − y. b) Đặt 1 1 1 1 1 1 S = 1+ + + 1+ + + ...+ 1+ + . 2 2 2 2 2 2 1 2 2 3 2017 2018 2 Ta có 1 1  1 1  2 1+ + = 1+ − + * (n ∈  ) 2 2 n (n + 1)   n n 1  +  n(n +1) 2  1 1  1 1 = 1+ − = 1+ −   .  n n + 1 n n + 1      
Áp dụng đẳng thức trên ta được 1 1 1 1 1 1 S = 1+ − +  1+ − +  ...+ 1+ −  1 2 2 3 2017 2018        THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 77 = 1 2018 −
< 2018. (điều phải chứng minh) 2018 Câu 59.
Từ giả thiết đã cho ta có: 1 1 1
+ = ⇔ xz + yz = xy ⇔ 2xy − 2xz − 2yz = 0 x y z ⇒ + + = + + + − − = ( + − )2 2 2 2 2 2 2 x y z x y z 2xy 2xz 2yz x y z = x + y − z 2 2 2
⇒ x + y + z là một số hữu tỉ
Vậy ta có điều phải chứng minh Câu 60. a) Rút gọn T:
Với a ≠ b,a > 0,b > 0 , ta có: 3 3 3 3 + − + − − − + + − ( a − b)( a + b a b ab a a b b a b a b a b ab ) a+b− ab T = : = ⋅ = a + b ( a − b)( a + b) a + b ab ( a − b) ab Vậy : a + b − ab T =
, với a ≠ b,a > 0,b > 0 . ab b) Chứng tỏ T > 1 Ta có: a + b − ab T =
, với a ≠ b,a > 0,b > 0 . (kết quả câu 1.a) ab ( − )2 + ( − )2 a b ab a b ⇔ T = =
+ 1 > 1(vì ab > 0, a − b ≠ 0 với ab ab a ≠ b,a > 0,b > 0 ) Vậy T > 1 Câu 61. Ta có ngay:
A = 4 20 − 45 + 3 125 − 2 405
= 8 5 − 3 5 + 15 5 −18 5 = 2 5 B = 9 − 4 2 + 9 + 4 2 = ( )2 − + + ( )2 2 2 2.2 2.1 1 2 2 + 2.2 2.1+ 1 = ( − )2 + ( + )2 2 2 1 2 2 1
= 2 2 −1 + 2 2 + 1 = 2 2 −1+ 2 2 + 1 = 4 2 (do2 2 −1 > 0) THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 78 Câu 62. Ta có: 2.3 1 2 1+ 2 = 3 = ⇒ = 2 1+ 2 2.3 3.4 1 2 1+ 2 + 3 = 6 = ⇒ = 2 1+ 2 + 3 3.4 ................. 2018.2019 1 2 1+ 2 + 3 + .....+ 2018 = ⇒ = 2
1+ 2 + 3 + ......+ 2018 2018.2019  2  2   2 P 1 1 ......1  = − − −  2.3 3.4 2018.2019       2.3 − 2 3.4 − 2 2018.2019 − 2 = . ....... 2.3 3.4 2018.2019 4 10 4074340 = . ........... 2.3 3.4 2018.2019 1.4 2.5 3.6 2016.2019 2017.2020 = . . ........ . 2.3 3.4 4.5 2017.2018 2018.2019
(1.2.......2017).(4.5.......2020) 1.2020 2020 1010 = ( = = =
2.3.......2018).(3.4.5.......2019) 2018.3 6054 3027 Câu 63.
a) Điều kiện x > 0; x ≠ 1 x + 1 1 − x + 1 A = : = − x x + x + x −x + x x (x+ x +1).( 2x x 2 ) x + 1 = − x.(x+ x +1). x (x x 1) x + 1 =
.( x −1)(x + x +1) = ( x +1)( x −1) = x −1 x + x + 1 b) Ta có: 2 T = B − 2A
= x − 5x − 8x + 2025 − 2(x −1)2 4 2 4 2 2
= x − 5x − 8x + 2025 − 2x + 4x − 2 4 2 = x − 7x − 4x + 2023 4 2 2
= x − 8x + 16 + x − 4x + 4 + 2003 = (x − 4)2 + (x − 2)2 2 + 2023 Vì ( − )2 ≥ ( − )2 2 x 4 0, x 2 ≥ 0 ⇒ T ≥ 2003 x = 2 2 x − 4 = 0 Dấu “=” xảy ra  ⇔  ⇔ x = 2 − ⇔ x = 2 x − 2 = 0 x =  2 Vậy với T = 2003 ⇔ x = 2 min THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 79 Câu 64. a) Rút gọn biểu thức 1 P : ( a + b)(a+b)
Điều kiện : a > 0,b > 0
ab.( a − b ) + ( a − b ) ( a − b )(1+ ab ) P = = = a − b 1 + ab 1 + ab 1 ⇒ P : ( = + + a + b ) . P ( a b )(a b) (a + b)
= ( a − b)( a + b)(a + b) = (a −b)(a + b) 2 2 = a − b b) Ta có:   a = + a = +  ( 2018 )2 1 2019 2 2018  a = 2018 +1  ⇔  ⇒  b  = 2020 + 2 2019 b  = ( +  )2  b = 2019 +1 2019 1
⇒ P = a − b = 2018 +1− ( 2019 + ) 1 = 2018 − 2019
Câu 65. 1) Điều kiện 0 < a < 1  1 + a 1 − a  1 1  2 Q =  + 
−1 −  a − 2a +1 2 2 1 + a − 1 −  a
1 − a −1 + a  a a    1 + a (1− a)2 2  1− a 1    = + 
−  a − a +
 1+ a − 1− a  a a a a a  1 − ( 1− − 1+ ) 2 2 1 2     2  1 + a 1 − a  1− a 1  =  +  −  (a − )2 1
1 + a − 1 − a 1 + a − 1 −  a a a     2 1 a 1  a 1 a 1  + + − − = . −  a −1 (do a > 0) 1 + a − 1 −  a a a    2 1 + a + 1 − a 1 − a −1 = − a do < . (1 ) ( 0 a < 1)
1 + a − 1 − a a
( +a + −a)( +a − −a) 2 1 1 1 1 1 − a −1 = ( − a
1 + a − 1 − a ) . (1 ) a 2 1 + a −1 + a 1 − a −1 = . .(1− a) 2 1 + +1 − − 2 1 − a a a a 2 2a 1 − a −1 = . (1 − a) 2 2 − 2 1− a a THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 80
= −(1− a) = a −1
2) Điều kiện 0 < a < 1 Ta có: = ( − )3 3 Q a 1 Xét hiệu : Q − Q = (a −1)3 3 − (a −1) (a 1)(a 1)2 1 = − − −
= (a −1)(a −1−1)(a −1+1) = a(a −1)(a − 2)   Mà a  > 0 0 a 1 a 
< < ⇒  −1 < 0 ⇒ a(a −1)(a − 2) > 0 a  − 2 < 0  3 3
⇒ Q − Q > 0 ⇔ Q > Q Vậy 3 Q > Q Câu 66.
A = (4+ 15)( 10 − 6) 4− 15 = 4+ 15. 2.( 5 − 3) (4+ 15)(4− 15)
= 8 + 2 15.( 5 − 3). 16 −15 = ( 5 + 3)2 .( 5 − 3).1
= ( 5 + 3).( 5 − 3) = 5− 3 = 2 Câu 67. a) Điều kiện a > 0  a a + a  4 − a P =  + .  a 2 a 3 a 2  + + +   a  a.( a +1  a ) 4−   a = +   ( a 1)( a 2) . a 2  + + + a   a a  4 − a =  + .  a 2 a 2  + +   a +
(2− a)(2+ a) a.( a +1)(2− a a a ) = . = a + 2 a a = ( a +1)(2 − a) = a − + a + 2
b) Điều kiện a > 0 . Ta có: 2  1  9 9 P = a − + a + 2 = − a − + ≤  2    4 4 Dấu “=” xảy ra 1 1 1
⇔ a − = 0 ⇔ a = ⇔ a = (tm) 2 2 4 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 81 Vậy 9 MaxP = khi 1 a = 4 4 Câu 68.
Điều kiện a > 0; x ≠ 1 2 2 a x = a + 1− 1+ a + (a+1)2 2 4 3 2 a + 2a + 1+ a + 2a + 2a = a + 1− 2 (a + 1) 4 3 2 2 a + 2a + a + 2a + 1+ 2a = a + 1− (a +1)2 (a +a+1)2 2 = a + 1− (a +1)2 2 2 2 a + a + 1 a + a + 1 a + a + 1  = a + 1− = a + 1− do > 0 a 1 a 1 a 1  + + +   2 2 a + 2a + 1− a − a −1 a = = < 1 a ∀ > 0 a + 1 a + 1 ⇒ 0 < x < 1 a ∀ > 0 2 x + ( x x 1) + x − 2 x + 1 + 1 − + 1 ⇒ P = = 2 x − 2x + 1 (x−1)2 x + x −1 + 1 x + 1− x + 1 2 2(a +1) = = = = = 2a + 2 x −1 1− x a a + 1− a 1− a+1 Vậy P = 2a + 2 Câu 69.  ( )2 ( )2 x y x y    + + −    y x  5  ( + + =   x y ).( x y) 2(x 2y)    x.  ( x y) y.( x y) + − + + + +  3    x + y + 2 xy + x + y − 2 xy y y + x x 5 ⇔ + = x − y + 2x + 4y xy.( x + y) 3 + ( x + y)(x+y− xy 2(x y) ) 5 ⇔ + = 3(x + y) xy.( x + y) 3 x + y − xy ⇔ = 1 xy THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 82 ⇔ x + y − xy = xy ⇔ x + y − 2 xy = 0 ⇔ ( x − y)2 = 0 x ⇔ x = y ⇒ = 1 y Vậy x = 1 y 2 2 2 2 4 2 2   a + a + b
a − a + b a − Câu 70. 4 =  −  a b P : , a > b > 0 2  2 2 2 2  − + + +   b a a b a a b
(a+ a +b )2 −(a− a +b )2 2 2 2 2 2 = b ( . a + 2 2 a + b )( 2 2
a − a + b ) 2 4 a ( 2 2 a − b ) 2 2 2 2 2
a + a + b + 2a a + b − ( 2 2 2 2 2
a + a + b − 2a a + b ) 2 = b . 2 a − ( 2 2 a − b ) 2 2
4. a . a − b 2 2 2 2 2 4a a + b b a a + = b . = 2 2 2 2 2 b
4. a . a − b a a − b 2 2  a +  b khi a > 0 2 2  a − =  b 2 2  a + − b khi a < 0  2 2  a − b Câu 71. ( − )2 ( + + − + + )2 2 2 x a x a a x 2x a a x 2x a A = + = + x x x x x − a + x + a = . x +) Với − + +
x ≥ a thì x − a = x − a nên A = x a x a 2x = = 2 x . x x
+) Với 0 < x < a thì x − a = −(x− a) = a −x
nên A = a − x + x + a 2 a = . x x Câu 72. THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 83
a) Với x > 0; x ≠ 4 , ta có:    x + 3 x + 2 1  1 x + 3 x + 2 x + 2 x +  4 A =  −  :   = − x . x x 8 x 2  − −    
x ( x −2)(x+2 x +4) ( x −2)(x+2 x +4) x − 2 x = ( = x − 2)(x + 2 x + 4) x . x + 2 x + 4 2 2
Ta có x = 14 + 6 5 = 9 + 2.3. 5 + 5 = (3+ 5) ⇒ x = (3+ 5) = 3+ 5 = 3+ 5. Khi đó, ta có: 3 + 5 3 + 5 3 + 5 1 A = = = =
14 + 6 5 + 2.(3+ 5)+ 4 24 + 8 5 8(3+ 5) . 8 b) Ta có = − + = ( − )2 2 A 24 8 4 2 3 2 3 2 ⇒ A = ±(2 3 − 2)
Do A < 0 nên A = 2 − 2 3 . Câu 73. + + + ( + )2 x 2 x ( x +1 x 4 x 4 x x ) a) + Biến đổi + = − x + x − 2 1− x
( x −1)( x +2) ( x −1)( x +1) = x + 2 x 2 − = x −1 x −1 x −1 + Biến đổi 1 1 2 x − = x + 1 1− x ( x +1)( x −1) ( x +1)( x −1 2 2 x 2 ) + Ta có A = : ( = − x + 1)( x −1) . x 1 x −1 2 x + Vậy x + 1 A =
, với điều kiện x > 0, x ≠ 1. x b) Ta có: 1+ 2018 1 1 1 1 A ≥ ⇔ 1+ ≥ 1+ ⇔ ≥ 2018 x 2018 x 2018
x ≤ 2018 ⇒ 0 < x ≤ 2018
Vì x > 0, x ≠ 1 và x nguyên nên x∈{2;3;4;...; }
2018 . Suy ra có 2017 giá trị nguyên của
x thỏa mãn bài toán. Câu 74. Ta có: THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 84 2 + 2 a 2a b + 2 ab A = : 1− ab 1− ab 2(1+ a) 1 = = 2 ab(1+ a) ab Khi a > 0; b > 0 , a + b 1 1 1 1 a + b = ab ⇔ = 1 ⇔ + = 1 ⇔ = 1− ab a b a b 2   Do đó 1 1 1 1 1 1 A = (1− ) = − 
−  ≤ . Dấu “ = “ xảy ra ⇔ b = 4; a = 4 . Vậy giá b b 4  b 2  4
trị lớn nhất của A là 1 khi a = b = 4 4 Câu 75. Ta có:  3 1 a  + a − 2 a + 1 P =  + 1− a  (a > 1)  a −1  a     (1 a )(1 a a)  + − +  ( a − 1)2 P =  ( + −  a 1)( a 1) 1 a . − +  a   1− a + a  a −1 P =  + 1− a .
(Do a > 1 ⇒ a > 1 ⇒ a −1 > 0)  a 1  −   a 1− a + a + a −1− a + a a −1 P = . a −1 a a a −1 P = . = 1 a −1 a Câu 76. x + 2 x + 3 3x + 4 x − 5 x + 2 x + 3 3x + 4 x − 5 a) P = − − = − − x + 1 5 − x x − 4 x − 5 x + 1 5 − x ( x +1)( x −5)
( x + 2)( x − 5) + ( x + 3)( x + 1) −(3x + 4 x − 5) = ( x + 1)( x − 5) −x − 3 x − 2 = ( x +1)( x −5) ( x + 1)( x + 2) x + 2 = − = − ( x + 1)( x − 5) x − 5 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 85 x + 2 x + 2  x < 5 Ta có P > 2 − ⇔ − > 2 − ⇔ 2 − > 0 ⇔  . x − 5 x − 5  x >  12
+ Với x < 5 ⇔ 0 ≤ x < 25 .
+ Với x > 12 ⇔ x > 144 . Câu 77.
Điều kiện : x > 0, x ≠ 1 2(x −1) 2 x − x 2x + x A = + − x −1 x + x + 1 x − = 2( x −1) x (x x 1) + − 2 x −1 x + x + 1 = + ( − ) 2 1 3  1  3 3 1
x. x 1 = x − x + + =  x − + ≥ 4 4 2    4 4 Vậy 3 A ≥ . Dấu " = " xảy ra 1 1 ⇔ x − = 0 ⇔ x = (tm) 4 2 4 Câu 78.   a) Ta có: x x y Q = − 1+  : 2 2  2 2  2 2 x − y x − y x − x − y   2 2 2 2 x x + x − y x − x − y = − ⋅ 2 2 2 2 x − y x − y y 2 2 2 x x − x + y = − 2 2 2 2 x − y y x − y x y = − 2 2 2 2 x − y x − y ( − )2 x y x − y = = x + y. x − y x + y x − y Vậy Q =
với x > y > 0 . x + y b) Ta có:
Thay x = 3y (thỏa mãn ĐK) vào biểu thức Q, ta được: 3y − y 2y 2 Q = = = 3y + y 4y 2 Vậy 2 Q = khi x = 3y . 2 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 86 Câu 79. ( − )3 x y + 2x x + y y 3 xy − 3y A = + với x,y ≥ 0 và x ≠ y x x + y y x − y 3 y ( x − − + − + + y x x 3x y 3y x y y 2x x y y ) = ( + x + y )(x − xy + y) ( x − y)( x + y) 3 x (x − xy + y) 3 y = ( + x + y )(x − xy + y) x + y 3 x 3 y = + x + y x + y 3 x + 3 y = = 3 x + y
Vậy giá trị của biểu thức A không phụ thuộc vào giá trị của biến với x,y ≥ 0 và x ≠ y. Câu 80.
a) ĐKXĐ: x ≥ 0; y ≥ 0,y ≠ 1,x + y ≠ 0.
x( x +1)− y(1− y)−xy( x + y) P = ( x + y)(1− y)( x +1)
( x + y)( x − y +x− xy +y−xy) = ( + )( − )( + ) = x + xy − y. x y 1 y x 1 b) P = 2 ⇔ x + xy − y = 2 ⇔
x (1+ y ) − ( y + ) 1 = 1 ⇔ ( x − ) 1 (1+ y ) =1
Ta có: 1+ y ≥ 1 ⇒ x −1 ≤ 1 ⇒ x ≤ 2 ⇔ x ≤ 4.
Kết hợp với điều kiện x ≥ 0 ⇒ 0 ≤ x ≤ 4 ⇔ x∈{0;1;2;3; } 4
Thay vào phương trình trên P = 2 Ta được (x; y)∈ ( { 4;0);(2;2)} Câu 81. THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 87 2 2  a − b a − b  a + b P =  + ⋅ (a > b > 0)  2 2  2 2  a + b + a − b a − b − a + b  a − b   2 2  a − b a − b  a + b = + ⋅  a + b + a − b a − b  ( a+b − a−b) 2 2  a − b 
(a − b).( a+b − a−b)+(a−b).( a+b + a−b) 2 2 a + b = ⋅
a − b ( a + b + a − b).( a + b − a − b) 2 2 a − b 2(a − b) 2 2 . a + b a + b 2 2 a + b = ⋅ = 2b a − b a − b. a + b b
Vì a – b = 1  a = b + 1 khi đó theo BĐT AM – GM: a + b ( + )2 2 2 2 2 b 1 + b 2b + 2b + 1 1 1 P = = =
= 2b + + 2 ≥ 2 2b⋅ + 2 = 2 2 + 2 b b b b b Câu 82.
a) ĐKXĐ: x ≥ 0; y ≥ 0, xy ≠ 1.
( x + y)(1+ xy)+( x − y)(1− xy) 1−xy+ x+ y+2xyP = :   1− xy  1− xyx + x y + y + y x + x − x y − y + y x 1− = xy . 1− xy
1+ x + y + xy 2 ( x + y x ) 2 x (1+ y) 2 = x ( = = 1+ x)(1+ y)
(1+ x)(1+ y) 1+ x 2(2 − 3 2 ) b) Với x = = +
( + )( − ) =4−2 3 =( 3−1)2. 2 3 2 3 2 3 = ( − )2 x 3 1 = 3 −1 = 3 −1 2( 3 −1) 2 3 −2 6 3 + 2 P = = = 1+ ( 3 −1) . 2 5 − 2 3 13 Câu 83. THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 88
 x + 3 x + 2 x + x   1 1  a) P =  −  : +     x + x − 2 x −1   x +1 x −1     x + 3 x + 2 x x −1+ x +    1  = ( −  x + 2)( x −1) : x 1 
 ( x +1)( x −1) −  + + − − ( x +1)( x −1 x 3 x 2 x 2 x ) = ( x+2)( x−1) . 2 x + ( x +1)( x −1 x 2 ) x +1 = ( = x + 2)( x −1). . 2 x 2 x x > 0; x ≠ 1 1 x + 1 b) 1  − ≥ ⇔  2 x x + 1 P 8 − ≥  1 (*)  x + 1 8 16 x − ( x +1)2 (*) 2 ⇔ ≥ ⇔ − ≤ ⇔ = 8( x +1) 1 ( x 3) 0 x 9 (tm) Vậy x = 9 thì 1 x + 1 − ≥ 1 P 8 Câu 84.
Với điều kiện x > 0,x ≠ 1, ta có: x − 2 x x + 1 2x − 2 x + 1 P = ( + + x −1)(x + x +1) x (x + x +1) x ( x −1)(x + x +1)
x (x − 2 x)+( x +1)( x −1)+ 2x − 2 x +1 = x ( x −1)(x + x +1) x (x + x − 2) = x( x−1)(x+ x+1) ( x −1)( x +2) x + 2 = ( = x −1)(x + x +1) . x + x + 1
Ta có với điều kiện x > 0,x ≠ 1 ⇒ x + x + 1 > x + 1 > 1 x + 2 x + 2 1 ⇒ 0 < P = < = 1+ < 2 x + x + 1 x + 1 x + 1 Do + P nguyên nên suy ra x 2 P = 1 ⇔ = 1 ⇔ x = 1 (loại). x + x + 1 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 89
Vậy không có giá trị của x để P nhận giá trị nguyên. Câu 85. 2 2 Ta có x − x x + x A = + = x ( x −1)+ x ( x +1) = 2x. x + x + 1 x − x + 1
Do đó B = 1− 2A − 4 x + 1 = 1− 2 x −1 = 1− (1−2 x) = 2 x. Câu 86. Ta có: 2
a = 3 + 5 + 2 3 + 3 − 5 + 2 3 + 2 9 − (5+ 2 3) = 6 + 2 4 − 2 3 = + ( − )2 = + ( − ) + =( + )2 6 2 3 1 6 2 3 1 4 2 3 1 3
Vì a > 0 nên a = 3 + 1. Do đó ( − )2 a 1 = 3hay 2 a − 2a − 2 = 0. Câu 87.  2 2 P 1 x 1 1 x 1 1 x  = − + − + − −     2 ⇒ P = (1− x)(2+2 1−( 2 1− x )) = 2(1−x)(1+ x ) Mà = − + ( − ) 2 − + − − ( − ) 2 P 1 x 1 x 1 x
1 x 1 x 1− x ≥ 0 ⇒ P = 2 (1− x) Với 1 2019 x = − ⇒ P = 2. 2019 2018 Câu 88.
Với n là số nguyên dương ta có: 1 n  1 1  1 n 1 1 ( = = − = − > − n + 1) n (n +1) n n   n n 1  +  n n + 1 n n + 1 Suy ra: 1 1 1 1 1 1 1 1 A = + + ...+ > 1− + − + ...+ − 2 1 3 2 2011 2010 2 2 3 2010 2011 1 2 87 = 1− > 1− = . 2011 89 89 Lại có: 1 2 2 2 ( < = − n + 1) n n + 1( n +1 + n) n n n + 1 2 2 2 2 2  1   1  88 ⇒ A < 2 − + − + ...+ − = 21−  < 21− = 2 2 3 2010 2011  2011  45    45 THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC 90 Câu 89. Ta có = ( − )2 1 5 A 2 2 5 + 20 − 20. = 2 2 − 5 + 2 5 − 20. 5 5
= 2( 5 − 2)+ 2 5 − 4 5 = 2 5 − 4 + 2 5 − 4 5 = 4 − THCS.TOANMATH.com TÀI LIỆU TOÁN HỌC
Document Outline

  • CHUYÊN ĐỀ: RÚT GỌN BIỂU THỨC CHỨA CĂN
  • VÀ BÀI TOÁN LIÊN QUAN
    • ( Dạng 1: Các bài toán biến đổi căn thức thường gặp
    • ( Dạng 2: Dùng ẩn phụ đơn giản hóa bài toán
    • ( Dạng 3: Các bài toán về tính tổng dãy có quy luật
    • ( Dạng 4: Bài toán rút gọn biểu thức chứa một hay nhiều ẩn
    • ( Dạng 4: Bài toán rút gọn biểu thức và bài toán liên quan
    • Ví dụ minh họa:
    • Do
    • a) Điều kiện:
    • b) Ta có:
    • A không âm với mọi giá trị .
    • Ví dụ minh họa:
    • ( BÀI TẬP VẬN DỤNG