Chuyên đề số phức – Bùi Trần Duy Tuấn Toán 12

Chuyên đề số phức – Bùi Trần Duy Tuấn Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

40 20 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 1

MỤC LỤC

A. CÁC PHÉP TOÁN CƠ BẢN TRÊN TẬP SỐ PHỨC ............................................ 3

I. LÝ THUYẾT ..................................................................................................................................... 3

II. CÁC DẠNG TOÁN VỚI PHÉP TOÁN CƠ BẢN ..................................................................... 5

III. SỬ DỤNG MÁY TÍNH CASIO 570 VN-PLUS ĐỂ GIẢI ..................................................... 14

IV. BÀI TẬP RÈN LUYỆN .............................................................................................................. 22

1. ĐỀ BÀI .................................................................................................................................... 22

2. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI CHI TIẾT ................................................................... 25

B. CĂN BẬC HAI VÀ PHƯƠNG TRÌNH BẬC HAI CỦA SỐ PHỨC ................. 28

I. CĂN BẬC HAI CỦA SỐ PHỨC ................................................................................................. 28

II. GIẢI PHƯƠNG TRÌNH BẬC HAI ........................................................................................... 30

1. GIẢI PHƯƠNG TRÌNH BẬC HAI TRÊN TẬP SỐ PHỨC .............................................. 30

2. ĐƯA PHƯƠNG TRÌNH BẬC CAO VỀ NHỮNG PHƯƠNG TRÌNH BẬC NHẤT,

PHƯƠNG TRÌNH BẬC HAI. .................................................................................................. 31

III. SỬ DỤNG MÁY TÍNH CASIO 570VN-PLUS ĐỂ GIẢI ...................................................... 38

IV. BÀI TẬP RÈN LUYỆN .............................................................................................................. 44

1. ĐỀ BÀI .................................................................................................................................... 44

2. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI CHI TIẾT ................................................................... 48

C. TẬP HỢP ĐIỂM CỦA SỐ PHỨC ......................................................................... 53

I. LÝ THUYẾT ................................................................................................................................... 53

II. MỘT SỐ BÀI TOÁN ĐIỂN HÌNH ........................................................................................... 54

III. SỬ DỤNG MÁY TÍNH CASIO 570 VN- PLUS ..................................................................... 61

IV. BÀI TẬP RÈN LUYỆN .............................................................................................................. 64

1. ĐỀ BÀI .................................................................................................................................... 64

2. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI CHI TIẾT ................................................................... 69

D. BÀI TOÁN CỰC TRỊ CỦA SỐ PHỨC ................................................................. 75

I. PHƯƠNG PHÁP QUY VỀ TÌM MIN-MAX CỦA HÀM MỘT BIẾN KẾT HỢP SỬ DỤNG

TÍNH CHẤT CỦA SỐ PHỨC. ....................................................................................................... 75

II. PHƯƠNG PHÁP HÌNH HỌC GIẢI BÀI TOÁN MIN-MAX................................................ 84

III. SỬ DỤNG MÁY TÍNH CASIO 570 VN-PLUS ĐỂ GIẢI ..................................................... 92

V. BÀI TẬP RÈN LUYỆN ................................................................................................................ 93

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 2

1. ĐỀ BÀI .................................................................................................................................... 93

2. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI ...................................................................................... 96

E. DẠNG LƯỢNG GIÁC CỦA SỐ PHỨC ............................................................. 101

I. LÝ THUYẾT ................................................................................................................................. 101

II. MỘT SỐ BÀI TOÁN ĐIỂN HÌNH ......................................................................................... 102

III. SỬ DỤNG MÁY TÍNH CASIO 570VN-PLUS ĐỂ GIẢI .................................................... 105

IV. MỘT SỐ BÀI TOÁN VỀ ỨNG DỤNG CỦA DẠNG LƯỢNG GIÁC ............................. 107

V. BÀI TẬP RÈN LUYỆN .............................................................................................................. 109

F. TUYỂN TẬP CÁC CÂU SỐ PHỨC VẬN DỤNG CAO ................................... 111

I. ĐỀ BÀI ......................................................................................................................................... 111

II. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI CHI TIẾT ....................................................................... 118

Tài liệu được tôi sưu tầm và biên soạn để làm tư liệu cho các em lớp 12 ôn thi kỳ thi

THPT

Quốc gia tham khảo, giúp các em ôn lại kiến thức nhanh chóng và hiệu quả hơn. Trong quá

tình tổng hợp và biên soạn không tránh khỏi những sai sót đáng tiếc do số lượng kiến thức và

bài tập khá nhiều. Mong các đọc giả thông cảm và đóng góp ý kiến để những tài liệu sau của

tôi được chỉnh chu hơn! Mọi đóng góp xin gửi về:

Facebook: https://web.facebook.com/duytuan.qna.

Hoặc qua Gmail: btdt94@gmail.com.

Các em có thể xem thêm các chuyên đề luyện thi Đại học môn Toán tại Website:

https://toanhocplus.blogspot.com/

Xin chân thành cảm ơn!!!

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 3

A. CÁC PHÉP TOÁN CƠ BẢN TRÊN TẬP SỐ PHỨC

I. LÝ THUYẾT

o Một số phức là một biểu thức dạng

z a bi 

với

,a b  

và

1i  

được gọi là đơn vị ảo,

được gọi là phần thực và

được gọi là phần ảo của số phức

z a bi 

Tập hợp các số phức được kí hiệu là



 

/ , ; 1

a bi a b i

    

 

o Chú ý: - Khi phần ảo

0b z a  

là số thực.

- Khi phần thực

0a z bi z   

là số thuần ảo.

- Số

0 0 0i 

vừa là số thực, vừa là số ảo.

o Hai số phức bằng nhau:



a c

a bi c di

b d









   











với

, , ,a b c d  

o Hai số phức

1 2

; z a bi z a bi    

được gọi là hai số phức đối nhau.

Số phức liên hợp của

z a bi 

với

,a b  

là

a bi

và được kí hiệu bởi

Một số tính chất của số phức liên hợp:

z z

' 'z z z z  

' 'z z z z  

. ' . 'z z z z

z z

 



















 

là số thực

z z 

;

là số thuần ảo

z z  

Ví dụ:

Số phức liên hợp của số phức

1 2z i 

là số phức

1 2z i 

Số phức liên hợp của số phức

5 3z i 

là số phức

5 3z i 

Trong mặt phẳng phức Oxy ( Ox là trục thực, Oy là trục ảo ), số phức

z a bi 

với

,a b  

được biểu diễn bằng điểm

 

;M a b

Ví dụ:

 

 1; 2

 

biểu diễn số phức

1 2z i 

 

B 0;3

biểu diễn số phức

3z i

 

C 3;1 

biểu diễn số phức

3z i  

 

D 1;2

biểu diễn số phức

1 2z i 

1. Định nghĩa

2. Số phức liên hợp

3. Biểu diễn hình học của số phức

Chuyên đề: SỐ PHỨC

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 4

o Môđun của số phức

 

 ,z a bi a b   

là

2 2

z a b  .

o Như vậy, môđun của số phức

là z chính là khoảng cách từ điểm M biểu diễn số phức

 

 ,z a bi a b   

đến gốc tọa độ O của mặt phẳng phức là:

2 2

OM a b zz  



o Một số tính chất của môđun:

1 2 1 2

 0; 0 0;

 ,  , 

 + 

 ' ' '

 . . 



z z z

z z z z z z

z z z z

z z z z z z

z z z z

    

    

  

     

 

Cho hai số phức

z a bi 

;

' ' ' z a b i 

với

, , ', 'a b a b  

và số

k  

o Tổng hai số phức:

' ' ( ')z z a a b b i    

o Hiệu hai số phức:

    ' ' ( ')z z a a b b i

o Số đối của số phức

z a bi 

là

z a bi   

o Nếu

, 'u u

 

theo thứ tự biểu diễn các số phức

, 'z z

thì

'u u

 

biểu diễn số phức

'z z

'u u

 

biểu diễn số phức

'z z

o Nhân hai số phức:

      

. ' ' ' . ' . ' . ' '.z z a bi a b i a a b b a b a b i      

o Số phức nghịch đảo:

z z





o Chia hai số phức:

Nếu

0z 

thì

' '.z z z

 , nghĩa là nếu muốn chia số phức

cho số phức

0z 

thì ta nhân

cả tử và mẫu của thương

cho z .

 Chú ý:

4 4 1 4 2 4 3

1;  ;  1;  (k )

k k k k

i i i i i i

  

       

5. Các phép toán trên tập số phức

4. Môđun của số phức

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 5

II. CÁC DẠNG TOÁN VỚI PHÉP TOÁN CƠ BẢN

1. PHƯƠNG PHÁP GIẢI TỔNG QUÁT

o Bước 1: Gọi số phức z cần tìm là

 

 ,z a bi a b

   

o Bước 2: Biến đổi theo điều kiện cho trước của đề bài (thường liên quan đến môđun, biểu

thức có chứa

, , ,...

z z z ) để đưa về phương trình hoặc hệ phương trình 2 ẩn theo

và

nhờ tính chất 2 số phức bằng nhau ( phần thực bằng nhau và phần ảo bằng nhau ), rồi từ

đó suy ra

và

và suy ra được số phức

cần tìm.

2. MỘT SỐ BÀI TOÁN ĐIỂN HÌNH

Tìm phần thực, phần ảo, số phức liên hợp và tính môđun của số phức

   

) 2 4 2 1 3 .a z i i i   

  

4 5

) 2 4 5 2

b z i i



   



Giải:

   

a) 2 4 2 1 3 2 4 2 6 2 6 6 8 6z i i i i i i i i            



Phần thực: 8 ; Phần ảo: 6 ; Số phức liên hợp:

8 6z i 

Môđun

2 2

8 6 10

z   

  

 



        



 

    

2 2

4 5 2

4 5

b) z 2 4 5 2 10 4 i 20 i 8 i

2 1

8 14 5 93 94



 18 16 .

5 5 5

i i



Phần thực:

; Phần ảo:

; Số phức liên hợp:

93 94

5 5

z i

 

Môđun

2 2

93 94 17485

5 5 5

   

 

 

 

  

 

 

 

 

 

   

Cho số phức

3 2z i 

. Tìm môđun số phức

 

  

1 2w zi z i

Giải:

 

1 2 (3 2 ) (3 2 )(1 2 )

 3 2 3 6 2 4 5 7

w zi z i i i i i

i i i i

       

       

Vậy

2 2

5 7 74

w   

Bài toán 1

Bài toán 2

Phương pháp

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 6

Gọi M, N lần lượt là hai điểm biểu diễn số phức

1 2

,z z

trên mặt phẳng phức. Mệnh đề nào

sau đây là đúng?

1 2 1 2

.  B.

C.  D.

A z z OM ON z z MN

z z OM MN z z OM MN

    

     

  

   

Giải:

M, N lần lượt là hai điểm biểu diễn số phức

1 2

,z z

trên mặt phẳng phức

nên



biểu diễn số phức



biểu diễn số phức

OM ON NM  

  

biểu diễn số phức

1 2

z z

1 2

z z NM MN

   

 

. Chọn B.

Cho ba số phức

1 2 3

,  , z z z

phân biệt thỏa mãn

1 2 3

z z z

  

và

1 2 3

1 1 1

z z z

 

. Biết

1 2 3

,  , z z z

lần lượt được biểu diễn bởi các điểm

,  , A B C

trên mặt phẳng phức. Tính góc



ACB

60 .



90 .



120 .



150 .



Giải:

Gọi

là điểm biểu diễn của số phức

(

là số phức

liên hợp của

). Khi đó

và

đối xứng nhau qua

.Ox

Gọi

',  ',  'A B C

lần lượt là điểm biểu diễn các số phức

1 2 3

,  ,  .z z z

Từ giả thiết

       

2 3

2 2 2

1 2 3

1 3

1 1 1

z z z

(do

1 2 3

z z z

  

Suy ra



  

  

' ' ' ' 'OA OB O OA C BC

là hình bình hành.

Mà 



 

  

' '

' ' '

OA OB O

OA C B

C là hình thoi với



' ' ' 120A C B 

Vậy



120ACB 

(do



ACB

và



' ' 'A C B

đối xứng qua

). Chọn C.

Tìm phần thực, phần ảo của số phức sau:

       

2 3 20

1 1 1 1 ... 1

i i i i

        

Giải:

Bài toán 5

Bài toán 4

Bài toán 3

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 7

     

 

           

 

2 20

21 2 10

10 10

1 1

1 1 1 ... 1

1 1 1 2 1 2 1

2 1 1

2 2 1

P i i i

i i i i i i

P i

 

        

 

        

 

 

  

     

Vậy phần thực là

2

và phần ảo là

2 1

Tính

2 3 2017

1009 2 3 ... 2017S i i i i     

Giải:

Cách 1:

   

       

2 3 4 2017

4 8 2016 5 9 2017

2 6 10 2014 3 7 11 2015

504 505 504 504

1 1 1 1

1009 2 3 4 ... 2017

1009 4 8 ... 2016 5 9 ... 2017 .....

2 6 10 ... 2014 3 7 11 ... 2015

1009 4 4 3 4 2 4 1

n n n n

S i i i i i

i i i i i i i

i i i i i i i i

n i n n i n

   

      

          

         

       

   

1009 509040 509545 508032 508536

2017 1009 .

i i

    

 

Cách 2:

Đặt

 

2 3 2017

1 ....f x x x x x

      

 

2 2016

1 2 3 ... 2017

f x x x x



    

   

2 3 2017

2 3 ... 2017 1

xf x x x x x



     

Mặt khác:

   

 

2017 2018

2018

2 3 2017

2017 2018

2018 1 1

1 ....

2018 1 1



 . 2

x x x

f x x x x x f x

x x x

xf x x

  





        



  



 



Thay

x i

vào

 

và

 

ta được:

(1) 1009; (1)=(2)S 

, nên:

 

  

  

     



2017 2018

2018 1 1

2018 2018 2

1009 . 1009 2017 1009 .

i i i

S i i i

Cho số phức

 

1 3

z i  

. Tính

 

    

2 3 2017

1 1 1 ... 1 .

w z z z z    

Giải :

Ta có

 

1 0

1 3 .

z z

z i





  



   











Bài toán 6

Bài toán 7

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 8

Do đó với mọi

k  

, ta có

3 3

3 1 3 1 2

3 2 2 3 2 2

1 1 2

1 1

k k

z z

z z z z z

 

   

      

  











   

Vì từ

đến

2017

có:

673

số chia

dư

672

số chia

dư

672

số chia hết cho

nên

 

    

 

673

672

2 3 2017 672 2 672 2018 672 3.672 2

1 1 1 ... 1 2 . . 2 . 2 .w z z z z z z z z



           

 

672 2 672 672 671

1 3

2 . 2 1 2 2 1 3

2 2

z z i i

 









       













 

Tìm số

sao cho:

(2 ) 3 5 (A,A 2014)

z i z i    

Giải:

Gọi số phức

cần tìm là

 

 ,z a bi a b

   

Ta có:

(2 ) 3 5 z i z i   

(2 )( ) 3 5 2 2 3 5

 3 ( ) 3 5

3 3 2



 2 3 .

5 3

a bi i a bi i a bi a bi ai bi i

a b a b i i

a b a

z i

a b b

              

     

 

 

  

 

    

 

 

   

 

 

Tìm số phức

khi nó thỏa mãn đồng thời các điều kiện sau:

(2 ) 10

z i   và

. 25z z 

Giải:

Gọi số phức cần tìm là

 

 ,z a bi a b

   

Ta có:

2 2

. 25(1)

z z z a b   

Lại có:

     

2 2

(2 ) 10 2 1 10 4 2 5 0 2

z i a b a b a b             

Thay (1) vào (2) ta được:

25 4 2 5 10 2 10a b b a       

Nên

2 2 2 2

 25 ( 2 10) 25a b a a      

5 0

5 40 75 0

3 4

a b

a a

a b

 

 

 

     

 

 

 

 

Vậy

5z 

hoặc

3 4z i 

Tìm các số thực

, ,a b c

sao cho hai phương trình

2 2

0,  16 16 0az bz c cz bz a i       

có nghiệm chung là

1 2z i 

Giải

Theo giả thiết phương trình

0az bz c  

có nghiệm

1 2z i 

khi đó:

Bài toán 8

Bài toán 9

Bài toán 10

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 9

       

3 0

1 2 1 2 0 3 4 2 0 1

4 2 0

a b c

a i b i c a b c a b i

a b



   



            



 





Tương tự phương trình

16 16 0cz bz a i    

có nghiệm

1 2z i 

khi đó:

     

1 2 1 2 16 16 0 3 4 2 16 16 0

3 16 0

3 16 2 2 8 0 2

2 8 0

c i b i a i c i b bi a i

a b c

a b c b c i

b c

               





   



        





  





Từ

   

1 , 2

suy ra

   

, , 1; 2;5 .

a b c

 

Cho

và

là số phức liên hợp của

. Biết

 

 

và

2 3

z z 

.Tìm

Giải :

Gọi

 

z a bi a b z a bi     



Ta có :

   

2 2 3 3

z z a bi a bi bi b

        

 

. .z z z z

   

. Ta có:

       

2 3

2 2 2 2 2

.1 .

z z z z z

      

Mà

   

 

2 3

3 3 2 3 2 2 3

3 3 3 3

z a a bi a bi bi a ab a b b i

       

2 3 2 2 2

2 2 2

3 0 3 0 1

3 3 3

a b b a b a

b b b

  

    

  

    

  

  

  

  

Tìm số phức z thỏa mãn điều kiện:

1 2 3 4z i z i

    

và

2z i

z i





là một số thuần ảo.

Giải :

Đặt

( ),z x yi x y 

. Theo bài ra ta có :

           

2 2 2 2

1 2 3 4 1 2 3 4 5

x y i x y i x y x y y x

                 

Số phức

 

    

 

2 2 1 2 3

x y i x y y x y i

z i

x y i

z i

x y

      



  

 



 

là một số ảo khi và chỉ khi

  

 

2 1 0

1 0

x y y

x y

y x







   



 



 

   

 

 



 

 









. Vậy

12 23

7 7

z i

  

Bài toán 11

Bài toán 12

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 10

Cho hai số phức

1 2

, z z

thỏa mãn

   

1 2 1 2

0,  0,  0z z z z

và

 



1 2 1 2

1 1 2

z z z z

Tính giá

trị biểu thức



Giải:

Từ giả thiết



   

 

2 1

1 2 1 2 1 2 1 2

1 1 2 1

z z

z z z z z z z z

   

  

 

 

 

 

       

 

 

 

 

  

1 1 1

1 2 1 2 2 1

2 2 2

. 2 1 1 2 .

z z z

z z z z z z

z z z

Đặt



, ta được phương trình

  

  1 1 2t t t





 



        



 





1 1

2 2

2 2 1 0

1 1

2 2

t i

t t t P

t i

Nếu số phức

thỏa mãn



và

1z 

thì phần thực của

1 z

bằng?

Giải:

Cách 1:

Đặt

 

,z a bi a b  



. Từ

2 2

1 1

z a b

   

Ta có:

  

 

1 1 1 1

1 1

a bi a bi

z a bi

a bi a bi

a b

   

  

  

   

 

Suy ra phần thực của

1 z

là:

 

a b



 

Ta có:

 

2 2 2

1 1 1 1

2 2 2

2 1

a a a

a a b

a b

  

  



  

 

Cách 2:

Gọi A là phần thực của

1 z

1 1 1 1 1 1 2 2

2 1

1 1 1

1 1 . 1

z z z z z z

z z z

z z z z z z z z

z z

      

       

  

      

 

a 

Bài toán 14

Bài toán 13

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 11

Cho hai số phức

1 2

, z z

thỏa mãn điều kiện

   

1 2 1 2

z z z z

Tính giá trị của biểu

thức

   

 

 

 

 

 

 

 

 

 

   

2 2

1 2

2 1

z z

Giải:

Cách 1:

Ta có

     

  

  

  

  

    

  

  

  

  

     

2 2 2

1 2 1 2

2 1 2 1

z z z z

 

Mà

    

1 2 1 2 2 1

1 2 2 1

2 2

2 1

z z z z z z

z z z z

z z

 

Theo giả thiết:

 

       

1 2 1 2 1 2 1 2 1 2

1 . .

z z z z z z z z z z

 

      

2 2

1 2 1 2 2 1 1 2 2 1

z z z z z z z z z z

 

Từ

 

và

 

suy ra

 1.P

Cách 2: Chuẩn hóa

Chọn



, còn

chọn sao cho thỏa mãn



và

 

1 2

z z

Ta chọn như sau: Đặt

 

z a bi

●

   

2 2

1 1

z a b

●

   

            

1 2 2

1 1 1 1 1 1 1.

z z z a bi a b

Từ đó giải hệ









   











1 3

2 2

z i

Thay



và

 

1 3

2 2

z i

vào

và bấm máy.

Hoặc ta cũng có thể chọn   

1 3

2 2

z i

và  

1 3

2 2

z i

Bài toán 15

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 12

Cho số phức

có môđun bằng

2018

và

là số phức thỏa mãn biểu thức

1 1 1

z w z w

 



Môđun của số phức

bằng?

Giải:

Từ giả thiết

 

1 1 1 1

0 0

z w zw

z w

z w z w zw z w

zw z w

 



      

 



2 2

2 2 2 2 2 2

1 3 1 3 1 3

0 0

4 4 2 4 2 2

i w

z w zw z zw w w z w w z w

 

   





 

 





 

               

 





 



 

 

 





   



 

Từ

1 3 1 3

2 2 2 2

i w i

z w z w

   

 

 

 





 

 



     



 

 



 







 

 

 

 

   

Lấy môđun hai vế, ta được

1 3

. 1. 2018.

2 2

z w w w w      

Cho số phức

,z w

khác 0 sao cho

z w z w  

. Phần thực của số phức



là ?

Giải :

Cách 1 : Gọi

 

,u a bi a b  



Ta có :

 

2 2

1 1

a b

z w z w

z w

a b







 



 



 

    

 

 



 

  

 

   









 

3 1

1 2 1

4 8

a a a a

        

Cách 2: Gọi

 

,w a bi a b  



Chọn

 

2 2

4 *

1 1 1 2

1 4

a b

z z w w a

a b



 



         



  





Thay



vào

 

15 1 1 15

2 8 8

1 15

2 2

b u i

     



Bài toán 17

Bài toán 16

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 13

Tính môđun của số phức

biết

z z

và

z z

có phần thực bằng

Giải:

Cách 1: Giả sử

z a bi 

 

, a b

 

Ta có

2 2

1 1

z z

a b a bi





  

     

2 2 2 2

2 2 2

2 2 2 2 2 2 2 2 2

a b a bi a b a b

a b a b a b a b a b a b

    

  

        

Theo giả thiết:

z z

có phần thực bằng 4 nên

 

2 2

2 2 2

a b a

a b a b

 



  

 

2 2 2 2

4 4

2 2

a b a a b a

a b a a b

a b a b a

   

   

  

  

2 2

1 1 1

4 .

8 8

a b z

a b

      



Cách 2: Nếu

z a bi 

thì

2z z a 

Áp dụng:

z z

có phần thực bằng

4 

1 1

z z z z

 

 

   

2 2 2

2 2

1 1

8 8 8

z z z z z z

z z z z

z z z z z z z z z z z

   

      

 

     

 

2 2

1 1

8 8 8 .

z z z z z z

z z z z

   

       

 

 

Nhận xét:

Trong bài toán tìm thuộc tính của số phức

thỏa mãn điều kiện K cho trước, nếu K là thuần

(tất cả đều

) hoặc thuần

thì đó là bài toán giải phương trình bậc nhất (phép cộng, trừ,

nhân, chia số phức) với ẩn

hoặc

. Còn nếu chứa hai loại trở lên (

) thì ta sẽ gọi

 

 ,z a bi a b

   

. Từ đó sử dụng các phép toán trên số phức để đưa về hai số phức bằng

nhau để giải.

Bài toán 18

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 14

III. SỬ DỤNG MÁY TÍNH CASIO 570 VN-PLUS ĐỂ GIẢI

Để thực hiện các phép toán trên tập số phức, ta chuyển qua chế độ CMPLX bằng cách bấm

o Bấm đơn vị ảo

bằng cách bấm phím

o Tính môđun của số phức bấm

o Để bấm số phức liên hợp của

bấm

q22

để hiện Conjg (liên hợp).

Sau đây là các bài toán điển hình cho các dạng tính toán cơ bản của số phức.

1. PHÉP CỘNG, TRỪ, NHÂN, CHIA

Tính

1 (3 2 ).z i i   

Hướng dẫn:

Ta lần lượt bấm các phím như sau:

1+bp(3+2b)

Và ta được kết quả là:

Tính

(1 3 )( 3 4 ).z i i   

Hướng dẫn:

Ta lần lượt bấm các phím tương tự như trên và ta thu được

kết quả như sau:

Tính

1 3

( 2 i)

2 7



  



Hướng dẫn:

Ta lần lượt nhập biểu thức

1 3

( 2 i)

2 7



  



vào máy ta thu

được kết quả:

PP CASIO

Bài toán 1

Bài toán 2

Bài toán 3

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 15

Cho số phức

z a bi 

. Số phức

có phần ảo là :

2 2

a b

2 2

2a b

2ab

Hướng dẫn:

 Vì đề bài cho ở dạng tổng quát nên ta tiến hành “cá biệt hóa” bài toán bằng cách chọn giá

trị cho

,a b

(lưu ý nên chọn các giá trị lẻ để tránh xảy ra trường hợp đặc biệt).

Chọn

1.25a 

và

2.1b 

ta có

1.25 2.1z i 

 Sử dụng máy tính Casio tính

1.25+2.1b)d=

Vậy phần ảo là

 Xem đáp số nào có giá trị là

thì đáp án đó chính xác. Ta có :

Vậy

ab 



Đáp án C là chính xác.

[Thi thử THPT Phan Chu Trinh – Phú Yên lần 1 năm 2017]

Cho số phức

z a bi 

. Số phức



có phần thực là :

a b

2 2

a b

2 2

a b





a b

Hướng dẫn:

 Vì đề bài mang tính chất tổng quát nên ta phải cá biệt hóa, ta chọn

1; 1.25a b 

 Với





Sử dụng máy tính Casio

a1R1+1.25b=

Ta thấy phần thực số phức



là :

đây là 1 giá trị dương. Vì ta chọn

0b a 

nên ta

thấy ngay đáp số C và D sai.

Thử đáp số A có

9 16

1 1.25

4 41

a b    

vậy đáp số A cũng sai



Đáp án chính xác là B

Bài toán 5

Bài toán 4

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 16

[Thi thử chuyên Khoa học tự nhiên lần 3 năm 2017]

Cho số phức

     

2 3 22

1 1 ... 1

z i i i

      

. Phần thực của số phức

là :

2

2 2 

2 2 

Hướng dẫn:

Dãy số trên là một cấp số nhân với

 

U i

 

, số số hạng là

và công bội là

1 i

. Thu

gọn

ta được :

 

1 1

. 1 .

1 1

z U i

 



  



 

 Sử dụng máy tính Casio tính

(1+b)dOa1p(1+b)^21R1

p(1+b)=

Vậy

2050 2048z i  



Phần ảo số phức

là

2050 2 2   



Đáp số chính xác là C

Bài toán 6

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 17

2. TÍNH MÔĐUN

Tìm môđun của số phức

(1 2 ) 2 6i z i   

Hướng dẫn:

6 2

(1 2 ) 2 6

1 2

i z i z z

 

      



.Nên ta thực hiện bấm như sau:

qcap6p2bR1p2b=

Ta thu được kết quả:

Tìm số phức

2. .

1 2

z z

 

. Biết

2 4 2(1 )

4 3 (1 ) ,

1 2

i i

z i i z

  

     



Hướng dẫn:

- Tính

4 3 (1 )

z i i

    và lưu vào biến A:

4p3b+(1pb)^3qJz

- Tính

2 4 2(1 )

i i

  





và lưu vào biến B

a2+4bp2(1pb)^3R1+bqJ

- Tính

2. .

1 2

z z

 

2q22q22Qz)OQx)=

Bài toán 1

Bài toán 2

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 18

3. PHƯƠNG TRÌNH BẬC NHẤT

Tìm môđun của số phức

thỏa mãn:

 

1 3 3 7 2

i z i i

   

. 1 . 4 . 2 .

A z B z C z D z   

Hướng dẫn:

Ta chuyển

về dạng:

7 2 3

1 3

i i

 





và tìm môđun.

Quy trình bấm máy:

Qca7bp2p3bR1p3b=

Màn hình hiển thị:

>>> Chọn C.

Cho số phức

thỏa mãn

(3 )( 1) (2 )( 3 ) 1 .i z i z i i      

Tìm môđun của số phức

i z







82 82 2 82 3 82

.  .  .  .

4 8 9 5

A B C D

Hướng dẫn:

Ở đây là sẽ cho phím X sẽ là đại diện cho số phức

Đây là phương trình bậc nhất của số phức.

Bước 1: Các em nhập lại phương trình này với máy tính lần lượt như sau:

(3 )(X 1) (2 )(C onj ( ) 3 ) (1 )i i g X i i      

(3pb)(Q)+1)+(2pb)(q2

2Q))+3b)p(1pb)

Màn hình hiển thị:

Bước 2:

Tìm số phức

z a bi 

nghĩa là đi tìm a và b.

Ta sẽ cho trước a=10000 và b=100 rồi từ đó suy ngược lại mối quan hệ của a và b bằng 1 hệ

phương trình 2 ẩn theo a và b, lúc đó tìm được a và b.

Cho

10000 100z i 

bằng cách nhập

r10000+100b=

Bài toán 1

Bài toán 2

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 19

Màn hình sẽ cho kết quả:

Nghĩa là:

(3 )( 1) (2 )( 3 ) (1 ) 50005 19894 5 5 (2 6)i z i z i i i a a b i             

Cho nên:

(3 )( 1) (2 )( 3 ) (1 ) 0

5 5 0 5 5 0

1, 8 1 8

2 6 0 2 6

i z i z i i

a a

a b z i

a b a b

       

 

 

   

 

         

 

 

    

 

 

Từ đó tính môđun của

>>> Chọn B.

Cho số phức

z a bi 

thỏa mãn điều kiện

     

2 3 4 1 3i z i z i

     

.Tìm

2P a b 

1

D. Đáp án khác

Giải:

 Phương trình

     

2 3 4 1 3 0

i z i z i

      

 Nhập vế trái vào máy tính Casio và CALC với

1000 100X i 

) ))(2p3b)Q +(4+b)q22Q

+(1+3b)dr1000+100b=

Vậy vế trái

6392 2194i 

với

6392 6.1000 4.100 8 6 4 8

2194 2.1000 2.100 6 2 2 6

a b





     







     





 Để vế trái

0

thì

6 4 8 0

2 2 6 0

a b





  







  





2; 5a b   

Vậy

2 5z i  



2 1P a b  



Đáp số chính xác là C.

Bài toán 3

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 20

4. BIỄU DIỄN HÌNH HỌC CỦA SỐ PHỨC

Các điểm

, ,M N P

lần lượt là điểm biểu diễn cho các số phức

;





  

1 1 2z i i  

; 1 2z i  

A. Tam giác vuông B.Tam giác cân C.Tam giác vuông cân D.Tam giác đều

Hướng dẫn:

 Rút gọn

bằng Casio

a4bRbp1=

Ta được

2 2z i 

vậy điểm

 

2; 2



 Rút gọn

bằng Casio

(1pb)(1+2b)=

Ta được

3z i 

vậy điểm

 

3;1

Tương tự

1 2z i  

và điểm

 

1;2



 Để phát hiện tính chất của tam giác

MNP

ta nên biểu diễn 3 điểm

, ,M N P

trên hệ trục tọa

độ

Dễ thấy tam giác MNP vuông cân tại P



đáp án C chính xác

Bài toán 1

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 21

Trong mặt phẳng tọa độ

Oxy

, gọi

là điểm biểu diễn số phức

3 4z i 

, điểm

là

điểm biểu diễn số phức

z z





. Tính diện tích

'OMM

OMM





OMM





OMM





OMM





Hướng dẫn:

 Điểm

biểu diễn số phức

3 4z i 



tọa độ

 

3; 4



Điểm

biểu diễn số phức

z z







tọa độ

7 1

;

2 2

 



















 

a1+bR2$O(3p4b)=

Gốc tọa độ

 

0;0

 Để tính diện tích tam giác

'OMM

ta ứng dụng tích có hướng của 2 vecto trong không gian.

Ta thêm cao độ 0 cho tọa độ mỗi điểm

, , 'O M M

là xong

 

3; 4;0

OM 



7 1

' ; ;0

2 2

 



















 



; '

S OM OM

 

 

 

 

 

Tính

; 'OM OM

 

 

 

 

w8113=p4=0=q51217P2=

p1P2=0=Cq53q57q54=

Vậy

25 1 25

; ' 12.5 ; '

2 2 4

OMM

OM OM S OM OM

   

    

   

   

   

Bài toán 2

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 22

IV. BÀI TẬP RÈN LUYỆN

1. ĐỀ BÀI

Câu 1. Cho hai số phức

1 2

1 2 ; 2 3z i z i   

. Khi đó số phức

1 2 1 2

3w z z z z  

có phần ảo

bằng bao nhiêu?

A. 9 B. 10 C.

9

10

Câu 2. Cho số phức

3 2z i 

, khi đó số phức

2 3w z z 

là

3 2i 

3 2i 

3 10i 

11 2i

Câu 3. Những số nào sau đây vừa là số thực và vừa là số ảo?

A. 0 và 1 B. chỉ có 0 C. chỉ có số 1 D.không có số nào

Câu 4. (Đề thử nghiệm 2017)Tìm số phức liên hợp của số phức

 

3 1z i i 

3z i 

3z i  

3z i 

3z i  

Câu 5. (Đề thử nghiệm 2017) Tìm môđun của số phức

thỏa mãn

 

2 13 1z i i  

34z 

5 34

z  D.

z 

Câu 6. (Đề minh họa 2017) Cho số phức

3 2z i 

. Tìm phần thực và phần ảo của số phức

A. Phần thực bằng

3

và phần ảo bằng

2i

B. Phần thực bằng

3

và phần ảo bằng

2

C. Phần thực bằng

và phần ảo bằng

D. Phần thực bằng

và phần ảo bằng

Câu 7. (Đề minh họa 2017)Cho hai số phức

1z i 

và

2 3z i 

. Tính môđun của số phức

1 2

z z

1 2

z z  B.

1 2

z z  C.

1 2

z z

 

1 2

z z

 

Câu 8. (Đề minh họa 2017)Cho số phức

2 5z i 

. Tìm số phức

w iz z 

7 3w i 

3 3w i  

3 7w i 

7 7w i  

Câu 9. Môđun của số phức

 

1 2

1 3

i i

 





là

5z 

2z 

1z 

Câu 10. Cho số phức

thỏa điều kiện

 

3 1 2 8 17i z i i    

. Khi đó hiệu phần thực và

phần ảo của

là

3

7

Câu 11. Cho số phức

thỏa mãn

 

2 1 2

1 2 7 8

i z i



   



. Môđun của số phức

1w z i  

là

Câu 12. Phần thực của số phức

 

4 2 1 2

2 2 3

i i i

i i

  

 

 

là



Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 23

Câu 13. Cho số phức

thỏa mãn

 

1 2 1 3 5i z i i   

. Khi đó điểm nào sau đây biểu diễn

số phức

 

2; 3



 

2;3

 

2;3



 

2; 3

 

Câu 14. Số phức

thỏa mãn

 

25 1 1

 





. Khi đó phần ảo của số phức

bằng bao

nhiêu?

31

17

Câu 15. Cho số phức

thỏa mãn

 

1 3 17z i i  

. Khi đó môđun của số phức

6 25w z i 

là

2 5

Câu 16. Cho số phức

thỏa mãn

  

1 2 1 2

1 1

i i i i

i i

   

 

 

. Trong các kết luận sau, kết

luận nào đúng?

z z

là số thuần ảo C.

| | 4z 



Câu 17. Cho hai số phức

1 2

3 2 , 2z i z i   

. Giá trị của biểu thức

1 1 2

| |z z z

là

130

10 3

2 30

3 10

Câu 18. Cho hai số phức

1 2

2 3 , 2z i z i   

. Giá trị của biểu thức

 là

Câu 19. Cho số phức

 

4 3 3

1 2

i i

  

 

 

. Môđun của số phức

w 1z iz  

là

85w 

4 5w 

6 3w 

56w 

Câu 20. Cho

là một số phức. Xét các mệnh đề sau :

(I) Nếu

z z

thì

là một số thực

(II) Môđun của

bằng độ dài đoạn

với

là gốc tọa độ và

là điểm biểu diễn của

số phức

(III)

.z z z

Trong 3 mệnh đề trên có bao nhiêu mệnh đề đúng?

A.0 B.1 C.2 D.3

Câu 21. Cho số phức

   

1 2z m m i   

với

m R

.Tìm tất cả các giá trị của

để

5z 

là.

1 0m 

. B.

0 m

hoặc

1m  

1 0m  

. D.

1m 

hoặc

0m 

Câu 22. Cho Số phức

z a bi 

với

,a b R

.Trong các mệnh đề sau,mệnh đề nào đúng.

2z z bi 

. B.

2z z a 

. C.

2 2

.z z a b 

. D.

z z



Câu 23. Cho số phức

2z i

. Lựa chọn phương án đúng





. B.

2 4

 

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 24

1 13

z z



  

. D.

64z 

Câu 24. Trong các kết luận sau kết luận nào sai?

A.Môđun số phức

là 1 số thực dương.

B.Môđun số phức

là 1 số thực.

C. Môđun số phức

là 1 số thực không âm.

D. Môđun số phức

là 1 số phức.

Câu 25. Số phức

2016 2018

1 1

i i

   

 

 

 

 

 

 

 







 

 

bằng

1 i

2

Câu 26. Cho

2 2017

1 ...P i i i    

, khẳng định nào sau đây là đúng

0P 

1P 

1P i 

2P i

Câu 27. Đẳng thức nào đúng trong các đẳng thức sau ?

 

2018

1009

1 2i i 

 

2018

1009

1 2i i  

 

2018

1009

1 2i  

 

2018

1009

1 2i 

Câu 28. Số phức

2017

4 2

i i

 





có tổng phần thực và phần ảo là

A.1 B.2 C.3 D.4

Câu 29. Số phức

 

2017

1008





có phần thực hơn phần ảo bao nhiêu đơn vị ?

A.0 B.1 C.2 D.

1008

Câu 30. Phần thực của số phức

       

2 3 2017

1 1 1 1 ... 1z i i i i         

là

2016

2

1008

2 1 

1008

2

Câu 31. Cho

2 4 4 2 4

1 ...

k k

A i i i i



     

với

k  

. Hỏi đâu là phương án đúng

2A ki

2A k

0A 

1A 

Câu 32. Với mọi số phức

, ta có

1z 

bằng

1z z 

2 1z z 

. 1z z z z  

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 25

2. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI CHI TIẾT

1B 2C 3B 4D 5A 6D 7A 8B

9D 10A 11B 12A 13B 14D 15A 16D

17A 18B 19A 20D 21C 22D 23C 24B

25C 26A 27D 28B 29C 30D 31D 32D

Câu 1.

Cách 1:Ta có

 

3 1 2 2 3 1 2 2 3 3 6 2 3 8 9 10w i i i i i i i i              

Suy ra

có phần ảo bằng 10.

Cách 2 : Sử dụng Casio (Để máy ở chế độ Mode 2 _CMPLX)

Nhập vào máy

 

3 1 2 2 3 1 2 2 3 9 10

Casio

i i i i i        

. Chọn B.

Câu 2.

Cách 1 :Ta có

 

2 3 2 3 3 2 6 4 9 6 3 10w i i i i i          

Cách 2 : Sử dụng Casio (Để máy ở chế độ Mode 2 _CMPLX)

Nhập vào máy

 

2 3 2 3 3 2 3 10

Casio

i i i       

. Chọn C.

Câu 3. Gọi

z a bi 

là số phức thỏa yêu cầu bài toán

 

,a b

 

Ta có

là số thực khi

0b 

;

là số ảo khi

0a 

0z 

. Chọn B.

Câu 4. Ta có

 

3 1 3 3 3z i i i i i z i          

. Chọn D.

Câu 5.

Cách 1:

 

2 2

1 13 1 13 2

2 13 1 3 5 3 5 34

2 1

i i i

z i i z i z

  

           





Cách 2 : Sử dụng Casio, Ta có

1 13

Casio



  



. Chọn A.

Câu 6. Ta có

3 2 3 2z i z i    

, suy ra phần thực bằng 3 và phần ảo bằng 2. Chọn D.

Câu 7. Ta có

2 2

1 2 1 2

3 2 3 2 13

z z i z z       

. Chọn A.

Câu 8. Ta có

 

2 5 2 5 2 5 2 5 3 3w i i i i i i          

. Chọn B.

Câu 9.

Cách 1:Ta có

 

2 2

1 2 3 3 1 3 3 4 3 4

1 3 1 3 5 5 5 5

1 3

i i i i i

z i z

i i

   

    

 

 

 

        

 

 

 

   

 



Cách 2: Dùng Casio,

 

1 2

1 3

Casio

i i

 

 



. Chọn D.

Câu 10. Ta có

 

8 17 1 2

cais

2 5

i i

z i

  

 

 

khi đó hiệu phần thực phần ảo là:

 

2 5 7  

Chọn A.

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 26

Câu 11.

 

2 2

2(1 2 )

7 8 : 2 3 2 w 1 4 3 4 3 5

z i i i z i i z

 









               













 

Chọn B

Câu 12.

4 2 (1 )(2 ) 29 11

2 2 3 13 13

i i i

z i

i i

  

   

 

. Chọn A.

Câu 13. Ta có

     

5 1 3 : 1 2 2 3 2;3

z i i i i N

 





      







 

. Chọn B.

Câu 14. Ta có

 

1 1

25 : 31 17

z i z

 













    





















 

có phần ảo bằng

17

. Chọn D.

Câu 15. Ta có

     

1 2 1 2

2 2

1 1

i i i i

z z

i i

   

      

 

. Chọn A.

Câu 16. Ta có

 

2 2

2 5 w 6 25 6 2 5 25 12 5 w 12 5 13

1 3

z i z i i i i



              



Chọn D.

Câu 17. Ta có

  

1 1 2

| z | 3 2 3 2 2 130

z z i i i      

. Chọn A.

Câu 18. Ta có

| | 2 3 5

2 3

z i



    



. Chọn B.

Câu 19. Ta có

   

4 3 3

2 4 2 4

1 2

i i

z i z i

i i

  

      

 

   

w 1 2 4 2 4 1 7 6 49 36 85

z iz i i i i            

. Chọn A.

Câu 20. Gọi

z a bi 

với

,a b R

1. 0

a a

z z b z a

b b









     





 







ĐÚNG

2 2

z a bi OM a b z

     



ĐÚNG

  

2 2

z z z a bi a bi a b z

      



ĐÚNG .Chọn D.

Câu 21. Ta có

   

2 2

5 1 2 5 0 1 0

z m m m m m

            

. Chọn C.

Câu 22. Ta có

 

  

2 2

z z a bi a bi a

z z a bi a bi bi

z z a bi a bi a b

     

     

    

Nên

, ,A B C

đều sai .Nên Chọn D.

Câu 23. Ta có

 

1 1 13

2 2 8 2

2 2 2

i i i i i i

       

Chọn C.

Câu 24. Gọi

z a bi 

với

,a b R

.khi đó

2 2

z a b

   

.Nên B sai. Chọn B.

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 27

Câu 25.

Ta có

   

2016 2018

1008 1009

2016 2018

2 2

1 1

1 1 0

1 1

i i

A i i i i

i i

   

 

 

 

 

         

 

 

 

 

 

 

   

. Chọn C.

Câu 26.

Cách 1:

2 3 2017

1 ...P i i i i     

2 3 2018

...iP i i i i    

 

1009

2018

1 2

1 1

1 1 1

P iP i P i

i i i



        

  

Cách 2:Do P la tổng của cấp số nhân

 

2018

Phần tử

2018

1 1

z i i



   



. Chọn A.

Câu 27. Ta có

     

 

1009

504

2018 2 1009

1009 2 1009

1 1 2 2 2

i i i i i i

 

     

 

 

. Chọn D.

Câu 28. Ta có

 

2017

504

2017 4

4 2 4 2

. 1 2

2 2

i i i i

i i i i z i

i i

   

      

 

. Chọn B.

Câu 29. Ta có

         

1008

2017 2 1008

1008

1 1 . 1 . 2 2 . 1

i i i i i

 

      

 

 

   

2017

1008

1008 1008

1 2 . 1

2 . 2 .

i i

z i

i i

 



    

. Vậy phần thực hơn phần ảo là 2. Chọn C.

Câu 30. Ta có

       

 

2017

2 3 2016

1 1

1 1 1 1 ... 1

1 1

z i i i i

 

          

 

         

1008

2017 2 1008

1008

1 1 . 1 . 2 2 . 1

i i i i i

 

      

 

 

 

2017

1008 1008 1008

1 1

2 . 2 2 .

1 1

z i

 



     



 

. Phần thực là

1008

2

. Chọn D.

Câu 31. Do A là tổng của một cấp số nhân (gồm

2 1k 

số hạng) với

u q i 

Suy ra

 

2 1

2 4 4 2 4

1 1

1 ... 1 1

1 1

k k

A i i i i





 

        



 

. Chọn D.

Câu 32. Gọi

; ,z a bi a b   

z a bi  

2 2

z z a b

z z a





 









 





 

2 2 2

1 1 1 2 1 . 1

z a bi a b a b a z z z z

              

Chú ý : Ngoài ra ta có thể viết

2 2 2

1 1 1

z a bi z z z

       

. Chọn D.

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 28

B. CĂN BẬC HAI VÀ PHƯƠNG TRÌNH BẬC HAI CỦA SỐ PHỨC

I. CĂN BẬC HAI CỦA SỐ PHỨC

1. LÝ THUYẾT

Cho số phức

. Mỗi số phức z thỏa mãn

z w

được gọi là một căn thức bậc 2 của

Mỗi số phức

0w 

0 có hai căn bậc hai là hai số phức đối nhau

 

 – .z và z

o Trường hợp

là số thực (

w a  

)

+ Khi

0a 

thì

có hai căn bậc hai là

và

a

+ Khi

0a 

nên

( )a a i 

, do đó

có hai căn bậc hai là

.a i

và

.a i 

Ví dụ: Hai căn bậc 2 của

1

là

và

–i

Hai căn bậc 2 của

( 0)a a 

là

,ai ai

o Trường hợp

( , ; 0)w a bi a b b   

Cách 1:

Gọi

( , )z x yi x y   

là căn bậc 2 của

khi và chỉ khi

z w

, tức là:

2 2

( )

...; ...

x yi a bi

x y a

x y

xy b

  





 



   











Mỗi cặp số thực

 

;x y

nghiệm đúng hệ phương trình đó cho ra một căn bậc hai

z x yi 

của số phức

w a bi 

Cách 2:

Có thể biến đổi

thành bình phương của một tổng, nghĩa là

w z

. Từ đó kết luận

căn bậc hai của

là

và -

2. MỘT SỐ BÀI TOÁN ĐIỂN HÌNH

Tìm các căn bậc

của

5 12i 

Giải:

o Cách 1:

Tìm các căn bậc 2 của

5 12i 

, tức là đi tìm các số phức

( , )x yi x y  

sao cho

( ) = 5 12x yi i  

nên ta cần giải hệ phương trình

2 2

2 12

x y





  













Rút y từ phương trình thứ hai thay vào phương trình thứ nhất, ta có:

Nội dung lý thuyết

Bài toán 1

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 29





 



 

   

  



 



 

  

 

  

  

 

  



  

 

 





4 2 2

5 36 0 4

6 6





x x x

y y

x x

Hệ này có 2 nghiệm:

(2;3)

và

( 2; 3) 

Vậy có 2 căn bậc hai của

5 12i 

là

2 3i

và

2 3i 

o Cách 2:

Ta có:

 

5 12 4 2.2.3 9 4 2.2.3 3 (2 3 ) .i i i i i

         

Từ đó dễ dàng suy ra hai căn bậc hai của

5 12i 

là

2 3i

và

2 3i 

Tìm căn bậc hai của số phức sau:

4 6 5w i 

Giải:

o Cách 1:

Gọi

 

,z x yi x y

   

là một căn bậc hai của

Khi đó ta có:

 

2 2

4 6 5

2 6 5

x y

x yi i





 



   











Giải hệ phương trình tìm được nghiệm:





































 











 









Vậy số phức đã cho có hai căn bậc hai là:

1 2

3 5;  3 5z i z i

    

o Cách 2:

Ta có:

 

4 6 5 9 2.3. 5 5 (3 5 ) .w i i i i

      

Suy ra

3 5i

là căn bậc của

4 6 5w i 

. Nên

3 5i 

là căn bậc của

4 6 5w i 

Vậy số phức đã cho có hai căn bậc hai là:

1 2

3 5; 3 5z i z i

    

Bài toán 2

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 30

II. GIẢI PHƯƠNG TRÌNH BẬC HAI

1. GIẢI PHƯƠNG TRÌNH BẬC HAI TRÊN TẬP SỐ PHỨC

Cho phương trình bậc 2:

0(1)Az Bz C  

trong đó

, ,A B C

là những số phức

0A 

Xét biệt thức

4B AC  

o Nếu

0 

thì phương trình (1) có 2 nghiệm phân biệt:

1 2

; 

2 2

B B

z z

A A

 

   

 

Trong đó



là một căn bậc 2 của



o Nếu

0 

thì phương trình (1) có nghiệm kép:

1 2



z z



 

CHÚ Ý:

o Mọi phương trình bậc n:

0 1 1

... 0

n n

A z A z A z A



    

luôn có n nghiệm phức

(không nhất thiết phân biệt).

o Hệ thức Vi-ét đối với phương trình bậc 2 số phức hệ số thực:

Cho phương trình bậc 2 :

0( , , ; 0)Az Bz C A B C A    

có 2 nghiệm phân

biệt (thực hoặc phức). Ta có:

1 2



S z z

P z z









  







 





MỘT SỐ BÀI TOÁN ĐIỂN HÌNH

Giải phương trình bậc hai sau:

2 3 0z z  

Giải:

Biệt thức

2 2

2 4.1.3 8 8i     

. Phương trình có 2 nghiệm phân biệt là:

1 2

2 4 2 4

1 2 ;  1 2

2 2

i i

z i z i

   

       

Giải phương trình bậc hai sau:

2 4 2 0z z i   

Giải:

Biệt thức:

2 2 2

2 4.1.(4 i 2) 4 16 8 12 16 16 2.4.2 4 (4 2 )i i i i i             

Chọn

4 2 .i  

Phương trình trên có hai nghiệm là :

1 2

2 4 2 2 4 2

1 i;  3 .

2 2 2 2

B i B i

z z i

A A

          

        

Phương pháp giải

Bài toán 1

Bài toán 2

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 31

2. ĐƯA PHƯƠNG TRÌNH BẬC CAO VỀ NHỮNG PHƯƠNG TRÌNH BẬC NHẤT,

PHƯƠNG TRÌNH BẬC HAI.

 Bước 1:

Để đưa phương trình thành nhân tử thì ta phải nhẩm nghiệm của phương trình. Có các

cách nhẩm nghiệm như sau:

o Tổng các hệ số của phương trình bằng 0 thì nghiệm của phương trình là

1x 

o Tổng các hệ số bậc chẳn bằng tổng hệ số bậc lẻ thì nghiệm của phương trình

1x  

o Định lý Bézout:

Phần dư trong phép chia đa thức

 

f x

cho

x a

bằng giá trị của đa thức

( )f x

tại

x a

. Tức là

       

f x x a g x f a  

Hệ quả: Nếu

 

f a



thì

   

f x x a



Nếu

   

f x

x a



thì

 

f a



o Sử dụng máy tính Casio để nhẩm nghiệm:

- Nhập phương trình vào máy tính.

- Bấm phím r rồi nhập 1 giá trị X bất kỳ, máy tính sẽ cho ra nghiệm của phương trình.

Sau đó dùng sơ đồ hoocne để phân tích thành nhân tử.

o Sơ đồ Hoocne:

Với đa thức f(x) =

-1 -2

-1 -2 1 0

...

n n n

a x a x a x a x a    

chia cho x - a thương là

g(x) =

-1 -2 -3

-1 -2 -3 1 0

...

n n n

b x b x b x b x b    

dư

Nếu

0r 

thì

   

f x g x



, nghĩa là:

     

f x x a g x 

Ta đi tìm các hệ số

-1 -2 -3 1 0

, , ... ,

n n n

b b b b b

bằng bảng sau đây.

-1n

-2n

...







1 -1



n n

ab a



 

2 -2



n n

ab a



 

2 2

b

ab a 

1 1

b

ab a 

0 0

r

ab a 

 Bước 2: Giải phương trình bậc nhất hoặc phương trình hai số phức, kết luận nghiệm.

MỘT SỐ BÀI TOÁN ĐIỂN HÌNH

Giải các phương trình:



27 0z

Giải:

 

3 2

2,3

– 27 0 – 1 3 9 0

3 3 3

z z z z







     

 









. Vậy p/t đã cho có 3 nghiệm.

a) Phương pháp phân tích đa thức thành nhân tử

Bài toán 1

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 32

Giải phương trình sau:

   

3 2

3 1 2 3 8 5 2 0.

z i z i z i

       

Giải:

Nhẩm nghiệm: Ta thấy tổng các hệ số của phương trình bằng 0 nên phương trình có nghiệm

 1z

Khi đó:

       

3 2 2

3 1 2 3 8 5 2 0 1 2 1 3 2 5 0

 1  v 2 5 .

z i z i z i z z i z i

z v z i z i

 

              

 

 

    

Vậy nghiệm của phương trình đã cho là :

1; ; 2 5 .z z i z i   

Cho phương trình sau:

     

  

3 2

2 – 2 5 – 4 – 10 0 1

z i z i z i

biết rằng phương trình có

nghiệm thuần ảo.

Giải:

Đặt

z yi

với

y  

. Phương trình (1) trở thành:

       

3 2

2 2 5 4 – 10 0

iy i yi i yi i

    



3 2 2

– 2 2 5 4 – 10 0 0 0iy y iy iy y i i      

Đồng nhất hoá hai vế ta được:

3 2

2 4 0

2 5 10 0

y y

y y y



  





    





Giải hệ này ta được nghiệm duy nhất

2y 

Suy ra phương trình (1) có nghiệm thuần ảo

2z i

* Vì phương trình (1) nhận nghiệm

 vế trái của (1) có thể phân tích dưới dạng:

     

 

3 2 2

2 – 2 5 – 4 – 10 – 2 , )

(z i z i z i z i z az b a b     



đồng nhất hoá hai vế ta giải

được

2a 

và

5b 

   

 

1 – 2 2 5 0 1 2

2 5 0

1 2

z i

z i z z z i

z z

z i







       

 

  

 

  





 

Vậy phương trình (1) có 3 nghiệm.

Giải

   

3 2

3 2 16 2 0

z i z i z i

      

biết rằng phương trình có 1 nghiệm thực.

Giải :

Gọi nghiệm thực là z

ta có:

   

3 2

0 0 0

3 2

0 0 0 0

3 2 16 0

3 2 16 2 0 2

2 0

z z z

z i z i z i z

z z





   



          





  





Bài toán 2

Bài toán 3

Bài toán 4

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 33

Khi đó ta có phương trình

   

 

2 5 8 0

z z i z i

     

Tìm được các nghiệm của phương trình là

2z  

;

2z i 

;

3 2z i 

Giải phương trình

   

3 2

2 3 3 1 2 9 0

z i z i z i

     

biết rằng phương trình có một

nghiệm thuần ảo.

Giải:

Giả sử phương trình có nghiệm thuần ảo là

, bi b  

Thay vào phương trình ta được:

       

 

2 3 2

3 2

 2 3 3 1 2 9 0

2 6 0

2 6 3 3 9 0 3 3

3 3 9 0

bi i bi i bi i

b b

b b b b b i b z i

b b b

     





 



              





    





Phương trình có thể phân tích thành

 

3 2 3 0

z i z z

   

Các nghiệm của phương trình là

3z i 

;

1 2z i 

Gọi

1 2 3 4

; ; ;z z z z

là 4 nghiệm phức của phương trình

 

   

4 2

4 4 0(1).

z m z m

Tìm tất cả

các giá trị

để

   

1 2 3 4

z z z z

Giải:

 

  



 



        

  





1,2

4 2 2 2

3,4

4 4 0 4 0

z i

z m z m z z m

z m

Nếu

 0m

thì (1) có nghiệm là



 



  





1,2

3,4

2z i

z m

Khi đó



      



  









1 2 3 4

6 4 2

z z z z m

Nếu

 0m

thì (1) có nghiệm là



 



 





1;2

3;4

z i

z i m

Khi đó



     



 









1 2 3 4

6 4 2

z z z z m

. Kết hợp lại

 1m

thỏa mãn bài toán.

Cho phương trình

4 2

4 4 0z mz  

trong tập số phức và

là tham số thực. Gọi

1 2 3 4

, , ,z z z z

lần lượt là 4 nghiệm của phương trình đã cho. Tìm tất cả các giá trị của

để

    

2 2 2 2

1 2 3 4

4 4 4 4 324

z z z z     .

Giải:

Bài toán 5

Bài toán 6

Bài toán 7

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 34

Cách 1:

Đặt

t z

, phương trình trở thành:

4 4 0t mt  

có 2 nghiệm

1 2

,t t

Ta có:

1 2

. 1

t t



  











. Do vai trò bình đẳng, giả sử ta có:

2 2 2 2

1 2 1 3 4 2

z z t z z t   

Yêu cầu bài toán

     

2 2

1 2 1 2 1 2

4 4 324 4 16 324

t t t t t t

 

        

 

 

17 18 1

17 18 .

17 18 35

m m



    

     



    





Cách 2:

Đặt

       

1 2 3 4

f z z z z z z z z z

    

  

1 1 1

4 2 2z z i z i

    nên

     

   

 

2 2 2 2

1 2 3 4

2 2

4 4 4 4 .  *

4 4

f i f i

z z z z



    

Mà

       

4 2

2 2 4 2 2 4 68 4 .f i f i i m i m

      

Vậy

 

68 4

* 324 .

4.4





 

  









Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 35

Cho pt bậc 4:

4 3 2

0Ax Bx Cx Dx E    

với

, , , , ; 0A B C D E A 

Tìm các nghiệm của phương trình. Biết phương trình có 1 nghiệm phức là

z a bi 

* Lưu ý:

Nếu phương trình trên có 1 nghiệm là

z a bi 

thì nó cũng có nghiệm

.z a bi 

Khi đó

2 2 2

1 2

z z x ax a b   

nên

4 3 2 2 2 2

( 2 ) ( )Ax Bx Cx Dx E x ax a b g x       

. Dùng

phép chia đa thức cho đa thức đã học ở lớp 8 để tìm

( )g x

Tiếp tục giải phương trình bậc hai :

( ) 0g x 

để tìm 2 nghiệm còn lại của phương trình.

BÀI TOÁN ĐIỂN HÌNH

Tìm phương trình bậc 4:

4 3 2

2 2 10 0z z z z    

.Tìm các nghiệm của phương trình.

Biết phương trình có 1 nghiệm phức là

2 .z i  

Hướng dẫn :

Phương trình trên có 1 nghiệm là

2z i  

thì nó cũng có nghiệm

2 .z i  

Khi đó

1 2

,z z

là nghiệm của phương trình:

  

1 2

4 5

z z z z z z

    

Nên

 

4 3 2 2

( 2 2 10) 4 5

z z z z z z g z

       .

Dùng phép chia đa thức cho đa thức đã học ở lớp 8 tìm được

 

2 2

g z z z

  

. Phương

trình

2 2 0z z  

có 2 nghiệm là

1 ; 1i i 

Vậy phương trình trên có 4 nghiệm là :

2 ; 2 ; 1 ; 1i i i i     

b) Phương pháp tìm nghiệm của phương trình bậc 4 hệ số thực

Bài toán

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 36

o Bước 1: Phân tích phương trình thành các đại lượng giống nhau.

o Bước 2: Đặt ẩn phụ, nêu điều kiện (nếu có).

o Bước 3: Đưa phương trình ban đầu về phương trình bậc nhất hoặc bậc 2 theo ẩn mới.

o Bước 4: Giải và kết luận nghiệm.

MỘT SỐ BÀI TOÁN ĐIỂN HÌNH

Giải phương trình sau:

2 2 2

( ) 4( ) 12 0z z z z    

Giải:

Đặt

 

t z z

, khi đó phương trình đã cho có dạng:

4

6 0

– 12 0

t z z

t t

z z



    



 





  





 

1 23



 





 











 



. Vậy p/t đã cho có 4

Giải phương trình sau trên tập số phức:

   

2 2 2

3  6 2 3  6  – 3 0

z z z z z z     

Giải:

Đặt

  

3 6t z z

phương trình đã cho có dang:

+ Với

    

3 6 – 0t z z z z



  

2 6 0z z





  



  



1 5

z i

+ Với



  



           



  



2 2

3 3

3 3 6 3 0 6 6 0

3 3

t z z z z z z

Vậy phương trình đã cho có 4 nghiệm.

Giải phương trình

( )( 3)( 2) 10z z z z   

Giải:

( 2)( 1)( 3) 10z z z z    

2 2

( 2 )( 2 3) 0z z z z    

Đặt

2t z z 

. Khi đó phương trình (8) trở thành:

c) Phương pháp đặt ẩn phụ

Bài toán 1

Bài toán 2

Bài toán 3

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 37

3 10 0

1 6

z i

t t



  

 



    





  





Vậy phương trình có các nghiệm:

1 6z   

;

1z i  

Giải phương trình sau trên tập số phức

4 3

1 0

z z z

    

Giải:

Nhận xét:

 0z

không là nghiệm của phương trình (1) vậy

 0z

Chia hai vế PT (1) cho

ta được: (

1 1 1

) ( ) 0

z z

    

(2)

Đặt

 

t z

. Khi đó

2 2

t z

  

2 2

z t

   

Phương trình (2) có dạng:



–

t t

(3)

1 4. 9 9

     

PT (3) có 2 nghiệm

t

1 3

i

t

1 3

i

+ Với

t

1 3

i

ta có

1 1 3

2 (1 3 ) 2 0

z z i z



      

(4)

Có

2 2 2

(1 3 ) 16 8 6 9 6 (3 )i i i i i          

PT (4) có 2 nghiệm:

z

(1 3 ) (3 )

i i

  

 

z

(1 3 ) (3 ) 1

4 2

i i i   



+ Với

t

1 3

i

ta có

1 1 3

2 (1 3 ) 2 0

z z i z



      

(5)

Có

2 2 2

(1 3 ) 16 8 6 9 6 (3 )i i i i i          

PT(5) có 2 nghiệm:

z

(1 3 ) (3 )

i i

  

 

z

(1 3 ) (3 ) 1

4 2

i i i    



Vậy PT đã cho có 4 nghiệm:

 1z i

;

 1z i

;

z

i 

;

z

i 

Bài toán 4

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 38

III. SỬ DỤNG MÁY TÍNH CASIO 570VN-PLUS ĐỂ GIẢI

Để thực hiện các phép toán trên tập số phức, ta chuyển qua chế độ CMPLX bằng cách bấm

o Bấm đơn vị ảo

bằng cách bấm phím

o Bấm

và lựa chọn các chức năng:

o Chọn

để bấm acgumen của

 

 arg

z z

o Chọn

để bấm số phức liên hợp của

 



z Conjg z

o Chọn

để chuyển từ dạng đại số sang dạng lượng giác.

o Chọn

để chuyển từ dạng lượng giác sang dạng đại số.

o Bấm dấu



bằng cách bấm:

Sau đây là cách giải các bài toán điển hình cho các dạng toán tìm căn bậc hai của một số phức;

giải phương trình bậc hai với hệ số thực và các dạng toán liên quan bằng máy tính casio.

1. BÀI TOÁN TÌM CĂN BẬC HAI CỦA MỘT SỐ PHỨC

Xây dựng công thức bấm:

Cho số phức

z a bi 

, có dạng lượng giác là z = r(cos



+isin



)

 

 0

. Với

2 2

r a b z  

.  là góc thoả mãn :

sin





















 được gọi là acgument của

, kí hiệu là

 

arg z

Khi đó z có hai căn bậc hai là:

os isin

2 2

r c

 

 



















 

và -

os isin

2 2

r c

 

 



















 

Hay được viết gọn là:



 

hay

 

arg

z 

Như vậy để tìm các căn bậc hai của số phức

z a bi 

, ta làm như sau:

o Nhập số phức

và lưu vào biến A (cái này đơn giản).

o Bấm theo công thức sau:

sqcQz$$qzaq21Qz)R2=

o Ta thu được kết quả của một căn thức của

, suy ra căn bậc hai còn lại.

Một số lưu ý

Cách 1

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 39

Tìm các căn bậc hai của số phức

3 4z i  

Hướng dẫn:

Quy trình bấm :

o Nhập số phức

3 4z i  

và lưu vào biến A:

p3+4bqJz

o Bấm theo công thức ở trên :

sqcQz$$qzaq21Qz)R2

o Màn hình cho kết quả:

Nên

1 2i

và

1 2i 

là 2 căn bậc hai của số phức

3 4z i  

o Nhập hàm X

Q)d

o Sử dụng phímr,nhập các giá trị vào, giá trị nào cho ra số phức

thì ta chọn đáp án đó.

Tìm các căn bậc hai của số phức

3 4z i  

.1 2 ;  1 2  .2 2 ;  1 2

.1 2 ;  1 2  . 2 ;  2

A i i B i i

C i i D i i

     

      

Hướng dẫn:

Q)d

Nhập lần lượt các số phức ở các đáp án vào nhé.

r1+2b=

màn hình sẽ cho kết quả:

Nên

1 2i

là căn bậc hai của số phức

3 4z i  

. Vì một số phức có hai căn bậc 2 đối nhau

nên

1 2i 

cũng là căn bậc hai của số phức

3 4z i  

>>> Chọn C.

Ví dụ

Cách 2

Ví dụ

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 40

Tìm các căn bậc hai của số phức

z a bi 

o Nhấp Shift + (Pol), ta nhập Pol(a,b).

o Dấu phẩy trong (a,b) bấm bằng cách

o Nhấp Shift - (Rec), ta nhập Rec(X,Y), ta thu được kết quả X=...;Y=...

o Kết luận các căn bậc 2 cần tìm.

Tìm các căn bậc hai của số phức

12 16z i  

Hướng dẫn:

q+p12q)16)=

màn hình hiện kết quả

qpsQ)$q)QnP2)=

thu được kết quả:

Suy ra các căn bậc hai của số phức

12 16z i  

là

2 4 ; 2 4i i  

Cách 3

Ví dụ

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 41

2. GIẢI PHƯƠNG TRÌNH BẬC HAI

a) Phương trình bậc hai với hệ số thực:

Giải phương trình bậc hai sau:

4 10 0z z  

Hướng dẫn:

Quy trình bấm:

w531=p4=10==

Thu được kết quả:

Gọi

1 2

,z z

là 2 nghiệm của phương trình :

1 0z z  

. Tính

2018 2018

1 2

.P z z 

Hướng dẫn :

Quy trình bấm như sau:

o Tìm nghiệm

1 2

,z z

w531=1=1==

Thu được kết quả:

o Lưu 2 nghiệm vào X và Y:

qJ)RqJn

o Màn hình hiển thị là đã lưu biến X thành công, tương tự

biến Y.

o Tính P .

o Sau đó vào

và nhập P và thu được kết quả:

Sau đây là Bài toán 3 tương tự Bài toán 2 nhưng giải theo dạng lượng giác của số phức. Cách này luôn

giải được với số mũ lớn bất kỳ, cách giải theo Bài toán 2 có thể không giải được với số mũ lớn nào đó.

Biết

là nghiệm của phương trình

  . Tính giá trị biểu thức

2009

P z

 

1P 

0P 

P   D.

P 

Bài toán 1

Bài toán 2

Bài toán 3

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 42

Hướng dẫn:

 Quy đồng phương trình

 

ta được phương trình bậc hai

1 0z z  

. Tính

nghiệm phương trình này với chức năng MODE 5 3

w531=p1=1==

 Ta thu được hai nghiệm

nhưng hai nghiệm này có vai trò như nhau nên chỉ cần lấy một

nghiệm

đại diện là được

Với

1 3

2 2

z i

  ta chuyển về dạng lượng giác

1 cos sin

3 3

z i

 

 







  











 

a1R2$+as3R2$bq23=

Vậy

2009 2009

1 cos2009. sin2009. cos2009. sin 2009.

3 3 3 3

z i i

   

   

 

 

 

    

 

 

 

 

 

   

Tính

2009

và lưu và biến

Wk2009OaqKR3$ +bj2009

OaqK

)

)R3$ =qJz

Tổng kết

P A

  

Qz+a1RQz=



Đáp số chính xác là A

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 43

b) Phương trình bậc hai với hệ số phức:

Giải phương trình :

8(1 ) 63 16 0z i z i    

Hướng dẫn:

o Tính

4B AC  

bằng máy tính , ta được:

o Sau đó gán kết quả của



vào A.

o Dùng công thức tìm căn bậc 2 đã học ở trên, thu được 1 căn bậc 2 của là

2 16i

o Gán kết quả này cho X.

o Nên 2 nghiệm của phương trình là :



Bài

toán

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 44

IV. BÀI TẬP RÈN LUYỆN

1. ĐỀ BÀI

Câu 1. Trong



, phương trình

1 0z  

có nghiệm là:

1; 2i 

2; 2i 

3; 4i 

1; i 

Câu 2. Trong



, căn bậc hai của

121

là:

11i

11i

11

11i

và

11i

Câu 3. Phương trình

8 4 1 0z z  

có nghiệm là:

1 2

1 1 5 1

;

4 4 4 4

z i z i

   

1 2

1 1 1 3

;

4 4 4 4

z i z i

   

1 2

1 1 1 1

;

4 4 4 4

z i z i

   

1 2

2 1 1 1

;

4 4 4 4

z i z i

   

Câu 4. Biết

1 2

;z z

là hai nghiệm của phương trình

2 3 3 0z z  

. Khi đó giá trị của

2 2

1 2

z z

là:



Câu 5. Phương trình

0z az b  

có một nghiệm phức là

1 2z i 

. Tổng 2 số

và

bằng:

3

C. 3 D.

4

Câu 6. Gọi

1 2

;z z

là hai nghiệm phức của phương trình

4 5 0z z  

. Khi đó phần thực của

2 2

1 2

z z

là:

A. 5 B. 6 C. 4 D. 7

Câu 7. Gọi

1 2

;z z

là hai nghiệm phức của phương trình

2 4 0z z  

. Khi đó

2 2

1 2

| | | |A z z 

có giá trị là

7

B. – 8 C.

4

D. 8

Câu 8. Phương trình

8z 

có bao nhiêu nghiệm phức với phần ảo âm?

A. 1 B. 2 C. 3 D. 0

Câu 9. Biết

1 2

,z z

là hai nghiệm của phương trình

2 3 3 0z z  

. Khi đó giá trị của

2 2

1 2

z z

là:

A. 4 B.

C. 9 D.



Câu 10. Phương trình sau có mấy nghiệm thực:

2 2 0z z  

A. 0 B. 1 C. 2 D. Vô số nghiệm.

Câu 11. Tìm các căn bậc hai của

9

3i

B. 3 C.

3

Câu 12. Trong



, phương trình

4 0z  

có nghiệm là:

   

1 4 ; 1 4i i   

 

1 2i 

;

 

1 2i 

   

1 3 ; 1 3i i   

D. ±

 

i

;

 

i 

Câu 13. Giải phương trình

2 7 0z z  

trên tập số phức ta được nghiệm là:

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 45

1 2 2z i 

1 6z i 

1 2z i 

1 7z i 

Câu 14. Căn bậc hai của số phức

4 6 5i

là:

 

3 5i

 

 

3 5i



 

3 5i

 

D. 2

Câu 15. Gọi z là căn bậc hai có phần ảo âm của

33 56i

. Phần thực của z là:

A. 6 B. 7 C. 4 D. –4

Câu 16. Tập nghiệm trong



của phương trình

3 2

1 0z z z   

là:

 

;i;1; 1

 

 

; ;1i i

 

; 1

 

 

; ; 1

i i

 

Câu 17. Trên tập số phức, phương trình bậc hai có hai nghiệm

4 3 ; 2i i     

là:

   

2 4 11 2 0

z i z i

    

   

2 4 11 2 0

z i z i

    

   

2 4 11 2 0

z i z i

    

   

2 4 11 2 0

z i z i

    

Câu 18. Có bao nhiêu số phức thỏa mãn điều kiện

2 2

| |z z z 

A. 3 B. 0 C. 1 D. 2

Câu 19. Phương trình

   

2 0 ,i z az b a b

     

có hai nghiệm là

3 i

và

1 2i

. Khi đó

?a 

9 2i 

15 5i

9 2i

15 5i

Câu 20. Cho số phức z thỏa mãn

6 13 0z z  

. Tính

z i



và 4 B.

và 5 C.

và 3 D.

và 2

Câu 21. Gọi

1 2

,z z

là các nghiệm phức của phương trình

   

1 3 2 1 0

z i z i

    

. Khi đó

2 2

1 2 1 2

w z z z z  

là số phức có môđun là:

A. 2 B.

2 13

Câu 22. Số nghiệm của phương trình với ẩn số phức z:

2 2

4 8 | z | 3 0z   

là:

A. 3 B. 2 C. 4 D. 1

Câu 23. Tìm số phức z để

z z z 

0; 1z z i  

0; 1z z i  

0; 1 ; 1z z i z i    

1 ; 1z i z i   

Câu 24. Với mọi số ảo z, số

2 2

| z |z 

là:

A. Số thực âm B. Số 0

C. Số thực dương D. Số ảo khác 0

Câu 25. Trong trường số phức phương trình

1 0z  

có mấy nghiệm?

A. 2 B. 3 C. 1 D. 0

Câu 26. Giá trị của các số thực b, c để phương trình

0z bz c  

nhận số phức

1z i 

làm

một nghiệm là:













 









 







 









 































Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 46

Câu 27. Trên tập hợp số phức, phương trình

7 15 0z z  

có hai nghiệm

1 2

,z z

. Giá trị biểu

thức

1 2 1 2

z z z z 

là:

A. –7 B. 8 C. 15 D. 22

Câu 28. Tìm số nguyên x, y sao cho số phức

z x yi 

thỏa mãn

18 26z i 













 

















 



























 







 





Câu 29. Trên tập số phức, cho phương trình sau:

 

4 0

z i z

  

. Có bao nhiêu nhận xét đúng

trong số các nhận xét sau?

1. Phương trình vô nghiệm trên trường số thực



2. Phương trình vô nghiệm trên trường số phức



3. Phương trình không có nghiệm thuộc tập số thực.

4. Phương trình có bốn nghiệm thuộc tập số phức.

5. Phương trình chỉ có hai nghiệm là số phức.

6. Phương trình có hai nghiệm là số thực

A. 0 B. 1 C. 3 D. 2

Câu 30. Phương trình

6 3

9 8 0z z  

có bao nhiêu nghiệm trên tập số phức?

A. 3 B. 4 C. 2 D. 6

Câu 31. Giả sử

1 2

,z z

là hai nghiệm của phương trình

2 5 0z z  

và A, B là các điểm biểu

diễn của

1 2

,z z

. Tọa độ trung điểm I của đoạn thẳng AB là:

 

1;1

 

1;0



 

0;1

 

1;0

Câu 32. Cho phương trình

6 0z mz i  

. Để phương trình có tổng bình phương hai nghiệm

bằng 5 thì m có dạng

  

,m a bi a b

    

. Giá trị

2a b

là:

A. 0 B. 1 C.

2

1

Câu 33. Gọi

1 2 2 4

, , ,z z z z

là các nghiệm phức của phương trình

z i

 























 

. Giá trị của

    

2 2 2 2

1 2 3 4

1 1 1 1

P z z z z

    

là:

Câu 34. Trong tập số phức, giá trị của m để phương trình bậc hai

0z mz i  

có tổng bình

phương hai nghiệm bằng

4i

là:

 

i 

 

i

 

i 

1 i 

Câu 35. Cho phương trình

2 1 0z mz m   

trong đó m là tham số phức. Giá trị của m để

phương trình có hai nghiệm

1 2

,z z

thỏa mãn

2 2

1 2

z z

  

là:

2 2 2m i 

2 2 2m i 

2 2 2m i 

2 2 2m i  

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 47

Câu 36. Gọi

1 2

,z z

là hai nghiệm của phương trình

2 8 0z z  

, trong đó

có phần ảo

dương. Giá trị của số phức

 

1 2 1

w z z z

 

là:

12 6i

B. 10 C. 8 D.

12 6i

Câu 37. Tổng bình phương các nghiệm của phương trình

1 0z  

trên tập số phức là bao

nhiêu?

A. 3 B. 1 C. 2 D. 0

Câu 38. Gọi

1 2

,z z

là hai nghiệm của phương trình

2 6 0z z  

. Trong đó

có phần ảo âm.

Giá trị biểu thức

1 1 2

| | | 3 |M z z z  

là:

6 2 21

6 2 21

6 4 21

6 4 21

Câu 39. Phương trình

4 2

2 24 72 0x x x   

trên tập số phức có các nghiệm là:

2 2i

hoặc

2 2 2i 

2 2i

hoặc

1 2 2i

hoặc

2 2 2i 

1 2 2i 

hoặc

2 2 2i 

Câu 40. Gọi

1 2

,z z

là các nghiệm phức của phương trình

3 7 0z z  

. Khi đó

4 4

1 2

A z z 

có

giá trị là:

A. 23 B.

C. 13 D.

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 48

2. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI CHI TIẾT

1.D

2.D

3.C

4.D

5.C

6.B

7.D

8.A

9.D

10.A

11.A

12.D

13.B

14.C

15.B

16.D

17.B

18.A

19.A

20.B

21.D

22.C

23.C

24.B

25.B

26.C

27.B

28.C

29.D

30.D

31.D

32.D

33.B

34.A

35.A

36.C

37.D

38.B

39.A

40.A

Câu 1.

  

 

4 2

1 1

1 0 1 1 1 0 1 1

1 0

z z

z z z z z z

z i



 



            



 

 





. Chọn D.

Câu 2.

Ta có:

 

121 11z z i

   

. Do đó z có hai căn bậc hai là

11 ; 11z i z i  

. Chọn D.

Câu 3.

1,2

2 2 1

' ' 4 8 4 0

8 4 4

i i

b ac z



           

. Chọn C.

Câu 4. Theo Viet, ta có:

1 2

S z z

P z z





     







  





2 2 2

1 2

3 9

2 3

4 4

z z S P

       

. Chọn D.

Câu 5. Vì

1 2z i 

là một nghiệm của phương trình

0z az b  

nên ta có:

   

1 2 1 2 0 2 3 4 3

i a i b a b ai i a b

            

. Chọn C.

Câu 6.Theo Viet, ta có:

1 2

. 5

S z z

P z z





    







  





2 2 2

1 2

2 16 2.5 6

z z S P

     

. Chọn B.

Câu 7.

 

2 2 2

1 2

2 4 0 1 3 0 1 3 | | | | 8

z z z z i A z z

              

. Chọn D.

Câu 8.

 

   

3 2

8 2 2 4 0 2 1 3 0

1 3

z z z z z z

z i







 



           

 





 

  

 





Do đó phương trình chỉ có một nghiệm phức có phần ảo âm. Chọn A.

Câu 9. Áp dụng định lý Viet, ta có:

1 2

S z z

P z z





     







  





2 2 2

1 2

3 9

2 3

4 4

z z S P

      

. Chọn D.

Câu 10.

' b' 1 2 1 0ac       

nên phương trình vô nghiệm trên tập số thực. Chọn A.

Câu 11. Ta có

9 9.i 

nên

9

có các căn bậc hai là

và

3i

. Chọn A.

Câu 12.

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 49

 

2 1

4 0

z i z i

z i



   



   



 

  





Chọn D.

Câu 13.

 

2 7 0 1 6 0 1 6z z z z i

         

. Chọn B.

Câu 14. Giả sử

là một căn bậc hai của

4 6 5i

. Ta có:

   

2 2

4 6 5 3 5 3 5w i w i w i

        

. Chọn C.

Câu 15. Ta có:

 

33 56 7 4i i

  

7 4z i  

. Do đó phần thực của z là 7. Chọn B.

Câu 16.

 

3 2 2

1 0 1 1 0

z z z z z

z i



 



        



 





. Chọn D

Câu 17. Áp dụng định lý Viet, ta có:

2 4

. 11 2

S i

P i

 





   







   





Do đó

, 

là hai nghiệm của phương trình:

   

2 2

0 2 4 11 2 0

z Sz P z i z i

        

Chọn B.

Câu 18. Gọi

 

,z a bi a b

   

là số phức thỏa mãn điều kiện trên. Ta có:

 

2 2 2 2 2 2

| | 2 2 0 2 2 0

2 0

z z z a bi a b a bi a b bi abi a b b ab i

a b

b ab

                  



 







 











 

 







  

 

 





  



 



 



 





 













 



 





















Vậy có 3 số phức thỏa mãn yêu cầu bài toán. Chọn A.

Câu 19. Theo Viet, ta có:

  

1 2

4 4 2 9 2

S z z i a i i a i

             



. Chọn A.

Câu 20.

 

6 13 0 3 4 0 3 2z z z z i         

+) Nếu

3 2z i 

6 6 9 15 18 72

3 2 1 4

3 3 3 3 18

1 4 17

i i

z i i

z i i i

z i

  

        

  

     



+) Nếu

3 2z i 

6 6 13 9 30 40 6

3 2 3 4 3 4 5

3 3 10

i i

z i i z i

z i i i z i

 

            

   

Chọn B.

Câu 21. Theo Viet, ta có:

 

1 2

1 3

. 2 1

S z z i

P z z i





      







    





Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 50

   

2 2 2

1 2 1 2

3 5 1 3 10 1 2 4 | | 4 16 20

w z z z z S P i i i w               

. Chọn D

Câu 22. Gọi

 

,z a bi a b

   

là nghiệm của phương trình. Ta có:

 

     

2 2 2 2 2 2

2 2

4 8 a 3 0 4 2 8 3 0

12 4 8 3 0

a bi b a b abi a b

a b abi

           

    

2 2 2 2

12 4 3 4 1

0 0

a b a b

ab ab

 

 

   

 

 

 

 

 

 

 

 

2 2

2 1

4 4 1

a b

a ab b























 

 











  





 



  



  





  





 

  

 





 



 























Vậy phương trình có 4 nghiệm phức.

Chọn C.

Câu 23. Gọi

 

,z a bi a b

   

là số phức thỏa mãn đẳng thức trên. Ta có:

 

2 2

a b

z z z a bi a bi a bi

ab b

















 











 



 











          

 





 







 





































z i







  



 





Chọn C.

Câu 24. Do z là số ảo nên z có dạng:

 

z bi b

  

Ta có:

 

2 2 2 2 2

| | 0

z z bi b b b

      

. Chọn B.

Câu 25.

 

3 2

1 0 1 1 0

1 3

z z z z







       











Vậy phương trình có ba nghiệm trong trường số phức. Chọn B.

Câu 26. Do

1z i 

là một nghiệm của

0z bz c  

nên ta có:

   

0 2

1 1 0 2 0

2 2

b c b

i b i c b c bi i

b c

 

 

   

 

           

 

 

  

 

 

. Chọn C.

Câu 27. Theo Viet, ta có:

1 2

S z z

P z z





     







  





1 2 1 2

7 15 8z z z z S P        

Chọn B.

Câu 28.

 

3 3 2 2 3

3 2 2 3

2 2

3 2

2 3

2 2

18 26 18 26 3 3 18 26

( 3 ) 3 18 26

3 18

3 26

z i x yi i x x yi xy y i i

x xy x y y i i

x x y

x xy

x y y

y x y

           

     





 



 

 

 

 

 

 









Do x, y nguyên nên

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 51

 

2 2

3 6

3 18

loai

3 3

x y

x x y

x y

 







 

 

 





   



















 

 







Mà

 

2 2

3 26 3; 1

y x y x y

    

. Chọn C.

Câu 29.

   

 

4 4

2 2

4 0 4

2 1 0

2 3

4 1 0

2 3 0

z i z z i z

z i iz z

z i

z iz

z i

z i iz

      



 

   



   



    



  



  







Do đó phương trình có 2 nghiệm thực và 4 nghiệm phức. Vậy nhận xét 4, 6 đúng. Chọn D.

Câu 30. Ta có:

  

6 3 2 2

9 8 0 1 2 1 2 4 0

1 3

z z z z z z z z













           





  



 





Chọn D.

Câu 31.

 

2 5 0 1 4 0 1 2z z z z i         

   

1;2 ; 1; 2

A B

 

Do đó tọa độ trung điểm I của đoạn thẳng AB là

 

1;0

. Chọn D.

Câu 32. Gọi

1 2

,z z

là hai nghiệm của phương trình đã cho

Theo Viet, ta có:

1 2

. 6

S z z m

P z z i





     







   





Theo bài cho, tổng bình phương hai nghiệm bằng 5. Ta có:

 

2 2 2 2 2 2

1 2

2 12 5 5 12 3 2

3 2

z z S P m i m i m i

m i

           

   

3; 2 2 3 4 1a b a b         

. Chọn D.

Câu 33. Với mọi



, ta có:

1 1

2 3

1 2 4

2 5

z i

i z

z i



  





 



  

 













  













 





 



  















    

 

   

2 2

2 2 2 2

1 2 3 4

1 2 4

1 1 1 1 1 1 1 1

9 25

i i

P z z z z i

   

 

   

 

   

           

 

   

 

 

   

   

 

9 2 13 16 425 17

1 2 .

9 25 9.25 9

i i

 

   

Chọn B.

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 52

Câu 34. Gọi

1 2

,z z

là hai nghiệm của phương trình.

Theo Viet, ta có:

1 2

S z z m

P z z i





     







  





2 2 2 2

1 2

2 2z z S P m i     

Ta có:

   

2 2 2

2 4 2 1 1

m i i m i m i m i            

Chọn A.

Câu 35. Theo Viet, ta có:

1 2

. 2 1

S z z m

P z z m





    







   





 

2 2 2 2 2

1 2

10 2 10 2 2 1 10 4 12 0

 2 8 0 2 2 2

z z S P m m m m

m m i

               

      

Chọn A.

Câu 36.

 

1 7

2 8 0 1 7 0 1 7

1 7

z i

z z z z i

z i





  



           





 





 

      

1 2 1

2 2 1 7 1 7 1 7 1 7 1 7

 1 7 8

w z z z i i i i i

 

             

 

 

  

. Chọn C.

Câu 37.

1 0

z i



 



  



 





Do đó tổng bình phương các nghiệm của phương trình là

1 1 0 

. Chọn D.

Câu 38.

 

1 2

1 1 2

2 6 0 1 5 0 1 5

1 5 ; 1 5

| | | 3 | 1 5 2 4 5 6 84 6 2 21

z z z z i

z i z i

M z z z i i

         

    

           

Chọn B.

Câu 39.

  

 

4 2 2 2

2 2

2 24 72 0 4 6 4 12 0

4 6 0 2 2 0 2 2

4 12 0

2 2 2

2 8 0

x x x x x x x

x x x x i

x x

x i

         



       



  



  



  



  







Chọn A.

Câu 40. Theo Viet, ta có:

1 2

. 7

S z z

P z z





     







  





 

4 4 2 2

1 2

2 2 3 2.7 2.49 23

A z z S P P        

. Chọn A.

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 53

C. TẬP HỢP ĐIỂM CỦA SỐ PHỨC

I. LÝ THUYẾT

Trong dạng này, ta gặp các bài toán biểu diễn hình học của số phức hay còn gọi là tìm tập

hợp điểm biểu diễn một số phức

trong đó số phức

thỏa mãn một hệ thức nào đó. Khi

đó ta giải bài toán này như sau:

1. Phương pháp tổng quát:

Đặt

    ,( )z x yi x y

. Khi đó số phức

biểu diễn trên mặt phẳng phức bởi điểm

 

;M x y

. Biến đổi điều kiện của bài toán thành để tìm mối liên hệ giữa

và

từ đó suy ra

tập hợp điểm M.

2. Giả sử các điểm M, A, B lần lượt là điểm biểu diễn của các số phức z, a, b

| | | |z a z b MA MB     

M thuộc đường trung trực của đoạn AB

| | | | ( , 0, | |)z a z b k k k k a b MA MB k          

( )M E 

nhận A, B

là hai tiêu điểm và có độ dài trục lớn bằng k.

3. Giả sử M và M’ lần lượt là điểm biểu diễn của số phức z và w = f(z)

Đặt z = x + yi và w = u + vi

( , , , )x y u v  

Hệ thức w = f(z) tương đương với hai hệ thức liên hệ giữa x, y, u, v

o Nếu biết một hệ thức giữa x, y ta tìm được một hệ thức giữa u, v và suy ra được tập

hợp các điểm M’

o Nếu biết một hệ thức giữa u, v ta tìm được một hệ thức giữa x, y và suy ra được tập

hợp điểm M’.

1. Các dạng phương trình đường thẳng

- Dạng tổng quát:

0ax by c  

. - Dạng đại số:

y ax b 

- Dạng tham số:

x x at

y y bt





 







 





- Dạng chính tắc:

0 0

x x y y

a b

 



- Phương trình đoạn chắn

x y

a b

 

- Phương trình đường thẳng đi qua 1 điểm

 

0 0 0

;M x y

biết hệ số góc k:

0 0

( )y k x x y  

2. Phương trình đường tròn tâm I(a;b) bán kính R:

2 2 2

( ) ( )x a y b R   

2 2

2 2 0x y ax by c     

với

2 2 2

c a b R  

Lưu ý điều kiện để phương trình:

2 2

2 2 0x y ax by c    

là phương trình đường tròn:

2 2

0a b c  

có tâm

 

,I a b 

và bán kính

2 2

R a b c  

3. Phương trình (Elip):

2 2

x y

a b

 

Với hai tiêu cự

1 2 1 2

( ;0), ( ; 0), 2F c F c F F c 

. Trục lớn 2a, trục bé 2b và

2 2 2

a b c 

Lý thuyết về tập hợp điểm của số phức

Nhắc lại kiến thức về hình học giải tích Oxy

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 54

II. MỘT SỐ BÀI TOÁN ĐIỂN HÌNH

Giả sử M là điểm trên mặt phẳng phức biểu diễn số phức

Tìm tập hợp các điểm M thỏa mãn một trong các điều kiện sau đây:

a) =2 b)

1 3 4z i  

Giải:

Đặt

( ),z x yi x y   

được biểu diễn bởi điểm

 

;M x y

a) Xét hệ thức:

  1 2z i

   

   

    

2 2

– 1 1 2

1 1 2.

1 1 4.

x y i

x y

 Tập hợp các điểm

 

M z

trên mặt phẳng tọa độ biểu diễn số phức

thỏa mãn (1) là

đường tròn có tâm tại

 

1; 1I

và bán kính

 2R

b) Xét hệ thức :

   

1 3 4 1 3 4z i x y i       

   

2 2

 1  1 4x y    

   

2 2

 1  1 16.x y   

Vậy tập hợp các điểm M trên mặt phẳng tọa độ biểu diễn số phức

là hình tròn có tâm là

 

1;1 ; bán kính

4r 

Nhận xét: Tập hợp các điểm biểu diễn số phức

thỏa mãn điều kiện:

1 3 4z i  

là tập

hình các điểm nằm trên và nằm ngoài đường tròn có tâm là

 

1;1 ; bán kính

4r 

c) Xét hệ thức:

  2 z z i

   

2 2

2 1

4 2 3 0.

x yi x y i

x y x y

x y

    

   



Vậy tập hợp các điểm M là đường thẳng

4 2 3 0.x y  

Nhận xét: Đường thẳng

4 2 3 0x y  

chính là đường trung trực của đoạn AB.

1z i 

2 1z i  

Bài toán 1

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 55

Trong mặt phẳng

Oxy

, tìm tập hợp điểm biểu diễn các số phức

thỏa mãn

 

z i i z

  

Giải:

Đặt

( , .)z x yi x y  

Ta có:

       

     

         

      

2 2 2

 1 1

z i i z x y i x y x y i

x y x y x y

 

2 2 2

2 1 0 1 2

x y xy x y

        

Vậy tập hợp các điểm M biểu diễn các số phức

là đường tròn có phương trình

 

1 2

x y

  

Cho các số phức

1 2 3

,  , z z z

có biểu diễn trên mặt phẳng phức là ba đỉnh của tam giác đều có

phương trình đường tròn ngoại tiếp là

   

2 2

2017 2018 1.

x y

   

Tổng phần thực và phần

ảo của số phức

1 2 3

w z z z  

bằng?

Giải:

Đường tròn đã cho có tâm

biểu diễn số phức

2017 2018z i  

Gọi

,  , A B C

lần lượt là điểm biểu diễn các số phức

1 2 3

,  , z z z

Ta có

3 3OA OB OC OG OI   

    

(do tam giác

ABC

đều nên

G I

Suy ra

 

1 2 3

3 2017 2018 6051 6054z z z i i       

Nên tổng phần thực và phần ảo của số phức

bằng 3.

Tìm tập hợp các điểm biểu diễn của số phức

sao cho

2 3z i

z i

 





là một số thuần ảo.

Giải :

Đặt

( ),z x yi x y   

, khi đó:

   

 

     

 

2 3 1

2 3

x y i x y i

x y i

x y

   

    

  

   

   

 

 

 

2 2

2 2 3 2 2 1



x y x y x y i

x y

      



 

Bài toán 2

Bài toán 4

Bài toán 3

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 56

u là số thuần ảo



 

   

2 2

2 2 3 0

1 1 5

1 0

; 0;1

x y x y

x y





    



   



 



 

 

  



 





Vậy tập hợp các điểm biểu diễn của

là đường tròn tâm

 ( 1; 1)I

, bán kính

trừ điểm

(0;1)

Trên mặt phẳng toạ độ, tìm tập hợp điểm biểu diễn số phức z thoả mãn điều kiện sau:

2 2z i z z i   

1 1 4

z z

   

Giải:

Đặt:

( , )z x yi x y R  

z

có điểm biểu diễn trên mặt phẳng phức là

 

M x; y .

2 2 2 ( 1) (1 )

z i z z i x y i y i y          

Vậy tập hợp điểm M là đường parabol (P) có phương trình

y 

   

2 2

1 1 4 1 1 4 (*)

z z x y x y          

Đặt

1 2

( 1; 0); (1;0)F F

1 2

(*) 4MF MF  

và

1 2

2F F 

Suy ra tập hợp M là elíp (E) có 2 tiêu điểm là

1 2

,F F

Gọi (E) có phương trình

2 2

2 2 2

2 2

1 (0 ; )

x y

b a b a c

a b

     

Ta có

1 2

2 2 2

1 2

2 2

2 1

MF MF a a

b a c

F F c c

 

 

  

 

    

 

 

 

 

 

Vậy (E) có phương trình

2 2

4 3

x y

 

Trong tập số phức



, gọi

và

các nghiệm của phương trình

2 10 0z z  

. Gọi

lần lượt là các điểm biểu diễn của

và số phức

k x iy 

trên mặt phẳng phức.

Để tam giác

MNP

đều thì số phức

là?

Giải:

Ta có

2 10 0z z  



1,2

1 3z i 

. Gọi

lần lượt là các điểm biểu diễn của

và số phức

k x iy 

trên mặt phẳng phức. Khi đó

 

1; 3

 

1; 3



 

;P x y

Để

MNP

đều



MN MP

MN NP





















2 2

MN MP

MN NP



















(1)

Bài toán 5

Bài toán 6

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 57

Ta có

 

0; 6

 



 

1; 3

MP x y

  



 

1; 3

NP x y

  



(2)

Từ (1) và (2)



   

2 2

1 3 36

x y





    







   







1 27





 















1 27k  

Trong mặt phẳng phức, cho

và

theo thứ tự là điểm biểu diễn của số phức

 z x yi

và







z i

Tìm tập hợp các điểm

sao cho:

là một số thực.

Giải:

Ta có:

 

   

 

   

 

  

   



   

   

1 2

1 1

2 2

x yi x y i

x yi

z x yi

z i

x yi i x y i

x y i x y i

     

 

     

 

 

1 2 2 2

x x y y y x i

x y

là một số thực khi và chỉ khi

  2 2 0y x

Tập hợp các điểm

biểu diễn số phức

 z x yi

là đường thẳng

     2 2 0 2 2y x y x

Tập hợp các điểm

biểu diễn số phức

thỏa mãn

z i z i

   

là?

Giải:

Ta có

   

2 2

4 1 1 4

z i z i x y x y

          

   

 

     

2 2

2 2 2

1 4

1 4 1

1 16 1 8 1

x y

x y x y

x y x y x y





  



       





        





 

   

 

2 2

1 16 1

1 16

4 4 2

2 1 4

4 3 12

3 4

x y

y y

x y y

x y





  





  



  



 

      

 

 

  







 

 







 













Tập hợp các điểm thỏa mãn

 

đều thỏa mãn

 

và

 

Vậy tập hợp những điểm

là elip

 

2 2

: 1.

3 4

x y

 

Bài toán 7

Bài toán 8

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 58

(ĐỀ MINH HỌA QUỐC GIA NĂM 2017)

Cho số phức

z  

thỏa mãn



. Biết tập hợp các điểm biểu diễn cho số phức

 

3 4

w i z i  

là đường tròn

, bán kính

. Khi đó.

 

0;1 , 2 5.

I R  B.

 

1;0 , 20

I R



 

0;1 , 20.

I R



 

1; 2 , 22.

I R

 

Giải:

Đặt

w a bi 

với

; ;a b c  

 

   

 

   

2 2

1 3 4

3 4

3 4 25

3 4 4 3 4 3

3 4 3

3 4 4

25 25 25

a b i i

a b i

w i z i z

a b b a

b a

a b

z i z

 

  

 

 

 

     



    

 

 

    

Mà

   

2 2

3 4 4 3 4 3

4 4 3 4 4 3 4 3 100

 2 399



a b b a

z a b b a

a b b

    

         

   

 

2 2

 1 20a b   

Vậy tập hợp các điểm biểu diễn của số phức

là đường tròn

 

0;1 , 20

I R



Có bao nhiêu số phức

thỏa mãn:

 

3 6 5

1 2 1 12 15

z i

i z i



  





   





Giải:

Gọi M là điểm biểu diễn số phức

, do M thỏa mãn phương trình

3 6 5

z i   nên thuộc

đường tròn tâm

 

3;6

A , bán kính



Ta có:

 

1 12 15

1 2 1 12 15 5 2 3 5

1 2

i z i z z i



          





M thuộc đường tròn tâm

 

5;2

B , bán kính

3 5R



Nhận thấy

   

2 2

5 3 2 6 2 5 'AB R R      

Vậy 2 đường tròn tiếp xúc trong tại M, hay chỉ có một số phức

thỏa mãn bài toán.

Bài toán 9

Bài toán 10

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 59

Cho số phức

thỏa mãn

1 2

 

. Biết rằng tập hợp các điểm biểu diễn số phức





1 3 2

w i z

  

là một đường tròn. Tính bán kính của đường tròn đó.

Giải:

Cách 1:

Ta có:





2 3 3

1 3 2 1

1 3 1 3

w w i

w i z z z

i i

  

       

 

Suy ra

3 3 3 3

3 3

1 2 3 3 4

1 3

w i w i

w i

z w i

   

 

        



Như vậy bán kính của đường tròn là 4.

Cách 2:

Ta có:









 









 

1 3 2 1 3 1 3 3 3 3 1 3 1

w i z w i z i w i i z

              

Lấy môđun hai vế ta được:





3 3 1 3 . 1 2.2 4

w i i z

      

Cho các số phức

thỏa mãn

1 3.

 

Biết rằng tập hợp các điểm biểu diễn các số phức

với

 

3 2 2

i w iz

  

là một đường tròn. Tìm tọa độ tâm

và bán kính

của đường

tròn đó.

Giải:

Ta có

 

2 2 3 6 4

3 2 2

3 2 3 2 13 13 13 13

i w iz w z w i z i

i i

 







           











 

 

   

2 3 4 7 4 7 2 3

1 1 .

13 13 13 13 13 13 13 13

w i z i w i i z

     

  

  

  

             

  

  

  

  

  

     

Lấy môđun, hai vế ta được



4 7 2 3 3

. 1

13 13 13 13

w i i z

 







      











 



Vậy tập hợp các số phức

thuộc đường tròn tâm

4 7

;

13 13

 

















 

, bán kính

r 

Nhận xét: Bài này có rất nhiều cách giải tự luận nhưng cách này là tối ưu nhất. Quý thầy cô nên

nghiên cứu kỹ phương pháp giải này để truyền đạt cho học sinh.

Bài toán 11

Bài toán 12

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 60

Cho hai số phức

1 2

, z z

thỏa mãn

z  ,



được biểu diễn trong mặt phẳng phức lần

lượt là các điểm

, M N

. Biết góc tạo bởi giữa hai vectơ



và



bằng

. Tính giá trị của

biểu thức

1 2

z z







Giải:

Cách 1:

Dựng hình bình hành

OMPN

trong mặt phẳng phức, khi đó

1 2

z z OP

z z MN





 







 





Ta có

2 2

1 2 1 2 1 2

2 2

1 2 1 2 1 2

2 cos 30 13

2 cos150 1

z z z z z z





    







    





1 2

z z



  



Nhận xét: Thầy cô nên giải thích rõ cho học sinh hiểu tại tại lại là góc

và góc

150 .

Cách 2:

Giả sử

 

1 1 1 1 1 1 1

2 2 2

2 2

; ;

;

z a b i M a b OM a b

z a b i

N a b

ON a b









  



 

 

  

  

 



  













Theo giả thiết, ta có

2 2

1 1

2 2

a b





 







 





và

 

1 2 1 2

2 2 2 2

1 1 2 2

cos , cos 30 3.

a a b b

OM ON a a b b

a b a b



    

 

 

Ta có

   

2 2

1 2 1 2 1 2 1 2

1 2

2 2

1 2

1 2 1 2

a a b b i

a a b b

z z

a a b b i

a a b b

     



  



  

   

 

   

 

2 2 2 2

1 1 2 2 1 2 1 2

2 2 2 2

1 1 2 2 1 2 1 2

3 4 2.3

13.

3 4 2.3

a b a b a a b b

    

 

  

 

    

Bài toán 13

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 61

III. SỬ DỤNG MÁY TÍNH CASIO 570 VN- PLUS

Đây là một trong những bài toán điển hình nhất dùng máy tính CASIO để giải bài toán tìm tập

hợp điểm của số phức. Các bài toán khác ta làm tương tự.

Trên mặt phẳng Oxy tìm tập hợp biểu diễn các số phức thỏa mãn điều kiện

 

2| |

– 2zi i

 

2 1 0x y  

   

2 2

1 – 2 9

x y

  

   

2 2

1 2 4

x y

   

3 4 2 0x y  

Hướng dẫn:

Ta giả sử:

z A Bi 

Nên điều kiện của bài toán được viết lại là:

   

 – 2 2 0.

A Bi i i

   

và nhập điều kiện vào:

 Thử đáp án A.

2 1 0 1 2x y x y    

Cho

1y 

ta được

1x  

Nhập

rp1=1=

thu được kết quả khác 0.

>>> Loại đáp án A.

 Thử đáp án B.

   

2 2

1 – 2 9

x y

  

Cho

1x  

ta được

5y 

hoặc

1y  

rp1=5=

ra kết quả khác 0.

>>> Loại đáp án B

 Thử đáp án C.

   

2 2

1 2 4

x y

   

Cho

1x 

ta được

0y 

và

4y  

r1=0=

và

r1=p4=

đều được kết quả bằng 0.

Vậy đáp án đúng là C.

Bài toán 1

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 62

[Đề minh họa của bộ GD-ĐT lần 1-2017]

Cho các số phức

thỏa mãn



. Biết rằng tập hợp các điểm biểu diễn các số phức

 

3 4

w i z i  

là một đường tròn. Tính bán kính

của đường tròn đó.

4r 

5r 

20r 

22r 

Hướng dẫn:

 Để xây dựng 1 đường tròn ta cần 3 điểm biểu diễn của

, vì

sẽ sinh ra

nên đầu tiên ta

sẽ chọn 3 giá trị đại diện của

thỏa mãn



 Chọn

4 0z i 

(thỏa mãn



). Tính

  

3 4 4 0

w i i i   

(3+4b)O4+b=

Ta có điểm biểu diễn của

là

 

12;17

 Chọn

4z i

(thỏa mãn



). Tính

  

3 4 4

w i i i  

(3+4b)O4b+b=

Ta có điểm biểu diễn của

là

 

16;13



 Chọn

4z i 

(thỏa mãn



). Tính

  

3 4 4

w i i i   

(3+4b)(p4b)+b=

Ta có điểm biểu diễn của

là

 

16; 11



Vậy ta có 3 điểm

, ,M N P

thuộc đường tròn biểu diễn số phức

 Đường tròn này sẽ có dạng tổng quát

2 2

0x y ax by c    

. Để tìm

, ,a b c

ta sử dụng

máy tính Casio với chức năng MODE 5 3

w5212=17=1=p12dp17d=p16=

13=1=p16dp13d=16=p11=1=

p16dp11d==

Vậy phương trình đường tròn biễu diễn số phức

là:

Bài toán 2

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 63

 

2 2 2 2

2 399 0 1 20

x y y x y       

Bán kính đường tròn tập hợp điểm biểu diễn số phức

là 20



Đáp án chính xác là C.

Tập hợp điểm biểu diễn số phức

thỏa mãn

2 1 2z z z i

   

là một Parabol có dạng:

3 6 2y x x  

y x 

 

y x x

  

Hướng dẫn:

 Đặt số phức

z x yi 

 Nếu đáp số A đúng thì đúng với mọi

z x yi 

thỏa mãn

3 6 2y x x  

Chọn một cặp

 

;x y

bất kì thỏa

3 6 2y x x  

ví dụ

 

0;2 2A z i 

Xét hiệu

2 1 2z z z i

   

2qc2bp1$pqc2bp(p2b)+2b=

Vậy

2 1 2 6 2 5 0

z z z i

       

2 1 2z z z i

    



Đáp số A sai

 Tương tự với đáp số B chọn

z i

 

. Xét hiệu

2 1 2z z z i

   

2qc1pabR2$p1$pqc1pab

R2$p(1+abR2$)+2b=

Vậy

2 1 2 0

z z z i

    

2 1 2z z z i

    



Đáp số B chính xác.

Bài toán 3

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 64

IV. BÀI TẬP RÈN LUYỆN

1. ĐỀ BÀI

Câu 1. Cho số phức

6 7z i 

. Số phức liên hợp của

có điểm biểu diễn là:

 

6;  7

. B.

 

6; 7

. C.

 

6; 7

. D.

 

6;  7 

Câu 2. Điểm biểu diễn của số phức

1 3





là

 

1; 3

. B.

1 3

;

5 5

 

















 

. C.

 

3; 2

. D.

 

4; 1

Câu 3. Số phức

3 4





có điểm biểu diễn là:

; 2

 



















 

. B.

 

3; 4

. C.

 

3; 4 

. D.

 

3; 4



Câu 4. Cho số phức

3 2z i 

có điểm biểu diễn hình học là:

 

2; 3



. B.

 

3;2

. C.

 

2;3

. D.

 

2; 3

 

Câu 5. Biểu diễn về dạng

z a bi 

của số phức

2016

(1 2 )





là số phức nào?

3 4

25 25



. B.

3 4

25 25

 

. C.

3 4

25 25



. D.

3 4

25 25

 

Câu 6. Điểm M biểu diễn số phức

2019

3 4i





có tọa độ là

3(4;M 

) B.

 

3; 4



 

3;4

 

4; 3



Câu 7. Điểm biểu diễn số phức

(2 3 )(4 )

3 2

i i

 





có tọa độ là

 

1; 4

. B.

 

1; 4 

. C.

 

1;4

. D.

 

1;4

Câu 8. Điểm biểu diễn hình học của số phức

z a ai 

nằm trên đường thẳng:

y x

2y x

y x 

2y x 

Câu 9. Gọi

là điểm biểu diễn của số phức

5 8i

và

là điểm biểu diễn của số phức

5 8 .i 

Chọn mệnh đề đúng trong các mệnh đề sau

A. Hai điểm

và

đối xứng với nhau qua trục hoành.

B. Hai điểm

và

đối xứng với nhau qua trục tung.

C. Hai điểm

và

đối xứng với nhau qua gốc toạ độ O.

D. Hai điểm

và

đối xứng với nhau qua đường thẳng

.y x

Câu 10. Gọi

là điểm biểu diễn của số phức

2 5z i 

và

là điểm biểu diễn của số phức

2 5z i



  

. Tìm mệnh đề đúng trong các mệnh đề sau:

A. Hai điểm

và

đối xứng với nhau qua trục hoành

B. Hai điểm

và

đối xứng với nhau qua trục tung

C. Hai điểm

và

đối xứng với nhau qua gốc toạ độ

D. Hai điểm

và

đối xứng với nhau qua đường thẳng

y x

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 65

Câu 11. Gọi

là điểm biểu diễn của số phức

3 2z i 

và

là điểm biểu diễn của số phức

2 3z i



 

Tìm mệnh đề đúng trong các mệnh đề sau:

A. Hai điểm

và

đối xứng với nhau qua trục hoành.

B. Hai điểm

và

đối xứng với nhau qua trục tung.

C. Hai điểm

và

đối xứng với nhau qua gốc toạ độ

D. Hai điểm

và

đối xứng với nhau qua đường thẳng

y x

Câu 12. Trên mặt phẳng tọa độ

Oxy

, cho số phức

z x yi 

 

,x y

 

các điểm biểu diễn

và

đối xứng nhau qua

A. trục

. B. trục

C. gốc tọa độ

. D. đường thẳng

y x

Câu 13. Điểm biểu diễn của các số phức

7z bi 

với

b  

, nằm trên đường thẳng có

phương trình là:

7x 

. B.

7y 

. C.

y x

. D.

7y x 

Câu 14. Điểm biểu diễn của các số phức

z n ni 

với

n  

, nằm trên đường thẳng có

phương trình là:

2y x

. B.

2y x 

. C.

y x

. D.

y x 

Câu 15. Cho số phức

z a a i 

với

a  

. Khi đó điểm biểu diễn của số phức liên hợp của

nằm trên:

A. Đường thẳng

2y x

. B. Đường thẳng

1y x  

C. Parabol

y x

. D. Parabol

y x 

Câu 16. Tập hợp các điểm trong mặt phẳng biểu diễn cho số phức

thỏa mãn điều kiện

z i

 

là:

A. Một đường thẳng. B. Một đường tròn.

C. Một đoạn thẳng. D. Một hình vuông.

Câu 17. Trong mặt phẳng phức, gọi

, ,A B C

lần lượt là các điểm biểu diễn của các số phức

1 3z i  

1 5z i 

4z i 

. Số phức với điểm biểu diễn

sao cho tứ giác

ABCD

là một hình bình hành là:

2 3i

. B.

2 .i

. C.

2 3 .i

. D.

3 5 .i

Câu 18. Gọi

và

là các nghiệm phức của phương trình

4 9 0z z  

. Gọi

,M N

là các điểm

biểu diễn của

và

trên mặt phẳng phức. Khi đó độ dài của

là:

4.MN 

. B.

5.MN 

2 5.MN  

2 5.MN 

Câu 19. Gọi

và

là các nghiệm của phương trình

4 9 0z z  

. Gọi

, ,M N P

lần lượt là các

điểm biểu diễn của

1 2

,z z

và số phức

k x yi 

trên mặt phẳng phức. Khi đó tập hợp

điểm

trên mặt phẳng phức để tam giác

MNP

vuông tại

là:

A. đường thẳng có phương trình

5.y x 

B. là đường tròn có phương trình

2 2

2 8 0.x x y   

C. là đường tròn có phương trình

2 2

2 8 0,x x y   

nhưng không chứa

, .M N

D. là đường tròn có phương trình

2 2

4 1 0x x y   

nhưng không chứa

, .M N

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 66

Câu 20. Giả sử

,A B

theo thứ tự là điểm biểu diễn của các số phức

1 2

,z z

. Khi đó độ dài của véctơ



bằng:

1 2

.z z

1 2

.z z

2 1

.z z

2 1

.z z

Câu 21. Biết

 

z i i z

  

, tập hợp điểm biểu diễn số phức

có phương trinh

2 2

2 1 0x y y    

. B.

2 2

2 1 0x y y   

2 2

2 1 0x y y   

. D.

2 2

2 1 0x y y  

Câu 22. Tập hợp điểm biểu diễn số phức

, biết

3 4 2

zi   là

A. điểm. B. đường thẳng. C. đường tròn. D. elip.

Câu 23. Trong mặt phẳng phức cho

ABC

vuông tại

. Biết rằng

lần lượt biểu diễn các

số phức

2 2z i 

2 4z i  

. Khi đó,

biểu diễn số phức:

2 4z i 

. B.

2 2z i  

. C.

2 4z i 

. D.

2 2z i  

Câu 24. Trên mặt phẳng tọa độ

Oxy

, tập hợp các điểm biểu diễn số phức

thỏa mãn điều kiện

số phức

 

2 2

zi i

  

là:

3 4 2 0x y  

. B.

   

2 2

1 2 9

x y

   

   

2 2

1 2 4

x y

   

. D.

2 1 0x y  

Câu 25. Trong mặt phẳng tọa độ

Oxy

, tập hợp điểm biểu diễn số phức

thỏa mãn

 

1 1

z i z

  

là:

A. Đường tròn có tâm

(0; 1)I 

, bán kính

2r 

B. Đường tròn có tâm

(0;1)I

, bán kính

2r 

C. Đường tròn có tâm

(1;0)I

, bán kính

2r 

D. Đường tròn có tâm

( 1;0)I 

, bán kính

2r 

Câu 26. Tập hợp các điểm trong mặt phẳng biểu diễn cho số phức

thỏa mãn điều kiện

1 2 4

z i

  

là:

A. Một đường thẳng B. Một đường tròn

C. Một đoạn thẳng D. Một hình vuông

Câu 27. Tập hợp các điểm trong mặt phẳng biểu diễn số phức

thỏa mãn điều kiện

là một

số thực âm là:

A. Trục hoành (trừ gốc

). B. Đường thẳng

y x

(trừ gốc

C. Trục tung (trừ gốc

). D. Đường thẳng

y x 

(trừ gốc

Câu 28. Giả sử

là điểm trên mặt phẳng phức biểu diễn số phức

. Tập hợp các điểm

thoả

mãn điều kiện sau đây:

1 2

z i

  

là một đường tròn:

A. Có tâm

 

1; 1 

và bán kính là 2. B. Có tâm

 

1; 1

và bán kính là

C. Có tâm

 

1; 1



và bán kính là 2. D. Có tâm

 

1; 1

và bán kính là 2.

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 67

Câu 29. Giả sử

 

M z

là điểm trên mặt phẳng phức biểu diễn số phức

. Tập hợp các điểm

 

M z

thoả mãn điều kiện sau đây:

2 1

z i  

là một đường thẳng có phương trình:

4 2 3 0x y  

. B.

4 2 3 0x y   

4 2 3 0x y  

. D.

2 2 0x y  

Câu 30. Tập hợp các điểm nằm trong mặt phẳng phức biểu diễn các số phức

thoả mãn điều

kiện sau đây:

3 4

z z

  

là hai đường thẳng:

 

và

 

. B.



và

 



và



. D.

 

và



Câu 31. Tập hợp các điểm nằm trong mặt phẳng phức biểu diễn các số phức

thoả mãn điều

kiện sau đây:

1 2

z z i

   

là hai đường thẳng:

1 3





và

1 3





. B.

1 3

 



và

1 3





1 3





và

1 3



 

. D.

1 3

 



và

1 3



 

Câu 32. Cho số phức

. ( , )z x y i x y   

. Tập hợp các điểm biểu diễn của

sao cho

z i





là

một số thực âm là:

A. Các điểm trên trục hoành với

1 1x  

B. Các điểm trên trục tung với

1 1y  

C. Các điểm trên trục hoành với



 









D. Các điểm trên trục tung với



 









Câu 33. Gọi

, ,M N P

lần lượt là các điểm biểu diễn cho các số phức

1 5z i 

3z i 

6z 

, ,M N P

là 3 đỉnh của tam giác có tính chất:

A. Vuông. B. Vuông cân. C. Cân. D. Đều.

Câu 34. Gọi

, , ,A B C D

lần lượt là các điểm biểu diễn cho các số phức

7 3z i 

8 4z i 

1 5z i 

2z i 

. Tứ giác

ABCD

là:

A. là hình vuông. B. là hình thoi.

C. là hình chữ nhật. D. là hình bình hành.

Câu 35. Gọi

, ,A B C

lần lượt là các điểm biểu diễn cho các số phức

1 2 3

1 3 ; 3 2 ; 4z i z i z i       

. Chọn kết luận sai:

A. Tam giác

ABC

vuông cân. B. Tam giác

ABC

cân.

C. Tam giác

ABC

vuông. D. Tam giác

ABC

đều.

Câu 36. Tập hợp các điểm

biểu diễn cho số phức

thoả mãn

z i z i

   

có dạng là

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 68

2 2

4 3

x y

 

. B.

2 2

16 9

x y

 

2 2

16 9

x y

 

. D.

2 2

4 3

x y

 

Câu 37. Gọi

, ,A B C

lần lượt là điểm biểu diễn của các số phức

1 2 3

3 2 , 2 3 , 5 4z i z i z i     

Chu vi của tam giác ABC là :

22 2 58 

. B.

26 2 58 

22 2 2 56 

. D.

26 2 2 58 

Câu 38. Cho các điểm

, ,A B C

trong mặt phẳng phức theo thứ tự được biểu diễn bởi các số:

1 ;2 4 ;6 5i i i  

. Tìm số phức biểu diễn điểm

sao cho tứ giác

ABDC

là hình bình

hành:

7 8i

. B.

5 2i

3

. D.

3 8i 

Câu 39. Cho

,  , A B M

lần lượt là điểm biểu diễn của các số phức

4; 4 ; 3i x i 

. Với giá trị thực

nào của

thì

,  , A B M

thẳng hàng :

1x 

. B.

2x  

1x  

. D.

2x 

Câu 40. Trong mặt phẳng

Oxy

cho điểm

biểu diễn số phức

1 2z i 

là điểm thuộc

đường thẳng

2y 

sao cho tam giác

OAB

cân tại

biểu diễn số phức nào sau đây:

1 2z i  

. B.

2z i 

1 2z i 

. D.

1 2z i  

Câu 41. Cho các số phức

21 3

1 3 ; 2+2 ; 1z i z i z i      

được biểu diễn lần lượt bởi các

điểm

,  , A B C

trên mặt phẳng. Gọi

là điểm thỏa mãn:

AM AB AC 

  

. Khi đó

điểm

biểu diễn số phức:

6z i 

. B.

2z 

2z  

. D.

6z i

Câu 42. Tromg mặt phẳng phức cho hai điểm

 

4; 0

 

0; 3



. Điểm

thỏa mãn:

OC OA OB 

  

. Khi đó điểm

biểu diễn số phức:

4 3z i 

. B.

3 4z i  

3 4z i  

. D.

4 3z i 

Câu 43. Trong mặt phẳng tọa độ

Oxy

, tập hợp điểm biểu diễn các số phức

thỏa mãn điều

kiện

 

3 4 2

z i

  

là:

5x 

   

2 2

3 4 4

x y

   

2y  

2 2

4x y 

Câu 44. Cho

, ,A B C

là ba điểm trong mặt phẳng phức theo thứ tự biểu diễn các số:

1 ; 1 ;2i i i   

. Tính

.AB BC

 

A. – 7. B. 5.

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 69

C. – 2. D. – 6.

Câu 45. Trong mặt phẳng tọa độ

Oxy

, tìm tập hợp điểm

biểu diễn số phức



thỏa mãn điều

kiện

 

1 2 3

i z

   

, biết z là số phức thỏa mãn

2 5

 

   

2 2

1 4 125

x y   

   

2 2

5 4 125

x y   

   

2 2

1 2 125

x y   

2x 

2. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI CHI TIẾT

10B

11D

12A

13A

14D

15C

16B

17A

18D

19D

20C

21B

22C

23A

24C

25D

26B

27C

28A

29A

30B

31A

32B

33A

34A

35D

36A

37D

38A

39C

40A

41D

42A

43B

44D

45A

Câu 1. Chọn A.

Câu 2. Ta có

2 1 3

1 3 5 5

z i

  



. Chọn B.

Câu 3. Số phức

3 4 3

2 2

z i



  

có tọa độ điểm biểu diễn là

; 2

 



 

 

. Chọn A.

Câu 4. Số phức..có tọa độ điểm biểu diễn là





2; 3



. Chọn A.

Câu 5. Ta có

2016

3 4

25 25

(1 2 )

z i

   



(Dùng Casio). Chọn D.

Câu 6.

2019 4.504 3 3

, 4 3i i i i z i



      

. Suy ra điểm biểu diễn có tọa độ là

 

4; 3

. Chọn D.

Câu 7. Ta có

(2 3 )(4 )

1 4

3 2

i i

z i

 

   



. Chọn B.

Câu 8. Ta có:

 

;M a a

biểu diễn nên

z a ai 

. Chọn A.

Câu 9. Tọa độ điểm

   

5;8 , 5;8

A B 

ta thấy hai điểm đối xứng nhau qua trục tung

 

. Chọn B.

Câu 10. Ta có:

   

2;5 & 2;5

 biểu diễn 2 số phức trên đối xứng qua

nên Chọn B.

Câu 11.

 

3 2 3;2

z i A  

;

 

2 3 2;3

z i B



  

5 5

;

2 2

 

















 

là trung điểm

nằm trên

y x

và

:AB d y x 

. Chọn D.

Câu 12. Số phức

z x yi 

 

,x y

 

có điểm biểu diễn là

 

;M x y

. Số phức

z x yi 

 

,x y 



có

điểm biểu diễn là

 

' ;

M x y



, 'M M

đối xứng qua

. Chọn A.

Câu 13. Điểm biểu diễn của các số phức

7z bi 

với



là

 

7;M b

nằm trên đường thẳng

7x 

. Chọn A.

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 70

Câu 14. Điểm biểu diễn của các số phức

z n ni 

với



là điểm

 

n, n



nằm trên đường

thẳng có phương trình là:

y x 

. Chọn D.

Câu 15. Điểm biểu diễn của các số phức

z a a i 

với



là điểm

 

,M a a

nằm trên

đường có phương trình là:

y x

. Chọn C.

Câu 16. Chọn B.

Câu 17. Gọi

 

; ;D x y z

là điểm biểu diễn số phức

; ,z x yi x y    

Ta có

     

1; 3 ; 1;5 ; 4;1

A B C

ABCD

là hình bình hành, nên

4 2 2

2 3

1 2 3

x x

AB CD z i

y y

 

 

  

 

     

 

 

  

 

 

 

. Chọn A.

Câu 18. Hai nghiệm phức của phương trình đã cho là

1 2

2 5 ; 2 5z i z i

   

Nên









2; 5 , 2; 5

M N 

2 5MN

 

. Chọn D.

Câu 19.

   

2; 5 , 2; 5

M N 

;

 

;P x y

. Tam giác

MNP

vuông tại

, nên

 

2 2 2

. 0 2 5 0 4 1 0

MP NP x y x x y

          

 

. Chọn D.

Câu 20. Giả sử:

   

1 1 2 2

; ; ;A x y B x y

là điểm biểu diễn hai số phức

1 1 1 2 2 2 1 2 1 2

; ; , , ,z x y i z x y i x x y y      

 

   

2 2

2 1 2 1

2 2

2 1 2 1 2 1

;

AB x x y y

z z x x y y i

z z x x y y



   

  





 

    

 



    





. Chọn C.

Câu 21. Gọi

 

;M x y

là điểm biểu diến số phức

; ;z x yi x y    

          

     

2 2 2

1 1 1 1

1 2 1 0

z i i z x y i i x yi x y i x y x y i

x y x y x y x y y

               

           

Chọn B.

Câu 22. Gọi

 

;M x y

là điểm biểu diến số phức

; ;z x yi x y    

 

2 2

3 4 2 3 4 2 4 3 3 2

4 2

4 3 9 2

3 9

zi i x yi y xi

y x x y

         

 

       

 

 

Chọn C.

Câu 23.

     

2; 2 ; 2;4 ; ;A B C x y

 

;

vuông tại nên

      

. 0 2 2 2 4 0

AC BC x x y y

       

 

. Chọn A.

Câu 24. Gọi

 

;M x y

là điểm biểu diến số phức

; ;z x yi x y    

       

2 2

2 2 2 1 2 1 2 4

zi i y x i x y

             

. Chọn C.

Câu 25. Gọi điểm

 

;M x y

là điểm biểu diễn cho số phức

 

, ,z x yi x y  



ABC

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 71

Ta có:

          

1 1 1 1 1

z i z x yi i x yi x yi x y x y i

               

       

2 2 2 2

1 2 1 0 1 2

x y x y x y x y x x y

               

Gọi điểm

 

;M x y

là điểm biểu diễn cho số phức

 

, ,z x yi x y

   

Ta có:

   

1 1 1 1 1 1

z i x yi i x y i x y

             

 

1 1

x y

   

là đường tròn . Chọn D.

Câu 26. Gọi điểm

 

;M x y

là điểm biểu diễn cho số phức

 

, ,z x yi x y  



Ta có:

   

1 2 4 1 2 4 1 2 4

z i x yi i x y i

            

       

2 2 2 2

1 2 4 1 2 16

x y x y

         

là đường tròn . Chọn B.

Câu 27. Đặt

 

,z a bi a b  



. Điểm biểu diễn số phức

là

 

;M a b

Khi đó

 

2 2 2

2z a bi a b abi

    

là một số thực âm khi

   

2 2

0; , 0

. 0

a b

M b b

a b





 

 

  

 









Vậy tập hợp điểm

biểu diễn số phức

là trục tung (trừ gốc tọa độ

). Chọn C.

Câu 28. Xét hệ thức:

1 2

z i

  

(1). Đặt

     

, 1 1 1z x yi x y z i x y i

         

Khi đó (1)



2 2

( 1) ( 1) 2x y   

   

2 2

1 1 4

x y

    



Tập hợp các điểm

trên mặt

phẳng toạ độ biểu diễn số phức

thoả mãn (1) là đường tròn có tâm tại

 

1; 1



và bán kính

2R 

. Chọn A.

Câu 29. Xét hệ thức

z z i  



( 2)

z z i   

(*)

Gọi

là điểm biểu diễn số -2, còn

là điểm biểu diễn số phức

   

2;0 , 0;1

A B

Đẳng thức (*) chứng tỏ

( ) ( )M z A M z B

Vậy tập hợp tất cả các điểm

 

M z

chính là đường trung trực của

Chú ý: Ta có thể giải cách khác như sau:

Giả sử

z x yi 

, khi đó:

(2)

       

2 2

2 1 2 1 4 2 3 0

x yi x y i x y x y x y

                

Vậy tập hợp các điểm

 

M z

là đường thẳng

4 2 3 0x y  

. Chọn A.

Nhận xét: Đường thẳng

4 2 3 0x y  

chính là phương trình đường trung trực của đoạn

Câu 30. Xét hệ thức:

3 4

z z

  

(1)

Đặt

 

,z x yi x y  





z x yi 

, do đó

   

3 4

x yi x yi

     

2 3 4

x x

    

hoặc

 

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 72

Vậy tập hợp tất cả các điểm

là hai đường thẳng song song với trục tung



và

 

Chọn B.

Câu 31. Xét hệ thức:

1 2

z z i

   

. Đặt

z x yi 



z x yi 

Khi đó: (2)

   

1 2 1 2 1 2 1 4 2 2 1 0

y i y y y

           



1 3





hoặc

1 3





. Vậy tập hợp các điểm

là hai đường thẳng song song với trục

hoành

1 3





. Chọn A.

Câu 32.

 

   

 

   

2 2

2 2 2

1 1

1 1 1

x y i x y i

x y

x y i

z i x

z i

x y i

x y x y x y

   

   

 

 



   

   

   



 

     

z i





là một số thực âm khi

 

2 2

1 1

1 0

x y



 











  

 

 

  

  

 









 





. Chọn B.

Câu 33.

     

1 2 3

1 5 1;5 ; 3 3; 1 ; 6 6; 0

z i M z i N z P

         

Ta có

   

2; 6 , 3;1

MN NP  

 

. 2.3 6.1 0, 4 36 40, 9 1 10MN NP MN NP MN

          

 

Vậy

MNP

là tam giác vuông tại

. Chọn A.

Câu 34.

 

7 3 7; 3

z i A

   

;

 

8 4 8;4

z i B  

 

1 5 1;5

z i C  

;

 

2 0; 2

z i D

   

Ta có

   

1;7 , 7;1

. 0

AB BC







   









 

Vậy

ABCD

là hình vuông. Chọn A.

Câu 35.

     

1 2 3

1 3 1; 3 ; 3 2 3; 2 ; 4 4;1

z i A z i B z i C

             

Suy ra

   

2; 5 , 5; 2

. 0

AB AC







     









 

Vậy tam giác

ABC

vuông cân tại

. Chọn D.

Câu 36. Đặt

 

,z x yi x y  



. Suy ra

 

;M x y

biểu diễn dố phức

Ta có:

4 4

z i z i x yi i x yi i

          

       

2 2

1 1 4 1 1 4 (*)

x y i x y i x y x y             

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 73

Đặt

   

1 2

0; 1 , 0;1

F F . Thì

2 1 1 2

(*) 4 2MF MF F F

    

. Suy ra tập hợp các điểm

là elip

 

có 2 tiêu điểm

. Phương trình chính tắc của

 

có dạng

 

2 2

2 2 2

2 2

1 0;

x y

a b b a c

a b

     

Ta có :

1 2

2 2 1F F c c   

2 2

2 1

4 2 2 3

MF MF a a b a c         .

Vậy

 

2 2

: 1

4 3

x y

 

. Chọn A.

Câu 37.

     

1 2 3

3 2 3;2 ; 2 3 2; 3 ; 5 4 5;4

z i A z i B z i C         

Suy ra ta được

     

1; 5 , 3;7 , 2;2

AB BC AC    

  

2 2 2 2 2 2

1 5 26, 3 7 58, 2 2 2 2AB BC AC

         

Vậy

26 2 2 58

ABC

ChuVi



  

. Chọn D.

Câu 38. Theo giả thiết ta có

     

1;1 , 2; 4 , 6;5

A B C

Gọi

 

;D x y

, khi đó

   

1; 3 , 6; 5

AB CD x y

   

 

Tứ giá

ABDC

là hình bình hành khi

1 6 7

3 5 8

x x

AB CD

y y

 

  

 

  

 

  

 

 

 

. Chọn A.

Câu 39: Theo giả thiết ta có

     

4;0 , 0;4 , ;3A B C x

 .Ta có

   

4;4 , 4;3

AB AC x  

 

, ,A B M

thẳng hằng

,AB AC



 

cùng phương

4 3

. 1

4 4

AB k AC k x



      

 

. Chọn C.

Câu 40.

Cách 1.

Theo giả thiết

   

1;2 , ;2 , 1

A B x x



thì

biểu diễn số phức

2z x i 

Tam giác

OAB

cân tại

2 2 2 2 2 2

2 1 2OB OA x     

1x 

(loại) hoặc

1x  

(nhận)

Vậy

1 2z i  

Cách 2.

Dễ thấy

,A B

cùng nằm trên

: 2d y 

nên tam giác

OAB

cân tại

khi và chỉ khi

,A B

đối xứng

qua

. Vậy

 

1;2

B 

và do đó

1 2z i  

. Chọn A.

Câu 41. Gọi

 

; , ,M x y x y

 

thì

biểu diễn cho số phức

z x yi 

Theo giả thiết

     

1;3 , 2;2 , 1; 1

A B C

  

Từ

1 1 0

3 3 6

x x

AM AB AC AM CB

y y

 

   

 

     

 

  

 

 

    

. Vậy

6z i

. Chọn D.

Câu 42. Gọi

 

; , ,C x y x y

 

thì

biểu diễn cho số phức

z x yi 

 

4;0

OA 



 

0; 3

 



. Suy ra

 

4; 3

OA OB

  

 

Theo giả thiết

   

4; 3 4; 3

OC OA OB OC C

      

   

.Vậy

4 3z i 

. Chọn A.

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 74

Câu 43: Gọi

 

; , ,M x y x y

 

thì

biểu diễn cho số phức

z x yi 

Ta có

             

2 2 2 2

3 4 2 3 4 2 3 4 2 3 4 4

z i x y i x y x y

                 

Chọn B.

Câu 44. Ta có

     

1;1 , 1; 1 , 0;2

A B C  

. Suy ra

   

0; 2 , 1;3

AB BC  

 

Do đó

       

. 0 . 1 2 . 3 6

AB BC

    

 

. Chọn D.

Câu 45. Gọi

 

; , ,M x y x y

 

thì

biểu diễn cho số phức

x yi



 

 

3 2 3 2 6

1 2 3

1 2 5 5

x yi x y x y

i z z i



     

      



Theo giả thiết

   

2 2

2 7 2 6

2 5 5 2 7 2 6 625

5 5

x y x y

z i x y x y

   

           

Suy ra

   

2 2

1 4 125

x y   

. Chọn A.

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 75

D. BÀI TOÁN CỰC TRỊ CỦA SỐ PHỨC

I. PHƯƠNG PHÁP QUY VỀ TÌM MIN-MAX CỦA HÀM MỘT BIẾN KẾT HỢP

SỬ DỤNG TÍNH CHẤT CỦA SỐ PHỨC.

Bài toán: Trong các số phức

thoả mãn điều kiện T. Tìm số phức

để biểu thức P đạt

giá trị nhỏ nhất, lớn nhất.

Phương pháp tổng quát: Đặt

 

;z x yi x y

   

Từ điều kiện T, biến đổi để tìm cách rút ẩn rồi thế vào biểu thức P để được hàm một biến.

Tìm giá trị lớn nhất (hoặc nhỏ nhất) tuỳ theo yêu cầu bài toán của hàm số một biến vừa

tìm được.

Sử dụngcác tính chất và các bất đẳng thức về môđun của số phức sau để giải quyết các bài

toán min-max:



 ' '

 . ' . '



z z

z z z z

z z

 

   

   

 

 

 

 

 

1 2 1 2

 0; 0 0;

 ,  , 

 + 

 ' ' '

 . . 



z z z

z z z z z z

z z z z

z z z z z z

z z z z

    

    

  

     

 

Kết hợp sử dụng các bất đẳng thức liên hệ giữa trung bình cộng và trung bình nhân, BĐT

Bunhia- Cốpxki.

 Bất đẳng thức Bunhiacopxki :Cho các số thực

, , ,a b x y

ta luôn có

 

  

2 2 2 2

ax by a b x y

   

. Dấu = xảy ra

a b

x y

 

 Bất đẳng thức Vectơ : Cho 2 vecto

 

;u x y



và

 

'; 'v x y



ta luôn có

u v u v  

  

   

2 2

2 2 2 2

' ' ' 'x y x y x x y y

       

Dấu = xảy ra

' '

x y

  

Phương pháp 1

Phương pháp 2

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 76

MỘT SỐ BÀI TOÁN ĐIỂN HÌNH

Trong các số phức

thoả mãn điều kiện

1 5 3

z i z i    

, tìm số phức

có môđun

nhỏ nhất.

Giải:

Gọi

 

;z x yi x y

   

2 2 2 2

1 5 3 ( 1) ( 5) ( 3) ( 1)

z i z i x y x y            

3 4 0 4 3x y x y      

2 2 2 2 2

6 8 2 10

(4 3 ) 10 24 16 10

5 5 5

z x y y y y y y

 







           











 

Đẳng thức xảy ra khi

6 2

5 5

y x

  

Vậy

đạt giá trị nhỏ nhất bằng

2 10

khi

2 6

5 5

z i

 

. Vậy

2 6

5 5

z i

 

là số phức cần tìm.

Cho các số phức

thỏa mãn

2 5

z m m

  

, với

là tham số thực. Biết rằng tập hợp

các điểm biểu diễn các số phức

 

3 4 2w i z i  

là một đường tròn. Bán kính nhỏ nhất

của đường tròn đó bằng?

Giải :

Cách 1 : Gọi

w x yi 

Từ giả thiết, ta có

 

3 4 8 4 3 6

3 4 2 .

3 4 25 25

x y i

x y x y

x yi i z i z i

 

   

       



   

2 2

3 4 8 4 3 6

x y x y

    

 

Mà

   

 

2 2

2 2 2

2 5 3 4 8 4 3 6 25 2 25

z m m x y x y m m           

     

2 2

2 2 2

2 2 2 2

4 4 25 1 4 2 25 1 4 400 20 .

x y y m x y m

   

              

   

   

Vậy bán kính nhỏ nhất của đường tròn đó là 20. Dấu

'' ''

xảy ra khi

1m  

Cách 2: Từ giả thiết, ta có

 

2 3 4w i i z  

Lấy môđun hai vế, ta được

 

2 3 4 . 5. 2 5 5 1 4 20.

w i i z m m m

 

         

 

 

Bài toán 1

Bài toán 2

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 77

Trong các số phức

có phần thực, phần ảo không âm và thoả mãn:

1 2

z i





 

Tìm số phức

sao cho biểu thức

 

2 2 2 2

. . (1 ) (1 )P z z z z i z i z i

 

      

 

 

đạt giá trị lớn

nhất, nhỏ nhất.

Giải:

Điều kiện:

1 2z i 

. Gọi

 

;z x yi x y



  





              

 

  

2 2 2 2

1 1 3 1 2 ( 3) ( 1) ( 2)

1 2

 1

z z i x y x y

z i

x y

(luôn thoả mãn điều kiện vì

1; 2x y  

không thoả mãn phương trình)

2 2 2 2

4 . 4z x yi z z xy i z z xy

       

(vì

;x y

không âm).

(1 ) (1 ) 2 2z i z i x y    

Do đó

2 2 2 2

16 4 .(2 2 ) 16 8P x y xy x y x y xy    

Đặt

2 4

x y

t xy t

 









    











 

, ta có

16 8 ; 0;

P t t t

 

 

  

 

 

+ Xét hàm số

( ) 16 8f t t t 

liên tục trên

 

 

 

'( ) 32 8 ; '( ) 0 0

f t t t f t t t

       

(loại)

1 1

0; 0;

4 4

1 33 33 1

(0) 0; max ( ) ; min ( ) 0 0

4 16 16 4

f f f t t f t t

   

   

   

 







        











 

Khi

0; 1

1 1

; Khi 0

1; 0

2 2

x y

t x y t

x y



 



     



 





Vậy P đạt giá trị lớn nhất bằng

33 1 1

khi

16 2 2

z i

 

P đạt giá trị nhỏ nhất bằng

0 khi 1 0z z  

Nhận xét: Bài tập này cũng có thể giải được bằng cách rút

1y x 

và thế vào biểu thức

ta được hàm số

2 2

( ) 16 (1 ) 8 (1 )g x x x x x   

rồi đi tìm giá trị lớn nhất, giá trị nhỏ nhất của

hàm số

( )g x

trên

0;1

 

 

 

Trong các số phức

thỏa mãn điều kiện

2 4 2z i z i   

.Tìm số phức

có môđun

nhỏ nhất.

Giải:

Giả sử số phức

cần tìm có dạng

    ,( )z x yi x y

được biểu diễn bởi điểm M(x;y).

Bài toán 3

Bài toán 4

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 78

Ta có

2 ( 4) ( 2)x y i x y i     

(1)

2 2 2 2

( 2) ( 4) ( 2)x y x y      

4y x   

Mặt khác

2 2 2 2 2

8 16 2 8 16

z x y x x x x x        

Hay

 

2 2 8 2 2

z x   

. Do đó

min

2 2

z x y

   

. Vậy

2 2z i 

Trong các số phức

thỏa mãn

 1.

Tìm số phức

để

  

1 3 1

z z

đạt giá trị lớn nhất

Giải:

Giả sử

 

   

, ,z x yi x y

Vì

      

2 2 2 2

1 1 1

z x y x y

Khi đó:

   

 

2 2

1 3 1 1 3 1

 1 1 3 1 1 2 1 3 1

z z x y x y

x x x x x x

        

           

Xét hàm số

 

   2 1 3 1

f x x x

trên đoạn

 



 

 

1;1

ta có:

   

 









     









 

 

1 3 4

' 2 ; ' 0

2 1 2 1

f x f x x

x x

Ta có:

 

 







   











 

1 6; 2 10

f f

Vậy





   

 



 











    















 



 



  





max

2 2

4 3

;

5 5

2 10

4 3

;

5 5

x y

f f

y x

x y

Vậy

     

4 3 4 3

, .

5 5 5 5

z i z i

Trong các số phức

thỏa:

3 4 ,z i z

  

biết rằng số phức

 

, ,z a bi a b

   

có

modul nhỏ nhất. Khi đó, giá trị của

P a b 

là ?

Giải:

Ta có

3 4 3 4

z i z a bi i a bi

        

   

2 2

25 6

3 4 25 6 8 0

a b a b a b b



           

2 2

25 6 25 75 625 5 15 25 25

8 16 16 64 4 8 4 4

z a a a a

   



 

 

 

         

 

 

 

 

 

   

Bài toán 5

Bài toán 6

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 79

Dấu

" "

xảy ra khi

a b

  

Khi đó

P a b

  

Cho số phức thỏa



. Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của

1 1P z z z    

Giải :

Đặt

 

2 2

; 1

z a bi a b a b

     



   

 1 1 2 1

z a b a

      

 

2 2 2 2 2 2

2 2

 1 2 2 2 1

 2 2 1

 2 1

z z a abi b a bi a b a a a bi

a a a b

a a b

             

   

  

2 1

 

Vậy

 

2 1 2 1

P a a

   

Xét

 

max 1 3

min 3

P P



 

 



 

 



 

 

 

 



 



. Xét

7 13

max

8 4

min 3

P P



 



 



 

 



 

  



 

 

 



 

 



 



Kết luận

13 7 15



4 8 8

1 3

 3

2 2

Max P z i

Min P z i





    







   





Số phức

 0z

thỏa mãn

 2.

Tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu thức





z i

Giải:

Ta có

          

1 1

1 1 1 1 1 1 .

i i i i

z z z z

z z

Mặt khác

  

1 1

suy ra

 

1 3

2 2

Suy ra giá trị lớn nhất và giá trị nhỏ nhất là

3 1

, .

2 2

Vậy tổng giá trị lớn nhất và giá trị nhỏ nhất

của biểu thức

là

Bài toán 7

Bài toán 8

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 80

Cho số phức

thỏa mãn

  2 3 1

z i

. Tìm giá trị lớn nhất của

  

P z i

Giải:

Ta có:

           2 3 2 3 2 3 2 3 1

z i z i z i z i

              

1 2 3 3 2 2 3 3 2 1 13

P z i z i i z i i

. Vậy

 

max

1 13

Trong các số phức

thoả mãn

3 4 4

z i

  

. Tìm giá trị lớn nhất, giá trị nhỏ nhất của

và xảy ra khi

bằng bao nhiêu?

Giải:

Ta có :

3 4 (3 4 ) 3 4 5

z i z i z i z

         

4 5 4 5 4 1 9

z z z

          

max 9

 

và

min 1



Đặt

   ( ; )z x yi x y

 TH

max 9





 



 

  

 

  

 

   

  



 



2 2

3 4 45

( 3) ( 4) 16

3 4 4

x y

z i

Giải hệ phương trình này ta thu được

  

27 36

; y

5 5

  

27 36

5 5

z i

Vậy

max 9



  

27 36

5 5

z i

 TH

min 1





 



 

  

 

  

 

   

  



 



2 2

3 4 45

( 3) ( 4) 16

3 4 4

x y

z i

Giải hệ phương trình này ta thu được

  

3 4

; y

5 5

  

3 4

5 5

z i

Vậy

min 1



  

3 4

5 5

z i

Cho số phức

thỏa mãn

 

2 1 1

i z

  

. Tổng giá trị lớn nhất và giá trị nhỏ nhất của



bằng bao nhiêu ?

Giải:

Ta có .

 

2 1

1 1 2 1

2 1 1

2 5 5

2 2

i z

i z z z

i i

 

          



 

Bài toán 9

Bài toán 10

Bài toán 11

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 81

1 1 1 1 1

1 2 1 2 2 1 2

5 5 5 5 5

z z z               

max min

1 1 2 2

z z   

Cho số phức

thỏa mãn

1 2 10

z i  

. Giá trị lớn nhất và giá trị nhỏ nhất của

1 4z i 

bằng bao nhiêu ?

Giải:

Ta có

1 2 1 2 (1 2 ) 1 2 1 2 10

z i z i z i z i z i              

Lại có :

   

1 2 1 4 2 2 1 4 2 2 1 4 2 2

z i z i i z i i z i               

10 1 4 2 2 10 1 4 2 2 10

 10 2 2

1 4 10 2 2

z i z i

z i

          

      

Vậy

max min

1 4 10 2 2;  1 4 10 2 2

z i z i       

Trong các số phức

có môđun bằng

2 2

. Tìm số phức

sao cho biểu thức

P z z i   

đạt giá trị lớn nhất.

Giải:

Gọi

 

;z x yi x y

   

2 2 2 2

2 2 2 2 8

z x y x y

      

2 2 2 2

1 ( 1) ( 1)

P z z i x y x y         

Áp dụng bất đẳng thức Bunhia-côpxki cho hai bộ số 1;1 và

2 2 2 2

( 1) ; ( 1)x y x y   

, ta

có:

2 2 2 2 2

2 ( 1) ( 1) 4(9 )P x y x y x y

 

        

 

 

Áp dụng bất đẳng thức Bunhia-cốpxki cho hai bộ số 1;1 và

;x y

, ta có:

 

2 2

2 4

x y x y

   

52 2 13P P   

. Đẳng thức xảy ra khi

2x y 

Vậy P đạt giá trị lớn nhất bằng

2 13 khi 2 2z i 

2 7 7

1 1 1 2

5 5 5 5 5 5

i i i

z z z z

 







              











 

Bài toán 12

Bài toán 13

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 82

Cho số phức

thỏa mãn

3 3 8

z z

   

. Gọi

lần lượt giá trị lớn nhất và nhỏ

nhất

Khi đó

M m

bằng ?

Giải:

Gọi

z x yi 

với

;x y  

Ta có

8 3 3 3 3 2 4

z z z z z z

          

Do đó

M max z

 

Mà

   

2 2

3 3 8 3 3 8 3 3 8

z z x yi x yi x y x y

                 

Áp dụng bất đẳng thức Bunhiacopxki, ta có

   

 

   

2 2 2 2

2 2 2 2 2 2

8 1. 3 1. 3 1 1 3 3

x y x y x y x y

 

            

 

 

   

2 2 2 2

8 2 2 2 18 2 2 2 18 64

x y x y       

2 2 2 2

7 7 7

x y x y z       

Do đó

M min z  .

Vậy

4 7M m  

Cho số phức

thỏa mãn

4 4 10

z z

   

. Giá trị lớn nhất và nhỏ nhất của

bằng?

Giải:

Cách 1: Giả sử

 

 ;z x yi x y

   

Ta có

10 4 4 4 4 2 5

z z z z z z

          

Áp dụng bất đẳng thức Bunhiacopxki, ta có

     

2 2 2

100 4 .1 4 .1 4 4 .2

z z z z

 

       

 

 

   

 

2 2

2 2 2 2

4 4 50 9 3

a b a b a b z

           

Cách 2: Giả sử

 

 ;z x yi x y

   

Từ giả thiết, ta có

   

2 2

4 4 10

x y x y     

 

Trong mặt phẳng với hệ tọa độ

Oxy

, gọi

 

;M x y

và

 

4; 0



 

4; 0



thì

 

có dạng

1 2

2.5MF MF 

. Vậy tợp hợp điểm

 

;M x y

biểu diễn số phức

là một Elip có độ dài trục lớn

5a 

, tiêu cự

1 2

8 4F F c  

. Suy ra độ dài trục bé

2 2

3b a c  

Khi đó ta luôn có

b OM a 

hay

3 5

 

Bài toán 14

Bài toán 15

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 83

Gọi T là tập hợp các số phức

thỏa mãn

1 3

 

và

1 5

 

. Gọi

1 2

,z z 

T lần lượt là

các số phức có môđun nhỏ nhất và lớn nhất. Tìm số phức

1 2

2z z



Giải:

Áp dụng bất đẳng thức:

1 2 1 2 1 2

z z z z z z

    

Ta có:

   

1 2

3 2

2 6

1 1 5 6

z i z i z

z z z

 

    

 

   

 

    

 

 

Dấu ”=” thứ nhất xảy ra khi

z i

 

, kết hợp với

1 5

 

ta được hệ:

1 1

1 3

1 5 2

z z i



 



    









Dấu ”=” thứ hai xảy ra khi

z i

 

, kết hợp với

1 3

 

ta được hệ:

2 2

1 5

1 3 6

z z



 



   









Suy ta

1 2

2 12 6z z i  

Bài toán 16

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 84

II. PHƯƠNG PHÁP HÌNH HỌC GIẢI BÀI TOÁN MIN-MAX

1. PHƯƠNG PHÁP:

Để giải được lớp bài toán này, chúng tôi cung cấp cho học sinh các bất đẳng thức hình học và

một số bài toán công cụ sau:

Cho đường tròn

( )T

cố định có tâm I bán kính R và điểm A cố định. Điểm M di động trên

đường tròn

( )T

. Hãy xác định vị trí điểm M sao cho AM lớn nhất, nhỏ nhất.

Giải:

TH1: A thuộc đường tròn (T)

Ta có: AM đạt giá trị nhỏ nhất bằng 0 khi M trùng với A

AM đạt giá trị lớn nhất bằng 2R khi M là điểm đối xứng với A qua I

TH2: A không thuộc đường tròn (T)

Gọi B, C là giao điểm của đường thẳng qua A,I và đường tròn (T);

Giả sử AB < AC.

+) Nếu A nằm ngoài đường tròn (T) thì với điểm M bất kì trên (T), ta có:

AM AI IM AI IB AB     .

Đẳng thức xảy ra khi

M B

AM AI IM AI IC AC     .

Đẳng thức xảy ra khi

M C

+) Nếu A nằm trong đường tròn (T) thì với điểm M bất kì trên

(T), ta có:

AM IM IA IB IA AB    

Đẳng thức xảy ra khi

M B

AM AI IM AI IC AC     .

Đẳng thức xảy ra khi

M C

Vậy khi M trùng với B thì AM đạt gía trị nhỏ nhất.

Vậy khi M trùng với C thì AM đạt gía trị lớn nhất.

Cho hai đường tròn

( )T

có tâm I, bán kính R

; đường tròn

( )T

có tâm J, bán kính R

. Tìm

vị trí của điểm M trên

( )T

, điểm N trên

( )T

sao cho MN đạt giá trị lớn nhất, nhỏ nhất.

Giải:

Gọi d là đường thẳng đi qua I, J; d cắt đường tròn

( )T

tại hai điểm phân biệt A, B (giả sử JA

> JB) ; d cắt

( )T

tại hai điểm phân biệt C, D ( giả sử ID > IC).

Với điểm M bất khì trên

( )T

và điểm N bất kì trên

( )T

Ta có:

1 2

MN IM IN IM IJ JN R R IJ AD        

Bài toán công cụ 1

Bài toán công cụ 2

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 85

Đẳng thức xảy ra khi M trùng với A và N trùng với D

1 2

MN IM IN IJ IM JN IJ R R BC        

Đẳng thức xảy ra khi M trùng với B và N trùng với

Vậy khi M trùng với A và N trùng với D thì MN đạt

giá trị lớn nhất.

khi M trùng với B và N trùng với C thì MN đạt giá

trị nhỏ nhất.

Cho hai đường tròn

( )T

có tâm I, bán kính R; đường thẳng



không có điểm chung với

( )T

. Tìm vị trí của điểm M trên

( )T

, điểm N trên



sao cho MN đạt giá trị nhỏ nhất.

Giải:

Gọi H là hình chiếu vuông góc của I trên d

Đoạn IH cắt đường tròn

( )T

tại J

Với M thuộc đường thẳng



, N thuộc đường tròn

( )T

, ta có:

MN IN IM IH IJ JH const      .

Đẳng thức xảy ra khi

;M H N I 

Vậy khi M trùng với H; N trùng với J thì MN đạt giá trị nhỏ nhất.

2. MỘT SỐ BÀI TOÁN ĐIỂN HÌNH

Trong các số phức

thoả mãn

3 4 4z i  

. Tìm giá trị lớn nhất, giá trị nhỏ nhất của

Giải:

 Cách 1

Gọi

 

;z x yi x y   

( ; )M x y

biểu diễn cho số phức

trong hệ toạ độ Oxy

2 2 2 2

3 4 4 ( 3) ( 4) 4 ( 3) ( 4) 16z i x y x y            

Vậy điểm M biểu diễn cho số phức

thuộc đường tròn (T) có tâm

(3; 4)I 

, bán kính R = 4.

2 2

z x y OM  

;

5OI R 

nên O nằm ngoài đường tròn (T)

lớn nhất khi OM lớn nhất, nhỏ nhất khi OM nhỏ nhất.

(Bài toán qui về Bài toán công cụ 1- Trường hợp 2)

Đường thẳng OI cắt đường tròn (T) tại hai điểm phân biệt

3 4 27 36

; ; ; 1; 9

5 5 5 5

A B OA OB

   

 

 

 

    

 

 

 

 

 

   

Với M di động trên (T), ta có: 1 9OA OM OB OM    

1 9z  

 OM nhỏ nhất khi M trùng với A; OM lớn nhất khi M trùng với B

Bài toán công cụ 3

Bài toán 1

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 86

Vậy

nhỏ nhất bằng 1 khi

3 4

5 5

z i

 

;

lớn nhất bằng 9 khi

27 36

5 5

z i

 

 Cách 2

Gọi

 

;z x yi x y

   



( ; )M x y

biểu diễn cho số phức

trong hệ toạ độ Oxy

3 4i   

(3; 4)A 

biểu diễn cho số phức



;  5

z OM OA z AM      

;

Theo giả thiết

3 4 4 4 4

z i z AM

       

Ta có:

4 4 4 4 1 9

OM OA AM OM OA OA OM OA OM

               

1 9

  

;



khi

3 4

5 5

z i

 

;



khi

27 36

5 5

z i

 

Vậy

nhỏ nhất bằng 1 khi

3 4

5 5

z i

 

;

lớn nhất bằng 9 khi

27 36

5 5

z i

 

Nhận xét: Ngoài ra bài toán trên có thể giải bằng phương pháp sử dụng bất đẳng thức

Bunhia-Cốpxki hoặc phương pháp lượng giác hoá.

Trong các số phức

thoả mãn điều kiện

( 2 4 )z z i 

là một số ảo, tìm số phức

sao cho

1z i   

có môđun lớn nhất.

Giải:

Gọi

 

;z x yi x y

   



( ; )M x y

biểu diễn cho số phức

trong hệ toạ độ

Oxy

( 2 4 ) ( ) ( 2) ( 4) ( 2) ( 4) ( 4) ( 2)z z i x yi x y i x x y y x y y x i

   

              

   

   

( 2 4 )z z i 

là một số ảo

2 2 2 2

( 2) ( 4) 0 2 4 0 ( 1) ( 2) 5x x y y x y x y x y              



M biểu diễn cho

thuộc đường tròn (T) có tâm

( 1;2)I 

, bán kính

5R 

2 2

1 ( 1) ( 1) ( 1) ( 1)

z i x y i x y AM

            

với

(1;1)A

5 ( )IA A T  

(Bài toán được qui về Bài toán công cụ 1 - trường hợp 1)

Vì M là điểm di động trên (T) nên

lớn nhất



là đường kính của (T)



đối xứng với

qua



là trung diểm của

Vậy lớn nhất bằng khi .

( 3;3) 3 3 4 2M z i i         



2 5

3 3z i  

Bài toán 2

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 87

Trong các số phức thoả mãn: , tìm số phức sao

cho đạt giá trị lớn nhất.

Giải:

Gọi là những số thực); được biểu diễn bởi điểm ;

được biểu diễn bởi điểm trong mặt phẳng toạ độ Oxy

M thuộc đường tròn tâm I(1; 1), bán kính R = 1.

M thuộc đường tròn tâm , bán kính .

(Bài toán được qui về Bài toán công cụ 2)

Đường thẳng IJ có phương trình . Đường thẳng IJ cắt đường tròn tâm I tại hai điểm

Đường thẳng IJ cắt đường tròn tâm J tại 2 điểm

Vậy thì đạt giá trị lớn nhất.

Cho các số phức thoả mãn: là một số thực. Tìm số phức

sao cho đạt giá trị nhỏ nhất.

Giải:

Gọi

lần lượt biểu diễn cho trong hệ toạ độ Oxy

M thuộc đường tròn có tâm O, bán kính R = 1

là số thực

1 2

,z z

1 2

1 1 ; 6 6 6

z i z i

     

1 2

,z z

1 2

z z



1 2

. ;  . ; ( , , ,z a b i z c d i a b c d   

 

;M a b

 

;N c d

2 2

1 1

1 1 1 1 ( 1) ( 1) 1

z i z i a b

           



2 2

6 6 6 6 6 36 ( 6) ( 6) 36

z i z i c d           



 

6;6

' 6R

2 2

1 2

( ) ( )

z z c a d b MN

     

y x

1 2

2 2 2 2 2 2 2 2

; ; ;

2 2 2 2

M M

   

     

 

 

 

 

 

 

 

 

 

   

   

1 2

6 3 2;6 3 2 ; 6 3 2;6 3 2

N N   

2 1 1 2

M N MN M N 

1 2

5 2 7 5 2 7

z z

     

    

1 2 1 2

max 5 2 7  ,

z z khi M M N N

 

1 2

2 2 2 2

; 6 3 2 6 3 2

2 2

z i z i

 

     

1 2

z z



1 2

;z z

1 2 2

1 ; (1 ) 6 2z z z i i

 

    

 

 

1 2

;z z

 

2 1 2 1 2

P z z z z z

  

 

1 2

; ;  , , ,z a bi z c di a b c d

     

( ; ), ( ; )M a b N c d

1 2

;z z

2 2 2 2

1 1 1

z a b a b

      



( )T

   

;

1 6 2 ( 1) ( 1) 2 6

( 1) ( 1) 2 ( 1) ( 1) 6

z c di

z z i i c di c d i i

c c d d c d d c i



 

 

           

 

 

 

         

 

 



( 1) ( 1) 6 0 6 0c d d c c d         

Bài toán 3

Bài toán 4

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 88

N thuộc đường thẳng

Ta có nên và không có điểm chung

(vì )

(Bài toán được qui về Bài toán công cụ 3)

Gọi H là hình chiếu vuông góc của O trên

Đoạn OH cắt đường tròn tại

Với N thuộc đường thẳng , M thuộc đường tròn , ta có:

Đẳng thức xảy ra khi

Vậy P đạt giá trị nhỏ nhất bằng khi .

Trong các số phức có môđun bằng . Tìm số phức sao cho biểu thức

đạt giá trị lớn nhất.

Giải:

Gọi

Xét . Khi đó:

. Đẳng thức xảy ra khi cùng hướng

Với thì ngược hướng (không thoả mãn)

Với thì cùng hướng (thoả mãn)

Vậy thì P đạt giá trị nhỏ nhất bằng 7.



: 6 0x y   

( ; ) 1d O  



( )T

1 2

1 2 1 2 1 2

( ) ;

( ) 2( )

z z ac bd bc ad i

z z ac bd bc ad i z z z z ac bd

   

        

2 2 2 2 2

2( ) ( ) ( ) 1 1P c d ac bd c a b d MN          

2 2

1a b 

: 6 0 (3; 3)x y H    

( )T

2 2

;

2 2

 





















 



( )T

   3 2 1MN ON OM OH OI IH      

;M I N H 

 

3 2 1 1 18 6 2

P     

1 2

2 2

; 3 3

2 2

z i z i

   

18 3 2

1 2

2 2

; 3 3

2 2

z i z i

   

1 1 7P z z i    

 

;z x yi x y

   

2 2 2 2

2 2 4

z x y x y

      

2 2 2 2

1 1 7 ( 1) ( 1) ( 7)

P z z i x y x y           

     

1; , 1 ; 7 0; 7

u x y v x y u v

       

   

P u v u v

    

   

,u v

 

( 1)( 7 ) (1 ) 1x y y x x       

3y  

1; 3x y 

,u v

 

1; 3x y  

,u v

 

1 3z i 

Bài toán 5

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 89

Cho số phức thỏa mãn . Gọi lần lượt là giá trị lớn nhất và giá trị

nhỏ nhất của . Tính giá trị .

Giải :

Gọi . Ta có : .

thuộc đường tròn có tâm và bán kính .

Mặt khác : .

Vậy thuộc đường thẳng .

Ta có : Để thì .

Trong các số phức thoả mãn điều kiện . Tìm số phức z có môđun lớn

nhất.

Giải:

Gọi

biểu diễn cho số phức z trong hệ toạ độ Oxy

(với ).

có tâm O, trục lớn bằng 10; tiêu cự bằng 6

lớn nhất

Vậy lớn nhất bằng 5 khi .

Biết rằng số phức thỏa mãn là một số thực. Tìm giá trị nhỏ

nhất của .

Giải:

Đặt ta có

Ta có:

 

3 4 5

z i  

,M m

2 2

P z z i   

2 2

A M m

 

 

,z a bi a b  



     

2 2

3 4 5 3 4 5

z i a b

       

z

 

3;4



   

2 2 2 2

2 2

2 2 1 4 2 3 0

P z z i a b a b a b P

              

 

: 4 2 3 0

a b P

    

 

z C











 





z

     

;

C d I R

 

      

 

 

5 13 33

2 5



    

1258A 

3 3 10

z z

   

 

;z x yi x y

   



( ; )M x y

2 2 2 2

1 2

3 3 10 ( 3) ( 3) 10

 10

z z x y x y

MF MF

          

  

1 2

( 3; 0);  (3;0)F F

( )M E 

2 2

( ) : 1

25 9

x y

M E

   

;

z OM OM

5 (5;0) ( 5;0)OM a M M     

5 5z z   

 

3 1 3u z i z i

    

    ,( )z x yi x y

         

2 2

3 1 1 3 4 4 6 2 4u x y i x y i x y x y x y i

   

               

   

   

4 0u R x y    

Bài toán 6

Bài toán 7

Bài toán 8

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 90

Tập hợp các điểm biểu diễn của là đường thẳng .

là điểm biểu diễn của , có môđun nhỏ nhất khi và chỉ khi độ dài OM nhỏ nhất

. Tìm được suy ra .

Tìm số phức có mô đun lớn nhất và thỏa mãn điều kiện .

Giải:

Gọi .

Gọi là điểm biểu diễn của trong mặt phẳng tọa độ Oxy.

là đường tròn có tâm và bán kính .

Gọi d là đường thẳng đi qua O và I .

Gọi là hai giao điểm của d và (C) và .

Ta thấy

Số phức cần tìm ứng với điểm biểu diễn hay .

Cho số phức thỏa mãn và đạt

giá trị nhỏ nhất . Tính .

Giải :

Ta có : .

Xét trong mặt phẳng phức , xét các điểm với điểm biểu

diễn số phức .

Ta có : .

Vậy ta tìm sao cho .

Do cùng thuộc một phía so với đường thẳng .

Gọi là điểm đối xứng của qua . Ta có : .

Dấu xảy ra khi .

  : 4 0d x y

 

;M x y

OM d 

 

2;2

  2 2z i

 

1 3 2

z i i   

( , )z x yi x y R z x yi     

2 2

13 39

(1 ) 3 2 5 0

2 8

z i i x y x y

         

 

;M x y

( )M C 

1 5

;

2 2

 

















 

R 

: 5d y x 

1 2

,M M

3 15

;

4 4

 



















 

1 5

;

4 4

 

















 

1 2

( ( ))

OM OM

OM OI R OM M C













   







3 15

4 4

z i

 

 

,z a bi a b

   

1 2z i z i   

2 3 1

P z i z

    

2P a b 

1 2 1

z i z i a b

      

     

2 2 2

2 3 1 2 3 1

P z i z a b a b

           

Oab

     

; , 2;3 , 1;0

M a b A B



 

: 1 0

z M d a b

    

     

2 2 2

2 3 1

MA MB a b a b

       

M d

 

min

MA MB



  

1 1 0 ,

A A B B

x y x y A B     



' 'MA MB MA MB A B   

" "

'M A B d 

3 1 5

; 2

2 2 2

M P a b

 







    











 

Bài toán 9

Bài toán 10

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 91

Cho hai số phức

1 2

, z z

thỏa mãn

2 3

z i

 

và

2 2

2 2 2 4z i z i    

. Giá trị nhỏ nhất

của biểu thức

1 2

P z z 

bằng?

Giải:

Đặt

1 1 1

z x y i 

và

2 2 2

z x y i 

với

1 2 1 2

,  ,  ,  .x x y y  

●

 

1 1 1

2 3 2 9

z i x y

      

tập hợp các số phức

là

đường tròn

   

: 2 9

C x y

  

●

2 2

2 2 2 4z i z i    

       

2 2 2 2

2 2 2 2 2

2 2 2 4 3 0

x y x y y

          



tập hợp các số phức

là đường thẳng

: 3d y  

Ta có

   

2 2

1 2 2 1 2 1

P z z x x y y

     

đây chính là khoảng cách từ điểm

 

2 2

;

B x y d

đến

điểm

   

1 1

;

A x y C

. Do đó

2 1 min

min

z z AB

 

Dựa vào hình vẽ ta tìm được

min

2AB 

khi

   

0; 1 ,  0; 3

A B

 

. Vậy

1 2

P z z 

khi

1 2

;  3z i z i   

Nhận xét: Ở bài này đường thẳng và đường tròn có vị trí đặc biệt nên vẽ hình sẽ nhận ra ngay được hai

điểm

, nếu không thì viết phương trình đường thẳng qua tâm

và vuông góc với

, sau đó tìm

giao điểm với

và

rồi loại điểm.

Bài toán 11

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 92

III. SỬ DỤNG MÁY TÍNH CASIO 570 VN-PLUS ĐỂ GIẢI

Trong các số phức có môđun bằng . Tìm số phức sao cho biểu thức

đạt giá trị lớn nhất.

Hướng dẫn:

o Chuyển qua chế độ số phức:

o Nhập biểu thức P :

qcQ)p1$+ qcQ)p1+7b

Màn hình hiển thị:

o Gán X cho từng đáp án, dùng phím:

o So sánh kết quả và ta tìm được giá trị lớn nhất là 7

Trong các số phức thoả mãn điều kiện . Tìm số phức z có môđun lớn

nhất.

Hướng dẫn:

o Chuyển qua chế độ số phức:

o Nhập biểu thức: vào máy tính:

qcQ)p3$ qcQ)+3$p10

Màn hình hiển thị:

o Dùng phím

để nhập các đáp án, nếu đáp án nào cho

kết quả bằng 0 thì thỏa mãn điều kiện .

Ta thấy 3 đáp án A,B,C thỏa mãn điều kiện đề bài nhưng

đáp án B có môđun lớn nhất. Chọn B.

1 1 7P z z i    

.1 i 3 .1  3 . 3  . 3A B i C i D i    

3 3 10

z z

   

9 12

.4  .5 .3  .3 5 i

5 5

A i B C i D  

3 3 10

z z

   

3 3 10

z z

   

Bài toán 1

Bài toán 2

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 93

V. BÀI TẬP RÈN LUYỆN

1. ĐỀ BÀI

Câu 1. Cho số phức thỏa mãn . Giá trị lớn nhất và giá trị nhỏ nhất của lần

lượt là

A. B. C. D.

Câu 2. Cho số phức thỏa mãn . Giá trị nhỏ nhất của lần lượt là

A. B. C. D.

Câu 3. Trong các số phức thỏa mãn: thì số phức có modul nhỏ nhất là

A. B. C. D.

Câu 4. Trong các số phức thỏa mãn: thì số phức có modul nhỏ nhất là

A. B. C. D.

Câu 5. Trong các số phức thỏa: biết rằng số phức có

modul nhỏ nhất. Khi đó, giá trị của là

A. B. C. D.

Câu 6. Trong các số phức thỏa mãn: , biết rằng số phức

có modul nhỏ nhất. Khi đó, tỉ số bằng

A. B. C. D.

Câu 7. Cho số phức thỏa mãn điều kiện . Giá trị lớn nhất của là

A. B. C. D.

Câu 8. Cho số phức thỏa mãn . Tổng giá trị lớn nhất và giá trị nhỏ nhất của

bằng

A. B. C. D.

Câu 9. Cho số phức thỏa mãn . Giá trị lớn nhất của bằng

A. B. C. D.

Câu 10. Cho số phức thỏa mãn . Gọi M và m lần lượt là giá trị lớn nhất và giá

trị nhỏ nhất của . Giá trị của là

A. B. C. D.

Câu 11. Trong mặt phẳng phức Oxy, tập hợp biểu diễn số phức Z thỏa mãn là

đường tròn . Diện tích S của đường tròn bằng bao nhiêu?

2 2 1

z i

  

2 2 1;2 2 1 

2 1; 2 1 

2;1

3 1; 3 1 

1 2 4 5

z i  

3 5

5 5

5 3

3 4

z i z  

z i 

z i 

z i

  

z i

  

2 4 2z i z i   

2 2z i  

2 2z i  

2 2z i 

2 2z i 

3 4 ,z i z

  

 

, ,z a bi a b

   

P a b 



 

1 5 3

z i z i    

 

, ,z a bi a b

   

2P  

2 1

z i

  



2 1

2 1

 

2 1 1

i z

  



2 2

2 3

1 2 10

z i  

1 4z i 

10 3

3 10

4 10

1 2 4

z i

  

z i 

2 2

T M m 

50T 

64T 

68T 

16T 

z z z

  

 

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 94

A. B. C. D.

Câu 12. Trong mặt phẳng phức Oxy, tập hợp biểu diễn số phức Z thỏa là hình

vành khăn. Chu vi P của hình vành khăn là bao nhiêu?

A. B. C. D.

Câu 13. Trong mặt phẳng phức Oxy, giả sử M là điểm biểu diễn số phức Z thỏa mãn

. Tập hợp những điểm M là?

A. B.

C. D.

Câu 14. Trong mặt phẳng phức Oxy, các số phức thỏa . Nếu số phức có môđun

nhỏ nhất thì phằng ảo bằng bao nhiêu?

A. B. C. D.

Câu 15. Trong mặt phẳng phức Oxy, các số phức thỏa . Tìm số phức được

biểu diễn bởi điểm M sao cho MA ngắn nhất với

A. B. C. D.

Câu 16. Trong mặt phẳng phức Oxy, trong các số phức thỏa . Nếu số phức có

môđun lớn nhất thì số phức có phần thực bằng bao nhiêu?

A. B. C. D.

Câu 17. Cho số phức z thỏa mãn : . Gọi A và B lần lượt là giá trị lớn nhất và nhỏ

nhất của . Khi đó có giá trị bằng

A. 20 B. 18 C. 24 D. 32

Câu 18. Cho số phức z thỏa mãn : . Gọi A và B lần lượt là giá trị lớn nhất và

nhỏ nhất của . Khi đó có giá trị bằng C.

A. 10 B. -10 C. 12 D. -12

Câu 19. Cho số phức z thỏa mãn : . Gọi A và B lần lượt là giá trị lớn nhất và

nhỏ nhất của . Khi đó có giá gần nhất bằng

A. 20 B. 18 C. 64 D. 32

Câu 20: Xét số phức thỏa mãn Tìm giá trị lớn nhất của

A. B. C. 4. D. 6.

Câu 21: Xét số phức thỏa mãn Tìm giá trị nhỏ nhất của

A. B. C. D.

Câu 22: Cho số phức thoã mãn . Gọi và lần lượt là giá trị lớn nhất và nhỏ

nhất của . Tính giá trị của biểu thức .

4S 

2S 

3S 

S 

1 1 2

z i

   

4P 

P 

2P 

3P 

2 2 8

z z

   

 

2 2

: 1

16 12

x y

 

 

2 2

: 1

12 16

x y

 

     

2 2

: 2 2 64

T x y   

     

2 2

: 2 2 8

T x y

   

5 3

z i

 

2 1

z i z i   

 

1;3

3 i

1 3i

2 3i

2 3i 

1 1

z i

  

2 2

 

2 2



2 2



2 2



1 2

z i  



2 2

A B

1 2 2 5

z i  

z i

.A B

 

1 1 2 2

z i i

   

1 3z i 

2 2

2A B

2 3 1.

z i

  

1 .

z i

 

1 13.

2 13.

1 4 2 .

z i z i

    

2 1 .

z i

 

102

7 10

470

3 4 2

z i

  

2P A B 

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 95

A. B. C. D.

Câu 23: Cho số phức thoã mãn . Gọi và lần lượt là giá trị lớn nhất và

nhỏ nhất của . Giá trị của biểu thức gần bằng.

A. 6 B. 7 C. 8 D. 9

Câu 24: Cho số phức thoã mãn . Giá trị lớn nhất của là.

A. B. C. D. 5

Câu 25: Trong tất cả các số phức thỏa mãn hãy tìm số phức có mođun nhỏ

nhất .

A. B. C. D.

Câu 26: Cho số phức thỏa mãn Giá trị lớn nhất của là

A. B. C. D.

Câu 27: Cho số phức thoã mãn điều kiện . Gọi là số phức thoã mãn

điều kiện . Giá trị nhỏ nhất của biểu thức là:

A. B. C. D.

Câu 28: Cho số phức thỏa mãn điều kiện . Gọi

lần lượt là giá trị lớn nhất, nhỏ nhất của biểu thức . Tổng bằng

A. B. C. D.

Câu 29: Gọi và là các nghiệm của phương trình Gọi lần lượt là các điểm

biểu diễn của trên mặt phẳng phứC. Khi đó độ dài là

A. B. C. D.

Câu 30 : Trong mặt phẳng tọa độ tìm tập hợp điểm biểu diễn số phức thỏa mãn điều kiện

biết là số phức thỏa mãn

A. B.

C. D.

43P 

80P 

8P 

48P 

1 2

z i  

z i 

2P A B 

1 2

z i



  



A z i  

2 2

5 2

2 5

 

2 1

i z



 



min



min

2 2

z  

min



min



2 3 1z i  

1z i 

13 2.

13 1.

2 1 2z i z i   

 

1 2

w i z

  

P w

min



min

P 

min

P 

min



 

,z x yi x y

   

1 2 3 5

z i z i     

,M m

.P x z



2M m

54.

27.

18.

9.

4 9 0.

z z

  

,M N

1 2

,z z



2 5.

MN 

,Oxy

 

1 2 3,

w i z

  

2 5.

 

   

2 2

1 4 125.

x y   

   

2 2

5 4 125.

x y   

   

2 2

1 2 125.

x y   



Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 96

2. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI

1A 2B 3B 4D 5A 6B 7A 8B 9C 10C

11D

12C

13A

14C

15A

16A 17C

18A

19C

20A

21C

22A

23C

24D

25A

26D

27B

28A

29C

30A

Câu 1. Ta có

Lại có Chọn A.

Câu 2. Ta có Chọn B.

Câu 3. Ta có

Chọn B.

Câu 4. Ta có

Chọn D.

Câu 5. Ta có

Chọn A.

Câu 6. Ta có

Chọn B.

Câu 7. Đặt , khi đó

Chọn A.

Câu 8. Ta có .

Đặt , khi đó

2 2 2 2 2 2 2 2 1.

z i z z i z z

           

2 2 2 2 2 2 2 2 1 2 2.

z i i z i i z z            

4 5 1 2 1 2 5 3 5.

z i z i z z         

   

2 2

8 25

3 4 3 4 25 6 8 0

a bi i a bi a b a b a b a



                

2 2

8 25 25 100 625 5 10 25 25 3

2 .

6 9 9 36 3 3 4 4 2

z b b b b b a

   



 

 

 

              

 

 

 

 

 

   

     

2 2 2

2 4 2 2 4 2

a bi i a bi i a b a b            

20 4 8 4 4 4 4 16 4a b b a b b a          

   

2 2 2

2 2

4 2 8 16 2 2 8 2 2.

z a a a a a a b

             

   

2 2

25 6

3 4 3 4 25 6 8 0

a bi i a bi a b a b a b b



                

2 2

25 6 25 75 625 5 15 25 3

8 16 16 64 4 8 4 2

z a a a a a b

   



 

 

 

            

 

 

 

 

 

   

       

2 2 2 2

1 5 3 1 5 3 1

a bi i a bi i a b a b              

26 2 10 10 6 2 4 12 16 4 3a b a b a b a b           

 

2 2

12 8 6 2

4 3 10 24 16 10 .

5 5 5

z b b b b b b a

 







             











 

1 1w z z w    

2 2

max

2 1 1 1 1 1 1 2.

z i w i w           

 

2 1

1 1 2 1

2 1 1

2 5 5

2 2

i z

i z z z

i i

 

          



 

1 1w z z w    

2 2

max

2 7 1 7 1 1 1

2 .

5 5 5 5 5 5

5 5 5

i i

z w w

   

 

 

 

           

 

 

 

 

 

   

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 97

Và Vậy Chọn B.

Câu 9. Ta có .

Đặt , khi đó

Vậy giá trị lớn nhất là Chọn C.

Câu 10. Đặt , khi đó

Suy ra Chọn C.

Câu 11. Đặt , ta có và .

Khi đó, giả thiết

Suy ra tập hợp biểu diễn số phức là đường tròn tâm , bán kính

Chọn D.

Câu 12. Đặt , khi đó ta có

Tập hợp các

điểm biểu diễn số phức nằm bên ngoài hình tròn có tâm , bán kính

Tập hợp các

điểm biểu diễn số phức nằm bên trong hình tròn có tâm , bán kính

Vì hai đường tròn đồng tâm nên chu vi hình vành khăn là

Chọn C.

Câu 13. Xét điểm và , ta có

Tập hợp điểm là Elip . Chọn A.

Câu 14. Giả sử M là điểm biểu diễn số phức . Xét điểm

Tập hợp điểm là các điểm không nằm ngoài đường tròn tâm bán kính

. Chọn C.

Câu 15. Xét điểm Tập hợp điểm là đường thẳng trung

được của .

2 2

max

7 1 1 1

2 .

5 5

   

 

 

 

    

 

 

 

 

 

   

min max

2 2.

w w 

1 2 10 1 2 10

z i z i      

 

1 2 . 1 2 10

z i z i     

 

1 2 . 1 2 10

z i z i     

1 2 . 1 2 10 1 2 10.

z i z i z i         

1 4 1 4w z i z w i      

1 2 2 6 10.

z i w i     

2 2

max max

10 2 6 3 10 1 4 3 10.

w z i       

2 2w z i z w i      

1 2 2 1 2 3 3 4.

z i w i i w i

          

2 2

max

2 2

min

3 3 4 3 2 4

68.

3 3 4 3 2 4

M w

M m

m w





     



  





     





 

,z x yi x y

   

z x yi 

2 2

z x y

 

 

2 2

2 2 2

0 0 1 1.

z z z x y x yi x yi x y

             

 

1;0

I 

 

1 .

R S   

 

,z x yi x y

   

         

2 2 2 2

1 1 1 1 1 1 1 1 1

z i x y i x y x y

                

 

1;1

I 

1.R 

         

2 2 2 2

1 1 1 1 1 2 1 1 4

z i x y i x y x y

                

 

1;1

I 

2.R 

 

2 2 2 1

2 2 .

P C C R R

     

 

2;0

 

2;0



1 2

8 2 4MF MF a a    

2 2 2

1 2

4 2 2 12

F F c c b a c

        

 

2 2

: 1

16 12

x y

 

 

0;5 3

A AM

 

3R 

5 3 2OM AO AM     

   

1; 2 , 0; 1B C MB MC

    

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 98

Ta có: và trung điểm là Phương trình đường trung trực

là:

. Lại có: .

Dấu bằng khi là hình chiếu của lên

Khi đó:

. Chọn A.

Câu 16. Giả sử M là điểm biểu diễn số phức . Xét điểm

Tập hợp điểm là các điểm không nằm ngoài đường tròn tâm bán kính

. Dấu bằng khi là giao điểm của và

(chọn điểm xa O hơn).

Chọn A.

Câu 17. Giả sử M là điểm biểu diễn số phức . Xét điểm và

Tập hợp điểm là các điểm không nằm ngoài đường tròn tâm bán kính

Ta có: . Chọn C.

Câu 18. Giả sử M là điểm biểu diễn số phức . Xét điểm và

Tập hợp điểm là các điểm không nằm ngoài đường tròn tâm bán kính

Ta có: . Chọn A.

Câu 19. Ta có

Giả sử M là điểm biểu diễn số phức . Xét điểm và

Tập hợp điểm là các điểm không nằm ngoài đường tròn tâm bán kính

Ta có: .

Chọn C.

Câu 20: Giả sử

Ta có

Chọn A

 

: 1 0

BC x y

  

1 3

;

2 2

 







 











 

: 2 0x y   

 

, 2 2

AM d A  



       

2 2 2 2

2 2 1 3 8 1 5 8

M M M M

AM x y x x

          

   

x 3 0 3 3;1

M M

x M     

 

1;1 1

A AM

  

 

1R 

2 1OM AO AM    

 

:OA y x 

   

2 2

2 2 2 2

2 2

1 1 1

M M

x y

x x

x y





 

   



    





   





 

2; 0



 

1; 1 2

E EM  

 

2R 

2 2

10 2 10 2 24

FE EM MF FE EM MF A B           

 

0; 1



 

1;2 2 5

E EM  

 

2 5R 

2 5 10 2 5 10 10

FE EM MF FE EM MF AB          

 

1 2 1 3

1 1 2 2 2

1 2 2

i i

z i i z z

 









         













 

 

1; 3

 

1 3

; 2

2 2

E EM

 







 











 

 

2R 

2 2

3 10 3 10

2 2 2 64

2 2

FE EM MF FE EM MF A B           

   

2 2

2 sin

2 3 1 2 3 1

3 cos

a x

a bi i a b

b x





 



         





 





       

2 2 2 2 2 2

1 1 1 1 3 sin 2 cosz i a bi i a b x x

             

 

  

2 2 2 2

14 2 3 sin 2 cos 14 2 3 2 sin cos 14 2 13 1 1 13.

x x x x z i             

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 99

Câu 21: Ta có

Khi đó

Chọn C

Câu 22: Tập hợp điểm biểu diễn số phức là đường tròn tâm bán kính

Khi đó ;

Suy ra . Chọn A.

Câu 23: Tập hợp điểm biểu diễn số phức là đường tròn tâm bán kính

Gọi khi đó ;

Do đó . Chọn C.

Câu 24: Ta có:

Tập hợp điểm biểu diễn số phức là đường tròn tâm bán kính

Gọi suy ra . Chọn D.

Câu 25:

Tập hợp điểm biểu diễn số phức là đường tròn tâm bán kính

Ta có: . Chọn A.

Câu 26: Tập hợp điểm biểu diễn số phức là đường tròn tâm bán kính .

Gọi . Gọi

Do đó . Chọn D.

Câu 27: Ta có:

. Gọi và suy ra nên tập hợp điểm

M là trung trực của AB có PT là:

Ta có: . Chọn B.

Câu 28: Đặt và suy ra

Từ giả thiết ta có

thuộc đường thẳng với .

       

2 2 2 2

1 4 2 1 1 2 4

a bi i a bi i a b a b              

2 2 2 20 4 8 2 6 18 0 3 9.a b a b a b a b             

       

2 2 2 2 2 2

2 1 2 1 1 2 3 8 2

z i a bi i a b b b              

22 98 98 7 10

10 44 68 10 2 1 .

5 5 5

b b b z i

 







          











 

 

3; 4



2R 

max

5 2 7

A z OI R

     

min

B z OI R

   

43P 

 

1;1

2R 

 

2; 1



max

2 5 2

A z i IK R      

5 2B  

2 8P A B  

1 2 1 2 . 1 2 1 2

z i iz i i z i z i



              



 

1; 1

 

2R 

 

2; 1



max

5A IK R  

   

1 2 1

2 1 1 2 1

1 1 1

i z i

z z i

i i i

 



       

  

 

0;2

1R 

min

z OI R

  

 

2; 3

1R 

   

1 1 1 1z x yi z i x yi i x y i

            

 

1;1



max

1 1 13

z i IK R     

   

2 1 2 1 2 2 1 1 3z i z i i z i i z i

           

4 2 1 3w i w i     

   

4; 2 ; 1;3

A B



 

M w

MA MB

 

3 5 5 0

x y d  

 

min

;

w OM OM d O d   

 

, ;

z x yi x y M x y    



   

1;1 , 2;3

A B 

5.AB 

       

2 2 2 2

1 2 3 1 1 2 3 .z i z i x y x y MA MB AB

               

M

 

: 2 1 0 2 1

AB x y y x

      

2; 1

 

  

 

 

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 100

Khi đó . Đặt .

Xét hàm số trên đoạn , có .

Suy ra là hàm số đồng biến trên Chọn A

Câu 29 : Ta có . Suy ra .

Chọn C

Câu 30 : Gọi với thì là điểm biểu diễn cho số phức

Ta có

Theo giả thuyết

Suy ra . Chọn A.

 

2 2

2 3 2

. . 2 1 5 4

P x z x x x x x x

 

      

 

 

 

3 2

5 4

f x x x x  

 

f x

2; 1

 

 

 

 

 

' 15 8 1 0; 2; 1

f x x x x

 

       

 

 

 

f x

2; 1

 

 

 

 

 

1 2

2 54.

2 26

M f

M m

m f





   



    





   





2 5

4 9 0

2 5

z i

z z

z i



 



   



 



   

2; 5 , 2; 5

M N

2 5MN 

 

;M x y

,x y  

w x yi 

 

1 2 3

w i z

  

   

3 1 2

3 2 3 2 6

1 2 5 5 5

x yi i

x yi x y x y

z i

 

  

     

 

 

    



   

2 2

2 7 2 6

2 5 5 2 7 2 6 625

5 5

x y x y

z i x y x y

   

           

   

2 2

1 4 125

x y   

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 101

E. DẠNG LƯỢNG GIÁC CỦA SỐ PHỨC

I. LÝ THUYẾT

Gọi là một điểm trong mặt phẳng phức biểu diễn số phức . Số đo (radian) của mỗi

góc lượng giác tia đầu là , tia cuối được gọi là một acgumen của .

Như vậy nếu  là một acgumen của , thì mọi acgumen đều có dạng: +2k,kZ.

Xét số phức z = a + bi  0 .

Dạng lượng giác có dạng: trong đó .

Để chuyển một số phức sang dạng lượng giác ta cần tìm r và ;

o Ta có :



là số thực thoả mãn : .

Nếu z = r(cos



+isin



) ;

= r’(cos



’ +isin



’) (r ≥ 0, r’ ≥ 0) thì:

. ’z z

= r.r[cos(



’) +isin(



’)]

[z = r(cos



+isin



)]

= r

(cos n



+isin n



)

Cho số phức z = r(cos



+isin



) (r>0)

Khi đó

có hai căn bậc hai là: và

- =

 ( , )a b

  c( )os sinz r i

 0r

r z

sin





















   

 

os ' + sin ' ; 0

' '

z r

c i khi r

z r

   

 

   

 

 

os isin

2 2

r c

 

 



















 

os isin

2 2

r c

 

 



















 

os isin

2 2

r c

 

 

 

   



  

 



 

   

 



 



 



 

 





   

 

1. Acgumen của số phức

2. Dạng lượng giác của số phức

3. Nhân và chia số phức dưới dạng lượng giác

4. Công thức Moivre

5. Căn bậc hai của số phức dưới dạng lượng giác

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 102

II. MỘT SỐ BÀI TOÁN ĐIỂN HÌNH

Viết các số phức sau dưới dạng lượng giác:

a. b. c.

Giải:

a) Ta có:

Chọn  là số thực thoả mãn .

b) Ta có = .

Chọn  là số thực thoả mãn

c)Ta có: .

Chọn  là số thực thoả mãn .

Viết các số phức sau dưới dạng lượng giác:

a) b) c)

Giải:

a) Ta có: ;

Áp dụng công tthức nhân, chia số phức ta được:

b) =

 

6 6z i



1 3

4 4

 



5 3 5

2 2



2 2

6 6 6 2.

r   

sin

c 





















6 2( )

4 4 4

cos s nz i i

  

    

1 3 1

4 4 2

 

 













 

















 



 

sin

c 







 













2 22

( )

3 33

12 .

cos isinz





 

   

5 3 5

2 2

 















  

















 



 

sin

c 





















5 cos sin

6 6 6

z i

  



 







    











 

 

 

(1 ) 1

i i

1 3





2 2i

1 i

 2

os isin

3 3

 

 

   

 

 

 

 

  

 

 

 

 

 

 

   

 

 

 

 

2 os i sin

4 4

 

 

 



 

 

(1 3i

 



) 1



2 2

os isin

12 12

 

 

   

 

 

 

 

  

 

 

 

 

 

 

   

 

 

1 3





7 7

os isin

12 12

 

 

   

 

 

 

 

  

 

 

 

 

 

 

   

 

 

Bài toán 1

Bài toán 2

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 103

c) = = = .

Tìm phần thực và phần ảo của mỗi số phức sau:

a) b)

Giải:

a) Xét số phức:

Vậy: phần thực bằng: và phần ảo bằng 0.

b) Xét số phức:

Vậy: phần thực bằng: 0 và phần ảo bằng 128.

Tính số phức sau: z =

Giải:

2 2i

(1 )

i

2 os isin

4 4 4

 

 

   

 

 

 

 

  

 

 

 

 

 

 

   

 

 

os isin

2 4 4

 

 

   

 

 

 

 

  

 

 

 

 

 

 

   

 

 

 

(1 )





5 7

os i sin (1 3 )

3 3

c i i

 

 







 











 

 

9 9

5 5

2 os- i sin

4 4

12 12

(1 )

3 3

2 os i sin

2 2

6 6



 

 

 



 



 



 



 





 











 

  

 

 

 

 

 







 





 

 











 

 







 

 

1 1



2 ( os i sin )c  

  





5 7

os i sin (1 3 )

3 3

c i i

 

 







 











 

7 7

os i sin 2 os i sin

3 3 3 3

7 7

2 os i sin os i sin

3 3 3 3

2 os2 i sin 2 2 .

c i c

c i i

   

 

 

   

 

 

 

 

  

 

 

 

 

 

 

   

 

 

   

     



   

  

 



  

     

  



  



 

  



  

  





     

 

 

 

 

  

 

 

 

(1 ) 3

1 3

i i

 

 

z

 

2 os i sin 2 os i sin

4 4 6 6

4 4

2 os isin

3 3

c c

   

 

 

     



   

  



  

   



  



  



  



  

  



     

 

 



















 

Bài toán 3

Bài toán 4

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 104

10 10 5 5

2 os i sin os i sin

4 4 6 6

40 40

 15

2 os isin

3 3

5 5

os i sin

3 3

( )  1( )

40 40

5  

os isin

3 3

cos p isin p

c c

   

 

 

     



   

  



  

   



  



  



  

  

  



     

 



 



















 

   

 

 

 

  

 

 

 

 

 

   

    



1.

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 105

III. SỬ DỤNG MÁY TÍNH CASIO 570VN-PLUS ĐỂ GIẢI

Đưa máy tính về dạng rađian

qw4

Để chuyển một số phức từ dạng đại số sang dạng lượng giác, trong chế độ CMPLX ta bấm

và chọn

Để chuyển một số phức từ dạng đại số sang dạng lượng

giác, trong chế độ CMPLX ta bấm

và chọn

Viết số phức dưới dạng lượng giác.

Hướng dẫn:

o Đưa máy tính về dạng rađian

qw4

o Vào chế độ CMPLX

o Nhập số phức z:

7+7b

o Nhấn

q23

để chuyển sang dạng lượng giác.

o Kết quả thu được là:

Số phức z đã được chuyển sang dạng lượng giác với và acgument là

Viết số phức z= (cos + isin ) dưới dạng đại số.

Hướng dẫn:

o Đưa máy tính về dạng rađian

qw4

o Vào chế độ CMPLX

o Nhập số phức

ở dạng lượng giác và chuyển số phức qua dạng đại số như sau:

s2$qzpaqKR4$q24=

o Màn hình cho kết quả là:

7 7z i 

7 2r 







7 2 os isin

4 4

z c

 

 

 

   





 

 

 





 

 

 



 



 

 



 

 





   

  

 



 



















 



 



















 

PP CASIO

Bài toán 1

Bài toán 2

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 106

Số phức

5 3 3

1 2 3







có một Acgument là :



Hướng dẫn:

 Thu gọn

về dạng tối giản

1 3z i   

a5+3bs3R1p2bs3=

 Tìm Acgument của

với lệnh SHIFT 2 1

q21p1+s3$b)=

Vậy

có 1 Acgument là



. Tuy nhiên khi so sánh kết quả ta lại không thấy có giá trị nào là



. Khi đó ta nhớ đến tính chất “Nếu góc



là một Acgument thì góc

2 

cũng là một

Acgument”



Đáp số chính xác là D vì

2 8

2 3

 

 

Bài toán 3

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 107

IV. MỘT SỐ BÀI TOÁN VỀ ỨNG DỤNG CỦA DẠNG LƯỢNG GIÁC

Giải phương trình:

 

5 4 3 2

1 0 1

z z z z z     

Giải:

Ta có: (1) 

     

4 2

1 1 1 0

z z z z z

     



 





4 2

1 1 0

z z z

   



Xét phương trình:

4 2

1 0z z  

 z



Từ z

= 

Từ z

= 

Tóm lại phương trình đã cho có tất cả 5 nghiệm:

1z  

;

z 

;

z 

;

z 

;

z 

Cho

và

là hai số phứ xác định bởi

1z i 

và

1 –z i



. Xác định dạng đại số và

dạng lượng giác của . Từ đó suy ra giá trị chính xác của: cos và sin .

Giải:

Ta có: = = .

Ta có: z

= 2(cos + isin ); z

= (cos + isin ) = (cos + isin ) 

cos = và sin = .

4 2

1 0

z z



 



  





1 3

 

1 3 2 2

os i sin

2 2 3 3

1 3 2 2

os i sin

2 2 3 3

z i c

 





    



   

 

 



 

      

 

 

 



 

 

   



2 2

os i sin

3 3

 



os i sin

3 3

os -i sin

3 3

z c

 





 



 





2 2

os i sin

3 3

 

   

 

 

 

  

 

 

 

 

 

   

os i sin

3 3

os -i sin

3 3

z c

 



   

 

 



 

   

 

 



 

 

 

   



   

 

 



 

   

 

 



 

 

 

   





1 3

2 2



1 3

2 2

 

1 3

2 2



1 3

2 2

 



1 3





1 3 1 3

2 2

 

  





















 



 



















 



 



















 



1 3





1 3



Bài toán 1

Bài toán 2

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 108

Nhận xét: Qua bài tập này ta thấy được một ứng dụng quan trọng của số phức, ta có thể tính

sin, cos của một góc bằng công cụ số phức thông qua sự liên hệ giữa dạng đại số và dạng

lượng giác của số phức.

Giải phương trình: .

Giải:

Ta có: :

6 6

64 0 64.z z    

Giả sử

cos( )sinz x yi r i

 

   

Ta có:

64 64 cos( )sini

 

  

Và cos6  + isin6  = cos  + isin   6  =  +2k  (k  Z)

  =

Với

0 2k z  

= +i

Với

1 2k z   

= -i

Với

1 2k z  

= 2i

Với

2 2k z   

= -2i

Với

3 2k z   

= - - i.

Tìm n là số nguyên dương và sao cho số phức là số thực.

Giải:

Ta có: 1 + i = 2  z = 2

Để z  R  2

.sin = 0  sin = 0

 n chia hết cho 3, mà n nguyên dương  [1;10]  n  [3;6;9].

64 0z  

6 6

 



os isi

6 6

c n

 

 



















 

os - isi

6 6

c n

 

 

   



  

 



 

  

 



 



 



 

 





   

 

os isi

2 2

c n

 

 



















 

os - isi

2 2

c n

 

 

   



  

 



 

  

 



 



 



 

 





   

 

5 5

os - isi -

6 6

c n

 

 

   



  

 



 

 

 



 



 



 

 





   

 

1,10

 



 

 

 

1 3

z i 

os i sin

3 3

 

 



















 

os i sin

3 3

n n

 

 



















 

n

Bài toán 3

Bài toán 4

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 109

V. BÀI TẬP RÈN LUYỆN

Câu 1: Số phức z = -1 + i viết dưới dạng lượng giác là:

A. z = B. z =

C. z = D. z =

Câu 2: Số phức z = 8i viết dưới dạng lượng giác là:

A. z = B. z =

C. z = D. z =

Câu 3: Dạng lượng giác của số phức z = là:

A. z = B. z =

C. z = D.

Câu 4: : Số phức z = 8i viết dưới dạng lượng giác là:

A. B.

C. D.

Câu 6: Cho số phức z = - 1 - i. Argumen của z (sai khác k2) bằng:

A. B. C. D.

Câu 7: Điểm biểu diễn của số phức z = có toạ độ là:

A. (1; -1) B. (-1; 1) C. (2; 2) D. (-2; 2)

Câu 8: Cho , . Tích

bằng:

A. 12(1 - i) B. C. D.

Câu 9: Cho , . Tích z

bằng:

A. 6(1 - 2i) B. 4i C. 6i D. 6(1 - i)

Câu 10: Cho , .Thương bằng:

A. 1 + i B. C. 1 - i D. 2(1 + i)

Câu 11: Cho , . Thương bằng:

A. 2i B. -2i C. 2(1 + i) D. 2(1 - i)

Câu 12: Tính (1 - i)

, ta được:

2 cos sin

6 6

 

 



















 

2 cos

4 4

isin

 

 



















 

3 3

2 cos sin

4 4

 

 



















 

3 cos sin

6 6

 

 



















 

3 3

8 cos sin

2 2

 

 



















 

8 cos sin

2 2

 

 



















 

 

8 cos 0 sin 0



 

8 cos sin

 

2 cos sin

6 6

 

 



















 

11 11

2 cos sin

6 6

 

 



















 

7 7

2 cos sin

6 6

 

 



















 

5 5

2 cos sin

6 6

 

 



















 

13 13

2 cos sin

6 6

 

 



















 

8 2 cos sin

6 6

 

 



















 

8 2 cos sin

4 4

 

 



















 

6 2 cos sin

5 5

 

 

 



















 

6 2 cos sin

7 7

 

 



















 



 

0 0

2 cos 315 sin 315

i

 

0 0

3 cos15 sin15

z i 

 

0 0

4 cos 30 sin 30

z i 

 

6 2 1

i

 

3 2 1 2i



 

2 2

i

 

0 0

3 cos20 sin 20

z i 

 

0 0

2 cos110 sin110

z i  

 

0 0

8 cos100 sin100

z i 

 

0 0

4 cos 40 sin 40

z i 

 

2 1 3

i

 

0 0

4 cos10 sin10

z i 

 

0 0

2 cos 280 sin 280

z i  

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 110

A. -1024 B. 1024i C. 512(1 + i) D. 512(1 - i)

Câu 13: Đẳng thức nào trong các đẳng thức sau đây là đúng?

A. (1+ i)

= -16 B. (1 + i)

= 16i

C. (1 + i)

= 16 D. (1 + i)

= -16i

Câu 14: Cho số phức z  0. Biết rằng số phức nghịch đảo của z bằng số phức liên hợp của nó.

Trong các kết luận nào đúng:

A. z  R B. z là một số thuần ảo

C. D.

Câu 15: Cho số phức z = cos + isin . kết luận nào sau đây là đúng:

A. B.

C. D. .

Đáp án:

6. C 7. A 8. B 9. C 10. A

11.

12.

13.

14.

15.



 

cos

n n

z z n



 

 

2 cos

n n

z z n

 

 

2 cos

n n

z z n



 

 

2 cos

n n

z z



 

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 111

F. TUYỂN TẬP CÁC CÂU SỐ PHỨC VẬN DỤNG CAO

I. ĐỀ BÀI

Câu 1. Cho các số phức

1 2

,z z

khác nhau thỏa mãn:

1 2

.z z

Chọn phương án đúng:

1 2

z z







1 2

z z





là số phức với phần thực và ảo đều khác

1 2

z z





là số thực D.

1 2

z z





là số thuần ảo

Câu 2. Cho số phức

thỏa mãn điều kiện

3 4 2.

z i

  

Trong mặt phẳng

Oxy

tập hợp điểm

biểu diễn số phức

2 1w z i  

là hình tròn có diện tích

9S 

. B.

12S 

. C.

16S 

. D.

25S 

Câu 3. Trong các số phức thỏa mãn điều kiện

3 2 .z i z i   

Tìm số phức có môđun nhỏ

nhất?

1 2z i 

. B.

1 2

5 5

z i

  

. C.

1 2

5 5

z i

 

. D.

1 2z i  

Câu 4. Cho số phức

thỏa mãn

2 3 1

z i

  

. Giá trị lớn nhất của

z i 

là

13 2

. B.

. C.

. D.

13 1

Câu 5. Cho

1 2 3

,  , z z z

là các số phức thỏa mãn

1 2 3

0z z z  

và

1 2 3

z z z

  

Khẳng

định nào dưới đây là sai ?

3 3 3 3 3 3

1 2 3 1 2 3

.z z z z z z

    

3 3 3 3 3 3

1 2 3 1 2 3

.z z z z z z

    

3 3 3 3 3 3

1 2 3 1 2 3

.z z z z z z

    

3 3 3 3 3 3

1 2 3 1 2 3

.z z z z z z

    

Câu 6. Cho

1 2 3

, ,z z z

là các số phức thỏa

1 2 3

z z z

  

Khẳng định nào dưới đây là đúng?

1 2 3 1 2 2 3 3 1

.z z z z z z z z z    

1 2 3 1 2 2 3 3 1

.z z z z z z z z z    

1 2 3 1 2 2 3 3 1

.z z z z z z z z z    

1 2 3 1 2 2 3 3 1

.z z z z z z z z z    

Câu 7. Cho

 

P z

là một đa thức với hệ số thực.Nếu số phức

thỏa mãn

 

P z



thì

 

P z



 



















 

 



















 

 

P z



Câu 8. Cho số phức

thỏa mãn



. Đặt

z i







. Mệnh đề nào sau đây đúng?



. B.



. C.



. D.



Câu 9. Cho số phức

thỏa mãn



. Tìm giá trị lớn nhất của biểu thức

1 .

 

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 112

Câu 10. Gọi

là điểm biểu diễn số phức

2 3

z z i



 





, trong đó

là số phức thỏa mãn

  

2 3

i z i i z    

. Gọi

là điểm trong mặt phẳng sao cho

 

, 2

Ox ON





 

, trong

đó

 

Ox OM

 

 

là góc lượng giác tạo thành khi quay tia

tới vị trí tia

. Điểm

nằm trong góc phần tư nào?

A. Góc phần tư thứ (I). B. Góc phần tư thứ (II).

C. Góc phần tư thứ (III). D. Góc phần tư thứ (IV).

Câu 11. Cho số phức

thỏa mãn



. Tìm giá trị lớn nhất

max

và giá trị nhỏ nhất

min

của

biểu thức

2 3

1 1 .

M z z z    

max min

5;  1.M M 

max min

5;  2.M M 

max min

4;  1.M M 

max min

4;  2.M M 

Câu 12. Cho số phức

thỏa



. Tìm tích của giá trị lớn nhất và nhỏ nhất của biểu thức

z i





. D.

Câu 13. Gọi

1 2 3 4

,  ,  , z z z z

là các nghiệm của phương trình

z i

 























 

Tính giá trị biểu thức

    

2 2 2 2

1 2 3 4

1 1 1 1

P z z z z

    

2.P 

P 

Câu 14. Cho số phức

thỏa mãn

1 2 3

z i

  

. Tìm môđun lớn nhất của số phức

2 .z i

26 6 17 .

26 6 17 .

26 8 17 .

26 4 17 .

Câu 15. Cho số phức

thỏa mãn



. Tìm giá trị lớn nhất của biểu thức

1 3 1 .P z z   

3 15

6 5

2 20.

Câu 16. Cho số phức

thỏa mãn



Gọi

và

lần lượt là giá trị lớn nhất và giá trị nhỏ

nhất của biểu thức

1 1 .

P z z z

    

Tính giá trị của

.M m

13 3

3 3.

Câu 17. Gọi điểm

, A B

lần lượt biểu diễn các số phức

và

 

;  0

z z z





 

trên mặt phẳng

tọa độ (

,  , A B C

và

,  , A B C

  

đều không thẳng hàng). Với

là gốc tọa độ, khẳng

định nào sau đây đúng?

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 113

A. Tam giác

OAB

đều. B. Tam giác

OAB

vuông cân tại

C. Tam giác

OAB

vuông cân tại

D. Tam giác

OAB

vuông cân tại

Câu 18. Cho số phức

thỏa mãn điều kiện Khẳng định nào sau đây là đúng?

A. B.

C. D.

Câu 19. Cho số phức thỏa mãn . Tìm môđun lớn nhất của số phức

A. B. C. D.

Câu 20. Cho là bốn điểm trong mặt phẳng tọa độ theo thứ tự biểu diễn các số phức

. Biết là tứ giác nội tiếp tâm Tâm biểu

diễn số phức nào sau đây?

A. B. C. D.

Câu 21. Trên mặt phẳng tọa độ lấy điểm là điểm biểu diễn số phức

và gọi là góc tạo bởi chiều dương trục hoành và vectơ Tính

A. B. C. D.

Câu 22. Cho là hai số phức liên hợp của nhau và thỏa mãn và

Tính môđun của số phức

A. B. C. D.

Câu 23. Cho số phức nguyên dương. Có bao nhiêu giá trị để là

số thuần ảo?

A. 24. B. 26. C. 25. D. 50.

Câu 24. Nếu thì

A. lấy mọi giá trị phức. B. là số thuần ảo.

C. bằng 0. D. lấy mọi giá trị thực.

Câu 25. Cho số phức thỏa mãn . Tìm môđun lớn nhất của số phức

A. B. C. D.

4 2 .z z

 

3 1 3 1

6 6

 

 

5 1 5 1.

   

6 1 6 1.

   

2 1 2 1

3 3

 

 

1 2 2

z i

  

9 4 5.

11 4 5

6 4 5

5 6 5

,  ,  , A B C D

1 2 ; 1 3 ; 1 3 ; 1 2i i i i     

ABCD

3.z 

1 3 .z i 

1.z 

1.z  

,Oxy

   

2 4

z i i  



.OM



cos2 .

425



475



425

1 2

, z z

 

1 2

2 3.

z z 

z 



z 

2 6

 























 

1;50

 



 

 





 

1 6 2 10

i z i   

4 5

3 5.

3 5

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 114

Câu 26. Gọi là số phức thỏa mãn hai điều kiện và

đạt giá trị lớn nhất. Tính tích

A. B. C. D.

Câu 27. Có bao nhiêu số phức thỏa và

A. 1. B. 2. C. 3. D. 4.

Câu 28. Gọi điểm lần lượt biểu diễn các số phức ; trên mặt phẳng tọa độ

( và đều không thẳng hàng) và . Với là gốc tọa độ,

khẳng định nào sau đây đúng?

A. Tam giác đều. B. Tam giác vuông cân tại

C. Tam giác vuông cân tại D. Diện tích tam giác không đổi.

Câu 29. Trong các số phức thỏa mãn điều kiện . Tìm môđun nhỏ nhất của

số phức

A. B. C. D.

Câu 30. Tìm điều kiện cần và đủ về các số thực để phương trình không

có nghiệm thực.

A. B. hoặc

C. D. hoặc

Câu 31. Nếu thì

A. lấy mọi giá trị phức. B. là số thuần ảo.

C. bằng 0. D. lấy mọi giá trị thực.

Câu 32. Cho số phức thỏa mãn . Tìm môđun nhỏ nhất của số phức

A. B. C. D.

Câu 33. Gọi là điểm biểu diễn số phức , trong đó là số phức thỏa mãn

. Gọi là điểm trong mặt phẳng sao cho , trong

 

 ,z x yi x y

   

2 2

2 2 26

z z   

3 3

2 2

z i

 

.xy

xy 

i z







z i







, A B

 

2 1 2

;  . 0

z z z



,  , A B C

  

2 2

1 2 1 2

.z z z z 

OAB

2 4 2z i z i   

2 .z i

3 5.

3 2

3 2

, m n

4 2

0z mz n  

4 0.m n 

4 0m n 

4 0

m n





 















4 0

0 .

m n





 















4 0m n 

4 0

m n





 















 

;  0

z a a

 

z a



1 2 3

z i

  

1 .z i 

2 2.

2 1z z i

z i



  





  

1 2

i z i i z    

 

, 2

Ox ON





 

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 115

đó là góc lượng giác tạo thành khi quay tia tới vị trí tia . Điểm

nằm trong góc phần tư nào?

A. Góc phần tư thứ (I). B. Góc phần tư thứ (II).

C. Góc phần tư thứ (III). D. Góc phần tư thứ (IV).

Câu 34. Biết số phức thỏa mãn đồng thời hai điều kiện và biểu thức

đạt giá trị lớn nhất. Tính môđun của số phức

A. B.

C. D.

Câu 35. Các điểm và lần lượt biểu diễn các số phức và

trên mặt phẳng tọa độ ( và đều không thẳng hàng). Biết

, khẳng định nào sau đây đúng?

A. Hai tam giác và bằng nhau.

B. Hai tam giác và có cùng trực tâm.

C. Hai tam giác và có cùng trọng tâm.

D. Hai tam giác và có cùng tâm đường tròn ngoại tiếp.

Câu 36. Trên mặt phẳng tọa độ lấy điểm là điểm biểu diễn số phức

và gọi là góc tạo bởi chiều dương trục hoành và vectơ Tính

A. B. C. D.

Câu 37. Cho số phức . Tìm môđun lớn nhất của

A. 1. B. 0. C. . D. 2.

Câu 38. Cho số phức có . Với tìm phần thực của số phức

A. B. C. D.

Câu 39. Cho số phức thỏa mãn , được biểu diễn trong mặt phẳng phức

lần lượt là các điểm . Biết , tính giá trị của biểu thức .

A. B. C. D.

 

Ox OM

 

 

3 4 5

z i  

2 2

M z z i   

.z i

2 41

z i 

3 5.

z i 

5 2

z i 

41.

z i 

,  , A B C

  

1 2 3

,  , z z z

1 2 3

,  , z z z

  

,  , A B C

  

1 2 3 1 2 3

z z z z z z

  

    

ABC

A B C

  

ABC

A B C

  

ABC

A B C

  

ABC

A B C

  

,Oxy

  

2 3 1

z i i  



.OM



sin2 .



 

1 2

m i

z m

m m i

 

 

 



 

;  0

z m m

 

; z m

m z

1 2

,z z

z 



,M N

 

OM ON



 

 

1 2

z z





7 3

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 116

Câu 40. Cho thỏa mãn thỏa mãn . Biết tập hợp các điểm biểu

diễn cho số phức là đường tròn , bán kính . Khi đó.

A. B.

C. D.

Câu 41. Trong các số phức thỏa , gọi là số phức có mô đun nhỏ nhất. Khi đó

A. Không tồn tại số phức . B. .

C. . D. .

Câu 42.

Tìm tập hợp các điểm biểu diễn hình học số phức trong mặt phẳng phức, biết số

phức thỏa mãn điều kiện:

A. Tập hợp các điểm cần tìm là đường tròn có tâm và có bán kính .

B. Tập hợp các điểm cần tìm là đường elip có phương trình

C. Tập hợp các điểm cần tìm là những điểm trong mặt phẳng thỏa mãn

phương trình

D. Tập hợp các điểm cần tìm là đường elip có phương trình

Câu 43. Trong mặt phẳng phức , các số phức thỏa . Tìm số phức

được biểu diễn bởi điểm sao cho ngắn nhất với .

A. . B. . C. . D. .

Câu 44. Trong mặt phẳng phức , tập hợp biểu diễn số phức Z thỏa là hình

vành khăn. Chu vi của hình vành khăn là bao nhiêu ?

A. . B. . C. . D. .

Câu 45. Trong mặt phẳng phức , tập hợp các điểm biểu diễn số phức thỏa mãn

là hai đường thẳng . Khoảng cách giữa 2 đường thẳng

là bao nhiêu ?

A. . B. . C. . D. .

Câu 46. Cho số phức thỏa mãn .Tính , với

A. . B. . C. . D. .

z  

 

2 1 2i z i

   

 

3 4 1 2w i z i   

 

1; 2

., 5

I R  

 

1;2 ,

I R 

 

1;2 , 5.

I R

 

 

1; 2 , 5.

I R

 

3 4 2

z i

  



4 4 10.

z z

   

 

0;0

4.R 

2 2

9 25

x y

 

 

;M x y

Oxy

   

2 2

4 4 12.

x y x y     

2 2

25 9

x y

 

Oxy

2 1

z i z i   

 

1, 3

3 i

1 3i

2 3i

2 3i 

Oxy

1 1 2

z i

   

4P 

P 

2P 

3P 

Oxy

 

2 16

z z z  

1 2

,d d

1 2

,d d

 

1 2

, 2

d d d



 

1 2

, 4

d d d



 

1 2

, 1

d d d



 

1 2

, 6

d d d



  

2 5 1 2 3 1

z z z i z i

      

min | |w

2 2w z i  

min | |



min | | 2w 

min | | 1w 

min | |



Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 117

Câu 47. Giả sử theo thứ tự là điểm biểu diễn của số phức , . Khi đó độ dài của

bằng

A. . B. . C. . D. .

Câu 48. Cho số phức thỏa mãn điều kiện . Tìm giá trị lớn nhất của

A. . B. . C. . D. .

Câu 49. Trên mặt phẳng tọa độ , tìm tập hợp các điểm biểu diễn các số phức thỏa mãn

điều kiện .

A. Đường tròn . B. Elip .

C. Đường tròn . D. Elip .

Câu 50. Tìm nghiệm phức thỏa mãn hệ phương trình phức:

A. . B. . C. . D. .

,A B



2 1

z z

2 1

z z

1 2

z z



1 2

z z



1 2

z  

T z i z i    

max 8 2T 

max 4T 

max 4 2T 

max 8T 

Oxy

2 2 10

z z

   

   

2 2

2 2 100

x y   

2 2

25 4

x y

 

   

2 2

2 2 10

x y   

2 2

25 21

x y

 

z z i

z i





  



















2z i 

1z i 

2z i 

1z i 

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 118

II. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI CHI TIẾT

1D 2C 3C 4D 5D 6A 7D 8A 9C 10A

11A

12A

13B 14A

15D

16A

17C

18B

19A

20C 21D

22C

23C 24B

25B 26D

27A

28A

29C

30D

31B 32C

33B

34D

35C 36A

37A

38D

39B

40C

41D

42D

43A

44C

45B

46C

47B

48B

49D

50D

Câu 1.

Phương pháp tự luận:

Vì và nên cả hai số phức đều khác .

Đặt và , ta có

Từ đó suy ra là số thuần ảo

Phương pháp trắc nghiệm:

Số phức khác nhau thỏa mãn nên chọn , suy ra

là số thuần ảo Chọn D.

Câu 2.

Giả sử , khi đó

Suy ra tập hợp điểm biểu diễn số phức là hình tròn tâm , bán kính

Vậy diện tích cần tìm là Chọn C.

Câu 3.

Phương pháp tự luận

Giả sử

1 2

z z

1 2

z z

1 2

z z







1 2

z z a 

2 2

1 2 1 2 1 2 1 2

1 2 2

1 2

a a

z z z z z z z z

w w

z z z z

a a

z z



 

  









     









 

 



1 2

,z z

1 2

z z

1 2

1;z z i 

1 2

z z

z z i



 

 



2 1

w i

w z i z

 

    

 

3 4 2 3 4 2 1 6 8 4 7 9 4 1

w i

z i i w i i w i

 

                

 

,w x yi x y

   

     

2 2

1 7 9 16

x y    

 

7; 9



4.r 

.4 16S   



 

,z x yi x y

   

           

2 2 2

3 2 3 2 1 3 2 1

z i z i x y i x y i x y x y                 

6 9 4 4 2 1 4 8 4 0 2 1 0 2 1y x y x y x y x y                

 

2 2 2 2

2 1 5

2 1 5 4 1 5

5 5 5

z x y y y y y y

 







           











 

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 119

Suy ra khi .Vậy Chọn C.

Phương pháp trắc nghiệm

Giả sử

Vậy tập hợp các điểm biểu diễn số phức thỏa điều kiện là đường thẳng

Phương án A: có điểm biểu diễn nên loại A.

Phương án B: có điểm biểu diễn nên loại B.

Phương án D: có điểm biểu diễn nên loại B.

Phương án C: có điểm biểu diễn

Câu 4. Gọi ta có .

Theo giả thiết nên điểm biểu diễn cho số phức nằm trên đường

tròn tâm bán kính .

Ta có .

Gọi và thì .

Do chạy trên đường tròn, cố định nên lớn nhất khi là giao của với đường

tròn.

Phương trình , giao của và đường tròn ứng với thỏa mãn:

nên .

Tính độ dài ta lấy kết quả Chọn D

Câu 5.

Cách 1: Ta có:

Mặt khác nên Chọn D.

Cách 2: thay thử vào các đáp án, thấy đáp án D bị sai

min

z 

2 1

5 5

y x

   

1 2

5 5

z i

 



 

,z x yi x y

   

           

2 2 2

3 2 3 2 1 3 2 1

z i z i x y i x y i x y x y                 

6 9 4 4 2 1 4 8 4 0 2 1 0y x y x y x y             

3 2

z i z i   

: 2 1 0d x y  

1 2z i 

 

1; 2

d 

1 2

5 5

z i

  

1 2

;

5 5

 







 











 

1 2z i  

 

1;2

d 

1 2

5 5

z i

 

1 2

;

5 5

 







 











 

z x yi 

 

2 3 2 3 2 3z i x yi i x y i         

   

2 2

2 3 1

x y

   

 

2;3

1R 

     

2 2

1 1 1 1 1 1

z i x yi i x y i x y             

 

;M x y

 

1;1



   

1 1

HM x y   

2 3

3 2

x t

y t





 







 





2 2

9 4 1

t t t    

3 2 3 2

2 ; 3 , 2 ; 3

13 13 13 13

M M

   

 

 

 

   

 

 

 

 

 

   

13 1HM  



1 2 3 2 3 1

0z z z z z z      

      

3 3 3

1 2 3 1 2 3 1 2 1 3 1 2 3 2 3 2 3

3 3

z z z z z z z z z z z z z z z z z

          

3 3 3

1 2 3 1 2 3

z z z z z z   

3 3 3

1 2 3 1 2 3

z z z z z z   

3 3 3

1 2 3 1 2 3 1 2 3

3 3 3

z z z z z z z z z

     

1 2 3

z z z

  

3 3 3

1 2 3

z z z

  



1 2 3

1z z z  

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 120

Câu 6.

Cách 1: Kí hiệu : là phần thực của số phức.

Ta có (1).

(2).

Từ và suy ra .

Các h khác: B hoặc C đúng suy ra D đúngLoại B, C.

Chọn  A đúng và D sai Chọn A.

Cách 2: thay thử vào các đáp án, thấy đáp án D bị sai

Câu 7.Giả sử có dạng

. Chọn D.

Câu 8. Đặt Có (do )

Ta chứng minh .

Thật vậy ta có

Dấu “=” xảy ra khi .Vậy Chọn A.

Câu 9. Ta có: Khi Chọn C.

Câu 10. Ta có:

Lúc đó: . Chọn A.

Câu 11. Ta có: , khi

Mặt khác: khi

Chọn A.

1 2 3

z z z

 

 

2 2 2

1 2 3 1 2 2 3 3 1

2 Re

z z z z z z z z z

     

 

1 2 2 3 3 1

3 2 Re

z z z z z z   

1 2 2 3 3 1

z z z z z z

 

 

2 2 2

1 2 2 3 3 1 1 2 2 3 2 3 3 1 3 1 1 2

2 Re

z z z z z z z z z z z z z z z z z z

     

2 2 2 2 2 2 2 2 2

1 2 2 3 3 1 1 2 3 2 3 1 3 1 2

. . . 2 Re

z z z z z z z z z z z z z z z

 





     







 

   

1 3 2 1 3 2 1 2 3 3 3 1

3 2 Re 3 2 Re

z z z z z z z z z z z z       

 

1 2 3 1 2 2 3 3 1

z z z z z z z z z    

1 2 3

z z z 



1 2 3

1z z z  

( 3; 3; 0)A  

 

0 1 2 0 1 2

... ; ; ;...; ; 0

n n n

P z a a z a z a z a a a a a      

 

2 2

0 1 2 0 1 2

0 ... 0 ... 0

n n

P z a a z a z a z a a z a z a z

            

 

0 1 2

... 0 0

a a z a z a z P z

       



 

2 2

, , 1

a a bi a b a b

     





   

 

2 2 1 4 2 1

2 2

a b i a b

z i

iz b ai

b a

   



  

  

 

 

4 2 1

a b

b a

 



 

 

   

2 2

2 2 2 2

4 2 1

1 4 2 1 2 1

a b

a b b a a b

b a

 

         

 

2 2

1a b 





5 5 5

1 1 1 6.

i i

z z

      

6.z i A  



  

5 1 5 1 1

2 3 1 ; tan .

4 4 4 4 5

i z i i z z i w i M 

 







             











 

2 2

2 tan 5 1 tan 12

sin 2 0;  cos 2 0

13 13

1 tan 1 tan

 



     

 



2 3

1 1 5

M z z z

     

max

1 5 5.z M M    

3 3 3 3 3

1 1 1 1 1

1 1,

2 2 2

z z z z z

M z

     

      



min

1 1 1.z M M     



Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 121

Câu 12. Ta có Mặt khác:

Vậy, giá trị nhỏ nhất của là , xảy ra khi giá trị lớn nhất của bằng xảy ra khi

Chọn A.

Câu 13. Ta có phương trình

Suy ra: . Vì

Mà Vậy từ Chọn B.

Câu 14. Gọi . Ta có:

Đặt

Chọn A.

Câu 15. Gọi . Ta có:

Ta có: .

Xét hàm số Hàm số liên tục trên và với

ta có:

Ta có: Chọn D.

Câu 16. Gọi . Ta có:

Đặt , ta có

Ta có

Suy ra .

Xét hàm số Bằng cách dùng đạo hàm, suy ra

Chọn A.

1 3

1 1 .

| | 2

z z

    

1 1

1 1 .

| | 2

z z

   

P

2 ;z i 

2 .z i



     

4 4

2 1 0.

f z z i z

     

      

1 2 3 4

f z z z z z z z z z    

  

   

 

1 1 1

1  1 .

225

f i f i

z z i z i P



     

         

4 4 4

1 5; 3 1 85.

f i i i f i i i         

 

1 .

P 



   

;  ; 2 2z x yi x y z i x y i        

 

   

2 2

1 2 9 1 2 9

z i x y

       

1 3 sin ;  2 3 cos ;  0;2 .

x t y t t



 

     

 

 

         

2 2 2

2 1 3 sin 4 3 cos 26 6 sin 4 cos 26 6 17 sin ;  .

z i t t t t t               



max

26 6 17 2 26 6 17 2 26 6 17 .

z i z i         



 

;  ;z x yi x y

    

2 2 2 2

1 1 1 1;1 .

z x y y x x

 

         

 

 

       

2 2

1 3 1 1 3 1 2 1 3 2 1

P z z x y x y x x

             

     

2 1 3 2 1 ;  1;1 .

f x x x x

 

     

 

 

1;1

 



 

 

 

1;1

 

 

   

 

1 3 4

0 1;1 .

2 1 2 1

f x x

x x



       

 

   

max

1 2;  1 6;  2 20 2 20.

f f f P

 







      











 



 

;  ;z x yi x y

    

1 . 1

z z z

  

t z

 

0 1 1 1 2 0;2 .

z z z t

 

        

 

 

  

1 1 1 . 2 2 .

t z z z z z z x x



          

 

2 2 2

1 . 1 2 1 2 1 3

z z z z z z z z z x x t

             

 

3 , 0;2 .

f t t t t

 

   

 

 

   

13 13 3

max ; min 3 . .

4 4

f t f t M n   



Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 122

Câu 17. Ta có:

Ta có:

Suy ra: và là tam giác vuông cân tại Chọn C.

Câu 18. Áp dụng bất đẳng thức ta được

Vậy, nhỏ nhất là khi và lớn nhất là khi

Chọn B.

Câu 19. Gọi . Ta có:

Đặt .

Lúc đó:

đạt được khi Chọn A.

Câu 20. Ta có biểu diễn số phức biểu diễn số phức . Mặt khác

nên . Tương tự (hay vì lí do đối xứng qua ), . Từ đó

suy ra là một đường kính của đường tròn đi qua

Vậy Chọn C.

Câu 21. Ta có:

Ta có: Chọn D.

Câu 22. Gọi . Không mất tính tổng quát ta gọi

Do là hai số phức liên hợp của nhau nên , mà

Ta có:

1 1 2

; . . .

2 2 2

i i

OA z OB z z z z

 



    

1 1 2

. .

2 2 2

i i

BA OA OB BA z z z z z z

 



        

  

2 2 2

OA OB AB 

AB OB OAB 



,u v u v  

2 2

2 4 4 4 2 4 0 5 1.

z z z z z z

             

2 2

2 4 4 2 4 0 5 1.

z z z z z z z

            

5 1,

5z i i  

5 1,

5.z i i 



 

;  ;z x yi x y

    

   

2 2

1 2 2 1 2 4.

z i x y

       

1 2 sin ; 2 2 cos ;  0;2

x t y t t



 

     

 

 

         

2 2 2

2 2

1 2 sin 2 2 cos 9 4 sin 8 cos 9 4 8 sin ; z t t t t t              



 

9 4 5 sin 9 4 5; 9 4 5

z t z

 

        

 

 

max

9 4 5

z  

5 2 5 10 4 5

5 5

z i

  

 





3 ;i



3 3i

3 3







. 0AB DB 

 

. 0DC AC 

 

,  ,  ,  .A B C D

 

1; 0 1.

I z

 



     

2 4 16 13 16;13 tan .

z i i i M        

1 tan 425

cos2 .

1 tan





 





 

1 2

;  ; z a bi z a bi a b

       

0.b 

1 2

2 3 2 2 3 3.

z z bi b     

1 2

, z z

1 2

.z z  

 

1 1

2 2

1 2

z z

   

 

 

   

3 3 2 2 3 2 3 2

2 2

3 3 3 0 1.

z a bi a ab a b b i a b b a

a b







            











Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 123

Vậy Chọn C.

Câu 23. Ta có:

là số thuần ảo khi và chỉ khi (do ).

Vậy có 25 giá trị thỏa yêu cầu đề bài. Chọn C.

Câu 24. Ta có: là số thuần ảo. Chọn B.

Câu 25. Gọi .

Ta có:

Đặt .

Lúc đó:

đạt được khi Chọn B.

Câu 26. Đặt Thay vào điều kiện thứ nhất, ta được

Đặt Thay vào điều kiện thứ hai, ta có

Dấu bằng xảy ra khi Chọn D.

Câu 27. Ta có:

Chọn A.

Câu 28. Ta có: . Do

(1)

2 2

z a b

  



2 6

(2 ) 2 .

m m m

z i i

 









  













 

2 1,m k k   

0; z m   



1 1

z z z

z z z z z

z z z z



       



 

;  ;z x yi x y

    

   

2 2

6 2

1 6 2 10 1 . 10 2 4 5

2 4 5.

i z i i z z i

x y

 

           



    

2 5 sin ; 4 5 cos ;  0;2

x t y t t



 

    

 

 

   

     

   

2 2

2 5 sin 4 5 cos

 25 4 5 sin 8 5 cos 25 4 5 8 5 sin ; 

z t t

t t t  

   

       



 

25 20 sin 5; 3 5

z t z

 

     

 

 

max

3 5

z 

3 6 .z i 



 

 , .

z x iy x y

   

2 2

36.x y 

3 cos , 3 sin .x t y t 

3 3

 18 18 sin 6.

2 2

P z i t



 







      











 

3 3 2 3 2

sin 1 .

4 4 2 2

t t z i

 

 







         











 



3 3

4 2 3 3

2 2

z i z x y

i z

z i

x y

z i z i z

















 





    





  

      

   

   

  

   

   











 



 







 

2 2 2

1 2 1 2 1 1 2 1 1 1 2 1

. ;  .

z z z z z z z z z z z z

      

1 2 1

0 ; 

z z z

   

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 124

Mặt khác: (do ) (2)

Từ (1) và (2) suy ra: . Vậy ta có: .

Chọn A.

Câu 29. Gọi .

Ta có:

khi Chọn C.

Câu 30. Phương trình không có nghiệm thực trong các trường hợp:

TH 1: Phương trình vô nghiệm, tức là

TH 2: Phương trình có hai nghiệm âm

Chọn D.

Câu 31. Ta có: là số thuần ảo. Chọn B.

Câu 32. Gọi . Ta có:

Đặt

, khi

Chọn C.

Câu 33. Ta có:

Lúc đó: . Chọn C.

Câu 34. Gọi . Ta có: :

tâm và

Mặt khác:

Do số phức thỏa mãn đồng thời hai điều kiện nên và có điểm chung

 

1 2 1 2 1 2 1 2 1 2

z z z z z z z z z z

       

0z 

2 2

2 1

1 2

z z

  

1 2 2 1

z z z z OA OB AB     



 

;  ;z x yi x y

    

     

2 2 2

2 4 2 2 4 2 4 0 4 .z i z i x y x y x y y x                 

     

2 2 2 2

2 2 2

2 2 6 2 12 36 2 3 18 18

z i x y x x x x x             

min

2 18 3 2

z i   

3 .z i 



4 2

0z mz n  

4 0.m n 

 

4 2 2

0; 

t mt n t z

   

0 4 0

0 0 .

0 0

m n

S m

P n

 

 

   

 

   

 

 

 

 

 



2 2 2 2

z a a a z a z

z z z z z

z z z z



       



     

;  ; 1 1 1z x yi x y z i x y i          

 

   

2 2

1 2 9 1 2 9

z i x y

       

1 3 sin ;  2 3 cos ;  0;2 .

x t y t t



 

     

 

 

   

2 2 2

min

1 3 sin 1 3 cos 10 6 cos 2 2 4 1 2

z i t t t z i z i

                

1 .z i 



  

7 19 7 19 19

1 2 3 ; tan .

82 82 82 82 7

i z i i z z i w i M 

 







               











 

2 2

2 tan 133 1 tan 156

sin 2 0;  cos2 0

205 205

1 tan 1 tan

 



      

 



 

;  ;z x yi x y

    

     

2 2

3 4 5 : 3 4 5

z i C x y

       

 

3;4

5.R 

 

2 2 2 2

2 2

2 2 1 4 2 3 : 4 2 3 0.

M z z i x y x y x y d x y M

 

                 

 

 

 

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 125

Chọn D.

Câu 35. Gọi .

Khi đó: , gọi là trọng tâm

Tương tự, gọi .

Khi đó: ,

gọi là trọng tâm

Chọn C.

Câu 36. Ta có:

Ta có: Chọn A.

Câu 37. Ta có:

Chọn A.

Câu 38. Gọi là phần thực của số phức

Ta xét:

Chọn D.

Câu 39. Dựng hình bình hành trong mặt phẳng phức, khi đó biểu diễn của :

Chọn B.

Câu 40. Đặt và , với .

 

; 5 23 10 13 33

2 5

d I d R M M



         

   

2 2

max

4 2 30 0

33 5 4 41.

3 4 5

x y

M z i i z i

x y







  







          

 

 

 

   

 









 

1 1 1 2 2 2 3 3 3

;  ;  ;  ;  ;  1; 3

k k

z x y i z x y i z x y i x y k

 

       

     

1 1 2 2 3 3

; ;  ; ;  ;A x y B x y C x y

1 2 3 1 2 3

; .

3 3

x x x y y y

ABC G

 

   









 









 

 

1 1 1 2 2 2 3 3 3

;  ;  ;  ;  ;  1;3

k k

z x y i z x y i z x y i x y k

          

       

     

1 1 2 2 3 3

; ;  ; ;  ;A x y B x y C x y

        



1 2 3 1 2 3

; .

3 3

x x x y y y

A B C G

 

     

   







   



 









 

       

1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3

z z z z z z x x x y y y i x x x y y y i

        

                

1 2 3 1 2 3

x x x x x x

G G

y y y y y y



  



    





  



  



    







    

2 3 1 5 5; 1 tan .

z i i i M          

2 tan 5

sin2 .

1 tan



  





 

2 2 2

max

1 1 ;  0.

1 1 1

1 2

m i m i

z z z z i m

m m m

m m i

 

          

  

 



 

Re z

  

1 1 1 1 2

m z m z m z z

m z m z m z m z

m z z mz mz

m z m z

 

    







    











   

  

  

 

2 2 1 1 1

Re .

m z z m z z

m m z m

m mz mz

m m z z

 

   







    













 

 



OMPN

1 2

z z OP

z z MN





 









 





 

2 2

1 2 1 2 1 2

2 2

1 2 1 2 1 2

2 cos 150 1

2 cos 30 1

z z z z z z





    







    





1 2

z z



  





z a bi 

z c

 

; ;a b c  

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 126

Lại có .

Gọi với .

Khi đó

Vậy tập hợp các điểm biểu diễn của số phức là đường tròn .

Khi đó chỉ có đáp án C có khả năng đúng và theo đó .

Thử vào phương trình (1) thì thỏa mãn Chọn C.

Câu 41.

Cách 1:

Đặt . Khi đó .

Suy ra biểu diễn hình học của số phức là đường tròn tâm và bán kính .

Gọi là điểm biểu diễn số phức . Ta có: .

Vậy bé nhất bằng 3 khi .

Cách 2:

Đặt .

Chọn D

Câu 42. Ta có: Gọi là điểm biểu diễn của số phức

Gọi là điểm biểu diễn của số phức

Khi đó: (*)

Hệ thức trên chứng tỏ tập hợp các điểm là elip nhận là các tiêu điểm.

Gọi phương trình của elip là

Từ (*) ta có:

Vậy quỹ tích các điểm là elip: Chọn D.

Câu 43. Gọi là điểm biểu diễn số phức

 

1 2

3 4 1 2

3 4

w i

w i z i z

 

     



w x yi 

;x y  

1 2

1 2 5

3 4

w i

z c c c x yi i c

 

         



       

2 2 2 2

1 2 5 1 2 25x y c x y c

         

 

1;2



5 5 5 1R c c    

1c 



( , )z a bi a b   

2 2

3 4 2 ( 3) ( 4) 4

z i a b

       

 

3; 4

 

5R 

 

M z

   

M z C

z OM OI R

   

   

M z C IM 

3 2 cos 3 2 cos

4 2 sin 4 2 sin

a a

b b

 

 

 

    

 



 

 

    

 

 

2 2 2 2

(2 cos 3) (2 sin 4) 29 12 cos 16 sin

z a b

   

         

3 4

29 20 cos sin 29 20 cos( ) 9

5 5

   

 







      











 

 



 

;M x y

.z x yi 

 

4; 0

4.z 

 

4; 0



4.z  

4 4 10 10.

z z MA MB

      

,A B

 

2 2

2 2 2

2 2

1, 0,

x y

a b a b c

a b

     

2 10 5.a a  

2 2 2

2 8 2 4 9AB c c c b a c        

 

2 2

: 1.

25 9

x y

 



 

,M x y

 

z x yi x y R  

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 127

Gọi là điểm biểu diễn số phức

Ta có: Tập hợp điểm biểu diễn số phức là đường trung

trục .

Để ngắn nhất khi tại => Chọn A.

Câu 44. Gọi là điểm biểu diễn số phức

Gọi là điểm biểu diễn số phức

. Tập hợp điểm biểu diễn là hình vành khăn giới hạn bởi 2

đường tròn đồng tâm có bán kính lần lượt là .

=> Chọn C.

Lưu ý cần nắm vững lý thuyết và hình vẽ của dạng bài này khi học trên lớp tránh nhầm lẫn sang tính

diện tích hình tròn.

Câu 45. Gọi là điểm biểu diễn số phức

Ta có:

. . Chọn B.

Ở đây lưu ý hai đường thẳng x = 2 và x = -2 song song với nhau.

Câu 46. Ta có

Trường hợp : .

Trường hợp 2:

Gọi (với ) khi đó ta được

Suy ra .

Từ , suy ra Chọn C.

Câu 47. Giả sử , , .

Theo đề bài ta có: , .

Chọn B.

Câu 48. .

 

1, 2



1 2i

 

0, 1



i

2 1

z i z i ME MF     



: 2 0EF x y  

MA EF

 

3,1 3

M z i   

 

,M x y

 

z x yi x y R  

 

1,1



1 i 

1 1 2

z i

   

1 2MA  

1 2

2, 1R R 

 

1 2 1 2

2 2

P P P R R

      

 

,M x y

 

z x yi x y R  

 

2 2 2 2 2 2 2

2 16 2 2 2 2 16

z z z x xyi y x xyi y x y           

4 16 2

x x

    



 

1 2

, 4

d d d





        

2 5 1 2 3 1 1 2 1 2 1 2 3 1

z z z i z i z i z i z i z i

                

   

1 2 0

1 2 3 1

z i

z i z i



  





    





1 2 0z i  

1 1

w w

    

 

1 2 3 1

z i z i

    

z a bi 

,a b  

         

2 2

1 2 1 3 2 3

a b i a b i b b b

             

 

3 9 3

2 2 2 2

2 4 2

w z i a i w a

          

 

min | | 1w 



z a bi 

z c di 

 

, , ,a b c d 



 

;A a b

 

;B c d

   

2 2

AB c a d b

    

   

2 1

z z a c d b i    

   

2 2

2 1

z z c a d b

     



       

2 1 1 1 1

T z i z i z i z i            

Biên soạn: Bùi Trần Duy Tuấn

https://facebook.com/duytuan.qna

Tổng hợp các chuyên đề luyện thi đại học Trang 128

Đặt . Ta có và .

Đặt . Khi đó .

Vậy Chọn B

Câu 49. Gọi là điểm biểu diễn số phức , .

Gọi là điểm biểu diễn số phức

Ta có: .

Ta có . Suy ra tập hợp điểm biểu diễn số phức là Elip với tiêu điểm là ,

, tiêu cự , độ dài trục lớn là , độ dài trục bé là

Vậy, tập hợp các điểm biểu diễn các số phức thỏa mãn điều kiện là Elip có

phương trình Chọn D.

Câu 50. Gọi là điểm biểu diễn số phức

Gọi lần lượt là điểm biểu diễn số phức và .

Gọi lần lượt là điểm biểu diễn số phức và

Ta có: với thuộc đường trung trực của

với thuộc đường trung trực

của

là giao điểm của thỏa hệ: => Chọn D.

1w z 



   

1 1

T w i w i     

.w x y i 

2 2

w x y  

       

 

       

 

2 2 2 2

2 2

1 1 1 1

1. 1 1 1. 1 1

1 1 1 1 1 1

2 2 2 4 4

T x y i x y i

x y x y

x y

       

 





        







 

   

max 4T 



 

;M x y

z x yi 

,x y  

2

2 2 10 10

z z MB MA

      

4AB 

 

2;0

 

2;0



4 2AB c 

10 2a

2 2

2 2 2 25 4 2 21b a c    

2 2 10

z z

   

2 2

25 21

x y

 



 

,M x y

 

z x yi x y R  

,A B

,C D

i

z z i MA MB    

   

1,0 ; 0,1

A B





1 3

z i

z i z i MC MD

z i



      



   

0, 1 ; 0,3

C D

M



1 2

; 

M

y x











 

1,1

M

1z i  

Bấm Tải xuống để xem toàn bộ.

| 1/129

| | Tải xuống

Preview text:

Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna MỤC LỤC
A. CÁC PHÉP TOÁN CƠ BẢN TRÊN TẬP SỐ PHỨC ............................................ 3
I. LÝ THUYẾT ..................................................................................................................................... 3
II. CÁC DẠNG TOÁN VỚI PHÉP TOÁN CƠ BẢN ..................................................................... 5
III. SỬ DỤNG MÁY TÍNH CASIO 570 VN-PLUS ĐỂ GIẢI ..................................................... 14
IV. BÀI TẬP RÈN LUYỆN .............................................................................................................. 22
1. ĐỀ BÀI .................................................................................................................................... 22
2. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI CHI TIẾT ................................................................... 25
B. CĂN BẬC HAI VÀ PHƯƠNG TRÌNH BẬC HAI CỦA SỐ PHỨC ................. 28
I. CĂN BẬC HAI CỦA SỐ PHỨC ................................................................................................. 28
II. GIẢI PHƯƠNG TRÌNH BẬC HAI ........................................................................................... 30
1. GIẢI PHƯƠNG TRÌNH BẬC HAI TRÊN TẬP SỐ PHỨC .............................................. 30
2. ĐƯA PHƯƠNG TRÌNH BẬC CAO VỀ NHỮNG PHƯƠNG TRÌNH BẬC NHẤT,
PHƯƠNG TRÌNH BẬC HAI. .................................................................................................. 31
III. SỬ DỤNG MÁY TÍNH CASIO 570VN-PLUS ĐỂ GIẢI ...................................................... 38
IV. BÀI TẬP RÈN LUYỆN .............................................................................................................. 44
1. ĐỀ BÀI .................................................................................................................................... 44
2. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI CHI TIẾT ................................................................... 48
C. TẬP HỢP ĐIỂM CỦA SỐ PHỨC ......................................................................... 53
I. LÝ THUYẾT ................................................................................................................................... 53
II. MỘT SỐ BÀI TOÁN ĐIỂN HÌNH ........................................................................................... 54
III. SỬ DỤNG MÁY TÍNH CASIO 570 VN- PLUS ..................................................................... 61
IV. BÀI TẬP RÈN LUYỆN .............................................................................................................. 64
1. ĐỀ BÀI .................................................................................................................................... 64
2. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI CHI TIẾT ................................................................... 69
D. BÀI TOÁN CỰC TRỊ CỦA SỐ PHỨC ................................................................. 75
I. PHƯƠNG PHÁP QUY VỀ TÌM MIN-MAX CỦA HÀM MỘT BIẾN KẾT HỢP SỬ DỤNG
TÍNH CHẤT CỦA SỐ PHỨC. ....................................................................................................... 75
II. PHƯƠNG PHÁP HÌNH HỌC GIẢI BÀI TOÁN MIN-MAX................................................ 84
III. SỬ DỤNG MÁY TÍNH CASIO 570 VN-PLUS ĐỂ GIẢI ..................................................... 92
V. BÀI TẬP RÈN LUYỆN ................................................................................................................ 93
Tổng hợp các chuyên đề luyện thi đại học Trang 1
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
1. ĐỀ BÀI .................................................................................................................................... 93
2. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI ...................................................................................... 96
E. DẠNG LƯỢNG GIÁC CỦA SỐ PHỨC ............................................................. 101
I. LÝ THUYẾT ................................................................................................................................. 101
II. MỘT SỐ BÀI TOÁN ĐIỂN HÌNH ......................................................................................... 102
III. SỬ DỤNG MÁY TÍNH CASIO 570VN-PLUS ĐỂ GIẢI .................................................... 105
IV. MỘT SỐ BÀI TOÁN VỀ ỨNG DỤNG CỦA DẠNG LƯỢNG GIÁC ............................. 107
V. BÀI TẬP RÈN LUYỆN .............................................................................................................. 109
F. TUYỂN TẬP CÁC CÂU SỐ PHỨC VẬN DỤNG CAO ................................... 111
I. ĐỀ BÀI ......................................................................................................................................... 111
II. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI CHI TIẾT ....................................................................... 118
Tài liệu được tôi sưu tầm và biên soạn để làm tư liệu cho các em lớp 12 ôn thi kỳ thi THPT
Quốc gia tham khảo, giúp các em ôn lại kiến thức nhanh chóng và hiệu quả hơn. Trong quá
tình tổng hợp và biên soạn không tránh khỏi những sai sót đáng tiếc do số lượng kiến thức và
bài tập khá nhiều. Mong các đọc giả thông cảm và đóng góp ý kiến để những tài liệu sau của
tôi được chỉnh chu hơn! Mọi đóng góp xin gửi về:
Facebook: https://web.facebook.com/duytuan.qna.
Hoặc qua Gmail: btdt94@gmail.com.
Các em có thể xem thêm các chuyên đề luyện thi Đại học môn Toán tại Website:
https://toanhocplus.blogspot.com/ Xin chân thành cảm ơn!!!
Tổng hợp các chuyên đề luyện thi đại học Trang 2
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
Chuyên đề: SỐ PHỨC
A. CÁC PHÉP TOÁN CƠ BẢN TRÊN TẬP SỐ PHỨC I. LÝ THUYẾT
1. Định nghĩa
o Một số phức là một biểu thức dạng z  a  bi với a,b   và 2 i  1.
o i được gọi là đơn vị ảo, a được gọi là phần thực và b được gọi là phần ảo của số phức
z  a bi .
Tập hợp các số phức được kí hiệu là  .    2 a  bi / , a b  ;  i    1 .
o Chú ý: - Khi phần ảo b  0  z  a là số thực.
- Khi phần thực a  0  z  bi  z là số thuần ảo.
- Số 0  0  0i vừa là số thực, vừa là số ảo. a   c 
o Hai số phức bằng nhau: a  bi  c  di   với a, , b , c d   . b   d 
o Hai số phức z  a  b ;
i z  a
 bi được gọi là hai số phức đối nhau. 1 2
2. Số phức liên hợp
Số phức liên hợp của z  a  bi với a,b   là a bi và được kí hiệu bởi z .
Một số tính chất của số phức liên hợp: a) z  z
b)z  z '  z  z ' c) z  z '  z  z '  z    z
c) z.z '  z.z ' d)     z ' z '
z là số thực  z  z ; z là số thuần ảo  z  z  Ví dụ:
Số phức liên hợp của số phức z  1  2i là số phức z  1  2i .
Số phức liên hợp của số phức z  5  3i là số phức z  5  3i .
3. Biểu diễn hình học của số phức
Trong mặt phẳng phức Oxy ( Ox là trục thực, Oy là trục ảo ), số phức z  a  bi với
a,b   được biểu diễn bằng điểm M a;b . Ví dụ:
 A1;2biểu diễn số phức z  12i .  B0;3biểu diễn số phức z  3i . 1 2  C3; 
1 biểu diễn số phức z  3
  i .  D1;2biểu diễn số phức z  1 2i . 3 4
Tổng hợp các chuyên đề luyện thi đại học Trang 3
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
4. Môđun của số phức
o Môđun của số phức z  a  bi a,b   là 2 2
z  a  b .
o Như vậy, môđun của số phức z là z chính là khoảng cách từ điểm M biểu diễn số phức 
z  a  bi a,b  đến gốc tọa độ O của mặt phẳng phức là: 2 2
OM  a  b  zz .
o Một số tính chất của môđun:
 z  0; z  0  z  0; 2 2
 z  z , z
  z , z  z
 z  z  z + z 1 2 1 2
 z  z '  z  z '  z  z '
 z .z  z . z 1 2 1 2 z z1 1   z z 2 2
5. Các phép toán trên tập số phức
Cho hai số phức z  a  bi ; z '  a ' b 'i với a, ,
b a ',b '   và số k   .
o Tổng hai số phức: z  z '  a  a ' (b  b ')i .
o Hiệu hai số phức: z  z '  a  a 
' (b b ')i .
o Số đối của số phức z  a  bi là z   a  bi .   o Nếu ,
u u ' theo thứ tự biểu diễn các số phức z,z ' thì  
u  u ' biểu diễn số phức z  z ' .  
u  u ' biểu diễn số phức z  z ' . o Nhân hai số phức:
z.z '  a  bia ' b 'i  a.a 'b.b '  a.b ' a '.bi .  1
o Số phức nghịch đảo: 1 z  z . 2 z o Chia hai số phức: z ' z '.z Nếu z  0 thì 
, nghĩa là nếu muốn chia số phức z ' cho số phức z  0 thì ta nhân 2 z z z '
cả tử và mẫu của thương cho z . z  Chú ý: 4k 4k 1  4k 2  4k 3 i  1; i  i; i  1; i  i  (k  )  .
Tổng hợp các chuyên đề luyện thi đại học Trang 4
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
II. CÁC DẠNG TOÁN VỚI PHÉP TOÁN CƠ BẢN
1. PHƯƠNG PHÁP GIẢI TỔNG QUÁT Phương pháp
o Bước 1: Gọi số phức z cần tìm là z  a  bi a,b  .
o Bước 2: Biến đổi theo điều kiện cho trước của đề bài (thường liên quan đến môđun, biểu
thức có chứa z, z, z ,... ) để đưa về phương trình hoặc hệ phương trình 2 ẩn theo a và b
nhờ tính chất 2 số phức bằng nhau ( phần thực bằng nhau và phần ảo bằng nhau ), rồi từ
đó suy ra a và b và suy ra được số phức z cần tìm.
2. MỘT SỐ BÀI TOÁN ĐIỂN HÌNH Bài toán 1
Tìm phần thực, phần ảo, số phức liên hợp và tính môđun của số phức z :  i
a) z  2  4i  2i 1  3i. b z    i  i 4 5 ) 2 4 5 2  . 2  i Giải:
z    i  i   i 2 a) 2 4 2 1
3  2  4i  2i  6i  2  6i  6  8  6i .
 Phần thực: 8 ; Phần ảo: 6 ; Số phức liên hợp: z  8  6i . Môđun 2 2 z  8  6  10 . 4 5 4  5i2   i i 
b) z  2  4i5  2i   10  4  i 20  2 i 8 i  2  2 i 2  2 1 8  14i  5 93 94  18  16i    i. 5 5 5  93 94 93 94 Phần thực: ; Phần ảo:
; Số phức liên hợp: z   i . 5 5 5 5 2 2 93 94     17485 Môđun z         .  5     5  5 Bài toán 2
Cho số phức z  3  2i . Tìm môđun số phức w  zi  z 1  2i. Giải:
w  zi  z 1  2i  (3  2i)i  (3  2i)(1  2i) .
 3i  2  3  6i  2i  4  5  7i Vậy 2 2 w  5  7  74 .
Tổng hợp các chuyên đề luyện thi đại học Trang 5
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna Bài toán 3
Gọi M, N lần lượt là hai điểm biểu diễn số phức z ,z trên mặt phẳng phức. Mệnh đề nào 1 2 sau đây là đúng?    .
A z  z  OM ON B. z  z  MN 1 2 1 2    
C. z  z  OM  MN D. z  z  OM  MN 1 2 1 2 Giải:
M, N lần lượt là hai điểm biểu diễn số phức z ,z trên mặt phẳng phức 1 2  
nên OM biểu diễn số phức z ,ON biểu diễn số phứcz 1 2   
OM ON  NM biểu diễn số phức z z 1 2  
 z  z  NM  MN . Chọn B. 1 2 Bài toán 4 1 1 1
Cho ba số phức z , z , z phân biệt thỏa mãn z  z  z  3 và   . Biết 1 2 3 1 2 3 z z z 1 2 3
z , z , z lần lượt được biểu diễn bởi các điểm , A ,
B C trên mặt phẳng phức. Tính góc 1 2 3  ACB ? A. 60 .  B. 90 .  C. 120 .  D. 150 .  Giải:
Gọi M là điểm biểu diễn của số phức z , N là điểm biểu diễn của số phức z (z là số phức
liên hợp của z ). Khi đó M và N đối xứng nhau qua Ox.
Gọi A', B ', C ' lần lượt là điểm biểu diễn các số phức z , z , z . 1 2 3 1 1 1 z z z Từ giả thiết  
 1  2  3  z  z  z (do z  z  z  3). 2 2 2 1 2 3 z z z 1 2 3 1 2 3 z z z 1 2 3   
Suy ra OA  OB '  OC '  OA 'C ' B ' là hình bình hành.     Mà 
OA  OB '  OC '  OA'C ' B ' là hình thoi với 0
A 'C ' B '  120 .    Vậy 0
ACB  120 (do ACB và A 'C ' B ' đối xứng qua Ox ). Chọn C. Bài toán 5 2 3 20
Tìm phần thực, phần ảo của số phức sau: 1  1  i  1  i  1  i  ...  1  i Giải:
Tổng hợp các chuyên đề luyện thi đại học Trang 6
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna 2 20 1 i21 
P     i    i     i 1 1 1 1 ... 1  i 20   
1  i21  1  i2 1  i  2i10 1  i 10  2 1  i    10 2  1i1 10  P   2   10 2   1 i i Vậy phần thực là 10 2 và phần ảo là 10 2  1 . Bài toán 6 Tính 2 3 2017
S  1009  i  2i  3i  ...  2017i . Giải: Cách 1: 2 3 4 2017
S  1009  i  2i  3i  4i  ...  2017i  1009   4 8 2016
4i  8i  ...  2016i  5 9 2017
i  5i  9i  ...  2017i .....   2 6 10 2014
2i  6i  10i  ...  2014i  3 7 11 2015
3i  7i  11i  ...  2015i  504
 1009  4n 505
 i4n   504 3  4n   504
2  i4n   1 n 1  n 1  n 1  n 1 
 1009  509040  509545i  508032  508536i  2017  1009i. Cách 2:
Đặt f x  2 3 2017
 1  x  x  x  ....  x  f x 2 2016
 1  2x  3x  ...  2017x
 xf x 2 3 2017
 x  2x  3x  ...  2017x  1 Mặt khác: 2017 2018x
x  1 2018 2018 x x    f x 1 1 2 3 2017
 1  x  x  x  ....  x 
 f x  x  1 x  2 1 2017 2018x
x  1 2018 x  
 xf x 1  x. 2 2   x  1
Thay x  i vào  
1 và 2 ta được: (1)  S  1009; (1)=(2) , nên: 2017 2018i
i  1 2018 i   1 2018  2018i  2
S  1009  i.  1009  i  2017  1009i.  2   2 1 i i Bài toán 7 1
Cho số phức z   1  i 3. Tính w    z 2  z  3  z   2017 1 1 1 ... 1  z . 2 Giải : 1 z
  z  1  0 
Ta có z   1  i 3 2  . 3 2 z   1 
Tổng hợp các chuyên đề luyện thi đại học Trang 7
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna  3k 3 z   1 1 k  z  2 
Do đó với mọi k   , ta có 3k 1  3k 1  2 z   z 1  z
 1  z  z  .   3k 2  2 3k 2  2 z   z 1  z
 1  z  z   
Vì từ 1 đến 2017 có: 673 số chia 3 dư 1 , 672 số chia 3 dư 2 , 672 số chia hết cho 3 nên w
 z z  z   z   z672 2 3 2017 672  2z673 672 2018 672 3.672 2 1 1 1 ... 1 2 . . 2 .z 2 .z              1 3  672 2 672
 2 .z  2 1  z 672 671  2   i    2   1 3i. 2 2    Bài toán 8
Tìm số z sao cho: z  (2  i)z  3  5i (A,A  2014) . 1 Giải:
Gọi số phức z cần tìm là z  a  bi a,b  .
Ta có: z  (2  i)z  3  5i 2
 a  bi  (2  i)(a bi)  3  5i  a  bi  2a  2bi  ai bi  3  5i
 3a  b  (a b)i  3  5i 3
 a b  3  a  2      
 z  2  3i.  a b  5 b   3    Bài toán 9
Tìm số phức z khi nó thỏa mãn đồng thời các điều kiện sau: z  (2  i)  10 và z.z  25 . Giải:
Gọi số phức cần tìm là z  a  bi a,b  . 2 Ta có: 2 2
z.z  z  a  b  25 (1). 2 2 Lại có: z   i 
 a    b   2 2 (2 ) 10 2
1  10  a  b  4a  2b  5  0 2
Thay (1) vào (2) ta được: 25  4a  2b  5  10  b  2  a  10 . a  5 b    0 Nên 2 2 2 2
a  b  25  a  (2a  10)  25 2 5a 40a 75 0         a  3 b    4  
Vậy z  5 hoặc z  3  4i . Bài toán 10
Tìm các số thực a, ,
b c sao cho hai phương trình 2 2
az  bz  c  0, cz  bz  a  16  16i  0 có nghiệm chung là z  1  2i Giải
Theo giả thiết phương trình 2
az bz  c  0 có nghiệm z  1  2i khi đó:
Tổng hợp các chuyên đề luyện thi đại học Trang 8
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna     a  i2 b  i c a b c  a b 3a b c 0 1 2 1 2 0 3 4 2 i 0                 1 4a  2b  0  Tương tự phương trình 2
cz  bz  a  16  16i  0 có nghiệm z  1  2i khi đó: c   i2 1 2
 b 1  2i  a  16 16i  0  c3  4i  b  2bi  a  16 16i  0        a b c  b c  a b 3c 16 0 3 16 2 2 8 i 0            2 b   2c  8  0  Từ  
1 ,2 suy ra a, , b c  1; 2  ;5. Bài toán 11 _ z
Cho z và z là số phức liên hợp của z . Biết
  và z  z  2 3 .Tìm z z2 Giải : _
Gọi z  a  bi  ,
a b    z  a bi .
Ta có : z  z  a  bi  a  bi 2
 2bi  2 3  b  3 . _ 2 3 z z z z z z z 3    z z 2 . .   . Ta có:  .1  . 
   z   .  2  2  2 2z z z z z.z2 2 3 Mà 3 3 2
z  a  a bi  a bi  bi 3 2
 a  ab   2 3 3 3 3
3a b  b i 2 3 2 2 2
3a b  b  0
3a  b  0 a   1           z  2 . 2 2 2 b  3 b  3 b  3       Bài toán 12 z  2i
Tìm số phức z thỏa mãn điều kiện: z  1  2i  z  3  4i và là một số thuần ảo. z  i Giải :
Đặtz  x  yi (x, y) . Theo bài ra ta có :
x   y  i  x     yi  x  2  y  2  x  2  y  2 1 2 3 4 1 2 3
4  y  x  5
x  y   2 2 i
x  y  2y  
1  x 2y    3 2 i z i Số phức w    z  i
x  1 yi
x  y  2 2 1  2 x   
y 2y  1  0  12  x      2   12 23 w 
là một số ảo khi và chỉ khi 2 x   y   7 1  0   z    i   . Vậy . 23 7 7 y   x  5 y         7
Tổng hợp các chuyên đề luyện thi đại học Trang 9
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna Bài toán 13 1 1 2
Cho hai số phức z , z thỏa mãn z  0, z  0, z  z  0 và   . Tính giá 1 2 1 2 1 2 z  z z z 1 2 1 2 z
trị biểu thức P  1 . z2 Giải: 1 1 2 1 z  2z Từ giả thiết     2 1 z  z z z z  z z z 1 2 1 2 1 2 1 2    z z z  z z  z z . z 2z 1 1 2 . 1 2   1 2    2 1  1  1  1           z z    z 2  2    2  z
Đặt t  1 , ta được phương trình t  t   1 1  2t z2   1 1 t   i 2 2 2 
 t  t     2 2 2 2 1 0  t   P   1 1 t   2 2  i  2 2 Bài toán 14 1
Nếu số phức z thỏa mãn z  1 và z  1 thì phần thực của bằng? 1  z Giải: Cách 1:
Đặt z  a  bi  , a b   . Từ 2 2
z  1  a  b  1. 1 1 1  a  bi 1  a  bi Ta có:    1  z 1  a  bi
1  a bi1  a  bi 1 a2 2  b 1 1  a Suy ra phần thực của là: . 1  z 1  a2 2  b 1  a 1  a 1  a 1 Ta có:    . 1  a2 2 2 2
a  2a  1  b 2  2a 2  b Cách 2: 1
Gọi A là phần thực của . 1  z 1 1 1 1
1  z  1  z 2  z  z 2  z  z 1 2A         1  a  . 2 2 1  z 1  z 1  z 1  z
1  z  z  z.z
1  z  z  z 2 2  z  z
Tổng hợp các chuyên đề luyện thi đại học Trang 10
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna Bài toán 15
Cho hai số phức z , z thỏa mãn điều kiện z  z  z  z  1. Tính giá trị của biểu 1 2 1 2 1 2  2  2 z z 1   2  thức P         . z      z 2     1  Giải: Cách 1:  2  2  2 z z z z 1   2   1 2 
Ta có P         2.   1 z          z z z 2         1     2 1  z z z z z z
Mà 1  2  1 2  2 1  z z  z z . 2 2 2 1 2 2 1 z z 2 1 z z 2 1 2
Theo giả thiết: 1  z  z  z z . z z z z . z z 1 2   1 2    1 2     1 2    1 2  2 2  z  z  z z z z z z z z 1. 3 1 2   1 2 2 1     1 2 2 1 Từ  
1 , 2 và 3 suy ra P  1.
Cách 2: Chuẩn hóa
Chọn z 1 , còn z chọn sao cho thỏa mãn z  1 và z  z  1. 1 2 2 1 2
Ta chọn như sau: Đặt z  a  bi . 2 ● z  1  2 a  2 b  1 . 2 2
● z  z  1
 z  1  1  a 1 bi 1 a 1 b 1. 1 2 2
         2   1 a   1 3 2 Từ đó giải hệ    z   i  .  2 3 2 2 b   2 1 3
Thay z  1 và z  
i vào P và bấm máy. 1 2 2 2 1 3 1 3
Hoặc ta cũng có thể chọn z    i và z   i . 1 2 2 2 2 2
Tổng hợp các chuyên đề luyện thi đại học Trang 11
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna Bài toán 16 1 1 1
Cho số phức z có môđun bằng 2018 và w là số phức thỏa mãn biểu thức   . z w z  w
Môđun của số phức w bằng? Giải:  z  w2 1 1 1 1  zw z w Từ giả thiết      0   z w z  w zw z  w
zw z  w 0 2 2 2 1 3  1    3  1     i 3w  2 2 2 2 2 2
 z  w  zw  0  z  zw  w  w  0  z
  w   w  z   w            4 4  2  4  2   2    2 2  1     i 3w     1 i 3  Từ z   w         z        .      w 2  2     2 2    1 i 3
Lấy môđun hai vế, ta được z   
. w  1. w  w  w  2018. 2 2 Bài toán 17 z
Cho số phức z,w khác 0 sao cho z  w  2 z  w . Phần thực của số phức u  là ? w Giải :
Cách 1 : Gọi u  a  bi  ,
a b   .  z  1 u      1 2 2  w 2 a     b   
Ta có : z  w  2 z  w     4  . z  w  z  w     u   a  2 2 1  b  1 1 1    w w   a  2 3 1 2 1 a  2  a  1   a  4 8
Cách 2: Gọi w  a  bi  ,
a b   . 2 2 a   b  4  * 1
Chọn z  1  z  1  1  w  2  w    a  . a  12 2  b  4 2  1 Thay a  vào   15 1 1 15 *  b   u    i . 2 2 8 8 1 15  i 2 2
Tổng hợp các chuyên đề luyện thi đại học Trang 12
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna Bài toán 18 1
Tính môđun của số phức z biết z  z và có phần thực bằng 4. z  z Giải:
Cách 1: Giả sử z  a  bi a, b  . 1 1 Ta có  2 2 z  z
a  b a bi 2 2 2 2
a  b a  bi
a  b a b    i. 
a  b  a2 b
 a b a2 b  a b a2 2 2 2 2 2 2 2 2 2  b 1 2 2
a  b a Theo giả thiết:
có phần thực bằng 4 nên  4 z  z
 a b a2 2 2 2  b 2 2 2 2
a  b a
a  b a   4   4 2 2 2 a  b  2 2 2 2  2a a  b 2 a  b  2 2
a  b a 1 1 1 2 2 
 4  a  b   z  . 2 2 8 8 2 a  b
Cách 2: Nếu z  a  bi thì z  z  2a . 1 1 1 Áp dụng:
có phần thực bằng 4    8 z  z z  z z  z
2 z  z  z 2 1 1
z  z  z    8   8   8 2 z  z z  z
z  z z  z  2  z.z
z  z z  z  2  z
2 z  z  z
2 z  z  z 1 1   8   8   8  z  . 2
2 z  z z  z 
z 2 z  z  z  z 8 Nhận xét:
Trong bài toán tìm thuộc tính của số phức z thỏa mãn điều kiện K cho trước, nếu K là thuần
z (tất cả đềuz ) hoặc thuần z thì đó là bài toán giải phương trình bậc nhất (phép cộng, trừ,
nhân, chia số phức) với ẩn z hoặc z . Còn nếu chứa hai loại trở lên (z , z , z ) thì ta sẽ gọi
z  a  bi a,b  . Từ đó sử dụng các phép toán trên số phức để đưa về hai số phức bằng nhau để giải.
Tổng hợp các chuyên đề luyện thi đại học Trang 13
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
III. SỬ DỤNG MÁY TÍNH CASIO 570 VN-PLUS ĐỂ GIẢI PP CASIO
Để thực hiện các phép toán trên tập số phức, ta chuyển qua chế độ CMPLX bằng cách bấm w2.
o Bấm đơn vị ảo i bằng cách bấm phím b.
o Tính môđun của số phức bấm qc.
o Để bấm số phức liên hợp của z bấm q22để hiện Conjg (liên hợp).
Sau đây là các bài toán điển hình cho các dạng tính toán cơ bản của số phức.
1. PHÉP CỘNG, TRỪ, NHÂN, CHIA Bài toán 1
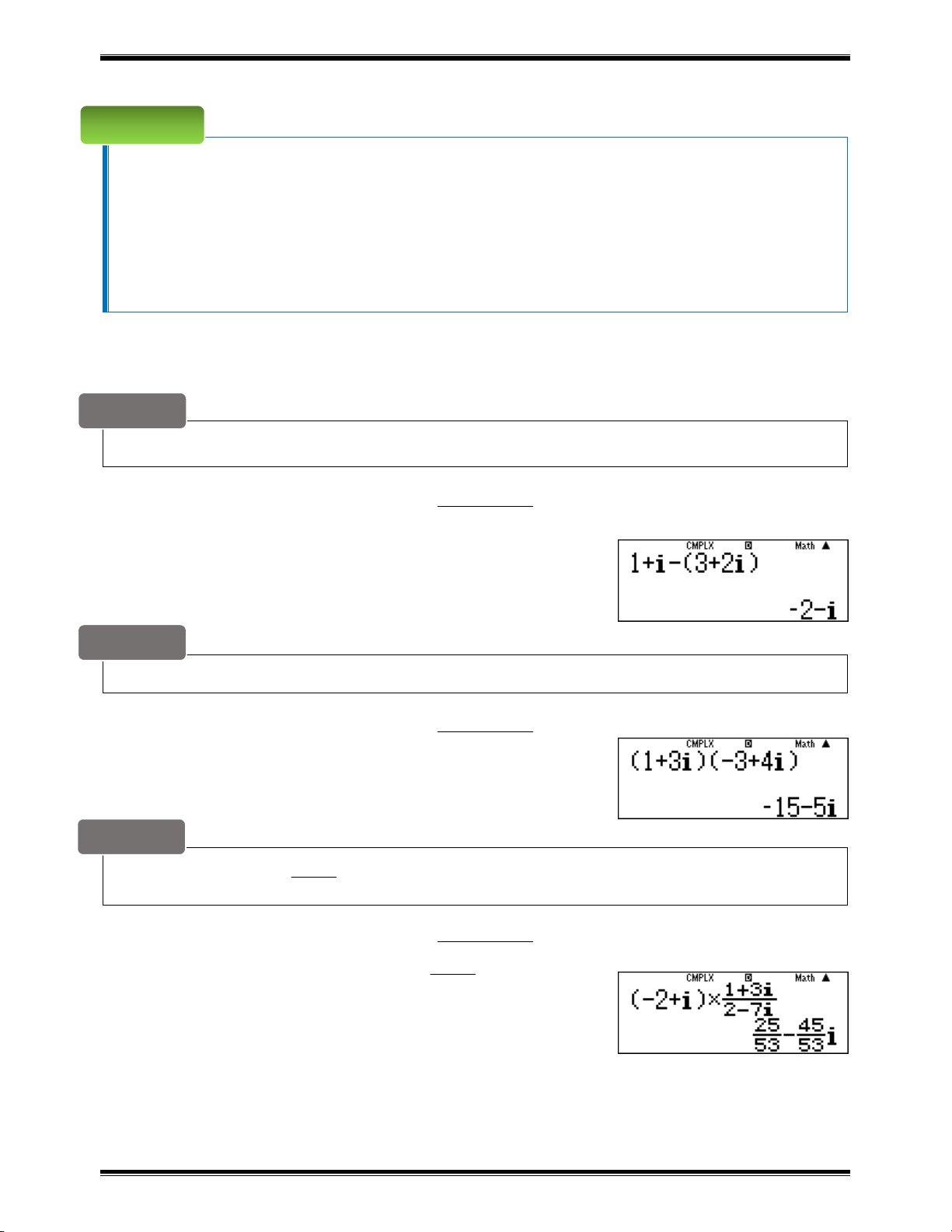
Tính z  1  i  (3  2i). Hướng dẫn:
Ta lần lượt bấm các phím như sau: 1+bp(3+2b)
Và ta được kết quả là: Bài toán 2
Tính z  (1  3i)(3  4i). Hướng dẫn:
Ta lần lượt bấm các phím tương tự như trên và ta thu được kết quả như sau: Bài toán 3 1  3i
Tính z  (2  i) . 2  7i Hướng dẫn: 1  3i
Ta lần lượt nhập biểu thức z  ( 2   i) vào máy ta thu 2  7i được kết quả:
Tổng hợp các chuyên đề luyện thi đại học Trang 14
Biên soạn: Bùi Trần Duy Tuấn
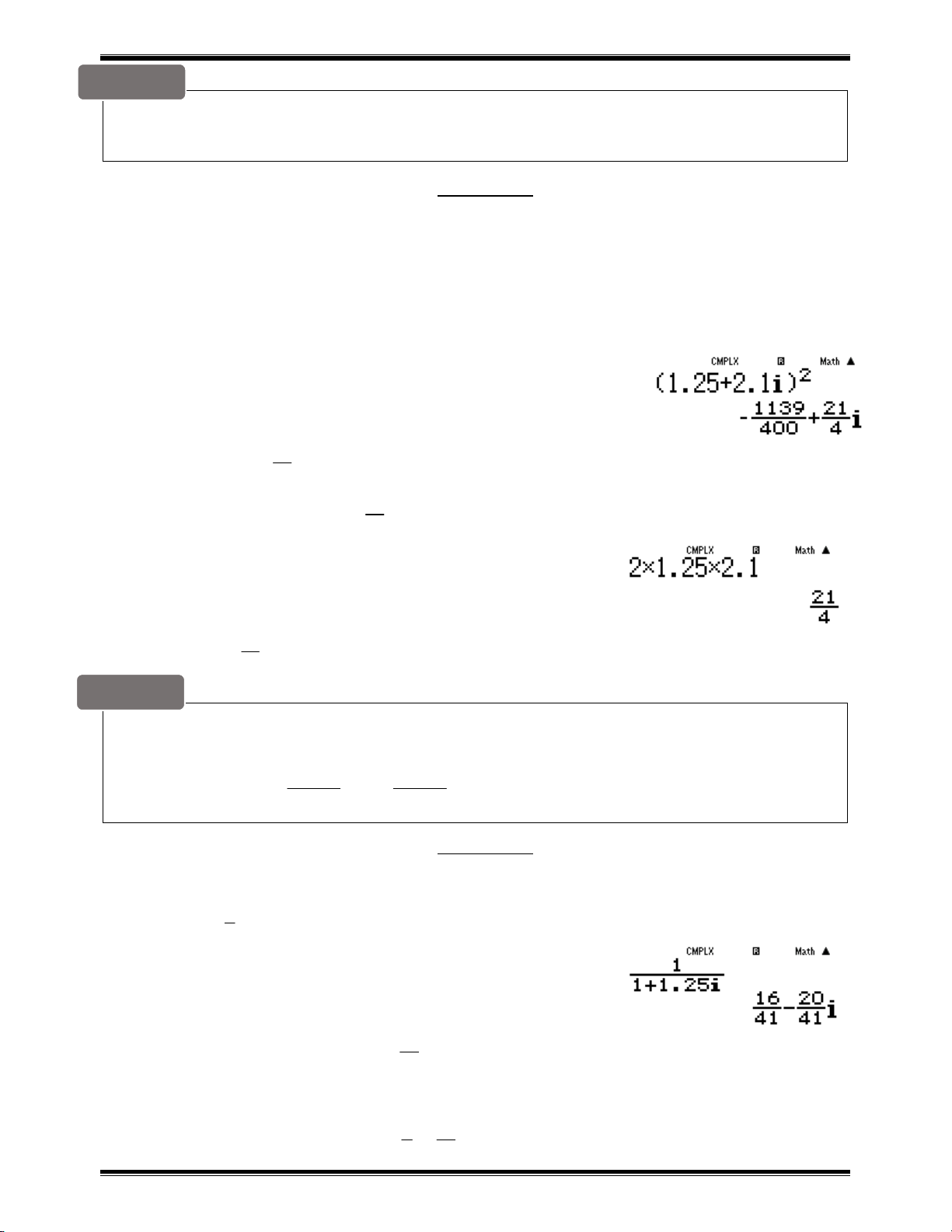
https://facebook.com/duytuan.qna Bài toán 4
Cho số phức z  a  bi . Số phức 2
z có phần ảo là : A. 2 2 a b B. 2 2 2a b C. 2ab D.ab Hướng dẫn:
 Vì đề bài cho ở dạng tổng quát nên ta tiến hành “cá biệt hóa” bài toán bằng cách chọn giá trị cho ,
a b (lưu ý nên chọn các giá trị lẻ để tránh xảy ra trường hợp đặc biệt).
Chọn a  1.25 và b  2.1 ta có z  1.25  2.1i
 Sử dụng máy tính Casio tính 2 z 1.25+2.1b)d= 21 Vậy phần ảo là 4 21
 Xem đáp số nào có giá trị là
thì đáp án đó chính xác. Ta có : 4 21 Vậy 2ab 
 Đáp án C là chính xác. 4 Bài toán 5
[Thi thử THPT Phan Chu Trinh – Phú Yên lần 1 năm 2017]
Cho số phức z  a  bi . Số phức 1
z có phần thực là : a b 
A.a  b B. C.
D.a  b 2 2 a  b 2 2 a  b Hướng dẫn:
 Vì đề bài mang tính chất tổng quát nên ta phải cá biệt hóa, ta chọn a  1;b  1.25 .  1  Với 1 z
 Sử dụng máy tính Casio z a1R1+1.25b= 16
Ta thấy phần thực số phức 1 z là :
đây là 1 giá trị dương. Vì ta chọn b  a  0 nên ta 41
thấy ngay đáp số C và D sai. 9 16
Thử đáp số A có a  b  1  1.25  
vậy đáp số A cũng sai  Đáp án chính xác là B 4 41
Tổng hợp các chuyên đề luyện thi đại học Trang 15
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna Bài toán 6
[Thi thử chuyên Khoa học tự nhiên lần 3 năm 2017] 2 3 22
Cho số phức z  1  i  1  i  ...  1  i . Phần thực của số phức z là : A. 11 2  B. 11 2  2 C. 11 2   2 D. 11 2 Hướng dẫn:
Dãy số trên là một cấp số nhân với U  1  i2 , số số hạng là 21 và công bội là 1  i . Thu 1 n 1   1 1  i q 21 2
gọn z ta được : z  U .  1  i . 1   1  q 1  1  i
 Sử dụng máy tính Casio tính z (1+b)dOa1p(1+b)^21R1 p(1+b)=
Vậy z  2050  2048i
 Phần ảo số phức z là 11 2  050  2 
 2  Đáp số chính xác là C
Tổng hợp các chuyên đề luyện thi đại học Trang 16
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna 2. TÍNH MÔĐUN Bài toán 1
Tìm môđun của số phức (1  2i)z  2i  6 . Hướng dẫn: 6   2i
(1  2i)z  2i  6
  z  z 
.Nên ta thực hiện bấm như sau: 1  2i qcap6p2bR1p2b= Ta thu được kết quả: Bài toán 2 3 3
2  4i  2(1  i)
Tìm số phức   2.z .
1 z2 . Biết z  4  3i  (1  i) , 1 z2   1  i Hướng dẫn: 3 - Tính  4  3  (1  ) 1 z i
i và lưu vào biến A: 4p3b+(1pb)^3qJz 3
2  4i  2(1  i) - Tính z2  và lưu vào biến B 1  i a2+4bp2(1pb)^3R1+bqJ x
- Tính   2.z . 1 z2 : 2q22q22Qz)OQx)=
Tổng hợp các chuyên đề luyện thi đại học Trang 17
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
3. PHƯƠNG TRÌNH BẬC NHẤT Bài toán 1
Tìm môđun của số phức z thỏa mãn: 1  3iz  3i  7i  2 . 5 .
A z  1 B. z  4 C. z  2 D. z  3 Hướng dẫn: 7i  2  3i
Ta chuyển z về dạng: z  và tìm môđun. 1  3i Quy trình bấm máy: Qca7bp2p3bR1p3b= Màn hình hiển thị: >>> Chọn C. Bài toán 2
Cho số phức z thỏa mãn (3  i)(z  1)  (2  i)(z  3i)  1  i. i  z
Tìm môđun của số phức w  . 1  z 82 82 2 82 3 82 . A B. C. . D 4 8 9 5 Hướng dẫn:
Ở đây là sẽ cho phím X sẽ là đại diện cho số phức z .
Đây là phương trình bậc nhất của số phức.
Bước 1: Các em nhập lại phương trình này với máy tính lần lượt như sau:
(3  i)(X 1)  (2  i)(C onjg(X )  3i)  (1  i) (3pb)(Q)+1)+(2pb)(q2 2Q))+3b)p(1pb) Màn hình hiển thị: Bước 2:
Tìm số phức z  a  bi nghĩa là đi tìm a và b.
Ta sẽ cho trước a=10000 và b=100 rồi từ đó suy ngược lại mối quan hệ của a và b bằng 1 hệ
phương trình 2 ẩn theo a và b, lúc đó tìm được a và b.
Cho z  10000  100i bằng cách nhập r10000+100b=
Tổng hợp các chuyên đề luyện thi đại học Trang 18
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
Màn hình sẽ cho kết quả: Nghĩa là:
(3  i)(z  1)  (2  i)(z  3i)  (1  i)  50005  19894i  5a  5  (2a b  6)i . Cho nên:
(3  i)(z  1)  (2  i)(z  3i)  (1  i)  0  5a  5  0 5  a  5  0        a  1
 ,b  8  z  1  8i 2
 a b  6  0 2a b  6  
Từ đó tính môđun của w : >>> Chọn B. Bài toán 3
Cho số phức z  a  bi thỏa mãn điều kiện   i z    i z     i2 2 3 4 1 3
.TìmP  2a  b A. 3 B.1 C.1 D. Đáp án khác Giải:
 Phương trình    iz    iz    i2 2 3 4 1 3  0
 Nhập vế trái vào máy tính Casio và CALC với X  1000  100i (2p3b) ) Q +(4+b)q22 ) Q ) +(1+3b)dr1000+100b=
Vậy vế trái  6392  2194i với 6392 
 6.1000  4.100  8  6a  4b  8  2
 194  2.1000  2.100  6  2a  2b  6  6
 a  4b  8  0 
 Để vế trái  0 thì   a  2  ;b  5 2
 a  2b  6  0  Vậy z  2
  5i  P  2a  b  1  Đáp số chính xác là C.
Tổng hợp các chuyên đề luyện thi đại học Trang 19
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
4. BIỄU DIỄN HÌNH HỌC CỦA SỐ PHỨC Bài toán 1 4i
Các điểm M,N,P lần lượt là điểm biểu diễn cho các số phức z 
; z  1  i 1  2i 2    1 i  1
;z  1  2i 3
A. Tam giác vuông B.Tam giác cân
C.Tam giác vuông cân D.Tam giác đều Hướng dẫn:
 Rút gọn z bằng Casio a4bRbp1= 1
Ta được z  2  2i vậy điểm M 2;2 1
 Rút gọn z bằng Casio (1pb)(1+2b)= 2
Ta được z  3  i vậy điểm N 3;  1 2
Tương tự z  1  2i và điểm P 1;2 2
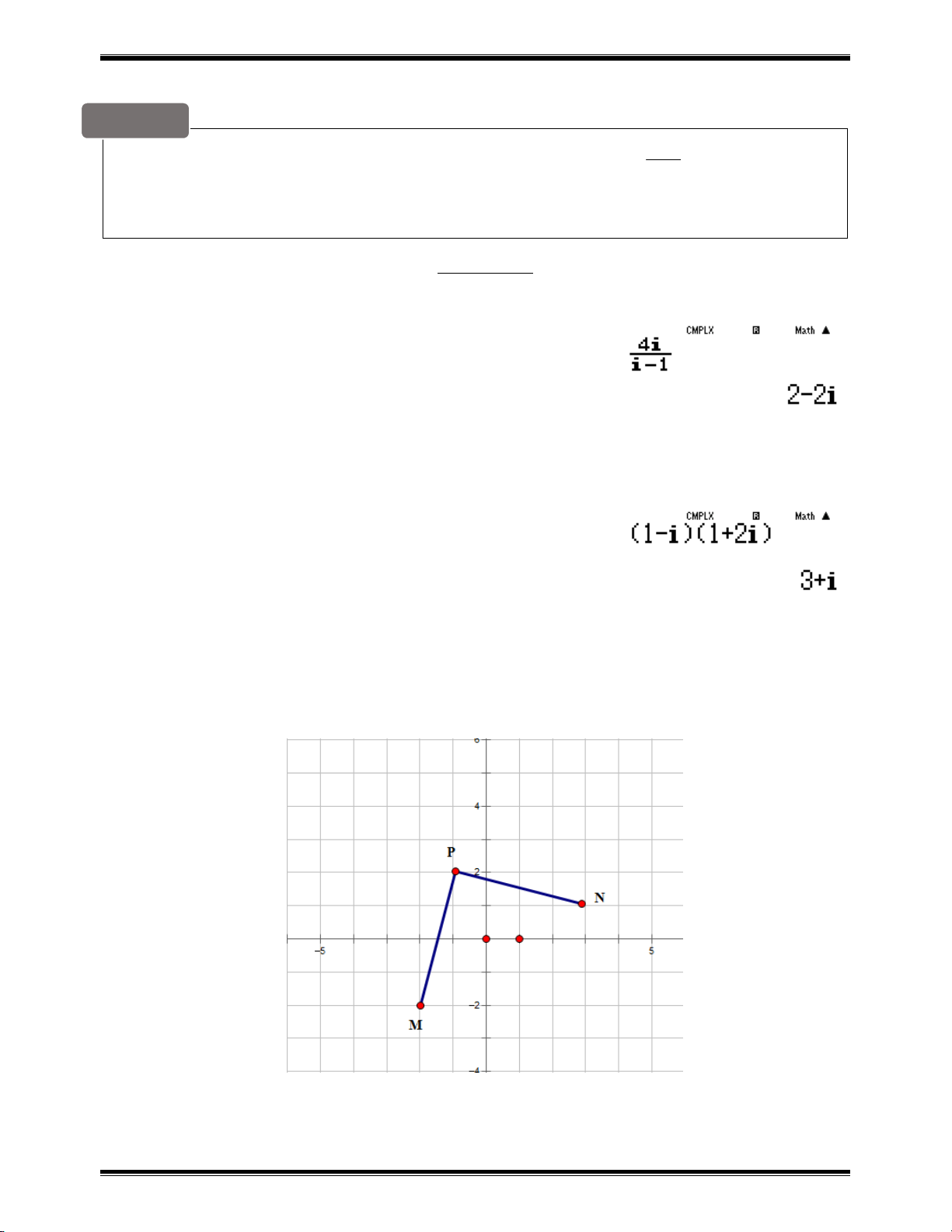
 Để phát hiện tính chất của tam giác MNP ta nên biểu diễn 3 điểm M,N,P trên hệ trục tọa độ
Dễ thấy tam giác MNP vuông cân tại P  đáp án C chính xác
Tổng hợp các chuyên đề luyện thi đại học Trang 20
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna Bài toán 2
Trong mặt phẳng tọa độ Oxy , gọi M là điểm biểu diễn số phức z  3  4i , điểm M ' là 1  i
điểm biểu diễn số phức z ' 
z . Tính diện tích OMM ' 2 25 25 15 15 A.S  B.S  C.S  S  O  MM ' 4 O  MM ' 2 OM  M ' 4 D. O  MM ' 2 Hướng dẫn:
 Điểm M biểu diễn số phức z  3  4i  tọa độ M 3;4 1 1  i 7 1  
Điểm M ' biểu diễn số phức z ' 
z  tọa độ N  ;  2 2 2 a1+bR2$O(3p4b)=
Gốc tọa độ O 0; 0
 Để tính diện tích tam giác OMM ' ta ứng dụng tích có hướng của 2 vecto trong không gian.
Ta thêm cao độ 0 cho tọa độ mỗi điểm ,
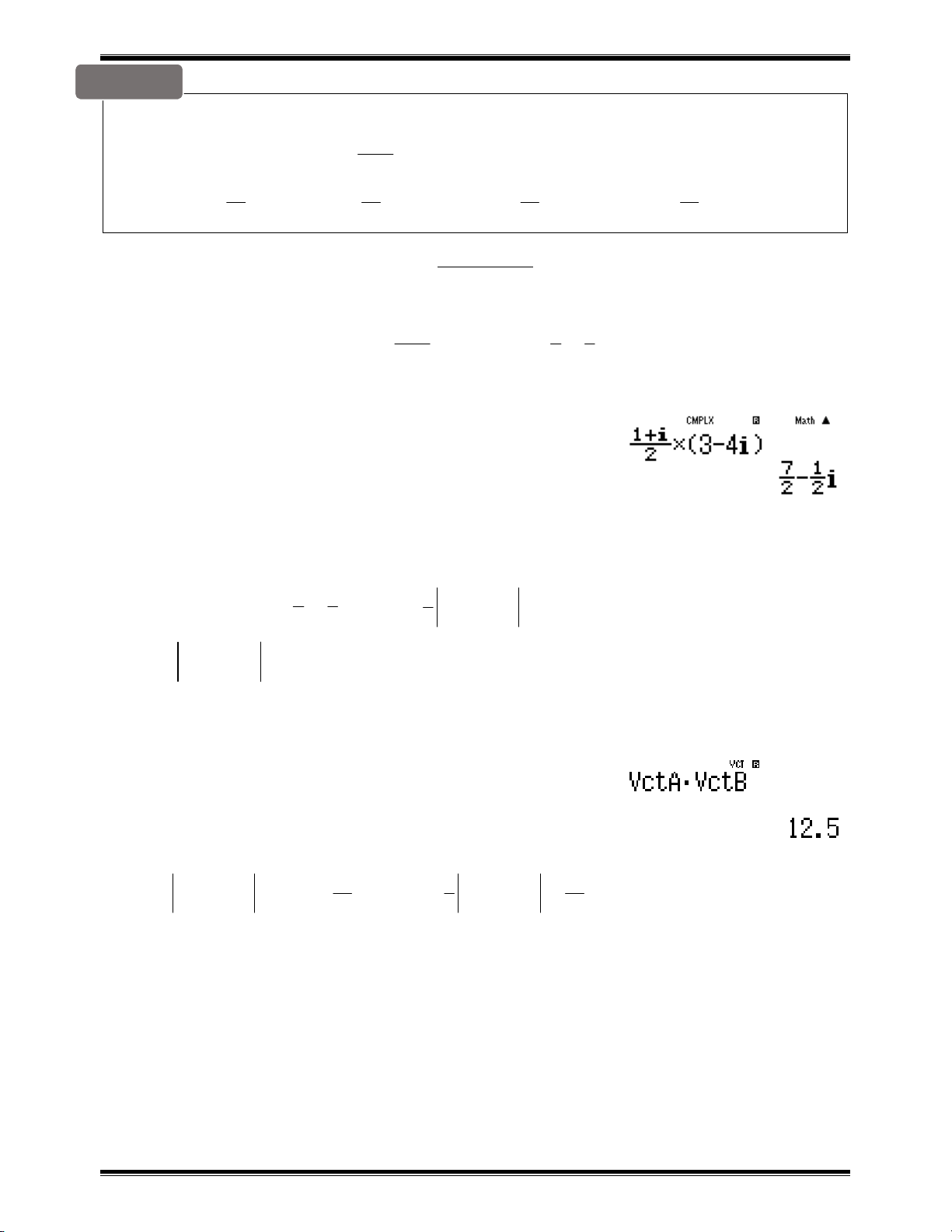
O M,M ' là xong   7 1  1   OM 3; 4  ;0     , OM ' ; ; 0   S  OM  ;OM '   2 2  2  
  Tính O  M;OM '   w8113=p4=0=q51217P2= p1P2=0=Cq53q57q54=
  25
1   25 Vậy OM  ;OM '  12.5   S  OM  ;OM '  OMM '   2 2   4
Tổng hợp các chuyên đề luyện thi đại học Trang 21
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
IV. BÀI TẬP RÈN LUYỆN 1. ĐỀ BÀI
Câu 1. Cho hai số phức z  1  2i; z  2  3i . Khi đó số phức w  3z  z  z z có phần ảo 1 2 1 2 1 2 bằng bao nhiêu? A. 9 B. 10 C. 9 D. 10
Câu 2. Cho số phức z  3  2i , khi đó số phức w  2z  3z là A. 3   2i B. 3  2i
C. 3  10i
D. 11  2i
Câu 3. Những số nào sau đây vừa là số thực và vừa là số ảo? A. 0 và 1 B. chỉ có 0 C. chỉ có số 1 D.không có số nào
Câu 4. (Đề thử nghiệm 2017)Tìm số phức liên hợp của số phức z  i 3i   1
A. z  3  i
B. z  3  i
C. z  3  i D. z  3   i
Câu 5. (Đề thử nghiệm 2017) Tìm môđun của số phức z thỏa mãn z 2  i  13i  1 5 34 34 A. z  34 B. z  34 C. z  D. z  3 3
Câu 6. (Đề minh họa 2017) Cho số phức z  3  2i . Tìm phần thực và phần ảo của số phức z
A. Phần thực bằng 3 và phần ảo bằng 2i
B. Phần thực bằng 3 và phần ảo bằng 2
C. Phần thực bằng 3 và phần ảo bằng 2i
D. Phần thực bằng 3 và phần ảo bằng 2
Câu 7. (Đề minh họa 2017)Cho hai số phức z  1  i và z  2  3i . Tính môđun của số phức 1 2 z  z 1 2
A. z  z  13
B. z  z  5
C. z  z  1
D. z  z  5 1 2 1 2 1 2 1 2
Câu 8. (Đề minh họa 2017)Cho số phức z  2  5i . Tìm số phức w  iz  z
A.w  7  3i
B.w  3  3i
C.w  3  7i D.w  7   7i
1  i2 i
Câu 9. Môđun của số phức z  là 1  3i A. z  5 B. z  5 C. z  2
D. z  1
Câu 10. Cho số phức z thỏa điều kiện   iz    i2 3 1 2
 8  17i . Khi đó hiệu phần thực và
phần ảo của z là A. 7 B.3 C. 3 D. 7  2 1  2i
Câu 11. Cho số phức z thỏa mãn 1  2i   z 
 7  8i . Môđun của số phức 1  i
w  z  i  1 là A. 3 B. 5 C. 4 D.13 4  2i
1i2  i
Câu 12. Phần thực của số phức z   là 2  i 2  3i 29 11 29 11 A. B. C. D. 13 13 13 13
Tổng hợp các chuyên đề luyện thi đại học Trang 22
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
Câu 13. Cho số phức z thỏa mãn   iz    i2 1 2 1 3
 5i . Khi đó điểm nào sau đây biểu diễn số phức z ? A. M 2; 3   B. M 2; 3 C.M  2  ;  3 D. M  2  ; 3   25 1 1
Câu 14. Số phức z thỏa mãn  
. Khi đó phần ảo của số phức z bằng bao z 1  i 2 i2 nhiêu? A. 31 B.17 C.31 D. 1  7
Câu 15. Cho số phức z thỏa mãn z 1  3i  17  i . Khi đó môđun của số phức w  6z  25i là A. 29 B.13 C.2 5 D. 5
1  i2  i 1i2 i
Câu 16. Cho số phức z thỏa mãn z  
. Trong các kết luận sau, kết 1  i 1  i luận nào đúng? 1
A. z  z
B. z là số thuần ảo C.| z | 4 D. z  z
Câu 17. Cho hai số phức z  3  2 ,
i z  2  i . Giá trị của biểu thức | z  z z |là 1 2 1 1 2 A. 130 B.10 3 C.2 30 D. 3 10 z
Câu 18. Cho hai số phức z  2  3 ,
i z  2  i . Giá trị của biểu thức 2 z  là 1 2 1 z1 A. 5 B. 5 C.13 D. 11
  i   i2 4 3 3
Câu 19. Cho số phức z  
. Môđun của số phức w  z  iz  1 là 1  2i i  A. w  85 B. w  4 5 C. w  6 3
D. w  56
Câu 20. Cho z là một số phức. Xét các mệnh đề sau :
(I) Nếu z  z thì z là một số thực
(II) Môđun của z bằng độ dài đoạn OM với O là gốc tọa độ và M là điểm biểu diễn của số phức z
(III) z  z.z
Trong 3 mệnh đề trên có bao nhiêu mệnh đề đúng? A.0 B.1 C.2 D.3
Câu 21. Cho số phức z  m  
1  m  2i với m  R .Tìm tất cả các giá trị của m để z  5là.
A. 1  m  0 .
B. 0  m hoặcm  1  .
C.1  m  0 .
D. m  1 hoặcm  0 .
Câu 22. Cho Số phức z  a bi với a,b  R .Trong các mệnh đề sau,mệnh đề nào đúng. 2
A. z  z  2bi .
B. z  z  2a . C. 2 2
z.z  a b . D. 2
z  z .
Câu 23. Cho số phức z  2i . Lựa chọn phương án đúng 1 A. 2 z  .
B. z  2  4 . 4
Tổng hợp các chuyên đề luyện thi đại học Trang 23
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna 1 13  i C. 3 z   z  . D. 6 z  64 . z 2
Câu 24. Trong các kết luận sau kết luận nào sai?
A.Môđun số phức z là 1 số thực dương.
B.Môđun số phức z là 1 số thực.
C. Môđun số phức z là 1 số thực không âm.
D. Môđun số phứcz là 1 số phức. 2016 2018 1 i    1 i     
Câu 25. Số phức z        bằng 1  i  1  i A.1  i B. 0 C.2 D.2 Câu 26. Cho 2 2017
P  1  i  i  ...  i
, khẳng định nào sau đây là đúng A. P  0 B. P  1
C.P  1  i
D. P  2i
Câu 27. Đẳng thức nào đúng trong các đẳng thức sau ?
A.  i2018 1009 1  2 i
B.  i2018 1009 1  2 i
C.  i2018 1009 1  2
D.  i2018 1009 1  2 2017 4  2i  i
Câu 28. Số phức z 
có tổng phần thực và phần ảo là 2  i A.1 B.2 C.3 D.4 1  i2017
Câu 29. Số phức z 
có phần thực hơn phần ảo bao nhiêu đơn vị ? 1008 2 i A.0 B.1 C.2 D. 1008 2 2 3 2017
Câu 30. Phần thực của số phức z  1  1  i  1  i  1  i  ...  1  i là A. 2016 2 B. 1008 2 C. 1008 2   1 D. 1008 2 Câu 31. Cho 2 4 4 2  4  1    ... k k A i i  i  i với *
k   . Hỏi đâu là phương án đúng
A. A  2ki
B. A  2k C.A  0
D. A  1 2
Câu 32. Với mọi số phức z , ta có z  1 bằng
A. z  z  1 B. 2 z  2z  1 2
C. z  2 z  1
D. z.z  z  z  1
Tổng hợp các chuyên đề luyện thi đại học Trang 24
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
2. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI CHI TIẾT 1B 2C 3B 4D 5A 6D 7A 8B 9D 10A 11B 12A 13B 14D 15A 16D 17A 18B 19A 20D 21C 22D 23C 24B 25C 26A 27D 28B 29C 30D 31D 32D Câu 1.
Cách 1:Ta có w  31  2i  2  3i  1  2i2  3i  3  6i  2  3i  8  i  9  10i
Suy ra w có phần ảo bằng 10.
Cách 2 : Sử dụng Casio (Để máy ở chế độ Mode 2 _CMPLX)
Nhập vào máy 31  2   2  3   1  2 2  3  Casio i i i
i   9  10i . Chọn B. Câu 2.
Cách 1 :Ta có w  23  2i  33  2i  6  4i  9  6i  3   10i .
Cách 2 : Sử dụng Casio (Để máy ở chế độ Mode 2 _CMPLX)
Nhập vào máy 23  2   33  2  Casio i
i   3  10i . Chọn C.
Câu 3. Gọi z  a bi là số phức thỏa yêu cầu bài toán a,b  
Ta có z là số thực khi b  0 ; z là số ảo khi a  0  z  0 . Chọn B.
Câu 4. Ta có z  i  i   2 3
1  3i  i  3
  i  z  3
  i . Chọn D. Câu 5. 1  13i
1 13i2  i
Cách 1:z 2  i 2 2
 13i  1  z  
 3  5i  z  3  5  34 . 2 2 2  i 2  1 1  13i
Cách 2 : Sử dụng Casio, Ta có Casio z 
  34 . Chọn A. 2  i
Câu 6. Ta có z  3  2i  z  3  2i , suy ra phần thực bằng 3 và phần ảo bằng 2. Chọn D. Câu 7. Ta có 2 2
z  z  3  2i  z  z  3  2  13 . Chọn A. 1 2 1 2
Câu 8. Ta có w  i 2  5i  2  5i  2i  5  2  5i  3  3i . Chọn B. Câu 9.
1 i2 i 3 i
3 i1 3i 2 2 3 4 3 4         
Cách 1:Ta có z   
  i  z        1 . 2 2 1  3i 1  3i        1 3 5 5 5 5
1  i2  i Cách 2: Dùng Casio, Casio
  1 . Chọn D. 1  3i
 i    i2 8 17 1 2 caisio
Câu 10. Ta có z 
2  5i khi đó hiệu phần thực phần ảo là:2  5  7 . 3  i  Chọn A.
Tổng hợp các chuyên đề luyện thi đại học Trang 25
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna  2(1 2i)    Câu 11. z  7   8i   :   2  i 2 2
 3  2i  w  z  i  1  4  3i  z  4  3  5  .  1  i  Chọn B 4  2i
(1  i)(2  i) 29 11 Câu 12. z     i . Chọn A. 2  i 2  3i 13 13  2 
Câu 13. Ta có z  5  i  
1  3i  :12i  2  3i  N 2;3   . Chọn B.    1 1 
Câu 14. Ta có z  25 :    
  31  17i  z có phần ảo bằng 1  7 . Chọn D. 1 i      2 i2    
1i2 i 1i2 i
Câu 15. Ta có z    2   z  2  . Chọn A. 1  i 1  i Câu 16. Ta có 17  i z 
 2  5i  w  6z  25i  62  5i 2 2         .  i 25i 12 5i w 12 5 13 1 3 Chọn D.
Câu 17. Ta có | z  z z | 3  2i  3  2i 2  i  130 . Chọn A. 1 1 2    z 5  i Câu 18. Ta có 2 | z  | 2  3i   5 . Chọn B. 1 z 2  3i 1
  i  i2 4 3 3
Câu 19. Ta có z  
 2  4i  z  2  4i . 1  2i i 
w  z  iz  1  2  4i  i 2  4i  1  7  6i  49  36  85 . Chọn A.
Câu 20. Gọi z  a bi với a,b  R a   a 
1. z  z  
 b  0  z  a  ĐÚNG b   b   2. 2 2
z  a  bi  OM  a  b  z  ĐÚNG
3. z  z z  a  bia bi 2 2 .
 a  b  z  ĐÚNG .Chọn D. 2 2
Câu 21. Ta có z 
 m    m   2 5 1
2  5  m  m  0  1
  m  0 . Chọn C. Câu 22. Ta có
z  z  a bi  a bi  2a
z  z  a  bi  a bi  2bi .
z.z  a bia bi 2 2  a  b Nên ,
A B,C đều sai .Nên Chọn D.
Câu 23. Ta có  i3 1 1 13 2 
 2i  8i  i  2i   i . Chọn C. 2i 2 2
Câu 24. Gọi z  a bi với a,b  R .khi đó 2 2
 z  a  b  0 .Nên B sai. Chọn B.
Tổng hợp các chuyên đề luyện thi đại học Trang 26
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna Câu 25. 2016 2018 1 i    1 i    2016 2018 1008 1009   Ta có A           . Chọn C.      i  i     2i   2i  1  1  0 1 i  1  i Câu 26. Cách 1: 2 3 2017
P  1  i  i  i  ...  i 2 3 2018
iP  i  i  i  ...  i 1 1   i i 1009 2 2018 2 2018
P  iP  1  i  P     1  i 1  i 1  i 1  i 2018 1  i
Cách 2:Do P la tổng của cấp số nhân2018Phần tử z  1  i
 1  i . Chọn A. 1  i 1009 2018 2 1009 504  
Câu 27. Ta có   i    i    i 1009 
 2i i 1009 1 1 2 2  2 i  . Chọn D.   4  2i  i 4  2i  i
Câu 28. Ta có i  i.i  2017 504 2017 4  i  z  
 1  2i . Chọn B. 2  i 2  i 1008 2017 2 1008  
Câu 29. Ta có   i
   i   i    i 1008 1 1 . 1 . 2  2 .1  i  .   1i2017 1008 2 .1  i 1  i z   
 1  i . Vậy phần thực hơn phần ảo là 2. Chọn C. 1008 1008 2 .i 2 .i i    i2017 2 3 2016 1 1
Câu 30. Ta có z  1  1  i  1  i  1  i  ...  1  i  . 1  1  i 1008   
 i2017    i   i2   i1008 1008 1 1 . 1 . 2  2 .1  i  .   1  1  i2017 1  i 1008 1008 1008  z  . Phần thực là 1008 2 . Chọn D.        i 2 . 2 2 .i 1 1 i 
Câu 31. Do A là tổng của một cấp số nhân (gồm 2k  1 số hạng) với 2
u  1;q  i . 1 k  k  1  i 1  1  2 4 4k 2  4k  2 1  2 1 2
Suy ra A  1  i  i  ...  i  i  1   1 . Chọn D. 2 1  i 1    1  2 2 z
 .z  a b 
Câu 32. Gọi z  a  bi;a,b    z  a  bi   . z
  z  2a  2 2 z   a bi   a  2 2 2 2 1 1
1  b  a  b  2a  1  z.z  z  z  1. 2 2 2
Chú ý : Ngoài ra ta có thể viết z  1  a  bi  1  z  z  z  1. Chọn D.
Tổng hợp các chuyên đề luyện thi đại học Trang 27
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
B. CĂN BẬC HAI VÀ PHƯƠNG TRÌNH BẬC HAI CỦA SỐ PHỨC
I. CĂN BẬC HAI CỦA SỐ PHỨC 1. LÝ THUYẾT
Nội dung lý thuyết
Cho số phức w . Mỗi số phức z thỏa mãn 2
z  w được gọi là một căn thức bậc 2 củaw .
Mỗi số phức w  0 0 có hai căn bậc hai là hai số phức đối nhau z và – z .
o Trường hợp w là số thực (w  a   )
+ Khi a  0 thì w có hai căn bậc hai là a và  a . + Khi a  0 nên 2 a  ( a
 )i , do đó w có hai căn bậc hai là a  .i và  a  .i .
Ví dụ: Hai căn bậc 2 của 1
 là i và –i . Hai căn bậc 2 của 2 a
 (a  0) là ai , ai .
o Trường hợp w  a  bi (a,b  ;  b  0) . Cách 1:
Gọi z  x  yi (x,y  )
 là căn bậc 2 của w khi và chỉ khi 2
z  w , tức là: 2
(x  yi)  a  bi  2 2 x   y  a   
 x  ...;y  ...  2xy  b 
Mỗi cặp số thực x;y  nghiệm đúng hệ phương trình đó cho ra một căn bậc hai
z  x  yi của số phức w  a bi . Cách 2:
Có thể biến đổi w thành bình phương của một tổng, nghĩa là 2
w  z . Từ đó kết luận
căn bậc hai của w là z và -z .
2. MỘT SỐ BÀI TOÁN ĐIỂN HÌNH Bài toán 1 Tìm các căn bậc 2 của 5   12i . Giải: o Cách 1: Tìm các căn bậc 2 của 5
  12i , tức là đi tìm các số phức x  yi (x,y  )  sao cho  2 2 x   y  5 2
(x  yi) =  5  12i 
nên ta cần giải hệ phương trình . 2xy  12 
Rút y từ phương trình thứ hai thay vào phương trình thứ nhất, ta có:
Tổng hợp các chuyên đề luyện thi đại học Trang 28
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna  36 2  4 2  x   5
x  5x  36  0  2 x    4  2  x      6   6   6   y  y   y   x      x x
Hệ này có 2 nghiệm: (2;3) và ( 2  ; 3  ) .
Vậy có 2 căn bậc hai của 5
  12i là 2  3i và 2   3i . o Cách 2: Ta có:   i   i    i   i2 2 5 12 4 2.2.3 9 4 2.2.3 3  (2  3i) .
Từ đó dễ dàng suy ra hai căn bậc hai của 5
  12i là 2  3i và 2   3i . Bài toán 2
Tìm căn bậc hai của số phức sau:w  4  6i 5 . Giải: o Cách 1:
Gọi z  x  yi x,y   là một căn bậc hai của 2 2  2 x  y  4 
Khi đó ta có:x  yi  4  6i 5   2  xy  6 5   x   3  y  5 
Giải hệ phương trình tìm được nghiệm:   x    3  y  5 
Vậy số phức đã cho có hai căn bậc hai là: z  3  i 5; z  3   i 5 . 1 2 o Cách 2:
Ta có: w   i   i   i2 2 4 6 5 9 2.3. 5 5  (3  5i) .
Suy ra 3  i 5 là căn bậc của w  4  6i 5 . Nên 3  i 5 là căn bậc củaw  4  6i 5
Vậy số phức đã cho có hai căn bậc hai là: z  3  i 5;z  3   i 5 . 1 2
Tổng hợp các chuyên đề luyện thi đại học Trang 29
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
II. GIẢI PHƯƠNG TRÌNH BẬC HAI
1. GIẢI PHƯƠNG TRÌNH BẬC HAI TRÊN TẬP SỐ PHỨC
Phương pháp giải Cho phương trình bậc 2: 2
Az  Bz C  0 (1) trong đó ,
A B,C là những số phứcA  0 . Xét biệt thức 2
  B  4AC
o Nếu   0 thì phương trình (1) có 2 nghiệm phân biệt: B    B    z  ; z  1 2 2A 2A
Trong đó  là một căn bậc 2 của  . B 
o Nếu   0 thì phương trình (1) có nghiệm kép: z  z  1 2 2A CHÚ Ý: n n
o Mọi phương trình bậc n: 1 A z  A z
 ...  A z  A  0 luôn có n nghiệm phức 0 1 n 1  n
(không nhất thiết phân biệt).
o Hệ thức Vi-ét đối với phương trình bậc 2 số phức hệ số thực: Cho phương trình bậc 2 : 2
Az  Bz  C  0 ( , A B,C  ;
 A  0) có 2 nghiệm phân  B  S
  z  z  1 2 
biệt (thực hoặc phức). Ta có: A  C P   z z  1 2  A
MỘT SỐ BÀI TOÁN ĐIỂN HÌNH Bài toán 1
Giải phương trình bậc hai sau: 2
z  2z  3  0 . Giải: Biệt thức 2 2   2  4.1.3  8
  8i . Phương trình có 2 nghiệm phân biệt là: 2  4i 2  4i z 
 1  2i; z   1  2i . 1 2 2 2 Bài toán 2
Giải phương trình bậc hai sau: 2
z  2z  4i  2  0 . Giải: Biệt thức: 2 2 2
  2  4.1.(4 i 2)  4  16i  8  12  16i  16  2.4.2i  4i  (4  2i) .
Chọn   4  2 .
i Phương trình trên có hai nghiệm là : B    2  4  2i B    2  4  2i z    1  i; z    3   i. 1 2 2A 2 2A 2
Tổng hợp các chuyên đề luyện thi đại học Trang 30
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
2. ĐƯA PHƯƠNG TRÌNH BẬC CAO VỀ NHỮNG PHƯƠNG TRÌNH BẬC NHẤT,
PHƯƠNG TRÌNH BẬC HAI.
a) Phương pháp phân tích đa thức thành nhân tử  Bước 1:
Để đưa phương trình thành nhân tử thì ta phải nhẩm nghiệm của phương trình. Có các
cách nhẩm nghiệm như sau:
o Tổng các hệ số của phương trình bằng 0 thì nghiệm của phương trình là x  1.
o Tổng các hệ số bậc chẳn bằng tổng hệ số bậc lẻ thì nghiệm của phương trình x  1  . o Định lý Bézout:
Phần dư trong phép chia đa thức f x cho x  a bằng giá trị của đa thức f (x) tại
x  a . Tức là f x  x ag x f a
Hệ quả: Nếu f a  0 thì f x x a.
Nếu f x  x a thì f a  0 .
o Sử dụng máy tính Casio để nhẩm nghiệm:
- Nhập phương trình vào máy tính.
- Bấm phím r rồi nhập 1 giá trị X bất kỳ, máy tính sẽ cho ra nghiệm của phương trình.
Sau đó dùng sơ đồ hoocne để phân tích thành nhân tử. o Sơ đồ Hoocne: Với đa thức f(x) = n n -1 n -2 a x  a x  a x  .. .  a
x  a chia cho x - a thương là n n -1 n -2 1 0 g(x) = n -1 n -2 n -3 b x  b x  b x  .. . 
b x  b dư r . n -1 n -2 n -3 1 0
Nếu r  0 thì f x g x , nghĩa là: f x   x ag x  .
Ta đi tìm các hệ số b ,b ,b . ..b
,b bằng bảng sau đây. n -1 n -2 n -3 1 0 a a a ... a a a n n-1 n -2 2 1 0 a b b b b b r n 1  n 2  n 3  1 0  a  ab a  ab  a  ab  a  ab  a  ab a 0 0 n n 1  n-1 n 2  n -2 2 2 1 1
 Bước 2: Giải phương trình bậc nhất hoặc phương trình hai số phức, kết luận nghiệm.
MỘT SỐ BÀI TOÁN ĐIỂN HÌNH Bài toán 1 Giải các phương trình: 3
z  27  0 . Giải:  z  1 3 z – 27 0 z – 1 2 z 3z 9 0       
. Vậy p/t đã cho có 3 nghiệm.  3   3 3i z  2,3  2
Tổng hợp các chuyên đề luyện thi đại học Trang 31
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna Bài toán 2 Giải phương trình sau: 3
z    i 2 3 1
2 z  3  8iz  5  2i  0. Giải:
Nhẩm nghiệm: Ta thấy tổng các hệ số của phương trình bằng 0 nên phương trình có nghiệm z  1. Khi đó: 3 z  i 2 z  iz i z  2 3 1 2 3 8 5 2 0 1 z 2 
1 3iz 2i 5                0  
 z  1 v z  i v z  2  5 . i
Vậy nghiệm của phương trình đã cho là : z  1 ; z  i ; z  2  5 . i Bài toán 3 Cho phương trình sau: 3 z   i 2
2 – 2 z  5 – 4iz – 10i  0 
1 biết rằng phương trình có nghiệm thuần ảo. Giải:
Đặt z  yi với y   . Phương trình (1) trở thành: 3 2
iy  2i  2yi   5  4i yi  – 10i  0  3 2 2 i
 y – 2y  2iy  5iy  4y – 10i  0  0  0i 2 
2y  4y  0 
Đồng nhất hoá hai vế ta được:  3 2 y 
 2y  5y  10  0  
Giải hệ này ta được nghiệm duy nhất y  2 .
Suy ra phương trình (1) có nghiệm thuần ảo z  2i .
* Vì phương trình (1) nhận nghiệm 2i .
 vế trái của (1) có thể phân tích dưới dạng: 3 z   i  2 z   i z i  z i  2 2 – 2 5 – 4 – 10 – 2
z  az  b ( ,
a b  ) đồng nhất hoá hai vế ta giải
được a  2 và b  5 .   z  2i  z  2i    
1  z – 2i 2
z  2z  5  0    z   1  2i 2
z  2z  5  0  z   1  2i   
Vậy phương trình (1) có 3 nghiệm. Bài toán 4 Giải 3
z    i 2 3
z  2  iz  16  2i  0 biết rằng phương trình có 1 nghiệm thực. Giải :
Gọi nghiệm thực là z0 ta có:  3 2 z
  3z  2z  16  0  3
z  3  i z  2  i z  16  2i  0    z  2 0   20   0 0 0 0 2 0 z   z  2  0  o 0 
Tổng hợp các chuyên đề luyện thi đại học Trang 32
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
Khi đó ta có phương trình z   2
2 z  5  iz  8  i  0
Tìm được các nghiệm của phương trình là z  2
 ; z  2  i ; z  3  2i . Bài toán 5 Giải phương trình 3
z    i 2 2
3 z  31  2iz  9i  0 biết rằng phương trình có một nghiệm thuần ảo. Giải:
Giả sử phương trình có nghiệm thuần ảo là b ,
i b   .
Thay vào phương trình ta được: 2
bi3 2  3ibi  31  2ibi  9i  0 2 2
 b  6b  0 2 2b 6b  3 2 b 3b 3b 9i 0             b  3   z  3  i 3 2  b
  3b  3b  9  0 
Phương trình có thể phân tích thành z  i 2
3 z  2z   3  0
Các nghiệm của phương trình là z  3
 i ; z  1  2i . Bài toán 6
Gọi z ;z ;z ;z là 4 nghiệm phức của phương trình 4
z    m 2 4
z  4m  0 (1). Tìm tất cả 1 2 3 4
các giá trị m để z  z  z  z  6. 1 2 3 4 Giải: z  2i 4 2 2 2 1,2
z  4  mz  4m  0  z  4z  m  0   z   m  3,4 z  2i 1,2
Nếu m  0 thì (1) có nghiệm là  . z   m  3,4 
6  z  z  z  z  4  2 m Khi đó 1 2 3 4   m  1 . m   0  z  2i 1;2
Nếu m  0 thì (1) có nghiệm là  z  i m  3;4 
6  z  z  z  z  4  2 m Khi đó 1 2 3 4 
 m  1 . Kết hợp lại m  1 thỏa mãn bài toán. m   0  Bài toán 7 Cho phương trình 4 2
4z  mz  4  0 trong tập số phức và m là tham số thực. Gọi
z ,z ,z ,z lần lượt là 4 nghiệm của phương trình đã cho. Tìm tất cả các giá trị của m để 1 2 3 4  2 z  4 2 z  4 2 z  4 2 z  4  324 . 1 2 3 4  Giải:
Tổng hợp các chuyên đề luyện thi đại học Trang 33
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna Cách 1: Đặt 2
t  z , phương trình trở thành: 2
4t  mt  4  0 có 2 nghiệm t ,t . 1 2  m t   t   Ta có: 1 2 
4 . Do vai trò bình đẳng, giả sử ta có: 2 2 2 2
z  z  t ,z  z  t . 1 2 1 3 4 2  t .t  1 1 2  2 2 2
Yêu cầu bài toán  t  4
t  4  324  t
 t  4 t  t  16  324 . 1   2  1 2  1 2     m   17  18 m   1    m   172 2  18     . m   17  18  m  35     Cách 2:
Đặt f z   4 z  z z  z z  z z  z . 1   2   3   4  f 2i f 2  i 2 2 2 2     Do 2
z  4  z  2i z  2i nên z  4 z  4 z  4 z  4  . * 1  2  3  4    1  1  1  4 4 4 2
Mà f 2i  f  2
 i   4 2i  m 2i  4  68  4 . m   m2 68 4 m   1  Vậy *  324    . 4.4 m  35 
Tổng hợp các chuyên đề luyện thi đại học Trang 34
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
b) Phương pháp tìm nghiệm của phương trình bậc 4 hệ số thực Cho pt bậc 4: 4 3 2
Ax  Bx Cx  Dx  E  0 với , A , B C, , D E  ;  A  0 .
Tìm các nghiệm của phương trình. Biết phương trình có 1 nghiệm phức là z  a  bi . 1 * Lưu ý:
Nếu phương trình trên có 1 nghiệm là z  a  bi thì nó cũng có nghiệm z  a b . i Khi đó 2 2 2 2
z z  x  2ax  a  b nên 4 3 2 2 2 2
Ax  Bx Cx  Dx  E  (x  2ax  a  b )g(x). Dùng 1 2
phép chia đa thức cho đa thức đã học ở lớp 8 để tìm g(x) .
Tiếp tục giải phương trình bậc hai : g(x)  0 để tìm 2 nghiệm còn lại của phương trình. BÀI TOÁN ĐIỂN HÌNH Bài toán
Tìm phương trình bậc 4: 4 3 2
z  2z  z  2z  10  0 .Tìm các nghiệm của phương trình.
Biết phương trình có 1 nghiệm phức là z  2  i. Hướng dẫn :
Phương trình trên có 1 nghiệm là z  2  i thì nó cũng có nghiệm z  2  i. Khi đó z ,z 1 2 1 2
là nghiệm của phương trình: z  z z  z  2
 z  4z  5. 1 2 Nên 4 3 2
z  z  z  z    2 ( 2 2 10) z  4z   5 g z.
Dùng phép chia đa thức cho đa thức đã học ở lớp 8 tìm được g z  2
 z  2z  2 . Phương trình 2
z  2z  2  0 có 2 nghiệm là 1  i; 1  i .
Vậy phương trình trên có 4 nghiệm là : 2   i ; 2  i; 1  ; i 1 i .
Tổng hợp các chuyên đề luyện thi đại học Trang 35
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
c ) Phương pháp đặt ẩn phụ
o Bước 1: Phân tích phương trình thành các đại lượng giống nhau.
o Bước 2: Đặt ẩn phụ, nêu điều kiện (nếu có).
o Bước 3: Đưa phương trình ban đầu về phương trình bậc nhất hoặc bậc 2 theo ẩn mới.
o Bước 4: Giải và kết luận nghiệm.
MỘT SỐ BÀI TOÁN ĐIỂN HÌNH Bài toán 1 Giải phương trình sau: 2 2 2
(z  z)  4(z  z)  12  0 . Giải: Đặt  2 t
z  z , khi đó phương trình đã cho có dạng:  1   23i z   2    2 t  6
z  z  6  0 2  1   23i
t  4t – 12  0        z
. Vậy p/t đã cho có 4 n . 2 t  2 
z  z  2  0  0     2  z  1   z  2   Bài toán 2 2
Giải phương trình sau trên tập số phức:  2 z 
z    z  2 z  z   2 3 6 2 3 6 – 3z  0 Giải: Đặt t  2
z  3z  6 phương trình đã cho có dang: z  1   5i
+ Với t  z  2
z  3z  6 – z  0  2
z  2z  6  0   z  1   5i z  3  3 2 2 
+ Với t  3z  z  3z  6  3z  0  z  6z  6  0   z  3   3
Vậy phương trình đã cho có 4 nghiệm. Bài toán 3 Giải phương trình 2
(z  z)(z  3)(z  2)  10 . Giải:
PT  z(z  2)(z 1)(z  3)  10 2 2
 (z  2z)(z  2z  3)  0 Đặt 2
t  z  2z . Khi đó phương trình (8) trở thành:
Tổng hợp các chuyên đề luyện thi đại học Trang 36
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna t  2
z  1  i   2
t  3t  10  0   t  5   z  1  6  
Vậy phương trình có các nghiệm: z  1  6 ; z  1   i . Bài toán 4 2 z
Giải phương trình sau trên tập số phức 4 3 z  z   z  1  0 . 2 Giải:
Nhận xét: z  0 không là nghiệm của phương trình (1) vậy z  0 . 1 1 1 Chia hai vế PT (1) cho 2 z ta được: ( 2 z  )  (z  )   0 (2) 2 z z 2 1 1 1
Đặtt  z  . Khi đó 2 2 t  z   2 2 2  z   t  2 z 2 z 2 z 5
Phương trình (2) có dạng: 2 t – t  (3) 2 5 2
  1  4.  9  9i 2 1  3i 1  3i
PT (3) có 2 nghiệm t  , t  . 2 2 1  3i 1 1  3i + Với t  ta có 2 z  
 2z  (1  3i)z  2  0 (4) 2 z 2 Có 2 2 2
  (1  3i)  16  8  6i  9  6i  i  (3  i)
(1  3i)  (3  i)
(1  3i)  (3  i) i  1
PT (4) có 2 nghiệm: z 
 1  i ,z   . 4 4 2 1  3i 1 1  3i + Với t  ta có 2 z  
 2z  (1  3i)z  2  0 (5) 2 z 2 Có 2 2 2
  (1  3i)  16  8  6i  9  6i  i  (3  i)
(1  3i)  (3  i)
(1  3i)  (3  i) i   1
PT(5) có 2 nghiệm: z 
 1  i ,z   . 4 4 2 i  1 i   1
Vậy PT đã cho có 4 nghiệm: z  1  i ; z  1  i ; z  ; z  . 2 2
Tổng hợp các chuyên đề luyện thi đại học Trang 37
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
III. SỬ DỤNG MÁY TÍNH CASIO 570VN-PLUS ĐỂ GIẢI
Một số lưu ý
Để thực hiện các phép toán trên tập số phức, ta chuyển qua chế độ CMPLX bằng cách bấm w2.
o Bấm đơn vị ảo i bằng cách bấm phím b
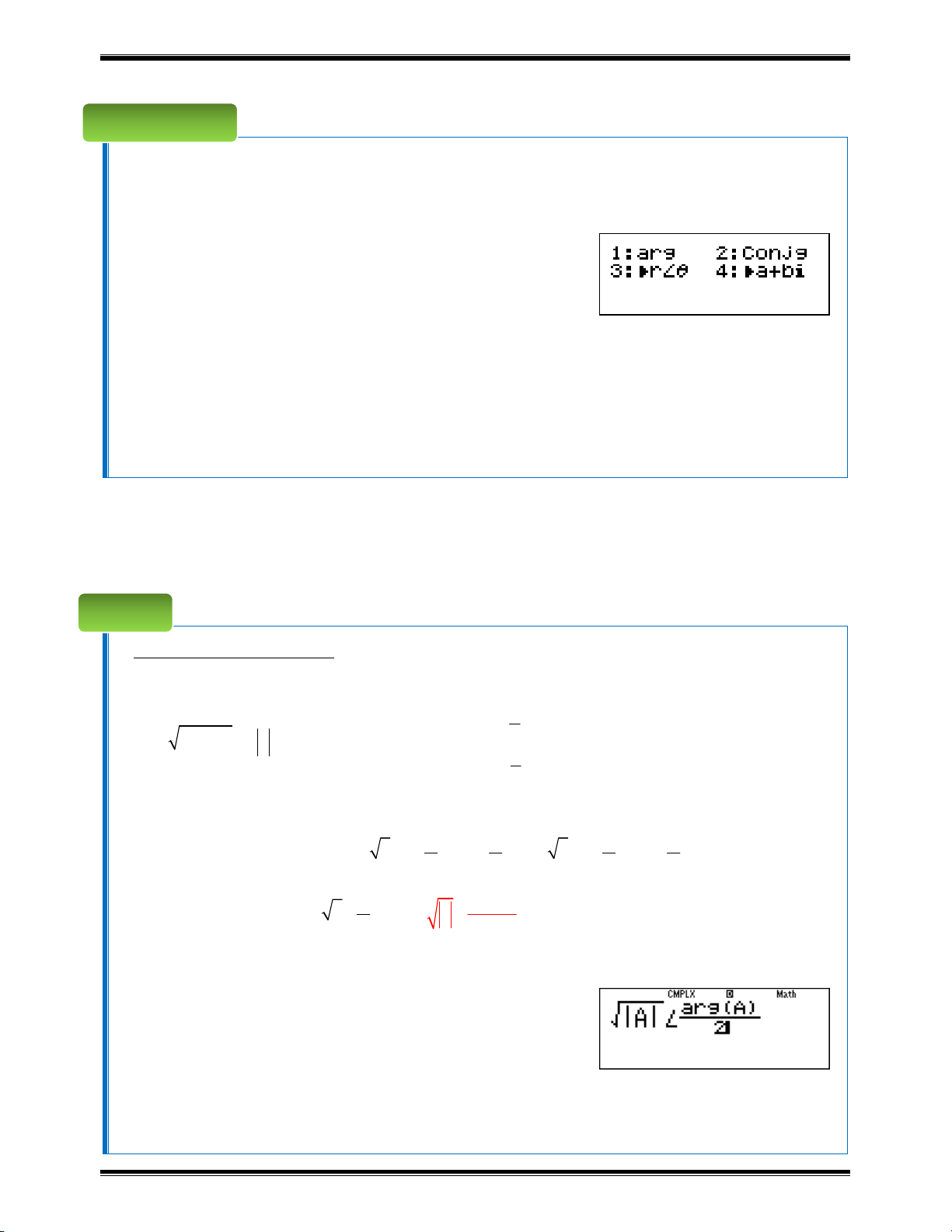
o Bấm q2 và lựa chọn các chức năng:
o Chọn 1 để bấm acgumen của z arg z  .
o Chọn 2 để bấm số phức liên hợp của z Conjg z  .
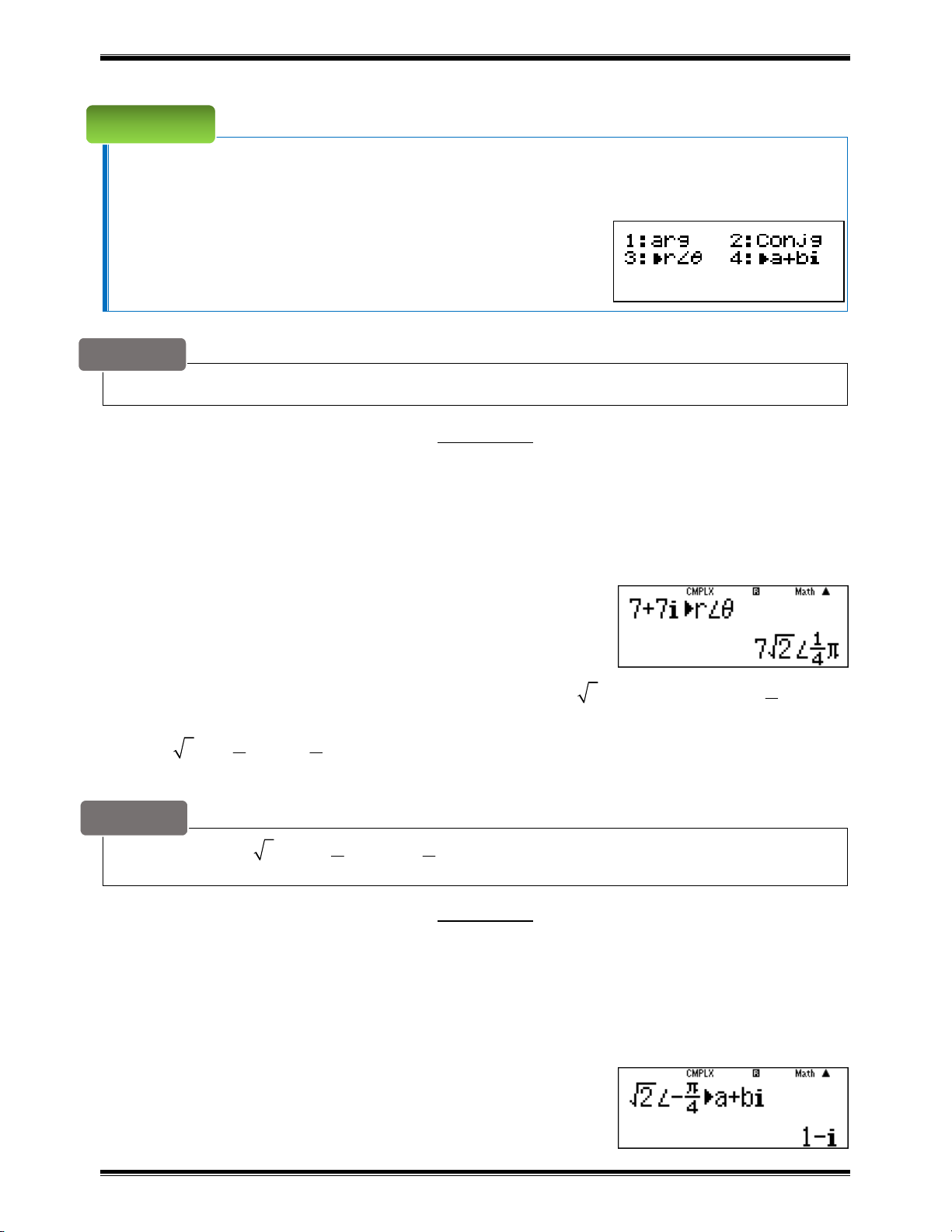
o Chọn 3 để chuyển từ dạng đại số sang dạng lượng giác.
o Chọn 4 để chuyển từ dạng lượng giác sang dạng đại số.
o Bấm dấu  bằng cách bấm: qz
Sau đây là cách giải các bài toán điển hình cho các dạng toán tìm căn bậc hai của một số phức;
giải phương trình bậc hai với hệ số thực và các dạng toán liên quan bằng máy tính casio.
1. BÀI TOÁN TÌM CĂN BẬC HAI CỦA MỘT SỐ PHỨC Cách 1
Xây dựng công thức bấm:
Cho số phức z  a bi , có dạng lượng giác là z = r(cos +isin)r  0. Với  a  os c   2 2
r  a  b  z  .  là góc thoả mãn : r  . b si  n   r
 được gọi là acgument của z , kí hiệu là arg z  .          
Khi đó z có hai căn bậc hai là: r  os c  isin   r c     và - os isin .  2 2   2 2   argz
Hay được viết gọn là:  r hay  z  2 2
Như vậy để tìm các căn bậc hai của số phức z  a bi , ta làm như sau:
o Nhập số phức z và lưu vào biến A (cái này đơn giản).
o Bấm theo công thức sau: sqcQz$$qzaq21Qz)R2=
o Ta thu được kết quả của một căn thức của z , suy ra căn bậc hai còn lại.
Tổng hợp các chuyên đề luyện thi đại học Trang 38
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna Ví dụ
Tìm các căn bậc hai của số phức z  3   4i . Hướng dẫn: Quy trình bấm :
o Nhập số phức z  3
  4i và lưu vào biến A: p3+4bqJz
o Bấm theo công thức ở trên : sqcQz$$qzaq21Qz)R2 = o Màn hình cho kết quả: Nên 1  2i và 1
 2i là 2 căn bậc hai của số phức z  3   4i . Cách 2 o Nhập hàm X2 : Q)d
o Sử dụng phímr,nhập các giá trị vào, giá trị nào cho ra số phức z thì ta chọn đáp án đó. Ví dụ
Tìm các căn bậc hai của số phức z  3   4i . .1
A  2i;  1  2i B.2  2i;  1  2i
C.1  2i;  1  2i D.  2  i;  2  i Hướng dẫn: o Q)d
o r Nhập lần lượt các số phức ở các đáp án vào nhé.
r1+2b= màn hình sẽ cho kết quả:
Nên 1  2i là căn bậc hai của số phức z  3
  4i . Vì một số phức có hai căn bậc 2 đối nhau nên 1
 2i cũng là căn bậc hai của số phức z  3   4i . >>> Chọn C.
Tổng hợp các chuyên đề luyện thi đại học Trang 39
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna Cách 3
Tìm các căn bậc hai của số phức z  a  bi . o w1
o Nhấp Shift + (Pol), ta nhập Pol(a,b).
o Dấu phẩy trong (a,b) bấm bằng cách q)
o Nhấp Shift - (Rec), ta nhập Rec(X,Y), ta thu được kết quả X=...;Y=...
o Kết luận các căn bậc 2 cần tìm. Ví dụ
Tìm các căn bậc hai của số phức z  1
 2  16i . Hướng dẫn: o w1
o q+p12q)16)= màn hình hiện kết quả
o qpsQ)$q)QnP2)= thu được kết quả:
Suy ra các căn bậc hai của số phức z  1
 2  16i là 2  4i ; 2   4i .
Tổng hợp các chuyên đề luyện thi đại học Trang 40
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
2. GIẢI PHƯƠNG TRÌNH BẬC HAI
a) Phương trình bậc hai với hệ số thực: Bài toán 1
Giải phương trình bậc hai sau: 2
z  4z  10  0 . Hướng dẫn:
Quy trình bấm: w531=p4=10== Thu được kết quả: Bài toán 2
Gọi z ,z là 2 nghiệm của phương trình : 2
z  z  1  0 . Tính 2018 2018 P  z  z . 1 2 1 2 Hướng dẫn : Quy trình bấm như sau:
o Tìm nghiệm z ,z 1 2 w531=1=1== Thu được kết quả:
o Lưu 2 nghiệm vào X và Y: qJ)RqJn
o Màn hình hiển thị là đã lưu biến X thành công, tương tự biến Y. o Tính P .
o Sau đó vào w2 và nhập P và thu được kết quả:
Sau đây là Bài toán 3 tương tự Bài toán 2 nhưng giải theo dạng lượng giác của số phức. Cách này luôn
giải được với số mũ lớn bất kỳ, cách giải theo Bài toán 2 có thể không giải được với số mũ lớn nào đó. Bài toán 3 1 1
Biết z là nghiệm của phương trình z 
 1 . Tính giá trị biểu thức 2009 P  z  z 2009 z 5 7 A. P  1 B.P  0 C.P   D.P  2 4
Tổng hợp các chuyên đề luyện thi đại học Trang 41
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna Hướng dẫn: 1
 Quy đồng phương trình z 
 0 ta được phương trình bậc hai 2
z  z  1  0 . Tính z
nghiệm phương trình này với chức năng MODE 5 3 w531=p1=1==
 Ta thu được hai nghiệm z nhưng hai nghiệm này có vai trò như nhau nên chỉ cần lấy một
nghiệm z đại diện là được 1 3      Với z  
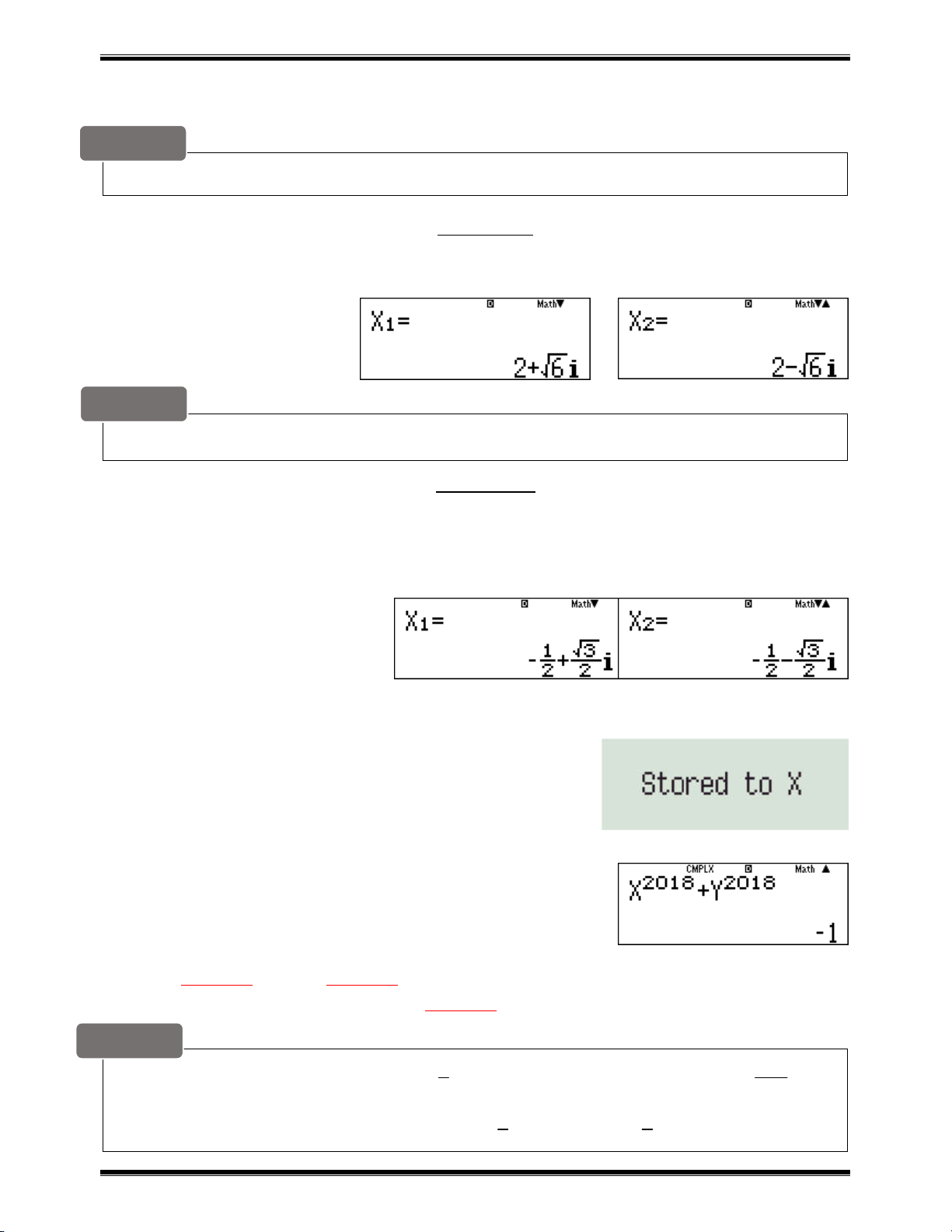
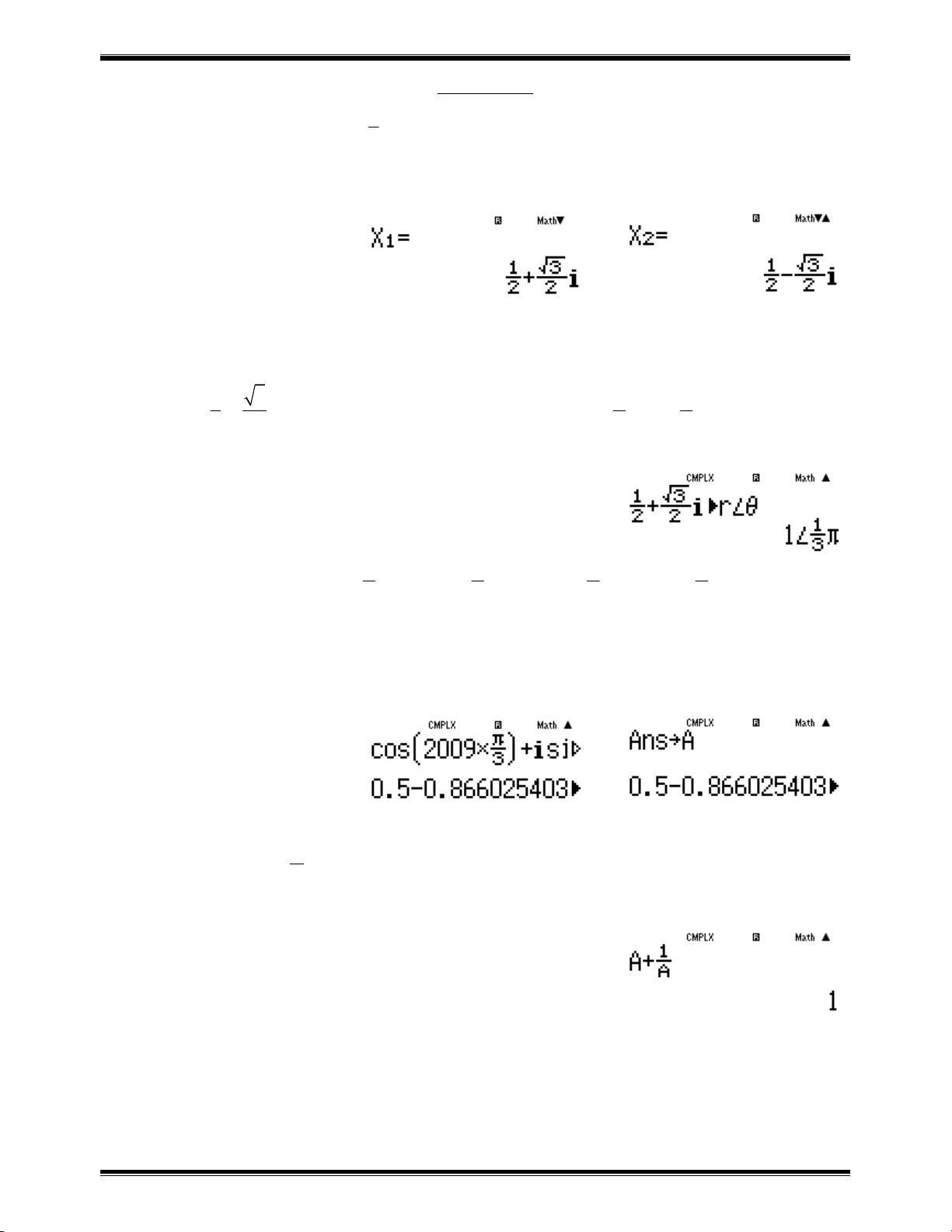
i ta chuyển về dạng lượng giác  z  1cos  i sin  2 2  3 3  a1R2$+as3R2$bq23=           Vậy 2009 2009  z  1
cos2009.  i sin 2009.   cos 2009.  i sin 2009.    3 3     3 3  Tính 2009 z
và lưu và biến A Wk2009OaqKR3$)+bj2009 OaqKR3$)=qJz 1
Tổng kết P  A   1 A Qz+a1RQz=
 Đáp số chính xác là A
Tổng hợp các chuyên đề luyện thi đại học Trang 42
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
b) Phương trình bậc hai với hệ số phức: Bài toán Giải phương trình : 2
z  8(1  i)z  63  16i  0 . Hướng dẫn: o Tính 2
  B  4AC bằng máy tính , ta được:
o Sau đó gán kết quả của  vào A.
o Dùng công thức tìm căn bậc 2 đã học ở trên, thu được 1 căn bậc 2 của  là 2  16i .
o Gán kết quả này cho X.
o Nên 2 nghiệm của phương trình là :
Tổng hợp các chuyên đề luyện thi đại học Trang 43
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
IV. BÀI TẬP RÈN LUYỆN 1. ĐỀ BÀI
Câu 1. Trong  , phương trình 4
z  1  0 có nghiệm là: A. 1  ; 2i B. 2  ; 2i C. 3  ; 4i D. 1  ; i
Câu 2. Trong  , căn bậc hai của 121 là: A. 11i B. 11i C. 11
D. 11i và 11i
Câu 3. Phương trình 2
8z  4z  1  0 có nghiệm là: 1 1 5 1 1 1 1 3 A z 
 i; z   i B. z 
 i; z   i 1 2 4 4 4 4 1 2 4 4 4 4 1 1 1 1 2 1 1 1 C. z 
 i; z   i D. z 
 i; z   i 1 2 4 4 4 4 1 2 4 4 4 4
Câu 4. Biết z ; z là hai nghiệm của phương trình 2
2z  3z  3  0 . Khi đó giá trị của 2 2 z  z 1 2 1 2 là: 9 9 A. B. 9 C. 4 D.  4 4
Câu 5. Phương trình 2
z  az  b  0 có một nghiệm phức là z  1  2i . Tổng 2 số a và b bằng: A. 0 B. 3 C. 3 D. 4
Câu 6. Gọi z ; z là hai nghiệm phức của phương trình 2
z  4z  5  0. Khi đó phần thực của 1 2 2 2 z  z là: 1 2 A. 5 B. 6 C. 4 D. 7
Câu 7. Gọi z ; z là hai nghiệm phức của phương trình 2
z  2z  4  0 . Khi đó 2 2 A |
 z |  | z | 1 2 1 2 có giá trị là A. 7  B. – 8 C. 4 D. 8
Câu 8. Phương trình 3
z  8 có bao nhiêu nghiệm phức với phần ảo âm? A. 1 B. 2 C. 3 D. 0
Câu 9. Biết z , z là hai nghiệm của phương trình 2
2z  3z  3  0 . Khi đó giá trị của 2 2 z  z 1 2 1 2 là: 9 9 A. 4 B. C. 9 D.  4 4
Câu 10. Phương trình sau có mấy nghiệm thực: 2
z  2z  2  0 A. 0 B. 1 C. 2
D. Vô số nghiệm.
Câu 11. Tìm các căn bậc hai của 9 . A. 3i B. 3 C. 3i D. 3
Câu 12. Trong  , phương trình 4
z  4  0 có nghiệm là:
A. 1  4i; 1  4i
B. 1  2i; 1  2i
C. 1  3i; 1  3i D. ±1  i; 1  i
Câu 13. Giải phương trình 2
z  2z  7  0 trên tập số phức ta được nghiệm là:
Tổng hợp các chuyên đề luyện thi đại học Trang 44
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
A. z  1  2 2i
B. z  1  6i
C. z  1  2i
D. z  1  7i
Câu 14. Căn bậc hai của số phức 4  6 5i là:
A. 3  5i
B. 3  5i
C. 3  5i D. 2
Câu 15. Gọi z là căn bậc hai có phần ảo âm của 33  56i . Phần thực của z là: A. 6 B. 7 C. 4 D. –4
Câu 16. Tập nghiệm trong  của phương trình 3 2
z  z  z  1  0 là: A.  i  ; i;1;  1 B.  i  ;i;  1 C.  i  ;  1 D.  i  ;i;  1
Câu 17. Trên tập số phức, phương trình bậc hai có hai nghiệm   4  3i;   2   i là: A. 2
z  2  4iz 11  2i  0 B. 2
z  2  4iz  11  2i  0 C. 2
z  2  4iz  11  2i  0 D. 2
z  2  4iz  11  2i  0
Câu 18. Có bao nhiêu số phức thỏa mãn điều kiện 2 2 z |  z | z  ? A. 3 B. 0 C. 1 D. 2 2
Câu 19. Phương trình 2  iz az b  0 , a b  
 có hai nghiệm là 3  i và 1  2i . Khi đó a  ? A. 9  2i B. 15  5i C. 9  2i
D. 15  5i 6
Câu 20. Cho số phức z thỏa mãn 2
z  6z 13  0. Tính z  z  i A. 17 và 4 B. 17 và 5 C. 17 và 3 D. 17 và 2
Câu 21. Gọi z ,z là các nghiệm phức của phương trình 2
z  1  3iz  21  i  0 . Khi đó 1 2 2 2
w  z  z  3z z là số phức có môđun là: 1 2 1 2 A. 2 B. 13 C. 2 13 D. 20
Câu 22. Số nghiệm của phương trình với ẩn số phức z: 2 2
4z  8 | z | 3  0 là: A. 3 B. 2 C. 4 D. 1
Câu 23. Tìm số phức z để 2
z  z  z .
A z  0;z  1  i
B. z  0;z  1  i
C. z  0;z  1  i;z  1  i
D. z  1  i;z  1  i
Câu 24. Với mọi số ảo z, số 2 2 z  | z | là:
A. Số thực âm B. Số 0 C. Số thực dương
D. Số ảo khác 0
Câu 25. Trong trường số phức phương trình 3
z  1  0 có mấy nghiệm? A. 2 B. 3 C. 1 D. 0
Câu 26. Giá trị của các số thực b, c để phương trình 2
z bz c  0 nhận số phức z  1  i làm một nghiệm là: b   2     b   2  b   2  b   2  A.  B.  C.  D.  c   2          c 2  c 2  c 2 
Tổng hợp các chuyên đề luyện thi đại học Trang 45
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
Câu 27. Trên tập hợp số phức, phương trình 2
z  7z 15  0 có hai nghiệm z ,z . Giá trị biểu 1 2
thức z  z  z z là: 1 2 1 2 A. –7 B. 8 C. 15 D. 22
Câu 28. Tìm số nguyên x, y sao cho số phức z  x  yi thỏa mãn 3
z  18  26i x   3     x   3  x   3  x   3  A.  B.  C.  D.  y   1           y 1  y 1  y 1 
Câu 29. Trên tập số phức, cho phương trình sau: z  i4 2
 4z  0 . Có bao nhiêu nhận xét đúng
trong số các nhận xét sau?
1. Phương trình vô nghiệm trên trường số thực  .
2. Phương trình vô nghiệm trên trường số phức  .
3. Phương trình không có nghiệm thuộc tập số thực.
4. Phương trình có bốn nghiệm thuộc tập số phức.
5. Phương trình chỉ có hai nghiệm là số phức.
6. Phương trình có hai nghiệm là số thực A. 0 B. 1 C. 3 D. 2
Câu 30. Phương trình 6 3
z  9z  8  0 có bao nhiêu nghiệm trên tập số phức? A. 3 B. 4 C. 2 D. 6
Câu 31. Giả sử z ,z là hai nghiệm của phương trình 2
z  2z  5  0 và A, B là các điểm biểu 1 2
diễn của z ,z . Tọa độ trung điểm I của đoạn thẳng AB là: 1 2 A. I 1;  1
B. I 1; 0 C. I 0;  1 D. I 1;  0
Câu 32. Cho phương trình 2
z  mz  6i  0 . Để phương trình có tổng bình phương hai nghiệm
bằng 5 thì m có dạng m  a bi ,
a b  . Giá trị a  2b là: A. 0 B. 1 C. 2 D. 1 4  z 1    
Câu 33. Gọi z ,z ,z , z là các nghiệm phức của phương trình    1. Giá trị của 1 2 2 4
2z  i P   2 z   1  2 z   1  2 z   1  2 z  1 là: 1 2 3 4  17 17 9 17i A. B. C. D. 8 9 17 9
Câu 34. Trong tập số phức, giá trị của m để phương trình bậc hai 2
z  mz  i  0 có tổng bình
phương hai nghiệm bằng 4i là:
A. 1  i
B. 1  i
C. 1  i
D. 1  i
Câu 35. Cho phương trình 2
z mz  2m 1  0 trong đó m là tham số phức. Giá trị của m để
phương trình có hai nghiệm z ,z thỏa mãn 2 2
z  z  10 là: 1 2 1 2
A. m  2  2 2i
B. m  2  2 2i
C. m  2  2 2i
D. m  2  2 2i
Tổng hợp các chuyên đề luyện thi đại học Trang 46
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
Câu 36. Gọi z ,z là hai nghiệm của phương trình 2
z  2z  8  0 , trong đó z có phần ảo 1 2 1
dương. Giá trị của số phức w  2z  z z là: 1 2  1
A. 12  6i B. 10 C. 8
D. 12  6i
Câu 37. Tổng bình phương các nghiệm của phương trình 4
z  1  0 trên tập số phức là bao nhiêu? A. 3 B. 1 C. 2 D. 0
Câu 38. Gọi z ,z là hai nghiệm của phương trình 2
z  2z  6  0 . Trong đó z có phần ảo âm. 1 2 1
Giá trị biểu thức M |
 z |  | 3z  z | là: 1 1 2 A. 6  2 21 B. 6  2 21 C. 6  4 21 D. 6  4 21
Câu 39. Phương trình 4 2
x  2x 24x  72  0 trên tập số phức có các nghiệm là:
A. 2  i 2 hoặc 2  2i 2
B. 2  i 2 hoặc 1  2i 2
C. 1  2i 2 hoặc 2  2i 2
D. 1  2i 2 hoặc 2  2i 2
Câu 40. Gọi z ,z là các nghiệm phức của phương trình 2
z  3z  7  0 . Khi đó 4 4
A  z  z có 1 2 1 2 giá trị là: A. 23 B. 23 C. 13 D. 13
Tổng hợp các chuyên đề luyện thi đại học Trang 47
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
2. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI CHI TIẾT 1.D 2.D 3.C 4.D 5.C 6.B 7.D 8.A 9.D 10.A 11.A 12.D 13.B 14.C 15.B 16.D 17.B 18.A 19.A 20.B 21.D 22.C 23.C 24.B 25.B 26.C 27.B 28.C 29.D 30.D 31.D 32.D 33.B 34.A 35.A 36.C 37.D 38.B 39.A 40.A z  1   z  1     Câu 1. 4
z  1  0  z   1 z   1  2 z   1  0  z   1  z  1   . Chọn D. 2  z   1  0 z  i    Câu 2. Ta có: z  
 z   i2 121 11
. Do đó z có hai căn bậc hai là z  11i;z  11i . Chọn D. 2  2i 1 i Câu 3. 2
 '  b ' ac  4  8  4   0  z    . Chọn C. 1,2 8 4 4  b 3 S
  z  z      1 2  3 9
Câu 4. Theo Viet, ta có: a 2  2 2 2
 z  z  S  2P   3    . Chọn D. c 3 1 2 4 4 P
  z .z   1 2  a 2
Câu 5. Vì z  1  2i là một nghiệm của phương trình 2
z  az  b  0 nên ta có:   i2 1 2
 a 1  2i  b  0  a  b  2ai  3  4i  a  b  3 . Chọn C.  b S
  z  z    4 1 2 
Câu 6.Theo Viet, ta có: a  c P
  z .z   5 1 2  a 2 2 2
z  z  S  2P  16  2.5  6 . Chọn B. 1 2
Câu 7. z  2z  4  0  z  2 2 2 2
1  3  0  z  1
  3i  A |
 z |  | z |  8 . Chọn D. 1 2 Câu 8. z      z 8 z  2 z 2z 4 0 z  2 z 2 2 3 2 1 3 0                  z   1   3i 
Do đó phương trình chỉ có một nghiệm phức có phần ảo âm. Chọn A.  b 3 S
  z  z      1 2 
Câu 9. Áp dụng định lý Viet, ta có: a 2  c 3 P   z z   1 2  a 2 3 9 2 2 2
z  z  S  2P   3   . Chọn D. 1 2 4 4 Câu 10. 2
'  b' ac  1  2  1
  0 nên phương trình vô nghiệm trên tập số thực. Chọn A. Câu 11. Ta có 2 9
  9.i nên 9 có các căn bậc hai là 3i và 3i . Chọn A. Câu 12.
Tổng hợp các chuyên đề luyện thi đại học Trang 48
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna 2 z  2i z    1  i 4     z  4  0     Chọn D. 2 z  2  i z 
  1  i  
Câu 13. z  z    z  2 2 2 7 0
1  6  0  z  1  6i . Chọn B.
Câu 14. Giả sử w là một căn bậc hai của 4  6 5i . Ta có: w  
i  w    i2 2 2 4 6 5 3 5
 w  3  5i . Chọn C. Câu 15. Ta có: 
i    i2 33 56 7 4
 z  7  4i . Do đó phần thực của z là 7. Chọn B. z   1 Câu 16. 3 2 z z z 1 0 z 1 2z 1 0           . Chọn D z   i   S
      2  4i 
Câu 17. Áp dụng định lý Viet, ta có: . P   .    11   2i  Do đó ,
  là hai nghiệm của phương trình: 2 2
z  Sz  P  0  z  2  4iz  11  2i  0 . Chọn B.
Câu 18. Gọi z  a  bi  ,
a b   là số phức thỏa mãn điều kiện trên. Ta có: z |  z | z
  a bi2 2 2 2 2 2
 a  b  a bi  a  2b bi  2abi  0   2
a  2b    b
  2abi  0   2 a  b  0 a   2b  0     2 a   2b  0    1   b  0  a               2 b 2ab 0 1    a     1     2  b       2
Vậy có 3 số phức thỏa mãn yêu cầu bài toán. Chọn A.
Câu 19. Theo Viet, ta có: a
S  z  z  
 4  i  a  i  4 i  2  a  9  2i . Chọn A. 1 2    2  i Câu 20. z  z    z  2 2 6 13 0
3  4  0  z  3  2i
+) Nếu z  3  2i : 6 6 9  15i 18  72i z   3  2i     1   4i z  i 3  3i 3  3i 18 6  z   1   4i  17 z  i
+) Nếu z  3  2i : 6 6 13  9i 30  40i 6 z   3  2i   
 3  4i  z 
 3  4i  5 Chọn B. z  i 3  i 3  i 10 z  i  b S
  z  z    1  3i 1 2 
Câu 21. Theo Viet, ta có: a  c P
  z .z   2  1  i 1 2    a
Tổng hợp các chuyên đề luyện thi đại học Trang 49
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
w  z  z  3z z  S  5P   1   3i2 2 2 2
 10 1  i  2  4i |
 w | 4  16  20 . Chọn D 1 2 1 2  
Câu 22. Gọi z  a  bi  ,
a b   là nghiệm của phương trình. Ta có:
4a bi2  8 2 2
a  b   3  0  4 2 2
a b  2abi  8 2 2
a  b   3  0 2 2
 12a  4b  8abi  3  0  a  0      
 2a  b  1   2 2    2 2 2   2 2  b  1 12a  4b  3 4  a b  1  
4a  4ab  b  1               a   0   ab   0 a  b  0 1          ab 0      a    b  0    4    b   0 
Vậy phương trình có 4 nghiệm phức. Chọn C.
Câu 23. Gọi z  a  bi  ,
a b   là số phức thỏa mãn đẳng thức trên. Ta có:  a   1  2 2 a  b  0       z  0 2 2            
z  z  z  a  bi a  bi  a bi2 a b 0 b 1 2     a   1    
 z  1  i . 2  ab  2b    a   0      b   0      z  1  i  b    0     Chọn C.
Câu 24. Do z là số ảo nên z có dạng: z  bi b  .
Ta có: z  z  bi2 2 2 2 2 2 | |  b  b
  b  0 . Chọn B. z  1  Câu 25. 3
z  1  0  z   1  2 z  z   1  0   1  3i z    2
Vậy phương trình có ba nghiệm trong trường số phức. Chọn B.
Câu 26. Do z  1  i là một nghiệm của 2
z  bz  c  0 nên ta có:         i2 b  i b c 0 b 2 1 1 c 0 b c bi 2i 0                 . Chọn C. b   2 c   2    b S
  z  z    7  1 2 
Câu 27. Theo Viet, ta có: a  c P
  z z   15 1 2  a
 z  z  z z  S  P  7  15  8 Chọn B. 1 2 1 2 Câu 28.
z  18  26i  x  yi3 3 3 2 2 3
 18  26i  x  3x yi  3xy  y i  18  26i 3 2
 (x  3xy )   2 3
3x y  y i  18  26i  3 2 x   3xy  18 x       2 2
x  3y   18     2 3 3
 x y  y  26 y      2 2
3x  y   26   Do x, y nguyên nên
Tổng hợp các chuyên đề luyện thi đại học Trang 50
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna x  3 x  3   2 2 x  3y  6 y  1    x  2 2
x  3y   18    x  6 x  6      loai 2 2
 x  3y  3    y   11  Mà y  2 2
3x  y   26  x  3;y  1 . Chọn C. Câu 29.
z  i4  4z  0  z i4 2 2  4z
z i2  2  2iz z  1  0 z   1  z   1             z i  
z  4iz  1  0  2iz 
z  2i2 2 2  3  0 z    2 3i   
Do đó phương trình có 2 nghiệm thực và 4 nghiệm phức. Vậy nhận xét 4, 6 đúng. Chọn D. Câu 30. Ta có: z   1 z  2 6 3 z 9z 8 0 z 1z  2  2 z z
1 2z 2z 4 0               3 Chọn D. z    1  1   i 3 
Câu 31. z  z    z  2 2 2 5 0
1  4  0  z  1  2i  A1;  2 ;B 1;  2
Do đó tọa độ trung điểm I của đoạn thẳng AB là I 1; 0. Chọn D.
Câu 32. Gọi z ,z là hai nghiệm của phương trình đã cho 1 2  b S
  z  z    m  1 2  Theo Viet, ta có: a  c P
  z .z   6i 1 2  a
Theo bài cho, tổng bình phương hai nghiệm bằng 5. Ta có:
z  z  S  2P  m  12i  5  m  5  12i  m  3  2i2 2 2 2 2 2 2 1 2
 m  3  2i
 a  3;b  2  a  2b  3  4  1 . Chọn D. z   1  i   z 1  1  i 4   i    1  1  z z     
Câu 33. Với mọi z  , ta có: 2z  i 3    1       2
2z  i   z  1  2  4i  i  z    2z  i  5 z   0   2   2        1  i   2  4i  P
z  1 z  1 z  1 z  1   1  i  1   1   1 . 1  2  3  4  2 2 2 2 2          9   25           i  i    i 9 2 13 16 425 17 1 2 .   Chọn B. 9 25 9.25 9
Tổng hợp các chuyên đề luyện thi đại học Trang 51
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
Câu 34. Gọi z ,z là hai nghiệm của phương trình. 1 2  b S
  z  z    m  1 2  Theo Viet, ta có: a  2 2 2 2
 z  z  S  2P  m  2i  c 1 2 P
  z .z   i 1 2  a 2 Ta có: 2 2 2
m  2i  4i  m  2i  m  1  i  m  1  i Chọn A.  b S
  z  z    m 1 2 
Câu 35. Theo Viet, ta có: a  c P
  z .z   2m 1 1 2  a 2 2 2 2 z  z  10 
 S  2P  10  m  22m   2
1  10  m  4m  12  0 1 2 Chọn A.
 m  22  8  0  m  2  2 2i z
  1 7i  Câu 36. 2
z  2z  8  0  z  2 1
1  7  0  z  1  7i   z   1 7i 2   
w  2z  z z  2 1
  7i  1  7i 1  7i  1   7i 1   7i 1 2  1          . Chọn C.  1  7  8 z  1 Câu 37. 4 z 1 0      . z  i  
Do đó tổng bình phương các nghiệm của phương trình là 1  1  0 . Chọn D. Câu 38.
z  2z  6  0  z  2 2
1  5  0  z  1  5i  z  1  5 ; i z  1  5i Chọn B. 1 2  M |
 z |  | 3z  z | 1  5i  2  4 5i  6  84  6  2 21 1 1 2 Câu 39. 4 2
x  2x  24x  72  0   2 x  4x   6  2 x  4x   12  0 
x  4x  6  0  x 22 2  2  0
x  2  2i  Chọn A.       2
x  4x  12  0  x  2 
2  8  0 x  2  2 2i    b S
  z  z     3 1 2 
Câu 40. Theo Viet, ta có: a  c P
  z .z   7 1 2  a
A  z  z  S  2P2  2P  3  2.72 4 4 2 2
 2.49  23 . Chọn A. 1 2
Tổng hợp các chuyên đề luyện thi đại học Trang 52
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
C. TẬP HỢP ĐIỂM CỦA SỐ PHỨC I. LÝ THUYẾT
Lý thuyết về tập hợp điểm của số phức
Trong dạng này, ta gặp các bài toán biểu diễn hình học của số phức hay còn gọi là tìm tập
hợp điểm biểu diễn một số phức z trong đó số phức z thỏa mãn một hệ thức nào đó. Khi
đó ta giải bài toán này như sau:
1. Phương pháp tổng quát:
Đặt z  x  yi (x,y  ) . Khi đó số phức z biểu diễn trên mặt phẳng phức bởi điểm
M x;y. Biến đổi điều kiện của bài toán thành để tìm mối liên hệ giữa x và y từ đó suy ra tập hợp điểm M.
2. Giả sử các điểm M, A, B lần lượt là điểm biểu diễn của các số phức z, a, b o | z  a | |
 z  b | MA  MB  M thuộc đường trung trực của đoạn AB o | z  a | |
 z b | k(k  ,  k  0,k |
 a b |)  MA  MB  k  M  (E) nhận A, B
là hai tiêu điểm và có độ dài trục lớn bằng k.
3. Giả sử M và M’ lần lượt là điểm biểu diễn của số phức z và w = f(z)
Đặt z = x + yi và w = u + vi (x,y,u,v  ) .
Hệ thức w = f(z) tương đương với hai hệ thức liên hệ giữa x, y, u, v
o Nếu biết một hệ thức giữa x, y ta tìm được một hệ thức giữa u, v và suy ra được tập hợp các điểm M’
o Nếu biết một hệ thức giữa u, v ta tìm được một hệ thức giữa x, y và suy ra được tập hợp điểm M’.
Nhắc lại kiến thức về hình học giải tích Oxy
1. Các dạng phương trình đường thẳng
- Dạng tổng quát: ax  by  c  0 . - Dạng đại số: y  ax  b . x
  x at  x  x y  y - Dạng tham số: 0  - Dạng chính tắc: 0 0  . y   y bt  a b 0  x y
- Phương trình đoạn chắn   1. a b
- Phương trình đường thẳng đi qua 1 điểm M x ;y biết hệ số góc k: y  k(x  x )  y 0  0 0  0 0
2. Phương trình đường tròn tâm I(a;b) bán kính R: 2 2 2
(x  a)  (y b)  R 2 2
 x  y  2ax  2by  c  0 với 2 2 2
c  a  b  R
Lưu ý điều kiện để phương trình: 2 2
x  y  2ax  2by  c  0 là phương trình đường tròn: 2 2
a  b c  0 có tâm I  a  , b   và bán kính 2 2
R  a  b  c . 2 2 x y
3. Phương trình (Elip):   1 2 2 a b
Với hai tiêu cự F ( ; c 0),F ( ;
c 0),F F  2c . Trục lớn 2a, trục bé 2b và 2 2 2
a  b  c . 1 2 1 2
Tổng hợp các chuyên đề luyện thi đại học Trang 53
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
II. MỘT SỐ BÀI TOÁN ĐIỂN HÌNH Bài toán 1
Giả sử M là điểm trên mặt phẳng phức biểu diễn số phức z .
Tìm tập hợp các điểm M thỏa mãn một trong các điều kiện sau đây:
a) z 1 i =2 b) z  1  3i  4 c) 2  z  1 i Giải:
Đặt z  x  yi (
x,y  ) được biểu diễn bởi điểm M x;y
a) Xét hệ thức: z  1  i  2 .  x –  1  y   1 i  2 2 2  x   1  y   1  2. 2 2  x   1  y   1  4.
 Tập hợp các điểm M z  trên mặt phẳng tọa độ biểu diễn số phức z thỏa mãn (1) là
đường tròn có tâm tại I 1; 
1 và bán kínhR  2 .
b) Xét hệ thức : z  1  3i  4  x   1  y   3 i  4 2 2  x   1  y   1  4 2 2  x   1  y   1  16.
Vậy tập hợp các điểm M trên mặt phẳng tọa độ biểu diễn số phức z là hình tròn có tâm là  1  ; 
1 ; bán kính r  4 .
Nhận xét: Tập hợp các điểm biểu diễn số phức z thỏa mãn điều kiện: z  1  3i  4 là tập
hình các điểm nằm trên và nằm ngoài đường tròn có tâm là 1;1 ; bán kính r  4 .
c) Xét hệ thức: 2  z  z  i
 x  2  yi  x  y  1i
 x  22  y  x  y  12 2 2
 4x  2y  3  0.
Vậy tập hợp các điểm M là đường thẳng
4x  2y  3  0.
Nhận xét: Đường thẳng 4x  2y  3  0 chính là đường trung trực của đoạn AB.
Tổng hợp các chuyên đề luyện thi đại học Trang 54
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna Bài toán 2
Trong mặt phẳng Oxy , tìm tập hợp điểm biểu diễn các số phức z thỏa mãn
z  i  1  iz . Giải:
Đặt z  x  yi ( x,y)  .  Ta có:
z  i  1  iz  x  y  
1 i  x y  x  yi 2 2 2  2
x  y  
1  x  y  x  y
 x  y  xy    x  y  2 2 2 2 2 1 0 1  2
Vậy tập hợp các điểm M biểu diễn các số phức z là đường tròn có phương trình
x  y  2 2 1  2 . Bài toán 3
Cho các số phức z , z , z có biểu diễn trên mặt phẳng phức là ba đỉnh của tam giác đều có 1 2 3 2 2
phương trình đường tròn ngoại tiếp là x  2017  y  2018  1. Tổng phần thực và phần
ảo của số phức w  z  z  z bằng? 1 2 3 Giải:
Đường tròn đã cho có tâm I biểu diễn số phức z  2  017  2018i . Gọi , A ,
B C lần lượt là điểm biểu diễn các số phức z , z , z . 1 2 3     
Ta có OA  OB  OC  3OG  3OI (do tam giác ABC đều nên G  I ).
Suy ra z  z  z  3 2017  2018i  6051  6054i . 1 2 3  
Nên tổng phần thực và phần ảo của số phức w bằng 3. Bài toán 4 z  2  3i
Tìm tập hợp các điểm biểu diễn của số phức z sao cho u  là một số thuần ảo. z  i Giải :
Đặt z  x  yi (
x,y)   , khi đó:
x  2 y  3i x 2 
 y 3i x    y  1 i        u   
x  y   1 i
x  y  2 2 1  2 2
x  y  2x  2y  
3  22x  y   1 i 
x  y  2 2 1
Tổng hợp các chuyên đề luyện thi đại học Trang 55
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna  2 2 x 
 y  2x  2y  3  0  x   2 1  y  2 1  5
u là số thuần ảo     x  y 2 2 1 0    
 x;y  0;  1  
Vậy tập hợp các điểm biểu diễn của z là đường tròn tâm I 
( 1;1) , bán kính 5 trừ điểm (0;1) . Bài toán 5
Trên mặt phẳng toạ độ, tìm tập hợp điểm biểu diễn số phức z thoả mãn điều kiện sau:
a) 2 z  i  z  z  2i b) z  1  z  1  4 Giải:
Đặt: z  x  yi (x,y  )
R  z có điểm biểu diễn trên mặt phẳng phức là Mx; y. 2 x
a) 2 z  i  z  z  2i  2 x  (y  1)i  (1  y)i  y  4 2 x
Vậy tập hợp điểm M là đường parabol (P) có phương trình y  . 4 2 2
b) z   z    x   2
 y  x   2 1 1 4 1 1  y  4 (*). Đặt F ( 1  ;0) ;F (1;0) 1 2
(*)  MF  MF  4 và F F  2 . 1 2 1 2
Suy ra tập hợp M là elíp (E) có 2 tiêu điểm là F ,F . 1 2 2 2 x y Gọi (E) có phương trình 2 2 2 
 1 (0  b  a; b  a c ) 2 2 a b MF   MF  2a a   2   Ta có 1 2 2 2 2   
 b  a c  3 F  F  2c c   1  1 2   2 2 x y Vậy (E) có phương trình   1 . 4 3 Bài toán 6
Trong tập số phức  , gọi z và z các nghiệm của phương trình 2
z  2z  10  0 . Gọi M , 1 2
N , P lần lượt là các điểm biểu diễn của z , z và số phức k  x  iy trên mặt phẳng phức. 1 2
Để tam giác MNP đều thì số phức k là? Giải: Ta có 2
z  2z  10  0  z  1  3i . Gọi M , N , P lần lượt là các điểm biểu diễn của z , 1,2 1
z và số phức k  x  iy trên mặt phẳng phức. Khi đó M 1;3, N 1; 3
 , P x;y 2 MN   MP  2 2  M  N  MP  Để M  NP đều     (1) MN   NP 2 2    MN  NP 
Tổng hợp các chuyên đề luyện thi đại học Trang 56
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna   
Ta có MN  0; 
6 , MP  x 1;y  
3 , NP  x 1;y   3 (2) x    2 1  y  2 3  36 x   1  27 Từ (1) và (2)    k       1 27 .  x  2 1  y  2 3  36 y   0   Bài toán 7
Trong mặt phẳng phức, cho m và M theo thứ tự là điểm biểu diễn của số phức z  x  yi z  1 và Z 
. Tìm tập hợp các điểm m sao cho: Z là một số thực. z  2i Giải: x  yi z    1 1 x  1  yi
x  1  yix  y  2i Ta có: Z     z  2i
x  yi  2i x  y  2i x  y  2ix  y  2i
x x  1  y y  2  y  2x  2i  Z  2 2
x  y  2
Z là một số thực khi và chỉ khi y  2x  2  0 .
Tập hợp các điểm m biểu diễn số phức z  x  yi là đường thẳng y  2x  2  0  y  2x  2 Bài toán 8
Tập hợp các điểm M biểu diễn số phức z thỏa mãn z  i  z  i  4 là? Giải: 2 2 Ta có 2
z  i  z  i   x  y   2 4
1  x  y   1  4  2 2
 x  y  1  4 2 2  2 2 x y 1 4 x y 1           x   y  2
1  16  x  y  2
1  8 x  y   2 2 2 2 1     2  2           x     y   2 2 x y 1 16 x y 1 16 1 2     2     1 16     y      4  y   4  2 . 2    2 2 x   
y  1  y  4    2 2  2 2  4
 x  3y  12 x y      1   3  3 4
Tập hợp các điểm thỏa mãn 3 đều thỏa mãn   1 và 2. x y
Vậy tập hợp những điểm M là elip E  2 2 :   1. 3 4
Tổng hợp các chuyên đề luyện thi đại học Trang 57
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna Bài toán 9
(ĐỀ MINH HỌA QUỐC GIA NĂM 2017)
Cho số phức z   thỏa mãn z  4 . Biết tập hợp các điểm biểu diễn cho số phức
w  3  4iz  i là đường tròn I , bán kính R . Khi đó. A. I 0; 
1 ,R  2 5. B. I 1;0,R  20 C. I 0; 
1 ,R  20. D. I 1;2,R  22. Giải:
Đặt w  a  bi với a; ; b c   .
a  b   1 i a   b 1i     3  4i w 3 4iz i z        3  4i 25 3b  4a a b     3 3 4 4
3a  4b  42 3b  4a  2 3  z   i  z  25 25 25 Mà
3a  4b  42 3b  4a  32 z  4 
 4  3a  4b  42  3b  4a  2 2 3  100 25 2 2
 a  b  2b  399
 a  b  2 2 2 1  20
Vậy tập hợp các điểm biểu diễn của số phức w là đường tròn I 0;  1 , R  20 . Bài toán 10 
z  3  6i  5 
Có bao nhiêu số phức z thỏa mãn:  ?
 1  2i  z  1  12i  15  Giải:
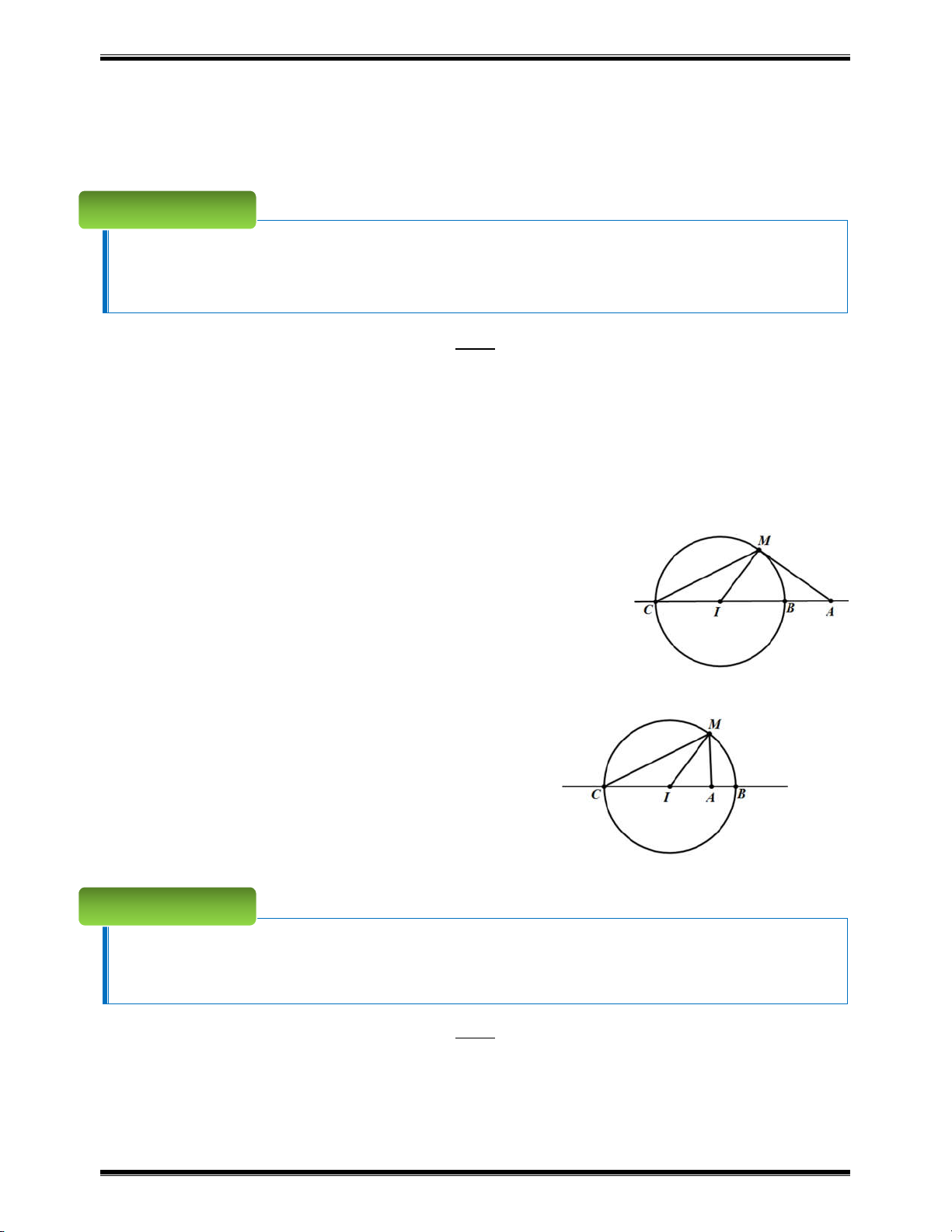
Gọi M là điểm biểu diễn số phức z , do M thỏa mãn phương trình z  3  6i  5 nên thuộc
đường tròn tâm A 3;6 , bán kính R  5 .  i Ta có:   i 1 12 15
1 2 z  1  12i  15  z  
 z  5  2i  3 5 1  2i 1  2i
 M thuộc đường tròn tâm B 5;2 , bán kính R  3 5 . 2 2
Nhận thấy AB  5  3  2  6  2 5  R ' R .
Vậy 2 đường tròn tiếp xúc trong tại M, hay chỉ có một số phức z thỏa mãn bài toán.
Tổng hợp các chuyên đề luyện thi đại học Trang 58
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
Bài toán 11
Cho số phức z thỏa mãn z  1  2 . Biết rằng tập hợp các điểm biểu diễn số phức
w  1  3iz  2 là một đường tròn. Tính bán kính của đường tròn đó. Giải: Cách 1: w  w   i
Ta có: w    i 2 3 3 1
3 z  2  z   z  1  1  3i 1  3i w  3  3i w  3  3  3  3 i w i Suy ra z  1    2   w  3  3i  4 2 1  3i 1  3i
Như vậy bán kính của đường tròn là 4. Cách 2:
Ta có: w  1  3iz  2  w  1  3iz  1  3  3i  w  3  3i  1  3iz  1.
Lấy môđun hai vế ta được: w  3  3i  1  3i . z  1  2.2  4 . Bài toán 12
Cho các số phức z thỏa mãn z  1  3. Biết rằng tập hợp các điểm biểu diễn các số phức
w với 3  2iw  iz  2 là một đường tròn. Tìm tọa độ tâm I và bán kính r của đường tròn đó. Giải: i     Ta có   i 2 2 3 6 4 3
2 w  iz  2  w  z   w     iz   i 3  2i 3  2i  13 13  13 13  2 3       w      i  z   4 7 4 7   2 3 1   i  w    i        i          z   1 . 13 13 13 13 13 13   13 13   4 7    2 3 3
Lấy môđun, hai vế ta được w    i    i . z  1   . 13 13  13 13  13
 3 1 13  4 7    3
Vậy tập hợp các số phức w thuộc đường tròn tâm I  ;   r  .  , bán kính 13 13 13
Nhận xét: Bài này có rất nhiều cách giải tự luận nhưng cách này là tối ưu nhất. Quý thầy cô nên
nghiên cứu kỹ phương pháp giải này để truyền đạt cho học sinh.
Tổng hợp các chuyên đề luyện thi đại học Trang 59
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna Bài toán 13
Cho hai số phức z , z thỏa mãn z  3 , z  2 được biểu diễn trong mặt phẳng phức lần 1 2 1 2  
lượt là các điểm M, N . Biết góc tạo bởi giữa hai vectơ OM và ON bằng 0 30 . Tính giá trị của z  z biểu thức 1 2 A  . z  z 1 2 Giải: Cách 1:
z  z  OP 
Dựng hình bình hành OMPN trong mặt phẳng phức, khi đó 1 2  .
z  z  MN  1 2   2 2 y 0
z  z  z  z  2 z z cos30  13 P  Ta có 1 2 1 2 1 2  N 2 2 0
 z  z  z  z  2 z z cos150  1  1 2 1 2 1 2  z  z z  z 1 2 1 2    13 . M x z  z z  z 1 2 1 2 O
Nhận xét: Thầy cô nên giải thích rõ cho học sinh hiểu tại tại lại là góc 0 30 và góc 0 150 . Cách 2:  z
  a b i M  a  ;b OM      a ;b 1 1 1   1 1   1 1 Giả sử      . z
  a  b i N  a ,b   2 2 2    2 2  ON    a ;b 2 2   2 2 a  b  3  Theo giả thiết, ta có 1 1  và 2 2 a  b  4  2 2    a a  b b cosOM,ON  0 1 2 1 2  cos 30 
 a a  b b  3. 1 2 1 2 2 2 2 2 a  b a  b 1 1 2 2 
a a b b i
a a 2 b b z z 2 1 2 1 2 1 2 1 2 Ta có 1 2 A    z  z
a a b b i
a a 2 b b 2 1 2 1 2 1 2 1 2 1 2  2 2
a  b    2 2
a  b  2 a a  b b 1 1 2 2   1 2 1 2 3  4  2.3    13.  2 2
a  b    2 2
a  b  2 a a  b b 3  4  2.3 1 1 2 2   1 2 1 2
Tổng hợp các chuyên đề luyện thi đại học Trang 60
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
III. SỬ DỤNG MÁY TÍNH CASIO 570 VN- PLUS
Đây là một trong những bài toán điển hình nhất dùng máy tính CASIO để giải bài toán tìm tập
hợp điểm của số phức. Các bài toán khác ta làm tương tự. Bài toán 1
Trên mặt phẳng Oxy tìm tập hợp biểu diễn các số phức thỏa mãn điều kiện | zi – 2  i | 2 2 2
A. x  2y  1  0 B. x  1  y – 2  9 2 2
C. x  1  y  2  4 D. 3x  4y  2  0 Hướng dẫn:
Ta giả sử: z  A  Bi .
Nên điều kiện của bài toán được viết lại là: A  Bii – 2  i  2  0. o
w2 và nhập điều kiện vào:
 Thử đáp án A. x  2y  1  0x  1  2y .
Cho y  1 ta được x  1  .
Nhập rp1=1=thu được kết quả khác 0.
>>> Loại đáp án A. 2 2
 Thử đáp án B. x  1  y – 2  9 . Cho x  1
 ta được y  5 hoặcy  1 .
rp1=5= ra kết quả khác 0.
>>> Loại đáp án B 2 2
 Thử đáp án C. x  1  y  2  4 .
Cho x  1 ta được y  0 và y  4 .
r1=0= và r1=p4= đều được kết quả bằng 0.
Vậy đáp án đúng là C.
Tổng hợp các chuyên đề luyện thi đại học Trang 61
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna Bài toán 2
[Đề minh họa của bộ GD-ĐT lần 1-2017]
Cho các số phức z thỏa mãn z  4 . Biết rằng tập hợp các điểm biểu diễn các số phức
w  3  4iz  i là một đường tròn. Tính bán kính r của đường tròn đó.
A.r  4 B.r  5
C.r  20 D.r  22 Hướng dẫn:
 Để xây dựng 1 đường tròn ta cần 3 điểm biểu diễn của w , vì z sẽ sinh ra w nên đầu tiên ta
sẽ chọn 3 giá trị đại diện của z thỏa mãn z  4
 Chọn z  4  0i (thỏa mãn z  4 ). Tính w  3  4i 4  0i  i 1    (3+4b)O4+b=
Ta có điểm biểu diễn của z là M 12;17 1
 Chọn z  4i (thỏa mãn z  4 ). Tính w  3  4i 4i  i 2    (3+4b)O4b+b=
Ta có điểm biểu diễn của z là N 16;13 2
 Chọn z  4i (thỏa mãn z  4 ). Tính w  3  4i 4i  i 3    (3+4b)(p4b)+b=
Ta có điểm biểu diễn của z là P 16;1  1 3
Vậy ta có 3 điểm M,N,P thuộc đường tròn biểu diễn số phức w
 Đường tròn này sẽ có dạng tổng quát 2 2
x  y  ax  by  c  0 . Để tìm , a , b c ta sử dụng
máy tính Casio với chức năng MODE 5 3 w5212=17=1=p12dp17d=p16= 13=1=p16dp13d=16=p11=1= p16dp11d==
Vậy phương trình đường tròn biễu diễn số phức w là:
Tổng hợp các chuyên đề luyện thi đại học Trang 62
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
x  y  y 
  x  y  2 2 2 2 2 2 399 0 1  20 .
Bán kính đường tròn tập hợp điểm biểu diễn số phức w là 20  Đáp án chính xác là C. Bài toán 3
Tập hợp điểm biểu diễn số phức z thỏa mãn 2 z  1  z  z  2i là một Parabol có dạng: 2 x 2 x 1 A. 2
y  3x  6x  2 B.y   x C.y   4 D. 2
y  x  2x  2 3 3 Hướng dẫn:
 Đặt số phức z  x  yi .
 Nếu đáp số A đúng thì đúng với mọi z  x  yi thỏa mãn 2
y  3x  6x  2 .
Chọn một cặp x;y bất kì thỏa 2
y  3x  6x  2 ví dụ A0;2  z  2i
Xét hiệu 2 z  1  z  z  2i 2qc2bp1$pqc2bp(p2b)+2b=
Vậy 2 z  1  z  z  2i  6  2 5  0
 2 z  1  z  z  2i  Đáp số A sai 1
 Tương tự với đáp số B chọn z  1  i . Xét hiệu2 z  1  z  z  2i 2 2qc1pabR2$p1$pqc1pab R2$p(1+abR2$)+2b=
Vậy 2 z  1  z  z  2i  0  2 z  1  z  z  2i  Đáp số B chính xác.
Tổng hợp các chuyên đề luyện thi đại học Trang 63
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
IV. BÀI TẬP RÈN LUYỆN 1. ĐỀ BÀI
Câu 1. Cho số phức z  6  7i . Số phức liên hợp của z có điểm biểu diễn là: A. 6;  7. B. 6; 7. C. 6; 7.
D. 6;  7. 2
Câu 2. Điểm biểu diễn của số phức z  là 1  3i 1 3   A. 1;3. B.  ;   3;2 4;1  . C.  . D.  . 5 5 3  4i
Câu 3. Số phức z 
có điểm biểu diễn là: 2 3    A.  ;  2  3; 4 3  ;  4 3  ; 4  . B.  . C.  . D.  . 2 
Câu 4. Cho số phức z  3i  2 có điểm biểu diễn hình học là: A. 2; 3. B.  3;2. C. 2; 3.
D. 2; 3. 2016 i
Câu 5. Biểu diễn về dạng z  a  bi của số phức z  là số phức nào? 2 (1  2i) 3 4 3 4 3 4 3 4 A.  i . B.   i . C.  i . D.   i . 25 25 25 25 25 25 25 25 3  4i
Câu 6. Điểm M biểu diễn số phức z  có tọa độ là 2019 i A. M (4;3 )
B. M 3;4 C. M 3; 4
D. M 4; 3
(2  3i)(4  i)
Câu 7. Điểm biểu diễn số phức z  có tọa độ là 3  2i A. 1;4. B. 1;4. C. 1; 4.
D. 1; 4.
Câu 8. Điểm biểu diễn hình học của số phức z  a  ai nằm trên đường thẳng:
A. y  x
B. y  2x
C. y  x 
D. y  2x
Câu 9. Gọi A là điểm biểu diễn của số phức 5  8i và B là điểm biểu diễn của số phức 5   8 . i
Chọn mệnh đề đúng trong các mệnh đề sau
A. Hai điểm A và B đối xứng với nhau qua trục hoành.
B. Hai điểm A và B đối xứng với nhau qua trục tung.
C. Hai điểm A và B đối xứng với nhau qua gốc toạ độ O.
D. Hai điểm A và B đối xứng với nhau qua đường thẳng y  x.
Câu 10. Gọi A là điểm biểu diễn của số phức z  2  5i và B là điểm biểu diễn của số phức
z   2  5i . Tìm mệnh đề đúng trong các mệnh đề sau:
A. Hai điểm A và B đối xứng với nhau qua trục hoành
B. Hai điểm A và B đối xứng với nhau qua trục tung
C. Hai điểm A và B đối xứng với nhau qua gốc toạ độ O
D. Hai điểm A và B đối xứng với nhau qua đường thẳng y  x
Tổng hợp các chuyên đề luyện thi đại học Trang 64
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
Câu 11. Gọi A là điểm biểu diễn của số phức z  3  2i và B là điểm biểu diễn của số phức
z   2  3i Tìm mệnh đề đúng trong các mệnh đề sau:
A. Hai điểm A và B đối xứng với nhau qua trục hoành.
B. Hai điểm A và B đối xứng với nhau qua trục tung.
C. Hai điểm A và B đối xứng với nhau qua gốc toạ độ O .
D. Hai điểm A và B đối xứng với nhau qua đường thẳng y  x .
Câu 12. Trên mặt phẳng tọa độ Oxy , cho số phức z  x  yi x,y  các điểm biểu diễn z và
z đối xứng nhau qua A. trục Ox . B. trục Oy .
C. gốc tọa độ O .
D. đường thẳng y  x .
Câu 13. Điểm biểu diễn của các số phức z  7  bi với b   , nằm trên đường thẳng có phương trình là: A. x  7 . B. y  7 .
C. y  x .
D. y  x  7 .
Câu 14. Điểm biểu diễn của các số phức z  n  ni với n   , nằm trên đường thẳng có phương trình là:
A. y  2x .
B. y  2x .
C. y  x .
D. y  x  .
Câu 15. Cho số phức 2
z  a  a i với a   . Khi đó điểm biểu diễn của số phức liên hợp của z nằm trên:
A. Đường thẳngy  2x .
B. Đường thẳng y  x   1 . C. Parabol 2 y  x . D. Parabol 2 y  x  .
Câu 16. Tập hợp các điểm trong mặt phẳng biểu diễn cho số phức z thỏa mãn điều kiện
z  i  1 là:
A. Một đường thẳng.
B. Một đường tròn.
C. Một đoạn thẳng.
D. Một hình vuông.
Câu 17. Trong mặt phẳng phức, gọi ,
A B,C lần lượt là các điểm biểu diễn của các số phức
z  1  3i , z  1  5i , z  4  i . Số phức với điểm biểu diễn D sao cho tứ giác 1 2 3
ABCD là một hình bình hành là: A. 2  3i . B. 2  i. . C. 2  3 . i .
D. 3  5i..
Câu 18. Gọi z và z là các nghiệm phức của phương trình 2
z  4z  9  0. Gọi M,N là các điểm 1 2
biểu diễn của z và z trên mặt phẳng phức. Khi đó độ dài của MN là: 1 2 A. MN  4.. B. MN  5. C. MN  2 5. D. MN  2 5.
Câu 19. Gọi z và z là các nghiệm của phương trình 2
z  4z  9  0 . Gọi M,N,P lần lượt là các 1 2
điểm biểu diễn của z ,z và số phức k  x  yi trên mặt phẳng phức. Khi đó tập hợp 1 2
điểm P trên mặt phẳng phức để tam giác MNP vuông tại P là:
A. đường thẳng có phương trình y  x  5.
B. là đường tròn có phương trình 2 2
x  2x  y  8  0.
C. là đường tròn có phương trình 2 2
x  2x  y  8  0, nhưng không chứa M,N.
D. là đường tròn có phương trình 2 2
x  4x  y  1  0 nhưng không chứa M,N.
Tổng hợp các chuyên đề luyện thi đại học Trang 65
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna Câu 20. Giả sử ,
A B theo thứ tự là điểm biểu diễn của các số phức z ,z . Khi đó độ dài của véctơ 1 2  AB bằng:
A. z  z .
B. z  z .
C. z  z .
D. z  z . 1 2 1 2 2 1 2 1
Câu 21. Biết z  i  1  iz , tập hợp điểm biểu diễn số phức z có phương trinh A. 2 2 x  y
  2y  1  0 . B. 2 2
x  y  2y  1  0 . C. 2 2
x  y  2y  1  0
x y  y   . D. 2 2 2 1 0 .
Câu 22. Tập hợp điểm biểu diễn số phức z , biết 3zi  4  2 là A. điểm. B. đường thẳng. C. đường tròn. D. elip.
Câu 23. Trong mặt phẳng phức cho ABC vuông tại C . Biết rằng A , B lần lượt biểu diễn các
số phức z  2  2i , z  2  4i . Khi đó, C biểu diễn số phức: 1 2
A. z  2  4i . B. z  2   2i .
C. z  2  4i .
D. z  2  2i .
Câu 24. Trên mặt phẳng tọa độ Oxy , tập hợp các điểm biểu diễn số phức z thỏa mãn điều kiện
số phức zi  2  i  2 là: 2 2
A. 3x  4y  2  0 . B. x  
1  y  2  9 . 2 2 C. x  
1  y  2  4 .
D. x  2y  1  0 .
Câu 25. Trong mặt phẳng tọa độOxy , tập hợp điểm biểu diễn số phức z thỏa mãn
z  1  1  iz là:
A. Đường tròn có tâm I (0;1), bán kính r  2
B. Đường tròn có tâm I (0;1) , bán kính r  2
C. Đường tròn có tâm I (1; 0) , bán kính r  2
D. Đường tròn có tâm I (1; 0), bán kính r  2
Câu 26. Tập hợp các điểm trong mặt phẳng biểu diễn cho số phức z thỏa mãn điều kiện
z  1  2i  4 là:
A. Một đường thẳng
B. Một đường tròn
C. Một đoạn thẳng
D. Một hình vuông
Câu 27. Tập hợp các điểm trong mặt phẳng biểu diễn số phức z thỏa mãn điều kiện 2 z là một số thực âm là:
A. Trục hoành (trừ gốc O ).
B. Đường thẳng y  x (trừ gốc O ).
C. Trục tung (trừ gốc O ).
D. Đường thẳng y  x
 (trừ gốc O ).
Câu 28. Giả sử M là điểm trên mặt phẳng phức biểu diễn số phức z . Tập hợp các điểm M thoả
mãn điều kiện sau đây: z  1  i  2 là một đường tròn: A. Có tâm  1  ;   1 và bán kính là 2.
B. Có tâm 1;   1 và bán kính là 2 . C. Có tâm  1  ;  1 và bán kính là 2.
D. Có tâm 1;  
1 và bán kính là 2.
Tổng hợp các chuyên đề luyện thi đại học Trang 66
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
Câu 29. Giả sử M z là điểm trên mặt phẳng phức biểu diễn số phức z . Tập hợp các điểm
M z thoả mãn điều kiện sau đây: 2  z  1  i là một đường thẳng có phương trình:
A. 4x  2y  3  0 .
B. 4x  2y  3  0 .
C. 4x  2y  3  0 .
D. 2x  y  2  0 .
Câu 30. Tập hợp các điểm nằm trong mặt phẳng phức biểu diễn các số phức z thoả mãn điều
kiện sau đây: z  z  3  4 là hai đường thẳng: 1 7 1 7
A. x   và x   . B. x  và x   . 2 2 2 2 1 7 1 7 C. x  và x  .
D. x   và x  . 2 2 2 2
Câu 31. Tập hợp các điểm nằm trong mặt phẳng phức biểu diễn các số phức z thoả mãn điều
kiện sau đây: z  z  1  i  2 là hai đường thẳng: 1  3 1  3 1  3 1  3 A. y  và y  . B. y  và y  . 2 2 2 2 1  3 1  3 1  3 1  3 C. y  và y   . D. y  và y   . 2 2 2 2 z  i
Câu 32. Cho số phức z  x  y.i(x,y  ). Tập hợp các điểm biểu diễn của z sao cho là z  i một số thực âm là:
A. Các điểm trên trục hoành với 1   x  1.
B. Các điểm trên trục tung với 1  y  1. x   1 
C. Các điểm trên trục hoành với  . x   1  y   1 
D. Các điểm trên trục tung với  . y   1 
Câu 33. Gọi M, N, P lần lượt là các điểm biểu diễn cho các số phức z  1  5i , z  3  i , 1 2
z  6 . M, N, P là 3 đỉnh của tam giác có tính chất: A. Vuông. B. Vuông cân. C. Cân. D. Đều. Câu 34. Gọi , A ,
B C, D lần lượt là các điểm biểu diễn cho các số phức z  7  3i , z  8  4i , 1 2
z  1  5i , z  2
 i . Tứ giác ABCD là: 3 4 A. là hình vuông. B. là hình thoi.
C. là hình chữ nhật.
D. là hình bình hành. Câu 35. Gọi ,
A B,C lần lượt là các điểm biểu diễn cho các số phức z  1   3 ; i z  3
  2i;z  4  i . Chọn kết luận sai: 1 2 3
A. Tam giác ABC vuông cân.
B. Tam giác ABC cân.
C. Tam giác ABC vuông.
D. Tam giác ABC đều.
Câu 36. Tập hợp các điểm M biểu diễn cho số phức z thoả mãn z  i  z  i  4 có dạng là
Tổng hợp các chuyên đề luyện thi đại học Trang 67
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna 2 2 x y 2 2 x y A.   1 . B.   1 . 4 3 16 9 2 2 x y 2 2 x y C.   1. D.   1. 16 9 4 3 Câu 37. Gọi ,
A B,C lần lượt là điểm biểu diễn của các số phứcz  3  2 , i z  2  3 , i z  5  4i 1 2 3
Chu vi của tam giác ABC là : A. 22  2  58 . B. 26  2  58 . C. 22  2 2  56 .
D. 26  2 2  58 .
Câu 38. Cho các điểm , A B,C
trong mặt phẳng phức theo thứ tự được biểu diễn bởi các số:
1  i;2  4i;6  5i . Tìm số phức biểu diễn điểm D sao cho tứ giác ABDC là hình bình hành: A. 7  8i . B. 5  2i . C. 3 . D. 3   8i . Câu 39. Cho ,
A B, M lần lượt là điểm biểu diễn của các số phức 4  ; 4 ;
i x  3i . Với giá trị thực nào củax thì ,
A B, M thẳng hàng : A. x  1 . B. x  2 . C. x  1.
D. x  2 .
Câu 40. Trong mặt phẳng Oxy cho điểm A biểu diễn số phứcz  1  2i , B là điểm thuộc 1
đường thẳng y  2 sao cho tam giác OAB cân tại O . B biểu diễn số phức nào sau đây: A. z  1   2i .
B. z  2  i .
C. z  1  2i .
D. z  1  2i .
Câu 41. Cho các số phức z  1  3i;z  2 +2i;z  1  i được biểu diễn lần lượt bởi các 1 2 3    điểm ,
A B, C trên mặt phẳng. Gọi M là điểm thỏa mãn: AM  AB  AC . Khi đó
điểm M biểu diễn số phức:
A. z  6i . B. z  2 . C. z  2 .
D. z  6i .
Câu 42. Tromg mặt phẳng phức cho hai điểm A4; 0 , B 0;3. Điểm C thỏa mãn:   
OC  OA OB . Khi đó điểm C biểu diễn số phức:
A. z  4  3i .
B. z  3  4i . C. z  3   4i .
D. z  4  3i .
Câu 43. Trong mặt phẳng tọa độ Oxy , tập hợp điểm biểu diễn các số phức z thỏa mãn điều
kiện z  3  4i  2 là: 2 2 A. x  5 . B. x  
3  y  4  4. C. y  2 . x  y  D. 2 2 4 . Câu 44. Cho , A ,
B C là ba điểm trong mặt phẳng phức theo thứ tự biểu diễn các số:  
1  i;1  i;2i . Tính AB.BC . A. – 7. B. 5.
Tổng hợp các chuyên đề luyện thi đại học Trang 68
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna C. – 2. D. – 6.
Câu 45. Trong mặt phẳng tọa độ Oxy , tìm tập hợp điểm M biểu diễn số phức  thỏa mãn điều
kiện   1  2iz  3 , biết z là số phức thỏa mãn z  2  5 . 2 2 2 2 A. x  
1  y  4  125 . B. x  
5  y  4  125. 2 2 C. x  
1  y  2  125. D. x  2 .
2. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI CHI TIẾT 1A 2B 3A 4A 5D 6D 7B 8A 9B
10B 11D 12A 13A 14D 15C
16B 17A 18D 19D 20C 21B 22C 23A 24C 25D 26B 27C 28A 29A 30B
31A 32B 33A 34A 35D 36A 37D 38A 39C 40A 41D 42A 43B 44D 45A Câu 1. Chọn A. 2 1 3
Câu 2. Ta cóz    i . Chọn B. 1  3i 5 5 3  4i 3  3 
Câu 3. Số phức z  
 2i có tọa độ điểm biểu diễn là ; 2  . Chọn A. 2 2  2   
Câu 4. Số phức..có tọa độ điểm biểu diễn là2; 3. Chọn A. 2016 i 3 4
Câu 5. Ta có z    
i (Dùng Casio). Chọn D. 2 (1  2i) 25 25 Câu 6. 2019 4.5043 3 i  i  i   , i z  4
  3i . Suy ra điểm biểu diễn có tọa độ là 4;3. Chọn D.
(2  3i)(4  i)
Câu 7. Ta có z   1
  4i . Chọn B. 3  2i
Câu 8. Ta có: M a; a biểu diễn nên z  a  ai . Chọn A.
Câu 9. Tọa độ điểmA5;8,B 5;8 ta thấy hai điểm đối xứng nhau qua trục tungOy . Chọn B.
Câu 10. Ta có: 2;5 &  2
 ; 5 biểu diễn 2 số phức trên đối xứng qua Oy nên Chọn B.
Câu 11. z  3  2i  A3;2 ; z  2  3i  B 2;3 5 5 M  ;  
AB  d y  x 
là trung điểm AB nằm trên y  x và : . Chọn D. 2 2
Câu 12. Số phức z  x  yi x,y   có điểm biểu diễn là M x;y. Số phức z  x  yi  , x y   có
điểm biểu diễn là M ' x; y
   M,M ' đối xứng qua Ox . Chọn A.
Câu 13. Điểm biểu diễn của các số phức z  7  bi với b   là M 7;b nằm trên đường thẳng
x  7 . Chọn A.
Tổng hợp các chuyên đề luyện thi đại học Trang 69
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
Câu 14. Điểm biểu diễn của các số phức z  n  ni với n   là điểm M n,  n nằm trên đường
thẳng có phương trình là: y  x . Chọn D.
Câu 15. Điểm biểu diễn của các số phức 2
z  a  a i với a   là điểm M  2 , a a  nằm trên
đường có phương trình là: 2
y  x . Chọn C. Câu 16. Chọn B.
Câu 17. Gọi D x;y;z  là điểm biểu diễn số phức z  x  yi;x,y   .
Ta có A1;3;B 1;5;C 4;1   4   x  2 x   2  
ABCD là hình bình hành, nên AB  CD    
 z  2  3i . Chọn A. 1   y  2 y   3  
Câu 18. Hai nghiệm phức của phương trình đã cho là z  2  5 ; i z  2  5i 1 2 .
Nên M 2; 5,N 2; 5  MN  2 5 . Chọn D.
Câu 19. M 2; 5,N 2; 5; P ;
x y . Tam giác MNP vuông tại P , nên  
MP NP   x  2 2 2 2 . 0
2  y  5  0  x  4x  y  1  0 . Chọn D.
Câu 20. Giả sử: A x ;y ;B x ;y 1 1 
 2 2  là điểm biểu diễn hai số phức
z  x  y i;z  x  y ; i x
 ,x ,y ,y   1 1 1 2 2 2 1 2 1 2 .    2 2 AB  
 x  x ;y  y AB  x  x  y  y 2 1 2 1    2 1   2 1     . Chọn C.
z  z  x  x  
y  y i  
z  z  x  x 2  y  y 2 2 1 2 1 2 1 2 1 2 1 2 1 
Câu 21. Gọi M  ;
x y là điểm biểu diến số phức z  x  yi; x;y   .
z  i  1  iz  x  y  1i  1  ix  yi  x  y  1i  x  y  x  yi Chọn B.
 x  y  2
1  x  y2  x  y2 2 2 2
 x  2y  y  1  0
Câu 22. Gọi M  ;
x y là điểm biểu diến số phức z  x  yi;x;y   .
3zi  4  2  3i x  yi  4  2  4  3y  3xi  2 2 Chọn C.      y 2 2 2 4 2 4 3
 9x  2  x  y    3  9  
Câu 23. A2;2;B  2
 ; 4;C x;y  ;  
ΔABC vuông tại C nên AC .BC  0  x  2 x  2  y  2 y  4  0 . Chọn A.
Câu 24. Gọi M x;y  là điểm biểu diến số phức z  x  yi;x;y   .
zi    i     y  x  i   x  2  y  2 2 2 2 1 2 1 2  4 . Chọn C.
Câu 25. Gọi điểm M x;y là điểm biểu diễn cho số phức z  x  ,
yi x,y  
Tổng hợp các chuyên đề luyện thi đại học Trang 70
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
Ta có: z  1  1  iz  x  yi  1  1  i x  yi  x  1  yi  x  y   x  y i
 x  2  y  x y2  x  y2  x  y  x    x  2 2 2 2 2 1 2 1 0 1  y  2
Gọi điểm M x;y  là điểm biểu diễn cho số phức z  x  y ,ix,y  
Ta có: z  i 
 x  yi  i 
 x  y  i   x  y  2 2 1 1 1 1 1  1
 x  y  2 2
1  1 là đường tròn . Chọn D.
Câu 26. Gọi điểm M x;y  là điểm biểu diễn cho số phức z  x  ,
yi x,y  
Ta có: z  1  2i  4  x  yi  1  2i  4  x  1  y  2i  4 2 2 2 2
 x  1  y  2  4  x  1  y  2  16 là đường tròn . Chọn B.
Câu 27. Đặt z  a  bi  ,
a b   . Điểm biểu diễn số phức z là M a;b .
Khi đó z  a  bi2 2 2 2
 a  b  2abi 2 2 a   b  0 a   0 2  
z là một số thực âm khi   
 M 0;b , b  0 a.b  0 b  0    
Vậy tập hợp điểm M biểu diễn số phức z là trục tung (trừ gốc tọa độ O ). Chọn C.
Câu 28. Xét hệ thức: z  1  i  2 (1). Đặt z  x  yi x,y    z  1  i  x  
1  y  1i 2 2 Khi đó (1)  2 2
(x  1)  (y  1)  2  x  1  y  1  4. Tập hợp các điểm M trên mặt
phẳng toạ độ biểu diễn số phức z thoả mãn (1) là đường tròn có tâm tại I 1; 1 và bán kính
R  2 . Chọn A.
Câu 29. Xét hệ thức 2  z  z  i  z  ( 2) 
 z  i (*)
Gọi A là điểm biểu diễn số -2, còn B là điểm biểu diễn số phức i : A 2  ; 0,B 0;  1
Đẳng thức (*) chứng tỏ M(z)A  M(z)B .
Vậy tập hợp tất cả các điểm M zchính là đường trung trực củaAB .
Chú ý: Ta có thể giải cách khác như sau:
Giả sử z  x  yi , khi đó: 2 2
(2)  x    yi  x
    yi  x   2 2 2 1
2  y  x  1  y  4x  2y  3  0
Vậy tập hợp các điểm M  z là đường thẳng 4x  2y  3  0 . Chọn A.
Nhận xét: Đường thẳng 4x  2y  3  0 chính là phương trình đường trung trực của đoạn AB .
Câu 30. Xét hệ thức: z  z  3  4 (1)
Đặt z  x  yi x,y   z  x  yi , do đó  x  yi   x  yi   3  4 1 7
 2x  3  4  x  hoặc x   . 2 2
Tổng hợp các chuyên đề luyện thi đại học Trang 71
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna 1 7
Vậy tập hợp tất cả các điểm M là hai đường thẳng song song với trục tung x  và x   . 2 2 Chọn B.
Câu 31. Xét hệ thức: z  z  1  i  2 . Đặtz  x  yi  z  x  yi . Khi đó: (2) 
  y  i     y  2 2 1 2 1 2 1 2
1  4  2y  2y  1  0 1 3 1 3 y   hoặc y  
. Vậy tập hợp các điểm M là hai đường thẳng song song với trục 2 2 1 3 hoành y   . Chọn A. 2 x     z i  y    1 i x  
y  1i x     y   2 1 i x     2y  1 2x  Câu 32.          i z i x y 1 i
x  y  2 1
x  y  2 1
x  y  2 2 2 2 1 2 x   2 y  1   0 z 2  i  2
x  y   x   0 x   0 1  
là một số thực âm khi     . Chọn B. z   i 2 2x y  1  0 1  y  1   0     x   y  12 2 
Câu 33. z  1  5i  M 1; 5 ; z  3  i  N 3; 1
 ; z  6  P 6; 0  1   2   3     Ta có MN  2; 6
 ,NP  3;  1  
 MN.NP  2.3  6.1  0, MN 
4  36  40,NP  9  1  10  MN
Vậy MNP là tam giác vuông tại N . Chọn A.
Câu 34. z  7  3i  A 7; 3  ;
z  8  4i  B 8; 4 2   1  
z  1  5i  C 1;5 ; z  2i  D 0; 2 4   3     A  B  BC 
Ta có AB  1;7,BC   7
 ;1    A  B.BC  0  
Vậy ABCD là hình vuông. Chọn A. Câu 35. z  1   3i  A 1  ;3 ; z  3   2i  B 3  ; 2
 ; z  4  i  C 4;1 1   2   3     A  B  AC  Suy ra AB   2  ; 5  ,AC  5; 2
     . A  B.AC  0  
Vậy tam giác ABC vuông cân tại A . Chọn D.
Câu 36. Đặt z  x  yi x,y   . Suy ra M x; y biểu diễn dố phức z .
Ta có: z  i  z  i  4  x  yi  i  x  yi  i  4 2 2
 x  y  i  x  y   2 i  
x  y   2 1 1 4
1  x  y  1  4 (*)
Tổng hợp các chuyên đề luyện thi đại học Trang 72
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna Đặt F 0; 1
 , F 0;1 . Thì (*)  MF  MF  4  2  F F . Suy ra tập hợp các điểm M là elip 1   2   2 1 1 2
E  có 2 tiêu điểm F , F . Phương trình chính tắc của E  có dạng 1 2 2 2 x y   1  2 2 2
a  b  0; b  a  c 2 2  a b
Ta có : F F  2c  2  c  1, 2 2
MF  MF  4  2a  a  2  b  a  c  3 . 1 2 2 1 2 2 x y Vậy E  :   1 . Chọn A. 4 3
Câu 37. z  3  2i  A 3;2 ; z  2  3i  B 2; 3 
; z  5  4i  C 5; 4 1   2   3     
Suy ra ta được AB   1  ; 5
 ,BC  3;7,AC  2;2 2 2 2 2 2 2  AB  1  5 
26,BC  3  7  58,AC  2  2  2 2 Vậy ChuVi 
26  2 2  58 . Chọn D. AB  C
Câu 38. Theo giả thiết ta có A 1;1,B 2;4,C 6;5  
Gọi D x;y  , khi đó AB  1; 3,CD  x  6;y  5   1   x  6 x   7  
Tứ giá ABDC là hình bình hành khi AB  CD    . Chọn A. 3 y 5 y     8      
Câu 39: Theo giả thiết ta có A 4
 ; 0,B 0;4,C x;3 .Ta có AB  4;4,AC  x  4;3.     x  4 3 , A ,
B M thẳng hằng  A ,
B AC cùng phươngAB  k.AC  k    x  1  . Chọn C. 4 4 Câu 40. Cách 1.
Theo giả thiết A1;2,B x;2,x  1 thì B biểu diễn số phức z  x  2i .
Tam giác OAB cân tại O 2 2 2 2 2 2
 OB  OA  x  2  1  2  x  1 (loại) hoặc x  1  (nhận) Vậy z  1   2i . Cách 2. Dễ thấy ,
A B cùng nằm trên d : y  2 nên tam giác OAB cân tại O khi và chỉ khi , A B đối xứng
qua Oy . Vậy B  1
 ;2 và do đó z  1
  2i . Chọn A.
Câu 41. Gọi M x;y ,x,y   thì M biểu diễn cho số phức z  x  yi .
Theo giả thiết A1;3,B 2;2,C  1  ; 1   .      x   1  1  x   0  
Từ AM  AB  AC  AM  CB   
. Vậy z  6i . Chọn D. y 3 3 y     6    
Câu 42. Gọi C x;y ,x,y   thì C biểu diễn cho số phức z  x  yi .    
OA  4;0, OB  0; 3
 . Suy ra OA OB  4;3.    
Theo giả thiết OC  OA  OB  OC  4; 3    C 4; 3
  .Vậy z  4  3i . Chọn A.
Tổng hợp các chuyên đề luyện thi đại học Trang 73
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
Câu 43: Gọi M x;y ,x,y   thì M biểu diễn cho số phức z  x  yi . Ta có
z    i   x    y  i   x  2  y  2   x  2  y  2 3 4 2 3 4 2 3 4 2 3 4  4 . Chọn B.  
Câu 44. Ta có A  1
 ;1,B 1;  
1 ,C 0;2 . Suy ra AB  0; 2
 ,BC  1;3 .   Do đó A .
B BC  0.  1   2  .3  6  . Chọn D.
Câu 45. Gọi M x;y ,x,y   thì M biểu diễn cho số phức   x  yi .           i x 3 yi x 2y 3 2x y 6
1 2 z  3  z    i . 1  2i 5 5 2 2 x  2y  7 2x  y  6
Theo giả thiết z  2  5  
i  5  x  2y  7  2x  y  6  625 5 5 2 2 Suy ra x  
1  y  4  125 . Chọn A.
Tổng hợp các chuyên đề luyện thi đại học Trang 74
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
D. BÀI TOÁN CỰC TRỊ CỦA SỐ PHỨC
I. PHƯƠNG PHÁP QUY VỀ TÌM MIN-MAX CỦA HÀM MỘT BIẾN KẾT HỢP
SỬ DỤNG TÍNH CHẤT CỦA SỐ PHỨC.
Phương pháp 1
Bài toán: Trong các số phức z thoả mãn điều kiện T. Tìm số phức z để biểu thức P đạt
giá trị nhỏ nhất, lớn nhất.
Phương pháp tổng quát: Đặt z  x  yi x;y  .
Từ điều kiện T, biến đổi để tìm cách rút ẩn rồi thế vào biểu thức P để được hàm một biến.
Tìm giá trị lớn nhất (hoặc nhỏ nhất) tuỳ theo yêu cầu bài toán của hàm số một biến vừa tìm được.
Phương pháp 2
Sử dụngcác tính chất và các bất đẳng thức về môđun của số phức sau để giải quyết các bài toán min-max:
 z  0; z  0  z  0; 2  z  z 2
 z  z , z
  z , z  z
 z  z '  z  z '
 z  z  z + z 1 2 1 2
 z  z '  z  z '  z  z '  z  z '  z  z '
 z.z '  z.z '
 z .z  z . z 1 2 1 2  z  z z z   1  1   z '    z ' z z 2 2
Kết hợp sử dụng các bất đẳng thức liên hệ giữa trung bình cộng và trung bình nhân, BĐT Bunhia- Cốpxki.
 Bất đẳng thức Bunhiacopxki :Cho các số thực , a ,
b x,y ta luôn có  a b  2   2 2   2 2 ax by a b
x  y  . Dấu = xảy ra   x y     
 Bất đẳng thức Vectơ : Cho 2 vecto u x;y và v x ';y ' ta luôn có u  v  u  v
 x  y  x  y  x  x 2  y  y 2 2 2 2 2 ' ' ' ' x y Dấu = xảy ra    0 x ' y '
Tổng hợp các chuyên đề luyện thi đại học Trang 75
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
MỘT SỐ BÀI TOÁN ĐIỂN HÌNH Bài toán 1
Trong các số phức z thoả mãn điều kiện z  1  5i  z  3  i , tìm số phức z có môđun nhỏ nhất. Giải:
Gọi z  x  yi x;y    . 2 2 2 2
z  1  5i  z  3  i  (x  1)  (y  5)  (x  3)  (y  1)
 x  3y  4  0  x  4  3y . 2  6   8 2 10 2 2 2 2 2
z  x  y  (4  3y)  y  10y  24y  16  10 y       .  5 5 5 6 2
Đẳng thức xảy ra khi y   x  . 5 5 2 10 2 6 2 6
Vậy z đạt giá trị nhỏ nhất bằng khi z 
 i . Vậy z   i là số phức cần tìm. 5 5 5 5 5 Bài toán 2
Cho các số phức z thỏa mãn 2
z  m  2m  5 , với m là tham số thực. Biết rằng tập hợp
các điểm biểu diễn các số phức w  3  4iz  2i là một đường tròn. Bán kính nhỏ nhất
của đường tròn đó bằng? Giải :
Cách 1 : Gọi w  x  yi .
x  y  2i 3x  4y  8 4x  3y  6
Từ giả thiết, ta có x  yi  3  4iz  2i  z    .i 3  4i 25 25
 x  y  2  x  y  2 3 4 8 4 3 6  z  . 25 2 2 Mà 2
z  m  m    x  y     x  y   2   2 2 5 3 4 8 4 3 6 25 m  2m   25 2 2    
 x  y  y  
m  2    x y  2  m  2 2 2 2 2 4 4 25 1 4 2 25 1  4  400  20 .     
Vậy bán kính nhỏ nhất của đường tròn đó là 20. Dấu '  ' xảy ra khi m  1 .
Cách 2: Từ giả thiết, ta có w  2i  3  4iz .  
Lấy môđun hai vế, ta được w  i 
 i z  m  m    m  2 2 2 3 4 . 5. 2 5 5 1  4  20.   
Tổng hợp các chuyên đề luyện thi đại học Trang 76
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna Bài toán 3 z  3
Trong các số phức z có phần thực, phần ảo không âm và thoả mãn:  1. z  1  2i
Tìm số phức z sao cho biểu thức 2 2 P z z  2 2 z
z .i.z(1 i) z (1 i)        
 đạt giá trị lớn nhất, nhỏ nhất. Giải:
Điều kiện: z  1  2i . Gọi z  x  yi  * x;y   .   z  z  3 3  1 
 1  z  3  z  1  2i  (x  2 3)  2 y  (x  2 1)  (y  2 2) z  1  2i z  1  2i
 x  y  1
(luôn thoả mãn điều kiện vì x  1;y  2 không thoả mãn phương trình) 2 2 2 2
z  x  yi  z  z  4xy.i  z  z  4xy (vì x;y không âm).
z(1  i)  z (1  i)  2x  2y Do đó 2 2 2 2
P  16x y  4xy.(2x  2y)  16x y  8xy . 2 x y     1  1
Đặt t  xy  0  t           P 16t 8t;t 0;  , ta có 2 .  2  4  4    1 + Xét hàm số 2
f (t)  16t  8t liên tục trên 0;   . 4   1
f '(t)  32t  8t; f '(t)  0  t  0  t   (loại) 4 1   33 33 1
f (0)  0; f   
 max f (t) 
 t  ; min f (t)  0  t  0      1  1 4 16  16 4  0; 0;   4  4     1 1 x   0;y  1 Khi t x y ; Khit 0        2 2 x   1;y  0  33 1 1
Vậy P đạt giá trị lớn nhất bằng khi z   i . 16 2 2
P đạt giá trị nhỏ nhất bằng 0 khi z  1  z  0 .
Nhận xét: Bài tập này cũng có thể giải được bằng cách rút y  1  x và thế vào biểu thức P ta được hàm số 2 2
g(x)  16x (1  x)  8x(1  x) rồi đi tìm giá trị lớn nhất, giá trị nhỏ nhất của
hàm số g(x) trên 0;1   . Bài toán 4
Trong các số phức z thỏa mãn điều kiện z  2  4i  z  2i .Tìm số phức z có môđun nhỏ nhất. Giải:
Giả sử số phức z cần tìm có dạng z  x  yi (x,y  ) được biểu diễn bởi điểm M(x;y).
Tổng hợp các chuyên đề luyện thi đại học Trang 77
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
Ta có x  2  (y  4)i  x  (y  2)i (1) 2 2 2 2
 (x  2)  (y  4)  x  (y  2)  y  x   4 . Mặt khác 2 2 2 2 2
z  x  y  x  x  8x  16  2x  8x  16 Hay z  x  2 2
2  8  2 2 . Do đó z
 x  2  y  2. Vậy z  2  2i . min Bài toán 5
Trong các số phức z thỏa mãn z  1. Tìm số phức z để 1  z  3 1  z đạt giá trị lớn nhất Giải:
Giả sử z  x  ,
yi x,y   . Vì z   2 x  2 y   2 x  2 1 1 y  1 Khi đó:
1  z  3 1  z  x  2
1  y  3 x  2 2 2 1  y  x  2
1  1  x  3 x  2 2 2
1  1  x  2  1  x  3 1 x 
Xét hàm số f x   2  1  x  3 1  x  trên đoạn     1; 1 ta có:   f x  1 3  4 '  2    
; f 'x   0  x     2 1  x 2 1  x  5 4 Ta có: f       1  6; f       2 10  . 5     4  4 3  
x   ;y   4 x      Vậy f  f        5 5 2 10 5 max     5    2 2  4 3 y  1  x x   ;y     5 5 4 3 4 3 Vậy z    ,
i z    i. 5 5 5 5 Bài toán 6
Trong các số phức z thỏa: z  3  4i  z , biết rằng số phức z  a  ,
bi a,b   có
modul nhỏ nhất. Khi đó, giá trị của 2
P  a b là ? Giải:
Ta có z  3  4i  z  a bi  3  4i  a  bi    2  a a 3  b  42 25 6 2 2
 a  b  25  6a  8b  0  b  8 2 2 2 25 6a 25 75 625 5 15      25 25 2 2
 z  a     a  a    a       8  16 16 64 4 8  4 4
Tổng hợp các chuyên đề luyện thi đại học Trang 78
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna 3
Dấu "  " xảy ra khi a   b  2 . 2 1 Khi đó 2
P  a b  . 4 Bài toán 7
Cho số phức thỏa z  1 . Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của 2
P  z  1  z  z  1 . Giải :
Đặt z  a  bi a b   2 2 ;
 a  b  1 . 
z   a  2 2 1
1  b  2a   1 2
 z  z  1   2 2
a  2abi  b   a  bi 2 2
 a  b   2
2a  a   2a   1 bi
 2a  a2  2a  2 2 2 1 b  2a  2 1  2 2
a  b   2a  1
Vậy P  2 a  1  2a  1 .   7   13 m
 ax P  P   1  3 max P   P  1      1  8 4 Xét a  ;1        1  . Xét a  1  ;  2 min P     P  3     2  1  2    min P  P  3     2       13 7 15 Ma  x P   z    i z 1   Kết luận 4 8 8  1 3 Min  P  3  z   i z 1    2 2 Bài toán 8
Số phức z  0 thỏa mãn z  2. Tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu thức z  i P  . z Giải: i i i 1 i 1 Ta có 1   1   1   1   1   1  . z z z z z z 1 1 1 3 Mặt khác z  2   suy ra  P  . z 2 2 2 3 1
Suy ra giá trị lớn nhất và giá trị nhỏ nhất là , . Vậy tổng giá trị lớn nhất và giá trị nhỏ nhất 2 2
của biểu thức P là 2.
Tổng hợp các chuyên đề luyện thi đại học Trang 79
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna Bài toán 9
Cho số phức z thỏa mãn z  2  3i  1 . Tìm giá trị lớn nhất của P  z  1  i Giải:
Ta có: z  2  3i  z  2  3i  z  2  3i  z  2  3i  1
P  z  1  i  z  2  3i  3  2i  z  2  3i  3  2i  1  13 . Vậy P  1  13 . max Bài toán 10
Trong các số phức z thoả mãn z  3  4i  4 . Tìm giá trị lớn nhất, giá trị nhỏ nhất của z
và xảy ra khi z bằng bao nhiêu? Giải:
Ta có : z  3  4i  z  (3  4i)  z  3  4i  z  5
 4  z  5  4  z  5  4  1  z  9  max  9 và min  1 z z
Đặt z  x  yi (x;y  )  TH max  9 z  z  9  2 x  2 y  81  2 x  2 y     81     2 2 
z  3  4i  4
(x  3)  (y  4)  16 3x  4y  45       27 36 27 36
Giải hệ phương trình này ta thu được x  ; y    z   i . 5 5 5 5 27 36
Vậy max  9  z   i . z 5 5  TH min  1 z  z  1  2 x  2 y  1  2 x  2 y     1     2 2 
z  3  4i  4
(x  3)  (y  4)  16 3x  4y  45       3 4 3 4
Giải hệ phương trình này ta thu được x  ; y    z   i . 5 5 5 5 3 4
Vậy min  1  z   i . z 5 5 Bài toán 11
Cho số phức z thỏa mãn 2  iz  1  1. Tổng giá trị lớn nhất và giá trị nhỏ nhất của
z  1 bằng bao nhiêu ? Giải:
2  iz 1 1 1 2 i 1
Ta có 2  iz  1  1    z   z    . 2  i 2  i 2  i 5 5 5
Tổng hợp các chuyên đề luyện thi đại học Trang 80
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna 2 i  7 i    7 i z    z  1   
   z  1     z  1  2   5 5  5 5 5 5 1 1 1 1 1   z  1  2 
 z  1  2   
 2  z  1  2  5 5 5 5 5 z  1  z  1  2 2 . max min Bài toán 12
Cho số phức z thỏa mãn z  1  2i  10 . Giá trị lớn nhất và giá trị nhỏ nhất của
z  1  4i bằng bao nhiêu ? Giải:
Ta có z  1  2i  z  1  2i  z  (1  2i)  z  1  2i  z  1  2i  10
Lại có : z  1  2i  z  1  4i  2  2i  z  1  4i  2  2i  z  1  4i  2 2
 10  z  1  4i  2 2  10  z  1  4i  2 2  10
 10  2 2  z  1  4i  10  2 2
Vậy z  1  4i
 10  2 2; z  1  4i  10  2 2 . max min Bài toán 13
Trong các số phức z có môđun bằng 2 2 . Tìm số phức z sao cho biểu thức
P  z  1  z  i đạt giá trị lớn nhất. Giải:
Gọi z  x  yi x;y    2 2 2 2
z  2 2  x  y  2 2  x  y  8 2 2 2 2
P  z  1  z  i  (x  1)  y  x  (y  1)
Áp dụng bất đẳng thức Bunhia-côpxki cho hai bộ số 1;1 và 2 2 2 2
(x  1)  y ; x  (y  1) , ta có: 2 2 2 2 2 P 2 (x 1) y x (y 1)       
 4(9  x  y)  
Áp dụng bất đẳng thức Bunhia-cốpxki cho hai bộ số 1;1 và x;y , ta có: x  y   2 2
2 x  y   4 2
 P  52  P  2 13 . Đẳng thức xảy ra khi x  y  2
Vậy P đạt giá trị lớn nhất bằng 2 13 khi z  2  2i .
Tổng hợp các chuyên đề luyện thi đại học Trang 81
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna Bài toán 14
Cho số phức z thỏa mãn z  3  z  3  8 . Gọi M , m lần lượt giá trị lớn nhất và nhỏ
nhất z . Khi đó M  m bằng ? Giải:
Gọi z  x  yi với x;y   .
Ta có 8  z  3  z  3  z  3  z  3  2z  z  4 .
Do đó M  max z  4 . 2 2 Mà z 
 z    x   yi  x   yi   x   2
 y  x   2 3 3 8 3 3 8 3 3  y  8 .
Áp dụng bất đẳng thức Bunhiacopxki, ta có    
x  2  y 
x  2 y     x  2 y x  2 2 2 2 2 2 2 8 1. 3 1. 3 1 1 3 3  y        2 2 x  y     2 2 8 2 2 2 18
2 2x  2y  18  64 2 2 2 2
 x  y  7  x  y  7  z  7 .
Do đó M  min z  7 .
Vậy M  m  4  7 . Bài toán 15
Cho số phức z thỏa mãn z  4  z  4  10 . Giá trị lớn nhất và nhỏ nhất của z bằng? Giải:
Cách 1: Giả sử z  x  yi x;y  .
Ta có 10  z  4  z  4  z  4  z  4  2z  z  5 . 2  2 2 
Áp dụng bất đẳng thức Bunhiacopxki, ta có 100   z  4 .1  z  4 . 
1   z  4    z  4   .2  
 a  2 b  a  2 2 2  b    2 2 4 4 50
a  b   9  z  3.
Cách 2: Giả sử z  x  yi x;y  . 2 2
Từ giả thiết, ta có x   2
 y  x   2 4 4  y  10 .   *
Trong mặt phẳng với hệ tọa độ Oxy , gọi M x;y và F 4;0 , F 4;0 thì   * có dạng 2   1  
MF  MF  2.5 . Vậy tợp hợp điểm M x;y biểu diễn số phức z là một Elip có độ dài trục lớn 1 2
a  5 , tiêu cự F F  8  c  4 . Suy ra độ dài trục bé 2 2
b  a  c  3 . 1 2
Khi đó ta luôn có b  OM  a hay 3  z  5 .
Tổng hợp các chuyên đề luyện thi đại học Trang 82
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna Bài toán 16
Gọi T là tập hợp các số phức z thỏa mãn z  1  3 và z  1  5 . Gọi z ,z  T lần lượt là 1 2
các số phức có môđun nhỏ nhất và lớn nhất. Tìm số phức z  2z . 1 2 Giải:
Áp dụng bất đẳng thức: z  z  z  z  z  z . 1 2 1 2 1 2   1 2
3  z  i  z  i 2   z   Ta có:     2  z  6 .
z  1  z  1  5 z  6    
Dấu ”=” thứ nhất xảy ra khi z  i  3 , kết hợp với z  1  5 ta được hệ:  z  1  3 1  z 
 1  5  z  2i . 1 1  z  2 1   z  1  5 2 
Dấu ”=” thứ hai xảy ra khi z  i  5 , kết hợp với z  1  3 ta được hệ: z 
 1  3  z  6 2 2  z  6 2 
Suy ta z  2z  12  6i . 1 2
Tổng hợp các chuyên đề luyện thi đại học Trang 83
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
II. PHƯƠNG PHÁP HÌNH HỌC GIẢI BÀI TOÁN MIN-MAX 1. PHƯƠNG PHÁP:
Để giải được lớp bài toán này, chúng tôi cung cấp cho học sinh các bất đẳng thức hình học và
một số bài toán công cụ sau:
Bài toán công cụ 1
Cho đường tròn (T ) cố định có tâm I bán kính R và điểm A cố định. Điểm M di động trên
đường tròn (T ) . Hãy xác định vị trí điểm M sao cho AM lớn nhất, nhỏ nhất. Giải:
TH1: A thuộc đường tròn (T)
Ta có: AM đạt giá trị nhỏ nhất bằng 0 khi M trùng với A
AM đạt giá trị lớn nhất bằng 2R khi M là điểm đối xứng với A qua I
TH2: A không thuộc đường tròn (T)
Gọi B, C là giao điểm của đường thẳng qua A,I và đường tròn (T); Giả sử AB < AC.
+) Nếu A nằm ngoài đường tròn (T) thì với điểm M bất kì trên (T), ta có:
AM  AI  IM  AI  IB  AB .
Đẳng thức xảy ra khi M  B
AM  AI  IM  AI  IC  AC .
Đẳng thức xảy ra khi M  C
+) Nếu A nằm trong đường tròn (T) thì với điểm M bất kì trên (T), ta có:
AM  IM  IA  IB  IA  AB .
Đẳng thức xảy ra khi M  B
AM  AI  IM  AI  IC  AC .
Đẳng thức xảy ra khi M  C
Vậy khi M trùng với B thì AM đạt gía trị nhỏ nhất.
Vậy khi M trùng với C thì AM đạt gía trị lớn nhất.
Bài toán công cụ 2
Cho hai đường tròn (T ) có tâm I, bán kính R
(T ) có tâm J, bán kính R 1 1; đường tròn 2 2. Tìm
vị trí của điểm M trên (T ), điểm N trên (T ) sao cho MN đạt giá trị lớn nhất, nhỏ nhất. 1 2 Giải:
Gọi d là đường thẳng đi qua I, J; d cắt đường tròn (T ) tại hai điểm phân biệt A, B (giả sử JA 1
> JB) ; d cắt (T ) tại hai điểm phân biệt C, D ( giả sử ID > IC). 2
Với điểm M bất khì trên (T ) và điểm N bất kì trên (T ) . 1 2
Ta có: MN  IM  IN  IM  IJ  JN  R  R  IJ  AD 1 2
Tổng hợp các chuyên đề luyện thi đại học Trang 84
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
Đẳng thức xảy ra khi M trùng với A và N trùng với D
MN  IM  IN  IJ  IM  JN  IJ  R  R  BC . 1 2
Đẳng thức xảy ra khi M trùng với B và N trùng với C.
Vậy khi M trùng với A và N trùng với D thì MN đạt giá trị lớn nhất.
khi M trùng với B và N trùng với C thì MN đạt giá trị nhỏ nhất.
Bài toán công cụ 3
Cho hai đường tròn (T ) có tâm I, bán kính R; đường thẳng  không có điểm chung với
(T ) . Tìm vị trí của điểm M trên (T ) , điểm N trên  sao cho MN đạt giá trị nhỏ nhất. Giải:
Gọi H là hình chiếu vuông góc của I trên d
Đoạn IH cắt đường tròn (T ) tại J
Với M thuộc đường thẳng  , N thuộc đường tròn (T ) , ta có:
MN  IN  IM  IH  IJ  JH  const .
Đẳng thức xảy ra khi M  H ;N  I
Vậy khi M trùng với H; N trùng với J thì MN đạt giá trị nhỏ nhất.
2. MỘT SỐ BÀI TOÁN ĐIỂN HÌNH Bài toán 1
Trong các số phức z thoả mãn z  3  4i  4 . Tìm giá trị lớn nhất, giá trị nhỏ nhất của z Giải:  Cách 1
Gọi z  x  yi x;y  
  M(x;y) biểu diễn cho số phức z trong hệ toạ độ Oxy 2 2 2 2
z  3  4i  4  (x  3)  (y  4)  4  (x  3)  (y  4)  16
Vậy điểm M biểu diễn cho số phức z thuộc đường tròn (T) có tâm I (3;4) , bán kính R = 4. 2 2
z  x  y  OM ;OI  5  R nên O nằm ngoài đường tròn (T)
z lớn nhất khi OM lớn nhất, nhỏ nhất khi OM nhỏ nhất.
(Bài toán qui về Bài toán công cụ 1- Trường hợp 2)
Đường thẳng OI cắt đường tròn (T) tại hai điểm phân biệt 3 4    27 36 A ; ;B    ;  
  OA  1;OB  9  5 5    5 5 
Với M di động trên (T), ta có: OA  OM  OB  1  OM  9  1  z  9
 OM nhỏ nhất khi M trùng với A; OM lớn nhất khi M trùng với B
Tổng hợp các chuyên đề luyện thi đại học Trang 85
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna 3 4 27 36
Vậy z nhỏ nhất bằng 1 khi z 
 i ; z lớn nhất bằng 9 khi z   i . 5 5 5 5  Cách 2
Gọi z  x  yi x;y   
 M(x;y) biểu diễn cho số phức z trong hệ toạ độ Oxy
  3  4i  (
A 3;4) biểu diễn cho số phức 
z  OM;   OA  5  z    AM ;
Theo giả thiết z  3  4i  4  z    4  AM  4 .
Ta có: OM OA  AM  4  OM OA  4  4 OA  OM  4  OA  1  OM  9 3 4 27 36
 1  z  9 ; z  1 khi z   i ; z  9 khi z   i . 5 5 5 5 3 4 27 36
Vậy z nhỏ nhất bằng 1 khi z 
 i ; z lớn nhất bằng 9 khi z   i . 5 5 5 5
Nhận xét: Ngoài ra bài toán trên có thể giải bằng phương pháp sử dụng bất đẳng thức
Bunhia-Cốpxki hoặc phương pháp lượng giác hoá. Bài toán 2
Trong các số phức z thoả mãn điều kiện z (z  2  4i) là một số ảo, tìm số phức z sao cho
  z 1 i có môđun lớn nhất. Giải:
Gọi z  x  yi x;y   
 M(x;y) biểu diễn cho số phức z trong hệ toạ độ Oxy z (z 2 4i) (x yi) (x 2) (y 4)i x(x 2) y(y 4)
x(y 4) y(x 2)                i    
z (z  2  4i)là một số ảo 2 2 2 2
 x(x  2)  y(y  4)  0  x  y  2x  4y  0  (x  1)  (y  2)  5
 M biểu diễn cho z thuộc đường tròn (T) có tâm I(1;2), bán kính R  5 2 2
  z 1  i  (x 1)  (y 1)i  (x 1)  (y 1)  AM với ( A 1;1)
IA  5  A  (T ) (Bài toán được qui về Bài toán công cụ 1 - trường hợp 1)
Vì M là điểm di động trên (T) nên AM lớn nhất
 AM là đường kính của (T)
 M đối xứng với A qua I
 I là trung diểm của AM  M(3;3)  z  3  3i    4  2i
Vậy  lớn nhất bằng 2 5 khi z  3   3i .
Tổng hợp các chuyên đề luyện thi đại học Trang 86
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna Bài toán 3
Trong các số phức z ,z
z  1  i 1 ; z  6  6i  6 z ,z 1 2 thoả mãn: , tìm số phức 1 2 sao 1 2
cho z  z đạt giá trị lớn nhất. 1 2 Giải:
Gọi z  a  b.i ; z  c  d.i ; (a, , b ,
c d là những số thực); z
M a;b
1 được biểu diễn bởi điểm ; 1 2 z
N c;d
2 được biểu diễn bởi điểm
trong mặt phẳng toạ độ Oxy 2 2 2
z  1  i  1  z  1  i  1  (a  1)  (b  1)  1 1 1
 M thuộc đường tròn tâm I(1; 1), bán kính R = 1. 2 2 2
z  6  6i  6  z  6  6i
 36  (c  6)  (d  6)  36 2 2
 M thuộc đường tròn tâmJ 6; 6, bán kính R '  6 . 2 2
z  z  (c  a)  (d  b)  MN . 1 2
(Bài toán được qui về Bài toán công cụ 2)
Đường thẳng IJ có phương trìnhy  x . Đường thẳng IJ cắt đường tròn tâm I tại hai điểm 2 2 2 2  2 2 2 2        M  ; ;M    ;      1 2  2 2     2 2   
Đường thẳng IJ cắt đường tròn tâm J tại 2 điểm N 6  3 2; 6  3 2 ;N 6  3 2;6  3 2 1   2 
M N  MN  M N  5 2  7  z  z  5 2  7 2 1 1 2 1 2 max z  z
 5 2  7 khi M  M ,N  N . 1 2 1 2 2  2 2  2 Vậy z  
i ; z  6  3 2  6  3 2 i z  z 1 2   thì
đạt giá trị lớn nhất. 2 2 1 2 Bài toán 4
Cho các số phức z ;z z 1 ;z z  (1 i)     6  2i 1 2 thoả mãn:
là một số thực. Tìm số phức 1 2  2   2 z ;z P  z  z z  z z 2  1 2 1 2 1 2 sao cho
đạt giá trị nhỏ nhất. Giải:
Gọi z  a bi ; z  c  di ; , a , b , c d   1 2  
 M(a;b),N(c;d) lần lượt biểu diễn cho z ;z 1 2 trong hệ toạ độ Oxy 2 2 2 2
z  1  a  b  1  a b  1  M thuộc đường tròn (T ) có tâm O, bán kính R = 1 1 z  c  ; di 2  z z  
1 i 6 2i  
c di (c 1) (d 1)i            2  6i      ( c c 1) d(d 1) 2  ( c d 1) d(c 1) 6           i  
 là số thực  (
c d  1)  d(c  1)  6  0  c  d  6  0
Tổng hợp các chuyên đề luyện thi đại học Trang 87
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
 N thuộc đường thẳng  : x  y  6  0 Ta có d(O; )
  1 nên  và (T ) không có điểm chung
z z  ac  bd  (bc  ad)i; 1 2
z z  ac  bd  ( b
 c  ad)i  z z  z z  2(ac  bd) 1 2 1 2 1 2 2 2 2 2 2
P  c  d  2(ac  bd)  (c  a)  (b  d)  1  MN  1 (vì 2 2 a  b  1 )
(Bài toán được qui về Bài toán công cụ 3)
Gọi H là hình chiếu vuông góc của O trên  : x  y  6  0  H (3; 3)  2 2
Đoạn OH cắt đường tròn (T ) tại I  ;     2 2   
Với N thuộc đường thẳng  , M thuộc đường tròn (T ) , ta có:
MN  ON OM  OH OI  IH  3 2  1 .
Đẳng thức xảy ra khi M  I;N  H  P    2 3 2 1  1  18  6 2 . 2 2
Đẳng thức xảy ra khi z  
i;z  3  3i 1 2 2 2 2 2
Vậy P đạt giá trị nhỏ nhất bằng 18  3 2 khi z  
i;z  3  3i . 1 2 2 2 Bài toán 5
Trong các số phức z có môđun bằng 2 . Tìm số phức z sao cho biểu thức
P  z  1  z  1  7i đạt giá trị lớn nhất. Giải:
Gọi z  x  yi x;y    2 2 2 2
z  2  x  y  2  x  y  4 2 2 2 2
P  z 1  z 1  7i  (x 1)  y  (x 1)  (y  7)    
Xét u x  1;y,v 1  x;7  y  u  v  0;7 . Khi đó:      
P  u  v  u  v  7 . Đẳng thức xảy ra khi u ,v cùng hướng
 (x  1)(7  y)  y(1  x)  x  1  y   3  
Với x  1;y  3 thì u ,v ngược hướng (không thoả mãn)  
Với x  1;y   3 thì u ,v cùng hướng (thoả mãn)
Vậy z  1  i 3 thì P đạt giá trị nhỏ nhất bằng 7.
Tổng hợp các chuyên đề luyện thi đại học Trang 88
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna Bài toán 6
Cho số phức z thỏa mãn z  3  4i  5 . Gọi M , m lần lượt là giá trị lớn nhất và giá trị 2 2
nhỏ nhất của P  z  2  z  i . Tính giá trị 2 2
A  M  m . Giải : 2 2
Gọi z  a  bi  ,
a b   . Ta có : z  3  4i  5  a  3  b  4  5 .
 z thuộc đường tròn C  có tâm I 3;4 và bán kính R  5 . 2 2 2 2
Mặt khác : P  z 
 z  i  a   2 2 2
2  b  a  b  
1  4a  2b  3  P  0 .
Vậy z thuộc đường thẳng  : 4a  2b  3  P  0 . z    C  Ta có :     Để z
 thì C       d I;      R . z         23  P  
5  13  P  33  A  1258 . 2 5 Bài toán 7
Trong các số phức z thoả mãn điều kiện z  3  z  3  10 . Tìm số phức z có môđun lớn nhất. Giải:
Gọi z  x  yi x;y   
 M(x;y) biểu diễn cho số phức z trong hệ toạ độ Oxy 2 2 2 2
z  3  z  3  10  (x  3)  y  (x  3)  y  10 (với F (3;0); F (3;0) ).
 MF  MF  10 1 2 1 2 2 2 x y
 M  (E) có tâm O, trục lớn bằng 10; tiêu cự bằng 6  M  (E) :   1 25 9
z  OM;OM lớn nhất  OM  a  5  M(5;0)  M(5;0)
Vậy z lớn nhất bằng 5 khi z  5  z  5  . Bài toán 8
Biết rằng số phức z thỏa mãn u  z  3  iz  1  3ilà một số thực. Tìm giá trị nhỏ nhất của z . Giải:
Đặt z  x  yi (x,y  ) ta có
u  x  
y  i   x    y    2 2 3 1 1
3 i  x  y  4x  4y  6  2   x  y   4i 
Ta có: u  R  x  y  4  0
Tổng hợp các chuyên đề luyện thi đại học Trang 89
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
Tập hợp các điểm biểu diễn của z là đường thẳngd : x  y  4  0 .
M x;y là điểm biểu diễn của z , z có môđun nhỏ nhất khi và chỉ khi độ dài OM nhỏ nhất
 OM  d . Tìm được M 2;2 suy ra z  2  2i . Bài toán 9
Tìm số phức z có mô đun lớn nhất và thỏa mãn điều kiện z   i 13 1  3  2i  . 2 Giải:
Gọi z  x  yi (x,y  R)  z  x  yi . 13 39 2 2
z (1  i)  3  2i 
 x  y  x  5y   0 . 2 8
Gọi M x;y là điểm biểu diễn của z trong mặt phẳng tọa độ Oxy.   26  M  1 5 (C )  
là đường tròn có tâm I  ;  và bán kính R  . 2 2 4
Gọi d là đường thẳng đi qua O và I  d : y  5x . 3 15   1 5   Gọi M ,M  M  ;  M  ;  1
2 là hai giao điểm của d và (C) và . 1 4 4  2 4 4 OM   OM  Ta thấy 1 2  OM 
 OI  R  OM(M  (C ))  1  3 15
 Số phức cần tìm ứng với điểm biểu diễn M z   i 1 hay . 4 4 Bài toán 10
Cho số phức z  a bi  ,
a b   thỏa mãn z  1  i  z  2i và P  z 2  3i  z 1 đạt
giá trị nhỏ nhất . Tính P  a  2b . Giải :
Ta có : z  1  i  z  2i  a  b  1 .
P  z   i  z   a  2  b  2  a  2 2 2 3 1 2 3 1  b .
Xét trong mặt phẳng phức Oab , xét các điểm M  ;
a b, A2;  3 , B  1  ; 
0 với M điểm biểu
diễn số phức z  M  d : a b  1  0 . 2 2 2
Ta có : MA  MB  a    b    a   2 2 3 1  b .
Vậy ta tìm M  d sao cho MA  MB . min
Do x  y  x  y    A B d A A 1 B B 1 0 ,
cùng thuộc một phía so với đường thẳng .
 GọiA ' là điểm đối xứng của A qua d . Ta có : MA  MB  MA' MB  A'B . 3 1   5
Dấu "  " xảy ra khi M  A' B  d  M  ;   P  a  2b  . 2 2 2
Tổng hợp các chuyên đề luyện thi đại học Trang 90
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna Bài toán 11
Cho hai số phức z , z thỏa mãn z  2i  3 và z  2  2i  z  2  4i . Giá trị nhỏ nhất 1 2 1 2 2
của biểu thức P  z  z bằng? 1 2 Giải:
Đặt z  x  y i và z  x  y i với x , x , y , y  .  1 1 1 2 2 2 1 2 1 2
● z  2i  3  x  y  22 2
 9  tập hợp các số phức z là 1 1 1 1
đường tròn C  x  y  2 2 : 2  9 .
● z  2  2i  z  2  4i 2 2
 x  22  y  22  x  22  y  42  y  3  0 2 2 2 2 2
 tập hợp các số phức z là đường thẳng d : y  3  . 2 2 2
Ta có P  z  z  x  x  y  y
đây chính là khoảng cách từ điểm B x ;y  d đến 2 2  1 2  2 1  2 1
điểm Ax ;y  C . Do đó z  z
 AB . Dựa vào hình vẽ ta tìm được AB  2 khi 1 1    2 1 min min min A0; 
1 , B 0;3. Vậy P  z  z khi z  i
 ; z  3i . 1 2 1 2
Nhận xét: Ở bài này đường thẳng và đường tròn có vị trí đặc biệt nên vẽ hình sẽ nhận ra ngay được hai
điểm A & B , nếu không thì viết phương trình đường thẳng qua tâm C và vuông góc với d , sau đó tìm
giao điểm với C và d rồi loại điểm.
Tổng hợp các chuyên đề luyện thi đại học Trang 91
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
III. SỬ DỤNG MÁY TÍNH CASIO 570 VN-PLUS ĐỂ GIẢI Bài toán 1
Trong các số phức z có môđun bằng 2 . Tìm số phức z sao cho biểu thức
P  z  1  z  1  7i đạt giá trị lớn nhất. .
A 1  i 3 B.1  i 3 C. 3  i D.  3  i Hướng dẫn:
o Chuyển qua chế độ số phức: w2 o Nhập biểu thức P : qcQ)p1$+ qcQ)p1+7b Màn hình hiển thị:
o Gán X cho từng đáp án, dùng phím: r
o So sánh kết quả và ta tìm được giá trị lớn nhất là 7 Bài toán 2
Trong các số phức z thoả mãn điều kiện z  3  z  3  10 . Tìm số phức z có môđun lớn nhất. 9 12 .4
A  i B.5 C.3 
i D.3  5 i 5 5 Hướng dẫn:
o Chuyển qua chế độ số phức: w2
o Nhập biểu thức: z  3  z  3  10 vào máy tính: qcQ)p3$ qcQ)+3$p10. Màn hình hiển thị:
o Dùng phím r để nhập các đáp án, nếu đáp án nào cho
kết quả bằng 0 thì thỏa mãn điều kiện z  3  z  3  10 .
Ta thấy 3 đáp án A,B,C thỏa mãn điều kiện đề bài nhưng
đáp án B có môđun lớn nhất. Chọn B.
Tổng hợp các chuyên đề luyện thi đại học Trang 92
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
V. BÀI TẬP RÈN LUYỆN 1. ĐỀ BÀI
Câu 1. Cho số phức z thỏa mãn z  2  2i  1 . Giá trị lớn nhất và giá trị nhỏ nhất của z lần lượt là
A. 2 2  1;2 2  1 B. 2  1; 2  1 C. 2;1
D. 3  1; 3  1
Câu 2. Cho số phức z thỏa mãn z  1  2i  4 5 . Giá trị nhỏ nhất của z lần lượt là A. 5 B. 3 5 C. 5 5 D. 5 3
Câu 3. Trong các số phức z thỏa mãn: z  3  4i  z thì số phức z có modul nhỏ nhất là 11 3 5 1 A. z   i B. z   2i C. z  5   i
D. z  3  i 2 2 2 6
Câu 4. Trong các số phức z thỏa mãn: z  2  4i  z  2i thì số phức z có modul nhỏ nhất là
A. z  2  2i B. z  2   2i
C. z  2  2i
D. z  2  2i
Câu 5. Trong các số phức z thỏa: z  3  4i  z , biết rằng số phức z  a  ,
bi a,b   có
modul nhỏ nhất. Khi đó, giá trị của 2
P  a  b là 1 1 1 1 A. P  B. P 
C. P  
D. P   4 2 4 2
Câu 6. Trong các số phức z thỏa mãn: z  1  5i  z  3  i , biết rằng số phức a z  a  ,
bi a,b   có modul nhỏ nhất. Khi đó, tỉ số bằng b 1 2 A. 3 B. C.
D. P   2 3 3
Câu 7. Cho số phức z thỏa mãn điều kiện z  2  i  1. Giá trị lớn nhất của z  1 là A. 2  1 B. 2  1 C. 2 D. 1
Câu 8. Cho số phức z thỏa mãn 2  iz  1  1. Tổng giá trị lớn nhất và giá trị nhỏ nhất của z  1 bằng 2 A. 3 B. 2 2 C. D. 2 3 5
Câu 9. Cho số phức z thỏa mãn z  1  2i  10 . Giá trị lớn nhất của z  1  4i bằng A. 10 B. 10 3 C. 3 10 D. 4 10
Câu 10. Cho số phức z thỏa mãn z  1  2i  4 . Gọi M và m lần lượt là giá trị lớn nhất và giá
trị nhỏ nhất của z  2  i . Giá trị của 2 2
T  M  m là
A. T  50
B. T  64
C. T  68
D. T  16 2
Câu 11. Trong mặt phẳng phức Oxy, tập hợp biểu diễn số phức Z thỏa mãn z  z  z  0 là
đường tròn C  . Diện tích S của đường tròn C  bằng bao nhiêu?
Tổng hợp các chuyên đề luyện thi đại học Trang 93
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
A. S  4
B. S  2
C. S  3
D. S  
Câu 12. Trong mặt phẳng phức Oxy, tập hợp biểu diễn số phức Z thỏa 1  z  1  i  2 là hình
vành khăn. Chu vi P của hình vành khăn là bao nhiêu?
A. P  4
B. P  
C. P  2
D. P  3
Câu 13. Trong mặt phẳng phức Oxy, giả sử M là điểm biểu diễn số phức Z thỏa mãn
z  2  z  2  8 . Tập hợp những điểm M là? x y x y A. E  2 2 :   1 B. E  2 2 :   1 16 12 12 16 2 2 2 2
C. T  : x   2  y   2  64
D. T  : x  2  y  2  8
Câu 14. Trong mặt phẳng phức Oxy, các số phức z thỏa z  5i  3 . Nếu số phức z có môđun
nhỏ nhất thì phằng ảo bằng bao nhiêu? A. 0 B. 3 C. 2 D. 4
Câu 15. Trong mặt phẳng phức Oxy, các số phức z thỏa z  2i  1  z  i . Tìm số phức z được
biểu diễn bởi điểm M sao cho MA ngắn nhất với A1; 3
A. 3  i
B. 1  3i
C. 2  3i
D. 2  3i
Câu 16. Trong mặt phẳng phức Oxy, trong các số phức z thỏa z  1  i  1. Nếu số phức z có
môđun lớn nhất thì số phức z có phần thực bằng bao nhiêu?  2  2 2  2 2  2 2  2 A. B. C. D. 2 2 2 2
Câu 17. Cho số phức z thỏa mãn : z  1  i  2 . Gọi A và B lần lượt là giá trị lớn nhất và nhỏ
nhất của z  2 . Khi đó 2 2
A  B có giá trị bằng A. 20 B. 18 C. 24 D. 32
Câu 18. Cho số phức z thỏa mãn : z  1  2i  2 5 . Gọi A và B lần lượt là giá trị lớn nhất và
nhỏ nhất của z  i . Khi đó .
A B có giá trị bằng C. A. 10 B. -10 C. 12 D. -12
Câu 19. Cho số phức z thỏa mãn : z 1  i  1  2i  2 . Gọi A và B lần lượt là giá trị lớn nhất và
nhỏ nhất của z  1  3i . Khi đó 2 2
2A  B có giá gần nhất bằng A. 20 B. 18 C. 64 D. 32
Câu 20: Xét số phức z thỏa mãn z  2  3i  1. Tìm giá trị lớn nhất của z  i  1 . A. 1  13. B. 2  13. C. 4. D. 6.
Câu 21: Xét số phức z thỏa mãn z  i  1  z  4i  2 . Tìm giá trị nhỏ nhất của z  2i  1 . 98 102 7 10 470 A. . B. . C. . D. . 5 5 5 5
Câu 22: Cho số phức z thoã mãn z  3  4i  2 . Gọi A và B lần lượt là giá trị lớn nhất và nhỏ
nhất của z . Tính giá trị của biểu thức 2
P  A  2B .
Tổng hợp các chuyên đề luyện thi đại học Trang 94
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
A. P  43 B. P  80 C. P  8
D. P  48
Câu 23: Cho số phức z thoã mãn z  1  i  2 . Gọi A và B lần lượt là giá trị lớn nhất và
nhỏ nhất của z  2  i . Giá trị của biểu thức 2
P  2A  B gần bằng. A. 6 B. 7 C. 8 D. 9 1  i
Câu 24: Cho số phức z thoã mãn
z  1  i  2 . Giá trị lớn nhất của A  z  2  i là. 1  i A. 2  2 B. 5  2 C. 2  5 D. 5 1 i z
Câu 25: Trong tất cả các số phức z thỏa mãn
 2  1 hãy tìm số phức z có mođun nhỏ 1 i nhất . A. z  1 B. z  2  2 C. z  0 D. z  2 min min min min
Câu 26: Cho số phức z thỏa mãn z  2  3i  1 Giá trị lớn nhất của z 1 i là A. 13  2. B. 4. C. 6. D. 13 1.
Câu 27: Cho số phức z thoã mãn điều kiện z  2i  z  1  2i . Gọi w là số phức thoã mãn
điều kiện w  1  iz  2 . Giá trị nhỏ nhất của biểu thức P  w là: 1 5 5 1 A. P  B. P  P  P  min C. min D. min 5 34 41 min 3
Câu 28: Cho số phức z  x  yi x,y   thỏa mãn điều kiện z  1  i  z  2  3i  5 . Gọi 2
M, m lần lượt là giá trị lớn nhất, nhỏ nhất của biểu thức P  x. z . Tổng M  2m bằng A. 54. B. 27. C. 18. D. 9.
Câu 29: Gọi z và z là các nghiệm của phương trình 2
z  4z  9  0. Gọi M , N lần lượt là các điểm 1 2
biểu diễn của z , z trên mặt phẳng phứC. Khi đó độ dài MN là 1 2
A. MN  4. B. MN  5.
C. MN  2 5.
D. MN  5.
Câu 30 : Trong mặt phẳng tọa độ Oxy, tìm tập hợp điểm M biểu diễn số phức w thỏa mãn điều kiện
w  1 2i z  3, biết z là số phức z thỏa mãn z  2  5. 2 2 2 2 A.  x   1
  y  4  125.
B.  x  5   y  4  125. 2 2 C.  x  
1   y  2  125.
D. x  2.
Tổng hợp các chuyên đề luyện thi đại học Trang 95
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
2. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI 1A 2B 3B 4D 5A 6B 7A 8B 9C
10C 11D 12C 13A 14C 15A 16A
17C 18A 19C 20A 21C 22A 23C 24D 25A 26D 27B 28A 29C 30A
Câu 1. Ta có z  2  2i  z
  z  2  2i  z  2 2  z  2 2  1.
Lại có z  2  2i  2i  2  z  2  2i  2i  2  z  z  1  2 2. Chọn A.
Câu 2. Ta có 4 5  z  1  2i  z  1  2i  z  5  z  3 5. Chọn B. Câu 3. Ta có b 
a  bi  3  4i  a  bi  a  32  b  42 8 25 2 2
 a  b  25  6a  8b  0  a  6 2 2 2 8b 25 25 100 625 5 10      25 25 3 2 2  z    b  b  b    b      b  2   a  .        6  9 9 36 3 3  4 4 2 Chọn B. 2 2 2
Câu 4. Ta có a  bi   i  a  bi  i  a    b   2 2 4 2 2
4  a  b   2
 20  4a  8b  4  4b  4a  4b  16  b  4 a 2
 z  a   a2  a  a   a  2 2 2 4 2 8 16 2
2  8  a  2  b  2. Chọn D. Câu 5. Ta có  a
a bi  3  4i  a  bi  a  32  b  42 25 6 2 2
 a  b  25  6a  8b  0  b  8 2 2 2 25 6a  25 75 625 5 15      25 3 2 2
 z  a     a  a    a     a   b  2.       Chọn A.  8  16 16 64 4 8  4 2 2 2 2 2
Câu 6. Ta có a  bi  1  5i  a bi  3  i  a  
1  b  5  a  3  b   1
 26  2a 10b  10  6a  2b  4a  12b  16  a  4  3b 2   2
 z  4  3b2 12   8 6 2 2 2
 b  10b  24b  16  b  10 
   b   a  .   Chọn B.     5 5 5 10
Câu 7. Đặt w  z  1  z  w  1, khi đó 2 2
z  2  i  w  1  i  1  w
 1  1  1  1  2. Chọn A. max
2  iz 1 1 1 2 i 1
Câu 8. Ta có 2  iz  1  1    z   z    . 2  i 2  i 2  i 5 5 5
Đặt w  z  1  z  w  1, khi đó 2 2 2 i 7 i 1 7 1     1 1 z    w     w         2  .       max 5 5 5 5 5 5 5  5 5
Tổng hợp các chuyên đề luyện thi đại học Trang 96
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna 2 2 7 1     1 1 Và w         2  .   w  w  2 2.     Vậy Chọn B. max 5 5 5 5 min max 2
Câu 9. Ta có z  1  2i  10  z  1  2i  10  z 1  2i.z 1  2i  10 .
 z 1  2i.z 1  2i  10  z 1  2i . z 1  2i  10  z 1  2i  10. .
Đặt w  z  1  4i  z  w  1  4i , khi đó z  1  2i  w  2  6i  10.
Vậy giá trị lớn nhất là 2 2 w
 10  2  6  3 10  z  1  4i  3 10. Chọn C. max max
Câu 10. Đặt w  z  2  i  z  w  2  i , khi đó
z  1  2i  w  2  i  1  2i  w  3  3i  4.  2 2 M   w
 3  3  4  3 2  4  Suy ra 2 2 max 
 M  m  68. Chọn C.  2 2 m   w
 3  3  4  3 2  4  min
Câu 11. Đặt z  x  yi x,y   , ta có z  x  yi và 2 2
z  x  y . 2 2 Khi đó, giả thiết 2 2
z  z  z   x  y  x  yi  x  yi   x   2 0 0 1  y  1.
Suy ra tập hợp biểu diễn số phức z là đường tròn tâm I 1; 
0 , bán kính R  1  S  .  C Chọn D.
Câu 12. Đặt z  x  yi x,y   , khi đó ta có
z   i  x   y  i  x  2  y  2   x  2  y  2 1 1 1 1 1 1 1 1  1  Tập hợp các
điểm biểu diễn số phức z nằm bên ngoài hình tròn có tâm I 1;1 R  1. 1   , bán kính 1
z   i  x   y  i  x  2  y  2   x  2  y  2 1 1 1 1 1 2 1 1  4  Tập hợp các
điểm biểu diễn số phức z nằm bên trong hình tròn có tâm I 1;1 R  2. 2  , bán kính 2
Vì hai đường tròn đồng tâm nên chu vi P hình vành khăn là P  C C  2 R  R  2 .  2 2  2 1  Chọn C.
Câu 13. Xét điểm F 2; 0 F 2  ;0
MF  MF  8  2a  a  4 2   1   và , ta có 1 2 x y 2 2 2
F F  4  2c  c  2  b  a  c  12  Tập hợp điểm là Elip E 2 2 :   1 . Chọn A. 1 2 16 12
Câu 14. Giả sử M là điểm biểu diễn số phức z . Xét điểm A0;5  AM  3
Tập hợp điểm M là các điểm không nằm ngoài đường tròn tâm A bán kính R  3
 OM  AO  AM  5  3  2 . Chọn C.
Câu 15. Xét điểm B 1;2,C 0; 
1  MB  MC  Tập hợp điểm M là đường thẳng trung được của BC .
Tổng hợp các chuyên đề luyện thi đại học Trang 97
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna 1 3  
Ta có: BC  : x  y  1  0 và trung điểm BC là H  ;   Phương trình đường trung trực 2 2 BC là:
 : x  y  2  0 . Lại có: AM  d  , A    2 2 .
Dấu bằng khi M là hình chiếu của A lên  2 2 2 2
Khi đó: AM  2 2  x   y    x   x   M 1  3 M  8  M 1  5 M  8   
  x   M M 2 x 3 0 3 M 3; 1. Chọn A.
Câu 16. Giả sử M là điểm biểu diễn số phức z . Xét điểm A1;  1  AM  1
Tập hợp điểm M là các điểm không nằm ngoài đường tròn C  tâm A bán kính R  1
 OM  AO  AM  2  1 . Dấu bằng khi M là giao điểm của C  và OA : y  x  x   y   M M 2  2 2  2    2 2  x   x  (chọn điểm xa O hơn).
x   y   M  1  M 1 1 M 2 M 2  Chọn A.
Câu 17. Giả sử M là điểm biểu diễn số phức z . Xét điểm F 2; 0 và E 1;  1  EM  2
Tập hợp điểm M là các điểm không nằm ngoài đường tròn C  tâm E bán kính R  2 Ta có: 2 2
FE  EM  MF  FE  EM  10  2  MF  10  2  A  B  24 . Chọn C.
Câu 18. Giả sử M là điểm biểu diễn số phức z . Xét điểm F 0;  1 và E  1  ;  2  EM  2 5
Tập hợp điểm M là các điểm không nằm ngoài đường tròn C  tâm E bán kính R  2 5
Ta có: FE  EM  MF  FE  EM  2 5  10  MF  2 5  10  AB  10 . Chọn A. i  i    
Câu 19. Ta có z   i 1 2 1 3 1
 1  2i  2  z 
 z      2   1  i 2 2     
Giả sử M là điểm biểu diễn số phức z . Xét điểm F 1; 1 3
3 và E  ;   EM  2 2 2
Tập hợp điểm M là các điểm không nằm ngoài đường tròn C  tâm E bán kính R  2 3 10 3 10 Ta có: 2 2
FE  EM  MF  FE  EM   2  MF 
 2  2A  B  64 . 2 2 Chọn C.  2 2 a   2  sin x 
Câu 20: Giả sử a  bi  2  3i  1  a  2  b  3  1   b   3  cosx  2 2 2 2 2 2
Ta có z  i  1  a bi  i  1  a   1  b  
1  3  sinx  2  cosx    x  x     2 2   2 2 14 2 3 sin 2 cos 14 2 3 2
sin x  cos x  14  2 13  z  i  1  1  13. Chọn A
Tổng hợp các chuyên đề luyện thi đại học Trang 98
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna 2 2 2 2
Câu 21: Ta có a  bi  i  1  a bi  4i  2  a   1  b  
1  a  2  b  4
 2  2a  2b  20  4a  8b  2a  6b  18  0  a  3  b  9. 2 2 2 2 2 2
Khi đó z  2i  1  a  bi  2i  1  a  
1  b  2  3b  8  b  2 2  22    98 98 7 10 2
 10b  44b  68  b  10    
 z  2i  1  .   Chọn C     5 5 5 10
Câu 22: Tập hợp điểm biểu diễn số phức z là đường tròn tâm I 3;4 bán kính R  2 Khi đó A  z
 OI  R  5  2  7 ; B  z
 OI  R  3 max min
Suy ra P  43 . Chọn A.
Câu 23: Tập hợp điểm biểu diễn số phức z là đường tròn tâm I 1;  1 bán kính R  2 Gọi K 2; 
1 khi đó A  z  2  i
 IK  R  5  2 ; B  5  2 max Do đó 2
P  2A  B  8 . Chọn C. 1  i Câu 24: Ta có:
z  1  i  2  iz  1  i  2  i . z  1  i  2  z  1  i  2 1  i
Tập hợp điểm biểu diễn số phức z là đường tròn tâm I 1;  1 bán kính R  2 Gọi K 2;  1 suy raA
 IK  R  5 . Chọn D. max 1  iz 2  1 1  i i  Câu 25:  2  1  z 
 1  z  2i  1 1  i 1  i 1  i
Tập hợp điểm biểu diễn số phức z là đường tròn tâm I 0;2 bán kính R  1 Ta có: z
 OI  R  1 . Chọn A. min
Câu 26: Tập hợp điểm biểu diễn số phức z là đường tròn tâm I 2; 3 bán kính R  1.
Gọi z  x  yi  z  1  i  x  1  yi  i  x   1  y  
1 i . Gọi K 1;  1
Do đó z  1  i
 IK  R  1  13 . Chọn D. max
Câu 27: Ta có: z  2i  z  1  2i  1  iz  2  2i  1  iz  1  3i
 w  4  2i  w  1  3i . Gọi A4;2;B 1;3 và M w suy ra MA  MB nên tập hợp điểm
M là trung trực của AB có PT là: 3x  5y  5  0 d 5
Ta có: w  OM  OM  d O;d  min   . Chọn B. 34
Câu 28: Đặt z  x  yi x,y    M  x;y A1;  1 , B 2;  3 AB  5. z  và suy ra   Từ giả thiết ta có
z   i  z   i  x  2  y  2  x  2  y  2 1 2 3 1 1 2
3  MA  MB  AB.  M 
thuộc đường thẳng AB : 2x  y  1  0  y  2x 1 với x   2;1   .  
Tổng hợp các chuyên đề luyện thi đại học Trang 99
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna 2  2  Khi đó 2
P  x z  x x   x   3 2 . . 2
1   5x  4x  x . Đặt f x 3 2
 5x  4x  x .     
Xét hàm số f x  trên đoạn 2;1 
 , có f x 2 '
 15x  8x  1  0; x   2;1   .        M   f   1  2
Suy ra f x  là hàm số đồng biến trên 2;1    
 M  2m  54. Chọn A  m   f   2  26 
z  2 i 5  Câu 29 : Ta có 2 1
z  4z  9  0  
. Suy ra M 2; 5,N 2; 5 MN  2 5 .
z  2  i 5 2  Chọn C
Câu 30 : Gọi M x;y với x,y   thì M là điểm biểu diễn cho số phức w  x  yi   x   3 yi     1  2 3 i x yi
 x 2y 3 2x y 6 
Ta có w  1  2iz  3  z     i 1  2i 5 5 5 Theo giả thuyết x  2y  7 2x  y  6 z  2  5  
i  5  x  2y  72  2x  y  62  625 5 5 2 2 Suy ra x  
1  y  4  125 . Chọn A.
Tổng hợp các chuyên đề luyện thi đại học Trang 100
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
E. DẠNG LƯỢNG GIÁC CỦA SỐ PHỨC I. LÝ THUYẾT
1. Acgumen của số phức
Gọi M là một điểm trong mặt phẳng phức biểu diễn số phức z . Số đo (radian) của mỗi
góc lượng giác tia đầu là Ox , tia cuối OM được gọi là một acgumen của z .
Như vậy nếu  là một acgumen của z , thì mọi acgumen đều có dạng: +2k,kZ.
2. Dạng lượng giác của số phức
Xét số phức z = a + bi  0 (a,b  ) .
Dạng lượng giác có dạng: z  r(cos   i sin ) trong đór  0 .
Để chuyển một số phức sang dạng lượng giác ta cần tìm r và ;
o Ta có : r  z  a  o c s   r
o  là số thực thoả mãn :  .  b sin     r
3. Nhân và chia số phức dưới dạng lượng giác
Nếu z = r(cos +isin) ; z ' = r’(cos’ +isin’) (r ≥ 0, r’ ≥ 0) thì:
z.z’ = r.r[cos( +’) +isin( +’)] z r  os
c   '+i sin  '    ;khi r    0 z ' r ' 
4. Công thức Moivre
[z = r(cos +isin)]n = rn(cos n +isin n)
5. Căn bậc hai của số phức dưới dạng lượng giác
Cho số phức z = r(cos +isin) (r>0)     
Khi đó z có hai căn bậc hai là: r c  os  isin  và  2 2                     - r c  os  isin  = r c
 os    isin               2 2    2   2  
Tổng hợp các chuyên đề luyện thi đại học Trang 101
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
II. MỘT SỐ BÀI TOÁN ĐIỂN HÌNH Bài toán 1
Viết các số phức sau dưới dạng lượng giác: 1 3 5 3 5
a. z  6  6i b. z    i c. z   i 1 2 4 4 3 2 2 Giải: a) Ta có: 2 2 r  6  6  6 2. 1  1  os c      
Chọn  là số thực thoả mãn 2    
 z  6 2(cos  s i n i ) .  2 1 4 4 4 sin     2 2 2  1      3  1 b) Ta có r =           . 2  4   4  2    1  os c     2 2 2 Chọn 2
 là số thực thoả mãn     z  ( 12 cos  isin ).  3 2 3 3 3 si  n   2 2 2 5 3 5       c)Ta có: r       5 . 3  2      2  3  os c          
Chọn  là số thực thoả mãn 2    
 z  5cos  i sin  .  1 3 6  6 6  sin     2 Bài toán 2
Viết các số phức sau dưới dạng lượng giác: 1  i 3 1
a)(1  i)1  i b) c) 1  i 2  2i Giải:               
a) Ta có: 1  i 3  2 os c     isin           1  i      ; 2 cos i sin   3   3      4 4  
Áp dụng công tthức nhân, chia số phức ta được:          
(1  i 3 )1  i  2 2 os c     isin              12  12    1i 3   7  7       b) = 2 cos     isin                 1i 12  12   
Tổng hợp các chuyên đề luyện thi đại học Trang 102
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna      1 1 1              2        c) = (1  i) = 2 o c s     isin                    = o c s isin .             2  2i 4 4 4  4         2 4  4    Bài toán 3
Tìm phần thực và phần ảo của mỗi số phức sau: 10 (1  i)      a) b) 5 7  o c s
 i sin i (1  3i)      3  i9  3 3  Giải: a) Xét số phức: 10         5 5  5 2  os- c  i sin  2      os- c  i sin    10 (1  i)  4 4     12 12         3  i9 9    3 3 9         2  os c  i sin  2 os c i sin         2 2   6 6     1 1    4 2 ( os
c   i sin ) 16 1
Vậy: phần thực bằng:  và phần ảo bằng 0. 16 b) Xét số phức:      5 7  o c s
 i sin i (1  3i)  3 3  7             os c
 i sin i 2 os c  i sin   3 3       3 3                  7 7  7  2  os c     i sin     i       os c  i sin                  . 3 3     3 3      7 7 2  os c 2 i sin 2   i  2 i.  
Vậy: phần thực bằng: 0 và phần ảo bằng 128. Bài toán 4
(1  i)  3  i5 10 Tính số phức sau: z =  1   i 310 Giải: 10                  2 5 10 5  os c     i sin     2       os c  i sin     4     4      6 6  z  10    10 4 4 2  os c  isin   3 3 
Tổng hợp các chuyên đề luyện thi đại học Trang 103
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna                 10 10 10 5 5 2  os c     i sin         os c  i sin     4     4     6 6      10 40 40 2  os c  isin   3 3   5    5 o c s     i sin      3     3    cos( 15
 p)  isin(15p)   1. 40 40 os c  isin 3 3
Tổng hợp các chuyên đề luyện thi đại học Trang 104
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
III. SỬ DỤNG MÁY TÍNH CASIO 570VN-PLUS ĐỂ GIẢI PP CASIO
Đưa máy tính về dạng rađian qw4
Để chuyển một số phức từ dạng đại số sang dạng lượng giác, trong chế độ CMPLX ta bấm q2 và chọn 3
Để chuyển một số phức từ dạng đại số sang dạng lượng
giác, trong chế độ CMPLX ta bấm q2 và chọn 4 Bài toán 1
Viết số phức z  7  7i dưới dạng lượng giác. Hướng dẫn:
o Đưa máy tính về dạng rađian qw4 o Vào chế độ CMPLX w2 o Nhập số phức z: 7+7b.
o Nhấn q23 để chuyển sang dạng lượng giác.
o Kết quả thu được là: 
Số phức z đã được chuyển sang dạng lượng giác với r  7 2 và acgument là   4                 z  7 2 o c s   isin               .    4  4      Bài toán 2        
Viết số phức z= 2 (cos    + isin  
 ) dưới dạng đại số.  4  4 Hướng dẫn:
o Đưa máy tính về dạng rađian qw4 o Vào chế độ CMPLX w2
o Nhập số phức z ở dạng lượng giác và chuyển số phức qua dạng đại số như sau: s2$qzpaqKR4$q24=
o Màn hình cho kết quả là:
Tổng hợp các chuyên đề luyện thi đại học Trang 105
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna Bài toán 3 5  3i 3 Số phức z  có một Acgument là : 1  2i 3    8 A. B. C. D. 6 4 2 3 Hướng dẫn:
 Thu gọn z về dạng tối giản  z  1  3i a5+3bs3R1p2bs3=
 Tìm Acgument của z với lệnh SHIFT 2 1 q21p1+s3$b)= 2
Vậy z có 1 Acgument là
. Tuy nhiên khi so sánh kết quả ta lại không thấy có giá trị nào là 3
2 . Khi đó ta nhớ đến tính chất “Nếu góc  là một Acgument thì góc  2 cũng là một 3 Acgument” 2 8
 Đáp số chính xác là D vì  2  2 3
Tổng hợp các chuyên đề luyện thi đại học Trang 106
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
IV. MỘT SỐ BÀI TOÁN VỀ ỨNG DỤNG CỦA DẠNG LƯỢNG GIÁC Bài toán 1 Giải phương trình: 5 4 3 2
z  z  z  z  z  1  0   1 Giải: 4 2
Ta có: (1)  z z  
1  z z   1  z   1  0  z   4 2
1 z  z  1  0 z  1    4 2
z  z  1  0  1   3i Xét phương trình: 4 2
z  z  1  0  z2 = 2  1 3 2 2  2 z    i  os c  i sin  2 2 3 3    1 3  2     2 2 z    i  os c     i sin      2 2  3     3       2 2 z  os c  i sin  Từ z2 = os c  i sin  3 3  3 3    z   os c -i sin   3 3                    z os c i sin 2   2             3   3 Từ z2 = cos     i sin       3     3          z  c  os   -i sin         3     3  
Tóm lại phương trình đã cho có tất cả 5 nghiệm: 1 3 1 3 1 3 1 3
z  1 ; z  
i ; z    i ; z  
i ; z    i . 2 2 2 2 2 2 2 2 Bài toán 2 Cho z z z  1  i z  1 – i
1 và 2 là hai số phứ xác định bởi 1 và 2
. Xác định dạng đại số và z 7 7
dạng lượng giác của 1 . Từ đó suy ra giá trị chính xác của: cos và sin . z 12 12 2 Giải: z 1  i 3 1 3 1 3     Ta có: 1 = =  i     . z 1  i 2  2  2             z 7 7 Ta có: z 1 1 = 2(cos + isin ); z2 = 2 (cos    + isin    ) = 2 (cos + isin )  3     3  4   4  z 12 12 2 7 1  3 7 1  3 cos = và sin = . 1 2 2 1 2 2
Tổng hợp các chuyên đề luyện thi đại học Trang 107
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
Nhận xét: Qua bài tập này ta thấy được một ứng dụng quan trọng của số phức, ta có thể tính
sin, cos của một góc bằng công cụ số phức thông qua sự liên hệ giữa dạng đại số và dạng
lượng giác của số phức. Bài toán 3 Giải phương trình: 6 z  64  0 . Giải: Ta có: : 6 6
z  64  0  z  64  .
Giả sử z  x  yi  r c ( os  i sin) Ta có: 6  4  64 c ( os  i sin)
Và cos6  + isin6  = cos  + isin   6  =  +2k  (k  Z)     =  2k 6 6     
Với k  0  z  2  o c s  isin  = 3 +i 1  6 6               Với k  1   z  2  os
c -   isin         3      = -i 1   6   6       
Với k  1  z  2  os c  isin  = 2i 1  2 2               Với k  2   z  2  os
c -   isin              = -2i 1   2   2      5     5      Với k  3   z  2  o c s-   isin -       3      = - - i. 1   6   6   Bài toán 4 n
Tìm n là số nguyên dương và n 1  ,10 
sao cho số phức z  1  i 3 là số thực.   Giải:       n n    Ta có: 1 + i 3 = 2 o c s  i sin   z = 2n os c  i sin   3 3   3 3  n n Để z  R  2n.sin = 0  sin = 0 3 3
 n chia hết cho 3, mà n nguyên dương  [1;10]  n  [3;6;9].
Tổng hợp các chuyên đề luyện thi đại học Trang 108
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna V. BÀI TẬP RÈN LUYỆN
Câu 1: Số phức z = -1 + i viết dưới dạng lượng giác là:            A. z = 2cos  i sin  B. z = 2 cos  isin   6 6   4 4   3 3        C. z = 2 cos  i sin  D. z = 3 cos  i sin   4 4   6 6 
Câu 2: Số phức z = 8i viết dưới dạng lượng giác là:  3 3         A. z = 8 cos  i sin  B. z = 8 cos  i sin   2 2   2 2 
C. z = 8cos 0  i sin 0
D. z = 8cos   i sin       
Câu 3: Dạng lượng giác của số phức z = 2 cos  i sin  là:  6 6   11 11     7 7   A. z = 2 cos  i sin  B. z = 2 cos  i sin   6 6   6 6   5 5     13 13    C. z = 2 cos  i sin  D. 2 cos  i sin   6 6   6 6 
Câu 4: : Số phức z = 8i viết dưới dạng lượng giác là:           A. 8 2 cos  i sin  B. 8 2 cos  i sin   6 6   4 4               C. 6 2 cos  i sin  D. 6 2 cos  i sin   5 5   7 7 
Câu 6: Cho số phức z = - 1 - i. Argumen của z (sai khác k2) bằng:  3 5 7 A. B. C. D. 4 4 4 4
Câu 7: Điểm biểu diễn của số phức z =  0 0
2 cos 315  i sin 315  có toạ độ là: A. (1; -1) B. (-1; 1) C. (2; 2) D. (-2; 2)
Câu 8: Cho z  3 0 0 cos15  i sin15 z  4 0 0 cos 30  i sin 30 2  1 , . Tích z1.z2 bằng: A. 12(1 - i) B. 6 2 1  i C. 3 2 1  2i D. 2 2  i
Câu 9: Cho z  3 0 0 cos 20  i sin 20 z  2 0 0 cos110  i sin110 2  1  , . Tích z1.z2 bằng: A. 6(1 - 2i) B. 4i C. 6i D. 6(1 - i) z
Câu 10: Cho z  8 0 0 cos100  i sin100 z  4 0 0 cos 40  i sin 40 1 2  1 , .Thương bằng: z2 A. 1 + i 3 B. 21  i 3 C. 1 - i 3 D. 2(1 + i) z
Câu 11: Cho z  4 0 0 cos10  i sin10 z  2   0 0 cos 280  i sin 280 1 2  1 , . Thương bằng: z2 A. 2i B. -2i C. 2(1 + i) D. 2(1 - i)
Câu 12: Tính (1 - i)20, ta được:
Tổng hợp các chuyên đề luyện thi đại học Trang 109
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna A. -1024 B. 1024i C. 512(1 + i) D. 512(1 - i)
Câu 13: Đẳng thức nào trong các đẳng thức sau đây là đúng? A. (1+ i)8 = -16 B. (1 + i)8 = 16i C. (1 + i)8 = 16 D. (1 + i)8 = -16i
Câu 14: Cho số phức z  0. Biết rằng số phức nghịch đảo của z bằng số phức liên hợp của nó.
Trong các kết luận nào đúng: A. z  R
B. z là một số thuần ảo C. z  1 D. z  2
Câu 15: Cho số phức z = cos + isin . kết luận nào sau đây là đúng: A. n   n z
z   n cos B. n   n z
z   2 cosn C. n   n z
z   2n cos D. n   n z
z   2 cos . Đáp án: 1. C 2. B 3. D 4. B 5. 6. C 7. A 8. B 9. C 10. A 11. B 12. A 13. C 14. C 15. B
Tổng hợp các chuyên đề luyện thi đại học Trang 110
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
F. TUYỂN TẬP CÁC CÂU SỐ PHỨC VẬN DỤNG CAO I. ĐỀ BÀI
Câu 1. Cho các số phức z ,z khác nhau thỏa mãn: z  z . Chọn phương án đúng: 1 2 1 2 z  z z  z A. 1 2  0 B. 1
2 là số phức với phần thực và ảo đều khác 0 z  z z  z 1 2 1 2 z  z z  z C. 1 2 là số thực D. 1
2 là số thuần ảo z  z z  z 1 2 1 2
Câu 2. Cho số phức z thỏa mãn điều kiện z  3  4i  2. Trong mặt phẳng Oxy tập hợp điểm
biểu diễn số phức w  2z  1  i là hình tròn có diện tích
A. S  9 .
B. S  12 .
C. S  16 .
D. S  25 .
Câu 3. Trong các số phức thỏa mãn điều kiện z  3i  z  2  i . Tìm số phức có môđun nhỏ nhất? 1 2 1 2
A. z  1  2i .
B. z    i . C. z   i .
D. z  1   2i . 5 5 5 5
Câu 4. Cho số phức z thỏa mãn z  2  3i  1. Giá trị lớn nhất của z  1  i là A. 13  2 . B. 4 . C. 6 . D. 13  1.
Câu 5. Cho z , z , z là các số phức thỏa mãn z  z  z  0 và z  z  z  1. Khẳng 1 2 3 1 2 3 1 2 3
định nào dưới đây là sai ? A. 3 3 3 3 3 3
z  z  z  z  z  z . B. 3 3 3 3 3 3
z  z  z  z  z  z . 1 2 3 1 2 3 1 2 3 1 2 3 C. 3 3 3 3 3 3
z  z  z  z  z  z . D. 3 3 3 3 3 3
z  z  z  z  z  z . 1 2 3 1 2 3 1 2 3 1 2 3
Câu 6. Cho z ,z ,z là các số phức thỏa z  z  z  1. Khẳng định nào dưới đây là đúng? 1 2 3 1 2 3
A. z  z  z  z z  z z  z z .
B. z  z  z  z z  z z  z z . 1 2 3 1 2 2 3 3 1 1 2 3 1 2 2 3 3 1
C. z  z  z  z z  z z  z z .
D. z  z  z  z z  z z  z z . 1 2 3 1 2 2 3 3 1 1 2 3 1 2 2 3 3 1
Câu 7. Cho P z là một đa thức với hệ số thực.Nếu số phức z thỏa mãn P z   0 thì 1   1  
A. P  z   0.
B. P    0.  P    0. P z   C. D.   0. z  z  2z  i
Câu 8. Cho số phức z thỏa mãn z  1. Đặt A 
. Mệnh đề nào sau đây đúng? 2  iz A. A  1 . B. A  1 . C. A  1 . D. A  1 . 5i
Câu 9. Cho số phức z thỏa mãn z  1 . Tìm giá trị lớn nhất của biểu thức A  1  . z A. 5. B. 4. C. 6. D. 8.
Tổng hợp các chuyên đề luyện thi đại học Trang 111
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
z  2z  3i
Câu 10. Gọi M là điểm biểu diễn số phức  
, trong đó z là số phức thỏa mãn 2 z  2  
2  iz  i  3 i  z . Gọi N là điểm trong mặt phẳng sao cho Ox,ON  2 , trong  
đó   Ox,OM  là góc lượng giác tạo thành khi quay tia Ox tới vị trí tia OM . Điểm N
nằm trong góc phần tư nào? A. Góc phần tư thứ (I).
B. Góc phần tư thứ (II).
C. Góc phần tư thứ (III).
D. Góc phần tư thứ (IV).
Câu 11. Cho số phức z thỏa mãn z  1 . Tìm giá trị lớn nhất M
và giá trị nhỏ nhất M của max min biểu thức 2 3
M  z  z  1  z  1 . A. M  5; M  1. B. M  5; M  2. max min max min C. M  4; M  1. D. M  4; M  2. max min max min z  2
Câu 12. Cho số phức z thỏa
. Tìm tích của giá trị lớn nhất và nhỏ nhất của biểu thức z  i P  . z 3 2 A. . B. 1. C. 2 . D. . 4 3 4  z 1    
Câu 13. Gọi z , z , z , z là các nghiệm của phương trình 
  1. Tính giá trị biểu thức 1 2 3 4
2z i P   2 z   1  2 z   1  2 z   1  2
z  1 . 1 2 3 4  17 16 15
A. P  2. B. P  . C. P  . D. P  . 9 9 9
Câu 14. Cho số phức z thỏa mãn z  1  2i  3 . Tìm môđun lớn nhất của số phức z  2i. A. 26  6 17 . B. 26  6 17 . C. 26  8 17 . D. 26  4 17 .
Câu 15. Cho số phức z thỏa mãn z  1 . Tìm giá trị lớn nhất của biểu thức P  1  z  3 1  z . A. 3 15 B. 6 5 C. 20 D. 2 20.
Câu 16. Cho số phức z thỏa mãn z  1. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 2
P  z  1  z  z  1 . Tính giá trị của M.m . 13 3 39 13 A. . B. . C. 3 3. D. . 4 4 4 1  i
Câu 17. Gọi điểm ,
A B lần lượt biểu diễn các số phức z và z 
z; z  0 trên mặt phẳng 2 tọa độ ( , A ,
B C và A , B , C  đều không thẳng hàng). Với O là gốc tọa độ, khẳng
định nào sau đây đúng?
Tổng hợp các chuyên đề luyện thi đại học Trang 112
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
A. Tam giác OAB đều.
B. Tam giác OAB vuông cân tại O.
C. Tam giác OAB vuông cân tại B.
D. Tam giác OAB vuông cân tại . A
Câu 18. Cho số phức z thỏa mãn điều kiện 2
z  4  2 z . Khẳng định nào sau đây là đúng? 3  1 3  1 A.  z  .
B. 5  1  z  5  1. 6 6 2  1 2  1
C. 6  1  z  6  1. D.  z  . 3 3
Câu 19. Cho số phức z thỏa mãn z  1  2i  2 . Tìm môđun lớn nhất của số phức z. A. 9  4 5. B. 11  4 5 C. 6  4 5 D. 5  6 5 Câu 20. Cho , A ,
B C, D là bốn điểm trong mặt phẳng tọa độ theo thứ tự biểu diễn các số phức
1  2i; 1  3  i; 1  3  i; 1  2i . Biết ABCD là tứ giác nội tiếp tâm I. Tâm I biểu
diễn số phức nào sau đây? A. z  3.
B. z  1  3i. C. z  1. D. z  1. 2
Câu 21. Trên mặt phẳng tọa độ Ox ,
y lấy điểm M là điểm biểu diễn số phức z  2  i 4  i 
và gọi  là góc tạo bởi chiều dương trục hoành và vectơ OM. Tính cos 2 .  425 475 475 425 A.  . B. . C.  . D. . 87 87 87 87 z
Câu 22. Cho z , z là hai số phức liên hợp của nhau và thỏa mãn 1   và z  z  2 3. 1 2 2 z 1 2 2
Tính môđun của số phức z . 1 5 A. z  5. B. z  3. C. z  2. D. z  . 1 1 1 1 2 m 2 6i   
Câu 23. Cho số phức z  
 , m nguyên dương. Có bao nhiêu giá trị m 1  ;50    để là
 3  i   z số thuần ảo? A. 24. B. 26. C. 25. D. 50. 2 z  1
Câu 24. Nếu z  1 thì z
A. lấy mọi giá trị phức. B. là số thuần ảo. C. bằng 0.
D. lấy mọi giá trị thực.
Câu 25. Cho số phức z thỏa mãn 1  iz  6  2i  10 . Tìm môđun lớn nhất của số phức z. A. 4 5 B. 3 5. C. 3. D. 3  5
Tổng hợp các chuyên đề luyện thi đại học Trang 113
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna 2 2
Câu 26. Gọi z  x  yi x,y   là số phức thỏa mãn hai điều kiện z  2  z  2  26 và 3 3 z   i xy.
đạt giá trị lớn nhất. Tính tích 2 2 9 13 16 9 A. xy  . B. xy  . C. xy  . D. xy  . 4 2 9 2 z  1 z  i
Câu 27. Có bao nhiêu số phức z thỏa  1 và  1? i  z 2  z A. 1. B. 2. C. 3. D. 4.
Câu 28. Gọi điểm ,
A B lần lượt biểu diễn các số phức z ; z ; z .z  0 2  1 2
 trên mặt phẳng tọa độ 1 ( , A ,
B C và A , B , C  đều không thẳng hàng) và 2 2
z  z  z .z . Với O là gốc tọa độ, 1 2 1 2
khẳng định nào sau đây đúng?
A. Tam giác OAB đều.
B. Tam giác OAB vuông cân tại O.
C. Tam giác OAB vuông cân tại B.
D. Diện tích tam giác OAB không đổi.
Câu 29. Trong các số phức thỏa mãn điều kiện z  2  4i  z  2i . Tìm môđun nhỏ nhất của số phức z  2 . i A. 5 B. 3 5. C. 3 2 D. 3  2
Câu 30. Tìm điều kiện cần và đủ về các số thực m, n để phương trình 4 2
z  mz  n  0 không có nghiệm thực.  2 m   4n  0  A. 2 m  4n  0. B. 2
m  4n  0 hoặc m   0 n   0   2 m   4n  0   2 m   4n  0     C. m   0 . D. 2
m  4n  0 hoặc m   0   n   0   n   0   2 z  a
Câu 31. Nếu z  a; a  0 thì z
A. lấy mọi giá trị phức. B. là số thuần ảo. C. bằng 0.
D. lấy mọi giá trị thực.
Câu 32. Cho số phức z thỏa mãn z  1  2i  3 . Tìm môđun nhỏ nhất của số phức z 1  i. A. 4. B. 2 2. C. 2. D. 2.
2z  z  1  i
Câu 33. Gọi M là điểm biểu diễn số phức  
, trong đó z là số phức thỏa mãn 2 z  i  
1iz i  2 i  z . Gọi N là điểm trong mặt phẳng sao cho Ox,ON  2, trong
Tổng hợp các chuyên đề luyện thi đại học Trang 114
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna  
đó   Ox,OM  là góc lượng giác tạo thành khi quay tia Ox tới vị trí tia OM . Điểm
N nằm trong góc phần tư nào? A. Góc phần tư thứ (I).
B. Góc phần tư thứ (II).
C. Góc phần tư thứ (III).
D. Góc phần tư thứ (IV).
Câu 34. Biết số phức z thỏa mãn đồng thời hai điều kiện z  3  4i  5 và biểu thức 2 2
M  z  2  z  i đạt giá trị lớn nhất. Tính môđun của số phức z  i.
A. z  i  2 41
B. z  i  3 5.
C. z  i  5 2
D. z  i  41. Câu 35. Các điểm , A ,
B C và A , B , C  lần lượt biểu diễn các số phức z , z , z và z , z , z  1 2 3 1 2 3
trên mặt phẳng tọa độ ( , A ,
B C và A , B , C  đều không thẳng hàng). Biết
z  z  z  z   z   z  , khẳng định nào sau đây đúng? 1 2 3 1 2 3
A. Hai tam giác ABC và AB C   bằng nhau.
B. Hai tam giác ABC và AB C
  có cùng trực tâm.
C. Hai tam giác ABC và AB C
  có cùng trọng tâm.
D. Hai tam giác ABC và AB C
  có cùng tâm đường tròn ngoại tiếp.
Câu 36. Trên mặt phẳng tọa độ Ox ,
y lấy điểm M là điểm biểu diễn số phức z  2  3i1  i 
và gọi  là góc tạo bởi chiều dương trục hoành và vectơ OM. Tính sin 2 .  5 5 12 12 A.  . B. . C. . D.  . 12 12 5 5 m   i
Câu 37. Cho số phức z 
m   . Tìm môđun lớn nhất của . z
 m m  i, 1 2 1 A. 1. B. 0. C. . D. 2. 2 1
Câu 38. Cho số phức z có z  m; m  0 . Với z  m; tìm phần thực của số phức . m  z 1 1 1 A. . m B. . C. .D. . m 4m 2m
Câu 39. Cho số phức z , z thỏa mãn z  3 , z  2 được biểu diễn trong mặt phẳng phức 1 2 1 2    z  z
lần lượt là các điểm M,N . Biết OM,ON   , tính giá trị của biểu thức 1 2 . 6 z  z 1 2 7 3 1 A. 13 B. 1 C. D. 2 13
Tổng hợp các chuyên đề luyện thi đại học Trang 115
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
Câu 40. Cho thỏa mãn z   thỏa mãn   i 10 2 z 
 1  2i . Biết tập hợp các điểm biểu z
w  3  4iz  1  2i I R diễn cho số phức
là đường tròn , bán kính . Khi đó.
A. I  1  ; 2  ,R  5.
B. I 1;2,R  5.
C. I 1;2,R  5.
D. I 1;2,R  5.
Câu 41. Trong các số phức z thỏa z  3  4i  2 , gọi z là số phức có mô đun nhỏ nhất. Khi đó 0
A. Không tồn tại số phứcz .
B. z  2 . 0 0
C. z  7 .
D. z  3 . 0 0
Câu 42. Tìm tập hợp các điểm M biểu diễn hình học số phức z trong mặt phẳng phức, biết số
phức z thỏa mãn điều kiện: z  4  z  4  10.
A. Tập hợp các điểm cần tìm là đường tròn có tâm O 0; 0 và có bán kính R  4. . 2 2 x y
B. Tập hợp các điểm cần tìm là đường elip có phương trình   1. 9 25
C. Tập hợp các điểm cần tìm là những điểm M x;y trong mặt phẳng Oxy thỏa mãn 2 2
phương trình x   2
 y  x   2 4 4  y  12. 2 2 x y
D. Tập hợp các điểm cần tìm là đường elip có phương trình   1. 25 9
Câu 43. Trong mặt phẳng phức Oxy , các số phức z thỏa z  2i  1  z  i . Tìm số phức z
được biểu diễn bởi điểm M sao cho MA ngắn nhất với A1, 3. A. 3  i . B. 1  3i . C. 2  3i . D. 2   3i .
Câu 44. Trong mặt phẳng phức Oxy , tập hợp biểu diễn số phức Z thỏa 1  z  1  i  2 là hình
vành khăn. Chu vi P của hình vành khăn là bao nhiêu ?
A. P  4 .
B. P   .
C. P  2 .
D. P  3 .
Câu 45. Trong mặt phẳng phức Oxy , tập hợp các điểm biểu diễn số phức Z thỏa mãn z  z2 2 2
 2 z  16 là hai đường thẳng d ,d . Khoảng cách giữa 2 đường thẳng d ,d 1 2 1 2 là bao nhiêu ?
A. d d ,d  2
d d ,d  4
d d ,d  1
d d ,d  6 1 2  1 2  1 2  1 2  . B. . C. . D. .
Câu 46. Cho số phức z thỏa mãn 2
z  2z  5  z  1  2iz  3i  1 .Tính min | w |, với
w  z  2  2i . 3 1
A. min | w | .
B. min | w | 2 .
C. min | w | 1 .
D. min | w | . 2 2
Tổng hợp các chuyên đề luyện thi đại học Trang 116
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna  Câu 47. Giả sử ,
A B theo thứ tự là điểm biểu diễn của số phức z , z . Khi đó độ dài của AB 1 2 bằng
A. z  z .
B. z  z .
C. z  z .
D. z  z . 2 1 2 1 1 2 1 2
Câu 48. Cho số phức z thỏa mãn điều kiện z  1  2 . Tìm giá trị lớn nhất của
T  z  i  z  2  i .
A. maxT  8 2 .
B. maxT  4 .
C. maxT  4 2 .
D. maxT  8 .
Câu 49. Trên mặt phẳng tọa độ Oxy , tìm tập hợp các điểm biểu diễn các số phức z thỏa mãn
điều kiện z  2  z  2  10 . 2 2 2 2 x y
A. Đường tròn x  2  y  2  100 . B. Elip   1 . 25 4 2 2 2 2 x y
C. Đường tròn x  2  y  2  10 . D. Elip   1 . 25 21
z 1  z  i 
Câu 50. Tìm nghiệm phức z thỏa mãn hệ phương trình phức:  z  3i   1  z  i 
A. z  2  i .
B. z  1  i .
C. z  2  i .
D. z  1  i .
Tổng hợp các chuyên đề luyện thi đại học Trang 117
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
II. ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI CHI TIẾT 1D 2C 3C 4D 5D 6A 7D 8A
9C 10A 11A 12A 13B 14A 15D
16A 17C 18B 19A 20C 21D 22C 23C 24B 25B 26D 27A 28A 29C 30D
31B 32C 33B 34D 35C 36A 37A 38D 39B 40C 41D 42D 43A 44C 45B 46C 47B 48B 49D 50D Câu 1.
Phương pháp tự luận:
Vì z  z và z  z nên cả hai số phức đều khác 0 . 1 2 1 2 z  z Đặt 1 2 w 
và z  z  a , ta có z  z 1 2 1 2 2 2 a a  z z     z  z z z z  z 1 2 1 2 1 2 1 2 w          w  2 2
z  z  z  z a a z  z 1 2 2 1 2 1  z z 1 2
Từ đó suy ra w là số thuần ảo
Phương pháp trắc nghiệm: z  z 1  i Số phức z ,z z  z
z  1;z  i 1 2   i 1 2 khác nhau thỏa mãn 1 2 nên chọn , suy ra 1 2 z  z 1  i 1 2
là số thuần ảo  Chọn D. w  1  i
Câu 2. w  2z  1  i  z  2 w  1  i
z  3  4i  2 
 3  4i  2  w  1  i  6  8i  4  w  7  9i  4   1 2 2 2
Giả sử w  x  yi x,y   , khi đó  
1  x  7  y   9  16
Suy ra tập hợp điểm biểu diễn số phức w là hình tròn tâm I 7; 
9 , bán kính r  4.
Vậy diện tích cần tìm là 2 S  .4 
 16  Chọn C. Câu 3.
Phương pháp tự luận
Giả sử z  x  yi x,y  
z  i  z   i  x  y  i  x    y  i  x  y  2  x  2  y  2 2 3 2 3 2 1 3 2 1
 6y  9  4x  4  2y  1  4x  8y  4  0  x  2y  1  0  x  2y  1 2  
z  x  y  2y  2 2   1 5 2 2 2 2
1  y  5y  4y  1  5 y       5 5 5
Tổng hợp các chuyên đề luyện thi đại học Trang 118
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna 5 2 1 1 2 Suy ra z 
khi y    x  .Vậy z 
 i.  Chọn C. min 5 5 5 5 5
Phương pháp trắc nghiệm
Giả sử z  x  yi x,y  
z  i  z   i  x  y  i  x    y  i  x  y  2  x  2  y  2 2 3 2 3 2 1 3 2 1
 6y  9  4x  4  2y  1  4x  8y  4  0  x  2y  1  0
Vậy tập hợp các điểm biểu diễn số phức z thỏa điều kiện z  3i  z  2  i là đường thẳng
d : x  2y  1  0 .
Phương án A: z  1  2i có điểm biểu diễn 1; 
2  d nên loại A. 1 2  1 2  
Phương án B: z    i có điểm biểu diễn   ;   d   nên loại B. 5 5  5 5 Phương án D: z  1
  2i có điểm biểu diễn 1; 
2  d nên loại B. 1 2 1 2   Phương án C: z 
 i có điểm biểu diễn  ;   d   5 5 5 5
Câu 4. Gọi z  x  yi ta có z  2  3i  x  yi  2  3i  x  2  y  3i . 2 2
Theo giả thiết x  
2  y  3  1 nên điểm M biểu diễn cho số phức z nằm trên đường
tròn tâm I 2; 3 bán kính R  1. 2 2
Ta có z  1  i  x  yi  1  i  x  1  1  yi  x   1  y   1 .
Gọi M x;y và H 1; 
1 thì HM  x    y  2 2 1 1 .
Do M chạy trên đường tròn, H cố định nên MH lớn nhất khi M là giao của HI với đường tròn. x   2  3t 
Phương trình HI : 
, giao của HI và đường tròn ứng với t thỏa mãn: y   3  2t  1  3 2     3 2  2 2
9t  4t  1  t     nên M 2   ; 3  ,M 2   ; 3         . 13  13 13   13 13 
Tính độ dài MH ta lấy kết quả HM  13  1  Chọn D Câu 5.
Cách 1: Ta có: z  z  z  0  z  z  z  1 2 3 2 3 1
z  z  z 3 3 3 3
 z  z  z  3 z z  z z
z  z  z  3z z z  z 1 2 3 1 2 3  1 2 1 3 1 2 3 2 3  2 3  3 3 3
 z  z  z  3z z z 3 3 3
 z  z  z  3z z z . 1 2 3 1 2 3 1 2 3 1 2 3 3 3 3
 z  z  z  3z z z  3 z z z  3 1 2 3 1 2 3 1 2 3 3 3 3
Mặt khác z  z  z  1 z  z  z  3  1 2 3 nên 1 2 3 Chọn D.
Cách 2: thay thử z  z  z  1 1 2 3
vào các đáp án, thấy đáp án D bị sai
Tổng hợp các chuyên đề luyện thi đại học Trang 119
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna Câu 6.
Cách 1: Kí hiệu Re : là phần thực của số phức. 2 2 2 2
Ta có z  z  z  z  z  z
 2 Re z z  z z  z z  3  2 Rez z  z z  z z 1 2 2 3 3 1  1 2 3  1 2 2 3 3 1 (1). 1 2 3 2 2 2 2
z z  z z  z z  z z  z z  z z
 2 Re z z z z  z z z z  z z z z 1 2 2 3 3 1  1 2 2 3 2 3 3 1 3 1 1 2 1 2 2 3 3 1 2 2 2 2 2 2  2 2 2   z . z  z . z  z . z  2 Re z
 z z  z z z  z z z  1 2 2 3 3 1  1 2 3 2 3 1 3 1 2   
 3  2 Rez z  z z  z z  3  2 Re z z  z z  z z 1 3 2 1 3 2   1 2 3 3 3 1  (2). Từ  
1 và 2 suy ra z  z  z  z z  z z  z z . 1 2 3 1 2 2 3 3 1
Các h khác: B hoặc C đúng suy ra D đúngLoại B, C.
Chọn z  z  z   1 2 3 A đúng và D sai Chọn A.
Cách 2: thay thử z  z  z  1 vào các đáp án, thấy đáp án D bị sai 1 2 3 Câu 7.Giả sử (
A 3;3; 0) có dạng P z 2
 a  a z  a z  ... n  a z
a ; a ; a ;...;a  ;  a  0 0 1 2 n  0 1 2 n n  P z 2 n 2
 0  a  a z  a z  ...  a z  0  a  a z  a z  ... n  a z  0 0 1 2 n 0 1 2 n 2
 a  a z  a z  ... n
 a z  0  P z  0  0 1 2 n   . Chọn D.
Câu 8. Đặt Có a  a  bi a b   2 2 , ,
 a b  1 (do z  1)
2a  2b   1 i 4a  2b z i   2 2 1 2 A    2  iz 2 b  ai 2 b2 2  a
4a  2b  2 2 1 Ta chứng minh  1 . 2 b2 2  a
4a  2b  2 2 1 2 2 Thật vậy ta có 2
 1  4a  2b  1  2 b  a  a  b  1 2     2 2 2 2 b 2  a Dấu “=” xảy ra khi 2 2
a  b  1 .Vậy A  1  Chọn A. 5i 5i 5
Câu 9. Ta có: A  1   1   1 
 6. Khi z  i  A  6.  Chọn C. z z z    
Câu 10. Ta có:   iz  i 5 1 5 1 1 2
 3  i  z  z  1  i  w 
 i  M  ;   tan  .   4 4 4 4 5 2 2 tan  5 1  tan  12 Lúc đó: sin 2    0; cos 2    0 . Chọn A. 2 2 1  tan  13 1  tan  13 2 3
Câu 11. Ta có: M  z  z  1  z  1  5 , khi z  1  M  5  M  5. max 3 3 3 3 3 1  z 1  z 1  z
1  z  1  z Mặt khác: 3 M   1  z     1, khi 1  z 2 2 2 z  1
  M  1  M  1.  min Chọn A.
Tổng hợp các chuyên đề luyện thi đại học Trang 120
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna i 1 3 i 1 1
Câu 12. Ta có P  1   1 
 . Mặt khác: 1   1   . z | z | 2 z | z | 2 1 3
Vậy, giá trị nhỏ nhất của P l
à , xảy ra khi z  2i
; giá trị lớn nhất của P bằng xảy ra khi 2 2
z  2i.  Chọn A. 4 4
Câu 13. Ta có phương trình  f z  2z  i  z   1  0.
Suy ra: f z   15z  z z  z z  z z  z 1  2  3  4  . Vì f i .f i  2    
z  1  z  i z  i  P  1 . 1  1  1    225 4 4 4 Mà f i 4
 i i   1  5; f  i     3
 i i   1  85. Vậy từ   17 1  P  .  Chọn B. 9
Câu 14. Gọi z  x  yi; x  ;
 y    z  2i  x  y  2i . Ta có:
z   i   x  2  y  2 1 2 9 1 2  9 . Đặt x 1 3 sin t; y 2 3 cost; t 0;2       .    2
 z  i    t2    t2 2 1 3 sin 4 3 cos
 26  6sint  4 cost  26  6 17 sint  ;   .
 26  6 17  z  2i  26  6 17  z  2i
 26  6 17 .  Chọn A. max
Câu 15. Gọi z  x  yi; x  ;
 y   . Ta có: 2 2 2 2 z 1 x y 1 y 1 x x  1;1           .    2 2 Ta có: P   z 
 z    x 2  y   x 2 1 3 1 1 3 1
 y  21  x  3 21 x .
Xét hàm số f x 
21 x 3 21 x; x  1;1       .    
 Hàm số liên tục trên    và với  1;1 1 3 4 x  1; 
1 ta có: f x  
 0  x    1;  1 .   x  x 5 2 1 2 1  4   Ta có: f   1  2; f   1  6; f     2 20  P  2 20.    Chọn D. max  5
Câu 16. Gọi z  x  yi; x  ;
 y   . Ta có: z  1  z.z  1
Đặt t  z  1 , ta có 0 z 1 z 1 z 1 2 t 0;2          .    t  2
Ta có t  1  z 1  z  2 2
 1  z.z  z  z  2  2x  x  . 2
Suy ra z  z 
 z  z  z z  z z   z   x  2 2 2 2 1 . 1 2
1  2x  1  t  3 .
Xét hàm số f t 2 t t 3 ,t 0;2    
. Bằng cách dùng đạo hàm, suy ra   f t 13  f t 13 3 max ; min
 3  M.n  .  Chọn A. 4 4
Tổng hợp các chuyên đề luyện thi đại học Trang 121
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna 1  i 1  i 2
Câu 17. Ta có: OA  z ; OB  z   .z  . z  z . 2 2 2    1  i 1  i 2
Ta có: BA  OA OB  BA  z  z   z  z  . z  z . 2 2 2 Suy ra: 2 2 2
OA  OB  AB và AB  OB  OAB là tam giác vuông cân tại B.  Chọn C.
Câu 18. Áp dụng bất đẳng thức u  v  u  v , ta được 2 2 2 2 z  4
  z  4  4  z  z  2 z  4  0  z  5  1. 2 2 2 2
2 z  z  z  4  z 
 4  z  2 z  4  0  z  5  1.
Vậy, z nhỏ nhất là 5  1, khi z  i
  i 5 và z lớn nhất là 5  1 k
, hi z  i  i 5.  Chọn B. 2 2
Câu 19. Gọi z  x  yi; x  ;
 y   . Ta có: z 1  2i  2  x  
1  y  2  4. Đặt x 1 2 sint;y 2 2 cost; t 0;2         .  Lúc đó: 2 z    t2    t2    t  t 2 2 1 2 sin 2 2 cos 9 4 sin
8 cos  9  4  8 sint  ;    2  
 z  9  4 5 sint    z    9  4 5; 9  4 5        z  9  5 2 5 10 4 5
4 5 đạt được khi z  
i.  Chọn A. max 5 5  
Câu 20. Ta có AB biểu diễn số phức 3  i; DB biểu diễn số phức 3  3i . Mặt khác 3  3i    
 3i nên AB.DB  0 . Tương tự (hay vì lí do đối xứng qua Ox ), DC.AC  0 . Từ đó 3  i
suy ra AD là một đường kính của đường tròn đi qua ,
A B, C, D.
Vậy I 1; 0  z  1.  Chọn C. 2 13
Câu 21. Ta có: z  2  i 4  i  16  13i  M 16;  13  tan   . 16 2 1  tan  425 Ta có: cos 2   .  Chọn D. 2 1  tan  87
Câu 22. Gọi z  a  bi  z  a  bi; a  ;  b   b  0. 1 2 
. Không mất tính tổng quát ta gọi
Do z  z  2 3  2bi  2 3  b  3. 1 2 3 z z Do z , z z .z   1 1 3     z  .  1
2 là hai số phức liên hợp của nhau nên 1 2 , mà 2 z2 z z122 1  3 b  0 Ta có: 3 z a bi a 3ab 3a b b i  3a b b 0              a  1. 1    3 2   2 3  2 3 2  2 2 3a  b 
Tổng hợp các chuyên đề luyện thi đại học Trang 122
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna Vậy 2 2
z  a  b  2.  Chọn C. 1 m 2 6i   
Câu 23. Ta có: z  
  (2i)m  2m. m i    3 i 
z là số thuần ảo khi và chỉ khi m  2k  1, k   (do *
z  0; m   ).
Vậy có 25 giá trị m thỏa yêu cầu đề bài.  Chọn C. 2 z  1 1 z z Câu 24. Ta có:
 z   z   z 
 z  z là số thuần ảo. Chọn B. 2 z z z.z z
Câu 25. Gọi z  x  yi; x  ;
 y   .   
 iz   i    i 6 2i 1 6 2 10 1 . z 
 10  z  2  4i  5 Ta có: 1  i
 x  22  y  42  5. Đặt x 2 5 sint;y 4 5 cost; t 0;2      .   Lúc đó:
z  2  5 sint2  4  5 cost2 2
 25  4 5 sint  8 5 cost  25  4 52  8 52 sint  ;    2 z 25 20 sint  z  5;3 5            z  3 5 z  3  6 . i  max đạt được khi Chọn B.
Câu 26. Đặt z  x  iy  x,y  . Thay vào điều kiện thứ nhất, ta được 2 2
x  y  36.
Đặt x  3 cost, y  3 sin t. Thay vào điều kiện thứ hai, ta có 3 3   P  z  
i  18  18 sin t       6.  4  2 2      3 3 2 3 2
Dấu bằng xảy ra khi sin t
    1  t    z    i.    Chọn D.  4  4 2 2  z  1   3   1     i  z   1     x z i z x  y         3 3  Câu 27. Ta có: 2       
 z    i.  z  i
 z  i  2  z 4
 x  2y  3  3 2 2   1     y    2  z  2   Chọn A.
Câu 28. Ta có: z  z  z .z  z  z z  z  2 2 2 2 ; z
 z . z  z 1 2 1 2 1 1 2 1 1 1 2 1 . Do 2 z2
z  0  z  z  ; 1 2 1 (1) z1
Tổng hợp các chuyên đề luyện thi đại học Trang 123
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna 2 2 z 2 1
Mặt khác: z  z z  z  z
 z . z  z  z  z  z  0 1 2  1 2  1 2 1 2 1 2 (do 2 ) (2) z2 2 2 z z 2 1 Từ (1) và (2) suy ra:   z  z
z  z  z  z  OA  OB  AB 1 2 . Vậy ta có: . z z 1 2 2 1 1 2  Chọn A.
Câu 29. Gọi z  x  yi; x  ;
 y   . 2 2 2
Ta có: z   i  z  i  x    y   2 2 4 2 2
4  x  y  2  x  y  4  0  y  4  x. 2 2 2 2 Ta có: 2
z  i  x  y   2
 x    x 2 2 2 6
 2x 12x  36  2x   3  18  18  z  2i
 18  3 2 khi z  3  i.  Chọn C. min
Câu 30. Phương trình 4 2
z  mz  n  0 không có nghiệm thực trong các trường hợp:
TH 1: Phương trình vô nghiệm, tức là 2 m  4n  0.   2   0 m   4n  0       TH 2: Phương trình 4 2
t  mt  n   2
0; t  z  có hai nghiệm âm S   0  m   0 .   P  0 n     0    Chọn D. 2 2 2 2 z  a a a z a z Câu 31. Ta có:  z   z   z 
 z  z là số thuần ảo. Chọn B. 2 z z z .z z
Câu 32. Gọi z  x  yi; x  ;
 y    z  1  i  x   1  y   1 i . Ta có:
z   i   x  2  y  2 1 2 9 1 2  9 . Đặt x 1 3 sin t; y 2 3 cost; t 0;2       .    2
 z  1  i  3sint2  1  3cost2  10  6cost  2  z  2i  4  z 1  i  2 , khi min
z  1  i.  Chọn C. Câu 33. Ta có:   
 iz  i 7 19 7 19   19 1
 2  i  z  z  3i  w    i  M   ;   tan  .   82 82  82 82 7 2 2 tan  133 1  tan  156 Lúc đó: sin 2    0; cos 2     0 . Chọn C. 2 2 1  tan  205 1  tan  205 2 2
Câu 34. Gọi z  x  yi; x  ;
 y   . Ta có: z  3  4i  5  C  : x  
3  y  4  5 :
tâm I 3; 4 và R  5. Mặt khác: 2 2   M  z 
 z  i  x  2  y  x   y  2 2 2 2 2
1   4x  2y  3  d : 4x  2y  3  M  0.  
Do số phức z thỏa mãn đồng thời hai điều kiện nên d và C  có điểm chung
Tổng hợp các chuyên đề luyện thi đại học Trang 124
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna    d 23 M d I;  R 
 5  23  M  10  13  M  33 2 5 4
 x  2y  30  0  x   5  M  33     2 2  
 z  i  5  4i  z  i  41.  Chọn D. max
x  3 y  4  5 y   5   
Câu 35. Gọi z  x  y i; z  x  y i; z  x  y i; x ; y  ;  k  1; 3 1 1 1 2 2 2 3 3 3  k k .
Khi đó: Ax ;y ; B x ;y ; C x ;y G 1 1 
 2 2  3 3 , gọi là trọng tâm x x x y y y       1 2 3 1 2 3 ABC  G  ;   .  3 3 
Tương tự, gọi z   x   y i; z   x   y i; z   x   y i
 ; x ; y  ;  k  1;3 1 1 1 2 2 2 3 3 3  k k .
Khi đó: Ax ;y ; B x ;y ; C  x ;y 1 1   2 2  3 3,
x  x  x y  y  y   
gọi G là trọng tâm 1 2 3 1 2 3 AB C    G  ;   .  3 3 
Do z  z  z  z   z   z   x  x  x
 y  y  y i  x   x   x   y  y  y i 1 2 3 1 2 3  1 2 3   1 2 3   1 2 3   1 2 3  x
  x  x  x  x  x  1 2 3 1 2 3  
 G  G .  Chọn C. y
  y  y  y  y  y  1 2 3 1 2 3 
Câu 36. Ta có: z    i  i   i  M    1 2 3 1 5
5; 1  tan    . 5 2 tan  5 Ta có: sin 2    .  Chọn A. 2 1  tan  12 Câu 37. Ta có: m   i m i 1 z     z   1  z
 1  z  i; m  0.
1  m m  2i 2 2 2 max m  1 m  1 m  1  Chọn A.
Câu 38. Gọi Rez  là phần thực của số phức z. 1  1    1 1
m  z  m  z
2m  z  z Ta xét:          m  z
m  z  m  z m  z
m zm z  2
m  z.z  mz  mz 2m z z 2m z z 1  1        1     Re   .    Chọn D. 2
2m  mz  mz
m 2m  z  z  m
m  z  2m
Câu 39. Dựng hình bình hành OMPN trong mặt phẳng phức, khi đó biểu diễn của :     2 2
z  z  OP 0  
 z  z  z  z  2 z z cos 150  1 z  z z  z 1 2 1 2 1 2    1 2    1 2 1 2    1
 z  z  MN   2 2 z  z z  z 1 2 
 z  z  z  z  2 z z cos   0 30  1 1 2 1 2 1 2 1 2 1 2    Chọn B.
Câu 40. Đặt z  a  bi và z  c  0 , với a; ; b c   .
Tổng hợp các chuyên đề luyện thi đại học Trang 125
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna w   i
Lại có w    i 1 2 3
4 z  1  2i  z  . 3  4i
Gọi w  x  yi với x;y   . w  1  2  1  2 i w i
Khi đó z  c   c 
 c  x  yi  1  2i  5c 3  4i 3  4i
 x  2  y  2  c  x  2  y  2 2 1 2 5 1 2  25c .
Vậy tập hợp các điểm biểu diễn của số phức w là đường tròn I  1  ;2 .
Khi đó chỉ có đáp án C có khả năng đúng và theo đó R  5  5c  5  c  1 .
Thử c  1 vào phương trình (1) thì thỏa mãn  Chọn C. Câu 41. Cách 1:
Đặt z  a  bi (a,b  ) . Khi đó 2 2
z  3  4i  2  (a  3)  (b  4)  4 .
Suy ra biểu diễn hình học của số phức z là đường tròn C  tâm I 3;4 và bán kính R  5 .
Gọi M z là điểm biểu diễn số phức z . Ta có: M z   C  .
z  OM  OI  R  3 .
Vậy z bé nhất bằng 3 khi M z   C   IM . Cách 2: a
  3  2cos a   3   2 cos   Đặt    . b   4  2 sin b   4   2 sin   2 2 2 2
 z  a  b  (2 cos  3)  (2 sin   4)  29  12 cos  16 sin  . 3 4 
 29  20 cos  sin  29  20 cos(  )  9 5 5  .
 z  3  Chọn D 0
Câu 42. Ta có: Gọi M x;y là điểm biểu diễn của số phức z  x  yi.
Gọi A4; 0 là điểm biểu diễn của số phức z  4.
Gọi B 4; 0 là điểm biểu diễn của số phức z  4.
Khi đó: z  4  z  4  10  MA  MB  10. (*)
Hệ thức trên chứng tỏ tập hợp các điểm M là elip nhận ,
A B là các tiêu điểm. 2 2 x y
Gọi phương trình của elip là   1, 2 2 2
a  b  0,a  b  c 2 2  a b
Từ (*) ta có: 2a  10  a  5. 2 2 2
AB  2c  8  2c  c  4  b  a c  9 x y
Vậy quỹ tích các điểm M là elip: E  2 2 :   1.  Chọn D. 25 9
Câu 43. Gọi M x,y là điểm biểu diễn số phức z  x  yi x,y  R
Tổng hợp các chuyên đề luyện thi đại học Trang 126
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
Gọi E 1,2 là điểm biểu diễn số phức 1  2i Gọi F 0, 
1 là điểm biểu diễn số phức i 
Ta có: z  2i  1  z  i  ME  MF  Tập hợp điểm biểu diễn số phức z là đường trung
trục EF : x  y  2  0 .
Để MA ngắn nhất khi MA  EF tại M  M 3, 
1  z  3  i => Chọn A.
Câu 44. Gọi M x,y là điểm biểu diễn số phức z  x  yi x,y  R Gọi A1, 
1 là điểm biểu diễn số phức 1   i
1  z  1  i  2  1  MA  2 . Tập hợp điểm biểu diễn là hình vành khăn giới hạn bởi 2
đường tròn đồng tâm có bán kính lần lượt là R  2,R  1  P  P  P  2 R  R  2 1 2  1 2  1 2 . => Chọn C.
Lưu ý cần nắm vững lý thuyết và hình vẽ của dạng bài này khi học trên lớp tránh nhầm lẫn sang tính
diện tích hình tròn.
Câu 45. Gọi M x,y là điểm biểu diễn số phức z  x  yi x,y  R
Ta có: z  z2 2 2 2 2 2 2 2 2
 2 z  16  x  2xyi  y  x  2xyi  y  2x  2y  16 2
 4x  16  x  2  .d d ,d  4  1 2  . Chọn B.
Ở đây lưu ý hai đường thẳng x = 2 và x = -2 song song với nhau.
Câu 46. Ta có 2
z  2z  5  z  1  2iz  3i  1  z  1  2iz  1  2i  z  1  2iz  3i  1 z   1  2i  0   .
 z  1  2i   z  3i   1 
Trường hợp 1: z  1  2i  0  w  1   w  1   1 .
Trường hợp 2: z  1  2i  z  3i  1
Gọi z  a  bi (với a,b   ) khi đó ta được
a   b  i  a    b  i  b  2  b  2 1 1 2 1 3 2 3  b   . 2
Suy ra w  z   i  a  
i  w  a  2 3 9 3 2 2 2 2   2 . 2 4 2 Từ  
1 , 2 suy ra min | w | 1  Chọn C.
Câu 47. Giả sử z  a  bi , z  c  di , a, , b , c d   . 1 2 2 2
Theo đề bài ta có: Aa;b , B c;d   AB  c a  d b . 2 2
z  z  a  c  d b i  z  z 
c a  d b  2 1     2 1     Chọn B.
Câu 48. T  z  i  z  2  i  z  
1  1  i  z  
1  1  i .
Tổng hợp các chuyên đề luyện thi đại học Trang 127
Biên soạn: Bùi Trần Duy Tuấn
https://facebook.com/duytuan.qna
Đặt w  z  1 . Ta có w  1 và T  w  1  i  w  1  i . 2
Đặt w  x  y.i . Khi đó 2 2
w  2  x  y .
T  x   1  y  
1 i  x   1  y   1 i  1. x  2 1  y  2 1  1. x  2 1  y  2 1  2 2 2 2    2 2 1  1    x  
1 y  1 x  1 y  1     2 2 2
2x  2y  4  4
Vậy maxT  4  Chọn B
Câu 49. Gọi M x;y là điểm biểu diễn số phức z  x  yi , x,y   .
Gọi A là điểm biểu diễn số phức 2
Gọi B là điểm biểu diễn số phức 2
Ta có: z  2  z  2  10  MB  MA  10 .
Ta có AB  4 . Suy ra tập hợp điểm M biểu diễn số phức z là Elip với 2 tiêu điểm là A2; 0 ,
B 2;0 , tiêu cự AB  4  2c , độ dài trục lớn là 10  2a , độ dài trục bé là 2 2
2b  2 a c  2 25  4  2 21 .
Vậy, tập hợp các điểm biểu diễn các số phức z thỏa mãn điều kiện z  2  z  2  10 là Elip có 2 2 x y phương trình   1.  Chọn D. 25 21
Câu 50. Gọi M  x, y là điểm biểu diễn số phức z  x  yi x,y  R Gọi ,
A B lần lượt là điểm biểu diễn số phức 1 và i .
Gọi C, D lần lượt là điểm biểu diễn số phức i và 3i
Ta có: z  1  z  i  MA  MB với A1, 0; B 0, 
1  M thuộc đường trung trực  của AB 1
z  3i  1  z i  z  3i  MC  MD với C0, 1;D0,3  M thuộc đường trung trực z  i  của CD 2  y  x
M là giao điểm của  ;   M thỏa hệ:   M 1, 
1  z  1  i => Chọn D. 1 2 y  1 
Tổng hợp các chuyên đề luyện thi đại học Trang 128

Chuyên đề số phức – Bùi Trần Duy Tuấn Toán 12

Thông tin :

Tài liệu liên quan:

Chuyên đề Số phức – Trung tâm LTĐH Vĩnh Viễn Toán 12

Các dạng bài tập cơ bản về Số phức – Đặng Việt Hùng Toán 12

600 câu hỏi trắc nghiệm chuyên đề số phức – Nhóm Toán

Bài tập trắc nghiệm chuyên đề số phức – Đặng Việt Đông Toán 12

4 đề trắc nghiệm chuyên đề số phức – Bùi Thế Việt Toán 12