Chuyên đề số phức dành cho học sinh trung bình – yếu – Dương Minh Hùng Toán 12

Chuyên đề số phức dành cho học sinh trung bình – yếu – Dương Minh Hùng Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

29 15 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 4: Số phức

Môn: Toán 12

Thông tin:

51 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 1
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 2
FB: Duong Hung
A - Bài tập minh họa:
Câu 1. Số phức có phần thực bằng 3 và phần ảo bằng 4 là
Ⓐ.
3 4 .zi=+
Ⓑ.
4 3 .zi=−
Ⓒ.
3 4 .zi=−
Ⓓ.
4 3 .zi=+
Lời giải
Chọn A
PP nhanh trắc nghiệm
Phần ảo là hệ số trước i, phần thực là số tự
do.
Câu 2. Cho số phức
. Tính
||z
.
Ⓐ.
5z =
. Ⓑ.
3z =
. Ⓒ.
2z =
. Ⓓ.
5z =
.
Lời giải
Chọn D
Ta có
22
1 2 5z = + =
.
PP nhanh trắc nghiệm
Tính theo công thức:
Casio: MODE 2
Bài ➀: ĐỊNH NGHĨA SỐ PHỨC
. Phương pháp:
. Số phức có dạng .
. Phần thực của là , phần ảo của là .
. Số phức có phần ảo bằng được coi là số thực và viết là .
. Số phức có phần thực bằng được gọi là số ảo (hay số thuần ảo) .
. Số 0 vừa là số thực, vừa là số ảo.
. Mô đun của số phức là .
. Số phức liên hợp của là .
. Cho hai số phức , . Khi đó:
Dạng ①: Xác định các yếu tố cơ bản của số phức
CHƯƠNG ④:
Full Chuyên
đề 12 new
2020-2021
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 3
SHIFT hyp
Câu 3. Số phức liên hợp của số phức là
Ⓐ.
3 4 .zi= − −
Ⓑ.
4 3 .zi=−
Ⓒ.
3 4 .zi=+
Ⓓ.
4 3 .zi=+
Lời giải
Chọn C
Ta có:
3 4 .zi=+
PP nhanh trắc nghiệm
Số phức liên hợp có phần thực bằng nhau và
phần ảo đối nhau.
Casio: Dùng chức năng tính liên hợp của số
phức :
MODE 2
SHIFT 22
B - Bài tập rèn luyện:
Câu 1: Số phức
3 7 .zi= − +
có phần ảo bằng
Ⓐ.
3
. Ⓑ.
7i
. Ⓒ.
3−
. Ⓓ.
7
.
Câu 2: Số phức
56zi=+
có phần thực bằng
Ⓐ.
5−
. Ⓑ.
5
. Ⓒ.
6−
. Ⓓ.
6
.
Câu 3: Cho số phức
;z a a=
. Khi đó khẳng định đúng là
Ⓐ. z là số thuần ảo. Ⓑ. z có phần thực là a, phần ảo là i.
Ⓒ.
za=
. Ⓓ.
za=
.
Câu 4: Số phức nào dưới đây là số thuần ảo?
Ⓐ.
32zi=+
. Ⓑ.
2zi=
. Ⓒ.
23zi= − +
. Ⓓ.
2z =−
.
Câu 5: Cho số phức
12zi=−
. Khẳng định nào sau đây là khẳng định đúng?.
Ⓐ. Phần thực của số phức z là . Ⓑ. Phần ảo của số phức là .
Ⓒ. Phần ảo của số phức là . Ⓓ. Số phức là số thuần ảo.
Câu 6: Số phức liên hợp của số phức
53zi=−
là
Ⓐ.
53i−−
. Ⓑ.
53i−+
. Ⓒ.
35i+
. Ⓓ.
53i+
.
Câu 7: Số phức liên hợp của số phức
21zi=−
là
34i−
1−
z
2i−
z
2−
z
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 4
Ⓐ.
21i +
. Ⓑ.
21i−+
. Ⓒ.
21i−−
. Ⓓ.
12i−+
.
Câu 8: Cho số phức
( , ).z a bi a b R= +
Tìm số phức
z
là số phức liên hợp của
z
.
Ⓐ.
.z a bi=−
Ⓑ.
.z a bi= − +
Ⓒ.
( ).z a bi= − +
Ⓓ.
22
.z a b i=−
Câu 9: Số phức
43zi=−
có môđun bằng
Ⓐ.
22
. Ⓑ.
25
. Ⓒ.
5
. Ⓓ.
8
.
Câu 10: Cho số phức
1 2 2.=−zi
. Tính
z
.
Ⓐ.
1 2 2=+z
. Ⓑ.
9=z
. Ⓒ.
10=z
. Ⓓ.
3=z
.
Câu 11: Cho số phức
14zi= − −
. Tìm phần thực của số phức
z
.
Ⓐ.
1−
. Ⓑ.
1
. Ⓒ.
4
. Ⓓ.
4−
.
Câu 12: Cho số phức
2zi= − +
. Tìm phần thực và phần ảo của số phức
z
.
Ⓐ. Phần thực bằng
2−
và phần ảo bằng
i−
. Ⓑ. Phần thực bằng
2−
và phần ảo bằng
1−
.
Ⓒ. Phần thực bằng
2
và phần ảo bằng
1
. Ⓓ. Phần thực bằng
2
và phần ảo bằng
i
.
Câu 13: Tìm phần ảo của số phức
z
biết
13zi=+
?
Ⓐ. Phần ảo bằng
3
. Ⓑ. Phần ảo bằng -
3i
. Ⓒ. Phần ảo bằng
3−
.
Ⓓ. Phần ảo bằng
i
.
Câu 14: Gọi
a
,
b
lần lượt là phần thực và phần ảo của số phức
32zi= − +
. Giá trị của
2ab+
bằng
Ⓐ.
1
. Ⓑ.
1−
. Ⓒ.
4−
. Ⓓ.
7−
.
Câu 15: Phần ảo của số phức liên hợp của
47zi=−
là
Ⓐ.
4−
. Ⓑ.
7−
. Ⓒ. 7. Ⓓ. 4.
Câu 16: Số phức
2 ( 1)z m m i= + −
, với
m
. Với giá trị nào m của thì
2z =
.
Ⓐ.
1m =−
. Ⓑ.
3
5
m =
. Ⓒ.
1
3
5
m
m
=
=−
. Ⓓ.
m
.
Câu 17: Cho số phức
z
có số phức liên hợp
32zi=−
. Tổng phần thực và phần ảo của số phức
z
bằng
Ⓐ.
5
. Ⓑ.
1−
. Ⓒ.
5−
. Ⓓ.
1
.
Câu 18: Cho số phức
24zi=+
. Hiệu phần thực và phần ảo của
z
bằng.
Ⓐ.
2
. Ⓑ.
25
. Ⓒ.
2−
. Ⓓ.
6
.
Câu 19: Số phức z nào sau đây thỏa
5z =
và phần thực gấp đôi phần ảo?.
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 5
Ⓐ.
1 2 .zi=+
Ⓑ.
2.zi=+
Ⓒ.
2 3 .zi=+
Ⓓ.
4 2 .zi=+
Câu 20: Tìm số thực
m
sao cho
( )
( )
2
11m m i− + +
là số ảo.
Ⓐ.
0m =
. Ⓑ.
1m =
. Ⓒ.
1m =
. Ⓓ.
1m =−
.
BẢNG ĐÁP ÁN
1.D
2.B
3.C
4.B
5.C
6.D
7.C
8.A
9.C
10.D
11.A
12.B
13.C
14.A
15.A
16.C
17.A
18.C
19.B
20.C
A - Bài tập minh họa:
Câu 1. Số phức
23zi=−
có điểm biểu diễn là
Ⓐ.
( )
2;3A
. Ⓑ.
( )
2; 3A −−
. Ⓒ.
( )
2; 3A −
. Ⓓ.
( )
2;3A −
.
Lời giải
Chọn C
Số phức
23zi=−
có phần thực bằng 2 và
phần ảo bằng -3
PP nhanh trắc nghiệm
Điểm biểu diễn có hoành độ bằng 2 và tung độ
bằng -3
Câu 2. Điểm trong hình vẽ bên là điểm biểu diễn của số phức . Tìm phần thực và phần ảo của
số phức .
Ⓐ. Phần thực là và phần ảo là .
Ⓑ. Phần thực là và phần ảo là .
Ⓒ. Phần thực là và phần ảo là .
Ⓓ. Phần thực là và phần ảo là .
Lời giải
Chọn C
Điểm
( )
3; 4M −
nên M là điểm biểu diễn của số
phức
34zi=−
.Vậy phần thực bằng 3 và phần
ảo bằng -4
PP nhanh trắc nghiệm
Hoành độ bằng phần thực ,tung độ bằng phần
ảo
M
z
z
4−
3
3
4− i
3
4−
4−
3i
. Phương pháp:
①. Biến đổi số phức cần biểu diễn về dạng z =a+bi
②. Điểm biểu diễn của số phức z là điểm M(a;b)
Dạng ②: Điểm biểu diễn của số phức
O
x
y
3
4−
M
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 6
Câu . Cho số phức
12zi=−
Tìm tọa độ biểu diễn của số phức trên mặt phẳng tọa độ.
Ⓐ.
( )
1; 2M −
Ⓑ.
( )
2;1M
Ⓒ.
( )
1;2M
Ⓓ.
( )
2; 1M −
Lời giải
Chọn C
Vì
12zi=−
nên
12zi=+
.Điểm biểu diễn của
là
( )
1;2M
PP nhanh trắc nghiệm
Nếu
z a bi=+
thì điểm biểu diễn của là
( )
;M a b−
B - Bài tập rèn luyện:
Câu 1: Số phức
34zi=+
có điểm biểu diễn là
Ⓐ.
( )
4;3M
Ⓑ.
( )
3;4M
Ⓒ.
( )
3;4M −
Ⓓ.
( )
4;3M −
Câu 2: Số phức
37zi
có điểm biểu diễn là
Ⓐ.
( )
3;7M
Ⓑ.
( )
3;7M −
. Ⓒ.
( )
3; 7M −
. Ⓓ.
( )
3; 7M −−
.
Câu 3: Điểm M biểu diễn số phức
32zi=+
trong mặt phẳng tọa độ là
Ⓐ.
(3;2)M
. Ⓑ.
(2;3)M
. Ⓒ.
(3; 2)M −
. Ⓓ.
( 3; 2)M −−
.
Câu 4: Cho số phức
21zi= − −
. Điểm biểu diễn của số phức
z
trong mặt phẳng là
Ⓐ.
( 1; 2)M −−
. Ⓑ.
( 1;2)M −
. Ⓒ.
( 2;1)M −
. Ⓓ.
(2; 1)M −
.
Câu 5: Cho số phức
5zi=−
. Điểm biểu diễn của số phức
z
trong mặt phẳng là
Ⓐ.
( 5;0)M −
. Ⓑ.
(0;5)M
. Ⓒ.
(0; 5)M −
. Ⓓ.
(5;0)M
.
Câu 6: Cho số phức
8z =−
. Điểm biểu diễn của số phức
z
trong mặt phẳng là
Ⓐ.
( 8;0)M −
. Ⓑ.
(8;0)M
. Ⓒ.
(0;8)M
. Ⓓ.
(0; 8)M −
.
Câu 7: Cho số phức
67zi=+
. Số phức liên hợp của có điểm biểu diễn là
Ⓐ.
( )
6;7
. Ⓑ.
( )
6; 7−
. Ⓒ.
( )
6;7−
. Ⓓ.
( )
6; 7−−
.
Câu 8: Cho số phức
21zi= − −
. Điểm biểu diễn số phức liên hợp của
z
là
Ⓐ.
( 1; 2)M −−
. Ⓑ.
( 1;2)M −
. Ⓒ.
( 2;1)M −
. Ⓓ.
(2; 1)M −
.
Câu 9: Cho số phức
2zi=−
. Điểm biểu diễn của số phức liên hợp của
z
là
Ⓐ.
(0; 2)M −
. Ⓑ.
(0;2)M
. Ⓒ.
( 2;0)M −
. Ⓓ.
(2;0)M
.
Câu 10: Cho điểm là điểm biểu diễn của số phức . Tìm phần thực và phần ảo của số phức .
Ⓐ. Phần thực là và phần ảo là .
Ⓑ. Phần thực là và phần ảo là .
Ⓒ. Phần thực là và phần ảo là .
z
z
z
z
M
z
z
4−
3i
3
4i−
4−
3
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 7
Ⓓ. Phần thực là và phần ảo là .
Câu 11:
Cho số phức có điểm biểu diễn là điểm trong hình vẽ bên.Tìm phần thực và phần ảo của
số phức
.
Ⓐ. Phần thực bằng , phần ảo bằng .
Ⓑ. Phần thực bằng , phần ảo bằng .
Ⓒ. Phần thực bằng , phần ảo bằng .
Ⓓ. Phần thực bằng , phần ảo bằng .
Câu 12: Gọi là điểm biểu diễn của số phức
25zi=+
và là điểm biểu diễn của số phức
25zi= − +
. Tìm mệnh đề đúng trong các mệnh đề sau.
Ⓐ. Hai điểm và đối xứng với nhau qua trục hoành.
Ⓑ. Hai điểm và đối xứng với nhau qua trục tung.
Ⓒ. Hai điểm và đối xứng với nhau qua gốc toạ độ .
Ⓓ. Hai điểm và đối xứng với nhau qua đường thẳng .
Câu 13: Trên mặt phẳng tọa độ cho điểm trong hình vẽ bên là điểm
biểu diễn của số phức . Tìm ?
Ⓐ.
z +
43zi= − +
. Ⓑ.
34zi=+
.
Ⓒ.
34zi=−
. Ⓓ.
34zi= − +
.
Câu 14: Trong mặt phẳng toạ độ, điểm
( )
1; 2A −
là điểm biểu diễn của số phức nào trong các số sau?
Ⓐ.
12zi= − −
. Ⓑ.
12zi=+
. Ⓒ.
12zi=−
. Ⓓ.
2zi= − +
.
Câu 15: Trong mặt phẳng phức, gọi lần lượt là điểm biểu diễn của các số phức
1
32zi=+
,
2
32zi=−
,
3
32zi= − −
. Khẳng định nào sau đây là sai?
Ⓐ. và đối xứng nhau qua trục tung.
Ⓑ. Trọng tâm của tam giác là điểm
2
1;
3
G



.
Ⓒ. và đối xứng nhau qua trục hoành.
Ⓓ. nằm trên đường tròn tâm là gốc tọa độ và bán kính bằng
13
.
Câu 16: Gọi A là điểm biểu diễn số phức
( )
,M x y
, B là điểm biểu diễn số phức
z x yi=+
. Trong các
khẳng định sau khẳng định nào sai?
Ⓐ. A và B đối xứng nhau qua trục hoành.
3
4−
z
A
z
3
2−
3
2
2
3i−
3
2i
A
B
A
B
A
B
A
B
O
A
B
yx=
Oxy
M
z
z
,,A B C
B
C
ABC
A
B
,,A B C
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 8
Ⓑ. A và B trùng gốc tọa độ khi
0z =
.
Ⓒ. A và B đối xứng qua gốc tọa độ.
Ⓓ. Đường thẳng AB đi qua gốc tọa độ.
Câu 17: Các điểm biểu diễn các số phức
( )
3z bi b= +
trong mặt phẳng tọa độ, nằm trên đường
thẳng có phương trình là
Ⓐ.
yb=
. Ⓑ.
3y =
Ⓒ.
xb=
. Ⓓ.
3x =
.
Câu 18: Trên mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức thỏa mãn điều kiện phần thực
của
z
bằng -2 là
Ⓐ.
2x =−
. Ⓑ.
2y =
. Ⓒ.
2yx=
Ⓓ.
2yx=+
Câu 19: Cho số phức
z a ai=+
. Tập hợp các điểm biểu diễn số phức liên hợp của z trong mặt phẳng
tọa độ là
Ⓐ.
0xy+=
. Ⓑ.
yx=
. Ⓒ.
xa=
. Ⓓ.
ya=
.
Câu 20: Tập hợp các điểm biểu diễn số phức z thỏa mãn
1z
trên mặt phẳng tọa độ là
Ⓐ. Hình tròn tâm
, bán kính
1R =
, không kể biên.
Ⓑ. Hình tròn tâm
, bán kính
1R =
, kể cả biên.
Ⓒ. Đường tròn tâm
, bán kính
1R =
.
Ⓓ. Đường tròn tâm bất kì, bán kính
1R =
.
BẢNG ĐÁP ÁN
1B
2.B
3.A
4.A
5.C
6.A
7.B
8.B
9.B
10.D
11.B
12.B
13.C
14.C
15.B
16.A
17.D
18.A
19.B
20.A
A - Bài tập minh họa:
Câu 1. Bộ số thực
( ; )xy
thỏa mãn
(3 ) (1 ) 1 3x y i i
, với
i
là đơn vị ảo là
Ⓐ.
(2; 2)
. Ⓑ.
( 2;2)
. Ⓒ.
(2;2)
. Ⓓ.
( 2; 2)
.
. Phương pháp:
Cho hai số phức , .
Khi đó:
Dạng ③: Hai số phức bằng nhau:
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 9
Lời giải
Chọn B
Ta có:
( ) ( )
3 1 1 3x y i i+ + + = +
31
13
x
y
+=
+=
2
2
x
y
=−
=
.
PP nhanh trắc nghiệm
Casio: Thay x, y trong các đáp án vào giả thiết
đã cho.
( )
3 2 (1 2) 1 3ii+ + − = +
(S)
( ) ( )
3 2 1 2 1 3ii− + + = +
(Đ), chọn B
Câu 2. Tìm điểm
( , )M x y
thỏa
2 1 (3 2) 5 .x y i i− + + = −
Ⓐ.
(3; 1).M −
Ⓑ.
(2; 1).M −
Ⓒ.
1
(3; ).
3
M
−
Ⓓ.
1
(2; ).
3
M
Lời giải
Chọn A
2 1 (3 2) 5x y i i− + + = −
2 1 5
3 2 1
x
y
−=
+ = −
3
1
x
y
=
=−
PP nhanh trắc nghiệm
Casio: Thay x, y trong các đáp án vào giả thiết
đã cho.
2.3 1 (3.( 1) 2) 5ii− + − + = −
(Đ), chọn A
Câu 3. Tìm hai số thực
x
và
y
thỏa mãn
3 2 2 2 3x yi i x i
với
i
là đơn vị ảo.
Ⓐ.
2; 2xy
. Ⓑ.
2; 1xy
. Ⓒ.
2; 2xy
. Ⓓ.
2; 1xy
.
Lời giải
Chọn C
Ta có
3 2 2 2 3
2 (2 4) 0
x yi i x i
x y i
2 0 2
2 4 0 2
xx
yy
+ = = −



+ = = −

PP nhanh trắc nghiệm
Casio: Thay x, y trong các đáp án vào giả thiết
đã ch
B - Bài tập rèn luyện:
Câu 1: Cho x là số thực. Hai số phức
3zi=+
và
z x i=+
bằng nhau khi
Ⓐ.
1x =
. Ⓑ.
2x =
. Ⓒ.
3x =
. Ⓓ.
1x =−
.
Câu 2: Cho y là số thực. Hai số phức
3zi=+
và
3z yi=−
bằng nhau khi
Ⓐ.
1y =−
. Ⓑ.
2y =−
. Ⓒ.
0y =
. Ⓓ.
1y =
.
Câu 3: Cho x, y là các số thực. Hai số phức
2z yi=+
và
2z x i=−
bằng nhau khi
Ⓐ.
2; 2xy
. Ⓑ.
2; 2xy
. Ⓒ.
2; 2xy
. Ⓓ.
2; 2xy
.
Câu 4: Cho hai số phức
2z x i=+
và
'
3z yi=−
. Hai số đó bằng nhau khi
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 10
Ⓐ.
2; 3xy
. Ⓑ.
3; 2xy
. Ⓒ.
3; 2xy
. Ⓓ.
3; 2xy
.
Câu 5: Cho hai số phức
2 3 , ( 1) 6i, , R.z yi z x x y
= − + = + −
Tìm
,xy
để
.zz
=
Ⓐ.
3, 9xy= = −
. Ⓑ.
3, 2xy= − = −
. Ⓒ.
1, 2xy= − =
. Ⓓ.
3, 2xy= = −
.
Câu 6: Cho hai số phức
2 3 , ( 1) 6i, , R.z yi z x x y
= + = + −
Tìm
,xy
để
.zz
=
Ⓐ.
3, 9xy= = −
. Ⓑ.
3, 2xy= − = −
. Ⓒ.
1, 2xy==
. Ⓓ.
1, 2xy= = −
.
Câu 7: Tìm điểm
( , )M x y
thỏa
2 1 ( 2) 5 .x y i i− + + = −
Ⓐ.
(3; 1).M −
Ⓑ.
(2; 1).M −
Ⓒ.
(3; 3).M −
Ⓓ.
(2;3).M
Câu 8: Tìm điểm
( , )M x y
thỏa
2 1 ( 2) 5 .x y i i+ + + = −
Ⓐ.
(3; 1).M −
Ⓑ.
(2; 3).M −
Ⓒ.
(3; 3).M −
Ⓓ.
(2;3).M
Câu 9: Cho
a
,
b
là hai số thực thỏa mãn
1 6 2 2a i bi+ + = −
, với
i
là đơn vị ảo. Tìm a và b.
Ⓐ.
1, 3ab= − = −
. Ⓑ.
1, 3ab==
. Ⓒ.
1, 3ab= = −
. Ⓓ.
1, 2xy= = −
.
Câu 10: Cho
a
,
b
là hai số thực thỏa mãn
6 2 2a i bi+ = −
, với
i
là đơn vị ảo. Giá trị của
ab+
bằng
Ⓐ.
1−
. Ⓑ. 1. Ⓒ.
4−
. Ⓓ. 5.
Câu 11: Tìm hai số thực
x
và
y
thỏa mãn
( ) ( ) 5 3x y x y i i
với
i
là đơn vị ảo.
Ⓐ.
4; 1xy
. Ⓑ.
1; 4xy
. Ⓒ.
2; 3xy
. Ⓓ.
2; 3xy
.
Câu 12: Với giá trị nào của x, y để 2 số phức
( ) (2 )z x y x y i
và
36zi
bằng nhau?
Ⓐ.
4; 1xy
. Ⓑ.
1; 4xy
. Ⓒ.
1; 4xy
. Ⓓ.
1; 4xy
.
Câu 13: Các số thực
,xy
thỏa mãn
( )
3 5 2 1x y xi y x y i+ + = − + −
là
Ⓐ.
( )
14
;;
77
xy

=−


. Ⓑ.
( )
24
;;
77
xy

=−


. Ⓒ.
( )
14
;;
77
xy

=


. Ⓓ.
( )
14
;;
77
xy

= − −


.
Câu 14: Tìm hai số thực
x
và
y
thỏa mãn
(3 2) (1 2 ) 2 3x y i x i
với
i
là đơn vị ảo.
Ⓐ.
2; 2xy
. Ⓑ.
2; 1xy
. Ⓒ.
2; 2xy
. Ⓓ.
2; 1xy
.
Câu 15: Tìm hai số thực
x
và
y
thỏa mãn
( ) ( )
3 4 2 5 2x yi i x i+ + − = +
với
i
là đơn vị ảo.
Ⓐ.
2x =−
;
4y =
. Ⓑ.
2x =
;
4y =
. Ⓒ.
2x =−
;
0y =
. Ⓓ.
2x =
;
0y =
.
Câu 16: Tìm hai số thực
x
và
y
thỏa mãn
( ) ( )
3 3 5 3 7 16x y x y i i+ − + + = −
Ⓐ.
1; 2xy
. Ⓑ.
1; 2xy
. Ⓒ.
2; 2xy
. Ⓓ.
2; 1xy
.
Câu 17: Cho hai số thực
x
và
y
thỏa mãn
( ) ( )
3 3 5 3 7 16x y x y i i+ − + + = −
. Tính xy?
Ⓐ.
3
. Ⓑ.
3−
. Ⓒ.
2
. Ⓓ.
7
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 11
Câu 18: Nếu hai số thực
,xy
thỏa mãn
( )
3 2 4 1 24x y x y i i+ + − = +
thì
xy−
bằng?
Ⓐ.
3
. Ⓑ.
3−
. Ⓒ.
7−
. Ⓓ.
7
Câu 19: Nếu hai số thực
,xy
thỏa mãn
( )
3 2 4 1 24x y x y i i+ + − = +
thì
xy+
bằng?
Ⓐ.
3
. Ⓑ.
3−
. Ⓒ.
7−
. Ⓓ.
7
Câu 20: Cho số thực
x
,
y
thỏa mãn
( ) ( )
2 2 2 3 2 1x y y x i x y y x i+ + − = − + + + +
. Khi đó giá trị của
22
4M x xy y= + −
là
Ⓐ.
1M =−
. Ⓑ.
1M =
. Ⓒ.
0M =
. Ⓓ.
2M =−
BẢNG ĐÁP ÁN
1.C
2.A
3.A
4.D
5.B
6.D
7.C
8.B
9.C
10.A
11.A
12.C
13.A
14.D
15.B
16.B
17.C
18.D
19.B
20.A
FB: Duong Hung
Full Chuyên
đề 12 new
2020-2021
CHƯƠNG
④
:
Bài ➁: PHÉP CỘNG-PHÉP NHÂN
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 12
A - Bài tập minh họa:
Câu 1: Cho hai số phức
1
2zi= − +
và
2
1zi=+
. Trên mặt phẳng tọa độ
Oxy
, điểm biểu diễn số phức
12
2zz+
có tọa độ là
Ⓐ.
( )
3;2−
. Ⓑ.
( )
2; 3−
. Ⓒ.
( )
3;3−
. Ⓓ.
( )
3; 3−
.
Lời giải
Chọn C
Ta có:
( ) ( )
12
2 2. 2 1 4 2 1 3 3z z i i i i i+ = − + + + = − + + + =− +
Vậy điểm biểu diễn số phức
12
2zz+
có tọa độ là
( )
3;3−
.
PP nhanh trắc nghiệm
Casio:
Câu 2: Cho hai số phức
1
12zi=+
và
2
34zi=−
. Số phức
1 2 1 2
23z z z z+−
là số phức nào sau đây?
Ⓐ.
10i
. Ⓑ.
10i−
. Ⓒ.
11 8i+
. Ⓓ.
11 10i−
.
Lời giải
Chọn B
Ta có
1 2 1 2
23z z z z+−
( ) ( ) ( )( )
2 1 2 3 3 4 1 2 3 4i i i i= + + − − + −
( )
11 8 11 2 10i i i= − − + = −
.
PP nhanh trắc nghiệm
Nhập vào máy tính
. Phương pháp:
①. Dạng đại số của số phức
: phần thực số phức ; : phần ảo của số phức ; : đơn vị ảo ( )
②. Các phép toán cộng, trừ, nhân các số phức: ( )
. Phép cộng 2 số phức:
. Phép trừ của 2 số phức:
. Số đối của số phức: ( ) là số phức .
. Phép nhân của số phức:
③. Nhận xét:
Với mọi số thực và mọi số phức ,
✓. ; ✓.
Dạng ①: Thực hiện các phép tính về số phức
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 13
Câu 3: Trên tập số phức, cho biểu thức
( )( )
1A a bi i= − −
(
, ab
là số thực). Khẳng định nào sau đây
đúng?
Ⓐ.
( )
.A a b a b i= + − +
Ⓑ.
( )
.A a b b a i= − + + −
Ⓒ.
( )
.A a b a b i= − − −
Ⓓ.
( )
.A a b a b i= − − +
Lời giải
Chọn D
( )( )
2
1A a bi i a ai bi bi= − − = − − +
( ) ( )
a b a b i= − − +
PP nhanh trắc nghiệm
Công thức
B - Bài tập rèn luyện:
Câu 1: Cho hai số phức
=−
1
43zi
và
=+
2
73zi
. Tìm số phức
=−
12
z z z
.
Ⓐ.
=+36zi
. Ⓑ.
= 11z
. Ⓒ.
= − −1 10zi
. Ⓓ.
= − −36zi
.
Câu 2: Cho số phức
= − +
3
1z i i
. Tìm phần thực
a
và phần ảo
b
của
z
.
Ⓐ.
= = −1, 2ab
. Ⓑ.
= − =2, 1ab
. Ⓒ.
==1, 0ab
. Ⓓ.
==0, 1ab
.
Câu 3: Cho số phức
32zi=+
. Giá trị của
.zz
bằng
Ⓐ.
5
. Ⓑ.
9
. Ⓒ.
13
. Ⓓ.
13
.
Câu 4: Cho số phức
32zi=−
. Trong mặt phẳng tọa độ
Oxy
, điểm nào dưới đây là điểm biểu diễn số
phức
iz
?
Ⓐ.
( )
2;3−
. Ⓑ.
( )
2; 3−
. Ⓒ.
( )
3; 2−
. Ⓓ.
( )
2;3i−
.
Câu 5: Trong hình vẽ bên, điểm
P
biểu diễn số phức
1
z
, điểm
Q
biểu
diễn số phức
2
z
. Tìm số phức
12
z z z=+
.
Ⓐ.
13i+
. Ⓑ.
3 i−+
.
Ⓒ.
12i−+
. Ⓓ.
2 i+
.
Câu 6: Số phức liên hợp của số phức
( )
12z i i=−
có điểm biểu diễn là điểm nào dưới đây?
Ⓐ.
( )
2; 1E −
. Ⓑ.
( )
1;2B −
. Ⓒ.
( )
1;2A
. Ⓓ.
( )
2;1F −
.
Câu 7: Cho hai số phức
1
1zi=+
và
2
1zi=−
. Giá trị của biểu thức
12
z iz+
bằng
Ⓐ.
22i−
. Ⓑ.
2i
. Ⓒ.
2
. Ⓓ.
22i+
.
Câu 8: Cho số phức thỏa mãn . Tổng phần thực và phần ảo của bằng
Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. .
z
1 14 2i z i
z
14
2
2
14
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 14
Câu 9: Môđun của số phức
( )
3
5 3 1z i i= + − +
là
Ⓐ.
25
. Ⓑ.
35
. Ⓒ.
53
. Ⓓ.
52
.
Câu 10: Số phức
(3 )z i i=−
biểu diễn trên mặt phẳng
Oxy
bởi điểm nào sau đây?
Ⓐ.
( 3;1)−
. Ⓑ.
(1;3)
. Ⓒ.
( 1; 3)−−
. Ⓓ.
(3; 1)−
.
Câu 11: Trong hình vẽ bên, điểm
A
biểu diễn số phức
1
z
, điểm
B
biểu diễn số phức
2
z
sao cho điểm
B
đối xứng với điểm
A
qua gốc tọa độ
O
.
Tìm
z
biết số phức
12
3z z z=+
.
Ⓐ.
4
. Ⓑ.
25
.
Ⓒ.
5
. Ⓓ.
17
.
Câu 12: Cho số phức
2 5 .zi=+
Tìm số phức
w iz z=+
Ⓐ.
73wi=−
. Ⓑ.
33wi= − −
. Ⓒ.
3 7 .wi=+
Ⓓ.
77wi= − −
.
Câu 13: Cho hai số phức
32zi=+
và
( )
2
11z a a i
= + −
. Tìm tất cả các giá trị thực của
a
để
zz
+
là
một số thực
Ⓐ.
3a =−
. Ⓑ.
3a =
.
Ⓒ.
3a =
hoặc
3a =−
. Ⓓ.
13a =
hoặc
13a =−
.
Câu 14: Cho số phức
12zi=+
. Tìm tổng phần thực và phần ảo của số phức
2w z z=+
.
Ⓐ. 3. Ⓑ. 5. Ⓒ. 1. Ⓓ. 2.
Câu 15: Điểm biểu diễn của số phức
z
là
( )
1;2M
. Tọa độ của điểm biểu diễn cho số phức
2w z z=−
là.
Ⓐ.
( )
2; 3−
. Ⓑ.
( )
2;1
. Ⓒ.
( )
1;6−
. Ⓓ.
( )
2;3
.
Câu 16: Cho
12
2 4 , 3 5z i z i= + = −
. Xác định phần thực của
2
12
.w z z=
Ⓐ.
120−
. Ⓑ.
32−
. Ⓒ.
88
. Ⓓ.
152−
.
Câu 17: Cho số phức
( ) ( )
2
1 1 2z i i= + +
. Số phức
z
có phần ảo là
Ⓐ.
2
. Ⓑ.
4
. Ⓒ.
2
. Ⓓ.
2i
.
Câu 18: Cho hai số phức
35zi=−
và
12wi= − +
. Điểm biểu diễn số phức
.z z w z
=−
trong mặt phẳng
Oxy
có tọa độ là
Ⓐ.
( )
6; 4−−
. Ⓑ.
( )
4; 6−
. Ⓒ.
( )
4; 6
. Ⓓ.
( )
4; 6−−
.
Câu 19: Tìm số phức
z
thỏa mãn
(2 ) 3 5z i z i+ + = −
.
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 15
Ⓐ.
23zi=+
. Ⓑ.
23zi= − +
. Ⓒ.
23zi=−
. Ⓓ.
23zi= − −
.
Câu 20: Trong mặt phẳng
( ) ( )
, 1;7 , 5;5Oxy A B −
lần lượt biểu diễn hai số phức
12
,.zz
C
biểu diễn số
phức
12
.zz+
Trong các mệnh đề sau, mệnh đề nào sai.
Ⓐ.
C
có tọa độ
( )
4;12−
. Ⓑ.
CB
biểu diễn số phức
1
z−
.
Ⓒ.
AB
biểu diễn số phức
12
zz−
. Ⓓ.
OACB
là hình thoi.
BẢNG ĐÁP ÁN
1.D
2.A
3.C
4.B
5.A
6.A
7.C
8.A
9.D
10.B
11.B
12.B
13.C
14.B
15.C
16.D
17.A
18.D
19.C
20.C
A - Bài tập minh họa:
Câu 1: Số phức
( ) ( )
2 3 5z i i= − − − +
có phần ảo bằng
Ⓐ.
2i−
. Ⓑ.
4i−
. Ⓒ.
4−
. Ⓓ.
2−
.
Lời giải
Chọn C
Ta có:
( ) ( ) ( ) ( )
2 3 5 2 5 3 1 i 7 4iz i i= − − − + = + − + = −
.
Nên phần ảo của số phức
z
là
4−
.
PP nhanh trắc nghiệm
Từ phép tính ta có phần ảo số phức
z
là
4−
.
Câu 2: Cho các số phức
1
12zi=−
,
2
z 2 3i= − +
. Số phức nào sau có phần ảo lớn hơn.
Ⓐ.
21
zz−
. Ⓑ.
1
z
. Ⓒ.
2
.z
Ⓓ.
21
zz+
.
. Phương pháp:
①. Số phức là biểu thức có dạng . Khi đó:
Phần thực của là , phần ảo của là và được gọi là đơn vị ảo.
②. Đặc biệt:
Số phức có phần ảo bằng được coi là số thực và viết là
Số phức có phần thực bằng được gọi là số ảo (hay số thuần ảo) và viết là
Số .
Số: vừa là số thực vừa là số ảo.
Dạng ②: Xác định các yếu tố cơ bản của số phức qua phép toán.
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 16
Lời giải
Chọn A
Số phức
( )
21
1 2 3 2z z i− = − − + +
, có phần
ảo là
32+
.
Số phức
1
12zi=−
, có phần ảo là
2−
.
Số phức
2
z 2 3i= − +
, có phần ảo là
3
.
Số phức
( )
21
1 2 3 2z z i+ = − + −
, có phần ảo
là
32−
.
Vậy số phức
21
zz−
có phần ảo lớn nhất.
PP nhanh trắc nghiệm
Nhập máy tính để tính
21
zz−
Nhập máy tính để tính
21
zz+
Câu 3: Tìm phần thực
a
của số phức
2 2019
...z i i= + +
.
Ⓐ.
1a =
. Ⓑ.
1009
2a =−
. Ⓒ.
1009
2a =
. Ⓓ.
1a =−
.
Lời giải
Chọn B
2 2019
...z i i= + +
Với
1n
, ta có:
4
1
n
i =
,
41n
ii
+
=
,
42
1
n
i
+
=−
,
43n
ii
+
=−
4 4 1 4 2 4 3
0
n n n n
i i i i
+ + +
+ + + =
( ) ( )
4 5 6 7 2016 2017 2018 2019
... 0i i i i i i i i + + + + + + + + =
2 2019 2 3
... 1z i i i i i = + + = + = − −
1a = −
.
PP nhanh trắc nghiệm
Ta có
2 2019
...z i i= + +
là tổng của dãy một
CSN với số hạng đầu tiên
1
1u =−
, công bội
qi=
và
2018n =
.
Do đó ta có
2018
2
1
1
1
i
z i i
i
−
= = − −
−
. Suy ra
1a =−
.
B - Bài tập rèn luyện:
Câu 1: Cho số phức
32zi=−
. Tìm phần ảo của số phức
( )
12w i z=+
Ⓐ.
4−
. Ⓑ.
7
. Ⓒ.
4
. Ⓓ.
4i
.
Câu 2: Cho số phức
( ) ( )
22
2 1 3z i i= − − +
. Tổng phần thực và phần ảo của
z
là
Ⓐ. 1. Ⓑ.
1−
. Ⓒ.
21−
. Ⓓ.
21
.
Câu 3: Phần ảo của số phức
3
5 2 (1 )z i i= + − +
bằng:
Ⓐ.
0
. Ⓑ.
7
. Ⓒ.
7−
. Ⓓ.
7
.
Câu 4: Cho hai số phức
1
23zi=+
;
2
1zi=+
. Tính
12
3zz+
.
Ⓐ.
12
3 61zz+=
. Ⓑ.
12
3 11zz+=
. Ⓒ.
12
3 11zz+=
. Ⓓ.
12
3 61zz+=
.
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 17
Câu 5: Số phức
( ) ( )
2 3 5z i i= − − − +
có phần ảo bằng:
Ⓐ.
2i−
. Ⓑ.
4i−
. Ⓒ.
4−
. Ⓓ.
2−
.
Câu 6: Cho số phức
( , )z a bi a b= +
. Tìm phần ảo của số phức
2
z
.
Ⓐ.
22
ab−
. Ⓑ.
22
ab+
. Ⓒ.
2ab−
. Ⓓ.
2ab
.
Câu 7: Cho hai số phức
1
12zi=+
và
2
23zi=−
. Phần ảo của số phức
12
w z z=+
là
Ⓐ.
5i
. Ⓑ.
5
. Ⓒ.
1−
. Ⓓ.
i−
.
Câu 8: Cho số phức
12zi= − +
. Môđun của số phức
iz z+
bằng
Ⓐ.
6
. Ⓑ.
32
. Ⓒ.
2
. Ⓓ.
18
.
Câu 9: Cho số phức
z
khác
0
. Khẳng định nào sau đây là sai?
Ⓐ.
z
z
là số thuần ảo. Ⓑ.
.zz
là số thực Ⓒ.
zz+
là số thực Ⓓ.
zz−
là số ảo.
Câu 10: Phần ảo của số phức
z
bằng bao nhiêu biết
( ) ( )
2
2 1 2z i i= + −
.
Ⓐ.
2
. Ⓑ.
2
. Ⓒ.
2−
. Ⓓ.
2−
.
Câu 11: Điểm nào trong hình vẽ dưới đây là điểm biểu diễn của số phức
( )( )
12z i i= + −
?
Ⓐ.
M
. Ⓑ.
P
.
Ⓒ.
N
. Ⓓ.
Q
.
Câu 12: Cho số phức
2z a bi=+
( )
,ab
. Khi đó phần thực của số phức
( )( )
23w z i i= + −
bằng
Ⓐ.
6 2 1ab++
. Ⓑ.
2 12 3ab− + +
. Ⓒ.
6 4 1ab++
. Ⓓ.
2 6 3ab− + +
.
Câu 13: Số nào trong các số phức sau là số thực?
Ⓐ.
( ) ( )
1 2 1 2ii+ + − +
. Ⓑ.
( ) ( )
3 2 3 2ii+ + −
.
Ⓒ.
( ) ( )
3 2 3 2ii+ − −
. Ⓓ.
( )
( )
5 2 5 2ii+ − −
.
Câu 14: Tìm số phức
z
thỏa mãn
2 2 4z z i+ = −
.
Ⓐ.
2
4
3
zi=−
. Ⓑ.
2
4
3
zi= − +
. Ⓒ.
2
4
3
zi=+
. Ⓓ.
2
4
3
zi= − −
.
Câu 15: Có bao nhiêu số phức
z
thỏa mãn
.2z z z z+=
?
Ⓐ.
1
. Ⓑ.
0
. Ⓒ.
3
. Ⓓ.
2
.
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 18
Câu 16: Cho hai số phức
12
2 3 , 3z i z i= + = −
. Số phức
12
2zz−
có phần ảo bằng
Ⓐ.
1
. Ⓑ.
3
. Ⓒ.
5
. Ⓓ.
7
.
Câu 17: Trong mặt phẳng tọa độ, điểm
( )
1; 2M −
biểu diễn số phức; Môđun của số phức
2
iz z−
bằng
Ⓐ.
6
. Ⓑ.
6
. Ⓒ.
26
. Ⓓ.
26
.
Câu 18: Nếu
23zi=−
thì
3
z
bằng
Ⓐ.
27 24 .i+
Ⓑ.
46 9 .i+
Ⓒ.
54 27 .i−
Ⓓ.
46 9 .i−−
Câu 19: Xét các khẳng định sau:
2
)z. ) ) 0i z z ii z z z iii z z +
Số khẳng định đúng là:
Ⓐ.
0
. Ⓑ.
1
. Ⓒ.
3
. Ⓓ.
2
.
Câu 20: Cho hai số phức
( )
,z a bi a b= +
và
( )
,z a b i a b

= +
. Điều kiện giữa
, , ,a b a b

để
zz
+
là một số thuần ảo là
Ⓐ.
0aa
+=
. Ⓑ.
'0
'0
aa
bb
+=
+
. Ⓒ.
'0
'0
aa
bb
+=
+=
. Ⓓ.
0bb
+=
.
BẢNG ĐÁP ÁN
1.C
2.C
3.A
4.A
5.C
6.D
7.C
8.B
9.A
10.D
11.D
12.C
13.B
14.C
15.D
16.C
17.D
18.D
19.D
20.B
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 19
A - Bài tập minh họa:
Câu 1: Nếu hai số thực
,xy
thỏa mãn
( ) ( )
3 2 1 4 1 24x i y i i+ + − = +
thì
xy−
bằng?
Ⓐ.
3
. Ⓑ.
3−
. Ⓒ.
7−
. Ⓓ.
7
Lời giải
Chọn D
Ta có:
( ) ( )
( )
3 2 1 4 1 24
3 2 4 1 24
3 1 2
2 4 24 5
x i y i i
x y x y i i
x y x
x y y
+ + − = +
+ + − = +
+ = =



− = = −

Vậy:
7xy−=
PP nhanh trắc nghiệm
Casio
Câu 2: Cho số phức z thỏa mãn
| | 5z =
và
| 3| | 3 10 |z z i+ = + −
. Tìm số phức
4 3 .w z i= − +
Ⓐ.
3 8 .wi= − +
Ⓑ.
1 3.wi=+
Ⓒ.
1 7 .wi= − +
Ⓓ.
4 8 .wi= − +
-Phương pháp:
①. Sử dụng tính chất hai số phức bằng nhau.
Cho hai số phức , . Khi đó:
②. Số phức liên hợp, mo đun của số phức: Cho số phức .
⬧.Số phức liên hợp của là ( ) .
⬧.Tổng và tích của và luôn là một số thực.
.
.
⬧. Mô đun của số phức .
; .
Dạng ③: Bài toán quy về giải phương trình, hệ phương trình
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 20
Lời giải
Chọn D
,( , )z x yi x y= +
. Theo đề bài ta có:
22
25xy+=
và
2 2 2 2
( 3) ( 3) ( 10)x y x y+ + = + + −
.
Giải hệ phương trình trên ta được
0; 5xy==
.
Vậy
5zi=
.
Từ đó ta có
48wi= − +
.
PP nhanh trắc nghiệm
Thử lần lượt các đáp án.
A
3 8 4 3 1 5w i z w i i= − + = + − = +
nên
| | 26z =
(loại).
Tương tự cho đáp án B và C,
D
4 8 4 3 5w i z w i i= − + = + − =
thỏa mãn
| | 5z =
và
| 3| | 3 10 |z z i+ = + −
.
Câu 3: Cho số phức
z
thỏa mãn
( )
( )
3 2 3 7 16z i i z i− − + = −
. Môđun của số phức
z
bằng.
Ⓐ.
5
. Ⓑ.
3
. Ⓒ.
5
. Ⓓ.
3
.
Lời giải
Chọn C
Gọi
z x yi=+
với
Ta có
( )
( )
( ) ( )( )
3 2 3 7 16
3 2 3 7 16
3 3 3 2 2 3 3 7 16
z i i z i
x yi i i x yi i
x yi i x yi xi y i
− − + = −
− − − + + = −
− − − − − + = −
( ) ( )
3 3 5 3 7 16
3 7 3 7 1
3 5 3 16 3 5 13 2
x y x y i i
x y x y x
x y x y y
+ − + + = −
+ = + = =
+ + = + = =
.
Do đó
12zi=+
. Vậy
5z =
.
PP nhanh trắc nghiệm
Casio: công thức nhanh
22
.c a bc
az bz c z
ab
−
+ = =
−
B - Bài tập rèn luyện:
Câu 1: Tìm hai số thực
x
và
y
thỏa mãn
( ) ( )
2 3 1 3 1 6x yi i i− + − = − +
với
i
là đơn vị ảo.
Ⓐ.
1x =
;
3y =−
. Ⓑ.
1x =−
;
3y =−
. Ⓒ.
1x =−
;
1y =−
. Ⓓ.
1x =
;
1y =−
.
Câu 2: Nếu hai số thực
,xy
thỏa mãn
( ) ( )
3 2 1 4 1 24x i y i i+ + − = +
thì
xy−
bằng?
Ⓐ.
3
. Ⓑ.
3−
. Ⓒ.
7−
. Ⓓ.
7
.
Câu 3: Cho cặp số
( )
;xy
thỏa mãn:
( ) ( )
2 1 2 3 7x y i y i i− + − = +
. Khi đó biểu thức
2
P x xy=−
nhận
giá trị nào sau đây:
Ⓐ.
30
. Ⓑ.
40
. Ⓒ.
10
. Ⓓ.
20
.
Câu 4: Tìm số phức thỏa mãn .
z
2 2 4z z i+ = −
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 21
Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. .
Câu 5: Tìm các số thực
và
thỏa mãn
với
là đơn vị ảo.
Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. .
Câu 6: Giả sử , là hai số thực thỏa mãn với là đơn vị ảo. Giá trị của ,
bằng
Ⓐ. , . Ⓑ. , . Ⓒ. , . Ⓓ. , .
Câu 7: Tìm các số thực , thỏa mãn .
Ⓐ. ; . Ⓑ. ; . Ⓒ. ; . Ⓓ. ; .
Câu 8: Tìm các số thực , thỏa mãn với là đơn vị ảo.
Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. .
Câu 9: Cho các số thực , thỏa mãn . Tính giá trị của .
Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. .
Câu 10: Các số thực , thỏa mãn đẳng thức
trong đó . Giá trị
của biểu thức
là
Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. .
Câu 11: Tìm các số thực và thỏa mãn với là đơn vị ảo.
Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. .
Câu 12: Cho hai số thực thỏa mãn . Giá trị bằng
Ⓐ. 3. Ⓑ. 2. Ⓒ. 4. Ⓓ. .
Câu 13: Cho số phức thỏa mãn . Tính môđun của số phức .
Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. .
Câu 14: Cho số phức thỏa mãn .Tính .
Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. .
Câu 15: Cho số phức thỏa mãn: . Tính
Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. .
Câu 16: Cho số phức thỏa mãn có phần thực là
2
4
3
zi= − −
2
4
3
zi=−
2
4
3
zi= − +
2
4
3
zi=+
a
b
( )
4 2 1 6ai bi i i+ − = +
i
1
,6
4
ab= − = −
1
,6
4
ab= − =
1, 1ab==
1, 1ab= = −
a
b
( )
2 3 4 5a b i i+ − = −
i
a
b
1a =
8b =
8a =
8b =
2a =
2b =−
2a =−
2b =
x
y
( ) ( )
1 3 2 1 2 3 6i x y y i i− − + + = − −
5x =−
4y =−
5x =
4y =
5x =
4y =−
5x =−
4y =
x
y
( )
2 1 2 1x y i i− + − = +
i
1; 1xy==
1; 2xy==
1; 3xy==
1; 3xy= − =
x
y
( )
4 3 2 4 2i x yi− = +
P x y=+
4P =
7P =
1P =−
8P =
x
y
( ) ( )
3 5 1 2 9 16x i y i i+ − + = +
2
1i =−
T x y=−
3
5
0
1
a
b
( )
2 1 2a b i i i+ + = +
i
0, 2ab==
1
,1
2
ab==
0, 1ab==
1, 2ab==
,xy
( ) ( )
3 2 1 4 1 24x i y i i+ + − = +
xy+
3−
z
( )
2 3 5z i z i+ + = +
z
13z =
5z =
13z =
5z =
( )
,,= + z a bi a b
( )
3 4 5 17 11z i z i− + = − +
ab
3ab =
6ab =
6ab =−
3ab =−
,,z a bi a b= +
( ) ( )
1 3 2 2 4i z i z i+ + + = − +
.P ab=
8I =
4P =−
8P =−
4P =
z
( )
2. 2 6z z z i+ + = −
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 22
Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. .
Câu 17: Cho số phức thỏa . Tính .
Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. .
Câu 18: Cho số phức thỏa mãn . Tính giá trị biểu thức ?
Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. .
Câu 19: Số phức (với ) thỏa mãn , giá trị của bằng
Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. .
Câu 20: Cho các số thực thỏa mãn đẳng thức với là đơn vị ảo. Giá trị
biểu thức bằng
Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. .
BẢNG ĐÁP ÁN
1.B
2.D
3.B
4.D
5.C
6.C
7.B
8.C
9.A
10.B
11.D
12.D
13.A
14.B
15.A
16.A
17.B
18.D
19.B
20.A
2
5
1−
3
4
6−
z a bi=+
( ; )a b R
( )
1 2 3 2i z z i+ + = +
P a b=+
1P =
1P =−
1
2
P =−
1
2
P =
( )
,z a bi a b= +
23z z i+ = +
3ab+
36ab+=
35ab+=
33ab+=
34ab+=
z x yi=+
,xy
( )
1 3 5i z i+ = +
22
xy+
34
17
34
17
,ab
( )
2 3 3 2 4 3a b i i i+ + − = −
i
2P a b=−
0
2
3
2
−
2−
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 23
A - Bài tập minh họa:
Câu 1:
Tìm tập hợp các điểm biểu diễn số phức
z
thỏa
| 3 | 2zi− + =
trong mặt phẳng
.Oxy
Ⓐ. Đường tròn
( ) ( )
22
3 1 4xy+ + − =
. Ⓑ. Đường tròn
( ) ( )
22
3 1 4xy− + + =
.
Ⓒ. Đường tròn
( ) ( )
22
3 1 2xy− + + =
. Ⓓ. Đường thẳng
3x y 2 0.− + =
Lời giải
Chọn B
Đặt
( )
,z x yi x y= +
. Ta có:
( ) ( )
( ) ( )
22
22
3 2 3 1 2
3 1 4.
z i x y
xy
− + = − + + =
− + + =
PP nhanh trắc nghiệm
-Phương pháp:
. Số phức có điểm biểu diễn trên mp là điểm .
.Số phức có mô đun .
.Số phức có phần ảo bằng được coi là số thực và viết là
. Số phức có phần thực bằng được gọi là số ảo (hay số thuần ảo) và
viết là
. Phương trình đường thẳng:
. Phương trình Elip:
. Phương trình đường tròn:
Dạng 1: có tâm , bán kính .
Dạng 2: có tâm , bán kính
(Với )
. Nhận dạng nhanh tâm và bán kính đường tròn :
. .
. .
Dạng ④: Bài toán tìm tập hợp điểm biểu diễn cho số phức
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 24
Câu 2: Tập hợp các điểm
M
biểu diễn số phức
z
sao cho
( )
2
2
zz=
là
Ⓐ. Trục tung và trục hoành. Ⓑ. Trục tung.
Ⓒ. Trục hoành. Ⓓ. Gốc tọa độ.
Lời giải
Chọn A
Đặt
( , )z x yi x y= +
nên
z x yi=−
.
Ta có:
( ) ( )
22
22
0z z z z= − =
( )( )
( ) ( )
0
2 . 2 0
0
0
z z z z
yi x
x
y
− + =
=
=
=
.
Vậy tập hợp các điểm
M
biểu diễn số phức
z
là trục tung
( )
0x =
và trục hoành
( )
0y =
.
PP nhanh trắc nghiệm
Nhận biết hằng đẳng thức
( ) ( )
22
22
0z z z z= − =
( )( )
0z z z z − + =
Casio:
Calc x=0; y=1 và x=1; y=0 đều cho kết quả
bằng 0 nên chọn Ⓐ.
Câu 3: Cho số phức
z
thỏa mãn
12z i z− + = +
. Trong mặt phẳng phức, quỹ tích điểm biểu diễn
các số phức
z
.
Ⓐ. là đường thẳng
3 1 0xy+ + =
. Ⓑ. là đường thẳng
3 1 0xy− + =
.
Ⓒ. là đường thẳng
3 1 0xy+ − =
. Ⓓ. là đường thẳng
3 1 0xy− − =
.
Lời giải
Chọn B
Giả sử số phức
z
có dạng:
( )
z x yi x,y= +
Ta có:
1 2 1 2z i z x yi i x yi− + = + + − + = + +
( ) ( ) ( )
1 1 2x y i x yi − + + = + +
( ) ( ) ( )
2 2 2
2
1 1 2x y x y − + + = + +
( ) ( ) ( )
2 2 2
2
1 1 2x y x y − + + = + +
2 2 2 2
2 1 2 1 4 4x x y y x x y − + + + + = + + +
6 2 2 0 3 1 0x y x y − + = − + =
Vậy tập hợp điểm biểu diễn số phức
z
là đường
thẳng
3 1 0xy− + =
.
PP nhanh trắc nghiệm
Casio: Chọn hai điểm đặc biệt thuộc đường
thẳng và calc.
Calc x=0;y=-1 loại A
Calc x=0;y=1 và x=-1/3; y=0
Ta chọn B
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 25
B - Bài tập rèn luyện:
Câu 1: Trong mặt phẳng phức với hệ tọa độ
Oxy
, điểm biểu diễn của các số phức
3z bi=+
với
b
luôn nằm trên đường có phương trình là
Ⓐ.
3x =
. Ⓑ.
yx=
. Ⓒ.
3y =
. Ⓓ.
3yx=+
.
Câu 2: Tập hợp các điểm biểu diễn số phức
z
thỏa mãn
23zi− + =
Ⓐ.
( ) ( )
22
2 1 9xy− + + =
. Ⓑ.
( ) ( )
22
2 1 1xy− + + =
.
Ⓒ.
( ) ( )
22
2 1 4xy− + + =
. Ⓓ.
( ) ( )
22
2 1 16xy− + + =
.
Câu 3: Tập hợp các điểm trong mặt phẳng biểu diễn cho số phức
z
thoả mãn điều kiện
1 2 4zi− + =
là.
Ⓐ. Một đường thẳng. Ⓑ. Một đoạn thẳng. Ⓒ. Một đường tròn. Ⓓ. Một hình vuông.
Câu 4: Tập hợp tất cả các điểm biểu diễn các số phức
z
thỏa mãn:
24zi+ − =
là đường tròn có tâm
I
và bán kính
R
lần lượt là:
Ⓐ.
( )
2; 1I −
;
2R =
. Ⓑ.
( )
2; 1I −−
;
2R =
.
Ⓒ.
( )
2; 1I −
;
4R =
. Ⓓ.
( )
2; 1I −−
;
4R =
.
Câu 5: Tìm tập hợp điểm biểu diễn số phức
z
thỏa
22zi− + =
.
Ⓐ. Tập hợp điểm biểu diễn số phức
z
là đường tròn
22
4 2 1 0x y x y+ − + + =
.
Ⓑ. Tập hợp điểm biểu diễn số phức
z
là đường tròn
22
4 2 1 0x y x y+ − − + =
.
Ⓒ. Tập hợp điểm biểu diễn số phức
z
là đường tròn
22
4 2 4 0x y x y+ − + − =
.
Ⓓ. Tập hợp điểm biểu diễn số phức
z
là đường tròn
22
4 2 4 0x y x y+ − − − =
.
Câu 6: Tập hợp các điểm
M
biểu diễn số phức
z
thoả mãn
2 5 4zi− + =
là:
Ⓐ. Đường tròn tâm
( )
2; 5I −
và bán kính bằng
2
.
Ⓑ. Đường tròn tâm
( )
2;5I −
và bán kính bằng
4
.
Ⓒ. Đường tròn tâm
O
và bán kính bằng
2
.
Ⓓ. Đường tròn tâm
( )
2; 5I −
và bán kính bằng
4
.
Câu 7: Trên mặt phẳng tọa độ, tập hợp điểm biểu diễn số phức
z
thỏa mãn điều kiện
2 5 6zi+ − =
là đường tròn có tâm và bán kính lần lượt là:
Ⓐ.
( 2;5), 6IR−=
. Ⓑ.
( 2;5), 36IR−=
. Ⓒ.
(2; 5), 36IR−=
. Ⓓ.
(2; 5), 6IR−=
.
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 26
Câu 8: Trên mặt phẳng phức tập hợp các 2018 phức
z x yi=+
thỏa mãn
23z i z i+ + = −
là đường
thẳng có phương trình
Ⓐ.
1yx= − +
. Ⓑ.
1yx= − −
. Ⓒ.
1yx=−
. Ⓓ.
1yx=+
.
Câu 9: Tìm tập hợp điểm biểu diễn số phức
z
thỏa mãn
23zi+ − =
.
Ⓐ. Đường tròn tâm
( )
2; 1I −
, bán kính
1R =
.
Ⓑ. Đường tròn tâm
( )
2;1I −
, bán kính
3R =
.
Ⓒ. Đường tròn tâm
( )
2;1I −
, bán kính
3R =
.
Ⓓ. Đường tròn tâm
( )
1; 2I −
, bán kính
3R =
.
Câu 10: Tập hợp các điểm trong mặt phẳng toạ độ biểu diễn các số phức
z
thoả mãn
4 8 2 5zi+ − =
là đường tròn có phương trình:
Ⓐ.
( ) ( )
22
4 8 2 5xy+ + − =
. Ⓑ.
( ) ( )
22
4 8 2 5xy− + + =
.
Ⓒ.
( ) ( )
22
4 8 20xy+ + − =
. Ⓓ.
( ) ( )
22
4 8 20xy− + + =
.
Câu 11: Cho số phức
z
thỏa mãn
( )
32iz i− − + =
. Trong mặt phẳng phức, quỹ tích điểm biểu diễn số
phức
z
là hình vẽ nào dưới đây?
Ⓐ. . Ⓑ. .
Ⓒ. . Ⓓ. .
Câu 12: Tìm tập hợp những điểm
M
biểu diễn số phức
z
trong mặt phẳng phức, biết số phức
z
thỏa
mãn điều kiện
21z i z− = +
.
Ⓐ. Tập hợp những điểm
M
là đường thẳng có phương trình
2 4 3 0xy+ + =
.
Ⓑ. Tập hợp những điểm
M
là đường thẳng có phương trình
4 2 3 0xy+ + =
.
Ⓒ. Tập hợp những điểm
M
là đường thẳng có phương trình
2 4 3 0xy+ − =
.
Ⓓ. Tập hợp những điểm
M
là đường thẳng có phương trình
4 2 3 0xy− + =
.
Câu 13: Tập hợp các điểm biểu diễn số phức
z
thỏa mãn
( )
1z i i z− = +
là một đường tròn, tâm của
đường tròn đó có tọa độ là
x
y
3
3
2
1
2
O
1
x
y
3
3
2
1
2
O
1
x
y
3
2
1
2
O
1
x
y
3
3
2
1
2
O
1
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 27
Ⓐ.
( )
1;1
. Ⓑ.
( )
0; 1−
. Ⓒ.
( )
0;1
. Ⓓ.
( )
1;0−
.
Câu 14: Tập hợp các điểm biểu diễn số phức
z
trên mặt phẳng tọa độ là đường tròn tâm
( )
0;1I
, bán
kính
3R =
. Mệnh đề nào dưới đây là đúng?
Ⓐ.
13z −=
. Ⓑ.
3zi−=
. Ⓒ.
3zi−=
. Ⓓ.
3zi+=
.
Câu 15: Tập hợp tất cả các điểm trong mặt phẳng toạ độ
Oxy
biểu diễn số phức
z
thoả mãn
1 2 3z i z− + = +
là đường thẳng có phương trình
Ⓐ.
2 1 0xy− + =
. Ⓑ.
2 1 0xy+ − =
. Ⓒ.
2 1 0xy− − =
. Ⓓ.
2 1 0xy+ + =
.
Câu 16: Trong mặt phẳng tọa độ, tập hợp điểm
( )
;M x y
biểu diễn số phức
z x yi=+
,
( )
,xy
thỏa
mãn
1 3 2z i z i− + = − −
Ⓐ. Đường tròn đường kính
AB
với
( )
1; 3A −
,
( )
2;1 .B
.
Ⓑ. Đường trung trực của đoạn thẳng
AB
với
( )
1; 3A −
,
( )
2;1 .B
.
Ⓒ. Trung điểm của đoạn thẳng
AB
với
( )
1; 3A −
,
( )
2;1 .B
.
Ⓓ. Đường trung trực của đoạn thẳng
AB
với
( )
1;3A −
,
( )
2; 1 .B −−
.
Câu 17: Cho số phức
z
thỏa mãn điều kiện
3 4 2zi− +
. Trong mặt phẳng tọa độ, tập hợp điểm biểu
diễn số phức
w 2 1zi= + −
là hình tròn có diện tích
Ⓐ.
9
. Ⓑ.
12
. Ⓒ.
16
. Ⓓ.
25
.
Câu 18: Cho số phức
z
thỏa mãn điều kiện
10z =
và
( ) ( )
2
6 8 1 2w i z i= + + −
. Tập hợp các điểm biểu
diễn số phức
w
là đường tròn có tâm là
Ⓐ.
( )
3; 4I −−
. Ⓑ.
( )
3;4I
. Ⓒ.
( )
1; 2I −
. Ⓓ.
( )
6;8I
.
Câu 19: Tập hợp tất cả các điểm biểu diễn số phức
z
mà
2
z
thuần ảo là
Ⓐ.
1
điểm duy nhất. Ⓑ.
1
đường thẳng duy nhất.
Ⓒ.
2
đường thẳng song song với nhau. Ⓓ.
2
đường thẳng vuông góc với nhau.
Câu 20: Cho số phức
z
thỏa mãn
5z =
. Biết tập hợp các điểm biểu diễn số phức
( )
12w i z i= + +
là
một đường tròn. Tìm bán kính
r
của đường tròn đó.
Ⓐ.
5r =
. Ⓑ.
10r =
. Ⓒ.
5r =
. Ⓓ.
25r =
.
BẢNG ĐÁP ÁN
1.A
2.A
3.C
4.D
5.A
6.D
7.A
8.C
9.B
10.C
11.C
12.C
13.B
14.B
15.B
16.B
17.C
18.A
19.D
20.C
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 28
FB: Duong Hung
A - Bài tập minh họa:
Câu 1. Thực hiện phép chia sau :
2
32
i
z
i
+
=
−
.
Ⓐ.
74
13 13
zi=+
. Ⓑ.
47
13 13
zi=+
. Ⓒ.
47
13 13
zi=−
. Ⓓ.
74
13 13
zi=−
.
Lời giải
Chọn B
( )( )
( )( )
2 3 2
2 4 7
3 2 2 3 2 13 13
ii
i
zi
i i i
++
+
= = = +
− + +
PP nhanh trắc nghiệm
Casio
Câu 2. Cho số phức
1
43
i
z
i
−
=
+
, khẳng định nào sau đây đúng.
Ⓐ.
17
25 25
zi=+
. Ⓑ.
17
25 25
zi=−
. Ⓒ.
17
25 25
zi= − −
. Ⓓ.
71
25 25
zi=−
.
Lời giải
Chọn B
1 1 7
.
4 3 25 25
i
zi
i
−
= = −
+
PP nhanh trắc nghiệm
Casio
Câu 3. Cho số phức
( )
,z a bi a b= +
thỏa
56
1
i
z
i
+
=
−
. Tính giá trị của
21P ab=−
.
Ⓐ.
13
2
P
−
=
. Ⓑ.
9
2
P =
. Ⓒ.
13
2
P =
. Ⓓ.
9
2
P =−
Full Chuyên
đề 12 new
2020-2021
CHƯƠNG
④
:
Bài ➂: PHÉP CHIA HAI SỐ PHỨC
. Phương pháp:
✓. Cho hai số phức và .
①.
②
. Sử dụng Casio: Chế độ số phức mode 2
Dạng ①: Thực hiện các phép tính về số phức
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 29
Lời giải
Chọn A
5 6 1 11
.
1 2 2
i
zi
i
+−
= = +
−
Ta có
1 11
;
22
ab
−
==
1 11 13
2 1 2 . 1
2 2 2
P ab
−−

= − = − =


PP nhanh trắc nghiệm
Casio
B - Bài tập rèn luyện:
Câu 1. Thu gọn
( )( )
3 2 6 2
1
ii
z
i
−+
=
+
ta được.
Ⓐ.
8 14zi=+
. Ⓑ.
8 14zi=−
. Ⓒ.
8 13zi= − +
. Ⓓ.
14zi=
.
Câu 2. Cho số phức
( )
,z a bi a b= +
thỏa
( ) ( )
23
1 . 2
2
ii
z
i
+
=
−+
. Tính giá trị của
2P a b=+
.
Ⓐ.
48
5
P =
. Ⓑ.
16
5
P =−
. Ⓒ.
48
5
P =−
. Ⓓ.
16P =−
.
Câu 3. Viết gọn
7 17
12
5
i
zi
i
−
= − +
−
.
Ⓐ.
3 5 .zi=+
Ⓑ.
3 5 .zi=−
Ⓒ.
3 5 .zi= − +
Ⓓ.
35zi= − −
.
Câu 4. Cho số phức
0z a bi= +
. Số phức
1
z
−
có phần thực là
Ⓐ.
.ab+
Ⓑ.
.ab−
Ⓒ.
22
a
ab+
Ⓓ.
22
b
ab
−
+
Câu 5. Cho số phức
0z a bi= +
. Số phức
1
z
có phần ảo là
Ⓐ.
22
.ab+
Ⓑ.
22
.ab−
Ⓒ.
22
a
ab
+
Ⓓ.
22
b
ab
−
+
Câu 6. Cho hai số phức
1
12zi=+
,
2
3zi=−
. Tìm số phức
2
1
z
z
z
=
.
Ⓐ.
17
55
zi=+
. Ⓑ.
17
10 10
zi=+
. Ⓒ.
17
55
zi=−
. Ⓓ.
17
10 10
zi= − +
.
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 30
Câu 7. Số phức nghịch đảo
1
z
−
của số phức
22zi=−
là
Ⓐ.
11
44
i−
. Ⓑ.
11
44
i−+
. Ⓒ.
11
44
i+
. Ⓓ.
11
44
i−−
.
Câu 8. Cho số phức
5 2 .zi=−
Số phức
1
z
có phần ảo là
Ⓐ.
29.
Ⓑ.
21.
Ⓒ.
5
.
29
Ⓓ.
2
.
29
Câu 9. Thực hiện phép chia sau:
2
32
i
z
i
+
=
−
Ⓐ.
47
.
13 13
zi=+
Ⓑ.
74
.
13 13
zi=+
Ⓒ.
47
.
13 13
zi=−
Ⓓ.
74
.
13 13
zi=−
Câu 10. Cho số phức
2 3 .zi=−
Hãy tìm nghịch đảo của số phức
z
Ⓐ.
23
.
11 11
i+
Ⓑ.
23
.
11 11
i−
Ⓒ.
32
.
11 11
i+
Ⓓ.
32
.
11 11
i−
Câu 11.Tìm số phức
34
4
i
i
z
−
=
−
.
Ⓐ.
16 13
17 17
zi=−
. Ⓑ.
16 11
15 15
zi=−
. Ⓒ.
94
55
zi=−
. Ⓓ.
9 23
25 25
zi=−
.
Câu 12. Tìm số phức
3
2
z
i
=
+
.
Ⓐ.
63
55
zi=+
. Ⓑ.
36
55
zi=+
. Ⓒ.
63
55
zi=−
. Ⓓ.
36
55
zi=−
.
Câu 13. Tìm số phức
3
z
i
=
.
Ⓐ.
3zi=
. Ⓑ.
zi=
. Ⓒ.
zi=−
. Ⓓ.
3z i= −
.
Câu 14. Nếu
23zi=+
thì
z
z
bằng
Ⓐ.
5 12
13
i−
. Ⓑ.
5 12
13
i+
. Ⓒ.
34
7
i−
. Ⓓ.
56
2
11
i
i
+
−
.
Câu 15. Viết số phức
23
32
i
z
ii
=−
−
dưới dạng đại số.
Ⓐ.
4 45
13 13
zi=−
. Ⓑ.
4 45
13 13
zi= − −
. Ⓒ.
4 45
z
13 13
i= − +
. Ⓓ.
4 45
13 13
zi=+
.
Câu 16. Viết số phức
2 4 3
3 2 3 2
i
z
ii
−
=−
−−
dưới dạng đại số.
Ⓐ.
10 3
13 13
zi= − +
. Ⓑ.
10 3
13 13
zi=−
. Ⓒ.
10 3
z
3 13
i=+
. Ⓓ.
10 7
13 13
zi= − +
.
Câu 17. Cho số phức z =
( )
7
32ii−
. Tìm số phức liên hợp của số phức
1
z
.
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 31
Ⓐ.
32
13 13
zi=−
. Ⓑ.
32
13 13
zi=+
. Ⓒ.
32
13 13
zi= − +
. Ⓓ.
32
13 13
zi= − −
.
Câu 18. Tính
2019
2
.
1
i
z
i
−
=
−
Ⓐ.
13
.
22
zi=+
Ⓑ.
31
.
22
zi=−
Ⓒ.
13
.
22
zi=−
Ⓓ.
31
.
22
zi=+
Câu 19. Biết
1
34
a bi
i
=+
+
,
( )
,ab
. Tính
ab
.
Ⓐ.
12
25
. Ⓑ.
12
625
. Ⓒ.
12
625
−
. Ⓓ.
12
25
−
.
Câu 20. Cho số phức
1zi=+
. Giá trị của biểu thức
1
z
z
+
là
Ⓐ.
31
22
i+
. Ⓑ.
11
22
i+
. Ⓒ.
31
22
i−
. Ⓓ.
11
22
i−
.
BẢNG ĐÁP ÁN
1.B
2.D
3.B
4.C
5.D
6.C
7.C
8.D
9.A
10.A
11.A
12.C
13.D
14.B
15.C
16.D
17.A
18.C
19.C
20.A
A - Bài tập minh họa:
. Phương pháp:
①. Casio FX 570 VN plus:
⬧ Để tính toán trên tập số phức : MODE 2
⬧Lệnh tính Modun của cố phức : SHIFT HYP
⬧Lệnh tìm số phức liên hợp là: SHIFT 2 2
②. Casio FX 580 VnX :
⬧ Để tính toán trên tập số phức : MENU 2
⬧ Lệnh tính Modun của cố phức : SHIFT Abs
⬧ Lệnh tìm Acgumen, số phức liên hợp , Phần thực, Phần ảo : OPTN
③. Công thức nhanh:
④. Chức năng lưu, xuất, tính toán: Sto, Alha, Calc
Dạng ②: Thực hiện phép tính và từ đó suy ra các yếu tố liên quan tới số
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 32
Câu 1: Điểm biểu diễn của số phức
1
23
z
i
=
−
là
Ⓐ.
( )
3; 2−
. Ⓑ.
23
;
13 13



. Ⓒ.
( )
2;3−
. Ⓓ.
( )
4; 1−
.
Lời giải
Chọn B
( )( )
1 2 3 2 3
2 3 2 3 2 3 13 13
i
zi
i i i
+
= = = +
− − +
.
Suy ra điểm biểu diễn của số phức
1
23
z
i
=
−
là:
23
;
13 13



.
PP nhanh trắc nghiệm
Casio
Dựa vào kết quả kết luận
23
;
13 13



Câu 2: Gọi
12
,zz
lần lượt có điểm biểu diễn là
,MN
trên mặt phẳng phức (hình
bên). Khi đó phần ảo của số phức
1
2
z
z
là
Ⓐ.
14
17
. Ⓑ.
1
4
−
.
Ⓒ.
5
17
−
. Ⓓ.
1
2
.
Lời giải
Chọn A
Dựa vào hình vẽ ta có được
1
12
2
3 2 5 14
3 2 , 1 4
1 4 17 17
z
i
z i z i i
zi
+
= + = − = = − +
−
.
PP nhanh trắc nghiệm
Dựa vào hình vẽ
12
3 2 , 1 4z i z i= + = −
Rồi bấm máy tính
Và dựa vào số chứa
i
trả lời phần ảo của z
Dựa vào định nghĩa trả lời phần ảo là
14
17
Câu 3: Cho số phức z thỏa mãn
13
.
1
i
z
i
−
+
=
−
Tính modun của số phức
w . ?i z z
−
=+
Ⓐ.
| w| = 4 2
. Ⓑ.
| w| = 2
. Ⓒ.
| w| = 3 2
. Ⓓ.
| w| = 2 2.
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 33
Lời giải
Chọn C
Ta có:
13
1 2 .
1
i
zi
i
−
+
= = − +
−
1 2 .zi = − −
w .( 1 2 ) ( 1 2 ) 3 3i i i i= − + + − − = − −
.
22
| w| = ( 3) ( 3) 18 3 2− + − = =
.
PP nhanh trắc nghiệm
Casio
B - Bài tập rèn luyện:
Câu 1. Cho
2
13
z
i
=
+
. Số phức liên hợp của
z
là.
Ⓐ.
13
22
i+
. Ⓑ.
13
44
i+
. Ⓒ.
13
44
i−
. Ⓓ.
13
22
i−
.
Câu 2. Cho số phức
34zi=+
. Khi đó môđun của
1
z
là.
Ⓐ.
1
5
. Ⓑ.
1
5
. Ⓒ.
1
4
. Ⓓ.
1
3
.
Câu 3. Cho số phức
32
1
i
z
i
−
=
+
, số phức liên hợp của z là.
Ⓐ.
15
22
i+
. Ⓑ.
15
22
i−+
. Ⓒ.
15
22
i−
. Ⓓ.
15
22
i +
.
Câu 4. Phần thực của số phức
34
4
i
z
i
−
=
−
bằng.
Ⓐ.
16
.
17
Ⓑ.
3
.
4
Ⓒ.
13
.
17
−
Ⓓ.
3
.
4
−
Câu 5. Số phức
1
57i−+
có phần ảo là.
Ⓐ.
5
74
−
. Ⓑ.
5
74
. Ⓒ.
7
74
. Ⓓ.
7
74
−
.
Câu 6. Cho hai số phức
2 , ' 2 3 .z i z i= + = − +
Thương số
'
z
z
có phần thực bằng.
Ⓐ.
3 2 2
13
−
. Ⓑ.
. Ⓒ.
2 3 2
13
−−
. Ⓓ.
2 3 2
13
+
.
Câu 7. Trên mặt phẳng tọa độ điểm nào biểu diễn cho số phức
34i
z
i
+
=
.
Ⓐ.
( )
4;3−
. Ⓑ.
( )
4; 3−−
. Ⓒ.
( )
4;3
. Ⓓ.
( )
4; 3−
.
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 34
Câu 8. Số phức
1
23i−+
có phần ảo là.
Ⓐ.
3
7
−
. Ⓑ.
3
7
. Ⓒ.
2
7
−
. Ⓓ.
2
7
.
Câu 9. Tìm số phức
z
, biết
23
1
i
z
i
−
=
+
.
Ⓐ.
15
22
zi=+
. Ⓑ.
15
22
zi= − −
. Ⓒ.
15
22
zi= − +
. Ⓓ.
15
22
zi=−
.
Câu 10. Cho số phức
12zi= − −
, phần ảo của số phức
z
z
bằng.
Ⓐ.
3
5
−
. Ⓑ.
4
5
. Ⓒ.
4
5
−
. Ⓓ.
3
5
.
Câu 11. Cho hai số phức
12
3
3 4 , 2
2
z i z i= − = +
và số phức
1
2
z
z
z
=
. Trong các mệnh đề sau mệnh đề nào sai.
Ⓐ.
z
là số thuần ảo. Ⓑ. Phần thực của
z
bằng
0
.
Ⓒ. Môđun của
z
bằng
2
. Ⓓ. Phần ảo của
z
bằng
2
.
Câu 12. Trên mặt phẳng tọa độ điểm nào biểu diễn cho số phức
55
13
i
z
i
+
=
−
.
Ⓐ.
( )
1;2−
. Ⓑ.
( )
1;2
. Ⓒ.
( )
1; 2−
. Ⓓ.
( )
1; 2−−
.
Câu 13. Cho 2 số phức
1
1zi=+
và
2
23zi=−
. Tính môđun của số phức
1
2
z
z
.
Ⓐ.
1
2
26
13
z
z
=
. Ⓑ.
1
2
2
13
z
z
=
. Ⓒ.
1
2
26
2
z
z
=
. Ⓓ.
1
2
6
z
z
=
.
Câu 14. Điểm biểu diễn của số phức
52i
z
i
−
=
có tọa độ là
Ⓐ.
( )
2; 5−
. Ⓑ.
( )
5; 2−−
. Ⓒ.
( )
2; 5−−
. Ⓓ.
( )
2;5−
.
Câu 15. Cho số phức
23zi=−
, phần ảo của số phức
1
z
bằng
Ⓐ.
2
13
. Ⓑ.
3
13
. Ⓒ.
3
13
i
. Ⓓ.
3
13
−
.
Câu 16. Số phức
25
1
i
z
i
−
=
+
có phần thực và phần ảo lần lượt là
Ⓐ.
37
22
và−−
. Ⓑ.
37
22
và −
. Ⓒ.
37
22
và −
. Ⓓ.
37
22
và
.
Câu 17. Số phức liên hợp của số phức
23i
z
i
−
=
.
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 35
Ⓐ.
32i−−
. Ⓑ.
32i−
. Ⓒ.
23i −
. Ⓓ.
23i +
.
Câu 18. Tính môđun của số phức
2
43
i
z
i
−
=
+
Ⓐ.
5
5
. Ⓑ.
1
5
. Ⓒ.
3
5
. Ⓓ.
2
5
.
Câu 19. Cho hai số phức
12
3 , 2z i z i= + = −
. Tính giá trị của biểu thức
1
2
z
z
Ⓐ.
4
. Ⓑ.
2
. Ⓒ.
2
. Ⓓ.
22
.
Câu 20. Điểm
M
trong hình vẽ bên là điểm biểu diễn của số phức nào sau đây
Ⓐ.
12zi=+
Ⓑ.
( )
12z i i=+
Ⓒ.
3
1
i
z
i
−
=
+
Ⓓ.
43
12
i
z
i
−−
=
+
BẢNG ĐÁP ÁN
1.A
2.B
3.C
4.A
5.D
6.A
7.D
8.A
9.C
10.B
11.D
12.A
13.A
14.C
15.B
16.A
17.C
18.A
19.C
20.C
A - Bài tập minh họa:
-2
1
x
y
O
M
. Phương pháp:
①. Phương trình: có nghiệm: .
②. Nếu điều kiện ban đầu có liên quan đến số phức thì ta gọi với
.
③. Sau đó tính rồi thay vào điều kiện, giải hệ tìm
④. Casio: Ấn MODE 2: CMPLX để vào chế độ tính toán với số phức.
Dạng ③: Giải phương trình bậc nhất – suy ra các yếu tố liên quan tới số
phức
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 36
Câu 1: Cho số phức
z
thỏa mãn:
(2 ) 13 1z i i− + =
. Tính mođun của số phức
z
Ⓐ.
34z =
. Ⓑ.
5 34
3
z =
. Ⓒ.
34z =
. Ⓓ.
34
3
z =
.
Lời giải
Chọn C
Ta có
1 13
(2 ) 13 1 3 5 .
2
i
z i i z i
i
−
− + = = = −
−
Do đó
22
3 5 34z = + =
.
PP nhanh trắc nghiệm
Casio
Câu 2: Cho số phức
z
thỏa
( )
2 2 3i z i+ − =
. Số phức liên hợp của
z
là:
Ⓐ.
81
55
i+
. Ⓑ.
47
55
i−
. Ⓒ.
81
55
i−
. Ⓓ.
81
55
i−+
.
Lời giải
Chọn C
Ta có
( )
3 2 8 1
2 2 3
2 5 5
i
i z i z i
i
+
+ − = = = +
+
Vậy Số phức liên hợp của
z
là:
81
55
i−
PP nhanh trắc nghiệm
Casio
Câu 3: Cho số phức
z
thỏa mãn
( )
1 4 0i z− − =
, phần thực và phần ảo của
z
lần lượt là.
Ⓐ. 2 và 2. Ⓑ. 2 và -2. Ⓒ. -2 và 2. Ⓓ.-2 và -2.
Lời giải
Chọn B
( )
4
21 4 0 2
1
i z z i
i
=
−
== +−−
Suy ra
22zi=−
Vậy z có phần thực và phần ảo lần lượt là:
2 và -2.
PP nhanh trắc nghiệm
Casio
Dựa vào kết quả trả lời đáp án
Câu 4: Cho số phức
z
thỏa mãn
1 1 5 0i z i
. Tính
.A z z
.
Ⓐ.
13A
. Ⓑ.
13A
. Ⓒ.
1 13A
. Ⓓ.
26A
.
Lời giải
Chọn B
Ta có
15
1 1 5 0 3 2
1
i
i z i z i
i
.
Suy ra
. 3 2 3 2 13A z z i i
.
PP nhanh trắc nghiệm
Casio
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 37
B - Bài tập rèn luyện:
Câu 1. Cho số phức
z
thỏa mãn
( )
1 4 2 0i z i− + − =
. Điểm biểu diễn của
z
có tọa độ là
Ⓐ.
( )
3; 1−
. Ⓑ.
( )
3;1−
. Ⓒ.
( )
3; 1−−
. Ⓓ.
( )
3;1
.
Câu 2. Cho số phức
z
thỏa mãn
( )
1 2 8i z i+ = +
. Hỏi điểm biểu diễn của số
phức
z
là điểm nào trong các điểm
, , ,M N P Q
ở hình bên.
Ⓐ. Điểm
M
. Ⓑ. Điểm
N
.
Ⓒ. Điểm
P
. Ⓓ. Điểm
Q
Câu 3. Nghiệm của phương trình
( )
2 5(3 2 )z i i− = −
là
Ⓐ.
8zi=−
. Ⓑ.
8zi=+
. Ⓒ.
8zi= − −
. Ⓓ.
8zi= − +
.
Câu 4. Tìm mô đun của số phức
z
thỏa mãn
( )
1 8 4z i i+ = − +
.
Ⓐ.
10
. Ⓑ.
22
. Ⓒ.
42
. Ⓓ.
2 10
.
Câu 5. Số phức
z
thỏa mãn
( ) ( )
4 7i z 5 2i 6iz+ − − =
là
Ⓐ.
18 13
77
i−
. Ⓑ.
18 13
17 17
i−
. Ⓒ.
18 13
7 17
i
−
+
. Ⓓ.
18 13
17 17
i+
.
Câu 6. Cho
s
ố phức
z
thỏa mãn
(1 2 ) 7 4z i i+ = +
.Tìm mô đun
s
ố phức
2zi
=+
.
Ⓐ. 4 Ⓑ.
17
Ⓒ.
24
Ⓓ.5
Câu 7. Tìm số phức thoả mãn
( ) ( )
3 2 4 5 7 3i z i i− + + = +
Ⓐ.
1z =
Ⓑ.
1z =−
Ⓒ.
zi=
Ⓓ.
zi=−
Câu 8. Nghiệm của phương trình là
Ⓐ.
1zi=+
Ⓑ.
1zi=−
Ⓒ.
1zi= − +
Ⓓ.
1zi= − −
z
13
2
i
i
z
+
=+
2
-3
3
x
y
-2
O
P
N
M
Q
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 38
Câu 9. Cho
s
ố phức
z
thỏa mãn:
( ) ( )
(1 3 ) 2 5 2i z i i z+ − + = +
.Phần ảo của số phức z là.
Ⓐ.
8
5
. Ⓑ.
9
5
. Ⓒ.
9
5
−
. Ⓓ.
8
5
−
.
Câu 10. Cho
s
ố phức
z
thỏa mãn:
( )
2 3 5 2
43
z
ii
i
+ − = −
−
.Phần thực của số phức z là.
Ⓐ.
5−
. Ⓑ.
5
. Ⓒ.
15
. Ⓓ.
3−
.
Câu 11. Nghiệm của phương trình
( ) ( )
3 4 1 3 2 5i z i i+ + − = +
là.
Ⓐ.
74
55
zi=−
. Ⓑ.
11 2
25 25
zi= − +
. Ⓒ.
11 2
25 25
zi=+
. Ⓓ.
74
55
zi=+
.
Câu 12. Cho số phức
z
thỏa
( )
1 2 4 2i z i+ + =
. Trong các mệnh đề sau mệnh đề nào sai.
Ⓐ.
z
là số thuần ảo. Ⓑ.
2z =
Ⓒ.
z
là số thực Ⓓ. Phần ảo của
z
bằng 2.
Câu 13. Phần thực, phần ảo của số phức
z
thỏa mãn
( ) ( )
1 2 . 5 3 1 2i z i i− = − −
lần lượt là
Ⓐ. 1;1. Ⓑ.
1; 2−
. Ⓒ. 1;2. Ⓓ.
1; 1−
.
Câu 14. Cho số phức
z
thỏa mãn điều kiện:
( )
1 1 3 0i z i+ − − =
. Phần ảo của số phức
1w iz z= − +
là
Ⓐ. 1. Ⓑ.
3−
. Ⓒ.
2−
. Ⓓ.
1−
.
Câu 15. Cho số phức
z
thỏa
( )
5
12
2
i
z
i
−
=
+
. Viết
z
dưới dạng
,,z a bi a b= +
. Khi đó tổng
2ab+
có
giá trị bằng bao nhiêu?
Ⓐ. 38. Ⓑ. 10. Ⓒ. 31. Ⓓ. 55.
Câu 16. Cho số phức
( )
2 4 8i z i i+ + = +
.Tìm mô đun của số phức
1w z i= + +
.
Ⓐ.
25w =
. Ⓑ.
6w =
. Ⓒ.
6w =
. Ⓓ.
5w =
.
Câu 17. Tìm số phức liên hợp của số phức
z
biết
( )
31
z
i
i
=+
.
Ⓐ.
3zi=−
. Ⓑ.
3zi= − +
. Ⓒ.
3zi=+
. Ⓓ.
3zi= − −
.
Câu 18. Tính môđun của số phức
z
thỏa mãn
( )
2 13 1z i i− + =
.
Ⓐ.
34z =
. Ⓑ.
34z =
. Ⓒ.
5 34
3
z =
. Ⓓ.
34
3
z =
.
Câu 19. Trong , phương trình
20iz i+ − =
có nghiệm là
Ⓐ.
12zi=−
Ⓑ.
2zi=+
Ⓒ.
12zi=+
Ⓓ.
43zi=−
Câu 20. Trong , phương trình
( )
1 2 1 3z i i+ = − +
có nghiệm là
Ⓐ.
11
22
zi=−
Ⓑ.
1zi=+
Ⓒ.
zi=
Ⓓ.
2zi=−
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 39
BẢNG ĐÁP ÁN
1.C
2.C
3.A
4.D
5.B
6.D
7.A
8.A
9.C
10.C
11.D
12.C
13.A
14.B
15.B
16.D
17.D
18.B
19.C
20.B
FB: Duong Hung
A - Bài tập minh họa:
Câu 1. Trong , căn bậc hai của
121−
là
Ⓐ.
11i−
Ⓑ.
11i
Ⓒ.
11−
Ⓓ.
11i
và
11i−
Full Chuyên
đề 12 new
2020-2021
CHƯƠNG
④
:
Bài ➃: PHƯƠNG TRÌNH BẬC HAI VỚI HỆ SỐ
THỰC
. Lý thuyết cần nắm:
①
. Căn bậc hai của là và vì và .
②. Căn bậc hai của số thực là và .
Căn bậc hai của
.Tổng quát :
Số phức được gọi là một căn thức bậc 2 của số phức nếu .
. Phương pháp giải:
①. Cách 1:
⬧ Gọi là căn bậc 2 của khi và chỉ khi
⬧ Mỗi cặp số thực nghiệm đúng hệ phương trình đó cho ra một căn bậc
hai của số phức .
②. Cách 2:
Có thể biến đổi . Từ đó kết luận căn bậc hai của là và .
③. Casio 570NV Plus
⬧ Cách 1: Lệnh Pol & Rec.
⬧ Cách 2: Mode 2 → dùng lệnh shift 2.
Dạng ①: Tìm Căn bậc hai của số thực âm
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 40
Lời giải
Chọn D
Ta có
22
121 121 0
11
11
zz
zi
zi
= − + =
=
=−
PP trắc nghiệm nhanh
Casio:
Câu 2. Trong , căn bậc hai của
3−
là
Ⓐ.
3i−
Ⓑ.
3i
Ⓒ.
3−
Ⓓ.
3i
và
3i−
Lời giải
Chọn D
Ta có
22
3 3 0
3
3
zz
zi
zi
= − + =
=
=−
PP trắc nghiệm nhanh
Casio:
B - Bài tập rèn luyện:
Câu 1. Tìm các căn bậc hai của
9−
.
Ⓐ.
3i
Ⓑ. 3 Ⓒ.
3i
Ⓓ.
3−
Câu 3. Căn bậc hai của số phức của số
8−
bằng bao nhiêu?
Ⓐ.
22i
Ⓑ.
22i−
Ⓒ.
2i
Ⓓ.
2−
Câu 4. Khẳng định nào sau đây đúng?
Ⓐ.
11−=
Ⓑ.
1 i−=
Ⓒ.
1 i− = −
Ⓓ.
1 i− =
Câu 5. Khẳng định nào sau đây sai?
Ⓐ.
33− = −
Ⓑ.
33i−=
Ⓒ.
42i−=
Ⓓ.
1 i−=
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 41
Câu 6. Căn bậc hai của số phức của số
5−
bằng bao nhiêu?
Ⓐ.
5.
Ⓑ.
4
5.i
Ⓒ.
5.i
Ⓓ.
5.i−
Câu 7. Trong tập số phức, mệnh đề nào dưới đây sai?
Ⓐ. Căn bậc hai của
25−
là
5.i
Ⓑ.
( )
2
6 36.i−=
Ⓒ. Căn bậc hai của
4−
là
2.i
Ⓓ. Căn bậc hai của 9 là
3.
Câu 8. Trong tập số phức, mệnh đề nào dưới đây đúng?
Ⓐ. Căn bậc hai của
16−
là
4.i
Ⓑ. Căn bậc hai của
100
là
10.
Ⓒ. Căn bậc hai của
10−
là
10 .i
Ⓓ.
2
3 9.i−=
BẢNG ĐÁP ÁN
1.A
2.A
3.D
4.A
5.A
6.B
7.A
8.C
A - Bài tập minh họa:
Câu 1: Kí hiệu
12
,zz
là hai nghiệm phức của phương trình
2
3z 5 0z − + =
. Giá trị của
12
zz+
bằng
Ⓐ.
25
. Ⓑ.
5
. Ⓒ.
3
. Ⓓ.
10
.
Quy trình bấm máy
Bấm máy
Màn hình hiển thị nghiệm
PP trắc nghiệm nhanh
Casio
+ Lúc giải phương trình là máy ở chế độ
tính toán bình thường, nhưng khi tính
12
zz+
thì phải chuyển tính năng máy
sang chế độ số phức mode 2
-Phương pháp:
①. Tính .
②. Áp dụng công thức nghiệm.
③. Casio: Dùng chức năng giải phương trình bậc hai trên máy tính Casio.
Sto các nghiệm vào A, B: vào mode 2 Alpha gọi nó ra tính các giá trị biểu thức liên quan đến
nghiệm
Dạng ②. Tìm nghiệm phức của phương trình bậc hai – tìm các yếu tố liên
quan tới hai nghiệm thức chứa lũy thừa.
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 42
Chọn A
Câu 2: Gọi
1
z
,
2
z
là hai nghiệm phức của phương trình
2
z 6z 10 0−+=
. Giá trị của
22
12
zz+
bằng
Ⓐ. 16. Ⓑ. 56. Ⓒ. 20. Ⓓ. 26.
Quy trình bấm máy.
Bấm máy
Màn hình hiển thị nghiệm.
+ Màn hình hiển thị kết quả :
Chọn A
PP trắc nghiệm nhanh
Casio
Bài này có thể nhẩm nhanh hơn bằng
định lý viet
( )
2
22
1 2 1 2 1 2
z z z z 2z z 16+ = + − =
Câu 3: Trong , phương trình
2
10zz− + =
có nghiệm là:
12
;zz
với
1
z
có phần ảo âm. Hãy tính
1
2
z
z
Ⓐ.
1 3 3 3
22
i
++
−+
Ⓑ.
1 3 3 3
22
i
++
−−
Ⓒ.
13
22
i
−
+
Ⓓ.
13
22
i
−
−
Quy trình bấm máy
Bấm máy
Màn hình hiển thị nghiệm.
PP trắc nghiệm nhanh
Casio
bấm MT ra hai nghiệm
gán hai nghiệm phù hợp
bấm mt
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 43
Chọn D
B - Bài tập rèn luyện:
Câu 1: Trong , cho phương trình bậc hai
( ) ( )
2
0 * 0az bz c a+ + =
. Gọi
2
4b ac = −
. Ta xét các
mệnh đề:
1) Nếu
là số thực âm thì phương trình (*) vô nghiệm
2) Nếu
0
thì phương trình có hai nghiệm số phân biệt
3) Nếu
0=
thì phương trình có một nghiệm kép
Trong các mệnh đề trên:
Ⓐ. Không có mệnh đề nào đúng Ⓑ. Có một mệnh đề đúng
Ⓒ. Có hai mệnh đề đúng Ⓓ. Cả ba mệnh đề đều đúng
Câu 2: Trong , phương trình
2
40z +=
có nghiệm là
Ⓐ.
2
2
zi
zi
=
=−
Ⓑ.
12
12
zi
zi
=+
=−
Ⓒ.
1
32
zi
zi
=+
=−
Ⓓ.
52
35
zi
zi
=+
=−
Câu 3: Trong , phương trình
2
10zz− + =
có nghiệm là
Ⓐ.
3
1
2
3
1
2
zi
zi
=+
=−
Ⓑ.
13
22
13
22
zi
zi
=+
=−
Ⓒ.
5
1
2
5
1
2
zi
zi
=+
=−
Ⓓ.
15
22
15
22
zi
zi
=+
=−
Câu 4: Gọi
1
z
,
2
z
là hai nghiệm phức của phương trình
2
2 10 0zz+ + =
. Giá trị của biểu thức
22
12
A z z=+
bằng
Ⓐ. . Ⓑ. . Ⓒ.
20
. Ⓓ. .
Câu 5: Gọi và
2
z
là hai nghiệm phức của phương trình
2
30zz− + =
. Giá trị của biểu thức bằng
12
zz+
bằng
Ⓐ.
3
. Ⓑ.
3
. Ⓒ.
33
. Ⓓ.
23
.
15
19
17
1
z
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 44
Câu 6. Gọi
1
z
,
2
z
là hai nghiệm phức của phương trình
2
5 8 5 0zz− + =
. Tính
1 2 1 2
S z z z z= + +
.
Ⓐ.
3S =
. Ⓑ.
15S =
. Ⓒ.
13
5
S =
. Ⓓ.
3
5
S =−
.
Câu 7. Giả sử
1
z
và
2
z
là hai nghiệm của phương trình
2
2 2 8 0zz− + =
. Giá trị của
22
1 2 1 2
A z z z z=+
bằng
Ⓐ.
16 2−
. Ⓑ.
16 2
. Ⓒ.
82
. Ⓓ.
82−
.
Câu 8: Trong , biết
12
,zz
là nghiệm của phương trình
2
6 34 0zz− + =
. Khi đó, tích của hai nghiệm
có giá trị bằng:
Ⓐ. -16 Ⓑ. 6 Ⓒ. 9 Ⓓ.34
Câu 9: Trong , biết
12
,zz
là nghiệm của phương trình
2
3 1 0zz− + =
. Khi đó, tổng bình phương
của hai nghiệm có giá trị bằng:
Ⓐ. 0 Ⓑ. 1 Ⓒ.
3
Ⓓ.
23
Câu 10: Trong , biết
12
,zz
là nghiệm của phương trình
2
2 5 0zz− + =
. Giá trị của biểu thức
( )
2
12
zz+
bằng:
Ⓐ. 0 Ⓑ. 1 Ⓒ. 2 Ⓓ.4
Câu 11: Phương trình sau có mấy nghiệm thực:
2
2 2 0zz+ + =
Ⓐ. 0 Ⓑ. 1 Ⓒ. 2 Ⓓ. Vô số nghiệm.
Câu 12: Gọi
12
,zz
là hai nghiệm của phương trình
2
2 6 0zz− + =
. Trong đó
1
z
có phần ảo âm.
Lúc đó
1
z
là
Ⓐ.
15i−
Ⓑ.
15i+
Ⓒ.
5 i−
Ⓓ.
5 i+
Câu 13: Gọi
12
,zz
là các nghiệm phức của phương trình
2
3 7 0zz+ + =
. Khi đó
12
A z z=+
có giá trị
là
Ⓐ.
3−
Ⓑ.
3
Ⓒ.
7
Ⓓ.
7−
Câu 14: Gọi
12
,zz
là các nghiệm phức của phương trình
2
2 9 0zz+ + =
. Khi đó
12
2A z z=+
có giá trị là
( với
1
z
có phần ảo dương).
Ⓐ.
3 2 2 2i+−
Ⓑ.
3 2 2 2i−−
Ⓒ.
3 2 2 2i− + −
Ⓓ.
3 2 2 2i++
Câu 15. Gọi
1
z
,
2
z
là hai nghiệm phức của phương trình
2
5 8 5 0zz− + =
. Tính
1 2 1 2
S z z z z= + +
.
Ⓐ.
3S =
. Ⓑ.
15S =
. Ⓒ.
13
5
S =
. Ⓓ.
3
5
S =−
.
Câu 16. Kí hiệu
12
,zz
là hai nghiệm phức của phương trình
2
2 9 0zz− + =
. Giá trị của
1 2 1 2
z z z z+ + −
bằng
Ⓐ.
2 4 2+
. Ⓑ.
2 4 2i+
. Ⓒ.
6
. Ⓓ.
2
.
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 45
Câu 17: Thương hai nghiệm
1
2
z
z
của phương trình
2
2 3 0zz− − − =
là (
1
z
có phần ảo dương)?
Ⓐ.
1 2 2
33
i
−
−
Ⓑ.
1 2 2
33
i
−
+
Ⓒ.
1 2 2
33
i−
Ⓓ.
1 2 2
33
i+
Câu 18: Gọi
12
,zz
là hai nghiệm của phương trình
2
2 3 0zz− − − =
. Khi đó môn đun của số phức có
phần ảo âm là
Ⓐ.
3
Ⓑ.
3−
Ⓒ. 2 Ⓓ.
1−
Câu 19: Gọi
12
,zz
là các nghiệm phức của phương trình
2
3 7 0zz+ + =
. Khi đó
44
12
A z z=+
có giá trị
là
Ⓐ. 23 Ⓑ.
23
Ⓒ. 13 Ⓓ.
13
Câu 20: Gọi
12
,zz
là hai nghiệm của phương trình
2
2 6 0zz− + =
. Trong đó
1
z
có phần ảo âm. Giá trị
biểu thức
1 1 2
| | | 3 |M z z z= + −
là
Ⓐ.
6 2 21−
Ⓑ.
6 2 21+
Ⓒ.
6 4 21+
Ⓓ.
6 4 21−
BẢNG ĐÁP ÁN
1.C
2.A
3.B
4.C
5.A
6.A
7.B
8.D
9.B
10.B
11.A
12.A
13.A
14.A
15.A
16.A
17.A
18.A
19.A
20.B
A - Bài tập minh họa:
Câu 1: Nghiệm của phương trình
42
20zz− − =
là
Ⓐ.
2; 1.−
Ⓑ.
2; .i
Ⓒ.
2; 1.i
Ⓓ.
2; .i
①. Phương pháp giải:
⬧Biến đổi phương trình về dạng phương trình tích, trong đó mỗi nhân tử là phương
trình bậc nhất hoặc bậc hai.
⬧Dùng phương pháp đặt ẩn phụ.
⬧Với phương trình trùng phương bậc bốn: : Đặt .
②. Casio:
⬧Thế các đáp án vào phương trình để loại suy.
⬧Với phương trình bậc ba: Dùng chức năng giải phương trình bậc ba trên máy tính.
⬧Với phương trình trùng phương: giải phương trình bậc bốn trên máy tính 580VNX
Dạng ③. Tìm nghiệm phương trình bậc 3, trùng phương
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 46
Lời giải
Chọn B
Ta có :
42
2
2
20
2
2
1
zz
z
z
zi
z
− − =
=
=

=
=−
PP nhanh trắc nghiệm
CÁCH 1:
CALC CÁC ĐÁP ÁN
CÁCH 2: dùng 580vnx
B - Bài tập rèn luyện:
Câu 1.Trong , nghiệm của phương trình
3
80−=z
là
Ⓐ.
1 2 3
2; 1 3 ; 1 3z z i z i= = + = −
Ⓑ.
1 2 3
2; 1 3 ; 1 3z z i z i= = − + = − −
Ⓒ.
1 2 3
2; 1 3 ; 1 3z z i z i= − = − + = − −
Ⓓ.
1 2 3
2; 1 3 ; 1 3z z i z i= − = + = −
Câu 2. Trong , phương trình
42
6 25 0− + =zz
có nghiệm là
Ⓐ.
8; 5i
Ⓑ.
3; 4i
Ⓒ.
5; 2i
Ⓓ.
( ) ( )
2 ; 2ii + −
Câu 3. Trong , phương trình
3
10+=z
có nghiệm thực là
Ⓐ.
1
Ⓑ.
1−
Ⓒ.
13
22
i+
Ⓓ.
13
22
i−
Câu 4. Trong , phương trình
4
10−=z
có nghiệm ảo là
Ⓐ.
1
Ⓑ.
i−
Ⓒ.
i
Ⓓ.
i
Câu 5. Phương trình
3
8z =
có bao nhiêu nghiệm phức với phần ảo âm?
Ⓐ. 1 Ⓑ. 2 Ⓒ. 3 Ⓓ. 0
Câu 6. Trong , phương trình
4
40+=z
có nghiệm là
Ⓐ.
( ) ( )
1 4 ; 1 4 − +ii
Ⓑ.
( )
12−i
;
( )
12+i
Ⓒ.
( ) ( )
1 3 ; 1 3 − +ii
Ⓓ. ±
( )
1−i
;
( )
1+i
Câu 7. Trong trường số phức phương trình
3
10z +=
có mấy nghiệm?
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 47
Ⓐ. 2. Ⓑ. 3. Ⓒ. 1. Ⓓ. 0.
Câu 8. Giải phương trình sau trên :
( )
( )( )
23
1 1 1 0z z z+ − + =
Ⓐ.
1
13
2
z
zi
i
z
=
=
−
=
Ⓑ.
1
13
2
z
zi
i
z
=
=
−
=
Ⓒ.
1
13
2
z
zi
i
z
=−
=−
−
=
Ⓓ.
1
13
2
z
zi
i
z
=
=
−
=
Câu 9. Tổng bình phương các nghiệm của phương trình
4
10z −=
trên tập số phức là bao nhiêu?
Ⓐ. 3. Ⓑ. 1. Ⓒ. 2. Ⓓ. 0.
Câu 10. Phương trình
63
9 8 0zz− + =
có bao nhiêu nghiệm trên tập số phức?
Ⓐ. 3. Ⓑ. 4. Ⓒ. 2. Ⓓ. 6.
Câu 11. Bộ số thực
( )
;;abc
để phương trình
32
0z az bz c+ + + =
nhận
1zi=+
và
2z =
làm nghiệm.
Ⓐ.
( )
4;6; 4−−
Ⓑ.
( )
4; 6;4−
Ⓒ.
( )
4; 6; 4−−−
Ⓓ.
( )
4;6;4
Câu 12. Trong , phương trình
4
10−=z
có nghiệm. Tổng của các nghiệm đó là
Ⓐ.
2−
. Ⓑ.
2
. Ⓒ.
2i
. Ⓓ. 0.
Câu 13. Giải phương trình sau trên :
( ) ( )
2 2 2
9 4 9 5 0z z z z z z+ + + + + − =
Ⓐ.
3
zi
zi
z
=
=−
=−
Ⓑ.
2
2
3
zi
zi
z
=
=−
=−
Ⓒ.
3
3
3
zi
zi
z
=
=−
=
Ⓓ.
3
3
3
zi
zi
z
=
=−
=−
Câu 14. Giải phương trình sau trên :
4 3 2
2 2 2 2 0z z z z− + + + =
Ⓐ.
1
11
22
zi
zi
=
= −
Ⓑ.
1
1
zi
zi
=+
=−
Ⓒ.
1
11
22
zi
zi
=+
= − +
Ⓓ.
1
11
22
zi
zi
=−
= − −
Câu 15. Tập nghiệm trong của phương trình
32
10z z z+ + + =
là
Ⓐ.
;i;1; 1i−−
Ⓑ.
; ;1ii−
Ⓒ.
;1i−−
Ⓓ.
; ; 1ii−−
Câu 16. Trong trường số phức phương trình
3
0zz+=
có mấy nghiệm?
Ⓐ. 2. Ⓑ. 3. Ⓒ. 1. Ⓓ. 0.
Câu 17. Tìm số nguyên x, y sao cho số phức
z x yi=+
thỏa mãn
3
18 26zi=+
Ⓐ.
3
1
x
y
=
=
Ⓑ.
3
1
x
y
=
=−
Ⓒ.
3
1
x
y
=
=
Ⓓ.
3
1
x
y
=−
=
Câu 18. Tập nghiệm của phương trình
42
2 8 0zz− − =
là
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 48
Ⓐ.
2; 4i
. Ⓑ.
2; 2i
. Ⓒ.
2 ; 2i
. Ⓓ.
2; 4i
.
Câu 19. Tập nghiệm của phương trình là
Ⓐ. Ⓑ. Ⓒ. Ⓓ.
Câu 20. Kí hiệu
1 2 3 4
, , ,z z z z
là 4 nghiệm phức của phương trình
42
12 0zz− − =
.
Tính tổng
1 2 3 4
T z z z z= + + +
Ⓐ.
4T =
Ⓑ.
23T =
Ⓒ.
4 2 3T =+
Ⓓ.
2 2 3T =+
BẢNG ĐÁP ÁN
1.B
2.D
3.B
4.D
5.A
6.D
7.B
8.B
9.D
10.D
11.A
12.D
13.D
14.A
15.D
16.B
17.C
18.C
19.D
20.C
A - Bài tập minh họa:
Câu1: Phương trình nào dưới đây nhận hai số phức
12i+
và
12i−
là nghiệm ?
Ⓐ.
2
2 3 0zz+ + =
Ⓑ.
2
2 3 0zz− − =
Ⓒ.
2
2 3 0zz− + =
Ⓓ.
2
2 3 0zz+ − =
Lời giải
Chọn C
Định lý viet
Quy trình bấm máy.
Nhập giải phương trình đáp án A
Màn hình hiển thị
42
2 3 0zz+ − =
1; 1;3 ; 3ii−−
1; 2; ;ii−−
1;3
1; 1; 3; 3ii−−
①. Phương pháp giải:
⬧Tìm các nghiệm của phương trình đã cho thay vào biểu thức
⬧Dùng định lý Vi-ét để giải quyết yêu cầu bài toánc Vi-ét đối với phương trình bậc 2 s:
⬧Với có 2 nghiệm phân biệt (thực hoặc phức). Ta có:
.Casio:
⬧ Dùng chức năng giải phương trình trên máy tính casio (với các phương trình bậc hai,
bậc ba, bốn) để suy ra nghiệm.
⬧Dùng chức năng tính toán trên môi trường số phức để suy ra kết quả.
Dạng ④. Mối liên hệ giữa hai nghiệm của phương trình bậc hai
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 49
( ) ( )
1 2 1 2 2ii+ + − =
( )( )
1 2 1 2 3ii+ − =
Theo ứng dụng định lý viet thì hai số đã cho là
nghiệm của phương trình
2
2 3 0zz− + =
Loại A
Nhập giải phương trình đáp án B
Màn hình hiển thị
Loại B
Nhập giải phương trình đáp án C
Màn hình hiển thị
Câu2: Nếu
=zi
là nghiệm phức của phương trình
2
0+ + =z az b
với
( )
, ab
thì
+ab
bằng
Ⓐ.
1−
. Ⓑ.
2−
. Ⓒ.
1
. Ⓓ.
2
.
Lời giải
Chọn C
Phương trình
2
0+ + =z az b
nhận
=zi
làm
nghiệm nên
2
0+ + =i ai b
10 + − =ai b
0
10
=
−=
a
b
0
1
=
=
a
b
1 + =ab
.
PP nhanh trắc nghiệm
Phương trình
2
0+ + =z az b
nhận
=zi
làm
nghiệm nên
2
0+ + =i ai b
10 + − =ai b
0
10
=
−=
a
b
0
1
=
=
a
b
1 + =ab
.
B - Bài tập rèn luyện:
Câu 1: Cho
12
, zz
là các nghiệm phức của phương trình
2
4 13 0zz+ + =
. Tính
( ) ( )
22
12
22m z z= − + −
.
Ⓐ.
25m =
. Ⓑ.
50m =
. Ⓒ.
10m =
. Ⓓ.
18m =
.
Câu 2: Gọi
12
,zz
là hai nghiệm phức của phương trình
2
2 4 3 0zz+ + =
. Tính giá trị của biểu thức
12
zz+
.
Ⓐ.
23
. Ⓑ.
3
. Ⓒ.
3
. Ⓓ.
6
.
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 50
Câu 3: Gọi
1
z
và
2
z
là hai nghiệm của phương trình
2
2 3 3 0+ + =zz
. Khi đó, giá trị
22
12
+zz
là
Ⓐ.
9
. Ⓑ.
4
. Ⓒ.
9
4
. Ⓓ.
9
4
−
.
Câu 4: Gọi
1
z
,
2
z
là hai nghiệm phức của phương trình
2
4 5 0zz− + =
. Giá trị của biểu thức
22
12
zz+
bằng.
Ⓐ.
10
. Ⓑ.
20
. Ⓒ.
6
. Ⓓ.
68i−
.
Câu 5: Gọi
1
z
và
2
z
là hai nghiệm phức của phương trình
2
2 10 0zz+ + =
, giá trị của biểu thức
22
12
A z z=+
là.
Ⓐ.
10
. Ⓑ.
20
. Ⓒ.
10
. Ⓓ.
20
.
Câu 6: Gọi
12
,zz
là hai nghiệm phức của phương trình
2
– 4 9 0.zz+=
Tổng
12
P z z=+
bằng:
Ⓐ.
18
. Ⓑ.
4
. Ⓒ.
6
. Ⓓ.
3
.
Câu 7:
G
ọi
1
z
và
2
z
là các nghiệm của phương trình
2
4 9 0zz− + =
. Gọi
M
,
N
là các điểm biểu diễn
của
1
z
và
2
z
trên mặt phẳng phứⒸ. Khi đó độ dài của
MN
là
Ⓐ.
25MN =
. Ⓑ.
4MN =
. Ⓒ.
25MN =−
. Ⓓ.
5MN =
.
Câu 8: Gọi
12
,zz
là 2 nghiệm phức của phương trình
2
2 3 7 0zz− + =
. Tính giá trị của biểu thức
1 2 1 2
z z z z+−
.
Ⓐ.
2−
. Ⓑ.
2.
Ⓒ.
5−
. Ⓓ.
5
.
Câu 9: Trong tập các số phức, cho phương trình
2
60z z m− + =
,
m
( )
1
. Gọi
0
m
là một giá trị
của
m
để phương trình
( )
1
có hai nghiệm phân biệt
1
z
,
2
z
thỏa mãn
1 1 2 2
..z z z z=
. Hỏi trong
khoảng
( )
0;20
có bao nhiêu giá trị
0
m
?
Ⓐ.
12
. Ⓑ.
10
. Ⓒ.
13
. Ⓓ.
11
.
Câu 10: Gọi
12
,zz
là hai nghiệm của phương trình
2
2 3 2 0zz− + =
trên tập số phức; Tính giá trị biểu
thức
22
1 1 2 2
P z z z z= + +
.
Ⓐ.
33
4
P =
. Ⓑ.
5
2
P =
. Ⓒ.
3
4
P =
. Ⓓ.
5
2
P =
.
Câu 11: Cho
1
z
,
2
z
là hai nghiệm của phương trình
2
2 2 0− + =zz
( )
z
. Tính giá trị của biểu
thức
1 2 1 2
2= + + −P z z z z
.
Ⓐ.
2 2 2=+P
. Ⓑ.
24=+P
. Ⓒ.
6=P
. Ⓓ.
3=P
.
Câu 12: Trong tập các số phức
1
z
,
2
z
lần lượt là 2 nghiệm của phương trình
2
4 5 0zz+ + =
. Tính
22
12
P z z=+
.
Ⓐ.
25P =
. Ⓑ.
6P =
. Ⓒ.
10P =
. Ⓓ.
50P =
.
Câu 13: Cho
12
, zz
là hai nghiệm của phương trình
2
2 3 0zz+ + =
. Tính
12
zz+
.
Ⓐ.
0
. Ⓑ.
1
. Ⓒ.
23
. Ⓓ.
6
.
Câu 14: Phương trình
2
4 5 0xx+ + =
có nghiệm phức mà tổng các mô đun của chúng bằng?
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 51
Ⓐ.
27
. Ⓑ.
25
. Ⓒ.
23
. Ⓓ.
22
.
Câu 15: Phương trình
2
2 6 0zz− + =
có các nghiệm
1
z
;
2
z
. Khi đó giá trị của biểu thức
22
12
22
12
zz
M
zz
=+
là.
Ⓐ.
2
3
. Ⓑ.
2
3
−
. Ⓒ.
2
9
. Ⓓ.
2
9
−
.
Câu 16: Cho phương trình
2
2 10 0zz+ + =
. Gọi
1
z
và
2
z
là hai nghiệm phức của phương trình đã
cho. Khi đó giá trị biểu thức
22
12
A z z=+
bằng:
Ⓐ.
4 10
. Ⓑ.
20
. Ⓒ.
10
. Ⓓ.
3 10
.
Câu 17: Gọi
1
z
,
2
z
là nghiệm phức của phương trình
2
2 10 0.zz+ + =
Tính giá trị của biểu thức
22
12
.zz+
.
Ⓐ.
25
. Ⓑ.
18
. Ⓒ.
20
. Ⓓ.
21
.
Câu 18: Gọi
1
z
và
2
z
lần lượt là hai nghiệm của phương trình
2
4 5 0zz− + =
. Giá trị của biểu thức
( )
1 2 2 1
2 . 4P z z z z= − −
bằng:
Ⓐ.
10−
Ⓑ.
10
Ⓒ.
5−
Ⓓ.
15−
Câu 19: Cho phương trình
2
2 3 0zz− + =
trên tập số phức, có hai nghiệm là
1
z
,
2
z
. Khi đó
22
12
zz+
có giá trị là:
Ⓐ.
6
. Ⓑ.
3
. Ⓒ.
2
. Ⓓ.
22
.
Câu 20: Gọi z
1
và z
2
là hai nghiệm phức của phương trình:
2
4 7 0zz+ + =
. Khi đó
22
12
zz+
bằng
Ⓐ.
7
. Ⓑ.
21
. Ⓒ.
14
. Ⓓ.
10
.
Câu 21: Gọi
12
,zz
là hai nghiệm phức của phương trình
2
4 5 0zz+ + =
. Tính giá trị của biểu thức
22
12
A z z=+
.
Ⓐ.
10
. Ⓑ.
6
. Ⓒ.
5
. Ⓓ.
25
.
Câu 22: Gọi
1
z
,
2
z
là nghiệm của phương trình
2
2 4 0zz− + =
. Tính giá trị của biểu thức
22
12
21
zz
P
zz
=+
Ⓐ.
4
Ⓑ.
4−
Ⓒ.
8
Ⓓ.
11
4
−
BẢNG ĐÁP ÁN
1.B
2.D
3.D
4.A
5.B
6.C
7.A
8.D
9.B
10.D
11.C
12.C
13.C
14.B
15.D
16.B
17.C
18.D
19.A
20.C
21.D
22.B
| 1/51
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
St-bs: Duong Hung - Word xinh 2020-2021 1
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung Full Chuyên đề 12 new 2020-2021 CHƯƠNG ④: FB: Duong Hung
Bài ➀: ĐỊNH NGHĨA SỐ PHỨC
Dạng ①: Xác định các yếu tố cơ bản của số phức . Phương pháp:
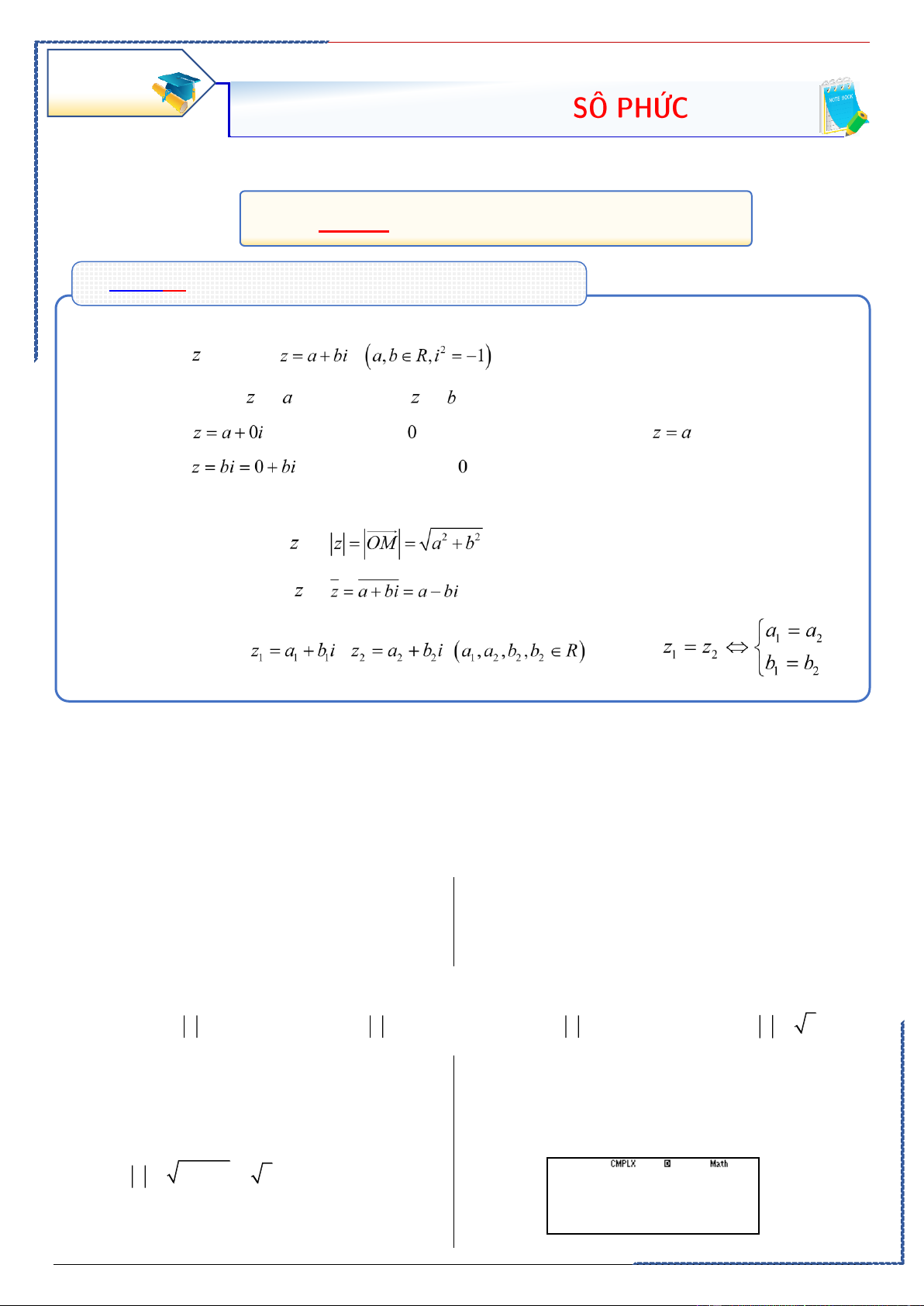
. Số phức có dạng .
. Phần thực của là , phần ảo của là . . Số phức
có phần ảo bằng được coi là số thực và viết là . . Số phức
có phần thực bằng được gọi là số ảo (hay số thuần ảo) .
. Số 0 vừa là số thực, vừa là số ảo.
. Mô đun của số phức là .
. Số phức liên hợp của là .
. Cho hai số phức , . Khi đó:
A - Bài tập minh họa:
Câu 1. Số phức có phần thực bằng 3 và phần ảo bằng 4 là
Ⓐ. z = 3+ 4 .i
Ⓑ. z = 4 −3 .i
Ⓒ. z = 3− 4 .i
Ⓓ. z = 4 + 3 .i Lời giải
PP nhanh trắc nghiệm Chọn A
 Phần ảo là hệ số trước i, phần thực là số tự do.
Câu 2. Cho số phức z = 2 + i . Tính | z |.
Ⓐ. z = 5 . Ⓑ. z = 3.
Ⓒ. z = 2.
Ⓓ. z = 5 . Lời giải
PP nhanh trắc nghiệm Chọn D
Tính theo công thức: Casio: MODE 2  Ta có 2 2 z = 1 + 2 = 5 .
St-bs: Duong Hung - Word xinh 2020-2021 2
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung SHIFT hyp
Câu 3. Số phức liên hợp của số phức 3− 4i là Ⓐ. z = 3 − − 4 .i
Ⓑ. z = 4 −3 .i
Ⓒ. z = 3+ 4 .i
Ⓓ. z = 4 + 3 .i Lời giải
PP nhanh trắc nghiệm Chọn C
Số phức liên hợp có phần thực bằng nhau và phần ảo đối nhau.
Ta có: z = 3 + 4 .i
Casio: Dùng chức năng tính liên hợp của số phức : MODE 2 SHIFT 22
B - Bài tập rèn luyện:
Câu 1: Số phức z = 3
− + 7 .i có phần ảo bằng Ⓐ. 3.
Ⓑ. 7i . Ⓒ. 3 − . Ⓓ. 7 .
Câu 2: Số phức z = 5 + 6i có phần thực bằng Ⓐ. 5 − . Ⓑ. 5. Ⓒ. 6 − . Ⓓ. 6 .
Câu 3: Cho số phức z = ; a a
. Khi đó khẳng định đúng là
Ⓐ. z là số thuần ảo.
Ⓑ. z có phần thực là a, phần ảo là i.
Ⓒ. z = a .
Ⓓ. z = a .
Câu 4: Số phức nào dưới đây là số thuần ảo?
Ⓐ. z = 3 + 2i .
Ⓑ. z = 2i . Ⓒ. z = 2 − +3i . Ⓓ. z = 2 − .
Câu 5: Cho số phức z = 1− 2i . Khẳng định nào sau đây là khẳng định đúng?.
Ⓐ. Phần thực của số phức z là 1 − .
Ⓑ. Phần ảo của số phức z là 2 − i .
Ⓒ. Phần ảo của số phức z là −2 .
Ⓓ. Số phức z là số thuần ảo.
Câu 6: Số phức liên hợp của số phức z = 5 − 3i là Ⓐ. 5 − − 3i . Ⓑ. 5 − + 3i . Ⓒ. 3+ 5i . Ⓓ. 5 + 3i .
Câu 7: Số phức liên hợp của số phức z = 2i −1 là
St-bs: Duong Hung - Word xinh 2020-2021 3
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung Ⓐ. 2i +1. Ⓑ. 2 − i +1. Ⓒ. 2 − i −1. Ⓓ. 1 − + 2i .
Câu 8: Cho số phức z = a + bi ( ,
a b R). Tìm số phức z là số phức liên hợp của z .
Ⓐ. z = a −b .i
Ⓑ. z = a − +b .i Ⓒ. z = ( − a + bi). Ⓓ. 2 2
z = a − b . i
Câu 9: Số phức z = 4 −3i có môđun bằng Ⓐ. 2 2 . Ⓑ. 25 . Ⓒ. 5. Ⓓ. 8 .
Câu 10: Cho số phức z = 1− 2 2.i . Tính z .
Ⓐ. z =1+ 2 2 . Ⓑ. z = 9 . Ⓒ. z = 10 . Ⓓ. z = 3 .
Câu 11: Cho số phức z = 1
− − 4i . Tìm phần thực của số phức z . Ⓐ. 1 − . Ⓑ. 1. Ⓒ. 4 . Ⓓ. −4.
Câu 12: Cho số phức z = 2
− + i . Tìm phần thực và phần ảo của số phức z .
Ⓐ. Phần thực bằng−2và phần ảo bằng −i . Ⓑ. Phần thực bằng−2và phần ảo bằng 1 − .
Ⓒ. Phần thực bằng 2 và phần ảo bằng 1.
Ⓓ. Phần thực bằng 2 và phần ảo bằng i .
Câu 13: Tìm phần ảo của số phức z biết z =1+ 3i ?
Ⓐ. Phần ảo bằng 3. Ⓑ. Phần ảo bằng -3i .
Ⓒ. Phần ảo bằng 3 − .
Ⓓ. Phần ảo bằng i .
Câu 14: Gọi a , b lần lượt là phần thực và phần ảo của số phức z = 3
− + 2i . Giá trị của a + 2b bằng Ⓐ. 1. Ⓑ. −1. Ⓒ. −4. Ⓓ. −7.
Câu 15: Phần ảo của số phức liên hợp của z = 4i − 7 là Ⓐ. 4 − . Ⓑ. 7 − . Ⓒ. 7. Ⓓ. 4.
Câu 16: Số phức z = 2m + (m −1)i , với m  . Với giá trị nào m của thì z = 2 . m = 1 Ⓐ. m = 1 − . Ⓑ. 3 m = . Ⓒ.  3 . Ⓓ. m. 5 m = −  5
Câu 17: Cho số phức z có số phức liên hợp z = 3− 2i . Tổng phần thực và phần ảo của số phức z bằng Ⓐ. 5 . Ⓑ. 1 − . Ⓒ. 5 − . Ⓓ. 1.
Câu 18: Cho số phức z = 2 + 4i . Hiệu phần thực và phần ảo của z bằng. Ⓐ. 2 . Ⓑ. 2 5 . Ⓒ. −2. Ⓓ. 6 .
Câu 19: Số phức z nào sau đây thỏa z = 5 và phần thực gấp đôi phần ảo?.
St-bs: Duong Hung - Word xinh 2020-2021 4
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
Ⓐ. z =1+ 2 .i
Ⓑ. z = 2+ .i
Ⓒ. z = 2 + 3 .i
Ⓓ. z = 4+ 2 .i
Câu 20: Tìm số thực m sao cho ( 2 m − ) 1 + (m + ) 1 i là số ảo. Ⓐ. m = 0. Ⓑ. m =1. Ⓒ. m = 1  . Ⓓ. m = 1 − . BẢNG ĐÁP ÁN 1.D 2.B 3.C 4.B 5.C 6.D 7.C 8.A 9.C 10.D 11.A 12.B 13.C 14.A 15.A 16.C 17.A 18.C 19.B 20.C
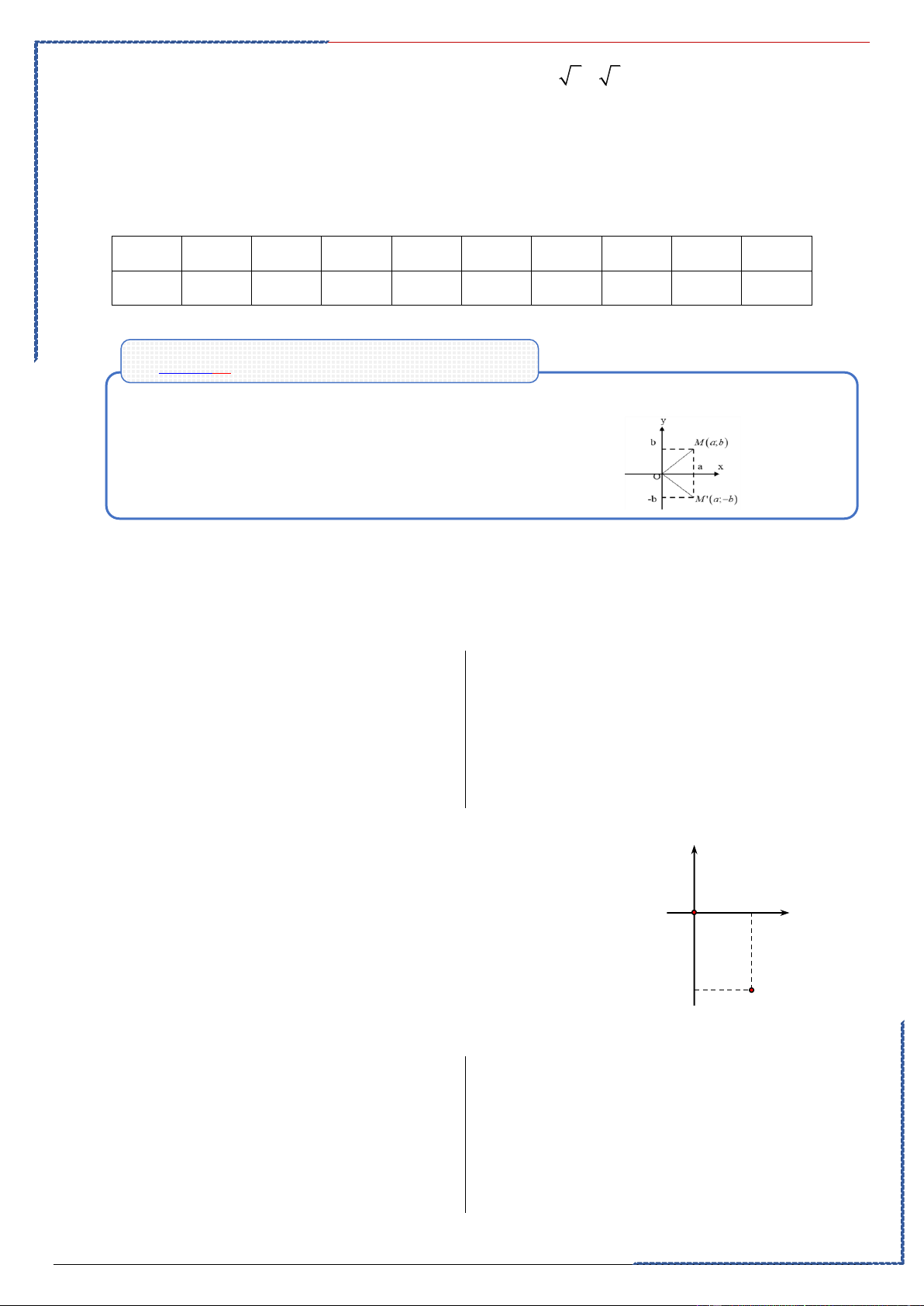
Dạng ②: Điểm biểu diễn của số phức . Phương pháp:
①. Biến đổi số phức cần biểu diễn về dạng z =a+bi
②. Điểm biểu diễn của số phức z là điểm M(a;b)
A - Bài tập minh họa:
Câu 1. Số phức z = 2 −3i có điểm biểu diễn là Ⓐ. A(2;3) . Ⓑ. A( 2 − ; 3 − ) . Ⓒ. A(2; 3 − ) . Ⓓ. A( 2 − ;3) . Lời giải
PP nhanh trắc nghiệm
Chọn C
Số phức z = 2 −3i có phần thực bằng 2 và
Điểm biểu diễn có hoành độ bằng 2 và tung độ phần ảo bằng -3 bằng -3
Câu 2. Điểm M trong hình vẽ bên là điểm biểu diễn của số phức z . Tìm phần thực và phần ảo của số phức z . y
Ⓐ. Phần thực là −4và phần ảo là 3. 3
Ⓑ. Phần thực là 3 và phần ảo là 4 − i . O x
Ⓒ. Phần thực là 3 và phần ảo là −4. 4 −
Ⓓ. Phần thực là −4và phần ảo là 3i . M Lời giải
PP nhanh trắc nghiệm Chọn C Điểm M (3; 4
− ) nên M là điểm biểu diễn của số  Hoành độ bằng phần thực ,tung độ bằng phần phức ảo
z = 3 − 4i .Vậy phần thực bằng 3 và phần ảo bằng -4
St-bs: Duong Hung - Word xinh 2020-2021 5
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu . Cho số phức z =1− 2i Tìm tọa độ biểu diễn của số phức z trên mặt phẳng tọa độ. Ⓐ. M (1; 2 − )
Ⓑ. M (2; )
Ⓒ. M (1;2)
Ⓓ. M (2;− ) 1 1 Lời giải
PP nhanh trắc nghiệm Chọn C
Vì z =1− 2i nên z = 1+ 2i .Điểm biểu diễn của  Nếu z = a +bi thì điểm biểu diễn của z là z là M (1; 2) M ( ; a b − )
B - Bài tập rèn luyện:
Câu 1: Số phức z = 3+ 4i có điểm biểu diễn là Ⓐ. M (4;3) Ⓑ. M (3;4) Ⓒ. M ( 3 − ;4) Ⓓ. M ( 4 − ;3)
Câu 2: Số phức z 3
7i có điểm biểu diễn là Ⓐ. M (3;7) Ⓑ. M ( 3 − ;7) . Ⓒ. M (3; 7 − ) . Ⓓ. M ( 3 − ; 7 − ) .
Câu 3: Điểm M biểu diễn số phức z = 3+ 2i trong mặt phẳng tọa độ là Ⓐ. M(3;2) . Ⓑ. M(2;3) . Ⓒ. M(3; 2 − ) . Ⓓ. M( 3 − ; 2 − ) .
Câu 4: Cho số phức z = 2
− i −1. Điểm biểu diễn của số phức z trong mặt phẳng là Ⓐ. M( 1 − ; 2 − ) . Ⓑ. M( 1 − ;2) . Ⓒ. M( 2 − ;1) . Ⓓ. M(2; 1 − ) .
Câu 5: Cho số phức z = 5
− i . Điểm biểu diễn của số phức z trong mặt phẳng là Ⓐ. M( 5 − ;0) . Ⓑ. M(0;5) . Ⓒ. M(0; 5 − ) . Ⓓ. M(5;0) .
Câu 6: Cho số phức z = 8
− . Điểm biểu diễn của số phức z trong mặt phẳng là Ⓐ. M( 8 − ;0) . Ⓑ. M(8;0) . Ⓒ. M(0;8) . Ⓓ. M(0; 8 − ) .
Câu 7: Cho số phức z = 6 + 7i . Số phức liên hợp của z có điểm biểu diễn là Ⓐ. (6;7) . Ⓑ. (6; 7 − ) . Ⓒ. ( 6 − ;7) . Ⓓ. ( 6 − ; 7 − ) .
Câu 8: Cho số phức z = 2
− i −1. Điểm biểu diễn số phức liên hợp của z là Ⓐ. M( 1 − ; 2 − ) . Ⓑ. M( 1 − ;2) . Ⓒ. M( 2 − ;1) . Ⓓ. M(2; 1 − ) .
Câu 9: Cho số phức z = 2
− i . Điểm biểu diễn của số phức liên hợp của z là Ⓐ. M(0; 2 − ) . Ⓑ. M(0;2). Ⓒ. M( 2 − ;0) . Ⓓ. M(2;0).
Câu 10: Cho điểm M là điểm biểu diễn của số phức z . Tìm phần thực và phần ảo của số phức z .
Ⓐ. Phần thực là −4 và phần ảo là 3i .
Ⓑ. Phần thực là 3 và phần ảo là 4 − i .
Ⓒ. Phần thực là −4 và phần ảo là 3.
St-bs: Duong Hung - Word xinh 2020-2021 6
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
Ⓓ. Phần thực là 3 và phần ảo là −4.
Câu 11: Cho số phức z có điểm biểu diễn là điểm A trong hình vẽ bên.Tìm phần thực và phần ảo của số phức z .
Ⓐ. Phần thực bằng 3, phần ảo bằng −2.
Ⓑ. Phần thực bằng 3, phần ảo bằng 2 .
Ⓒ. Phần thực bằng 2 , phần ảo bằng 3 − i .
Ⓓ. Phần thực bằng 3, phần ảo bằng 2i .
Câu 12: Gọi A là điểm biểu diễn của số phức z = 2 + 5i và B là điểm biểu diễn của số phức z = 2 − + 5i
. Tìm mệnh đề đúng trong các mệnh đề sau.
Ⓐ. Hai điểm A và B đối xứng với nhau qua trục hoành.
Ⓑ. Hai điểm A và B đối xứng với nhau qua trục tung.
Ⓒ. Hai điểm A và B đối xứng với nhau qua gốc toạ độ O .
Ⓓ. Hai điểm A và B đối xứng với nhau qua đường thẳng y = x .
Câu 13: Trên mặt phẳng tọa độ Oxy cho điểm M trong hình vẽ bên là điểm
biểu diễn của số phức z . Tìm z ?
Ⓐ. z + z = 4
− + 3i . Ⓑ. z = 3+ 4i .
Ⓒ. z = 3−4i . Ⓓ. z = 3 − + 4i .
Câu 14: Trong mặt phẳng toạ độ, điểm A(1; 2
− ) là điểm biểu diễn của số phức nào trong các số sau? Ⓐ. z = 1 − − 2i .
Ⓑ. z =1+2i .
Ⓒ. z =1−2i. Ⓓ. z = 2 − + i .
Câu 15: Trong mặt phẳng phức, gọi , A ,
B C lần lượt là điểm biểu diễn của các số phức z = 3 + 2i , 1
z = 3 − 2i , z = 3
− − 2i . Khẳng định nào sau đây là sai? 2 3
Ⓐ. B và C đối xứng nhau qua trục tung. Ⓑ.  
Trọng tâm của tam giác ABC là điểm 2 G 1;   .  3 
Ⓒ. A và B đối xứng nhau qua trục hoành. Ⓓ. , A ,
B C nằm trên đường tròn tâm là gốc tọa độ và bán kính bằng 13 .
Câu 16: Gọi A là điểm biểu diễn số phức M (x, y) , B là điểm biểu diễn số phức z = x + yi . Trong các
khẳng định sau khẳng định nào sai?
Ⓐ. A và B đối xứng nhau qua trục hoành.
St-bs: Duong Hung - Word xinh 2020-2021 7
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
Ⓑ. A và B trùng gốc tọa độ khi z = 0.
Ⓒ. A và B đối xứng qua gốc tọa độ.
Ⓓ. Đường thẳng AB đi qua gốc tọa độ.
Câu 17: Các điểm biểu diễn các số phức z = 3 + bi (b ) trong mặt phẳng tọa độ, nằm trên đường
thẳng có phương trình là
Ⓐ. y = b. Ⓑ. y = 3
Ⓒ. x = b . Ⓓ. x = 3.
Câu 18: Trên mặt phẳng tọa độ, tập hợp điểm biểu diễn các số phức thỏa mãn điều kiện phần thực của z bằng -2 là Ⓐ. x = 2 − . Ⓑ. y = 2 .
Ⓒ. y = 2x
Ⓓ. y = x + 2
Câu 19: Cho số phức z = a + ai . Tập hợp các điểm biểu diễn số phức liên hợp của z trong mặt phẳng tọa độ là
Ⓐ. x + y = 0.
Ⓑ. y = x .
Ⓒ. x = a .
Ⓓ. y = a .
Câu 20: Tập hợp các điểm biểu diễn số phức z thỏa mãn z  1 trên mặt phẳng tọa độ là
Ⓐ. Hình tròn tâm , bán kính R =1, không kể biên.
Ⓑ. Hình tròn tâm, bán kính R =1, kể cả biên.
Ⓒ. Đường tròn tâm, bán kính R =1.
Ⓓ. Đường tròn tâm bất kì, bán kính R =1. BẢNG ĐÁP ÁN 1B 2.B 3.A 4.A 5.C 6.A 7.B 8.B 9.B 10.D 11.B 12.B 13.C 14.C 15.B 16.A 17.D 18.A 19.B 20.A
Dạng ③: Hai số phức bằng nhau: . Phương pháp:
Cho hai số phức , .  Khi đó:
A - Bài tập minh họa:
Câu 1. Bộ số thực ( ; x y) thỏa mãn (3 x) (1 y)i 1
3i , với i là đơn vị ảo là Ⓐ. (2; 2) . Ⓑ.( 2;2) . Ⓒ. (2;2) . Ⓓ. ( 2; 2) .
St-bs: Duong Hung - Word xinh 2020-2021 8
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung Lời giải
PP nhanh trắc nghiệm Chọn B
 Casio: Thay x, y trong các đáp án vào giả thiết đã cho.
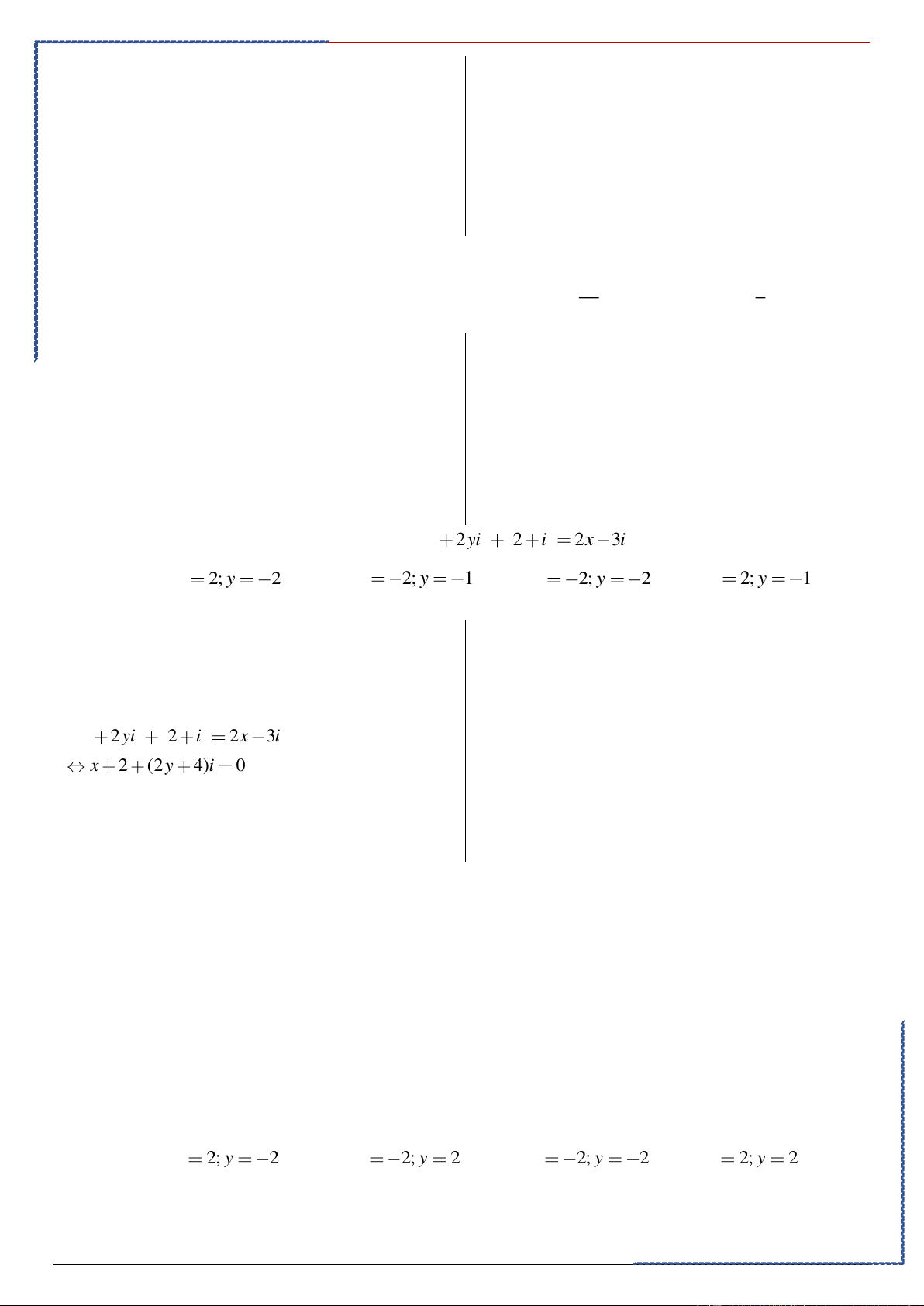
Ta có: (3+ x) + (1+ y)i =1+ 3i
(3+ 2) + (1− 2)i =1+ 3i (S) 3  + x =1  = −  x 2    . (3− 2) + (1+ 2) 1  + y = 3 y = 2
i = 1 + 3i (Đ), chọn B
Câu 2. Tìm điểm M ( ,
x y) thỏa 2x −1+ (3y + 2)i = 5 − . i Ⓐ. − M (3; 1 − ). Ⓑ. M(2; 1 − ). Ⓒ. 1 M (3; ). Ⓓ. 1 M (2; ). 3 3 Lời giải
PP nhanh trắc nghiệm Chọn A
 Casio: Thay x, y trong các đáp án vào giả thiết đã cho.  x − =
 2x −1+ (3y + 2)i = 5 − 2 1 5 i   − + − + = − (Đ), chọn A 3  y + 2 = 1 − 2.3 1 (3.( 1) 2)i 5 ix = 3  y = 1 −
Câu 3. Tìm hai số thực x và y thỏa mãn 3x 2yi 2 i 2x
3i với i là đơn vị ảo. Ⓐ. x 2; y 2 . Ⓑ. x 2; y 1. Ⓒ. x 2; y 2 . Ⓓ. x 2; y 1 . Lời giải
PP nhanh trắc nghiệm Chọn C
 Casio: Thay x, y trong các đáp án vào giả thiết đã ch  Ta có 3x 2 yi 2 i 2x 3i x 2 (2 y 4)i 0 x + 2 = 0 x = 2 −     2y + 4 = 0 y = 2 −
B - Bài tập rèn luyện:
Câu 1: Cho x là số thực. Hai số phức z = 3 + i và z = x + i bằng nhau khi Ⓐ. x =1. Ⓑ. x = 2 . Ⓒ. x = 3. Ⓓ. x = 1 − .
Câu 2: Cho y là số thực. Hai số phức z = 3 + i và z = 3 − yi bằng nhau khi Ⓐ. y = 1 − . Ⓑ. y = 2 − . Ⓒ. y = 0.
Ⓓ. y =1.
Câu 3: Cho x, y là các số thực. Hai số phức z = 2 + yi và z = x − 2i bằng nhau khi
Ⓐ. x 2; y 2 . Ⓑ. x 2; y 2 . Ⓒ. x 2; y
2 . Ⓓ. x 2; y 2 .
Câu 4: Cho hai số phức z = x + 2i và 'z = 3 − yi . Hai số đó bằng nhau khi
St-bs: Duong Hung - Word xinh 2020-2021 9
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung Ⓐ. x 2; y 3. Ⓑ. x 3; y 2 .
Ⓒ. x 3; y 2 .
Ⓓ. x 3; y 2 .
Câu 5: Cho hai số phức z = 2
− + 3yi, z = (x +1) − 6i, ,
x y  R . Tìm x, y để z = z .
Ⓐ. x = 3, y = 9 − . Ⓑ. x = 3 − , y = 2 − . Ⓒ. x = 1 − , y = 2 .
Ⓓ. x = 3, y = 2 − .
Câu 6: Cho hai số phức z = 2 + 3yi, z = (x +1) − 6i, ,
x y  R . Tìm x, y để z = z .
Ⓐ. x = 3, y = 9 − . Ⓑ. x = 3 − , y = 2 − .
Ⓒ. x =1, y = 2.
Ⓓ. x =1, y = 2 − .
Câu 7: Tìm điểm M ( ,
x y) thỏa 2x −1+ (y + 2)i = 5 − .i Ⓐ. M (3; 1 − ). Ⓑ. M(2; 1 − ). Ⓒ. M (3; 3 − ). Ⓓ. M(2;3).
Câu 8: Tìm điểm M ( ,
x y) thỏa 2x +1+ (y + 2)i = 5 − .i Ⓐ. M (3; 1 − ). Ⓑ. M(2; 3 − ). Ⓒ. M (3; 3 − ). Ⓓ. M(2;3).
Câu 9: Cho a , b là hai số thực thỏa mãn a +1+ 6i = 2 − 2bi , với i là đơn vị ảo. Tìm a và b. Ⓐ. a = 1 − ,b = 3 − .
Ⓑ. a =1,b = 3 .
Ⓒ. a =1,b = 3 − .
Ⓓ. x =1, y = 2 − .
Câu 10: Cho a , b là hai số thực thỏa mãn a + 6i = 2 − 2bi , với i là đơn vị ảo. Giá trị của a + b bằng Ⓐ. 1 − . Ⓑ. 1. Ⓒ. −4. Ⓓ. 5.
Câu 11: Tìm hai số thực x và y thỏa mãn (x y) (x y)i 5
3i với i là đơn vị ảo.
Ⓐ. x 4; y 1. Ⓑ. x 1; y
4 . Ⓒ. x 2; y 3 .
Ⓓ. x 2; y 3 .
Câu 12: Với giá trị nào của x, y để 2 số phức z (x y) (2x
y)i và z 3 6i bằng nhau?
Ⓐ. x 4; y 1. Ⓑ. x 1; y
4 . Ⓒ. x 1; y 4 . Ⓓ. x 1; y 4 .
Câu 13: Các số thực x, y thỏa mãn 3x + y + 5xi = 2y −1+ (x − y)i là Ⓐ.         ( x y) 1 4 ; = − ; 
 . Ⓑ. ( x y) 2 4 ; = − ; 
 . Ⓒ. ( x y) 1 4 ; = ;  . Ⓓ. ( x y) 1 4 ; = − ;−   .  7 7   7 7   7 7   7 7 
Câu 14: Tìm hai số thực x và y thỏa mãn (3x 2) (1 2y)i 2x
3i với i là đơn vị ảo. Ⓐ. x 2; y
2 . Ⓑ. x 2; y 1. Ⓒ. x 2; y 2 .
Ⓓ. x 2; y 1 .
Câu 15: Tìm hai số thực x và y thỏa mãn (3x + yi) + (4 − 2i) = 5x + 2i với i là đơn vị ảo. Ⓐ. x = 2 − ; y = 4 .
Ⓑ. x = 2 ; y = 4 . Ⓒ. x = 2 − ; y = 0.
Ⓓ. x = 2 ; y = 0.
Câu 16: Tìm hai số thực x và y thỏa mãn ( x + 3y) − (3x + 5y + 3)i = 7 −16i
Ⓐ. x 1; y 2 .
Ⓑ. x 1; y 2.
Ⓒ. x 2; y 2.
Ⓓ. x 2; y 1 .
Câu 17: Cho hai số thực x và y thỏa mãn ( x + 3y) − (3x + 5y + 3)i = 7 −16i . Tính xy? Ⓐ. 3. Ⓑ. 3 − . Ⓒ. 2 . Ⓓ. 7
St-bs: Duong Hung - Word xinh 2020-2021 10
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 18: Nếu hai số thực x, y thỏa mãn 3x + y + (2x − 4y)i = 1+ 24i thì x − y bằng? Ⓐ. 3. Ⓑ. 3 − . Ⓒ. 7 − . Ⓓ. 7
Câu 19: Nếu hai số thực x, y thỏa mãn 3x + y + (2x − 4y)i = 1+ 24i thì x + y bằng? Ⓐ. 3. Ⓑ. 3 − . Ⓒ. 7 − . Ⓓ. 7
Câu 20: Cho số thực x , y thỏa mãn 2x + y + (2y − x)i = x − 2y + 3+ ( y + 2x + )
1 i . Khi đó giá trị của 2 2
M = x + 4xy − y là Ⓐ. M = 1 − . Ⓑ. M =1. Ⓒ. M = 0 . Ⓓ. M = 2 − BẢNG ĐÁP ÁN 1.C 2.A 3.A 4.D 5.B 6.D 7.C 8.B 9.C 10.A 11.A 12.C 13.A 14.D 15.B 16.B 17.C 18.D 19.B 20.A Full Chuyên đề 12 new 2020-2021 CHƯƠNG ④: FB: Duong Hung
Bài ➁: PHÉP CỘNG-PHÉP NHÂN
St-bs: Duong Hung - Word xinh 2020-2021 11
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
Dạng ①: Thực hiện các phép tính về số phức . Phương pháp:
①. Dạng đại số của số phức
 : phần thực số phức ;  : phần ảo của số phức ;  : đơn vị ảo ( )
②. Các phép toán cộng, trừ, nhân các số phức: ( )
. Phép cộng 2 số phức:
. Phép trừ của 2 số phức:
. Số đối của số phức: ( ) là số phức .
. Phép nhân của số phức: ③. Nhận xét:
 Với mọi số thực và mọi số phức , ✓. ; ✓.
A - Bài tập minh họa:
Câu 1: Cho hai số phức z = 2
− + i và z =1+ i . Trên mặt phẳng tọa độ Oxy , điểm biểu diễn số phức 1 2
2z + z có tọa độ là 1 2 Ⓐ. ( 3 − ;2). Ⓑ. (2;−3) . Ⓒ. ( 3 − ;3) . Ⓓ. (3;−3). Lời giải
PP nhanh trắc nghiệm Chọn C Casio: Ta có: 2z + z = 2. 2
− + i + 1+ i = 4
− + 2i +1+ i =− 3+3i 1 2 ( ) ( )
Vậy điểm biểu diễn số phức 2z + z có tọa độ là 1 2 ( 3 − ;3) .
Câu 2: Cho hai số phức z =1+ 2i và z = 3− 4i . Số phức 2z + 3z − z z là số phức nào sau đây? 1 2 1 2 1 2 Ⓐ. 10i . Ⓑ. 10 − i .
Ⓒ. 11+8i . Ⓓ. 11−10i . Lời giải
PP nhanh trắc nghiệm Chọn B
Nhập vào máy tính
Ta có 2z + 3z − z z 1 2 1 2
= 2(1+ 2i) + 3(3− 4i) −(1+ 2i)(3− 4i) =
11− 8i − (11+ 2i) = 1 − 0i .
St-bs: Duong Hung - Word xinh 2020-2021 12
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 3: Trên tập số phức, cho biểu thức A = (a − bi)(1− i) ( a, b là số thực). Khẳng định nào sau đây đúng?
Ⓐ. A = a +b −(a +b) .i
Ⓑ. A = −a +b + (b − a) .i
Ⓒ. A = a −b −(a −b) .i
Ⓓ. A = a −b −(a +b) .i Lời giải
PP nhanh trắc nghiệm Chọn D Công thức
A = (a − bi)( − i) 2 1
= a − ai − bi + bi
= (a − b) − (a + b)i
B - Bài tập rèn luyện:
Câu 1: Cho hai số phức z = 4 − 3i và z = 7 + 3i . Tìm số phức z = z − z . 1 2 1 2
Ⓐ. z = 3+6i . Ⓑ. z = 11.
Ⓒ. z = −1−10i.
Ⓓ. z = −3−6i.
Câu 2: Cho số phức z = − i + 3 1
i . Tìm phần thực a và phần ảo b của z .
Ⓐ. a = 1,b = −2 .
Ⓑ. a = −2,b = 1.
Ⓒ. a = 1,b = 0 .
Ⓓ. a = 0,b = 1.
Câu 3: Cho số phức z = 3+ 2i . Giá trị của z.z bằng Ⓐ. 5. Ⓑ. 9. Ⓒ. 13. Ⓓ. 13 .
Câu 4: Cho số phức z = 3− 2i . Trong mặt phẳng tọa độ Oxy , điểm nào dưới đây là điểm biểu diễn số phức iz ? Ⓐ. ( 2 − ;3). Ⓑ. (2;−3). Ⓒ. (3;− 2). Ⓓ. ( 2 − ;3i) .
Câu 5: Trong hình vẽ bên, điểm P biểu diễn số phức z , điểm Q biểu 1
diễn số phức z . Tìm số phức z = z + z . 2 1 2 Ⓐ. 1+3i . Ⓑ. 3 − + i . Ⓒ. 1 − + 2i . Ⓓ. 2+i .
Câu 6: Số phức liên hợp của số phức z = i (1− 2i) có điểm biểu diễn là điểm nào dưới đây? Ⓐ. E (2;− ) 1 . Ⓑ. B( 1 − ;2) . Ⓒ. A(1;2) . Ⓓ. F ( 2 − ) ;1 .
Câu 7: Cho hai số phức z = 1+ i
z = 1− i . Giá trị của biểu thức z + iz 1 và 2 1 2 bằng Ⓐ. 2− 2i . Ⓑ. 2i . Ⓒ. 2 . Ⓓ. 2+ 2i .
Câu 8: Cho số phức z thỏa mãn 1 i z 14 2i . Tổng phần thực và phần ảo của z bằng Ⓐ. 14 . Ⓑ. 2 . Ⓒ. 2 . Ⓓ. 14.
St-bs: Duong Hung - Word xinh 2020-2021 13
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 9: Môđun của số phức z = + i − ( + i)3 5 3 1 là Ⓐ. 2 5 . Ⓑ. 3 5 . Ⓒ. 5 3 . Ⓓ. 5 2 .
Câu 10: Số phức z = i(3− i) biểu diễn trên mặt phẳng Oxy bởi điểm nào sau đây? Ⓐ. ( 3 − ;1) . Ⓑ. (1;3) . Ⓒ. ( 1 − ;−3) . Ⓓ. (3;−1) .
Câu 11: Trong hình vẽ bên, điểm A biểu diễn số phức z , điểm B biểu diễn số phức z sao cho điểm 1 2
B đối xứng với điểm A qua gốc tọa độ O .
Tìm z biết số phức z = z + 3z . 1 2 Ⓐ. 4 . Ⓑ. 2 5 . Ⓒ. 5. Ⓓ. 17 .
Câu 12: Cho số phức z = 2 + 5 .i Tìm số phức w = iz + z
Ⓐ. w = 7−3i . Ⓑ. w = 3 − −3i .
Ⓒ. w = 3+7 .i Ⓓ. w = 7 − − 7i .
Câu 13: Cho hai số phức z = 3+ 2i và z = a + ( 2 a − )
11 i . Tìm tất cả các giá trị thực của a để z + z là một số thực Ⓐ. a = 3 − . Ⓑ. a = 3.
Ⓒ. a = 3 hoặc a = 3 − .
Ⓓ. a = 13 hoặc a = − 13 .
Câu 14: Cho số phức z =1+ 2i . Tìm tổng phần thực và phần ảo của số phức w = 2z + z . Ⓐ. 3. Ⓑ. 5. Ⓒ. 1. Ⓓ. 2.
Câu 15: Điểm biểu diễn của số phức z là M (1;2) . Tọa độ của điểm biểu diễn cho số phức w = z − 2z là. Ⓐ. (2; 3 − ). Ⓑ. (2; ) 1 . Ⓒ. ( 1 − ;6) . Ⓓ. (2;3).
Câu 16: Cho z = 2 + 4i, z =3−5i . Xác định phần thực của 2 w = z .z 1 2 1 2 Ⓐ. 120 − . Ⓑ. 32 − . Ⓒ. 88. Ⓓ. 152 − .
Câu 17: Cho số phức z = ( + i)2 1
(1+ 2i). Số phức z có phần ảo là Ⓐ. 2 . Ⓑ. 4 . Ⓒ. 2. Ⓓ. 2i .
Câu 18: Cho hai số phức z = 3−5i và w = 1
− + 2i . Điểm biểu diễn số phức z = z − .
w z trong mặt phẳng
Oxy có tọa độ là Ⓐ. ( 6 − ; − 4) . Ⓑ. (4; −6) . Ⓒ. (4; 6). Ⓓ. ( 4 − ; − 6).
Câu 19: Tìm số phức z thỏa mãn z + (2 + i)z = 3−5i .
St-bs: Duong Hung - Word xinh 2020-2021 14
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
Ⓐ. z = 2+3i . Ⓑ. z = 2 − + 3i .
Ⓒ. z = 2−3i . Ⓓ. z = 2 − −3i .
Câu 20: Trong mặt phẳng Oxy, A(1;7), B( 5
− ;5) lần lượt biểu diễn hai số phức z , z . C biểu diễn số 1 2
phức z + z . Trong các mệnh đề sau, mệnh đề nào sai. 1 2
Ⓐ. C có tọa độ ( 4 − ;12).
Ⓑ. CB biểu diễn số phức −z . 1
Ⓒ. AB biểu diễn số phức z − z .
Ⓓ. OACB là hình thoi. 1 2 BẢNG ĐÁP ÁN 1.D 2.A 3.C 4.B 5.A 6.A 7.C 8.A 9.D 10.B 11.B 12.B 13.C 14.B 15.C 16.D 17.A 18.D 19.C 20.C
Dạng ②: Xác định các yếu tố cơ bản của số phức qua phép toán. . Phương pháp:
①. Số phức là biểu thức có dạng . Khi đó:
 Phần thực của là , phần ảo của là và được gọi là đơn vị ảo.
②. Đặc biệt:  Số phức
có phần ảo bằng được coi là số thực và viết là  Số phức
có phần thực bằng được gọi là số ảo (hay số thuần ảo) và viết là  Số .  Số:
vừa là số thực vừa là số ảo.
A - Bài tập minh họa:
Câu 1: Số phức z = (2 − 3i) − ( 5
− + i) có phần ảo bằng Ⓐ. 2 − i . Ⓑ. 4 − i . Ⓒ. −4. Ⓓ. −2. Lời giải
PP nhanh trắc nghiệm Chọn C Ta có:
z = (2 − 3i) − ( 5
− + i) = (2 + 5) −(3+ ) 1 i = 7 − 4i .
Nên phần ảo của số phức z là −4 .
Từ phép tính ta có phần ảo số phức z là −4 .
Câu 2: Cho các số phức z = 1− i 2 , z = − 2 + i 3 . Số phức nào sau có phần ảo lớn hơn. 1 2
Ⓐ. z − z . Ⓑ. z . Ⓒ. z .
Ⓓ. z + z . 2 1 1 2 2 1
St-bs: Duong Hung - Word xinh 2020-2021 15
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung Lời giải
PP nhanh trắc nghiệm Chọn A
Nhập máy tính để tính z − z 2 1
Số phức z − z = 1
− − 2 + 3 + 2 i , có phần 2 1 ( ) ảo là 3 + 2 .
Số phức z = 1− i 2 , có phần ảo là − 2 . 1
Nhập máy tính để tính z + z Số phức 2 1
z = − 2 + i 3 , có phần ảo là 3 . 2
Số phức z + z = 1− 2 +
3 − 2 i , có phần ảo 2 1 ( ) là 3 − 2 .
Vậy số phức z − z có phần ảo lớn nhất. 2 1
Câu 3: Tìm phần thực a của số phức 2 2019
z = i + ... + i .
Ⓐ. a =1. Ⓑ. 1009 a = 2 − . Ⓒ. 1009 a = 2 . Ⓓ. a = 1 − . Lời giải
PP nhanh trắc nghiệm Chọn B Ta có 2 2019
z = i + ... + i là tổng của dãy một
CSN với số hạng đầu tiên − , công bội =  2 2019 u = 1 q i
z = i + ... + i 1 và n = 2018 . Với n 1, ta có: 2018 i −1 2 4n i =1, 4n 1
i + = i , 4n 2 i + = 1 − , 4n+3 i = i −
Do đó ta có z = i
= −1− i . Suy ra a = 1 − . i −1 4n 4n 1 + 4n+2 4n+3  i + i + i + i = 0  ( 4 5 6 7
i + i + i + i ) + + ( 2016 2017 2018 2019 ... i + i + i + i ) = 0 2 2019 2 3
z = i +...+ i = i + i = 1 − −i a = 1 − .
B - Bài tập rèn luyện:
Câu 1: Cho số phức z = 3− 2i . Tìm phần ảo của số phức w = (1+ 2i) z Ⓐ. −4. Ⓑ. 7 . Ⓒ. 4 . Ⓓ. 4i .
Câu 2: Cho số phức z = ( i − )2 − ( + i)2 2 1 3
. Tổng phần thực và phần ảo của z là Ⓐ. 1. Ⓑ. 1 − . Ⓒ. −21. Ⓓ. 21.
Câu 3: Phần ảo của số phức 3
z = 5 + 2i − (1+ i) bằng: Ⓐ. 0 . Ⓑ. 7 . Ⓒ. 7 − . Ⓓ. 7 .
Câu 4: Cho hai số phức z = 2 + 3i ; z =1+ i . Tính z + 3z . 1 2 1 2
Ⓐ. z +3z = 61. Ⓑ. z + 3z =11.
Ⓒ. z +3z = 11 . Ⓓ. z + 3z = 61. 1 2 1 2 1 2 1 2
St-bs: Duong Hung - Word xinh 2020-2021 16
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 5: Số phức z = (2 − 3i) − ( 5
− + i) có phần ảo bằng: Ⓐ. 2 − i . Ⓑ. 4 − i . Ⓒ. −4. Ⓓ. −2.
Câu 6: Cho số phức z = a + bi ( ,
a b  ) . Tìm phần ảo của số phức 2 z . Ⓐ. 2 2 a − b . Ⓑ. 2 2 a + b . Ⓒ. 2 − ab . Ⓓ. 2ab .
Câu 7: Cho hai số phức z =1+ 2i và z = 2 − 3i . Phần ảo của số phức w = z + z là 1 2 1 2 Ⓐ. 5i . Ⓑ. 5. Ⓒ. 1 − . Ⓓ. −i .
Câu 8: Cho số phức z = 1
− + 2i . Môđun của số phức iz + z bằng Ⓐ. 6 . Ⓑ. 3 2 . Ⓒ. 2 . Ⓓ. 18.
Câu 9: Cho số phức z khác 0 . Khẳng định nào sau đây là sai?
Ⓐ. z là số thuần ảo. Ⓑ. .zz là số thực
Ⓒ. z + z là số thực Ⓓ. z − z là số ảo. z 2
Câu 10: Phần ảo của số phức z bằng bao nhiêu biết z = ( 2 + i) (1−i 2) . Ⓐ. 2 . Ⓑ. 2 . Ⓒ. −2. Ⓓ. − 2 .
Câu 11: Điểm nào trong hình vẽ dưới đây là điểm biểu diễn của số phức
z = (1+ i)(2 − i) ? Ⓐ. M . Ⓑ. P . Ⓒ. N . Ⓓ. Q .
Câu 12: Cho số phức z = a + 2bi (a, b ) . Khi đó phần thực của số phức w = (2z + i)(3− i) bằng
Ⓐ. 6a + 2b+1. Ⓑ. 2 − a +12b + 3.
Ⓒ. 6a + 4b+1. Ⓓ. 2 − a + 6b + 3.
Câu 13: Số nào trong các số phức sau là số thực? Ⓐ. (1+ 2i)+( 1 − + 2i) .
Ⓑ. (3+ 2i)+(3− 2i).
Ⓒ. ( 3 + 2i)−( 3 −2i).
Ⓓ. (5+ 2i)−( 5 −2i).
Câu 14: Tìm số phức z thỏa mãn z + 2z = 2 − 4i . Ⓐ. 2 z = − 4i . Ⓑ. 2 z = − + 4i . Ⓒ. 2 z = + 4i . Ⓓ. 2 z = − − 4i . 3 3 3 3
Câu 15: Có bao nhiêu số phức z thỏa mãn z + z.z = 2z ? Ⓐ. 1. Ⓑ. 0 . Ⓒ. 3. Ⓓ. 2 .
St-bs: Duong Hung - Word xinh 2020-2021 17
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 16: Cho hai số phức z = 2 + 3i, z = 3− i . Số phức 2z − z có phần ảo bằng 1 2 1 2 Ⓐ. 1. Ⓑ. 3. Ⓒ. 5. Ⓓ. 7 .
Câu 17: Trong mặt phẳng tọa độ, điểm M (1;− 2) biểu diễn số phức; Môđun của số phức 2
i z − z bằng Ⓐ. 6 . Ⓑ. 6 . Ⓒ. 26 . Ⓓ. 26 .
Câu 18: Nếu z = 2 −3i thì 3 z bằng Ⓐ. 27+ 24 .i Ⓑ. 46+9 .i Ⓒ. 54−27 .i Ⓓ. 4 − 6−9 .i
Câu 19: Xét các khẳng định sau: 2 i) z.z z  
ii)z + z z  
iii)z  0  z
Số khẳng định đúng là: Ⓐ. 0 . Ⓑ. 1. Ⓒ. 3. Ⓓ. 2 .
Câu 20: Cho hai số phức z = a + bi (a, b ) và z = a + b i (a, b ) . Điều kiện giữa , a , b a ,  b để
z + z là một số thuần ảo là Ⓐ. a + a ' = 0 a + a ' = 0
a + a = 0 . Ⓑ. . Ⓒ. .
Ⓓ. b+b = 0. b  + b'  0 b  + b' = 0 BẢNG ĐÁP ÁN 1.C 2.C 3.A 4.A 5.C 6.D 7.C 8.B 9.A 10.D 11.D 12.C 13.B 14.C 15.D 16.C 17.D 18.D 19.D 20.B
St-bs: Duong Hung - Word xinh 2020-2021 18
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
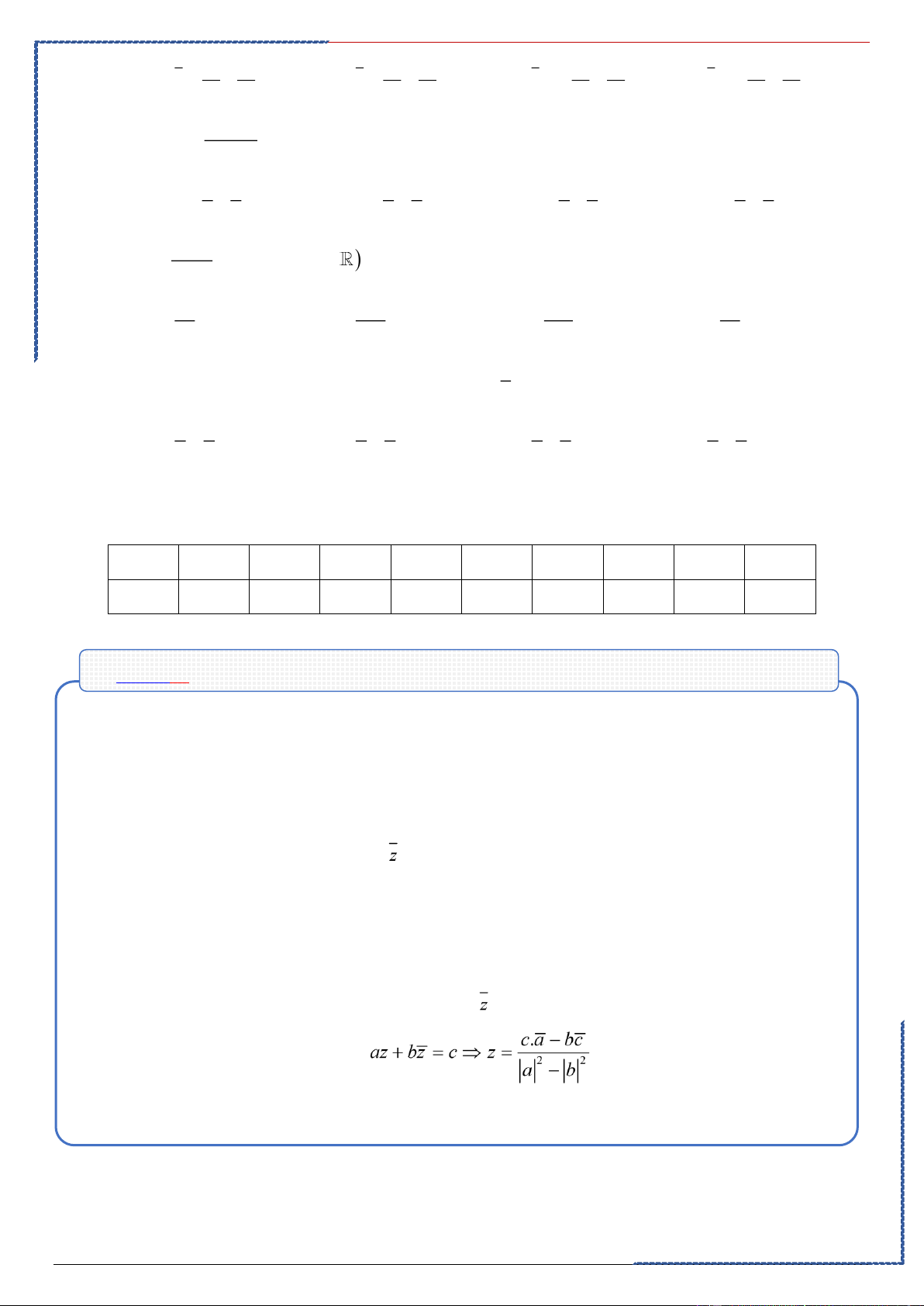
Dạng ③: Bài toán quy về giải phương trình, hệ phương trình
-Phương pháp:
①. Sử dụng tính chất hai số phức bằng nhau. Cho hai số phức , . Khi đó:
②. Số phức liên hợp, mo đun của số phức: Cho số phức .
⬧.Số phức liên hợp của là ( ) .
⬧.Tổng và tích của và luôn là một số thực.  .  .
⬧. Mô đun của số phức .  ; .
A - Bài tập minh họa:
Câu 1: Nếu hai số thực x, y thỏa mãn x (3+ 2i) + y (1− 4i) =1+ 24i thì x − y bằng? Ⓐ. 3. Ⓑ. 3 − . Ⓒ. 7 − . Ⓓ. 7 Lời giải
PP nhanh trắc nghiệm Chọn D Casio Ta có:
x (3 + 2i) + y (1− 4i) = 1+ 24i
 3x + y + (2x − 4y)i =1+ 24i 3  x + y =1 x = 2    
2x − 4y = 24 y = 5 −
Vậy: x − y = 7
Câu 2: Cho số phức z thỏa mãn | z |= 5 và | z + 3| |
= z + 3−10i | . Tìm số phức w = z − 4 +3 .i Ⓐ. w = 3 − +8 .i
Ⓑ. w =1+3 .i Ⓒ. w = 1 − + 7 .i Ⓓ. w = 4 − +8 .i
St-bs: Duong Hung - Word xinh 2020-2021 19
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung Lời giải
PP nhanh trắc nghiệm Chọn D
 Thử lần lượt các đáp án.
z = x + yi,( ,
x y  ) . Theo đề bài ta có: A w = 3
− +8i z = w+ 4 −3i =1+ 5i 2 2 x + y = 25 và 2 2 2 2
(x + 3) + y = (x + 3) + ( y −10) .
nên | z |= 26 (loại).
Giải hệ phương trình trên ta được x = 0; y = 5.
Tương tự cho đáp án B và C,
Vậy z = 5i .  D = − +  = + − = Từ đó ta có w 4 8i z w 4 3i 5i w = 4 − +8i .
thỏa mãn | z |= 5 và | z + 3 | |
= z + 3−10i | .
Câu 3: Cho số phức z thỏa mãn 3(z −i) −(2 + 3i) z = 7 −16i . Môđun của số phức z bằng. Ⓐ. 5. Ⓑ. 3. Ⓒ. 5 . Ⓓ. 3 . Lời giải
PP nhanh trắc nghiệm Chọn C
Casio: công thức nhanh
Gọi z = x + yi với , x y  . . c a − bc
az + bz = c z = 2 2  Ta có a − b
3(z − i) − (2 + 3i) z = 7 −16i
 3( x − yi − i) − (2 + 3i)(x + yi) = 7 −16i
 3x − 3yi − 3i − 2x − 2yi − 3xi + 3y = 7 −16i
 (x + 3y) − (3x + 5y + 3)i = 7 −16ix + 3y = 7 x + 3y = 7 x =1       . 3
x + 5y + 3 =16 3  x + 5y =13 y = 2
Do đó z =1+ 2i . Vậy z = 5 .
B - Bài tập rèn luyện:
Câu 1: Tìm hai số thực x và y thỏa mãn (2x − 3yi) + (1− 3i) = 1
− + 6i với i là đơn vị ảo.
Ⓐ. x =1; y = 3 − . Ⓑ. x = 1 − ; y = 3 − . Ⓒ. x = 1 − ; y = 1
− . Ⓓ. x =1; y = 1 − .
Câu 2: Nếu hai số thực x, y thỏa mãn x (3+ 2i) + y (1− 4i) =1+ 24i thì x − y bằng? Ⓐ. 3. Ⓑ. 3 − . Ⓒ. 7 − . Ⓓ. 7 .
Câu 3: Cho cặp số ( x; y) thỏa mãn: (2x − y)i + y (1− 2i) = 3+ 7i . Khi đó biểu thức 2
P = x − xy nhận
giá trị nào sau đây: Ⓐ. 30. Ⓑ. 40 . Ⓒ. 10. Ⓓ. 20 .
Câu 4: Tìm số phức z thỏa mãn z + 2z = 2 − 4i .
St-bs: Duong Hung - Word xinh 2020-2021 20
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung Ⓐ. 2 z = − − 2 4i . Ⓑ. z = − 2 4i . Ⓒ. z = − + 2 4i .
Ⓓ. z = + 4i . 3 3 3 3
Câu 5: Tìm các số thực a và b thỏa mãn 4ai + (2 −bi)i =1+ 6i với
i là đơn vị ảo. Ⓐ. 1 1 a = − , b = 6 − .
Ⓑ. a = − ,b = 6 .
Ⓒ. a =1,b =1.
Ⓓ. a =1,b = 1 − . 4 4
Câu 6: Giả sử a , b là hai số thực thỏa mãn 2a + (b −3)i = 4 −5i với i là đơn vị ảo. Giá trị của a , b bằng
Ⓐ. a =1, b = 8.
Ⓑ. a = 8, b = 8 .
Ⓒ. a = 2 , b = 2 − . Ⓓ. a = 2 − , b = 2 .
Câu 7: Tìm các số thực x , y thỏa mãn (1− 3i) x − 2y + (1+ 2y)i = 3 − − 6i . Ⓐ. x = 5 − ; y = 4 − .
Ⓑ. x = 5; y = 4 .
Ⓒ. x = 5; y = 4 − . Ⓓ. x = 5 − ; y = 4 .
Câu 8: Tìm các số thực x , y thỏa mãn 2x −1+ ( y − 2)i =1+ i với i là đơn vị ảo.
Ⓐ. x =1; y =1.
Ⓑ. x =1; y = 2.
Ⓒ. x =1; y = 3. Ⓓ. x = 1 − ; y = 3 .
Câu 9: Cho các số thực x , y thỏa mãn 4(3i − 2) = 4x + 2yi . Tính giá trị của P = x + y . Ⓐ. P = 4 . Ⓑ. P = 7 . Ⓒ. P = 1 − . Ⓓ. P = 8.
Câu 10: Các số thực x , y thỏa mãn đẳng thức x (3+ 5i) − y (1+ 2i) = 9 +16i trong đó 2 i = 1 − . Giá trị
của biểu thức T = x − y là Ⓐ. 3 . Ⓑ. 5 . Ⓒ. 0 . Ⓓ. 1.
Câu 11: Tìm các số thực a và b thỏa mãn 2a + (b + i)i =1+ 2i với i là đơn vị ảo.
Ⓐ. a = 0, b = 1 2 .
Ⓑ. a = , b =1.
Ⓒ. a = 0, b =1.
Ⓓ. a =1, b = 2 . 2
Câu 12: Cho hai số thực x, y thỏa mãn x (3+ 2i) + y (1− 4i) =1+ 24i . Giá trị x + y bằng Ⓐ. 3. Ⓑ. 2. Ⓒ. 4. Ⓓ. 3 − .
Câu 13: Cho số phức z thỏa mãn z + (2 + i) z = 3+ 5i . Tính môđun của số phức z . Ⓐ. z =13 . Ⓑ. z = 5 . Ⓒ. z = 13 . Ⓓ. z = 5 .
Câu 14: Cho số phức z = a + bi,(a,b ) thỏa mãn 3z − (4 + 5i) z = 1
− 7 +11i .Tính ab . Ⓐ. ab = 3. Ⓑ. ab = 6 . Ⓒ. ab = 6 − . Ⓓ. ab = 3 − .
Câu 15: Cho số phức z = a + bi, , a b
thỏa mãn: (1+ 3i) z + (2 + i) z = 2
− + 4i . Tính P = . a b Ⓐ. I = 8. Ⓑ. P = 4 − . Ⓒ. P = 8 − . Ⓓ. P = 4 .
Câu 16: Cho số phức z thỏa mãn z + 2.(z + z) = 2 − 6i có phần thực là
St-bs: Duong Hung - Word xinh 2020-2021 21
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung Ⓐ. 2 . Ⓑ. 1 − 3 . Ⓒ. . Ⓓ. 6 − . 5 4
Câu 17: Cho số phức z = a + bi ( ;
a b R) thỏa (1+ i) z + 2z = 3+ 2i . Tính P = a + b . Ⓐ. 1 1 P = 1 . Ⓑ. P = 1 − .
Ⓒ. P = − .
Ⓓ. P = . 2 2
Câu 18: Cho số phức z = a + bi (a,b ) thỏa mãn 2z + z = 3+i . Tính giá trị biểu thức 3a + b ?
Ⓐ. 3a +b = 6.
Ⓑ. 3a +b = 5.
Ⓒ. 3a +b = 3.
Ⓓ. 3a +b = 4.
Câu 19: Số phức z = x + yi (với , x y
) thỏa mãn (1+ i) z = 3 + 5i , giá trị của 2 2
x + y bằng Ⓐ. 34. Ⓑ. 17 . Ⓒ. 34 . Ⓓ. 17 .
Câu 20: Cho các số thực a,b thỏa mãn đẳng thức 2a + 3 + (3b − 2i)i = 4 − 3i với i là đơn vị ảo. Giá trị
biểu thức P = 2a −b bằng Ⓐ. − 3 0 . Ⓑ. 2 . Ⓒ. . Ⓓ. −2 . 2 BẢNG ĐÁP ÁN 1.B 2.D 3.B 4.D 5.C 6.C 7.B 8.C 9.A 10.B 11.D 12.D 13.A 14.B 15.A 16.A 17.B 18.D 19.B 20.A
St-bs: Duong Hung - Word xinh 2020-2021 22
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
Dạng ④: Bài toán tìm tập hợp điểm biểu diễn cho số phức
-Phương pháp: . Số phức
có điểm biểu diễn trên mp là điểm . .Số phức có mô đun . .Số phức
có phần ảo bằng được coi là số thực và viết là  . Số phức
có phần thực bằng được gọi là số ảo (hay số thuần ảo) và viết là
. Phương trình đường thẳng: . Phương trình Elip:
. Phương trình đường tròn:
Dạng 1: có tâm , bán kính .
Dạng 2: có tâm , bán kính (Với )
. Nhận dạng nhanh tâm và bán kính đường tròn : . . . .
A - Bài tập minh họa:
Câu 1: Tìm tập hợp các điểm biểu diễn số phức z thỏa | z − 3+ i |= 2 trong mặt phẳng Ox . y Ⓐ. Đường tròn ( 2 2
x + )2 + ( y − )2 3 1 = 4.
Ⓑ. Đường tròn (x −3) +( y + ) 1 = 4 .
Ⓒ. Đường tròn (x − )2 +( y + )2 3 1 = 2.
Ⓓ. Đường thẳng 3x− y+ 2 = 0. Lời giải
PP nhanh trắc nghiệm Chọn B
Đặt z = x + yi ( x, y  ) . Ta có:
z − 3 + i = 2  ( x − 3)2 + ( y + )2 1 = 2
 (x −3)2 + ( y + )2 1 = 4.
St-bs: Duong Hung - Word xinh 2020-2021 23
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 2: Tập hợp các điểm M biểu diễn số phức z sao cho = ( )2 2 z z là
Ⓐ. Trục tung và trục hoành.
Ⓑ. Trục tung.
Ⓒ. Trục hoành.
Ⓓ. Gốc tọa độ. Lời giải
PP nhanh trắc nghiệm Chọn A
Nhận biết hằng đẳng thức
Đặt z = x + yi ( , x y  ) nên 2 2
z = x − yi . 2 z = ( z) 2
z − (z) = 0 2 2 Ta có: 2 z = ( z) 2
z − (z) = 0
 (z − z)(z + z) = 0
 (z − z)(z + z) = 0  Casio:
 (2yi).(2x) = 0 . x = 0  y =0
Vậy tập hợp các điểm M biểu diễn số phức z
Calc x=0; y=1 và x=1; y=0 đều cho kết quả
là trục tung ( x = 0) và trục hoành ( y = 0) .
bằng 0 nên chọn Ⓐ.
Câu 3: Cho số phức z thỏa mãn z −1+ i = z + 2 . Trong mặt phẳng phức, quỹ tích điểm biểu diễn
các số phức z .
Ⓐ. là đường thẳng 3x + y +1= 0.
Ⓑ. là đường thẳng 3x − y +1= 0.
Ⓒ. là đường thẳng 3x + y −1= 0.
Ⓓ. là đường thẳng 3x − y −1= 0 . Lời giải
PP nhanh trắc nghiệm Chọn B
Casio: Chọn hai điểm đặc biệt thuộc đường thẳng và calc.
Giả sử số phức z có dạng:
z = x + yi (x,y ) Ta có:
z −1+ i = z + 2  x + yi −1+ i = x + yi + 2  (x − ) 1 + ( y + )
1 i = ( x + 2) + yi Calc x=0;y=-1 loại A
 (x − )2 + ( y + )2 = (x + )2 2 1 1 2 + y
 (x − )2 + ( y + )2 = (x + )2 2 1 1 2 + y 2 2 2 2
x − 2x +1+ y + 2y +1= x + 4x + 4 + y  Calc x=0;y=1 và x=-1/3; y=0
6x − 2y + 2 = 0  3x − y +1 = 0
Vậy tập hợp điểm biểu diễn số phức z là đường
thẳng 3x − y +1 = 0 . Ta chọn B
St-bs: Duong Hung - Word xinh 2020-2021 24
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
B - Bài tập rèn luyện:
Câu 1: Trong mặt phẳng phức với hệ tọa độ Oxy , điểm biểu diễn của các số phức z = 3+ bi với b
luôn nằm trên đường có phương trình là Ⓐ. x = 3. Ⓑ. y = x . Ⓒ. y = 3. Ⓓ. y = x +3.
Câu 2: Tập hợp các điểm biểu diễn số phức z thỏa mãn z − 2 + i = 3 Ⓐ. ( 2 2
x − )2 + ( y + )2 2 1 = 9 .
Ⓑ. (x − 2) +( y + ) 1 =1. Ⓒ. ( 2 2
x − )2 + ( y + )2 2 1 = 4 .
Ⓓ. (x − 2) +( y + ) 1 = 16 .
Câu 3: Tập hợp các điểm trong mặt phẳng biểu diễn cho số phức z thoả mãn điều kiện z −1+ 2i = 4 là.
Ⓐ. Một đường thẳng. Ⓑ. Một đoạn thẳng. Ⓒ. Một đường tròn. Ⓓ. Một hình vuông.
Câu 4: Tập hợp tất cả các điểm biểu diễn các số phức z thỏa mãn: z + 2 − i = 4 là đường tròn có tâm
I và bán kính R lần lượt là: Ⓐ. I (2;− ) 1 ; R = 2 . Ⓑ. I ( 2 − ;− ) 1 ; R = 2 . Ⓒ. I (2;− ) 1 ; R = 4 . Ⓓ. I ( 2 − ;− ) 1 ; R = 4 .
Câu 5: Tìm tập hợp điểm biểu diễn số phức z thỏa z − 2 + i = 2 .
Ⓐ. Tập hợp điểm biểu diễn số phức z là đường tròn 2 2
x + y − 4x + 2 y +1 = 0 .
Ⓑ. Tập hợp điểm biểu diễn số phức z là đường tròn 2 2
x + y − 4x − 2 y +1 = 0 .
Ⓒ. Tập hợp điểm biểu diễn số phức z là đường tròn 2 2
x + y − 4x + 2 y − 4 = 0 .
Ⓓ. Tập hợp điểm biểu diễn số phức z là đường tròn 2 2
x + y − 4x − 2 y − 4 = 0 .
Câu 6: Tập hợp các điểm M biểu diễn số phức z thoả mãn z − 2 + 5i = 4 là:
Ⓐ. Đường tròn tâm I (2; 5
− ) và bán kính bằng 2 .
Ⓑ. Đường tròn tâm I ( 2
− ;5) và bán kính bằng 4 .
Ⓒ. Đường tròn tâm O và bán kính bằng 2 .
Ⓓ. Đường tròn tâm I (2; 5
− ) và bán kính bằng 4 .
Câu 7: Trên mặt phẳng tọa độ, tập hợp điểm biểu diễn số phức z thỏa mãn điều kiện z + 2 − 5i = 6
là đường tròn có tâm và bán kính lần lượt là: Ⓐ. I( 2 − ;5), R = 6. Ⓑ. I( 2
− ;5), R = 36 . Ⓒ. I(2; 5
− ), R = 36 . Ⓓ. I(2; 5 − ), R = 6 .
St-bs: Duong Hung - Word xinh 2020-2021 25
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 8: Trên mặt phẳng phức tập hợp các 2018 phức z = x + yi thỏa mãn z + 2 + i = z − 3i là đường
thẳng có phương trình
Ⓐ. y = −x +1.
Ⓑ. y = −x −1.
Ⓒ. y = x −1. Ⓓ. y = x +1.
Câu 9: Tìm tập hợp điểm biểu diễn số phức z thỏa mãn z + 2 − i = 3.
Ⓐ. Đường tròn tâm I (2;− ) 1 , bán kính R = 1 .
Ⓑ. Đường tròn tâm I ( 2 − ; ) 1 , bán kính R = 3 .
Ⓒ. Đường tròn tâm I ( 2 − ; ) 1 , bán kính R = 3 .
Ⓓ. Đường tròn tâm I (1; 2
− ) , bán kính R = 3.
Câu 10: Tập hợp các điểm trong mặt phẳng toạ độ biểu diễn các số phức z thoả mãn z + 4 − 8i = 2 5
là đường tròn có phương trình: Ⓐ. ( 2 2
x + )2 + ( y − )2 4 8 = 2 5 .
Ⓑ. (x − 4) + ( y + 8) = 2 5 . Ⓒ. ( 2 2
x + )2 + ( y − )2 4 8 = 20 .
Ⓓ. (x − 4) + ( y + 8) = 20.
Câu 11: Cho số phức z thỏa mãn iz − ( 3
− + i) = 2 . Trong mặt phẳng phức, quỹ tích điểm biểu diễn số
phức z là hình vẽ nào dưới đây? y y 3 3 2 2 1 1 O x 1 2 3 O x 1 2 3 Ⓐ. . Ⓑ. . y y 3 3 2 2 1 1 x x O 1 2 3 O 1 2 Ⓒ. . Ⓓ. .
Câu 12: Tìm tập hợp những điểm M biểu diễn số phức z trong mặt phẳng phức, biết số phức z thỏa
mãn điều kiện z − 2i = z +1 .
Ⓐ. Tập hợp những điểm M là đường thẳng có phương trình 2x + 4y +3 = 0 .
Ⓑ. Tập hợp những điểm M là đường thẳng có phương trình 4x + 2y +3 = 0 .
Ⓒ. Tập hợp những điểm M là đường thẳng có phương trình 2x + 4y −3 = 0.
Ⓓ. Tập hợp những điểm M là đường thẳng có phương trình 4x −2y +3 = 0.
Câu 13: Tập hợp các điểm biểu diễn số phức z thỏa mãn z − i = (1+ i) z là một đường tròn, tâm của
đường tròn đó có tọa độ là
St-bs: Duong Hung - Word xinh 2020-2021 26
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung Ⓐ. (1 ) ;1 . Ⓑ. (0;− )1 . Ⓒ. (0 ) ;1 . Ⓓ. ( 1 − ;0) .
Câu 14: Tập hợp các điểm biểu diễn số phức z trên mặt phẳng tọa độ là đường tròn tâm I (0; ) 1 , bán
kính R = 3. Mệnh đề nào dưới đây là đúng? Ⓐ. z −1 = 3.
Ⓑ. z −i = 3 .
Ⓒ. z −i = 3 . Ⓓ. z +i = 3 .
Câu 15: Tập hợp tất cả các điểm trong mặt phẳng toạ độ Oxy biểu diễn số phức z thoả mãn
z −1+ 2i = z + 3 là đường thẳng có phương trình
Ⓐ. 2x − y +1= 0.
Ⓑ. 2x + y −1= 0.
Ⓒ. 2x − y −1= 0 .
Ⓓ. 2x + y +1= 0.
Câu 16: Trong mặt phẳng tọa độ, tập hợp điểm M ( ;
x y) biểu diễn số phức z = x + yi , ( x, y  ) thỏa
mãn z −1+ 3i = z − 2 − i
Ⓐ. Đường tròn đường kính AB với A(1; 3 − ) , B(2 ) ;1 . .
Ⓑ. Đường trung trực của đoạn thẳng AB với A(1; 3 − ) , B(2 ) ;1 . .
Ⓒ. Trung điểm của đoạn thẳng AB với A(1; 3 − ) , B(2 ) ;1 . .
Ⓓ. Đường trung trực của đoạn thẳng AB với A( 1 − ;3) , B( 2 − ;− ) 1 . .
Câu 17: Cho số phức z thỏa mãn điều kiện z − 3 + 4i  2 . Trong mặt phẳng tọa độ, tập hợp điểm biểu
diễn số phức w = 2z +1− i là hình tròn có diện tích Ⓐ. 9 . Ⓑ. 12 . Ⓒ. 16 . Ⓓ. 25 .
Câu 18: Cho số phức z thỏa mãn điều kiện z = 10 và w = ( + i) z + ( − i)2 6 8 1 2
. Tập hợp các điểm biểu
diễn số phức w là đường tròn có tâm là Ⓐ. I ( 3 − ;− 4) . Ⓑ. I (3;4) . Ⓒ. I (1;− 2). Ⓓ. I (6;8) .
Câu 19: Tập hợp tất cả các điểm biểu diễn số phức z mà 2
z thuần ảo là
Ⓐ. 1 điểm duy nhất.
Ⓑ. 1 đường thẳng duy nhất.
Ⓒ. 2 đường thẳng song song với nhau.
Ⓓ. 2 đường thẳng vuông góc với nhau.
Câu 20: Cho số phức z thỏa mãn z = 5 . Biết tập hợp các điểm biểu diễn số phức w = (1+ 2i) z + i là
một đường tròn. Tìm bán kính r của đường tròn đó. Ⓐ. r = 5 . Ⓑ. r =10. Ⓒ. r = 5 . Ⓓ. r = 2 5 . BẢNG ĐÁP ÁN 1.A 2.A 3.C 4.D 5.A 6.D 7.A 8.C 9.B 10.C 11.C 12.C 13.B 14.B 15.B 16.B 17.C 18.A 19.D 20.C
St-bs: Duong Hung - Word xinh 2020-2021 27
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung Full Chuyên đề 12 new 2020-2021 CHƯƠNG ④: FB: Duong Hung
Bài ➂: PHÉP CHIA HAI SỐ PHỨC
Dạng ①: Thực hiện các phép tính về số phức . Phương pháp:
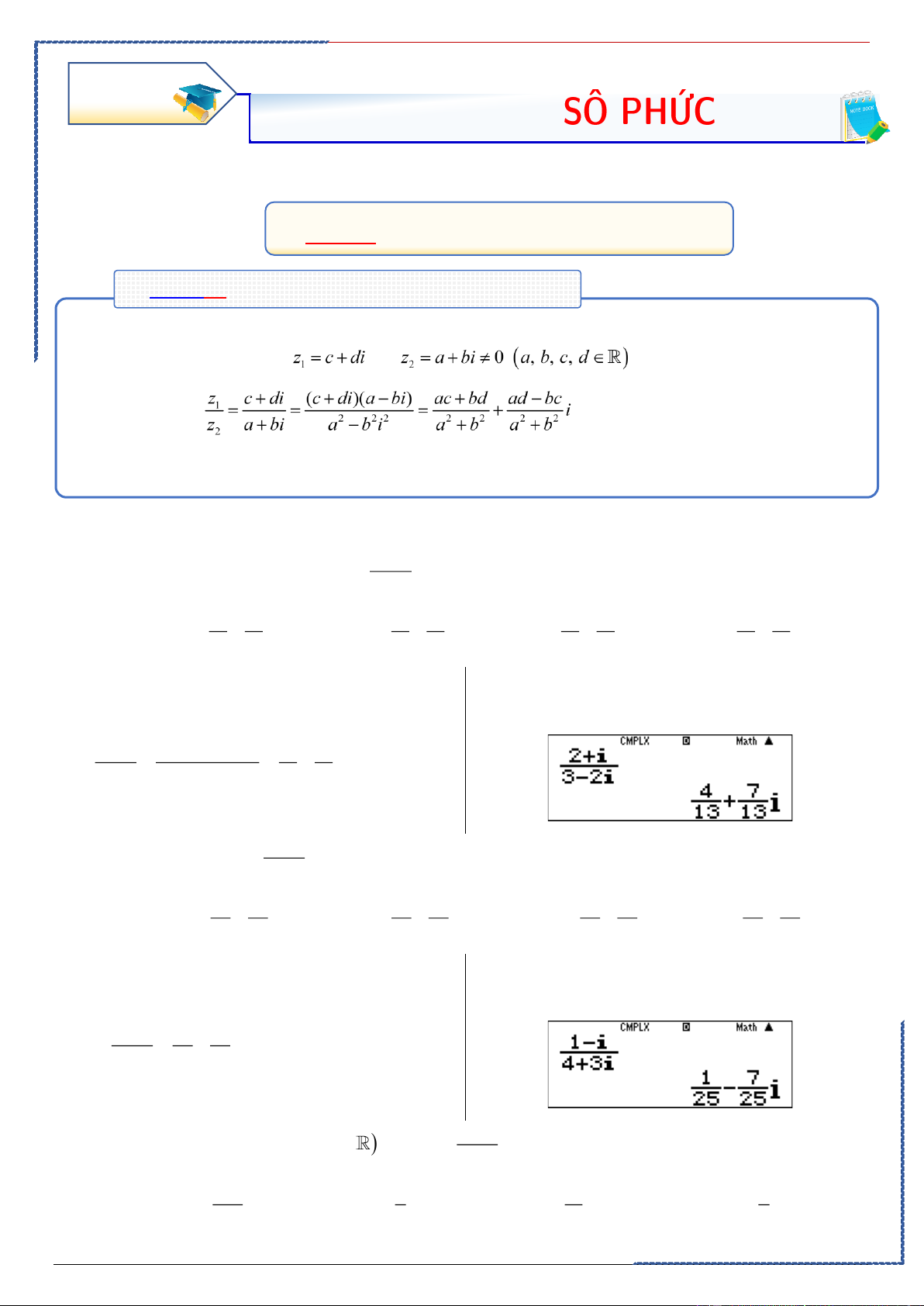
✓. Cho hai số phức và . ①.
②. Sử dụng Casio: Chế độ số phức mode 2
A - Bài tập minh họa: +
Câu 1. Thực hiện phép chia sau : 2 i z = . 3 − 2i Ⓐ. 7 4 4 7 z = + i . Ⓑ. z = + i . Ⓒ. 4 7 z = − i . Ⓓ. 7 4 z = − i . 13 13 13 13 13 13 13 13 Lời giải
PP nhanh trắc nghiệm Chọn B Casio 2 + i (2+i)(3+ 2i) 4 7 z = = = + i 3 − 2i
(2+i)(3+ 2i) 13 13 −
Câu 2. Cho số phức 1 i z =
, khẳng định nào sau đây đúng. 4 + 3i Ⓐ. 1 7 z = + i . Ⓑ. 1 7 z = − i . Ⓒ. 1 7 z = − − i . Ⓓ. 7 1 z = − i . 25 25 25 25 25 25 25 25 Lời giải
PP nhanh trắc nghiệm Chọn B Casio − i 1 1 7 z = = − . i 4 + 3i 25 25 +
Câu 3. Cho số phức i
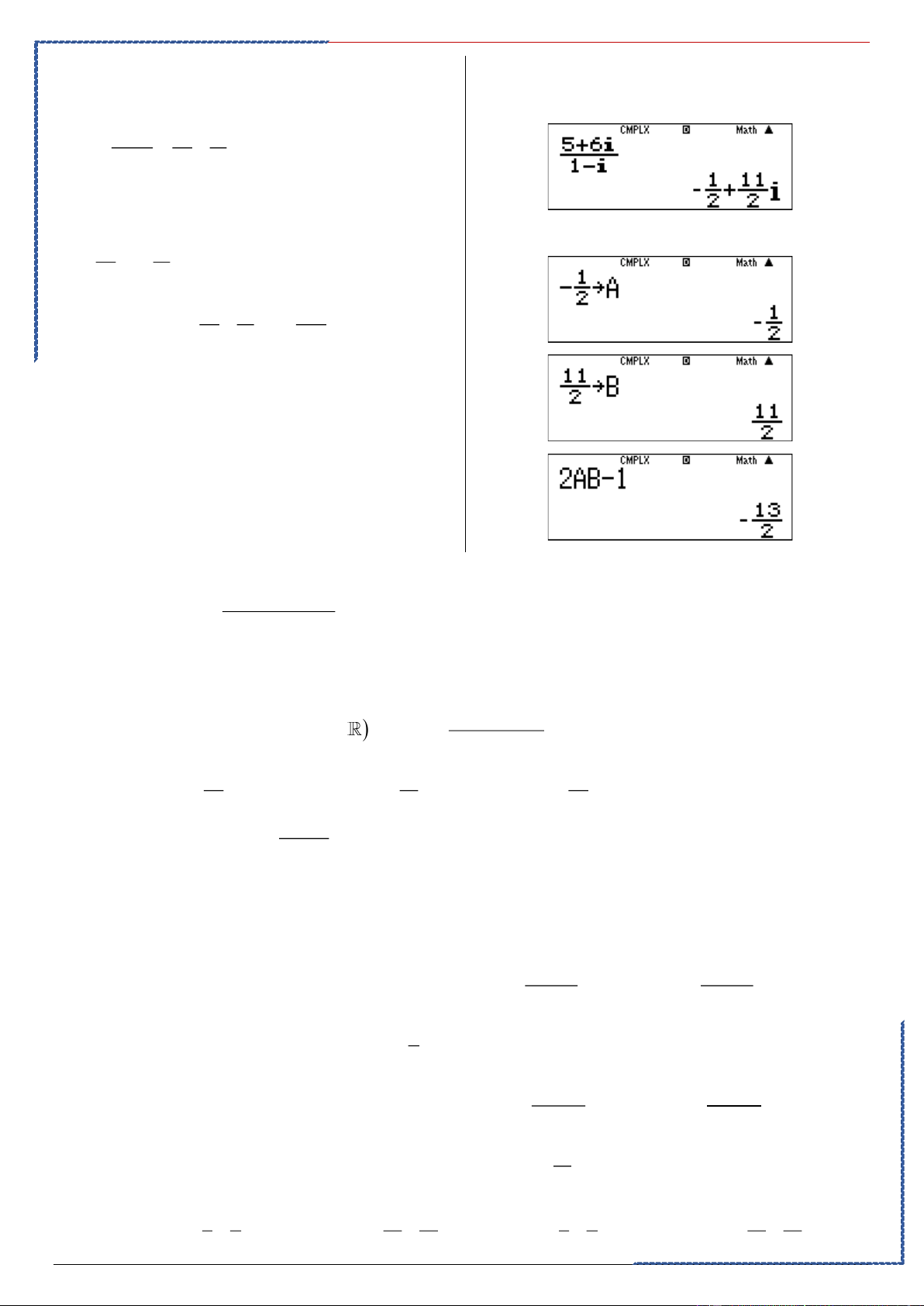
z = a + bi (a,b  ) thỏa 5 6 z =
. Tính giá trị của P = 2ab −1 . 1− i Ⓐ. − 13 P = . Ⓑ. 9 P = . Ⓒ. 13 P = . Ⓓ. 9 P = − 2 2 2 2
St-bs: Duong Hung - Word xinh 2020-2021 28
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung Lời giải
PP nhanh trắc nghiệm Chọn A Casio + i −  5 6 1 11 z = = + . i 1− i 2 2  Ta có 1 − 11 a = ;b = 2 2  1 −  11 1 − 3
P = 2ab −1 = 2 . −1 =    2  2 2
B - Bài tập rèn luyện:
(3− 2i)(6 + 2i)
Câu 1. Thu gọn z = ta được. 1+ i
Ⓐ. z = 8+14i .
Ⓑ. z = 8−14i . Ⓒ. z = 8 − +13i . Ⓓ. z =14i . ( +i)2 ( i)3 1 . 2
Câu 2. Cho số phức z = a + bi (a,b ) thỏa z =
. Tính giá trị của P = 2a + b . 2 − + i Ⓐ. 48 P = . Ⓑ. 16 P = − . Ⓒ. 48 P = − . Ⓓ. P = 16 − . 5 5 5 − Câu 3. Viết gọn 7 17i z = 1− 2i + . 5 − i
Ⓐ. z = 3+5 .i
Ⓑ. z = 3−5 .i Ⓒ. z = 3 − +5 .i Ⓓ. z = 3 − −5i .
Câu 4. Cho số phức z = a + bi  0. Số phức 1
z− có phần thực là Ⓐ. a −b a + . b Ⓑ. a − . b Ⓒ. Ⓓ. 2 2 a + b 2 2 a + b
Câu 5. Cho số phức z = a + bi  0 . Số phức 1 có phần ảo là z Ⓐ. − 2 2 a b a + b . Ⓑ. 2 2 a − b . Ⓒ.  Ⓓ.  2 2 a + b 2 2 a + b
Câu 6. Cho hai số phức z
z = 1+ 2i , z = 3 − i . Tìm số phức 2 z = . 1 2 z1 Ⓐ. 1 7 z = + i . Ⓑ. 1 7 z = + i . Ⓒ. 1 7 z = − i . Ⓓ. 1 7 z = − + i . 5 5 10 10 5 5 10 10
St-bs: Duong Hung - Word xinh 2020-2021 29
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 7. Số phức nghịch đảo 1
z− của số phức z = 2 − 2i là Ⓐ. 1 1 − i . Ⓑ. 1 1 − + i . Ⓒ. 1 1 + i . Ⓓ. 1 1 − − i . 4 4 4 4 4 4 4 4
Câu 8. Cho số phức z = 5− 2 .i Số phức 1 có phần ảo là z Ⓐ. 29. Ⓑ. 21. Ⓒ. 5 . Ⓓ. 2 . 29 29 +
Câu 9. Thực hiện phép chia sau: 2 i z = 3 − 2i Ⓐ. 4 7 z = + . i Ⓑ. 7 4 z = + . i Ⓒ. 4 7 z = − . i Ⓓ. 7 4 z = − . i 13 13 13 13 13 13 13 13
Câu 10. Cho số phức z = 2 − 3 .i Hãy tìm nghịch đảo của số phức z Ⓐ. 2 3 + . i Ⓑ. 2 3 − . i Ⓒ. 3 2 + . i Ⓓ. 3 2 − . i 11 11 11 11 11 11 11 11 −
Câu 11.Tìm số phức 3 4i z = . 4 − i Ⓐ. 16 13 z = − i . Ⓑ. 16 11 z = − i . Ⓒ. 9 4 z = − i . Ⓓ. 9 23 z = − i . 17 17 15 15 5 5 25 25
Câu 12. Tìm số phức 3 z = . 2 + i Ⓐ. 6 3 z = + i . Ⓑ. 3 6 z = + i . Ⓒ. 6 3 z = − i . Ⓓ. 3 6 z = − i . 5 5 5 5 5 5 5 5
Câu 13. Tìm số phức 3 z = . i
Ⓐ. z = 3i.
Ⓑ. z = i .
Ⓒ. z = i − . Ⓓ. z = 3 − i .
Câu 14. Nếu z = 2i + 3 thì z bằng z Ⓐ. − + − + 5 12i .
Ⓑ. 5 12i .
Ⓒ. 3 4i .
Ⓓ. 5 6i − 2i . 13 13 7 11
Câu 15. Viết số phức 2i 3 z =
− dưới dạng đại số. 3 − 2i i Ⓐ. 4 45 z = − i . Ⓑ. 4 45 z = − − i . Ⓒ. 4 45 z = − + i . Ⓓ. 4 45 z = + i . 13 13 13 13 13 13 13 13 −
Câu 16. Viết số phức 2i 4 3 z = − dưới dạng đại số. 3 − 2i 3i − 2 Ⓐ. 10 3 z = − + i . Ⓑ. 10 3 z = − i . Ⓒ. 10 3 z = + i . Ⓓ. 10 7 z = − + i . 13 13 13 13 3 13 13 13
Câu 17. Cho số phức z = ( i − ) 7 3
2 i . Tìm số phức liên hợp của số phức 1 . z
St-bs: Duong Hung - Word xinh 2020-2021 30
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung Ⓐ. 3 2 z = − i . Ⓑ. 3 2 z = + i . Ⓒ. 3 2 z = − + i . Ⓓ. 3 2 z = − − i . 13 13 13 13 13 13 13 13 − Câu 18. Tính 2 i z = . 2019 1− i Ⓐ. 1 3 z = + .i Ⓑ. 3 1 z = − .i Ⓒ. 1 3 z = − .i Ⓓ. 3 1 z = + .i 2 2 2 2 2 2 2 2 Câu 19. Biết 1
= a + bi , (a,b ) . Tính ab . 3 + 4i Ⓐ. 12 . Ⓑ. 12 . Ⓒ. 12 − . Ⓓ. 12 − . 25 625 625 25
Câu 20. Cho số phức z =1+ i . Giá trị của biểu thức 1 z + là z Ⓐ. 3 1 + i . Ⓑ. 1 1 + i . Ⓒ. 3 1 − i . Ⓓ. 1 1 − i . 2 2 2 2 2 2 2 2 BẢNG ĐÁP ÁN 1.B 2.D 3.B 4.C 5.D 6.C 7.C 8.D 9.A 10.A 11.A 12.C 13.D 14.B 15.C 16.D 17.A 18.C 19.C 20.A
Dạng ②: Thực hiện phép tính và từ đó suy ra các yếu tố liên quan tới số
. Phương pháp:
①. Casio FX 570 VN plus:
⬧ Để tính toán trên tập số phức : MODE 2
⬧Lệnh tính Modun của cố phức : SHIFT HYP
⬧Lệnh tìm số phức liên hợp là: SHIFT 2 2
②. Casio FX 580 VnX :
⬧ Để tính toán trên tập số phức : MENU 2
⬧ Lệnh tính Modun của cố phức : SHIFT Abs
⬧ Lệnh tìm Acgumen, số phức liên hợp , Phần thực, Phần ảo : OPTN
③. Công thức nhanh:
④. Chức năng lưu, xuất, tính toán: Sto, Alha, Calc
A - Bài tập minh họa:
St-bs: Duong Hung - Word xinh 2020-2021 31
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 1: Điểm biểu diễn của số phức 1 z = là 2 − 3i Ⓐ.   (3; 2 − ) . Ⓑ. 2 3 ;  . Ⓒ. ( 2 − ;3) . Ⓓ. (4; ) 1 − . 13 13  Lời giải
PP nhanh trắc nghiệm Chọn B Casio 1 2 + 3i 2 3  z = = = + i 2 − 3i
(2 −3i)(2 +3i) 13 13 .
Suy ra điểm biểu diễn của số phức 1 z = là: 2 − 3i  2 3  ;  .   13 13 
Dựa vào kết quả kết luận 2 3 ;   13 13 
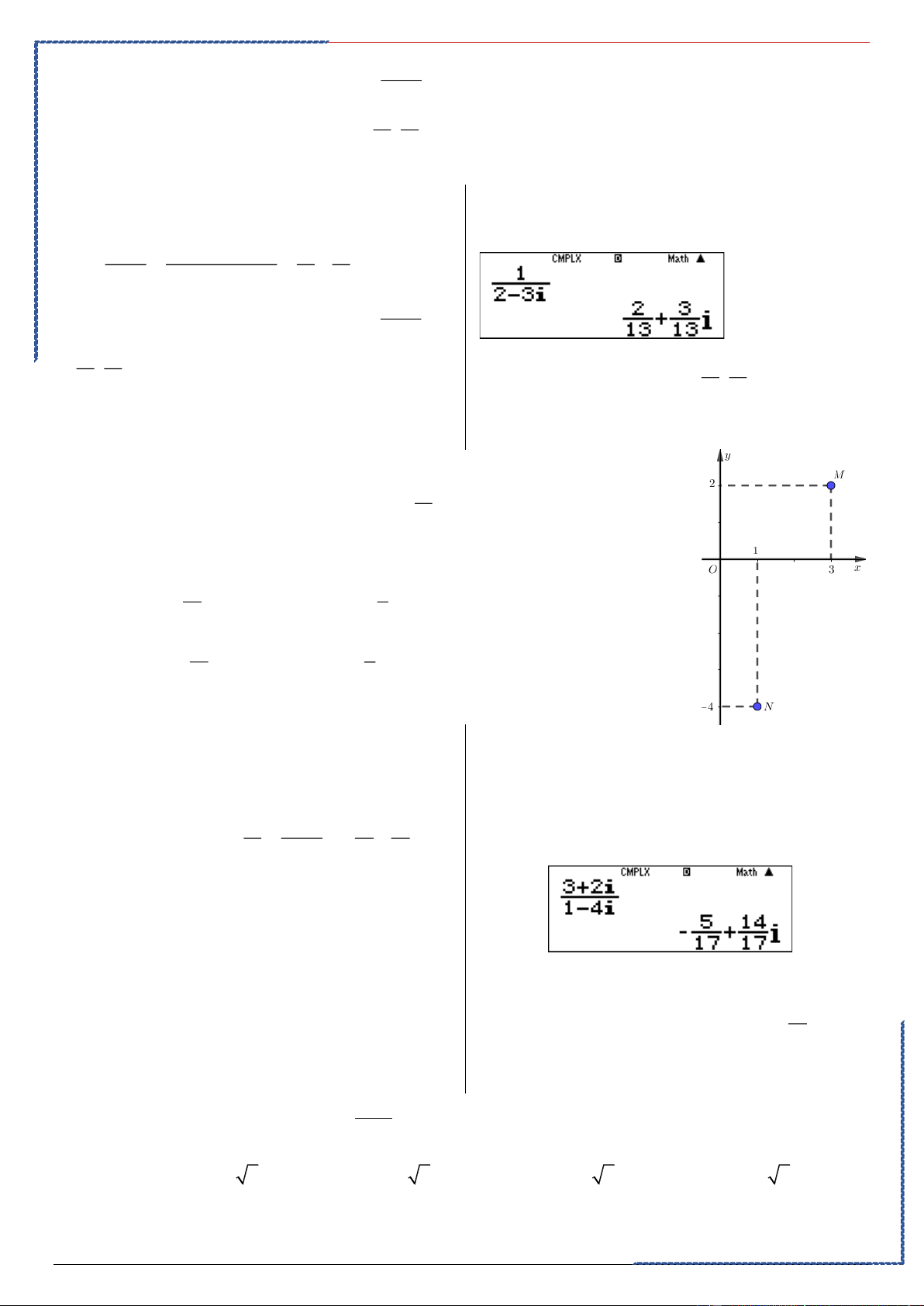
Câu 2: Gọi z , z lần lượt có điểm biểu diễn là M , N trên mặt phẳng phức (hình 1 2
bên). Khi đó phần ảo của số phức z1 là z2 Ⓐ. 14 . Ⓑ. 1 − . 17 4 Ⓒ. 5 − . Ⓓ. 1 . 17 2 Lời giải
PP nhanh trắc nghiệm Chọn A
Dựa vào hình vẽ
Dựa vào hình vẽ ta có được
z = 3 + 2i, z = 1− 4i 1 2 z 3 + 2i 5 14 1
z = 3 + 2i, z = 1− 4i  = = − + i . 1 2 Rồi bấm máy tính z 1− 4i 17 17 2
Và dựa vào số chứa i trả lời phần ảo của z
Dựa vào định nghĩa trả lời phần ảo là 14 17 − + −
Câu 3: Cho số phức z thỏa mãn 1 3i z =
. Tính modun của số phức w = .
i z+ z ? 1− i Ⓐ. | w| = 4 2 . Ⓑ. | w| = 2 . Ⓒ. | w| = 3 2 . Ⓓ. | w| = 2 2.
St-bs: Duong Hung - Word xinh 2020-2021 32
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung Lời giải
PP nhanh trắc nghiệm Chọn C Casio − + i Ta có: 1 3 z = = 1 − + 2 .i 1− iz = 1 − − 2 .i  w = .i( 1 − + 2i) + ( 1 − − 2i) = 3 − −3i .  2 2 | w| = ( 3 − ) + ( 3 − ) = 18 = 3 2 .
B - Bài tập rèn luyện: 2 Câu 1. Cho z =
. Số phức liên hợp của z là. 1+ i 3 Ⓐ. 1 3 + i . Ⓑ. 1 3 + i . Ⓒ. 1 3 − i . Ⓓ. 1 3 − i . 2 2 4 4 4 4 2 2
Câu 2. Cho số phức z = 3+ 4i . Khi đó môđun của 1 là. z Ⓐ. 1 . Ⓑ. 1 . Ⓒ. 1 . Ⓓ. 1 . 5 5 4 3 −
Câu 3. Cho số phức 3i 2 z =
, số phức liên hợp của z là. i +1 Ⓐ. 1 5 + 1 5 1 5 i . Ⓑ. − i + . Ⓒ. − i . Ⓓ. 1 5 i + . 2 2 2 2 2 2 2 2 −
Câu 4. Phần thực của số phức 3 4i z = bằng. 4 − i Ⓐ. 16 . Ⓑ. 3. Ⓒ. 13 − . Ⓓ. 3 − . 17 4 17 4 Câu 5. Số phức 1 có phần ảo là. 5 − + 7i Ⓐ. − − 5 . Ⓑ. 5 . Ⓒ. 7 . Ⓓ. 7 . 74 74 74 74
Câu 6. Cho hai số phức z
z = 2 + i, z ' = 2
− +3 .i Thương số có phần thực bằng. z ' Ⓐ. − + − − + 3 2 2 . Ⓑ. 3 2 2 . Ⓒ. 2 3 2 . Ⓓ. 2 3 2 . 13 13 13 13 +
Câu 7. Trên mặt phẳng tọa độ điểm nào biểu diễn cho số phức 3 4i z = . i Ⓐ. ( 4 − ;3) . Ⓑ. ( 4 − ; 3 − ) . Ⓒ. (4;3). Ⓓ. (4; 3 − ) .
St-bs: Duong Hung - Word xinh 2020-2021 33
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung 1 Câu 8. Số phức có phần ảo là. 2 − + 3i Ⓐ. − − 3 . Ⓑ. 3 . Ⓒ. 2 . Ⓓ. 2 . 7 7 7 7 −
Câu 9. Tìm số phức i z , biết 2 3 z = . 1+ i Ⓐ. 1 5 1 5 z = + i . Ⓑ. 1 5 z = − − i .
Ⓒ. z = − + i . Ⓓ. 1 5 z = − i . 2 2 2 2 2 2 2 2
Câu 10. Cho số phức z = 1
− − 2i , phần ảo của số phức z bằng. z Ⓐ. 3 − . Ⓑ. 4 . Ⓒ. 4 − . Ⓓ. 3 . 5 5 5 5
Câu 11. Cho hai số phức 3 z
z = 3 − 4i, z = 2 + i và số phức 1 z =
. Trong các mệnh đề sau mệnh đề nào sai. 1 2 2 z2
Ⓐ. z là số thuần ảo.
Ⓑ. Phần thực của z bằng 0 .
Ⓒ. Môđun của z bằng 2 .
Ⓓ. Phần ảo của z bằng 2 . +
Câu 12. Trên mặt phẳng tọa độ điểm nào biểu diễn cho số phức 5 5i z = . 1− 3i Ⓐ. ( 1 − ;2) . Ⓑ. (1;2) . Ⓒ. (1; 2 − ) . Ⓓ. ( 1 − ; 2 − ).
Câu 13. Cho 2 số phức z
z = 1+ i và z = 2 − 3i . Tính môđun của số phức 1 . 1 2 z2 Ⓐ. z 26 z 2 z 26 z 1 = . Ⓑ. 1 = . Ⓒ. 1 = . Ⓓ. 1 = 6 . z 13 z 13 z 2 z 2 2 2 2 −
Câu 14. Điểm biểu diễn của số phức 5 2i z = có tọa độ là i Ⓐ. (2; 5 − ) . Ⓑ. ( 5 − ; 2 − ) . Ⓒ. ( 2 − ; 5 − ) . Ⓓ. ( 2 − ;5) .
Câu 15. Cho số phức z = 2 −3i , phần ảo của số phức 1 bằng z Ⓐ. − 2 . Ⓑ. 3 . Ⓒ. 3 i . Ⓓ. 3 . 13 13 13 13 − Câu 16. Số phức 2 5i z =
có phần thực và phần ảo lần lượt là 1+ i Ⓐ. 3 7 − và − . Ⓑ. 3 7 và − . Ⓒ. 3 7 và − . Ⓓ. 3 7 và . 2 2 2 2 2 2 2 2 −
Câu 17. Số phức liên hợp của số phức 2 3i z = . i
St-bs: Duong Hung - Word xinh 2020-2021 34
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung Ⓐ. 3 − − 2i . Ⓑ. 3−2i . Ⓒ. 2i −3. Ⓓ. 2i +3. −
Câu 18. Tính môđun của số phức 2 i z = 4 + 3i Ⓐ. 5 . Ⓑ. 1 . Ⓒ. 3 . Ⓓ. 2 . 5 5 5 5
Câu 19. Cho hai số phức z
z = 3 + i, z = 2 − i . Tính giá trị của biểu thức 1 1 2 z2 Ⓐ. 4 . Ⓑ. 2 . Ⓒ. 2 . Ⓓ. 2 2 .
Câu 20. Điểm M trong hình vẽ bên là điểm biểu diễn của số phức nào sau đây y 1 O x -2 M Ⓐ. − − − i i
z =1+ 2i
Ⓑ. z = i(1+ 2i) Ⓒ. 3 z = Ⓓ. 4 3 z = 1+ i 1+ 2i BẢNG ĐÁP ÁN 1.A 2.B 3.C 4.A 5.D 6.A 7.D 8.A 9.C 10.B 11.D 12.A 13.A 14.C 15.B 16.A 17.C 18.A 19.C 20.C
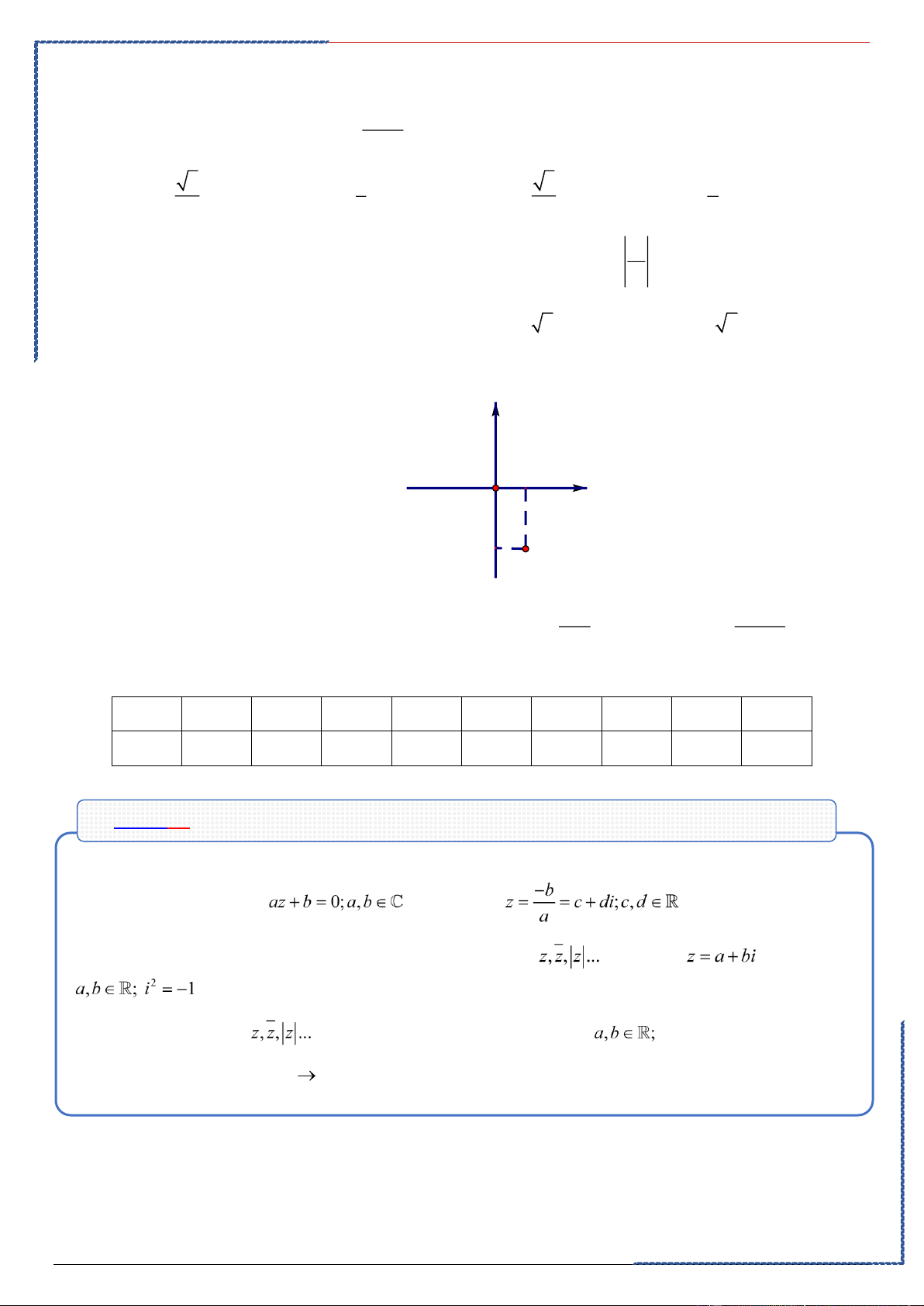
Dạng ③: Giải phương trình bậc nhất – suy ra các yếu tố liên quan tới số phức
. Phương pháp:
①. Phương trình: có nghiệm: .
②. Nếu điều kiện ban đầu có liên quan đến số phức thì ta gọi với . ③. Sau đó tính
rồi thay vào điều kiện, giải hệ tìm
④. Casio: Ấn MODE
2: CMPLX để vào chế độ tính toán với số phức.
A - Bài tập minh họa:
St-bs: Duong Hung - Word xinh 2020-2021 35
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 1: Cho số phức z thỏa mãn: z(2 −i) +13i =1. Tính mođun của số phức z
Ⓐ. z = 34 . Ⓑ. 5 34 z = .
Ⓒ. z = 34 . Ⓓ. 34 z = . 3 3 Lời giải
PP nhanh trắc nghiệm Chọn C Casio − i Ta có 1 13
z(2 − i) +13i = 1  z = = 3− 5 .i 2 − i Do đó 2 2 z = 3 + 5 = 34 .
Câu 2: Cho số phức z thỏa (2 + i) z − 2i = 3 . Số phức liên hợp của z là: Ⓐ. 8 1 + 4 7 8 1 i . Ⓑ. − i . Ⓒ. 8 1 − i . Ⓓ. − + i . 5 5 5 5 5 5 5 5 Lời giải
PP nhanh trắc nghiệm Chọn C Casio + i
Ta có ( + i) 3 2 8 1 2
z − 2i = 3  z = = + i 2 + i 5 5
Vậy Số phức liên hợp của z là: 8 1 − i 5 5
Câu 3: Cho số phức z thỏa mãn (1− i) z − 4 = 0 , phần thực và phần ảo của z lần lượt là. Ⓐ. 2 và 2. Ⓑ. 2 và -2. Ⓒ. -2 và 2. Ⓓ.-2 và -2. Lời giải
PP nhanh trắc nghiệm Chọn B Casio (1− i) 4
z − 4 = 0  z = = 2 + 2i 1− i
Suy ra z = 2 − 2i
Vậy z có phần thực và phần ảo lần lượt là:
Dựa vào kết quả trả lời đáp án 2 và -2.
Câu 4: Cho số phức z thỏa mãn 1 i z 1 5i 0 . Tính A . z z . Ⓐ. A 13 . Ⓑ. A 13. Ⓒ. A 1 13 . Ⓓ. A 26 . Lời giải
PP nhanh trắc nghiệm Chọn B Casio i Ta có 1 5 1 i z 1 5i 0 z 3 2i . 1 i Suy ra A . z z 3 2i 3 2i 13 .
St-bs: Duong Hung - Word xinh 2020-2021 36
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
B - Bài tập rèn luyện:
Câu 1. Cho số phức z thỏa mãn (1− i) z + 4 − 2i = 0 . Điểm biểu diễn của z có tọa độ là Ⓐ. (3; ) 1 − . Ⓑ. ( 3 − ) ;1 . Ⓒ. ( 3 − ;− ) 1 . Ⓓ. (3 ) ;1 .
Câu 2. Cho số phức z thỏa mãn (1+ 2i) z = 8 + i . Hỏi điểm biểu diễn của số y
phức z là điểm nào trong các điểm M, N, , P Q ở hình bên. M 3 N -2 2 x O Ⓐ. Điểm M . Ⓑ. Điểm N . Ⓒ. Điểm Q -3 P P . Ⓓ. Điểm Q
Câu 3. Nghiệm của phương trình z (2 − i) = 5(3− 2i) là
Ⓐ. z = 8−i .
Ⓑ. z = 8+i . Ⓒ. z = 8 − −i . Ⓓ. z = 8 − + i .
Câu 4. Tìm mô đun của số phức z thỏa mãn z (1+ i) = 8 − + 4i . Ⓐ. 10 . Ⓑ. 2 2 . Ⓒ. 4 2 . Ⓓ. 2 10 .
Câu 5. Số phức z thỏa mãn (4 + 7i)z − (5 − 2i) = 6iz là Ⓐ. 18 13 − − i . Ⓑ.18 13 − i . Ⓒ. 18 13 + i . Ⓓ.18 13 + i . 7 7 17 17 7 17 17 17
Câu 6. Cho số phức z thỏa mãn z (1+ 2i) = 7 + 4i .Tìm mô đun số phức  = z + 2i . Ⓐ. 4 Ⓑ. 17 Ⓒ. 24 Ⓓ.5
Câu 7. Tìm số phức z thoả mãn (3− 2i) z + (4 + 5i) = 7 + 3i Ⓐ. z =1 Ⓑ. z = 1 −
Ⓒ. z = i
Ⓓ. z = i − 1+ 3i
Câu 8. Nghiệm của phương trình = 2 + i là z
Ⓐ. z =1+i
Ⓑ. z =1−i Ⓒ. z = 1 − +i Ⓓ. z = 1 − −i
St-bs: Duong Hung - Word xinh 2020-2021 37
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 9. Cho số phức z thỏa mãn: (1+ 3i)z − (2 + 5i) = (2 + i) z .Phần ảo của số phức z là. Ⓐ. 8 . Ⓑ. 9 . Ⓒ. 9 − . Ⓓ. 8 − . 5 5 5 5
Câu 10. Cho số phức z z thỏa mãn:
+ (2 −3i) = 5 − 2i .Phần thực của số phức z là. 4 − 3i Ⓐ. 5 − . Ⓑ. 5. Ⓒ. 15. Ⓓ. 3 − .
Câu 11. Nghiệm của phương trình (3+ 4i) z + (1− 3i) = 2 + 5i là. Ⓐ. 7 4 z = − i . Ⓑ. 11 2 z = − + i . Ⓒ. 11 2 z = + i . Ⓓ. 7 4 z = + i . 5 5 25 25 25 25 5 5
Câu 12. Cho số phức z thỏa (1+ 2i) z + 4 = 2i . Trong các mệnh đề sau mệnh đề nào sai.
Ⓐ. z là số thuần ảo. Ⓑ. z = 2
Ⓒ. z là số thực
Ⓓ. Phần ảo của z bằng 2.
Câu 13. Phần thực, phần ảo của số phức z thỏa mãn (1− 2i).z = 5−3i(1− 2i) lần lượt là Ⓐ. 1;1. Ⓑ. 1; 2 − . Ⓒ. 1;2. Ⓓ. 1; 1 − .
Câu 14. Cho số phức z thỏa mãn điều kiện: (1+ i) z −1−3i = 0. Phần ảo của số phức w =1−iz + z là Ⓐ. 1. Ⓑ. 3 − . Ⓒ. −2. Ⓓ. 1 − . ( − i)5 1 2
Câu 15. Cho số phức z thỏa z =
. Viết z dưới dạng z = a + bi, , a b
. Khi đó tổng a + 2b có 2 + i giá trị bằng bao nhiêu? Ⓐ. 38. Ⓑ. 10. Ⓒ. 31. Ⓓ. 55.
Câu 16. Cho số phức (2 + i) z + i = 4 + 8i .Tìm mô đun của số phức w = z +1+i . Ⓐ. w = 25. Ⓑ. w = 6.
Ⓒ. w = 6 . Ⓓ. w = 5 .
Câu 17. Tìm số phức liên hợp của số phức z z biết = (3i + ) 1 . i
Ⓐ. z = 3−i . Ⓑ. z = 3 − +i . Ⓒ. z = 3+i . Ⓓ. z = 3 − −i .
Câu 18. Tính môđun của số phức z thỏa mãn z (2 − i) +13i =1. Ⓐ. z = 34 . Ⓑ. z = 34 . Ⓒ. 5 34 z = . Ⓓ. 34 z = . 3 3
Câu 19. Trong , phương trình iz + 2 −i = 0 có nghiệm là Ⓐ. z =1−2i Ⓑ. z = 2+i Ⓒ. z =1+2i
Ⓓ. z = 4−3i
Câu 20. Trong , phương trình z (1+ 2i) = 1
− + 3i có nghiệm là Ⓐ. 1 1 z = − i Ⓑ. z =1+i Ⓒ. z = i
Ⓓ. z = 2−i 2 2
St-bs: Duong Hung - Word xinh 2020-2021 38
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung BẢNG ĐÁP ÁN 1.C 2.C 3.A 4.D 5.B 6.D 7.A 8.A 9.C 10.C 11.D 12.C 13.A 14.B 15.B 16.D 17.D 18.B 19.C 20.B Full Chuyên đề 12 new 2020-2021 CHƯƠNG ④: FB: Duong Hung
Bài ➃: PHƯƠNG TRÌNH BẬC HAI VỚI HỆ SỐ THỰC
Dạng ①: Tìm Căn bậc hai của số thực âm
. Lý thuyết cần nắm:
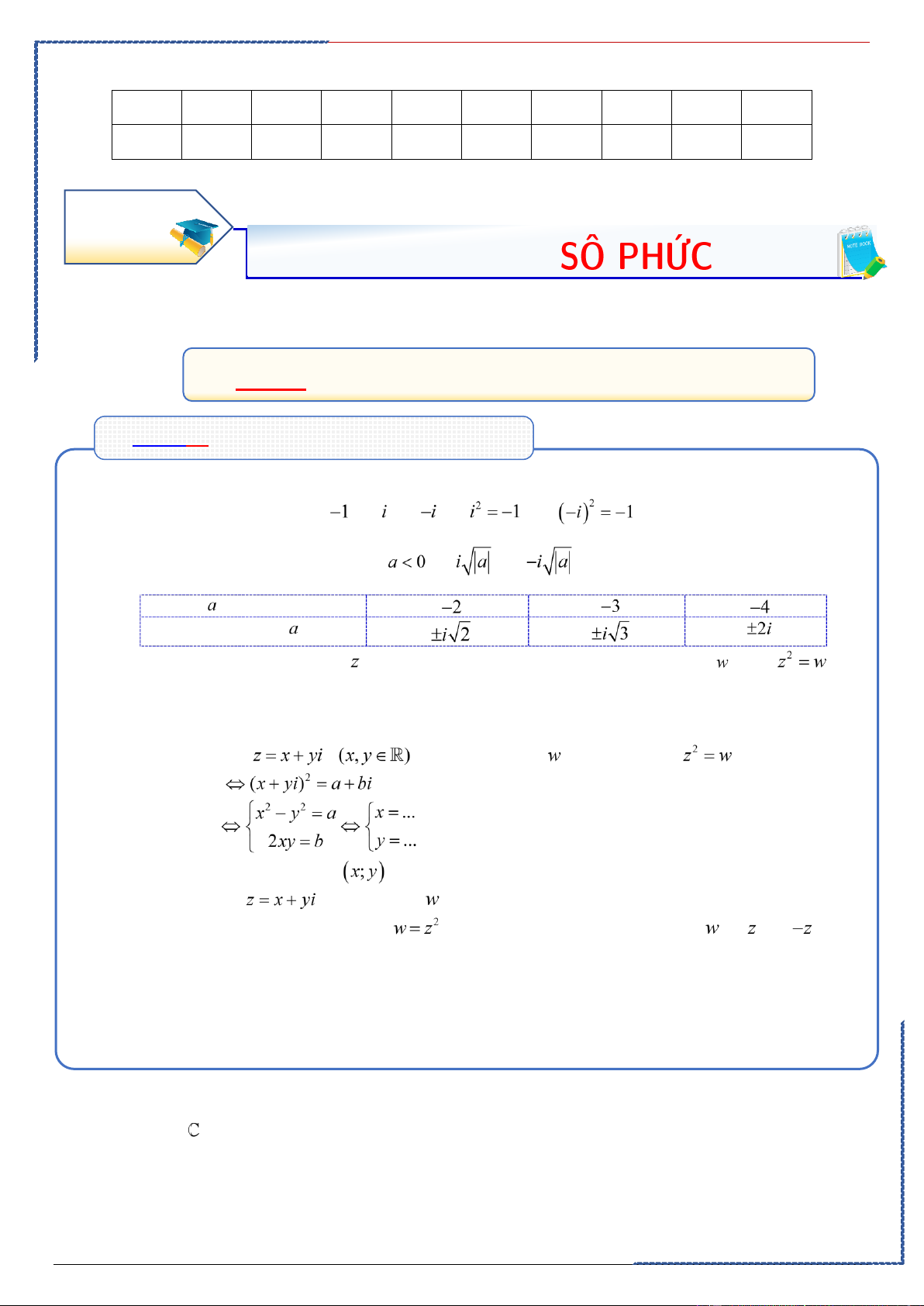
①. Căn bậc hai của là và vì và .
②. Căn bậc hai của số thực là và .
Căn bậc hai của
.Tổng quát : Số phức được gọi là một căn thức bậc 2 của số phức nếu .
. Phương pháp giải: ①. Cách 1: ⬧ Gọi
là căn bậc 2 của khi và chỉ khi
⬧ Mỗi cặp số thực
nghiệm đúng hệ phương trình đó cho ra một căn bậc hai của số phức .
②. Cách 2: Có thể biến đổi
. Từ đó kết luận căn bậc hai của là và .
③. Casio 570NV Plus
⬧ Cách 1: Lệnh Pol & Rec.
⬧ Cách 2: Mode 2 → dùng lệnh shift 2.
A - Bài tập minh họa:
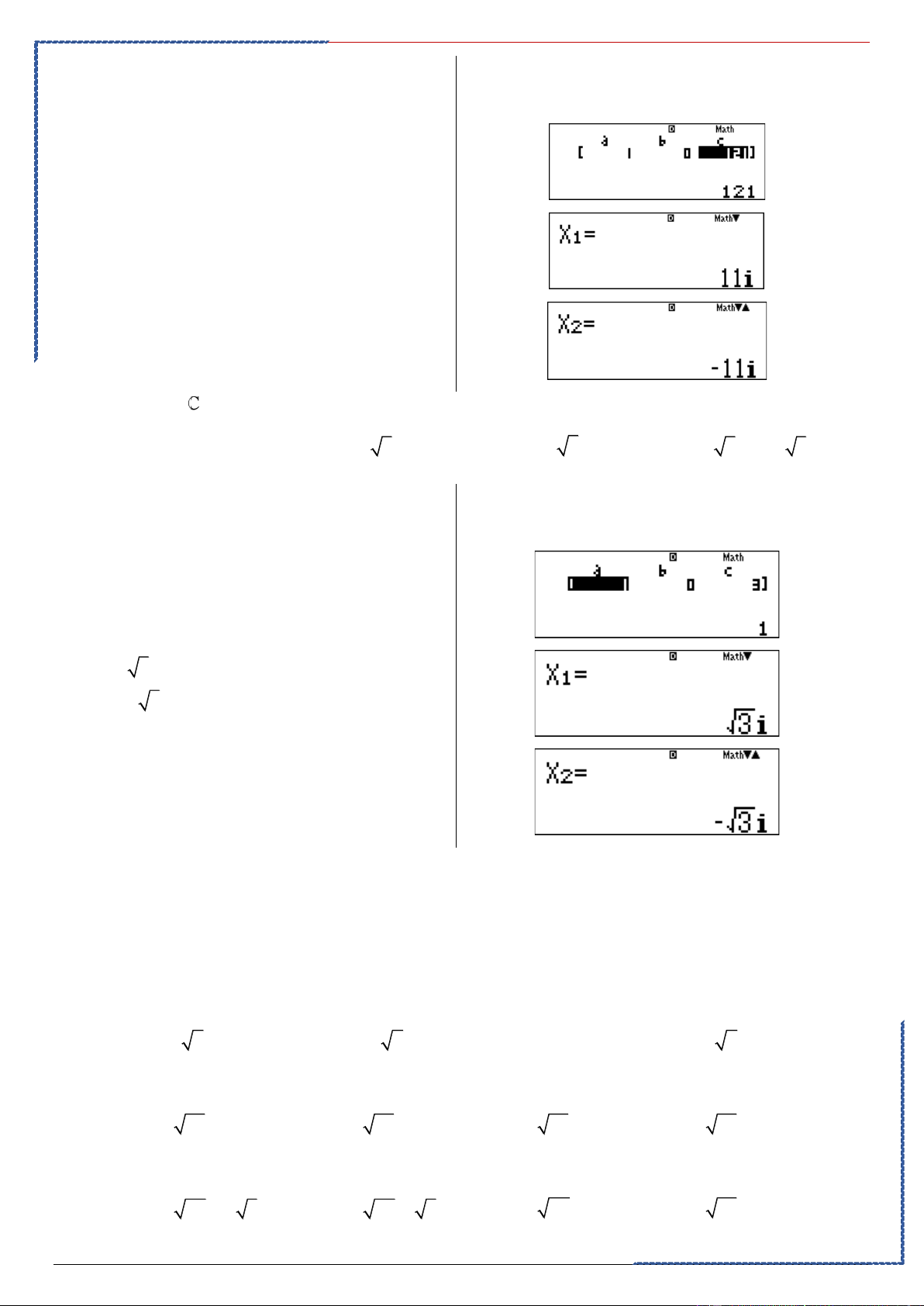
Câu 1. Trong , căn bậc hai của 121 − là Ⓐ. 11 − i Ⓑ. 11i Ⓒ. −11 Ⓓ. 11i và 11 − i
St-bs: Duong Hung - Word xinh 2020-2021 39
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung Lời giải
PP trắc nghiệm nhanh Chọn D Casio: Ta có 2 2 z = 121 −  z +121 = 0 z = 11i   z = 11 − i
Câu 2. Trong , căn bậc hai của 3 − là Ⓐ. 3
− i Ⓑ. 3i Ⓒ. − 3
Ⓓ. 3i và − 3i Lời giải
PP trắc nghiệm nhanh Casio: Chọn D Ta có 2 2 z = 3 −  z + 3 = 0 z = 3i   z = − 3i
B - Bài tập rèn luyện:
Câu 1. Tìm các căn bậc hai của 9 − . Ⓐ. 3  i Ⓑ. 3 Ⓒ. 3i Ⓓ. 3 −
Câu 3. Căn bậc hai của số phức của số 8 − bằng bao nhiêu? Ⓐ. 2 2i Ⓑ. −2 2i Ⓒ. 2i Ⓓ. − 2
Câu 4. Khẳng định nào sau đây đúng? Ⓐ. −1 =1
Ⓑ. −1 = i
Ⓒ. −1 = −i
Ⓓ. −1 = i
Câu 5. Khẳng định nào sau đây sai? Ⓐ. 3 − = − 3 Ⓑ. 3 − = 3i
Ⓒ. −4 = 2i
Ⓓ. −1 = i
St-bs: Duong Hung - Word xinh 2020-2021 40
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 6. Căn bậc hai của số phức của số − 5 bằng bao nhiêu? Ⓐ.  5. Ⓑ. 4  5 .i Ⓒ. 5 .i Ⓓ. − 5 .i
Câu 7. Trong tập số phức, mệnh đề nào dưới đây sai? Ⓐ. Căn bậc hai của 25 − là 5 .i Ⓑ. −( i)2 6 = 36.
Ⓒ. Căn bậc hai của −4 là 2  .i
Ⓓ. Căn bậc hai của 9 là 3. 
Câu 8. Trong tập số phức, mệnh đề nào dưới đây đúng? Ⓐ. Căn bậc hai của 16 − là 4 .i
Ⓑ. Căn bậc hai của 100 là 10. Ⓒ. Căn bậc hai của 10 − là  10 .i Ⓓ. 2 3 − i = 9. BẢNG ĐÁP ÁN 1.A 2.A 3.D 4.A 5.A 6.B 7.A 8.C
Dạng ②. Tìm nghiệm phức của phương trình bậc hai – tìm các yếu tố liên
quan tới hai nghiệm thức chứa lũy thừa.
-Phương pháp: ①. Tính .
②. Áp dụng công thức nghiệm.
③. Casio: Dùng chức năng giải phương trình bậc hai trên máy tính Casio.
Sto các nghiệm vào A, B: vào mode 2 Alpha gọi nó ra tính các giá trị biểu thức liên quan đến nghiệm
A - Bài tập minh họa:
Câu 1: Kí hiệu z , z là hai nghiệm phức của phương trình 2
z − 3z + 5 = 0 . Giá trị của z + z bằng 1 2 1 2 Ⓐ. 2 5 . Ⓑ. 5 . Ⓒ. 3. Ⓓ. 10. Quy trình bấm máy
PP trắc nghiệm nhanh  Bấm máy  Casio
 Màn hình hiển thị nghiệm
+ Lúc giải phương trình là máy ở chế độ
tính toán bình thường, nhưng khi tính
z + z thì phải chuyển tính năng máy 1 2
sang chế độ số phức mode 2
St-bs: Duong Hung - Word xinh 2020-2021 41
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung Chọn A
Câu 2: Gọi z , z là hai nghiệm phức của phương trình 2
z − 6z +10 = 0 . Giá trị của 2 2 z + z bằng 1 2 1 2 Ⓐ. 16. Ⓑ. 56. Ⓒ. 20. Ⓓ. 26. Quy trình bấm máy.
PP trắc nghiệm nhanh  Bấm máy Casio
 Màn hình hiển thị nghiệm.
 Bài này có thể nhẩm nhanh hơn bằng định lý viet z + z = (z + z )2 2 2 − 2z z =16 1 2 1 2 1 2
+ Màn hình hiển thị kết quả : Chọn A
Câu 3: Trong , phương trình 2 z
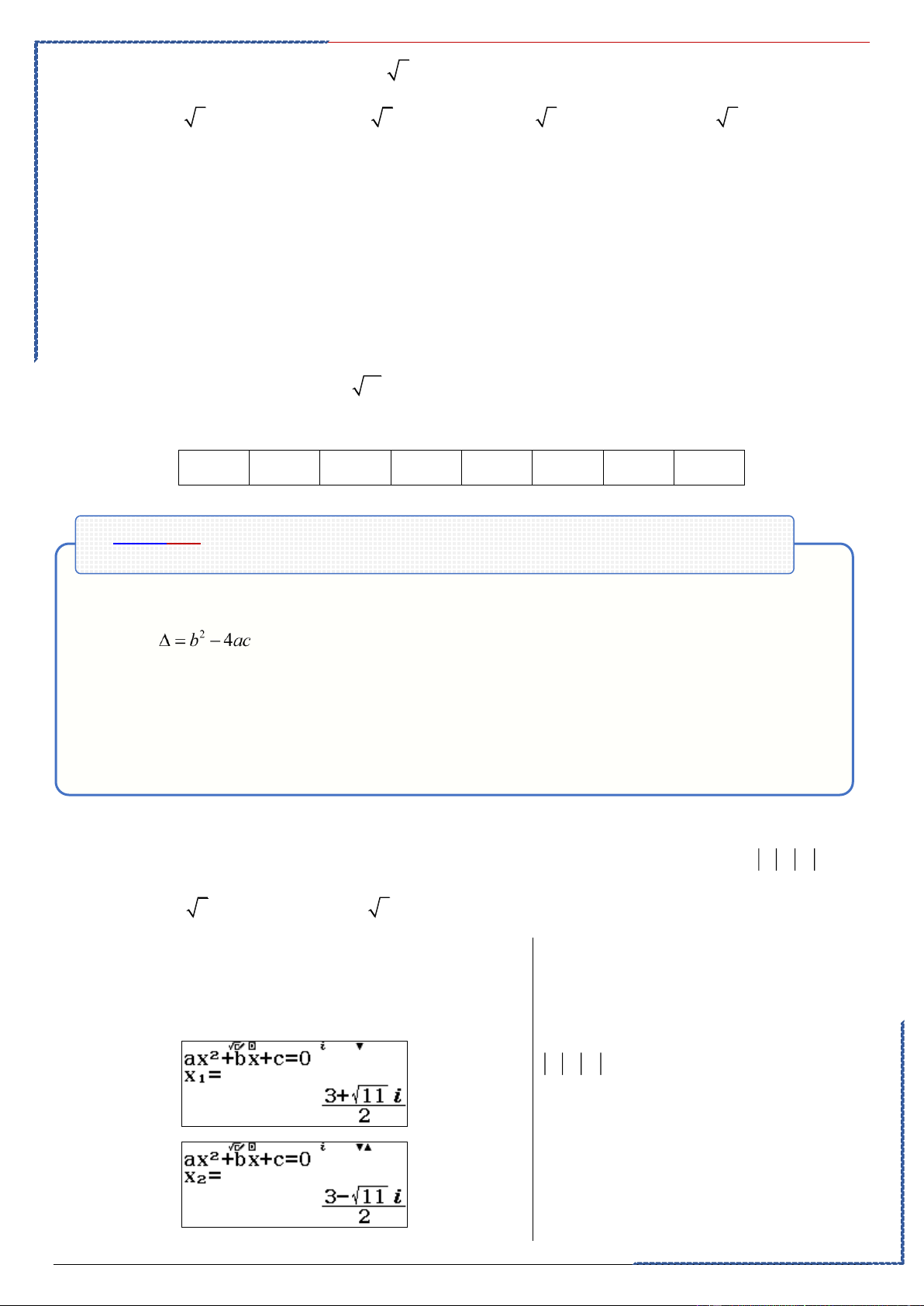
z − z +1 = 0 có nghiệm là: z ; z với z có phần ảo âm. Hãy tính 1 1 2 1 z2 Ⓐ. + + + + 1 3 3 3 − + i Ⓑ. 1 3 3 3 − − i 2 2 2 2 − − Ⓒ. 1 3 + i Ⓓ. 1 3 − i 2 2 2 2 Quy trình bấm máy
PP trắc nghiệm nhanh  Bấm máy Casio
 Màn hình hiển thị nghiệm.  bấm MT ra hai nghiệm
 gán hai nghiệm phù hợp  bấm mt
St-bs: Duong Hung - Word xinh 2020-2021 42
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung Chọn D
B - Bài tập rèn luyện:
Câu 1: Trong , cho phương trình bậc hai 2
az + bz + c = 0 ( ) * (a  0) . Gọi 2
 = b − 4ac . Ta xét các mệnh đề:
1) Nếu  là số thực âm thì phương trình (*) vô nghiệm
2) Nếu   0thì phương trình có hai nghiệm số phân biệt
3) Nếu  = 0 thì phương trình có một nghiệm kép
Trong các mệnh đề trên:
Ⓐ. Không có mệnh đề nào đúng
Ⓑ. Có một mệnh đề đúng
Ⓒ. Có hai mệnh đề đúng
Ⓓ. Cả ba mệnh đề đều đúng
Câu 2: Trong , phương trình 2
z + 4 = 0 có nghiệm là Ⓐ. z = 2iz =1+ 2iz =1+ iz = 5 + 2i Ⓑ.  Ⓒ.  Ⓓ. z = 2 − iz =1− 2iz = 3 − 2iz = 3− 5i
Câu 3: Trong , phương trình 2
z − z +1 = 0 có nghiệm là  3  1 3  5  1 5 z = 1+ iz = + iz = 1+ iz = + i Ⓐ. 2  Ⓑ. 2 2  Ⓒ. 2  Ⓓ. 2 2   3  1 3  5  1 5 z = 1− iz = − iz = 1− iz = − i  2  2 2  2  2 2
Câu 4: Gọi z , z là hai nghiệm phức của phương trình 2
z + 2z +10 = 0 . Giá trị của biểu thức 1 2 2 2 A = z + z bằng 1 2 Ⓐ. 15 . Ⓑ. 19 . Ⓒ. 20 . Ⓓ. 17 .
Câu 5: Gọi z và z là hai nghiệm phức của phương trình 2
z − z + 3 = 0 . Giá trị của biểu thức bằng 1 2 z + z bằng 1 2 Ⓐ. 3. Ⓑ. 3 . Ⓒ. 3 3 . Ⓓ. 2 3 .
St-bs: Duong Hung - Word xinh 2020-2021 43
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 6. Gọi z , z là hai nghiệm phức của phương trình 2
5z − 8z + 5 = 0 . Tính S = z + z + z z . 1 2 1 2 1 2 Ⓐ. S = 3. Ⓑ. S =15 . Ⓒ. 13 S = . Ⓓ. 3 S = − . 5 5
Câu 7. Giả sử z và z là hai nghiệm của phương trình 2
z − 2 2z + 8 = 0 . Giá trị của 2 2
A = z z + z z 1 2 1 2 1 2 bằng Ⓐ. −16 2 . Ⓑ. 16 2 . Ⓒ. 8 2 . Ⓓ. −8 2 .
Câu 8: Trong , biết z , z là nghiệm của phương trình 2
z − 6z + 34 = 0 . Khi đó, tích của hai nghiệm 1 2 có giá trị bằng: Ⓐ. -16 Ⓑ. 6 Ⓒ. 9 Ⓓ.34
Câu 9: Trong , biết z , z là nghiệm của phương trình 2
z − 3z +1 = 0 . Khi đó, tổng bình phương 1 2
của hai nghiệm có giá trị bằng: Ⓐ. 0 Ⓑ. 1 Ⓒ. 3 Ⓓ.2 3
Câu 10: Trong , biết z , z là nghiệm của phương trình 2
z − 2z + 5 = 0 . Giá trị của biểu thức ( z + z 1 2 )2 1 2 bằng: Ⓐ. 0 Ⓑ. 1 Ⓒ. 2 Ⓓ.4
Câu 11: Phương trình sau có mấy nghiệm thực: 2 z + 2z + 2 = 0 Ⓐ. 0 Ⓑ. 1 Ⓒ. 2
Ⓓ. Vô số nghiệm.
Câu 12: Gọi z , z là hai nghiệm của phương trình 2
z − 2z + 6 = 0 . Trong đó z có phần ảo âm. 1 2 1
Lúc đó z là 1
Ⓐ. 1− 5i
Ⓑ. 1+ 5i
Ⓒ. 5 −i
Ⓓ. 5 + i
Câu 13: Gọi z , z là các nghiệm phức của phương trình 2
z + 3z + 7 = 0 . Khi đó A = z + z có giá trị 1 2 1 2 là Ⓐ. − 3 Ⓑ. 3 Ⓒ. 7 Ⓓ. 7 −
Câu 14: Gọi z , z là các nghiệm phức của phương trình 2
z + 2z + 9 = 0 . Khi đó A = 2z + z có giá trị là 1 2 1 2
( với z có phần ảo dương). 1 Ⓐ. 3+ 2 2 − 2i Ⓑ. 3− 2 2 − 2i Ⓒ. 3
− + 2 2 − 2i Ⓓ. 3+ 2 2 + 2i
Câu 15. Gọi z , z là hai nghiệm phức của phương trình 2
5z − 8z + 5 = 0 . Tính S = z + z + z z . 1 2 1 2 1 2 Ⓐ. S = 3. Ⓑ. S =15 . Ⓒ. 13 S = . Ⓓ. 3 S = − . 5 5
Câu 16. Kí hiệu z , z là hai nghiệm phức của phương trình 2
z − 2z + 9 = 0 . Giá trị của z + z + z − z bằng 1 2 1 2 1 2 Ⓐ. 2 + 4 2 .
Ⓑ. 2 + 4i 2 . Ⓒ. 6 . Ⓓ. 2 .
St-bs: Duong Hung - Word xinh 2020-2021 44
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 17: Thương hai nghiệm z1 của phương trình 2
−z − 2z −3 = 0 là ( z có phần ảo dương)? z 1 2 Ⓐ. − − 1 2 2 − i Ⓑ. 1 2 2 + i Ⓒ. 1 2 2 − i Ⓓ. 1 2 2 + i 3 3 3 3 3 3 3 3
Câu 18: Gọi z , z là hai nghiệm của phương trình 2
−z − 2z −3 = 0 . Khi đó môn đun của số phức có 1 2 phần ảo âm là Ⓐ. 3 Ⓑ. − 3 Ⓒ. 2 Ⓓ. 1 −
Câu 19: Gọi z , z là các nghiệm phức của phương trình 2
z + 3z + 7 = 0 . Khi đó 4 4
A = z + z có giá trị 1 2 1 2 là Ⓐ. 23 Ⓑ. 23 Ⓒ. 13 Ⓓ. 13
Câu 20: Gọi z , z là hai nghiệm của phương trình 2
z − 2z + 6 = 0 . Trong đó z có phần ảo âm. Giá trị 1 2 1 biểu thức M |
= z | + | 3z − z | là 1 1 2 Ⓐ. 6 −2 21 Ⓑ. 6 + 2 21 Ⓒ. 6 + 4 21 Ⓓ. 6 −4 21 BẢNG ĐÁP ÁN 1.C 2.A 3.B 4.C 5.A 6.A 7.B 8.D 9.B 10.B 11.A 12.A 13.A 14.A 15.A 16.A 17.A 18.A 19.A 20.B
Dạng ③. Tìm nghiệm phương trình bậc 3, trùng phương
①. Phương pháp giải:
⬧Biến đổi phương trình về dạng phương trình tích, trong đó mỗi nhân tử là phương
trình bậc nhất hoặc bậc hai.
⬧Dùng phương pháp đặt ẩn phụ.
⬧Với phương trình trùng phương bậc bốn: : Đặt . ②. Casio:
⬧Thế các đáp án vào phương trình để loại suy.
⬧Với phương trình bậc ba: Dùng chức năng giải phương trình bậc ba trên máy tính.
⬧Với phương trình trùng phương: giải phương trình bậc bốn trên máy tính 580VNX
A - Bài tập minh họa:
Câu 1: Nghiệm của phương trình 4 2
z − z − 2 = 0 là Ⓐ. 2; 1 − .
Ⓑ.  2; .i Ⓒ. i  2; 1  . Ⓓ. 2; .i
St-bs: Duong Hung - Word xinh 2020-2021 45
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung Lời giải
PP nhanh trắc nghiệm
Chọn B  4 2
z − z − 2 = 0 CÁCH 1: Ta có : 2 z = 2 z =  2     2 z = 1 − z = i CALC CÁC ĐÁP ÁN CÁCH 2: dùng 580vnx
B - Bài tập rèn luyện:
Câu 1.Trong , nghiệm của phương trình 3 z − 8 = 0 là
Ⓐ. z = 2; z =1+ 3 ;i z =1− 3i
Ⓑ. z = 2; z = 1 − + 3 ;i z = 1 − − 3i 1 2 3 1 2 3 Ⓒ. z = 2 − ; z = 1 − + 3 ;i z = 1 − − 3i Ⓓ. z = 2
− ; z =1+ 3 ;i z =1− 3i 1 2 3 1 2 3
Câu 2. Trong , phương trình 4 2
z − 6z + 25 = 0 có nghiệm là Ⓐ. 8  ; 5i Ⓑ. 3  ; 4i Ⓒ. 5  ; 2i
Ⓓ. (2+i);(2−i)
Câu 3. Trong , phương trình 3
z +1 = 0 có nghiệm thực là Ⓐ. 1 Ⓑ. 1 − Ⓒ. 1 3 + i Ⓓ. 1 3 − i 2 2 2 2
Câu 4. Trong , phương trình 4
z −1 = 0 có nghiệm ảo là Ⓐ. 1  Ⓑ. −i Ⓒ. i Ⓓ. i
Câu 5. Phương trình 3
z = 8 có bao nhiêu nghiệm phức với phần ảo âm? Ⓐ. 1 Ⓑ. 2 Ⓒ. 3 Ⓓ. 0
Câu 6. Trong , phương trình 4
z + 4 = 0 có nghiệm là
Ⓐ. (1− 4i);(1+ 4i)
Ⓑ. (1− 2i); (1+ 2i)
Ⓒ. (1−3i);(1+3i)
Ⓓ. ±(1−i) ; (1+ i)
Câu 7. Trong trường số phức phương trình 3
z +1 = 0 có mấy nghiệm?
St-bs: Duong Hung - Word xinh 2020-2021 46
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung Ⓐ. 2. Ⓑ. 3. Ⓒ. 1. Ⓓ. 0.
Câu 8. Giải phương trình sau trên : ( z + )( 2 z − )( 3 1 1 z + ) 1 = 0         z = 1 =  = − =  z 1  z 1  z 1 
Ⓐ. z = i
Ⓑ. z = i
Ⓒ. z = i −
Ⓓ. z = i     1 −  i 3  −1 i 3  1 −  i 3  1 −  i 3  z = =  = =  z z z  2  2  2  2
Câu 9. Tổng bình phương các nghiệm của phương trình 4
z −1 = 0 trên tập số phức là bao nhiêu? Ⓐ. 3. Ⓑ. 1. Ⓒ. 2. Ⓓ. 0.
Câu 10. Phương trình 6 3
z − 9z + 8 = 0 có bao nhiêu nghiệm trên tập số phức? Ⓐ. 3. Ⓑ. 4. Ⓒ. 2. Ⓓ. 6.
Câu 11. Bộ số thực (a; ;
b c) để phương trình 3 2
z + az + bz + c = 0 nhận z = 1+ i và z = 2 làm nghiệm. Ⓐ. ( 4 − ;6; 4 − ) Ⓑ. (4; 6 − ;4) Ⓒ. ( 4 − ; 6 − ; 4 − ) Ⓓ.(4;6;4)
Câu 12. Trong , phương trình 4
z −1 = 0 có nghiệm. Tổng của các nghiệm đó là
Ⓐ. −2 . Ⓑ. 2 . Ⓒ. 2i . Ⓓ. 0.
Câu 13. Giải phương trình sau trên : ( 2
z + z + ) + z ( 2 z + z + ) 2 9 4 9 − 5z = 0 z = iz = 2iz = 3iz = 3i Ⓐ.     z = −i
Ⓑ. z = −2i
Ⓒ. z = −3i
Ⓓ. z = −3i  z = −3  z = −3  z = 3  z = −3 
Câu 14. Giải phương trình sau trên : 4 3 2
2z − 2z + z + 2z + 2 = 0 z =1 iz =1+ iz =1− i Ⓐ. z =1+ i    1 1  Ⓑ.  Ⓒ. 1 1 Ⓓ. 1 1 z = −  iz =1− iz = − + iz = − − i  2 2  2 2  2 2
Câu 15. Tập nghiệm trong của phương trình 3 2
z + z + z +1 = 0 là Ⓐ.  ;i − i;1;−  1 Ⓑ.  i − ;i;  1 Ⓒ.  ;i − −  1 Ⓓ.  i − ;i;−  1
Câu 16. Trong trường số phức phương trình 3
z + z = 0 có mấy nghiệm? Ⓐ. 2. Ⓑ. 3. Ⓒ. 1. Ⓓ. 0.
Câu 17. Tìm số nguyên x, y sao cho số phức z = x + yi thỏa mãn 3 z = 18 + 26i Ⓐ. x = 3 x = 3 x = 3 x = −3  Ⓑ.  Ⓒ.  Ⓓ.   y = 1  y = −1 y =1  y = 1
Câu 18. Tập nghiệm của phương trình 4 2
z − 2z − 8 = 0 là
St-bs: Duong Hung - Word xinh 2020-2021 47
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung Ⓐ.  2  ; 4  i .
Ⓑ.  2; 2 i.
Ⓒ.  2i;  2 . Ⓓ.  2  ; 4  i .
Câu 19. Tập nghiệm của phương trình 4 2
z + 2z − 3 = 0 là Ⓐ. 1; 1 − ;3 ;i 3 −  i Ⓑ. 1; 2 − ; ;i−  i Ⓒ. 1;  3 Ⓓ.1; 1 − ;i 3; i − 3
Câu 20. Kí hiệu z , z , z , z là 4 nghiệm phức của phương trình 4 2
z − z −12 = 0 . 1 2 3 4
Tính tổng T = z + z + z + z 1 2 3 4 Ⓐ. T = 4 Ⓑ. T = 2 3
Ⓒ. T = 4 + 2 3 Ⓓ. T = 2+ 2 3 BẢNG ĐÁP ÁN 1.B 2.D 3.B 4.D 5.A 6.D 7.B 8.B 9.D 10.D 11.A 12.D 13.D 14.A 15.D 16.B 17.C 18.C 19.D 20.C
Dạng ④. Mối liên hệ giữa hai nghiệm của phương trình bậc hai
①. Phương pháp giải:
⬧Tìm các nghiệm của phương trình đã cho thay vào biểu thức
⬧Dùng định lý Vi-ét để giải quyết yêu cầu bài toánc Vi-ét đối với phương trình bậc 2 s: ⬧Với
có 2 nghiệm phân biệt (thực hoặc phức). Ta có:  .Casio:
⬧ Dùng chức năng giải phương trình trên máy tính casio (với các phương trình bậc hai,
bậc ba, bốn) để suy ra nghiệm.
⬧Dùng chức năng tính toán trên môi trường số phức để suy ra kết quả.
A - Bài tập minh họa:
Câu1: Phương trình nào dưới đây nhận hai số phức 1 + 2i và 1 − 2i là nghiệm ? Ⓐ. 2 z + 2z + 3 = 0 Ⓑ. 2
z − 2z − 3 = 0 Ⓒ. 2
z − 2z + 3 = 0 Ⓓ. 2
z + 2z − 3 = 0 Lời giải
Quy trình bấm máy. Chọn C
 Nhập giải phương trình đáp án A Định lý viet  Màn hình hiển thị
St-bs: Duong Hung - Word xinh 2020-2021 48
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
(1+ 2i)+(1− 2i) = 2
(1+ 2i)(1− 2i)=3
 Theo ứng dụng định lý viet thì hai số đã cho là Loại A
nghiệm của phương trình
 Nhập giải phương trình đáp án B 2
z − 2z + 3 = 0  Màn hình hiển thị Loại B
 Nhập giải phương trình đáp án C  Màn hình hiển thị
Câu2: Nếu z = i là nghiệm phức của phương trình 2
z + az + b = 0 với (a,b  ) thì a + b bằng Ⓐ. 1 − . Ⓑ. −2. Ⓒ. 1. Ⓓ. 2 . Lời giải
PP nhanh trắc nghiệm
z + az + b = Chọn C Phương trình 2
0 nhận z = i làm nghiệm nên 2
i + ai + b = 0 Phương trình 2 a = a =
z + az + b = 0 nhận 0 0 z = i làm
ai +b −1= 0    
a + b =1. nghiệm nên 2
i + ai + b = 0 b −1 = 0 b = 1 a = a =  0 0
ai + b −1 = 0    
a + b =1. b −1 = 0 b = 1
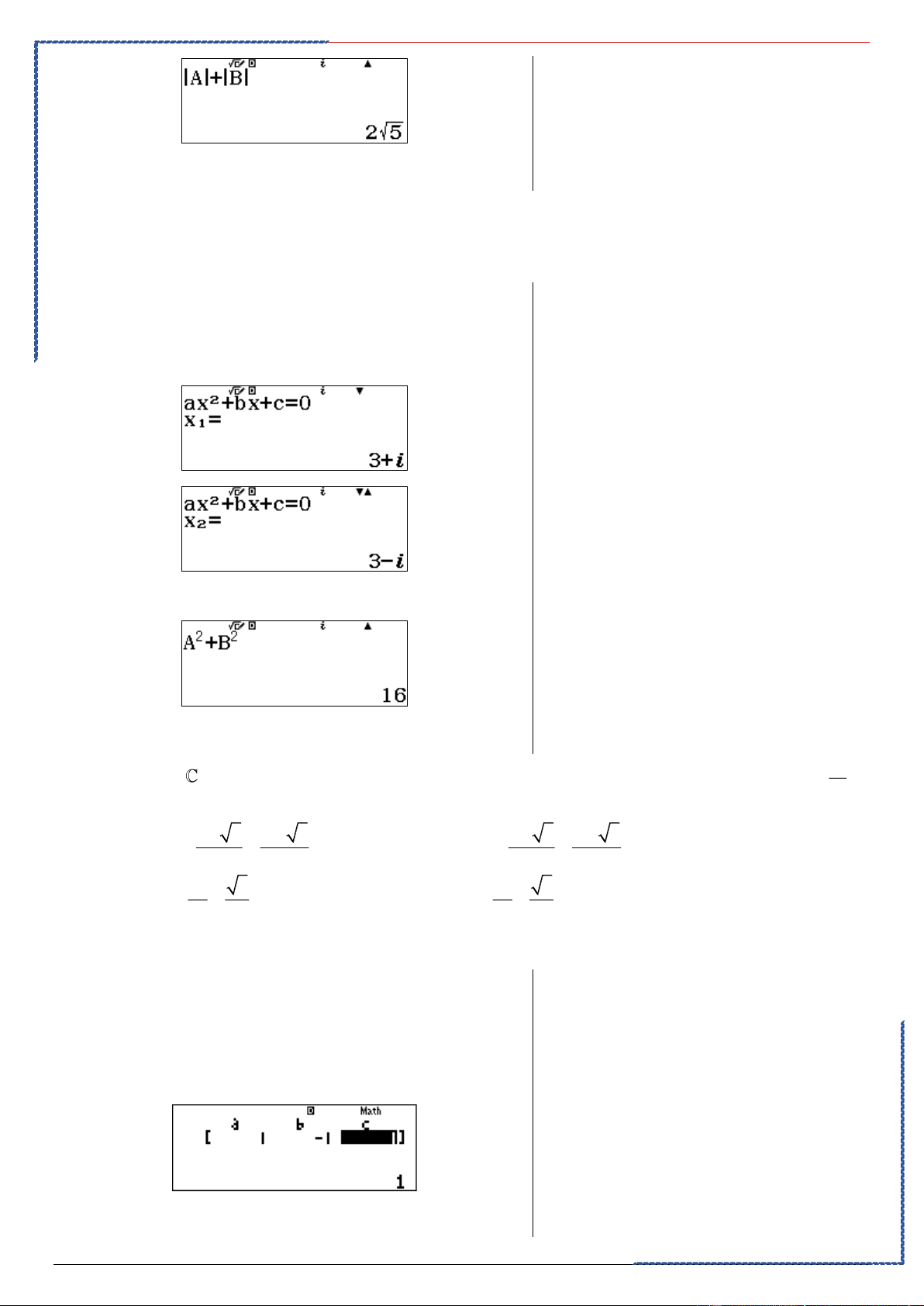
B - Bài tập rèn luyện: Câu 1: Cho 2 2
z , z là các nghiệm phức của phương trình 2
z + 4z +13 = 0 . Tính m = ( z − 2 + z − 2 . 1 ) ( 2 ) 1 2 Ⓐ. m = 25 .
Ⓑ. m = 50.
Ⓒ. m =10.
Ⓓ. m =18.
Câu 2: Gọi z , z là hai nghiệm phức của phương trình 2
2z + 4z + 3 = 0 . Tính giá trị của biểu thức 1 2 z + z . 1 2 Ⓐ.2 3 . Ⓑ. 3 . Ⓒ. 3. Ⓓ. 6 .
St-bs: Duong Hung - Word xinh 2020-2021 49
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung
Câu 3: Gọi z và z là hai nghiệm của phương trình 2
2z + 3z + 3 = 0 . Khi đó, giá trị 2 2
z + z là 1 2 1 2 Ⓐ.9. Ⓑ. 4 . Ⓒ. 9 . Ⓓ. 9 − . 4 4
Câu 4: Gọi z , z là hai nghiệm phức của phương trình 2
z − 4z + 5 = 0 . Giá trị của biểu thức 1 2 2 2
z + z bằng. 1 2 Ⓐ.10. Ⓑ. 20 . Ⓒ. 6 .
Ⓓ. 6−8i .
Câu 5: Gọi z và z là hai nghiệm phức của phương trình 2
z + 2z +10 = 0 , giá trị của biểu thức 1 2 2 2 A = z + z là. 1 2 Ⓐ. 10 . Ⓑ. 20 . Ⓒ. 10. Ⓓ. 20 .
Câu 6: Gọi z , z là hai nghiệm phức của phương trình 2
z – 4z + 9 = 0. Tổng P = z + z bằng: 1 2 1 2 Ⓐ.18. Ⓑ. 4 . Ⓒ. 6 . Ⓓ. 3.
Câu 7: Gọi z và z là các nghiệm của phương trình 2
z − 4z + 9 = 0 . Gọi M , N là các điểm biểu diễn 1 2
của z và z trên mặt phẳng phứⒸ. Khi đó độ dài của MN là 1 2 Ⓐ. MN = 2 5 .
Ⓑ. MN = 4. Ⓒ. MN = 2 − 5 .
Ⓓ. MN = 5.
Câu 8: Gọi z , z là 2 nghiệm phức của phương trình 2
2z − 3z + 7 = 0 . Tính giá trị của biểu thức 1 2
z + z − z z . 1 2 1 2 Ⓐ. 2 − . Ⓑ. 2. Ⓒ. 5 − . Ⓓ. 5.
Câu 9: Trong tập các số phức, cho phương trình 2
z − 6z + m = 0 , m ( )
1 . Gọi m là một giá trị 0
của m để phương trình ( )
1 có hai nghiệm phân biệt z , z thỏa mãn z .z = z .z . Hỏi trong 1 2 1 1 2 2
khoảng (0;20) có bao nhiêu giá trị m  ? 0 Ⓐ.12. Ⓑ. 10. Ⓒ. 13. Ⓓ. 11.
Câu 10: Gọi z , z là hai nghiệm của phương trình 2
2z − 3z + 2 = 0 trên tập số phức; Tính giá trị biểu 1 2 thức 2 2 P =
z + z z + z . 1 1 2 2 Ⓐ. 3 3 P = . Ⓑ. 5 P = . Ⓒ. 3 P = . Ⓓ. 5 P = . 4 2 4 2
Câu 11: Cho z , z là hai nghiệm của phương trình 2
z − 2z + 2 = 0 ( z  ) . Tính giá trị của biểu 1 2
thức P = 2 z + z + z − z . 1 2 1 2
Ⓐ. P = 2 2 + 2 .
Ⓑ. P = 2 + 4 .
Ⓒ. P = 6 .
Ⓓ. P = 3.
Câu 12: Trong tập các số phức z , z lần lượt là 2 nghiệm của phương trình 2
z + 4z + 5 = 0 . Tính 1 2 2 2 P = z + z . 1 2 Ⓐ. P = 2 5 .
Ⓑ. P = 6 .
Ⓒ. P =10.
Ⓓ. P = 50.
Câu 13: Cho z , z là hai nghiệm của phương trình 2
z + 2z + 3 = 0 . Tính z + z . 1 2 1 2 Ⓐ.0 . Ⓑ. 1. Ⓒ. 2 3 . Ⓓ. 6 .
Câu 14: Phương trình 2
x + 4x + 5 = 0 có nghiệm phức mà tổng các mô đun của chúng bằng?
St-bs: Duong Hung - Word xinh 2020-2021 50
Tài liệu giảng dạy HS TB-Yếu hiệu quả cao – FB Duong Hung Ⓐ. 2 7 . Ⓑ. 2 5 . Ⓒ. 2 3 . Ⓓ. 2 2 . 2 2 Câu 15: z z Phương trình 2
z − 2z + 6 = 0 có các nghiệm z ; z . Khi đó giá trị của biểu thức 1 2 M = + 1 2 2 2 z1 z2 là. Ⓐ. 2 − . Ⓑ. 2 . Ⓒ. 2 . Ⓓ. 2 − . 3 3 9 9
Câu 16: Cho phương trình 2
z + 2z +10 = 0 . Gọi z và z là hai nghiệm phức của phương trình đã 1 2
cho. Khi đó giá trị biểu thức 2 2 A = z + z bằng: 1 2 Ⓐ. 4 10 . Ⓑ. 20 . Ⓒ. 10 . Ⓓ. 3 10 .
Câu 17: Gọi z , z là nghiệm phức của phương trình 2
z + 2z +10 = 0. Tính giá trị của biểu thức 1 2 2 2 z + z . . 1 2 Ⓐ. 25 . Ⓑ. 18. Ⓒ. 20 . Ⓓ. 21.
Câu 18: Gọi z và z lần lượt là hai nghiệm của phương trình 2
z − 4z + 5 = 0 . Giá trị của biểu thức 1 2
P = ( z − 2z .z − 4z bằng: 1 2 ) 2 1 Ⓐ. 10 − Ⓑ. 10 Ⓒ. 5 − Ⓓ. 15 −
Câu 19: Cho phương trình 2
z − 2z + 3 = 0 trên tập số phức, có hai nghiệm là z , z . Khi đó 2 2 z + z 1 2 1 2 có giá trị là: Ⓐ.6 . Ⓑ. 3. Ⓒ. 2 . Ⓓ. 2 2 .
Câu 20: Gọi z1 và z2 là hai nghiệm phức của phương trình: 2
z + 4z + 7 = 0 . Khi đó 2 2 z + z bằng 1 2 Ⓐ.7 . Ⓑ. 21. Ⓒ. 14. Ⓓ. 10.
Câu 21: Gọi z , z là hai nghiệm phức của phương trình 2
z + 4z + 5 = 0 . Tính giá trị của biểu thức 1 2 2 2 A = z + z . 1 2 Ⓐ.10. Ⓑ. 6 . Ⓒ. 5. Ⓓ. 2 5 . 2 2 Câu 22: z z
Gọi z , z là nghiệm của phương trình 2
z − 2z + 4 = 0 . Tính giá trị của biểu thức 1 2 P = + 1 2 z z 2 1 Ⓐ. 4 Ⓑ. −4 Ⓒ. 8 Ⓓ. 11 − 4 BẢNG ĐÁP ÁN 1.B 2.D 3.D 4.A 5.B 6.C 7.A 8.D 9.B 10.D 11.C 12.C 13.C 14.B 15.D 16.B 17.C 18.D 19.A 20.C 21.D 22.B
St-bs: Duong Hung - Word xinh 2020-2021 51