Chuyên đề thể tích khối đa diện dành cho học sinh trung bình – yếu – Dương Minh Hùng Toán 12

Tài liệu gồm 67 trang, được biên soạn bởi thầy giáo Dương Minh Hùng, hướng dẫn giải các bài toán trắc nghiệm thuộc chuyên đề khối đa diện và thể tích của chúng, dành cho học sinh trung bình – yếu, ôn thi THPT Quốc gia môn Toán năm học 2020 – 2021.Mời bạn đọc đón xem.

Chủ đề:

Chương 1: Khối đa diện 172 tài liệu

Môn:

Toán 12 3.8 K tài liệu

Thông tin:
67 trang 1 năm trước
Tác giả:
L
Lan Tường
docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Chuyên đề thể tích khối đa diện dành cho học sinh trung bình – yếu – Dương Minh Hùng Toán 12

Tài liệu gồm 67 trang, được biên soạn bởi thầy giáo Dương Minh Hùng, hướng dẫn giải các bài toán trắc nghiệm thuộc chuyên đề khối đa diện và thể tích của chúng, dành cho học sinh trung bình – yếu, ôn thi THPT Quốc gia môn Toán năm học 2020 – 2021.Mời bạn đọc đón xem.

34 17 lượt tải Tải xuống

Chủ đề: Chương 1: Khối đa diện 172 tài liệu

Môn: Toán 12 3.8 K tài liệu

Thông tin:

67 trang 1 năm trước

Tác giả:

Profile Lan Tường
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 1
FB: Duong Hung
A - Bài tập minh họa:
Câu 1: Trong các hình dưới đây, hình nào là hình đa diện?
Ⓐ.
Hình 4.
Ⓑ.
Hình 2.
Ⓒ.
Hình 1.
Ⓓ.
Hình 3.
Full Chuyên
đề 12 new
2020-2021
CHƯƠNG ①:
KH
Ố
I ĐA DI
Ệ
N
Bài
:
KHÁI NI
Ệ
M KH
Ố
I ĐA DI
Ệ
N
. Lý thuyết cần nắm:
.Kết quả 1: Một khối đa diện bất kì có ít nhất 4 mặt.
.Kết quả 2:Mỗi hình đa diện có ít nhất 4 đỉnh.
.Kết quả 3: Cho là đa diện mà các mặt của nó là những đa giác có p cạnh. Nếu số mặt
của là lẻ thì p phải là số chẵn.
.Kết quả 4: Cho là đa diện có m mặt, mà các mặt của nó là những đa giác có p cạnh. Khi
đó số cạnh của là .
.Kết quả 5: Mỗi khối đa diện có các mặt là các tam giác thì tổng số các mặt của nó phải là
một số chẵn.
.Kết quả 6: Mỗi khối đa diện bất kì luôn có thể được phân chia được thành những khối tứ
diện.
.Kết quả 7: Mỗi đỉnh của một hình đa diện là đỉnh chung của ít nhất 3 cạnh.
.Kết quả 8: Nếu khối đa diện có mỗi đỉnh là đỉnh chung của ba cạnh thì số đỉnh phải là số
chẵn.
.Kết quả 9: Mỗi hình đa diện có ít nhất 6 cạnh.
.Kết quả 10: Không tồn tại hình đa diện có 7 cạnh.
.Kết quả 11: Với mỗi số nguyên luôn tồn tại hình đa diện có 2k cạnh.
.Kết quả 12: Với mỗi số nguyên luôn tồn tại hình đa diện có cạnh.
.Kết quả 13: Không tồn tại một hình đa diện có
+ Số mặt lớn hơn hoặc bằng số cạnh.
+ Số đỉnh lớn hơn hoặc bằng số cạnh.
.Kết quả 14: Tồn tại khối đa diện có 2n mặt là những tam giác đều.
Dạng
①
: Nhận diện đa diện lồi.
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 2
Lời giải.
Chọn D
Hình 4 không phải là hình đa diện vì có một cạnh là cạnh chung
của 4 đa giác, loại A
Hình 2 không phải là hình đa diện vì có một cạnh là cạnh chung của
3 đa giác, loại B
Hình 1 không phải là hình đa diện vì có một cạnh là cạnh chung của
4 đa giác, loại C
Hình 3 là hình đa diện vì nó thỏa mãn khái niệm hình đa diện.
(Hình đa diện là hình gồm hữu hạn các đa giác phẳng thỏa mãn hai
tính chất:
Bài học kinh nghiệm
Quan sát kỹ sử dụng các
kết quả chính xác để
Hai đa giác phân biệt chỉ
có thể hoặc không có điểm
chung, hoặc chỉ có một đỉnh
chung, hoặc chỉ có một cạnh
chung.
Mỗi cạnh của đa giác nào
cũng là cạnh chung của
đúng hai đa giác).
Câu 2: Trong các mệnh đề sau, mệnh đề nào sai?
Ⓐ.
Tồn tại một hình đa diện có số đỉnh bằng số mặt .
Ⓑ.
Tồn tại một hình đa diện có số cạnh gấp đôi số mặt.
Ⓒ.
Số đỉnh của một hình đa diện bất kì luôn lớn hơn hoặc bằng 4.
Ⓓ.
Tồn tại một hình đa diện có số cạnh bằng số mặt.
Lời giải.
Chọn D
Ⓐ.
Đúng vì tồn tại hình tứ diện.
Ⓑ.
Đúng vì tồn tại hình lập phương.
Ⓒ.
Đúng.
Ⓓ.
Sai.
Bài học kinh nghiệm
Quan sát kỹ sử dụng các
kết quả chính xác để
Câu 3: Mỗi cạnh của hình đa diện là cạnh chung của đúng
Ⓐ.
năm mặt.
Ⓑ.
ba mặt.
Ⓒ.
bốn mặt.
Ⓓ.
hai mặt.
Lời giải.
Chọn D
Trong một đa diện, mỗi cạnh nào cũng là cạnh chung của đúng hai
mặt.
Bài học kinh nghiệm
Quan sát kỹ sử dụng các
kết quả chính xác để
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 3
Câu 4: Hình nào dưới đây là hình đa diện?
Ⓐ.
Hình 3.
Ⓑ.
Hình 1.
Ⓒ.
Hình 2.
Ⓓ.
Hình 4.
Lời giải.
Chọn D
Hình 4 thỏa mãn, loại trừ hình 1,2,3 khá dễ.
Bài học kinh nghiệm
Quan sát
B - Bài tập rèn luyện:
Câu 1: Hình nào trong các hình sau không phải là hình đa diện?
Ⓐ.
Hình chóp.
Ⓑ.
Hình vuông.
Ⓒ.
Hình lập phương.
Ⓓ.
Hình lăng trụ.
Câu 2: Cho các hình sau:
Hình 1 Hình 2 Hình 3 Hình 4
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), hình đa diện
là
Ⓐ.
Hình 1.
Ⓑ.
Hình 2.
Ⓒ.
Hình 3.
Ⓓ.
Hình 4.
Câu 3: Cho các hình khối sau:
(a) (b) (c) (d)
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), số đa diện lồi là
Ⓐ.
1
.
Ⓑ.
2
.
Ⓒ.
3
.
Ⓓ.
4
.
Câu 4: Cho các hình sau:
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 4
Hình 1 Hình 2 Hình 3 Hình 4
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), số hình đa diện là
Ⓐ.
1
.
Ⓑ.
2
.
Ⓒ.
3
.
Ⓓ.
4
.
Câu 5: Vật thể nào trong các vật thể sau không phải là khối đa diện?
Ⓐ.
Ⓑ.
Ⓒ.
Ⓓ.
Câu 6: Hình đa diện trong hình vẽ bên có bao nhiêu mặt?
Ⓐ.
11.
Ⓑ.
12.
Ⓒ.
13.
Ⓓ.
14.
Câu 7: Khối đa diện nào sau đây có số mặt nhỏ nhất?
Ⓐ.
Khối tứ diện đều.
Ⓑ.
Khối chóp tứ giác.
Ⓒ.
Khối lập phương.
Ⓓ.
Khối 12 mặt đều.
Câu 8: Hình đa diện trong hình vẽ bên có bao nhiêu cạnh?
Ⓐ.
8.
Ⓑ.
9.
Ⓒ.
12.
.
Ⓓ.
16.
Câu 9: Hình đa diện trong hình vẽ bên có bao nhiêu mặt?
Ⓐ.
6
.
Ⓑ.
10
.
Ⓒ.
12
.
Ⓓ.
11
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 5
Câu 10: Trong không gian chỉ có 5 loại khối đa diện đều như hình vẽ
Khối tứ diện đều Khối lập phương Bát diện đều Hình
12
mặt đều Hình
20
mặt đều
Mệnh đề nào sau đây đúng?
Ⓐ.
Mọi khối đa diện đều có số mặt là những số chia hết cho 4.
Ⓑ.
Khối lập phương và khối bát diện đều có cùng số cạnh.
Ⓒ.
Khối tứ diện đều và khối bát diện đều có 1 tâm đối xứng.
Ⓓ.
Khối mười hai mặt đều và khối hai mươi mặt đều có cùng số đỉnh.
BẢNG ĐÁP ÁN
1.B 2.A 3.B 4.C 5.C 6.B 7.A 8.D 9.D 10.B
A - Bài tập minh họa:
Câu 1: Hình đa diện trong hình vẽ có bao nhiêu mặt?
Ⓐ.
12
.
Ⓑ.
10
.
Ⓒ.
6
.
Ⓓ.
11
.
Lời giải.
Chọn D
Dựa vào hình ta đếm được
11
mặt
Bài học kinh nghiệm
Quan sát
Câu 2: Tìm số mặt của hình đa diện ở hình vẽ bên?
Ⓐ.
11.
Ⓑ.
10.
Ⓒ.
12.
Ⓓ.
9.
Lời giải.
Chọn D
Bài học kinh nghiệm
Quan sát
_ Dạng 2. Xác định số đỉnh, cạnh, mặt bên của một khối đa diện.
-Phương pháp: Sử dụng các kết quả thừa nhận
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 6
Hình đa diện trên có 9 mặt gồm các mặt là
; ; ; ; ;
; ; ; .
ABD BDC ADC ABFE BFGC
ACGE HFE HFG EHG
Câu 3: Hình chóp có 50 cạnh thì có bao nhiêu mặt?
Ⓐ.
26
.
Ⓑ.
21
.
Ⓒ.
25
.
Ⓓ.
49
.
Lời giải.
Chọn A
Gọi
n
là số cạnh của đa giác đáy hình chóp đã cho. Ta có
Số cạnh đáy bằng số cạnh bên nên tổng số cạnh của hình chóp bằng
2n
.
Từ giả thiết, suy ra
2 50 25n n
.
Vậy số tổng số mặt của hình chóp là:
26
.
Bài học kinh nghiệm
Công thức
Câu 4: Hình bát diện đều có bao nhiêu cạnh ?
Ⓐ.
16
.
Ⓑ.
12
.
Ⓒ.
10
.
Ⓓ.
14
.
Lời giải.
Chọn B
Hình bát diện đều có 6 đỉnh, 8 mặt, 12 cạnh
Bài học kinh nghiệm
Quan sát
B - Bài tập rèn luyện:
Câu 1: Hình đa diện trong hình vẽ bên có bao nhiều mặt?
Ⓐ.
12
.
Ⓑ.
8
.
Ⓒ.
11
.
Ⓓ.
10
.
Câu 2: Hỏi hình đa diện ở hình vẽ bên có bao nhiêu mặt?
Ⓐ.
10m
.
Ⓑ.
12m
.
Ⓒ.
11m
.
Ⓓ.
20m
.
Câu 3: Khối lăng trụ ngũ giác có bao nhiêu mặt?
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 7
Ⓐ.
9
mặt.
Ⓑ.
7
mặt.
Ⓒ.
5
mặt.
Ⓓ.
6
mặt.
Câu 4: Số mặt phẳng cách đều tất cả các đỉnh của một hình lăng trụ tam giác là
Ⓐ.
2
.
Ⓑ.
3
.
Ⓒ.
4
.
Ⓓ.
1
.
Câu 5: Khối tám mặt đều có tất cả bao nhiêu đỉnh?
Ⓐ.
6
.
Ⓑ.
8
.
Ⓒ.
12
.
Ⓓ.
16
.
Câu 6: Hình lăng trụ lục giác có bao nhiêu mặt?
Ⓐ.
8
.
Ⓑ.
7
.
Ⓒ.
9
.
Ⓓ.
6
.
Câu 7: Mỗi cạnh của một hình đa diện là cạnh chung của đúng
n
mặt của hình đa diện đó.
Mệnh đề nào dưới đây đúng?
Ⓐ.
2n
.
Ⓑ.
5n
.
Ⓒ.
3n
.
Ⓓ.
4n
.
Câu 8: Một hình lăng trụ có đúng
11
cạnh bên thì hình lăng trụ đó có tất cả bao nhiêu
cạnh?
Ⓐ.
33
.
Ⓑ.
31
.
Ⓒ.
30
.
Ⓓ.
22
.
Câu 9: Mỗi đỉnh của hình đa diện thuộc ít nhất bao nhiêu mặt?
Ⓐ.
4.
Ⓑ.
5.
Ⓒ.
2.
Ⓓ.
3.
Câu 10: Hình lăng trụ lục giác có bao nhiêu mặt?
Ⓐ.
8
.
Ⓑ.
7
.
Ⓒ.
9
.
Ⓓ.
6
.
Câu 11: Khối chóp ngũ giác có số cạnh là
Ⓐ.
20
.
Ⓑ.
15
.
Ⓒ.
5
.
Ⓓ.
10
.
Câu 12: Cho một hình đa diện. Khẳng định nào sau đây là sai?
Ⓐ.
Mỗi cạnh là cạnh chung của ít nhất ba mặt.
Ⓑ.
Mỗi đỉnh là đỉnh chung của ít nhất ba cạnh.
Ⓒ.
Mỗi đỉnh là đỉnh chung của ít nhất ba mặt.
Ⓓ.
Mỗi mặt có ít nhất ba cạnh.
Câu 13: Mỗi hình đa diện có ít nhất
Ⓐ.
3
cạnh.
Ⓑ.
6
cạnh.
Ⓒ.
5
cạnh.
Ⓓ.
4
cạnh.
Câu 14: Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất bao nhiêu mặt?
Ⓐ.
3
.
Ⓑ.
1
.
Ⓒ.
4
.
Ⓓ.
2
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 8
Câu 15: Hình bát diện đều có bao nhiêu cạnh?
Ⓐ.
8
.
Ⓑ.
24
.
Ⓒ.
16
.
Ⓓ.
12
.
Câu 16: Số đỉnh của hình đa diện dưới đây là
Ⓐ.
8.
Ⓑ.
9.
Ⓒ.
10.
Ⓓ.
11.
Câu 17: Một hình lăng trụ có đúng
11
cạnh bên thì hình lăng trụ đó có tất cả bao nhiêu
cạnh?
Ⓐ.
31
.
Ⓑ.
30
.
Ⓒ.
22
.
Ⓓ.
33
.
Câu 18: Một hình đa diện có ít nhất bao nhiêu đỉnh?
Ⓐ.
6
.
Ⓑ.
3
.
Ⓒ.
5
.
Ⓓ.
4
.
Câu 19: Hình đa diện trong hình vẽ dưới đây có bao nhiêu mặt?
Ⓐ.
4.
Ⓑ.
10.
Ⓒ.
8.
Ⓓ.
9.
Câu 20: Cho hình chóp có
20
cạnh. Số mặt của hình chóp đó là
Ⓐ.
12
.
Ⓑ.
10
.
Ⓒ.
11
.
Ⓓ.
20
.
BẢNG ĐÁP ÁN THAM KHẢO
1.D 2.C 3.B 4.C 5.A 6.A 7.A 8.A 9.D 10.A
11.D 12.A 13.B 14.A 15.D 16.C 17.D 18.D 19.C 20.C
A - Bài tập minh họa:
Câu 1: Số mặt phẳng đối xứng của hình tứ diện đều là
Ⓐ.
4
mặt phẳng.
Ⓑ.
6
mặt phẳng.
Ⓒ.
8
mặt phẳng.
Ⓓ.
10
mặt phẳng.
Lời giải.
Chọn B
Bài học kinh nghiệm
Quan sát cẩn thận
_ Dạng 3. Mặt phẳng đối xứng.
-Phương pháp: Do tính chất đối xứng nhau, nên cứ đi từ trung điểm các cạnh ra mà tìm. Đảm
b
ả
o r
ằ
ng n
ế
u ch
ọ
n 1 m
ặ
t ph
ẳ
ng đ
ố
i x
ứ
ng nào thì các
đi
ể
m còn d
ư ph
ả
i chia đ
ề
u v
ề
2 phía.
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 9
Các mặt phẳng đối xứng của hình tứ diện đều là các mặt phẳng chứa một
cạnh và qua trung điểm cạnh đối diện.
Vậy hình tứ diện đều có 6 mặt phẳng đối xứng
Câu 2: Hình lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng?
Ⓐ.
4
mặt phẳng.
Ⓑ.
1
mặt phẳng.
Ⓒ.
2
mặt phẳng.
Ⓓ.
3
mặt phẳng.
Lời giải.
Chọn A
Hình lăng trụ tam giác đều có
4
mặt phẳng đối xứng (hình vẽ bên dưới).
Bài học kinh nghiệm
Quan sát cẩn thận
Câu 3: Hình hộp chữ nhật có ba kích thước đôi một khác nhau có bao nhiêu mặt phẳng đối xứng?
Ⓐ.
4
mặt phẳng.
Ⓑ.
6
mặt phẳng.
Ⓒ.
9
mặt phẳng.
Ⓓ.
3
mặt phẳng.
Lời giải.
Chọn D
Hình hộp chữ nhật (không là hình lập phương) có các mặt phẳng đối xứng là
các mặt các mặt phẳng trung trực của các cặp cạnh đối.
Bài học kinh nghiệm
Quan sát cẩn thận
Câu 4: Một hình hộp đứng có đáy là hình thoi (không phải là hình vuông) có bao nhiêu mặt phẳng đối
xứng?
Ⓐ.
4
mặt phẳng.
Ⓑ.
1
mặt phẳng.
Ⓒ.
2
mặt phẳng.
Ⓓ.
3
mặt phẳng.
Lời giải.
Chọn D
Bài học kinh nghiệm
Quan sát cẩn thận
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 10
Hình hộp đứng có đáy là hình thoi (không phải là hình chữ nhật) có 3 mặt
phẳng đối xứng bao gồm:
2 mặt phẳng chứa đường chéo của đáy và vuông góc với đáy.
Một mặt phẳng là mặt phẳng trung trực của cạnh bên.
B - Bài tập rèn luyện:
Câu 1: Số mặt phẳng đối xứng của hình bát diện đều là
Ⓐ.
4
.
Ⓑ.
6.
.
Ⓒ.
12.
.
Ⓓ.
9.
Câu 2: Hình đa diện nào dưới đây không có tâm đối xứng?
Ⓐ.
Tứ diện đều.
Ⓑ.
Bát diện đều.
Ⓒ.
Hình lập phương.
Ⓓ.
Lăng trụ lục giác đều.
Câu 3: Gọi
1 2 3
, , n n n
lần lượt là số trục đối xứng của khối tứ diện đều, khối chóp tứ giác đều và khối
lập phương. Mệnh đề nào sau đây là đúng?
Ⓐ.
1 2 3
0, 0, 6.n n n
Ⓑ.
1 2 3
0, 1, 9.n n n
Ⓒ.
1 2 3
3, 1, 9.n n n
Ⓓ.
1 2 3
0, 1, 3.n n n
Câu 4: Hình chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng?
Ⓐ.
4
mặt phẳng.
Ⓑ.
1
mặt phẳng.
Ⓒ.
2
mặt phẳng.
Ⓓ.
3
mặt phẳng.
Câu 5: Số mặt phẳng đối xứng của hình tứ diện đều là
Ⓐ.
4
mặt phẳng.
Ⓑ.
6
mặt phẳng.
Ⓒ.
8
mặt phẳng.
Ⓓ.
10
mặt phẳng.
Câu 6: Hình lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng?
Ⓐ.
4
mặt phẳng.
Ⓑ.
1
mặt phẳng.
Ⓒ.
2
mặt phẳng.
Ⓓ.
3
mặt phẳng.
Câu 7: Hình hộp chữ nhật có ba kích thước đôi một khác nhau có bao nhiêu mặt phẳng đối xứng?
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 11
Ⓐ.
4
mặt phẳng.
Ⓑ.
6
mặt phẳng.
Ⓒ.
9
mặt phẳng.
Ⓓ.
3
mặt phẳng.
Câu 8: Một hình hộp đứng có đáy là hình thoi (không phải là hình vuông) có bao nhiêu mặt phẳng
đối xứng?
Ⓐ.
4
mặt phẳng.
Ⓑ.
1
mặt phẳng.
Ⓒ.
2
mặt phẳng.
Ⓓ.
3
mặt phẳng.
Câu 9: Hình lập phương có tất cả bao nhiêu mặt phẳng đối xứng?
Ⓐ.
8
mặt phẳng.
Ⓑ.
9
mặt phẳng.
Ⓒ.
10
mặt phẳng.
Ⓓ.
12
mặt phẳng.
Câu 10: Số mặt phẳng đối xứng của hình bát diện đều là:
Ⓐ.
4
mặt phẳng.
Ⓑ.
9
mặt phẳng.
Ⓒ.
6
mặt phẳng.
Ⓓ.
12
mặt phẳng.
BẢNG ĐÁP ÁN
1.D 2.A 3.C 4.A 5.B 6.A 7.D 8.D 9.B 10.B
. Bài tập minh họa:
Câu 1: Cho khối lập phương
.ABCD A B C D
. Mặt phẳng
ACC
chia khối
lập phương trên thành những khối đa diện nào?
Ⓐ.
Hai khối lăng trụ tam giác
.ABC A B C
và
.BCD B C D
.
Ⓑ.
Hai khối lăng trụ tam giác
.ABC A B C
và
.ACD A C D
.
Ⓒ.
Hai khối chóp tam giác
.C ABC
và
.C ACD
.
Ⓓ.
Hai khối chóp tứ giác
.C ABCD
và
.C ABB A
.
Câu 2: Mặt phẳng
A BC
chia khối lăng trụ
.ABC A B C
thành hai khối
chóp.
Ⓐ.
.A ABC
và
.A BCC B
.
Ⓑ.
.A A B C
và
.A BCC B
.
Ⓒ.
.A A BC
và
.A BCC B
.
Ⓓ.
.A A B C
và
.A BCC B
.
_ Dạng 4. Phân chia lắp ghép khối đa diện
-Phương pháp: Sử dụng các kết quả thừa nhận và các tính chất của hình học.
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 12
Câu 3: Cho hình lăng trụ
. ' ' 'ABC A B C
. Mặt phẳng
'A BC
chia khối lăng
trụ đã cho thành các khối đa diện nào?
Ⓐ.
Hai khối chóp tam giác.
Ⓑ.
Một khối chóp tam giác, một khối chóp tứ giác.
Ⓒ.
Một khối chóp tam giác, một khối chóp ngũ giác.
Ⓓ.
Hai khối chóp tứ giác.
Câu 4: Mặt phẳng nào sau đây chia khối hộp
. ' ' ' 'ABCD A B C D
thành hai
khối lăng trụ
Ⓐ.
A BC
.
Ⓑ.
ABC
.
Ⓒ.
AB C
.
Ⓓ.
A BD
.
Câu 5: Cho khối lập phương
. ' ' ' 'ABCD A B C D
. Mặt phẳng
( ' ')BDD B
chia khối lập phương thành
Ⓐ.
Hai khối lăng trụ tam giác.
Ⓑ.
Hai khối tứ diện.
Ⓒ.
Hai khối lăng trụ tứ giác.
Ⓓ.
Hai khối chóp tứ giác.
Câu 6: Phân chia khối lập phương ABCDA’B’C’D’ bởi ba mặt phẳng
' 'CB D
,
'A BD
,
' 'BDB D
ta được những khối đa diện nào?
Ⓐ.
Hai khối tứ diện và hai khối chóp tứ giác.
Ⓑ.
Hai khối tứ diện và một khối lăng trụ tam giác.
Ⓒ.
Ba khối tứ diện và một khối lăng trụ tam giác.
Ⓓ.
Hai khối tứ diện và một khối lăng trụ tứ giác
BẢNG ĐÁP ÁN
1.B 2.C 3.B 4.B 5.A 6.A
Hướng dẫn giải
Câu 1: Cho khối lập phương
.ABCD A B C D
. Mặt phẳng
ACC
chia khối lập phương trên thành
những khối đa diện nào?
Ⓐ.
Hai khối lăng trụ tam giác
.ABC A B C
và
.BCD B C D
.
Ⓑ.
Hai khối lăng trụ tam giác
.ABC A B C
và
.ACD A C D
.
A
D
B
C
B'
C'
A'
D'
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 13
Ⓒ.
Hai khối chóp tam giác
.C ABC
và
.C ACD
.
Ⓓ.
Hai khối chóp tứ giác
.C ABCD
và
.C ABB A
.
Lời giải
Chọn B
Ta có mặt phẳng
ACC ACC A
.
Cho nên mặt phẳng
ACC A
phân chia khối lập phương
.ABCD A B C D
thành hai khối
lăng trụ tam giác
.ABC A B C
và
.ACD A C D
.
Câu 2: Mặt phẳng
A BC
chia khối lăng trụ
.ABC A B C
thành hai khối chóp.
Ⓐ.
.A ABC
và
.A BCC B
.
Ⓑ.
.A A B C
và
.A BCC B
.
Ⓒ.
.A A BC
và
.A BCC B
.
Ⓓ.
.A A B C
và
.A BCC B
.
Lời giải
Chọn C
Mặt phẳng
A BC
chia khối lăng trụ
.ABC A B C
thành hai khối chóp
.A A BC
và
.A BCC B
.
Câu 3: Cho hình lăng trụ
. ' ' 'ABC A B C
. Mặt phẳng
'A BC
chia khối lăng trụ đã cho thành các khối
đa diện nào?
Ⓐ.
Hai khối chóp tam giác.
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 14
Ⓑ.
Một khối chóp tam giác, một khối chóp tứ giác.
Ⓒ.
Một khối chóp tam giác, một khối chóp ngũ giác.
Ⓓ.
Hai khối chóp tứ giác.
Lời giải
Chọn B
Mặt phẳng
'A BC
chia khối lăng trụ đã cho thành một khối chóp tam giác và một khối
chóp tứ giác.
Câu 4: Mặt phẳng nào sau đây chia khối hộp ABCD.A'B'C'D' thành hai khối lăng trụ
Ⓐ.
A BC
.
Ⓑ.
ABC
.
Ⓒ.
AB C
.
Ⓓ.
A BD
.
Lời giải
Chọn B
Mặt phẳng
ABC
là mặt phẳng
ABC D
chia khối hộp thành hai khối lăng trụ là
.BCC ADD
và
.BB C AA D
.
Câu 5: Cho khối lập phương
. ' ' ' 'ABCD A B C D
. Mặt phẳng
( ' ')BDD B
chia khối lập phương thành
Ⓐ.
Hai khối lăng trụ tam giác.
Ⓑ.
Hai khối tứ diện.
Ⓒ.
Hai khối lăng trụ tứ giác.
Ⓓ.
Hai khối chóp tứ giác.
Lời giải
Chọn A
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 15
.
Câu 6: Phân chia khối lập phương ABCDA’B’C’D’ bởi ba mặt phẳng
' 'CB D
,
'A BD
,
' 'BDB D
ta được những khối đa diện nào?
Ⓐ.
Hai khối tứ diện và hai khối chóp tứ giác.
Ⓑ.
Hai khối tứ diện và một khối lăng trụ tam giác.
Ⓒ.
Ba khối tứ diện và một khối lăng trụ tam giác.
Ⓓ.
Hai khối tứ diện và một khối lăng trụ tứ giác
Lời giải
Chọn A
A
D
B
C
B'
C'
A'
D'
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 16
FB: Duong Hung
. Bài tập minh họa:
Câu 1: Hình nào dưới đây không phải là hình đa diện?
Ⓐ.
Ⓑ.
Ⓒ.
Ⓓ.
.
Câu 2: Trong các hình dưới đây hình nào không phải đa diện lồi?
Ⓐ.
Hình (II).
Ⓑ.
Hình (I).
Ⓒ.
Hình (IV).
Ⓓ.
Hình (III).
Câu 3: Hình nào dưới đây không phải là một khối đa diện?
Full Chuyên
đề 12 new
2020-2021
CHƯƠNG ①:
KH
Ố
I ĐA DI
Ệ
N
Bài
2
:
KH
Ố
I ĐA DI
Ệ
N L
Ồ
I VÀ ĐA DI
Ệ
N Đ
Ề
U
. Lý thuyết cần nắm:
Khối đa diện được gọi là khối đa diện lồi nếu đoạn thẳng nối hai điểm bất kì của
luôn thuộc . Khi đó đa diện giới hạn được gọi là đa diện lồi.
①. Khối đa diện không lồi
②. Khối đa diện lồi
Dạng
①
: Nhận diện hình đa diện, khối đa diện lồi.
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 17
Ⓐ.
.
Ⓑ.
.
Ⓒ.
.
Ⓓ.
.
Câu 4: Vật thể nào trong các vật thể sau không phải là khối đa diện?
Ⓐ.
.
Ⓑ.
.
Ⓒ.
.
Ⓓ.
.
Câu 5: Số hình đa diện lồi trong các hình dưới đây là
Ⓐ.
3
Ⓑ.
0
Ⓒ.
1
Ⓓ.
2
Câu 6: Hình nào trong các hình sau không phải là hình đa diện?
Ⓐ.
Hình chóp.
Ⓑ.
Hình vuông.
Ⓒ.
Hình lập phương.
Ⓓ.
Hình lăng trụ.
Câu 7: Cho các hình sau:
Hình 1 Hình 2 Hình 3 Hình 4
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 18
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), hình đa diện
là:
Ⓐ.
Hình 1.
Ⓑ.
Hình 2.
Ⓒ.
Hình 3.
Ⓓ.
Hình 4.
Câu 8: Cho các hình sau:
Hình 1 Hình 2 Hình 3 Hình 4
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), hình không
phải đa diện là
Ⓐ.
Hình 1.
Ⓑ.
Hình 2.
Ⓒ.
Hình 3.
Ⓓ.
Hình 4.
Câu 9: Cho các hình khối sau:
(a) (b) (c) (d)
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), hình không
phải đa diện lồi là
Ⓐ.
hình (a).
Ⓑ.
hình (b).
Ⓒ.
hình (c).
Ⓓ.
hình (d).
Câu 10: Cho các hình sau:
Hình 1 Hình 2 Hình 3 Hình 4
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), số hình đa
diện là:
Ⓐ.
1
.
Ⓑ.
2
.
Ⓒ.
3
.
Ⓓ.
4
.
Câu 11: Cho các hình khối sau:
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 19
(a) (b) (c) (d)
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), số đa diện lồi là
Ⓐ.
1
.
Ⓑ.
2
.
Ⓒ.
3
.
Ⓓ.
4
.
BẢNG ĐÁP ÁN
1.B 2.C 3.C 4.B 5.C 6.B 7.A 8.D 9.B 10.C 11.B
. Lý thuyết cần nắm:
. Khối đa diện đều là khối đa diện lồi có hai tính chất sau đây:
Các mặt là những đa giác đều có đúng cạnh
Mỗi đỉnh là đỉnh chung của đúng cạnh
. Khối đa diện đều như vậy gọi là khối đa diện đều loại
Khối đa diện đều Số đỉnh Số cạnh Số mặt Loại
Tứ diện đều
4 6 4
Khối lập phương
8 12 6
Bát diện đều
6 12 8
Mười hai mặt đều
20 30 12
Hai mươi mặt đều
12 30 20
. Chú ý: Giả sử khối đa diện đều loại có đỉnh, cạnh và mặt
. Công thức Euler: D + M = C + 2 .
Dạng
②
: Nhận diện khối đa diện đều
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 20
A - Bài tập minh họa:
Câu 1: Khối bát diện đều có bao nhiêu mặt phẳng đối xứng?
Ⓐ.
4.
Ⓑ.
6.
Ⓒ.
8.
Ⓓ.
9.
Lời giải.
Chọn D
Có 9 mặt phẳng đối xứng
Bài học kinh nghiệm
Câu 2: Số đỉnh của hình mười hai mặt đều là
Ⓐ.
12
.
Ⓑ.
30
.
Ⓒ.
20
.
Ⓓ.
16
.
Lời giải
Chọn C
Hình mười hai mặt đều có 20 đỉnh.
Bài học kinh nghiệm
Câu 3: Hình bát diện đều kí hiệu là
Ⓐ.
3;5
.
Ⓑ.
5;3
.
Ⓒ.
3;4
.
Ⓓ.
4;3
Lời giải.
Chọn C
Khối bát diện đều hay khối tám mặt đều
Bài học kinh nghiệm
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 21
Câu 4: Khối đa diện đều nào sau đây có các mặt không phải là tam giác đều?
Ⓐ.
Bát diện đều.
Ⓑ.
Tứ diện đều.
Ⓒ.
Nhị thập diện đều.
Ⓓ.
Thập nhị diện đều.
Lời giải.
Chọn D
Các khối bát diện đều, tứ diện đều và khối nhị thập diện đều có
các mặt bên là tam giác.
Khối thập nhị diện đều có các mặt là ngũ giác
Bài học kinh nghiệm
B - Bài tập rèn luyện:
Câu 1: Cho khối hai mươi mặt đều
H
. Biết mỗi mặt của nó là một đa giác đều
p
cạnh, mỗi đỉnh
của nó là đỉnh chung của đúng
q
mặt. Ta có
;p q
nhận giá trị nào sau đây.
Ⓐ.
4;q 3p
.
Ⓑ.
3;q 5p
.
Ⓒ.
3;q 4p
.
Ⓓ.
5;q 3p
.
Câu 2: Khối đa diện đều loại
4;3
có tên gọi là
Ⓐ.
Khối thập nhị diện đều.
Ⓑ.
Khối bát diện đều
Ⓒ.
Khối lập phương.
Ⓓ.
Khối tứ diện đều.
Câu 3: Cho khối đa diện đều loại
;p q
, chỉ số
q
là
Ⓐ.
Số mặt của đa diện.
Ⓑ.
Số đỉnh của đa diện.
Ⓒ.
Số cạnh của đa diện.
Ⓓ.
Số các mặt đi qua
mỗi đỉnh.
Câu 4: Hình bát diện đều có bao nhiêu đỉnh?
Ⓐ.
10
.
Ⓑ.
8
.
Ⓒ.
12
.
Ⓓ.
6
Câu 5: Khối tứ diện đều thuộc loại khối đa diện nào dưới đây?
Ⓐ.
3;4
.
Ⓑ.
4;3
.
Ⓒ.
5;3
.
Ⓓ.
3;3
.
Câu 6: Khối đa diện đều loại
3;5
là khối nào sau đây?
Ⓐ.
Tám mặt đều.
Ⓑ.
Hai mươi mặt đều.
Ⓒ.
Tứ diện đều.
Ⓓ.
Lập phương.
Câu 7: Khối bát diện đều thuộc loại khối đa diện đều nào dưới đây?
Ⓐ.
5;3
.
Ⓑ.
4;3
.
Ⓒ.
3;4
.
Ⓓ.
3;3
.
Câu 8: Khối tứ diện đều thuộc loại khối đa diện nào dưới đây?
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 22
Ⓐ.
3;4
.
Ⓑ.
4;3
.
Ⓒ.
5;3
.
Ⓓ.
3;3
.
Câu 9: Khối đa diện đều loại
5;3
có số đỉnh là
D
và số cạnh là
C
. Tính
T D C
.
Ⓐ.
50T
.
Ⓑ.
32T
.
Ⓒ.
42T
.
Ⓓ.
18T
.
Câu 10: Đa diện đều loại
5;3
có tên gọi nào dưới đây?
Ⓐ.
Lập phương.
Ⓑ.
Hai mươi mặt đều.
Ⓒ.
Mười hai mặt đều.
Ⓓ.
Tứ diện đều.
Câu 11: Có tất cả bao nhiêu khối đa diện đều?
Ⓐ.
6.
Ⓑ.
5.
Ⓒ.
7.
Ⓓ.
4.
Câu 12: Khối đa diện đều loại
4;3
là
Ⓐ.
Khối lập phương.
Ⓑ.
Khối bát diện đều.
Ⓒ.
Khối hộp chữ nhật.
Ⓓ.
Khối tứ diện đều.
Câu 13: Hỏi khối đa diện đều loại
4; 3
có bao nhiêu mặt?
Ⓐ.
4.
Ⓑ.
20.
Ⓒ.
6.
Ⓓ.
12.
Câu 14: Khối đa diện đều loại
4;3
có số đỉnh, số cạnh và số mặt lần lượt bằng:
Ⓐ.
6,12,8
.
Ⓑ.
8,12,6
.
Ⓒ.
12,30,20
.
Ⓓ.
4,6,4
.
Câu 15: Số đỉnh của một hình bát diện đều là bao nhiêu?
Ⓐ.
10.
Ⓑ.
8.
Ⓒ.
6.
Ⓓ.
12.
Câu 28 Hình lập phương thuộc dạng đa diện nào dưới đây?
Ⓐ.
6;3
.
Ⓑ.
3;4
.
Ⓒ.
3;3
.
Ⓓ.
4;3
.
Câu 16: Hình bát diện đều có số cạnh là
Ⓐ.
6.
Ⓑ.
10.
Ⓒ.
12.
Ⓓ.
8.
Câu 17: Khối tứ diện đều thuộc loại
Ⓐ.
3;4
.
Ⓑ.
4;3
.
Ⓒ.
3;3
.
Ⓓ.
3;5
.
Câu 18: Khối đa diện đều loại { 5;3} có tên gọi là
Ⓐ.
Khối hai mươi mặt đều.
Ⓑ.
Khối mười hai mặt đều.
Ⓒ.
Khối lập phương.
Ⓓ.
Khối bát diện đều.
Câu 19: Khối đa diện đều loại
4;3
có bao nhiêu mặt?
Ⓐ.
6.
Ⓑ.
20.
Ⓒ.
12.
Ⓓ.
8.
Câu 20: Trong các mệnh đề sau, mệnh đề nào sai?
Ⓐ.
Chỉ có năm loại khối đa diện đều.
Ⓑ.
Mỗi khối đa diện đều là một khối đa diện lồi.
Ⓒ.
Mỗi cạnh của hình đa diện là cạnh chung của đúng hai mặt
Ⓓ.
Hình chóp tam giác đều là hình chóp có bốn mặt là các tam giác đều.
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 23
Câu 21: Khối đa diện đều loại
3;4
có số đỉnh, số cạnh và số mặt tương ứng là
Ⓐ.
6, 12, 8.
Ⓑ.
4, 6, 4.
Ⓒ.
8, 12, 6.
Ⓓ.
8, 12, 6.
Câu 22: Hình bát diện đều có bao nhiêu cạnh?
Ⓐ.
10
.
Ⓑ.
12
.
Ⓒ.
8
.
Ⓓ.
20
.
Câu 23: Khối mười hai mặt đều (hình vẽ dưới đây) là khối đa diện đều loại
Ⓐ.
3;4
.
Ⓑ.
3;5
.
Ⓒ.
5;3
.
Ⓓ.
4;3
.
Câu 24: Khối
20
mặt đều có bao nhiêu đỉnh?
Ⓐ.
12
.
Ⓑ.
16
.
Ⓒ.
20
.
Ⓓ.
30
.
Câu 25: Số cạnh của hình mười hai mặt đều là
Ⓐ.
Mười sáu.
Ⓑ.
Ba mươi.
Ⓒ.
Hai mươi.
Ⓓ.
Mười hai.
Câu 26: Một hình lăng trụ có đúng 11 cạnh bên thì hình lăng trụ đó có tất cả bao nhiêu cạnh?
Ⓐ.
33.
Ⓑ.
31.
Ⓒ.
30.
Ⓓ.
22
Câu 27: Cho một khối đa diện lồi có
10
đỉnh,
7
mặt. Hỏi khối đa diện này có mấy cạnh?
Ⓐ.
20
.
Ⓑ.
18
.
Ⓒ.
15
.
Ⓓ.
12
.
Câu 28: Khối đa diện đều loại
5;3
có số đỉnh là
D
và số cạnh là
C
. Tính
T D C
.
Ⓐ.
50T
.
Ⓑ.
32T
.
Ⓒ.
42T
.
Ⓓ.
18T
.
BẢNG ĐÁP ÁN
1.B 2.C 3.D 4.D 5.D 6.B 7.C 8.D 9.A 10.C
11.B 12.A 13.C 14.B 15.C 16.C 17.C 18.B 19.A 20.D
21.A 22.B 23.C 24.A 25.B 26.A 27.C 28.A
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 24
FB: Duong Hung
. Bài tập minh họa:
Câu 1: Cho khối chóp có
vuông góc với đáy, , , và . Tính thể
tích khối chóp .
Ⓐ.
.
Ⓑ.
.
Ⓒ.
.
Ⓓ.
.
Lời giải
Chọn C
PP nhanh trắc nghiệm
.
S ABC
SA
4
SA
6
AB
10
BC
8
CA
.
S ABC
40
V
192
V
32
V
24
V
8
6
10
4
A
C
B
S
Full Chuyên
đề 12 new
2020-2021
CHƯƠNG ①:
KH
Ố
I ĐA DI
Ệ
N
Bài 3:
TH
Ể
TÍCH KH
Ố
I CHÓP CÓ C
Ạ
NH BÊN VUÔNG GÓC ĐÁY
_ Dạng 1. Chóp có đáy là tam giác.
-Phương pháp:
. Tính diện tích đáy:
. Tính chiều cao của chóp:
①
. Diện tích tam giác vuông.
S= nửa tích 2 cạnh góc vuông.
Pitago:
2 2 2
AB AC AC
②
. Diện tích tam giác đều.
S= (cạnh)
2
.
√
h= (cạnh).
√
1
.
3
V B h
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 25
Ta có suy ra tam giác vuông
tại ,do đó diện tích tam giác là:
Vậy .
Câu 2: Cho khối chóp có vuông góc với , đáy là tam giác vuông cân tại ,
, góc giữa và là . Tính thể tích khối chóp .
Ⓐ.
.
Ⓑ.
.
Ⓒ.
.
Ⓓ.
.
Lời giải
Chọn A
Ta có là hình chiếu của lên suy ra góc giữa và
là góc .
Tam giác vuông cân tại , .
Xét vuông tại có .
Ta có . Vậy .
PP nhanh trắc nghiệm
Câu 3: Cho hình chóp có tam giác vuông tại , , . vuông góc với
mặt phẳng đáy và . Tính thể tích của khối chóp .
Ⓐ.
.
Ⓑ.
.
Ⓒ.
.
Ⓓ.
.
Lời giải
Chọn C
PP nhanh trắc nghiệm
2 2 2 2 2 2
6 8 10
AB AC BC
ABC
A
ABC
1 1
. .6.8 24
2 2
S AB AC
1 1
. . .4.24 32
3 3
SABC ABC
V SA S
.
S ABC
SA
ABC
ABC
A
2
BC a
SB
ABC
30
.
S ABC
3
6
9
a
3
6
3
a
3
3
3
a
3
2
4
a
30°
A
C
B
S
AB
SB
ABC
SB
ABC
30
SBA
ABC
A
2
BC a
2
AB AC a
SAB
A
3 6
.tan30 2.
3 3
a
SA AB a
2 2
1
2
ABC
S AB
a
3
2
.
1 1 6 6
. . . .
3 3 3 9
S ABC ABC
a a
V SA S a
.
S ABC
ABC
A
AB a
2
AC a
SA
ABC
3
SA a
V
.
S ABC
3
3
V a
3
2 3
3
V a
3
3
3
V a
3
3
4
V a
S
a 3
2a
a
A
B
C
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 26
Vì . Tam giác vuông tại nên
Ta có: .
Câu 4: Cho khối chóp có đáy là tam giác đều cạnh . Cạnh bên vuông góc với đáy
và . Tính thể tích của khối chóp .
Ⓐ.
.
Ⓑ.
.
Ⓒ.
.
Ⓓ.
.
Lời giải
Chọn D
Có , và .
. Vậy .
PP nhanh trắc nghiệm
B - Bài tập rèn luyện:
Câu 1: Thể tích của khối chóp có diện tích mặt đáy bằng
B
, chiều cao bằng
h
được tính bởi công
thức:
Ⓐ.
1
3
V Bh
.
Ⓑ.
V Bh
.
Ⓒ.
1
2
V Bh
.
Ⓓ.
3V Bh
.
Câu 2: Thể tích khối chóp có độ dài đường cao bằng 6, diện tích đáy bằng 8 là
Ⓐ.
12
.
Ⓑ.
48
.
Ⓒ.
16
.
Ⓓ.
24
.
Câu 3: Khối chóp S.ABC có đáy ABC là tam giác vuông cân tại B,
AB a
, cạnh bên
( )SA ABC
và
2SA a
. Thể tích V của khối chóp đã cho bằng
Ⓐ.
3
1
.
3
V a
Ⓑ.
3
2
.
3
V a
Ⓒ.
3
2 2
.
3
V a
Ⓓ.
3
.V a
Câu 4: Cho hình chóp có vuông tại , . Biết rằng vuông góc
với mặt phẳng và . Tính thể tích khối chóp .
Ⓐ.
.
Ⓑ.
.
Ⓒ.
.
Ⓓ.
.
3
SA ABC h SA a
ABC
A
2
1 1
. . . .2
2 2
ABC
S AB AC a a a
2 3
.
1 1 3
. . . . 3
3 3 3
S ABC ABC
V S SA a a a

.
S ABC
ABC
2
a
SA
3
SA a
V
.
S ABC
3
3
V a
3
4
a
V
3
3
V a
3
V a
C
B
A
S
1
.
3
ABC
V SA S
3
SA a
2
2 3
4
ABC
a
S
2
3
2 3
1
3
3 4
a
V a a
3
V a
.
S ABC
ABC
A
, 3
AB a AC a
SA
ABC
5
SB a
.
S ABC
3
3
2
a
3
3
6
a
3
3
3
a
3
3
a
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 27
Câu 5: Cho khối chóp
.S ABC
có thể tích bằng
3
6
a
và diện tích tam giác
ABC
bằng
2
.
2
a
Tính chiều
cao
h
kẻ từ
S
của khối chóp
. .S ABC
Ⓐ.
h a
.
Ⓑ.
3
a
h
.
Ⓒ.
3h a
.
Ⓓ.
2
3
a
h
.
Câu 6: Cho hình chóp
.S ABC
có
SA ABC
, biết
4SA
và diện tích tam giác
ABC
bằng
8
. Tinh
thể tích
V
của khối chóp
.S ABC
.
Ⓐ.
32V
.
Ⓑ.
4V
.
Ⓒ.
32
3
V
.
Ⓓ.
8
3
V
.
Câu 7: Cho hình chóp
.S ABC
có
6, 8, 10AB BC AC
. Cạnh bên
SA
vuông góc với đáy và
4SA
. Tính thể tích
V
của khối chóp
.S ABC
.
Ⓐ.
40V
.
Ⓑ.
32V
.
Ⓒ.
192V
.
Ⓓ.
24V
.
Câu 8: Cho tứ diện
OABC
có
,OA
,OB
OC
đôi một vuông góc và
,OA a
,OB b
.OC c
Tính thể
tích khối tứ diện
.OABC
Ⓐ.
3
abc
.
Ⓑ.
abc
.
Ⓒ.
6
abc
.
Ⓓ.
2
abc
.
Câu 9: Cho hình chóp
.S ABC
có cạnh bên
SA
vuông góc với mặt đáy,
3SA a
,
AB a
,
3AC a
,
2
BC a
. Thể tích khối chóp
.
S ABC
bằng?
Ⓐ.
3
3
6
a
.
Ⓑ.
3
2
a
.
Ⓒ.
3
3
2
a
.
Ⓓ.
3
3
4
a
.
Câu 10: Cho hình chóp
.S ABC
có
SA
vuông góc với mặt đáy. Tam giác
ABC
vuông tại
B
. Biết
3 ; 2SA AB a BC a
. Thể tích hình chóp
.S ABC
là
Ⓐ.
3
9a
.
Ⓑ.
3
6a
.
Ⓒ.
3
a
.
Ⓓ.
3
3a
.
Câu 11: Cho khối chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
2a
. Cạnh bên
SA
vuông góc với đáy
và
3SA a
. Tính thể tích
V
của khối chóp
.S ABC
.
Ⓐ.
3
3V a
.
Ⓑ.
3
4
a
V
.
Ⓒ.
3
3V a
.
Ⓓ.
3
V a
.
Câu 12: Cho khối chóp
.S ABC
có ba cạnh
, ,SA SB SC
cùng có độ dài bằng a và vuông góc với nhau
từng đôi một. Thể tích của khối chóp
.S ABC
bằng
Ⓐ.
3
2
a
Ⓑ.
3
3
a
Ⓒ.
3
6
a
Ⓓ.
3
.a
Câu 13: Cho khối chóp tam giác
.S ABC
có đáy là tam giác đều cạnh
2a
, cạnh bên
SA
vuông góc với
mặt phẳng chứa mặt đáy, cạnh
2 5SC a
. Thể tích khối chóp
.S ABC
bằng
Ⓐ.
3
3
6
a
.
Ⓑ.
3
2 3
3
a
.
Ⓒ.
3
8 3
3
a
.
Ⓓ.
3
4 3
3
a
.
Câu 14: Cho khối chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
a
và hai mặt bên
SAB
,
SAC
cùng vuông góc với đáy. Tính thể tích khối chóp
.S ABC
biết 3SC a .
Ⓐ.
3
3
2
a
.
Ⓑ.
3
2 6
9
a
.
Ⓒ.
3
3
4
a
.
Ⓓ.
3
6
12
a
.
Câu 15: Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
a
, 3SA a và
SA
vuông góc với mặt
phẳng đáy. Tính thể tích của khối chóp
.S ABC
.
Ⓐ.
3
3
.
4
a
Ⓑ.
3
.
2
a
Ⓒ.
3
3
.
4
a
Ⓓ.
3
.
4
a
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 28
Câu 16: Cho khối chóp
.S ABC
có đáy
ABC
là tam giác vuông cân tại
B
, độ dài cạnh
AB BC a
,
cạnh bên
SA
vuông góc với đáy và
2SA a
. Tính thể tích
V
của khối chóp
.S ABC
.
Ⓐ.
3
3
a
V .
Ⓑ.
3
2
a
V .
Ⓒ.
4V
.
Ⓓ.
16
3
V
.
Câu 17: Cho hình chóp tam giác đều
.S ABC
có cạnh đáy bằng
a
và chiều cao của hình chóp là
2a
.
Tính theo
a
thể tích của khối chóp
.S ABC
.
Ⓐ.
3
6
.
6
a
Ⓑ.
3
6
.
12
a
Ⓒ.
3
6
.
4
a
Ⓓ.
3
2
.
12
a
BẢNG ĐÁP ÁN THAM KHẢO
1.A 2.C 3.A 4.C 5.A 6.C 7.B 8.C 9.B 10.D
11.D 12.C 13.D 14.D 15.D 16.A 17.B
① - Bài tập minh họa chóp có đáy là hình vuông:
Câu 1: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh bằng
a
. Biết cạnh bên
2
SA a
và vuông góc với mặt phẳng đáy. Tính thể tích của khối chóp
.S ABCD
.
Ⓐ.
3
4
3
a
.
Ⓑ.
3
2a
.
Ⓒ.
3
3
a
.
Ⓓ.
3
2
3
a
.
_ Dạng 2. Chóp có đáy là hình vuông, chữ
nhật, thoi, thang.
-Phương pháp:
1
.
3
V B h
. Tính diện tích đáy:
. Tính chiều cao của chóp:
①. Diện tích hình vuông:
. S= (cạnh)
2
. Pitago:
2 2 2
AB AD BD
.Đường chéo hình vuông bằng cạnh.
2
②. Diện tích hình chữ nhật:
. S= dài x rộng.
③. Diện tích hình thoi:
.
1
. .
2
S AC BD
. S= 2.S
ABC
=2.S
ADC
④. Diện tích hình thang:
. S= nửa chiều cao x (đáy lớn+bé)
.
1
.
2
S AH AB CD
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 29
Lời giải
Chọn D
Ta có
3
2
.
1 1 2
. .2
3 3 3
S ABCD ABCD
a
V S SA a a
.
PP nhanh trắc nghiệm
Câu 2: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
a
, cạnh bên
SA
vuông góc với
mặt phẳng đáy và
2SA a
. Tính thể tích
V
của hình chóp
.S ABCD
.
Ⓐ.
3
2
6
a
V
.
Ⓑ.
3
2
4
a
V
.
Ⓒ.
3
2V a
.
Ⓓ.
3
2
3
a
V
.
Lời giải
Chọn D
Ta có
3
2
1 1 2
. 2.
3 3 3
ABCD
a
V SA S a a
PP nhanh trắc nghiệm
Câu 3: Cho khối chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
3a
, cạnh
SA
vuông góc với mặt
phẳng
ABCD
và
SB
tạo với đáy một góc
60
. Tính thể tích
V
của khối chóp
.
S ABCD
.
Ⓐ.
3
9V a
.
Ⓑ.
3
3
4
a
V .
Ⓒ.
3
9
2
a
V .
Ⓓ.
3
3V a
.
Lời giải
Chọn D
SA ABCD AB
là hình chiếu vuông góc của
SB
lên mặt
phẳng
ABCD
.
PP nhanh trắc nghiệm
A
B
D
C
S
a 3
60
0
D
C
B
A
S
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 30
, , 60SB ABCD SB AB SBA .
Trong tam giác vuông
SAB
,
tan60 . 3. 3 3SA AB a a
.
2
2 2
3 3
ABCD
S AB a a .
Vậy thể tích
V
của khối chóp
.
S ABCD
là
2 .3
1 1
. . .3 .3 3
3 3
ABCD
V S SA a a a
.
. Bài tập rèn luyện:
Câu 1: Tính thể tích khối chóp
.S ABCD
có
SA ABCD
, đáy là hình vuông cạnh
a
, 5SB a
Ⓐ.
3
6
3
a
.
Ⓑ.
3
2
3
a
.
Ⓒ.
3
2a
.
Ⓓ.
3
3
a
.
Câu 2: Cho hình chóp tứ giác
.S ABCD
có đáy
ABCD
là hình vuông cạnh , cạnh bên vuông
góc với mặt đáy và
2SA a
. Tính thể tích của khối chóp
.S ABCD
.
Ⓐ.
3
2
6
a
.
Ⓑ.
3
2
4
a
.
Ⓒ.
3
2a
.
Ⓓ.
3
2
3
a
.
Câu 3: Cho hình chóp tứ giác
.S ABCD
có đáy
ABCD
là hình vuông cạnh , cạnh bên vuông
góc với mặt đáy và . Tính thể tích của khối chóp
.S ABCD
Ⓐ.
3
2
3
a
V .
Ⓑ.
3
3
a
V .
Ⓒ.
3
2V a
.
Ⓓ.
2
4
3
a
V .
Câu 4: Cho hình chóp tứ giác
.S ABCD
có đáy
ABCD
là hình vuông, cạnh bên
SA
vuông góc với mặt
đáy và
2SA AC a
. Tính thể tích của khối chóp
.S ABCD
Ⓐ.
3
2
3
a
V
.
Ⓑ.
3
6
9
a
V
.
Ⓒ.
3
2V a
.
Ⓓ.
3
6
3
a
V
Câu 5: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
. Biết
SA ABCD
và
3SB a
. Tính thể tích khối chóp
.S ABCD
.
Ⓐ.
3
2
2
a
V
.
Ⓑ.
3
3a .
Ⓒ.
3
2
3
a
V
.
Ⓓ.
3
2
6
a
V
.
Câu 6: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
. Hai mặt phẳng
SAC
và
SAB
cùng vuông góc với
ABCD
. Góc giữa
SCD
và
ABCD
là
60
. Tính thể tích của
khối chóp
.S ABCD
.
Ⓐ.
3
3
3
a
.
Ⓑ.
3
6
3
a
.
Ⓒ.
3
3
6
a
.
Ⓓ.
3
3
3
a
.
Câu 7: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SA
vuông góc với đáy
ABCD
.
Mặt bên
SCD
hợp với đáy một góc
60
. Tính thể tích của khối chóp
.S ABCD
.
Ⓐ.
3
3
6
a
V
.
Ⓑ.
3
3
3
a
V
.
Ⓒ.
3
3
12
a
V
.
Ⓓ.
3
2
6
a
V
a
SA
V
2
a
SA
5
SC a
V
V
V
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 31
Câu 8: Cho khối chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,cạnh bên
SA
vuông góc với mặt
phẳng đáy,góc giữa mặt phẳng
SBD
và mặt phẳng đáy bằng
60
. Tính thể tích
V
của khối
chóp
.
S ABCD
.
Ⓐ.
3
6
6
a
V
.
Ⓑ.
3
3
2
a
V
.
Ⓒ.
3
3
12
a
V
.
Ⓓ.
3
3
7
a
V
Câu 9: Cho khối chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
, cạnh bên
SA
vuông góc với mặt
phẳng đáy. Đường thẳng
SD
tạo với mặt phẳng
SAB
một góc
30
. Tính thể tích
V
của
khối chóp
.S ABCD
.
Ⓐ.
3
3
2
a
V
.
Ⓑ.
3
3
4
a
V
.
Ⓒ.
3
3
12
a
V
.
Ⓓ.
3
3
3
a
V
Câu 10: Cho khối chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
,
SA
vuông góc với mặt phẳng
đáy và cạnh bên
SB
tạo với mặt phẳng đáy góc
45
. Thể tích của khối chóp
.S ABCD
bằng
Ⓐ.
3
2
3
a
.
Ⓑ.
3
2
6
a
.
Ⓒ.
3
3
a
.
Ⓓ.
3
a
.
BẢNG ĐÁP ÁN THAM KHẢO
1.B 2.D 3.A 4.A 5.C 6.A 7.B 8.A 9.D 10.C
②- Bài tập minh họa chóp có đáy là hình chữ nhật:
Câu 1: Cho hình chóp
.S ABCD
có đáy là hình chữ nhật có cạnh
2, 4AB AD
. Cạnh bên
2
SA
và vuông góc với đáy (tham khảo hình vẽ). Thể tích
V
của khối chóp
.S ABCD
bằng
Ⓐ.
16V
.
Ⓑ.
16
3
V
.
Ⓒ.
8
3
V
.
Ⓓ.
8V
.
Lời giải
Chọn C
Do
SA
vuông góc với mặt phẳng đáy nên hình chiếu của
SB
trên
ABCD
là
AB
.
PP nhanh trắc nghiệm
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 32
Suy ra,
, , 45SB ABCD SB AB SBA .
Dễ thấy
SAB
vuông, cân tại
A
, suy ra
SA AB a
.
Vậy
3
2
.
1 1
. .
3 3 3
S ABCD ABCD
a
V SA S a a (đvtt).
Câu 2: Cho khối chóp
.S ABCD
có đáy là hình chữ nhật
AB a
,
2AD a
,
SA
vuông góc với đáy
và góc giữa
SD
và mặt phẳng
ABCD
bằng
0
45
. Tính thể tích
V
của khối chóp
.
S ABCD
.
Ⓐ.
3
4
3
a
V .
Ⓑ.
3
2
3
a
V
.
Ⓒ.
3
2 6V a .
Ⓓ.
3
4 3
3
a
V
.
Lời giải
Chọn A
Vì
SA ABCD
góc giữa
SD
và mặt phẳng
ABCD
bằng
góc giữa
SD
và
AD
.
0
45 SDA
SDA
vuông cân nên
2 SA AD a
.
3
.
1 1 4
. .2 . .2
3 3 3
S ABCD ABCD
a
V V SA S a a a .
PP nhanh trắc nghiệm
Câu 3: Cho khối chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật,
AB a
, 3AD a ,
SA
vuông góc
với mặt phẳng đáy và mặt phẳng
SBC
tạo với đáy một góc
o
60
. Tính thể tích
V
của
khối chóp
.S ABCD
.
Ⓐ.
3
3V a
.
Ⓑ.
3
3
3
a
V
.
Ⓒ.
3
V a
.
Ⓓ.
3
3
a
V .
Lời giải
Chọn C
PP nhanh trắc nghiệm
45
0
2a
a
A
D
C
B
S
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 33
Ta có
2
. . 3 3
ABCD
S AB AD a a a
.
Dễ thấy
o
; 60BC AB BC SB SBA
.
Xét tam giác vuông
1
SAB A v
có:
o o
tan60 tan 60 3
SA
SA AB a
AB
Vậy
2 3
.
1 1
. 3. 3
3 3
S ABCD ABCD
V S SA a a a
.
. Bài tập rèn luyện:
Câu 1: Cho hình chóp tứ giác
.S ABCD
có đáy là hình chữ nhật,
AB a
,
3AD a
,
SA
vuông góc với
mặt phẳng đáy và
2SA a
. Tính theo
a
thể tích khối chóp
.S ABCD
.
Ⓐ.
3
6a
.
Ⓑ.
3
3a
.
Ⓒ.
3
2a
.
Ⓓ.
3
a
.
Câu 2: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật
AB a
,
2 , 2BC a SA a
,
SA
vuông
góc với mặt phẳng
( )ABCD
. Tính thể tích khối chóp
.S ABCD
theo
a
.
Ⓐ.
3
4.a
.
Ⓑ.
3
8
3
a
.
Ⓒ.
3
6
3
a
.
Ⓓ.
3
4
3
a
.
Câu 3: Cho khối chóp
.S ABCD
có đáy là hình chữ nhật. Cạnh bên
SA
vuông góc với đáy.
3AB a
;
4AD a
; 3 3SC a .Thể tích của khối chóp
.S ABCD
bằng:
Ⓐ.
3
4 2a
.
Ⓑ.
3
4a
.
Ⓒ.
3
4 2
3
a
.
Ⓓ.
3
2 2
3
a
.
Câu 4: Cho hình chóp
.S ABCD
có đáy là hình chữ nhật với
, 2AB a AD a
và
2
a
SA
,
SA ABCD
. Tính thể tích của khối chóp
.S ABC
.
Ⓐ.
3
2
12
a
V
.
Ⓑ.
3
2
2
a
V
.
Ⓒ.
3
2
3
a
V
.
Ⓓ.
3
2
6
a
V
.
Câu 5: Cho hình chóp có đáy là tam giác cân tại , , , cạnh
bên vuông góc với mặt đáy và . Tính thể tích của khối chóp .
Ⓐ.
.
Ⓑ.
.
Ⓒ.
.
Ⓓ.
.
60
a
a 3
D
A
B
C
S
.
S ABC
ABC
A
2 3
BC a
120
BAC
SA
2
SA a
V
.
S ABC
3
2 3
3
a
V
3
3
V a
3
3
2
a
V
3
3
6
a
V
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 34
Câu 6: Cho hình chóp
.S ABCD
có đáy là hình chữ nhật có cạnh
2, 4AB AD
. Cạnh bên
2SA
và vuông góc với đáy (tham khảo hình vẽ). Thể tích
V
của khối
chóp
.S ABCD
bằng
Ⓐ.
16V
.
Ⓑ.
16
3
V
.
Ⓒ.
8
3
V
.
Ⓓ.
8V
.
Câu 7: Cho khối chóp
.S ABCD
có đáy là hình chữ nhật. Cạnh bên
SA
vuông góc với đáy.
3AB a
;
4AD a
;
3 3SC a
.Thể tích của khối chóp
.S ABCD
bằng:
Ⓐ.
3
4 2a
.
Ⓑ.
3
4a
.
Ⓒ.
3
4 2
3
a
.
Ⓓ.
3
2 2
3
a
.
Câu 8: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật tâm
, , 3, 3 .O AB a AD a SA a
SO
vuông góc với mặt phẳng đáy
.ABCD
Tính thể tích của khối chóp
. .S ABC
Ⓐ.
3
6
.
3
a
Ⓑ.
3
2 6
.
3
a
Ⓒ.
3
6.a
Ⓓ.
3
2 6.a
Câu 9: Cho hình chóp
.
S ABCD
có đáy là hình chữ nhật,
SA
vuông góc với đáy,
AB a
,
2
AD a
.
Góc giữa
SB
và đáy bằng
45
. Thể tích khối chóp là
Ⓐ.
3
2
3
a
.
Ⓑ.
3
2
3
a
.
Ⓒ.
3
2
6
a
.
Ⓓ.
3
3
a
.
Câu 10: Cho hình chóp
.S ABCD
có đáy là hình chữ nhật với
2AB a
,
AD a
. Hình chiếu của
S
lên
ABCD
là trung điểm
H
của
AB
,
SC
tạo với đáy một góc
45
. Thể tích khối chóp
.S ABCD
là
Ⓐ.
3
3
a
.
Ⓑ.
3
2 2
3
a
.
Ⓒ.
3
2
3
a
.
Ⓓ.
3
3
2
a
.
BẢNG ĐÁP ÁN THAM KHẢO
1.C 2.A 3.A 4.A 5.A 6.B 7.A 8.A 9.B 10.B
③. Bài tập minh họa chóp có đáy là hình thoi, thang vuông:
Câu 1: Cho khối chóp
.S ABCD
có đáy là hình thoi tâm
O
,
AB a
,
60BAD
,
SO ABCD
,
mặt phẳng
SCD
tạo với mặt phẳng đáy góc
60
. Thể tích khối chóp đã cho bằng
A.
3
3
8
a
.
Ⓑ.
3
3
24
a
. C.
3
3
48
a
.
Ⓓ.
3
3
12
a
Lời giải
Chọn A
PP nhanh trắc nghiệm
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 35
Ta có
ABCD
là hình thoi tâm
O
,
AB a
,
0
60BAD
nên
tam giác
,ABD CBD
đều cạnh a.
Gọi
BK
là đường cao của tam giác
CBD
, ta có
3
2
a
BK
.
Gọi H là hình chiếu của O lên DC
Ta có
0
, , 60
DC OH
DC SOH DC SH
DC SO
SCD ABCD OH SH SHO
.
Có
0 0
3
.tan60 .tan60
2 4
BK a
SO OH
;
2
3
2
2
ABCD ABD
a
S S
.
2 3
.
1 1 3 3 3
. . . .
3 3 2 4 8
S ABCD ABCD
a a a
V S SO
.
Câu 2: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thang vuông tại
A
và
, 1, 2.
B AB BC AD
Cạnh bên
2SA
và vuông góc với mặt đáy. Thể tích
V
của khối chóp
.S ABCD
bằng
Ⓐ.
3
2
V
.
Ⓑ.
1V
.
Ⓒ.
1
3
V
.
Ⓓ.
2V
.
Lời giải
Chọn B
ABCD
là hình thang vuông tại
A
và
, 1, 2B AB BC AD
1 3
1 2 .
2 2
ABCD
S
.
1 1 3
. .2. 1
3 3 2
S ABCD ABCD
V V SA S
.
PP nhanh trắc nghiệm
2
2
1
D
C
B
A
S
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 36
Câu 3: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thang vuông tại
A
và
B
,
2AB BC
,
3
AD
.
Cạnh bên
2SA
và vuông góc với đáy. Tính thể tích khối chóp
.S ABCD
.
Ⓐ.
4V
.
Ⓑ.
10
3
V
.
Ⓒ.
10 3
3
V
.
Ⓓ.
17
6
.
Lời giải
Chọn B
Ta có:
2 3
. .2 5
2 2
ABCD
AB CD
S AD
Thể tích:
.
1 1 10
. . .2.5
3 3 3
S ABCD ABCD
V SA S
.
PP nhanh trắc nghiệm
. Bài tập rèn luyện:
Câu 1: Cho hình chóp
.S ABCD
có
SA
vuông góc với mặt phẳng
,ABCD
đáy
ABCD
là hình thang
vuông tại
A
và
B
có
, 3 , .AB a AD a BC a
Biết
3,
SA a
tính thể tích khối chóp
.S BCD
theo
.a
Ⓐ.
3
3
.
6
a
Ⓑ.
3
2 3
.
3
a
Ⓒ.
3
3
.
4
a
Ⓓ.
3
2 3 .a
Câu 2: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thang vuông tại
A
và
D
,
AB AD a
,
3SA CD a
,
SA
vuông góc với mặt phẳng
ABCD
. Thể tích khối chóp
.S ABCD
bằng.
Ⓐ.
3
1
3
a
.
Ⓑ.
3
2a
.
Ⓒ.
3
6a
.
Ⓓ.
3
1
6
a
.
Câu 3: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thoi cạnh
a
và góc
60BAD ,
SA ABCD
. Biết rằng khoảng cách từ
A
đến cạnh
SC
bằng
a
. Thể tích khối chóp
.S ABCD
là
Ⓐ.
3
2
4
a
.
Ⓑ.
3
2
12
a
.
Ⓒ.
3
3
6
a
.
Ⓓ.
3
3a .
BẢNG ĐÁP ÁN
1.A 2.B 3.A
A
D
C
B
S
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 37
FB: Duong Hung
A - Bài tập minh họa:
Câu 1: Cho khối chóp
.S ABC
có đáy
ABC
là tam giác vuông tại
A
, biết
, 2AB a AC a
. Mặt bên
SAB
là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Tính theo
a
thể tích khối
chóp
.S ABC
.
Ⓐ.
3
3
2
a
.
Ⓑ.
3
3
6
a
.
Ⓒ.
3
3
4
a
.
Ⓓ.
3
3
3
a
.
Lời giải
Chọn B
Gọi
I
là trung điểm của đoạn thẳng
AB
. Ta có:
,SI SAB SI AB
SAB ABC AB SI ABC
SAB ABC
.
.
3
1 1 1 1
. . . . .
3 3 2 6
1 3 3
. . .2
6 2 6
S ABC ABC
V SI S SI AB AC SI AB AC
a a
a a
PP nhanh trắc nghiệm
Casio
B
C
A
S
I
Full Chuyên
đề 12 new
2020-2021
CHƯƠNG ①:
KH
Ố
I ĐA DI
Ệ
N
Bài
4
:
TH
Ể
TÍCH KH
Ố
I CHÓP CÓ
M
Ặ
T
BÊN VUÔNG GÓC ĐÁY
_ Dạng 1. Chóp có đáy là tam giác.
-Phương pháp:
1
.
3
V B h
Tính diện tích đáy: B
Tính chiều cao của chóp: h
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 38
Câu 2: Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông cân tại
, 2 ,B AC a
mặt bên
SAC
là tam giác đều và
.SAC ABC
Tính thể tích khối chóp
. .S ABC
Ⓐ.
3
2 2
3
a
.
Ⓑ.
3
2 10
3
a
.
Ⓒ.
3
10a .
Ⓓ.
3
3
3
a
Lời giải
Chọn D
Kẻ
.SH AC
Do
( ) ( ) ( ). SAC ABC SH ABC
Tam giác
SAC
đều cạnh
2AC a
nên
2 . 3
3.
2
a
SH a
Tam giác
ABC
là tam giác vuông cân tại,
2 2AC a AB BC a
.
Do đó:
2
1
S .
2
ABC
AB BC a
(đvdt)
3
2
.
1 1 3
. . 3.
3 3 3
S ABC ABC
a
V SH S a a
(đvtt).
PP nhanh trắc nghiệm
Casio
Câu 3: Cho hình chóp
.S ABC
có
.SA SB SC
Tam giác
ABC
vuông cân tại
, 2A AB AC a
và
SB
tạo với mặt phẳng
ABC
một góc
0
60
. Tính thể tích khối chóp
. .S ABC
Ⓐ.
3
3
6
a
.
Ⓑ.
3
3
3
a
.
Ⓒ.
3
2 3
3
a
.
Ⓓ.
3
2
6
a
.
Lời giải
Chọn B
Gọi
H
là trung điểm
.
BC
PP nhanh trắc nghiệm
Casio
A
B
C
S
H
60°
H
B
C
A
S
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 39
Theo giả thiết
0
, 60 .
BA CA
SH ABC SB ABC SBH
SA SB SC
Áp dụng pitago cho tam giác vuông
2 2
2 2
: 2 2 4 2 .ABC BC a a a BC a BH a
Áp dụng hệ thức lượng cho tam giác vuông
0
: tan 60 3.SBH SH BH a
2
1
. .
2
ABC
S AB AC a
Vậy thể tích của khối chóp là:
3
2
1 1 3
. 3. .
3 3 3
ABC
a
V SH S a a
B - Bài tập rèn luyện:
Câu 1: Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
2a
, tam giác
SAB
là tam giác đều
và nằm trong mặt phẳng vuông góc với mặt đáy. Tính thể tích khối chóp
.S ABC
.
Ⓐ.
3
2
a
V
.
Ⓑ.
3
V a
.
Ⓒ.
3
3
2
a
V
.
Ⓓ.
3
3V a
.
Câu 2: Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông cân tại
, 2A BC a
. Mặt bên
SBC
là
tam giác vuông cân tại
S
và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối
chóp
.S ABC
.
Ⓐ.
3
.V a
Ⓑ.
3
2
.
3
a
V
Ⓒ.
3
2
.
3
a
V
Ⓓ.
3
.
3
a
V
Câu 3: Cho hình chóp
.S ABC
có
SA a
, tam giác
ABC
đều, tam giác
SAB
vuông cân tại
S
và nằm
trong mặt phẳng vuông góc với mặt phẳng đáy. Thể tích khối chóp
.S ABC
bằng
Ⓐ.
3
6
4
a
.
Ⓑ.
3
6
24
a
.
Ⓒ.
3
6
12
a
.
Ⓓ.
3
6
8
a
.
Câu 4: Cho hình chóp
.S ABC
có đáy là tam giác
ABC
vuông tại
B
,
AB a
,
2AC a
. Hình chiếu
vuông góc của
S
lên
ABC
là trung điểm
M
của
AC
. Góc giữa
SB
và đáy bằng
60
. Thể
tích
.S ABC
là bao nhiêu?
Ⓐ.
3
3
2
a
.
Ⓑ.
3
2
a
.
Ⓒ.
3
4
a
.
Ⓓ.
3
2
12
a
.
Câu 5: Cho hình chóp
.S ABC
có tam giác
ABC
là tam giác đều cạnh
a
. Hình chiếu của
S
trên mặt
phẳng
ABC
là trung điểm của cạnh
A
, góc tạo bởi cạnh
SC
và mặt phẳng đáy
ABC
bằng
0
30
. Tính thể tích của khối chóp
.S ABC
.
Ⓐ.
3
3
8
a
.
Ⓑ.
3
2
8
a
.
Ⓒ.
3
3
24
a
.
Ⓓ.
3
3
2
a
.
Câu 6: Cho hình chóp
.S ABC
có
SAB
và
ABC
là hai tam giác đều và nằm trong hai mặt phẳng
vuông góc với nhau,
6
2
a
SC
. Tính thể tích
V
của khối chóp
.S ABC
.
Ⓐ.
3
12
a
V
.
Ⓑ.
3
4
a
V
.
Ⓒ.
3
3
8
a
V
.
Ⓓ.
3
8
a
V
.
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 40
Câu 7: Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều; mặt bên
SAB
nằm trong mặt phẳng
vuông góc với mặt phẳng đáy và tam giác
SAB
vuông tại
S
,
3SA a
,
SB a
. Tính thể
tích khối chóp
.S ABC
.
Ⓐ.
3
6
6
a
.
Ⓑ.
3
6
3
a
.
Ⓒ.
3
2
a
.
Ⓓ.
3
6
2
a
.
Câu 8: Cho hình chóp
.S ABC
có đáy là
ABC
tam giác vuông cân đỉnh
,A AB AC a
. Hình chiếu
vuông góc của
S
lên mặt phẳng
ABC
là trung điểm
H
của
BC
. Mặt phẳng
SAB
hợp
với mặt phẳng đáy một góc bằng
60
. Tính thể tích khối chóp
.S ABC
.
Ⓐ.
3
2
.
12
a
V
Ⓑ.
3
3
.
4
a
V
Ⓒ.
3
3
.
6
a
V
Ⓓ.
3
3
.
12
a
V
BẢNG ĐÁP ÁN
1.B 2.D 3.D 4.B 5.C 6.D 7.C 8.D
A - Bài tập minh họa:
Câu 1: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông đường chéo
2 2AC a
. Mặt bên
SAB
là tam giác đều và nằm trong mặt phẳng vuông góc với
( )ABCD
. Thể tích của khối chóp
.S ABCD
là
Ⓐ.
3
a
.
Ⓑ.
3
4 3
3
a
.
Ⓒ.
3
3
6
a
.
Ⓓ.
3
2 3
3
a
.
Lời giải
Chọn B
Hạ đường cao SH của tam giác SAB thì SH là đường cao của hình
chóp
PP nhanh trắc nghiệm
C
S
A
B
D
H
_ Dạng 2. Chóp có đáy là tứ giác.
-Phương pháp:
1
.
3
V B h
Tính diện tích đáy: B
Tính chiều cao của chóp: h
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 41
Trong hình vuông ABCD:
2
2 2 2 ; 4
ABCD
AC a AB a S a
Trong tam giác đều ABC:
3
2 2 . 3
2
AB a SH a a
⇒
3
2
.
1 4 3
. 3.4
3 3
S ABCD
a
V a a
⇒ Chọn B
Câu 2: Cho khối chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
. Tam giác
SAB
cân tại
S
và nằm
trong mặt phẳng vuông góc với đáy,
2SA a
. Tính theo
a
thể tích khối chóp
.S ABCD
.
Ⓐ.
3
2V a
.
Ⓑ.
3
15
12
a
V
.
Ⓒ.
3
15
6
a
V
.
Ⓓ.
3
2
3
a
V
.
Lời giải
Chọn C
Gọi
H
là trung điểm của
AB
.
Ta có
SAB ABCD
SAB ABCD AB SH ABCD
SH AB
.
Xét tam giác vuông
SAH
:
2
2 2 2
15
4
4 2
a a
SH SA AH a
.
Thể tích khối chóp
.S ABCD
là
3
2
1 1 15 15
. . . .
3 3 2 6
ABCD
a a
V SH S a
(đvtt).
PP nhanh trắc nghiệm
Câu 3: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
2a
,
SA a
, 3SB a . Biết rằng
SAB ABCD
. Gọi
,M N
lần lượt là trung điểm của các cạnh
,AB BC
. Tính theo
a
thể tích của khối
chóp
.S BMDN
.
Ⓐ.
3
3
6
a
.
Ⓑ.
3
3
3
a
.
Ⓒ.
3
2 3a
.
Ⓓ.
3
3
4
a
.
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 42
Lời giải
Chọn B
Ta có
2 2 2
SA SB AB SAB
vuông tại
S
.
Gọi
H
là hình chiếu của
S
trên
. 3
2
SA SB a
AB SH ABCD SH
AB
.
2 2
1
2 4 2. . 2
2
BMDN ABCD NCD
S S S a NC CD a
Vậy
3
2
.
1 1 3 3
. .2 .
3 3 2 3
S BMDN BMDN
a a
V S SH a
.
PP nhanh trắc nghiệm
Câu 1: Cho hình chóp
.S ABCD
có đáy là hình thang vuông tại
A
và
B
,
AB BC a
,
2AD a
. Hình
chiếu của
S
lên mặt phẳng
ABCD
trùng với trung điểm cạnh
AB
. Biết rằng 5SC a . Tính theo
a
thể tích
V
của khối chóp
.S ABCD
Ⓐ.
3
5
4
a
V
Ⓑ.
3
15
3
a
V
.
Ⓒ.
3
15
4
a
V
.
Ⓓ.
3
2 5
3
a
V
.
Câu 2: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật. Tam giác
SAB
đều và nằm trong mặt
phẳng vuông góc với mặt phẳng đáy
ABCD
. Biết 2 3SD a và góc tạo bởi đường thẳng
SC
và
mặt phẳng
ABCD
bằng
0
30
. Tính thể tích
V
của khối chóp
.S ABCD
Ⓐ.
3
2 3
7
a
V
.
Ⓑ.
3
3
13
a
V
.
Ⓒ.
3
3
4
a
V
Ⓓ.
3
4 6
3
a
V
Câu 3: Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Mặt bên SAB là tam giác đều cạnh a và nằm
trong mặt phẳng vuông góc với (ABCD). Tính thể tích của khối chóp S.ABCD
Ⓐ.
3
3
6
a
.
Ⓑ.
3
3
2
a
.
Ⓒ.
3
3
a
.
Ⓓ.
3
a
.
Câu 4: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh 2 3a , mặt bên
SAB
là tam giác đều
và nằm trong mặt phẳng vuông góc với đáy. Thể tích của khối chóp
.S ABCD
là:
Ⓐ.
3
12a
.
Ⓑ.
14a
3
.
Ⓒ.
3
15a
.
Ⓓ.
3
17a
.
Câu 5: Cho khối chóp
.S ABCD
có
ABCD
là hình vuông cạnh
3a
. Tam giác
SAB
cân tại
S
và nằm trong
mặt phẳng vuông góc với đáy. Tính thể tích
V
của khối chóp
.S ABCD
, biết góc giữa
SC
và
ABCD
bằng
o
60
.
N
M
A
D
C
B
S
H
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 43
Ⓐ.
3
18 3.V a
Ⓑ.
3
9 15
.
2
a
V
Ⓒ.
3
9 3V a
Ⓓ.
3
18 15.V a
Câu 6: Cho hình chóp
.S ABCD
có đáy là tam giác vuông cân tại
B
,
AB a
. Gọi
I
là trung điểm
AC
,
tam giác
SAC
cân tại
S
và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp
.S ABC
, biết góc giữa
SB
và mặt phẳng đáy băng
45
.
Ⓐ.
3
3
12
a
.
Ⓑ.
3
2
12
a
.
Ⓒ.
3
2
4
a
.
Ⓓ.
3
3
4
a
.
Câu 7: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật với
2AB a
,
AD a
. Hình chiếu của
S
lên mặt phẳng
ABCD
là trung điểm
H
của cạnh
AB
, đường thẳng
SC
tạo với đáy một góc
0
45
. Tính thể tích
V
của khối chóp
.S ABCD
.
Ⓐ.
3
2 2
3
a
V
.
Ⓑ.
3
3
a
V
.
Ⓒ.
3
2
3
a
V
.
Ⓓ.
3
3
2
a
V
Câu 8: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật, biết
AB a
, 3AD a . Hình chiếu
S
lên đáy là trung điểm
H
của cạnh
AB
, góc tạo bởi
SD
và đáy là 60
0
. Tính thể tích của khối chóp
.S ABCD
.
Ⓐ.
3
13
2
a
.
Ⓑ.
3
2
a
.
Ⓒ.
3
5
5
a
.
Ⓓ.
3
15
5
a
.
Câu 9: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật. Tam giác
SAB
đều và nằm trong mặt phẳng
vuông góc với mặt phẳng đáy
ABCD
. Biết 2 3SD a và góc tạo bởi đường thẳng
SC
và mặt
phẳng
ABCD
bằng
0
30
. Tính thể tích
V
của khối chóp
.S ABCD
.
Ⓐ.
3
2 3
7
a
V
.
Ⓑ.
3
3
13
a
V
.
Ⓒ.
3
3
4
a
V
.
Ⓓ.
3
4 6
3
a
V
.
Câu 10: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
a
; hình chiếu của
S
trên
ABCD
trùng với trung điểm của cạnh
AB
; cạnh bên
3
2
a
SD
. Tính theo
a
thể tích của khối chóp
.S ABCD
.
Ⓐ.
3
7
3
a
.
Ⓑ.
3
3
a
.
Ⓒ.
3
3
3
a
.
Ⓓ.
3
5
3
a
.
Câu 11: Cho hình chóp
.S ABCD
có đáy là hình chữ nhật với
2 , .AB a AD a
Tam giác
SAB
cân tại
S
và nằm trong mặt phẳng vuông góc với đáy,
SC
tạo với đáy một góc
45
. Thể tích khối chóp
.S ABCD
là
Ⓐ.
3
3
2
a
.
Ⓑ.
3
2 2
3
a
.
Ⓒ.
3
2 2a
.
Ⓓ.
3
2
3
a
.
Câu 12: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật,
SAB
đều cạnh a nằm trong mặt phẳng
vuông góc với
ABCD
. Biết
SCD
tạo với
ABCD
một góc bằng
0
30
. Tính thể tích
V
của
khối chóp
. .S ABCD
Ⓐ.
3
3
.
8
a
V
Ⓑ.
3
3
.
4
a
V
Ⓒ.
3
3
.
2
a
V
Ⓓ.
3
3
.
3
a
V
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 44
Câu 13: Cho hình chóp
.S ABCD
có đáy là hình chữ nhật với
2 ;AB a AD a
. Tam giác
SAB
là tam giác
cân tại S và nằm trong mặt phẳng vuông góc với mặt đáy. Góc giữa mặt phẳng
SBC
và
ABCD
bằng
0
45
. Khi đó thể tích khối chóp
.S ABCD
là:
Ⓐ.
3
3
3
a
.
Ⓑ.
3
1
3
a
.
Ⓒ.
3
2a
.
Ⓓ.
3
2
3
a
.
Câu 14: Cho khối chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh
2a
,
SAD
cân tại
S
và nằm trong
mặt phẳng vuông góc với đáy. Góc giữa
SBC
và mặt đáy bằng
o
60
. Tính thể tích
.S ABCD
bằng:
Ⓐ.
3
2 3
3
a
.
Ⓑ.
3
8 3
3
a
.
Ⓒ.
3
4 3
3
a
.
Ⓓ.
3
2 3a .
BẢNG ĐÁP ÁN
1.C 2.D 3.A 4.A 5.B 6.B 7.A 8.A 9.D 10.B
11.C 12.B 13.D 14.B
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 45
FB: Duong Hung
A - Bài tập minh họa:
Câu 1: Tính thể tích của khối tứ diện đều có tất cả các cạnh đều bằng
a
.
A.
3
2
12
a
. B.
3
3
12
a
. C.
3
2
4
a
. D.
3
3
4
a
.
Lời giải
Chọn A
Gọi
M
là trung điểm của
BC
,
H
là trọng tâm tam giác
BCD
.
Ta có
AH BCD
,
2 3
3 3
a
BH BM
2 2
AH AB BH
2
2
3
3
a
a
6
3
a
Vậy thể tích tứ diện là
1
.
3
ABCD BCD
V S AH
2
1 3 6
. .
3 4 3
a a
3
2
12
a
.
PP nhanh trắc nghiệm
Casio
Câu 2: Cho khối tứ diện đều có tất cả các cạnh bằng
2a
. Thể tích khối tứ diện đã cho bằng
a
M
B
D
C
H
A
Full Chuyên
đề 12 new
2020-2021
CHƯƠNG ①:
KH
Ố
I ĐA DI
Ệ
N
Bài
5
:
TH
Ể
TÍCH KH
Ố
I CHÓP
Đ
Ề
U
_ Dạng 1. Chóp có đáy là tam giác đều.
-Phương pháp:
1
.
3
V B h
Tính diện tích đáy: B
Tính chiều cao của chóp: h
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 46
A.
3
2
6
a
. B.
3
2
12
a
. C.
3
2
3
a
. D.
3
2 2
3
a
.
Lời giải
Chọn D
Gọi
O
là trọng tâm tam giác
ABC
.
Do tứ diện
ABCD
là tứ diện đều nên ta có
( )AO BCD
.
Ta có :
2
2
(2 ) 3
3
4
BCD
a
S a
.
2 2
2 2 2 3 2 3 2 6
.
3 3 2 3 3
a a a
BO BM AO AB BO
.
Ta có :
3
2
1 1 2 6 2 2
. . 3.
3 3 3 3
ABCD BCD
a a
V S AO a
(đvtt).
PP nhanh trắc nghiệm
Casio
Câu 3: Hình chóp tam giác đều
.S ABC
có cạnh đáy là
a
và mặt bên tạo với đáy góc
45
. Tính theo
a
thể tích khối chóp
.S ABC
.
A.
3
8
a
. B.
3
24
a
. C.
3
12
a
. D.
3
4
a
.
Lời giải
Chọn B
Gọi
M
là trung điểm
BC
và
O
là tâm đường tròn ngoại tiếp tam
giác
ABC
.
Suy ra
SO ABC
.
PP nhanh trắc nghiệm
Casio
2a
B
D
C
A
M
O
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 47
Góc giữa mặt bên
SBC
và mặt đáy
ABC
là góc
45 SMO
.
Xét tam giác vuông
ABM
:
2
2 2 2
3
4 2
a a
AM AB BM a .
Mặt khác
1 3
3 6
a
OM AM OM
.
Xét tam giác vuông
SOM
:
3 3
.tan .tan 45
6 6
a a
SO OM SMO
.
Diện tích tam giác
ABC
:
2
1 3
. . .sin 60
2 4
ABC
a
S a a
.
Vậy thể tích khối chóp
.S ABC
là
2 3
.
1 1 3 3
. . .
3 3 6 4 24
S ABC ABC
a a a
V SO S
.
B - Bài tập rèn luyện:
Câu 1: Cho hình chóp tam giác đều
.S ABC
có cạnh đáy bằng
2a
, cạnh bên tạo với mặt đáy góc
0
60
. Tính theo
a
thể tích khối chóp
.S ABC
.
A.
3
3
4
a
. B.
3
2 3
3
a
. C.
3
3
3
a
. D.
3
3a
.
Câu 2: Hình chóp tam giác đều
.S ABC
có cạnh đáy là
a
và mặt bên tạo với đáy góc
45
. Tính theo
a
thể tích khối chóp
.S ABC
.
A.
3
8
a
. B.
3
24
a
. C.
3
12
a
. D.
3
4
a
.
Câu 3: Cho hình chóp tam giác đều
.S ABC
có cạnh đáy bằng
2a
, cạnh bên tạo với đáy một góc
60
. Thể tích khối chóp
.S ABC
là
A.
3
2 3
3
a
. B.
3
3
3
a
. C.
3
3
4
a
. D.
3
3a
.
Câu 4: Cho khối chóp tam giác đều có tất cả các cạnh đều bằng
2a
. Thể tích của khối chóp đó bằng
A.
3
2 2
3
a
. B.
3
2
3
a
. C.
3
2
12
a
. D.
3
2 6
9
a
.
Câu 5: Cho khối chóp tam giác đều có cạnh đáy bằng
a
, cạnh bên bằng 3a . Thể tích của khối chóp
đó bằng
A.
3
2 2
3
a
. B.
3
2
3
a
. C.
3
2
6
a
. D.
3
2
12
a
.
Câu 6: Cho hình chóp tam giác đều có cạnh đáy bằng
a
và cạnh bên bằng
2a
. Thể tích khối chóp là
A.
3
5
6
a
. B.
3
11
24
a
. C.
3
5
12
a
. D.
3
11
12
a
.
Câu 7: Tính thể tích của khối tứ diện đều có tất cả các cạnh đều bằng
a
.
A.
3
2
12
a
. B.
3
3
12
a
. C.
3
2
4
a
. D.
3
3
4
a
.
Câu 8: Cho khối chóp tam giác đều
.S ABC
có cạnh đáy bằng
a
và cạnh bên bằng
2a
. Tính thể tích
V
của khối chóp
.S ABC
A.
3
13
12
a
V
. B.
3
11
12
a
V
. C.
3
11
6
a
V
. D.
3
11
4
a
V
.
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 48
Câu 9: Tính thể tích của chóp tam giác đều có tất cả các cạnh đều bằng
a
.
A.
3
2
12
a
. B.
3
2
4
a
. C.
3
2
6
a
. D.
3
2
2
a
.
Câu 10: Cho hình chóp tam giác đều
.S ABC
có cạnh đáy bằng 3a , cạnh bên bằng
2a
. Tính thể tích
V
của khối chóp
.S ABC
.
A.
3
3
4
a
V
. B.
3
3 3
2
a
V
. C.
3
3 3
4
a
V
. D.
3
3
4
a
V
.
Câu 11: Cho hình chóp tam giác đều có cạnh đáy bằng
a
và cạnh bên tạo đáy góc
0
60
. Thể tích của
khối chóp đó bằng:
A.
3
3
12
a
. B.
3
3
6
a
. C.
3
3
36
a
. D.
3
3
18
a
.
Câu 12: Cho hình chóp đều
.S ABC
có cạnh đáy bằng
,a
cạnh bên bằng
2.a
Thể tích khối chóp
.S ABC
là
A.
3
3
6
a
. B.
3
3
12
a
. C.
3
5
6
a
. D.
3
5
12
a
.
BẢNG ĐÁP ÁN
1.B 2.B 3.A 4.A 5.C 6.D 7.A 8.B 9.A 10.D
11.A 12.D
A - Bài tập minh họa:
Câu 1: Cho một hình chóp tứ giác đều có cạnh đáy bằng
2a
và cạnh bên tạo với mặt phẳng đáy
một góc bằng
45
. Thể tích của khối chóp đó là
A.
3
2
8
a
. B.
3
2 2a
. C.
3
4 2
3
a
. D.
3
2
6
a
.
Lời giải
Chọn C
Gọi
O AC BD
, vì hình chóp tứ giác đều nên ta có
SO ABCD
PP nhanh trắc nghiệm
_ Dạng 2. Chóp có đáy là hình vuông.
-Phương pháp:
1
.
3
V B h
Tính diện tích đáy: B
Tính chiều cao của chóp: h
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 49
Vì là hình chiếu vuông góc của trên mặt đáy
ABCD
nên
SDO
là góc giữa cạnh bên và mặt đáy
ABCD
Theo đề ra tam giác vuông tại và có
45SDO
nên tam giác
vuông cân tại.
Do vậy
2SO OD a
Vậy
3
2
.
1 1 4 2
. . 2.4
3 3 3
S ABCD ABCD
a
V SO S a a
.
Câu 2: Tính thể tích khối chóp tứ giác đều
.S ABCD
biết
AB a
,
SA a
.
A.
3
2
2
a
. B.
3
2
6
a
. C.
3
3
a
. D.
3
a
.
Lời giải
Chọn B
Ta có
2 2
SO SA OA
2
2
2
2 2
a a
a
Ta có:
.
1
.
3
S ABCD ABCD
V SO S
3
2
1 2 2
. .
3 2 6
a a
a
( đvtt )
PP nhanh trắc nghiệm
Câu 3: Cho khối chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
a
. Biết
90ASC , tính thể tích
V
của khối chóp đó.
A.
3
3
a
. B.
3
2
3
a
V
. C.
3
2
6
a
V
. D.
3
2
12
a
V
.
Lời giải
Chọn C
PP nhanh trắc nghiệm
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 50
Ta có
; 2.SO ABCD AC a
Tam giác
ASC
vuông cân tại
S
nên
2
.
2 2
AC a
SO
Vậy
3
2
1 1 2 2
. . . .
3 3 2 6
ABCD
a a
V S SO a
B - Bài tập rèn luyện:
Câu 1: Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
a
, góc giữa cạnh bên và mặt đáy bằng
60
. Thể tích khối chóp
.S ABCD
là
A.
3
6
6
a
. B.
3
3
6
a
. C.
3
6
12
a
. D.
3
6
2
a
.
Câu 2: Cho hình chóp tứ giác đều
.S ABCD
có diện tích đáy bằng
2
16 cm và diện tích một mặt bên
bằng
2
8 3 cm
. Thể tích của khối chóp là
A.
3
32 11
cm
3
. B.
3
4 cm . C.
3
32 2
cm
3
. D.
3
32 13
cm
3
.
Câu 3: Cho khối chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
a
, các mặt bên tạo với mặt đáy bằng
60
. Tính thể tích khối chóp đó.
A.
3
3
2
a
. B.
3
3
12
a
. C.
3
3
6
a
. D.
3
3
3
a
.
Câu 4: Cho khối chóp tứ giác đều có cạnh đáy bằng
2a
cạnh bên bằng
3a
. Thể tích của khối chóp
đã cho bằng
A.
3
2 7
3
a
. B.
3
4
3
a
. C.
3
4 7
3
a
. D.
3
2 2
3
a
.
Câu 5: Cho hình chóp tứ giác đều
SABCD
có độ dài cạnh đáy bằng
a
. Góc tạo bởi cạnh bên và đáy
bằng
60
. Tính thể tích khối chóp
.
S ABCD
theo
a
.
A.
3
5
6
a
. B.
3
3
6
a
. C.
3
6
6
a
. D.
3
2
6
a
.
Câu 6: Cho khối chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
a
. Biết
90ASC , tính thể tích
V
của
khối chóp đó.
A.
3
3
a
. B.
3
2
3
a
V
. C.
3
2
6
a
V
. D.
3
2
12
a
V
.
Câu 7: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật tâm
, , 3, 3 .O AB a AD a SA a
SO
vuông góc với mặt phẳng đáy
.ABCD
Tính thể tích của khối chóp
. .S ABC
A.
3
6
.
3
a
B.
3
2 6
.
3
a
C.
3
6.a
D.
3
2 6.a
a
S
O
D
C
B
A
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 51
Câu 8: Cho khối chóp tứ giác đều cạnh đáy bằng
,a
góc giữa mặt bên với mặt đáy bằng
45
. Tính
thể tích của khối chóp đó.
A.
3
6
a
. B.
3
3
a
. C.
3
2a
. D.
3
2
2
a
.
Câu 9: Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
a
và cạnh bên tạo với mặt phẳng đáy
một góc
0
60
. Tính thể tích
V
của khối chóp
.S ABCD
.
A.
3
6
2
a
V
. B.
3
6
3
a
V
. C.
3
3
2
a
V
. D.
3
6
6
a
V
Câu 10: Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
2a
, cạnh bên bằng
3a
. Tính thể tích
V
của khối chóp đã cho
A.
3
4 7V a
. B.
3
4 7
9
a
V
. C.
3
4
3
a
V
. D.
3
4 7
3
a
V
.
Câu 11: Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
2a
, góc giữa mặt bên và mặt đáy bằng
60
0
. Tính theo a thể tích khối chóp
.S ABCD
A.
3
2 3
3
a
. B.
3
2 6
3
a
. C.
3
4 3
3
a
. D.
3
3
3
a
.
Câu 12: Tính thể tích của khối chóp tứ giác đều có cạnh bên bằng 2a, góc giữa cạnh bên và mặt đáy
bằng
0
60
.
A.
3
2 3a
. B.
3
2a
. C.
3
2 3
3
a
. D.
3
6a
.
Câu 13: Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng 2a, góc giữa cạnh bên và mặt phẳng
đáy bằng
0
45
. Thể tích của khối chóp đó là
A.
3
4 2
3
a
. B.
3
8 2
3
a
. C.
3
3
3
a
. D.
3
3
6
a
.
Câu 14: Cho hình chóp tứ giác đều
.S ABCD
có cạnh đáy bằng
a
, góc giữa cạnh bên và mặt đáy bằng
. Khi đó thể tích khối chóp
.S ABCD
bằng
A.
3
2
tan
2
a
. B.
3
tan
6
a
. C.
3
2
tan
6
a
. D.
3
2
cot
6
a
.
Câu 15: Cho hình chóp tứ giác đều
.S ABCD
, đáy
ABCD
có diện tích
2
16cm
, diện tích một mặt bên
là
2
8 3 cm .
Tính thể tích
V
của khối chóp
.S ABCD
.
A.
3
32 2
cm .
3
V
B.
3
32 13
cm .
3
V
C.
3
32 11
cm .
3
V
D.
3
32 15
cm .
3
V
Câu 16: Cho một hình chóp tứ giác đều có góc tạo bởi mặt bên và mặt đáy bằng
0
60
và diện tích xung
quanh bằng
2
8 .a
Tính diện tích
S
của mặt đáy hình chóp.
A.
2
4 3a . B.
2
4a
. C.
2
2a
. D.
2
2 3a .
BẢNG ĐÁP ÁN
1.A 2.A 3.C 4.C 5.C 6.C 7.A 8.A 9.D 10.D
11.C 12.C 13.A 14.C 15.C 16.B
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 52
FB: Duong Hung
A - Bài tập minh họa:
Câu 1: Cho khối lăng trụ đứng
.ABC A B C
có
BB a
, đáy
ABC
là tam giác vuông cân tại
B
và
2AC a
. Tính thể tích
V
của khối lăng trụ đã cho.
Ⓐ.
3
6
a
V
.
Ⓑ.
3
2
a
V
.
Ⓒ.
3
V a
.
Ⓓ.
3
3
a
V
.
Lời giải
Chọn B
Ta có:
2 2 2 2 2 2 2
2 2AC BA BC a AB AB a
.
3
2
.
1
. . .
2 2
ABC A B C ABC
a
V BB S a a
.
PP nhanh trắc nghiệm
Thuộc Công thức. Xác
định và tính nhanh các yếu
tố.
Câu 2: Cho khối lăng trụ đứng
.ABC A B C
có
BB a
, đáy
ABC
là tam giác vuông cân tại
B
và
2AC a
. Tính thể tích
V
của khối lăng trụ đã cho.
Ⓐ.
3
V a
.
Ⓑ.
3
3
a
V
.
Ⓒ.
3
6
a
V
.
Ⓓ.
3
2
a
V
.
Lời giải
Chọn D
PP nhanh trắc nghiệm
Thuộc Công thức. Xác
định và tính nhanh các yếu
tố.
Full Chuyên
đề 12 new
2020-2021
CHƯƠNG ①:
KH
Ố
I ĐA DI
Ệ
N
Bài
6
:
TH
Ể
TÍCH KH
Ố
I
LĂNG TR
Ụ
Đ
Ứ
NG
_ Dạng 1. Lăng trụ đứng có đáy là tam giác.
-Phương pháp:
.V B h
Tính diện tích đáy: B
Tính chiều cao của chóp: h
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 53
Do
ABC
là tam giác vuông cân tại
B
và
2AC a
AB BC a
.
3
.
1 1
. . . . . . .
2 2 2
ABC A B C ABC
a
V BB S BB BA BC a a a
.
Câu 3: Cho khối lăng trụ đều .ABC A B C
có cạnh đáy bằng
a
. Khoảng cách từ điểm
A
đến mặt phẳng
AB C
bằng
2 3
19
a
. Thể tích khối lăng trụ đã cho là
Ⓐ.
3
3
4
a
.
Ⓑ.
3
3
6
a
.
Ⓒ.
3
3
2
a
.
Ⓓ.
3
2
a
.
Lời giải
Chọn C
Gọi
M
là trung điểm của B C
,
H
là hình chiếu của
A
lên
AM
.
Ta có
A M B C
B C AA M AB C AA M
A H AB C
AA B C
A H AM
Suy ra
2 3
,
19
a
d A AB C A H
.
Khi đó
2 2 2 2 2 2 2
1 1 1 1 1 1 1
2
4
AA a
A H AA AM AA A H AM a
Vậy thể tích khối lăng trụ đã cho là:
2 3
3 3
. .2a
4 2
ABC
a a
V S AA
.
PP nhanh trắc nghiệm
Thuộc Công thức. Xác
định nhanh khoảng cách và
tính các yếu tố.
B - Bài tập rèn luyện:
Câu 1: Cho hình lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác vuông tại
A
, biết
AB a
,
2AC a
và
3
A B a
. Tính thể tích của khối lăng trụ
.
ABC A B C
.
Ⓐ.
3
2 2
3
a
.
Ⓑ.
3
5
3
a
.
Ⓒ.
3
5a
.
Ⓓ.
3
2 2a
.
C'
A
B
C
A'
B'
M
C'
B'
A
C
B
A'
H
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 54
Câu 2: Cho hình lăng trụ đứng
.ABC A B C
có tam giác
ABC
vuông tại
A
,
AB BB a
,
2AC a
.
Tính thể tích khối lăng trụ đã cho.
Ⓐ.
3
2
3
a
.
Ⓑ.
3
3
a
.
Ⓒ.
3
2a
.
Ⓓ.
3
a
.
Câu 3: Cho hình lăng trụ
ABC.A' B' C'
có đáy là tam giác đều cạnh
a
, cạnh bên bằng 2
a
và hợp với
mặt đáy một góc 60
o
. Thể tích của khối lăng trụ
ABC.A' B' C'
tính theo
a
bằng:
Ⓐ.
3
2
3
a
.
Ⓑ.
3
4
3
a
.
Ⓒ.
3
3
4
a
.
Ⓓ.
3
5
3
a
Câu 4: Cho hình lăng trụ tam giác đều
. ' ' 'ABC A B C
có
2 ,AB a
' 3AA a . Tính thể tích
V
của
khối lăng trụ
. ' ' 'ABC A B C
theo
.a
Ⓐ.
3
V a
.
Ⓑ.
3
3V a
.
Ⓒ.
3
4
a
V .
Ⓓ.
3
3
4
a
V .
Câu 5: Cho hình lăng trụ đứng .ABC A B C
có đáy
ABC
là tam giác vuông tại
A
, biết
AB a
,
2AC a
và 3A B a
. Tính thể tích của khối lăng trụ .ABC A B C
.
Ⓐ.
3
2 2
3
a
.
Ⓑ.
3
5
3
a
.
Ⓒ.
3
5a
.
Ⓓ.
3
2 2a
.
Câu 6: Cho lăng trụ đứng
.ABC A B C
có
AB a
,
2AC a
,
120BAC
, biết
C A
hợp với đáy một
góc
45
. Thể tích của khối lăng trụ là
Ⓐ.
3
2 3a
.
Ⓑ.
3
2 3
3
a
V
.
Ⓒ.
3
3
3
a
.
Ⓓ.
3
3a
.
Câu 7: Cho lăng trụ đứng
.ABC A B C
có
ABC
là tam giác vuông tại
A
,
AC a
,
30 , ABC BC
hợp với mặt bên
ACC A
một góc
30
, thể tích của khối lăng trụ là
V
. Khi đó
3
6
V
a
bằng
Ⓐ.
1
.
Ⓑ.
3 .
Ⓒ.
3
3
.
Ⓓ.
1
3
.
Câu 8: Cho khối lăng trụ đứng
.
ABC A B C
và có
3B C a
, đáy
ABC
là tam giác vuông cân tại
B
và
2AC a
. Tính thể tích
V
của khối lăng trụ
.ABC A B C
.
Ⓐ.
3
2V a
.
Ⓑ.
3
2V a
.
Ⓒ.
3
2
3
a
V
.
Ⓓ.
3
6 2
a
.
Câu 9: Cho lăng trụ đứng
.ABC A B C
có ABC là tam giác vuông tại
B
,
; 2AB a BC a
. Mặt
phẳng
A BC
hợp với mặt đáy
ABC
một góc
30
. Tính thể tích khối lăng trụ.
Ⓐ.
3
6
3
a
.
Ⓑ.
3
6
6
a
.
Ⓒ.
3
3
3
a
.
Ⓓ.
3
3
6
a
.
Câu 10: Tính theo
a
thể tích khối lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác vuông cân tại
A
, mặt bên
BCC B
là hình vuông cạnh
2a
.
Ⓐ.
3
2a
.
Ⓑ.
3
2
3
a
.
Ⓒ.
3
4a
.
Ⓓ.
3
2a
.
Câu 11: Cho khối lăng trụ đứng
.ABC A B C
có đáy là tam giác cân
ABC
với
AB AC a
, góc
0
120BAC , mặt phẳng
AB C
tạo với đáy một góc
0
30
. Tính thể tích
V
của lăng trụ đã
cho.
Ⓐ.
3
6
a
V .
Ⓑ.
3
8
a
V .
Ⓒ.
3
3
8
a
V .
Ⓓ.
3
4
a
V .
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 55
Câu 12: Tính theo
a
thể tích khối lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác vuông cân tại
A
, mặt bên
BCC B
là hình vuông cạnh
2a
.
Ⓐ.
3
2a
.
Ⓑ.
3
2
3
a
.
Ⓒ.
3
a
.
Ⓓ.
3
2a
.
Câu 13: Cho khối lăng trụ đứng
. ' ' 'ABC A B C
có
' 2BB a
, đáy
ABC
là tam giác vuông cân tại
B
và
2AC a
. Tính thể tích
V
của khối lăng trụ đã cho.
Ⓐ.
3
2V a
.
Ⓑ.
3
2
3
a
V .
Ⓒ.
3
3
a
V .
Ⓓ.
3
V a
.
Câu 14: Cho lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác vuông tại
B
;
AB a
;
2BC a
;
mặt phẳng
A BC
hợp với đáy
ABC
góc
30
. Tính theo
a
thể tích của khối lăng trụ đã
cho.
Ⓐ.
3
6
12
a
.
Ⓑ.
3
6
3
a
.
Ⓒ.
3
6
6
a
.
Ⓓ.
3
6a .
Câu 15: Cho hình lăng trụ tam giác đều
.ABC A B C
có cạnh đáy bằng
2a
và mặt phẳng
A BC
tạo
với mặt phẳng
ABC
một góc
60
o
. Tính thể tích khối lăng trụ
.ABC A B C
.
Ⓐ.
3
3a
.
Ⓑ.
3
2 3a
.
Ⓒ.
3
3 3a
.
Ⓓ.
3
2a
.
Câu 16: Cho khối lăng trụ đứng
.ABC A B C
có
2CC a
, đáy
ABC
là tam giác vuông cân tại
B
và
2AC a
. Tính thể tích
V
của khối lăng trụ đã cho.
Ⓐ.
3
V a
.
Ⓑ.
3
2
a
V .
Ⓒ.
3
2V a
.
Ⓓ.
3
3
a
V .
Câu 17: Cho khối lăng trụ đều
.ABC A B C
có cạnh đáy bằng
a
, góc tạo bởi
A B
và đáy bằng
0
60
.
Tính thể tích khối lăng trụ
.
ABC A B C
.
Ⓐ.
3
3
4
a
.
Ⓑ.
3
3
4
a
.
Ⓒ.
3
3a
.
Ⓓ.
3
3a
.
Câu 18: Cho hình lăng trụ đều
. ' ' 'ABC A B C
có cạnh đáy bằng
a
,
'A C
hợp với mặt đáy một góc
60
o
. Thể tích của khối lăng trụ
. ' ' 'ABC A B C
tính theo
a
bằng:
Ⓐ.
3
3
4
a
.
Ⓑ.
3
4
a
.
Ⓒ.
3
2
3
a
.
Ⓓ.
3
3
8
a
.
Câu 19: Cho hình lăng trụ đứng
. ' ' 'ABC A B C
có cạnh đáy là tam giác vuông cân tại
B
,
AB a
. Cạnh
SC
hợp với mặt phẳng đáy một góc bằng
30
o
. Thể tích của khối lăng trụ
.ABC A B C
tính
theo
a
bằng:
Ⓐ.
3
3
3
a
.
Ⓑ.
3
3
6
a
.
Ⓒ.
3
6
3
a
.
Ⓓ.
3
2 3
3
a
.
BẢNG ĐÁP ÁN
1.D 2.D 3.C 4.B 5.D 6.D 7.A 8.B 9.B 10.A
11.B 12.A 13.D 14.C 15.C 16.A 17.A 18.A 19.C
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 56
A - Bài tập minh họa:
Câu 1: Tính thể tích khối lập phương
.ABCD A B C D
biết 3 .BD a
Ⓐ.
3
27a
.
Ⓑ.
3
a
.
Ⓒ.
3
3 3a
.
Ⓓ.
3
9a
.
Lời giải
Chọn B
Gọi cạnh của khối lập phương là
x
ta có
2 2
2.
x xB xD
Tam giác
BDD
vuông tại
D
suy ra
2 2 2 2 2 2 2
3 2 3 .BD DD x xBD a x a x
Vậy thể tích của khối lập phương
.ABCD A B C D
là
.
3
. . .
ABCD A B C D
V a a a a
PP nhanh trắc nghiệm
Thuộc Công thức. Xác
định và tính nhanh các yếu
tố.
Câu 2: Cho hình hộp chữ nhật
.ABCD A B C D
có đáy là hình vuông cạnh
2a
và
3A B a
. Tính
thể tích khối hộp chữ nhật
.ABCD A B C D
theo
a
.
A.
3
4 5V a
.
Ⓑ.
3
12V a
.
Ⓒ.
3
2 5V a
.
Ⓓ.
3
4 5
3
a
V
.
Lời giải
Chọn A
PP nhanh trắc nghiệm
Thuộc Công thức. Xác
định và tính nhanh các yếu
tố.
3a
2a
D
C
B
A
D
'
C
'
B
'
A
'
_ Dạng 2. Lăng trụ có đáy là tứ giác
-Phương pháp:
.V B h
Tính diện tích đáy: B
Tính chiều cao của chóp: h
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 57
Xét tam giác vuông
A BB
, ta có:
2 2
2 2
3 2 5BB A B A B a a a
Thể tích khối hộp chữ nhật
.ABCD A B C D
là:
3
. 2 .2 . 5 4 5
ABCD
V S BB a a a a
Câu 3: Cho hình lập phương
.ABCD A B C D
với
O
là tâm hình vuông
A B C D
. Biết rằng tứ
diện
.O BCD
có thể tích bằng
3
6a
. Tính thể tích
V
của khối lập phương
.
ABCD A B C D
.
Ⓐ.
3
12V a
.
Ⓑ.
3
36V a
.
Ⓒ.
3
54V a
.
Ⓓ.
3
18V a
.
Lời giải
Chọn B
Ta có
3
.
1 1 1 1
. . . 36
3 2 6 6
O BCD ABCD ABCD
V AA S AA S V V a
PP nhanh trắc nghiệm
Thuộc Công thức. Xác
định và tính nhanh các yếu
tố.
B - Bài tập rèn luyện:
Câu 1: Thể tích của khối lăng trụ đứng tam giác đều có tất cả các cạnh bằng
a
bằng
Ⓐ.
3
3
4
a
.
Ⓑ.
3
3
a
.
Ⓒ.
3
3
6
a
.
Ⓓ.
3
2
3
a
.
Câu 2: Cho hình lăng trụ đứng
.ABCD A B C D
có đáy là hình thoi, biết
4 , 2 ,AA a AC a BD a
.
Thể tích
V
của khối lăng trụ là
Ⓐ.
3
8V a
.
Ⓑ.
3
2V a
.
Ⓒ.
3
8
3
V a
.
Ⓓ.
3
4V a
.
Câu 3: Cho hình lăng trụ đứng
.ABCD A B C D
có đáy
ABCD
là hình chữ nhật,
AB a
,
2AD a
,
5AB a
(tham khảo hình vẽ). Tính theo
a
thể tích
V
của khối lăng trụ đã cho.
Ⓐ.
3
2V a
.
Ⓑ.
3
2 2V a
.
Ⓒ.
3
10V a
.
Ⓓ.
3
2 2
3
a
V
.
Câu 4: Cho hình hộp đứng có cạnh bên độ dài
3a
, đáy là hình thoi cạnh
a
và có một góc
60
. Khi
đó thể tích khối hộp là
O'
D
C
B
A
D'
C'
B'
A'
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 58
Ⓐ.
3
3 3
4
a
.
Ⓑ.
3
3
3
a
.
Ⓒ.
3
3
2
a
.
Ⓓ.
3
3 3
2
a
.
Câu 5: Thể tích khối lăng trụ đứng tam giác
.ABC A B C
có tất cả các cạnh bằng
a
là
Ⓐ.
3
3
4
a
.
Ⓑ.
3
3
6
a
.
Ⓒ.
3
3
3
a
.
Ⓓ.
3
4
a
.
Câu 6: Cho hình lăng trụ đứng .ABCD A B C D
, có
ABCD
là hình vuông cạnh
2a
, cạnh
2 3AC a
.Thể tích khối lăng trụ .ABC A B C
bằng
Ⓐ.
3
8a
.
Ⓑ.
3
3a
.
Ⓒ.
3
2a
.
Ⓓ.
3
a
.
Câu 7: Khối lập phương
. ' ' ' 'ABCD A B C D
có độ dài đoạn
' 2aAB
. Thế tích của khối đó là:
Ⓐ.
3
2 2a
.
Ⓑ.
3
8a
.
Ⓒ.
3
3 3a .
Ⓓ.
3
3 2a
.
Câu 8: Cho lăng trụ đứng tam giác
.
ABC A B C
, đáy là tam giác vuông tại
0
, , 60A AC a ACB
,
3
AC a
. Thể tích khối lăng trụ đó là:
Ⓐ.
3
4 6
3
a
.
Ⓑ.
3
6a .
Ⓒ.
3
2 6
3
a
.
Ⓓ.
3
6
3
a
.
Câu 9: Cho khối hộp chữ nhật
.ABCD A B C D
có
AB a
,
2AD a
,
3AA a
. Tính thể tích
V
của
khối tứ diện
.B A C D
.
Ⓐ.
3
6V a
.
Ⓑ.
3
2V a
.
Ⓒ.
3
V a
.
Ⓓ.
3
3V a
.
BẢNG ĐÁP ÁN
1.A 2.D 3.B 4.D 5.A 6.A 7.A 8.B 9.C
B'
C'
A'
B
A
D
C
D'
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 59
FB: Duong Hung
A - Bài tập minh họa:
Full Chuyên
đề 12 new
2020-2021
CHƯƠNG ①:
KH
Ố
I ĐA DI
Ệ
N
Bài
7
:
T
Ỷ
S
Ố
TH
Ể
TÍCH
①. M, N bất
kỳ trên AB,
AC
②. Đường
trung bình
MN
③. M, N, P
là trung
điểm của
AB, AC, BC
④. Trọng
tâm G
Dạng ①: Tỷ số cơ bản trong tam giác.
①. M, N, P lần lượt
thuộc SA, SC, SB
②. N thuộc SC
D
ạ
ng
②
: T
ỷ
s
ố
cơ b
ả
n c
ủ
a kh
ố
i
Chóp tam giác
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 60
Câu 1: Cho hình chóp
.S ABC
. Gọi
, ,M N P
lần lượt là trung điểm
,SA SB
và
SC
. Khi đó tỉ số thể tích
giữa khối chóp
.S MNP
và khối chóp
.S ABC
bằng
Ⓐ.
1
4
.
Ⓑ.
1
8
.
Ⓒ.
1
6
.
Ⓓ.
1
2
.
Lời giải
Chọn B
Hai khối tứ diện cần tính tỉ số là
.S MNP
và
.S ABC
M, N, P lần lượt là trung điểm của SA,
SB, SC nên
1 1 1
; ;
2 2 2
SM SN SP
SA SB SC
.
.
1 1 1 1
. . . .
2 2 2 8
S MNP
S ABC
V
SM SN SP
V SA SB SC
PP nhanh trắc nghiệm
Xác định tỉ số
.
.
1 1 1 1
. . . .
2 2 2 8
S MNP
S ABC
V
SM SN SP
V SA SB SC
Câu 2: Cho khối tứ diện
ABCD
có thể tích
V
và điểm
E
trên cạnh
AB
sao cho
3AE EB
. Tính thể
tích khối tứ diện
.E BCD
theo
V
.
Ⓐ.
3
4
V
.
Ⓑ.
3
2
V
.
Ⓒ.
3
V
.
Ⓓ.
4
V
.
Lời giải
Chọn D
Hai khối tứ diện cần tính tỉ số là
A.ECD
và
.A BCD
3AE EB
nên AB chia làm 4 phần
AE 3 phần EB 1 phần
3
4
AE
AB
3
4
AECD
ABCD
V
AE AC AD
V AB AC AD
3
4
AECD ABCD
V V
. Do đó
. . . .
3 1
4 4
E BCD A BCD A ECD A BCD ABCD ABCD
V V V V V V
.
PP nhanh trắc nghiệm
Xác định tỉ số
3
4
AECD
ABCD
V AE AC AD
V AB AC AD
. . .
.
3 1
4 4
E BCD A BCD A ECD
A BCD ABCD ABCD
V V V
V V V
Câu 3: Cho hình chóp
.S ABC
. Gọi
M
,
N
lần lượt là trung điểm của
SA
,
SB
. Tính tỉ số
.
.
S ABC
S MNC
V
V
.
Ⓐ.
1
2
.
Ⓑ.
1
4
.
Ⓒ.
2
.
Ⓓ.
4
.
Lời giải
Chọn D
Hai khối tứ diện cần tính tỉ số là
.S ABC
và
.S MNP
PP nhanh trắc nghiệm
Xác định tỉ số
.
.
. . 2.2 4
S ABC
S MNC
V
SA SB SC
V SM SN SC
E
B
D
C
A
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 61
M, N, P lần lượt là trung điểm của SA, SBnên
2; 2
SA SB
SM SN
.
.
. . 2.2 4
S ABC
S MNC
V
SA SB SC
V SM SN SC
Câu 4: Cho hình chóp
.S ABC
có
A
và
B
lần lượt là trung điểm của
SA
và
SB
. Biết thể tích khối chóp
.S ABC
bằng
24
. Tính thể tích
V
của khối chóp
.S A B C
.
Ⓐ.
12V
.
Ⓑ.
8V
.
Ⓒ.
6V
.
Ⓓ.
3V
.
Lời giải
Chọn C
Ta có
.
.
. .
S A B C
S ABC
V
SA SB SC
V SA SB SC
1 1
.
2 2
1
4
Vậy
. .
1
.
4
S A B C S ABC
V V
1
.24
4
6
.
PP nhanh trắc nghiệm
.
.
. .
S A B C
S ABC
V
SA SB SC
V SA SB SC
B - Bài tập rèn luyện:
Câu 1: Cho hình chóp
.S ABC
có
ASB ASC
60BSC
và
2SA
;
3SB
;
7SC
. Tính thể tích
V
của khối chóp.
Ⓐ.
4 2V
.
Ⓑ.
7 2
2
V
.
Ⓒ.
7 2
3
V
.
Ⓓ.
7 2V
.
Câu 2: Cho hình chóp
.S ABC
có
A
và
B
lần lượt là trung điểm của
SA
và
SB
. Biết thể tích khối
chóp
.S ABC
bằng
24
. Tính thể tích
V
của khối chóp
.S A B C
.
Ⓐ.
3V
Ⓑ.
12V
Ⓒ.
8V
Ⓓ.
6V
Câu 3: Cho khối chóp
.S ABC
,
M
là trung điểm của cạnh
.BC
Thể tích của khối chóp
.S MAB
là
3
2 .a
Thể tích khối chóp
.S ABC
bằng.
Ⓐ.
3
2a
.
Ⓑ.
3
4a
.
Ⓒ.
3
4
a
.
Ⓓ.
3
1
2
a
.
Câu 4: Cho tứ diện
ABCD
có thể tích bằng
12
và
I
là trung điểm
CD
,
M
là trung điểm
BI
. Tính
thể tích
V
của khối chóp
.A MCD
.
Ⓐ.
4V
.
Ⓑ.
6V
.
Ⓒ.
3V
.
Ⓓ.
5V
.
Câu 5: Cho tứ diện
ABCD
có
1; .DA DA ABC ABC
là tam giác đều, có cạnh bằng
1
. Trên
cạnh
, ,DA DB DC
lấy 3 điểm
, ,M N P
sao cho
1 1 3
; ; .
2 3 4
DM DN DP
DA DB DC
Thể tích của tứ
diện
MNPD
bằng
Ⓐ.
2
96
V
.
Ⓑ.
3
12
V
.
Ⓒ.
3
96
V
.
Ⓓ.
2
12
V
.
A'
B'
A
B
C
S
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 62
Câu 6: Cho khối chóp
.S ABCD
có thể tích là
3
a
. Gọi
, , ,M N P Q
theo thứ tự là trung điểm của
, , , .SA SB SC SD
Thể tích khối chóp
.S MNPQ
là:
Ⓐ.
3
16
a
Ⓑ.
3
.
8
a
Ⓒ.
2
.
4
a
Ⓓ.
3
6
a
Câu 7: Cho khối chóp
.S ABC
. Gọi
A
,
B
lần lượt là trung điểm của
SA
và
SB
. Khi đó tỉ số thể tích
của hai khối chóp
.S A B C
và
.S ABC
bằng:
Ⓐ.
1
4
.
Ⓑ.
1
6
.
Ⓒ.
1
2
.
Ⓓ.
1
3
.
Câu 8: Cho tứ điện
MNPQ
. Gọi
, ,I J K
lần lượt là trung điểm các cạnh
, ,MN MP MQ
. Tính tỉ số thể
tích
MIJK
MNPQ
V
V
.
Ⓐ.
1
6
.
Ⓑ.
1
3
.
Ⓒ.
1
4
.
Ⓓ.
1
8
.
Câu 9: Cho tứ diện
ABCD
. Gọi
B
và
C
lần lượt là trung điểm của
,AB AC
. Khi đó tỉ số thể tích
của khối tứ diện
AB C D
và khối
ABCD
bằng:
Ⓐ.
1
2
.
Ⓑ.
1
4
.
Ⓒ.
1
6
.
Ⓓ.
1
8
.
Câu 10: Cho khối tứ diện
OABC
với
, ,OA OB OC
vuông góc từng đôi một và
,OA a 2 ,OB a
3OC a
. Gọi
,M N
lần lượt là trung điểm của hai cạnh
,AC BC
. Thể tích của khối tứ diện
OCMN
tính theo
a
bằng:
Ⓐ.
3
3
4
a
Ⓑ.
3
a
Ⓒ.
3
2
3
a
Ⓓ.
3
4
a
Câu 11: Cho khối chóp
.S ABC
. Trên ba cạnh
SA
,
SB
,
SC
lần lượt lấy ba điểm
A
,
B
,
C
sao cho
1
3
SA SA
;
1
4
SB SB
;
1
2
SC SC
. Gọi
V
và
'V
lần lượt là thể tích của các khối chóp
.S ABC
và
.S A B C
. Khi đó tỉ số
'
V
V
là
Ⓐ.
1
12
.
Ⓑ.
24
.
Ⓒ.
1
24
.
Ⓓ.
12
.
BẢNG ĐÁP ÁN
1.B 2.D 3.B 4.B 5.C 6.B 7.A 8.D 9.B 10.D 11.B
12.D
Hướng dẫn giải
Câu 1: Cho hình chóp
.S ABC
có
ASB ASC
60BSC
và
2SA
;
3SB
;
7SC
. Tính thể tích
V
của khối chóp.
Ⓐ.
4 2V
.
Ⓑ.
7 2
2
V
.
Ⓒ.
7 2
3
V
.
Ⓓ.
7 2V
.
Lời giải
Chọn B
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 63
Lấy hai điểm
B
,
A
lần lượt trên hai cạnh
SB
và
SC
sao cho
2SB
,
2SC
.
Ta có hình chóp
.S AB C
là hình tứ diện đều có cạnh bằng
2
.
3
.
2 2
12
S AB C
V
2 2
3
.
Ta lại có:
.
.
. .
S AB C
S ABC
V
SA SB SC
V SA SB SC
2 2
.
3 7
4
21
.
.
.
21
4
S AB C
S ABC
V
V
21.2 2
3.4
7 2
2
.
Câu 2: Cho hình chóp
.S ABC
có
A
và
B
lần lượt là trung điểm của
SA
và
SB
. Biết thể tích khối
chóp
.S ABC
bằng
24
. Tính thể tích
V
của khối chóp
.S A B C
.
Ⓐ.
3V
Ⓑ.
12V
Ⓒ.
8V
Ⓓ.
6V
Lời giải
Chọn D
Ta có
.
.
. .
S A B C
S ABC
V
SA SB SC
V SA SB SC
1 1
.
2 2
1
4
Vậy
. .
1
.
4
S A B C S ABC
V V
1
.24
4
6
.
Câu 3: Cho khối chóp
.S ABC
,
M
là trung điểm của cạnh
.BC
Thể tích của khối chóp
.S MAB
là
3
2 .a
Thể tích khối chóp
.S ABC
bằng.
Ⓐ.
3
2a
.
Ⓑ.
3
4a
.
Ⓒ.
3
4
a
.
Ⓓ.
3
1
2
a
.
Lời giải
2
3
7
A
B
C
S
B'
C'
A'
B'
A
B
C
S
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 64
Chọn B
3
.
2 4
S ABC SMAB
V V a
.
Câu 4: Cho tứ diện
ABCD
có thể tích bằng
12
và
I
là trung điểm
CD
,
M
là trung điểm
BI
. Tính
thể tích
V
của khối chóp
.A MCD
.
Ⓐ.
4V
.
Ⓑ.
6V
.
Ⓒ.
3V
.
Ⓓ.
5V
.
Lời giải
Chọn B
Câu 5: Cho tứ diện
ABCD
có
1; .DA DA ABC ABC
là tam giác đều, có cạnh bằng
1
. Trên cạnh
, ,DA DB DC
lấy 3 điểm
, ,M N P
sao cho
1 1 3
; ; .
2 3 4
DM DN DP
DA DB DC
Thể tích của tứ diện
MNPD
bằng
Ⓐ.
2
96
V
.
Ⓑ.
3
12
V
.
Ⓒ.
3
96
V
.
Ⓓ.
2
12
V
.
Lời giải
Chọn C
1 3 3
. .1 .
3 4 12
ABCD
V
1 1 3 1
. . . . .
2 3 4 8
DMNP
DABC
V
DM DN DP
V DA DB DC
Suy ra
1 3 3
. .
8 12 96
DMNP
V
Câu 6: Cho khối chóp
.S ABCD
có thể tích là
3
a
. Gọi
, , ,M N P Q
theo thứ tự là trung điểm của
, , , .SA SB SC SD
Thể tích khối chóp
.S MNPQ
là:
Ⓐ.
3
16
a
Ⓑ.
3
.
8
a
Ⓒ.
2
.
4
a
Ⓓ.
3
6
a
Chọn B
Ta có: Tứ giác
MNPQ
đồng dạng với tứ giác
ABCD
với tỉ số
1
2
k
.
Đường cao
h
của hình chóp
.S MNPQ
bằng
1
2
đường cao
h
hình chóp
.S ABCD
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 65
Từ đó:
2
.
1 1 1
. . . . .
3 3 2 2
S MNPQ MNPQ ABCD
h
V S h S
3
.
1
8 8
S ABCD
a
V .
Câu 7: Cho khối chóp
.S ABC
. Gọi
A
,
B
lần lượt là trung điểm của
SA
và
SB
. Khi đó tỉ số thể tích
của hai khối chóp
.S A B C
và
.S ABC
bằng:
Ⓐ.
1
4
.
Ⓑ.
1
6
.
Ⓒ.
1
2
.
Ⓓ.
1
3
.
Lời giải
Chọn A
Ta có
.
.
1 1 1
. .
2 2 4
S A B C
S ABC
V
SA SB
V SA SB
.
Câu 8: Cho tứ điện
MNPQ
. Gọi
, ,I J K
lần lượt là trung điểm các cạnh
, ,MN MP MQ
. Tính tỉ số thể
tích
MIJK
MNPQ
V
V
.
Ⓐ.
1
6
.
Ⓑ.
1
3
.
Ⓒ.
1
4
.
Ⓓ.
1
8
.
Lời giải
Chọn D
Ta có:
1
. .
8
MIJK
MNPQ
V
MI MJ MK
V MN MP MQ
.
Câu 9: Cho tứ diện
ABCD
. Gọi
B
và
C
lần lượt là trung điểm của
,AB AC
. Khi đó tỉ số thể tích của
khối tứ diện
AB C D
và khối
ABCD
bằng:
Ⓐ.
1
2
.
Ⓑ.
1
4
.
Ⓒ.
1
6
.
Ⓓ.
1
8
.
Lời giải
Chọn B
Ta có
' '
1 1 1
. .
2 2 4
AB C D
ABCD
V
AB AC
V AB AC
.
.
K
J
I
M
P
Q
N
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 66
Câu 10: Cho khối tứ diện
OABC
với
, ,OA OB OC
vuông góc từng đôi một và
,OA a 2 ,OB a
3OC a
. Gọi
,M N
lần lượt là trung điểm của hai cạnh
,AC BC
. Thể tích của khối tứ diện
OCMN
tính theo
a
bằng:
Ⓐ.
3
3
4
a
Ⓑ.
3
a
Ⓒ.
3
2
3
a
Ⓓ.
3
4
a
Lời giải
Chọn D
Ta có
3
1 1
. . .
3 2
OABC
V OAOB OC a
(đvtt)
.
Ta có
. 1
. 4
OCMN
OCAB
V
CM CN
V CA CB
.Vậy
3
1
4 4
OCMN OABC
a
V V
.
Câu 11: Cho khối chóp
.S ABC
. Trên ba cạnh
SA
,
SB
,
SC
lần lượt lấy ba điểm
A
,
B
,
C
sao cho
1
3
SA SA
;
1
4
SB SB
;
1
2
SC SC
. Gọi
V
và
'V
lần lượt là thể tích của các khối chóp
.S ABC
và
.S A B C
. Khi đó tỉ số
'
V
V
là
Ⓐ.
1
12
.
Ⓑ.
24
.
Ⓒ.
1
24
.
Ⓓ.
12
.
Lời giải
Chọn B
Ta có
. . 3.4.2 24
' ' ' '
V SA SB SC
V SA SB SC
.
Câu 12: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành.
M
là trung điểm
SC
, mặt phẳng
P
chứa
AM
và song song với
BD
, cắt
SB
và
SD
lần lượt tại
B
và
D
. Tỷ số
. ' '
.
S AB MD
S ABCD
V
V
là
Ⓐ.
3
4
.
Ⓑ.
2
3
.
Ⓒ.
1
6
.
Ⓓ.
1
3
.
Lời giải
Chọn D
Gọi
O
là tâm hình bình hành đáy.
I AO SO
Đường thẳng qua I và song song
BD
cắt
,SB SD
tại
,B D
.
Ta có
SAB MD SAB M SAMD
V V V
2 1 1
3 2 3
SAB M
SABC
V
SB SM
V SB SC
nên
1
6
SABCD
SAB M
V V
D'
B'
I
M
D
O
A
C
B
S
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 67
Tương tự
4
1
3
SAMD
S CD
V
V
nên
1
6
SABCD
SAMD
V V
do dó
1
3
SABCD
SAB MD
V V
.
| 1/67

Tài liệu khác của Toán 12

Preview text:

Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung Full Chuyên đề 12 new 2020-2021
CHƯƠNG ①: KHỐI ĐA DIỆN FB: Duong Hung
Bài 1: KHÁI NIỆM KHỐI ĐA DIỆN
 Dạng ①: Nhận diện đa diện lồi.
. Lý thuyết cần nắm:
.Kết quả 1: Một khối đa diện bất kì có ít nhất 4 mặt.
.Kết quả 2:Mỗi hình đa diện có ít nhất 4 đỉnh. .Kết quả 3: Cho
là đa diện mà các mặt của nó là những đa giác có p cạnh. Nếu số mặt của
là lẻ thì p phải là số chẵn. .Kết quả 4: Cho
là đa diện có m mặt, mà các mặt của nó là những đa giác có p cạnh. Khi đó số cạnh của là .
.Kết quả 5: Mỗi khối đa diện có các mặt là các tam giác thì tổng số các mặt của nó phải là một số chẵn.
.Kết quả 6: Mỗi khối đa diện bất kì luôn có thể được phân chia được thành những khối tứ diện.
.Kết quả 7: Mỗi đỉnh của một hình đa diện là đỉnh chung của ít nhất 3 cạnh.
.Kết quả 8: Nếu khối đa diện có mỗi đỉnh là đỉnh chung của ba cạnh thì số đỉnh phải là số chẵn.
.Kết quả 9: Mỗi hình đa diện có ít nhất 6 cạnh.
.Kết quả 10: Không tồn tại hình đa diện có 7 cạnh.
.Kết quả 11: Với mỗi số nguyên
luôn tồn tại hình đa diện có 2k cạnh.
.Kết quả 12: Với mỗi số nguyên
luôn tồn tại hình đa diện có cạnh.
.Kết quả 13: Không tồn tại một hình đa diện có
+ Số mặt lớn hơn hoặc bằng số cạnh.
+ Số đỉnh lớn hơn hoặc bằng số cạnh.
.Kết quả 14: Tồn tại khối đa diện có 2n mặt là những tam giác đều. A - Bài tập minh họa:
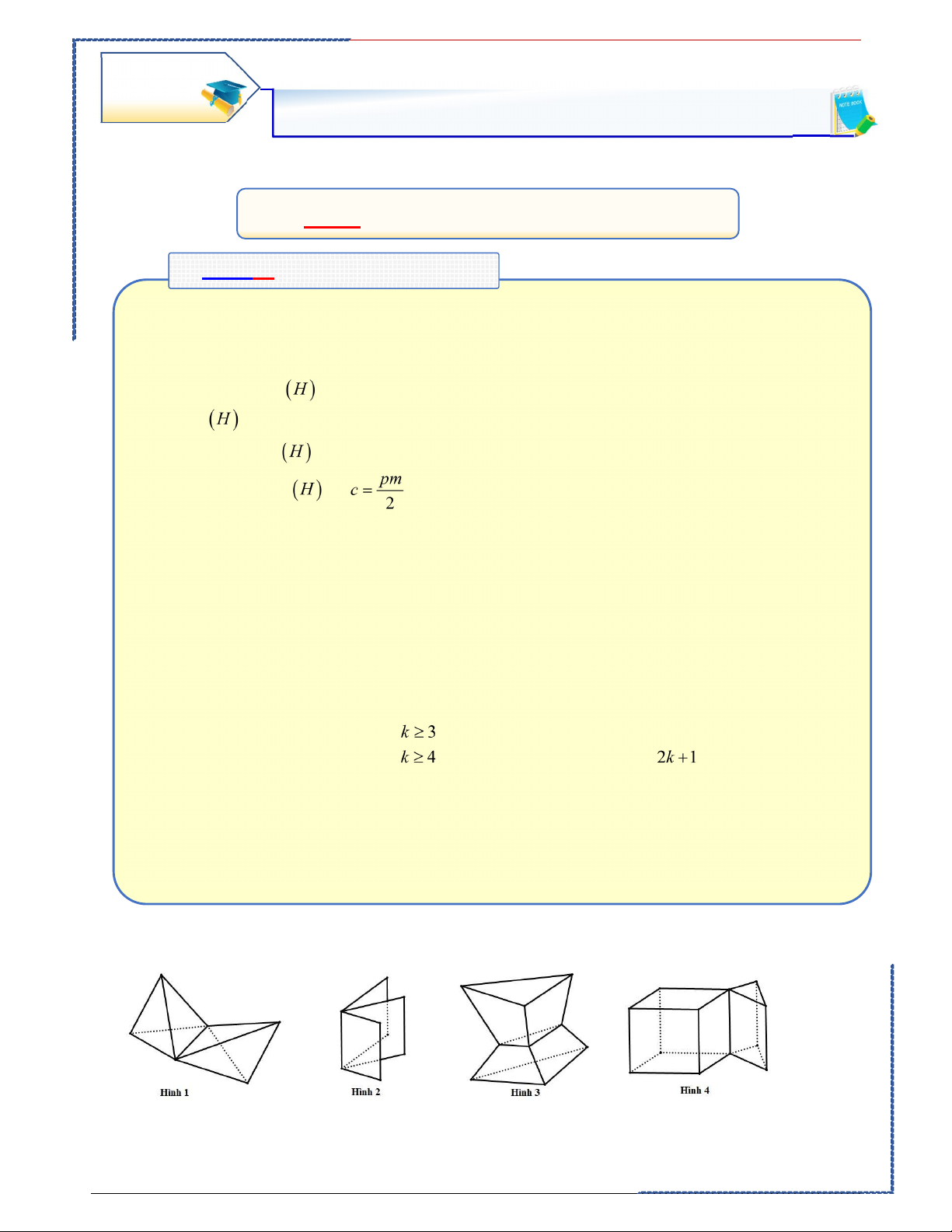
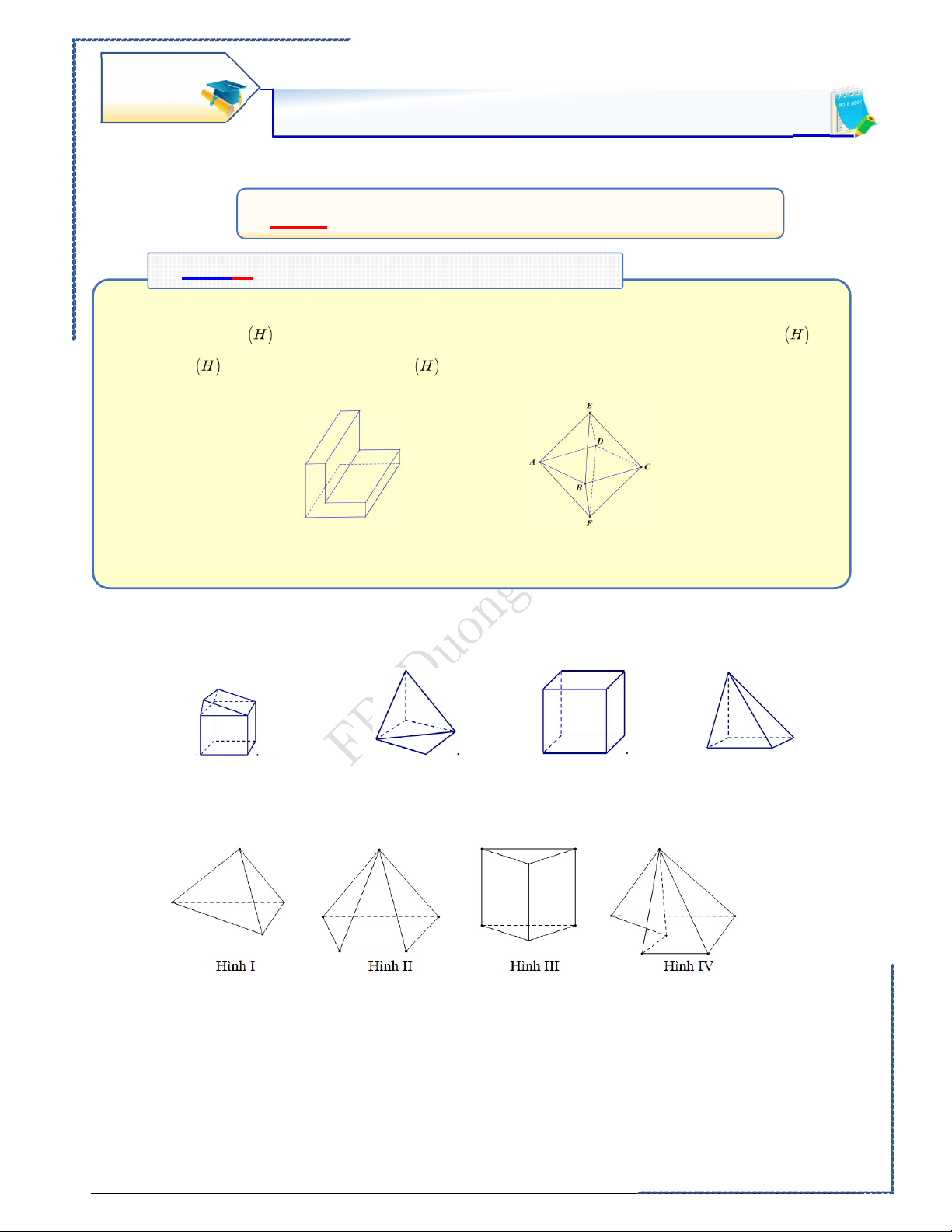
Câu 1: Trong các hình dưới đây, hình nào là hình đa diện? Ⓐ. Hình 4. Ⓑ. Hình 2. Ⓒ. Hình 1. Ⓓ. Hình 3.
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 1
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung Lời giải. Bài học kinh nghiệm Chọn D
 Quan sát kỹ sử dụng các kết quả chính xác để
Hình 4 không phải là hình đa diện vì có một cạnh là cạnh chung của 4 đa giác, loại A
Hình 2 không phải là hình đa diện vì có một cạnh là cạnh chung của  Hai đa giác phân biệt chỉ 3 đa giác, loại B
có thể hoặc không có điểm
chung, hoặc chỉ có một đỉnh
Hình 1 không phải là hình đa diện vì có một cạnh là cạnh chung của chung, hoặc chỉ có một cạnh 4 đa giác, loại C chung.
Hình 3 là hình đa diện vì nó thỏa mãn khái niệm hình đa diện.
 Mỗi cạnh của đa giác nào
(Hình đa diện là hình gồm hữu hạn các đa giác phẳng thỏa mãn hai cũng là cạnh chung của tính chất: đúng hai đa giác).
Câu 2: Trong các mệnh đề sau, mệnh đề nào sai?
Ⓐ. Tồn tại một hình đa diện có số đỉnh bằng số mặt .
Ⓑ. Tồn tại một hình đa diện có số cạnh gấp đôi số mặt.
Ⓒ. Số đỉnh của một hình đa diện bất kì luôn lớn hơn hoặc bằng 4.
Ⓓ. Tồn tại một hình đa diện có số cạnh bằng số mặt. Lời giải. Bài học kinh nghiệm Chọn D
 Quan sát kỹ sử dụng các
Ⓐ. Đúng vì tồn tại hình tứ diện. kết quả chính xác để
Ⓑ. Đúng vì tồn tại hình lập phương. Ⓒ. Đúng. Ⓓ. Sai.
Câu 3: Mỗi cạnh của hình đa diện là cạnh chung của đúng Ⓐ. năm mặt. Ⓑ. ba mặt. Ⓒ. bốn mặt. Ⓓ. hai mặt. Lời giải. Bài học kinh nghiệm
 Quan sát kỹ sử dụng các kết quả chính xác để  Chọn D
Trong một đa diện, mỗi cạnh nào cũng là cạnh chung của đúng hai mặt.
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 2
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
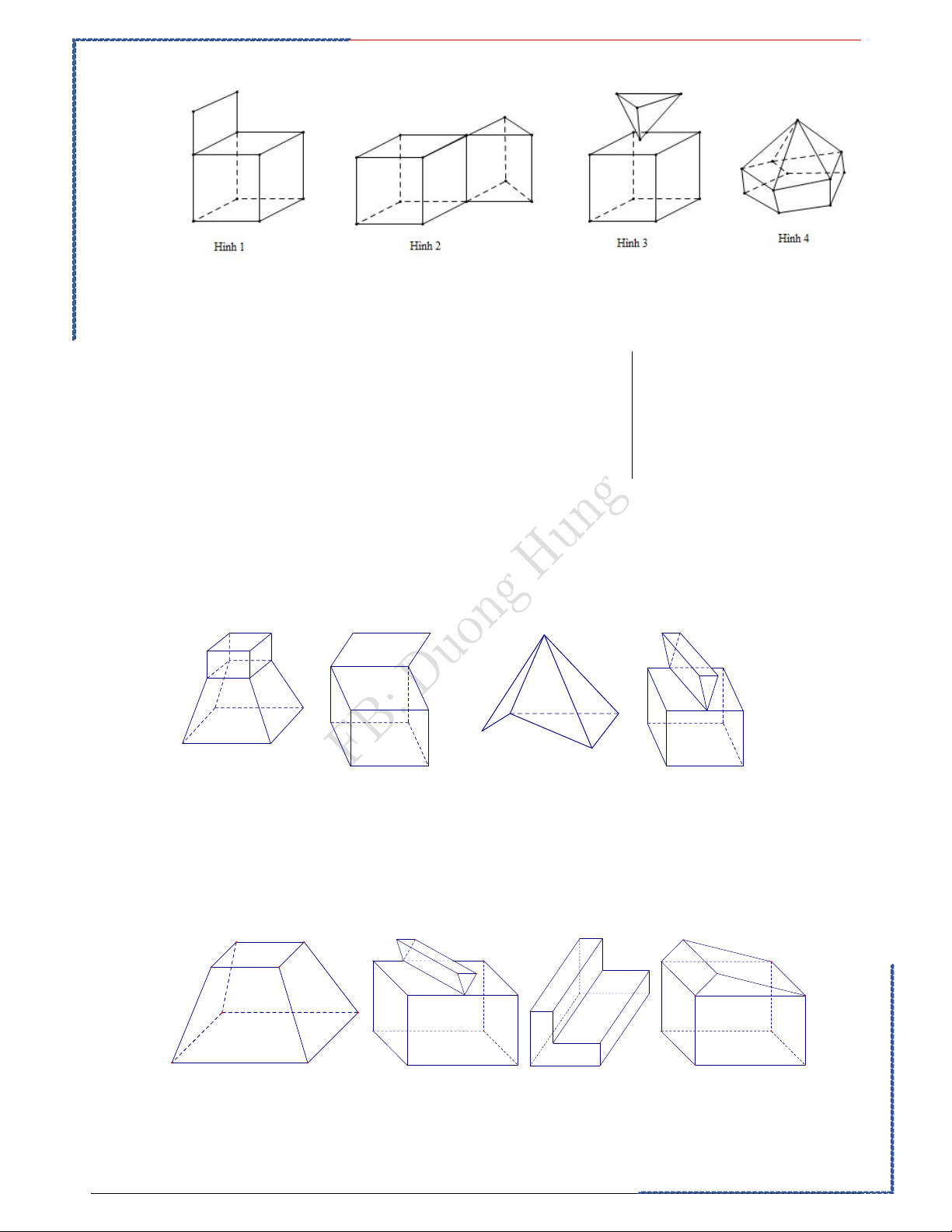
Câu 4: Hình nào dưới đây là hình đa diện? Ⓐ. Hình 3. Ⓑ. Hình 1. Ⓒ. Hình 2. Ⓓ. Hình 4. Lời giải. Bài học kinh nghiệm  Quan sát Chọn D
Hình 4 thỏa mãn, loại trừ hình 1,2,3 khá dễ.
B - Bài tập rèn luyện:
Câu 1: Hình nào trong các hình sau không phải là hình đa diện? Ⓐ. Hình chóp. Ⓑ. Hình vuông.
Ⓒ. Hình lập phương. Ⓓ. Hình lăng trụ. Câu 2: Cho các hình sau: Hình 1 Hình 2 Hình 3 Hình 4
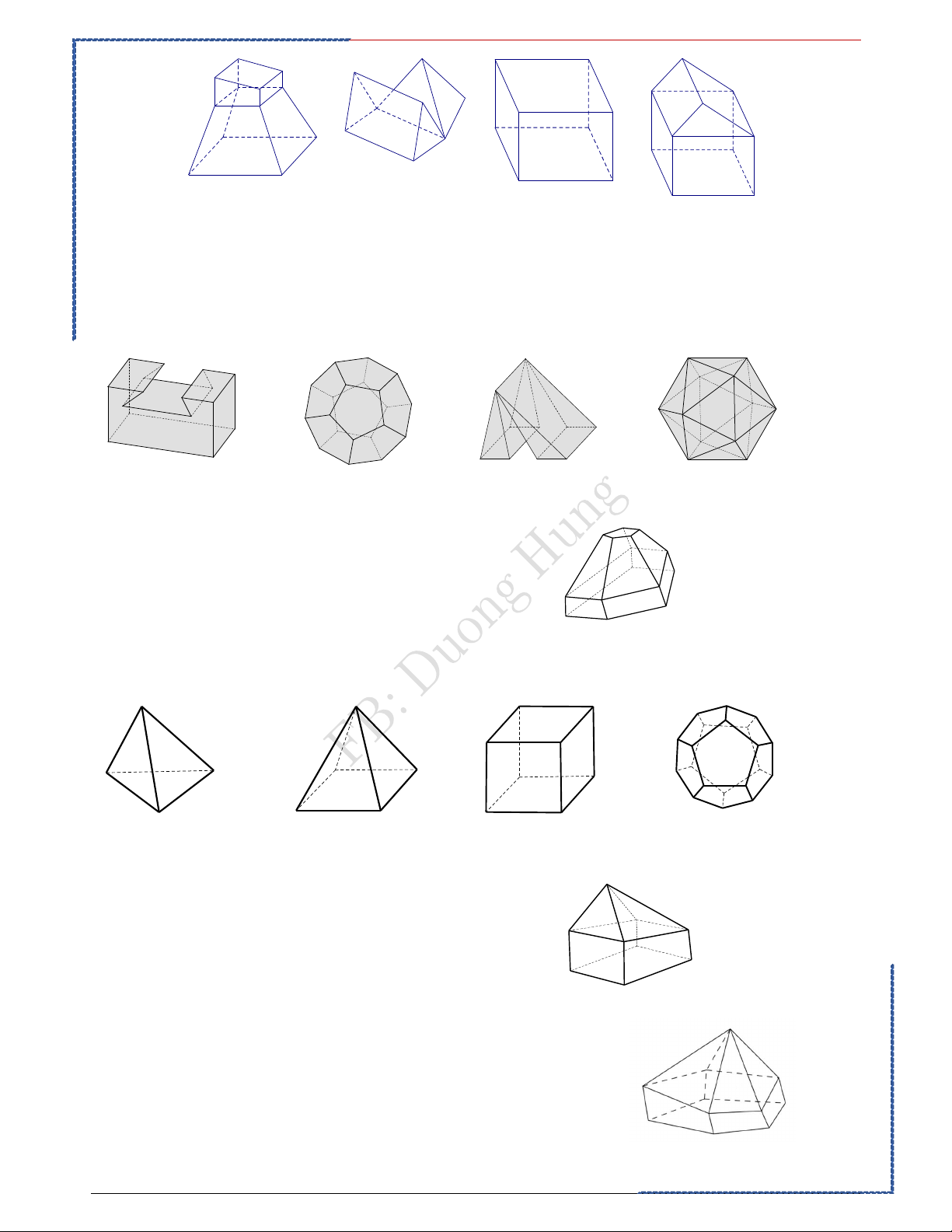
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), hình đa diện là Ⓐ. Hình 1. Ⓑ. Hình 2. Ⓒ. Hình 3. Ⓓ. Hình 4.
Câu 3: Cho các hình khối sau: (a) (b) (c) (d)
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), số đa diện lồi là Ⓐ. 1. Ⓑ. 2 . Ⓒ. 3 . Ⓓ. 4 . Câu 4: Cho các hình sau:
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 3
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung Hình 1 Hình 2 Hình 3 Hình 4
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), số hình đa diện là Ⓐ. 1 . Ⓑ. 2 . Ⓒ. 3. Ⓓ. 4 .
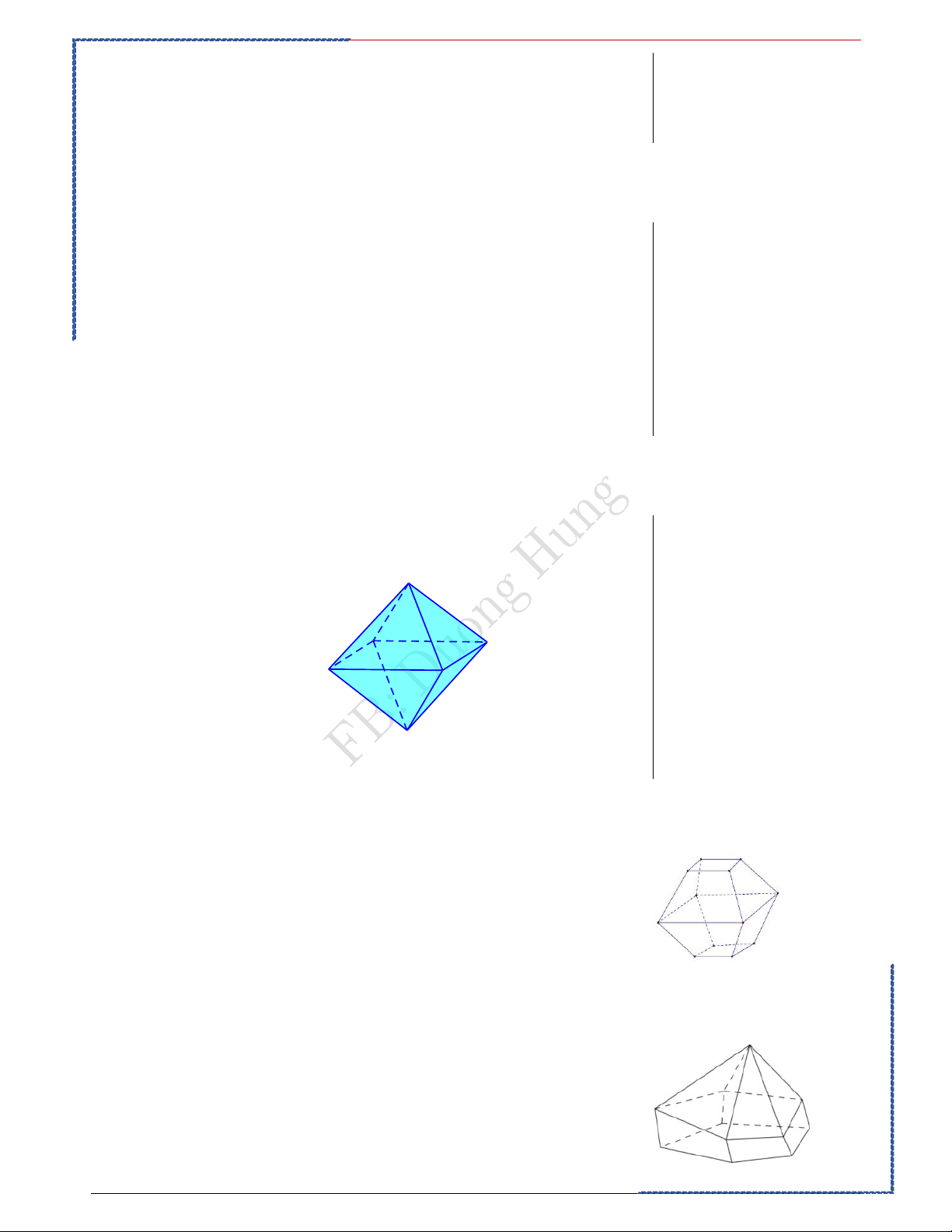
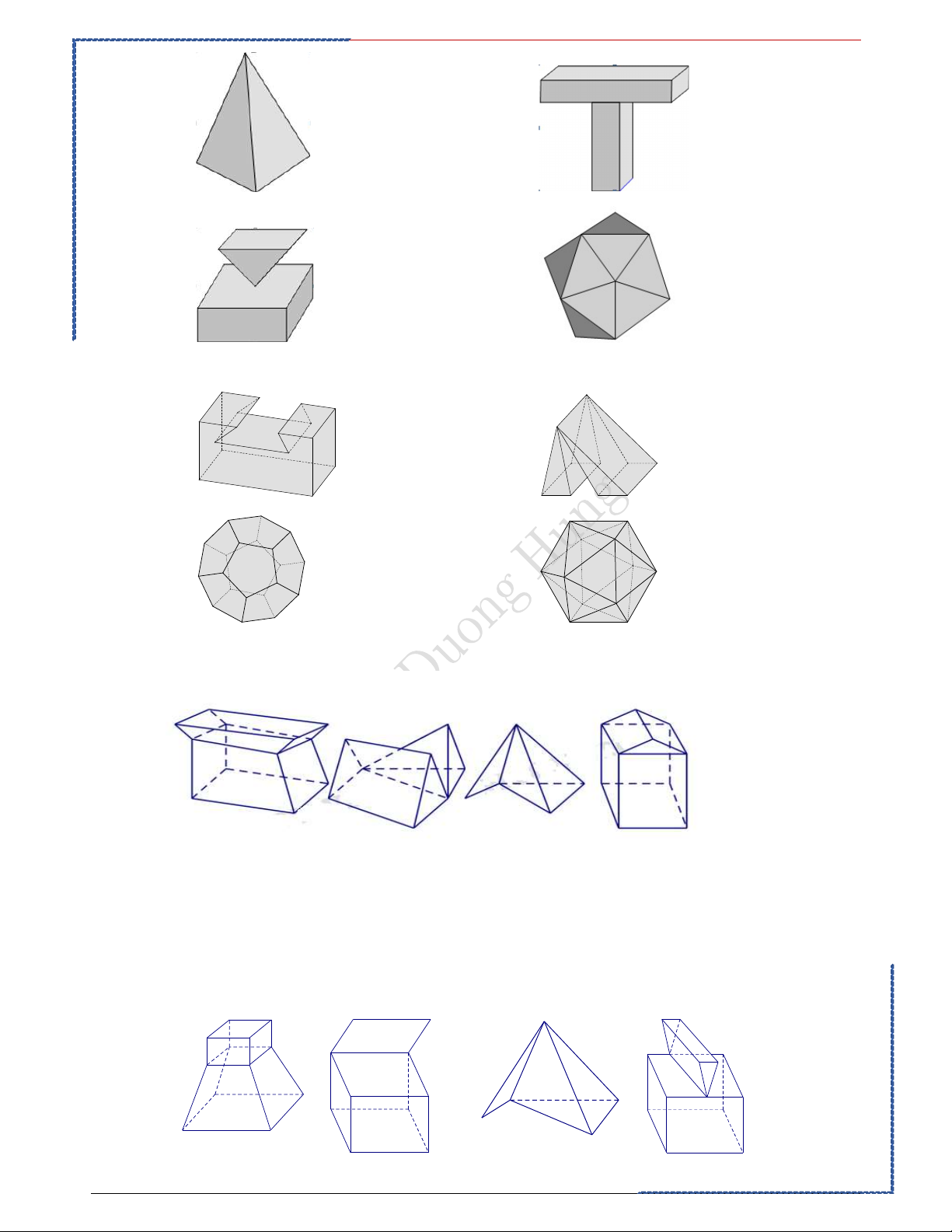
Câu 5: Vật thể nào trong các vật thể sau không phải là khối đa diện? Ⓐ. Ⓑ. Ⓒ. Ⓓ. Câu 6:
Hình đa diện trong hình vẽ bên có bao nhiêu mặt? Ⓐ. 11. Ⓑ. 12. Ⓒ. 13. Ⓓ. 14.
Câu 7: Khối đa diện nào sau đây có số mặt nhỏ nhất?
Ⓐ. Khối tứ diện đều. Ⓑ. Khối chóp tứ giác. Ⓒ. Khối lập phương. Ⓓ. Khối 12 mặt đều.
Câu 8: Hình đa diện trong hình vẽ bên có bao nhiêu cạnh? Ⓐ. 8. Ⓑ. 9. Ⓒ. 12. . Ⓓ. 16.
Câu 9: Hình đa diện trong hình vẽ bên có bao nhiêu mặt? Ⓐ. 6. Ⓑ. 10 . Ⓒ. 12 . Ⓓ. 11
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 4
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
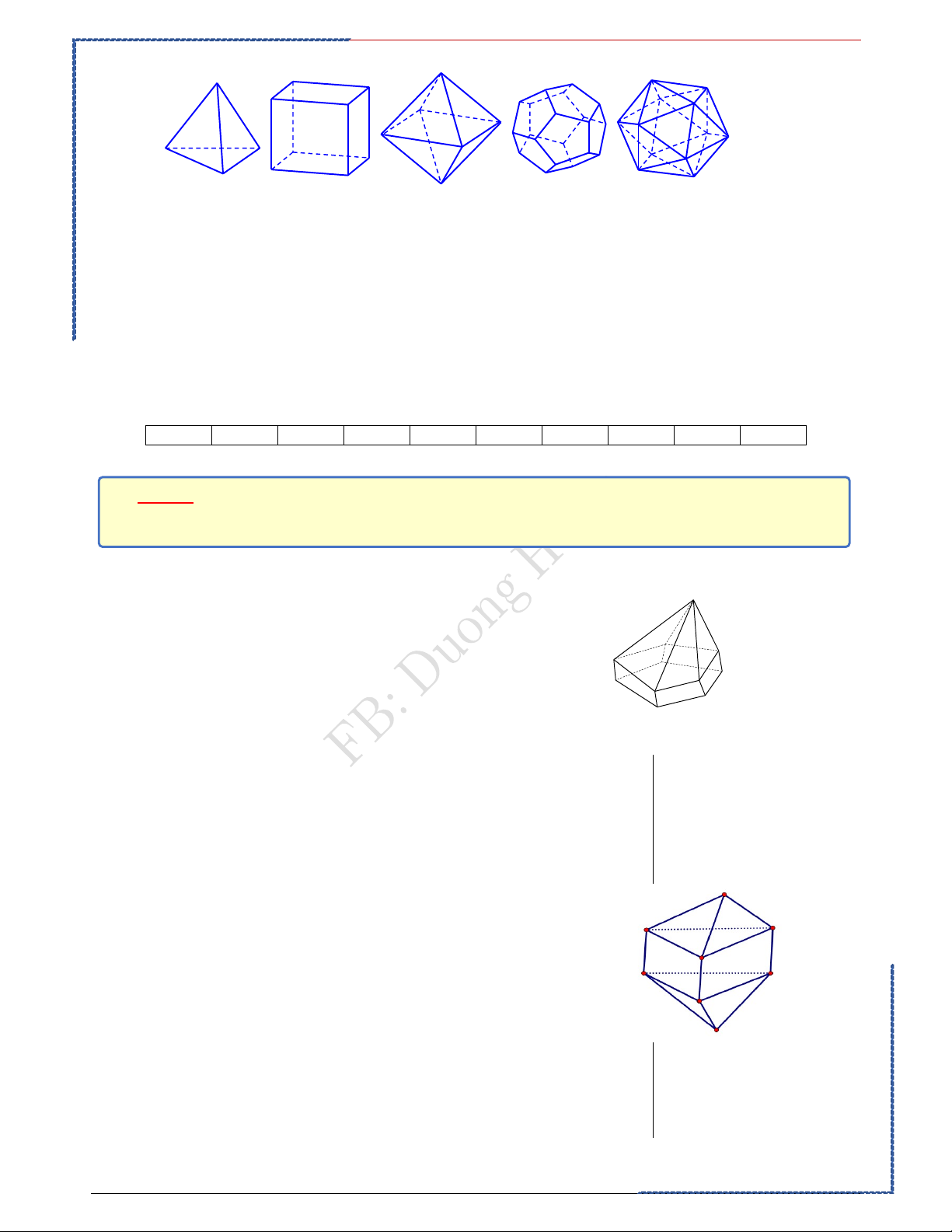
Câu 10: Trong không gian chỉ có 5 loại khối đa diện đều như hình vẽ
Khối tứ diện đều Khối lập phương Bát diện đều Hình 12 mặt đều Hình 20 mặt đều
Mệnh đề nào sau đây đúng?
Ⓐ. Mọi khối đa diện đều có số mặt là những số chia hết cho 4.
Ⓑ. Khối lập phương và khối bát diện đều có cùng số cạnh.
Ⓒ. Khối tứ diện đều và khối bát diện đều có 1 tâm đối xứng.
Ⓓ. Khối mười hai mặt đều và khối hai mươi mặt đều có cùng số đỉnh. BẢNG ĐÁP ÁN 1.B 2.A 3.B 4.C 5.C 6.B 7.A 8.D 9.D 10.B
_ Dạng 2. Xác định số đỉnh, cạnh, mặt bên của một khối đa diện.
-Phương pháp: Sử dụng các kết quả thừa nhận A - Bài tập minh họa:
Câu 1: Hình đa diện trong hình vẽ có bao nhiêu mặt? Ⓐ. 12 . Ⓑ. 10. Ⓒ. 6. Ⓓ. 11. Lời giải. Bài học kinh nghiệm Chọn D  Quan sát
 Dựa vào hình ta đếm được 11 mặt
Câu 2: Tìm số mặt của hình đa diện ở hình vẽ bên? Ⓐ. 11. Ⓑ. 10. Ⓒ. 12. Ⓓ. 9. Lời giải. Bài học kinh nghiệm Chọn D  Quan sát
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 5
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
 Hình đa diện trên có 9 mặt gồm các mặt là
 ABD;BDC; ADC;ABFE;BFGC; 
ACGE;HFE ;HFG;EHG.
Câu 3: Hình chóp có 50 cạnh thì có bao nhiêu mặt? Ⓐ. 26 . Ⓑ. 21. Ⓒ. 25 . Ⓓ. 49 . Lời giải. Bài học kinh nghiệm Chọn A  Công thức
 Gọi n là số cạnh của đa giác đáy hình chóp đã cho. Ta có
 Số cạnh đáy bằng số cạnh bên nên tổng số cạnh của hình chóp bằng 2n .
 Từ giả thiết, suy ra 2n  50  n  25 .
 Vậy số tổng số mặt của hình chóp là: 26 .
Câu 4: Hình bát diện đều có bao nhiêu cạnh ? Ⓐ. 16. Ⓑ. 12. Ⓒ. 10 . Ⓓ. 14. Lời giải. Bài học kinh nghiệm Chọn B  Quan sát
 Hình bát diện đều có 6 đỉnh, 8 mặt, 12 cạnh
B - Bài tập rèn luyện:
Câu 1: Hình đa diện trong hình vẽ bên có bao nhiều mặt? Ⓐ. 12. Ⓑ. 8 . Ⓒ. 11. Ⓓ. 10.
Câu 2: Hỏi hình đa diện ở hình vẽ bên có bao nhiêu mặt? Ⓐ. m 10. Ⓑ. m 12. Ⓒ. m 11. Ⓓ. m  20 .
Câu 3: Khối lăng trụ ngũ giác có bao nhiêu mặt?
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 6
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung Ⓐ. 9mặt. Ⓑ. 7 mặt. Ⓒ. 5mặt. Ⓓ. 6 mặt.
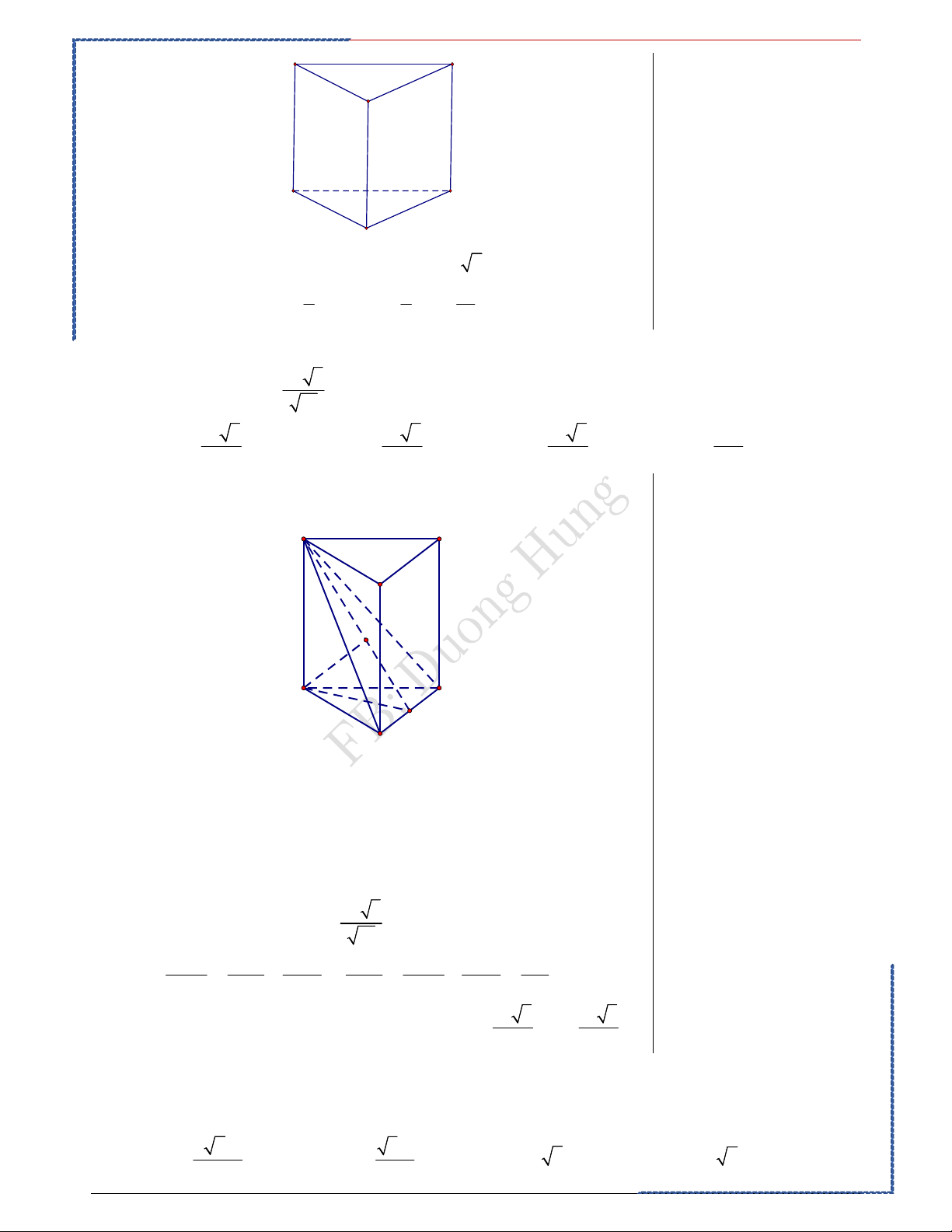
Câu 4: Số mặt phẳng cách đều tất cả các đỉnh của một hình lăng trụ tam giác là Ⓐ. 2 . Ⓑ. 3. Ⓒ. 4 . Ⓓ. 1.
Câu 5: Khối tám mặt đều có tất cả bao nhiêu đỉnh? Ⓐ. 6 . Ⓑ. 8. Ⓒ. 12. Ⓓ. 16.
Câu 6: Hình lăng trụ lục giác có bao nhiêu mặt? Ⓐ. 8. Ⓑ. 7 . Ⓒ. 9. Ⓓ. 6 .
Câu 7: Mỗi cạnh của một hình đa diện là cạnh chung của đúng n mặt của hình đa diện đó.
Mệnh đề nào dưới đây đúng? Ⓐ. n  2. Ⓑ. n  5. Ⓒ. n  3. Ⓓ. n  4.
Câu 8: Một hình lăng trụ có đúng 11 cạnh bên thì hình lăng trụ đó có tất cả bao nhiêu cạnh? Ⓐ. 33. Ⓑ. 31. Ⓒ. 30. Ⓓ. 22.
Câu 9: Mỗi đỉnh của hình đa diện thuộc ít nhất bao nhiêu mặt? Ⓐ. 4. Ⓑ. 5. Ⓒ. 2. Ⓓ. 3.
Câu 10: Hình lăng trụ lục giác có bao nhiêu mặt? Ⓐ. 8. Ⓑ. 7 . Ⓒ. 9. Ⓓ. 6 .
Câu 11: Khối chóp ngũ giác có số cạnh là Ⓐ. 20 . Ⓑ. 15 . Ⓒ. 5. Ⓓ. 10.
Câu 12: Cho một hình đa diện. Khẳng định nào sau đây là sai?
Ⓐ. Mỗi cạnh là cạnh chung của ít nhất ba mặt.
Ⓑ. Mỗi đỉnh là đỉnh chung của ít nhất ba cạnh.
Ⓒ. Mỗi đỉnh là đỉnh chung của ít nhất ba mặt.
Ⓓ. Mỗi mặt có ít nhất ba cạnh.
Câu 13: Mỗi hình đa diện có ít nhất Ⓐ. 3cạnh. Ⓑ. 6 cạnh. Ⓒ. 5 cạnh. Ⓓ. 4 cạnh.
Câu 14: Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất bao nhiêu mặt? Ⓐ. 3. Ⓑ. 1. Ⓒ. 4. Ⓓ. 2
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 7
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
Câu 15: Hình bát diện đều có bao nhiêu cạnh? Ⓐ. 8 . Ⓑ. 24. Ⓒ. 16. Ⓓ. 12.
Câu 16: Số đỉnh của hình đa diện dưới đây là Ⓐ. 8. Ⓑ. 9. Ⓒ. 10. Ⓓ. 11.
Câu 17: Một hình lăng trụ có đúng 11 cạnh bên thì hình lăng trụ đó có tất cả bao nhiêu cạnh? Ⓐ. 31. Ⓑ. 30. Ⓒ. 22 . Ⓓ. 33.
Câu 18: Một hình đa diện có ít nhất bao nhiêu đỉnh? Ⓐ. 6 . Ⓑ. 3. Ⓒ. 5. Ⓓ. 4.
Câu 19: Hình đa diện trong hình vẽ dưới đây có bao nhiêu mặt? Ⓐ. 4. Ⓑ. 10. Ⓒ. 8. Ⓓ. 9.
Câu 20: Cho hình chóp có 20 cạnh. Số mặt của hình chóp đó là Ⓐ. 12. Ⓑ. 10. Ⓒ. 11. Ⓓ. 20 . BẢNG ĐÁP ÁN THAM KHẢO 1.D 2.C 3.B 4.C 5.A 6.A 7.A 8.A 9.D 10.A 11.D 12.A 13.B 14.A 15.D 16.C 17.D 18.D 19.C 20.C
_ Dạng 3. Mặt phẳng đối xứng.
-Phương pháp: Do tính chất đối xứng nhau, nên cứ đi từ trung điểm các cạnh ra mà tìm. Đảm
bảo rằng nếu chọn 1 mặt phẳng đối xứng nào thì các điểm còn dư phải chia đều về 2 phía. A - Bài tập minh họa:
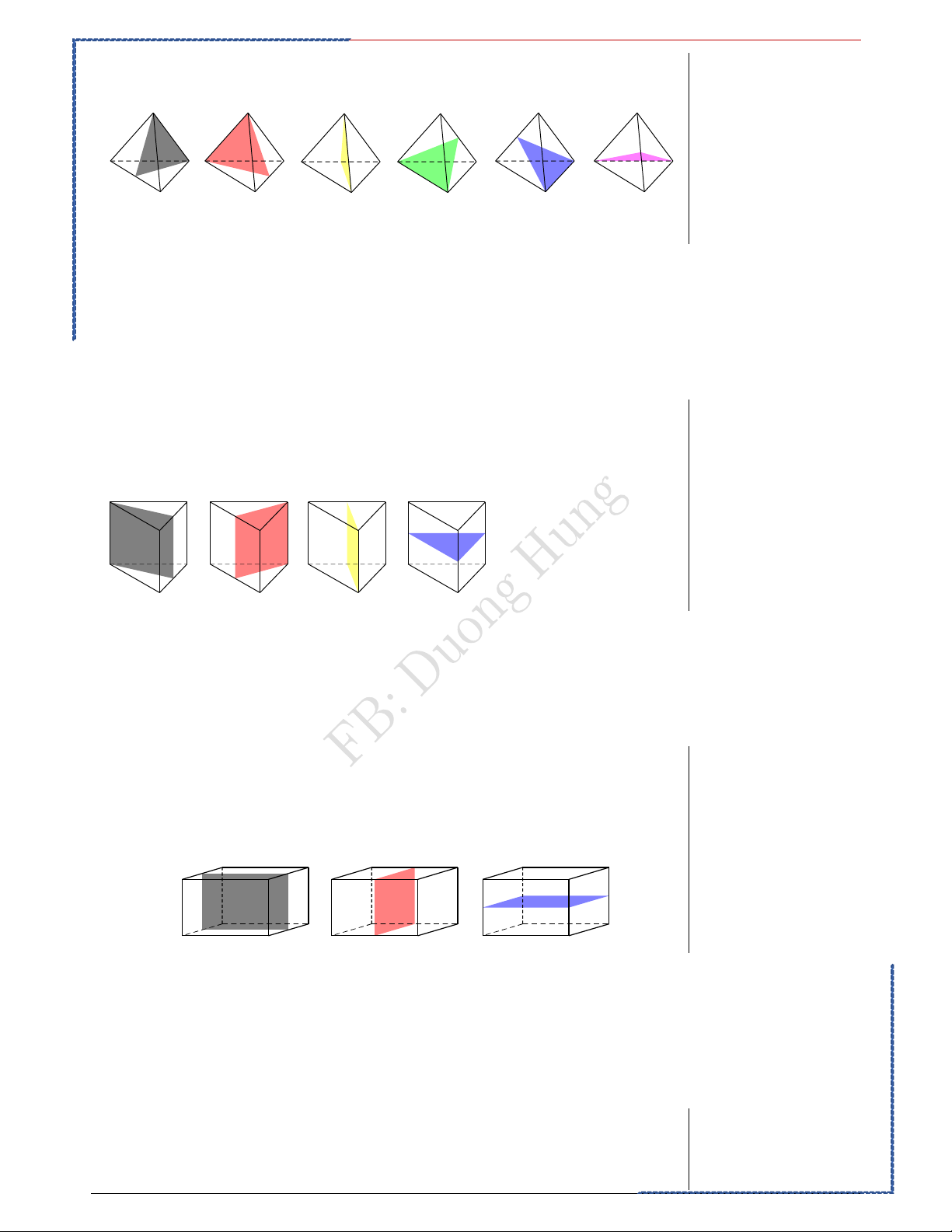
Câu 1: Số mặt phẳng đối xứng của hình tứ diện đều là Ⓐ. 4 mặt phẳng. Ⓑ. 6 mặt phẳng. Ⓒ. 8 mặt phẳng. Ⓓ. 10 mặt phẳng. Lời giải. Bài học kinh nghiệm Chọn B  Quan sát cẩn thận
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 8
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
Các mặt phẳng đối xứng của hình tứ diện đều là các mặt phẳng chứa một
cạnh và qua trung điểm cạnh đối diện.
Vậy hình tứ diện đều có 6 mặt phẳng đối xứng
Câu 2: Hình lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng? Ⓐ. 4 mặt phẳng. Ⓑ. 1 mặt phẳng. Ⓒ. 2 mặt phẳng. Ⓓ. 3 mặt phẳng. Lời giải. Bài học kinh nghiệm Chọn A  Quan sát cẩn thận
Hình lăng trụ tam giác đều có 4 mặt phẳng đối xứng (hình vẽ bên dưới).
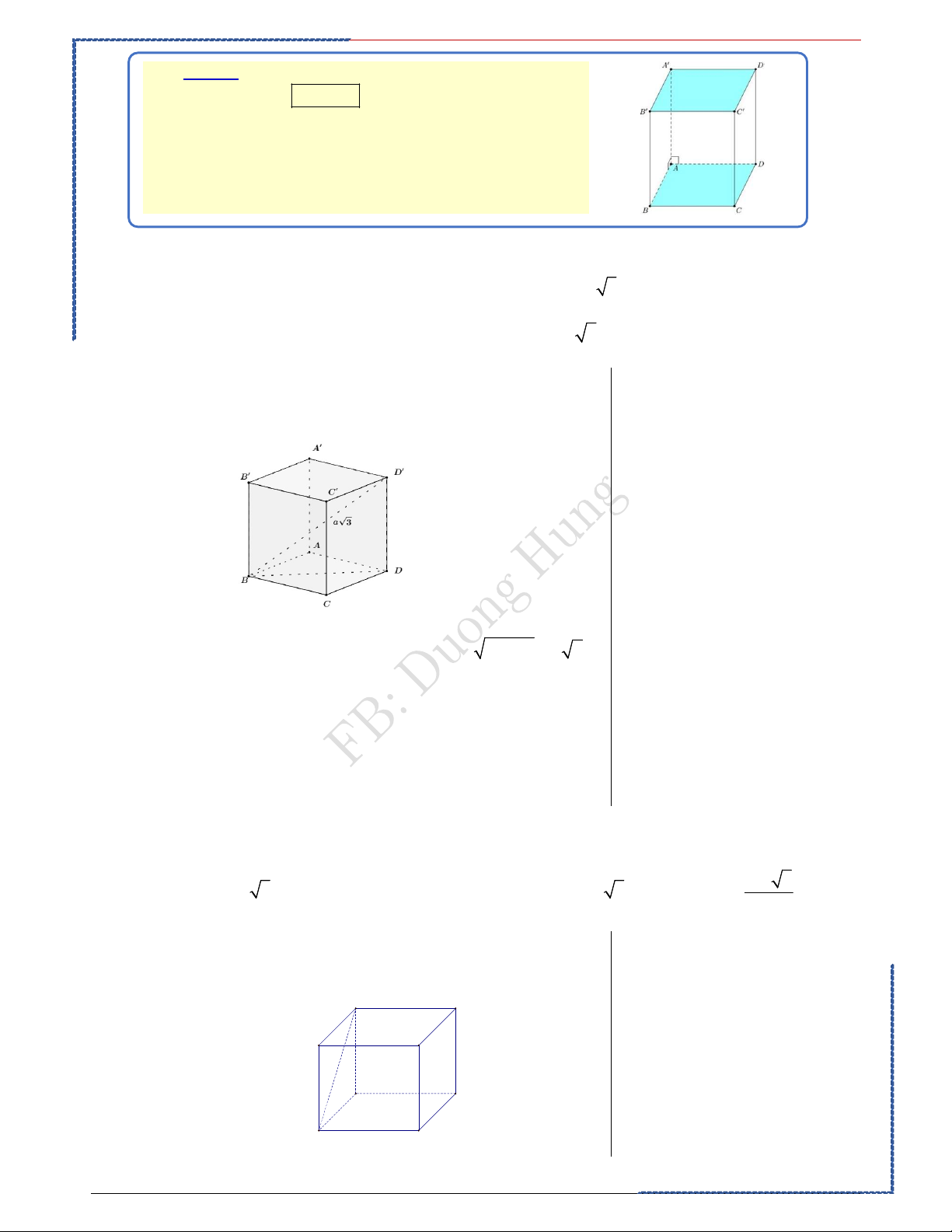
Câu 3: Hình hộp chữ nhật có ba kích thước đôi một khác nhau có bao nhiêu mặt phẳng đối xứng? Ⓐ. 4 mặt phẳng. Ⓑ. 6 mặt phẳng. Ⓒ. 9 mặt phẳng. Ⓓ. 3 mặt phẳng. Lời giải. Bài học kinh nghiệm Chọn D Quan sát cẩn thận
Hình hộp chữ nhật (không là hình lập phương) có các mặt phẳng đối xứng là
các mặt các mặt phẳng trung trực của các cặp cạnh đối.
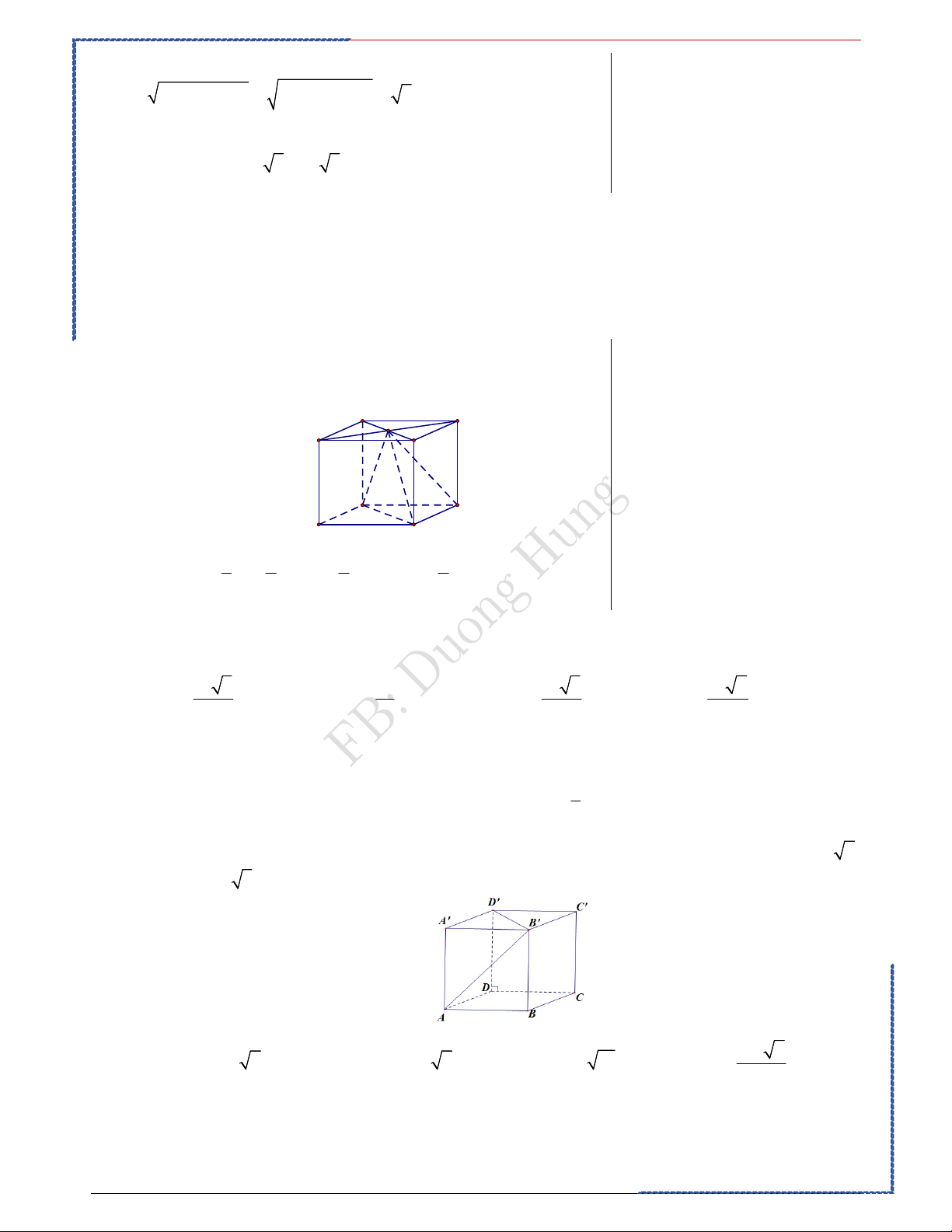
Câu 4: Một hình hộp đứng có đáy là hình thoi (không phải là hình vuông) có bao nhiêu mặt phẳng đối xứng? Ⓐ. 4 mặt phẳng. Ⓑ. 1 mặt phẳng. Ⓒ. 2 mặt phẳng. Ⓓ. 3 mặt phẳng. Lời giải. Bài học kinh nghiệm Chọn D  Quan sát cẩn thận
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 9
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
Hình hộp đứng có đáy là hình thoi (không phải là hình chữ nhật) có 3 mặt
phẳng đối xứng bao gồm:
2 mặt phẳng chứa đường chéo của đáy và vuông góc với đáy.
Một mặt phẳng là mặt phẳng trung trực của cạnh bên.
B - Bài tập rèn luyện:
Câu 1: Số mặt phẳng đối xứng của hình bát diện đều là Ⓐ. 4 . Ⓑ. 6.. Ⓒ. 12.. Ⓓ. 9.
Câu 2: Hình đa diện nào dưới đây không có tâm đối xứng?
Ⓐ. Tứ diện đều. Ⓑ. Bát diện đều. Ⓒ. Hình lập phương.
Ⓓ. Lăng trụ lục giác đều.
Câu 3: Gọi n , n , n lần lượt là số trục đối xứng của khối tứ diện đều, khối chóp tứ giác đều và khối 1 2 3
lập phương. Mệnh đề nào sau đây là đúng? Ⓐ. n 0, n 0, n 6. Ⓑ. n 0, n 1, n 9. 1 2 3 1 2 3 Ⓒ. n 3, n 1, n 9. Ⓓ. n 0, n 1, n 3. 1 2 3 1 2 3
Câu 4: Hình chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng? Ⓐ. 4 mặt phẳng. Ⓑ. 1 mặt phẳng. Ⓒ. 2 mặt phẳng. Ⓓ. 3 mặt phẳng.
Câu 5: Số mặt phẳng đối xứng của hình tứ diện đều là Ⓐ. 4 mặt phẳng. Ⓑ. 6 mặt phẳng. Ⓒ. 8 mặt phẳng. Ⓓ. 10 mặt phẳng.
Câu 6: Hình lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng? Ⓐ. 4 mặt phẳng. Ⓑ. 1 mặt phẳng. Ⓒ. 2 mặt phẳng. Ⓓ. 3 mặt phẳng.
Câu 7: Hình hộp chữ nhật có ba kích thước đôi một khác nhau có bao nhiêu mặt phẳng đối xứng?
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 10
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung Ⓐ. 4 mặt phẳng. Ⓑ. 6 mặt phẳng. Ⓒ. 9 mặt phẳng. Ⓓ. 3 mặt phẳng.
Câu 8: Một hình hộp đứng có đáy là hình thoi (không phải là hình vuông) có bao nhiêu mặt phẳng đối xứng? Ⓐ. 4 mặt phẳng. Ⓑ. 1 mặt phẳng. Ⓒ. 2 mặt phẳng. Ⓓ. 3 mặt phẳng.
Câu 9: Hình lập phương có tất cả bao nhiêu mặt phẳng đối xứng? Ⓐ. 8 mặt phẳng. Ⓑ. 9 mặt phẳng. Ⓒ. 10 mặt phẳng. Ⓓ. 12 mặt phẳng.
Câu 10: Số mặt phẳng đối xứng của hình bát diện đều là: Ⓐ. 4 mặt phẳng. Ⓑ. 9 mặt phẳng. Ⓒ. 6 mặt phẳng. Ⓓ. 12 mặt phẳng. BẢNG ĐÁP ÁN 1.D 2.A 3.C 4.A 5.B 6.A 7.D 8.D 9.B 10.B
_ Dạng 4. Phân chia lắp ghép khối đa diện
-Phương pháp: Sử dụng các kết quả thừa nhận và các tính chất của hình học. . Bài tập minh họa:
Câu 1: Cho khối lập phương ABC . D AB C  D
  . Mặt phẳng  ACC chia khối
lập phương trên thành những khối đa diện nào?
Ⓐ. Hai khối lăng trụ tam giác ABC.A B  C   và BC . D B C  D   .
Ⓑ. Hai khối lăng trụ tam giác ABC.A B  C   và AC . D A C  D  .
Ⓒ. Hai khối chóp tam giác C .ABC và C .ACD .
Ⓓ. Hai khối chóp tứ giác C .ABCD và C .ABB A   . Câu 2: Mặt phẳng  A B
 C chia khối lăng trụ ABC.A B  C   thành hai khối chóp. Ⓐ. A.ABC và . A BCC B   . Ⓑ. . A AB C   và . A BCC B   . Ⓒ. . A A B  C và A .BCC B  . Ⓓ. . A AB C   và A .BCC B   .
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 11
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
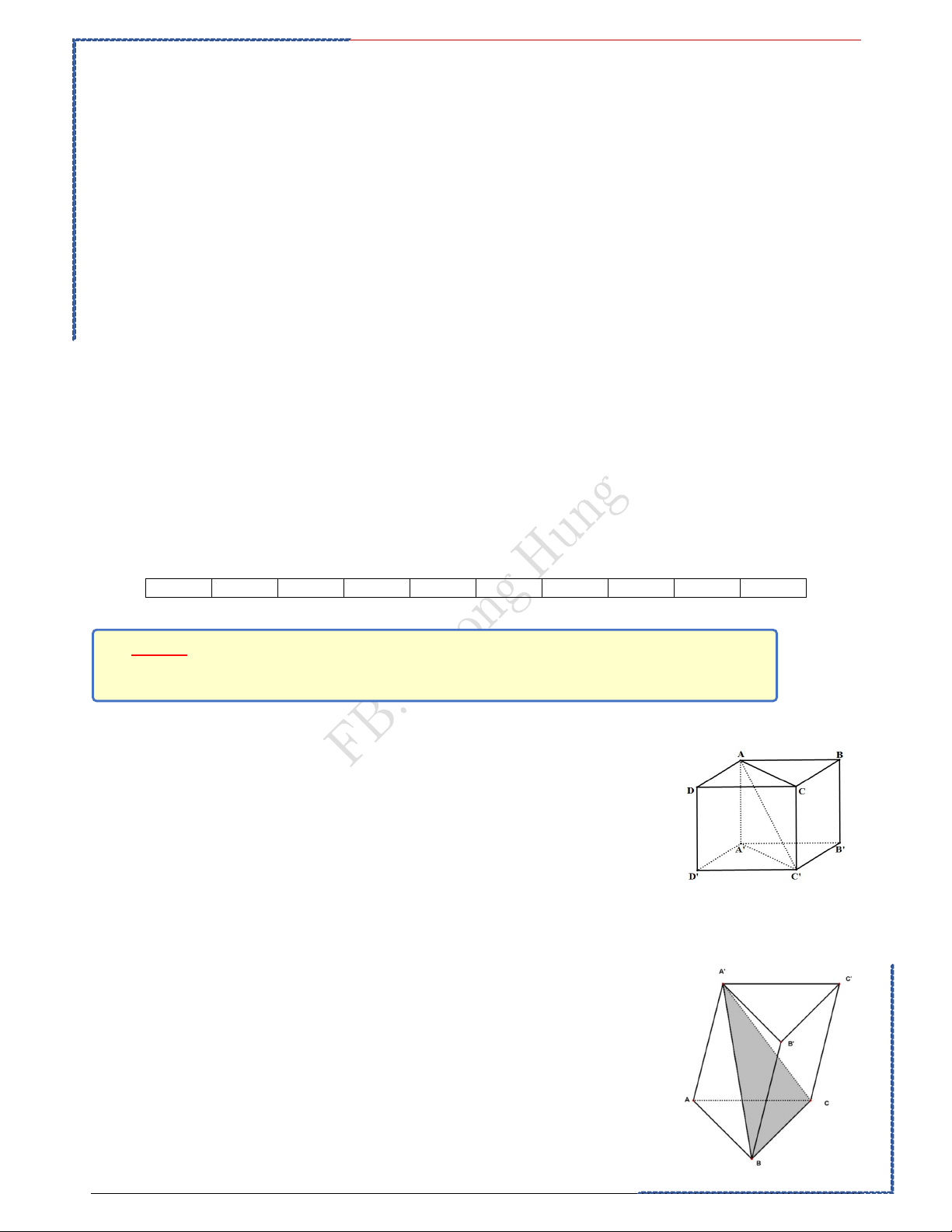
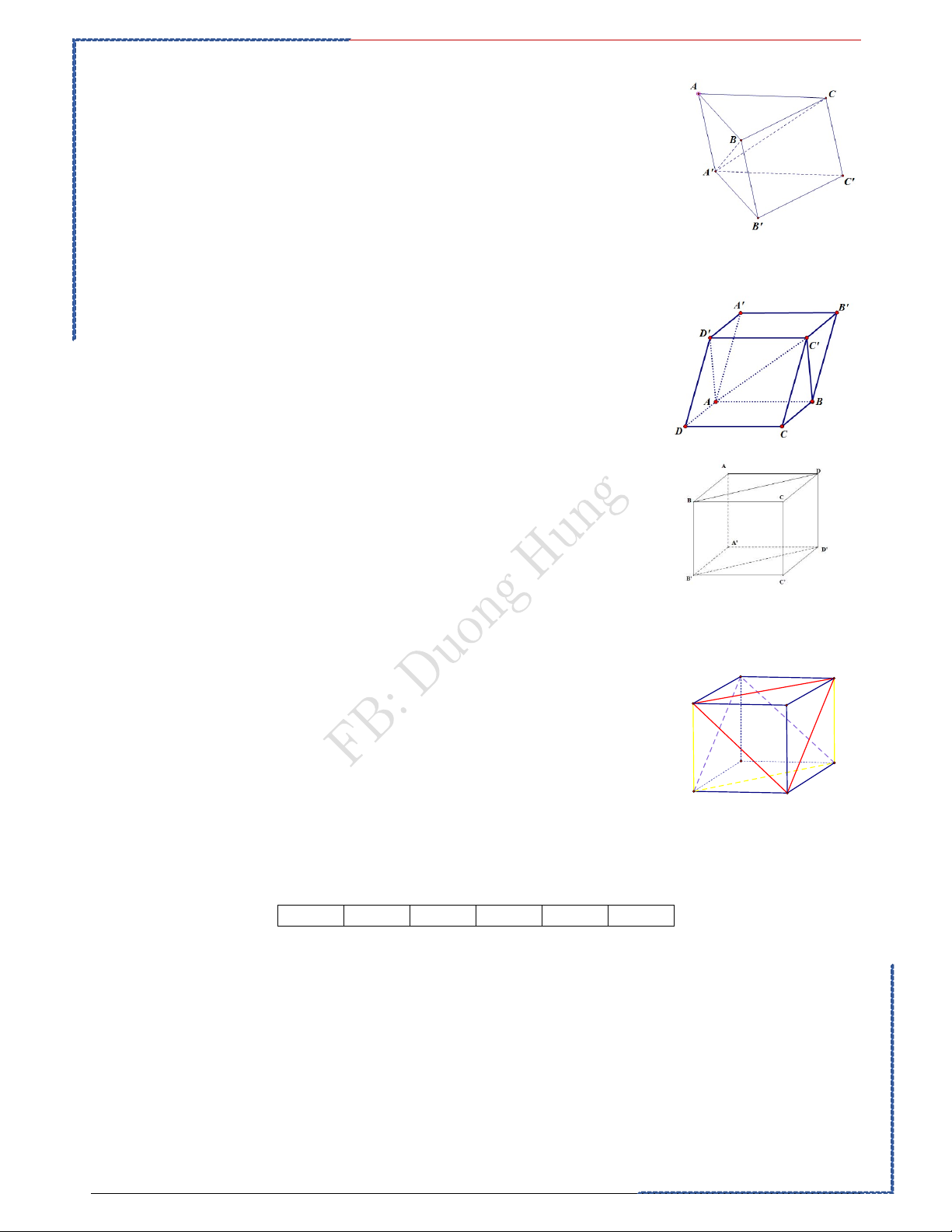
Câu 3: Cho hình lăng trụ ABC.A' B 'C '. Mặt phẳng  A' BC chia khối lăng
trụ đã cho thành các khối đa diện nào?
Ⓐ. Hai khối chóp tam giác.
Ⓑ. Một khối chóp tam giác, một khối chóp tứ giác.
Ⓒ. Một khối chóp tam giác, một khối chóp ngũ giác.
Ⓓ. Hai khối chóp tứ giác.
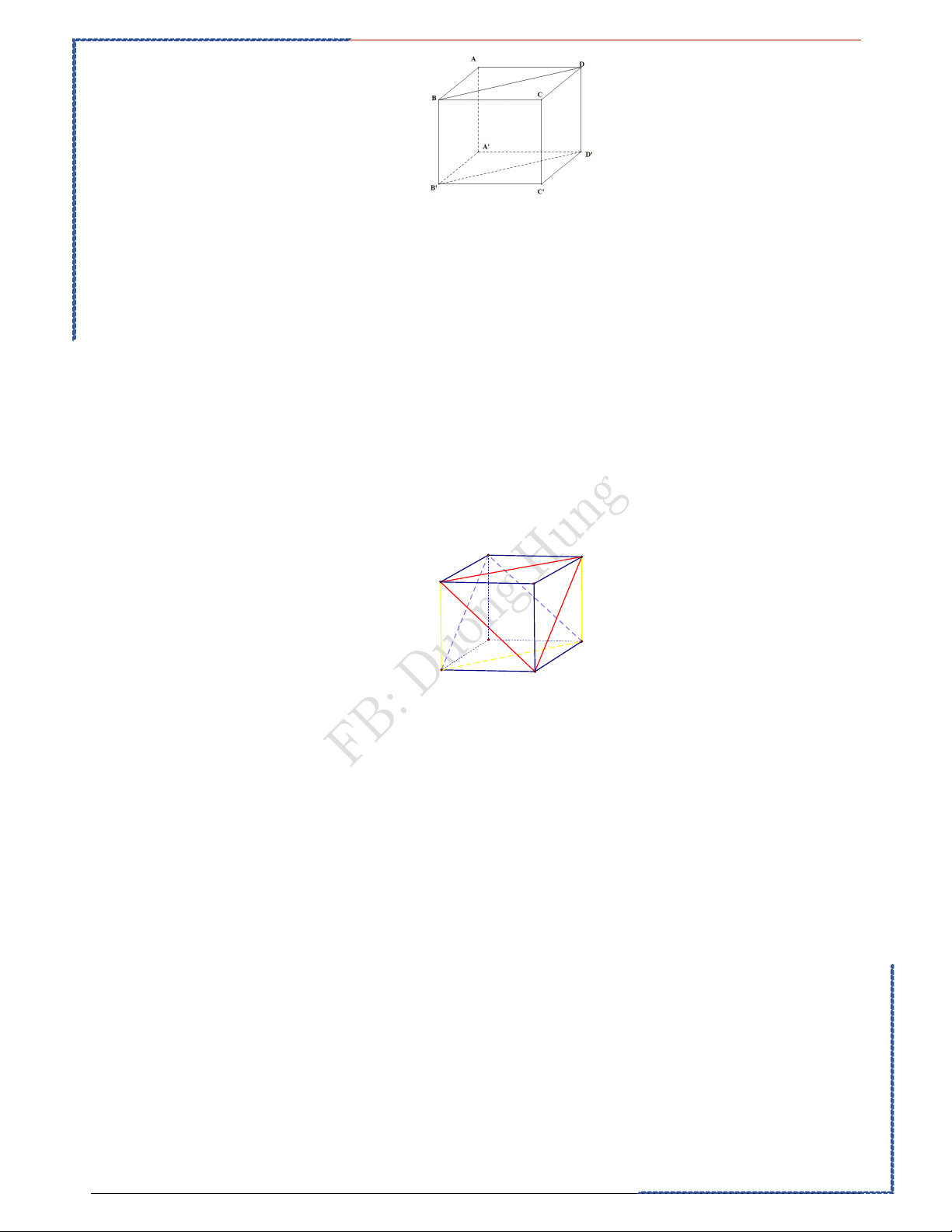
Câu 4: Mặt phẳng nào sau đây chia khối hộp ABC . D A' B 'C ' D ' thành hai khối lăng trụ Ⓐ.  ABC . Ⓑ.  ABC . Ⓒ.  AB C   . Ⓓ.  ABD.
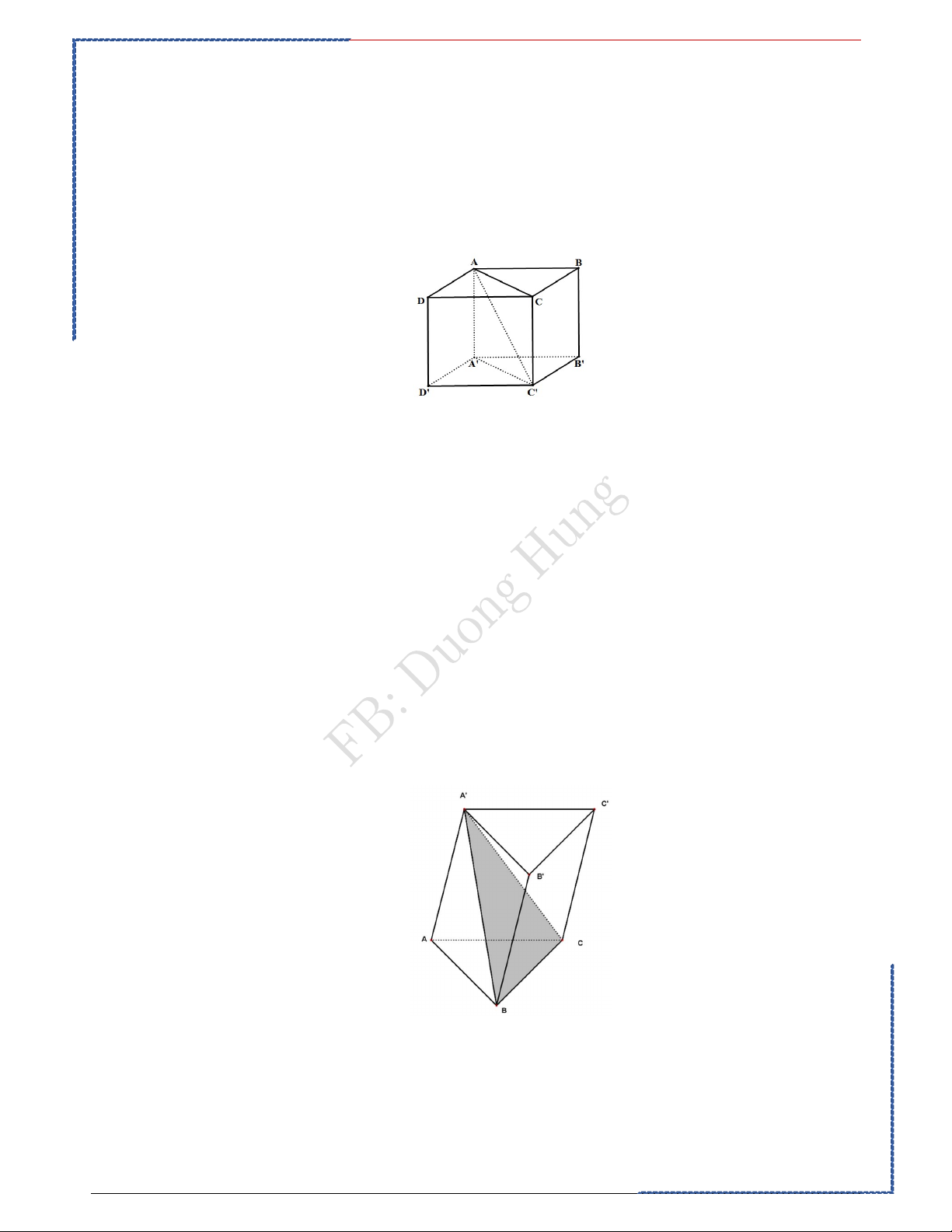
Câu 5: Cho khối lập phương ABC .
D A' B 'C ' D ' . Mặt phẳng (BDD ' B ')
chia khối lập phương thành
Ⓐ. Hai khối lăng trụ tam giác. Ⓑ. Hai khối tứ diện.
Ⓒ. Hai khối lăng trụ tứ giác.
Ⓓ. Hai khối chóp tứ giác.
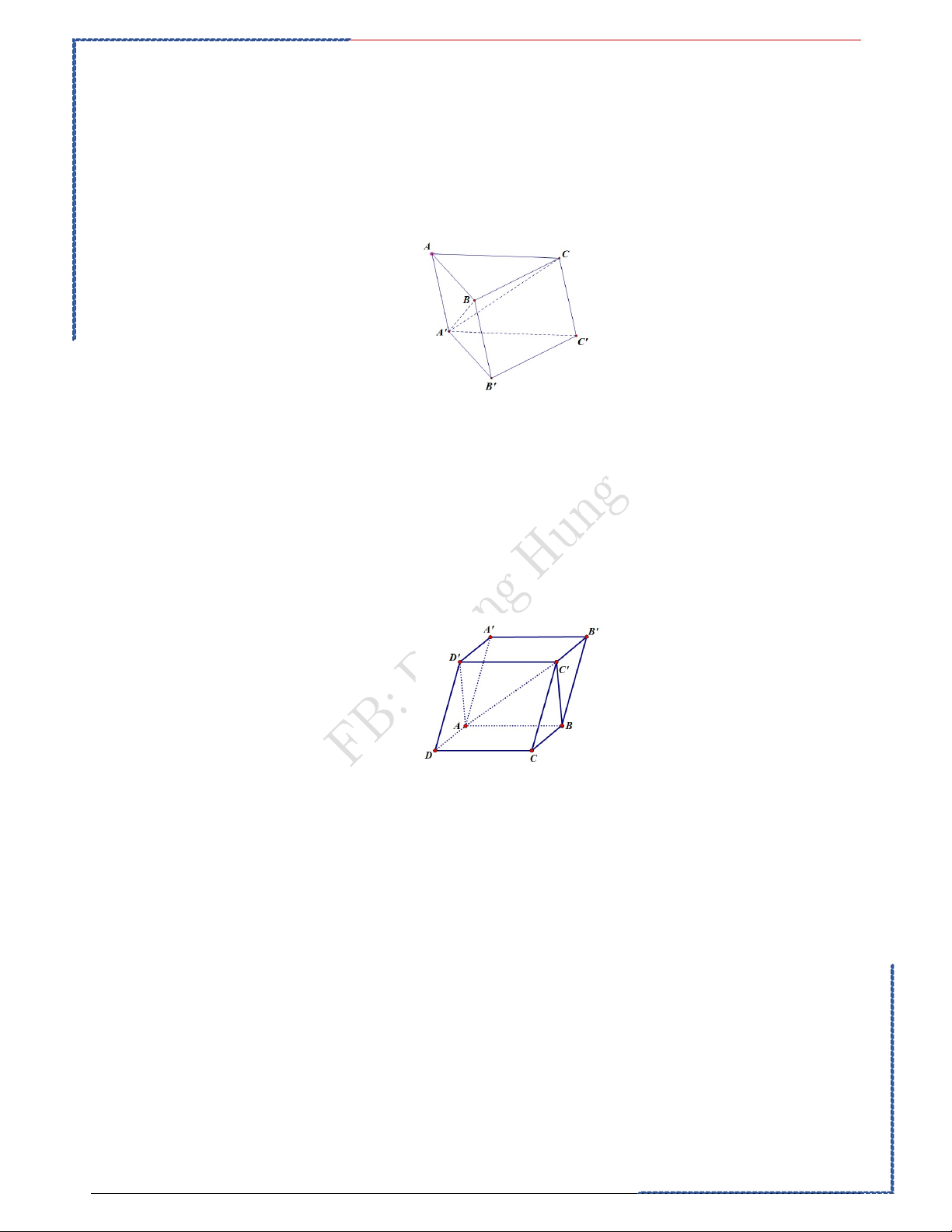
Câu 6: Phân chia khối lập phương ABCDA’B’C’D’ bởi ba mặt phẳng CB ' D ' , A' BD ,
BDB'D' ta được những khối đa diện nào? D' A' C' Ⓐ. B'
Hai khối tứ diện và hai khối chóp tứ giác.
Ⓑ. Hai khối tứ diện và một khối lăng trụ tam giác. A D
Ⓒ. Ba khối tứ diện và một khối lăng trụ tam giác. B C
Ⓓ. Hai khối tứ diện và một khối lăng trụ tứ giác BẢNG ĐÁP ÁN 1.B 2.C 3.B 4.B 5.A 6.A Hướng dẫn giải
Câu 1: Cho khối lập phương ABC . D AB C  D
  . Mặt phẳng  ACC chia khối lập phương trên thành
những khối đa diện nào?
Ⓐ. Hai khối lăng trụ tam giác ABC.A B  C   và BC . D B C  D   .
Ⓑ. Hai khối lăng trụ tam giác ABC.A B  C   và AC . D A C  D  .
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 12
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
Ⓒ. Hai khối chóp tam giác C .ABC và C .ACD .
Ⓓ. Hai khối chóp tứ giác C .ABCD và C .ABB A   . Lời giải Chọn B
Ta có mặt phẳng  ACC   ACC A   .
Cho nên mặt phẳng  ACC A
  phân chia khối lập phương ABC . D AB C  D   thành hai khối lăng trụ tam giác ABC.A B  C   và AC . D A C  D  .
Câu 2: Mặt phẳng  ABC chia khối lăng trụ ABC.A B  C
  thành hai khối chóp. Ⓐ. A.ABC và . A BCC B   . Ⓑ. . A AB C   và . A BCC B   . Ⓒ. . A A B  C và A .BCC B  . Ⓓ. . A AB C   và A .BCC B   . Lời giải Chọn C Mặt phẳng  A B
 C chia khối lăng trụ ABC.A B  C
  thành hai khối chóp . A ABC và A .BCC B  .
Câu 3: Cho hình lăng trụ ABC.A' B 'C ' . Mặt phẳng  A' BC chia khối lăng trụ đã cho thành các khối đa diện nào?
Ⓐ. Hai khối chóp tam giác.
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 13
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
Ⓑ. Một khối chóp tam giác, một khối chóp tứ giác.
Ⓒ. Một khối chóp tam giác, một khối chóp ngũ giác.
Ⓓ. Hai khối chóp tứ giác. Lời giải Chọn B
Mặt phẳng  A' BC chia khối lăng trụ đã cho thành một khối chóp tam giác và một khối chóp tứ giác.
Câu 4: Mặt phẳng nào sau đây chia khối hộp ABCD.A'B'C'D' thành hai khối lăng trụ Ⓐ.  ABC . Ⓑ.  ABC . Ⓒ.  AB C   . Ⓓ.  A B  D . Lời giải Chọn B
Mặt phẳng  ABC là mặt phẳng  ABC D
  chia khối hộp thành hai khối lăng trụ là
BCC .ADD và BB C  .AA D   .
Câu 5: Cho khối lập phương ABC .
D A' B 'C ' D ' . Mặt phẳng (BDD ' B ') chia khối lập phương thành
Ⓐ. Hai khối lăng trụ tam giác. Ⓑ. Hai khối tứ diện.
Ⓒ. Hai khối lăng trụ tứ giác.
Ⓓ. Hai khối chóp tứ giác. Lời giải Chọn A
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 14
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung .
Câu 6: Phân chia khối lập phương ABCDA’B’C’D’ bởi ba mặt phẳng CB ' D ' , A' BD , BDB ' D '
ta được những khối đa diện nào?
Ⓐ. Hai khối tứ diện và hai khối chóp tứ giác.
Ⓑ. Hai khối tứ diện và một khối lăng trụ tam giác.
Ⓒ. Ba khối tứ diện và một khối lăng trụ tam giác.
Ⓓ. Hai khối tứ diện và một khối lăng trụ tứ giác Lời giải Chọn A D' A' C' B' A D B C
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 15
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung Full Chuyên đề 12 new 2020-2021
CHƯƠNG ①: KHỐI ĐA DIỆN FB: Duong Hung
Bài 2: KHỐI ĐA DIỆN LỒI VÀ ĐA DIỆN ĐỀU
 Dạng ①: Nhận diện hình đa diện, khối đa diện lồi.
. Lý thuyết cần nắm: Khối đa diện
được gọi là khối đa diện lồi nếu đoạn thẳng nối hai điểm bất kì của luôn thuộc
. Khi đó đa diện giới hạn
được gọi là đa diện lồi.
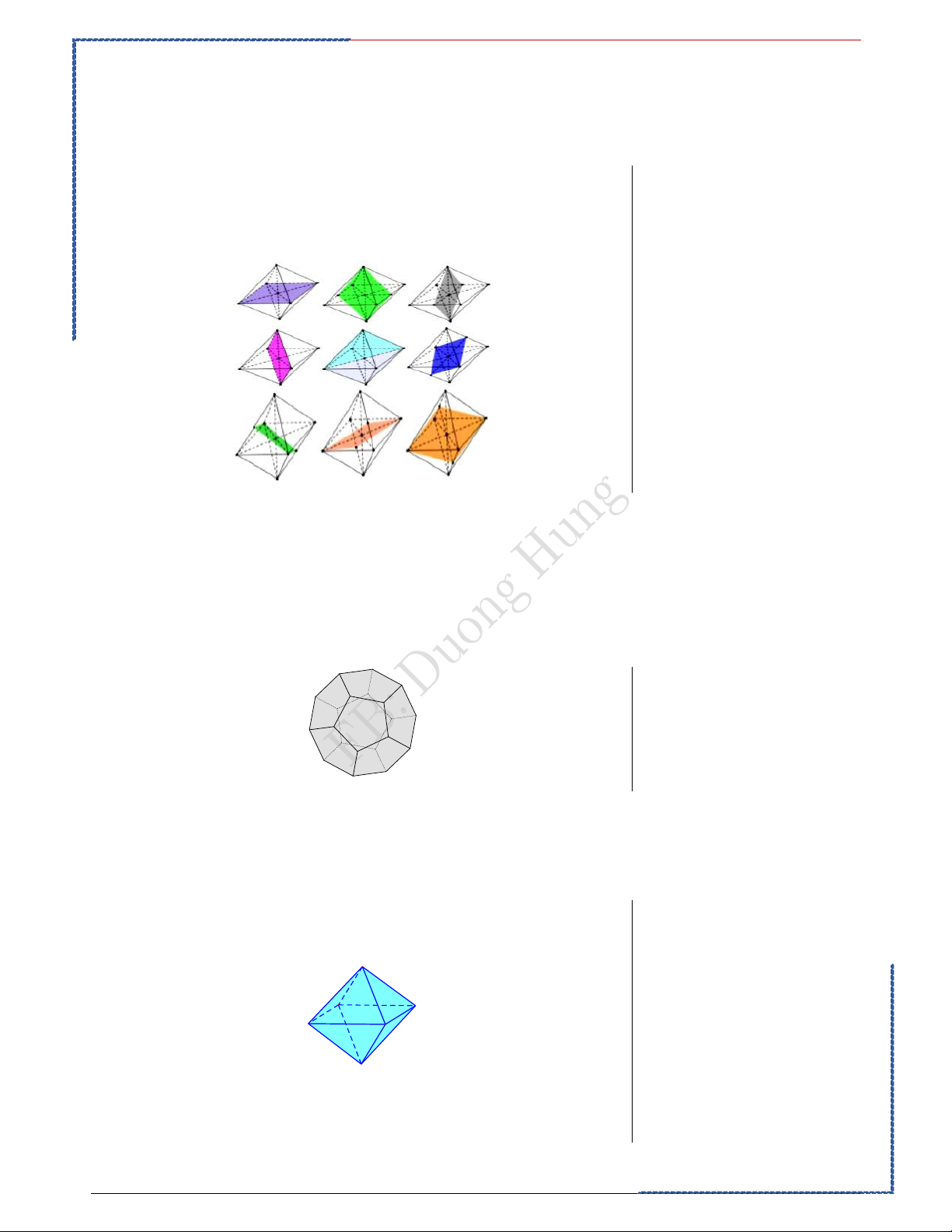
①. Khối đa diện không lồi ②. Khối đa diện lồi . Bài tập minh họa:
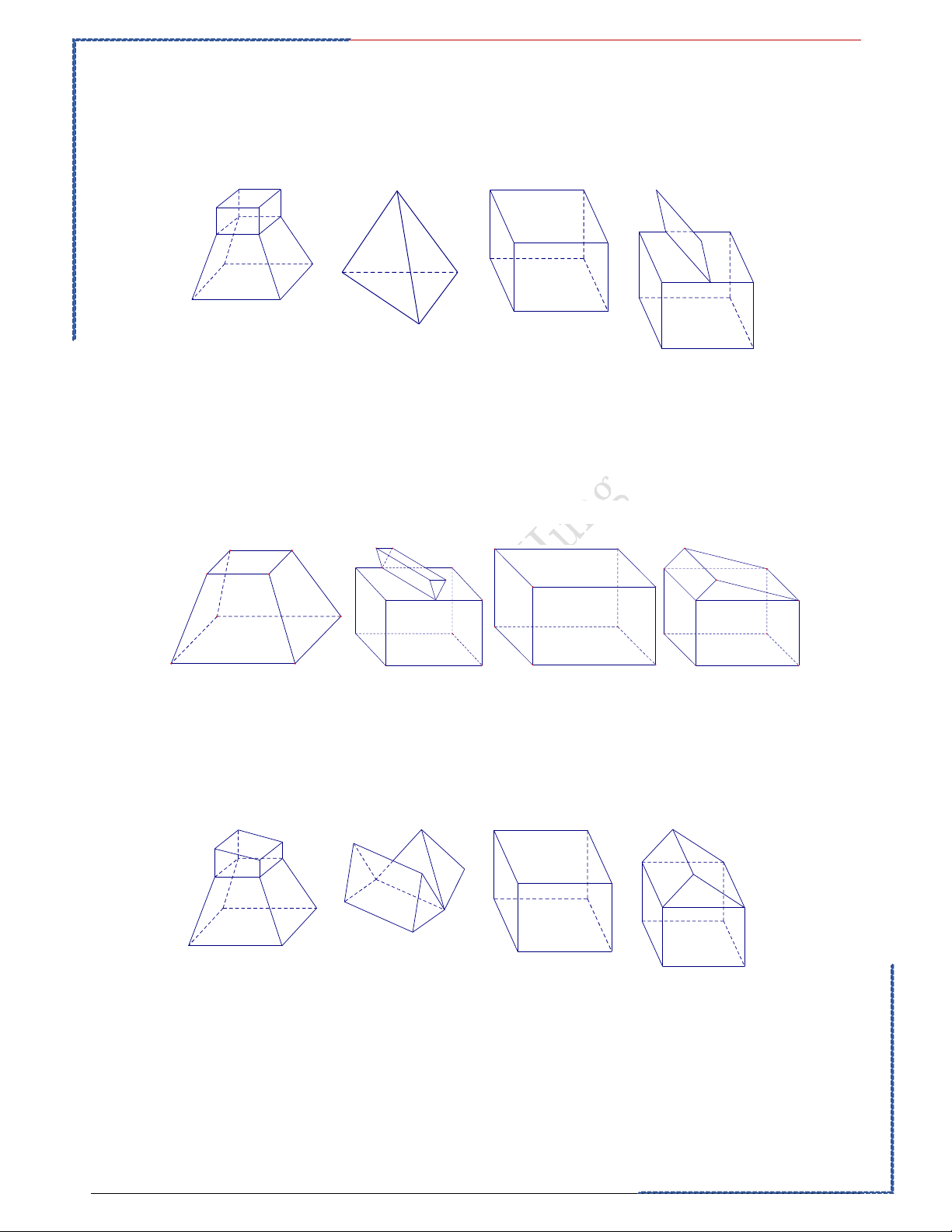
Câu 1: Hình nào dưới đây không phải là hình đa diện? Ⓐ. Ⓑ. Ⓒ. Ⓓ. .
Câu 2: Trong các hình dưới đây hình nào không phải đa diện lồi? Ⓐ. Hình (II). Ⓑ. Hình (I). Ⓒ. Hình (IV). Ⓓ. Hình (III).
Câu 3: Hình nào dưới đây không phải là một khối đa diện?
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 16
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. .
Câu 4: Vật thể nào trong các vật thể sau không phải là khối đa diện? Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. .
Câu 5: Số hình đa diện lồi trong các hình dưới đây là Ⓐ. 3 Ⓑ. 0 Ⓒ. 1 Ⓓ. 2
Câu 6: Hình nào trong các hình sau không phải là hình đa diện? Ⓐ. Hình chóp. Ⓑ. Hình vuông.
Ⓒ. Hình lập phương. Ⓓ. Hình lăng trụ. Câu 7: Cho các hình sau: Hình 1 Hình 2 Hình 3 Hình 4
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 17
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), hình đa diện là: Ⓐ. Hình 1. Ⓑ. Hình 2. Ⓒ. Hình 3. Ⓓ. Hình 4. Câu 8: Cho các hình sau: Hình 1 Hình 2 Hình 3 Hình 4
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), hình không phải đa diện là Ⓐ. Hình 1. Ⓑ. Hình 2. Ⓒ. Hình 3. Ⓓ. Hình 4.
Câu 9: Cho các hình khối sau: (a) (b) (c) (d)
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), hình không phải đa diện lồi là Ⓐ. hình (a). Ⓑ. hình (b). Ⓒ. hình (c). Ⓓ. hình (d). Câu 10: Cho các hình sau: Hình 1 Hình 2 Hình 3 Hình 4
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), số hình đa diện là: Ⓐ. 1. Ⓑ. 2 . Ⓒ. 3. Ⓓ. 4 .
Câu 11: Cho các hình khối sau:
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 18
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung (a) (b) (c) (d)
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), số đa diện lồi là Ⓐ. 1. Ⓑ. 2 . Ⓒ. 3 . Ⓓ. 4 . BẢNG ĐÁP ÁN 1.B 2.C 3.C 4.B 5.C 6.B 7.A 8.D 9.B 10.C 11.B
 Dạng ②: Nhận diện khối đa diện đều
. Lý thuyết cần nắm:
. Khối đa diện đều là khối đa diện lồi có hai tính chất sau đây:
 Các mặt là những đa giác đều có đúng cạnh
 Mỗi đỉnh là đỉnh chung của đúng cạnh
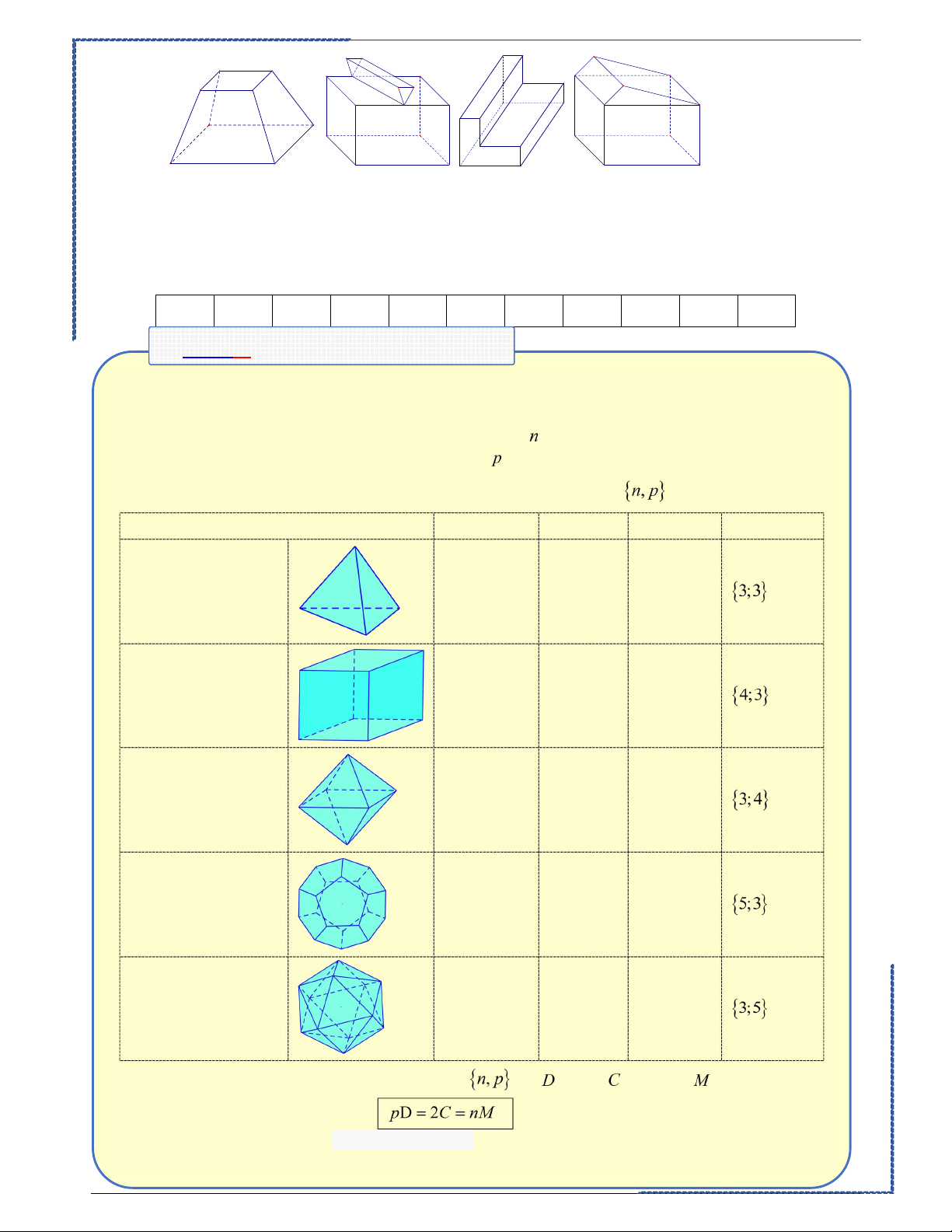
. Khối đa diện đều như vậy gọi là khối đa diện đều loại Khối đa diện đều Số đỉnh Số cạnh Số mặt Loại Tứ diện đều 4 6 4 Khối lập phương 8 12 6 Bát diện đều 6 12 8 Mười hai mặt đều 20 30 12 Hai mươi mặt đều 12 30 20
. Chú ý: Giả sử khối đa diện đều loại có đỉnh, cạnh và mặt
. Công thức Euler: D + M = C + 2 .
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 19
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung A - Bài tập minh họa:
Câu 1: Khối bát diện đều có bao nhiêu mặt phẳng đối xứng? Ⓐ. 4. Ⓑ. 6. Ⓒ. 8. Ⓓ. 9. Lời giải. Bài học kinh nghiệm Chọn D
Có 9 mặt phẳng đối xứng
Câu 2: Số đỉnh của hình mười hai mặt đều là Ⓐ. 12. Ⓑ. 30. Ⓒ. 20 . Ⓓ. 16. Lời giải Chọn C
Hình mười hai mặt đều có 20 đỉnh. Bài học kinh nghiệm
Câu 3: Hình bát diện đều kí hiệu là Ⓐ. 3;  5 . Ⓑ. 5;  3 . Ⓒ. 3;  4 . Ⓓ. 4;  3 Lời giải. Bài học kinh nghiệm Chọn C
Khối bát diện đều hay khối tám mặt đều
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 20
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
Câu 4: Khối đa diện đều nào sau đây có các mặt không phải là tam giác đều?
Ⓐ. Bát diện đều. Ⓑ. Tứ diện đều.
Ⓒ. Nhị thập diện đều.
Ⓓ. Thập nhị diện đều. Lời giải. Bài học kinh nghiệm Chọn D
Các khối bát diện đều, tứ diện đều và khối nhị thập diện đều có
các mặt bên là tam giác.
Khối thập nhị diện đều có các mặt là ngũ giác
B - Bài tập rèn luyện:
Câu 1: Cho khối hai mươi mặt đều H  . Biết mỗi mặt của nó là một đa giác đều p cạnh, mỗi đỉnh
của nó là đỉnh chung của đúng q mặt. Ta có  ;
p q nhận giá trị nào sau đây. Ⓐ. p  4;q  3. Ⓑ. p  3;q  5. Ⓒ. p  3;q  4 . Ⓓ. p  5;q  3.
Câu 2: Khối đa diện đều loại 4;  3 có tên gọi là
Ⓐ.Khối thập nhị diện đều.
Ⓑ. Khối bát diện đều Ⓒ.Khối lập phương.
Ⓓ. Khối tứ diện đều.
Câu 3: Cho khối đa diện đều loại  p;  q , chỉ số q là
Ⓐ.Số mặt của đa diện.
Ⓑ. Số đỉnh của đa diện.
Ⓒ.Số cạnh của đa diện. Ⓓ. Số các mặt đi qua mỗi đỉnh.
Câu 4: Hình bát diện đều có bao nhiêu đỉnh? Ⓐ.10. Ⓑ. 8 . Ⓒ.12. Ⓓ. 6
Câu 5: Khối tứ diện đều thuộc loại khối đa diện nào dưới đây? Ⓐ.3;  4 . Ⓑ. 4;  3 . Ⓒ.5;  3 . Ⓓ. 3;  3 .
Câu 6: Khối đa diện đều loại 3;  5 là khối nào sau đây? Ⓐ.Tám mặt đều. Ⓑ. Hai mươi mặt đều. Ⓒ.Tứ diện đều. Ⓓ. Lập phương.
Câu 7: Khối bát diện đều thuộc loại khối đa diện đều nào dưới đây? Ⓐ.5;  3 . Ⓑ. 4;  3 . Ⓒ.3;  4 . Ⓓ. 3;  3 .
Câu 8: Khối tứ diện đều thuộc loại khối đa diện nào dưới đây?
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 21
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung Ⓐ.3;  4 . Ⓑ. 4;  3 . Ⓒ.5;  3 . Ⓓ. 3;  3 .
Câu 9: Khối đa diện đều loại 5; 
3 có số đỉnh là D và số cạnh là C . Tính T  D  C . Ⓐ.T  50 . Ⓑ. T  32 . Ⓒ.T  42 . Ⓓ. T 18.
Câu 10: Đa diện đều loại 5; 
3 có tên gọi nào dưới đây? Ⓐ.Lập phương. Ⓑ. Hai mươi mặt đều. Ⓒ.Mười hai mặt đều. Ⓓ. Tứ diện đều.
Câu 11: Có tất cả bao nhiêu khối đa diện đều? Ⓐ.6. Ⓑ. 5. Ⓒ.7. Ⓓ. 4.
Câu 12: Khối đa diện đều loại 4;  3 là Ⓐ.Khối lập phương.
Ⓑ. Khối bát diện đều.
Ⓒ.Khối hộp chữ nhật.
Ⓓ. Khối tứ diện đều.
Câu 13: Hỏi khối đa diện đều loại 4;  3 có bao nhiêu mặt? Ⓐ.4. Ⓑ. 20. Ⓒ.6. Ⓓ. 12.
Câu 14: Khối đa diện đều loại 4; 
3 có số đỉnh, số cạnh và số mặt lần lượt bằng: Ⓐ.6,12,8. Ⓑ. 8,12,6. Ⓒ.12,30,20 . Ⓓ. 4,6,4.
Câu 15: Số đỉnh của một hình bát diện đều là bao nhiêu? Ⓐ.10. Ⓑ. 8. Ⓒ.6. Ⓓ. 12.
Câu 28 Hình lập phương thuộc dạng đa diện nào dưới đây? Ⓐ.6;  3 . Ⓑ. 3;  4 . Ⓒ.3;  3 . Ⓓ. 4;  3 .
Câu 16: Hình bát diện đều có số cạnh là Ⓐ.6. Ⓑ. 10. Ⓒ.12. Ⓓ. 8.
Câu 17: Khối tứ diện đều thuộc loại Ⓐ.3;  4 . Ⓑ. 4;  3 . Ⓒ.3;  3 . Ⓓ. 3;  5 .
Câu 18: Khối đa diện đều loại { 5;3} có tên gọi là
Ⓐ.Khối hai mươi mặt đều.
Ⓑ. Khối mười hai mặt đều. Ⓒ.Khối lập phương.
Ⓓ. Khối bát diện đều.
Câu 19: Khối đa diện đều loại 4;  3 có bao nhiêu mặt? Ⓐ.6. Ⓑ. 20. Ⓒ.12. Ⓓ. 8.
Câu 20: Trong các mệnh đề sau, mệnh đề nào sai?
Ⓐ.Chỉ có năm loại khối đa diện đều.
Ⓑ. Mỗi khối đa diện đều là một khối đa diện lồi.
Ⓒ.Mỗi cạnh của hình đa diện là cạnh chung của đúng hai mặt
Ⓓ. Hình chóp tam giác đều là hình chóp có bốn mặt là các tam giác đều.
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 22
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
Câu 21: Khối đa diện đều loại 3; 
4 có số đỉnh, số cạnh và số mặt tương ứng là Ⓐ.6, 12, 8. Ⓑ. 4, 6, 4. Ⓒ.8, 12, 6. Ⓓ. 8, 12, 6.
Câu 22: Hình bát diện đều có bao nhiêu cạnh? Ⓐ.10. Ⓑ. 12. Ⓒ.8. Ⓓ. 20 .
Câu 23: Khối mười hai mặt đều (hình vẽ dưới đây) là khối đa diện đều loại Ⓐ.3;  4 . Ⓑ. 3;  5 . Ⓒ.5;  3 . Ⓓ. 4;  3 .
Câu 24: Khối 20 mặt đều có bao nhiêu đỉnh? Ⓐ.12. Ⓑ. 16. Ⓒ. 20 . Ⓓ. 30.
Câu 25: Số cạnh của hình mười hai mặt đều là Ⓐ.Mười sáu. Ⓑ. Ba mươi. Ⓒ.Hai mươi. Ⓓ. Mười hai.
Câu 26: Một hình lăng trụ có đúng 11 cạnh bên thì hình lăng trụ đó có tất cả bao nhiêu cạnh? Ⓐ.33. Ⓑ. 31. Ⓒ.30. Ⓓ. 22
Câu 27: Cho một khối đa diện lồi có 10 đỉnh, 7 mặt. Hỏi khối đa diện này có mấy cạnh? Ⓐ. 20 . Ⓑ. 18. Ⓒ.15. Ⓓ. 12.
Câu 28: Khối đa diện đều loại 5; 
3 có số đỉnh là D và số cạnh là C . Tính T  D  C . Ⓐ.T  50 . Ⓑ. T  32 . Ⓒ.T  42 . Ⓓ. T 18. BẢNG ĐÁP ÁN 1.B 2.C 3.D 4.D 5.D 6.B 7.C 8.D 9.A 10.C 11.B 12.A 13.C 14.B 15.C 16.C 17.C 18.B 19.A 20.D 21.A 22.B 23.C 24.A 25.B 26.A 27.C 28.A
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 23
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung Full Chuyên đề 12 new 2020-2021
CHƯƠNG ①: KHỐI ĐA DIỆN FB: Duong Hung
Bài 3: THỂ TÍCH KHỐI CHÓP CÓ CẠNH BÊN VUÔNG GÓC ĐÁY
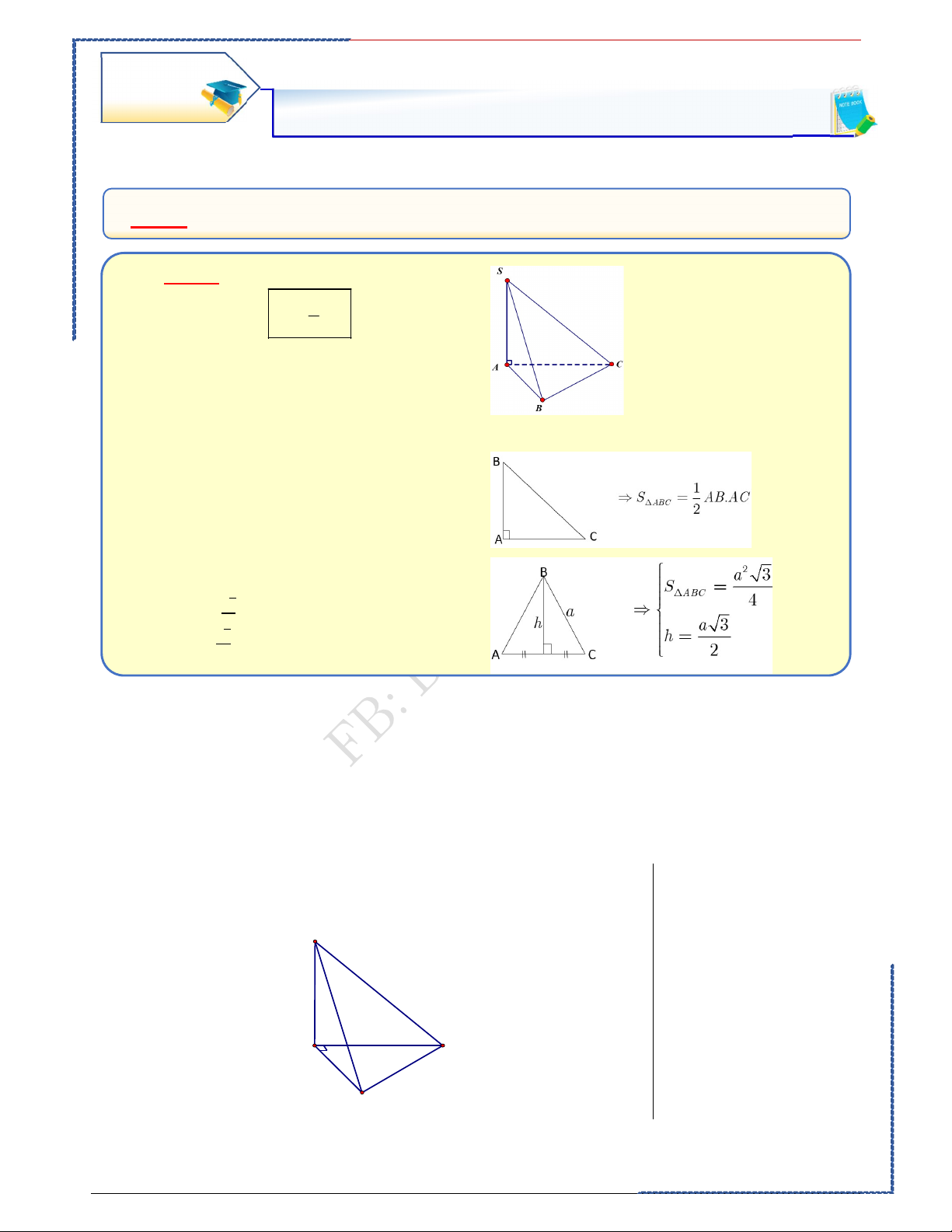
_ Dạng 1. Chóp có đáy là tam giác. 1 -Phương pháp: V  B.h 3
. Tính diện tích đáy:
. Tính chiều cao của chóp:
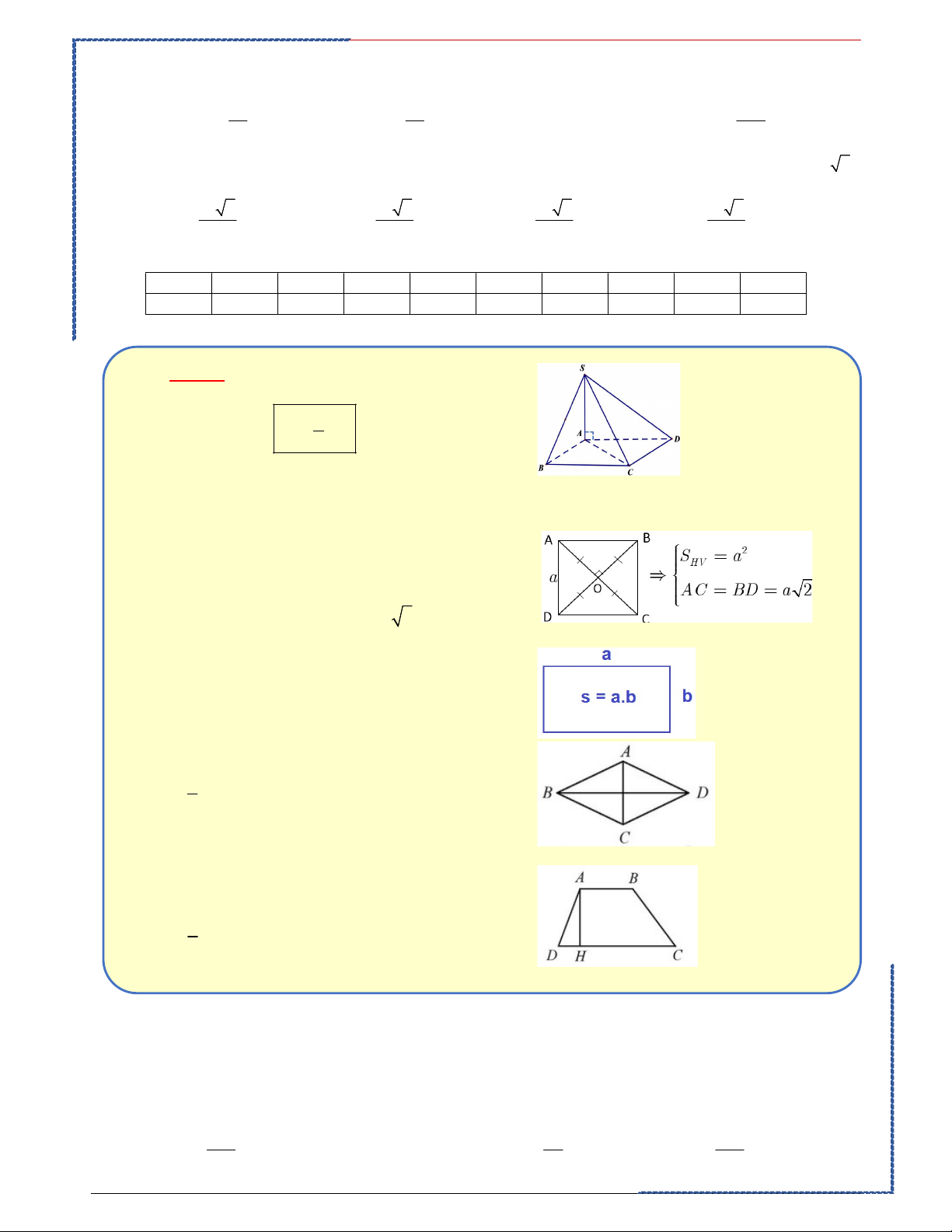
①. Diện tích tam giác vuông.
 S= nửa tích 2 cạnh góc vuông.  Pitago: 2 2 2 AB AC  AC
②. Diện tích tam giác đều.  S= (cạnh)2.√  h= (cạnh).√ . Bài tập minh họa:
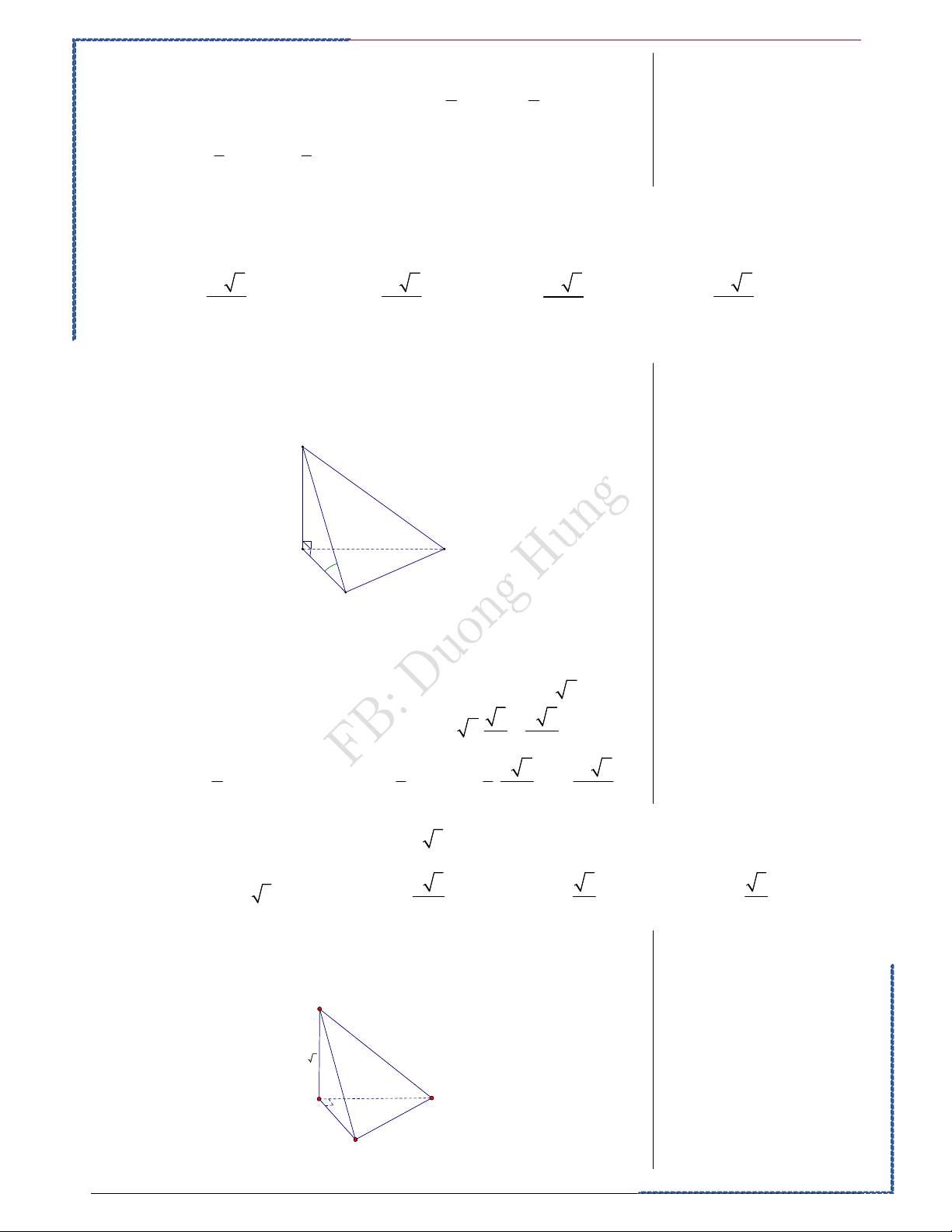
Câu 1: Cho khối chóp S.ABC có SA vuông góc với đáy, SA  4 , AB  6 , BC 10 và CA  8. Tính thể tích khối chóp S.ABC . Ⓐ. V  40 . Ⓑ. V 192 . Ⓒ.V  32 . Ⓓ. V  24 . Lời giải PP nhanh trắc nghiệm Chọn C  S 4 8 A C 6 10 B
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 24
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung Ta có 2 2 2 2 2 2
AB  AC  6  8  10  BC suy ra tam giác ABC vuông 1 1
tại A ,do đó diện tích tam giác ABC là: S  A . B AC  .6.8  24 2 2 1 1 Vậy V  .S . A S  .4.24  32. SABC 3 ABC 3
Câu 2: Cho khối chóp S.ABC có SA vuông góc với  ABC , đáy ABC là tam giác vuông cân tại A ,
BC  2a , góc giữa SB và  ABC là 30 . Tính thể tích khối chóp S.ABC . 3 3 3 3 Ⓐ. a 6 a 6 a 3 a 2 . Ⓑ. . Ⓒ. . Ⓓ. . 9 3 3 4 Lời giải PP nhanh trắc nghiệm Chọn A S  A C 30° B
Ta có AB là hình chiếu của SB lên  ABC suy ra góc giữa SB và  ABC là góc  SBA  30 .
Tam giác ABC vuông cân tại A , BC  2a  AB  AC  a 2 . 3 a 6 Xét S
 AB vuông tại A có SA  A . B tan 30  a 2.  . 3 3 1 3 1 1 a 6 a 6 Ta có 2 2 S  AB  a . Vậy 2 V  .S . A S  . .a  . ABC 2 S.ABC 3 ABC 3 3 9
Câu 3: Cho hình chóp S.ABC có tam giác ABC vuông tại A , AB  a , AC  2a . SA vuông góc với
mặt phẳng đáy  ABC và SA  a 3 . Tính thể tích V của khối chóp S.ABC . Ⓐ. 2 3 3 3 3 V  a 3 . Ⓑ. 3 V  a . Ⓒ. 3 V  a . Ⓓ. 3 V  a . 3 3 4 Lời giải PP nhanh trắc nghiệm Chọn C S  a 3 2a A C a B
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 25
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
Vì SA   ABC  h  SA  a 3 . Tam giác ABC vuông tại A nên 1 1 2 S  .AB.AC  .a.2a  a ABC 2 2 1 1 3 Ta có: 2 3 V .S .SA  .a .a 3  a . S.ABC 3 ABC 3 3
Câu 4: Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh 2a . Cạnh bên SA vuông góc với đáy
và SA  a 3 . Tính thể tích V của khối chóp S.ABC . 3 Ⓐ. a 3 V  3a . Ⓑ. V  . Ⓒ. 3 V  a 3 . Ⓓ. 3 V  a . 4 Lời giải PP nhanh trắc nghiệm Chọn D S  A C B 1  a2 2 3 Có V  S . A S , SA  a 3 và S  . 3 ABC ABC 4 1 2a2 3 3  V  a 3  a . Vậy 3 V  a . 3 4
B - Bài tập rèn luyện:
Câu 1: Thể tích của khối chóp có diện tích mặt đáy bằng B, chiều cao bằng h được tính bởi công thức: Ⓐ. 1 V  Bh . Ⓑ. V  Bh . Ⓒ. 1 V  Bh . Ⓓ. V  3Bh . 3 2
Câu 2: Thể tích khối chóp có độ dài đường cao bằng 6, diện tích đáy bằng 8 là Ⓐ. 12 . Ⓑ. 48 . Ⓒ.16. Ⓓ. 24 .
Câu 3: Khối chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB  a , cạnh bên SA  ( ABC)
và SA  2a . Thể tích V của khối chóp đã cho bằng Ⓐ. 1 2 2 3 2 V  a . Ⓑ. 3 V  a . Ⓒ. 3 V  a . Ⓓ. 3 V  a . 3 3 3
Câu 4: Cho hình chóp S.ABC có A
 BC vuông tại A , AB  a, AC  a 3 . Biết rằng SA vuông góc
với mặt phẳng  ABC và SB  a 5 . Tính thể tích khối chóp S.ABC . 3 3 3 Ⓐ. a 3 a 3 a 3 . Ⓑ. . Ⓒ. . Ⓓ. 3 a 3 . 2 6 3
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 26
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung 3 a 2 a
Câu 5: Cho khối chóp S.ABC có thể tích bằng
và diện tích tam giác ABC bằng . Tính chiều 6 2
cao h kẻ từ S của khối chóp S.ABC. Ⓐ. a 2a h  a . Ⓑ. h  . Ⓒ. h  3a . Ⓓ. h  . 3 3
Câu 6: Cho hình chóp S.ABC có SA   ABC , biết SA  4 và diện tích tam giác ABC bằng 8 . Tinh
thể tích V của khối chóp S.ABC . Ⓐ. 8 V  32 . Ⓑ. V  4 . Ⓒ. 32 V  . Ⓓ. V  . 3 3
Câu 7: Cho hình chóp S.ABC có AB  6, BC  8, AC  10 . Cạnh bên SA vuông góc với đáy và
SA  4 . Tính thể tích V của khối chóp S.ABC . Ⓐ. V  40 . Ⓑ. V  32. Ⓒ.V 192. Ⓓ. V  24 .
Câu 8: Cho tứ diện OABC có OA, O ,
B OC đôi một vuông góc và OA  a, OB  b, OC  c. Tính thể
tích khối tứ diện OABC. Ⓐ. abc abc abc . Ⓑ. abc . Ⓒ. . Ⓓ. . 3 6 2
Câu 9: Cho hình chóp S.ABC có cạnh bên SA vuông góc với mặt đáy, SA  a 3 , AB  a , AC  a 3
, BC  2a . Thể tích khối chóp S.ABC bằng? 3 3 3 3 Ⓐ. a 3 a a 3 a 3 . Ⓑ. . Ⓒ. . Ⓓ. . 6 2 2 4
Câu 10: Cho hình chóp S.ABC có SA vuông góc với mặt đáy. Tam giác ABC vuông tại B . Biết
SA  AB  3a; BC  2a . Thể tích hình chóp S.ABC là Ⓐ. 3 9a . Ⓑ. 3 6a . Ⓒ. 3 a . Ⓓ. 3 3a .
Câu 11: Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh 2a . Cạnh bên SA vuông góc với đáy
và SA  a 3 . Tính thể tích V của khối chóp S.ABC . 3 Ⓐ. a 3 V  3a . Ⓑ. V  . Ⓒ. 3 V  a 3 . Ⓓ. 3 V  a . 4
Câu 12: Cho khối chóp S.ABC có ba cạnh S ,
A SB, SC cùng có độ dài bằng a và vuông góc với nhau
từng đôi một. Thể tích của khối chóp S.ABC bằng 3 3 3 Ⓐ. a  a a Ⓑ.  Ⓒ.  Ⓓ. 3 a . 2 3 6
Câu 13: Cho khối chóp tam giác S.ABC có đáy là tam giác đều cạnh 2a , cạnh bên SA vuông góc với
mặt phẳng chứa mặt đáy, cạnh SC  2a 5 . Thể tích khối chóp S.ABC bằng 3 3 3 3 Ⓐ. a 3 2a 3 8a 3 4a 3 . Ⓑ. . Ⓒ. . Ⓓ. . 6 3 3 3
Câu 14: Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a và hai mặt bên SAB , SAC
cùng vuông góc với đáy. Tính thể tích khối chóp S.ABC biết SC  a 3 . 3 3 3 3 Ⓐ. a 3 2a 6 a 3 a 6 . Ⓑ. . Ⓒ. . Ⓓ. . 2 9 4 12
Câu 15: Cho hình chóp S.ABC có đáy là tam giác đều cạnh a , SA  a 3 và SA vuông góc với mặt
phẳng đáy. Tính thể tích của khối chóp S.ABC . 3 3 3 3 Ⓐ. 3a a a 3 a . Ⓑ. . . Ⓓ. . 4 2 Ⓒ. 4 4
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 27
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
Câu 16: Cho khối chóp S.ABC có đáy ABC là tam giác vuông cân tại B , độ dài cạnh AB  BC  a ,
cạnh bên SA vuông góc với đáy và SA  2a . Tính thể tích V của khối chóp S.ABC . 3 3 Ⓐ. a a 16 V  . Ⓑ. V  . Ⓒ.V  4 . Ⓓ. V  . 3 2 3
Câu 17: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và chiều cao của hình chóp là a 2 .
Tính theo a thể tích của khối chóp S.ABC . Ⓐ. 3 a 6 3 a 6 a 3 a 2 . Ⓑ. . Ⓒ. 3 6 . Ⓓ. . 6 12 4 12 BẢNG ĐÁP ÁN THAM KHẢO 1.A 2.C 3.A 4.C 5.A 6.C 7.B 8.C 9.B 10.D 11.D 12.C 13.D 14.D 15.D 16.A 17.B
_ Dạng 2. Chóp có đáy là hình vuông, chữ nhật, thoi, thang. 1 -Phương pháp: V  B.h 3
. Tính diện tích đáy:
. Tính chiều cao của chóp:
①. Diện tích hình vuông: . S= (cạnh)2 . Pitago: 2 2 2 AB  AD  BD
.Đường chéo hình vuông bằng cạnh. 2
②. Diện tích hình chữ nhật: . S= dài x rộng. ③. Diện tích hình thoi: 1 . S  .AC.BD 2 . S= 2.SABC=2.SADC
④. Diện tích hình thang:
. S= nửa chiều cao x (đáy lớn+bé) 1 . S  AH .AB CD 2
① - Bài tập minh họa chóp có đáy là hình vuông:
Câu 1: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a . Biết cạnh bên SA  2a
và vuông góc với mặt phẳng đáy. Tính thể tích của khối chóp S.ABCD . 3 3 3 Ⓐ. 4a a 2a . Ⓑ. 3 2a . Ⓒ. . Ⓓ. . 3 3 3
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 28
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung Lời giải PP nhanh trắc nghiệm Chọn D 3 1 1 2a Ta có 2 V  S .SA  a .2a  .  S. ABCD 3 ABCD 3 3
Câu 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , cạnh bên SA vuông góc với
mặt phẳng đáy và SA  a 2 . Tính thể tích V của hình chóp S.ABCD . 3 2a 3 2a 3 2a Ⓐ. V  . Ⓑ. V  . Ⓒ. 3 V  2a . Ⓓ. V  . 6 4 3 Lời giải PP nhanh trắc nghiệm Chọn D S  A B D C 3 1 1 a 2 Ta có 2 V  S . A S  a 2.a  3 ABCD 3 3
Câu 3: Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a 3 , cạnh SA vuông góc với mặt
phẳng  ABCD và SB tạo với đáy một góc 60 . Tính thể tích V của khối chóp S.ABCD . 3 3 Ⓐ. 3a 9a 3 V  9a . Ⓑ. V  . Ⓒ.V  . Ⓓ. 3 V  3a . 4 2 Lời giải PP nhanh trắc nghiệm Chọn D S  a 3 600 A B D C
 SA   ABCD  AB là hình chiếu vuông góc của SB lên mặt phẳng  ABCD .
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 29
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung  SB, ABCD   SB, AB    SBA  60 .
Trong tam giác vuông SAB ,  SA  tan 60 .  AB  3.a 3  3a . S  AB  a 2 2 2 3  3a . ABCD
Vậy thể tích V của khối chóp S.ABCD là 1 1 2 .3 V  .S .SA  .3a .3a  3a . 3 ABCD 3 . Bài tập rèn luyện:
Câu 1: Tính thể tích khối chóp S.ABCD có SA   ABCD , đáy là hình vuông cạnh a , SB  a 5 3 3 3 Ⓐ. a 6 2a a . Ⓑ. . Ⓒ. 3 2a . Ⓓ. . 3 3 3
Câu 2: Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh a , cạnh bên SA vuông
góc với mặt đáy và SA  a 2 . Tính thể tích V của khối chóp S.ABCD . 3 3 3 Ⓐ. a 2 a 2 a 2 . Ⓑ. . Ⓒ. 3 a 2 . Ⓓ. . 6 4 3
Câu 3: Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh a 2 , cạnh bên SA vuông
góc với mặt đáy và SC  a 5 . Tính thể tích V của khối chóp S.ABCD 3 3 2 Ⓐ. 2a a 4a V  . Ⓑ. V  . Ⓒ. 3 V  2a . Ⓓ. V  . 3 3 3
Câu 4: Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông, cạnh bên SA vuông góc với mặt
đáy và SA  AC  a 2 . Tính thể tích V của khối chóp S.ABCD 3 3 3 Ⓐ. a 2 a 6 a 6 V  . Ⓑ. V  . Ⓒ. 3 V  a 2 . Ⓓ. V  3 9 3
Câu 5: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Biết SA   ABCD và
SB  a 3 . Tính thể tích khối chóp S.ABCD . 3 3 3 Ⓐ. a 2 a 2 a 2 V  . Ⓑ. 3 a 3 . Ⓒ.V  . Ⓓ. V  . 2 3 6
Câu 6: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Hai mặt phẳng SAC và
SAB cùng vuông góc với ABCD . Góc giữa SCD và  ABCD là 60. Tính thể tích của khối chóp S.ABCD . 3 3 3 3 Ⓐ. a 3 a 6 a 3 a 3 . Ⓑ. . Ⓒ. . Ⓓ. . 3 3 6 3
Câu 7: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với đáy ABCD .
Mặt bên SCD hợp với đáy một góc 60 . Tính thể tích V của khối chóp S.ABCD . 3 3 3 3 Ⓐ. a 3 a 3 a 3 a 2 V  . Ⓑ. V  . Ⓒ.V  . Ⓓ. V  6 3 12 6
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 30
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
Câu 8: Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a ,cạnh bên SA vuông góc với mặt
phẳng đáy,góc giữa mặt phẳng SBD và mặt phẳng đáy bằng 60 . Tính thể tích V của khối chóp S.ABCD . 3 3 3 3 Ⓐ. a 6 a 3 a 3 a 3 V  . Ⓑ. V  . Ⓒ.V  . Ⓓ. V  6 2 12 7
Câu 9: Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a , cạnh bên SA vuông góc với mặt
phẳng đáy. Đường thẳng SD tạo với mặt phẳng SAB một góc 30 . Tính thể tích V của khối chóp S.ABCD . 3 3 3 3 Ⓐ. a 3 a 3 a 3 a 3 V  . Ⓑ. V  . Ⓒ.V  . Ⓓ. V  2 4 12 3
Câu 10: Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với mặt phẳng
đáy và cạnh bên SB tạo với mặt phẳng đáy góc 45 . Thể tích của khối chóp S.ABCD bằng 3 3 3 Ⓐ. a 2 a 2 a . Ⓑ. . Ⓒ. . Ⓓ. 3 a . 3 6 3 BẢNG ĐÁP ÁN THAM KHẢO 1.B 2.D 3.A 4.A 5.C 6.A 7.B 8.A 9.D 10.C
②- Bài tập minh họa chóp có đáy là hình chữ nhật:
Câu 1: Cho hình chóp S.ABCD có đáy là hình chữ nhật có cạnh AB  2, AD  4 . Cạnh bên SA  2
và vuông góc với đáy (tham khảo hình vẽ). Thể tích V của khối chóp S.ABCD bằng Ⓐ. 16 V 16 . Ⓑ. V  . Ⓒ. 8 V  . Ⓓ. V  8 . 3 3 Lời giải PP nhanh trắc nghiệm Chọn C 
Do SA vuông góc với mặt phẳng đáy nên hình chiếu của SB trên  ABCD là AB .
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 31
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
Suy ra, SB, ABCD   SB, AB    SBA  45 . Dễ thấy S
 AB vuông, cân tại A , suy ra SA  AB  a . 3 1 1 a  Vậy 2 V  S . A S  . a a  (đvtt). S.ABCD 3 ABCD 3 3
Câu 2: Cho khối chóp S.ABCD có đáy là hình chữ nhật AB  a , AD  2a , SA vuông góc với đáy
và góc giữa SD và mặt phẳng  ABCD bằng 0
45 . Tính thể tích V của khối chóp S.ABCD . 3 3 3 Ⓐ. 4a a 2 4 3 a V  . Ⓑ. V  . Ⓒ. 3 V  2 6a . Ⓓ. V  . 3 3 3 Lời giải PP nhanh trắc nghiệm Chọn A  S 450 D a A B 2a C
Vì SA   ABCD  góc giữa SD và mặt phẳng  ABCD bằng góc giữa SD và AD .   0
SDA  45  SDA vuông cân nên SA  AD  2a . 3 1 1 4a V  V  S . A S  .2 . a . a 2a  . S.ABCD 3 ABCD 3 3
Câu 3: Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật, AB  a , AD  a 3 , SA vuông góc
với mặt phẳng đáy và mặt phẳng SBC tạo với đáy một góc o
60 . Tính thể tích V của khối chóp S.ABCD . 3 3 Ⓐ. 3a a 3 V  3a . Ⓑ. V  . Ⓒ. 3 V  a . Ⓓ. V  . 3 3 Lời giải PP nhanh trắc nghiệm Chọn C 
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 32
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung S A a 60 B a 3 D C Ta có 2 S  A . B AD  . a a 3  3a . ABCD
Dễ thấy BC  AB BC  SB   o ; SBA  60 .
Xét tam giác vuông SAB  A1v có: SA o o tan 60   SA  AB tan 60  a 3 AB 1 1 Vậy 2 3 V  S .SA  a 3.a 3  a . S.ABCD 3 ABCD 3 . Bài tập rèn luyện:
Câu 1: Cho hình chóp tứ giác S.ABCD có đáy là hình chữ nhật, AB  a , AD  3a , SA vuông góc với
mặt phẳng đáy và SA  2a . Tính theo a thể tích khối chóp S.ABCD . Ⓐ. 3 6a . Ⓑ. 3 3a . Ⓒ. 3 2a . Ⓓ. 3 a .
Câu 2: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB  a , BC  2a, SA  2a , SA vuông
góc với mặt phẳng ( ABCD) . Tính thể tích khối chóp S.ABCD theo a . 3 3 3 Ⓐ. 3 8a 4.a 6a 4a . Ⓑ. . Ⓒ. . Ⓓ. . 3 3 3
Câu 3: Cho khối chóp S.ABCD có đáy là hình chữ nhật. Cạnh bên SA vuông góc với đáy. AB  3a ;
AD  4a ; SC  3 3a .Thể tích của khối chóp S.ABCD bằng: 3 3 Ⓐ. 4 2a 2 2a 3 4 2a . Ⓑ. 3 4a . Ⓒ. . Ⓓ. . 3 3 a
Câu 4: Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB  , a AD  a 2 và SA  , 2 SA ABC 
D . Tính thể tích của khối chóp S.ABC . 3 3 3 3 Ⓐ. a 2 a 2 a 2 a 2 V  . Ⓑ. V  . Ⓒ.V  . Ⓓ. V  . 12 2 3 6
Câu 5: Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A , BC  2a 3 ,  BAC  120 , cạnh
bên SA vuông góc với mặt đáy và SA  2a . Tính thể tích V của khối chóp S.ABC . 3 3 3 Ⓐ. 2a 3 a 3 a 3 V  . Ⓑ. 3 V  a 3 . Ⓒ.V  . Ⓓ. V  3 2 6 .
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 33
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
Câu 6: Cho hình chóp S.ABCD có đáy là hình chữ nhật có cạnh AB  2, AD  4 . Cạnh bên SA  2
và vuông góc với đáy (tham khảo hình vẽ). Thể tích V của khối chóp S.ABCD bằng Ⓐ. 16 V 16 . Ⓑ. V  . 3 Ⓒ. 8 V  . Ⓓ. V  8 . 3
Câu 7: Cho khối chóp S.ABCD có đáy là hình chữ nhật. Cạnh bên SA vuông góc với đáy. AB  3a ;
AD  4a ; SC  3 3a .Thể tích của khối chóp S.ABCD bằng: 3 3 Ⓐ. 4 2a 2 2a 3 4 2a . Ⓑ. 3 4a . Ⓒ. . Ⓓ. . 3 3
Câu 8: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O, AB  a, AD  a 3, SA  3 . a
SO vuông góc với mặt phẳng đáy ABC .
D Tính thể tích của khối chóp S.ABC. 3 3 Ⓐ. a 6 2a 6 . Ⓑ. . Ⓒ. 3 a 6. Ⓓ. 3 2a 6. 3 3
Câu 9: Cho hình chóp S.ABCD có đáy là hình chữ nhật, SA vuông góc với đáy, AB  a , AD  2a .
Góc giữa SB và đáy bằng 45 . Thể tích khối chóp là 3 3 3 3 Ⓐ. a 2 2a a 2 a . Ⓑ. . Ⓒ. . Ⓓ. . 3 3 6 3
Câu 10: Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB  2a , AD  a . Hình chiếu của S lên
 ABCD là trung điểm H của AB , SC tạo với đáy một góc 45. Thể tích khối chóp S.ABCD là 3 3 3 3 Ⓐ. a 2 2a 2a a 3 . Ⓑ. . Ⓒ. . Ⓓ. . 3 3 3 2 BẢNG ĐÁP ÁN THAM KHẢO 1.C 2.A 3.A 4.A 5.A 6.B 7.A 8.A 9.B 10.B
③. Bài tập minh họa chóp có đáy là hình thoi, thang vuông:
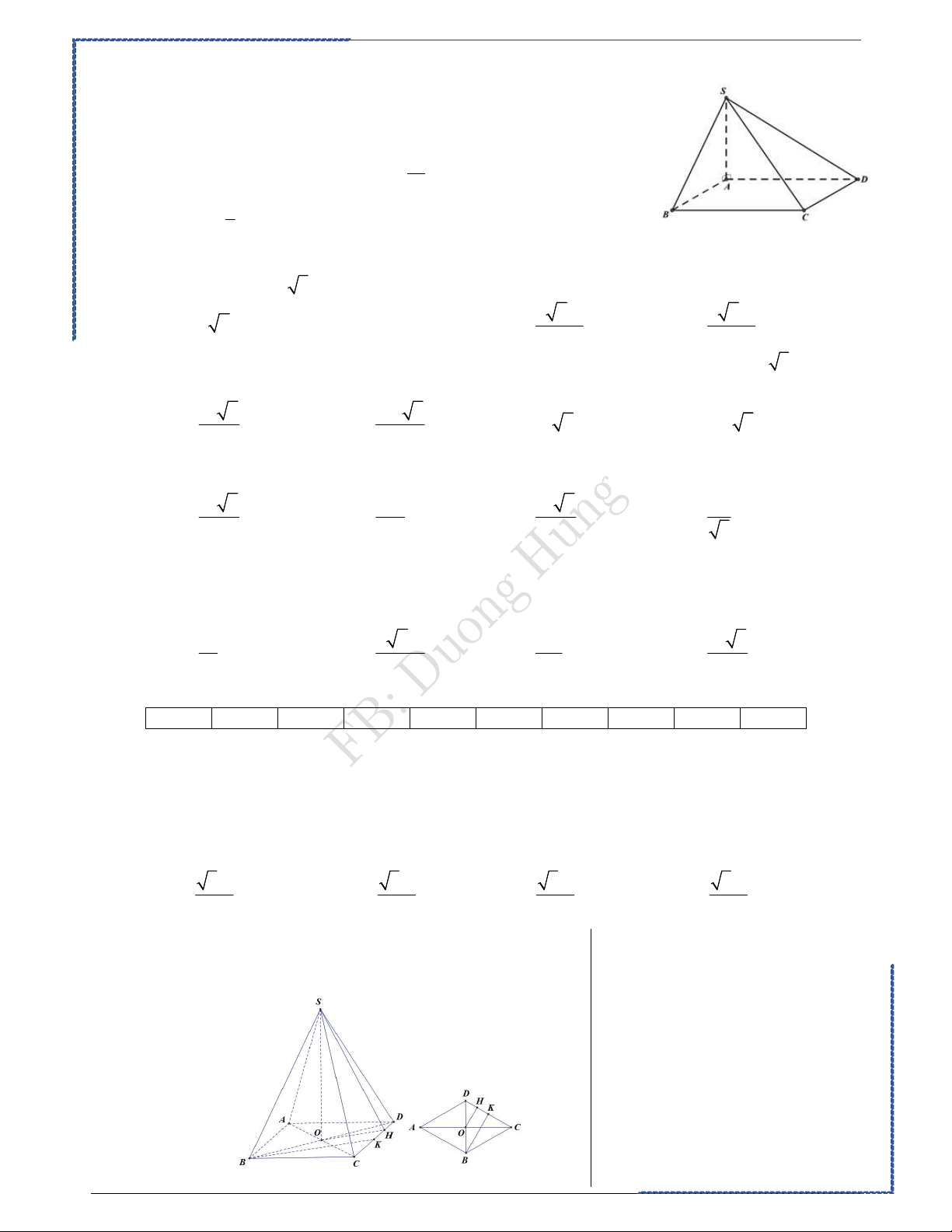
Câu 1: Cho khối chóp S.ABCD có đáy là hình thoi tâm O , AB  a , 
BAD  60 , SO ABCD,
mặt phẳng SCD tạo với mặt phẳng đáy góc 60. Thể tích khối chóp đã cho bằng 3 3a 3 3a 3 3a 3 3a A. . Ⓑ. . C. . Ⓓ. 8 24 48 12 Lời giải PP nhanh trắc nghiệm Chọn A 
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 34
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
Ta có ABCD là hình thoi tâm O , AB  a ,  0 BAD  60 nên
tam giác ABD, CBD đều cạnh a. a 3
Gọi BK là đường cao của tam giác CBD , ta có BK  . 2
Gọi H là hình chiếu của O lên DC Ta có
DC  OH DC SOH DC  SH DC  SO  .
 SCD ABCD OH SH  0 , ,  SHO  60 BK 3a Có 0 0 SO  OH.tan 60  .tan 60  ; 2 4 2 a 3 S  2S  . ABCD ABD 2 2 3 1 1 a 3 3a a 3 V  .S .SO  . .  . S.ABCD 3 ABCD 3 2 4 8
Câu 2: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, AB  BC 1, AD  2.
Cạnh bên SA  2 và vuông góc với mặt đáy. Thể tích V của khối chóp S.ABCD bằng Ⓐ. 3 V  . Ⓑ. V 1. Ⓒ. 1 V  . Ⓓ. V  2 . 2 3 Lời giải PP nhanh trắc nghiệm Chọn B S  2 A 2 D B 1 C
 ABCD là hình thang vuông tại A và
B, AB  BC 1, AD  2  S    ABCD   1 3 1 2 . 2 2 1 1 3 V V  S . A S  .2. 1. S.ABCD 3 ABCD 3 2
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 35
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
Câu 3: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B , AB  BC  2 , AD  3.
Cạnh bên SA  2 và vuông góc với đáy. Tính thể tích khối chóp S.ABCD . Ⓐ. 10 17 V  4 . Ⓑ. V  . Ⓒ. 10 3 V  . Ⓓ. . 3 3 6 Lời giải PP nhanh trắc nghiệm Chọn B S  A D B C AB  CD  Ta có: 2 3 S  .AD  .2  5 ABCD 2 2 1 1 10 Thể tích: V  .S . A S  .2.5  . S. ABCD 3 ABCD 3 3 . Bài tập rèn luyện:
Câu 1: Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng  ABCD, đáy ABCD là hình thang
vuông tại A và B có AB  a, AD  3a, BC  .
a Biết SA  a 3, tính thể tích khối chóp S.BCD theo . a 3 3 3 Ⓐ. 3a 2 3a 3a . Ⓑ. . Ⓒ. . Ⓓ. 3 2 3a . 6 3 4
Câu 2: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D , AB  AD  a ,
SA  CD  3a , SA vuông góc với mặt phẳng  ABCD . Thể tích khối chóp S.ABCD bằng. Ⓐ. 1 1 3 a . Ⓑ. 3 2a . Ⓒ. 3 6a . Ⓓ. 3 a . 3 6
Câu 3: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và góc 
BAD  60 , SA   ABCD
. Biết rằng khoảng cách từ A đến cạnh SC bằng a . Thể tích khối chóp S.ABCD là 3 3 3 Ⓐ. a 2 a 2 a 3 . Ⓑ. . Ⓒ. . Ⓓ. 3 a 3 . 4 12 6 BẢNG ĐÁP ÁN 1.A 2.B 3.A
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 36
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung Full Chuyên đề 12 new 2020-2021
CHƯƠNG ①: KHỐI ĐA DIỆN FB: Duong Hung
Bài 4: THỂ TÍCH KHỐI CHÓP CÓ MẶT BÊN VUÔNG GÓC ĐÁY
_ Dạng 1. Chóp có đáy là tam giác. 1 -Phương pháp: V  B.h 3
 Tính diện tích đáy: B
 Tính chiều cao của chóp: h A - Bài tập minh họa:
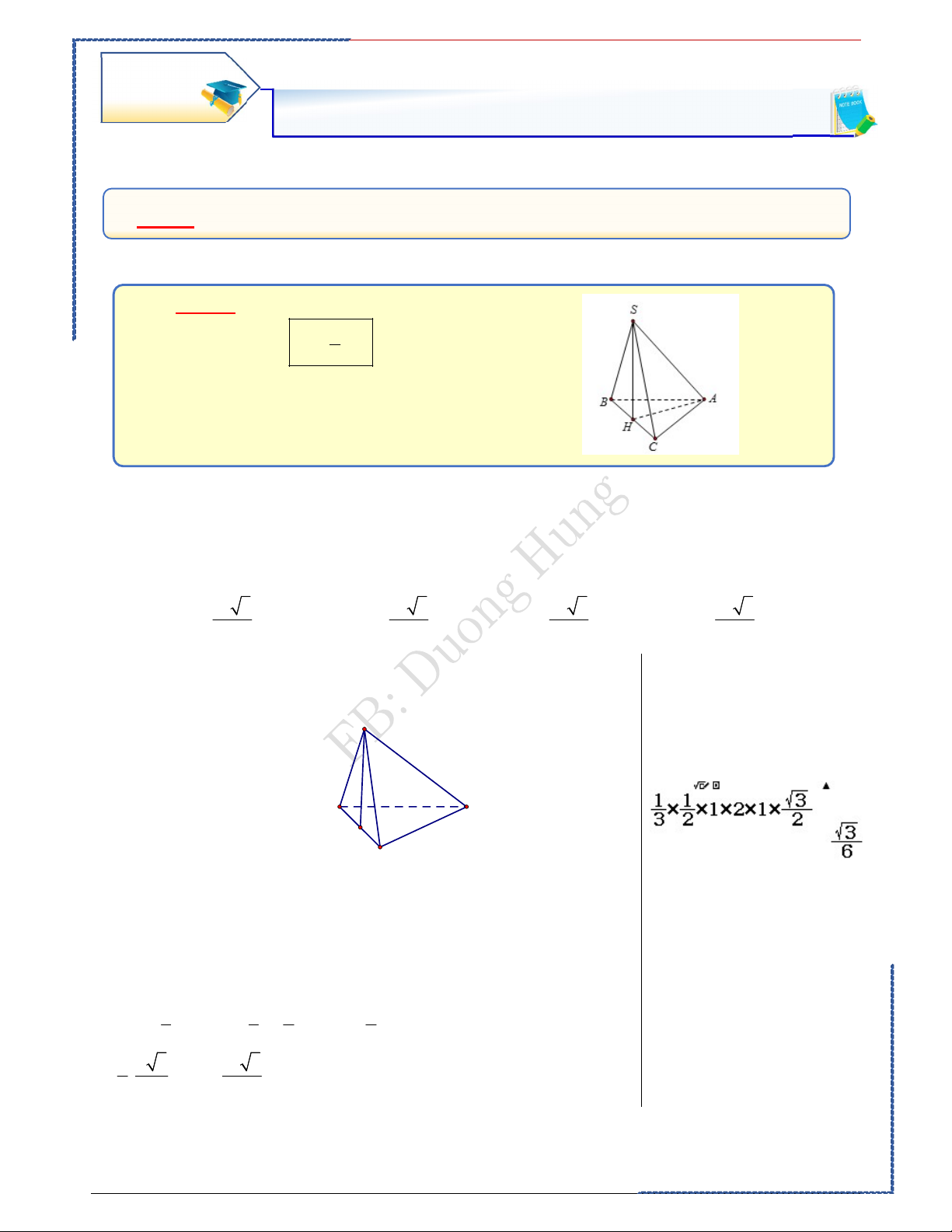
Câu 1: Cho khối chóp S.ABC có đáy ABC là tam giác vuông tại A , biết AB  , a AC  2a . Mặt bên
SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Tính theo a thể tích khối chóp S.ABC . 3 3 3 3 Ⓐ. a 3 a 3 a 3 a 3 . Ⓑ. . Ⓒ. . Ⓓ. . 2 6 4 3 Lời giải PP nhanh trắc nghiệm Chọn B S  Casio B C I A
Gọi I là trung điểm của đoạn thẳng AB . Ta có: SI  SAB, SI  AB  
 SAB  ABC  AB  SI   ABC .   SAB    ABC 1 1 1 1 V  SI.S  SI. A . B AC  SI.A . B AC S.ABC 3 A  BC 3 2 6 3 1 a 3 a 3  . . . a 2a  6 2 6
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 37
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
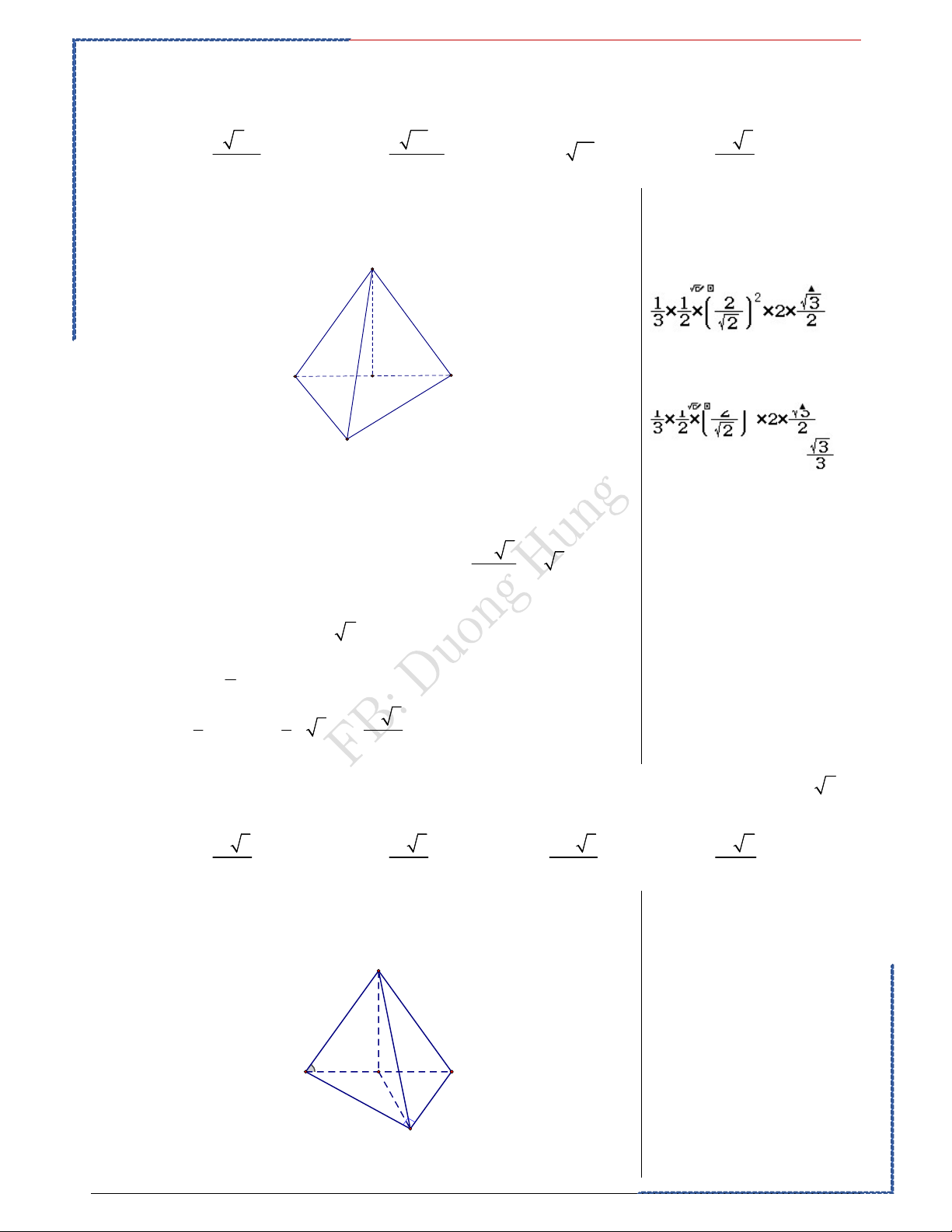
Câu 2: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại , B AC  2 , a mặt bên SAC
là tam giác đều và SAC   ABC. Tính thể tích khối chóp S.ABC. 3 3 3 Ⓐ. 2 2a 2 10a a 3 . Ⓑ. . Ⓒ. 3 a 10 . Ⓓ. 3 3 3 Lời giải PP nhanh trắc nghiệm Chọn D S  Casio A C H B Kẻ SH  A . C
Do (SAC)  (ABC)  SH  (ABC). 2 . a 3
Tam giác SAC đều cạnh AC  2a nên SH   a 3. 2
Tam giác ABC là tam giác vuông cân tại,
AC  2a  AB  BC  a 2 . 1 Do đó: 2 S  A . B BC  a (đvdt) ABC 2 3 1 1 a 3 2  V  SH.S  .a 3.a  (đvtt). S.ABC 3 ABC 3 3
Câu 3: Cho hình chóp S.ABC có SA  SB  SC. Tam giác ABC vuông cân tại , A AB  AC  a 2 và
SB tạo với mặt phẳng  ABC một góc 0
60 . Tính thể tích khối chóp S.AB . C 3 3 3 3 Ⓐ. a 3 a 3 2a 3 a 2 . Ⓑ. . Ⓒ. . Ⓓ. . 6 3 3 6 Lời giải PP nhanh trắc nghiệm Chọn B S  Casio 60° B C H A
Gọi H là trung điểm BC.
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 38
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung Theo giả thiết BA  CA 
 SH   ABC  SB  ABC     0 , SBH  60 . SA   SB  SC
Áp dụng pitago cho tam giác vuông
ABC BC  a 2  a 2 2 2 : 2
2  4a  BC  2a  BH  . a
Áp dụng hệ thức lượng cho tam giác vuông 0
SBH : SH  BH tan 60  a 3. 1  2 S  A . B AC  a . ABC 2 3 1 1 a 3
Vậy thể tích của khối chóp là: 2 V  SH.S  a 3.a  . 3 ABC 3 3
B - Bài tập rèn luyện:
Câu 1: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2a , tam giác SAB là tam giác đều
và nằm trong mặt phẳng vuông góc với mặt đáy. Tính thể tích khối chóp S.ABC . 3 3 Ⓐ. a 3a V  . Ⓑ. 3 V  a . Ⓒ. V  . Ⓓ. 3 V  3a . 2 2
Câu 2: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại ,
A BC  2a . Mặt bên SBC là
tam giác vuông cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABC . 3 3 3 Ⓐ. 2a 2a a 3 V  a . Ⓑ. V  . Ⓒ. V  . Ⓓ. V  . 3 3 3
Câu 3: Cho hình chóp S.ABC có SA  a , tam giác ABC đều, tam giác SAB vuông cân tại S và nằm
trong mặt phẳng vuông góc với mặt phẳng đáy. Thể tích khối chóp S.ABC bằng 3 3 3 3 Ⓐ. 6a 6a 6a 6a . Ⓑ. . Ⓒ. . Ⓓ. . 4 24 12 8
Câu 4: Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại B , AB  a , AC  2a . Hình chiếu
vuông góc của S lên  ABC là trung điểm M của AC . Góc giữa SB và đáy bằng 60. Thể tích S.ABC là bao nhiêu? 3 3 3 3 Ⓐ. a 3 a a a 2 . Ⓑ. . Ⓒ. . Ⓓ. . 2 2 4 12
Câu 5: Cho hình chóp S.ABC có tam giác ABC là tam giác đều cạnh a . Hình chiếu của S trên mặt
phẳng  ABC  là trung điểm của cạnh A , góc tạo bởi cạnh SC và mặt phẳng đáy  ABC  bằng 0
30 . Tính thể tích của khối chóp S.ABC . 3 3 3 3 Ⓐ. a 3 a 2 a 3 a 3 . Ⓑ. . Ⓒ. . Ⓓ. . 8 8 24 2
Câu 6: Cho hình chóp S.ABC có SAB và ABC là hai tam giác đều và nằm trong hai mặt phẳng a 6 vuông góc với nhau, SC 
. Tính thể tích V của khối chóp S.ABC . 2 3 3 3 3 Ⓐ. a a 3a a V  . Ⓑ. V  . Ⓒ. V  . Ⓓ. V  . 12 4 8 8
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 39
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
Câu 7: Cho hình chóp S.ABC có đáy ABC là tam giác đều; mặt bên SAB nằm trong mặt phẳng
vuông góc với mặt phẳng đáy và tam giác SAB vuông tại S , SA  a 3 , SB  a . Tính thể tích khối chóp S.ABC . 3 3 3 3 Ⓐ. 6a 6a a 6a . Ⓑ. . Ⓒ. . Ⓓ. . 6 3 2 2
Câu 8: Cho hình chóp S.ABC có đáy là ABC tam giác vuông cân đỉnh ,
A AB  AC  a . Hình chiếu
vuông góc của S lên mặt phẳng  ABC là trung điểm H của BC . Mặt phẳng SAB hợp
với mặt phẳng đáy một góc bằng 60 . Tính thể tích khối chóp S.ABC . 3 3 3 3 Ⓐ. a 2 a 3 a 3 a 3 V  . Ⓑ. V  . Ⓒ. V  . Ⓓ. V  . 12 4 6 12 BẢNG ĐÁP ÁN 1.B 2.D 3.D 4.B 5.C 6.D 7.C 8.D
_ Dạng 2. Chóp có đáy là tứ giác. 1 -Phương pháp: V  B.h 3
 Tính diện tích đáy: B
 Tính chiều cao của chóp: h A - Bài tập minh họa:
Câu 1: Cho hình chóp S. ABCD có đáy ABCD là hình vuông đường chéo AC  2 2 a . Mặt bên SAB
là tam giác đều và nằm trong mặt phẳng vuông góc với (ABCD) . Thể tích của khối chóp S. ABCD là 3 3 3 Ⓐ. 4 3 a 3 a 2 3 a 3 a . Ⓑ. . Ⓒ. . Ⓓ. . 3 6 3 Lời giải PP nhanh trắc nghiệm Chọn B  S B C H A D
Hạ đường cao SH của tam giác SAB thì SH là đường cao của hình chóp
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 40
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung Trong hình vuông ABCD: 2 AC  2 2 a  AB  2 ; a S  4a ABCD 3
Trong tam giác đều ABC: AB  2 a  SH  2 . a  a 3 2 3 1 4 3 a ⇒ 2 V  .a 3.4a  ⇒ Chọn B S .ABCD 3 3
Câu 2: Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Tam giác SAB cân tại S và nằm
trong mặt phẳng vuông góc với đáy, SA  2a . Tính theo a thể tích khối chóp S.ABCD . 3 3 3 Ⓐ. a 15 a 15 2a 3 V  2a . Ⓑ. V  . Ⓒ. V  . Ⓓ. V  . 12 6 3 Lời giải PP nhanh trắc nghiệm Chọn C 
Gọi H là trung điểm của AB .   SAB   ABCD  Ta có 
 SAB  ABCD  AB  SH   ABCD . SH  AB  2 a a 15
Xét tam giác vuông SAH : 2 2 2 SH  SA  AH  4a   . 4 2
Thể tích khối chóp S.ABCD là 3 1 1 a 15 a 15 2 V  .SH.S  . .a  (đvtt). 3 ABCD 3 2 6
Câu 3: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a , SA  a , SB  a 3 . Biết rằng
SAB  ABCD. Gọi M , N lần lượt là trung điểm của các cạnh AB,BC. Tính theo a thể tích của khối chóp S.BMDN . 3 3 3 Ⓐ. a 3 a 3 a 3 . Ⓑ. . Ⓒ. 3 2a 3 . Ⓓ. . 6 3 4
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 41
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung Lời giải PP nhanh trắc nghiệm Chọn B  S A D H M B N C Ta có 2 2 2
SA  SB  AB  SAB vuông tại S .
Gọi H là hình chiếu của S trên AB  SH   ABCD S . A SB a 3  SH   . AB 2 1 2 2 S  S  2S  4a  2. NC.CD  2a BMDN ABCD NCD 2 3 1 1 a 3 a 3 Vậy 2 V  S .SH  .2a .  . S.BMDN 3 BMDN 3 2 3
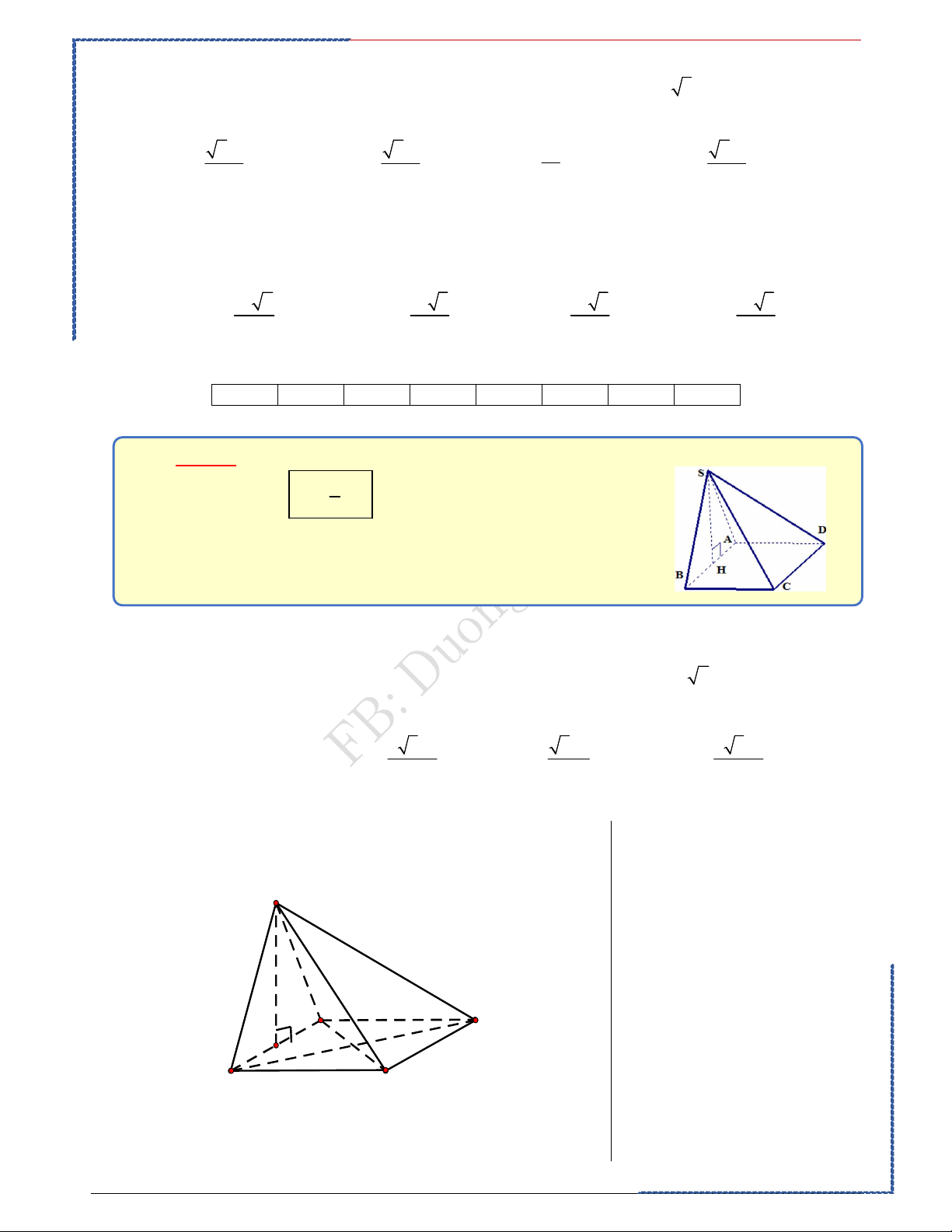
Câu 1: Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B , AB  BC  a , AD  2a . Hình
chiếu của S lên mặt phẳng  ABCD trùng với trung điểm cạnh AB . Biết rằng SC  a 5 . Tính theo
a thể tích V của khối chóp S.ABCD 3 3 3 3 Ⓐ. a 5 a 15 a 15 2a 5 V  Ⓑ. V  . Ⓒ. V  . Ⓓ. V  . 4 3 4 3
Câu 2: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Tam giác SAB đều và nằm trong mặt
phẳng vuông góc với mặt phẳng đáy  ABCD . Biết SD  2a 3 và góc tạo bởi đường thẳng SC và
mặt phẳng  ABCD bằng 0
30 . Tính thể tích V của khối chóp S.ABCD 3 3 3 3 Ⓐ. 2a 3 a 3 a 3 4a 6 V  . Ⓑ. V  . Ⓒ. V  Ⓓ. V  7 13 4 3
Câu 3: Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Mặt bên SAB là tam giác đều cạnh a và nằm
trong mặt phẳng vuông góc với (ABCD). Tính thể tích của khối chóp S.ABCD 3 3 3 Ⓐ. a 3 a 3 a . Ⓑ. . Ⓒ. . Ⓓ. 3 a . 6 2 3
Câu 4: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a 3 , mặt bên SAB là tam giác đều
và nằm trong mặt phẳng vuông góc với đáy. Thể tích của khối chóp S.ABCD là: Ⓐ. 3 12a . Ⓑ. 14a3. Ⓒ. 3 15a . Ⓓ. 3 17a .
Câu 5: Cho khối chóp S.ABCD có ABCD là hình vuông cạnh 3a . Tam giác SAB cân tại S và nằm trong
mặt phẳng vuông góc với đáy. Tính thể tích V của khối chóp S.ABCD , biết góc giữa SC và  ABCD bằng o 60 .
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 42
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung 3 Ⓐ. 9a 15 3 V  18a 3. Ⓑ. V  . Ⓒ. 3 V  9a 3 Ⓓ. 3 V  18a 15. 2
Câu 6: Cho hình chóp S.ABCD có đáy là tam giác vuông cân tại B , AB  a . Gọi I là trung điểm AC ,
tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp
S.ABC , biết góc giữa SB và mặt phẳng đáy băng 45 . 3 3 3 3 Ⓐ. a 3 a 2 a 2 a 3 . Ⓑ. . Ⓒ. . Ⓓ. . 12 12 4 4
Câu 7: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB  2a , AD  a . Hình chiếu của S
lên mặt phẳng  ABCD là trung điểm H của cạnh AB , đường thẳng SC tạo với đáy một góc 0 45
. Tính thể tích V của khối chóp S.ABCD . 3 3 3 3 Ⓐ. 2 2a a 2a 3a V  . Ⓑ. V  . Ⓒ. V  . Ⓓ. V  3 3 3 2
Câu 8: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, biết AB  a , AD  a 3 . Hình chiếu S
lên đáy là trung điểm H của cạnh AB , góc tạo bởi SD và đáy là 600. Tính thể tích của khối chóp S.ABCD . 3 3 3 3 Ⓐ. a 13 a a 5 a 15 . Ⓑ. . Ⓒ. . Ⓓ. . 2 2 5 5
Câu 9: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Tam giác SAB đều và nằm trong mặt phẳng
vuông góc với mặt phẳng đáy  ABCD . Biết SD  2a 3 và góc tạo bởi đường thẳng SC và mặt phẳng  ABCD bằng 0
30 . Tính thể tích V của khối chóp S.ABCD . 3 3 3 3 Ⓐ. 2 3a a 3 3a 4 6a V  . Ⓑ. V  . Ⓒ. V  . Ⓓ. V  . 7 13 4 3
Câu 10: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a ; hình chiếu của S trên  ABCD 3a
trùng với trung điểm của cạnh AB ; cạnh bên SD 
. Tính theo a thể tích của khối chóp 2 S.ABCD . 3 3 3 3 Ⓐ. a 7 a a 3 a 5 . Ⓑ. . Ⓒ. . Ⓓ. . 3 3 3 3
Câu 11: Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB  2a, AD  . a Tam giác SAB cân tại S
và nằm trong mặt phẳng vuông góc với đáy, SC tạo với đáy một góc 45. Thể tích khối chóp S.ABCD là 3 3 3 Ⓐ. a 3 a 2 2 2a . Ⓑ. . Ⓒ. 3 2 2a . Ⓓ. . 2 3 3
Câu 12: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, S
 AB đều cạnh a nằm trong mặt phẳng
vuông góc với  ABCD . Biết SCD tạo với  ABCD một góc bằng 0
30 . Tính thể tích V của khối chóp S.ABC . D 3 3 3 3 Ⓐ. a 3 a 3 a 3 a 3 V  . Ⓑ. V  . Ⓒ. V  . Ⓓ. V  . 8 4 2 3
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 43
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
Câu 13: Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB  2 ;
a AD  a . Tam giác SAB là tam giác
cân tại S và nằm trong mặt phẳng vuông góc với mặt đáy. Góc giữa mặt phẳng SBC  và  ABCD bằng 0
45 . Khi đó thể tích khối chóp S.ABCD là: Ⓐ. 3 1 2 3 a . Ⓑ. 3 a . Ⓒ. 3 2a . Ⓓ. 3 a . 3 3 3
Câu 14: Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a , S
 AD cân tại S và nằm trong
mặt phẳng vuông góc với đáy. Góc giữa SBC  và mặt đáy bằng o
60 . Tính thể tích S.ABCD bằng: 3 3 3 Ⓐ. 2a 3 8a 3 4a 3 . Ⓑ. . Ⓒ. . Ⓓ. 3 2a 3 . 3 3 3 BẢNG ĐÁP ÁN 1.C 2.D 3.A 4.A 5.B 6.B 7.A 8.A 9.D 10.B 11.C 12.B 13.D 14.B
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 44
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung Full Chuyên đề 12 new 2020-2021
CHƯƠNG ①: KHỐI ĐA DIỆN FB: Duong Hung
Bài 5: THỂ TÍCH KHỐI CHÓP ĐỀU
_ Dạng 1. Chóp có đáy là tam giác đều. 1 -Phương pháp: V  B.h 3
 Tính diện tích đáy: B
 Tính chiều cao của chóp: h A - Bài tập minh họa:
Câu 1: Tính thể tích của khối tứ diện đều có tất cả các cạnh đều bằng a . 3 a 2 3 a 3 3 a 2 3 a 3 A. . B. . C. . D. . 12 12 4 4 Lời giải PP nhanh trắc nghiệm Chọn A A  Casio a B D H M C
Gọi M là trung điểm của BC , H là trọng tâm tam giác BCD . 2 a 3
Ta có AH  BCD , BH  BM  2 2  AH  AB  BH 3 3 2  a 3  a 6 2  a      3    3 1 2 1 a 3 a 6 3 a 2
Vậy thể tích tứ diện là V  S .AH  . .  . ABCD 3 BCD 3 4 3 12
Câu 2: Cho khối tứ diện đều có tất cả các cạnh bằng 2a . Thể tích khối tứ diện đã cho bằng
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 45
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung 3 a 2 3 a 2 3 a 2 3 2a 2 A. . B. . C. . D. . 6 12 3 3 Lời giải PP nhanh trắc nghiệm Chọn D A  Casio 2a B D O M C
Gọi O là trọng tâm tam giác ABC .
Do tứ diện ABCD là tứ diện đều nên ta có AO  (BC ) D . 2 (2a) 3 Ta có : 2 S   a 3 . BCD 4 2 2 2a 3 2a 3 2a 6 2 2 BO  BM  .   AO  AB  BO  . 3 3 2 3 3 3 1 1 2a 6 2a 2 Ta có : 2 V  S .AO  .a 3.  (đvtt). ABCD 3 B  CD 3 3 3
Câu 3: Hình chóp tam giác đều S.ABC có cạnh đáy là a và mặt bên tạo với đáy góc 45 . Tính theo
a thể tích khối chóp S.ABC . 3 a 3 a 3 a 3 a A. . B. . C. . D. . 8 24 12 4 Lời giải PP nhanh trắc nghiệm Chọn B  Casio
 Gọi M là trung điểm BC và O là tâm đường tròn ngoại tiếp tam giác ABC .
 Suy ra SO   ABC .
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 46
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
 Góc giữa mặt bên SBC  và mặt đáy  ABC là góc  SMO  45 . 2 a a 3
Xét tam giác vuông ABM : 2 2 2 AM  AB  BM  a   . 4 2 1 3 Mặt khác    a OM AM OM . 3 6
Xét tam giác vuông SOM : SO  OM  a 3 a 3 .tan SMO  .tan 45  . 6 6 2 1 a 3
Diện tích tam giác ABC : S  . . a . a sin 60  . ABC 2 4
Vậy thể tích khối chóp S.ABC là 2 3 1 1 a 3 a 3  a V S . O S  . .  . S.ABC 3 ABC 3 6 4 24
B - Bài tập rèn luyện:
Câu 1: Cho hình chóp tam giác đều .
S ABC có cạnh đáy bằng 2a , cạnh bên tạo với mặt đáy góc 0 60
. Tính theo a thể tích khối chóp . S ABC . 3 a 3 3 2a 3 3 a 3 A. . B. . C. . D. 3 a 3 . 4 3 3
Câu 2: Hình chóp tam giác đều S.ABC có cạnh đáy là a và mặt bên tạo với đáy góc 45 . Tính theo
a thể tích khối chóp S.ABC . 3 a 3 a 3 a 3 a A. . B. . C. . D. . 8 24 12 4
Câu 3: Cho hình chóp tam giác đều .
S ABC có cạnh đáy bằng 2a , cạnh bên tạo với đáy một góc 6  0 . Thể tích khối chóp . S ABC là 3 2a 3 3 a 3 3 a 3 A. . B. . C. . D. 3 a 3 . 3 3 4
Câu 4: Cho khối chóp tam giác đều có tất cả các cạnh đều bằng 2a . Thể tích của khối chóp đó bằng 3 2 2a 3 2a 3 2a 3 2 6a A. . B. . C. . D. . 3 3 12 9
Câu 5: Cho khối chóp tam giác đều có cạnh đáy bằng a , cạnh bên bằng 3a . Thể tích của khối chóp đó bằng 3 2 2a 3 2a 3 2a 3 2a A. . B. . C. . D. . 3 3 6 12
Câu 6: Cho hình chóp tam giác đều có cạnh đáy bằng a và cạnh bên bằng 2a . Thể tích khối chóp là 3 a 5 3 a 11 3 a 5 3 a 11 A. . B. . C. . D. . 6 24 12 12
Câu 7: Tính thể tích của khối tứ diện đều có tất cả các cạnh đều bằng a . 3 a 2 3 a 3 3 a 2 3 a 3 A. . B. . C. . D. . 12 12 4 4
Câu 8: Cho khối chóp tam giác đều S.ABC có cạnh đáy bằng a và cạnh bên bằng 2a . Tính thể tích V của khối chóp S.ABC 3 13a 3 11a 3 11a 3 11a A. V  . B. V  . C. V  . D. V  . 12 12 6 4
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 47
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
Câu 9: Tính thể tích của chóp tam giác đều có tất cả các cạnh đều bằng a . 3 a 2 3 a 2 3 a 2 3 a 2 A. . B. . C. . D. . 12 4 6 2
Câu 10: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a 3 , cạnh bên bằng 2a . Tính thể tích V của khối chóp S.ABC . 3 a 3 3 3a 3 3 3a 3 3 3a A. V  . B. V  . C. V  . D. V  . 4 2 4 4
Câu 11: Cho hình chóp tam giác đều có cạnh đáy bằng a và cạnh bên tạo đáy góc 0 60 . Thể tích của khối chóp đó bằng: 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 12 6 36 18
Câu 12: Cho hình chóp đều S.ABC có cạnh đáy bằng a, cạnh bên bằng a 2. Thể tích khối chóp S.ABC là 3 3 3 3 A. a 3 . B. a 3 . C. a 5 . D. a 5 . 6 12 6 12 BẢNG ĐÁP ÁN 1.B 2.B 3.A 4.A 5.C 6.D 7.A 8.B 9.A 10.D 11.A 12.D
_ Dạng 2. Chóp có đáy là hình vuông. 1 -Phương pháp: V  B.h 3
 Tính diện tích đáy: B
 Tính chiều cao của chóp: h A - Bài tập minh họa:
Câu 1: Cho một hình chóp tứ giác đều có cạnh đáy bằng 2a và cạnh bên tạo với mặt phẳng đáy
một góc bằng 45 . Thể tích của khối chóp đó là 3 a 2 3 4a 2 3 a 2 A. . B. 3 2a 2 . C. . D. . 8 3 6 Lời giải PP nhanh trắc nghiệm Chọn C 
Gọi O  AC  BD , vì hình chóp tứ giác đều nên ta có SO   ABCD
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 48
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
Vì là hình chiếu vuông góc của trên mặt đáy  ABCD nên 
SDO là góc giữa cạnh bên và mặt đáy  ABCD
Theo đề ra tam giác vuông tại và có  SDO  45 nên tam giác vuông cân tại. Do vậy SO  OD  a 2 3 1 1 4a 2 Vậy 2 V  S . O S  .a 2.4a  S .ABCD 3  . ABCD 3 3
Câu 2: Tính thể tích khối chóp tứ giác đều S.ABCD biết AB  a , SA  a . 3 a 2 3 a 2 3 a A. . B. . C. . D. 3 a . 2 6 3 Lời giải PP nhanh trắc nghiệm Chọn B  2 a a Ta có 2 2 SO  SA  OA 2 2  a   2 2 1 3 1 a 2 a 2 Ta có: V  S . O S 2  . .a  ( đvtt ) S .ABCD 3 ABCD 3 2 6
Câu 3: Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a . Biết 
ASC  90 , tính thể tích V của khối chóp đó. 3 a 3 a 2 3 a 2 3 a 2 A. . B. V  . C. V  . D. V  . 3 3 6 12 Lời giải PP nhanh trắc nghiệm  Chọn C
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 49
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung S B C O A a D
Ta có SO   ABCD; AC  a 2. AC a 2
Tam giác ASC vuông cân tại S nên SO   . 2 2 3 1 1 a 2 a 2 Vậy 2 V  S .SO  .a .  . 3 ABCD 3 2 6
B - Bài tập rèn luyện:
Câu 1: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a , góc giữa cạnh bên và mặt đáy bằng
60 . Thể tích khối chóp S.ABCD là 3 a 6 3 a 3 3 a 6 3 a 6 A. . B. . C. . D. . 6 6 12 2
Câu 2: Cho hình chóp tứ giác đều S.ABCD có diện tích đáy bằng 2
16 cm và diện tích một mặt bên bằng 2
8 3 cm . Thể tích của khối chóp là 32 11 32 2 32 13 A. 3 cm . B. 3 4 cm . C. 3 cm . D. 3 cm . 3 3 3
Câu 3: Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a , các mặt bên tạo với mặt đáy bằng
60 . Tính thể tích khối chóp đó. 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 2 12 6 3
Câu 4: Cho khối chóp tứ giác đều có cạnh đáy bằng 2a cạnh bên bằng 3a . Thể tích của khối chóp đã cho bằng 3 2 7a 3 4a 3 4 7a 3 2 2a A. . B. . C. . D. . 3 3 3 3
Câu 5: Cho hình chóp tứ giác đều SABCD có độ dài cạnh đáy bằng a . Góc tạo bởi cạnh bên và đáy
bằng 60 . Tính thể tích khối chóp S.ABCD theo a . 3 a 5 3 a 3 3 a 6 3 a 2 A. . B. . C. . D. . 6 6 6 6
Câu 6: Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a . Biết 
ASC  90 , tính thể tích V của khối chóp đó. 3 a 3 a 2 3 a 2 3 a 2 A. . B. V  . C. V  . D. V  . 3 3 6 12
Câu 7: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O, AB  a, AD  a 3, SA  3 . a
SO vuông góc với mặt phẳng đáy ABC .
D Tính thể tích của khối chóp S.ABC. 3 a 6 3 2a 6 A. . B. . C. 3 a 6. D. 3 2a 6. 3 3
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 50
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
Câu 8: Cho khối chóp tứ giác đều cạnh đáy bằng a, góc giữa mặt bên với mặt đáy bằng 45. Tính
thể tích của khối chóp đó. 3 a 3 a 3 a 2 A. . B. . C. 3 a 2 . D. . 6 3 2
Câu 9: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và cạnh bên tạo với mặt phẳng đáy một góc 0
60 . Tính thể tích V của khối chóp S.ABCD . 3 a 6 3 a 6 3 a 3 3 a 6 A. V  . B. V  . C. V  . D. V  2 3 2 6
Câu 10: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a , cạnh bên bằng 3a . Tính thể tích V của khối chóp đã cho 3 4 7a 3 4a 3 4 7a A. 3 V  4 7a . B. V  . C. V  . D. V  . 9 3 3
Câu 11: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a , góc giữa mặt bên và mặt đáy bằng
600. Tính theo a thể tích khối chóp S.ABCD 3 2a 3 3 2a 6 3 4a 3 3 a 3 A. . B. . C. . D. . 3 3 3 3
Câu 12: Tính thể tích của khối chóp tứ giác đều có cạnh bên bằng 2a, góc giữa cạnh bên và mặt đáy bằng 0 60 . 3 2a 3 A. 3 2a 3 . B. 3 2a . C. . D. 3 6a . 3
Câu 13: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, góc giữa cạnh bên và mặt phẳng đáy bằng 0
45 . Thể tích của khối chóp đó là 3 4 2a 3 8 2a 3 a 3 3 a 3 A. . B. . C. . D. . 3 3 3 6
Câu 14: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a , góc giữa cạnh bên và mặt đáy bằng
 . Khi đó thể tích khối chóp S.ABCD bằng 3 a 2 3 a 3 a 2 3 a 2 A. tan . B. tan . C. tan . D. cot . 2 6 6 6
Câu 15: Cho hình chóp tứ giác đều S.ABCD , đáy ABCD có diện tích 2
16 cm , diện tích một mặt bên là 2
8 3 cm . Tính thể tích V của khối chóp S.ABCD . 32 2 32 13 32 11 32 15 A. 3 V  cm . B. 3 V  cm . C. 3 V  cm . D. 3 V  cm . 3 3 3 3
Câu 16: Cho một hình chóp tứ giác đều có góc tạo bởi mặt bên và mặt đáy bằng 0 60 và diện tích xung quanh bằng 2
8a . Tính diện tích S của mặt đáy hình chóp. A. 2 4a 3 . B. 2 4a . C. 2 2a . D. 2 2a 3 . BẢNG ĐÁP ÁN 1.A 2.A 3.C 4.C 5.C 6.C 7.A 8.A 9.D 10.D 11.C 12.C 13.A 14.C 15.C 16.B
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 51
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung Full Chuyên đề 12 new 2020-2021
CHƯƠNG ①: KHỐI ĐA DIỆN FB: Duong Hung
Bài 6: THỂ TÍCH KHỐI LĂNG TRỤ ĐỨNG
_ Dạng 1. Lăng trụ đứng có đáy là tam giác. -Phương pháp: V  B.h
 Tính diện tích đáy: B
 Tính chiều cao của chóp: h A - Bài tập minh họa:
Câu 1: Cho khối lăng trụ đứng ABC. AB C
  có BB  a , đáy ABC là tam giác vuông cân tại B và
AC  a 2 . Tính thể tích V của khối lăng trụ đã cho. 3 3 3 Ⓐ. a a a V  . Ⓑ. V  . Ⓒ. 3 V  a . Ⓓ. V  . 6 2 3 Lời giải PP nhanh trắc nghiệm Chọn B
 Thuộc Công thức. Xác
định và tính nhanh các yếu tố. Ta có: 2 2 2 2 2 2 2
AC  BA  BC  2a  2AB  AB  a . 3 1 a  2 V        BB .S . a .a . ABC. A B C A  BC 2 2
Câu 2: Cho khối lăng trụ đứng ABC.AB C
  có BB  a , đáy ABC là tam giác vuông cân tại B và
AC  a 2 . Tính thể tích V của khối lăng trụ đã cho. Ⓐ. 3 3 3 3 a a a V  a . Ⓑ. V  . Ⓒ. V  . Ⓓ. V  . 3 6 2 Lời giải PP nhanh trắc nghiệm Chọn D Thuộc Công thức. Xác
định và tính nhanh các yếu tố.
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 52
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung A' C' B' C A B
Do ABC là tam giác vuông cân tại B và AC  a 2  AB  BC  a . 3 1 1 a V          BB .S BB . .B . A BC . a . . a a . ABC.A B C ABC 2 2 2
Câu 3: Cho khối lăng trụ đều ABC.AB C
  có cạnh đáy bằng a . Khoảng cách từ điểm A đến mặt phẳng AB C  2a 3 bằng
. Thể tích khối lăng trụ đã cho là 19 3 3 3 3 Ⓐ. a 3 a 3 a 3 a . Ⓑ. . Ⓒ. . Ⓓ. . 4 6 2 2 Lời giải PP nhanh trắc nghiệm Chọn C
 Thuộc Công thức. Xác A C
định nhanh khoảng cách và tính các yếu tố. B H A' C' M B'
Gọi M là trung điểm của B C
  , H là hình chiếu của A lên AM . Ta có AM  B C    
 B C AAMAB CAAM AA  B C       AH AB C     AH  AM  a Suy ra d A AB C   2 3 ,  AH  . 19 1 1 1 1 1 1 1 Khi đó        AA  2a 2 2 2 2 2 2 2 AH AA AM AA A H AM 4a 2 3 a 3 a 3
Vậy thể tích khối lăng trụ đã cho là: V  S .AA  .2 a  . A  BC 4 2
B - Bài tập rèn luyện:
Câu 1: Cho hình lăng trụ đứng ABC. 
A BC có đáy ABC là tam giác vuông tại A , biết AB  a , AC  2a và 
A B  3a . Tính thể tích của khối lăng trụ ABC.  A BC . 3 3 Ⓐ. 2 2a 5a . Ⓑ. . Ⓒ. 3 5a . Ⓓ. 3 2 2a . 3 3
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 53
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
Câu 2: Cho hình lăng trụ đứng ABC.A B  C
  có tam giác ABC vuông tại A , AB  BB  a , AC  2a .
Tính thể tích khối lăng trụ đã cho. 3 3 Ⓐ. 2a a . Ⓑ. . Ⓒ. 3 2a . Ⓓ. 3 a . 3 3
Câu 3: Cho hình lăng trụ ABC.A' B' C' có đáy là tam giác đều cạnh a , cạnh bên bằng 2 a và hợp với
mặt đáy một góc 60o. Thể tích của khối lăng trụ ABC.A' B' C' tính theo a bằng: 3 3 3 3 Ⓐ. 2a 4a 3a 5a . Ⓑ. . Ⓒ. . Ⓓ. 3 3 4 3
Câu 4: Cho hình lăng trụ tam giác đều ABC.A' B 'C ' có AB  2a, AA'  a 3 . Tính thể tích V của
khối lăng trụ ABC.A' B 'C ' theo . a 3 3 Ⓐ. a 3a 3 V  a . Ⓑ. 3 V  3a . Ⓒ. V  . Ⓓ. V  . 4 4
Câu 5: Cho hình lăng trụ đứng ABC.AB C
  có đáy ABC là tam giác vuông tại A, biết AB  a ,
AC  2a và AB  3a . Tính thể tích của khối lăng trụ ABC.AB C   . 3 3 Ⓐ. 2 2a 5a . Ⓑ. . Ⓒ. 3 5a . Ⓓ. 3 2 2a . 3 3 
Câu 6: Cho lăng trụ đứng ABC.A B  C
  có AB  a , AC  2a, BAC 120, biết C A  hợp với đáy một
góc 45 . Thể tích của khối lăng trụ là 3 3 Ⓐ. 3 2a 3 a 3 2a 3 . Ⓑ. V  . Ⓒ. . Ⓓ. 3 a 3 . 3 3
Câu 7: Cho lăng trụ đứng ABC.A B  C
  có ABC là tam giác vuông tại A , AC  a ,  ABC  30 ,  BC V
hợp với mặt bên  ACC A
  một góc 30 , thể tích của khối lăng trụ là V . Khi đó bằng 3 a 6 Ⓐ. 3 1 1 . Ⓑ. 3 . Ⓒ. . Ⓓ. . 3 3
Câu 8: Cho khối lăng trụ đứng ABC.  A BC và có B C
  3a , đáy ABC là tam giác vuông cân tại B
và AC  a 2 . Tính thể tích V của khối lăng trụ ABC.A B  C  . 3 Ⓐ. 3 3 2a a V  2a . Ⓑ. 3 V  2a . Ⓒ. V  . Ⓓ. . 3 6 2
Câu 9: Cho lăng trụ đứng ABC.A B  C
  có ABC là tam giác vuông tại B , AB  a; BC  a 2 . Mặt
phẳng  ABC hợp với mặt đáy  ABC một góc 30 . Tính thể tích khối lăng trụ. 3 3 3 3 Ⓐ. a 6 a 6 a 3 3a . Ⓑ. . Ⓒ. . Ⓓ. . 3 6 3 6
Câu 10: Tính theo a thể tích khối lăng trụ đứng ABC.AB C
  có đáy ABC là tam giác vuông cân tại A , mặt bên BCC B
  là hình vuông cạnh 2a . 3 Ⓐ. 2a 3 2a . Ⓑ. . Ⓒ. 3 4a . Ⓓ. 3 a 2 . 3
Câu 11: Cho khối lăng trụ đứng ABC.A B  C
  có đáy là tam giác cân ABC với AB  AC  a , góc  0
BAC  120 , mặt phẳng  AB C
  tạo với đáy một góc 0
30 . Tính thể tích V của lăng trụ đã cho. 3 3 3 3 Ⓐ. a a 3a a V  . Ⓑ. V  . Ⓒ. V  . Ⓓ. V  . 6 8 8 4
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 54
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
Câu 12: Tính theo a thể tích khối lăng trụ đứng ABC.AB C
  có đáy ABC là tam giác vuông cân tại A , mặt bên BCC B
  là hình vuông cạnh 2a . 3 Ⓐ. 3 2a 2a . Ⓑ. . Ⓒ. 3 a . Ⓓ. 3 a 2 . 3
Câu 13: Cho khối lăng trụ đứng ABC.A' B 'C ' có BB '  2a , đáy ABC là tam giác vuông cân tại B và
AC  a 2 . Tính thể tích V của khối lăng trụ đã cho. 3 3 Ⓐ. 2a a 3 V  2a . Ⓑ. V  . Ⓒ. V  . Ⓓ. 3 V  a . 3 3
Câu 14: Cho lăng trụ đứng ABC.A B  C
  có đáy ABC là tam giác vuông tại B ; AB  a ; BC  a 2 ;
mặt phẳng  ABC hợp với đáy  ABC góc 30 . Tính theo a thể tích của khối lăng trụ đã cho. 3 3 3 Ⓐ. a 6 a 6 a 6 . Ⓑ. . Ⓒ. . Ⓓ. 3 a 6 . 12 3 6
Câu 15: Cho hình lăng trụ tam giác đều ABC. AB C
  có cạnh đáy bằng 2a và mặt phẳng  ABC tạo
với mặt phẳng  ABC một góc 60o . Tính thể tích khối lăng trụ AB . C A B  C   . Ⓐ. 3 a 3 . Ⓑ. 3 2a 3 . Ⓒ. 3 3a 3 . Ⓓ. 3 2a .
Câu 16: Cho khối lăng trụ đứng ABC.AB C
  có CC  2a , đáy ABC là tam giác vuông cân tại B và
AC  a 2 . Tính thể tích V của khối lăng trụ đã cho. 3 3 Ⓐ. 3 a a V  a . Ⓑ. V  . Ⓒ. 3 V  2a . Ⓓ. V  . 2 3
Câu 17: Cho khối lăng trụ đều ABC.A B  C
 có cạnh đáy bằng a , góc tạo bởi AB và đáy bằng 0 60 .
Tính thể tích khối lăng trụ ABC.A B  C  . 3 3 Ⓐ. 3a a 3 . Ⓑ. . Ⓒ. 3 a 3 . Ⓓ. 3 3a . 4 4
Câu 18: Cho hình lăng trụ đều ABC.A' B 'C ' có cạnh đáy bằng a , A'C hợp với mặt đáy một góc 60o
. Thể tích của khối lăng trụ ABC.A' B 'C ' tính theo a bằng: 3 3 3 3 Ⓐ. 3a a 2a 3a . Ⓑ. . Ⓒ. . Ⓓ. . 4 4 3 8
Câu 19: Cho hình lăng trụ đứng ABC.A' B 'C ' có cạnh đáy là tam giác vuông cân tại B , AB  a . Cạnh
SC hợp với mặt phẳng đáy một góc bằng 30o . Thể tích của khối lăng trụ ABC.A B  C   tính theo a bằng: 3 3 3 3 Ⓐ. a 3 a 3 a 6 2a 3 . Ⓑ. . Ⓒ. . Ⓓ. . 3 6 3 3 BẢNG ĐÁP ÁN 1.D 2.D 3.C 4.B 5.D 6.D 7.A 8.B 9.B 10.A 11.B 12.A 13.D 14.C 15.C 16.A 17.A 18.A 19.C
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 55
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
_ Dạng 2. Lăng trụ có đáy là tứ giác -Phương pháp: V  B.h
 Tính diện tích đáy: B
 Tính chiều cao của chóp: h
A - Bài tập minh họa:
Câu 1: Tính thể tích khối lập phương ABC . D AB C  D   biết BD  3 . a Ⓐ. 3 27a . Ⓑ. 3 a . Ⓒ. 3 3a 3 . Ⓓ. 3 9a . Lời giải PP nhanh trắc nghiệm Chọn B
 Thuộc Công thức. Xác
định và tính nhanh các yếu tố.
Gọi cạnh của khối lập phương là x ta có 2 2 BD  x  x  x 2.
Tam giác BDD vuông tại D suy ra 2 2 2 2 2 2 2
BD  BD  DD  3a  2x  x  3x  a  . x
Vậy thể tích của khối lập phương ABC . D AB C  D   là 3 V       . a . a a a . ABCD.A B C D
Câu 2: Cho hình hộp chữ nhật ABC . D A B  C  D
  có đáy là hình vuông cạnh 2a và A B   3a . Tính
thể tích khối hộp chữ nhật ABC . D A B  C  D   theo a . 3 4a 5 A. 3 V  4a 5 . Ⓑ. 3 V  12a . Ⓒ. 3 V  2a 5 . Ⓓ. V  . 3 Lời giải PP nhanh trắc nghiệm Chọn A B C
 Thuộc Công thức. Xác
định và tính nhanh các yếu A D tố. 3a B' C' 2a A' D'
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 56
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
Xét tam giác vuông ABB , ta có: BB  A B   A B
    a2  a2 2 2 3 2  5a
Thể tích khối hộp chữ nhật ABC . D A B  C  D   là: 3 V  S .BB  2 . a 2 . a 5a  4 5a ABCD
Câu 3: Cho hình lập phương ABC . D A B  C  D
  với O là tâm hình vuông A B  C  D   . Biết rằng tứ
diện O .BCD có thể tích bằng 3
6a . Tính thể tích V của khối lập phương ABC . D AB C  D   . Ⓐ. 3 V  12a . Ⓑ. 3 V  36a . Ⓒ. 3 V  54a . Ⓓ. 3 V  18a . Lời giải PP nhanh trắc nghiệm Chọn B B' C'
 Thuộc Công thức. Xác O' A'
định và tính nhanh các yếu D' tố. B C A D 1 1 1 1 Ta có 3 V         AA . .S AA .S V V 36a O .BCD 3 2 ABCD 6 ABCD 6
B - Bài tập rèn luyện:
Câu 1: Thể tích của khối lăng trụ đứng tam giác đều có tất cả các cạnh bằng a bằng 3 3 3 3 Ⓐ. a 3 a a 3 a 2 . Ⓑ. . Ⓒ. . Ⓓ. . 4 3 6 3
Câu 2: Cho hình lăng trụ đứng ABCD.AB C  D
  có đáy là hình thoi, biết AA  4a, AC  2a, BD  a .
Thể tích V của khối lăng trụ là Ⓐ. 3 8 V  8a . Ⓑ. 3 V  2a . Ⓒ. 3 V  a . Ⓓ. 3 V  4a . 3
Câu 3: Cho hình lăng trụ đứng ABC . D A B  C  D
  có đáy ABCD là hình chữ nhật, AB  a , AD  a 2
, AB  a 5 (tham khảo hình vẽ). Tính theo a thể tích V của khối lăng trụ đã cho. 3 Ⓐ. 3 2a 2 V  a 2 . Ⓑ. 3 V  2a 2 . Ⓒ. 3 V  a 10 . Ⓓ. V  . 3
Câu 4: Cho hình hộp đứng có cạnh bên độ dài 3a , đáy là hình thoi cạnh a và có một góc 60 . Khi
đó thể tích khối hộp là
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 57
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung 3 3 3 3 Ⓐ. 3a 3 a 3 a 3 3a 3 . Ⓑ. . Ⓒ. . Ⓓ. . 4 3 2 2
Câu 5: Thể tích khối lăng trụ đứng tam giác ABC.ABC có tất cả các cạnh bằng a là 3 3 3 3 Ⓐ. a 3 a 3 a 3 a . Ⓑ. . Ⓒ. . Ⓓ. . 4 6 3 4
Câu 6: Cho hình lăng trụ đứng ABC . D AB C  D
  , có ABCD là hình vuông cạnh 2a , cạnh
AC  2a 3 .Thể tích khối lăng trụ ABC.AB C   bằng Ⓐ. 3 8a . Ⓑ. 3 3a . Ⓒ. 3 2a . Ⓓ. 3 a .
Câu 7: Khối lập phương ABC .
D A' B 'C ' D ' có độ dài đoạn AB '  2a . Thế tích của khối đó là: Ⓐ. 3 2 2a . Ⓑ. 3 8a . Ⓒ. 3 3 3a . Ⓓ. 3 3 2a .
Câu 8: Cho lăng trụ đứng tam giác ABC. 
A BC , đáy là tam giác vuông tại A AC  a  0 , , ACB  60 ,
AC  3a . Thể tích khối lăng trụ đó là: 3 3 3 Ⓐ. 4 6a 2 6a 6a . Ⓑ. 3 6a . Ⓒ. . Ⓓ. . 3 3 3
Câu 9: Cho khối hộp chữ nhật ABC . D AB C  D
  có AB  a , AD  2a , AA  3a . Tính thể tích V của khối tứ diện . B A C  D   . A B D C B' A' D' C' Ⓐ. 3 V  6a . Ⓑ. 3 V  2a . Ⓒ. 3 V  a . Ⓓ. 3 V  3a . BẢNG ĐÁP ÁN 1.A 2.D 3.B 4.D 5.A 6.A 7.A 8.B 9.C
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 58
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung Full Chuyên đề 12 new 2020-2021
CHƯƠNG ①: KHỐI ĐA DIỆN FB: Duong Hung Bài 7: TỶ SỐ THỂ TÍCH
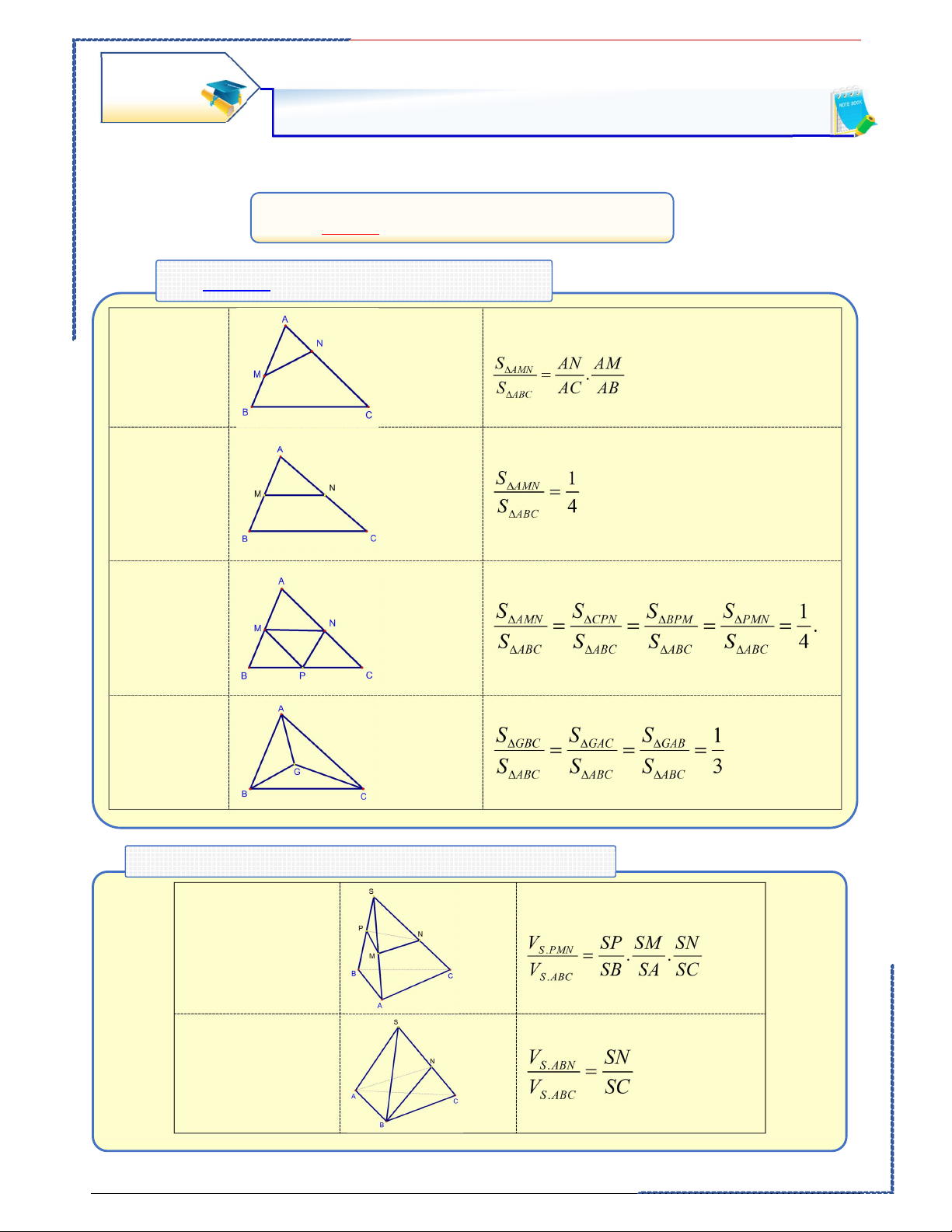
 Dạng ①: Tỷ số cơ bản trong tam giác. ①. M, N bất kỳ trên AB, AC ②. Đường trung bình MN ③. M, N, P là trung điểm của AB, AC, BC ④. Trọng tâm G
 Dạng ②: Tỷ số cơ bản của khối Chóp tam giác ①. M, N, P lần lượt thuộc SA, SC, SB ② . N thuộc SC A - Bài tập minh họa:
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 59
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
Câu 1: Cho hình chóp S.ABC . Gọi M , N, P lần lượt là trung điểm S ,
A SB và SC . Khi đó tỉ số thể tích
giữa khối chóp S.MNP và khối chóp S.ABC bằng Ⓐ. 1 1 . Ⓑ. . Ⓒ. 1 . Ⓓ. 1 . 4 8 6 2 Lời giải PP nhanh trắc nghiệm Chọn B  Xác định tỉ số
 Hai khối tứ diện cần tính tỉ số là V SM SN SP 1 1 1 1 S.MNP  . .  . .  S.MNP và S.ABC V SA SB SC 2 2 2 8 S.ABC
 M, N, P lần lượt là trung điểm của SA, SM 1 SN 1 SP 1 SB, SC nên  ;  ;  SA 2 SB 2 SC 2 V SM SN SP 1 1 1 1 S.MNP  . .  . .  V SA SB SC 2 2 2 8 S.ABC
Câu 2: Cho khối tứ diện ABCD có thể tích V và điểm E trên cạnh AB sao cho AE  3EB . Tính thể
tích khối tứ diện E.BCD theo V . Ⓐ. 3V 3V V V . Ⓑ. . Ⓒ. . Ⓓ. . 4 2 3 4 Lời giải PP nhanh trắc nghiệm Chọn D A  Xác định tỉ số
 Hai khối tứ diện cần tính tỉ số là V AE AC AD 3 AECD     A.ECD và . A BCD V AB AC AD 4 ABCD
 AE  3EB nên AB chia làm 4 phần V  V V AE 3 E.BCD . A BCD . A ECD AE 3 phần EB 1 phần  E 3 1 AB 4  V  V  V . A BCD 4 ABCD 4 ABCD V AE AC AD 3 AECD     B D V AB AC AD 4 ABCD 3  V  V . Do đó C AECD 4 ABCD 3 1 V  V V  V  V  V . E.BCD A.BCD A.ECD A.BCD 4 ABCD 4 ABCD V
Câu 3: Cho hình chóp S.ABC . Gọi M , N lần lượt là trung điểm của SA , SB . Tính tỉ số S.ABC . VS.MNC Ⓐ. 1 1 . Ⓑ. . Ⓒ.2. Ⓓ.4. 2 4 Lời giải PP nhanh trắc nghiệm Chọn D  Xác định tỉ số V SA SB SC S.ABC  . .  2.2  4 V SM SN SC S.MNC
 Hai khối tứ diện cần tính tỉ số là S.ABC và S.MNP
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 60
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung SA SB
 M, N, P lần lượt là trung điểm của SA, SBnên  2;  2 SM SN V SA SB SC  S.ABC  . .  2.2  4 V SM SN SC S.MNC
Câu 4: Cho hình chóp S.ABC có A và B lần lượt là trung điểm của SA và SB . Biết thể tích khối chóp
S.ABC bằng 24 . Tính thể tích V của khối chóp S.AB C  . Ⓐ. V  12. Ⓑ. V  8. Ⓒ.V  6 . Ⓓ.V  3. Lời giải Chọn C PP nhanh trắc nghiệm S V     SA SB SC  S.A B C  . . V SA SB SC S.ABC A' B' A B C V     SA SB SC 1 1  Ta có S.A B C  . .  1 .  V SA SB SC 2 2 4 S.ABC 1  Vậy V  1   .   .V .24 6 S . A B C S . 4 ABC 4
B - Bài tập rèn luyện:
Câu 1: Cho hình chóp S.ABC có  ASB   ASC  
BSC  60 và SA  2 ; SB  3 ; SC  7 . Tính thể tích V của khối chóp. Ⓐ. 7 2 V  4 2 . Ⓑ. V  . Ⓒ. 7 2 V  . Ⓓ. V  7 2 . 2 3
Câu 2: Cho hình chóp S.ABC có A và B lần lượt là trung điểm của SA và SB . Biết thể tích khối
chóp S.ABC bằng 24 . Tính thể tích V của khối chóp S.AB C  . Ⓐ. V  3 Ⓑ. V 12 Ⓒ.V  8 Ⓓ. V  6
Câu 3: Cho khối chóp S.ABC , M là trung điểm của cạnh BC. Thể tích của khối chóp S.MAB là 3 2a .
Thể tích khối chóp S.ABC bằng. 3 Ⓐ. a 1 3 2a . Ⓑ. 3 4a . Ⓒ. . Ⓓ. 3 a . 4 2
Câu 4: Cho tứ diện ABCD có thể tích bằng 12 và I là trung điểm CD , M là trung điểm BI . Tính
thể tích V của khối chóp . A MCD . Ⓐ. V  4 . Ⓑ. V  6. Ⓒ.V 3. Ⓓ.V 5.
Câu 5: Cho tứ diện ABCD có DA  1; DA   ABC. A
 BC là tam giác đều, có cạnh bằng 1 . Trên DM 1 DN 1 DP 3
cạnh DA, DB, DC lấy 3 điểm M , N , P sao cho  ;  ;  . Thể tích của tứ DA 2 DB 3 DC 4 diện MNPD bằng Ⓐ. 2 3 V  . Ⓑ. V  . Ⓒ. 3 V  . Ⓓ. 2 V  . 96 12 96 12
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 61
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
Câu 6: Cho khối chóp S.ABCD có thể tích là 3
a . Gọi M , N , P, Q theo thứ tự là trung điểm của
SA, SB, SC, SD. Thể tích khối chóp S.MNPQ là: 3 3 2 3 Ⓐ. a a a a Ⓑ. . Ⓒ. . Ⓓ. 16 8 4 6
Câu 7: Cho khối chóp S.ABC . Gọi A , B lần lượt là trung điểm của SA và SB . Khi đó tỉ số thể tích
của hai khối chóp S.AB C  và S.ABC bằng: Ⓐ. 1 1 . Ⓑ. . Ⓒ. 1 . Ⓓ. 1 . 4 6 2 3
Câu 8: Cho tứ điện MNPQ . Gọi I , J , K lần lượt là trung điểm các cạnh MN , MP, MQ . Tính tỉ số thể V tích MIJK . VMNPQ Ⓐ. 1 1 . Ⓑ. . Ⓒ. 1 . Ⓓ. 1 . 6 3 4 8
Câu 9: Cho tứ diện ABCD . Gọi 
B và C lần lượt là trung điểm của AB, AC . Khi đó tỉ số thể tích
của khối tứ diện ABCD và khối ABCD bằng: Ⓐ. 1 1 . Ⓑ. . Ⓒ. 1 . Ⓓ. 1 . 2 4 6 8
Câu 10: Cho khối tứ diện OABC với O ,
A OB,OC vuông góc từng đôi một và OA  a, OB  2a, OC  3a
. Gọi M , N lần lượt là trung điểm của hai cạnh AC, BC . Thể tích của khối tứ diện OCMN tính theo a bằng: 3 3 3 Ⓐ. 3a 2a a Ⓑ. 3 a Ⓒ. Ⓓ. 4 3 4
Câu 11: Cho khối chóp S.ABC . Trên ba cạnh SA , SB , SC lần lượt lấy ba điểm A , B , C sao cho 1 1 1
SA  SA ; SB  SB ; SC  SC . Gọi V và V ' lần lượt là thể tích của các khối chóp 3 4 2 S.ABC V và S.AB C
 . Khi đó tỉ số là V ' Ⓐ. 1 . Ⓑ. 24 . Ⓒ. 1 . Ⓓ. 12. 12 24 BẢNG ĐÁP ÁN 1.B 2.D 3.B 4.B 5.C 6.B 7.A 8.D 9.B 10.D 11.B 12.D Hướng dẫn giải
Câu 1: Cho hình chóp S.ABC có  ASB   ASC  
BSC  60 và SA  2 ; SB  3 ; SC  7 . Tính thể tích V của khối chóp. Ⓐ. 7 2 V  4 2 . Ⓑ. V  . Ⓒ. 7 2 V  . Ⓓ.V  7 2 . 2 3 Lời giải Chọn B
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 62
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung S C' 3 7 2 A C B' B
Lấy hai điểm B , A lần lượt trên hai cạnh SB và SC sao cho SB  2 , SC  2 . Ta có hình chóp S.AB C
  là hình tứ diện đều có cạnh bằng 2 . 3 2 2  V  2 2  . S .AB C   12 3 V     SA SB SC Ta lại có: S.AB C  2 2 . .  4 .  . V SA SB SC 3 7 21 S .ABC 21V  S .AB C V     21.2 2  7 2  . S .ABC 4 3.4 2
Câu 2: Cho hình chóp S.ABC có A và B lần lượt là trung điểm của SA và SB . Biết thể tích khối
chóp S.ABC bằng 24 . Tính thể tích V của khối chóp S.AB C  . Ⓐ. V  3 Ⓑ. V 12 Ⓒ.V  8 Ⓓ.V  6 Lời giải Chọn D S A' B' A B C V     SA SB SC Ta có S.A B C  1 1 . .  1 .  V SA SB SC 2 2 4 S.ABC 1 Vậy V  1     .V .24 6 . S .A B C S . 4 ABC 4
Câu 3: Cho khối chóp S.ABC , M là trung điểm của cạnh BC. Thể tích của khối chóp S.MAB là 3 2a .
Thể tích khối chóp S.ABC bằng. 3 Ⓐ. a 1 3 2a . Ⓑ. 3 4a . Ⓒ. . Ⓓ. 3 a . 4 2 Lời giải
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 63
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung Chọn B  3 V  2V  4a . S.ABC SMAB
Câu 4: Cho tứ diện ABCD có thể tích bằng 12 và I là trung điểm CD , M là trung điểm BI . Tính
thể tích V của khối chóp . A MCD . Ⓐ. V  4 . Ⓑ. V  6. Ⓒ.V 3. Ⓓ.V 5. Lời giải Chọn B
Câu 5: Cho tứ diện ABCD có DA  1; DA   ABC. A
 BC là tam giác đều, có cạnh bằng 1 . Trên cạnh DM 1 DN 1 DP 3
DA, DB, DC lấy 3 điểm M , N , P sao cho  ;  ;
 . Thể tích của tứ diện DA 2 DB 3 DC 4 MNPD bằng Ⓐ. 2 3 V  . Ⓑ. V  . Ⓒ. 3 V  . Ⓓ. 2 V  . 96 12 96 12 Lời giải Chọn C 1 3 3 V  . .1  . ABCD 3 4 12 V DM DN DP 1 1 3 1  DMNP  . .  . .  . V DA DB DC 2 3 4 8 DABC 1 3 3 Suy ra V  .  . DMNP 8 12 96
Câu 6: Cho khối chóp S.ABCD có thể tích là 3
a . Gọi M , N , P, Q theo thứ tự là trung điểm của
SA, SB, SC, SD. Thể tích khối chóp S.MNPQ là: 3 3 2 3 Ⓐ. a a a a Ⓑ. . Ⓒ. . Ⓓ. 16 8 4 6 Chọn B 1
Ta có: Tứ giác MNPQ đồng dạng với tứ giác ABCD với tỉ số k  . 2 1
Đường cao h của hình chóp S.MNPQ bằng đường cao h hình chóp S.ABCD 2
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 64
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung 2 1 1  1  h Từ đó: V  .S .h  . .S . S .MNPQ   3 MNPQ 3  2 ABCD  2 3 1 a  V  . S. 8 ABCD 8
Câu 7: Cho khối chóp S.ABC . Gọi A , B lần lượt là trung điểm của SA và SB . Khi đó tỉ số thể tích
của hai khối chóp S.AB C  và S.ABC bằng: Ⓐ. 1 1 . Ⓑ. . Ⓒ. 1 . Ⓓ. 1 . 4 6 2 3 Lời giải Chọn A V     SA SB 1 1 1 Ta có S.A B C  .  .  . V SA SB 2 2 4 S .ABC
Câu 8: Cho tứ điện MNPQ . Gọi I , J , K lần lượt là trung điểm các cạnh MN , MP, MQ . Tính tỉ số thể V tích MIJK . VMNPQ Ⓐ. 1 1 . Ⓑ. . Ⓒ. 1 . Ⓓ. 1 . 6 3 4 8 Lời giải Chọn D VMIJK MI MJ MK 1 Ta có:  . .  . V MN MP MQ 8 MNPQ
Câu 9: Cho tứ diện ABCD . Gọi 
B và C lần lượt là trung điểm của AB, AC . Khi đó tỉ số thể tích của
khối tứ diện ABCD và khối ABCD bằng: Ⓐ. 1 1 . Ⓑ. . Ⓒ. 1 . Ⓓ. 1 . 2 4 6 8 Lời giải Chọn B V AB AC 1 1 1 Ta có AB'C 'D  .  .  . V AB AC 2 2 4 ABCD M K I J N Q P .
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 65
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung
Câu 10: Cho khối tứ diện OABC với O ,
A OB,OC vuông góc từng đôi một và OA  a, OB  2a, OC  3a
. Gọi M , N lần lượt là trung điểm của hai cạnh AC, BC . Thể tích của khối tứ diện OCMN tính theo a bằng: 3 3 3 Ⓐ. 3a 2a a Ⓑ. 3 a Ⓒ. Ⓓ. 4 3 4 Lời giải Chọn D 1  1  Ta có 3 V  . O . AOB .OC  a (đvtt) OABC   3  2  . V CM .CN 1 3 1 a Ta có OCMN   V  V  V C . A CB 4 .Vậy OCMN 4 OABC 4 . OCAB
Câu 11: Cho khối chóp S.ABC . Trên ba cạnh SA , SB , SC lần lượt lấy ba điểm A , B , C sao cho 1 1 1
SA  SA ; SB  SB ; SC  SC . Gọi V và V ' lần lượt là thể tích của các khối chóp 3 4 2 S.ABC V và S.AB C
 . Khi đó tỉ số là V ' Ⓐ. 1 . Ⓑ. 24 . Ⓒ. 1 . Ⓓ.12. 12 24 Lời giải Chọn B V SA SB SC Ta có  . .  3.4.2  24 . V ' SA' SB ' SC '
Câu 12: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. M là trung điểm SC , mặt phẳng P V
chứa AM và song song với BD , cắt SB và SD lần lượt tại B và D . Tỷ số S.AB'MD' là VS.ABCD Ⓐ. 3 2 . Ⓑ. . Ⓒ. 1 . Ⓓ. 1 . 4 3 6 3 Lời giải Chọn D
Gọi O là tâm hình bình hành đáy. I  AO  SO S
Đường thẳng qua I và song song BD cắt SB, SD tại B, D . M D' B' Ta có V   I   V  V SAB MD SAB M SAMD A D V  O  SB SM 2 1 1 1  SAB M      nên V  B C  V V SB SC 3 2 3 SAB M 6 SABCD SABC
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 66
Tài liệu giảng dạy, học tập hiệu quả cao – FB Duong Hung V  1 1 1
Tương tự SAMD  nên V  do dó V    V  V V 3 SAMD 6 SABCD SAB MD 3 SABCD S 4CD .
St-bs: Duong Hung – Zalo: 0774.860.155 – Word xinh 2021 67