Chuyên đề thể tích khối đa diện – Lê Minh Tâm

Tài liệu gồm 127 trang, được biên soạn bởi thầy giáo Lê Minh Tâm, tổng hợp kiến thức cần nhớ, các dạng toán kèm phương pháp giải và bài tập chuyên đề thể tích khối đa diện.Mời bạn đọc đón xem.

66 33 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Khối đa diện

Môn: Toán 12

Thông tin:

127 trang 8 tháng trước

Tác giả:

Profile Lan Tường
TÀI LIỆU LƯU HÀNH NỘI BỘ
CHƯƠNG 01.
THỂ TÍCH
KHỐI ĐA DIỆN
LÊ MINH TÂM
THỂ TÍCH KHỐI ĐA DIỆN
Biên soạn:
LÊ MINH TÂM
Trang 2
MỤC LỤC
CHUYÊN ĐỀ. THỂ TÍCH KHỐI ĐA DIỆN ................................................................................ 3
I. KIẾN THỨC CẦN NHỚ. .................................................................................................. 3
II. CÁC DẠNG BÀI TẬP. ..................................................................................................... 6
Dạng toán 1. CHÓP CÓ CẠNH BÊN VUÔNG GÓC VỚI ĐÁY. ................................. 6
Dạng toán 2. CHÓP CÓ MẶT BÊN VUÔNG GÓC VỚI ĐÁY. .................................... 8
Dạng toán 3. CHÓP ĐỀU. .................................................................................................. 11
Dạng toán 4. TỶ SỐ THỂ TÍCH. ...................................................................................... 14
Dạng toán 5. TỔNG HIỆU THỂ TÍCH. ............................................................................ 18
Dạng toán 6. THỂ TÍCH LĂNG TRỤ ĐỨNG. ............................................................... 24
Dạng toán 7. THỂ TÍCH LĂNG TRỤ XIÊN. .................................................................. 29
Dạng toán 8. THỂ TÍCH KHỐI LẬP PHƯƠNG – KHỐI HỘP. .................................. 33
Dạng toán 9. KHỐI ĐA DIỆN ĐƯỢC CẮT RA TỪ KHỐI LĂNG TRỤ. ................... 37
Dạng toán 10. MAX – MIN THỂ TÍCH. ..................................................................... 44
III. BÀI TẬP RÈN LUYỆN. ................................................................................................. 50
IV. BẢNG ĐÁP ÁN THAM KHẢO. .............................................................................. 127
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 3
LÊ MINH TÂM
CHUYÊN ĐỀ
I. KIẾN THỨC CẦN NHỚ.
Các định nghĩa.
– Hình chóp là hình có đáy là một đa giác và các mặt bên là các tam giác có chung một đỉnh.
– Hình lăng trụ là hình có hai đáy là hai đa giác bằng nhau nằm trên hai mặt phẳng song song
với nhau và các mặt bên đều là các hình bình hành.
– Hình hộp là hình lăng trụ có đáy là hình bình hành.
Thể tích khối chóp.
Công thức tính thể tích khối chóp:
Trong đó: là diện tích đáy và là chiều cao khối chóp (khoảng cách từ đỉnh đến mặt đáy).
Cách xác định đường cao khối chóp:
a. Chóp có cạnh bên vuông góc chiều cao chính là cạnh bên.
b. Chóp có hai mặt bên vuông góc đáy đường cao là giao tuyến của hai mặt bên vuông góc
đáy.
c. Chóp có mặt bên vuông góc đáy: chiều cao của mặt bên vuông góc đáy.
d. Chóp đều chiều cao hạ từ đỉnh đến tâm đa giác đáy.
e. Chóp có hình chiếu vuông góc của một đỉnhlên xuống mặt đáy thuộc cạnh mặt đáy đường
cao là từ đỉnh tới hình chiếu.
Thể tích khối lăng trụ.
Công thức tính thể tích khối lăng trụ:
Trong đó: là diện tích đáy và là chiều cao khối chóp (khoảng cách từ đỉnh đến mặt đáy).
● Thể tích khối hộp chữ nhật: .
● Thể tích khối lập phương: .
S
h
.V S h
S
h
..V a b c
3
Va
THỂ TÍCH KHỐI ĐA DIỆN
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 4
Công thức diện tích đáy.
Ta có các đa giác thường gặp sau:
Tam giác
với là bán kính đường tròn ngoại tiếp .
với là nửa chu vi và là bán kính đường tròn nội tiếp .
với hoặc
22
22
1
4
S a b c c a b
vuông tại : .
đều, cạnh : ;
Chiều cao tam giác đều .
Hình vuông cạnh .
Hình chữ nhật.
( : dài và rộng)
Hình bình hành .
Hình thoi .
Hình thang:
(a, b: hai đáy, h: chiều
cao)
Tứ giác có hai
đường chéo vuông góc
111
222
. . .
a b c
S a h b h c h
1 1 1
2 2 2
.sinA .sinB .sinCS ba ca ba
2
2
4
R .sinA.sin .sin
R
abc
S B C
R
ABC
.S p r
p
r
ABC
S p p a p b p c
2
a b c
p

ABC
A
11
22
..S AB AC BC AH
ABC
x
2
3
4
x
S
3
2
x
h
x
2
Sx
.S x y
;xy
ABCD
. .sinS AB AD BAD
ABCD
1
2
. .sin .S AB AD BAD AC BD
1
2
.S a b h
ABCD
1
2
.S AC BD
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 5
LÊ MINH TÂM
Tỷ số diện tích
AM trung tuyến,
đặt .
G là trọng tâm,
đặt .
đặt .
.
.
.
12
2
ABC
S
S S S S 
1 2 3
3
ABC
S
S S S S S 
NM MN NC
1 2 3
3
ABC
S
S S S S S
1 2 3 4
4
ABCD
S
S S S S S S
1 2 3 4
4
ABC
S
S S S S S S
AMN
ABC
S
AM AN
S AB AC

Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 6
II. CÁC DẠNG BÀI TẬP.
Dạng toán 1. CHÓP CÓ CẠNH BÊN VUÔNG GÓC VỚI ĐÁY.
Phương pháp giải
Khối chóp có sẵn chiều cao và diện tích đáy.
Áp dụng công thức:
Ví dụ 01.
Cho khối chóp có đáy là
hình vuông cạnh . Biết vuông góc với
và . Thể tích của khối chóp
là:
A. .
B. .
C. .
D. .
Lời giải
Chọn D
Thể tích khối chóp .
Ví dụ 02.
Cho hình chóp tứ giác có đáy là
hình vuông cạnh , vuông góc với mặt
phẳng đáy và . Thể tích khối chóp
bằng:
A. .
B. .
C. .
D. .
Lời giải
Chọn D
.
.S ABCD
ABCD
a
SA
ABCD
3SA a
.S ABCD
3
4
a
3
3a
3
3
6
a
3
3a
3
13
33
.
.
S ABCD ABCD
a
V S SA
.S ABCD
a
SA
2SA a
.S ABCD
3
4
3
a
3
2a
3
3
a
3
2
3
a
3
2
1 1 2
2
3 3 3
.S ABCD ABCD
a
V S SA a a
S
A
B
C
D
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 7
LÊ MINH TÂM
Ví dụ 03.
Cho hình chóp có đáy là
hình chữ nhật , cạnh bên
vuông góc với đáy và . Tính thể
tích khối chóp .
A. .
B. .
C. .
D. .
Lời giải
Chọn D
Diện tích đáy: . Thể tích: .
Ví dụ 04.
Cho hình chóp có đáy là
hình vuông cạnh . Cạnh bên vuông
góc với đáy và có độ dài bằng . Thể tích
khối tứ diện là:
A. . B. .
C. . D. .
Lời giải
Chọn D
Ta có: . Suy ra .
Ví dụ 05.
Cho hình chóp có đáy là
hình vuông tâm cạnh . Biết vuông
góc với mặt phẳng đáy và Tính
thể tích khối chóp .
A. . B. .
C. . D. .
Lời giải
Chọn A
.S ABCD
ABCD
2,AB a BC a
SA
2SA a
.S ABCD
3
23
3
a
3
2a
3
22a
3
22
3
a
2
2.
ABCD
S AB BC a
3
1 2 2
33
.
ABCD
a
V S SA
.S ABCD
ABCD
a
SA
2a
.S BCD
3
4
a
3
8
a
3
6
a
3
3
a
2
1
22
BCD ABCD
a
SS
23
11
2
3 3 2 3
.
. . .
S ABCD BCD
aa
V SA S a
.S ABCD
ABCD
O
2a
SA
2.SA a
.S ABO
3
2
3
a
3
22
12
a
3
2
12
a
3
42
3
a
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 8
Ta có: .
Vậy: .
Dạng toán 2. CHÓP CÓ MẶT BÊN VUÔNG GÓC VỚI ĐÁY.
Phương pháp giải
Khối chóp có mặt bên vuông góc mặt phẳng đáy.
+ Áp dụng công thức: .
+ Chiều cao khối chóp là đoạn thẳng từ đỉnh của chóp ta kẻ vuông góc vào giao tuyến của mặt
bên và mặt đáy.
Một số kiểu thường gặp:
Mặt bên vuông với đáy và là tam giác
đều cạnh với là trung
điểm .
Mặt bên vuông với đáy và là tam giác
cân tại với là trung điểm .
Ví dụ 01.
Hình chóp đáy là hình chữ nhật có
. Mặt bên là tam giác
đều và nằm trong mặt phẳng vuông góc với
đáy. Thể tích khối chóp là.
A. .
B. .
C. .
D. .
Lời giải
Chọn D
Gọi là trung diểm của .
Tam giác là tam giác đều cạnh nên .
Vậy thể tích khối chóp là .
2
1
2 2 2
22
. .OB a
OAB
AC
AC a OA OB a S OA
23
1 1 2
2
3 3 3
.
. . . .
S OAB OAB
V SA S a a a
SAB
ABCD
SAB
x
SH ABCD
3
2
x
h SH
H
AB
SAB
ABCD
SAB
S
SH ABCD
h SH
H
AB
.S ABCD
2 3 2; AB a AD a
SAB
.S ABD
3
23
3
a
3
43a
3
4a
3
23a
H
AB
SH ABCD
SAB
23a
2 3 3
3
2
a
SH a

SABD
3
1 1 1
3 2 3 2 2 3
3 3 2
ABD
V SH S a a a a
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 9
LÊ MINH TÂM
Ví dụ 02.
Cho hình chóp có đáy là hình vuông
cạnh hình chiếu của trên trng
với trung điểm của cạnh cạnh bên
. Thể tích của khối chóp tính theo
bằng:
A. . B. .
C. . D. .
Lời giải
Chọn D
Gọi là trung điểm của nên .
Lại có .
Xt tam giác vuông tại .
.
Ví dụ 03.
Cho hình chóp có đáy là hình
vuông cạnh , , .
Tính thể tích của khối chóp biết
.
A. .
B. .
C. .
D. .
Lời giải
Chọn D
Ta có:
.
.S ABCD
;a
S
ABCD
;AB
3
2
a
SD
.S ABCD
a
3
5
3
a
3
3
3
a
3
7
3
a
3
3
a
H
AB
SH ABCD
2
2
5
22
a
DH a a



SDH
HL
2
2
2 2 3
3 5 1 1
2 2 3 3
.
ABCD
SH SH DH a a a V S SH a







.S ABCD
ABCD
a
SAD ABCD
SA SD
V
.S ABCD
21
2
a
SC
3
7
2
a
V
3
2Va
3
7
6
a
V
3
2
3
a
V
3
2
5 1 2
22
2 3 3
..
aa
HC SH a V a a
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 10
Ví dụ 04.
Cho tứ diện có là tam giác vuông
cân tại và nằm trong mặt phẳng vuông góc
với mặt phẳng , tam giác là tam
giác đều và có cạnh bằng . Tính thể tích của
khối tứ diện .
A. . B. .
C. . D. .
Lời giải
Chọn B
Gọi là trung điểm của . Ta có và .
vuông cân tại .
Ví dụ 05.
Cho chóp có là hình vuông
cạnh . cân tại và nằm trong mặt
phẳng vuông góc với đáy. Tính thể tích
, biết góc giữa và bằng
A. B. .
C. . D. .
Lời giải
Chọn C
Ta có
Gọi H là trung điểm
CH là hình chiếu vuông góc của SC trên
Xét vuông tại H có
,
.
ABCD
ABC
C
ABD
ABD
2a
ABCD
3
2a
3
3
3
a
3
3a
3
3
9
a
H
AB
DH ABC
3DH a
ABC
3
22
13
22
33
.
ABCD ABC
a
C CA AB AC BC a V DH S
.S ABCD
ABCD
3a
SAB
S
V
.S ABCD
SC
ABCD
0
60
3
18 15Va
3
18 3Va
3
9 15
2
a
V
3
93Va
2
2
39
ABCD
S a a
AB SH ABCD
ABCD
60,,SC ABCD SC CH SCH
SCH
22
35
2
a
CH BC BH
3 15
2
tan
a
SH CH SCH
3
1 9 15
32
.
.
S ABCD ABCD
a
V S SH
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 11
LÊ MINH TÂM
Dạng toán 3. CHÓP ĐỀU.
Phương pháp giải
Khối chóp có các cạnh bên bằng nhau
+ Áp dụng công thức: .
+ Chiều cao khối chóp là đoạn thẳng từ đỉnh của chóp hạ vuông góc xuống tâm mặt đáy.
Một số kiểu thường gặp:
Chóp đều , góc giữa mặt phẳng bên và mặt đáy là hoặc góc giữa cạnh bên và
mặt đáy là .
Chóp đều , góc giữa mặt phẳng bên và mặt đáy là hoặc góc giữa cạnh bên và
mặt đáy là .
Một số công thức tính nhanh:
Chóp đều cạnh , đáy là tam giác
Chóp đều cạnh , đáy là tứ giác
.
.
Chóp đều có cạnh bên bằng , đáy là tam
giác cạnh .
Chóp đều có cạnh bên bằng , đáy là tứ
giác cạnh .
.
.
Chóp đều có các mặt bên cùng tạo với đáy
một góc , đáy là tam giác cạnh .
Chop đều có các mặt bên cng tạo với
đáy một góc , đáy là tứ giác cạnh .
.
.
.S ABCD
.S ABC
x
x
3
2
12
x
V
3
2
6
x
V
x
y
x
y
22
2
3
12
yyx
V
22
3
24
6
yyx
V
x
x
3
24
tanx
V
3
6
tanx
V
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 12
Ví dụ 01.
Tính chiều cao của hình chóp tứ giác đều có
cạnh đáy bằng và cạnh bên bằng ?
A. .
B. .
C. .
D. .
Lời giải
Chọn B
Gọi là tâm hình vuông ,
Do S.ABCD là hình chóp tứ giác đều nên .
Ta có .
Ví dụ 02.
Tính thể tích của khối chóp tứ giác đều có cạnh
đáy bằng và cạnh bên bằng là:
A. .
B. .
C. .
D. .
Lời giải
Chọn B
là chóp tứ giác đều nên .
là đường cho hình vuông cạnh nên .
Ta có .
.
a
b
22
42
2
ba
22
42
2
ba
22
4
2
ba
22
4
2
ba
H
ABCD
SH ABCD
2
22
2 2 2
42
2
2
a b a
SH SC HC b



a
b
2 2 2
2
6
a b a
2 2 2
42
6
a b a
2 2 2
42
6
a b a
2 2 2
4
6
a b a
.S ABCD
SO ABCD
BD
a
2
2
2
a
BD a OB
2
22
2 2 2
42
2
2
a b a
SO SB OB b



2 2 2 2 2
2
1 1 4 2 4 2
3 3 2 6
. . . .
ABCD
b a a b a
V SH S a

Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 13
LÊ MINH TÂM
Ví dụ 03.
Cho hình chóp đều có cạnh đáy bằng
và cạnh bên tạo với đáy một góc . Thể tích
của hình chóp đều đó là:
A. .
B. .
C. .
D. .
Lời giải
Chọn A
Gọi
.
Ví dụ 04.
Cho hình chóp tứ giác đều có cạnh đáy
bằng . Gọi điểm là giao điểm của và
. Biết khoảng cách từ đến bằng .
Tính thể tích khối chóp .
A. . B. .
C. . D. .
Lời giải
Chọn D
là hình chiếu của lên nên ,
là hình vuông có
vuông tại có là đường cao
.
.
.S ABCD
a
60
3
6
6
a
3
3
6
a
3
3
2
a
3
6
2
a
O AC BD SO ABCD
60 60 3 3
2
tan .
SO a
SCO SO OC
OC
3
2
1 3 6
3 2 6
.
a
V a a
.S ABCD
a
O
AC
BD
O
SC
6
a
.S ABC
3
6
a
3
4
a
3
8
a
3
12
a
H
O
SC
6
a
OH
ABCD
12
22
a
OC AC
SOC
O
OH
2 2 2
1 1 1
2
a
SO
OH SO OC
 
3
1 1 1
3 3 2 12
.
. . .
S ABCD ABC ABCD
a
V S SO S SO
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 14
Ví dụ 05.
Một hình chóp tam giác đều có cạnh bên bằng
và cạnh bên tạo với mặt phẳng đáy một góc
. Thể tích của hình chóp đó là
A. .
B. .
C. .
D. .
Lời giải
Chọn D
Xt tam giác vuông tại , ta có:
.
Mà: .
.
Dạng toán 4. TỶ SỐ THỂ TÍCH.
Phương pháp giải
A. Cho khối chóp có lần lượt là nằm trên khi đó:
1. Nếu và thì
(Hai khối chóp chung đỉnh và chung mặt đáy).
2. Định lý SIMSON cho khối chóp tam giác
.
3. Cắt khối chóp bởi mặt phẳng song song với đáy sao cho thì
b
3
3
4
cos sinb
32
3
4
sin cosb
32
3
4
cos sinb
32
3
4
cos sinb
SHA
H
sin sin
cos cos
SH SA b
AH SA b


33
22
cosAM AH b
32
3
2
3
cos
AB AM
AM AB
2
32
33
1 1 3
3 3 4 4
cos
. . . sin . cos sin
SABC ABC
b
V SH S b b
.S ABC
;;A B C
;;SA SB SC
;A A B B


CC
.
.
S A B C A B C
S ABC ABC
V
VS
S
.
.
S A B C
S ABC
SB SC
V SB SC
V
SA
SA


1
1
SB
k
SA
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 15
LÊ MINH TÂM
B. Mặt phẳng cắt các cạnh của khối chóp tứ giác có đáy là hình bình hành lần lượt tại
sao cho :
và
.
Ví dụ 01.
Cho hình chóp . Gọi lần lượt là
trung điểm của . Tỉ số thể tích
bằng
A. .
B. .
C. .
D. .
Lời giải
Chọn C
Ta có .
12
12
3
. ...
. ...
n
n
S B B B
S A A A
k
V
V
.S ABCD
; ; ;M N P Q
; ; ;
SM SN SP SQ
SA SB SC SD
1 1 1 1
4
.
.
. . .
S MNPQ
S ABCD
V
V



1 1 1 1
.S ABC
,,M N P
,,SA SB SC
.
.
S ABC
S MNP
V
V
12
2
8
3
2 2 2 8
.
.
. . . .
S ABC
S MNP
V
SA SB SC
V SM SN SP
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 16
Ví dụ 02.
Cho tứ diện . Gọi ; ; lần lượt là
trung điểm của các cạnh ; ; . Tỉ số
thể tích bằng
A.
B.
C.
D.
Lời giải
Chọn D
Ta có: .
Ví dụ 03.
Cho khối tứ diện có thể tích bằng . Gọi là
thể tích của khối đa diện có các đỉnh là các
trung điểm của các cạnh của khối tứ diện đã
cho, tính tỉ số .
A. .
B. .
C. .
D. .
Lời giải
Chọn B
Cách 1.
Đặc biệt hóa tứ diện cho là tứ diện đều cạnh .
Hình đa diện cần tính có được bằng cách cắt góc của tứ diện, mỗi góc cũng là một
tứ diện đều có cạnh bằng .
Do đó thể tích phần cắt bỏ là .
MNPQ
I
J
K
MN
MP
MQ
MIJK
MNPQ
V
V
1
3
1
4
1
6
1
8
1 1 1 1
2 2 2 8
.
.
. . . .
M IJK
M NPQ
V
MI MJ MK
V MN MP MQ
V
V
V
V
2
3
V
V
5
8
V
V
1
2
V
V
1
4
V
V
a
4
2
a
4
82
.
VV
V


Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 17
LÊ MINH TÂM
Vậy .
Cách 2.
Khối đa diện là hai khối chóp tứ giác có cng đáy là hình bình hành úp lại.
Suy ra:
Cách 3.
Ta có
.
Ví dụ 04.
Cho hình chóp . Gọi , , , theo
thứ tự là trung điểm của , , , . Tính
tỉ số thể tích của hai khối chóp và
.
A. B.
C. D.
Lời giải
Chọn C
Ta có .
Và .
Suy ra .
Ví dụ 05.
Cho hình chóp có đáy là hình bình
hành. Gọi lần lượt là trọng tâm của
các tam giác . Gọi là điểm
bất kỳ trên mặt phẳng đáy . Biết thể tích
khối chóp bằng . Tính thể tích khối
chóp .
A. . B. .
C. . D. .
1
22
VV
V
V
1 1 1
2 4 4 4
2 4 2
. . .
. . . .
N MEPF N MEP P MNE
V V V V V V
. . . .
'
A QEP B QMF C MNE D NPF
V V V V V
V
VV
1
..
..
A QEP B QMF
C MNE D NPF
VV
VV
V V V V
1 1 1 1 1 1 1 1 1 1 1 1 1
1
2 2 2 2 2 2 2 2 2 2 2 2 2
. . . . . . . .
.S ABCD
A
B
C
D
SA
SB
SC
SD
.S A B C D
.S ABCD
1
16
1
4
1
8
1
2
1
8
.
.
..
S A B D
S ABD
V
SA SB SD
V SA SB SD

1
16
.
.
S A B D
S ABCD
V
V

1
8
.
.
..
S B D C
S BDC
V
SB SD SC
V SB SD SC

1
16
.
.
S B D C
S ABCD
V
V

1 1 1
16 16 8
..
..
S A B D S B D C
S ABCD S ABCD
VV
VV
1
8
.
.
S A B C D
S ABCD
V
V

SABCD
, , ,M N P Q
, , ,SAB SBC SCD SDA
O
ABCD
OMNPQ
V
SABCD
27
8
V
27
2
V
9
4
V
27
4
V
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 18
Lời giải
Chọn B
Ta có
+ .
+ .
.
Ta có: .
Khi đó,
Nên .
Dạng toán 5. TỔNG HIỆU THỂ TÍCH.
Phương pháp giải
Trong quá trình tính thể tích một khối đa diện lồng ghép trong khối chóp ta gặp khó khăn
với cách tính thực tiếp thì khi đó:
Ta có thể tách khối chóp ra thành các khối nhỏ và tính trực tiếp từng khối đã tách.
Phần cần tính sẽ là phần khối chóp bỏ đi những khối nhỏ đã tính.
Ví dụ minh họa: Cho khối chóp , mặt phẳng chia khối chóp thành 2 phần ;
. Tính thể tích khối .
Giải.
Để tính trực tiếp thể tích khối ta sẽ khó áp
dụng công thức vì thế ta sẽ cắt khối chóp thành
hai phần:
+ là phần chứa đỉnh .
+ là phần dưới mặt phẳng .
Gọi thể tích khối chóp là , vậy
.
2 2 2 // , ,
SMNPQ OMNPQ
MNPQ ABCD d S MNPQ d O MNPQ V V V
2 2 2 8 8
3 3 3 27 27
. . . .
SMNQ
SMNQ SEFK
SEFK
V
SM SN SQ
VV
V SE SF SK
2 2 2 8 8
3 3 3 27 27
. . . .
SNPQ
SNPQ SFGK
SFGK
V
SN SP SQ
VV
V SF SG SK
8 8 8 27 27
27 27 27 8 4
SMNQ SNPQ SEFK SFGK SMNPQ SEFGK SEFGK SMNPQ
V V V V V V V V V
1
1 1 1
2
1
4 4 8
2
. .sin
. .sin
EBF
EBF ABC ABCD
ABC
BE BF B
S
S S S
S
BA BC B
4
EFGK ABCD ABF FCG GDK KAE ABCD EBF
S S S S S S S S
1
2
EFGK ABCD
SS
1
1 27
3
2
1
22
3
,
,
EFGK
SEFGK
SABCD SEFGK
SABCD
ABCD
d S EFGK S
V
V V V
V
d S ABCD S
.S ABCD
1
V
2
V
2
V
2
V
1
V
S
2
V
.S ABCD
V
1 2 2 1
V V V V V V
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 19
LÊ MINH TÂM
Ví dụ 01.
Cho tứ diện đều có cạnh bằng . Trên
và lần lượt lấy các điểm và sao
cho và . Mặt phẳng
chứa và song song với chia khối
tứ diện thành hai khối đa diện, trong đó
khối đa diện chứa đỉnh có thể tích là . Tính
.
A. . B. .
C. . D. .
Lời giải
Chọn B
Từ kẻ ,
kẻ , . Mặt phẳng là
Ta có
Ta có
Vậy .
Ví dụ 02.
Cho hình chóp có đáy là hình
vuông cạnh , và . Gọi
là trung điểm , là điểm thuộc cạnh
sao cho . Tính thể tích của tứ diện
.
A. . B. .
C. . D. .
ABCD
1
AB
CD
M
N
0MA MB
2NC ND
P
MN
AC
ABCD
A
V
V
2
18
V
11 2
216
V
72
216
V
2
108
V
N
//NP AC
N AD
M
//MQ AC
Q BC
P
MPNQ
12
3 12
.
ABCD ABCD
V AH S
ACMPNQ AMPC MQNC MPNC
V V V V V
..
AMPC ABCD
AM AP
VV
AB AD
1 2 1
2 3 3
.
ABCD ABCD
VV
11
22
..
MQNC AQNC ABCD
CQ CN
V V V
CB CD

1 1 2 1
2 2 3 2
.
ABCD ABCD
VV
2 2 1
3 3 3
.
MPNC MPCD MACD
V V V
21
33
..
ABCD
AM
V
AB
2 1 1 1
3 3 2 9
.
ABCD ABCD
VV
1 1 1
3 6 9
ABCD
VV



11 11 2
18 216
ABCD
VV
.S ABCD
ABCD
a
SA a
SA ABCD
M
SB
N
SD
2SN ND
V
ACMN
3
12
a
V
3
6
a
V
3
8
a
V
3
36
a
V
O
N
M
C
A
B
D
S
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 20
Lời giải
Chọn A
là trung điểm , là điểm thuộc cạnh sao cho nên
Ta có:
Lại có:
Do đó: .
Ví dụ 03.
Cho hình chóp có đáy là hình
chữ nhật với cạnh . Biết hai mặt
phẳng , cng vuông góc với mặt
đáy và đoạn ; góc giữa và mặt
đáy bằng . Hai điểm lần lượt là trung
điểm của . Thể tích khối đa diện
bằng
A. . B. .
C. . D. .
Lời giải
Chọn D
Gọi . Do .
Theo tính chất hình chữ nhật: và .
Khi đó diện tích đáy: .
Gọi là trung điểm của . Do
.
M
SB
N
SD
2SN ND
12
23
,
SM SN
SB SD

22
. . . . . .C AMN O AMN S ABD S AMN M AOB N AOD
V V V V V V
3 3 3
1
3 3 6 12
. . . .
. . . ,
S ABCD S ABD S AOB S AOD
a a a
V SA AB AD V V V
3
1 2 1 1
2 3 3 3 18
.
..
.
..
S AMN
S AMN S ABD
S ABD
V
SM SN a
VV
V SB SD
3
11
2 2 24
.
..
.
M AOB
M AOB S AOB
S AOB
V
MB a
VV
V SB
3
11
3 3 36
.
..
.
N AOD
N AOD S AOD
S AOD
V
ND a
VV
V SD
3 3 3 3 3
22
6 18 24 36 12
..C AMN O AMN
a a a a a
VV



.S ABCD
ABCD
2AD CD
SAC
SBD
6BD
SCD
60
,MN
,SA SB
ABCDMN
108 15
25
128 15
15
16 15
15
18 15
5
O AC BD
,SAC ABCD SBD ABCD
SO ABCD
2 2 2
AD CD BD
22
6
56
5
CD CD
12
5
AD
72
5
.
ABCD
S AD CD
I
CD
,CD SO CD OI CD SOI
CD SI
60,,SCD ABCD SI OI SIO
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 21
LÊ MINH TÂM
Trong tam giác vuông tại , có: .
Thể tích là: .
Ta có .
Do .
Do là trung điểm của .
Ta có: .
Ví dụ 04.
Cho hình chóp có là hình thoi
cạnh và . Biết rằng ,
và . là trọng tâm tam
giác . Tính thể tích của tứ diện .
A.
B.
C.
D.
Lời giải
Chọn B
Ta có .
* Tính ?
Gọi , do .
Kẻ , do nên .
Suy ra .
Do và là trung tuyến nên tam giác vuông cân tại .
Khi đó và .
Mà tam giác vuông tại có đường cao nên .
SOI
O
6
60
2
5
,
AD
OI SIO
63
60
5
.tanSO OI
.S ABCD
1 1 72 6 3 144 15
3 3 5 25
5
. . . .
ABCD
V S SO
2
..S ABD S BCD
V
VV
1
4
SMN SAB
SS
11
48
SMND SABD
V V V
N
SB
1
2
,,d N SCD d B SCD
11
24
SCDN SBCD
V V V
3
8
.S CDMN SMND SCDN
V V V V
3 5 18 15
8 8 5
ABCDMN
V V V V
.S ABCD
ABCD
a
60ABC
SA SC
SB SD
SAB SBC
G
SAD
V
GSAC
3
2
96
a
V
3
2
48
a
V
3
2
24
a
V
3
2
12
a
V
1
3
,.
GSAC SAC
V d G SAC S
SAC
S
O AC BD
SA SC SO AC
SO ABCD
SB SD SO BD

OH SB
AC SBD
SB AHC
90,,SAB SBC AH CH AHC


OH AC
OH
AHC
H
1
22
a
OH AC
3
2
a
OB
SOB
O
OH
2 2 2
1 1 1 6
4
a
SO
OH OS OB
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 22
Vậy .
* Tính ?
Gọi là trung điểm của thì .
Gọi là trung điểm của thì .
Suy ra .
Vậy .
Ví dụ 05.
Cho tứ diện đều cạnh . Mặt phẳng
chứa cạnh cắt cạnh tại . Biết góc giữa
hai mặt phẳng và có số đo là thỏa
mãn . Gọi thể tích của hai tứ diện
và tứ diện lần lượt là và .
Tính tỉ số .
A. . B. .
C. . D. .
Lời giải
Chọn B
Gọi , lần lượt là hình chiếu vuông góc của , trên mặt phẳng . Khi đó
, với là trung điểm .
Ta tính được , , .
Ta có góc giữa với . Khi đó .
Gọi .
Khi đó .
2
1 1 6 6
2 2 4 8
. . . .
SAC
aa
S SO AC a
,d E SAC
E
AD
2
3
,
,
d G SAC SG
SE
d E SAC

F
OA
EF SAC
13
24
,
a
d E SAC EF OD
2 2 3 3
3 3 4 6
, , .
aa
d G SAC d E SAC
23
1 1 3 6 2
3 3 6 8 48
.
, . . .
G SAC SAC
a a a
V d G SAC S
ABCD
a
P
BC
AD
E
P
BCD
52
7
tan
ABCE
BCDE
1
V
2
V
1
2
V
V
1
8
3
5
5
8
3
8
H
I
A
E
BCD
H
I DM
M
BC
6
3
a
AH
3
3
a
DH
3
6
a
MH
P
BCD
,P BCD EMD
52
7
tan
EI
MI

DE x
DE EI DI
AD AH DH
6
6
3
3
3
3
3
3
.
.
.
.
a
x
DE AH x
EI
AD a
a
x
DE DH x
DI
AD a
33
23
ax
MI DM DI
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 23
LÊ MINH TÂM
Vậy .
Khi đó: .
Ví dụ 06.
Cho tứ diện và các điểm , , lần
lượt thuộc các cạnh , , sao cho
, , . Tính tỉ số thể
tích hai phần của khối tứ diện được
phân chia bởi .
A. .
B. .
C. .
D. .
Lời giải
Chọn A
Gọi , , do đó mặt phẳng cắt tứ diện theo thiết
diện là tứ giác .
Gọi là trung điểm thì và ,
Do nên suy ra .
Bởi vậy
Từ là trung điểm và suy ra .
Kẻ với , ta có .
Mặt khác nên suy ra . Do đó .
Từ và suy ra .
Gọi là thể tích khối tứ diện , là thể tích khối đa diện , là thể
tích khối đa diện .
52
7
tan
EI
MI

6
52
3
7
33
23
x
ax

5
8
xa
5
8
DBCE
ABCD
V
DE
V AD

3
5
ABCE
BCDE
V
V

ABCD
M
N
P
BC
BD
AC
4BC BM
3AC AP
2BD BN
ABCD
mp MNP
7
13
7
15
8
15
8
13
E MN CD
Q EQ AD
MNP
ABCD
MNQP
I
CD
NI CB
1
2
NI BC
4BC BM
2
3
NI MC
2
3
.
EN EI NI
EM EC MC
I
CD
2
3
EI
EC
1
3
ED
EC
DK AC
K EP
1
3
EK KD ED
EP AC EC
3AC AP
2
3
KD
AP
2
3
QD QK KD
QA QP AP
2
3
QK
QP
1
3
EK
EP
3
5
EQ
EP
V
ABCD
1
V
ABMNQP
2
V
CDMNQP
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 24
Ta có .
Vì nên . Do đó :
.
, nên suy ra .
Từ đó ta có .
Và .
Như vậy :
Dạng toán 6. THỂ TÍCH LĂNG TRỤ ĐỨNG.
Phương pháp giải
Áp dụng công thức chính: .
Trong đó: là diện tích đáy và là chiều cao khối chóp (khoảng cách từ đỉnh đến mặt đáy).
Tính được diện tích đáy ta xem lại “Công thức tính diện tích đáy”
Lăng trụ đứng sẽ có các đường cao song song nhau, ty vào trường hợp đề ra ta sẽ sử
dụng đường cao hợp lý.
Định nghĩa
Tính chất
Hình lăng trụ đứng
Là hình lăng trụ có cạnh bên
vuông góc với mặt đáy.
Các mặt bên của hình lăng trụ đứng
là các hình chữ nhật và vuông góc
với mặt đáy.
Hình lăng trụ đều
Là hình lăng trụ đứng có đáy là
đa giác đều.
Các mặt bên của hình lăng trụ đều
là các hình chữ nhật bằng nhau và
vuông góc với mặt đáy.
Xem lại cách xác định góc giữa đường – mặt; mặt – mặt để tính được chiều cao.
Ví dụ 01.
Khối lăng trụ có đáy là hình vuông cạnh đường cao bằng có thể tích bằng
A. . B. . C. . D. .
Lời giải
Chọn B
3 2 1 1
4 3 2 2
..
CMP
CMP CAB
CAB
S
CM CP
SS
S CB CA
1
3
ED
EC
3
2
;;d E ABC d D ABC
1 1 1 3 3 1 3
3 3 2 2 4 3 4
.
. ; . . . ; . . ;
E CMP CMP CAB CAB
V S d E ABC S d D ABC S d D ABC V
1 2 3 2
3 3 5 15
.
.
. . . .
E DNQ
E CMP
V
ED EN EQ
V EC EM EP
2 2 3 1
15 15 4 10
..
.
E DNQ E CMP
V V V V
2
3 1 13
4 10 20
..E CMP E DNQ
V V V V V V
12
13 7
20 20
V V V V V V
1
2
7
13
V
V
.V S h
S
h
,a
3a
3
3
3
a
3
3a
3
23a
3
3
6
a
23
33. . .V S h a a a
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 25
LÊ MINH TÂM
Ví dụ 02.
Cho hình lăng trụ đứng có .
Đáy là tam giác vuông cân tại và
. Tính thể tích của khối lăng trụ đã
cho.
A. . B. .
C. . D. .
Lời giải
Chọn C
Theo giả thiết là lăng trụ đứng có đáy là tam giác vuông cân tại .
Suy ra thể tích của khối lăng trụ là .
Ví dụ 03.
Cho lăng trụ đứng có đáy là
tam giác vuông tại . Biết
cạnh bên của lăng trụ bằng . Thể tích khối
lăng trụ là.
A. .
B. .
C. .
D. .
Lời giải
Chọn C
Xét tam giác vuông tại có .
Trong đó .
Vậy .
Ví dụ 04.
Cho lăng trụ đứng có đáy là
tam giác vuông cân tại Thể
tích của khối lăng trụ bằng?
A. .
B. .
C. .
D. .
.ABC A B C
AA a
ABC
A
AB a
V
3
3
a
V
3
6
a
V
3
2
a
V
3
Va
.ABC A B C
ABC
A
3
1
22
. . . .
ABC
a
V AA S AA AB AC

.ABC A B C
ABC
2 30; ; A BC a ABC
23a
3
23a
3
3a
3
3a
3
6a
.ABC
A
2 30.sin ;AC a a
2 30 3.cos .AB a a
23.h AA a

2
13
22
.
ABC
S AB AC a
3
3
lt
Va
. ' ' 'ABC A B C
ABC
23, , ' .A BC a A B a
. ' ' 'ABC A B C
3
2a
3
2
3
a
3
6a
3
7a
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 26
Lời giải
Chọn D
Tam giác vuông cân tại .
Tam giác vuông tại .
.
Ví dụ 05.
Cho khối lăng trụ đứng có đáy là
tam giác vuông vuông tại , ,
. Đường thẳng tạo với mặt phẳng
góc . Tính thể tích khối lăng trụ đã
cho.
A. . B. .
C. D. .
Lời giải
Chọn A
Ta có , dễ thấy góc giữa đường thẳng tạo với mặt phẳng là góc
.
Suy ra .
Vậy .
Ví dụ 06.
Cho lăng trụ đứng có đáy là
tam giác vuông tại , . Mặt
phẳng hợp với mặt phẳng một
góc . Tính thể tích khối lăng trụ đã cho.
A. . B. .
C. . D. .
Lời giải
Chọn B
ABC
2
2
.
BC
A AB AC a
'A AB
2 2 2 2
9 2 7''A A A A B AB a a a
3
17
7 2 2 7
22
. ' ' '
' . . . . . .
ABC A B C ABC
a
V A A S a AB AC a a a
.ABC A B C
ABC
A
AC a
60ACB 
BC
A C CA

30
3
6a
3
3
2
a
3
3
3
a
3
23a
3AB a
BC
A C CA

30BC A

3
30tan
a
AC

3AC a

22C C a

1
2 2 3
2
.
..
ABC A B C
V a a a
3
6a
.ABC A B C
ABC
A
23,AB a AC a
A BC
A B C
60
3
6 39
13
a
3
18 39
13
a
3
9 39
26
a
3
3 39
26
a
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 27
LÊ MINH TÂM
Ta có
.
Dựng
.
Dựng .
Góc mặt phẳng với mặt phẳng
là .
Ta có .
Ta có .
Vậy .
Ví dụ 07.
Cho khối lăng trụ đứng có đáy
là tam giác cân với ,
, mặt phẳng tạo với đáy một
góc . Tính thể tích của khối lăng trụ đã
cho.
A. . B. .
C. . D. .
Lời giải
Chọn D
Gọi , , lần lượt là trung điểm của , , .
là điểm đối xứng với qua , là điểm đối xứng với qua .
Khi đó mặt phẳng .
góc giữa mặt phẳng với đáy là góc giữa mặt phẳng với đáy.
Ta có tứ giác là hình thoi
Vì nên tam giác là tam giác đều cạnh bằng .
Mà
Nên
Vậy góc giữa mặt phẳng với đáy là góc
Xt tam giác , có:
// // //
;
A A BC A B C
B C BC A BC A B C A d BC B C
B C A B C BC A BC


dA H B C A H A
A K BC A K A d
A BC
A B C
60KA H KA H

22
22
6 13
13
.A B A C
A H a
A B A C

6 39
60
13
tan .BB HK A H a

3
1 1 6 39 18 39
23
2 2 13 13
.
.S .A . .
ABC A B C ABC
V BB AB C BB a a a a

.ABC A B C
ABC
AB AC a
120BAC 
A B C
60
V
3
33
8
a
V
3
3
8
a
V
3
9
8
a
V
3
3
8
a
V
M
I
I
AC

BC
BC

D
A
I
D
A
I
A BC A BDC
A BC
A BDC

A B D C
120B A C

A C D
a
D M A C

A C DD
A C DM

A BDC

60DMD

A C D
3
2
3
2
a
D M C I
C B a
a
AI




Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 28
Xt tam giác vuông tại có là nửa tam giác đều có
đường cao .
.
.
Ví dụ 08.
Một nhà kho có dạng khối hộp chữ nhật đứng
, nền là hình chữ nhật có
, , chiều cao , chắp
thêm một lăng trụ tam giác đều mà một mặt
bên là và là một cạnh đáy của
lăng trụ. Tính thể tích của nhà kho ?
A. . B. .
C. . D. .
Lời giải
Chọn C
Ta có :
.
.
MDD
D
60DMD

DMD
DD
3
3
2
.
a
DD D M

2
1 1 3
3
2 2 2 4
. . .
A B C
aa
S A I B C a
23
1 1 3 3 3
3 3 4 2 8
.
. . .
ABC A B C A B C
a a a
V S DD
.ABCD A B C D
ABCD
3mAB
6mBC
3mAA
A B C D
AB

9 12 3
2
3
m
54
3
m
27 4 3
2
3
m
27 3
2
3
m
..kho ABCD A B C D A B J D C I
V V V

.
..
ABCD A B C D
V AB AD A A
336..
54
3
m
.
.
A B J D C I A B J
V S A D

2
3
36
4
..




27 3
2
3
m
27 4 3
2
3
m
kho
V

Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 29
LÊ MINH TÂM
Dạng toán 7. THỂ TÍCH LĂNG TRỤ XIÊN.
Phương pháp giải
Áp dụng công thức chính: .
Trong đó: là diện tích đáy và là chiều cao khối chóp (khoảng cách từ đỉnh đến mặt đáy).
Tính được diện tích đáy ta xem lại “Công thức tính diện tích đáy”
Lăng trụ xiên sẽ có các đường cao đề ra cụ thể.
Xem lại cách xác định góc giữa đường – mặt; mặt – mặt để tính được chiều cao.
Ví dụ 01.
Cho hình lăng trụ tứ giác có đáy là hình vuông cạnh và thể tích
bằng . Tính chiều cao của lăng trụ đã cho.
A. . B. . C. . D. .
Lời giải
Chọn D
Ta có: .
Ví dụ 02.
Cho lăng trụ tam giác có đáy là tam
giác đều cạnh . Độ dài cạnh bên bằng . Mặt
phẳng vuông góc với đáy và
. Thể tích khối chóp là:
A. . B. .
C. . D. .
Lời giải
Chọn D
Gọi là hình chiếu của trên . Từ giả thiết suy ra: .
.
Mặt khác: .
.
.
.V S h
S
h
.ABCD A B C D
ABCD
a
3
3a
h
9ha
3
a
h
ha
3ha
.
.
ABCD A B C D ABCD
V S h
.ABCD A B C D
ABCD
V
h
S

3
2
3a
a
3a
.ABC A B C
a
4a
BCC B

30B BC

.ACC B

3
3
2
a
3
3
12
a
3
3
18
a
3
3
6
a
H
B
BC
B H ABC
1
2
. .sin
BB C
S BB BC B BC

1
4 30
2
. .sinaa
2
a
1
2
.
BB C
S B H BC
2
BB C
S
BH
BC

2
2
2
a
a
a

.
LT ABC
V B H S
2
3
2
4
.
a
a
3
3
2
a
1
2
..A CC B A CC B B
VV
1 2 1
2 3 3
.
LT LT
VV
3
13
32
.
a
3
3
6
a
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 30
Ví dụ 03.
Cho lăng trụ có đáy là tam
giác đều cạnh bằng , biết .
Tính thể tích khối lăng trụ ?
A. .
B. .
C. .
D. .
Lời giải
Chọn B
Gọi là trọng tâm tam giác .
Theo giả thiết ta có là tam giác đều cạnh bằng và nên
là tứ diện đều cạnh hay là đường cao của khối chóp
.
Xét tam giác vuông ta có .
Diện tích tam giác là .
Thể tích khối lăng trụ là .
Ví dụ 04.
Cho hình lăng trụ có đáy là
tam giác vuông tại . cạnh và
. Biết tứ giác là hình thoi có
nhọn. Biết vuông góc với
và tạo với góc . Thể tích của
khối lăng trụ bằng
A. . B. .
C. . D. .
Lời giải
Chọn C
Do là tam giác vuông tại cạnh và nên , .
Gọi là hình chiếu vuông góc của lên thuộc đoạn (do nhọn)
.ABC A B C
ABC
a
A A A B AC a
.ABC A B C
3
3
4
a
3
2
4
a
3
3
4
a
3
4
a
H
ABC
ABC
a
A A A B AC a
.A ABC
a
A H ABC
AH
.A ABC
A HA
22
A H A A AH


6
3
a
ABC
1
60
2
. .sin
ABC
S a a
2
3
4
a
.ABC A B C
2
36
43
.ABC A B C
aa
V
3
2
4
a
.ABC A B C
ABC
A
2BC a
60ABC 
BCC B

B BC
BCC B

ABC
ABB A

ABC
45
.ABC A B C
3
37
a
3
7
a
3
3
7
a
3
6
7
a
ABC
,A
2BC a
60ABC 
AB a
3AC a
H
B
BC
H
BC
B BC
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 31
LÊ MINH TÂM
(do vuông góc với ).
Kẻ song song (do là tam giác vuông tại ).
Ta có vuông tại
Mặt khác song song
Từ (1), (2) và (3) suy ra .
Vậy .
Ví dụ 05.
Cho lăng trụ có đáy là tam
giác vuông tại , . Điểm là
trung điểm , tam giác đều cạnh
và nằm trong mặt phẳng vuông góc với
đáy. Thể tích khối lăng trụ là
A. . B. .
C. . D. .
Lời giải
Chọn A
Gọi là trung điểm của .
Ta có .
Tam giác đều cạnh
Đặt , tam giác vuông tại có
Áp dụng công thức tính độ dài trung tuyến ta có
.
Suy ra .
Do đó .
B H ABC

BCC B

ABC
HK
AC
K AB
HK AB
ABC
A
45, (1)ABB A ABC B KH B H KH



BB H
H
22
4 (2)BH a B H
HK
AC
BH HK
BC AC

2
3
.
(3)
HK a
BH
a

22
2
4
3
.B H a
a B H
a

12
7
B H a

3
13
2
7
. ' '
. . .
ABC A B C ABC
a
V S B H AB AC B H

.ABC A B C
ABC
A
30ABC 
M
AB
MA C
23a
.ABC A B C
3
72 2
7
a
3
24 3
7
a
3
72 3
7
a
3
24 2
7
a
H
MC
A H MC
A MC ABC A H ABC
A MC ABC MC


MA C
23a
23
3
MC a
A H a
0AC x
ABC
A
30ABC 
2
3
BC x
AB x
2 2 2 2 2 2
22
4 3 4 3
12
2 4 2 4
7
CA CB AB x x x a
CM a x

2
1 1 12 4 3 24 3
2 2 7
77
. . .
ABC
a a a
S AB AC
3
72 3
7
.
.
ABC A B C ABC
a
V A H S

Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 32
Ví dụ 06.
Cho hình lăng trụ tam giác có đáy
là tam giác đều cạnh , hình chiếu của
trên mặt phẳng là trung điểm cạnh
. Biết góc giữa hai mặt phẳng và
bằng . Tính thể tích của khối chóp
.
A. . B. .
C. . D. .
Lời giải
Chọn B
Ta có : .
Mà .
Gọi là trung điểm của , là trung điểm của và là trung điểm của .
Khi đó : .
Mặt khác : .
, .
Góc giữa hai mặt phẳng và chính là góc giữa và và bằng
nên tam giác vuông cân tại .
Trong tam giác :
Trong tam giác vuông cân : .
.
.
.ABC A B C
ABC
2a
A
ABC
BC
ABA
ABC
45
V
.A BCC B

3
3
2
a
3
Va
3
3a
3
23
3
a
. . .ABC A B C A A B C A BCC B
V V V

..A ABC A BCC B
VV

..A BCC B A BCC B
VV
..A A B C A ABC
VV

M
BC
I
AB
K
IB
A M ABC
//MK CI
MK AB
CI AB

MK AB
A M AB
A K AB

ABA
ABC
AK
KM
A KM
45
A KM
M
ABC
1 1 2 3 3
2 2 2 2
..
aa
MK CI
A KM
3
2
a
A M MK

1
3
..
.
A ABC ABC A B C
VV
23
1 2 2 2 3
3
3 3 3 3 2
. . . .
. . . .
A BCC B ABC A B C ABC A B C ABC A B C ABC
a
V V V V S A M a a
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 33
LÊ MINH TÂM
Dạng toán 8. THỂ TÍCH KHỐI LẬP PHƯƠNG – KHỐI HỘP.
Phương pháp giải
Áp dụng công thức chính: .
Trong đó: là diện tích đáy và là chiều cao khối chóp (khoảng cách từ đỉnh đến mặt đáy).
● Thể tích khối hộp chữ nhật: .
● Thể tích khối lập phương cạnh a: .
Định nghĩa
Tính chất
Hình hộp đứng
Là hình hộp có cạnh bên vuông
góc với mặt đáy
Có 2 đáy là hình bình hành, 4 mặt
xung quanh là 4 hình chữ nhật.
Hình hộp chữ nhật
Là hình hộp đứng có đáy là
hình chữ nhật.
Có 6 mặt là 6 hình chữ nhật.
Hình lập phương
Là hình hộp chữ nhật đáy và
mặt bên đều là hình vuông
Có 6 mặt đều là hình vuông.
Đường chéo hình hộp với là ba kích thước của hình hộp.
Hệ quả: Đường chéo hình lập phương với là cạnh của hình lập phương.
Ví dụ 01.
Tổng diện tích các mặt của một hình lập phương bằng 150. Thể tích của khối lập phương đó
là.
A. . B. . C. . D. .
Lời giải
Chọn D
Gọi cạnh hình lập phương là . Ta có .
Thể tích khối lập phương là .
Ví dụ 02.
Tính theo a thể tích V của khối lập phương
biết
A. .
B. .
C. .
D. .
Lời giải
Chọn D
Ta có .
.V S h
S
h
..V a b c
3
Va
2
4
222
d r c
;;d r c
3a
a
200
100
625
125
a
2
6 150 5aa
3
125Va
.ABCD A B C D
.AC a
3
27
a
V
3
3
3
a
V
3
33Va
3
3
9
a
V
3
3
a
AC AB AB
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 34
Thể tích khối lập phương là: .
Ví dụ 03.
Cho hình lập phương có diện
tích tam giác bằng . Tính thể tích V
của hình lập phương.
A. .
B. .
C. .
D. .
Lời giải
Chọn B
Giả sử cạnh của hình lập phương có độ dài là .
Ta có ,
Diện tích tam giác là .
Khi đó, ta có .
Vậy .
Ví dụ 04.
Cho hình lập phương . Tính thể
tích của hình lập phương biết rằng khoảng
cách từ trung điểm của đến mặt phẳng
bằng .
A. .
B. .
C. .
D. .
Lời giải
Chọn D
Gọi các điểm như hình vẽ bên trong đó .
Đặt cạnh suy ra . Vậy .
3
33
3
3
9
3 3 3
a a a
V AB



.ABCD A B C D
ACD
2
3a
3
33Va
3
22Va
3
Va
3
8Va
x
2AC x
22
6
2
x
OD OD A A

ACD
2
1 1 6 3
2
2 2 2 2
..
ACD
xx
S OD AC x
22
22
3
32
22
xx
a a x a
33
22V x a
.ABCD A B C D
V
I
AB
A B CD

2
a
3
3
a
V
3
2Va
3
2Va
3
Va
IH I J
AB x
22
xa
IH x a
3
Va
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 35
LÊ MINH TÂM
Ví dụ 05.
Cho hình lập phương , khoảng
cách từ đến mặt phẳng bằng
Tính theo thể tích khối lập phương
A.
B.
C.
D.
Lời giải
Chọn A
Gọi là giao điểm của và
Trong mặt phẳng ; cắt tại
Do song song và nên
Suy ra là trọng tâm tam giác ,
Mà tam giác đều (có các cạnh là các đường cho của những hình vuông bằng
nhau)
Nên và
Suy ra
Do đó khoảng cách từ đến mặt phẳng là
Mặt khác Vậy
Ví dụ 06.
Cho hình lập phương cạnh .
Các điểm theo thứ tự đó thuộc các cạnh
sao cho . Tìm
diện tích thiết diện của hình lập phương khi
cắt bởi mặt phẳng .
A. B.
C. D.
Lời giải
Chọn A
.ABCD A B C D
C
A BD
43
2
.
a
a
..ABCD A B C D
3
8 .Va
3
33a.V
3
83a.V
2
216 .Va
I
AC
.BD
ACC A

AC
AI
.G
AI
AC
1
2
AI AC
1
2
.IG GA
G
A BD
A BD
GA GB GD

AA AB AD

( ).AG A BD
C
A BD
'.CG
2 2 4 3
32
3 3 3
' ' .
a
C G AC AB AB a
3
8 .Va
. ' ' ' 'ABCD A B C D
a
,,M N P
',BB
' ',C D DA
3
'
a
BM C N DP
S
()MNP
2
11 3
18
.
a
S
2
53
18
.
a
S
2
13 3
18
.
a
S
2
17 3
18
.
a
S
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 36
Ta có , do đó theo định lý ta-let trong không gian thì ,
, lần lượt cng song song với một mặt phẳng.
Mà và nên ta có .
Chứng minh tương tự ta có .
Do đó .
Qua , kẻ . Qua , kẻ .
Qua , kẻ .
Khi đó ta có thiết diện tạo bởi mặt phẳng với hình lập phương là lục giác
.
Dễ thấy , và tam giác là tam giác
đều vì .
Do đó
Suy ra: .
Tương tự thì .
Ta có .
1
BM MB BB
C N ND C D

BC
MN
BD

//B D BC D
BC BC D

//MN BC D
//NP BC D
//MNP BC D
P
// ,PQ BD Q AB
N
//C ,NF D F D D

M
//BC ,ME E B C
MNP
MENFPQ
2
3
a
EN PF MQ
22
3
a
NF PQ ME
BC D
2BC BD DC a

60ENF NFP FPQ PQM QME MEN
2 2 2 2
2
2 60
3
. . .cosEF EN NF EN NF a
6
3
a
EF
6
3
a
FQ QE
3.
MENFPQ ENF EFQ
S S S
2
1 2 2 2 3 3 2
3
2 3 3 2 4 3
. . . . .
a a a

2
53
18
a
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 37
LÊ MINH TÂM
Dạng toán 9. KHỐI ĐA DIỆN ĐƯỢC CẮT RA TỪ KHỐI LĂNG TRỤ.
Phương pháp giải
A. Một số mối liên hệ thường gặp giữa chóp – lăng trụ và chóp – thể tích:
Mối liên hệ giữa
Công thức
Hình minh họa
Chóp
Lăng trụ
4 điểm thuộc mặt đáy
3 điểm thuộc mặt đáy
Chóp
Hình hộp
Với 3 điểm thuộc đáy và 1 điểm
thuộc mặt bên
Với 3 điểm thuộc mặt chéo
5
2
3
d
.L Tr
C
VV
1
3
4d
.L Tr
C
VV
1
6
4d
Hop
C
VV
1
3
4d
Hop
C
VV
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 38
Với 4 điểm thuộc mặt bên hoặc
mặt đáy
Với 4 điểm thuộc mặt chéo
B. Mặt phẳng cắt các cạnh của khối lăng trụ tam giác lần lượt tại sao cho
:
C. Mặt phẳng cắt các cạnh của khối hộp lần lượt tại sao cho
:
và .
1
3
5d
Hop
C
VV
1
3
5d
Hop
C
VV
.ABC A B C
;;M N P
;;
AM BN CP
AA BB CC
3
.
.
ABC MNP
ABC A B C
V
V

.ABCD A B C D
; ; ;M N P Q
; ; ;
AM BN CP DQ
AA BB CC DD
4
.
.
ABCD MNPQ
ABCD A B C D
V
V
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 39
LÊ MINH TÂM
Ví dụ 01.
Hình lập phương cạnh . Tính
thể tích khối tứ diện .
A.
B.
C.
D.
Lời giải
Chọn D
Ta có .
Mà và .
Do đó .
Ví dụ 02.
Cho hình lập phương cạnh
bằng . Gọi là giao điểm của và . Thể
tích của tứ diện bằng
A. . B. .
C. . D. .
Lời giải
Chọn C
Ví dụ 03.
Cho khối lăng trụ có thể tích bằng
. Tính thể tích khối đa diện .
A. . B. .
C. . D. .
ABCDA B C D
a
ACB D

3
4
.
a
3
2
.
a
3
6
.
a
3
3
.
a
. . . . .ACBD ABCD A B C D B ABC C B C D D ACD A A B D
V V V V V V
3
.ABCD A B C D
Va
23
1 1 1 1
3 3 2 6
. . . .
. . . .
B ABC C B C D D ACD A A B D A B D
V V V V A A S a a a
3
33
4
63
ACB D
a
V a a

.ABCD A B C D
a
O
AC
BD
OA BC
3
6
a
3
4
a
3
12
a
3
24
a
3
1 1 2 2
6 6 2 2 12
. '.
. . . . .
O A BC A OBC
a a a
V V AA OBOC a
.ABC A B C
V
ABCB C

2
3
V
2
V
4
V
3
4
V
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 40
Lời giải
Chọn A
Ta có:
Ví dụ 04.
Cho khối lăng trụ có thể tích là .
Gọi là điểm bất kỳ trên đường thẳng .
Tính thể tích khối chóp theo .
A. .
B. .
C. .
D. .
Lời giải
Chọn C
Gọi , lần lượt là đường cao của hai hình chóp , thì là
đường cao của lăng trụ .
Ta có:
Suy ra .
Ví dụ 05.
Cho khối lăng trụ tam giác . Tính tỉ
số thể tích giữa khối đa diện và khối
lăng trụ .
A. .
B. .
C. .
D. .
Lời giải
Chọn D
2
3 3 3
ABCB C B ABC C B AC
V V V
V V V
.ABC A B C
V
M
CC
.M ABB A
V

V
3
V
2
9
V
2
3
V
2
V
1
h
2
h
.M ABC
.M A B C
12
h h h
.ABC A B C
. . .M ABC M ABB A M A B C
V V V V
1 2 1 2
1 1 1 1
3 3 3 3
. . .
. . . .
ABC M ABB A A B C ABC M ABB A M ABB A
S h V S h S h h V V V
2
3
.M ABB A
V
V

.ABC A B C
A B C BC
.ABC A B C
1
3
1
2
5
6
2
3
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 41
LÊ MINH TÂM
Ta có: , .
Ta có: .
Ví dụ 06.
Cho khối lăng trụ tam giác . Gọi
, lần lượt là trung điểm của và . Mặt
phẳng chia khối lăng trụ thành hai
phần. Gọi là thể tích của khối đa diện chứa
đỉnh và là thể tích khối đa diện còn lại.
Tính tỉ số .
A. . B. .
C. . D. .
Lời giải
Chọn A
Gọi là trung điểm của và , , lần lượt là thể tích khối lăng trụ
khối lăng trụ và thể tích khối chóp . Khi đó
.
Lại có ; suy ra từ đó ta có
. Vậy .
Ví dụ 07.
Cho khối lăng trụ có thể tích bằng
2018. Gọi là trung điểm ; lần lượt
là các điểm nằm trên các cạnh , sao cho
, . Tính thể tích khối đa
diện .
A. .
B. .
C. .
D. .
Lời giải
1
3
.
. . ,
A ABC ABC
V S d A ABC
1
3
. . .
.,
A B C ABC ABC A ABC A B C ABC
V S d A ABC V V
..A ABC A B C BC A B C ABC
V V V

2
3
.A B C BC A B C ABC
VV

.ABC A B C
M
N
BB
CC
AMN
1
V
B
2
V
1
2
V
V
1
2
2
V
V
1
2
1
3
V
V
1
2
5
2
V
V
1
2
7
2
V
V
K
AA
V
.ABC KMN
V
.A MNK
V
.ABC A B C
.ABC KMN
.A MNK
2 ..ABC KMN A MNK
V V V
1
2
.ABC KMN
VV
11
36
..A MNK ABC KMN
V V V
2
1 1 1
2 6 3
V V V V
1
12
33
V V V V
1
2
2
V
V
.ABC A B C
M
AA
,NP
BB
CC
2BN B N
3CP C P
.ABC MNP
40360
27
4036
3
23207
18
32288
27
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 42
Chọn C
Ta có . Vậy .
Ví dụ 08.
Cho hình hộp chữ nhật có thể
tích bằng và là trọng tâm của tam giác
. Thể tích của khối chóp là
A. .
B. .
C. .
D. .
Lời giải
Chọn D
Gọi là trung điểm của theo tính chất trọng tâm của ta có
.
Ví dụ 09.
Cho khối lăng trụ có thể tích
. Mặt phẳng và chia
khối lăng trụ thành khối đa diện. Tính thể
tích khối đa diện có chứa một mặt là hình bình
hành .
A. .
B. .
C. .
D. .
Lời giải
Chọn A
Gọi , .
Ta có .
Mặt khác .
Ta lại có .
1 23
3 36
.
.
ABC MNP
ABC A B C
V
AM BN CP
V AA BB CC



23207
18
.ABC MNP
V
.ABCD A B C D
1
G
BCD
V
.'G ABC
1
3
V
1
6
V
1
12
V
1
18
V
M
BD
G
1
3
GM CM
1 1 1 1 1
3 3 3 3 2
. . .
. . . .
G ABC C ABC A BCC
V V V AB CBCC
1 1 1
18 18 18
.
..
ABCD A B C D
AB BC CC V
.ABC A B C
3
36 cmV
AB C

A BC
4
BCC B

3
15 cm
3
9 cm
3
12 cm
3
18 cm
I AB A B


J A C AC


' ' . ' ' .IJBB C C A BB C C A BCIJ
V V V
. . .A A B C A BCC B ABC A B C
V V V

2
3
..A BCC B ABC A B C
VV

2
24
3
V
1 1 1
36 3
4 4 3
.
.
.
. . .
A IJA
A IJA
A A B C
V
AI AJ
V
V AB AC

Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 43
LÊ MINH TÂM
.
Vậy .
Ví dụ 10.
Cho hình lăng trụ . Gọi , ,
lần lượt là các điểm thuộc các cạnh , ,
sao cho , , .
Gọi , lần lượt là thể tích của hai khối đa
diện và . Tính tỉ số .
A. . B. .
C. . D. .
Lời giải
Chọn C
Gọi là thể tích khối lăng trụ . Ta có .
.
.
Do là hình bình hành và , nên .
Suy ra
Từ đó
.
Như vậy . Bởi vậy: .
1
36 3 9
3
. . .
.
A IJBC A ABC A IJA
V V V

3
24 9 15
''
cm
IJBB C C
V
.ABC A B C
M
N
P
AA
BB
CC
2AM MA
2NB NB
PC PC
1
V
2
V
ABCMNP
A B C MNP
1
2
V
V
1
2
2
V
V
1
2
1
2
V
V
1
2
1
V
V
1
2
2
3
V
V
V
.ABC A B C
1 ..M ABC M BCPN
V V V
1 1 2 2
3 3 3 9
.
. , . . ,
M ABC ABC ABC
V S d M ABC S d A ABC V
1 1 1 1
3 3 3 9
.
. , . . ,
M A B C A B C A B C
V S d M A B C S d M A B C V
BCC B

2NB NB
PC PC
7
5
B C PN BCPN
SS

7
5
..M B C PN M BCPN
VV

. . . .M ABC M BCPN M A B C M B C PN
V V V V V
2 1 7 5
9 9 5 18
. . .M BCPN M BCPN M BCPN
V V V V V V V
12
2 5 1 1
9 18 2 2
V V V V V V
1
2
1
V
V
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 44
Dạng toán 10. MAX – MIN THỂ TÍCH.
Phương pháp giải
Ta có thể dng các phương pháp sau:
BĐT
Bunyakovsky
Dạng
Dấu “=” xảy ra khi
BĐT
AM – GM
Khảo sát hàm
số trên khoảng
xác định
Tính đạo hàm rồi lập BBT, từ đó kết luận theo yêu cầu bài toán.
Ví dụ 01.
Cho hình chóp có đáy là hình
chữ nhật với , cạnh bên vuông góc
với mặt phẳng đáy và . Tính thể
tích lớn nhất của khối chóp đã cho.
A.
B.
C.
D.
Lời giải
Chọn A
Cách 1.
Đặt cạnh Tam giác vuông có
Tam giác vuông có
Diện tích hình chữ nhật
Thể tích khối chóp
2
2 2 2 2
a b c d ac bd
ab
cd
2
2 2 2 2 2 2
1 2 1 2 1 1 2 2
... ... ...
n n n n
a a a b b b a b a b a b
12
12
...
n
n
a
aa
b b b
2
ab
ab
ab
12
12
1
...
. .....
n
n
n
a a a
a a a n
n

12
...
n
a a a
.S ABCD
ABCD
4AB
SA
ABCD
6SC
max
V
40
3
max
.V
80
3
max
.V
20
3
max
.V
24
max
.V
0.BC x
,ABC
22
16 .AC x
,SAC
2 2 2
20 .SA SC AC x
4..
ABCD
S AB BC x
2
14
20
33
.
..
S ABCD ABCD
V S SA x x
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 45
LÊ MINH TÂM
Áp dụng BĐT Côsi, ta có .
Suy ra
Dấu xảy ra . Vậy .
Cách 2. Xét hàm số trên
Ví dụ 02.
Cho hình chóp có đáy là tam giác
đều và có . Tính thể tích lớn
nhất của khối chóp đã cho.
A.
B.
C.
D.
Lời giải
Chọn C
Gọi là tâm đường tròn ngoại tiếp tam giác đều
Vì là hình chóp đều .
Đặt Diện tích tam giác đều
Gọi là trung điểm
Tam giác vuông có
Khi đó
Xét hàm trên , ta được
Cách 2. Ta có
2
22
2
20
20 10
2
.
xx
xx

4 40
10
33
.
..
S ABCD
V 
""
2
20 10x x x
40
3
max
V
2
4
20
3
f x x x
0 2 5;.
.S ABC
ABC
1SA SB SC
max
V
1
6
max
.V
2
12
max
.V
3
12
max
.V
1
12
max
.V
O
.ABC
.S ABC
SO ABC
0.AB x
2
3
4
.
ABC
x
S
M
3 2 3
2 3 3
.
xx
BC AM OA AM
,SOA
2
22
1
3
.
x
SO SA OA
22
22
1 1 3 3 1
3
3 3 4 12
3
.
. . . .
S ABC ABC
xx
V S SO x x
22
1
3
12
.f x x x
03;
03
1
2
6
;
max .f x f
3
2 2 2
2 2 2 2 2
1 1 6 2
3 6 2 2
3
22
. . .
x x x
x x x x x



Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 46
Ví dụ 03.
Cho hình chóp có đáy là hình
chữ nhật với và mặt bên
là tam giác cân tại và nằm trong mặt phẳng
vuông góc với đáy. Tính thể tích lớn nhất
của khối chóp đã cho.
A. B.
C. D.
Lời giải
Chọn D
Gọi là trung điểm của Mà
Giả sử . Suy ra
Tam giác vuông có
Khi đó
Ví dụ 04.
Người ta cần trang trí một kim tự tháp hình
chóp tứ giác đều cạnh bên bằng
, góc bằng đường gấp khúc dây đèn
led vòng quanh kim tự tháp .
Trong đó điểm cố định và (tham
khảo hình vẽ). Hỏi khi đó cần dung ít nhất bao
nhiêu mt dây đèn led để trang trí?
A. mét.
B. mét.
C. mét.
D. mét.
Lời giải
Chọn C
Ta sử dụng phương pháp trải đa diện
Cắt hình chóp theo cạnh bên rồi trải ra mặt phẳng hai lần, ta có hình vẽ sau
.S ABCD
ABCD
46,AB SC
SAD
S
max
V
40
3
max
.V
40
max
.V
80
max
.V
80
3
max
.V
H
.AD SH AD
.SAD ABCD SH ABCD
0AD x
2
22
16
4
.
x
HC HD CD
,SHC
2
22
20
4
.
x
SH SC HC
11
33
.
. . .
S ABCD ABCD
V S SH AB AD SH
2
2 2 2
1 1 1 80
4 20 2 80 80
3 4 3 3 3
. . .
x
x x x x x
.S ABCD
200m
15ASB 
AEFGHIJKLS
L
40mLS
40 67 40
20 111 40
40 31 40
40 111 40
SA
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 47
LÊ MINH TÂM
Từ đó suy ra chiều dài dây đèn led ngắn nhất là bằng .
Từ giả thiết về hình chóp đều ta có .
Ta có .
Nên .
Vậy, chiều dài dây đèn led cần ít nhất là mét.
Ví dụ 05.
Cho hình chóp có đáy là hình bình
hành và có thể tích là . Điểm là trung điểm
của . Một mặt phẳng qua cắt hai cạnh
và lần lượt tại và . Gọi là thể
tích của khối chóp . Tìm giá trị nhỏ
nhất của .
A. . B. .
C. . D. .
Lời giải
Chọn A
Đặt , , .
Ta có (1)
Lại có (2).
Suy ra .
Từ điều kiện , ta có , hay .
AL LS
.S ABCD
120ASL 
2 2 2 2 2
2 200 40 2 200 40 120 49600. .cos . . .cosAL SA SL SASL ASL
49600 40 31AL 
40 31 40
.S ABCD
V
P
SC
AP
SB
SD
M
N
1
V
.S AMPN
1
V
V
1
3
1
8
2
3
3
8
SM
x
SB
SN
y
SD
01,xy
1
..S AMP S ANP
VV
V
VV
22
..
..
S AMP S ANP
S ABC S ADC
VV
VV

1
2
..
SM SP SN SP
SB SC SD SC




1
4
xy
1
..S AMN S PMN
VV
V
VV
22
..
..
S AMN S PMN
S ABD S CBD
VV
VV

1
2
. . .
SM SN SM SN SP
SB SD SB SD SC




3
4
xy
13
44
x y xy
3x y xy
31
x
y
x

01y
1
31
x
x
1
2
x
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 48
Thay vào (2) ta được tỉ số thể tích .
Đặt , ta có , .
, , do đó .
Ví dụ 06.
Cho hình hộp chữ nhật có
. Gọi là trung
điểm của , mặt phẳng đi qua và cắt
các tia tương ứng tại ba điểm
phân biệt . Tìm giá trị nhỏ nhất của
biểu thức .
A. . B. .
C. . D. .
Lời giải
Chọn C
Đặt .
ta có
Ta có
Do không đồng phẳng nên
2
1
3
4 3 1
.
V
x
Vx
2
31
1
4 3 1 2
. , ;
x
f x x
x




2
2
3 3 2
4
31
.
xx
fx
x
0
0
2
3
()
()
xL
fx
xN

13
1
28
ff




21
33
f



1
1
1
2
;
min min
x
V
fx
V



21
33
f




.ABCD A B C D
23,,AB a AD a AA a
G
BD
P
G
,,AD CD D B
,,H I K
2 2 2
1 1 1
' ' '
T
D H D K D I
2
1
3
T
a
2
4
T
a
2
4
3
T
a
2
1
12
T
a
,,
D H D I D K
x y z
D A D C D B
1 1 1 1
2 2 2 2
D G D B D A D C D D
D H xD A x D D D A
1
D H D D D A
x
D I yD C y D D D C
1
D I D D D C
y
D K zD A z D A D C
1
D K D A D C
z
1 1 1
4 4 4
D G D H D I D K
x y z
, , ,DG DH DI DK
1 1 1
1
4 4 4xyz
4
D A D C D B
D H D I D K
2
2 2 2 2
2 2 2
1 1 1
4
D A D C D B
D A D C D B
D H D I D K
D H D I D K
2 2 2 2 2
16 16 4
12 3
T
D A D C D B a a

Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 49
LÊ MINH TÂM
Ví dụ 07.
Cho hình chóp . Một mặt phẳng song
song mặt đáy cắt các cạnh lần
lượt tại . Gọi lần lượt là
hình chiếu của lên mặt đáy. Tìm tỉ số
để thể tích khối đa điện
lớn nhất.
A. . B. .
C. . D.
Lời giải
Chọn B
Đặt . Suy ra .
Gọi lần lượt là chiều cao hình chóp và chiều cao khối đa diện .
Do nên ta có .
Tương tự ta có
Ta có ( Vì tam giác đồng dạng tam giac )
Mặt khác ta có
Ta có
Do không thay đổi nên đạt giá trị lớn nhất khi và chỉ khi
đạt lớn nhất.
Ta có
Dấu xảy ra khi và chỉ khi .
.S ABCD
; ; ;SA SB SC SD
, , ,M N P Q
', ', ', 'M N P Q
, , ,M N P Q
SM
SA
. ' ' ' 'MNPQ M N P Q
3
4
SM
SA
2
3
SM
SA
1
2
SM
SA
1
3
SM
SA
SM
x
SA
SN SP SQ
x
SB SC SD
,'hh
. ' ' ' 'MNPQ M N P Q
//MN AB
.
SM MN MN
x MN x AB
SA AB AB
.BC x NP
22
.
MNP ABC MNPQ ABCD
S x S S x S
MNP
ABC
11
' ' '
'
AM h SA SM h h
x h x h
AS h SA h h
22
11
. ' ' ' '
'. . . . .
MNPQ M N P Q MNPQ ABCD ABCD
V h S x h x S x x h S
,
ABCD
hS
. ' ' ' 'MNPQ M N P Q
V
2
1 xx
3
2
1
22
4
1 4 1 4
2 2 27 27
..
xx
x
xx
x x x



2
1
23
x
xx
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 50
III. BÀI TẬP RÈN LUYỆN.
Câu 1. Hình lăng trụ tam giác có tất cả bao nhiêu cạnh?
A. . B. . C. . D. .
Lời giải
Chọn D
Lăng trụ tam giác có cạnh.
Câu 2. Cho hình chóp có đáy là hình vuông cạnh , vuông góc với mặt phẳng
, . Tính thể tích khối chóp
A. . B. . C. . D. .
Lời giải
Chọn D
Diện tích đáy: .
Thể tích khối chóp là: .
Câu 3. Cho hình chóp có đáy là hình vuông cạnh và chiều cao bằng . Thể tích khối chóp đã cho
bằng
A. . B. . C. . D. .
Lời giải
Chọn A
Ta có .
Câu 4. Một khối lăng trụ có diện tích đáy và có thể tích bằng thì chiều cao bằng :
A. . B. . C. . D. .
Lời giải
Chọn A
Chiều cao của khối lăng trụ bằng .
Câu 5. Cho khối chóp có diện tích đáy và thể tích bằng . Chiều cao của khối chóp bằng
A. 6. B. 2. C. 3. D. 12.
Lời giải
Chọn B
Ta có thể tích khối chóp .
Câu 6. Cho khối hộp chữ nhật có ba kích thước . Thể tích của khối hộp đã cho bằng
A. . B. . C. . D. .
Lời giải
Chọn A
Thể tích của khối hộp đã cho là .
Câu 7. Cho khối chóp có đáy là tam giác đều cạnh và chiều cao bằng . Thể tích của khối
chóp bằng
12
10
6
9
9
.S ABCD
ABCD
a
SA
ABCD
3SA a
.S ABCD
3
3a
3
9
a
3
3
a
3
a
2
ABCD
Sa
.S ABCD
23
1
3
3
.V a a a
a
4a
3
4
3
a
3
16a
3
4a
3
16
3
a
2
4,B a h a
23
1 1 4
4
3 3 3
..V B h a a a
3
6
2
3
4
6
6
2
3
V
h
S
3B
6
6
2
3
.
V
V B h h
B
2 4 6;;
8
16
48
12
2 4 6 48..V 
a
3a
V
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 51
LÊ MINH TÂM
A. . B. . C. . D. .
Lời giải
Chọn D
Diện tích đáy bằng .
Thể tích khối chóp là .
Câu 8. Hình chóp
có chiều cao , diện tích tam giác
là . Tính thể tích khối chóp
A. . B. . C. . D. .
Lời giải
Chọn B
Ta có:
Câu 9. Chiều cao của khối lăng trụ có thể tích bằng , diện tích đáy là
A. . B. . C. . D. .
Lời giải
Chọn D
Ta có: .
Câu 10. Thể tích khối hộp chữ nhật có ba kích thước lần lượt là
A. . B. . C. . D. .
Lời giải
Chọn C
Thể tích khối hộp chữ nhật có ba kích thước lần lượt là .
Câu 11. Cho hình lăng trụ đều có cạnh đáy bằng và cạnh bên bằng . Thể tích của
khối lăng trụ đã cho là
A. . B. . C. . D. .
Lời giải
Chọn D
Thể tích khối lăng trụ đã cho là .
Câu 12. Một hình hộp chữ nhật có ba kích thước là , và . Thể tích của khối hộp chữ nhật đó
bằng
A. . B. . C. . D. .
Lời giải
Chọn D
Thể tích khối hộp chữ nhật là: .
3
2
a
V
3
Va
3
3
4
a
V
3
4
a
V
ABC
BS
1
2
. .sinAB AC A
1
60
2
. .sinaa
2
3
4
a
1
3
V Bh
2
13
3
34
a
a
3
4
a
.S ABC
ha
ABC
2
3a
..S ABC
3
2
a
3
a
3
3a
3
3
2
a
23
11
3
33
. . . .V B h a a a
12V
4B
8
9
1
3
12
3
4
.
V
V B h h
B
,,a b c
3
V a bc
1
3
V abc
V abc
1
2
V abc
,,a b c
V abc
.ABC A B C
a
2a
3
3
4
a
3
3
6
a
3
3
3
a
3
3
2
a
23
33
2
42
. . a
aa
V B h
a
2a
3a
3
a
3
3a
3
2a
3
6a
3
6aV
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 52
Câu 13. Cho hình chóp có đáy là hình vuông cạnh , và vuông góc
với . Thể tích của khối chóp bằng
A. . B. . C. . D. .
Lời giải
Chọn B
Thể tích khối chóp .
Câu 14. Mặt phẳng chia khối lăng trụ thành các khối đa diện nào?
A. Hai khối chóp tam giác.
B. Một khối chóp tam giác và một khối chóp ngũ giác.
C. Một khối chóp tam giác và một khối chóp tứ giác.
D. Hai khối chóp tứ giác.
Lời giải
Chọn C
Mặt phẳng chia khối lăng trụ thành hai khối đó là chóp tam giác và chóp
tứ giác .
Câu 15. Cho khối lăng trụ tam giác đều có cạnh đáy bằng , cạnh bên bằng . Thể tích của khối
lăng trụ đã cho bằng
A. B. C. D.
Lời giải
Chọn A
.S ABCD
ABCD
a
32SA a
SA
ABCD
.S ABCD
3
2
2
a
3
2a
3
32a
3
43
3
a
23
11
3 2 2
33
.
. . .
S ABCD ABCD
V S SA a a a
AB C

.ABC A B C
AB C

.A A B C
.A B C CB

2a
a
3
3
2
.
a
3
3
3
.
a
3
3
12
.
a
3
3.a
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 53
LÊ MINH TÂM
Trong ta có .
Vậy thể tích khối lăng trụ tam giác đều là
Câu 16. Cho hình chóp có tam giác vuông tại . .
Thể tích của hình chóp là
A. . B. . C. . D. .
Lời giải
Chọn D
Thể tích khối chóp
Câu 17. Tính thể tích của khối chóp có chiều cao bằng và diện tích đáy bằng .
A. . B. . C. . D. .
Lời giải
Chọn B
Thể tích của khối chóp cần tìm là:
Câu 18. Cho hình hộp chữ nhật có đáy là hình vuông cạnh a, chiều cao bằng . Tính thể tích hình
hộp chữ nhật.
A. . B. . C. . D. .
Lời giải
Chọn A
Thể tích hình hộp chữ nhật là .
ABC
22
33
44
ABC
AB a
S 
23
33
2
42
.
'. . .
ABC A B C ABC
aa
V AA S a
.S ABC
ABC
A
23; ; ; ( )AB a AC a SA a SA ABC
3
3Va
3
6Va
3
2Va
3
Va
3
1 1 1 1
23
3 3 2 6
. . . . . . . . .
SABC ABC
V S SA AB AC SA a a a a
V
5cm
2
12cm
3
60cmV
3
20cmV
3
30cmV
3
40cmV
3
11
5 12 20
33
. . cmV Bh
2a
3
2a
3
6a
3
2
3
a
2
2a
23
22..V B h a a a
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 54
Câu 19. Cho khối lăng trụ có diện tích đáy là ,chiều cao là . Tính thể tích khối lăng trụ
A. . B. . C. . D. .
Lời giải
Chọn C
.
Câu 20. Cho khối lăng trụ tam giác đều có tất cả các cạnh bằng . Thể tích của khối lăng trụ đã cho
bằng
A. . B. . C. . D. .
Lời giải
Chọn B
Ta có diện tích đáy .Suy ra thể tích khối lăng trụ là .
Câu 21. Cho khối hộp chữ nhật có , , . Thể tích của khối hộp
đã cho bằng
A. . B. . C. . D. .
Lời giải
Chọn C
Áp dụng định lý Pytago cho tam giác vuông , ta có .
Khi đó, thể tích của khối hộp chữ nhật là .
Câu 22. Cho khối lăng trụ có thể tích bằng 18, thể tích khối chóp bằng
A. . B. . C. . D. .
Lời giải
Chọn A
Ta có: .
Câu 23. Cho khối chóp tứ giác đều có cạnh đáy bằng và cạnh bên bằng . Thể tích khối chóp
bằng
8
6
16
36
48
24
6 8 48..V B h
a
3
2
3
a
3
3
4
a
2
3
4
a
3
a
2
3
4
a
B
23
33
44
..
aa
V B h a
.ABCD A B C D
3AB
5AC
8AA
120
32
96
60
ABC
22
5 3 4BC
3 4 8 96. . . .V AB BC AA
1 1 1
.ABC A B C
1
.A ABC
6
9
12
3
1 1 1 1
1
1 1 1
18 6
3 3 3
..
. . . . .
A ABC ABC ABC A B C
V S d A ABC V
2
6
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 55
LÊ MINH TÂM
A. . B. . C. . D. .
Lời giải
Chọn C
Áp dụng công thức:
Đáy là hình vuông nên: ;
.
Câu 24. Thể tích của khối chóp có diện tích đáy bằng và chiều cao bằng là
A. . B. . C. . D. .
Lời giải
Chọn D
Thể tích của khối chóp cần tìm là .
Câu 25. Cho một khối chóp có diện tích đáy , chiều cao . Thể tích khối chóp đã cho bằng
A. . B. . C. . D. .
Lời giải
Chọn A
Thể tích khối chóp đã cho là .
Câu 26. Số cạnh của hình bát diện đều là
A. . B. . C. . D. .
Lời giải
Chọn B
Câu 27. Cho khối lăng trụ có diện tích đáy và chiều cao . Thể tích của khối lăng trụ đã cho
bằng:
A. . B. . C. . D. .
Lời giải
Chọn A
Thể tích của khối lăng trụ đã cho là: .
Câu 28. Thể tích của khối chóp có diện tích đáy , chiều cao là
A. . B. . C. . D. .
8
4
3
8
3
4
1
3
V Bh
2
24B 
2
2
22
22
6 6 2 2
2
h SO SA AO




18
42
33
..V 
V
2
6a
a
3
12Va
3
6Va
3
18Va
3
2Va
23
11
62
33
..V Sh a a a
2
6Ba
3ha
3
6a
3
18a
3
9a
3
54a
23
11
6 3 6
33
.V Bh a a a
8
12
10
20
8B
6h
48
16
24
14
8 6 48..V Bh
B
h
.Bh
1
2
.Bh
1
3
.Bh
4
3
.Bh
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 56
Lời giải
Chọn C
Thể tích của khối chóp có diện tích đáy , chiều cao là .
Câu 29. Cho khối chóp có chiều cao và diện tích đáy . Thể tích của khối chóp đã cho bằng
A. . B. . C. . D. .
Lời giải
Chọn A
Thể tích của khối chóp là: .
Câu 30. Tính thể tích của khối lập phương biết .
A. . B. . C. . D. .
Lời giải
Chọn A
Ta có .
Câu 31. Cho khối chóp có diện tích đáy và chiều cao . Thể tích của khối chóp đã cho
bằng
A. B. C. D.
Lời giải
Chọn D
Thể tích của khối chóp là .
Câu 32. Thể tích của khối lăng trụ có diện tích đáy bằng và chiều cao bằng là:
A. . B. . C. . D. .
Lời giải
Chọn A
Thể tích khối lăng trụ đã cho là .
Câu 33. Cho khối chóp
có đáy là hình vuông cạnh , và vuông góc với
mặt phẳng đáy. Thể tích của khối chóp
là
A. . B. . C. . D. .
Lời giải
Chọn B
Ta có là đường cao của hình chóp.
Thể tích khối chóp là: .
Câu 34. Cho khối lăng trụ tam giác đều có độ dài tất cả các cạnh bằng . Thể tích khối lăng trụ đã
cho bằng
A. . B. . C. . D. .
Lời giải
B
h
1
3
.Bh
3h
2B
2
3
12
6
11
2 3 2
33
..V Bh
V
.ABCD A B C D
3AC a
3
Va
3
4
a
V
3
36
4
a
V
3
33Va
3
3 3 3.AC a AB a AB a V a
6B
10h
6.
24.
10.
20.
11
6 10 20
33
. . .V B h
B
h
V Bh
1
3
V Bh
1
2
V Bh
4
3
V Bh
V Bh
.S ABCD
ABCD
a
3SA a
SA
.S ABCD
3
3a
3
a
3
3
a
3
6a
SA ABCD SA
.S ABCD
23
11
3
33
. . .
ABCD
V SA S a a a
3
93
4
27 3
4
27 3
2
93
2
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 57
LÊ MINH TÂM
Chọn B
Thể tích khối lăng trụ tam giác cạnh bằng là: .
Câu 35. Thể tích của khối lập phương cạnh bằng
A. . B. . C. . D. .
Lời giải
Chọn B
Thể tích của khối lập phương cạnh là .
Câu 36. Thể tích khối lập phương có cạnh bằng
A. . B. . C. . D. .
Lời giải
Chọn A
Thể tích khối lập phương có cạnh là (đvtt).
Câu 37. Cho khối lăng trụ có diện tích đáy và chiều cao Thể tích của khối lăng trụ đã cho
bằng
A. B. C. D.
Lời giải
Chọn B
Thể tích của khối lăng trụ đã cho là:
Câu 38. Cho khối lăng trụ có diện tích đáy và chiều cao . Thể tích khối lăng trụ đã cho
bằng
A. . B. . C. . D. .
Lời giải
Chọn D
Thể tích khối lăng trụ đã cho bằng .
Câu 39. Một khối lăng trụ có diện tích đáy bằng và chiều cao bằng . Thể tích khối lăng trụ đã cho
bẳng:
A. . B. . C. . D. .
Lời giải
Chọn B
Ta có thể tích khối lăng trụ đã cho là:
Câu 40. Cho khối chóp có đáy là hình vuông cạnh , và vuông góc với
đáy. Thể tích khối chóp là
A. . B. . C. . D. .
Lời giải
Chọn B
.
Câu 41. Thể tích của khối lăng trụ có chiều cao bằng và diện tích đáy bằng là
A.
B. C.
D.
3
2
33
3
4
.V
27 3
4
a
2
a
3
a
4
a
5
a
a
3
a
23
24 3
54 2
8
18 2
23
3
2 3 24 3V 
5B
6.h
15
30
150
10
5 6 30..V Bh
6S
10h
20
40
30
60
6 10 60..V S h
6
5
90
30
10
15
6 5 30xV 
.S ABCD
ABCD
a
3SA a
SA
.S ABCD
3
3a
3
a
3
3
a
3
6a
23
11
3
33
.
..
S ABCD
V Bh a a a
h
B
1
3
.Bh
1
6
.Bh
.Bh
3 .Bh
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 58
Lời giải
Chọn C
Thể tích khối lăng trụ là
Câu 42. Khối lăng trụ có diện tích đáy là S, chiều cao h có thể tích V là
A. B. C. D.
Lời giải
Chọn C
Ta có
Câu 43. Thể tích khối lăng trụ được tính theo công thức nào sau đây?
A. . B. . C. . D. .
Lời giải
Chọn B
Câu 44. Cho hình chóp có đáy là tam giác,diện tích đáy bằng và thể tích bằng . Tính
chiều cao của hình chóp đã cho.
A. . B. . C. . D. .
Lời giải
Chọn C
Ta có: .
Câu 45. Thể tích của khối lăng trụ tam giác đều có cạnh đáy bằng và cạnh bên bằng là
A. . B. . C. . D. .
Lời giải
Chọn B
Ta có: Diện tích đáy
Suy ra: .
Câu 46. Cho hình chóp có và , diện tích tứ giác là bằng . Thể
tích khối chóp bằng
A. . B. . C. . D. .
Lời giải
Chọn A
Ta có:
Câu 47. Tính thể tích của một khối lăng trụ biết khối lăng trụ đó có đường cao bằng , diện tích mặt
đáy bằng .
A. . B. . C. . D. .
Lời giải
V Bh
2
V Sh
1
2
V Sh
V Sh
1
3
V Sh
V Sh
1
3
.V B h
.V B h
1
2
.V B h
1
6
.V B h
.S ABC
2
3a
3
a
h
3
6
a
h
3
2
a
h
3a
3
3
a
1
3
.
ABC
V h S
3
ABC
V
h
S

3
2
3
3
a
a
3a
V
a
2a
3
3
3
a
V
3
3
2
a
V
3
3Va
3
3
4
a
V
2
3
4
ABC
a
S
23
33
2
42
..
ABC
aa
V AA S a
.S ABCD
SA SBCD
2SA a
ABCD
2
3a
.S ABCD
3
2a
2
6a
3
6a
2
2a
23
11
3 2 2
33
.
. . . . .
S ABCD ABCD
V S SA a a a
3a
2
4a
3
4a
2
4a
3
12a
2
12a
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 59
LÊ MINH TÂM
Chọn C
Gọi là diện tích mặt đáy, là độ dài đường cao của khối trụ đã cho.
Khi đó thể tích của khối lăng trụ đã cho là .
Câu 48. Tính thể tích của khối chóp có diện tích đáy bằng 12 và chiều cao bằng 4 là
A. . B. . C. . D. .
Lời giải
Chọn D
Ta có .
Câu 49. Tính thể tích của khối lập phương có cạnh .
A. . B. . C. D. .
Lời giải
Chọn D
Ta có: .
Câu 50. Một khối lăng trụ có diện tích đáy bằng và chiều cao bằng . Thể tích của khối lăng trụ
đó bằng
A. . B. . C. . D. .
Lời giải
Chọn B
.
Câu 51. Cho khối chóp có và vuông góc với mặt phẳng , tam giác
vuông tại và có . Tính thể tích của khối chóp bằng
A. . B. . C. . D. .
Lời giải
Chọn B
Câu 52. Một khối lăng trụ có chiều cao bằng và diện tích đáy bằng . Thể tích của khối lăng
trụ đó bằng
A. . B. . C. . D. .
Lời giải
Chọn D
Thể tích cuả khối lăng trụ (đvtt)
Câu 53. Mặt phẳng chia khối lăng trụ thành các khối đa diện nào?
A. Hai khối chóp tam giác.
B. Một khối chóp tam giác và một khối chóp tứ giác.
C. Hai khối chóp tứ giác.
D. Một khối chóp tam giác và một khối chóp ngũ giác.
Lời giải
Chọn B
S
h
23
4 3 12..V S h a a a
V
8V
48V
24V
16V
1
12 4 16
3
..V 
V
.ABCD A B C D
AB a
3
6
a
V
3
3
a
V
3
2
a
V
3
Va
23
.V Bh a a a
3
4
4
12
36
6
3 4 12..V S h
.S ABC
3SA a
SA
ABC
ABC
A
34,AB a AC a
.S ABC
3
18a
3
6a
3
36a
3
2a
3
1 1 1
3 4 3 6
3 3 2
. . . .V B h a a a a
6
2 14
2 14
4 14
6 14
12 14
2 14 6 12 14.V Bh
A BC
.ABC A B C
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 60
Mặt phẳng chia khối lăng trụ thành một khối chóp tam giác
và một khối chóp tứ giác
Câu 54. Cho khối chóp có đáy là tam giác cân tại , , . Cạnh bên
vuông góc với mặt đáy, . Thể tích khối chóp đã cho bằng
A. . B. . C. . D. .
Lời giải
Chọn C
Diện tích đáy bằng .
Thể tích khối chóp là .
Câu 55. Cho khối chóp tứ giác đều có cạnh đáy bằng , cạnh bên gấp hai lần cạnh đáy. Tính thể tích
của khối chóp đã cho:
A. . B. . C. . D. .
Lời giải
Chọn A
Xt hình chóp đều có đáy là hình vuông tâm cạnh
Từ gt và ;
Vậy thể tích của khối chóp là: .
A BC
.ABC A B C
.A ABC
.A BB C C
.S ABC
ABC
A
BAC
30
AB a
SA
22SA a
3
2
12
a
3
2
4
a
3
2
6
a
3
2
2
a
ABC
BS
1
2
. .sinAB AC A
1
30
2
. .sinaa
2
4
a
1
3
V Bh
1
3
.BSA
2
1
22
34
a
a
3
2
6
a
a
V
3
14
6
a
V
3
2
6
a
V
3
2
2
a
V
3
14
2
a
V
.S ABCD
ABCD
H
a
SH ABCD
2SA a
2
2
a
AH
22
14
2
a
SH SA AH
V
.S ABCD
3
2
1 1 14 14
3 3 2 6
. . .
ABCD
aa
V SH S a
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 61
LÊ MINH TÂM
Câu 56. Cho khối chóp có đáy là hình vuông cạnh , vuông góc mới mặt phẳng đáy,
tạo với mặt phẳng một góc . Tính thể tích khối chóp
A. . B. . C. . D. .
Lời giải
Chọn B
Ta có .
Do đó góc giữa với mặt phẳng là góc .
Trong tam giác vuông tại , ta có .
.
Thể tích khối chóp .
Câu 57. Khối chóp tam giác có thể tích là: và chiều cao . Tìm diện tích đáy của khối chóp
tam giác đó.
A. . B. . C. . D. .
Lời giải
Chọn C
.
Vậy diện tích đáy của khối chóp tam giác đấy là .
Câu 58. Cho hình chóp có đáy
là hình vuông tâm cạnh . Cạnh bên vuông
góc với đáy, góc . Thể tích khối chóp đã cho bằng
A. . B. . C. . D. .
Lời giải
Chọn C
.S ABCD
a
SA
SC
SAB
30
.S ABCD
3
6
3
a
3
2
3
a
3
2a
3
2
3
a
a
a
D
A
B
C
S
,BC AB BC SA BC SAB
SC
SAB
30BSC 
BSC
B
30 3
30
tan
tan
BC BC
SB a
SB
22
2SA SB AB a
3
2
1 1 2
2
3 3 3
.
. . . .
S ABCD ABCD
a
V S SA a a
3
2
3
a
3a
2
3a
2
23a
2
23
3
a
2
23
9
a
32
2 1 1 2 3
3
3 3 3 3
. . . .
chóp đáy đáy đáy
aa
V h S a S S
2
23
3
a
.S ABCD
ABCD
O
a
SA
60SBD
3
2
3
a
3
3
2
a
3
3
a
3
a
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 62
Do tứ giác
là hình vuông tâm cạnh nên và .
Vì .
Ta có . Mà đều.
Suy ra
Vậy .
Câu 59. Cho khối chóp có đáy là hình vuông cạnh , vuông góc với mặt phẳng đáy và
tạo với đáy một góc bằng Thể tích của khối chóp đã cho bằng
A. . B. . C. . D. .
Lời giải
Chọn D
Áp dụng công thức:
Với: ,
Vậy:
Câu 60. Cho khối chóp có đáy là hình vuông tâm , cạnh , vuông góc với mặt
phẳng đáy và . Gọi lần lượt là trung điểm của . Thể tích khối tứ diện
bằng
A. . B. . C. . D. .
Lời giải
Chọn A
ABCD
O
a
2BD a
2
ABCD
Sa
,SA ABCD SA AB SA AD
2 2 2 2
;SB SA AB SD SA AD SB SD
60SBD SBD
22
2SB BD a SA SB AB a
3
1
33
.
..
S ABCD ABCD
a
V SA S
.S ABCD
a
SA
SC
60
3
6
6
a
3
6
9
a
3
6a
3
6
3
a
1
3
V Bh
2
ABCD
B S a
60 2 3 6.tan .h SA AC a a
3
2
16
6
33
..
a
V a a
.S ABCD
ABCD
O
a
SA
3SA a
,MN
,SC SD
SOMN
3
16
a
3
8
a
3
3
8
a
3
3
16
a
O
B
S
A
D
C
M
N
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 63
LÊ MINH TÂM
Ta có:
Lại có:
Câu 61. Cho khối lăng trụ tam giác đều có cạnh đáy là và khoảng cách từ đến mặt
phẳng bằng . Tính thể tích của khối lăng trụ .
A. . B. . C. . D. .
Lời giải
Chọn B
Gọi là trung điểm của
Ta có , vì đều và nên .
Dựng , khi đó , do đó
vuông tại với đường cao nên
Thể tích khối lăng trụ là:
Câu 62. Cho lăng trụ tam giác có đáy là tam giác vuông tại , , cạnh bên
bằng . Hình chiếu vuông góc của trên mặt phẳng là trung điểm cạnh . Tính
thể tích của khối lăng trụ
A. . B. . C. . D. .
Lời giải
Chọn C
3
2
1 1 1 1 1
3
4 4 3 4 3 4
..
. . . . . . .
S OCD S ABCD ABCD
a
V V SA S a a
1 1 1
2 2 4
.
.
..
S OMN
S OCD
V
SM SN
V SC SD
33
11
4 4 4 16
..
.
S OMN S OCD
aa
VV
.ABC A B C
2a
A
A BC
a
.ABC A B C
3
22a
3
32
2
a
3
2
2
a
3
2
2
a
M
BC

B C A M
ABC
B C AA
B C AA M
A E AM
A E AB C
;d A AB C A E a

AA M
A
AH
2 2 2 2 2 2 2
2
1 1 1 1 1 1 1 1 6
2
3()
a
AA
A H AA A M AA A E A M a
a
.ABC A B C
23
6 2 3 3 2
2 4 2
()a a a
V
.ABC A B C
ABC
A
AB a
2a
A
ABC
BC
.ABC A B C
3
2
2
a
3
2
6
a
3
14
4
a
3
14
12
a
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 64
Gọi là trung điểm của cạnh
vuông cân tại .
Ta có
.
Câu 63. Cho hình chóp đều có đáy là hình vuông cạnh , cạnh bên . Thể tích của
khối chóp.
A. . B. . C. . D. .
Lời giải
Chọn A
Gọi là tâm của hình vuông
Ta có:
Vậy thể tích khối chóp là: .
Câu 64. Cho hình lập phương có cạnh bằng . Thể tích khối tứ diện bằng
H
A'
B'
C'
C
A
B
H
BC
A H ABC

ABC
A
2BC a
2
22
BC a
AH
2
2
22
2 14
2
22
aa
A H A A AH a





23
14 1 14
2 2 4
.
.
ABCD A B C D
a
V a a
.S ABCD
a
2SA a
3
14
6
a
3
2a
3
14
2
a
3
7
2
.a
O
ABCD SO ABCD
11
2
22
.OA AC a
2
2
22
2 14
2
22
aa
SO SA OA a




23
1 1 14 14
3 3 2 6
.
. .S . .
S ABCD ABCD
a
V SO a a
.ABCD A B C D
a
ABDB
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 65
LÊ MINH TÂM
A. . B. . C. . D. .
Lời giải
Chọn A
Ta có: .
Câu 65. Lăng trụ đều cạnh , góc giữa đường thẳng và mặt phẳng đáy bằng
. Hỏi thể tích lăng trụ.
A. . B. . C. . D. .
Lời giải
Chọn B
Ta có là hình chiếu vuông góc của trên do đó
.
Diện tích tam giác : . Vậy
Câu 66. Cho khối chóp tứ giác đều có cạnh đáy và chiều cao Thể tích của khối chóp bằng
A. B. C. D.
Lời giải
Chọn B
Do khối chóp tứ giác đều nên đáy của khối chóp là hình vuông có cạnh đáy là .
Diện tích đáy của khối chóp là: .
Chiều cao của khối chóp là:
Vậy thể tích của khối chóp bằng: .
Câu 67. Cho hình lăng trụ có cạnh bên bằng và tạo với mặt phẳng đáy một
góc bằng , diện tích tam giác bằng . Tính thể tích khối lăng trụ
bằng
A. . B. . C. . D. .
Lời giải
Chọn C
3
6
a
3
2
3
a
3
2
a
3
3
a
3
2
1 1 1 1
3 3 2 6 6
. . . . . .
ABDB ABD ABCD
a
V B B S B B S a a

. ' ' 'ABC A B C
AB a
'AB
0
60
3
3
12
a
3
3
4
a
3
4
a
3
3
4
a
AA mp ABC A

'A
mp ABC
0
60' , 'A B ABC A BA
0
60 3' tanAA AB a
ABC
2
3
4
ABC
a
S
3
3
4
. ' ' 'ABC A B C
a
V
3a
5.h
15
15
45
45
3a
22
39Ba
5.h
11
9 5 15
33
. . .V B h
. ' ' 'ABC A B C
2'AA a
0
60
ABC
2
a
. ' ' 'ABC A B C
3
3
3
a
3
a
3
3a
3
3
a
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 66
Giả sử đường cao là . Vì cạnh bên
tạo với đáy một góc
nên . Xét
tam giác vuông
Vậy thể tích lăng trụ là:
Câu 68. Biết rằng thể tích của một khối lập phương bằng 27. Tính tổng diện tích các mặt của hình lập
phương đó.
A. B. C. D.
Lời giải
Chọn C
Thể tích khối lập phương cạnh .
Diện tích các mặt (diện tích toàn phần) hình lập phương là .
Câu 69. Cho hình chóp đều có cạnh đáy bằng và cạnh bên tạo với đáy một góc . Thể
tích của hình chóp đều đó là
A. . B. . C. . D. .
Lời giải
Chọn C
Đáy là hình vuông nên diện tích đáy là
(đvdt).
Gọi là tâm của đáy
là hình chiếu vuông góc của lên mặt
phẳng góc giữa cạnh bên và đáy là góc .
.
A
A'
C
B
B'
C'
H
'AA
'AA
0
60
0
60'AA H
'AA H
0
60 3sin
'
AH
AH a
AA
23
33.V a a a
27
16
54
36
3
27 3x V x x
3 3 6 54..
.S ABCD
a
60
3
3
6
a
3
3
2
a
3
6
6
a
3
6
2
a
ABCD
2
Ba
O
SO DABC
OB
SB
ABCD
SB
60SBO
26
60 3
22
.tan .
aa
h SO OB
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 67
LÊ MINH TÂM
Vậy thể tích khối chóp là
(đvtt).
Câu 70. Cho hình chóp có , tam giác vuông cân tại , . Tính
theo thể tích
của khối chóp .
A. . B. . C. . D. .
Lời giải
Chọn A
Đáy là tam giác vuông cân tại nên .
(đvdt).
Vậy thể tích khối chóp là
(đvtt).
Câu 71. Diện tích toàn phần của một hình lập phương bằng . Khối lập phương đã cho có thể
tích bằng
A. . B. . C. . D. .
Lời giải
Chọn C
Gọi là cạnh của hình lập phương.
.
Vậy .
Câu 72. Cho tứ diện có , , đôi một vuông góc với nhau và ,
. Thể tích khối tứ diện đã cho bằng:
A. . B. . C. . D. .
Lời giải
Chọn D
Do tứ diện có , , đôi một vuông góc với nhau nên thể tích khối tứ diện
là: .
Câu 73. Cho khối tứ diện đều có cạnh bằng . Thể tích của khối tứ diện đã cho bằng
3
16
36
a
V Bh
.S ABC
SA ABC
ABC
A
SA BC a
a
V
.S ABC
3
12
a
V
3
4
a
V
3
2Va
3
2
a
V
ABC
A
2
2
2
BC a
AB AC
2
1
24
.
ABC
a
B S AB AC
3
11
3 3 12
.
ABC
a
V Bh S SA
2
96 cm
3
84 cm
3
48 cm
3
64 cm
3
91 cm
x
0x
2
6 96 4
tp
S x x
33
4 64V cm
OABC
OA
OB
OC
6OB OC a
OA a
3
3a
3
2a
3
6a
3
a
OABC
OA
OB
OC
OABC
3
11
66
66
. . . .
OABC
V OAOBOC a a a a
3a
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 68
A. . B. . C. . D. .
Lời giải
Chọn D
Gọi H là trọng tâm của
Gọi M là giao điểm của BH và CD ta có:
Xét vuông tại H có:
Ta có: .
Câu 74. Cho khối chóp có đáy là hình chữ nhật, biết vuông
góc với mặt phẳng đáy và tạo với đáy một góc . Thể tích của khối chóp bằng
A. B. C. D.
Lời giải
Chọn D
Ta có là hình chiếu của lên mặt phẳng đáy
Vậy thể tích của khối chóp
Câu 75. Cho khối lăng trụ đứng có đáy là tam giác đều cạnh a và . Thể tích của
khối lăng trụ đã cho bằng
A. . B. . C. . D. .
Lời giải
Chọn A
3
2
4
a
3
3
4
a
3
6
12
a
3
6
4
a
BCD AH BCD
3 3 3 2 2 3
2 2 3 3 2
.
.
a a a
BM BH BM a
ABH
2 2 2 2 2 2
3 2 2AH AB BH a a a AH a
2
3
33
1 1 6
2
3 3 4 4
. . .
ABCD BCD
a
a
V AH S a
.S ABCD
ABCD
3,,AB a AD a SA
SC
60
o
.S ABCD
3
6 .a
3
3.a
3
3
3
.
a
3
2 .a
AC
SC
60 60 2 3, , .tan .
oo
SC ABCD SC AC SCA SA AC a
3
11
3 2 3 2
33
.
. . . . . .
S ABCD ABCD
V S SA a a a a
.S ABCD
3
2 .a
.ABC A B C
2AA a
3
3
2
a
3
3
6
a
3
3a
3
3
3
a
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 69
LÊ MINH TÂM
Gọi M là trung điểm của .
Diện tích tam giác là: .
Thể tích của khối lăng trụ là: .
Câu 76. Cho khối tứ diện và gọi là trung điểm của đoạn thẳng , khi đó mặt phẳng
chứa cạnh , song song với chia khối tứ diện thành
A. Một khối tứ diện và một khối lăng trụ.
B. Hai khối chóp tứ giác.
C. Một khối tứ diện và một khối chóp tứ giác.
D. Hai khối tứ diện.
Lời giải
Chọn C
Ta có khi đó mặt phẳng chứa cạnh , song song với nên giao tuyến của mặt
phẳng và mặt phẳng là đường thẳng đi qua và song song với , cắt
tại .
Khi đó mặt phẳng . Vậy mặt phẳng chia khối tứ diện thành khối
tứ diện và khối chóp tứ giác
Câu 77. Cho khối chóp có đáy là tam giác đều cạnh bằng , tam giác đều và nằm
trong mặt phẳng vuông góc với mặt phẳng đáy. Thể tích của khối chóp đã cho bằng
BC

A B C
2
1 1 3 3
2 2 2 4
. . . .
A B C
aa
S A M B C a
.ABC A B C
23
33
2
42
..
A B C
aa
V S AA a
ABCD
M
AB
P
CM
BD
ABCD
P
CM
BD
P
ABD
M
BD
AD
H
P CMH
P
ABCD
AMCH
.C MHDB
.S ABC
3
SAC
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 70
A. . B. . C. . D. .
Lời giải
Chọn B
Gọi là trung điểm của , hai tam giác và là hai tam giác đều, bằng nhau và
.
Ba đường thẳng , , đôi một vuông góc với nhau, suy ra:
.
Câu 78. Cho hình chóp có , và . Thể tích khối
chóp bằng
A. . B. . C. . D. .
Lời giải
Chọn B.
Ta có .
Vậy .
Câu 79. Cho tứ diện , gọi lần lượt là trung điểm các cạnh , , và là
trọng tâm tam giác . Tính tỉ số thể tích .
A. . B. . C. . D. .
Lời giải
Chọn B
3
12
33
8
33
4
3
8
H
AC
SAC
ABC
33
22
AB
HS HB
AC
HS
HB
1 1 3 3 3 3
3
6 6 2 2 8
.
. . . .
S ABC
V AC HB HS
.S ABC
SA ABC
2 ,SA AC a AB a
60BAC 
.S ABC
3
2
3
a
3
3
3
a
3
3
6
a
3
3a
2
1 1 3
2 60
2 2 2
. .sin . . .sin
ABC
a
S AB AC BAC a a
23
1 1 3 3
2
3 3 2 3
.
. . . .
S ABC ABC
aa
V SA S a
ABCD
,,M N P
AB
AC
AD
O
BCD
OMNP
ABCD
V
V
1
6
1
8
1
12
1
4
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 71
LÊ MINH TÂM
Dễ thấy . Do lần lượt là trung điểm các cạnh , , cho
nên
.
.
Câu 80. Cho lăng trụ đều có tất cả các cạnh đều bằng . Thể tích khối lăng trụ
là
A. . B. . C. . D. .
Lời giải
Chọn A
Vì tam giác đều cạnh , suy ra .
Chiều cao của lăng trụ là .
Thể tích khối lăng trụ bằng .
Câu 81. Tính thể khối đa diện , biết đôi một vuông góc và có độ dài lần lượt là
2, 3,4?
A. . B. . C. . D. .
Lời giải
Chọn D
Do đôi một vuông góc nên suy ra là đường cao của khối đa
diện . Không mất tính tổng quát ta chọn .
Ta có .
Vậy (đvtt).
K
I
P
N
M
O
J
B
C
D
A
//MNP BCD
,,M N P
AB
AC
AD
;;
OMNP AMNP
d A MNP d O MNP V V
1 1 1 1
2 2 2 8
OMNP AMNP
ABCD ABCD
VV
AM AN AP
V V AB AC AD
.ABC A B C
a
.ABC A B C
3
3
4
a
V
3
3
2
a
V
3
3
6
a
V
3
3
3
a
V
ABC
a
2
3
4
ABC
a
S
.ABC A B C
AA a
.ABC A B C
3
3
4
.
ABC
a
V S AA

ABCD
,,AB AC AD
8
24
3
4
,,AB AC AD
()AD ABC
AD
ABCD
2 3 4,,AB AC AD
1
3
2
.
ABC
S AB AC
1
4
3
.
ABCD ABC
V AD S
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 72
Câu 82. Cho khối chóp có đáy là hình vuông cạnh , vuông góc với đáy và
. Thể tích khối chóp là
A. . B. . C. . D. .
Lời giải
Chọn B
Ta có là chiều cao của hình chóp.
Diện tích đáy: .
Thể tích của khối chóp : .
Câu 83. Cho hình lăng trụ đứng tất cả các cạnh bằng . Thể tích của khối lăng trụ
bằng
A. . B. C. . D. .
Lời giải
Chọn A
Ta có
Do đó thể tích của khối lăng trụ bằng .
Câu 84. Cho khối lăng trụ đứng tam giác có đáy là tam giác vuông tại với
. Biết hợp với mặt phẳng một góc . Thể tích khối lăng trụ đã
cho bằng
A. . B. . C. . D. .
Lời giải
Chọn B
.S ABCD
ABCD
a
SA
6SA a
3
a
3
2a
3
3a
3
6a
6a
a
B
C
A
D
S
SA ABCD SA
2
ABCD
Sa
.S ABCD
23
11
62
33
.
. . . .
S ABCD ABCD
V S SA a a a
. ' ' 'ABC A B C
2a
. ' ' 'ABC A B C
3
6
2
a
3
3
12
a
3
3
4
a
3
6
6
a
2
2
33
22
42
. ; ' .
ABC
B S a a h AA a
. ' ' 'ABC A B C
23
36
2
22
. . .B h a a a
.ABC A B C
ABC
B
22BC BA a
AB
ABC
60
3
23a
3
3a
3
3
3
a
3
23
3
a
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 73
LÊ MINH TÂM
Hình chiếu của lên là , do đó góc giữa và là .
Tam giác vuông tại nên .
Do đó thể tích khối lăng trụ là .
Câu 85. Tính thể tích khối lăng trụ tam giác đều , biết mặt bên của khối lăng trụ là hình
vuông và có chu vi bằng .
A. . B. . C. . D. .
Lời giải
Chọn C
Ta có là hình vuông cạnh có chu vi bằng .
Tam giác đều cạnh nên có .
Vậy thể tích của khối lăng trụ là .
Câu 86. Cho khối chóp tứ giác đều có cạnh đáy và cạnh bên đều bằng . Thể tích của khối
chóp trên bằng
A. . B. . C. . D. .
Lời giải
Chọn D
AB
ABC
AB
AB
ABC
60A BA

A BA
A
60 3tanAA AB a
3
11
2 3 3
22
ABC
V S AA BA BC AA a a a a

.ABC A B C
8
43V
26V
23V
16 3V
ABB A

a
4 8 2a a AB AA
ABC
2
2
23
3
4
ABC
S 
23.
ABC
V AA S

.DS ABC
6a
3
36 3a
3
108 2a
3
18 2a
3
36 2a
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 74
Ta có .
Khi đó thể tích khối chóp đã cho là .
Câu 87. Cho khối chóp có đáy là tam giác vuông tại , , . Biết
rằng góc giữa đường thẳng và mặt phẳng đáy bằng , thể tích khối chóp đã cho bằng
A. . B. . C. . D. .
Lời giải
Chọn C
Ta có
Giả sử là hình chiếu của lên
là hình chữ nhật
Ta có: là hình chiếu của lên mặt phẳng
;
Vậy thể tích khối chóp đã cho bằng
Câu 88. Cho hình lăng trụ có đáy là tam giác đều cạnh Hình chiếu của lên mặt
phẳng trùng với trung điểm cạnh góc giữa và mặt đáy của hình lăng trụ
đã cho bằng Tính thể tích của khối chóp
A. B. C. D.
Lời giải.
Chọn A
22
6 2 3 2 3 2a a aAC OC SO SC OC
23
11
3 2 36 36 2
33
. a . aV Sh a
.S ABC
B
90SAB SCB
2,AB a BC a
SB
60
3
a
3
15
6
a
3
15
3
a
3
5
6
a
90 ,SAB SCB SA AB SC CB
D
S
()ABC
( ) ,SD ABC SD AB SD BC
()
()
CB SCD CB CD
ABCD
AB SAD AB AD





BD
SD
()ABCD
60( ;( )) ( ; )SB ABCD SB BD SBD
2 2 2 2
25()BD BC CD a a a
60 15tanSD BD a
3
15
1 1 1
15 2
3 3 2 3
.
. . . . . .
S ABC ABC
a
V SDS a a a
. ' ' 'ABC A B C
.a
'A
ABC
,AB
'AA
60 .
o
V
'. ' '.A BCC B
3
4
.
a
V
3
8
.
a
V
3
3
4
.
a
V
3
3
8
.
a
V
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 75
LÊ MINH TÂM
Ta có:
Vậy
Câu 89. Một khối hộp có thể tích bằng . Gọi là trung điểm của cạnh .
Mặt phẳng chia khối hộp thành hai khối đa diện. Tính thể tích
phần khối đa diện chứa đỉnh .
A. . B. . C. . D. .
Lời giải
Chọn C
Gọi .
Ta có: là trung điểm của .
là trung điểm của .
là trung điểm của và .
Ta có: .
3
60 60
2
', ', ' ' .tan .
oo
a
AA ABC AA AH A AH A H AH
23
3 3 3
4 2 8
. ' ' '
. ' . .
ABC A B C ABC
a a a
V S A H
3
12
3 3 4
. ' ' . ' ' ' . ' ' ' . ' ' ' . ' ' ' . ' ' '
.
A BCC B ABC A B C A A B C ABC A B C ABC A B C ABC A B C
a
V V V V V V
3
4
.
a
V
.ABCD A B C D
2019
M
AB
MB D

.ABCD A B C D
A
4711
4
5045
6
4711
8
10090
17
N
M
D
C
B
D'
A'
B'
C'
A
E
;B M A A E ED AD N
M
AB
M
EB
N
ED
AD
1
8
.
.
..
E AMN
E A B D
V
EA EM EN
V EA EB ED


Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 76
.
Câu 90. Cho khối tứ diện , và là các điểm thuộc các cạnh và sao cho
, , là mặt phẳng qua và song song với . Kí hiệu và là các
khối đa diện có được khi chia khối tứ diện bởi mặt phẳng , trong đó chứa
điểm , chứa điểm ; và lần lượt là thể tích của và . Tính tỉ số
A. . B. . C. . D. .
Lời giải
Chọn B
Mặt phẳng qua và song song với cắt và lần lượt tại và thỏa
mãn và .
Gọi là thể tích của khối tứ diện . Xét .
.
Câu 91. Cho hình lập phương
cạnh bằng . Gọi
là trung điểm cạnh . Mặt
phẳng
cắt cạnh
tại . Thể tích khối đa diện lồi
bằng
A. . B. . C. . D. .
Lời giải
Chọn D
7 7 7 1
22
8 8 8 6
. . . .
. . . .
AMN A B D E A B D A A B D ABCD A B C D
V V V V
7 4711
24 8
.ABCD A B C D
V

SABC
M
N
SA
SB
2SMA M
2SN NB
MN
SC
1
H
2
H
SABC
1
H
S
2
H
A
1
V
2
V
1
H
2
H
1
2
V
V
5
4
4
5
3
4
4
3
MN
SC
BC
AC
P
Q
MQ SC
NP SC
V
SABC
2 ..MNABPQ N ABPQ Q AMN
V V V V
2
5
1
9
..
. . . .
S
N ABPQ Q AMN
VV
V
CQ CP BN AM SN QA
V V V CA CB B AS SB CA



1
2
4
5
V
V

. ' ' ' 'ABCD A B C D
1
M
'BB
( ' )MA D
BC
K
' ' ' 'A B C D MKCD
7
24
7
17
1
24
17
24
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 77
LÊ MINH TÂM
Kéo dài và cắt nhau tại . Suy ra
Dễ thấy là trung điểm và là trung điểm
Có
Câu 92. Cho hình chóp tứ giác có đáy là hình vuông, mặt bên
là tam giác đều và nằm
trong mặt phẳng vuông góc với đáy. Biết khoảng cách từ điểm đến mặt phẳng
bằng . Thể tích của khối chóp
là
A. . B. . C. . D. .
Lời giải
Chọn B
Gọi lần lượt là trung điểm của và , là hình chiếu của trên ta có
; và .
Đặt . Vì tam giác vuông tại nên .
Suy ra .
Diện tích đáy ; chiều cao
Vậy thể tích của khối chóp
là .
K
E
M
D
A
D'
C
A'
B
B'
C'
'AM
AB
E
.K DE BC
B
EA
K
BC
1 1 7 17
11
3 24 24 24
' ' ' ' 'ADMBK '. .
.
A B C D MKCD A A ADE M BEK
V V V V V V



.S ABCD
SAB
A
SCD
37
7
a
V
.S ABCD
3
2
3
Va
3
3
2
Va
3
Va
3
1
3
Va
S
I
D
H
B
A
C
K
,HI
AB
CD
K
H
SI
SH ABCD
HK SCD
37
7
a
HK
23AB x SH x
SHI
H
2 2 2
1 1 1
HK SH HI

2 2 2
7 1 1 3
2
9 3 4
a
x
a x x
2
2
33S a a
3
2
h SH a
V
.S ABCD
3
13
32
.
a
V S h
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 78
Câu 93. Cho lăng trụ tam giác có thể tích . Gọi là trọng tâm tam giác , là
tâm của mặt bên . Tính thể tích của khối tứ diện theo .
A. . B. . C. . D. .
Lời giải
Chọn B
Ta có: .
Khi đó: .
Khi đó:
.
.
Vậy ta có .
Câu 94. Cho hình lăng trụ có tam giác vuông tại , , , .
Hình chiếu vuông góc của điểm trên mặt phẳng trùng với trung điểm của
đoạn (tham khảo hình vẽ dưới đây). Khoảng cách giữa hai đường thẳng và
bằng
.ABC A B C
V
G
A B C
M
ABB A

GMBC
V
2
9
V
1
9
V
1
3
V
1
6
V
. . . .C BKA C BMG C MGA C BGK
V V V V

1 1 1 1
3 6 6 3
. . . .C BKA ABC A B C ABCA C CKA B BKA
V V V V V V V V V V
1
3
.
d ; .
C MGA A MG
V C A MG S

1 1 1 1 1 1 1 1
3 3 3 3 3 3 3 9
d ; . . d ; . .
A BK A BK CA BK
C A MG S C A MG S V V V


1 1 1
3 3 3
.
d ; . d ; .
C BGK BGK A BK
V C BGK S C BGK S


1 1 1 1 1 1
3 3 3 3 3 9
. d ; . .
A BK CA BK
C A BK S V V V

1 1 1 1
3 9 9 9
. . . .C BMG C BKA C MGA C BGK
V V V V V V V V

.ABC A B C
ABC
A
AB a
3AC a
2'AA a
A
A B C
H
BC

AA
BC
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 79
LÊ MINH TÂM
A. B. C. D.
Lời giải
Chọn D
Vì nên .
Trong có .
Trong có .
Trong có .
Trong có .
Thể tích lăng trụ là .
Mà .
Câu 95. Cho hình chóp có đáy là hình bình hành. Mặt bên là tam giác đều cạnh
. là tam giác vuông tại có cạnh , góc giữa và bằng . Thể
tích khối chóp bằng
A. . B. . C. . D. .
Lời giải
Chọn B
Cách 1:
5
5
.
a
5
3
.
a
15
3
.
a
15
5
.
a
//AA BB

,
', ,
AA BC
AA BB C C A BB C C
d d d


A B C
22
2'B C A B A C a A H a
AA H
22
3AH AA A H a

AHC
22
6CH AC AH a
C HC
2
2
15
15
4
C HC BCC B
a
S p p a p b p c S a
3
13
33
22
.
. . . .
ABC A B C A B C
a
V AH S a a a
3
3
2
2 1 3 15
3 3 5
15
'. .
,,
..
A BB C C ABC A B C BB C C
A BB C C A BB C C
aa
V V d S a d
a
.S ABCD
ABCD
SAB
3a
ABC
A
AC a
AD
SAB
30
.S ABCD
3
3
6
a
3
3
2
a
3
3
4
a
3
a
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 80
Từ giả thiết bài toán ta có
Gọi lần lượt là trung điểm của khi đó .
Từ đó ta có là hình chiếu của lên mặt phẳng mà .
Vậy .
Cách 2:
Gọi là hình chiếu của lên , khi đó
Câu 96. Cho hình chóp có đáy là hình bình hành. Gọi là một điểm thuộc cạnh
sao cho Mặt phẳng qua song song với cắt lần lượt tại
Biết khối chóp đã cho có thể tích Tính theo thể tích khối chóp .
A. . B. . C. . D. .
Lời giải
Chọn A
I
H
D
A
B
C
S
30 .ABC 
,HI
,AB BC
30,,AD SAB BI SAB HBI
HB
IB
SAB
SH AB SH BI
SH ABCD
3
1 3 3 3
3
3 2 2
.
.
. . . .
S ABCD
aa
V a a
D
A
B
C
S
K
K
C
SAB
30, , .AD SAB BC SAB CBK
3
13
30 2 2
32
..
sin . . . .
S ABCD S ABC SAB
a
CK BC a V V CK S
.S ABCD
ABCD
N
SD
2 .DN SN
P
,BN
AC
,SA SC
,.ME
.V
V
.S BMNE
6
V
12
V
4
V
3
V
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 81
LÊ MINH TÂM
Gọi , khi đó chính là mặt phẳng .
Gọi là trung điểm , ta có hay là trung điểm . Do
nên lần lượt là trung điểm và .
Ta thấy , tương tự .
Do đó hay .
Câu 97. Cho khối chóp có , vuông góc với mặt phẳng , vuông tại
, , cân. Thể tích khối chóp bằng
A. . B. . C. . D. .
Lời giải
Chọn C
Vì và
vuông tại ; vuông tại
Lại có: ; , mà (do vuông tại )
Từ , và cân cân tại . Khi đó
Ta lại có:
M
E
I
O
B
C
A
D
S
K
N
,O AC BD I SO ME
P
BMNE
K
ND
// //OK BN IN OK
I
SO
//ME AC
,ME
SA
SC
1 1 1
1
2 3 6
.
.
. . . .
S BMN
S BAD
V
SB SM SN
V SB SA SD
1
6
.
.
S BNE
S BDC
V
V
1
6
. . .
. . .
S BMN S BNE S BMNE
S BAD S BDC S ABCD
V V V
V V V

6
.S BMNE
V
V
.S ABC
3SA a
SA
ABC
ABC
B
AB a
SBC
.S ABC
3
3a
3
23
3
a
3
3
3
a
3
3
6
a
SA ABC
SA AB
SA AC
ABC
B
AC BC
SAC
A
SC AC
SC BC
1
2 2 2
SC SA AC
2 2 2
SB SA AB
AC AB
ABC
B
22
SC SB
SC SB
2
1
2
SBC
SBC
B
BC SB
2 2 2 2 2
3 4 2SB SA AB a a a a
2BC a
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 82
Diện tích là
Vậy thể tích khối chóp là .
Câu 98. Cho hình lăng trụ có đáy là tam giác đều cạnh , hình chiếu của trên
mặt phẳng là tâm của tam giác . Gọi là tâm của tam giác là
trung điểm của , là trọng tâm tam giác . Biết . Tính chiều cao của
lăng trụ.
A. . B. . C. . D. .
Lời giải
Chọn B
Gọi và lần lượt là trung điểm của và . Ta có
suy ra
hay .
Câu 99. Cho hình chóp , gọi lần lượt là trung điểm của các cạnh .
Tính thể tích khối chóp biết rằng thể tích khối chóp là .
A. . B. . C. . D. .
Lời giải
Chọn D
ABC
2
11
2
22
AB BC a a a
.S ABC
3
2
13
3
33
a
V a a
.ABC A B C
ABC
a
A
ABC
O
ABC
O
,A B C M
AA
G
B C C

3
.O OMG
Va
h
24 3ha
36 3ha
93ha
18 3ha
G
O'
O
M
I
I'
A'
C'
B'
A
C
B
I
I
BC
BC

//AA OO G

. . . .O OMG M OO G A OO G G AOO
V V V V
1 1 2 1
2 2 3 3
. . .
.
G AOO A G AII A G AII A
V V V

3
1 1 1 2 2
3 3 9 3 27
. . .
..
C AII A AIC A I C AIC A I C
V V V a
3
27
2
.AIC A I C
Va

2
3
1 3 27
2 4 2
.
a
ha
3
27
4
.ha
27 4
36 3
3
..a
ha
.S ABCD
, , ,I J K H
, , ,SA SB SC SD
.S ABCD
.S IJKH
1
4
2
16
8
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 83
LÊ MINH TÂM
Ta có:
Từ và
Khi đó .
Câu 100. Cho khối chóp có đáy là hình bình hành . Gọi lần lượt là trọng
tâm các tam giác . Biết thể tích khối chóp là , khi đó thể tích
của khối chóp là
A. . B. . C. . D.
Lời giải
Chọn A
Giải bài toán trong trường hợp đặc biệt. Ta có hình vuông cũng là một hình bình hành đặc
biệt nên xem đáy là hình vuông.
Khi đó, khối chóp
là chóp đều và có chiều cao , cạnh đáy .
H
K
J
I
A
D
B
C
S
1 1 1 1
2 2 2 8
.
.
. . . .
S IJK
S ABC
V
SI SJ SK
V SA SB SC
1
1
8
..
.
S IJK S ABC
VV
1 1 1 1
2 2 2 8
.
.
. . . .
S IKH
S ACD
V
SI SK SH
V SA SC SD
1
2
8
..
.
S IKH S ACD
VV
1
2
1
8
. . . . .S IJKH S IJK S IKH S ABC S ACD
V V V V V
11
88
.
.
.
.
S IJKH
S ABCD
S ABCD
V
V
V
88
..
.
S ABCD S IJKH
VV
.S ABCD
ABCD
, , ,M N P Q
, , ,SAB SBC SCD SDA
.S MNPQ
V
.S ABCD
27
4
V
2
9
2
V



9
4
V
81
8
V
ABCD
.S ABCD
h
1AB
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 84
Suy ra, khối chóp có chiều cao bằng và cạnh đáy .
Xt tỉ số .
Câu 101. Cho hình chóp có đáy là hình vuông cạnh , và vuông góc với
đáy. Gọi là trung điểm của , thuộc cạnh . Tính của khối tứ diện
.
A. . B. . C. . D. .
Lời giải
Chọn B
. Ta có
Vậy .
Câu 102. Ông An muốn xây một bể nước dạng hình hộp chữ nhật có nắp với dung tích mét khối.
Đáy bể là một hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thuê nhân công để xây bể
là đồng cho mỗi mét vuông. Hỏi chi phí thấp nhất ông An cần bỏ ra để xây bể nước
là bao nhiêu?
A. đồng. B. đồng. C. đồng. D. đồng.
Lời giải
Chọn A
.S MNPQ
2
3
h
2 1 2
3 2 3
.MN AC
2
3 3 27 27
2 4 4
2
.
.
.
.
S ABCD
S ABCD
S MNPQ
V
VV
V



.S ABCD
ABCD
a
SA a
SA
M
SB
N
2SN ND
V
ACMN
3
1
36
Va
3
1
12
Va
3
1
8
Va
3
1
6
Va
.ACMN S ABCD SAMN DNAC BAMC SMCN
V V V V V V
11
36
.
SAMN
SAMN SABCD
SABD
V
SM SN
VV
V SB SD
11
36
DACN
SAMN SABCD
DACS
V
ND
VV
V SD
11
24
BACM
SAMN SABCD
BACS
V
BM
VV
V BS
11
36
.
SMCN
SAMN SABCD
SBCD
V
SM SN
VV
V BS SD
3
11
4 12
ACMN SABCD
V V a
3
500000
6490123
7500000
6500000
5151214
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 85
LÊ MINH TÂM
Gọi là chiều rộng của đáy bể, suy ra chiều dài của đáy bể là và gọi là chiều
cao của bể.
Diện tích xây dựng là diện tích toàn phần của bể
Ta có . Thay vào , ta được hàm , với
Ta có .
Dấu “=” xảy ra khi và chỉ khi .
Khi đó chi phí thấp nhất là (đồng).
Câu 103. Cho hình lập phương cạnh , gọi là trung điểm của và thuộc
cạnh sao cho . Mặt phẳng cắt tại . Thể tích khối đa diện
bằng
A. . B. . C. . D. .
Lời giải
Chọn A
Gọi ta có .
0xx
2x
h
2
2 2 2 2 2 4 6 1. . . .S xh xh x x x xh
2
3
3 2 2
2
..V x x h h
x
2
1
2
9
4S x x
x

0x
2 2 2
3
3
9 9 9 9 9
4 4 3 4 3 81
2 2 2 2
..S x x x x
x x x x x
3
2
99
4
22
xx
x
3
3 81 500000 6490123
.ABCD A B C D
2a
M
BB
P
DD
1
4
DP DD
AMP
CC
N
AMNPBCD
3
3a
3
11
3
a
3
2a
3
9
4
a
N
P
M
D
B
C
D'
C'
B'
A'
A
; ;
BM CN DP
b c d
BB CC DD
1 1 3
2 4 4
c b d
3
3
3
23
48
.
. . .
AMNPBCD ABCD A B C D
b c d
V V a a

Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 86
Câu 104. Cho khối lăng trụ đứng có , và . Gọi là trung
điểm của , biết khoảng các từ đến mặt phẳng bằng . Thể tích khối
lăng trụ bằng
A. . B. . C. . D. .
Lời giải
Chọn B
Gọi là giao điểm của và .Ta có , suy ra:
Từ kẻ đường cao của tam giác , kẻ vuông góc với đường thẳng . Khi
đó .
Mặt khác .
Tam giác vuông tại có đường cao :
.
Vậy .
Câu 105. Cho hình chóp có đáy là hình vuông cạnh , , ,
và tổng diện tích hai tam giác và bằng . Tính thể tích của
khối chóp .
A. . B. . C. . D. .
Lời giải
Chọn D
.ABC A B C
60BAC 
3AB a
4AC a
M
BC

M
B AC
3 15
10
a
3
7a
3
27a
3
4a
3
9a
N
BM
BC
1
2
MN B M
BN BC

3 15
2
5
;;
a
d B AB C d M AB C


B
BH
ABC
BK
HB
3 15
5
;
a
BK d B AB C

33
3 60
2
.sin .sin
a
BH AB HAB a
HBB
B
BK
2 2 2 2 2 2
1 1 1 25 4 1
9 15 9 3 27. . .B B BK BH a a a
33B B a

3
1
60 27
2
.
. . . .sin
ABC A B C ABC
V BB S BB AB AC a

.S ABCD
ABCD
a
SA SB
SC SD
SAB SCD
SAB
SCD
2
7
10
a
V
.S ABCD
3
4
15
a
V
3
20Va
3
12
25
a
V
3
4
25
a
V
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 87
LÊ MINH TÂM
Gọi lần lượt là trung điểm của .
Ta có:
Kẻ
(vì
Mặt khác ta có:
.
Ta lại có:
Có: . Vậy: .
Câu 106. Cho hình chóp đều với là tâm đáy. Khoảng cách từ đến mặt bên bằng 1 và
góc giữa mặt bên với đáy bằng . Thể tích của khối chóp bằng
A. . B. . C. . D. .
Lời giải
Chọn B
N
M
H
C
A
D
B
S
,MN
,AB CD
SM AB SAB can
SMN ABCD
SN CD SCD can

SH MN SH ABCD h SH
0
90MSN
0
90,SAB SCD SAB SCD
.SM SN
h SH
MN
2
1 1 7
2 2 10
..
SAB SCD
a
S S AB SM CD SN SM SN
2
7
5
a
SM SN
2
22
2
2 2 2
12
2 25
.
SM SN SM SN
a
SM SN MN SM SN
12
25
SH a
3
14
3 25
..
ABCD
a
V S SH
.S ABCD
O
O
0
45
.S ABCD
42
3
V
82
3
V
23V
43
3
V
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 88
Gọi là trung điểm của
Kẻ tại
Ta có
Xét tam giác vuông
Ta có là tam giác vuông cân tại
Vậy
Câu 107. Cho hình lăng trụ đứng có thể tích bằng Các điểm lần lượt thuộc
các cạnh sao cho . Thể tích khối đa diện
bằng
A. B. C. . D. .
Lời giải
Chọn D
Gọi là hình chiếu của trên .
Khi đó
I
2,.CD OI CD CD OI
OH SI
1,.H OH SCD d O SCD OH
0
45, , , .
,
SCD ABCD CD
SI SCD SI CD SCD ABCD SI OI SIO
OI ABCD OI CD


0
1
2 2 2 2
45
.
sin
sin
OH
HIO OI CD OI
SIO
SIO
2.O SO OI
2
2
1 1 8 2
2 2 2
3 3 3
.
. . .
S ABCD
V CD SO
.ABC A B C
.V
,,M N P
;;AA BB CC
12
23
;
AM BN CP
AA BB CC
.ABC MNP
2
3
V
9
16
V
20
27
V
11
18
V
K
P
AA
2
3
.ABC KPN
VV
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 89
LÊ MINH TÂM
.
Do đó
Câu 108. Cho hình chóp có đáy là hình vuông. Các điểm lần lượt là trung
điểm của . Điểm thuộc miền trong của hình vuông . Biết rằng
. Thể tích khối chóp nằm trong khoảng nào
dưới đây?
A. . B. . C. . D. .
Lời giải
Chọn B
Ta thấy rằng:
Do đó, .
Câu 109. Cho hình chóp có đáy là hình thoi cạnh bằng . Biết rằng
. Thể tích khối chóp bằng.
A. . B. . C. . D. .
Lời giải
Chọn C
Gọi . Ta có
Suy ra: .
Lại có: .
1 1 1 1 1
3 3 2 6 18
,
. . .
M KPN KNP ABC
V MK S AA S V



2 1 11
3 18 18
.ABC MNP
V V V V
.S ABCD
ABCD
, , ,M N P Q
, , ,AB BC CD DA
E
ABCD
75 42 60
. . .
,,
S EMAQ S EMBN S EQDP
V V V
.S EPCN
35 40;
25 30;
30 35;
20 25;
EMQ ENP EPQ EMN AEMQ CENP EQDP EMBN
S S S S S S S S
42 60 75 27 25 30
. . . . .
;
S AEMQ S CENP S EQDP S EMBN S CENP
V V V V V
.S ABCD
ABCD
a
3, , ,SA a SA AD SB a AC a
.S ABCD
3
2
2
a
3
2
3
a
3
2
6
a
3
6
2
a
23O AC BD BD BO a
22
2SD SA AD a
2 2 2 2 2 2 2
2
3 2 3 7
2 4 2 4 4
SB SD BD a a a a
SO

2 2 2 2 2 2 2
2
7
3
2 4 2 4 4
SA SC AC a SC a a
SO SC a

Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 90
Xét vuông tại vì và nên hình chiếu của lên
là điểm trung điểm .
Do đó, .
Câu 110. Cho khối chóp , đáy là tam giác có ,
, , cạnh bên
vuông góc với đáy, Gọi là mặt phẳng đi qua đỉnh vuông góc với cạnh
, mặt phẳng chia khối chóp thành 2 khối đa diện có thể tích , (trong đó
là thể tích khối đa diện chứa đỉnh ). Tỷ số bằng
A. . B. . C. . D. .
Lời giải
Chọn A
Gọi .
Gọi là hình chiếu vuông góc của lên , kẻ với .
; .
Tam giác có
.
Do tam giác vuông cân tại nên .
Ta lại có .
SCD
D
2 2 2
SC SD DC
AS AD AC
A
SCD
H
SC
2 3 3
1 1 2 3 2
2
3 3 2 2 12 6
. . . .
. . . .
A SDC S ADC SDC S ABCD S ADC
a a a a
V V AH S V V
.S ABC
ABC
32AB
12AC
0
45BAC
SA
12.SA
A
SC
.S ABC
1
V
2
V
1
V
S
1
2
V
V
2
3
2
1
3
1
2
F SC AF SC
H
B
SC
//EF BH
E SB
AFE
9 2 12 2;SB SC
2 2 0
2 45 3 10. .cosBC AB AC AB AC
SBC
2 2 2 2
SB SH BC HC
2 2 2
2
9 2 3 10 12 2SH SH
15 2
2
SH
SAC
A
12 2SC
12 2
2
SF
12 2
4
2
5
15 2
2
SE SF
SB SH
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 91
LÊ MINH TÂM
. Vậy .
Câu 111. Cho hình chóp tứ giác đều có mặt bên hợp với mặt đáy một góc và
khoảng cách từ điểm đến mặt phẳng bằng . Thể tích khối chóp bằng
A. . B. . C. . D. .
Lời giải
Chọn D
Gọi là trung điểm cạnh , khi đó: tại trong và tại
trong .
Khi đó: . Suy ra: vuông cân tại .
Trong , dựng tại .
Ta có: .
Suy ra: .
Câu 112. Cho khối chóp có đáy là hình vuông cạnh , vuông góc với mặt phẳng
đáy. Gọi lần lượt là hình chiếu vuông góc của lên . Biết góc giữa hai mặt
phẳng và bằng . Thể tích khối chóp bằng
A. . B. . C. . D. .
Lời giải
Chọn A
3
1
4 1 2 3
5 2 5 5
..
..
S ABC S ABC
V
V
SE SF
V SB SC V
1
2
2
3
V
V
.S ABCD
SCD
45
A
SCD
3a
.S ABCD
3
4
3
a
3
2
3
a
3
23a
3
6a
M
SC
SM CD
M
SCD
OM CD
M
ABCD
45,,SCD ABCD SM OM SMO
SOM
O
SOM
OH SM
H
3
3 2 2
2
,,
a
a d A SCD d O SCD OH OH
2
23
6 1 1 6 6
26
2 3 3 2 2
.
. . . . .
S ABCD
a a a
SO OM V SO AD a




.S ABCD
ABCD
a
SA
,HK
A
,SB SD
ABCD
AHK
0
30
.S ABCD
3
6
3
a
3
6
9
a
3
2
3
a
3
6
2
a
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 92
Ta có: và suy ra .
Mặt khác suy ra .
Chứng minh tương tự ta cũng có .
Vậy .
Mà .
Do đó góc giữa hai mặt phẳng và là góc giữa hai đường thẳng và (
theo định nghĩa góc giữa hai mặt phẳng) và bằng . Vậy .
Xét tam giác có .
.
Câu 113. Cho hình chóp có đáy là hình chữ nhật có , , vuông góc
với đáy, khoảng cách từ đến bằng . Tính thể tích khối chóp theo .
A. . B. . C. . D. .
Lời giải
Chọn A
K
H
D
C
B
A
S
BC AB
BC SA
BC SAB BC AH
AH SB
AH SBC SC AH
AK SCD SC AK
SC AHK
SA ABCD
ABCD
AHK
SA
SC
ASC
0
30ASC
SAC
2
2
3
2
2
cos
SA SA
ASC
SC
SA a
6SA a
3
2
1 1 6
6
3 3 3
.
. . .
S ABCD ABCD
a
V SA S a a
.S ABCD
ABCD
AB a
2AD a
SA
A
SCD
2
a
a
3
4 15
45
a
3
4 15
15
a
3
25
15
a
3
25
45
a
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 93
LÊ MINH TÂM
Kẻ .
Ta có .
Từ , ta có .
Trong ta có .
Vậy thể tích khối chóp là .
Câu 114. Cho hình chóp có đáy là hình chữ nhật với , , tam giác
nhọn và nằm trong mặt phẳng vuông góc với đáy. Biết hai mặt phẳng ,
tạo với nhau góc thỏa mãn và cạnh . Thể tích khối bằng:
A. . B. . C. . D. .
Lời giải
Chọn B
. Kẻ vuông góc với tại .
Ta có: , ,
.
.
.
Vậy .
Câu 115. Cho hình chóp có đáy là hình thoi tâm cạnh , góc ,
và . Khi đó thể tích của khối chóp là
AH SD
1
CD AD
CD SA
CD SAD
CD AH
2
1
2
AH SCD
,d A SCD AH
2
a
AH
SAD
2 2 2
1 1 1
AH SA AD

22
.AH AD
SA
AD AH

2
2
2
2
4
4
a
a
a
a
2 15
15
a
.S ABCD
1
3
..V SA AB AD
1 2 15
2
3 15
..
a
aa
3
4 15
45
a
.S ABCD
ABCD
6AB
3AD
SAC
SAB
SAC
3
4
tan
3SC
.S ABCD
4
3
8
3
33
53
3
22
. . .S ABCD S ABC B SAC
V V V
BH
AC
H
3AC
2BH
1 HC
42
3
KH
22
3
sin
KH
SAC
HA

1
3
cosSAC
2 2 2
2 . .cosSC SA AC AS AC SAC
2SA
1
2
. .sin
SAC
S SA AC SAC
1 2 2
2 3 2 2
23
...
18
2 2 2 2
33
.
. . .
S ABCD
V 
.S ABCD
ABCD
O
a
30BCA 
SO ABCD
3
4
a
SO
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 94
A. . B. . C. . D. .
Lời giải
Chọn B
Theo giả thiết là hình thoi tâm cạnh , góc nên ; đều
suy ra , , .
Ta có ; với suy ra
.
Câu 116. Cho hình chóp có đáy là tam giác vuông tại và có . Mặt bên
là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng . Tính thể
tích của khối khóp .
A. . B. . C. . D. .
Lời giải
Chọn C
Gọi là trung điểm của đoạn . Vì là tam giác đều nên .
theo giao tuyến .
3
2
4
a
3
3
8
a
3
2
8
a
3
3
4
a
s
A
B
C
D
O
30
a
3
4
a
ABCD
O
a
30BCA 
60BCD 
BCD
BD a
3
2
a
CO
23AC CO a
1
2
.
ABCD
S AC BD
2
13
3
22
..
a
aa
1
3
.
.
S ABCD ABCD
V SO S
3
4
a
SO
23
1 3 3 3
3 4 2 8
.S ABCD
a a a
V
.S ABC
ABC
A
3,AB a BC a
SAB
ABC
V
.S ABC
3
26
12
a
V
3
6
6
a
V
3
6
12
a
V
3
6
4
a
V
K
AB
SAB
SK AB
SAB ABC
AB
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 95
LÊ MINH TÂM
.
vuông tại có
.
là tam giác đều .
.
Câu 117. Cho hình chóp có đáy là hình vuông cạnh , hình chiếu vuông góc của lên mặt
phẳng trùng với trung điểm cạnh , cạnh bên hợp với đáy một góc . Tính
theo thể tích của khối chóp .
A. . B. . C. . D. .
Lời giải
Chọn B
Gọi là trung điểm của là hình chiếu vuông góc của
trên .
.
vuông tại .
vuông tại
.
Câu 118. Cho hình chóp có đáy là tam giác vuông cân tại , , . Biết
góc giữa đường thẳng và mặt phẳng bằng . Thể tích khối chóp bằng
A. . B. . C. . D. .
Lời giải
1
3
.
.
S ABC ABC
SK ABC V SK S
ABC
A
22
32,AB a BC a AC BC AB a
2
1 1 2
2
2 2 2
..
ABC
a
S AB AC a a
SAB
3
2
a
SK
23
1 1 3 2 6
3 3 2 2 12
.
. . .
S ABC ABC
a a a
V SK S
.S ABCD
a
S
ABCD
AD
SB
60
a
V
.S ABCD
3
15
2
a
V
3
15
6
a
V
3
15
4
a
V
3
5
6
a
V
H
AD
SH ABCD
BH
SB
ABCD
60,SBH SB ABCD
ABH
A
2
2 2 2
5
42
aa
BH AB AH a
SBH
H
15
60
2
.tan .
a
SH HB
3
1 15
36
.
..
S ABCD ABCD
a
V SH S
.S ABC
ABC
B
SA ABC
AB a
AC
SBC
30
.S ABC
3
6
a
3
3
a
3
a
3
3
6
a
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 96
Chọn A
Từ kẻ tại .
Ta có .
Lại có .
Từ đó suy ra .
Tam giác vuông cân tại nên .
Xét vuông tại .
Xét vuông tại .
Diện tích tam giác là .
Thể tích khối chóp là .
Câu 119. Cho hình chóp tứ giác đều có cạnh đáy bằng . Góc giữa đường thẳng và
mặt phẳng bằng . Thể tích của khối chóp bằng
A. . B. . C. . D. .
Lời giải
Chọn B
Gọi là giao điểm hai đường cho của hình vuông . Suy ra .
A
C
B
S
H
A
AH SB
B
BC AB
BC SAB BC AH
BC SA
AH SB
AH SBC
AH BC

30,,AC SBC AC HC ACH
ABC
B
22AC AB a
AHC
2
2 30
2
: .sin .sin
a
H AH AC ACH a
SAB
2 2 2 2 2
1 1 1 1 1
:A SA a
AH SA AB SA a
ABC
2
2
1
22
ABC
a
S AB
.S ABC
3
1
36
.
.
S ABC ABC
a
V S SA
.S ABCD
2a
AC
SBC
30
.S ABCD
3
4a
3
4
3
a
3
26
9
a
3
26
3
a
K
O
C
A
D
B
S
H
O
ABCD
SO ABCD
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 97
LÊ MINH TÂM
Gọi là trung điểm của . Từ kẻ tại .
Ta có .
Lại có .
Suy ra .
Ta có .
Xét vuông tại .
Xét vuông tại .
Diện tích hình vuông .
Thể tích khối chóp .
Câu 120. Cho hình chóp có đáy là tam giác đều, cạnh bên vuông góc với mặt đáy và
, góc giữa mặt phẳng bằng . Thể tích khối chóp bằng
A. B. C. D.
Lời giải
Chọn D
Gọi là trung điểm của
Do tam giác đều nên
Kẻ
Ta có
K
BC OK BC
O
OH SK
H
BC OK
BC SOK BC OH
BC SO
OH SK
OH SBC
OH BC

30,,,AC SBC OC SBC OC HC OCH
11
22
22
.OC AC AB a
OHC
2
2 30
2
: .sin .sin
a
H OH OC OCH a
SOK
2 2 2 2 2
1 1 1 1 1
:O SO a
OH SO OK SO a
2
22
24:
ABCD
ABCD S AB a a
23
1 1 4
4
3 3 3
.
. : . . .
S ABCD ABCD
S ABCD V S SO a a a
.S ABC
ABC
SA
3SA a
SA
()SBC
0
45
.S ABC
3
3.a
3
3
12
.
a
3
33
12
.
a
3
.a
M
BC
ABC
AM BC
()
AM BC
BC SAM
SA BC

AH SM
0
45( ) ,( ) ,
BC AH
AH SBC SA SBC SA SH ASH
SM AH
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 98
Suy ra vuông cân tại
Ta c
Suy ra
Vậy
Câu 121. Cho hình chóp có đáy là hình vuông cạnh . Cạnh bên vuông góc với mặt
phẳng đáy, cạnh bên tạo với mặt phẳng một góc . Thể tích của khối chóp đó
bằng
A. . B. . C. . D. .
Lời giải
Chọn D
Vì và nên . Từ đó
Trong tam giác , ta có
Vậy thể tích khối chóp là
Câu 122. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thang vuông tại
A
và
D
. Biết
42,AB a AD CD a
. Cạnh bên
3SA a
và
SA
vuông góc với mặt phẳng đáy. Gọi
G
là
trọng tâm tam giác
SBC
,
M
là điểm sao cho
2MA MS
và
E
là trung điểm cạnh
CD
(tham khảo hình vẽ). Tính thể tích
V
của khối đa diện
MGABE
.
ASM
A
3SA AM a
2AB BC AC a
3
1
3
.
..
S ABC ABC
V S SA a
.S ABCD
a
SA
SC
SAB
30
3
3
3
a
3
2
4
a
3
2
2
a
3
2
3
a
BC SA
BC AB
BC SAB
30,,SC SAB SC SB BSC
SCB
22
30 3 2tan ;
a
SB a SA SB AB a
SB
3
12
33
.
SABCD ABCD
a
V SA S
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 99
LÊ MINH TÂM
A.
3
27
8
a
. B.
3
10
3
a
. C.
3
13
4
a
. D.
3
25
9
a
.
Lời giải
Chọn B
Ta có
MGABE GABE GABM GAEM
V V V V
.
2
1
2 4 4
2
..
ABE
S a a a
3
2
1 1 1 1 4
43
3 3 3 9 3
. . . .
GABE SABE ABE
a
V V S SA a a
.
2
1
4 2 4
2
..
ABM
S a a a
3
2
1 1 1 1 8
42
3 3 3 9 9
. . . .
GABM CABM ABM
a
V V S DA a a
.
Gọi
I
là trung điểm của
BC
.
22
45AE a a a
;
22
16 4
5
22
BD a a
EI a
.
2 2 2 2 2 2
22
8 16 8
10 10
2 4 2 4
AC AB BC a a a
AI a AI a

.
Dựng
EH AI
H
là trung điểm của
AI
.
2
2
10 10
5
22
aa
EH a




;
2
1 1 10 5
10
2 2 2 2
. . .
AEI
a
S EH AI a a
.
3
2
2 2 2 1 2 5 10
2
3 3 3 3 9 2 9
. . . .
GAEM IAEM MAEI AEI
a
V V V S MA a a
.
Vậy
3 3 3 3
4 8 10 10
3 9 9 3
MGABE
a a a a
V
.
Câu 123. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật.
E
là điểm trên cạnh
AD
sao cho
BE
vuông góc với
AC
tại
H
và
AB AE
, cạnh
SH
vuông góc với mặt phẳng đáy, góc
45BSH 
. Biết
2
5
a
AH
,
5BE a
. Thể tích khối chóp
.S ABCD
bằng
A.
3
5
15
a
. B.
3
16
35
a
. C.
3
32
5
a
. D.
3
85
5
a
.
Lời giải
Chọn B
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 100
Đặt
AE x
,
AB y
yx
.
Tam giác
ABE
vuông tại
A
, có đường cao
AH
. Áp dụng các hệ thức lượng trong tam giác
vuông ta có:
+)
2 2 2
2 2 2
1 1 1
BE AE AB
AH AE AB


2 2 2
2 2 2
5
5 1 1
4
a x y
a x y


2 2 2
2
5
2
x y a
xy a

2
3
2
x y a
xy a

2
xa
ya
.
+)
22
4 4 5
5
5
AB a a
BH
BE
a
4 5 5
5
55
aa
EH BE BH a
.
Tam giác
SHB
vuông cân tại
H
(có
45BSH 
), suy ra:
45
5
a
SH
.
+)
44
BC BH
BC a
EA EH
.
Vậy
3
1 1 1 4 5 16 5
24
3 6 6 5 15
.
. . . . . . . .
S ABCD ABCD
aa
V SH S SH AB BC a a
.
Câu 124. Cho khối hộp
.ABCD A B C D
có thể tích bằng
V
. Gọi
M
,
N
,
P
lần lượt là trung điểm của
AB
,
BC

,
DD
. Gọi thể tích khối tứ diện
CMNP
là
V
, khi đó tỉ số
V
V
bằng
A.
1
16
. B.
3
16
. C.
1
64
. D.
3
64
.
Lời giải
Chọn B
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 101
LÊ MINH TÂM
Ta có:
. . . . . . . .B HN BMQ A HD AMD N MQC P NCC P D C N P D HN P HNM P MDC
V V V V V V V V V V
.
Gọi
S
là diện tích đáy và
h
là chiều cao khối hộp.
Xét:
1
8
.B HN BMQ
V Sh
,
1
4
.A HD AMD
V Sh

,
1
24
.N MQC
V Sh
,
1
12
.P NCC
V Sh
,
1
24
.P D C N
V Sh

,
1
16
.P D HN
V Sh
,
1
8
. . .P HNM D HNM M HND
V V V Sh

,
1
12
.P MDC
V Sh
.
Suy ra:
13 3 3
16 16 16
V
V V V V V
V

.
Câu 125. Cho tứ diện
SABC
và hai điểm
,MN
lần lượt thuộc các cạnh
,SA SB
sao cho
1
2
SM
AM
,
2
SN
BN
. Mặt phẳng
()P
đi qua hai điểm
,MN
và song song với cạnh
SC
cắt
,AC BC
lần
lượt tại
,LK
. Gọi
,VV
lần lượt là thể tích các khối đa diện
,SCMNKL SABC
. Tỉ số
V
V
bằng
A.
2
3
. B.
4
9
. C.
1
4
. D.
1
3
.
Lời giải
Chọn B
I
K
L
A
C
B
S
M
N
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 102
Gọi
I
là giao điểm của
,,AB MN KL
.
Do
ML
SC
và
NK
SC
nên ta có
2
3
AM AL
AS AC

và
1
3
BN BK
BS BC

.
Ta có
1..
MA NS IB
MS NB IA
suy ra
1
4
IB
IA
.
Ta có
13
11
31
. . . .
CL BA KI KI
KL KI
CA BI KL KL
suy ra
MN NI
hay
1
2
IN IK
IM IL

.
Xét hình chóp
IAML
ta có
1 1 1 1
4 2 2 16
.
.
..
..
..
I BNK
I AML
V
IB IN IK
V IA IM IL
.
Mặt khác ta có
1 1 4 2 2 16
3 3 3 3 3 27
;( ) . . ;( ) . .
IAML AML SAC SABC
V d I AML S d B AML S V
.
Suy ra
1 16 1
16 27 27
.
.
I BNK
SABC
V
V

. Suy ra
1 16 1 5
27 27 27 9
.
..
I BNK BNKAML
V V V V V V
.
Ta có
54
99
SCMNKL BNKAML
V V V V V V
.
Từ đó ta có
4
9
V
V
.
Câu 126. Cho lăng trụ
.ABC A B C
. Gọi
M
,
N
,
Q
,
R
lần lượt là trung điểm của các cạnh
AB
,
AB

,
BC
,
BC

và
P
,
S
lần lượt là trọng tâm của các tam giác
AA B
,
CC B
. Tỉ số thể tích khối đa
diện
MNRQPS
và khối lăng trụ
.ABC A B C
là
A.
1
9
. B.
5
54
. C.
1
10
. D.
2
27
.
Lời giải
Chọn B
Đặt:
.ABC A B C
VV
;
12
33
.
.d ,
B AA C C AA C C
V S B AA C C V

1 1 1 1
3 3 2 2
.
. .d , . d ,
B MNRQ MNRQ AA C C
V S B MNRQ S B AA C C

1 1 1 2 1
3 4 4 3 6
. .d , . .
AA C C
S B AA C C V V




1 1 1 1 1
3 3 3 6 18
. . .
. . .
P MNRQ A MNRQ B MNRQ
V V V V V

12
33
.
.d ,
A BB C C BB C C
V S A BB C C V


Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 103
LÊ MINH TÂM
11
24
QRC QRC C BB C C
S S S

;
1 1 1 1
3 3 4 12
.
QRS QRC BB C C BB C C
S S S S
1 1 1
3 3 12
.
.d , . d ,
A QRS QRS BB C C
V S A QRS S A BB C C






1 1 1 2 1
3 12 12 3 18
. .d , . .
BB C C
S A BB C C V V





2 1 1
3 18 27
..
..
P QRS A QRS
PB
V V V V
AB
1 1 5
18 27 54
..MNRQPS P MNRQ P QRS
V V V V V V
Vậy:
5
54
.
MNRQPS
ABC A B C
V
V
.
Câu 127. Cho hình lăng trụ đứng
.ABC A B C
có
21,AB CB AC
. Một mặt phẳng
()P
cắt các
đường thẳng
,,AA BB CC
lần lượt tại
,,M N P
sao cho tam giác
MNP
đều. Gọi là góc
tạo bởi mặt phẳng
()P
và mặt phẳng
()ABC
, khi đó
A.
3
3
cos
. B.
5
3
cos
. C.
5
5
cos
. D.
10
5
cos
.
Lời giải
Chọn C
Ta có:
21,AB CB AC
ABC
cân tại
B
1 15
24
. ( ;( )).
ABC
S d B AC AC
.
Ta có: Mặt phẳng
()P
cắt các đường thẳng
,,AA BB CC
lần lượt tại
,,M N P
; Gọi mặt
phẳng
()
qua
N
song song với mặt đáy cắt
,AA CC

lần lượt tại
,IJ
; Gọi
H
là giao
điểm của
IJ
và
MP
thì
H
là trung điểm của
IJ
và
MP
.
Ta đặt:
0MN x
2
4IM x PJ
,
22
1 15
44
MH IM x
.
Mà
H
là trung điểm
IJ
nên
H
cũng là trung điểm
MP
2
2 4 15MP MH x
.
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 104
Do đề cho tam giác
MNP
đều nên ta có phương trình:
2
4 15 5MP MN x x x
.
Suy ra
2
3 5 3
44
MNP
x
S

.
Đến đây ta nhận thấy, do
ABC
là hình chiếu của
MNP
lên mặt phẳng đáy nên suy ra:
15 4 5
45
53
cos .
ABC
MNP
S
S
.
Câu 128. Cho khối chóp tứ giác
.S ABCD
có cạnh đáy bằng
a
và cạnh bên bằng
2a
. Gọi
M
là điểm
đối xứng của
C
qua
D
,
N
là trung điểm của
SC
. Mặt phẳng
()BMN
chia khi chóp đã cho
thành
2
phần. Thể tích của phần chứa đỉnh
S
bằng
A.
3
3 14
32
a
. B.
3
5 14
72
a
. C.
3
7 14
96
a
. D.
3
7 14
72
a
.
Lời giải
Chọn D
Giả sử các điểm như hình vẽ.
F BMN AD
; Kẻ
OH SF
;
Gọi
E SD MN E
là trọng tâm
SCM
,
//DF BC F
là trung điểm
BM
.
Ta có:
2
2
2 2 2 2
2 14
24
2 2 2
()
a a a
SO SD DO a a




2
2
22
14 15
2 2 2
a a a
SF SO OF







2
2 210 1 15
4 4 4
15 2 4
.
( ;( )) . ( ;( )) ; . .
SAD
SO OF a a
d M SBC d O SAD OH S SF AD
SF
.
2 1 1 1 1
3 2 2 6 6
. . . . .
MEFD
MEFD MNBC
MNBC
V
MD
ME MF
VV
V MN MB MC
3
5 5 1 1 5 1 1 5 14
4
6 6 3 2 6 3 2 72
. . . ( ;( )). . . . . .
BFDCNE MNBC SBC SAD
a
V V d M SBC S OH S

.
33
1 14 7 14
3 6 72
..
..
S ABCD ABCD SABFEN S ABCD BFDCNE
aa
V SO S V V V
.
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 105
LÊ MINH TÂM
Câu 129. Cho hình chóp
.S ABC
có
3AB a
,
4BC a
,
5CA a
, các mặt bên tạo với đáy góc
60
, hình
chiếu vuông góc của
S
lên mặt phẳng
ABC
thuộc miền trong của tam giác
ABC
. Tính thể
tích hình chóp
.S ABC
.
A.
3
23a
. B.
3
63a
. C.
3
12 3a
. D.
3
22a
.
Lời giải
Chọn A
Ta có
2 2 2 2 2 2
25 9 16AC a a a AB BC
, vậy tam giác
ABC
vuông tại
B
.
Gọi
H
là hình chiếu của
S
trên mặt phẳng
ABC
. Vì các mặt bên tạo với đáy góc
60
suy
ra:
; ; ;d H AC d H BC d H AB
và
H
thuộc miền trong của tam giác
ABC
nên
H
là
tâm đường tròn nội tiếp tam giác
ABC
.
Từ
H
kẻ đường thẳng vuông góc với
BC
tại
M
, suy ra:
BC HM
BC SHM BC SM
BC SH
.
Suy ra:
60;SMH SBC ABC
.
Đoạn
HM
là bán kính đường tròn nội tiếp tam giác
ABC
, suy ra:
3
3 4 12
3 4 5 12
..
ABC
S
AB BC a a a
HM a
p AB BC CA a a a a
.
60 3.tanSH HM a
.
Vậy
3
11
3 4 3 2 3
66
.
. . . . .
S ABC
V AB BC SH a a a a
.
Câu 130. Cho hình lăng trụ
. ' ' ' 'ABCD A B C D
đáy là hình bình hành. Với
,AC BC a
0
2 3 90, ' , ' ' ' 'CD a AC a CA B A D C
. Thể tích khối tứ diện
'BCDA
là
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 106
A.
3
6
a
. B.
3
a
. C.
3
2
3
a
. D.
3
6 a
.
Lời giải
Chọn A
Ta có tam giác
ABC
vuông cân tại
C
Gọi
O
là trung điểm của
3
2
a
AC OC OA

Gọi
H
là chân đường cao hạ từ
C
xuống mặt
A B C D
.
Ta có:
A D CH
A D HD
A D D C


.
Lại có:
A B A C
A B A H
A B CH


.
Ta có:
00
90 90;HA H A B HA B A D
. Tam giác
A D H

vuông cân tại
D
Giả sử
22
2CH x CA x a
2 2 2
CC x a

2 2 2 2 2 2 2 2 2 2 2
3 2 2
2 4 4 2 4 4
CC C A CA a x a a x a x a
CO
2 2 2
23x a a x a CH
C'
B'
D'
D
A
B
C
A'
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 107
LÊ MINH TÂM
3
11
6 6 6
.
..
BCDA ABCD A B C D ABCD
a
V V CH S
.
Câu 131. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều có cạnh
6
. Biết rằng các mặt bên của
hình chóp có diện tích bằng nhau và một trong các cạnh bên bằng
32
. Tính thể tích nhỏ
nhất của khối chóp
.S ABC
.
A. 4. B. 3. C.
22
. D.
23
.
Lời giải
Chọn B
Gọi H là hình chiếu vuông góc của S lên
mp ABC
.
,,E F M
lần lượt là hình chiếu vuông
góc của H lên
,,AB AC BC
Khi đó ta có
,,AB SE AC SF BC SM
.
Vì
SAB ASAC SBC
S S S
,
6AB AC BC
suy ra
SE SF SM
SHE SHF SHM
HE HF HM
nên H là tâm đường tròn nội tiếp hoặc H là
tâm đường tròn bàng tiếp góc
A
hoặc B, hoặc C của
ABC
.
Trường hợp 1: H là tâm đường tròn nội tiếp
ABC
. Do
ABC
đều nên H cũng là trọng
tâm
ABC
và
.S ABC
là hình chóp đều.
Ta có
2
2
22
23
6 2 3 2 2 4
32
.,HA SH SA HA
.
2
3 3 3
6
42
ABC
S 
1 1 3 3
4 2 3
3 3 2
.
..
S ABC ABC
V SH S
.
Trường hợp 2: H là tâm đường tròn bàng tiếp
ABC
. Giả sử H là tâm đường tròn bàng tiếp
góc A.
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 108
Ta có
0
60HBC
,
0
6 3 2
60 3
22
tan .HM BM
3 2 3 2
32
22
AH AM HM
,
0
6
60cos
BI
HB 
. Hình chóp
.S ABC
có một cạnh bên bằng
3 2 3 2SB SC
(Vì
32SA AH
) suy ra
2
2
22
3 2 6 2 3SH SB BH
,
1 1 3 3
2 3 3
3 3 2
.
..
S ABC ABC
V SH S
.
Vậy thể tích khói chóp
.S ABC
nhỏ nhất bằng 3.
Câu 132. Cho hình lăng trụ
.ABC A B C
có đáy là tam giác đều. Hình chiếu vuông góc của
A
trên
ABC
là trung điểm của
BC
. Mặt phẳng
P
vuông góc với các cạnh bên và cắt các cạnh
bên của hình lăng trụ lần lượt tại
D
,
E
,
F
. Biết mặt phẳng
ABBA
vuông góc với mặt
phẳng
ACC A

và chu vi của tam giác
DEF
bằng 4, thể tích khối lăng trụ
.ABC A B C
bằng
A.
12 10 7 2
. B.
4 10 7 2
. C.
6 10 7 2
. D.
12 10 7 2
.
Lời giải
Chọn A
Gọi
H
và
H
lần lượt là trung điểm của
BC
và
BC

.
Khi đó ta có
BC A H
BC AA
BC AH

,BC BB BC CC

,
Suy ra
BB C C

là hình chữ nhật.
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 109
LÊ MINH TÂM
Vì
E BB
,
F CC
, và
EF BB
,
EF CC
(do
EF P
vuông góc với các cạnh bên của
lăng trụ),
Suy ra
//EF BC
và
EF BC
a
(giả sử cạnh đáy của lăng trụ là
a
).
Gọi
I
là trung điểm của
HH
I
cũng là trung điểm của
EF
.
Kẻ
ED AA
,
D AA
, suy ra
DF AA
.
Do
ABB A ACC A
nên suy ra
ED DF
. Hơn nữa dễ thấy
DE DF
, nên
DEF
vuông cân tại
D
. Suy ra
2 2 2
2ED EF a
2
2
a
ED
.
Chu vi
DEF
bằng
24DE DF EF a a
4 2 1a
.
Xét hình bình hành
AA H H

, kẻ
A K HH

. Ta thấy,
ID AA ID HH

,
Suy ra
//A K ID
22
EF a
A K ID
(do
DEF
vuông cân tại
D
).
Khi đó, ta có diện tích hình bình hành
AA H H

bằng:
..AK AA A H AH
3
22
..
aa
AA A H


3AA A H


.
Mà
2 2 2
AA A H AH


2
22
3
2
4
a
A H AH
3
22
a
AH

.
2
3
4
ABC
a
S
.
Suy ra
2
33
4
22
.
..
ABC A B C ABC
aa
V A H S

.
Với
4 2 1a 
thì
2
4 2 1 16 2 1 3
12 10 7 2
4
22
.
.
.
ABC A B C
V

.
Câu 133. Cho khối chóp
.S ABC
có đáy là tam giác vuông cân tại
B
. Khoảng cách từ điểm
A
đến mặt
phẳng
SBC
bằng
2a
.
90
o
SAB SCB
. Thể tích khối chóp
.S ABC
có giá trị nhỏ nhất bằng
A.
3
6
2
a
. B.
3
6
6
a
. C.
3
6
4
a
. D.
3
6a
.
Lời giải
Chọn C
Dựng điểm
D
sao cho
ABCD
là hình vuông.
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 110
Ta có
,AB SA AB AD AB SD
,BC SC BC CD BC SD
Suy ra
SD ABCD
.
Vì
// , ,AD SBC d A SBC d D SBC
.
Kẻ
2,DH SC DH SBC d D SBC DH a
.
Đặt
AB x
.
22
2 2 2 2 2 2 2 2 2 2
1 1 1 1 1 1 1 1 2
22
xa
DH SD DC SD DH DC a x a x
22
2ax
SD
xa

.
3
2
2 2 2 2
1 1 2 1 2
3 3 2 6
. . . .
SABC ABC
ax a x
V SD S x
x a x a

.
Xét hàm số
3
22
x
fx
xa
với
xa
.
4 2 2
2 2 2 2
23x x a
fx
x a x a

,
6
0
2
a
f x x
.
Vậy thể tích khối chóp
.S ABC
có giá trị nhỏ nhất bằng
23
2 3 3 6
6 2 4
.
a a a
.
Câu 134. Cho hình chóp
.S ABC
,
O
là trung điểm của
AB
. Điểm
M
di động trên cạnh
SB
. Đặt
SM
x
SB
. Mặt phẳng qua
A
,
M
song song với
OC
, cắt
SC
tại
N
. Thể tích khối chóp
ABMN
lớn
nhất khi
A.
31x 
. B.
1x
. C.
35x 
. D.
12x
.
Lời giải
Chọn D
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 111
LÊ MINH TÂM
Trong mặt phẳng
SAB
, gọi
I
là giao điểm của
SO
và
AM
.
Mặt phẳng qua
,AM
, song song với
SO
, cắt
SOC
theo giao tuyến là đường thẳng qua
I
,
đường thẳng đó cắt
SC
tại
N
.
Áp dụng định lý Menelauyt đối với tam giác
SOB
và bộ ba điểm thẳng hàng
,,A I M
ta có
2 2 2
1
1 1 1
SM BA OI SI SM BA x SN x NS x
MB AO IS OI MB AO x CN x CS x
.
Thể tích khối chóp
1
3
.
,
ABMN N ABM ABM
V V S d N ABM
1 2 2
11
3 1 1
.
,
SAB S ABC
xx
x S d C SAB x V
xx

4
2 1 6
1
.S ABC
xV
x



4
2 2 1 6 6 4 2
1
..S ABC S ABC
x V V
x




Do đó thể tích khối chóp
ABMN
lớn nhất bằng
6 4 2
.S ABC
V
khi
4
2 1 1 2 2 1
1
x x x
x
.
Câu 135. Cho hình hộp
. ' ' ' 'ABCD A B C D
. Gọi
G
là trọng tâm của tam giác
ABD
. Mặt phẳng
P
đi
qua hai điểm
',CG
và song song với đường thẳng
BD
, chia khối hộp thành hai phần có thể
thể tích
1
V
,
2
V
12
VV
. Tỉ số
1
2
V
V
bằng
A.
1
2
1
2
V
V
. B.
1
2
7
17
V
V
. C.
1
2
2
3
V
V
. D.
1
2
31
77
V
V
.
Lời giải
Chọn D
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 112
Gọi
V
là thể tích khối hộp
. ' ' ' 'ABCD A B C D
Dựng
P ABCD
, ta có
//BD
(do
//P BD
. Gọi
, , ,M J K N
lần lượt là giao
điểm của với
, , ,BC AB AD DC
và
,FE
lần lượt là giao điểm của
'MC
với
'BB
và
'NC
với
'DD
.
Ta có
4
3
CM CN
CB CD

. Suy ra
2
4 16
39
.
CMN CBD CBD
S S S




.
Mặt khác
1
2
JB JM
JA JK

. Suy ra
2
11
24
.
JBM JAK JAK
S S S




.
Mà
2
3
AJ AK
AB AD

. Suy ra
2
24
39
.
AJK ABD ABD
S S S




. Suy ra
1 4 1
4 9 9
.
JBM ABD ABD
S S S
.
Tương tự
1
9
NKD ABD
SS
.
Ta lại có
44
',
'
', ,
,
d C ABCD
MC
h d C ABCD d F ABCD
MF
d F ABCD
.
Tương tự
4', ,h d C ABCD d E ABCD
Thể tích
1
1 16 1 1 1 31
2
3 9 3 9 4 54
'. . .
. . . . . .
C CMN F MBJ E KDN BCD BCD BCD
V V V V S h S h S h
2
31 31 77
108 108 108
.
ABCD
S h V V V
.
Vậy
1
2
31
77
V
V
.
Câu 136. Cho khối chóp
.S ABC
. Có
23,AB AC
và
120 ,BAC SA
vuông góc với mặt phẳng đáy.
Gọi
,MN
lần lượt là hình chiếu của
A
trên
SB
và
SC
. Biết góc giữa mặt phẳng
ABC
và
AMN
bằng
60
. Thể tích của khối chóp đã cho bằng
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 113
LÊ MINH TÂM
A.
57
. B.
3 57
. C.
57
3
. D.
3 57
2
.
Lời giải
Chọn C
Ttrong mặt phẳng
()ABC
: Kẻ
,HC AC HB AB
.
,HB SAB HC SAC
,AM SBH AN SCH SH AMN
Mà
90,SA ABC ASH
,,AMN ABC SA SH ASH
22
60 2 120 19; . . .cosASH BC AB AC AB AC
2
1 1 3 3 3 3 3
120 2 3
2 2 2 2
19
. . .sin . . .
ABC
ABC
S
S AB AC AI
BC
2 3 2 19
3 3 3
19
..
sin
AB AB AB AC
AH
AI
AI
BCA
AC
2 19
2 19 1 1 2 19 3 3 57
3
60 3 3 3 3 2 3
3
.
. . . .
tan
S ABC ABC
AH
SA V SA S
Câu 137. Cho hình chóp tứ giác đều có cạnh đáy bằng . Gọi là chiều cao của hình
chóp, khoảng cách từ trung điểm của đến mặt bên bằng . Tính thể tích
của khối chóp .
A. . B. .
C. . D. .
Lời giải
Chọn B
.S ABCD
a
SH
I
SH
SBC
b
V
.S ABCD
22
3 16
ab
V
ab
3
22
2
3 16
ab
V
ab
22
16
ab
V
ab
22
2
16
ab
V
ab
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 114
Vì là hình chóp tứ giác đều suy ra là tâm của hình vuông .
Gọi là trung điểm , là hình chiếu vuông góc của lên .
Ta có: .
, mà .
Suy ra , ta có.
. Vậy .
Câu 138. Cho khối lăng trụ tứ giác đều
.ABCD A B C D
có đáy là hình vuông; khoảng cách và góc
giữa hai đường thẳng
AC
và
DC
lần lượt bằng
37
7
a
và với
2
4
cos
. Thể tích khối
lăng trụ đã cho bằng
A.
3
3a
. B.
3
9a
. C.
3
33a
. D.
3
3a
.
Lời giải
Chọn B
, , ,d AC DC d AC A C D d A A C D

3
7
,
a
d D A C D

.
A C D

với
2
4
cos
.
Đặt
3
7
,
a
DD x D E


, ta có
2 2 2 2
1 1 1 7
9DD D O D E a
2 2 2
1 1 7
9x D O a
22
3
79
ax
DO
xa

2 2 2
2
22
22
97
79
79
.a x x
DO x
xa
xa
H
A
D
C
S
B
M
K
I
J
.S ABCD
H
ABCD
M
BC
K
H
SM
BC SH
BC SHM
BC HM

SBC SHM
HK SM HK SBC
22HK IJ b
22
22
22
2
16
.HK HM ab
SH
HM HK
ab

3
22
2
3 16
ab
V
ab
O
D
C
A
B
B'
A'
C'
D'
E
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 115
LÊ MINH TÂM
và
2
1
17tan
cos
.
Khi đó
7
73
3
tan
DO x
xa
OC a
.
Vì
3AA a
và
22
32
3
79
ax
AB a
xa

nên
3
9
.
.
ABCD A B C D ABCD
V AA S a

.
Câu 139. Cho khối lăng trụ đứng
. ' ' 'ABC A B C
có đáy tam giác vuông cân tại
C
.
2BA a
và góc tạo
bởi
'ABC
và
ABC
bằng
60
o
. Gọi
,MN
lần lượt là trung điểm của
''AC
và
BC
. Mặt
AMN
chia khối lăng trụ thành hai phần. Tìm thể tích phần nhỏ.
A.
3
73
24
a
. B.
3
76
24
a
C.
3
3
3
a
. D.
3
6
6
a
.
Lời giải
Chọn A
Kẻ
/ / ' 'MP A B
Góc tạo bởi
'ABC
và
ABC
là góc
0
60'C JC
với
J
là trung điểm
AB
.
0
60 3' .tanCC CJ a
2
1
2
.
ABC
S CJ AB a
2
1
11
22
ACN ABC
S S S a
2
2
1 1 1
4 2 8
'
' . '
C MP ABC
S S S C M C P a
3
1 2 1 2
73
3 24
'CC a
V S S S S
Câu 140. Cho hình lăng trụ
.ABC A B C
có thể tích bằng
2
. Gọi
,MN
là các điểm lần lượt nằm trên
các cạnh
,AA BB

sao cho
M
là trung điểm của
AA
và
1
2
BN B N
. Đường thẳng
CM
cắt
đường thẳng
AC

tại điểm
P
, đường thẳng
CN
cắt đường thẳng
AB

tại
Q
. Tính thể tích
của khối đa diện
A MPB NQ

bằng.
A.
13
18
. B.
23
9
. C.
21
9
. D.
7
18
.
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 116
Lời giải
Chọn B
Đặt
ABC
SS
và
( ,( ))h d C A B C
ta có
2
.ABC A B C
V hS

.
Trong mặt phẳng
AA C C

ta có
1
2
//
A M CC
A M CC


nên ta có
A
là trung điểm của
PC
.
Tương tự trong mặt mặt phẳng
BCC B

ta có
1
3
C B C Q
.
Từ đây ta có diện tích tam giác
C PQ
là
6
C PQ
SS
do vậy thể tích khối tứ diện
CC PQ
là
1
6 2 4
3
.
CC PQ
V h S hS
.
Trong khối lăng trụ
.ABC A B C
ta có
11
0
5
23
3 18
.
CABMN
CAB C A B
V
V


suy ra
55
18 9
.
.
CABMN CAB C A B
VV

do đó thể tích khối
A B C MNC
bằng
5 13
2
99

.
Do vậy thể tích của khối đa diện
A MPB NQ

bằng
13 23
4
99

.
Câu 141. Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh
a
, mặt bên
SAB
là tam giác đều và nằm
trong mặt phẳng vuông góc với đáy. Gọi
,,H M O
lần lượt là trung điểm các cạnh
AB
,
SA
,
AC
và
G
là trọng tâm tam giác
SBC
. Thể tích khối tứ diện
GHMO
bằng
A.
3
3
64
a
. B.
3
3
128
a
. C.
3
128
a
. D.
3
64
a
.
Lời giải
Chọn D
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 117
LÊ MINH TÂM
Gọi
,NE
lần lượt là trung điểm của
CB
và
SB
.
Ta có:
23
1 1 3 3
3 3 4 2 8
.
. . .
S ABC ABC
a a a
V S SH
.
+)
3
11
2 2 16
..OAHN ABC S OAHN S ABC
a
S S V V
,
3
1
2 32
. . .S AHN S OAN S AHNO
a
V V V
.
+)
3
2 1 1 1
3 2 3 3 96
.
..
.
. . .
S GMH
S GMH S NAH
S NAH
V
SG SM SH a
VV
V SN SA SH
.
+)
3
2 1 1 1
3 2 3 3 96
.
..
.
. . .
S GMO
S GMH S OAH
S NAO
V
SG SM SO a
VV
V SN SA SO
.
+)
3
1 1 1 1 1 1 1
3 3 3 4 12 3 12 96
..
; . . . . .
G ONH ONH ABC ABC S ABC
a
V d G ABC S SH S SH S V
.
+)
3
1 1 1 1 1 1 1
3 3 2 4 8 3 8 64
..
; . . . . .
M OAH OAH ABC ABC S ABC
a
V d M ABC S SH S SH S V
.
Vậy
3 3 3 3
3
16 96 64 64
. . . . .
.
GMOHN S HNO S GMH S GMO G HNO G HAO
a a a a
V V V V V V
.
Câu 142. Cho hình chóp
.S ABC
có
AB BC a
, góc
120ABC 
,
90SAB SCB
và khoảng cách từ
B
đến mặt phẳng
SAC
bằng
2
21
a
. Tính thể tích khối
.S ABC
.
A.
3
5
10
a
V
. B.
3
15
10
a
V
. C.
3
15
5
a
V
. D.
3
5
2
a
V
.
Lời giải
Chọn B
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 118
Gọi
D
là hình chiếu vuông góc của
S
lên mặt phẳng
ABC
.
Có
BC SC
BC SD
BC CD
.
Có
AB SD
AB SA
AB AD
.
Gọi
I
là giao điểm của
BD
và
AC
(
BD
là đường phân giác của góc
ABC
)
2
60cos
BC
BD a
;
60
2
cos
a
BI BC
.
Gọi
H
là hình chiếu vuông góc của
D
lên
SI
.
SAC SBC
SAC SBC SI
DH SI

DH SAC
hay
;DH d D SAC
Ta có:
26
3
21 21
;;
DI a a
d D SAC d B SAC DH
BI
.
Suy ra:
2 2 2 2
36
65
2
21
5
9 12
47
aa
DI DH a
SD
DI DH a a
.
Vậy
3
1 1 6 5 1 3 15
3 3 5 2 2 10
.S ABC ABC
aa
V SD S a a
.
Câu 143. Cho tứ diện
ABCD
. Hai điểm
,MN
lần lượt di động trên hai đoạn thẳng
BC
và
BD
sao
cho
2 3 10..
BC BD
BM BN

. Gọi
12
,VV
lần lượt là thể tích của các khối tứ diện
ABMN
và
ABCD
. Tìm giá trị nhỏ nhất của
1
2
.
V
V
A.
3
8
.
B.
2
7
.
C.
6
25
.
D.
5
8
.
Lời giải
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 119
LÊ MINH TÂM
Chọn C
Cách 1
Vì
,M BC N BD
nên ta đặt
1
BD
aa
BN

.
Suy ra
10 3 3 8
1 5 1
2 2 3
.
BC a
aa
BM
1
2
2
1 1 1
33
55
22
..
ABMN
ABCD
V
V
BM BN
V V BC BD a
a a a

.
2
1
2
3
5
2
min
max
V
aa
V







. Tìm
2
8
1
3
3
5
2
;
max a a






.
Xt hàm số
2
38
51
23
,;f a a a a



;
5
5 3 0
3
' ; ' .f a a f a a
Suy ra
8
1
3
25
6
;
max .fa



Vậy
1
2
6
25
min
.
V
V



Cách 2
1
2
1
2
1
2
. . .sin
.
.
. . .sin
ABMN BMN
ABCD BCD
BM BN B
VS
V
BM BN
V V S BC BD
BC BD B
.
1
2
min
min
..
.
..
max
V
BM BN BC BD
V BC BD BM BN




Theo giả thiết;
2 3 2 3
10 2 2 6
. . . .
. . . . .
BC BD BC BD BC BD
BM BN BM BN BM BN
.
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 120
25
56
6
..
..
..
BC BD BC BD
BM BN BM BN
Do đó
1
2
6
25
min
.
V
V



Đẳng thức xảy ra
2 3 2
5
3
2 3 10
5
..
.
. . .
BC BD
BM BC
BM BN
BC BD
BN BD
BM BN









.
Câu 144. Cho hình lăng trụ
.ABC A B C
có đáy ABC là tam giác đều cạnh bằng 2,
2AA A B A C
, M là trung điểm của
AA
. Tính thể tích phần chung của 2 khối đa diện
.A M BCCB
và
.A A B C
.
A.
17 2
27
. B.
17 3
18
. C.
17 3
27
. D.
52
3
.
Lời giải
Chọn A
Gọi H là hình chiếu vuông góc của
A
lên mặt phẳng (ABC). Vì
A A AB AC

nên H
trùng với tâm đường tròn ngoại tiếp tam giác ABC cũng là trọng tâm tam giác ABC. Gọi I là
trung điểm BC.
Ta có:
2 2 3
3
33
AI AH AI
;
22
12 2 6
4
93
A H AA AH

;
26
3 2 2
3
.
..
ABC A B C ABC
V A H S
;
1 2 2
33
..A A B C ABC A B C
VV

;
Gọi
P AB BM

;
Q AC CM

. Khi đó phần chung của 2 khối đa diện
.A M BCCB
và
.A A B C
là khối đa diện
.MPQ A B C
.
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 121
LÊ MINH TÂM
Ta có:
1 1 1 1 17 17 2 2 17 2
2 3 3 18 18 18 3 27
.
..
.
. . . . .
A MPQ
MPQ A B C A A B C
A A B C
V
AM AP AQ
VV
V AA AB AC
.
Câu 145. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thang vuông tại
A
và
B
,
AB BC a
,
2AD a
,
SA
vuông góc với đáy,
2SA a
. Gọi
'B
là điểm đối xứng của
B
qua mặt phẳng
SCD
. Tính thể tích khối đa diện
'.SB ABCD
bằng
A.
3
52
6
a
. B.
3
72
3
a
. C.
3
2a
. D.
3
22
3
a
.
Lời giải
Chọn D
Ta có:
11
33
'. . '
. . ',
SB ABCD S ABCD B SCD ABCD SCD
V V V SAS S d B SCD
11
33
. . ,
ABCD SCD
SA S S d B SCD
(vì
'B
là điểm đối xứng của
B
qua mặt phẳng
SCD
)
+
3
2
11
2
3 3 2
2
.
. . .
S ABCD ABCD
a a a
a
V SA S a
+ Gọi
M
là giao điểm của
AB
và
CD
, dễ dàng chứng minh được
B
là trung điểm của
MA
11
22
,,d B SCD d A SCD AH
Lại có tam giác
SAC
vuông cân tại
A
( vì
2SA AC a
)
1 1 1 1
2
2 2 4 4 2
, , .
a
d B SCD d A SCD AH SC a
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 122
33
1 1 1 1 2
22
3 3 2 2 6 2 6
32
'.
. . ', . . . . . . .
B SCD SCD
a a a a
V S d B SCD SC CD a a
3 3 3
22
3
2 3 2
'. . 'SB ABCD S ABCD B SCD
a a a
V V V
.
Câu 146. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh bằng 1, biết khoảng cách từ
A
đến
mặt phẳng
SBC
bằng
6
4
, khoảng cách từ
B
đến mặt phẳng
SCA
bằng
15
10
, khoảng
cách từ
C
đến mặt phẳng
SAB
bằng
30
20
và hình chiếu vuông góc của
S
xuống đáy nằm
trong tam giác
ABC
. Tính thể tích khối chóp
.S ABC
V
.
A.
1
24
. B.
1
12
. C.
1
36
. D.
1
48
.
Lời giải
Chọn D
Gọi
H
là hình chiếu của
S
trên
ABC
.
,,F G K
lần lượt là hình chiếu của
H
trên
,,AB BC CA
.
Đặt
.
;
S ABC
V V h SH
Ta có
3 . ,( ) . ,( ) . ,( ) .
ABC SBC SAC SAB
V hS d A SBC S d SAC S d SAB S BC
3 6 1 15 1 30 1
4 4 2 10 2 20 2
. . . . . .h SF SG SK
2 5 10 2 3; ; ; ;SF h SG h SK h HF h HG h HK h
.
Mặt khác
3 1 1 1 3
4 2 2 2 12
ABC HAB HBC HCA
S S S S HF HG HK h
.
Vậy
1 3 3 1
3 12 4 48
.
..
S ABC
V 
.
Câu 147. Cho hình chóp tam giác đều
.S ABC
, cạnh đáy bằng
a
. Các điểm
,MN
lần lượt là trung điểm
của
,SA SC
. Biết rằng
BM
vuông góc với
AN
. Thể tích của khối chóp bằng
A.
3
7
24
a
. B.
3
7
8
a
. C.
3
14
8
a
. D.
3
14
24
a
.
A
B
C
S
H
F
G
K
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 123
LÊ MINH TÂM
Lời giải
Chọn D
Gọi
D
sao cho
MNAD
là hình bình hành.
BM
vuông góc với
AN
nên tam giác
DMB
vuông cân tại
M
. Suy ra:
2
2
3
2
14
4
22
.
a
a
BD a
BM




Gọi cạnh
0, .SA x x
BM
là đường trung tuyến tam giác
SAB
nên ta có:
2
2 2 2 2 2 2
2
22
14 6
4 4 4 2
.
BA BS SA a x x
aa
BM x




22
42
6
a
SH SA AH
. Vậy
23
1 42 3 14
3 6 4 24
.
..
S ABC
a a a
V 
.
Câu 148. Cho khối chóp
.S ABCD
có đáy là hình bình hành, có thể tích bằng
24
cm
3
. Gọi
E
là trung
điểm
SC
. Một mặt phẳng chứa
AE
cắt các cạnh
SB
và
SD
lần lượt tại
M
và
N
. Tìm giá trị
nhỏ nhất của thể tích khối chóp
.S AMEN
.
A.
9
cm
3
. B.
8
cm
3
. C.
6
cm
3
. D.
7
cm
3
.
Lời giải
Chọn B
Mặt đáy
ABCD
là hình bình hành
ADC
và
ABC
có cùng diện tích
..S ADC S ABC
VV
(hai khối chóp có cùng chiều cao và có diện tích mặt đáy bằng nhau).
D
N
M
H
A
C
B
S
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 124
Mà
24
. . .S ABCD S ADC S ABC
V V V
cm
3
24
12
22
.
..
S ABCD
S ADC S ABC
V
VV
(cm
3
).
Gọi
O
là giao điểm của
AC
và
BD
;
I
là giao điểm của
SO
và
AE
I
là trọng tâm của
SAC
và
I
thuộc
MN
. Gọi
SM
a
SB
và
SN
b
SD
(
0a
;
0b
).
Ta có:
1
1
22
.
.
S ANE
S ADC
V
SA SN SE b
b
V SA SD SC
và
1
1
22
.
.
S AME
S ABC
V
SA SM SE a
a
V SA SB SC
12 2
.S ANE
V
b

và
12 2
.S AME
V
a
6
.S ANE
Vb
(cm
3
) và
6
.S AME
Va
(cm
3
).
Do đó:
6 6 6
. . .S AMEN S AME S ANE
V V V a b a b
(cm
3
).
Mặt khác:
ISM
và
ISB
có chung chiều cao kẻ từ
I
và có đáy
SM
a
SB
ISM
ISB
S
a
S

.
Mà
I
là trọng tâm của
SAC
2
3
SI
SO

2
3
ISB
SOB
S
S

2
3
ISM
SOB
S
a
S

.
Chứng minh tương tự ta có:
2
3
ISN
SOD
S
b
S
.
O
là trung điểm của
DB
2
SDB
SOB SOD
S
SS
hay
22
SDB SOB SOD
SSS
2
2 2 2
22
3 3 2 2
ISM ISN
ISM ISN ISM ISN SNM
SOB SOD SOB SOD SDB SDB
SS
S S S S S
ab
S S S S S S
3
3
33
sin
sin
SNM
SDB
S
SN SM MSN SN SM
a b ab
S SD SB
SD SB BSD


.
Theo bất đẳng thức AM-GM, ta có:
2
4
ab
ab
2
3
3
4
ab
a b ab
34ab
(do
0ab
)
4
3
ab
68ab
hay
8
.S AMEN
V
(cm
3
).
Dấu
""
xảy ra khi và chỉ khi
2
3
ab
2
3
SM SN
SB SD
MN
đi qua
I
và
MN BD
.
Vậy giá trị nhỏ nhất của thể tích khối chóp
.S AMEN
là
8
cm
3
.
Câu 149. Tứ diện
ABCD
có
00
120 60,,AB AC AD a BAC BAD
và tam giác
BCD
là tam giác
vuông tại
D
. Tính thể tích khối tứ diện
ABCD
.
A.
3
2
4
a
. B.
3
2
3
a
. C.
3
2
6
a
. D.
3
2
12
a
.
Lời giải
Chọn D
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 125
LÊ MINH TÂM
Gọi
H
là hình chiếu của
A
lên
BCD
.
Dễ thấy,
AHB AHC AHD HB HC HD
.
Do đó,
H
là tâm đường tròn ngoại tiếp
BCD
H
là trung điểm của
BC
.
Xét tam giác
ABC
, có
2 2 2 2 2 2
2 2 120 3. .cos . .cosBC AB AC AB AC BAC a a a a a
.
3
3
2
a
BC a BH
.
Xét
AHB
vuông tại
H
, có
2
2 2 2
3
22
aa
AH AB BH a




.
Xét vuông tại , có .
Xét
,ABD
có và là tam giác đều cạnh .
(đvdt).
Vậy (đvtt).
Câu 150. Cho hình chóp có đáy là hình vuông cạnh bằng tam giác vuông
tại và nằm trong mặt phẳng vuông góc với đáy, đường thẳng tạo với mặt phẳng
một góc . Thể tích của khối chóp đã cho bằng
A. . B. . C. . D. .
Lời giải
Chọn C
Kẻ
BDC
D
2 2 2 2
32CD BC BD a a a
AB AD a
60BAD ABD
a BD a
2
12
2
22
..
BDC
a
S a a
23
1 1 2 2
3 3 2 2 12
. . .
ABCD BCD
a a a
V AH S
.S ABCD
ABCD
3 ,a
SBC
S
SD
SBC
60
3
26a
3
6a
3
32a
3
3a
,.SH BH H BC
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
LÊ MINH TÂM
Trang 126
Ta có
Mà và
Suy ra là hình chiếu của lên
Khi đó
Tam giác vuông tại có
Tam giác vuông tại có
Mà
Vậy thể tích của khối chóp đã cho là (đvtt).
------------------ HẾT ------------------
.
SBC ABCD
SBC ABCD BC SH ABCD
SH BC
CD BC
CD SBC
CD SH

.SD SBC S
SC
SD
.SBC
60, , .SD SBC SD SC CSD
SCD
C
3
3
60
3
.
tan
CD a
SC a
SBC
S
22
6.SB BC SC a
63
2
3
..
.
SB SC a a
SH a
BC a
2
3
11
2 3 3 2
33
. . .
ABCD
V SH S a a a
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trang 127
LÊ MINH TÂM
IV. BẢNG ĐÁP ÁN THAM KHẢO.
BẢNG ĐÁP ÁN
1
2
3
4
5
6
7
8
9
10
D
D
A
A
B
C
D
B
D
C
11
12
13
14
15
16
17
18
19
20
D
D
B
C
A
D
B
A
C
B
21
22
23
24
25
26
27
28
29
30
C
A
C
D
A
B
A
C
A
A
31
32
33
34
35
36
37
38
39
40
D
A
B
B
B
A
B
D
B
B
41
42
43
44
45
46
47
48
49
50
C
C
B
C
B
A
C
D
D
B
51
52
53
54
55
56
57
58
59
60
B
D
B
C
A
B
C
C
D
A
61
62
63
64
65
66
67
68
69
70
B
C
A
A
B
B
C
C
C
A
71
72
73
74
75
76
77
78
79
80
C
D
D
D
A
C
B
B
B
A
81
82
83
84
85
86
87
88
89
90
D
B
A
B
C
D
C
A
C
B
91
92
93
94
95
96
97
98
99
100
D
B
B
D
B
A
C
B
D
A
101
102
103
104
105
106
107
108
109
110
B
A
A
B
D
B
D
B
C
A
111
112
113
114
115
116
117
118
119
120
D
A
A
B
B
C
B
A
B
D
121
122
123
124
125
126
127
128
129
130
D
B
B
B
B
B
C
D
A
A
131
132
133
134
135
136
137
138
139
140
B
A
C
D
D
C
B
B
A
B
141
142
143
144
145
146
147
148
149
150
D
B
C
A
D
D
D
B
D
C
| 1/127
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

LÊ MINH TÂM CHƯƠNG 01. THỂ TÍCH KHỐI ĐA DIỆN
TÀI LIỆU LƯU HÀNH NỘI BỘ THỂ TÍCH KHỐI ĐA DIỆN MỤC LỤC
CHUYÊN ĐỀ. THỂ TÍCH KHỐI ĐA DIỆN ................................................................................ 3
I. KIẾN THỨC CẦN NHỚ. .................................................................................................. 3
II. CÁC DẠNG BÀI TẬP. ..................................................................................................... 6
Dạng toán 1. CHÓP CÓ CẠNH BÊN VUÔNG GÓC VỚI ĐÁY. ................................. 6
Dạng toán 2. CHÓP CÓ MẶT BÊN VUÔNG GÓC VỚI ĐÁY. .................................... 8
Dạng toán 3. CHÓP ĐỀU. .................................................................................................. 11
Dạng toán 4. TỶ SỐ THỂ TÍCH. ...................................................................................... 14
Dạng toán 5. TỔNG HIỆU THỂ TÍCH. ............................................................................ 18
Dạng toán 6. THỂ TÍCH LĂNG TRỤ ĐỨNG. ............................................................... 24
Dạng toán 7. THỂ TÍCH LĂNG TRỤ XIÊN. .................................................................. 29
Dạng toán 8. THỂ TÍCH KHỐI LẬP PHƯƠNG – KHỐI HỘP. .................................. 33
Dạng toán 9. KHỐI ĐA DIỆN ĐƯỢC CẮT RA TỪ KHỐI LĂNG TRỤ. ................... 37
Dạng toán 10. MAX – MIN THỂ TÍCH. ..................................................................... 44
III. BÀI TẬP RÈN LUYỆN. ................................................................................................. 50
IV. BẢNG ĐÁP ÁN THAM KHẢO. .............................................................................. 127
Biên soạn: LÊ MINH TÂM Trang 2
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN CHUYÊN ĐỀ THỂ TÍCH KHỐI ĐA DIỆN
I. KIẾN THỨC CẦN NHỚ.
Các định nghĩa.
– Hình chóp là hình có đáy là một đa giác và các mặt bên là các tam giác có chung một đỉnh.
– Hình lăng trụ là hình có hai đáy là hai đa giác bằng nhau nằm trên hai mặt phẳng song song
với nhau và các mặt bên đều là các hình bình hành.
– Hình hộp là hình lăng trụ có đáy là hình bình hành.
Thể tích khối chóp.
Công thức tính thể tích khối chóp: 1 V  . . S h 3
Trong đó: S là diện tích đáy và h là chiều cao khối chóp (khoảng cách từ đỉnh đến mặt đáy).
Cách xác định đường cao khối chóp:
a. Chóp có cạnh bên vuông góc chiều cao chính là cạnh bên.
b. Chóp có hai mặt bên vuông góc đáy đường cao là giao tuyến của hai mặt bên vuông góc đáy.
c. Chóp có mặt bên vuông góc đáy: chiều cao của mặt bên vuông góc đáy.
d. Chóp đều chiều cao hạ từ đỉnh đến tâm đa giác đáy.
e. Chóp có hình chiếu vuông góc của một đỉnhlên xuống mặt đáy thuộc cạnh mặt đáy đường
cao là từ đỉnh tới hình chiếu.
Thể tích khối lăng trụ.
Công thức tính thể tích khối lăng trụ: V  . S h
Trong đó: S là diện tích đáy và h là chiều cao khối chóp (khoảng cách từ đỉnh đến mặt đáy).
● Thể tích khối hộp chữ nhật: V  . a . b c .
● Thể tích khối lập phương: 3 V a . Trang 3 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Công thức diện tích đáy.
Ta có các đa giác thường gặp sau: 1 1 1 S  . a h  . b h  . c h 2 a 2 b 2 c 1 1 1 S b . a sin A  c . a sin B  b . a sin C Tam giác 2 2 2 abc 2 S   2R .sin A.sin . B sinC 4R
với R là bán kính đường tròn ngoại tiếp ABC . S  . p r
với p là nửa chu vi và r là bán kính đường tròn nội tiếp ABC .   a b c
S pp ap bp c với p  hoặc 2 1 S
a b2 c  c a b2 2 2       4     1 1
ABC vuông tại A : S A . B AC BC.AH . 2 2 x2 3
ABC đều, cạnh x :S  ; 4 x 3
Chiều cao tam giác đều h  . 2
Hình vuông cạnh x .   2 S x
Hình chữ nhật.
S  x.y ( x; y : dài và rộng)
Hình bình hành ABCD . S A . B A . D sin BAD 1
Hình thoi ABCD . S A . B A . D sin BAD AC.BD 2 1
S  a b.h (a, b: hai đáy, h: chiều Hình thang: 2 cao)
Tứ giác ABCD có hai 1 S AC.BD
đường chéo vuông góc 2 LÊ MINH TÂM Trang 4
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Tỷ số diện tích AM trung tuyến, S đặt SS 
S S  . ABC 1 2 2 G là trọng tâm, S đặt SS 
S S S  . ABC 1 2 3 3
NM MN NC S đặt S
S S S S  . ABC 1 2 3 3 S S
S S S S S  . ABCD 1 2 3 4 4 S S
S S S S S  . ABC 1 2 3 4 4 SAMN AM AN   . S AB AC ABC Trang 5 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
II. CÁC DẠNG BÀI TẬP.
Dạng toán 1. CHÓP CÓ CẠNH BÊN VUÔNG GÓC VỚI ĐÁY.
Phương pháp giải
Khối chóp có sẵn chiều cao và diện tích đáy. 1
Áp dụng công thức: V  . . S h 3
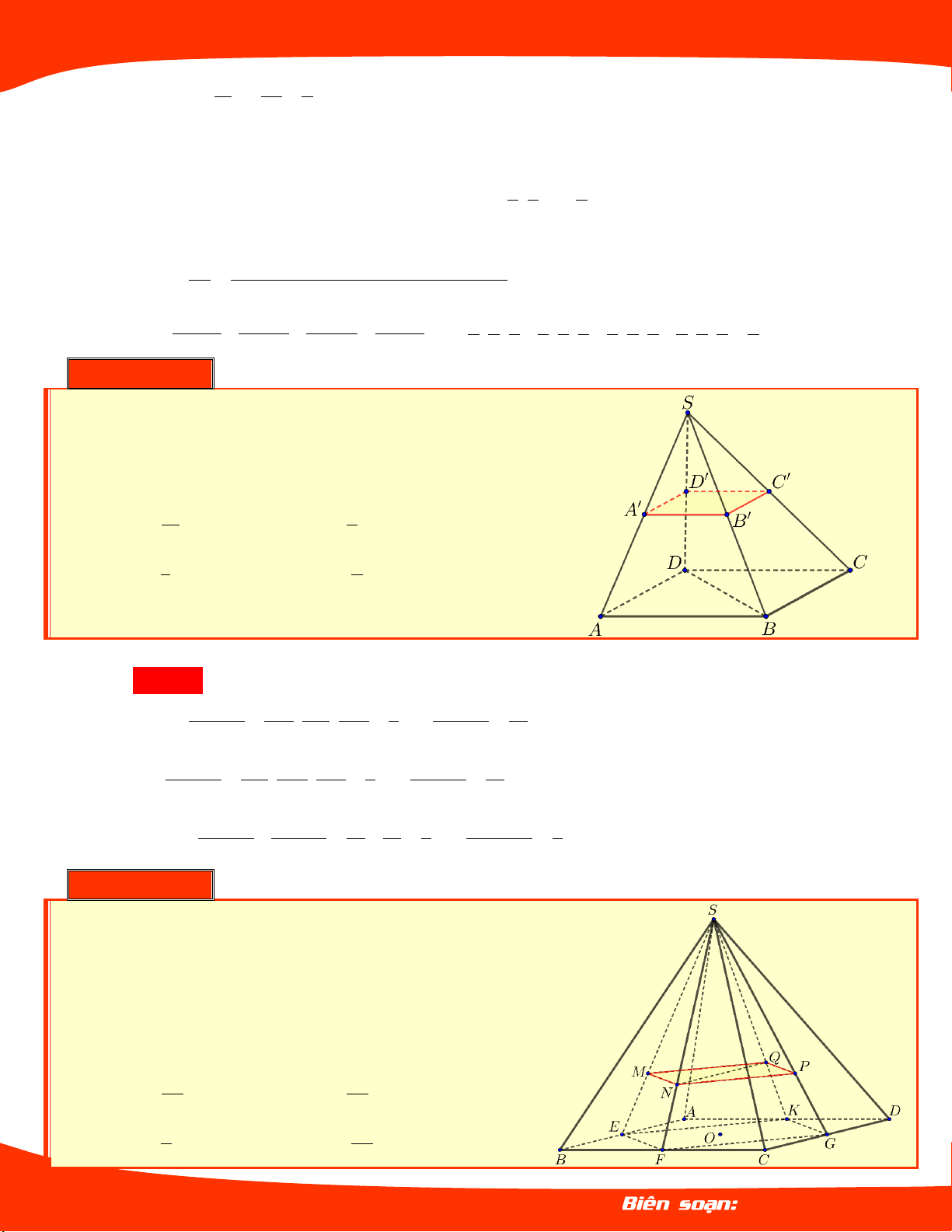
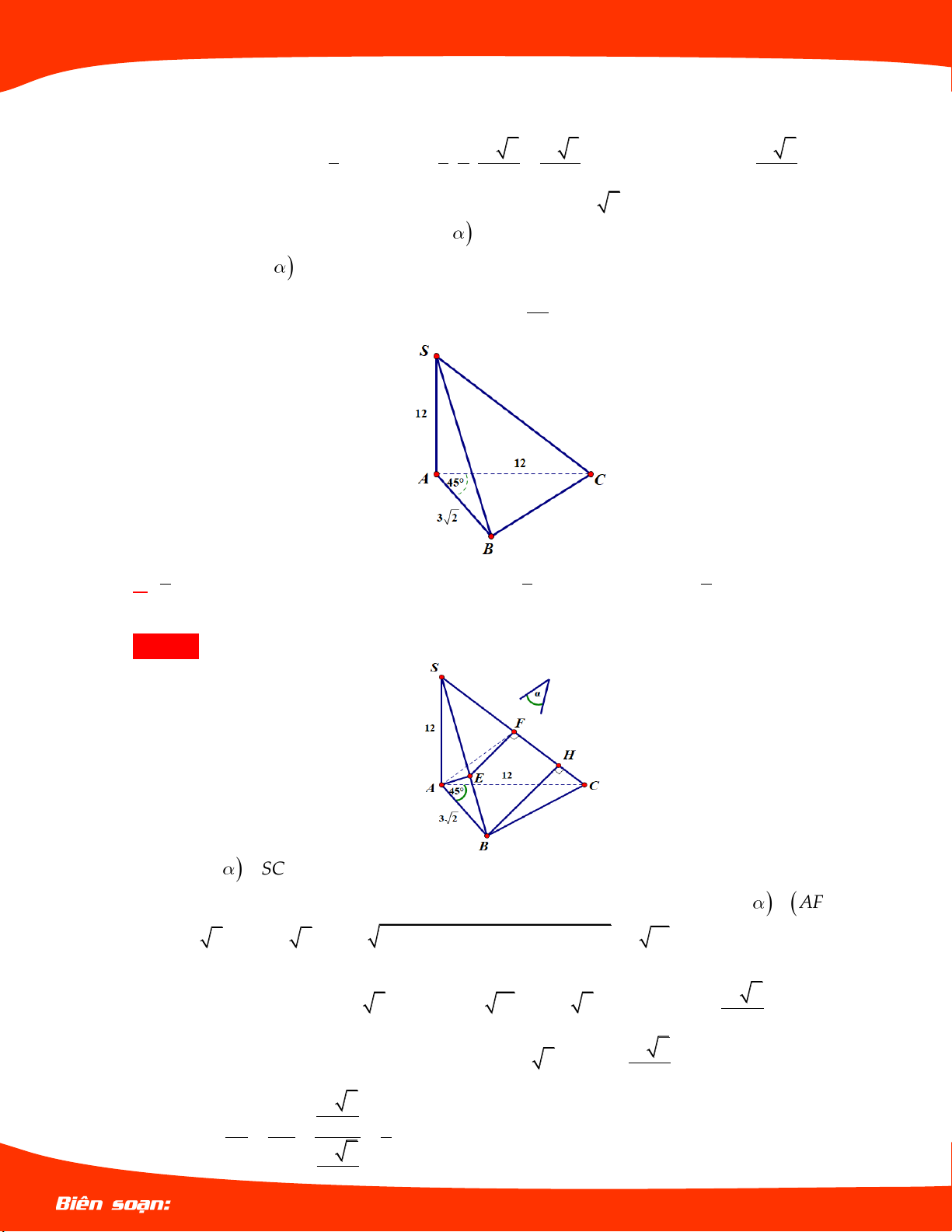
Ví dụ 01. Cho khối chóp .
S ABCD có đáy ABCD là S
hình vuông cạnh a . Biết SA vuông góc với
ABCD và SAa 3 . Thể tích của khối chóp . S ABCD là: 3 a A. . 4 B. 3 a 3 . A D 3 a 3 C. . 6 B C D. 3 3a . Lời giải Chọn D 3 1 a 3
Thể tích khối chóp VS .SA  . S.ABCD 3 ABCD 3
Ví dụ 02. Cho hình chóp tứ giác . S ABCD có đáy là
hình vuông cạnh a , SA vuông góc với mặt
phẳng đáy và SA  2a . Thể tích khối chóp . S ABCD bằng: 3 4a A. . 3 B. 3 2a . 3 a C. . 3 3 2a D. . 3 Lời giải Chọn D 3 1 1 2a 2 VS
SA  a 2a   . S.ABCD 3 ABCD 3 3 LÊ MINH TÂM Trang 6
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Ví dụ 03. Cho hình chóp .
S ABCD có đáy ABCD là
hình chữ nhật AB a, BC  2a , cạnh bên SA
vuông góc với đáy và SA a 2 . Tính thể tích khối chóp . S ABCD . 3 2a 3 A. . 3 B. 3 a 2 . C. 3 2a 2 . 3 2a 2 D. . 3 Lời giải Chọn D 3 1 2a 2 Diện tích đáy: 2 SA .
B BC  2a . Thể tích: V S .SA  . ABCD 3 ABCD 3
Ví dụ 04. Cho hình chóp .
S ABCD có đáy ABCD là
hình vuông cạnh a . Cạnh bên SA vuông
góc với đáy và có độ dài bằng 2a . Thể tích khối tứ diện . S BCD là: 3 a 3 a A. . B. . 4 8 3 a 3 a C. . D. . 6 3 Lời giải Chọn D 2 1 a 2 3 1 1 a a Ta có: SS  . Suy ra V  . SA S  2 . . a  . BCD 2 ABCD 2 S.ABCD 3 BCD 3 2 3
Ví dụ 05. Cho hình chóp .
S ABCD có đáy ABCD là
hình vuông tâm O cạnh 2a. Biết SA vuông
góc với mặt phẳng đáy và SA a 2. Tính thể tích khối chóp . S ABO. 3 a 2 3 2a 2 A. . B. . 3 12 3 a 2 3 4a 2 C. . D. . 12 3 Lời giải Chọn A Trang 7 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN AC 1 Ta có: 2 AC  2 .
a 2  OA OB   a 2  SO . A OB  a . 2 OAB 2 1 1 2 Vậy: 2 3 V  . SA S  .a 2.a  .a . S.OAB 3 OAB 3 3
Dạng toán 2. CHÓP CÓ MẶT BÊN VUÔNG GÓC VỚI ĐÁY.
Phương pháp giải
Khối chóp có mặt bên vuông góc mặt phẳng đáy. 1
+ Áp dụng công thức: V  . . S h . 3
+ Chiều cao khối chóp là đoạn thẳng từ đỉnh của chóp ta kẻ vuông góc vào giao tuyến của mặt bên và mặt đáy.
Một số kiểu thường gặp:
 Mặt bên SAB vuông với đáy ABCD và SAB là tam giác x 3
đều cạnh x SH  ABCD  h SH  với H là trung 2 điểm AB .
 Mặt bên SAB vuông với đáy ABCD và SAB là tam giác
cân tại S SH  ABCD  h SH với H là trung điểm AB .
Ví dụ 01. Hình chóp .
S ABCD đáy là hình chữ nhật có
AB  2a 3; AD  2a . Mặt bên SAB là tam giác
đều và nằm trong mặt phẳng vuông góc với
đáy. Thể tích khối chóp . S ABD là. 2 3 A. 3 a . 3 B. 3 4 3a . C. 3 4a . D. 3 2 3a . Lời giải Chọn D
Gọi H là trung diểm của AB SH  ABCD . 2a 3  3
Tam giác SAB là tam giác đều cạnh 2a 3 nên SH   3a . 2 1 1 1
Vậy thể tích khối chóp SABD là 3
V  SH S
 3a 2a 3 2a  2 3a . 3 ABD 3 2 LÊ MINH TÂM Trang 8
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Ví dụ 02. Cho hình chóp .
S ABCD có đáy là hình vuông
cạnh a; hình chiếu của S trên ABCD trùng 3a
với trung điểm của cạnh ;
AB cạnh bên SD  2
. Thể tích của khối chóp .
S ABCD tính theo a bằng: 3 a 5 3 a 3 A. . B. . 3 3 3 a 7 3 a C. . D. . 3 3 Lời giải Chọn D
Gọi H là trung điểm của AB nên SH  ABCD . 2  a  5 Lại có 2 DH a     a .  2  2
Xét tam giác SDH vuông tại HL . 2 2  3   5  1 1 2 2 3
SH SH DH   a   
a   a V S
.SH a . 2  2    3 ABCD 3  
Ví dụ 03. Cho hình chóp .
S ABCD có đáy ABCD là hình
vuông cạnh a , SAD  ABCD , SA SD .
Tính thể tích V của khối chóp . S ABCD biết a 21 SC  . 2 3 a 7 A. V  . 2 B. 3
V  2a . 3 a 7 C. V  . 6 3 2a D. V  . 3 Lời giải Chọn D 3 a 5 1 2a Ta có: 2 HC
SH  2a V  .a 2 . a  . 2 3 3 Trang 9 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
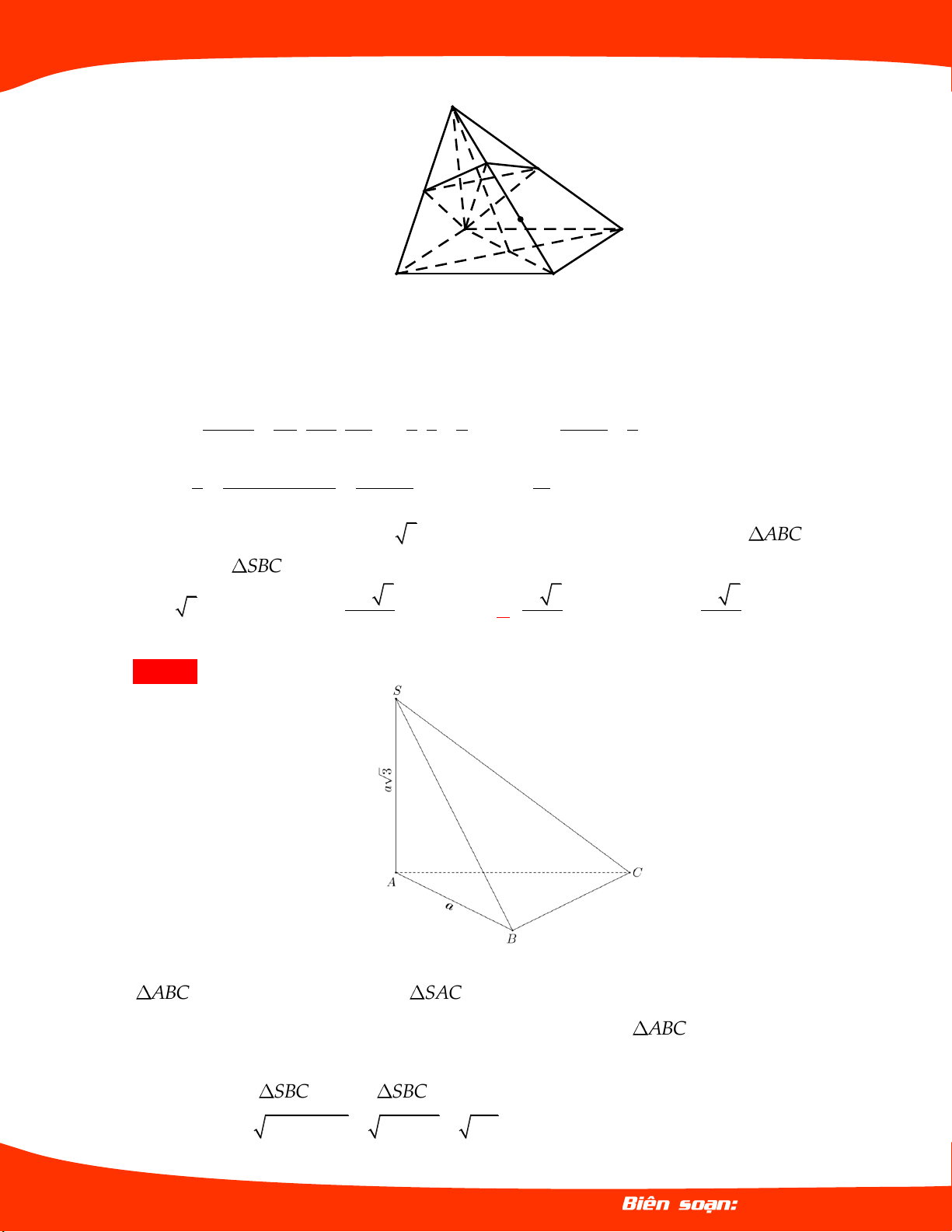
Ví dụ 04.
Cho tứ diện ABCD có ABC là tam giác vuông
cân tại C và nằm trong mặt phẳng vuông góc
với mặt phẳng  ABD , tam giác ABD là tam
giác đều và có cạnh bằng 2a . Tính thể tích của
khối tứ diện ABCD . 3 a 3 A. 3 a 2 . B. . 3 3 a 3 C. 3 a 3 . D. . 9 Lời giải Chọn B
Gọi H là trung điểm của AB . Ta có DH  ABC và DH a 3 . 3 1 a 3 ABC vuông cân tại 2 2
C  2CA AB AC BC a 2  VDH.S  . ABCD 3 ABC 3
Ví dụ 05. Cho chóp .
S ABCD có ABCD là hình vuông cạnh 3a .
SAB cân tại S và nằm trong mặt
phẳng vuông góc với đáy. Tính thể tích V .
S ABCD , biết góc giữa SC và ABCD bằng 0 60 A. 3
V 18a 15 B. 3 V  18a 3 . 3 9a 15 C. V  . D. 3 V  9a 3 . 2 Lời giải Chọn C Ta có Sa a ABCD  2 2 3 9
Gọi H là trung điểm AB SH  ABCD
CH là hình chiếu vuông góc của SC trên ABCD
 SC,ABCD  SC,CH  SCH  60
Xét SCH vuông tại H có 3a 5 a 2 2
CH BC BH  3 15
, SH CH tanSCH  2 2 3 1 9a 15 VS .SH  . S.ABCD 3 ABCD 2 LÊ MINH TÂM Trang 10
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Dạng toán 3. CHÓP ĐỀU.
Phương pháp giải
Khối chóp có các cạnh bên bằng nhau 1
+ Áp dụng công thức: V  . . S h . 3
+ Chiều cao khối chóp là đoạn thẳng từ đỉnh của chóp hạ vuông góc xuống tâm mặt đáy.
Một số kiểu thường gặp:  Chóp đều .
S ABCD, góc giữa mặt phẳng bên và mặt đáy là hoặc góc giữa cạnh bên và mặt đáy là .  Chóp đều .
S ABC , góc giữa mặt phẳng bên và mặt đáy là hoặc góc giữa cạnh bên và mặt đáy là .
Một số công thức tính nhanh:
Chóp đều cạnh x , đáy là tam giác
Chóp đều cạnh x , đáy là tứ giác x3 2 x3 2 V . V  . 12 6
Chóp đều có cạnh bên bằng x , đáy là tam
Chóp đều có cạnh bên bằng x , đáy là tứ
giác cạnh y . giác cạnh y .  3 y2 2 2 3x yy 2 2 4x  2y V . V  . 12 6
Chóp đều có các mặt bên cùng tạo với đáy
Chop đều có các mặt bên cùng tạo với
một góc , đáy là tam giác cạnh x .
đáy một góc , đáy là tứ giác cạnh x . x3tan x3tan V . V  . 24 6 Trang 11 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Ví dụ 01.
Tính chiều cao của hình chóp tứ giác đều có
cạnh đáy bằng a và cạnh bên bằng b ? 2 2 4b  2a A. . 2 2 2 4b  2a B. . 2 2 2 4b a C. . 2 2 2 4b a D. . 2 Lời giải Chọn B
Gọi H là tâm hình vuông ABCD ,
Do S.ABCD là hình chóp tứ giác đều nên SH  ABCD . 2 2 2  a  4b  2a Ta có 2 2 2
SH SC HC b     .  2  2
Ví dụ 02.
Tính thể tích của khối chóp tứ giác đều có cạnh
đáy bằng a và cạnh bên bằng b là: 2 2 2 a b  2a A. . 6 2 2 2 a 4b  2a B. . 6 2 2 2 a 4b  2a C. . 6 2 2 2 a 4b a D. . 6 Lời giải Chọn B .
S ABCD là chóp tứ giác đều nên SO  ABCD . a 2
BD là đường chéo hình vuông cạnh a nên BD a 2  OB  . 2 2 2 2  a  4b  2a Ta có 2 2 2
SO SB OB b     .  2  2 2 2 2 2 2 1 1 4b  2a a 4b  2a 2
V  .SH.S  . .a  . 3 ABCD 3 2 6 LÊ MINH TÂM Trang 12
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Ví dụ 03. Cho hình chóp đều .
S ABCD có cạnh đáy bằng
a và cạnh bên tạo với đáy một góc 60. Thể tích
của hình chóp đều đó là: 3 a 6 A. . 6 3 a 3 B. . 6 3 a 3 C. . 2 3 a 6 D. . 2 Lời giải Chọn A
Gọi O AC BD SO  ABCDSO a
SCO  60  tan60 
SO OC 3  . 3 OC 2 3 1 3 a 6 2  V a .a  . 3 2 6
Ví dụ 04.
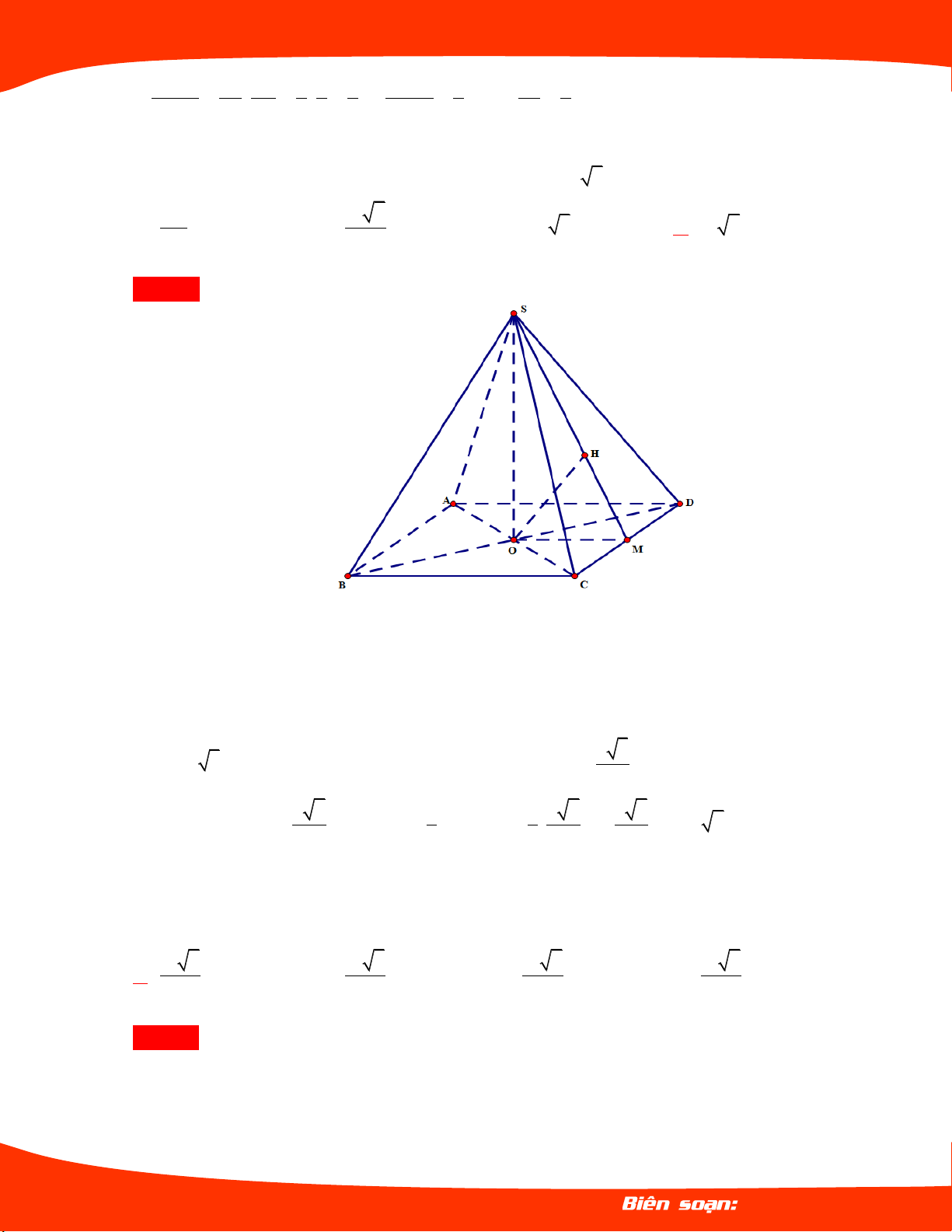
Cho hình chóp tứ giác đều .
S ABCD có cạnh đáy
bằng a . Gọi điểm O là giao điểm của AC và a
BD . Biết khoảng cách từ O đến SC bằng . 6
Tính thể tích khối chóp . S ABC . 3 a 3 a A. . B. . 6 4 3 a 3 a C. . D. . 8 12 Lời giải Chọn D a
H là hình chiếu của O lên SC nên OH  , 6 1 a 2
ABCD là hình vuông có OC AC  2 2
SOC vuông tại O có OH là đường cao 1 1 1 a      SO  . 2 2 2 OH SO OC 2 3 1 1 1 a  V
S .SO  . S .SO  . S.ABCD 3 ABC 3 2 ABCD 12 Trang 13 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Ví dụ 05.
Một hình chóp tam giác đều có cạnh bên bằng
b và cạnh bên tạo với mặt phẳng đáy một góc
. Thể tích của hình chóp đó là 3 A. 3 b cos sin . 4 3 B. 3 2 b sin cos . 4 3 C. 3 2 b cos sin . 4 3 D. 3 2 b cos sin . 4 Lời giải Chọn D S
H SAsin  bsin
Xét tam giác SHAvuông tại H , ta có: 
AH SA cos   b cos 3 3
AM AH bcos . 2 2 AB 3 2AM Mà: AM   AB   3 cos . 2 3 3  3 1 1 b cos 2 3 3 2 V  .SH.S  .bsin .  b cos sin SABC ABC . 3 3 4 4
Dạng toán 4. TỶ SỐ THỂ TÍCH.
Phương pháp giải
A. Cho khối chóp .
S ABC có A; B;C lần lượt là nằm trên SA;SB;SC khi đó:
1. Nếu A A; B B và C C thì V    S S.A B C A BC   
(Hai khối chóp chung đỉnh và chung mặt đáy). V S S.ABC ABC
2. Định lý SIMSON cho khối chóp tam giác V       SA SB SC S.A B C    . V SA SB SC S.ABC SB
3. Cắt khối chóp bởi mặt phẳng song song với đáy sao cho 1  k thì SA1 LÊ MINH TÂM Trang 14
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
VS. 1B 2B... nB 3  k VS. 1A 2 A ... n A
B. Mặt phẳng cắt các cạnh của khối chóp tứ giác .
S ABCD có đáy là hình bình hành lần lượt tại SM SN SP SQ
M ; N ; P ;Q sao cho  ;  ;  ;  : SA SB SC SD V   S.MNPQ . . . 1 1 1 1       và V 4   S.ABCD 1 1 1 1    .
Ví dụ 01. Cho hình chóp .
S ABC . Gọi M, N, P lần lượt là V trung điểm của S , A S ,
B SC . Tỉ số thể tích S.ABC VS.MNP bằng A. 12 . B. 2 . C. 8 . D. 3 . Lời giải Chọn C V SA SB SC Ta có S.ABC  . .  2 2 . 2 .  8 . V SM SN SP S.MNP Trang 15 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Ví dụ 02.
Cho tứ diện MNPQ . Gọi I ; J ; K lần lượt là
trung điểm của các cạnh MN ; MP ; MQ . Tỉ số V thể tích MIJK bằng VMNPQ 1 A. 3 1 B. 4 1 C. 6 1 D. 8 Lời giải Chọn D VM.IJK MI MJ MK 1 1 1 1 Ta có:  . .  . .  . V MN MP MQ 2 2 2 8 M.NPQ
Ví dụ 03.
Cho khối tứ diện có thể tích bằng V . Gọi V là
thể tích của khối đa diện có các đỉnh là các
trung điểm của các cạnh của khối tứ diện đã V  cho, tính tỉ số . V V  2 A.  . V 3 V  5 B.  . V 8 V  1 C.  . V 2 V  1 D.  . V 4 Lời giải Chọn B Cách 1.
Đặc biệt hóa tứ diện cho là tứ diện đều cạnh a .
Hình đa diện cần tính có được bằng cách cắt 4 góc của tứ diện, mỗi góc cũng là một a
tứ diện đều có cạnh bằng . 2 V V
Do đó thể tích phần cắt bỏ là V   4.  . 8 2 LÊ MINH TÂM Trang 16
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN V V  1 Vậy V     . 2 V 2 Cách 2.
Khối đa diện là hai khối chóp tứ giác có cùng đáy là hình bình hành úp lại. 1 1 1
Suy ra: V   2V  4.V  4.V
 4. . V V N.MEPF N.MEP P.MNE 2 4 2 Cách 3. V ' V VVVV Ta có A.QEP B.QMF C.MNE D.NPFV V V V V V  1 A.QEP B.QMF C.MNE D.NPF     1 1 1 1 1 1 1 1 1 1 1 1 1
1 . .  . .  . .  . .  . V V V V 2 2 2 2 2 2 2 2 2 2 2 2 2
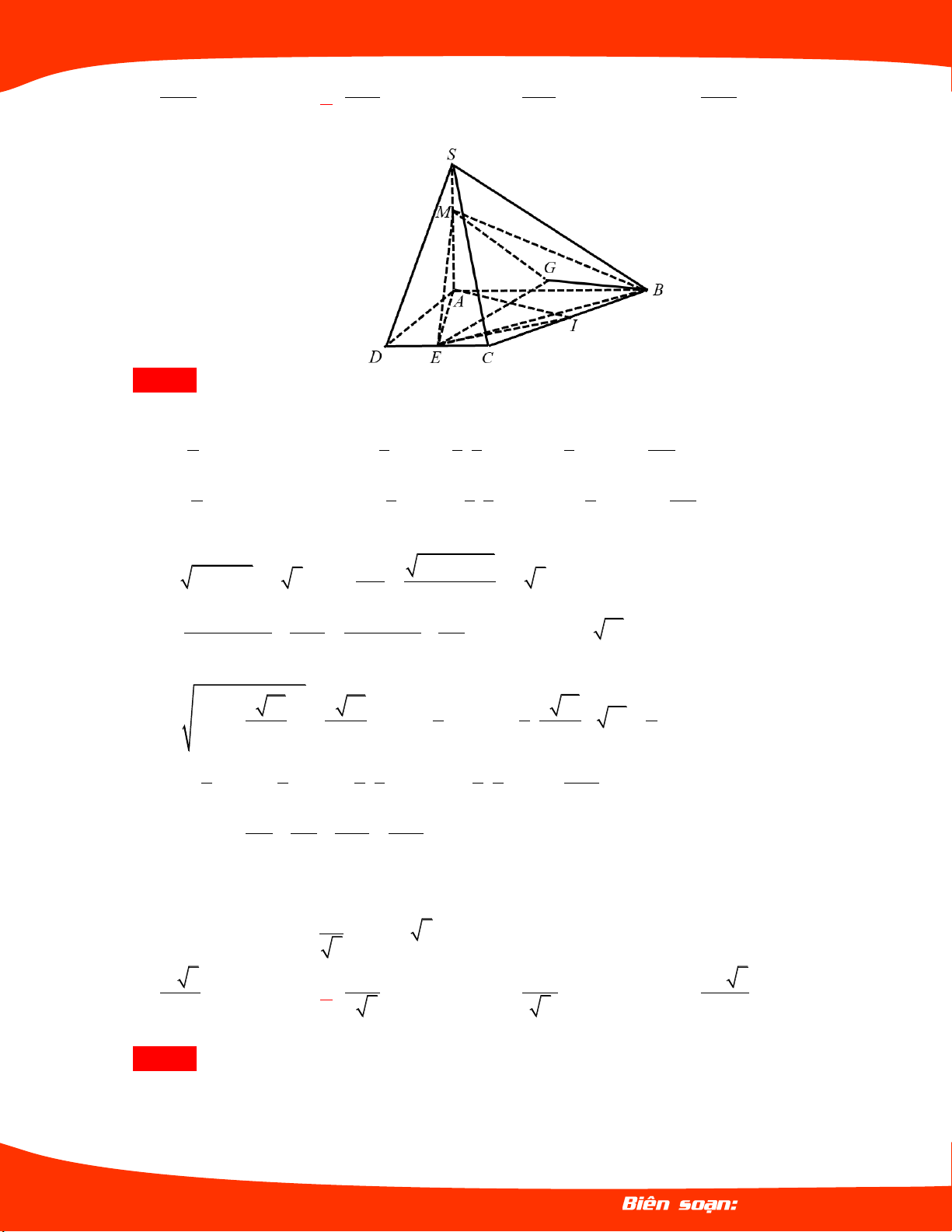
Ví dụ 04. Cho hình chóp .
S ABCD . Gọi A , B , C , D theo
thứ tự là trung điểm của SA , SB, SC , SD. Tính
tỉ số thể tích của hai khối chóp . S A BCD   và . S ABCD . 1 1 A. B. 16 4 1 1 C. D. 8 2 Lời giải Chọn C V       SA SB SD 1 V
Ta có S.A B D  . .     1 S.A B D   . V SA SB SD 8 V 16 S.ABD S.ABCD V       SB SD SC 1 V Và S.B D C  . .     1 S.B D C   . V SB SD SC 8 V 16 S.BDC S.ABCD
V    V    1 1 1 V Suy ra S.A B D S.  BDC        1 S.A B C D   . V V 16 16 8 V 8 S.ABCD S.ABCD S.ABCD
Ví dụ 05.
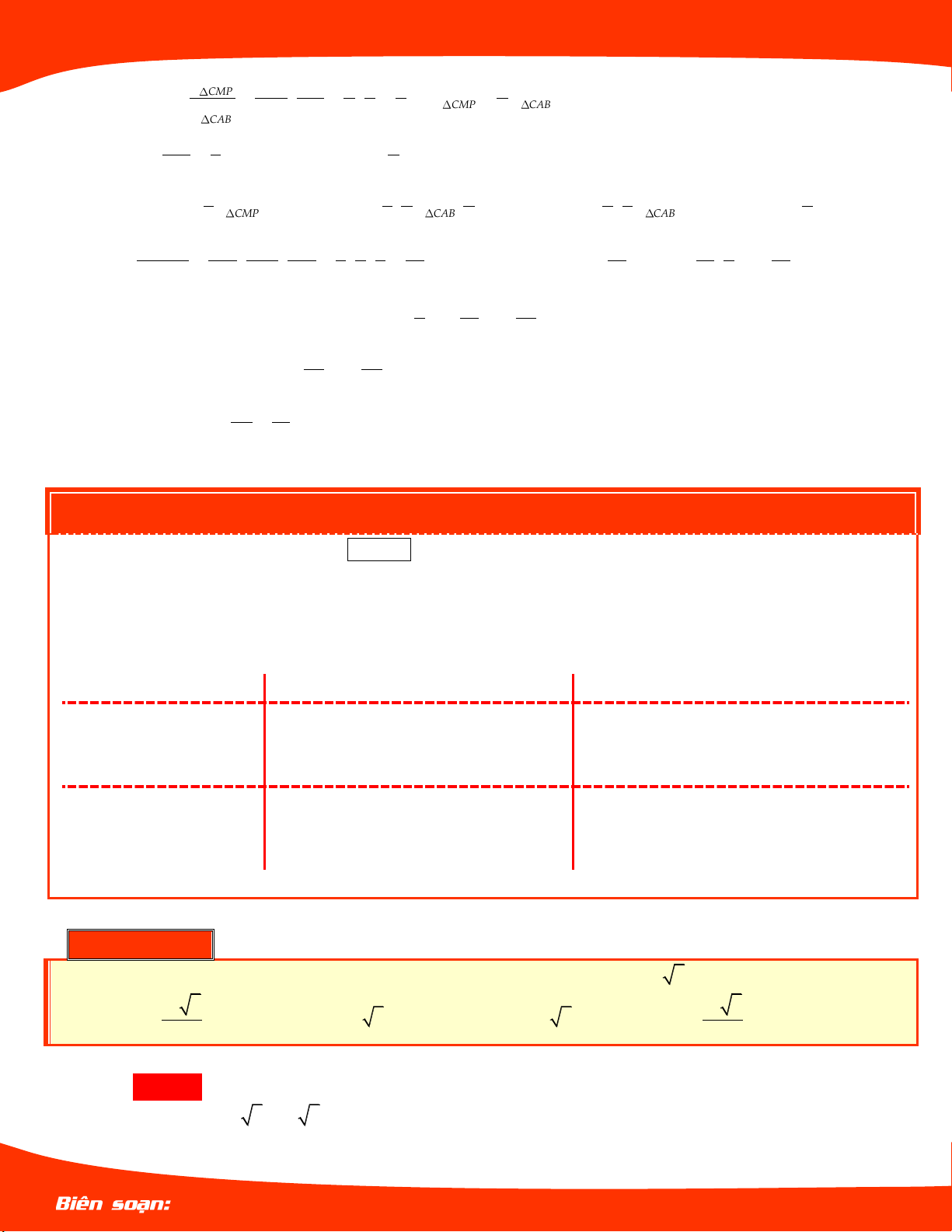
Cho hình chóp SABCD có đáy là hình bình
hành. Gọi M, N, P,Q lần lượt là trọng tâm của
các tam giác SAB,SBC,SCD,SDA . Gọi O là điểm
bất kỳ trên mặt phẳng đáy ABCD . Biết thể tích
khối chóp OMNPQ bằng V . Tính thể tích khối chóp SABCD. 27 27 A. V . B. V . 8 2 9 27 C. V . D. V . 4 4 Trang 17 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN Lời giải Chọn B
Ta có MNPQ //  ABCD  dS,MNPQ  2dO,MNPQ  V  2V  2V SMNPQ OMNPQ VSMNQ SM SN SQ 2 2 2 8 8 +  . .  . .   VV . V SE SF SK 3 3 3 27 SMNQ 27 SEFK SEFK VSNPQ SN SP SQ 2 2 2 8 8 +  . .  . .   VV . V SF SG SK 3 3 3 27 SNPQ 27 SFGK SFGK 8 8 8 27 27  VVVVVVV VV . SMNQ SNPQ 27 SEFK 27 SFGK SMNPQ 27 SEFGK SEFGK 8 SMNPQ 4 1 B . E BF.sin B S 1 1 1 Ta có: EBF 2    SSS . S 1 4 EBF 4 ABC 8 ABCD ABC B . A BC.sin B 2 Khi đó, SSSSSSSS EFGK ABCDABF FCG GDK KAE 4 ABCD EBF 1  SS EFGK 2 ABCD
1 dS,EFGKSEFGK V 1 27 Nên SEFGK 3    V  2VV . V 1 dSABCD SEFGK SABCD S, ABCD 2 2 S 3 ABCD
Dạng toán 5. TỔNG HIỆU THỂ TÍCH.
Phương pháp giải
 Trong quá trình tính thể tích một khối đa diện lồng ghép trong khối chóp ta gặp khó khăn
với cách tính thực tiếp thì khi đó:
 Ta có thể tách khối chóp ra thành các khối nhỏ và tính trực tiếp từng khối đã tách.
 Phần cần tính sẽ là phần khối chóp bỏ đi những khối nhỏ đã tính.
Ví dụ minh họa: Cho khối chóp .
S ABCD , mặt phẳng   chia khối chóp thành 2 phần V1 ; V V 2 . Tính thể tích khối 2 . Giải.
Để tính trực tiếp thể tích khối V2 ta sẽ khó áp
dụng công thức vì thế ta sẽ cắt khối chóp thành hai phần: + V S 1 là phần chứa đỉnh . + V  
2 là phần dưới mặt phẳng .
Gọi thể tích khối chóp .
S ABCD là V , vậy
V V V V V V . 1 2 2 1 LÊ MINH TÂM Trang 18
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Ví dụ 01.
Cho tứ diện đều ABCD có cạnh bằng 1. Trên
AB và CD lần lượt lấy các điểm M và N sao
cho MA MB  0 và NC  2  ND . Mặt phẳng
P chứa MN và song song với AC chia khối
tứ diện ABCD thành hai khối đa diện, trong đó
khối đa diện chứa đỉnh A có thể tích là V . Tính V . 2 A. V  11 2 . B. V  . 18 216 7 2 C. V  2 . D. V  . 216 108 Lời giải Chọn B
Từ N kẻ NP//AC , N AD
M kẻ MQ//AC , Q BC . Mặt phẳng P là MPNQ 1 2 Ta có VAH.SABCD 3 ABCD 12 V VVVV ACMPNQ AMPC MQNC MPNC AM AP Ta có V  1 2 1 . .V  . VV AMPC ABCD AB AD 2 3 ABCD 3 ABCD 1 1 CQ CN VV  1 1 2 1 . .V  . VV MQNC 2 AQNC 2 ABCD CB CD 2 2 3 ABCD 2 ABCD 2 2 1 AM VV  2 1 . V  2 1 1 1 . .V  . VV MPNC 3 MPCD 3 3 MACD 3 3 ABCD AB 3 3 2 ABCD 9 ABCD  1 1 1  11 11 2 Vậy V     VV V  .  3 6 9 ABCD  18 ABCD 216
Ví dụ 02. Cho hình chóp .
S ABCD có đáy ABCD là hình S
vuông cạnh a , SA a và SA  ABCD. Gọi M
là trung điểm SB , N là điểm thuộc cạnh SD
sao cho SN  2ND. Tính thể tích V của tứ diện M ACMN . 3 a 3 a A. V  . B. V  . 12 6 A N B 3 a 3 a C. V  . D. V  . O 8 36 D C Trang 19 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN Lời giải Chọn A
M là trung điểm SB , N là điểm thuộc cạnh SD sao cho SN  2ND nên SM 1 SN 2  ,  SB 2 SD 3 Ta có: V  2V  2 VVVV C.AMN O.AMN
S.ABD S.AMN M.AOB N.AOD Lại có: 3 3 3 1 a a a V  . . SA A . B AD   V  , VVS.ABCD 3 3 S.ABD 6 S.AOB S.AOD 12 3 V SM SN 1 2 1 1 a S.AMN  .  .   VVV SB SD 2 3 3 S.AMN 3 S.ABD 18 S.ABD 3 V MB 1 1 a M.AOB    VVM.AOB S.AOB V SB 2 2 24 S.AOB 3 V ND 1 1 a N.AOD    VVV SD 3 N.AOD 3 S.AOD 36 S.AOD 3 3 3 3 3  a a a a a Do đó: V  2V  2      C.AMN O.AMN . 6 18 24 36 12  
Ví dụ 03. Cho hình chóp .
S ABCD có đáy ABCD là hình
chữ nhật với cạnh AD  2CD . Biết hai mặt
phẳng SAC , SBD cùng vuông góc với mặt
đáy và đoạn BD  6 ; góc giữa SCD và mặt
đáy bằng 60. Hai điểm M, N lần lượt là trung
điểm của SA,SB . Thể tích khối đa diện ABCDMN bằng 108 15 128 15 A. . B. . 25 15 16 15 18 15 C. . D. . 15 5 Lời giải Chọn D
Gọi O AC BD. Do SAC  ABCD ,SBD  ABCD  SO  ABCD . 6
Theo tính chất hình chữ nhật: 2 2 2
AD CD BD 2 2
 5CD  6  CD  12 và AD  . 5 5 72
Khi đó diện tích đáy: SA . D CD  . ABCD 5
Gọi I là trung điểm của CD . Do CD SO,CD OI CD  SOI CD SI
  SCD,ABCD  SI,OI  SIO  60 . LÊ MINH TÂM Trang 20
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN AD 6
Trong tam giác SOI vuông tại O , OI   ,SIO  60 6 3
có: SO OI.tan 60  . 2 5 5 1 1 72 6 3 144 15 Thể tích .
S ABCD là: V  .S .SO  . .  ABCD . 3 3 5 5 25 V Ta có VV  . S.ABD S.BCD 2 1 Do S  1 1 SVVV . SMN 4 SAB SMND 4 SABD 8 1
Do N là trung điểm của SB dN,SCD  1 1
dB,SCD  VVV . 2 SCDN 2 SBCD 4 3 Ta có: VVV  3 5 18 15 V V
V V V  . S.CDMN SMND SCDN 8 ABCDMN 8 8 5
Ví dụ 04. Cho hình chóp .
S ABCD có ABCD là hình thoi
cạnh a và ABC  60 . Biết rằng SA SC ,
SB SD và SAB  SBC . G là trọng tâm tam
giác SAD . Tính thể tích V của tứ diện GSAC . 3 a 2 A. V 96 3 a 2 B. V 48 3 a 2 C. V 24 3 a 2 D. V 12 Lời giải Chọn B 1 Ta có V
dG,SAC.S . GSAC 3 SAC * Tính S ? SAC SA
SC SO AC
Gọi O AC BD, do 
SO  ABCD .
SB SD SO   BD
Kẻ OH SB, do AC  SBD nên SB   AHC . Suy ra 
SAB ,SBC   AH,CH  AHC  90 .
Do OH AC và OH là trung tuyến nên tam giác AHC vuông cân tại H . 1 a a
Khi đó OH AC  3 và OB  . 2 2 2 1 1 1 a 6
Mà tam giác SOB vuông tại O có đường cao OH nên    SO  . 2 2 2 OH OS OB 4 Trang 21 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN 2 1 1 a 6 a 6 Vậy S  .S . O AC  . .a  . SAC 2 2 4 8
* Tính dE,SAC ?
d G,SAC  SG 2
Gọi E là trung điểm của AD thì   .
d E,SAC SE 3 a
Gọi F là trung điểm của OA thì EF  SAC  dE,SAC 1 3
EF OD  . 2 4 2 2 a 3 a 3
Suy ra dG,SAC  dE,SAC  .  . 3 3 4 6 a a a Vậy V
dG,SAC 2 3 1 1 3 6 2 .S  . .  . G.SAC 3 SAC 3 6 8 48
Ví dụ 05.
Cho tứ diện đều ABCD cạnh a . Mặt phẳng P
chứa cạnh BC cắt cạnh AD tại E . Biết góc giữa
hai mặt phẳng P và BCD có số đo là thỏa 5 2 mãn tan 
. Gọi thể tích của hai tứ diện 7
ABCE và tứ diện BCDE lần lượt là V V 1 và 2 . V Tính tỉ số 1 . V2 1 3 A. . B. . 8 5 5 3 C. . D. . 8 8 Lời giải Chọn B
Gọi H , I lần lượt là hình chiếu vuông góc của A , E trên mặt phẳng BCD . Khi đó
H , I DM với M là trung điểm BC . a 6 a a
Ta tính được AH  3 , DH  3 , MH  . 3 3 6 EI
Ta có góc giữa P với BCD   P ,BCD  EMD  5 2 . Khi đó tan   . MI 7  a 6  . x . DE AH x 6 3 EI     Gọi DE DE EI DI x    AD a 3   . AD AH DHa 3 . x  . DE DH x 3 3 DI     AD a 3 a 3 x 3
Khi đó MI DM DI   . 2 3 LÊ MINH TÂM Trang 22
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN x 6 EI 5 2 5 2 5 Vậy tan   3    x a . MI 7 a 3 x 3 7 8  2 3 V DE 5 V Khi đó: DBCE   3 ABCE   . V AD 8 V 5 ABCD BCDE
Ví dụ 06.
Cho tứ diện ABCD và các điểm M , N , P lần
lượt thuộc các cạnh BC , BD , AC sao cho
BC  4BM , AC  3AP , BD  2BN . Tính tỉ số thể
tích hai phần của khối tứ diện ABCD được
phân chia bởi mpMNP . 7 A. . 13 7 B. . 15 8 C. . 15 8 D. . 13 Lời giải Chọn A
Gọi E MN CD , Q EQ AD , do đó mặt phẳng MNP cắt tứ diện ABCD theo thiết
diện là tứ giác MNQP . 1
Gọi I là trung điểm CD thì NI CB và NI BC , 2 Do BC  2
4BM nên suy ra NI MC . 3 EN EI NI 2 Bởi vậy    . EM EC MC 3 EI 2 ED
Từ I là trung điểm CD và  1 suy ra  . EC 3 EC 3 EK KD ED
Kẻ DK AC với K  1 EP , ta có    . EP AC EC 3 KD QD QK KD Mặt khác AC  2 3AP nên suy ra  2 . Do đó    . AP 3 QA QP AP 3 QK 2 EK EQ Từ  1 và  3 suy ra  . QP 3 EP 3 EP 5
Gọi V là thể tích khối tứ diện ABCD , V ABMNQP V
1 là thể tích khối đa diện , 2 là thể
tích khối đa diện CDMNQP . Trang 23 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN S CM CP 3 2 1 1 Ta có CMP  .  .   SS CMP CAB . S CB CA 4 3 2 2 CAB ED 1 3 Vì  nên d ;
E ABC  dD;ABC . Do đó : EC 3 2 1 VS .d ; E ABC  . S . .d ; D ABC  . S .d ; D ABC V E.CMP CMP    1 1 3 CAB    3 1 CAB    3 . 3 3 2 2 4 3 4 VE.DNQ ED EN EQ 1 2 3 2  . .  . .  2 2 3 1 , nên suy ra VV  . V V . V EC EM EP 3 3 5 15 E.DNQ 15 E.CMP 15 4 10 E.CMP 3 1 13
Từ đó ta có V VVV V V 2 . E.CMP E.DNQ 4 10 20 13 7
Và V V V V V V 1 2 . 20 20 V 7 Như vậy : 1  V 13 2
Dạng toán 6. THỂ TÍCH LĂNG TRỤ ĐỨNG.
Phương pháp giải
 Áp dụng công thức chính: V  . S h .
Trong đó: S là diện tích đáy và h là chiều cao khối chóp (khoảng cách từ đỉnh đến mặt đáy).
 Tính được diện tích đáy ta xem lại “Công thức tính diện tích đáy”
 Lăng trụ đứng sẽ có các đường cao song song nhau, tùy vào trường hợp đề ra ta sẽ sử
dụng đường cao hợp lý. Định nghĩa Tính chất
Các mặt bên của hình lăng trụ đứng
Là hình lăng trụ có cạnh bên
Hình lăng trụ đứng
là các hình chữ nhật và vuông góc
vuông góc với mặt đáy. với mặt đáy.
Các mặt bên của hình lăng trụ đều
Là hình lăng trụ đứng có đáy là
Hình lăng trụ đều
là các hình chữ nhật bằng nhau và đa giác đều.
vuông góc với mặt đáy.
 Xem lại cách xác định góc giữa đường – mặt; mặt – mặt để tính được chiều cao.
Ví dụ 01.
Khối lăng trụ có đáy là hình vuông cạnh a, đường cao bằng a 3 có thể tích bằng 3 a 3 3 a 3 A. . B. 3 a 3 . C. 3 2a 3 . D. . 3 6 Lời giải Chọn B 2 3 V  .
S h a .a 3  a 3. LÊ MINH TÂM Trang 24
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Ví dụ 02.
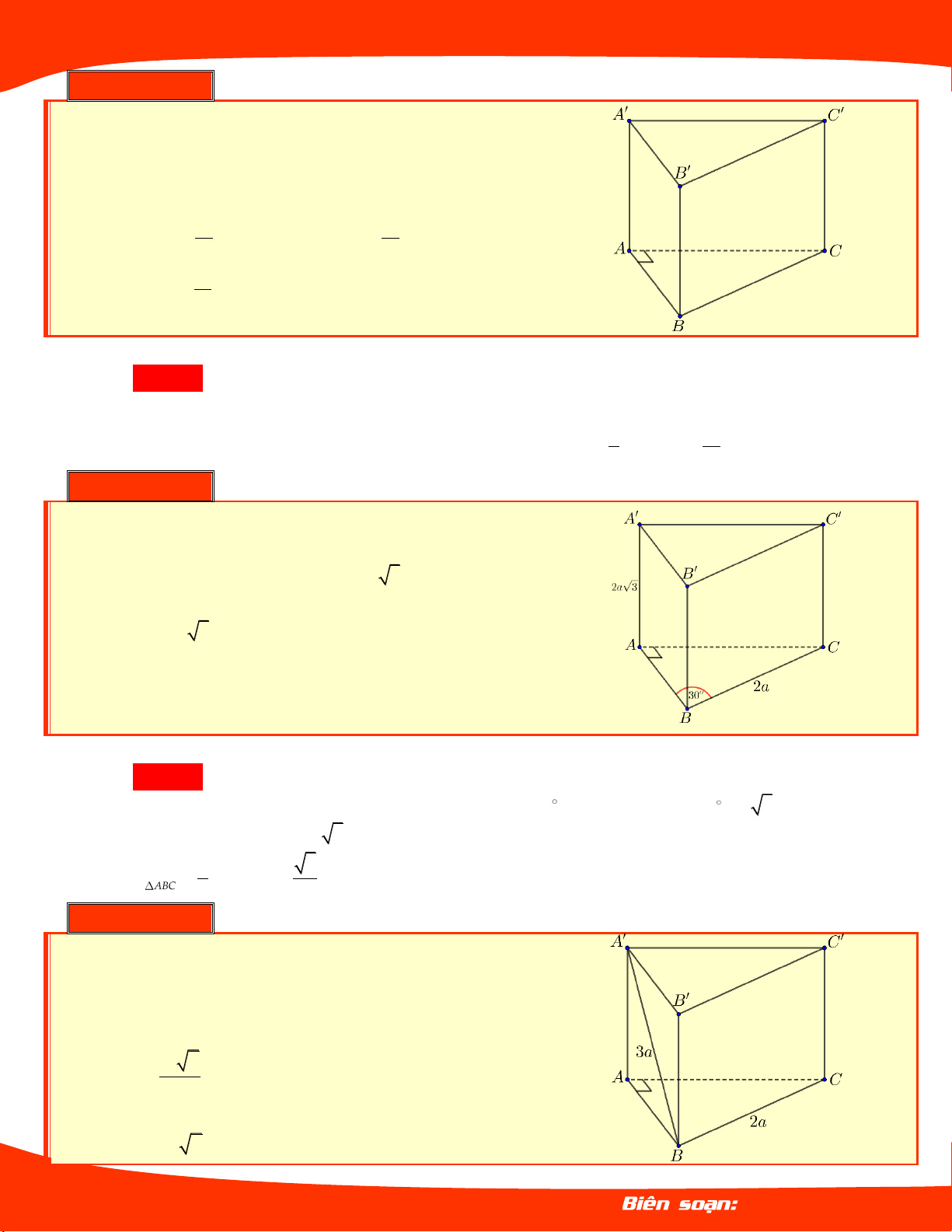
Cho hình lăng trụ đứng AB . C A BC
  có AA  a .
Đáy ABC là tam giác vuông cân tại A và
AB a . Tính thể tích V của khối lăng trụ đã cho. 3 a 3 a A. V  . B. V  . 3 6 3 a C. V  . D. 3
V a . 2 Lời giải Chọn C Theo giả thiết AB . C A BC
  là lăng trụ đứng có đáy là tam giác ABC vuông cân tại A . 3 1 a
Suy ra thể tích của khối lăng trụ là V AA .SAA . .A . B AC  . ABC 2 2
Ví dụ 03.
Cho lăng trụ đứng AB . C A BC
  có đáy ABC là tam giác vuông tại ; A BC  2 ;
a ABC  30 . Biết
cạnh bên của lăng trụ bằng 2a 3 . Thể tích khối lăng trụ là. A. 3 2a 3 . B. 3 3a . C. 3 3a . D. 3 6a . Lời giải Chọn C Xét tam giác AB .
C vuông tại A có AC  2 . a s 3
in 0  a; AB  2 . a co 3 s 0  a 3..
Trong đó h AA  2a 3. . 1 3 2 SABAC a . Vậy 3 V  3a . ABC 2 2 lt
Ví dụ 04.
Cho lăng trụ đứng AB .
C A' B'C' có đáy ABC là
tam giác vuông cân tại A, BC  2a, A' B  3 . a Thể
tích của khối lăng trụ AB .
C A' B'C' bằng? A. 3 2a . 3 a 2 B. . 3 C. 3 6a . D. 3 a 7 . Trang 25 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN Lời giải Chọn D BC
Tam giác ABC vuông cân tại A AB AC   a 2.. 2
Tam giác A' AB vuông tại 2 2 2 2
A A' A A' B AB  9a  2a a 7 . 1 a 7 3  VA' . A Sa 7. A . B AC
.a 2.a 2  a 7. .
ABC.A'B'C' ABC 2 2
Ví dụ 05.
Cho khối lăng trụ đứng AB . C A BC   có đáy là
tam giác vuông ABC vuông tại A , AC a ,
ACB  60 . Đường thẳng BC tạo với mặt phẳng
A CCA góc 30. Tính thể tích khối lăng trụ đã cho. 3 a 3 A. 3 a 6 . B. . 2 3 a 3 C. D. 3 2 3a . 3 Lời giải Chọn A
Ta có AB a 3 , dễ thấy góc giữa đường thẳng BC tạo với mặt phẳng A CCA là góc BC A   30 . a 3 Suy ra tan30 
AC  3a C C   2 2a . AC 1 Vậy V  2 2 3     . a .
a a 3 a 6 . ABC.A B C 2
Ví dụ 06.
Cho lăng trụ đứng AB . C A BC
  có đáy ABC là
tam giác vuông tại A , AB  2a, AC  3a . Mặt phẳng A B
C hợp với mặt phẳng A BC   một
góc 60. Tính thể tích khối lăng trụ đã cho. 3 6a 39 3 18a 39 A. . B. . 13 13 3 9a 39 3 3a 39 C. . D. . 26 26 Lời giải Chọn B LÊ MINH TÂM Trang 26
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN AA B
CA BC    Ta có B C  //BC  A B
CA BC
   A d//BC//B C   . B C    A BC
 ;BC  A BC  Dựng A H   B C    A H   Ad . Dựng A K
  BC A K   A d  .
Góc mặt phẳng A B
C với mặt phẳng A BC   là KA H   KA H   60 . 2 2 A B   .A C   6 13 Ta có A H    a . 2 2 A B    A C   13 6 39
Ta có BB  HK  tan 60 .  A H   a . 13 1 1 6 39 18 39 Vậy 3 V          BB .S A . B AC.BB 2a 3 . a a a . ABC.A B C ABC 2 2 13 13
Ví dụ 07.
Cho khối lăng trụ đứng AB . C A BC   có đáy
ABC là tam giác cân với AB AC a ,
BAC 120 , mặt phẳng A BC
  tạo với đáy một
góc 60. Tính thể tích V của khối lăng trụ đã cho. 3 3 3a 3 3a A. V  . B. V  . 8 8 3 9a 3 a 3 C. V  . D. V  . 8 8 Lời giải Chọn D
Gọi M , I , I lần lượt là trung điểm của A C
  , BC , B C   .
D là điểm đối xứng với A qua I , D là điểm đối xứng với A qua I.
Khi đó mặt phẳng A B
C  A BDC .
góc giữa mặt phẳng A BC với đáy là góc giữa mặt phẳng A B
DC với đáy. Ta có tứ giác A BDC   là hình thoi Vì B AC
   120 nên tam giác A CD
  là tam giác đều cạnh bằng a D M   A C   . Mà A C    DD Nên A C    DM
Vậy góc giữa mặt phẳng A B
DC với đáy là góc DMD  60  a 3 D M    C I  Xét tam giác A CD   , có: 2   C B    a 3  a A I     2 Trang 27 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Xét tam giác MDD vuông tại D có DMD  60  DMD là nửa tam giác đều có a đường cao DD 3
DD  D . M 3  . 2 2 1 1 a a 3 S           A I .B C . .a 3 . A B C 2 2 2 4 2 3 1 1 a 3 3a a 3 V        S   .DD . . . ABC.A B C 3 A B C 3 4 2 8
Ví dụ 08.
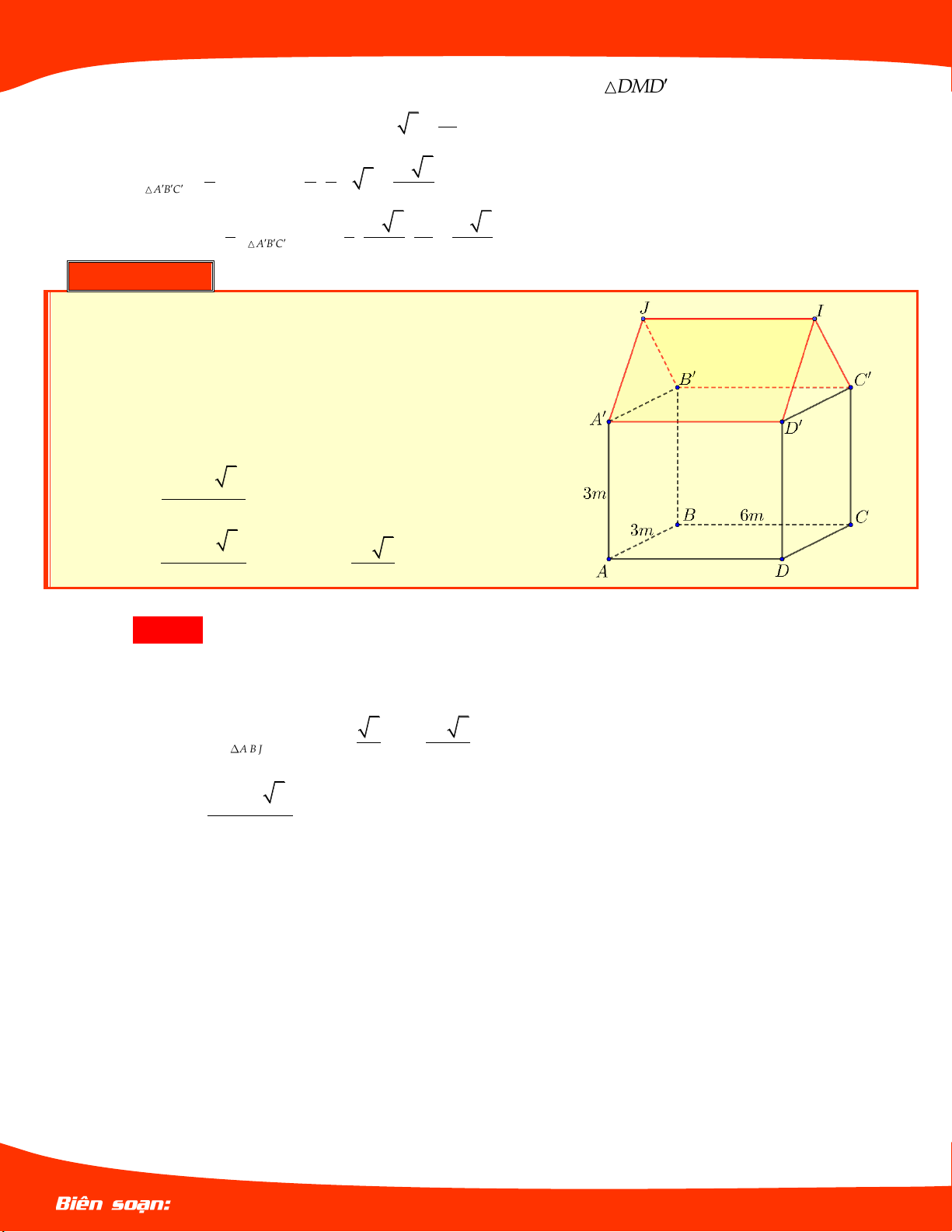
Một nhà kho có dạng khối hộp chữ nhật đứng ABC . D A BCD
  , nền là hình chữ nhật ABCD có
AB  3m , BC  6m , chiều cao AA  3m , chắp
thêm một lăng trụ tam giác đều mà một mặt bên là A BCD   và A B
  là một cạnh đáy của
lăng trụ. Tính thể tích của nhà kho ? 9 12  3 A. 3 m . B. 54 3 m . 2 27 4  3 27 3 C. 3 m . D. 3 m . 2 2 Lời giải Chọn C Ta có : VV      V     kho ABCD.A B C D A B J.D C I V    3 3 . 6 .  54 3     A . B A . D A A m . ABC . D A B C D  3  27 3 V    2    3      S   .A D 3 . 6 . m . A B J.D C I A B J  4    2 27 4  3 3  V  m kho 2 LÊ MINH TÂM Trang 28
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Dạng toán 7. THỂ TÍCH LĂNG TRỤ XIÊN.
Phương pháp giải
 Áp dụng công thức chính: V  . S h .
Trong đó: S là diện tích đáy và h là chiều cao khối chóp (khoảng cách từ đỉnh đến mặt đáy).
 Tính được diện tích đáy ta xem lại “Công thức tính diện tích đáy”
 Lăng trụ xiên sẽ có các đường cao đề ra cụ thể.
 Xem lại cách xác định góc giữa đường – mặt; mặt – mặt để tính được chiều cao.
Ví dụ 01.
Cho hình lăng trụ tứ giác ABC . D A BCD
  có đáy ABCD là hình vuông cạnh a và thể tích bằng 3
3a . Tính chiều cao h của lăng trụ đã cho. a
A. h  9a .
B. h  .
C. h a .
D. h  3a . 3 Lời giải Chọn D V 3 3a Ta có: VABCD.A BCD           S .h h 3a . ABC . D A B C D ABCD S 2 a ABCD
Ví dụ 02.
Cho lăng trụ tam giác AB . C A BC   có đáy là tam
giác đều cạnh a . Độ dài cạnh bên bằng 4a . Mặt phẳng BCC B
  vuông góc với đáy và B B
C  30 . Thể tích khối chóp . A CC B   là: 3 a 3 3 a 3 A. . B. . 2 12 3 a 3 3 a 3 C. . D. . 18 6 Lời giải Chọn D
Gọi H là hình chiếu của B trên BC . Từ giả thiết suy ra: B H   ABC . 1 1 S      2   BB .B . C sin B BC 4 . a . a sin 30 a . BB C 2 2 1 2S 2 2a Mặt khác: S   BB C        B H.BC B H 2a . BB C 2 BC a 2 a 3 3 a 3 V B . H S  2 . a  . LT ABC 4 2 1 3 1 a 3 3 a 3 V  1 2 1       V   . V V . . A.CC B 2 A.CC B B 2 3 LT 3 LT 3 2 6 Trang 29 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Ví dụ 03. Cho lăng trụ AB . C A BC
  có đáy ABC là tam
giác đều cạnh bằng a , biết A A   A B   A C   a.
Tính thể tích khối lăng trụ AB . C A BC  ? 3 3a A. . 4 3 a 2 B. . 4 3 a 3 C. . 4 3 a D. . 4 Lời giải Chọn B
Gọi H là trọng tâm tam giác ABC .
Theo giả thiết ta có ABC là tam giác đều cạnh bằng a và A A   A B   A C   a nên
A .ABC là tứ diện đều cạnh a A H
  ABC hay A H
 là đường cao của khối chóp A .ABC . a
Xét tam giác vuông A HA ta có 2 2 A H   A A   6 AH  . 3 1 2 a 3
Diện tích tam giác ABC là S  . a . a sin 60  . ABC 2 4 2 a 3 a 6 3 a 2
Thể tích khối lăng trụ AB . C A BC   là V      . ABC.A B C 4 3 4
Ví dụ 04.
Cho hình lăng trụ AB . C A BC
  có đáy ABC là
tam giác vuông tại A . cạnh BC  2a và
ABC  60 . Biết tứ giác BCC B   là hình thoi có B B
C nhọn. Biết BCC B
  vuông góc với ABC và ABB A
  tạo với ABC góc 45. Thể tích của khối lăng trụ AB . C A BC  bằng 3 a 3 a A. . B. . 3 7 7 3 3a 3 6a C. . D. . 7 7 Lời giải Chọn C
Do ABC là tam giác vuông tại A, cạnh BC  2a và ABC  60 nên AB a , AC a 3 .
Gọi H là hình chiếu vuông góc của B lên BC H thuộc đoạn BC (do B BC nhọn) LÊ MINH TÂM Trang 30
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN  B H
  ABC (do BCC B
  vuông góc với ABC ).
Kẻ HK song song AC K AB  HK AB (do ABC là tam giác vuông tại A ).     ABB A
 ,ABC  B K
H  45  B H   KH (1)   Ta có BB H  vuông tại H 2 2
BH  4a B H  (2) BH HK HK. a
Mặt khác HK song song AC   2  BH  (3) BC AC a 3 B H  2 . a Từ (1), (2) và (3) suy ra 2 2 4a B H   12  B H   a . a 3 7 3 1 3a Vậy V       S .B H A . B AC.B H .
ABC.A' B'C ABC 2 7
Ví dụ 05. Cho lăng trụ AB . C A BC
  có đáy ABC là tam
giác vuông tại A , ABC  30 . Điểm M là
trung điểm AB , tam giác MA C  đều cạnh
2a 3 và nằm trong mặt phẳng vuông góc với
đáy. Thể tích khối lăng trụ AB . C A BC   là 3 72 2a 3 24 3a A. . B. . 7 7 3 72 3a 3 24 2a C. . D. . 7 7 Lời giải Chọn A
Gọi H là trung điểm của MC . A H   MC  Ta có   A MC    ABC  A H   ABC. A MC   ABC   MC
MC  2a 3 Tam giác MA C
 đều cạnh 2a 3   A H   3a BC  2x
Đặt AC x  0 , tam giác ABC vuông tại A có ABC  30   AB x 3
Áp dụng công thức tính độ dài trung tuyến ta có 2 2 2 2 2 2 CA CB AB x  4x 3x 4a 3 2 2 CM    12a    x  . 2 4 2 4 7 2 1 1 12a 4a 3 24a 3 Suy ra SA . B AC  . .  . ABC 2 2 7 7 7 3 72a 3 Do đó V       A H.S . ABC.A B C ABC 7 Trang 31 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Ví dụ 06.
Cho hình lăng trụ tam giác AB . C A BC   có đáy
ABC là tam giác đều cạnh 2a, hình chiếu của
A trên mặt phẳng ABC là trung điểm cạnh
BC . Biết góc giữa hai mặt phẳng ABA và
ABC bằng 45. Tính thể tích V của khối chóp . A BCC B   . 3 A. 3 a . B. 3
V a . 2 3 2 3a C. 3 a 3 . D. . 3 Lời giải Chọn B Ta có : V        V    V   V V    . ABC.A B C A.A B C A.BCC B A .ABC A .BCC B Mà V       V  
V    V  . A .BCC B . A BCC B . A A B C A .ABC
Gọi M là trung điểm của BC , I là trung điểm của AB và K là trung điểm của IB . Khi đó : A M   ABC. MK // CI  Mặt khác :
  MK AB . CI AB
MK AB , A M
  AB A K   AB.
Góc giữa hai mặt phẳng ABA và ABC chính là góc giữa A K  và KM và bằng A K
M  45 nên tam giác A K
M vuông cân tại M . 1 1 2a 3 a 3
Trong tam giác ABC : MK CI  .  . 2 2 2 2 a
Trong tam giác vuông cân A K  3 M : A M   MK  . 2 1 V   .V    . A .ABC 3 ABC.A B C 1 2 2 2 a 3 2 3  V           V    V    V    .S .A M .a 3. a  . A .BCC B ABC.A B C 3 ABC.A B C 3 ABC.A B C 3 ABC 3 2 LÊ MINH TÂM Trang 32
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Dạng toán 8. THỂ TÍCH KHỐI LẬP PHƯƠNG – KHỐI HỘP.
Phương pháp giải
 Áp dụng công thức chính: V  . S h .
Trong đó: S là diện tích đáy và h là chiều cao khối chóp (khoảng cách từ đỉnh đến mặt đáy).
● Thể tích khối hộp chữ nhật: V  . a . b c .
● Thể tích khối lập phương cạnh a: 3 V a . Định nghĩa Tính chất
Là hình hộp có cạnh bên vuông
Có 2 đáy là hình bình hành, 4 mặt
Hình hộp đứng góc với mặt đáy
xung quanh là 4 hình chữ nhật.
Là hình hộp đứng có đáy là
Hình hộp chữ nhật
Có 6 mặt là 6 hình chữ nhật. hình chữ nhật.
Là hình hộp chữ nhật 2 đáy và 4
Hình lập phương
Có 6 mặt đều là hình vuông.
mặt bên đều là hình vuông
 Đường chéo hình hộp 2 2 2
d r c với d;r ;c là ba kích thước của hình hộp.
Hệ quả: Đường chéo hình lập phương  a 3 với a là cạnh của hình lập phương.
Ví dụ 01.
Tổng diện tích các mặt của một hình lập phương bằng 150. Thể tích của khối lập phương đó là. A. 200 . B. 100. C. 625. D. 125. Lời giải Chọn D
Gọi cạnh hình lập phương là a . Ta có 2
6a 150  a  5 .
Thể tích khối lập phương là 3
V a 125 .
Ví dụ 02.
Tính theo a thể tích V của khối lập phương ABC . D A BCD
  biết AC  .a 3 a A. V  . 27 3 3a B. V  . 3 C. 3
V  3 3a . 3 3a D. V  . 9 Lời giải Chọn D a
Ta có AC  AB 3  AB  . 3 Trang 33 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN 3 3 3  a a a 3
Thể tích khối lập phương là: 3 V AB      .  3  3 3 9
Ví dụ 03.
Cho hình lập phương ABC . D A BCD   có diện
tích tam giác ACD bằng 2 a
3 . Tính thể tích V của hình lập phương. A. 3
V  3 3a . B. 3
V  2 2a . C. 3
V a . D. 3
V  8a . Lời giải Chọn B
Giả sử cạnh của hình lập phương có độ dài là x . x 6
Ta có AC x 2 , 2 2
OD  OD A A   2 2 1 1 x 6 x 3
Diện tích tam giác ACD là S      OD .AC x 2. . ACD 2 2 2 2 2 2 x 3 x Khi đó, ta có 2 2 a 3   a   x a 2 . 2 2 Vậy 3 3
V x  2a 2 .
Ví dụ 04.
Cho hình lập phương ABC . D A BCD   . Tính thể
tích V của hình lập phương biết rằng khoảng
cách từ trung điểm I của AB đến mặt phẳng  a A BCD bằng . 2 3 a A. V  . 3 B. 3 V a 2 . C. 3
V  2a . D. 3
V a . Lời giải Chọn D
Gọi các điểm như hình vẽ bên trong đó IH I J . x a
Đặt cạnh AB x suy ra IH  
x a . Vậy 3 V a . 2 2 LÊ MINH TÂM Trang 34
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Ví dụ 05.
Cho hình lập phương ABC . D A BCD   , khoảng a
cách từ C đến mặt phẳng A B  4 3 D bằng . 2
Tính theo a thể tích khối lập phương ABC . D A BCD  . A. 3
V  8a . B. 3 V  3 3 a . C. 3 V  8 3 a . D. 2
V  216a . Lời giải Chọn A
Gọi I là giao điểm của AC và . BD
Trong mặt phẳng ACC A
  ; AC cắt A I tại . G
Do AI song song AC 1 và AI  1
AC nên IG G . A 2 2
Suy ra G là trọng tâm tam giác A BD, Mà tam giác A B
D đều (có các cạnh là các đường chéo của những hình vuông bằng nhau)
Nên GA  GB GD và AA  AB AD
Suy ra AG  (A BD  ).
Do đó khoảng cách từ C đến mặt phẳng A B
D là C' . G 2 2 4a 3
Mặt khác C 'G AC '  AB 3   AB  2 . a Vậy 3
V  8a . 3 3 3
Ví dụ 06.
Cho hình lập phương ABC .
D A' B'C' D' cạnh a .
Các điểm M, N, P theo thứ tự đó thuộc các cạnh a
BB', C' D', DA   
sao cho BM C ' N DP . Tìm 3
diện tích thiết diện S của hình lập phương khi
cắt bởi mặt phẳng (MNP) . 2 11 3a 2 5 3a A. S  . B. S  . 18 18 2 13 3a 2 17 3a C. S  . D. S  . 18 18 Lời giải Chọn A Trang 35 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN    BM MB BB Ta có  
1, do đó theo định lý ta-let trong không gian thì BC , C NNDC D   MN , B D
  lần lượt cùng song song với một mặt phẳng.  Mà B D  //BC D
  và BC  BC D
  nên ta có MN//BC D   .
 Chứng minh tương tự ta có NP// BC D   .
Do đó MNP // BC D  .
 Qua P , kẻ PQ//BD,QAB . Qua N , kẻ NF//C D  ,F D D  .
 Qua M , kẻ ME//BC,EB C   .
Khi đó ta có thiết diện tạo bởi mặt phẳng MNP với hình lập phương là lục giác MENFPQ . a 2 a
Dễ thấy EN PF MQ  2 2
, NF PQ ME  và tam giác BC D  là tam giác 3 3
đều vì BC  BD DC  a 2 .
Do đó ENF NFP FPQ PQM QME MEN  60 2 a Suy ra: 2 2 2 2
EF EN NF  2.EN.NF.cos 60  6 a EF  . 3 3 a 6
Tương tự thì FQ QE  . 3 2 1 2a 2 a 2 3 3 2a 5 3 Ta có S  3.SS  3. . . .  . 2  a . MENFPQ ENF EFQ 2 3 3 2 4 3 18 LÊ MINH TÂM Trang 36
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Dạng toán 9. KHỐI ĐA DIỆN ĐƯỢC CẮT RA TỪ KHỐI LĂNG TRỤ.
Phương pháp giải
A. Một số mối liên hệ thường gặp giữa chóp – lăng trụ và chóp – thể tích:
Mối liên hệ giữa Công thức
Hình minh họa 2 VV 5d 3 L.Tr C
4 điểm thuộc mặt đáy Chóp Lăng trụ 1 VV 4d 3 L.Tr C
3 điểm thuộc mặt đáy 1 VV 4d 6 Hop C
Với 3 điểm thuộc đáy và 1 điểm thuộc mặt bên Chóp Hình hộp 1 VV 4d 3 Hop C
Với 3 điểm thuộc mặt chéo Trang 37 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN 1 VV 5d 3 Hop C
Với 4 điểm thuộc mặt bên hoặc mặt đáy 1 VV 5d 3 Hop C
Với 4 điểm thuộc mặt chéo
B. Mặt phẳng cắt các cạnh của khối lăng trụ tam giác AB . C A BC
  lần lượt tại M;N;P sao cho AM BN CP  ;  ;  : AABBCCV   ABC.MNP V 3 ABC.A BC  
C. Mặt phẳng cắt các cạnh của khối hộp ABC . D A BCD
  lần lượt tại M;N;P;Q sao cho AM BN CP DQ  ;  ;  ;  : AABBCCDDV    ABCD.MNPQ V 4 ABCD.A BCD   và    . LÊ MINH TÂM Trang 38
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Ví dụ 01.
Hình lập phương ABCDA BCD
  cạnh a . Tính
thể tích khối tứ diện ACB D   . 3 a A. . 4 3 a B. . 2 3 a C. . 6 3 a D. . 3 Lời giải Chọn D Ta có V        V     V
V    V V ACB D ABCD.A B C D
B.ABC C.BCD D.ACD A.ABD. 1 1 1 1 Mà 3 V  2 3            a và V
V    V V    .A . A S    . . a a a . ABCD.A B C D B .ABC C.B C D D .ACD A.A B D 3 A B D 3 2 6 3 4 a Do đó 3 3 V      a a . ACB D 6 3
Ví dụ 02.
Cho hình lập phương ABC . D A BCD   cạnh
bằng a . Gọi O là giao điểm của AC và BD . Thể
tích của tứ diện OA BC bằng 3 a 3 a A. . B. . 6 4 3 a 3 a C. . D. . 12 24 Lời giải Chọn C 3 1 1 a 2 a 2 a V       V AA .O . B OC . . a . O.A BC A'.OBC 6 6 2 2 12
Ví dụ 03.
Cho khối lăng trụ AB . C A BC
  có thể tích bằng
V . Tính thể tích khối đa diện ABCB C  . 2V V A. . B. . 3 2 V 3V C. . D. . 4 4 Trang 39 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN Lời giải Chọn A V V 2V Ta có: V        V V   ABCB C B ABC C B AC 3 3 3
Ví dụ 04.
Cho khối lăng trụ AB . C A BC
  có thể tích là V .
Gọi M là điểm bất kỳ trên đường thẳng CC .
Tính thể tích khối chóp V V M.ABB A   theo . V A. . 3 2V B. . 9 2V C. . 3 V D. . 2 Lời giải Chọn C Gọi h h . M ABC . M A BC  
h h h 1 ,
2 lần lượt là đường cao của hai hình chóp , thì 1 2 là
đường cao của lăng trụ AB . C A BC  . Ta có: V VV    V    M.ABC M.ABB A M.A B C 1 1 1 1  .S .h V         .S   .h S h h V   V V ABC 1 M.ABB A A B C 2 ABC  1 2    3 3 3 M.ABB A 3 M.ABB A 2V Suy ra V    . M.ABB A 3
Ví dụ 05.
Cho khối lăng trụ tam giác AB . C A BC  . Tính tỉ
số thể tích giữa khối đa diện A BCBC và khối lăng trụ AB . C A BC  . 1 A. . 3 1 B. . 2 5 C. . 6 2 D. . 3 Lời giải Chọn D LÊ MINH TÂM Trang 40
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN 1 Ta có: V   V        S .d A , ABC V V A B C .ABC ABC    1  .S .d A , ABC A .ABC ABC   ,    . 3 A .ABC 3 A B C .ABC Ta có: V   2    V    V    V    V    . A .ABC A B C BC A B C .ABC A B C BC 3 A B C .ABC
Ví dụ 06.
Cho khối lăng trụ tam giác AB . C A BC  . Gọi M
, N lần lượt là trung điểm của BB và CC . Mặt
phẳng AMN chia khối lăng trụ thành hai
phần. Gọi V1 là thể tích của khối đa diện chứa
đỉnh B và V2 là thể tích khối đa diện còn lại. V Tính tỉ số 1 . V2 V V 1 A. 1  2 . B. 1  . V V 3 2 2 V 5 V 7 C. 1  . D. 1  . V 2 V 2 2 2 Lời giải Chọn A
Gọi K là trung điểm của AA và V , V V ABC.KMN ,
lần lượt là thể tích khối lăng trụ . A MNK AB . C A BC
  khối lăng trụ AB .
C KMN và thể tích khối chóp . A MNK . Khi đó V VV . 2 ABC.KMN . A MNK 1 1 1 1 Lại có V  1 1 V ; VV
V suy ra V V V V từ đó ta có ABC.KMN 2 A.MNK 3 ABC.KMN 6 2 2 6 3 1 2 V
V V V V . Vậy 1  2 . 1 3 3 V2
Ví dụ 07.
Cho khối lăng trụ AB . C A BC
  có thể tích bằng
2018. Gọi M là trung điểm AA; N, P lần lượt
là các điểm nằm trên các cạnh BB , CC sao cho BN  2B N
 , CP  3C P
 . Tính thể tích khối đa diện AB . C MNP . 40360 A. . 27 4036 B. . 3 23207 C. . 18 32288 D. . 27 Lời giải Trang 41 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN Chọn C V 1  AM BN CP  23 23207
Ta có ABC.MNP       . Vậy V  . V 3    ABC.MNP     AA BB CC  36 18 ABC.A B C
Ví dụ 08.
Cho hình hộp chữ nhật ABC . D A BCD   có thể
tích bằng 1 và G là trọng tâm của tam giác
BCD . Thể tích V của khối chóp . G ABC' là 1
A. V  . 3 1
B. V  . 6 1 C. V  . 12 1 D. V  . 18 Lời giải Chọn D 1
Gọi M là trung điểm của BD theo tính chất trọng tâm của G ta có GM CM 3 1 1 1 1 1  1 1 1 V          VV  . .A . B C . B CC A . B BC.CC V     . G.ABC 3 C.ABC 3 A.BCC 3 3 2 18 18 ABCD.A B C D 18
Ví dụ 09.
Cho khối lăng trụ AB . C A BC   có thể tích 3
V  36 cm . Mặt phẳng AB C   và A BC chia
khối lăng trụ thành 4 khối đa diện. Tính thể
tích khối đa diện có chứa một mặt là hình bình hành BCC B   . A. 3 15 cm . B. 3 9 cm . C. 3 12 cm . D. 3 18 cm . Lời giải Chọn A
Gọi I AB  A B  , J A C   AC . Ta có VVV . IJBB'C 'C
A.BB'C 'C A.BCIJ Mặt khác V   2   2      V   V    V   V    V 24 . . A A B C . A BCC B ABC.A B C A.BCC B 3 ABC.A B C 3 VA.IJAAI AJ 1 1 1 Ta lại có  .   V    . 3 . 6 3 . V      AB AC 4 A.IJA 4 3 A.A B C LÊ MINH TÂM Trang 42
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN 1 VV      V 3  . 6 3 9 . A.IJBC A .ABC A.IJA 3 Vậy V    C C  3 24 9 15 cm IJBB' ' .
Ví dụ 10.
Cho hình lăng trụ AB . C A BC
 . Gọi M , N , P
lần lượt là các điểm thuộc các cạnh AA, BB ,
CC sao cho AM  2MA , NB  2NB , PC PC . Gọi V V 1 ,
2 lần lượt là thể tích của hai khối đa V
diện ABCMNP và A BCM
NP. Tính tỉ số 1 . V2 V V 1 A. 1  2 . B. 1  . V V 2 2 2 V V 2 C. 1  1. D. 1  . V V 3 2 2 Lời giải Chọn C
Gọi V là thể tích khối lăng trụ AB . C A BC
 . Ta có V VV 1 M.ABC M.BCPN . 1 V
S .d M, ABC  . S .d A, ABC V M.ABC ABC    1 2 ABC    2 . 3 3 3 9 1 V            
S   .d M, A B C
. S   .d M, A B C V M.A B C A B C    1 1 ABC    1 . 3 3 3 9 Do BCC B
  là hình bình hành và NB  2NB , PC  7 PC nên S    S . B C PN 5 BCPN 7 Suy ra V    V M.B C PN 5 M.BCPN
Từ đó V VVV     V   M.ABC M.BCPN M.A B C M.B C PN 2 1 7 5
V V VV VVV . 9 M.BCPN 9 5 M.BCPN M.BCPN 18 2 5 1 1 V
Như vậy V V
V V V V . Bởi vậy: 1  1. 1 2 9 18 2 2 V2 Trang 43 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Dạng toán 10. MAX – MIN THỂ TÍCH.
Phương pháp giải
 Ta có thể dùng các phương pháp sau: Dạng
Dấu “=” xảy ra khi a b BĐT
        2 2 2 2 2 a b c d ac bd c d Bunyakovskya a a
a a  ...  a b b  ... b   a b a b  ... a b 1 2   ... nn n n n 2 2 2 2 2 2 2 1 2 1 2 1 1 2 2 b b b 1 2 n
a b ab a b BĐT 2 AM – GM
a a  ...  a 1 2 n n
a .a .....a n  1
a a  ...  a 1 2 n   n 1 2 n
Khảo sát hàm
số trên khoảng Tính đạo hàm rồi lập BBT, từ đó kết luận theo yêu cầu bài toán. xác định
Ví dụ 01. Cho hình chóp .
S ABCD có đáy ABCD là hình
chữ nhật với AB  4 , cạnh bên SA vuông góc
với mặt phẳng đáy ABCD và SC  6. Tính thể tích lớn nhất V của khối chóp đã cho. max 40 A. V  . max 3 80 B. V  . max 3 20 C. V  . max 3 D. V  24. max Lời giải Chọn A Cách 1.
Đặt cạnh BC x  0. Tam giác vuông ABC, có 2 2
AC 16  x .
Tam giác vuông SAC, có 2 2 2
SA SC AC  20  x .
Diện tích hình chữ nhật SA . B BC  4 . x ABCD 1 4 Thể tích khối chóp 2 VS
.SA x 20  x . S.ABCD 3 ABCD 3 LÊ MINH TÂM Trang 44
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN x  20  x 2  2 2 2
Áp dụng BĐT Côsi, ta có . x 20  x  10 . 2 4 40 Suy ra V  10 .  . S.ABCD 3 3 Dấu "  " xảy ra 2
x  20  x x  40 10 . Vậy V  . max 3 4
Cách 2. Xét hàm số f x 2
x 20  x trên 0;2 5. 3
Ví dụ 02. Cho hình chóp .
S ABC có đáy ABC là tam giác
đều và có SA SB SC 1. Tính thể tích lớn nhất V của khối chóp đã cho. max 1 A. V  . max 6 2 B. V  . max 12 3 C. V  . max 12 1 D. V  . max 12 Lời giải Chọn C
Gọi O là tâm đường tròn ngoại tiếp tam giác đều AB . C Vì .
S ABC là hình chóp đều  SO  ABC . 2 x 3
Đặt AB x  0. Diện tích tam giác đều S  .  ABC 4 x 3 2 x 3
Gọi M là trung điểm BC AM
OA AM  . 2 3 3 2 x
Tam giác vuông SOA, có 2 2
SO SA OA  1 . 3 2 2 1 1 x 3 3  x 1 Khi đó 2 2 VS .SO  . .  .x 3  x S.ABC 3 ABC 3 4 3 12 1 1
Xét hàm f x 2 2  .x
3  x trên 0; 3 , ta được max f x  f  2  . 12 0; 3 6 3 2 2 2 1 1
x x  6  2x
Cách 2. Ta có 2 2 2 2 x 3  x x .x . 2 6  2x      2. 2 2 3   Trang 45 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Ví dụ 03. Cho hình chóp .
S ABCD có đáy ABCD là hình
chữ nhật với AB  4, SC  6 và mặt bên SAD
là tam giác cân tại S và nằm trong mặt phẳng
vuông góc với đáy. Tính thể tích lớn nhất V max của khối chóp đã cho. 40 A. V  . B. V  40. max 3 max C. V  80 80. D. V  . max max 3 Lời giải Chọn D
Gọi H là trung điểm của AD SH A .
D Mà SAD  ABCD  SH  ABCD. 2 x
Giả sử AD x  0 . Suy ra 2 2
HC HD CD  16. 4 2 x
Tam giác vuông SHC, có 2 2
SH SC HC  20  . 4 1 1 Khi đó VS .SH A . B A . D SH S.ABCD 3 ABCD 3 2 1 x 1  4 . .x 20    1 80 2
2x 80  x    2 2
x  80  x   . 3 4 3 3 3
Ví dụ 04.
Người ta cần trang trí một kim tự tháp hình chóp tứ giác đều .
S ABCD cạnh bên bằng 200m
, góc ASB 15 bằng đường gấp khúc dây đèn
led vòng quanh kim tự tháp AEFGHIJKLS .
Trong đó điểm L cố định và LS  40m (tham
khảo hình vẽ). Hỏi khi đó cần dung ít nhất bao
nhiêu mét dây đèn led để trang trí?
A. 40 67  40 mét. B. 20 111  40 mét.
C. 40 31  40 mét. D. 40 111  40 mét. Lời giải Chọn C
Ta sử dụng phương pháp trải đa diện
Cắt hình chóp theo cạnh bên SA rồi trải ra mặt phẳng hai lần, ta có hình vẽ sau LÊ MINH TÂM Trang 46
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Từ đó suy ra chiều dài dây đèn led ngắn nhất là bằng AL LS .
Từ giả thiết về hình chóp đều .
S ABCD ta có ASL  120 . Ta có 2 2 2 2 2
AL SA SL  2S . A S .
L cos ASL  200  40  2 2 . 00 4 . 0.co 1 s 20  49600 .
Nên AL  49600  40 31 .
Vậy, chiều dài dây đèn led cần ít nhất là 40 31  40 mét.
Ví dụ 05. Cho hình chóp .
S ABCD có đáy là hình bình
hành và có thể tích là V . Điểm P là trung điểm
của SC . Một mặt phẳng qua AP cắt hai cạnh
SB và SD lần lượt tại M và N . Gọi V1 là thể tích của khối chóp .
S AMPN . Tìm giá trị nhỏ V nhất của 1 . V 1 1 A. . B. . 3 8 2 3 C. . D. . 3 8 Lời giải Chọn A SM Đặt x SN , y
, 0  x, y   1 . SB SD V VV V VSM SP SN SP  1 Ta có 1 S.AMP S.ANPS.AMP S.ANP   1  .   .
  x y (1) V V 2V 2V 2  SB SC SD SC  4 S.ABC S.ADC V VV V V
SM SN SM SN SP  3 Lại có 1 S.AMN S.PMNS.AMN S.PMN   1  .   . .   xy (2). V V 2V 2V 2  SB SD SB SD SC  4 S.ABD S.CBD 1 3 x
Suy ra x y  xy x y  3xy y  . 4 4 3x 1 x 1
Từ điều kiện 0  y 1 , ta có 1, hay x  . 3x 1 2 Trang 47 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN 2 V 3 x
Thay vào (2) ta được tỉ số thể tích 1  . . V 4 3x 1 x  0 ( ) L x   2 3 3x  2x Đặt  f x 2 3 1  . , x  ;1 
 , ta có f x  .
, f x  0  2 . 4 3x 1  2  4   3x  2 1 x  (N)  3  1   2  1 V   ff   3 1    , f    , do đó 1 min  2 1
min f x  f    .  2  8  3  3 1 V    3  3 x 1  ;  2 
Ví dụ 06.
Cho hình hộp chữ nhật ABC . D A BCD   có
AB a, AD a 2 , AA  a 3 . Gọi G là trung
điểm của BD , mặt phẳng P đi qua G và cắt
các tia AD,CD, D B
  tương ứng tại ba điểm
phân biệt H, I,K . Tìm giá trị nhỏ nhất của 1 1 1 biểu thức T    . 2 2 2 D' H D' K D' I 1 4 A. T  . B. T  . 2 3a 2 a 4 1 C. T  . D. T  . 2 3a 2 12a Lời giải Chọn C D HD ID K  Đặt  x,  y,  z . D AD CD B   1 1 1 1 ta có D G   D B   D A   D C   D D  2 2 2 2 Ta có D H   xD A   xD D   1 D A    D H   D D   D Ax D I   yD C   yD D   1 D C
   D I  D D   D C   y D K   zD A   zD A    1 D C    D K   D A    D C   z 1 1 1  D G   D H   D I   D K  4x 4y 4z 1 1 1 D AD CD B
Do DG, DH, DI, DK không đồng phẳng nên   1     4 4x 4y 4z D HD ID K  2  D AD CD B    1 1 1  2  4        2 2 2 D A   D C       D B   2 2 2   D HD ID K    D HD ID K   16 16 4  T    2 2 2 2 2 D A   D C   D B   12a 3a LÊ MINH TÂM Trang 48
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
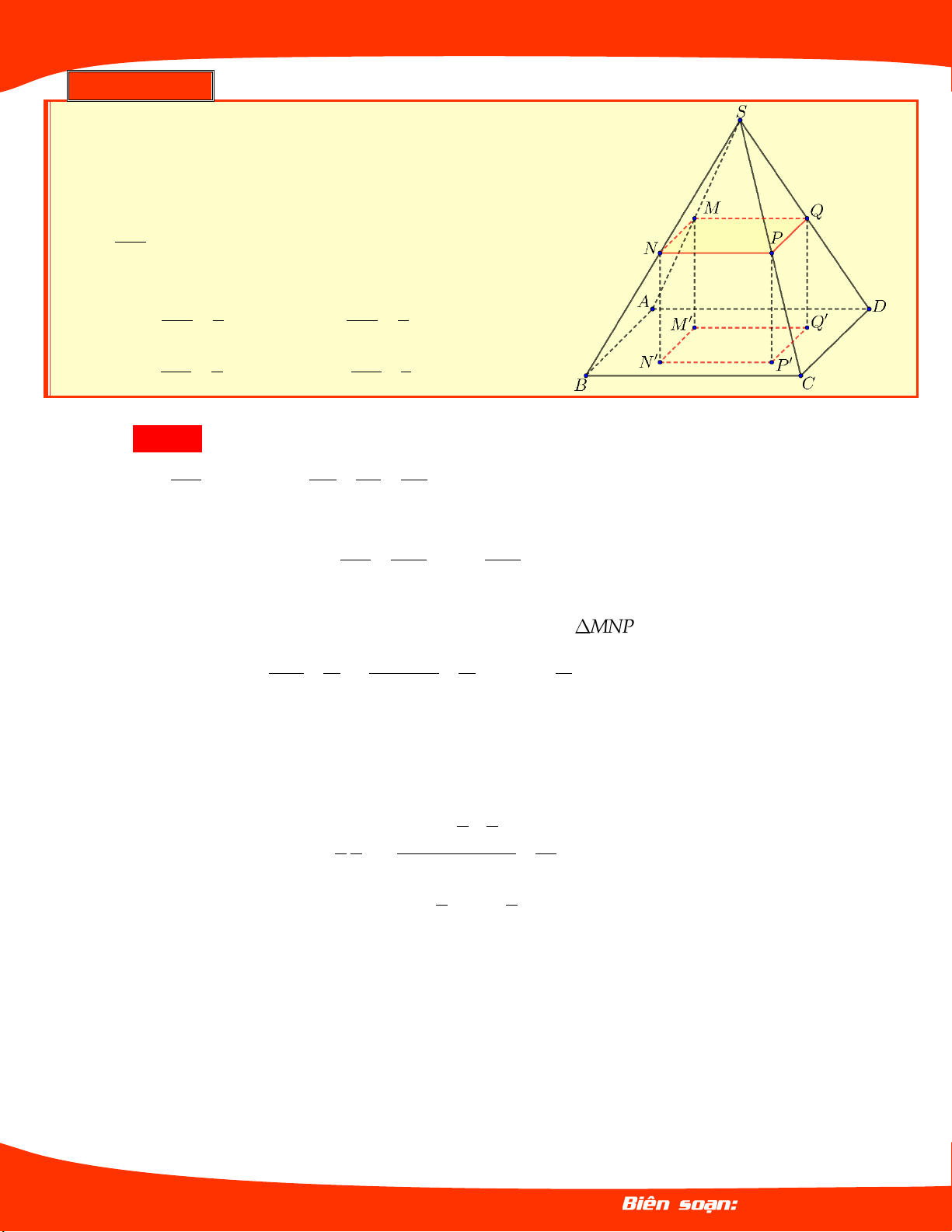
Ví dụ 07. Cho hình chóp .
S ABCD . Một mặt phẳng song
song mặt đáy cắt các cạnh S ; A S ; B SC;SD lần
lượt tại M, N, P,Q . Gọi M ', N ', P',Q' lần lượt là
hình chiếu của M, N, P,Q lên mặt đáy. Tìm tỉ số
SM để thể tích khối đa điện M .
NPQ M ' N ' P 'Q' SA lớn nhất. SM 3 SM A.  2 . B.  . SA 4 SA 3 SM 1 SM C.  1 . D. SA 2 SA 3 Lời giải Chọn B SM Đặt  SN SP SQ x . Suy ra    x . SA SB SC SD
Gọi h, h' lần lượt là chiều cao hình chóp và chiều cao khối đa diện M .
NPQ M ' N ' P 'Q' . SM MN MN
Do MN / /AB nên ta có   x   MN  . x AB . SA AB AB
Tương tự ta có BC  . x NP Ta có 2 2 Sx .SSx S
( Vì tam giác MNP đồng dạng tam giac ABC ) MNP ABC MNPQ ABCD AM h' SA SM h' h' Mặt khác ta có    1 x
h'  1 xh AS h SA h h Ta có Vh'.S   x h x S   x x h S M N P Q MNPQ   2 . . ABCD   2 1 1 . . MNPQ. ' ' ' ' ABCD Do h,S
không thay đổi nên V
đạt giá trị lớn nhất khi và chỉ khi    2 1 x x ABCD
MNPQ.M ' N ' P'Q' đạt lớn nhất. 3  x x  1 x     x x  2 2  4 Ta có 1 x 2
x  4.1 x  4.  2 2 27 27 x Dấu  2
xảy ra khi và chỉ khi 1 x   x  . 2 3 Trang 49 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
III. BÀI TẬP RÈN LUYỆN. Câu 1.
Hình lăng trụ tam giác có tất cả bao nhiêu cạnh? A. 12 . B. 10 . C. 6 . D. 9 . Lời giải Chọn D
Lăng trụ tam giác có 9 cạnh. Câu 2. Cho hình chóp .
S ABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với mặt phẳng
ABCD, SA3a. Tính thể tích khối chóp .SABCD 3 a 3 a A. 3 3a . B. . C. . D. 3 a . 9 3 Lời giải Chọn D Diện tích đáy: 2 Sa . ABCD 1 Thể tích khối chóp . S ABCD là: 2 3 V a 3 . a a . 3 Câu 3.
Cho hình chóp có đáy là hình vuông cạnh a và chiều cao bằng 4a . Thể tích khối chóp đã cho bằng 4 16 A. 3 a . B. 3 16a . C. 3 4a . D. 3 a . 3 3 Lời giải Chọn A 1 1 4 Ta có 2
B a ,h  4a 2 3  V  . B h a 4 . a a . 3 3 3 Câu 4.
Một khối lăng trụ có diện tích đáy 3 và có thể tích bằng 6 thì chiều cao bằng : A. 2 . B. 3 . C. 4 . D. 6 . Lời giải Chọn A V 6
Chiều cao của khối lăng trụ bằng h    2 . S 3 Câu 5.
Cho khối chóp có diện tích đáy B  3 và thể tích bằng 6 . Chiều cao của khối chóp bằng A. 6. B. 2. C. 3. D. 12. Lời giải Chọn B V 6
Ta có thể tích khối chóp V  . B h h    2 . B 3 Câu 6.
Cho khối hộp chữ nhật có ba kích thước 2; 4; 6 . Thể tích của khối hộp đã cho bằng A. 8 . B. 16 . C. 48 . D. 12 . Lời giải Chọn A
Thể tích của khối hộp đã cho là V  2 4 . 6 .  48 . Câu 7.
Cho khối chóp có đáy là tam giác đều cạnh a và chiều cao bằng a 3 . Thể tích V của khối chóp bằng LÊ MINH TÂM Trang 50
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN 3 a 3 3a 3 a A. V  . B. 3
V a . C. V  . D. V  . 2 4 4 Lời giải Chọn D 2 a 3
Diện tích đáy bằng B  1 S  1 A . B AC.sin A  . a . a sin 60  . ABC 2 2 4 1 2 1 a 3 3 a
Thể tích khối chóp là V Bh a 3  . 3 3 4 4 Câu 8. Hình chóp . S ABC
có chiều cao h a , diện tích tam giác ABC 2
là 3a . Tính thể tích khối chóp . S AB . C 3 a 3 A. . B. 3 a . C. 3 3a . D. 3 a . 2 2 Lời giải Chọn B 1 1 Ta có: 2 3 V  . B h  3
. a .a a . 3 3 Câu 9.
Chiều cao của khối lăng trụ có thể tích bằng V 12 , diện tích đáy B  4 là A. 8 . B. 9 . C. 1. D. 3 . Lời giải Chọn D V 12 Ta có: V  . B h h    3 . B 4
Câu 10. Thể tích khối hộp chữ nhật có ba kích thước lần lượt a, b, c là A. 3 V  1 a bc .
B. V abc . C. V  1 abc .
D. V abc . 3 2 Lời giải Chọn C
Thể tích khối hộp chữ nhật có ba kích thước lần lượt a, b, c là V abc .
Câu 11. Cho hình lăng trụ đều AB . C A BC
 có cạnh đáy bằng a và cạnh bên bằng 2a . Thể tích của
khối lăng trụ đã cho là 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 4 6 3 2 Lời giải Chọn D 2 3 a 3 a 3
Thể tích khối lăng trụ đã cho là V  . B h  2 . a  . 4 2
Câu 12. Một hình hộp chữ nhật có ba kích thước là a , 2a và 3a . Thể tích của khối hộp chữ nhật đó bằng A. 3 a . B. 3 3a . C. 3 2a . D. 3 6a . Lời giải Chọn D
Thể tích khối hộp chữ nhật là: 3 V  6a . Trang 51 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Câu 13. Cho hình chóp .
S ABCD có đáy ABCD là hình vuông cạnh a , SA  3a 2 và SA vuông góc
với  ABCD . Thể tích của khối chóp . S ABCD bằng 3 a 2 3 4a 3 A. . B. 3 a 2 . C. 3 3a 2 . D. . 2 3 Lời giải Chọn B 1 1 Thể tích khối chóp 2 3 VS .SA  .a 3 . a 2  a 2 . S.ABCD 3 ABCD 3
Câu 14. Mặt phẳng AB C
  chia khối lăng trụ AB . C A BC
  thành các khối đa diện nào?
A. Hai khối chóp tam giác.
B. Một khối chóp tam giác và một khối chóp ngũ giác.
C. Một khối chóp tam giác và một khối chóp tứ giác.
D. Hai khối chóp tứ giác. Lời giải Chọn C Mặt phẳng AB C
  chia khối lăng trụ thành hai khối đó là chóp tam giác . A A BC   và chóp tứ giác . A B CCB .
Câu 15. Cho khối lăng trụ tam giác đều có cạnh đáy bằng 2a , cạnh bên bằng a . Thể tích của khối lăng trụ đã cho bằng 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. 3 a 3. 2 3 12 Lời giải Chọn A LÊ MINH TÂM Trang 52
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN 2 2 AB 3 a 3 Trong ABC ta có S   . ABC 4 4 2 3 a 3 a 3
Vậy thể tích khối lăng trụ tam giác đều là V       AA'.S 2 . a . ABC.A B C ABC 4 2
Câu 16. Cho hình chóp .
S ABC có tam giác ABC vuông tại A . AB  2a; AC a;SA  3a;SA  (ABC) .
Thể tích của hình chóp là A. 3 V  3a . B. 3 V  6a . C. 3 V  2a . D. 3 V a . Lời giải Chọn D 1 1 1 1 Thể tích khối chóp 3 VS .SA  . .A . B AC.SA  2 . . a a 3 . a a .  SABC 3 ABC 3 2 6
Câu 17. Tính thể tích V của khối chóp có chiều cao bằng 5cm và diện tích đáy bằng 2 12 cm . A. 3 V  60cm . B. 3 V  20cm . C. 3 V  30cm . D. 3 V  40cm . Lời giải Chọn B 1 1
Thể tích của khối chóp cần tìm là: V Bh  5 . 1 . 2  20 3 cm  3 3
Câu 18. Cho hình hộp chữ nhật có đáy là hình vuông cạnh a, chiều cao bằng 2a . Tính thể tích hình hộp chữ nhật. 3 2a A. 3 2a . B. 3 6a . C. . D. 2 2a . 3 Lời giải Chọn A
Thể tích hình hộp chữ nhật là 2 3 V  . B h a 2 . a  2a . Trang 53 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Câu 19. Cho khối lăng trụ có diện tích đáy là 8 ,chiều cao là 6 . Tính thể tích khối lăng trụ A. 16 . B. 36 . C. 48 . D. 24 . Lời giải Chọn C V  . B h  6 8 .  48 .
Câu 20. Cho khối lăng trụ tam giác đều có tất cả các cạnh bằng a . Thể tích của khối lăng trụ đã cho bằng 3 a 2 3 a 3 2 a 3 A. . B. . C. . D. 3 a . 3 4 4 Lời giải Chọn B 2 a 3 2 3 a 3 a 3
Ta có diện tích đáy B
.Suy ra thể tích khối lăng trụ là V  . B h  .a  . 4 4 4
Câu 21. Cho khối hộp chữ nhật ABC . D A BCD
  có AB  3, AC  5, AA  8. Thể tích của khối hộp đã cho bằng A. 120. B. 32 . C. 96 . D. 60 . Lời giải Chọn C
Áp dụng định lý Pytago cho tam giác vuông ABC , ta có 2 2 BC  5  3  4 .
Khi đó, thể tích của khối hộp chữ nhật là V A . B B . C AA  3 4 . 8 .  96.
Câu 22. Cho khối lăng trụ ABC.A B C có thể tích bằng 18, thể tích khối chóp A .ABC bằng 1 1 1 1 A. 6 . B. 9 . C. 12 . D. 3 . Lời giải Chọn A 1 1 1  Ta có: V
 .S .d A . ABC  .V  1 . 8  6 A .ABC ABC 1 ABC.A B C 1    . 1 1 1 3 3 3
Câu 23. Cho khối chóp tứ giác đều có cạnh đáy bằng 2 và cạnh bên bằng 6 . Thể tích khối chóp bằng LÊ MINH TÂM Trang 54
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN 4 8 A. 8 . B. . C. . D. 4 . 3 3 Lời giải Chọn C 1
 Áp dụng công thức: V Bh 3    2 2 Đáy là hình vuông nên: 2
B  2  4 ; h SO SA AO   6 2 2 2 2     6  2  2  2    1 8  V  4 . 2 .  . 3 3
Câu 24. Thể tích V của khối chóp có diện tích đáy bằng 2
6a và chiều cao bằng a là A. 3 V 12a . B. 3 V  6a . C. 3 V 18a . D. 3 V  2a . Lời giải Chọn D 1 1
Thể tích của khối chóp cần tìm là 2 3 V Sh  6
. a .a  2a . 3 3
Câu 25. Cho một khối chóp có diện tích đáy 2
B  6a , chiều cao h  3a . Thể tích khối chóp đã cho bằng A. 3 6a . B. 3 18a . C. 3 9a . D. 3 54a . Lời giải Chọn A 1 1
Thể tích khối chóp đã cho là 2 3
V Bh  6a 3 . a  6a . 3 3
Câu 26. Số cạnh của hình bát diện đều là A. 8 . B. 12 . C. 10 . D. 20 . Lời giải Chọn B
Câu 27. Cho khối lăng trụ có diện tích đáy B  8 và chiều cao h  6 . Thể tích của khối lăng trụ đã cho bằng: A. 48 . B. 16 . C. 24 . D. 14 . Lời giải Chọn A
Thể tích của khối lăng trụ đã cho là: V  . B h  8 6 .  48 .
Câu 28. Thể tích của khối chóp có diện tích đáy B , chiều cao h là 1 1 4 A. . B h . B. . B h . C. . B h . D. . B h . 2 3 3 Trang 55 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN Lời giải Chọn C 1
Thể tích của khối chóp có diện tích đáy B , chiều cao h là . B h . 3
Câu 29. Cho khối chóp có chiều cao h  3 và diện tích đáy B  2 . Thể tích của khối chóp đã cho bằng A. 2 . B. 3 . C. 12 . D. 6 . Lời giải Chọn A 1 1
Thể tích của khối chóp là: V Bh  2 . 3 .  2 . 3 3
Câu 30. Tính thể tích V của khối lập phương ABC . D A BCD
  biết AC  a 3 . 3 a 3 3 6a A. 3 V a . B. V  . C. V  . D. 3 V  3 3a . 4 4 Lời giải Chọn A Ta có 3
AC  a 3  A .
B 3  a 3  AB a V a .
Câu 31. Cho khối chóp có diện tích đáy B  6 và chiều cao h 10 . Thể tích của khối chóp đã cho bằng A. 6. B. 24. C. 10. D. 20. Lời giải Chọn D 1 1
Thể tích của khối chóp là V  . B h  6 . 1 . 0  20 . 3 3
Câu 32. Thể tích của khối lăng trụ có diện tích đáy bằng B và chiều cao bằng h là: A. V  1 Bh . B. V  1 Bh . C. V  4 Bh .
D. V Bh . 3 2 3 Lời giải Chọn A
Thể tích khối lăng trụ đã cho là V Bh .
Câu 33. Cho khối chóp .
S ABCD có đáy ABCD là hình vuông cạnh a , SA  3a và SA vuông góc với
mặt phẳng đáy. Thể tích của khối chóp . S ABCD là 3 a A. 3 3a . B. 3 a . C. . D. 3 6a . 3 Lời giải Chọn B
 Ta có SA  ABCD  SA là đường cao của hình chóp. 1 1  Thể tích khối chóp .
S ABCD là: 2 3 V S . A S  3 . .
a a a . 3 ABCD 3
Câu 34. Cho khối lăng trụ tam giác đều có độ dài tất cả các cạnh bằng 3 . Thể tích khối lăng trụ đã cho bằng 9 3 27 3 27 3 9 3 A. . B. . C. . D. . 4 4 2 2 Lời giải LÊ MINH TÂM Trang 56
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN Chọn B 2 3 3
Thể tích khối lăng trụ tam giác cạnh bằng 3 là: V  27 3 3 .  . 4 4
Câu 35. Thể tích của khối lập phương cạnh a bằng A. 2 a . B. 3 a . C. 4 a . D. 5 a . Lời giải Chọn B
Thể tích của khối lập phương cạnh a là 3 a .
Câu 36. Thể tích khối lập phương có cạnh 2 3 bằng A. 24 3 . B. 54 2 . C. 8 . D. 18 2 . Lời giải Chọn A
Thể tích khối lập phương có cạnh 2 3 là V   3 2 3  24 3 (đvtt).
Câu 37. Cho khối lăng trụ có diện tích đáy B  5 và chiều cao h  6. Thể tích của khối lăng trụ đã cho bằng A. 15 B. 30 C. 150 D. 10 Lời giải Chọn B
Thể tích của khối lăng trụ đã cho là: V  . B h  5 6 .  30
Câu 38. Cho khối lăng trụ có diện tích đáy S  6 và chiều cao h 10 . Thể tích khối lăng trụ đã cho bằng A. 20 . B. 40 . C. 30 . D. 60 . Lời giải Chọn D
Thể tích khối lăng trụ đã cho bằng V  . S h  6 1 . 0  60 .
Câu 39. Một khối lăng trụ có diện tích đáy bằng 6 và chiều cao bằng 5 . Thể tích khối lăng trụ đã cho bẳng: A. 90 . B. 30 . C. 10 . D. 15 . Lời giải Chọn B
Ta có thể tích khối lăng trụ đã cho là: V  6 5 x  30
Câu 40. Cho khối chóp .
S ABCD có đáy ABCD là hình vuông cạnh a , SA  3a và SA vuông góc với
đáy. Thể tích khối chóp . S ABCD là 3 a A. 3 3a . B. 3 a . C. . D. 3 6a . 3 Lời giải Chọn B 1 1 2 3 VBh  .a 3 . a a . S.ABCD 3 3
Câu 41. Thể tích của khối lăng trụ có chiều cao bằng h và diện tích đáy bằng B là 1 1 A. . Bh B. . Bh C. . Bh D. 3 . Bh 3 6 Trang 57 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN Lời giải Chọn C
Thể tích khối lăng trụ là V Bh
Câu 42. Khối lăng trụ có diện tích đáy là S, chiều cao h có thể tích V là A. 2 V  1 Sh
B. V Sh C. V  1 Sh
D. V Sh 2 3 Lời giải Chọn C
Ta có V Sh
Câu 43. Thể tích khối lăng trụ được tính theo công thức nào sau đây? 1 A. V  . B h . B. V  1 . B h . C. V  1 . B h . D. V  . B h . 3 2 6 Lời giải Chọn B
Câu 44. Cho hình chóp .
S ABC có đáy là tam giác,diện tích đáy bằng 2 a 3 và thể tích bằng 3 a . Tính
chiều cao h của hình chóp đã cho. 3a a 3a A. h  3 . B. h  . C. 3a . D. . 6 2 3 Lời giải Chọn C 1 V 3 3a Ta có: V  3 . h S      h 3a . 3 ABC S 2 ABC a 3
Câu 45. Thể tích V của khối lăng trụ tam giác đều có cạnh đáy bằng a và cạnh bên bằng 2a là 3 a 3 3 a 3 3 a 3 A. V . B. V . C. 3 V a 3 . D. V . 3 2 4 Lời giải Chọn B 2 a 3
Ta có: Diện tích đáy SABC 4 2 3 a 3 a 3
Suy ra: V AA .S  2 . a  . ABC 4 2
Câu 46. Cho hình chóp .
S ABCD có SA  SBCDvà SA  2a, diện tích tứ giác là ABCD bằng 2 3a . Thể tích khối chóp . S ABCD bằng A. 3 2a . B. 2 6a . C. 3 6a . D. 2 2a . Lời giải Chọn A 1 1 Ta có: 2 3 V  .S .SA  3 . a 2 . a  2a . S.ABCD 3 ABCD 3
Câu 47. Tính thể tích của một khối lăng trụ biết khối lăng trụ đó có đường cao bằng 3a , diện tích mặt đáy bằng 2 4a . A. 3 4a . B. 2 4a . C. 3 12a . D. 2 12a . Lời giải LÊ MINH TÂM Trang 58
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN Chọn C
Gọi S là diện tích mặt đáy, h là độ dài đường cao của khối trụ đã cho.
Khi đó thể tích của khối lăng trụ đã cho là 2 3 V  . S h  4a 3 . a 12a .
Câu 48. Tính thể tích V của khối chóp có diện tích đáy bằng 12 và chiều cao bằng 4 là A. V  8 . B. V  48 . C. V  24 . D. V 16 . Lời giải Chọn D 1 Ta có V  1 . 2 4 .  16 . 3
Câu 49. Tính thể tích V của khối lập phương ABC . D A BCD
  có cạnh AB a . 3 a 3 a 3 a A. V  . B. V  . C. V D. 3 V a . 6 3 2 Lời giải Chọn D Ta có: 2 3
V Bh a .a a .
Câu 50. Một khối lăng trụ có diện tích đáy bằng 3 và chiều cao bằng 4 . Thể tích của khối lăng trụ đó bằng A. 4 . B. 12 . C. 36 . D. 6 . Lời giải Chọn B V  . S h  3 4 . 12.
Câu 51. Cho khối chóp .
S ABC có SA  3a và SA vuông góc với mặt phẳng ABC , tam giác ABC
vuông tại A và có AB  3a, AC  4a . Tính thể tích của khối chóp . S ABC bằng A. 3 18a . B. 3 6a . C. 3 36a . D. 3 2a . Lời giải Chọn B 1 1 1 3 V  . B h  . 3a 4 . a 3
. a  6a 3 3 2
Câu 52. Một khối lăng trụ có chiều cao bằng 6 và diện tích đáy bằng 2 14 . Thể tích của khối lăng trụ đó bằng A. 2 14 . B. 4 14 . C. 6 14 . D. 12 14 . Lời giải Chọn D
Thể tích cuả khối lăng trụ V Bh  2 14 6 .  12 14 (đvtt)
Câu 53. Mặt phẳng A B
C chia khối lăng trụ AB . C A BC
  thành các khối đa diện nào?
A. Hai khối chóp tam giác.
B. Một khối chóp tam giác và một khối chóp tứ giác.
C. Hai khối chóp tứ giác.
D. Một khối chóp tam giác và một khối chóp ngũ giác. Lời giải Chọn B Trang 59 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN Mặt phẳng A B
C chia khối lăng trụ AB . C A BC
  thành một khối chóp tam giác A.ABC
và một khối chóp tứ giác A .BB CC
Câu 54. Cho khối chóp .
S ABC có đáy là tam giác ABC cân tại A , BAC  30 , AB a . Cạnh bên SA
vuông góc với mặt đáy, SA  2a 2 . Thể tích khối chóp đã cho bằng 3 a 2 3 a 2 3 a 2 3 a 2 A. . B. . C. . D. . 12 4 6 2 Lời giải Chọn C 2 a
Diện tích đáy bằng B  1 S  1 A . B AC.sin A  . a . a sin 30  . ABC 2 2 4 1 2 1 a 3 a 2
Thể tích khối chóp là V  1 Bh  . B SA  2a 2  . 3 3 3 4 6
Câu 55. Cho khối chóp tứ giác đều có cạnh đáy bằng a , cạnh bên gấp hai lần cạnh đáy. Tính thể tích
V của khối chóp đã cho: 3 14a 3 2a 3 2a 3 14a A. V  . B. V  . C. V  . D. V  . 6 6 2 2 Lời giải Chọn A Xét hình chóp đều .
S ABCD có đáy ABCD là hình vuông tâm H cạnh a a a 14
Từ gt  SH  ABCD và SA  2 2a; AH   2 2
SH SA AH  2 2 3 1 1 a 14 14a
Vậy thể tích V của khối chóp . S ABCD là: 2
V SH.S  . .a  . 3 ABCD 3 2 6 LÊ MINH TÂM Trang 60
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Câu 56. Cho khối chóp .
S ABCD có đáy là hình vuông cạnh a ,SA vuông góc mới mặt phẳng đáy, SC
tạo với mặt phẳng SAB một góc 30. Tính thể tích khối chóp . S ABCD 3 6a 3 2a 3 2a A. . B. . C. 3 2a . D. . 3 3 3 Lời giải Chọn B S A D a B a C
Ta có BC AB, BC SA BC  SAB.
Do đó góc giữa SC với mặt phẳng SAB là góc BSC  30 . BC BC
Trong tam giác BSC vuông tại B , ta có tan 30   SB   a 3 . SB tan 30 2 2
SA SB AB a 2 . 3 1 1 2a Thể tích khối chóp 2 V  .S
.SA  .a .a 2  . S.ABCD 3 ABCD 3 3 3 2a
Câu 57. Khối chóp tam giác có thể tích là:
và chiều cao a 3 . Tìm diện tích đáy của khối chóp 3 tam giác đó. 2 2 3a 2 2 3a A. 2 3a . B. 2 2 3a . C. . D. . 3 9 Lời giải Chọn C 3 2 2a 1 1 2 3a V   . . h S
 .a 3.S S  . chóp 3 3 đáy 3 đáy đáy 3 2 2 3a
Vậy diện tích đáy của khối chóp tam giác đấy là . 3
Câu 58. Cho hình chóp .
S ABCD có đáy ABCD là hình vuông tâm O cạnh a . Cạnh bên SA vuông
góc với đáy, góc SBD  60. Thể tích khối chóp đã cho bằng 3 2a 3 a 3 3 a A. . B. . C. . D. 3 a . 3 2 3 Lời giải Chọn C Trang 61 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN  Do tứ giác ABCD  2 
là hình vuông tâm O cạnh a nên BD a 2 và S a . ABCD
 Vì SA  ABCD  SA AB,SA AD . Ta có 2 2 2 2
SB SA AB ;SD SA AD SB SD . Mà SBD  60  SBD đều. Suy ra 2 2
SB BD a 2  SA SB AB a 3  1 a Vậy V  . . SA S  . S.ABCD 3 ABCD 3
Câu 59. Cho khối chóp .
S ABCD có đáy là hình vuông cạnh a , SA vuông góc với mặt phẳng đáy và
SC tạo với đáy một góc bằng 60 Thể tích của khối chóp đã cho bằng 3 6a 3 6a 3 6a A. . B. . C. 3 6a . D. . 6 9 3 Lời giải Chọn D 1
 Áp dụng công thức: V Bh 3  Với: 2 B S
a , h SA A .
C tan60  a 2. 3  a 6 ABCD 3  1 a 6 Vậy: 2
V  .a .a 6  3 3
Câu 60. Cho khối chóp .
S ABCD có đáy ABCD là hình vuông tâm O , cạnh a , SA vuông góc với mặt
phẳng đáy và SA  3a . Gọi M, N lần lượt là trung điểm của SC,SD . Thể tích khối tứ diện SOMN bằng 3 a 3 a 3 3a 3 3a A. . B. . C. . D. . 16 8 8 16 Lời giải Chọn A S N M A D O B C LÊ MINH TÂM Trang 62
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN 3  1 1 1 1 1 a Ta có: 2 V  .V  . . . SA S  . 3 . . a a S.OCD 4 S.ABCD 4 3 ABCD 4 3 4 V SM SN 1 1 1 3 3  1 1 a a
Lại có: S.OMN  .  .   VV  .  V SC SD 2 2 4 S.OMN 4 S.OCD 4 4 16 S.OCD
Câu 61. Cho khối lăng trụ tam giác đều AB . C A BC
  có cạnh đáy là 2a và khoảng cách từ A đến mặt phẳng A B
C bằng a . Tính thể tích của khối lăng trụ AB . C A BC  . 3 3a 2 3 a 2 3 2a A. 3 2 2a . B. . C. . D. . 2 2 2 Lời giải Chọn B
 Gọi M là trung điểm của B C    Ta có B C    A M  , vì A
BC đều và B C
   AA nên B C    AA M   .  Dựng A E
  AM, khi đó A E   AB C
  , do đó dA ;AB C    A E   a AA M
 vuông tại A với đường cao A H  nên 1 1 1 1 1 1 1 1  a 6         AA   2 2   2 2   2  2 2 2 A H AA A M AA A E A M a (a 3 2 ) 2 3  a 6 (2a) 3 3a 2
Thể tích khối lăng trụ AB . C A BC   là: V    2 4 2
Câu 62. Cho lăng trụ tam giác AB . C A BC
  có đáy ABC là tam giác vuông tại A , AB a , cạnh bên
bằng 2a . Hình chiếu vuông góc của A trên mặt phẳng  ABC là trung điểm cạnh BC . Tính
thể tích của khối lăng trụ AB . C A BC   3 a 2 3 a 2 3 a 14 3 a 14 A. . B. . C. . D. . 2 6 4 12 Lời giải Chọn C Trang 63 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN B' C' A' B H C A
Gọi H là trung điểm của cạnh BC A H   ABCBC a A
BC vuông cân tại A BC  2 a 2  AH   . 2 2 2   2 a 2 a 14 Ta có 2 2 A H   A A
AH  2a     2  2   a 14 1 14 2 3  V       . a a . ABCD.A B C D 2 2 4
Câu 63. Cho hình chóp đều .
S ABCD có đáy là hình vuông cạnh a , cạnh bên SA  2a. Thể tích của khối chóp. 14 3 14a 7 A. 3 a . B. 3 2a . C. . D. 3 a . . 6 2 2 Lời giải Chọn A
 Gọi O là tâm của hình vuông ABCD SO  ABCD 1 1
 Ta có: OAAC  .a 2 2 2 2    2 a 2 a 14 2 2
SO SA OA  2a      2  2    1 1 a 14 14
Vậy thể tích khối chóp là: 2 3 V  .S . O S  . .a a . S.ABCD 3 ABCD 3 2 6
Câu 64. Cho hình lập phương ABC . D A BCD
  có cạnh bằng a . Thể tích khối tứ diện ABDB bằng LÊ MINH TÂM Trang 64
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN 3 a 3 2a 3 a 3 a A. . B. . C. . D. . 6 3 2 3 Lời giải Chọn A 3  1 1 1 1 a Ta có: 2 V        .B . B S .B . B S . . a a . ABDB 3 ABD 3 2 ABCD 6 6
Câu 65. Lăng trụ đều AB .
C A' B'C' cạnh AB a , góc giữa đường thẳng A' B và mặt phẳng đáy bằng 0
60 . Hỏi thể tích lăng trụ. 3 a 3 3 3a 3 a 3 a 3 A. . B. . C. . D. . 12 4 4 4 Lời giải Chọn B
Ta có AA  mpABC  A là hình chiếu vuông góc của A' trên mpABC do đó
A'B,ABC 0  A'BA  60 0
AA'  ABtan60  a 3 . 2 a 3 3 3a
Diện tích tam giác ABC : S  . Vậy V ABC 4
ABC.A'B'C ' 4
Câu 66. Cho khối chóp tứ giác đều có cạnh đáy a  3 và chiều cao h  5. Thể tích của khối chóp bằng A. 15 B. 15 C. 45 D. 45 Lời giải Chọn B
Do khối chóp tứ giác đều nên đáy của khối chóp là hình vuông có cạnh đáy là a  3.
Diện tích đáy của khối chóp là: 2 2
B a  3  9 .
Chiều cao của khối chóp là: h  5. 1 1
Vậy thể tích của khối chóp bằng: V  . B h  9 . 5 .  15 . 3 3
Câu 67. Cho hình lăng trụ AB .
C A' B'C' có cạnh bên bằng AA'  2a và tạo với mặt phẳng đáy một góc bằng 0
60 , diện tích tam giác ABC bằng 2
a . Tính thể tích khối lăng trụ AB .
C A' B'C' bằng 3 3a 3 3 a A. . B. a . C. 3 3a . D. . 3 3 Lời giải Chọn C Trang 65 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN A B C A' B' H C'
Giả sử đường cao là AA' . Vì cạnh bên AA' tạo với đáy một góc 0 60 nên 0
AA' H  60 . Xét
tam giác vuông AA' H AH 0 sin 60   AH a 3 AA'
Vậy thể tích lăng trụ là: 2 3
V a .a 3  a 3
Câu 68. Biết rằng thể tích của một khối lập phương bằng 27. Tính tổng diện tích các mặt của hình lập phương đó. A. 27 B. 16 C. 54 D. 36 Lời giải Chọn C
 Thể tích khối lập phương cạnh 3
x V x  27  x  3 .
Diện tích các mặt (diện tích toàn phần) hình lập phương là 3 3 . 6 .  54 .
Câu 69. Cho hình chóp đều .
S ABCD có cạnh đáy bằng a và cạnh bên tạo với đáy một góc 60 . Thể
tích của hình chóp đều đó là 3 a 3 3 a 3 3 a 6 3 a 6 A. . B. . C. . D. . 6 2 6 2 Lời giải Chọn C
 Đáy ABCD là hình vuông nên diện tích đáy là 2
B a (đvdt).
 Gọi O là tâm của đáy SO  AB D
C   OB là hình chiếu vuông góc của SB lên mặt
phẳng ABCD  góc giữa cạnh bên SB và đáy là góc SBO  60 . a 2 a 6
h SO O . B tan 60  . 3  . 2 2 LÊ MINH TÂM Trang 66
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN 3  1 a 6
Vậy thể tích khối chóp là V Bh  (đvtt). 3 6
Câu 70. Cho hình chóp .
S ABC có SA  ABC , tam giác ABC vuông cân tại A , SA BC a. Tính
theo a thể tích V của khối chóp . S ABC . 3 a 3 a 3 a A. V  . B. V  . C. 3 V  2a . D. V  . 12 4 2 Lời giải Chọn A BC a 2
 Đáy ABC là tam giác vuông cân tại A nên AB AC   . 2 2 2 1 aB SA . B AC  (đvdt). ABC 2 4 3  1 1 a
Vậy thể tích khối chóp là V Bh S .SA ABC (đvtt). 3 3 12
Câu 71. Diện tích toàn phần của một hình lập phương bằng  2
96 cm  . Khối lập phương đã cho có thể tích bằng A.  3 84 cm  . B.  3 48 cm  . C.  3 64 cm  . D.  3 91 cm  . Lời giải Chọn C
Gọi x x  0 là cạnh của hình lập phương. 2
S  6x  96  x  4 . tp Vậy 3 V    3 4 64 cm  .
Câu 72. Cho tứ diện OABC có OA , OB , OC đôi một vuông góc với nhau và OB OC a 6 , OA a
. Thể tích khối tứ diện đã cho bằng: A. 3 3a . B. 3 2a . C. 3 6a . D. 3 a . Lời giải Chọn D
Do tứ diện OABC có OA, OB , OC đôi một vuông góc với nhau nên thể tích khối tứ diện 1 1 OABC là: 3 VO . A O . B OC  .
a a 6.a 6  a . OABC 6 6
Câu 73. Cho khối tứ diện đều có cạnh bằng a 3 . Thể tích của khối tứ diện đã cho bằng Trang 67 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN 3 a 2 3 a 3 3 a 6 3 a 6 A. . B. . C. . D. . 4 4 12 4 Lời giải Chọn D
Gọi H là trọng tâm của B
CD AH  BCDa 3. 3 3a 2 2 3a
Gọi M là giao điểm của BH và CD ta có: BM  
BH BM  .  a 2 2 3 3 2 Xét A
BH vuông tại H có: 2 2 2 2 2 2
AH AB BH  3a a  2a AH a 2 1 1
a 32 3 3a 6 Ta có: VAH.S  .a 2.  ABCD BCD . 3 3 4 4
Câu 74. Cho khối chóp .
S ABCD có đáy ABCD là hình chữ nhật, biết AB a, AD a 3,SA vuông
góc với mặt phẳng đáy và SC tạo với đáy một góc 60o . Thể tích của khối chóp . S ABCD bằng 3 a 3 A. 3 6a . B. 3 a 3. C. . D. 3 2a . 3 Lời giải Chọn D
Ta có AC là hình chiếu của SC lên mặt phẳng đáy   ,   ,    60o   .tan 60o SC ABCD SC AC SCA SA AC  2a 3. 1 1  V  .S .SA  . . a a . aa . S.ABCD ABCD  3 3 2 3 2 3 3
Vậy thể tích của khối chóp . S ABCD 3 2a .
Câu 75. Cho khối lăng trụ đứng AB . C A BC
  có đáy là tam giác đều cạnh a và AA  2a . Thể tích của
khối lăng trụ đã cho bằng 3 3a 3 3a 3 3a A. . B. . C. 3 3a . D. . 2 6 3 Lời giải Chọn A LÊ MINH TÂM Trang 68
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Gọi M là trung điểm của B C   . 2 1 1 a 3 a 3
Diện tích tam giác A BC   là: S          .A M.B C . .a . A B C 2 2 2 4 2 3 a 3 a 3
Thể tích của khối lăng trụ AB . C A BC
  là: V S      .AA 2 . a . A B C 4 2
Câu 76. Cho khối tứ diện ABCD và gọi M là trung điểm của đoạn thẳng AB , khi đó mặt phẳng
P chứa cạnh CM, song song với BD chia khối tứ diện ABCD thành
A. Một khối tứ diện và một khối lăng trụ.
B. Hai khối chóp tứ giác.
C. Một khối tứ diện và một khối chóp tứ giác.
D. Hai khối tứ diện. Lời giải Chọn C
Ta có khi đó mặt phẳng P chứa cạnh CM , song song với BD nên giao tuyến của mặt
phẳng P và mặt phẳng  ABD là đường thẳng đi qua M và song song với BD , cắt AD tại H .
Khi đó mặt phẳng P  CMH . Vậy mặt phẳng P chia khối tứ diện ABCD thành khối
tứ diện AMCH và khối chóp tứ giác . C MHDB
Câu 77. Cho khối chóp .
S ABC có đáy là tam giác đều cạnh bằng 3 , tam giác SAC đều và nằm
trong mặt phẳng vuông góc với mặt phẳng đáy. Thể tích của khối chóp đã cho bằng Trang 69 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN 3 3 3 3 3 3 A. . B. . C. . D. . 12 8 4 8 Lời giải Chọn B
Gọi H là trung điểm của AC , hai tam giác SAC và ABC là hai tam giác đều, bằng nhau và AB 3 3 HS HB   . 2 2
Ba đường thẳng AC , HS , HB đôi một vuông góc với nhau, suy ra: 1 1 3 3 3 3 VAC.H . B HS  3. .  . S.ABC 6 6 2 2 8
Câu 78. Cho hình chóp .
S ABC có SA  ABC , SA AC  2a, AB a và BAC  60 . Thể tích khối chóp . S ABC bằng 3 2a 3 3a 3 3a A. . B. . C. . D. 3 3a . 3 3 6 Lời giải Chọn B. 2 1 1 3a Ta có SA .
B AC.sin BAC  . . a 2 . a sin 60  . ABC 2 2 2 2 3 1 1 3a 3a Vậy V  .S . A S  2 . . a  . S.ABC 3 ABC 3 2 3
Câu 79. Cho tứ diện ABCD , gọi M, N, P lần lượt là trung điểm các cạnh AB , AC , AD và O là V
trọng tâm tam giác BCD . Tính tỉ số thể tích OMNP . VABCD 1 1 1 1 A. . B. . C. . D. . 6 8 12 4 Lời giải Chọn B LÊ MINH TÂM Trang 70
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN A M P K I N B D O J C
Dễ thấy MNP // BCD. Do M,N,P lần lượt là trung điểm các cạnh AB , AC , AD cho nên
d A;MNP  dO;MNP  VV . OMNP AMNP V V AM AN AP 1 1 1 1 OMNP AMNP         . V V AB AC AD 2 2 2 8 ABCD ABCD
Câu 80. Cho lăng trụ đều AB . C A BC
  có tất cả các cạnh đều bằng a . Thể tích khối lăng trụ AB . C A BC   là 3 3a 3 3a 3 3a 3 3a A. V  . B. V  . C. V  . D. V  . 4 2 6 3 Lời giải Chọn A 2 a 3
Vì tam giác ABC đều cạnh a , suy ra S  . ABC 4
Chiều cao của lăng trụ AB . C A BC
  là AA  a . 3 3a
Thể tích khối lăng trụ AB . C A BC
  bằng V S .AA  . ABC 4
Câu 81. Tính thể khối đa diện ABCD , biết A ,
B AC, AD đôi một vuông góc và có độ dài lần lượt là 2, 3,4? A. 8 . B. 24 . C. 3 . D. 4 . Lời giải Chọn D Do A ,
B AC, AD đôi một vuông góc nên AD  (ABC) suy ra AD là đường cao của khối đa
diện ABCD . Không mất tính tổng quát ta chọn AB  2, AC  3, AD  4. 1 Ta có SA . B AC  3 . ABC 2 1 Vậy VA . D S  4 (đvtt). ABCD 3 ABC Trang 71 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Câu 82. Cho khối chóp .
S ABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với đáy và
SA  6a . Thể tích khối chóp là A. 3 a . B. 3 2a . C. 3 3a . D. 3 6a . Lời giải Chọn B S 6a A D a B C
Ta có SA  ABCD  SA là chiều cao của hình chóp. Diện tích đáy: 2 Sa . ABCD 1 1
Thể tích của khối chóp . S ABCD : 2 3 V  .S .SA  .a 6 . a  2a . S.ABCD 3 ABCD 3
Câu 83. Cho hình lăng trụ đứng AB .
C A' B'C' tất cả các cạnh bằng 2a . Thể tích của khối lăng trụ AB .
C A' B'C' bằng 6 3 3 6 A. 3 a . B. 3 a C. 3 a . D. 3 a . 2 12 4 6 Lời giải Chọn A 3 3 Ta có B Saa h AA a ABC  2 2 2 . ; ' 2 . 4 2 3 6
Do đó thể tích của khối lăng trụ AB .
C A' B'C' bằng 2 3 . B h a . . 2a a . 2 2
Câu 84. Cho khối lăng trụ đứng tam giác AB . C A BC
  có đáy ABC là tam giác vuông tại B với
BC  2BA  2a . Biết A B
 hợp với mặt phẳng ABC một góc 60. Thể tích khối lăng trụ đã cho bằng 3 a 3 3 2a 3 A. 3 2a 3 . B. 3 a 3 . C. . D. . 3 3 Lời giải Chọn B LÊ MINH TÂM Trang 72
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN Hình chiếu của A B
 lên ABC là AB, do đó góc giữa A B
 và ABC là A BA  60 . Tam giác A B
A vuông tại A nên AA  AB tan 60  a 3 . 1 1
Do đó thể tích khối lăng trụ là 3 V S
AA   BABC AA  a2aa 3  a 3 . ABC 2 2
Câu 85. Tính thể tích khối lăng trụ tam giác đều AB . C A BC
 , biết mặt bên của khối lăng trụ là hình
vuông và có chu vi bằng 8 . A. V  4 3 . B. V  2 6 . C. V  2 3 . D. V 16 3 . Lời giải Chọn C Ta có ABB A
  là hình vuông cạnh a có chu vi bằng 4a  8  a  2  AB AA. 2 2 3
Tam giác ABC đều cạnh 2 nên có S   3 . ABC 4
Vậy thể tích của khối lăng trụ là V AA .S  2 3 . ABC
Câu 86. Cho khối chóp tứ giác đều . S AB D
C có cạnh đáy và cạnh bên đều bằng 6a . Thể tích của khối chóp trên bằng A. 3 36 3a . B. 3 108 2a . C. 3 18 2a . D. 3 36 2a . Lời giải Chọn D Trang 73 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN Ta có 2 2
AC  6a 2  OC  3a 2  SO SC OC  3a 2 . 1 1
Khi đó thể tích khối chóp đã cho là 2 3 V Sh  3 . a 2 3 . 6a  36 2a . 3 3
Câu 87. Cho khối chóp .
S ABC có đáy là tam giác vuông tại B , SAB SCB  90 , AB a, BC  2a . Biết
rằng góc giữa đường thẳng SB và mặt phẳng đáy bằng 60 , thể tích khối chóp đã cho bằng 3 a 15 3 a 15 3 a 5 A. 3 a . B. . C. . D. . 6 3 6 Lời giải Chọn C
 Ta có SAB SCB  90  SA A , B SCCB
 Giả sử D là hình chiếu của S lên (ABC)  SD (ABC)  SDA , B SD BC CB  (SCD) CBCD    
ABCD là hình chữ nhật AB (SA ) D AB   AD
Ta có: BD là hình chiếu của SD lên mặt phẳng (ABC ) D (S ; B (ABC ) D )  (S ; B B ) D SBD   60 ; 2 2 2 2
BDBC CD a  (2a)  a 5
SDBD tan 60  a 15 3 1 1 1 a 15
Vậy thể tích khối chóp đã cho bằng V  .S . DS  .a 15. . . a 2a S.ABC  3 ABC 3 2 3
Câu 88. Cho hình lăng trụ AB .
C A' B'C' có đáy là tam giác đều cạnh .
a Hình chiếu của A' lên mặt
phẳng  ABC trùng với trung điểm cạnh AB, góc giữa AA' và mặt đáy của hình lăng trụ
đã cho bằng 60o. Tính thể tích V của khối chóp A'.BCC' B'. 3 a 3 a 3 3a 3 3a A. V  . B. V  . C. V  . D. V  . 4 8 4 8 Lời giải. Chọn A LÊ MINH TÂM Trang 74
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN Ta có: ',   ',  3  '  60o  '  .tan 60o a AA ABC AA AH A AH A H AH  . 2 2 3 a 3 a 3 3aVS .A' H  .  .
ABC.A'B'C' ABC 4 2 8 3 1 2 a 3  a VVVVVV  . Vậy V  . A.BCC' B'
ABC.A' B'C'
A.A' B'C'
ABC.A' B'C'
3 ABC.A'B'C'
3 ABC.A'B'C' 4 4
Câu 89. Một khối hộp ABC . D A BCD
  có thể tích bằng 2019. Gọi M là trung điểm của cạnh AB. Mặt phẳng MB D
  chia khối hộp ABC . D A BCD
  thành hai khối đa diện. Tính thể tích
phần khối đa diện chứa đỉnh A . 4711 5045 4711 10090 A. . B. . C. . D. . 4 6 8 17 Lời giải Chọn C E A N D M B C A' D' B' C'  Gọi B M   A A
  E ; ED AD N .
 Ta có: M là trung điểm của AB .
Mlà trung điểm của EB .
N là trung điểm của ED và AD . V EA EM EN 1
 Ta có: E.AMN  . .  . V      EA EB ED 8 E.A B D Trang 75 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN 7 7 7 1  V    7 4711      V 2    . .V 2    . . V     V     . AMN.A B D 8 E.A B D 8 A.A B D 8 6 ABCD.A B C D 24 ABCD.A B C D 8
Câu 90. Cho khối tứ diện SABC , M và N là các điểm thuộc các cạnh SA và SB sao cho MA  2SM
, SN  2NB,   là mặt phẳng qua MN và song song với SC . Kí hiệu HH2 1  và là các
khối đa diện có được khi chia khối tứ diện SABC bởi mặt phẳng   , trong đó H1 chứa V điểm S , H A V VHH 1 2  1  2  chứa điểm ; và
lần lượt là thể tích của và . Tính tỉ số 1 2 V2 5 4 3 4 A. . B. . C. . D. . 4 5 4 3 Lời giải Chọn B
Mặt phẳng   qua MN và song song với SC cắt BC và AC lần lượt tại P và Q thỏa
mãn MQ SC và NP SC .
Gọi V là thể tích của khối tứ diện SABC . Xét V VVV . 2 MNABPQ N.ABPQ Q.AMN V V V   N.ABPQ Q.AMN CQ CP BN AM SN QA 5 V 4 2    1 . .  . .    1   . V V VCA CB  S B AS SB CA 9 V 5 2
Câu 91. Cho hình lập phương ABC .
D A' B'C' D' cạnh bằng 1. Gọi M là trung điểm cạnh BB' . Mặt
phẳng (MA' D) cắt cạnh BC tại K . Thể tích khối đa diện lồi A'B'C'D' MKCD bằng 7 7 1 17 A. . B. . C. . D. . 24 17 24 24 Lời giải Chọn D LÊ MINH TÂM Trang 76
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN A' D' B' C' M A D B K C E
 Kéo dài A' Mvà AB cắt nhau tại E . Suy ra K DEB . C
 Dễ thấy B là trung điểm EA và K là trung điểm BC    Có VV VV VV         .
A' B'C ' D' MKCD A'ADMBK
A'.ADE M.BEK  1 1 7 17 1 1  3 24  24 24
Câu 92. Cho hình chóp tứ giác .
S ABCD có đáy là hình vuông, mặt bên SAB là tam giác đều và nằm
trong mặt phẳng vuông góc với đáy. Biết khoảng cách từ điểm A đến mặt phẳng SCD 3 7a bằng
. Thể tích V của khối chóp . S ABCD là 7 2 3 1 A. 3 V a . B. 3 V a . C. 3 V a . D. 3 V a . 3 2 3 Lời giải Chọn B S K B C H I A D
 Gọi H, I lần lượt là trung điểm của AB và CD , K là hình chiếu của H trên SI ta có 3 7a
SH  ABCD ; HK  SCD và HK  . 7 1 1 1
 Đặt AB  2x SH x 3 . Vì tam giác SHI vuông tại H nên   . 2 2 2 HK SH HI 7 1 1 a 3 Suy ra    x  . 2 2 2 9a 3x 4x 2
 Diện tích đáy S  a 2 2 3  3
3a ; chiều cao h SH a 2 3  1 3a
Vậy thể tích V của khối chóp .
S ABCD là V  . S h  . 3 2 Trang 77 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Câu 93. Cho lăng trụ tam giác AB . C A BC
  có thể tích V . Gọi G là trọng tâm tam giác A BC   , M là
tâm của mặt bên ABB A
  . Tính thể tích của khối tứ diện GMBC theo V . 2 1 1 1 A. V . B. V . C. V . D. V . 9 9 3 6 Lời giải Chọn B  Ta có: V     V VV . C.BKA C.BMG C.MGA C.BGK 1 1 1 1  Khi đó: V           V    VV   V   V V V V V . C.BKA ABC.A B C ABCA C .CKA B .BKA 3 6 6 3 1  Khi đó: V   
d C; A MG .S C.MGA      3 A MG 1  dC;A MG 1 1 1 . S        . d C A MG S  V V V A BK  ;  1 1 1 1 . . . 3 3 3 3 A BK 3 CA BK 3 3 9 1 V
 d C; BGK .S
 d C; BGK . S C.BGK    1 BGK    1   3 3 3 A BK 1 1
 . dC;A BK 1 1 1 1 .S      V  . V V . 3 3 A BK 3 CA BK 3 3 9 1 1 1 1  Vậy ta có VV        VV V V V V . C.BMG C.BKA C.MGA C.BGK 3 9 9 9
Câu 94. Cho hình lăng trụ AB . C A BC
  có tam giác ABC vuông tại A , AB a , AC a 3 , AA'  2a.
Hình chiếu vuông góc của điểm A trên mặt phẳng A BC
  trùng với trung điểm H của đoạn B C
  (tham khảo hình vẽ dưới đây). Khoảng cách giữa hai đường thẳng AA và BC bằng LÊ MINH TÂM Trang 78
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN a 5 a 5 a 15 a 15 A. . B. . C. . D. . 5 3 3 5 Lời giải Chọn D
Vì AA//BB nên ddd   . AA ,BC
AA',BB CC
A,BB CC Trong ABC   có 2 2
B'C  A B    A C
   2a A H   a. Trong AA H  có 2 2
AH AA  A H   a 3 . Trong AHC có 2 2
CH AC AH a 6 . a 15 Trong CHC có S         p p a p b p c S   a C HC     2 2 15 . 4 BCC B 3 1 3a
Thể tích lăng trụ là V      
AH.S    a 3. . . a a 3 . ABC.A B C A B C 2 2 3 2 1 3a a 15 Mà 3 V         V    .d .S      a d . A'.BB C C ABC.A B C
A ,BB C C BB C C
A,BB CC 2 3 3 a 15 5
Câu 95. Cho hình chóp .
S ABCD có đáy ABCD là hình bình hành. Mặt bên SAB là tam giác đều cạnh
3a . ABC là tam giác vuông tại A có cạnh AC a , góc giữa AD và SAB bằng 30. Thể tích khối chóp . S ABCD bằng 3 3a 3 3a 3 3a A. . B. . C. . D. 3 a . 6 2 4 Lời giải Chọn B Cách 1: Trang 79 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN S A B H I D C
Từ giả thiết bài toán ta có ABC  30 . 
Gọi H, I lần lượt là trung điểm của AB, BC khi đó AD,SAB  BI,SAB  30  HBI .
Từ đó ta có HB là hình chiếu của IB lên mặt phẳng SAB mà SH AB SH BI .
Vậy SH  ABCD . a . a V  . a .a .  . S.ABCD   3 1 3 3 3 3 3 2 2 Cách 2: S K A B D C
Gọi K là hình chiếu của C lên SAB , khi đó AD,SAB  BC,SAB  CBK  30 .  3 1 a 3
CK BC sin30  a V  2V  2. .CK.S  . S.ABCD S.ABC 3 SAB 2
Câu 96. Cho hình chóp .
S ABCD có đáy ABCD là hình bình hành. Gọi N là một điểm thuộc cạnh
SD sao cho DN  2S .
N Mặt phẳng P qua BN, song song với AC cắt SA,SC lần lượt tại M, .
E Biết khối chóp đã cho có thể tích V. Tính theo V thể tích khối chóp . S BMNE . V V V V A. . B. . C. . D. . 6 12 4 3 Lời giải Chọn A LÊ MINH TÂM Trang 80
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN S N E M I K C B O A D
Gọi O AC BD, I SO ME , khi đó P chính là mặt phẳng BMNE .
Gọi K là trung điểm ND , ta có OK // BN IN // OK hay I là trung điểm SO. Do
ME // AC nên M, E lần lượt là trung điểm SA và SC . V SB SM SN 1 1 1 V
Ta thấy S.BMN  . . 1. .  1
, tương tự S.BNE  . V SB SA SD 2 3 6 V 6 S.BAD S.BDC 1 VV V V Do đó S.BMN S.BNE S.BMNE   hay V  . 6 VV V S.BMNE 6 S.BAD S.BDC S.ABCD
Câu 97. Cho khối chóp .
S ABC có SA a 3 , SA vuông góc với mặt phẳng ABC , ABC vuông tại
B , AB a , SBC cân. Thể tích khối chóp . S ABC bằng 3 2a 3 3 a 3 3 a 3 A. 3 a 3 . B. . C. . D. . 3 3 6 Lời giải Chọn C
Vì SA  ABC SA AB và SA AC
ABC vuông tại B AC BC ; SAC vuông tại A SC AC SC BC   1 Lại có: 2 2 2
SC SA AC ; 2 2 2
SB SA AB , mà AC AB (do ABC vuông tại B ) 2 2
SC SB SC SB 2 Từ  
1 , 2 và SBC cân  SBC cân tại B . Khi đó BC SB Ta lại có: 2 2 2 2 2
SB SA AB  3a a  4a  2a BC  2a Trang 81 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN  1 1 Diện tích ABC là 2
ABBC  a2a a 2 2 3 1 a 3
Vậy thể tích khối chóp . S ABC là 2
V   a a 3  . 3 3
Câu 98. Cho hình lăng trụ AB . C A BC
  có đáy ABC là tam giác đều cạnh a , hình chiếu của A trên
mặt phẳng  ABC là tâm O của tam giác ABC . Gọi O là tâm của tam giác A BC  ,M là
trung điểm của AA, G là trọng tâm tam giác B CC  . Biết 3 Vh
a . Tính chiều cao của O .OMG lăng trụ.
A. h  24a 3 .
B. h  36a 3 .
C. h  9a 3 .
D. h  18a 3 . Lời giải Chọn B A' C' O' I' B' M G A C O I B
Gọi I và I lần lượt là trung điểm của BC và B C
  . Ta có AA//OO G   suy ra V    1 1 2 1     VVV V   . V   V O .OMG M.OO G . A OO G G.AOO   2 G.AOO A 2 3 G.AII A 3 G.AII A 1 1 1 2 2 27 3  . V    3      . V    V    a V    a 3 3 C .AII A 9 3 AIC.A I C 27 AIC.A I C AIC.A I C 2 2 1 a 3 27 . .a hay 3 . h  3 a  . h  27 4 27a h   36a 3 . 2 4 2 4 3
Câu 99. Cho hình chóp .
S ABCD , gọi I, J, K, H lần lượt là trung điểm của các cạnh SA,SB,SC,SD .
Tính thể tích khối chóp .
S ABCD biết rằng thể tích khối chóp . S IJKH là 1. A. 4 . B. 2 . C. 16 . D. 8 . Lời giải Chọn D LÊ MINH TÂM Trang 82
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN S H I K J A D C B VS.IJK SI SJ SK 1 1 1 1 Ta có:  . .  . .  V SA SB SC 2 2 2 8 S.ABC 1  V  .V S.IJK S.ABC   1 8 V SI SK SH 1 1 1 1 S.IKH  . .  . .  V SA SC SD 2 2 2 8 S.ACD 1  V  .V S.IKH S.ACD  2 8 1 V Từ   . 1 và 2  VVVV  1 1 V  . S IJKH V   S.IJKH S.IJK S.IKH
S.ABC S.ACD 8 8 S.ABCD V 8 S.ABCD Khi đó V  8.V  8 . S.ABCD S.IJKH
Câu 100. Cho khối chóp .
S ABCD có đáy là hình bình hành ABCD . Gọi M, N, P,Q lần lượt là trọng
tâm các tam giác SAB,SBC,SCD,SDA . Biết thể tích khối chóp .
S MNPQ là V , khi đó thể tích của khối chóp . S ABCD là 2 27V  9  9V 81V A. . B.   V . C. . D. 4  2  4 8 Lời giải Chọn A
Giải bài toán trong trường hợp đặc biệt. Ta có hình vuông cũng là một hình bình hành đặc
biệt nên xem đáy ABCD là hình vuông. Khi đó, khối chóp .
S ABCD là chóp đều và có chiều cao h , cạnh đáy AB 1. Trang 83 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN 2 2 1 2 Suy ra, khối chóp .
S MNPQ có chiều cao bằng h và cạnh đáy MN  . AC  . 3 3 2 3 2 V 3  3  27 27
Xét tỉ số S.ABCD  .    VV . V 2 S.ABCD   S.MNPQ 2 4 4
Câu 101. Cho hình chóp .
S ABCD có đáy ABCD là hình vuông cạnh a , SA a và SA vuông góc với
đáy. Gọi M là trung điểm của SB , N thuộc cạnh SN  2ND. Tính V của khối tứ diện ACMN . 1 1 1 1 A. 3 V a . B. 3 V a . C. 3 V a . D. 3 V a . 36 12 8 6 Lời giải Chọn B VVVVVV . Ta có ACMN . S ABCD SAMN DNAC BAMC SMCN V SM SN 1 1 SAMN  .   VV V SB SD 3 SAMN 6 SABCD SABD V ND 1 1 DACN    VV V SD 3 SAMN 6 SABCD DACS V BM 1 1 BACM    VV V BS 2 SAMN 4 SABCD BACS V SM SN 1 1 SMCN  .   VV V BS SD 3 SAMN 6 SABCD SBCD 1 1 Vậy 3 VVa . ACMN 4 SABCD 12
Câu 102. Ông An muốn xây một bể nước dạng hình hộp chữ nhật có nắp với dung tích 3 mét khối.
Đáy bể là một hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thuê nhân công để xây bể
là 500000 đồng cho mỗi mét vuông. Hỏi chi phí thấp nhất ông An cần bỏ ra để xây bể nước là bao nhiêu? A. 6490123 đồng. B. 7500000 đồng. C. 6500000 đồng. D. 5151214 đồng. Lời giải Chọn A LÊ MINH TÂM Trang 84
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Gọi xx  0 là chiều rộng của đáy bể, suy ra chiều dài của đáy bể là 2x và gọi h là chiều cao của bể.
Diện tích xây dựng là diện tích toàn phần của bể 2 S  2 2
. xh  2.xh  2 2 . .
x x  4x  6xh   1 3 9 Ta có V  3  2 . x . x h h  2 2  1 Sx 2  4x x  0 2 
. Thay vào , ta được hàm , với 2x x 9 9 9 9 9 Ta có Sx 2 2 2 3 3
 4x   4x    3 4x . .  3 81 . x 2x 2x 2x 2x 3 9 9
Dấu “=” xảy ra khi và chỉ khi 2 4x   x  . 2x 2
Khi đó chi phí thấp nhất là 3
3 81500000  6490123 (đồng).
Câu 103. Cho hình lập phương ABC . D A BCD
  cạnh 2a, gọi M là trung điểm của BB và P thuộc cạnh DD 1 sao cho DP
DD. Mặt phẳng AMP cắt CC tại N . Thể tích khối đa diện 4 AMNPBCD bằng 3 a 11 3 a 9 A. 3 3a . B. . C. 3 2a . D. . 3 4 Lời giải Chọn A C' B' N M D' A' C B P D A BM CN DP 1 1 3 Gọi b  ; c  ; d
ta có c b d    . BBCCDD 2 4 4
b c d 3 V  .V       . a a . AMNPBCD ABCD.A B C D 2 3 3 3 4 8 Trang 85 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Câu 104. Cho khối lăng trụ đứng AB . C A BC
  có BAC  60 , AB  3a và AC  4a. Gọi M là trung a điểm của B C
  , biết khoảng các từ M đến mặt phẳng B A  3 15 C bằng . Thể tích khối 10 lăng trụ bằng A. 3 7a . B. 3 27a . C. 3 4a . D. 3 9a . Lời giải Chọn B MN B M
Gọi N là giao điểm của BM và B C  1 .Ta có   , suy ra: BN BC 2  a d ; B AB C
   dM;AB C   3 15 2  5
Từ B kẻ đường cao BH của tam giác ABC , kẻ BK vuông góc với đường thẳng HB . Khi a
đó BK d  ; B AB C   3 15  . 5 3a 3
Mặt khác BH A .
B sin HAB  3 . a sin 60  . 2
Tam giác HBB vuông tại B có đường cao BK : 1 1 1 25 4 1       B B   a . 2 2 2 2 2 2 B B  3 3 BK BH 9a 1 . 5 9.a 3 . 27a 1 Vậy 3 V          BB .S BB . A . B AC.sin 60 27a . ABC.A B C ABC 2
Câu 105. Cho hình chóp .
S ABCD có đáy ABCD là hình vuông cạnh a , SA SB , SC SD ,  2 7a
SAB  SCD và tổng diện tích hai tam giác SAB và SCD bằng
. Tính thể tích V của 10 khối chóp . S ABCD . 3 4a 3 12a 3 4a A. V  . B. 3
V  20a . C. V  . D. V  . 15 25 25 Lời giải Chọn D LÊ MINH TÂM Trang 86
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN S A D M N H B C
Gọi M, N lần lượt là trung điểm của AB,CD . SM  
AB SAB can Ta có: 
SMN ABCD SN   CD   SCD can    
Kẻ SH MN SH  ABCD  h SH 0
MSN  90 (vì SAB  SCD   SAB ,SCD 0  90 S . M SNh SH MN a Mặt khác ta có: SS  A . B SM C . D SN SM SN SAB SCD    2 1 1 7 2 2 10 2 7a
SM SN  . 5
SM SN2  SM SN 12a 2 2 2  2 2  2
Ta lại có: SM SN MN SM.SN   2 25 12 3 1 4a Có: SH
a . Vậy: V  .S .SH  . 25 3 ABCD 25
Câu 106. Cho hình chóp đều .
S ABCD với O là tâm đáy. Khoảng cách từ O đến mặt bên bằng 1 và
góc giữa mặt bên với đáy bằng 0
45 . Thể tích của khối chóp . S ABCD bằng 4 2 A. V  8 2 . B. V  . C. V  4 3 2 3 . D. V  . 3 3 3 Lời giải Chọn B Trang 87 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Gọi I là trung điểm của CD OI CD ,CD  2OI.
Kẻ OH SI tại H OH  SCD  d O,SCD  OH  1.
SCDABCD  CD
Ta có  SI  SCD ,SI CD   SCD ,ABCD  SI,OI 0  SIO  45 . OI  
ABCD,OI CD OH 1
Xét tam giác vuông HIO OI  
 2  CD  2OI  2 2. 0 sin SIO sin 45 Ta có S
IO là tam giác vuông cân tại O SO OI  2. 1 1 8 2 Vậy VCD .SO  .  . S.ABCD   2 22 2 2 3 3 3
Câu 107. Cho hình lăng trụ đứng AB . C A BC
  có thể tích bằng V. Các điểm M,N,P lần lượt thuộc AM BN CP
các cạnh AA ; BB ;CC 1 2 sao cho  ; 
 . Thể tích khối đa diện ABC MNP AA 2 BBCC . 3 bằng 2 9 20 11 A. V B. V C. V . D. V . 3 16 27 18 Lời giải Chọn D
Gọi K là hình chiếu của P trên AA. 2 Khi đó VV ABC.KPN 3 LÊ MINH TÂM Trang 88
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN 1 1  1 1  1 VMK.S   .AA .S    V . M ,KPN 3 KNP 3  2 6 ABC  18 2 1 11 Do đó VV V V ABC.MNP 3 18 18
Câu 108. Cho hình chóp .
S ABCD có đáy ABCD là hình vuông. Các điểm M, N, P,Q lần lượt là trung điểm của A ,
B BC,CD, DA . Điểm E thuộc miền trong của hình vuông ABCD . Biết rằng V  75,V  42,V
 60. Thể tích khối chóp .
S EPCN nằm trong khoảng nào S.EMAQ S.EMBN S.EQDP dưới đây? A. 35; 40 . B. 25;30 . C. 30;35 . D. 20; 25 . Lời giải Chọn B Ta thấy rằng: SSSSSSSS EMQ ENP EPQ EMN AEMQ CENP EQDP EMBN Do đó, VVVVV  42  60  75  27 S AEMQ S CENP S EQDP S EMBN S CENP 25;30 . . . . . .
Câu 109. Cho hình chóp .
S ABCD có đáy ABCD là hình thoi cạnh bằng a . Biết rằng
SA a,SA A ,
D SB a 3, AC a . Thể tích khối chóp . S ABCD bằng. 3 a 2 3 a 2 3 a 2 3 a 6 A. . B. . C. . D. . 2 3 6 2 Lời giải Chọn C
Gọi O AC BD BD  2BO a 3 . Ta có 2 2
SD SA AD a 2 2 2 2 2 2 2 2 SB SD BD 3a  2a 3a 7a Suy ra: 2 SO      . 2 4 2 4 4 2 2 2 2 2 2 2 SA SC AC a SC a 7a Lại có: 2 SO     
SC a 3 . 2 4 2 4 4 Trang 89 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN Xét S
CD vuông tại D vì 2 2 2
SC SD DC và AS AD AC nên hình chiếu của A lên
SCD là điểm H trung điểm SC . 2 3 3 1 1 a a 2 a 3 a 2 Do đó, VV  .AH.S  . .   V  2V  . A.SDC S.ADC  3 SDC 3 2 2 12 S.ABCD S.ADC 6
Câu 110. Cho khối chóp .
S ABC , đáy ABC là tam giác có AB  3 2 , 0
AC 12 , BAC  45 , cạnh bên
SA vuông góc với đáy, SA 12. Gọi   là mặt phẳng đi qua đỉnh A vuông góc với cạnh
SC , mặt phẳng   chia khối chóp .
S ABC thành 2 khối đa diện có thể tích V , V (trong đó 1 2 V
V là thể tích khối đa diện chứa đỉnh S ). Tỷ số 1 bằng 1 V2 2 1 1 A. . B. 2 . C. . D. . 3 3 2 Lời giải Chọn A
 Gọi F   SC AF SC .
 Gọi H là hình chiếu vuông góc của B lên SC , kẻ EF // BH với ESB     AFE.
SB  9 2;SC 12 2 ; 2 2 0
BC AB AC  2A . B AC.cos 45  3 10 .  Tam giác SBC có 2 2 2 2 2 2 2
SB SH BC HC    2 9 2
SH  3 10 12 2  15 2
SH   SH  . 2
 Do tam giác SAC vuông cân tại A nên SC  12 2 12 2  SF  . 2 12 2  SE SF 4 Ta lại có 2    . SB SH 15 2 5 2 LÊ MINH TÂM Trang 90
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN V SE SF 4 1 2 V 3 V 2  1 3  .  .    . Vậy 1  . V SB SC 5 2 5 V 5 V 3 S.ABC S.ABC 2
Câu 111. Cho hình chóp tứ giác đều .
S ABCD có mặt bên SCD hợp với mặt đáy một góc 45 và
khoảng cách từ điểm A đến mặt phẳng SCD bằng a 3 . Thể tích khối chóp . S ABCD bằng 3 4a 3 a 2 A. . B. . C. 3 2a 3 . D. 3 a 6 . 3 3 Lời giải Chọn D
Gọi M là trung điểm cạnh SC , khi đó: SM CD tại M trong SCD và OM CD tại M trong  ABCD .
Khi đó:  SCD ,ABCD  SM,OM  SMO  45 . Suy ra: S
OM vuông cân tại O .
Trong SOM, dựng OH SM tại H . a Ta có: a
dA,SCD  dO,SCD 3 3 2
 2OH OH  . 2 2 a 6 1 1 a 6  a 6  Suy ra: 2 3 SO OM   V  . . SO AD  . . 2.   a 6 . 2 S.ABCD 3 3 2  2   
Câu 112. Cho khối chóp .
S ABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với mặt phẳng
đáy. Gọi H, K lần lượt là hình chiếu vuông góc của A lên SB,SD . Biết góc giữa hai mặt
phẳng  ABCD và  AHK bằng 0
30 . Thể tích khối chóp . S ABCD bằng 3 a 6 3 a 6 3 a 2 3 a 6 A. . B. . C. . D. . 3 9 3 2 Lời giải Chọn A Trang 91 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN S K H D A B C
Ta có: BC AB và BC SA suy ra BC  SAB  BC AH .
Mặt khác AH SB suy ra AH  SBC  SC AH .
Chứng minh tương tự ta cũng có AK  SCD  SC AK .
Vậy SC  AHK .
Mà SA  ABCD.
Do đó góc giữa hai mặt phẳng  ABCD và  AHK là góc giữa hai đường thẳng SA và SC (
theo định nghĩa góc giữa hai mặt phẳng) và bằng ASC . Vậy 0 ASC  30 . SA SA 3
Xét tam giác SAC có cos ASC    SA a 6 . SC
SA  a 22 2 2 3 1 1 a 6 2 V  . SA S  .a 6.a  . S.ABCD 3 ABCD 3 3
Câu 113. Cho hình chóp .
S ABCD có đáy ABCD là hình chữ nhật có AB a , AD  2a , SA vuông góc a
với đáy, khoảng cách từ A đến SCD bằng . Tính thể tích khối chóp theo a . 2 4 15 4 15 2 5 2 5 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 45 15 15 45 Lời giải Chọn A LÊ MINH TÂM Trang 92
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Kẻ AH SD   1 . CD AD Ta có 
CD  SAD CD AH 2 . CD   SA a Từ  
1 , 2 ta có AH  SCD  d A,SCD  AH AH  . 2 a  1 1 1 2a AH.AD 2a 15 Trong SAD ta có    SA  2   . 2 2 2 AH SA AD 2 2 AD AH 2 15 2 a 4a  4 1 a 4 15
Vậy thể tích khối chóp .
S ABCD là V  1 2 15 S . A A . B AD   .a 2 . a 3  a . 3 3 15 45
Câu 114. Cho hình chóp .
S ABCD có đáy ABCD là hình chữ nhật với AB  6 , AD  3 , tam giác
SAC nhọn và nằm trong mặt phẳng vuông góc với đáy. Biết hai mặt phẳng SAB , SAC 3
tạo với nhau góc thỏa mãn tan 
và cạnh SC  3 . Thể tích khối . S ABCD bằng: 4 4 8 5 3 A. . B. . C. 3 3 . D. . 3 3 3 Lời giải Chọn B V  2V  2V
. Kẻ BH vuông góc với AC tại H . S.ABCD S.ABC . B SAC
Ta có: AC  3, BH  2 , HC  4 2 1  KH  3 KH 2 2 sinSAC   1  cosSAC  . HA 3 3 2 2 2
SC SA AC  2A . S A .
C cosSAC SA  2 . 1 S  1 2 2 S . A AC.sinSAC  2 . 3 . .  2 2 . SAC 2 2 3 1 8 Vậy V  2. 2 . 2. 2  . S.ABCD 3 3
Câu 115. Cho hình chóp .
S ABCD có đáy ABCD là hình thoi tâm O cạnh a , góc BCA  30 , 3a
SO  ABCD và SO
. Khi đó thể tích của khối chóp là 4 Trang 93 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN 3 a 2 3 a 3 3 a 2 3 a 3 A. . B. . C. . D. . 4 8 8 4 Lời giải Chọn B s 3a 4 B A 30 O C a D
Theo giả thiết ABCD là hình thoi tâm O cạnh a , góc BCA  30 nên BCD  60 ; BCD đều a suy ra BD  3 a , CO
, AC  2CO a 3 . 2 1 2 1 a 3 a Ta có S
AC.BD  . . a a 3  1 ; V  3 S . O S với SO  suy ra ABCD 2 2 2 S.ABCD 3 ABCD 4 2 3 1 3a a 3 a 3 V     . S.ABCD 3 4 2 8
Câu 116. Cho hình chóp .
S ABC có đáy ABC là tam giác vuông tại A và có AB a, BC a 3 . Mặt bên
SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng ABC . Tính thể
tích V của khối khóp . S ABC . 3 2a 6 3 a 6 3 a 6 3 a 6 A. V  . B. V  . C. V  . D. V  . 12 6 12 4 Lời giải Chọn C
Gọi K là trung điểm của đoạn AB . Vì S
AB là tam giác đều nên SK AB.
SAB ABC theo giao tuyến AB. LÊ MINH TÂM Trang 94
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN SK  ABC 1  VSK.S . S.ABC 3 ABC A
BC vuông tại A có 2 2
AB a, BC a 3  AC BC AB a 2 2 1 1 a 2 SA . B AC  . a a 2  . ABC 2 2 2 a S  3
AB là tam giác đều  SK  . 2 2 3 1 1 a 3 a 2 a 6 VSK.S  . .  . S.ABC  3 ABC 3 2 2 12
Câu 117. Cho hình chóp .
S ABCD có đáy là hình vuông cạnh a , hình chiếu vuông góc của S lên mặt
phẳng  ABCD trùng với trung điểm cạnh AD , cạnh bên SB hợp với đáy một góc 60. Tính
theo a thể tích V của khối chóp . S ABCD . 3 a 15 3 a 15 3 a 15 3 a 5 A. V  . B. V  . C. V  . D. V  . 2 6 4 6 Lời giải Chọn B
Gọi H là trung điểm của AD SH  ABCD  BH là hình chiếu vuông góc của SB trên  ABCD .
SBH  SB,ABCD  60 . 2 a a 5 A
BH vuông tại A 2 2 2
BH AB AH a   . 4 2 a 15 S
BH vuông tại H SH H . B tan 60  . 2 3 1 a 15 V  .SH.S  . S.ABCD 3 ABCD 6
Câu 118. Cho hình chóp .
S ABC có đáy ABC là tam giác vuông cân tại B , SA  ABC , AB a . Biết
góc giữa đường thẳng AC và mặt phẳng SBC bằng 30. Thể tích khối chóp . S ABC bằng 3 a 3 a 3 a 3 A. . B. . C. 3 a . D. . 6 3 6 Lời giải Trang 95 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN Chọn A S H A C B
Từ A kẻ AH SB tại B . BC AB Ta có 
BC  SAB  BC AH . BC   SAAH SB Lại có 
AH  SBC. AH   BC
Từ đó suy ra  AC,SBC   AC,HC  ACH  30 .
Tam giác ABC vuông cân tại B nên AC AB 2  a 2 . a 2
Xét AHC vuông tại H : AH AC.sin ACH a 2.sin 30  . 2 1 1 1 1 1
Xét SAB vuông tại A :      SA a . 2 2 2 2 2 AH SA AB SA a 2 1 a
Diện tích tam giác ABC là 2 SAB  . ABC 2 2 3 1 a Thể tích khối chóp . S ABC là VS .SA  . S.ABC 3 ABC 6
Câu 119. Cho hình chóp tứ giác đều .
S ABCD có cạnh đáy bằng 2a. Góc giữa đường thẳng AC và
mặt phẳng SBC bằng 30. Thể tích của khối chóp . S ABCD bằng 4 3 2 6a 3 2 6a A. 3 4a . B. 3 a . C. . D. . 3 9 3 Lời giải Chọn B S H A D O B K C
Gọi O là giao điểm hai đường chéo của hình vuông ABCD . Suy ra SO  ABCD . LÊ MINH TÂM Trang 96
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Gọi K là trung điểm của BC OK BC . Từ O kẻ OH SK tại H . BC OK Ta có 
BC  SOK  BC OH . BC   SO OH   SK Lại có 
OH  SBC . OH   BC
Suy ra AC,SBC  OC,SBC  OC,HC  OCH  30 . 1 1 Ta có OC
AC  .AB 2  a 2 . 2 2 a 2
Xét OHC vuông tại H : OH OC.sinOCH a 2.sin 30  . 2 1 1 1 1 1
Xét SOK vuông tại O :      SO a . 2 2 2 2 2 OH SO OK SO a
Diện tích hình vuông ABCD : S
AB a a ABCD  2 2 2 2 4 . 1 1 4 Thể tích khối chóp 2 3 . S ABCD : VS .SO  4
. a .a a . S.ABCD 3 ABCD 3 3
Câu 120. Cho hình chóp .
S ABC có đáy ABC là tam giác đều, cạnh bên SA vuông góc với mặt đáy và
SA a 3 , góc giữa SA mặt phẳng (SBC) bằng 0
45 . Thể tích khối chóp . S ABC bằng 3 a 3 3 3a 3 A. 3 a 3. B. . C. . D. 3 a . 12 12 Lời giải Chọn D
Gọi M là trung điểm của BC
Do tam giác ABC đều nên AM BC
AM BC BC (SAM) SA BC  Kẻ AH SM BC AH  Ta có
  AH  (SBC)  SA,(SBC)  SA,SH 0  ASH  45 SM AHTrang 97 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Suy ra ASM vuông cân tại A
Ta c SA AM a 3
Suy ra AB BC AC  2a 1 Vậy 3 V
S .SA a . S.ABC 3 ABC
Câu 121. Cho hình chóp .
S ABCD có đáy là hình vuông cạnh a . Cạnh bên SA vuông góc với mặt
phẳng đáy, cạnh bên SC tạo với mặt phẳng SAB một góc 30. Thể tích của khối chóp đó bằng 3 a 3 3 a 2 3 a 2 3 a 2 A. . B. . C. . D. . 3 4 2 3 Lời giải Chọn D
Vì BC SA và BC AB nên BC  SAB. Từ đó SC,SAB  SC,SB  BSC  30 a
Trong tam giác SCB , ta có 2 2 tan 30 
SB a 3 ; SA SB AB a 2 SB 3 1 a 2
Vậy thể tích khối chóp là VS . A S SABCD 3 ABCD 3
Câu 122. Cho hình chóp .
S ABCD có đáy ABCD là hình thang vuông tại A và D . Biết
AB  4a, AD CD  2a . Cạnh bên SA  3a và SA vuông góc với mặt phẳng đáy. Gọi G là
trọng tâm tam giác SBC , M là điểm sao cho MA  2MS và E là trung điểm cạnh CD
(tham khảo hình vẽ). Tính thể tích V của khối đa diện MGABE. LÊ MINH TÂM Trang 98
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN 3 27a 3 10a 3 13a 3 25a A. . B. . C. . D. . 8 3 4 9 Lời giải Chọn B Ta có VVVV . MGABE GABE GABM GAEM 1 3 1 1 1 1 4a 2 S  2 . a 4 . a  4a  2 VV
 . S .SA  4 . a 3 . a  . ABE 2 GABE 3 SABE 3 3 ABE 9 3 1 3 1 1 1 1 8a 2 S  4 . a 2 . a  4a 2  VV  . S .DA  4 . a 2 . a  . ABM 2 GABM 3 CABM 3 3 ABM 9 9
Gọi I là trung điểm của BC . 2 2 BD 16a  4a 2 2
AE  4a a a 5 ; EI    a 5 . 2 2 2 2 2 2 2 2 AC AB BC 8a 16a 8a 2 2 AI    
10a AI a 10 . 2 4 2 4
Dựng EH AI H là trung điểm của AI . 2  a 10  a 10 1 1 a 10 5 2
EH  5a      ; 2 SEH.AI  . .a 10  a . 2  2 AEI   2 2 2 2 3 2 2 2 1 2 5 10a 2 VVV
 . S .MA  . a 2 . a  . GAEM 3 IAEM 3 MAEI 3 3 AEI 9 2 9 3 3 3 3 4a 8a 10a 10a Vậy V     . MGABE 3 9 9 3
Câu 123. Cho hình chóp .
S ABCD có đáy ABCD là hình chữ nhật. E là điểm trên cạnh AD sao cho
BE vuông góc với AC tại H và AB AE , cạnh SH vuông góc với mặt phẳng đáy, góc 2a
BSH  45 . Biết AH
, BE a 5 . Thể tích khối chóp . S ABCD bằng 5 3 a 5 3 16a 3 32a 3 8a 5 A. . B. . C. . D. . 15 3 5 5 5 Lời giải Chọn B Trang 99 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Đặt AE x , AB y y x .
Tam giác ABE vuông tại A , có đường cao AH . Áp dụng các hệ thức lượng trong tam giác vuông ta có: 2 2 2
BE AE AB 2 2 2 5
a x y   2 2 2
x y  5a
x y  3ax a +)  1 1 1         .   5 1 1     2 xy  2a 2 xy  2ay  2a 2 2 2  AH AE AB 2 2 2 4  a x y 2 2 AB 4a 4 5a a a +) BH    4 5 5
EH BE BH a 5   . BE a 5 5 5 5 4 5a
Tam giác SHB vuông cân tại H (có BSH  45 ), suy ra: SH  . 5 BC BH +) 
 4  BC  4a . EA EH 3 1 1 1 4 5a 16 5a Vậy V  .SH.S  .SH.A . B BC  . 2 . a 4 . a  . S.ABCD 3 ABCD 6 6 5 15
Câu 124. Cho khối hộp ABC . D A BCD
  có thể tích bằng V . Gọi M , N , P lần lượt là trung điểm của V AB , B C
 , DD. Gọi thể tích khối tứ diện CMNP là V , khi đó tỉ số bằng V 1 3 1 3 A. . B. . C. . D. . 16 16 64 64 Lời giải Chọn B LÊ MINH TÂM Trang 100
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Ta có: V V   V         V   V VV   VV V . B HN.BMQ A HD .AMD N.MQC P.NCC P.D C N P.D HN P.HNM P.MDC
Gọi S là diện tích đáy và h là chiều cao khối hộp. 1 1 1 1 1 Xét: V       Sh , V   Sh , V Sh , VSh , V   Sh , B HN.BMQ 8 A HD .AMD 4 N.MQC 24 P.NCC 12 P.D C N 24 1 1 1 V       Sh , V V VSh , V Sh . P.D HN 16 P.HNM D .HNM M.HND 8 P.MDC 12 13 3 V  3
Suy ra: V V   V V   V   . 16 16 V 16 SM 1
Câu 125. Cho tứ diện SABC và hai điểm M, N lần lượt thuộc các cạnh SA, SB sao cho  , AM 2
SN  2. Mặt phẳng (P) đi qua hai điểm M, N và song song với cạnh SC cắt AC, BC lần BN V
lượt tại L, K . Gọi V , V  lần lượt là thể tích các khối đa diện SCMNKL, SABC . Tỉ số V bằng 2 4 1 1 A. . B. . C. . D. . 3 9 4 3 Lời giải Chọn B S M N L A C K B I Trang 101 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Gọi I là giao điểm của A , B MN, KL . AM AL 2 BN BK 1
Do ML SC và NK SC nên ta có   và   . AS AC 3 BS BC 3 MA NS IB IB 1 Ta có . . 1 suy ra  . MS NB IA IA 4 CL BA KI 1 3 KI IN IK 1 Ta có . . 1  . .
1  KL KI suy ra  MN NI hay   . CA BI KL 3 1 KL IM IL 2 V I . B IN.IK 1 1 1 1
Xét hình chóp IAML ta có I.BNK   . .  . V I . A IM.IL 4 2 2 16 I.AML 1 1 4 2 2 16 Mặt khác ta có V
dI;(AM ) L .S  . d B AML SV . AML  ;( ). . IAML 3 3 3 3 3 SAC 27 SABC V 1 16 1 1 16 1 5 Suy ra I.BNK  .  . Suy ra V  .V   VV  
.V   V . V 16 27 27 I.BNK 27 BNKAML 27 27 9 SABC 5 4 Ta có VV  V
V  V  V . SCMNKL BNKAML 9 9 V 4 Từ đó ta có  V  . 9
Câu 126. Cho lăng trụ AB . C A BC
 . Gọi M , N , Q , R lần lượt là trung điểm của các cạnh AB , A B  , BC , B C
  và P , S lần lượt là trọng tâm của các tam giác AA B  , CC B
 . Tỉ số thể tích khối đa
diện MNRQPS và khối lăng trụ AB . C A BC   là 1 5 1 2 A. . B. . C. . D. . 9 54 10 27 Lời giải Chọn B  1 2 Đặt: V V ; V        
S   .d B , AA C C V B .AA C C AA C C    ABC.A BC   3 3 1     V        .S .d B , MNRQ
S   . d B , AA C C B .MNRQ MNRQ    1 1 1 AA C C    3 3  2   2   1   .S         .d B AA C C V V AA C C  ,  1 1 2 1 . .  3  4 4 3 6 1 1 1 1 1 V  .V     .V  . V V P.MNRQ 3 A .MNRQ 3 B .MNRQ 3 6 18  1 2 V      
S   .d A, BB C C V A.BB C C BB C C    3 3 LÊ MINH TÂM Trang 102
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN 1 1 1 1 1 1 S       SS ; S S  . S   S QRC     2 QRC C 4 BB C C QRS 3 QRC 3 4 BB C C 12 BB C C 1   VS
.d A, QRS   S  
   . d A, BB C C A.QRS QRS  
 1 1 BBCC     3 3 12   1   .S        .d A BB C C V V BB C C  ,  1 1 2 1 . .  3  12 12 3 18 PB 2 1 1 V  .V  . V V P.QRS A.QRS AB 3 18 27  1 1 5 VVVV V V MNRQPS P.MNRQ P.QRS 18 27 54 VMNRQPS 5 Vậy:  . V 54 ABC.A BC  
Câu 127. Cho hình lăng trụ đứng AB . C A BC
  có AB CB  2, AC 1. Một mặt phẳng (P) cắt các
đường thẳng AA, BB, CC lần lượt tại M, N, P sao cho tam giác MNP đều. Gọi là góc tạo bởi mặt phẳng ( )
P và mặt phẳng (ABC) , khi đó 3 5 5 10 A. cos  . B. cos  . C. cos  . D. cos  . 3 3 5 5 Lời giải Chọn C 1 15
Ta có: AB CB  2, AC 1  A
BC cân tại B S  . ( d ;
B (AC)).AC  . ABC 2 4
Ta có: Mặt phẳng (P) cắt các đường thẳng AA, BB, CC lần lượt tại M, N, P ; Gọi mặt
phẳng ( ) qua N song song với mặt đáy cắt AA, CC lần lượt tại I, J ; Gọi H là giao
điểm của IJ và MP thì H là trung điểm của IJ và MP . 1 15
Ta đặt: MN x  0 2
IM x  4  PJ , 2 2 MHIM   x  . 4 4
Mà H là trung điểm IJ nên H cũng là trung điểm MP 2
MP  2MH  4x 15 . Trang 103 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Do đề cho tam giác MNP đều nên ta có phương trình: 2
MP MN x  4x 15  x  5 . 2 x 3 5 3 Suy ra S   . MNP 4 4
Đến đây ta nhận thấy, do A
BC là hình chiếu của M
NP lên mặt phẳng đáy nên suy ra: S 15 4 5 cos ABC   .  . S 4 MNP 5 3 5
Câu 128. Cho khối chóp tứ giác .
S ABCD có cạnh đáy bằng a và cạnh bên bằng 2a . Gọi M là điểm
đối xứng của C qua D , N là trung điểm của SC . Mặt phẳng (BMN) chia khi chóp đã cho
thành 2 phần. Thể tích của phần chứa đỉnh S bằng 3 3 14a 3 5 14a 3 7 14a 3 7 14a A. . B. . C. . D. . 32 72 96 72 Lời giải Chọn D
Giả sử các điểm như hình vẽ. F  BMN  AD ; Kẻ OH SF ;
Gọi E SDMN E là trọng tâm S
CM , DF / /BC F là trung điểm BM. 2 2  a 2  a a 14 Ta có: 2 2 2 2
SO SD DO  (2a)     4a    2  2 2   2 2
a 14   a a 15 2 2
SF SO OF         2     2  2 2 S . O OF 2a 210 1 a 15  (
d M;(SBC))  4. ( d ; O (SA )
D )  4OH  4  ;S  .SF.AD . SF  15 SAD 2 4 V ME MF MD 2 1 1 1 1 MEFD   . .  . .   V  .V V MN MB MC 3 2 2 6 MEFD 6 MNBC MNBC 3 5 5 1 1 5 1 1 5a 14  V  .V  . . (
d M;(SBC)). .S  . .4OH. .S  . BFDCNE   6 MNBC 6 3 2 SBC 6 3 2 SAD 72 3 3 1 a 14 7a 14 V  .S . O S   VVV  . S.ABCD 3 ABCD 6 SABFEN S.ABCD BFDCNE 72 LÊ MINH TÂM Trang 104
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Câu 129. Cho hình chóp .
S ABC có AB  3a , BC  4a, CA  5a , các mặt bên tạo với đáy góc 60 , hình
chiếu vuông góc của S lên mặt phẳng ABC thuộc miền trong của tam giác ABC . Tính thể tích hình chóp . S ABC . A. 3 2a 3 . B. 3 6a 3 . C. 3 12a 3 . D. 3 2a 2 . Lời giải Chọn A Ta có 2 2 2 2 2 2
AC  25a  9a 16a AB BC , vậy tam giác ABC vuông tại B .
Gọi H là hình chiếu của S trên mặt phẳng ABC . Vì các mặt bên tạo với đáy góc 60 suy
ra: dH; AC  dH; BC  dH; AB và H thuộc miền trong của tam giác ABC nên H là
tâm đường tròn nội tiếp tam giác ABC .
Từ H kẻ đường thẳng vuông góc với BC tại M , suy ra: BC HM
BC  SHM  BC SM . BC   SH
Suy ra: SMH   SBC;ABC  60.
Đoạn HM là bán kính đường tròn nội tiếp tam giác ABC , suy ra: 3 S A . B BC 3a 4 . a 12a ABC HM      a p
AB BC CA 3a  4a  . 5a 12a SH H .
M tan60  a 3 . 1 1 Vậy 3 VA . B B . C SH  3 . a 4 . . a a 3  2a 3 . S.ABC 6 6
Câu 130. Cho hình lăng trụ ABC .
D A' B'C' D' đáy là hình bình hành. Với AC BC a, 0
CD a 2, AC '  a 3,CA' B'  A' D'C  90 . Thể tích khối tứ diện BCDA' là Trang 105 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN A' D' C' B' A D B C 3 a 3 2a A. . B. 3 a . C. . D. 3 6 a . 6 3 Lời giải Chọn A
Ta có tam giác ABC vuông cân tại C a 3
Gọi O là trung điểm của AC  OC  OA  2
Gọi H là chân đường cao hạ từ Cxuống mặt  A BCD  . A D    CH Ta có:   A D    HD. A D     D C  A B    A C  Lại có:   A B    A H  . A B     CH Ta có: 0 0 A H   A B    HA B    90 ; A D
 H  90 . Tam giác A DH
 vuông cân tại D Giả sử 2 2
CH x CA  x  2a 2 2 2
CC  x a 2 2 2 2 2 2 2 2 2 2 2 CC  C A   CA 3a
x a a x  2a x  2a C O        2 4 4 2 4 4 2 2 2
x  2a  3a x a CH LÊ MINH TÂM Trang 106
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN 3 1 1 a V     V    .CH.S . BCDA 6 ABCD.A B C D 6 ABCD 6
Câu 131. Cho hình chóp .
S ABC có đáy ABC là tam giác đều có cạnh 6 . Biết rằng các mặt bên của
hình chóp có diện tích bằng nhau và một trong các cạnh bên bằng 3 2 . Tính thể tích nhỏ nhất của khối chóp . S ABC . A. 4. B. 3. C. 2 2 . D. 2 3 . Lời giải Chọn B
Gọi H là hình chiếu vuông góc của S lên mpABC . E,F, M lần lượt là hình chiếu vuông
góc của H lên AB, AC, BC
Khi đó ta có AB SE, AC SF, BC SM . Vì SSS
, AB AC BC  6 suy ra SE SF SM SAB ASAC SBC
SHE SHF SHM HE HF HM nên H là tâm đường tròn nội tiếp hoặc H là
tâm đường tròn bàng tiếp góc A hoặc B, hoặc C của ABC .
Trường hợp 1: H là tâm đường tròn nội tiếp ABC . Do ABC đều nên H cũng là trọng tâm ABC và .
S ABC là hình chóp đều. 2 3 2 3 3 3 Ta có HA
. 6  2 ,SH SA HA  3 22 2 2 2  2  4 . S  6  3 2 ABC 4 2 1 1 3 3  VSH.S  4.  2 3 . S.ABC 3 ABC 3 2
Trường hợp 2: H là tâm đường tròn bàng tiếp ABC . Giả sử H là tâm đường tròn bàng tiếp góc A. Trang 107 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN 6 3 2 Ta có 0 HBC  60 , 0
HM BM tan 60  . 3  3 2 3 2
AH AM HM    3 2 , 2 2 2 2 BI HB   6 . Hình chóp .
S ABC có một cạnh bên bằng 3 2  SB SC  3 2 (Vì 0 cos 60
SA AH  3 2 ) suy ra SH SB BH   2 2 2 2 3 2  6  2 3 , 1 1 3 3 VSH.S  2 3.  3. S.ABC 3 ABC 3 2
Vậy thể tích khói chóp .
S ABC nhỏ nhất bằng 3.
Câu 132. Cho hình lăng trụ AB . C A BC
  có đáy là tam giác đều. Hình chiếu vuông góc của A trên
ABC là trung điểm của BC . Mặt phẳng P vuông góc với các cạnh bên và cắt các cạnh
bên của hình lăng trụ lần lượt tại D , E , F . Biết mặt phẳng ABBA vuông góc với mặt phẳng  ACC A
  và chu vi của tam giác DEF bằng 4, thể tích khối lăng trụ AB . C A BC   bằng
A. 1210  7 2 .
B. 410  7 2  . C. 610  7 2 .
D. 1210  7 2  . Lời giải Chọn A
Gọi H và H lần lượt là trung điểm của BC và B C  . BC A H  Khi đó ta có 
BC AA  BC BB,BC CC, BC   AH Suy ra BB CC  là hình chữ nhật. LÊ MINH TÂM Trang 108
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Vì EBB , F CC , và EF BB, EF CC (do EF  P vuông góc với các cạnh bên của lăng trụ),
Suy ra EF // BC và EF BC a (giả sử cạnh đáy của lăng trụ là a ).
Gọi I là trung điểm của HH  I cũng là trung điểm của EF .
Kẻ ED AA , D AA , suy ra DF AA . Do ABB A    ACC A
  nên suy ra ED DF . Hơn nữa dễ thấy DE DF , nên DEF a
vuông cân tại D . Suy ra 2 2 2 2ED EF  2 a ED  . 2
Chu vi DEF bằng DE DF EF a 2  a  4  a  4 2   1 .
Xét hình bình hành AA HH  , kẻ A K
  HH . Ta thấy, ID AA  ID HH , EF a Suy ra A K
 // ID A K   ID
 (do DEF vuông cân tại D ). 2 2
Khi đó, ta có diện tích hình bình hành AA HH  bằng: A .
K AA  A . H AH a a 3  .AA  .A H
  AA  3A H  . 2 2 2 3a a Mà 2 2 2 AA  A H   AH 2 2  2A H   AH  3  A H   . 4 2 2 2 a 3 S  . ABC 4 2 a 3 a 3 Suy ra V       A H.S . . ABC.A B C ABC 2 2 4      2 4 2 1 16 2 1 . 3
Với a  4 2   1 thì V       . 12 . ABC.A B C 10 7 2 2 2 4
Câu 133. Cho khối chóp .
S ABC có đáy là tam giác vuông cân tại B . Khoảng cách từ điểm A đến mặt
phẳng SBC bằng a 2 .   90o SAB SCB . Thể tích khối chóp .
S ABC có giá trị nhỏ nhất bằng 3 a 6 3 a 6 3 a 6 A. . B. . C. . D. 3 a 6 . 2 6 4 Lời giải Chọn C
Dựng điểm D sao cho ABCD là hình vuông. Trang 109 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Ta có AB SA, AB AD AB SD
BC SC, BC CD BC SD
Suy ra SD  ABCD .
Vì AD // SBC  dA,SBC  dD,SBC .
Kẻ DH SC DH  SBC   d D,SBC   DH a 2 .
Đặt AB x . 2 2 1 1 1 1 1 1 1 1 x  2a         ax 2  SD  . 2 2 2 2 2 2 2 2 2 2 DH SD DC SD DH DC 2a x 2a x 2 2 x a 3 1 1 ax 2 1 a 2 x 2 V  .S . D S  . x  . . SABC ABC 2 2 2 2 3 3 2 6 x a x a x
Xét hàm số f x 3 
với x a . 2 2 x a   4 2 2 2x  3x a a f x    , f x 6  0  x  . 2 2
x a   2 2 x a  2 2 3 a 2 3a 3 a 6
Vậy thể tích khối chóp .
S ABC có giá trị nhỏ nhất bằng .  . 6 2 4 SM
Câu 134. Cho hình chóp .
S ABC , O là trung điểm của AB . Điểm M di động trên cạnh SB. Đặt  x SB
. Mặt phẳng qua A , M song song với OC , cắt SC tại N . Thể tích khối chóp ABMN lớn nhất khi
A. x  3 1. B. x 1.
C. x  3  5 . D. x  1   2 . Lời giải Chọn D LÊ MINH TÂM Trang 110
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Trong mặt phẳng SAB , gọi I là giao điểm của SO và AM .
Mặt phẳng qua A, M , song song với SO, cắt SOC theo giao tuyến là đường thẳng qua I ,
đường thẳng đó cắt SC tại N .
Áp dụng định lý Menelauyt đối với tam giác SOB và bộ ba điểm thẳng hàng A, I, M ta có SM BA OI SI SM BA 2x SN 2x NS 2x   1        . MB AO IS OI MB AO 1 x CN 1 x CS x 1 1
Thể tích khối chóp VV  Sd N, ABM ABMN N.ABM ABM    3 1     2x   x x S d C, SAB   x V SAB     2 1 1 3 x 1
x 1 S.ABC   4       x   4 2 1   6 V    2  2x   1   6 V   V S ABC 6 4 2  x 1 S.ABC   x 1 . S.ABC  
Do đó thể tích khối chóp ABMN lớn nhất bằng 6  4 2 V khi S.ABCx  4 2 1 
x 1 2  x  2 1. x 1
Câu 135. Cho hình hộp ABC .
D A' B'C' D' . Gọi G là trọng tâm của tam giác ABD . Mặt phẳng P đi
qua hai điểm C ',G và song song với đường thẳng BD , chia khối hộp thành hai phần có thể V
thể tích V , V V V . Tỉ số 1 bằng 1 2  1 2 V2 V 1 V 7 V 2 V 31 A. 1  . B. 1  . C. 1  . D. 1  . V 2 V 17 V 3 V 77 2 2 2 2 Lời giải Chọn D Trang 111 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
 Gọi V là thể tích khối hộp ABC .
D A' B'C' D'
 Dựng  PABCD , ta có / /BD (do P / /BD . Gọi M, J,K,N lần lượt là giao điểm của
với BC, AB, AD, DC và F, E lần lượt là giao điểm của MC' với BB' và NC' với DD' . 2    CM CN 4 4 16 Ta có   . Suy ra S  .S    S . CB CD 3 CMN  3 CBD  9 CBD 2 JB JM 1  1  1 Mặt khác   . Suy ra S  .S    S . JA JK 2 JBM  2 JAK  4 JAK 2 AJ AK 2  2  4 1 4 1 Mà   . Suy ra S  .S    S . Suy ra S  . SS . AB AD 3 AJK  3 ABD  9 ABD JBM 4 9 ABD 9 ABD  1 Tương tự SS . NKD 9 ABD
d C ', ABCD  MC ' Ta lại có      . d  4
h d C ', ABCD  4dF, ABCD F, ABCD    MF
 Tương tự h dC',ABCD  4dE,ABCD  1 16 1 1 1 31
Thể tích V VVV
 . S .h  2. . S . h S .h 1 C'.CMN F.MBJ E.KDN 3 9 BCD 3 9 BCD 4 54 BCD 31 31 77  S .h V V V . ABCD 2 108 108 108 V 31 Vậy 1  . V 77 2
Câu 136. Cho khối chóp .
S ABC . Có AB  2, AC  3 và BAC  120,SA vuông góc với mặt phẳng đáy.
Gọi M , N lần lượt là hình chiếu của A trên SB và SC . Biết góc giữa mặt phẳng ABC và
AMN bằng 60. Thể tích của khối chóp đã cho bằng LÊ MINH TÂM Trang 112
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN 57 3 57 A. 57 . B. 3 57 . C. . D. . 3 2 Lời giải Chọn C
Ttrong mặt phẳng (ABC) : Kẻ HC AC, HB AB.
HB  SAB,HC  SAC
AM  SBH, AN  SCHSH  AMN
Mà SA   ABC  , ASH  90
 AMN,ABC  SA,SH  ASH 2 2  ASH  60 ;
BC AB AC  2.A . B A . C cos120  19 1 1 3 3 3 2S 3 3 S  .A . B AC.sin120  2 . 3 . . ABC   AI   ABC 2 2 2 2 BC 19 AB AB A . B AC 2 3 . 2 19 AH      sin AI AI BCA 3 3 3 AC 19 2 19 AH 3 2 19 1 1 2 19 3 3 57 SA     V  .S . A S  . .  tan 60 S.ABC ABC  3 3 3 3 3 2 3
Câu 137. Cho hình chóp tứ giác đều .
S ABCD có cạnh đáy bằng a . Gọi SH là chiều cao của hình
chóp, khoảng cách từ trung điểm I của SH đến mặt bên SBC bằng b . Tính thể tích V của khối chóp . S ABCD . ab 3 2a b A. V  . B. V  . 2 2 3 a 16b 2 2 3 a 16b ab 2ab C. V  . D. V  . 2 2 a 16b 2 2 a 16b Lời giải Chọn B Trang 113 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN S J I D K C H A M B Vì .
S ABCD là hình chóp tứ giác đều suy ra H là tâm của hình vuông ABCD .
Gọi M là trung điểm BC , K là hình chiếu vuông góc của H lên SM . BC SH  Ta có:
  BC  SHM . BC HM
 SBC  SHM, mà HK SM HK  SBC .
Suy ra HK  2IJ  2b , ta có. 2 2 HK .HM 2ab 3 2a b SH   . Vậy V  . 2 2 2 2 HM HK a 16b 2 2 3 a 16b
Câu 138. Cho khối lăng trụ tứ giác đều ABC . D A BCD
  có đáy là hình vuông; khoảng cách và góc 3 7a 2
giữa hai đường thẳng AC và DC lần lượt bằng và với cos  . Thể tích khối 7 4 lăng trụ đã cho bằng A. 3 3a . B. 3 9a . C. 3 3 3a . D. 3 3a . Lời giải Chọn B D C A B E D' C' O A' B'a
d AC, DC  d AC, A CD
   dA,A CD
   dD,A CD   3  . 7  2  A CD  với cos  . 4  3a 1 1 1 7 1 1 7
Đặt DD  x, D E   , ta có       2 2 2 2 2 2 2 7 DDD OD E  9a x D O  9a 3ax 2 2 2  9a x x . 7 D O   2  DO   x  2 2 2 2 7x  9a 2 2 7x  9a 7x  9a LÊ MINH TÂM Trang 114
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN 1 và tan  1  7 . 2 cos DO x 7 Khi đó tan  
 7  x  3a OC . 3a 3ax 2
Vì AA  3a và AB   a 3 nên 3 V        AA .S 9a . 2 2 ABCD.A B C D ABCD 7x  9a
Câu 139. Cho khối lăng trụ đứng AB .
C A' B'C' có đáy tam giác vuông cân tại C . BA  2a và góc tạo
bởi ABC' và ABC bằng 60o . Gọi M,N lần lượt là trung điểm của A'C' và BC . Mặt
AMN chia khối lăng trụ thành hai phần. Tìm thể tích phần nhỏ. 3 7 3a 3 7 6a 3 3a 3 6a A. . B. C. . D. . 24 24 3 6 Lời giải Chọn A
Kẻ MP / / A' B'
Góc tạo bởi ABC' và ABC là góc 0
C ' JC  60 với J là trung điểm AB . 0
CC '  CJ.tan 60  a 3 1 2 S
CJ.AB a ABC 2 1 1 2 S SSa 1 ACN 2 ABC 2 1 1 1 2 S SS
C' M.C'P a 2 C' MP 4 ABC 2 8 CC '      3 7 3a V S S S S  1 2 1 2 3 24
Câu 140. Cho hình lăng trụ AB . C A BC
  có thể tích bằng 2 . Gọi M,N là các điểm lần lượt nằm trên 1
các cạnh AA, BB sao cho M là trung điểm của AA và BN B N
 . Đường thẳng CM cắt 2 đường thẳng A C
  tại điểm P , đường thẳng CN cắt đường thẳng A B
  tại Q . Tính thể tích
của khối đa diện A MPB NQ  bằng. 13 23 21 7 A. . B. . C. . D. . 18 9 9 18 Trang 115 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN Lời giải Chọn B Đặt S S và h  ( d C,(A BC  )) ta có V      hS 2 . A BC   ABC.A B C  1 A M   CC
Trong mặt phẳng AA CC   ta có  2
nên ta có A là trung điểm của PC. A M  //CC  1
Tương tự trong mặt mặt phẳng BCC B   ta có C B    C Q  . 3
Từ đây ta có diện tích tam giác C PQ là S  6  
S do vậy thể tích khối tứ diện CC PQ là C PQ 1 V     h 6 . S 2hS 4 . CC PQ 3 1 1   0 V 5
Trong khối lăng trụ AB . C A BC   ta có CABMN 2 3   suy ra V 3 18 CAB.C AB   5 5 5 13 V  .V
 do đó thể tích khối A BCM
NC bằng 2   . CABMN    18 CAB.C A B 9 9 9 13 23
Do vậy thể tích của khối đa diện A MPB NQ  bằng 4   . 9 9
Câu 141. Cho hình chóp .
S ABC có đáy là tam giác đều cạnh a , mặt bên SAB là tam giác đều và nằm
trong mặt phẳng vuông góc với đáy. Gọi H, M,O lần lượt là trung điểm các cạnh AB , SA ,
AC và G là trọng tâm tam giác SBC . Thể tích khối tứ diện GHMO bằng 3 3a 3 3a 3 a 3 a A. . B. . C. . D. . 64 128 128 64 Lời giải Chọn D LÊ MINH TÂM Trang 116
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Gọi N, E lần lượt là trung điểm của CB và SB. 2 3 1 1 a 3 a 3 a Ta có: VS .SH  . .  . S.ABC 3 ABC 3 4 2 8 3 1 1 a 3 1 a +) SSVV  , VVV  . OAHN 2 ABC S.OAHN 2 S.ABC 16 S.AHN S.OAN 2 S.AHNO 32 3 V SG SM SH 2 1 1 1 a +) S.GMH  . .  .   VV  . V SN SA SH 3 2 3 S.GMH 3 S.NAH 96 S.NAH 3 V SG SM SO 2 1 1 1 a +) S.GMO  . .  .   VV  . V SN SA SO 3 2 3 S.GMH 3 S.OAH 96 S.NAO a +) V
d G; ABC .S  . SH. S  . SH.SV  . G.ONH    3 1 1 1 1 1 1 1 3 ONH 3 3 4 ABC 12 3 ABC 12 S.ABC 96 a +) V
d M; ABC .S  . SH. S  . SH.SV  . M.OAH    3 1 1 1 1 1 1 1 3 OAH 3 2 4 ABC 8 3 ABC 8 S.ABC 64 3 3 3 3 a a a a Vậy VVVVVV   3.   . GMOHN S.HNO S.GMH S.GMO G.HNO G.HAO 16 96 64 64
Câu 142. Cho hình chóp .
S ABC có AB BC a , góc ABC 120, SAB SCB  90 và khoảng cách từ 2a
B đến mặt phẳng SAC bằng . Tính thể tích khối . S ABC . 21 3 a 5 3 a 15 3 a 15 3 a 5 A. V  . B. V  . C. V  . D. V  . 10 10 5 2 Lời giải Chọn B Trang 117 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Gọi D là hình chiếu vuông góc của S lên mặt phẳng ABC . BC SC Có   BC CD. BC   SDAB SD Có 
AB AD . AB   SA
Gọi I là giao điểm của BD và AC ( BD là đường phân giác của góc ABC ) BC a BD
 2a; BI BC cos60  . cos 60 2
Gọi H là hình chiếu vuông góc của D lên SI .
SAC  SBC
SACSBC  SI DH SAC hay DH dD;SAC DH SI  DI a a
Ta có: dD;SAC  d ; B SAC 2 6  3   DH . BI 21 21 3a 6aDI DH 2 21 6a 5 Suy ra: SD    . 2 2 2 2 5 DI DH 9a 12a  4 7 3 1 1 6a 5 1 3 a 15 Vậy VSDS    aa  . S.ABC 3 ABC 3 5 2 2 10
Câu 143. Cho tứ diện ABCD . Hai điểm M, N lần lượt di động trên hai đoạn thẳng BC và BD sao BC BD cho 2.  3.
10 . Gọi V ,V lần lượt là thể tích của các khối tứ diện ABMN và ABCD BM BN 1 2 V
. Tìm giá trị nhỏ nhất của 1 . V2 3 2 6 5 A. . B. . C. . D. . 8 7 25 8 Lời giải LÊ MINH TÂM Trang 118
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN Chọn C Cách 1 BD
Vì M BC , N BD nên ta đặt
aa   1 . BN BC 10  3a 3 8 Suy ra 1  
 5  a 1 a  . BM 2 2 3  V V BM BN 1 1 1 1 ABMN   .  .  . V V BC BD a 3 3 2 2 ABCD 5  a 5a a 2 2        V 3 3 1 2    5
a a  . Tìm 2 max 5a   a .  V   2   8   2  2 min max 1;   3     3 8
Xét hàm số f a 2
 5a a ,a 1
 ;  ; f 'a   ;
a f 'a 5 5 3  0  a  . 2  3  3  25
Suy ra max f a  .  8  6 1;   3     V 6 Vậy 1    .  V 25 2 min Cách 2
1 .BM.BN.sin BV V S BM.BN 1 ABMN BMN 2     . V V S 1 BC.BD 2 ABCD BCD .BC.B . D sin B 2        V BM.BN BC.BD 1         .  V   BC.BD   BM.BN  2 min min max  2.BC 3.BD 2.BC 3.BD BC BD Theo giả thiết; 10    2. .  2. 6. . . BM BN BM BN BM BN Trang 119 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN BC.BD BC.BD 25  5  6.   . BM.BN BM.BN 6    V 6 Do đó 1    .  V 25 2 min 2.BC 3.BD  2  BM  .BC      Đẳng thức xảy ra BM BN 5     . BC BD 3 2. 3. 10    BN  .BD  BM BN  5
Câu 144. Cho hình lăng trụ AB . C A BC
  có đáy ABC là tam giác đều cạnh bằng 2, A A   A B   A C   2
, M là trung điểm của AA. Tính thể tích phần chung của 2 khối đa diện A . M BCC B   và . A A BC   . 17 2 17 3 17 3 5 2 A. . B. . C. . D. . 27 18 27 3 Lời giải Chọn A
 Gọi H là hình chiếu vuông góc của A lên mặt phẳng (ABC). Vì A A   A B   A C  nên H
trùng với tâm đường tròn ngoại tiếp tam giác ABC cũng là trọng tâm tam giác ABC. Gọi I là
trung điểm BC.  Ta có: 2 2 3 12 2 6
AI  3  AH AI  ; 2 2 A H
  AA  AH  4   ; 3 3 9 3 2 6 1 2 2 V          A H.S . 3 2 2 ; V    V ; ABC.A B C ABC    3 A.A B C 3 ABC.A B C 3
 Gọi P ABBM ; Q AC CM . Khi đó phần chung của 2 khối đa diện A . M BCC B   và . A A BC
  là khối đa diện MP . Q A BC   . LÊ MINH TÂM Trang 120
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN VA.MPQ AM AP AQ 1 1 1 1 17 17 2 2 17 2 Ta có:  . .  . .   V       V    . V    .    AA AB AC 2 3 3 18 MPQ.A B C 18 A.A B C 18 3 27 A.A B C
Câu 145. Cho hình chóp .
S ABCD có đáy ABCD là hình thang vuông tại A và B , AB BC a ,
AD  2a , SA vuông góc với đáy, SA a 2 . Gọi B' là điểm đối xứng của B qua mặt phẳng
SCD. Tính thể tích khối đa diện SB'.ABCD bằng 3 5 2a 3 7 2a 3 2 2a A. . B. . C. 3 2a . D. . 6 3 3 Lời giải Chọn D 1 1 Ta có: VVVS . A S
S .d B', SCD SB'.ABCD S.ABCD B'SCD ABCD SCD    3 3 1 1  S . A S
S .dB, SCD (vì B' là điểm đối xứng của B qua mặt phẳng SCD ) ABCD SCD   3 3 1 1 aa 3 2 a a + V  . SA S  .a 2.  S.ABCD 3 ABCD 3 2 2
+ Gọi M là giao điểm của AB và CD , dễ dàng chứng minh được B là trung điểm của MA
dB,SCD 1
dA,SCD 1  AH 2 2
Lại có tam giác SAC vuông cân tại A ( vì SA AC a 2 )   a
d B,SCD 1
dA,SCD 1 1 1
AH SC  2 . a  2 2 4 4 2 Trang 121 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN a a a aV
 .S .d B', SCD  . .SC.C . D  . . a a .   B'.SCD SCD    3 3 1 1 1 1 2 2 2 3 3 2 2 6 2 6 3 2 3 3 3 a a 2 2a VVV    . SB'.ABCD S.ABCD B'SCD 2 3 2 3
Câu 146. Cho hình chóp .
S ABC có đáy ABC là tam giác đều cạnh bằng 1, biết khoảng cách từ A đến 6 15
mặt phẳng SBC bằng
, khoảng cách từ B đến mặt phẳng SCA bằng , khoảng 4 10 30
cách từ C đến mặt phẳng SAB bằng
và hình chiếu vuông góc của S xuống đáy nằm 20
trong tam giác ABC . Tính thể tích khối chóp V . S.ABC 1 1 1 1 A. . B. . C. . D. . 24 12 36 48 Lời giải Chọn D S K A C H F G B
Gọi H là hình chiếu của S trên ABC . F,G,K lần lượt là hình chiếu của H trên
AB, BC,CA . Đặt V V ; h SH S.ABC Ta có 3V  . h S
dA,(SBC).S
dB,(SAC).S
dC,(SA ) B .S ABC SBC SAC SAB 3 6 1 15 1 30 1  h  . .SF  . .SG  . .SK 4 4 2 10 2 20 2
SF h 2;SG h 5;SK h 10  HF  ; h HG  2 ; h HK  3h . 3 1 1 1 3 Mặt khác SSSS
HF HG HK h  . ABC HAB HBC HCA 4 2 2 2 12 1 3 3 1 Vậy V  . .  . S.ABC 3 12 4 48
Câu 147. Cho hình chóp tam giác đều .
S ABC , cạnh đáy bằng a . Các điểm M, N lần lượt là trung điểm
của SA,SC . Biết rằng BM vuông góc với AN . Thể tích của khối chóp bằng 7 7 14 14 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 24 8 8 24 LÊ MINH TÂM Trang 122
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN Lời giải Chọn D S M N D C A H B
Gọi D sao cho MNAD là hình bình hành. BM vuông góc với AN nên tam giác DMB 2  a 3  2 a     2  BD   a 14
vuông cân tại M . Suy ra: BM    . 2 2 4
Gọi cạnh SA x, x  0. BM là đường trung tuyến tam giác SAB nên ta có:
2BA BS  2 2 2 2 SA   2 14  2 2 a x  2  x a a 6 2 BM       x  . 4  4  4 2   a 42 2 3 1 a 42 a 3 a 14 2 2
SH SA AH  . Vậy V  . .  . 6 S.ABC 3 6 4 24
Câu 148. Cho khối chóp .
S ABCD có đáy là hình bình hành, có thể tích bằng 24 cm3. Gọi E là trung
điểm SC . Một mặt phẳng chứa AE cắt các cạnh SB và SD lần lượt tại M và N . Tìm giá trị
nhỏ nhất của thể tích khối chóp . S AMEN . A. 9 cm3. B. 8 cm3. C. 6 cm3. D. 7 cm3. Lời giải Chọn B
Mặt đáy  ABCD là hình bình hành  ADC và ABC có cùng diện tích  VV
(hai khối chóp có cùng chiều cao và có diện tích mặt đáy bằng nhau). S.ADC S.ABC Trang 123 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN V 24 Mà VVV  24 cm3 S.ABCDVV   12 (cm3). . S ABCD . S ADC . S ABC S.ADC S.ABC 2 2
Gọi O là giao điểm của AC và BD ; I là giao điểm của SO và AE I là trọng tâm của SM SN
SAC và I thuộc MN . Gọi  a và
b ( a  0; b  0). SB SD V SA SN SE 1 b V SA SM SE 1 a
Ta có: S.ANE   
1b  và S.AME    1 a  V SA SD SC 2 2 V SA SB SC 2 2 S.ADC S.ABC V b V a S.ANE
 và S.AME   V
 6b (cm3) và V  6a (cm3). 12 2 12 2 S.ANE S.AME Do đó: VVV
 6a  6b  6 a b (cm3). S.AMEN S.AME S.ANE   SM S
Mặt khác: ISM và ISB có chung chiều cao kẻ từ I và có đáy  a ISMa  . SB SISB SI 2 S S a
Mà I là trọng tâm của SAC   2 ISB   2 ISM   . SO 3 S 3 S 3 SOB SOB S 2b
Chứng minh tương tự ta có: ISN  . S 3 SOD S
O là trung điểm của DB SDBSS  hay S  2S  2S SOB SOD 2 SDB SOB SOD 2a 2b S S 2S 2S 2 SS S ISM ISN ISM ISN ISM ISN  2 SNM         3 3 S S 2S 2S S S SOB SOD SOB SOD SDB SDB 3S
3SN SM  sin MSN SN SM SNMa b    3   3ab . S SD SB BSD SD SB SDB sin ab2 ab2 3
Theo bất đẳng thức AM-GM, ta có: ab
a b  3ab  4 4  4
3a b  4 (do a b  0 )  a b   6a b  8 hay V  8 (cm3). 3 S.AMEN 2 SM SN
Dấu "  " xảy ra khi và chỉ khi a b  2   
MN đi qua I và MN BD. 3 SB SD 3
Vậy giá trị nhỏ nhất của thể tích khối chóp . S AMEN là 8 cm3.
Câu 149. Tứ diện ABCD có 0 0
AB AC AD a, BAC  120 , BAD  60 và tam giác BCD là tam giác
vuông tại D . Tính thể tích khối tứ diện ABCD . 3 a 2 3 a 2 3 a 2 3 a 2 A. . B. . C. . D. . 4 3 6 12 Lời giải Chọn D LÊ MINH TÂM Trang 124
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
Gọi H là hình chiếu của A lên BCD .
Dễ thấy, AHB AHC AHD HB HC HD.
Do đó, H là tâm đường tròn ngoại tiếp BCD H là trung điểm của BC .
Xét tam giác ABC , có 2 2 2 2 2 2
BC AB AC  2A . B A .
C cos BAC a a  2 . a .
a cos120  3a . a 3
BC a 3  BH  . 2 2  a 3  a
Xét AHB vuông tại H , có 2 2 2
AH AB BH a      . 2  2  
Xét BDC vuông tại D , có 2 2 2 2
CD BC BD  3a a a 2 .
Xét ABD, có AB AD a và BAD  60  ABD là tam giác đều cạnh a BD a . 2 1 a 2  S  . . a a 2  (đvdt). BDC 2 2 2 3 1 1 a a 2 a 2 Vậy VAH.S  . .  (đvtt). ABCD 3 BCD 3 2 2 12
Câu 150. Cho hình chóp .
S ABCD có đáy ABCD là hình vuông cạnh bằng 3a, tam giác SBC vuông
tại S và nằm trong mặt phẳng vuông góc với đáy, đường thẳng SD tạo với mặt phẳng
SBC một góc 60. Thể tích của khối chóp đã cho bằng A. 3 2a 6 . B. 3 a 6 . C. 3 3a 2 . D. 3 a 3 . Lời giải Chọn C
Kẻ SH BH, H B . C Trang 125 LÊ MINH TÂM
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
SBC  ABCD  Ta có 
SBC   ABCD  BC SH   ABCD. SH BC  CD   BC Mà 
CD  SBC và SDSBC   S . CD   SH
Suy ra SC là hình chiếu của SD lên SBC.
Khi đó SD,SBC  SD,SC  CSD  60 .  CD 3a
Tam giác SCD vuông tại C có SC    a 3. tan 60 3
Tam giác SBC vuông tại S có 2 2
SB BC SC a 6. . SB SC a 6.a 3 Mà SH    a 2. BC 3a 1 1
Vậy thể tích của khối chóp đã cho là V SH.S
 .a 2. a a ABCD 3 2 3 3 2 (đvtt). 3 3
------------------ HẾT ------------------ LÊ MINH TÂM Trang 126
Chuyên Đề. THỂ TÍCH KHỐI ĐA DIỆN
IV. BẢNG ĐÁP ÁN THAM KHẢO. BẢNG ĐÁP ÁN 1 2 3 4 5 6 7 8 9 10 D D A A B C D B D C 11 12 13 14 15 16 17 18 19 20 D D B C A D B A C B 21 22 23 24 25 26 27 28 29 30 C A C D A B A C A A 31 32 33 34 35 36 37 38 39 40 D A B B B A B D B B 41 42 43 44 45 46 47 48 49 50 C C B C B A C D D B 51 52 53 54 55 56 57 58 59 60 B D B C A B C C D A 61 62 63 64 65 66 67 68 69 70 B C A A B B C C C A 71 72 73 74 75 76 77 78 79 80 C D D D A C B B B A 81 82 83 84 85 86 87 88 89 90 D B A B C D C A C B 91 92 93 94 95 96 97 98 99 100 D B B D B A C B D A 101 102 103 104 105 106 107 108 109 110 B A A B D B D B C A 111 112 113 114 115 116 117 118 119 120 D A A B B C B A B D 121 122 123 124 125 126 127 128 129 130 D B B B B B C D A A 131 132 133 134 135 136 137 138 139 140 B A C D D C B B A B 141 142 143 144 145 146 147 148 149 150 D B C A D D D B D C Trang 127 LÊ MINH TÂM