


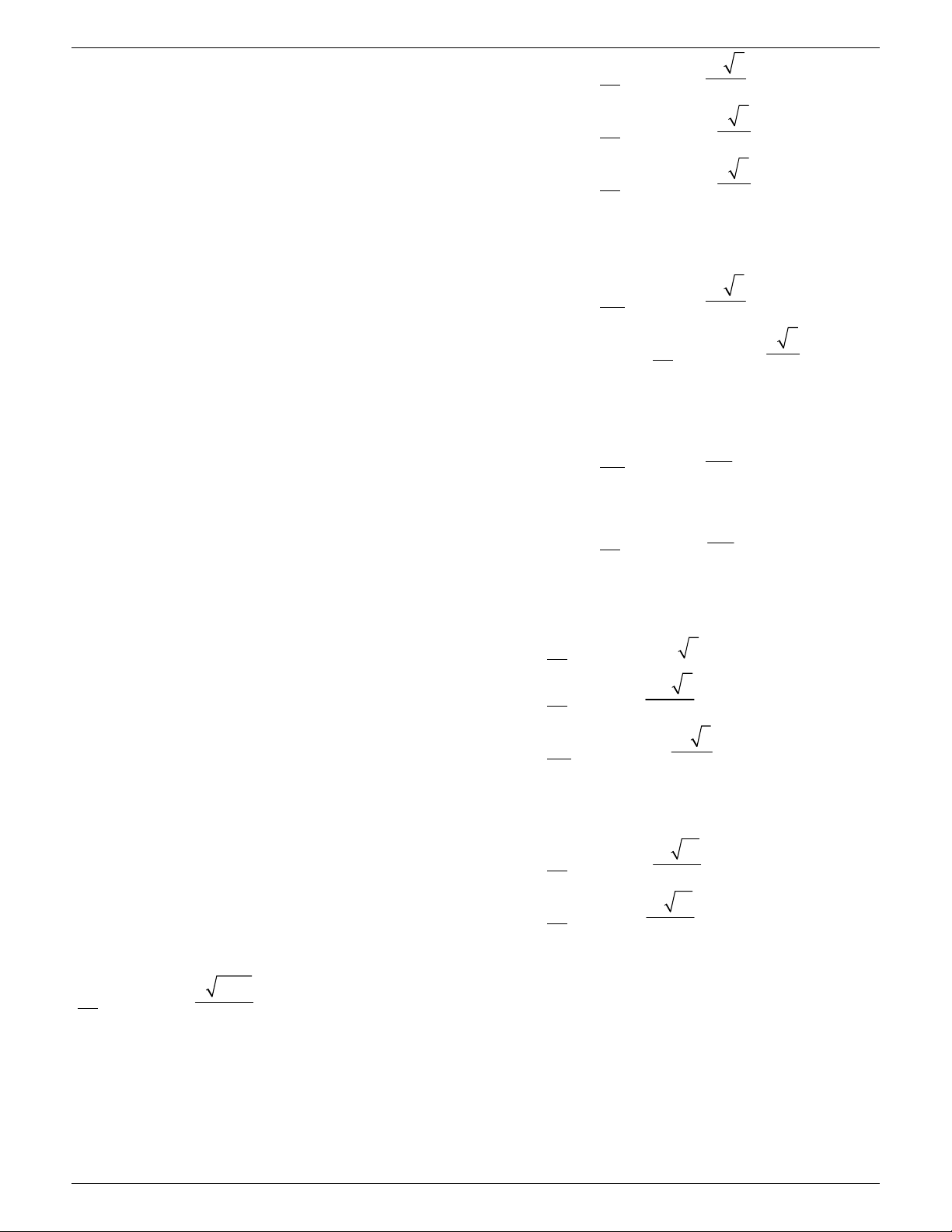



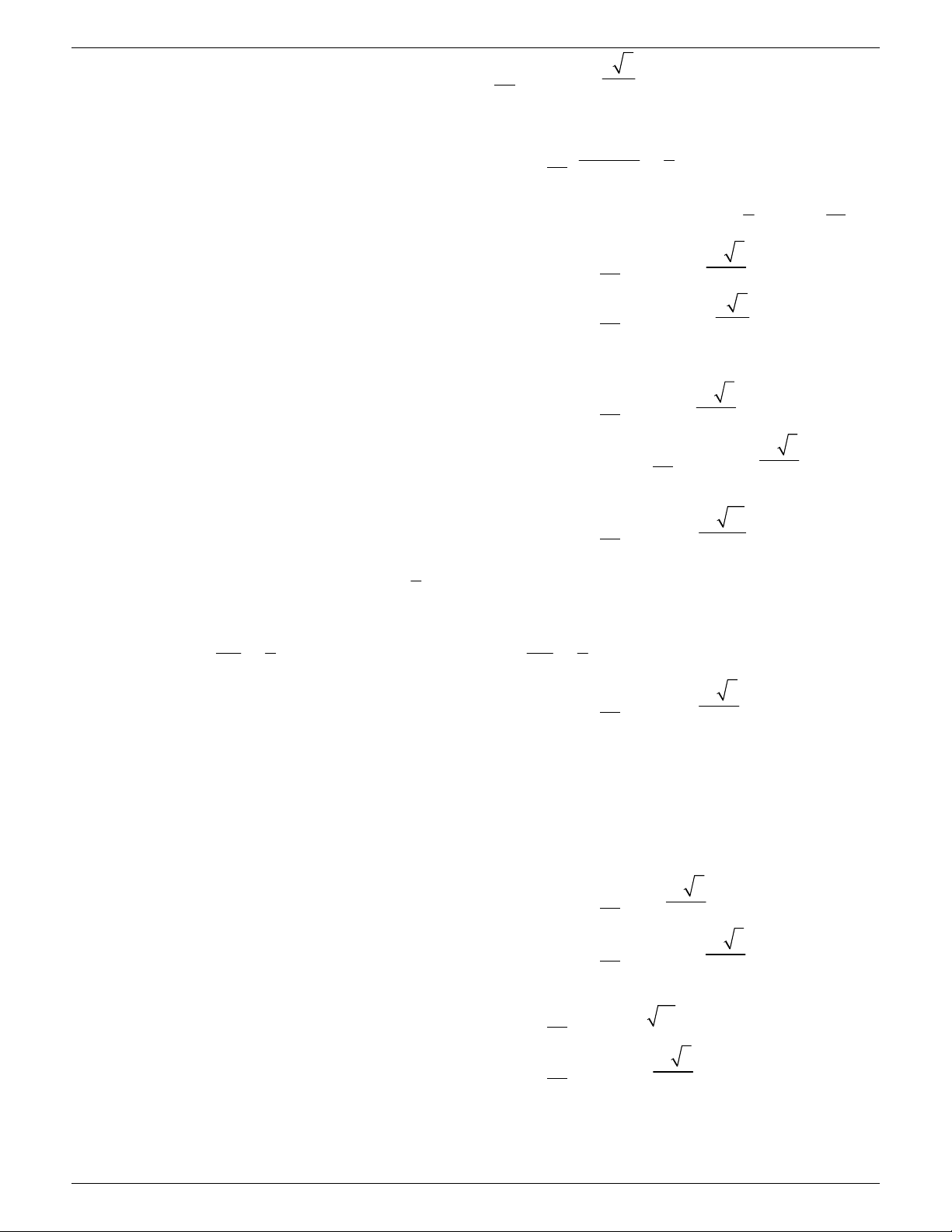



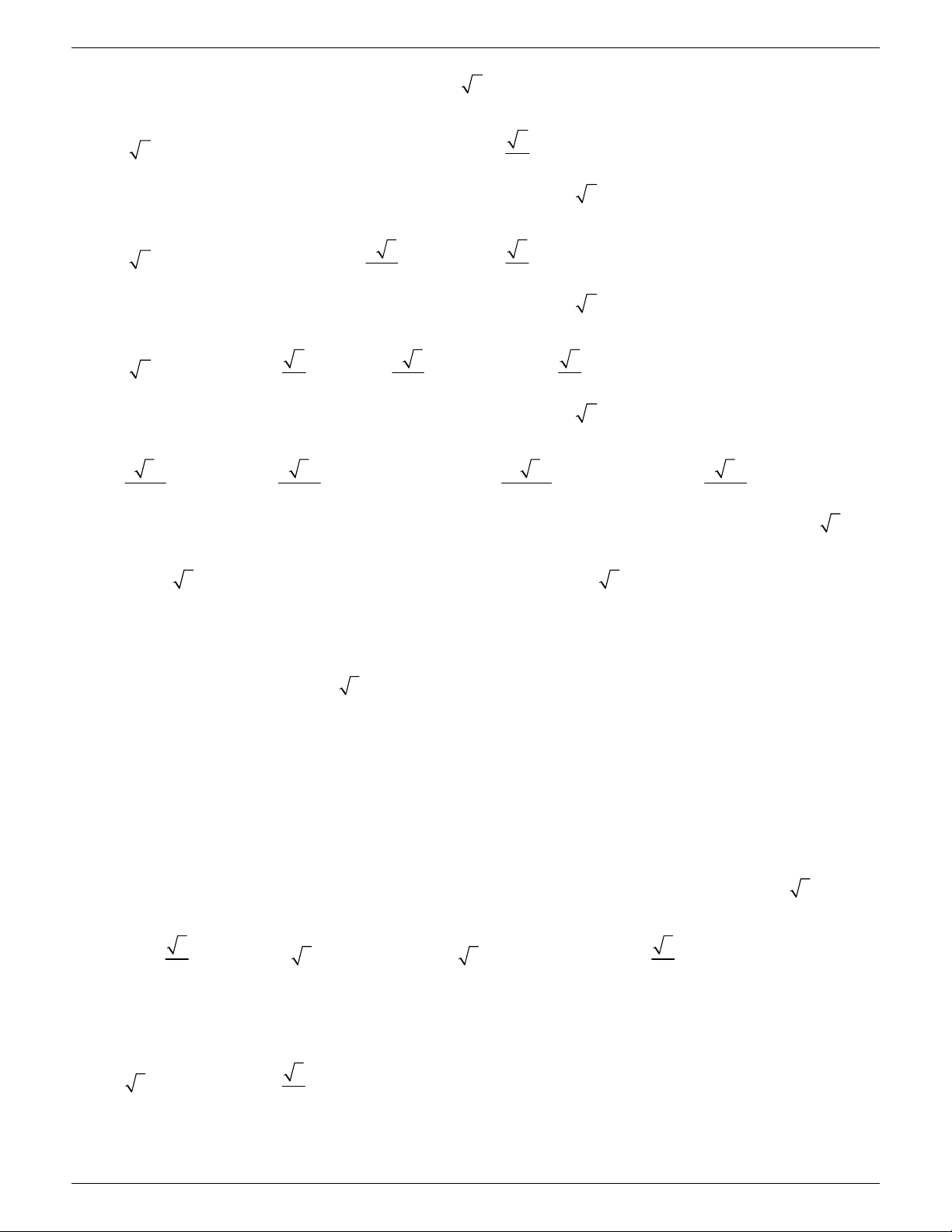
Preview text:
Chuyên đề Thể tích khối đa diện
VẤN ĐỀ 1: ÔN TẬP HÌNH HỌC PHẲNG
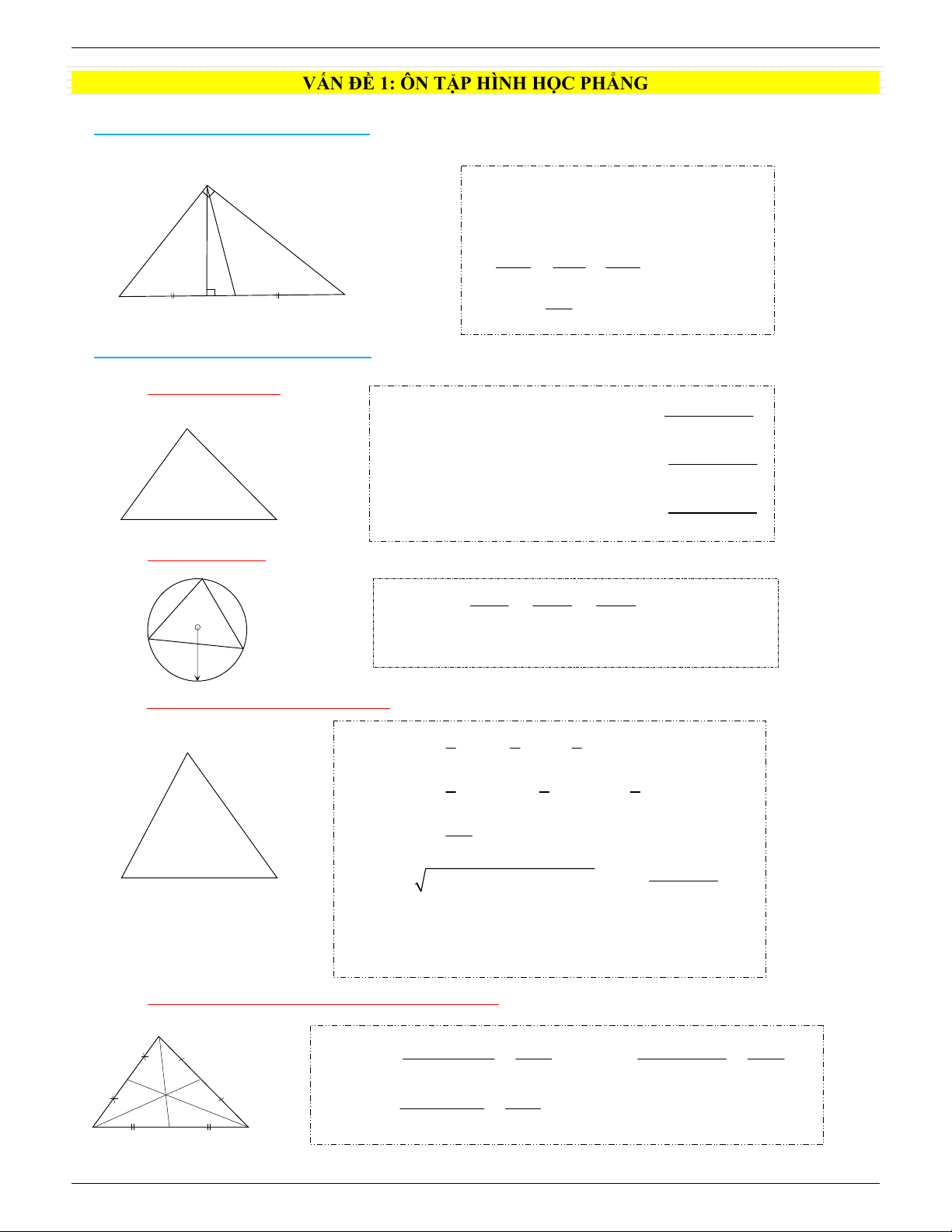
1/ Các hê ̣ thức lượng trong tam giác vuông Cho AB D
C vuông ta ̣i A, AH là đường cao, AM là đường trung tuyến. Ta có: A 2 2 2
BC = AB + AC (Pitago)
AH.BC = AB.AC 2 2
AB = BH.BC, AC = CH.CB 1 1 1 = + , 2
AH = HB.HC 2 2 2 AH AB AC B C BC H M AM = 2
2/ Các hê ̣ thức lượng trong tam giác bất kỳ
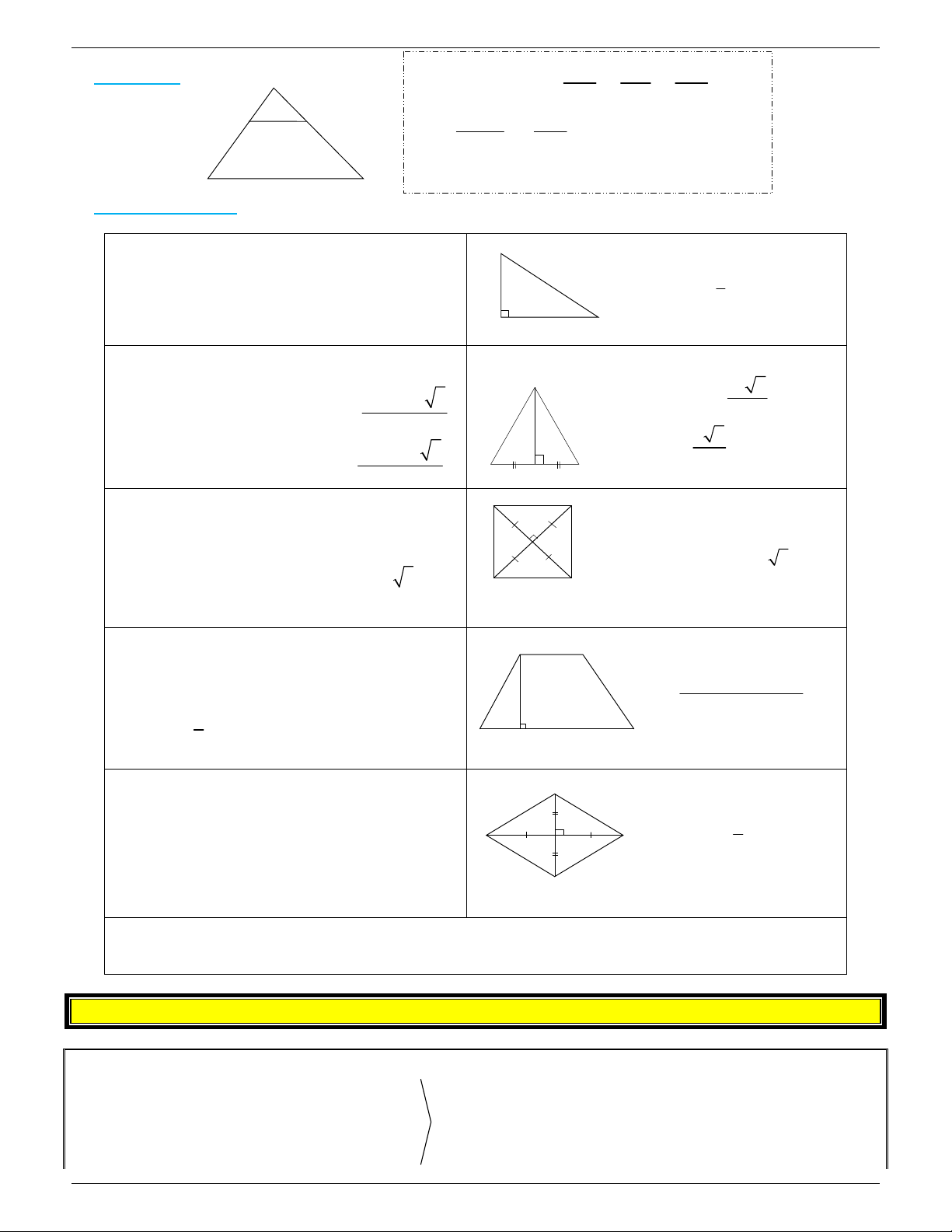
a) Đi ̣nh lı́ hàm số cosin 2 2 2 b + c -a * 2 2 2
a = b + c - 2bc cos A cos A = A 2bc 2 2 2 a + c -b c b * 2 2 2
b = a + c - 2ac cos B cos B = 2ac 2 2 2 a + b -c 2 2 2 B a C
* c = a + b - 2ab cosC cosC = 2ab
b) Đi ̣nh lı́ hàm số sin A a b c c = = = 2R b sin A sin B sinC B C
(R là bán kı́nh đường tròn ngoa ̣i tiếp ABC) R a
c) Công thức tı́nh diê ̣n tı́ch của tam giác A 1 1 1 S = a.h = . b h = . c h AB D C 2 a 2 b 2 c 1 1 1 c b S
= ab sinC = bc sin A = ac sin B AB D C 2 2 2 abc S = , S = . p r AB D C 4 A D BC R B a C æ
a + b + c ö = - - - ç = ÷ S p (p a)(p b)(p c), p AB D C ç ÷ çè 2 ø p – nư ̉ a chu vi
r – bán kı́nh đường tròn nô ̣i tiếp
R – bk đường ngoại nô ̣i tiếp
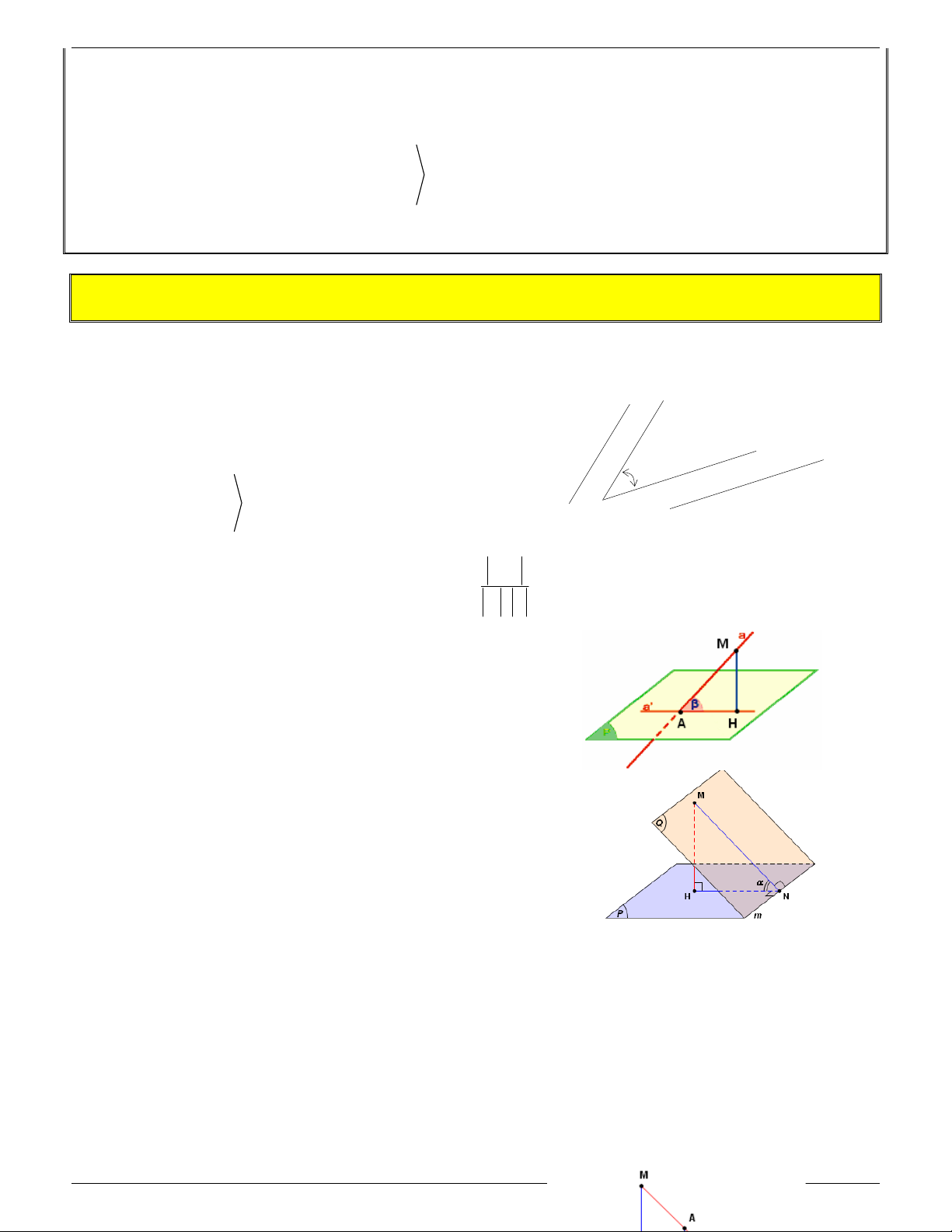
d) Công thức tı́nh độ dài đường trung tuyến của tam giác A 2 2 2 2 2 2 . . AB + AC BC BA + BC AC * 2 AM = - * 2 BN = - K N 2 4 . 2 4 2 2 2 CA +CB AB * 2 CK = - B M C 2 4
Nguyễn Văn Thân Trang 1
Chuyên đề Thể tích khối đa diện 3/ Đi ̣nh lı́ Talet AM AN MN A * MN / /BC = = = k AB AC BC 2 S æAM ö M N ç ÷ * AM D N 2 = ç ÷ = k ç ÷ ç ÷ S è AB ø AB D C B C (Tı
̉ diê ̣n tı́ch bằng tı̉ bı̀nh phương đồng dạng)
4/ Diê ̣n tı́ch của đa giác a/ Diê ̣n tı B ́ch tam giác vuông 1 S = AB.AC
Diê ̣n tı́ch tam giác vuông bằng ½ tı́ch 2 ca ̣nh góc AB D C 2 vuông. A C
b/ Diê ̣n tı́ch tam giác đều B 2 ìï a 3 . (ca ̣nh)2 3 S ïï = + Diê D ̣n tı ABC
́ch tam giác đều: S đều = ïï 4 D 4 a í h ïï a 3 . (ca ̣nh) 3 h ï = ï
+ Chiều cao tam giác đều: h đều = A C ïî 2 D 2 A B
c/ Diê ̣n tı́ch hı̀nh vuông và hı̀nh chữ nhâ ̣t 2 S ìï = a HV ï a í
+ Diê ̣n tı́ch hı̀nh vuông bằng ca ̣nh bı̀nh phương. O AC ï = BD = a 2 ïïî + Đươ D C
̀ ng chéo hı̀nh vuông bằng ca ̣nh nhân 2 .
+ Diê ̣n tı́ch hı̀nh chữ nhâ ̣t bằng dài nhân rô ̣ng. d/ Diê ̣n tı A D ́ch hı̀nh thang
(AD + BC ).AH
Diê ̣n tı́ch hı̀nh thang: S = 2 1
SHı̀nh Thang = .(đáy lớn + đáy bé) . chiều cao 2 B H C B
e/ Diê ̣n tı́ch tứ giác có hai đường chéo vuông góc 1
+ Diê ̣n tı́ch tứ giác có hai đường chéo vuông góc nhau A C S = AC.BD H .Thoi bằng ½ tı 2 ́ch hai đường chéo.
+ Hı̀nh thoi có hai đường chéo vuông góc nhau ta ̣i
trung điểm của mỗi đường. D
Lưu ý: Trong tı́nh toán diê ̣n tı́ch, ta có thể chia đa giác thành những hı̀nh đơn giản dễ tı́nh diê ̣n tı́ch, sau đó
cô ̣ng các diê ̣n tı́ch được chia này, ta được diê ̣n tı́ch đa giác.
VẤN ĐỀ 2: ÔN TẬP HÌNH HỌC KHÔNG GIAN 11
1/ Chứng minh đường thẳng d // m ( p a) d ìïï // d ' ïï
a. Phương pháp 1: Chứng minh d í ' Ì (a) d // m ( p a) (ïïïd Ë (a ï )) ïî
Nguyễn Văn Thân Trang 2
Chuyên đề Thể tích khối đa diện d ìï Ì (b) ï
b. Phương pháp 2: Chứng minh (í ïï ) d // m ( p ) a b // ( ) a ïî
c. Phương pháp 3: Chứng minh d và (a) cùng vuông góc với mô ̣t đường thẳng hoă ̣c cùng vuông góc với mô ̣t mă ̣t phẳng. 2/ Chứng minh ( mp a /
) / mp (b)
a. Phương pháp 1: Chứng minh ( mp )
a chứa hai đường thẳng cắt nhau song song với mp (b).
b. Phương pháp 2: Chứng minh (
mp a) và mp (b) cùng song song với 1 mă ̣t phẳng hoă ̣c cùng vuông góc với 1 đường thẳng.
3/ Chứng minh hai đường thẳng song song:
a. Phương pháp 1: Hai ( mp )
a ,(b) có điểm chung S và lần lượt chứa 2 đường thẳng song song a,b thı̀
(a) Ç (b) = Sx // a // b . a ìï // m ( p a) ïïï
b. Phương pháp 2: Chứng minh a í Ì mp (b) a// b . ï(ïï )aÇ ï (b) = b ïî
c. Phương pháp 3: Hai mă ̣t phẳng cùng song song với mô ̣t đường thẳng thı̀ giao tuyến của chúng song song với đường thẳng đó.
d. Phương pháp 4: Mô ̣t mă ̣t phẳng cắt hai mă ̣t phẳng song song theo giao tuyến song song.
e. Phương pháp 5: Hai đường thẳng cùng vuông góc với mô ̣t mă ̣t phẳng thı̀ song song với nhau.
f. Phương pháp 6: Sử du ̣ng phương pháp hı̀nh ho ̣c phẳng: Đường trung bı̀nh, đi ̣nh lı́ Talét đảo, …
4/ Chứng minh đường thẳng d ^ mp (a) d ìï ^ a ïïdïï ^b
a. Phương pháp 1: Chư ï ́ ng minh: í
d ^ mp (a) a ï Ç b
ïïaïï,b Ìmp(a) ïî d ìï // d ' ï
b. Phương pháp 2: Chứng minh: í
d ^ mp (a) d ï ' ^ mp ï (a) ïî d ìï ^ mp ï (b)
c. Phương pháp 3: Chứng minh: í
d ^ mp (a) mp
ïï (b) // mp(a) ïî
d. Phương pháp 4: Hai mă ̣t phẳng cắt nhau cùng vuông góc với mă ̣t phẳng thứ 3 thı̀ giao tuyến của chúng vuông (ìïa) ^ ï (P) ïï
góc với mă ̣t phẳng thứ 3: ( í b) ^ (P) d ^ (P) (ïïïa ï ) Ç (b) = d ïî
e. Phương pháp 5: Có hai mă ̣t phẳng vuông góc, đường thẳng nào nằm trong mă ̣t phẳng này và vuông góc với giao (ìïa) ^ ï (b) (ïïïa ï ) Ç (b) = a
tuyến của 2 mặt phẳng, cũng vuông góc với mă ̣t phẳng kia: í ^ b d ï Ì ï (a) d ( ) ïdïï ^ a ïî
5/ Chứng minh đường thẳng d ^ d '
a. Phương pháp 1: Đường thẳng d ^ (a) thì d ^ tất cả các đường thẳng nằm trong mp (a).
Nguyễn Văn Thân Trang 3
Chuyên đề Thể tích khối đa diện
b. Phương pháp 2: Sử du ̣ng đi ̣nh lý ba đường vuông góc.
c. Phương pháp 3: Chứng tỏ góc giữa d và d ' bằng 0 90 .
d. Phương pháp 4: Sử du ̣ng hı̀nh ho ̣c phẳng.
6/ Chứng minh mp (a) ^ mp (b) (ìïa ï ) É d
a. Phương pháp 1: Chứng minhí a ^
b (chứng minh mp chứa 1 đường thẳng vuông d ï ^ ï (b) mp ( ) mp( ) ïî góc với mp kia)
b. Phương pháp 2: Chứng tỏ góc giữa hai mă ̣t phẳng bằng 0 90 .
PHƯƠNG PHÁP XÁC ĐỊNH GÓC VÀ KHOẢNG CÁCH
(Phần này cần nắm cho thật vững) I. TÍNH GÓC
1. Tính góc giữa hai đường thẳng a và b chéo nhau
Phương pháp : Có thể sử dụng một trong các cách sau: a. Cách
1: (theo phương pháp hình học)
+ Góc giữa hai đường thẳng song song hoặc trùng nhau thì bằng 0 + Go
́c giữa hai đường thẳng chéo nhau: Là góc tạo bởi hai đường a ' a
thẳng cắt nhau lần lượt vẽ cùng phương với hai đường thẳng đó: a ìï // a ' ï b ' í
(a,b) = (a ',b ') = f b b ï // b ' ïî
(chú ý: Góc giữa hai đường thẳng chỉ lấy góc nhọn không lấy góc tù) a b
b. Cách 2 : (theo phương pháp véc tơ): cosa,b . a b
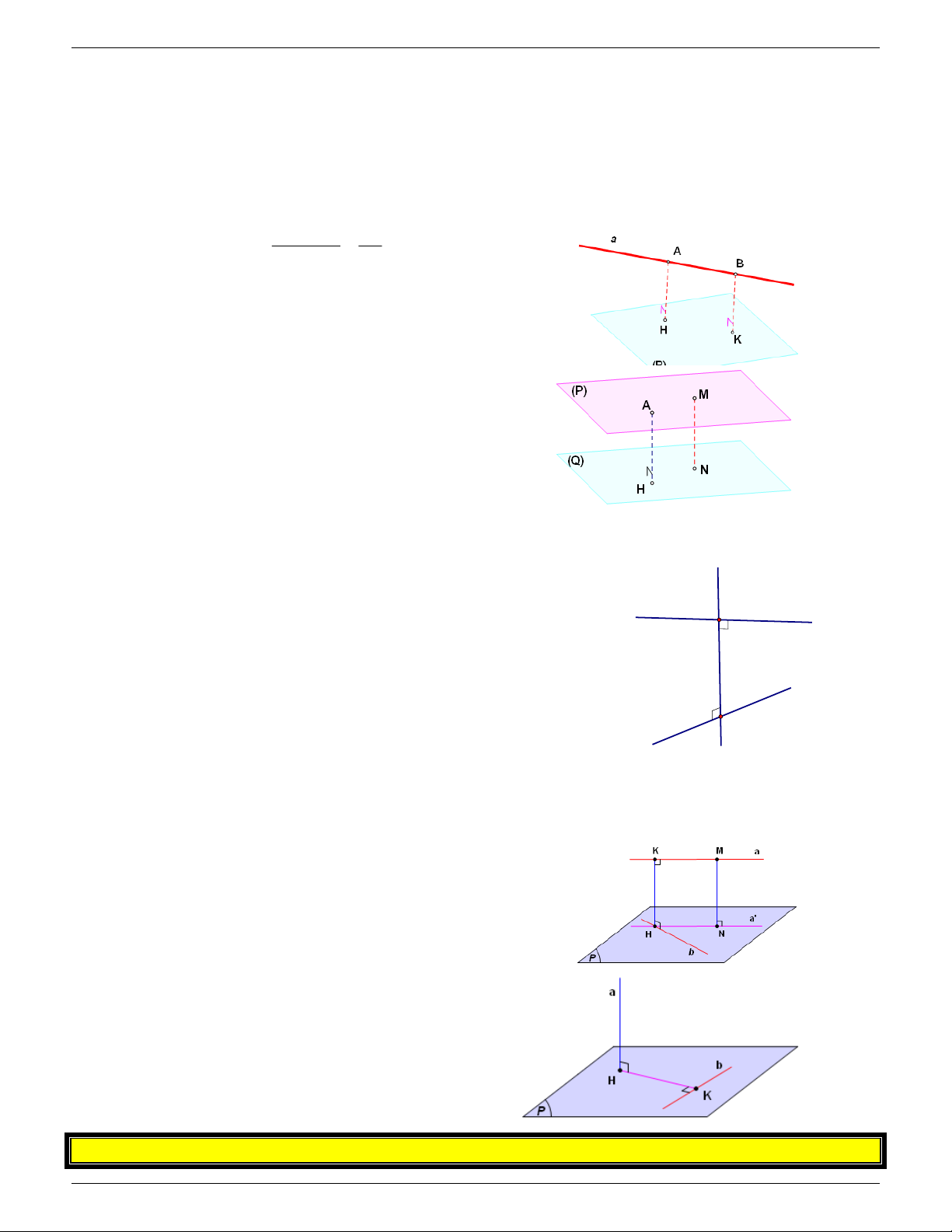
2. Tính góc giữa đường thẳng a và mặt phẳng P
Phương pháp xác định :
+ a P A
+ Trên đường thẳng a lấy điểm M bất kỳ.
+ Tìm điểm H là hình chiếu của M trên mp P MH P + ;
a P MAH
Chú ý: đường thẳng song song hoặc trùng với mặt phẳng thì góc bằng 0
3. Xác định góc giữa hai mặt phẳng P và Q Phương pháp :
+ Tìm giao tuyến của 2 mặt phẳng P và Q
+ Tìm 2 đường thẳng nằm trong 2 mặt phẳng P và Q
đồng thời 2 đường thẳng này cùng vuông góc với giao tuyến chung
của 2 mặt phẳng P và Q
+ Góc của 2 mặt phẳng P và Q là góc của 2 đường thẳng
cùng vuông góc với giao tuyến chung của 2 mặt phẳng P và Q
Chú ý: 2 mặt phẳng song song hoặc trùng nhau thì góc bằng 0 II. TÍNH KHOẢNG CÁCH
1. Tính các khoảng cách giữa một điểm và mặt phẳng
Phương pháp : Để tính khoảng cách từ một điểm đến một mặt phẳng , ta phải đi tìm đoạn vuông góc vẽ từ điểm đó
đến mặt phẳng , ta hay dùng một trong hai cách sau : Cách 1 :
+ Tìm một mặt phẳng (Q) chứa M và vuông góc với (P) .
Nguyễn Văn Thân Trang 4
Chuyên đề Thể tích khối đa diện
+ Xác định mPQ .
+ Dựng MH mPQ , MH P
Suy ra MH là đoạn cần tìm .
Cách 2: Dựng MH // AK P Chú ý :
+ Nếu MA / / P d d . M ,P M ,P
dM ,P IM
+ Nếu MAPI d , IA M P
2. Khoảng cách từ một đường thẳng đến một mặt phẳng: +
Khi a //P d d với A P . a,P , A P
+ Khi đường thẳng aP hoặc aP thì khoảng cách bằng 0
3. Khoảng cách từ một mặt phẳng đến một mặt phẳng : +
Khi P//Q d d
với A P .
P,Q M ,Q
PQ + Khi d PQ 0 P ,Q 4.
Khoảng cách giữa hai đường thẳng ' a. Khi d . ' 0 , '
b. Khi / / ' d (a) với M , N ' . d d , ' M ,' N ,
c. Khi hai đường thẳng chéo nhau : M
+ Đường vuông góc chung của hai đường thẳng chéo nhau
và ' là đường thẳng a cắt ở M và cắt ' ở N
đồng thời vuông góc với cả và ' . '
+ Đoạn MN được gọi là đoạn vuông góc chung của hai đường
thẳng chéo nhau và ' . N
+ Khoảng cách giữa hai đường thẳng chéo nhau là độ dài đoạn
vuông góc chung của hai đường thẳng đó .
Phương pháp :
+ Cách 1 : Dựng mặt phẳng (P) chứa đường thẳng a và song song với b .Tính khoảng cách từ b đến mp(P)
+ Cách 2 : Dựng hai mặt phẳng song song và lần lượt chứa hai đường thẳng . Khoảng cách giữa hai mặt phẳng đó là
khoảng cách cần tìm .
+ Cách 3 : Dựng đoạn vuông góc chung và tính độ dài đoạn đó .
* Cách dựng đoạn vuông góc chung của hai đường thẳng chéo nhau :
+ Dựng Pb,P//a .
+ Dựng a 'hc h a P
, bằng cách lấy M a
+ Dựng đoạn MN , lúc đó a’ là đường thẳng đi qua N và song song a .
+ Gọi H a 'b , dựng HK //MN
HK là đoạn vuông góc chung cần tìm
( Hay MN là đoạn vuông góc chung cần tìm) . *
Nếu hai đường thẳng chéo nhau và vuông góc nhau thì:
+ Dựng một mpPb,Pa tại H .
+ Trong (P) dựng HK b tại K .
+ Đoạn HK là đoạn vuông góc chung của a và b .
VẤN ĐỀ 3: TÍNH CHẤT CỦA MỘT SỐ HÌNH ĐẶC BIỆT
Nguyễn Văn Thân Trang 5
Chuyên đề Thể tích khối đa diện I. HÌNH CHÓP ĐỀU
1/ Đi ̣nh nghı̃a: Mô ̣t hı̀nh chóp được go ̣i là hı̀nh chóp đều nếu có đáy là một đa giác đều và có chân đường cao trùng với
tâm của đa giác đáy. Nhận xét:
+ Hı̀nh chóp đều có các mặt bên là những tam giác cân bằng nhau.
+ Các mặt bên tạo với đáy các góc bằng nhau.
+ Các cạnh bên của hı̀nh chóp đều tạo với mặt đáy các góc bằng nhau.
+ Đáy là đa giác đều (tam giác đều, hình vuông ...) S
2/ Hai hı̀nh chóp đều thường gă ̣p
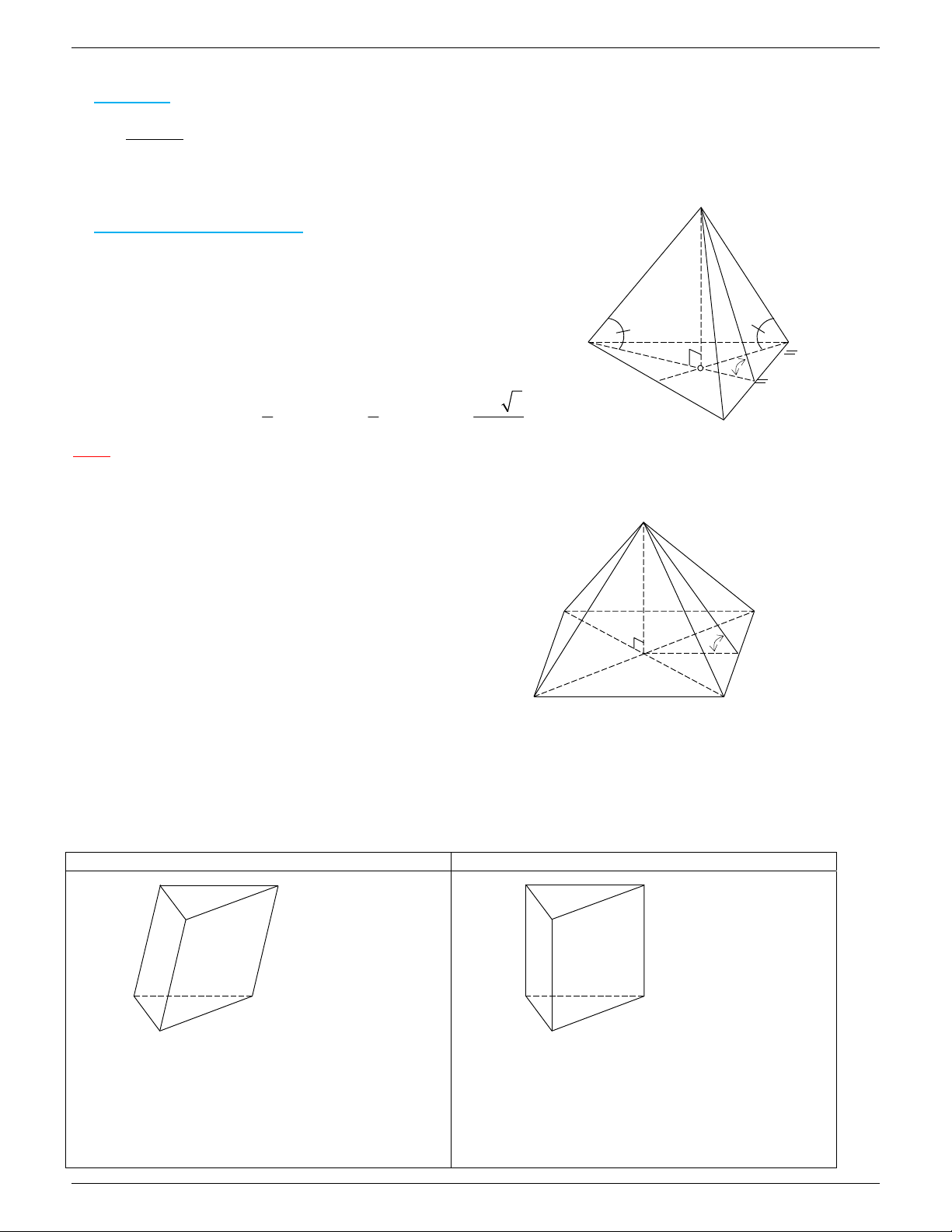
a/ Hı̀nh chóp tam giác đều:
Cho hı̀nh chóp tam giác đềuS.ABC . Khi đó:
+ ĐáyABC là tam giác đều.
+ Các mă ̣t bên là các tam giác cân ta ̣iS .
+ Chiều cao: SO .( O là tâm của đáy) A + Go
SAO = SBO = SCO . C
́c giữa ca ̣nh bên và mă ̣t đáy:
+ Góc giữa mă ̣t bên và mă ̣t đáy: SHO . O H 2 1 AB 3
+ Tı́nh chất: AO = AH, OH = AH, AH = . 3 3 2 B
Lưu ý: Hı̀nh chóp tam giác đều khác với tứ diê ̣n đều:
+ Tứ diê ̣n đều có các mă ̣t là các tam giác đều.
+ Tứ diê ̣n đều là hı̀nh chóp tam giác đều có ca ̣nh bên bằng ca ̣nh đáy. S
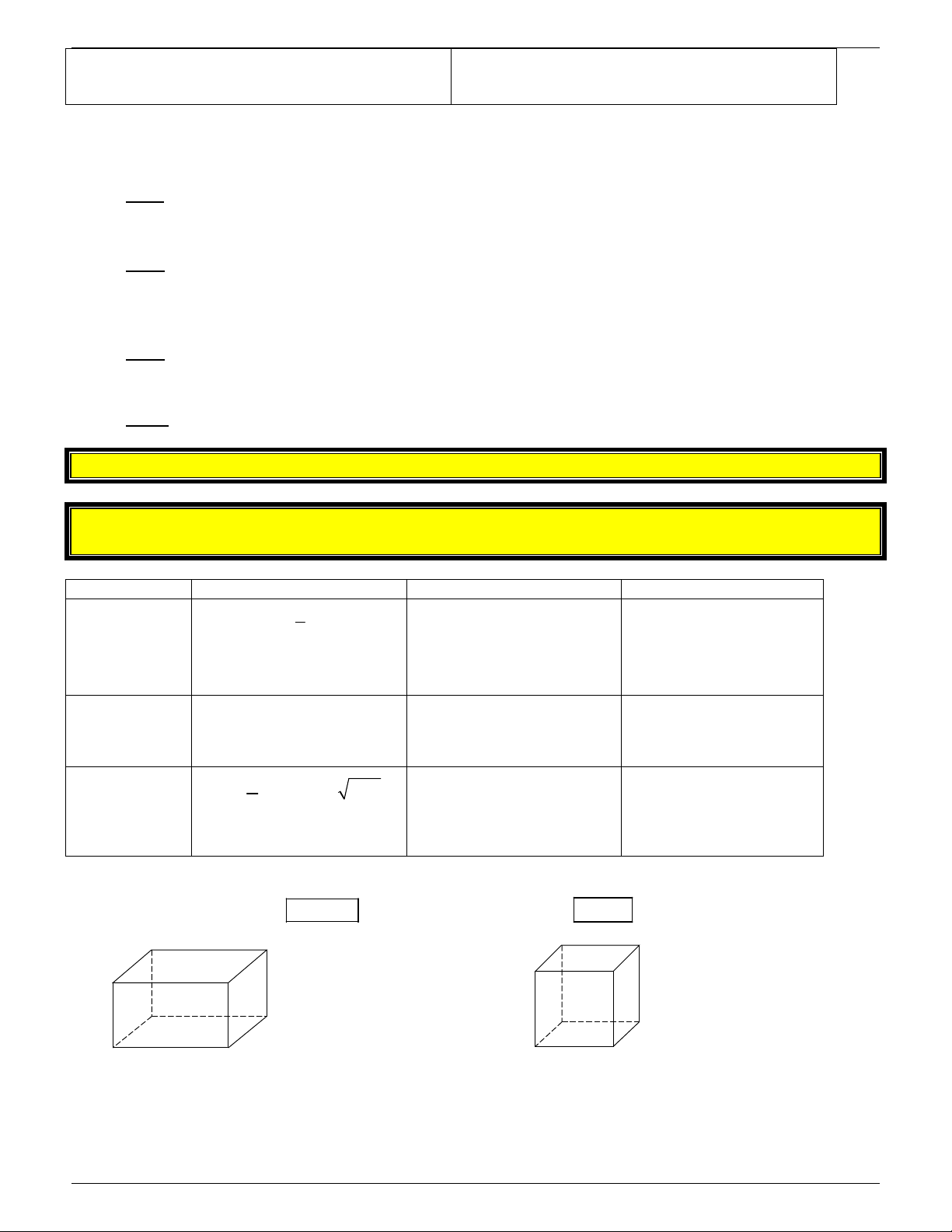
b/ Hı̀nh chóp tứ giác đều:
Cho hı̀nh chóp tam giác đềuS.ABCD .
+ ĐáyABCD là hı̀nh vuông.
+ Các mă ̣t bên là các tam giác cân ta ̣iS . A D + Chiều cao: SO .
+ Góc giữa ca ̣nh bên và mă ̣t đáy: H O
SAO = SBO = SCO = SDO . B C
+ Góc giữa mă ̣t bên và mă ̣t đáy: SHO .
II. TỨ DIỆN ĐỀU:
+ Tứ diê ̣n đều có 4 mă ̣t là các tam giác đều
+ Khi hı̀nh chóp tam giác đều có ca ̣nh bên bằng ca ̣nh đáy thì đó là tứ diê ̣n đều. Do đó tứ diê ̣n đều có tính chất như hình chóp tam giác.
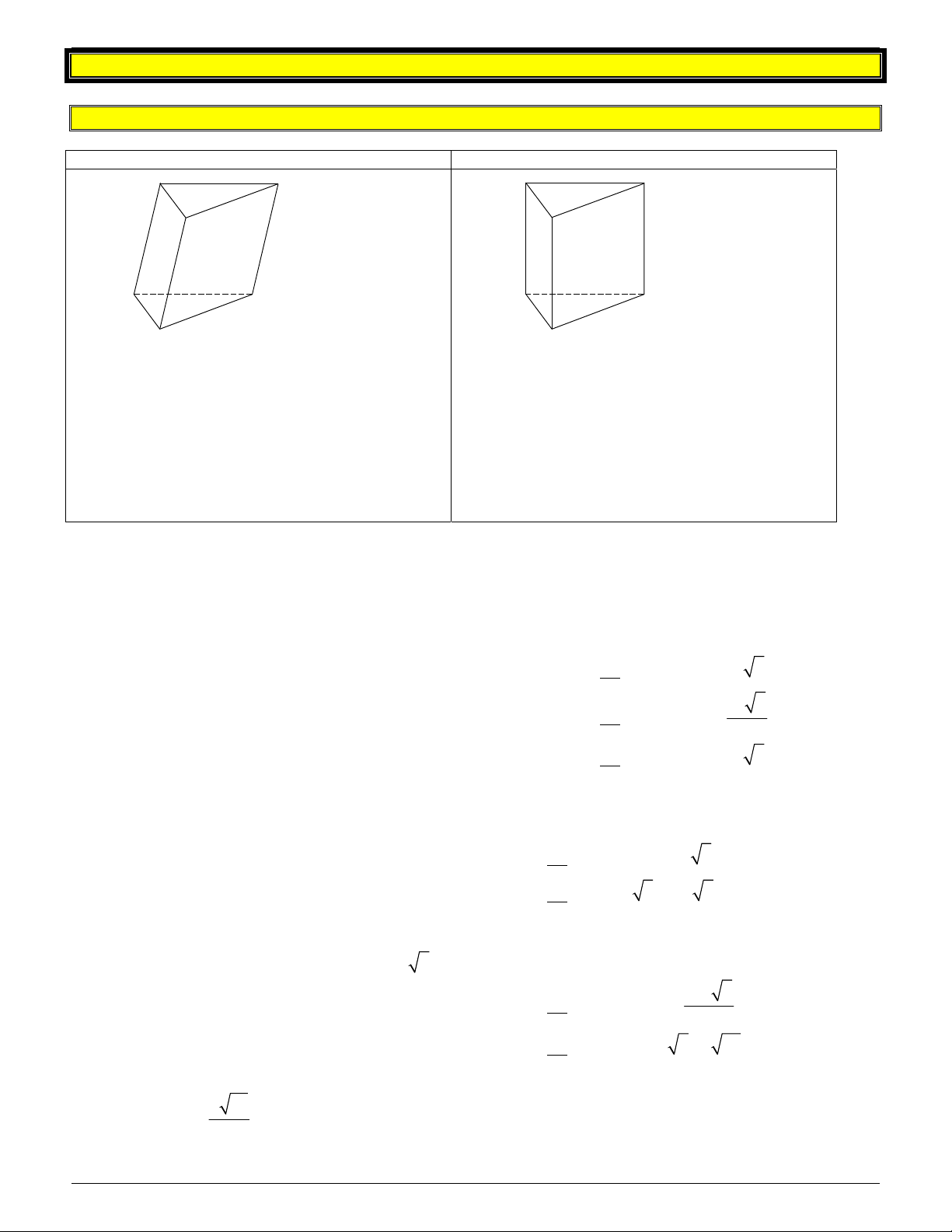
III. HÌNH LĂNG TRỤ VÀ HÌNH LĂNG TRỤ ĐỨNG HÌNH LĂNG TRỤ
HÌNH LĂNG TRỤ ĐỨNG
+ 2 mặt đáy là đa giác song song và bằng nhau.
+ 2 mặt đáy là đa giác song song và bằng nhau.
+ các cạnh bên song song và bằng nhau
+ các cạnh bên song song và bằng nhau
+ các mặt bên là hình bình hành
+ các mặt bên là hình bình chữ nhật và vuông góc với 2 mặt đáy
+ Chiều cao là khoảng cách của 2 mặt đáy + Chiều cao là cạnh bên
Hình hộp: là hình lăng trụ có 2 đáy là hình bình hành
Hình hộp chữ nhật : là hình lăng trụ đứng có 2 đáy là
Nguyễn Văn Thân Trang 6
Chuyên đề Thể tích khối đa diện hình chữ nhật
Hình lập phương: là hình lăng trụ đứng có 6 mặt là hình vuông.
IV. CHIỀU CAO CỦA MỘT SỐ HÌNH CHÓP CÓ TÍNH CHẤT ĐẶC BIỆT
1/ Hı̀nh chóp có mô ̣t ca ̣nh bên vuông góc với đáy: Chiều cao của hı̀nh chóp là độ dài cạnh bên vuông góc với đáy
Vı́ du ̣: Hı̀nh chópS.ABCD có ca ̣nh bên SA ^ (ABCD)thı̀ chiều cao là SA.
2/ Hı̀nh chóp có mô ̣t mă ̣t bên vuông góc với mă ̣t đáy: Chiều cao của hı̀nh chóp là chiều cao của tam giác chứa
trong mặt bên vuông góc với đáy.
Vı́ du ̣: Hı̀nh chópS.ABC có mă ̣t bên(SAB) vuông góc với mă ̣t đáy(ABC )thı̀ chiều cao của hı̀nh chóp là chiều cao của SA D B .
3/ Hı̀nh chóp có hai mă ̣t bên vuông góc với đáy: Chiều cao của hı̀nh chóp là giao tuyến của hai mặt bên cùng
vuông góc với đáy.
Vı́ du ̣: Hı̀nh chópS.ABCD có hai mă ̣t bên (SAB)và(SAD) cùng vuông góc với mă ̣t đáy(ABCD)thı̀ chiều cao
là SA. 4/ Hı̀nh chóp đều và tứ diện đều: Chiều cao của hı̀nh chóp là đoạn thẳng nối đı̉nh và tâm của đáy.
Vı́ du ̣: Hı̀nh chóp tứ giác đềuS.ABCD có tâm mă ̣t phẳng đáy là giao điểm O của hai đường chéo hı̀nh
vuông ABCD thı̀ có đường cao là SO .
THỂ TÍCH KHỐI ĐA DIỆN
LÝ THUYẾT: THỂ TÍCH KHỐI ĐA DIỆN, DIỆN TÍCH XUNG QUANH,
DIỆN TÍCH TOÀN PHẦN Thể tích
Diện tích xung quanh
Diện tích toàn phần 1 V . B h 3 KHỐI CHÓP
Sxq = Tổng diện tích các mặt bên
Stp = Sxq + Diện tích mặt đáy
+ B là diện tích đáy
+ h đường cao hình chóp V . B h KHỐI LĂNG
+ B là diện tích đáy S TRỤ
+ h là đường cao lăng trụ
xq = Tổng diện tích các mặt bên
Stp = Sxq + Diện tích 2 mặt đáy h
V = (B + B '+ BB ') KHỐI CHÓP 3 S CỤT
xq = Tổng diện tích các mặt bên
Stp = Sxq + Diện tích mặt đáy +Với ,
B B ' là diê ̣n tı́ch hai đáy
+ h đường cao hình chóp Chú ý:
I. Thể tı́ch hı̀nh hô ̣p chữ nhâ ̣t: V = a. .
b c Thể tı́ch khối lâ ̣p phương: 3 V = a a a b a a c Hình hộp chữ nhật Hình lập phương
II. 4 phương pháp thường dùng tı́nh thể tı́ch
1.Tı́nh thể tı́ch bằng công thức.
+ Tı́nh các yếu tố cần thiết: đô ̣ dài ca ̣nh, diê ̣n tı́ch đáy, chiều cao,….
+ Sử du ̣ng công thức tı́nh thể tı́ch.
Nguyễn Văn Thân Trang 7
Chuyên đề Thể tích khối đa diện
+ Cần năm vững các công thức tính diện tích tam giác, tứ giác, ....
2. Tı́nh thể tı́ch bằng cách chia nhỏ: Ta chia khối đa diê ̣n thành nhiều khối đa diê ̣n nhỏ mà có thể dễ dàng tı́nh thể
tı́ch của chúng. Sau đó, ta cô ̣ng kết quả la ̣i, ta sẽ có kết quả cần tı̀m.
3. Tı́nh thể tı́ch bằng cách bổ sung: Ta có thể ghép thêm vào khối đa diê ̣n mô ̣t khối đa diê ̣n khác, sao cho khối đa
diê ̣n thêm vào và khối đa diê ̣n mới có thể dễ dàng tı́nh được thể tı́ch.
4. Tı́nh thể tı́ch bằng tı̉ số thể tı́ch.
* Trong nhiều bài toán, viê ̣c tı́nh trực tiếp thể tı́ch khối đa diê ̣n có thể gặp khó khăn vı̀ hai lı́ do: +
Hoặc là khó xác đi ̣nh và tı́nh được chiều cao. +
Hoặc tı́nh được diê ̣n tı́ch đáy nhưng cũng không dễ dàng. * Khi
đó, ta có thể làm theo các phương pháp sau:
+ Phân chia khối cần tı́nh thể tı́ch thành tổng hoặc hiê ̣u các khối cơ bản (hı̀nh chóp hoặc hı̀nh lăng trụ) mà
các khối này dễ tı́nh hơn. +
Hoặc là so sánh thể tı́ch khối cần tı́nh với một đa diê ̣n khác đã biết trước hoặc dễ dàng tı́nh thể tı́ch.
* Trong dạng này, ta thường hay sử dụng phương pháp tỉ số, lấy kết quả của bài toán sau: V
SA' SB ' SC '
Cho hı̀nh chóp S.ABC. Lấy A’, B’, C’ tương ứng trên ca ̣nh SA, SB, SC. Khi đó: S.A'B 'C ' = . . . V SA SB SC S .ABC Chứng minh:
Kẻ A’H’ và AH cùng vuông góc với mă ̣t phẳng (SBC).
Khi đó: A’H // AH và S, H’, H thẳng hàng. S 1 S .A' H ' H’ V V SB D 'C ' Ta co S A B C A SB C 3 ́: . ' ' ' ' ' ' = = A’ B’ V V 1 S .ABC . A SBC S .AH 3 SBC D C’ H 1 A B SB '.SC '.sin . a A'H '
SB '.SC '.SA' 2 = = (Ðpcm). 1 SB.SC.SA SB.SC.sin . a AH C 2
Trong đó: a = B 'SC ' = BSC .
Lưu ý: Kết quả trên vẫn đúng nếu như trong các điểm A’, B’, C’ có thể có điểm A º A',B º B ',C º C ' .
Thông thường, đối với loại này, đề thường cho điểm chia đoạn theo tı̉ lê ̣, song song, hı̀nh chiếu,…
III. Sử dụng phương pháp thể tích khối đa diện để tính khoảng cách
* Các bài toán tı̀m khoảng cách: Khoảng cách từ mô ̣t điểm đến mô ̣t mă ̣t phẳng, khoảng cách giữa hai đường
thẳng, trong nhiều trường hợp có thể qui về bài toán thể tı́ch khối đa diê ̣n. Viê ̣c tı́nh khoảng cách này dựa vào công thức 3V hiển nhiên: h = , ở đâyV, ,
B h lần lượt là thể tı́ch, diê ̣n tı́ch đáy và chiều cao của một hı̀nh chóp nào đó (hoă ̣c B V h =
đối với hı̀nh lăng trụ). S
* Phương pháp này áp dụng được trong trường hợp sau: Giả sử có thể qui bài toán tı̀m khoảng cách về bài toán
tı̀m chiều cao của mô ̣t hı̀nh chóp (hoă ̣c mô ̣t lăng trụ) nào đó. Dı̃ nhiên, các chiều cao này thường là không tı́nh được trực tiếp
bằng cách sử dụng các phương pháp thông thường như đi ̣nh lı́ Pitago, công thức lượng giác,… Tuy nhiên, các khối đa diê ̣n
này la ̣i dễ dàng tı́nh được thể tı́ch và diê ̣n tı́ch đáy. Như vâ ̣y, chiều cao của nó sẽ được xác đi ̣nh bởi công thức đơn giản trên.
* Phương pháp: Sử du ̣ng các đi ̣nh lı́ của hı̀nh ho ̣c trong không gian sau đây:
+ Nếu AB // mp (P)trong đo é ù
́ mp (P)chứaCD thı̀d (A , B CD) = d A , B ê (P) ë úû . + Nếu
mp (P) // mp(Q) trong đó mp(P),mp(Q) lần lượt chứa AB và CD thı̀: d (A , B CD) d m
é p(P),mp(Q)ù = êë úû .
+ Từ đó, qui bài toán tı̀m khoảng cách theo yêu cầu bài toán về viê ̣c tı̀m chiều cao của khối chóp (hoă ̣c mô ̣t khối lăng tru ̣) nào đó.
Nguyễn Văn Thân Trang 8
Chuyên đề Thể tích khối đa diện
+ Giả sử bài toán đã được qui về tı̀m chiều cao kẻ từ đı̉nhS của mô ̣t hı̀nh chóp (hoă ̣c mô ̣t lăng trụ). Ta tı̀m thể tı́ch
của hı̀nh chóp (lăng tru ̣) này theo mô ̣t con đường khác mà không dựa vào đı̉nh S này, chẳng ha ̣n như quan niê ̣m hı̀nh chóp
ấy có đı̉nhS ' ¹ S . Sau đó, tı́nh diê ̣n tı́ch đáy đối diê ̣n với đı̉nhS . Như thế, ta suy ra được chiều cao kẻ từS cần tı̀m.
CHỦ ĐỀ 1: CÁC DẠNG TOÁN KHỐI CHÓP
DẠNG 1: HÌNH CHÓP CÓ CẠNH BÊN VUÔNG GÓC VỚI ĐÁY
Bài 1. Cho hı̀nh chóp S.ABC có đáy là AB D C vuông cân ở ,
B AC = a 2,SA ^ mp (ABC ),SA = a . 3 a
a. Tı́nh thể tı́ch khối chóp S.ABC . ĐS: V = . S .ABC (đvtt) 6
b. Go ̣i G là tro ̣ng tâm của SB D
C , mp (a)đi quaAG và song song với BC cắt SC,SB lần lượt ta ̣i M,N . Tı́nh 3 2a
thể tı́ch khối chóp S.AMN . ĐS: V = . SAMN (đvtt) 27
Bài 2. Cho hı̀nh chóp S.ABC có đáy là AB D
C đều ca ̣nh a và SA ^ (ABC ),SA = 2a . Gọi H,K lần lượt là hı̀nh
chiếu vuông góc của điểm A lần lượt lên ca ̣nh , SB SC . 3 a 3
a. Tı́nh thể tı́ch khối chóp H.ABC theo a . ĐS: V = . H .ABC (đvtt) 30 3 3a 3
b. Tı́nh thể tı́ch khối . ABCKH theo a . ĐS: V = . . A BCKH (đvtt) 50 a 3
c. Tính khoảng cách từ H đếnmp (SAC ). ĐS: d = . é ù (đvđd) H ê ( , SAC ) ë úû 10
Bài 3. Cho tứ diê ̣n ABCD có ca ̣nh AD vuông góc với mp (ABC ) , AC = AD = 4(cm),AB = 3(cm) , 6 34
BC = 5(cm). Tı́nh khoảng cách từ A đến mp(BCD). ĐS: d = (cm é ù ) A ê ( , DBC ) ë úû 17
Bài 4. Cho hı̀nh chóp S.ABC có đáyABC là tam giác có AC = a, AB = 3a , 0
BAC = 60 . Go ̣i H là hình chiếu
của S trên (ABC ) biết H Î AB và AH = 2HB . Cạnh bên SC hợp với đáy một góc 0 45 .
a. Tı́nh thể tı́ch khối chóp S.ABC
b. Tı́nh khoảng cách từ A đến mp (SBC ).
Bài 5. Cho hı̀nh chóp S.ABC có đáy AB D
C là tam giác vuông ta ̣i B và SA ^ (ABC )với 0 ACB = 60 ,
BC = a,SA = a 3 . Go ̣i M là trung điểm của ca ̣nh SB .
a. Chứng minh rằng: mp (SAB) ^ mp (SBC ) . 3 a
b. Tı́nh thể tı́ch khối chóp S.ABC . ĐS: V = . S .ABC (đvtt) 2 3 a
c. Tı́nh thể tı́ch khối tứ diê ̣nMABC . ĐS: V = . MABC (đvtt) 4 a
d. Tı́nh khoảng cách từ điểm M đến mp (SAC ). ĐS: d = é ù (đvđd) M ê (,SAC) ë úû 2
Bài 6. Cho hı̀nh chóp S.ABCD có đáyABCD là hı̀nh vuông ca ̣nh a ,SA ^ (ABCD), SA = a 3 . Gọi O là giao
điểm của hai đường chéo hình vuông ABCD . 3 a 3
a. Tı́nh thể tı́ch khối chóp S.ABCD theo a . ĐS: V = . S .ABCD (đvtt) 3
Nguyễn Văn Thân Trang 9
Chuyên đề Thể tích khối đa diện 3 a 3
b. Tı́nh thể tı́ch khối chóp S.OBC theo a . ĐS: V = . S .ABCD (đvtt) 12 a 3
c. Tı́nh khoảng cách từ điểm A đến mp (SBC ). ĐS: d = é ù (đvđd) A ê ( , SBC ) ë úû 2 a 3
d. Tı́nh khoảng cách từ điểm O đến mp (SBC ). ĐS: d = é ù (đvđd) A ê ( , SBC ) ë úû 4
Bài 7. Cho hı̀nh chóp S.ABCD có đáyABCD là hı̀nh vuông ca ̣nh a ,SA ^ (ABCD). Cạnh SC tạo với mặt phẳng
đáy (ABCD) một góc 0 60 . 3 a 6
a. Tı́nh thể tı́ch khối chóp S.ABCD theo a . ĐS: V = . S .ABCD (đvtt) 3 a 3
b. Xác đi ̣nh và tı́nh đô ̣ dài đoa ̣n vuông góc chung của hai đường thẳng SC và BD . ĐS: ( d = SC ;BD) 4
Bài 8. Cho hı̀nh chóp S.ABCD có đáy là hı̀nh vuông ca ̣nh bằng a , chiều cao SA = 2a . Go ̣i N là trung điểm của SC .
a. Tính diện tích toàn phần hình chóp S.ABCD . 3 2a
b. Tı́nh thể tı́ch khối chóp S.ABCD theo a . ĐS: V = . S .ABCD (đvtt) 3
c. Mă ̣t phẳng (P) chứa AN và song song với BD lần lượt cắt SB,SD ta ̣i M,P . Tı́nh thể tı́ch khối chóp 3 2a
S.AMNP theo a . ĐS: V = . S .AMNP (đvtt) 9
Bài 9. Cho hı̀nh chóp S.ABCD có đáy ABCD là hı̀nh chữ nhâ ̣t tâm ,
O SA ^ mp (ABCD). Biết AB = 3a , góc 0
BAC = 60 . Mặt bên (SBC ) hợp với đáy một góc 0 45 .
a. Tı́nh thể tı́ch khối chóp S.ABCD theo a . ĐS: 3 V = 9a 3 . S .ABCD (đvtt) 3 9a 3
b. Tı́nh thể tı́ch khối chóp SOAD . ĐS: V = . S .OAD (đvtt) 4 3a 2
c. Tı́nh khoảng cách từ điểm O đếnmp (SBC ). ĐS: d = é ù (đvđd) O ê ( , SBC ) ë úû 2
Bài 10. Cho khối chóp S.ABCD có đáy ABCD là hı̀nh chữ nhâ ̣t. Biết rằng SA ^ (ABCD),SC hợp với mă ̣t phẳng
chứa đáy ABCD mô ̣t góc 0
30 vàAB = a,BC = 2a . 3 a 15
a. Tı́nh thể tı́ch khối chóp S.ABCD . ĐS: V = . S .ABCD (đvtt) 3 3 a 15
b. Tı́nh thể tı́ch khối chóp S.ABC . ĐS: V = . S .ABC (đvtt) 6
c. Gọi O là giao điểm của AC và BD . Tı́nh khoảng cách từ điểm O đến mp (SCD). a 1140 ĐS: d = é ù (đvđd) O ê ( , SCD) ë úû 60
Nguyễn Văn Thân Trang 10
Chuyên đề Thể tích khối đa diện
DẠNG 2: HÌNH CHÓP CÓ MỘT MẶT VUÔNG GÓC VỚI ĐÁY Chú ý: (ìïïP) ^ (Q) ï(ïïP ï ) Ç (Q) = a - í ^ b ï Ì ï (P) b (Q) ïbïï ^ a ïî
- Tam giác BAC cân tại A , I là trung điểm BC AI vừa đường cao vừa đường trung tuyến vừa đường phân giác AB D C .
- Tam giác ABC đều , G là trọng tâm AB D
C , M,N,P lần lượt là trung điểm cạnh BC,AC,AB . Ta cần nhớ: ìï 1 2 AG ïï = GM = AM ïï 3 3 ïï 1 2 + BG ïí = GN = BN ï 3 3 ïïï 1 2 CG ï = GP = CP ïï 3 3 ïî
+ AM,BN,CP vừa đường cao vừa đường trung tuyến vừa đường phân giác của AB D C .
Bài 1. Cho hı̀nh chóp S.ABCD có đáyABCD là hı̀nh vuông ca ̣nh a . Mă ̣t bên SAB là tam giác đều nằm trong mă ̣t
phẳng vuông góc với mă ̣t phẳng đáy(ABCD).
a. Chứng minh rằng chân đường cao của khối chóp đã cho trùng với trung điểm của ca ̣nh AB . 3 a 3
b. Tı́nh thể tı́ch khối chóp S.ABCD . ĐS: V = . S .ABCD (đvtt) 6 3 a 3
c. Tı́nh thể tı́ch khối chóp S.BCD . ĐS: V = . S .BCD (đvtt) 12 a 3
d. Tı́nh khoảng cách từ D đến mp (SBC ). ĐS: d = . é ù (đvđd) D ê ( , SBC ) ë úû 2
Bài 2. Cho hı̀nh chópS.ABCD có đáyABCD là hı̀nh chữ nhâ ̣t. Mă ̣t bên SAB là tam giác đều ca ̣nh là a và nằm trong
mă ̣t phẳng vuông góc vớimp (ABCD). Cạnh bên SC hợp với mp (ABCD)mô ̣t góc bằng 0 30 . 3 a 30
a. Tı́nh thể tı́ch khối chópS.ABCD đã cho. ĐS: V = . S .ABCD 12 a 3
b. Tı́nh khoảng cách của điểm C đến mp (SAD) ĐS: d = . é ù (đvđd) C ê ( , SAD) ë úû 2 a 390
c. Tı́nh khoảng cách của điểm B đến mp (SAC ) ĐS: d = . é ù (đvđd) B ê ( , SAC ) ë úû 13 0
Bài 3. Cho hı̀nh chóp S.ABC có 0
BAC = 90 ,ABC = 30 , SBC D
là tam giác đều ca ̣nh a và
mp (SAB) ^ mp(ABC ). 3 a 39
a. Tı́nh thể tı́ch khối chóp S.ABC . ĐS: V = . S .ABC (đvtt) 96 a 39
b. Tính khoảng cách từ B đến mp (SAC ). ĐS: d = . é ù (đvđd) B ê ( , SAC ) ë úû 8
c. Gọi G là trọng tâm SB D
C . Tı́nh khoảng cách của điểm G đến mp (SAC ).
Bài 4. Cho hı̀nh chóp S.ABC có đáyABC là tam giác vuông cân ta ̣iB , cóBC = a . Mă ̣t bên (SAC ) vuông góc với
mă ̣t phẳng đáy, mă ̣t bên (SAB) ta ̣o với mă ̣t phẳng đáy mô ̣t góc 0 45 . Biết SA D
C cân tại S .
Nguyễn Văn Thân Trang 11
Chuyên đề Thể tích khối đa diện
a. Gọi H là trung điểm AC . Chứng minh SH ^ (ABC ). 3 a
b. Tı́nh thể tı́ch khối chóp S.ABC . ĐS: V = . S .ABC (đvtt) 12 a 2
c. Tính khoảng cách từ H đến mp (SBC ). ĐS: d = . é ù (đvđd) H ê ( , SBC ) ë úû 4
Bài 5. Cho hı̀nh chóp S.ABCD có đáy ABCD là hı̀nh vuông ca ̣nh a ,mp (SAB) ^ mp (ABCD), SA = SB , góc
giữa đường thẳng SC và mă ̣t phẳng đáy bằng 0 45 . 3 a 5
a. Tı́nh theo a thể tı́ch của khối chóp S.ABCD . ĐS: V = . S .ABCD (đvtt) 6 a 30
b. Tính khoảng cách từ D đến mp (SBC ). ĐS: d = . é ù (đvđd) D ê ( , SBC ) ë úû 6 2a 5
c. Gọi G là trọng tâm SAB D
. Tı́nh khoảng cách của điểm G đến mp (SCD). ĐS: d = . G é (,SCD)ù êë úû 9
Bài 6. Cho hı̀nh chóp S.ABCD có đáy ABCD là hı̀nh vuông ca ̣nh a ,mp (SAC ) ^ mp (ABCD), SAC D , vuông cân tại S . 3 a 2
a. Tı́nh theo a thể tı́ch của khối chóp S.ABCD . ĐS: V = . S .ABCD (đvtt) 6 3 a 2
b. Tı́nh theo a thể tı́ch của khối chóp S.BCD . ĐS: V = . S .BCD (đvtt) 12 a 6
b. Tính khoảng cách từ B đến mp (SAD). ĐS: d = . é ù (đvđd) B ê ( , SAD) ë úû 12
DẠNG 3: HÌNH CHÓP CÓ HAI MẶT VUÔNG GÓC VỚI ĐÁY
(Q) ^ (P) üïïïï
Chú ý: (R) (P) ^
ý a ^ (P) ( ï
Q) Ç (R) = aïïïþ
Bài 1. Cho hı̀nh chóp S.ABC có SA = AB = AC = BC = a . Hai ( mp SAB) và (
mp SAC ) cùng vuông góc với ( mp SBC ). 3 a 3
a. Tı́nh thể tı́ch của hı̀nh chóp S.ABC . ĐS: V = S .ABC (đvtt) 12
b. Tính góc giữa đường thẳng SB và ( mp ABC ) . ĐS: SB (ABC ) 0 , = 45 . a 15
c. Tính khoảng cách từ A đến mp (SBC ). ĐS: d = . é ù (đvđd) A ê ( , SBC ) ë úû 5
Bài 2. Cho hình chópS.ABCD có đáy ABCD là hình chữ nhật có AB = a,BC = 2a . Hai mp (SAB) và
mp (SAD)cùng vuông góc với mă ̣t phẳng đáy, cạnh SC hợp với đáy một góc 0 60 . 3 2a 15
a. Tính thể tích khối chóp S.ABCD theo a . ĐS: V = ABCD (đvtt) 3 3 a 15
b. Gọi {O} = AC Ç BD . Tính thể tích khối chóp S.OBC theo a . ĐS: V = S .OBC (đvtt) 6 a 60
c. Tính khoảng cách từ O đến mp (SCD). ĐS: d = . é ù (đvđd) O ê ( , SCD) ë úû 2 19
Nguyễn Văn Thân Trang 12
Chuyên đề Thể tích khối đa diện
Bài 3. Cho hı̀nh chópS.ABC có đáyABC là tam giác vuông cân ta ̣iA . Hai mă ̣t phẳng(SAB)và(SAC )cùng vuông góc
với mă ̣t phẳng đáy(ABC ), cho BC = a 2 , mă ̣t bên(SBC ) ta ̣i với đáy(ABC )mô ̣t góc 0 60 .
a. Tı́nh thể tı́ch của khối chóp S.ABC
b. Tı́nh khoảng cách từ điểm A đến mă ̣t phẳng (SBC ) . 2
c. Trên cạnh AB lấy điểm D sao cho: AD =
AB . Tı́nh khoảng cách từ điểm D đến mă ̣t phẳng (SAC ). 3
Bài 4. Cho hı̀nh chóp S.ABCD có đáyABCD là hı̀nh vuông ca ̣nh a , hai mă ̣t bên(SAB)và(SAD) cùng vuông góc
với(ABCD). Cho SB = 3a . Go ̣i M là trung điểm của CD .
a. Tı́nh thể tı́ch của khối chóp S.ABCM .
b. Tı́nh khoảng cách của điểm M đến mp (SBC )
Bài 5. Cho hı̀nh chóp S.ABCD có đáy ABCD là hı̀nh chữ nhâ ̣t, các mă ̣t bên (SAB) và (SAD) cùng vuông góc với
mă ̣t đáy (ABCD), choAB = a,AD = 2a,SC ta ̣o với mă ̣t đáy (ABCD) mô ̣t góc 0 45 .
a. Tı́nh thể tı́ch của khối chóp S.ABCD theo a .
b. Gọi H là hình chiếu của A trên cạnh BD . Tính thể tı́ch của khối chóp S.AHCD theo a .
c. Tı́nh khoảng cách của điểm C đến mp (SAH ).
d. Tı́nh khoảng cách 2 đường thẳng SB và AH .
Bài 6. Cho hı̀nh chóp S.ABCD có đáy ABCD là hı̀nh thoi cạnh a , 0
BAD = 120 . Biết mặt bên(SAB) và (SAD)
cùng vuông góc với mặt đáy (ABCD). Cạnh bên SC tạo với đáy một góc 0 60 . 3 a
a. Tı́nh thể tı́ch khối chóp S.ABCD . ĐS: V = . S .ABCD (đvtt) 2 3 a
b. Tı́nh thể tı́ch khối chóp S.BCD . ĐS: V = . S .BCD (đvtt) 4 a 3
c. Tính khoảng cách từ C đến mp (SAB) . ĐS: d = . é ù (đvđd) C ê ( , SAB) ë úû 2
DẠNG 4: HÌNH CHÓP ĐỀU Định nghĩa:
+ đáy là đa giác đều (tam giác đều, hình vuông, ngũ giác đều ...)
+ các mặt bên là tam giác cân tại đỉnh của hình chóp.
+ đường cao là đường hạ từ đỉnh đến tâm của đa giác đều.
+ các cạnh bên tạo với đáy 1 góc đều bằng nhau.
+ các mặt bên tạo với đáy 1 góc đều bằng nhau. Chú ý:
+ Tứ diện đều là hình chóp tam giác đều có cạnh đáy bằng cạnh bên.
+ Hình chóp đều khác với hình chóp có đáy là đa giác đều (hình chóp có đáy là tứ giác đều là hình
chóp chỉ có đáy là đa giác đều )
Bài 1. Cho hình chóp đều S.ABCD có cạnh đáy 2a , góc giữa mặt bên và mặt đáy bằng 0
60 . Gọi G là trọng tâm tam giác SAC D . 3 4a 3
a. Tính thể tích của hình chópS.ABCD . ĐS: V = . S .ABCD (đvtt) 3
b. Tính khoảng cách từ A đến mp (SBC ). ĐS: d = a 3 . é ù (đvđd) A ê ( , SBC ) ë úû
Nguyễn Văn Thân Trang 13
Chuyên đề Thể tích khối đa diện a 3
c. Tính khoảng cách từ G đến mp (SAB) ĐS: d = . é ù (đvđd) G ê ( , SAB) ë úû 3
Bài 2. Cho khối chóp tứ giác đều S.ABCD . Mô ̣t mă ̣t phẳng (P) qua ,
A B và trung điểm M của SC . Tı́nh tı̉ số thể tı́ch V 3
của hai phần khối chóp bi ̣ phân chia bởi mă ̣t phẳng đó. ĐS: S.ABMN = V 5 ABCDNM a 2a
Bài 3. Cho tứ diê ̣n đều ABCD có ca ̣nh a . Lấy các điểm B ',C ' trên AB và AC sao cho AB ' = , AC ' = . 2 3 3 a 2
a. Tı́nh thể tı́ch khối tứ diê ̣n AB 'C 'D . ĐS: V = . AB 'C ' D (đvtt) 36 a 6
b. Tı́nh khoảng cách từ B ' đến mp (ACD). ĐS: d đvđd B'; ACD 6
Bài 4. Cho khối tứ diê ̣n đều ABCD ca ̣nh bằng a . Go ̣iM là trung điểm của ca ̣nhDC . 3 a 2
a. Tı́nh thể tı́ch khối tứ diê ̣n đều ABCD . ` ĐS: V = . ABCD (đvtt) 12 3 a 2
b. Tı́nh khoảng cách từ M đến mp (ABC ) . Suy ra thể tı́ch hı̀nh chópM.ABC . ĐS: V = M .ABC 24
Bài 5. Cho khối chóp tam giác đều S.ABC biết ca ̣nh đáy bằng a , ca ̣nh bên bằng 2a . 3 a 11
a. Tı́nh thể tı́ch khối chóp S.ABC . ĐS: V = . S .ABC (đvtt) 2 1
b. Trên cạnh AC lấy điểm E sao cho: AE =
AC . Tı́nh khoảng cách từ E đến mp(SBC ). 3
Bài 6. Cho khối chóp tam giác đều S.ABC biết ca ̣nh đáy bằng a , mă ̣t bên hợp với đáy mô ̣t góc 0 60 . Trên cạnh SB SE 1 SF 2
lấy điểm E sao cho:
= , trên cạnh SC lấy điểm F sao cho: = . SB 3 SC 3 3 a 3
a. Tı́nh thể tı́ch khối chóp S.ABC . ĐS: V = . S .ABC (đvtt) 24
b. Tı́nh thể tı́ch khối chóp S.AEF .
Bài 7. Cho hı̀nh chóp tứ giác đều S.ABCD có ca ̣nh đáy bằng a , góc giữa mă ̣t bên và mă ̣t đáy bằng 0 60 .
a. Tı́nh thể tı́ch của khối chóp S.ABCD theo a .
b. Gọi O là tâm của đáy ABCD . Tı́nh thể tı́ch của khối tứ diện SOAB .
c. Tı́nh khoảng cách từ điểm A đến mp (SBC ). Bài 8. Cho hı 0
̀nh chóp tứ giác đều S.ABCD có ca ̣nh đáy bằng a và BSA = 60 . 2 a 3
a. Tı́nh diện tích xung quanh của hı̀nh chóp đều này. ĐS: S = (đvdt). 3 3 a 2
b. Tı́nh thể tı́ch của khối chóp S.ABCD . ĐS: V = . S .ABCD (đvtt) 6
Bài 9. Cho hı̀nh chóp tứ giác đều S.ABCD có ca ̣nh đáy bằng a và ca ̣nh bên hợp với đáy mô ̣t góc 0 60 .
a. Tı́nh diện tích toàn phần của hı̀nh chóp đều này. ĐS: 2 S = a ( 10 + ) 1 . tp (đvdt) 3 a 6
b. Tı́nh thể tı́ch của khối chóp S.ABCD . ĐS: V = . S .ABCD (đvtt) 6
Nguyễn Văn Thân Trang 14
Chuyên đề Thể tích khối đa diện
CHỦ ĐỀ 2: THỂ TÍCH CỦA KHỐI LĂNG TRỤ
DẠNG 1: LĂNG TRỤ ĐỨNG HÌNH LĂNG TRỤ
HÌNH LĂNG TRỤ ĐỨNG
+ 2 mặt đáy là đa giác song song và bằng nhau.
+ 2 mặt đáy là đa giác song song và bằng nhau.
+ các cạnh bên song song và bằng nhau
+ các cạnh bên song song và bằng nhau
+ các mặt bên là hình bình hành
+ các mặt bên là hình bình chữ nhật và vuông góc với 2 mặt đáy
+ Chiều cao là khoảng cách của 2 mặt đáy + Chiều cao là cạnh bên
Hình hộp: là hình lăng trụ có 2 đáy là hình bình hành
Hình hộp chữ nhật : là hình lăng trụ đứng có 2 đáy là hình chữ nhật
Hình lập phương: là hình lăng trụ đứng có 6 mặt là hình vuông.
Chú ý: + Hình lăng trụ tam giác đều là hình lăng trụ đứng có 2 đáy là tam giác đều.
+ Hình lăng trụ có đáy tam giác đều là hình lăng trụ xiên có 2 đáy là tam giác đều.
+ Hình lăng trụ tứ giác đều là hình lăng trụ đứng có 2 đáy là hình vuông.
Bài 1. Cho hı̀nh lăng trụ đứng ABC.A'B 'C ' có đáy ABC là tam giác đều. Biết ca ̣nh bên AA' = a . Tı́nh thể tich khối
lăng tru ̣ trong các trường hợp sau:
a. mp (A'BC )hợp với đáy mă ̣t phẳng chứa đáyABC mô ̣t góc 0 60 . ĐS: 3 V = a 3
ABC .A' B 'C ' (đvtt) 3 a 3
b. Đường thẳngA'B hợp vớimp (ABC ) mô ̣t góc 0 45 . ĐS: V =
ABC .A' B 'C ' (đvtt) 4
c. Chiều cao kẻ từA' của A
D ' BC bằng đô ̣ dài ca ̣nh đáy của lăng trụ. ĐS: 3 V = a 3
ABC .A' B 'C ' (đvtt)
Bài 2. Cho hình lăng trụ đứng ABC.A' B 'C ' có đáy ABC là tam giác vuông tại 0 ,
A AC = a,ACB = 60 . Đường
chéo BC ' của mặt bên (BC 'C 'C ) tạo với mặt phẳng mp (AA'C 'C ) một góc 0 30 .
a. Tính thể tích của khối lăng trụ theo a . ĐS: 3 V = a 6 .
ABC .A' B 'C ' (đvtt)
b. Tính diện tích xung quanh hình lăng trụ. ĐS: S = ( + ) 2 2 2 3 3 a xq (đvdt)
Bài 3. Cho hình lăng trụ đứng ABC.A ' B 'C ' có đáy ABC là tam giác vuông tại ,
B BC = a , mp (A'BC ) tạo với đáy một góc 0 30 và A
D ' BC có diện tích bằng 2 a 3 . 3 3a 3
a. Tính thể tích khối lăng trụ ABC.A' B 'C ' . ĐS: V =
ABC .A' B 'C ' (đvtt) 2
b. Tính diện tích toàn phần hình lăng trụ. ĐS: S = ( + + ) 2 3 4 3 30 a tp (đvdt)
Bài 4. Cho hı̀nh lăng trụ tam giác đều ABC.A'B 'C ' có ca ̣nh đáy bằng a . Biết khoảng cách giữa hai đường thẳng a 15
AB và A'C bằng . 5
Nguyễn Văn Thân Trang 15
Chuyên đề Thể tích khối đa diện 3 3a
a. Tı́nh thể tı́ch khối lăng trụ ABC.A'B 'C ' . ĐS: V = .
ABC .A' B 'C ' (đvtt) 4
b. Tı́nh thể tı́ch khối đa diện A'BCB 'C ' .
c. Tı́nh khoảng cách từ A đến mp (A'BC ).
Bài 5. Cho lăng tru ̣ đứng ABC.A' B 'C ' có đáy ABC là tam giác đều ca ̣nh a . Biết rằng AB ' hợp với mă ̣t bên
(BCC 'B ') một góc 0 30 .
a. Tı́nh đô ̣ dài đoa ̣n thẳng AB ' .
ĐS: AB ' = a 3 (đvđd). 3 a 3
b. Tı́nh thể tı́ch khối lăng trụ ABC.A'B 'C ' . ĐS: V = .
ABC .A' B 'C ' (đvtt) 2
c. Tı́nh khoảng cách từ C đến mp (AB 'C ').
Bài 6. Cho lăng tru ̣ đứng ABC.A' B 'C ' có đáy ABC là tam giác vuông ta ̣iA . Biết 0
AB = a;ACB = 60 và đường
thẳng BC ' hợp với mă ̣t bên (AA'C 'C ) mô ̣t góc 0 30 .
a. Thể tı́ch khối lăng trụ ABC.A'B 'C ' ĐS: 3 V = a 6
ABC .A' B 'C ' (đvtt) 2 3a 3
b. Tı́nh diê ̣n tı́ch tam giácABC ' . ĐS: S = . AB D C ' (đvdt) 2
Bài 7. Cho hı̀nh lăng trụ đứngABC.A'B 'C ' có đáyABC là tam giác vuông ta ̣i ,
B AB = a,AA' = 2a , A'C = 3a .
Go ̣i M là trung điểm đoa ̣n thẳngA'C ' vàI là giao điểm củaAM vàA'C . 3 4a
a. Tı́nh thể tı́ch của khối tứ diê ̣n IABC . ĐS: V = IABC (đvtt) 9 2a 5
b. Tı́nh khoảng cách từ A đến mp (IBC ) theo a . ĐS: d = (đvđd) ( A (,IBC ) 5
Bài 8. Cho hı̀nh lăng trụ đứng ABC.A'B 'C ' có đáy ABC là tam giác vuông cân ta ̣i B ;AC = 2a . Biết rằng
mp (A'BC ) hợp với mp(ABC ) một góc 0 45 .
a. Tı́nh thể tı́ch khối lăng trụ ABC.A'B 'C ' . ĐS: 3 V = a 2 .
ABC .A' B 'C ' (đvtt)
b. Tính diện tích toàn phần hình lăng trụ.
Bài 9. Cho lăng tru ̣ đứng ABC.A' B 'C ' có đáy ABC là tam giác vuông ta ̣i A , góc 0
ACB = 30 , AA' = 3a , AC = 2a .
a. Tı́nh thể tı́ch khối lăng trụ ABC.A'B 'C ' .
b. Tı́nh thể tı́ch khối chóp A'BCC 'B ' .
c. Mă ̣t phẳng (A'BC ) chia khối lăng trụ ABC.A'B 'C ' thành hai khối đa diê ̣n. Tı́nh thể tı́ch của mỗi khối đa diê ̣n.
Bài 10. Cho lăng tru ̣ đứng có đáy là tam giác đều, biết rằng tất cả các ca ̣nh của lăng tru ̣ bằng a . 3 a 3
a. Tı́nh thể tı́ch và tổng diê ̣n tı́ch các mă ̣t bên của lăng trụ. ĐS: 2 V = ;S = 3a . 4 xq
b. Tı́nh thể tı́ch khối tứ diện ABCB ' .
DẠNG 2: HÌNH LĂNG TRỤ XIÊN
Bài 1. Cho hı̀nh lăng tru ̣ tam giác ABC.A'B 'C ' có đáy ABC là tam giác đều với tâm O . Cạnh bên CC ' = a và hợp
với mă ̣t phẳng chứa đáy ABC mô ̣t góc 0
60 . Hı̀nh chiếu của điểm C ' lên mp (ABC ) trùng với O . 2 a 3
a. Chứng minh rằng: AA'B 'B là hı̀nh chữ nhâ ̣t. Tı́nh diê ̣n tı́ch hı̀nh chữ nhâ ̣t này. ĐS: S = . 2
b. Chứng minh hình chóp O.A' B 'C ' là hình chóp tam giác đều. 3 3a 3
c. Tı́nh thể tı́ch khối lăng trụ ABC.A'B 'C ' này. ĐS: V = . 8
Nguyễn Văn Thân Trang 16
Chuyên đề Thể tích khối đa diện
Bài 2. Cho hình lăng trụ ABC.A' B 'C ' có đáy ABC là tam giác đều cạnh bằnga . Điểm H là hình chiếu vuông góc
của A' xuống mp (ABC ) là trung điểm của AB . Mặt bên (AA'C 'C ) tạo với đáy một góc bằng 45 . 3 3a
a. Tính thể tích của khối lăng trụ này. ĐS: V =
ABC .A' B 'C ' (đvtt) 16 a 3
b. Tính khoảng cách từ điểm C ' đến mp AHA' . ĐS: d = é ù (đvđd) C ê (',AHA') ë úû 2
Bài 3. Cho hı̀nh lăng trụ tam giác ABC.A'B 'C ' có đáy ABC là tam giác đều ca ̣nh a . Biết ca ̣nh bên bằng a 3 và nó
hợp với mă ̣t phẳng chứa đáy ABC mô ̣t góc 0 60 . 3 3a 3
a. Tı́nh thể tı́ch khối lăng trụ ABC.A'B 'C ' . ĐS: V = .
ABC .A' B 'C ' (đvtt) 8 a 15
b. Tính khoảng cách từ điểm A đến mp A' BC . ĐS: d = é ù (đvđd) A ê ( , A' BC ) ë úû 5
Bài 4. Cho hı̀nh lăng trụ tam giác ABC.A'B 'C ' có đáy ABC là tam giác đều ca ̣nh a . Hı̀nh chiếu của điểm A' trên
mp (ABC ) trùng với trọng tâm G của AB D
C . Biết cạnh bên AA' = a 2 .
a. Tı́nh thể tı́ch khối lăng trụ ABC.A'B 'C ' .
b. Tı́nh thể tı́ch khối chóp G.A'B 'C ' .
Bài 5. Cho hı̀nh lăng trụ tam giác ABC.A'B 'C ' có đáy ABC là tam giác đều ca ̣nh a . Hı̀nh chiếu của điểm A' xuống
mp (ABC )trùng với tâm O của đường tròn ngoa ̣i tiếp AB D
C và biết rằng đường thẳng AA' ta ̣o với mă ̣t phẳng chứa
đáyABC mô ̣t góc 0
45 .Tı́nh thể tı́ch khối lăng trụ ABC.A'B 'C ' đã cho.
CHỦ ĐỀ 3: MỘT SỐ BÀI TẬP TRẮC NGHIỆM
Câu 1. Tính thể tích V của khối lập phương ABCD.A’B’C’D’, biết AB 2a . 2 2 A. 3
V 2 2a B. 3
V 2a C. 3
V 2a D. 3 V a 3
Câu 2. Tính thể tích V của khối lập phương ABCD.A’B’C’D’, biết BB ' 2m . 8 A. 3
V 8m B. 3
V 2m C. 3 V m D. 3
V 6m 3
Câu 3. Hỏi khi các cạnh của khối lập phương tăng lên 5 lần, thì lúc đó thể tích của khối lập phương sẽ tăng lên bao nhiêu lần? A. 125 lần. B. 15 lần. C. 25 lần. D. 5 lần.
Câu 4. Trong không gian, cho tam giác ABC vuông tại A, AB a 2 và AC = a 5 .Tính độ dài đường sinh l của hình
nón, nhận được khi quay tam giác ABC xung quanh trục AB.
A. l 7a
B. l 10a C. l 3a
D. l 7a
Câu 5. Trong không gian, cho tam giác ABC vuông tại B, AB a 2 và BC = a 6 .Tính độ dài đường sinh l của hình
nón, nhận được khi quay tam giác ABC xung quanh trục AB.
A. l 2a
B. l 2 2a C. l 4a
D. l 3a
Câu 6. Trong không gian, cho hình chữ nhật ABCD có AB 1m và AD 2m. Gọi M, N lần lượt là trung điểm của AD
và BC. Quay hình chữ nhật đó xung quanh trục MN, ta được một hình trụ. Tính diện tích toàn phần Stp của hình trụ đó. A. Stp 2 2 m . B. Stp 2 m . C. Stp 6 2 m . D. Stp 10 2 m .
Câu 7. Trong không gian, cho khối hộp chữ nhật ABCD.A’B’C’D’ có số đo các cạnh là AB 1m, AD 2m và AA’=3m.
Tính thể tích V của khối hộp chữ nhật ABCD.A’B’C’D’. A. 3
V 6m B. 3
V 2m C. 3 V m D. 3
V 12m
Nguyễn Văn Thân Trang 17
Chuyên đề Thể tích khối đa diện
Câu 8. Cho khối chóp S.ABCD có SA (ABCD), SC 2a và ABCD là hình vuông cạnh a . Tính bán kính R của mặt
cầu ngoại tiếp khối chóp S.ABCD. 2
A. R a
B. R 2a C. R 2a D. R a 2
Câu 9. Trong không gian, cho hình hộp chữ nhật ABCD.A’B’C’D’ có số đo các cạnh là AB 1m, AD 2m và AA’=3m.
Tính diện tích toàn phần Stp hình hộp chữ nhật ABCD.A’B’C’D’. A. Stp 22 2 m . B. Stp 6 2 m . C. Stp 2 2 m . D. Stp 11 2 m .
Câu 10. Tính diện tích toàn phần S
tp hình lập phương ABCD.A’B’C’D’, biết AB 2a . A. 3 S 12a B. 3 S 64a C. 3 S 2a D. 3 S 8a tp tp tp tp
Câu 11. Tính diện tích toàn phần S
tp hình lập phương ABCD.A’B’C’D’, biết AA ' 2m . A. 3 S 24m B. 3 S 64m C. 3 S 12m D. 3 S 8m tp tp tp tp
Câu 12. Cho khối chóp S.ABCD có SA (ABCD), SC 2a và ABCD là hình vuông cạnh a . Tính thể tích V của khối
cầu ngoại tiếp hình chóp S.ABCD. 4 4 A. 3 V a B. 3
V a C. 3 V 4 a D. 3 V 4a 3 3
Câu 13. Cho khối chóp S.ABCD có SA (ABCD), SA 2a và ABCD là hình vuông cạnh a . Tính bán kính R của mặt
cầu ngoại tiếp khối chóp S.ABCD. 2
A. R 2a
B. R a C. R 2a D. R a 2
Câu 14. Tính thể tích V của khối lập phương ABCD.A’B’C’D’, biết AC 2a . 2 2 A. 3
V 2a B. 3
V 2 2a C. 3
V 2a D. 3 V a 3
Câu 15. Tính thể tích V của khối lập phương ABCD.A’B’C’D’, biết BC ' 2 2m . 8 2 A. 3
V 2 2m B. 3
V 8m C. 3 V m D. 3
V 6 2m 3
Câu 16. Hỏi khi thể tích của khối lập phương tăng lên 8 lần, thì lúc đó các cạnh của khối lập phương sẽ tăng lên bao nhiêu lần? A. 8 lần. B.2 lần. C. 4 lần. D. 24 lần.
Câu 17. Trong không gian, cho tam giác ABC vuông tại A, AC a 2 và AB = a 5 .Tính thể tích V của khối nón nhận
được khi quay tam giác ABC xung quanh trục AB. 2 5 2 5 10 A. 3 V a B. 3 V a C. 3
V 2 5 a D. 3 V a 3 3 3
Câu 18. Trong không gian, cho tam giác ABC vuông tại B, AB 3m và BC = 2m . Tính thể tích V của khối nón nhận
được khi quay tam giác ABC xung quanh trục AB. A. 3
V 12m B. 3
V 12 m C. 3
V 6m D. 3
V 2 m
Câu 19. Trong không gian, cho hình chữ nhật ABCD có AB 1m và AC 3 m. Gọi M, N lần lượt là trung điểm của
AD và BC. Quay hình chữ nhật đó xung quanh trục MN, ta được một hình trụ. Tính diện tích toàn phần Stp của hình trụ đó. 3 A. S 2 tp 2 2 m . B. Stp 3 2 m . C. Stp 2 3 2 m . D. Stp m . 3
Câu 20. Trong không gian, cho khối hộp chữ nhật ABCD.A’B’C’D’ có số đo các cạnh là AB 1m, AA’=3m và có độ dài
đường chéo AC 3 m. Tính thể tích V của khối hộp chữ nhật ABCD.A’B’C’D’.
Nguyễn Văn Thân Trang 18
Chuyên đề Thể tích khối đa diện A. 3
V 2m B. 3
V 6m C. 3 V m D. 3
V 12m
Câu 21. Cho khối chóp S.ABCD có SA (ABCD), SA 2a và ABCD là hình vuông cạnh a . Tính bán kính R của mặt
cầu ngoại tiếp khối chóp S.ABCD.. 2
A. R 2a
B. R a C. R 2a D. R a 2
Câu 22. Cho khối chóp tứ giác đều S.ABCD có ABCD là hình vuông cạnh 2a . Góc giữa đường thẳng SA và mặt phẳng
(ABCD) bằng 600. Tính bán kính R của mặt cầu ngoại tiếp khối chóp S.ABCD. 2 3 3
A. R 2a
B. R a C. R a D. R a 3 2
Câu 23. Cho hình chóp tứ giác đều S.ABCD có ABCD là hình vuông cạnh 2a . Góc giữa đường thẳng SA và mặt phẳng
(SBD) bằng 300. Tính bán kính R của mặt cầu ngoại tiếp khối chóp S.ABCD. 6 2 3 3
A. R 2a B. R
a C. R a D. R a 3 3 2
Câu 24. Cho khối chóp tứ giác đều S.ABCD có ABCD là hình vuông cạnh 2a . Góc giữa đường thẳng SA và mặt phẳng
(ABCD) bằng 600. Tính thể tích V của khối cầu ngoại tiếp hình chóp S.ABCD. 8 3 2 3 32 3 2 3 A. 3 V a B. 3 V a C. 3 V a D. 3 V a 9 9 27 9
Câu 25. Trong không gian, cho hình hộp chữ nhật ABCD.A’B’C’D’ có số đo các cạnh là AB 1m, AC 5 m và
AA’=3m. Tính thể tích V của khối chóp D.A’B’C’D’. A. 3
V 3 5m B. 3
V 6m C. 3
V 2m D. 3
V 5m
Câu 26. Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh 1m, cạnh bên SA vuông góc với mặt phẳng
đáy và góc giữa đường thẳng SB và mặt phẳng (ABCD) bằng 600. Tính diện tích toàn phần Stp của mặt cầu ngoại tiếp hình chóp S.ABCD. A. Stp 5 2 m . B. Stp 3 2 m . C. Stp 5 2 m . D. Stp 1 2 m .
Câu 27. Cho hình chóp S.ABC có ABC là tam giác vuông cân tại B, cạnh AB = 6a. có SA (ABC), SB 10a . Tính diện
tích toàn phần Stp của mặt cầu ngoại tiếp hình chóp S.ABC. A. Stp 544 a2 B. Stp 60 a2
C. Stp 136 a2 D. Stp 30a2
Câu 28. Cho hình chóp S.ABC có ABC là tam giác đều cạnh 2a. Hình chiếu vuông góc của S trên (ABC) là điểm H thuộc
cạnh BC sao cho HC = HB. Góc giữa đường thẳng SA và mặt phẳng (ABC) bằng 600. Tính diện tích toàn phần Stp của khối
nón nhận được khi quay tam giác SHA xung quanh trục SH.
A. Stp 6 a2 B. Stp 9a2 C. Stp a2 D. Stp 9a2
Câu 29. Trong không gian, cho hình hộp chữ nhật ABCD.A’B’C’D’ có số đo các cạnh là AB 1m, AC 5 m và Góc
giữa mặt (A’BC) và mặt phẳng (ABCD) bằng 600. Tính thể tích V của khối chóp D.A’B’C’D’. 5 3 A. 3 V m B. 3
V 2 5m C. 3
V 2 3m D. 3 V m 3 3
Câu 30. Cho hình chóp S.ABC có ABC là tam giác đều cạnh 2m. Hình chiếu vuông góc của S trên (ABC) là điểm H thuộc
cạnh BC sao cho HC = HB. Góc giữa đường thẳng SA và mặt phẳng (ABC) bằng 600. Tính thể tích V của khối nón nhận
được khi quay tam giác SHB xung quanh trục SH. 3 A. 3
V 3m B. 3 V m C. 3
V 3m D. 3 V m 3
Nguyễn Văn Thân Trang 19




