Chuyên đề thể tích khối lăng trụ – Trần Đình Cư Toán 12

Tài liệu gồm 34 trang với các dạng toán về thể tích khối lăng trụ: lăng trụ đứng, lăng trụ đều, lăng trụ xiên, các bài tập có đáp án và lời giải chi tiết.Mời các bạn đón xem.

80 40 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Khối đa diện

Môn: Toán 12

Thông tin:

34 trang 8 tháng trước

Tác giả:

Profile Lan Tường
Chuyên đề: Hình học không gian Chủ đề 3: Thể tích khối lăng trụ
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 1
Chuyên đề: Hình học không gian Chủ đề 3: Thể tích khối lăng trụ
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 2
MỤC LỤC
CHỦ ĐỀ 3. THỂ TÍCH KHỐI LĂNG TRỤ ......................................................................... 3
DẠNG 1. KHỐI LĂNG TRỤ ĐỨNG ................................................................................ 4
DẠNG 2. KHỐI LĂNG TRỤ ĐỀU .................................................................................. 18
DẠNG 3. KHỐI LĂNG TRỤ XIÊNG .............................................................................. 23
Chuyên đề: Hình học không gian Chủ đề 3: Thể tích khối lăng trụ
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 3
CHỦ ĐỀ 3. THỂ TÍCH KHỐI LĂNG TRỤ
1. Định nghĩa: Cho hai mặt song song
()
và
( ')
. Trên
()
ta lấy đa giác lồi
1 2 n
A A ...A
,
qua các đỉnh này ta dựng các đường thẳng song song cắt
( ')
tại
' ' '
1 2 n
A ,A ,...,A
.
Hình bao gồm hai đa giác
1 2 n 1 2 n
A A ...A ,A' A' ...A'
và các hình bình hành
''
1 2 2 1
A A A A ,...
Được gọi là hình lăng trụ. Kí hiệu là:
1 2 n 1 2 n
A A ...A .A' A' ...A'
.
Nhận xét:
Các mặt bên của hình lăng trụ bằng nhau và song song với nhau
Các mặt bên là các hình bình hành
Hai đáy hình lăng trụ là hai đa giác bằng nhau
2. Hình lăng trụ đứng - hình lăng trụ đều, hình hộp chữ nhật và hình lập phương
a) Hình lăng trụ đứng: là hình lăng trụ có cạnh bên vuông góc với đáy. Độ dài cạnh
bên được gọi là chiều cao của hình lăng trụ. Lúc đó các mặt bên của hình lăng trụ
đứng là các hình chữ nhật
b) Hình lăng trụ đều: là hình lăng trụ đứng có đáy là đa giác đều. Các mặt bên của
lăng trụ đều là các hình chữ nhật bằng nhau. Ví dụ: hình lăng trụ tam giác đều, tứ
giác đều... thì ta hiểu là hình lăng trụ đều
c) Hình hộp : Là hình lăng trụ có đáy là hình bình hành
d) Hình hộp đứng: là hình lăng trụ đứng có đáy là hình bình hành
e) Hình hộp chữ nhật: là hình hộp đứng có đáy là hình chữ nhật
f) Hình lăng trụ đứng có đáy là hình vuông và các mặt bên đều là hình vuông được
gọi là hình lập phương (hay hình chữ nhật có ba kích thước bằng nhau được gọi là
hình lập phương)
Nhận xét:
Hình hộp chữ nhật
hình lăng trụ đứng (Có tất cả các mặt là hình chữ nhật
Hình lập phương
hình lăng trụ đều (tất cả các cạnh bằng nhau)
Hình hộp đứng
hình lăng trụ đứng (mặt bên là hình chữ nhật, mặt đáy là
hình bình hành)
3. Thể tích khối lăng trụ:
V B.h
: Với B là diện tích đáy và h là chiều cao
'
A'
3
A'
4
A'
2
A'
5
A
1
A
5
A
4
A
3
A
2
A'
1
Chuyên đề: Hình học không gian Chủ đề 3: Thể tích khối lăng trụ
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 4
4. So sánh khối lăng trụ đứng và khối lăng trụ đều:
ĐỊNH NGHĨA:
TÍNH CHẤT
Hình lăng trụ đứng là
hình lăng trụ có cạnh bên
vuông góc với mặt đáy
Các mặt bên hình lăng trụ
đứng là hình chữ nhật
Các mặt bên hình lăng trụ
đứng vuông góc với mặt
đáy
Chiều cao là cạnh bên
Hình lăng trụ đều là hình
lăng trụ đứng có đáy là đa
giác đều
Các mặt bên của hình lăng
trụ đều là các hình chữ
nhật bằng nhau
Chiều cao là cạnh bên
DẠNG 1. KHỐI LĂNG TRỤ ĐỨNG
Câu 1. Cho hình lăng trụ đứng
ABC.A’B’C’
có thể tích là
V. Trong các khối chóp dưới đây, khối chóp có thể tích
2V
3
là:
A.
A.A'B'C'
B.
C'.ABC
C.
A'.BCC'B'
D.
I.ABB'A'
Hướng dẫn giải
Ta có:
ABC.A'B'C' A'.BCC'B' A'.ABC
V V V
.
Mà
A'.ABC ABC.A'B'C' A'.BCC'B' ABC.A'B'C'
1 2 2
V V V V V
3 3 3
.
Vậy chọn đáp án C.
Câu 2. Cho hình hộp đứng có các cạnh
AB 3a;AD 2a;AA' 2a
như hình vẽ. Thể tích của khối
A’.ACD’
là:
A.
3
a
B.
3
2a
C.
3
3a
D.
3
6a
Hướng dẫn giải
Ta có:
3
A’.ACD’ C.ADD'A' ABCD.A'B'C'D'
1 1 1 1
V V . .V .3a.2a.2a 2a .
2 2 3 6
Vậy chọn đáp án B.
I
B'
C'
A'
C
B
A
A'
D'
C'
B'
D
C
B
A
Chuyên đề: Hình học không gian Chủ đề 3: Thể tích khối lăng trụ
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 5
Câu 3. Cho hình lăng trụ đứng ABC.A’B’C’ có
0
AC 3a,BC a,ACB 150
, đường thẳng
B'C
tạo với mặt phẳng
ABB'A'
một góc
thỏa mãn
1
sin
4

. Thể tích khối lăng trụ
ABC.A’B’C’ là:
A.
3
a 105
28
B.
3
a 105
14
C.
3
a 339
14
D.
3
a 339
28
Hướng dẫn giải
Ta có
ABC
2
0
1
S AC.BC.sinACB
2
1 3a
a 3.a.sin150
24

Kẻ
CH AB
CH ABB'A'
nên B’H là hình chiếu vuông góc
của B’C lên
ABB'A'
B'C, ABB'A' B'C,B'H CB'H
2 2 2 0 2
AB AC BC 2AC.BC.cos150 7a AB a 7
ABC
2.S
a 21
CH
AB 14

CH 2a 21
B'C
sin 7
Xét
BB'C
vuông tại B có:
22
a 35
BB' B'C BC
7
.
Do đó
23
ABC
3a a 35 a 105
V S .AA' .
4 7 28
Chọn đáp án A
Câu 4. Khối lập phương có độ dài đường chéo bằng d thì thể tích của khối lập phương là:
A.
3
Vd
;
B.
3
3d
;
C.
3
3d
;
D.
3
d3
V
9
Hướng dẫn giải
Khối lập phương có cạnh là
d
a.
3
Do đó khối lập phương có thể tích là
3
3
d d 3
V.
9
3




Vậy chọn đáp án D.
Câu 5. Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác cân,
AB AC a
,
0
BAC 120
.
Mặt phẳng
AB'C'
tạo với mặt đáy góc
0
60
. Tính thể tích lăng trụ ABC.A’B’C’.
A.
3
8
a;
3
B.
3
3
a;
8
C.
3
a
;
8
D.
3
3
a;
8
A
B
C
A'
C'
B'
H
Chuyên đề: Hình học không gian Chủ đề 3: Thể tích khối lăng trụ
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 6
Hướng dẫn giải
Xác định góc giữa
AB'C'
và mặt đáy
là
0
AKA' AKA' 60
Tính
0
1a
A'K A'C'
22
a3
AA' A'K.tan60
2

3
ABC.A'B'C' ABC
3a
V AA'.S
8

.
Vậy chọn đáp án B.
Câu 6. Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác cân tại A,
BC a
,
AA' a 2
và
5
cosBA'C
6
. Tính thể tích hình lăng trụ ABC.A’B’C’.
A.
3
a6
4
B.
3
a3
4
C.
3
3a 6
4
D.
3
3a 3
4
Hướng dẫn giải
Đặt
AB x
thì
2 2 2 2
A'B A'C x 2a
Áp dụng định lí hàm số cosin trong
A'BC
, ta có:
2 2 2
2 2 2
22
A'B A'C BC
cosBA'C
2A'B.A'C
2x 4a a 5
xa
6
2 x 2a


Suy ra
ABC
đều nên
2
ABC
a3
S
4
Vậy thể tích hình lăng trụ ABC.A’B’C’ là
3
a6
V
4
Vậy chọn đáp án A.
Câu 7. Cho hình lăng trụ đứng ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a,
0
a 2 2
BAD 45 , AA'
2

. Thể tích của khối lăng trụ ABCD.A’B’C’D’ là
A.
3
a 2 1
22
B.
3
a 2 1
2
C.
3
a 2 1
4
D.
3
a 2 1
2
Hướng dẫn giải
a
3
a
A'
C'
B
A
C
B'
60
0
120
0
a
a
K
A'
C'
B
A
C
B'
Chuyên đề: Hình học không gian Chủ đề 3: Thể tích khối lăng trụ
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 7
Ta có:
ABCD ABD
S 2S
2
ABD
1a
S AB.AD.sinBAD
2
22

Do ABCD.A’B’C’D’ là hình lăng trụ
đứng nên
ABCD.A'B'C'D' ABCD
23
V AA'.S
a 2 2 a a 2 1
.
22
2


Vậy chọn đáp án D.
Câu 8. Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông cân tại B. Biết
AB 3cm, BC' 3 2cm
. Thể tích khối lăng trụ đã cho là
A.
27
3
cm
B.
27
2
3
cm
C.
27
4
3
cm
D.
27
8
3
cm
Hướng dẫn giải
Diện tích đáy của khối lăng trụ:
2
ABC
9
S cm
a
Chiều cao của khối lăng trụ:
22
h CC' BC' BC 3 cm
Thể tích của khối lăng trụ đã cho:
3
ABC
9 27
V S .h .3 cm
22
.
Vậy chọn đáp án C.
Câu 9. Cho hình hộp chữ nhật ABCD.A’B’C’D’ có
AB a, BC b, AA' c
. Gọi M và N
theo thứ tự là trung điểm của A’B’ và B’C’. Tính tỉ số giữa thể tích khối chóp D’.DMN và
thể tích khối hộp chữ nhật ABCD.A’B’C’D’
A.
1
2
B.
1
5
C.
1
8
D.
1
4
Hướng dẫn giải
Thể tích khối chóp D’.DMN bằng thể tích khối chóp D.D’MN
Ta có
D'MN A'B'C'D' D'A'M D'C'N B'MN
S S S S S
a
2-
2
2
45
0
O'
O
B'
C'
D'
C
D
A
B
A'
3
3
3
2
A'
B'
A
C
B
A'
N
M
B'
N
M
B
A
B
C
D
D'
C'
A'
A'
D'
C'
Chuyên đề: Hình học không gian Chủ đề 3: Thể tích khối lăng trụ
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 8
ab ab ab 3ab
ab
4 4 8 8



Thể tích khối chóp D’.DMN là:
1 D'MN
1 1 3ab abc
V S .DD' . .c
3 3 8 8
Thể tích của khối hộp chữ nhật ABCD.A’B’C’D’ là
V abc
1
V
1
V8

. Vậy chọn đáp án C.
Câu 10. Cho hình lăng trụ đứng ABC.A’B’C’, có đáy ABC là tam giác cân tại A,
AB AC a, BAC
. Gọi M là trung điểm của AA’, tam giác C’MB vuông. Thể tích của
khối lăng trụ ABC.A’B’C’ là
A.
3
a sin . cos
B.
3
a cos . sin
C.
3
a cot . sin
D.
3
a tan . cos
Hướng dẫn giải
Diện tích đáy của khối lăng trụ là:
2
1
S a sin
2

Đặt
A'A x
. Ta có:
2
2
x
BM C'M a
4
,
22
BC' BC x
Trong đó
BC 2asin
2
. Tam giác C’MB
vuông tại M, ta có:
2
2
2 2 2 2 2 2 2
x
2 a BC x x 4a 2 2asin x 4a cos x 2a cos
42







Thể tích
của khối lăng trụ là
3
V a sin . cos
.
Vậy chọn đáp án A.
Câu 11. Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác vuông tại B,
AB a, BC 2a, AA' 3a
. Mặt phẳng
qua A vuông góc với CA’ lần lượt cắt các đoạn
thẳng CC’ và BB’ tại M và N. Diện tích tam giác AMN là
A.
2
a 14
6
B.
2
a 14
3
C.
2
a 14
9
D.
2
a 14
7
Hướng dẫn giải
α
M
B'
C'
A
C
B
A'
Chuyên đề: Hình học không gian Chủ đề 3: Thể tích khối lăng trụ
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 9
Gọi
H A'C
Trong tam giác A’AH ta có:
22
2 2 2
A'A 9a
A'H
A'C
a 4a 9a
9a
A'H
14



Ta có:
A'.AMN
AMN
3V
S
A'H
. Mà
NB AA'∥
nên:
3
A'.AMN M.A'AN M.A'AB C.A'AB ABC A'.AMN
1
V V V V AA'.S V a
3
Vì vậy
32
AMN
3a a 14
S
9a
3
14

. Vậy chọn đáp án B.
Câu 12. Cho hình hộp chữ nhật ABCD.A’B’C’D’,
AB a, AD a 3
, khoảng cách từ A đến
mặt phẳng (A’BD) bằng
a
2
. Thể tích khối hộp ABCD.A’B’C’D’ là
A.
3
a2
8
B.
3
3a 2
2
C.
3
3a 2
4
D.
3
3a 2
8
Giải
Gọi K là hình chiếu của A lên BD, H
là hình chiếu của A lên A’K
Vì
BD AK
BD AKA'
BD AA'

BD AH
Mà
AH A'K AH A'BD
a
AH
2

Trong tam giác vuông A’AK ta có:
2 2 2
1 1 1
AH A'A AK

2 2 2
1 1 1
A'A AB AD
Suy ra
2 2 2 2 3
1 4 1 1 8
A'A a a 3a 3a
a6
A'A
4

Vậy
3
ABCD.A'B'C'D'
a 6 3a 2
V A'A.AB.AD .a.a 3
44
.
Vậy chọn đáp án C.
H
B'
C'
A
C
B
A'
M
N
C'
D'
B'
C
A
B
D
A'
K
H
Chuyên đề: Hình học không gian Chủ đề 3: Thể tích khối lăng trụ
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 10
Câu 13. Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại A và
AB a, AC a 3
, mặt phẳng (A’BC) tạo với đáy một góc
0
30
. Thể tích của khối lăng trụ
ABC.A’B’C’ là
A.
3
a3
4
B.
3
2a 3
3
C.
3
3a 2
7
D.
3
3a 2
7
Hướng dẫn giải
Ta có
2
ABC
1 a 3
S AB.AC
22

.
Gọi M là hình chiếu của A trên
BC.
Suy ra
BC A'MA
0
A'MA A'BC , ABC 30
Do
0
a 3 a
AM AA' AMtan30
22
Vậy
23
ABC.A'B'C' ABC
a a 3 a 3
V AA'.S .
2 2 4
.
Vậy chọn đáp án A.
Câu 14. Cho lăng trụ đứng tam giác đều ABC.A’B’C’, có cạnh đáy bằng a, đường chéo BC’
của mặt bên (BCC’B’) tạo với mặt phẳng (ABB’A’) một góc
0
30
. Thể tích khối lăng trụ
ABC.A’B’C’ theo a.
A.
3
a6
3
B.
3
a6
8
C.
3
a6
6
D.
3
a6
4
Hướng dẫn giải
Gọi I’ là trung điểm của A’B’, thì
C'I' A'B'
(do
ABC
đều)
C'I' AA' C'I' ABB'A'
suy
ra
I'BC'
là góc giữa BC’ và mặt
phẳng (ABB’A’)
Suy ra
0
I'BC' 30
. Ta có
a3
C'I'
2
,
0
C'I'
BC' a 3
sin30

Trong
BCC'
vuông:
2 2 2 2
CC' BC' BC 2a CC' a 2
B'
C'
A
C
B
A'
M
a
30
0
I'
B'
C'
A
C
B
A'
Chuyên đề: Hình học không gian Chủ đề 3: Thể tích khối lăng trụ
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 11
Thể tích của khối lăng trụ ABC.A’B’C’ là:
3
ABC
a6
V CC'.S
4

.
Vậy chọn đáp án D.
Câu 15. Đáy của lăng trụ đứng tam giác
ABC.A'B'C'
là tam giác
ABC
vuông cân tại
A
có cạnh
BC a 2
và biết
A'B 3a
. Tính thể tích khối lăng trụ
A.
3
a2
B.
3
a6
8
C.
3
a6
6
D.
3
a6
4
Hướng dẫn giải
Ta có
ABC
vuông cân tại A nên
AB AC a
ABC.A'B'C'
là lăng trụ đứng
AA' AB
Trong
2 2 2 2
AA'B: AA' A'B AB 8a
AA' 2a 2
.
Vậy
ABC
3
AA'.SV a 2
Vậy chọn đáp án A.
Câu 16. Đáy của lăng trụ đứng tam giác
ABC.A'B'C'
là tam giác đều cạnh
a4
và biết
diện tích tam giác
A'BC
bằng 8. Tính thể tích khối lăng trụ.
A.
8
B.
83
3
C.
83
D.
3
Hướng dẫn
Gọi
I
là trung điểm
BC
. Ta có
ABC
đều nên
AB 3
AI 2 3 , AI BC A'I BC
2
A'BC
A'BC
2S
1
S BC.A'I A'I 4
2 BC
AA' (ABC) AA' AI
.
22
A'AI AA' A'I AI 2
Vậy
ABC
AA'.SV 8 3
.
Vậy chọn đáp án C.
Câu 17. Cho lăng trụ đứng tam giác
ABC.A'B'C'
có đáy
ABC
là tam giác vuông cân tại
B
với
BA BC a
,biết
A'B
hợp với đáy
ABC
một góc 60
0
. Tính thể tích lăng trụ.
A.
3
a3
4
B.
3
a3
2
C.
3
2a 3
D.
3
a3
Hướng dẫn giải
3a
a
2
a
a
A'
B'
C'
A
B
C
Chuyên đề: Hình học không gian Chủ đề 3: Thể tích khối lăng trụ
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 12
Ta có
A'A (ABC) A'A AB
và
AB
là hình chiếu của
A'B
trên đáy
ABC
.
Vậy
o
ABA'A'B,(ABC) 60
.
Trong
0
ABA': AA' AB.tan60 a 3
2
ABC
1a
S BA.BC
22

.
Vậy
ABC
3
V AA'.S
a3
2

. Vậy chọn đáp án B.
Câu 18. Cho lăng trụ đứng tam giác
ABC.A'B'C'
có đáy
ABC
là tam giác vuông tại
A
với
AC a
,
0
ACB 60
, biết
BC'
hợp với
AA'C'C
một góc
0
30
. Thể tích lăng trụ là
A.
3
3a 3
B.
3
2a 6
C.
3
a3
D.
3
a6
Hướng dẫn giải
o
a3ABC AB AC.tan60
.
Ta có:
AB AC;AB AA' AB (AA'C'C)
nên
AC'
là hình chiếu của
BC'
trên
AA'C'C
.
0
BC', AA'C'C BC'A 30
o
AB
AC'B AC' 3a
tan30
Trong
22
AA'C': AA' AC' A'C' 2a 2
ABC
là nửa tam giác đều nên
2
ABC
a3
S
2
.
Vậy
3
V a 6
. Vậy chọn đáp án D.
Câu 19. Cho lăng trụ đứng tam giác
ABC.A'B'C'
có đáy
ABC
là tam giác vuông cân tại
B
với
BA BC a
,biết
A'BC
hợp với đáy
ABC
một góc 60
0
.Tính thể tích lăng trụ.
A.
3
3a 3
2
B.
3
a3
2
C.
3
a3
3
D.
3
a
3
Hướng dẫn
Chuyên đề: Hình học không gian Chủ đề 3: Thể tích khối lăng trụ
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 13
Ta có
A'A (ABC)&BC AB BC A'B
o
(A'BC),(ABC) ABA' 60
0
ABA' AA' AB.tan60 a 3
2
ABC
1a
S BA.BC
22

. Vậy
3
a3
V
2
Vậy chọn đáp án B.
Câu 20. Đáy của lăng trụ đứng tam giác
ABC.A'B'C'
là tam giác đều cạnh
x
. Mặt
A'BC
tạo với đáy một góc 30
0
và diện tích tam giác
A'BC
bằng 8. Tính thể tích khối
lăng trụ
A.
3
x3
3
B.
3
3x 3
C.
3
x3
D.
3
x
3
Hướng dẫn giải
ABC
đều
AI BC
mà
AA' ABC
nên
A'I BC
.
Vậy
0
A'BC , ABC A'IA 30
Ta có
BC x
. Ta có
0
A'A AItan30 x
. Ta có
3
ABC.A'B'C'
V x 3
.
Mà
A'BC
S BI.A'I x.2x 8 x 2
. Do đó
3
ABC.A'B'C'
V x . 3
Vậy chọn đáp án C.
Câu 21. Cho lăng trụ đứng
ABC.A'B'C'
có đáy ABC là tam giác vuông,
AB BC a
, cạnh
bên
AA' a 2.
Tính theo a thể tích của khối lăng trụ
A.
3
2
a
2
B.
3
2a
C.
3
2a
D.
3
2 2a
Hướng dẫn giải
Ta có
2
ABC
1 1 1
S BA.BC a.a a .
2 2 2
23
ABC.A'B'C' ABC
12
V AA'.S a 2. a a .
22
Vậy chọn đáp án A.
Câu 22. Cho hình hộp đứng có đáy là hình thoi cạnh a và có góc nhọn bằng 60
0
. Đường
chéo lớn của đáy bằng đường chéo nhỏ của lăng trụ.Tính thể tích hình hộp .
3
2
32
x
x
AI
x
xAI
AIIAAIA 2
3
32
3
2
30cos:':'
0
C'
B'
A'
C
B
A
o
60
x
o
30
I
C'
B'
A'
C
B
A
Chuyên đề: Hình học không gian Chủ đề 3: Thể tích khối lăng trụ
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 14
A.
3
3a 6
2
B.
3
a6
3
C.
3
a6
2
D.
3
2a 6
3
Hướng dẫn giải
Ta có tam giác ABD đều nên : BD = a
và SABCD = 2SABD =
2
a3
2
Theo đề bài BD' = AC =
a3
2 a 3
2
22
DD'B DD' BD' BD a 2
Vậy V = SABCD.DD' =
3
a6
2
.
Vậy chọn đáp án C.
Câu 23. Cho lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là hình vuông cạnh a và đường
chéo BD' của lăng trụ hợp với đáy ABCD một góc 30
0
. Tính tổng diên tích của các mặt bên
của lăng trụ .
A.
2
a6
2
B.
3
a6
3
C.
2
a6
4
D.
2
4a 6
3
Hướng dẫn giải
Ta có ABCD A'B'C'D' là lăng trụ đứng nên ta có:
DD' (ABCD) DD' BD
và BD là hình chiếu của BD' trên ABCD .
Vậy góc [BD';(ABCD)] =
0
DBD' 30
0
a6
BDD' DD' BD.tan30
3
S = 4SADD'A' =
2
4a 6
3
. Vậy chọn đáp án D.
Câu 24. Cho hình hộp đứng ABCD A'B'C'D' có đáy ABCD là hình thoi cạnh a và
BAD
=
60
o
biết AB' hợp với đáy (ABCD) một góc 30
o
. Tính thể tích của hình hộp
A.
3
3a
B.
3
a
4
C.
3
3a
2
D.
3
a
Hướng dẫn
ABD
đều cạnh a
2
ABD
a3
S
4

2
ABCD ABD
a3
S 2S
2
ABB'
vuông tại B
a
o
30
o
60
D'
C'
B'
A'
D
C
B
A
Chuyên đề: Hình học không gian Chủ đề 3: Thể tích khối lăng trụ
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 15
2a
o
30
o
60
D'
C'
B'
A'
D
C
B
A
o
BB' ABtan30 a 3
Vậy
3
ABCD
3a
V B.h S .BB'
2
. Vậy chọn đáp án C.
Câu 25. Cho hình hộp chữ nhật ABCD.A'B'C'D' có AA' = 2a ; mặt phẳng (A'BC) hợp với
đáy (ABCD) một góc 60
o
và A'C hợp với đáy (ABCD) một góc 30
o
.Tính thể tích khối hộp
chữ nhật.
A.
3
3
16a 2
B.
3
16a 2
9
C.
3
16a 2
3
D.
3
16a 2
8
Hướng dẫn giải
Ta có AA'
(ABCD)
AC là hình chiếu của A'C trên (ABCD) .
Vậy góc[A'C,(ABCD)] =
o
A'CA 30
BC
AB
BC
A'B (đl 3
) .
Vậy góc[(A'BC),(ABCD)] =
o
A'BA 60
A'AC
AC = AA'.cot30
o
=
2a 3
A'AB
AB = AA'.cot60
o
=
2a 3
3
22
4a 6
ABC BC AC AB
3
.
Vậy
3
V AB.BC.A
16
3
A'
a2

.Vậy chọn đáp án C.
Câu 26. Cho lăng trụ đứng ABC.A
/
B
/
C
/
có đáy ABC là tam giác vuông tại B, AB=a, AC=a
3
, cạnh A
/
B = 2a. Tính thể tích khối lăng trụ
A.
3
3a 6
2
B.
3
a6
4
C.
3
a6
2
D.
3
2a 6
2
Hướng dẫn
* Tam giác ABC vuông tại B
BC =
22
AC AB a 2
2
ABC
1 a 2
S AB.BC
22

* Tam giác A
/
AB vuông tại A
/ / 2 2
A A A B AB a 3
*
3
/
/ / / ABC
ABC.A B C
a6
V S .A A
2

.
Vậy chọn đáp án C.
2 a
a
3
a
B
/
C
/
A
/
A
C
B
Chuyên đề: Hình học không gian Chủ đề 3: Thể tích khối lăng trụ
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 16
Câu 27. Cho lăng trụ đứng ABC.A
/
B
/
C
/
có đáy ABC là tam giác vuông tại B, AB=a,
BC a 2
, mặt bên (A
/
BC) hợp với mặt đáy (ABC) một góc 30
0
. Tính thể tích khối lăng
trụ.
A.
3
a6
9
B.
3
a6
4
C.
3
a6
3
D.
3
a6
6
Hướng dẫn giải
Ta có A
/
A
(ABC)
/
(A BC) (ABC) BC
AB
BC Mà AB =
/
(ABC)
hc A B
nên
A
/
B
BC
/ / 0
(A BC),(ABC) A BA 30




* Tam giác ABC vuông tại B
2
ABC
1 a 2
S AB.BC
22

* Tam giác A
/
AB vuông tại A
/0
a3
A A AB.tan30
3

*
3
/
/ / / ABC
ABC.A B C
a6
V S .A A
6

. Vậy chọn đáp án D.
Câu 28. Cho hình hộp chữ nhật ABCD.A’B’C’D’ có , AD = a, AA’ = a, O là
giao điểm của AC và BD. Tính thể tích khối OBB’C’.
A.
3
a2
9
B.
3
a2
4
C.
3
a2
3
D.
3
a2
12
Hướng dẫn giải
M là trung điểm BC
Vậy chọn đáp án D.
Câu 29. Cho hình lập phương ABCD.A’B’C’D’có cạnh bằng a. Tính thể tích khối tứ diện
ACB’D’.
3AB a
22
ó : 2ABD c DB AB AD a
( ' ')OM BB C
23
' ' ' '
1 1 3 3
. . .
3 3 2 2 12
OBB C BB C
a a a
V S OM
30
0
A
/
C
/
B
/
a
a
2
2a
B
C
A
M
O
D'
C'
B'
A'
D
C
B
A
Chuyên đề: Hình học không gian Chủ đề 3: Thể tích khối lăng trụ
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 17
A.
3
a
2
B.
3
a
6
C.
3
a
3
D.
3
a
4
Hướng dẫn giải
Hình lập phương được chia thành: khối ACB’D’ và bốn
khối CB’D’C’, BB’AC, D’ACD, AB’A’D’.
Các khối CB’D’C’, BB’AC, D’ACD, AB’A’D’ có diện tích
đáy và chiều cao bằng nhau nên có cùng
thể tích.
Khối CB’D’C’ có
Khối lập phương có thể tích:
Vậy chọn đáp án C.
Câu 30. Cho hình lăng trụ đứng tam giác có các cạnh bằng a. E là trung điểm cạnh AC,
mp(A’B’E) cắt BC tại F. Tính thể tích khối CA’B’FE
A.
3
a3
5
B.
3
a3
4
C.
3
a3
16
D.
3
a3
15
Hướng dẫn giải
Khối CA’B’FE: phân ra hai khối
CEFA’ và CFA’B’.
Khối A’CEFcó đáy là CEF, đường
cao A’A nên
Gọi J là trung điểm B’C’.
Ta có khối A’B’CF có đáy là CFB’, đường cao JA’ nên ;
Vậy : . Vậy chọn đáp án C.
23
1
1 1 1
..
3 2 6
V a a a
3
2
Va
3 3 3
''
11
4.
63
ACB D
V a a a
' EF EF
1
.'
3
A C C
V S A A
2
EF
13
4 16
C ABC
a
SS
3
' EF
3
48
AC
a
V
' ' F FB'
1
.'
3
A B C C
V S A J
2
FB' '
1
24
C CBB
a
SS
23
' ' F
1 3 3
3 4 2 24
A B C
a a a
V
3
A'B'FE
3
16
C
a
V
a
D'
C'
B'
A'
D
C
B
A
J
I
F
E
C'
B'
A'
C
B
A
Chuyên đề: Hình học không gian Chủ đề 3: Thể tích khối lăng trụ
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 18
DẠNG 2. KHỐI LĂNG TRỤ ĐỀU
Câu 1. Cho khối lăng trụ tam giác đều ABC.A’B’C’. Mặt phẳng (A’BC) chia khối lăng trụ
thành hai phần. Tỉ số thể tích của hai phần đó bằng:
A.
1
;
2
B.
C.
1
;
4
D.
3
5
Hướng dẫn giải
Mặt phẳng (A’BC) chia khối lăng trụ
ABC.A’B’C’ thành hai phần là
A'.ABC
và
A'B'C'BC
Ta có:
A'.ABC ABC.A'B'C'
A'B'C'BC ABC.A'B'C'
1
VV
3
2
VV
3

Suy ra tỉ số thể tích của hai phần đó
bằng
Vậy chọn đáp án A.
Câu 2. Cho khối lăng trụ tam giác đều ABC.A’B’C’. Gọi M là trung điểm cạnh AA’. Mặt
phẳng (MBC) chia khối lăng trụ thành hai phần. Tỉ số thể tích cua hai phần đó bằng:
A.
1
;
3
B.
C.
1
;
6
D.
3
5
Hướng dẫn giải
Mặt phẳng (MBC) chia khối lăng trụ thành hai
phần
M.ABC
Và
MA'B'C'BC
.
Ta có:
M.ABC ABC ABC.A'B'C
1 1 1
V . h.S V
3 2 6

Suy ra:
MA'B'C'BC ABC.A'B'C'
5
VV
6
Tỉ số thể tích cua hai phần đó bằng:
Vậy ta chọn đáp án B.
Câu 3. Cho hình lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy bằng a và chiều cao bằng
a6
2
. Thể tích khối tứ diện ACA’B’ là
A.
3
a2
8
B.
3
a2
4
C.
3
a
8
D.
3
a2
2
Hướng dẫn giải
M
B
C
A'
B'
C'
A
B
C
A'
B'
C'
A
Chuyên đề: Hình học không gian Chủ đề 3: Thể tích khối lăng trụ
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 19
ACA'B' C.AA'B' AA'B'
1
V V S .d C, AA'B'
3

Ta có
CM AB
(vì tam giác ABC là tam
giác đều)
CM AA'B'B
hay
CM AA'B'
CM d C, AA'B'
ACA'B' AA'B'
3
1 1 1
V S .CM . AA'.A'B'.CM
3 3 2
1 a 6 a 3 a 2
. .a.
6 2 2 8


Vậy chọn đáp án A.
Câu 4. Cho khối lăng trụ tứ giác đều ABCD.A’B’C’D’ có khoảng cách giữa hai đường
thẳng AB và A’D bằng 2 và độ dài đường chéo của mặt bên bằng 5. Vẽ
AK A'D K A'D
. Lúc đó độ dài
AK
là
A. 1
B. 2
C. 3
D. 4
Hướng dẫn giải
AB A'B' AB A'B'D∥∥
d A, A'B'D d AB,A'D
Ta có
A'B' AA'D'D
A'B' AK
Ta còn có
A'D AK
(giả thiết)
AK A'B'D
Vậy
AK d A, A'B'D
d AB,A'D 2
. Vậy chọn đáp án B.
Câu 5. Cho hình lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy bằng a. Mặt phẳng (ABC’)
hợp với mặt phẳng (BCC’B’) một góc
. Diện tích xung quanh của khối lăng trụ là
A.
2
2
3 3a
tan 3
B.
2
2
3a
tan 3
C.
2
2
3 3a
tan 3
D.
2
2
3a
tan 3
Hướng dẫn giải
a
6
2
a
M
B
C
A'
B'
C'
A
C'
D'
B'
C
A
D
A'
B
K
Chuyên đề: Hình học không gian Chủ đề 3: Thể tích khối lăng trụ
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 20
Gọi H, K lần lượt là hình chiếu của A lên
BC, BC’.
Ta có
AH BCC'B' AH BC'
, do đó
AKH BC' AKH
Tam giác AKH vuông tại H và
a3
AH
2
nên
a3
AK
2sin
Đặt
AA' x
. Xét tam giác C’AB có:
22
C'A CB x a
,
AB a
.
Nên từ
a3
AK
2sin
ta tính được
2
a3
x
tan 3

Diện tích xung quanh của khối lăng trụ
2
xq
2
3 3a
S
tan 3

.
Vậy chọn đáp án C.
Câu 6. Cho lăng trụ tứ giác đều
ABCD.A'B'C'D'
có cạnh bên bằng
4a
và đường chéo
.
Tính thể tích khối lăng trụ này
A.
3
8a
B.
3
9a
C.
3
18a
D.
3
21a
Hướng dẫn giải
ABCD.A'B'C'D'
là lăng trụ đứng nên
BD
2
= BD'
2
- DD'
2
= 9a
2
BD 3a
ABCD là hình vuông
3a
AB
2

Suy ra B = SABCD =
2
9a
2
Vậy
3
ABCD
V B.h S .AA' 18a
Vậy chọn đáp án C.
Câu 7. Cho lăng trụ tứ giác đều ABCD.A'B'C'D' có cạnh đáy a và mặt phẳng (BDC') hợp
với đáy (ABCD) một góc 60
o
. Tính thể tích khối hộp chữ nhật.
A.
3
a6
2
B.
3
a6
4
C.
3
a6
3
D.
3
a6
12
Hướng dẫn giải
a
α
H
A'
C'
B
C
A
B'
K
Chuyên đề: Hình học không gian Chủ đề 3: Thể tích khối lăng trụ
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 21
Gọi O là tâm của ABCD . Ta có
ABCD là hình vuông nên
OC BD
CC'
(ABCD) nên OC'
BD (đl 3
).
Vậy góc[(BDC');(ABCD)] =
COC'
= 60
o
Ta có V = B.h = SABCD.CC'
ABCD là hình vuông nên SABCD = a
2
OCC'
vuông nên CC' = OC.tan60
o
=
a6
2
. Vậy V =
3
a6
2
.
Vậy chọn đáp án A.
Câu 8. Cho hình lăng trụ tứ giác đều ABCD.A’B’C’D’ có chiều cao bằng h và góc của hai
đường chéo của hai mặt bên kề nhau phát xuất từ một đỉnh là
. Tính thể tích của lăng trụ
theo h và
là
A.
3
h (1 sin )
sin

B.
3
h (1 sin )
sin

C.
3
h (1 cos )
cos

D.
3
h (1 cos )
cos

Hướng dẫn giải
Gọi x là cạnh của đáy, ta có
B’D’ = x
22
2, AB' AD' h x
2 2 2
22
AB'D':
B'D' AB' AD' 2AB'.AD'.cos
2AB' 2AB' cos
2 2 2 2 2
2 2 2 2 2
2x 2(h x ) 2(h x )cos
x (h x ) (h x )cos
2
2
h (1 cos )
x
cos


.
Vậy V = x
2
.h =
3
h (1 cos )
cos

.Vậy chọn đáp án C.
Câu 9. Tính thể tích lăng trụ đều ABC.A’B’C’ biết (ABC’) hợp với đáy góc 60
0
và diện tích
tam giác ABC
'
bằng
2
3a
A.
3
6
a
4
B.
3
36
a
8
C.
3
36
a
4
D.
3
36
a
2
Hướng dẫn giải
a
0
60
O
A'
D'
B'
C'
C
A
D
B
B'
h
D'
C'
A'
O
B
D
C
A
Chuyên đề: Hình học không gian Chủ đề 3: Thể tích khối lăng trụ
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 22
Gọi H là trung điểm AB
CH AB
C'H AB
(ABC'),(ABC) (CH,C'H)
0
CHC' 60


22
ABC'
3a HC'.AB 2 3a
S
(1)
Xét
HCC'
vuông tại C:
0
HC
HC' AB 3
cos60

(2)
0
32
CC' HC'.sin60 a
2

;
2 0 2
ABC
13
AB sin60 a
22
S

Từ (1),(2)
AB a 2;HC' a 6
3
ABC.A'B'C' ABC
36
.CC' a
4
VS

(đvtt). Vậy chọn đáp án C.
A
H
B
C
C’
B’
A’
Chuyên đề: Hình học không gian Chủ đề 3: Thể tích khối lăng trụ
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 23
DẠNG 3. KHỐI LĂNG TRỤ XIÊNG
Câu 1. Gọi V là thể tích khối hộp ABCD.A’B’C’D’ và
1
V
là thể tích của khối tứ diện có
cùng đáy và chiều cao với khối hộp. Hệ thức nào sau đây là đúng:
A.
1
V 6V
;
B.
1
V 5V
;
C.
1
V 4V
;
D.
1
V 3V
Hướng dẫn giải
Ta có:
B'.BCD BCD
ABCD ABCD.A'B'C'D'
1
V h.S
3
11
h.S V
66

Hay
1
V 6V
.
Vậy chọn đáp án A.
Câu 2. Cho khối lăng trụ tam giác
ABC.A'B'C'
có thể tích V. Trên đáy
A'B'C'
lấy điểm M
bất kỳ. Thể tích khối chóp
M.ABC
tính theo V bằng
A.
V
2
;
B.
2V
3
;
C.
V
3
;
D.
3V
4
Hướng dẫn giải
Ta có:
M.ABC ABC
11
V h.S V
33

.
Vậy ta chọn đáp án C
Câu 3. Cho hình lăng trụ ABC.A’B’C’, đáy ABC có
AC a 3, BC 3a
,
0
ACB 30
. Cạnh
bên hợp với mặt phẳng đáy góc
0
60
và mặt phẳng
A'BC
vuông góc với mặt phẳng
ABC
. Điểm H trên cạnh BC sao cho
HC 3BH
và mặt phẳng
A'AH
vuông góc với
mặt phẳng
ABC
. Thể tích khối lăng trụ ABC.A’B’C’ là
A.
3
3a
4
B.
3
9a
4
C.
3
9a
2
D.
3
3 3a
4
Hướng dẫn giải
D
C
B
B'
A'
D'
A
B
C
A'
B'
C'
A
M
Chuyên đề: Hình học không gian Chủ đề 3: Thể tích khối lăng trụ
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 24
A'BC ABC
A'AH ABC A'H ABC
A'H A'BC A'AH

Suy ra
0
A'AH 60
2 2 2 0 2
0
23
ABC.A'B'C' ABC
AH AC HC 2AC.HC.cos30 a AH a
A'H AH.tan60 a 3
3a 3 9a
V S .A'H .a 3
44
Vậy chọn đáp án B.
Câu 4. Cho hình lăng trụ ABC.A’B’C’,
ABC
đều có cạnh bằng a,
AA' a
và đỉnh A’ cách
đều A, B, C. Gọi M là trung điểm của cạnh BC. Thể tích khối lăng trụ ABC.A’B’C’ là
A.
3
a2
2
B.
3
a2
4
C.
3
a2
8
D.
3
2a
3
Hướng dẫn giải
Gọi O là tâm tam giác đều ABC
A'O ABC
Ta có
a 3 2 a 3
AM , AO AM
2 3 3
2
2 2 2
a a 6
A'O AA' AO a
33
;
2
ABC
a3
S
4
Thể tích khối lăng trụ ABC.A’B’C’:
23
ABC
a 3 a 6 a 2
V S .A'O .
4 3 4
.
Vậy chọn đáp án B.
Câu 5. Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác vuông tại B,
0
AB a, ACB 30
; M là trung điểm cạnh AC. Góc giữa cạnh bên và mặt đáy của lăng trụ
bằng
0
60
. Hình chiếu vuông góc của đỉnh A’ lên mặt phẳng (ABC) là trung điểm H của
BM. Thể tích khối lăng trụ ABC.A’B’C’ là
A.
3
3a 3
4
B.
3
a3
4
C.
3
3a 3
D.
3
a3
Hướng dẫn giải
O
M
B
C
A'
B'
C'
A
C'
B'
B
C
A
A'
H
Chuyên đề: Hình học không gian Chủ đề 3: Thể tích khối lăng trụ
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 25
A'H ABC A'H
là đường cao của
hình lăng trụ.
AH là hình chiếu vuông góc của AA’ lên
(ABC)
0
A'AH 60
ABC.A'B'C' ABC
V A'H.S
AC 2a, MA MB AB a
a 3 3a
AH A'H
22
2 2 3
ABC ABC.A'B'C'
1 1 a 3 3a a 3 3a 3
S BA.BC a.a 3 V .
2 2 2 2 2 4
Vậy chọn đáp án A.
Câu 6. Cho hình lăng trụ ABC.A’B’C’ có
a 10
AB 2a, AC a, AA'
2
,
0
BAC 120
. Hình
chiếu vuông góc của C’ lên mặt phẳng (ABC) là trung điểm của cạnh BC. Tính thể tích
khối lăng trụ ABC.A’B’C’ theo a và tính số đo góc giữa hai mặt phẳng (ABC) và (ACC’A’).
A.
3
a3
4
B.
3
3a
4
C.
3
3a 3
4
D.
3
a3
Hướng dẫn giải
Gọi H là trung điểm BC. Từ giả
thiết suy ra
C'H ABC
. Trong
ABC
ta có:
2
0
ABC
2 2 2 0 2
22
1 a 3
S AB.AC.sin120
22
BC AC AB 2AC.AB.cos120 7a
a7
BC a 7 CH
2
a3
C'H C'C CH
2

Suy ra thể tích lăng trụ
3
ABC
3a
V C'H.S
4

. Vậy chọn đáp án B.
Câu 7. Cho hình lăng trụ ABCD.A’B’C’D’ có đáy ABCD là hình vuông cạnh bằng a. Hình
chiếu vuông góc của điểm A’ trên mặt phẳng ABCD là trung điểm I của cạnh AB. Biết A’C
tạo với mặt phẳng đáy một góc
với
2
tan
5

. Thể tích khối chóp A’.ICD là
A.
3
a
6
B.
3
a3
6
C.
3
a3
3
D.
3
a
3
30
0
60
0
H
M
B
C
A'
B'
C'
A
120
0
a
10
2
a
2a
H
A
B
A'
B'
C'
C
Chuyên đề: Hình học không gian Chủ đề 3: Thể tích khối lăng trụ
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 26
Hướng dẫn giải
heo bài ra ta có IC là hình chiếu
vuông góc của A’C trên mặt
phẳng (ABCD). Suy ra
A'C, ABCD A'C,CI A'CI
Xét ta giác vuông A’IC:
a 5 2
A'I IC.tanA'CI IC.tan . a
2
5
Thể tích khối chóp A’.ICD là:
23
A'.ICD ICD
1 1 a a
V A'I.S a.
3 3 2 6
(đvtt)
Vậy chọn đáp án A.
Câu 8. Cho khối lăng trụ tam giác ABC.A’B’C’ mà mặt bên ABB’A’ có diện tích bằng 4.
Khoảng cách giữa cạnh CC’ và mặt (ABB’A’) bằng 7. Thể tích khối lăng trụ là
A. 10
B. 12
C. 14
D. 16
Hướng dẫn giải
Dựng khối hộp ABCD.A’B’C’D’ ta
có:
ABC.A'B'C' ABCD.A'B'C'D'
1
VV
2
Xem khối hộp ABCD.A’B’C’D’ là
khối lăng trụ có hai đáy là ABB’A’
và DCC’D’.
Vậy
ABCD.A'B'C'D' ABB'A'
V S .h
trong đó
h d CDD'C' , ABB'A' d CC', ABB'A' 7
và
ABB'A'
S4
ABC.A'B'C'
1
V .4.7 14
2
. Vậy chọn đáp án C.
Câu 9. Cho lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, và
7
A'A A'B A'C a
12
. Thể tích khối lăng trụ ABC.A’B’C’ theo a là
A.
3
a
8
B.
3
a3
8
C.
3
3a 3
8
D.
3
a3
4
Hướng dẫn giải
α
I
D
C
B
C'
B'
A'
D'
A
D'
C'
A'
D
B
C
B'
A
Chuyên đề: Hình học không gian Chủ đề 3: Thể tích khối lăng trụ
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 27
Gọi H là hình chiếu của A trên (ABC)
Vì
A'A A'B A'C
nên
HA HB HC
,
suy ra H là tâm của tam giác đều ABC.
Gọi I, J lần lượt là trung điểm của BC,
AB.
22
22
22
7a a a
A'J AA' AJ
12 4
3
1 1 a 3 a 3 a
HJ CJ . A'H A'J HJ
3 3 2 6 2
Thể tích khối lăng trụ ABC.A’B’C’ là:
23
ABC
a a 3 a 3
V A'H.S .
2 4 8
Vậy chọn đáp án B.
Câu 10. Cho lăng trụ ABC.A’B’C’ có đáy ABC là tam giác cân
AB AC a
,
0
BAC 120
và
AB’ vuông góc với đáy (A’B’C’). Mặt phẳng (AA’C’) tạo với mặt phẳng (ABC) một góc
0
30
. Thể tích khối lăng trụ ABC.A’B’C’ là
A.
3
a3
3
B.
3
8a
3
C.
3
a3
8
D.
3
a3
2
Hướng dẫn giải
Ta có
2 2 2 2
BC AB AC 2AB.ACcosA 3a
BC a 3
Gọi K là hình chiếu của B’ lên
A’C’, suy ra
A'C' AB'K
Do đó:
0
AKB' A'B'C' , AA'C' 30
Trong tam giác A’KB’ có
0
KA'B' 60
,
A'B' a
nên
0
a3
B'K A'B'sin60
2

. Suy ra
0
a
AB' B'K.tan30
2

.
Thể tích khối lăng trụ:
3
ABC
a3
V AB'.S
8

.
Vậy chọn đáp án C.
Câu 11. Cho lăng trụ ABC.A’B’C’ có đáy ABC là tam giác cân tại A,
0
AB AC a, BAC 120
, hình chiếu của A’ lên mặt phẳng (ABC) trùng với trọng tâm tam
giác ABC, cạnh bên
AA' 2a
. Thể tích của khối lăng trụ là
120
0
a
a
A
C
A'
B'
C'
B
K
I
H
J
A'
C'
B
C
A
B'
Chuyên đề: Hình học không gian Chủ đề 3: Thể tích khối lăng trụ
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 28
A.
3
3a 3
4
B.
3
3a
4
C.
3
a
4
D.
3
a3
4
Hướng dẫn giải
Gọi H là tâm của đáy, M là trung điểm
của cạnh BC,
SH ABC
0
a3
AM ABsin60 BC a 3
2
Áp dụng định lý sin ta có:
0
22
BC
HA R a,
2sin120
A'H A'A AH a 3
2
0
ABC
1 a 3
S AB.ACsin120
24

. Vậy
3
ABC.A'B'C' ABC
3a
V A'H.S
4

Vậy chọn đáp án B.
Câu 12. Cho hình lăng trụ tam giác ABC.A’B’C’ có
BB' a
, góc giữa đường thẳng BB’ và
mặt phẳng (ABC) bằng
0
60
, tam giác ABC vuông tại C và
0
BAC 60
. Hình chiếu vuông
góc của điểm B’ lên mặt phẳng (ABC) trùng với trọng tâm của tam giác ABC. Thể tích khối
tứ diện A’.ABC là
A.
3
3a
208
B.
3
9a
208
C.
3
a
108
D.
3
9a
108
Hướng dẫn giải
Gọi D là trung điểm AC, G là trọng
tâm tam giác ABC
0
B'G ABC B'BG 60
a3
B'G BB'sinB'BG ;
2
a 3a
BG BD
24
Trong
ABC
ta có:
AB 3
BC
2
,
AB AB
AC CD
24
2 2 2
2 2 2
2
ABC
3AB AB 9a
BC BD BD
4 16 16
3a 13 3a 13 9a 3
AB , AC , S
13 26 104
M
A'
C'
B
C
A
B'
H
60
0
G
D
A'
C'
B
C
A
B'
Chuyên đề: Hình học không gian Chủ đề 3: Thể tích khối lăng trụ
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 29
Thể tích khối tứ diện A’.ABC là:
3
A'.ABC ABC
1 9a
V B'G.S
3 208

.
Vậy chọn đáp án B.
Câu 13. Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác đều cạnh a, cạnh bên bằng
a3
và hình chiếu của A’ lên mặt phẳng (ABC) trùng với trung điểm của BC. Tính thể tích của
khối lăng trụ đó.
A.
3
3a
8
B.
3
a3
8
C.
3
3a 3
8
D.
3
a
8
Hướng dẫn giải
Gọi H là trung điểm của cạnh BC
A'H ABC
Tam giác vuông A’HA:
2
2 2 2
3a 3a
AH A'A AH 3a
42
2
ABC
a3
S
4
nên
23
ABC.A'B'C' ABC
3a a 3 3a 3
V A'H.S .
2 4 8

Vậy chọn đáp án C.
Câu 14. Cho hình lăng trụ ABC.A’B’C’ có độ dài tất cả các cạnh bằng a và hình chiếu của
đỉnh C trên mặt phẳng (ABB’A’) là tâm của hình bình hành ABB’A’. Tính thể tích của khối
lăng trụ.
A.
3
a
4
B.
3
a2
2
C.
3
a2
4
D.
3
a
2
Hướng dẫn giải
Gọi O là tâm hình bình hành ABB’A’. Ta
có
CO ABB'A'
.
Vì
CA CB
nên
OA OB
, suy ra hình
thoi ABB’A’ là hình vuông.
Do đó
AB a
OA
22

. Suy ra:
2
2 2 2
a
OC AC AO
2
a
OC
2

.
Vậy thể tích của khối chóp:
3
C.ABA' ABA'
1 a 2
V CO.S
3 12

H
B'
C'
A
C
B
A'
O
B'
C'
A
C
B
A'
Chuyên đề: Hình học không gian Chủ đề 3: Thể tích khối lăng trụ
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 30
Mà
ABC.A'B'C' C.ABA'
V 3V
nên thể tích của khối lăng trụ ABC.A’B’C’ là:
3
ABC.A'B'C'
a2
V
4
. Vậy chọn đáp án C.
Câu 15. Cho hình hộp ABCD.A’B’C’D’ có các cạnh bằng a,
0
BAD 60
,
0
BAA' 90
,
0
DAA' 120
. Thể tích khối hộp là
A.
3
a
2
B.
3
a
4
C.
3
a2
4
D.
3
a2
2
Hướng dẫn giải
Từ giả thiết ta tính được
BD a
,
A'B a 2
,
A'D a 3
nên tam giác
A’BD vuông tại B.
Vì
AB AD AA'
nên hình chiếu
vuông góc của A lên mặt phẳng
(A’BD) trung với tâm H của đường
tròn ngoại tiếp tam giác A’BD (do tam
giác đó vuông nên H là trung điểm
của A’D)
Ta có
0
a
AH AA'cos60
2

,
2
A'BD
1 a 2
S BA'.BD
22

,
Do đó thể tích khối tứ diện A’.ABD là
3
A'.ABD
a2
V
12
.
Ta đã biết
ABCD.A'B'C'D' A'.ABD
V 6V
nên
3
ABCD.A'B'C'D'
a2
V
2
.
Vậy chọn đáp án D.
Câu 16. Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác đều cạnh a. Hình chiếu vuông
góc của A’ lên mặt phẳng (ABC) trùng với tâm O của đường tròn ngoại tiếp tam giác ABC.
Cho
0
BAA' 45
. Thể tích của khối lăng trụ đã cho là
A.
3
a2
4
B.
3
a2
8
C.
3
a
8
D.
3
a
4
Hướng dẫn giải
H
C'
B'
D'
C
A
B
A'
D
Chuyên đề: Hình học không gian Chủ đề 3: Thể tích khối lăng trụ
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 31
Gọi E là trung điểm của AB, ta có:
OE AB
A'O AB do A'O ABC
AB A'OE AB A'E

Tam giác vuông A’EA có
0
A 45
nên là tam giác vuông cân tại E
Suy ra
a a 2
A'E EA , AA'
22
Tam giác vuông A’OE (vuông tại O) có:
2
2 2 2 2
2 2 2
a 1 a 3 a 3a 6a a 6
A'O A'E OE . A'O
4 3 2 4 36 36 6




Thể tích của khối lăng trụ ABC.A’B’C’:
23
ABC
a 3 a 6 a 2
V S .A'O .
4 6 8
. Vậy chọn đáp án B.
Câu 18. Cho lăng trụ xiên tam giác ABC.A'B'C' có đáy ABC là tam giác đều cạnh a , biết
cạnh bên là
a3
và hợp với đáy ABC một góc 60
o
. Tính thể tích lăng trụ.
A.
3
3a 3
8
B.
3
a3
8
C.
3
3a
8
D.
3
a
8
Hướng dẫn giải
Ta có
C'H (ABC) CH
là hình chiếu của CC' trên (ABC)
Vậy
o
C'CH[CC',(ABC)] 60
0
3a
CHC' C'H CC'.sin60
2
;
SABC =
2
3a
4
.
Vậy V = SABC.C'H =
3
3a 3
8
. Vậy chọn đáp án A.
Câu 19. Cho lăng trụ xiên tam giác ABC.A'B'C' có đáy ABC là tam giác đều cạnh a . Hình
chiếu của A' xuống (ABC) là tâm O đường tròn ngoại tiếp tam giác ABC biết AA' hợp với
đáy ABC một góc 60 . Tính thể tích khối lăng trụ
A.
3
a3
3
B.
3
a3
4
C.
3
a3
8
D.
3
a3
2
Hướng dẫn giải
a
O
E
B
C
A'
B'
C'
A
H
o
60
a
B'
A'
C'
C
B
A
Chuyên đề: Hình học không gian Chủ đề 3: Thể tích khối lăng trụ
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 32
Ta có
A'O (ABC) OA
là hình chiếu của AA' trên (ABC).
Vậy
o
OAA'[AA',(ABC)] 60
Ta có BB'CC' là hình
bình hành ( vì mặt bên của lăng trụ)
AO BC
tại trung điểm H của BC nên
BC A'H
(đl 3
)
BC (AA'H) BC AA'
mà AA'//BB' nên
BC BB'
.
Vậy BB'CC' là hình chữ nhật.
ABC
đều nên
2 2 a 3 a 3
AO AH
3 3 2 3
o
AOA' A'O AOtan60 a
. Vậy V = SABC.A'O =
3
a3
4
.
Vậy chọn đáp án B.
Câu 20. Cho hình hộp ABCD.A’B’C’D’ có đáy là hình chữ nhật với
AB 3
,
AD 7
.
Hai mặt bên (ABB’A’) và (ADD’A’) lần lượt tạo với đáy những góc 45
0
và 60
0
.
Tính thể tích
khối hộp nếu biết cạnh bên bằng 1.
A.
3
B.
2
C.
4
D.
8
Hướng dẫn giải
Kẻ A’H ,
HM
oo
A'MH 45 ,A'NH 60 
Đặt A’H = x . Khi đó
A’N = x : sin 60
0
=
AN =
Mà HM = x.cot 45
0
= x
Nghĩa là x = .
Vậy VABCD.A’B’C’D’ = AB.AD.x = .Vậy chọn đáp án A.
)(ABCD
ADHNAB ,
ADNAABMA ','
3
2x
HM
x
NAAA
3
43
''
2
22
7
3
3
43
2
x
x
3
3. 7. 3
7
H
O
o
60
C'
A
a
B'
A'
C
B
Chuyên đề: Hình học không gian Chủ đề 3: Thể tích khối lăng trụ
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 33
Câu 22. Cho lăng trụ ABC.A
/
B
/
C
/
có đáy ABC là tam giác đều cạnh 2a
3
, hình chiếu
vuông góc của A
/
lên mặt phẳng (ABC) trùng với trọng tâm của tam giác ABC, cạnh A
/
A
hợp với mặt đáy (ABC) một góc 30
0
. Tính thể tích khối lăng trụ.
A.
3
6a
B.
3
8a
C.
3
4a
D.
3
2a
Giải
* Gọi M là trung điểm BC, G là trọng tâm của tam giác ABC
Ta có A
/
G
(ABC)
GA =
/
(ABC)
hc A A
/ / 0
A A,(ABC) A AG 30




* Tam giác ABC đều cạnh 2a
3
2
2
ABC
3
S 2a 3 . 3a 3
4

* Tam giác A
/
AG vuông tại G có
0
2 2 3
A 30 ,AG AM .2a 3. 2a
3 3 2
/0
2a 3
A G AG.tan30
3

.Vậy
/3
/ / / ABC
ABC.A B C
V S .A A 6a
.
Vậy chọn đáp án A.
30
0
2a
3
C
/
A
/
B
/
M
A
C
B
G
Chuyên đề: Hình học không gian Chủ đề 3: Thể tích khối lăng trụ
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 34
Để sử dụng file word, quý thầy cô vui lòng đóng góp chút kinh phí để tạo
động lực cho tác giả ra đời những chuyên đề khác hay hơn
TÊN TÀI LIỆU
GIÁ
MÃ SỐ
TRẮC NGHIỆM THỂ
TÍCH KHỐI LĂNG TRỤ
50K
HHKG_TTLT
Quà tăng đính kèm:
File Word 5 đề thi thử THPT Quốc gia 2017 có đáp án và lời giải chi tiết {ĐỀ 15-19}
Hướng dẫn thanh toán
Quý thầy cô thanh toán cho mình qua ngân hàng. Sau khi chuyển khoản, mình sẽ lập tức
gửi tài liệu cho quý thầy cô.
Nếu trong ngày mà thầy cô chưa nhận được thì vui lòng gọi điện trực tiếp cho mình.
Thầy cư. SĐT: 01234332133
NGÂN HÀNG
TÊN TÀI KHOẢN
TRẦN ĐÌNH CƯ
TRẦN ĐÌNH CƯ
TRẦN ĐÌNH CƯ
SỐ TÀI KHOẢN
4010205025243
0161000381524
55110000232924
CHI NHÁNH
THỪA THIÊN HUẾ
THỪA THIÊN HUẾ
THỪA THIÊN HUẾ
Nội dung: Họ và tên_email_ma tai liệu
Ví dụ: Nguyễn Thị B_nguyenthib@gmail.com_HHKG_TTKC
Lưu ý:
Thầy cô đọc kỹ file PDF trước khi mua, tài liệu mua chỉ
dùng với mục đích cá nhân, không được bán lại hoặc
chia sẻ cho người khác.
CHÚC QUÝ THẦY CÔ DẠY TỐT VÀ THÀNH CÔNG TRONG
SỰ NGHIỆP TRỒNG NGƯỜI
| 1/34
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Chuyên đề: Hình học không gian
Chủ đề 3: Thể tích khối lăng trụ T
hs. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 1
Chuyên đề: Hình học không gian
Chủ đề 3: Thể tích khối lăng trụ MỤC LỤC
CHỦ ĐỀ 3. THỂ TÍCH KHỐI LĂNG TRỤ ......................................................................... 3
DẠNG 1. KHỐI LĂNG TRỤ ĐỨNG ................................................................................ 4
DẠNG 2. KHỐI LĂNG TRỤ ĐỀU .................................................................................. 18
DẠNG 3. KHỐI LĂNG TRỤ XIÊNG .............................................................................. 23
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 2
Chuyên đề: Hình học không gian
Chủ đề 3: Thể tích khối lăng trụ
CHỦ ĐỀ 3. THỂ TÍCH KHỐI LĂNG TRỤ
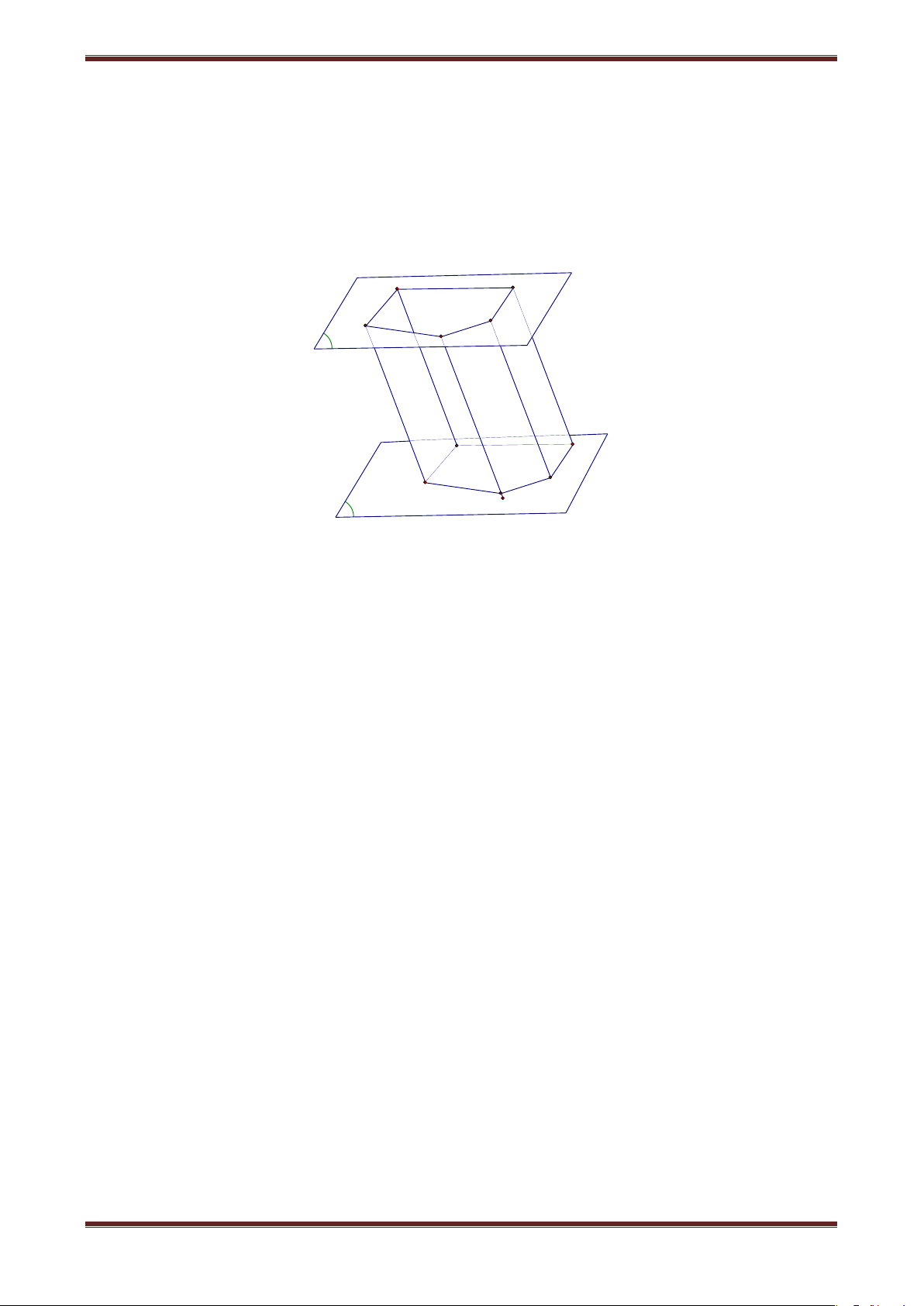
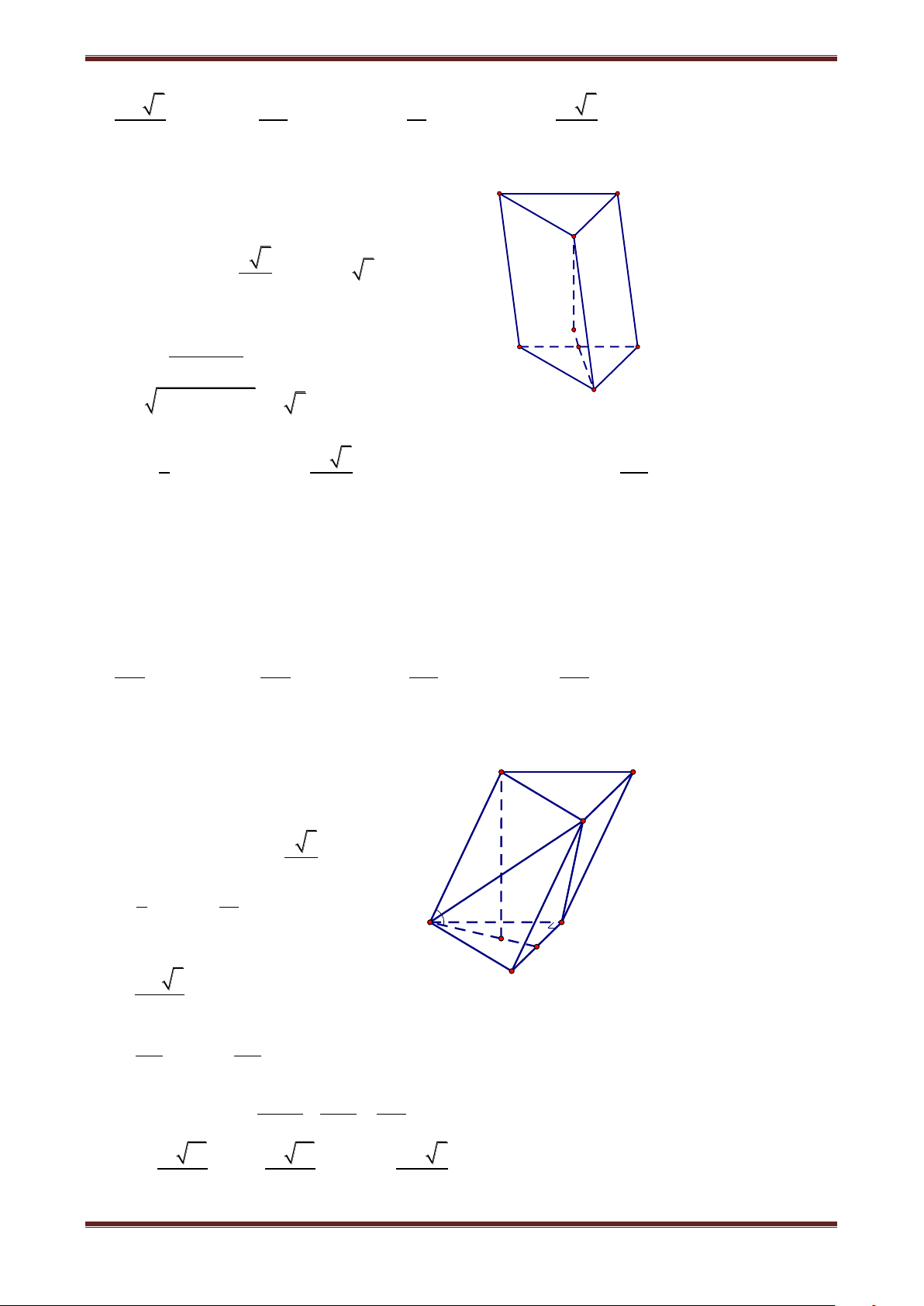
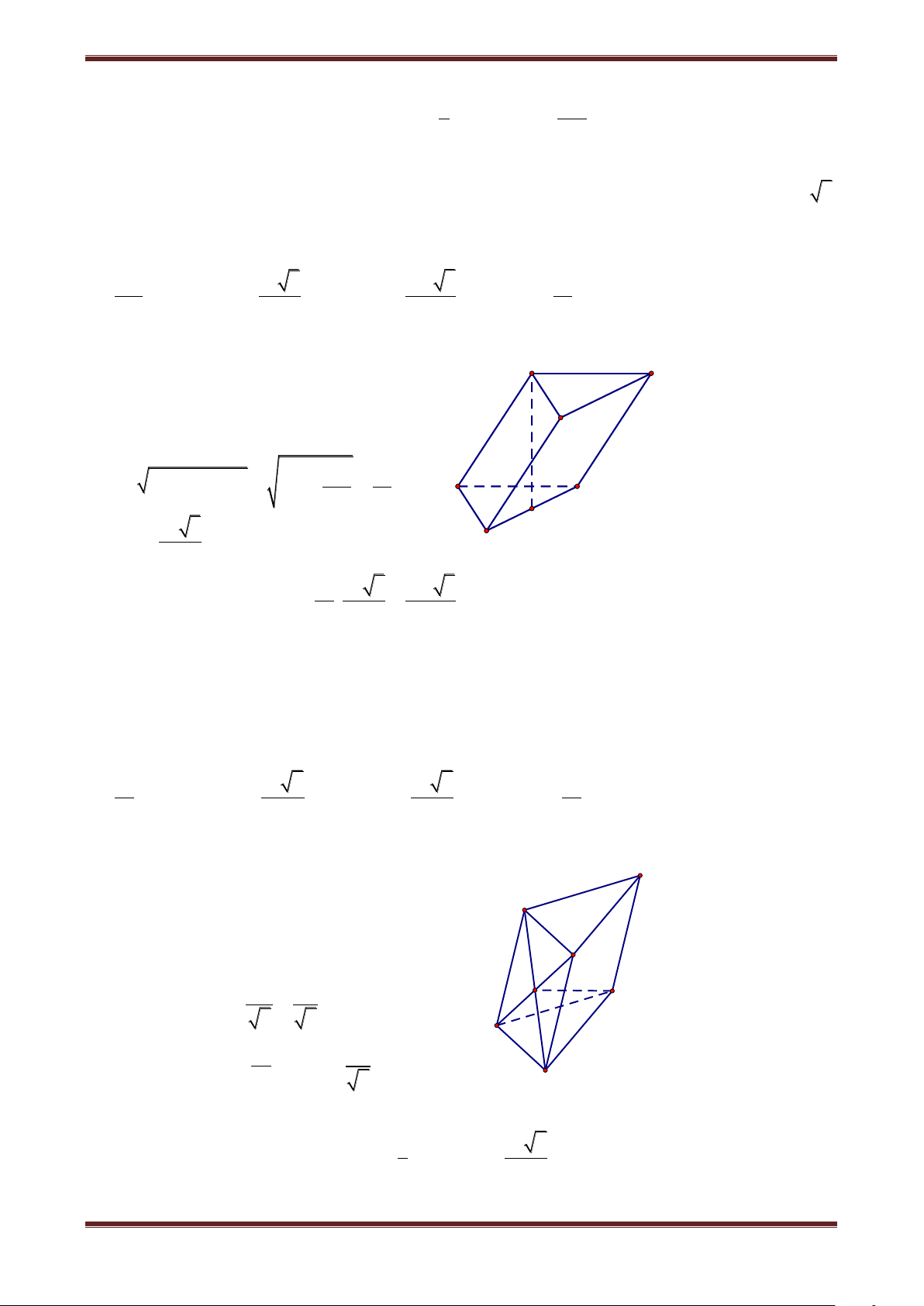
1. Định nghĩa: Cho hai mặt song song () và ( ') . Trên () ta lấy đa giác lồi 1 A A2...An , ' ' '
qua các đỉnh này ta dựng các đường thẳng song song cắt ( ') tại 1 A ,A2,...,An . ' ' Hình bao gồm hai đa giác 1
A A2...An,A 1' A 2' ...A'n và các hình bình hành 1 A A2A2 1 A ,...
Được gọi là hình lăng trụ. Kí hiệu là: 1 A A2...An.A 1'A 2' ...A'n . A A 3 2 A A 4 1  A5 A'3 A'2 A'4 A'1 A'  5 ' Nhận xét:
 Các mặt bên của hình lăng trụ bằng nhau và song song với nhau
 Các mặt bên là các hình bình hành
 Hai đáy hình lăng trụ là hai đa giác bằng nhau
2. Hình lăng trụ đứng - hình lăng trụ đều, hình hộp chữ nhật và hình lập phương
a) Hình lăng trụ đứng: là hình lăng trụ có cạnh bên vuông góc với đáy. Độ dài cạnh
bên được gọi là chiều cao của hình lăng trụ. Lúc đó các mặt bên của hình lăng trụ
đứng là các hình chữ nhật
b) Hình lăng trụ đều: là hình lăng trụ đứng có đáy là đa giác đều. Các mặt bên của
lăng trụ đều là các hình chữ nhật bằng nhau. Ví dụ: hình lăng trụ tam giác đều, tứ
giác đều... thì ta hiểu là hình lăng trụ đều
c) Hình hộp : Là hình lăng trụ có đáy là hình bình hành
d) Hình hộp đứng: là hình lăng trụ đứng có đáy là hình bình hành
e) Hình hộp chữ nhật: là hình hộp đứng có đáy là hình chữ nhật
f) Hình lăng trụ đứng có đáy là hình vuông và các mặt bên đều là hình vuông được
gọi là hình lập phương (hay hình chữ nhật có ba kích thước bằng nhau được gọi là hình lập phương) Nhận xét:
 Hình hộp chữ nhật  hình lăng trụ đứng (Có tất cả các mặt là hình chữ nhật
 Hình lập phương  hình lăng trụ đều (tất cả các cạnh bằng nhau)
 Hình hộp đứng  hình lăng trụ đứng (mặt bên là hình chữ nhật, mặt đáy là hình bình hành)
3. Thể tích khối lăng trụ:
V  B.h: Với B là diện tích đáy và h là chiều cao
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 3
Chuyên đề: Hình học không gian
Chủ đề 3: Thể tích khối lăng trụ
4. So sánh khối lăng trụ đứng và khối lăng trụ đều: ĐỊNH NGHĨA: TÍNH CHẤT
 Hình lăng trụ đứng là
 Các mặt bên hình lăng trụ
hình lăng trụ có cạnh bên
đứng là hình chữ nhật vuông góc với mặt đáy
 Các mặt bên hình lăng trụ
đứng vuông góc với mặt đáy
 Chiều cao là cạnh bên
 Hình lăng trụ đều là hình
 Các mặt bên của hình lăng
lăng trụ đứng có đáy là đa
trụ đều là các hình chữ giác đều nhật bằng nhau
 Chiều cao là cạnh bên
DẠNG 1. KHỐI LĂNG TRỤ ĐỨNG
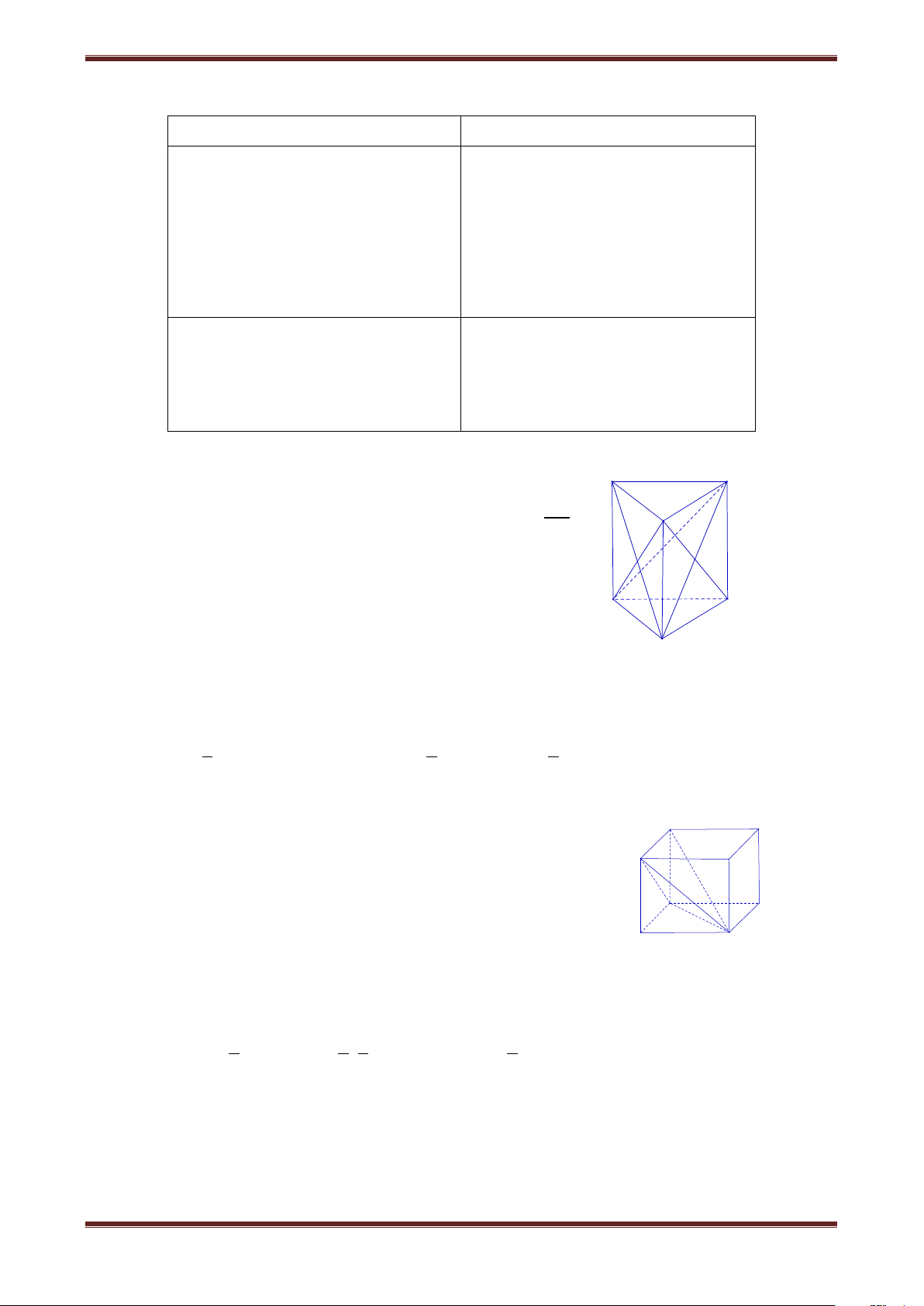
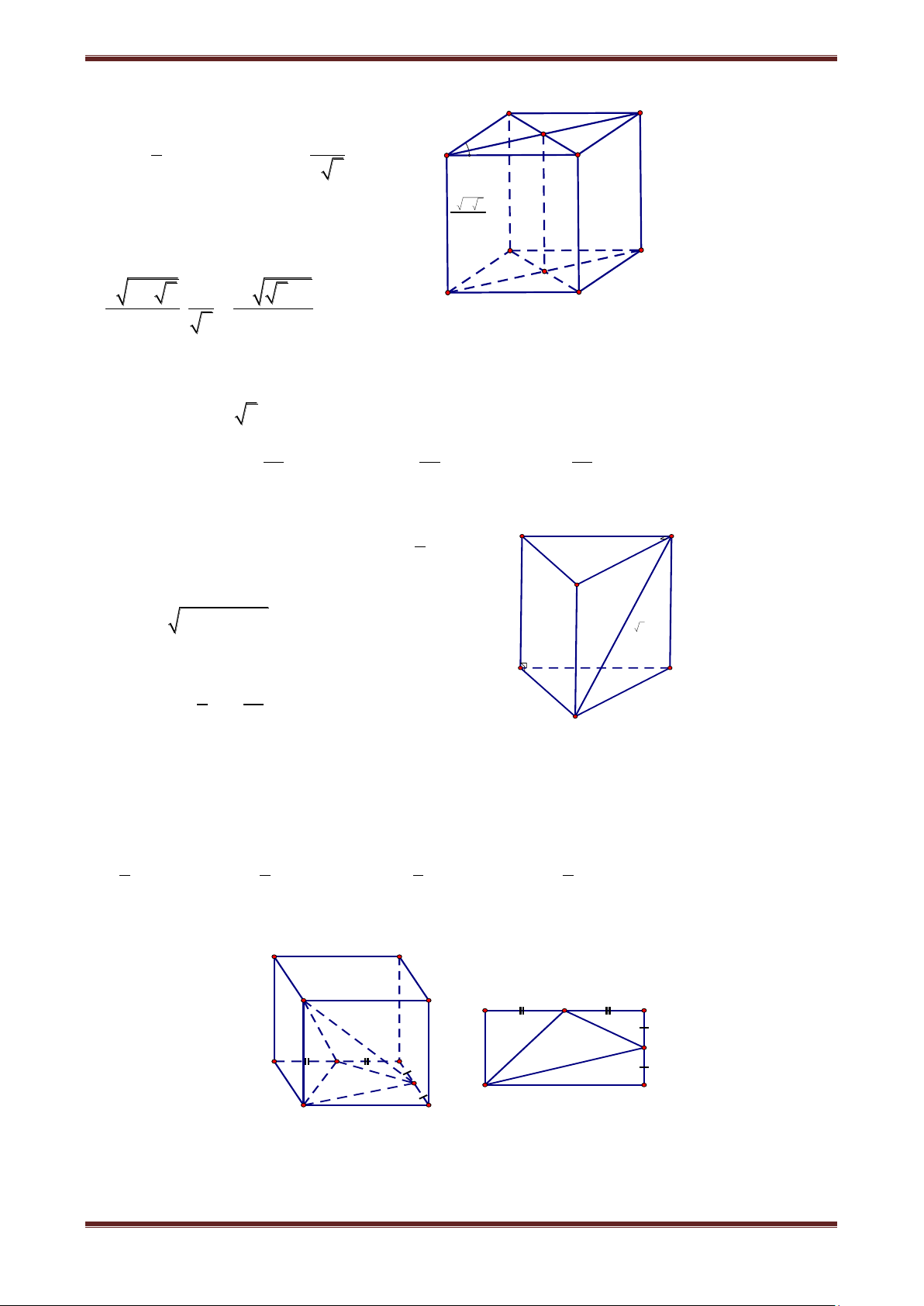
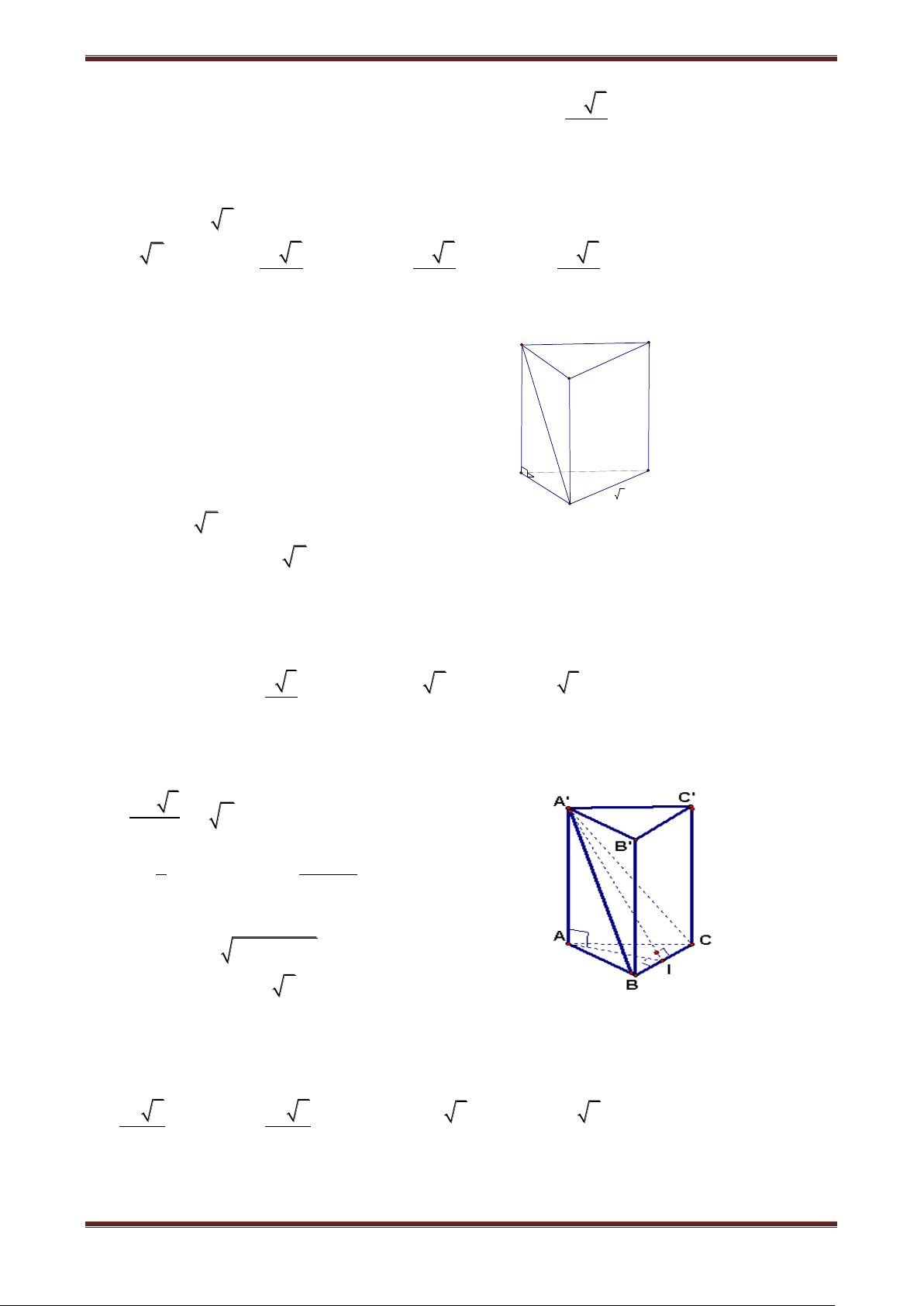
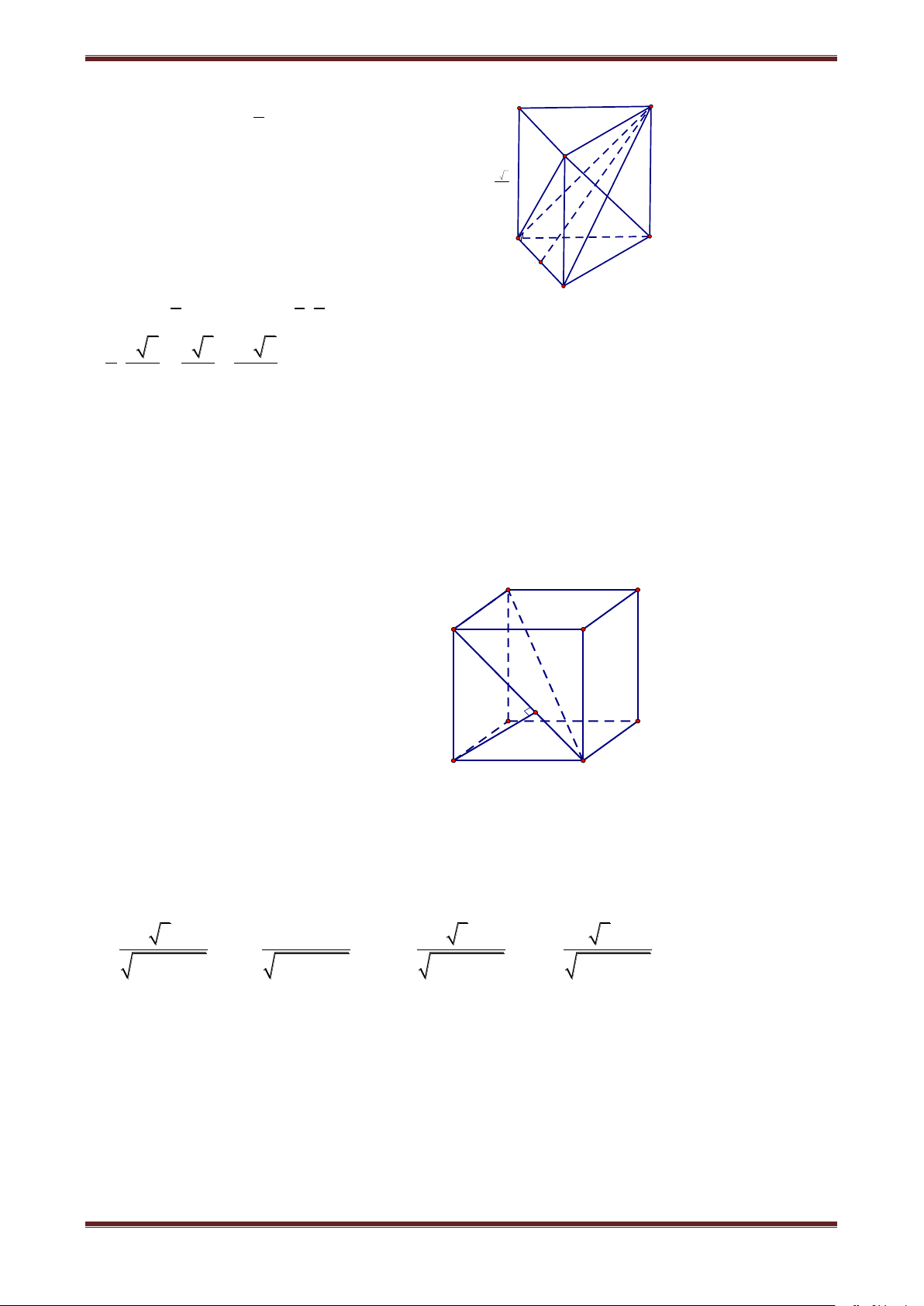
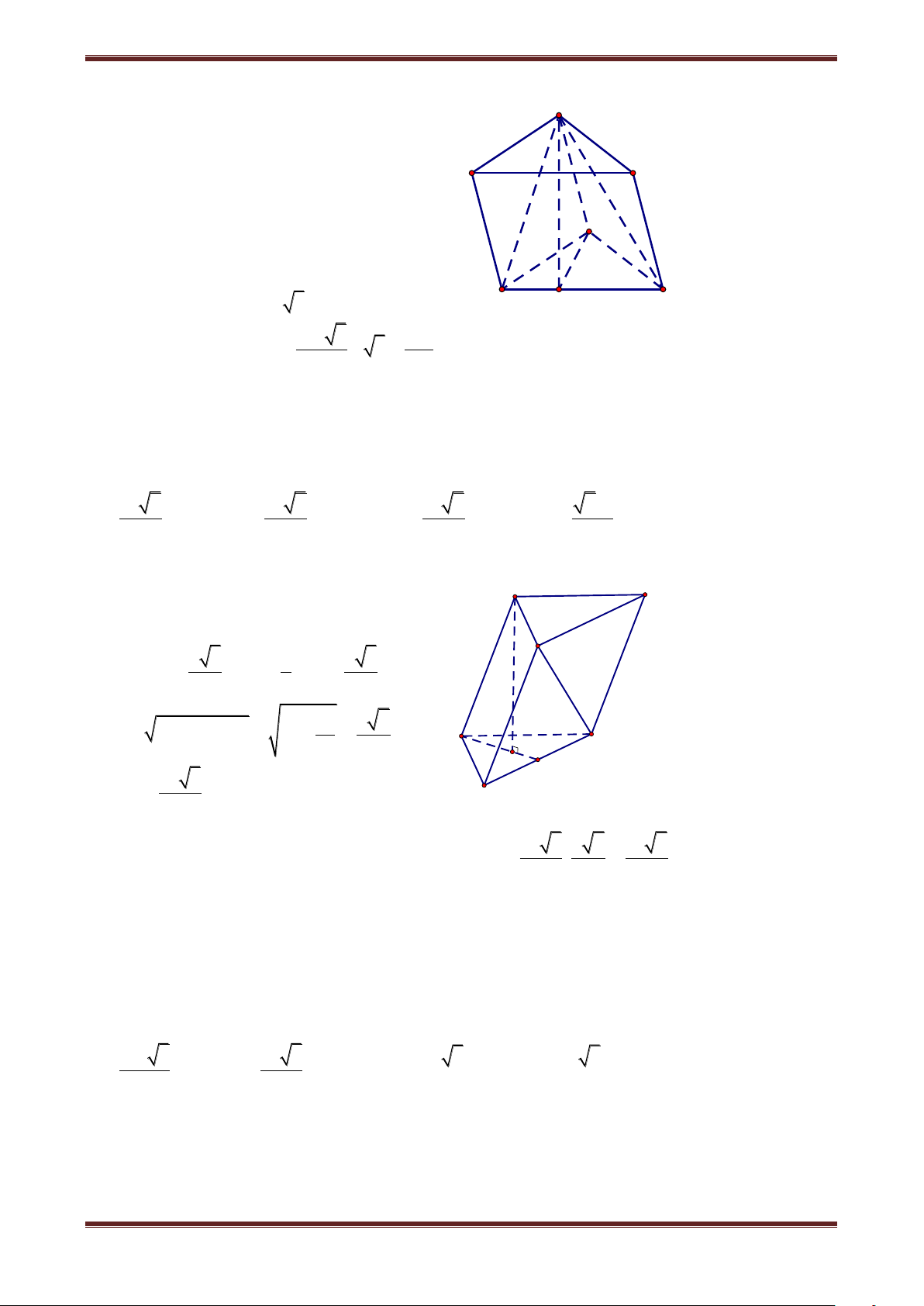
Câu 1. Cho hình lăng trụ đứng ABC.A’B’C’ có thể tích là B' C' 2V
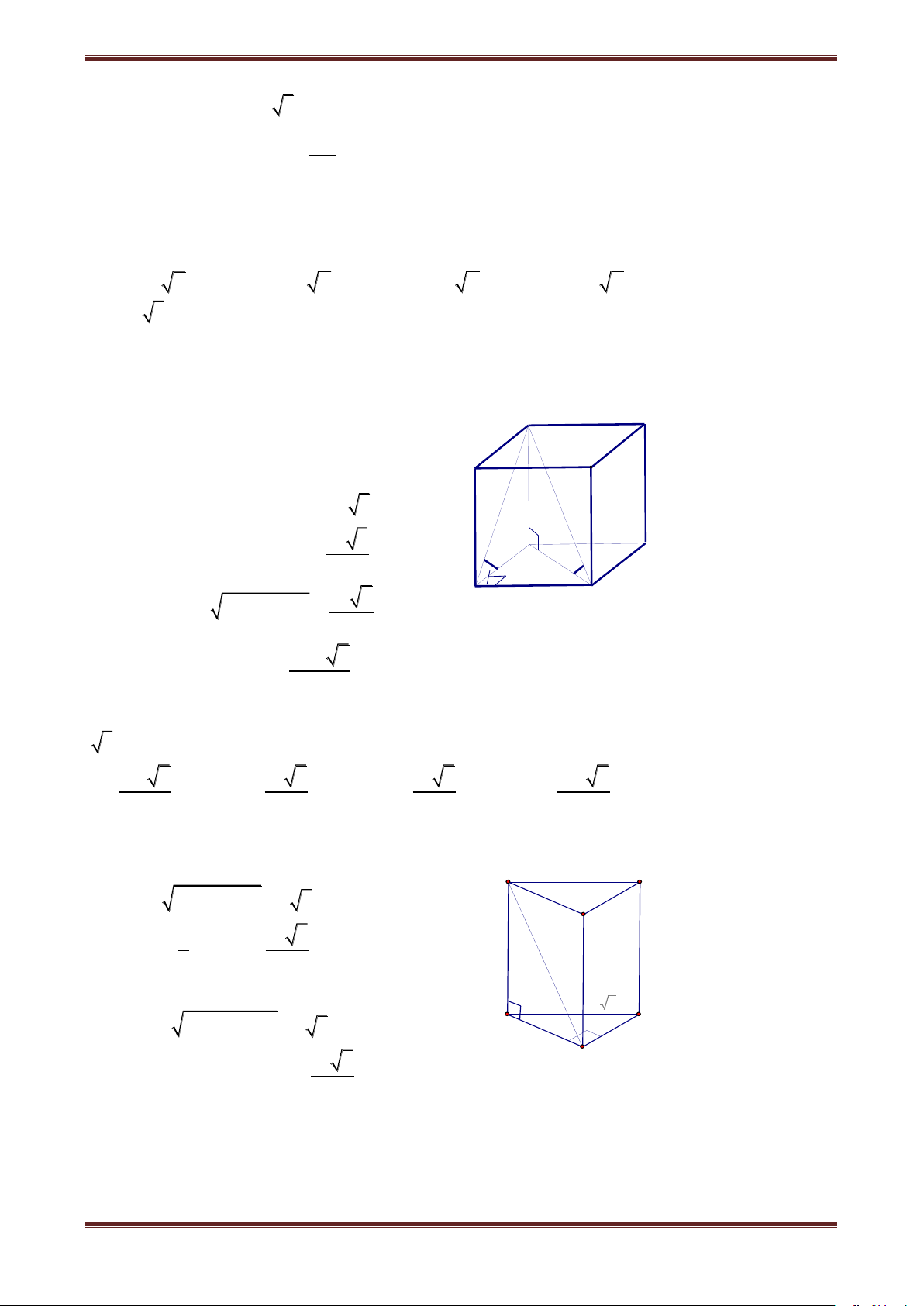
V. Trong các khối chóp dưới đây, khối chóp có thể tích A' 3 là: I A. A.A'B'C' B. C'.ABC B C C. A'.BCC'B' D. I.ABB'A' A Hướng dẫn giải Ta có: A V BC.A'B'C'  A V '.BCC'B'  A V '.ABC . 1 2 2 Mà A V '.ABC  A V BC.A'B'C'  A V '.BCC'B'  A V BC.A'B'C'  V 3 3 3 .
Vậy chọn đáp án C. Câu 2. Cho hình hộp đứng có các cạnh A' B'
AB  3a;AD  2a;AA'  2a như hình vẽ. Thể tích của khối D' C' A’.ACD’ là: 3 3 B A. a B. 2a A 3 3 D C C. 3a D. 6a Hướng dẫn giải 1 1 1 1 3 Ta có: A V ’.ACD’  C V .ADD'A'  . . A
V BCD.A'B'C'D'  .3a.2a.2a  2a . 2 2 3 6
Vậy chọn đáp án B.
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 4
Chuyên đề: Hình học không gian
Chủ đề 3: Thể tích khối lăng trụ 0
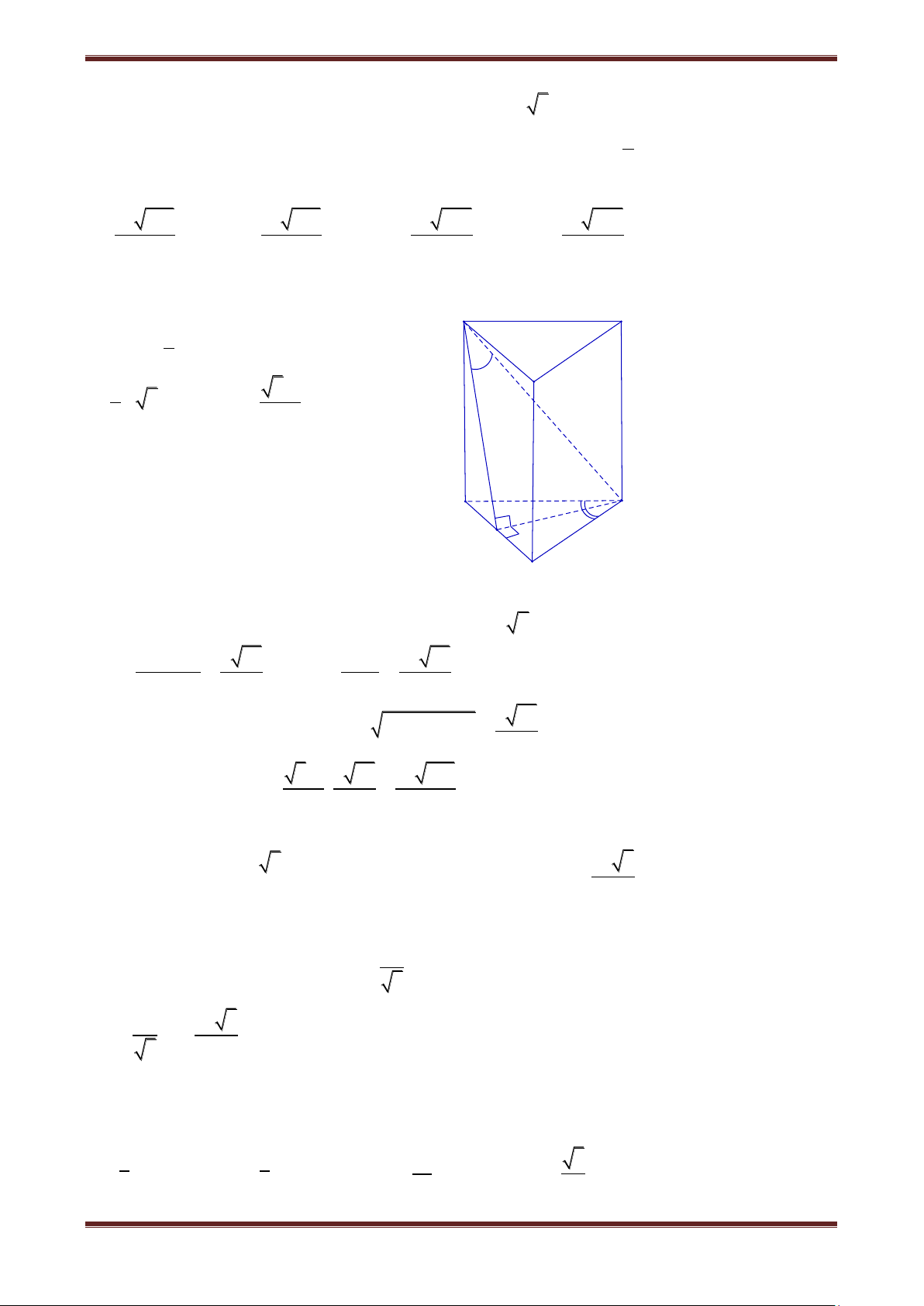
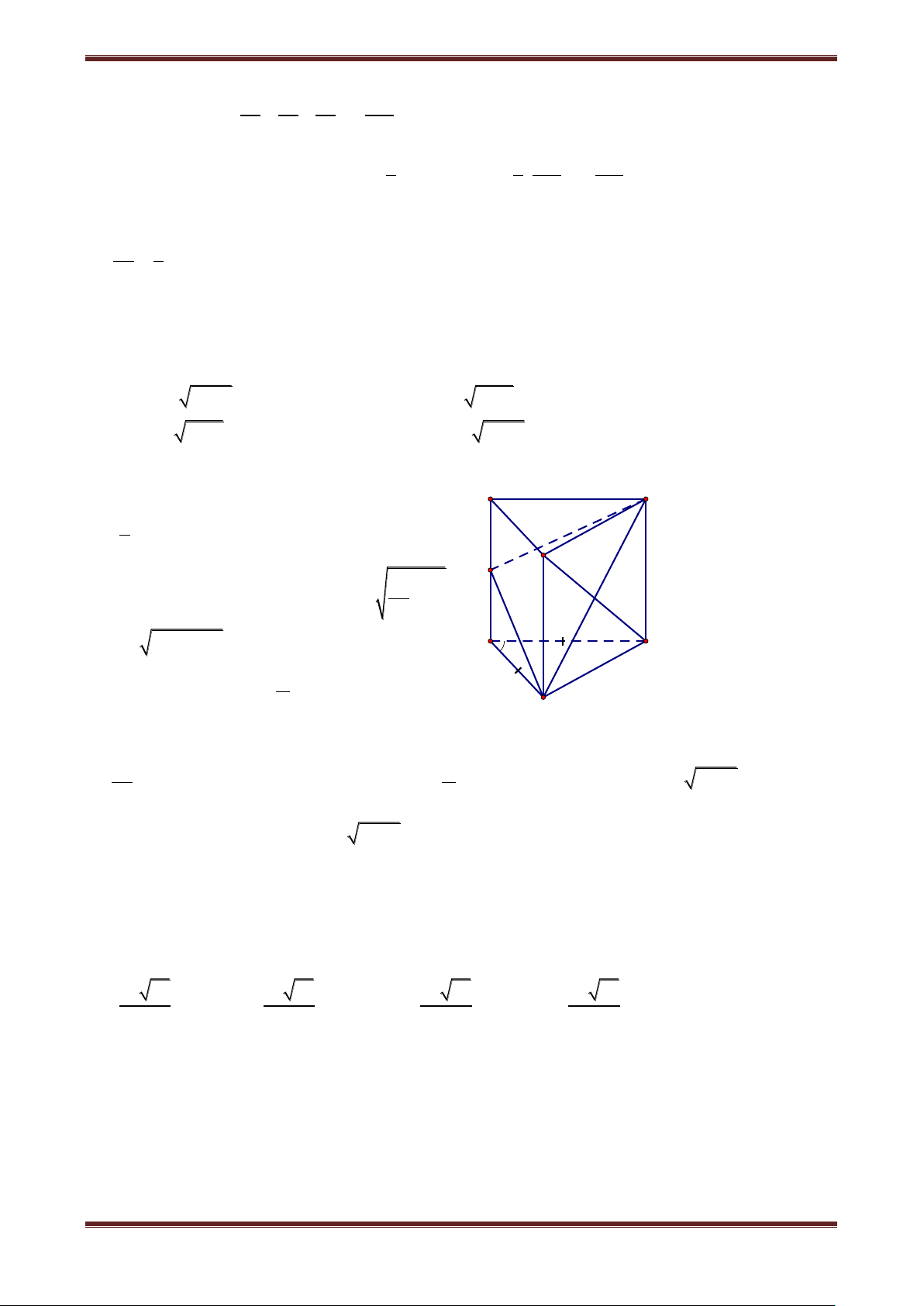
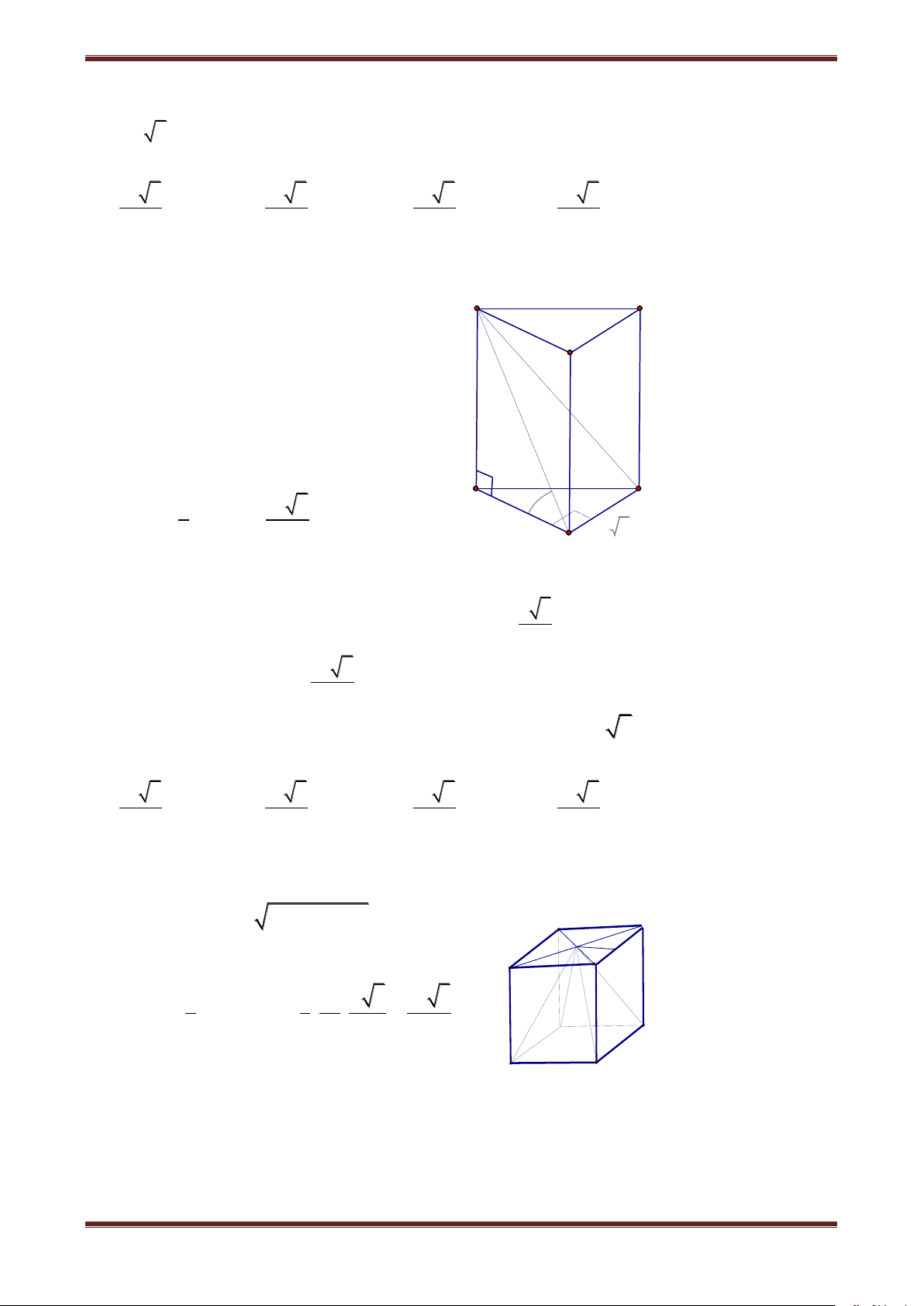
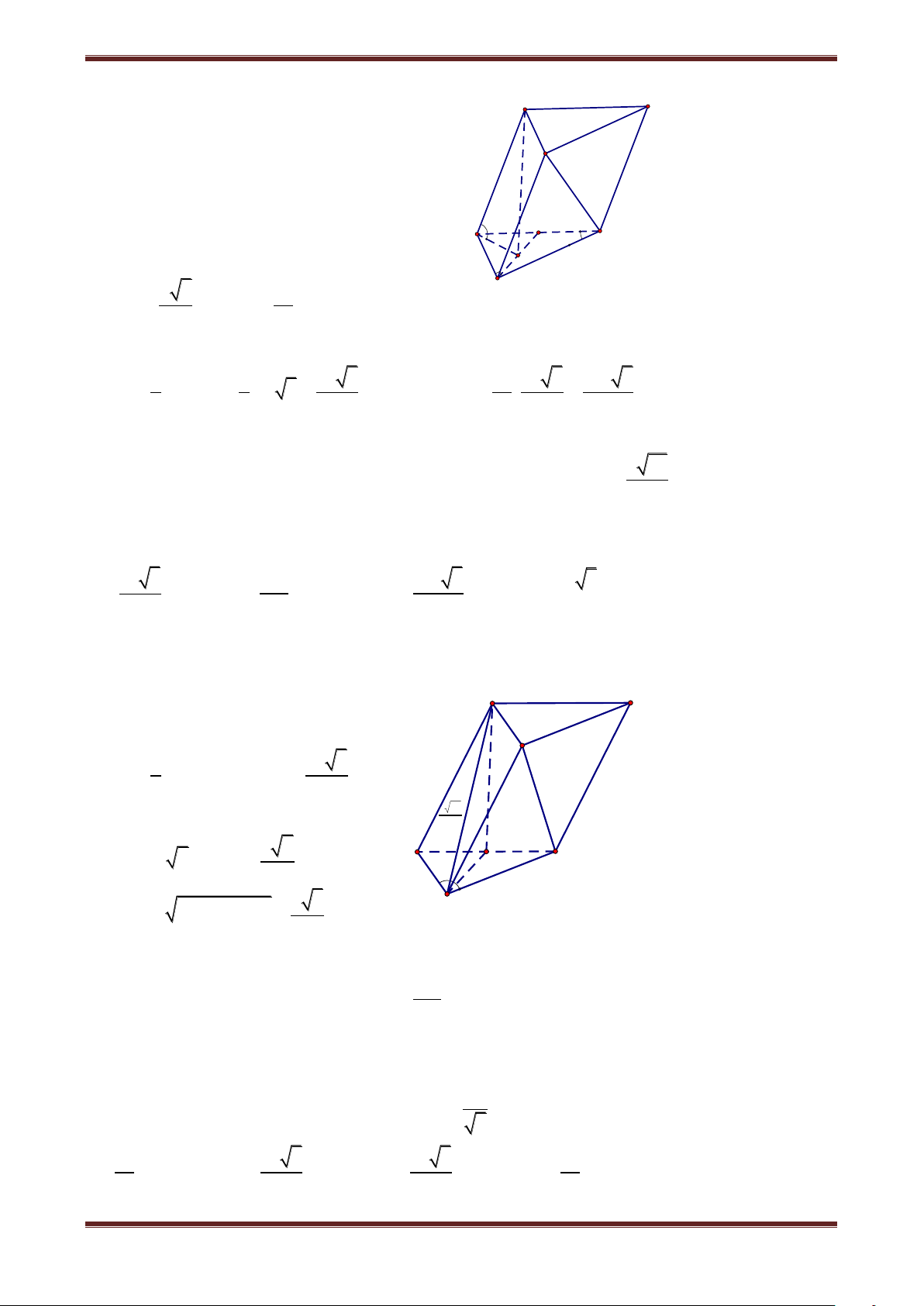
Câu 3. Cho hình lăng trụ đứng ABC.A’B’C’ có AC  3a,BC  a,ACB  150 , đường thẳng 1
B'C tạo với mặt phẳng ABB'A' một góc  thỏa mãn sin  4 . Thể tích khối lăng trụ AB C.A’B’C’ là: 3 a 105 3 a 105 3 a 339 3 a 339 A. 28 B. 14 C. 14 D. 28 Hướng dẫn giải Ta có B' C' 1 S A  BC  AC.BC.sin ACB 2 A' 2 1 0 3a  a 3.a.sin150  2 4
Kẻ CH  AB  CH  ABB'A'
nên B’H là hình chiếu vuông góc
của B’C lên ABB'A' B C
 B'C,ABB'A'  B'C,B'H  CB'H   H A 2 2 2 0 2
AB  AC  BC  2AC.BC.cos150  7a  AB  a 7 2.S A  BC a 21 CH CH 2a 21    B'C   AB 14 sin  7 2 2 a 35 Xét B
 B'C vuông tại B có: BB'  B'C  BC  7 . 2 3 3a a 35 a 105 Do đó V  S A  BC.AA '  .   4 7 28
Chọn đáp án A
Câu 4. Khối lập phương có độ dài đường chéo bằng d thì thể tích của khối lập phương là: 3 3 3 3 A. V  d ; B. 3d ; C. 3d ; d 3 D. V  9 Hướng dẫn giải d
Khối lập phương có cạnh là a 
. Do đó khối lập phương có thể tích là 3 3 3  d  d 3 V    
. Vậy chọn đáp án D.  3 9  0
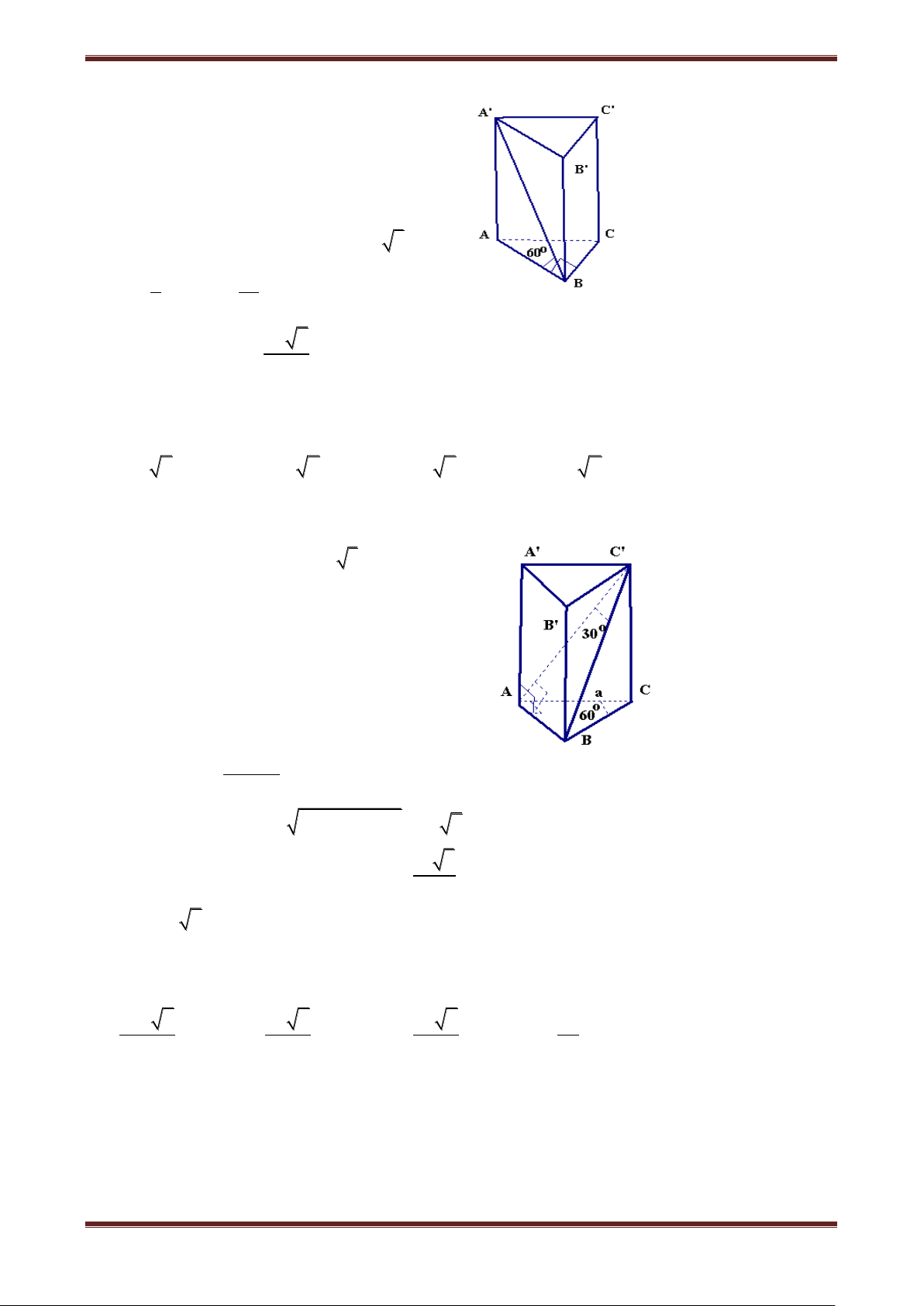
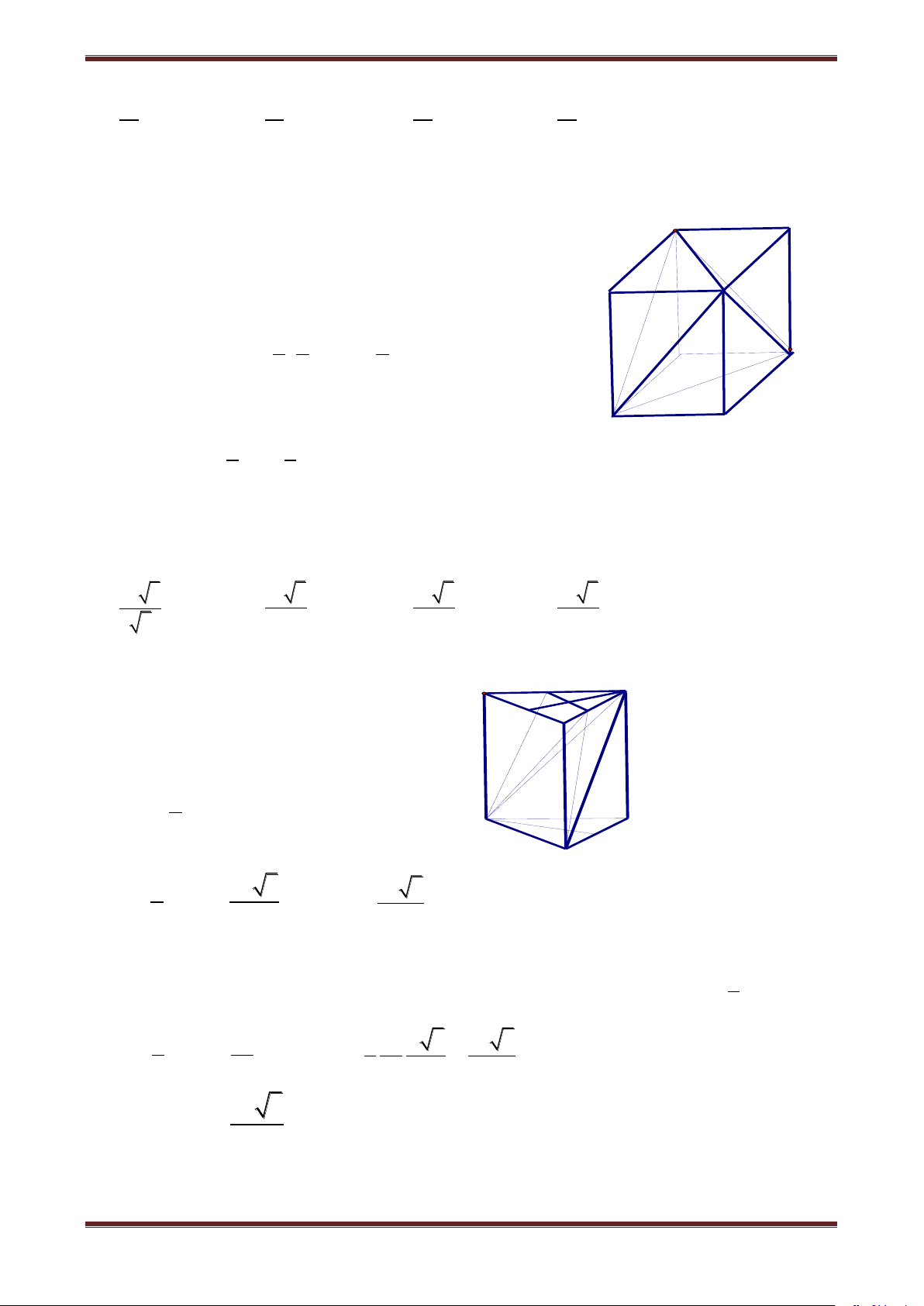
Câu 5. Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác cân, AB  AC  a , BAC  120 . 0
Mặt phẳng AB'C' tạo với mặt đáy góc 60 . Tính thể tích lăng trụ ABC.A’B’C’. 8 3 3 3 3 a 3 A. a ; a ; 3 3 B. 8 C. ; a ; 8 D. 8
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 5
Chuyên đề: Hình học không gian
Chủ đề 3: Thể tích khối lăng trụ Hướng dẫn giải
Xác định góc giữa AB'C' và mặt đáy B C 0 là AKA'  AKA'  60 a 1200 Tính a A 1 a A'K  A'C'  2 2 0 a 3  AA'  A'K.tan 60  600 B' C' 2 K 3 3a A V BC.A'B'C'  AA'. A S BC  A' 8 .
Vậy chọn đáp án B.
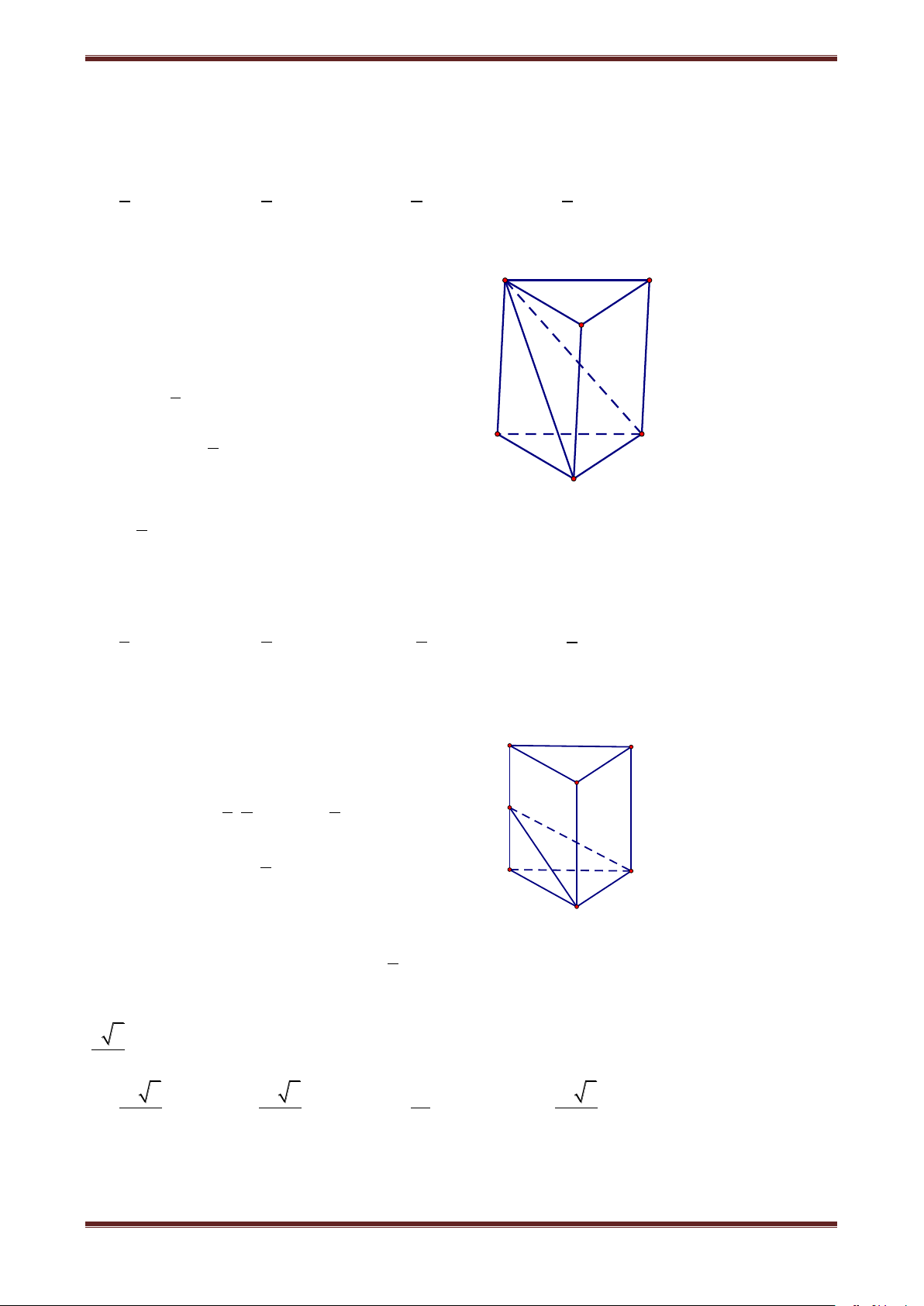
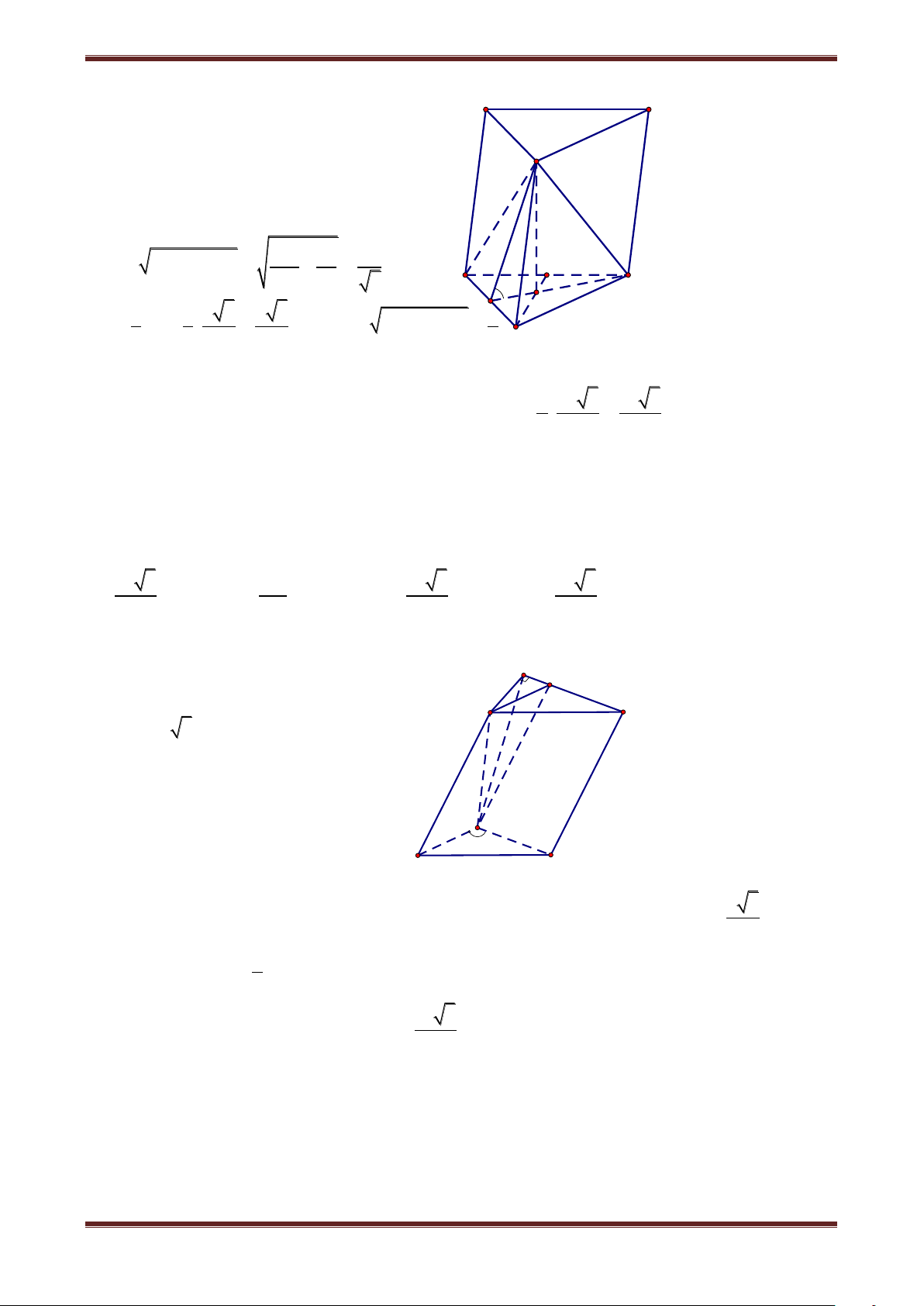
Câu 6. Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác cân tại A, BC  a, 5
AA'  a 2 và cosBA'C  6 . Tính thể tích hình lăng trụ ABC.A’B’C’. 3 a 6 3 a 3 3 3a 6 3 3a 3 A. 4 B. 4 C. 4 D. 4 Hướng dẫn giải 2 2 2 2
Đặt AB  x thì A'B  A'C  x  2a B a C
Áp dụng định lí hàm số cosin trong A  'BC , ta có: A 2 2 2 A'B  A'C  BC a 3 cosBA'C  2A'B.A'C 2 2 2 2x  4a  a 5     x  a B' C' 2 2   6 2 x 2a 2 a 3 A' Suy ra A  BC đều nên A S BC  4 3 a 6
Vậy thể tích hình lăng trụ ABC.A’B’C’ là V  4
Vậy chọn đáp án A.
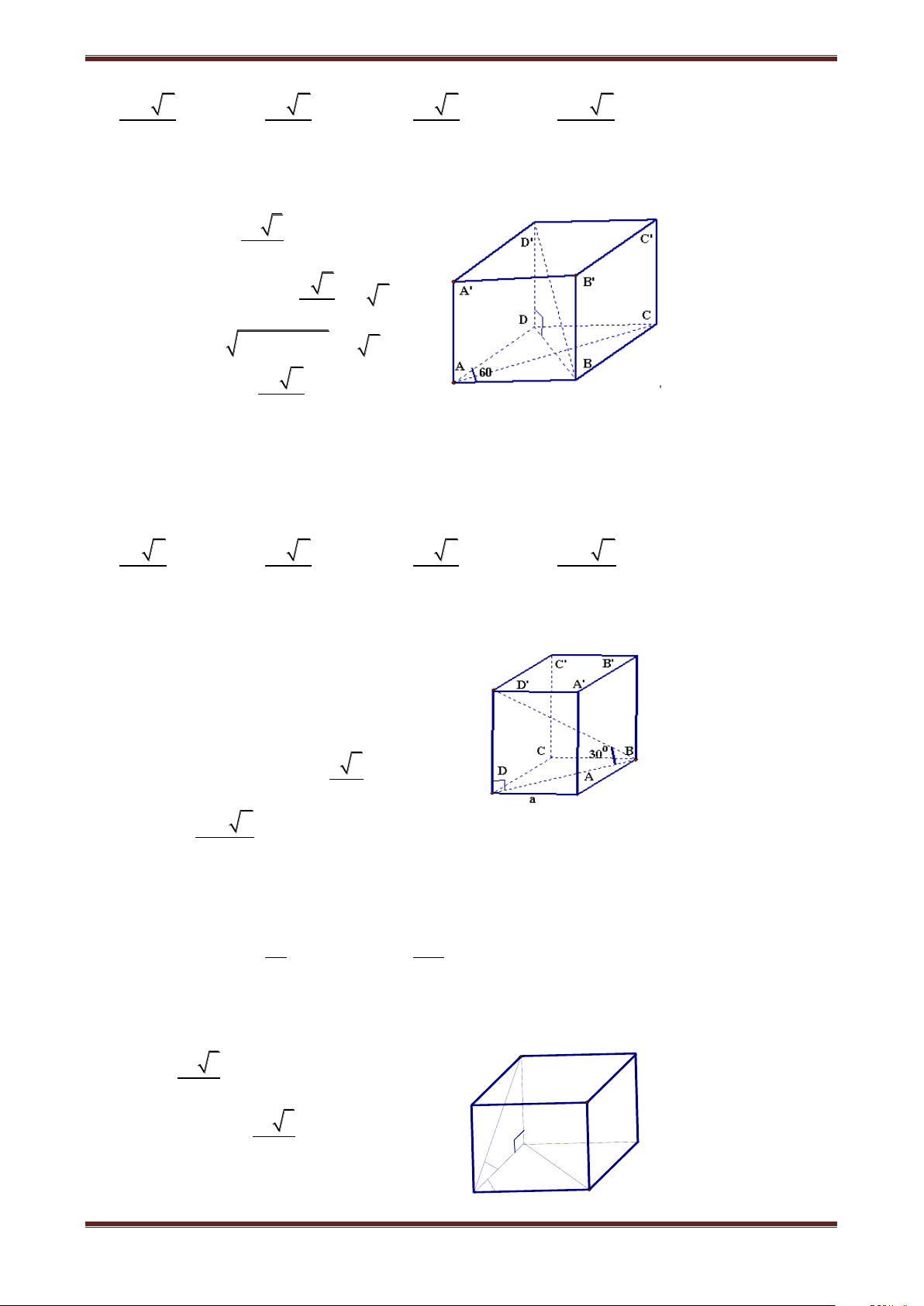
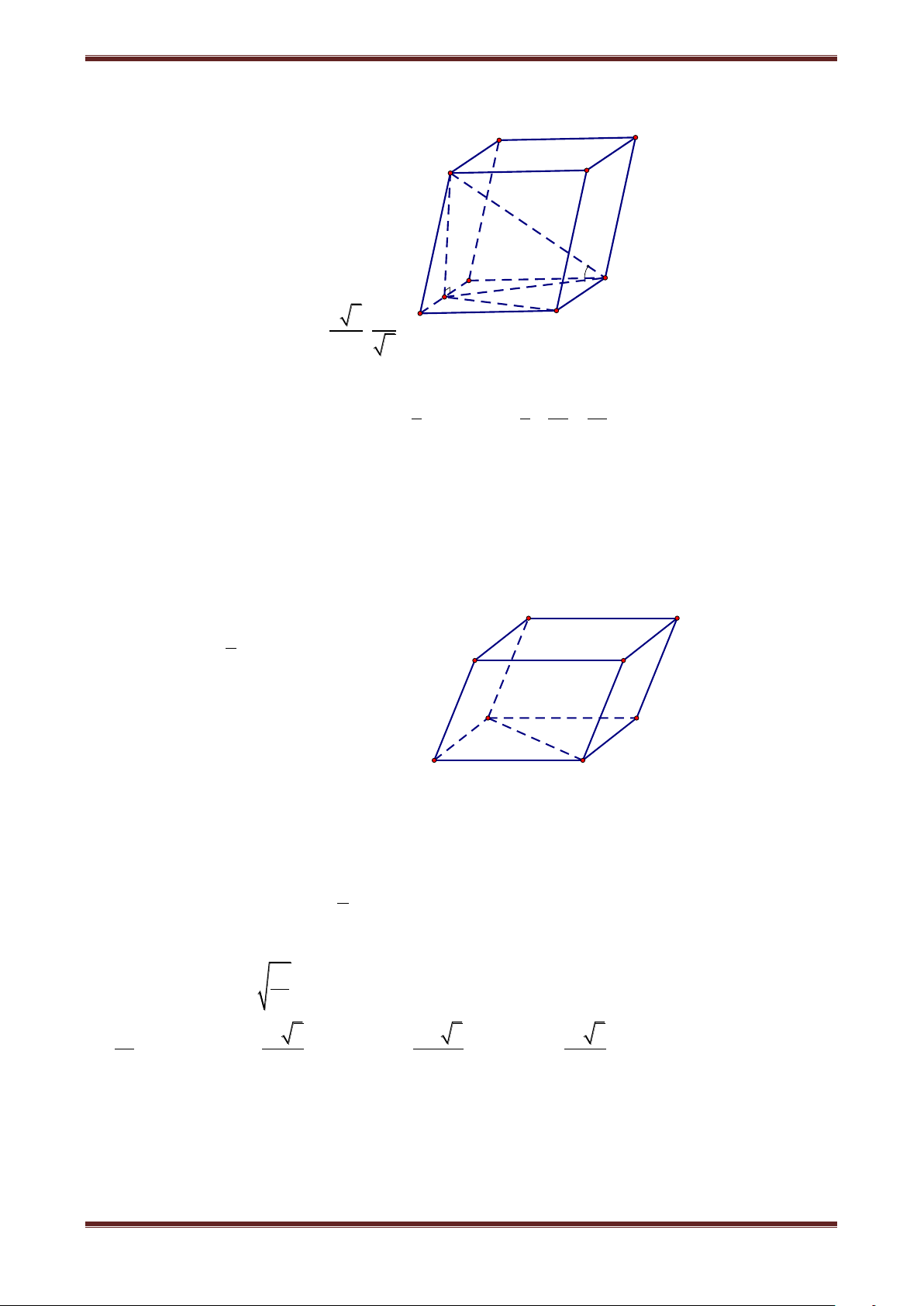
Câu 7. Cho hình lăng trụ đứng ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a, 0 a 2  2 BAD  45 , AA'  2
. Thể tích của khối lăng trụ ABCD.A’B’C’D’ là 3 a 2 1 3 a 2 1 3 a 2 1 3 a 2 1 A. B. C. D. 2 2 2 4 2 Hướng dẫn giải
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 6
Chuyên đề: Hình học không gian
Chủ đề 3: Thể tích khối lăng trụ Ta có: A S BCD  2 A S BD D C O 2 1 a 450 A A S BD  AB.AD.sinBAD  2 2 2 B
Do ABCD.A’B’C’D’ là hình lăng trụ a 2- 2 đứng nên 2 D' A V BCD.A'B'C'D'  AA'. A S BCD C' 2 3 a 2  2 a a 2 1 O'  .  A' B' 2 2 2
Vậy chọn đáp án D.
Câu 8. Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông cân tại B. Biết
AB  3cm, BC' 3 2cm . Thể tích khối lăng trụ đã cho là 3 A. 27 cm  27 3 27 3 27 3 B. cm  cm  cm  2 C. 4 D. 8 Hướng dẫn giải 9 2 A 3 B
Diện tích đáy của khối lăng trụ: A S BC  cm  a 3
Chiều cao của khối lăng trụ: C 2 2
h  CC'  BC'  BC  3 cm 3 2
Thể tích của khối lăng trụ đã cho: A' B' 9 27 V  S .h  .3   3 ABC cm  2 2 . A'
Vậy chọn đáp án C.
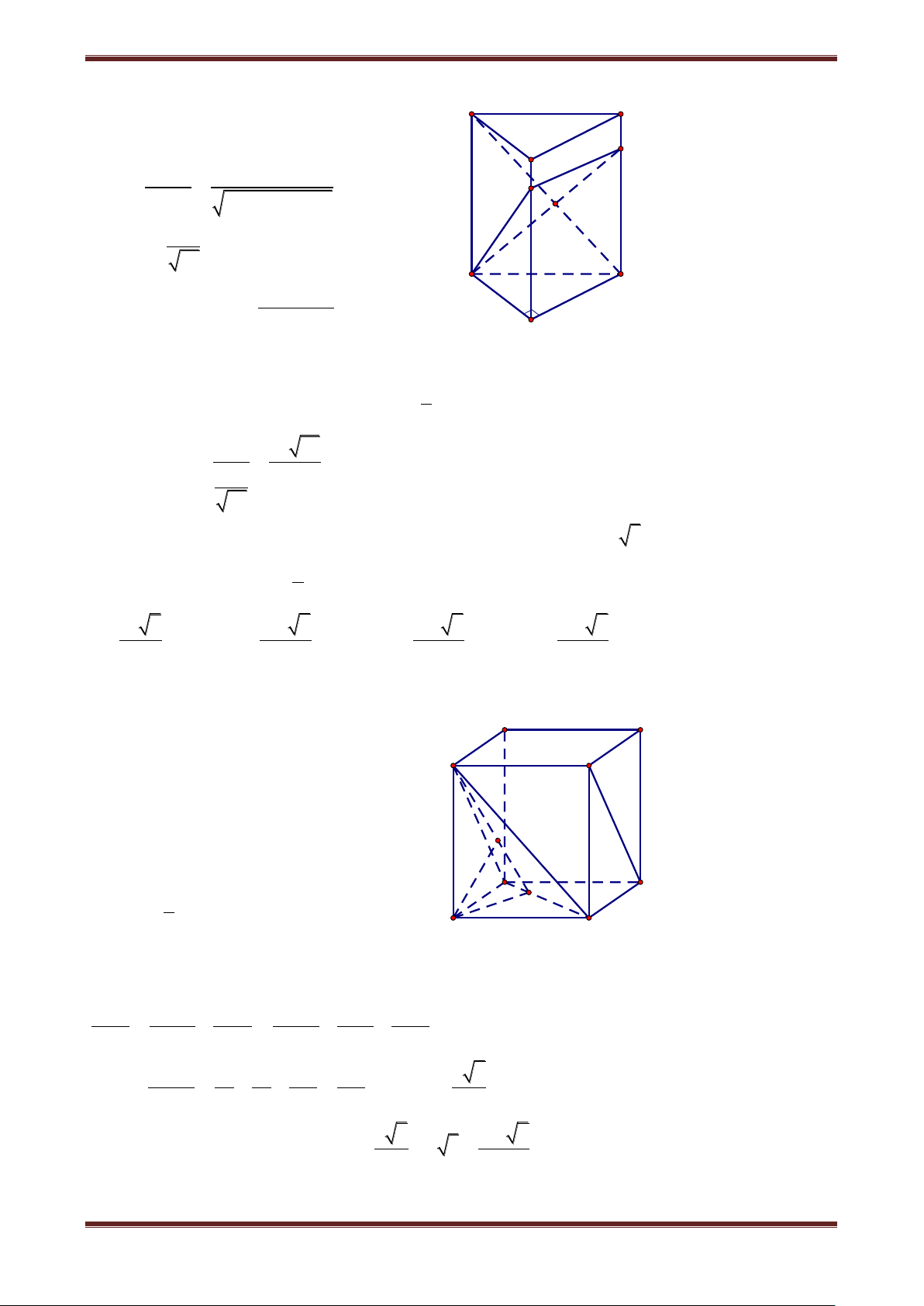
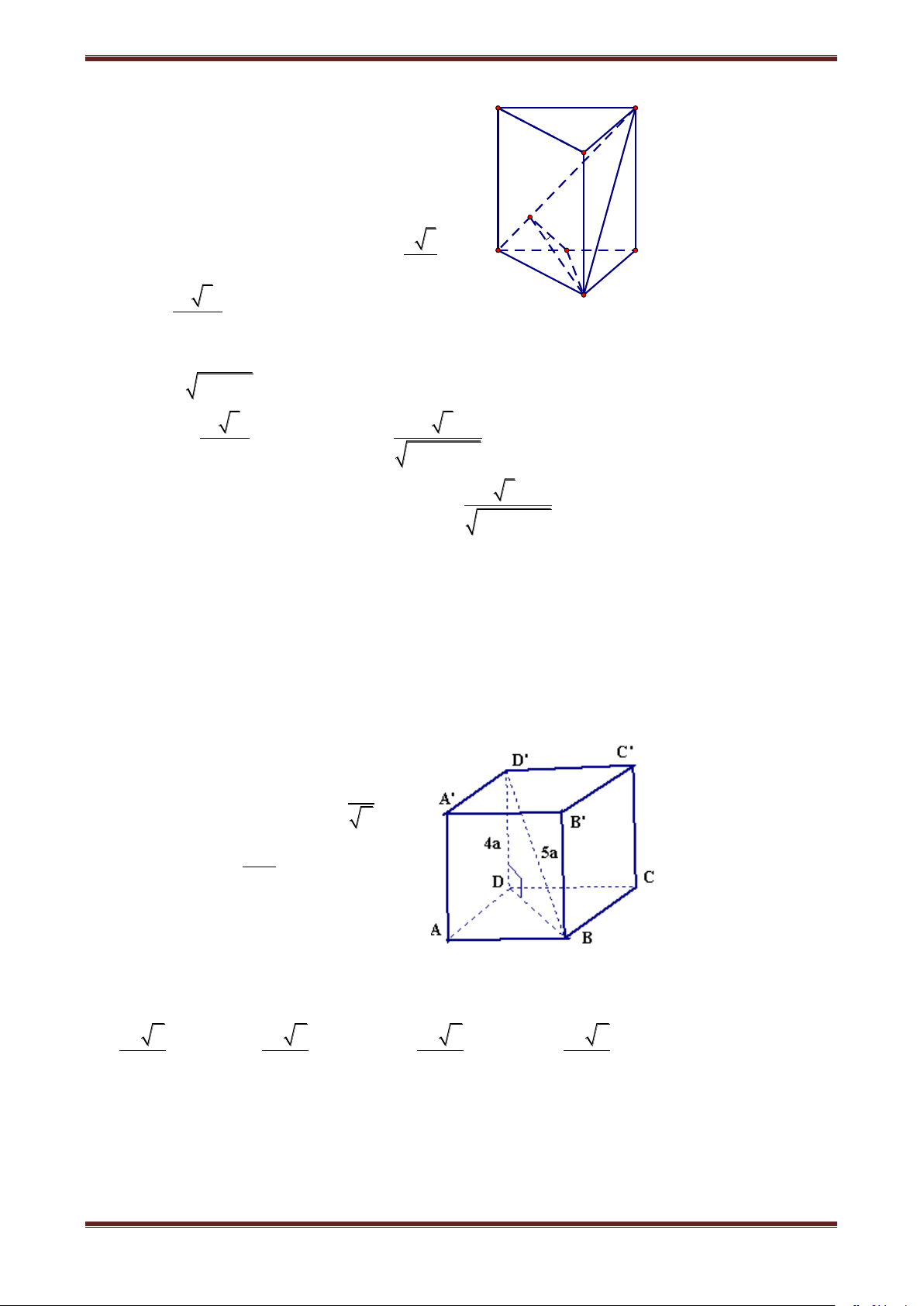
Câu 9. Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB  a, BC  b, AA'  c . Gọi M và N
theo thứ tự là trung điểm của A’B’ và B’C’. Tính tỉ số giữa thể tích khối chóp D’.DMN và
thể tích khối hộp chữ nhật ABCD.A’B’C’D’ 1 1 1 1 A. 2 B. 5 C. 8 D. 4 Hướng dẫn giải A B C D M A' B' N M B A' N D' C' D' C'
Thể tích khối chóp D’.DMN bằng thể tích khối chóp D.D’MN Ta có D S 'MN  A S 'B'C'D'  D S 'A'M  D S 'C'N  B S 'MN 
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 7
Chuyên đề: Hình học không gian
Chủ đề 3: Thể tích khối lăng trụ  ab ab ab  3ab  ab      4 4 8    8 1 1 3ab abc
Thể tích khối chóp D’.DMN là: 1 V  S D  'MN.DD'  . .c  3 3 8 8
Thể tích của khối hộp chữ nhật ABCD.A’B’C’D’ là V  abc 1 V 1  
V 8 . Vậy chọn đáp án C.
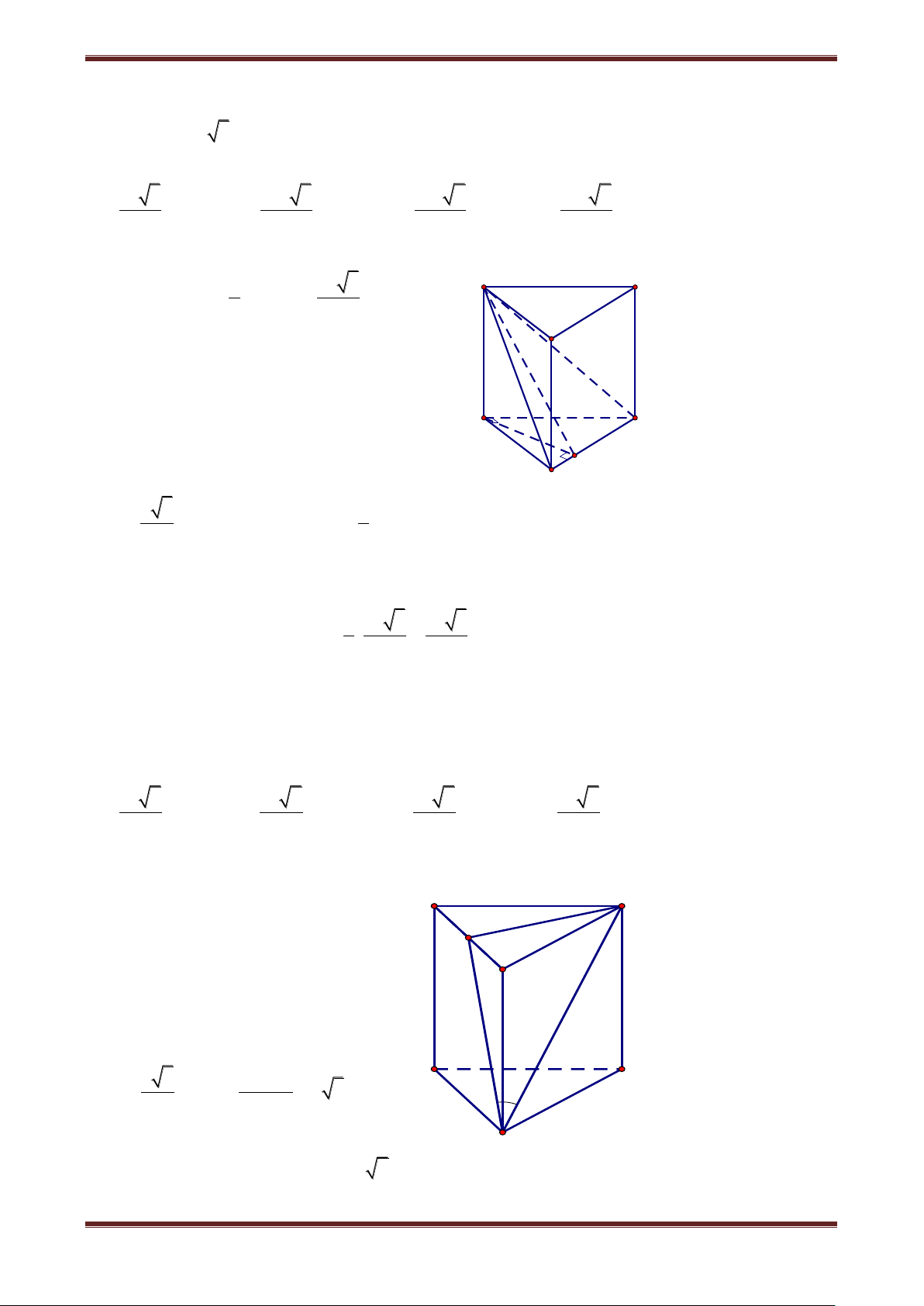
Câu 10. Cho hình lăng trụ đứng ABC.A’B’C’, có đáy ABC là tam giác cân tại A,
AB  AC  a, BAC   . Gọi M là trung điểm của AA’, tam giác C’MB vuông. Thể tích của
khối lăng trụ ABC.A’B’C’ là 3 3 A. a sin .  cos B. a cos .  sin 3 3 C. a cot .  sin D. a tan .  cos Hướng dẫn giải
Diện tích đáy của khối lăng trụ là: C' A' 1 2 S  a sin 2 2 M B' x 2
Đặt A'A  x . Ta có: BM  C' M   a 4 , 2 2 BC'  BC  x A α C
Trong đó BC  2asin 2 . Tam giác C’MB B vuông tại M, ta có: 2  2 x  2 2 2 2 2    2 2 2
 a   BC  x  x  4a  2 2asin
 x  4a cos  x  2a cos 4  2    Thể tích     3
của khối lăng trụ là V  a sin .  cos .
Vậy chọn đáp án A.
Câu 11. Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác vuông tại B,
AB  a, BC  2a, AA'  3a. Mặt phẳng  qua A vuông góc với CA’ lần lượt cắt các đoạn
thẳng CC’ và BB’ tại M và N. Diện tích tam giác AMN là 2 a 14 2 a 14 2 a 14 2 a 14 A. 6 B. 3 C. 9 D. 7 Hướng dẫn giải
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 8
Chuyên đề: Hình học không gian
Chủ đề 3: Thể tích khối lăng trụ Gọi H    A'C A' C'
Trong tam giác A’AH ta có: B' M 2 2 A'A 9a A'H   N A'C 2 2 2 a  4a  9a H 9a  A'H  14 3V A C Ta có: A'.AMN AMN S  A'H . Mà B NB A ∥ A' nên: 1 3 A V '.AMN  M V .A'AN  M V .A'AB  C V .A'AB  AA'. A S BC  A V '.AMN  a 3 3 2 3a a 14 Vì vậy AMN S   9a 3
. Vậy chọn đáp án B. 14
Câu 12. Cho hình hộp chữ nhật ABCD.A’B’C’D’, AB  a, AD  a 3 , khoảng cách từ A đến a
mặt phẳng (A’BD) bằng 2 . Thể tích khối hộp ABCD.A’B’C’D’ là 3 a 2 3 3a 2 3 3a 2 3 3a 2 A. 8 B. 2 C. 4 D. 8 Giải
Gọi K là hình chiếu của A lên BD, H D' C'
là hình chiếu của A lên A’K A' B' BD  AK Vì   BD  AKA' BD  AA'  BD  AH H
Mà AH  A'K  AH  A'BD C D a  AH  K 2 A B
Trong tam giác vuông A’AK ta có: 1 1 1 1 1 1      2 2 2 AH A'A AK 2 2 2 A'A AB AD 1 4 1 1 8 a 6 Suy ra      A'A  2 2 2 2 3 A'A a a 3a 3a 4 3 a 6 3a 2 Vậy A
V BCD.A'B'C'D'  A'A.AB.AD  .a.a 3  4 4 .
Vậy chọn đáp án C.
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 9
Chuyên đề: Hình học không gian
Chủ đề 3: Thể tích khối lăng trụ
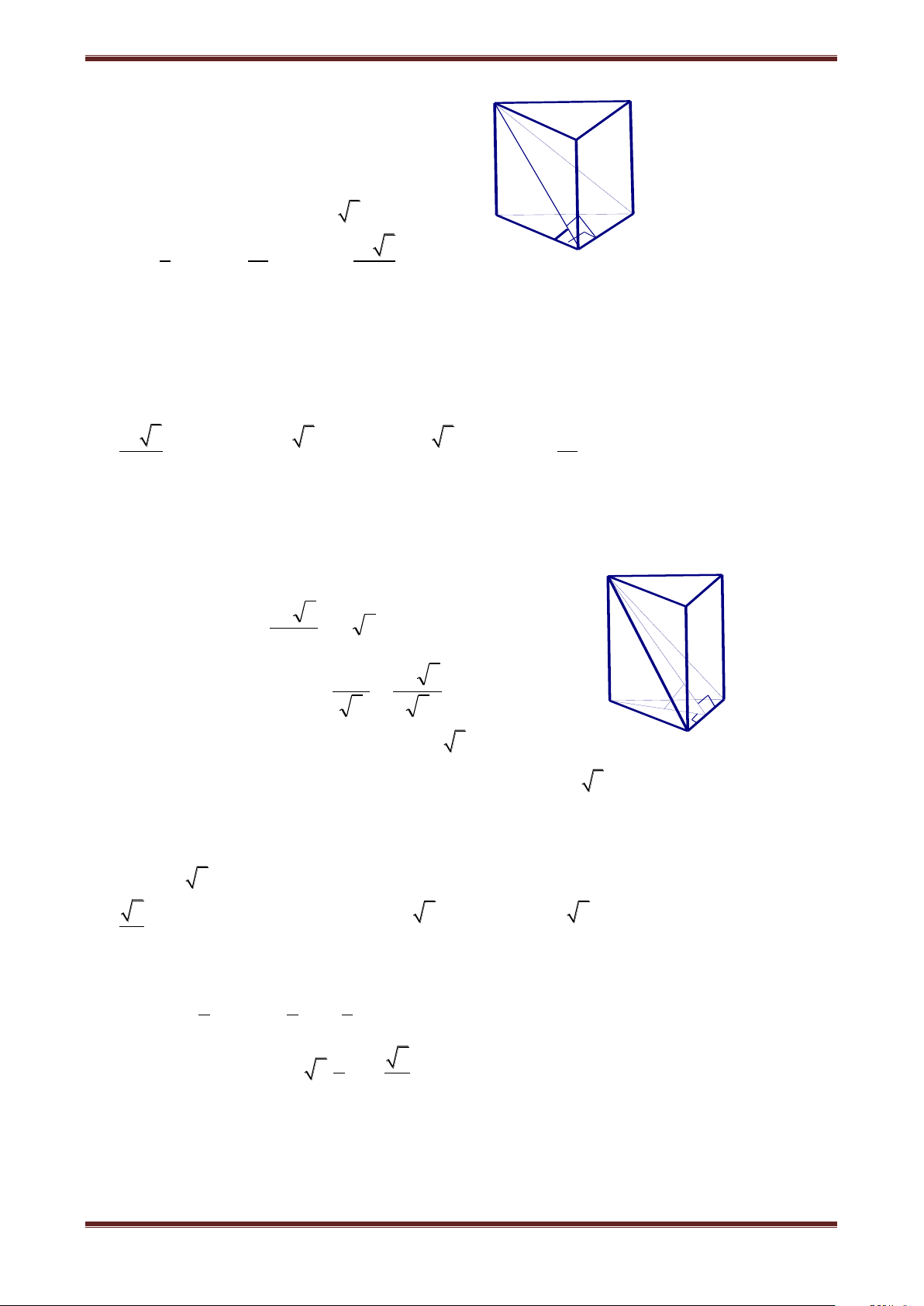
Câu 13. Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại A và AB  a, AC  a 3 0
, mặt phẳng (A’BC) tạo với đáy một góc 30 . Thể tích của khối lăng trụ ABC.A’B’C’ là 3 a 3 3 2a 3 3 3a 2 3 3a 2 A. 4 B. 3 C. 7 D. 7 Hướng dẫn giải 2 1 a 3 A' C' Ta có S A  BC  AB.AC  2 2 . B'
Gọi M là hình chiếu của A trên BC. Suy ra BC  A'MA A C       0 A'MA A'BC , ABC  30 M Do B a 3 0 a AM   AA'  AMtan30  2 2 2 3 a a 3 a 3 Vậy A V BC.A'B'C'  AA'.S A  BC  .  2 2 4 .
Vậy chọn đáp án A.
Câu 14. Cho lăng trụ đứng tam giác đều ABC.A’B’C’, có cạnh đáy bằng a, đường chéo BC’ 0
của mặt bên (BCC’B’) tạo với mặt phẳng (ABB’A’) một góc 30 . Thể tích khối lăng trụ ABC.A’B’C’ theo a. 3 a 6 3 a 6 3 a 6 3 a 6 A. 3 B. 8 C. 6 D. 4 Hướng dẫn giải
Gọi I’ là trung điểm của A’B’, thì A' C' C'I'  A'B' (do A  BC đều)
C'I'  AA'  C'I'  ABB'A' suy I'
ra I' BC' là góc giữa BC’ và mặt B' phẳng (ABB’A’) 0 Suy ra I'BC'  30 . Ta có a 3 C'I' C'I'  BC'   a 3 A C 2 , 0 300 sin30 a Trong B  CC' vuông: B 2 2 2 2
CC'  BC'  BC  2a  CC'  a 2
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 10
Chuyên đề: Hình học không gian
Chủ đề 3: Thể tích khối lăng trụ 3 a 6
Thể tích của khối lăng trụ ABC.A’B’C’ là: V  CC'.S A  BC  4 .
Vậy chọn đáp án D.
Câu 15. Đáy của lăng trụ đứng tam giác ABC.A'B'C' là tam giác ABC vuông cân tại A
có cạnh BC  a 2 và biết A' B  3a. Tính thể tích khối lăng trụ 3 3 3 3 A. a 2 a 6 a 6 a 6 B. 8 C. 6 D. 4 Hướng dẫn giải Ta có ABC 
vuông cân tại A nên A' C' AB  AC  a B' ABC.A'B'C' là lăng trụ đứng  AA'  AB 3a Trong a 2 2 2 2 A A
 A'B: AA'  A'B AB  8a C a a 2  AA'  2a 2 B . 3 Vậy V  AA'.  a 2 A S BC
Vậy chọn đáp án A.
Câu 16. Đáy của lăng trụ đứng tam giác ABC.A'B'C' là tam giác đều cạnh a  4 và biết
diện tích tam giác A'BC bằng 8. Tính thể tích khối lăng trụ. A. 8 8 3 C. 8 3 D. 3 B. 3 Hướng dẫn
Gọi I là trung điểm BC . Ta có A  BC đều nên AB 3 AI 
 2 3 , AI  BC  A'I  BC 2 1 A 2S 'BC A S 'BC  BC.A'I  A'I   4 2 BC AA'  (ABC)  AA'  AI. 2 2 A
 'AI  AA'  A'I  AI  2 Vậy V  AA'.S  8 3 ABC .
Vậy chọn đáp án C.
Câu 17. Cho lăng trụ đứng tam giác ABC.A'B'C' có đáy ABC là tam giác vuông cân tại
B với BA  BC  a ,biết A'B hợp với đáy ABC một góc 600. Tính thể tích lăng trụ. 3 a 3 3 a 3 3 3 C. 2a 3 D. a 3 A. 4 B. 2 Hướng dẫn giải
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 11
Chuyên đề: Hình học không gian
Chủ đề 3: Thể tích khối lăng trụ
Ta có A'A  (ABC)  A'A  AB và
AB là hình chiếu của A'B trên đáy ABC . Vậy A'B,(ABC) o  ABA'  60 . 0 Trong A
 BA' : AA'  AB.tan60  a 3 2 1 a A S BC  BA.BC  2 2 . 3 a 3 Vậy V  AA '. A
S BC  2 . Vậy chọn đáp án B.
Câu 18. Cho lăng trụ đứng tam giác ABC.A'B'C' có đáy ABC là tam giác vuông tại A 0 0
với AC  a , ACB  60 , biết BC' hợp với AA'C'C một góc 30 . Thể tích lăng trụ là 3 3 3 3 A. 3a 3 B. 2a 6 C. a 3 D. a 6 Hướng dẫn giải o A
 BC  AB  AC.tan60  a 3 . Ta có:
AB AC;AB AA'  AB  (AA'C'C)
nên AC' là hình chiếu của BC' trên AA'C'C.     0 BC', AA'C'C  BC'A  30 AB A  C'B  AC'   3a o t an30 2 2 Trong A
 A'C' : AA'  AC'  A'C'  2a 2 2 a 3 A
 BC là nửa tam giác đều nên A S BC  2 . 3 Vậy V  a
6 . Vậy chọn đáp án D.
Câu 19. Cho lăng trụ đứng tam giác ABC.A'B'C' có đáy ABC là tam giác vuông cân tại
B với BA  BC  a ,biết A'B 
C hợp với đáy ABC một góc 600 .Tính thể tích lăng trụ. 3 3a 3 3 a 3 3 a 3 3 a A. 2 B. 2 C. 3 D. 3 Hướng dẫn
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 12
Chuyên đề: Hình học không gian
Chủ đề 3: Thể tích khối lăng trụ Ta có A' C'
A'A  (ABC)& BC  AB  BC  A'B B'    o (A'BC),(ABC)  ABA'  60 0 A
 BA'  AA'  AB.tan60  a 3 A C o 60 2 1 a 3 a 3 B A S BC  BA.BC  V  2 2 . Vậy 2
Vậy chọn đáp án B.
Câu 20. Đáy của lăng trụ đứng tam giác ABC.A'B'C' là tam giác đều cạnh x . Mặt
A'BCtạo với đáy một góc 300 và diện tích tam giác A'BCbằng 8. Tính thể tích khối lăng trụ 3 x 3 3 3 3 B. 3x 3 C. x 3 x A. 3 D. 3 Hướng dẫn giải ABC 
đều  AI BC mà AA'  ABC nên A'I  BC. Vậy     0 A'BC , ABC A'IA 3  0 A' C' 2x 3 B'
Ta có BC  x  AI   x 3 . Ta có 2 0 2AI 2x 3 A
 ' AI : A' I AI : cos30    2x o A 30 C 3 3 I 0 x A'A  AItan30  x 3 B . Ta có A V BC.A'B'C'  x 3 . 3 Mà A
S 'BC  BI.A'I  x.2x  8 x  2 . Do đó A V BC.A'B'C'  x . 3
Vậy chọn đáp án C.
Câu 21. Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông, AB  BC  a , cạnh
bên AA'  a 2. Tính theo a thể tích của khối lăng trụ 2 3 3 3 3 B. 2a C. 2a D. 2 2a A. a 2 Hướng dẫn giải 1 1 1 2 Ta có A S BC  BA.BC  a.a  a . 2 2 2 1 2 2 3 A V BC.A'B'C'  AA'. A S BC  a 2. a  a . 2 2
Vậy chọn đáp án A.
Câu 22. Cho hình hộp đứng có đáy là hình thoi cạnh a và có góc nhọn bằng 600 . Đường
chéo lớn của đáy bằng đường chéo nhỏ của lăng trụ.Tính thể tích hình hộp .
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 13
Chuyên đề: Hình học không gian
Chủ đề 3: Thể tích khối lăng trụ 3 3a 6 3 a 6 3 a 6 3 2a 6 A. 2 B. 3 C. 2 D. 3 Hướng dẫn giải
Ta có tam giác ABD đều nên : BD = a 2 a 3 và SABCD = 2SABD = 2 a 3 Theo đề bài BD' = AC = 2  a 3 2 2 2 D
 D'B  DD'  BD'  BD  a 2 3 a 6 Vậy V = SABCD.DD' = 2 .
Vậy chọn đáp án C.
Câu 23. Cho lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là hình vuông cạnh a và đường
chéo BD' của lăng trụ hợp với đáy ABCD một góc 300. Tính tổng diên tích của các mặt bên
của lăng trụ . 2 a 6 3 a 6 2 a 6 2 4a 6 A. 2 B. 3 C. 4 D. 3 Hướng dẫn giải
Ta có ABCD A'B'C'D' là lăng trụ đứng nên ta có: DD'  (ABCD)  DD'  BD
và BD là hình chiếu của BD' trên ABCD . 0
Vậy góc [BD';(ABCD)] = DBD'  30 0 a 6 B
 DD'  DD'  BD.tan30  3 2 4a 6 S = 4SADD'A' =
3 . Vậy chọn đáp án D.
Câu 24. Cho hình hộp đứng ABCD A'B'C'D' có đáy ABCD là hình thoi cạnh a và BAD =
60o biết AB' hợp với đáy (ABCD) một góc 30o. Tính thể tích của hình hộp 3 3 3 3 A. 3a a 3a D. a B. 4 C. 2 Hướng dẫn A  BD đều cạnh a C' 2 B' a 3  A S BD  4 A' D' 2 a 3  A S BCD  2 A S BD  C 2 B o 30 A  BB' vuông tại B o 60 A D a
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 14
Chuyên đề: Hình học không gian
Chủ đề 3: Thể tích khối lăng trụ o
 BB'  ABt an30  a 3 3 3a Vậy V  B.h  A
S BCD.BB'  2 . Vậy chọn đáp án C.
Câu 25. Cho hình hộp chữ nhật ABCD.A'B'C'D' có AA' = 2a ; mặt phẳng (A'BC) hợp với
đáy (ABCD) một góc 60o và A'C hợp với đáy (ABCD) một góc 30o .Tính thể tích khối hộp chữ nhật. 3 16a 2 3 16a 2 3 16a 2 3 16a 2 A. B. 3 9 C. 3 D. 8 Hướng dẫn giải
Ta có AA'  (ABCD)  AC là hình chiếu của A'C trên (ABCD) . o
Vậy góc[A'C,(ABCD)] = A'CA  30 A' D'
BC  AB  BC  A'B (đl 3  ) . C' B' o
Vậy góc[(A'BC),(ABCD)] = A'BA  60 2a A
 'AC  AC = AA'.cot30o = 2a 3 A D 2a 3 o A  'ABAB = AA'.cot60o = 60 o 30 C 3 B 2 2 4a 6 A
 BC  BC  AC  AB  3 . 3 a 2 Vậy V  AB.BC.A 16 A'  3
.Vậy chọn đáp án C.
Câu 26. Cho lăng trụ đứng ABC.A/B/C/ có đáy ABC là tam giác vuông tại B, AB=a, AC=a
3 , cạnh A/B = 2a. Tính thể tích khối lăng trụ 3 3a 6 3 a 6 3 a 6 3 2a 6 A. 2 B. 4 C. 2 D. 2 Hướng dẫn
* Tam giác ABC vuông tại B C/ A/  2 2 BC = AC  AB  a 2 B/ 2 1 a 2  2a A S BC  AB.BC  2 2
* Tam giác A/AB vuông tại A a 3 A C  / / 2 2 A A  A B  AB  a 3 a 3 B / a 6 * V / / /  A S BC.A A  . ABC.A B C 2
Vậy chọn đáp án C.
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 15
Chuyên đề: Hình học không gian
Chủ đề 3: Thể tích khối lăng trụ
Câu 27. Cho lăng trụ đứng ABC.A/B/C/ có đáy ABC là tam giác vuông tại B, AB=a,
BC  a 2 , mặt bên (A/BC) hợp với mặt đáy (ABC) một góc 300. Tính thể tích khối lăng trụ. 3 a 6 3 a 6 3 a 6 3 a 6 A. 9 B. 4 C. 3 D. 6 Hướng dẫn giải Ta có A/A  (ABC) A/ C/ / (A BC)(ABC)  BC B/ / AB  BC Mà AB = h ( c ABC)A B nên A/B  BC 2a   /  / 0
(A BC),(ABC)  A BA  30  
* Tam giác ABC vuông tại B C 2 1 a 2 A  300 A S BC  AB.BC  a 2 2 a 2 B / 0 a 3
* Tam giác A/AB vuông tại A  A A  AB.tan 30  3 3 / a 6 * V / / /  A S BC.A A 
. Vậy chọn đáp án D. ABC.A B C 6
Câu 28. Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB a 3 , AD = a, AA’ = a, O là
giao điểm của AC và BD. Tính thể tích khối OBB’C’. 3 a 2 3 a 2 3 a 2 3 a 2 A. 9 B. 4 C. 3 D. 12 Hướng dẫn giải 2 2 ABD ó c :DB
AB AD  2a A B O
M là trung điểm BC  OM  (BB 'C ') M D C 2 3 1 1 a a 3 a 3 VS .OM  . .  O BB'C ' BB'C ' B' 3 3 2 2 12 A' C'
Vậy chọn đáp án D. D'
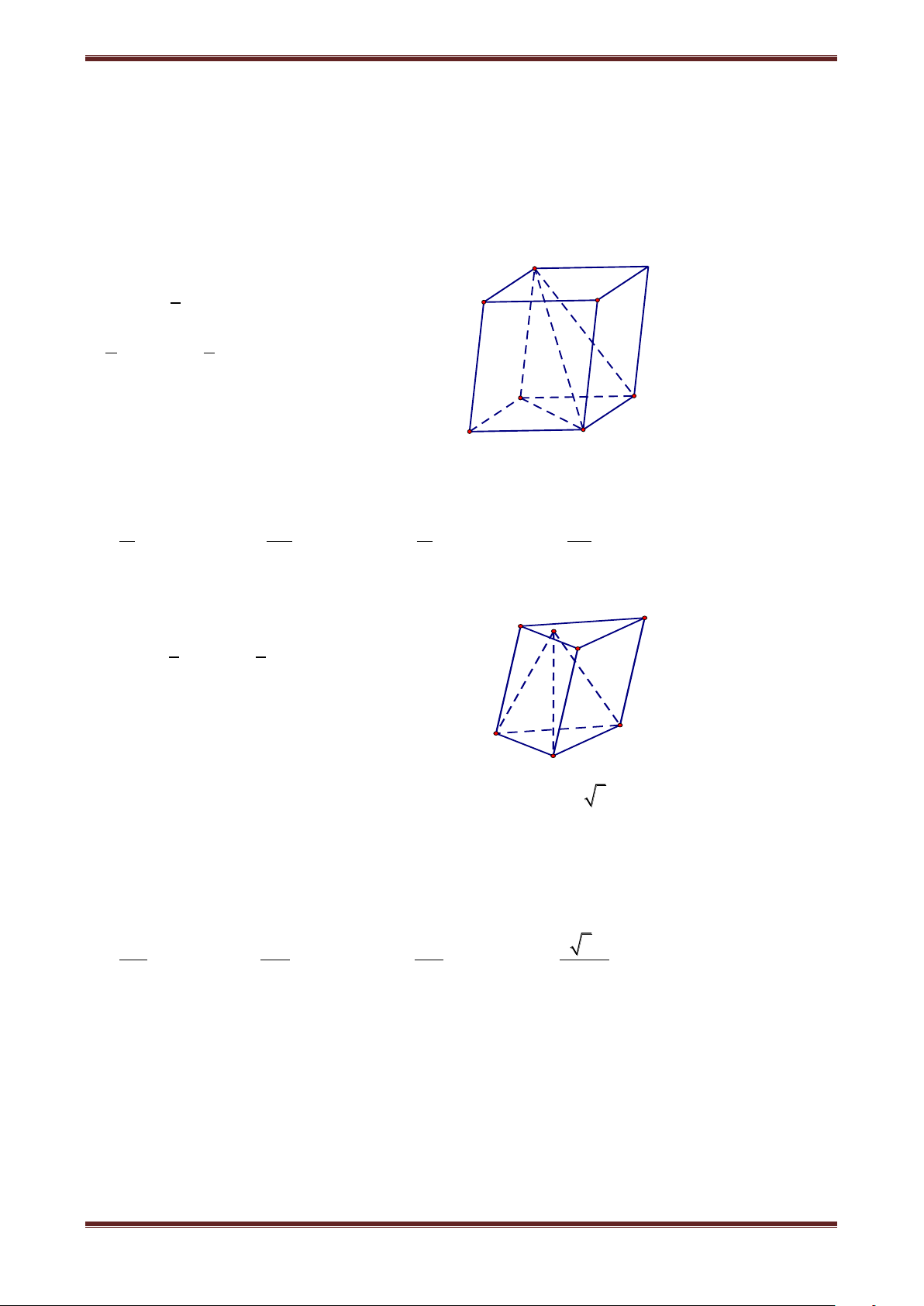
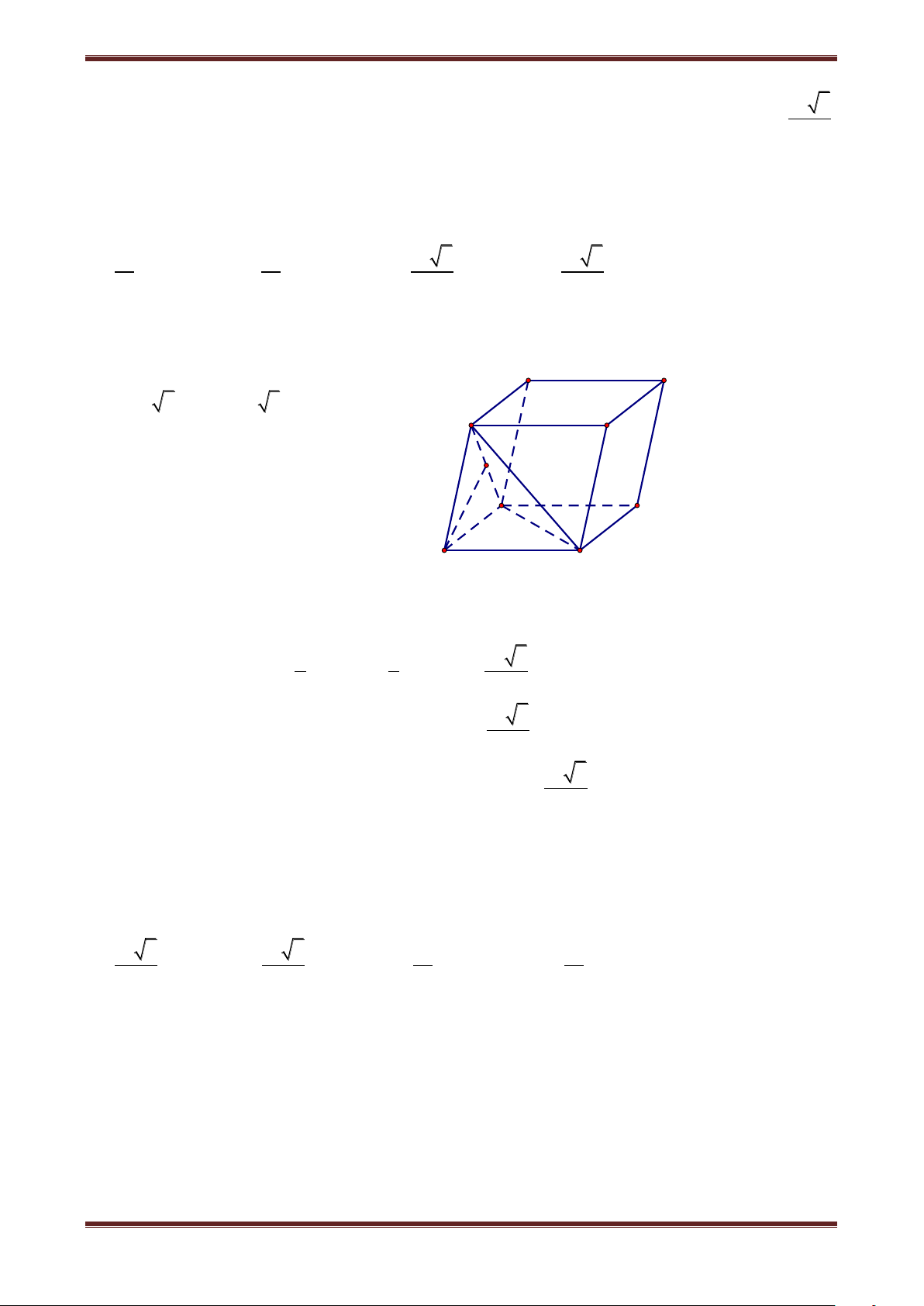
Câu 29. Cho hình lập phương ABCD.A’B’C’D’có cạnh bằng a. Tính thể tích khối tứ diện ACB’D’.
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 16
Chuyên đề: Hình học không gian
Chủ đề 3: Thể tích khối lăng trụ 3 a 3 a 3 a 3 a A. 2 B. 6 C. 3 D. 4 Hướng dẫn giải
Hình lập phương được chia thành: khối ACB’D’ và bốn
khối CB’D’C’, BB’AC, D’ACD, AB’A’D’. B A
Các khối CB’D’C’, BB’AC, D’ACD, AB’A’D’ có diện tích
đáy và chiều cao bằng nhau nên có cùng D C thể tích. 1 1 1 2 3   A' B'
Khối CB’D’C’ có V . a .a a 1 3 2 6 C' 3  Khối lập phương có thể tích: V aD' 2 a 1 1 3 3 3 V
a  4. a a ACB ' D ' 6 3
Vậy chọn đáp án C.
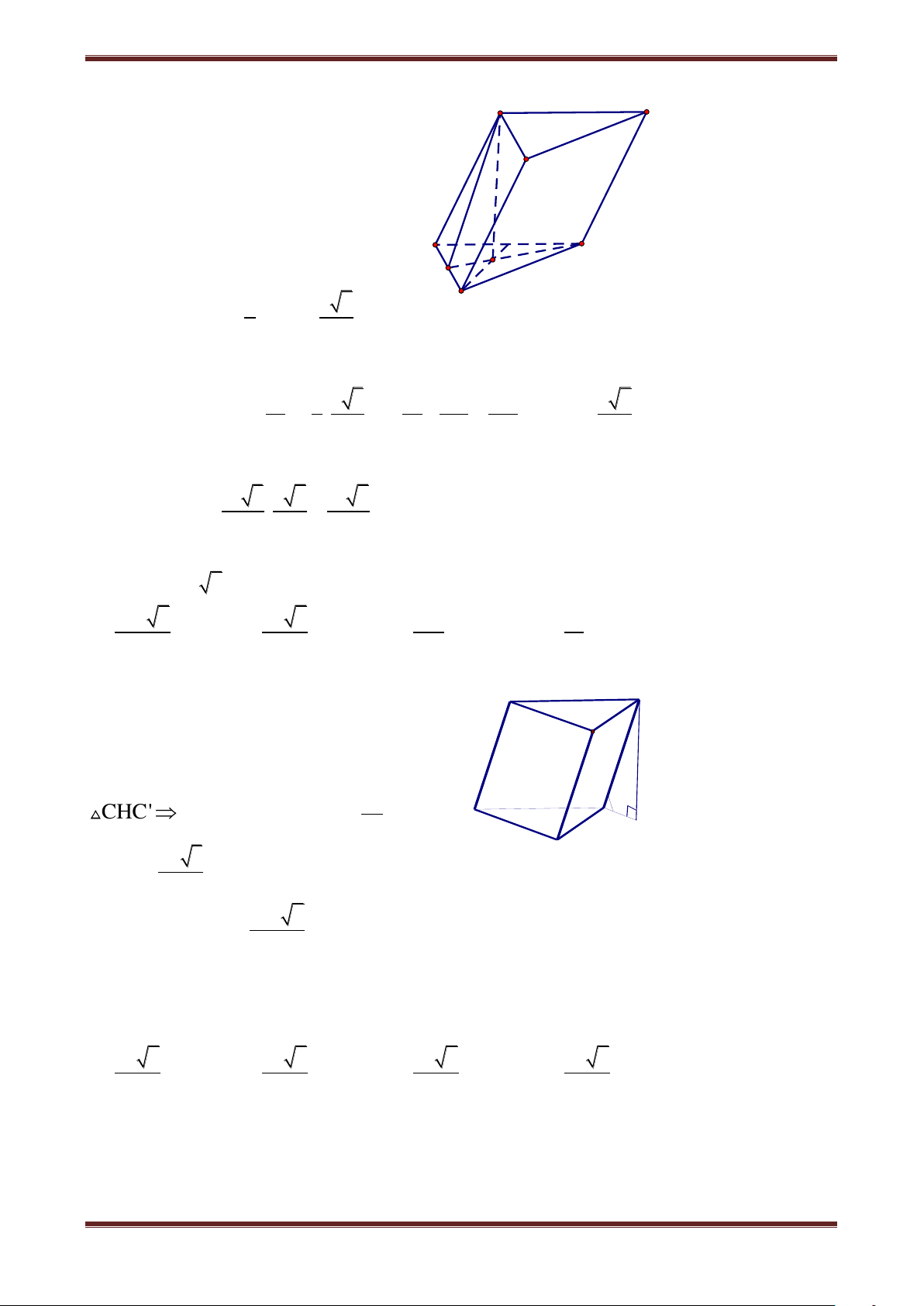
Câu 30. Cho hình lăng trụ đứng tam giác có các cạnh bằng a. E là trung điểm cạnh AC,
mp(A’B’E) cắt BC tại F. Tính thể tích khối CA’B’FE 3 a 3 3 a 3 3 a 3 3 a 3 A. B. 5 4 C. 16 D. 15 Hướng dẫn giải
Khối CA’B’FE: phân ra hai khối E B A CEFA’ và CFA’B’. I F C
Khối A’CEFcó đáy là CEF, đường cao A’A nên 1 V
S .A' A B' A' E C F E C F A' 3 J C' 2 1 a 3 3 a 3 SS  V  EF C ABC A' E C F 4 16 48
Gọi J là trung điểm B’C’. 1
Ta có khối A’B’CF có đáy là CFB’, đường cao JA’ nên VS .A' J A' B ' F C F C B' ; 3 2 1 a 2 3 1 a a 3 a 3 SS  V   F C B' CBB ' A' B ' F C 2 4 3 4 2 24 3 a 3 Vậy : V  A C 'B'FE
. Vậy chọn đáp án C. 16
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 17
Chuyên đề: Hình học không gian
Chủ đề 3: Thể tích khối lăng trụ
DẠNG 2. KHỐI LĂNG TRỤ ĐỀU
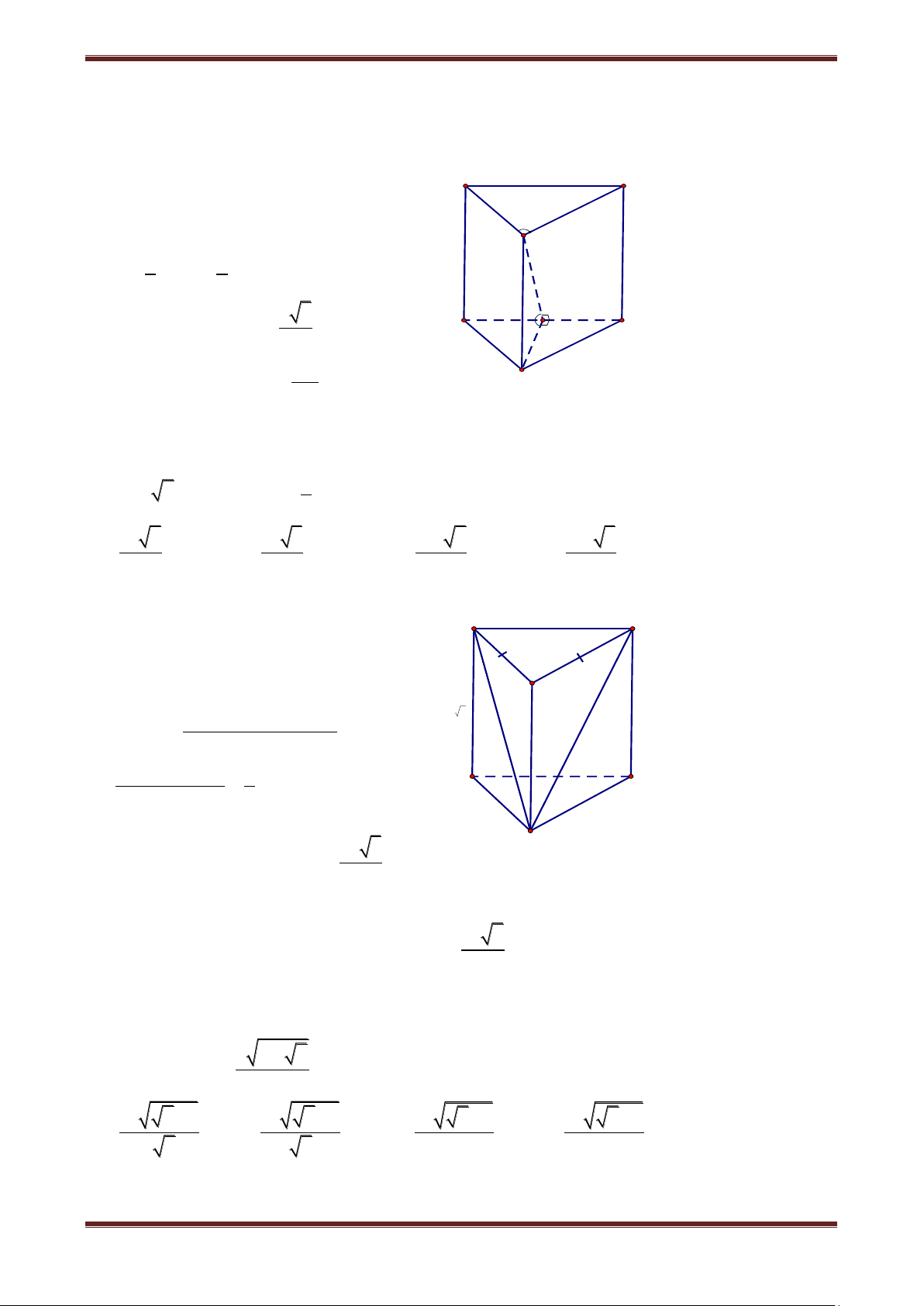
Câu 1. Cho khối lăng trụ tam giác đều ABC.A’B’C’. Mặt phẳng (A’BC) chia khối lăng trụ
thành hai phần. Tỉ số thể tích của hai phần đó bằng: 1 1 1 3 A. ; ; ; 2 B. 3 C. 4 D. 5 Hướng dẫn giải
Mặt phẳng (A’BC) chia khối lăng trụ A' C'
ABC.A’B’C’ thành hai phần là A'.ABC B' và A'B'C'BC Ta có: 1 A V '.ABC  A V BC.A'B'C' 3 2  A C A V 'B'C'BC  A V BC.A'B'C' 3
Suy ra tỉ số thể tích của hai phần đó B 1 bằng .
2 Vậy chọn đáp án A.
Câu 2. Cho khối lăng trụ tam giác đều ABC.A’B’C’. Gọi M là trung điểm cạnh AA’. Mặt
phẳng (MBC) chia khối lăng trụ thành hai phần. Tỉ số thể tích cua hai phần đó bằng: 1 1 1 3 A. ; ; ; 3 B. 5 C. 6 D. 5 Hướng dẫn giải
Mặt phẳng (MBC) chia khối lăng trụ thành hai A' C' phần M.ABC Và MA'B'C'BC . B' 1 1 1 Ta có: M M V .ABC  . h. A S BC  A V BC.A'B'C 3 2 6 5 Suy ra: M V A'B'C'BC  A V BC.A'B'C' 6 A C B 1
Tỉ số thể tích cua hai phần đó bằng: .
5 Vậy ta chọn đáp án B.
Câu 3. Cho hình lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy bằng a và chiều cao bằng a 6
2 . Thể tích khối tứ diện ACA’B’ là 3 a 2 3 a 2 3 a 3 a 2 A. 8 B. 4 C. 8 D. 2 Hướng dẫn giải
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 18
Chuyên đề: Hình học không gian
Chủ đề 3: Thể tích khối lăng trụ 1 A' C' A V CA'B'  C
V .AA'B'  S AA'B'.dC,AA'B' 3  B'
Ta có CM  AB (vì tam giác ABC là tam a 6 giác đều) 2  CM  AA'B'  B hay CM  AA'B' C
 CM  dC,AA'B' A a M 1 1 1 B A V CA'B'  S A
 A'B'.CM  . AA '.A ' B'.CM 3 3 2 3 1 a 6 a 3 a 2  . .a.  6 2 2 8
Vậy chọn đáp án A.
Câu 4. Cho khối lăng trụ tứ giác đều ABCD.A’B’C’D’ có khoảng cách giữa hai đường
thẳng AB và A’D bằng 2 và độ dài đường chéo của mặt bên bằng 5. Vẽ
AK  A'D KA'D. Lúc đó độ dài AK là A. 1 B. 2 C. 3 D. 4 Hướng dẫn giải AB A B' C' ∥ 'B'  AB  ∥ A'B'D
 dA,A'B'D  dAB,A'D D' A' Ta có A'B'  AA'D'D  A'B'  AK K B C
Ta còn có A'D  AK (giả thiết)  AK  A'B'D A D
Vậy AK  d A,A'B'D  dAB,A'D  2 . Vậy chọn đáp án B.
Câu 5. Cho hình lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy bằng a. Mặt phẳng (ABC’)
hợp với mặt phẳng (BCC’B’) một góc  . Diện tích xung quanh của khối lăng trụ là 2 3 3a 2 3a 2 3 3a 2 3a A. B. C. D. 2 tan   3 2 tan   3 2 tan   3 2 tan   3 Hướng dẫn giải
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 19
Chuyên đề: Hình học không gian
Chủ đề 3: Thể tích khối lăng trụ
Gọi H, K lần lượt là hình chiếu của A lên B' C' BC, BC’. A'
Ta có AH  BCC'B'  AH  BC' , do đó
AKH BC'  AKH K a 3 α H
Tam giác AKH vuông tại H và AH  2 B C a a 3 nên AK  A 2sin 
Đặt AA'  x . Xét tam giác C’AB có: 2 2
C'A  CB  x  a , AB  a . a 3 a 3 Nên từ AK  x  2sin ta tính được  2 tan   3 2 3 3a
Diện tích xung quanh của khối lăng trụ xq S  . 2 tan   3
Vậy chọn đáp án C.
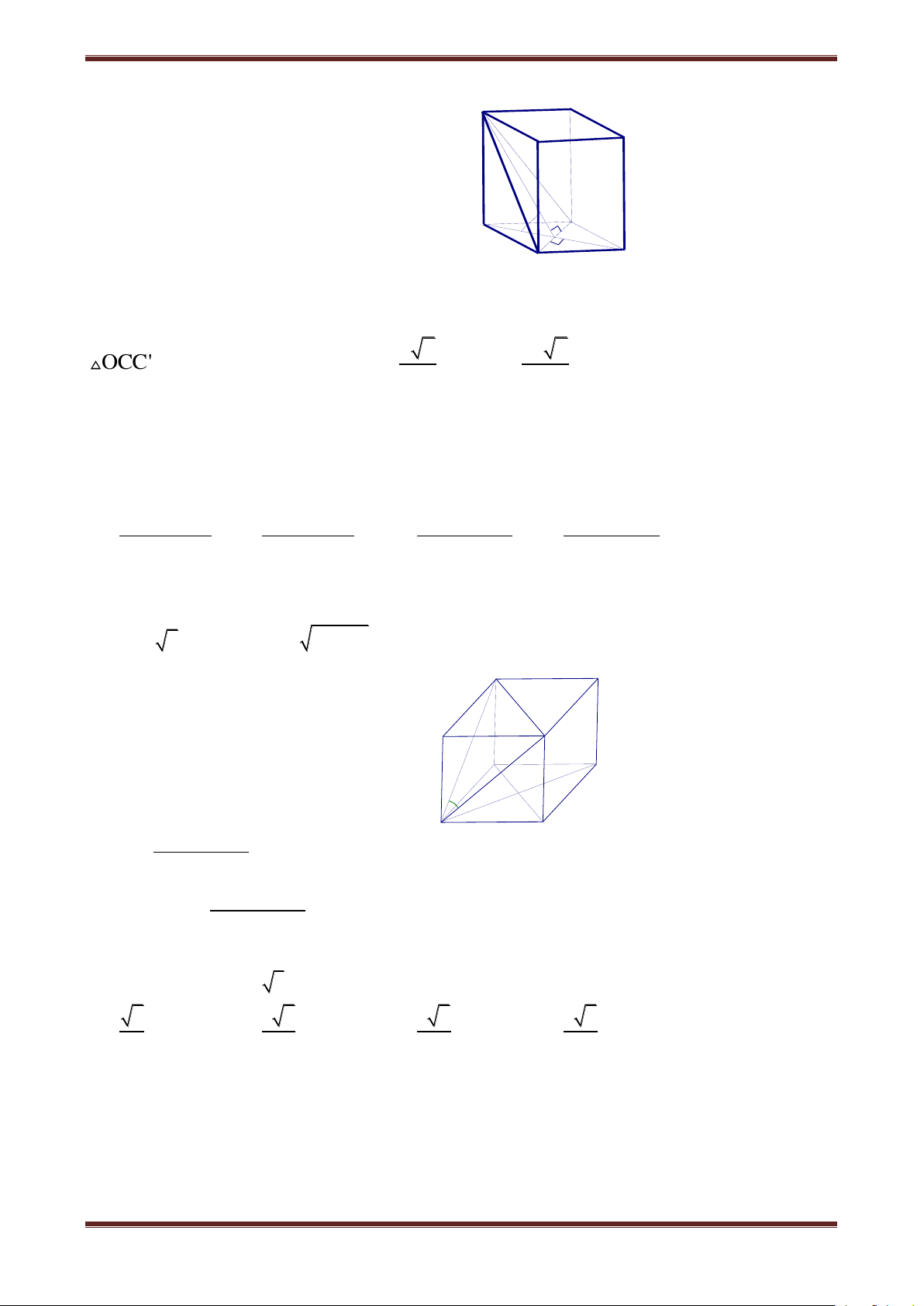
Câu 6. Cho lăng trụ tứ giác đều ABCD.A'B'C'D' có cạnh bên bằng 4a và đường chéo 5a .
Tính thể tích khối lăng trụ này 3 3 3 3 A. 8a B. 9a C. 18a D. 21a Hướng dẫn giải
ABCD.A'B'C'D' là lăng trụ đứng nên
BD2 = BD'2 - DD'2 = 9a2  BD  3a 3a
ABCD là hình vuông  AB  2 2 9a Suy ra B = SABCD = 2 3
Vậy V  B.h  SABCD.AA' 1  8a
Vậy chọn đáp án C.
Câu 7. Cho lăng trụ tứ giác đều ABCD.A'B'C'D' có cạnh đáy a và mặt phẳng (BDC') hợp
với đáy (ABCD) một góc 60o. Tính thể tích khối hộp chữ nhật. 3 a 6 3 a 6 3 a 6 3 a 6 A. 2 B. 4 C. 3 D. 12 Hướng dẫn giải
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 20
Chuyên đề: Hình học không gian
Chủ đề 3: Thể tích khối lăng trụ
Gọi O là tâm của ABCD . Ta có C' D'
ABCD là hình vuông nên OC  BD A' B'
CC'  (ABCD) nên OC'  BD (đl 3  ).
Vậy góc[(BDC');(ABCD)] = COC' = 60o D 0 C Ta có V = B.h = S 60 ABCD.CC' O A a B
ABCD là hình vuông nên SABCD = a2 3 OCC' a 6 a 6
vuông nên CC' = OC.tan60o = 2 . Vậy V = 2 .
Vậy chọn đáp án A.
Câu 8. Cho hình lăng trụ tứ giác đều ABCD.A’B’C’D’ có chiều cao bằng h và góc của hai
đường chéo của hai mặt bên kề nhau phát xuất từ một đỉnh là  . Tính thể tích của lăng trụ theo h và  là 3 h (1 sin) 3 h (1 sin) 3 h (1 cos) 3 h (1 cos) A. sin B. C. D.  sin cos cos Hướng dẫn giải
Gọi x là cạnh của đáy, ta có 2 2
B’D’ = x 2, AB'  AD'  h  x A  B'D' : D' C' 2 2 2
B'D'  AB'  AD'  2AB'.AD'.cos 2 2  2AB'  2AB' cos A' B' 2 2 2 2 2
 2x  2(h  x )  2(h  x )cos D C h O 2 2 2 2 2
 x  (h  x )  (h  x )cos A 2 B 2 h (1 cos)  x  cos . 3 h (1 cos) Vậy V = x2.h = cos
.Vậy chọn đáp án C.
Câu 9. Tính thể tích lăng trụ đều ABC.A’B’C’ biết (ABC’) hợp với đáy góc 600 và diện tích ' 2 tam giác ABC bằng 3a 6 3 3 6 3 3 6 3 3 6 3 A. a a a a 4 B. 8 C. 4 D. 2 Hướng dẫn giải
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 21
Chuyên đề: Hình học không gian
Chủ đề 3: Thể tích khối lăng trụ Gọi H là trung điểm AB A’ C’ CH  AB   C'H  AB B’
 (ABC'),(ABC)  (CH,C'H) 0  CHC'  60 A C 2 2  3a  HC'.AB  2 3a S (1) A  BC' H B Xét H  CC' vuông tại C: HC HC'   AB 3 0 (2) cos60 0 3 2 1 3 CC'  HC'.sin 60  a ; 2 0 2  AB sin 60  a S 2 A  BC 2 2
Từ (1),(2)  AB  a 2;HC'  a 6 3 6 3  .CC'  a V
(đvtt). Vậy chọn đáp án C. ABC.A'B'C' S ABC 4
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 22
Chuyên đề: Hình học không gian
Chủ đề 3: Thể tích khối lăng trụ
DẠNG 3. KHỐI LĂNG TRỤ XIÊNG
Câu 1. Gọi V là thể tích khối hộp ABCD.A’B’C’D’ và 1
V là thể tích của khối tứ diện có
cùng đáy và chiều cao với khối hộp. Hệ thức nào sau đây là đúng: A. V  6 1 V ; B. V  5 1 V ; C. V  4 1 V ; D. V  3 1 V Hướng dẫn giải Ta có: B' 1 A' B V '.BCD  h. B S CD 3 D' 1 1  h. A S BCD  A V BCD.A'B'C'D' 6 6 Hay V  6 1 V . B C
Vậy chọn đáp án A. A D
Câu 2. Cho khối lăng trụ tam giác ABC.A'B'C' có thể tích V. Trên đáy A'B'C' lấy điểm M
bất kỳ. Thể tích khối chóp M.ABC tính theo V bằng V 2V V 3V A. 2 ; B. 3 ; C. 3 ; D. 4 Hướng dẫn giải Ta có: C' A' M 1 1 B' M V .ABC  h. A S BC  V 3 3 .
Vậy ta chọn đáp án C C A B 0
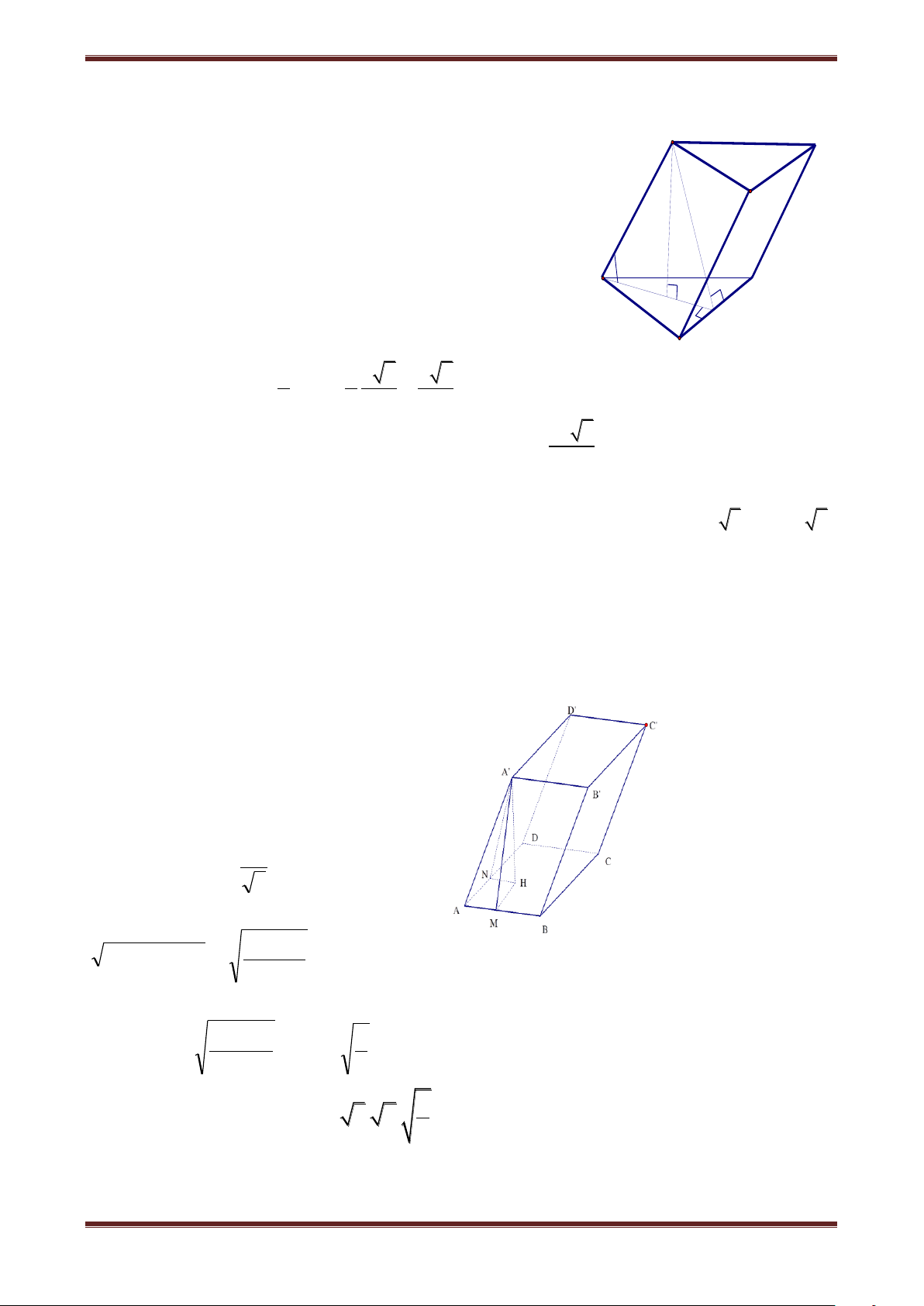
Câu 3. Cho hình lăng trụ ABC.A’B’C’, đáy ABC có AC  a 3, BC  3a , ACB  30 . Cạnh 0
bên hợp với mặt phẳng đáy góc 60 và mặt phẳng A'BC vuông góc với mặt phẳng
ABC. Điểm H trên cạnh BC sao cho HC3BH và mặt phẳng A'AH vuông góc với
mặt phẳng ABC . Thể tích khối lăng trụ ABC.A’B’C’ là 3 3a 3 9a 3 9a 3 3 3a A. 4 B. 4 C. 2 D. 4 Hướng dẫn giải
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 23
Chuyên đề: Hình học không gian
Chủ đề 3: Thể tích khối lăng trụ A'BC  ABC A'
A'AH  ABC  A'H  ABC A'H  A'BC  B' C'  A'AH 0 A Suy ra A'AH  60 2 2 2 0 2
AH  AC  HC  2AC.HC.cos30  a  AH  a 0  A'H  AH.tan 60  a 3 B C H 2 3 3a 3 9a A V BC.A'B'C'  A S BC.A'H  .a 3  4 4
Vậy chọn đáp án B.
Câu 4. Cho hình lăng trụ ABC.A’B’C’, A
 BC đều có cạnh bằng a, AA'  a và đỉnh A’ cách
đều A, B, C. Gọi M là trung điểm của cạnh BC. Thể tích khối lăng trụ ABC.A’B’C’ là 3 a 2 3 a 2 3 a 2 3 2a A. 2 B. 4 C. 8 D. 3 Hướng dẫn giải
Gọi O là tâm tam giác đều ABC A' C'  A'O  ABC B' a 3 2 a 3 Ta có AM  , AO  AM  2 3 3 2 2 2 2 a a 6 A'O  AA'  AO  a   3 3 ; C A O 2 a 3 M S A  BC  4 B 2 3 a 3 a 6 a 2
Thể tích khối lăng trụ ABC.A’B’C’: V  S A  BC.A 'O  .  4 3 4 .
Vậy chọn đáp án B.
Câu 5. Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác vuông tại B, 0
AB  a, ACB  30 ; M là trung điểm cạnh AC. Góc giữa cạnh bên và mặt đáy của lăng trụ 0
bằng 60 . Hình chiếu vuông góc của đỉnh A’ lên mặt phẳng (ABC) là trung điểm H của
BM. Thể tích khối lăng trụ ABC.A’B’C’ là 3 3a 3 3 a 3 3 3 C. 3a 3 D. a 3 A. 4 B. 4 Hướng dẫn giải
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 24
Chuyên đề: Hình học không gian
Chủ đề 3: Thể tích khối lăng trụ
A'H  ABC  A'H là đường cao của A' C' hình lăng trụ. B'
AH là hình chiếu vuông góc của AA’ lên 0 (ABC)  A'AH  60 A V BC.A'B'C'  A'H. A S BC 600 300 A M C
AC  2a, MA  MB  AB  a H a 3 3a B  AH   A'H  2 2 2 2 3 1 1 a 3 3a a 3 3a 3 A S BC  BA.BC  a.a 3   A V BC.A'B'C'  .  2 2 2 2 2 4
Vậy chọn đáp án A. a 10 0
Câu 6. Cho hình lăng trụ ABC.A’B’C’ có AB  2a, AC  a, AA '  BAC  120 2 , . Hình
chiếu vuông góc của C’ lên mặt phẳng (ABC) là trung điểm của cạnh BC. Tính thể tích
khối lăng trụ ABC.A’B’C’ theo a và tính số đo góc giữa hai mặt phẳng (ABC) và (ACC’A’). 3 a 3 3 3a 3 3a 3 3 D. a 3 A. 4 B. 4 C. 4 Hướng dẫn giải
Gọi H là trung điểm BC. Từ giả
thiết suy ra C'H  ABC. Trong A' C' A  BC ta có: B' 2 1 0 a 3 A S BC  AB.AC.sin120  2 2 2 2 2 0 2
BC  AC  AB  2AC.AB.cos120  7a a 10 2 a 7  BC  a 7  CH  C H B 2 1200 a 2a 2 2 a 3  C'H  C'C  CH  A 2 3 3a
Suy ra thể tích lăng trụ V  C' H. A
S BC  4 . Vậy chọn đáp án B.
Câu 7. Cho hình lăng trụ ABCD.A’B’C’D’ có đáy ABCD là hình vuông cạnh bằng a. Hình
chiếu vuông góc của điểm A’ trên mặt phẳng ABCD là trung điểm I của cạnh AB. Biết A’C 2
tạo với mặt phẳng đáy một góc  với tan  
. Thể tích khối chóp A’.ICD là 5 3 a 3 a 3 3 a 3 3 a A. 6 B. 6 C. 3 D. 3
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 25
Chuyên đề: Hình học không gian
Chủ đề 3: Thể tích khối lăng trụ Hướng dẫn giải
heo bài ra ta có IC là hình chiếu B' C'
vuông góc của A’C trên mặt A' phẳng (ABCD). Suy ra D'
A'C,ABCDA'C,CIA'CI  B α Xét ta giác vuông A’IC: C I a 5 2
A'I  IC.tan A'CI  IC.tan  .  a A D 2 5 2 3 1 1 a a
Thể tích khối chóp A’.ICD là: A
V '.ICD  A'I.S ICD  a.  3 3 2 6 (đvtt)
Vậy chọn đáp án A.
Câu 8. Cho khối lăng trụ tam giác ABC.A’B’C’ mà mặt bên ABB’A’ có diện tích bằng 4.
Khoảng cách giữa cạnh CC’ và mặt (ABB’A’) bằng 7. Thể tích khối lăng trụ là A. 10 B. 12 C. 14 D. 16 Hướng dẫn giải
Dựng khối hộp ABCD.A’B’C’D’ ta A' D' 1 có: A V BC.A'B'C'  A V BCD.A'B'C'D' 2 B' C'
Xem khối hộp ABCD.A’B’C’D’ là
khối lăng trụ có hai đáy là ABB’A’ A D và DCC’D’. B Vậy C A V BCD.A'B'C'D'  A S BB'A'.h trong đó
h  d CDD'C',ABB'A'  dCC',ABB'A'  7 1 và A S BB'A'  4  A V BC.A'B'C'  .4.7 14 2
. Vậy chọn đáp án C.
Câu 9. Cho lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, và 7
A'A  A'B  A'C  a 12 . Thể tích khối lăng trụ ABC.A’B’C’ theo a là 3 a 3 a 3 3 3a 3 3 a 3 A. 8 B. 8 C. 8 D. 4 Hướng dẫn giải
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 26
Chuyên đề: Hình học không gian
Chủ đề 3: Thể tích khối lăng trụ
Gọi H là hình chiếu của A trên (ABC) B' C'
Vì A'A  A'B  A'C nên HA  HB  HC , A'
suy ra H là tâm của tam giác đều ABC.
Gọi I, J lần lượt là trung điểm của BC, AB. 2 2 2 2 7a a a A'J  AA'  AJ    I 12 4 3 B C 1 1 a 3 a 3 H 2 2 J a HJ  CJ  .   A'H  A'J  HJ  3 3 2 6 2 A 2 3 a a 3 a 3
Thể tích khối lăng trụ ABC.A’B’C’ là: V  A ' H.S A  BC  .  2 4 8
Vậy chọn đáp án B. 0
Câu 10. Cho lăng trụ ABC.A’B’C’ có đáy ABC là tam giác cân AB  AC  a , BAC  120 và
AB’ vuông góc với đáy (A’B’C’). Mặt phẳng (AA’C’) tạo với mặt phẳng (ABC) một góc 0
30 . Thể tích khối lăng trụ ABC.A’B’C’ là 3 a 3 3 8a 3 a 3 3 a 3 A. 3 B. 3 C. 8 D. 2 Hướng dẫn giải Ta có K B' 2 2 2 2
BC  AB  AC 2AB.ACcosA  3a A' C'  BC  a 3
Gọi K là hình chiếu của B’ lên
A’C’, suy ra A'C'  AB'K Do đó: A a a 1200      0 AKB' A'B'C' , AA'C'  30 B C 0 0 a 3
Trong tam giác A’KB’ có KA'B'  60 , A' B'  a nên B'K  A ' B'sin 60  2 . Suy ra 0 a AB'  B'K.tan30  2. 3 a 3
Thể tích khối lăng trụ: V  AB'.S A  BC  8 .
Vậy chọn đáp án C.
Câu 11. Cho lăng trụ ABC.A’B’C’ có đáy ABC là tam giác cân tại A, 0
AB  AC  a, BAC 120 , hình chiếu của A’ lên mặt phẳng (ABC) trùng với trọng tâm tam
giác ABC, cạnh bên AA'  2a. Thể tích của khối lăng trụ là
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 27
Chuyên đề: Hình học không gian
Chủ đề 3: Thể tích khối lăng trụ 3 3a 3 3 3a 3 a 3 a 3 A. 4 B. 4 C. 4 D. 4 Hướng dẫn giải
Gọi H là tâm của đáy, M là trung điểm B' C'
của cạnh BC, SH  ABC A' 0 a 3 AM  ABsin60   BC  a 3 2
Áp dụng định lý sin ta có: BC H M HA  R   a, B C 0 2sin120 2 2 A'H  A'A  AH  a 3 A 2 1 3 0 a 3 S 3a A V  A'H.S  BC  AB.ACsin120   2 4 . Vậy ABC.A'B'C' A  BC 4
Vậy chọn đáp án B.
Câu 12. Cho hình lăng trụ tam giác ABC.A’B’C’ có BB'  a , góc giữa đường thẳng BB’ và 0 0
mặt phẳng (ABC) bằng 60 , tam giác ABC vuông tại C và BAC  60 . Hình chiếu vuông
góc của điểm B’ lên mặt phẳng (ABC) trùng với trọng tâm của tam giác ABC. Thể tích khối tứ diện A’.ABC là 3 3a 3 9a 3 a 3 9a A. 208 B. 208 C. 108 D. 108 Hướng dẫn giải
Gọi D là trung điểm AC, G là trọng B' C' tâm tam giác ABC     0 B'G ABC  B'BG  60 A' a 3  B'G  BB'sin B'BG  ; 2 a 3a BG   BD  2 4 600 B C Trong A  BC ta có: G D AB 3 BC  A 2 , AB AB AC   CD  2 4 2 2 2 2 2 2 3AB AB 9a BC  BD  BD    4 16 16 2 3a 13 3a 13 9a 3  AB  , AC  , S A  BC  13 26 104
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 28
Chuyên đề: Hình học không gian
Chủ đề 3: Thể tích khối lăng trụ 3 1 9a
Thể tích khối tứ diện A’.ABC là: A V '.ABC  B'G.S A  BC  3 208 .
Vậy chọn đáp án B.
Câu 13. Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác đều cạnh a, cạnh bên bằng a 3
và hình chiếu của A’ lên mặt phẳng (ABC) trùng với trung điểm của BC. Tính thể tích của khối lăng trụ đó. 3 3a 3 a 3 3 3a 3 3 a A. 8 B. 8 C. 8 D. 8 Hướng dẫn giải
Gọi H là trung điểm của cạnh BC A' C'  A'H  ABC B' Tam giác vuông A’HA: 2 2 2 2 3a 3a AH  A'A  AH  3a   4 2 A C 2 a 3 H S A  BC  4 nên B 2 3 3a a 3 3a 3 A V BC.A'B'C'  A'H.S A  BC  .  2 4 8
Vậy chọn đáp án C.
Câu 14. Cho hình lăng trụ ABC.A’B’C’ có độ dài tất cả các cạnh bằng a và hình chiếu của
đỉnh C trên mặt phẳng (ABB’A’) là tâm của hình bình hành ABB’A’. Tính thể tích của khối lăng trụ. 3 a 3 a 2 3 a 2 3 a A. 4 B. 2 C. 4 D. 2 Hướng dẫn giải
Gọi O là tâm hình bình hành ABB’A’. Ta C' có CO  ABB'A' . A'
Vì CA  CB nên OA  OB , suy ra hình B'
thoi ABB’A’ là hình vuông. AB a O Do đó OA   . Suy ra: C 2 2 A 2 2 2 2 a OC a  AC  AO   OC  2 . 2 B 3 1 a 2
Vậy thể tích của khối chóp: C V .ABA'  CO. A S BA'  3 12
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 29
Chuyên đề: Hình học không gian
Chủ đề 3: Thể tích khối lăng trụ 3 a 2 Mà A V BC.A'B'C'  3 C
V .ABA' nên thể tích của khối lăng trụ ABC.A’B’C’ là: A V BC.A'B'C'  4
. Vậy chọn đáp án C. 0 0
Câu 15. Cho hình hộp ABCD.A’B’C’D’ có các cạnh bằng a, BAD  60 , BAA '  90 , 0
DAA'  120 . Thể tích khối hộp là 3 a 3 a 3 a 2 3 a 2 A. 2 B. 4 C. 4 D. 2 Hướng dẫn giải
Từ giả thiết ta tính được BD  a , D' C'
A'B  a 2 , A'D  a 3 nên tam giác A' A’BD vuông tại B. B'
Vì AB  AD  AA' nên hình chiếu H
vuông góc của A lên mặt phẳng C
(A’BD) trung với tâm H của đường D
tròn ngoại tiếp tam giác A’BD (do tam A B
giác đó vuông nên H là trung điểm của A’D) 2 0 a 1 a 2 Ta có AH  AA ' cos60  S  BA'.BD  2 , A'BD 2 2 , 3 a 2
Do đó thể tích khối tứ diện A’.ABD là A V '.ABD  12 . 3 a 2 Ta đã biết A V BCD.A'B'C'D'  A 6V '.ABD nên A V BCD.A'B'C'D'  2 .
Vậy chọn đáp án D.
Câu 16. Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác đều cạnh a. Hình chiếu vuông
góc của A’ lên mặt phẳng (ABC) trùng với tâm O của đường tròn ngoại tiếp tam giác ABC. 0
Cho BAA'  45 . Thể tích của khối lăng trụ đã cho là 3 a 2 3 a 2 3 a 3 a A. 4 B. 8 C. 8 D. 4 Hướng dẫn giải
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 30
Chuyên đề: Hình học không gian
Chủ đề 3: Thể tích khối lăng trụ
Gọi E là trung điểm của AB, ta có: A' C' OE  AB   B' A'O  AB  do A'O   ABC
 AB  A'OE  AB  A'E 0
Tam giác vuông A’EA có A  45 A C
nên là tam giác vuông cân tại E O a E a a 2 B
Suy ra A ' E  EA  , AA '  2 2
Tam giác vuông A’OE (vuông tại O) có: 2 2 2 2 2   2 2 2 a 1 a 3 a 3a 6a a 6 A'O  A'E  OE    .      A'O  4  3 2  4 36 36 6  
Thể tích của khối lăng trụ ABC.A’B’C’: 2 3 a 3 a 6 a 2 V  A S BC.A'O  .  4 6
8 . Vậy chọn đáp án B.
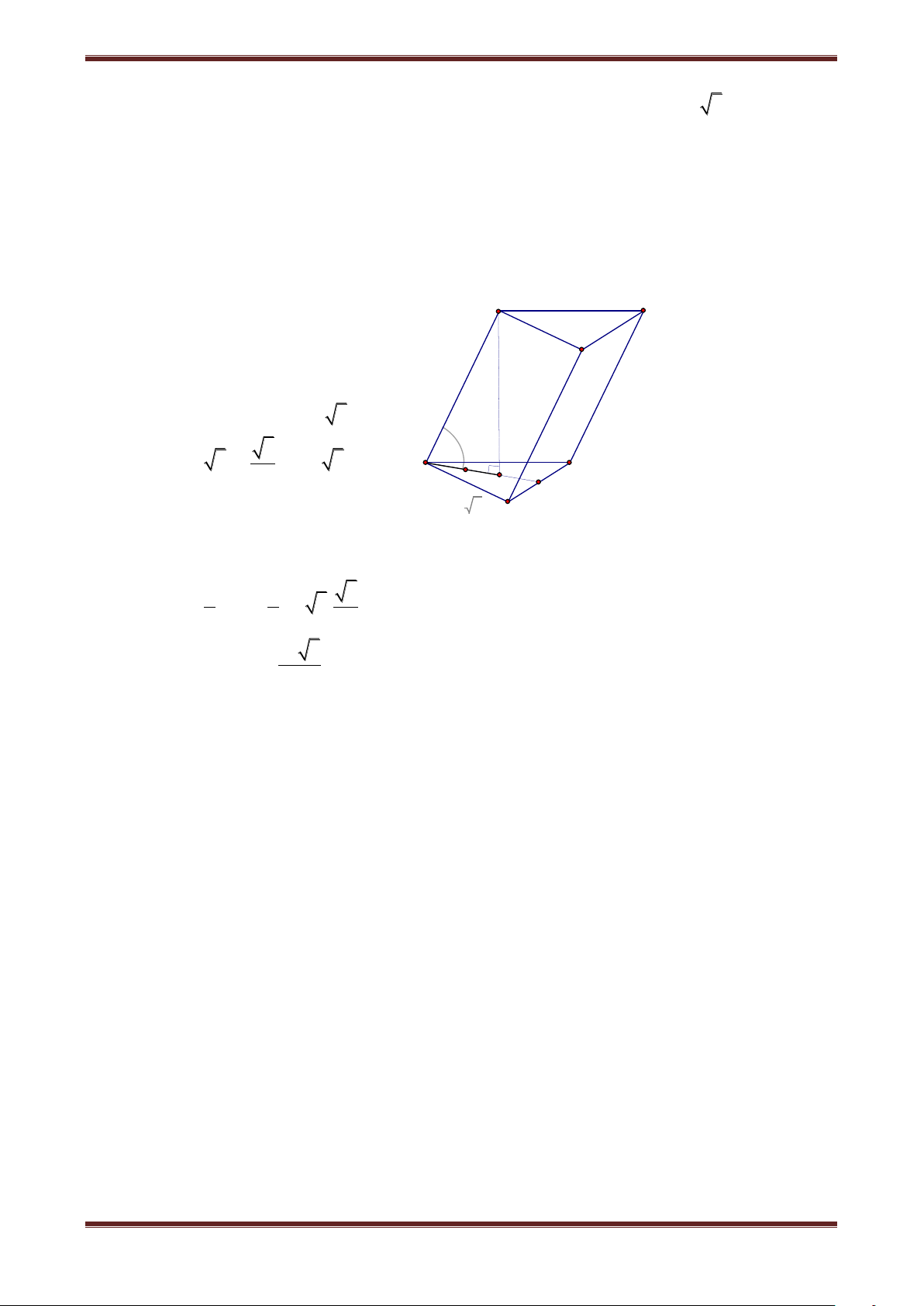
Câu 18. Cho lăng trụ xiên tam giác ABC.A'B'C' có đáy ABC là tam giác đều cạnh a , biết
cạnh bên là a 3 và hợp với đáy ABC một góc 60o . Tính thể tích lăng trụ. 3 3a 3 3 a 3 3 3a 3 a A. 8 B. 8 C. 8 D. 8 Hướng dẫn giải
Ta có C'H  (ABC) CH A' C'
là hình chiếu của CC' trên (ABC) B' o
Vậy [CC',(ABC)]  C'CH  60 0 3a o CHC' C'H  CC'.sin60  C A 60 2 ; H a B 2 a 3 S  ABC = 4 . 3 3a 3 Vậy V = SABC.C'H =
8 . Vậy chọn đáp án A.
Câu 19. Cho lăng trụ xiên tam giác ABC.A'B'C' có đáy ABC là tam giác đều cạnh a . Hình
chiếu của A' xuống (ABC) là tâm O đường tròn ngoại tiếp tam giác ABC biết AA' hợp với
đáy ABC một góc 60 . Tính thể tích khối lăng trụ 3 a 3 3 a 3 3 a 3 3 a 3 A. 3 B. 4 C. 8 D. 2 Hướng dẫn giải
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 31
Chuyên đề: Hình học không gian
Chủ đề 3: Thể tích khối lăng trụ Ta có A'O  (ABC) OA
là hình chiếu của AA' trên (ABC). A' C' o Vậy [AA',(ABC)]  OAA' 6  0 Ta có BB'CC' là hình
bình hành ( vì mặt bên của lăng trụ) B'
AO  BC tại trung điểm H của BC nên BC  A'H (đl 3  ) o 60
 BC  (AA'H) BC  AA' A mà AA'//BB' nên C BC  BB' . O a H
Vậy BB'CC' là hình chữ nhật. B A 2 2 a 3 a 3
 BC đều nên AO  AH   3 3 2 3 o 3 A
 OA'  A'O  AOtan60  a a 3 . Vậy V = SABC.A'O = 4 .
Vậy chọn đáp án B.
Câu 20. Cho hình hộp ABCD.A’B’C’D’ có đáy là hình chữ nhật với AB  3 , AD  7 .
Hai mặt bên (ABB’A’) và (ADD’A’) lần lượt tạo với đáy những góc 450 và 600. Tính thể tích
khối hộp nếu biết cạnh bên bằng 1. A. 3 B. 2 C. 4 D. 8 Hướng dẫn giải
Kẻ A’H  (ABCD) ,
HM  AB, HN AD
A' M AB, A' N AD o o  A'MH  45 ,A'NH  60 Đặt A’H = x . Khi đó 2x A’N = x : sin 600 = 3 AN = 2 2 3  4x2
AA'  A' N   HM 3 Mà HM = x.cot 450 = x 3  4 2 x 3 Nghĩa là x =  x  . 3 7 3 Vậy V 3. 7.  3
ABCD.A’B’C’D’ = AB.AD.x =
.Vậy chọn đáp án A. 7
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 32
Chuyên đề: Hình học không gian
Chủ đề 3: Thể tích khối lăng trụ
Câu 22. Cho lăng trụ ABC.A/B/C/ có đáy ABC là tam giác đều cạnh 2a 3 , hình chiếu
vuông góc của A/ lên mặt phẳng (ABC) trùng với trọng tâm của tam giác ABC, cạnh A/A
hợp với mặt đáy (ABC) một góc 300. Tính thể tích khối lăng trụ. 3 3 3 3 A. 6a B. 8a C. 4a D. 2a Giải
* Gọi M là trung điểm BC, G là trọng tâm của tam giác ABC Ta có A/G  (ABC) A/ C/ / GA = h ( c ABC)A A B/   /  / 0
 A A,(ABC)  A AG  30  
* Tam giác ABC đều cạnh 2a 3 3  300 S  2a 32 2 ABC .  3a 3 4 A C G M
* Tam giác A/AG vuông tại G có 2a 3 B 0 2 2 3 A  30 ,AG  AM  .2a 3.  2a 3 3 2  / 0 2a 3 / 3 A G  AG.tan 30  V  S .A A  6a 3 .Vậy / / / ABC . ABC.A B C
Vậy chọn đáp án A.
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 33
Chuyên đề: Hình học không gian
Chủ đề 3: Thể tích khối lăng trụ
Để sử dụng file word, quý thầy cô vui lòng đóng góp chút kinh phí để tạo
động lực cho tác giả ra đời những chuyên đề khác hay hơn TÊN TÀI LIỆU GIÁ MÃ SỐ TRẮC NGHIỆM THỂ 50K HHKG_TTLT
TÍCH KHỐI LĂNG TRỤ
Quà tăng đính kèm:
File Word 5 đề thi thử THPT Quốc gia 2017 có đáp án và lời giải chi tiết {ĐỀ 15-19}
Hướng dẫn thanh toán
Quý thầy cô thanh toán cho mình qua ngân hàng. Sau khi chuyển khoản, mình sẽ lập tức
gửi tài liệu cho quý thầy cô.
Nếu trong ngày mà thầy cô chưa nhận được thì vui lòng gọi điện trực tiếp cho mình.
Thầy cư. SĐT: 01234332133 NGÂN HÀNG TÊN TÀI KHOẢN TRẦN ĐÌNH CƯ TRẦN ĐÌNH CƯ TRẦN ĐÌNH CƯ SỐ TÀI KHOẢN 4010205025243 0161000381524 55110000232924 CHI NHÁNH THỪA THIÊN HUẾ
THỪA THIÊN HUẾ THỪA THIÊN HUẾ
Nội dung: Họ và tên_email_ma tai liệu
Ví dụ: Nguyễn Thị B_nguyenthib@gmail.com_HHKG_TTKC Lưu ý:
Thầy cô đọc kỹ file PDF trước khi mua, tài liệu mua chỉ
dùng với mục đích cá nhân, không được bán lại hoặc chia sẻ cho người khác.
CHÚC QUÝ THẦY CÔ DẠY TỐT VÀ THÀNH CÔNG TRONG
SỰ NGHIỆP TRỒNG NGƯỜI
Ths. Trần Đình Cư. Gv Chuyên luyện thi THPT Quốc gia, TP Huế. SĐT: 01234332133 Page 34