Chuyên đề trắc nghiệm biểu diễn hình học của số phức Toán 12

Chuyên đề trắc nghiệm biểu diễn hình học của số phức Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

15 8 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 4: Số phức

Môn: Toán 12

Thông tin:

24 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
CHỦ ĐỀ 18: BIỂU DIỄN HÌNH HỌC CỦA SỐ PHỨC
1)Định nghĩa
Mỗi số phức
z x yi= +
được biểu diễn một điểm
( )
;M xy
khi đó
( )
;
OM x y=

trên mặt phẳng phức. Ta
viết
( )
M x yi+
hoặc
( )
Mz
.
Khi đó
22
z OM x y= = +

Nếu điểm
( )
1
Mz
là điểm biểu diễn số phức
1
z
và điểm
là điểm biểu diễn số phức
2
z
thì
12 12
,z z OM ON NM z z OM ON−= − = += +
    
.
2)Phương pháp giải toán
Bài toán 1: Tìm tập hợp điểm biểu diễn số phức
z
thỏa mãn
( ) ( )
;;f zz g zz=
hoặc
( )
;f zz
là số
thực, hoặc
(
)
;
f zz
là số ảo
Phương pháp giải: Đặt
( )
;
z x yi x y z x yi=+ ∈ ⇒=−
thế vào biểu thức ban đầu, biến đổi và kết luận.
Mối liên hệ giữa
x
và
y
Kết luận tập hợp điểm
( )
;M xy
○
0
Ax By C+ +=
Là đường thẳng
0
Ax By C+ +=
○
(
)
( )
22
2
22
22 0
xa yb R
x y ax by c
− +− =
+ − − +=
Là đường tròn
( )
C
có tâm
( )
;I ab
và bán kính
22
R abc= +−
○
( ) ( )
22
2
22
22 0
xa yb R
x y ax by c
−+−≤
+ − − +≤
Là hình tròn
( )
C
có tâm
( )
;I ab
và bán kính
22
R abc= +−
(bao gồm đường tròn và các điểm
bên trong).
○
( ) ( )
22
22
12
R xa yb R≤−+−≤
Là những điểm thuộc miền có hình vành khăn tạo
bởi hai đường tròn đồng tâm
( )
;I ab
và bán kính
lần lượt
1
R
và
2
R
○
2
y ax bx c
= ++
Là một parabol
( )
P
có đỉnh
;
24
b
I
aa
∆

−−


○
22
22
1
xy
ab
+=
với
12
12
2
22
MF MF a
FF c a
+=
= <
Là một elíp có trục lớn
2a
trục bé
2b
và tiêu cự là
( )
22
12
22 ; 0FF c a b a b= = + >>
Một số trường hợp đặc biệt:
Tìm tập hợp điểm biểu diễn số phức
z
thỏa mãn
( ) ( )
z a bi z c di−+ =−+
Gọi
( ) ( ) ( )
; ;; ;M z Aab B cd
lần lượt là các điểm biểu diễn số phức
;z a bi+
và
c di+
.
Khi đó
( )
(
)
z a bi z c di MA MB
−+ =−+ ⇔ = ⇒
Tập hợp điểm biểu diễn số phức
z
là trung trực của
AB
.
Tìm tập hợp điểm biểu diễn số phức
z
thỏa mãn
(
)
(
)
0z a bi R R−+ = >
Gọi
( )
(
)
;;M z I ab
lần lượt là các điểm biểu diễn số phức
z
và
a bi+
Khi đó
(
)
z a bi R MI R
−+ =⇔ =⇒
Tập hợp điểm biểu diễn số phức
z
là đường tròn tâm
( )
;I ab
bán
kính
R
.
Bài toán 2: Tìm tập hợp điểm biểu diễn số phức
w
biết
12
.w zz z
= +
và số phức
z
thỏa mãn
z a bi R−− =
Ta có:
2
1
wz
z
z
−
=
suy ra
( )
2
21 1
1
wz
z a bi R a bi R w z z a bi R z
z
−
−− = ⇔ −− = ⇔ − − + =
Tập hợp điểm biểu diễn
w
là đường tròn bán kính
1
Rz
,
Tổng quát: Tìm tập hợp điểm biểu diễn số phức
w
biết
12
.w zz z= +
và số phức
z
thỏa mãn
0
.
z z a bi R−− =
(thêm yếu tố
0
z
)
Ta có:
2
1
wz
z
z
−
=
suy ra
(
)
1
1
2
00 2
10 0 0
.
z a bi
Rz
wz
a bi
z z a bi R z R w z
zz z z
+
−
+
−− = ⇔ − = ⇔ − − =
Tập hợp điểm biểu diễn
w
là đường tròn bán kính
1
0
Rz
z
.
3)Các ví dụ minh họa
Ví dụ 1: Gọi
M
là điểm biểu diễn của số phức
z
thỏa mãn
3 23zi zz i+= −+
. Tập hợp tất cả các điểm
M
như vậy là:
A. một đường tròn B. một parabol C. một đường thẳng D. một elip
Lời giải
Gọi
( )
;z x yi x y=+∈
khi đó ta có:
( )
( )
32 3x yi i x yi x yi i+ += − − + +
( ) (
) ( ) ( )
22
22
3 1 33 9 9 1 9 1xyixyi x y x y⇔++=−−⇔++=+−
22
4
8 18 0
9
xy y x⇔ + =⇔=−
nên tập hợp là Parabol. Chọn B.
Ví dụ 2: Tìm tập hợp các điểm biểu diễn số phức
z
sao cho
( )
( )
11zz
−+
là số thực.
A. một đường tròn B. một parabol C. một đường thẳng D. một elip
Lời giải
Đặt
z x yi= +
ta có:
( )
( )
( )( ) ( ) ( )
11 1 1 1 1z z x yi x yi x yi x yi

− += +− −+= −+ +−

( )
(
) (
)
(
)
(
)
2
11 1 1x x y x y yx i

= − ++ + − −+ +

là số thực nên ta có:
0xy y xy y− ++ +=
0y⇔=
. Vậy điểm biểu diễn số phức
z
là đường thẳng
0
y =
. Chọn C.
Ví dụ 3: Gọi
M
là điểm biểu diễn của số phức
z
thỏa mãn
22zi zz i−= −+
. Tập hợp tất cả các điểm
M
như vậy là:
A. một đường tròn B. một parabol C. một đường thẳng D. một elip
Lời giải
Đặt
( )
;z x yi x y z x yi=+ ∈ ⇒=−
Ta có:
( ) ( ) ( )
2
22
2
2 2 2 1 22 1 1
4
x
z i z z i x y i yi i x y y y−=−+⇔ +− = +⇔+− =+ ⇔=
Tập hợp điểm biểu diễn
z
là parabol
2
4
x
y =
. Chọn B.
Ví dụ 4: Gọi
M
là điểm biểu diễn của số phức
z
thỏa mãn
( )
1z i iz−= +
. Tập hợp tất cả các điểm
M
như vậy là đường tròn có bán kính
A.
2
R =
B.
2R =
C.
4R
=
D.
1R =
Lời giải
Đặt
( )
;z x yi x y=+∈
. Ta có:
( )
( )
1 12zi iz zi iz z−= + ⇒ −= + =
(
)
2
22 2 2 2
2 12 2
x yi i x y x y x y⇒ + −= + ⇔ + − = +
(
)
2
2
12xy⇔+− =⇒
Tập hợp điểm
M
là đường tròn có bán kính
2R =
. Chọn B.
Ví dụ 5: Biết điểm biểu diễn số phức
z
thỏa mãn
( )
( )
21z iz+−
là số thực là một đường thẳng, khoảng
cách từ gốc tọa độ đến đường thẳng đó bằng
A.
2d =
B.
2
5
d =
C.
2d =
D.
4
5
d =
Lời giải
Đặt
( )
;z x yi x y=+∈
ta có:
( ) ( )
21x y i x yi

+ + −−

là số thực
( )( )
12 0x y xy⇒− +−=
2 2 0 2 20xy y x xy x y⇔ −+ −− =⇔ −−=
Vậy tập hợp các điểm biểu diễn
z
là đường thẳng
(
) ( )
2
2 20 ;
5
x y dO− − = ∆⇒ ∆=
. Chọn B.
Ví dụ 6: Trong mặt phẳng tọa độ
Oxy
, tập hợp điểm biểu diễn các số phức
z
thỏa mãn điều kiện
( )
22
zi i−+=
là đường tròn
A.
( ) ( )
22
1 24xy− ++ =
B.
( ) ( )
22
1 24xy− +− =
C.
( )
( )
22
1 24
xy+ ++ =
D.
( ) (
)
22
1 24
xy+ +− =
Lời giải
Ta có:
( )
2
2 2 . 2 12 2
i
zi i i z z i
i
+
− + = ⇔ − = ⇔ −+ =
Do đó tập hợp điểm biểu diễn
z
là đường tròn
( ) ( )
22
1 24
xy− ++ =
. Chọn A.
Ví dụ 7: [Đề thi THPT Quốc gia năm 2018] Xét các số phức
z
thỏa mãn
( )
( )
2ziz
++
là số thuần ảo.
Trên mặt phẳng tọa độ, tập hợp tất cả các điểm biểu diễn số phức
z
là một đường tròn có bán kính bằng
A. 1 B.
5
,
4
C.
5
2
D.
3
2
Lời giải
Đặt
( )
;z x yi x y=+∈
ta có:
(
)
( )
( )( )
22
w z i z x yi i x yi
=+ +=−+ ++
( )
( )
12x y i x yi

= +− + +

Phần thực của số phức
w
là:
( )
2
1x yy−−
Do
w
là số thuần ảo nên phần thực của nó bằng 0 suy ra
(
)
(
) (
)
2
2
22
15
21 2 0 1
24
xx yy x y x y x y

+ −− = + + −=⇔ + + − =


Do đó tập hợp điểm biểu diễn số phức
z
là đường tròn tâm
1
1;
2
I

−


bán kính
5
2
R =
. Chọn C.
Ví dụ 8: [Đề minh họa BGD và ĐT 2017]
Cho các số phức
z
thỏa mãn
4z =
. Biết rằng tập hợp các
điểm biểu diễn số phức
( )
34w iz i=++
là một đường tròn. Tìm bán kính của đường tròn đó
A.
4r =
B.
5
r =
C.
20r =
D.
22r =
Lời giải
Ta có:
4 20
34 34 5
wi
wi wi
z z wi
ii
−
−−
= ⇒ = = =⇔ −=
++
⇒
tập hợp là đường tròn
( )
0;1 ; 20Ir=
.
Chọn C.
Ví dụ 9: Cho các số phức
z
thỏa mãn
2z =
và số phức
w
thỏa mãn
( )
. 34 2iw i z i=−+
. Biết rằng tập hợp
điểm biểu diễn số phức
w
là một đường tròn. Tính bán kính đường tròn đó:
A.
5R =
B.
10R =
C.
14R =
D.
20R =
Lời giải
Ta có:
( ) ( )
2 3 4 3 4 5.2 10iw i i z i z−=− =− = =
Do đó
. 2 10 2 10iw w
−= ⇔ −=
, đặt
( )
;w x yi x y=+∈
thì
2 10x yi−−=
( )
2
2
2 100 10xy R
⇔ − + = ⇒=
. Chọn C.
Ví dụ 10: Cho số phức
z
thỏa mãn
3
2 10
12
i
z
i
−
+=
−
. Biết tập hợp các điểm biểu diễn số phức
w
thỏa mãn
( )
1 10i w iz+ − +=
là một đường tròn. Tìm bán kính của đường tròn đó.
A.
52R =
B.
5R =
C.
10R =
D.
50R =
Lời giải
Ta có:
( ) ( )
3
2 10 1 2 10 1 1 10 1 5 2 1
12
i
z iz izi zi
i
−
+ = ⇔ + + = ⇔ + +− = ⇔ +− =
−
Lại có:
( )
( )
11
1
iw
z iw i
i
++
= =−−
thế vào (1) ta được
( )
1 1 2 52iw i+ +− =
( )
13 13
1 52 5
22 22
iwi wi⇔ − −+ = ⇔ −+ =
. Do đó suy ra
5
R
=
. Chọn B.
Ví dụ 11: Cho số phức
z
thỏa mãn
55z i iz+= −
. Biết rằng tập hợp các điểm biểu diễn cho số phức
w
thỏa mãn
(
) ( )
1 68 3 2w i iz i−= − ++
là một đường tròn. Xác định tọa độ tâm
I
của đường tròn đó
A.
( )
1; 5I −
B.
( )
1; 5I −
C.
15
;
22
I

−


D.
15
;
22
I

−


Lời giải
Ta có:
(
)
(
) ( )
22
22
5 5 5 51 5 25 51 5z i iz x y i xi y x y x y
+=−⇔++=−+⇔ ++=++
( )
22 22
24 24 1 1xy xy z
⇔ + = ⇔+=⇔=
Khi đó
( ) ( )
( )
( )
1 68 3 2 1 3 2 68w i iz i w i i iz
− = − + +⇔ −− −= −
Lấy modun 2 vế ta được
( )
32
1 3 2 10 1 10
1
i
w i i iw
i
+
−− − = ⇔− − =
−
15
52
22
wi
−

⇔− + =


. Do đó tập hợp điểm biểu diễn
z
là đường tròn tâm
15
; ; 52
22
IR

−=


Chọn
D.
Ví dụ 12: Cho số phức
z
thỏa mãn
3
43 5
1
i
zi
i
+
++ =
−
. Biết rằng tập hợp các điểm biểu diễn số phức
w
thỏa mãn
( )
34 2w iz i=++
là một đường tròn. Phương trình đường tròn đó là:
A.
( ) ( )
22
10 3 5xy
+ ++ =
B.
( ) ( )
22
10 3 25xy+ ++ =
C.
( )
( )
22
10 3 5
xy− +− =
D.
( ) (
)
22
10 3 25
xy− +− =
Lời giải
Ta có:
(
)
3
43 5 12 43 5 12 2 5 2 1
1
i
z i iz i izi zi
i
+
++ = ⇔ + ++ = ⇔+ +−= ⇔ +−=
−
Mặt khác
2
34
wi
z
i
−
=
+
suy ra
10 3
2
2 1 1 10 3 5
34 34
wi
wi
i wi
ii
++
−
+−=⇔ =⇔ + + =
++
Do đó phương trình đường tròn biểu diễn
w
là
( ) ( )
22
10 3 25
xy
+ ++ =
. Chọn B.
Ví dụ 13: Tập hợp điểm biểu diễn số phức
23
wz i= +−
, biết
2
2 3. 1z i zz
+= +
là đường tròn có tâm
A.
B.
(
)
3; 5I
−
C.
( )
3; 1I −−
D.
( )
3; 5
I −
Lời giải
Đặt
( ) ( )
,, ,w x yi x y z a bi a b=+ ∈=+ ∈
. Ta có:
( )
23
23
21
xa
x yi a bi i
yb
= +
+ = + +−⇔
= −
Ta có:
(
)
(
)
(
)
2
2
2
22 2 2 2
2 3.1 2 21 3 1 4 21 3 3 1z i zz a b a b a b a b
+ = +⇔ + + = + +⇔ + + = + +
( ) ( )
( )
22
2 22
22 2
31
4 0 2 4 2 4 3 5 16
22
xy
ab b a b x y
−+

⇔++=⇔++ =⇔ + + =⇔− ++ =


Vậy tập hợp các điểm biểu diễn
w
là đường tròn tâm
( )
3; 5
I −
, bán kính
4
R =
. Chọn D.
Ví dụ 14:
Tập hợp các điểm biểu diễn số phức
(
)
12w iz
= +
biết rằng số phức
z
thỏa mãn điều kiện
2
2z i zz+− =
là đường thẳng
d
. Khoảng cách từ
O
đến
d
bằng
A.
5
4
B.
5
2
C.
25
4
D.
25
2
Lời giải
Đặt
w x yi= +
và
( )
;;;z a bi a b x y=+∈
ta có:
( )
( ) ( )
12 2 2x yi iabi a b abi+=+ + =−+ +
2
2
5
22
5
yx
b
xa b
y ab x y
a
−
=
= −
⇔⇔

=++
=
Mặt khác
( ) ( )
( )
22
2
22
2 2 1 4 2 50z i zz a b a b a b+− = ⇔ + + − = + ⇔ − +=
48 24
50 8 6 250
55
xy yx
xy
+−
⇔ − +=⇔ + + =
Vậy tập hợp điểm biểu diễn số phức
w
là đường thẳng
( )
:8 6 25 0dxy++=
Do đó
( )
25 5
;
10 2
d Od
= =
. Chọn B.
Ví dụ 15: Cho các số phức
z
thỏa mãn
12zi z i
− = −+
. Tập hợp các điểm biểu diễn số phức
(
)
21w iz
=−+
trên mặt phẳng tọa độ là một đường thẳng. Diện tích tam giác tạo bởi đường thẳng đó với
các trục tọa độ bằng
A.
81
7
B.
9
7
C.
9
14
D.
81
14
Lời giải
Ta có:
( )
1
21
2
w
w iz z
i
−
= − +⇒ =
−
Do đó
( )( )
11
12 12 w1 (2i) 1 2 12
22
ww
zi z i i i i w i i
ii
−−
− = −+ ⇔ − = −+ ⇔ −− − = −+ − −
−−
22 15
w iw i⇔ − − = −+
Do đó tập hợp điểm biểu diễn của
w
là trung trực
d
của
AB
với
( ) ( )
2; 2 ; 1; 5AB−
Ta có: trung điểm của
AB
là
( )
33
; ; 1; 7 : 7 9 0
22
n AB d x y

− = = ⇒ + +=



Khi đó
d
cắt các trục tọa độ tại
(
)
9 1 81
0; ; 9; 0 .
7 2 14
OMN
M N S OM ON
−

−⇒ = =


. Chọn D.
Ví dụ 16:
Biết tập hợp các điểm
M
biểu diễn hình học số phức
z
thỏa
4 4 10zz
++−=
là mộ
t Elip
( )
E
. Phương trình Elip
( )
E
là:
A.
22
1
53
xy
+=
B.
22
1
25 16
xy
+=
C.
22
1
25 9
xy
+=
D.
22
1
16 9
xy
+=
Lời giải
Gọi
( ) ( )
12
4; 0 ; 4; 0FF−
và lần lượt là các điểm biểu diễn số phức
4; 4−
và
z
Ta có:
1 2 12
4 4 10 10 8z z MF MF F F++−= ⇔ + = > =
Khi đó tập hợp điểm
M
là Elip có
22
5
2 10; 2 8 4
3
a
ac c
b ab
=
= =⇒=
= −=
Phương trình Elip là:
22
1
25 9
xy
+=
. Chọn C.
Ví dụ 17: Trên mặt phẳng phức, gọi
M
là điểm biểu diễn số phức
( ) ( )
2
24zii=+−
và gọi
ϕ
là góc tạo
bởi chiều dương trục hoành và véc-tơ
OM

. Tính
cos 2
ϕ
.
A.
87
cos 2
475
ϕ
= −
B.
87
cos 2
475
ϕ
=
C.
87
cos 2
425
ϕ
= −
D.
87
cos 2
425
ϕ
=
Lời giải
Ta có
( )
16 13 16;13
z iM
=+⇒
và nằm ở góc phần tư thứ nhất nên ta có
( )
2
22
16 16 87
cos cos ; cos 2 2cos 1
425
425
16 13
OM i
ϕ ϕϕ
= = = ⇒ = −=
+

. Chọn D.
Ví dụ 18: Trên mặt phẳng tọa độ
Oxy
, lấy
M
là điểm biểu diễn số phức
12zi=−+
và gọi
ϕ
là góc lượng
giác tia đầu
Ox
, tia cuối
OM
. Tính
tan 2
ϕ
.
A.
4
tan 2
3
ϕ
= −
B.
3
tan 2
4
ϕ
= −
C.
4
tan 2
3
ϕ
=
D.
tan 2 1
ϕ
= −
Lời giải
Ta có
( )
1 2 1; 2z iM=−+ ⇒ −
và nằm ở góc phần tư thứ III nên ta có
(
)
(
)
2
2
1 1 sin 2 4
cos cos ; tan 2
cos 2 3
5
12
OM i
ϕ
ϕϕ
ϕ
−
= = =−⇒ = =
−+

. Chọn C.
Ví dụ 19: Cho hai số phức
12
,zz
thỏa mãn
12
2, 3zz
= =
và nếu gọi
,
MN
lần lượt là điểm biểu diễn
của
12
,z iz
thì
30MON = °
, Tính
22
12
4
Pz z= +
.
A.
5
P =
B.
47P
=
C.
33P =
D.
52
P =
Lời giải
Ta có
( )
2
2 22
12
4 4 2. 2P z iz a b a b a b=− =−=− +
. Với
12
2; 3a z a b iz b=⇒= = ⇒=
Lại có
22 2
2 4. . .cos 30 4 4 2 2ab a ab b ab− = − ° + = → − =
Và
22 2
2 4. . .cos30 4 28 2 2 7
ab a ab b ab+ = + ° + = → + =
Vậy
2 . 2 2.2 7 4 7P a ba b=− += =
. Chọn B.
BÀI TẬP TỰ LUYỆN
Câu 1: Giả sử
,
AB
theo thứ tự là điểm biểu diễn của số phức
12
,zz
. Tính độ dài của
AB

.
A.
21
zz+
B.
21
zz−
C.
12
zz
+
D.
12
zz−
Câu 2: (Sở GD & ĐT TP. Hồ Chí Minh 2017) Tìm điểm biểu diễn của
5
34
z
i
=
−
A.
34
;
55
M

−


B.
34
;
55
N



C.
34
;
55
P

−


D.
( )
3; 4Q −
Câu 3: Tìm điểm biểu diễn của số phức
z
thỏa mãn
( )
2
12zi i= +
A.
( )
1
4; 3M −−
B.
( )
2
4; 3M −
C.
( )
3
4;3M −
D.
(
)
4
4;3M
Câu 4: Tìm điểm biểu diễn của số phức
z
thỏa mãn
( ) ( )
95 72 0iz i+ +− =
A.
( )
1; 2M
B.
(
)
1;1N
C.
( )
2; 2P
D.
11
;
22
Q

−


Câu 5: Tìm điểm biểu diễn của số phức
z
thỏa mãn
( )
1 53iz i−=+
A.
( )
1; 2M
B.
(
)
4;1
N
C.
(
)
1; 4P
D.
( )
1; 4Q −−
Câu 6: Điểm
M
trong hình vẽ bên là điểm biểu diễn số phức
A.
2zi=−+
B.
12
zi= −
C.
2zi= +
D.
12zi
= +
Câu 7: Điểm
M
trong hình vẽ bên là điểm biểu diễn số phức
A.
42zi= +
B.
24
zi= +
C.
24zi=−+
D.
42zi= −
Câu 8: Điểm
M
trong hình vẽ bên là điểm biểu diễn số phức
A.
12zi=−+
B.
12zi= +
C.
12zi= −
D.
2zi= +
Câu 9: Điểm
M
trong hình vẽ bên là điểm biểu diễn số phức
A.
3zi=−+
B.
13zi
= −
C.
13
zi=−−
D.
13zi= +
Câu 10: Điểm
M
trong hình vẽ bên là điểm biểu diễn số phức
A.
( )( )
12z ii=+−
B.
( )( )
1 23zi i
=+−
C.
32i
z
i
−
=
D.
23
i
z
i
=
+
Câu 11: (Đề thi THPTQG năm 2017 – Đề 101) Cho số phức
12zi= −
. Điểm nào dưới đây là điểm biểu
diễn của số phức
w iz=
trên mặt phẳng tọa độ?
A.
( )
1; 2Q
B.
(
)
2;1
N
C.
(
)
1; 2M −
D.
( )
2;1P
−
Câu 12: (Đề thi THPTQG năm 2017 – Đề 104) Cho hai số phức
12
1 2, 3z iz i=− =−+
. Tìm điểm biểu
diễn của số phức
12
zz z= +
trên mặt phẳng tọa độ
A.
( )
4; 3N −
B.
( )
2; 5M
−
C.
( )
2; 1P −−
D.
( )
1; 7Q −
Câu 13: Điểm
M
trong hình vẽ bên là điểm biểu diễn số phức
z
. Tìm số phức
z
A.
13zi=−−
B.
3zi= −
C.
13zi= +
D.
13zi= +
Câu 14: Điểm
M
trong hình vẽ bên là điểm biểu diễn số phức
z
. Tìm số phức
z
A.
1zi= −
B.
1zi=−−
C.
1zi
= +
D.
1zi=−+
Câu 15: Điểm
M
trong hình vẽ bên là điểm biểu diễn số phức
z
. Tìm số phức
z
A.
3zi= −
B.
3zi=
C.
3z = −
D.
3z =
Câu 16: Điểm
M
trong hình vẽ bên là điểm biểu diễn số phức
z
. Tìm số phức
z
A.
2zi=
B.
2z =
C.
2z = −
D.
2zi= −
Câu 17: Các điểm
, .,
M NPQ
trong hình vẽ bên là điểm biểu
diễn lần lượt của các số phức
1234
,,,zz zz
. Khi đó số phức
1234
3w zz z z= +++
bằng
A.
64wi=−+
B.
34wi= −
C.
64wi
= +
D.
43wi= −
Câu 18: (Đề minh họa lần 2 – Bộ GDĐT năm 2017) Điểm
M
trong hình vẽ bên
là điểm biểu diễn số phức
z
. Tìm phần thực và phần ảo của
z
.
A. Phần thực là
4−
và phần ảo là 3.
B. Phần thực là 3 và phần ảo là
4
i
−
.
C. Phần thực là 3 và phần ảo là
4−
.
D. Phần thực là
4
−
và phần ảo là
3i
.
Câu 19: (Đề minh họa lần 1 – Bộ GDĐT năm 2017) Cho số phức
z
thỏa mãn
điều kiện
(
)
13iz i
+=−
. Hỏi điểm biểu diễn của
z
là điểm nào trong các điểm
, .,M NPQ
ở hình bên?
A. Điểm
P
B. Điểm
Q
C. Điểm
M
D. Điểm
N
Câu 20: Gọi
,MN
lần lượt là điểm biểu diễn của các số phức
12
,zz
khác 0.
Khi đó khẳng định nào sau đây là sai?
A.
2
z ON=
B.
12
z z MN−=
C.
12
z z MN+=
D.
1
z OM=
Câu 21: Cho số phức
2zi= −
. Tìm điểm biểu diễn của số phức
iz
ω
=
A.
( )
1; 2M
−
B.
( )
2; 1N
−
C.
( )
2;1P
D.
( )
1; 2Q
Câu 22: Cho số phức
32zi= +
. Tìm điểm biểu diễn của số phức
iz z
ω
= −
A.
(
)
5; 5M
B.
( )
5; 5N −
C.
( )
5; 5P −
D.
( )
5; 5Q −−
Câu 23: Cho số phức
32
zi= −
. Tìm điểm biểu diễn của số phức
.z iz
ω
= +
A.
( )
1; 5M −
B.
( )
5; 5
N −
C.
( )
1;1P
D.
( )
5;1Q
Câu 24: Tìm điểm biểu diễn của số phức
z
thỏa mãn
(
)
( )
21 3iz i i i
+ −= −
A.
( )
3
1; 0M
B.
( )
1
0;1M
C.
( )
4
0; 2M
D.
( )
2
0; 1M −
Câu 25: Tìm điểm biểu diễn của số phức
z
thỏa mãn
( )( )
2 1 42i iz i− ++=−
A.
(
)
1
1; 3M
−−
B.
(
)
2
1; 3
M
−
C.
( )
3
1; 3M −
D.
(
)
4
1; 3
M
Câu 26: Gọi
,MN
lần lượt là điểm biểu diễn của các số phức
12
,zz
khác 0. Khi đó khẳng định nào sau đây
là sai?
A.
2
z ON=
B.
12
z z MN−=
C.
12
z z MN+=
D.
1
z OM=
Câu 27: Cho số phức
z
thỏa
2 10z =
. Hỏi điểm biểu diễn của
z
là
điểm nào trong hình?
A. Điểm
P
B. Điểm
M
C. Điểm
N
D. Điểm
Q
Câu 28: Trong mặt phẳng tọa độ, điểm
M
là điểm biểu diễn của số phức
z
. Điểm
nào trong hình vẽ là điểm biểu diễn của số phức
2z
A. Điểm
N
B. Điểm
Q
C. Điểm
E
D. Điểm
P
Câu 29: Số phức
z
được biểu diễn trên mặt phẳng tọa độ như hình vẽ. Hỏi
điểm biểu diễn của số phức
i
w
z
=
nằm ở góc phần tư thứ mấy trong hệ trục tọa
độ
Oxy
?
A. Thứ nhất
B. Thứ hai
C. Thứ ba
D. Thứ tư
Câu 30: Cho số phức
2zi
=
được biểu diễn bởi điểm nào trong hình vẽ bên?
A. Điểm
M
B. Điểm
N
C. Điểm
P
D. Điểm
Q
Câu 31: Cho số phức
z
thỏa
( )
13 2 4iz i+ +=−
. Điểm nào sau đây biểu diễn cho
z
trong các điểm
, ,,
M N PQ
ở hình bên?
A. Điểm
M
B. Điểm
N
C. Điểm
P
D. Điểm
Q
Câu 32: Cho số phức
z
thỏa
( )
23 19z iz i−+ =−
. Số phức
( )
1
5.w iz
−
=
có điểm biểu diễn là điểm nào trong các điểm
, ,,M N PQ
ở hình vẽ?
A. Điểm
N
B. Điểm
Q
C. Điểm
M
D. Điểm
P
Câu 33: Cho hai điểm
,MN
trong mặt phẳng phức như hình vẽ, gọi
P
là điểm sao cho
OMNP
là hình
bình hành. Hỏi điểm
P
biểu thị cho số phức nào sau đây?
A.
4
43zi= −
B.
3
2
zi=−+
C.
2
43zi= +
D.
1
2zi
= −
Câu 34: Trong mặt phẳng phức gọi
M
là điểm biểu diễn cho số phức
z a bi= +
với
, ,0a b ab∈≠
và
M
′
là điểm biểu diễn cho số phức
z
. Mệnh đề nào sau đây đúng?
A.
M
′
đối xứng với
M
qua
Oy
B.
M
′
đối xứng với
M
qua
Ox
C.
M
′
đối xứng với
M
qua
O
D.
M
′
đối xứng với
M
qua đường
yx=
Câu 35: Cho số phức
z
thỏa mãn điều kiện
17
12
13
i
iz i
i
+
=+−
−
. Xác định tọa độ điểm
A
biểu diễn số phức
liên hợp
z
.
A.
( )
1; 3A −
B.
( )
1; 3A −−
C.
( )
1; 3A −
D.
( )
1; 3A
Câu 36: Biết điểm
( )
1; 2
M
−
biểu diễn số phức
z
. Tính môđun của số phức
2
.iz z
ω
= −
A. 26 B. 6 C.
26
D.
6
Câu 37: Cho hai số phức
12
1 3, 4 6
z iz i=− =−−
có các điểm biểu diễn trên mặt phẳng tọa độ lần lượt là hai
điểm
M
và
N
. Gọi
z
là số phức mà có điểm biểu diễn là trung điểm của đoạn
MN
. Hỏi
z
là số phức nào
trong các số phức dưới đây?
A.
39zi=−−
B.
13
zi
=−−
C.
53
22
zi
= +
D.
39
22
zi
=−−
Câu 38: Trong mặt phẳng tọa độ
Oxy
, cho số phức
z
thỏa mãn
3zi z i−= +
. Tìm tập hợp điểm biểu diễn
số phức
z
.
A. Một đường thẳng B. Một đường tròn C. Một hyperbol D. Một elip
Câu 39: Trong mặt phẳng phức, tập hợp các điểm biểu diễn của số phức
z
thỏa mãn điều kiện
2z iz+=−
là đường thẳng có phương trình nào sau đây?
A.
2 4 13 0xy+ +=
B.
4 2 30
xy+ +=
C.
2 4 13 0xy−+ −=
D.
4 2 30xy− +=
Câu 40: Tìm tập hợp những điểm
M
biểu diễn số phức
z
trong mặt phẳng phức, biết số phức
z
thỏa mãn
điều kiện
21ziz−=+
A. Tập hợp những điểm
M
là đường thẳng có phương trình
4 2 30xy+ +=
.
B. Tập hợp những điểm
M
là đường thẳng có phương trình
4 2 30xy− +=
C. Tập hợp những điểm
M
là đường thẳng có phương trình
2 4 30xy+ −=
D. Tập hợp những điểm
M
là đường thẳng có phương trình
2 4 30xy+ +=
Câu 41: Tìm tập hợp các điểm biểu diễn số phức
z
thỏa mãn điều kiện
2z iz+=−
A. Đường thẳng
3
2
2
yx=−−
B. Đường thẳng
23yx=−−
C. Đường thẳng
3
2
2
yx= −
D. Đường thẳng
3
2
2
yx= +
Câu 42: Tìm tập hợp các điểm biểu diễn số phức
z
trong mặt phẳng phức thỏa mãn điều kiện
( )
( )
2 ziz−+
là số thực
A. Đường thẳng
20xy+−=
B. Đường thẳng
20xy−+=
C. Đường thẳng
2 20xy− +=
D. Đường thẳng
2 20xy+ −=
Câu 43: Tìm tập hợp các điểm trên mặt phẳng tọa độ biểu diễn các số phức
z
thỏa mãn điều kiện
( )( )
2v zi i=−+
là một số thuần ảo
A. Đường tròn
22
2xy+=
B. Đường thẳng
2 20xy+ −=
C. Đường thẳng
2 10xy− +=
D. Đường parabol
2
2xy=
Câu 44: Trên mặt phẳng tọa độ
Oxy
, tìm tập hợp các điểm biểu diễn các số phức
z
thỏa mãn điều kiện số
phức
( )
23 5wz i i= + +−
là số thuần ảo
A. Đường tròn
22
5xy+=
B. Đường thẳng
2 3 50xy− +=
C. Đường tròn
(
) (
)
22
3 25
xy− +− =
D. Đường thẳng
3 2 10
xy+ −=
Câu 45: Tìm tất cả các số phức
z
thỏa mãn
25zi−=
và điểm biểu diễn của
z
thuộc đường thẳng
:3 1 0d xy− +=
.
A.
14zi= −
B.
14zi= +
và
21
55
zi=−−
C.
21
55
zi=−+
D.
12zi=−−
và
2 11
55
zi
= +
Câu 46: Cho số phức
z
thỏa mãn
12zi z i− = −+
. Trong mặt phẳng phức, tập hợp các điểm biểu diễn số
phức
( )
21w iz=−+
là một đường thẳng. Viết phương trình đường thẳng đó.
A.
7 90xy− −=
B.
7 90xy+ −=
C.
7 90xy+ +=
D.
7 90xy
− +=
Câu 47: Cho số phức
v a bi= +
. Tìm tập hợp các điểm trên mặt phẳng tọa độ biểu diễn các số phức
z
thỏa
mãn điều kiện
1
zv−=
A. Đường thẳng
( ) ( )
1xa yb
−+−=
B. Đường thẳng
yb
=
C. Đường tròn
( ) ( )
22
1xa yb− +− =
D. Đường thẳng
xa=
Câu 48: Tập hợp các điểm
M
biểu diễn số phức
z
sao cho
( )
2
2
zz=
là
A. Gốc tọa độ B. Trục hoành
C. Trục tung D. Trục tung và trục hoành
Câu 49: Trong mặt phẳng phức với hệ tọa độ
Oxy
, tìm tập hợp các điểm biểu diễn số phức
z
thỏa mãn điều
kiện
z
là số ảo
A. Trục ảo
B. Trục thực và trục ảo
C. Đường phân giác góc phần tư thứ nhất và thứ ba
D. Hai đường phân giác của các gốc tọa độ
Câu 50: Tìm tập hợp các điểm biểu diễn bằng số phức
z
thỏa mãn
( )
1zi+
là số thực.
A. Đường tròn bán kính bằng 1 B. Trục hoành
Ox
C. Đường thẳng
yx= −
D. Đường thẳng
yx=
Câu 51: Xác định tập hợp các điểm biểu diễn số phức
z
thỏa mãn
zi
zi
−
+
là số thực
A. Đường tròn phương trình
22
1xy
+=
bỏ đi điểm
( )
0; 1A −
B. Hyperbol phương trình
22
1xy
−=−
bỏ đi điểm
( )
0; 1A −
C. Trục tung
Oy
bỏ đi điểm
(
)
0; 1
A −
D. Trục hoành
Ox
bỏ đi điểm
( )
0; 1A −
Câu 52: Cho số phức
z
thỏa mãn
1
zi
zi
−
=
+
. Tìm tập hợp các điểm biểu diễn số phức
z
trong mặt phẳng
phức
A. Đường tròn B. Trục thực C. Trục ảo D. Một điểm
Câu 53: Cho hai số phức
,zz
′
thỏa mãn phần thực của
z
bằng phần ảo của
z
′
và phần ảo của
z
bằng phần
thực của
z
′
. Nếu tập hợp của các điểm biểu diễn số phức
z
là đường thẳng
2 30
xy+ −=
thì tập hợp các
điểm biểu diễn số phức
z
′
là đường thẳng có phương trình nào sau đây?
A.
2 30
xy− +=
B.
2 30
xy+−=
C.
2 30
xy− −=
D.
2 30
xy
++=
Câu 54: Cho số phức
z
thỏa
2
2
z =
và điểm
A
trong hình vẽ bên là điểm
biểu diễn của
z
. Biết rằng ở hình vẽ bên, điểm biểu diễn của số phức
1
w
iz
=
là
1 trong bốn điểm
, ,,M N PQ
. Khi đó điểm biểu diễn của số phức
w
là điểm
nào sau đây?
A. Điểm
Q
B. Điểm
M
C. Điểm
N
D. Điểm
P
Câu 55: Cho số phức
z
có điểm biểu diễn là
M
. Biết số phức
1
w
z
=
được biểu diễn bởi một trong bốn điểm
,,,PQRS
như hình vẽ. Hỏi điểm
biểu diễn của
w
là điểm nào?
A. Điểm
S
B. Điểm
Q
C. Điểm
P
D. Điểm
R
Câu 56: Cho số phức
( )
,z a bi a b=+∈
. Để điểm biểu diễn của
z
nằm trong dải
( )
2; 2−
như phần gạch
sọc của hình vẽ thì điều kiện của
,ab
phải thỏa mãn là gì?
A.
22a−< <
và
b ∈
B.
2
2
a
b
≥
≥
C.
2
2
a
b
≤−
≤−
D.
( )
, 2; 2ab∈−
Câu 57: Cho hình vuông
ABCD
có tâm
H
và
,,, ,
ABC DH
lần lượt là điểm biểu diễn cho các số phức
,,, ,
abc dh
. Biết
2 , 13a ih i=−+ =+
và số phức
b
có phần ảo dương. Khi đó, môđun của số phức
b
A.
13
B.
10
C.
26
D.
37
Câu 58: Trên mặt phẳng tọa độ
Oxy
lấy
M
là điểm biểu diễn số phức
( )( )
21zii= − −+
và gọi
ϕ
là góc
tạo bởi chiều dương của trục hoành với véc tơ
OM

. Tính
sin 2
ϕ
.
A.
3
5
B.
3
5
−
C.
3 10
10
D.
3 10
10
−
Câu 59: Trên mặt phẳng phức, gọi
M
là điểm biểu diễn số phức
( )( )
23 1z ii=−+
và
ϕ
và góc tạo bởi
chiều dương trục hoành và véc tơ
OM

. Tính
sin 2
ϕ
.
A.
5
sin 2
13
ϕ
= −
B.
5
sin 2
13
ϕ
=
C.
13
sin 2
5
ϕ
=
D.
13
sin 2
5
ϕ
= −
Câu 60: Gọi
(
)
H
là tập hợp tất cả các điểm trong mặt phẳng tọa độ
Oxy
biểu diễn số phức
( )
,z a bi a b=+∈
thỏa mãn
22
1a b ab+ ≤≤ −
. Tính diện tích hình
( )
H
.
A.
31
42
π
+
B.
4
π
C.
1
42
π
−
D. 1
Câu 61: Biết tập hợp các điểm
M
biểu diễn hình học số phức
z
thỏa mãn
2 2 10zz−++=
là một elip
( )
E
. Hãy viết phương trình elip đó.
A.
( )
22
:1
25 16
xy
E +=
B.
( )
22
:1
25 21
xy
E +=
C.
(
)
22
:1
21 16
xy
E +=
D.
( )
22
:1
16 9
xy
E +=
Câu 62: Tập hợp các điểm biểu diễn số phức
z
thỏa mãn
2 25zz++−=
trên mặt phẳng tọa độ là một
elip có phương trình chính tắc nào sau đây?
A.
( )
22
:1
25 9
xy
E +=
B.
( )
22
:4
25 9
xy
E +=
C.
( )
22
44
:1
25 9
xy
E +=
D.
( )
22
3
:1
25 3
xy
E +=
Câu 63: Tập hợp các điểm
M
biểu diễn hình học số phức
z
thỏa
1 18zi zi−+ + +− =
là một elip
( )
E
.
Hãy viết phương trình elip đó.
A.
( )
22
:1
16 13
xy
E +=
B.
( )
22
:1
16 14
xy
E
+=
C.
( )
22
:1
16 12
xy
E +=
D.
( )
22
:1
16 15
xy
E +=
Câu 64: Biết tập hợp các điểm
M
biểu diễn hình học số phức
z
thỏa
4zi zi−+ +=
là một elip
(
)
E
. Hãy
viết phương trình elip đó.
A.
( )
22
:1
94
xy
E +=
B.
( )
22
:1
43
xy
E +=
C.
( )
22
:1
93
xy
E +=
D.
( )
22
:1
42
xy
E +=
LỜI GIẢI CHI TIẾT
Câu 1:
21
AB z z= −

. Chọn B.
Câu 2:
( )
( )(
)
53 4
5 3 4 34
;
34 34 34 5 5 55
i
zi
i ii
+

= = =+⇒

− −+

là điểm biểu diễn. Chọn B.
Câu 3:
(
)
( ) (
)
2
1 2 3 4 4 3 4; 3zi i i i i
= + = −+ =−− ⇒− −
là điểm biểu diễn. Chọn A.
Câu 4:
( ) (
)
2 7 1 1 11
95 72 0 ;
9 5 2 2 22
i
iz i z z i
i
−

+ + − =⇔= ⇔=−+ ⇒−

+

là điểm biểu diễn. Chọn D.
Câu 5:
( )
( )
53
1 5 3 1 4 1; 4
1
i
iz i z z i
i
+
− =+ ⇔= ⇔=+ ⇒
−
là điểm biểu diễn. Chọn C.
Câu 6: Ta có
( )
2;1 1 2M zi− ⇒ =−+
. Chọn A.
Câu 7: Ta có
( )
2; 4 2 4M zi⇒=+
. Chọn B.
Câu 8: Ta có
(
)
2;1 2M zi
⇒=+
. Chọn D.
Câu 9: Ta có
( )
1; 3 1 3M zi−⇒=−
. Chọn B.
Câu 10: Ta có
( )
32
2; 3 2 3
i
M zi
i
−
− − ⇒ =−− =
. Chọn C.
Câu 11:
(
) ( )
2
1 2 2 2 2;1
w iz i i i i i N= = − =− = +⇒
. Chọn B.
Câu 12:
( ) ( ) ( )
12
1 2 3 2 2; 1zz z i i i= + = − +−+ =−−⇒− −
. Chọn C.
Câu 13:
( )
1; 3 1 3 1 3M z iz i− ⇒ =−+ ⇒ =−−
. Chọn A.
Câu 14:
( )
1;1 1 1M z iz i− ⇒ =−+⇒ =−−
. Chọn B.
Câu 15:
( )
3; 0 3Mz− ⇒=−
. Chọn C.
Câu 16:
(
)
0; 2 2 2
M ziz i⇒= ⇒=−
. Chọn D.
Câu 17:
1 2 3 4 1234
3 2, 2 , 3 , 2 2 3 6 4z iz iz iz i w z z z z i=−+ =−− = + = − ⇒ = + + + =−+
. Chọn A.
Câu 18:
( )
3; 4 3 4M zi−⇒=− ⇒
phần thực là 3 và phần ảo là
4−
. Chọn C.
Câu 19:
( )
( )(
)
( )( )
( )
31
3 24
1 3 1 2 1; 2
1 11 2
ii
ii
iz i z z i Q
i ii
−−
−−
+ =−⇔= ⇔= = =− ⇒ −⇒
+ +−
. Chọn B.
Câu 20: Ta có
12
z z MN+≠
nên đáp án C sai. Chọn C.
Câu 21:
( ) ( )
2 1 2 1; 2iz i i i
ω
== −=+⇒
là điểm biểu diễn. Chọn D.
Câu 22:
( ) ( ) ( )
32 32 55 5;5
iz z i i i i
ω
= − = + − − =−+ ⇒−
là điểm biểu diễn. Chọn B.
Câu 23:
( ) ( ) ( )
. 3 2 3 2 1 1;1z iz i i i i
ω
= + = − + + =+⇒
là điểm biểu diễn. Chọn C.
Câu 24:
( ) ( ) (
)
( )
1
2 1 3 1 1 0;1
1
i
iziii zi iz zi
i
+
+ −= −⇔ −=+⇔= ⇔=⇒
−
là điểm biểu diễn. Chọn B.
Câu 25:
( )
(
)
( )
2 1 4 2 1 3 1 3 1; 3i iz i z i z i
− ++=− ⇔=− ⇒=+ ⇒
là điểm biểu diễn. Chọn D.
Câu 26: Ta có
12
z z MN−=
nên đáp án C sai. Chọn C.
Câu 27: Với
(
)
6; 2 6 2 2 10
Q z iz−⇒=− ⇒ =
. Chọn D.
Câu 28: Điểm biểu diễn số phức
2
z
là
E
. Chọn C.
Câu 29: Giả sử
z x yi= +
với
,0xy>
. Ta có
( )
22 22 22
i x yi
ii y x
wi
xyixy xy xy
z
+
=== =−+
− + ++
Điểm biểu diễn của
w
là
2222
;
yx
xyxy

−

++

nằm ở góc phần tư thứ 2. Chọn B.
Câu 30: Điểm biểu diễn của số phức là
(
)
0; 2
là điểm
N
. Chọn B.
Câu 31: Ta có
( )
(
)
42
1 3 2 4 1 1;1
13
i
iz i z z i
i
−−
+ + =−⇔= ⇔=−+⇒−
+
là điểm biểu diễn. Chọn A.
Câu 32: Giả sử
z x yi z x yi=+ ⇒=−
Ta có
( ) ( ) ( )( )
23 19 23 19z i z i x yi i x yi i−+ =−⇔+ −+ − =−
( ) ( )
2 3 3 2 19 3 3 3 19x yi x y xi yi i x y x y i i⇔+− − − + =−⇔−− +−+ =−
31 2
33 9 1
xy x
xy y
−− = =

⇔⇔

−+ =− =−

Do đó
( )
(
)
(
)
1
55 5
2 5 . 1 2 1; 2
2 12
z i w iz i
iz i i i
−
= −⇒ = = = = =− ⇒ −
−+
là điểm biểu diễn. Chọn C.
Câu 33: Ta có
(
)
2; 1 2OM P N P z i= ⇒ −⇒=−
 
. Chọn D.
Câu 34:
( ) ( )
;, ;M ab M a b
′
−⇒
đối xứng nhau qua trục
Ox
. Chọn B.
Câu 35:
( )
17
12 12 2 3 13 13
13
i
iz i iz i i iz i z i z i
i
+
=+− ⇔=+−−+⇔=+⇔=−⇒=+
−
Do đó tọa độ điểm
A
là
( )
1; 3
. Chọn D.
Câu 36:
( ) ( ) ( )
2
2
12 . 12 12 2 34 15 26z i iz z i i i i i i
ωω
=− ⇒ = − = + − − =−+−−− =+ ⇒ =
. Chọn C.
Câu 37: Gọi
I
là trung điểm
3 9 39
;
2 2 22
MN I z i

⇒ − − ⇒=−−


. Chọn D.
Câu 38: Gọi
( ) (
)
; 0;1Mz A
và
( )
0; 3B −
là các điểm biểu diễn số phức
;zi
và
3i−
Khi đó
MA MB= ⇒
tập hợp điểm biểu diễn số phức
z
là đường trung trực của
AB
có phương trình
1y = −
. Chọn A.
Câu 39: Đặt
( )
;
z x yi x y
=+∈
ta có:
(
)
2
x yi y x yi
++=− +
(
) (
)
22
22
2 1 4 2 30x yx y xy
⇔ + + = + − ⇔ + +=
Do đó tập hợp điểm
( )
;M xy
biểu diễn số phức
z
là đường thẳng
4 2 30xy+ +=
. Chọn B.
Câu 40: Đặt
( )
;z x yi x y z x yi=+ ∈ ⇔=−
ta có:
21x yi i x yi+− =−+
( ) (
)
22
22
2 1 2 4 30
x y x y xy
⇔ + − = + + ⇔ + −=
Do đó tập hợp điểm
(
)
;M xy
biểu diễn số phức
z
là đường thẳng
2 4 30xy+ −=
. Chọn B.
Câu 41: Đặt
(
)
;
z x yi x y=+∈
ta có:
(
)
2x yi i x yi++=− +
( ) (
)
22
22
3
2 1 4 2 30 2
2
x yx y xy y x
⇔ + + = + − ⇔ + +=⇔ =− −
Do đó tập hợp điểm
(
)
;M xy
biểu diễn số phức
z
là đường thẳng
3
2
2
yx
=−−
. Chọn A.
Câu 42: Đặt
( )
;z x yi x y=+∈
ta có:
(
)
( )
( )(
)
22w z i z x yi i x yi= − + = −− +−
(
) ( )
21x yi x y i

= − − +−

Phần ảo của số phức
w
là:
( )( )
2 1 22x y xy x y− − − =−− +
Số phức
w
là số ảo khi
2 20 2 20xy xy−− + = ⇔ + − =
Vậy tập hợp điểm biểu diễn số phức
z
thỏa mãn
( )
( )
2 ziz−+
là số thực là đường thằng
2 20xy+ −=
.
Chọn D.
Câu 43: Đặt
(
)
;z x yi x y=+∈
ta có:
( )( )
( )( )
22vziixyiii=−+=+−+
(
)
( )
2 12 1
x y y i xi
= − −+ − +
Số phức
( )
( )
2v zi i
=−+
là một số thuần ảo khi phần thực
(
)
2 10xy
− −=
hay
2 10xy− +=
.
Do đó tập hợp điểm biểu diễn số phức
z
là đường thẳng
2 10xy− +=
. Chọn C.
Câu 44: Đặt
( )
;z x yi x y=+∈
ta có:
( ) ( )( )
23 5 23 5wziixyi ii= + +−= + + +−
( ) ( )
22 3 35 235 321x yi xi y i x y x y i=+ + −+−= −++ +−
Số phức
( )
23 5wz i i
= + +−
là số thuần ảo khi phần thực
2 3 50xy− +=
Do đó tập hợp điểm biểu diễn số phức
z
là đường thẳng
2 3 50xy− +=
. Chọn B.
Câu 45: Đặt
( )
;z x yi x y=+∈
ta có:
( )
2
2
2 5 25zi x y−= ⇔+− =
Giải hệ phương trình
( ) ( ) ( )
22 2
222
25 25 3125
3 10 31 31
xy xy x x
xy yx yx

+−= +−= ++−=

⇔⇔

− += = + = +


2
14
10 6 4 0
21
31
55
xy
xx
xy
yx
=⇒=
− −=
⇔⇔
−

= ⇒=−
= +
Do đó
14zi= +
và
21
55
zi
−
= −
là các số phức cần tìm. Chọn B.
Câu 46:
( )
1
21
2
w
w iz z
i
−
= − +⇔ =
−
Suy ra
( )( )
2
1 12 2
1 1 12
12 12
22 2 2
w ii
w w w ii
zi z i i i
ii i i
−− − −
− − −− +
− = −+ ⇔ − = −+ ⇔ =
−− − −
22 15w iw i⇔ − − = −+
Đặt
( )
;w x yi x y=+∈
ta có:
( ) ( ) ( ) ( )
2 22 2
22 15 2 2 1 5
w iw i x y x y−−=−+⇔− +− =−++
2 14 18 0 7 9 0x y xy⇔ + + =⇔+ +=
Do đó tập hợp điểm biểu diễn
w
là đường thẳng
7 90xy+ +=
. Chọn C.
Câu 47: Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn các số phức
z
thỏa mãn điều kiện
1zv−=
là
đường tròn tâm
( ) ( )
;I v I ab=
bán kính
1R =
. Chọn C.
Câu 48: Đặt
( )
;
z x yi x y z x yi=+ ∈ ⇒=−
ta có:
( )
( ) ( )
2
22
2
z z x yi x yi= ⇔+ =−
0
2 2 40 0
0
x
xyi xyi xyi xy
y
=
⇔=−⇔=⇔=⇔
=
Do đó tập hợp điểm biểu diễn số phức
z
là trục hoành và trục tung. Chọn D.
Câu 49: Đặt
( )
;
z x yi x y=+∈
khi đó
z
là số ảo khi phần thực
0x =
Do đó tập hợp điểm biểu diễn
z
là đường thẳng
0x =
hay là trục ảo. Chọn A.
Câu 50: Đặt
( )
;z x yi x y=+∈
ta có:
( ) (
)( ) (
)
11
z i x yi i x y y x i+= + +=−+ +
là số thực khi phần ảo
0xy y x+=⇔=−
Do đó tập hợp điểm biểu diễn
z
là đường thẳng
yx
= −
. Chọn C.
Câu 51: Đặt
( )
;z x yi x y=+∈
ta có:
( )
( )
1
1
xy i
z i x yi i
zixyiix y i
+−
− +−
= =
+++++
(ĐK
zi≠−
)
( ) ( )
( )
( )
( ) ( )
( )
22
22
22
1 11
11
11
x y xy xy i
x y ix y i
xy xy

− −+ −− +

+− −+


= =
++ ++
là số thực khi phần ảo
(
)
2
2
00
1
xy x xy x
x
xy
−− −
=⇔=
++
Do đó tập hợp điểm biểu diễn
z
là đường thẳng
0x =
(trục tung) bỏ đi điểm
. Chọn C.
Câu 52: Ta có:
1
zi
zi zi
zi
−
=⇔ −= +
+
(với
zi
≠−
)
Đặt
( )
;z x yi x y=+∈
ta có:
( )
( )
22
22
1 10x yi i x yi i x y x y y+−=++⇔ +− =++ ⇔=
Do đó tập hợp điểm biểu diễn
z
là đường thẳng
0y
=
(trục thực) bỏ đi điểm
. Chọn B.
Câu 53: Đặt
( )
; ; ;;z x yi z x y i x x y y
′′′ ′ ′
=+=+ ∈
Khi đó
xy
yx
′
=
′′
=
, mặt khác
2 30 2 30 2 30
x y y x xy
′ ′ ′′
+ −=⇒ + −=⇔ + −=
Do đó tập hợp điểm biểu diễn
z
′
là đường thẳng có phương trình
2 30xy+−=
. Chọn B.
Câu 54: Đặt
(
)
;
z x yi x y=+∈
ta có:
( )
22
11y xi
w
i x yi y xi x y
−−
= = =
+ −+ +
Lại có:
22
22 22
1 11
.2w yx
xy xy z
= += ==
++
Dựa vào hình vẽ ta thấy
0; 0xy> >⇒
phần thực và phần ảo của
w
đều âm
Mặt khác
2wz
=
nên điểm biểu diễn
w
trong 4 điểm chỉ có thể là điểm
P
. Chọn D.
Câu 55: Đặt
( )
1z yi y=+∈
. Dựa vào hình vẽ ta thấy
0
y
>
Ta có:
2
111
11
yi
w
z yi y
−
= = = ⇒
++
phần thực của
w
bằng
2
1
1 y+
suy ra
2
1
01
1 y
<<
+
, phần ảo của
w
bằng
2
0
1
y
y
−
<
+
nên trong 4 điểm chỉ điểm
Q
có tọa độ thỏa mãn 2 yêu cầu trên. Chọn B.
Câu 56: Dựa vào hình vẽ ta thấy các điểm nằm trong dải
(
)
2; 2
−
đều thỏa mãn
2 2;xy−< < ∈
Do đó
22
a−< <
và
b ∈
. Chọn A.
Câu 57: Do
( )
( )
2 , 1 3 2; 1 ; 1; 3a ih i A H=−+ =+ ⇒ −
Đường thẳng
BD
là trung trực của
AC
đi qua
( )
1; 3H
và có VTPT là:
(
)
3; 2AH =

Suy ra
:3 2 9 0BD x y+ −=
, gọi
93
;
2
t
B t BD
−

∈


ta có:
HB HA=
( ) (
) ( )
( )
22
2 2 22
93 33 9
1 3 13 1 13 1 1 13 1 4
2 24
tt
t t tt
−−

⇒− + − = ⇔− + = ⇔+ − = ⇔− =


( )
( )
3; 0
3
1
1; 6
B
t
t
B
=
⇔⇒
= −
−
Do đó phức
b
có phần ảo dương nên
( )
1; 6 37B b OM− ⇒= =
. Chọn D.
Câu 58:
( )
1 3 1; 3z iM=−+ ⇒ −
và nằm ở góc phần tư thứ (II) nên ta có
(
)
( )
2
2
11 3
cos cos ; sin
10 10
13
OM i
ϕϕ
−
= = =−⇒ =
−+

. Vậy
3
sin 2
5
ϕ
= −
. Chọn B.
Câu 59:
( )
5 5; 1z iM= −⇒ −
và nằm ở góc phần tư thứ (IV) nên ta có
( )
( )
2
2
55 1
cos cos ; sin
26 26
51
OM i
ϕϕ
= = =⇒=−
+−

. Vậy
5
sin 2
13
ϕ
= −
. Chọn A.
Câu 60: Vẽ đường tròn
( )
22
:1
Cx y+=
và đường thẳng
10xy
− −=
Đồng thời xét miền bất đẳng thức, ta được hình
( )
H
có diện tích là
1
42
S
π
= −
. Chọn C.
Câu 61: Gọi
( ) ( )
0; 2 , 0; 2 10 2 5A B MA MB a a− ⇒ + = = → =
Và
2 22
2 4 2 21
AB c c b a c= = → = ⇒ = − =
. Vậy
( )
22
:1
25 21
xy
E +=
. Chọn B.
Câu 62: Gọi
( ) ( )
5
0; 2 , 0; 2 5 2
2
A B MA MB a a− ⇒ + = = → =
Và
2 22
9
24 2
4
AB c c b a c
= = → = ⇒ = − =
. Vậy
(
)
22
44
:1
25 9
xy
E
+=
. Chọn C.
Câu 63: Gọi
( ) ( )
1;1 , 1; 1 8 2 4
A B MA MB a a− − ⇒ + = = → =
Và
2 22
2 2 2 2 14AB c c b a c= = → = ⇒ = − =
. Vậy
( )
22
:1
16 14
xy
E +=
. Chọn B.
Câu 64: Gọi
( ) ( )
0; 1 , 0;1 4 2 2A B MA MB a a− ⇒ + = = → =
Và
2 22
22 1 3AB c c b a c
= = → = ⇒ = − =
. Vậy
( )
22
:1
43
xy
E +=
. Chọn B.
| 1/24
| | Tải xuống

Có thể bạn quan tâm:

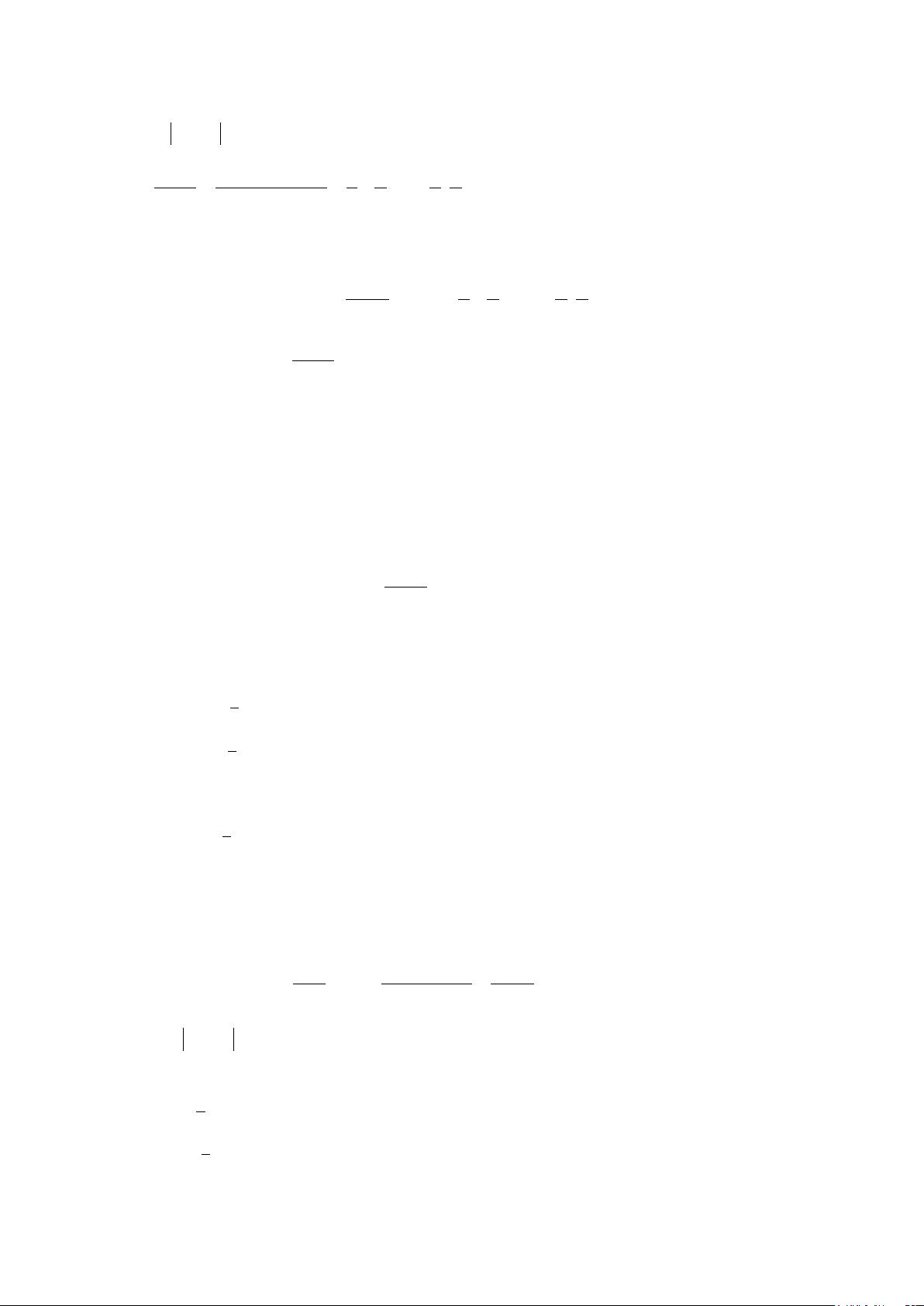
Preview text:

CHỦ ĐỀ 18: BIỂU DIỄN HÌNH HỌC CỦA SỐ PHỨC 1)Định nghĩa 
Mỗi số phức z = x + yi được biểu diễn một điểm M ( ;
x y) khi đó OM = ( ;
x y) trên mặt phẳng phức. Ta
viết M (x + yi) hoặc M (z).  Khi đó 2 2
z = OM = x + y
Nếu điểm M (z là điểm biểu diễn số phức z và điểm N (z là điểm biểu diễn số phức z thì 2 ) 1 ) 1 2
    
z − z = OM − ON = NM , z + z = OM + ON . 1 2 1 2
2)Phương pháp giải toán
Bài toán 1: Tìm tập hợp điểm biểu diễn số phức z thỏa mãn f (z; z) = g (z; z) hoặc f (z; z) là số
thực, hoặc f (z;z) là số ảo
Phương pháp giải: Đặt z = x + yi( ;
x y ∈) ⇒ z = x − yi thế vào biểu thức ban đầu, biến đổi và kết luận.
Mối liên hệ giữa x và y
Kết luận tập hợp điểm M ( ; x y)
○ Ax + By + C = 0
Là đường thẳng Ax + By + C = 0
(x − a)2 +( y −b)2 2 = R
Là đường tròn (C) có tâm I ( ; a b) và bán kính ○  2 2
x + y − 2ax − 2by + c = 0 2 2
R = a + b − c
(x − a)2 +( y −b)2 2 ≤ R
Là hình tròn (C) có tâm I (a;b) và bán kính ○  2 2
x + y − 2ax − 2by + c ≤ 0 2 2
R = a + b − c (bao gồm đường tròn và các điểm bên trong).
○ R ≤ (x − a)2 + ( y −b)2 2 2 ≤ R
Là những điểm thuộc miền có hình vành khăn tạo 1 2
bởi hai đường tròn đồng tâm I (a;b) và bán kính
lần lượt R và R 1 2 ○ 2
y = ax + bx + c
Là một parabol (P) có đỉnh  b I ; ∆  − −  2a 4a    2 2
MF + MF = 2a
Là một elíp có trục lớn 2a trục bé 2b và tiêu cự là ○ x y + = 1 với 1 2 2 2 a bFF = 2c <  2a 1 2 2 2
F F = 2c = 2 a + b ; a > b > 0 1 2 ( )
Một số trường hợp đặc biệt:
 Tìm tập hợp điểm biểu diễn số phức z thỏa mãn z − (a + bi) = z − (c + di)
Gọi M (z); A(a;b); B( ;
c d ) lần lượt là các điểm biểu diễn số phức z; a + bi và c + di .
Khi đó z − (a + bi) = z −(c + di) ⇔ MA = MB ⇒ Tập hợp điểm biểu diễn số phức z là trung trực của AB .
 Tìm tập hợp điểm biểu diễn số phức z thỏa mãn z − (a + bi) = R(R > 0)
Gọi M (z); I (a;b) lần lượt là các điểm biểu diễn số phức z và a + bi
Khi đó z − (a + bi) = R ⇔ MI = R ⇒ Tập hợp điểm biểu diễn số phức z là đường tròn tâm I ( ; a b) bán kính R .
Bài toán 2: Tìm tập hợp điểm biểu diễn số phức w biết w = z .z + z và số phức z thỏa mãn 1 2
z − a − bi = R Ta có: w − z w − z 2 z = suy ra 2
z − a − bi = R ⇔
− a − bi = R ⇔ w − z − z a + bi = R z 2 1 ( ) z 1 z 1 1
Tập hợp điểm biểu diễn w là đường tròn bán kính R z , 1
Tổng quát: Tìm tập hợp điểm biểu diễn số phức w biết w = z .z + z và số phức z thỏa mãn 1 2
z.z − a − bi = R (thêm yếu tố z ) 0 0 w − z a + bi z a + bi R z 2 1 ( ) Ta có: w − z2 z = suy ra 1
z.z − a − bi = R ⇔ z −
= R ⇔ w − z − = z 0 0 2 z z z z 1 1 0 0 0 R z
Tập hợp điểm biểu diễn w là đường tròn bán kính 1 . z0
3)Các ví dụ minh họa
Ví dụ 1: Gọi M là điểm biểu diễn của số phức z thỏa mãn 3 z + i = 2z − z + 3i . Tập hợp tất cả các điểm M như vậy là:
A. một đường tròn B. một parabol
C. một đường thẳng D. một elip Lời giải
Gọi z = x + yi( ;
x y ∈) khi đó ta có: 3 x + yi + i = 2(x − yi) −(x + yi) + 3i
⇔ x + ( y + )i = x − ( y − )i ⇔ x + ( y + )2 = x + ( y − )2 2 2 3 1 3 3 9 9 1 9 1 2 4 2
⇔ 8x +18y = 0 ⇔ y = − x nên tập hợp là Parabol. Chọn B. 9
Ví dụ 2: Tìm tập hợp các điểm biểu diễn số phức z sao cho (z − ) 1 (z + ) 1 là số thực.
A. một đường tròn B. một parabol
C. một đường thẳng D. một elip Lời giải
Đặt z = x + yi ta có: (z − ) 1 (z + )
1 = (x + yi − ) 1 (x − yi + )
1 = (x − )1+ yi   ( x + ) 1 − yi = (x − )(x + ) 2 1
1 + y + (x − )
1 (−y) + y(x + 
)1i là số thực nên ta có: −xy + y + xy + y = 0
⇔ y = 0 . Vậy điểm biểu diễn số phức z là đường thẳng y = 0. Chọn C.
Ví dụ 3: Gọi M là điểm biểu diễn của số phức z thỏa mãn 2 z − i = z − z + 2i . Tập hợp tất cả các điểm M như vậy là:
A. một đường tròn B. một parabol
C. một đường thẳng D. một elip Lời giải
Đặt z = x + yi( ;
x y ∈) ⇒ z = x − yi 2 Ta có: − = − + ⇔ + ( − ) = + ⇔ + ( − )2 = ( + )2 2 2 2 2 1 2 2 1 1 x z i z z i x y i yi i x y y ⇔ y = 4 2
Tập hợp điểm biểu diễn z là parabol x y = . Chọn B. 4
Ví dụ 4: Gọi M là điểm biểu diễn của số phức z thỏa mãn z − i = (1+ i) z . Tập hợp tất cả các điểm M
như vậy là đường tròn có bán kính A. R = 2 B. R = 2 C. R = 4 D. R =1 Lời giải
Đặt z = x + yi( ;
x y ∈) . Ta có: z −i = (1+ i) z ⇒ z −i = (1+ i) z = 2 z
⇒ x + yi − i =
x + y ⇔ x + ( y − )2 2 2 2 2 2 2 1 = 2x + 2y
⇔ x + ( y − )2 2
1 = 2 ⇒ Tập hợp điểm M là đường tròn có bán kính R = 2 . Chọn B.
Ví dụ 5: Biết điểm biểu diễn số phức z thỏa mãn (z + 2i)(z − )1 là số thực là một đường thẳng, khoảng
cách từ gốc tọa độ đến đường thẳng đó bằng A. d = 2 B. 2 d = C. d = 2 D. 4 d = 5 5 Lời giải
Đặt z = x + yi( ;
x y ∈) ta có: x +  ( y + 2)i   ( x − )
1 − yi là số thực ⇒ (x − )1( y + 2)− xy = 0
⇔ xy − y + 2x − 2 − xy = 0 ⇔ 2x − y − 2 = 0
Vậy tập hợp các điểm biểu diễn z là đường thẳng x − y − = (∆) ⇒ d (O ∆) 2 2 2 0 ; = . Chọn B. 5
Ví dụ 6: Trong mặt phẳng tọa độ Oxy , tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện
zi − (2 + i) = 2 là đường tròn
A. (x − )2 + ( y + )2 1 2 = 4
B. (x − )2 + ( y − )2 1 2 = 4
C. (x + )2 + ( y + )2 1 2 = 4
D. (x + )2 + ( y − )2 1 2 = 4 Lời giải Ta có: − ( + ) 2 2 = 2 ⇔ . + i zi i i z −
= 2 ⇔ z −1+ 2i = 2 i
Do đó tập hợp điểm biểu diễn z là đường tròn (x − )2 + ( y + )2 1 2 = 4 . Chọn A.
Ví dụ 7: [Đề thi THPT Quốc gia năm 2018] Xét các số phức z thỏa mãn (z +i)(z + 2) là số thuần ảo.
Trên mặt phẳng tọa độ, tập hợp tất cả các điểm biểu diễn số phức z là một đường tròn có bán kính bằng A. 1 B. 5 , C. 5 D. 3 4 2 2 Lời giải
Đặt z = x + yi( ;
x y ∈) ta có: w = (z +i)(z + 2) = (x − yi +i)(x + yi + 2) = x +  (1− y)i 
 ( x + 2) + yi
Phần thực của số phức w là: 2
x − (1− y) y
Do w là số thuần ảo nên phần thực của nó bằng 0 suy ra 2
x(x + ) − ( − y) y = x + y + x − y = ⇔ (x + )2 2 2  1  5 2 1 2 0 1 + y − =  2    4
Do đó tập hợp điểm biểu diễn số phức z là đường tròn tâm 1 I  1;  −  bán kính 5 R = . Chọn C. 2    2
Ví dụ 8: [Đề minh họa BGD và ĐT 2017] Cho các số phức z thỏa mãn z = 4. Biết rằng tập hợp các
điểm biểu diễn số phức w = (3+ 4i) z + i là một đường tròn. Tìm bán kính của đường tròn đó A. r = 4 B. r = 5 C. r = 20 D. r = 22 Lời giải w − i w − i w − i Ta có: z = ⇒ z = =
= 4 ⇔ w − i = 20 ⇒ tập hợp là đường tròn I (0; ) 1 ; r = 20. 3+ 4i 3+ 4i 5 Chọn C.
Ví dụ 9: Cho các số phức z thỏa mãn z = 2 và số phức w thỏa mãn .iw = (3− 4i) z + 2i . Biết rằng tập hợp
điểm biểu diễn số phức w là một đường tròn. Tính bán kính đường tròn đó: A. R = 5 B. R =10 C. R =14 D. R = 20 Lời giải
Ta có: iw − 2i = (3− 4i) z = (3− 4i) z = 5.2 =10
Do đó i . w − 2 =10 ⇔ w − 2 =10 , đặt w = x + yi( ;
x y ∈) thì x − yi − 2 =10 ⇔ (x − )2 2
2 + y =100 ⇒ R =10. Chọn C.
Ví dụ 10: Cho số phức z thỏa mãn 3− i z + 2 =10 . Biết tập hợp các điểm biểu diễn số phức w thỏa mãn 1− 2i
(1+i)w−iz +1= 0 là một đường tròn. Tìm bán kính của đường tròn đó. A. R = 5 2 B. R = 5 C. R =10 D. R = 50 Lời giải
Ta có: 3− i z + 2 =10 ⇔ (1+ i) z + 2 =10 ⇔ 1+ i z +1−i =10 ⇔ z +1−i = 5 2 ( ) 1 1− 2i (1+i)w+1 Lại có: z =
= (1− i) w − i thế vào (1) ta được (1+ i) w +1− 2i = 5 2 i ⇔ ( − i) 1 3 1 3 1
w − + i = 5 2 ⇔ w − + i = 5 . Do đó suy ra R = 5. Chọn B. 2 2 2 2
Ví dụ 11: Cho số phức z thỏa mãn 5z + i = 5 − iz . Biết rằng tập hợp các điểm biểu diễn cho số phức w
thỏa mãn w(1−i) = (6 −8i) z + 3i + 2 là một đường tròn. Xác định tọa độ tâm I của đường tròn đó A. I ( 1; − 5) B. I (1; 5 − ) C. 1 5 I  ;  −   D. 1 5 I  −  ; 2 2      2 2  Lời giải
Ta có: z + i = − iz ⇔ x + ( y + )i = − xi + y ⇔ x + ( y + )2 = x + ( y + )2 2 2 5 5 5 5 1 5 25 5 1 5 ⇔ ( 2 2 x + y ) 2 2 24
= 24 ⇔ x + y =1 ⇔ z =1
Khi đó w(1−i) = (6 −8i) z + 3i + 2 ⇔ w(1−i) −3i − 2 = (6 −8i) z
Lấy modun 2 vế ta được w( −i) 3i + 2 1
− 3i − 2 =10 ⇔ 1− i w − =10 i −1  1 − 5 w  ⇔ − + i =    
5 2 . Do đó tập hợp điểm biểu diễn z là đường tròn tâm 1 5 I − ; ; R =   5 2 Chọn  2 2   2 2  D.
Ví dụ 12: Cho số phức +
z thỏa mãn 3 i z + 4 + 3i = 5 . Biết rằng tập hợp các điểm biểu diễn số phức w 1− i
thỏa mãn w = (3+ 4i) z + 2i là một đường tròn. Phương trình đường tròn đó là:
A. (x + )2 + ( y + )2 10 3 = 5
B. (x + )2 + ( y + )2 10 3 = 25
C. (x − )2 + ( y − )2 10 3 = 5
D. (x − )2 + ( y − )2 10 3 = 25 Lời giải
Ta có: 3+ i z + 4 + 3i = 5 ⇔ (1+ 2i) z + 4 + 3i = 5 ⇔ 1+ 2i z + 2 −i = 5 ⇔ z + 2 −i =1 1− i w − 2i w +10 + 3i Mặt khác w − 2i z = suy ra + 2 − i =1 ⇔
= 1 ⇔ w +10 + 3i = 5 3+ 4i 3+ 4i 3+ 4i
Do đó phương trình đường tròn biểu diễn w là (x + )2 + ( y + )2 10 3 = 25. Chọn B.
Ví dụ 13: Tập hợp điểm biểu diễn số phức w = 2z + 3− i , biết 2
2z + i = 3z.z +1 là đường tròn có tâm A. I (3;5) B. I ( 3 − ;5) C. I ( 3 − ;− ) 1 D. I (3; 5 − ) Lời giảix = a +
Đặt w = x + yi(x, y ∈), z = a + bi(a,b∈) . Ta có: x + yi = (a + bi) 2 3 2 + 3− i ⇔  y = 2b −1 Ta có: 2
z + i = z z + ⇔ a + ( b + ) 2 = ( 2 2 a + b ) 2
+ ⇔ a + ( b + )2 2 2 2 3 . 1 2 2 1 3 1 4
2 1 = 3a + 3b +1 2 2 ( )2  x −   y a b b a b +  ⇔ + + = ⇔ + + = ⇔ + +
= ⇔ (x − )2 + ( y + )2 2 2 2 3 1 4 0 2 4 2 4 3 5 =     16  2   2 
Vậy tập hợp các điểm biểu diễn w là đường tròn tâm I (3; 5
− ) , bán kính R = 4 . Chọn D.
Ví dụ 14: Tập hợp các điểm biểu diễn số phức w = (1+ 2i) z biết rằng số phức z thỏa mãn điều kiện 2
z + 2 − i = zz là đường thẳng d . Khoảng cách từ O đến d bằng A. 5 B. 5 C. 25 D. 25 4 2 4 2 Lời giải
Đặt w = x + yi và z = a + bi(a; ; b ;
x y ∈) ta có: x + yi = (1+ 2i)(a + bi) = a − 2b + (2a + b)i y − 2x  = − 2 b x a b =  5 ⇔  ⇔ y 2a b  = + x + 2ya =  5 Mặt khác 2
z + − i = zz ⇔ (a + )2 + (b − )2 = ( 2 2 2 2 1
a + b ) ⇔ 4a − 2b + 5 = 0
4x + 8y 2y − 4x ⇔ −
+ 5 = 0 ⇔ 8x + 6y + 25 = 0 5 5
Vậy tập hợp điểm biểu diễn số phức w là đường thẳng (d ):8x + 6y + 25 = 0
Do đó d (O d ) 25 5 ; = = . Chọn B. 10 2
Ví dụ 15: Cho các số phức z thỏa mãn z − i = z −1+ 2i . Tập hợp các điểm biểu diễn số phức
w = (2 −i) z +1 trên mặt phẳng tọa độ là một đường thẳng. Diện tích tam giác tạo bởi đường thẳng đó với
các trục tọa độ bằng A. 81 B. 9 C. 9 D. 81 7 7 14 14 Lời giải
Ta có: w = ( −i) w −1 2 z +1⇒ z = 2 − i Do đó w −1 w −1
z − i = z −1+ 2i ⇔ − i =
−1+ 2i ⇔ w −1− i(2 − i) = w −1+ (2i − ) 1 (2 −i) 2 − i 2 − i
⇔ w − 2 − 2i = w −1+ 5i
Do đó tập hợp điểm biểu diễn của w là trung trực d của AB với A(2;2); B(1; 5 − )  
Ta có: trung điểm của AB là  3 3 ;  −
; n = AB = (1;7) ⇒ d : x + 7y + 9 =   0  2 2  Khi đó  −
d cắt các trục tọa độ tại 9 MN (− ) 1 81 0; ; 9;0 ⇒ S = OM ON =   . Chọn D. OMN .  7  2 14
Ví dụ 16: Biết tập hợp các điểm M biểu diễn hình học số phức z thỏa z + 4 + z − 4 =10 là một Elip
(E). Phương trình Elip (E) là: 2 2 2 2 2 2 2 2 A. x y + = 1 B. x y + = 1 C. x y + = 1 D. x y + = 1 5 3 25 16 25 9 16 9 Lời giải Gọi F 4;
− 0 ; F 4;0 và lần lượt là các điểm biểu diễn số phức 4; − 4 và 1 ( ) 2 ( ) z
Ta có: z + 4 + z − 4 =10 ⇔ MF + MF =10 > F F = 8 1 2 1 2 a = 5 
Khi đó tập hợp điểm M là Elip có 2a =10;2c = 8 ⇒ c = 4  2 2 b
 = a − b = 3 2 2
Phương trình Elip là: x y + = 1. Chọn C. 25 9
Ví dụ 17: Trên mặt phẳng phức, gọi M là điểm biểu diễn số phức z = ( + i)2 2
(4−i) và gọi ϕ là góc tạo 
bởi chiều dương trục hoành và véc-tơ OM . Tính cos 2ϕ . A. 87 cos 2ϕ = − B. 87 cos 2ϕ = C. 87 cos 2ϕ = − D. 87 cos 2ϕ = 475 475 425 425 Lời giải
Ta có z =16 +13i ⇒ M (16;13) và nằm ở góc phần tư thứ nhất nên ta có   ϕ = (OM i) 16 16 2 87 cos cos ; = = ⇒ cos 2ϕ = 2cos ϕ −1 = . Chọn D. 2 2 16 +13 425 425
Ví dụ 18: Trên mặt phẳng tọa độ Oxy , lấy M là điểm biểu diễn số phức z = 1
− + 2i và gọi ϕ là góc lượng
giác tia đầu Ox , tia cuối OM . Tính tan 2ϕ . A. 4 tan 2ϕ = − B. 3 tan 2ϕ = − C. 4 tan 2ϕ = D. tan 2ϕ = 1 − 3 4 3 Lời giải Ta có z = 1
− + 2i ⇒ M ( 1;
− 2) và nằm ở góc phần tư thứ III nên ta có   = ( − ϕ ϕ OM i) 1 1 sin 2 4 cos cos ; = = − ⇒ tan 2ϕ = = . Chọn C. (− )2 2 + 5 cos 2ϕ 3 1 2
Ví dụ 19: Cho hai số phức z , z thỏa mãn z = 2, z = 3 và nếu gọi M , N lần lượt là điểm biểu diễn 1 2 1 2
của z , iz thì  MON = 30°, Tính 2 2
P = z + 4z . 1 2 1 2 A. P = 5 B. P = 4 7 C. P = 3 3 D. P = 5 2 Lời giải
Ta có P = z − 4(iz )2 2 2 2
= a − 4b = a − 2b . a + 2b . Với a = z ⇒ a = 2; b = iz ⇒ b = 3 1 2 1 2 Lại có 2 2 2
a − 2b = a − 4. a . b .cos30° + 4 b = 4 
→ a − 2b = 2 Và 2 2 2
a + 2b = a + 4. a . b .cos30° + 4 b = 28 
→ a + 2b = 2 7
Vậy P = a − 2b . a + 2b = 2.2 7 = 4 7 . Chọn B.
BÀI TẬP TỰ LUYỆN  Câu 1: Giả sử ,
A B theo thứ tự là điểm biểu diễn của số phức z , z . Tính độ dài của AB . 1 2
A. z + z
B. z − z
C. z + z
D. z − z 2 1 2 1 1 2 1 2
Câu 2: (Sở GD & ĐT TP. Hồ Chí Minh 2017) Tìm điểm biểu diễn của 5 z = 3− 4i A. 3 4 M  ;  −    B. 3 4 N  ; C. 3 4 P ;− D. Q(3; 4 − ) 5 5       5 5   5 5 
Câu 3: Tìm điểm biểu diễn của số phức z thỏa mãn z = i( + i)2 1 2 A. M 4; − 3 − B. M 4; 3 − C. M 4; − 3 D. M 4;3 4 ( ) 3 ( ) 2 ( ) 1 ( )
Câu 4: Tìm điểm biểu diễn của số phức z thỏa mãn (9 + 5i) z + (7 − 2i) = 0 A. M (1;2) B. N (1; ) 1 C. P(2;2) D. 1 1 Q ;  −  2 2   
Câu 5: Tìm điểm biểu diễn của số phức z thỏa mãn (1−i) z = 5+ 3i A. M (1;2) B. N (4; ) 1 C. P(1;4) D. Q( 1; − 4 − )
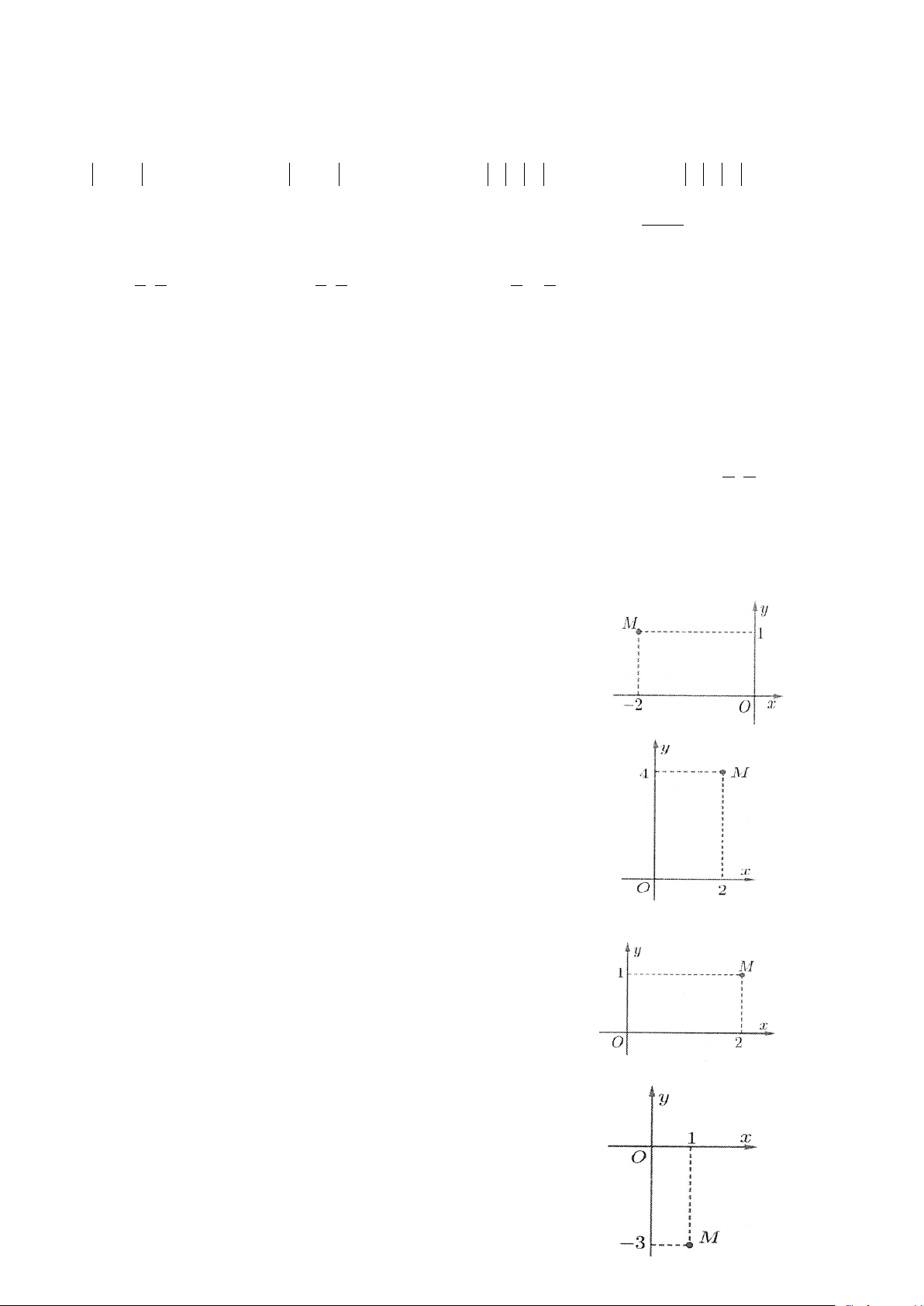
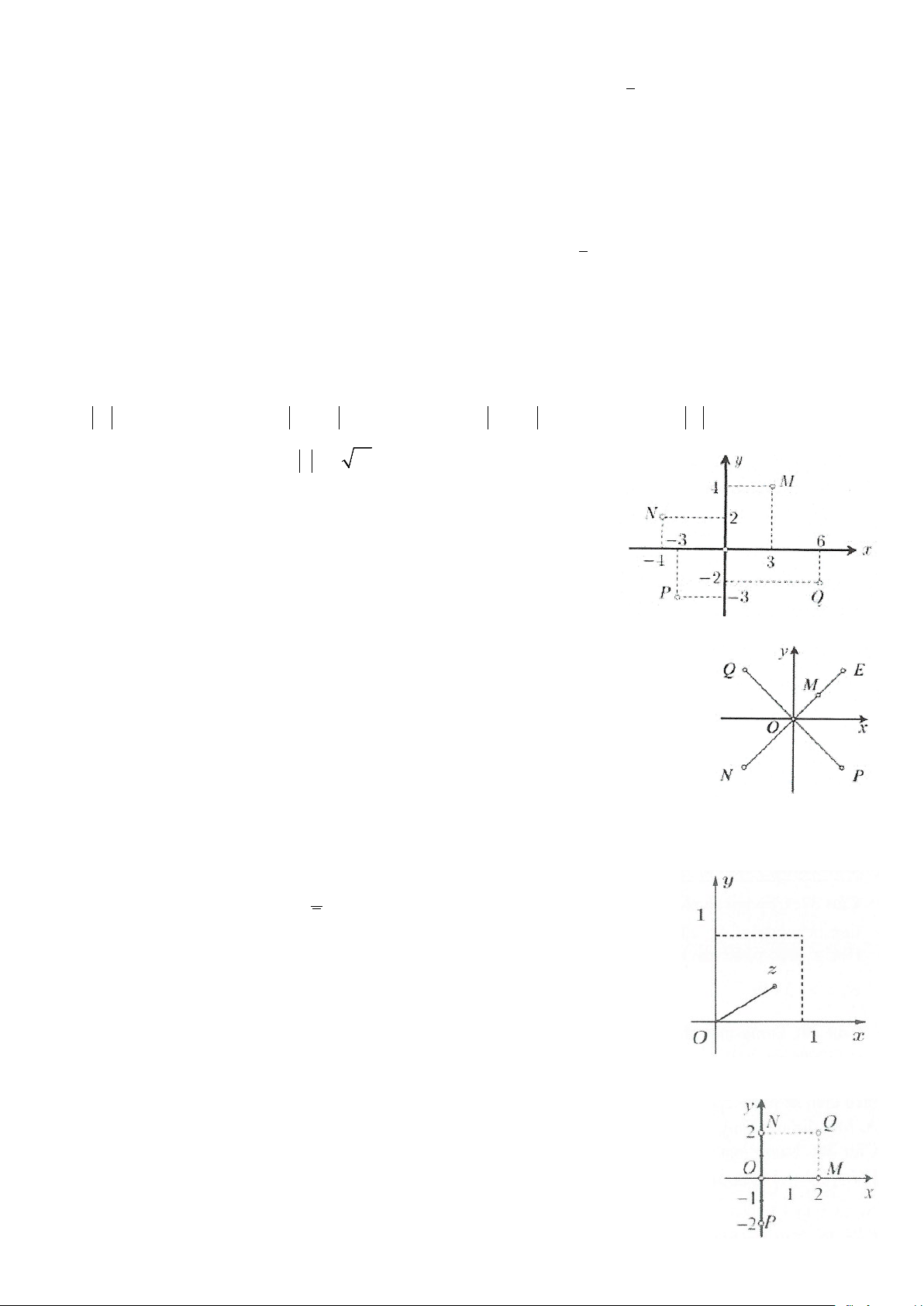
Câu 6: Điểm M trong hình vẽ bên là điểm biểu diễn số phức A. z = 2 − + i
B. z =1− 2i
C. z = 2 + i
D. z =1+ 2i
Câu 7: Điểm M trong hình vẽ bên là điểm biểu diễn số phức
A. z = 4 + 2i
B. z = 2 + 4i C. z = 2 − + 4i
D. z = 4 − 2i
Câu 8: Điểm M trong hình vẽ bên là điểm biểu diễn số phức A. z = 1 − + 2i
B. z =1+ 2i
C. z =1− 2i
D. z = 2 + i
Câu 9: Điểm M trong hình vẽ bên là điểm biểu diễn số phức A. z = 3 − + i
B. z =1− 3i C. z = 1 − − 3i
D. z =1+ 3i
Câu 10: Điểm M trong hình vẽ bên là điểm biểu diễn số phức
A. z = (1+ i)(2 −i)
B. z = (1+ i)(2 −3i) C. 3− 2i z = i D. i z = 2 + 3i
Câu 11: (Đề thi THPTQG năm 2017 – Đề 101) Cho số phức z =1− 2i . Điểm nào dưới đây là điểm biểu
diễn của số phức w = iz trên mặt phẳng tọa độ? A. Q(1;2) B. N (2; ) 1 C. M (1; 2 − ) D. P( 2; − ) 1
Câu 12: (Đề thi THPTQG năm 2017 – Đề 104) Cho hai số phức z =1− 2i, z = 3
− + i . Tìm điểm biểu 1 2
diễn của số phức z = z + z trên mặt phẳng tọa độ 1 2 A. N (4; 3 − ) B. M (2; 5 − ) C. P( 2; − − ) 1 D. Q( 1; − 7)
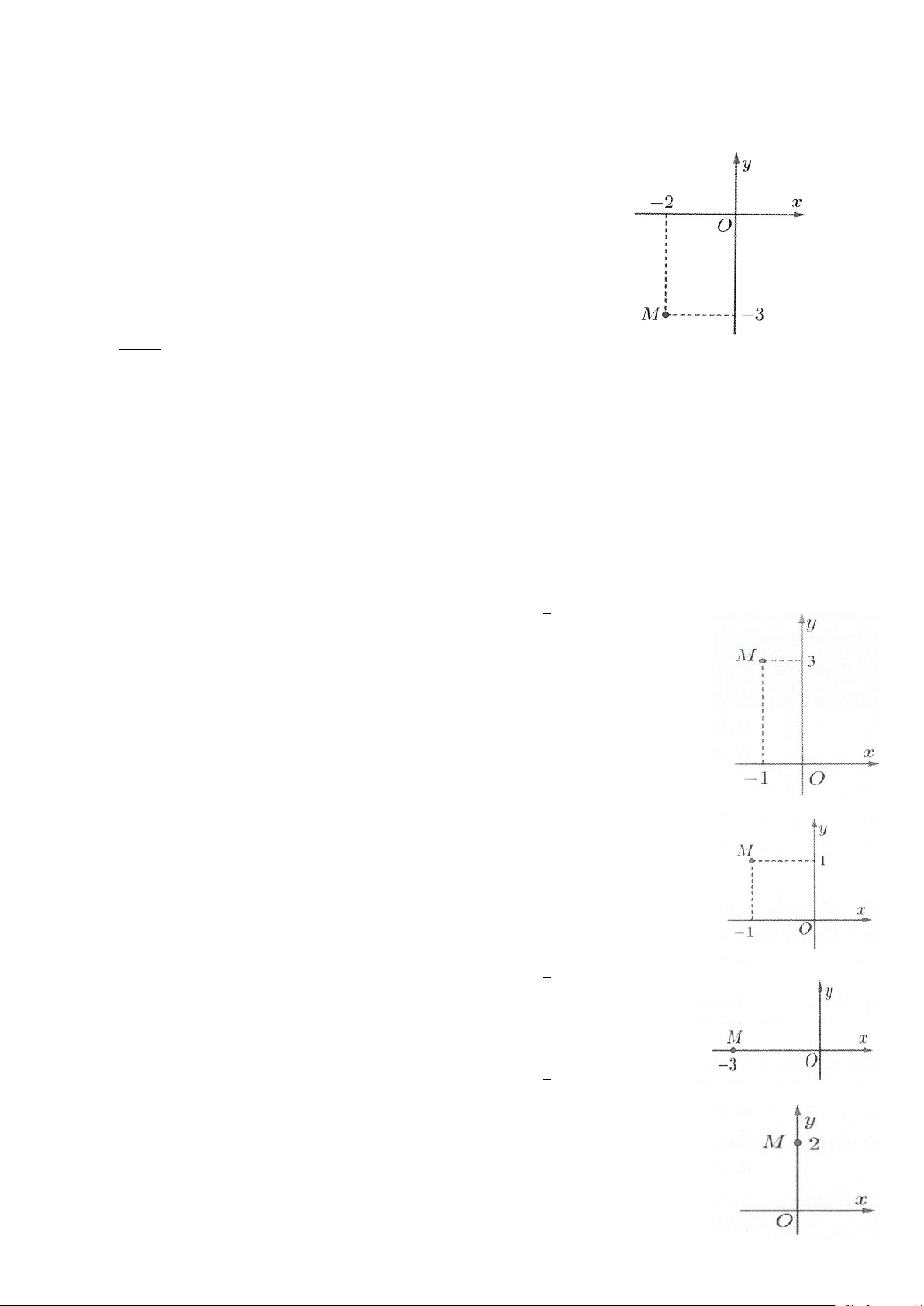
Câu 13: Điểm M trong hình vẽ bên là điểm biểu diễn số phức z . Tìm số phức z A. z = 1 − − 3i
B. z = 3− i
C. z =1+ 3i
D. z =1+ 3i
Câu 14: Điểm M trong hình vẽ bên là điểm biểu diễn số phức z . Tìm số phức z
A. z =1− i B. z = 1 − − i
C. z =1+ i D. z = 1 − + i
Câu 15: Điểm M trong hình vẽ bên là điểm biểu diễn số phức z . Tìm số phức z A. z = 3 − i
B. z = 3i C. z = 3 − D. z = 3
Câu 16: Điểm M trong hình vẽ bên là điểm biểu diễn số phức z . Tìm số phức z
A. z = 2i B. z = 2 C. z = 2 − D. z = 2 − i
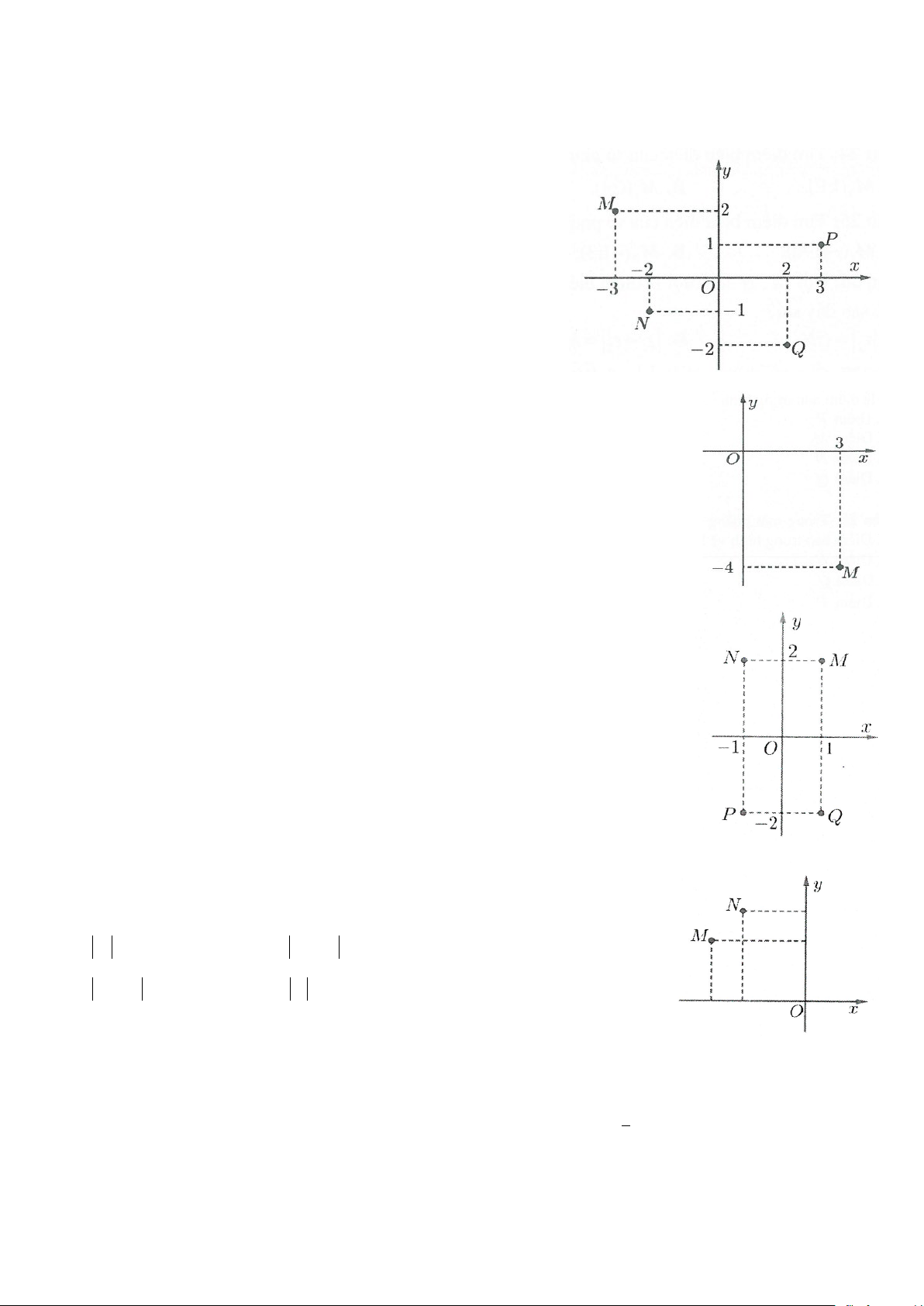
Câu 17: Các điểm M , N. P, Q trong hình vẽ bên là điểm biểu
diễn lần lượt của các số phức z , z , z , z . Khi đó số phức 1 2 3 4
w = 3z + z + z + z bằng 1 2 3 4 A. w = 6 − + 4i
B. w = 3− 4i
C. w = 6 + 4i
D. w = 4 − 3i
Câu 18: (Đề minh họa lần 2 – Bộ GDĐT năm 2017) Điểm M trong hình vẽ bên
là điểm biểu diễn số phức z . Tìm phần thực và phần ảo của z . A. Phần thực là 4 − và phần ảo là 3.
B. Phần thực là 3 và phần ảo là 4 − i .
C. Phần thực là 3 và phần ảo là 4 − . D. Phần thực là 4
− và phần ảo là 3i .
Câu 19: (Đề minh họa lần 1 – Bộ GDĐT năm 2017) Cho số phức z thỏa mãn
điều kiện (1+ i) z = 3−i . Hỏi điểm biểu diễn của z là điểm nào trong các điểm
M , N. P, Q ở hình bên? A. Điểm P B. Điểm Q C. Điểm M D. Điểm N
Câu 20: Gọi M , N lần lượt là điểm biểu diễn của các số phức z , z khác 0. 1 2
Khi đó khẳng định nào sau đây là sai?
A. z = ON
B. z − z = MN 2 1 2
C. z + z = MN
D. z = OM 1 2 1
Câu 21: Cho số phức z = 2 − i . Tìm điểm biểu diễn của số phức ω = iz A. M ( 1; − 2) B. N (2;− ) 1 C. P(2; ) 1 D. Q(1;2)
Câu 22: Cho số phức z = 3+ 2i . Tìm điểm biểu diễn của số phức ω = iz − z A. M (5;5) B. N ( 5; − 5) C. P(5; 5 − ) D. Q( 5; − 5 − )
Câu 23: Cho số phức z = 3− 2i . Tìm điểm biểu diễn của số phức ω = z + .iz A. M (1; 5 − ) B. N (5; 5 − ) C. P(1; ) 1 D. Q(5; ) 1
Câu 24: Tìm điểm biểu diễn của số phức z thỏa mãn 2i + z (1−i) = i(3−i) A. M 1;0 B. M 0;1 C. M 0;2 D. M 0; 1 − 2 ( ) 4 ( ) 1 ( ) 3 ( )
Câu 25: Tìm điểm biểu diễn của số phức z thỏa mãn (2 −i)(1+ i) + z = 4 − 2i A. M 1; − 3 − B. M 1; − 3 C. M 1; 3 − D. M 1;3 4 ( ) 3 ( ) 2 ( ) 1 ( )
Câu 26: Gọi M , N lần lượt là điểm biểu diễn của các số phức z , z khác 0. Khi đó khẳng định nào sau đây 1 2 là sai?
A. z = ON
B. z − z = MN
C. z + z = MN
D. z = OM 2 1 2 1 2 1
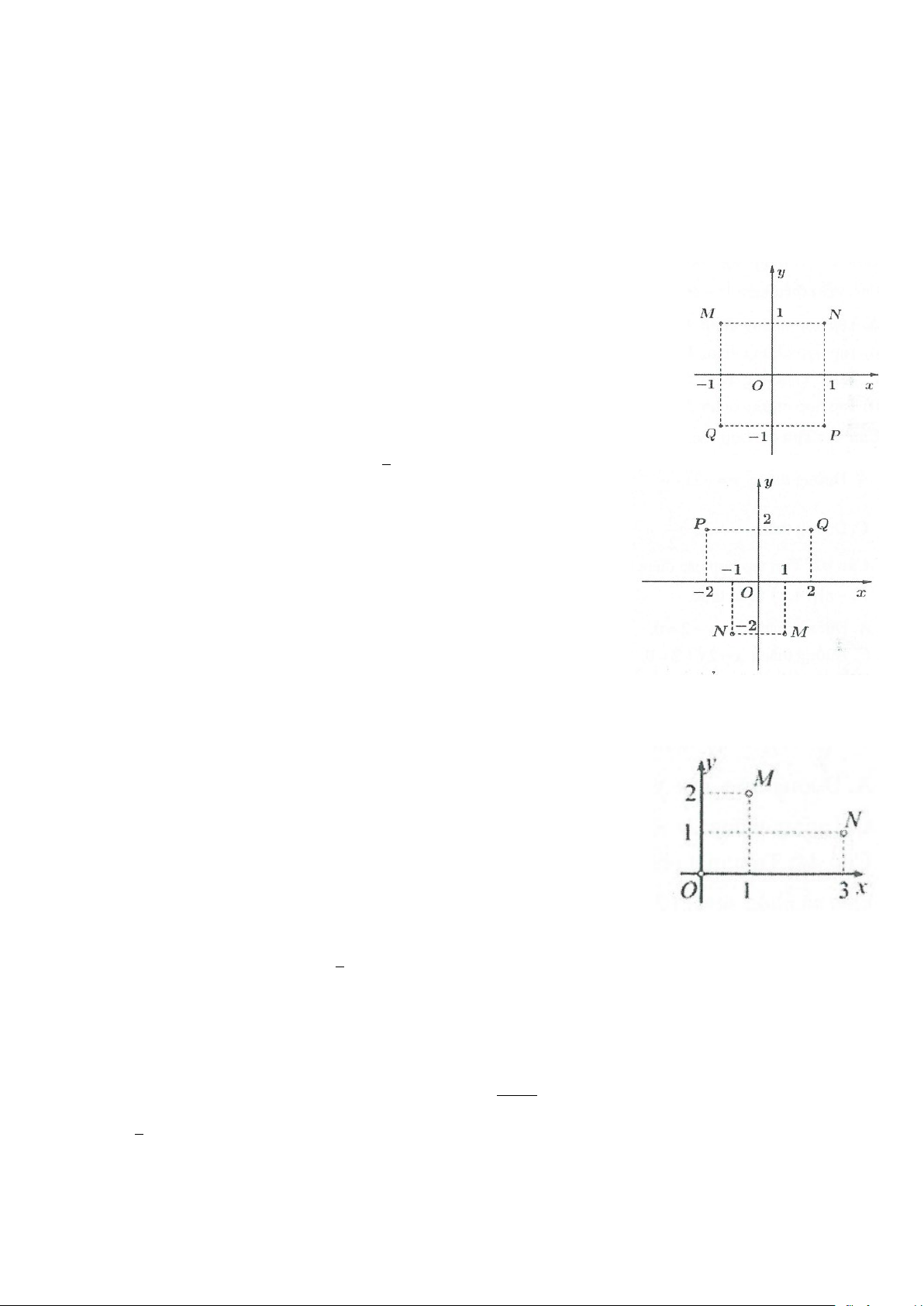
Câu 27: Cho số phức z thỏa z = 2 10 . Hỏi điểm biểu diễn của z là điểm nào trong hình? A. Điểm P B. Điểm M C. Điểm N D. Điểm Q
Câu 28: Trong mặt phẳng tọa độ, điểm M là điểm biểu diễn của số phức z . Điểm
nào trong hình vẽ là điểm biểu diễn của số phức 2z A. Điểm N B. Điểm Q C. Điểm E D. Điểm P
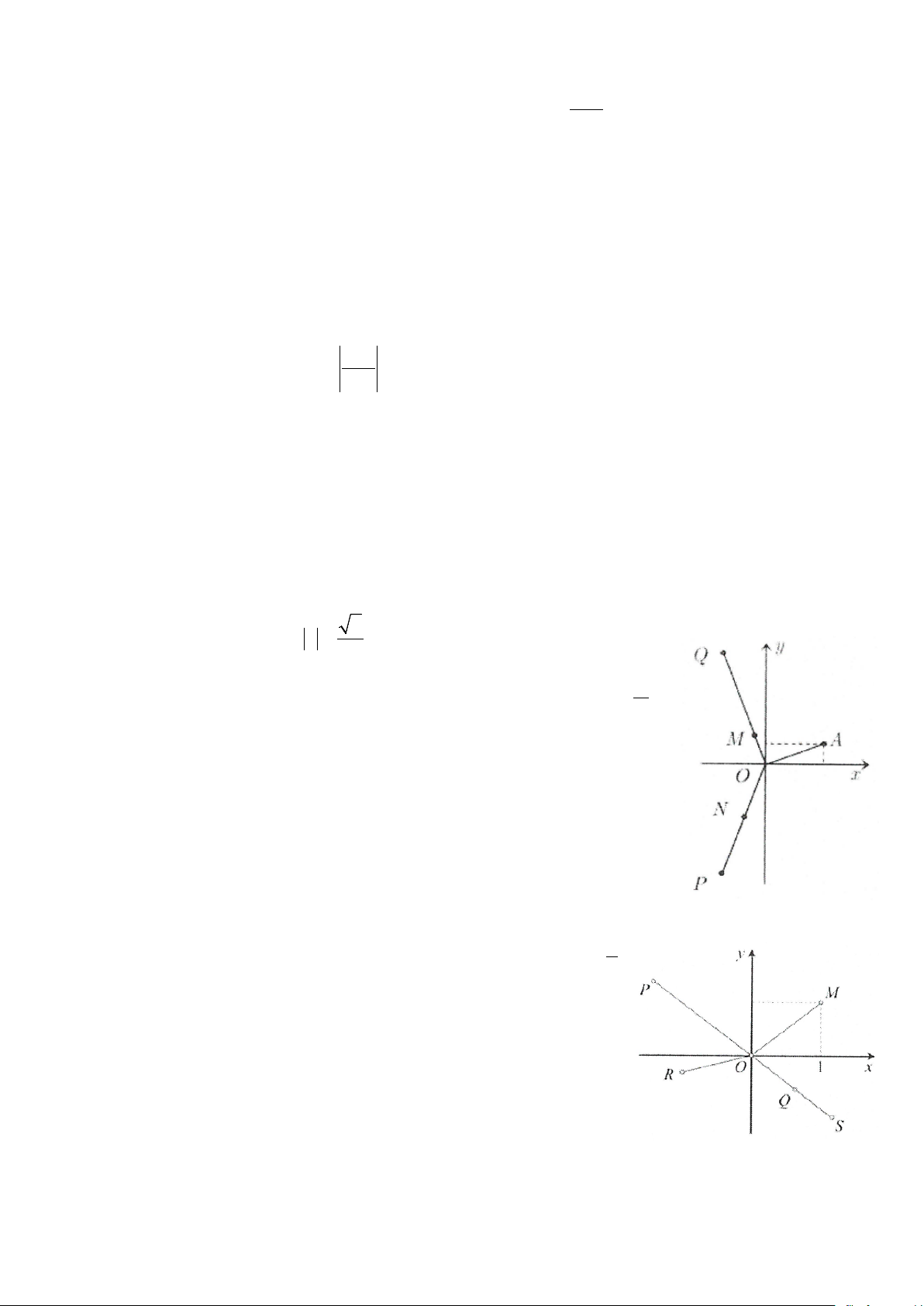
Câu 29: Số phức z được biểu diễn trên mặt phẳng tọa độ như hình vẽ. Hỏi
điểm biểu diễn của số phức i
w = nằm ở góc phần tư thứ mấy trong hệ trục tọa z độ Oxy ? A. Thứ nhất B. Thứ hai C. Thứ ba D. Thứ tư
Câu 30: Cho số phức z = 2i được biểu diễn bởi điểm nào trong hình vẽ bên? A. Điểm M B. Điểm N C. Điểm P D. Điểm Q
Câu 31: Cho số phức z thỏa (1+ 3i) z + 2i = 4
− . Điểm nào sau đây biểu diễn cho z trong các điểm
M , N, P, Q ở hình bên? A. Điểm M B. Điểm N C. Điểm P D. Điểm Q
Câu 32: Cho số phức z thỏa z − (2 + 3i) z =1−9i . Số phức w (iz) 1 5. − =
có điểm biểu diễn là điểm nào trong các điểm M , N, P, Q ở hình vẽ? A. Điểm N B. Điểm Q C. Điểm M D. Điểm P
Câu 33: Cho hai điểm M , N trong mặt phẳng phức như hình vẽ, gọi P là điểm sao cho OMNP là hình
bình hành. Hỏi điểm P biểu thị cho số phức nào sau đây?
A. z = 4 − 3i 4 B. z = 2 − + i 3
C. z = 4 + 3i 2
D. z = 2 − i 1
Câu 34: Trong mặt phẳng phức gọi M là điểm biểu diễn cho số phức z = a + bi với a, b∈, ab ≠ 0 và
M ′ là điểm biểu diễn cho số phức z . Mệnh đề nào sau đây đúng?
A. M ′ đối xứng với M qua Oy
B. M ′ đối xứng với M qua Ox
C. M ′ đối xứng với M qua O
D. M ′ đối xứng với M qua đường y = x
Câu 35: Cho số phức +
z thỏa mãn điều kiện 1 7 = 1+ 2 i iz i −
. Xác định tọa độ điểm A biểu diễn số phức 1− 3i liên hợp z . A. A( 1; − 3) B. A( 1; − 3 − ) C. A(1; 3 − ) D. A(1;3)
Câu 36: Biết điểm M (1; 2
− ) biểu diễn số phức z . Tính môđun của số phức 2 ω = .iz − z A. 26 B. 6 C. 26 D. 6
Câu 37: Cho hai số phức z =1− 3i, z = 4
− − 6i có các điểm biểu diễn trên mặt phẳng tọa độ lần lượt là hai 1 2
điểm M và N . Gọi z là số phức mà có điểm biểu diễn là trung điểm của đoạn MN . Hỏi z là số phức nào
trong các số phức dưới đây? A. z = 3 − − 9i B. z = 1 − − 3i C. 5 3 z = + i D. 3 9 z = − − i 2 2 2 2
Câu 38: Trong mặt phẳng tọa độ Oxy , cho số phức z thỏa mãn z −i = z + 3i . Tìm tập hợp điểm biểu diễn số phức z .
A. Một đường thẳng
B. Một đường tròn C. Một hyperbol D. Một elip
Câu 39: Trong mặt phẳng phức, tập hợp các điểm biểu diễn của số phức z thỏa mãn điều kiện
z + 2 = i − z là đường thẳng có phương trình nào sau đây?
A. 2x + 4y +13 = 0
B. 4x + 2y + 3 = 0 C. 2
− x + 4y −13 = 0
D. 4x − 2y + 3 = 0
Câu 40: Tìm tập hợp những điểm M biểu diễn số phức z trong mặt phẳng phức, biết số phức z thỏa mãn
điều kiện z − 2i = z +1
A. Tập hợp những điểm M là đường thẳng có phương trình 4x + 2y + 3 = 0 .
B. Tập hợp những điểm M là đường thẳng có phương trình 4x − 2y + 3 = 0
C. Tập hợp những điểm M là đường thẳng có phương trình 2x + 4y − 3 = 0
D. Tập hợp những điểm M là đường thẳng có phương trình 2x + 4y + 3 = 0
Câu 41: Tìm tập hợp các điểm biểu diễn số phức z thỏa mãn điều kiện z + 2 = i − z A. Đường thẳng 3 y = 2 − x −
B. Đường thẳng y = 2 − x − 3 2 C. Đường thẳng 3 y = 2x − D. Đường thẳng 3 y = 2x + 2 2
Câu 42: Tìm tập hợp các điểm biểu diễn số phức z trong mặt phẳng phức thỏa mãn điều kiện (2 − z)(i + z) là số thực
A. Đường thẳng x + y − 2 = 0
B. Đường thẳng x − y + 2 = 0
C. Đường thẳng x − 2y + 2 = 0
D. Đường thẳng x + 2y − 2 = 0
Câu 43: Tìm tập hợp các điểm trên mặt phẳng tọa độ biểu diễn các số phức z thỏa mãn điều kiện
v = (z −i)(2 + i) là một số thuần ảo A. Đường tròn 2 2 x + y = 2
B. Đường thẳng x + 2y − 2 = 0
C. Đường thẳng 2x − y +1 = 0 D. Đường parabol 2 2x = y
Câu 44: Trên mặt phẳng tọa độ Oxy , tìm tập hợp các điểm biểu diễn các số phức z thỏa mãn điều kiện số
phức w = z (2 + 3i) + 5 −i là số thuần ảo A. Đường tròn 2 2 x + y = 5
B. Đường thẳng 2x − 3y + 5 = 0
C. Đường tròn (x − )2 + ( y − )2 3 2 = 5
D. Đường thẳng 3x + 2y −1 = 0
Câu 45: Tìm tất cả các số phức z thỏa mãn z − 2i = 5 và điểm biểu diễn của z thuộc đường thẳng
d :3x − y +1 = 0.
A. z =1− 4i
B. z =1+ 4i và 2 1 z = − − i 5 5 C. 2 1 z = − + i D. z = 1 − − 2i và 2 11 z = + i 5 5 5 5
Câu 46: Cho số phức z thỏa mãn z − i = z −1+ 2i . Trong mặt phẳng phức, tập hợp các điểm biểu diễn số
phức w = (2 −i) z +1 là một đường thẳng. Viết phương trình đường thẳng đó.
A. x − 7y − 9 = 0
B. x + 7y − 9 = 0
C. x + 7y + 9 = 0
D. x − 7y + 9 = 0
Câu 47: Cho số phức v = a + bi . Tìm tập hợp các điểm trên mặt phẳng tọa độ biểu diễn các số phức z thỏa
mãn điều kiện z − v =1
A. Đường thẳng (x − a) + ( y −b) =1
B. Đường thẳng y = b
C. Đường tròn (x − a)2 + ( y −b)2 =1
D. Đường thẳng x = a
Câu 48: Tập hợp các điểm M biểu diễn số phức z sao cho = ( )2 2 z z là A. Gốc tọa độ B. Trục hoành C. Trục tung
D. Trục tung và trục hoành
Câu 49: Trong mặt phẳng phức với hệ tọa độ Oxy , tìm tập hợp các điểm biểu diễn số phức z thỏa mãn điều
kiện z là số ảo A. Trục ảo
B. Trục thực và trục ảo
C. Đường phân giác góc phần tư thứ nhất và thứ ba
D. Hai đường phân giác của các gốc tọa độ
Câu 50: Tìm tập hợp các điểm biểu diễn bằng số phức z thỏa mãn z (1+ i) là số thực.
A. Đường tròn bán kính bằng 1
B. Trục hoành Ox
C. Đường thẳng y = −x
D. Đường thẳng y = x
Câu 51: Xác định tập hợp các điểm biểu diễn số phức −
z thỏa mãn z i là số thực z + i
A. Đường tròn phương trình 2 2
x + y =1 bỏ đi điểm A(0;− ) 1
B. Hyperbol phương trình 2 2 x − y = 1
− bỏ đi điểm A(0;− ) 1
C. Trục tung Oy bỏ đi điểm A(0;− ) 1
D. Trục hoành Ox bỏ đi điểm A(0;− ) 1
Câu 52: Cho số phức z thỏa mãn z − i =1. Tìm tập hợp các điểm biểu diễn số phức z trong mặt phẳng z + i phức A. Đường tròn B. Trục thực C. Trục ảo D. Một điểm
Câu 53: Cho hai số phức z, z′ thỏa mãn phần thực của z bằng phần ảo của z′ và phần ảo của z bằng phần
thực của z′. Nếu tập hợp của các điểm biểu diễn số phức z là đường thẳng x + 2y − 3 = 0 thì tập hợp các
điểm biểu diễn số phức z′ là đường thẳng có phương trình nào sau đây?
A. x − 2y + 3 = 0
B. 2x + y − 3 = 0
C. x − 2y − 3 = 0
D. 2x + y + 3 = 0
Câu 54: Cho số phức z thỏa 2 z =
và điểm A trong hình vẽ bên là điểm 2
biểu diễn của z . Biết rằng ở hình vẽ bên, điểm biểu diễn của số phức 1 w = là iz
1 trong bốn điểm M , N, P, Q . Khi đó điểm biểu diễn của số phức w là điểm nào sau đây? A. Điểm Q B. Điểm M C. Điểm N D. Điểm P
Câu 55: Cho số phức z có điểm biểu diễn là M . Biết số phức 1 w = z
được biểu diễn bởi một trong bốn điểm P, Q, R, S như hình vẽ. Hỏi điểm
biểu diễn của w là điểm nào? A. Điểm S B. Điểm Q C. Điểm P D. Điểm R
Câu 56: Cho số phức z = a + bi(a, b∈) . Để điểm biểu diễn của z nằm trong dải ( 2; − 2) như phần gạch
sọc của hình vẽ thì điều kiện của a, b phải thỏa mãn là gì? A. 2
− < a < 2 và b∈  a ≥ 2 B. b   ≥ 2 a ≤ 2 − C. b   ≤ 2 −
D. a, b∈( 2; − 2)
Câu 57: Cho hình vuông ABCD có tâm H và ,
A B, C, D, H lần lượt là điểm biểu diễn cho các số phức a, ,
b c, d, h . Biết a = 2
− + i, h =1+ 3i và số phức b có phần ảo dương. Khi đó, môđun của số phức b A. 13 B. 10 C. 26 D. 37
Câu 58: Trên mặt phẳng tọa độ Oxy lấy M là điểm biểu diễn số phức z = (2 −i)( 1
− + i) và gọi ϕ là góc 
tạo bởi chiều dương của trục hoành với véc tơ OM . Tính sin 2ϕ . A. 3 B. 3 − C. 3 10 D. 3 10 − 5 5 10 10
Câu 59: Trên mặt phẳng phức, gọi M là điểm biểu diễn số phức z = (2 −3i)(1+ i) và ϕ và góc tạo bởi 
chiều dương trục hoành và véc tơ OM . Tính sin 2ϕ . A. 5 sin 2ϕ = − B. 5 sin 2ϕ = C. 13 sin 2ϕ = D. 13 sin 2ϕ = − 13 13 5 5
Câu 60: Gọi (H ) là tập hợp tất cả các điểm trong mặt phẳng tọa độ Oxy biểu diễn số phức
z = a + bi(a, b∈) thỏa mãn 2 2
a + b ≤1≤ a − b . Tính diện tích hình (H ) . A. 3π 1 π π + B. C. 1 − D. 1 4 2 4 4 2
Câu 61: Biết tập hợp các điểm M biểu diễn hình học số phức z thỏa mãn z − 2 + z + 2 =10 là một elip
(E). Hãy viết phương trình elip đó. 2 2 2 2 2 2 2 2 A. ( ): x y E + =1 B. ( ): x y E + = 1 C. ( ): x y E + = 1 D. ( ): x y E + = 1 25 16 25 21 21 16 16 9
Câu 62: Tập hợp các điểm biểu diễn số phức z thỏa mãn z + 2 + z − 2 = 5 trên mặt phẳng tọa độ là một
elip có phương trình chính tắc nào sau đây? 2 2 2 2 2 2 2 2 A. ( ): x y E + =1 B. ( ): x y E + = 4 C. ( ) 4x 4 : y E + =1 D. ( ) 3 : x y E + = 1 25 9 25 9 25 9 25 3
Câu 63: Tập hợp các điểm M biểu diễn hình học số phức z thỏa z − i +1 + z + i −1 = 8 là một elip (E).
Hãy viết phương trình elip đó. 2 2 2 2 2 2 2 2 A. ( ): x y E + = 1 B. ( ): x y E + = 1 C. ( ): x y E + = 1 D. ( ): x y E + = 1 16 13 16 14 16 12 16 15
Câu 64: Biết tập hợp các điểm M biểu diễn hình học số phức z thỏa z − i + z + i = 4 là một elip (E). Hãy
viết phương trình elip đó. 2 2 2 2 2 2 2 2 A. ( ): x y E + = 1 B. ( ): x y E + = 1 C. ( ): x y E + = 1 D. ( ): x y E + = 1 9 4 4 3 9 3 4 2
LỜI GIẢI CHI TIẾT 
Câu 1: AB = z − z . Chọn B. 2 1 5 5(3+ 4i) Câu 2: 3 4  3 4 z  = = = + ⇒
là điểm biểu diễn. Chọn B. i ( i)( i) i  ; 3 4 3 4 3 4 5 5 5 5  − − +  
Câu 3: z = i( + i)2 1 2 = i( 3 − + 4i) = 4 − − 3i ⇒ ( 4; − 3
− ) là điểm biểu diễn. Chọn A. Câu 4: ( i) z ( i) 2i − 7 1 1  1 1 9 5 7 2 0 z z i  ;  + + − = ⇔ = ⇔ = − + ⇒ −
là điểm biểu diễn. Chọn D. 9 5i 2 2 2 2  +   Câu 5: ( − ) 5 + 3 1 = 5 + 3 i i z i ⇔ z =
⇔ z =1+ 4i ⇒ (1;4) là điểm biểu diễn. Chọn C. 1− i
Câu 6: Ta có M ( 2; − ) 1 ⇒ z = 1
− + 2i . Chọn A.
Câu 7: Ta có M (2;4) ⇒ z = 2 + 4i . Chọn B.
Câu 8: Ta có M (2; )
1 ⇒ z = 2 + i . Chọn D.
Câu 9: Ta có M (1; 3
− ) ⇒ z =1− 3i . Chọn B.
Câu 10: Ta có (− − ) 3− 2 2; 3 ⇒ = 2 − − 3 i M z i = . Chọn C. i
Câu 11: w = iz = i( − i) 2
1 2 = i − 2i = 2 + i ⇒ N (2; ) 1 . Chọn B.
Câu 12: z = z + z = 1− 2i + 3 − + i = 2 − − i ⇒ 2; − 1 − . Chọn C. 1 2 ( ) ( ) ( ) Câu 13: M ( 1; − 3) ⇒ z = 1
− + 3i ⇒ z = 1
− − 3i . Chọn A. Câu 14: M ( 1; − ) 1 ⇒ z = 1
− + i ⇒ z = 1
− − i . Chọn B. Câu 15: M ( 3 − ;0) ⇒ z = 3 − . Chọn C.
Câu 16: M (0;2) ⇒ z = 2i ⇒ z = 2
− i . Chọn D. Câu 17: z = 3 − + 2i, z = 2
− − i, z = 3+ i, z = 2 − 2i ⇒ w = 3z + z + z + z = 6
− + 4i . Chọn A. 1 2 3 4 1 2 3 4 Câu 18: M (3; 4
− ) ⇒ z = 3− 4i ⇒ phần thực là 3 và phần ảo là 4 − . Chọn C. 3− i 3− i 1− i Câu 19: ( + ) ( )( ) 2− 4 1 = 3 i i z − i ⇔ z = ⇔ z = =
= − i ⇒ − ⇒ Q . Chọn B. 1+ i (1+i)(1−i) 1 2 (1; 2) 2
Câu 20: Ta có z + z ≠ MN nên đáp án C sai. Chọn C. 1 2
Câu 21: ω = iz = i(2 −i) =1+ 2i ⇒ (1;2) là điểm biểu diễn. Chọn D.
Câu 22: ω = iz − z = i(3+ 2i) −(3− 2i) = 5 − + 5i ⇒ ( 5
− ;5) là điểm biểu diễn. Chọn B.
Câu 23: ω = z + .iz = (3− 2i) + i(3+ 2i) =1+ i ⇒ (1; )
1 là điểm biểu diễn. Chọn C.
Câu 24: + ( − ) = ( − ) ⇔ ( − ) 1 2 1 3 1 = 1 + i i z i i i z i + i ⇔ z =
⇔ z = i ⇒ (0; )
1 là điểm biểu diễn. Chọn B. 1− i
Câu 25: (2 −i)(1+ i) + z = 4 − 2i ⇔ z =1−3i ⇒ z =1+ 3i ⇒ (1;3) là điểm biểu diễn. Chọn D.
Câu 26: Ta có z − z = MN nên đáp án C sai. Chọn C. 1 2
Câu 27: Với Q(6; 2
− ) ⇒ z = 6 − 2i ⇒ z = 2 10 . Chọn D.
Câu 28: Điểm biểu diễn số phức 2z là E . Chọn C. i i i(x + yi)
Câu 29: Giả sử z = x + yi với x, y > 0 . Ta có y x w = = = = − + i 2 2 2 2 2 2 z x − yi x + y x + y x + y  
Điểm biểu diễn của w là y −  ; x
nằm ở góc phần tư thứ 2. Chọn B. 2 2 2 2  x y x y  + + 
Câu 30: Điểm biểu diễn của số phức là (0;2) là điểm N . Chọn B. Câu 31: Ta có ( + ) 4 − − 2 1 3 + 2 = 4 i i z i − ⇔ z = ⇔ z = 1 − + i ⇒ ( 1; − )
1 là điểm biểu diễn. Chọn A. 1+ 3i
Câu 32: Giả sử z = x + yi ⇒ z = x − yi
Ta có z − (2 + 3i) z =1−9i ⇔ (x + yi) −(2 + 3i)(x − yi) =1−9i
⇔ x + yi − 2x − 3y − 3xi + 2yi =1− 9i ⇔ (−x − 3y) + ( 3
− x + 3y)i =1− 9i
−x − 3y =1 x = 2 ⇔  ⇔  3x 3y 9  − + = − y = 1 −
Do đó z = − i ⇒ w = (iz) 1− 5 5 5 2 5. = = ( =
= − i ⇒ − là điểm biểu diễn. Chọn C. iz i 2 − i) 1 2 (1; 2) 1+ 2i  
Câu 33: Ta có OM = PN ⇒ P(2;− )
1 ⇒ z = 2 − i . Chọn D. Câu 34: M ( ;
a b), M ′(a; b
− ) ⇒ đối xứng nhau qua trục Ox . Chọn B. Câu 35: 1+ 7 = 1+ 2 i iz i −
⇔ iz =1+ 2i − ( 2
− + i) ⇔ iz = 3+ i ⇔ z =1− 3i ⇒ z =1+ 3i 1− 3i
Do đó tọa độ điểm A là (1;3). Chọn D.
Câu 36: z = − i ⇒ ω = i z − z = i( + i) −( − i)2 2 1 2 . 1 2 1 2 = 2 − + i − ( 3
− − 4i) =1+ 5i ⇒ ω = 26 . Chọn C.
Câu 37: Gọi I là trung điểm  3 9  3 9
MN ⇒ I − ;− ⇒ z = − −   i . Chọn D.  2 2  2 2
Câu 38: Gọi M (z); A(0; ) 1 và B(0; 3
− ) là các điểm biểu diễn số phức z; i và 3 − i
Khi đó MA = MB ⇒ tập hợp điểm biểu diễn số phức z là đường trung trực của AB có phương trình y = 1 − . Chọn A.
Câu 39: Đặt z = x + yi( ;
x y ∈) ta có: x + yi + 2 = y −(x + yi)
⇔ (x + )2 + y = x + ( y − )2 2 2 2
1 ⇔ 4x + 2y + 3 = 0
Do đó tập hợp điểm M ( ;
x y) biểu diễn số phức z là đường thẳng 4x + 2y + 3 = 0 . Chọn B.
Câu 40: Đặt z = x + yi( ;
x y ∈) ⇔ z = x − yi ta có: x + yi − 2i = x − yi +1
⇔ x + ( y − )2 = (x + )2 2 2 2
1 + y ⇔ 2x + 4y − 3 = 0
Do đó tập hợp điểm M ( ;
x y) biểu diễn số phức z là đường thẳng 2x + 4y − 3 = 0. Chọn B.
Câu 41: Đặt z = x + yi( ;
x y ∈) ta có: x + yi + 2 = i −(x + yi)
⇔ (x + )2 + y = x + ( y − )2 2 2 3 2
1 ⇔ 4x + 2y + 3 = 0 ⇔ y = 2 − x − 2
Do đó tập hợp điểm M ( ;
x y) biểu diễn số phức z là đường thẳng 3 y = 2
− x − . Chọn A. 2
Câu 42: Đặt z = x + yi( ;
x y ∈) ta có: w = (2 − z)(i + z) = (2− x − yi)(i + x − yi)
= (2− x)− yi x +   (1− y)i
Phần ảo của số phức w là: (2 − x)(1− y) − xy = −x − 2y + 2
Số phức w là số ảo khi −x − 2y + 2 = 0 ⇔ x + 2y − 2 = 0
Vậy tập hợp điểm biểu diễn số phức z thỏa mãn (2 − z)(i + z) là số thực là đường thằng x + 2y − 2 = 0. Chọn D.
Câu 43: Đặt z = x + yi( ;
x y ∈) ta có: v = (z −i)(2 + i) = (x + yi −i)(2 + i)
= 2x − ( y − ) 1 + 2( y − ) 1 i + xi
Số phức v = (z −i)(2 + i) là một số thuần ảo khi phần thực 2x −( y − )
1 = 0 hay 2x − y +1 = 0 .
Do đó tập hợp điểm biểu diễn số phức z là đường thẳng 2x − y +1 = 0 . Chọn C.
Câu 44: Đặt z = x + yi( ;
x y ∈) ta có: w = z (2 + 3i) + 5 −i = (x + yi)(2 + 3i) + 5 −i
= 2x + 2yi + 3xi − 3y + 5 − i = (2x − 3y + 5) + (3x + 2y − ) 1 i
Số phức w = z (2 + 3i) + 5 −i là số thuần ảo khi phần thực 2x −3y + 5 = 0
Do đó tập hợp điểm biểu diễn số phức z là đường thẳng 2x − 3y + 5 = 0 . Chọn B.
Câu 45: Đặt z = x + yi( ;
x y ∈) ta có: z − i =
⇔ x + ( y − )2 2 2 5 2 = 5
x + ( y − 2)2 = 5 x +( y − 2)2 = 5 x +(3x +1− 2)2 2 2 2 Giải hệ phương trình = 5  ⇔  ⇔  3
 x − y +1 = 0 y = 3x +1 y = 3x +1 2 x =1⇒ y = 4 10
x − 6x − 4 = 0  ⇔  ⇔  2 − 1 y = 3x +1 x = ⇒ y = −  5 5 Do đó − z =1+ 4i và 2 1 z =
− i là các số phức cần tìm. Chọn B. 5 5
Câu 46: w = ( −i) w −1 2 z +1 ⇔ z = 2 − i 2 w −1 w −1
w −1− 2i + i
w −1− (1− 2i)(2 − i)
Suy ra z − i = z −1+ 2i ⇔ − i = −1+ 2i ⇔ = 2 − i 2 − i 2 − i 2 − i
⇔ w − 2 − 2i = w −1+ 5i
Đặt w = x + yi( ;
x y ∈) ta có: w − − i = w − + i ⇔ (x − )2 + ( y − )2 = (x − )2 + ( y + )2 2 2 1 5 2 2 1 5
⇔ 2x +14y +18 = 0 ⇔ x + 7y + 9 = 0
Do đó tập hợp điểm biểu diễn w là đường thẳng x + 7y + 9 = 0 . Chọn C.
Câu 47: Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn các số phức z thỏa mãn điều kiện z − v =1 là
đường tròn tâm I (v) = I ( ;
a b) bán kính R =1. Chọn C.
Câu 48: Đặt z 2 = x + yi( ;
x y ∈) ⇒ z = x − yi ta có: = ( ) ⇔ ( + )2 = ( − )2 2 z z x yi x yi x = 0 ⇔ 2xyi = 2
− xyi ⇔ 4xyi = 0 ⇔ xy = 0 ⇔   y = 0
Do đó tập hợp điểm biểu diễn số phức z là trục hoành và trục tung. Chọn D.
Câu 49: Đặt z = x + yi( ;
x y ∈) khi đó z là số ảo khi phần thực x = 0
Do đó tập hợp điểm biểu diễn z là đường thẳng x = 0 hay là trục ảo. Chọn A.
Câu 50: Đặt z = x + yi( ;
x y ∈) ta có: z (1+ i) = (x + yi)(1+ i) = x − y + ( y + x)i là số thực khi phần ảo
x + y = 0 ⇔ y = −x
Do đó tập hợp điểm biểu diễn z là đường thẳng y = −x . Chọn C.
z − i x + yi − i x + ( y − ) 1 i
Câu 51: Đặt z = x + yi( ; x y ∈) ta có: = = (ĐK z ≠ i − )
z + i x + yi + i x + ( y + ) 1 ix + 
( y − )1i x −   ( y + ) 2 1 ix − 
( 2y − )1+ x(y− )1− x(y+ )1i = =
là số thực khi phần ảo x + ( y + )2 1 x + ( y + )2 2 2 1
xy − x − xy − x = 0 ⇔ x = 0 x + ( y + )2 2 1
Do đó tập hợp điểm biểu diễn z là đường thẳng x = 0 (trục tung) bỏ đi điểm (0; ) 1 − . Chọn C.
Câu 52: Ta có: z − i =1 ⇔ z − i = z + i (với z ≠ i − ) z + i
Đặt z = x + yi( ;
x y ∈) ta có: x + yi −i = x + yi + i ⇔ x + ( y − )2 = x + ( y + )2 2 2 1 1 ⇔ y = 0
Do đó tập hợp điểm biểu diễn z là đường thẳng y = 0 (trục thực) bỏ đi điểm (0; ) 1 − . Chọn B.
Câu 53: Đặt z = x + yi; z′ = x′ + y i′( ;
x x ;′ y; y′∈) x′ = y Khi đó 
, mặt khác x + 2y − 3 = 0 ⇒ y′ + 2x′ − 3 = 0 ⇔ 2x′ + y′ − 3 = 0 y′ = x′
Do đó tập hợp điểm biểu diễn z′ là đường thẳng có phương trình 2x + y − 3 = 0. Chọn B.
Câu 54: Đặt z − − = x + yi( ; x y ∈ 1 1 y xi ) ta có: w = = = i(x + yi) 2 2
− y + xi x + y Lại có: 1 2 2 1 1 w = . y + x = = = 2 2 2 2 2 x + y x + y z
Dựa vào hình vẽ ta thấy x > 0; y > 0 ⇒ phần thực và phần ảo của w đều âm
Mặt khác w = 2 z nên điểm biểu diễn w trong 4 điểm chỉ có thể là điểm P . Chọn D.
Câu 55: Đặt z =1+ yi( y ∈) . Dựa vào hình vẽ ta thấy y > 0 Ta có: 1 1 1− yi w = = =
⇒ phần thực của w bằng 1 suy ra 1 0 <
< 1, phần ảo của w bằng 2
z 1+ yi 1+ y 2 1+ y 2 1+ y
− y < 0 nên trong 4 điểm chỉ điểm Q có tọa độ thỏa mãn 2 yêu cầu trên. Chọn B. 2 1+ y
Câu 56: Dựa vào hình vẽ ta thấy các điểm nằm trong dải ( 2; − 2) đều thỏa mãn 2
− < x < 2; y ∈ Do đó 2
− < a < 2 và b∈  . Chọn A.
Câu 57: Do a = 2
− + i, h =1+ 3i ⇒ A( 2 − ; ) 1 ; H (1;3) 
Đường thẳng BD là trung trực của AC đi qua H (1;3) và có VTPT là: AH = (3;2) Suy ra  −
BD :3x + 2y − 9 = 0 , gọi 9 3 ; t B t ∈ 
BD ta có: HB = HA  2  2 2
(t )2  9−3t
(t )2  3−3t   9 1 3 13 1 13 1  ⇒ − + − = ⇔ − + = ⇔ + (t − )2 1 =13 ⇔ (t − )2 1 =       4  2   2   4  t = 3 B(3;0) ⇔ ⇒   t = 1 − B  ( 1; − 6)
Do đó phức b có phần ảo dương nên B( 1;
− 6) ⇒ b = OM = 37 . Chọn D. Câu 58: z = 1
− + 3i ⇒ M ( 1;
− 3) và nằm ở góc phần tư thứ (II) nên ta có   ϕ = (OM i) 1 − 1 3 cos cos ; = = − ⇒ sinϕ = . Vậy 3
sin 2ϕ = − . Chọn B. (− )2 2 + 10 10 1 3 5
Câu 59: z = 5 − i ⇒ M (5;− )
1 và nằm ở góc phần tư thứ (IV) nên ta có   ϕ = (OM i) 5 5 1 cos cos ; = = ⇒ sinϕ = − . Vậy 5 sin 2ϕ = − . Chọn A. + (− )2 2 26 26 5 1 13
Câu 60: Vẽ đường tròn (C) 2 2
: x + y =1 và đường thẳng x − y −1 = 0
Đồng thời xét miền bất đẳng thức, ta được hình ( π
H ) có diện tích là 1
S = − . Chọn C. 4 2
Câu 61: Gọi A(0; 2
− ), B(0;2) ⇒ MA + MB =10 = 2a  →a = 5 2 2 Và 2 2 2
AB = 2c = 4 
→c = 2 ⇒ b = a − c = 21. Vậy ( ) : x y E + = 1. Chọn B. 25 21
Câu 62: Gọi A( − ) B( ) 5 0; 2 ,
0;2 ⇒ MA + MB = 5 = 2a  →a = 2 2 2 Và 2 2 2 9
AB = 2c = 4 
→c = 2 ⇒ b = a − c = . Vậy ( ) 4x 4 : y E + =1. Chọn C. 4 25 9
Câu 63: Gọi A( 1; − ) 1 , B(1;− )
1 ⇒ MA + MB = 8 = 2a  →a = 4 2 2 Và 2 2 2
AB = 2c = 2 2 
→c = 2 ⇒ b = a − c =14 . Vậy ( ) : x y E + = 1. Chọn B. 16 14
Câu 64: Gọi A(0;− ) 1 , B(0; )
1 ⇒ MA + MB = 4 = 2a  →a = 2 2 2 Và 2 2 2
AB = 2c = 2 
→c =1⇒ b = a − c = 3 . Vậy ( ) : x y E + = 1. Chọn B. 4 3
Document Outline

  • ITMTTL~1
  • IIBITP~1
  • IIILIG~1