Chuyên đề trắc nghiệm cực trị số phức Toán 12

Chuyên đề trắc nghiệm cực trị số phức Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

19 10 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 4: Số phức

Môn: Toán 12

Thông tin:

27 trang 7 tháng trước

Tác giả:

Profile Mai Nguyệt
CHỦ ĐỀ 19: BÀI TOÁN CỰC TRỊ SỐ PHỨC
Dạng 1: Cho số phức
z
thỏa mãn
zz zz
−=−
12
. Tìm số phức thỏa mãn
zz−
0
nhỏ nhất.
Phương pháp: Đặt
M(z); A(z ); B(z )
12
là các điểm biểu diễn số
phức
1
z; z
và
z
2
. Khi đó từ giả thiết
zz zz−=−
12
suy ra
MA MB=
, tập hợp điểm biểu diễn số phức
z
là đường trung
trực ∆ của AB.
Gọi
N(z )
0
là điểm biểu diễn số phức
Ta có
MN z z= −
0
nhỏ nhất khi
min
MN
khi M là hình chiếu
vuông góc của N trên d và
min
MN d(N; )
= ∆
Ví dụ 1: Cho số phức
z
thỏa mãn
4−−= +z i zi
. Gọi
(; )z a bi a b=+∈
là số phức thỏa mãn
13−+zi
nhỏ nhất. Giá trị của biểu thức
23= +T ab
là:
A.
4
−
B. 4 C. 0 D. 1
Lời giải
Đặt
( ); (4;1), B(0; 1)
Mz A −
là các điểm biểu diễn số phức
;4zi+
và
−i
. Khi đó từ giả thiết suy ra
=MA MB
, tập hợp điểm biểu diễn số phức
z
là đường trung
trực của AB đi qua
I(2; 0)
và có VTPT là
( 4; 2) : 2 4 0= − − ⇒∆ + − =n AB x y

Gọi
(1; 3)−N
là điểm biểu diễn số phức
13− i
Ta có
13−+zi
nhỏ nhất khi
min
MN
khi M là hình chiếu vuông
góc của N trên
∆
, suy ra
:x 2y 1 0− +=MN
Giải hệ
( )
2 40 3
3; 2 3 2 2 3 0
2 70 2
+−= =

⇒ ⇒ −⇒=− ⇒ + =

− −= =−

xy x
M z i ab
xy y
. Chọn C.
Ví dụ 2: Cho các số phức
z
thỏa mãn
22−=+ziz
. Gọi
z
là số phức thỏa mãn
(2 ) 5−+iz
nhỏ nhất.
Khi đó :
A.
01<<z
B.
12<<z
C.
23
<<z
D.
3>z
Lời giải
Gọi
(x; y); (0; 2), B( 2;0)−MA
là các điểm biểu diễn số phức
;2zi
và
2−
.
Từ giả thiết
⇒
= ⇒∈
MA MB M
trung trực của AB có phương trình
:0∆ +=xy
Lại có:
5
(2 ) 5 2 5 2
2
= − + = − + = ++
−
P iz iz z i
i
, gọi
( 2; 1)−−N
là điểm biểu diễn số phức
2−−i
suy ra
5=P MN
Ta có P nhỏ nhất khi
min
MN
khi M là hình chiếu vuông góc của N trên
∆
, suy ra phương trình
:x y 1 0−+=MN
Giải hệ
1
0
11 1 1 2
2
;
10 1
22 2 2 2
2
−
=
+=
−−

⇒ ⇒ ⇒= + ⇒ =


− +=

=
x
xy
M z iz
xy
y
. Chọn A.
Dạng 2: Cho số phức
z
thỏa mãn
zz R−=
0
. Tìm số phức thỏa mãn
P zz= −
1
đạt giá trị lớn nhất,
nhỏ nhất.
Phương pháp: Đặt
M(z); I(z );E(z )
01
là các điểm biểu diễn số
phức
0
z; z
và
z
1
. Khi đó từ giả thiết
0
z z R MI R−=⇔ =
M⇒
thuộc đường tròn tâm I bán kính R. Ta có:
P ME=
lớn
nhất
max
ME⇔
và P nhỏ nhất
min
ME⇔
. Khi đó:
max
P IE R M M= +⇔ ≡
2
và
min
P IE R M M= −⇔≡
1
(Điểm E có thể nằm trong hoặc ngoài đường tròn).
Ví dụ 1: Cho số phức
z
thỏa mãn
32 3−+ =iz i
. Tìm giá trị nhỏ nhất của biểu thức:
1
= −−Pz i
A.
min
P = 3
B.
min
P 13 3= −
C.
min
P = 2
D.
min
P = 10
Lời giải
Ta có:
3
32 3 2 3 23 3−+ =⇔ − + =⇔ ++ =⇒iz i i z z i
i
tập hợp điểm M biểu diễn số phức
z
là đường
tròn tâm
( 2; 3)
−−I
bán kính
3=R
Gọi
E( ; )11
là điểm biểu diễn số phức
min
12+⇒ = ⇒ = − =i P ME P EI R
Ví dụ 2: Cho số phức
z
thỏa mãn
25+−=
zi
. Gọi
1
z
và
2
z
lần lượt là 2 số phức làm cho biểu thức
23= −−Pz i
đạt giá trị nhỏ nhất và lớn nhất. Tính
12
32= +Tz z
A.
T = 20
B.
T = 6
C.
T =
14
D.
T = 24
Lời giải
Ta có:
25+−= ⇒zi
tập hợp điểm M biểu diễn số phức
z
là đường tròn tâm
( 2;1)
−I
bán kính
5=R
. Gọi
E(2; 3) P ME⇒=
Phương trình đường thẳng
: 2 40− +=
IE x y
Dựa vào hình vẽ ta có
max
P IE R M M= +⇔ ≡
2
Giải hệ
2 min
22
1 min
2 40
( 4; 0) 3 5
( 2) ( 1) 5
(0; 2) P 5
− +=
−⇒=
⇒
+ +− =
⇒=
xy
MP
xy
M
.
Do đó
12
3 2 3.2 2.4 14= + =+=Tz z
. Chọn C.
Dạng 3: Cho số phức
z
thỏa mãn
zz zz−=−
12
. Tìm số phức thỏa mãn
P zz zz=− +−
34
đạt giá
trị nhỏ nhất.
Phương pháp: Đặt
M(z); A(z ); B(z ); H(z ); K(z )
12 3 4
là các điểm biểu diễn số phức
z;z ;z ;z
123
và
z
4
. Khi
đó từ giả thiết
12
zz zz−=−
suy ra
MA MB=
, tập hợp điểm biểu diễn số phức
z
là đường trung trực ∆
của AB;
P z z z z MH MK
=− +− = +
34
TH1: H, K nằm khác phía so với đường thẳng ∆
Ta có:
P MH MK HK
=+≥
Dấu bằng xảy ra
o
M M HK ( )⇔ ≡ = ∩∆
Khi đó
min
P HK
=
TH2: H, K nằm cùng phía so với đường thẳng ∆
Gọi H’ là điểm đối xứng của ∆
Khi đó:
P MH MK MH ' MK H 'K=+=+≥
Dấu bằng xảy ra
o
M M H'K ( )⇔ ≡ = ∩∆
Khi đó
min
P H'K=
Ví dụ 1: Cho số phức
z
thỏa mãn
12 32
−+ = + −z iz i
. Gọi
= +z a bi
(; )∈ab
sao cho
24 1= − − + +−Pz iz i
đạt giá trị nhỏ nhất. Khi đó
+
ab
là:
A. 3 B. 5 C. 8 D. 4
Lời giải
Đặt
( ); (1; 2), B( 3; 2)−−Mz A
tử giả thiết suy ra
=MA MB
nên M thuộc đường thẳng trung trực của AB có
phương trình
: 10∆ − +=xy
, gọi
H(2; 4)
và
K( 1; 1)−
là các điểm
biểu diễn số phức
24+ i
và
1−+i
Ta có
P MH MK= +
và 2 điểm H, K cùng phía so với đường thẳng ∆
Gọi H’ là điểm đối xứng của
: 10∆ − +=xy
Ta có:
HH' : 6 0+−=xy
tọa độ trung điểm của HH’ là nghiệm hệ
phương trình
10
57
;
60
22
− +=

⇒

+−=

xy
I
xy
Suy ra
H'(3; 3)
Lại có:
P MH MK MH ' MK H 'K=+=+≥
Dấu bằng xảy ra
M H'K d
⇔= ∩
. Phương trình đường thẳng H’K là:
': 2 30− +=
HK x y
Suy ra
o
M H'K M ( ; ) z i= ∩∆⇒ ⇒ = +
0
12 1 2
. Khi đó
min
' 25= =P HK
. Chọn A.
Ví dụ 2: Cho số phức
z
thỏa mãn
24 2−+ = −z i iz
. Gọi
= +z a bi
(; )∈ab
sao cho
13= −+ ++P zi z i
đạt giá trị nhỏ nhất. Giá trị nhỏ nhất đấy bằng
A.
53
B.
37
C. 4 D.
41
Lời giải
Ta có:
2
24 2 24 2−+ = − ⇔ −+ = − = +
z iiz z iiz zi
i
Gọi
( ); (2; 4), B(0; 2)
−−
Mz A
từ giả thiết suy ra
=MA MB
nên M thuộc đường thẳng trung trực của AB có
phương trình
: 40∆ −−=xy
, gọi
H(0;1)
và
K( 1; 3)−−
là
các điểm biểu diễn số phức
i
và
13−−
i
Ta có:
P MH MK= +
và 2 điểm H, K cùng phía so với
đường thẳng ∆
Gọi H’ là điểm đối xứng của
: 50∆ −−=xy
Ta có:
HH' : 1 0+ −=xy
tọa độ trung điểm của HH’ là
nghiệm hệ phương trình
40
53
;
10
22
−−=

⇒−

+ −=

xy
I
xy
Suy ra
H'(5; 4)−
Lại có:
P MH MK MH ' MK H 'K 37=+=+≥ =
. Chọn B.
Dạng 4: Cho số phức
z
thỏa mãn
zz zz−=−
12
. Tìm số phức thỏa mãn
22
34
P zz zz
=− +−
đạt
giá trị nhỏ nhất.
Phương pháp: Đặt
M(z); A(z ); B(z ); H(z ); K(z )
12 3 4
là các
điểm biểu diễn số phức
z;z ;z ;z
123
và
z
4
. Khi đó từ giả
thiết
zz zz− ≡−
12
suy ra
MA MB
=
, tập hợp điểm biểu
diễn số phức
z
là đường trung trực ∆ của AB;
22
22
34
P z z z z MH MK=− +− = +
Gọi I là trung điểm của
222 2
2 22 2
2
24 2
+
⇒ = − ⇒= + = +
MH MK HK HK
HK MI P MH MK MI
nhỏ nhất khi
min
⇔MI M
là hình chiếu vuông góc của I xuống
∆
.
Ví dụ 1: Cho số phức
z
thỏa mãn
24 2+− = −z izi
. Gọi z là số phức thoả mãn biểu thức
22
4
= − + −+P zi z i
đạt giá trị nhỏ nhất. Tính
2
z
.
A.
2
12
=z
B.
2
10
=z
C.
2
2=z
D.
2
5=
z
Lời giải
Gọi
( ); ( 2; 4), B(0; 2)−
Mz A
là các điểm biểu diễn số phức
;2 4−+zi
và
2i
Khi đó
24 2
+−=−⇔ = ⇒
z i z i MA MB M
thuộc trung trực
của AB có phương trình
: 40
∆ −+=xy
Gọi
( ) ( )
2
22 2
0;1 , 4; 1 2
2
−⇒= + = +
HK
H K P MH MK MI
(với
( )
2; 0I
là trung điểm của HK)
Do đó
min min
⇔P ME
hay M là hình chiếu vuông góc của I xuống
∆
, khi đó
( )
2
2
: 2 0 1; 3 10+ − = ⇒ = ∩∆⇒ − ⇒ = =IM x y M IM M z OM
. Chọn B.
Ví dụ 2:
Cho số phức
z
thỏa mãn
13 2−+ = + +z iz i
. Giá trị nhỏ nhất của biểu thức
22
24 2
= −+ + +Pz i z i
là:
A.
min
8=P
B.
min
9=P
C.
min
16
=P
D.
min
25=P
Lời giải
Gọi
( ); (1; 3) , B( 1; 1)
− −−Mz A
là các điểm biểu diễn số phức
;1 3zi+
và
1−−i
Khi đó
13 1−+ = ++ ⇔ = ⇒z i z i MA MB M
thuộc trung trực
của AB có phương trình
: 20
∆ −−=xy
Gọi
( ) ( )
2
22 2
2; 4 , 0; 2 2
2
− −⇒= + = +
HK
H K P MH MK MI
(với
( )
1; 3−I
là trung điểm của HK)
Do đó
min min
⇔P ME
hay M là hình chiếu vuông góc của I
xuống
∆
, khi đó
( )
2
2
min
2; 8
2
= ∆+ =


HK
P dI
. Chọn A.
Dạng 5: Cho số phức
z
thỏa mãn
0
zz R−=
. Tìm số phức thỏa mãn
22
12
P zz zz=− +−
đạt giá trị
lớn nhất, nhỏ nhất.
Phương pháp: Đặt
( )
1 20
M(z); A(z ); B(z ); I z
là các điểm biểu diễn số
phức
12
z;z ;z
và
0
z
.
Khi đó từ giả thiết
0
z z R MI R M−=⇔ =⇒
thuộc đường tròn tâm I
bán kính R.
Gọi E là trung điểm của AB ta có:
2
2
2
2
= +
AB
P ME
lớn nhất
max
⇔ ME
và P nhỏ nhất
min
⇔ ME
.
Khi đó
2
⇔≡
max
P MM
và
min 1
⇔≡P MM
.
Ví dụ 1: Cho số phức
z
thỏa mãn
12 2−+ =zi
. Gọi
( )
;=+∈z a bi a b
là số thức thỏa mãn biểu thức
22
23 5= −− + −
Pz i zi
đạt giá trị lớn nhất. Tính
= +T ab
A.
1=T
B.
3=T
C.
1= −T
D.
3= −T
Lời giải
Gọi
( ) ( )
; 1; 2−Mz I
khi đó
2= ⇔MI M
thuộc đường tròn tâm
( )
1; 2−
I
bán kính
2=R
Đặt
( ) ( )
22
2;3 ; 0;5 ⇒= +A B P MA MB
Gọi
( )
1; 4H
là trung điểm của AB ta có :
2
2
2
2
= +
AB
P MH
lớn nhất
max
⇔ MH
Do
max 2
≤ +⇔ ⇔≡MH MI IH MH M M
Ta có:
:1=IH x
Giải hệ
( ) ( )
( )
( )
1
22
2
1
1; 0
1; 4
1 24
=

⇒

−
− ++ =
x
M
M
xy
. Do đó
3+=−ab
. Chọn D.
Ví dụ 2: Cho số phức
z
thỏa mãn
13
3
2
−+=zi
. Gọi
( )
;=+∈z a bi a b
là số thức thỏa mãn biểu thức
22
23= −− + −Pz i zi
đạt giá trị nhỏ nhất. Tính
= +
T ab
A.
5
2
=
T
B.
3
2
=T
C.
13
2
=T
D.
9
2
=
T
Lời giải
Gọi
( ) ( )
; 3; 1
−Mz I
khi đó
13
2
= ⇔MI M
thuộc đường tròn tâm
( )
3; 1−I
bán kính
13
2
=R
Đặt
( ) ( )
22
2;1 ; 0;3 ⇒= +A B P MA MB
Gọi
( )
1; 2E
là trung điểm của AB ta có :
2
2
2
2
= +
AB
P ME
nhỏ nhất
min
⇔ ME
Do
min 1
≥ −⇔ ⇔≡ME MI IE ME M M
Ta có:
:3 2 7 0+ −=IE x y
. Giải hệ
(
)
( )
1
22
2
1
2;
3 2 70
2
13
31
5
4;
4
2

− −=


⇒

− ++ =
−




M
xy
xy
M
. Do đó
5
2
+=ab
. Chọn A.
Dạng 6: Cho hai số phức
12
z ;z
thỏa mãn
10
zz R−=
và
21 2 2
ww−=−zz
;
trong đó
0; 1 2
w ;wz
là các số phức đã biết. Tìm giá trị nhỏ nhất của biểu thức
12
z= −Pz
Phương pháp: Đặt
( )
12
M(z ); N z
lần lượt là các điểm biểu diễn
số phức
1
z
và
2
z
.
Điểm M thuộc đường tròn tâm
(
)
0
Iz
bán kính
R
,
N
thuộc trung
trực
∆
của AB với
(
)
( )
12
w; wAB
Lại có:
min ( ; )∆
=⇒= −
t
P MN P d R
Ví dụ 1: Cho số phức
1
z
thỏa mãn
22
21− −+ =z zi
và số phức
2
z
thỏa mãn
45−−=zi
. Tìm giá trị
nhỏ nhất của
12
−zz
A.
25
5
B.
5
C.
25
D.
35
5
Lời giải
Gọi
(; )Mzy
là điểm biểu diễn số phức
1
z
. Khi đó
22
21− −+ =z zi
2 22 2
(x 2) ( 1) 1 4 2 2 ( ) : 2 1 0⇔ − + − − + = ⇔− − =− ⇔ ∆ + − =y x y x y xy
Gọi
N(a; b)
là điểm biểu diễn số phức
2
z
. Khi đó
22
4 5 ( 4) ( 1) 5−−= ⇔ − + − =
zi a b
Hay tập hợp điểm N trong mặt phẳng Oxy là đường tròn
22
( ) : (x 4) (y 1) 5− +− =C
Ta có
( )
() ( )
8
;( ) 5
5
∆= > =
cC
dI R
( )
⇒∆
không cắt đường tròn
( )
C
.
Lại có
12
=−⇒MN z z
dựa vào hình vẽ ta thấy
( )
( )
( )
( )
min
;⇔ = ∆−
CC
MN MN d I R
Hay
12
min
85 35
5
55
− = −=zz
. Chọn D.
Bài toán có thể hỏi thêm là tìm số phức
1
z
hoặc
để
12
min
−zz
thì ta chỉ cần viết phương trình đường
thẳng
( )
⊥∆MN
sau đó tìm giao điểm
(
)
( )
=∆∩
= ∩
M MN
N C MN
.
Ví dụ 2: Cho hai số phức
12
;
zz
thỏa mãn
1
55+=z
và
22
13 36
+− = −−
z iz i
. Tìm giá trị nhỏ nhất của
biểu thức
12
= −Pzz
A.
min
5
2
=
P
B.
min
15
2
=P
C.
min
3=P
D.
min
10=
P
Lời giải
Gọi
( ) ( )
12
;Mz Nz
lần lượt là các điểm biểu diễn các số phức
1
z
và
2
z
.
Điểm M thuộc đường thẳng tròn tâm
( )
5; 0−I
bán kính
5=R
.
Điểm N thuộc đường thẳng trung trực
∆
của AB với
( ) ( )
35
1; 3 ; B 3; 6 : 4 3 0
2
− ⇒∆ + − =A xy
Lại có:
(
)
;
5
2
∆
= ⇒ = −=
min
I
P MN P d R
. Chọn A.
Dạng 7: Cho hai số phức
12
z ;z
thỏa mãn
11 1
zw R−=
và
21 2
w−=
zR
trong đó
12
w ;w
là các số
phức đã biết. Tìm giá trị lớn nhất, nhỏ nhất của biểu thức
12
= −Pzz
.
Phương pháp: Đặt
( )
12
M(z ); N z
lần lượt là các điểm biểu diễn số phức
1
z
và
2
z
.
Điểm M thuộc đường tròn tâm
( )
1
C
tâm
( )
1
wI
bán kính
1
R
và
N
thuộc đường tròn
( )
2
C
tâm
(
)
2
wK
bán kính
2
⇒=R P MN
. Dựa vào các vị trí tương đối của 2 đường tròn để tìm
min
;
max
MN MN
Ví dụ 1: Cho hai số phức
;w
z
thỏa mãn
.1=zz
và
w34 2−+ =i
. Tìm giá trị lớn nhất của biểu thức
w= −Pz
A.
5=
max
P
B.
max
8=P
C.
max
10=P
D.
max
52= +P
Lời giải
Ta có:
.1 1=⇔=zz z
Gọi
( ) ( )
;wMz N
lần lượt là các điểm biểu diễn các số phức
z
và
w
.
Điểm M thuộc đường tròn tâm
( )
1
C
tâm
( )
0; 0O
bán kính
1
1
=
R
và
N
thuộc đường tròn
( )
2
C
tâm
(3; 4)−K
bán kính
2
2
=⇒=
R P MN
.
Dễ thấy
12
5=>+OK R R
nên
( )
1
C
và
( )
2
C
nằm ngoài nhau suy ra
12
8= ++ =
max
MN OK R R
. Chọn B.
Ví dụ 2: [Đề tham khảo Bộ GD & ĐT 2018] Xét các số phức
( )
,b=+∈z a bi a
thỏa mãn điều kiện
43 5−− =zi
. Tính
= +
P ab
khi giá trị biểu thức
13 1+− + −+z iz i
đạt giá trị lớn nhất
A.
10=P
B.
4
=
P
C.
6=P
D.
8
=P
Lời giải
Gọi
( )
;M xy
là điểm biểu diễn số phức
z
Từ giả thiết, ta có
( )
(
)
22
43 5 4 3 5−−=⇔−+−=⇒zi x y M
thuộc đường tròn
( )
C
tâm
( )
4;3I
, bán
kính
5=R
. Khi đó
= +P MA MB
, với
( ) ( )
1; 3 , 1; 1−−AB
.
Ta có
(
)
222 22
2. 2 .
=++ ≤ +P MA MB MA MB MA MB
Gọi
(
)
0;1
E
là trung điểm
222
2
24
+
⇒= −
MA MB AB
AB ME
.
Do đó
2 22
4.≤+
P ME AB
mà
35
≤=ME CE
suy ra
( ) ( )
22
2
4. 3 5 2 5 200≤ +=P
.
Với C là giao điểm của đường thẳng EI với đường tròn
( )
C
.
Vậy
10 2≤P
. Dấu
""=
xảy ra
( )
6; 4 10
=
⇒ ⇒+=
≡
MA MB
M ab
MC
. Chọn A.
Ví dụ 3: [Đề tham khảo Bộ GD & ĐT 2017] Xét các số phức
z
thỏa mãn điều kiện:
2 4 7 62+−+ −− =z iz i
. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
1−+zi
. Tính
= +
PMm
A.
13 73= +P
B.
52 273
2
+
=P
C.
5 2 73
= +P
D.
5 2 73
2
+
=P
Lời giải
Đặt
( )
,=+∈z x yi x y
và gọi
( ) ( ) ( )
; , 2;1 , 4; 7−M xy A B
suy ra
62=AB
.
Ta có
(
) ( )
6; 6 1; 1= ⇒= −⇒

AB n
phương trình đường thẳng
AB là
30−+=xy
.
Từ giả thiết, ta có
62+= →+=MA MB MA MB AB
suy ra M thuộc đoạn thẳng AB.
Gọi
(
)
(
) (
)
min
22
max
max
1
1; 1 1 1 1
1
−+ =
− ⇒ −+ = − + + = ⇒
−+ =
min
z i MN
N z i x y MN
z i MN
.
Độ dài đoạn thẳng MN nhỏ nhất khi và chỉ khi M là hình chiếu của N trên AB.
Hay
( )
( )
( )
( )
min
2
2
1 13
52 52
;
22
11
−− +
= = = →=
+−
MN d N AB m
Độ dài đoạn thẳng MN lớn nhất khi và chỉ khi
≡
MA
hoặc
≡MB
.
Ta có
13
73 73.
73
≡→ = =
⇒ = →=
≡→ = =
max
M A MN AN
MN M
M B MN BN
Vậy giá trị biểu thức
52 273
2
+
= +=
PMm
. Chọn B.
Ví dụ 4: Xét các số phức
z
thỏa mãn điều kiện:
1 7 4 35−−+ − − =z iz i
. Gọi M, m lần lượt là giá trị lớn
nhất và giá trị nhỏ nhất của
52−+
zi
. Tính
= +PMm
A.
5 10= +P
B.
2 5 10
2
+
=
P
C.
( )
2 5 10= +P
D.
5 2 10
2
+
=P
Lời giải
Đặt
( )
,
=+∈z x yi x y
và gọi
(
) (
)
( )
; , 1;1 , 7; 4
M xy A B
suy ra
35=AB
.
Ta có
( ) (
)
()
6; 3 1; 2
AB
AB n= ⇒ = −⇒

phương trình đường
thẳng AB là
2 10− +=xy
.
Từ giả thiết, ta có
35+= →+=
MA MB MA MB AB
suy ra M thuộc đoạn thẳng AB.
Gọi
( )
min
max
52
5; 2 5 2
52
−+ =
− ⇒ −+ = ⇒
−+ =
min
max
z i MN
N z i MN
z i MN
.
Độ dài đoạn thẳng MN nhỏ nhất khi và chỉ khi M là hình chiếu của N trên AB.
Hay
( )
( )
( )
( )
min
2
2
52 2 1
; 25 25
12
−−+
= = = →=
+−
MN d N AB m
Độ dài đoạn thẳng MN lớn nhất khi và chỉ khi
≡MA
hoặc
≡MB
.
Ta có
5
2 10 2 10.
2 10
≡→ = =
⇒ = →=
≡→ = =
max
M A MN AN
MN M
M B MN BN
Vậy giá trị biểu thức
( )
2 5 10 .= += +PMm
Chọn C.
Ví dụ 5: Biết số phức
z
thỏa mãn đồng thời hai điều kiện
34 5−− =zi
và biểu thức
22
2
=+ −−
M z zi
đạt giá trị lớn nhất. Tính môđun của số phức
+zi
.
A.
z i 2 41+=
B.
z i 35+=
C.
z i 52+=
D.
z i 41+=
Lời giải
Gọi
( )
,=+∈z x yi x y
Ta có:
( ) (
)
22
34 5 3 4 5−− = ⇔ − + − =⇒zi x y
tập hợp điểm biểu diễn số phức
z
là dường tròn
( )
C
tâm
(
)
3; 4I
và
5
=R
.
Mặt khác:
( )
( )
( )
22
22
22
2 2 1 423

=+ −− = + + − + − = + +

M z zi x y x y x y
:4 2 3 0⇔ + +− =dx y M
Do số phức
z
thỏa mãn đồng thời hai điều kiện nên d và
( )
C
có điểm chung
( )
23
; R 5 23 10 13 33
25
−
⇔ ≤⇔ ≤ ⇔ − ≤ ⇔≤ ≤
M
d Id M M
(
) ( )
22
4 2 30 0
5
33 5 4 41
5
3 45
max
xy
x
M zi i zi
y
xy
+−=
=
⇒ = ⇔ ⇔ ⇒ += − ⇒ + =

= −
− +− =
. Chọn D.
Ví dụ 6: Cho hai số phức
1
z
và
2
z
thỏa mãn
12
86+=+zz i
và
12
2−=zz
. Tìm giá trị lớn nhất của
12
?= +
Pz z
A.
P 46=
B.
P 5 35= +
C.
P 2 26=
D.
P 34 3 2= +
Lời giải
Đặt
( ) ( )
12
A;z Bz
theo giả thiết ta có:
(8; 6); 2;+= − = =+
 
 
OA OB OA OB P OA OB
( )
( )
( )
( )
22
2
22 2
104 2 104 2 26=++−= +≥+=⇒≤=
   
OA OB OA OB OA OB OA OB P P
. Chọn C.
Ví dụ 7: [Đề thi thử chuyên Đại học Vinh 2018] Giả sử
12
,zz
là hai trong các số phức
z
thỏa mãn
21+ −=
iz i
và
12
2−=zz
. Giá trị lớn nhất của
12
+zz
bằng
A. 3 B.
23
C.
32
D. 4
Lời giải
Ta có:
( )
21 21+ −=⇔ + + −=iz i i x yi i
(với
( )
;
=+∈z x yi x y
)
(
)
( )
( )
2
2
1 2 1 x;⇔− +− =⇒x y My
biểu diễn
z
thuộc đường tròn tâm
( )
1; 2I
bán kính
1=R
.
Giả sử
( ) ( )
12
A;z Bz
do
12
2 22−=⇒ ==z z AB R
nên
AB
là đường kính của đường tròn
( )
;IR
Lại có:
12
+=+z z OA OB
Mặt khác theo công thức trung tuyến ta có:
22 2
2 22
8
24
+
= − ⇒+=
OA OB AB
OI OA OB
Theo BĐT Bunhiascopky ta có:
( )
( )
2
22
24+ ≥ + ⇒+≤OA OB OA OB OA OB
. Chọn D.
Ví dụ 8: Cho
12
,zz
là hai trong các số phức
z
thỏa mãn điều kiện
53 5−− =zi
và
12
8
−=zz
. Giá trị nhỏ
nhất của biểu thức
12
+
zz
là:
A.
6 34−
B.
2 34 6−
C.
2 34 6+
D.
34 6+
Lời giải
Giả sử
12
w = +zz
Đặt
11
22
w 53
w 53
= −−
= −−
zi
zi
suy ra
1212 12
w w 10 6 w 10 6 w w w 10 6+ =+−−=−−⇔ + = −−zz i i i
Mà
12
1 2 12
ww5
ww 8zz
= =
− =−=
mà
(
)
2 2 22 2
12 12 1 2 12
w w w w 2 w w w w 36.+ +− = + ⇒+ =
Vậy
12
w 10 6 w w 36 6 w
−−= + = =⇒i
thuộc đường tròn tâm
( )
10; 6I
, bán kính
6
=R
.
Cách 2: Gọi
( ) ( )
12
A;z Bz
biểu diễn số phức
12
;zz
Ta có: tập hợp
z
là đường tròn tâm
(
)
5; 3I
bán kính
5, 8= =R AB
Gọi H là trung điểm của
( )
12
w 21⇒=+= + =
  
AB z z OA OB OH
Mặt khác
22
3
= −=⇒IH IA HA
tập hợp điểm H là đường tròn
( ) ( ) ( )
22
5 39− +− =xy C
.
Giả sử
( ) (
)
( ) ( ) ( )
22
22
w ; , 1 ; 5 3 9 10 6 36.
22 2 2

⇒ ∈ ⇒ − + − =⇔− +− =


ab a b
ab H C a b
Do đó tập hợp điểm biểu diễn w thuộc đường tròn tâm
( )
10; 6I
, bán kính
6=R
.
Ta có:
min
w 2 34 6.= −= −
OI R
Chọn B.
Ví dụ 9: Cho
12
,zz
là hai nghiệm của phương trình
63 2 69− + = −−i iz z i
, thỏa mãn điều kiện
12
8
5
−=zz
. Giá trị lớn nhất của
12
+zz
A.
31
5
B.
56
5
C.
42
D.
5
Lời giải
Đặt
( )
;=+∈z x yi x y
suy ra
( ) ( )
( )
63 63 6 3
2 69 2 2 69 2 6 2 9
−+=−+ + =−+ −
−− = + −− = −+ −
iiz iix yi y x i
z ixyi ix y i
Khi đó, giả thiết
( ) ( ) (
) ( ) ( ) (
) ( )
22 2 2 22
3 6 26 29 3 4 1xy x y xy C⇔− +− = − + − ⇔− +− =
.
Tập hợp
z
là đường tròn tâm
(
)
3; 4I
bán kính
8
1,
5
= =R AB
Đặt
12
w = +
zz
gọi H là trung điểm của
( )
12
w 21⇒=+= + =
  
AB z z OA OB OH
Mặt khác
22
3
5
= −=⇒IH IA HA
tập hợp điểm H là đường tròn
( )
( )
(
)
22
9
34
25
xy C− +− =
.
Giả sử
(
) (
) ( ) (
)
( )
22
22
9 36
w ; ,1 ; 3 4 6 8 .
2 2 2 2 25 25

⇒ ∈ ⇒ − + − = ⇔− +− =


ab a b
ab H C a b
Do đó tập hợp điểm biểu diễn w thuộc đường tròn tâm
( )
6;8I
, bán kính
6
5
=R
.
Ta có:
6 56
w 10 .
55
= += +=
max
OI R
Chọn B.
Ví dụ 10: [Đề thi thử chuyên Đại học Vinh 2018] Cho số phức
z
thỏa mãn
z
không phải là số thực và
2
w
2
=
+
z
z
là số thực. Giá trị lớn nhất của biểu thức
1
= +−Mz i
là
A.
2
B.
22
C.
2
D. 8
Lời giải
Ta có
( )
2
22
ww 1
22
2
= ⇒= =
++
+
z zz
zz
z
. Vì w là số thực nên
( )
w w2=
.
Từ (1), (2) suy ra
(
)
( )
( ) ( )
2
2
2
2
w 2 22 .
2
2
= = ⇔ += +⇔ −= −
+
+
zz
z z z z zz zzzz
z
z
( )
( )
22
20 2 2
⇔− −=⇔ =⇔=zz z z z
(vì
z
không là số thực nên
0−≠zz
).
Đặt
w 1 w1= +−⇔ = −+z iz i
nên
22
w 1 2 w 2 1 1 22
−+ = ⇒ = + + =
max
i
. Chọn B.
Cách 2: Ta có w là số thực nên
12
w
= +z
z
là số thực.
Đặt
( )
22
2
1
w
−
=+⇒ =++
+
a bi
z a bi a bi
ab
là số thực khi
( )
22
22
0/
2
0
22
=
−=⇔
+
+=⇒=
b kot mycbt
b
b
ab
ab z
Tập hợp điểm biểu diễn z là đường tròn
(
)
0; 0 ; 2
=OR
Đặt
( ) ( )
; 1;1 2 2− ⇒ = +=
max
M z A MA AO R
. Chọn B.
Ví dụ 11: Cho số phức
z
thỏa mãn
1=z
. Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
biểu thức
2
11= ++ −+Pz z z
. Tính giá trị của M.m
A.
13 3
4
B.
39
4
C.
33
D.
13
4
Lời giải
Gọi
( )
;;=+ ∈∈z x yi x y
. Ta có:
1 .1=⇔=z zz
.
Đặt
1,
= +tz
ta có
[
]
0 1 1 1 2 0; 2= −≤ + ≤ += ⇒∈zzz t
.
Ta có
( )
( )
2
2
2
1 1 1 . 22
2
−
= + + =+ ++=+ ⇒ =
t
t z z zzzz x x
Suy ra
( )
2
22 2
1 . 1 21 21 3−+= −+ = −+ = − = −= −zz zzzzzz z x x t
Xét hàm số
( )
[ ]
2
3 , 0; 2=+− ∈ft t t t
. Bằng cách dùng đạo hàm, suy ra
( )
( )
13 13 3
max ;min 3 . .
44
= =⇒=ft ft Mn
Chọn A.
Ví dụ 12:
Cho số phức z thỏa mãn
1=
z
. Tìm giá trị lớn nhất của biểu thức
12 1= ++ −
Tz z
A.
MaxT=2 5
B.
MaxT=2 10
C.
MaxT=3 5
D.
MaxT=3 2
Lời giải
( )
( ) ( )
22 2
2
1 2 1 1 2 1 1 5.2 1 2 5= ++ −≤ + + + − = + =Tz z z z z
(BĐT Cauchy-Swart)
Chú ý:
( )
22 2
22
1 1 2 2 22 1+ +− = + += +z z xy z
với
= +z x yi
Cách 2: Đặt
= +
z x yi
. Ta có :
22 22
1 2 1 ( 1) 2 ( 1)=+++ −−= +++ −+
T x yi x yi x y x y
Lại có
( )
22
1 22222+ =⇒ = ++ − +=x y T x x fx
Ta có:
( )
12 6
' 0 25
10
2 2 22
−
= − =⇔= ⇒ =
+−
max
fx x T
xx
. Chọn A.
Ví dụ 13:
Cho số phức z thỏa mãn
4 4 10−++=
zz
. Giá trị lớn nhất và giá trị nhỏ nhất của
lần lượt
là :
A. 10 và 4 B. 5 và 4 C. 4 và 3 D. 5 và 3
Lời giải
Đặt
( )
; ; (; )=+ ∈⇒z x yi xy Mxy
biểu diễn
z
Ta có:
4 4 10 4 4 10−++= ⇔+ −++ +=z z z yi x yi
Gọi
1 2 12
F ( 4;0); F (4; 0) MF MF 10− ⇒+=
Khi đó điểm biểu diễn
z
là Elip có trục lớn
12
2 10 5; 2 8= ⇒= = =a a FF c
22
43⇒=⇒= − =c b ac
. Do đó
3 53 5≤ ≤⇒≤ ≤
OM z
. Chọn D.
BÀI TẬP TỰ LUYỆN
Câu 1: Trong mặt phẳng tọa độ, hãy tìm số phức
z
có môđun nhỏ nhất, biết rằng số phức
z
thỏa mãn điều
kiện
24 5−− =zi
A.
12=−−zi
B.
12= −zi
C.
12= +zi
D.
12=−+zi
Câu 2: Cho số phức
z
thỏa mãn
34 4−+ =zi
. Tìm giá trị lớn nhất của biểu thức
=Pz
A.
9
=
max
P
B.
5
=
max
P
C.
12=
max
P
D.
3=
max
P
Câu 3: Cho số phức
z
thỏa mãn
22 1−+ =zi
. Tìm giá trị lớn nhất của
z
A.
42 2−
B.
22 1+
C.
22+
D.
32 1+
Câu 4: Trong các số phức
z
thỏa mãn
34 2++ =zi
.Gọi
0
z
là số phức của môđun nhỏ nhất. Tìm môđun của
số phức
A.
4=
o
z
B.
2
=
o
z
C.
7=
o
z
D.
3=
o
z
Câu 5: Cho số phức
z
thỏa mãn
23 1−− =zi
. Tìm giá trị lớn nhất của
1= ++Pz i
A.
13 2
+
B.
4
C. 3 D.
13 1+
Câu 6: Cho số phức
z
thỏa mãn điều kiện
32−=zz
và
12 2−+ = +max z i a b
. Tính
+ab
A. 4 B.
42
C. 3 D.
4
3
Câu 7: Cho số phức
z
có
2=z
thì số phức
3wz i= +
có môđun nhỏ nhất và lớn nhất lần lượt là bao nhiêu?
A. 2 và 5 B. 1 và 6 C. 2 và 6 D. 1 và 5
Câu 8: Trong tất cả các số phức có dạng
3 ( 2)= −− −zm m i
với
∈m
, hãy tìm số phức
z
có môđun nhỏ
nhất ?
A.
11
22
= −zi
B.
11
22
=−+zi
C.
11
22
=−−zi
D.
11
22
= +zi
Câu 9: Cho số phức
( 1) ( 2) ,= −+ − ∈z m m im
. Tìm giá trị của m để môđun của số phức
z
có giá trị lớn
nhất là
5
A.
30−≤ ≤m
B.
03≤≤m
C.
3
0
≤−
≥
m
m
D.
6
2
≤−
≥
m
m
Câu 10: Cho số phức
( 3) ,=+− ∈
z m m im
. Tìm m để
z
đạt giá trị nhỏ nhất?
A.
0=
m
B.
3=m
C.
3
2
=
m
D.
3
2
= −
m
Câu 11: Cho số phức
z
thỏa mãn
23−− = −z i zi
. Gọi
(; )=+∈z a bi a b
là số phức thỏa mãn
22++zi
nhỏ nhất. Giá trị của biểu thức
3+ab
là:
A. 4 B. 3 C. 6 D. 0
Câu 12: Biết số phức
(, )
=+∈z a bi a b
thỏa mãn điều kiện
24 2−− = −z izi
có môđun nhỏ nhất của.
Tính
22
= +
Ma b
A.
8=
M
B.
10=M
C.
16=M
D.
26=M
Câu 13: Cho số phức
z
có điểm biểu diễn nằm trên đường thẳng
3 4 30− −=xy
. Tìm giá trị nhỏ nhất của
z
A.
1
5
B.
3
5
C.
4
5
D.
2
5
Câu 14: Xét số phức
,( , )=+∈z a bi a b
thỏa mãn
24 2−− = −z izi
. Tìm giá trị nhỏ nhất của
z
A. 4 B.
22
C. 10 D. 8
Câu 15: Cho số phức
z
thỏa mãn
12−+ = − −z iz i
. Gọi
,( , )=+∈z a bi a b
là số phức thỏa mãn
−zi
nhỏ nhất. Giá trị của biểu thức
+ab
là:
A.
7
10
−
B.
9
10
C.
3
10
D.
7
10
Câu 16: Cho các số phức
,z
ω
thỏa mãn
22 4
+− = −z izi
. Gọi
,( , )=+∈z a bi a b
là số phức thỏa mãn
1+
iz
nhỏ nhất. Tính giá trị của biểu thức
22
+ab
A. 4 B.
5
2
C. 5 D. 2
Câu 17: Cho số phức
z
thỏa mãn
1+= +z zi
. Tìm giá trị nhỏ nhất của
12−−
zi
A.
1
3
B.
3
C.
1
2
D.
2
Câu 18: Cho số phức
(x, y )=+∈z x yi
thỏa mãn
1−= +z zi
. Biết
2−zi
nhỏ nhất, tính
2= +Sx y
A.
2=S
B.
3=S
C.
1=S
D.
4=S
Câu 19: Xét các số phức
,( , )=+∈z a bi a b
thỏa mãn
12−+ = −z i zi
. Tính
2
2= −
P ab
khi
z
đạt giá
trị nhỏ nhất
A.
1
25
=P
B.
19
25
=P
C.
4
25
= −P
D.
14
25
=P
Câu 20: Cho các số phức
,z
ω
thỏa mãn
22 4+− = −z izi
và
1w iz= +
. Tính giá trị nhỏ nhất của
w
A.
min
2w
=
B.
min
2
2
w =
C.
min
22w =
D.
min
32
2
w =
Câu 21: Cho số phức
z
thỏa mãn
2
2 5 ( 1 2 )( 3 1)− + = −+ + −z z z iz i
. Tính
min w
, biết
22wz i=−+
A.
3
min
2
w =
B.
min 2w =
C.
min 1w =
D.
1
min
2
w =
Câu 22: Cho số phức
z
thỏa mãn
32
−=
zz
và
12 2−+ = +max z i a b
. Tính
+ab
A. 4 B.
42
C. 3 D.
4
3
Câu 23: Cho số phức
z
thỏa mãn
z
không phải số thực và
2
2
z
w
z
=
+
là số thực. Biểu thức
1+−zi
đạt giá
trị lớn nhất khi
,( , )=+∈z a bi a b
. Tính
2
2= −Pa b
A.
2−
B.
1
C.
3
D.
5−
Câu 24: Cho số phức
z
thỏa mãn
11−+ = +−zizi
. Gọi
,( , )
=+∈
z a bi a b
sao cho
15 2
= −− + + +Pz iz i
đạt giá trị nhỏ nhất. Khi đó
+
ab
bằng
A.
6
5
B.
6
5
−
C.
3
5
−
D.
3
5
Câu 25: Cho số phức
z
thỏa mãn
23−+= −z izi
. Gọi
,( , )=+∈z a bi a b
sao cho
2
= −+ −P zi z
đạt
giá trị nhỏ nhất. Khi đó
2 −ab
bằng
A.
1
5
B.
7
5
−
C.
1
5
−
D.
3
5
Câu 26: Cho số phức
z
thỏa mãn
12 1−− = +z iz
. Gọi
,( , )=+∈z a bi a b
là số phức thỏa mãn biểu thức
22
12= −+ + −
P z i zi
đạt giá trị nhỏ nhất. Tổng
+ab
là
A.
0+=
ab
B.
1
+=ab
C.
2+=ab
D.
3+=ab
Câu 27: Cho số phức
z
thỏa mãn
31−− = ++z iz i
. Gọi
,( , )=+∈z a bi a b
là số phức thỏa mãn biểu
thức
22
12= −− + + +
Pz i z i
đạt giá trị nhỏ nhất. Tổng
+
ab
là
A.
13
10
+=ab
B.
1
10
+=ab
C.
1+=
ab
D.
2+=ab
Câu 28: Cho số phức
z
thỏa mãn
12 5−+ =
zi
và
1= ++zi
ω
có môđun lớn nhất. Tính môđun của số
phức
z
A.
25=z
B.
32=z
C.
6=z
D.
52=z
Câu 29: Cho số phức
z
thỏa mãn
1=z
. Tìm giá trị lớn nhất của
12 1= ++ −Tz z
A.
max 2 5=T
B.
max 2 10=T
C.
max 3 5
=T
D.
max 3 2=
T
Câu 30: Cho số phức
z
thỏa mãn
2
2 5 ( 1 2 )( 3 1)− + = −+ + −z z z iz i
. Tính
min
ω
, với
22=−=zi
ω
A.
3
min
2
=
ω
B.
min 2=
ω
C.
min 1=
ω
D.
1
min
2
=
ω
Câu 31: Cho số phức
z
thỏa mãn
2
1−=
zi
. Tìm giá trị lớn nhất của
z
A.
5
B. 2 C.
22
D.
2
Câu 32: Cho số phức
z
thỏa mãn
22
4
11
+ ++ =
−−
iz iz
ii
. Gọi M, m lần lượt là giá trị lớn nhất và nhỏ nhất
z
. Tính Mm.
A.
2Mm =
B.
1
Mm =
C.
22Mm =
D.
23Mm =
Câu 33: Cho số phức
z
thỏa mãn
2
2
−
−
zi
z
là số ảo. Tìm giá trị lớn nhất của
1= −+ −P z zi
A.
52
B.
32
C.
25
D.
35
Câu 34: Gọi S là tập hợp tất cả các giá trị thực của tham số m để tồn tại duy nhất số phức
z
thỏa mãn
.1=
zz
và
3− +=z im
. Tìm số phần tử của S.
A. 2 B. 4 C. 1 D. 3
Câu 35: Biết rằng tồn tại hai số phức
z
thỏa mãn
21 3+= ++z zz
và
8−
z
đạt giá trị nhỏ nhất. Tính tổng
hai phần thực của hai số phức đó.
A. 7 B. 0 C. 14 D. 8
Câu 36: Cho số phức
(x, y )=+∈z x yi
thay đổi thỏa mãn
1=z
. Hãy tính tổng giá trị lớn nhất và giá trị
nhỏ nhất của biểu thức
= −Pxy
A. 0 B. 12 C.
5
D.
25
Câu 37: Cho số phức
z
thỏa mãn
1=z
. Tìm giá trị lớn nhất của biểu thức
22 2=++ −Tz z
A.
25
B.
2 10
C.
35
D.
52
LỜI GIẢI BÀI TẬP TỰ LUYỆN
Câu 1: Tập hợp điểm M biểu diễn số phức
z
là đường tròn
()C
tâm
(2; 4)I
bán kính
5
=
R
Ta có:
=z OM
, mặt khác
OM
đạt giá trị lớn nhất và nhỏ nhất khi
()
= ∩
M OI C
Phương trình đường thẳng
:2=OI y x
, phương trình đường tròn
22
( ) : (x 2) (y 4) 5− +− =C
Giải hệ phương trình:
22 22
22
( 2) ( 4) 5 ( 2) ( 4) 5
= =

⇔

− +− = − +− =

yx yx
xy xy
1
2
5
12
36
35
=
=⇒=
⇔⇒
=⇒=
=
OM
xy
xy
OM
suy ra
1
12= +zi
là số phức thỏa mãn điều kiện
24 5−− =zi
Và có môđun nhỏ nhất,
2
36= +zi
là số phức có môđun lớn nhất. Chọn C.
Câu 2: Tập hợp điểm M biểu diễn số phức
z
là đường tròn
()C
tâm
(3; 4)−I
bán kính
4
=R
Ta có:
=z OM
, khi đó
549= = + =+=
max max
P OM OI R
. Chọn A.
Câu 3: Tập hợp điểm M biểu diễn số phức
z
là đường tròn
()
C
tâm
(2; 2)
−
I
bán kính
1=
R
Ta có:
=z OM
, khi đó
22 1= = += +
max
max
z OM OI R
. Chọn B.
Câu 4: Tập hợp điểm M biểu diễn số phức
z
là đường tròn
()C
tâm
( 3; 4)−−I
bán kính
2=R
Ta có:
=z OM
, khi đó
min
min
52 2= = − =−=z OM OI R
. Chọn D.
Câu 5: Đặt
= +
z x yi
(x, y )∈
, ta có :
22
2 3 1 ( 2) ( 3) 1zi x y−−=⇔−+−=
Tập hợp điểm M biểu diễn số phức
z
là đường tròn
()C
tâm
(2; 3)I
bán kính
1=R
Lại có:
2 2 22
1 ( 1) (1 ) ( 1) (y 1)=−++= ++− = ++−P x yi i x y x
Gọi
( 1; 1) 13 1− ⇒= → = += +
max
K P MK P IK R
. Chọn D.
Câu 6: Đặt
= +z x yi
(x, y )∈
, ta có :
32 32−= ⇔+ −= +
z z x yi x yi
22 22 2 2 22
(3) 4( )3 3 690 230⇔ − + = + ⇔ + + −=⇔ + + −=x y xy x y x xy x
22
( 1) 4⇔+ +=⇒xy
Tập hợp điểm M biểu diễn số phức
z
là đường tròn tâm
( 1; 0 )−I
bán kính
2=R
Gọi
2
(1; 2) 1 2 2 2 2 4
2
max
a
K z i MK MK IK R a b
b
=
⇒ −= = → = + = + ⇒ ⇒ + =
=
.
Chọn A.
Câu 7: Tập hợp điểm M biểu diễn số phức
z
là đường tròn tâm
(0; 0)O
bán kính
2=R
Gọi
(0; 3) 3K w z i MK−⇒ =+ =
Ta có:
min
5; 1= += = − =
max
MK OI R MK OK R
. Chọn D.
Câu 8:
2
2
2 22
5 11
( 3) ( 2) 2 10 13 2
2 22

= − + − = − + = − +≥


zm m m m m
Do đó
min
1 5 11
2 22
2
= ⇔ = ⇒=−−z mz i
. Chọn C.
Câu 9:
2
2 22 2
(1)( 2)2 6 552 6 00 3
= − + − = − +≤⇔ − ≤⇔≤ ≤z m m mm mm m
. Chọn B.
Câu 10:
2
2
2 22
3 99
( 3) 2 6 9 2
2 22

= + − = − += − + ≥


zmm m m m
Do đó
min
33
2
2
= ⇔=zm
. Chọn C.
Câu 11: Đặt
( ); (2; 3), B(0;1)Mz A
là các điểm biểu diễn số phức
;2 3+zi
và
i
. Khi đó từ giả thiết suy ra
=
MA MB
, tập hợp điểm biểu diễn số
phức
z
là đường trung trực của AB đi qua
I(1; 2 )
và có VTCP là
(1; 1) : 3 0
⇒ +−=n dx y
Gọi
( 2; 2)−−N
là điểm biểu diễn số phức
22−−i
Ta có
22++
zi
nhỏ nhất khi
min
MN
khi M là hình chiếu vuông góc của
N trên d, suy ra
:x y 0
−=MN
Giải hệ
3
0
33 3 3
2
; 36
30 3
22 2
2
=
−=
+

⇒ ⇒ ⇒= ⇒+ =


+−=

=
x
xy
i
M z ab
xy
y
. Chọn C.
Câu 12: Tập hợp điểm M biểu diễn số phức
z
là trung trực ∆ của AB với
(2; 4), B(0; 2)A
Trung điểm của AB là
1
(1; 3); (1; 1) : 4 0
2
=− = ⇒∆ + − =I n AB x y

Mặt khác
=z OM
nhỏ nhất khi M là hình chiếu vuông góc của O xuống ∆
Khi đó
2
: 0 (2; 2) 8
2
=
− = ⇒ = ∩∆= ⇒ ⇒ =
=
o
a
OM x y M OM M
b
. Chọn A.
Câu 13: Ta có
=z OM
nhỏ nhất khi M là hình chiếu vuông góc của O xuống
:3 4 3 0∆ − −=xy
Khi đó
min
min
22
33
(O; )
5
34
= = ∆= =
+
z OM d
. Chọn B.
Câu 14: Tập hợp điểm M biểu diễn số phức
z
là trung trực ∆ của AB với
(2; 4), B(0; 2)A
Trung điểm của AB là
1
(1; 3); (1; 1) : 4 0
2
=− = ⇒∆ + − =I n AB x y

Mặt khác
=z OM
nhỏ nhất khi M là hình chiếu vuông góc của O xuống ∆
Khi đó
min
4
(;) 22
2
= ∆= =OM d O
. Chọn B.
Câu 15: Đặt
( ); (1; 1), B( 2;1)−
Mz A
là các điểm biểu diễn số phức
;1 i−z
và
2
+ i
. Khi đó từ giả thiết suy ra
=MA MB
, tập hợp điểm biểu diễn số phức
z
là đường trung trực của AB
đi qua
3
I ;0
2



và có VTCP là
3
(1; 2) : 2 0
2
⇒ + −=n dx y
Gọi
(0;1)
N
là điểm biểu diễn số phức
i
Ta có
−zi
nhỏ nhất khi
min
MN
khi M là hình chiếu vuông góc của N trên
d, suy ra
:2x y 1 0−+=MN
Giải hệ
1
3
20
14 1 4 7
10
;
2
4
10 5 10 5 10
2 10
5
−
=
+ −=
−−


⇒ ⇒ ⇒= + ⇒+=




− +=
=
x
xy
i
M z ab
xy
y
. Chọn D.
Câu 16: Gọi
I(x; y); M( 2; 2), N(0; 4)−
là điểm biểu diễn các số phức
; 2 2 ;4
−+z ii
Từ giả thiết
⇒ = ⇒∈IM IN I
trung trực của MN là
: 20+−=dx y
Khi đó
22
1 1 1 ( 1)+=−+ +⇒ + = + − =iz y xi iz x y NM
với
(0;1)N
Ta có
1+iz
nhỏ nhất khi
min
MN
khi M là hình chiếu vuông góc của N trên d, suy ra
:x y 1 0
−+=MN
Giải hệ
22
1
20
13 1 3 5
2
;
10 3
22 2 2 2
2
=
+−=

⇒ ⇒ ⇒=+ ⇒ + =


− +=

=
x
xy
M z i ab
xy
y
. Chọn B
Câu 17: Gọi
= +
z x yi
(x, y )∈
222 2
1 ( 1)
( 1) ( 1) 0
⇒ ++ = + +
⇔ + + = + + ⇔−=
x yi x y i
x y x y xy
()
⇒ Mz
có quỹ tích là đường thẳng
:x y 0−=d
Với
' 1 2 ( ') (1; 2)=+⇒ =z i Nz
Ta có
min
min
⇔ ⇔⊥z NM NM d
min
1
(;)
2
⇒= =z dNd
. Chọn C.
Câu 18: Gọi
= +z x yi
(x, y )∈
222 2
1 ( 1)
( 1) ( 1) 0
⇒ −+ = + +
⇔−+=++⇔+=
x yi x y i
x y x y xy
()⇒ Mz
có quỹ tích là đường thẳng
:x y 0+=d
Với
' 2 ( ') (0; 2)=⇒=z i Nz
Ta có
min
min
:0⇔ ⇔ ⊥⇒ −+=z NM NM d MN x y k
Mà MN qua
(0; 2) k 2 MN : x y 2 0⇒ = ⇒ −+ =N
Tọa độ M là nghiệm của hệ
20 1
( 1; 1) 1
01
−+= =−

⇒ − ⇒ ⇒=

+= =

xy x
MS
xy y
. Chọn C.
Câu 19: Đặt
() (;)=M z M ab
và
(1; 2), B(0;1) MA MB− ⇒=A
Suy ra tập hợp điểm biểu diễn số phức
z
là đường thẳng trung trực của AB
( ): 3 2 0⇒ − −=
dx y
Gọi H là hình chiếu của O trên (d)
⇒
Phương trình đường thẳng
:3 0+=OH x y
Ta có
= ≥z OM OH
. Dấu bằng xay ra khi và chỉ khi
()≡⇒ = ∩
M H M d OH
Khi đó, tọa độ điểm M là nghiệm của hệ
1
3 20
5
30 3
5
=
− −=
⇒

+=
= −
a
ab
ab
b
. Vậy
1
25
=P
. Chọn A.
Câu 20: Đặt
() (;)
=M z M ab
và
( 2; 2), B(0; 4) MA MB− ⇒=A
Suy ra tập hợp điểm biểu diễn số phức
z
là đường thẳng trung trực của AB
( ): 2 0⇒ +−=dxy
Ta có
1
1
11
w iz
w iz w iz w z MC
ii i
+
=+⇔=+⇔ = ⇔=+=
, với
(0;1)C
Gọi H là hình chiếu của C trên (d)
⇒
≥CM CH
. Dấu = xảy ra
⇔≡MH
Vậy
min
22
0.1 1.1 2
2
( ;( ))
2
11
w CH d C d
+−
= = = =
+
. Chọn B.
Câu 21:
2
2 5 (z 1 2i)(z 3i 1) ( 1 2 )( 1 2 ) (z 1 2i)(z 3i 1)
− + = −+ + − ⇔ −+ −− = −+ + −
z z z iz i
12 0 12 1 1
12 13 12 13 (*)
z i z iw w
z iz i z iz i
−+ = =− ⇒ =−→ =
⇔⇔

−− = −+ −− = −+


Đặt
() (;)=M z M ab
và
(1; 2) , B(1; 3) (*) MA MB−⇒ ⇔ =A
Suy ra tập hợp điểm biểu diễn số phức
z
là đường thẳng trung trực của AB
( ):2 1 0⇒ +=dy
Ta có
22 22wziwziMC=−+ ⇔ = −+ =
, với
(2; 2)−C
Gọi H là hình chiếu của C trên (d)
⇒
≥CM CH
. Dấu = xảy ra
⇔≡MH
Khi đó
min
22
2.0 2.( 2) 1
3
( ;( ))
2
02
w CH d C d
+ −+
= = = =
+
. Vậy
min 1w =
. Chọn C.
Câu 22: Đặt
= +z x yi
(x, y )∈
khi đó
2
2
3 2 ( 3) 4−= ⇔ − =z zz z
22 22 22 22
(x3)4() 230(1)4⇔−+= + ⇔++−=⇔++=y xy xy x x y
(C)
⇒
Tập hợp điểm M biểu diễn số phức
z
là đường tròn (C) tâm
( 1; 0 )−I
, bán kính
2=R
Gọi
(1; 2 ) 2 2−⇒ = >⇒A IA R A
nằm ngoài đường tròn (C)
2 22⇒ = +=+
max
MA IA R
Mặt khác
max 1 2 2 2
−+ = + → = =
z i ab a b
. Vậy
4
+=ab
. Chọn A.
Câu 23: Vì
w
là số thực suy ra
2
12 2
z
z
wz z
+
= = +
là số thực
22
2
⇔+=+⇔ =
zz z
zz
Suy ra tập hợp điểm M biểu diễn số phức
z
là đường tròn (C) :
22
2
+=
xy
với
(0; 0)
2
=
I
R
Gọi
( 1; 1) 1− ⇒ +− =A z i MA
và
2= = ⇒IA R A
nằm trên đường tròn (C)
Khi đó
max
MA 2 2= +=IA R
. Dấu bằng xảy ra khi I là trung điểm MA
(1; 1)⇒−M
Vậy
1
= −zi
thì
2
1
1 2 2 1 2.( 1) 3
1
=
+− = → ⇒ = − − =
= −
a
zi P
b
. Chọn C.
Câu 24: Gọi
( ); A(1; 1) ; ( 1;1)−−Mz B
từ giả thiết suy ra MA = MB nên M thuộc đường thẳng trung trực của
AB có phương trình
()=
y xd
.
Gọi
(1; 5) ; ( 2; 1)−−⇒ = +H K P MH MK
, 2 điểm H, K cùng phía so với đường thẳng d
Gọi H’ là điểm đối xứng của
:
=dy x
Ta có:
': x y 6 0 I(3;3) H'(5;1)+−= ⇒ ⇒
HH
Lại có:
''=+= +≥P MH MK MH MK H K
Dấu bằng xảy ra
'⇔= ∩M HK d
Phương trình đường thẳng H’K là:
2 7 30− −=xy
Suy ra
33 6
;
55 5
−

=− − ⇒+=


M ab
. Chọn B.
Câu 25: Ta có:
2 333
−+=−=−=+z izizizi
Gọi
( ); A(2; 1); (0; 3)−−
Mz B
suy ra MA = MB nên M thuộc
đường thẳng trung trực của AB có phương trình
1 0( )
+ +=zy d
.
Gọi
(0;1); (2; 0)
⇒= +H K P MH MK
, 2 điểm H, K cùng phía so
với đường thẳng d
Gọi H’ là điểm đối xứng của
:z y 1 0++=d
Ta có:
':x y1 0 I(1;0) H'(2;1)−+= ⇒ − ⇒ − −HH
Lại có:
''=+= +≥P MH MK MH MK H K
Dấu bằng xảy ra
'⇔= ∩M HK d
Phương trình đường thẳng H’K là:
4 20
− −=xy
Suy ra
23 1
;2
55 5

=− − ⇒ −=−


M ab
. Chọn C.
Câu 26: Gọi
( ); (1; 2 ), B( 1; 0 )−Mz A
Khi đó
12 1−− = + ⇔ = ⇒z i z MA MB M
thuộc trung trực của AB có
phương trình
10+ −=xy
(d)
Gọi
2
22 2
IJ
(1; 2);J(0;1) P MI 2
2
− ⇒= + = +I MJ ME
(với
11
;
22
−



E
là trung điểm của IJ)
Do đó
min min
⇔P ME
hay M là hình chiếu vuông góc của E xuống d, khi đó
:x y 1 0−−=
EM
( )
1; 0 1⇒ = ∩⇒ ⇒+=M EM d M a b
. Chọn A.
Câu 27: Gọi
( ); (3;1), B( 1; 1)−−Mz A
Khi đó
31−− = ++ ⇔ = ⇒z i z i MA MB M
thuộc trung trực của AB có phương trình
2 20+−=
xy
(d)
Gọi
2
22 2
IJ
(1;1); J( 2; 1) P MI 2
2
−−⇒ = + = +I MJ ME
(với
1
;0
2
−



E
là trung điểm của IJ)
Do đó
min min
⇔P ME
hay M là hình chiếu vuông góc của E xuống d, khi
đó
1
:x 2y 0
2
− +=EM
7 3 13
;
10 5 10

⇒ = ∩⇒ ⇒+=


M EM d M a b
. Chọn A.
Câu 28: Ta có
11= ++⇔ = −−z iz i
ωω
nên
12 1 12 2−+ = −−−+ = − +zi ii i
ωω
Khi đó
12 5 2 5−+ = ⇔ − + =zi i
ω
nên
25 4 2= ⇔=−
max
i
ωω
Suy ra
22
1 4 2 1 3 3 3 ( 3) 3 2= −−= − −−= − → = +− =
z i i i iz
ω
. Chọn B.
Câu 29: Xét hai cách giải:
Cách 1: Gọi
(, ) (, )z x yixy Mxy=+ ∈⇒
Và
( 1; 0 ), B(1; 0)−A
. Ta có
22
11 1=⇒+ =⇔ + =z x yi x y
⇒
M thuộc đường tròn đường kính AB.
⇒
222
4+==MA MB AB
. Khi đó, theo Bunhiacopxki, ta có
22 2 2
2 (1 2 )( ) 5.4 2 5T MA MB MA MB=+ ≤+ + = =
Vậy giá trị lớn nhất của biểu thức
maxT=2 5
. Chọn A.
Cách 2: Đặt
= +z x yi
22
(x, y ) 1 (x 1)∈ ⇒ += + +zy
và
22
1 (x 1)−= − +zy
Mặt khác
22 22
1 11=⇔ +=⇔+=z xy xy
, khi đó
22 22 22 22 22
(x 1) 2 ( 1) (1 2 ) ( 1) ( 1)

= +++ −+≤ + +++−+

T yxy xyxy
22
10( 1) 10.2 2 5 max 2 5
= + += = ⇒ =xy T
Câu 30:
2 2 22
25(1)4(1)(2) (12)(12)− + = − + = − − = −+ −−
z z z z i z iz i
Khi đó, giả thiết
12
( 1 2)( 1 2) ( 1 2)( 3 1)
12 3 1
= −
⇔ −+ −− = −+ + − ⇔
−− = + −
zi
z iz i z iz i
z izi
TH1. Với
12= −
zi
, ta có
22 12 22 1 1
wz i i i w=−+ =− −+ =−⇒ =
TH2. Với
12 3 1−− = + −z izi
(*), đặt
= +z x yi
(x, y )∈
, ta có
(*)
22 22
1
1 ( 2) 1 ( 3) ( 1) (y 2) ( 1) (y 3)
2
⇔ −+ − = −+ + ⇔ − + − = − + + ⇔ =−
xyixyix x y
Do đó
2
1 3 93
22 22 2 ( 2)
2 2 42
wz ix i ix i w x=−+ =− −+ =−+ ⇒ = − + ≥
So sánh hai trường hợp, ta được giá trị nhỏ nhất của
ω
bằng 1. Chọn A.
Câu 31: Đặt
= +z x yi
(x, y )∈
nên
22
1( ) 1
−=⇔ + −=
z i z yi i
22 222 2 22
(2 1) 1 ( ) ( 2 1) 1 2⇔−+−=⇔−+−=⇔+=x y xy i x y xy x y xy
22 22 22
2 2( ) 2 2⇔ + = ≤+≤ + ⇔ + ≤ ⇔ ≤xy xyxy xy xy z
. Chọn D.
Câu 32: Ta có
22
4 1 14 1 1 4
11
+ ++ =⇔+++−−=⇔+−+−+=
−−
iz iz iz i iz i z i z i
ii
Gọi
( 1;1), (1; 1)−−AB
có trung điểm là
(0; 0)O
. Điểm M biểu diễn số phức
z
Theo công thức trung tuyến thì
222
2
2
24
+
= = −
MA MB AB
z OM
Ta có
(
)
2
2
22
4
8
22
+
+≥ ==
MA MB
MA MB
. Do đó
2
88
22
24
≥−=⇔ ≥zz
Lại có
4 1 1 1 12 2= +−+ −+ ≥ +−+ −+ = ⇔ ≤zizizizizz
Vậy
2; 2 . m 2 2==→=Mm M
. Chọn C.
Câu 33: Đặt
= +z x yi
(x, y )∈
, khi đó
[
][ ]
22
( 2) 2
2 ( 2)
2 2 ( 2)
+ − −−
− +−
= =
− −+ − +
x y i x yi
z ix y i
z x yi x y
22
22
2 2 2( 2)
( 2)
+ − − − +−
=
−+
x y x y xy i
xy
là số ảo
22 22
2 2 0 2( )⇔+−−=⇔+= +xy xy xy xy
Suy ra
2
22 2
()
2() ()4()0 4
2
+
+ = + ≥ ⇔ + − + ≤⇔+≤
xy
xy x y xy xy xy
Ta có
22 2 2 22 22
1 ( 1) ( 1) 2 1 2 1=−+−= −++ +− = +−++ +−+Pz zi x y x y xy x xy y
2 1 2 12 124125= ++ +≤ ++= +=y x xy
. Vậy
25=
max
P
. Chọn C.
Câu 34:
.1 1=⇔=zz z
nên tập hợp biểu diễ số phức
z
là đường tròn
1
()
C
tâm O, R = 1
Lại có
3− +=z im
nên tập hợp biểu diễn số phức
z
là đường tròn
2
()C
tâm
( 3; 1), R' m−=I
Yêu cầu bài toán
12
(C ), ( )⇔ C
tiếp xúc trong hoặc tiếp xúc ngoài
'1
'3
=+=

⇔⇔

+= =

OI R R m
OI R R m
Chọn A.
Câu 35: Đặt
= +z x yi
(x, y )∈
, ta có
2 1 3 2 12 2 3+ = + + ⇔ ++ = +
z z z x yi x
2
22
2
2 2 2 22 2
(2 1) (2 ) (2 3) 1 8 ( 8) 9
22

⇔ + + = + ⇔ = −⇒ − = − + = − +


yy
x yx x z x y y
Xét hàm số
2
2
2 42 2 2
11
( ) 9 8 81 ( 16) 17 17
24 4

= − + = − +≥ − +≥


y
fx y y y y
Suy ra
min ( ) 17=
fy
. Dấu bằng xảy ra khi
2
47
16
47
=→=
= ⇔
=−→ =
yx
y
yx
Vậy tổng hai phần thực của hai số phức là 14. Chọn C.
Câu 36:
22
4= +zxy
mà
22
1 41=⇔+ =z xy
(*)
Lại có
=−⇔=−P xy y xP
thế vào (*), ta được
22
4( ) 1+−=x xP
22 2 2 2
4 8Px 4P 1 5 8 . 4P 1 0⇔ + − + =⇔ − + −=
x x x Px
(**)
Phương trình (**) có nghiệm
22
' ( 4 ) 5(4 1) 0
⇔∆ = − − − ≥PP
2
55 5 5
5 4 P 0 min ;max
22 2 2
⇔ − ≥ ⇔− ≤ ≤ → =− =
PP
. Chọn A.
Câu 37: Đặt
= +z x yi
22 22
(x, y ) 2 ( 2) ; 2 ( 2)∈ ⇒+= + + −= − + z x yz x y
Mặt khác
22 22
1 11=⇔ +=⇔+=z xy xy
, khi đó
22 22 22 22 22
( 2) 2 ( 2) (1 2 ) ( 2) ( 2)

= +++ −+≤ + +++−+

Txyxy xyxy
22
10( 4) 10.5 5 2 max 5 2
= ++= = ⇒ =xy T
Vậy giá trị lớn nhất của biểu thức T là
52=T
. Chọn D.
| 1/27
| | Tải xuống

Có thể bạn quan tâm:

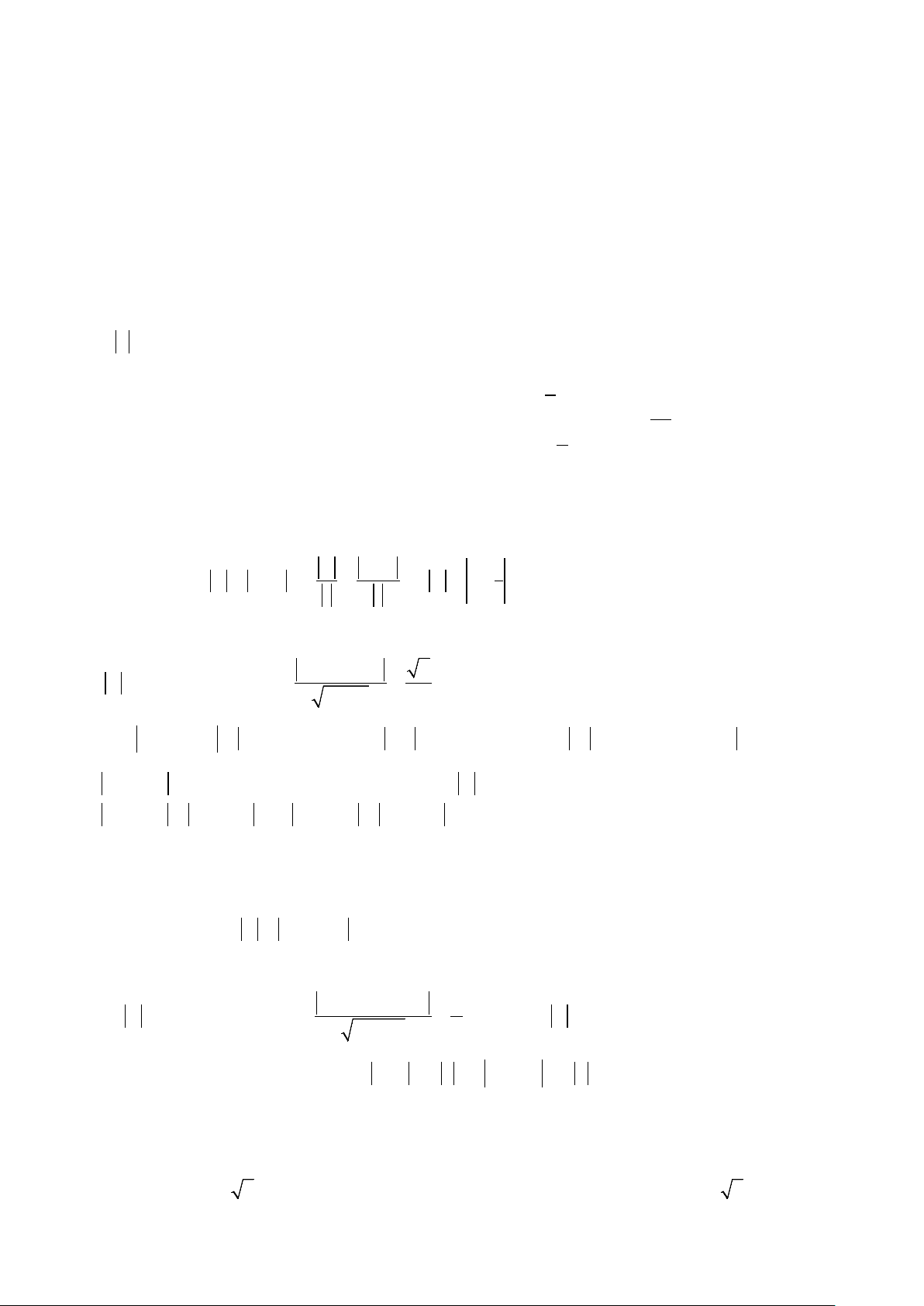
Preview text:

CHỦ ĐỀ 19: BÀI TOÁN CỰC TRỊ SỐ PHỨC
Dạng 1: Cho số phức z thỏa mãn z − z = z −
. Tìm số phức thỏa mãn z − z nhỏ nhất. 1 z2 0
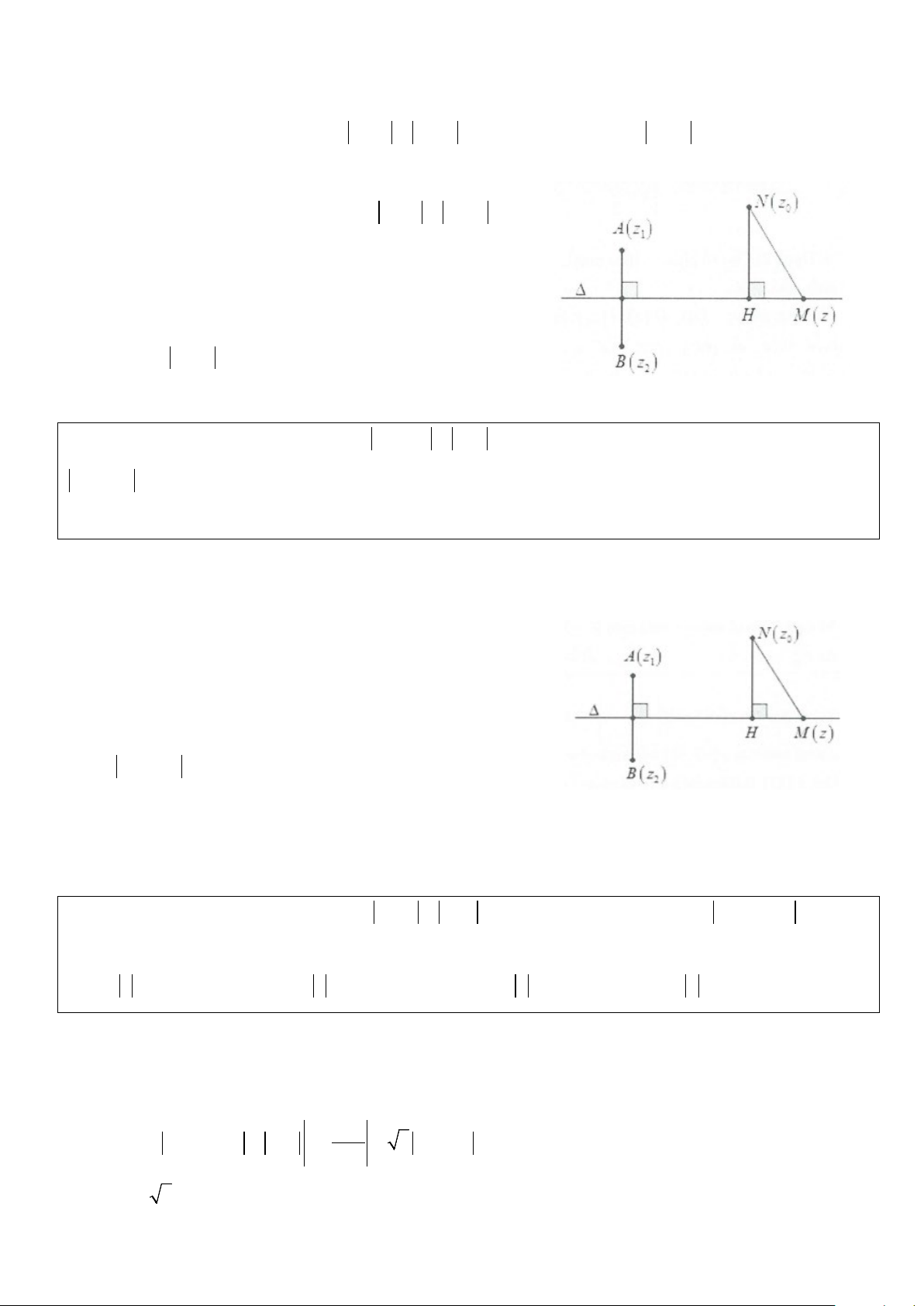
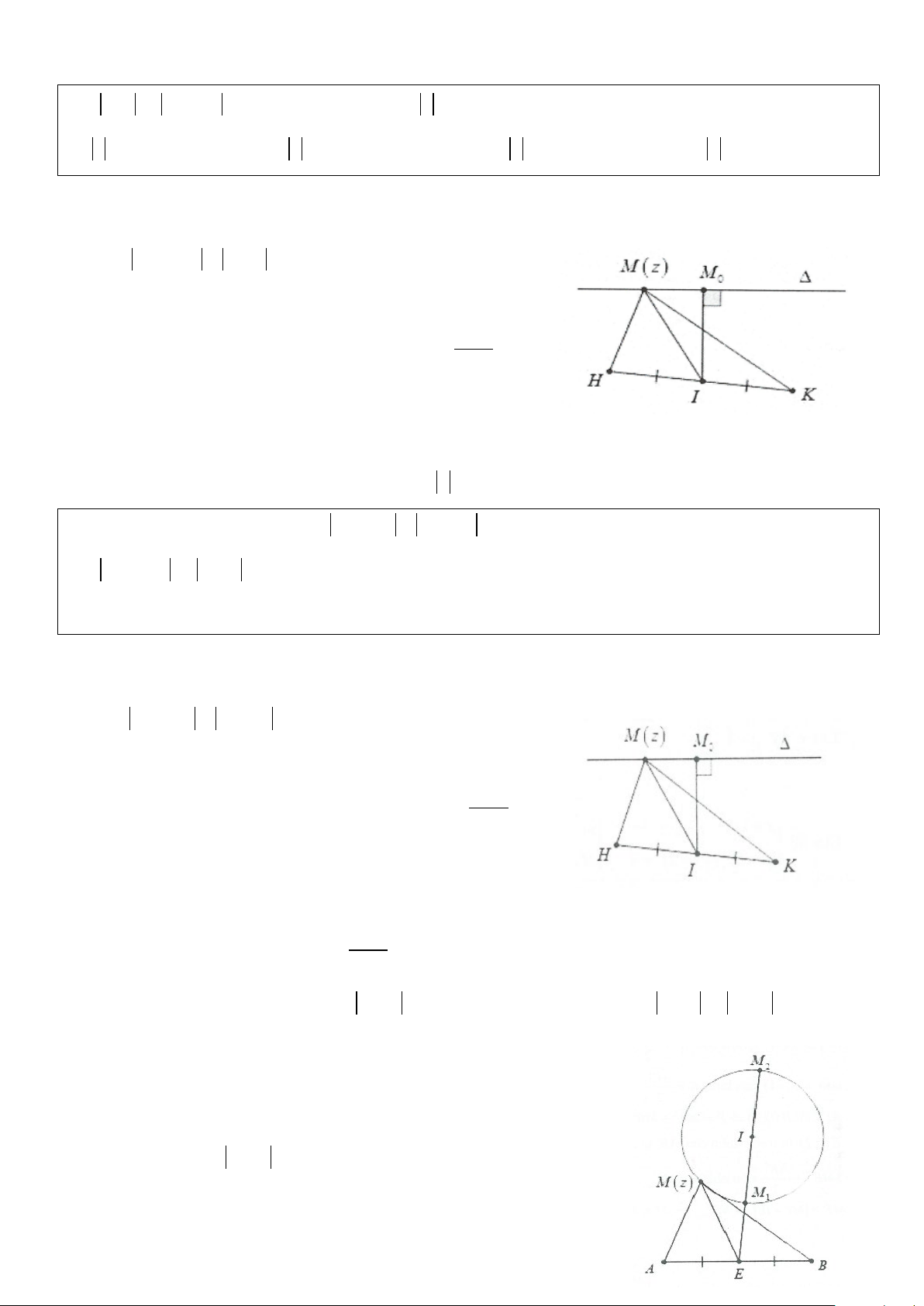
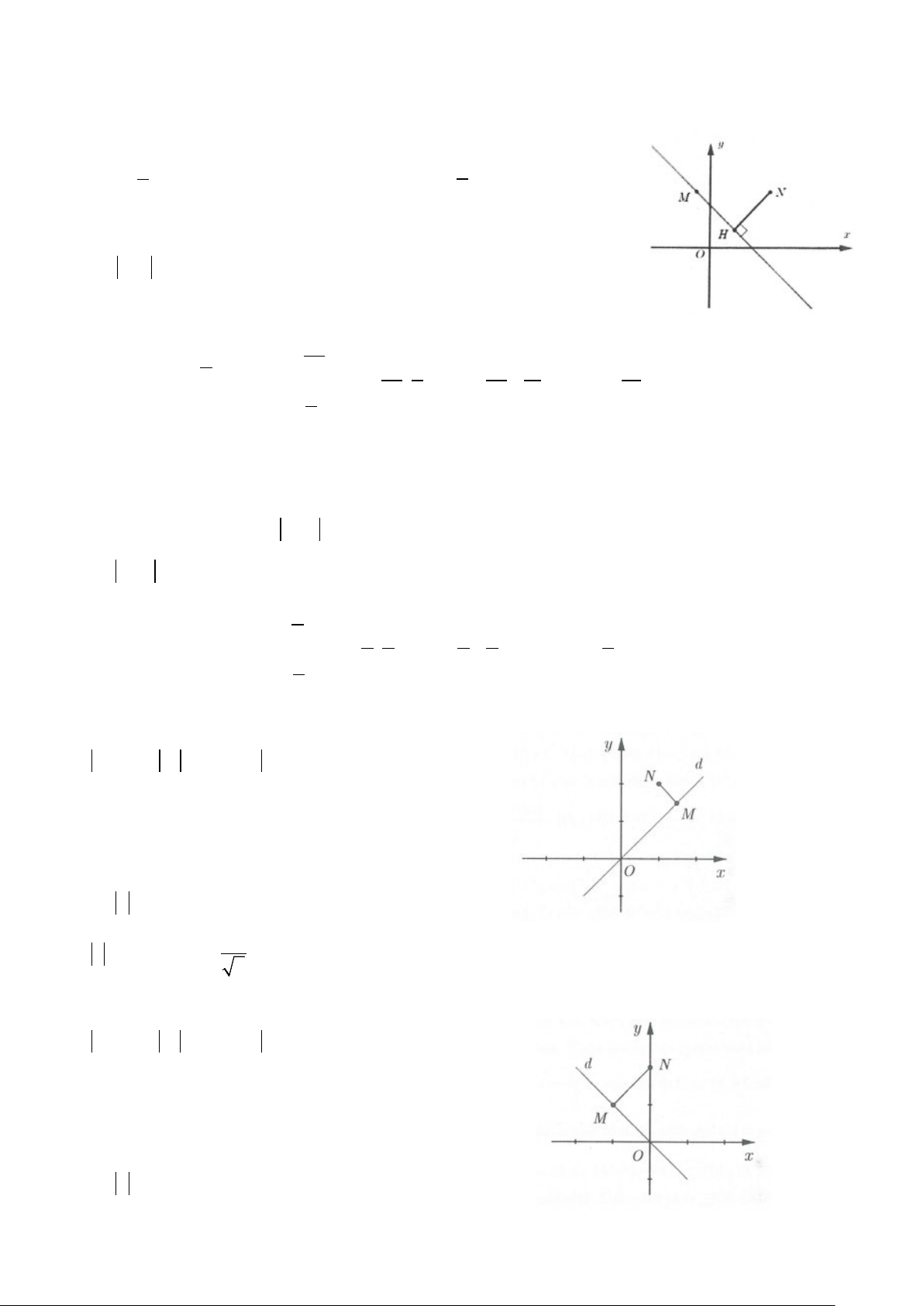
Phương pháp: Đặt M(z);A(z
là các điểm biểu diễn số 1); B(z2)
phức z; z và z . Khi đó từ giả thiết z − z = z − suy ra 1 z 1 2 2
MA = MB , tập hợp điểm biểu diễn số phức z là đường trung trực ∆ của AB.
Gọi N(z là điểm biểu diễn số phức z 0) 0
Ta có MN = z − z nhỏ nhất khi MN khi M là hình chiếu 0 min
vuông góc của N trên d và MN = d(N;∆) min
Ví dụ 1: Cho số phức z thỏa mãn z − 4 − i = z + i . Gọi z = a + bi ( ;
a b∈) là số phức thỏa mãn
z −1+ 3i nhỏ nhất. Giá trị của biểu thức T = 2a + 3b là: A. 4 − B. 4 C. 0 D. 1 Lời giải Đặt M (z); ( A 4;1), B(0; 1)
− là các điểm biểu diễn số phức z; 4 + i và −i . Khi đó từ giả thiết suy ra
MA = MB , tập hợp điểm biểu diễn số phức z là đường trung
trực của AB đi qua I(2;0) và có VTPT là   n = AB( 4; − 2
− ) ⇒ ∆ : 2x + y − 4 = 0 Gọi N(1; 3
− ) là điểm biểu diễn số phức 1− 3i
Ta có z −1+ 3i nhỏ nhất khi MN khi M là hình chiếu vuông min
góc của N trên ∆, suy ra MN : x− 2 y+1= 0
2x + y − 4 = 0 x = 3 Giải hệ  ⇒  ⇒ M (3; 2
− ) ⇒ z = 3− 2i ⇒ 2a + 3b = 0 . Chọn C.
x − 2y − 7 = 0 y = 2 −
Ví dụ 2: Cho các số phức z thỏa mãn z − 2i = z + 2 . Gọi z là số phức thỏa mãn (2 − i)z + 5 nhỏ nhất. Khi đó :
A. 0 < z <1
B. 1< z < 2
C. 2 < z < 3 D. z > 3 Lời giải Gọi M (x; y); ( A 0;2),B( 2;
− 0) là các điểm biểu diễn số phức z; 2i và 2 − .
Từ giả thiết ⇒ MA = MB ⇒ M ∈trung trực của AB có phương trình ∆ : x + y = 0 Lại có: 5
P = (2 − i)z + 5 = 2 − i z +
= 5 z + 2 + i , gọi N( 2 − ; 1)
− là điểm biểu diễn số phức 2 − − i 2 − i suy ra P = 5MN
Ta có P nhỏ nhất khi MN khi M là hình chiếu vuông góc của N trên min ∆, suy ra phương trình MN : x− y+1 = 0  1 − x + y = 0 x =  Giải hệ  2  1 − 1  1 − 1 2  ⇒ 
⇒ M  ; ⇒ z = + i ⇒ z = . Chọn A. x y 1 0 1 2 2  − + =    2 2 2 y =  2
Dạng 2: Cho số phức z thỏa mãn z − z = . Tìm số phức thỏa mãn P = z − z đạt giá trị lớn nhất, 0 R 1 nhỏ nhất.
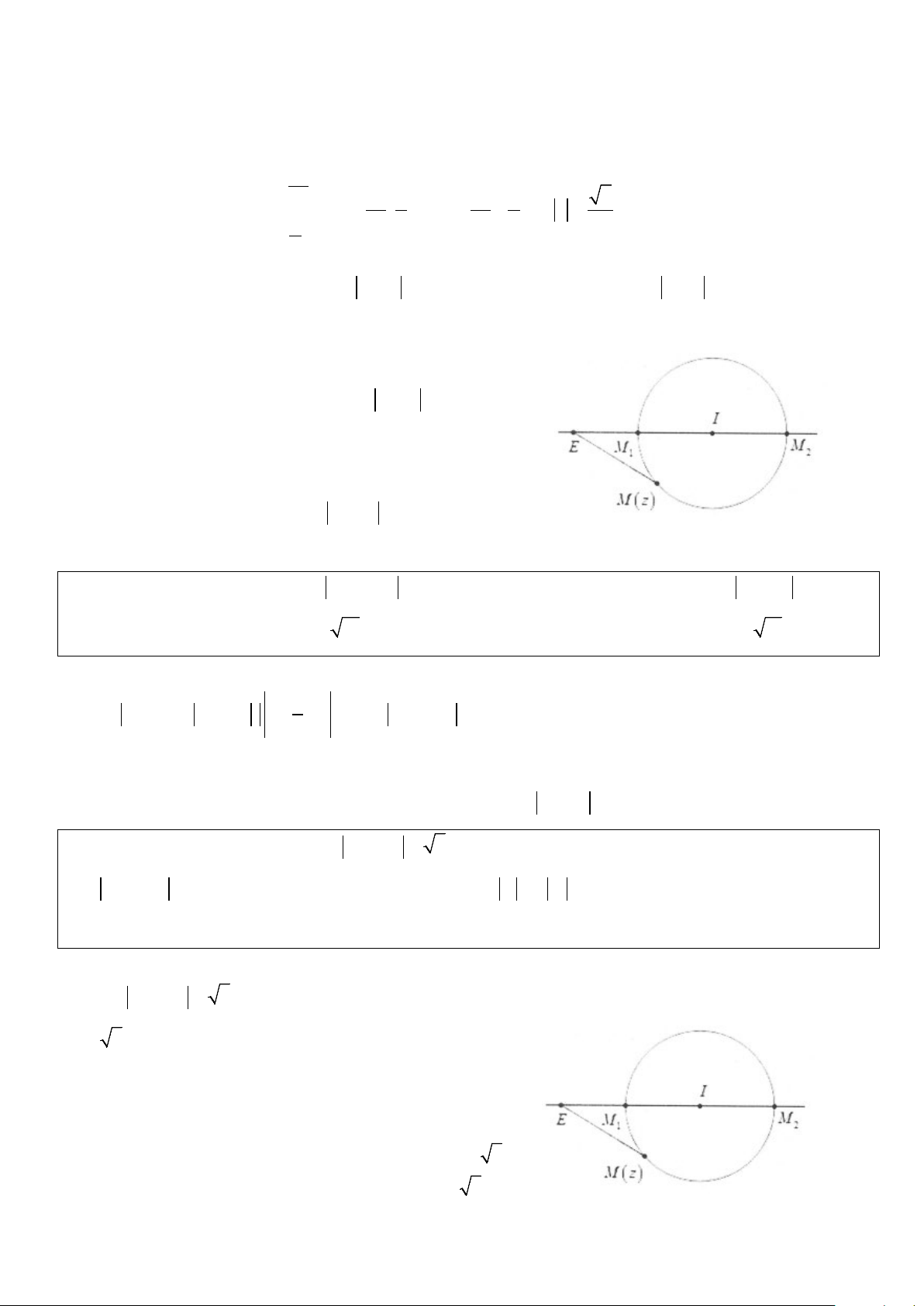
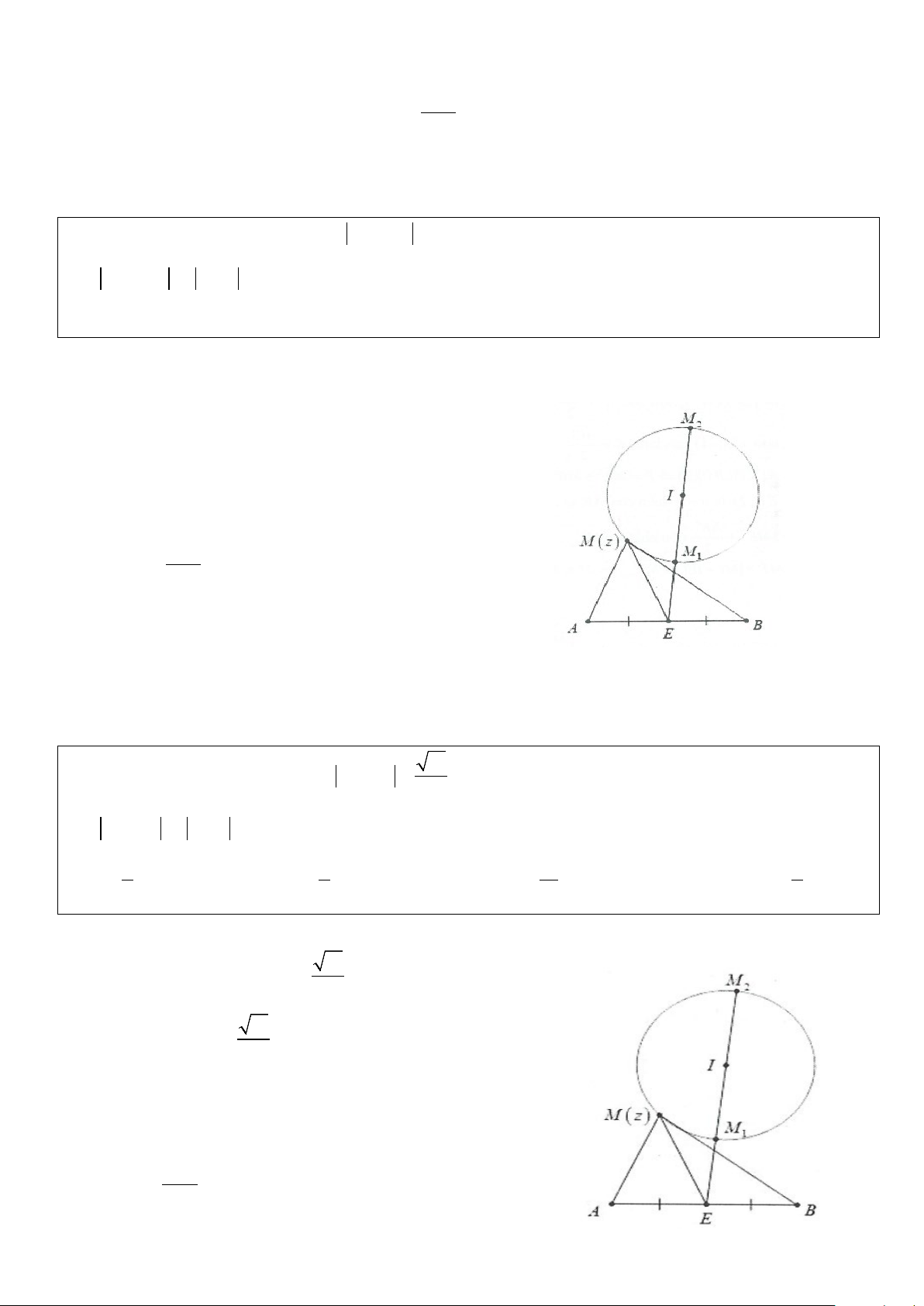
Phương pháp: Đặt M(z);I(z
là các điểm biểu diễn số 0); E(z1)
phức z; z và z . Khi đó từ giả thiết z − z = R ⇔ MI = R 0 1 0
⇒ M thuộc đường tròn tâm I bán kính R. Ta có: P = ME lớn
nhất ⇔ ME và P nhỏ nhất ⇔ ME . Khi đó: max min
P = IE + R ⇔ M ≡ M và P = IE − R ⇔ M ≡ M max 2 min 1
(Điểm E có thể nằm trong hoặc ngoài đường tròn).
Ví dụ 1: Cho số phức z thỏa mãn iz − 3+ 2i = 3. Tìm giá trị nhỏ nhất của biểu thức: P = z −1− i A. P = 3 B. P = 13 − 3 C. P = 2 D. P = 10 min min min min Lời giải Ta có: 3
iz − 3+ 2i = 3 ⇔ i z − + 2 = 3 ⇔ z + 2 + 3i = 3 ⇒ tập hợp điểm M biểu diễn số phức z là đường i tròn tâm I( 2; − 3) − bán kính R = 3 Gọi E( ; )
11 là điểm biểu diễn số phức 1+ i ⇒ P = ME ⇒ P = EI − R = 2 min
Ví dụ 2: Cho số phức z thỏa mãn z + 2 − i = 5 . Gọi z và z lần lượt là 2 số phức làm cho biểu thức 1 2
P = z − 2 − 3i đạt giá trị nhỏ nhất và lớn nhất. Tính T = 3 z + 2 z 1 2 A. T = 20 B. T = 6 C. T = 14 D. T = 24 Lời giải
Ta có: z + 2 − i = 5 ⇒ tập hợp điểm M biểu diễn số phức z là đường tròn tâm I( 2 − ;1) bán kính
R = 5 . Gọi E(2;3) ⇒ P = ME
Phương trình đường thẳng IE : x − 2y + 4 = 0
Dựa vào hình vẽ ta có P = IE + R ⇔ M ≡ M max 2
x − 2y + 4 = 0 M ( 4; − 0) ⇒ P = 3 5 Giải hệ 2 min  ⇒  . 2 2
(x + 2) + (y −1) = 5 M (0;2) ⇒ P = 5 1 min
Do đó T = 3 z + 2 z = 3.2 + 2.4 =14 . Chọn C. 1 2
Dạng 3: Cho số phức z thỏa mãn z − z = z −
. Tìm số phức thỏa mãn P = z − z + z − đạt giá 3 z 1 z2 4 trị nhỏ nhất.
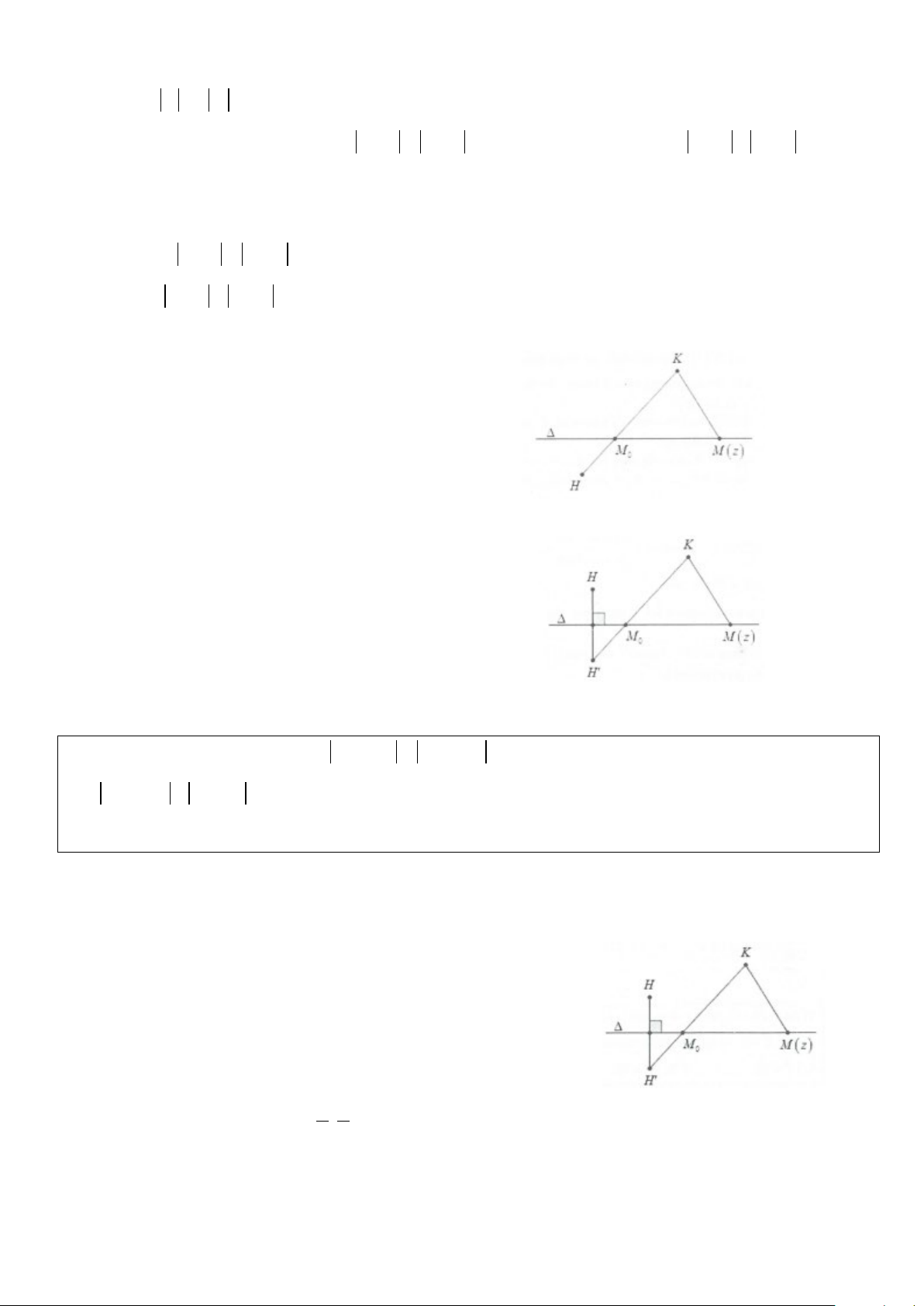
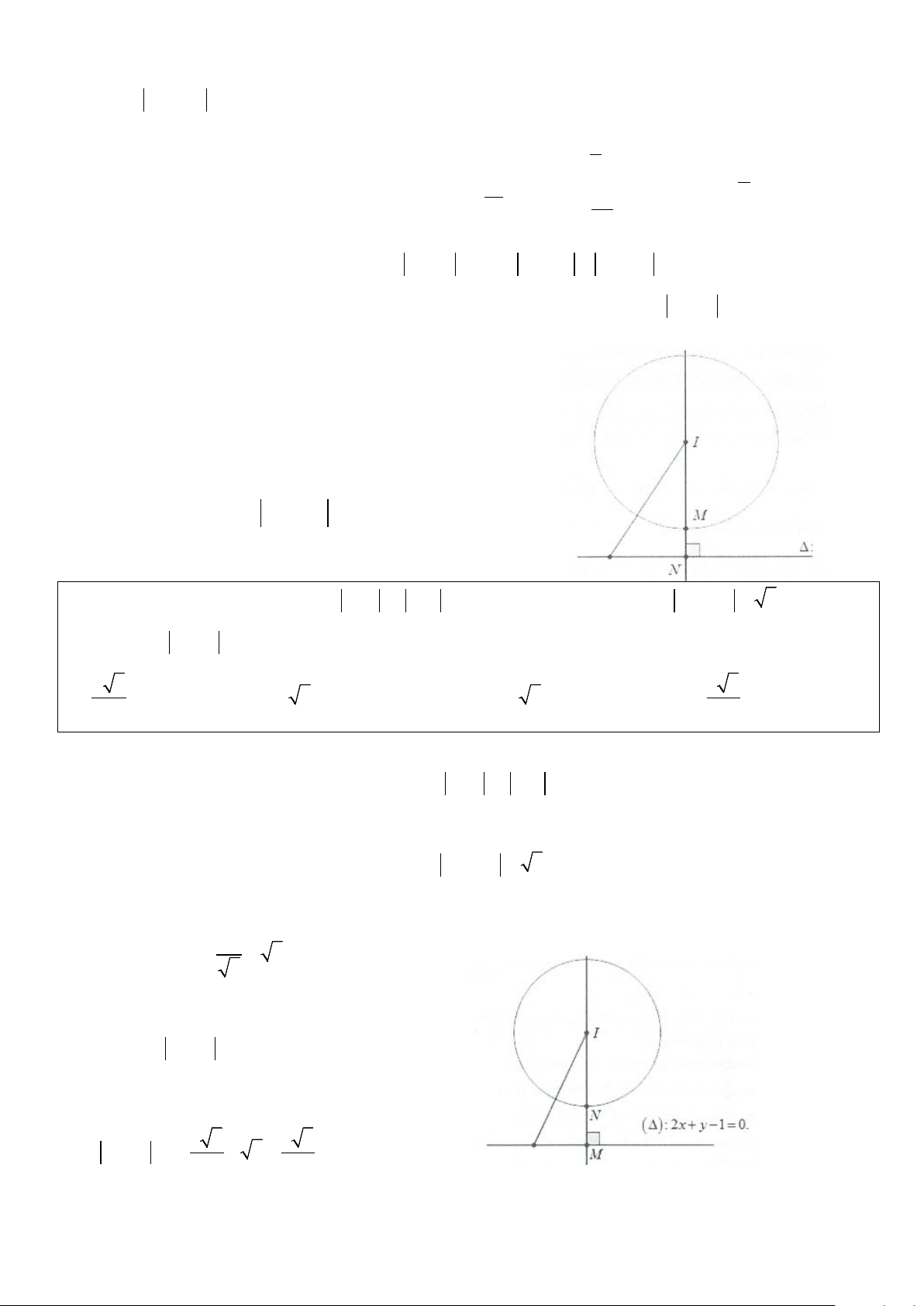
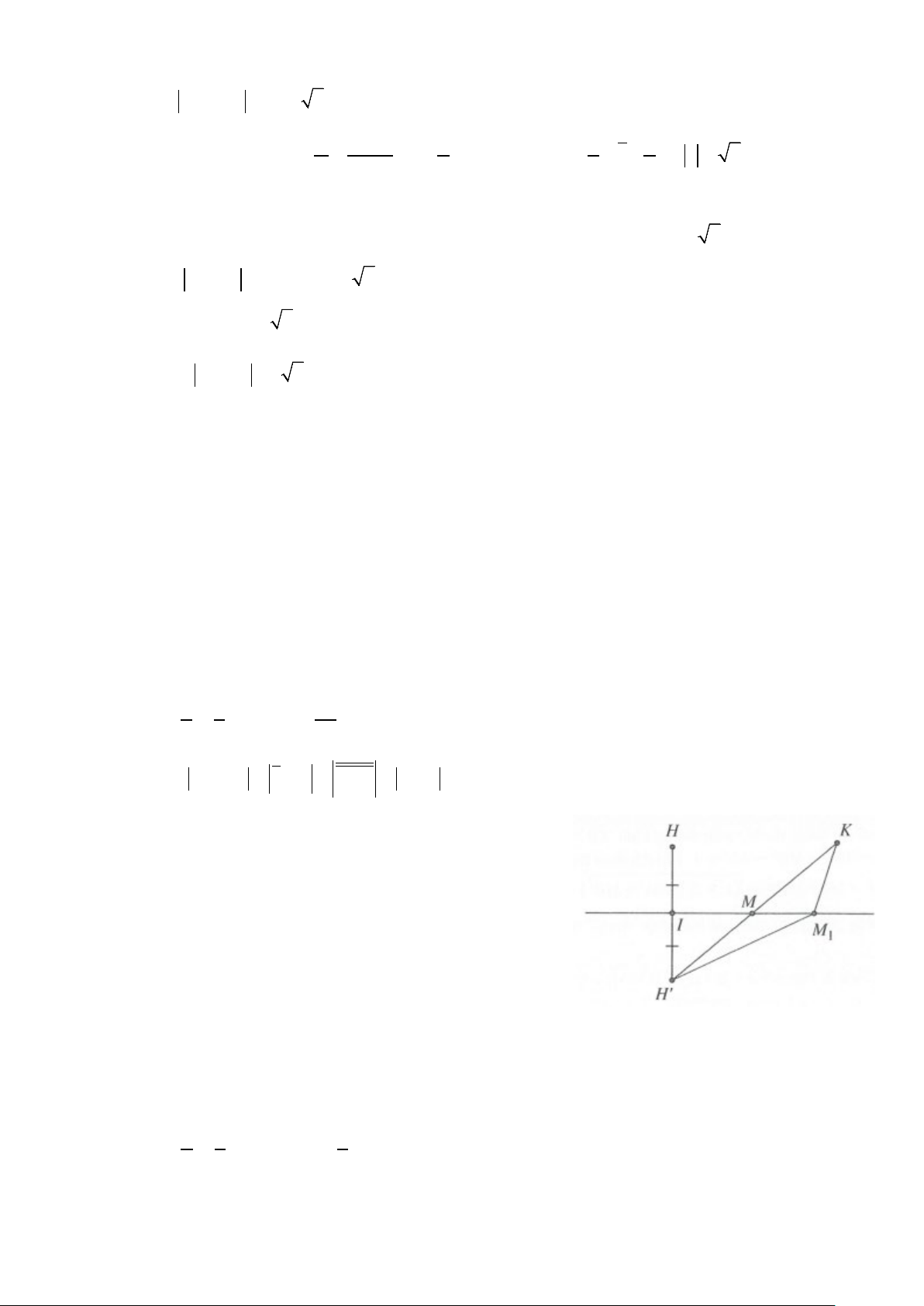
Phương pháp: Đặt M(z);A(z
là các điểm biểu diễn số phức z;z ;z và z . Khi 1 2;z 1); B(z2); H(z3); K(z4) 3 4
đó từ giả thiết z − z = z − z suy ra MA = MB , tập hợp điểm biểu diễn số phức z là đường trung trực 1 2 ∆
của AB; P = z − z + z − z = MH + 3 4 MK
TH1: H, K nằm khác phía so với đường thẳng ∆ Ta có: P = MH + MK ≥ HK
Dấu bằng xảy ra ⇔ M ≡ M = HK ∩ (∆) o Khi đó P = HK min
TH2: H, K nằm cùng phía so với đường thẳng ∆
Gọi H’ là điểm đối xứng của ∆
Khi đó: P = MH + MK = MH '+ MK ≥ H 'K
Dấu bằng xảy ra ⇔ M ≡ M = H 'K ∩ (∆) o Khi đó P = H 'K min
Ví dụ 1: Cho số phức z thỏa mãn z −1+ 2i = z + 3− 2i . Gọi z = a + bi ( ; a b∈) sao cho
P = z − 2 − 4i + z +1− i đạt giá trị nhỏ nhất. Khi đó a + b là: A. 3 B. 5 C. 8 D. 4 Lời giải Đặt M (z); ( A 1; 2 − ),B( 3
− ;2) tử giả thiết suy ra MA = MB nên M thuộc đường thẳng trung trực của AB có
phương trình ∆ : x − y +1 = 0 , gọi H(2;4) và K( 1; − 1) là các điểm
biểu diễn số phức 2 + 4i và 1 − + i
Ta có P = MH + MK và 2 điểm H, K cùng phía so với đường thẳng ∆
Gọi H’ là điểm đối xứng của ∆ : x − y +1 = 0
Ta có: HH': x + y − 6 = 0 tọa độ trung điểm của HH’ là nghiệm hệ
x − y +1 = 0 phương trình  5 7  I  ;  ⇒ x y 6 0 2 2  + − =   Suy ra H'(3;3)
Lại có: P = MH + MK = MH '+ MK ≥ H 'K
Dấu bằng xảy ra ⇔ M = H 'K ∩ d . Phương trình đường thẳng H’K là: H 'K : x − 2y + 3 = 0
Suy ra M = H 'K ∩ ∆ ⇒ M ( ;1 ) 2 ⇒ z = +
1 2 . Khi đó P = H 'K = 2 5 . Chọn A. 0 i o min
Ví dụ 2: Cho số phức z thỏa mãn z − 2 + 4i = iz − 2 . Gọi z = a + bi ( ; a b∈) sao cho
P = z − i + z +1+ 3i đạt giá trị nhỏ nhất. Giá trị nhỏ nhất đấy bằng A. 53 B. 37 C. 4 D. 41 Lời giải Ta có: 2
z − 2 + 4i = iz − 2 ⇔ z − 2 + 4i = i z − = z + 2i i Gọi M (z); ( A 2; 4 − ),B(0; 2
− ) từ giả thiết suy ra MA = MB nên M thuộc đường thẳng trung trực của AB có
phương trình ∆ : x − y − 4 = 0, gọi H(0;1) và K( 1; − 3 − ) là
các điểm biểu diễn số phức i và 1 − − 3i
Ta có: P = MH + MK và 2 điểm H, K cùng phía so với đường thẳng ∆
Gọi H’ là điểm đối xứng của ∆ : x − y − 5 = 0
Ta có: HH': x + y −1 = 0 tọa độ trung điểm của HH’ là
x − y − 4 = 0 nghiệm hệ phương trình  5 3  I  ;  ⇒ − x y 1 0 2 2  + − =   Suy ra H'(5; 4 − )
Lại có: P = MH + MK = MH '+ MK ≥ H 'K = 37 . Chọn B.
Dạng 4: Cho số phức z thỏa mãn z − z = z −
. Tìm số phức thỏa mãn 2 2 P = z − z + z − z đạt 1 z2 3 4 giá trị nhỏ nhất.
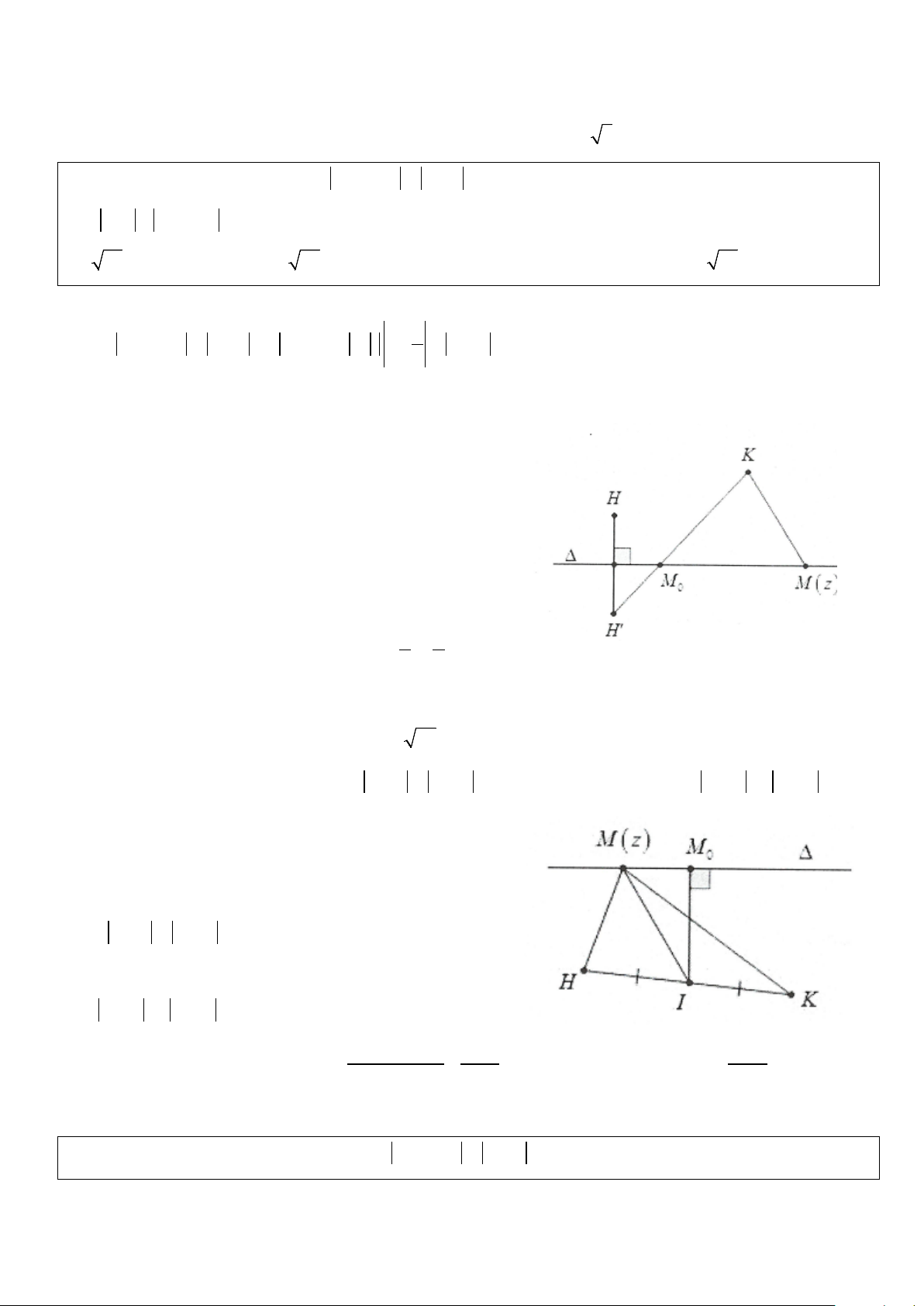
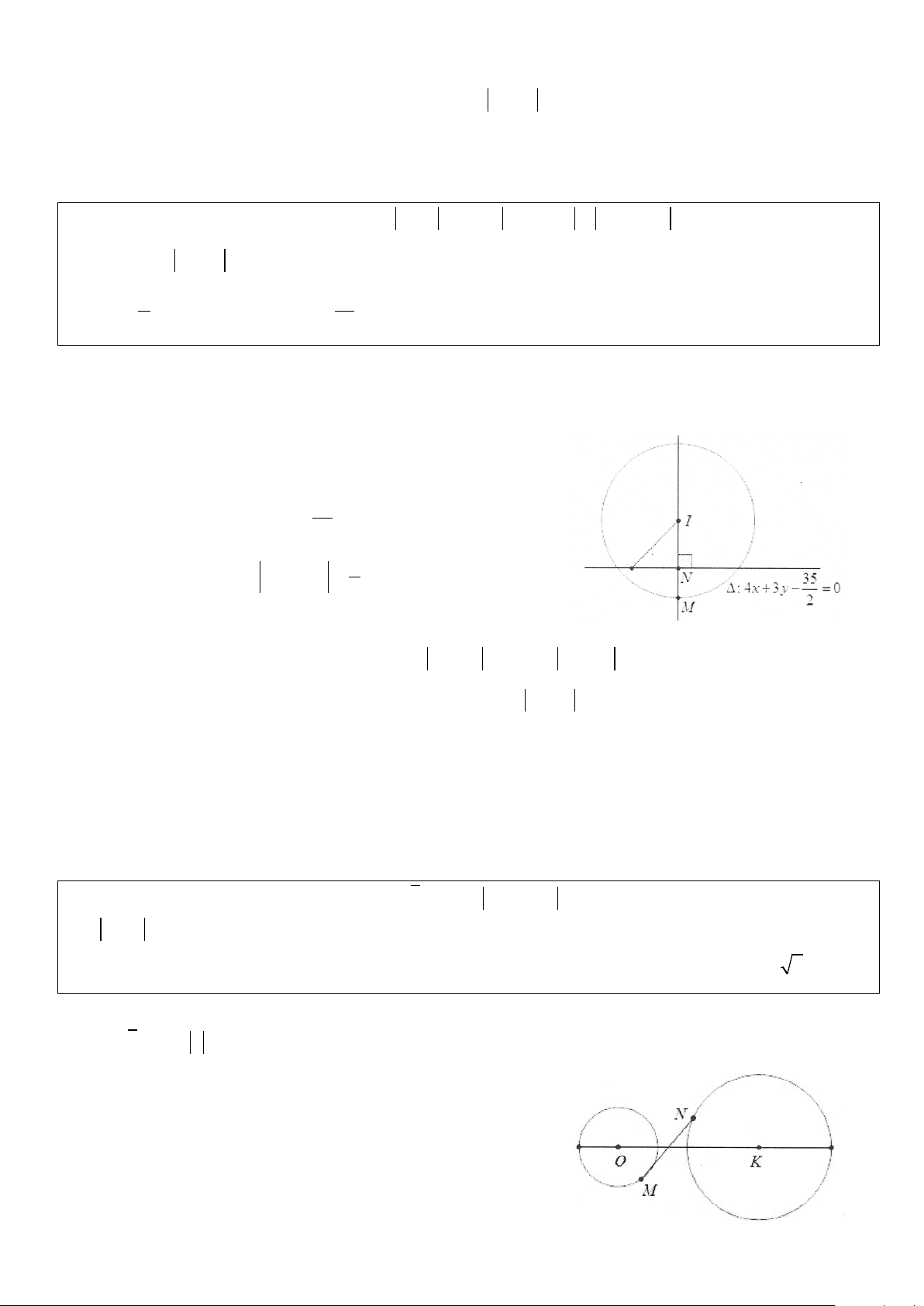
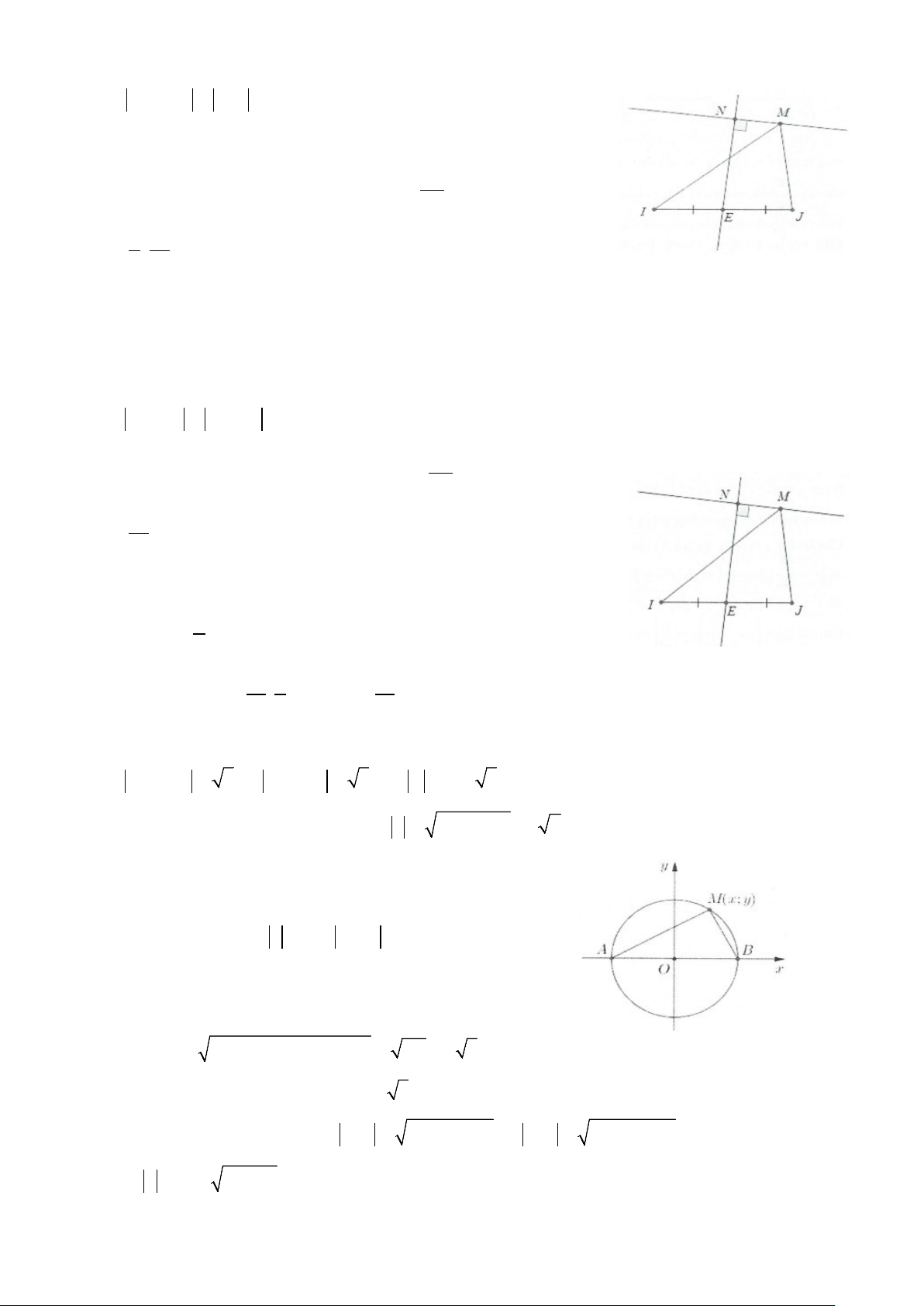
Phương pháp: Đặt M(z);A(z là các 1); B(z2); H(z3); K(z4)
điểm biểu diễn số phức z;z ;z và z . Khi đó từ giả 1 2;z3 4
thiết z − z ≡ z − suy ra MA = MB , tập hợp điểm biểu 1 z2
diễn số phức z là đường trung trực ∆ của AB; 2 2 2 2
P = z − z + z − z = MH + MK 3 4 2 2 2 2
Gọi I là trung điểm của 2 MH + MK HK 2 2 2 ⇒ = − ⇒ = + = 2 + HK HK MI P MH MK MI 2 4 2
nhỏ nhất khi MI ⇔ M là hình chiếu vuông góc của I xuống ∆ . min
Ví dụ 1: Cho số phức z thỏa mãn z + 2 − 4i = z − 2i . Gọi z là số phức thoả mãn biểu thức 2 2
P = z − i + z − 4 + i đạt giá trị nhỏ nhất. Tính 2 z . A. 2 z =12 B. 2 z =10 C. 2 z = 2 D. 2 z = 5 Lời giải Gọi M (z); ( A 2;
− 4),B(0;2) là các điểm biểu diễn số phức z; 2
− + 4i và 2i
Khi đó z + 2 − 4i = z − 2i ⇔ MA = MB ⇒ M thuộc trung trực
của AB có phương trình ∆ : x − y + 4 = 0 2 Gọi ( ) ( − ) 2 2 2 0;1 , 4; 1 ⇒ = + = 2 + HK H K P MH MK MI 2
(với I (2;0) là trung điểm của HK)
Do đó P ⇔ ME hay M là hình chiếu vuông góc của I xuống ∆ , khi đó min min
IM x + y − = ⇒ M = IM ∩ ∆ ⇒ M (− ) 2 2 : 2 0
1;3 ⇒ z = OM =10 . Chọn B.
Ví dụ 2: Cho số phức z thỏa mãn z −1+ 3i = z + 2 + i . Giá trị nhỏ nhất của biểu thức 2 2
P = z − 2 + 4i + z + 2i là: A. P = 8 B. P = 9 C. P =16 D. P = 25 min min min min Lời giải Gọi M (z); ( A 1; 3 − ),B( 1; − 1
− ) là các điểm biểu diễn số phức z; 1+ 3i và 1 − − i
Khi đó z −1+ 3i = z +1+ i ⇔ MA = MB ⇒ M thuộc trung trực
của AB có phương trình ∆ : x − y − 2 = 0 2 Gọi ( − ) ( − ) 2 2 2 2; 4 , 0; 2 ⇒ = + = 2 + HK H K P MH MK MI 2 (với I (1; 3
− )là trung điểm của HK)
Do đó P ⇔ ME hay M là hình chiếu vuông góc của I min min 2 xuống ∆ , khi đó = 2  HK Pd (I;∆) 2  + = 8. Chọn A. min  2
Dạng 5: Cho số phức z thỏa mãn z − z = R . Tìm số phức thỏa mãn 2 2
P = z − z + z − z đạt giá trị 0 1 2 lớn nhất, nhỏ nhất.
Phương pháp: Đặt M(z);A(z );B(z );I z là các điểm biểu diễn số 1 2 ( 0) phức z;z ;z và z . 1 2 0
Khi đó từ giả thiết z − z = R ⇔ MI = R ⇒ M thuộc đường tròn tâm I 0 bán kính R. 2
Gọi E là trung điểm của AB ta có: 2 = 2 + AB P ME
lớn nhất ⇔ ME và P nhỏ nhất ⇔ ME . 2 max min
Khi đó P ⇔ M ≡ M và P ⇔ M ≡ M . max 2 min 1
Ví dụ 1: Cho số phức z thỏa mãn z −1+ 2i = 2 . Gọi z = a + bi(a;b∈) là số thức thỏa mãn biểu thức 2 2
P = z − 2 − 3i + z − 5i đạt giá trị lớn nhất. Tính T = a + b A. T =1 B. T = 3 C. T = 1 − D. T = 3 − Lời giải
Gọi M (z); I (1; 2
− ) khi đó MI = 2 ⇔ M thuộc đường tròn tâm I (1; 2 − ) bán kính R = 2 Đặt A( ) B( ) 2 2
2;3 ; 0;5 ⇒ P = MA + MB
Gọi H (1;4) là trung điểm của AB ta có : 2 2 = 2 + AB P MH lớn nhất ⇔ MH 2 max
Do MH ≤ MI + IH ⇔ MH ⇔ M ≡ M max 2
Ta có: IH : x =1 x =1   M 1;0 1 ( ) Giải hệ (
. Do đó a + b = 3 − . Chọn D.x −  ) ⇒ 2  1 + ( y + 2)2 = 4 M 1; 4 −  2 ( )
Ví dụ 2: Cho số phức z thỏa mãn 13 z − 3+ i =
. Gọi z = a + bi(a;b∈) là số thức thỏa mãn biểu thức 2 2 2
P = z − 2 − i + z − 3i đạt giá trị nhỏ nhất. Tính T = a + b A. 5 T = B. 3 T = C. 13 T = D. 9 T = 2 2 2 2 Lời giải
Gọi M (z); I (3; ) 1 − khi đó 13 MI =
⇔ M thuộc đường tròn tâm 2 I (3; ) 1 − bán kính 13 R = 2 Đặt A( ) B( ) 2 2
2;1 ; 0;3 ⇒ P = MA + MB
Gọi E (1;2) là trung điểm của AB ta có : 2 2 = 2 + AB P ME nhỏ nhất ⇔ ME 2 min
Do ME ≥ MI − IE ⇔ ME ⇔ M ≡ M min 1   1  3
x − 2y − 7 = 0 M  2; 1    2 
Ta có: IE :3x + 2y − 7 = 0 . Giải hệ  (  . Do đó 5
a + b = . Chọn A.x )2 ( y )2 13 ⇒ 3 1  − + + =   5 −  2  4 M 4; 2  2    
Dạng 6: Cho hai số phức z ;z thỏa mãn z − z = R và z − w = z − w ; 1 2 1 0 2 1 2 2
trong đó z w ;w là các số phức đã biết. Tìm giá trị nhỏ nhất của biểu thức P = z − z 0; 1 2 1 2
Phương pháp: Đặt M(z ); N z lần lượt là các điểm biểu diễn 1 ( 2) số phức z và z . 1 2
Điểm M thuộc đường tròn tâm I (z bán kính R , N thuộc trung 0 )
trực ∆ của AB với A(w ; B w 1 ) ( 2)
Lại có: P = MN ⇒ P = d − R min (t;∆)
Ví dụ 1: Cho số phức z thỏa mãn 2 2
z − 2 − z + i =1 và số phức z thỏa mãn z − 4 − i = 5 . Tìm giá trị 1 2
nhỏ nhất của z − z 1 2 A. 2 5 B. 5 C. 2 5 D. 3 5 5 5 Lời giải
Gọi M (z; y)là điểm biểu diễn số phức z . Khi đó 2 2
z − 2 − z + i =1 1 2 2 2 2
⇔ (x− 2) + y − x − (y +1) =1 ⇔ 4 − x − 2y = 2
− ⇔ (∆) : 2x + y −1 = 0
Gọi N(a;b) là điểm biểu diễn số phức z . Khi đó 2 2
z − 4 − i = 5 ⇔ (a − 4) + (b −1) = 5 2
Hay tập hợp điểm N trong mặt phẳng Oxy là đường tròn 2 2
(C) : (x− 4) + (y−1) = 5 Ta có d ( 8 I R c ;(∆) = > 5 = ( ) ) (C) 5
⇒ (∆) không cắt đường tròn(C).
Lại có MN = z − z ⇒ dựa vào hình vẽ ta thấy 1 2
MN ⇔ MN = d I ; ∆ − R min ( C ( )) ( ) (C) Hay 8 5 3 5 z − z = − 5 = . Chọn D. 1 2 min 5 5
Bài toán có thể hỏi thêm là tìm số phức z hoặc z để z − z
thì ta chỉ cần viết phương trình đường 1 2 1 2 min M =  (∆)∩ MN
thẳng MN ⊥ (∆) sau đó tìm giao điểm  . N =  (C)∩ MN
Ví dụ 2: Cho hai số phức z ; z thỏa mãn z + 5 = 5 và z +1− 3i = z − 3− 6i . Tìm giá trị nhỏ nhất của 1 2 1 2 2
biểu thức P = z − z 1 2 A. 5 P = B. 15 P = C. P = 3 D. P =10 min 2 min 2 min min Lời giải
Gọi M (z ; N z lần lượt là các điểm biểu diễn các số phức z và z . 1 ) ( 2) 1 2
Điểm M thuộc đường thẳng tròn tâm I ( 5;
− 0) bán kính R = 5.
Điểm N thuộc đường thẳng trung trực ∆ của AB với A(− ) ( ) 35
1;3 ;B 3;6 ⇒ ∆ : 4x + 3y − = 0 2 Lại có: 5
P = MN ⇒ P = d( − R = . Chọn A. min I ;∆) 2
Dạng 7: Cho hai số phức z ;z thỏa mãn z − w = R và z − w = R trong đó w ;w là các số 1 2 1 1 1 2 1 2 1 2
phức đã biết. Tìm giá trị lớn nhất, nhỏ nhất của biểu thức P = z − z . 1 2
Phương pháp: Đặt M(z ); N z lần lượt là các điểm biểu diễn số phức z và z . 1 ( 2) 1 2
Điểm M thuộc đường tròn tâm (C tâm I (w bán kính R và N thuộc đường tròn (C tâm K (w 2 ) 2 ) 1 ) 1 ) 1
bán kính R ⇒ P = MN . Dựa vào các vị trí tương đối của 2 đường tròn để tìm MN MN max ; 2 min
Ví dụ 1: Cho hai số phức z;w thỏa mãn z.z =1 và w − 3+ 4i = 2 . Tìm giá trị lớn nhất của biểu thức P = z − w A. P = B. P = 8 C. P =10 D. P = 5 + 2 max 5 max max max Lời giải
Ta có: z.z =1 ⇔ z =1
Gọi M (z); N (w) lần lượt là các điểm biểu diễn các số phức z và w .
Điểm M thuộc đường tròn tâm (C tâm O(0;0) bán kính R =1 và N thuộc đường tròn (C tâm 2 ) 1 ) 1 K(3; 4
− ) bán kính R = 2 ⇒ P = MN . 2
Dễ thấy OK = 5 > R + R nên (C và (C nằm ngoài nhau suy ra MN = OK + R + R = . Chọn B. max 8 2 ) 1 ) 1 2 1 2
Ví dụ 2: [Đề tham khảo Bộ GD & ĐT 2018] Xét các số phức z = a + bi(a,b∈) thỏa mãn điều kiện
z − 4 − 3i = 5 . Tính P = a + b khi giá trị biểu thức z +1− 3i + z −1+ i đạt giá trị lớn nhất A. P =10 B. P = 4 C. P = 6 D. P = 8 Lời giải Gọi M ( ;
x y) là điểm biểu diễn số phức z
Từ giả thiết, ta có z − − i =
⇔ (x − )2 + ( y − )2 4 3 5 4
3 = 5 ⇒ M thuộc đường tròn (C)tâm I (4;3) , bán
kính R = 5 . Khi đó P = MA + MB , với A( 1; − 3), B(1;− ) 1 . Ta có 2 2 2
P = MA + MB + MA MB ≤ ( 2 2 2 . 2 MA + MB ). 2 2 2 Gọi E (0; ) 1 là trung điểm 2 MA + ⇒ = MB − AB AB ME . 2 4 Do đó 2 2 2 2 2
P ≤ 4.ME + AB mà ME ≤ CE = 3 5 suy ra 2
P ≤ 4.(3 5) +(2 5) = 200.
Với C là giao điểm của đường thẳng EI với đường tròn(C). MA = MB
Vậy P ≤10 2 . Dấu" = " xảy ra 
⇒ M (6;4) ⇒ a + b =10. Chọn A.M ≡ C
Ví dụ 3: [Đề tham khảo Bộ GD & ĐT 2017] Xét các số phức z thỏa mãn điều kiện:
z + 2 − i + z − 4 − 7i = 6 2 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của z −1+ i . Tính
P = M + m A. P + + = 13 + 73 B. 5 2 2 73 P = C. P = 5 2 + 73 D. 5 2 73 P = 2 2 Lời giải
Đặt z = x + yi(x, y ∈) và gọi M ( ; x y), A( 2; − )
1 , B(4;7) suy ra AB = 6 2 .  
Ta có AB = (6;6) ⇒ n = (1;− )
1 ⇒ phương trình đường thẳng
AB là x − y + 3 = 0 .
Từ giả thiết, ta có MA + MB = 6 2 → MA + MB = AB
suy ra M thuộc đoạn thẳng AB.  z −  1+ i = MN Gọi N (1;− )
1 ⇒ z −1+ i = (x − )2 1 + ( y + )2 min min 1 = MN ⇒  . z −1+ i =  MN max max
 Độ dài đoạn thẳng MN nhỏ nhất khi và chỉ khi M là hình chiếu của N trên AB. 1− 1 − + 3 Hay 5 2 5 2
MN = d N; AB = = → m = min ( ( )) ( ) 2 + (− )2 2 2 1 1
 Độ dài đoạn thẳng MN lớn nhất khi và chỉ khi M ≡ A hoặc M ≡ B .
M ≡ A → MN = AN = 13 Ta có  ⇒ MN = M max 73 → = 73.
M ≡ B → MN = BN = 73
Vậy giá trị biểu thức 5 2 + 2 73
P = M + m = . Chọn B. 2
Ví dụ 4: Xét các số phức z thỏa mãn điều kiện: z −1− i + z − 7 − 4i = 3 5 . Gọi M, m lần lượt là giá trị lớn
nhất và giá trị nhỏ nhất của z − 5 + 2i . Tính P = M + m A. P + + = 5 + 10 B. 2 5 10 P =
C. P = 2( 5 + 10) D. 5 2 10 P = 2 2 Lời giải
Đặt z = x + yi(x, y ∈) và gọi M ( ; x y), A(1; ) 1 , B(7;4) suy ra AB = 3 5 .  
Ta có AB = (6;3) ⇒ n =
− ⇒ phương trình đường AB 1; 2 ( ) ( )
thẳng AB là x − 2y +1 = 0 .
Từ giả thiết, ta có MA + MB = 3 5 → MA + MB = AB
suy ra M thuộc đoạn thẳng AB.  z −  5 + 2i = MN Gọi N (5; 2 − ) min min
⇒ z − 5 + 2i = MN ⇒  . z − 5 + 2i =  MN max max
 Độ dài đoạn thẳng MN nhỏ nhất khi và chỉ khi M là hình chiếu của N trên AB. 5 − 2 2 − +1
Hay MN = d N; AB = = 2 5 → m = 2 5 min ( ( )) ( ) 2 1 + ( 2 − )2
 Độ dài đoạn thẳng MN lớn nhất khi và chỉ khi M ≡ A hoặc M ≡ B .
M ≡ A → MN = AN =  5 Ta có  ⇒ MN = M max 2 10 → = 2 10.
M ≡ B → MN = BN = 2 10
Vậy giá trị biểu thức P = M + m = 2( 5 + 10). Chọn C.
Ví dụ 5: Biết số phức z thỏa mãn đồng thời hai điều kiện z − 3− 4i = 5 và biểu thức 2 2
M = z + 2 − z − i
đạt giá trị lớn nhất. Tính môđun của số phức z + i . A. z + i = 2 41 B. z + i = 3 5 C. z + i = 5 2 D. z + i = 41 Lời giải
Gọi z = x + yi(x, y ∈)
Ta có: z − − i =
⇔ (x − )2 + ( y − )2 3 4 5 3
4 = 5 ⇒ tập hợp điểm biểu diễn số phức z là dường tròn (C)
tâm I (3;4) và R = 5 . Mặt khác: 2 2 M = z +
− z − i = (x + )2 2 + y − ( 2 2 2 x ) + ( y − )2
1  = 4x + 2y + 3  
⇔ d : 4x + 2y + 3− M = 0
Do số phức z thỏa mãn đồng thời hai điều kiện nên d và (C) có điểm chung d (I d ) 23− M ⇔ ; ≤ R ⇔
≤ 5 ⇔ 23− M ≤10 ⇔ 13 ≤ M ≤ 33 2 5
4x + 2y − 30 = 0  x = 5 ⇒ M = ⇔  ⇔ 
⇒ z + i = − i ⇒ z + i = . Chọn D. max 33 (  x − 3  ) 5 4 41
2 + ( y − 4)2 = 5 y = 5 −
Ví dụ 6: Cho hai số phức z và z thỏa mãn z + z = 8 + 6i và z − z = 2. Tìm giá trị lớn nhất của 1 2 1 2 1 2
P = z + z ? 1 2 A. P = 4 6 B. P = 5 + 3 5 C. P = 2 26 D. P = 34 + 3 2 Lời giải    
Đặt A(z ; B z theo giả thiết ta có: OA+ OB = (8;6); OA−OB = 2; P = OA+ OB 1 ) ( 2)    
= (OA+ OB)2 + (OA−OB)2 = ( 2 2
OA + OB ) ≥ (OA+ OB)2 2 104 2
= P ⇒ P ≤ 104 = 2 26 . Chọn C.
Ví dụ 7: [Đề thi thử chuyên Đại học Vinh 2018] Giả sử z , z là hai trong các số phức z thỏa mãn 1 2
iz + 2 − i =1 và z − z = 2. Giá trị lớn nhất của z + z bằng 1 2 1 2 A. 3 B. 2 3 C. 3 2 D. 4 Lời giải
Ta có: iz + 2 − i =1 ⇔ i(x + yi) + 2 −i =1 (với z = x + yi( ; x y ∈) )
⇔ (x − ) + ( y − )2 2 1
2 =1⇒ M (x; y) biểu diễn z thuộc đường tròn tâm I (1; 2) bán kính R =1.
Giả sử A(z ; B z do z − z = 2 ⇒ AB = 2 = 2R nên AB là đường kính của đường tròn(I; R) 1 ) ( 2) 1 2
Lại có: z + z = OA + OB 1 2 2 2 2
Mặt khác theo công thức trung tuyến ta có: 2 OA + OB AB 2 2 OI = − ⇒ OA + OB = 8 2 4
Theo BĐT Bunhiascopky ta có: ( 2 2
2 OA + OB ) ≥ (OA+ OB)2 ⇒ OA+ OB ≤ 4. Chọn D.
Ví dụ 8: Cho z , z là hai trong các số phức z thỏa mãn điều kiện z − 5 − 3i = 5và z − z = 8 . Giá trị nhỏ 1 2 1 2
nhất của biểu thức z + z là: 1 2 A. 6 − 34 B. 2 34 − 6 C. 2 34 + 6 D. 34 + 6 Lời giải
Giả sử w = z + z 1 2
w = z − 5 − 3i Đặt 1 1 
suy ra w + w = z + z −10 − 6i = w −10 − 6i ⇔ w + w = w −10 − 6i w = z − 5 −  3i 1 2 1 2 1 2 2 2  w = w =  5 Mà 1 2  mà 2 2 w + w + w − w = 2 w + w ⇒ w + w = 36. 1 2 1 2 ( 2 2 1 2 ) 2
 w − w = z − z = 8 1 2  1 2 1 2
Vậy w −10 − 6i = w + w = 36 = 6 ⇒ w thuộc đường tròn tâm I (10;6) , bán kính R = 6 . 1 2
Cách 2: Gọi A(z ; B z biểu diễn số phức z ; z 1 ) ( 2) 1 2
Ta có: tập hợp z là đường tròn tâm I (5;3) bán kính R = 5, AB = 8   
Gọi H là trung điểm của AB ⇒ w = z + z = OA + OB = 2OH 1 1 2 ( ) Mặt khác 2 2
IH = IA − HA = 3 ⇒ tập hợp điểm H là đường tròn (x − )2 + ( y − )2 5 3 = 9(C) . 2 2 Giả sử (a b) ( )  a b H
(C)  a   b  ⇒ ∈ ⇒ − + −
= ⇔ (a − )2 + (b − )2 w ; , 1 ; 5 3 9 10 6 =       36.  2 2   2   2 
Do đó tập hợp điểm biểu diễn w thuộc đường tròn tâm I (10;6) , bán kính R = 6 . Ta có: w
= OI − R = 2 34 − 6. Chọn B. min
Ví dụ 9: Cho z , z là hai nghiệm của phương trình 6 − 3i + iz = 2z − 6 − 9i , thỏa mãn điều kiện 1 2 8
z − z = . Giá trị lớn nhất của z + z 1 2 5 1 2 A. 31 B. 56 C. 4 2 D. 5 5 5 Lời giải
6 −3i + iz = 6 −3i + i(x + yi) = 6 − y + (x −3)i
Đặt z = x + yi( ; x y ∈) suy ra 
2z − 6 − 9i = 2x + 2yi − 6 − 9i = 2x − 6 +  (2y −9)i
Khi đó, giả thiết ⇔ (x − )2 + ( y − )2 = ( x − )2 + ( y − )2 ⇔ (x − )2 + ( y − )2 3 6 2 6 2 9 3 4 =1 (C) .
Tập hợp z là đường tròn tâm I (3;4) bán kính 8 R =1, AB =
5   
Đặt w = z + z gọi H là trung điểm của AB ⇒ w = z + z = OA + OB = 2OH 1 1 2 ( ) 1 2 Mặt khác 2 2 3
IH = IA − HA = ⇒ tập hợp điểm H là đường tròn (x − )2 + ( y − )2 9 3 4 = (C) . 5 25 2 2 Giả sử (a b) ( )  a b  ⇒ H ∈(C)  a   b  9 ⇒ − + − =
⇔ (a − )2 + (b − )2 36 w ; , 1 ; 3 4 6 8 =       .  2 2   2   2  25 25
Do đó tập hợp điểm biểu diễn w thuộc đường tròn tâm I (6;8) , bán kính 6 R = . 5 Ta có: 6 56 w = OI + R =10 + = . max 5 5 Chọn B.
Ví dụ 10: [Đề thi thử chuyên Đại học Vinh 2018] Cho số phức z thỏa mãn z không phải là số thực và
w = z là số thực. Giá trị lớn nhất của biểu thức M = z +1− i là 2 2 + z A. 2 B. 2 2 C. 2 D. 8 Lời giải
Ta có w = z ⇒ w = z = z
1 . Vì w là số thực nên w = w (2) . 2 2 2 ( ) 2 + z 2 + z 2 + z
Từ (1), (2) suy ra w = z = z ⇔ z 2 + z = z 2 + z ⇔ 2 z − z = z.z z − z 2 ( 2) ( 2 2 ) ( ) ( ) 2 + z 2 + z ⇔ (z − z)( 2 z − ) 2
2 = 0 ⇔ z = 2 ⇔ z = 2 (vì z không là số thực nên z − z ≠ 0 ).
Đặt w = z +1− i ⇔ z = w −1+ i nên 2 2 w −1+ i = 2 ⇒ w
= 2 + 1 +1 = 2 2 . Chọn B. max
Cách 2: Ta có w là số thực nên 1 2 = z + là số thực. w z 1 2(a −bi) b = 0(kot / 2 mycbt b )
Đặt z = a + bi ⇒ = a + bi +
là số thực khi b − = 0 ⇔  2 2 w a + b 2 2 2 2 a + b
a + b = 2 ⇒ z = 2 
Tập hợp điểm biểu diễn z là đường tròn O(0;0); R = 2
Đặt M (z); A( 1; − )
1 ⇒ MA = AO + R = . Chọn B. max 2 2
Ví dụ 11: Cho số phức z thỏa mãn z =1. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 2
P = z +1 + z − z +1 . Tính giá trị của M.m A. 13 3 B. 39 C. 3 3 D. 13 4 4 4 Lời giải
Gọi z = x + yi;(x∈ ;
y ∈). Ta có: z =1 ⇔ z.z =1.
Đặt t = z +1 , ta có 0 = z −1≤ z +1 ≤ z +1 = 2 ⇒ t ∈[0;2]. Ta có = ( + )( + ) 2 2 − 2 1 1
=1+ . + + = 2 + 2 ⇒ = t t z z z z z z x x 2 Suy ra 2 2
z − z + = z − z + z z = z z − + z = ( x − )2 2 1 . 1
2 1 = 2x −1 = t − 3
Xét hàm số f (t) 2
= t + t − 3 ,t ∈[0;2]. Bằng cách dùng đạo hàm, suy ra f (t) 13 = f (t) 13 3 max ;min = 3 ⇒ M.n = . 4 4 Chọn A.
Ví dụ 12: Cho số phức z thỏa mãn z =1. Tìm giá trị lớn nhất của biểu thức T = z +1 + 2 z −1 A. MaxT=2 5 B. MaxT=2 10 C. MaxT=3 5 D. MaxT=3 2 Lời giải
T = z + + z − ≤ ( 2 1 2 1 1+ 2 )( 2 2
z +1 + z −1 ) = 5.2( 2
z + )1 = 2 5 (BĐT Cauchy-Swart) Chú ý: 2 2 2 2
z +1 + z −1 = 2x + 2y + 2 = 2( 2
z + )1 với z = x + yi
Cách 2: Đặt z = x + yi . Ta có : 2 2 2 2
T = x + yi +1 + 2 x − yi −1 = (x +1) + y + 2 (x −1) + y Lại có 2 2
x + y =1⇒ T = 2x + 2 + 2 2
− x + 2 = f (x) Ta có: f (x) 1 2 6 ' 0 − = − = ⇔ x = ⇒ T = . Chọn A. max 2 5 2x + 2 2 − 2x 10
Ví dụ 13: Cho số phức z thỏa mãn z − 4 + z + 4 =10 . Giá trị lớn nhất và giá trị nhỏ nhất của z lần lượt là : A. 10 và 4 B. 5 và 4 C. 4 và 3 D. 5 và 3 Lời giải
Đặt z = x + yi;( ;
x y ∈) ⇒ M ( ;
x y) biểu diễn z
Ta có: z − 4 + z + 4 =10 ⇔ z + yi − 4 + x + yi + 4 =10 Gọi F ( 4
− ;0);F (4;0) ⇒ MF + MF =10 1 2 1 2
Khi đó điểm biểu diễn z là Elip có trục lớn
2a =10 ⇒ a = 5; F F = 2c = 8 1 2 2 2
⇒ c = 4 ⇒ b = a − c = 3. Do đó 3 ≤ OM ≤ 5 ⇒ 3 ≤ z ≤ 5. Chọn D.
BÀI TẬP TỰ LUYỆN
Câu 1: Trong mặt phẳng tọa độ, hãy tìm số phức z có môđun nhỏ nhất, biết rằng số phức z thỏa mãn điều
kiện z − 2 − 4i = 5 A. z = 1 − − 2i
B. z =1− 2i
C. z =1+ 2i D. z = 1 − + 2i
Câu 2: Cho số phức z thỏa mãn z − 3+ 4i = 4. Tìm giá trị lớn nhất của biểu thức P = z A. P = B. P = C. P = D. P = max 3 max 12 max 5 max 9
Câu 3: Cho số phức z thỏa mãn z − 2 + 2i =1. Tìm giá trị lớn nhất của z A. 4 2 − 2 B. 2 2 +1 C. 2 + 2 D. 3 2 +1
Câu 4: Trong các số phức z thỏa mãn z + 3+ 4i = 2 .Gọi z là số phức của môđun nhỏ nhất. Tìm môđun của 0 số phức z 0 A. z = B. z = C. z = D. z = o 3 o 7 o 2 o 4
Câu 5: Cho số phức z thỏa mãn z − 2 − 3i =1. Tìm giá trị lớn nhất của P = z +1+ i A. 13 + 2 B. 4 C. 3 D. 13 +1
Câu 6: Cho số phức z thỏa mãn điều kiện z − 3 = 2 z và max z −1+ 2i = a + b 2 . Tính a + b A. 4 B. 4 2 C. 3 D. 4 3
Câu 7: Cho số phức z có z = 2 thì số phức w = z + 3i có môđun nhỏ nhất và lớn nhất lần lượt là bao nhiêu? A. 2 và 5 B. 1 và 6 C. 2 và 6 D. 1 và 5
Câu 8: Trong tất cả các số phức có dạng z = m − 3− (m − 2)i với m∈ , hãy tìm số phức z có môđun nhỏ nhất ? A. 1 1 z = − i B. 1 1 z = − + i C. 1 1 z = − − i D. 1 1 z = + i 2 2 2 2 2 2 2 2
Câu 9: Cho số phức z = (m −1) + (m − 2)i,m∈ . Tìm giá trị của m để môđun của số phức z có giá trị lớn nhất là 5 m ≤ 3 − m ≤ 6 − A. 3 − ≤ m ≤ 0
B. 0 ≤ m ≤ 3 C.D.  m ≥ 0 m ≥ 2
Câu 10: Cho số phức z = m + (m − 3)i,m∈ . Tìm m để z đạt giá trị nhỏ nhất? A. m = 0 B. m = 3 C. 3 m = D. 3 m = − 2 2
Câu 11: Cho số phức z thỏa mãn z − 2 − 3i = z − i . Gọi z = a + bi( ;
a b∈) là số phức thỏa mãn
z + 2 + 2i nhỏ nhất. Giá trị của biểu thức a + 3b là: A. 4 B. 3 C. 6 D. 0
Câu 12: Biết số phức z = a + bi(a,b∈) thỏa mãn điều kiện z − 2 − 4i = z − 2i có môđun nhỏ nhất của. Tính 2 2
M = a + b A. M = 8 B. M =10 C. M =16 D. M = 26
Câu 13: Cho số phức z có điểm biểu diễn nằm trên đường thẳng 3x − 4y − 3 = 0 . Tìm giá trị nhỏ nhất của z A. 1 B. 3 C. 4 D. 2 5 5 5 5
Câu 14: Xét số phức z = a + bi,(a,b∈) thỏa mãn z − 2 − 4i = z − 2i . Tìm giá trị nhỏ nhất của z A. 4 B. 2 2 C. 10 D. 8
Câu 15: Cho số phức z thỏa mãn z −1+ i = z − 2 − i . Gọi z = a + bi,(a,b∈) là số phức thỏa mãn z −i
nhỏ nhất. Giá trị của biểu thức a + b là: A. 7 − B. 9 C. 3 D. 7 10 10 10 10
Câu 16: Cho các số phức z,ω thỏa mãn z + 2 − 2i = z − 4i . Gọi z = a + bi,(a,b∈) là số phức thỏa mãn
iz +1 nhỏ nhất. Tính giá trị của biểu thức 2 2 a + b A. 4 B. 5 C. 5 D. 2 2
Câu 17: Cho số phức z thỏa mãn z +1 = z + i . Tìm giá trị nhỏ nhất của z −1− 2i A. 1 B. 3 C. 1 D. 2 3 2
Câu 18: Cho số phức z = x + yi(x, y∈) thỏa mãn z −1 = z + i . Biết z − 2i nhỏ nhất, tính S = x + 2y A. S = 2 B. S = 3 C. S =1 D. S = 4
Câu 19: Xét các số phức z = a + bi,(a,b∈) thỏa mãn z −1+ 2i = z −i . Tính 2
P = 2a − b khi z đạt giá trị nhỏ nhất A. 1 P = B. 19 P = C. 4 P = − D. 14 P = 25 25 25 25
Câu 20: Cho các số phức z,ω thỏa mãn z + 2 − 2i = z − 4i và w = iz +1. Tính giá trị nhỏ nhất của w A. w = 2 B. 2 w = C. w = 2 2 D. 3 2 w = min min 2 min min 2
Câu 21: Cho số phức z thỏa mãn 2
z − 2z + 5 = (z −1+ 2i)(z + 3i −1) . Tính min w , biết w = z − 2 + 2i A. 3 min w = B. min w = 2 C. min w =1 D. 1 min w = 2 2
Câu 22: Cho số phức z thỏa mãn z − 3 = 2 z và max z −1+ 2i = a + b 2 . Tính a + b A. 4 B. 4 2 C. 3 D. 4 3
Câu 23: Cho số phức z thỏa mãn z không phải số thực và z w =
là số thực. Biểu thức z +1− i đạt giá 2 2 + z
trị lớn nhất khi z = a + bi,(a,b∈). Tính 2
P = a − 2b A. 2 − B. 1 C. 3 D. 5 −
Câu 24: Cho số phức z thỏa mãn z −1+ i = z +1−i . Gọi z = a + bi,(a,b∈) sao cho
P = z −1− 5i + z + 2 + i đạt giá trị nhỏ nhất. Khi đó a + b bằng A. 6 B. 6 − C. 3 − D. 3 5 5 5 5
Câu 25: Cho số phức z thỏa mãn z − 2 + i = z − 3i . Gọi z = a + bi,(a,b∈) sao cho P = z −i + z − 2 đạt
giá trị nhỏ nhất. Khi đó 2a − b bằng A. 1 B. 7 − C. 1 − D. 3 5 5 5 5
Câu 26: Cho số phức z thỏa mãn z −1− 2i = z +1 . Gọi z = a + bi,(a,b∈) là số phức thỏa mãn biểu thức 2 2
P = z −1+ 2i + z − i đạt giá trị nhỏ nhất. Tổng a + b là
A. a + b = 0
B. a + b =1
C. a + b = 2
D. a + b = 3
Câu 27: Cho số phức z thỏa mãn z − 3− i = z +1+ i . Gọi z = a + bi,(a,b∈) là số phức thỏa mãn biểu thức 2 2
P = z −1− i + z + 2 + i đạt giá trị nhỏ nhất. Tổng a + b là A. 13 a + b = B. 1 a + b =
C. a + b =1
D. a + b = 2 10 10
Câu 28: Cho số phức z thỏa mãn z −1+ 2i = 5 và ω = z +1+ i có môđun lớn nhất. Tính môđun của số phức z A. z = 2 5 B. z = 3 2 C. z = 6 D. z = 5 2
Câu 29: Cho số phức z thỏa mãn z =1. Tìm giá trị lớn nhất của T = z +1 + 2 z −1 A. maxT = 2 5 B. maxT = 2 10 C. maxT = 3 5 D. maxT = 3 2
Câu 30: Cho số phức z thỏa mãn 2
z − 2z + 5 = (z −1+ 2i)(z + 3i −1) . Tính min ω , với ω = z − 2 = 2i A. 3 min ω = B. min ω = 2 C. min ω =1 D. 1 min ω = 2 2
Câu 31: Cho số phức z thỏa mãn 2
z − i =1. Tìm giá trị lớn nhất của z A. 5 B. 2 C. 2 2 D. 2
Câu 32: Cho số phức z thỏa mãn 2 2 iz + + iz +
= 4 . Gọi M, m lần lượt là giá trị lớn nhất và nhỏ nhất 1− i i −1 z . Tính Mm. A. Mm = 2 B. Mm =1 C. Mm = 2 2 D. Mm = 2 3
Câu 33: Cho số phức z − z thỏa mãn
2i là số ảo. Tìm giá trị lớn nhất của P = z −1 + z −i z − 2 A. 5 2 B. 3 2 C. 2 5 D. 3 5
Câu 34: Gọi S là tập hợp tất cả các giá trị thực của tham số m để tồn tại duy nhất số phức z thỏa mãn
z.z =1 và z − 3 + i = m . Tìm số phần tử của S. A. 2 B. 4 C. 1 D. 3
Câu 35: Biết rằng tồn tại hai số phức z thỏa mãn 2z +1 = z + z + 3 và z −8 đạt giá trị nhỏ nhất. Tính tổng
hai phần thực của hai số phức đó. A. 7 B. 0 C. 14 D. 8
Câu 36: Cho số phức z = x + yi(x, y∈) thay đổi thỏa mãn z =1. Hãy tính tổng giá trị lớn nhất và giá trị
nhỏ nhất của biểu thức P = x − y A. 0 B. 12 C. 5 D. 2 5
Câu 37: Cho số phức z thỏa mãn z =1. Tìm giá trị lớn nhất của biểu thức T = z + 2 + 2 z − 2 A. 2 5 B. 2 10 C. 3 5 D. 5 2
LỜI GIẢI BÀI TẬP TỰ LUYỆN
Câu 1: Tập hợp điểm M biểu diễn số phức z là đường tròn (C)tâm I(2;4) bán kính R = 5
Ta có: z = OM , mặt khác OM đạt giá trị lớn nhất và nhỏ nhất khi M = OI ∩ (C)
Phương trình đường thẳng OI : y = 2x , phương trình đường tròn 2 2
(C) : (x− 2) + (y− 4) = 5 y = 2xy = 2x
Giải hệ phương trình:  ⇔ 2 2  2 2
(x − 2) + (y − 4) = 5
(x − 2) + (y − 4) = 5 x =1⇒ y = 2 OM = 5 1 ⇔ ⇒ 
suy ra z =1+ 2i là số phức thỏa mãn điều kiện z − 2 − 4i = 5
x = 3 ⇒ y = 6  1 OM =  3 5 2
Và có môđun nhỏ nhất, z = 3+ 6i là số phức có môđun lớn nhất. Chọn C. 2
Câu 2: Tập hợp điểm M biểu diễn số phức z là đường tròn (C) tâm I(3; 4 − ) bán kính R = 4
Ta có: z = OM , khi đó P = OM
= OI + R = 5 + 4 = . Chọn A. max max 9
Câu 3: Tập hợp điểm M biểu diễn số phức z là đường tròn (C) tâm I(2; 2 − ) bán kính R =1
Ta có: z = OM , khi đó z = OM
= OI + R = 2 2 + . Chọn B. max max 1
Câu 4: Tập hợp điểm M biểu diễn số phức z là đường tròn (C) tâm I( 3 − ; 4 − ) bán kính R = 2
Ta có: z = OM , khi đó z = OM
= OI − R = 5 − 2 = 2 . Chọn D. min min
Câu 5: Đặt z = x + yi (x, y∈) , ta có : 2 2
z − 2 − 3i =1 ⇔ (x − 2) + (y − 3) =1
Tập hợp điểm M biểu diễn số phức z là đường tròn (C)tâm I(2;3) bán kính R =1 Lại có: 2 2 2 2
P = x − yi +1+ i = (x +1) + (1− y) = (x +1) + (y−1) Gọi K( 1;
− 1) ⇒ P = MK → P = IK + R = 13 + . Chọn D. max 1
Câu 6: Đặt z = x + yi (x, y∈) , ta có : z −3 = 2 z ⇔ x + yi −3 = 2 x + yi 2 2 2 2 2 2 2 2
⇔ (x − 3) + y = 4(x + y ) ⇔ 3x + 3y + 6x − 9 = 0 ⇔ x + y + 2x − 3 = 0 2 2
⇔ (x +1) + y = 4 ⇒ Tập hợp điểm M biểu diễn số phức z là đường tròn tâm I( 1;
− 0) bán kính R = 2 a = 2
Gọi K(1;2) ⇒ z −1 = 2i = MK → MK = IK + R = + ⇒  ⇒ a + b = . max 2 2 2 4 b  = 2 Chọn A.
Câu 7: Tập hợp điểm M biểu diễn số phức z là đường tròn tâm O(0;0) bán kính R = 2 Gọi K(0; 3)
− ⇒ w = z + 3i = MK Ta có: MK
= OI + R = 5;MK = OK − R = . Chọn D. max 1 min 2 Câu 8: 2 2 2 2  5  1 1
z = (m − 3) + (m − 2) = 2m −10m +13 = 2 m − + ≥  2    2 2 Do đó 1 5 1 1 z =
⇔ m = ⇒ z = − − i . Chọn C. min 2 2 2 2 Câu 9: 2 2 2 2 2
z = (m −1) + (m − 2) = 2m − 6m + 5 ≤ 5 ⇔ 2m − 6m ≤ 0 ⇔ 0 ≤ m ≤ 3. Chọn B. 2 Câu 10: 2 2 2 2  3  9 9
z = m + (m − 3) = 2m − 6m + 9 = 2 m − + ≥  2    2 2 Do đó 3 3 z =
⇔ m = . Chọn C. min 2 2
Câu 11: Đặt M (z); (
A 2;3),B(0;1) là các điểm biểu diễn số phức z;2 + 3i
và i . Khi đó từ giả thiết suy ra MA = MB , tập hợp điểm biểu diễn số
phức z là đường trung trực của AB đi qua I(1;2) và có VTCP là
n(1;1)⇒ d :x+ y−3= 0 Gọi N( 2; − 2
− ) là điểm biểu diễn số phức 2 − − 2i
Ta có z + 2 + 2i nhỏ nhất khi MN khi M là hình chiếu vuông góc của min
N trên d, suy ra MN : x− y = 0  3 x − y = 0 x =  Giải hệ  2  3 3  3+ 3i  ⇒ 
⇒ M  ; ⇒ z = ⇒ a + 
3b = 6. Chọn C.
x + y − 3 = 0 3   2 2  2 y =  2
Câu 12: Tập hợp điểm M biểu diễn số phức z là trung trực ∆ của AB với ( A 2;4),B(0;2)   Trung điểm của AB là 1
I(1;3);n = − AB = (1;1) ⇒ ∆ : x + y − 4 = 0 2
Mặt khác z = OM nhỏ nhất khi M là hình chiếu vuông góc của O xuống ∆ a = 2
Khi đó OM : x − y = 0 ⇒ M = OM ∩ ∆ = M . Chọn A. o (2;2) ⇒  ⇒ = 8 b = 2
Câu 13: Ta có z = OM nhỏ nhất khi M là hình chiếu vuông góc của O xuống ∆ :3x − 4y − 3 = 0 Khi đó 3 3 z = OM = d(O;∆) = = . Chọn B. min min 2 2 3 + 4 5
Câu 14: Tập hợp điểm M biểu diễn số phức z là trung trực ∆ của AB với ( A 2;4),B(0;2)   Trung điểm của AB là 1
I(1;3);n = − AB = (1;1) ⇒ ∆ : x + y − 4 = 0 2
Mặt khác z = OM nhỏ nhất khi M là hình chiếu vuông góc của O xuống ∆ Khi đó 4 OM = d( ; O ∆) = = 2 2 . Chọn B. min 2
Câu 15: Đặt M (z); ( A 1; 1)
− ,B(2;1) là các điểm biểu diễn số phức z;1− i và 2 + i . Khi đó từ giả thiết suy ra
MA = MB , tập hợp điểm biểu diễn số phức z là đường trung trực của AB  đi qua  3 I ;0  và có VTCP là 3
n(1;2) ⇒ d : x + 2y − = 0 2    2
Gọi N(0;1) là điểm biểu diễn số phức i
Ta có z − i nhỏ nhất khi MN khi M là hình chiếu vuông góc của N trên min
d, suy ra MN : 2 x− y+1 = 0  1  3 − x
x + 2y − = 0 =  Giải hệ  10  1 − 4  1 − 4i 7  2 ⇒ 
⇒ M  ; ⇒ z = + ⇒ a + b = . Chọn D. 4 10 5 
 x − y + =    10 5 10 2 1 0 y =  5
Câu 16: Gọi I(x; y);M( 2;
− 2), N(0;4) là điểm biểu diễn các số phức z; 2 − + 2i;4i
Từ giả thiết ⇒ IM = IN ⇒ I ∈trung trực của MN là d : x + y − 2 = 0 Khi đó 2 2
iz +1 = −y + xi +1⇒ iz +1 = x + (y −1) = NM với N(0;1)
Ta có iz +1 nhỏ nhất khi MN khi M là hình chiếu vuông góc của N trên d, suy ra MN : x− y+1 = 0 min  1
x + y − 2 = 0 x =  Giải hệ  2  1 3  1 3 2 2 5  ⇒ 
⇒ M  ; ⇒ z = + i ⇒ a + b = . Chọn B x y 1 0 3 2 2  − + =    2 2 2 y =  2
Câu 17: Gọi z = x + yi (x, y∈)
⇒ x +1+ yi = x + (y +1)i 2 2 2 2
⇔ (x +1) + y = x + (y +1) ⇔ x − y = 0
⇒ M (z) có quỹ tích là đường thẳng d : x− y = 0
Với z ' =1+ 2i ⇒ N(z ') = (1;2) Ta có z ⇔ NM ⇔ NM ⊥ d min min 1 ⇒ z
= d(N;d) = . Chọn C. min 2
Câu 18: Gọi z = x + yi (x, y∈)
⇒ x −1+ yi = x + (y +1)i 2 2 2 2
⇔ (x −1) + y = x + (y +1) ⇔ x + y = 0
⇒ M (z)có quỹ tích là đường thẳng d : x+ y = 0
Với z ' = 2i ⇒ N(z ') = (0;2) Ta có z ⇔ NM
⇔ NM ⊥ d ⇒ MN : x − y + k = 0 min min
Mà MN qua N(0;2) ⇒ k = 2 ⇒ MN : x− y+ 2 = 0
Tọa độ M là nghiệm của hệ
x − y + 2 = 0 x = 1 −  ⇒ M ( 1; − 1) ⇒ 
⇒ S =1. Chọn C.x + y = 0 y = 1
Câu 19: Đặt M (z) = M (a;b) và ( A 1; 2 − ),B(0;1) ⇒ MA = MB
Suy ra tập hợp điểm biểu diễn số phức z là đường thẳng trung trực của AB ⇒ (d) : x − 3y − 2 = 0
Gọi H là hình chiếu của O trên (d) ⇒ Phương trình đường thẳng OH :3x + y = 0
Ta có z = OM ≥ OH . Dấu bằng xay ra khi và chỉ khi M ≡ H ⇒ M = (d) ∩OH  1
a − 3b − 2 = 0 a = 
Khi đó, tọa độ điểm M là nghiệm của hệ  5  ⇒ . Vậy 1 P = . Chọn A. 3  a b 0  + = 3 b = − 25  5
Câu 20: Đặt M (z) = M (a;b) và ( A 2; − 2),B(0;4) ⇒ MA = MB
Suy ra tập hợp điểm biểu diễn số phức z là đường thẳng trung trực của AB ⇒ (d) : x + y − 2 = 0 w iz +1 Ta có 1
w = iz +1 ⇔ w = iz +1 ⇔ =
⇔ w = z + = MC , với C(0;1) i i i
Gọi H là hình chiếu của C trên (d) ⇒ CM ≥ CH . Dấu = xảy ra ⇔ M ≡ H 0.1+1.1− 2 Vậy 2 w
= CH = d(C;(d)) = = . Chọn B. min 2 2 1 +1 2 Câu 21: 2
z − 2z + 5 = (z−1+ 2i)(z+ 3i−1) ⇔ (z −1+ 2i)(z −1− 2i) = (z−1+ 2i)(z+ 3i−1)
z −1+ 2i = 0
z =1− 2i ⇒ w = 1 − → w =1 ⇔  ⇔ 
z −1− 2i = z −1+ 3i
z −1− 2i = z −1+ 3i (*) 
Đặt M (z) = M (a;b) và ( A 1;2),B(1; 3 − ) ⇒ (*) ⇔ MA = MB
Suy ra tập hợp điểm biểu diễn số phức z là đường thẳng trung trực của AB ⇒ (d) : 2y +1 = 0
Ta có w = z − 2 + 2i ⇔ w = z − 2 + 2i = MC , với C(2; 2 − )
Gọi H là hình chiếu của C trên (d) ⇒ CM ≥ CH . Dấu = xảy ra ⇔ M ≡ H 2.0 + 2.( 2) − +1 Khi đó 3 w
= CH = d(C;(d)) =
= . Vậy min w =1. Chọn C. min 2 2 0 + 2 2
Câu 22: Đặt z = x + yi (x, y∈) khi đó 2 2
z − 3 = 2 z ⇔ (z − 3) = 4 z 2 2 2 2 2 2 2 2
⇔ (x− 3) + y = 4(x + y ) ⇔ x + y + 2x − 3 = 0 ⇔ (x +1) + y = 4 (C)
⇒ Tập hợp điểm M biểu diễn số phức z là đường tròn (C) tâm I( 1;
− 0) , bán kính R = 2 Gọi ( A 1; 2
− ) ⇒ IA = 2 2 > R ⇒ A nằm ngoài đường tròn (C) ⇒ MA = IA + R = 2 + max 2 2
Mặt khác max z −1+ 2i = a + b 2 → a = b = 2 . Vậy a + b = 4 . Chọn A. 2
Câu 23: Vì w là số thực suy ra 1 2 + z 2 = = z + là số thực 2 2
⇔ z + = z + ⇔ z = 2 w z z z z I(0;0)
Suy ra tập hợp điểm M biểu diễn số phức z là đường tròn (C) : 2 2
x + y = 2 với  R = 2 Gọi ( A 1;
− 1) ⇒ z +1− i = MA và IA = 2 = R ⇒ Anằm trên đường tròn (C) Khi đó MA
= IA + R = 2 2 . Dấu bằng xảy ra khi I là trung điểm MA ⇒ M (1; 1 − ) max a =1
Vậy z =1− i thì 2
z +1− i = 2 2 →  ⇒ P =1 − 2.( 1 − ) = 3. Chọn C. b = 1 −
Câu 24: Gọi M (z);A(1; 1 − ); B( 1;
− 1) từ giả thiết suy ra MA = MB nên M thuộc đường thẳng trung trực của
AB có phương trình y = x(d) .
Gọi H (1;5); K( 2 − ; 1
− ) ⇒ P = MH + MK , 2 điểm H, K cùng phía so với đường thẳng d
Gọi H’ là điểm đối xứng của d : y = x
Ta có: HH ': x+ y− 6 = 0 ⇒ I(3;3) ⇒ H'(5;1)
Lại có: P = MH + MK = MH '+ MK ≥ H 'K
Dấu bằng xảy ra ⇔ M = H 'K ∩ d
Phương trình đường thẳng H’K là: 2x − 7y − 3 = 0 Suy ra  3 3  6 M = − ; − − ⇒ a + b =  . Chọn B. 5 5    5
Câu 25: Ta có: z − 2 + i = z − 3i = z − 3i = z + 3i
Gọi M (z);A(2; 1 − ); B(0; 3)
− suy ra MA = MB nên M thuộc
đường thẳng trung trực của AB có phương trình z + y +1 = 0(d) .
Gọi H (0;1); K(2;0) ⇒ P = MH + MK , 2 điểm H, K cùng phía so với đường thẳng d
Gọi H’ là điểm đối xứng của d : z+ y+1 = 0
Ta có: HH ': x− y+1 = 0 ⇒ I( 1 − ;0) ⇒ H'( 2 − ; 1 − )
Lại có: P = MH + MK = MH '+ MK ≥ H 'K
Dấu bằng xảy ra ⇔ M = H 'K ∩ d
Phương trình đường thẳng H’K là: x − 4y − 2 = 0 Suy ra  2 3  1 M = − ;− ⇒  2a − b = −  . Chọn C.  5 5  5
Câu 26: Gọi M (z); ( A 1;2),B( 1; − 0)
Khi đó z −1− 2i = z +1 ⇔ MA = MB ⇒ M thuộc trung trực của AB có
phương trình x + y −1 = 0 (d) 2 Gọi 2 2 2 IJ I(1; 2
− );J(0;1) ⇒ P = MI + MJ = 2ME + 2 (với  1 1 E ; −  
là trung điểm của IJ) 2 2   
Do đó P ⇔ ME hay M là hình chiếu vuông góc của E xuống d, khi đó EM : x− y−1 = 0 min min
⇒ M = EM ∩ d ⇒ M (1;0) ⇒ a + b =1. Chọn A.
Câu 27: Gọi M (z); (3 A ;1),B( 1 − ; 1 − )
Khi đó z − 3− i = z +1+ i ⇔ MA = MB ⇒ M thuộc trung trực của AB có phương trình 2x + y − 2 = 0 (d) 2 Gọi 2 2 2 IJ I(1;1);J( 2 − ; 1)
− ⇒ P = MI + MJ = 2ME + 2 (với  1 − E ;0 
là trung điểm của IJ) 2   
Do đó P ⇔ ME hay M là hình chiếu vuông góc của E xuống d, khi min min đó 1 EM : x− 2 y+ = 0 2  7 3  13
⇒ M = EM ∩ d ⇒ M ; ⇒ a + b =  . Chọn A. 10 5    10
Câu 28: Ta có ω = z +1+ i ⇔ z = ω −1− i nên z −1+ 2i = ω −1− i −1+ 2i = ω − 2 + i
Khi đó z −1+ 2i = 5 ⇔ ω − 2 + i = 5 nên ω
= 2 5 ⇔ ω = 4 − 2i max Suy ra 2 2
z = ω −1− i = 4 − 2i −1− i = 3− 3i → z = 3 + ( 3) −
= 3 2 . Chọn B.
Câu 29: Xét hai cách giải:
Cách 1: Gọi z = x + yi (x, y ∈) ⇒ M (x, y) Và ( A 1; − 0),B(1;0). Ta có 2 2
z =1⇒ x + yi =1 ⇔ x + y =1
⇒ M thuộc đường tròn đường kính AB. ⇒ 2 2 2
MA + MB = AB = 4 . Khi đó, theo Bunhiacopxki, ta có 2 2 2 2
T = MA + 2MB ≤ (1 + 2 )(MA + MB ) = 5.4 = 2 5
Vậy giá trị lớn nhất của biểu thức maxT=2 5 . Chọn A.
Cách 2: Đặt z = x + yi 2 2
(x, y∈) ⇒ z +1 = (x+1) + y và 2 2
z −1 = (x−1) + y Mặt khác 2 2 2 2
z =1 ⇔ x + y =1 ⇔ x + y =1, khi đó 2 2 2 2 2 2 2 2 2 2
T = (x+1) + y + 2 (x −1) + y ≤ (1 + 2 ) (x +1) + y + (x −1) + y    2 2
= 10(x + y +1) = 10.2 = 2 5 ⇒ maxT = 2 5 Câu 30: 2 2 2 2
z − 2z + 5 = (z −1) + 4 = (z −1) − (2i) = (z −1+ 2i)(z −1− 2i) z =1− 2i
Khi đó, giả thiết ⇔ (z −1+ 2i)(z −1− 2i) = (z −1+ 2i)(z + 3i −1) ⇔ 
z −1− 2i = z + 3i −1 
TH1. Với z =1− 2i , ta có w = z − 2 + 2i =1− 2i − 2 + 2i = 1 − ⇒ w =1
TH2. Với z −1− 2i = z + 3i −1 (*), đặt z = x + yi (x, y∈) , ta có (*) 2 2 2 2 1
⇔ x −1+ (y − 2)i = x −1+ (y + 3)i ⇔ (x −1) + (y− 2) = (x −1) + (y+ 3) ⇔ y = − 2 Do đó 1 3 2 9 3
w = z − 2 + 2i = x − i − 2 + 2i = x − 2 + i ⇒ w = (x − 2) + ≥ 2 2 4 2
So sánh hai trường hợp, ta được giá trị nhỏ nhất của ω bằng 1. Chọn A.
Câu 31: Đặt z = x + yi (x, y∈) nên 2 2
z − i =1 ⇔ (z + yi) − i =1 2 2 2 2 2 2 2 2
⇔ x − y + (2xy −1)i =1 ⇔ (x − y ) + (2xy −1) =1 ⇔ x + y = 2 xy 2 2 2 2 2 2
⇔ x + y = 2 xy ≤ x + y ≤ 2(x + y ) ⇔ x + y ≤ 2 ⇔ z ≤ 2 . Chọn D. Câu 32: Ta có 2 2 iz + + iz +
= 4 ⇔ iz + i +1 + iz − i −1 = 4 ⇔ z +1− i + z −1+ i = 4 1− i i −1 Gọi ( A 1; − 1), B(1; 1
− ) có trung điểm là O(0;0) . Điểm M biểu diễn số phức z 2 2 2
Theo công thức trung tuyến thì 2 2 MA + = = MB − AB z OM 2 4 MA + MB 2 2 ( )2 2 Ta có 4 MA + MB ≥ = = 8 . Do đó 2 8 8
z ≥ − = 2 ⇔ z ≥ 2 2 2 2 4
Lại có 4 = z +1− i + z −1+ i ≥ z +1− i + z −1+ i = 2 z ⇔ z ≤ 2
Vậy M = 2;m = 2 → M.m = 2 2 . Chọn C.
z − 2i x + (y − 2)i [x + (y − 2)i][x − 2 − yi]
Câu 33: Đặt z = x + yi (x, y∈) , khi đó = = 2 2 z − 2 x − 2 + yi (x − 2) + y 2 2
x + y − 2x − 2y − 2(x + y − 2) = i là số ảo 2 2 2 2
⇔ x + y − 2x − 2y = 0 ⇔ x + y = 2(x + y) 2 2 (x − 2) + y 2 Suy ra 2 2 (x + y) 2
2(x + y) = x + y ≥
⇔ (x + y) − 4(x + y) ≤ 0 ⇔ x + y ≤ 4 2 Ta có 2 2 2 2 2 2 2 2
P = z −1 + z − i = (x −1) + y + x + (y −1) = x + y − 2x +1 + x + y − 2y +1
= 2y +1 + 2x +1 ≤ 2 x + y +1 = 2 4 +1 = 2 5 . Vậy P = . Chọn C. max 2 5
Câu 34: z.z =1 ⇔ z =1 nên tập hợp biểu diễ số phức z là đường tròn (C ) tâm O, R = 1 1
Lại có z − 3 + i = m nên tập hợp biểu diễn số phức z là đường tròn (C ) tâm I( 3; −1),R' = m 2
OI = R + R ' m =1
Yêu cầu bài toán ⇔ (C ),(C ) tiếp xúc trong hoặc tiếp xúc ngoài ⇔ ⇔ 1 2  OI R R '  + = m = 3 Chọn A.
Câu 35: Đặt z = x + yi (x, y∈) , ta có 2z +1 = z + z + 3 ⇔ 2x +1+ 2yi = 2x + 3 2 2 2 yy  2 2 2 2 2 2 2
⇔ (2x +1) + (2y) = (2x + 3) ⇔ x =
−1⇒ z −8 = (x −8) + y =  −9 + y 2  2  2 2  y  Xét hàm số 2 1 4 2 1 2 2
f (x) =  −9 + y = y −8y +81≥ (y −16) +17 ≥17  2  4 4
y = 4 → x = 7
Suy ra min f (y) =17 . Dấu bằng xảy ra khi 2 y =16 ⇔   y = 4 − → x = 7
Vậy tổng hai phần thực của hai số phức là 14. Chọn C. Câu 36: 2 2
z = x + 4y mà 2 2
z =1 ⇔ x + 4y =1 (*)
Lại có P = x − y ⇔ y = x − P thế vào (*), ta được 2 2
x + 4(x − P) =1 2 2 2 2 2
⇔ x + 4x −8Px+ 4P =1 ⇔ 5x −8 . P x + 4P −1 = 0 (**)
Phương trình (**) có nghiệm 2 2 ⇔ ∆ ' = ( 4
− P) − 5(4P −1) ≥ 0 2 5 5 5 5 ⇔ 5 − 4P ≥ 0 ⇔ − ≤ P ≤ → min P = − ;max = . Chọn A. 2 2 2 2
Câu 37: Đặt z = x + yi 2 2 2 2
(x, y∈) ⇒ z + 2 = (x + 2) + y ; z − 2 = (x − 2) + y Mặt khác 2 2 2 2
z =1 ⇔ x + y =1 ⇔ x + y =1, khi đó 2 2 2 2 2 2 2 2 2 2
T = (x + 2) + y + 2 (x − 2) + y ≤ (1 + 2 ) (x + 2) + y + (x − 2) + y    2 2
= 10(x + y + 4) = 10.5 = 5 2 ⇒ maxT = 5 2
Vậy giá trị lớn nhất của biểu thức T là T = 5 2 . Chọn D.
Document Outline

  • ITMTTL~1
  • IIBITP~1
  • IIILIG~1