Chuyên đề trắc nghiệm thể tích khối chóp

Tài liệu gồm 48 trang, trình bày lý thuyết trọng tâm, các dạng toán trọng tâm kèm phương pháp giải và bài tập trắc nghiệm tự luyện chuyên đề thể tích khối chóp, có đáp án và lời giải chi tiết.Mời bạn đọc đón xem.

53 27 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Khối đa diện

Môn: Toán 12

Thông tin:

48 trang 8 tháng trước

Tác giả:

Profile Lan Tường
CHỦ ĐỀ 7: THỂ TÍCH KHỐI CHÓP
I. LÝ THUYẾT TRỌNG TÂM
Công thức tính thể tích khối chóp: V =
1
.
3
Sh
Trong đó: S là diện tích đáy và h là chiều cao của khối chóp.
II. CÁC DẠNG TOÁN TRỌNG TÂM VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: Thể tích khối chóp có đường cao sẵn có
Ví dụ 1: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với đáy, đường
thẳng SC tạo với đáy một góc
60
°
. Thể tích khối chóp S.ABC bằng?
A.
3
8
a
. B.
3
4
a
. C.
3
2
a
. D.
3
3
4
a
.
Lời giải:
Chú ý: Nếu tam giác ABC đều cạnh a thì độ dài đường trung tuyến
bằng m =
3
2
a
Ta có:
2
23
3
tan 60 tan 60 3,S
A4
1 13
. 3.
3 3 44
ABC
ABC
SA a
SA AC a
C
aa
V SA S a
⇒ °= ⇒ = °= =
⇒= = =
Chọn B
Ví dụ 2: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, hình chiếu vuông góc của S lên mặt phẳng
(ABCD) trùng với trung điểm của cạnh AD, cạnh bên SB hợp với đáy một góc
60°
. Tính theo a thể tích V
của khối chóp S.ABCD
A. V
3
15
2
a
=
. B. V
3
15
6
a
=
. C. V
3
5
4
=
a
. D. V
3
15
18
a
=
.
Lời giải
Gọi H là trung điểm của
()AD AH ABCD⇒⊥
Ta có:
2
2
5
22
aa
BH a

= +=


3
2
.
5 15
tan 60 . 3
22
1 1 15 15
. . .a
3 32 6
S ABCD ABCD
aa
SH BH
aa
V SH S
= °= =
= = =
Chọn B.
Ví dụ 3: Cho hình chóp S.ABC có đáy là tam giác đều cạnh a,
()SA ABC⊥
. Biết mặt phẳng
()SBC
tạo với đáy một góc
60°
. Thể tích khối chóp S.ABC là
A.
3
3
24
a
. B.
3
3
8
a
. C.
3
3
6
a
. D.
3
3
18
a
.
Lời giải:
Gọi M là trung điểm của
BC AM BC⇒⊥
và
3
.
2
a
AM
=
Lại có:
( ) (( );( )) 60⊥⇒ ⊥ ⇒ = =°BC SA BC SMA SBC ABC SMA
.
Khi đó
2
33
tan 60 ,S .
24
ABC
aa
SA AM= °= =
Thể tích khối chóp là:
3
13
.
48
ABC
a
V SA S= =
. Chọn B.
Ví dụ 4: Cho hình chóp S.ABC có đáy là tam giác vuông tại B có AB=a, BC=
3a
. Hình chiếu của đỉnh
S trên mặt phẳng đáy trùng với trung điểm của cạnh AC. Biết SB tạo với đáy một góc
30°
. Thể tích khối
chóp S.ABC là:
A.
3
2
a
. B.
3
4
a
. C.
3
3
6
a
. D.
3
6
a
.
Lời giải:
Gọi H là trung điểm của
( ).AC AH ABC⇒⊥
Khi đó
( );( )) .
SB ABC SBH=
Ta
có:
22
2.AC AB BC a
= +=
Tam giác ABC có đường trung tuyến BH ứng với cạnh
huyền nên
.
2
AC
BH a
= =
Do
30 tan 30 .
3
a
SBH SH HB
= °⇒ = °=
Lại có:
2
13
.
22
ABC
a
S BA BC= =
Suy ra:
23
.
1 13
.S . . .
3 3 26
3
S ABC ABC
aa a
V SH= = =
Chọn D.
Ví dụ 5: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có AB= 2a, AD=
3a
, cạnh bên SA
vuông góc với đáy, gọi M là trung điểm của cạnh CD. Biết SM tạo với mặt phẳng (ABCD) một góc
60°
,
tính thể tích V của khối chóp S.ABCD.
A. V=
3
2a
. B. V=
3
43a
. C. V=
3
12a
. D. V=
3
4a
.
Lời giải:
Do
()(;()) 60.⊥⇒ ==°SA ABCD SM ABCD SMA
Ta có:
22
2AM AD DM a
= +=
tan 60 2 3SA AM a⇒= =
.
Mặt khác
2
. 23
ABCD
S AB AD a= =
.
23
.
1
.2 3.2 3 4
3
S ABCD
V aa a= =
. Chọn D.
Ví dụ 6: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt đáy, SD tạo với
mặt phẳng (SAB) một góc bằng
30
°
.Tính thể tích V của khối chóp S.ABCD.
A. V=
3
6
18
a
. B. V=
3
3a
. C. V=
3
6
3
a
D. V=
3
3
3
a
.
Lời giải:
Ta có:
()
AD AB
AD SAB
AD SA
⊥
⇒⊥
⊥
Khi đó:
( )
;( ) 30SD SAB DSA= = °
suy ra
tan 30 3SA AD SA a°= ⇒ =
Do đó
3
.
13
.
33
S ABCD ABCD
a
V SA S= =
. Chọn D.
Ví dụ 7: Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD có AB= 2a. Hình chiếu vuông góc của
đỉnh S xuống mặt đáy là trung điểm của AB. Biết rằng SA=
a7
và mặt phẳng (SCD) tạo với đáy một
góc
60°
. Thể tích khối chóp là:
A.
3
46
3
a
. B.
3
23
3
a
. C.
3
26
3
a
. D.
3
43
3
a
.
Lời giải:
Ta có:
22
6SH SA HA a= −=
.
Dựng
HK CD⊥
ta có:
HK CD
SH CD
⊥
⊥
Suy ra
( ) 60CD SHK SKH⊥ ⇒=°
.
Khi đó
6
tan 60 2
3
a
HK SH HK a AD°= ⇒ = = =
.
Khi đó
3
2
1 43
22 .
33
ABCD ABCD
a
S a V SH S= ⇒= =
.
Chọn D.
Ví dụ 8: Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B có AD = 2AB= 2CD= 2a và
(ABCD)SA ⊥
. Biết SA tạo với (SCD) một góc
30°
. Thể tích khối chóp
.S ABCD
là:
A.
3
6
6
a
. B.
3
6
3
a
. C.
3
3
3
a
. D.
3
6
2
a
.
Lời giải:
Ta có:
22
2AC AB BC a= +=
Gọi I là trung điểm của
AD ABCI⇒
là hình vuông cạnh
2
AD
a CI a ACD⇒ = = ⇒∆
vuông tại C.
Khi đó:
()
CD SA
CD SAC
CD AC
⊥
⇒⊥
⊥
.
Dựng
( )
;( ) 30AN SC SA SCD ASN ASC⊥⇒ = = =°
.
Suy ra
cot 30 6SA AC a= °=
.
Lại có:
2
3
.
22
ABCD
AD BC a
S AB
+
= =
.
Do đó
3
.
16
.
32
S ABCD ABCD
a
V SA S= =
. Chọn D.
Ví dụ 9: Cho khối chóp S.ABCD có đáy là hình vuông có cạnh a, SA vuông góc với đáy và SC tạo với
mặt phẳng (SAB) một góc
30°
. Tính thể tích V của khối chóp đã cho.
A. V=
3
6
3
a
. B. V=
3
2
3
a
. C. V=
3
2a
. D. V=
3
2
3
a
.
Lời giải:
Ta có:
()
⊥
⇒⊥
⊥
BC AB
BC SAB
BC SA
Do đó
( )
;( ) 30
SC SAB SCB= = °
Khi đó:
22
.cot 30 3 2SB BC a SA SB AB a= °= ⇒ = − =
Mặt khác
2
ABCD
Sa
= ⇒
3
.
2
3
S ABCD
a
V =
. Chọn D.
Ví dụ 10: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O cạnh a, hình chiếu vuông góc của
đỉnh S lên mặt phẳng đáy trùng với tâm H của tam giác đều ABC, biết mặt phẳng (SDC) tạo với mặt
phẳng (ABCD) một góc
60°
. Thể tích khối chóp S.ABCD là:
A.
3
3
6
a
. B.
3
3
6
a
. C.
3
6
a
. D.
3
3
12
a
.
Lời giải:
Ta có
ABC∆
đều cạnh a nên H là trực tâm của tam giác
ABC CH AB CH BC⇒⊥⇒⊥
( ) 60CD SHC SCH⇒⊥ ⇒ =°
.
Ta có:
3 23
3
2 33
aa
OB BD a HB HC OB= ⇒= ⇒== =
.
Khi đó:
2
33
.tan 60 ,S 2
32
= °= = =
ABCD ABC
aa
SH a S
23
.
1 33
.a.
32 6
= =
S ABCD
aa
V
. Chọn A.
Ví dụ 11: Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), đáy ABC tam giác vuông tại B
có AB= a, BC=
3a
, biết góc giữa hai mặt phẳng (SAC) và (SBC) bằng
60°
. Tính thể tích khối chóp
S.ABC.
A..
3
6
12
a
. B.
3
6
4
a
. C.
3
2
12
a
. D.
3
6
8
a
.
Lời giải:
Dựng
()BH AC BH SAC⊥⇒⊥
Dựng
( ) 60HK SC HKB SC HKB⊥⇒ ⊥⇒ =°
.
Ta có:
33
sin 60
22
aa
BH BK BK a= ⇒ °= ⇒ =
.
Do
BC AB
BC SB
BC SA
⊥
⇒⊥
⊥
. Khi đó
SBC∆
vuông tại B nên ta
có:
22
22 2
11 1 3
2
2
a
SB a SA SB AB
SB BC BK
+ = ⇒= ⇒= − =
3
2
.
11 6
.. 3
3 2 12
2
S ABCD
aa
Va= =
. Chọn A.
Ví dụ 12: Cho hình chóp tứ giác S.ABCD có đáy là hình vuông ABCD tâm O cạnh 4a, M là một điểm
thuộc cạnh AB sao cho MA=3MB, hình chiếu vuông góc của H lên mặt phẳng (ABCD) là trung điểm
của cạnh OM. Biết góc giữa hai mặt phẳng (SBC) và đáy là
60°
. Thể tích khối chóp S.ABCD là:
A.
3
43a
. B.
3
83
3
a
. C.
3
83a
. D.
3
4a
.
Lời giải:
Dựng
,HE BC OF BC⊥⊥
Ta có
(SHE) 60
BC SEH⊥⇒ =°
Mặt khác ME là đường trung bình của hình thang MOFB
3
22
MB OF a
ME
+
⇒= =
Ta có:
33
.tan 60
2
a
SH HE
= °=
.
V
23
S.
13 3
. .16 8 3
32
ABCD
a
aa= =
. Chọn C.
Ví dụ 13: Cho hình chóp S.ABCD có đáy là nửa lục giác đều cạnh a, AD= 2a,
()SA ABCD⊥
. Mặt
phẳng
(SCD)
tạo với đáy một góc
45°
. Thể tích khối chóp S.ACD là:
A.
3
2
a
. B.
3
4
a
. C.
3
3
4
a
. D.
3
a
.
Lời giải:
Gọi O là trung điểm của AD dễ thấy
1
2
OC AB a AD ACD= = = ⇒∆
vuông tại C
Khi đó
()
CD AC
CD SAC
CD SA
⊥
⇒⊥
⊥
Do vậy
45SCA = °
. Lại có tam giác ACD vuông tại C
nên
22
AC 3 3.tan 45 3AD CD a SA a a= − = ⇒ = °=
Ta có:
3
( ; ) sin .sin 60
2
a
d C AD CD CDA CD= = °=
.
Do đó
2
33 3
.
224
ABCD
AD BC a a
S
+
= =
Vậy
3
.
13
.
34
S ABCD ABCD
a
V SA S= =
. Chọn C.
Dạng 2: Thể tích khối chóp có mặt bên vuông góc với đáy
Phương pháp giải:
Giả sử hình chóp S.ABC có mặt phẳng
( ) (ABC)SAB ⊥
. Ta dựng
SH AB⊥
(trong trường hợp
SAB∆
cân
tại S thì H là trung điểm của AB).
Khi đó
( )
( )
( )
( ) (ABC)
SH AB
⊥
⊥ ⇒⊥
= ∩
SAB
SH ABC
AB SAB ABC
.
Ví dụ 1: Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại B có AB=
3a
, BC= a. Tam giác SAC
cân tại S và thuộc mặt phẳng vuông góc với đáy, mặt phẳng (SAB) tạo với đáy một góc bằng
60
o
. Thể
tích khối chóp S.ABC là:
A.
3
3
2
a
. B.
3
4
a
. C.
3
3
3
a
. D.
3
2a
.
Lời giải:
Gọi H là trung điểm của AC ta có
SH AC⊥
Mặt khác
( ) ( )
SAC ABC⊥
suy ra
( )
SH ABC⊥
Dựng
HE AB
⊥
khi đó HE là đường trung bình của tam giác ABC.
Do đó:
22
BC a
HE = =
Mặt khác:
( ) 60
AB HE
AB SHE SEH
AB SH
⊥
⇒⊥ ⇒ =°
⊥
.
Do đó
2
3 .3
.tan 60 ,S
2 22
ABC
a AB BC a
SH HE= °= = =
⇒
3
.
1
.
34
S ABC ABC
a
V SH S
= =
. Chọn B.
Ví dụ 2: Cho hình chóp S.ABC có đáy là tam giác ABC có AB= AC= 2a và BC=
23a
, gọi M là trung
điểm của BC. Tam giác SAM cân tại S và thuộc mặt phẳng vuông góc với đáy. Khoảng cách từ A đến
mặt phẳng (SBC) bằng
3
2
a
. Thể tích khối chóp S.ABC là:
A.
3
6
a
. B.
3
3
2
a
. C.
3
3
2
a
. D.
3
2
a
.
Lời giải:
Gọi H là trung điểm của AM ta có
SH AM⊥
Mặt khác
( ) ( )
SAM ABC⊥
nên
( )
SH ABC⊥
Ta có:
22
3BM MC a AM AB BM a
==⇒= − =
2
1
.3
2
ABC
S AM BC a⇒= =
. Dựng
(
)
HK SM HK SBC
⊥⇒⊥
.
Khi đó
(
)
( )
( )
(
)
A;2;2
d SBC d H SBC HK= =
22 2
31 1 1 3
42
aa
HK SH
SH HK HM
⇒ = ⇒ = − ⇒=
.
2
3.
ABC
Sa=
Do đó
3
.
1
.
32
S ABC ABC
a
V SH S= =
. Chọn D.
Ví dụ 3: Cho khối chóp S.ABC có đáy là tam giác ABC vuông tại A, tam giác SAB vuông tại S và thuộc
mặt phẳng vuông góc với đáy. Biết SA=
6a
, SB=
3a
và AC=
2a
. Thể tích khối chóp S.ABC là:
A.
3
2a
. B.
3
32a
. C.
3
2
2
a
. D.
3
2
3
a
.
Lời giải:
Dựng
SH AB
⊥
. Mặt khác
( ) ( )
SAB ABC⊥
suy ra
( )
SH ABC⊥
. Ta có:
22
3AB SA SB a= +=
. Áp dụng hệ thức
lượng trong tam giác vuông SAB ta có:
2
2
SA
HA a
AB
= =
22 2
.
2,S 3
2
ABC
AB AC
SH SA HA a a⇒= − = = =
.
Khi đó
3
.
1
.2
3
= =
S ABC ABC
V SH S a
.Chọn A.
Ví dụ 4: Cho hình chóp S.ABC có mặt phẳng (SAC) vuông góc với mặt phẳng (ABC), SAB là tam giác
đều cạnh
3a
, BC=
3a
,đường thẳng SC tạo với mặt phẳng (ABC) góc
60°
. Thể tích của khối chóp
S.ABC bằng:
A.
3
3
3
a
. B.
3
26a
. C.
3
6
2
a
. D.
3
6
6
a
.
Lời giải:
Ta có
( )
( )
; ; 60SC ABC SC AC SCA= = = °
.
Gọi H là trung điểm của AB mà
ABC∆
cân
( )
BH SAC
⇒⊥
.
Gọi K là trung điểm của SA mà
SAB∆
đều
BK SA⇒⊥
Suy ra
( )
SA BHK SA HK⊥ ⇒⊥
mà
HK SC SA SC⇒⊥
.
Tam giác SAC vuông tại S, có
60
2
AC
SCA SC SH a= °⇒ = = =
.
Diện tích tam giác ABC là
2
13
..
22
∆
= =
ABC
a
S AB AC
.
Tam giác ABH vuông tại H, có
22
2= −=BH AB AH a
Vậy thể tích khối chóp S.ABC là
3
16
.BH.S
36
ABC
a
V
∆
= =
.
Chọn D.
Ví dụ 5: Cho khối chóp S.ABC có đáy là tam giác đều. Tam giác SAC cân tại S và thuộc mặt phẳng
vuông góc với đáy, đường thẳng SB tạo với đáy một góc
60°
. Biết khoảng cách từ S đến mặt đáy (ABC)
là h. Thể tích khối chóp tính theo h là:
A.
3
3
3
h
. B.
3
3
9
h
. C.
3
3
27
h
. D.
3
3
18
h
.
Lời giải:
Gọi H là trung điểm của AC ta có
SH AC⊥
Mặt khác
( ) ( )
SAC ABC⊥
nên
( )
SH ABC⊥
Khi đó SH=
h
. Mặt khác
60
SBH = °
Do vậy
tan 60
3
h
HB h HB
°= ⇒ =
.
Đặt AB=
32
23
3
ah h
a HB a⇒ = = ⇒=
. Do đó
22
33
49
ABC
ah
S = = ⇒
3
.
13
.
3 27
S ABC ABC
h
V SH S= =
.
Chọn C.
Ví dụ 6: Cho khối chóp S.ABC có đáy là tam giác đều cạnh a. Gọi M là trung điểm của BC. Tam giác
SAM vuông tại S và thuộc mặt phẳng vuông góc với đáy. Biết SA=
2
a
, thể tích khối chóp S.ABC là:
A.
3
2
4
a
. B.
3
2
12
a
. C.
3
2
18
a
. D.
3
2
24
a
.
Lời giải:
Dựng
SH AM⊥
ta có
( ) ( )
SAM ABC⊥
nên
( )
SH ABC⊥
Mặt khác
3
2
a
AM =
Suy ra
22
2
a
SM AM SA= −=
Lại có:
22
.
6
SA SM a
SH
SA SM
= =
+
Vậy
3
.
12
.
3 24
S ABC ABC
a
V SH S= =
. Chọn D.
Ví dụ 7: Cho khối chóp S.ABCD có đáy là hình chữ nhật ABCD. Tam giác SAB đều cạnh
2a
và thuộc
mặt phẳng vuông góc với đáy. Đường thẳng SC tạo với đáy một góc
30°
. Thể tích khối chóp S.ABCD là:
A.
3
46
3
a
. B.
3
26
3
a
. C.
3
46
6
a
. D.
3
42
3
a
.
Lời giải:
Gọi H là trung điểm của AB ta có
SH AB⊥
.
Mặt khác
( )
( )
SAB ABC⊥
nên
( )
,3SH ABC SH a⊥=
.
Đường thẳng SC tạo với đáy một góc
30°
Do đó
tan 30 3HC SH HC a°= ⇒ =
.
Khi đó
22
22BC HC HB a= −=
Do vậy
3
.
1 46
.
33
S ABCD ABCD
a
V SH S= =
.Chọn A.
Ví dụ 8: Cho khối chóp S.ABCD có đáy là hình chữ nhật. Tam giác SAB vuông tại S và thuộc mặt phẳng
đáy. Biết rằng SA= 3 và SB= 4, mặt phẳng (SCD) tạo với đáy một góc
60°
. Thể tích khối chóp S.ABCD
là:
A.
16 3
15
. B.
43
5
. C.
16
5
. D.
16 3
5
.
Lời giải:
Dựng
SH AB⊥
ta có
(
) ( )
SAB ABC⊥
nên
( )
SH ABC⊥
. Mặt khác
22
5AB SA SB= +=
Khi đó:
22
. 12
5
SA SB
SH
SA SB
= =
+
.
Dựng
HK CD⊥
ta có:
( )
CD SH
CD SHK
CD HK
⊥
⇒⊥
⊥
Do đó
60 tan 60= °⇒ °=SKH HK SH
43
tan 60 5
SH
HK AD⇒== =
°
Vậy
.
1 16 3
.
35
S ABCD ABCD
V SH S
= =
. Chọn D.
Ví dụ 9: Cho khối chóp S.ABCD có đáy là hình thoi ABCD có AC=
2a
, BD=
23
a
. Tam giác SAC cân
tại S và thuộc mặt phẳng vuông góc với đáy. Biết khoảng cách từ D đến mặt phẳng (SAB) bằng
2 15
5
a
.Thể tích khối chóp S.ABCD là:
A.
3
2 15a
. B.
3
4a
. C.
3
22
a
. D.
3
2
a
.
Lời giải:
Gọi H là trung điểm của AC ta có
SH AC⊥
. Mặt khác
( ) ( )
SAC ABC
⊥
nên
( )
SH ABC⊥
. Ta có:
2DB HB=
Do vậy
( )
( )
( )
( )
; 2;d D SAB d H SAB=
Dựng
HE AB⊥
;
HF SE⊥
. Khi đó
( )
( )
( )
( )
1 15
;;
25
a
HF d H SAB d D SAB= = =
.
Lại có:
2 22
1 11
HF HE SH
= +
Mặt khác
2 2 22 2 2 22
1 114 1 111
3
33
SH a
HE HA HB a SH HF HE a
=+ =⇒ = − =⇒=
2
.
23
2
ABCD
AC BD
Sa= = ⇒
3
.
1
.2
3
S ABCD ABCD
V SH S a= =
. Chọn D.
Ví dụ 10: Cho khối chóp S.ABCD có đáy là hình thang ABCD vuông tại A và D có AB= BC=
2a
, AD=
3a
. Tam giác SAB cân tại A và thuộc mặt phẳng vuông góc với đáy. Gọi M là trung điểm của CD.
Đường thẳng SM tạo với đáy một góc
60°
. Thể tích khối chóp S.ABCD là:
A.
3
25 3
6
a
. B.
3
25 3
2
a
. C.
3
53
12
a
. D.
3
53
6
a
.
Lời giải:
Gọi H là trung điểm của AB ta có
SH AB⊥
.
Mặt khác
( )
(
)
SAB ABC⊥
nên
( )
SH ABC
⊥
.
Do
( )
; 60 60SM ABCD SMH= °⇒ = °
Lại có
5
22
AD BC a
HM
+
= =
53
tan tan 60
2
a
SH HM SMH HM⇒ = = °=
Ta có
2
.5
2
ABCD
AD BC
S AB a
+
= =
.
3
.
1 25 3
.
36
S ABCD ABCD
a
V SH S= =
. Chọn A.
Ví dụ 11: Cho khối chóp S.ABCD có đáy là hình thang ABCD vuông tại A và B có AB=
3a
, AD=
3a
,
BC=
a
. Tam giác SBD cân tại S và thuộc mặt phẳng vuông góc với đáy. Đường thẳng SA tạo với đáy một
góc. Thể tích khối chóp S.ABCD là:
A.
3
6a
. B.
3
2
3
a
. C.
3
3
2
a
. D.
3
2a
.
Lời giải:
Gọi H là trung điểm của BD ta có
SH BD
⊥
. Mặt khác
( )
( )
SBD ABC⊥
nên
( )
SH ABC⊥
Lại có
22
23BD AB AD a= +=
1
3
2
AH BD a⇒= =
.
Do SA tạo với đáy góc
45 45 3SAH SH a°⇒ = °⇒ =
Mặt khác
2
. 23
2
ABCD
AD BC
S AB a
+
= = ⇒
3
.
1
.2
3
S ABCD ABCD
V SH S a
= =
.Chọn D.
Ví dụ 12: Cho khối chóp S.ABCD có đáy là nửa lục giác đều đường kính AD=
2
a
. Tam giác SAD cân
tại S và thuộc mặt phẳng vuông góc với đáy. Biết khoảng cách từ A đến mặt phẳng (SCD) bằng
3
2
a
.
Thể tích khối chóp S.ABCD là:
A.
3
33
8
a
. B.
3
3
8
a
. C.
3
3
2
a
. D.
3
3
4
a
.
Lời giải:
Gọi H là trung điểm của AD ta có
SH AD⊥
.
Mặt khác
(
)
( )
SAD ABC
⊥
nên
( )
SH ABC⊥
.
Do
( )
( )
( )
(
)
2 A; 2 ;
AD HD d SCD d H SCD=⇒=
.
Dựng
,HE CD HF SE⊥⊥
( )
( )
( )
( )
13
H; A;
24
a
d SCD HF d SCD
⇒== =
.
Mặt khác HCD là tam giác đều cạnh
a
nên E là trung điểm
của CD và HE=
3
2
a
Suy ra
2
a
SH =
⇒
3
.
11 3
. .3
33 8
S ABCD ABCD HCD
a
V SH S SH S
= = =
.
Chọn B.
Dạng 3: Thể tích khối chóp đều
Phương pháp giải:
Khối chóp đều là khối chóp có đáy là đa giác đều và các cạnh bên bằng nhau.
• Khối chóp tam giác đều
Khối chóp tam giác đều là khối chóp có đáy là tam giác đều và các cạnh bên bằng nhau.
Nếu cho khối chóp đều S.ABC thì ta có:
- Tam giác ABC là tam giác đều và các cạnh bên SA=SB=SC.
- Hình chiếu vuông góc của đỉnh S xuống mặt đáy trùng với trọng tâm G (cũng là trực tâm, tâm đường
tròn ngoại tiếp, nội tiếp) của tam giác đều ABC tức là SG
⊥
(ABC).
- Các cạnh bên bằng nhau và đều tạo với đáy một góc bằng nhau.
- Các mặt bên là tam giác cân bằng nhau và các mặt phẳng bên đều tạo với đáy các góc bằng nhau.
Tứ diện đều là tứ diện có tất cả các cạnh bằng nhau.
Như vậy khối tứ diện đều là một trường hợp đặc biệt của khối chóp tam giác đều.
Khối tứ diện đều là khối chóp tam giác đều có cạnh bên bằng cạnh đáy.
• Khối chóp tứ giác đều
Khối chóp tứ giác đều là khối chóp có đáy là hình vuông và các cạnh bên bằng nhau.
Nếu cho khối chóp đều S.ABCD thì ta có:
- Tứ giác ABCD là hình vuông và các cạnh bên SA = SB = SC = SD.
- Hình chiếu vuông góc của đỉnh S xuống mặt đáy trùng với tâm O của hình vuông ABCD tức là SO
⊥
(ABCD).
- Các cạnh bên bằng nhau và đều tạo với đáy một góc bằng nhau.
- Các mặt bên là các tam giác cân bằng nhau và các mặt phẳng bên đều tạo với đáy các góc bằng nhau.
Ví dụ 1: Cho khối chóp tứ giác đều có cạnh đáy bằng
a
, cạnh bên gấp hai lần cạnh đáy. Tính thể tích V
của khối chóp đã cho.
A. V=
3
14
6
a
. B. V=
3
2
6
a
. C. V=
3
14
2
a
D. V=
3
2
2
a
.
Lời giải:
Giả sử khối chóp S.ABCD đều có đáy là hình vuông cạnh
a
tâm O và cạnh bên SD=
2a
. Khi đó SO
⊥
(ABCD).
Ta có:
( )
22
2
22
7
2 ;2
2 22
aa
OD a OD SO a a=⇒ = = −=
2
ABCD
Sa=
;
3
2
.
1 1 7 14
..
3 32 6
S ABCD ABCD
a
V SO S a a= = =
.
Chọn A.
Ví dụ 2: Cho khối chóp tam giác đều S.ABC có cạnh đáy bằng
a
, cạnh bên bằng
2a
. Tính thể tích V của
khối chóp S.ABC
A. V=
3
13
12
a
. B. V=
3
11
12
a
. C. V=
3
11
6
a
. D. V=
3
11
4
a
.
Lời giải:
Gọi H là trọng tâm của
∆
ABC và M là trung điểm của BC.
Ta có AM=
3
2
a
⇒
AH=
2
3
AM=
3
3
a
;
2
3
4
ABC
a
S =
.
Mặt khác:
2
22 2
3 33
4
33
aa
SH SA AH a

= −=− =



.
Do đó
3
.
1 11
.
3 12
S ABC ABC
a
V SH S= =
. Chọn B.
Ví dụ 3: Cho hình chóp đều S.ABC có đáy là tam giác đều cạnh
a
, cạnh bên tạo với đáy một góc bằng
60°
. Tính thể tích khối chóp đã cho.
A.
3
3
4
a
. B.
3
3
8
a
. C.
3
3
12
a
. D.
3
3
24
a
.
Lời giải:
Gọi H là trọng tâm tam giác ABC suy ra
(
)
SH ABC
⊥
.
Gọi M là trung điểm của BC ta có
3
2
a
AM =
.
Khi đó
2 23 3
.
3 32 3
=⇒=
aa
AH AM
.
Lại có
60 tan 60=⇒= =
oo
SAH SH HA a
Suy ra:
23
.
1 133
..
3 3 4 12
= = =
S ABC ABC
aa
V SH S a
Chọn C.
Ví dụ 4: Cho hình chóp đều S.ABC có đáy là tam giác đều cạnh
a
, cạnh bên tạo với đáy một góc bằng
60°
. Tính thể tích khối chóp đã cho.
A.
3
3
4
a
. B.
3
3
8
a
. C.
3
3
12
a
. D.
3
3
24
a
.
Lời giải:
Gọi H là trọng tâm tam giác ABC suy ra
( )
SH ABC⊥
.
Gọi M là trung điểm của BC ta có
3
2
a
AM =
.
Khi đó
1 13 3
.
3 32 6
aa
HM AM=⇒=
.
Lại có
( )
BC SA
BC SAM
BC AM
⊥
⇒⊥
⊥
Do đó
( ) ( )
( )
; 60 tan 60
2
a
SMH SBC ABC SH HM= = °⇒ = °=
Do đó
23
.
1 1 33
. ..
3 3 2 4 24
S ABC ABC
aa a
V SH S
= = =
. Chọn D.
Ví dụ 5: Cho hình chóp đều S.ABCD có đáy là hình vuông cạnh
a
, mặt bên tạo với đáy một góc bằng
30°
. Tính thể tích V của khối chóp S.ABCD theo
a
và
30°
.
A.V=
3
3
6
a
. B. V=
3
3
9
a
. C.V=
3
3
12
a
. D. V=
3
3
18
a
.
Lời giải:
Gọi O là tâm của hình vuông ABCD khi đó
( )
SO ABCD⊥
và
2
ABCD
Sa
=
.
Dựng
OE CD⊥
, lại có
SOCD ⊥
( )
CD SEO⇒⊥
.
Khi đó ta có:
( ) ( )
( )
, 30SCD ABCD SEO= = °
.
Mặt khác
2
BC
OE =
(đường trung bình trong tam giác)
nên
tan 30
tan 30
22
23
a aa
OE SO OE
°
=⇒= = =
.
Khi đó
33
.
13
.
3 18
63
S ABCD ABCD
aa
V SO S= = =
. Chọn D.
Ví dụ 6: Cho khối chóp tứ giác đều có tất cả các cạnh bằng 2a. Thể tích khối chóp đã cho bằng:
A.
3
42
3
a
. B.
3
8
3
a
. C.
3
82
3
a
. D.
3
22
3
a
.
Lời giải:
Gọi O =
AC BD
∩
, ta có
()SO ABCD⊥
và đáy
ABCD là hình vuông.
Ta có:
2
4
ABCD
Sa
=
,
2
2
BC
OB a= =
.
22
2SO SB OB a⇒= − =
.
⇒
3
2
.
1 1 42
. . 2.
33 3
S ABCD ABCD
a
V SO S a AB
= = =
Chọn A.
Ví dụ 7: Cho hình chóp đều S.ABCD có đáy là hình vuông cạnh 4a. Khoảng cách từ điểm D đến mặt
phẳng (SAB) bằng
4
5
a
. Thể tích khối chóp đã cho là:
A.
3
3
a
. B.
3
2
3
a
. C.
3
16
3
a
. D.
3
4
3
a
.
Lời giải:
Gọi H là tâm của hình vuông suy ra
()SH ABCD⊥
Khi đó ta có:
(
)
( )
( )
( )
d ; 2 H;D SAB d SAB
=
Dựng
HE AB⊥
và
HF SE⊥
ta chứng minh được
( )
( )
( )
( )
4
d H; D; 2
5
a
SAB HF d SAB HF=⇒==
Do vậy
2
5
a
HF =
. Lại có
2HE a=
Ta có:
22 2
11 1
SH a
HE SH HF
+ = ⇒=
Vậy
3
.
1 16
.
33
S ABCD ABCD
a
V SH S= =
. Chọn C.
Ví dụ 8: Cho hình chóp đều S.ABCD có mặt bên tạo với đáy một góc
60°
. Cạnh bên SA=
5a
. Thể tích
khối chóp S.ABCD là:
A.
3
6
3
a
. B.
3
3
3
a
. C.
3
22
3
a
. D.
3
43
3
a
.
Lời giải:
Gọi H là tâm của hình vuông suy ra
(
)
SH ABCD⊥
.
Đặt
2AB x=
. Dựng
HK AB
⊥
Ta có:
( )
SH AB HK SAB⊥⇒ ⊥
Do vậy
( )
( )
( )
; 60SAB ABCD SKH
= = °
Lại có
tan 60 3HK x SH x x= ⇒ = °=
.
Khi đó
2 2 2222
325SA SH HA x x x= + =+=
3x a SH a⇒=⇒ =
,
22
4
ABCD
S AB a
= =
.
⇒
3
.
1 43
.
33
S ABCD ABCD
a
V SH S= =
. Chọn D.
Ví dụ 9: Cho khối chóp đều S.ABCD có đáy là hình vuông cạnh
2a
, biết diện tích của tam giác SCD là
2
3
a
. Thể tích khối chóp S.ABCD là:
A.
3
3
8
a
. B.
3
82
3
a
. C.
3
33
4
a
. D.
3
42
3
a
.
Lời giải:
Gọi H là tâm của hình vuông suy ra
()SH ABCD⊥
.
Gọi K là trung điểm của CD. Khi đó ta có
SK CD⊥
.
Lại có:
2
1
. .3
2
ACD
S CD SK a SK a= = =
22
3 22
SK a SH SK HK a
⇒=⇒= − =
,
2
4
ABCD
Sa
=
Vậy
3
.
1 82
.
33
S ABCD ABCD
a
V SH S= =
. Chọn B.
Ví dụ 10: Cho hình chóp S.ABC có đáy là tam giác đều cạnh
a
. Khoảng cách từ điểm A đến mặt phẳng
(SBC) bằng
3
4
a
. Thể tích khối chóp đã cho là:
A.
3
3
6
a
. B.
3
3
8
a
. C.
3
3
12
a
. D.
3
3
24
a
.
Lời giải:
Gọi H là trọng tâm tam giác đều ABC ta có:
()SH ABC⊥
.
Khi đó
( )
(
)
( )
(
)
3
A; 3 ;
4
a
d SBC d H SBC= =
Suy ra
( )
( )
d;
4
a
H SBC =
. Gọi I là trung điểm của BC dễ thấy
AI BC⊥
.
Dựng
HK SI⊥
Ta có:
.
Do vậy
( )
( )
H;
4
a
d SBC HK= =
;
3
6
a
HI =
Mặt khác
2 22
1 11
2
a
SH
HK SH HI
= + ⇒=
.
Vậy
23
.
1 1 33
. ..
3 3 2 4 24
S ABC ABC
aa a
V SH S
= = =
. Chọn D.
Ví dụ 11: Cho hình chóp đều S.ABC có đáy là tam giác đều cạnh a. Biết tam giác ASB vuông, thể tích
khối chóp S.ABC là:
A.
3
2
24
a
. B.
3
2
32
a
. C.
3
2
16
a
. D.
3
2
8
a
.
Lời giải:
Gọi H là trọng tâm của tam giác ABC
Khi đó
()SH ABC⊥
. Do
SA SB=
nên tam giác SAB
vuông khi và chỉ khi tam giác ASB vuông tại S
Khi đó gọi K là trung điểm của AB ta có:
SK
22
AB a
= =
. Mặt khác
33
26
aa
CK HK
= ⇒=
Suy ra
22
6
a
SH SK HK
= −=
.
Do đó
3
.
12
.
3 24
S ABC ABC
a
V SH S= =
. Chọn A.
Dạng 4: Thể tích một số khối chóp đặc biệt
• Khối chóp có các cạnh bên bằng nhau
Cho khối chóp
12
. ...
n
S AA A
có tất cả các cạnh bên bằng nhau:
12
...
n
SA SA SA= = =
.
Dựng đường cao
( )
12n
SH A A A⊥
của khối chóp.
Khi đó theo định lý Pytago ta có:
22 2 2 2 2 2
112 2
....
nn
SH SA HA SA HA SA HA=−=−==−
.
Lại có
12
...
n
SA SA SA= = =
suy ra
12
...
n
HA HA HA= = =
.
Như vậy: Hình chiếu vuông góc của đỉnh S xuống mặt đáy trùng với
tâm đường tròn ngoại tiếp của đa giác
12
...
n
AA A
.
Khi đó
tan
đ
RSH h
α
= =
.
• Khối chóp có các cạnh bên tạo với đáy các góc bằng nhau
Cho khối chóp
12
. ...
n
S AA A
có tất cả các cạnh bên
đều tạo với đáy một góc
α
.
Dựng đường cao
( )
12n
SH A A A⊥
của khối chóp.
Khi đó:
12
....
n
SA H SA H SA H
α
= = = =
suy ra
12
tan tan .... tan
n
SH HA HA HA
αα α
= = = =
.
Do đó
12
...
n
HA HA HA= = =
suy ra hình chiếu
vuông góc của đỉnh S xuống mặt đáy trùng với
tâm đường tròn ngoại tiếp của đa giác
12
...
n
AA A
.
Khi đó
tan
đ
RSH h
α
= =
.
• Khối chóp có các mặt bên đều tạo với đáy các góc bằng nhau
Cho khối chóp
12
. ...
n
S AA A
có tất cả các mặt bên đều tạo với đáy
một góc
α
Dựng đường cao
( )
12
n
SH A A A⊥
của khối chóp. Dựng
1 12
HK A A⊥
,
2 23
HK A A⊥
,… ,
1
⊥
nn
HK A A
Do
( )
1 12
12 1 1
12
α
⊥
⇒⊥ ⇒ =
⊥
HK A A
A A SK H SK H
A A SH
.
Tương tự như vậy ta có:
12
....
n
SK H SK H SK H
α
= = = =
.
Suy ra
12
tan tan .... tan
n
SH HK HK HK
αα α
= = =
do đó
12
...
n
HK HK HK= = =
.
Suy ra điểm H trùng với tâm đường tròn tiếp xúc với tất cả các
cạnh (hay đường tròn nội tiếp) của đa giác
12
...
n
AA A
.
Khi đó
tan
đ
SH h r
α
= =
.
Ví dụ 1: Cho hình chóp S.ABC có đáy là tam giác ABC, các cạnh bên SA=SB=SC=
a
. Biết rằng
60
ASB BSC= = °
,
90ASC = °
. Thể tích khối chóp đã cho là:
A.V=
3
3
6
a
. B. V=
3
2
6
a
. C. V=
3
2
12
a
. D.V=
3
3
12
a
.
Lời giải:
Dễ thấy các tam giác ASB, BSC là tam giác đều do đó
AB = BC =
a
.
Mặt khác:
22 2 2
2AC SA SC a AB BC= +== +
Do đó tam giác ABC vuông tại B.
Mặt khác SA = SB = SC =
a
nên hình chiếu vuông
góc của đỉnh S xuống mặt đáy là tâm đường tròn ngoại
tiếp tam giác ABC và là trung điểm của cạnh huyền
AC.
Ta có:
2
2
a
SH =
;
2
2
ABC
a
S =
⇒
3
.
2
12
S ABC
a
V =
.
Chọn C.
Ví dụ 2: Cho hình chóp S.ABC có đáy là tam giác ABC, các cạnh bên SA=SB=SC=
a
. Biết rằng
60ASB = °
,
90BSC = °
,
120ASC = °
. Thể tích khối chóp đã cho là:
A.V=
3
3
6
a
. B. V=
3
2
6
a
. C. V=
3
2
12
a
. D.V=
3
3
12
a
.
Lời giải:
Tam giác SAB đều nên AB=
a
,
∆
SBC vuông tại S nên
22
2BC SB SC a= +=
.
Mặt khác
22
2 . cos ASC 3AC SA SC SA SC a
= +− =
Do
222
= +AC AB BC
nên tam giác ABC vuông tại B.
Mặt khác SA=SB=SC=
a
nên hình chiếu vuông góc của đỉnh
S xuống mặt đáy là tâm đường tròn ngoại tiếp tam giác ABC
và là trung điểm của cạnh huyền AC.
Ta có:
2
2
2
ABC
a
S
=
,
22
2
a
SH SA HA
= −=
.
⇒
3
.
12
.
3 12
S ABC ABC
a
V SH S= =
. Chọn C.
Ví dụ 3: Cho hình chóp S.ABC có đáy là tam giác ABC, có AB=AC=
a
,
120BAC = °
. Các cạnh bên đều
tạo với đáy một góc
60
°
.Thể tích khối chóp S.ABC là:
A.V=
3
4
a
. B. V=
3
3
4
a
. C. V=
3
3
8
a
. D.V=
3
3
12
a
.
Lời giải:
Diện tích tam giác ABC là:
2
13
. .sin
24
ABC
a
S AB AC BAC= =
.
Do các cạnh bên đều tạo với đáy một góc bằng
60°
⇒
hình chiếu vuông góc của đỉnh S xuống mặt đáy
là tâm đường tròn ngoại tiếp tam giác ABC.
Lại có:
22
3
2 .A 3
2sin 2sin120
cos
ABC
BC a
BC AB AC AB C a R a
A
BAC
= +− =⇒= = =
°
.
Suy ra
.tan 60 3
ABC
SH R a= °=
⇒
3
.
1
.
34
S ABC ABC
a
V SH S
= =
. Chọn A.
Ví dụ 4: Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại B có AB = 3, BC = 4. Biết rằng các
mặt bên của khối chóp đều tạo với đáy một góc bằng nhau và bằng
60°
. Thể tích khối chóp đã cho là
A.V=
53
3
. B. V=
53
6
. C. V=
53
2
. D.V=
53
12
.
Lời giải:
Ta có: H là tâm đường tròn nội tiếp tam giác ABC.
Lại có
.
ABC
pr S=
.
Trong đó
1
.B 6
2
ABC
S AB C= =
;
22
5
AC AB BC
= +=
Suy ra
5
6
26
AB BC CA
p r HK
++
= =⇒= =
.
Khi đó
53
tan 60
6
SH r= °=
Do đó
1 53
.
33
ABC
V SH S= =
. Chọn A.
Ví dụ 5: Cho hình chóp S.ABC có đáy là tam giác ABC cân tại A có AB = AC= 10, BC= 12. Các mặt
bên của khối chóp đều tạo với đáy một góc bằng nhau và bằng
30
o
. Thể tích khối chóp đã cho là
A.
18 3
. B.
48 3
. C.
16 3
. D.
93
.
Lời giải:
Do các mặt bên của khối chóp đều tạo với đáy một góc bằng nhau
nên hình chiếu vuông góc của đỉnh S xuống mặt đáy trùng với tâm
đường tròn nội tiếp tam giác ABC.
Gọi M là trung điểm của BC
⇒
AM
⊥
BC
Ta có:
2 2 22
10 6 8AM AB BM= − = −=
.
Khi đó:
1 48
.B 48 3
10 10 12
2
2
= =⇒== =
++
ABC ABC
S
S AM C r
p
tan 30 3
SH r⇒ = °=
⇒
1
. 16 3
3
ABC
V SH S= =
.Chọn C.
BÀI TẬP TỰ LUYỆN
Câu 1: Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt
phẳng đáy và SA=
2
a
. Tính thể tích V của khối chóp S.ABCD.
A. V=
3
2
6
a
. B. V=
3
2
4
a
. C. V=
3
2a
. D. V=
3
2
3
a
.
Câu 2: Cho khối chóp S.ABC có SA vuông góc với mặt phẳng (ABC), tam giác ABC vuông tại B và
AB=a;AC=
3a
.Tính thể tích khối chóp S.ABC biết SB=
5a
.
A.
3
2
3
a
. B.
3
36
4
a
. C.
3
6
6
a
. D.
3
15
6
a
.
Câu 3: Cho khối chóp S.ABC có SA vuông góc với mặt phẳng (ABC), tam giác ABC vuông tại B và AB=a
AC=
3a
.Tính thể tích khối chóp S.ABC biết SC=
6a
.
A.
3
6
6
a
. B.
3
6
2
a
. C.
3
6
3
a
. D.
3
15
6
a
.
Câu 4: Cho khối chóp S.ABC có đáy là tam giác ABC đều cạnh a. Hai mặt phẳng (SAB) và ( SAC) cùng
vuông góc với đáy. Tính thể tích khối chóp S.ABC biết SC=
3a
A.
3
26
9
a
. B.
3
6
12
a
. C.
3
3
4
a
. D.
3
3
2
a
.
Câu 5: Cho khối chóp S.ABCD có đáy là hình chữ nhật; AD=2AB=2a; Gọi H là trung điểm của AD, biết
SH vuông góc với mặt phẳng đáy. Tính thể tích khối chóp S.ABCD biết SA=
5a
.
A.
3
23
3
a
. B.
3
43
3
a
. C.
3
4
3
a
. D.
3
2
3
a
.
Câu 6: Cho khối chóp S.ABCD có đáy là hình vuông cạnh 2a. Gọi H là trung điểm của AB, biết SH vuông
góc với mặt phẳng đáy. Tính thể tích khối chóp S.ABCD biết tam giác SAB đều.
A.
3
23
3
a
. B.
3
43
3
a
. C.
3
6
a
. D.
3
3
a
.
Câu 7: Cho khối chóp S.ABC có SA vuông góc với mặt phẳng (ABC), tam giác ABC vuông tại B và AB=a,
AC=
3a
.Tính thể tích khối chóp S.ABC biết góc giữa SB và (ABC) bằng
30°
.
A.
3
6
9
a
. B.
3
6
6
a
’ C.
3
6
18
a
. D.
3
26
3
a
.
Câu 8: Cho khối chóp S.ABC có đáy là tam giác ABC đều cạnh a. Hai mặt phẳng (SAB) và ( SAC) cùng
vuông góc với đáy. Tính thể tích khối chóp S.ABC biết SB hợp với đáy một góc
30°
.
A.
3
3
6
a
. B.
3
3
12
a
. C.
3
4
a
. D.
3
12
a
.
Câu 9: Cho khối chóp S.ABC có đáy là tam giác ABC đều cạnh a. Hai mặt phẳng (SAB) và ( SAC) cùng
vuông góc với đáy. Tính thể tích khối chóp S.ABC biết SM hợp với đáy một góc
60°
, với M là trung điểm
của BC.
A.
3
6
8
a
. B.
3
3
4
a
. C.
3
3
8
a
. D.
3
6
24
a
.
Câu 10: Cho khối chóp S.ABC có SA vuông góc với mặt phẳng (ABC), tam giác ABC vuông tại A và
BC=2AB=2a. Tính thể tích khối chóp S.ABC biết góc giữa SC và (ABC) bằng
45°
.
A.
3
2
a
. B.
3
3
2
a
. C.
3
33
2
a
. D.
3
6
a
.
Câu 11: Cho khối chóp S.ABC có SA vuông góc với mặt phẳng (ABC), tam giác ABC vuông tại A và
BC=2AB=2a. Tính thể tích khối chóp S.ABC biết góc giữa SM và (ABC) bằng
60°
với M là trung điểm của
BC.
A.
3
2
a
. B.
3
3
6
a
. C.
3
3
2
a
. D.
3
6
a
.
Câu 12: Cho khối chóp S.ABCD có đáy là hình chữ nhật tâm O; AC=2AB=2a, SA vuông góc với mặt
phẳng đáy. Tính thể tích khối chóp S.ABCD. Biết góc giữa SC và (ABCD) bằng
45°
A.
3
23
3
a
. B.
3
43
3
a
. C.
3
a
. D.
3
3
a
.
Câu 13: Cho khối chóp S.ABCD có đáy là hình chữ nhật tâm O; AC=2AB=2a, SA vuông góc với mặt
phẳng đáy. Tính thể tích khối chóp S.ABCD biết góc giữa SO và (ABCD) bằng
60°
.
A.
3
23
3
a
B.
3
3
3
a
C.
3
a
D.
3
3
a
Câu 14: Cho khối chóp S.ABCD có đáy là hình vuông cạnh a. Hai mặt phẳng (SAB) và (SAD) cùng vuông
góc với đáy. Tính thể tích khối chóp S.ABCD biết SC hợp với đáy một góc
45
°
.
A.
3
2
6
a
. B.
3
2
3
a
. C.
3
6
a
. D.
3
3
a
Câu 15: Cho khối chóp S.ABCD có đáy là hình vuông cạnh a. Hai mặt phẳng (SAB) và (SAC) cùng vuông
góc với đáy. Tính thể tích khối chóp S.ABCD biết SM hợp với đáy một góc
60°
, v ới M là trung điểm của
BC.
A.
3
15
6
a
. B.
3
15
3
a
. C.
3
6
a
. D.
3
3
a
.
Câu 16: Cho khối chóp S.ABCD có đáy là hình vuông cạnh 2a. Gọi H là trung điểm của AB và SH vuông
góc với đáy. Tính thể tích khối chóp S.ABCD biết SC hợp với đáy một góc
60°
.
A.
3
2 15
3
a
. B.
3
4 15
3
a
. C.
3
6
a
. D.
3
3
a
.
Câu 17: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB=a. Cạnh bên SA vuông góc với
mặt phẳng đáy một góc, SC tạo với mặt phẳng đáy một góc
45°
và SC=
22
a
. Thể tích khối chóp S.ABCD
bằng.
A.
3
4
3
a
. B.
3
23
3
a
. C.
3
3
3
a
. D.
3
3
3
a
.
Câu 18: Cho hình chóp tam giác S.ABC có SA, SB, SC đôi một vuông góc và SA=SB=SC=a. Khi đó, thể
tích khối chóp trên bằng:
A.
3
6
a
. B.
3
9
a
. C.
3
3
a
. D.
3
2
3
a
.
Câu 19: Đáy của hình chóp S.ABCD là một hình vuông cạnh a. Cạnh bên SA vuông góc với đáy và có độ
dài bằng a. Thể tích khối tứ diện S.BCD bằng
A.
3
3
a
. B.
3
8
a
. C.
3
6
a
. D.
3
4
a
.
Câu 20: Cho hình chóp S.ABCD có đáy là một hình vuông cạnh a. Các mặt phẳng (SAB) và (SAD) cùng
vuông góc với mặt phẳng đáy, còn cạnh bên SC tạo với mặt phẳng (SAB) một góc
30°
. Thể tích hình chóp
đó bằng
A.
3
3
3
a
. B.
3
2
2
a
. C.
3
2
4
a
. D.
3
2
3
a
Câu 21:Cho hình chóp S.ABCD có đáy là một hình vuông cạnh a. Các mặt phẳng (SAB) và (SAD) cùng
vuông góc với mặt phẳng đáy, còn cạnh bên SC tạo với mặt phẳng đáy một góc bằng
30°
. Thể tích hình
chóp đó bằng
A.
3
6
5
a
. B.
3
6
3
a
. C.
3
6
4
a
. D.
3
6
9
a
.
Câu 22: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, biết SA vuông góc với đáy (ABC) và
(SBC) hợp với đáy (ABC) một góc
60
°
. Tính thể tích hình chóp
A.
3
3
8
a
. B.
3
5
9
a
. C.
3
3
a
. D. Đáp án khác.
Câu 23: Cho hình chóp tam giác S.ABC có SA, SB, SC đôi một vuông góc, SA=a, SB=b, SC=c. Thể tích
khối chóp bằng:
A.
1
3
abc
. B.
1
9
abc
. C.
1
6
abc
. D.
2
3
abc
.
Câu 24: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt phẳng đáy, góc
giữa đường thẳng SB và (ABC) bằng
60°
. Tính thể tích khối chóp
A.
3
3
12
a
. B.
3
4
a
. C.
3
2
a
. D.
3
3
6
a
.
Câu 25: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SD=
13
2
a
. Hình chiếu S lên
(ABCD) là trung điểm H của cạnh AB. Tính thể tích khối chóp
A.
3
12a
. B.
3
2
3
a
. C.
3
2
3
a
. D.
3
2
a
.
Câu 26: Hình chóp tam giác S.ABC có đáy là tam giác đều cạnh a, SA
⊥
(ABC). Góc giữa (SBC) và (ABC)
bằng
60°
. Thể tích khối chóp S.ABC bằng.
A.
3
3
8
a
. B.
3
33
8
a
. C.
3
4
a
. D.
3
3
4
a
.
Câu 27: Cho hình chóp S.MNPQ có đáy MNPQ là hình vuông, SM
⊥
(MNPQ). Biết MN =a, SM =
2a
.
Thể tích khối chóp là
A.
3
2
6
a
. B.
3
2
2
a
. C.
3
3
2
a
. D.
3
2
3
a
.
Câu 28: Một hình chóp tam giác có đường cao bằng 100cm và các cạnh đáy bằng 20cm, 21cm,29cm. Thể
tích khối chóp đó bằng
A.
3
7000cm
. B.
3
6213
cm
. C.
3
6000
cm
. D.
3
7000 2cm
.
Câu 29: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = 2a, AD = a . Hình chiếu của S lên
(ABCD) là trung điểm H của AB, SC tạo với đáy một góc
45°
. Thể tích khối chóp S.ABCD là
A.
3
2
3
a
. B.
3
22
3
a
. C.
3
3
a
. D.
3
3
2
a
.
Câu 30: Cho tứ diện S.ABC có các cạnh SA,SB,SC đôi một vuông góc với nhau và AB = 5, BC = 6, CA =
7. Khi đó thể tích tứ diện S.ABC bằng
A.
210
. B.
210
3
. C.
95
3
. D.
95
.
Câu 31: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a, AD =
3a
. Đường thẳng SA
vuông góc với đáy. Cạnh bên SB tạo với mặt phẳng (SAC) góc
30°
. Thể tích khối chóp S.ABCD là
A.
3
6a
. B.
3
6
6
a
. C.
3
6
2
a
. D.
3
6
3
a
.
Câu 32: Cho hình chóp S.ABCD có đáy là hình thoi,
60ABC = °
, SA=SB=SC. Gọi H là hình chiếu vuông
góc của S trên mặt phẳng đáy. Khoảng cách từ H đến (SAB) bằng 2cm và thể tích khối chóp S.ABCD bằng
3
60
cm
. Diện tích tam giác SAB bằng:
A. 5. B. 15. C. 30. D.
15
2
.
Câu 33: Cho khối chóp S.ABCD có đáy là hình chữ nhật, AD = 2a, AB = a. H là trung điểm của AD và SH
vuông góc với đáy. Tính thể tích khối chóp S.ABCD biết SD hợp với đáy một góc
45°
A.
3
23
2
a
. B.
3
3
a
. C.
3
2
3
a
. D.
3
3
a
.
Câu 34: Cho khối chóp S.ABCD có đáy là hình chữ nhật, AD = 2a, AB = a. H là trung điểm của AD và SH
vuông góc với đáy. Tính thể tích khối chóp S.ABCD biết SD hợp với đáy một góc
60°
A.
3
46
3
a
. B.
3
26
3
a
. C.
3
6
a
. D.
3
3
a
.
Câu 35: Cho hình chóp S.ABCD có đáy là hình vuông. Tam giác SAB đều và nằm trong mặt phẳng vuông
góc với đáy. Biết diện tích của tam giác SAB là
93
(cm
3
). Thể tích khối chóp S.ABCD là:
A.
18 3
. B.
36 3
. C.
81 3
. D.
93
.
Câu 36: Cho khối chóp S.ABCD có ABCD là hình vuông có cạnh đáy bằng 3a. Tam giác SAB cân tại S và
nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp biết tam giác SAB đều.
A.
3
93a
. B.
3
93
2
a
. C.
3
9
a
. D.
3
9
2
a
.
Câu 37: Cho khối chóp S.ABCD có ABCD là hình vuông có cạnh đáy bằng 3a. Tam giác SAB cân tại S và
nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp biết tam giác SAB vuông.
A.
3
93a
. B.
3
93
2
a
. C.
3
9a
. D.
3
9
2
a
.
Câu 38: Cho khối chóp S.ABCD có ABCD là hình vuông có cạnh đáy bằng 3a. Tam giác SAB cân tại S và
nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp biết góc giữa SC và mặt phẳng (ABCD)
bằng
60°
.
A.
3
18 3a
. B.
3
9 15
2
a
. C.
3
93a
. D.
3
18 15a
.
Câu 39: Cho khối chóp S.ABCD có ABCD là hình chữ nhật, AB = 2a. Tam giác SAB nằm trong mặt phẳng
vuông góc với đáy và SA = a; SB =
3a
. Tính thể tích khối chóp biết AD=3a.
A.
3
3
a
. B.
3
9 15
2
a
C.
3
23
a
. D.
3
18 15a
.
Câu 40: Cho khối chóp S.ABCD có ABCD là hình chữ nhật, AB = a; AD =
3a
. Tam giác SBD vuông tại
S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp biết góc giữa SD và đáy bằng
30°
.
A.
3
3a
. B.
3
a
. C.
3
3
3
a
. D.
3
2
a
.
Câu 41: Cho hình chóp S.ABC có đáy ABC là tam giác đều. Mặt bên SAB nằm trong mặt phẳng vuông góc
với mặt phẳng đáy và tam giác SAB vuông tại S, SA =
3a
, SB = a. Tính thể tích hình chóp S.ABC.
A.
3
4
a
. B.
3
3
a
. C.
3
6
a
. D.
3
2
a
.
Câu 42: Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 2a. Mặt phẳng (SAB) vuông góc với đáy,
tam giác SAB cân tại A. Biết thể tích khối chóp S.ABC bằng
3
4
3
a
. Khi đó, độ dài SC bằng:
A.
3
a
. B.
6a
. C.
2
a
. D. Đáp số khác.
Câu 43: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, AB = 3a, BC = 5a và (SAC) vuông góc
với đáy. Biết SA=2a,
30SAC = °
. Thể tích khối chóp là:
A.
3
3
9
a
. B.
3
23a
. C.
3
3a
D.
3
2a
.
Câu 44: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, AB = 3a, BC = 5a, mặt phẳng (SAC)
vuông góc với đáy. Biết SA = 2a
3
,
30SAC = °
. Thể tích khối chóp là:
A.
3
23
a
. B.
3
3a
. C.
3
2
a
. D.
3
3
3
a
.
Câu 45: Cho khối chóp đều S.ABC cạnh đáy bằng
3a
. Tính thể tích của khối chóp S.ABC biết mặt bên là
tam giác vuông cân.
A.
3
21
36
a
. B.
3
21
12
a
. C.
3
6
8
a
. D.
3
6
4
a
.
Câu 46: Cho hình chóp tứ giác đều S.ABCD có cạnh AB = a và đường cao h=
3
2
a
Diện tích toàn phần của
hình chóp bằng.
A.
2
5
2
a
. B.
2
3a
. C.
2
2a
. D.
2
3
2
a
.
Câu 47: Cho một hình chóp tứ giác đều có cạnh đáy bằng a và diện tích xung quanh gấp đôi diện tích đáy.
Khi đó thể tích của khối chóp là:
A.
3
3
6
a
. B.
3
3
3
a
. C.
3
2
3
a
. D.
3
3
12
a
.
Câu 48: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a. Gọi SH là đường cao của hình chóp.
Khoảng cách từ trung điểm của SH đến (SBC) bằng b. Thể tích của khối chóp S.ABCD là.
A.
3
22
2
3 16
ab
ab−
. B.
3
22
3 16
ab
ab−
. C.
3
22
2
16
ab
ab−
. D.
2
3
ab
.
Câu 49: Thể tích khối tứ diện đều cạnh a là:
A.
3
2
12
a
. B.
3
3
8
a
. C.
3
6
a
. D.
3
3
a
.
Câu 50: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng
ϕ
.
Khi đó thể tích khối chóp S.ABCD bằng.
A.
3
2
tan
6
a
ϕ
. B.
3
6
a
tan
ϕ
. C.
3
2
cot
6
a
ϕ
. D.
3
2
tan
2
a
ϕ
.
Câu 51: Cho khối chóp S.ABCD có ABCD là hình thang vuông tại A,B. Hai mặt phẳng (SAB) và (SAD)
cùng vuông góc với đáy. Biết AD = 2BC= 2a, BD =
5
a
. Tính thể tích khối chóp S.ABCD biết góc giữa
SB và mặt phẳng đáy bằng
30°
.
A.
3
3
6
a
B.
3
3
2
a
C.
3
22
3
a
D.
3
2
3
a
Câu 52: Cho khối chóp S.ABCD có ABCD là hình thang vuông tại A,B. Hai mặt phẳng (SAB) và (SAD)
cùng vuông góc với đáy. Biết AD = 2BC= 2a, BD =
5
a
. Tính thể tích khối chóp S.ABCD biết góc giữa
SO và mặt phẳng đáy bằng
45
°
, với O là giao điểm của AC và BD.
A.
3
3
3
a
B.
3
23
3
a
C.
3
2
3
a
D.
3
3
2
a
Câu 53: Cho khối chóp S.ABCD có ABCD là hình thoi cạnh bằng a, tâm O,
60BAD = °
. Gọi I là giao
điểm của hai đường chéo AC và BD. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) là điểm H, sao cho
H là trung điểm của BI. Góc giữa SC và mặt phẳng đáy bằng
45°
. Thể tích khối chóp S.ABCD là.
A.
3
39
12
a
B.
3
39
48
a
C.
3
39
24
a
D.
3
39
36
a
Câu 54: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Mặt phẳng (SAB), (SAD) cùng vuông
góc với mặt phẳng (ABCD). Đường thẳng SC tạo với đáy góc
45°
. Gọi M, N lần luợt là trung điểm của AB,
AD. Thể tích khối chóp S.MCDN là bao nhiêu?
A.
3
52
12
a
B.
3
52
6
a
C.
3
52
8
a
D.
3
52
24
a
Câu 55: Cho hình chóp S.ABC đáy ABC là tam giác đều cạnh 4cm. Cạnh bên SA vuông góc với đáy và
SA= 4cm. Lấy điểm M trên cạnh AB sao cho
45ACM = °
. Gọi H là hình chiếu của S trên CM. Gọi I, K theo
thứ tự là hình chiếu của A trên SC,SH. Thể tích của khối tứ diện SAIK tính theo cm
3
bằng.
A.
16
3
B. 9 C. 8 D.
16
9
Câu 56: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA = a, AB = a. Hình chiếu vuông
góc của đỉnh S trên ABCD là điểm H thuộc cạnh AC sao cho AC= 4AH. Gọi CM là đường cao của tam giác
SAC. Tính thể tích tứ diện SMBC.
A.
3
2
15
a
B.
3
48
a
C.
3
14
15
a
D.
3
14
48
a
Câu 57: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O, AB = a, AD =
3
a
, SO
⊥
(ABCD). Khoảng cách giữa AB và SD bằng
3
4
a
. Thể tích khối đa diện S.ABCD bằng
A.
3
15
30
a
B.
3
3
8
a
C.
3
3
3
a
D.
3
3
6
a
Câu 58: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA
⊥
(ABCD), AB = SA= 1, AD =
2
.
Gọi M, N lần luợt là trung điểm của AD, SC, I là giao điểm của BM và AC. Tính thể tích khối tứ diện ANIB
là
A.
3
2
36
a
B.
2
12
C.
2
18
D.
2
36
Câu 59: Cho hình chóp tam giác S.ABC có AB = 5a, BC = 6a, CA = 7a. Các mặt bên (SAB), (SBC), (SCA)
tạo với đáy một góc
60
°
. Tính thể tích khối chóp
A.
3
83a
B.
3
63a
C.
3
73a
D.
3
53a
.
LỜI GIẢI BÀI TẬP TỰ LUYỆN
Câu 1: Ta có
2
= ⇒
ABCD
Sa
3
2
.
11 2
. . 2.
33 3
= = =
S ABCD ABCD
a
V SA S a a
. Chọn D.
Câu 2:
22
2SA SB AB a= −=
,
22
2
BC AC AB a
= −=
2
12
.
22
⇒= =
ABC
a
S AB BC
Ta có
23
.
1 1 22
. .2 .
3 32 3
S ABC ABC
aa
V SA S a= = =
. Chọn A.
Câu 3:
2 2 22
3; 2
= −= = −=
SA SC AC a BC AC AB a
2
12
.
22
ABC
a
S AB BC
⇒= =
Ta có:
23
.
1 1 26
. . 3.
3 3 26
S ABC ABC
aa
V SA S a= = =
. Chọn A.
Câu 4: Ta có
( ) ( )
( ) ( )
( )
SAB ABC
SH ABC
SAC ABC
⊥
⇒⊥
⊥
Ta có
22
2SA SC AC a= −=
Ta có
2
3
4
ABC
a
S = ⇒
33
.
1 1 36
. . 2.
3 3 4 12
S ABC ABC
aa
V SA S a= = =
. Chọn B.
Câu 5:
22
2SH SA AH a= −=
.
Ta có
2
.2
ABCD
S AB AD a= = ⇒
3
2
.
1 14
. .2 .2
3 33
S ABCD ABCD
a
V SH S a a= = =
. Chọn C.
Câu 6:
23
3
2
a
SH a= =
,
22
(2 ) 4
= =
ABCD
S aa
⇒
3
2
.
1 1 43
. . 3.4
33 3
S ABCD ABCD
a
V SH S a a= = =
.Chọn B.
Câu 7:
(
) { }
SB ABC B∩=
và
(
) ( )
(
)
( )
, , 30SA ABC SB ABC SB AB SBA⊥⇒ = ==°
3
tan tan
3
SA a
SBA SA AB SBA
AB
= ⇒= =
2
22
12
2.
22
ABC
a
BC AC AB a S AB BC= −=⇒= =
23
.
1 13 2 6
. ..
3 3 3 2 18
= = =
S ABC ABC
aa a
V SA S
. Chọn C.
Câu 8: Ta có
( ) ( )
( )
( )
( )
SAB ABC
SA ABC
SAC ABC
⊥
⇒⊥
⊥
.
(
) { }
SB ABC B∩=
và
( ) ( )
( )
( )
, , 30SA ABC SB ABC SB AB SBA⊥⇒ = ==°
3
tan tan
3
SA a
SBA SA AB SBA
AB
= ⇒= =
2
3
4
ABC
a
S = ⇒
23
.
1 13 3
. ..
3 3 3 4 12
= = =
S ABC ABC
aa a
V SA S
. Chọn D.
Câu 9: Ta có
( ) ( )
( ) ( )
( )
SAB ABC
SA ABC
SAC ABC
⊥
⇒⊥
⊥
.
( ) { }
SM ABC M∩=
và
( ) ( )
( )
( )
, , 60SA ABC SM ABC SM AB SMA⊥⇒ = ==°
tan tan
SA
SMA SA AM SMA
AM
= ⇒=
mà
3 33
.tan 60
22 2
= ⇒ = °=
aa a
AM SA
2
3
4
ABC
a
S =
⇒
23
.
1 13 3 3
. ..
3 32 4 8
= = =
S ABC ABC
aa a
V SA S
. Chọn C.
Câu 10:
( ) { }
SC ABC C∩=
và
( ) ( )
( )
( )
, , 45SA ABC SC ABC SC AC SCA⊥⇒ = ==°
22
3AC BC AB a= −=
.
tan tan 3
SA
SCA SA AC SCA a
AC
= ⇒= =
2
13
.
22
ABC
a
S AB AC= = ⇒
23
.
1 13
. . 3.
3 3 22
= = =
S ABC ABC
aa
V SA S a
. Chọn A.
Câu 11:
( ) { }
SM ABC M∩=
và
( ) ( )
(
)
(
)
, , 60SA ABC SM ABC SM AB SMA⊥⇒ = ==°
tan tan
SA
SMA SA AM SMA
AM
= ⇒=
mà
1
.tan 60 3
2
= = ⇒ = °=AM BC a SA a a
2
3
4
ABC
a
S = ⇒
23
.
1 13 3 3
. ..
3 32 4 8
= = =
S ABC ABC
aa a
V SA S
.Chọn C.
Câu 12:
( ) { }
SC ABCD C∩=
và
( ) ( )
( )
( )
, , 45SA ABCD SC ABCD SC AC SCA⊥⇒ = ==°
tan tan 2
SA
SCA SA AC SCA a
AC
= ⇒= =
22
3BC AC AB a= −=
⇒
2
.B 3
ABCD
S AB C a
= = ⇒
3
2
.
1 1 23
. .2 a .a 3
33 3
S ABCD ABCD
a
V SA S
= = =
. Chọn A.
Câu 13:
( ) { }
SO ABCD O∩=
và
( ) (
)
( )
( )
, , 60SA ABCD SO ABCD SO OA SOA⊥⇒ = ==°
1
2
OA AC a= =
tan tan 3
SA
SOA SA OA SOA a
OA
= ⇒= =
22 2
3 .3
ABCD
BC AC AB a S AB BC a= −=⇒ = =
⇒
23
.
11
. .a 3.a 3
33
S ABCD ABCD
V SA S a= = =
. Chọn C.
Câu 14: Ta có:
( ) ( )
( ) ( )
( )
SAB ABCD
SA ABCD
SAD ABCD
⊥
⇒⊥
⊥
( ) { }
SC ABCD C∩=
và
( ) ( )
( )
( )
, , 45SA ABCD SC ABCD SC AC SCA⊥⇒ = ==°
22
2AC AB BC a= +=
tan tan 2
SA
SCA SA AC SCA a
AC
= ⇒= =
2
ABCD
Sa
= ⇒
3
2
.
11 2
. .a 2.a
33 3
S ABCD ABCD
a
V SA S
= = =
. Chọn B.
Câu 15: Ta có:
( ) ( )
( ) ( )
( )
SAB ABCD
SA ABCD
SAD ABCD
⊥
⇒⊥
⊥
(
)
{
}
SM ABCD M
∩=
và
( ) ( )
( )
( )
, , 60SA ABCD SM ABCD SM AM SMA⊥⇒ = ==°
22
5
2
a
AM AB BM= +=
.
15
tan tan
2
SA a
SMA SA AM SMA
AM
= ⇒= =
2
ABCD
Sa= ⇒
3
2
.
1 1 15 15
. . .a
3 32 6
S ABCD ABCD
aa
V SA S= = =
. Chọn A.
Câu 16:
( )
{ }
SC ABCD C∩=
và
( ) ( )
( )
( )
, , HC 60SH ABCD SC ABCD SC SCH⊥⇒ = ==°
22
5CH BC BH a
= +=
.
tan tan 15
SH
SCH SH CH SCH a
CH
= ⇒= =
( )
2
2
24
ABCD
S aa= = ⇒
3
2
.
1 1 4 15
. . 15.4 a
33 3
= = =
S ABCD ABCD
a
V SH S a
. Chọn B.
Câu 17:
( ) { } ( ) ( )
( )
( )
; , , AC 45∩=⊥⇒ = ==°SC ABCD C SA ABCD SC ABCD SC SCA
22
sin sin 2 2
SA
SCA SA SC SCA a AC SC SA a
SC
= ⇒= =⇒ = − =
22 2
3 .3
ABCD
BC AC AB a S AB BC a= −=⇒ = = ⇒
3
.
1 23
.
33
S ABCD ABCD
a
V SA S= =
.Chọn B.
Câu 18: Ta có
3
.
1
..
66
S ABC
a
V SA SB SC= =
. Chọn A.
Câu 19: Ta có
2
1
.
22
BCD
a
S BC CD= = ⇒
23
.
11
. .a.
3 326
S BCD BCD
aa
V SA S= = =
. Chọn C.
Câu 20: Ta có
( ) ( )
( ) ( )
( )
SAB ABCD
SA ABCD
SAD ABCD
⊥
⇒⊥
⊥
Lại có
(
)
BC AB
BC SAB
BC SA
⊥
⇒⊥
⊥
mà
( ) { } ( )
( )
(
)
, , 30
∩=⇒ = ==°SC SAB S SC ABC SC SB CSB
22
tan 3 2
tan
BC BC
CSB SB a SA SB AB a
SB
CSB
= ⇒= = ⇒= − =
2
ABCD
Sa= ⇒
3
2
.ABCD
11 2
. .a 2.
33 3
S ABCD
a
V SA S a= = =
. Chọn D.
Câu 21: Ta có
( ) ( )
(
) ( )
( )
SAB ABCD
SA ABCD
SAD ABCD
⊥
⇒⊥
⊥
( )
{ } (
) ( )
( )
( )
; , , AC 30∩=⊥⇒ = ==°
SC ABCD C SA ABCD SC ABCD SC SCA
22
2AC AB BC a= +=
.
6
tan tan
3
SA a
SCA SA AC SCA
AC
= ⇒= =
2
ABCD
Sa= ⇒
3
2
.ABCD
1 1a 6 6
. ..
3 33 9
= = =
S ABCD
a
V SA S a
.Chọn D.
Câu 22:
Gọi M là trung điểm của BC
Ta có
( )
BC AM
BC SAM
BC SA
⊥
⇒⊥
⊥
( ) (
)
( )
( )
, , AM 60SBC ABC SM SMA
⇒===°
33
tan tan . tan 60
22
SA a a
SMA SA AM SMA
AM
= ⇒ = = °=
2
3
4
ABC
a
S = ⇒
23
.ABC
1 1 3a 3 3
. ..
3 33 4 8
= = =
S ABC
aa
V SA S
. Chọn
A.
Câu 23: Ta có
.ABC
1
..
66
S
abc
V SA SB SC= =
. Chọn C.
Câu 24:
( ) { }
SB ABC B∩=
và
( ) ( )
( )
( )
, , AB 60SA ABC SB ABC SB SBA⊥⇒ = ==°
tan tan 3
SA
SBA SA AB SBA a
AB
= ⇒= =
.
2
ABC
3
4
a
S = ⇒
3
.ABC
1
.
34
S ABC
a
V SA S= =
. Chọn B.
Câu 25: Ta có
22 22
53
22
aa
HD AH AD SH SD HD= + = ⇒= − =
Lại có
2
ABCD
Sa= ⇒
3
.ABCD
1
.
32
S ABCD
a
V SH S= =
. Chọn D.
Câu 26:
Gọi M là trung điểm của BC
Ta có
( )
BC AM
BC SAM
BC SA
⊥
⇒⊥
⊥
( ) ( )
( )
( )
, , AM 60SBC ABC SM SMA⇒===°
3
tan tan
2
SA a
SMA SA AM SMA
AM
= ⇒= =
3
.tan 60
2
a
°=
2
ABC
3
4
a
S = ⇒
23
.ABC
1 13 3 3
. ..
3 32 4 8
S ABC
aa a
V SA S
= = =
.
Chọn A.
Câu 27: Ta có:
2
MNPQ
Sa
= ⇒
3
.MNPQ
12
.
33
S MNPQ
a
V SM S= =
. Chọn D.
Câu 28: Ta có:
22 2
20 21 29
+=⇒
đáy là tam giác vuông.
S
day=
1
.20.21 210
2
= ⇒
V=
1
.100.210 7000
3
=
. Chọn A.
Câu 29:
( ) {
}
SC ABCD C∩=
và
( ) ( )
( )
( )
, , 45SH ABCD SC ABCD SC HC SCH⊥⇒ = ==°
22
2HC HB BC a= +=
.
tan tan 2
SH
SCH SH HC SCH a
HC
= ⇒= =
2
.2
ABCD
S AB AD a= = ⇒
3
2
.
1 1 22
. . 2.2
33 3
S ABCD ABCD
a
V SH S a a= = =
. Chọn B.
Câu 30:
22 2 2
22 2 2
22 2 2
19
25 19
36 6 6
49 30
30
SA
SA SB AB SA
SB SC BC SB SB
SA SC AB SC
SC
=

+= = =

+= =⇔ =⇔=


+== =
=

⇒
.
1
. . 95
6
S ABC
V SA SB SC= =
.Chọn D.
Câu 31: Kẻ BH
⊥
AC ta có
( )
BH AC
BH SAC
BH SA
⊥
⇒⊥
⊥
mà
(
) { }
( )
(
)
( )
SB, ,SH 30SB SAC S SAC SB SBH∩=⇒ = ==°
.
2 2 22
1 114 3
32
a
BH
BH BC BA a
= + =⇒=
3
tan
2
tan
BH BH a
BSH SH
SH
BSH
= ⇒= =
.
22
2
a
AH AB BH= −=
;
22
2SA SH AH a= −=
.
2
.3
ABCD
S AB AD a= = ⇒
3
.
16
.
33
S ABCD ABCD
a
V SA S= =
.
Chọn D.
Câu 32: Ta có ngay tâm H là đường tròn ngoại tiếp
∆
ABC.
Kẻ HK
⊥
AB, HP
⊥
SK
⇒
( )
( )
;2d H SAB HP= =
.
tan 30
3 23
HK BK AB
HK
BK
°= ⇒ = =
.
2
.ABC
2
1 1 3 120 3
30 . .
3 34
S ABC
AB
V SH S SH SH
AB
== = ⇒=
2
120 3
.
1 1 .1
23
. . . 15
22 22
ABC
AB
SH HK
AB
S SK AB AB AB
HP
= = = =
.
Chọn B.
Câu 33:
( ) { }
SD ABCD D∩=
và
(
) ( )
( )
( )
, , 45SH ABCD SD ABCD SD HD SDH⊥⇒ = ==°
tan tan
SH
SDH SH HD SDH
HD
= ⇒=
mà
1
2
HD AD a SH a= =⇒=
2
.2
ABCD
S AB AD a= = ⇒
3
2
.
1 12
. . .2
3 33
S ABCD ABCD
a
V SH S a a= = =
. Chọn C.
Câu 34:
( ) { }
SC ABCD C∩=
và
( ) ( )
( )
(
)
, , 60SH ABCD SC ABCD SC HC SCH⊥⇒ = ==°
tan tan
SH
SCH SH HC SCH
HC
= ⇒=
mà
22
26HC HD CD a SH a= + = ⇒=
2
.2
ABCD
S AB AD a= = ⇒
3
2
.
1 1 26
. . 6.2
33 3
S ABCD ABCD
a
V SH S a a= = =
. Chọn B.
Câu 35: Gọi H là trung điểm của AB
⇒
SH
⊥
AB
Ta có:
( ) ( )
(
)
SAB ABCD
SH ABCD
SH AB
⊥
⇒⊥
⊥
2
33
93 6 33
42
ABC
AB AB
S AB SH= = ⇔=⇒= =
2
36
ABCD
S AB= = ⇒
.
11
. .3 3.36 36 3
33
S ABC D ABCD
V SH S= = =
.Chọn B
Câu 36:
Gọi H là trung điểm của AB
⇒
SH
⊥
AB
Ta có:
( ) ( )
( )
SAB ABCD
SH ABCD
SH AB
⊥
⇒⊥
⊥
333
22
AB a
SH = =
,
22
9
ABCD
S AB a= =
3
2
.
1 13 3 9 3
. . .9
3 32 2
S ABCD ABCD
aa
V SH S a= = =
Chọn B
Câu 37: Gọi H là trung điểm của AB
⇒
SH
⊥
AB
Ta có:
( ) ( )
( )
SAB ABCD
SH ABC D
SH AB
⊥
⇒⊥
⊥
13
22
a
SH AB= =
,
22
9
ABCD
S AB a= =
3
2
.
1 13 9
. . .9
3 32 2
S ABCD ABCD
aa
V SH S a= = =
. Chọn D.
Câu 38
Gọi H là trung điểm của AB
⇒
SH
⊥
AB
Ta có:
( ) ( )
( )
SAB ABCD
SH ABC D
SH AB
⊥
⇒⊥
⊥
( )
{ }
SC ABCD C
∩=
và
( )
⊥SH ABCD
( )
( )
(
)
, , 60
o
SC ABCD SC HC SCH
⇒===
22
35
2
a
CH BH BC= +=
3 15
tan tan
2
SH a
SCH SH HC SCH
HC
= ⇒= =
22
9
ABCD
S AB a= = ⇒
3
2
.
1 1 3 15 9 15
. . .9
3 32 2
S ABCD ABCD
aa
V SH S a= = =
Chọn B.
Câu 39:
Kẻ SH
⊥
AB ta có
( )
(
)
(
)
SAB ABCD
SH ABCD
SH AB
⊥
⇒⊥
⊥
Dễ thấy
22 22
4SA SB AB a+= =
⇒
∆
SAB vuông tại S
2 222
1 114 3
32
a
SH
SH SA SB a
= + = ⇒=
2
.6
ABCD
S AB AD a= =
23
.
1 13
. . .6 3
3 32
S ABCD ABCD
a
V SH S a a= = =
.Chọn A.
Câu 40:
Kẻ SH
⊥
BD
Ta có
( ) ( )
( )
SBD ABCD
SH ABCD
SH BD
⊥
⇒⊥
⊥
( )
{
}
SD ABCD D∩=
và
(
)
( )
(
)
(
)
, , DH 30
SH ABCD SD ABCD SD SDH
⊥⇒ = ==°
22
D2B AB AD a= +=
sin sin SD 3
SB
SDH SB BD SDH a a
BD
= ⇒= =⇒=
2222
1 114 3
32
a
SH
SH SB SD a
= + = ⇒=
2
.3
ABCD
S AB AD a= = ⇒
3
2
.
1 13
. . .3
3 32 2
S ABCD ABCD
aa
V SH S a
= = =
. Chọn D.
Câu 41:
Kẻ SH
⊥
AB
Ta có
(
) ( )
( )
SAB ABC
SH ABC
SH AB
⊥
⇒⊥
⊥
2 222
1 114 3
32
a
SH
SH SA SB a
= + = ⇒=
2
22 2
3
23
4
ABC
AB
AB SA SB a S a= +=⇒ = =
3
2
.
1 13
. . .3
3 32 2
S ABC ABC
aa
V SH S a
= = =
. Chọn D.
Câu 42:
Gọi H là trung điểm của AB
⇒
SH
⊥
AB
Ta có
( ) ( )
( )
SAB ABCD
SH ABCD
SH AB
⊥
⇒⊥
⊥
22
11
(2 ) 2
22
ABC ABCD
S S aa= = =
.
.
3
1
.2
3
S ABC
S ABC ABC
ABC
V
V SH S SH a
S
= ⇒= =
22 2 2
53HC BH BC a SC SH HC a= + = ⇒= + =
.Chọn A.
Câu 43:
Kẻ SH
⊥
AC
Ta có
( ) ( )
( )
SAC ABC
SH ABC
SH AC
⊥
⇒⊥
⊥
sin sin
SH
SAC SH SA SAC a
SA
=⇒= =
22
4AC BC AB a
= −=
2
1
.AC 6 a
2
⇒= =
ABC
S AB
23
.
11
. . .6 2
33
S ABC ABC
V SA S a a a= = =
. Chọn D.
Câu 44:
Kẻ SH
⊥
AC
Ta có
( ) ( )
( )
SAC ABC
SH ABC
SH AC
⊥
⇒⊥
⊥
sin sin 3
SH
SAC SH SA SAC a
SA
=⇒= =
22 2
1
4 .AC 6 a
2
= −=⇒= =
ABC
AC BC AB a S AB
23
.
11
. . 3.6 2 3
33
S ABC ABC
V SH S a a a= = =
. Chọn A.
Câu 45: Gọi H là tâm đường tròn ngoại tiếp
∆
ABC
⇒
SH
⊥
(ABC)
Gọi M là trung điểm của AB
13
22
a
SM AB= =
,
1 1 3. 3
.
3 32 2
aa
MH CM= = =
22
2
2
a
SH SM MH
= −=
( )
2
2
33
33
44
ABC
a
a
S
= =
23
.
1 1 23 3 6
. ..
3 32 4 8
S ABC ABC
aa a
V SH S= = =
.Chọn C.
Câu 46: Diện tích đáy hình chóp S
đ
= a
2
Gọi O là tâm của hình vuông ABCD
⇒
SO
⊥
(ABCD).
Dựng OE
⊥
CD, CD
⊥
SO
⇒
CD
⊥
SE
Ta có:
22
22
3
44
aa
SE h OE a= + = +=
.
Diện tích một mặt bên là:
2
1
.
22
a
S OE CD= =
.
Diện tích toàn phần của hình chóp :
2
22
4. 3
2
a
Sa a=+=
. Chọn B.
Câu 47: Diện tích đáy hình chóp S
đ
= a
2
Gọi O là tâm của hình vuông ABCD
⇒
SO
⊥
(ABCD).
Dựng OE
⊥
CD, CD
⊥
SO
⇒
CD
⊥
SE.
4 2. 2.
xq SCD
S S SE CD SE a= = =
Mặt khác S
xq
=2S
đ
2
2. . 2
SE a a SE a⇒ = ⇒=
Do đó
2
222
3
22
aa
SO SE OE a

= −=− =


.
Thể tích khối chóp là: V=
3
13
.
36
ABCD
a
SO S =
. Chọn A.
Câu 48:
Gọi H =
(
)
AC BD SH ABCD∩⇒⊥
.
Dựng HE
⊥
BC, HF
⊥
SE
⇒
BC SH
BC HF
BC HE
⊥
⇒⊥
⊥
Mặt khác HF
⊥
SE
⇒
HF
⊥
(SBC)
⇒
( )
( )
;d H SBC HF=
.
Do I là trung điểm của
SH
( )
(
)
( )
( )
;2I;2d H SBC d SBC b HF⇒===
Lại có:
2 22
22 2
2
1 11 .
4
4
= + ⇒= =
−
−
HE HF ab
SH
HF HE SH
HE HF a
b
Do đó
3
.
22
1 2.
..
33
16
S ABCD ABCD
ab
V SH S
ab
= =
−
. Chọn A.
Câu 49:
Giả sử tứ diện S.ABC đều cạnh a.
Gọi H là trọng tâm tam giác ABC suy ra SH
⊥
(ABC)
Gọi M là trung điểm của BC ta có
3
2
a
AM =
Khi đó
2 23 3
.
3 32 3
aa
AH AM=⇒=
.
Lại có
2
2 22
6
33
aa
SH SA AH a= − = −=
.
23
.
1 16 3 2
. ..
3 3 3 4 12
⇒= = =
S ABC ABC
aa a
V SH S
. Chọn A.
Câu 50:
Gọi O là tâm của hình vuông ABCD khi đó SO
⊥
(ABCD) suy ra
(
)
( )
;SDO SD ABCD
ϕ
= =
.
Lại có
2
2
22
BD a
BD a OD= ⇒==
.
Suy ra
2 tan
tan
2
a
SO OD
ϕ
ϕ
= =
.
Khi đó
3
.
12
. tan
36
S ABCD ABCD
a
V SO S
ϕ
= =
. Chọn A.
Câu 51: Ta có
( ) ( )
( ) ( )
( )
SAB ABCD
SA ABCD
SAD ABCD
⊥
⇒⊥
⊥
(
)
{ }
∩=SB ABC D B
và
( )
SA ABCD⊥
( )
( )
( )
, , 30SB ABCD SB BA SBA⇒===°
22
AB BD AD
= −
a=
3
tan tan
3
SA a
SBA SA AB SBA
AB
= ⇒= =
2
13
.( )
22
ABCD
a
S AB AD BC= +=
23
.
1 1 33 3
.. . .
3 33 2 6
S ABCD ABCD
a aa
V SA S= = =
. Chọn A.
Câu 52: Ta có
( ) ( )
( ) ( )
( )
SAB ABCD
SA ABCD
SAD ABCD
⊥
⇒⊥
⊥
( ) { }
SO ABCD O∩=
và
(
)
SA ABCD⊥
( )
( )
( )
, , AO 45
SO ABCD SO SOA⇒===°
22 22
2AB BD AD a AC AB BC a= − =⇒= + =
2 22
33
a
AO AC= =
22
tan tan
3
SA a
SOA SA AO SOA
AO
= ⇒= =
.
2
13
.( )
22
ABCD
a
S AB AD BC= +=⇒
23
.
1 12 23 2
. ..
3 33 2 3
S ABCD ABCD
a aa
V SA S= = =
.Chọn C.
Câu 53:
( ) { }
SC ABCD C∩=
và
( )
SH ABCD⊥
( )
( )
( )
, , CH 45SC ABCD SC SCH⇒===°
60BAD BD a= °⇒ =
,
3AC a=
. Ta có
1
44
a
IH BD
= =
2
13
.
22
ABCD
a
S AC BD= =
22
13
4
a
HC IH IC= +=
13
tan tan
4
SH a
SCH SH HC SCH
HC
= ⇒= =
23
.
1 1 13 3 39
.. . .
3 3 4 2 24
S ABCD ABC D
aa a
V SH S= = =
. Chọn C
Câu 54:
( ) { }
SC ABCD C∩=
và
( )
SA ABCD⊥
( )
( )
( )
, , AC 45SC ABCD SC SCA⇒===°
22
2AC AB BC a= +=
tan tan 2
SA
SCA SA AC SCA a
AC
= ⇒= =
2
1
.AN
28
AMN
a
S AM= =
,
2
1
.BC
24
BCM
a
S BM= =
2
5
8
MCDN ABCD AMN BCM
a
S S SS= −−=
23
.
1 1 5 52
.S . 2.
3 3 8 24
S MCDN MCDN
aa
V SH a= = =
.
Chọn D.
Câu 55:
Cách 1: Ta có
CM SA
SM AH AHC
CM SA
⊥
⇒ ⊥ ⇒∆
⊥
vuông cân tại H.
Mặt khác
( )
()CM SAH AK CM AK SHC
⊥ ⇒⊥ ⇒⊥
.
Do đó
AK K I
AK SC
⊥
⊥
. Lại có
()SC AI SC AIK
⊥⇒⊥
.
Hình chóp S.AIK có đường cao là SI và đáy là tam giác AKI vuông tại
K.
Ta có:
22
.
22
SA AC
AI
SA AC
= =
+
,
22AH HC= =
.
22
22
. 4 26
3
3
SA AH
AK KI AI AK
SA AH
= = ⇒= − =
+
.
Tam giác SAC vuông cân tại A nên I là trung điểm của
SC
22
2
SC
SI⇒= =
.
1 42
.
23
AKI
S AK KI= = ⇒
.
1 16
..
39
S AIK AKI
V SI S= =
.
Cách 2:
( )
2
.
1 1 1 16
. . .4. . 2 2
3 32 3
S AHC AHC
V SA S= = =
.
Lại có:
22
2
22
42
..
4 83
SA SK
SA SK SH SI SC
SH SH
= = ⇒== =
+
;
2
2
1
2
SA SI
SC SC
= =
Khi đó
.
.
1
.
3
S AIK
S AHC
V
SK SI
V SH SC
= =
..
1 16
39
S AIK S AHC
VV⇒= =
. Chọn D.
Câu 56:
SA a=
,
12
2
44
a
AC a AH AC= ⇒= =
.
Do đó
22
14
4
a
SH SA AH= −=
.Mặt khác
14
. . 2 . .2
4
SAC
a
SA CM SH AC S a CM a= =⇔=
Do đó
22
7
22
aa
CM AM AC CM
= ⇒= − =
⇒
M là
trung điểm của SA.
Ta có:
23
. ABC
1 1 14 14
.S . .
3 3 4 2 24
S ABC
a aa
V SH= = =
.Do đó:
.MS BC
V
=
1
2
3
.
14
48
=
S ABC
a
V
. Chọn D.
Câu 57:
Do
( ) ( )
( )
/ / ; AB;⇒=AB CD d AB SD d SCD
( )
( )
(
)
(
)
A; 2 ;
d SCD d O SCD= =
(Do
2AC OC
=
)
Mặt khác
( ) (
)
( )
33
;;
48
aa
d AB SD d O SCD=⇒=
.
Dựng
OE CD⊥
,
( )
OF SE CD OF OF SCD⊥⇒ ⊥ ⇒ ⊥
.
Khi đó
( )
( )
3
;
8
= =
a
d O SCD OF
mà
3
22
= =
AD a
OE
và
22 2
11 1 5
SO
10
+ = ⇒=
a
SO OE OF
.
Mặt khác
2
3
ABCD
Sa=
⇒
3
.
1 15
.
3 30
S ABCD ABCD
a
V SO S= =
. Chọn
A.
Câu 58: Gọi O là tâm hình chữ nhật thì NO là đường trung
bình của tam giác SAC và
1
22
SA
NO
= =
.
Do
I AO BM=∩⇒
I là trọng tâm
∆
SBD.
Ta có:
21 1
33 3
AIB ACB
AI AO AC S S= = ⇒=
.
Mặt khác:
1 2 12
.
2 2 36
ABC ABI ABC
S AB BC S S= =⇒= =
.
Thể tích khối chóp ANIB là:
V=
1 11 2 2
. ..
3 3 2 6 36
ABI
NO S = =
. Chọn D.
Câu 59:Nửa chu vi tam giác ABC là:
9
2
AB BC CA
pa
++
= =
Diện tích tam giác ABC tính theo công thức He-rông là:
2
( )( )( ) 6 6
ABC
S pp a p b p c a= − − −=
.
Gọi H là hình chiếu vuông góc của S trên mặt phẳng (ABC).
Dựng
HM AB⊥
,
HN AC⊥
,
60HP BC SMH SNH SPH⊥⇒ = = =°
.Khi đó
∆ =∆=∆
SHM SHN SHP
suy ra
HM HN HP= = ⇒
H là tâm
đường tròn nội tiếp tam giác ABC
2
6 626
93
Sa a
HM r
pa
⇒=== =
.
Suy ra
tan 60 2 2SH HM a= °= ⇒
3
.
1
. 83
3
= =
S ABC ABC
V SH S a
.Chọn A.
| 1/48
| | Tải xuống

Có thể bạn quan tâm:

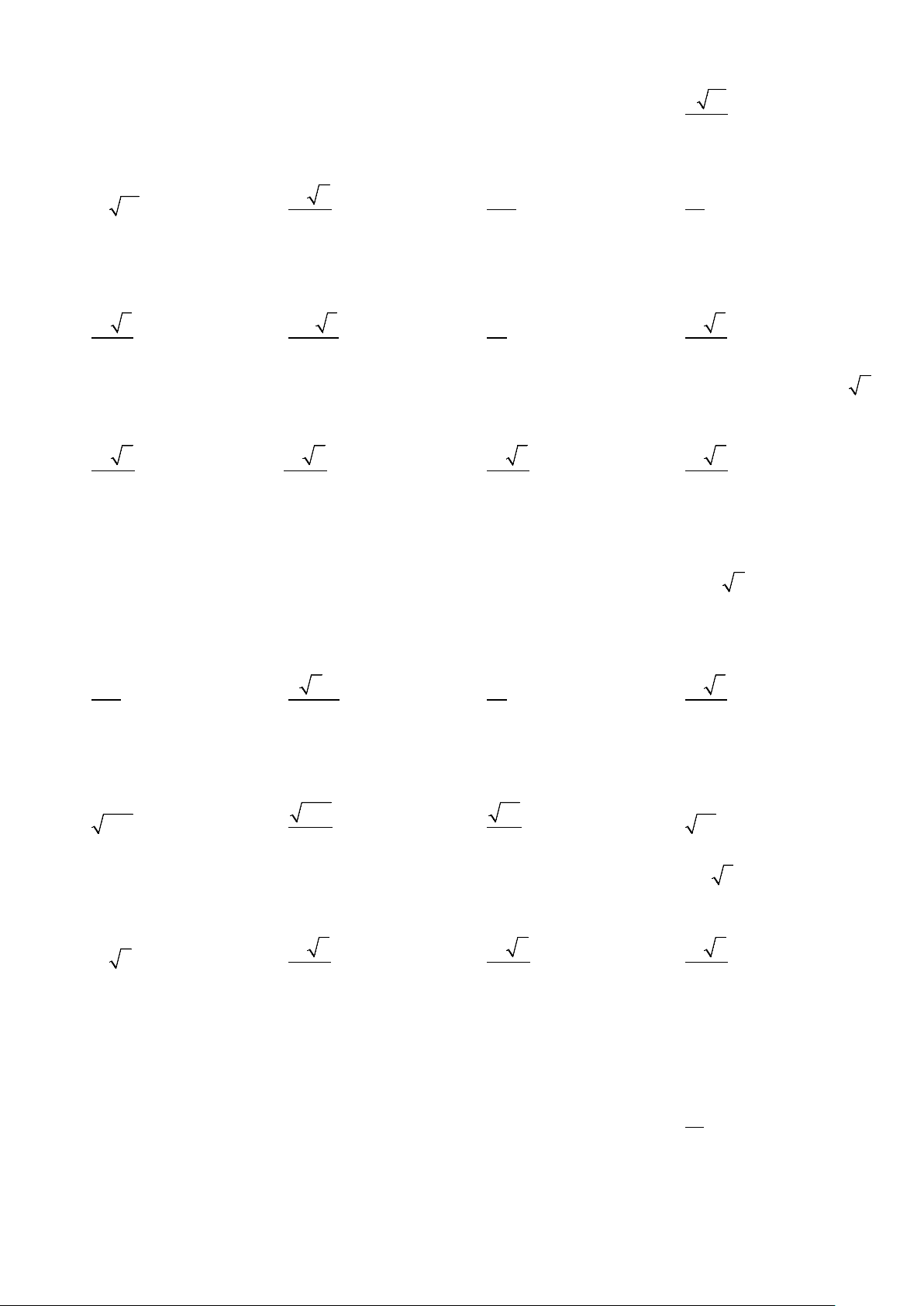
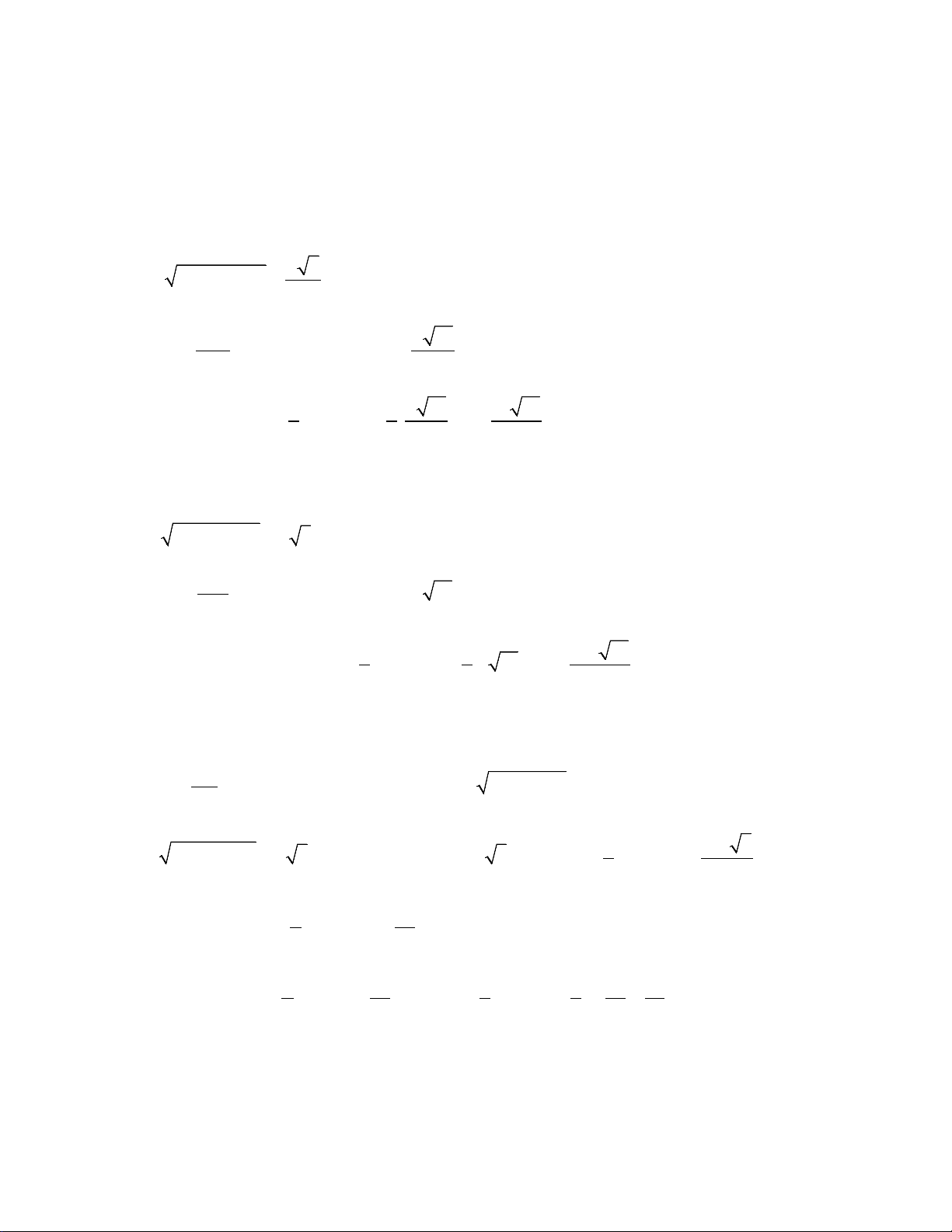
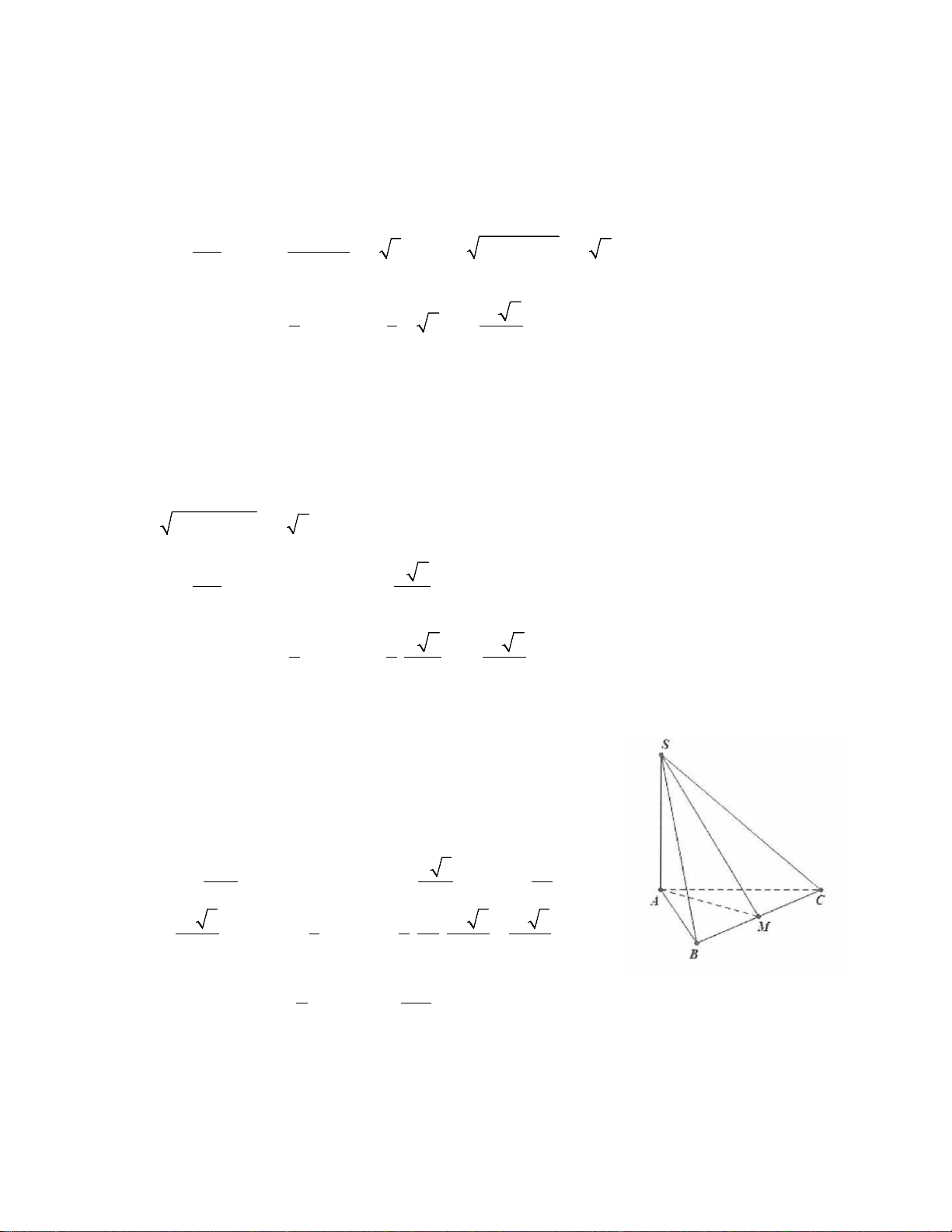
Preview text:

CHỦ ĐỀ 7: THỂ TÍCH KHỐI CHÓP
I. LÝ THUYẾT TRỌNG TÂM
Công thức tính thể tích khối chóp: V = 1 S.h 3
Trong đó: S là diện tích đáy và h là chiều cao của khối chóp.
II. CÁC DẠNG TOÁN TRỌNG TÂM VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: Thể tích khối chóp có đường cao sẵn có
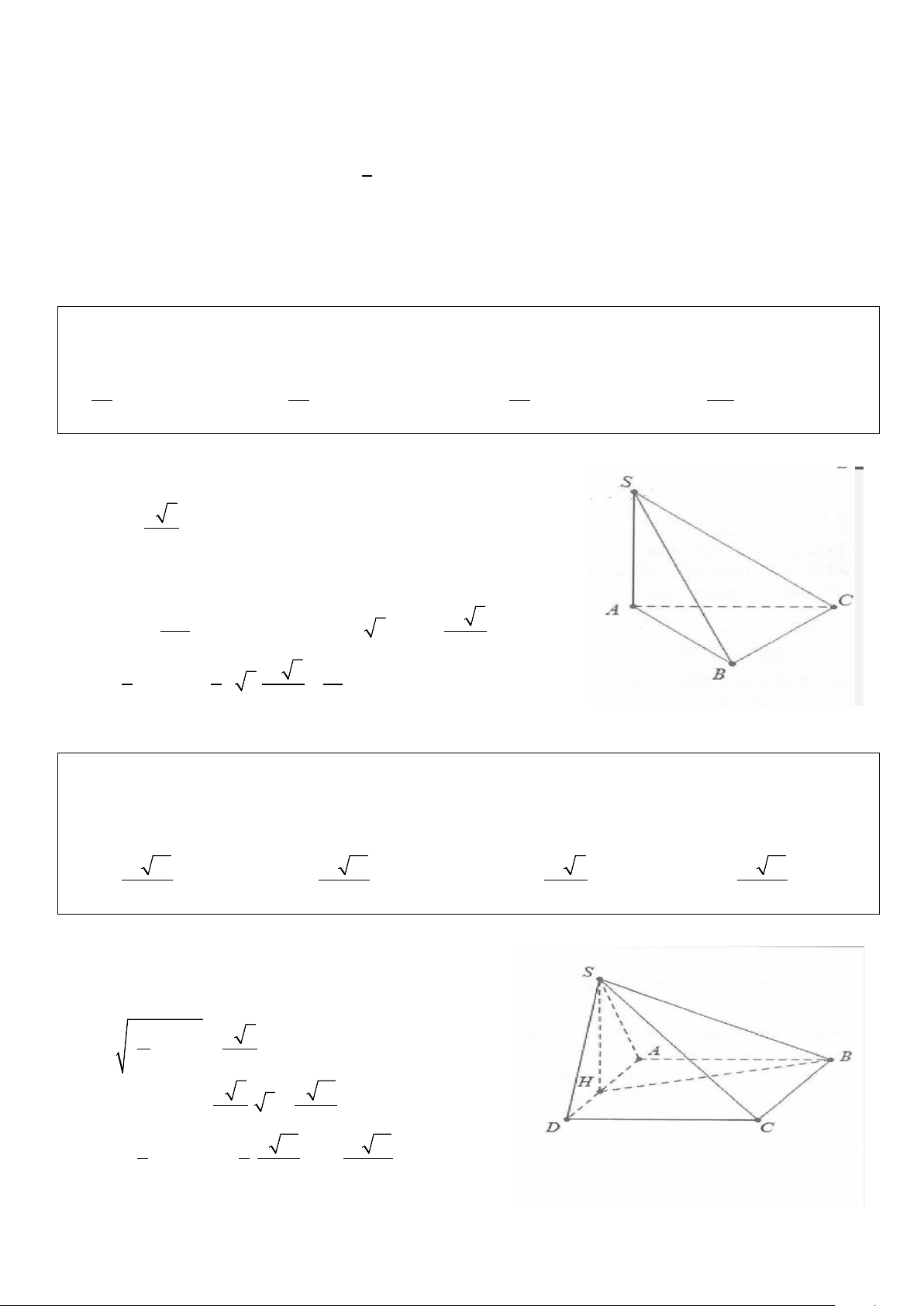
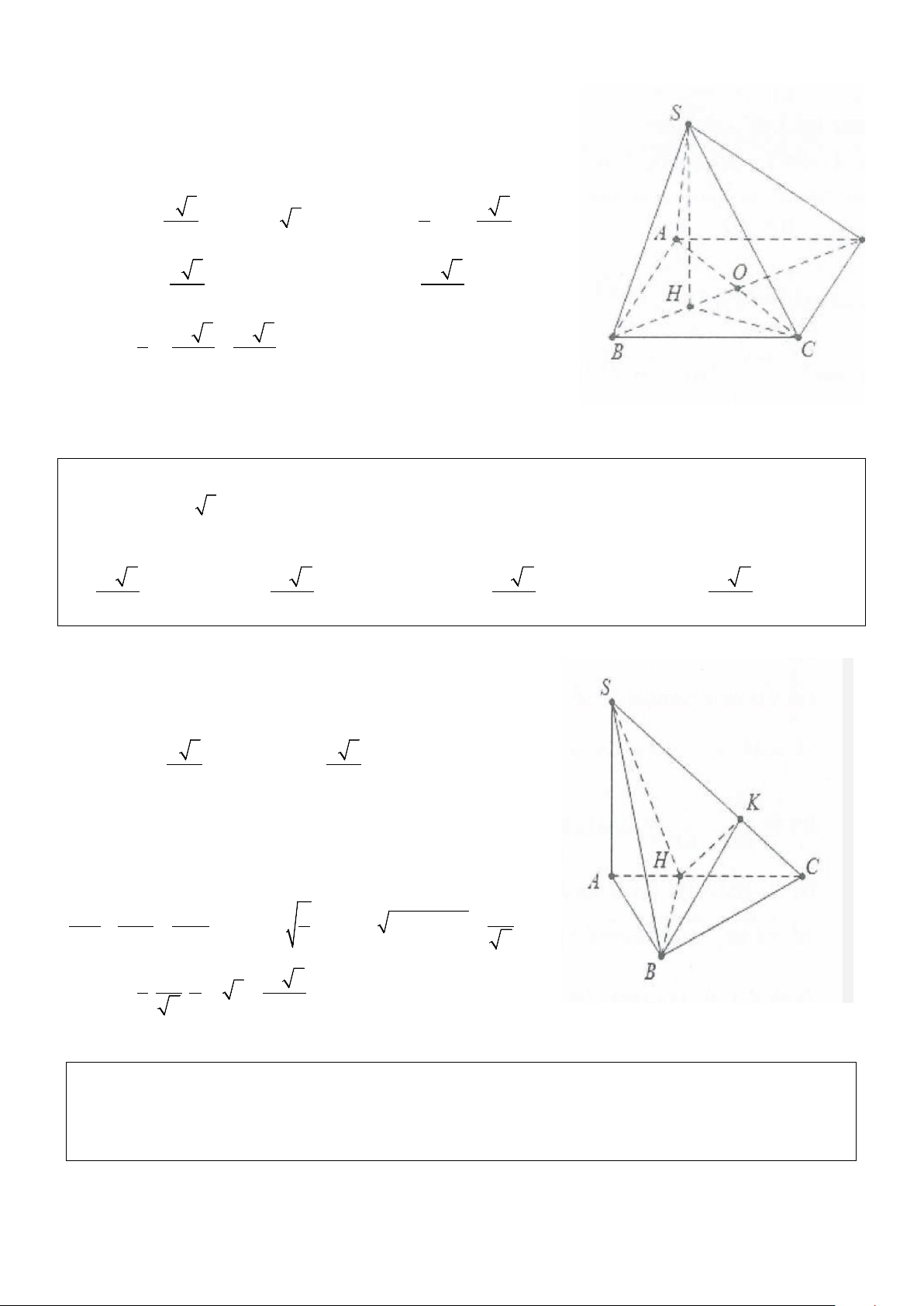
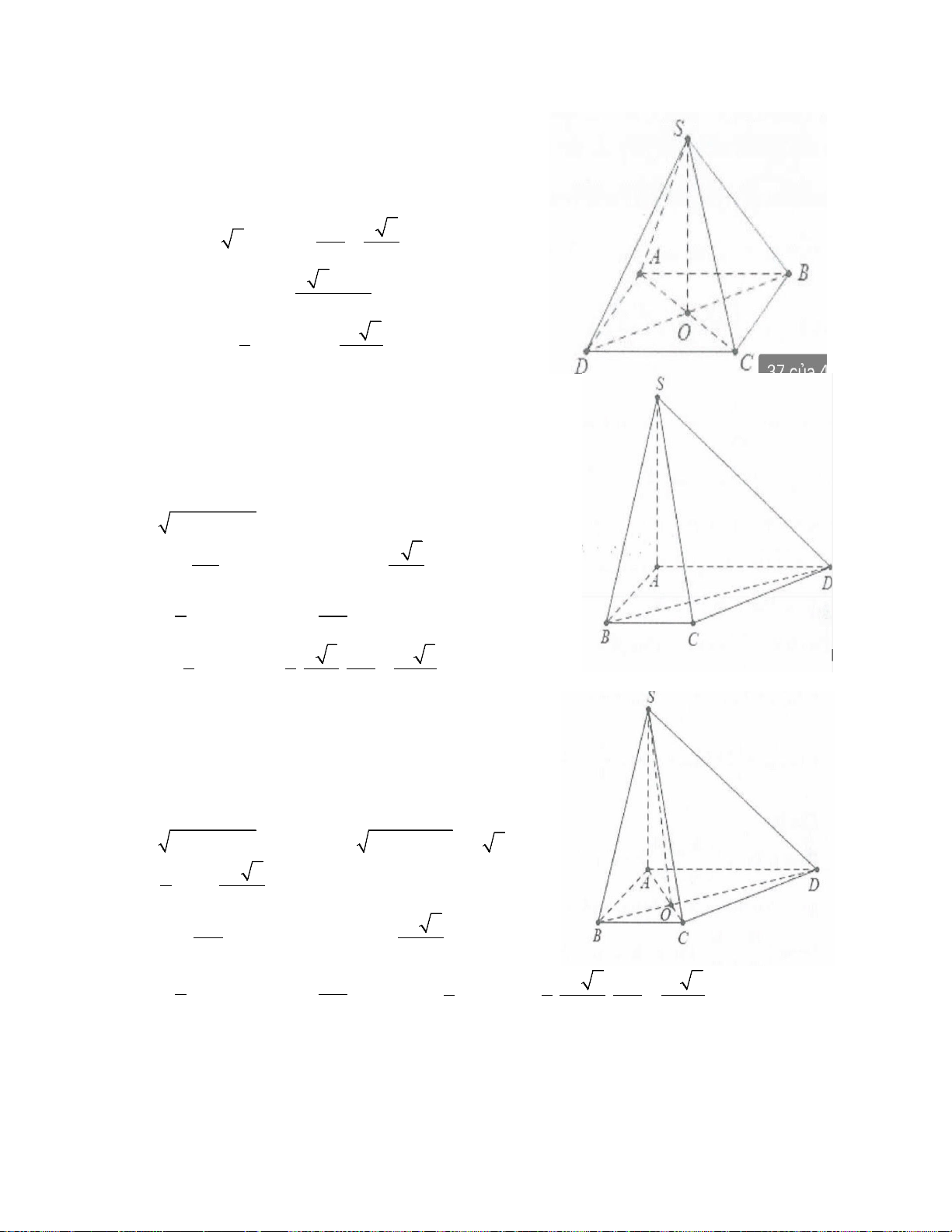
Ví dụ 1: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với đáy, đường
thẳng SC tạo với đáy một góc 60°. Thể tích khối chóp S.ABC bằng? 3 3 3 3 A. a . B. a . C. a . D. 3a . 8 4 2 4
Lời giải:
Chú ý: Nếu tam giác ABC đều cạnh a thì độ dài đường trung tuyến bằng m = a 3 2 Ta có: ⊥ ⇒  =  SA (ABC) (SC;(ABC)) SCA = 60° 2 SA a 3 ⇒ tan 60° =
⇒ SA = AC tan 60° = a 3,S = A ABC C 4 2 3 1 1 a 3 ⇒ = . a V SA S = a = ABC 3. 3 3 4 4 Chọn B
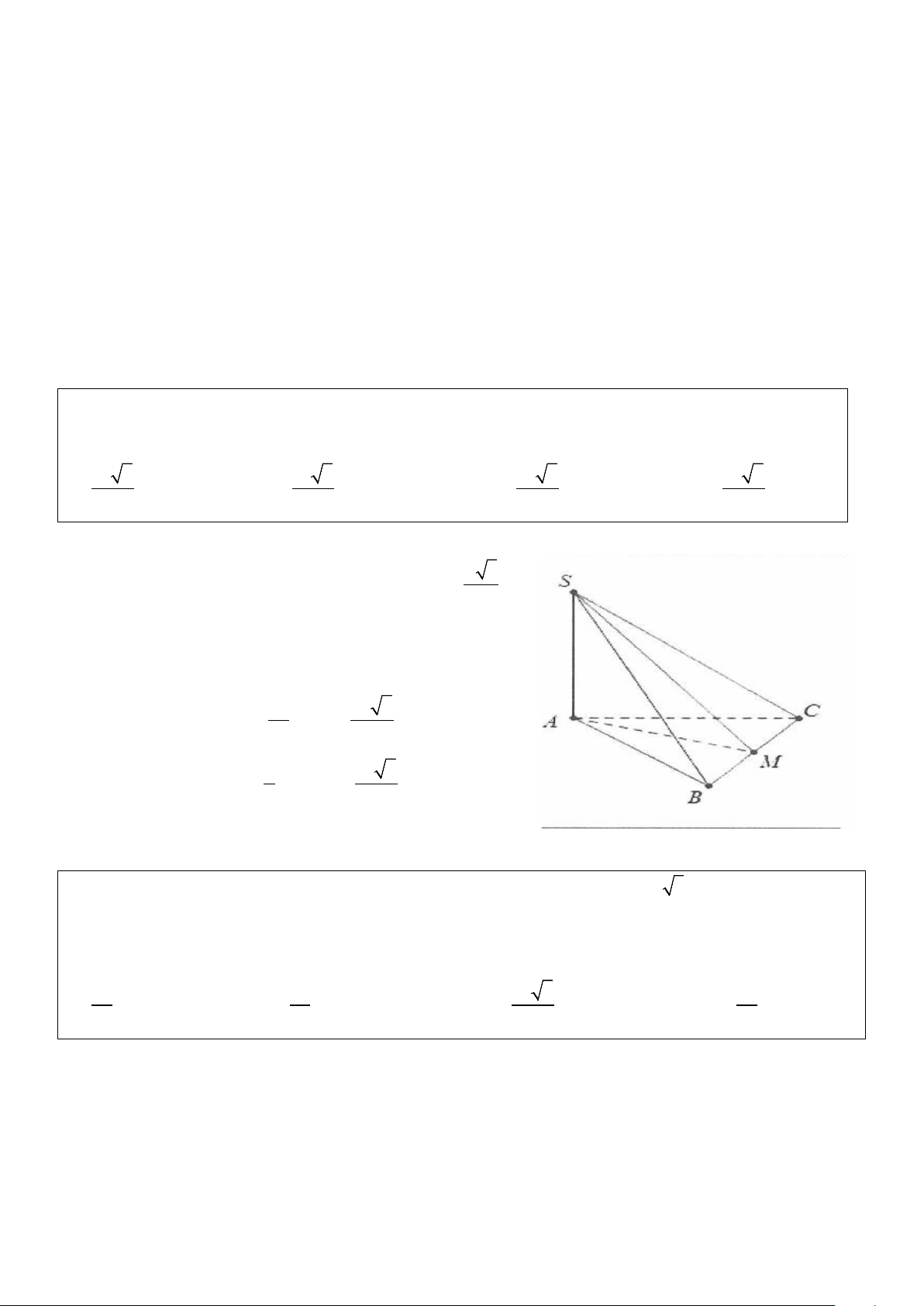
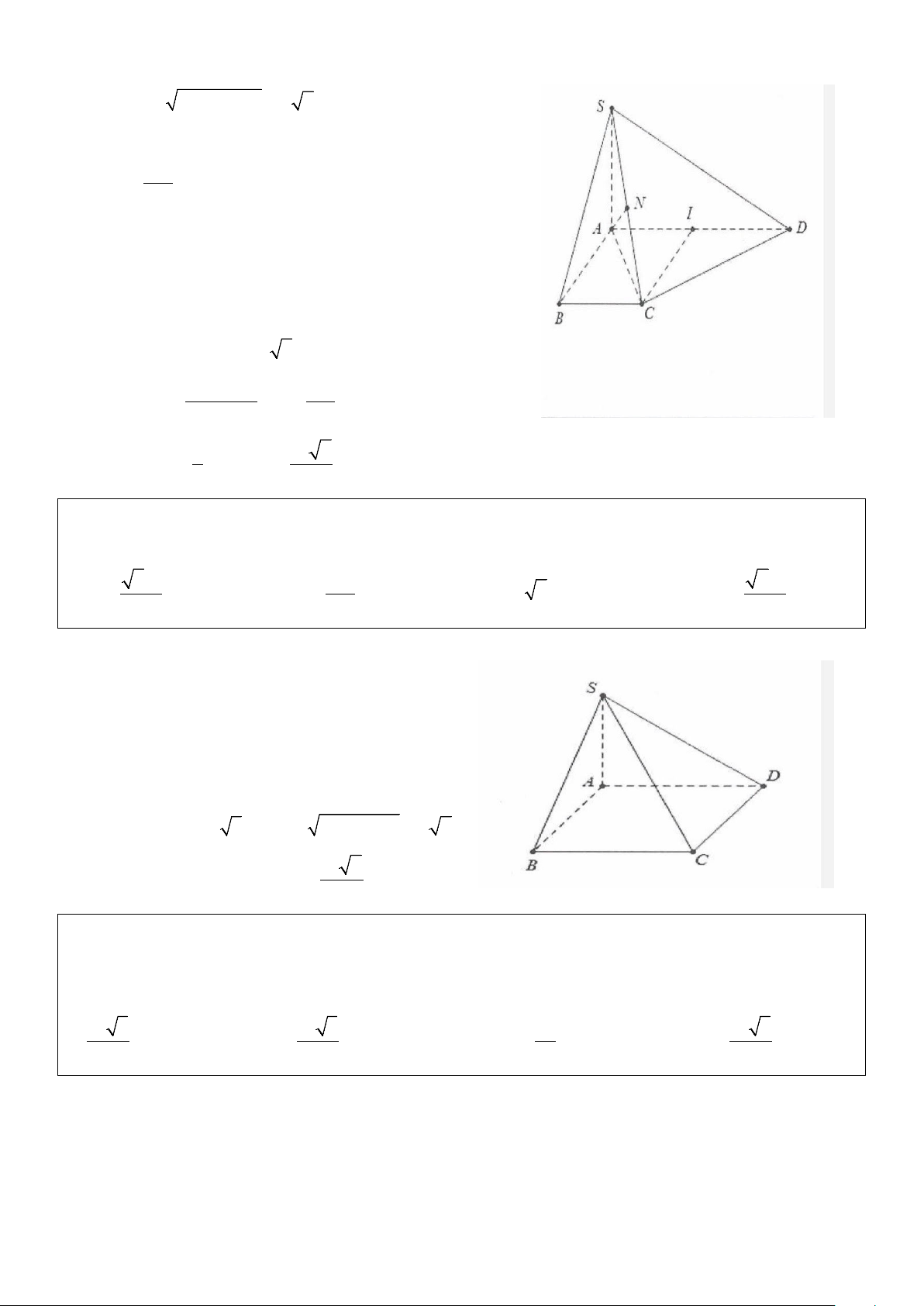
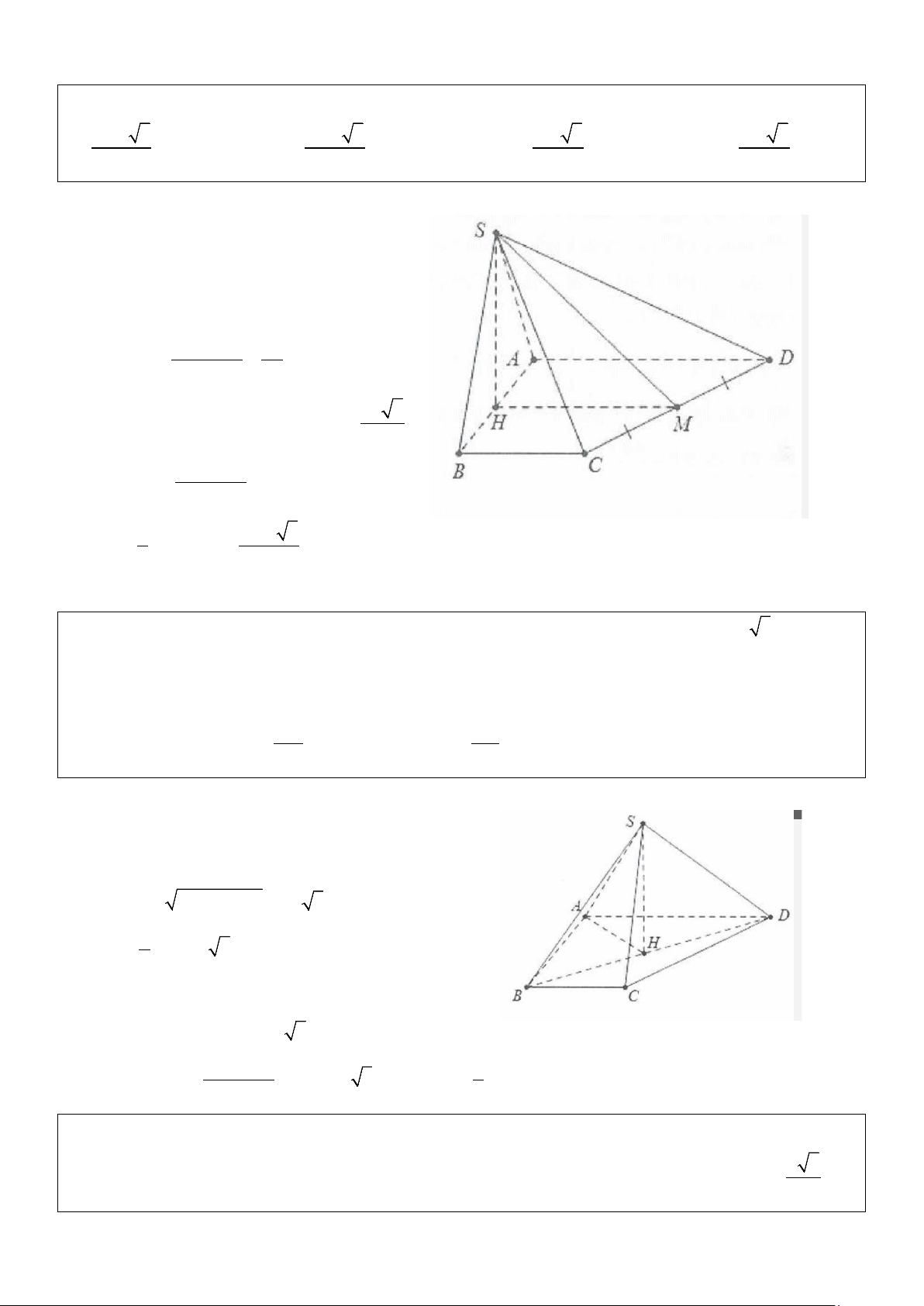
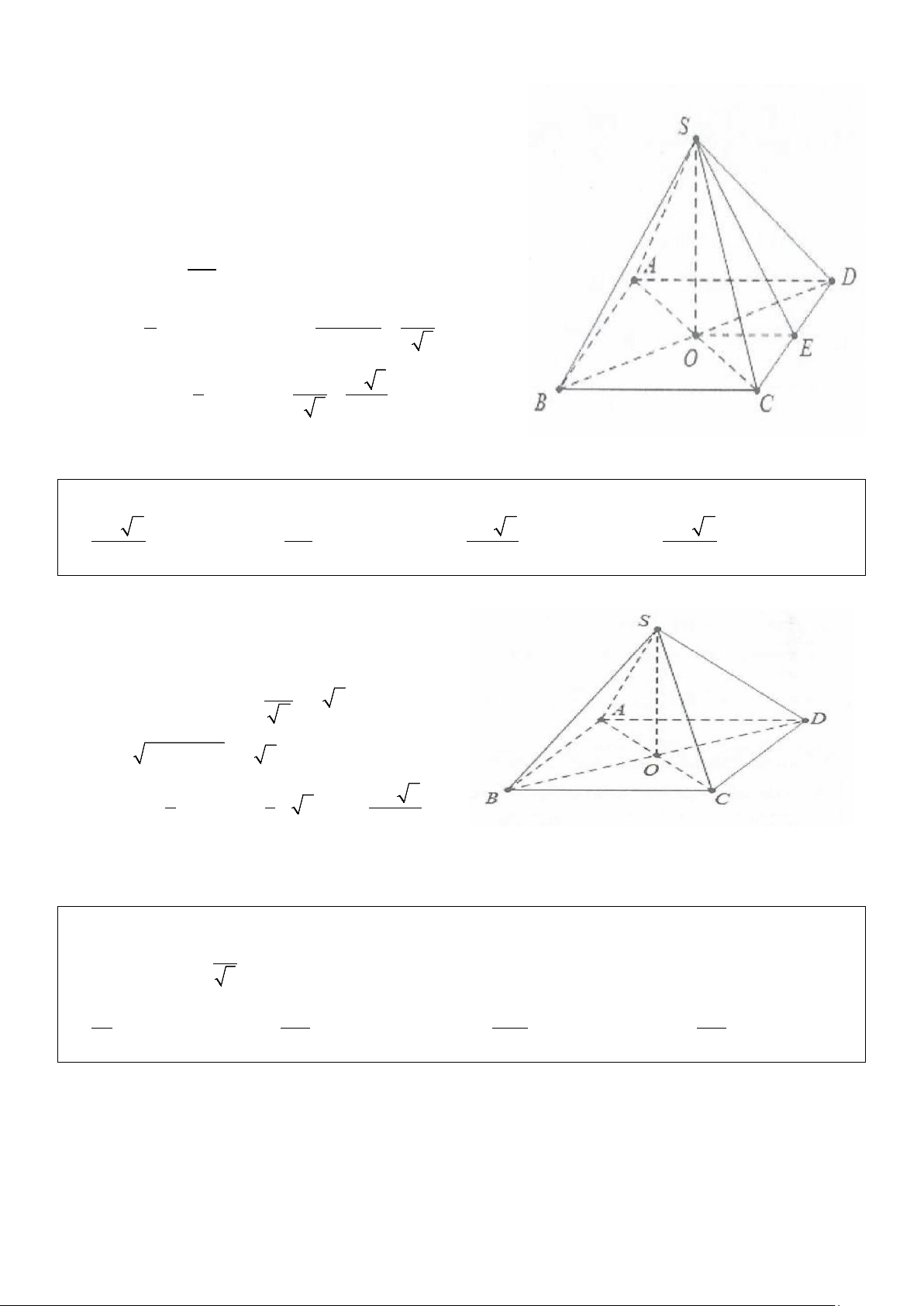
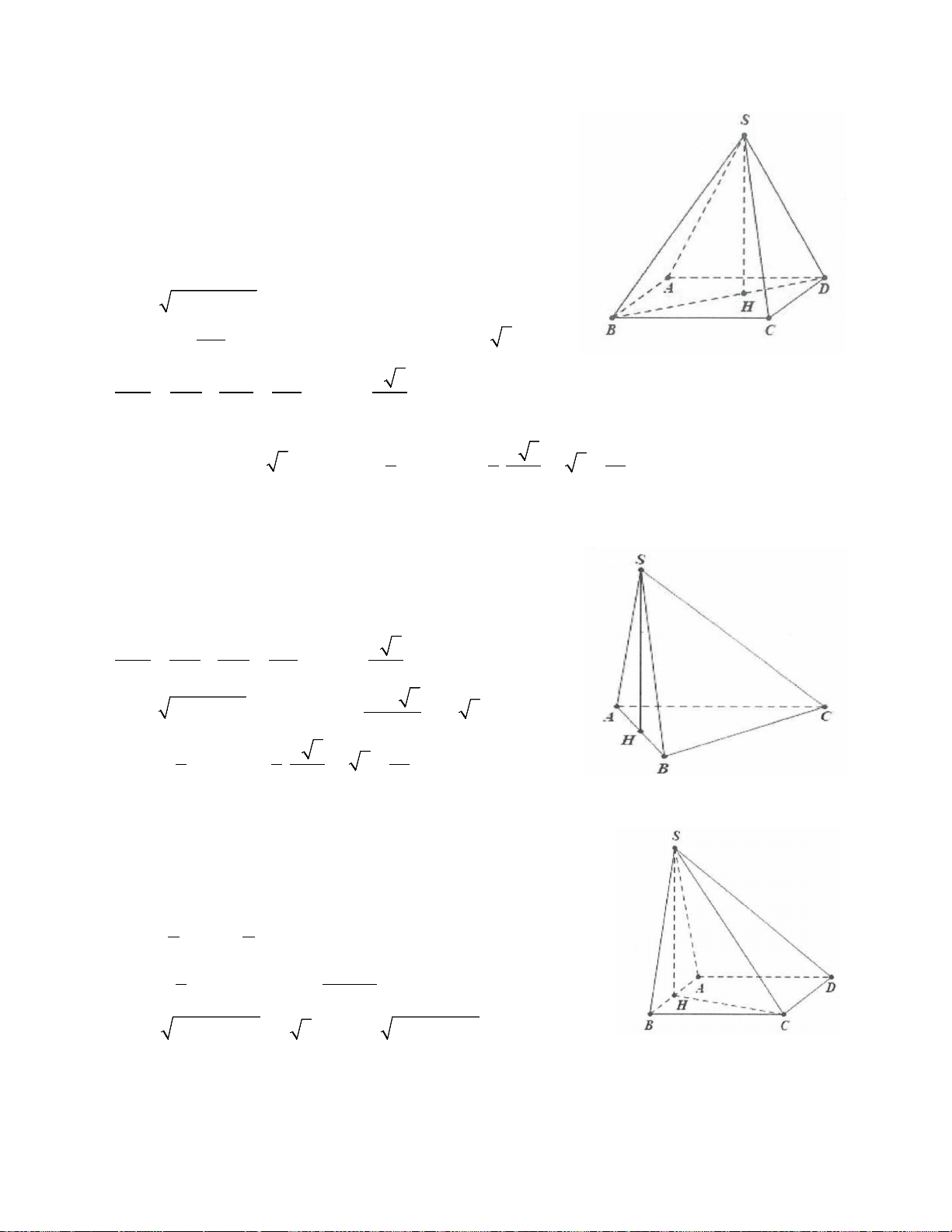
Ví dụ 2: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, hình chiếu vuông góc của S lên mặt phẳng
(ABCD) trùng với trung điểm của cạnh AD, cạnh bên SB hợp với đáy một góc 60°. Tính theo a thể tích V
của khối chóp S.ABCD 3 3 3 3 A. V a 15 = . B. V a 15 = . C. V 5 = a . D. V a 15 = . 2 6 4 18 Lời giải
Gọi H là trung điểm của AD ⇒ AH ⊥ (ABCD) Ta có: 2  a  2 a 5 BH = +  a =   2  2 a 5 a 15
SH = BH tan 60° = . 3 = 2 2 3 1 1 a 15 2 a 15 V = SH S = = S ABCD . ABCD . .a . 3 3 2 6 Chọn B.
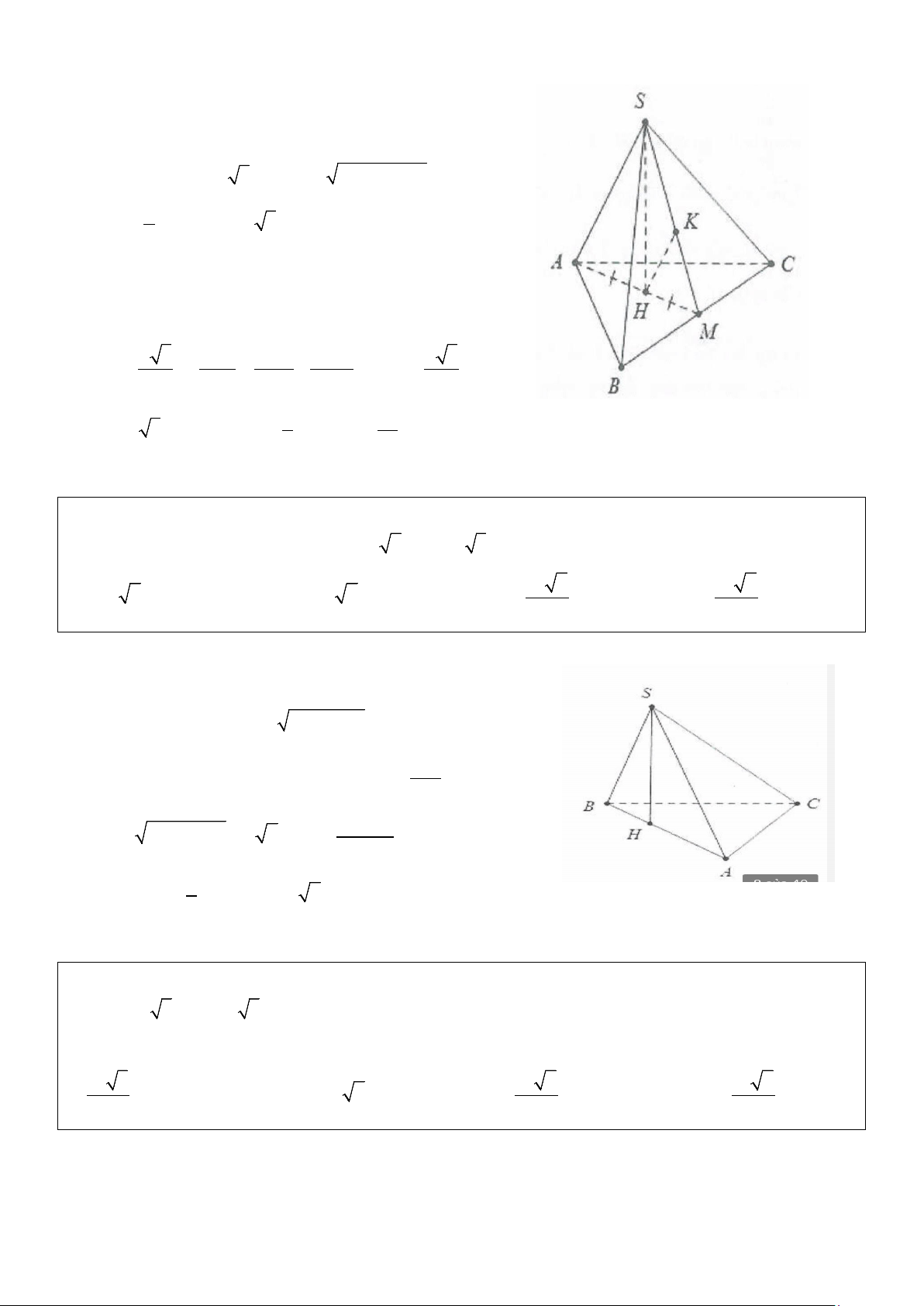
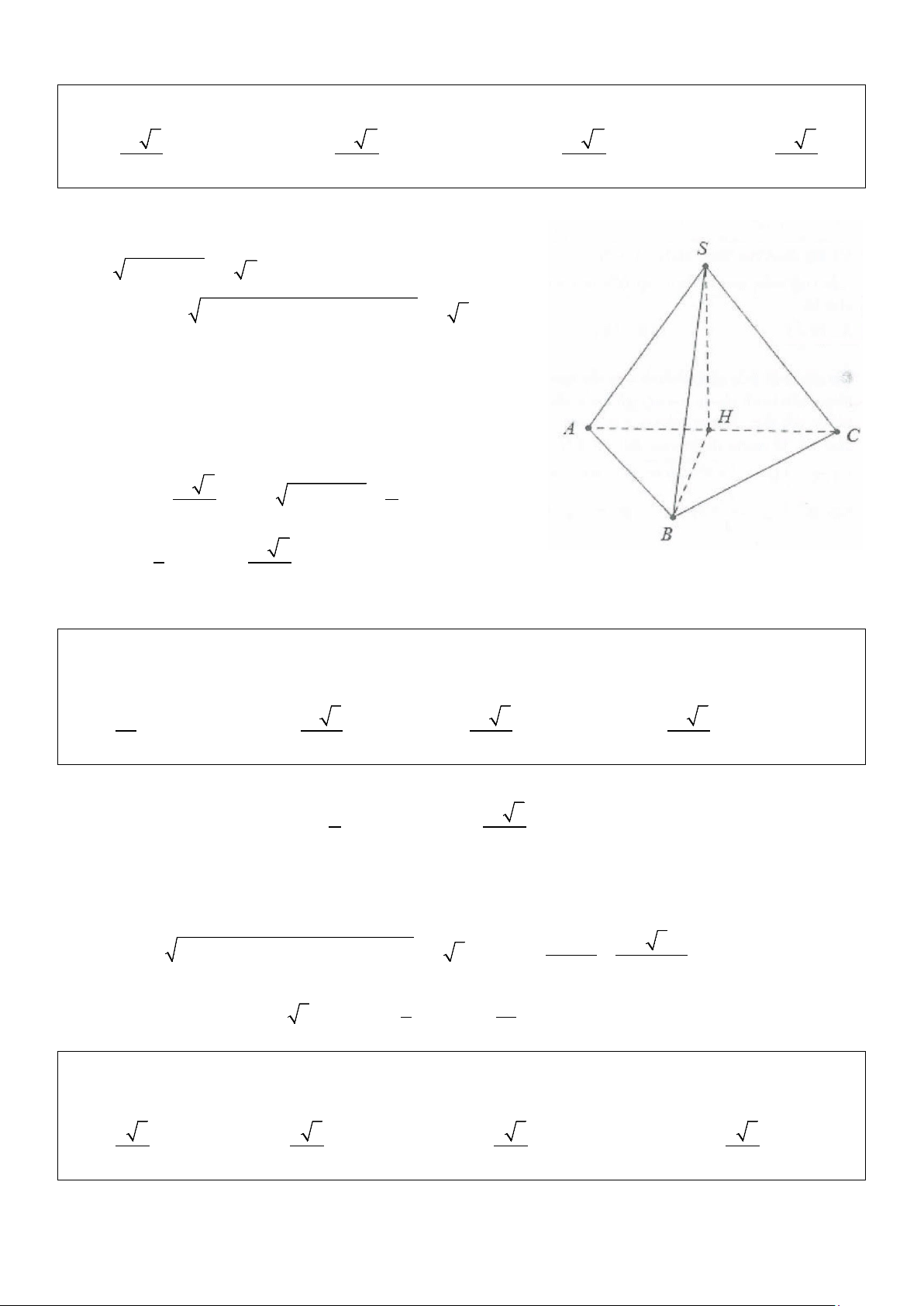
Ví dụ 3: Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, SA ⊥ (ABC) . Biết mặt phẳng (SBC)
tạo với đáy một góc 60°. Thể tích khối chóp S.ABC là 3 3 3 3
A. a 3 . B. a 3 . C. a 3 . D. a 3 . 24 8 6 18 Lời giải:
Gọi M là trung điểm của BC ⇒ AM ⊥ BC và a 3 AM = . 2 Lại có:
BC ⊥ SA ⇒ BC ⊥ SMA ⇒  SBC ABC =  ( ) (( );( )) SMA = 60°. 2 Khi đó 3a a 3
SA = AM tan 60° = ,S = ABC . 2 4 3 Thể tích khối chóp là: 1 a 3 V = . SA S = . Chọn B. 4 ABC 8
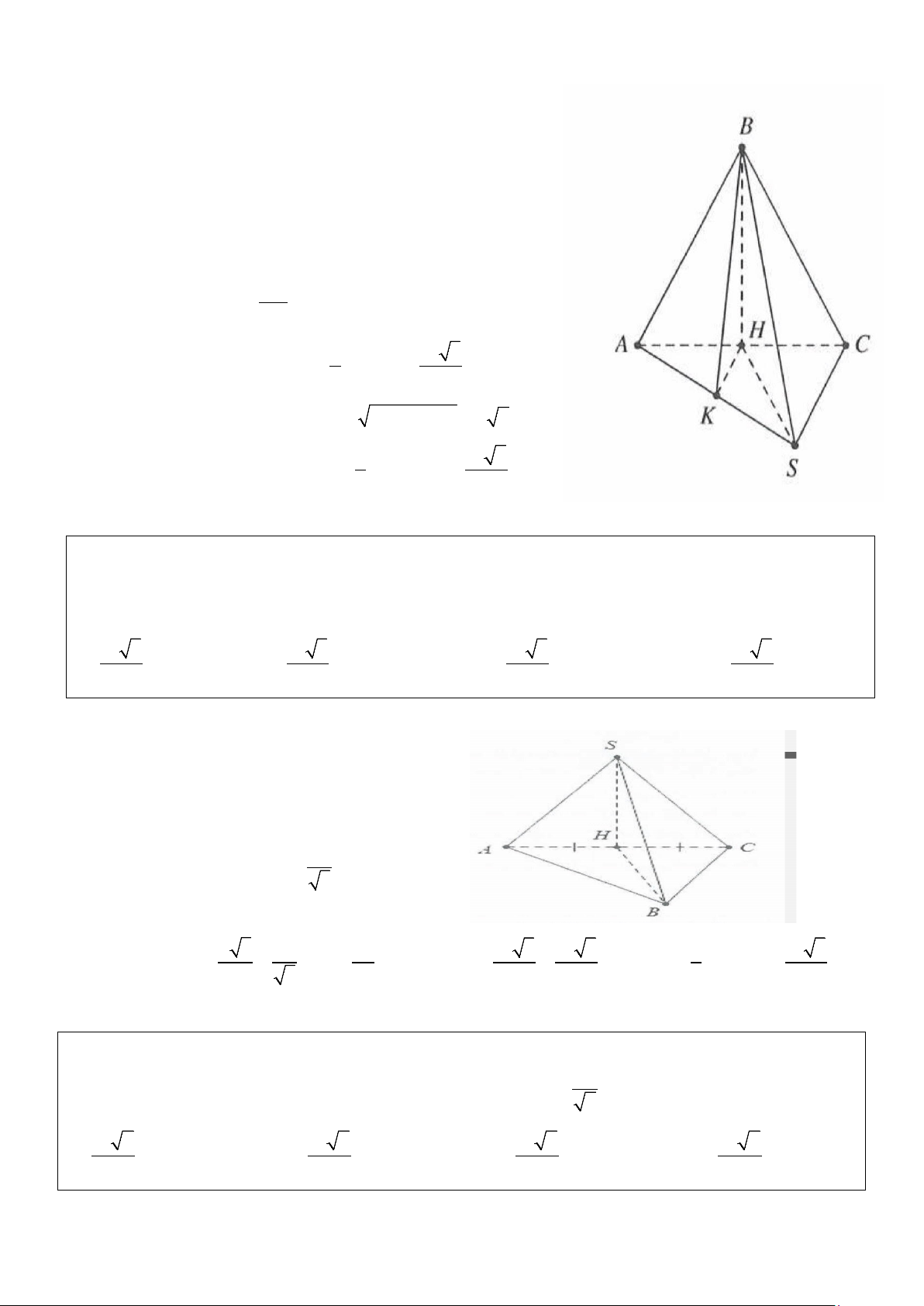
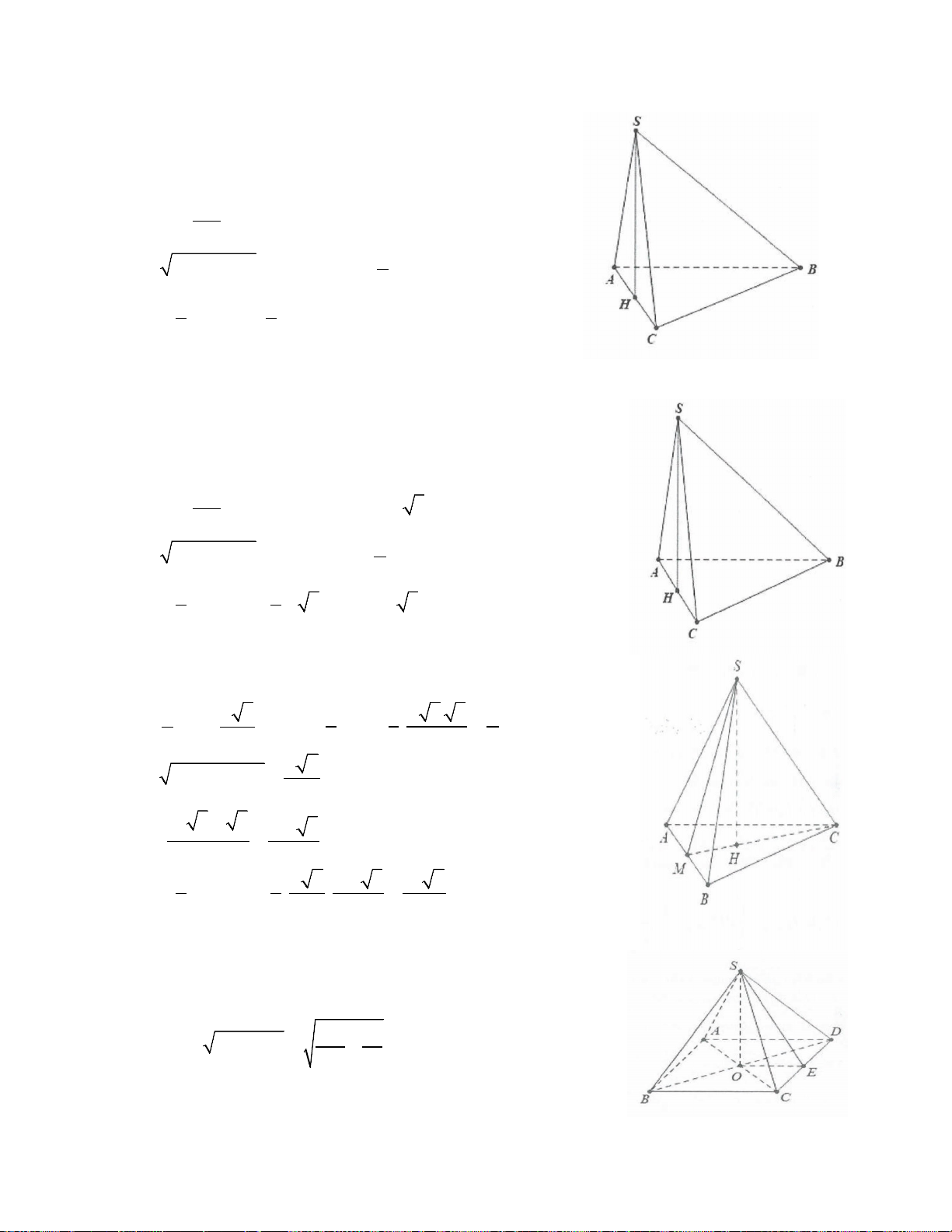
Ví dụ 4: Cho hình chóp S.ABC có đáy là tam giác vuông tại B có AB=a, BC= a 3 . Hình chiếu của đỉnh
S trên mặt phẳng đáy trùng với trung điểm của cạnh AC. Biết SB tạo với đáy một góc 30° . Thể tích khối chóp S.ABC là: 3 3 3 3
A. a . B. a . C. a 3 . D. a . 2 4 6 6 Lời giải:
Gọi H là trung điểm của AC ⇒ AH ⊥ (ABC). Khi đó  = 
(SB);(ABC)) SBH. Ta có: 2 2
AC = AB + BC = 2 . a
Tam giác ABC có đường trung tuyến BH ứng với cạnh huyền nên AC BH = = . a Do  = 30° ⇒ = tan 30 a SBH SH HB ° = . 2 3 2 Lại có: 1 a 3 S = BA BC = ABC . 2 2 2 3 Suy ra: 1 1 a a 3 a V = SH = = Chọn D. S ABC .SABC . . . . 3 3 3 2 6
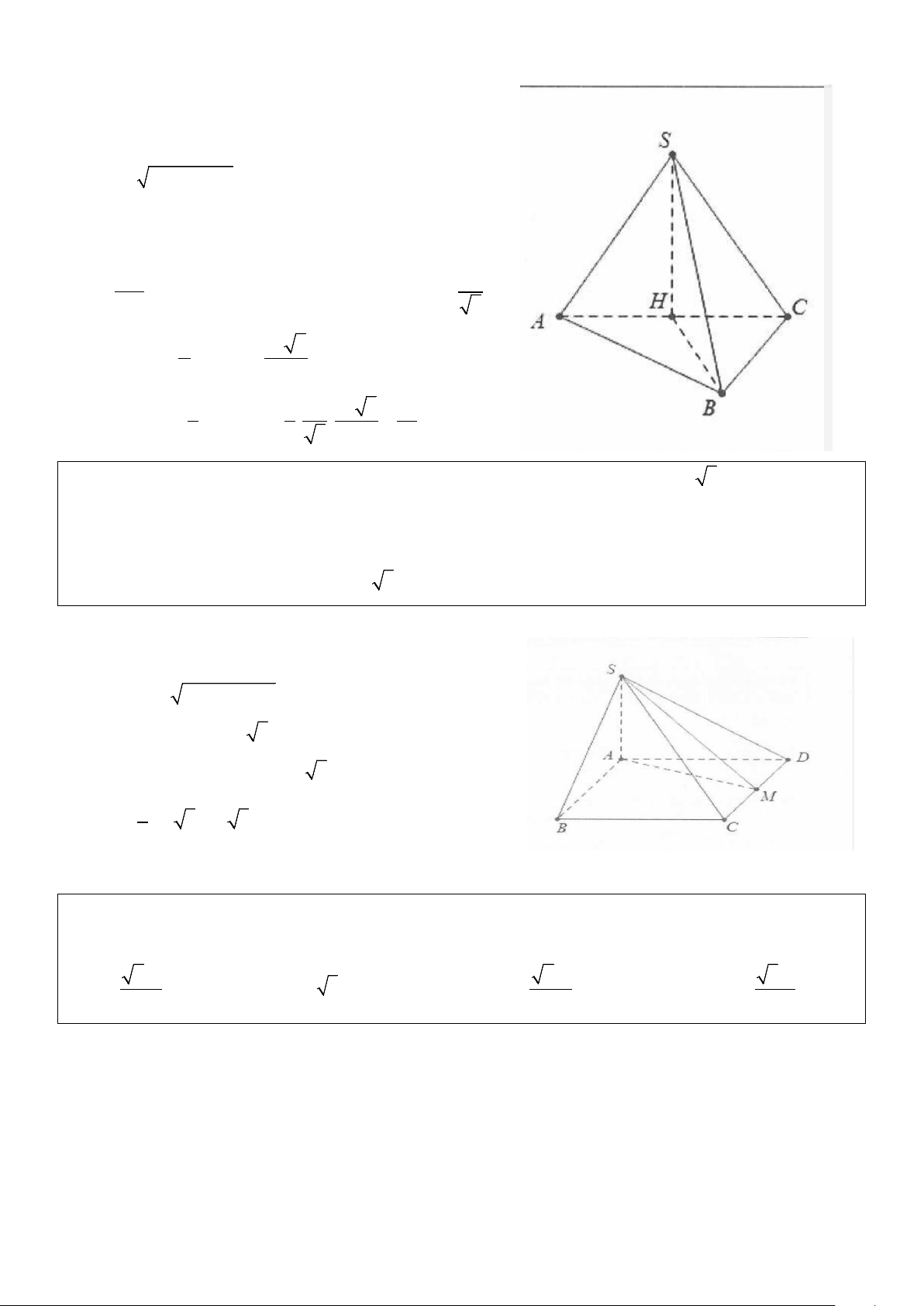
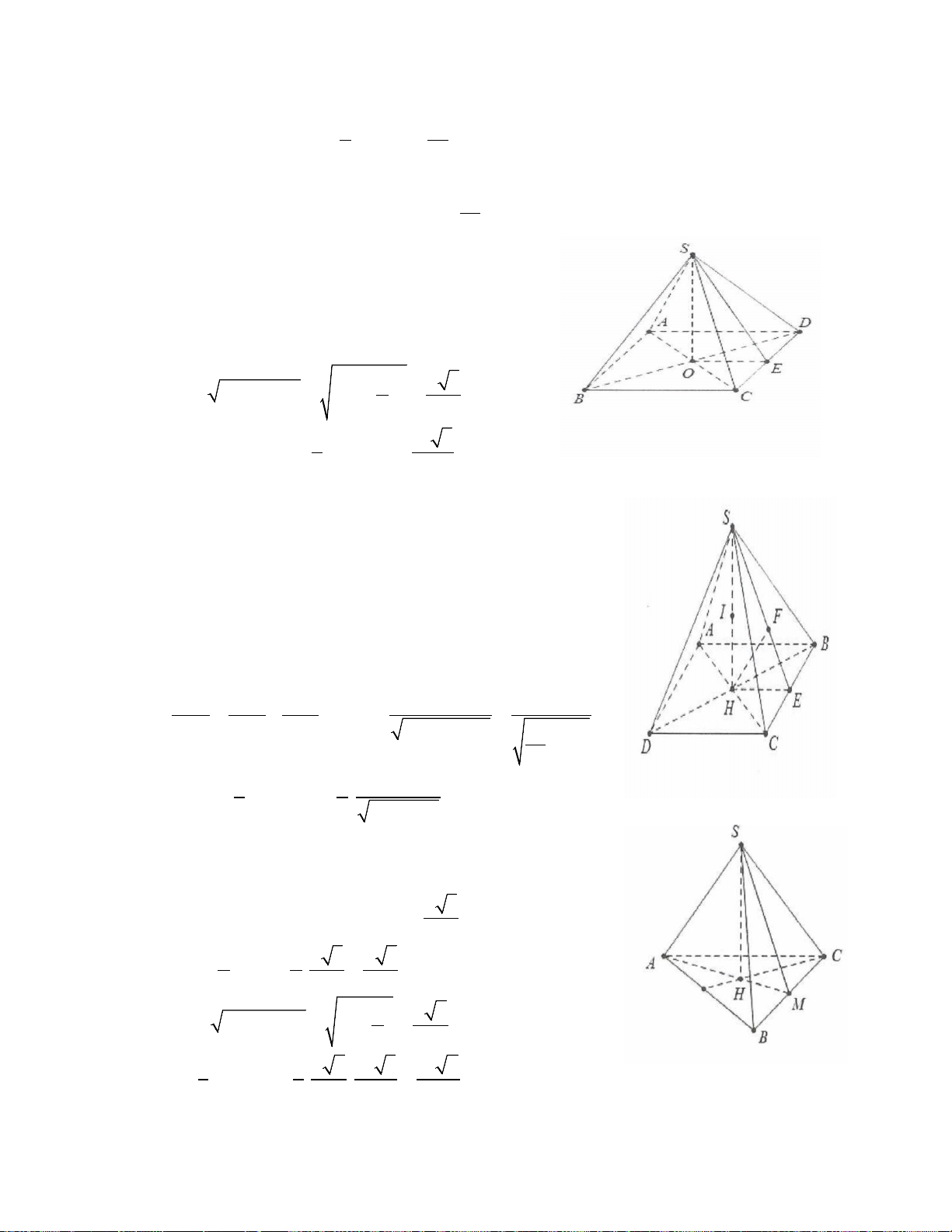
Ví dụ 5: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có AB= 2a, AD= a 3 , cạnh bên SA
vuông góc với đáy, gọi M là trung điểm của cạnh CD. Biết SM tạo với mặt phẳng (ABCD) một góc 60°,
tính thể tích V của khối chóp S.ABCD. A. V= 3 2a . B. V= 3 4a 3 . C. V= 3 12a . D. V= 3 4a . Lời giải:
Do SA ⊥ ABCD ⇒  SM ABCD =  ( ) ( ;( )) SMA = 60 .° Ta có: 2 2
AM = AD + DM = 2a
⇒ SA = AM tan 60 = 2a 3 . Mặt khác 2 S = AB AD = a . ABCD . 2 3 1 2 3 V = a a = a . Chọn D. S ABCD .2 3.2 3 4 . 3
Ví dụ 6: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt đáy, SD tạo với
mặt phẳng (SAB) một góc bằng 30° .Tính thể tích V của khối chóp S.ABCD. 3 3 3
A. V= 6a . B. V= 3
3a . C. V= 6a D. V= 3a . 18 3 3 Lời giải: AD ⊥ AB Ta có: 
⇒ AD ⊥ (SAB) AD ⊥ SA Khi đó:  (SD SAB )=  ;( ) DSA = 30°suy ra
SAtan 30° = AD ⇒ SA = a 3 3 Do đó 1 a 3 V = SA S = . Chọn D. S ABCD . . 3 ABCD 3
Ví dụ 7: Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD có AB= 2a. Hình chiếu vuông góc của
đỉnh S xuống mặt đáy là trung điểm của AB. Biết rằng SA= a 7 và mặt phẳng (SCD) tạo với đáy một
góc 60°. Thể tích khối chóp là: 3 3 3 3
A. 4a 6 . B. 2a 3 . C. 2a 6 . D. 4a 3 . 3 3 3 3 Lời giải: Ta có: 2 2
SH = SA − HA = a 6 . HK ⊥ CD
Dựng HK ⊥ CD ta có:  SH ⊥ CD Suy ra ⊥ ⇒  CD (SHK) SKH = 60° . Khi đó a 6
HK tan 60° = SH ⇒ HK = = a 2 = AD . 3 3 Khi đó 2 1 4a 3 S = a ⇒ V = SH S = . ABCD 2 2 . 3 ABCD 3 Chọn D.
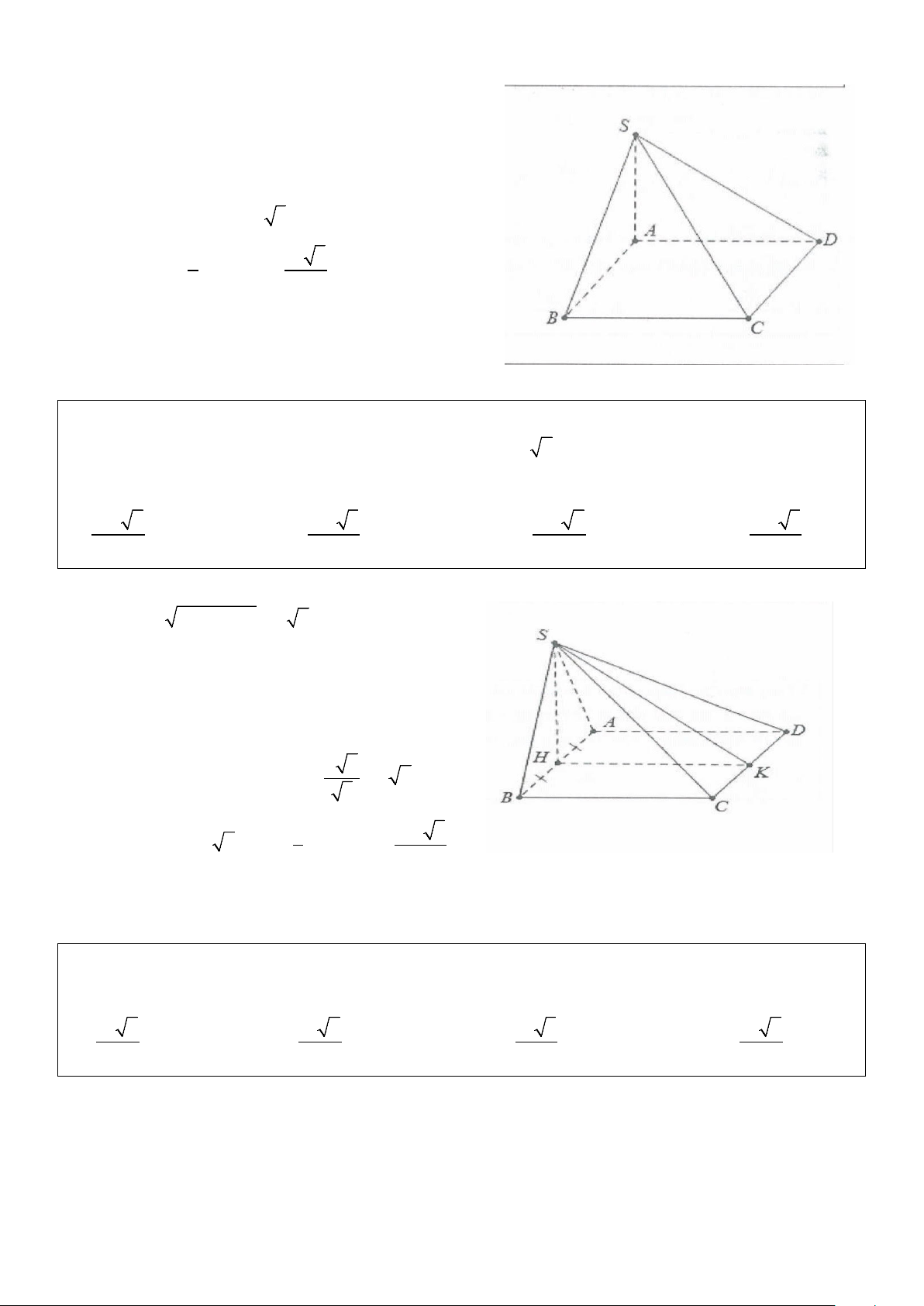
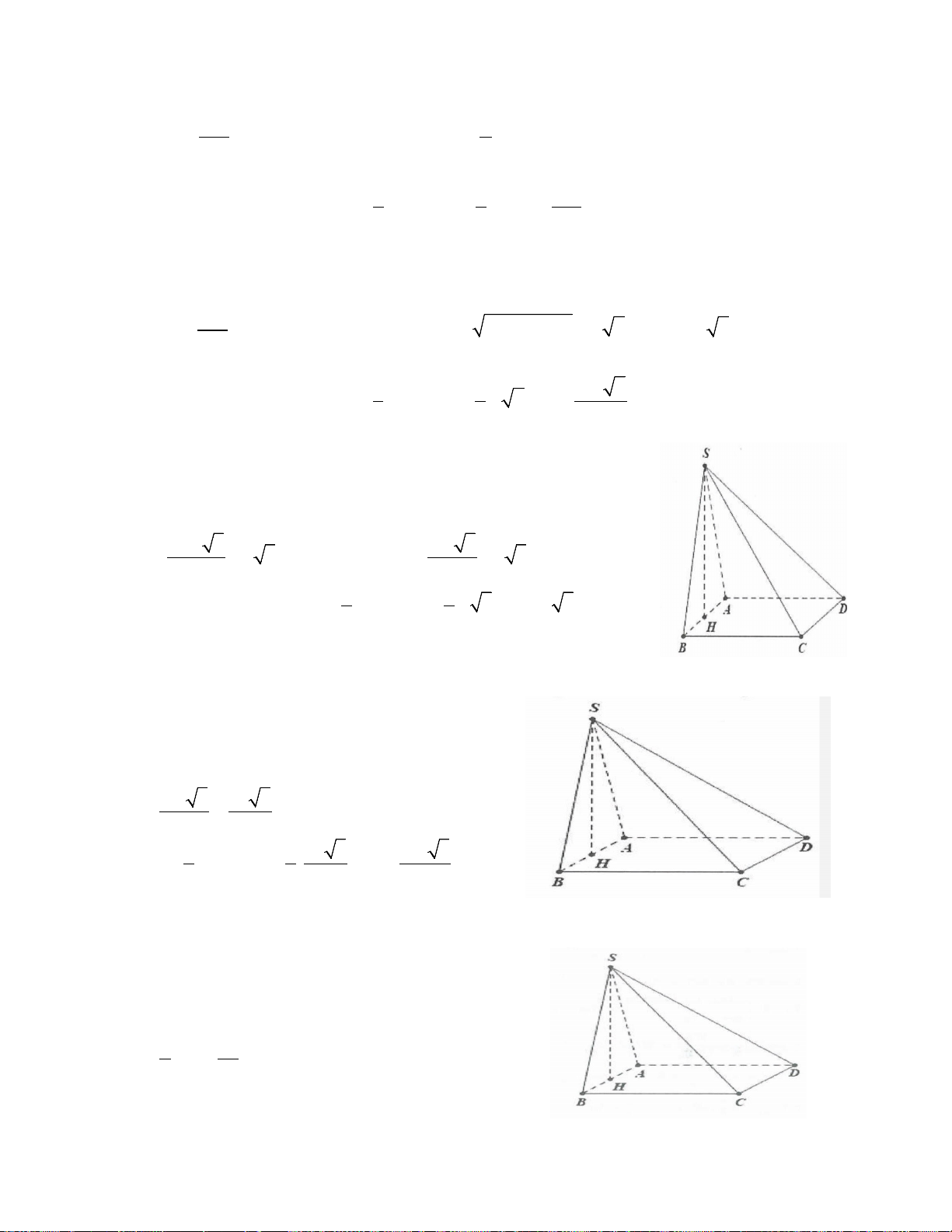
Ví dụ 8: Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B có AD = 2AB= 2CD= 2a và
SA ⊥ (ABCD) . Biết SA tạo với (SCD) một góc 30°. Thể tích khối chóp S.ABCD là: 3 3 3 3
A. a 6 . B. a 6 . C. a 3 . D. a 6 . 6 3 3 2 Lời giải: Ta có: 2 2
AC = AB + BC = a 2
Gọi I là trung điểm của AD ⇒ ABCI là hình vuông cạnh AD a ⇒ CI = = a ⇒ A
∆ CD vuông tại C. 2 CD ⊥ SA Khi đó: 
⇒ CD ⊥ (SAC). CD ⊥ AC Dựng ⊥ ⇒  AN SC (SA SCD )=  =  ;( ) ASN ASC = 30° .
Suy ra SA = AC cot 30° = a 6 . 2 Lại có: AD + BC 3a S = AB = . ABCD . 2 2 3 Do đó 1 a 6 V = SA S = . Chọn D. S ABCD . . 3 ABCD 2
Ví dụ 9: Cho khối chóp S.ABCD có đáy là hình vuông có cạnh a, SA vuông góc với đáy và SC tạo với
mặt phẳng (SAB) một góc 30° . Tính thể tích V của khối chóp đã cho. 3 3 3
A. V= 6a . B. V= 2a . C. V= 3
2a . D. V= 2a . 3 3 3 Lời giải: BC ⊥ AB Ta có: 
⇒ BC ⊥ (SAB) BC ⊥ SA Do đó  (SC SAB )=  ;( ) SCB = 30° Khi đó: 2 2
SB = BC.cot 30° = a 3 ⇒ SA = SB − AB = a 2 3 Mặt khác 2 a 2 S = a ⇒ V = . Chọn D. ABCD S.ABCD 3
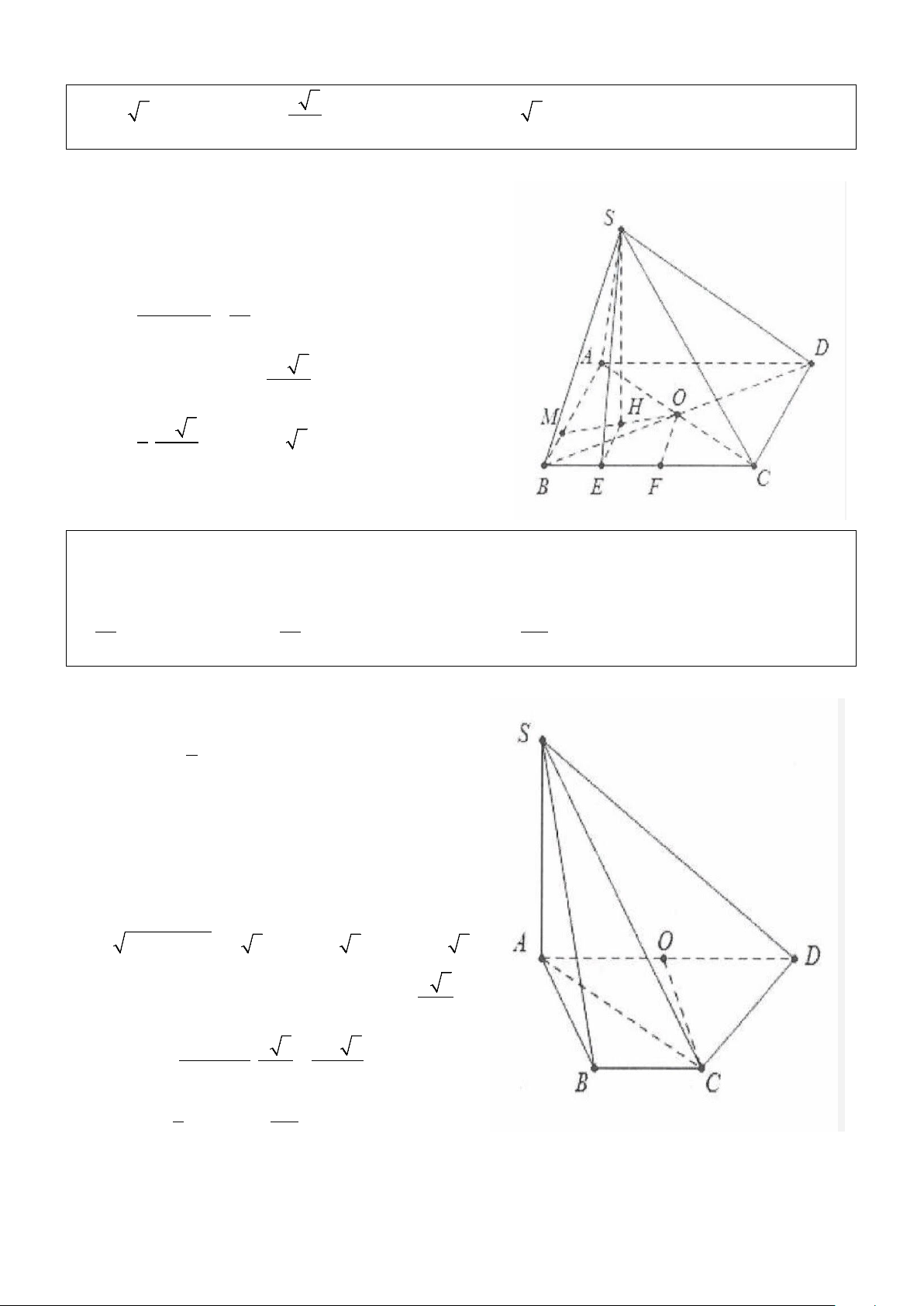
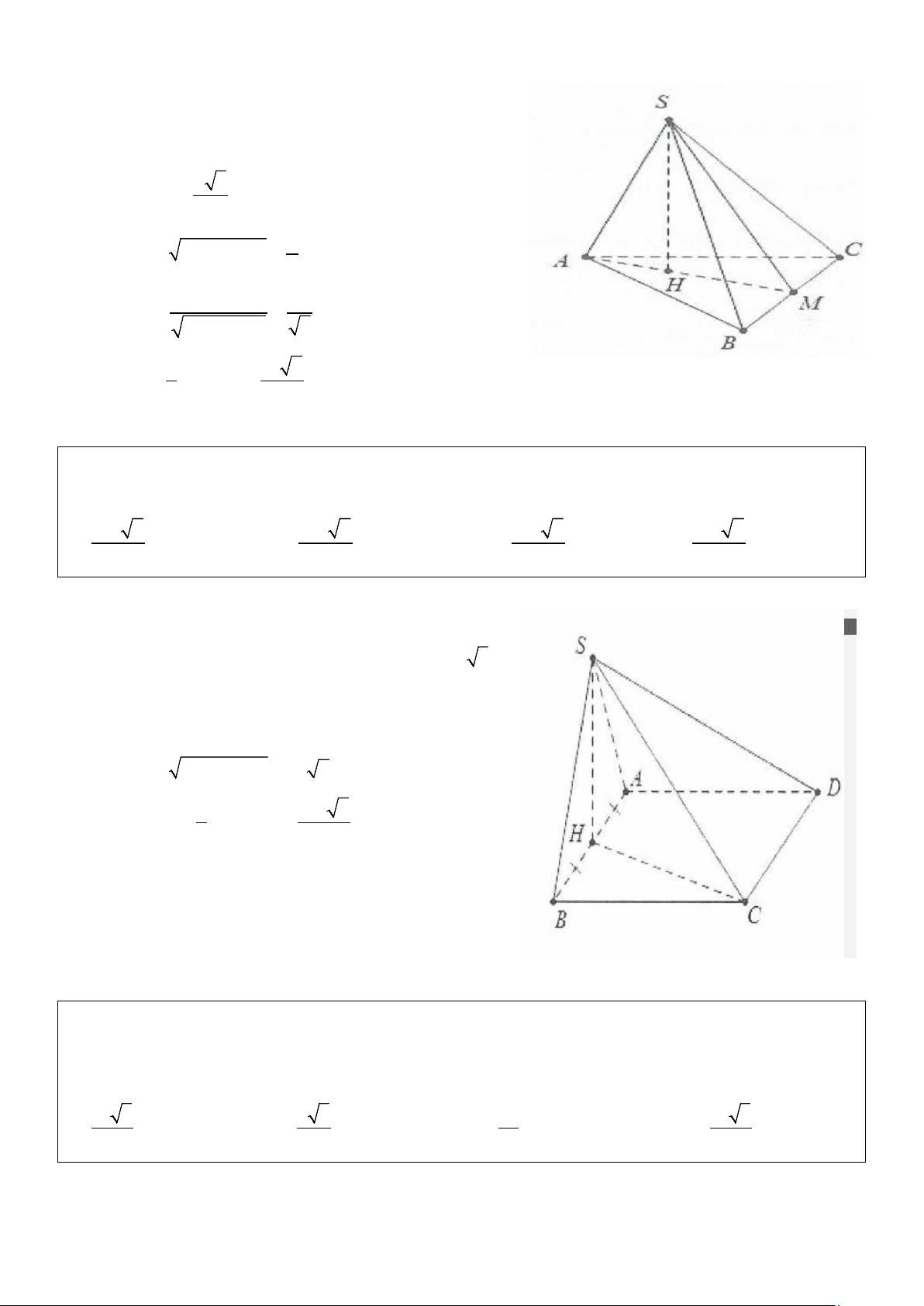
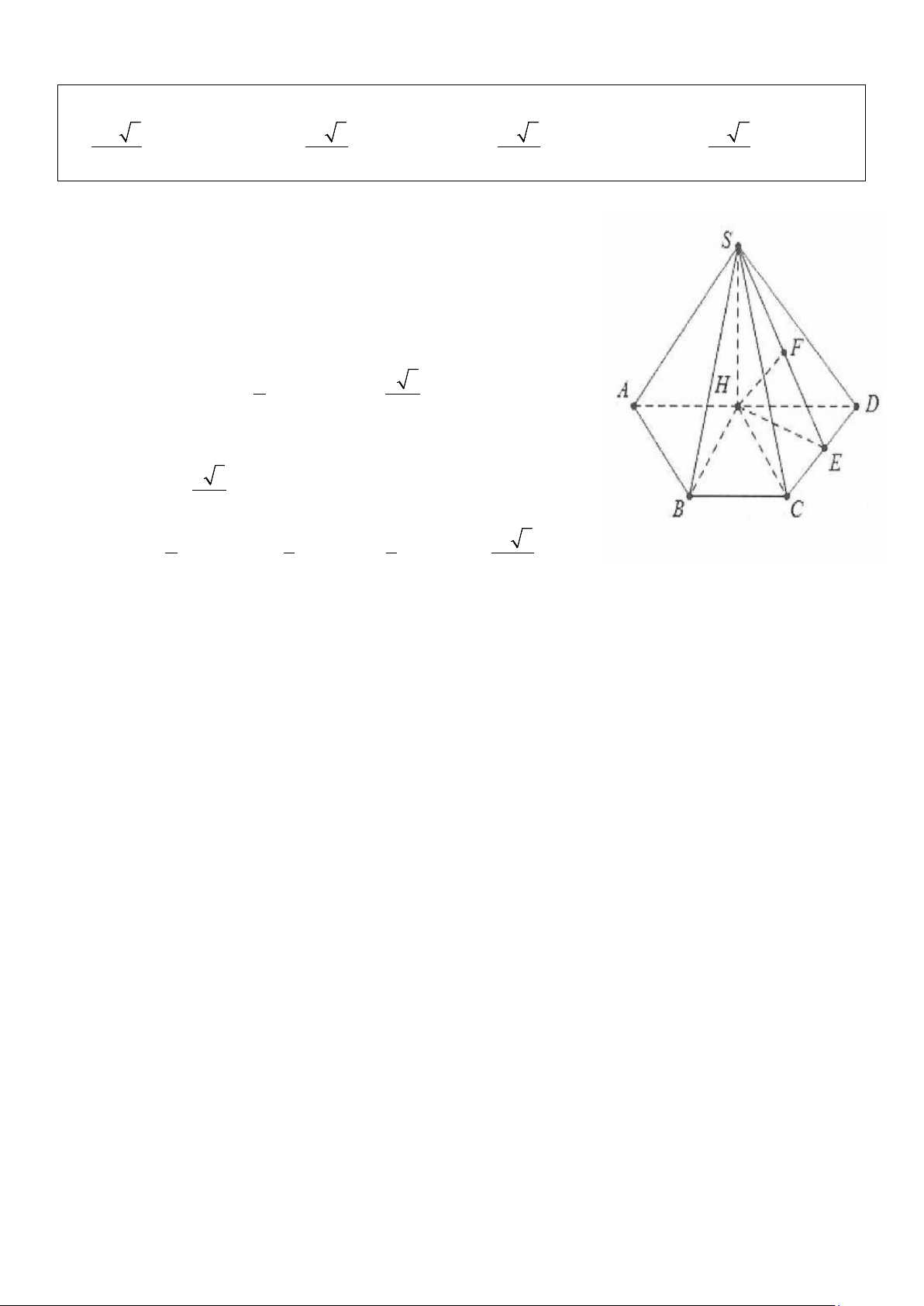
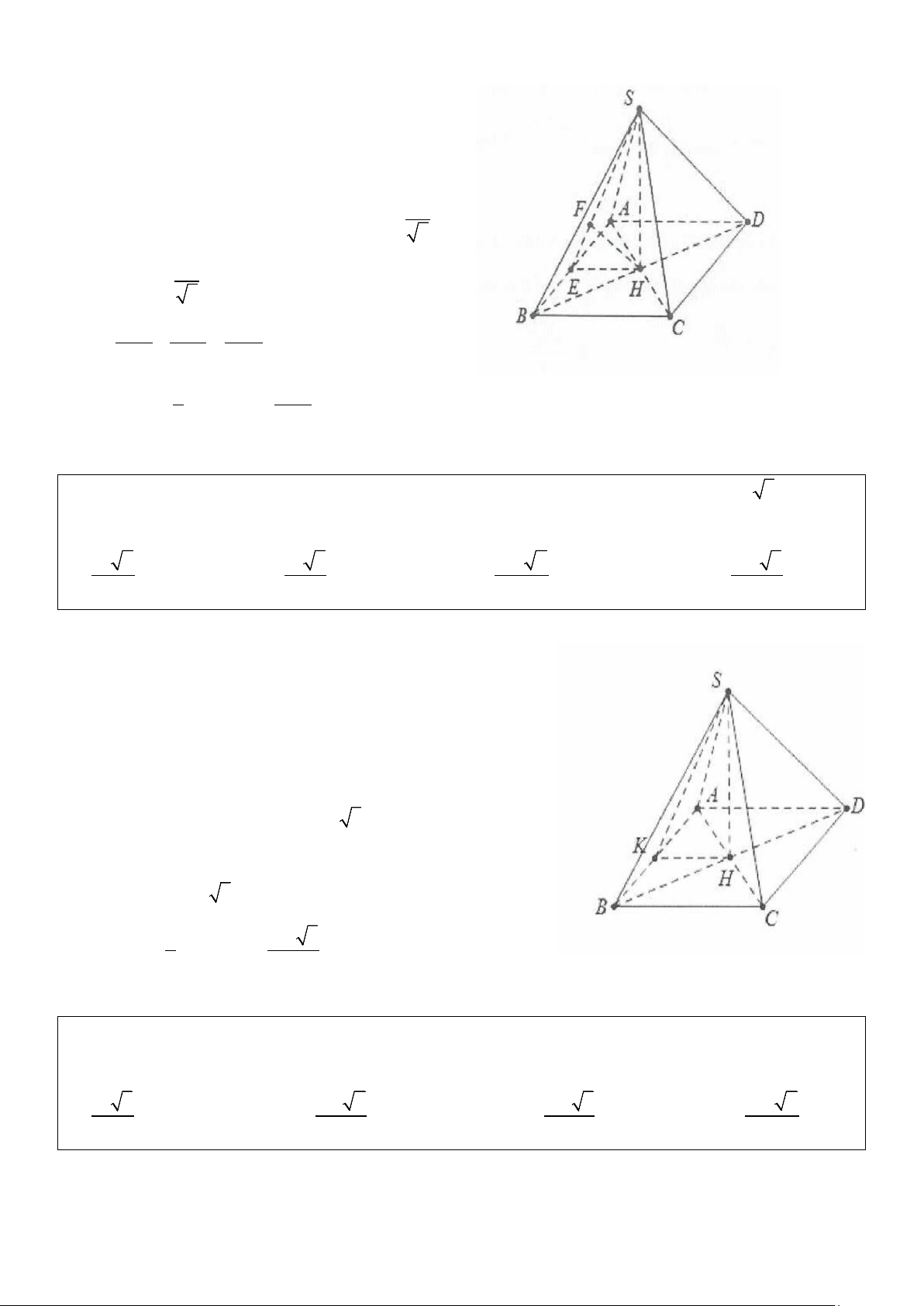
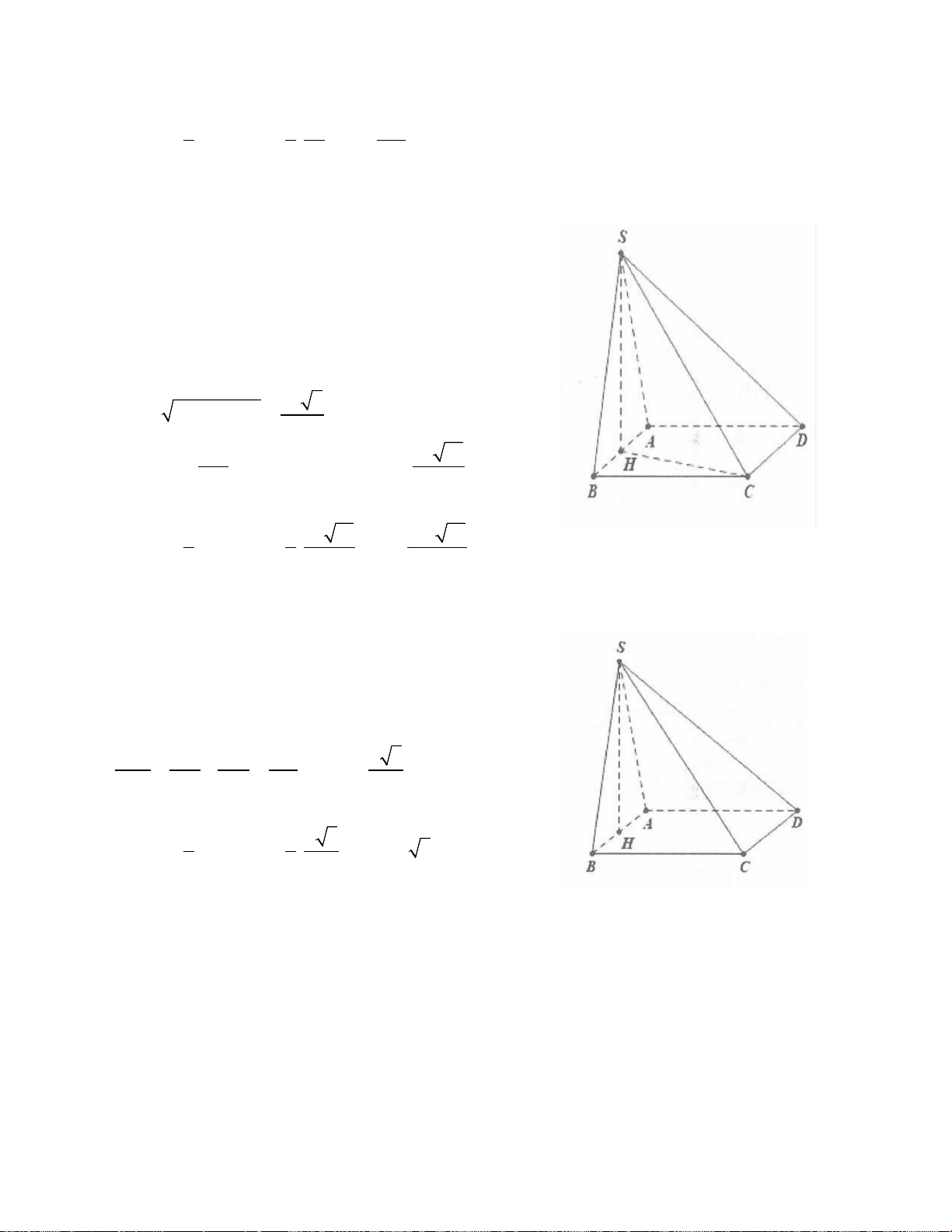
Ví dụ 10: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O cạnh a, hình chiếu vuông góc của
đỉnh S lên mặt phẳng đáy trùng với tâm H của tam giác đều ABC, biết mặt phẳng (SDC) tạo với mặt
phẳng (ABCD) một góc 60°. Thể tích khối chóp S.ABCD là: 3 3 3 3
A. a 3 . B. a 3 . C. a . D. a 3 . 6 6 6 12 Lời giải: Ta có A
∆ BC đều cạnh a nên H là trực tâm của tam giác
ABC ⇒ CH ⊥ AB ⇒ CH ⊥ BC ⇒ ⊥ ⇒  CD (SHC) SCH = 60° . Ta có: a 3 2 a 3 OB =
⇒ BD = a 3 ⇒ HB = HC = OB = . 2 3 3 2 Khi đó: a 3 a 3 SH = .tan 60° = a,S = S ABCD 2 = 3 ABC 2 2 3 1 a 3 a 3 V = . Chọn A. ABCD .a. = S. 3 2 6
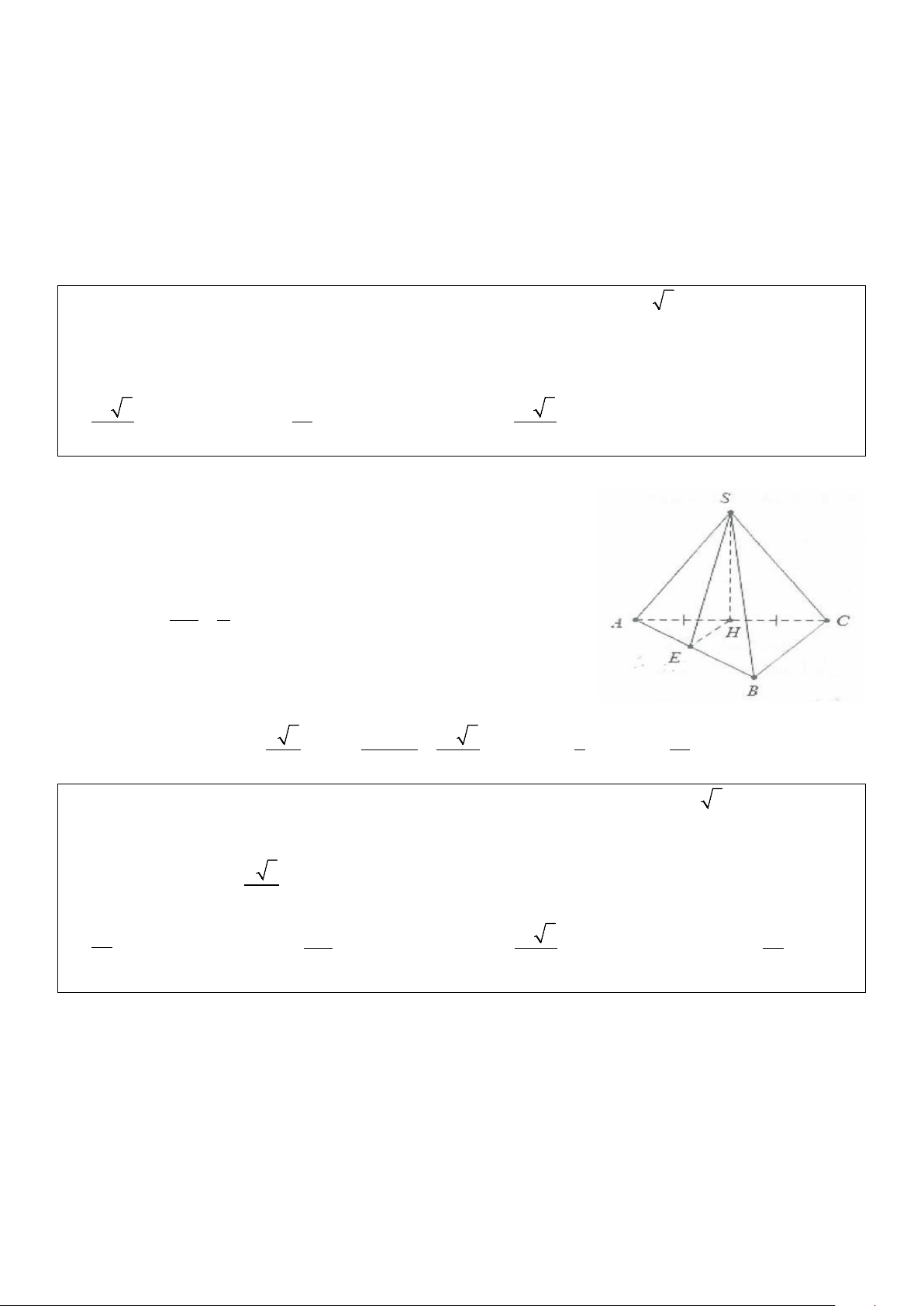
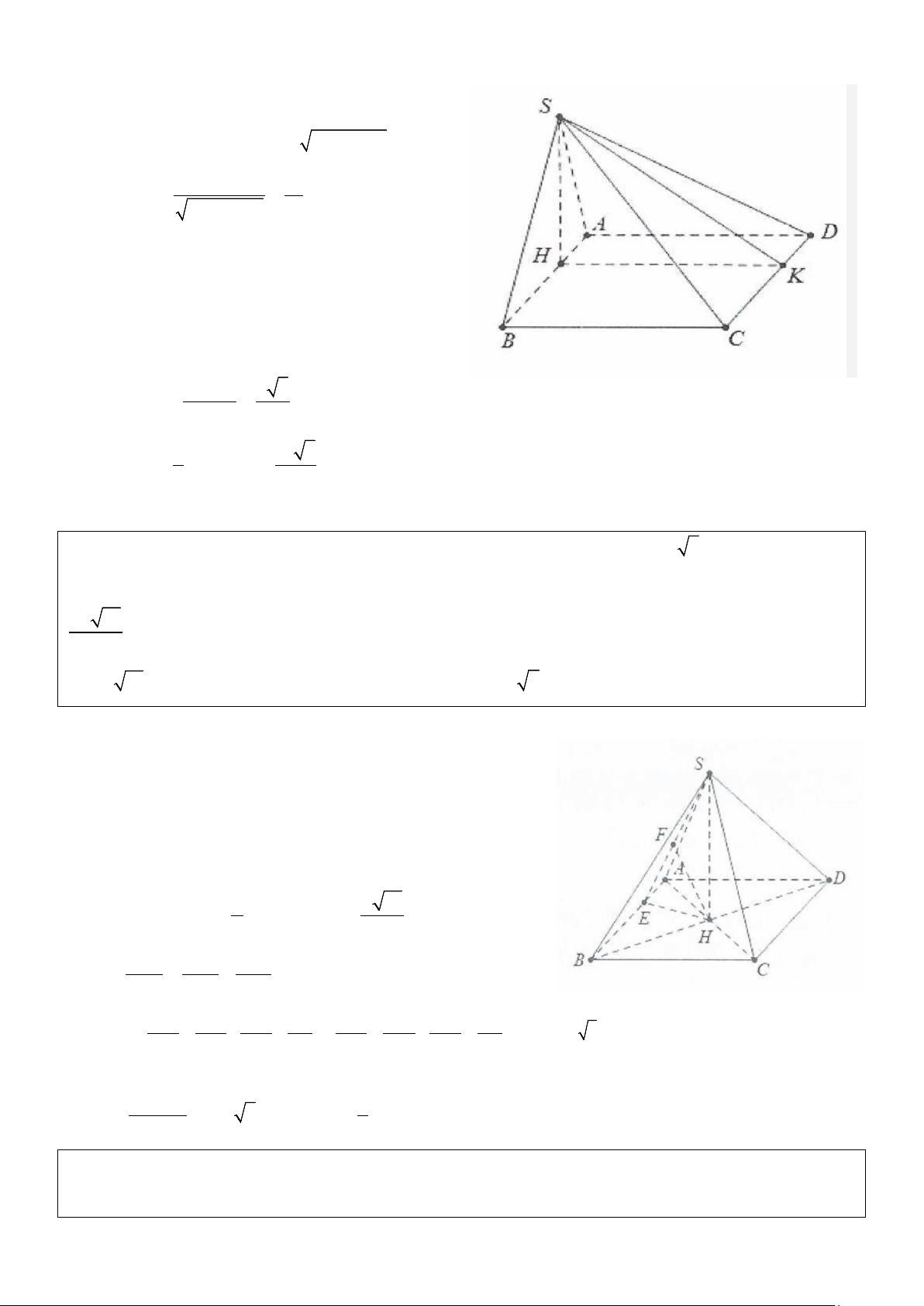
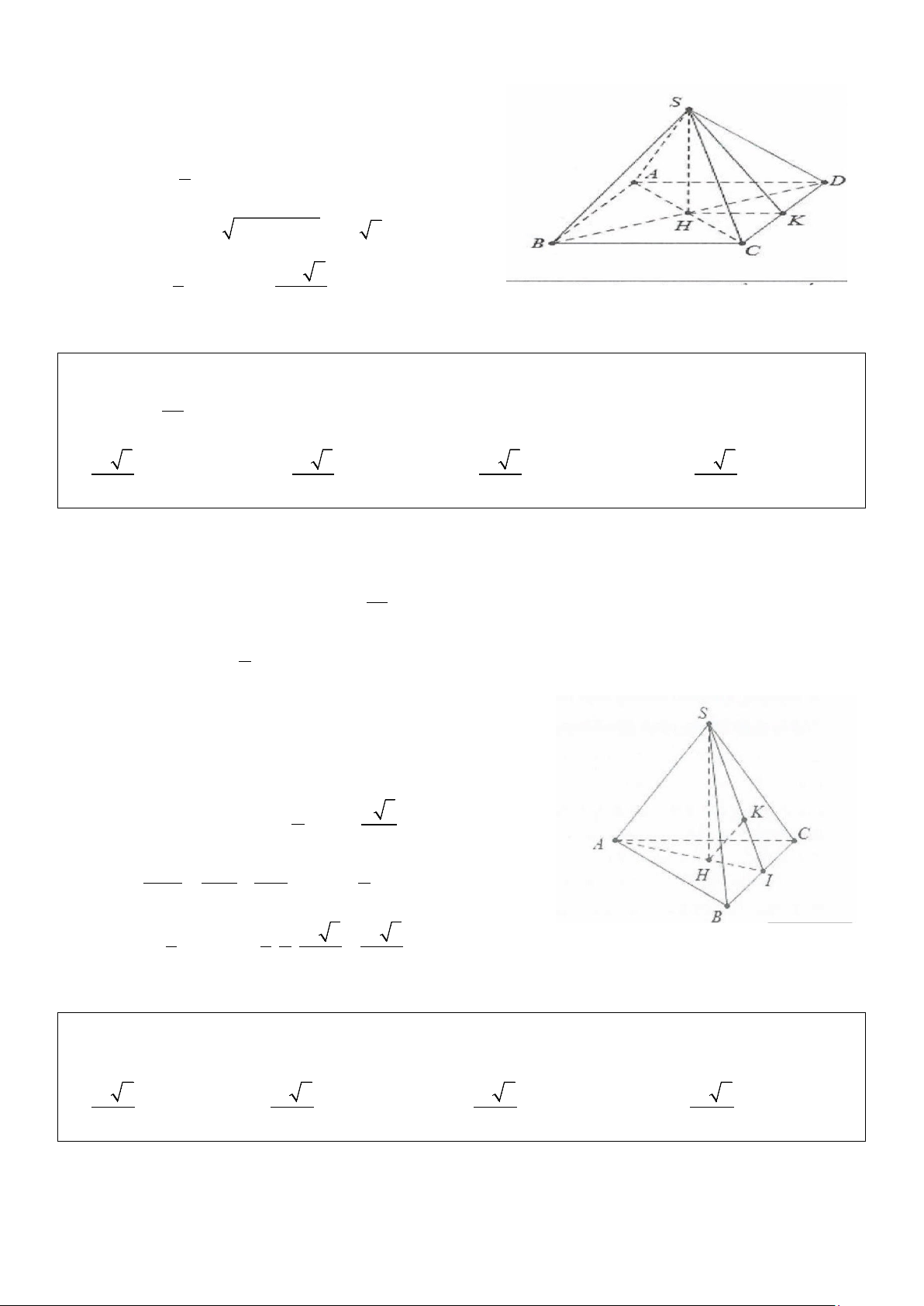
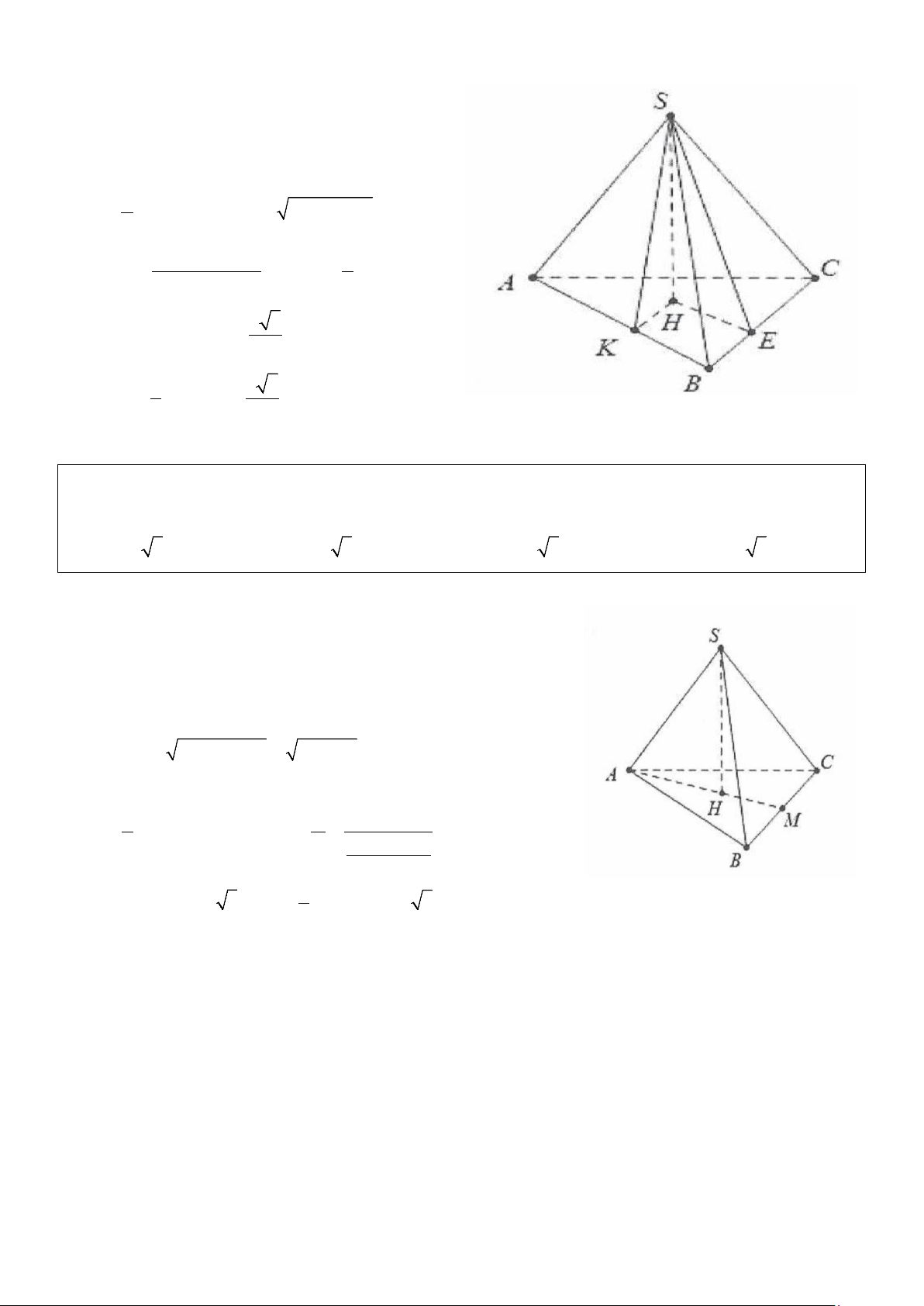
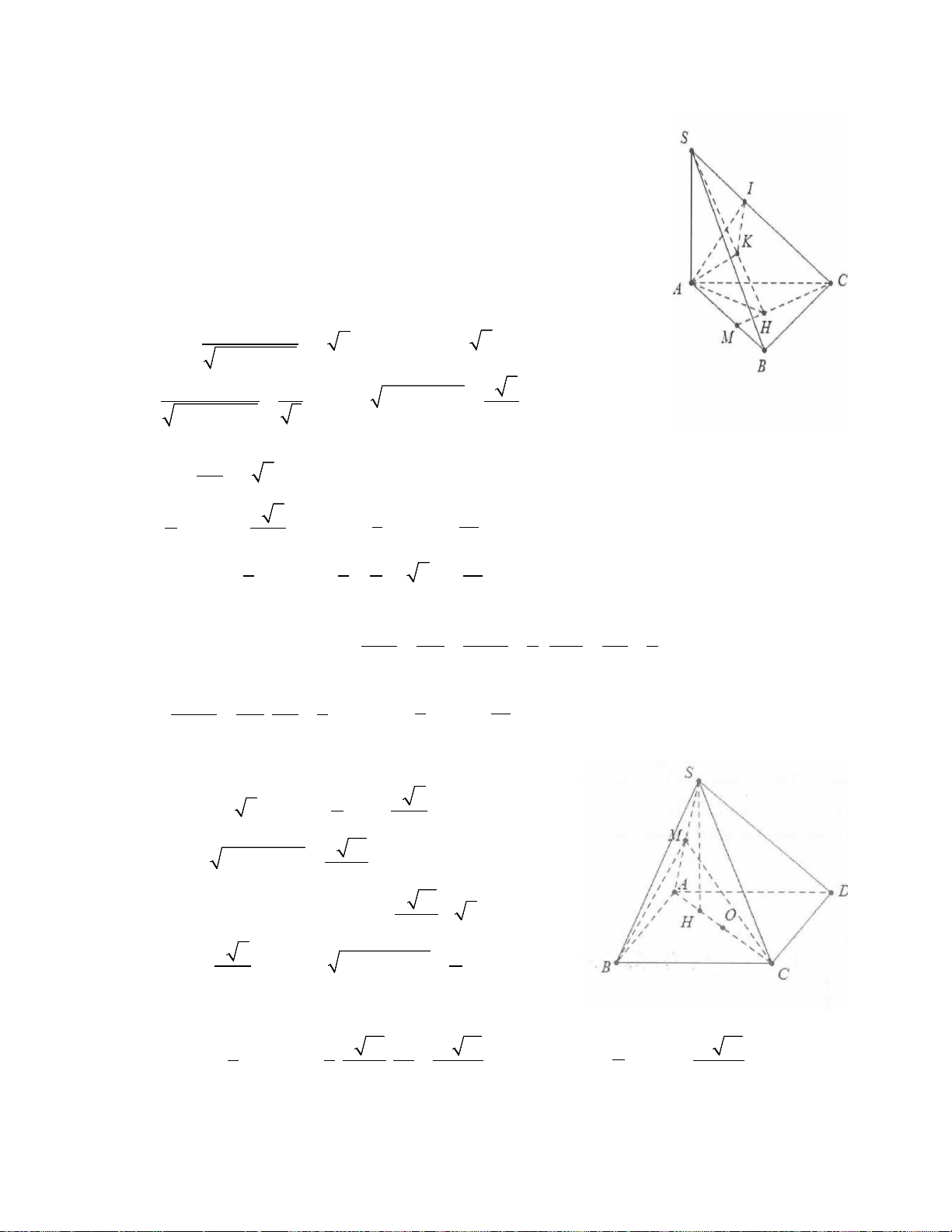
Ví dụ 11: Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), đáy ABC tam giác vuông tại B
có AB= a, BC= a 3 , biết góc giữa hai mặt phẳng (SAC) và (SBC) bằng 60°. Tính thể tích khối chóp S.ABC. 3 3 3 3
A.. a 6 . B. a 6 . C. a 2 . D. a 6 . 12 4 12 8 Lời giải:
Dựng BH ⊥ AC ⇒ BH ⊥ (SAC) Dựng ⊥ ⇒ ⊥ ⇒  HK SC (HKB) SC HKB = 60° . Ta có: a 3 a 3 BH = ⇒ BK sin 60° = ⇒ BK = a . 2 2 BC ⊥ AB Do 
⇒ BC ⊥ SB . Khi đó S
∆ BC vuông tại B nên ta BC ⊥ SA có: 1 1 1 3 2 2 a + = ⇒ SB = a
⇒ SA = SB − AB = 2 2 2 SB BC BK 2 2 3 1 a 1 2 a 6 V = a = . Chọn A. S ABCD . . 3 . 3 2 2 12
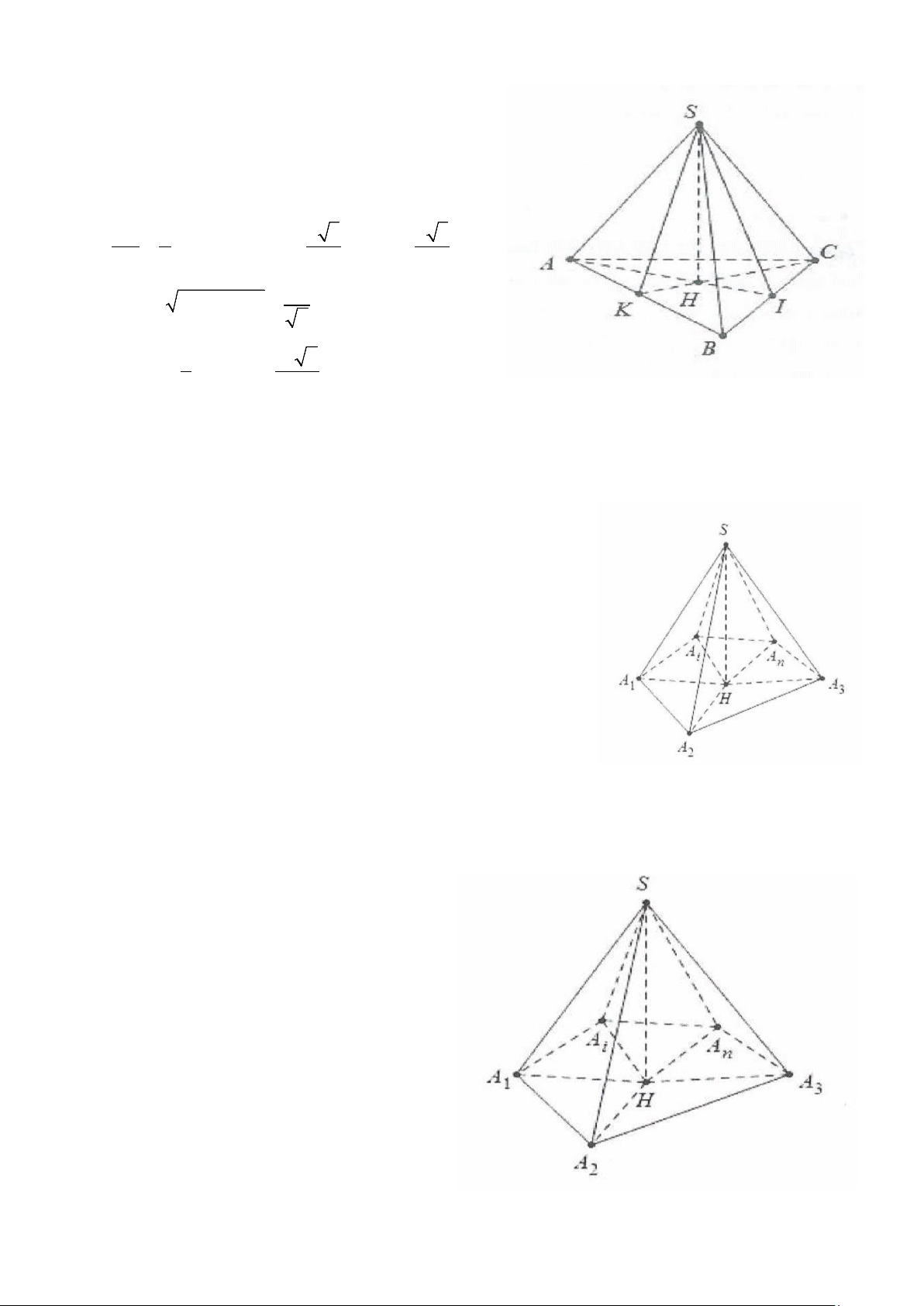
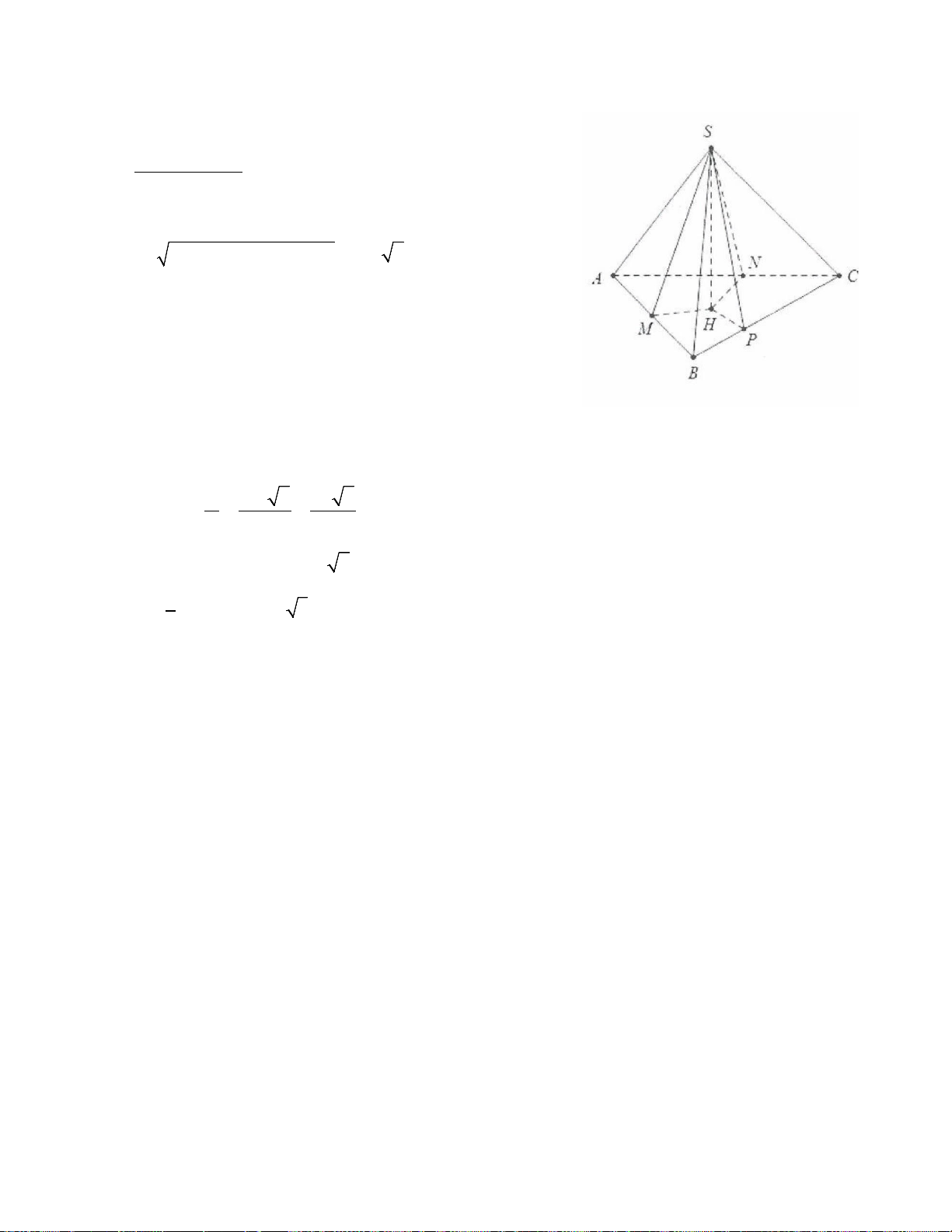
Ví dụ 12: Cho hình chóp tứ giác S.ABCD có đáy là hình vuông ABCD tâm O cạnh 4a, M là một điểm
thuộc cạnh AB sao cho MA=3MB, hình chiếu vuông góc của H lên mặt phẳng (ABCD) là trung điểm
của cạnh OM. Biết góc giữa hai mặt phẳng (SBC) và đáy là 60°. Thể tích khối chóp S.ABCD là: A. 3 4a 3 . B. 8 3 3 a . C. 3 8a 3 . D. 3 4a . 3 Lời giải:
Dựng HE ⊥ BC,OF ⊥ BC Ta có ⊥ ⇒  (SHE) BC SEH = 60°
Mặt khác ME là đường trung bình của hình thang MOFB MB OF 3a ME + ⇒ = = 2 2 Ta có: 3a 3
SH = HE.tan 60° = . 2 V 1 3a 3 2 3 = a = a . Chọn C. ABCD . .16 8 3 S. 3 2
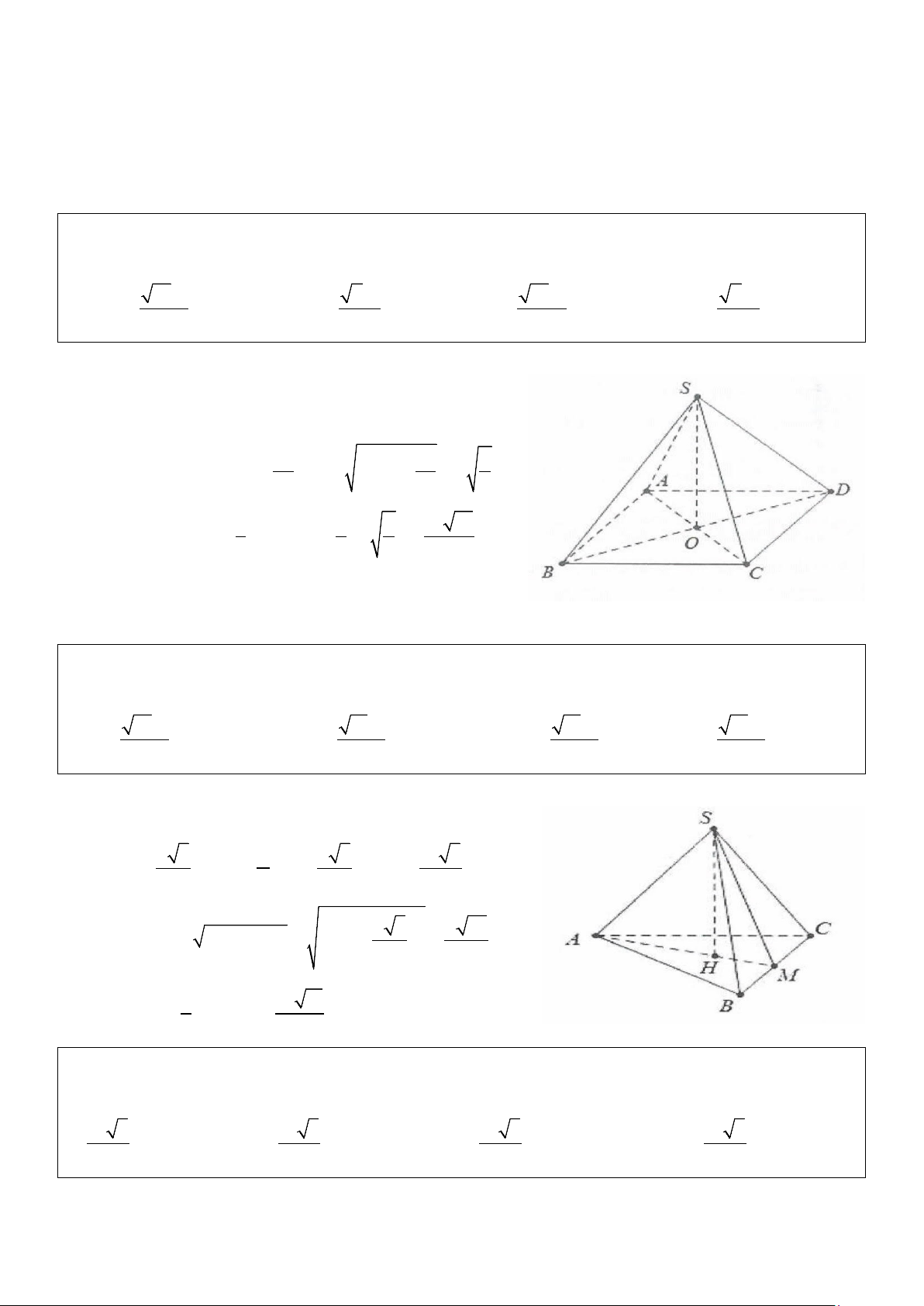
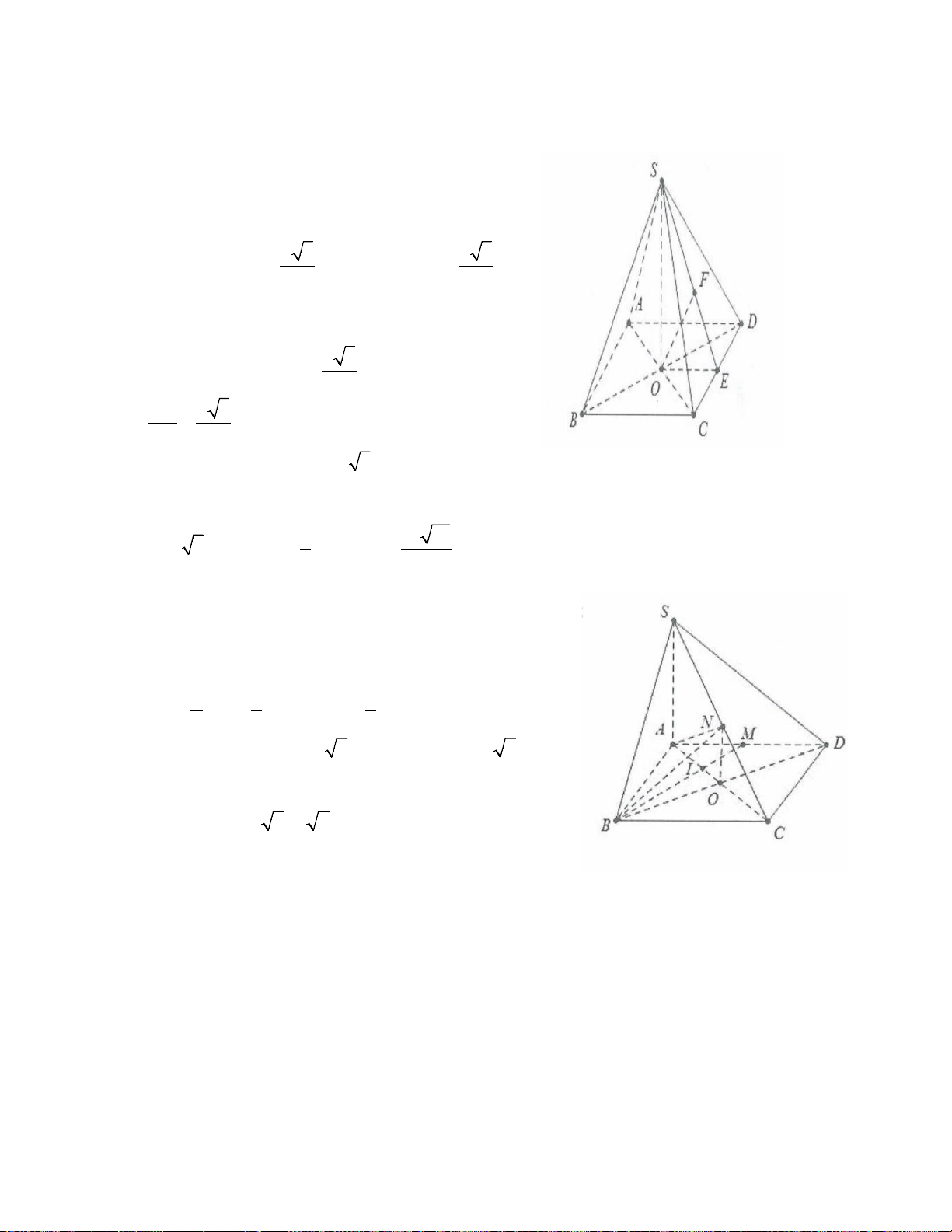
Ví dụ 13: Cho hình chóp S.ABCD có đáy là nửa lục giác đều cạnh a, AD= 2a, SA ⊥ (ABCD) . Mặt
phẳng (SCD) tạo với đáy một góc 45°. Thể tích khối chóp S.ACD là: 3 3 3
A. a . B. a . C. 3a . D. 3 a . 2 4 4 Lời giải:
Gọi O là trung điểm của AD dễ thấy 1
OC = AB = a = AD ⇒ A ∆ CD vuông tại C 2 CD ⊥ AC Khi đó 
⇒ CD ⊥ (SAC) CD ⊥ SA Do vậy 
SCA = 45° . Lại có tam giác ACD vuông tại C nên 2 2
AC = AD − CD = a 3 ⇒ SA = a 3.tan 45° = a 3 Ta có: =  a 3
d(C; AD) CDsin CDA = . CD sin 60° = . 2 2 Do đó AD BC a 3 3a 3 S + = = ABCD . 2 2 4 3 Vậy 1 3a V = SA S = . Chọn C. S ABCD . . 3 ABCD 4
Dạng 2: Thể tích khối chóp có mặt bên vuông góc với đáy Phương pháp giải:
Giả sử hình chóp S.ABC có mặt phẳng (SAB) ⊥ (ABC) . Ta dựng SH ⊥ AB (trong trường hợp S ∆ AB cân
tại S thì H là trung điểm của AB). (SAB) ⊥ (ABC) Khi đó S   H ⊥ AB
⇒ SH ⊥ ( ABC) . AB = (SAB)∩  ( ABC)
Ví dụ 1: Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại B có AB= a 3 , BC= a. Tam giác SAC
cân tại S và thuộc mặt phẳng vuông góc với đáy, mặt phẳng (SAB) tạo với đáy một góc bằng 60o . Thể tích khối chóp S.ABC là: 3 3 3
A. a 3 . B. a . C. a 3 . D. 3 2a . 2 4 3 Lời giải:
Gọi H là trung điểm của AC ta có SH ⊥ AC
Mặt khác (SAC) ⊥ ( ABC) suy ra SH ⊥ ( ABC)
Dựng HE ⊥ AB khi đó HE là đường trung bình của tam giác ABC. Do đó: BC a HE = = 2 2 AB ⊥ HE Mặt khác:  ⇒ ⊥ ⇒  AB (SHE) SEH = 60° . AB ⊥ SH 2 3 Do đó a 3 A . B BC a 3
SH = HE.tan 60° = ,S = = ⇒ 1 a V = SH S = . Chọn B. S ABC . 2 ABC 2 2 . 3 ABC 4
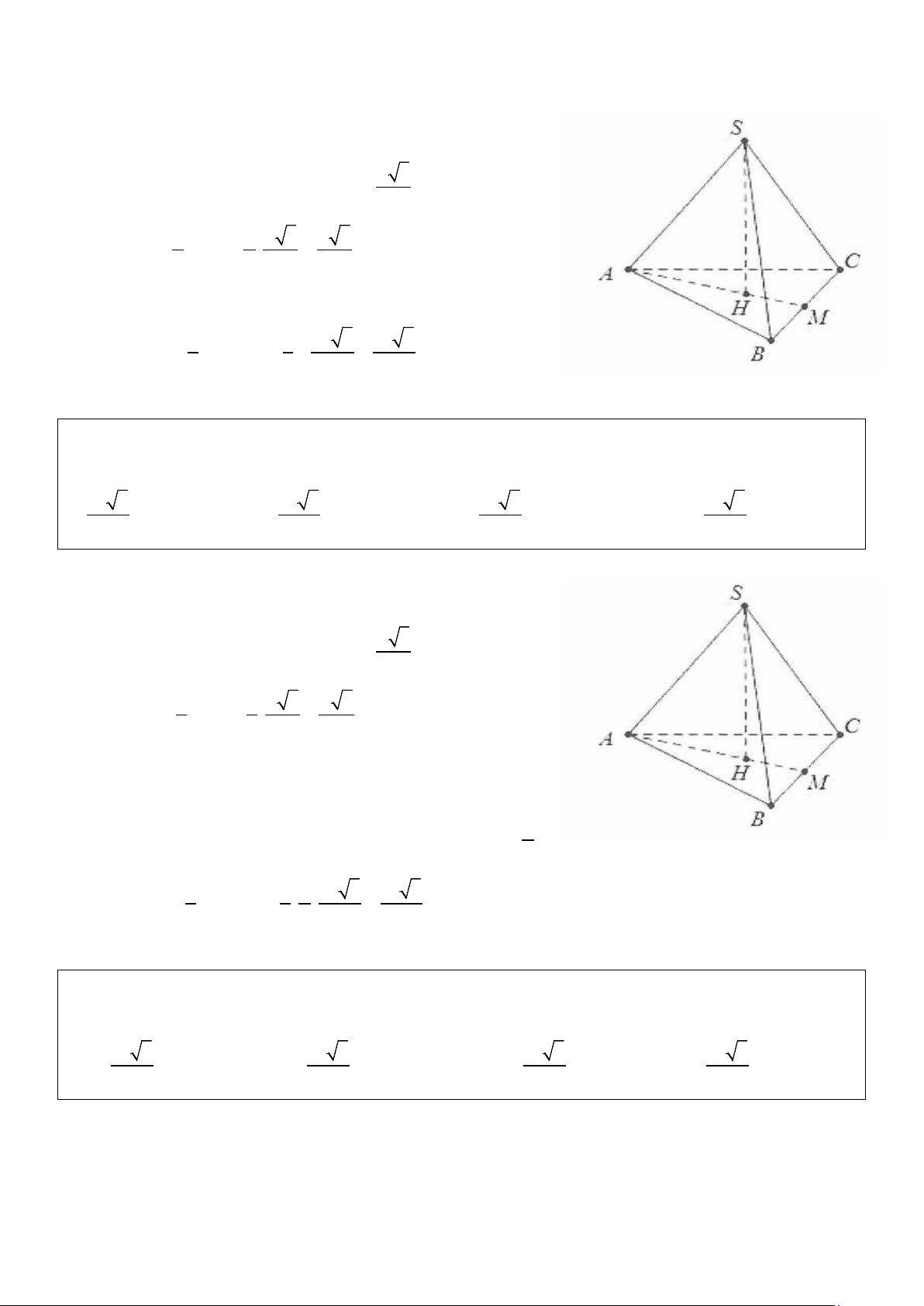
Ví dụ 2: Cho hình chóp S.ABC có đáy là tam giác ABC có AB= AC= 2a và BC= 2a 3 , gọi M là trung
điểm của BC. Tam giác SAM cân tại S và thuộc mặt phẳng vuông góc với đáy. Khoảng cách từ A đến
mặt phẳng (SBC) bằng a 3 . Thể tích khối chóp S.ABC là: 2 3 3 3 3
A. a . B. 3a . C. a 3 . D. a . 6 2 2 2 Lời giải:
Gọi H là trung điểm của AM ta có SH ⊥ AM
Mặt khác (SAM ) ⊥ ( ABC)nên SH ⊥ ( ABC) Ta có: 2 2
BM = MC = a 3 ⇒ AM = AB − BM = a 1 2 ⇒ S = AM BC = a . Dựng ABC . 3 2
HK ⊥ SM ⇒ HK ⊥ (SBC) .
Khi đó d (A;(SBC)) = 2d (H;(SBC)) = 2HK a 3 1 1 1 a 3 ⇒ HK = ⇒ = − ⇒ SH = . 2 2 2 4 SH HK HM 2 3 2 1 a S = a Do đó V = SH S = . Chọn D. S ABC . ABC 3. . 3 ABC 2
Ví dụ 3: Cho khối chóp S.ABC có đáy là tam giác ABC vuông tại A, tam giác SAB vuông tại S và thuộc
mặt phẳng vuông góc với đáy. Biết SA= a 6 , SB= a 3 và AC= 2a . Thể tích khối chóp S.ABC là: 3 3 A. 3 a 2 . B. 3
3a 2 . C. a 2 . D. a 2 . 2 3 Lời giải:
Dựng SH ⊥ AB . Mặt khác (SAB) ⊥ ( ABC) suy ra
SH ⊥ ( ABC) . Ta có: 2 2
AB = SA + SB = 3a . Áp dụng hệ thức 2
lượng trong tam giác vuông SAB ta có: SA HA = = 2a AB 2 2 A . B AC 2
⇒ SH = SA − HA = a 2,S = = a . ABC 3 2 Khi đó 1 3 V = SH.S = a .Chọn A. S ABC ABC 2 . 3
Ví dụ 4: Cho hình chóp S.ABC có mặt phẳng (SAC) vuông góc với mặt phẳng (ABC), SAB là tam giác
đều cạnh a 3 , BC= a 3 ,đường thẳng SC tạo với mặt phẳng (ABC) góc 60°. Thể tích của khối chóp S.ABC bằng: 3 3 3
A. a 3 . B. 3
2a 6 . C. a 6 . D. a 6 . 3 2 6 Lời giải: Ta có SC ( ABC)  = (SC AC)  =  ; ; SCA = 60° .
Gọi H là trung điểm của AB mà A
∆ BC cân ⇒ BH ⊥ (SAC) .
Gọi K là trung điểm của SA mà S
∆ AB đều ⇒ BK ⊥ SA
Suy ra SA ⊥ (BHK ) ⇒ SA ⊥ HK mà HK SC ⇒ SA ⊥ SC .
Tam giác SAC vuông tại S, có  = 60 AC SCA ° ⇒ SC = SH = = a . 2 2
Diện tích tam giác ABC là 1 a 3 S = AB AC = . ∆ABC . . 2 2
Tam giác ABH vuông tại H, có 2 2
BH = AB − AH = a 2 3
Vậy thể tích khối chóp S.ABC là 1 a 6 V = .BH.S = . 3 ABC ∆ 6 Chọn D.
Ví dụ 5: Cho khối chóp S.ABC có đáy là tam giác đều. Tam giác SAC cân tại S và thuộc mặt phẳng
vuông góc với đáy, đường thẳng SB tạo với đáy một góc 60°. Biết khoảng cách từ S đến mặt đáy (ABC)
là h. Thể tích khối chóp tính theo h là: 3 3 3 3
A. h 3 . B. h 3 . C. h 3 . D. h 3 . 3 9 27 18 Lời giải:
Gọi H là trung điểm của AC ta có SH ⊥ AC
Mặt khác (SAC) ⊥ ( ABC) nên SH ⊥ ( ABC)
Khi đó SH= h . Mặt khác  SBH = 60° Do vậy tan 60 h HB ° = h ⇒ HB = . 3 2 2 3 Đặt AB= a 3 h 2h a ⇒ HB = = ⇒ a = . Do đó a 3 h 3 S = = ⇒ 1 h 3 V = SH S = . S ABC . 2 3 3 ABC 4 9 . 3 ABC 27 Chọn C.
Ví dụ 6: Cho khối chóp S.ABC có đáy là tam giác đều cạnh a. Gọi M là trung điểm của BC. Tam giác
SAM vuông tại S và thuộc mặt phẳng vuông góc với đáy. Biết SA= a , thể tích khối chóp S.ABC là: 2 3 3 3 3
A. a 2 . B. a 2 . C. a 2 . D. a 2 . 4 12 18 24 Lời giải:
Dựng SH ⊥ AM ta có (SAM ) ⊥ ( ABC)nên SH ⊥ ( ABC) Mặt khác a 3 AM = 2 Suy ra 2 2 a
SM = AM − SA = 2 Lại có: . SA SM a SH = = 2 2 SA + SM 6 3 Vậy 1 a 2 V = SH S = . Chọn D. S ABC . . 3 ABC 24
Ví dụ 7: Cho khối chóp S.ABCD có đáy là hình chữ nhật ABCD. Tam giác SAB đều cạnh 2a và thuộc
mặt phẳng vuông góc với đáy. Đường thẳng SC tạo với đáy một góc 30° . Thể tích khối chóp S.ABCD là: 3 3 3 3
A. 4a 6 . B. 2a 6 . C. 4a 6 . D. 4a 2 . 3 3 6 3 Lời giải:
Gọi H là trung điểm của AB ta có SH ⊥ AB .
Mặt khác (SAB) ⊥ ( ABC) nên SH ⊥ ( ABC), SH = a 3 .
Đường thẳng SC tạo với đáy một góc 30°
Do đó HC tan 30° = SH ⇒ HC = 3a . Khi đó 2 2
BC = HC − HB = 2a 2 3 Do vậy 1 4a 6 V = SH S = .Chọn A. S ABCD . . 3 ABCD 3
Ví dụ 8: Cho khối chóp S.ABCD có đáy là hình chữ nhật. Tam giác SAB vuông tại S và thuộc mặt phẳng
đáy. Biết rằng SA= 3 và SB= 4, mặt phẳng (SCD) tạo với đáy một góc 60°. Thể tích khối chóp S.ABCD là:
A. 16 3 . B. 4 3 . C. 16 . D.16 3 . 15 5 5 5 Lời giải:
Dựng SH ⊥ AB ta có (SAB) ⊥ ( ABC) nên
SH ⊥ ( ABC) . Mặt khác 2 2
AB = SA + SB = 5 Khi đó: . SA SB 12 SH = = . 2 2 SA + SB 5
Dựng HK ⊥ CD ta có: CD ⊥ SH
⇒ CD ⊥ (SHK ) CD ⊥ HK Do đó 
SKH = 60° ⇒ HK tan 60° = SH SH 4 3 ⇒ HK = AD = = tan 60° 5 Vậy 1 16 3 V = SH S = . Chọn D. S ABCD . . 3 ABCD 5
Ví dụ 9: Cho khối chóp S.ABCD có đáy là hình thoi ABCD có AC= 2a , BD= 2a 3 . Tam giác SAC cân
tại S và thuộc mặt phẳng vuông góc với đáy. Biết khoảng cách từ D đến mặt phẳng (SAB) bằng
2a 15 .Thể tích khối chóp S.ABCD là: 5 A. 3 2a 15 . B. 3 4a . C. 3 2a 2 . D. 3 2a . Lời giải:
Gọi H là trung điểm của AC ta có SH ⊥ AC . Mặt khác
(SAC) ⊥ ( ABC)nên SH ⊥ ( ABC). Ta có: DB = 2HB Do vậy d ( ;
D (SAB)) = 2d (H;(SAB))
Dựng HE ⊥ AB ; HF ⊥ SE . Khi đó
HF = d (H (SAB)) 1
= d (D (SAB)) a 15 ; ; = . 2 5 Lại có: 1 1 1 = + 2 2 2 HF HE SH 1 1 1 4 1 1 1 1 Mặt khác = + = ⇒ = − = ⇒ SH = a 3 2 2 2 2 2 2 2 2 HE HA HB 3a SH HF HE 3a AC.BD 2 S = = a ⇒ 1 3 V = SH S = a . Chọn D. S ABCD . ABCD 2 ABCD 2 3 2 . 3
Ví dụ 10: Cho khối chóp S.ABCD có đáy là hình thang ABCD vuông tại A và D có AB= BC= 2a , AD=
3a . Tam giác SAB cân tại A và thuộc mặt phẳng vuông góc với đáy. Gọi M là trung điểm của CD.
Đường thẳng SM tạo với đáy một góc 60°. Thể tích khối chóp S.ABCD là: 3 3 3 3
A. 25a 3 . B. 25a 3 . C. 5a 3 . D. 5a 3 . 6 2 12 6 Lời giải:
Gọi H là trung điểm của AB ta có SH ⊥ AB .
Mặt khác (SAB) ⊥ ( ABC) nên SH ⊥ ( ABC) . Do SM ( ABCD)  = ° ⇒  ; 60 SMH = 60° Lại có AD BC 5a HM + = = 2 2 ⇒ =  5a 3
SH HM tan SMH = HM tan 60° = 2 Ta có AD + BC 2 S = AB = a . ABCD . 5 2 3 1 25a 3 V = SH S = . Chọn A. S ABCD . . 3 ABCD 6
Ví dụ 11: Cho khối chóp S.ABCD có đáy là hình thang ABCD vuông tại A và B có AB= a 3 , AD= 3a ,
BC= a . Tam giác SBD cân tại S và thuộc mặt phẳng vuông góc với đáy. Đường thẳng SA tạo với đáy một
góc. Thể tích khối chóp S.ABCD là: 3 3 A. 3
6a . B. 2a . C. 3a . D. 3 2a . 3 2 Lời giải:
Gọi H là trung điểm của BD ta có SH ⊥ BD . Mặt khác
(SBD) ⊥ ( ABC) nên SH ⊥ ( ABC) Lại có 2 2
BD = AB + AD = 2a 3 1
⇒ AH = BD = a 3 . 2 Do SA tạo với đáy góc ° ⇒  45
SAH = 45° ⇒ SH = a 3 Mặt khác AD + BC 2 S = AB = a ⇒ 1 3 V = SH S = a .Chọn D. S ABCD . ABCD 2 ABCD . 2 3 2 . 3
Ví dụ 12: Cho khối chóp S.ABCD có đáy là nửa lục giác đều đường kính AD= 2a . Tam giác SAD cân
tại S và thuộc mặt phẳng vuông góc với đáy. Biết khoảng cách từ A đến mặt phẳng (SCD) bằng a 3 . 2
Thể tích khối chóp S.ABCD là: 3 3 3 3
A. 3a 3 . B. a 3 . C. a 3 . D. a 3 . 8 8 2 4 Lời giải:
Gọi H là trung điểm của AD ta có SH ⊥ AD .
Mặt khác (SAD) ⊥ ( ABC)nên SH ⊥ ( ABC) .
Do AD = 2HD ⇒ d (A;(SCD)) = 2d (H;(SCD)).
Dựng HE ⊥ CD, HF ⊥ SE ⇒ d ( (SCD)) 1
= HF = d ( (SCD)) a 3 H; A; = . 2 4
Mặt khác HCD là tam giác đều cạnh a nên E là trung điểm của CD và HE= a 3 2 3 Suy ra a SH = ⇒ 1 1 a 3 V = SH S = SH S = . S ABCD . ABCD .3 2 . 3 3 HCD 8 Chọn B.
Dạng 3: Thể tích khối chóp đều Phương pháp giải:
Khối chóp đều là khối chóp có đáy là đa giác đều và các cạnh bên bằng nhau.
• Khối chóp tam giác đều
Khối chóp tam giác đều là khối chóp có đáy là tam giác đều và các cạnh bên bằng nhau.
Nếu cho khối chóp đều S.ABC thì ta có:
- Tam giác ABC là tam giác đều và các cạnh bên SA=SB=SC.
- Hình chiếu vuông góc của đỉnh S xuống mặt đáy trùng với trọng tâm G (cũng là trực tâm, tâm đường
tròn ngoại tiếp, nội tiếp) của tam giác đều ABC tức là SG ⊥ (ABC).
- Các cạnh bên bằng nhau và đều tạo với đáy một góc bằng nhau.
- Các mặt bên là tam giác cân bằng nhau và các mặt phẳng bên đều tạo với đáy các góc bằng nhau.
Tứ diện đều là tứ diện có tất cả các cạnh bằng nhau.
Như vậy khối tứ diện đều là một trường hợp đặc biệt của khối chóp tam giác đều.
Khối tứ diện đều là khối chóp tam giác đều có cạnh bên bằng cạnh đáy.
• Khối chóp tứ giác đều
Khối chóp tứ giác đều là khối chóp có đáy là hình vuông và các cạnh bên bằng nhau.
Nếu cho khối chóp đều S.ABCD thì ta có:
- Tứ giác ABCD là hình vuông và các cạnh bên SA = SB = SC = SD.
- Hình chiếu vuông góc của đỉnh S xuống mặt đáy trùng với tâm O của hình vuông ABCD tức là SO ⊥ (ABCD).
- Các cạnh bên bằng nhau và đều tạo với đáy một góc bằng nhau.
- Các mặt bên là các tam giác cân bằng nhau và các mặt phẳng bên đều tạo với đáy các góc bằng nhau.
Ví dụ 1: Cho khối chóp tứ giác đều có cạnh đáy bằng a , cạnh bên gấp hai lần cạnh đáy. Tính thể tích V của khối chóp đã cho. 3 3 3 3
A. V= 14a . B. V= 2a . C. V= 14a D. V= 2a . 6 6 2 2 Lời giải:
Giả sử khối chóp S.ABCD đều có đáy là hình vuông cạnh
a tâm O và cạnh bên SD= 2a . Khi đó SO ⊥ (ABCD). 2 2 Ta có: 2 2 a
OD = a ⇒ OD =
SO = ( a)2 a 7 2 ; 2 − = a 2 2 2 3 1 1 7 a 14 2 S = a ; 2 V = SO S = a a = . S ABCD . ABCD . ABCD . 3 3 2 6 Chọn A.
Ví dụ 2: Cho khối chóp tam giác đều S.ABC có cạnh đáy bằng a , cạnh bên bằng 2a . Tính thể tích V của khối chóp S.ABC 3 3 3 3
A. V= 13a . B. V= 11a . C. V= 11a . D. V= 11a . 12 12 6 4 Lời giải:
Gọi H là trọng tâm của ∆ ABC và M là trung điểm của BC. 2
Ta có AM= a 3 ⇒ AH= 2 AM= a 3 ; a 3 S = . 2 3 3 ABC 4 2   Mặt khác: 2 2 2 a 3 a 33
SH = SA − AH = 4a −   =  . 3  3   3 Do đó 1 a 11 V = SH S = . Chọn B. S ABC . . 3 ABC 12
Ví dụ 3: Cho hình chóp đều S.ABC có đáy là tam giác đều cạnh a , cạnh bên tạo với đáy một góc bằng
60°. Tính thể tích khối chóp đã cho. 3 3 3 3
A. a 3 . B. a 3 . C. a 3 . D. a 3 . 4 8 12 24 Lời giải:
Gọi H là trọng tâm tam giác ABC suy ra SH ⊥ ( ABC) .
Gọi M là trung điểm của BC ta có a 3 AM = . 2 Khi đó 2 2 a 3 a 3 AH = AM ⇒ . = . 3 3 2 3 Lại có  = 60o ⇒ = tan 60o SAH SH HA = a 2 3 Suy ra: 1 1 a 3 a 3 V = SH S a Chọn C. ABC . = ABC . = S. 3 3 4 12
Ví dụ 4: Cho hình chóp đều S.ABC có đáy là tam giác đều cạnh a , cạnh bên tạo với đáy một góc bằng
60°. Tính thể tích khối chóp đã cho. 3 3 3 3
A. a 3 . B. a 3 . C. a 3 . D. a 3 . 4 8 12 24 Lời giải:
Gọi H là trọng tâm tam giác ABC suy ra SH ⊥ ( ABC) .
Gọi M là trung điểm của BC ta có a 3 AM = . 2 Khi đó 1 1 a 3 a 3 HM = AM ⇒ . = . 3 3 2 6 BC ⊥ SA Lại có 
⇒ BC ⊥ (SAM ) BC ⊥ AM Do đó  = (( ) ( ))  ; = 60° ⇒ = tan 60 a SMH SBC ABC SH HM ° = 2 2 3 Do đó 1 1 a a 3 a 3 V = SH S = = . Chọn D. S ABC . ABC . . . 3 3 2 4 24
Ví dụ 5: Cho hình chóp đều S.ABCD có đáy là hình vuông cạnh a , mặt bên tạo với đáy một góc bằng
30°. Tính thể tích V của khối chóp S.ABCD theo a và 30°. 3 3 3 3
A.V= a 3 . B. V= a 3 . C.V= a 3 . D. V= a 3 . 6 9 12 18 Lời giải:
Gọi O là tâm của hình vuông ABCD khi đó
SO ⊥ ( ABCD) và 2 S = a . ABCD
Dựng OE ⊥ CD , lại có CD ⊥ SO ⇒ CD ⊥ (SEO) .
Khi đó ta có: ((SCD) ( ABCD))  =  , SEO = 30° . Mặt khác BC OE =
(đường trung bình trong tam giác) 2 nên a a tan 30 tan 30 a OE SO OE ° = ⇒ = = = . 2 2 2 3 3 3 Khi đó 1 a a 3 V = SO S = = . Chọn D. S ABCD . . 3 ABCD 6 3 18
Ví dụ 6: Cho khối chóp tứ giác đều có tất cả các cạnh bằng 2a. Thể tích khối chóp đã cho bằng: 3 3 3 3
A. 4a 2 . B. 8a . C. 8a 2 . D. 2a 2 . 3 3 3 3 Lời giải:
Gọi O = AC ∩ BD , ta có SO ⊥ (ABCD) và đáy ABCD là hình vuông. Ta có: 2 BC S = a , OB = = a 2 . ABCD 4 2 2 2
⇒ SO = SB − OB = a 2 . 3 ⇒ 1 1 2 4a 2 V = SO S = a AB = S ABCD . ABCD . 2. . 3 3 3 Chọn A.
Ví dụ 7: Cho hình chóp đều S.ABCD có đáy là hình vuông cạnh 4a. Khoảng cách từ điểm D đến mặt
phẳng (SAB) bằng 4a . Thể tích khối chóp đã cho là: 5 3 3 3 3
A. a . B. 2a . C. 16a . D. 4a . 3 3 3 3 Lời giải:
Gọi H là tâm của hình vuông suy ra SH ⊥ (ABCD) Khi đó ta có: d( ;
D (SAB)) = 2d (H;(SAB))
Dựng HE ⊥ AB và HF ⊥ SE ta chứng minh được ( ( )) = ⇒ ( ( )) 4 d H; D; = 2 a SAB HF d SAB HF = 5 Do vậy 2a HF =
. Lại có HE = 2a 5 Ta có: 1 1 1 + = ⇒ SH = a 2 2 2 HE SH HF 3 Vậy 1 16a V = SH S = . Chọn C. S ABCD . . 3 ABCD 3
Ví dụ 8: Cho hình chóp đều S.ABCD có mặt bên tạo với đáy một góc 60°. Cạnh bên SA= a 5 . Thể tích khối chóp S.ABCD là: 3 3 3 3
A. a 6 . B. a 3 . C. 2a 2 . D. 4a 3 . 3 3 3 3 Lời giải:
Gọi H là tâm của hình vuông suy ra SH ⊥ ( ABCD).
Đặt AB = 2x . Dựng HK ⊥ AB
Ta có: SH ⊥ AB ⇒ HK ⊥ (SAB)
Do vậy ((SAB) ( ABCD))  =  ; SKH = 60°
Lại có HK = x ⇒ SH = x tan 60° = x 3 . Khi đó 2 2 2 2 2 2
SA = SH + HA = 3x + 2x = 5x
⇒ x = a ⇒ SH = a 3 , 2 2 S = AB = a . ABCD 4 3 ⇒ 1 4a 3 V = SH S = . Chọn D. S ABCD . . 3 ABCD 3
Ví dụ 9: Cho khối chóp đều S.ABCD có đáy là hình vuông cạnh 2a , biết diện tích của tam giác SCD là 2
3a . Thể tích khối chóp S.ABCD là: 3 3 3 3
A. a 3 . B. 8a 2 . C. 3a 3 . D. 4a 2 . 8 3 4 3 Lời giải:
Gọi H là tâm của hình vuông suy ra SH ⊥ (ABCD).
Gọi K là trung điểm của CD. Khi đó ta có SK ⊥ CD . Lại có: 1 2 S
= CD SK = a SK = a ACD . . 3 2 2 2
⇒ SK = 3a ⇒ SH = SK − HK = 2a 2 , 2 S = a ABCD 4 3 Vậy 1 8a 2 V = SH S = . Chọn B. S ABCD . . 3 ABCD 3
Ví dụ 10: Cho hình chóp S.ABC có đáy là tam giác đều cạnh a . Khoảng cách từ điểm A đến mặt phẳng
(SBC) bằng 3a . Thể tích khối chóp đã cho là: 4 3 3 3 3
A. a 3 . B. a 3 . C. a 3 . D. a 3 . 6 8 12 24 Lời giải:
Gọi H là trọng tâm tam giác đều ABC ta có: SH ⊥ (ABC) . Khi đó ( ( )) = ( ( )) 3 A; 3 ; a d SBC d H SBC = 4 Suy ra d( ;( )) a
H SBC = . Gọi I là trung điểm của BC dễ thấy AI ⊥ BC . 4
Dựng HK ⊥ SI BC ⊥ SH Ta có: 
⇒ BC ⊥ HK ⇒ HK ⊥ (SBC). BC ⊥ AI Do vậy (H;( )) a d SBC = HK = ; a 3 HI = 4 6 Mặt khác 1 1 1 a = + ⇒ SH = . 2 2 2 HK SH HI 2 2 3 Vậy 1 1 a a 3 a 3 V = SH S = = . Chọn D. S ABC . ABC . . . 3 3 2 4 24
Ví dụ 11: Cho hình chóp đều S.ABC có đáy là tam giác đều cạnh a. Biết tam giác ASB vuông, thể tích khối chóp S.ABC là: 3 3 3 3
A. a 2 . B. a 2 . C. a 2 . D. a 2 . 24 32 16 8 Lời giải:
Gọi H là trọng tâm của tam giác ABC
Khi đó SH ⊥ (ABC) . Do SA = SB nên tam giác SAB
vuông khi và chỉ khi tam giác ASB vuông tại S
Khi đó gọi K là trung điểm của AB ta có: SK AB a = = . Mặt khác a 3 a 3 CK = ⇒ HK = 2 2 2 6 Suy ra 2 2 a
SH = SK − HK = . 6 3 Do đó 1 a 2 V = SH S = . Chọn A. S ABC . . 3 ABC 24
Dạng 4: Thể tích một số khối chóp đặc biệt
• Khối chóp có các cạnh bên bằng nhau
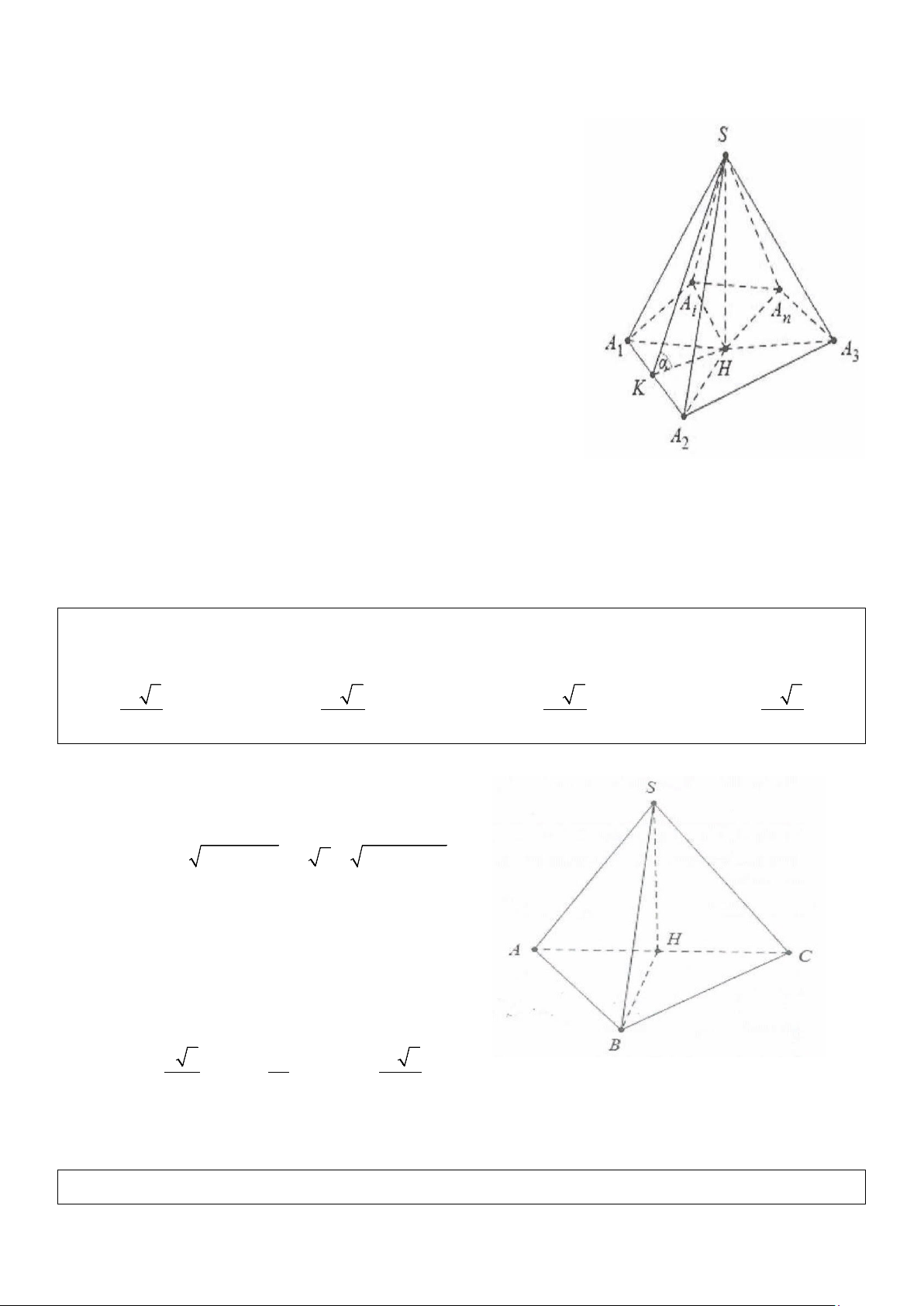
Cho khối chóp S.A A ...A có tất cả các cạnh bên bằng nhau: 1 2 n
SA = SA = ... = SA . 1 2 n
Dựng đường cao SH ⊥ ( A A A của khối chóp. 1 2 n )
Khi đó theo định lý Pytago ta có: 2 2 2 2 2 2 2
SH = SA − HA = SA − HA = .... = SA − HA . 1 1 2 2 n n
Lại có SA = SA = ... = SA suy ra HA = HA = ... = HA . 1 2 n 1 2 n
Như vậy: Hình chiếu vuông góc của đỉnh S xuống mặt đáy trùng với
tâm đường tròn ngoại tiếp của đa giác A A ...A . 1 2 n
Khi đó SH = h = R α . đ tan
• Khối chóp có các cạnh bên tạo với đáy các góc bằng nhau
Cho khối chóp S.A A ...A có tất cả các cạnh bên 1 2 n
đều tạo với đáy một góc α .
Dựng đường cao SH ⊥ ( A A A của khối chóp. 1 2 n ) Khi đó:  =  = = 
SA H SA H .... SA H = α suy ra 1 2 n
SH = HA tanα = HA tanα = . . = HA α . n tan 1 2
Do đó HA = HA = ... = HA suy ra hình chiếu 1 2 n
vuông góc của đỉnh S xuống mặt đáy trùng với
tâm đường tròn ngoại tiếp của đa giác A A ...A . 1 2 n
Khi đó SH = h = R α . đ tan
• Khối chóp có các mặt bên đều tạo với đáy các góc bằng nhau
Cho khối chóp S.A A ...A có tất cả các mặt bên đều tạo với đáy 1 2 n một gócα
Dựng đường cao SH ⊥ ( A A A của khối chóp. Dựng 1 2 n )
HK ⊥ A A , HK ⊥ A A ,… , HK ⊥ A A 1 1 2 2 2 3 n n 1 HK ⊥ A A Do 1 1 2 
⇒ A A ⊥ SK H ⇒ SK H = α 1 2 ( 1 )  1 . A A ⊥  SH 1 2
Tương tự như vậy ta có:  =  = = 
SK H SK H .... SK H = α . 1 2 n
Suy ra SH = HK tanα = HK tanα. . = HK α do đó n tan 1 2
HK = HK = ... = HK 1 2 n .
Suy ra điểm H trùng với tâm đường tròn tiếp xúc với tất cả các
cạnh (hay đường tròn nội tiếp) của đa giác A A ...A . 1 2 n
Khi đó SH = h = r α . đ tan
Ví dụ 1: Cho hình chóp S.ABC có đáy là tam giác ABC, các cạnh bên SA=SB=SC= a . Biết rằng  =  ASB BSC = 60° , 
ASC = 90° . Thể tích khối chóp đã cho là: 3 3 3 3
A.V= a 3 . B. V= a 2 . C. V= a 2 . D.V= a 3 . 6 6 12 12 Lời giải:
Dễ thấy các tam giác ASB, BSC là tam giác đều do đó AB = BC = a . Mặt khác: 2 2 2 2
AC = SA + SC = a 2 = AB + BC
Do đó tam giác ABC vuông tại B.
Mặt khác SA = SB = SC = a nên hình chiếu vuông
góc của đỉnh S xuống mặt đáy là tâm đường tròn ngoại
tiếp tam giác ABC và là trung điểm của cạnh huyền AC. 2 3 Ta có: a 2 SH = ; a S = ⇒ a 2 V = . 2 ABC 2 S.ABC 12 Chọn C.
Ví dụ 2: Cho hình chóp S.ABC có đáy là tam giác ABC, các cạnh bên SA=SB=SC= a . Biết rằng  ASB = 60° ,  BSC = 90° , 
ASC =120°. Thể tích khối chóp đã cho là: 3 3 3 3
A.V= a 3 . B. V= a 2 . C. V= a 2 . D.V= a 3 . 6 6 12 12 Lời giải:
Tam giác SAB đều nên AB= a , ∆ SBC vuông tại S nên 2 2
BC = SB + SC = a 2 . Mặt khác 2 2 = + −  AC SA SC 2 .
SA SC cos ASC = a 3 Do 2 2 2
AC = AB + BC nên tam giác ABC vuông tại B.
Mặt khác SA=SB=SC= a nên hình chiếu vuông góc của đỉnh
S xuống mặt đáy là tâm đường tròn ngoại tiếp tam giác ABC
và là trung điểm của cạnh huyền AC. 2 Ta có: a 2 S a = , 2 2
SH = SA − HA = . ABC 2 2 3 ⇒ 1 a 2 V = SH S = . Chọn C. S ABC . . 3 ABC 12
Ví dụ 3: Cho hình chóp S.ABC có đáy là tam giác ABC, có AB=AC= a , 
BAC =120° . Các cạnh bên đều
tạo với đáy một góc 60°.Thể tích khối chóp S.ABC là: 3 3 3 3
A.V= a . B. V= a 3 . C. V= a 3 . D.V= a 3 . 4 4 8 12 Lời giải:
Diện tích tam giác ABC là: =  2 1 a 3 S AB AC BAC = . ABC . .sin 2 4
Do các cạnh bên đều tạo với đáy một góc bằng 60° ⇒ hình chiếu vuông góc của đỉnh S xuống mặt đáy
là tâm đường tròn ngoại tiếp tam giác ABC. Lại có: 2 2 = + −  BC a 3 BC AB AC 2A .A
B C cos BAC = a 3 ⇒ R = = = a . ABC 2sin A 2sin120° 3 Suy ra SH = R ° = a ⇒ 1 a V = SH S = . Chọn A. S ABC . ABC . tan 60 3 . 3 ABC 4
Ví dụ 4: Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại B có AB = 3, BC = 4. Biết rằng các
mặt bên của khối chóp đều tạo với đáy một góc bằng nhau và bằng 60°. Thể tích khối chóp đã cho là
A.V= 5 3 . B. V= 5 3 . C. V= 5 3 . D.V= 5 3 . 3 6 2 12 Lời giải:
Ta có: H là tâm đường tròn nội tiếp tam giác ABC. Lại có . p r = S . ABC Trong đó 1 S = AB C = ; 2 2
AC = AB + BC = 5 ABC .B 6 2 Suy ra
AB + BC + CA 5 p =
= 6 ⇒ r = = HK . 2 6 Khi đó 5 3
SH = r tan 60° = 6 Do đó 1 5 3 V = SH.S = . Chọn A. 3 ABC 3
Ví dụ 5: Cho hình chóp S.ABC có đáy là tam giác ABC cân tại A có AB = AC= 10, BC= 12. Các mặt
bên của khối chóp đều tạo với đáy một góc bằng nhau và bằng 30o . Thể tích khối chóp đã cho là
A. 18 3 . B. 48 3 . C. 16 3 . D.9 3 . Lời giải:
Do các mặt bên của khối chóp đều tạo với đáy một góc bằng nhau
nên hình chiếu vuông góc của đỉnh S xuống mặt đáy trùng với tâm
đường tròn nội tiếp tam giác ABC.
Gọi M là trung điểm của BC⇒ AM ⊥ BC Ta có: 2 2 2 2
AM = AB − BM = 10 − 6 = 8 . Khi đó: 1 S 48 S = AM C r ABC .B = 48 ⇒ = = = ABC 3 2 p 10 +10 +12 2
⇒ SH = r tan 30° = 3 ⇒ 1 V = SH.S = 16 3 .Chọn C. 3 ABC
BÀI TẬP TỰ LUYỆN
Câu 1: Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt
phẳng đáy và SA= 2a . Tính thể tích V của khối chóp S.ABCD. 3 3 3 A. V= 2a . B. V= 2a . C. V= 3 2a . D. V= 2a . 6 4 3
Câu 2: Cho khối chóp S.ABC có SA vuông góc với mặt phẳng (ABC), tam giác ABC vuông tại B và
AB=a;AC= a 3 .Tính thể tích khối chóp S.ABC biết SB= a 5 . 3 3 3 3 A. a 2 . B. 3a 6 . C. a 6 . D. a 15 . 3 4 6 6
Câu 3: Cho khối chóp S.ABC có SA vuông góc với mặt phẳng (ABC), tam giác ABC vuông tại B và AB=a
AC= a 3 .Tính thể tích khối chóp S.ABC biết SC= a 6 . 3 3 3 3 A. a 6 . B. a 6 . C. a 6 . D. a 15 . 6 2 3 6
Câu 4: Cho khối chóp S.ABC có đáy là tam giác ABC đều cạnh a. Hai mặt phẳng (SAB) và ( SAC) cùng
vuông góc với đáy. Tính thể tích khối chóp S.ABC biết SC= a 3 3 3 3 3 A. 2a 6 . B. a 6 . C. a 3 . D. a 3 . 9 12 4 2
Câu 5: Cho khối chóp S.ABCD có đáy là hình chữ nhật; AD=2AB=2a; Gọi H là trung điểm của AD, biết
SH vuông góc với mặt phẳng đáy. Tính thể tích khối chóp S.ABCD biết SA= a 5 . 3 3 3 3 A. 2a 3 . B. 4a 3 . C. 4a . D. 2a . 3 3 3 3
Câu 6: Cho khối chóp S.ABCD có đáy là hình vuông cạnh 2a. Gọi H là trung điểm của AB, biết SH vuông
góc với mặt phẳng đáy. Tính thể tích khối chóp S.ABCD biết tam giác SAB đều. 3 3 3 3 A. 2a 3 . B. 4a 3 . C. a . D. a . 3 3 6 3
Câu 7: Cho khối chóp S.ABC có SA vuông góc với mặt phẳng (ABC), tam giác ABC vuông tại B và AB=a,
AC= a 3 .Tính thể tích khối chóp S.ABC biết góc giữa SB và (ABC) bằng 30° . 3 3 3 3 A. a 6 . B. a 6 ’ C. a 6 . D. 2a 6 . 9 6 18 3
Câu 8: Cho khối chóp S.ABC có đáy là tam giác ABC đều cạnh a. Hai mặt phẳng (SAB) và ( SAC) cùng
vuông góc với đáy. Tính thể tích khối chóp S.ABC biết SB hợp với đáy một góc 30° . 3 3 3 3 A. a 3 . B. a 3 . C. a . D. a . 6 12 4 12
Câu 9: Cho khối chóp S.ABC có đáy là tam giác ABC đều cạnh a. Hai mặt phẳng (SAB) và ( SAC) cùng
vuông góc với đáy. Tính thể tích khối chóp S.ABC biết SM hợp với đáy một góc 60°, với M là trung điểm của BC. 3 3 3 3 A. a 6 . B. a 3 . C. a 3 . D. a 6 . 8 4 8 24
Câu 10: Cho khối chóp S.ABC có SA vuông góc với mặt phẳng (ABC), tam giác ABC vuông tại A và
BC=2AB=2a. Tính thể tích khối chóp S.ABC biết góc giữa SC và (ABC) bằng 45°. 3 3 3 3 A. a . B. a 3 . C. 3a 3 . D. a . 2 2 2 6
Câu 11: Cho khối chóp S.ABC có SA vuông góc với mặt phẳng (ABC), tam giác ABC vuông tại A và
BC=2AB=2a. Tính thể tích khối chóp S.ABC biết góc giữa SM và (ABC) bằng 60° với M là trung điểm của BC. 3 3 3 3 A. a . B. a 3 . C. a 3 . D. a . 2 6 2 6
Câu 12: Cho khối chóp S.ABCD có đáy là hình chữ nhật tâm O; AC=2AB=2a, SA vuông góc với mặt
phẳng đáy. Tính thể tích khối chóp S.ABCD. Biết góc giữa SC và (ABCD) bằng 45° 3 3 3 A. 2a 3 . B. 4a 3 . C. 3 a . D. a . 3 3 3
Câu 13: Cho khối chóp S.ABCD có đáy là hình chữ nhật tâm O; AC=2AB=2a, SA vuông góc với mặt
phẳng đáy. Tính thể tích khối chóp S.ABCD biết góc giữa SO và (ABCD) bằng 60°. 3 3 3 A. 2a 3 B. a 3 C. 3 a D. a 3 3 3
Câu 14: Cho khối chóp S.ABCD có đáy là hình vuông cạnh a. Hai mặt phẳng (SAB) và (SAD) cùng vuông
góc với đáy. Tính thể tích khối chóp S.ABCD biết SC hợp với đáy một góc 45°. 3 3 3 3 A. a 2 . B. a 2 . C. a . D. a 6 3 6 3
Câu 15: Cho khối chóp S.ABCD có đáy là hình vuông cạnh a. Hai mặt phẳng (SAB) và (SAC) cùng vuông
góc với đáy. Tính thể tích khối chóp S.ABCD biết SM hợp với đáy một góc 60°, v ới M là trung điểm của BC. 3 3 3 3 A. a 15 . B. a 15 . C. a . D. a . 6 3 6 3
Câu 16: Cho khối chóp S.ABCD có đáy là hình vuông cạnh 2a. Gọi H là trung điểm của AB và SH vuông
góc với đáy. Tính thể tích khối chóp S.ABCD biết SC hợp với đáy một góc 60°. 3 3 3 3 A. 2a 15 . B. 4a 15 . C. a . D. a . 3 3 6 3
Câu 17: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB=a. Cạnh bên SA vuông góc với
mặt phẳng đáy một góc, SC tạo với mặt phẳng đáy một góc 45° và SC= 2a 2 . Thể tích khối chóp S.ABCD bằng. 3 3 3 3 A. 4a . B. 2 3a . C. 3a . D. a 3 . 3 3 3 3
Câu 18: Cho hình chóp tam giác S.ABC có SA, SB, SC đôi một vuông góc và SA=SB=SC=a. Khi đó, thể
tích khối chóp trên bằng: 3 3 3 3 A. a . B. a . C. a . D. 2a . 6 9 3 3
Câu 19: Đáy của hình chóp S.ABCD là một hình vuông cạnh a. Cạnh bên SA vuông góc với đáy và có độ
dài bằng a. Thể tích khối tứ diện S.BCD bằng 3 3 3 3 A. a . B. a . C. a . D. a . 3 8 6 4
Câu 20: Cho hình chóp S.ABCD có đáy là một hình vuông cạnh a. Các mặt phẳng (SAB) và (SAD) cùng
vuông góc với mặt phẳng đáy, còn cạnh bên SC tạo với mặt phẳng (SAB) một góc 30° . Thể tích hình chóp đó bằng 3 3 3 3 A. a 3 . B. a 2 . C. a 2 . D. a 2 3 2 4 3
Câu 21:Cho hình chóp S.ABCD có đáy là một hình vuông cạnh a. Các mặt phẳng (SAB) và (SAD) cùng
vuông góc với mặt phẳng đáy, còn cạnh bên SC tạo với mặt phẳng đáy một góc bằng 30° . Thể tích hình chóp đó bằng 3 3 3 3 A. a 6 . B. a 6 . C. a 6 . D. a 6 . 5 3 4 9
Câu 22: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, biết SA vuông góc với đáy (ABC) và
(SBC) hợp với đáy (ABC) một góc 60°. Tính thể tích hình chóp 3 3 3 A. a 3 . B. a 5 . C. a . D. Đáp án khác. 8 9 3
Câu 23: Cho hình chóp tam giác S.ABC có SA, SB, SC đôi một vuông góc, SA=a, SB=b, SC=c. Thể tích khối chóp bằng: A. 1 abc . B. 1 abc . C. 1 abc . D. 2 abc . 3 9 6 3
Câu 24: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt phẳng đáy, góc
giữa đường thẳng SB và (ABC) bằng 60°. Tính thể tích khối chóp 3 3 3 3 A. a 3 . B. a . C. a . D. a 3 . 12 4 2 6
Câu 25: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SD= a 13 . Hình chiếu S lên 2
(ABCD) là trung điểm H của cạnh AB. Tính thể tích khối chóp 3 3 3 A. 3 a 12 . B. a 2 . C. 2a . D. a . 3 3 2
Câu 26: Hình chóp tam giác S.ABC có đáy là tam giác đều cạnh a, SA ⊥ (ABC). Góc giữa (SBC) và (ABC)
bằng 60° . Thể tích khối chóp S.ABC bằng. 3 3 3 3 A. a 3 . B. 3a 3 . C. a . D. a 3 . 8 8 4 4
Câu 27: Cho hình chóp S.MNPQ có đáy MNPQ là hình vuông, SM ⊥ (MNPQ). Biết MN =a, SM = a 2 . Thể tích khối chóp là 3 3 3 3 A. a 2 . B. a 2 . C. a 3 . D. a 2 . 6 2 2 3
Câu 28: Một hình chóp tam giác có đường cao bằng 100cm và các cạnh đáy bằng 20cm, 21cm,29cm. Thể
tích khối chóp đó bằng A. 3 7000cm . B. 3 6213cm . C. 3 6000cm . D. 3 7000 2cm .
Câu 29: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = 2a, AD = a . Hình chiếu của S lên
(ABCD) là trung điểm H của AB, SC tạo với đáy một góc 45° . Thể tích khối chóp S.ABCD là 3 3 3 3 A. 2a . B. 2 2a . C. a . D. a 3 . 3 3 3 2
Câu 30: Cho tứ diện S.ABC có các cạnh SA,SB,SC đôi một vuông góc với nhau và AB = 5, BC = 6, CA =
7. Khi đó thể tích tứ diện S.ABC bằng A. 210 . B. 210 . C. 95 . D. 95 . 3 3
Câu 31: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a, AD = a 3 . Đường thẳng SA
vuông góc với đáy. Cạnh bên SB tạo với mặt phẳng (SAC) góc 30° . Thể tích khối chóp S.ABCD là 3 3 3 A. 3 a 6 . B. a 6 . C. a 6 . D. a 6 . 6 2 3
Câu 32: Cho hình chóp S.ABCD có đáy là hình thoi, 
ABC = 60° , SA=SB=SC. Gọi H là hình chiếu vuông
góc của S trên mặt phẳng đáy. Khoảng cách từ H đến (SAB) bằng 2cm và thể tích khối chóp S.ABCD bằng 3
60cm . Diện tích tam giác SAB bằng: A. 5. B. 15. C. 30. D. 15 . 2
Câu 33: Cho khối chóp S.ABCD có đáy là hình chữ nhật, AD = 2a, AB = a. H là trung điểm của AD và SH
vuông góc với đáy. Tính thể tích khối chóp S.ABCD biết SD hợp với đáy một góc 45° 3 3 3 A. 2a 3 . B. 3 a 3 . C. 2a . D. a . 2 3 3
Câu 34: Cho khối chóp S.ABCD có đáy là hình chữ nhật, AD = 2a, AB = a. H là trung điểm của AD và SH
vuông góc với đáy. Tính thể tích khối chóp S.ABCD biết SD hợp với đáy một góc 60° 3 3 3 3 A. 4a 6 . B. 2a 6 . C. a . D. a . 3 3 6 3
Câu 35: Cho hình chóp S.ABCD có đáy là hình vuông. Tam giác SAB đều và nằm trong mặt phẳng vuông
góc với đáy. Biết diện tích của tam giác SAB là 9 3 (cm3). Thể tích khối chóp S.ABCD là: A. 18 3 . B. 36 3 . C. 81 3 . D. 9 3 .
Câu 36: Cho khối chóp S.ABCD có ABCD là hình vuông có cạnh đáy bằng 3a. Tam giác SAB cân tại S và
nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp biết tam giác SAB đều. 3 3 A. 3 9a 3 . B. 9a 3 . C. 3 9a . D. 9a . 2 2
Câu 37: Cho khối chóp S.ABCD có ABCD là hình vuông có cạnh đáy bằng 3a. Tam giác SAB cân tại S và
nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp biết tam giác SAB vuông. 3 3 A. 3 9a 3 . B. 9a 3 . C. 3 9a . D. 9a . 2 2
Câu 38: Cho khối chóp S.ABCD có ABCD là hình vuông có cạnh đáy bằng 3a. Tam giác SAB cân tại S và
nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp biết góc giữa SC và mặt phẳng (ABCD) bằng 60°. 3 A. 3 18a 3 . B. 9a 15 . C. 3 9a 3 . D. 3 18a 15 . 2
Câu 39: Cho khối chóp S.ABCD có ABCD là hình chữ nhật, AB = 2a. Tam giác SAB nằm trong mặt phẳng
vuông góc với đáy và SA = a; SB = a 3 . Tính thể tích khối chóp biết AD=3a. 3 A. 3 a 3 . B. 9a 15 C. 3 2a 3 . D. 3 18a 15 . 2
Câu 40: Cho khối chóp S.ABCD có ABCD là hình chữ nhật, AB = a; AD = a 3 . Tam giác SBD vuông tại
S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp biết góc giữa SD và đáy bằng 30° . 3 3 A. 3 a 3 . B. 3 a . C. a 3 . D. a . 3 2
Câu 41: Cho hình chóp S.ABC có đáy ABC là tam giác đều. Mặt bên SAB nằm trong mặt phẳng vuông góc
với mặt phẳng đáy và tam giác SAB vuông tại S, SA = a 3 , SB = a. Tính thể tích hình chóp S.ABC. 3 3 3 3 A. a . B. a . C. a . D. a . 4 3 6 2
Câu 42: Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 2a. Mặt phẳng (SAB) vuông góc với đáy, 3
tam giác SAB cân tại A. Biết thể tích khối chóp S.ABC bằng 4a . Khi đó, độ dài SC bằng: 3 A. 3a . B. 6a . C. 2a . D. Đáp số khác.
Câu 43: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, AB = 3a, BC = 5a và (SAC) vuông góc với đáy. Biết SA=2a, 
SAC = 30° . Thể tích khối chóp là: 3 A. a 3 . B. 3 2a 3 . C. 3 a 3 D. 3 2a . 9
Câu 44: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, AB = 3a, BC = 5a, mặt phẳng (SAC)
vuông góc với đáy. Biết SA = 2a 3 , 
SAC = 30° . Thể tích khối chóp là: 3 A. 3 2a 3 . B. 3 a 3 . C. 3 2a . D. a 3 . 3
Câu 45: Cho khối chóp đều S.ABC cạnh đáy bằng a 3 . Tính thể tích của khối chóp S.ABC biết mặt bên là tam giác vuông cân. 3 3 3 3 A. a 21 . B. a 21 . C. a 6 . D. a 6 . 36 12 8 4
Câu 46: Cho hình chóp tứ giác đều S.ABCD có cạnh AB = a và đường cao h= a 3 Diện tích toàn phần của 2 hình chóp bằng. 2 2 A. 5a . B. 2 3a . C. 2 2a . D. 3a . 2 2
Câu 47: Cho một hình chóp tứ giác đều có cạnh đáy bằng a và diện tích xung quanh gấp đôi diện tích đáy.
Khi đó thể tích của khối chóp là: 3 3 3 3 A. 3a . B. 3a . C. 2a . D. 3a . 6 3 3 12
Câu 48: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a. Gọi SH là đường cao của hình chóp.
Khoảng cách từ trung điểm của SH đến (SBC) bằng b. Thể tích của khối chóp S.ABCD là. 3 3 3 A. 2a b . B. a b . C. 2a b . D. 2ab . 2 2 3 a −16b 2 2 3 a −16b 2 2 a −16b 3
Câu 49: Thể tích khối tứ diện đều cạnh a là: 3 3 3 3 A. 2a . B. 3a . C. a . D. a . 12 8 6 3
Câu 50: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng ϕ .
Khi đó thể tích khối chóp S.ABCD bằng. 3 3 3 3 A. a 2 tanϕ . B. a tanϕ . C. a 2 cot ϕ . D. a 2 tanϕ . 6 6 6 2
Câu 51: Cho khối chóp S.ABCD có ABCD là hình thang vuông tại A,B. Hai mặt phẳng (SAB) và (SAD)
cùng vuông góc với đáy. Biết AD = 2BC= 2a, BD = a 5 . Tính thể tích khối chóp S.ABCD biết góc giữa
SB và mặt phẳng đáy bằng 30° . 3 3 3 3 A. a 3 B. a 3 C. 2a 2 D. a 2 6 2 3 3
Câu 52: Cho khối chóp S.ABCD có ABCD là hình thang vuông tại A,B. Hai mặt phẳng (SAB) và (SAD)
cùng vuông góc với đáy. Biết AD = 2BC= 2a, BD = a 5 . Tính thể tích khối chóp S.ABCD biết góc giữa
SO và mặt phẳng đáy bằng 45°, với O là giao điểm của AC và BD. 3 3 3 3 A. a 3 B. 2a 3 C. a 2 D. a 3 3 3 3 2
Câu 53: Cho khối chóp S.ABCD có ABCD là hình thoi cạnh bằng a, tâm O, 
BAD = 60° . Gọi I là giao
điểm của hai đường chéo AC và BD. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) là điểm H, sao cho
H là trung điểm của BI. Góc giữa SC và mặt phẳng đáy bằng 45°. Thể tích khối chóp S.ABCD là. 3 3 3 3 A. a 39 B. a 39 C. a 39 D. a 39 12 48 24 36
Câu 54: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Mặt phẳng (SAB), (SAD) cùng vuông
góc với mặt phẳng (ABCD). Đường thẳng SC tạo với đáy góc 45°. Gọi M, N lần luợt là trung điểm của AB,
AD. Thể tích khối chóp S.MCDN là bao nhiêu? 3 3 3 3 A. 5a 2 B. 5a 2 C. 5a 2 D. 5a 2 12 6 8 24
Câu 55: Cho hình chóp S.ABC đáy ABC là tam giác đều cạnh 4cm. Cạnh bên SA vuông góc với đáy và
SA= 4cm. Lấy điểm M trên cạnh AB sao cho 
ACM = 45° . Gọi H là hình chiếu của S trên CM. Gọi I, K theo
thứ tự là hình chiếu của A trên SC,SH. Thể tích của khối tứ diện SAIK tính theo cm 3 bằng. A. 16 B. 9 C. 8 D. 16 3 9
Câu 56: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA = a, AB = a. Hình chiếu vuông
góc của đỉnh S trên ABCD là điểm H thuộc cạnh AC sao cho AC= 4AH. Gọi CM là đường cao của tam giác
SAC. Tính thể tích tứ diện SMBC. 3 3 3 3 A. a 2 B. a C. a 14 D. a 14 15 48 15 48
Câu 57: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O, AB = a, AD = a 3 , SO ⊥
(ABCD). Khoảng cách giữa AB và SD bằng a 3 . Thể tích khối đa diện S.ABCD bằng 4 3 3 3 3 A. a 15 B. a 3 C. a 3 D. a 3 30 8 3 6
Câu 58: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA ⊥ (ABCD), AB = SA= 1, AD = 2 .
Gọi M, N lần luợt là trung điểm của AD, SC, I là giao điểm của BM và AC. Tính thể tích khối tứ diện ANIB là 3 A. a 2 B. 2 C. 2 D. 2 36 12 18 36
Câu 59: Cho hình chóp tam giác S.ABC có AB = 5a, BC = 6a, CA = 7a. Các mặt bên (SAB), (SBC), (SCA)
tạo với đáy một góc 60°. Tính thể tích khối chóp A. 3 8a 3 B. 3 6a 3 C. 3 7a 3 D. 3 5a 3 .
LỜI GIẢI BÀI TẬP TỰ LUYỆN 3 Câu 1: Ta có 2 S = a ⇒ 1 1 2 a 2 V = SA S a a . Chọn D. S ABCD . = ABCD . 2. = ABCD . 3 3 3 2 Câu 2: 2 2
SA = SB − AB = 2a , 2 2
BC = AC − AB = a 2 1 a 2 ⇒ S = A . B BC = ABC 2 2 2 3 Ta có 1 1 a 2 a 2 V = SA S = a = . Chọn A. S ABC . ABC .2 . . 3 3 2 3 2 Câu 3: 2 2 2 2
SA = SC − AC = a 3; BC = AC − AB = a 2 1 a 2 ⇒ S = AB BC = ABC . 2 2 2 3 Ta có: 1 1 a 2 a 6 V = SA S = a = . Chọn A. S ABC . ABC . 3. . 3 3 2 6 (
 SAB) ⊥ ( ABC) Câu 4: Ta có 
⇒ SH ⊥ ( ABC) (  SAC  ) ⊥ ( ABC) Ta có 2 2
SA = SC − AC = a 2 2 3 3 Ta có a 3 S = ⇒ 1 1 a 3 a 6 V = SA S = a = . Chọn B. S ABC . ABC . 2. ABC 4 . 3 3 4 12 Câu 5: 2 2
SH = SA − AH = 2a . 3 Ta có 2 1 1 4 S a = AB AD = a ⇒ 2 V = SH S = a a = . Chọn C. S ABCD . ABCD .2 .2 ABCD . 2 . 3 3 3 Câu 6: 2a 3 3 SH = = a 3 , 2 2 S = (2a) = a ⇒ 1 1 2 4a 3 V = SH S = a a = .Chọn B. S ABCD . ABCD . 3.4 ABCD 4 2 . 3 3 3
Câu 7: SB ∩( ABC) = { }
B và SA ⊥ ( ABC) ⇒ (SB ( ABC))  = (SB AB)  =  , , SBA = 30°  SA = ⇒ =  a 3 tan SBA SA AB tan SBA = AB 3 2 2 2 1 a 2
BC = AC − AB = a 2 ⇒ S = AB BC = ABC . 2 2 2 3 1
1 a 3 a 2 a 6 V = SA S . Chọn C. ABC . = ABC . . = S. 3 3 3 2 18 (
 SAB) ⊥ ( ABC) Câu 8: Ta có 
⇒ SA ⊥ ( ABC) ( .  SAC  ) ⊥ ( ABC)
SB ∩( ABC) = { }
B và SA ⊥ ( ABC) ⇒ (SB ( ABC))  = (SB AB)  =  , , SBA = 30°  SA = ⇒ =  a 3 tan SBA SA AB tan SBA = AB 3 2 a 3 2 3 S = ⇒ 1 1 a 3 a 3 = a V SA S . Chọn D. S ABC . = ABC . . = ABC 4 . 3 3 3 4 12 (
 SAB) ⊥ ( ABC) Câu 9: Ta có 
⇒ SA ⊥ ( ABC) ( .  SAC  ) ⊥ ( ABC)
SM ∩( ABC) = {M}và SA ⊥ ( ABC) ⇒ (SM ( ABC))  = (SM AB)  =  , , SMA = 60°  SA = ⇒ =  tan SMA
SA AM tan SMA mà a 3 a 3 3 = ⇒ = .tan 60° = a AM SA AM 2 2 2 2 a 3 2 3 S = ⇒ 1 1 3a a 3 a 3 V = SA S . Chọn C. S ABC . = ABC . . = ABC 4 . 3 3 2 4 8
Câu 10: SC ∩( ABC) = {C}và SA ⊥ ( ABC) ⇒ (SC ( ABC))  = (SC AC)  =  , , SCA = 45° 2 2
AC = BC − AB = a 3 . SA = ⇒ =  tan SCA
SA AC tan SCA = a 3 AC 2 1 a 3 2 3 S = AB AC = ⇒ 1 1 a 3 = a V SA S a . Chọn A. S ABC . = ABC . 3. = ABC . 2 2 . 3 3 2 2
Câu 11: SM ∩( ABC) = {M} và SA ⊥ ( ABC) ⇒ (SM ( ABC))  = (SM AB)  =  , , SMA = 60°  SA = ⇒ =  tan SMA
SA AM tan SMA mà 1
AM = BC = a ⇒ SA = .
a tan 60° = a 3 AM 2 2 a 3 2 3 S = ⇒ 1 1 3a a 3 a 3 V = SA S .Chọn C. S ABC . = ABC . . = ABC 4 . 3 3 2 4 8
Câu 12: SC ∩( ABCD) = {C} và SA ⊥ ( ABCD) ⇒ (SC ( ABCD))  = (SC AC)  =  , , SCA = 45°  SA = ⇒ =  tan SCA
SA AC tan SCA = 2a AC 2 2
BC = AC − AB = a 3 ⇒ 2 S = AB C = a ⇒ ABCD .B 3 3 1 1 2 2a 3 V = SA S = = . Chọn A. S ABCD . ABCD .2a.a 3 . 3 3 3
Câu 13: SO ∩( ABCD) = { }
O và SA ⊥ ( ABCD) ⇒ (SO ( ABCD))  = (SO OA)  =  , , SOA = 60° 1
OA = AC = a 2  SA = ⇒ =  tan SOA
SA OAtan SOA = a 3 OA 2 2 2
BC = AC − AB = a 3 ⇒ S = AB BC = a ABCD . 3 ⇒ 1 1 2 3 V = SA S = = a . Chọn C. S ABCD . ABCD .a 3.a 3 . 3 3 (
 SAB) ⊥ ( ABCD) Câu 14: Ta có: 
⇒ SA ⊥ ( ABCD) (  SAD  ) ⊥ ( ABCD)
SC ∩( ABCD) = {C}và SA ⊥ ( ABCD) ⇒ (SC ( ABCD))  = (SC AC)  =  , , SCA = 45° 2 2
AC = AB + BC = a 2  SA = ⇒ =  tan SCA
SA AC tan SCA = a 2 AC 3 2 S = a ⇒ 1 1 2 a 2 V = SA S = = . Chọn B. S ABCD . ABCD .a 2.a ABCD . 3 3 3 (
 SAB) ⊥ ( ABCD) Câu 15: Ta có: 
⇒ SA ⊥ ( ABCD) (  SAD  ) ⊥ ( ABCD)
SM ∩( ABCD) = {M}và SA ⊥ ( ABCD) ⇒ (SM ( ABCD))  = (SM AM )  =  , , SMA = 60° 2 2 a 5
AM = AB + BM = . 2  SA = ⇒ =  a 15 tan SMA SA AM tan SMA = AM 2 3 2 S = a ⇒ 1 1 a 15 2 a 15 V = SA S = = . Chọn A. S ABCD . ABCD . .a ABCD . 3 3 2 6
Câu 16: SC ∩( ABCD) = {C}và SH ⊥ ( ABCD) ⇒ (SC ( ABCD))  = (SC )  =  , ,HC SCH = 60° 2 2
CH = BC + BH = a 5 .  SH = ⇒ =  tan SCH
SH CH tan SCH = a 15 CH 3 S = a = a ⇒ 1 1 2 4a 15 V = SH S = a = . Chọn B. ABCD ( )2 2 2 4 S ABCD . ABCD . 15.4a . 3 3 3
Câu 17: SC ∩( ABCD) = {C} SA ⊥ ( ABCD) ⇒ (SC ( ABCD))  = (SC )  =  ; , ,AC SCA = 45° SA = ⇒ =  2 2 sin SCA
SA SC sin SCA = 2a ⇒ AC = SC − SA = 2a SC 3 2 2 2
BC = AC − AB = a 3 ⇒ S = AB BC = a ⇒ 1 2a 3 = = .Chọn B. ABCD . 3 V SA S S ABCD . . 3 ABCD 3 3 Câu 18: Ta có 1 a V = SA SB SC = . Chọn A. S ABC . . . 6 6 2 2 3 Câu 19: Ta có 1 a S = BC CD = ⇒ 1 1 a a V = SA S = = . Chọn C. S BCD . BCD .a. BCD . 2 2 . 3 3 2 6 (
 SAB) ⊥ ( ABCD) Câu 20: Ta có 
⇒ SA ⊥ ( ABCD) (  SAD  ) ⊥ ( ABCD) BC ⊥ AB Lại có 
⇒ BC ⊥ (SAB) mà BC ⊥ SA
SC ∩(SAB) = {S} ⇒ (SC ( ABC))  = (SC SB)  =  , , CSB = 30° BC BC 2 2 tan CSB = ⇒ SB = = ⇒ = − = SBa 3 SA SB AB a 2 tan CSB 3 2 S = a ⇒ 1 1 2 a 2 V = SA S = a = . Chọn D. S . ABCD .a 2. ABCD .ABCD 3 3 3 (
 SAB) ⊥ ( ABCD)
Câu 21: Ta có
⇒ SA ⊥ ( ABCD) ( SAD  ) ⊥ ( ABCD)
SC ∩( ABCD) = {C} SA ⊥ ( ABCD) ⇒ (SC ( ABCD))  = (SC )  =  ; , ,AC SCA = 30° 2 2
AC = AB + BC = a 2 . SA = ⇒ =  a 6 tan SCA SA AC tan SCA = AC 3 3 2 S = a ⇒ 1 1 a 6 2 a 6 V = SA S a .Chọn D. S . = ABCD . . = ABCD .ABCD 3 3 3 9 Câu 22:
Gọi M là trung điểm của BC BC ⊥ AM Ta có 
⇒ BC ⊥ (SAM ) BC ⊥ SA
⇒ ((SBC) ( ABC))  = (SM )  =  , ,AM SMA = 60°  SA = ⇒ =  a 3 3 tan tan = .tan 60 a SMA SA AM SMA ° = AM 2 2 2 a 3 2 3 S = ⇒ 1 1 3a a 3 a 3 V = SA S . Chọn S . = ABC . . = ABC 4 .ABC 3 3 3 4 8 A. Câu 23: Ta có 1 abc V = SA SB SC = . Chọn C. S . . .ABC 6 6
Câu 24: SB ∩( ABC) = { }
B và SA ⊥ ( ABC) ⇒ (SB ( ABC))  = (SB )  =  , ,AB SBA = 60° SA = ⇒ =  tan SBA
SA AB tan SBA = a 3 . AB 2 a 3 3 1 a S = ⇒ V = SA S = . Chọn B. S . ABC 4 .ABC 3 ABC 4 Câu 25: Ta có 2 2 a 5 2 2 3a
HD = AH + AD =
⇒ SH = SD − HD = 2 2 3 Lại có 2 1 S a = a ⇒ V = SH S = . Chọn D. S . ABCD .ABCD 3 ABCD 2 Câu 26:
Gọi M là trung điểm của BC BC ⊥ AM Ta có 
⇒ BC ⊥ (SAM ) BC ⊥ SA
⇒ ((SBC) ( ABC))  = (SM )  =  , ,AM SMA = 60°  SA 3a = ⇒ =  a 3 tan SMA SA AM tan SMA = .tan 60° = AM 2 2 2 a 3 2 3 S = ⇒ 1 1 3a a 3 a 3 V = SA S = = . S . ABC . . ABC 4 .ABC 3 3 2 4 8 Chọn A. 3 Câu 27: Ta có: 2 S = a ⇒ 1 a 2 = = . Chọn D. MNPQ V SM S S . .MNPQ 3 MNPQ 3 Câu 28: Ta có: 2 2 2
20 + 21 = 29 ⇒ đáy là tam giác vuông. S 1
day= .20.21 = 210 ⇒ V= 1 .100.210 = 7000 . Chọn A. 2 3
Câu 29: SC ∩( ABCD) = {C}và SH ⊥ ( ABCD) ⇒ (SC ( ABCD))  = (SC HC)  =  , , SCH = 45° 2 2
HC = HB + BC = a 2 .  SH = ⇒ =  tan SCH
SH HC tan SCH = a 2 HC 3 2 S = AB AD = a ⇒ 1 1 2 2a 2 V = SH S = a a = . Chọn B. S ABCD . ABCD . 2.2 ABCD . 2 . 3 3 3 2 2 2 2
SA + SB = AB = 25 SA =19 SA = 19    Câu 30: 2 2 2 2 SB SC BC 36 SB 6  + = = ⇔ = ⇔ SB = 6  2 2 2  2 SA SC AB 49 SC 30  + = = = SC =   30  ⇒ 1 V = SA SB SC = .Chọn D. S ABC . . 95 . 6 BH ⊥ AC
Câu 31: Kẻ BH ⊥ AC ta có 
⇒ BH ⊥ (SAC) mà BH ⊥ SA
SB ∩(SAC) = {S} ⇒ ( (SAC))  = (SB )  =  SB, ,SH SBH = 30°. 1 1 1 4 a 3 = + = ⇒ BH = 2 2 2 2 BH BC BA 3a 2  BH BH 3 tan a BSH = ⇒ SH = = . SH  tan BSH 2 2 2 a
AH = AB − BH = ; 2 2
SA = SH − AH = a 2 . 2 3 2 S = AB AD = a ⇒ 1 a 6 V = SA S = S ABCD . ABCD . 3 . 3 ABCD 3 . Chọn D.
Câu 32: Ta có ngay tâm H là đường tròn ngoại tiếp ∆ ABC.
Kẻ HK ⊥ AB, HP ⊥ SK ⇒ d (H;(SAB)) = HP = 2 . tan 30 HK BK AB ° = ⇒ HK = = . BK 3 2 3 2 1 1 AB 3 120 3 V = = SH S = SH ⇒ SH = S 30 . ABC . .ABC 2 3 3 4 AB 120 3 . AB 2 1 1 SH.HK 1 AB 2 3 S = SK AB = AB = AB = . ABC . . . 15 2 2 HP 2 2 Chọn B.
Câu 33: SD ∩( ABCD) = { }
D và SH ⊥ ( ABCD) ⇒ (SD ( ABCD))  = (SD HD)  =  , , SDH = 45°  SH = ⇒ =  tan SDH
SH HD tan SDH mà 1
HD = AD = a ⇒ SH = a HD 2 3 2 1 1 2 S a = AB AD = a ⇒ 2 V = SH S = a a = . Chọn C. S ABCD . ABCD . .2 ABCD . 2 . 3 3 3
Câu 34: SC ∩( ABCD) = {C}và SH ⊥ ( ABCD) ⇒ (SC ( ABCD))  = (SC HC)  =  , , SCH = 60°  SH = ⇒ =  tan SCH
SH HC tan SCH mà 2 2
HC = HD + CD = a 2 ⇒ SH = a 6 HC 3 2 S = AB AD = a ⇒ 1 1 2 2a 6 V = SH S = a a = . Chọn B. S ABCD . ABCD . 6.2 ABCD . 2 . 3 3 3
Câu 35: Gọi H là trung điểm của AB ⇒SH ⊥ AB (
 SAB) ⊥ ( ABCD) Ta có: 
⇒ SH ⊥ ( ABCD) SH ⊥ AB 2 AB 3 AB 3 S = =
⇔ AB = ⇒ SH = = ABC 9 3 6 3 3 4 2 2 S 1 1 = AB = ⇒ V = SH S = = .Chọn B S ABC D . ABCD .3 3.36 36 3 ABCD 36 . 3 3 Câu 36:
Gọi H là trung điểm của AB⇒SH ⊥ AB (
 SAB) ⊥ ( ABCD) Ta có: 
⇒ SH ⊥ ( ABCD) SH ⊥ AB AB 3 3a 3 SH = = , 2 2 S
= AB = a ABCD 9 2 2 3 1 1 3a 3 2 9a 3 V = SH S = a = S ABCD . ABCD . .9 . 3 3 2 2 Chọn B
Câu 37: Gọi H là trung điểm của AB⇒SH ⊥ AB (
 SAB) ⊥ ( ABCD) Ta có: 
⇒ SH ⊥ ( ABCD) SH ⊥ AB 1 3a SH = AB = , 2 2 S
= AB = a ABCD 9 2 2 3 1 1 3a 2 9a V = SH S = a = S ABCD . ABCD . .9 . . Chọn D. 3 3 2 2 Câu 38
Gọi H là trung điểm của AB⇒SH ⊥ AB (
 SAB) ⊥ ( ABCD) Ta có: 
⇒ SH ⊥ ( ABCD) SH ⊥ AB
SC ∩(ABCD) = {C} và SH ⊥ ( ABCD) ⇒ ( ( ))  = ( )   , , = = 60o SC ABCD SC HC SCH 2 2 3a 5
CH = BH + BC = 2  SH = ⇒ =  3a 15 tan SCH SH HC tan SCH = HC 2 2 2 S = AB = a ⇒ ABCD 9 3 1 1 3a 15 2 9a 15 V = SH S = a = S ABCD . ABCD . .9 . 3 3 2 2 Chọn B. Câu 39: Kẻ SH ⊥ AB ta có (
 SAB) ⊥ ( ABCD) 
⇒ SH ⊥ ( ABCD) SH ⊥ AB Dễ thấy 2 2 2 2
SA + SB = AB = 4a ⇒ ∆ SAB vuông tại S 1 1 1 4 a 3 = + = ⇒ SH = 2 2 2 2 SH SA SB 3a 2 2 S = AB AD = a ABCD . 6 1 1 a 3 2 3 V = SH S = a = a .Chọn A. S ABCD . ABCD . .6 3 . 3 3 2 Câu 40: Kẻ SH ⊥ BD (
 SBD) ⊥ ( ABCD) Ta có 
⇒ SH ⊥ ( ABCD) SH ⊥ BD
SD ∩( ABCD) = { } D và
SH ⊥ ( ABCD) ⇒ (SD ( ABCD))  = (SD )  =  , ,DH SDH = 30° 2 2 D
B = AB + AD = 2a SB = ⇒ =  sin SDH
SB BDsin SDH = a ⇒ SD = a 3 BD 1 1 1 4 a 3 = + = ⇒ SH = 2 2 2 2 SH SB SD 3a 2 3 2 S = AB AD = a ⇒ 1 1 a 3 2 a = = = . Chọn D. ABCD . 3 V SH S a S ABCD . ABCD . . 3 . 3 3 2 2 Câu 41: Kẻ SH ⊥ AB (
 SAB) ⊥ ( ABC) Ta có 
⇒ SH ⊥ ( ABC) SH ⊥ AB 1 1 1 4 a 3 = + = ⇒ SH = 2 2 2 2 SH SA SB 3a 2 2 2 2 AB 3 2
AB = SA + SB = 2a ⇒ S = = a ABC 3 4 3 1 1 a 3 2 a V = SH S = a = . Chọn D. S ABC . ABC . . 3 . 3 3 2 2 Câu 42:
Gọi H là trung điểm của AB ⇒SH ⊥ AB (
 SAB) ⊥ ( ABCD) Ta có 
⇒ SH ⊥ ( ABCD) SH ⊥ AB 1 1 2 2 S = S = a = a ABC ABCD (2 ) 2 2 2 1 3VS. V = SH. ABC S ⇒ SH = = a S ABC ABC 2 . 3 SABC 2 2 2 2
HC = BH + BC = a 5 ⇒ SC = SH + HC = 3a .Chọn A. Câu 43: Kẻ SH ⊥ AC (
 SAC) ⊥ ( ABC) Ta có
⇒ SH ⊥ ( ABC) SH ⊥ ACSH = ⇒ =  sin SAC
SH SAsin SAC = a SA 2 2
AC = BC − AB = 4a 1 2 ⇒ S = A . B AC = ABC 6a 2 1 1 2 3 V = SA S
= a a = a . Chọn D. S ABC . ABC . .6 2 . 3 3 Câu 44: Kẻ SH ⊥ AC (
 SAC) ⊥ ( ABC) Ta có
⇒ SH ⊥ ( ABC) SH ⊥ ACSH = ⇒ =  sin SAC
SH SAsin SAC = a 3 SA 2 2 1 2
AC = BC − AB = 4a ⇒ S = A . B AC = ABC 6a 2 1 1 2 3 V = SH S = a a = a . Chọn A. S ABC . ABC . 3.6 2 3 . 3 3
Câu 45: Gọi H là tâm đường tròn ngoại tiếp ∆ ABC⇒SH ⊥ (ABC)
Gọi M là trung điểm của AB 1 a 3 SM = AB = , 1 1 a 3. 3 = = . a MH CM = 2 2 3 3 2 2 2 2 a 2
SH = SM − MH = 2 (a 3)2 3 2 3a 3 S = = ABC 4 4 2 3 1
1 a 2 3a 3 a 6 V = SH S = = .Chọn C. S ABC . ABC . . . 3 3 2 4 8
Câu 46: Diện tích đáy hình chóp Sđ= a2
Gọi O là tâm của hình vuông ABCD ⇒SO ⊥ (ABCD).
Dựng OE ⊥ CD, CD ⊥ SO⇒ CD ⊥ SE 2 2 Ta có: 2 2 3a a
SE = h + OE = + = a . 4 4 2
Diện tích một mặt bên là: 1 = . a S OE CD = . 2 2 2
Diện tích toàn phần của hình chóp : 2 a 2 S = a + 4.
= 3a . Chọn B. 2
Câu 47: Diện tích đáy hình chóp Sđ= a2
Gọi O là tâm của hình vuông ABCD ⇒SO ⊥ (ABCD).
Dựng OE ⊥ CD, CD ⊥ SO⇒ CD ⊥ SE. S = 4S
= 2SE.CD = 2SE.a xq SCD Mặt khác S 2
xq=2Sđ ⇒ 2.SE.a = 2a ⇒ SE = a 2 Do đó 2 2 2 a a 3 SO SE OE a   = − = − =  . 2    2 3
Thể tích khối chóp là: V= 1 a 3 . SO S = . Chọn A. 3 ABCD 6 Câu 48:
Gọi H = AC ∩ BD ⇒ SH ⊥ ( ABCD) . BC ⊥ SH
Dựng HE ⊥ BC, HF ⊥ SE⇒  ⇒ BC ⊥ HF BC ⊥ HE
Mặt khác HF ⊥ SE⇒HF ⊥ (SBC)⇒ d (H;(SBC)) = HF . Do I là trung điểm của
SH⇒ d (H;(SBC)) = 2d (I;(SBC)) = 2b = HF Lại có: 1 1 1 HE. = + ⇒ = HF = ab SH 2 2 2 2 2 2 HF HE SH HE − HF a 2 − 4b 4 3 Do đó 1 2 a .b V = SH S = . Chọn A. S ABCD . ABCD . . 2 2 3 3 a −16b Câu 49:
Giả sử tứ diện S.ABC đều cạnh a.
Gọi H là trọng tâm tam giác ABC suy ra SH ⊥ (ABC)
Gọi M là trung điểm của BC ta có a 3 AM = 2 Khi đó 2 2 a 3 a 3 AH = AM ⇒ . = . 3 3 2 3 2 Lại có 2 2 2 a a 6
SH = SA − AH = a − = . 3 3 2 3 1
1 a 6 a 3 a 2 ⇒ V = SH S . Chọn A. ABC . = ABC . . = S. 3 3 3 4 12 Câu 50:
Gọi O là tâm của hình vuông ABCD khi đó SO ⊥ (ABCD) suy ra 
SDO = (SD ( ABCD))  ; = ϕ . Lại có BD a 2
BD = a 2 ⇒ OD = = . 2 2 Suy ra a 2 tanϕ SO = OD tanϕ = . 2 3 Khi đó 1 a 2 V = SO S = ϕ . Chọn A. S ABCD . ABCD tan . 3 6 (
 SAB) ⊥ ( ABCD)
Câu 51: Ta có
⇒ SA ⊥ ( ABCD) ( SAD  ) ⊥ ( ABCD)
SB ∩( ABCD) = { }
B và SA ⊥ ( ABCD) ⇒ (SB ( ABCD))  = (SB BA)  =  , , SBA = 30° 2 2
AB = BD − AD = a SA = ⇒ =  a 3 tan SBA SA AB tan SBA = AB 3 2 1 3a S = AB AD + BC = ABCD .( ) 2 2 2 3 1 1 a 3 3a a 3 V = SA S = = . Chọn A. S ABCD . .ABCD . . . 3 3 3 2 6 (
 SAB) ⊥ ( ABCD)
Câu 52: Ta có
⇒ SA ⊥ ( ABCD) ( SAD  ) ⊥ ( ABCD)
SO ∩( ABCD) = { }
O và SA ⊥ ( ABCD) ⇒ (SO ( ABCD))  = (SO )  =  , ,AO SOA = 45° 2 2 2 2
AB = BD − AD = a ⇒ AC = AB + BC = a 2 2 2a 2 AO = AC = 3 3  SA = ⇒ =  2a 2 tan SOA SA AO tan SOA = . AO 3 2 1 3a 2 3 S = AB AD + BC = ⇒ 1 1 2a 2 3a a 2 = = = .Chọn C. ABCD .( ) V SA S S ABCD . ABCD . . 2 2 . 3 3 3 2 3
Câu 53: SC ∩( ABCD) = {C}và SH ⊥ ( ABCD) ⇒ (SC ( ABCD))  = (SC )  =  , ,CH SCH = 45°
BAD = 60° ⇒ BD = a , AC = a 3 . Ta có 1 a
IH = BD = 4 4 2 1 a 3 S = AC BD = ABCD . 2 2 2 2 a 13
HC = IH + IC = 4  SH = ⇒ =  a 13 tan SCH SH HC tan SCH = HC 4 2 3 1
1 a 13 a 3 a 39 V = SH S = = . Chọn C S ABCD . .ABCD . . . 3 3 4 2 24 Câu 54:
SC ∩( ABCD) = {C}và SA ⊥ ( ABCD) ⇒ (SC ( ABCD))  = (SC )  =  , ,AC SCA = 45° 2 2
AC = AB + BC = a 2 SA = ⇒ =  tan SCA
SA AC tan SCA = a 2 AC 2 1 a 2 S = AM = , 1 a S = BM = BCM .BC AMN .AN 2 8 2 4 2 5a S = S − S − S = MCDN ABCD AMN BCM 8 2 3 1 1 5a 5a 2 V = SH = a = . S MCDN .SMCDN . 2. . 3 3 8 24 Chọn D. Câu 55: CM ⊥ SA
Cách 1: Ta có
⇒ SM ⊥ AH ⇒ A
∆ HC vuông cân tại H. CM ⊥ SA
Mặt khác CM ⊥ (SAH ) ⇒ AK ⊥ CM ⇒ AK ⊥ (SHC) . AK ⊥ KI Do đó 
. Lại có SC ⊥ AI ⇒ SC ⊥ (AIK) . AK ⊥ SC
Hình chóp S.AIK có đường cao là SI và đáy là tam giác AKI vuông tại K. Ta có: S . A AC AI =
= 2 2 , AH = HC = 2 2 . 2 2 SA + AC S . A AH 4 2 2 2 6 AK = =
⇒ KI = AI − AK = . 2 2 SA + AH 3 3
Tam giác SAC vuông cân tại A nên I là trung điểm của SC SC ⇒ SI = = 2 2 . 2 1 4 2 1 16 S = AK KI = ⇒ V = SI S = . S AIK . . AKI . 2 3 . 3 AKI 9 Cách 2: 1 1 1 V = SA S = = . S AHC AHC ( )2 16 . . .4. . 2 2 . 3 3 2 3 2 2 2 Lại có: 2 SA SK 4 2
SA = SK.SH = SI.SC ⇒ = = = ; SA SI 1 = = 2 2 SH SH 4 + 8 3 2 SC SC 2 Khi đó V SK SI 1 16 S AIK 1 . = . = ⇒ V = V = . Chọn D. V SH SC S.AIK S. 3 AHC 9 S AHC 3 . Câu 56: SA = a , 1 a 2
AC = a 2 ⇒ AH = AC = . 4 4 Do đó 2 2 a 14
SH = SA − AH = .Mặt khác 4 a 14 .
SACM = SH.AC = 2S ⇔ a CM = a SAC . . 2 4 Do đó a 7 2 2 a CM =
⇒ AM = AC − CM = ⇒ M là 2 2 trung điểm của SA. 2 3 3 Ta có: 1 1 a 14 a a 14 V = SH = = .Do đó: V = 1 a 14 V = . Chọn D. S ABC .S . . . ABC 3 3 4 2 24 S.M BC 2 S.ABC 48 Câu 57: Do
AB / /CD ⇒ d ( A ;
B SD) = d (AB;(SCD))
= d (A;(SCD)) = 2d ( ;
O (SCD))(Do AC = 2OC )
Mặt khác d ( AB SD) a 3 =
⇒ d (O (SCD)) a 3 ; ; = . 4 8 Dựng
OE ⊥ CD ,OF ⊥ SE ⇒ CD ⊥ OF ⇒ OF ⊥ (SCD). Khi đó ( ( )) 3 ; = = a d O SCD OF mà 8 AD a 3 OE = = 2 2 và 1 1 1 5 + = ⇒ SO = a . 2 2 2 SO OE OF 10 Mặt khác 3 2 S = a ⇒ 1 a 15 = = . Chọn ABCD 3 V SO S S ABCD . . 3 ABCD 30 A.
Câu 58: Gọi O là tâm hình chữ nhật thì NO là đường trung
bình của tam giác SAC và SA 1 NO = = . 2 2
Do I = AO ∩ BM ⇒I là trọng tâm ∆ SBD. Ta có: 2 1 1
AI = AO = AC ⇒ S = S . 3 3 AIB 3 ACB Mặt khác: 1 2 1 2 S = AB BC = ⇒ S = S = . ABC . 2 2 ABI 3 ABC 6
Thể tích khối chóp ANIB là: V= 1 1 1 2 2 . NO S = = . Chọn D. ABI . . 3 3 2 6 36
Câu 59:Nửa chu vi tam giác ABC là:
AB + BC + CA p = = 9a 2
Diện tích tam giác ABC tính theo công thức He-rông là: 2 S
= p p − a p − b p − c = a . ABC ( )( )( ) 6 6
Gọi H là hình chiếu vuông góc của S trên mặt phẳng (ABC). Dựng
HM ⊥ AB , HN ⊥ AC , ⊥ ⇒  =  =  HP BC
SMH SNH SPH = 60°.Khi đó
∆SHM = ∆SHN = ∆SHP suy ra HM = HN = HP ⇒ H là tâm
đường tròn nội tiếp tam giác ABC 2
S 6a 6 2a 6 ⇒ HM = r = = = . p 9a 3
Suy ra SH = HM tan 60° = 2a 2 ⇒ 1 3 V = SH.S = a .Chọn A. S ABC ABC 8 3 . 3
Document Outline

  • ITMTTL~1
  • IIBITP~1
  • IIILIG~1