









Preview text:
CHỦ ĐỀ 9: TỈ SỐ THỂ TÍCH
I. LÝ THUYẾT TRỌNG TÂM
Chú thích V = Thể tích cũ, V =Thể tích mới (dùng cho kỹ thuật chuyển đỉnh và đáy). 1 2
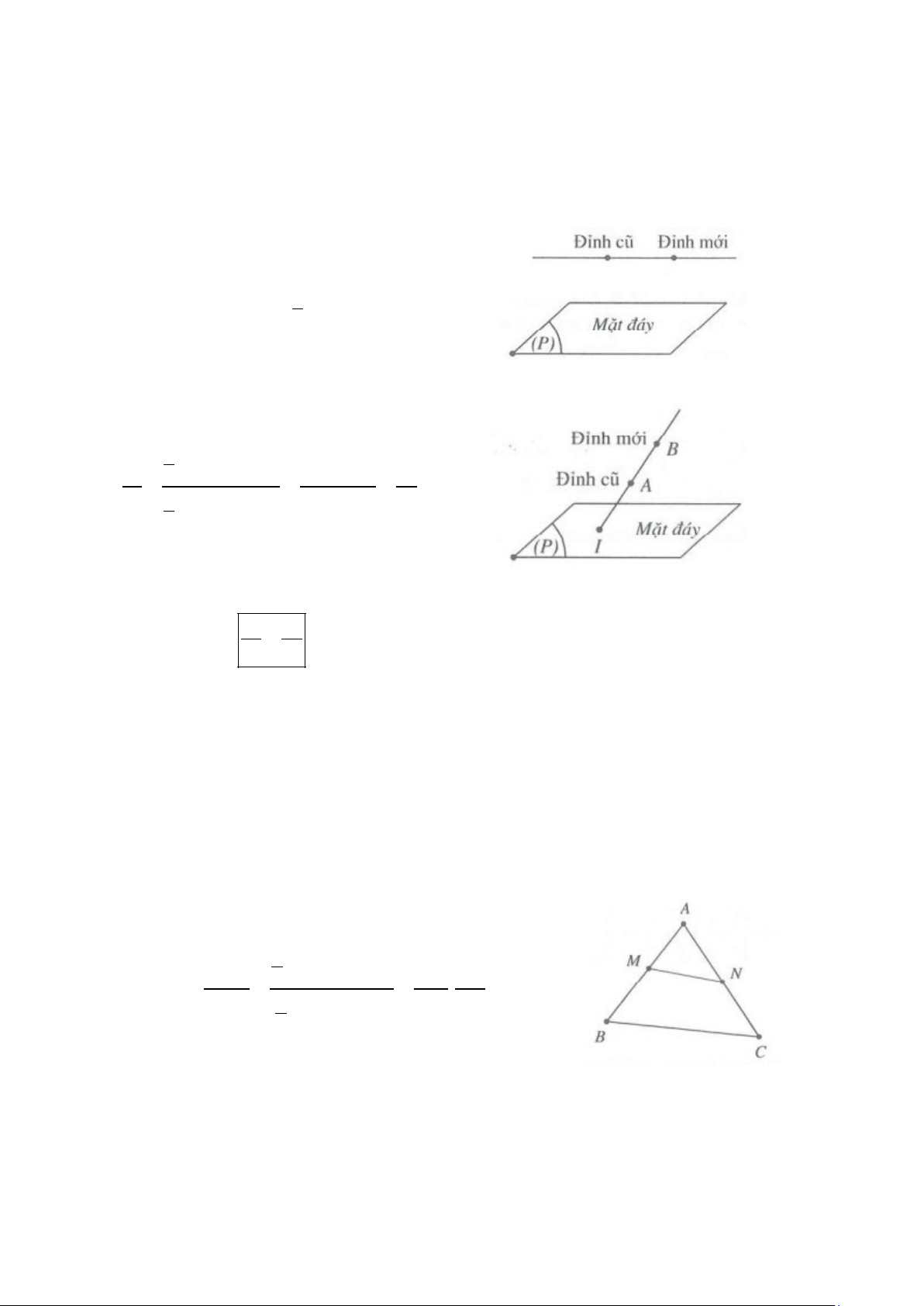
1. Kỹ thuật đổi đỉnh (đáy không đổi) a. Song song với đáy 1
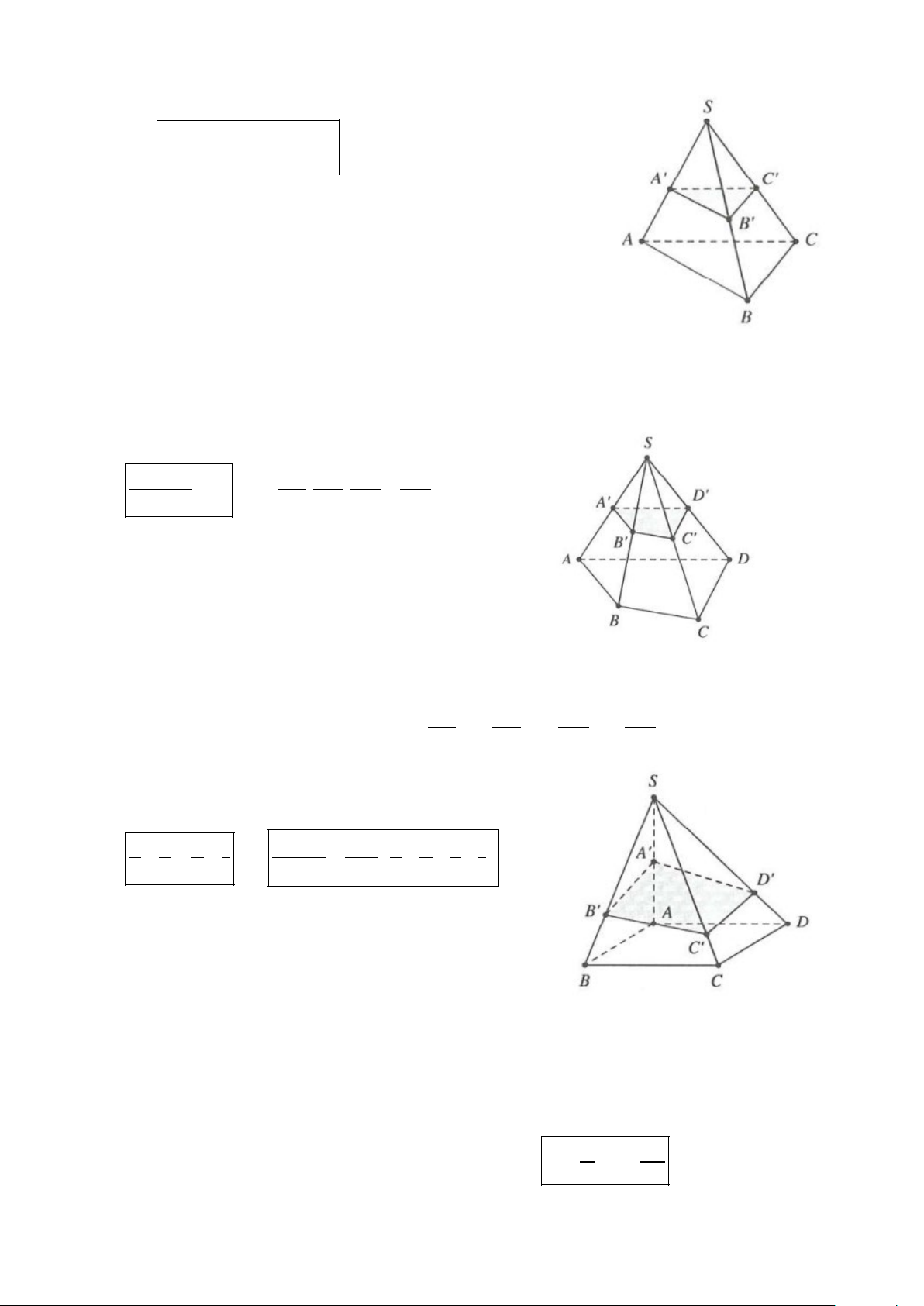
V = V = B . h 1 2 3 b. Cắt đáy
1.d ( ;A(P)).Sđ V d ( ; A (P)) 1 3 IB = = = . V 1 d B P IA 2 .d ( ; B (P)) ( ;( )) .S 3 đ
2. Kỹ thuật chuyển đáy (đường cao không đổi) V S 1 1 =
;với S là diện tích đáy cũ; S là diện tích đáy mới V S 1 2 2 2 Chú ý:
i. Đưa hai khối đa diện về cùng một đỉnh; hai đáy mới và cũ nằm trong cùng một mặt phẳng (thường
thì đáy cũ chứa đáy mới). Áp dụng công thức tính diện tích của đa giác để so sánh tỉ số giữa đáy cũ và đáy mới.
ii. Nếu tăng (hoặc giảm) mỗi cạnh của đa giác (tam giác, tứ giác), k lần thì diện tích đa giác sẽ tăng (hoặc giảm) 2 k lần.
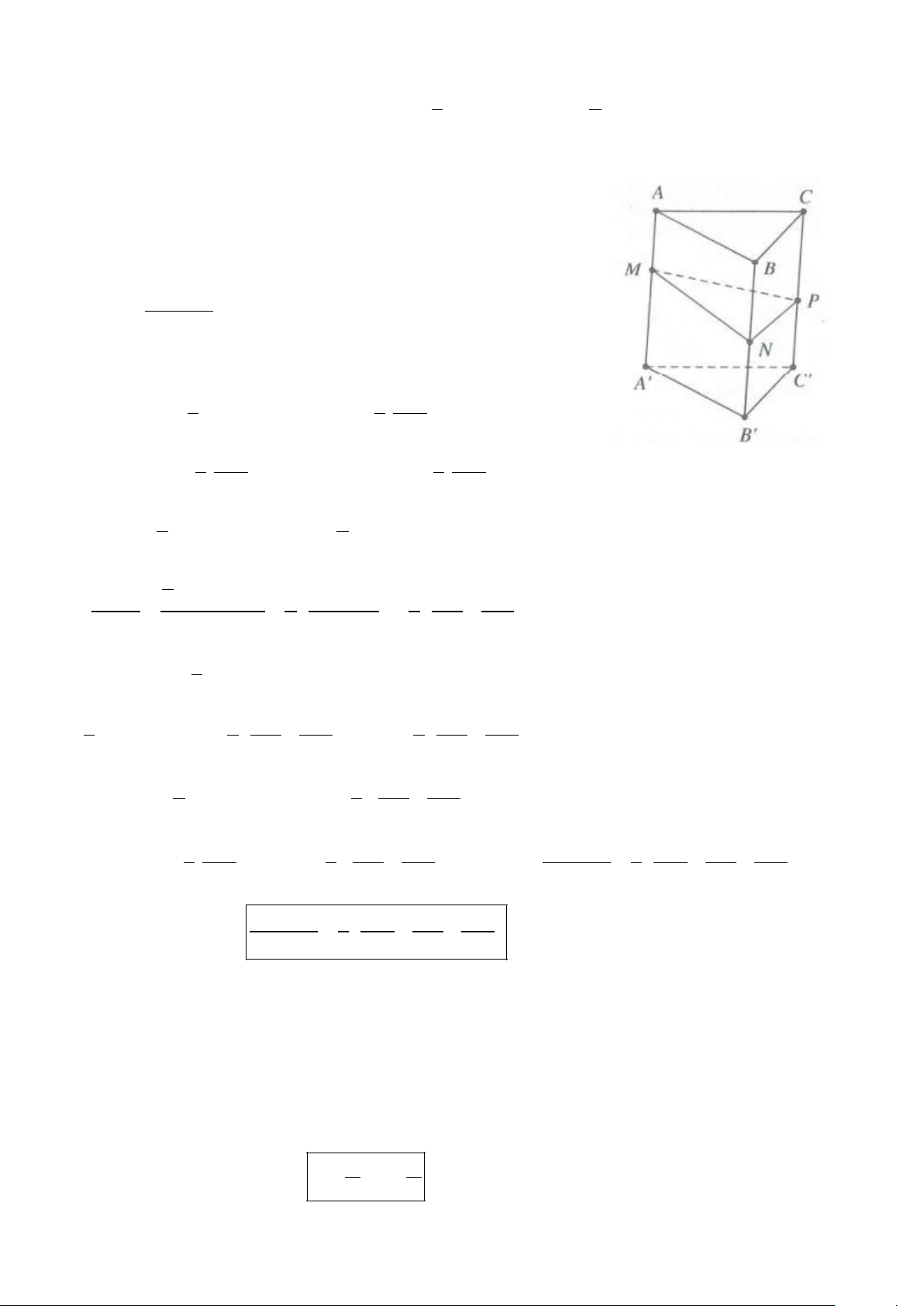
iii. Tỉ số đa giác hay gặp là tỉ số diện tích của hai tam giác.
1 .AM.AN.sin A S A∆MN 2 AM = = . AN . S 1 ∆ AB AC ABC .A . B AC.sin A 2
3. Tỉ số thể tích của khối chóp
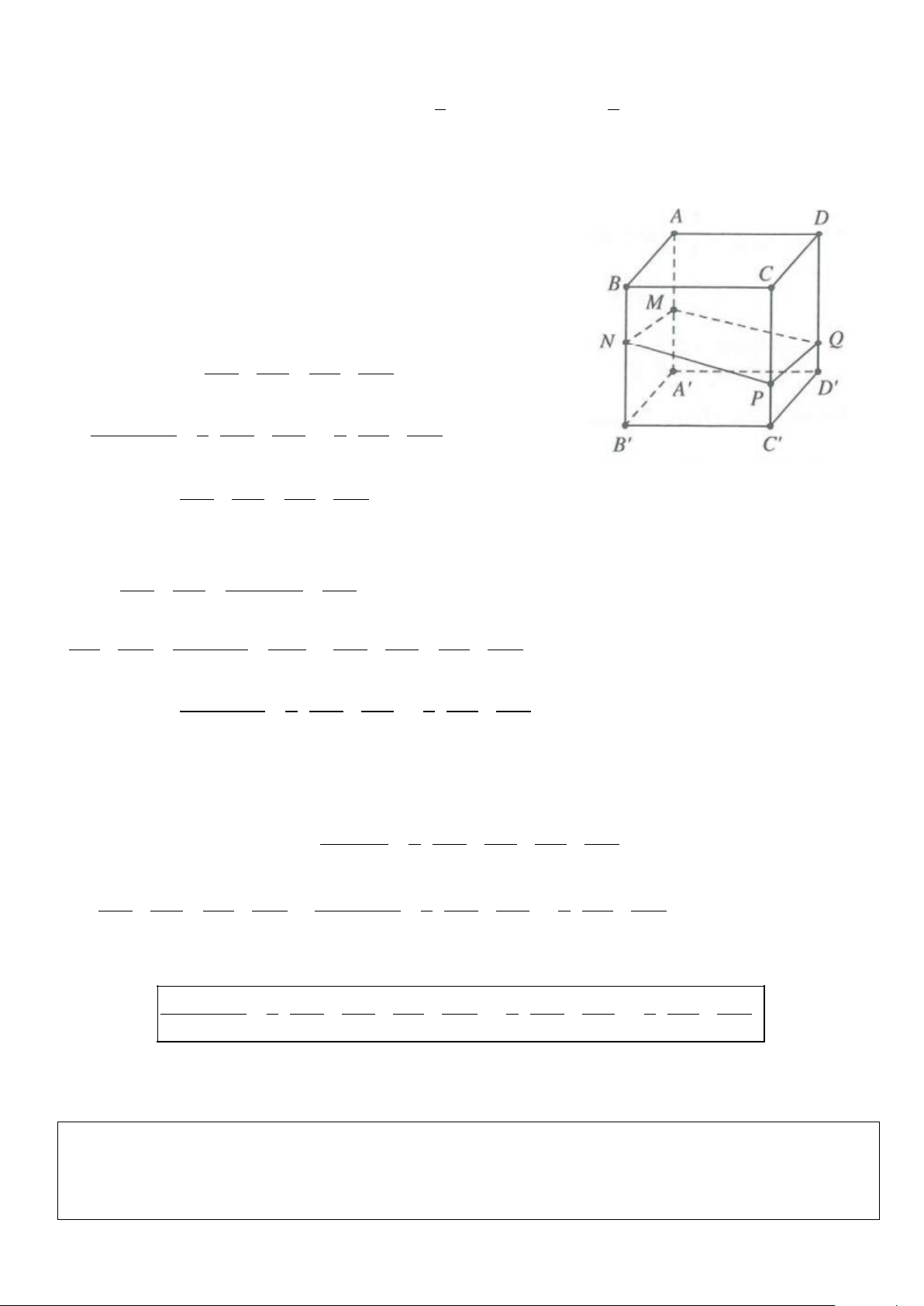
a. Tỉ số thể tích của khối chóp tam giác ′ ′ ′
Công thức: VS.A′BC′′ SA = . SB . SC V SA SB SC S.ABC
Lưu ý: Công thức chỉ áp dụng với khối chóp có đáy là tam giác nên
trong nhiều trường hợp ta cần chia nhỏ các khối đa diện thành các
hình chóp tam giác khác nhau rồi mới áp dụng.
b. Tỉ số thể tích của khối chóp tứ giác
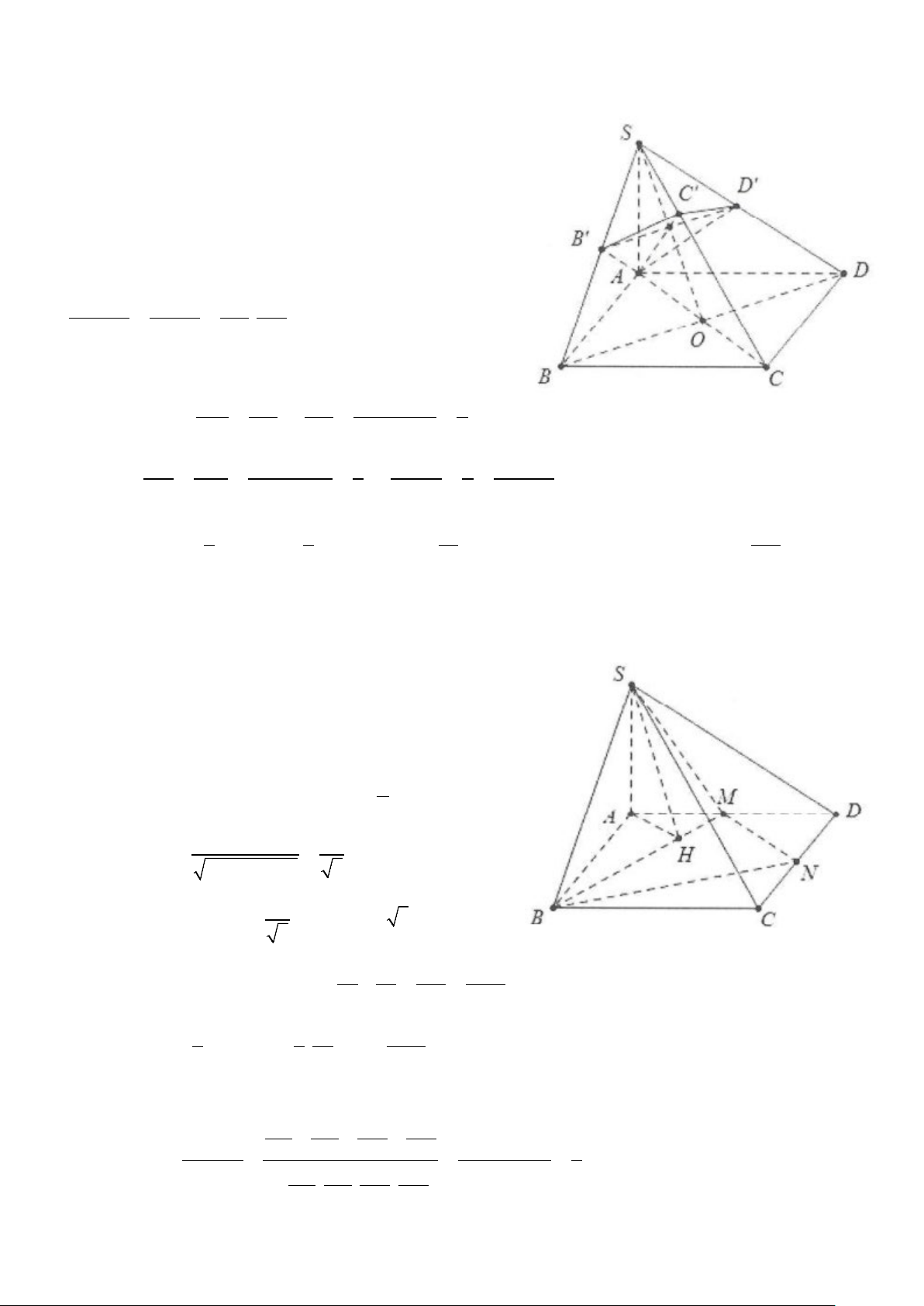
Trường hợp đặc biệt: Cho hình chóp S.ABCD có đáy ABCD (hoặc đa giác bất kỳ), mặt phẳng (P)
song song với đáy cắt các cạnh bên ,
SA SB, SC, SD lần lượt tại A ,′ B ,′C ,′ D′ . ′ ′ ′ ′
Khi đó VS.A′BC′ D′′ 3
= k ; với SA . SB . SC SD = = k . V SA SB SC SD S.ABCD
Chú ý: Công thức trên đúng với đáy n giác.
Trường hợp đáy là hình bình hành (hay gặp)
Bài toán: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Mặt phẳng (P) cắt các cạnh ′ ′ ′ ′ ,
SA SB, SC, SD lần lượt tại A ,′ B ,′C ,′ D′ sao cho SA = ; SB = ; SC = ; SD x y z = t. SA SB SC SD VS MNPQ xyzt Khi đó 1 1 1 1 + = + và . 1 1 1 1 = + + + x z y t V x y z t S ABCD 4 .
4. Tỉ số thể tích của khối lăng trụ a. Lăng trụ tam giác
Kết quả 1:
Gọi V là thể tích khối lăng trụ, V là thể tích khối chóp tạo thành từ 4 trong 6 đỉnh của lăng trụ, V là thể 1 2
tích khối chóp tạo thành từ 5 trong 6 đỉnh của lăng trụ. Khi đó: V 2 = ; V V V = 1 2 3 3
Ví dụ: Hình lăng trụ 1 2
ABC.A′B C ′ ′ →V = = ′ ′ V ′ ′ ′ V ′ ′ V A B BC ABC A B C ; . A B ABC ABC. 3 3 A′B C ′ ′ Kết quả 2:
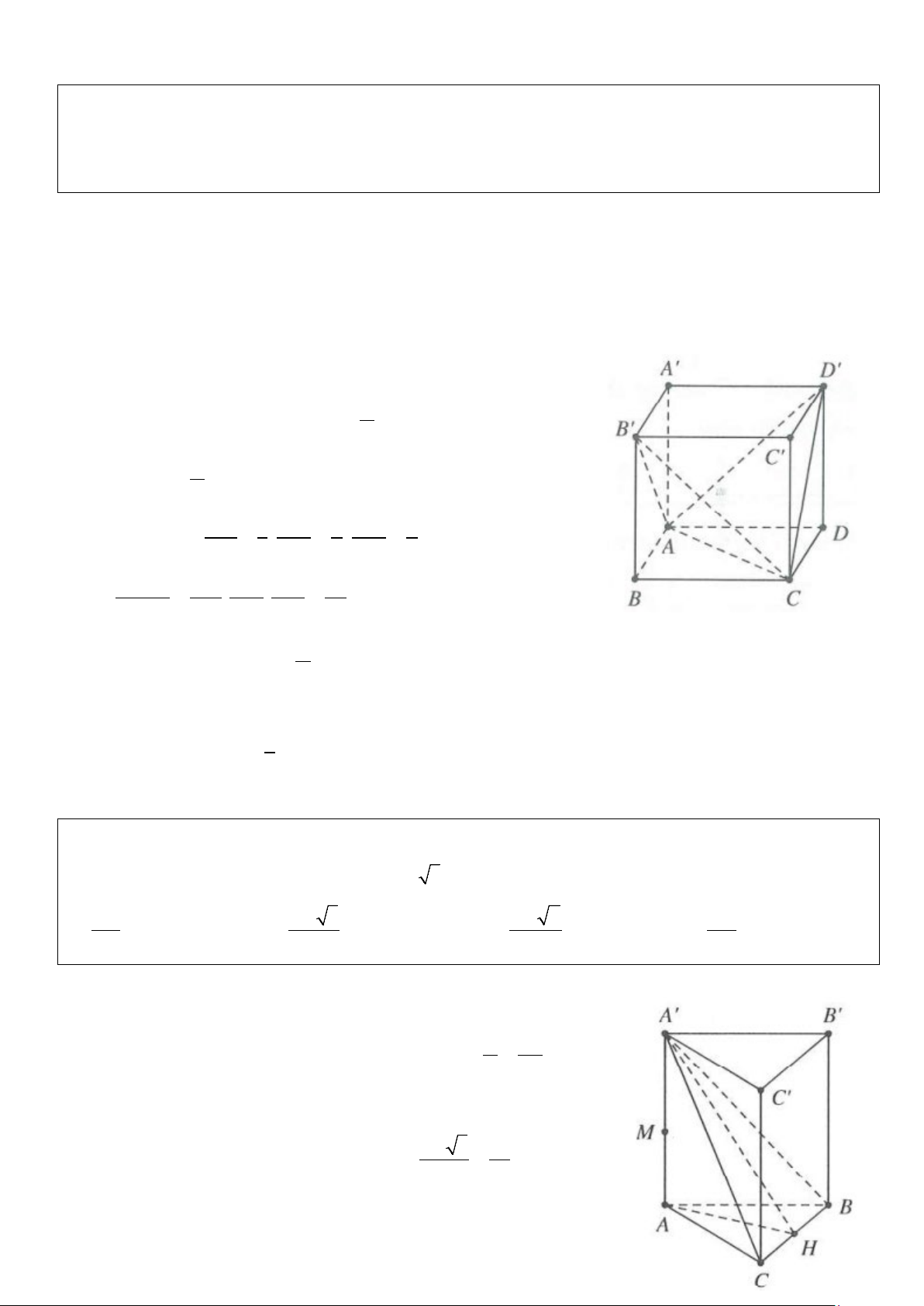
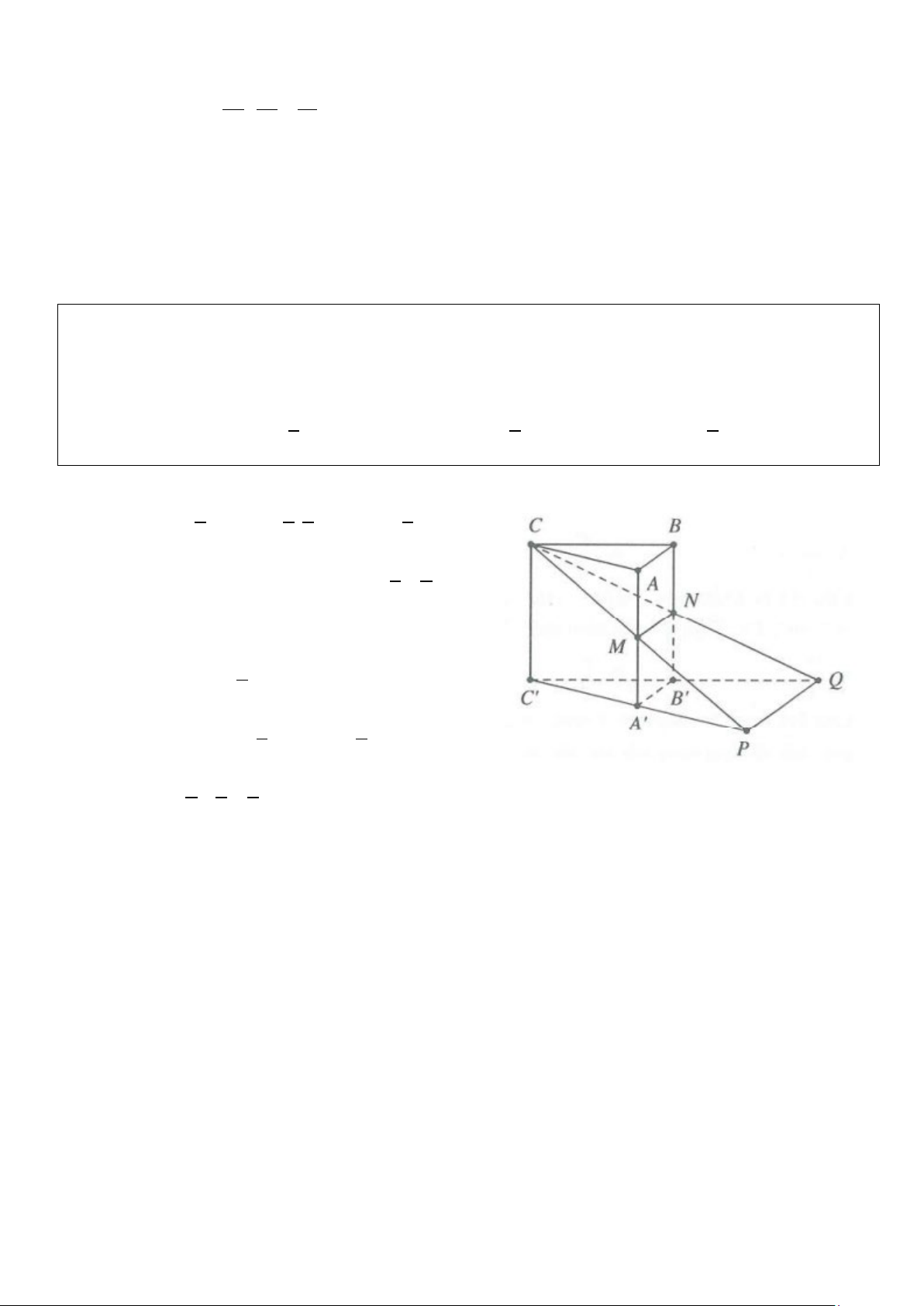
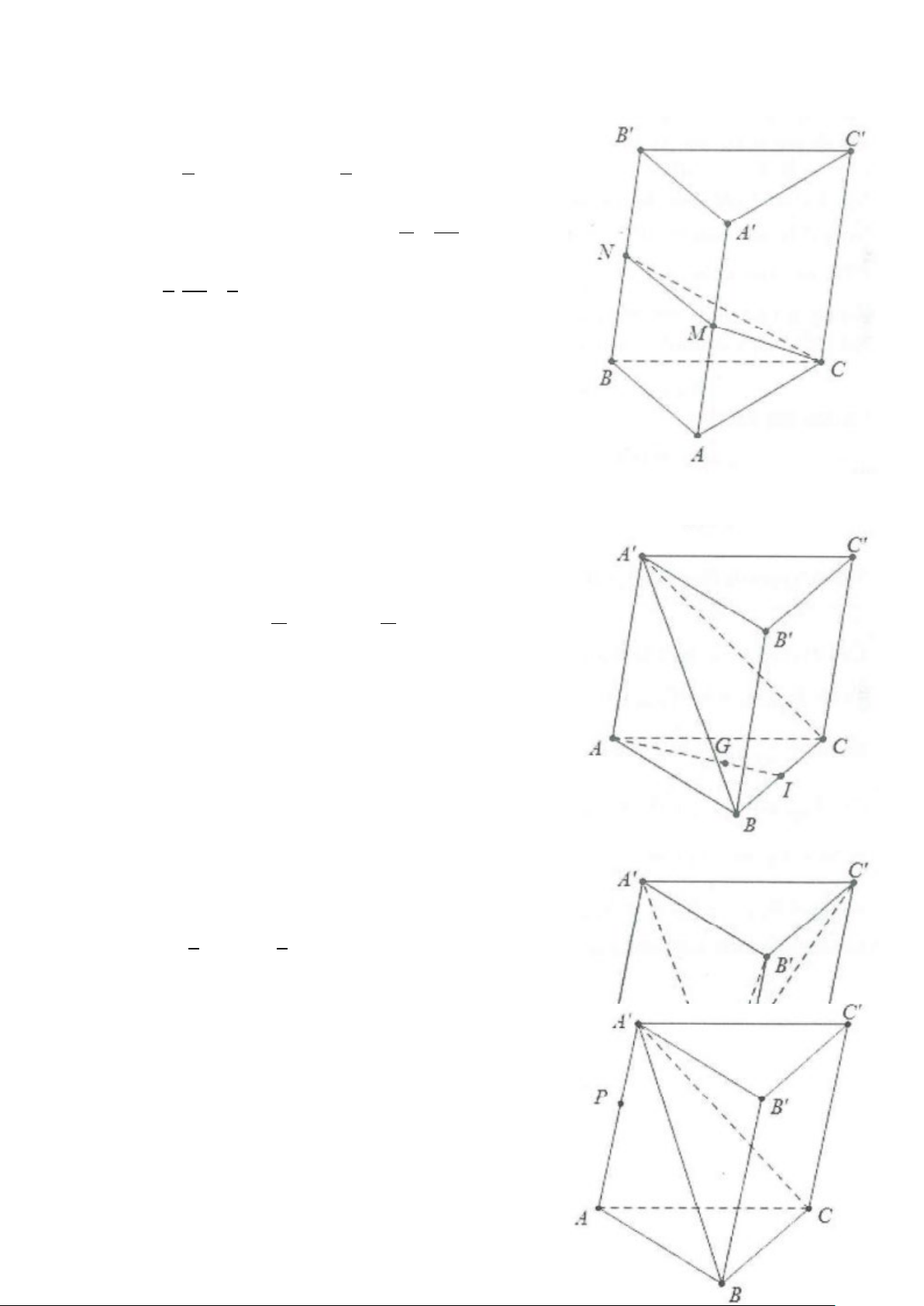
Cho hình lăng trụ tam giác ABC.A′B C
′ ′ . Mặt phẳng (α ) cắt các đường
thẳng AA ,′ BB ,′CC′ lần lượt tại M , N, P (tham khảo hình vẽ bên).
Tính tỉ số VABC.MNP .
VABC.A′BC′′ HD: Ta có V = V + V ABC.MNP M .ABC . A BNPC Lại có 1 1 AM V = d M ABC S = ′ ∆ d A ABC S M ABC . ; . ABC . . ; . . ( ( )) ( ( )) 3 3 ABC AA ∆ ′ 1 AM 1 = . . AM V → = ′ ′ ′ V V ABC A B C M ABC . . . . ABC. 3 AA′ 3 A′B C AA ′ ′ ′ Và h S = BN + CP h S = ′ + ′ = ′ ′ ′ BB CC h BB BCC B .( ) . BNPC .( ); 2 2
h .(BN +CP) S + BNPC 2
1 BN CP 1 BN CP ⇒ = = = + . S ′ ′ ′ ′ ′ ′ h BB BB BB CC BCC B . 2 2 Suy ra 1 V = d A BCC B ′ ′ S A BNPC . ; . . ( ( )) 3 BNPC 1 = ( ( )) 1 BN CP 1 . ; . + . BN CP d A BCC B S ′ ′ = + ′ ′ V BCC B . . 3
2 BB′ CC′ 2 A BCC B BB′ CC ′ ′ ′ Mà 2 1 BN CP V = ⇒ = + ′ ′ V ′ ′ ′ V V A BCC B ABC A B C A BNPC . . . . . ABC. 3 3 A′B C BB′ CC ′ ′ ′ Vậy 1 AM 1 BN CP VABC.MNP 1 AM BN CP V V = + + ⇒ = + + ′ ′ ′ V ABC MNP . . ABC ABC . . . . ABC. 3 AA 3 A′B C BB CC ′ ′ V ′ ′ ′ ′ ′ ′ ′ ′ ′ AA BB CC ABC A B C 3 .
Công thức tính nhanh VABC.MNP 1 AM BN CP = + + V ′ ′ ′ ′ ′ ′ AA BB CC ABC A B C 3 . b. Khối hộp
Kết quả 1:
Gọi V là thể tích khối hộp, V là thể tích khối chóp tạo thành từ 4 trong 8 đỉnh của khối hộp gồm hai 1
đường chéo của hai mặt song song, V là thể tích khối chóp tạo thành từ 4 trong 8 đỉnh của khối hộp ở 2
các trường hợp còn lại. Khi đó: V = ; V V V = 1 2 3 6
Ví dụ: Hình hộp 1 1 ABC . D A′B C ′ D ′ ′ →V = = ′ V
′ ′ ′ ′ V ′ ′ ′ V A C BD ABCD A B C D ; ' . A C D D ABCD. 3 6 A′B C ′ D ′ ′ Kết quả 2:
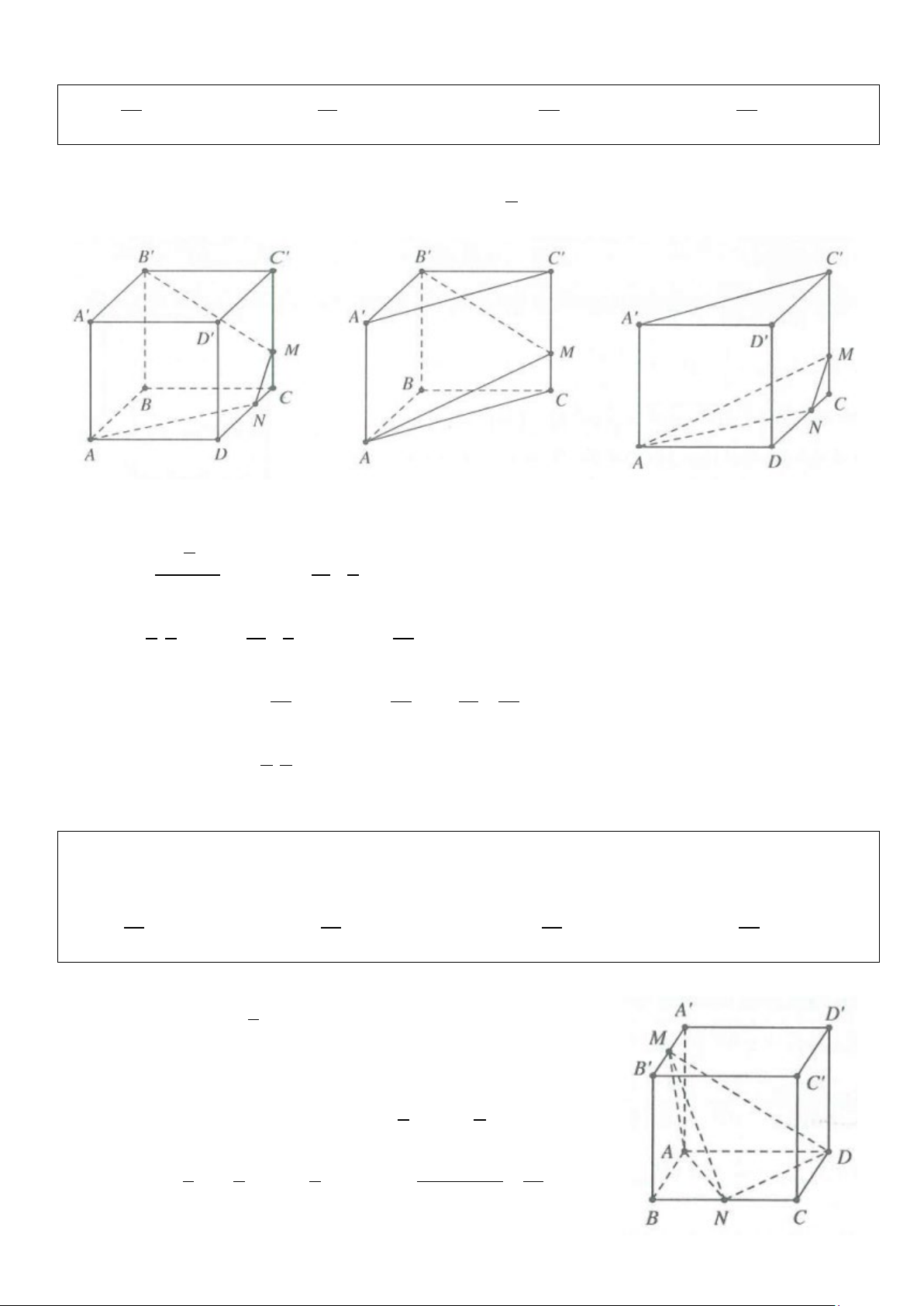
Cho hình lăng trụ tam giác ABC . D A′B C ′ D
′ ′ . Mặt phẳng (α ) cắt
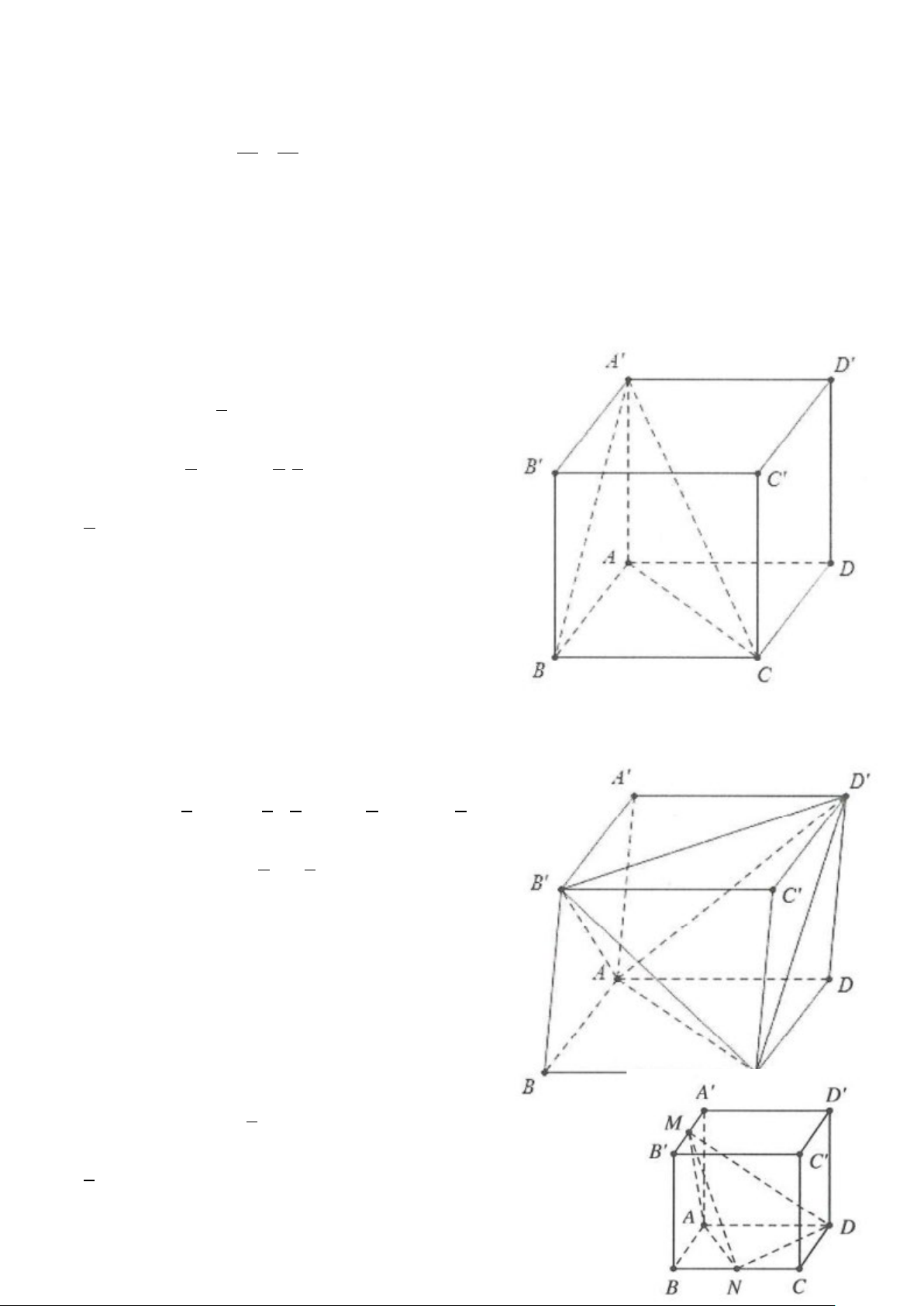
các đường thẳng AA ,′ BB ,′CC ,′ DD′ lần lượt tại M , N, P,Q (tham khảo hình vẽ bên). Chứng minh rằng AM CP BN DQ + = +
AA′ CC′ BB′ DD′ V và ABCD.MNPQ 1 AM CP 1 BN DQ = + = + V ′ ′ ′ ′ ′ ′ ′ ′ AA CC BB DD ABCD A B C D 2 2 . • Chứng minh AM CP BN DQ + = +
AA′ CC′ BB′ DD′
Gọi I là tâm hình vuông ABCD; I′ là tâm hình vuông A′B C ′ D ′ ′. Ta có: AM CP
AM + PC 2OI + = = ; AA′ CC′ AA′ AA′ BN DQ
BN + DQ 2OI ′ AM CP BN DQ + = = ⇒ + = + . BB′ DD′ BB′ BB′
AA′ CC′ BB′ DD′ V
• Chứng minh ABCD.MNPQ 1 AM CP 1 BN DQ = + = + V ′ ′ ′ ′ ′ ′ ′ ′ AA CC BB DD ABCD A B C D 2 2 .
Chia khối đa diện ABC .
D MNPQ thành hai khối đa diện ABC.MNP và AC . D MPQ ;
Làm tương tự với thể tích khối lăng trụ tam giác;
Cộng thể tích hai khối đa diện VABC.MNP 1 AM CP BN DQ ⇒ = + + + V ′ ′ ′ ′ ′ ′ ′ AA CC BB DD ABC A B C 4 . AM CP BN DQ V Mà ABCD.MNPQ 1 AM CP 1 BN DQ + = + ⇒ = + = + AA CC BB DD V ′ ′ ′ ′ ′ ′ ′ ′ ′ ′ ′ ′ AA CC BB DD ABCD A B C D 2 2 .
Công thức tính nhanh VABCD.MNPQ 1 AM CP BN DQ 1 AM CP 1 BN DQ = + + + = + = + V ′ ′ ′ ′ ′ ′ ′ ′ ′ ′ ′ ′ AA CC BB DD AA CC BB DD ABCD A B C D 4 2 2 .
II. CÁC DẠNG TOÁN TRỌNG TÂM VÀ PHƯƠNG PHÁP GIẢI
Dạng 1. Tỉ số thể tích của khối chóp
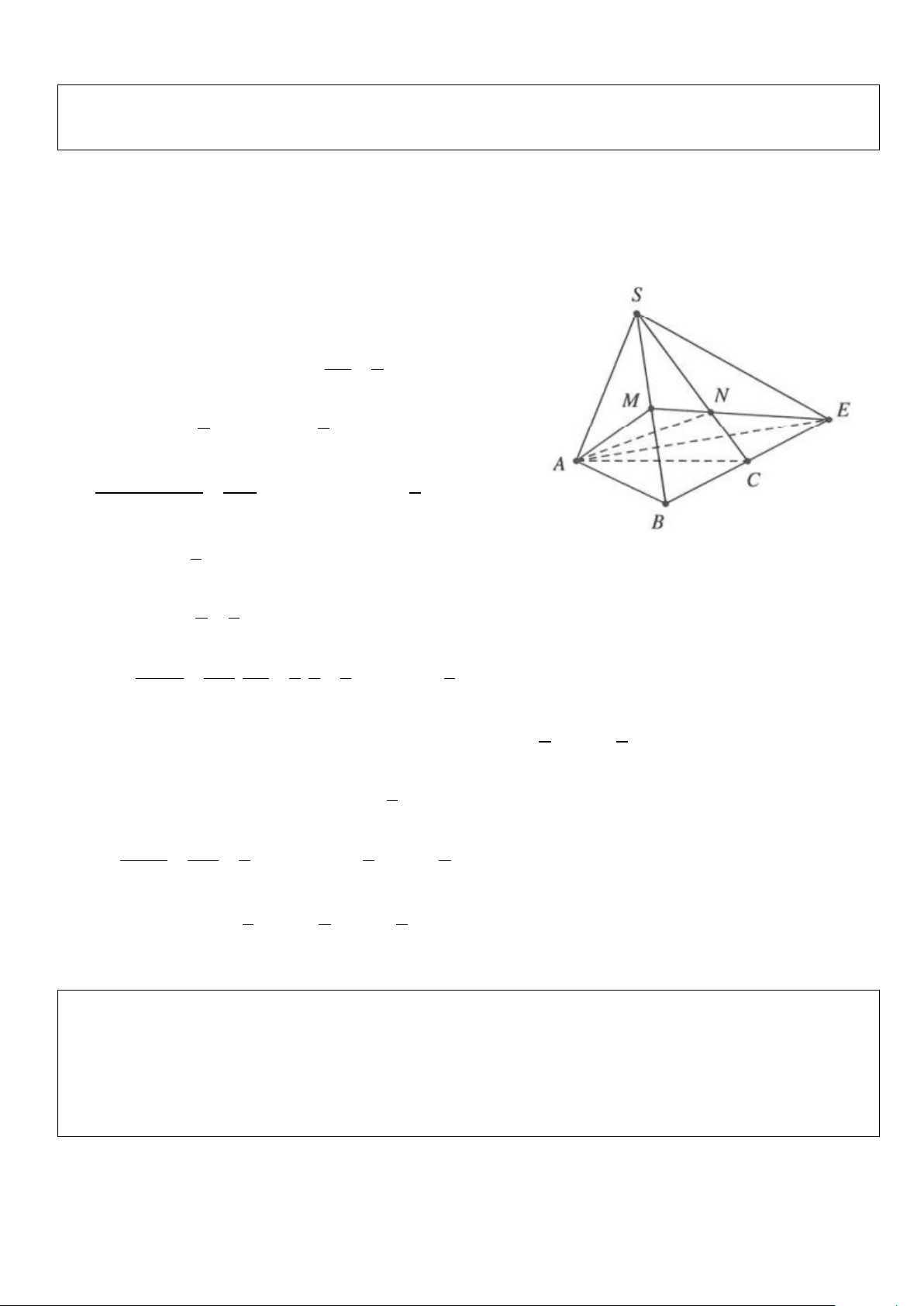
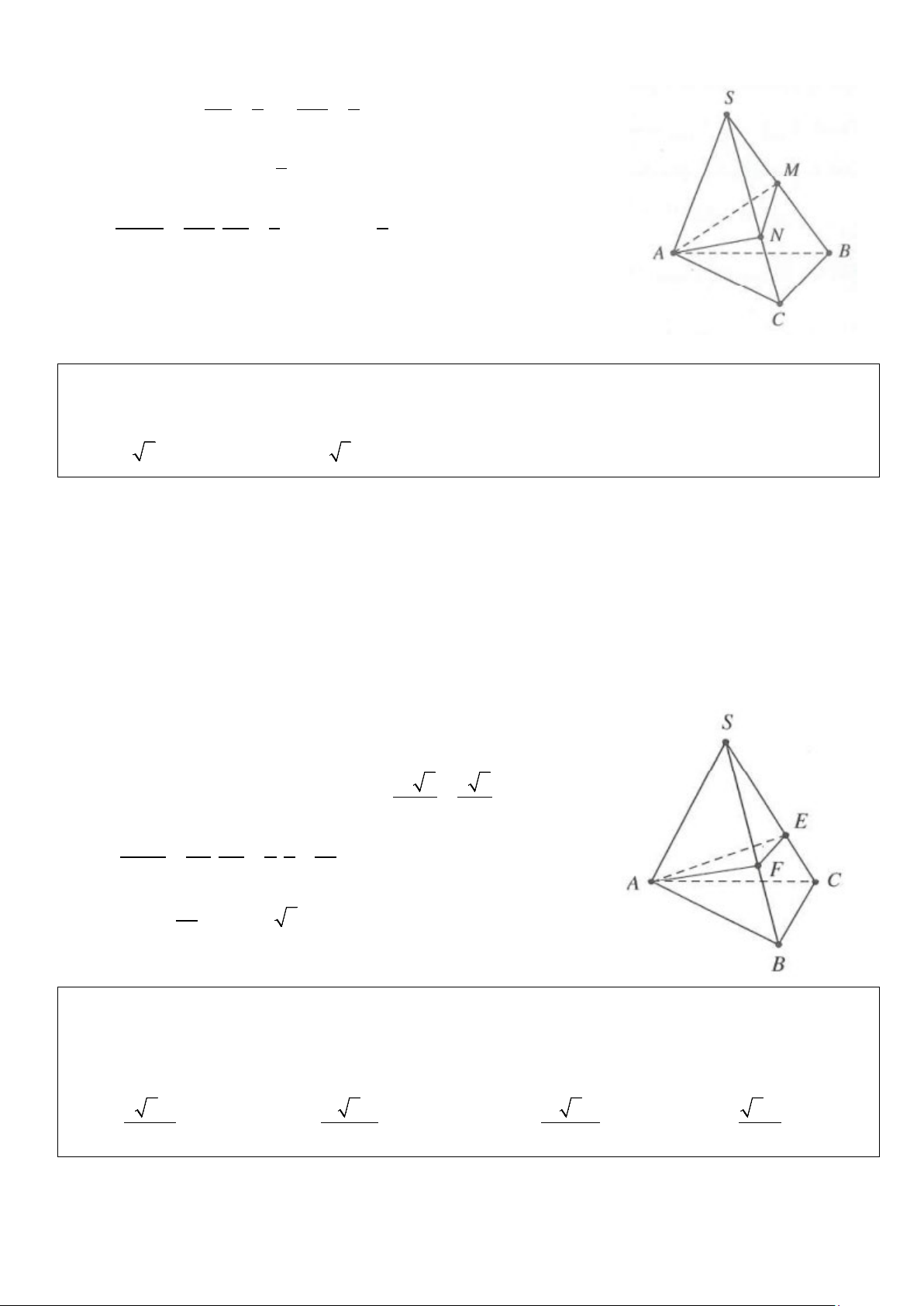
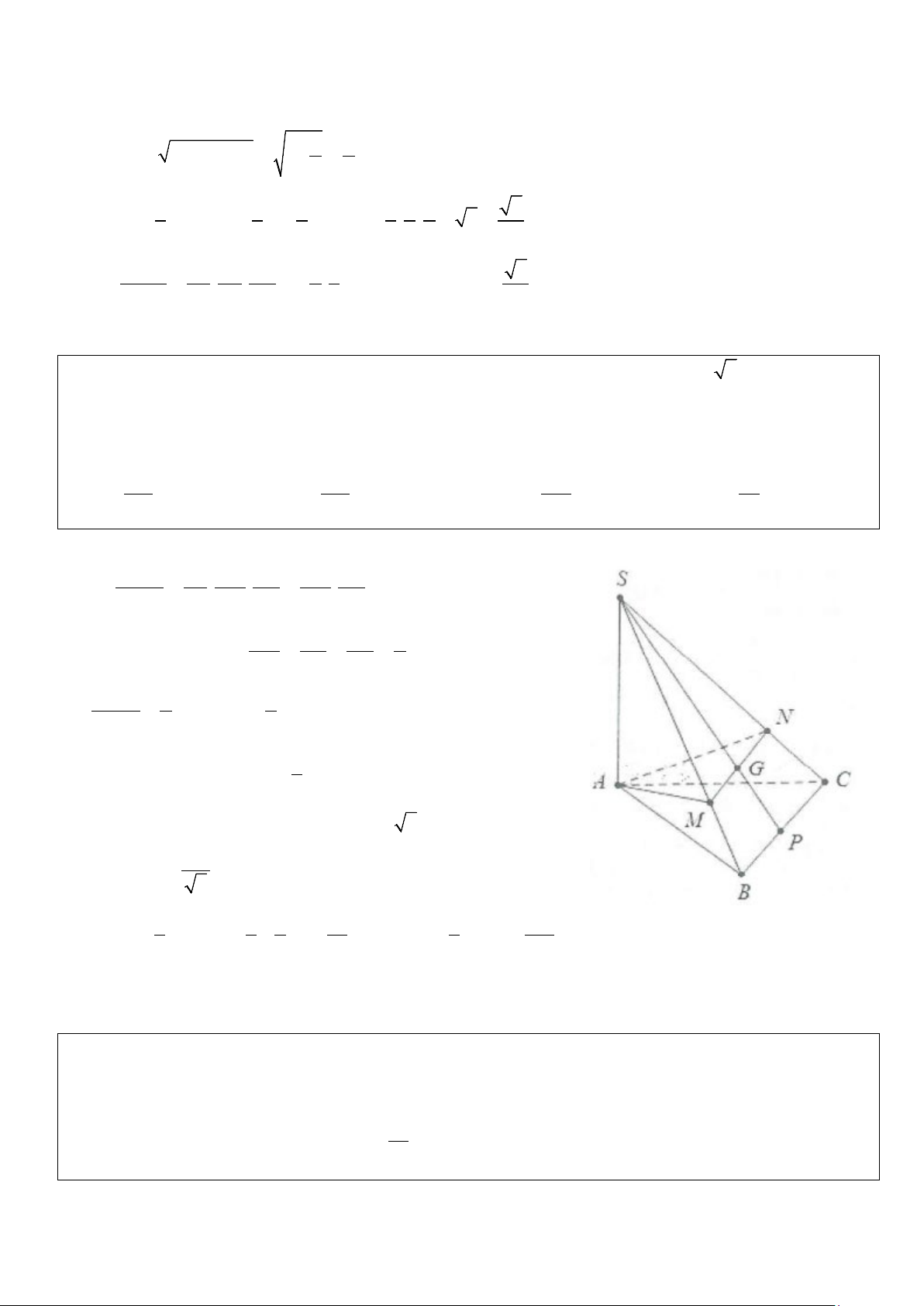
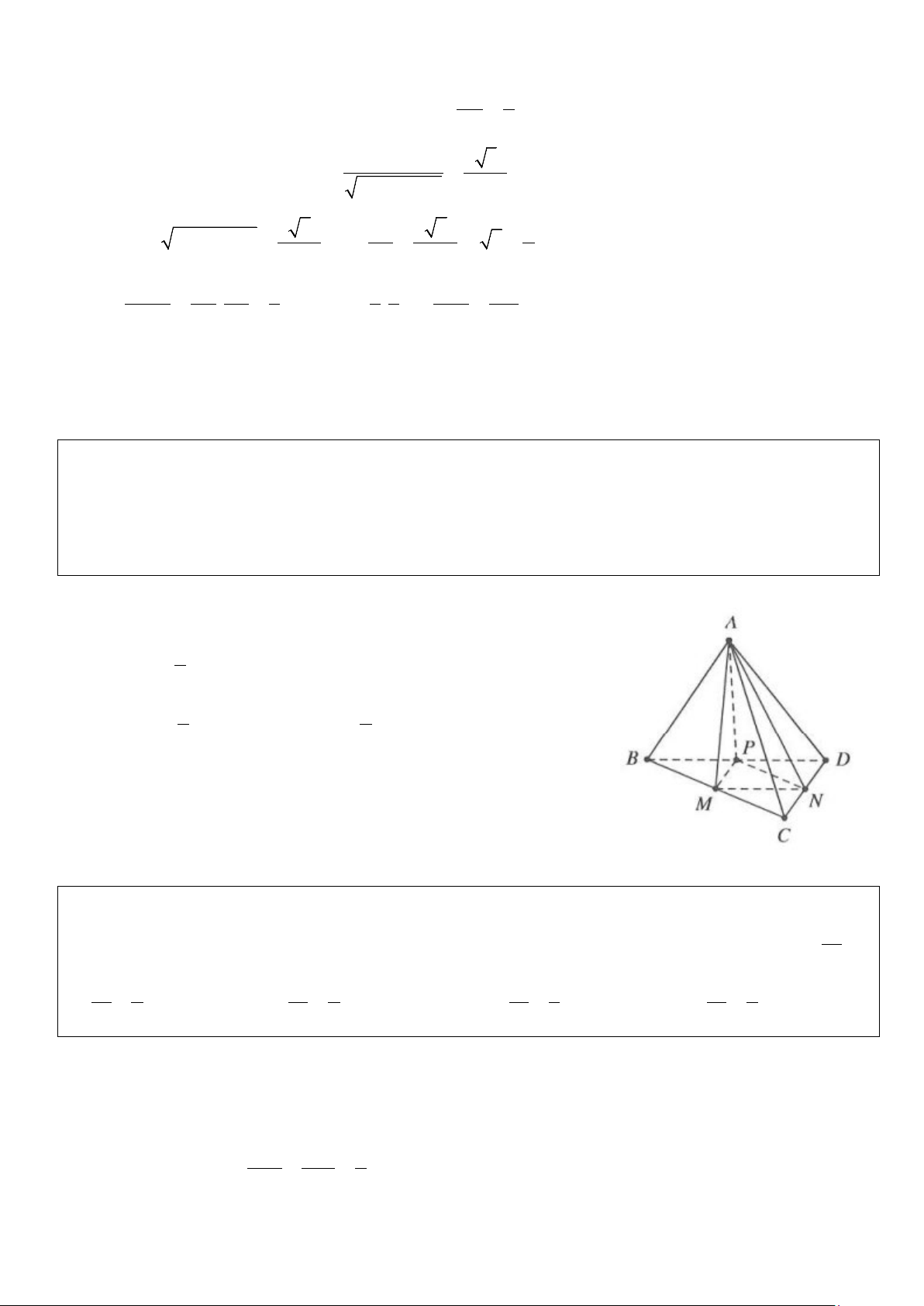
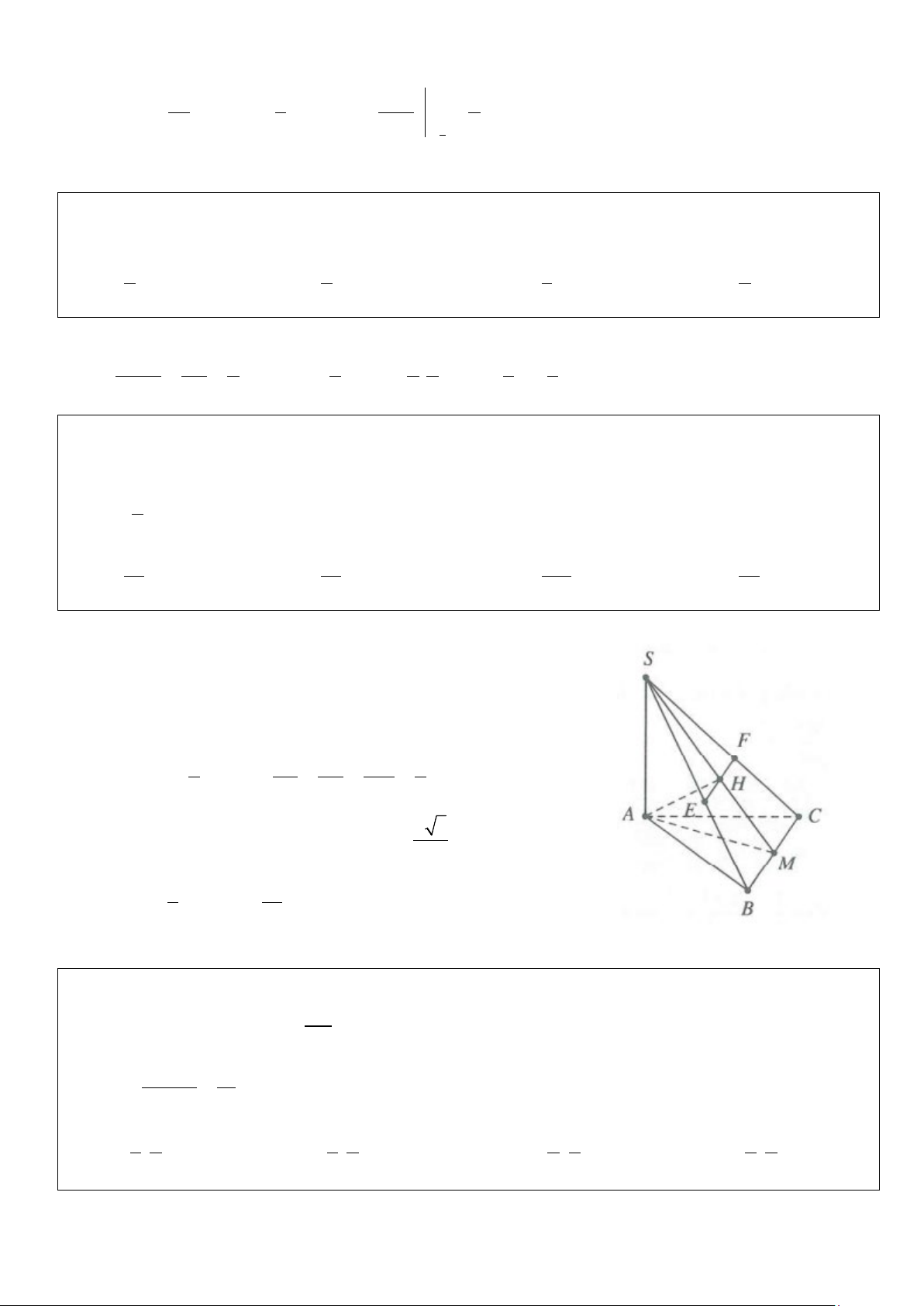
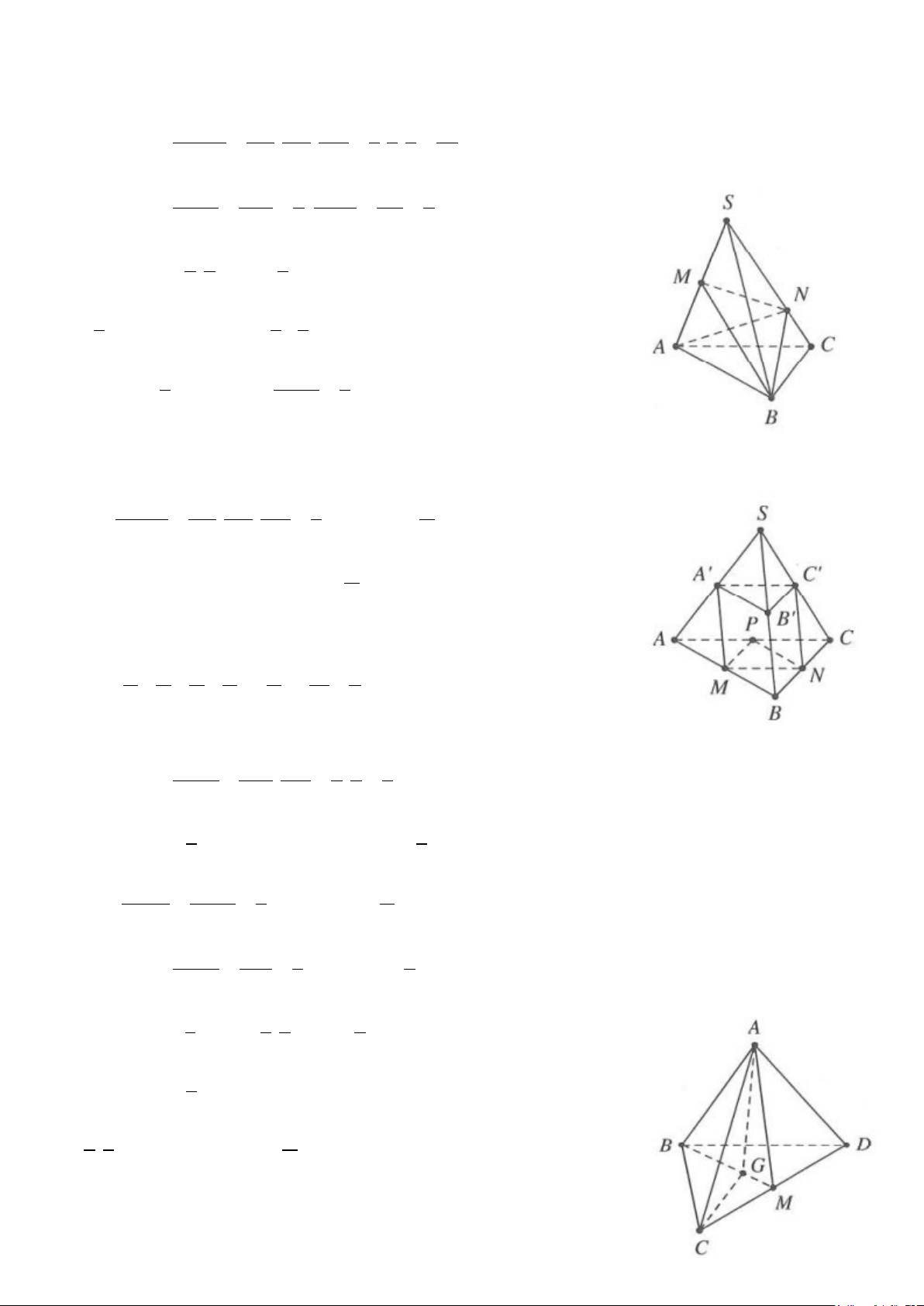
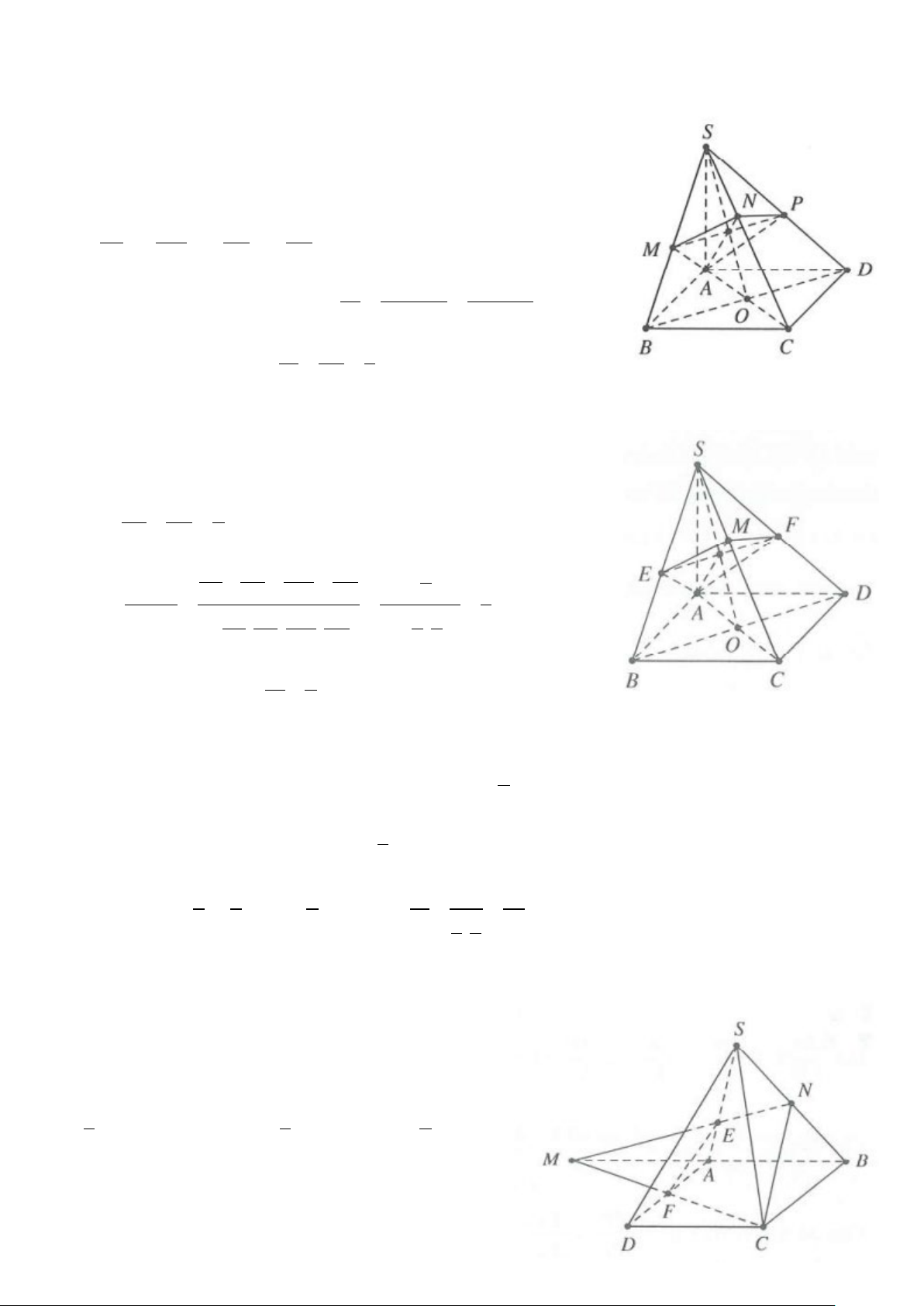
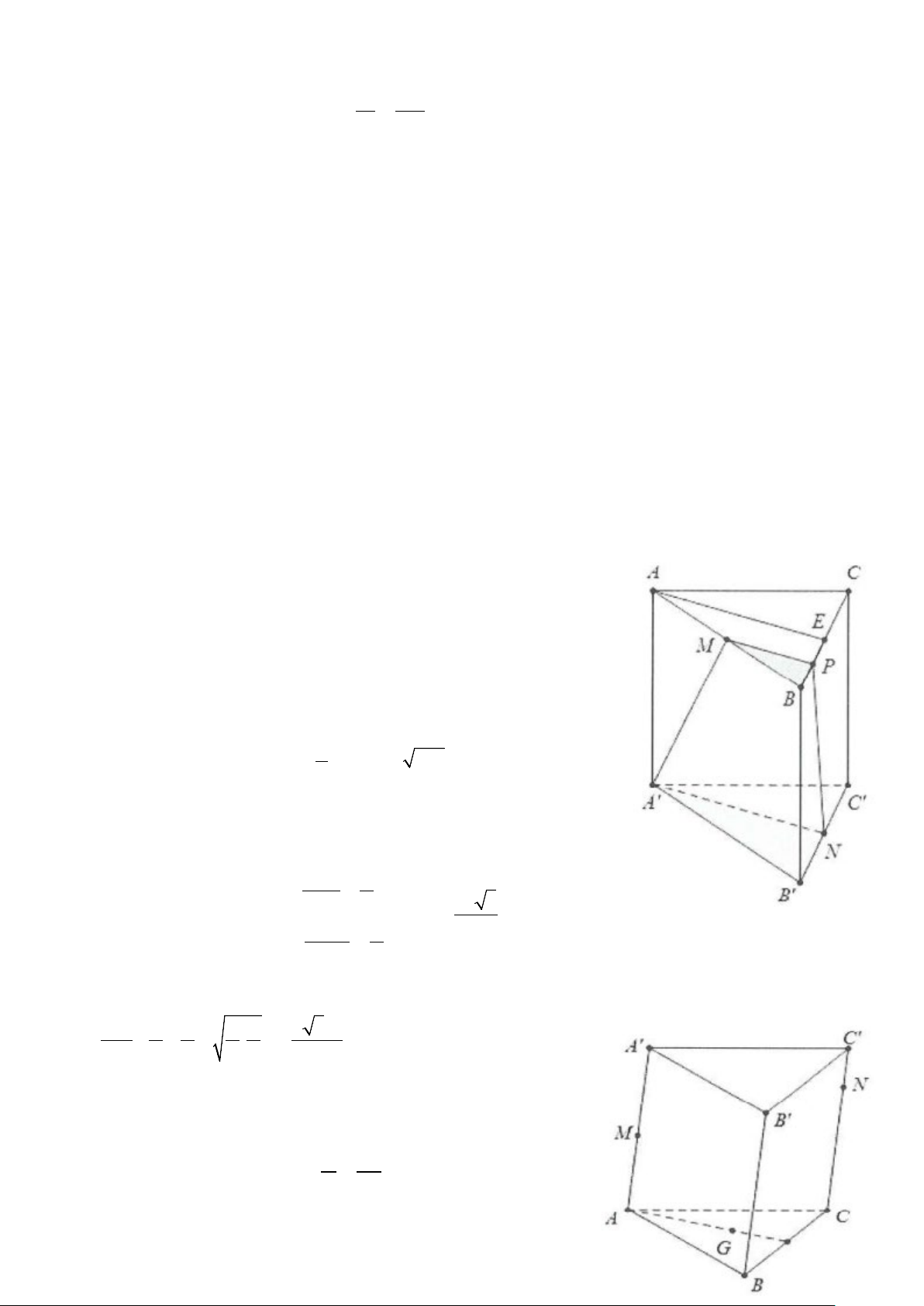
Ví dụ 1: Cho hình chóp S.ABC có thể tích V = 18. Gọi M là trung điểm của SA, E là điểm đối xứng với B
qua C. Gọi N là giao điểm của hai đường thẳng SB và ME.
a) Tính thể tích khối chóp MABE
b) Tính thể tích khối chóp AMNBC
c) Tính thể tích khối chóp SANE Lời giải
Vì E đối xứng với B qua C ⇒ C là trung điểm của BE.
Mà M là trung điểm của SB. SC ∩ ME = N
Suy ra N là trọng tâm SN 2 S ∆ BE → = . SC 3 a) Ta có: 1 1 S = = = ∆ d → BE d → BC S SBE A BC . 2 A BC . 2. 2 2 ABC
d (S;( ABC)) Và SB 1 = ⇒ = d (
d (M; ABC )
d (S;( ABC)) M ;( ABC)) ( ) BM 2 Khi đó 1 V = d M ABC S M ABE ; . . ( ( )) 3 S ∆ BE 1 1
= .2. d (M;( ABC)).S = = ∆ V 18. . 2 3 ABC S ABC b) Ta có VS.AMN SM SN 1 2 1 1 = . = . = ⇒ V = V S.AMN S. V SB SC ABC 2 3 3 3 ABC S. Lại có 2 2 V = V + V →V = V −V = V = = S ABC S AMN AMNBC AMNBC S ABC S AMN S ABC .18 12 . . . . . 3 3 c) Ta có 1 V = V −V = V − V S.ANE S.AME S.AMN S.AME S. 3 ABC Lại có VS.AME SM 1 1 1 = = →V = V = V = V S AME S ABE .2 . . S.ABC S. V SB ABE 2 2 2 ABC S. Do đó 1 2 2 V = V − V = V = = S ANE S ABC S ABC S ABC .18 12 . . . . 3 3 3
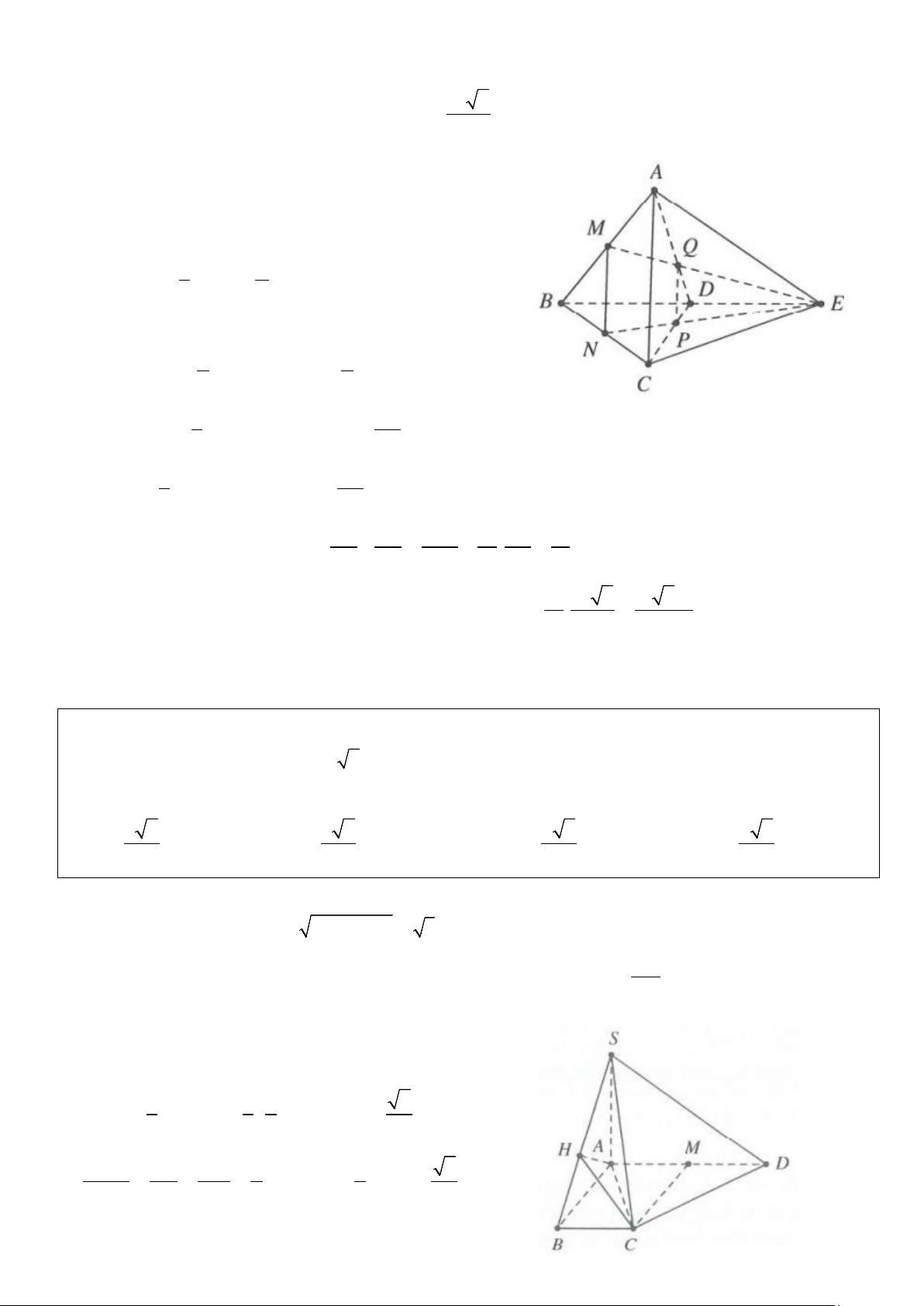
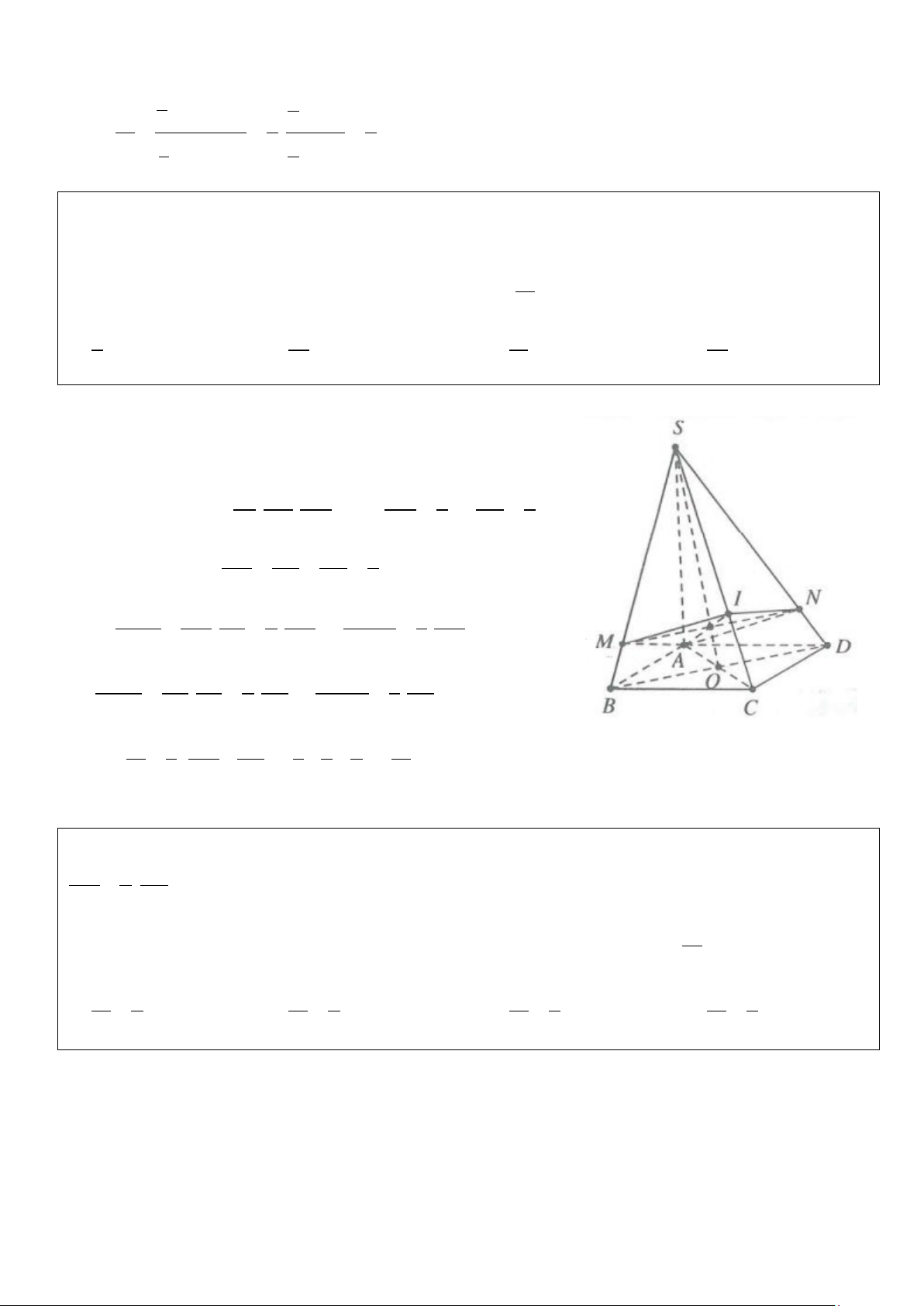
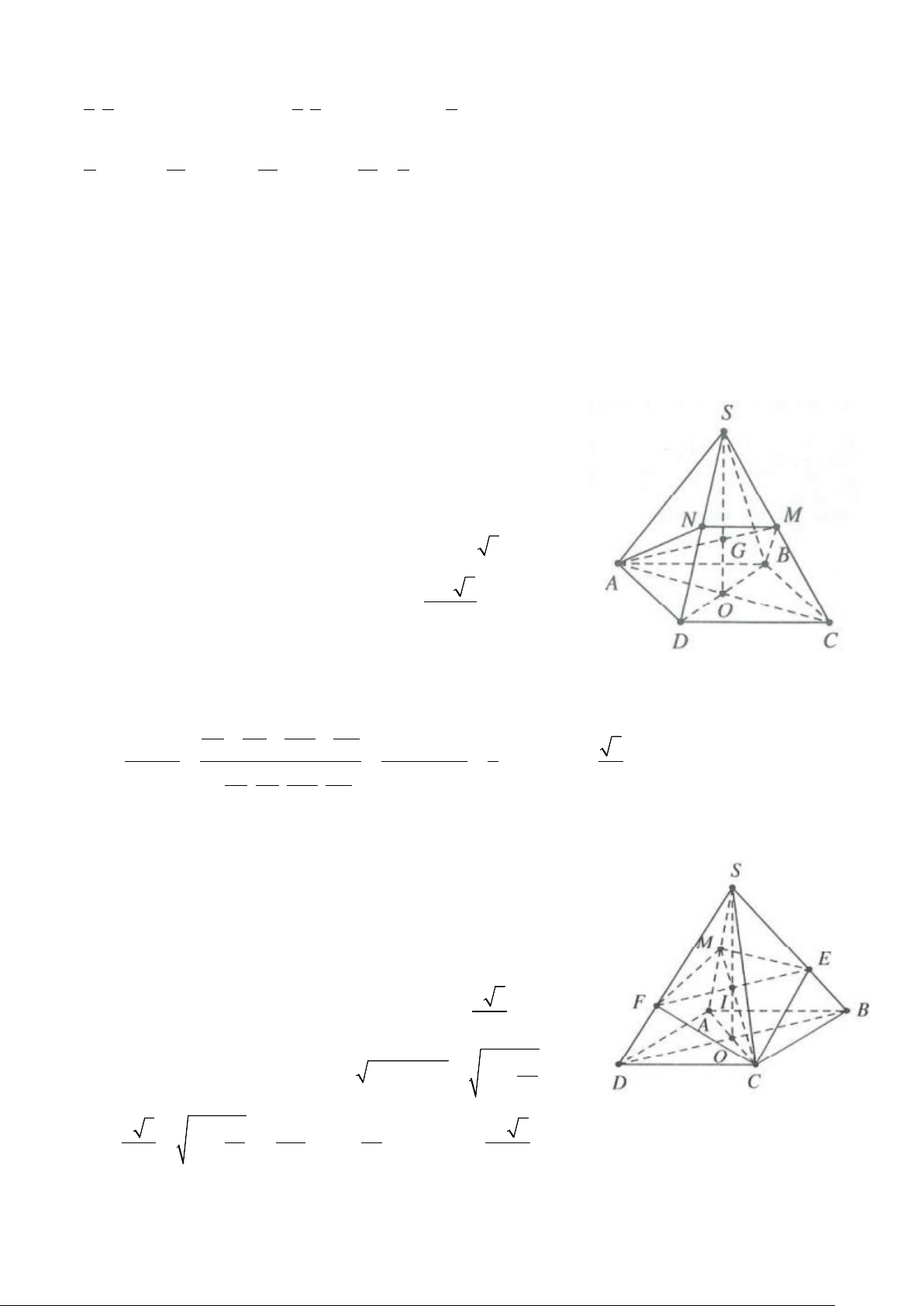
Ví dụ 2: Cho hình chóp đều S.ABC có đáy cạnh bằng a, cạnh bên bằng 2a.
a) Gọi M, N lần lượt thuộc AB, AC sao cho 2AM = AB, AN = 2NC. Tính V S.MBCN
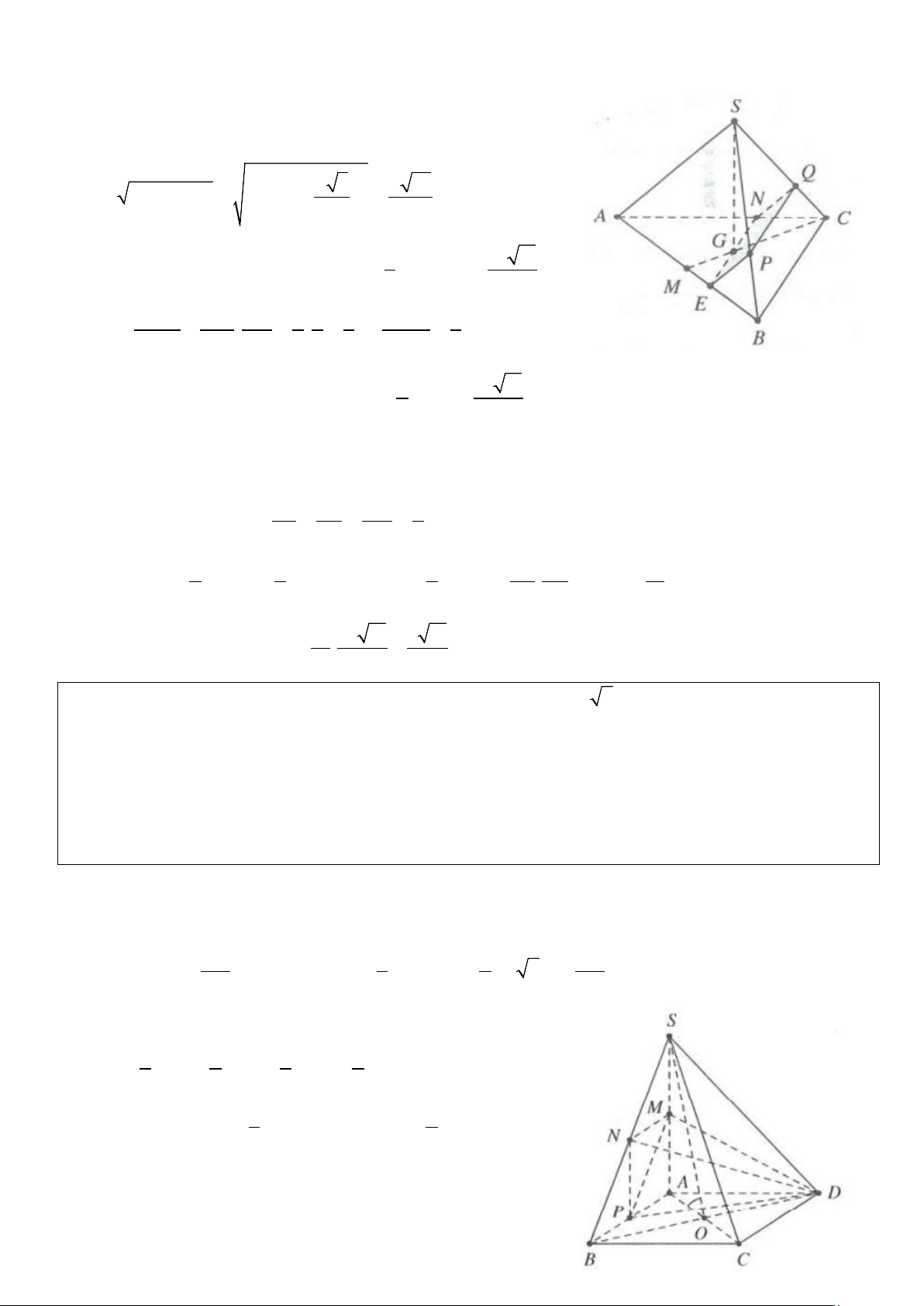
b) Mặt phẳng (P) đi qua trọng tâm của tam giác ABC, song song với SA và BC, biết (P) cắt SB, SC lần
lượt tại P, Q. Tính thể tích khối chóp MPQCB Lời giải
Gọi G là trọng tâm tam giác ABC ⇒ SG ⊥ ( ABC) .
Tam giác SAG vuông tại G, có 2 2 2
SG = SA − AG = ( a)2 a 3 a 33 2 − = . 3 3 3
⇒ Thể tích khối chóp S.ABC là 1 a 11 V = SG S = S ABC . . . 3 ABC ∆ 12 a) Ta có S∆ AM AN V AMN 1 2 1 S.AMN 1 = . = . = ⇒ = S∆ AB AC V ABC 2 3 3 S ABC 3 . 3 Mà 2 a 11 V = V + V →V = V = S.ABC S.AMN S.MBCN S.MBCN S. 3 ABC 18
b) Qua G kẻ đường thẳng song song với BC, cắt AB, AC lần lượt tại E, N. Tương tự, từ E, N kẻ các đường
thẳng song song với BC cắt SB, SC lần lượt tại P, Q.
Dễ dàng chứng minh được SP SQ AN 2 = = = . SB SC AC 3 Ta có: 1 1 1 SP SQ 5 V = V = V −V = V − V = V MPQCB A PQCB S ABC S APQ S ABC . . S ABC S ABC . . ( . . ) . . . 2 2 2 SB SC 18 3
Vậy thể tích cần tìm là 5 a 11 5 11 3 V = = a . MPQCB . 18 12 216
Ví dụ 3: Cho hình chóp S.ABC có đáy ABCD là hình vuông cạnh a 2 , cạnh bên SA vuông góc với đáy.
Góc giữa hai mặt phẳng (SBD) và ( ABCD) bằng 45°.
a) Gọi M, N, P lần lượt là trung điểm của SA, SB, AB. Tính V . MNPD
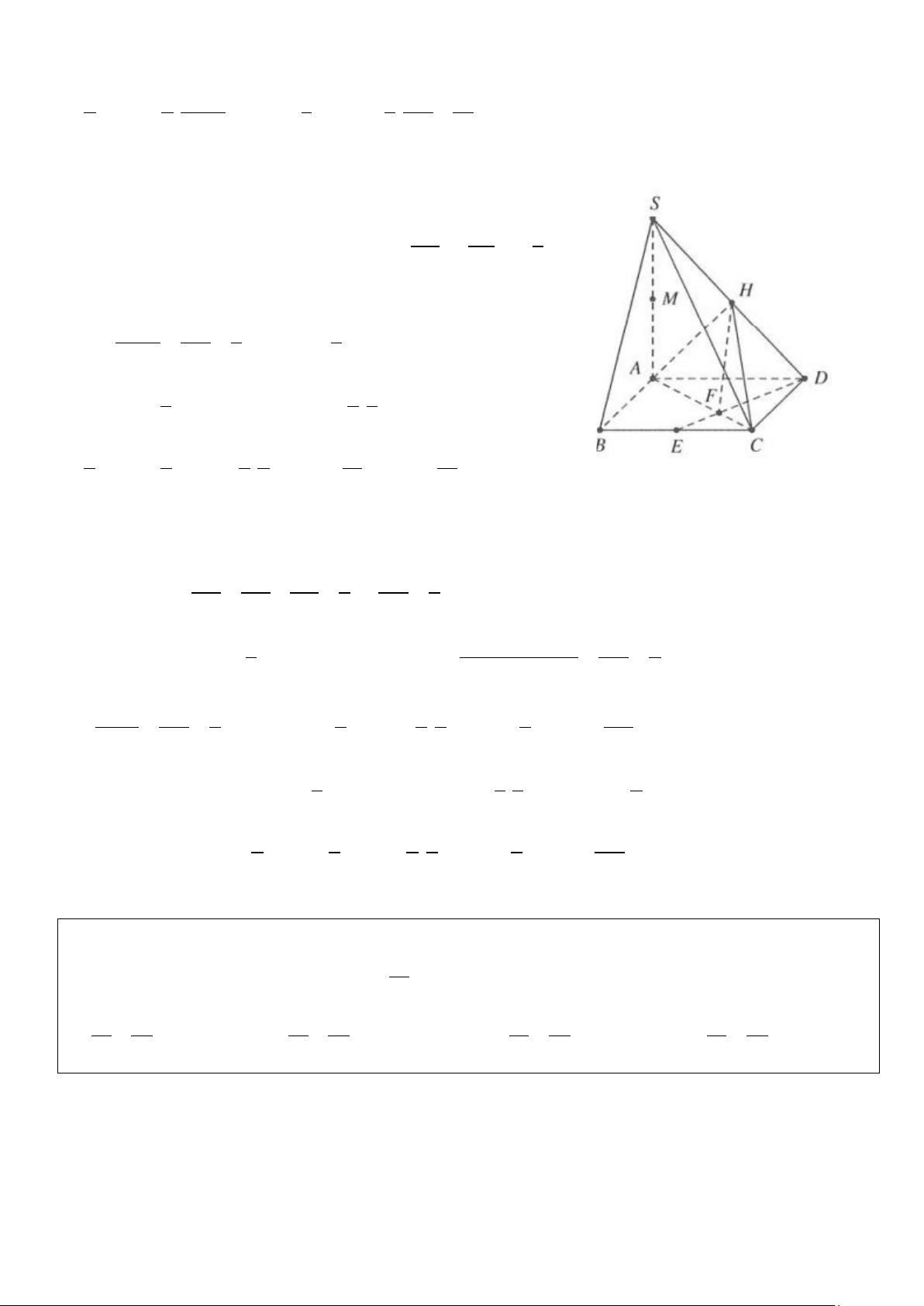
b) Gọi H là hình chiếu của A trên SD; E là trung điểm của BC. Nối AC cắt DE tại F. Tính thể tích các khối đa diện MHCD, HFCD. Lời giải
Gọi O là tâm hình vuông ABCD ⇒ (SBD) ( ABCD) = ; SOA = 45° Suy ra AC 1 a a SA = OA = = a →V = SA S = a = S ABCD ABCD ( ) 3 2 2 . . . 2 . . 2 3 3 3 a) Ta có S = − − − ∆ S∆ S∆ S∆ S MNP SAB SMN AMP BPN ∆ 1 1 1 1 = S − − − = ∆ S∆ S∆ S∆ S SAB SAB SAB SAB S ∆ AB . 4 4 4 4 Lại có 1 1 V = V = d D SAB S = ∆ V MNPD D MNP ; . . ( ( )) MNP D. 3 4 SAB 3 3 1 1 S ABD ∆ 1 1 2a a = V = V = V = = S ABD . . S ABCD S ABCD . . . . . 4 4 SABCD 8 8 3 12 2 b) Xét S
∆ AD vuông tại A, đường cao AH SH SA 1 ⇒ = = . SD SD 3
• Tính thể tích khối chóp MHCD. Ta có S HC ∆ D HD 1 1 = = ⇒ S = ∆ S S∆ SD 3 HCD 3 S∆CD SCD 1 1 1 ⇒ V = d M SCD S = ∆ d A SCD S M HCD . ; . HCD . . ; . . ( ( )) ( ( )) 3 6 3 S ∆ CD 3 1 1 1 1 1 a = V = V = V = V = A SCD S ACD . S ABCD . S ABCD . . . . . 6 6 6 2 12 18
• Tính thể tích khối chóp HFCD. Vì EC CF EF 1 DF 2 EC / / AD ⇒ = = = ⇒ = . AD AC FD 2 DE 3
d (H;( ABCD)) Cách 1. Ta có 1 V = d H ABCD S mà HD 2 = = . H FCD . ; . . ( ( )) 3 FC ∆ D
d (S;( ABCD)) SD 3 3 Và S FC ∆ D DF 2 4 4 1 1 2a = = →V = V = V = V = H FCD . S ECD . S ABCD S ABCD . . . . . S∆ DE ECD 3 9 9 4 9 27 Cách 2. Ta có 1 1 1 2 V = V = d F SCD S = ∆ d A SCD S H FCD F HCD . ; . HCD . ; . . . ( ( )) ( ( )) 3 3 3 3 S∆CD 3 2 2 2 1 1 2a = V = V = V = V = A SCD S ACD . S ABCD S ABCD . . . . . 9 9 9 2 9 27
Ví dụ 4: Cho tứ diện ABCD có thể tích V. Gọi V ′ là thể tích của khối tứ diện có các đỉnh là trọng tâm của ′
các mặt của khối tứ diện ABCD. Tính tỉ số V . V ′ ′ ′ ′ A. V 8 = . B. V 23 = . C. V 1 = . D. V 4 = . V 27 V 27 V 27 V 27 Lời giải
Gọi M là trung điểm AC; E, F lần lượt là trọng tâm của tam giác ABC,
ACD. Trong tam giác MBD có 1 EF = B . D 3
Tương tự ta có các cạnh còn lại của tứ diện mới sinh ra bằng 1 cạnh của 3 3 ′
tứ diện ban đầu. Do đó V 1 1 = = . Chọn C. V 3 27
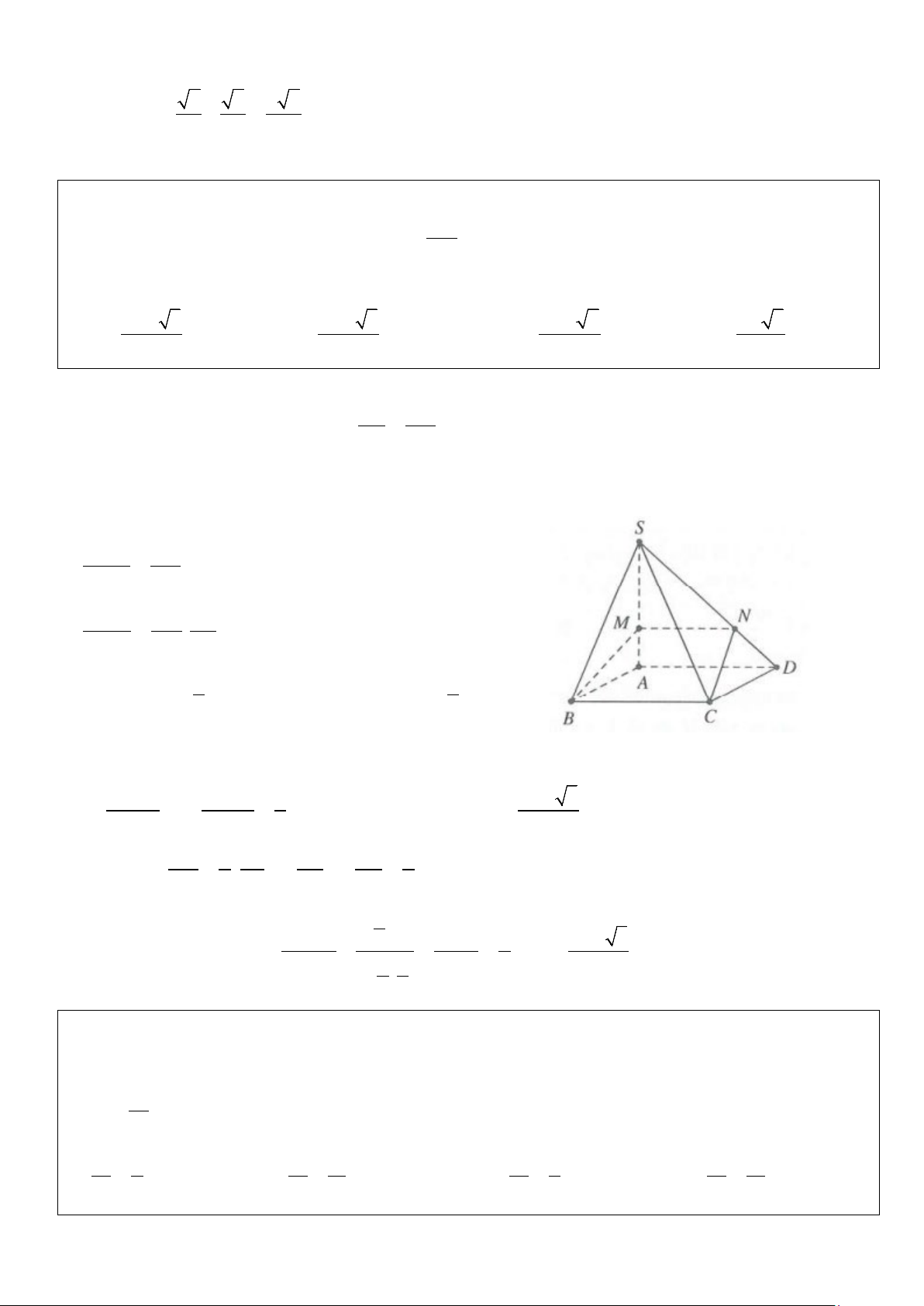
Ví dụ 5: Cho tứ diện ABCD có AB, AC, AD đôi một vuông góc và AB = 6a, AC = 9a, AD = 3 . a Gọi M, N,
P lần lượt là trọng tâm của các tam giác ABC, ACD, ADB. Tính thể tích V của khối tứ diện AMNP. A. 2 V = 8a . B. 2 V = 4a . C. 2 V = 6a . D. 2 V = 2a . Lời giải Ta có: 1 3 V = AB AC AD = a ABCD . . 27 . 6
Gọi E, F, G lần lượt là trung điểm của BC, CD, DB. Suy ra 1 27 3 V = V = a AEFG ABCD . 4 4
Do M, N, P là trọng tâm của các tam giác ABC, ACD, ADB. Nên ta có: AM AN AP 2 = = = . AE AF AG 3
Lại có: V .AMNP AM AN AP 8 = . . = . V AE AF AG A EFG 27 . 8 3 →V = V = a Chọn D. A MNP . A EFG 2 . . . 27
Ví dụ 6: Cho hình chóp S.ABCD có chiều cao bằng 9, diện tích đáy bằng 5. Gọi M là trung điểm của cạnh
SB và N thuộc cạnh SC sao cho NS = 2NC. Tính thể tích V của khối chóp A.BMNC. A. V = 15. B. V = 5. C. V = 10. D. V = 6. Lời giải
Từ giả thiết, ta có SN 2 = và SM 1 = . SC 3 SB 2 Thể tích khối chóp 1 V = = S ABC .9.5 15 . 3 Ta có VS.AMN SM SN 1 2 = . = ⇒ V = V = Chọn C. ABMNC S ABC 10. . V SB SC S ABC 3 3 .
Ví dụ 7: Cho hình chóp S.ABC có SA = 3, SB = 4, SC = 5 và = =
ASB BSC CSA = 60 .° Tính thể tích V của khối chóp đã cho. A. V = 5 2. B. V = 5 3. C. V = 10. D. V = 15. Lời giải
Trên SB, SC lần lượt lấy các điểm E, F sao cho SE = SF = 3..
Khi đó S.AEF là khối tứ diện đều có cạnh a = 3. 3
Suy ra thể tích khối chóp S.AEF là a 2 9 2 V = = S AEF . . 12 4 Ta có: VS.AEF SE SF 3 3 9 = . = . = . V SB SC S ABC 4 5 20 . 20 →V = V = Chọn A. S ABC . S AEF 5 2. . . 9
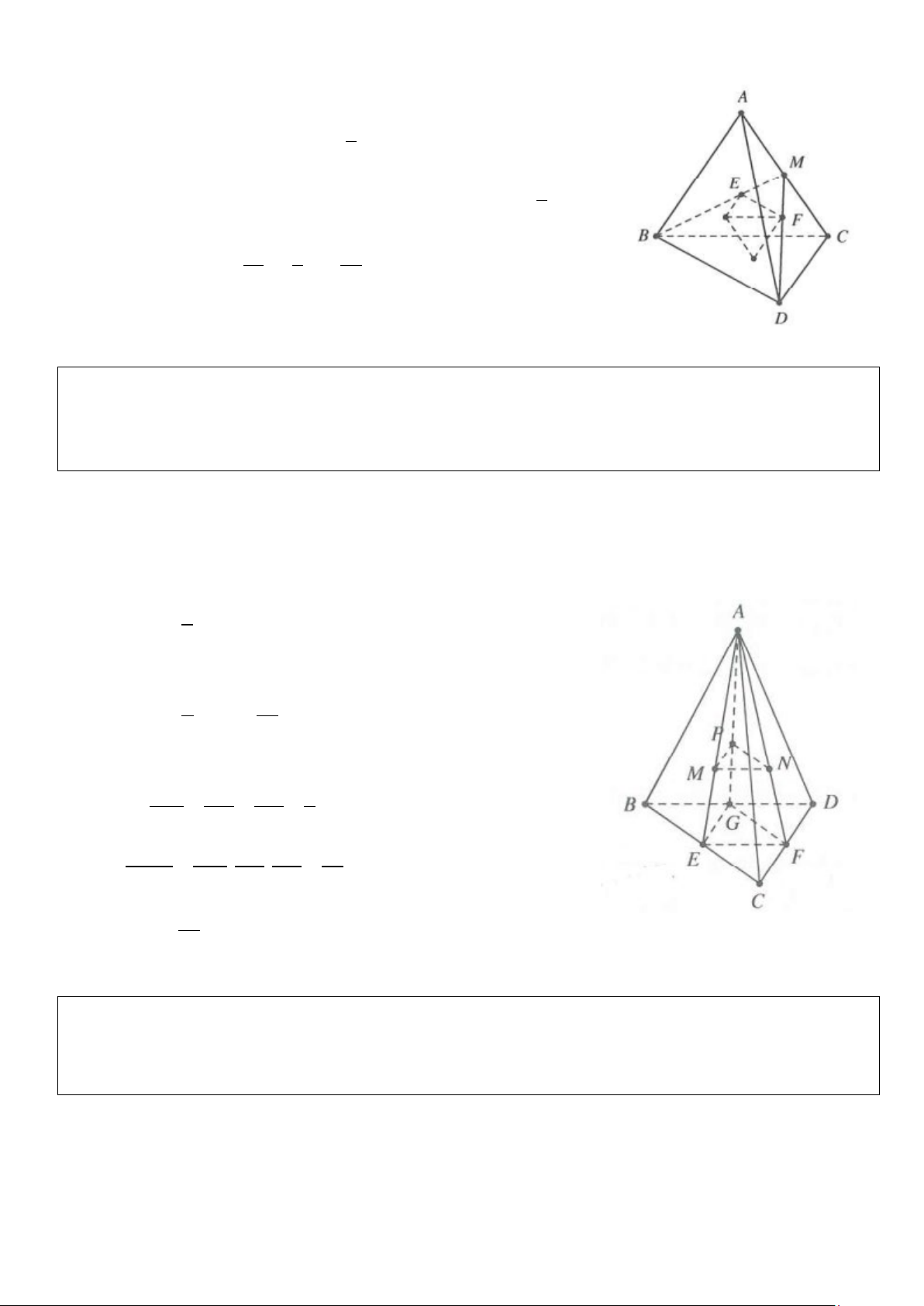
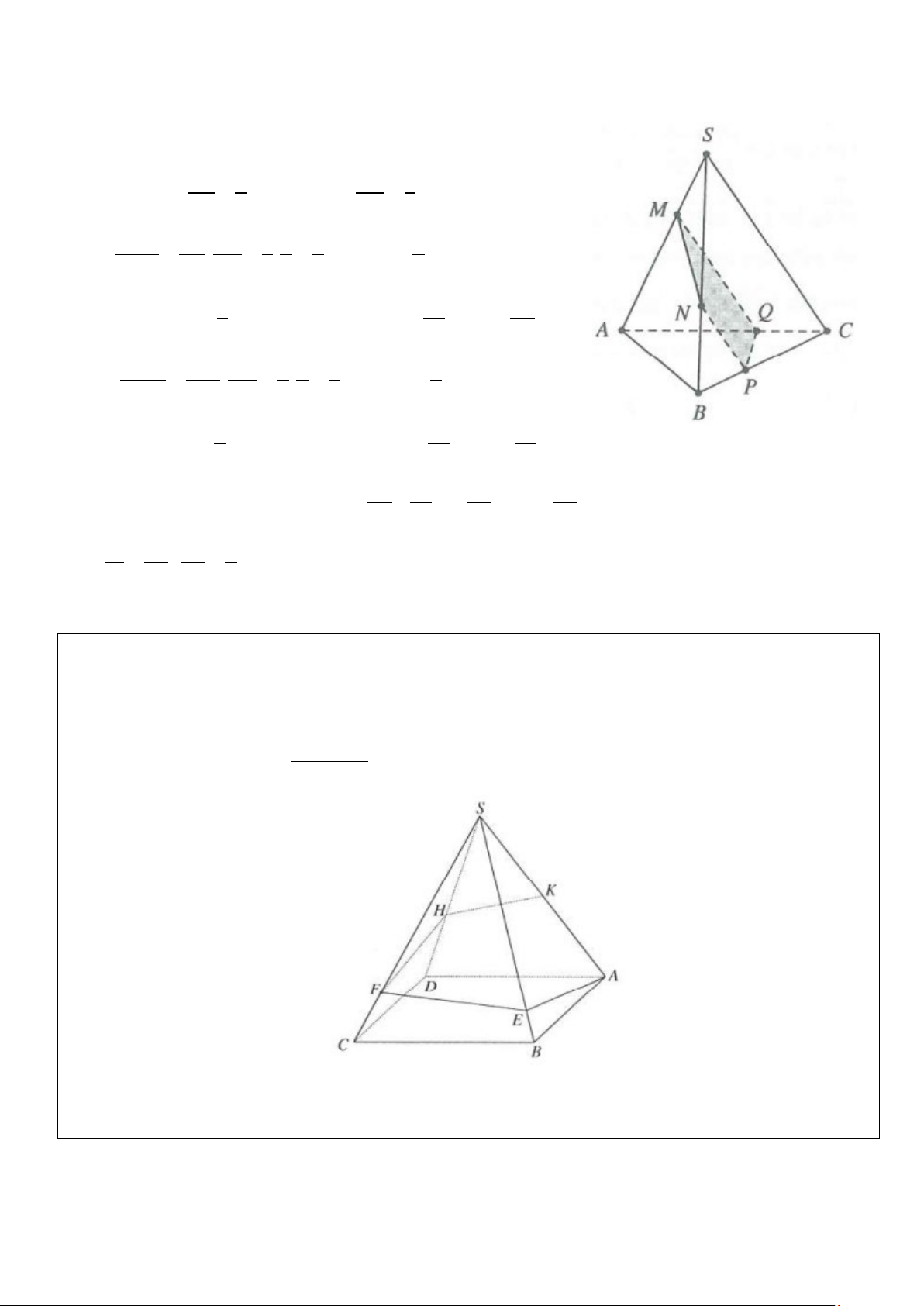
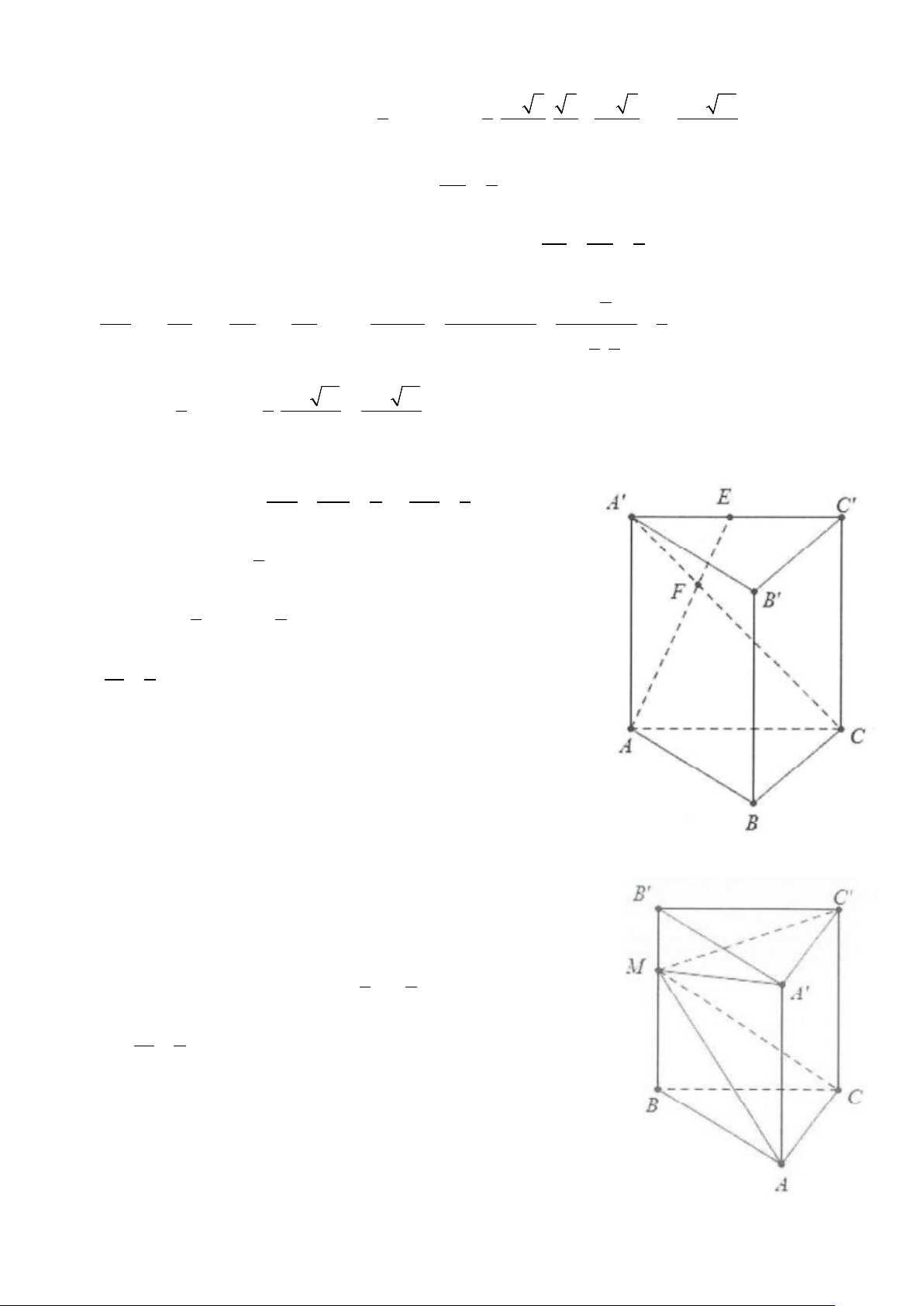
Ví dụ 8: Cho tứ diện đều cạnh ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC
và E là điểm đối xứng với B qua D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện,
trong đó khối đa diện chứa đỉnh A có thể tích V. Tính V 3 3 3 3 A. 7 2a V = B. 11 2a V = C. 13 2a V = D. 2a V = 216 216 216 18 Lời giải 3
Thể tích khối tứ diện đều ABCD cạnh a là a 2 V = ABCD 12
Gọi P = EN ∩ CD và Q = EM ∩ AD .
⇒ P, Q lần lượt là trọng tâm của B ∆ CE và A ∆ BE
Gọi S là diện tích tam giác BCD ⇒ S = = ∆ S∆ S CDE BNE . Ta có: 1 = = S S S ∆PDE . ∆CDE . 3 3
Gọi h là chiều cao của tứ diện ABCD, suy ra ; ( ) h = ; ; ( ) h d M BCD d Q BCD = . 2 3 Khi đó 1 S.h V = S = ; ∆ d M BCD M BNE BNE . ; . ( ( )) 3 6 Và 1 S.h V = S = ∆ d Q BCD Q PDE PDE . ; . ( ( )) 3 27 Suy ra
S.h S.h 7S.h 7 S.h 7 V = V −V = − = = = V PQD NMB M BNE Q PDE . . ABCD. . . . 6 27 54 18 3 18 3 3
Vậy thể tích khối đa diện chứa đỉnh A là 11 a 2 11 2a V = V −V = = . Chọn B. ABCD PQD NMB . . 18 12 216
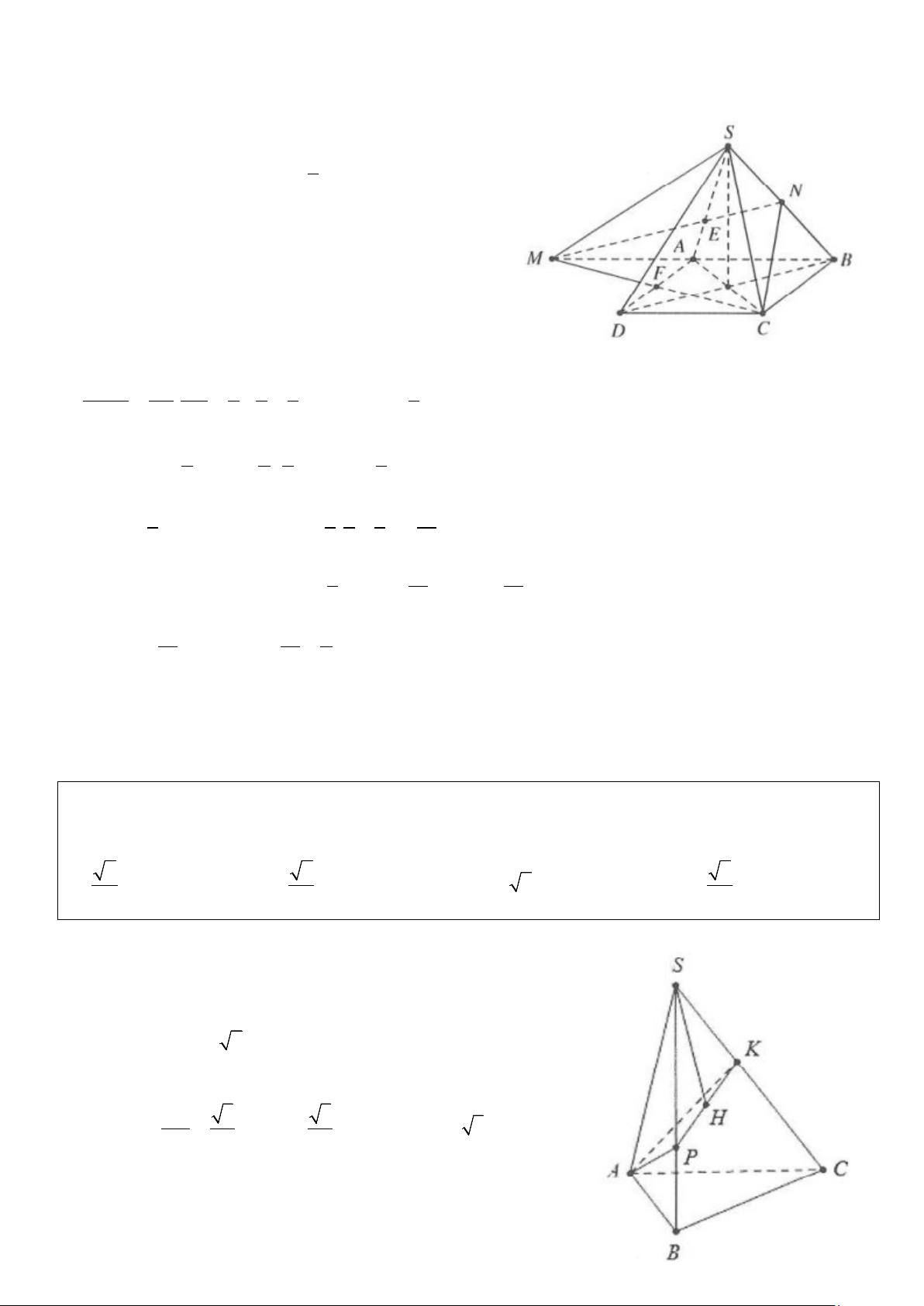
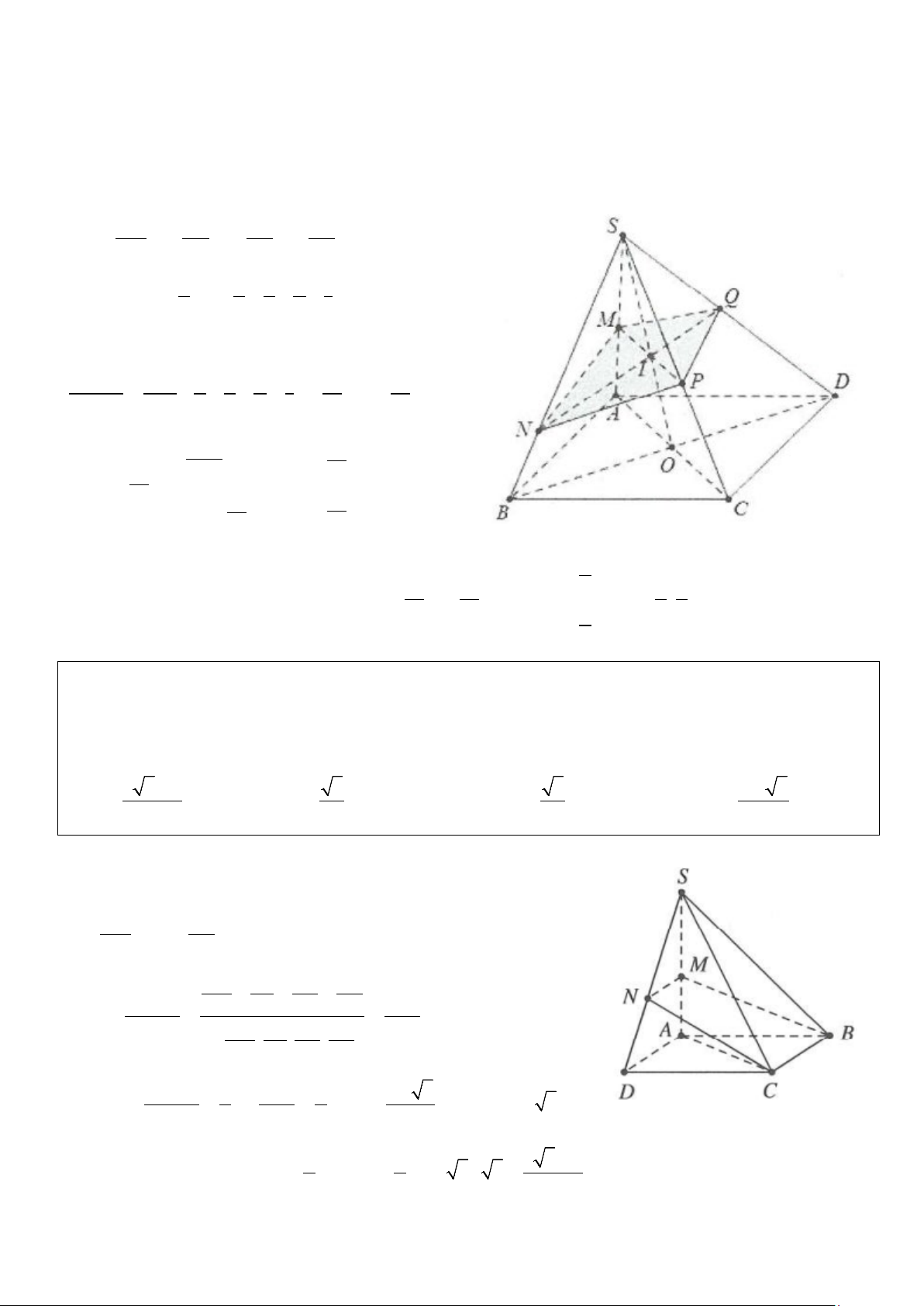
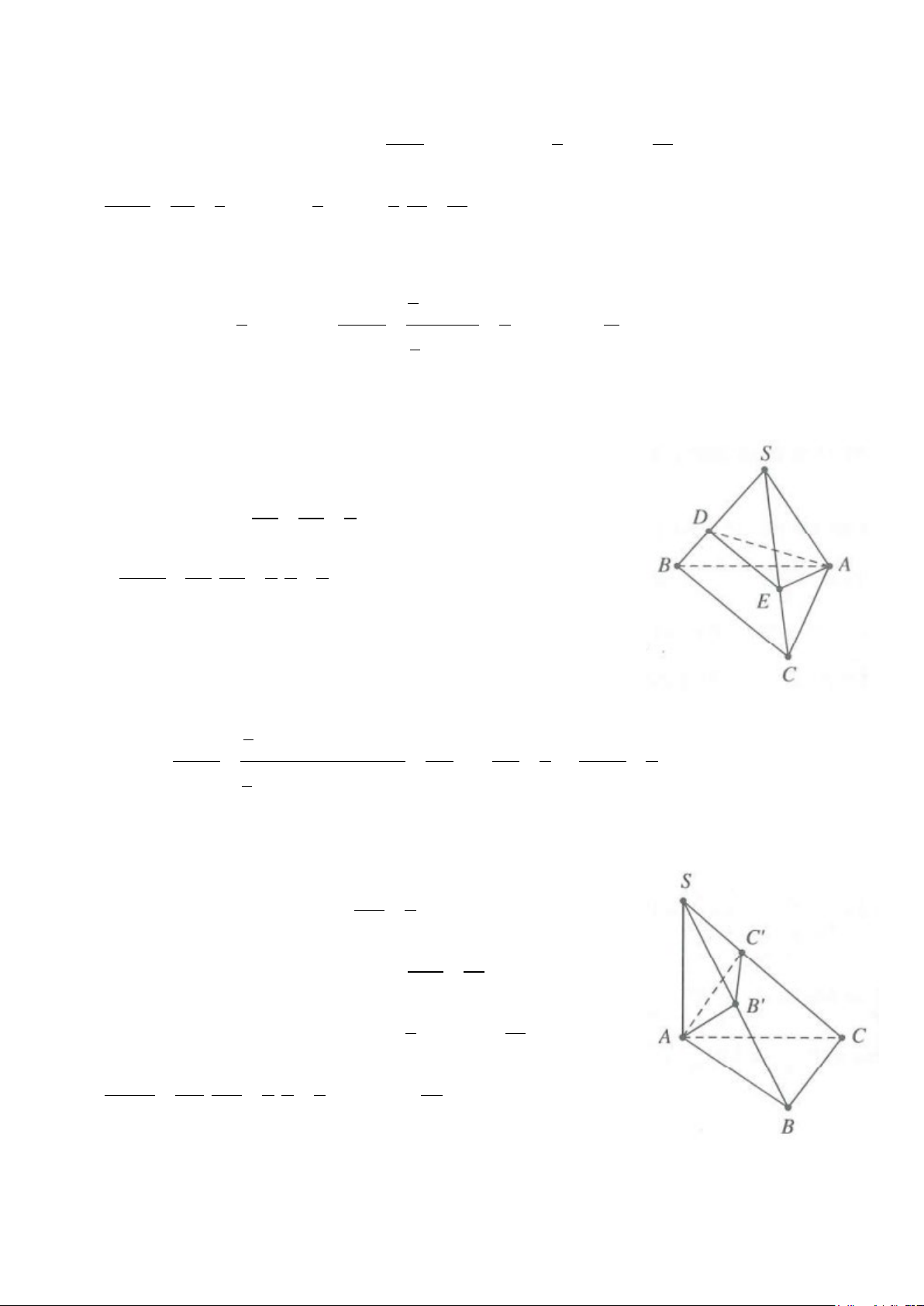
Ví dụ 9: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, AD = 2, BA = BC = 1. Cạnh
bên SA vuông góc với đáy và SA = 2 . Gọi H là hình chiếu vuông góc của A trên SB. Tính thể tích V của
khối đa diện SAHCD. A. 2 2 V = . B. 4 2 V = . C. 4 2 V = . D. 2 2 V = . 3 9 3 9 Lời giải
Tam giác vuông SAB, có 2 2
SB = SA + AB = 3
Gọi M là trung điểm của AD ⇒ ABCM là hình vuông nên AD
CM = AB = a = . 2
→ Tam giác ACD vuông tại C. Ta có V = V +V S.AHCD S.ACD S.AHC • 1 1 1 2 V = S = = ∆ SA AD AB SA S ACD ACD . . . 3 3 2 3 2 V • S.AHC SH SA 2 2 2 = = = ⇒ V = V = 2 S.AHC S. V SB SB 3 3 ABC S ABC 9 . Vậy 2 2 4 2 V = + = Chọn B S AHCD . . 3 9 9
Ví dụ 10: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA = a vuông góc với mặt phẳng
đáy ( ABCD) . Điểm M thuộc cạnh SA sao cho SM = k . Xác định k sao cho mặt phẳng (MBC) chia khối SA
chóp đã cho thành hai phần có thể tích bằng nhau. A. 1 3 k − + = . B. 1 5 k − + = . C. 1 2 k − + = . D. 1 5 k + = . 2 2 2 4 Lời giải
Cách 1. Kẻ MN / / ( ∈ ) SN SM AD N SD → = = k. SD SA
Khi đó mặt phẳng (MBC) chia khối chóp thành hai phần là S.MBCN và AMBDNC. Ta có V = V + V S MBCN S MBC S MCN . . . . V • S.MBC SM = = k ⇒ V = k V S MBC . S ABC. . . V SA S.ABC V • S.MCN SM SN 2 2 = . = k ⇒ V = k V S MCN . S ACD. . . V SA SD S.ACD Lại có 1 2 1 V = V ⇒ k V + k V = V S MBCN . S ABCD . S ABC . S ACD . . . . . S. 2 2 ABCD V V − + S.ABCD 2 S.ABCD 1 2 ⇒ k. + k . = . 1 5 V
→ k + k = ⇒ k = S ABCD 1 . . 2 2 2 2
Cách 2: Với SA 1 SB SC SD 1 = ; = 1; = 1; = SM k SB SC SN k 1 2. + 2 2
Áp dụng công thức, ta được V + − + S.MBCN k k 1 1 1 5 = = = ⇒ k = . Chọn B. V 1 1 S ABCD 2 2 2 . 4. . k k
Ví dụ 11: Cho hình chóp đều S.ABCD. Gọi N là trung điểm SB, M là điểm đối xứng với B qua A. Mặt
phẳng (MNC) chia khối chóp S.ABCD thành hai phần có thể tích lần lượt là V ,V với V < V . Tính tỉ số 1 2 1 2 thể tích V1 . V2 A. V V V V 1 5 = B. 1 5 = C. 1 5 = D. 1 5 = V 7 V 11 V 9 V 13 2 2 2 2 Lời giải
Gọi h, S lần lượt là chiều cao và diện tích đáy của khối chóp S.ABCD. Khi đó 1 V = S h S ABCD . . . 3
Nối MN cắt SA tại E, MC cắt AD tại F.
Tam giác SBM có A, N lần lượt là trung điểm của BM và
SB. Suy ra E là trọng tâm tam giác SBM.
Vì ACDM là hình bình hành nên F là trung điểm MC. Ta có V = V + V BNC.AEF ABCEN E.ACF V • S.ENC SE SN 2 1 1 1 = . = × = →V = V S.ENC S. V SA SB ABC 3 2 3 3 ABC S. 2 2 1 1 →V = V = V = V ABCEN S ABC S ABCD S ABCD . . . . 3 3 2 3 • 1 1 1 1 1 V = S = = ∆ d E ACF S h V E ACF ACF . ; . . . S ABCD. . ( ( )) . 3 3 4 3 12 Do đó 1 1 5 V = V + V = V + V = V = V BNC AEF ABCEN E ACF S ABCD . S ABCD . S ABCD . . . . . . 1 3 12 12 Suy ra 7 V1 5 V = .V → = Chọn A. S ABCD . 2 . 12 V 7 2
Ví dụ 12: Cho hình chóp S.ABC có = = = = ° = °
SA 1, SB 2, SC 3, ASB 60 , ASC 90 ,CSB = 120 .° Thể tích của
khối chóp S.ABC bằng? A. 2 . B. 2 . C. 2 D. 2 . 4 2 6 Lời giải
Kí hiệu như hình vẽ với SA = SP = SK = 1 ⇒ Hình chiếu vuông góc
H hạ từ S xuống ( APK ) trùng với tâm đường tròn ngoại tiếp A ∆ PK .
Ta có AP = 1, AK = 2
Gọi H là trung điểm của cạnh PK HP 3 3 ⇒ sin 60° = = ⇒ HP =
⇒ PK = 2HP = 3 SP 2 2 Như vậy 2 2 2
AP + AK = 1+ 2 = PK ⇒ AP ⊥ AK
⇒ H là tâm đường tròn ngoại tiếp A
∆ PK ⇒ SH ⊥ ( APK ). Cạnh 2 2 3 1
SH = SP − HP = 1− = 4 2 1 1 1 1 1 1 2 ⇒ V = SH S = SH AP AK = = . S APK . APK . . . . .1. 2 . 3 3 2 3 2 2 12 Ta có: VS.APK SA SP SK 1 1 2 = . . = 1. . ⇒ V = V = Chọn B. S ABC 6 S APK . . . V SA SB SC S ABC 2 3 2 .
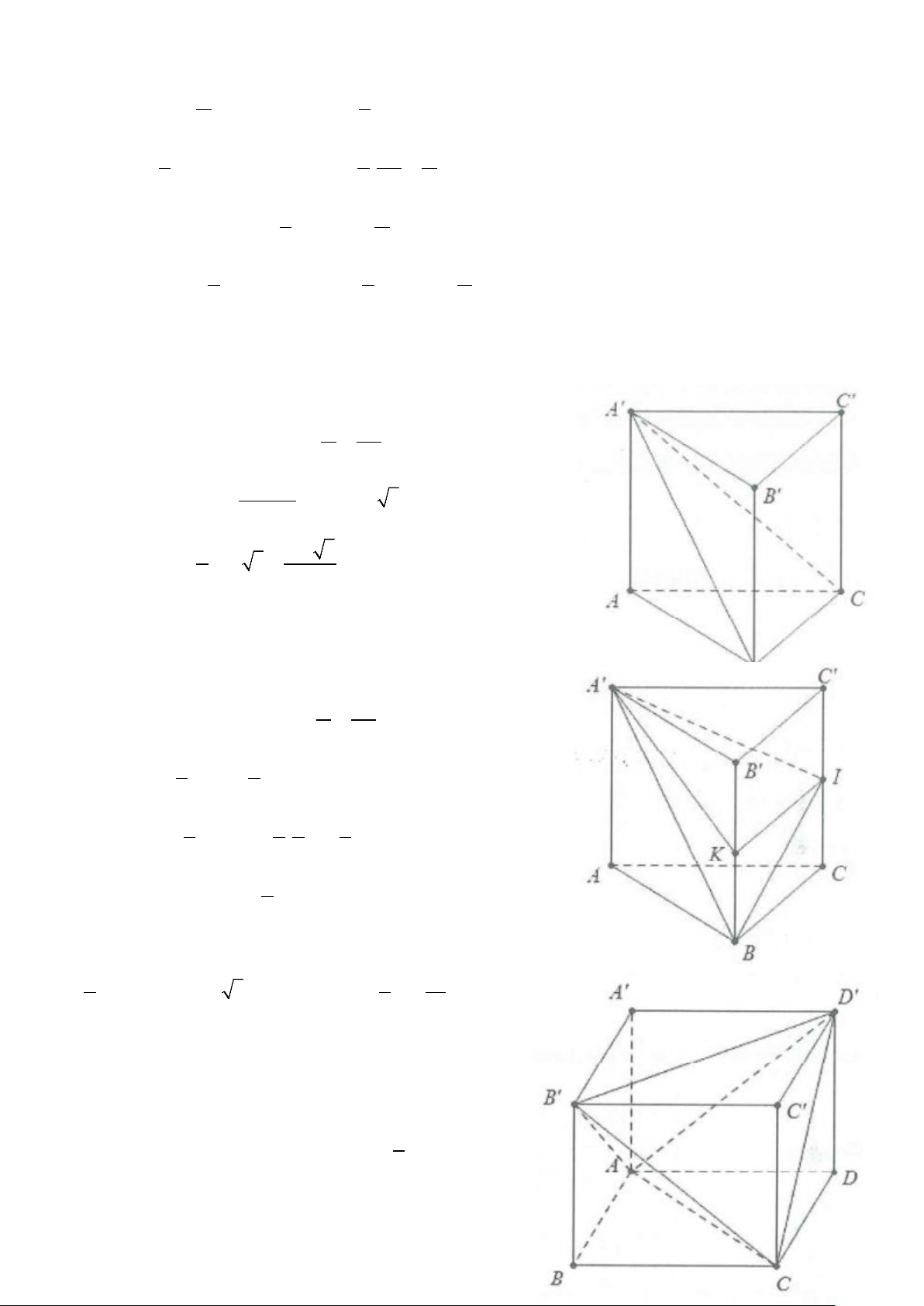
Ví dụ 13: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, với AC = a 2. Cạnh SA = a và
vuông góc với mặt phẳng đáy. Gọi G là trọng tâm của tam giác SBC, mặt phẳng (α ) qua A, G và song song
với BC cắt SB, SC lần lượt tại M và N. Tính theo a thể tích V của khối chóp A.BCNM 3 3 3 3 A. 5a V = . B. 5a V = . C. 2a V = . D. a V = . 54 27 27 18 Lời giải Ta có VS.AMN SA = . SM . SN SM = . SN . V SA SB SC SB SC S.ABC Bài ra có: SM SN SG 2 MN / /BC ⇒ = = = . SB SC GP 3 VS.AMN 4 4 ⇒ = ⇒ V = V S.AMN S. V ABC 9 9 ABC S. 5 ⇒ V = V −V = V A BCNM S ABC S AMN S ABC . . . . . 9
Tam giác ABC vuông cân tại B, với AC = a 2. AC ⇒ AB = BC = = a 2 3 3 1 1 1 2 a 5 5a ⇒ V = SA S = a a = ⇒ V = V = Chọn A. S ABC . ABC . A BCNM S ABC . . . . 3 3 2 6 9 54
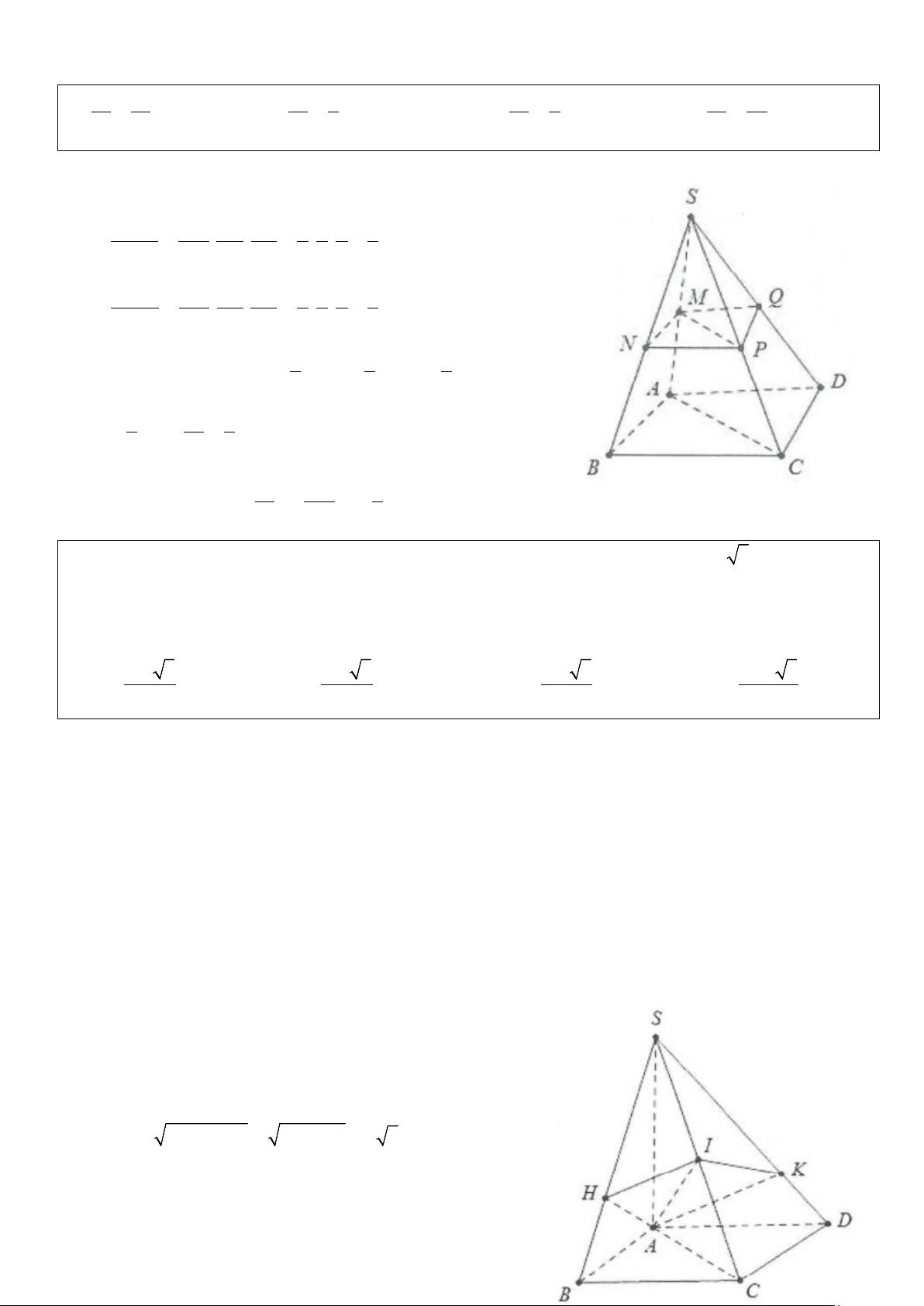
Ví dụ 14: Cho hình chóp S.ABCD, trên cạnh SA lấy điểm M sao cho SM = AM . Mặt phẳng (α ) đi qua M
và song song với mặt phẳng đáy cắt SB, SC, SD lần lượt tại N, P, Q. Kí hiệu V và V lần lượt là thể tích của 1 2
khối chóp S.MNPQ và S.ABCD. Tính tỉ số V1 . V2 A. V V V V 1 1 = . B. 1 1 = . C. 1 1 = . D. 1 1 = . V 16 V 8 V 4 V 24 2 2 2 2 Lời giải
Ta có N, P, Q lần lượt là trung điểm của SB, SC, SD. Tỉ số VS.MNP SM SN SP 1 1 1 1 = . . = . . = . V SA SB SC S ABC 2 2 2 8 . V Tỉ số S.MPQ SM SP SQ 1 1 1 1 = . . = . . = . V SA SC SD S ACD 2 2 2 8 . 1 1 1 ⇒ V = V + V = V + V = V S.MNPQ S.MNP S.MPQ S.ABC S. 8 8 ACD 8 SABCD 1 V1 1 ⇒ V = V ⇒ = 1 2 8 V 8 2 2
Hoặc áp dụng công thức V1 SM 1 = = . Chọn B V SA 8 2
Ví dụ 15: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, với AB = a, AD = a 3. Cạnh SA = 2a
và vuông góc với mặt phẳng đáy. Mặt phẳng (α ) qua A và vuông góc với SC cắt SB, SC, SD lần lượt tại H,
I, K. Tính theo a thể tích V của khối chóp S.AHIK. 3 3 3 3 A. 4a 3 V = . B. 6a 3 V = . C. 8a 3 V = . D. 12a 3 V = . 35 35 35 35 Lời giải
Ta có SC ⊥ ( AHIK ) ⇒ SC ⊥ AI, SC ⊥ AH ⇒ AH ⊥ SC. BC ⊥ AB Lại có
⇒ BC ⊥ (SAB) ⇒ BC ⊥ AH ⇒ AH ⊥ BC. BC ⊥ SA AH ⊥ SC Như vậy
⇒ AH ⊥ (SBC) ⇒ AH ⊥ SB, tương tự AH ⊥ BC thì AK ⊥ S . D Cạnh 2 2 2 2
SB = SA + AB = 4a + a = a 5 2 2 SA 4a 4a SB 5 ⇒ SH = = = ⇒ = SB a 5 5 SH 4
Mà SA = 2a ⇒ SA = AC ⇒ SA
∆ C vuông cân tại A
⇒ I là trung điểm của cạnh SC SC ⇒ = 2. SI Do đó SA SC SB SD SD 7 + = + ⇒ = . SA SI SH SK SK 4
Áp dụng công thức, ta được: 5 7 1+ + 2 V + S.AHIK 4 4 12 = = . V 5 7 S ABCD 35 . 4.1. .2. 4 4 3 Do đó 12 1 4 8a 3 V = SA S = a a a = Chọn C. S AHIK . . ABCD .2 . . 3 . . 35 3 35 35
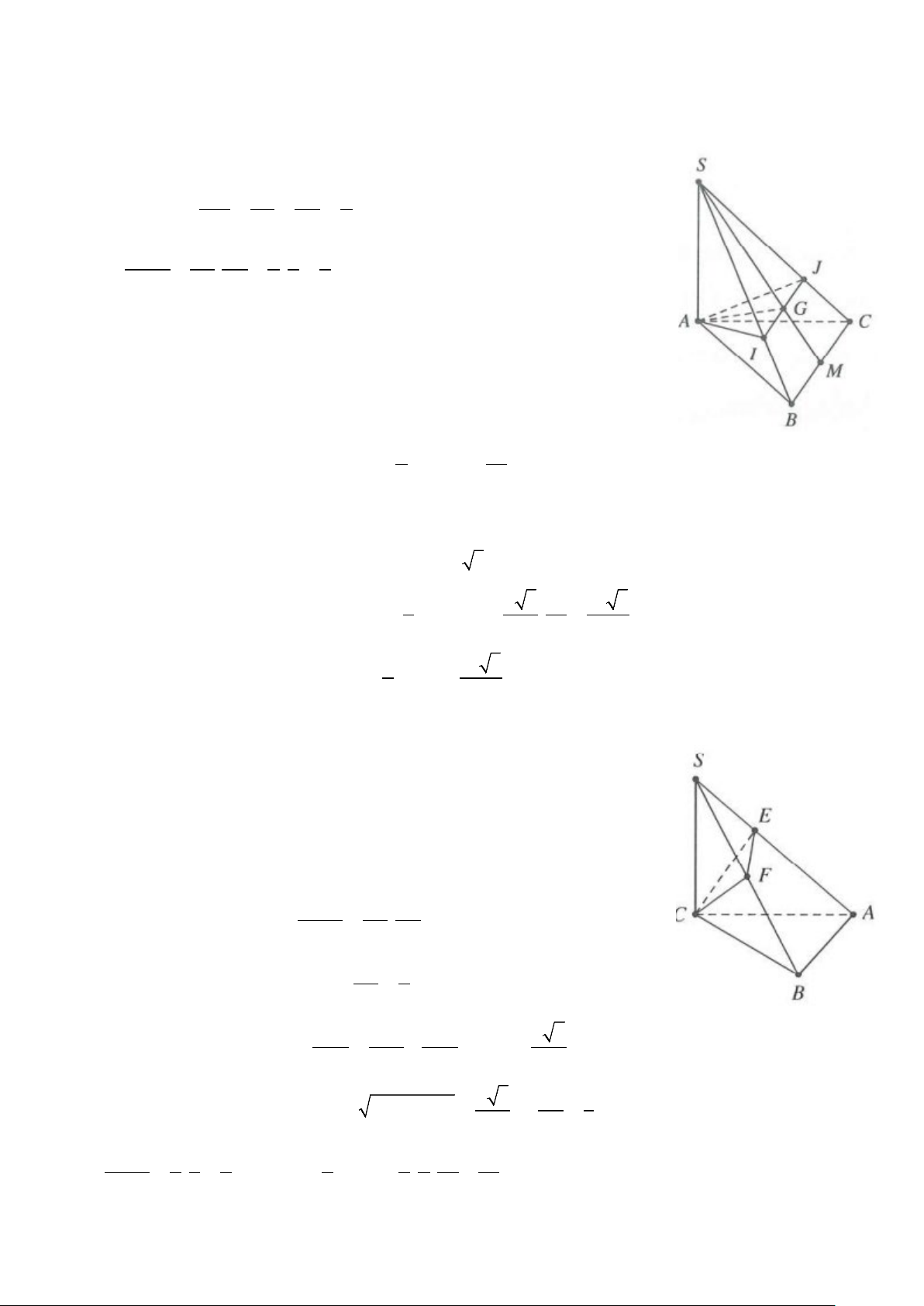
Ví dụ 16: Cho hình chóp S.ABC có SA = 6, SB = 2, SC = 4, AB = 2 10 và = °
SBC 90 , ASC = 120 .° Mặt
phẳng (P) đi qua B và trung điểm N của SC đồng thời vuông góc với mặt phẳng (SAC), cắt cạnh SA tại V
M. Tính tỉ số thể tích S.BMN k = . VS.ABC A. 2 k = B. 2 k = C. 1 k = D. 1 k = 9 5 6 4 Lời giải
Gọi D thuộc SA sao cho SA = 3.SD ⇒ SD = 2. Xét S
∆ BC vuông tại B, có SB 1 = = ⇒ cos BSC BSC = 60 .° SC 2 Và 2 2 2
AB = SA + SB ⇒ SA
∆ B vuông tại S ⇒ ASB = 90°
Xét tứ diện S.BND có = ° = °
DSB 90 , BSN 60 , DSN = 120° 2 2 2
⇒ BD + BN = DN ⇒ B
∆ DN vuông tại B
Mà SB = SN = SD ⇒hình chiếu của S trên mặt phẳng (BDN ) trùng
với tâm đường tròn ngoại tiếp tam giác BDN.
Gọi H là trung điểm DN ⇒ SH ⊥ (BDN ) ⇒ (SDN ) ⊥ (BDN )
Hay (BDN ) ⊥ (SAC) ⇒ mp(P) ≡ (BDN ) ⇒ M ≡ . D Vậy
VS.BMN SN SM 1 1 1 k = = . = . = . Chọn C. V SC SD S ABC 2 3 6 .
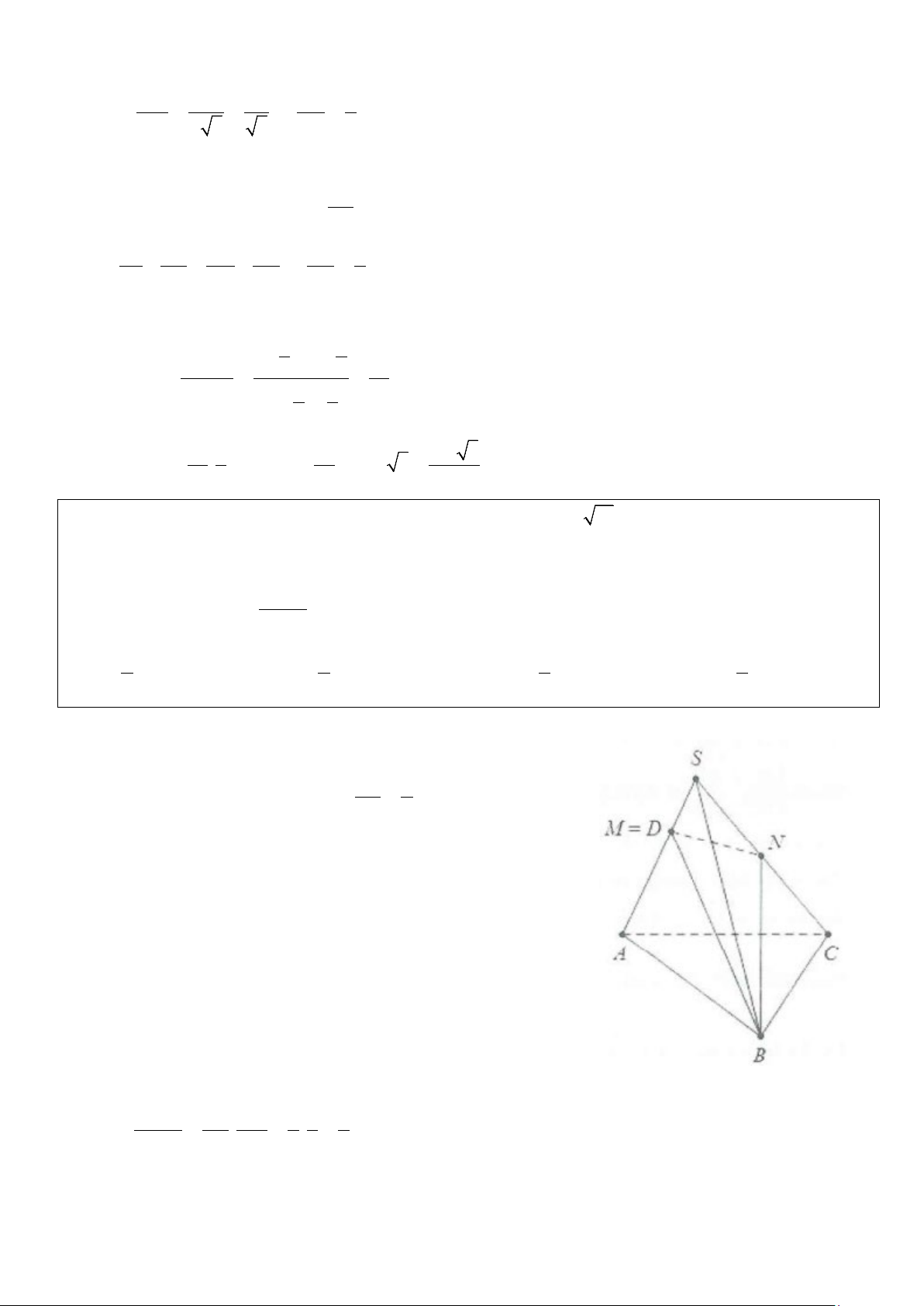
Ví dụ 17: Cho khối tứ diện ABCD có AB, AC, AD đôi một vuông góc với nhau và AB = 2a, AC = AD = 4 .
a Gọi H, K lần lượt là hình chiếu của A lên BC và BD. Thể tích của khối tứ diện ABHK là 3 3 3 3 A. 16a B. 32a C. 2a D. 3a 75 75 3 2 Lời giải Ta có 2 2
BD = AB + AD = (2a)2 + (4a)2 = 2a 5 2 2 Và 2 BK AB 2a 1
AB = BK.BD ⇒ = = = . BD BD 2a 5 5
Tương tự, được BH 1 = . BC 5 3 Lại có 1 16a V = V = a a a = B ACD D ABC .4 .4 .2 . . . 6 3 3 3 Vậy VB.AKH BK BH 1 1 1 1 16a 16 = . = . a = ⇒ V = = ABHK . . V BD BC B ACD 5 5 25 25 3 75 . Chọn A.
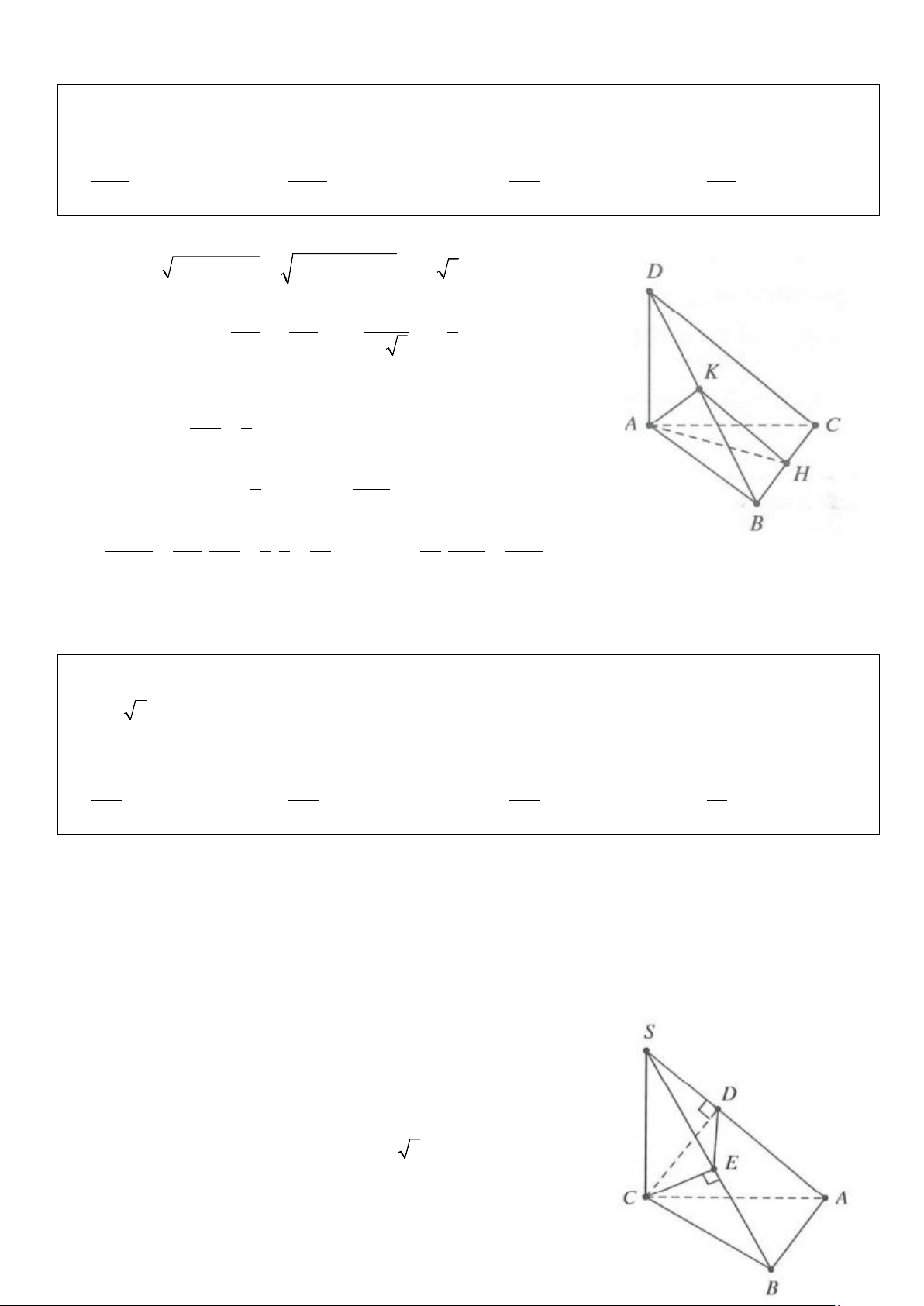
Ví dụ 18: Cho hình hộp S.ABC có SC = 2a và SC ⊥ ( ABC). Đáy ABC là tam giác vuông cân tại B có
AB = a 2 . Mặt phẳng (α ) đi qua C và vuông góc với SA, (α ) cắt SA, SB lần lượt tại D, E. Tính thể tích khối chóp S.CDE 3 3 3 3 A. 4a B. 2a C. 2a D. a 9 3 9 3 Lời giải SC ⊥ AB Ta có
⇒ AB ⊥ (SBC) ⇒ CE ⊥ AB BC ⊥ AB
Mà SA ⊥ (α ) ⇒ SA ⊥ CE suy ra CE ⊥ (SAB) ⇒ CE ⊥ SB
Tam giác ABC vuông cân tại B ⇒ AC = AB 2 = 2a
Suy ra SC = AC ⇒ S
∆ AC cân tại C SD 1 ⇒ SD = DA ⇔ = . SA 2
Tam giác SBC vuông tại C, có SC.BC 2 3a CE = = . 2 2 SC + BC 3 Do đó 2 2 2 6a SE 2 6a 2
SE = SC − CE = → = : a 6 = . 3 SB 3 3 2 3 Khi đó VS.CDE SD SE 1 1 1 AB 2 = . a = ⇒ V = SC = S CDE . . . . V SA SB S CAB 3 3 3 2 9 . Chọn C.
Ví dụ 19: Cho tứ diện ABCD có các cạnh AB, AC và AD đôi một vuông góc. Các điểm M, N, P lần lượt là
trung điểm các đoạn thẳng BC, CD, BD. Biết rằng AB = 4a, AC = 6a, AD = 7 .
a Tính thể tích của khối tứ diện AMNP. A. 3 V = 7a B. 3 V = 28a C. 3 V = 14a D. 3 V = 21a Lời giải
Tứ diện ABCD có các cạnh AB, AC và AD đôi một vuông góc 1 3 →V = AB AC AD = a ABCD . . 28 6 Ta có 1 S = suy ra 1 3 V = V = a Chọn A. AMNP A BCD 7 . ∆ S MNP B ∆ CD , 4 . 4
Ví dụ 20: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm SB và G là trọng
tâm của tam giác SBC. Gọi V ,V ′ lần lượt là thể tích của các khối chóp M.ABC và G.ABD. Tính tỉ số V V ′ A. V 3 = B. V 4 = C. V 5 = D. V 2 = V ′ 2 V ′ 3 V ′ 3 V ′ 3 Lời giải
Gọi H và K lần lượt là hình chiếu của M và G trên mp( ABCD) Suy ra MH CM 3 MH / /GK → = = . GK CG 2 1 1 MH.S∆ S ABC ABCD Ta có V 3 3 2 3 = = . = . Chọn D V ′ 1 2 1 2 GK.S∆ S 3 ABD 2 ABCD
Ví dụ 21: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. I nằm trên cạnh SC sao cho IS = 2IC .
Mặt phẳng (P) chứa cạnh AI cắt cạnh SB, SD lần lượt tại M, N. Gọi V ,′V lần lượt là thể tích khối chóp ′
S.AMIN và S.ABCD. Tính giá trị nhỏ nhất của tỷ số thể tích V V A. 4 B. 5 C. 8 D. 5 5 54 15 24 Lời giải
Gọi O là tâm của hình bình hành ABCD.
Gọi H = SK ∩ AI, qua H kẻ d / /BD cắt SB, SD tại M, N.
Xét tam giác SAC, có IS AC OH OH 1 SH 4 . . = 1 ⇒ = ⇒ = . IC OC SH SC 4 SC 5 Mà SM SN SH 4 MN / /BD → = = = SB SD SO 5 Ta có V SM SI SM V S.AMI 2 S.AMI 1 = . = . ⇒ = . SM V SB SC SB V SB S ABC 3 S ABCD 3 . . Và V SN SI SN V S.ANI 2 S.ANI 1 = . = . ⇒ = . SN V SD SC SD V SD S ACD 3 S ABCD 3 . . ′ Suy ra V
1 SM SN 1 4 4 8 = + = . + = . Chọn C. V
3 SB SD 3 5 5 15
Ví dụ 22: Cho điểm M nằm trên cạnh SA, điểm N nằm trên cạnh SB của khối chóp tam giác S.ABC sao cho SM 1
= ; SN = 2. Mặt phẳng (α ) đi qua MN và song song với SC chia khối chóp thành 2 phần. Gọi V là MA 2 NB 1
thể tích của khối đa diện chứa A, V
V là thể tích của khối đa diện còn lại. Tính tỉ số 1 ? 2 V2 A. V V V V 1 4 = B. 1 5 = C. 1 5 = D. 1 6 = V 5 V 4 V 6 V 5 2 2 2 2 Lời giải
Kẻ NP / /SC (P ∈ BC), kẻ MQ / /SC (Q ∈ SC).
Khi đó, mặt phẳng (α ) cắt hình chóp theo thiết diện là MNPQ. Vì CP 2 CQ 1 NP / /SC ⇒ = ;MQ / /SC ⇒ = . CB 3 CA 3 S Ta có C ∆ PQ CP CQ 1 2 2 2 = . = . = ⇒ S = ∆ S CPQ . S∆ CB CA 3 3 9 9 ABC ∆ CBA Và ( ( )) 1 = ( ( )) 2 2 ; . ; V d N ABC d S ABC ⇒ V = V = N CPQ S ABC . . . 3 27 27 S Lại có A ∆ MQ AM AQ 2 2 4 5 = . = . = ⇒ S = S SMQC SA ∆ C . S∆ SA AC ASC 3 3 9 9
Và d (N (SAC)) 2
= d (B (SAC)) 10 10 ; . ; ⇒ V = V = V N SMQC S ABC . . . 3 27 27 Do đó 2V 10 4V 5V V = V = V + V = + V = ⇒ V = SCMNPQ N CPQ N SMQC . 2 . . 1 27 27 9 9
Vậy V1 5V 4V 5 = : = . Chọn B V 9 9 4 2
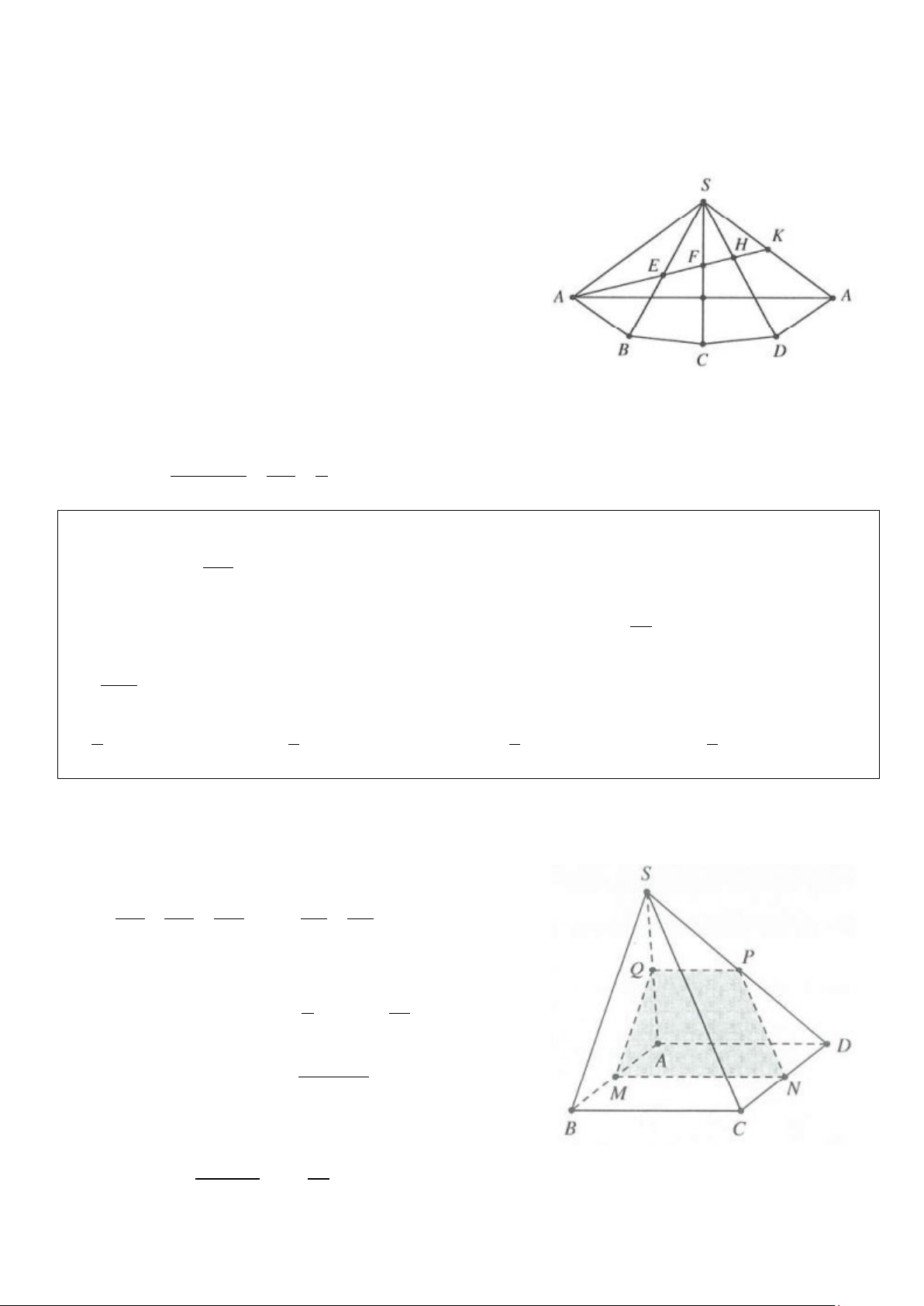
Ví dụ 23: Thị xã Từ Sơn xây dựng một ngọn tháp đèn lộng lẫy hình chóp tứ giác S.ABCD có cạnh bên SA = 12m và
ASB = 30° . Người ta cần mắc một đường dây điện từ điểm A đến trung điểm K của SA gồm
AE, EF, FH, HK như hình vẽ. Để tiết kiệm chi phí người ta cần thiết kế được chiều dài con đường từ A đến
K là ngắn nhất. Tính tỉ số HF + HK k = EA + EF A. 3 k = B. 1 k = C. 1 k = D. 2 k = 4 2 3 3 Lời giải
Giả sử ngọn tháp được làm bằng bìa nên ta cắt được ngọn tháp
theo các đường SA, AB, BC, CD, DA. Và trải các mặt bên SAB,
SBC, SCD, SDA lên cùng một mặt phẳng. Vì = = =
ASB BSC CSA DSA = 30° nên khi trải ra mặt phẳng
ta thu được một tam giác cân SAA có góc ở đỉnh
S = 4.30° =120° như hình vẽ bên.
Để độ dài đoạn gấp khúc AE + EF + FH + HK nhỏ nhất khi
và chỉ khi A, E, F, H, K thẳng hàng.
Vì K là trung điểm của SA ⇒ F = SC ∩ AK ⇒ F là trọng tâm của tam giác SAA Vậy tỉ số HF + HK FK 1 k = = = . Chọn B. EA + EF AF 2
Ví dụ 24: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành có thể tích là V. Gọi M là một điểm trên
cạnh AB sao cho MA = x,0 < x < 1. Biết rằng mặt phẳng (α ) qua M và song song với (SBC) chia khối MB
chóp S.ABCD thành hai phần trong đó phần chứa điểm A có thể tích bằng 4 V . Tính giá trị của biểu thức 27 1− x P = . 1+ x A. 1 B. 1 C. 1 D. 3 2 5 3 5 Lời giải
Kẻ MN / /BC (N ∈CD), NP / /SC (P ∈ SD), MQ / /SB(Q ∈ SA).
⇒ mp(α ) cắt chóp S.ABCD theo thiết diện là MNPQ. Ta có MA AQ ND SQ SP = = = x ⇒ = = 1− x AB SA CD SA SD Mặt khác A ∆ MN = A ∆ DN 2 x x ⇒ V = V = xV = V = V Q AMN P ADN . S AMN S AMND . . . . . 2 2 2 x 1− x Và V
= x − x ×V = V N APQ 1 N SAD . . ( ) ( ) . 2 Do đó V = V + V + V AQM .DPN Q.AMN P.AND N.APQ 2 3 3x − x 4 = ×V = V 2 27 3 2 8 1 − ⇒ x − 3x + = 0 ⇒ x = . Vậy 1 x 1 P = = . Chọn A. 27 3 1+ x 1 = 2 x 3
Ví dụ 25: Cho hình chóp S.ABCD có đáy là hình bình hành và có thể tích bằng 1. Trên cạnh SC lấy điểm E
sao cho SE = 2EC. Tính thể tích V của khối tứ diện SEBD. A. 2 V = . B. 1 V = . C. 1 V = . D. 4 V = . 3 6 3 3 Lời giải Ta có VS.EBD SE 2 2 2 1 1 1 = = ⇒ V = V = S = = Chọn C. S EBD S BCD . ABCD .1 . . . V SC S BCD 3 3 3 2 3 3 .
Ví dụ 26: Cho hình chóp S.ABCD có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt đáy. Gọi M là
trung điểm của BC. Mặt phẳng (P) đi qua A và vuông góc với SM cắt SB, SC lần lượt tại E, F. Biết 1 V = V
. Tính thể tích V của khối chóp S.ABC. S.AEF S. 4 ABC 3 3 3 3 A. a V = B. a V = C. 2a V = D. a V = 2 8 5 12 Lời giải
Dựng AH ⊥ SM , dựng đường thẳng qua H song song với BC cắt SB,
SC lần lượt tại E, F.
Khi đó EF / /BC ⊥ SM ⇒ mp( AEF ) ⊥ SM. Lại có: 1 SE SF SH 1 V = V ⇒ = = = S AEF S ABC . . . 4 SB SC SM 2 Do đó S
∆ AM vuông cân tại a 3
A ⇒ SA = SM = 2 3 Vậy 1 a V = SA S = Chọn B. S ABC . . ABC . . 3 8
Ví dụ 27: Cho hình chóp S.ABCD có đáy là hình bình hành, gọi M, P lần lượt là trung điểm của SA và SC.
Điểm N thuộc cạnh SB sao cho SN = k. Mặt phẳng (MNP) cắt khối chóp theo thiết diện là tứ giác MNPQ. SB V
Biết rằng S.MNPQ 2 =
, giá trị của k là: VS ABCD 15 . A. 1 2 k ; ∈ . B. 1 2 k ∈ ; . C. 2 2 k ∈ ; . D. 3 2 k ∈ ; . 3 3 3 5 3 5 5 5 Lời giải
Ta có SM = ; SN = ; SP = ; SQ x y z = t. SA SB SC SD Ta có: 1 x = z = . mà 1 1 1 1 + + + = 4. 2 x z y t
Áp dụng công thức nhanh ta có:
VS.MNPQ xyzt 1 1 1 1 yt 2 = . + + + = .2.4 = . V x z y t S ABCD 4 16 15 . y + t 4 = 4 = 4 yt yt 15 ⇔ yt = ⇒ ⇔ 15 4 16 yt = yt = 15 15 2 X =
Khi đó y, t là nghiệm của phương trình 2 16 4 3 2 2 X X 0 k ; − + = ⇒ ⇒ ∈ . Chọn C 15 15 2 5 3 X = 5
Ví dụ 28: Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = 1, AD = 2, SA vuông góc với mặt
phẳng đáy ( ABCD) và SA = 2 . Điểm M trên cạnh SA sao cho (MBC) chia khối chóp S.ABCD thành hai
phần có thể tích bằng nhau. Tính diện tích S của tam giác MAC. A. 3 5 5 S − = . B. 5 S = . C. 5 S = . D. 5 5 S − = . 2 2 3 4 Lời giải
Qua M kẻ đường thẳng d / /BC, cắt SD tại N ⇒ N ∈(MBC) Đặt SA SD = k ⇒ = k SM SN SA SB SC SD + + + Khi đó V + S.MBCN SM SB SC SN k 1 = = 2 V SA SB SC SD k S ABCD 2 . 4. . . . SM SB SC SN Theo bài: V + + S.MBCN 1 k 1 1 1 5 = ⇒ = ⇔ k = ⇒ MA = 3 − 5 2 V k S ABCD 2 2 2 2 .
Diện tích tam giác MAC là 1 1
S = MA AC = ( − ) 3 5 − 5 . . 3 5 . 5 = . Chọn A. 2 2 2
Ví dụ 29: Cho khối chóp S.ABCD có đáy ABCD là hình bình hành, M thuộc cạnh SA, P thuộc cạnh SC sao
cho 2SM = AM , SP = PC. Mặt phẳng (α ) chứa MP, chia khối chóp S.ABCD thành hai khối đa diện. Gọi
V , V lần lượt là thể tích khối đa diện chứa đỉnh S và thể tích khối chóp S.ABCD. Giá trị nhỏ nhất của biểu 1 thức V1 là V A. 5 B. 1 C. 1 D. 2 12 25 15 25 Lời giải
Giả sử mặt phẳng (α ) chứa MP, cắt đường thẳng SB, SD lần lượt tại N, Q. Khi đó SA SC SB SD + = +
⇔ 3 + 2 = x + y ⇔ x + y = 5. SM SP SN SQ SA SB SC SD V + + + Và S.MNPQ SM SN SP SQ
x + y + 5 x + y + 5 5 = = = = V SA SB SC SD x xy xy S ABCD 4.3. .2.y 24 12 . 4. . . . SM SN SP SQ
Ta có xy ≤ (x + y)2 5 5 1 4
= 25 ⇔ 12xy ≤ 75 → ≥ = 12xy 75 15
Vậy tỉ số V1 đạt giá trị nhỏ nhất bằng 1 . Chọn C. V 15
Ví dụ 30: Cho khối chóp S.ABCD có đáy ABCD là hình bình hành, M là điểm thuộc cạnh SB, N là điểm
thuộc cạnh SD sao cho SB = 3BM , SN = 2N .
D Mặt phẳng ( AMN ) chia khối chóp S.ABCD thành hai khối đa diện. Gọi V
V , V lần lượt là thể tích khối đa diện chứa đỉnh S và đỉnh C. Tính tỉ số 1 1 2 V2 A. 2 B. 2 C. 1 D. 1 3 3 2 Lời giải
Giả sử mặt phẳng ( AMN ) cắt đường thẳng SC tại P. Khi đó SA SC SB SD SC 3 3 + = + ⇔ 1 SC + = + ⇔ = 2 SA SP SM SN SP 2 2 SP SA SB SC SD 3 3 + + + 1+ + 2 + Và VS.AMPN SA SM SP SN 2 2 6 1 = = = = ⇒ V = V S ABCD 3 . 1 V SA SB SC SD 3 3 S ABCD 18 3 . 4. . . . 4.1. .2. SA SM SP SN 2 2 Mà V1 1 V = V + V
= V +V = V ⇔ V = V ⇔ = Chọn D. S ABCD S AMPN AMPN BCD 3 2 . . . . 1 2 1 2 1 V 2 2
Dạng 2: Tỉ số thể tích khối lăng trụ
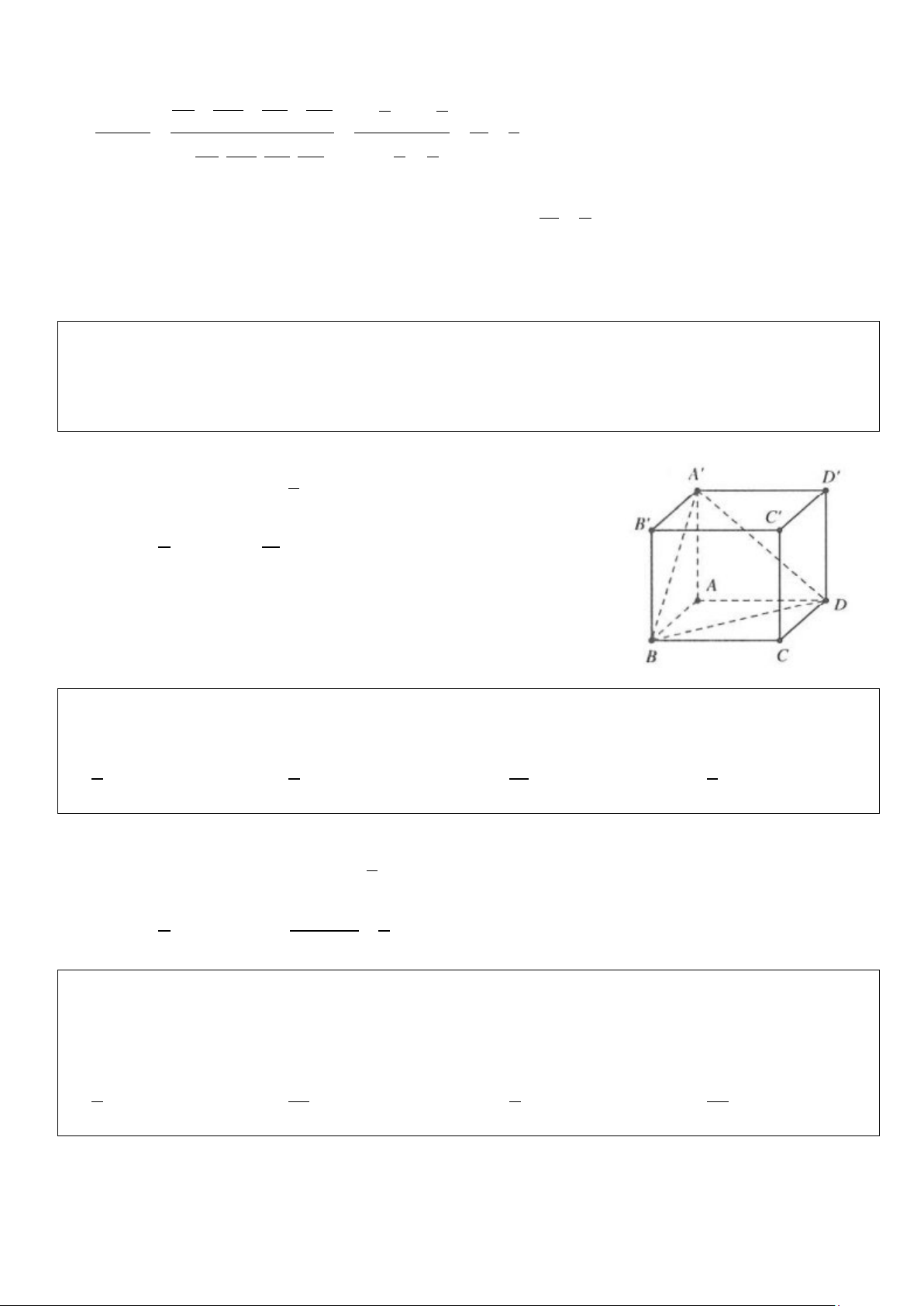
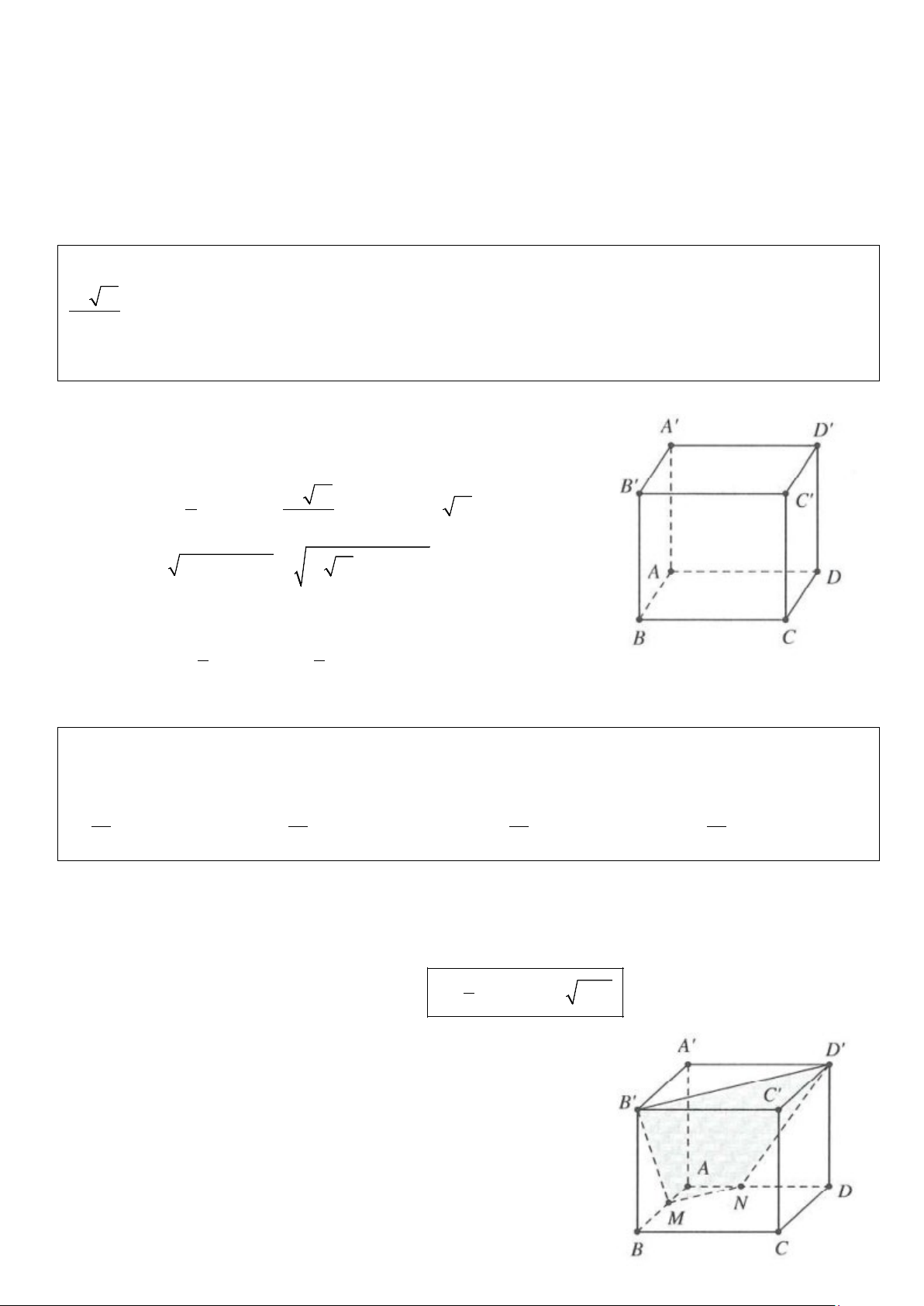
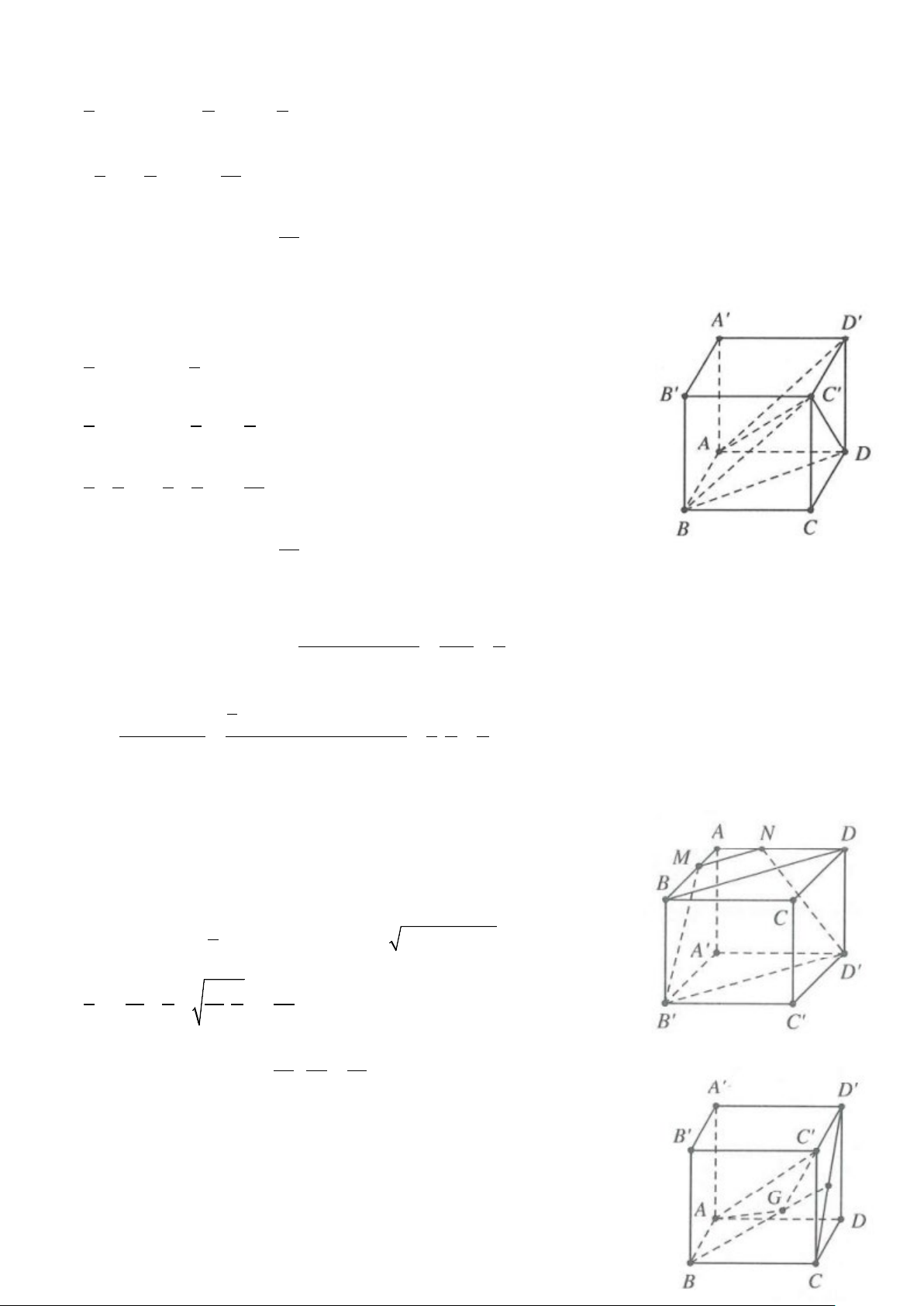
Ví dụ 1: Gọi V là thể tích của hình lập phương ABC . D A′B C ′ D
′ ,′V là thể tích tứ diện A′ABD . Hệ thức nào 1 sau đây đúng?
A. V = 6V
B. V = 4V
C. V = 3V
D. V = 2V 1 1 1 1 Lời giải Ta có V = S AA′ và 1 V = S ′ ∆ .AA ABCD . 1 3 ABD Mà 1 V S = → = ∆ S ABD ABCD 6 2 V1
Suy ra V = 6V . Chọn A. 1
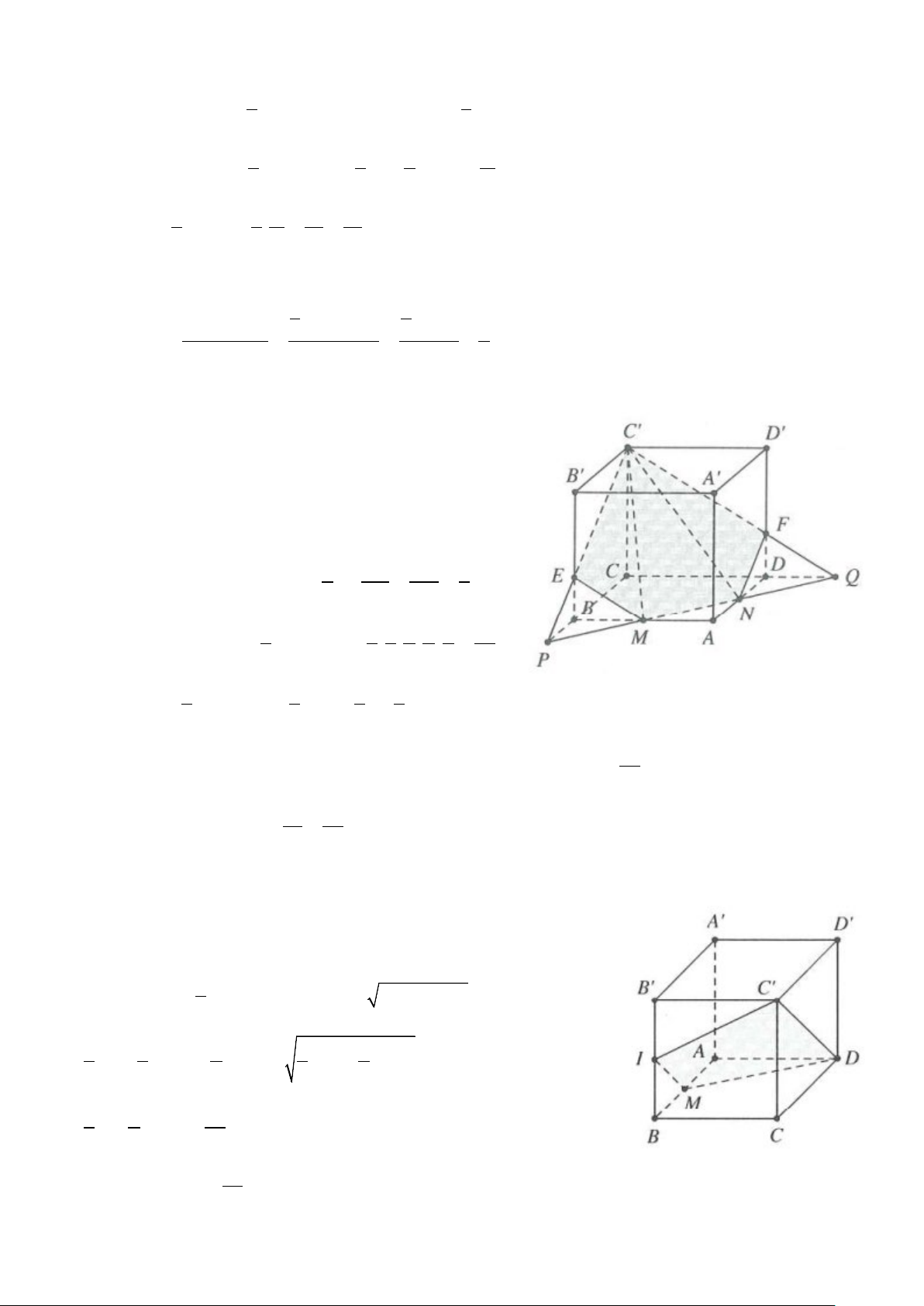
Ví dụ 2: Cho hình lăng trụ đứng ABC.A′B C
′ ′ . Gọi D là trung điểm của AC. Tính tỉ số thể tích khối tứ diện B B
′ AD và thể tích khối lăng trụ đã cho. A. 1 B. 1 C. 1 D. 1 4 6 12 3 Lời giải Ta có V = ′ và 1 V = ′ ′ S∆ BB B BAD BAD . . ′ ′ ′ S∆ BB ABC A B C ABC . . 3 Mà 1 VBBAD ′ 1 S = → = = Chọn B. ∆ S∆ k BAD ABC . 2
VABC A′BC′′ 6 .
Ví dụ 3: Cho khối lăng trụ ABC.A′B C
′ ′ . Đường thẳng đi qua trọng tâm của tam giác ABC và song song
với BC cắt các cạnh AB, AC lần lượt tại M, N. Mặt phẳng ( A′MN ) chia khối lăng trụ thành hai phần. Tính
tỉ số thể tích (phần bé chia phần lớn) của chúng. A. 2 B. 4 C. 4 D. 4 3 23 9 27 Lời giải
Gọi G là trọng tâm của tam giác ABC.
Gọi E là trung điểm của BC AG 2 ⇒ = AE 3
Qua G kẻ đường thẳng d / /BC, cắt AB, AC lần lượt tại M, N. AM AN AG 2 ⇒ = = = (định lí Talet) AB AC AE 3 2 AM = AB 3 4 ⇒ ⇒ S = (1). ∆ S 2 AMN 9 ABC ∆ AN = AC 3 Ta có V = và 1 V = (2). ′ S∆ AA A AMN AMN . ' ′ ′ ′ S∆ AA ABC A B C ABC . ' . . 3 Từ (1) và (2) 4 23 ⇒ V = ⇒ = ′ V ′ ′ ′ V ′ ′ ′ V A .AMN ABC.A B C BMNC,A B C ABC. 27 27 A′B C ′ ′
Vậy tỉ số cần tìm là 4 23 4 : = . Chọn B. 27 27 23
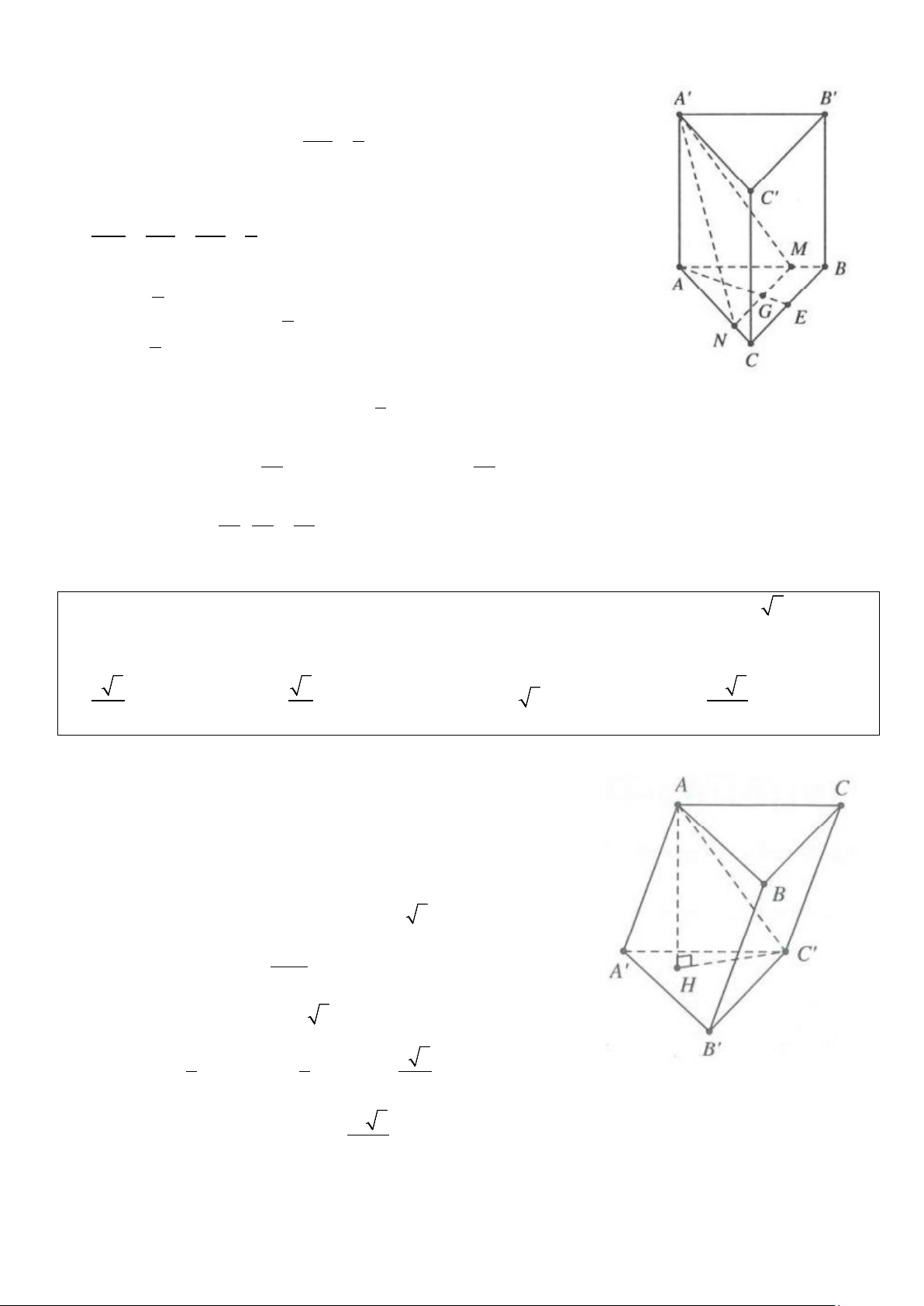
Ví dụ 4: Cho hình lăng trụ ABC.A′B C
′ ′ có đáy ABC là tam giác vuông cân tại A, AC = 2 2. Biết AC′
tạo với mặt phẳng ( ABC) một góc 60° và AC′ = 4 . Tính thể tích của khối đa diện ABCC B ′ ′ . A. 8 3 B. 3 C. 2 3 D. 16 3 3 3 3 Lời giải
Gọi H là hình chiếu của A trên mặt phẳng ( A′B C ′ ′).
Suy ra HC′ là hình chiếu của AC′ trên mặt phẳng ( A′B C ′ ′).
Do đó ( AC′ ( ABC))
= (AC′ HC′) = ; ; AHC′ = 60° Tam giác AHC′, có = ′ AH AC sin AC H ′ = 2 3 2 Diện tích tam giác AC S = = ABC ∆ 4 2 Suy ra V = = ′ ′ ′ S∆ AH ABC A B C ABC . 8 3 . Ta có 1 1 8 3 V = = = ′ ′ ′
S∆ ′ ′ ′ AH V A A B C A B C . ABC A′B C ′ ′ . . . 3 3 3 Suy ra 16 3 V = − = . Chọn D. ′ ′ V ′ ′ ′ V ABCC B ABC.A B C . A A′B C ′ ′ 3
Ví dụ 5: Cho hình hộp chữ nhật ABC . D A′B C ′ D
′ ′ có thể tích V. Các điểm M, N, P lần lượt thuộc các cạnh
AC, AB ,′ AD′ sao cho AM = 2AC, AN = 3AB ,′ AP = 4AD .′ Tính thể tích của khối tứ diện AMNP theo V. A. V = V B. V = V C. V = V D. V = V AMNP 12 AMNP 6 AMNP 4 AMNP 8 Lời giải Ta có V = V + + + + ′ ′ ′
V ′ ′ ′ V ′ ′ ′ V ′ V AB D C ( AABD CC B D D DAC B BAC ′ ). Mà V V = = = = ′ ′ ′
V ′ ′ ′ V ′ V AA B D CC B D D DAC B BAC ′ . 6 Suy ra V V = AB D ′ C ′ ′ . 3 ′ ′
Từ gia thiết, ta có AB 1 AC 1 AD 1 = ; = ; = . AN 3 AM 2 AP 4 ′ ′
Ta có V .ABD′C′′ AB AD AC 1 = . . = . V AN AP AM A NPM 24 . V →V = V = = Chọn A. ′ ′ ′ V A NPM 24 A BDC 24. 8 . . . 3
Nhận xét: Công thức giải nhanh: Thể tích của khối tứ diện (4 đỉnh nằm trên hai đường chéo của hai mặt
đối diện) có thể tích bằng 1 của khối lăng trụ tam giác. 3
Ví dụ 6: Cho lăng trụ tam giác đều ABC.A′B C
′ ′ có góc giữa hai mặt phẳng ( A′BC) và ( ABC) bằng 30° .
Điểm M nằm trên cạnh AA′. Biết cạnh AB = a 3, thể tích khối đa diện MBCC B ′ ′ bằng 3 3 3 3 A. 3a . B. 3a 3 . C. 3a 2 . D. 2a . 4 2 4 3 Lời giải
Gọi V là thể tích khối lăng trụ ABC.A′B C ′ ′ . Do V 2 ′ / / V AA BB′ ⇒ V = = − = − = ′ ′
V ′ ′ ′ V V ′ V M .BCB C A .BCC B A .ABC 3 3
Dựng AH ⊥ BC mà AA′ ⊥ BC ⇒ BC ⊥ ( A′HA) Do đó ( ′ ) ( ) = AB 3 3 ; ′ = 30 a A BC ABC A HA ° ⇒ AH = = . 2 2 3 Khi đó a 3 9 ′ = .tan 30° = ⇒ = . a AA AH V AA′ S = ABC ∆ . 2 8 3
Vậy thể tích cần tính là V 3a V = = Chọn A. M BCC B ′ ′ 2 . . 3 4
Ví dụ 7: Cho hình lăng trụ ABC.A′B C
′ ′ có thể tích bằng V. Các điểm M, N, P lần lượt thuộc các cạnh
AA ,′ BB ,′CC′ sao cho AM 1 BN CP 2 = ; =
= . Tính thể tích của khối đa diện ABC.MNP
AA′ 2 BB′ CC′ 3 A. 2 V ′ = V B. 9 V ′ = V C. 20 V ′ = V D. 11 V ′ = V 3 16 27 18 Lời giải Công thức giải nhanh
m + n + p V = AM BN CP V với m = ,n = , p = . ABC.MNP 3 AA′ BB′ CC′ Áp dụng với: 1 2 2
m = ;n = ; p = , ta được 11 V = V . Chọn D. 2 3 3 ABC.MNP 18
Ví dụ 8: Cho hình lập phương ABC . D A′B C ′ D
′ ′ cạnh 2a, gọi M là trung điểm của BB′ và P thuộc cạnh DD′ sao cho 1
DP = DD′ . Mặt phẳng ( AMP) cắt CC′ tại N. Thể tích khối đa diện AMNPBCD bằng 4 3 3 A. 3 V = 2a B. 3 V = 3a C. 11a V = D. 9a V = 3 4 Lời giải
Áp dụng công thức tính nhanh, ta được VAMNPBCD 1 BM DP 1 1 1 3 3 = + = . + = →V = a = a . Chọn B AMNPBCD .(2 )3 3 3 V ′ ′ ′ ′ ′ ′ BB DD ABCD A B C D 2 2 2 4 8 8 .
Ví dụ 9: Cho hình hộp ABC . D A′B C ′ D
′ ′ . Gọi M là điểm thuộc CC′ thỏa mãn CC′ = 4CM . Mặt phẳng ( AB M
′ ) chia khối hộp thành hai phần có thể tích là V và V . Gọi V là phần thể tích có chứa điểm B. Tính 1 2 1 tỉ số V1 k = . V2 A. 7 k = B. 7 k = C. 7 k = D. 25 k = 32 16 25 32 Lời giải
Trong mặt phẳng (CDD C
′ ′), kẻ MN / /C . D ′ Suy ra 1
CN = CD và V là khối đa diện ABB N ′ CM. 4 1
Ta chia khối hộp thành hai phần (như hình vẽ). Khi đó V = + ′ V ′ V ABB NCM ABB CM MACN . . 1 0 + +1 • 4 5 1 V = = ′ V ′ ′ ′ V ABB CM . ABC ABC . . 3 12 2 • 1 1 1 1 1 V = V = = ′ V ′ ′ ′ V MACN . C ADC . ADC A D C . . . 4 4 16 3 96 Vậy 7 25 V1 7 V = V + = → = → = Chọn C ′ V V V ABCMB MACN . 1 2 32 32 V 25 2
Nhận xét: Ta có 1 1 V = V
vì diện tích giảm 4 lần và chiều cao giảm 4 lần MACN . C . 4 4 ′ ADC
Ví dụ 10: Cho hình lập phương ABC . D A′B C ′ D
′ ′ cạnh a. Gọi M là trung điểm của A′B ,′ N là trung điểm
của BC. Tính thể tích của khối tứ diện ADMN. 3 3 3 3 A. a V = . B. a V = . C. a V = . D. a V = . 3 12 6 2 Lời giải Ta có 1 V = V = d M ABCD S ADMN M ADN . ; . . ( ( )) 3 AM ∆ D
Lại có d (M;( ABCD)) = d ( A ;′( ABCD)) = AA′ Và 1 1 S = − − = − = ∆ S S∆ S∆ S S S AMD ABCD ABN CDN ABCD 2 ABCD 2 ABCD 3 Do đó 1 1 1 VABCD. = . . = . A B C D a V AA S AA S ′ ′ ′ ′ ′ ′ = = ADMN ABCD ABCD . 3 2 6 6 6 Chọn C.
Ví dụ 11: Cho hình hộp chữ nhật ABC . D A′B C ′ D
′ ′ có AB = a, AD = 2 .
a Diện tích tam giác A′DC bằng 2
a 13 . Tính thể tích khối chóp A.′BCC B′′ theo a. 2 A. 3 a B. 3 2a C. 3 3a D. 3 6a Lời giải C D ⊥ DD′ Ta có
⇒ CD ⊥ ( ADD A
′ ′) ⇒ CD ⊥ A′ . D CD ⊥ AD 2 Suy ra 1 a 13 S = ′ = → ′ = ∆ ′ A D CD A D a A CD . . 13 2 2 2 Do đó 2 2
AA′ = A′D − AD = (a 13) − (2a)2 = 3 .a
Thể tích của khối hộp ABC . D A′B C ′ D ′ ′ là 3
V = AA .′A . B AD = 6a . Lại có 1 1 3 3 V = = = Chọn B. ′ ′ ′ V ′ ′ ′ ′ a a A BCC B ABCD A B C D .6 2 . . . 3 3
Ví dụ 12: Cho khối hộp ABC . D A′B C ′ D
′ ′ . Gọi M thuộc cạnh AB sao cho MB = 2 .
MA Mặt phẳng (MB D ′ ′)
chia khối hộp thành hai phần. Tính tỉ số thể tích của hai phần đó. A. 5 . B. 7 . C. 13 . D. 5 . 12 17 41 17 Lời giải Lý thuyết bổ sung:
Cho hình chóp cụt ABC.A′B C
′ ′ có chiều cao h, S là diện tích tam giác ABC, S là diện tích tam giác 1 2 A′B C
′ .′ Thể tích khối chóp cụt ABC.A′B C ′ ′ là 1
V = h(S + S + S S 1 2 1 2 ) 3
Qua M kẻ đường thẳng d / /BD, cắt AD tại N
Suy ra thiết diện cắt bởi mặt phẳng (MB D ′ ′) là MND B ′ ′ Khi đó V = + ′ ′ ′ ′ V ′ ′ ′ V ABCD.A B C D AMN.A B D B C ′ D ′ .′MBCDN Đặt AA′ = ; h S = S →V = ′ ′ ′ ′ S h ABCD ABCD A B C D . .
Áp dụng công thức tính thể tích chóp cụt, ta có 1 V = ′ + + ′ ′ ′ AA S∆ S∆ ′ ′ ′ S∆ S AMN A B D . AMN A B D AMN . . ( A ∆ ′B D ′ ′ ) 3 Mà S A ∆ MN AM AN 1 1 = . S = ⇒ S = = ∆ S AMN ABD ∆ . S∆ AB AD ABD 9 9 18 Và S 1 S S S S 13 S = → = + + = ∆ ′ ′ ′ V ′ ′ ′ h V A B D AMN A B D . . 2 3 18 2 18 2 54
Vậy tỉ số thể tích cần tính là 13 13 13 : 1− = . Chọn C. 54 54 41
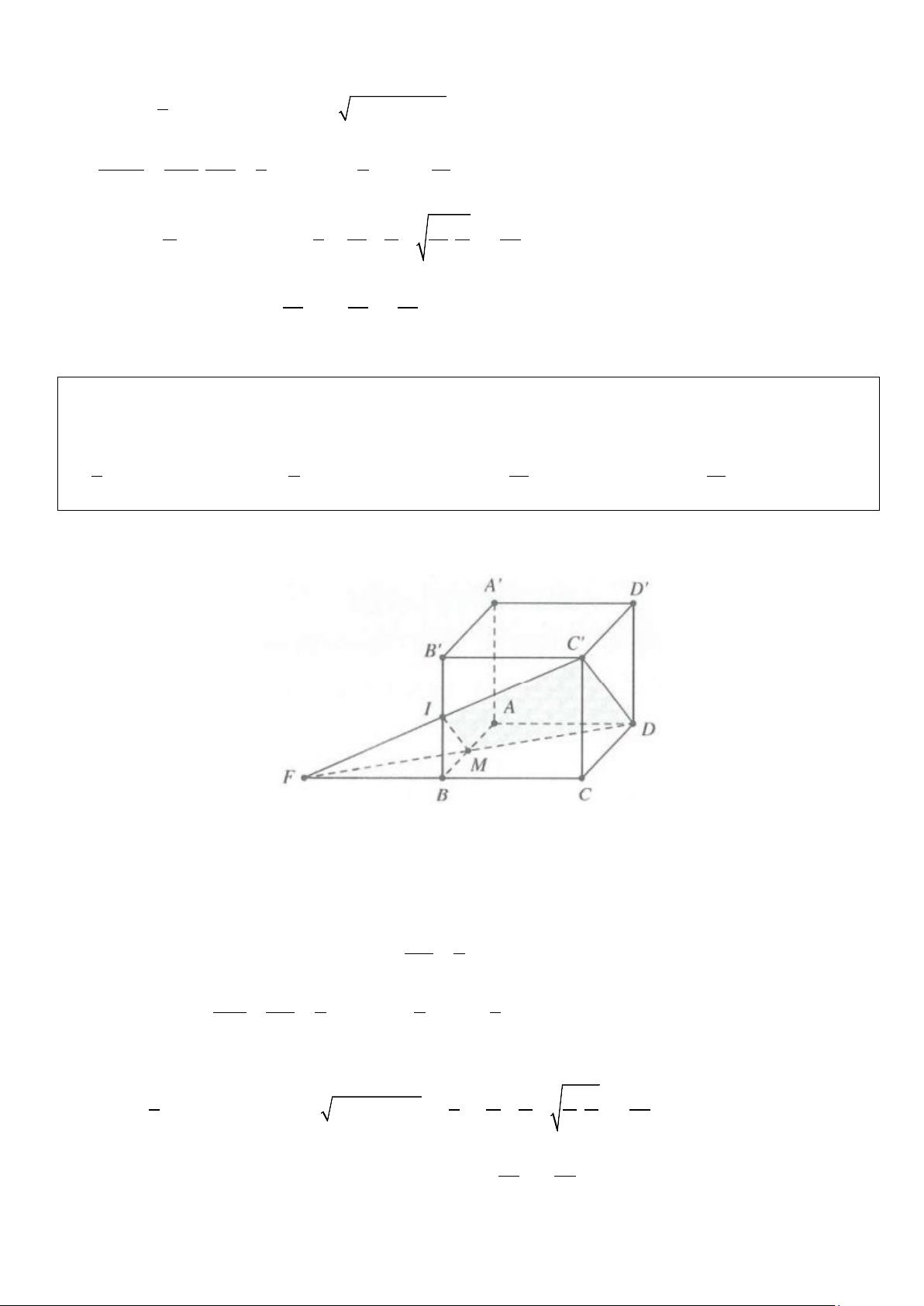
Ví dụ 13: Cho hình lập phương ABC . D A′B C ′ D
′ ′ . Gọi I là trung điểm của BB ,′ mặt phẳng (DIC′) chia
khối lập phương thành 2 phần có tỉ số thể tích phần bé chia phần lớn bằng A. 3 B. 2 C. 7 . D. 5 8 3 17 12 Lời giải
Tham khảo hình vẽ dưới đây: Đặt AA′ = ; h S = S →V = ′ ′ ′ ′ S h ABCD ABCD A B C D . .
Nối IC′ cắt BC tại F; nối FD cắt AB tại M.
Suy ra mp(DIC′) chia khối lập phương thành hai khối IBM.C C
′ D và IMAA′B .′C D ′ D′
Vì M là trung điểm của AB mà FB 1 BM / /CD ⇒ = . FC 2 Ta có IB FB 1 1 1 BI / /CC′ ⇒ = = ⇒ S = = ∆ S∆ ′ S CC′ FC 2 IBM 4 BAB 8 ABBA′′
Áp dụng công thức tính thể tích chóp cụt, ta được 1 1 S S S S 7 V = + + = + + = ′ BC S∆ S∆ ′ S∆ S∆ ′ h Sh IBM C CD . IBM C CD IBM . C CD . . . . ( ) 3 3 8 2 8 2 24
Do đó, thể tích khối IMAA′B .′C D ′ D′ là 7 17 V = − = ′ ′ ′ ′ V V V IMAA B C DD . . 24 24
Vậy tỉ số cần tính là 7 17 7 : = . Chọn C. 24 24 17
Ví dụ 14: Cho khối lăng trụ ABC.A′B C
′ ′ có thể tích bằng 1. Gọi M, N lần lượt là trung điểm của các đoạn
thẳng AA′ và BB′. Đường thẳng CM cắt đường thẳng C A
′ ′ tại P, đường thẳng CN cắt đường thẳng C B ′ ′
tại Q. Thể tích của khối đa diện lồi A′MPB N ′ Q bằng: A. 1 B. 1 C. 1 D. 2 3 2 3 Lời giải Ta có: 1 1 2 1 V = V = = ′ ′ V C ABNM C ABB A . ABC A′B C ′ ′ . . . . 2 2 3 3 Suy ra 1 2 V = − = − = ′ ′ ′ V ′ ′ ′ V CMN A B C ABC A B C C ABNM 1 . . . . 3 3 Lại có V = + ′ V ′ ′ ′ V C.C PQ CMN.A B C A′MPB N ′ Q 2 ⇒ V = − Mà S = ∆ ′ S C PQ 4 ′ ′ V A MPB NQ C C PQ ′ . . 3 A′B C ′ ′ 1 4 ⇒ V = = = ′ V ′ ′ ′ ′ V C C PQ
4 C ABC 4. ABC A′BC′′ . . . . 3 3 Vậy 4 2 2 V = − = Chọn D. A′MPB N ′ Q . 3 3 3
BÀI TẬP TỰ LUYỆN
Câu 1: Cho khối chóp S.ABC, trên ba cạnh SA, SB, SC lần lượt lấy ba điểm A ,′ B ,′C′ sao cho 1 1 1 SA′ = ,
SA SB′ = SB, SC′ = SC. Gọi V và V ′ lần lượt là thể tích của các khối chóp S.ABC và S.A′B C ′ ′. 3 3 3 Tính tỉ số V V ′ A. 1 B. 1 C. 1 D. 1 3 27 9 6
Câu 2: Cho hình chóp S.ABC. Gọi M là trung điểm canh SA và N là điểm trên cạnh SC sao cho SN = 3NC.
Tính tỉ số k giữa thể tích khối chóp ABMN và thể tích khối chóp S.ABC. A. 3 k = B. 2 k = C. 1 k = D. 3 k = 8 5 3 4
Câu 3: Cho khối tứ diện có thể tích bằng V. Gọi V ′ là thể tích của khối đa diện có các đỉnh là các trung ′
điểm của các cạnh của khối tứ diện đã cho, tính tỉ số V . V ′ ′ ′ ′ A. V 1 = B. V 1 = C. V 2 = D. V 5 = V 2 V 4 V 3 V 8
Câu 4: Cho khối chóp S.ABC có thể tích bằng V. Điểm M là trung điểm của đoạn thẳng AB, N là điểm nằm ′
giữa AC sao cho AN = 2NC. Gọi V ′ là thể tích khối chóp S.AMN. Tính tỉ số V . V ′ ′ ′ ′ A. V 1 = B. V 1 = C. V 1 = D. V 2 = V 3 V 2 V 6 V 3
Câu 5: Cho tứ diện ABCD có thể tích bằng V và G là trọng tâm tam giác BCD, M là trung điểm CD. Thể
tích khối chóp AGMC là A. V B. V C. V D. V 18 9 6 3
Câu 6: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AC = 2a, SA vuông góc với đáy,
SA = a , I thuộc cạnh SB sao cho 1 SI = .
SB Tính thể tích khối chóp S.ACI. 3 3 3 3 3 A. a B. a C. a D. a 3 6 12 9
Câu 7: Cho khối chóp S.ABC có thể tích bằng V. Gọi M, N, K lần lượt là trung điểm của AB, BC, CA. Tính
thể tích khối chóp A. V B. V C. V D. V 2 3 4 8
Câu 8: Cho hình chóp đều S.ABC có SA = 3 .
a D thuộc cạnh SB và DB = .
a Mặt phẳng (α ) đi qua AD và
song song với BC cắt SC tại E. Tính tỉ số giữa thể tích khối tứ diện SADE và thể tích khối chóp S.ABC. A. 2 B. 4 C. 1 D. 1 9 9 3 4
Câu 9: Cho khối tứ diện ABCD có thể tích là V và điểm E trên cạnh AB sao AE = 3E .
B Tính thể tích V ′ của
khối tứ diện EBCD theo V. A. V V ′ = B. V V ′ = C. V V ′ = D. V V ′ = 2 5 3 4
Câu 10: Cho hình chóp S.ABC, SA ⊥ ( ABC),SA = a, A
∆ BC vuông cân, AB = AC = a, B′ là trung điểm của
SB, C′ là chân đường cao hạ từ A của S
∆ AC . Tính thể tích của khối chóp S.AB C ′ ′ 3 3 3 3 A. a B. a C. a D. a 9 12 36 24
Câu 11: Cho khối chóp S.ABC. Gọi G là trọng tâm của tam giác SBC. Mặt phẳng (α ) qua AG và song song
với BC cắt SB, SC lần lượt tại I, J. Tính tỉ số của hai khối tứ diện SAIJ và S.ABC. A. 2 B. 2 C. 4 D. 8 9 3 9 27
Câu 12: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB = .
a Đường thẳng SA vuông
góc với mặt phẳng ( ABC), góc giữa đường thẳng SB và mặt phẳng ( ABC) bằng 60°. Tính thể tích V của
khối chóp M.ABC, với M là trung điểm của SB. 3 3 3 3 A. 3a V = . B. 3a V = . C. 3a V = . D. 3a V = . 2 4 12 6
Câu 13: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân, AB = AC = a, SC vuông góc với mặt
phẳng ( ABC) và SC = .
a Mặt phẳng qua C, vuông góc với SB và cắt SA, SB lần lượt tại E, F. Tính thể tích khối chóp S.CEF. 3 3 3 3 A. a 2 B. a 2 C. a D. a 12 36 36 12
Câu 14: Cho hình chóp S.ABC có thể tích V. Gọi H, K lần lượt là trung điểm của SB và SC. Tính thể tích
khối chóp S.AHK theo V. A. 1 V = V B. 1 V = V C. 1 V = V D. 1 V = V S.AHK 2 S.AHK 4 S.AHK 12 S.AHK 6
Câu 15: Cho khối chóp S.ABCD có thể tích là 3
3a . Gọi G là trọng tâm của tam giác SAB. Thể tích của khối chóp G.ABCD là A. 3 V = a B. 3 V = 2a C. 1 3 V = a D. 4 3 V = a 3 3
Câu 16: Cho hình chóp đều S.ABCD có độ dài cạnh bên và cạnh đáy đều bằng a. Gọi M, N, O lần lượt là
trung điểm SC, SD, AC. Tính tỉ số thể tích VS.OMN . VS.ABCD A. 1 B. 1 C. 1 D. 1 6 4 12 16
Câu 17: Cho hình chóp S.ABC có SC = 2a và SC ⊥ ( ABC). Đáy ABC là tam giác vuông cân tại B và có
AB = a 2. Mặt phẳng (α ) đi qua C vuông góc với SA và cắt SA, SB lần lượt tại D, E. Tính thể tích khối chóp S.CDE. 3 3 3 3 A. 4a B. 2a C. 2a D. a 9 3 9 9
Câu 18: Cho hình chóp S.ABC có đáy là tam giác ABC thoả mãn AB = 2a, BC = 4a, AC = 2 5 . a Cạnh bên
SA vuông góc với đáy và SA = 2a . Gọi M, N lần lượt là hình chiếu vuông góc của A trên SB, SC. Tính thể
tích V của khối chóp S.AMN. 3 3 3 3 A. 2a V = B. a V = C. a 5 V = D. a 5 V = 9 12 2 3
Câu 19: Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B, cạnh SA vuông góc với đáy, góc
ACB = 60 ,° BC = a, SA = a 3. Gọi M là trung điểm của SB. Tính thể tích V của khối tứ diện MABC. 3 3 3 3 A. a V = B. a V = C. a V = D. a V = 2 3 6 4
Câu 20: Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, SA = 2a và SA vuông góc với đáy ( ABC).
Gọi M, N lần lượt là trung điểm của SA, SB và P là hình chiếu vuông góc của A lên SC. Tính thể tích V của khối chóp S.MNP. A. 3 3 a B. 3 3 a C. 3 3 a D. 3 3 a 30 6 15 10
Câu 21: Cho hình chóp tam giác S.ABC có = = °
ASB CSB 60 , ASC = 90°. SA = SB = 1 , SC = 3. Gọi M là
điểm trên cạnh SC sao cho 1
SM = SC. Khi đó, thể tích của khối chóp S.ABM bằng 3 A. 6 V = B. 3 V = C. 2 V = D. 2 V = 36 36 12 4
Câu 22: Cho hình chóp S.ABC có SA = 4, SB = 5, SC = 6 , = ASB BSC = 45°,
CSA = 60 .° Các điểm M, N, P
thỏa mãn đẳng thức AB = 4AM ; BC = 4BN;CA = 4C .
P Tính thể tích khối chóp S.MNP. A. 128 2 B. 35 C. 245 D. 35 2 3 8 32 8
Câu 23: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, SA ⊥ ( ABC). Biết AB = a,
SA = 2a, mặt phẳng đi qua A và vuông góc với SC và cắt SB, SC lần lượt tại H và K. Tính thể tích V của hình chóp S.AHK. 3 3 3 3 A. 8a V = B. 8a V = C. 3a V = D. 4a V = 15 45 15 45
Câu 24: (Sở GD và ĐT Bắc Giang) Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = 1,
AD = 2, SA vuông góc với mặt phẳng đáy ( ABCD) và SA = 2. Điểm M điểm trên cạnh SA sao cho mặt
phẳng (MBC) chia khối chóp S.ABCD thành hai phần có thể tích bằng nhau. Tính diện tích S của tam giác MAC. A. 3 5 5 S − = B. 5 S = C. 5 S = D. 5 5 S − = 2 2 3 4
Câu 25: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt đáy, SA = .
a Mặt phẳng (P) qua A và vuông góc với SC cắt SB, SC, SD lần lượt tại B ,′C ,′ D′. Tính thể tích V
của khối đa diện ABCDD C ′ B ′ .′ 3 3 3 3 A. 5a V = B. 5a V = C. 5a V = D. 5a V = 18 9 12 6
Câu 26: Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA vuông góc với mặt phẳng ( ABC) và SA = .
a Gọi M, N lần lượt là trung điểm của AD, DC. Góc giữa mặt phẳng (SBM ) và mặt phẳng ( ABC)
bằng 45°. Tính thể tích khối chóp S.ABNM. 3 3 3 3 A. 25a B. 25a C. 25a D. 25a 8 16 18 24
Câu 27: Cho hình chóp S.ABCD. Gọi A ,′ B ,′C ,′ D′ theo thứ tự là trung điểm của các cạnh SA, SB, SC, SD.
Tính tỉ số thể tích của hai khối chóp S.A′B C ′ D
′ ′ và S.ABCD A. 1 B. 1 C. 1 D. 1 4 16 8 2
Câu 28: Cho hình chóp S.ABCD có thể tích V, có đáy ABCD là hình bình hành. Gọi N là trung điểm của SC.
Một mặt phẳng đi qua AN cắt các cạnh SB, SD lần lượt tại M, P. Gọi V ′ là thể tích của khối chóp S.AMNP. ′
Tính giá trị nhỏ nhất của V T = V A. 3 B. 1 C. 2 D. 1 8 3 3 8
Câu 29: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, M là trung điểm của SC. Mặt phẳng (P)
chứa AM và song song với BD chia khối chóp thành hai phần. Gọi V là thể tích của phần chứa đỉnh S và V 1 2
là thể tích phần còn lại. Tính tỉ số V1 . V2 A. 2 B. 2 C. 1 D. 1 9 3 3 2
Câu 30: Cho hình chóp S.ABCD có đáy là hình tứ giác lồi với O là giao điểm của AC và BD. Gọi M, N, P, Q
lần lượt là trọng tâm các tam giác SAB, SBC, SCD và SDA. Gọi V , V lần lượt là thể tích của khối chóp 1 2
S.ABCD và O.MNPQ. Tính tỉ số V1 . V2 A. 8 B. 27 C. 27 D. 9 4 2
Câu 31: Cho hình chóp tứ giác đều S.ABCD. Gọi N là trung điểm của SB, M là điểm đối xứng với B qua A.
Mặt phẳng (MNC) chia khối S.ABCD thành hai phần có thể tích lần lượt là V , V với V <V . Tính tỉ số 1 2 1 2 V1 k = . V2 A. 5 k = B. 5 k = C. 5 k = D. 5 k = 7 9 11 13
Câu 32: (Sở GD và ĐT Thừa Thiên Huế 2017) Cho hình chóp đều S.ABCD có cạnh đáy bằng 2a. Mặt bên
hình chóp tạo với đáy một góc bằng 60°. Mặt phẳng (P) chứa AB đi qua trọng tâm G của tam giác SAC cắt
SC, SD lần lượt tại M, N. Tính theo a thể tích V của khối chóp S.ABMN. A. 3 V = 3a B. 3 3 V = a C. 3 3 V = a D. 3 3 3 V = a 4 2 2
Câu 33: Cho hình chóp đều S.ABCD có SA = a, góc giữa mặt bên và mặt đáy là 60°. Gọi M là trung điểm
SA, mặt phẳng (P) đi qua CM và song song với BD cắt SB, SD lần lượt tại E, F. Tính thể tích khối chóp S.CEMF 3 3 3 3 A. a 15 B. a 15 C. 4a 15 D. 4a 15 75 225 225 75
Câu 34: Cho khối lăng trụ tam giác ABC.A′B C
′ ′ có thể tích là V . Gọi E là trung điểm của A′C ,′ F là giao 1 điểm của AE và V
A′C. Biết khối chóp F.A′B C
′ ′ có thể tích là V . Tính tỉ số 2 2 V1 A. V V V V 2 1 = B. 2 1 = C. 2 2 = D. 2 1 = V 3 V 6 V 9 V 9 1 1 1 1
Câu 35: (Sở GD&ĐT Cần Thơ 2017) Cho khối lăng trụ đứng ABC.A′B C
′ ′ và M là điểm tùy ý thuộc cạnh
bên BB′. Gọi V ,V ′ lần lượt là thể tích của khối lăng trụ ABC.A′B C
′ ′ và khối chóp M.AA′C C ′ . Tính tỉ số V ′ k = V A. 2 k = B. 1 k = C. 5 k = D. 1 k = 3 6 6 3
Câu 36: Cho lăng trụ ABC.A′B C
′ ′ có thể tích bằng 18. Gọi M, N lần lượt là trung điểm của AA ,′ BB .′ Tính
thể tích V của khối đa diện CNMA′B C ′ ′ . A. 12 B. 6 C. 9 D. 15
Câu 37: Cho lăng trụ ABC.A′B C
′ ′ có thể tích bằng V. Gọi G là trọng tâm tam giác ABC. Tính thể tích khối chóp .
G A′BC theo V. A. V B. V C. V D. V 12 6 5 9
Câu 38: Cho hình lăng trụ ABC.A′B C
′ ′ có thể tích V. Gọi G là trọng tâm của tam giác ABC. Khi đó thể tích khối chóp . G A′B C ′ ′ là A. V B. 3V C. 2V D. V 3 2
Câu 39: Cho khối lăng trụ tam giác ABC.A′B C
′ ′ có thể tích V . Gọi P là một điểm trên đường thẳng AA′. 0
Tính thể tích khối chóp tứ giác . P BCC B ′ ′ theo V 0 A. 2V V V V 0 B. 0 C. 0 D. 0 3 2 3 4
Câu 40: Cho hình lăng trụ tam giác đều ABC.A′B C
′ ′ có tất cả các cạnh đều bằng a. Gọi M, N lần lượt là
trung điểm của các cạnh AB, B C
′ . Mặt phẳng ( A′MN ) cắt cạnh BC tại P. Tính thể tích của khối đa diện MB . P A′B N ′ 3 3 3 3 A. 7a 3 B. a 3 C. 7a 3 D. 7a 3 32 32 68 96
Câu 41: Cho khối lăng trụ tam giác ABC.A′B C
′ ′ . Gọi M, N lần lượt là các điểm thuộc các cạnh bên
AA ,′CC′ sao cho MA = MA′ và NC = 4NC .′ Gọi G là trọng tâm tam giác ABC. Trong bốn khối tứ diện GA′B C ′ ′, BB MN ′ , ABB C
′ ′, A′BCN khối nào có thể tích nhỏ nhất?
A. Khối A′BCN
B. Khối GA′B C ′ ′ C. Khối ABB C ′ ′ D. Khối BB MN ′
Câu 42: Cho khối lăng trụ ABC.A′B C
′ ′ có đáy ABC là tam giác vuông tại B. AB = BC = 2a, AA′ = a 3.
Tính thể tích V của khối chóp . A BCC B ′ ′theo a. 3 3 A. 4a 3 V = B. 3 V = a 3 C. 2a 3 V = D. 3 V = 2a 3 3 3
Câu 43: Cho hình lăng trụ đứng ABC.A′B C
′ ′ có AB = a, AC = 2a, AA′ = 2a 3 ,
BAC = 120° . Gọi K, I lần
lượt là trung điểm của các cạnh CC ,′ BB .′ Tính thể tích V của khối tứ diện IA′BK 3 3 3 3 A. a V = B. a 3 V = C. a 5 V = D. a V = 2 6 2 6
Câu 44: Cho hình lập phương ABC . D A′B C ′ D
′ ′ có cạnh bằng a. Tính thể tích V của khối tứ diện ACD B ′ ′ 3 3 3 A. 1 3 V = a B. a 2 V = C. a V = D. a 6 V = 3 3 4 4
Câu 45: Cho khối hộp chữ nhật ABC . D A′B C ′ D
′ ′ . Tỉ số thể tích của khối tứ diện A′ABC và khối hộp chữ nhật ABC . D A′B C ′ D ′ ′ bằng A. 1 B. 1 C. 1 D. 1 4 6 2 3
Câu 46: Cho hình hộp V ABC . D A′B C ′ D
′ ′ có thể tích V. Gọi V là thể tích của tứ diện ACB D ′ .′ Tính tỉ số 1 . 1 V A. 1 B. 2 C. 1 D. 4 3 3 5 5
Câu 47: Cho hình lập phương ABC . D A′B C ′ D
′ ′ cạnh a. Gọi M là trung điểm của A′B′ và N là trung điểm
của BC. Tính thể tích của khối tứ diện ADMN. 3 3 3 3 A. a V = B. a V = C. a V = D. a V = 3 12 6 2
Câu 48: Cho hình lập phương ABC . D A′B C ′ D
′ ′ có cạnh a.Tính thể tích của khối tứ giác . D ABC D ′ ′ . 3 3 3 3 A. a B. a 2 C. a 2 D. a 3 6 3 4
Câu 49: Cho hình lập phương ABC . D A′B C ′ D
′ ′ . Gọi M là điểm trên đường chéo CA′ sao cho MC = 3 − MA′
Tính tỉ số giữa thể tích V của khối chóp M.ABCD và thể tích V của khối lập phương. 1 2 A. V V V V 1 1 = B. 1 3 = C. 1 1 = D. 1 1 = V 3 V 4 V 9 V 4 2 2 2 2
Câu 50: Cho hình hộp ABC . D A′B C ′ D
′ ′ . Gọi M thuộc cạnh AB sao cho MB = 2 .
MA Mặt phẳng (MB D ′ ′)
chia khối hộp thành hai phần. Tính tỉ số thể tích của hai phần đó. A. 5 B. 7 C. 13 D. 5 12 17 41 17
Câu 51: Cho hình hộp chữ nhật ABC . D A′B C ′ D
′ ′ có thể tích bằng 1 và G là trọng tâm của tam giác BCD′.
Tính thể tích V của khối chóp GABC′ A. 1 V = B. 1 V = C. 1 V = D. 1 V = 18 12 3 6
Câu 52: Cho hình hộp chữ nhật ABC . D A′B C ′ D
′ ′ . Tỉ số thể tích của khối tứ diện A′ABC khối hộp chữ nhật ABC . D A′B C ′ D ′ ′ bằng A. 1 B. 1 C. 1 D. 1 4 6 2 3
Câu 53: Cho hình lập phương ABC . D A′B C ′ D
′ ′ . Gọi M, N lần lượt là trung điểm của AB và AD, mặt phẳng (C MN ′
) chia khối lập phương thành hai khối đa diện. Gọi V là thể tích của khối đa diện có thể tích nhỏ 1 hơn, V
V là thể tích của khối đa diện có thể tích lớn. Tính 1 . 2 V2 A. V V V V 1 1 = B. 1 13 = C. 1 1 = D. 1 25 = V 3 V 23 V 2 V 47 2 2 2 2
Câu 54: Cho hình lập phương ABC . D A′B C ′ D
′ ′ . Gọi I là trung điểm của BB′, mặt phẳng (DIC′) chia khối
lập phương thành hai phần có tỉ số thể tích phần bé chia phần lớn bằng A. 3 B. 2 C. 7 D. 5 8 3 17 12
LỜI GIẢI BÀI TẬP TỰ LUYỆN ′ ′ ′
Câu 1: Ta có VS.A′BC′′ SA SB SC 1 1 1 1 = . . = . . = . Chọn B V SA SB SC S ABC 3 3 3 27 .
Câu 2: Ta có S∆ AM S AMN 1 S ∆ AN SN 3 = = ; = = . S∆ SA S∆ SC SAN 2 SAC 4 Suy ra 1 3 3 S = = ∆ S∆ S AMN .
2 4 SAC 8 S∆AC 1
⇔ d (B (SAC)) 3 1 ; .S = × ∆ d B SAC S AMN ( ;( )). 3 8 3 S ∆ AC 3 VABMN 3 ⇔ V = V ⇔ k = = Chọn A B AMN B SAC . . . 8 VS ABC 8 .
Câu 3: Kí hiệu tứ diện và các điểm như hình vẽ. ′ ′ ′
Ta có VS.A′BC′′ SA SB SC 1 = . . V = ⇒ V = S. V SA SB SC 8 A′B C ′ ′ S ABC 8 . Tương tự V V = = = ′ V ′ V . A A MP B.B MN C.C N ′ P 8
Do đó V ′ = V − V + + + ′ ′ ′ V ′ V ′ V S.ABC ( S.ABC . A A MP B.B MN C.C N ′ P ) V V V V V V ′ 1 = V − + + + = ⇒ = . Chọn A 8 8 8 8 2 V 2
Câu 4: Ta có S A ∆ MN AM AN 1 2 1 = . = . = S∆ AB AC ABC 2 3 3 Lại có 1 1 V = d A ABC S = ∆ V d A ABC S S AMN ; . AMN ; S ABC ; . . ( ( )) . ( ( )) 3 3 ABC ∆ Suy ra V S S.AMN A ∆ MN 1 V = = →V = Chọn A S AMN . . V S S ABC ABC ∆ 3 3 .
Câu 5: Ta có S MC ∆ G MG 1 = = mà 1 S = ∆ S S MCB 2 B ∆ CD ∆ MB MCB 3 Suy ra 1 1 1 1 S = = = ∆ S∆ S∆ S MCG MCB . 3 3 2 BCD 6 B ∆ CD Lại có 1 V = d A BCD S A GMC ; . . ( ( )) 3 MG ∆ C 1 1 = . ( ;( )). V d A BCD S = . Chọn C 6 3 BC ∆ D 6 2 3
Câu 6: Diện tích tam giác ABC là AC 2 1 a S = = ⇒ = = ∆ a V SA S ABC S ABC . . . 4 3 ABC ∆ 3 3 3 Vậy VS.AIC SI 1 1 1 a a = = ⇒ V = V = = . Chọn D S AIC S ABC . . . V SB S ABC 3 3 3 3 9 . 1 .hS MN ∆ K Câu 7: Ta có 1 VS.MNK 3 1 V S = → = = ⇒ = . Chọn C ∆ S∆ V MNK ABC S. 3 V 1 4 MNK S ABC 4 . . h S 3 ABC ∆
Câu 8: Qua D kẻ đường thẳng d / /BC, cắt SC tại E
⇒ Mặt phẳng (α ) cắt khối chóp theo thiết diện là A ∆ DE
Theo định lí Talet, ta có SD SE 2 = = SB SC 3 Do đó VS.ADE SD SE 2 2 4 = . = . = . Chọn B V SB SC S ABC 3 3 9 .
1 d (E;(BCD)).S BC ∆ D Câu 9: Ta có V EB V E.BCD 3 AE = = mà 1 E.BCD 1 = ⇒ = . Chọn D V 1 AB AB 4 VA BCD 4 . A BCD .d ( ;
A (BCD)).S . 3 BC ∆ D
Câu 10: Tam giác SAC cân tại A mà AC′ ⊥ SC ′
Suy ra C′ là trung điểm của SC 1 SC → = SC 2 2 2
Tam giác ABC vuông cân tại AB a A → S = = ABC ∆ 2 2 3
Do đó, thể tích khối chóp S.ABC là 1 a V = SA S = S ABC . . . 3 ABC ∆ 6 3
Vậy VS.ABC′′ SB SC 1 1 1 = . = . a = ⇒ V = Chọn D S AB C ′ ′ . . V SB′ SC′ S ABC 2 2 4 24 .
Câu 11: Qua G kẻ đường thẳng d / /BC, cắt SB, SC tại I, J. Ta có SG SI SJ 2 d / /BC ⇒ = =
= (M là trung điểm của BC) SM SB SC 3 Khi đó VS.AIJ SI SJ 2 2 4 = . = . = . Chọn C V SB SC S ABC 3 3 9 . 2
Câu 12: Diện tích tam giác ABC là 1 a S = = ∆ AB BC ABC . . 2 2
Ta có SA ⊥ ( ABC) ⇒ SB ( ABC) = (SB AB) = ; ; SBA = 60°
Tam giác SAB vuông tại A, có = SA A .
B tan SBA = a 3 2 3
Suy ra thể tích khối chóp S.ABC là 1 a 3 a a 3 V = SA S = = S ABC . . ABC ∆ . . 3 3 2 6 3
Vì M là trung điểm của 1 a 3 SB →V = V = Chọn C M ABC S ABC . . . 2 12
Câu 13: Kẻ CF ⊥ SB(F ∈ SB) SC ⊥ AB Ta có
⇒ AB ⊥ (SAC) AC ⊥ AB
Kẻ CE ⊥ SA(E ∈ SA) mà AB ⊥ CE ⇒ CE ⊥ (SAB) ⇒ CE ⊥ SB Do đó V
C, E, F đồng phẳng S.CEF SE ⇒ = . SF V SA SB S.CAB
Tam giác SAC vuông cân tại SE 1 C → = SA 2
Tam giác SBC vuông tại C , có 1 1 1 a 6 = + ⇒ CF = 2 2 2 CF SC BC 3
Tam giác SCF vuông tại F , có 2 2 a 3 SF 1
SF = SC − CF = ⇒ = 3 SB 3 2 3 Vậy VS.CEF 1 1 1 1 1 = . a a a = ⇒ V = V = = Chọn C S CEF S ABC . . . . . VS CAB 2 3 6 6 6 3 2 36 .
Câu 14: Ta có VS.AHK SA SH SK 1 1 1 = . . = 1. . = V SA SB SC S ABC 2 2 4 . Do đó 1 1 V = V = V Chọn B S AHK S ABC . . . 4 4
Câu 15: Gọi M là trung điểm của AB ⇒ , A G, M thẳng
hàng và SM = GM ⇒ d (G ( ABC)) 1 3 ;
= d (S;( ABC)) 3 Ta có: 1 V = d G ABCD S G ABCD ; . . ( ( )) 3 ABCD 1 1 = . d ( ; A ( ABCD)) 1 3 .S = V = a . Chọn A ABCD S. 3 3 3 ABCD Câu 16: Do S = S ⇒ V = V ABCD 4 OCD S ABCD 4 . S.OCD
Mặt khác VS.OMN SO SM SN 1 = . . = V SO SC SD S OCD 4 . VS.OCD 1 ⇒ V = = V . Chọn D S.OMN S. 4 16 ABCD
Câu 17: BC = AB = a 2, AC = AB 2 = 2a AB ⊥ BC Do ⇒ AB ⊥ CE. AB ⊥ SC
Mặt khác CE ⊂ (α ) ⇒ CE ⊥ SA ⇒ CE ⊥ (SAB) ⇒ CE ⊥ SB
Tam giác SCB vuông tại S có đường cao CE có: 2 2 2 SC SE SE SC 4
SC = SE.SB ⇒ = ⇒ = = 2 2 2 SB SB SB SC + BC 6
SC = AC ⇒ SC
∆ A vuông cân tại C nên D là trung điểm của SA Suy ra VS.CED SC SE SD 4 1 1 = . . = . = V SC SB SA S CBA 6 2 3 . Mặt khác 1 1 1 V = SC S = a a = a ⇒ V =
a = a Chọn C S CAB . . ABC .2 . ( 2)2 2 3 1 2 3 2 3 S CDE . . . . 3 2 2 3 3 3 9 Câu 18: Ta có 2 2 2 2
AB + BC = AC = 20a ⇒ A
∆ BC vuông tại B 3 Do đó 1 2 1 8a S
= AB BC = a ⇒ V = SA S = ABC . 4 S ABC . ABC . . 2 3 3
Xét tam giác SAB vuông tại S có đường cao AM có: 2 2 2 SA SM SM SA 1
SA = SM.SB ⇒ = ⇒ = = 2 2 2 SB SB SB SA + AB 2 2 Tương tự SN SA 4 1 = = = 2 2 SC SA + AC 4 + 20 6 3 3
Mặt khác VS.AMN SM SN 1 1 8a 2 = . a = ⇒ V = = S AMN . . . V SB SC S ABC 12 12 3 9 . Chọn A. Câu 19: A
∆ BC vuông tại B
⇒ AB = BC tan B = tan 60° = a 3 2 1 a 3 S = AB BC = ABC . 2 2
Gọi H là trung điểm của AB ⇒ MH là đường trung bình của tam
MH / /SA ⇒ MH ⊥ ( ABC) giác SAB ⇒ SA a 3 MH = = . 2 2 3 Do đó 1 a V = MH S = Chọn D. M ABC . ABC . . 3 4
Câu 20: Xét tam giác SAC vuông tại S có đường cao AP có: 2 2 2 SA SP SP SA 4 4 SA = . SP SC ⇒ = ⇒ = = = . 2 2 2 SC SC SC SA + AC 4 +1 5 Do đó VS.MNP SM SN SP 1 1 4 1 = . . = . . = V SA SB SC S ABC 2 2 5 5 . 2 3 Lại có a 3 1 a 3 S = ⇒ V = SA S = ABC S ABC . ABC . . 4 3 6 3 3 Suy ra 1 a 3 a 3 V = = Chọn A. S MNP . . . 5 6 30
Câu 21: Ta có SA = SB = SM = 1 ⇒ hình chiếu của đỉnh S
xuống mặt phẳng ( ABM ) là tâm đường tròn ngoại tiếp A ∆ BM . Mặt khác 2 2
ASC = 90° ⇒ AS ⊥ SM ⇒ AM ⊥ SA + SM = 2.
Các tam giác ASB, ASM là các tam giác đều nên AB = BM = 1. Suy ra 2 2 2
AB + BM = AM = 2 ⇒ A ∆ BM vuông tại . B
Khi đó SH ⊥ ( ABM ) thì H là trung điểm của cạnh huyền AM. Ta có 2 2 2 2 AH =
⇒ SH = SA − AH = . 2 2 1 1 2 A . B BM 2 V = SH S = = Chọn C. S ABM . ABM . . . . 3 3 2 2 12
Câu 22: Trên SB lấy điểm E sao cho SE = 1 Dựng EF ⊥ ,
SA EG ⊥ SC (F ∈ , SA G ∈ SC). Khi đó S ∆ EF, S
∆ EG vuông cân tại E .
Ta có EF = EG = 1 ⇒ SF = SG = 2 Do = ° ⇒ CSA 60 FSG = 60° ⇒ F
∆ SG đều suy ra FG = 2. Khi đó E
∆ FG vuông cân tại 1 1 E ⇒ S = EF FG = EFG . 2 2 1 1 ⇒ V = SE S = S EFG . EFG . . 3 6 Ta có VS.EFG SF SE SG 2 1 2 1 = . . = . . = . V SA SB SC S ABC 4 5 6 60 . Suy ra V = V = S ABC 60 S EFG 10 . . Mặt khác SAMP AM AP 3 3 = . = ⇒ S = S S AB AC 16 AMP 16 ABC ABC Tương tự 3 3 7 ⇒ S = S = S = S ⇒ S = − S = S AMP BMN CNP ABC MNP 1 3. 16 16 ABC 16 ABC Suy ra 7 7 35 V = V = = Chọn B. S MNP . S ABC .10 . . . 16 16 8
Câu 23: Dễ dàng chứng minh được AH ⊥ SB,
AC = AB 2 = a 2 .
Tam giác SAB vuông tại A , có đường cao AH nên 2 2 2 SA SH SA 4
SA = SH.SB ⇒ = = = . 2 2 2 SB SB SA + AB 5 2
Tương tự, ta tính được SK SA 2 = = 2 2 SC SA + AC 3 2 3 Vậy VS.AHK SH SK 4 2 8 8 1 a 8 = . = . a = ⇒ V = a = S AHK . .2 . . . V SB SC S ABC 5 3 15 15 3 2 45 . Chọn B.
Câu 24: Gọi N = (MBC) ∩ S . D
Ta có: BC / / AD ⇒ (MAC) ∩ (SAD) = MN suy ra V
MN / /BC / / A . D S.ABCD V = V = S ABC S ACD . . . 2 Đặt SM V = .
x Ta có S.ACM SM = = . x SA V SA S.ABC VS.ACM x ⇒ = x ⇒ V = V S ACM S ABCD . . . VS.ABCD 2 2 2
Lại có: VS.CMN SM SN 2 = . x = x ⇒ V = V S.CMN S. V SA SD CAD 2 ABCD S. 2 2 x x 1 x x 1 1 − + 5 ⇒ V = + V = ⇒ + = ⇒ x = ⇒ SM = − + S ACNM S ABCD 1 5 . . 2 2 2 2 2 2 2
Lại có AC = 1+ 4 = 5, MA = 2 − ( 1
− + 5) = 3− 5, AC = 5 Suy ra 1 3 5 5 S MA AC − = = Chọn A. MAC . . 2 2 BC ⊥ AB Câu 25: Do
⇒ BC ⊥ AB′ BC ⊥ SA AB′ ⊥ SC Ta có:
⇒ AB′ ⊥ (SBC) ⇒ AB′ ⊥ SB AB′ ⊥ BC
Do hình chóp có (SAC) là mặt phẳng đối xứng nên V ′ ′ ′ ′ ′ V S.AB C D S.AB C ′ ′ SB = = . SC . V V SB SC S.ABCD S.ABC
Xét tam giác SAB vuông tại S có đường cao AB′ có: 2 2 ′ ′ 2 SA SB SB SA 1
SA = SB .′SB ⇒ = ⇒ = = 2 2 2 SB SB SB SA + AB 2 2 2 ′ Tương tự SC SA SA 1 V ′ ′ V S.AB C 1 S.AB C ′ D ′ ′ = = = ⇒ = = 2 2 2 SC SC SA + AC 3 V V S ABC 6 . S.ABCD 3 Mặt khác 1 1 3 1 3 5a V = SA S = a ⇒ V = ⇒ = − = . ′ ′ ′ a V ′ ′ ′ V V ABCD . ABCD S.AB C D AB C D .ABCD S.ABCD S. 3 3 18 AB C ′ D ′ ′ 18 Chọn A.
Câu 26: Dựng AH ⊥ BM
Ta có BM ⊥ SA ⇒ BM ⊥ (SHA).
Khi đó (SBM ) ( ABCD) ( )= ; SHA = 45° Đặt x
AB = AD = x ⇒ AM = MD = DN = 2 Mặt khác AM.AB x AH = = 2 2 AM + AB 5 Suy ra = tan 45 x SA AH ° =
= a ⇒ x = a 5 5 2 2 2 2 2 x x 5x 25a S = S − S − S = x − − = = AMNB ABCD DMN BCN 8 4 8 8 3 Do đó 1 1 25 2 25a V = S SA = a a = Chọn D. S ABNM ABNM . . . . . 3 3 8 24
SA SB′ SC′ SD + + +
Câu 27: Ta có V ′ ′ + + + S.AB C ′ D ′ ′ SA SB SC SD 2 2 2 2 1 = = = . Chọn C. V
SA SB′ SC′ SD S ABCD 4.2.2.2.2 8 . 4. . . .
SA′ SB SC SD′
Câu 28: Gọi O là tâm hình bình hành ABCD
Nối AN ∩ SO = I ⇒ I là trọng tâm tam giác SAC
Qua I kẻ đường thẳng d cắt SB, SD lần lượt tại M , P
Đặt SA = 1; SB = ; SC = 2; SD x = y SA SM SN SP ′ Suy ra 1 + + + +
+ 2 = x + y ⇔ x + y = 3 và V x y 3 x y 3 = = V 8xy 8xy ′
Ta có xy ≤ (x + y)2 V 2.3 1 4 = 9 ⇒ ≥ = . Chọn B. V 2.9 3
Câu 29: Nối AN ∩ SO = I ⇒ I là trọng tâm tam giác SAC
Qua I kẻ đường thẳng d / /BD, cắt SB, SD lần lượt tại E, F Suy ra SE SF 2 =
= ; E, F thuộc mặt phẳng (P) SB SD 3 SA SB SC SD 3 + + + 1+ 2. + 2 Khi đó V1 SA SE SM SF 2 1 = = = V SA SB SC SD 3 3 S ABCD 3 . 4. . . . 4.1. . .2 SA SE SM SF 2 2 Mà V1 1 V = V +V → = Chọn D. S ABCD . . 1 2 V 2 2
Câu 30: Ta có (MNPQ) ( ABCD) ⇒ d (S (MNPQ)) 2 / / ;
= d (S;( ABCD)) 3
Mà O ∈( ABCD)
→ d (O (MNPQ)) 1 ;
= d (S;( ABCD)) 3 2 Lại có 2 1 2 V1 1 27 S = S = S → = = Chọn C MNPQ . ABCD ABCD . 3 2 9 V 1 2 2 2 . 3 9
Câu 31: Nối MN ∩ SA = E ⇒ E là trọng tâm S ∆ MB
Nối MC ∩ AD = F ⇒ F là trung điểm AD Ta có V = V −V AEF.BNC N.MBC E.MAF 1
= d (N ( ABCD)) 1 S − ∆ d ABCD S MBC ( ( )) 1 . ; . . E; . 3 3 4 MA ∆ F 1 1 =
d (S ( ABCD)) 1 1 S − d A ABCD S ABCD ( ( )) 1 . ; . . . ; . 3 2 3 3 4 ABCD 1 1 5 V1 5 = V − V = V ⇒ = . Chọn A. S.ABCD S.ABCD S. 2 12 12 ABCD V 7 2
Câu 32: Gọi O là tâm hình vuông ABCD ⇒ SO ⊥ ( ABCD)
Gọi E là trung điểm BC ⇒ BC ⊥ (SEO)
Do đó (SNO) ( ABCD) = (SN ON) = ; ; SNO = 60°
Tam giác SEO vuông tại O, có =
SO OE.tan SEO = a 3 3
Suy ra thể tích khối chóp S.ABCD là 4a 3 V = S.ABCD 3
Vì (P) chứa AG nên (P) ∩ SC = M là trung điểm của SC
Qua M kẻ đường thẳng d / /CD, cắt SD tại N SA SB SC SD + + + Khi đó V + + + S.ABMN SA SB SM SN 1 1 2 2 3 3 3 = = = ⇒ V = a . Chọn C S. V SA SB SC SD 4.1.1.2.2 8 ABMN S ABCD 2 . . a . . . SA SB SM SN
Câu 33: Gọi O là tâm hình vuông ABCD ⇒ SO ⊥ ( ABCD)
Gọi N là trung điểm BC ⇒ BC ⊥ (SNO)
Do đó (SNO) ( ABCD) = (SN ON) = ; ; SNO = 60°
Tam giác SNO vuông tại O, có = x 3 SO ON.tan SNO = 2 2
Tam giác SAO vuông tại O, có 2 2 2 x
SO = SA − OA = a − 2 2 2 2 Suy ra x 3 2 x 3x 2 x 2a 5 = a − ⇔ = a − ⇔ AB = x = 2 2 4 2 5 2 3
Thể tích khối chóp S.ABCD là 1 1 2a 5 3 2a 5 4a 15 V = SO S = = S ABCD . . ABCD . . . . 3 3 5 2 5 75
Nối SO ∩ CM = I
→ I là trọng tâm SI 2 S ∆ AC ⇒ = . SO 3
Qua I kẻ đường thẳng d / /BD, cắt SB, SD lần lượt tại SE SF 2 E, F ⇒ = = SB SD 3 3 2 + 2. +1 Đặt SA SB SC SD V + + + S.MECF x y z t 2 1 = ; x = y; = z; = t ⇒ = = = SM SE SC SF V xyzt S ABCD 4 3 3 3 . 4.2. . .1 2 2 3 3 Vậy 1 1 4a 15 4a 15 V = V = = Chọn C S MECF . S ABCD . . . . 3 3 75 225 ′ ′ ′ Câu 34: Do FA A E 1 FA 1
A′E / / AC ⇒ = = ⇒ = FC AC 2 CA′ 3
Do đó d (F ( A′B C ′ ′)) 1 ;
= d (C;( A′B C ′ ′)) 3 Suy ra 1 1 V = = ′ ′ V ′ ′ ′ V F AB C C A B C ABCD ABC′ . . . . 3 9 Vậy V2 1 = . Chọn D V 9 1
Câu 35: Ta có MB′ / / ( ACC A ′ ′) nên
d (M;( A′AC)) = d (B ;′( A′AC)). Do đó 1 2 V ′ = V = − = − = ′ ′ ′ V V ′ V V V B .ACC A B .ABC 3 3 ′ Vậy V 2 k = = . Chọn A V 3
Câu 36: Gọi V là thể tích của khối trụ. Ta có: 1 1 S = S ⇒ = ′ ′ V V MNBA A B BA C MNBA C A′B BA ′ . . . 2 2 Mặt khác V 2V V = − = − = ′ ′ V ′ ′ V ′ ′ ′ V C.A B BA ABC.A BC C.A B C 3 3 1 2V 1 ⇒ V = = = C MNBA . .18 6 . 2 3 3 Do đó V = − = Chọn A. ′ ′ V V CNMAB C C MNBA 12. .
Câu 37: Gọi I là trung điểm của BC ⇒ AI = 3GI Khi đó d ( ;
A ( A′BC)) = 3d (G;( A′BC)) ⇒ V = ′ V A A BC 3 . G A ′ ′B C ′ ′ Mặt khác V V V = = ⇒ = Chọn D ′ V ′ V . A A BC A ABC G. 3 A′BC 9
Câu 38: Do ( ABC) / / ( A′B C
′ ′) ⇒ d (G;( A′B C
′ ′)) = h với h là
chiều cao khối lăng trụ. Do đó 1 1 V = = . Chọn A ′ ′ h S ′ ′ ′ V G AB C . ABC . . 3 3
Câu 39: Do AA′ / / (BCC B
′ ′) và P ∈ AA′ nên ta có: V 2V 0 0 V = = − = − = Chọn A. ′ ′
V ′ ′ ′ V V ′ V P BCC B A BCC B A ABC . . . 0 . 0 3 3
Câu 40: Gọi E là trung điểm của BC, F là trung điểm của BE.
Khi đó MF / / AE mà AE / / A′N nên MF / / A′N
Suy ra các điểm A ,′ M , F, N thuộc cùng một mặt phẳng.
Vậy ( A′MN ) cắt cạnh BC tại điểm P ⇒ P trùng với F .
Công thức tổng quát tính thể tích khối đa diện
“Thể tích khối chóp cụt là h
V = (B + B′ + BB′) với h là chiều cao, 3
B, B′ lần lượt là diện tích hai đáy”
Xét khối chóp cụt MB . P A′B N
′ có chiều cao h = BB′ = a . SABC S B = S = = MBP 2 Và diện tích đáy 8 8 a 3 với S = S 4 A B C S B′ = S ′ ′ ′ = = A′B N ′ ′ 2 2 Thể tích khối đa diện MB . P A′B N ′ là 3 BB′ S S S S 7 3 = . + + . a V = . Chọn D 3 8 2 8 2 96
Câu 41: Gọi V là thể tích khối lăng trụ ABC.A′B C ′ ′ Ta có: V 2V V = − = − = ′ ′ V V ′ V . A BCC B A .ABC 3 3 Khi đó V 1 V = = = ′ ′ ′ V ′ V ′ ′ V G A B C , . M .BB N A .BB N A . 3 2 ′ BCC B′′ (Do 1 S = ). Do đó 1 2V V V = = M BB N ′ . . ′ S NBB 2 CC B′B′ . 2 3 3 Tương tự 1 V V = = = ′ ′ V ′ ′ ′ V A C B B A C B B
. A′ BCCB′′ . . . . 2 3 Do 1 1 V S < S = ⇒ < = ′ S ′ ′ V ′ V BCN BCC BCC B A BCN
. A′ BCCB′′ . . . 2 2 3
Vậy khối chóp BB MN ′
có thể tích nhỏ nhất. Chọn D
Câu 42: Gọi V là thể tích khối chóp ABC.A′B C ′ ′ Ta có: V 2V V = − = − = ′ ′ V V ′ V . A BCC B A .ABC 3 3 Lại có A . B AC 3 V = S AA′ = AA′ = a ABC . . 2 3 2 3 Suy ra 2 3 4a 3 V = = . Chọn A ′ ′ a A BCC B .2 3 . 3 3
Câu 43: Gọi V là thể tích khối chóp ABC.A′B C ′ ′ Ta có V 2V V = − = − = ′ ′ V V ′ V . A BCC B A .ABC 3 3 Lại có: 1 1 S = S = S IKB
2 KICB 4 BCC B′′ Suy ra 1 1 2 1 V = = = ′ V ′ ′ V V A IKB A BCC B . . . 4 4 3 6 Mặt khác 1 = ′ = V S AA AB AC BAC AA′ ABC . . .sin . 2 3 1 3 1 = . .2 .sin120 .2 ° 3 = 3 a a a a a ⇒ V = = Chọn ′ V A IKB . . 2 6 2 A.
Câu 44: Thể tích khối lập phương là 3 V = a . Ta có 1 3 V = = = = ′ ′ ′ V ′ V ′ V ′ ′ ′ a . A A B D B .ABC D .ACD D .B C C 6 V = − − − − ′ ′ V ′ ′ ′ ′
V ′ ′ ′ V ′ V ′ V ACD B ABCD.A B C D A,A B D B .ABC D .ACD D .′B C ′ C ′ 3 3 Suy ra 3 a a V = − = . Chọn A ′ ′ a ACD B 4. 6 3 Câu 45: Ta có S = S ⇒ V = ′ V ABCD 2 ABC A ABCD 2 . A .′ABC Mặt khác 1 V = ′ V A .ABCD ABCD. 3 A B ′ C ′ D ′ ′ Do đó 1 1 1 V = = ′ V ′ V A ABC A ABCD . . . ABCD. 2 2 3 A′B C ′ D ′ ′ 1 = V Chọn B ′ ′ ′ ′ . . 6 ABCD ABC D
Câu 46: Gọi h là chiều cao của khối hộp Ta có 1 1 1 1 1 V = = = = ′ h S h S h S V B ABC . ABC . ABCD . . 3 3 2 6 ABCD 6 1 1
V = V − 4.V = − = Chọn A ′ V V V B ABC 4. . 1 . 6 3 Câu 47: Ta có 1 V
= d M ABCD S ADMN . ; ( ) . 3 AN ∆ D 1 = .AA .′(S − S − ∆ S∆ ) 3 ABCD ABN NCD 1 1 1 = .AA . S − S − S ′ 3 ABCD
4 ABCD 4 ABCD 3 = 1 1 = . . a AA′ S = 3 2 ABCD 6 3
Vậy thể tích cần tính là a V = . Chọn C 6 Câu 48: Ta có V = + ′ ′ V ′ V D.ABC D C .ABD C .′ADD′ 1 1 = CC .′S + ′ ′ ∆ C D S ABD . 3 3 AD ∆ D′ 1 1 1 = CC .′S + C D ′ ′ S ABCD . . 3 3 2 AA′DD′ 3 1 1 2 1 1 2 = . + . a a a a a = 3 2 3 2 3 3
Vậy thể tích cần tính là a V = . Chọn A 3
d (M;( ABCD)) Câu 49: Ta có MC 3 MC = 3MA′ ⇒ = =
d (A ;′( ABCD)) A′C 4
1 d (M;(ABCD)).SABCD Do đó VM.ABCD 3 1 3 1 = = . = , Chọn D V ′ ABCD A′B C ′ D ′ ′ d A ; ABCD S 3 4 4 . ( ( )) ABCD
Câu 50: Chuẩn hóa thành hình lập phương ABC . D A′B C ′ D ′ ′ cạnh I
Qua M kẻ đường thẳng d / /BD, cắt AD tại N ⇒ MN / /BD, Mà BD / /B D
′ ′ ⇒ MN / /B D
′ ′ ⇒ M , N, B ,′ D′ đồng phẳng Dó đó 1 V = ′ + + ′ ′ ′ AA S∆ S∆ ′ ′ ′ S∆ S AMN A B D . AMN A B D AMN . . ( A ∆ ′B D ′ ′ ) 3 1 1 1 1 1 13 = .1. + + . = 3 18 2 18 2 54
⇒ Thể tích khối còn lại là 13 41 13 : = . Chọn C 54 54 41
Câu 51: Dễ thấy AB / /C D ′ ′ ⇒ ,
A B,C ,′ D′ đồng phẳng Do đó d G ( ABC′) 1 = d C ( ABC′) 1 ; ; ⇒ V = ′ V G.ABC C. 3 3 ABC′ Ta có 1 1 1 V V = = ′ = ′ = ′ V ′ CC S∆ CC S C ABC C ABC . ABC . . . 3 3 2 ABCD 6 Vậy 1 1 V V 1 V = = = = Chọn A. ′ V G ABC C ABC′ . . . . 3 3 6 18 18 1 1 .AA .′S∆ S ABC . ABC ∆
Câu 52: Ta có VA.′ABC 3 3 1 = = = . Chọn B V ′ ′ ′ ′ ′ AA S S ABCD A B C D . ABCD 2. ABC ∆ 6 .
Câu 53: Chọn AB = 1
Nối MN ∩ BC = ;
P MN ∩ CD = Q Nối C P
′ ∩ BB′ = E,C Q
′ ∩ DD′ = F
Do đó thiết diện cắt bởi mp(C MN ′
) là C E′MNF Dễ thấy 1 PB QD 1
BM = BP = DQ = DN = ⇒ = = 2 PC QC 3 Khi đó 1 1 1 1 1 1 1 V = V = EB S = = E PM F DQN . . BPM ∆ . . . . .B . 3 3 3 2 2 2 72 Ta có 1 1 1 3 V = ′ = + = ′ CC S C CPQ . C ∆ PQ .1.1 . 3 3 8 8
Gọi V là thể tích đa diện chứa điểm 25
C ⇒ V = V − − = ′ V V 0 0 C .CPQ E.B PM F.DQN 72
Vậy tỉ số thể tích cần tính là V1 25 = . Chọn D V 72 2
Câu 54: Gọi M là trung điểm AB ⇒ IM / / AB′ / /C D ′
Do đó mp(DIC′) cắt hình lập phương theo thiết diện IMDC′ Ta có 1 V = + + ′ BC S∆ S∆ ′ S∆ S IBM C CD . IBM C CD IBM . . ( C ∆ C ′ D ) 3 1 1 1 1 1 = BC. S + S + S S ABCD ABCD ABCD . 3 8 2 8 2 ABCD 1 7 7 = BC. S = V ABCD ABCD. 3 8 24 A′B C ′ D ′ ′
Vậy tỉ số cần tính là 7 . Chọn C 17
Document Outline
- ITMTTL~1
- IIBITP~1
- IIILIG~1




