Chuyên đề trắc nghiệm tích có hướng của hai vectơ và ứng dụng Toán 12
Chuyên đề trắc nghiệm tích có hướng của hai vectơ và ứng dụng Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Chủ đề: Chương 3: Phương pháp tọa độ trong không gian
Môn: Toán 12
Thông tin:
Tác giả:
Thông tin :
Chủ đề:
Chương 3: Phương pháp tọa độ trong không gian
Môn:
Tác giả:
Tài liệu liên quan:
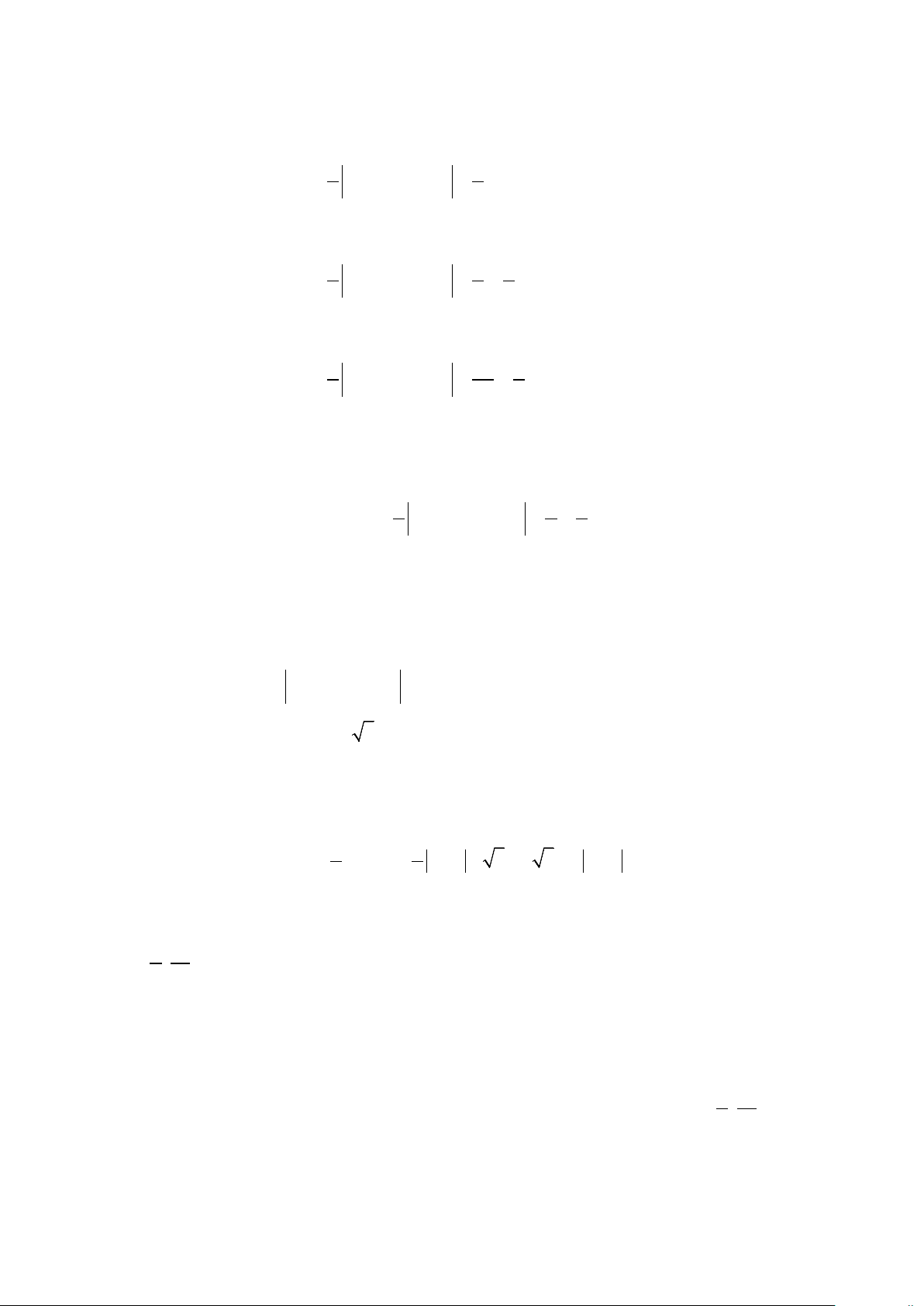
Preview text:
CHỦ ĐỀ 12: TÍCH CÓ HƯỚNG VÀ ỨNG DỤNG a b
1) Công thức định thức: = ad − . bc c d
2) Định nghĩa tích có hướng của 2 vectơ: Cho 2 vectơ: u = (x ; y ; z ;v = x ; y ;z . 1 1 1 ) ( 2 2 2)
Khi đó tích có hướng của 2 vectơ u = (x ; y ; z ;v = x ; y ;z ký hiệu: u,v là một vectơ và được tính 1 1 1 ) ( 2 2 2) y z z x x y như sau: 1 1 1 1 1 1 u,v = ; ;
= ( y z − y z ; z x − z x ; x y − x y 1 2 2 1 1 2 2 1 1 2 2 1 ) y z z x x y 2 2 2 2 2 2
3) Tính chất: u,v ⊥ u; u,v ⊥ ;
v u,v = − v,u
Độ dài của vectơ tích có hướng u,v = u . v .sin(u,v).
Hai vectơ u; v cùng phương ⇔ u,v = 0 (0;0;0). Ba vectơ ; a ;
b c đồng phẳng khi a,b.c = 0.
Từ đó suy ra 4 điểm A, B, C, D là 4 đỉnh của một tứ diện khi 3 vectơ A ;
B AC; AD không đồng phẳng
hay AB, AC.AD ≠ 0
và 4 điểm A, B, C, D đồng phẳng khi AB, AC.AD = 0. 4) Ứng dụng:
Diện tích hình bình hành ABCD : S = AB AD ABCD , . Diện tích tam giác 1 ABC : S = AB AC ABC , . 2
Thể tích khối hộp ABC .
D A'B 'C 'D ': V
= AB AD AA ABCD A B C D , . ' . . ' ' ' '
Thể tích tứ diện ABCD: 1 V
= AB AC AD ABCD , . . 6
Ví dụ 1: Tính tích có hướng của các cặp vectơ sau: a) a = (1;0; 2 − );b = (0;1;3).
b) a = (3;1;− ) 1 ;b = (2;1; 2 − ). c) a = ( 3 − ;1;4);b = (1; 1; − 2).
d) a = (1;3;5);b = (2; 1 − ;3). Lời giải: 0 2 − 2 − 1 1 0
a) a,b = ; ; = (2; 3 − ; ) 1 . 1 3 3 0 0 1 1 1 − 1 − 3 3 1
b) a,b = ; ; = ( 1; − 4; ) 1 . 1 2 − 2 − 2 2 1 1 4 4 3 − 3 − 1
c) a,b = ; ; = (6;10;2). 1 − 2 2 1 1 1 −
d) a,b = ( 4 − ;13; 7 − ). Ví dụ 2:
a) Cho 3 vectơ u = (2; 1; − ) 1 ;v = ( ; m 3;− ) 1 ;w = (1;2; )
1 . Tìm m để 3 vectơ đồng phẳng.
b) Cho 3 vectơ u = (1;2;3);v = (2;1;m);w = (2; ; m )
1 . Tìm m để 3 vectơ không đồng phẳng. Lời giải:
a) Ta có: u,v = ( 2;
− m + 2;m + 6) ⇒ u,v.w = 2
− + 2m + 4 + m + 6 = 3m + 8 Ba vectơ u; ; v w đồng phẳng 8
⇔ 3m + 8 = 0 ⇔ m = − . 3
b) Ta có: u v = ( m − − m − ) 2 2 , 2 3;6
; 3 ⇒ u,v.w = 4m − 6 + 6m − m − 3 = −m +10m − 9 m ≠ 1 Để 3 vectơ u; ;
v w không đồng phẳng thì 2
u,v.w ≠ 0 ⇔ −m +10m −9 ≠ 0 ⇔ . m ≠ 9
Ví dụ 3: Trong không gian với hệ trục tọa độ Oxyz, cho 4 điểm: A(1;0;1); B ( 1; − 1;2); C ( 1; − 1;0); D (2; 1; − 2 − ).
a) Chứng minh rằng A, B, C, D là 4 đỉnh của một tứ diện.
b) Tính thể tích tứ diện ABCD. Suy ra độ dài đường cao của tứ diện qua đỉnh A. Lời giải:
a) Ta có: AB = ( 2 − ;1;1); AC = ( 2 − ;1; 1 − ); AD = (1; 1; − 3 − ).
Suy ra AB, AC = ( 2; − 4;
− 0) ⇒ AB, AC.AD = 2 ≠ 0 ⇒ A ; B AC; AD không đồng phẳng
Do đó A, B, C, D là 4 đỉnh của một tứ diện.
b) Thể tích tứ diện ABCD là: 1 1 V
= AB AC AD = đvtt ABCD , . ( ). 6 3 Lại có: BC = (0;0; 2 − ); BD = (3; 2; − 4
− ) ⇒ BC, BD = ( 4; − 6; − 0) 1 3VABCD 13 ⇒ S = = ⇒ = = ∆ BC BD d A BCD BCD , 13 ( ,( )) . 2 S BC ∆ D 13
Ví dụ 4: Trong không gian với hệ trục tọa độ Oxyz, cho 4 điểm: A( 3
− ;5;15), B (0;0;7), C (2; 1 − ;4), D (4; 3
− ;0). Chứng minh rằng AB và CD cắt nhau. Lời giải: Ta có: AB = (3; 5 − ; 8 − ); AC = (5; 6 − ; 1 − 1); AD = (7; 8 − ; 1 − 5) và CD = (2; 2; − 4 − )
Do AB, AC = (7; 7;
− 7) ⇒ AB, AC.AD = 0 ⇒ A ; B AC; AD đồng phẳng (1)
Mặt khác AB ≠ k.CD ⇒ AB và CD không cùng phương (2)
Từ (1) và (2) suy ra AB và CD cắt nhau.
Ví dụ 5: Cho 3 vectơ u = (3;7;0); v = (2;3;1); w = (3; 2 − ;4).
a) Chứng minh 3 vectơ u; ;
v w không đồng phẳng.
b) Biểu thị vectơ a = ( 4; − 1
− 2;3) theo 3 vectơ u; ; v . w Lời giải:
a) Ta có: u,v = (7; 3 − ; 5)
− ⇒ u,v.w = 7 ≠ 0 ⇒ 3 vectơ u; ;
v w không đồng phẳng.
b) Giả sử a = . m u + . n v + . p w ⇔ ( 4; − 1 − 2;3) = (3 ; m 7 ; m 0) + (2 ; n 3 ; n n) + (3p; 2 − p;4 p) 3
m + 2n + 3p = 4 − m = 5 −
7m 3n 2 p 7 ⇔ + − =
⇔ n = 7 . Vậy a = 5.
− u + 7.v − . w n 4p 3 + = p = 1 −
Ví dụ 6: Cho 4 điểm A(1;1;0); B (0;2;1); C (1;0;2); D (1;1;1)
a) Chứng minh 4 điểm đã cho đồng phẳng, tính thể tích tứ diện ABCD.
b) Tính diện tích các mặt của tứ diện ABCD.
c) Tính độ dài các đường cao của tứ diện ABCD. Lời giải:
a) Ta có: AB = ( 1; − 1;0); AC = (0; 1; − 2); AD = (0;0;1)
Suy ra AB, AC.AD = (3;2;1).(0;0;1) =1⇒ A ; B AC; AD không đồng phẳng
Do đó 4 điểm A, B, C, D không đồng phẳng
Thể tích tứ diện ABCD là: 1 1 V
= AB AC AD = ABCD , . . 6 6 b) Ta có: 1 14 1 1 S = = = = ∆ AB AC S∆ AC AD ABC , ; ACD , . 2 2 2 2 1 2 1 3 S = = = = ∆ AD AB S∆ BC BD ADB , ; BCD , . 2 2 2 2 c) Ta có 1 3V
V = Sh ⇒ h =
. Gọi h h h h lần lượt là độ dài đường cao hạ từ A, B, C, D của tứ diện
A; B ; C ; 3 S D thì ta có: 3V 3 3V 3V 1 3V 1 h = = h = = h = = h = = A ; B 1; C ; D . S S S S BCD 3 ACD ABD 2 ABC 14
Ví dụ 7: Cho 3 điểm A(1;0;0); B (0;0;1) và C (2;1;1).
a) Chứng minh 3 điểm A, B, C là 3 đỉnh của một tam giác, tính diện tích tam giác đó.
b) Tính độ dài đường cao h kẻ từ đỉnh A của tam giác ABC. A Lời giải: a) AB = ( 1;
− 0;1); AC = (1;1;1) ⇒ AB, AC = ( 1; − 2; 1 − ) ≠ 0 ⇒ A ; B AC
không cùng phương hay 3 điểm
A, B, C là 3 đỉnh của một tam giác.
Diện tích tam giác ABC là 1 6 S = AB AC = ABC , . 2 2 b) Ta có: 2SABC 6 30 h = = = A . BC 5 5
Ví dụ 8: Cho tứ diện ABCD có A(2;1; 1
− ), B (3;0;1), C (2; 1
− ;3) và điểm D thuộc trục Oy. Biết V = ABCD 5.
Tìm tọa độ điểm D. Lời giải:
Gọi D(0; y;0)∈Oy ta có: AB = (1; 1; − 2); AD = ( 2
− ; y −1;1); AC = (0; 2 − ;4)
Suy ra AB, AC = (0; 4; − 2
− ) ⇒ AB, AC.AD = 4 − (y −1) − 2 = 4 − y + 2 1 y = 7 − Do V = ⇒ − y + = ⇔ ABCD 5 . 4 2 5 . 6 y = 8 Vậy D (0; 7
− ;0) hoặc D (0;8;0).
Ví dụ 9: Chứng minh đẳng thức: 2 2
a . b − ( .ab)2 2 = a,b . Lời giải: Ta có: 2 2 2 2 2 2 = a b − a b a b = a b ( − (a b) 2 2 2 2 2 VT . . cos ( , ) . 1 cos ,
= a . b .sin (a,b)
Lại có: a,b = a . b .sin (a,b) Do đó 2 2
a . b − ( .ab)2 2 = a,b (đpcm).
Ví dụ 10: Trong không gian tọa độ Oxyz cho 3 vectơ a (m + 2;3;2m); b (2; 1
− ;m); c (1;2;1) . Gọi S là tập
hợp các giá trị của tham số m để 3 vectơ trên đồng phẳng. Số phần tử của tập hợp S là: a) 0. b) 1. c) 2. d) 3. Lời giải: Ta có: a b = ( 2 , 5 ;2
m m − m ;−m −8)
Ba vectơ đã cho đồng phẳng khi 2
a,b.c = 0 ⇔ 5m + 4m − 2m − m −8 = 0 2 ⇔ 2
− m + 8m −8 = 0 ⇔ m = 2.
Do đó tập hợp S có một phần tử. Chọn B.
Ví dụ 11: Cho 2 vectơ u = (1;2; 1 − ); v = (1; 3
− ; x). Tìm x biết rằng u,v = 30. A. x = 1. − B. x =1. C. x = 2. − D. x = 2. Lời giải:
Ta có: u,v = (2x − 3; x +1; 5 − ) Do đó 2 2 2
u,v = (2x −3) + (x +1) + 25 = 30 ⇔ 5x −10x + 5 = 0 ⇔ x =1. Chọn B.
Ví dụ 12: Cho 3 vectơ u = (1; ; x 1
− ); v = (0;2;1); w = ( ;
x 7;2). Tìm x biết rằng u,v.w = 0. x =1 x = 3 A. x = 1. ± B. x = 3. ± C. . D. . x = 3 − x = 1 Lời giải: x =1 2 2
u,v = (x + 2; 1;
− 2) ⇒ u,v.w = x + 2x − 7 + 4 = 0 ⇔ x + 2x − 3 = 0 ⇔ . Chọn C. x = 3 −
Ví dụ 13: Cho 2 vectơ u và v biết u = 2; v = 3. Góc giữa 2 vectơ u và v là 45o , độ dài vectơ 5u, 3 − v là: A. 7 2. B. 15. C. 15 2. D. 45. Lời giải:
Do ( , ) = 45o ⇒ (5 , 3 − ) =135 .o u v u v
Ta có: u − v = u − v ( u − v) 0 5 , 3
5 . 3 .sin 5 , 3 = 5 2.9.sin135 = 45. Chọn D.
Ví dụ 14: Trong không gian tọa độ Oxyz, cho các điểm A(3;1; 1
− ); B (1;0;2); C (5;0;0). Tính diện tích tam giác ABC. A. 21. B. 21 . C. 42. D. 2 21. 3 Lời giải: Ta có: AB = ( 2; − 1 − ;3); AC = (2; 1
− ;1) ⇒ AB, AC = (2;8;4).
Vậy diện tích tam giác ABC là 1 S = AB AC = Chọn A. ABC . , 21. 2
Ví dụ 15: Trong không gian tọa độ Oxyz cho 4 điểm A(0;1;1); B ( 1; − 0;2); C ( 1;
− 1;1); D (1;4;7). Khoảng
cách từ điểm D đến mặt phẳng (ABC) là: A. 9 2 h = B. h = C. 9 2 h = D. h = D 9 2. D . D 9. D . 2 4 Lời giải: Ta có: AB = ( 1; − 1; − 1); AC = ( 1; − 0;0); AD = (1;3;6)
Lại có: AB AC = ( − − ) 1 3 , 0; 1; 1 ⇒ V
= AB AC AD = ABCD , . . 6 2 Mặt khác: 1 2 3V 9 9 2 S = = ⇒ = = = = Chọn A. ∆ AB AC d h ABC , D ABC D . ( ;( )) 2 2 SABC 2 2
Ví dụ 16: Trong không gian tọa độ Oxyz cho 3 điểm A(1;1;1), B ( 1; − 7; 3
− ), C (m +1; ;
m 0). Biết diện tích
tam giác ABC bằng 3 3. Tổng tất cả các giá trị của tham số m thỏa mãn yêu cầu bài toán là: A. 1. B. 2. C. 3. D. 4. Lời giải: Ta có: AB = ( 2; − 6; 4 − ); AC = ( ; m m −1; 1 − )
Khi đó AB, AC = (4m −10;2 + 4 ; m 8 − m + 2) 1 1 2 2 2 ⇒ S = AB AC = m − + + m + − m + = ABC , (4 10) (2 4 ) ( 8 2) 3 3. 2 2 m =1 2 2 2 2
⇔ (2m − 5) + (1+ 2m) + ( 4
− m +1) = 3 3 ⇔ 24m − 24m + 27 = 27 ⇔ ⇒ T = 1. Chọn A. m = 0
Ví dụ 17: Trong không gian tọa độ Oxyz cho 4 điểm A(m −1; ;
m 2m −1); B ( 1; − 0;2); C ( 1; − 1;0); D (2;1; 2 − ).
Biết thể tích của tứ diện ABCD bằng 5 . Tổng tất cả các giá trị của tham số m thỏa mãn yêu cầu bài toán là: 6 A. 1. B. 9 . C. 9. D. 5 . 7 7 Lời giải: Ta có: BC = (0;1; 2 − ); BD = (3;1; 4
− ) ⇒ BC, BD = ( 2; − 6; − 3) −
Lại có: 1 1 BA = ( ; m ;
m 2m − 3) ⇒ V
= BC BD BA = − m − m − m + ABCD , . 2 6 6 9 6 6 m =1 1 5 14m 9 9 14m 5 = − + = ⇔ − = ⇔ 2 . Chọn B. 6 6 m = 7
Ví dụ 18: Trong không gian tọa độ Oxyz cho 3 điểm A(1;1;1); B ( 1; − 7; 3
− ); C (2;1;0). Tìm điểm D thuộc Oz
sao cho bốn điểm A, B, C, D đồng phẳng. A. D(1;2;0). B. D(0;0;3). C. D(0;0; 3) − . D. D(0;0;2). Lời giải:
Do điểm D ∈Oz ⇒ D (0;0;d) Ta có: AB = ( 2 − ;6; 4 − ); AC = (1;0; 1 − ); AD = ( 1; − 1; − d −1)
Để bốn điểm A, B, C, D đổng phẳng thì AB, AC.AD = 0 ⇔ ( 6; − 6; − 6 − ).( 1 − ; 1
− ;d −1) = 0 ⇔ 6 + 6 − 6d + 6 = 0 ⇔ d = 3 ⇒ D (0;0;3). Chọn B.
Ví dụ 19: Trong không gian Oxyz, cho 3 điểm A(1;0;3); B ( 1
− ;2;1); C (0;1;4). Biết H (x y z là trực
o ; o ; o )
tâm của tam giác ABC. Tính P = x − y o o. A. P =1. B. 1 P − = . C. 1 P = . D. P = 2. 2 2 Lời giải:
Gọi H (a; ;
b c) là trực tâm tam giác ABC thì A ;
B AC; AH đồng phẳng Ta có: AB( 2 − ;2; 2 − ) = 2 − (1; 1; − 1); AC = ( 1; − 1;1);
CH = (a;b −1;c − 4); BH = (a +1;b − 2;c −1); AH = (a −1; ; b c − 3)
Suy ra AB, AC = (4;4;0) = 4(1;1;0) 1
= , = 0 a AB AC AH 4
a + b −1 = 0 Mặt khác 3 1 C H.AB = 0
⇔ a −b +1+ c − 4 = 0 ⇔ b
= ⇒ P = − . Chọn B. 4 2 BH.AC = 0
a 1 b 2 c 1 0 − − + − + − = 7 c = 2
Ví dụ 20: Trong không gian Oxyz, cho 3 điểm A(2;0; 2 − ); B (3; 1 − ; 4 − ); C ( 2;
− 2;0). Điểm D nằm trong mặt
phẳng (Oyz) có cao độ âm sao cho thể tích của khối tứ diện ABCD bằng 2 và khoảng cách từ D đến mặt
phẳng (Oxy) bằng 1. Khi đó có tọa độ điểm D thỏa mãn bài toán là A. D(0;3; 1) − . B. D(0; 3 − ; 1 − ). C. D(0;1; 1 − ). D. D(0;2; 1 − ). Lời giải:
Vì D ∈(Oyz) ⇒ D (0; ;
b c), do cao độ âm nên c < 0.
Khoảng cách từ D đến mặt phẳng c và bằng 1 ⇒ c =1⇒ c = 1
− (do c < 0) ⇒ D (0; ; b 1) − . AB = (1; 1; − 2 − )
Ta có AC = ( 4;
− 2;2) ⇒ AB, AC = (2;6;−2) ⇒ AB, AC.AD = −4 + 6b − 2 = 6b − 6 = 6(b −1) AD = (− 2; ; b 1)
1 ⇒ V
= AB AC AD = b − ABCD , . 1 6 b = 3 D (0;3; 1) − Mặt khác V = ⇔ b − = ⇔ ⇔ Chọn A. ABCD 2 1 2 . b = 1 − D (0; 1 − ; 1 − )
BÀI TẬP TỰ LUYỆN
Câu 1: Trong không gian với hệ tọa độ Oxyz, cho a, b là các vectơ khác 0. Kết luận nào là sai?
A. a,b = b,a.
B. a,b
không vuông góc với a và b .
C. ka,b = k a,b.
D. a,b = a . b sin(a,b) .
Câu 2: Cho a = ( 2; − 5;3), b = ( 4; − 1; 2
− ). Kết quả của biểu thức a,b là A. 216. B. 405. C. 749. D. 708.
Câu 3: Cho a = (1;t;2), b = (t +1;2;1), c = (0;t − 2;2). Xác định t để a, , b c đồng phẳng A. t =1. B. t = 2. − C. 1 t = . D. 2 t = . 2 5
Câu 4: Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;2 −1), B (3;0;4), C (2;1; 1 − ). Độ dài đường
cao hạ từ đỉnh A của A ∆ BC là A. 6. B. 33. C. 5 6 . D. 50. 50 9 33
Câu 5: Trong không gian với hệ tọa độ Oxyz, cho A(1;0; 1 − ), B (1; 2
− ;2). Diện tích tam giác OAB bằng: A. 17 . B. 11. C. 6. D. 6 . 2 2
Câu 6: Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC với A(1;0;1), B (0;2;3), C (2;1;0). Độ dài
đường cao kẻ từ C của tam giác ABC là A. 26. B. 26 . C. 26 . D. 26. 2 3
Câu 7: Cho tam giác ABC biết A(2;0;0), B (0;3;1), C ( 1
− ;4;2). Độ dài trung tuyến AM và đường cao AH lần lượt là: A. 83 và 2 2. B. 83 và 2. C. 79 và 2. D. 79 và 2 2. 2 2 2 2
Câu 8: Trong không gian với hệ tọa độ Oxyz, cho hình bình hành ABCD có A(2;4; 4 − ), B (1;1; 3) − , C ( 2;
− 0;5). Diện tích hình bình hành ABCD bằng A. 245. B. 345. C. 615. D. 618. Câu 9:
Trong không gian Oxyz, cho 4 điểm không đồng phẳng A(2; 1; − 2 − ), B ( 1; − 1;2), C ( 1;
− 1;0), S (1;0;1). Độ dài đường cao của hình chóp S.ABC xuất phát từ đỉnh S bằng A. 1 B. 1 . C. 2 . D. 13. 3 3. 13 13
Câu 10: Trong không gian Oxyz, cho 4 điểm A(1;0;0), B (0;1;0), C (0;1;1), D (1;1;1) không đồng phẳng. Tứ
diện ABCD có thể tích là A. 1 . B. 2 . C. 2. D. 1. 6 3 3
Câu 11: Trong không gian với hệ tọa độ Oxyz, cho 4 điểm A(1; 2; − 2), B (0; 1 − ;2), C (0; 2; − 3) và D ( 2 − ; 1;
− 1). Thể tích tứ diện ABCD là A. 1 . B. 5. C. 5 . D. 1 . 2 3 6 6
Câu 12: Cho A(3;0;0); B (0;3;0); C (0;0;3); D (1; 1
− ;0) thì thể tích của tứ diện ABCD là A. 1 . B. 27. C. 9 . D. 3. 2 2
Câu 13: Trong không gian với hệ tọa độ Oxyz, cho hình hộp chữ nhật ABCD.A’B’C’D’ có
A(0;0;0), B (1;0;0), D (0;1;0), A'(0;0;2) thì thể tích V của tứ diện ABA’C’ bằng: A. 1. B. 2 . C. 1. D. 1 . 3 3 6
Câu 14: Trong không gian Oxyz, cho A(1;1; 6 − ), B (0;0; 2 − ), C ( 5 − ;1;2), D '(2;1; 1
− ). Nếu ABCD.A’B’C’D’
là hình hộp thì thể tích của nó là: A. 36 (đvtt). B. 38 (đvtt). C. 40 (đvtt). D. 42 (đvtt).
Câu 15: Trong không gian Oxyz, cho hai điểm A(5;3; 4
− ) và điểm B (1;3;4) . Tìm tọa độ điểm C thuộc mặt
phẳng (Oxy) sao cho tam giác ABC cân tại C và có diện tích bằng 8 5. C (3;7;0) C (3;7;0) C ( 3 − ; 7 − ;0) C ( 3 − ; 7 − ;0) A. . B. . C. . D. . C(3;1;0) C(3; 1; − 0) C( 3 − ; 1; − 0) C(3; 1; − 0)
Câu 16: Trong không gian với hệ tọa độ Oxyz, cho 4 điểm A(2;4; 1 − ), B (1;4; 1
− ), C (2;4;3), D (2;2; 1 − ).
Tìm tọa độ điểm M để 2 2 2 2
MA + MB + MC + MD đạt giá trị nhỏ nhất. A. 7 14 M ; ;0 . B. 7 4 M ; ;0. C. 7 14 M ; ;0. D. M (0;0;1). 3 3 3 3 4 4
Câu 17: Trong không gian với hệ tọa độ Oxyz, cho điểm A(3; 1 − ;1), B (0; 3
− ;3), C (1;7;1). Biết rằng tọa độ
điểm M thỏa mãn MA + 2MB + MC đạt giá trị nhỏ nhất có dạng M ( ;
a 0;b), (a,b∈). Khi đó 2 2 a + 3b bằng A. 16. B. 4. C. 11. D. 13.
LỜI GIẢI BÀI TẬP TỰ LUYỆN
Câu 1: Theo lý thuyết SGK thì hiển nhiên A sai, B đúng, C đúng, D đúng. Chọn A. 5 3 3 2 − 2 − 5
Câu 2: Ta có a,b = ; ; = ( 13 − ; 16
− ;18) ⇒ a,b = 749. Chọn C. 1 2 2 4 4 1 − − − −
Câu 3: Để a, b, c đồng phẳng khi và chỉ khi a,b.c = 0. t 2 2 1 1 t
Ta có a,b = ; ; = ( 2
t − 4;2t +1;2 − t − t ) 2 1 1 t +1 t + 1 2 Suy ra 2 2
a,b.c = (2t +1)(t − 2) + 2(2 −t −t ) = 0 ⇔ t = . Chọn D. 5
Câu 4: Diện tích tam giác ABC là 1 5 2 S = = ∆ AB AC ABC , . 2 2 Ta có 2.S ABC ∆ 5 6 BC = ( 1; − 1; 5
− ) ⇒ BC = 27 → d( , A BC) = = . Chọn C. BC 9 Câu 5: Ta có 1 1 2 2 2 17 S = = − + − + − = Chọn A. ∆ OA OB OAB , ( 2) ( 3) ( 2) . 2 2 2
Câu 6: Diện tích tam giác ABC là 1 26 S = = ∆ AB AC ABC , . 2 2 Ta có 2.S ABC ∆ 26 AB = ( 1
− ;2;2) ⇒ AB = 3
→d(C, AB) = = . Chọn C. AB 3
Câu 7: Diện tích tam giác ABC là 1 6 S = = ∆ AB AC ABC , . 2 2 Ta có: 2. BC ( 1;1;1) BC 3 d( , A BC) S ABC ∆ = − ⇒ = → = = 2. BC
Tọa độ trung điểm M của BC là 1 7 3 83 M − ; ; ⇒ AM = . Chọn B. 2 2 2 2 Câu 8: AB = ( 1 − ; 3 − ;1); AC = ( 4; − 4; − 9)
Diện tích hình bình hành ABCD bằng: S = 2S = AB AC = − − = Chọn D. ABC , ( 23;5; 8) 618.
Câu 9: SA = (1; 1; − 3 − ); SB = ( 2 − ;1;1); SC = ( 2 − ;1; 1 − )
Thể tích hình chóp S.ABC là 1 1 V
= SA SB SC = S ABC , . . . 6 3 Mặt khác 1 AB = ( 3 − ;2;4); AC = ( 3 − ;2;2) ⇒ S = AB AC = ABC , 13. 2 Khi đó 3V 1 h = = Chọn B. S . S 13
Câu 10: AB = ( 1; − 1;0); AC = ( 1; − 1;1); AD = (0;1;1)
Thể tích tứ diện ABCD là: 1 1 V
= AB AC AD = Chọn A. ABCD , . . 6 6
Câu 11: AB = ( 1; − 1;0); AC = ( 1; − 0;1); AD = ( 3 − ;1; 1 − )
Thể tích tứ diện ABCD là: 1 3 1 V
= AB AC AD = = Chọn A. ABCD , . . 6 6 2
Câu 12: AB = ( 3 − ;3;0); AC = ( 3 − ;0;3); AD = ( 2 − ; 1 − ;0)
Thể tích tứ diện ABCD là: 1 27 9 V
= AB AC AD = = Chọn C. ABCD , . . 6 6 2
Câu 13: AB = (1;0;0); AD = (0;1;0); AA' = (0;0;2)
Do ABCD.A’B’C’D’ là hình hộp chữ nhật nên AB + AD + AA' = AC ' = (1;1;2)
Thể tích V của tứ diện ABA’C’ bằng : 1 2 1
V = AB, AA'.AC ' = = . Chọn C. 6 6 2
Câu 14: Do ABCD.A’B’C’D’ là hình hộp nên ABCD là hình bình hành
Ta có AB = DC = ( 1; − 1; − 4) ⇒ ( 5 − − x − y − z = − − D ;1 D ; 2 D ) ( 1; 1;4) Suy ra D ( 4; − 2; 2
− ) khi đó DD ' = (6; 1; − 1); DA = (5; 1; − 4 − ); DC = ( 1; − 1; − 4)
Thể tích của khối hộp là V = ,
DA DC DD ' = 38. Chọn B.
Câu 15: Ta có AB = ( 4; − 0;8); AB = 4 5.
Gọi I (3;3;0) là trung điểm của AB và C ( ;
x y;0) ta có: CA = CB ⇒ CI ⊥ AB ⇔ ( 4 − ;0;8).(3− ;
x 3− y;0) ⇔ x = 3. 1 1 y = 7
Suy ra C (3; y;0), mặt khác S = CI AB = y − = ⇔ y − = ⇔ Chọn B. ABC . 3 .4 5 8 3 3 4 . 2 2 y = 1 −
Câu 16: Gọi G là trọng tâm tứ diện khi đó GA + GB + GC + GD = 0 Khi đó 7 14 G ; ;0 , ta có: 2 2 2 2 2 2 2 2
MA + MB + MC + MD = MA + MB + MC + MD 4 4
= (MG +GA)2 +(MG +GB)2 +(MG +GC)2 +(MG +GD)2
2 2 2 2 2
= 4MG + 2MG(GA + GB + GC + GD) + GA + GB + GC + GD 2 2 2 2 2
= 4MG + GA + GB + GC + GD nhỏ nhất 2 ⇔ MG nhỏ nhất 7 14 MG 0 M G ; ;0 ⇔ = ⇔ ≡ . Chọn C. 4 4
Câu 17: Gọi I là điểm thỏa mãn IA + 2IB + IC = 0 ⇔ I (1;0;2)
Khi đó MA + 2MB + MC = MI + IA + 2MI + 2IB + MI + IC = 4MI nhỏ nhất ⇔ MI nhỏ nhất a =1 Suy ra 2 2
M ≡ I (1;0;2) ⇒
⇒ a + 3b =13. Chọn D. b = 2
Document Outline
- ITMTTL~1
- IIBITP~1
- IIILIG~1