Competitive Firm Analysis and Cost Calculations | Microeconomics | Trường Đại học Quốc tế, Đại học Quốc gia Thành phố Hồ Chí Minh

Họ và tên: Nguyễn Xuân Tố Uyên Lớp: EBBA 16.2 PERSONAL ASSIGNMENT 7
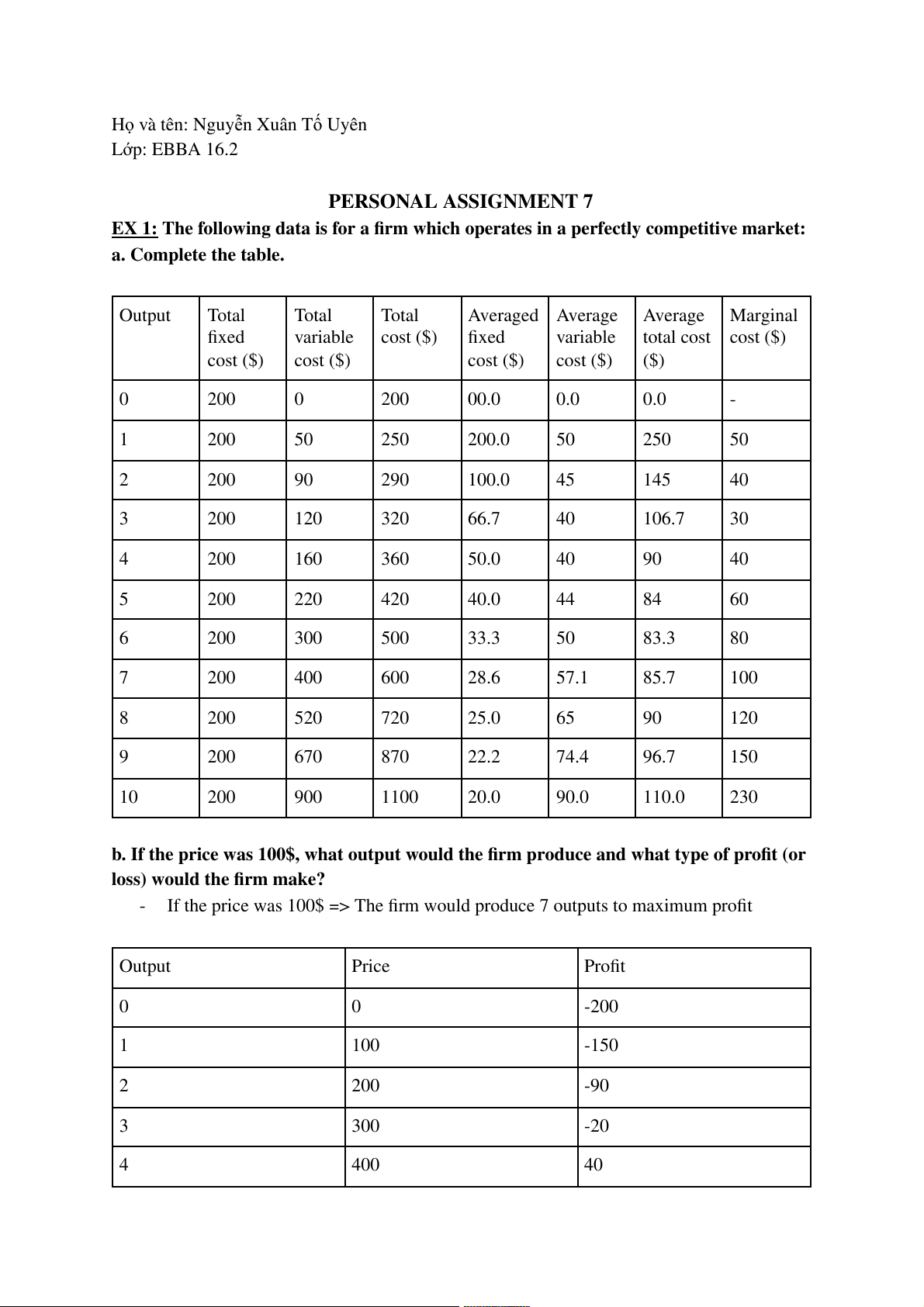
EX 1: The following data is for a firm which operates in a perfectly competitive market: a. Complete the table. Output Total Total Total Averaged Average Average Marginal fixed variable cost ($) fixed variable total cost cost ($) cost ($) cost ($) cost ($) cost ($) ($) 0 200 0 200 00.0 0.0 0.0 - 1 200 50 250 200.0 50 250 50 2 200 90 290 100.0 45 145 40 3 200 120 320 66.7 40 106.7 30 4 200 160 360 50.0 40 90 40 5 200 220 420 40.0 44 84 60 6 200 300 500 33.3 50 83.3 80 7 200 400 600 28.6 57.1 85.7 100 8 200 520 720 25.0 65 90 120 9 200 670 870 22.2 74.4 96.7 150 10 200 900 1100 20.0 90.0 110.0 230
b. If the price was 100$, what output would the firm produce and what type of profit (or
loss) would the firm make? -
If the price was 100$ => The firm would produce 7 outputs to maximum profit Output Price Profit 0 0 -200 1 100 -150 2 200 -90 3 300 -20 4 400 40 5 500 80 6 600 100 7 700 100 8 800 80 9 900 30 10 1000 -100
c. Does the profitable situation in the question b exist in the long – run? Why? -
The profitable situation in question b cannot exist in the long- run. Because in the
long-term, the process of entering the market causes market supply to increase pull
prices down. => If the firm continues keep the price of 100$, it would be losses EX 2:
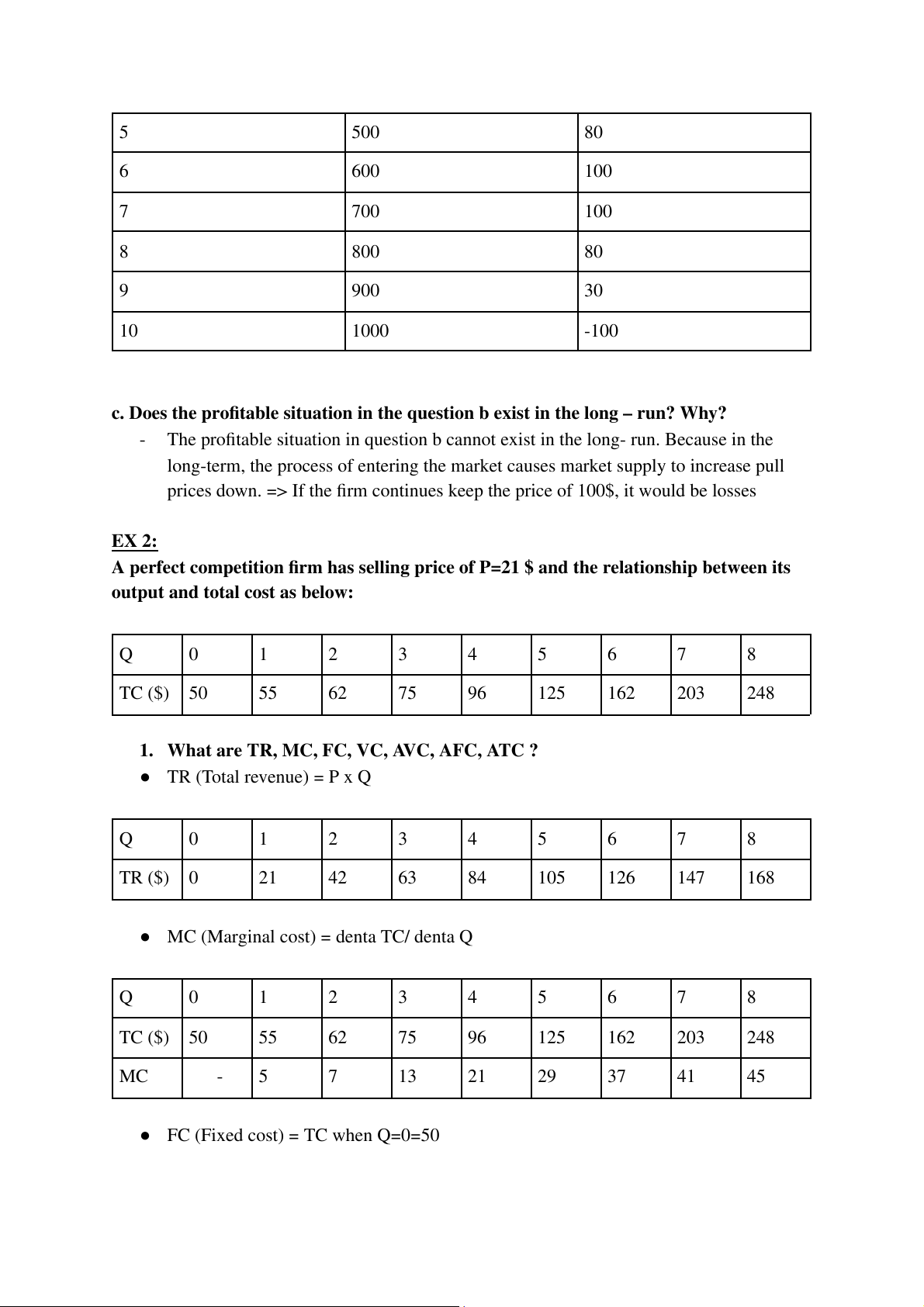
A perfect competition firm has selling price of P=21 $ and the relationship between its
output and total cost as below: Q 0 1 2 3 4 5 6 7 8 TC ($) 50 55 62 75 96 125 162 203 248
1. What are TR, MC, FC, VC, AVC, AFC, ATC ? ● TR (Total revenue) = P x Q Q 0 1 2 3 4 5 6 7 8 TR ($) 0 21 42 63 84 105 126 147 168
● MC (Marginal cost) = denta TC/ denta Q Q 0 1 2 3 4 5 6 7 8 TC ($) 50 55 62 75 96 125 162 203 248 MC - 5 7 13 21 29 37 41 45
● FC (Fixed cost) = TC when Q=0=50 ● VC (Variable cost) = TC-FC Q 0 1 2 3 4 5 6 7 8 VC ($) 0 5 12 25 46 75 112 153 198
● AVC (Average variable cost) = VC/Q Q 1 2 3 4 5 6 7 8 AVC 5 6 8.33 11.5 15 18.67 21.86 24.75
● AFC (Average fixed cost) = FC/ Q Q 1 2 3 4 5 6 7 8 AFC 50 25 16.67 12.5 10 8.33 7.14 6.25 ($)
● ATC (Average total cost) = TC/Q Q 1 2 3 4 5 6 7 8 ATC ($) 55 31 25 24 25 27 29 31
2. Identify optimal output level (Q *) that gives the firm profit maximization? What
is the maximum profit ? - In perfect competition, MR=P. Q TR ($) TC ($) Profit ($) = TR - TC MC ($) 0 0 50 -50 - 1 21 55 -34 5 2 42 62 -20 7 3 63 75 -12 13 4 84 96 -12 21 5 105 125 -20 29 6 126 162 -36 37 7 147 203 -56 41 8 168 248 -80 45 -
The profits are maximized at Q=3 because it has the highest profit (least negative)
before profit becomes negative. -
Maximum profit at Q=3: Profit=TR−TC=63−75=−12
3. With the above profit (in the question 2), should the firm continue the production? Why? -
Since the firm is incurring a loss of $12 at the optimal output level, we need to
consider whether the firm should continue production:
+ Short-Run Decision: A firm should continue production in the short run if it can cover its variable costs. - At Q=3:
+ Total Variable Cost (TVC): VC=25 + Total Revenue (TR): 63 -
Since TR>TVC, the firm can cover its variable costs and contributes to fixed costs,
even though it is making an overall loss. -
Conclusion: The firm should continue production in the short run because it is covering its variable costs.
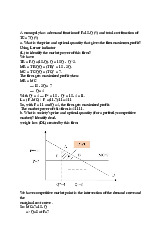
EX 3: A perfect competition firm has a demand equaltion of P=8 ($) and total cost
equation of TC= Q2+ 2Q+ 4 ($)
1. Identify TR and MR equation - Total Revenue (TR): TR=P×Q=8Q - Marginal Revenue (MR):
+ In perfect competition, MR is constant and equal to the price: MR=8
2. Identify MC, VC, AVC, AFC, ATC equation -
Marginal Cost (MC): We find MC by taking the derivative of the total cost - Variable Cost (VC): VC=TC−FC - Average Variable Cost (AVC): - Average Fixed Cost (AFC): - Average Total Cost (ATC):
3. Optimal Output Level (Q∗) for Profit Maximization -
To find the optimal output level, set MR=MC: 8=2Q+2 - Solving for Q: 2Q=8−2 2Q=6 Q=3 -
Maximum Profit: TR and TC at Q=3: + TR = 8Q = 8 × 3 = 24 - Profit =TR−TC=24−19=5
4. What is break even price and break even quantity? -
A firm breaks even when TR=TC. - Set TR equal to TC: -> Q1 ≈5.24 Q2 ≈0.76 -
Using P=8 (constant price), both break-even quantities ≈5.24 and ≈0.76 yield a break-even price of P=8. - Conclusion: + Break-even price = 8
+ Break-even quantities ≈ 5.24 and 0.76
5. If market price decrease to P= 4$, should the firm continue the production? Why? - Set MR=MC: 4=2Q+2 ->Q=1 - At Q=1:
+ Total Revenue (TR): TR=P×Q=4×1=4
+ Total Cost (TC): TC=Q=1+2+4=7 -
Profit=TR−TC=4−7=−3 -> The firm incurs a loss of 3 -
Variable Cost (VC) at Q=1: VC=3 -> Average Variable Cost (AVC): AVC=3 -
Since the market price is greater than the average variable cost, the firm can cover its variable costs.
-> The firm should continue production.