Thi Thử MIỄN PHÍ tại http://thiquocgia.vn 1
CÔNG THỨC TÍNH NHANH THỂ TÍCH
KHỐI TRÒN XOAY (tập 3)
1. Thể tích khối cầu
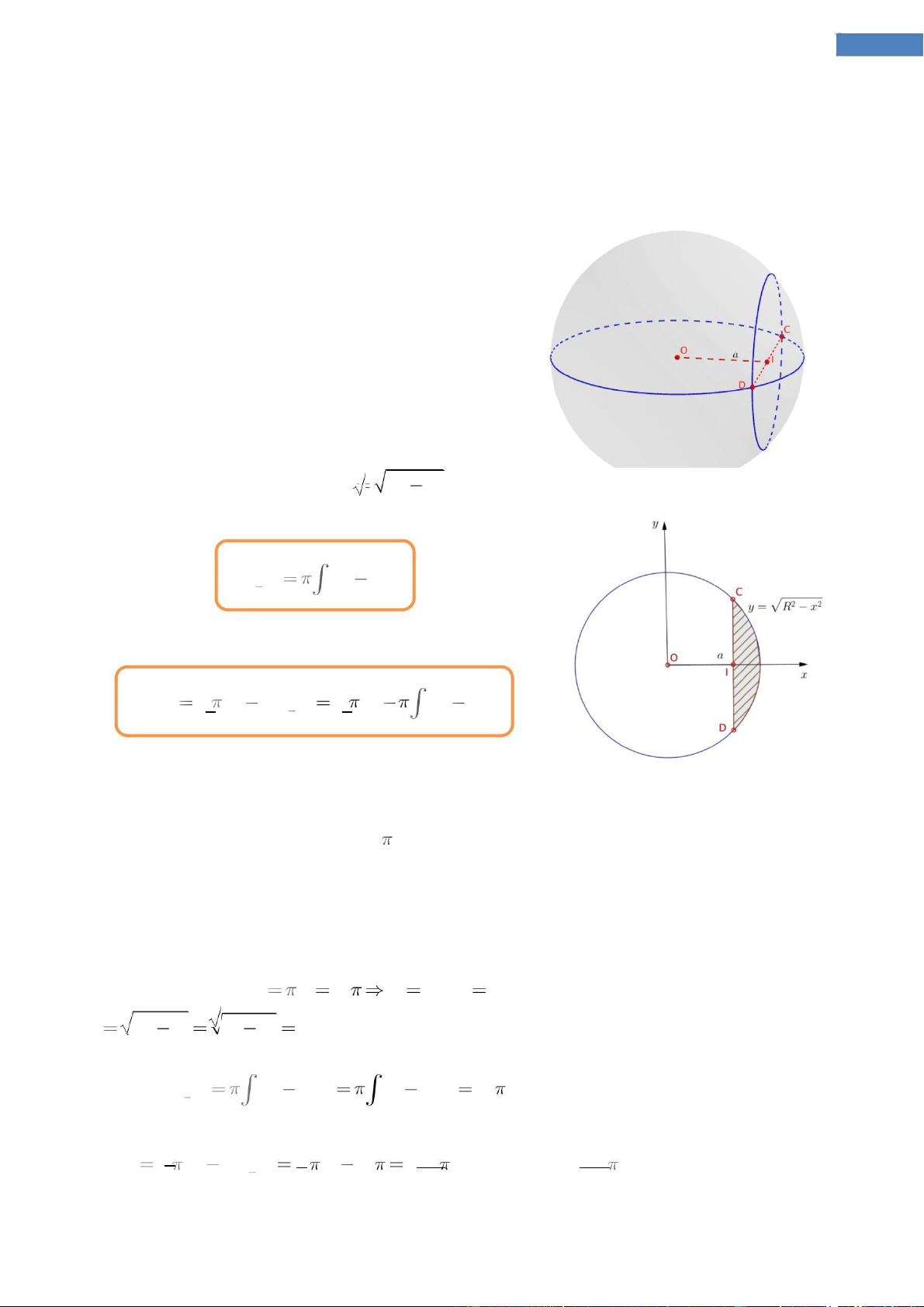
Bài toán gốc. Cho khối cầu có bán kính R, cắt một
chỏm cầu theo mặt phẳng cách tâm khối cầu một
đoạn bằng a. Tính thể tích khối còn lại và thể tích phần cắt đi. Công thức giải.
Phần bị cắt đi (tính dựa vào thể tích vật thể tròn
xoay tạo bởi phần đường tròn y R2 x2 quay
xung quanh Ox từ a đến R): R Vcut out
R2 x 2 dx a Phần còn lại: R Vremain 4 R 3 Vcut out 4 R 3
R2 x 2 dx 3 3 a
Bài toán 1. Một khối cầu bằng thủy tinh có bán kính 4dm, người ta muốn cắt bỏ một
chỏm cầu có diện tích mặt cắt là 15 (dm2 ) để lấy phần còn lại làm chậu nuôi cá. Hỏi thể
tích nước tối đa mà chậu cá này có thể chứa là bao nhiêu? (giả sử bề dày chậu không đáng kể) Giải.
Diện tích mặt cắt là S r 2 15 r 2
15 (r OC) . Khi đó, tính được a R2 r2 16 15 1. R 4 Khi đó: Vcut out
R2 x 2 dx
16 x 2 dx 27 (dm3 ) a 1 V 4 R 3 V 4 43 27
175 ( dm3 ) . Đáp số: 175 ( dm3 ) . remain 3 cut out 3 3 3
Thi Thử MIỄN PHÍ tại http://thiquocgia.vn2
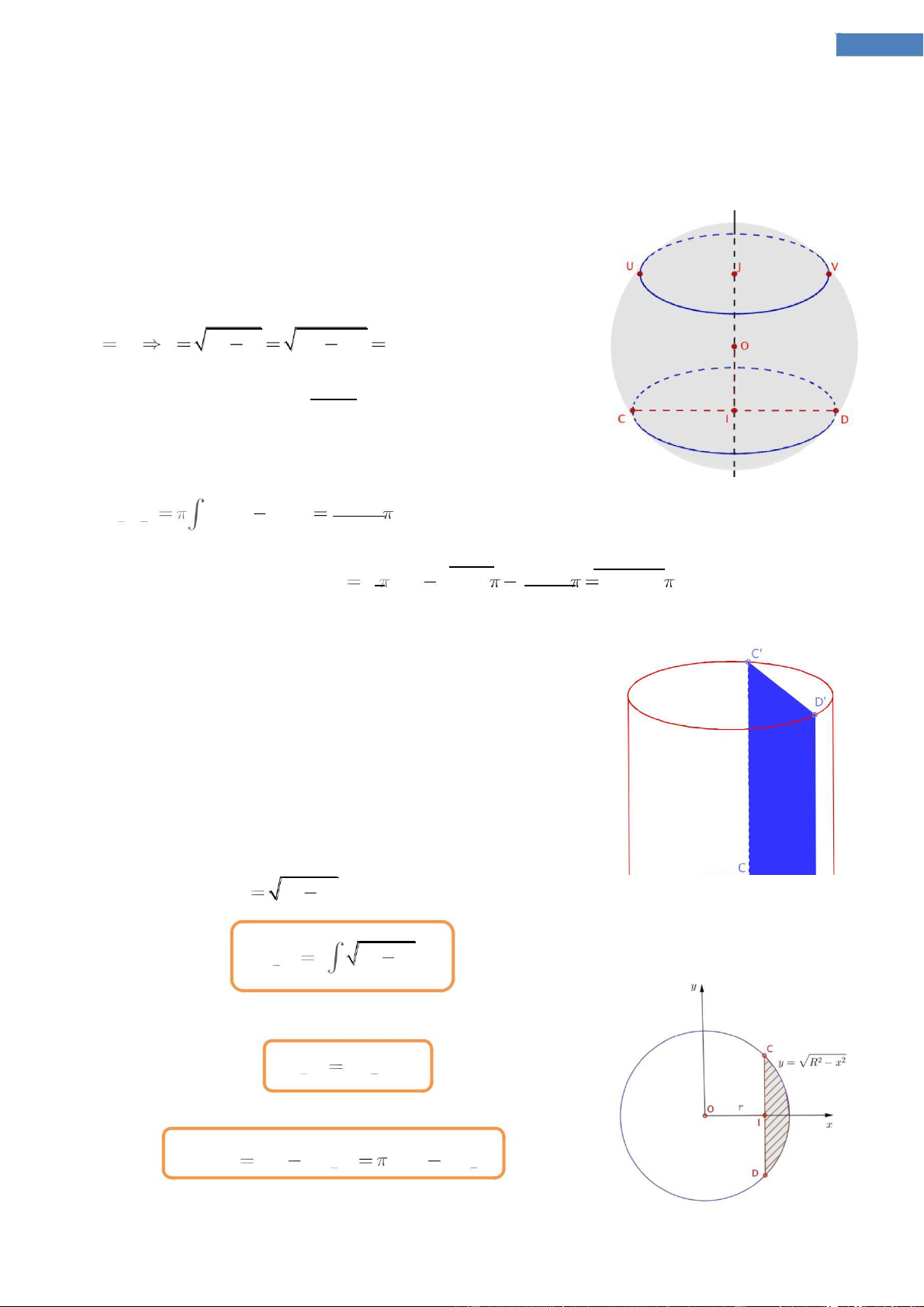
Bài toán 2. Nhà sản xuất muốn tạo một cái lu đựng nước bằng cách cắt bỏ hai chỏm cầu
của một khối cầu để tạo phần đáy và miệng lu như hình vẽ. Biết bán kính khối cầu là 50
cm, phần mặt cắt ở đáy là hình tròn có bán kính 30cm và mặt phẳng ở miệng lu cách tâm
khối cầu 30cm. Tính thể tích nước tối đa mà cái lu có thể chứa. (giả sử độ dày của lu không đáng kể) Giải. Xét phần đáy lu. Ta có, r 30 a R2r2 502 302 40 V  50
cut  out 1
 40 (50 2  x 2 )dx  14000  (cm3 ) 3
Xét phần miệng lu. Ta có: Vcut out 2
50 ( 502 x 2 )dx 52000 ( cm3 ) . 30 3 14000 434000
Suy ra phần thể tích còn lại V 4 .503 52000 ( cm3 ) . remain 3 3 3 3
2. Thể tích khối trụ
Bài toán gốc. Cho một khối trụ có bán kính đáy bằng R và
chiều cao h. Cắt khối trụ theo một mặt phẳng song song với
trục và cách trục (tâm) một khoảng r. Tính thể tích phần
còn lại và phần bị cắt đi. Công thức giải.
Diện tích phần bị cắt đi (bằng 2 lần diện tích hình tạo bởi
phần đường tròn y R2x2
và trục Ox tính từ r đến R): R S
2 R2 x 2 dx. cut out r
Thể tích phần bị cắt đi: V S cut out cut out .h.
Thể tích phần còn lại: V V V .R2 .h V remain tru cut out cut out
Bài toán 3. Một bồn trụ đang chứa dầu được đặt nằm ngang
Thi Thử MIỄN PHÍ tại http://thiquocgia.vn 3
có chiều dài bồn là 5m, bán kính đáy 1m. Người ta rút dầu ra trong bồn tương ứng với
0,5m của đường kính đáy. Tính thể tích gần đúng nhất của thể tích dầu trong bồn (theo đơn vị m3)
A. 11, 781m3
B. 12 , 637m3
C. 14 , 923m3
D. 8 , 703m3
Giải. Ta có: Vcut  out  S cut out .h  2. 1 1 x 2 dx.5  3, 071 0,5 Thể tích dầu: V V V .R2 .h V
.1.5 3 , 071 12 , 637(m3 ) . Đáp án B. dau cut out cut out
3. Thể tích khối nón
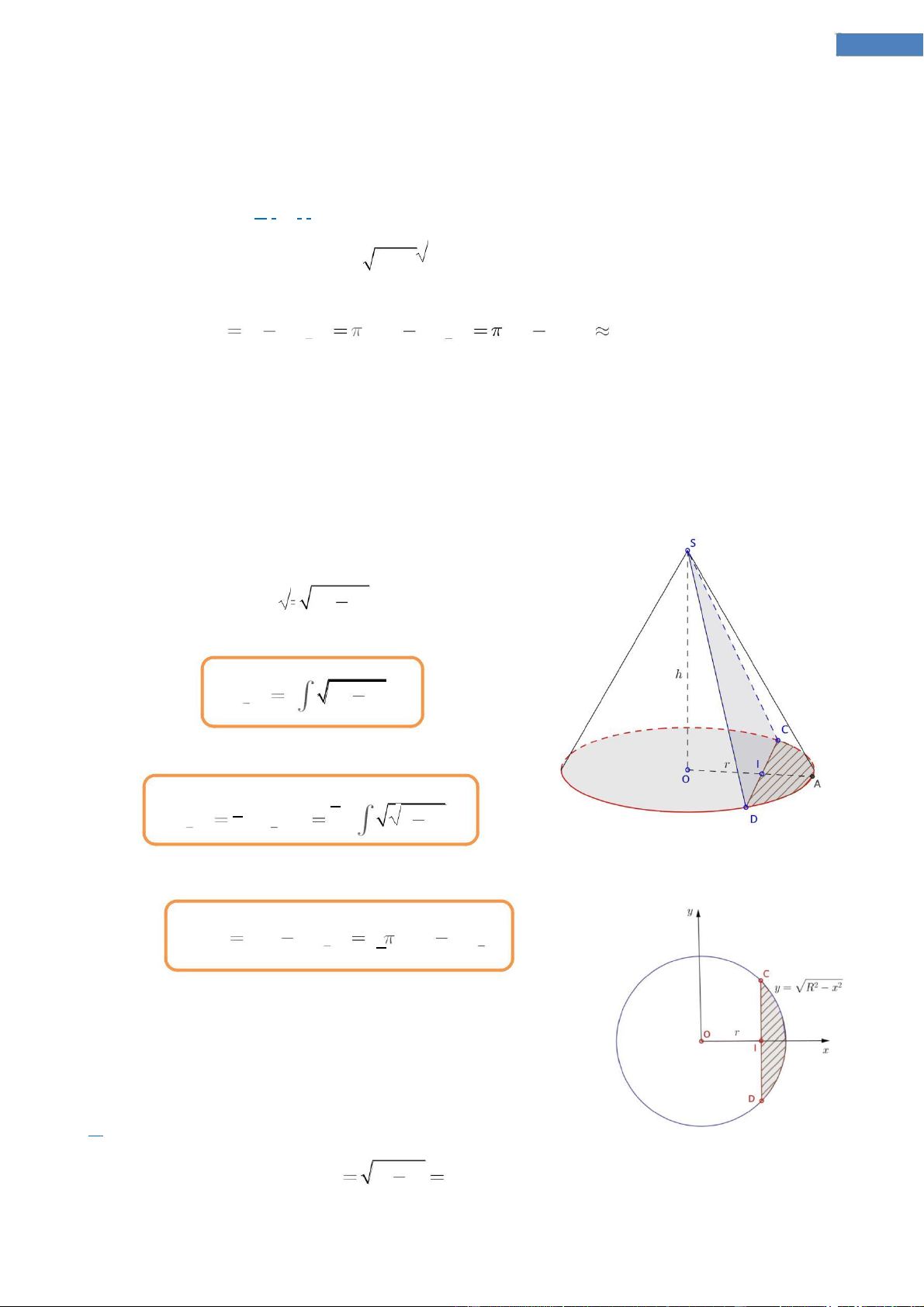
Bài toán gốc. Cho một khối nón có bán kính đáy bằng R và chiều cao h. Cắt khối nón
theo một mặt phẳng đi qua đỉnh và cắt đường tròn đáy theo một dây cung cách tâm
một khoảng r. Tính thể tích phần còn lại và phần bị cắt đi. Công thức giải.
Diện tích phần bị cắt đi (bằng 2 lần diện tích hình tạo
bởi phần đường tròn y R2 x2 và trục Ox tính từ r đến R): R S 2
R2 x 2 dx. cut out r
Thể tích phần bị cắt đi: 2 R V 1 S .h h.
R2 x 2 dx. r 3 cut out cut out 3
Thể tích phần còn lại: V V V remain non cut out
1 .R2 .h Vcut out 3
Bài toán 4. Một khối nón bán kính bằng 5cm, đường cao bằng
4cm. Cắt khối nón theo một mặt phẳng từ đỉnh xuống
đáy và cắt đáy theo dây cung có độ dài bằng 6cm. Thể
tích phần còn lại của khối nón là:
A. 99 , 27cm3 B. 5 , 45cm3 C. 297 , 81cm3 D. 88 , 37cm3
Giải. Thể tích phần bị cắt đi ( r 52 32 4 ): 4
Thi Thử MIỄN PHÍ tại http://thiquocgia.vn 1 R 5 S .h V 1 .2
R2 x 2 dx.h 8
25 x 2 dx 5 , 45 (cm3) cut 3 cut 3 3 4 r
Thể tích phần còn lại: V V V 1 .R2 .h V
1 .25.4 5 , 45 99 , 27( cm3 ) . Chọn A. remain non cut 3 cut 3
Nhận xét. Trong các bài toán trên, việc tính tích phân giải nhanh bằng Casio. Ta hoàn R
toàn có thể giải tay tích phân S 2R2
x 2 dx bằng đổi biến x R sin t. cut out r BÀI TOÁN MỞ RỘNG
Bài toán về: 2 khối cầu giao nhau, 2 khối trụ giao nhau, khối cầu giao khối trụ, khối cầu
giao khối nón, khối nón giao khối trụ… (còn tiếp…)
Follow facebook: https://www.facebook.com/thiquocgiatoan/                               