






Preview text:
Chương 3. Thống kê
3.4. Kiểm định tham số

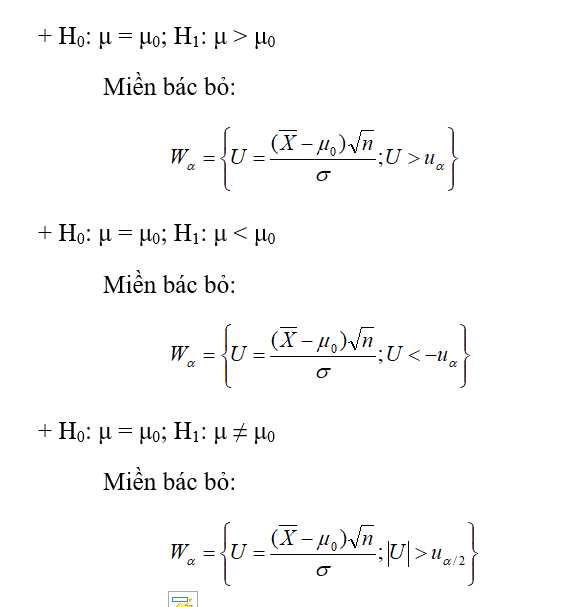


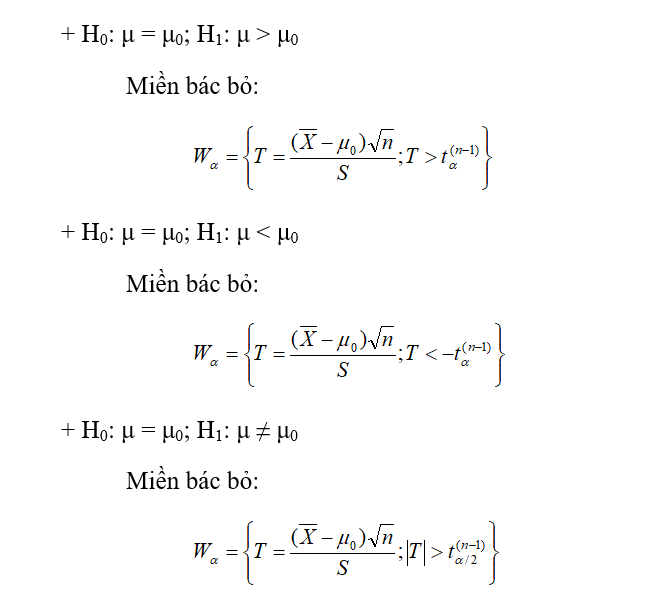




Vd12:
- Tỷ lệ phế phẩm gốc (theo thiết kế):
- Cỡ mẫu:
- Số phế phẩm quan sát:
- Mức ý nghĩa:
Bài giải:
1. Tính tỷ lệ mẫu:
2. Đặt giả thuyết:
- Giả thuyết không (): Tỷ lệ phế phẩm không tăng.
- Giả thuyết đối (): Tỷ lệ phế phẩm đã tăng lên.
Đây là kiểm định một phía (phải).
3. Chọn tiêu chuẩn kiểm định: Vì kiểm định tỷ lệ với mẫu nhỏ, ta dùng thống kê:
(Thống kê này xấp xỉ N(0,1) khi n đủ lớn, nhưng ở đây n nhỏ nên cần lưu ý).
4. Tính giá trị quan sát:
5. Xác định miền bác bỏ:
Với và kiểm định một phía phải, tra bảng giá trị tới hạn chuẩn:
Miền bác bỏ:
6. So sánh và kết luận:
Ta có:
So sánh:
=> thuộc miền bác bỏ .
Vậy, ta bác bỏ và chấp nhận .
Kết luận: Với mức ý nghĩa 5%, có đủ cơ sở thống kê để cho rằng tỷ lệ phế phẩm của máy đã tăng lên
Ví dụ 13: So sánh hiệu quả thuốc A và B
Thông tin:
- Tỷ lệ khỏi bệnh của thuốc A:
- Thuốc B: Số bệnh nhân điều trị , số khỏi
- Mức ý nghĩa:
Bài giải:
1. Tính tỷ lệ mẫu của thuốc B:
2. Đặt giả thuyết:
- : Thuốc B không hiệu quả hơn thuốc A.
- : Thuốc B hiệu quả hơn thuốc A.
Đây là kiểm định một phía (phải).
3. Chọn tiêu chuẩn kiểm định: So sánh tỷ lệ với một giá trị cố định.
4. Tính giá trị quan sát:
5. Xác định miền bác bỏ:
Với và kiểm định một phía phải:
Miền bác bỏ:
6. So sánh và kết luận:
Ta có:
So sánh:
=> thuộc miền bác bỏ .
Vậy, ta bác bỏ và chấp nhận .
Kết luận: Với mức ý nghĩa 5%, có đủ cơ sở thống kê để kết luận rằng thuốc B hiệu quả hơn thuốc A.
Ví dụ 14: So sánh tỷ lệ thôi việc giữa hai xí nghiệp
Thông tin:
- Xí nghiệp A: , số người xin chuyển
- Xí nghiệp B: , số người xin chuyển
- Mức ý nghĩa:
Bài giải:
1. Tính tỷ lệ mẫu:
2. Đặt giả thuyết:
- : Tỷ lệ thôi việc ở A bằng hoặc cao hơn ở B.
- : Tỷ lệ thôi việc ở A thấp hơn ở B.
Đây là kiểm định một phía (trái) để so sánh hai tỷ lệ.
3. Chọn tiêu chuẩn kiểm định: So sánh hai tỷ lệ độc lập.
4. Tính giá trị quan sát:
5. Xác định miền bác bỏ:
Với và kiểm định một phía trái:
Miền bác bỏ cho kiểm định trái là:
6. So sánh và kết luận:
Ta có:
So sánh: (Vì -1.065 nằm bên phải -1.645 trên trục số)
=> KHÔNG thuộc miền bác bỏ .
Vậy, ta chưa đủ cơ sở để bác bỏ .
Kết luận: Với mức ý nghĩa 5%, chưa có đủ bằng chứng thống kê để cho rằng tỷ lệ công nhân thôi việc ở xí nghiệp A thấp hơn xí nghiệp B.




