Dạng toàn phương | Môn Toán cao cấp 1 - Đại học Sư phạm Kỹ thuật Thành phố Hồ Chí Minh

lOMoAR cPSD| 58794847
§11. DẠNG TOÀN PHƯƠNG
Trong bài này, bạn sẽ học:
Tích vô hướng Euclide trong Rn;
Quá trình trực giao Gram-Schmidt;
Ma trận đối xứng, ma trận trực giao;
Dạng toàn phương, dạng chính tắc của dạng toàn phương;
Xét dấu dạng toàn phương.
……………………………………………………………………………………………………………………………………………
……………………………
1. Tích vô hướng Euclide trong Rn.
Tröôùc tieân, nhaéc laïi tích voâ höôùng cuøng vôùi caùc tính chaát vaø caùc khaùi nieäm
nhö ñoä daøi vectô, goùc giöõa hai vectô , tröïc giao, trực chuẩn,… cuûa caùc vectô hình hoïc.
Trong mặt phẳng Oxy 2
Trong khoâng gian Oxyz 3 →
a = (a1,a2) , →b = (b1,b2) 2; k → → → → → →
a = (a1,a2,a3) , →b = (b1,b2,b3) 3;k
Tập{ i , j } trực chuẩn,a = a → → → → → → →
1 i + a2 j
Tập{ i , j, k }trực chuẩn,a = a1 i + a2 j+ a3 k lOMoAR cPSD| 58794847 Tích voâ höôùng Tích voâ höôùng → → → → b b a.b = a )
1 1 + a2 2 (tích voâ höôùng hai vectô laø moät soá thöïc a.b = a b b b )
1 1 + a2 2 + a3 3 (tích voâ höôùng hai vectô laø moät soá thöïc Tính chaát → → → → Tính chaát → → → →
i) a.b = b.a → → → → → → →
i) a.b = b.a → → → → → → →
ii) (a+ c).b = a.b+ c .b
ii) (a+ c).b = a.b+ c .b → → → → → → → →
iii) (k a) b = k a.b
iii) (k a) b = k a.b → → → → → → → → → → → →
iv) a.a 0; a.a= 0 a= 0
iv) a.a 0; a.a= 0 a= 0 Ñoä daøi vectô Ñoä daøi vectô → → → a → → → = a 2 2
1 +a2 = a.a 2 + 2 + 2 → →
a = a1 a2 a3 = a.a → →
Goùc giöõa hai vectô : ( a , b ) = thoûa → →
Goùc giöõa hai vectô : ( a , b ) = thoûa → → a.b → → → →
a.b → → → → cos = hay a.b = a
cos = hay a.b = a b cos b cos → → → → a b a b
Hai vectô vuoâng goùc (tröïc giao)
Hai vectô vuoâng goùc (tröïc giao) → → → → → → → →
a ⊥ b a . b = 0
a ⊥ b a . b = 0 → → → → → → →→
Tích coù höôùng cuûa hai vectô a vaø b kyù hieäu a b hay a b hay a,b , laø moät
vectô xaùc ñònh nhö sau: →→
• Phöông: Vuoâng goùc vôùi maët phaúng coù phöông xaùc ñònh bôûi a, b →→ → →
• Chieàu : Ñöôïc xaùc ñònh sao cho a, b , a b taïo thaønh tam dieän thuaän. lOMoAR cPSD| 58794847 → → → → → → • a b a . b a , b → → → → a b = v b S → a → → → i j k ; ; = Nếu a
→a = (a1,a2,a3), →b = (b1,b2,b3) thì →a →b = ab22 ab33ab33 ab11ab11 ab22 b11 ab22 ab33.
1.1.Định nghĩa
i) Tích vô hướng (còn gọi là tích vô hướng Euclide) trên n xác như sau: u = (u1,u2,....,un) n, v = (v1,v2,....,vn) n ÑN
u,v = u1v1 +u2v2 +...+unvn
ii) Chuaån hay ñoä daøi 1 2 n vectô u = (u ,u ,....,u ) 2 2 2 , kyù hieäu u nhö sau 1 2 n u
= u,u = u +u +...+u Vectơ u gọi là vectơ đơn vị nếu u = 1.
iii) Góc giữa hai vectơ u = (u1,u2,....,un) n, v = (v1,v2,....,vn) n là góc (0 ) thỏa lOMoAR cPSD| 58794847 cos = u,v =
u1v1 +u2v2 +...+unvn
|| u || .|| v || u 2 2 2 2 2 2
1 +u2 + ...+un . v1 +v2 +...+vn
iv) Hai vectô u vaø v goïi laø tröïc giao nhau, kyù hieäu u ⊥ v, neáu u,v = 0
v) Vectô v vaø taäp A goïi laø tröïc giao nhau, kyù hieäu v ⊥ A hoaëc A ⊥ v, neáu u,v = 0, u A
vi) Hai taäp Avaø B goïi laø tröïc giao nhau, kyù hieäu A⊥B , neáu
= 0, u A vaø v B vii) A goïi laø
taäp tröïc giao neáu: u, u' A maø u u’ thì < u,u’> = 0 viii) A goïi laø
taäp tröïc chuaån neáu A laø taäp tröïc giao vaø u = 1, u A.
Ví duï 1 Xeùt tích voâ höôùng Euclide:
a) Trong khoâng gian 3 , hai vectô u = (1,−2,1) vaø v = (3,3,3) tröïc giao nhau vì u,v =1.3+ (−2).3+1.3 = 0. → →
b) Trong khoâng gian 3, taäp A = a = (a1, a2 , a3), b = (b1, b2, a3) vaø vectơ → a2
a3a3 a1a1 a2 → → → → , , v =
b2 b3b3 b1b1 b2
= a b = [ a , b ] tröïc giao nhau.
c) Trong khoâng gian 2, {i = (1,0), j = (0,1)} laø taäp tröïc giao và trực chuẩn.
d) Trong khoâng gian 3, {i = (1,0,0), j = (0,1,0),k = (0,0,1)} laø taäp tröïc giao và trực chuẩn.
e) Trong khoâng gian n, {e1 =(1,0,...,0),e2 =(0,1,...,0),...,en =(0,0,...,1)} laø taäp tröïc giao và trực chuẩn.
f) Trong khoâng gian 4, cho caùc taäp A={(1,0,1,0),(1,0,−1,0)} vaø B ={(0,1,0,2),(0,−2,0,1)}.
Deã thaáy moãi taäp A,Blaø taäp tröïc giao vaø taäp Atröïc giao taäp B . Lưu ý lOMoAR cPSD| 58794847
i) Trên không gian n có nhiều tích vô hướng khác nhau. Chẳng hạn như:
u = (u1, u2,…, un) n, v =(v1, v2,…, vn) n vaø 1, 2, …, n laø caùc soá thöïc döông. Khi ñoù ÑN
= 1u1 v1 + 2u2 v2 + .….+ nun vn
cũng laø moät tích voâ höôùng treân n.
Khi 1= 2= …= n = 1 thì tích voâ höôùng treân trôû thaønh tích voâ höôùng Euclide ÑN
u,v = u1v1 +u2v2 +...+unvn
ii) Tổng quát: Một tích vô hướng trên không gian vectơ là một ánh xạ < , > :
→ (tích vô hướng của hai vectơ cho kết quả là một số thực) (u,v)
u,v thỏa mãn 4 tính
chất sau : u, v, w ; k
i) u,v = v,u
ii) u + w,v = u,v + w,v iii) ku,v = k u,v
iv) u,u 0 ; u,u = 0 u = 0V
Không gian vectơ được trang bị một tích vô hướng gọi là không gian Euclide.
Ví duï 2 (Minh hoïa yù nghóa trong kinh teá )
Moät loaïi saûn phaåm saûn xuaát töø boán loaïi nguyeân lieäu I, II, III, IV vôùi giaù moãi ñôn
vò nguyeân lieäu laàn löôït laø x1,x2,x3,x4 vaø löôïng nguyeân lieäu caàn ñeå saûn xuaát moãi
saûn phaåm laàn löôït laø y1, y2, y3, y4; veùctô x =(x1,x2,x3,x4)laø veùctô ñôn giaù vaø y = (y1, y2,
y3, y4) laø veùctô nguyeân lieäu. Khi ñoù
Chi phí nguyeân lieäu ñeå saûn xuaát moãi saûn phaåm bieåu dieãn bôûi tích voâ
höôùng Euclide
x, y = x1y1 + x2y2 + x3y3 + x4y4
Khi giaù nguyeân lieäu I taêng 10%, nguyeân lieäu II taêng 12%, nguyeân lieäu III giaûm
10%, nguyeân lieäu loaïi IV taêng 5% thì chi phí nguyeân lieäu ñeå saûn xuaát moãi saûn
phaåm bieåu dieãn bôûi tích voâ höôùng lOMoAR cPSD| 58794847 x, y
=1,10x1y1 +1,12x2y2 + 0,9x3y3 +1,05x4y4
1.2.Tính chaát
Tích vô hướng trong n thỏa mãn các tính chất sau: u, v, w ; k i)
u,v = v,u i’) 0V ,v = 0 ; u
0 ; u =0 u =0V . ii)
u + w,v = u,v + w,v
ii’) u,v+w = u,v + u,w iii) ku,v = k
u,v iii’) u,kv =k u,v ; u,kv
= k u,v iv) u,u 0 ; u,u = 0 u =
0V ix’) ku = k. u v) u,v
u . v (Baát ñaúng thöùc Cauchy – Schwarz)
Daáu “ = “ xaûy ra khi u vaø v phuï thuoäc tuyeán tính (cuøng phöông)
vi) u + v u + v (Baát ñaúng thöùc tam giaùc).
Daáu “ = “ xaûy ra khi u vaø v cuøng chieàu (u = kv hay v = ku vôùi k
0) vii) Neáu A laø taäp tröïc giao vaø 0v A thì A laø taäp ñoäc laäp
tuyeán tính. viii) Neáu A laø taäp tröïc chuaån thì A ñoäc laäp tuyeán tính.
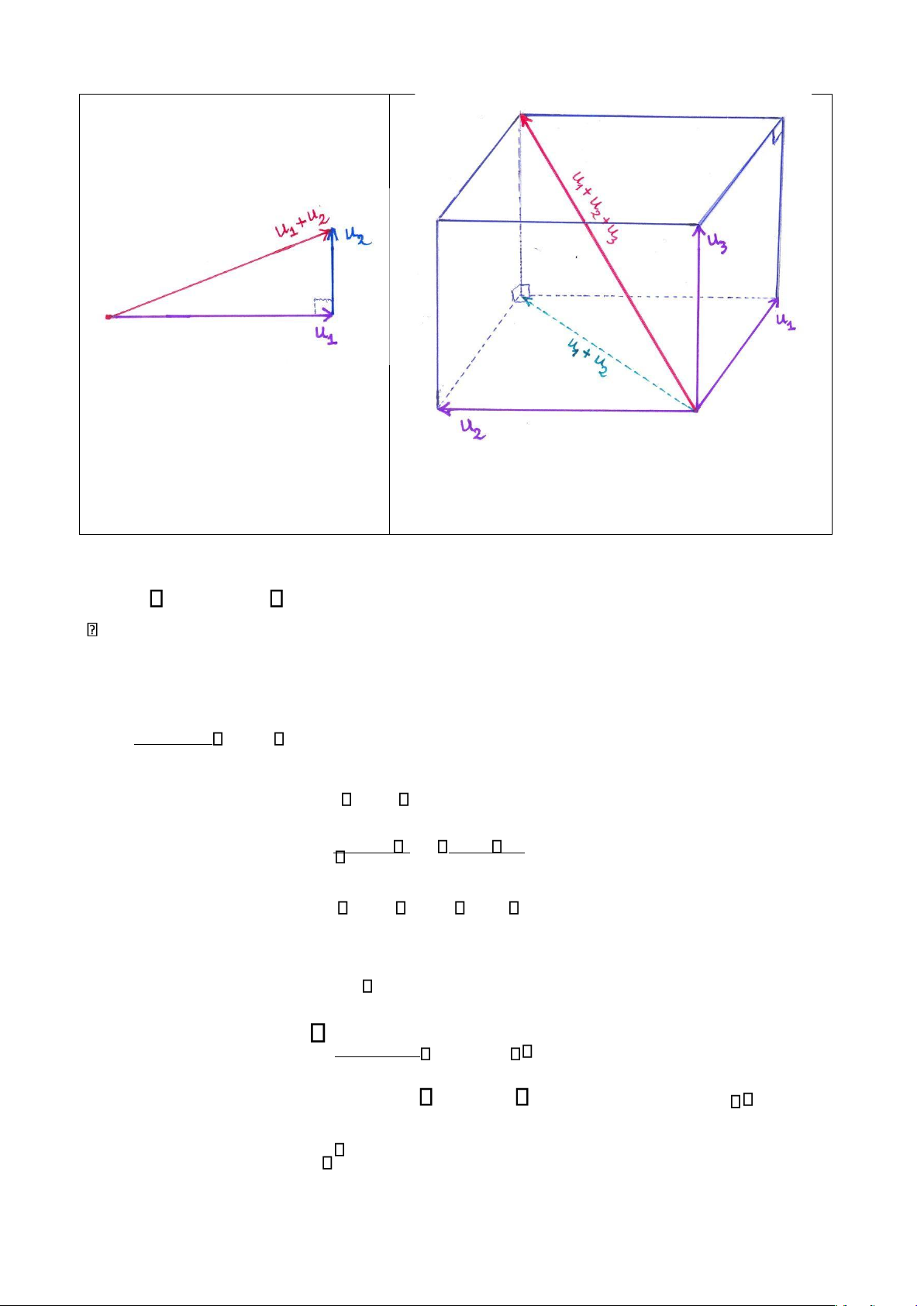
ix) Neáu A = u1,u2,.....,um laø taäp tröïc giao thì u 2 2 2 2 1 + u 2 +...+ u m
= u1 + u 2 +...+ u m (Ñònh lyù Pitago môû roäng )
Caùc caïnh goùc vuoâng: u1,u2,.....,um Caïnh huyeàn: u1 + u2 +...+ um Vaäy,
bình phöông caïnh huyeàn baèng toång bình phöông caùc caïnh goùc vuoâng.
Minh hoïa hình hoïc cho m = 2
Minh hoïa hình hoïc cho m = 3 lOMoAR cPSD| 58794847
Bình phöông caïnh huyeàn baèng
toång bình phöông hai caïnh goùc vuoâng.
Bình phöông ñöôøng cheùo hình hoäp chöõ nhaät
baèng toång bình phöông cuûa ba kích thöôùc.
1.3.Thuaät toaùn tröïc giao Gram – Schmidt (Gram-Schmidt orthogonalization algorithm)
Cho S = u1,u 2 ,......,u m laø moät heä vectô ñoäc laäp tuyeán tính trong khoâng gian Euclide . Ñaët: v1 = u1 v2 = u2 - u2 ,v1 v1 v1,v1 u3,v1 v u ,v 1- 3 2 v2 v3 = u3 - v1,v1 v2,v2  m−1 u vm = um - vmk,,vvkk vk. , k=1 Khi đó:
v1,v2,....,vm laø heä vectô tröïc giao; 1 v1 1 v2,...., 1 vm laø heä vectô tröïc lOMoAR cPSD| 58794847 v1 v2 vm chuẩn.
Ví duï 3 Aùp duïng thuaät toaùn tröïc giao Gram – Schmidt, haõy xaây döïng moät hệ vectơ
tröïc giao vaø moät hệ vectơ tröïc chuaån cuûa 3 töø tập B= u1 =(1,0,1),u2 =(0,1,1),u3 =(1,1,1) . Giaûi
v1 = u1 = (1,0,1) u2 ,v1 v 1
1= (0,1,1)- (1,0,1) = (− 1 ,1, 1) v2 = u2 - v1,v1 2 2 2 3 , v 1 u , v 3 2 2 2 1 1 1 1 1 u v u v v ( , 1 , 1 ) 1 1 ( 0 , 1 , ( , , 1 ) ( , , 3 = 3 1 2 ) − ) − 1 v , v 2 2 v1,v 2 3 3 1 v v v 1 = 2 2 = 3 = 2 2 2 3 3 3 3 1
Hệ vectơ tröïc giao E = {v1 = (1,0,1),v2 = (− ,1, ),v3 = ( , ,− )}. 2 1 1 1 2 1 1 1 1 , , 0 , , −
Hệ vectơ tröïc chuaån F = {w 1 = 2 2 (),w2 6 6 6 = 3 3 3 (− , ,),w3 = ()}
2. Ma trận đối xứng, ma trận trực giao
2.1. Định nghĩa
i) Ma traän vuoâng A = [aij]nxn goïi laø ma traän ñoái xöùng neáu AT = A (töùc laø aij = aji vôùi
i =1,n vaø j =1,n).
ii) Ma traän vuoâng A = [aij]nxn goïi laø ma traän tröïc giao neáu AT = A-1 (töùc laø AT A = I n = AAT ). lOMoAR cPSD| 58794847
2.2. Định lý
Ma traän thöïc A = [aij]nxn laø ma traän tröïc giao khi vaø chæ khi caùc vectô haøng (hay caùc
vectô coät) cuûa A laø heä vectô tröïc chuaån(theo tích voâ höôùng Euclide trong n).
Ví du 3 3 2 −2 1 1 2 2 − 1 1
a) A = 2 4 1 laø ma traän ñoái xöùng. b) A = 2 laø ma traän tröïc giao. −2 1 5 2
2.3 -Định lý Neáu A = [aij]nxn laø ma traän ñoái xöùng thöïc vuoâng caáp n thì:
i) Taát caû caùc trò rieâng cuûa A ñeàu laø soá thöïc. ii) Caùc vectô rieâng öùng vôùi caùc trò
rieâng khaùc nhau cuûa A thì tröïc giao (theo tích voâ höôùng Euclide trong n).
iii) Neáu laø trò rieâng boäi k cuûa A (töùc laø laø nghieäm boäi k cuûa phöông trình
ñaëc tröng cuûa A) thì öùng vôùi seõ coù k vectô rieâng ñoäc laäp tuyeán tính. iv) A seõ
coù n vectô rieâng tröïc chuaån.
v) A ñoàng daïng tröïc giao vôùi ma traän cheùo. Töùc laø, toàn taïi ma traän tröïc giao P sao cho
P−1AP = D = PTAP, với D laø ma traän cheùo. Ma traän P laø ma traän goàm caùc coät laø
caùc vectô rieâng tröïc chuaån cuûa A. Khi ñoù ta noùi A cheùo hoùa tröïc giao ñöôïc.
2.4 Thuaät toaùn cheùo hoùa tröïc giao ma traän ñoái xöùng
thöïc Cho ma traän ñoái xöùng thöïc A = [aij]nxn.
Böôùc 1 Giaûi phöông trình det(A - I) = 0 ñeå tìm caùc trò rieâng cuûa A.
Böôùc 2
Bước 2a) Neáu 1, 2, ..., k laø trò rieâng phaân bieät cuûa A thì laàn löôït giaûi k heä phöông trình
thuaàn nhaát (A - iI)X = 0 vôùi i =1,k ñeå tìm n vectô rieâng ñoäc laäp tuyeán tính cuûa A.
Bước 2b) Tröïc giao vaø sau ñoù chuaån hoùa caùc vectô rieâng ñoäc laäp tuyeán tính coù
ñöôïc ôû böôùc 2 (chæ caàn tröïc giao caùc vectô rieâng cuøng trò rieâng).
Böôùc 3 Neáu Y1, Y2, ..., Yn laø n vectô rieâng tröïc chuaån (coù ñöôïc ôû böôùc 3) laàn löôït öùng vôùi lOMoAR cPSD| 58794847
caùc trò rieâng 1, 2, ..., n thì ta ñaët ma traän P = (Y1, Y2, ..., Yn). 1 0  0 2 0     = D.
Khi ñoù P laø ma traän tröïc giao (PT = P-1) vaø: P-1AP = 0 0   n 0 0 1 1
Ví du 4 Cheùo hoùa tröïc giao ma traän A = 10 1 1 1 0 Giaûi - 1 1 2 2) = 0
λλ==−21 det(A - I) = 0 1 − 1 = 0 ( +1) ( − 1 1 − lOMoAR cPSD| 58794847 x 1 1 1 1 x1 0
= -1: X= x2 , (A +1I)X = 0 1 1 1 x2 = 0 x3 = -x1 – x2 x3 1 11 x3 0 1 X1 = 0 x1 1 0 −1  X2 = 1 X1 X2 −1 Suy ra X = x2 = x1 0 +x2 1 x1 -2 1 1 x1 0 0 − = 2: X = x 2 2 , (A–2I)X = 0 1 − x1 − x2 1 x2 = 0 −1 −1 x3 1 1 − 2 x3 0 x3 1 1 1 x1 =x3 1 X3 = X = x3 = x3 x2 =x3 x3 1 1 X3 1 ' 0 1 − 1 ,X1
Tröïc giao Ñaët X '1 = X1 = 0 ; X '2 = X2 - XX12' ,X1' X1' = −11 - 12 −01 = −1122 −1 lOMoAR cPSD| 58794847 1 Chuaån hoùa: Y1= X' 1 Y2= 1 Y3= Ñaët P = (Y1 Y2 Y3 ) = Khi ñoù P AP = 0 −1 0 = P AP. 0 0 2
3. Dạng toàn phương –1 T
3.1 . Ñònh nghóa Moät daïng toaøn phöông thöïc f (x1,x2,...,xn) cuûa n bieán (x1,x2,...,xn) laø
moät ña thöùc ñaúng caáp baäc hai theo caùc bieán x1,x2,...,xn . Töùc laø noù coù daïng n n
f (x) = f (x1,x2,...,xn) =
a ij xi x j vôùi aij = aji , i= 1,n vaø j=1,n i=1 j=1 Ví duï 5 x2 y2
a) f (x, y) = +
laø daïng toaøn phöông theo hai bieán x, y. 4 9 x2 y2 z2
b) f (x, y, z) = + +
laø daïng toaøn phöông theo ba bieán x, y, z. 4 9 16 lOMoAR cPSD| 58794847
c) f (x1,x2,x3)= x +x +x + x x + x x − x x laø daïng toaøn phöông theo ba bieán
x1, x2, x3.
3.2 . Ma traän cuûa daïng toaøn phöông n n
Cho daïng toaøn phöông f (x) = f (x1,x2,...,xn)= a ij xi x j vôùi aij = aji . i=1 j=1 x1 Neáu goïi
x2 ñaët= X → XT = (x1 x2 …… xn) xn
Khi ñoù daïng toaøn phöông f (x1,x2,...,xn)coù theå vieát laïi döôùi daïng ma traän laø n n
f (x) = f (x1,x2,...,xn)= a ij x i x j = XTAX i=1 j=1
a11 a12  a1n a22   a2n Trong ñoù ma traän A =  an2
 = [aij]nxn goïi laø ma traän cuûa daïng toaøn a 21   phöông an1 ann
f(x1,x2, … ,xn). Vì aij = aji neân A laø ma traän ñoái xöùng thöïc (töùc laø AT = A).
- Haïng cuûa ma traän A goïi laø haïng cuûa daïng toaøn phöông f, kyù hieäu r(f).
- Daïng toaøn phöông f goïi laø khoâng suy bieán neáu r(f) = n, daïng toaøn phöông f goïi
laø suy bieán neáu r(f) < n. Ví duï 6 1 x2 y2 410
a) Daïng toaøn phöông f (x, y) = + coù ma traän A= 4 9 0 lOMoAR cPSD| 58794847 9 1 0 0 x2 y2 z2 04
b) Daïng toaøn phöông f (x, y, z) = + + coù ma traän A= 4 9 16 0 0 1 0 16
c) Daïng toaøn phöông f (x 2 2 2
1,x2,x3)= x1 + 3x2 + 5x3 + 2x1x2 + 4x1x3 − 2x2x3 coù ma traän 1 1 2 3 A= 1 −1 −1 . 2 5
d) Với hàm số hai biến z = f (x, y) , vi phân toàn phần cấp hai d2 f (x, y)=f ' ' 2f 2 2 2f dxdy + 2f dy2= d2z là dạng toàn
xxdx2 + 2fxy' ' dxdy + fyy' ' dy2 = x2 x y y2 dx +
phương hai biến dx,dy và có ma trận là 2f 2f x y x2 =H -ma trận Hessian 2f 2f x y y2
e) Với hàm số ba biến u = f (x, y,z) , vi phân toàn phần cấp hai
d2 f (x, y,z)= fxx' ' dx2 +fyy' ' dy2 +fzz' ' dz2 + 2fxy' ' dxdy + 2fxz' ' dxdz + 2fyz' ' dydz lOMoAR cPSD| 58794847 = x2f dx2 + y2f dy2 + z2f2 dz2 + 2 x2 fy dxdy + 2 x2 fz dxdz + 2 y2 fz dydz 2 2
là dạng toàn phương ba biến dx,dy,dz và có ma trận là 2f 2f 2f 2 x y x z x 2f 2f 2f 2 y z = H -ma trận Hessian y y x 2f 2f 2f x z y z z2
3.3. Daïng chính taéc cuûa moät daïng toaøn phöông
Daïng toaøn phöông fCT(y) goïi laø chính taéc neáu trong moät cô sôû B naøo ñoù noù y coù daïng f 2 2
CT (y) = 1 1 + 2 y 2 + ...+ n y 2n 1 0  0 y1 2   0 y2  Ñaët D = 0 0   ,Y =  YT = (y1 y2 .... .yn)  0 n yn
Khi ñoù daïng toaøn phöông fCT(y) coù theå vieát laïi döôùi daïng ma traän laø 1 0  0 y1 fCT(y) = (y1 y2 … .yn)
0 2  0 y2 = YTDY 0 0  n yn lOMoAR cPSD| 58794847
Ma traän D chính laø ma traân cuûa fCT trong cô sôû B. Ñaëc bieät khi λi = 1 hay λi = 0vôùi
i =1,n thì daïng toaøn phöông fCT goïi laø daïng chuaån.
Cho daïng toaøn phöông f(x) = XTAX . Giaû söû coù ma traän khaû nghòch P sao cho
PTAP = D laø ma traän cheùo. Thöïc hieän pheùp ñoåi bieán X = PY , suy ra XT =YTPT , ta
ñöôïc f(x) = XTAX = YTPTAPY = YTDY = fCT(y). Khi ñoù ta noùi pheùp ñoåi bieán (tuyeán tính
khoâng suy bieán) X = PY ñöa daïng toaøn phöông f veà daïng chính taéc laø fCT.
3.4. Thuật toán đưa dạng toàn phương về dạng chính tắc bằng phép
biến đổi trực giao
Cho daïng toaøn phöông thöïc trong cô sôû chính taéc E cuûa n laø n n f (x)
= f (x1,x2,...,xn) = a ij xi x j i=1 j=1
Böôùc 1 Vieát ma traän A cuûa f , giaûi phöông trình det(A-λI ) = 0 ñeå tìm caùc trò rieâng cuûa A. Böôùc 2
Bước 2a) Neáu λ1 , λ2,..., λk laø k trò rieâng phaân bieät cuûa A thì laàn löôït giaûi k heä phöông x1 x trình tuyeán tính (A-λ 2 i I )X = 0 vôùi X= 
, i = 1,k ñeå tìm caùc vectô treân cô sôû cuûa A. xn
Bước 2b) Tröïc giao vaø chuaån hoùa caùc vectô rieâng cô sôû coù ñöôïc ôû böôùc 2(chæ
caàn tröïc giao caùc vectô rieâng cuøng trò rieâng). Böôcù 3
Bước 3a) Neáu Y1, Y2, ….., Yn laø caùc vectô rieâng cô sôû tröïc chuaån cuûa A(coù ñöôïc ôû
böôùc3) laàn löôït töông öùng vôùi caùc trò rieâng λ1 , λ2,....., λn thì ñaët P =( Y1,Y2 , … ,Yn). Khi đó P laø 1 0  0 lOMoAR cPSD| 58794847  0
ma traän tröïc giao ( PT = P−1) và P-1AP = 0 2      = D. 0 0  n x1 y1 x y
Bước 3b) Khi ñoù vôùi X = 2 2  , Y = 
thì pheùp bieán ñoåi tröïc giao X = PY ñöa daïng xn yn
toaøn phöông f veà daïng chính taéc laø f 2
CT(y) = λ1y1 + λ 2 y22 +... + λ n y2n
. Ví duï 7 Cho daïng toaøn phöông f(x 2 2 2
1,x2,x3)= 2x1 + 5x2 + 2x3 + 4x1x2 + 2x1x3 + 4x2 x3
Ñöa daïng toaøn phöông f veà daïng chính taéc baèng phöông phaùp bieán ñoåi tröïc giao. Giaûi 2 2 1
Ma traän daïng toaøn phöông f laø A = 2 5 2 1 2 2 2 - 2 1 det(A - I) = 0 2 5 − 2 = 0 1 2 2 − 1 x1 0 x1 1 2 4 2 x2 = 0
= 1: X = x2 ,(A–1I)X = 0 2 2 1 x3 0 x3 1 ( −1)2 ( − 7) = 0 λλ ==17
x1 + 2x2 + x3 = 0 x3 = -x1 – 2x2 1 lOMoAR cPSD| 58794847 x1 1 0 1 = −01 X X = x2 = x1 0 +x2 1 0 − x1 − 2x2 −1 −2 X2 = 1 X1 X − 2 2 x1 - 5 2 1 x1 0
= 7: X = x2 , (A–7I)X = 0 2 − 2 2 x2 = 0 x3 1 2 − 5 x3 0 x3 1 1 x1 = x3 X = 2x3 = x3 2 X3 = 2 x2 = 2x3 x3 1 1 X 3 Tröïc giao 1 ' Ñaët X1 = X1 = −01 ; X '2 = X2 - XX12' ,,XX11' X1' = −102 - 22 −101 = −−111 1 Chuanå hoùa Y1= ' X1' = −021 ⎯Trò⎯ rieâng⎯⎯
töông⎯⎯ öùng⎯→ = 1 1 lOMoAR cPSD| 58794847 X1 2 −1 3 1 Y2= 1X '2 = 3
⎯Trò⎯ rieâng⎯⎯ töông⎯⎯ öùng⎯→ = 1 X'2 −1 3 1 6
Trò rieâng töông öùng = 7 Y3= X3= 1 2 ⎯⎯⎯⎯⎯⎯⎯→ X3 1 6 6 1 −1 1 2 3 6 1 0 1 0 0 3 6 − 1 − 1 1 2 TAP = 0 2 3 6 1 0 = D. Ñaët P = (Y1 Y2 Y3 ) =
laø ma traän tröïc giao và P 0 0 7 x1 y1
Vôùi X = x2 , Y = y2 , pheùp ñoåi bieán tröïc giao X = PY ñöa daïng toaøn phöông f veà daïng x3 y3 chính taéc laø f 2 2 CT(y) = y1 + y 22 + 7y3 .
Ví duï 8 Cho daïng toaøn phöông :f(x 2 2
1,x2) = 4x1 + 4x2 + 2x1x2 lOMoAR cPSD| 58794847
Ñöa daïng toaøn phöông f veà daïng chính taéc baèng phöông phaùp bieán ñoåi tröïc giao.
Tính Anvôùi A laø ma traän daïng toaøn phöông. Giaûi 4 1
Ma traän daïng toaøn phöông f laø: A = 1 4 4 − 1 det(A - I) = 0 = 0 Trò rieâng = 3; = 5 1 4 − = 3: X = xx12 ,(A–3I)X = 0 11 11 xx12 = 00 X = −xx11 = x1 −11 X1 = 5: X = xx12 ,(A–5I)X = 0 −11 −11 xx12 = 00 X = xx22 = x2 11 X2
= 3⎯⎯vectô⎯ rieâng⎯ cô⎯⎯ sôû → X1 = −11 , = 5 ⎯⎯vectô⎯
rieâng⎯ cô⎯⎯ sôû → X2 = 11 1 Chuaån 1 hoùa Y = −11 , Y2 = 1 11 2 2 1 1 2 2 1 1 2 2 Ñaët P =
laø ma traän tröïc giao. Khi ñoù P − -1AP = 0350 = D = PTAP .