Đề 1 - Ôn tập full lớp 12 môn Toán ứng dụng | Trường Đại học Sư phạm Thành phố Hồ Chí Minh

lOMoAR cPSD| 22014077 ĐỀ SỐ 59
ĐỀ RÈN LUYỆN MÔN TOÁN 12
HƯỚNG ĐẾN KÌ THI THPT QUỐC GIA
Trắc nghiệm: 50 câu Nội dung:
Thời gian: 90 phút
FULL KIẾN THỨC TOÁN 12+
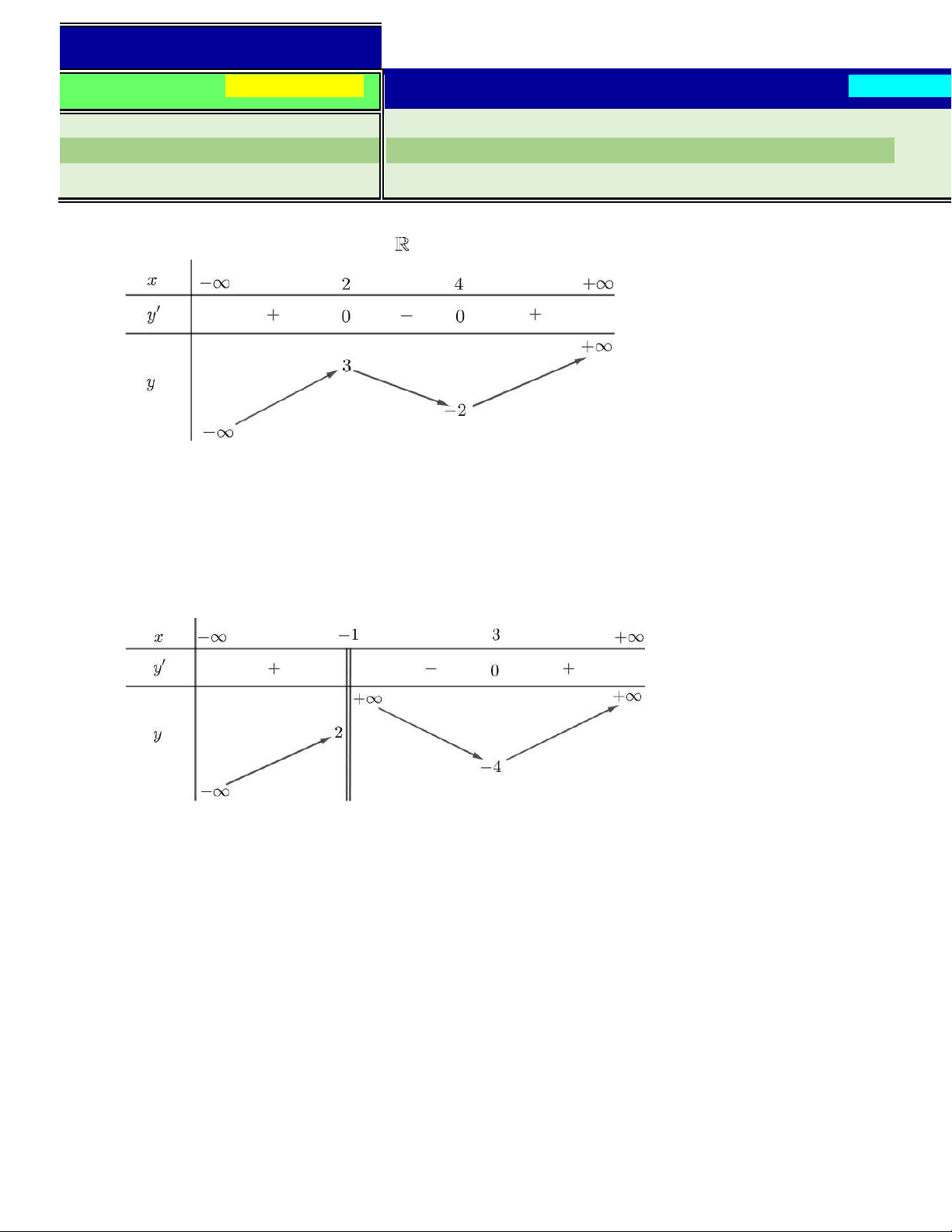
Câu 1. Cho hàm s ố y = ()
fx liên t ụ c trên và có b ả ng bi ế n thiên sau
Khẳng ịnh nào sau ây là úng?
A. Hàm số ạt cực ại tại x =3.
B. Hàm số ạt cực ại tại x = 2.
C. Hàm số ạt cực ại tại x = −2.
D. Hàm số ạt cực ại tại x = 4.
Câu 2. Cho hàm số y = f x( ) có bảng biến thiên như sau. Tổng các giá trị nguyên của m ể ường thẳng
y = m−1 cắt ồ thị hàm số y = f x( ) tại ba iểm phân biệt bằng A. 6 . B. 1. C. 0 . D. 3.
Câu 3. Tìm phương trình mặ 3
t cầu có tâm là iểm I (1;2; ) và tiếp xúc với trục Oz .
A. (x− + − + − =1)2 (y 2)2 (z 3)2 5.
B. (x− + − + − =1)2 (y 2)2 (z 3)2 13.
C. (x− + − + − =1)2 (y 2)2 (z 3)2 14.
D. (x− + − + − =1)2 (y 2)2 (z 3)2 10.
Câu 4. Cho hàm số y = f x( ) có bảng biến thiên như sau: lOMoAR cPSD| 22014077
Tổng số ường tiệm cận ứng và tiệm cận ngang của ồ thị hàm số ã cho là A. 2 . B. 3. C. 4 . D. 1.
Câu 5. Trong không gianOxyz . ab
, gọi là góc giữa hai vectơ a và b , với a và b khác 0 , khi ó B. cos bằng . ab
A. ab. . . C. ab. . D. 3 5 4
ab. . a b.a + b a b. x
Câu 6. Rút gọn biểu thức P = x với x 0.
A. P = x .
B. P = x .
C. P = x .
D. P = x .
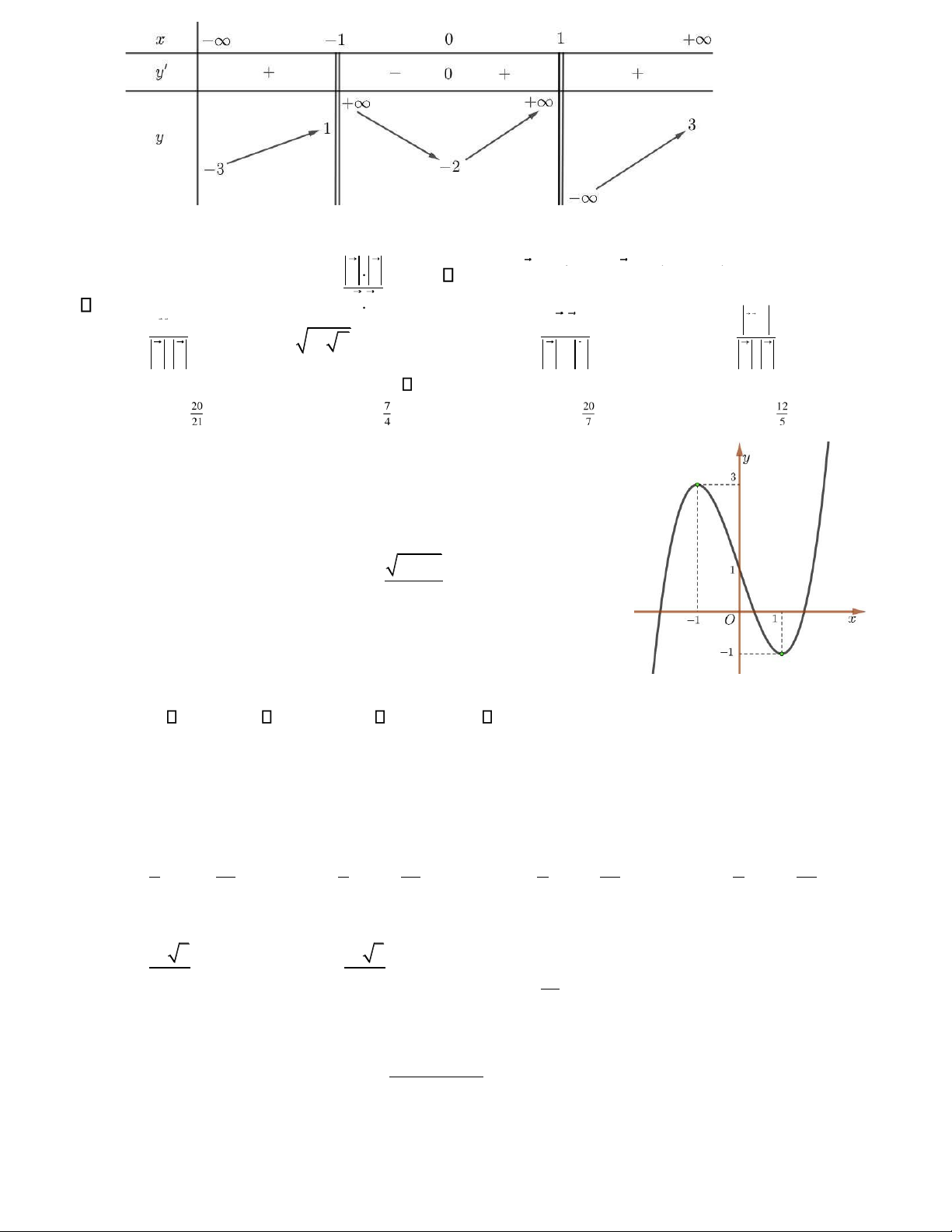
Câu 7. Hình bên là ồ thị của hàm số nào trong các hàm số ược liệt kê ở bốn
phương án A, B, C, D dưới ây?
A. y = −x3 +3x−1. B. y = −x3 −3x+1. C. y = x3 −3x+1.
D. y = x3 +3x+1.
Số tiệm cận của ồ thị hàm số y =
4− x2 là Câu 8. x+3 A. 0 . B. 1. C. 2 . D. 3.
Câu 9. Tìm tất cả các giá trị của m ể phương trình 2025x = m có nghiệm thực. A. m 1. B. m 0. C. m 0. D. m 0.
Câu 10. Có bao nhiêu cách chọn hai học sinh từ nhóm 41 học sinh? A.412 . B. A 2 2 41 . C.241. D. C41 .
Câu 11. Trong không gianOxyz , cho các iểm A(4; 3;− 2), B(6;1;−7),C(2;8;−1). Viết phương trình ường thẳng
i qua gốc tọa ộ O và trọng tâm G của tam giác ABC . x x x x A. = =y z . B. = =y z . C. = =y z . D. = =y z . 2 − −1 1 2 1 −1 2 3 −1 4 1 −3
Câu 12. Tính thể tích khối chóp tứ giác ều cạnh áy bằng a, chiều cao bằng 3a . A. a3 3 a3 3 a3 3 . . B. . C. . D. a 12 4 3 = 1
Câu 13. Tìm họ nguyên hàm của hàm số y
sin2 x .cos2 x . lOMoAR cPSD| 22014077
A.2cot2x+C .
B. −cot2x C+ .
C. cot2x+C .
D. −2cot2x C+ .
Câu 14. Trong không gian Oxyz , iểm nào dưới ây nằm trên mặt phẳng ( )P :2x − y + z −2 = 0 .
A. Q(1; 2;− 2).
B. N (1; 1;−−1).
C. P(2; 1;− −1).
D. M (1;1;−1). 4044 4044 Câu 15. Cho biết 2022 2 f x( )− 1x
dx = 2a với a , khi ó 2022
f x( )dx bằng: A. a+ln2. B. a−ln2. C. a + ln2. D. a + ln2. =
Câu 16. Cho tập hợp A 10;10 ;10 ;...102 3 10 .
tích các phần tử của tập S . Gọi S là A. 60 B. 24 tập các C. 120 D. 720 . số
Câu 17. Tính ạo hàm của hàm số y = ln sin( ) x . nguyên có dạng A. y ' = 1.
B. y ' = −12 .
C. y' = tan x .
D. y' = cot x . log 100 m với m A . Tính sin x sin x
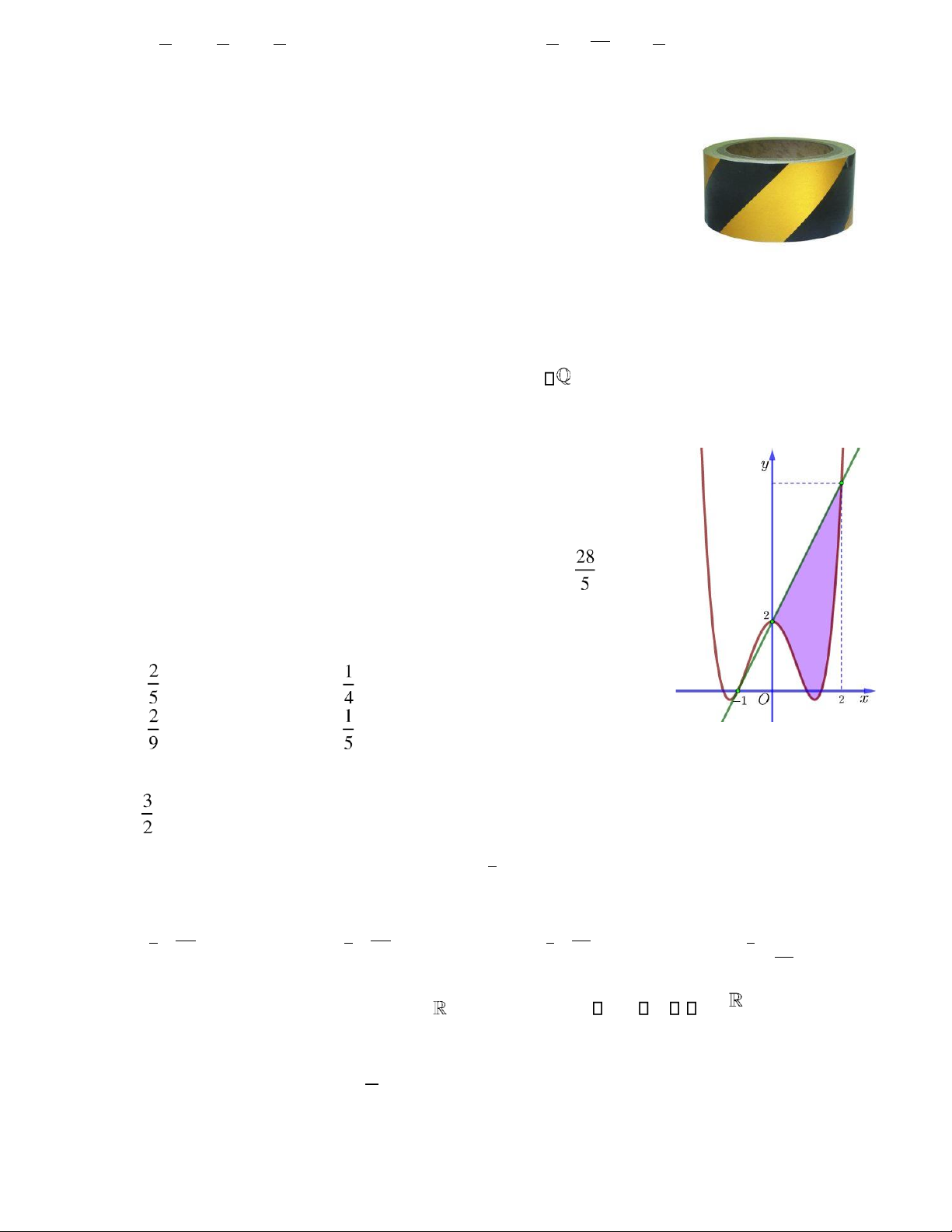
Câu 18. Cho ồ thị hàm số y = f x( ). Diện tích S của hình phẳng (phần tô ậm trong hình vẽ) là 1 3 A. S = −
f x( )dx+ f x( )dx. 0 1 1 3 B. S =
f x( )dx− f x( )dx . 0 1 3 C. S = f x( )dx. 0 1 3 D. S =
f x( )dx+ f x( )dx. 0 1 lOMoAR cPSD| 22014077
Câu 19. Cho cấp số cộng (u ) = = n
, biết u2 3 và u4 7. Giá trị của u15 bằng A. 27. B. 31. C. 35. D. 29.
Câu 20. Thể tích của khối nón có chiều cao bằng 4 và ường sinh bằng 5 bằng A. 16 . B. 48 . C. 12 . D. 36 . 2 Câu 21. Tích phân 2 dx bằng. 0 2x+1 A. 2ln5. B. ln5 . C. ln5. D. 4ln5.
Câu 22. Tiếp tuyến của ồ thị hàm số y x= − +3 3x2 1 có hệ số góc nhỏ nhất là ường thẳng A.
D. y =− +3x 2. y=0.
B. y =− −3x 2. C. y x= .
Câu 23. Số giao iểm của ồ thị hàm số y=− + +x x4 2 2024 và trục hoành là A. 2. B. 4. C. 3. D. 1.
Câu 24. Hàm số y = (x+1) 12 xác ịnh khi A. x −1. B. x . C. x 1. D. x −1. m Câu 25. Nếu
(2x −1)dx = 2 thì m có giá trị bằng 0 m=1 m =1 m = −1 m=−1 A. =−2. B. m = 2 . C. m = 2 . m D. =−2. m
Câu 26. Cho hình nón có bán kính áy R , ường cao h . Diện tích xung quanh của hình nón này là A. Rh. B. 2 Rh.
C. R R2 + h2 .
D. 2 R R2 + h2 .
Câu 27. Tập nghiệm của bất phương trình log22 x−3log2 x+2 0 là A.(2;4). B.(1;4) . C.(1;2) . D.(0;2). sin2x+sin x
Câu 28. Cho tích phân I = 2
dx . Thực hiện phép biến ổi t = 1 3+ cosx , ta có thể ưa I về dạng 0 1+3cos x nào sau ây? 2 2 2 2 A. ( ( ( ( I = 1
2t2 +1)dt . B. I = 1
t2 + 2)dt . C. I = 2
2t2 +1)dt . D. I = 2 t2 + 2)dt . 2 9 2 9 1 9 1 9 lOMoAR cPSD| 22014077
Câu 29. Xét hình trụ T có thiết diện qua trục của hình trụ là hình vuông cạnh bằng a. Tính diện tích toàn phần S của hình trụ. 2.
B. S = a2 .
C. S = a2 .
D. S = 3 a2 .
A. S = 4 a 2 2
Câu 30. Cho a là một số thực dương khác 1. Có bao nhiêu mệnh ề úng trong các mệnh ề sau?
1. Hàm số y =loga x có tập xác ịnh là D = (0;+ ).
2. Hàm số y =loga x ơn iệu trên khoảng (0;+ ).
3. Đồ thị hàm số y =loga x và ồ thị hàm số y = ax ối xứng nhau qua ường thẳng y x= .
4. Đồ thị hàm số y =loga x nhận trục Ox là một tiệm cận. A. 3. B. 1. C. 4 . D. 2 .
Câu 31. Điều kiện cần và ủ ể hàm số y = ax4 +bx2 +c có hai iểm cực ại và một iểm cực tiểu là
A. a 0, b 0.
B. a 0, b 0.
C. a 0, b 0.
D. a 0, b 0.
Câu 32. Trong không gian Oxyz , cho mặt phẳng ( ) :3x −2y + z +6 = 0 . Hình chiếu vuông góc của iểm A(2;
1;− 0) lên mặt phẳng ( ) có tọa ộ là A. (1;0;3). B. (2; 2;− 3). C. (1;1;−1) . D. (−1;1;−1) .
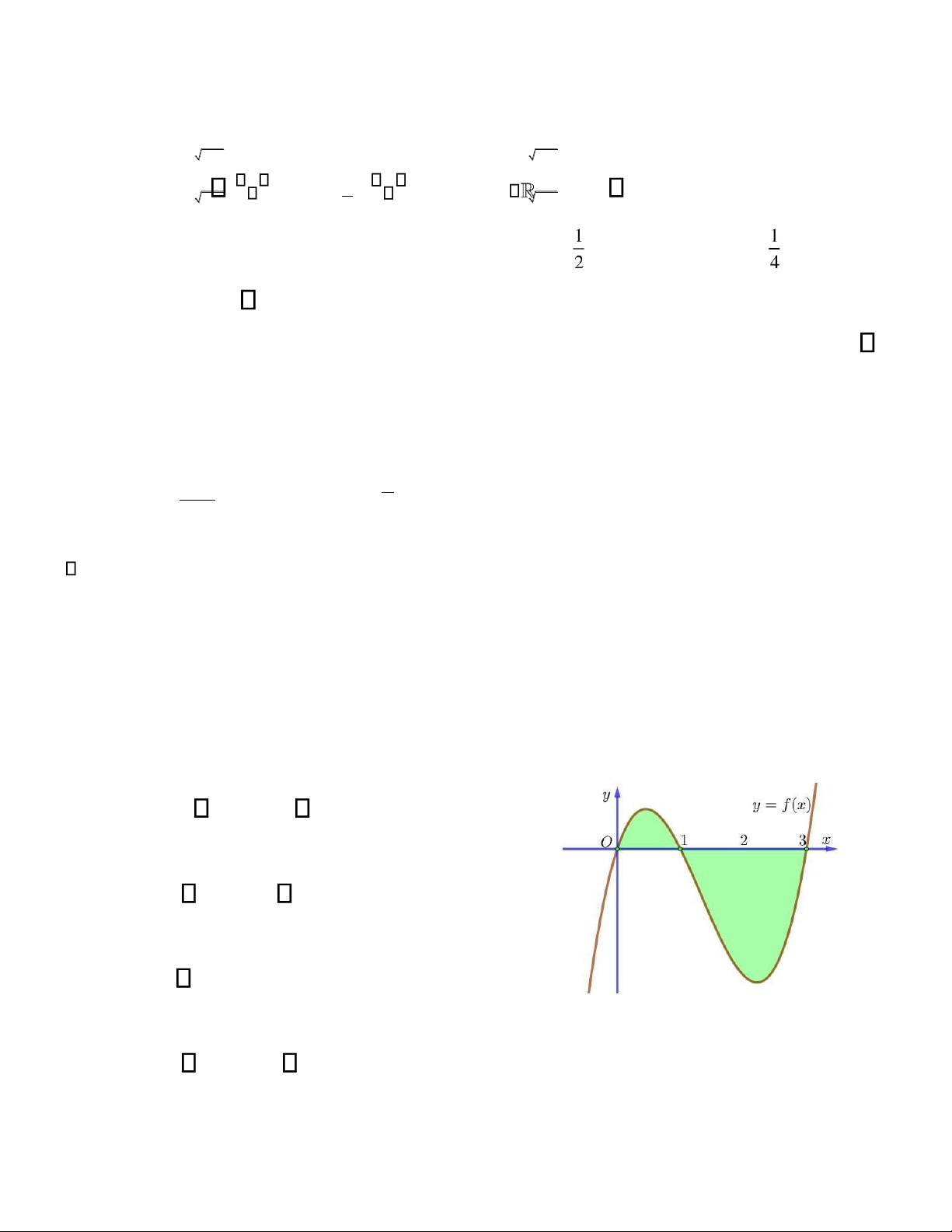
Câu 33. Trong mặt phẳng tọa ộ, cho iểm M như hình vẽ bên là iểm biểu
diễn của số phức z . Tính (1+ z)2
A. (1+ z)2 =−2i.
B. (1+ z)2 =−8i. C. (1+ z) =− + 2 1 i .
D. (1+ z)2 =− +2 2i.
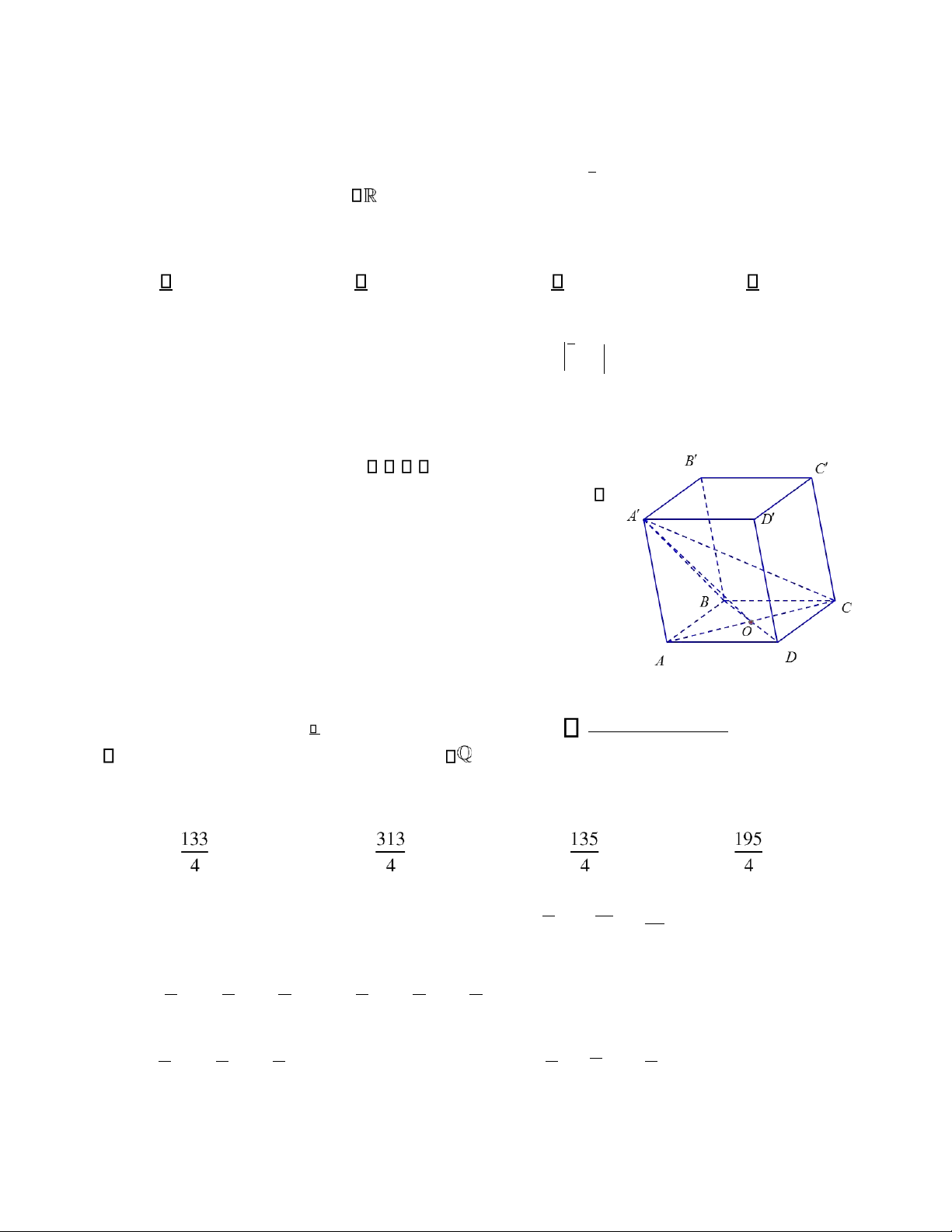
Câu 34. Cho hình chóp S ABC.
có SA a= 3, SA vuông góc với mặt phẳng (ABC), tam giác ABC vuông tại
B AB, = a , tam giác SBC cân. Thể tích khối chóp S ABC. bằng a 3 a 3 A. . B. a3 3. C. 3 . D. 3 . 3 6 1
Câu 35. Cho x a b,
, là các số thực dương thỏa mãn log = 7 2log7
a −6log49 b. Khi ó giá trị của x là x 3 2 = b = a
A. x = 2a−3b. B. x 2 . C. x
3 . D. x = a b2 3. a b lOMoAR cPSD| 22014077
Câu 36. Cho tứ diện ABCD có AB AC AD, , ôi một vuông góc với nhau và AB = AC = AD . Góc giữa CD và ( ) ABC bằng 0 B. 30 .0 C. 60 .0 D. 90 .0 A. 45 .
Câu 37. Cho số phức z = a+bi với a b,
thỏa mãn (1+i z) +(2−i z) =13+2i . Tính tổng a b+ A. a b+ =1. B. a b+ = −2.
C. a+b = 2. D. a b+ = 0.
Câu 38. Tính diện tích mặt cầu ngoại tiếp một hình lăng trụ tam giác ều có các cạnh ều bằng a. 7 a2 7 a2 7 a2 3 a2 A. . B. . C. . D. . 3 6 5 7
Câu 39. Tập hợp tất cả các iểm biểu diễn các số phức z thỏa mãn: z + 2−i = 4 là ường tròn có tâmI và bán kính
R lần lượt là:
A. I (−2;−1) ; R=4.
B. I (−2;−1) ;R=2.
C. I (2;−1); R=4.
D. I (2;−1); I (2;−1).
Câu 40. Cho khối lăng trụ ABCD ABCD. có thể tích bằng 12, áy
ABCD là hình vuông tâm O. Thể tích của khối chóp A BCO . bằng A. 1. B. 4 . C. 3. D. 2 . = )
Câu 41. Biết rằng tích phân I 4
ln sin( x+215cos x
dx = a +bln2+cln3+d ln5, trong ó a b c d, , , . 0 cos x
Tính T = a+b+c+d . A. T = . B. T = . C. T = . D. . x−1
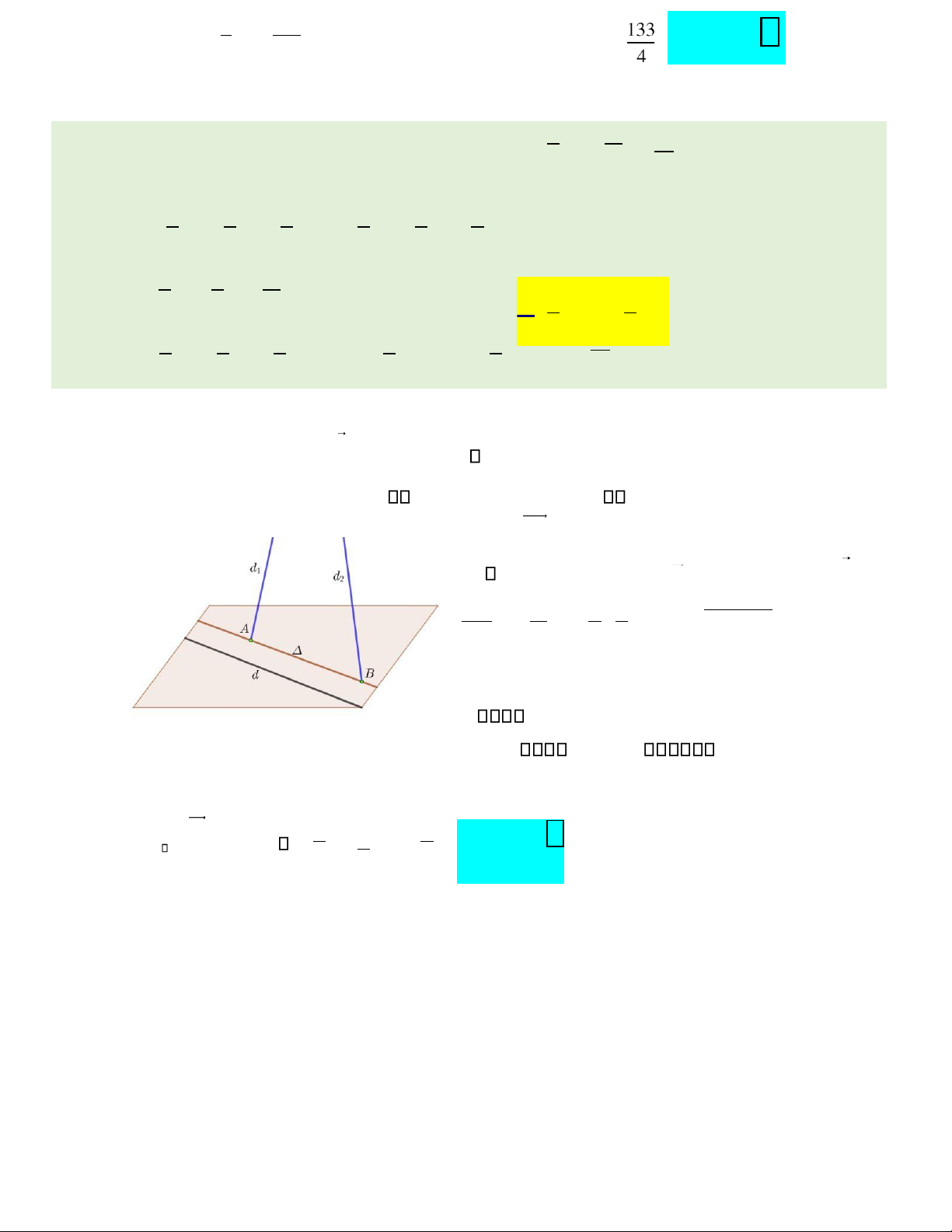
Câu 42. Phương trình ường thẳng song song với ường thẳng d :
= y+ 2 = z và cắt hai ường thẳng 1 1 −1
d1 : x +1 = y +1 = z −2 ; d2 : x −1 = y −2 = z −3 là: 2 1 −1 −1 1 3
A. x +1 = y +1 = z −2 .
B. x −1 = y = z −1. −1 −1 1 1 1 −1 lOMoAR cPSD| 22014077
C. x −1 = y −2 = z −3 . D. x −1 = y = z −1. 1 1 −1 1 −1 1
Câu 43. Một tấm ề can hình chữ nhật ược cuộn tròn lại theo chiều dài tạo thành
một khối trụ có ường kính 50 (cm). Người ta trải ra 250 vòng ể cắt chữ và
in tranh cổ ộng, phần còn lại là một khối trụ có ường kính 45 (cm). Hỏi
phần ã trải ra dài bao nhiêu mét (làm tròn ến hàng ơn vị)? A. 373 (m). B. 187 (m). C. 384 (m). D. 192 (m).
Câu 44. Cho hàm số y = x4 +2mx2 +m (với mlà tham số thực). Tập tất cả các giá trị của tham số m ể ồ thị hàm
số ã cho cắt ường thẳng y =−3 tại bốn iểm phân biệt, trong ó có một iểm có hoành ộ lớn hơn 2 còn ba iểm kia có hoành ộ ;
nhỏ hơn 1, là khoảng (a b ) (với a b,
; a,b là phân số tối giản). Khi ó, 15ab nhận
giá trị nào sau ây? A. −63. B. 63. C. 95. D. −95.
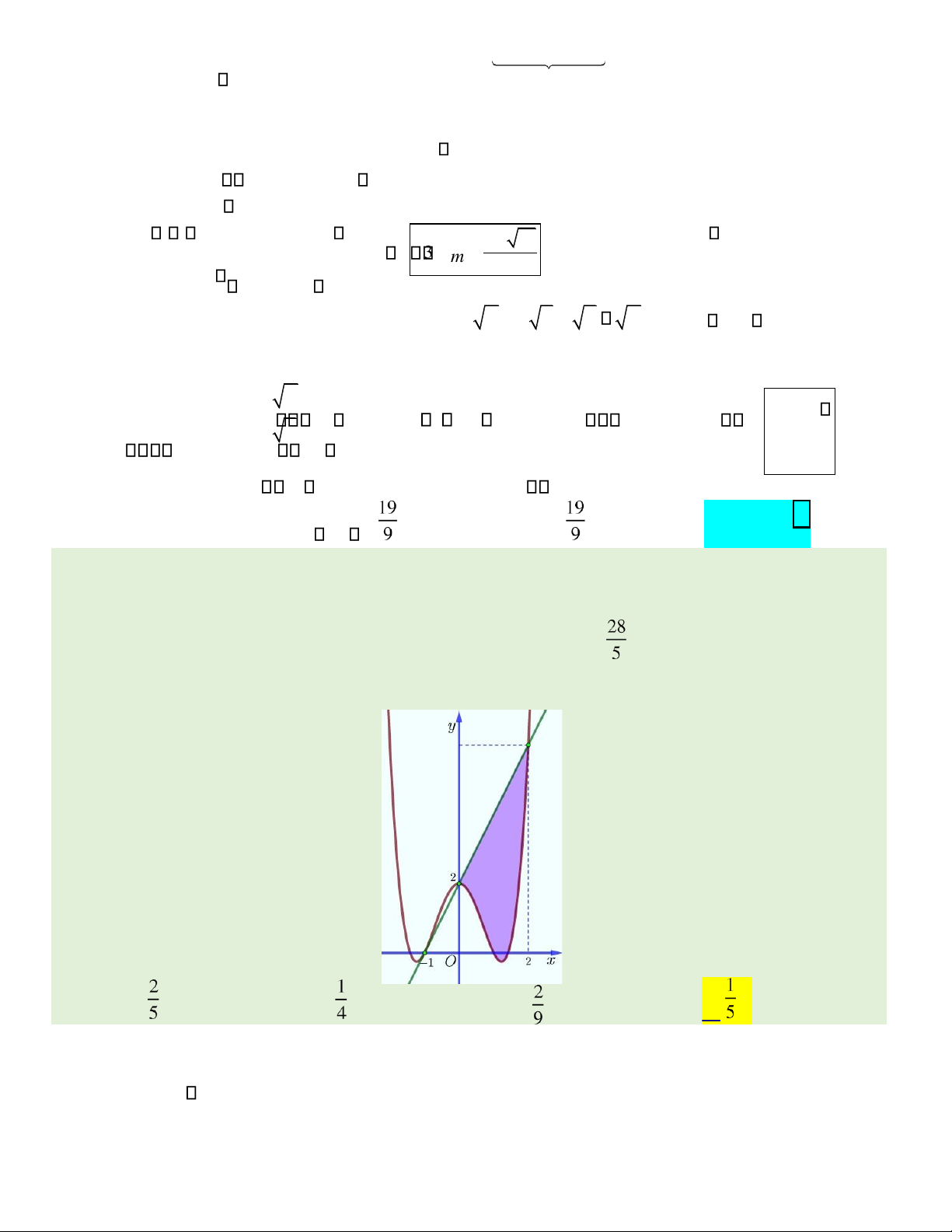
Câu 45. Cho hàm số y = ax4 +bx2 +c có ồ thị ( )C , biết rằng ( )C i qua iểm 0
A(−1; ). Biết tiếp tuyến d tại A của ( )C cắt ( )C tại hai iểm có hoành
ộ lần lượt là 0 và 2 ; ồng thời diện tích hình phẳng giới hạn bởi ường
thẳng d , ồ thị ( )C và hai ường thẳng x = 0, x = 2 có bằng (phần tô
màu trong hình vẽ). Diện tích hình phẳng giới hạn bởi d, ( )C và hai
ường thẳng x = −1, x = 0 bằng A. . B. . C. . D. .
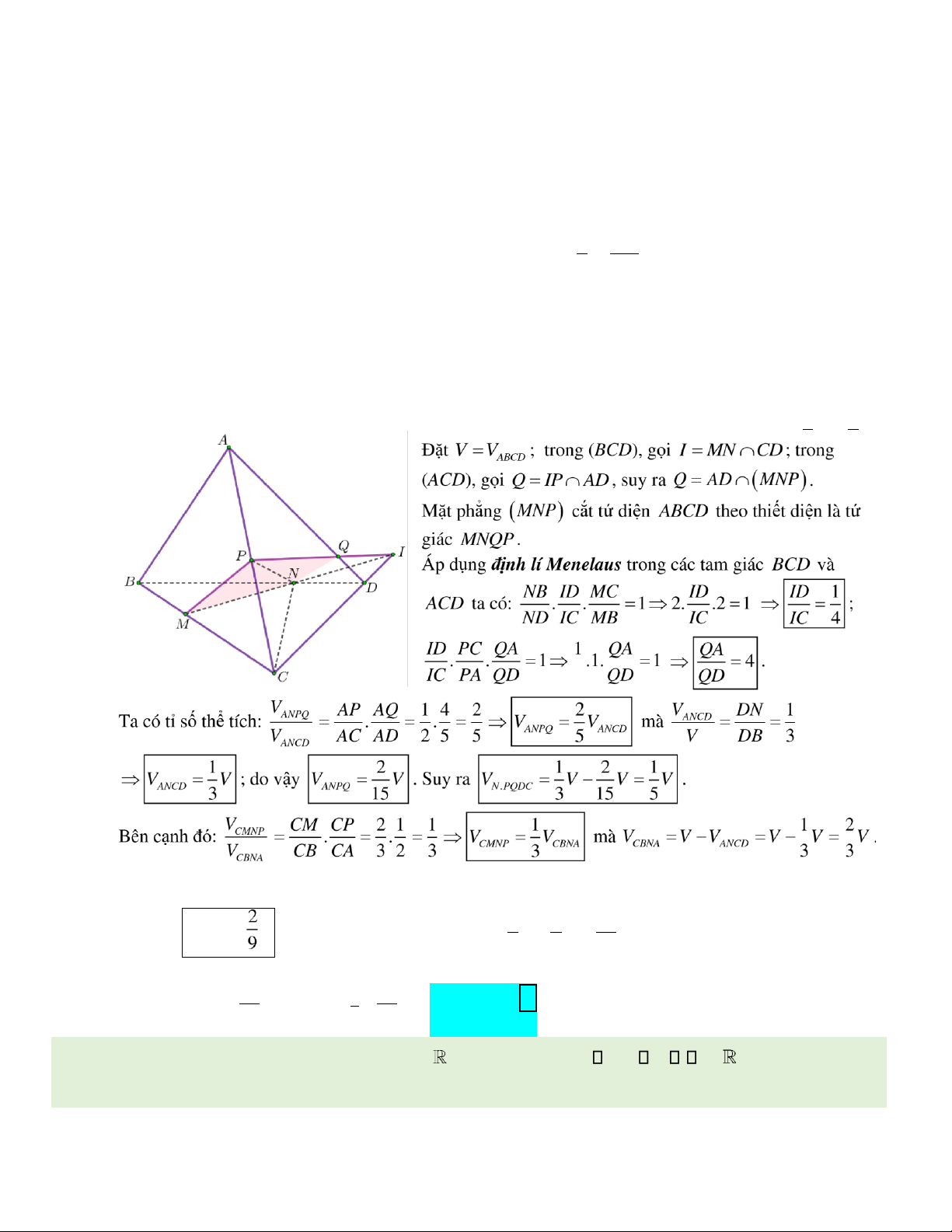
Câu 46. Cho tứ diện ABCD, trên các cạnh BC , BD, AC lần lượt lấy các iểm M , N , P sao cho BC =3BM , BD
= BN , AC = 2AP. Mặt phẳng ( )
MNP chia khối tứ diện ABCD thành hai phần có thể tích là V1, V2 với V V 1
1 là thể tích khối a diện chứa ỉnh B. Tính tỉ số . V2 A. V = = = = 1 26 . B. V1 26 . C. V1 3 . D. V1 15 . V2 13 V2 19 V2 19 V2 19
Câu 47. Cho hàm số f x( ) có ạo hàm liên tục trên thỏa mãn f x( )+ f ( )x 1, x và f ( )0 = 0. Tìm giá
trị lớn nhất của f ( )1 . 2e −1 e 1− lOMoAR cPSD| 22014077 A.
. B. . C. e 1− . D. 2e−1. e e ;2;3 , 4
Câu 48. Trong không gian Oxyz , cho hai iểm A(1 ) ( ) B 2;3;
. Một mặt cầu ( )S bán kính R luôn tiếp xúc
với ba mặt phẳng tọa ộ và oạn thẳng AB luôn nằm trong ( )S (mọi iểm thuộc oạn thẳng AB ều nằm
trong ( )S ). Giá trị nguyên lớn nhất của R ạt ược là: A. 4. B. 6. C. 5. D. 3.
Câu 49. Cho ba số thực dương a b c, ,
thỏa mãn abc =10. Biết giá trị lớn nhất của biểu thức m F =5log .loga
b+2log .logb c+log .logc a bằng với m n,
nguyên dương và m tối giản. Tổng n n
m+n bằng A. 7 . B. 10. C. 13. D. 16. .
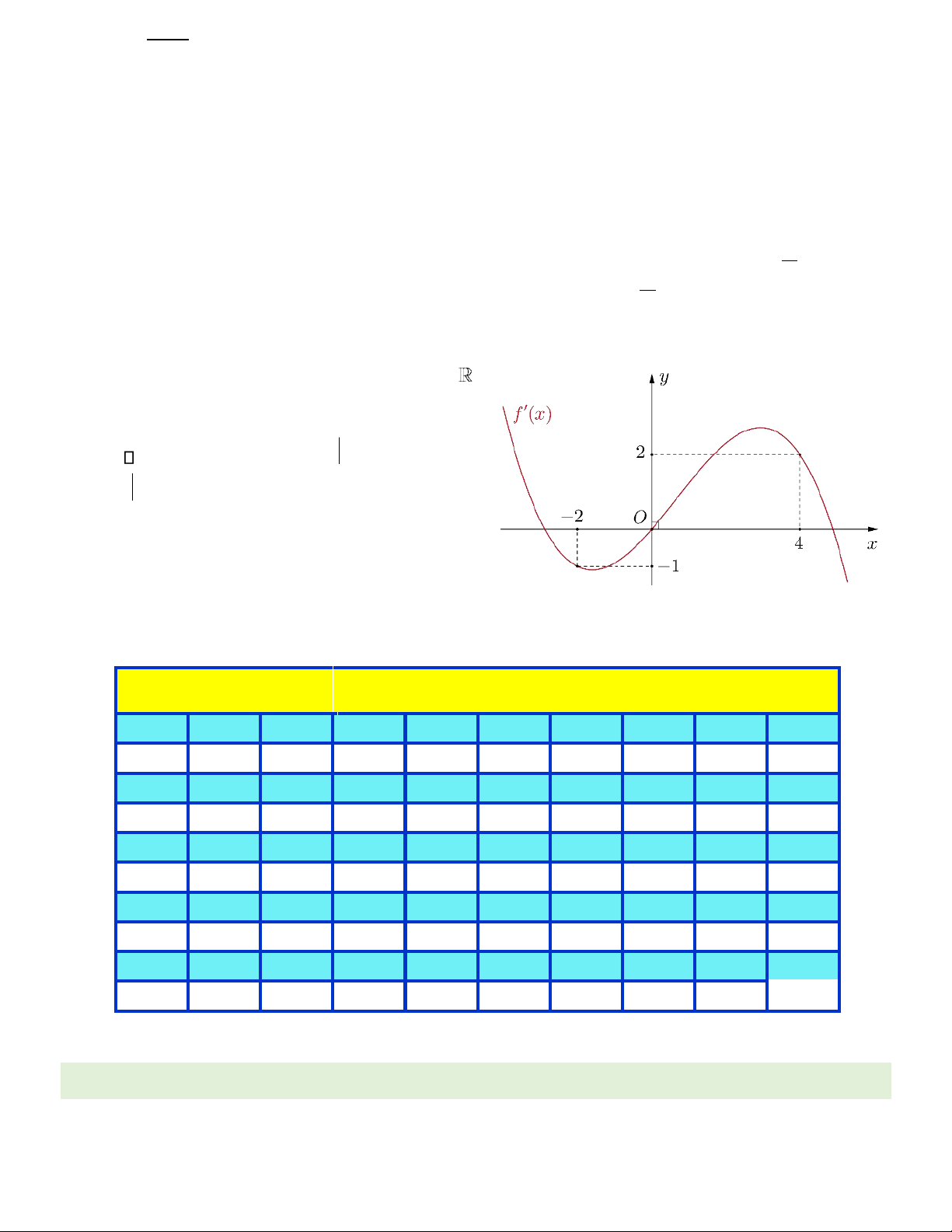
Câu 50. Cho hàm số a thức f x( ) có ạo hàm trên ()
Biết f (−2) = 0 và ồ thị của hàm số y = f
x như hình vẽ. Hàm số y =4 f x( )− +x2
4 có bao nhiêu iểm cực trị? A. 3. B. 5. C. 4. D. 2.
__________________HẾT__________________ AP AN E SO` 59 1 2 3 4 5 6 7 8 9 10 B C A C A B C A C D 11 12 13 14 15 16 17 18 19 20 B D D B D C D B D C 21 22 23 24 25 26 27 28 29 30 C D A A C C A C D A 31 32 33 34 35 36 37 38 39 40 A D A C B A A A A A 41 42 43 44 45 46 47 48 49 50 A B A C D B B A A B
Lłi giaßi cau hoßi van dung cao æe soÆ 59 lOMoAR cPSD| 22014077 = 4 ln sin( + )
x 215cos x dx = a +bln2+cln3+d ln5, trong ó a b c d, , , . Câu 41. Biết rằng tích phân I 0 cos x
Tính T = a b c++ +d . A. T = . B. T = . C. T = . D. . Hướng dẫn giải: ) Đặ dv d u t u ==ln sincos( 1 +x == 2 xx 15cos x dv
tansincosCx=15x+ =x+ − 15 sin x 15 15 cos
sin xxdcos+x15xcos x . ( ) tan x+15)ln sin( x+15cosx − 4 04 cosx−15sin x dx Khi ó: I = 0 cosx sin x d cos
=16ln8 2 −15ln15− 4 dx+15 4
dx =16ln8 2 −15ln15− − 15 4 ( x) 4 0 0 cos x 0 cos x 4 1
=16ln8 2 −15ln15− −15ln cos x =16ln8 2 −15ln15− −15ln 404 2 =−
+16ln2 72 −15ln5 15ln3 15ln− − 2− 12
=− 1 +127 ln2−15ln3 15ln− 5. 4 2 lOMoAR cPSD| 22014077
⎯Choïn⎯⎯→A
Suy ra a = − 1 , b = 127 , c = −15, d = −15 . Vậy T = a +b+c + d =. 4 2 x −1
Câu 42. Phương trình ường thẳng song song với ường thẳng d :
= y + 2 = z và cắt hai ường thẳng 1 1 −1
d1 : x +1 = y +1 = z −2 ; d2 : x −1 = y −2 = z −3 là: 2 1 −1 −1 1 3
A. x+1 = y+1 = z− 2 . . −1 −1 1
B. x−1 = =y z−1 1 1 −1
C. x −1 = y −2 = z −3 . D. x −1 = y = z −1. 1 1 −1 1 −1 1 Hướng dẫn giải:
Vectơ chỉ phương của d là u = ( d
1;1;−1). Gọi là ường thẳng cần tìm.
Gọi A(− +1 2a;− +1 a;2− a) = d 1
, B(1−b;2+b;3+3b) = d2 . Suy ra: AB = − −( b
2a+2;b−a+3;3b+a+1).
Vì song song với d nên AB cùng phương với ud , suy ra:
− −b 2a + 2 = b−a +3 = 3b+ a +1 1 1 −1
b− − + = − +b− + =− − −a2a3 2 3bb aa 13 ba=−=11 BA((12;0;;1;10)).
Phương trình chính tắc của Δ qua A và có vectơ chỉ −
⎯Choïn⎯⎯→ phương x −1 1 B u = (1;1;−1) là : = y = z− 1 . 1 1 lOMoAR cPSD| 22014077
Câu 43. Một tấm ề can hình chữ nhật ược cuộn tròn lại theo chiều dài tạo thành một khối trụ có ường kính
50 (cm). Người ta trải ra 250 vòng ể cắt chữ và in tranh cổ ộng, phần còn lại là một khối trụ có ường
kính 45 (cm). Hỏi phần ã trải ra dài bao nhiêu mét (làm tròn ến hàng ơn vị)? A. 373 (m). B. 187 (m). C. 384 (m). D. 192 (m). Hướng dẫn giải:
☺ Cách giải 1: Gọi a là bề dày của tấm ề can, sau mỗi vòng ược quấn thì ường kính của vòng mới
sẽ ược tăng lên 2a. Vì vậy: 2a 250 = 50−45 a = = 0,01 (cm) .
Gọi l là chiều dài ã trải ra và h là chiều rộng của tấm ề can (tức chiều cao hình trụ).
⎯Choïn⎯⎯→A Khi ó ta có: lha = 502 ) 2 h− 452 2 h l = (5042a−452 37306 (cm) 373 (m).
☺ Cách giải 2: Gọi a là bề dày của tấm ề can, sau mỗi vòng ược quấn thì ường kính của vòng mới
sẽ ược tăng lên 2a. Vì vậy: 2a 250 = 50−45 a = = 0,01 (cm) .
Chiều dài của phần trải ra là tổng chu vi của 250 ường tròn có bán kính là một cấp số cộng có số hạng ầu bằng r = 1
25, công sai là d =−0,01 (do khi trải ra thì bán kính các vòng tròn ngày càng
giảm với ộ giảm bằng bề dày của tấm ề can). Do ó chiều dài của phần ề can ã trải ra là: l = 2 r + + + + 1 r2 (2r1 249 ).250d = 2 (2.25 −249.0,01) 250 37314 (cm) 373 (m). ... r = 250 2 . 2 2 S 250
Câu 44. Cho hàm số y x= +4 2mx m2 + (với mlà tham số thực). Tập tất cả các giá trị của tham số m ể ồ thị hàm
số ã cho cắt ường thẳng y = −3 tại bốn iểm phân biệt, trong ó có một iểm có hoành ộ lớn hơn 2 còn ba iể ;
m kia có hoành ộ nhỏ hơn 1, là khoảng (a b ) (với a b,
; a,b là phân số tối giản). Khi ó, 15ab
nhận giá trị nào sau ây? A. −63. B. 63. C. 95. D. −95. Hướng dẫn giải: lOMoAR cPSD| 22014077
Xét phương trình hoành ộ giao iểm của hai ồ thị hàm số: x4 +2mx m2 + =−3 (1).
Đặt t = x2 , t 0. Khi ó phương trình trở thành t2 + 2mt + m+3 = 0 ( )2 . f t( )
Phương trình (1) có bốn nghiệm phân biệt Phương trình ( )2 có hai nghiệm thỏa mãn
=(1) m2 − −m 3 0 0 t =− 1 t2 S(1) 2m 0 1 − 13 − 3 m (*). 2 P = +m3 0
Khi ó, bốn nghiệm của phương trình (1) 2 1 1 t
2 là: − t − t t . x1 x2 x3 x4 2 m Từ giả thiết, ta có t 2 hay t 1 1 4 t2 . Suy ra: f ( )( )14 00 −19 93mm++194 00 (**). 9 t1 1 f
⎯Choïn⎯⎯→C
Từ (*) và (**) suy ra: −3 m −
. Do ó: a = −3, b = − nên 15ab =95. 0
Câu 45. Cho hàm số y ax bx c= 4 + +2 có ồ thị ( )C , biết rằng ( )C i qua iểm A(−1; ). Biết tiếp tuyến d tại A
của ( )C cắt ( )C tại hai iểm có hoành ộ lần lượt là 0 và 2 ; ồng thời diện tích hình phẳng giới hạn bởi
ường thẳng d , ồ thị ( )C và hai ường thẳng x = 0, x = 2 có bằng (phần tô màu trong hình vẽ). Diện
tích hình phẳng giới hạn bởi d, ( )C và hai ường thẳng x = −1, x = 0 bằng C. . A. . B. . D. . Hướng dẫn giải:
Ta có: y = 4ax3 +2bx; tiếp tuyến của (C) tại A là d y: = −( 4a −2b)(x +1). lOMoAR cPSD| 22014077
Phương trình hoành ộ giao iểm của d và ( )C là: (−4a − 2b)(x +1) = ax4 +bx2 + c ( )1 . Theo giả
thiết, ta có: Phương trình ( )1 nhận x = 0, x = 2 làm nghiệm (ngoài một nghiệm là x = −1)
−−124aa−−26bb==c16a + 4b+c
28 10− − − =4 2aa+ b cb c+ =00 ( )( )23 .
Mặt khác, diện tích phần tô màu là: 285 = (− − − 02
4a−2b)(x+1)−ax4 bx2 c dx
285 = −( 2a−b)(x+1) − + + 2 02 ax55 bx33 cx
02 285 = 4(−4a −2b)− 325 a − 83b−2c
( 112 32 28 a+ b+2c = −
)4 . Từ (2), (3), (4) suy ra a =1, b = −3, c = 2. 5 3 5 Khi ó ta xác
ịnh ược ( )C : y = x4 −3x2 + 2 và d y: = 2(x +1). 0
⎯Choïn⎯⎯→D )
Diện tích cần tìm là S =
x4 −3x2 + 2−2(x +1 dx = 0 (x4 −3x2 −2x dx) =. −1 −1
Câu 46. Cho tứ diện ABCD, trên các cạnh BC , BD, AC lần lượt lấy các iểm M , N , P sao cho BC =3BM , BD
= BN , AC = 2AP. Mặt phẳng ( )
MNP chia khối tứ diện ABCD thành hai phần có thể tích là V1, V2 với V V 1
1 là thể tích khối a diện chứa ỉnh B. Tính tỉ số . V2 A. V = = = = 1 26 . B. V1 C. V1 3 . D. V1 15 . V 26 . 2 13 V2 19 V2 19 V2 19 Hướng dẫn giải: lOMoAR cPSD| 22014077 4 QD Vì vậy . Ta có: V = CMNP V V = + = 2 VN PQDC. VCMNP
1V + 2V = 19V . 5 9 45 Do ó V V V = − = = 1 2 26V . Vậy V1
26 . ⎯Choïn⎯⎯→B 45 V2 19
Câu 47. Cho hàm số f x( ) có ạo hàm liên tục trên thỏa mãn f x( )+ f ( )x 1, x và f ( )0 = 0. Tìm
giá trị lớn nhất của f ( )1 . lOMoAR cPSD| 22014077 2e −1 e 1− A. . B. . C. e 1− . D. 2e−1. e e Hướng dẫn giải:
Ta có: x , f x( )+ f ( )x 1 ex f x( )+ ex f ( )x ex ex f x( ) (ex ) ( ) 10 ex f x( )
dx 10 ex dx ex f x( ) 10 ex 10 e.f ( )1 e −1 f ( )1 e−1. e
⎯Choïn⎯⎯→ Do ó giá trị e 1− B
lớn nhất của f ( )1 là . e ;2;3 , 4
Câu 48. Trong không gian Oxyz , cho hai iểm A(1 ) ( ) B 2;3;
. Một mặt cầu ( )S bán kính R luôn tiếp xúc
với ba mặt phẳng tọa ộ và oạn thẳng AB luôn nằm trong ( )S (mọi iểm thuộc oạn thẳng AB ều nằm
trong ( )S ). Giá trị nguyên lớn nhất của R ạt ược là: A. 4. B. 6. C. 5. D. 3. Hướng dẫn giải:
Do mặt cầu luôn tiếp xúc với ba mặt phẳng tọa ộ nên tọa ộ tâm mặt cầu là I a a a( , , ), suy ra bán kính
mặt cầu R = a .
Mặt khác, mọi iểm thuộc oạn thẳng AB ều nằm trong mặt cầu( )S nên ta có: IA R IA ( +( +( − 22 a22 1−a)22 2−a)22 3−a)22 a22 2a22 12a +14 0 IB R IB a
(2−a) +(3−a) +(4−a) a 2a −18a +29 0 3− 2 a 2 3+ 9 − 23 3 + 9 23 a + 2 9− 23 2 . 4,414 2 2, 102 a 2
⎯Choïn⎯⎯→
Giá trị nguyên lớn nhất của R là R=4. A lOMoAR cPSD| 22014077
Câu 49. Cho ba số thực dương a b c, ,
thỏa mãn abc =10. Biết giá trị lớn nhất của biểu thức m F =5log .loga
b+2log .logb c+log .logc a bằng với m n,
nguyên dương và m tối giản. Tổng n n
m+n bằng A. 7 . B. 10. C. 13. D. 16. Hướng dẫn giải:
Đặt x = log ,a y = log ,b z = logc. Suy ra x + y + z = log(abc) = log10 =1.
Khi ó: F = 5xy + 2yz + zx = 5xy + 2y(1− x − y)+ x(1− x − y) = −2y2 − x2 + 2xy + 2y + x = − x
2y2 − x2 +2xy +2y + x = −2(y2 − xy − y)− x2 + x ???=−2 y − 2 − 12 2 − 12(x−2)2 + 52 52
Dấu “=” xảy ra x = 2, y = 3, z = − 5 . 2 2 Do ó: F = max
m = 5 m = 5,n = 2 m+ n = 7 . ⎯Choïn⎯⎯→A n 2
 Lưu ý: Bằng cách nào ta có thể phân tích ược các hằng ẳng thức như trên? 
Trước hết ta cần dự oán ược iểm rơi trong biểu thức F, mà biểu thức này vốn là
hàm hai biến x, y; vì vậy ta sử dụng cách thức tìm cực trị của hàm hai biến: F = −= − xy
24xy++22yx+ =+12 =00 (*). Giải hệ (*), ta
ược: x= 2, y= 32 . F 
Từ ây, ta xây dựng ược các hằng ẳng thức phù hợp cho ánh giá của mình. lOMoAR cPSD| 22014077
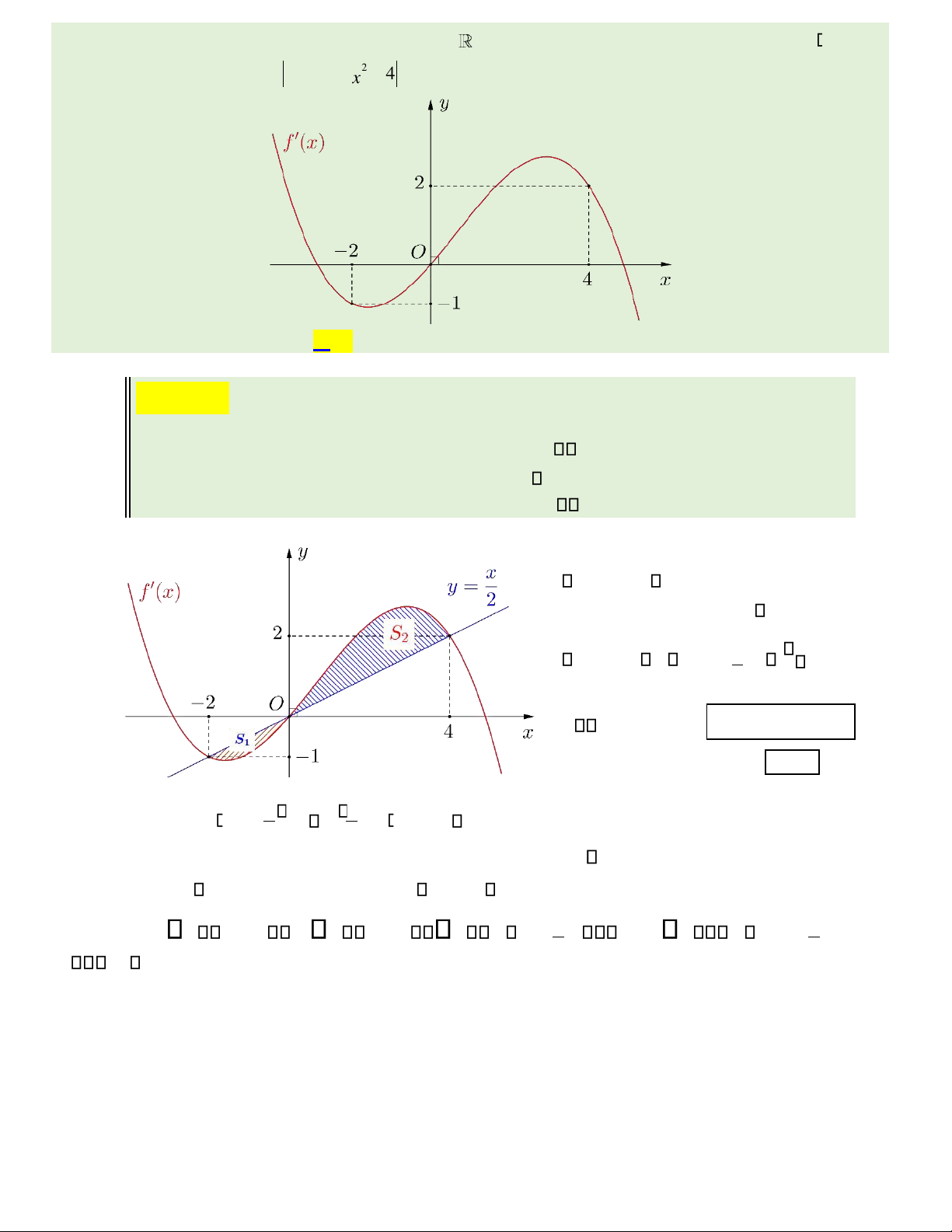
Câu 50. Cho hàm s ố a thứ c ()
fx có ạ o hàm trên . Bi ế t ( 2) 0
f − = và ồ th ị c ủ a hàm s ố y = f () x như hình v ẽ . Hàm s ố = 4 y () 2 fx −+ 4 x
có bao nhiêu iể m c ự c tr ị ? A. 3. B. 5. C. 4. D. 2.
Hướng dẫn giải:
 Ghi nhớ: Số iểm cực trị của hàm số y = f x( ) bằng số cực trị của hàm số y = f x( ) cộng y = f x( )
với số giao iểm (không kể tiếp iểm) hai ồ thị hàm số . y = 0 (Oy) Đặt g
x( ) = 4 f x( )− x2 + 4, suy ra
g ( )x = 4 f ( )x − 2x ; x = −2 x
g ( )x = 0 f ( )x = 2 x = 0 .
x = 4 Do vậy, hàm số g x( ) có ba cực trị (*). Ta có: g(− =2 4)
f (− − − + =2) ( 2)2 4 0. Suy ra: () x x f − d x x − f () d x x
() Từ ồ thị ta so sánh các phần diện tích và thấy 2 S S 2 1. 04 2 − 02 04
f x − 2x dx+ − 02 f ( )x − 2x dx 0 lOMoAR cPSD| 22014077 x 4 ( 2 f ( )x − 2 dx 0 −
42 4 f ( )x −2x)dx 0 g( )4 − g(−2) 0 g( )4 g(−2) = 0 . −
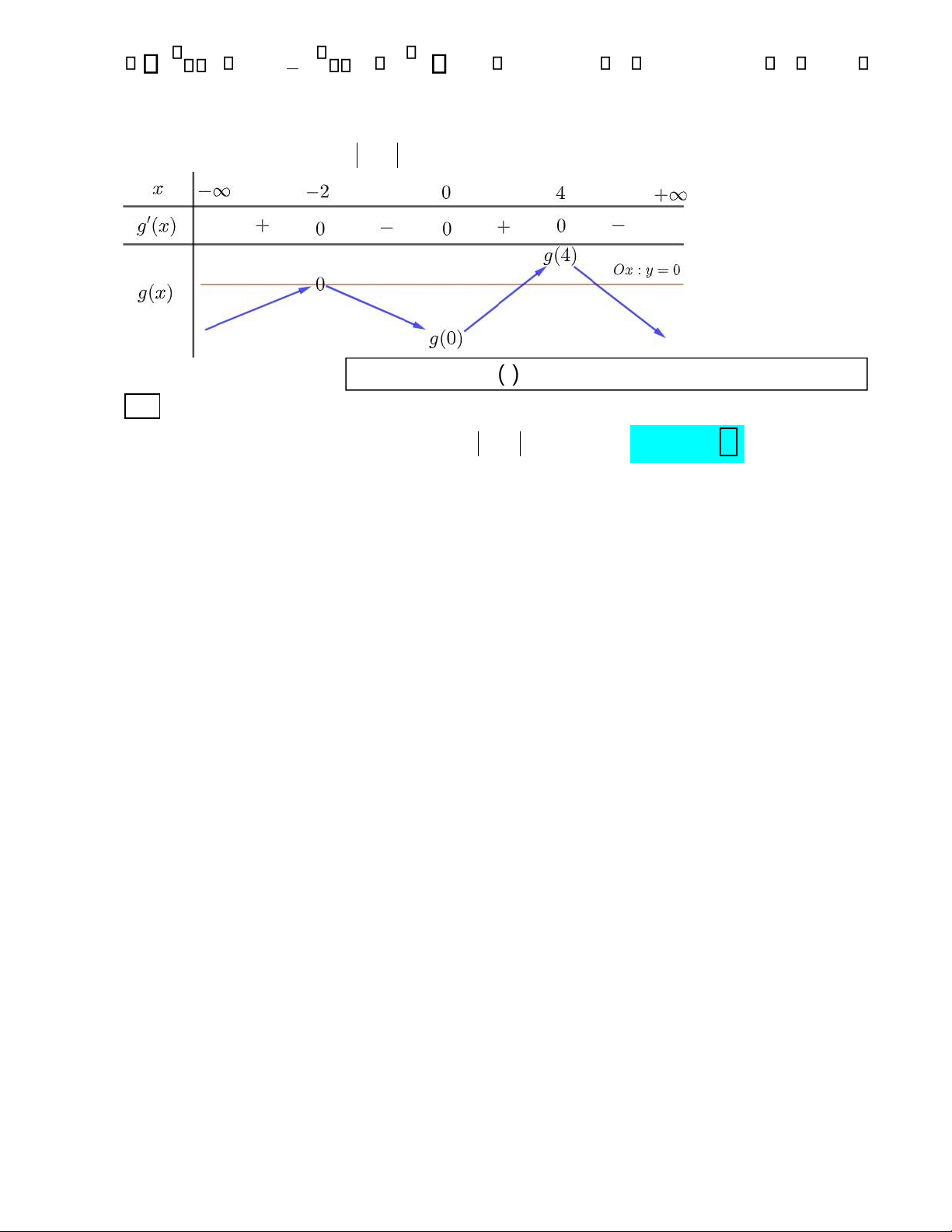
B ả ng bi ế n thiên hàm () gx và () gx :
Theo b ả ng bi ế n thiên, ta th ấ y ồ th ị hàm s ố = ( ) có hai giao iể m v ớ i tr ụ c O y (không tính ti ế p y g x xúc) (**).
⎯Choïn⎯⎯→B
Từ (*) và (**) suy ra số cực trị của hàm số y = g x( ) là: 3 + 2 = 5.