Đề chọn học sinh giỏi tỉnh Toán 11 năm 2024 – 2025 sở GD&ĐT Hà Nam

UBND TỈNH HÀ NAM
KỲ THI CHỌN HỌC SINH GIỎI LỚP 10, 11 THPT
SỞ GIÁO DỤC VÀ ĐÀO TẠO VÀ LỚP 12 GDTX CẤP TỈNH NĂM HỌC 2024 - 2025 Môn: Toán 11 ĐỀ CHÍNH THỨC
Thời gian làm bài: 180 phút
(Đề thi gồm 02 trang)
Câu I. (4,0 điểm)
1. Một chiếc cầu bắc qua sông, mặt dưới gầm cầu có dạng cung AB của đồ thị hàm số 8 3 cos x y = + 2 với x ∈[ 6 − ;
π 6π] được mô tả trong hệ trục toạ độ Oxy với đơn 3 12
vị trục là mét (trục Ox mô tả mặt nước sông) như hình minh họa dưới đây y A B x - 6π O 6π
Một sà lan chở khối hàng hóa được xếp thành hình hộp chữ nhật với độ cao 6 mét so
với mặt nước sông sao cho sà lan có thể đi qua được gầm cầu. Chứng minh rằng
chiều rộng của khối hàng hoá đó phải nhỏ hơn 12,6 mét.
2. Cho phương trình sin3x + cos2x − msin x =1 với m là tham số. Tìm tất cả các giá  π trị của 
m để phương trình có đúng 7 nghiệm khác nhau thuộc khoảng −  ;2π . 2   
Câu II. (4,0 điểm)
1. Một quả bóng cao su được thả từ độ cao 22,5mét. Giả sử sau mỗi lần chạm đất quả
bóng cao su lại nảy lên độ cao bằng 80% độ cao của lần rơi trước. Tính chiều dài
quãng đường quả bóng cao su di chuyển từ khi được thả đến khi không nảy nữa. u   2025
2. Cho dãy số u xác định bởi 1  . n 
nu       u u n n n  2 n  * 3 , 1  
Tìm số hạng tổng quát của dãy số (u và tính lim un . n ) 2 n
Câu III. (2,0 điểm) + 2 Cho hàm số f (x) 1
(x + x) f (x) + 2
f (x) thỏa mãn lim = 16. Tính lim . x 1 → x −1 x 1 → x −1
Câu IV. (2,0 điểm)
Ba cầu thủ đá phạt đền 11m, mỗi người đá một lần với xác suất ghi bàn tương ứng là
x, y và 0,6 (với x > y ). Biết xác suất để ít nhất một trong ba cầu thủ ghi bàn là
0,976 và xác suất để cả ba cầu thủ đều ghi bàn là 0,336 . Tính xác suất để có đúng
hai cầu thủ ghi bàn. Trang 1/2
Câu V. (6,0 điểm)
1. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O . Mặt phẳng (α)
không đi qua S cắt các cạnh ,
SA SB,SC,SD lần lượt tại M , N, P,Q sao cho
SA = 2SM và SC = 3SP . Tính SB SD + . SN SQ
2. Cho hình lăng trụ tam giác ABC.A′B C
′ ′ , điểm M nằm trên cạnh AC sao cho
AM = kMC. Mặt phẳng (P) đi qua M song song với hai đường thẳng AB′ và A′C. Gọi NB
N là giao điểm của mặt phẳng (P) và đường thẳng BC .Tìm k để 5 = . NC 3
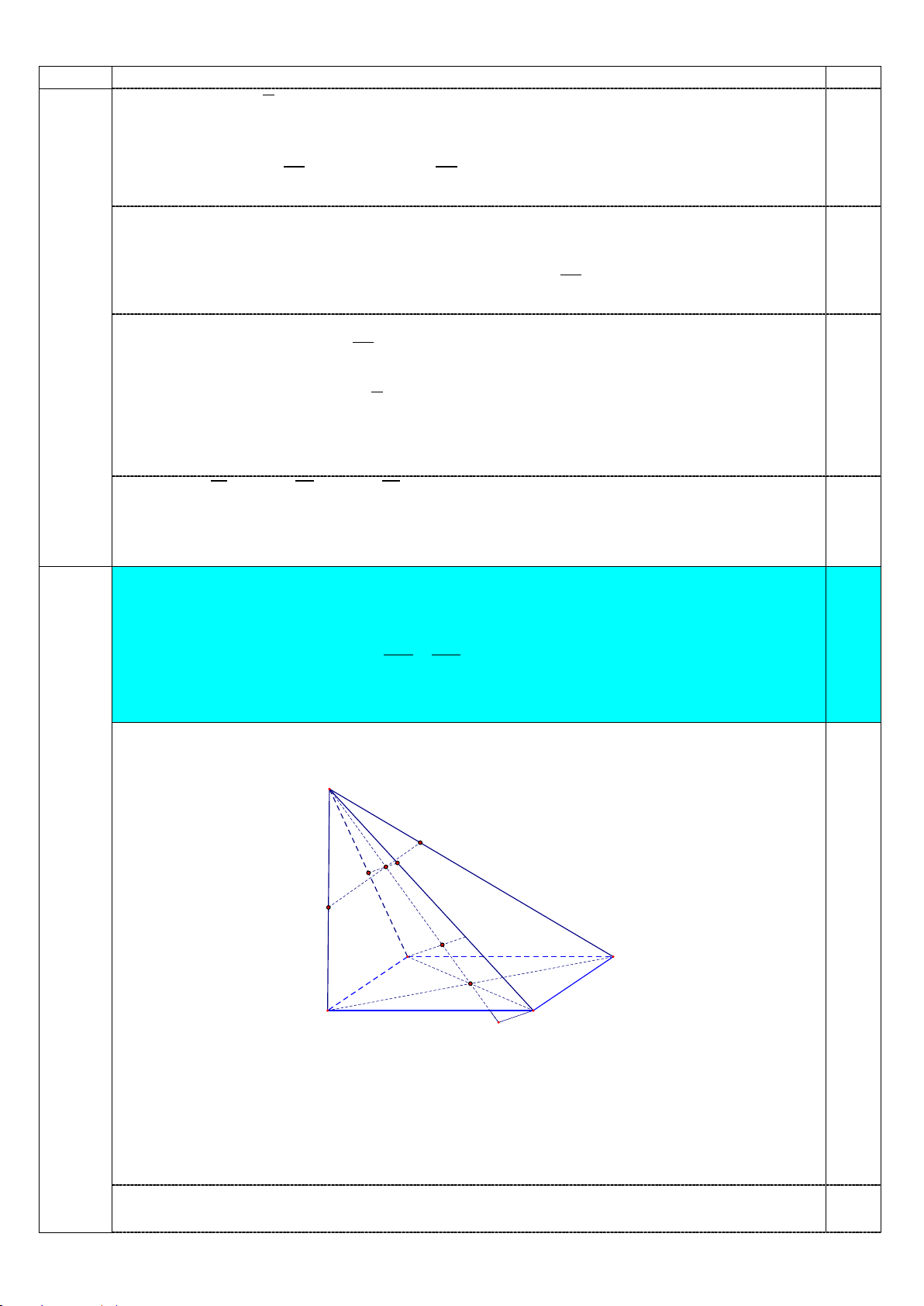
3. Cho tứ diện OABC có các cạnh ,
OA OB,OC đôi một vuông góc. Gọi M là một
điểm bất kì thuộc miền trong tam giác ABC . Tìm giá trị nhỏ nhất của biểu thức 2 2 2 MA MB MC T = + + . 2 2 2 OA OB OC
Câu VI. (2,0 điểm)
Cho a,b,c là các số thực dương thỏa mãn 1 1 1 + + = 6. 3a 2b c
Tìm giá trị lớn nhất của biểu thức a b c P = + + . a + 4bc b + 9ca c + 36ab --- HẾT---
Họ và tên thí sinh:………………………………Số báo danh:.................................................
Cán bộ coi thi số 1:…………………………….. Cán bộ coi thi số 2:..……………................ Trang 2/2 UBND TỈNH HÀ NAM
KỲ THI CHỌN HỌC SINH GIỎI LỚP 10, 11 THPT
SỞ GIÁO DỤC VÀ ĐÀO TẠO
VÀ LỚP 12 GDTX CẤP TỈNH NĂM HỌC 2024 – 2025
HƯỚNG DẪN CHẤM MÔN TOÁN LỚP 11
(Hướng dẫn chấm gồm 10 trang)
I. HƯỚNG DẪN CHUNG
o Hướng dẫn chấm chỉ trình bày sơ lược các bước giải, lời giải của học sinh cần lập luận chặt chẽ,
hợp logic. Nếu học sinh trình bày cách làm khác mà đúng thì vẫn được điểm theo thang điểm tương ứng.
o Đối với bài toán hình học nếu học sinh chứng minh có sử dụng đến hình vẽ thì yêu cầu phải vẽ
hình, nếu học sinh vẽ hình sai hoặc không vẽ hình thì không cho điểm phần tương ứng.
o Điểm toàn bài không làm tròn.
II. ĐÁP ÁN VÀ THANG ĐIỂM Câu
Sơ lược lời giải Điểm
1. Một chiếc cầu bắc qua sông, mặt dưới gầm cầu có dạng cung AB của đồ thị hàm số 8 3 cos x y = + 2 với x ∈[ 6 − ;
π 6π] được mô tả trong hệ trục toạ độ Oxy với đơn vị 3 12
trục là mét (trục Ox mô tả mặt nước sông) như hình minh họa dưới đây y A B 2,0 - 6π O 6π
Một sà lan chở khối hàng hóa được xếp thành hình hộp chữ nhật với độ cao 6 mét so
với mặt nước sông sao cho sà lan có thể đi qua được gầm cầu. Chứng minh rằng I
chiều rộng của khối hàng hoá đó phải nhỏ hơn 12,6 mét. (4,0
điểm) Xét điểm M ( ;
x y) nằm trên cung AB , khoảng cách từ điểm M đến mặt nước tương
ứng với giá trị tung độ y của điểm M. Xét phương trình 8 3 cos x y   = + 2 =   6 . 3 12  x 3 ⇔ cos = x 3 ⇔ cos = 12 2 12 2 0,5 Vì [ 6 ;6 ] x x  π ;π ∈ − π π ⇒ ∈ − 0,5 12  2 2    π nên ta có x 3 cos x = ⇔ = ± ⇔ x = 2 ± π hay x = 2π. 12 2 12 6 0,5
Do sà lan có thể đi qua được gầm cầu nên chiều rộng khối hàng hoá là
2 x < 4π =12,56 <12,6. 0,5 Trang 1/10 Câu
Sơ lược lời giải Điểm
2. Cho phương trình sin3x + cos2x − msin x =1 với m là tham số.
Tìm tất cả các giá trị của m để phương trình có đúng 7 nghiệm khác nhau thuộc 2,0 khoảng  π ;2π  −  . 2   
sin3x + cos2x − msin x =1 3 2
⇔ 3sin x − 4sin x +1− 2sin x − msin x =1 0,25 3 2
⇔ 4sin x + 2sin x + (m − 3)sin x = 0 t = 0
Đặt sin x = t với t ∈[ 1; − ] 1 . Ta có ⇔  2 4t + 2t +  (m −3) = 0(*) 0,25 Với  π 
t = 0 thì sin x = 0 ⇔ x = kπ , có 2 nghiệm là 0;π thuộc −  ;2π . 2    0,25 Với mỗi giá trị  π t  ∈( 1;
− 0) thì phương trình sin x = t có 3 nghiệm thuộc −  ;2π . 2    0,25 Với mỗi giá trị  π t  ∈(0; )
1 thì phương trình sin x = t có 2 nghiệm thuộc −  ;2π . 2    0,25
Để pt có đúng 7 nghiệm thỏa mãn thì phương trình (*) phải có 2 nghiệm t ;t thỏa 1 2 mãn điều kiện: 1
− < t < 0 < t <1. 0,25 1 2 ( ) 2 * ⇔ m = 4
− t − 2t + 3 = f (t)
Từ bảng biến thiên trên ta có m∈(1;3). 0,5
1. Một quả bóng cao su được thả từ độ cao 22,5 mét. Giả sử sau mỗi lần chạm đất quả
bóng lại nảy lên độ cao bằng 80% độ cao của lần rơi trước. Tính chiều dài quãng 2,0
đường quả bóng cao su di chuyển từ khi thả đến khi không nảy nữa. II (4,0 *
điểm) Gọi h là độ dài đường đi của quả bóng ở lần rơi xuống thứ n(n∈ ) . n
Gọi l là độ dài đường đi của quả bóng ở lần nảy lên thứ ( * n n∈  ) . n Trang 2/10 Câu
Sơ lược lời giải Điểm
Theo bài ra ta có h = 22,5, 4
l = .22,5 =18 và các dãy số (h , (l là các cấp số nhân n ) n ) 1 1 5
lùi vô hạn với công bội 4 q = . 5 0,5
Tổng quãng đường rơi xuống h1 h = = 112,5 4 1− 0,5 5
Tổng quãng đường nảy lên l1 l = = 90 4 1− 0,5 5
Từ đó ta suy ra tổng độ dài đường đi của quả bóng là:
S = h + l = 202,5(m) . 0,5 u   2025
2. Cho dãy số u xác định bởi 1  . n 
nu       u u n n n  2 n  * 3 , 1   2,0
Tìm số hạng tổng quát của dãy số(u và tính lim un . n ) 2 n
Từ giả thiết ta có: nu     u u n n 2 n 3 1    . n u = + + + n u n 2 n 6 1 ( ) u + u n n 6 1 ⇔ = + n + 2 n n(n + 2) u + u n n 6 1 ⇔ ( = + n + )
1 (n + 2) n(n + ) 1 n(n + ) 1 (n + 2) 0,5 +) Đặt un * v = n∈ n  n(n + ) , 1  2025 v =  1  2 Ta được dãy (v n ) :  6 * v = + ∀ ∈ + v n n n , 1   n  (n + )1(n + 2) Ta có 6 6 6 v = v + ;v = v + ;v = v + 2 1 3 2 n n 1 1.2.3 2.3.4 − ( 0,5 n − ) 1 .n(n + ) 1
Cộng theo vế các đẳng thức trên ta được Trang 3/10 Câu
Sơ lược lời giải Điểm  1 1 1  v = v +  + + + n 6 ... 1 1.2.3 2.3.4 (   n ) 1 n(n ) 1  − +   2025 6  1 1 1 1 1 1  v = +  − + − + + − n ... 2 2 1.2 2.3 2.3 3.4 (   n ) 1 n n(n ) 1  − +   3 v = − n 1014 n(n+ )1 Do đó u = n n + − 0,5 n 1014 ( )1 3 u 1014n(n + ) 1 − 3 n ⇒ = 2 2 n n u 1014n n + − n ( ) 1 3 Vậy lim = lim = 1014 2 2 n n 0,5 + 2 Cho hàm số f (x) 1
(x + x) f (x) + 2
f (x) thỏa mãn lim = 16. Tính lim . x 1 → x −1 x 1 2,0 → x −1 2 2
(x + x) f (x) + 2
(x + x)( f (x) + ) 2
1 − x − x + 2 lim = lim 0,25 x 1 → − x 1 x 1 → x −1 2 2 III
(x + x)( f (x) + ) 1 x + x − 2 = lim − lim 0,5 (2,0 x 1 → − x 1 x 1 → x −1 điểm) 2
(x + x)( f (x) + ) 1 +/ 2 f (x) +1 lim = lim(x + x).lim = 2.16 = 32 0,5 x 1 → − x 1 → x 1 x 1 → x −1 2 +/ x + x − 2 (x −1)(x + 2) lim = lim = lim(x + 2) = 3 0,5 x 1 → − x 1 → − x 1 x 1 x 1 → 2 Vậy
(x + x) f (x) + 2 lim = 32 − 3 = 29 0,25 x 1 → x −1
Ba cầu thủ đá phạt đền 11m, mỗi người đá một lần với xác suất ghi bàn tương ứng là
x , y và 0,6 (với x > y ). Biết xác suất để ít nhất một trong ba cầu thủ ghi bàn là
0,976 và xác suất để cả ba cầu thủ đều ghi bàn là 0,336. Tính xác suất để có đúng hai 2,0 cầu thủ ghi bàn.
Gọi A là biến cố: “ Có ít nhất một trong ba cầu thủ ghi bàn” IV
B “ Cả ba cầu thủ đều ghi bàn” (2,0
điểm) C “Có đúng hai cầu thủ ghi bàn”
Gọi A là biến cố “người thứ i ghi bàn” với i =1,2,3 . i
Ta có các A độc lập với nhau và P( A = x, P A = y, P A = 0,6 . 0,25 1 ) ( 2) ( 3) i
Ta có: A = A .A .A ⇒ P A = P A .P A .P A = 0,4(1− x)(1− y) 1 2 3 ( ) ( 1) ( 2) ( 3) 0,25 Trang 4/10 Câu
Sơ lược lời giải Điểm Nên P( )
A =1− P( A) =1−0,4(1− x)(1− y) = 0,976 Suy ra 3 47
(1− x)(1− y) =
⇔ xy − x − y = − (1). 50 50 0,25
Tương tự: B = A .A .A , suy ra: 1 2 3
P(B) = P( A .P A .P A = 0,6xy = 0,336 hay là 14 1 ) ( 2) ( 3) xy = (2) 0,25 25  14 xy = 
Từ (1) và (2) ta có hệ:  25  3 x + y =  2
giải hệ này kết hợp với x > y ta tìm được x = 0,8 và y = 0,7 0,5
Ta có: C = A A A + A A A + A A A 1 2 3 1 2 3 1 2 3 0,5
Nên P(C) = (1− x) .0
y ,6 + x(1− y).0,6 + x .0 y ,4 = 0,452 .
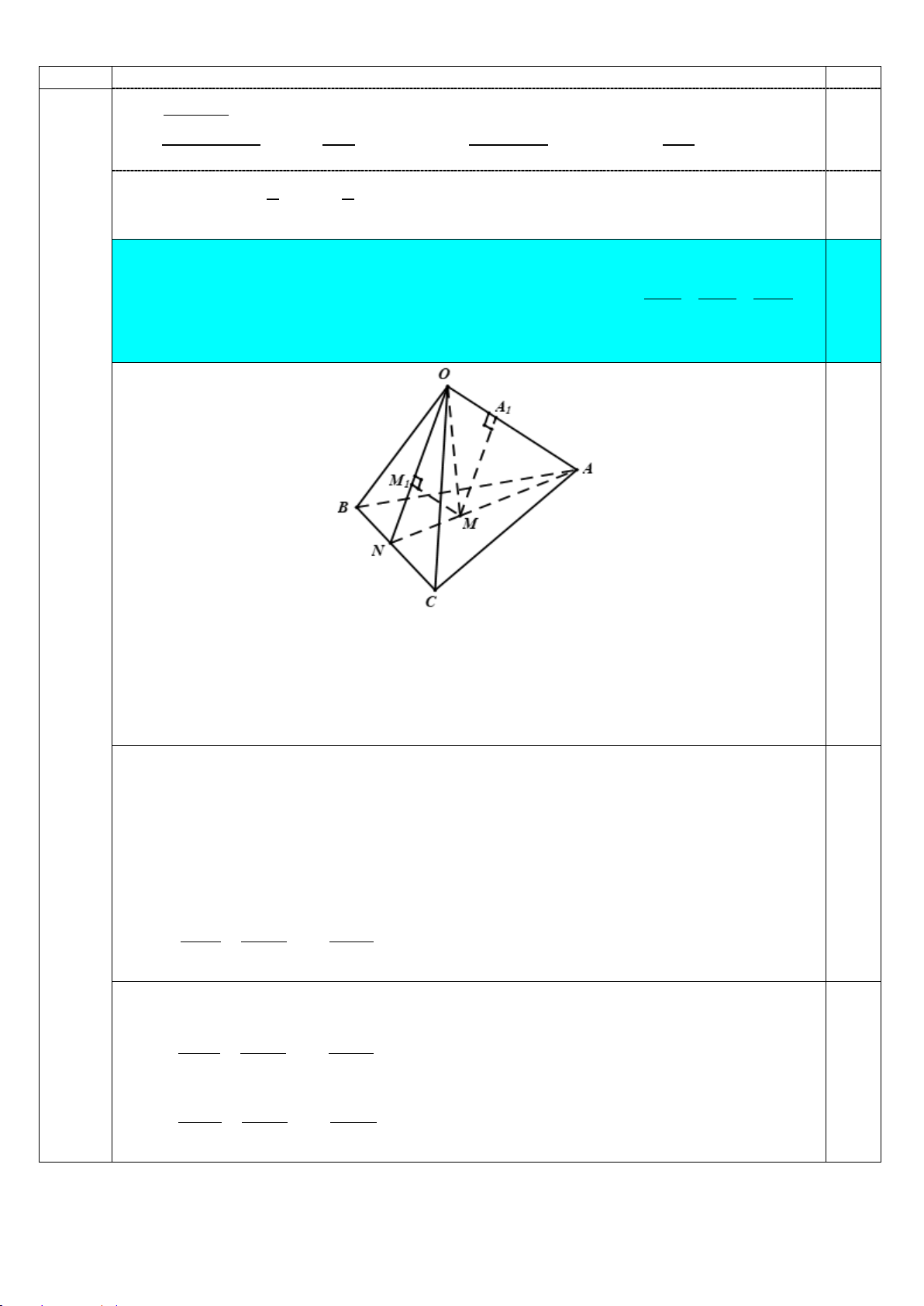
1. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O . Mặt phẳng (α)
không đi qua S cắt các cạnh ,
SA SB,SC,SD lần lượt tại M , N, P,Q sao cho
SA = 2SM và SC = 3SP . Tính SB SD + . 2,0 SN SQ S N V M P G (6,0 điểm) Q E A B O D C F
Trong mặt phẳng (SAC) gọi G = SO ∩ MP
Ba mặt phẳng (SAC),(SBD),(α) đôi một cắt nhau theo 3 giao tuyến SO,MP, NQ nên
SO,MP, NQ đồng quy tại G 0,25
Trong mặt phẳng (SAC) vẽ AE,CF song song với MP (E, F thuộc SO) Trang 5/10 Câu
Sơ lược lời giải Điểm
Vì AE  MP nên ta có : SA SE = . SM SG
CF  MP nên ta có: SC SF = 0,25 SP SG
Cộng vế với vế hai đẳng thức trên ta được:
SA SC SE + SF SO −OE + SO + OF + = = (1) 0,25 SM SP SG SG Xét A ∆ OE và C
∆ OF có : OA = OC,  =  AOE COF ,  =  EAO FCO ⇒ A ∆ OE = C
∆ OF ⇒ OE = OF (2) 0,5
Từ (1) và (2) ta có: SA SC + = 2 SO SM SP SG 0,25 SB SD SO Tương tự + = 2 SN SQ SG SB SD SA SC Suy ra + = + = 2 + 3 = 5 0,5 SN SQ SM SP
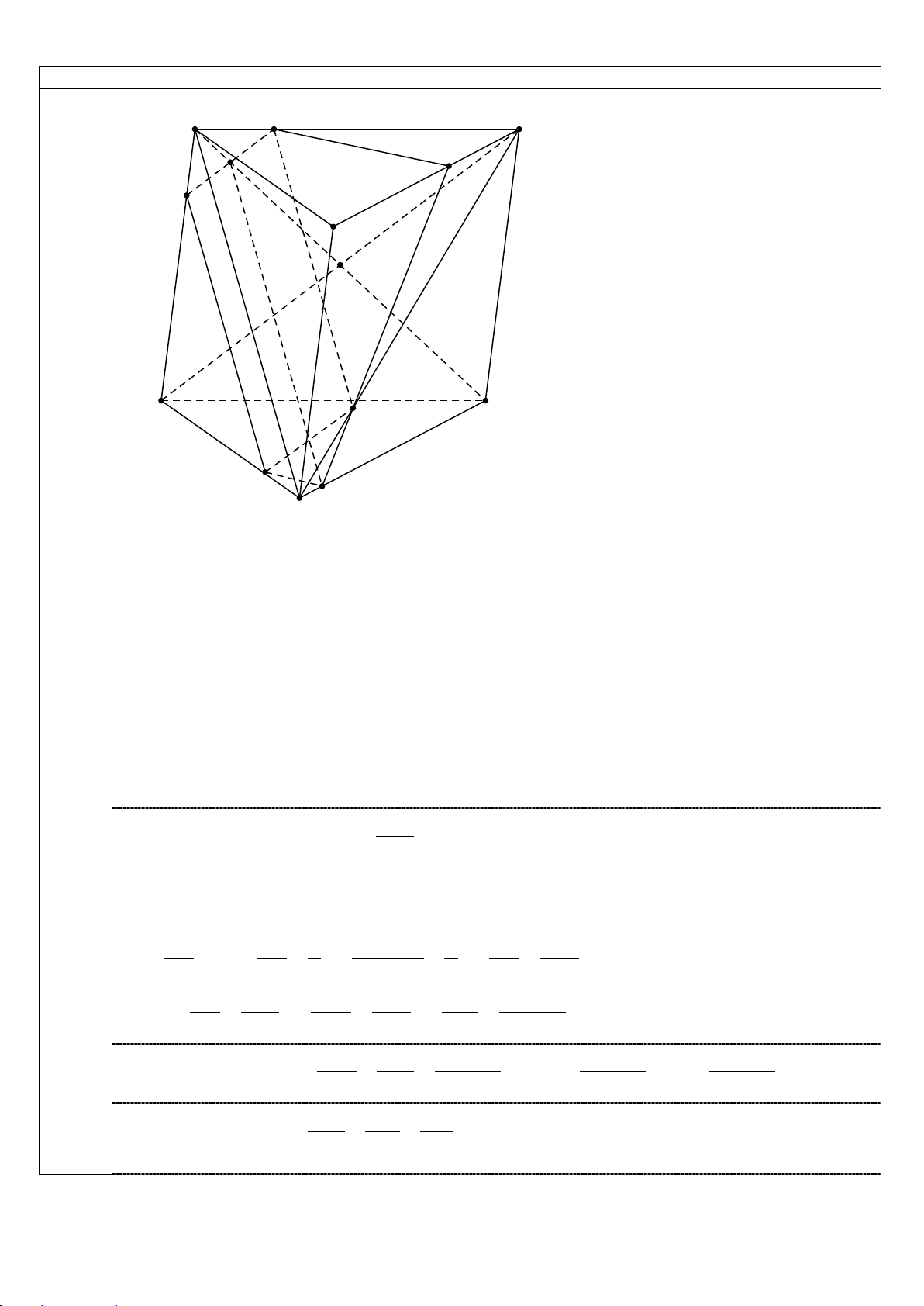
2. Cho hình lăng trụ tam giác ABC.A′B C
′ ′ , điểm M nằm trên cạnh AC sao cho
AM = kMC. Mặt phẳng (P) đi qua M song song với hai đường thẳng AB′ và A′C . Gọi NB N là 2,0
giao điểm của mặt phẳng (P) và đường thẳng BC .Tìm k để 5 = . NC 3 Trang 6/10 Câu
Sơ lược lời giải Điểm A M C N E R B I A' F C' Q P B'
Giao tuyến của (P) và ( ACC A
′ ′) là đường thẳng đi qua M song song với A′C cắt AA′ tại .
R Cắt AC′ tại E.
Giao tuyến của (P) và ( ABB A
′ ′) là đường thẳng đi qua R song song với AB′ cắt A′B′ tại . Q Giao tuyến của (
P) và ( ACB′)là đường thẳng đi qua M song song với AB′ cắt CB′ tại F.
Giao tuyến của (P) và ( AC B
′ ′)là đường thẳng đi qua E song song với AB′ cắt C B ′ ′ tại . P
Nối P với F cắt BC tại N. 0,5
Nối N với M . Theo bài ta có AM = k . MC
Gọi I = AC′ ∩ A′C.
Do MR / / A′C nên ta có AE EI 1 AI − AE 1 AI k +1 = k ⇔ = ⇔ = ⇔ = EI AE k AE k AE k AE k 2AE k AE k ⇔ = ⇔ = ⇔ = 0,5 AI k +1 AC ' k +1 AC ' 2(k + ) 1 Vì B'
EP / / AB′ nên ta có P AE k k k = = ( ⇒ ′ = ′ ′ = ′ ′ k + ) B P (k + ).B C (k + ).BC B C AC ' 2 1 2 1 2 1 0,25 ′ ′
Lại có MF / / AB′ nên AM B F B P = = = k MC FC NC 0,25 Trang 7/10 Câu
Sơ lược lời giải Điểm k BC 2(k + ) 1 Vậy BC = ⇔ = 2( + ) 1 BN + NC ⇔ = 2( + ) 1 NB k k k ⇔ = 2k +1 0,25 NC NC NC NC Theo bài 5 1
2k +1 = ⇔ k = . 3 3 0,25
3. Cho tứ diện OABC có các cạnh ,
OA OB,OC đôi một vuông góc. M là một điểm bất 2 2 2
kì thuộc miền trong tam giác ABC . Tìm giá trị nhỏ nhất của = MA + MB + MC T . 2 2 2 2,0 OA OB OC
Gọi N = AM ∩ BC , kẻ MM  OA (M ∈ON)thì ta có 1 1 OA  ⊥ (OBC) 
⇒ MM ⊥ (OBC) 0,25 1 MM  OA 1 Kẻ MA ⊥ ,
OA A ∈OA . Khi đó 1 1 2 2 2 2 2 2
AM = AA + MA = AA + MO − OA = (AA − OA )(AA + OA ) 1 1 1 1 1 1 1 1 2 = OM + ( OA OA − 2OA ) 1 2 2
= OM + OA − 2O . AOA1 2 2 Suy ra MA OM 2OA1 = +1− (1) 2 2 OA OA OA 0,25
Tương tự gọi B ,C A 1
1 là các điểm tương tự như 1 thì ta có 2 2 MB OM 2OB1 = +1− (2) 2 2 OB OB OB 2 2 MC OM 2OC1 = +1− (3) 0,25 2 2 OC OC OC Trang 8/10 Câu
Sơ lược lời giải Điểm Từ ( ) 1 ,(2),(3) ta có 2  1 1 1   OA OB OC 1 1 1 T OM 2  = + + − + + +     3 2 2 2  OA OB OC   OA OB OC  0,25
Gọi H là trực tâm của tam giác ABC thì ta có 1 1 1 1 + + = 2 2 2 2 OA OB OC OH 2 Nên OM  OA OB OC 1 1 1 T 2  = − + + +   3 2 OH  OA OB OC  0,25 Mặt khác OA NM S 1 MBC = = OA NA S ABC Tương tự OB S OC S 1 MAC 1 = , MAB = 0,25 OB S OC S ABC ABC Nên OA OB OC 1 1 1 + + = 1 OA OB OC 0,25 2 Do đó OM T =
+1 ≥ 2 do OM ≥ OH . 2 OH
Vậy MinT = 2 khi M ≡ H . 0,25
Cho a,b,c là các số thực dương thỏa mãn 1 1 1 + + = 6 3a 2b c 2,0
Tìm giá trị lớn nhất của biểu thức a b c P = + + . a + 4bc b + 9ca c + 36ab 1 1 1 P = 4bc + 9ca + 36 1+ 1+ 1 ab + a b c 1 1 1 . VI = + + 0,25 (2,0 2 2 2  bc   ca   ab  điểm) 1+ 2  1+ 3  1+ 6 a b c       
Đặt = 2 bc , = 3 ca , = 6 ab x y z ⇒ xy = 6 ; c yz =18 ; a zx =12b . a b c Theo giả thiết ta có: 1 1 1 1 1 1 + + = 6 ⇔ + + = 1 3a 2b c
18a 12b 6c 1 1 1 . ⇔ + +
= 1 ⇔ x + y + z = xyz 0,25 yz zx xy Trang 9/10 Câu
Sơ lược lời giải Điểm Vậy tồn tại ba góc ,
A B,C của một tam giác sao cho x = tan ,
A y = tan B, z = tanC . 0,25 1 1 1 P = + +
= cos A + cos B + cosC 0,25 2 2 2 1+ tan A 1+ tan B 1+ tan C π π C + C π A B A B − + − 3 3
cos A + cos B + cosC + cos = 2cos .cos + 2cos .cos 3 2 2 2 2 π C π A B + + 3
⇒ cos A + cos B + cosC + cos ≤ 2cos + 2cos 3 2 2 π π A B C A B C π + + + + − − 3 3
⇒ cos A + cos B + cosC + cos ≤ 4cos cos 0,25 3 4 4 π
⇒ cos A + cos B + cosC + cos ≤ 2 3 3 0,25
⇒ cos A + cos B + cosC ≤ 2  yz zx xy 1  = = = Dấu bằng xảy ra khi π 1
A = B = C = ⇒  x y z
3 ⇒ x = y = z = . 3 3 
x + y + z = 1  bc  =  3 2 3 bc = a a   4  a = 1/ 6  ca  1 3  3 ca b b  = ⇔ = ⇔  =1/ 4 b 3    Khi đó c =  1/ 2   1 6 ab 3 ab = = c   12 0,25  c  1 a =  6  Giá trị lớn nhất của  1 P là 3 khi b  = 2 4 0,25   1 c =  2 -----HẾT----- Trang 10/10
Xem thêm: ĐỀ THI HSG TOÁN 11
https://toanmath.com/de-thi-hsg-toan-11
Document Outline

• ĐỀ CHÍNH THỨC TOÁN 11 NĂM 2024_2025
• HDC_ĐỀ CHÍNH THỨC TOÁN 2024_2025
• HSG 11