Đề chọn HSG Toán 11 năm 2024 – 2025 trường THPT Phùng Khắc Khoan – Hà Nội

SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
KỲ THI CHỌN HSG CẤP TRƯỜNG
TRƯỜNG THPT PHÙNG KHẮC KHOAN
KHỐI 10, 11-NĂM HỌC 2024-2025 - THẠCH THẤT
ĐỀ THI MÔN: TOÁN – LỚP 11
Thời gian làm bài 150 phút ĐỀ CHÍNH THỨC
(không kể thời gian giao đề) (Đề thi gồm 02 trang)
Số báo danh:..................... Họ và tên ............................................................................. Câu 1. (2,0 điểm ) .   
a.Tìm tập xác định D của hàm số y  tan 2x    .  4  sin x  tan x
b. Xét tính chẵn, lẻ của hàm số y  . sin x  cot x
Câu 2. (2,0 điểm). Tìm nghiệm lớn nhất của phương trình 2cos 2x 1  0 trong đoạn 0; . Câu 3. (4,0 điểm). 1
a. Tìm số hạng thứ 10 và xét tính tăng, giảm của dãy số u  . n 2 n  n
b. Một quả bóng cao su được thả từ độ cao 81 mét. Mỗi lần chạm đất quả bóng lại nảy lên hai
phần ba độ cao của lần rơi trước. Tính tổng các khoảng cách rơi và nảy của quả bóng từ lúc
thả bóng cho đến lúc bóng không nảy nữa. Câu 4. (1,5 điểm).
Một người gửi vào ngân hàng số tiền tiết kiệm là 73 triệu đồng theo hình thức lãi kép, nhằm
mục đích sau 5 năm thu được số tiền là 100 triệu đồng . Tuy nhiên vì kế hoạch tài chính thay
đổi nên người đó không rút tiền ra mà để sau 10 năm mới rút toàn bộ gốc và lãi. Giả sử trong
suốt quá trình gửi 10 năm, lãi suất của ngân hàng không thay đổi. Tính số tiền cả gốc và lãi
mà người đó nhận về sau 10 năm gửi ? (kết quả làm tròn đến hàng đơn vị và tính theo đơn vị triệu đồng). Câu 5. (4,0 điểm). 1 1 1 1 a. Tính limu với u     . n n 1.3 3.5 5.7 2n  12n  1 3  1 x  1 x  khi x  0 
b. Tìm m đề hàm số f x x  
liên tục tại điểm x  0 . 3 0  x  3x 1 m  h k i x  0  x  2 Câu 6. (6,5 điểm).
a. Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình thang, đáy lớn AB . Gọi I, J , K là
ba điểm lần lượt nằm trên các cạnh S ,
A AB, BC . Tìm giao tuyến của SAK với SBD , giao
điểm của IK với SBD , giao điểm của SD với IJK  .
b. Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình thang, đáy lớn AD và AD  2 BC
.Gọi O là giao điểm của AC và BD . Gọi G là trọng tâm tam giác SCD .Chứng minh OG / / (SBC). Đề thi môn Toán 11 Trang 1/2 trang
c. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, mặt bên SAB là tam giác
vuông tại A, SA  a 3 , SB  2a . Điểm M nằm trên đoạn AD sao cho AM  2MD . Gọi
P là mặt phẳng qua M và song song với SAB . Tính diện tích thiết diện của hình chóp
cắt bởi mặt phẳng P .
------------- HẾT -------------
(Thí sinh không dùng tài liệu, cán bộ coi thi không giải thích gì thêm) Đề thi môn Toán 11 Trang 2/2 trang ĐÁP ÁN. Câu 1. (2,0 điểm ) .   
a.Tìm tập xác định D của hàm số y  tan 2x    .  4  sin x  tan x
b. Xét tính chẵn, lẻ của hàm số: y  sin x  cot x         0,5 a.Hàm số y  tan 2x  
 xác định khi và chỉ khi cos 2x   0  2x    k   .  4   4  4 2 điểm 3 k 0,5 Suy ra x   . 8 2 điểm 3 k 
Vậy tập xác định của hàm số là D   \   , k  .  8 2  b.Hàm số xác định khi 0,5 cos x  0 cos x  0 điểm   cos x  0 k s  in x  0  s  in x  0    x  ,k  .  s    in x  0 2 2 sin x  cot x  0  s  in x  cos x  0 k 
Tập xác định: D   \  , k   ; x   D  x  D  2  sin x  tan x sin x  tan x sin x - tan x 0,5 Ta có: f x         f x
sin x  cot x  
sin x  cot x sin x  cot x điểm
Do đó hàm số đã cho là hàm số chẵn.
Câu 2. (2,0 điểm). Tìm nghiệm lớn nhất của phương trình 2cos 2x 1  0 trong đoạn 0; .     1,0 2x   k2  x   k  điểm
Phương trình 2cos 2x 1  1 0  cos 2x  3   6   . 2    2x    k2       x k  3  6    1  5   1,0 0   k     k     x k  0  điểm Xét x 0;  6   6 6   mà k   suy ra 6   .    1 7 k  1 5 0    k       k  x   6 6 6  6 Đề thi môn Toán 11 Trang 3/2 trang 5
Vậy nghiệm lớn nhất của phương trình 2cos 2x 1  0 trong đoạn 0;  là x  . 6 Câu 3. (4,0 điểm). 1
a. Tìm số hạng thứ 10 và xét tính tăng, giảm của dãy số u  . n 2 n  n
b. Một quả bóng cao su được thả từ độ cao 81 mét. Mỗi lần chạm đất quả bóng lại nảy lên
hai phần ba độ cao của lần rơi trước. Tính tổng các khoảng cách rơi và nảy của quả bóng từ
lúc thả bóng cho đến lúc bóng không nảy nữa. 1 1 1,0
a. Số hạng thứ 10 của dãy số là u   10 2 10 10 110 điểm 1 1 1 1 1,0 Ta có u  u     n 1  n n  2 1  n   2 1 n  n
n  1n  2 nn   1 điểm 2    với n  1. nn  n   0 1 2 Do đó u là dãy giảm. n  2 n 1 2    1,0
b.Gọi r là khoảng cách lần rơi thứ i . Ta có r  81, r  .81,…, r  .81 i 1 2   3 n  3  điểm ,…
Suy ra tổng các khoảng cách rơi của quả bóng từ lúc thả bóng cho đến lần rơi thứ 2 n   1    3 n bằng 81.  . 2 1 3 2  2  2 0,5
Gọi t là khoảng cách lần nảy thứ i . Ta có t  .81, t  . 81,…, i 1   3 2  3  3 điểm n 1 2    2 t  .81,… n    3  3
Suy ra tổng các khoảng cách nảy của quả bóng từ lúc thả bóng cho đến đến lần nảy n 1 2    1 2    3 thứ n bằng .81.  . 3 2 1 3 Đề thi môn Toán 11 Trang 4/2 trang
Vậy tổng các khoảng cách rơi và nảy của quả bóng từ lúc thả bóng cho đến lúc 0,5 n n 1 2 2        điểm  1 1        3  2  3
bóng không nảy nữa bằng S lim 81. .81.      2 3 2  1 1  3 3    1 0 2 1 0  81.  .81.  405m. 2 3 2 1 1 3 3 Câu 4. (1,5 điểm).
Một người gửi vào ngân hàng số tiền tiết kiệm là 73 triệu đồng theo hình thức lãi kép, nhằm
mục đích sau 5 năm thu được số tiền là 100 triệu đồng . Tuy nhiên vì kế hoạch tài chính
thay đổi nên người đó không rút tiền ra mà để sau 10 năm mới rút toàn bộ gốc và lãi. Giả sử
trong suốt quá trình gửi 10 năm, lãi suất của ngân hàng không thay đổi. Tính số tiền cả gốc
và lãi mà người đó nhận về sau 10 năm gửi ? (kết quả làm tròn đến hàng đơn vị và tính theo đơn vị triệu đồng).
Gọi r (r  0) là lãi suất gửi tiền, từ giả thiết của bài toán, theo công thức lãi kép ta 0,75 có: điểm 73.1 r5 100 100 5 5 100  1 r   r  1. 73 73
Suy ra tổng số tiền người đó thu được sau 10 năm là: 0,75 2    điểm  r10 100 73. 1  73.  137   (triệu đồng).  73  Câu 5. (4,0 điểm). 1 1 1 1 a. Tính limu với u     . n n 1.3 3.5 5.7 2n  12n  1 3  1 x  1 x  khi x  0 
b. Tìm m đề hàm số f x x  
liên tục tại điểm x  0 . 3 0  x  3x 1 m  h k i x  0  x  2 Đề thi môn Toán 11 Trang 5/2 trang 1 1 1 1 1,0 a. Ta có u     n 13 35 5 7 2n  12n   1 điểm 1  1 1 1 1 1  1  1   1      1     2  3 3 5 2n 1 2n 1 2  2n 1 1  1  1 1,0 limu  lim 1  . n   2  2n 1 2 điểm b. 0,5
+)Tập xác định D   1  ;  \  0 . điểm +) f   1 0  m  2     1 x  1 3 0,5 3 1 1 1 1  x x x  ) lim f x  lim  lim điểm x 0 x 0 x 0 x     x 3 1 x 1 1 1 x  lim  lim x 0 x 0 x    x  x
 1 x  1 1 x   1 1 1 1 x 1 ) lim  lim  lim x 0 x 0 x  x 1 x   x 0 1     x 1 x   1 1 1  lim  x 0  1 x 1 2  0,5 1 1 x  1  1 x     1 x2 3 3 3        3 1 1 x  điểm ) lim  lim   x 0 x 0 x    x 1  1 x  1 x 2 3 3          1 1 x 1  1   lim  lim  x 0   x 1   1 x   31 x2 x0 3  3
1 1 x   3 1 x 2 3     ilm f x 1 1 1    . x 0  2 3 6 3     0,5 f  x x 3x 1 1 lim  lim m    m  . điểm x 0 x 0    x  2  2 1 1 1
Để hàm số liên tục tại x  0 thì lim  lim f x  f 0  m    m   . x 0 x 0   2 6 3 1 Vậy m   . 3 Câu 6. (6,5 điểm).
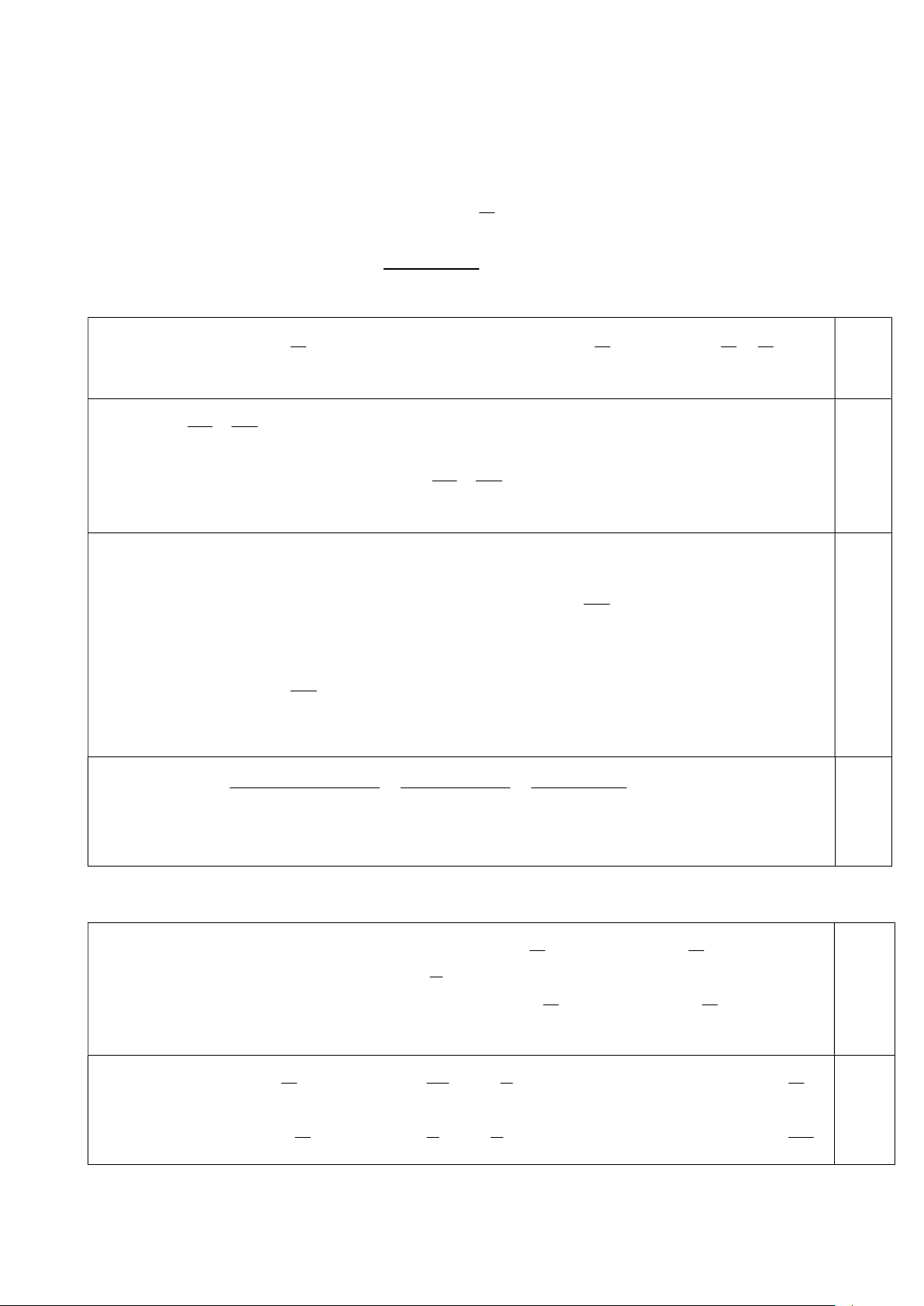
a. Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình thang, đáy lớn AB . Gọi I, J , K là
ba điểm lần lượt nằm trên các cạnh S ,
A AB, BC . Tìm giao tuyến của SAK với SBD , giao
điểm của IK với SBD , giao điểm của SD với IJK  . Đề thi môn Toán 11 Trang 6/2 trang
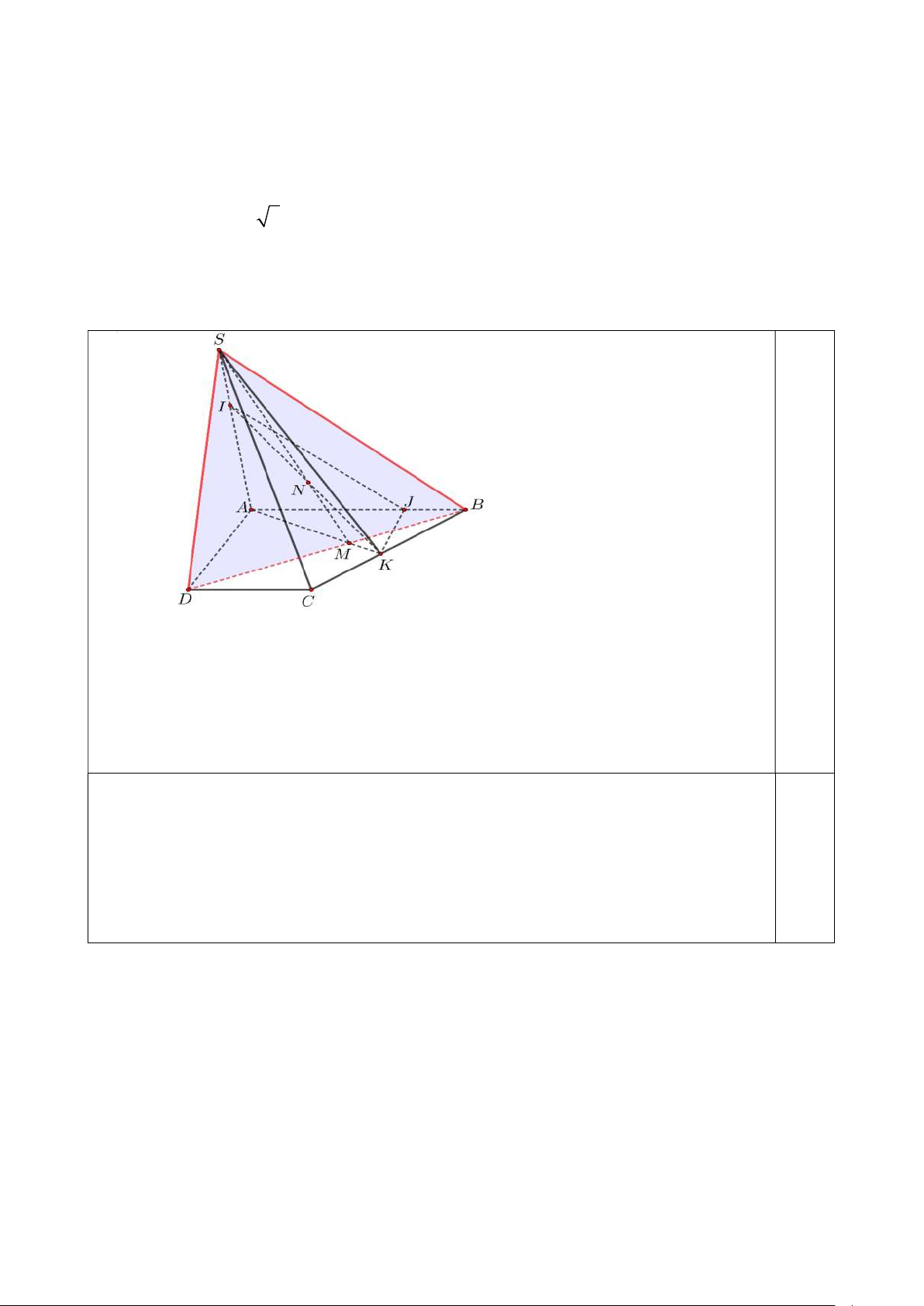
b. Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình thang, đáy lớn AD và AD  2 BC
.Gọi O là giao điểm của AC và BD . Gọi G là trọng tâm tam giác SCD . Chứng minh OG / / (SBC).
c. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, mặt bên SAB là tam giác
vuông tại A, SA  a 3 , SB  2a . Điểm M nằm trên đoạn AD sao cho AM  2MD . Gọi
P là mặt phẳng qua M và song song với SAB . Tính diện tích thiết diện của hình chóp
cắt bởi mặt phẳng P . 0,5 điểm a.
Trong mặt phẳng  ABCD , gọi M là giao điểm của BD và AK . M  BD M SBD Ta có :       M  AK M  
SAK  M SBD SAK .
Mặt khác : S  SBD  SAK .
SM  SBD  SAK  hay SM là giao tuyến của 2 mặt phẳng SBD và SAK .
Trong mặt phẳng SAK , gọi N là giao điểm của SM và IK . 0,75 N  SM  (SBD) điểm 
 N  IK SBD.  N  IK
Vậy N là giao điểm của IK và SBD . Đề thi môn Toán 11 Trang 7/2 trang 0,75 điểm
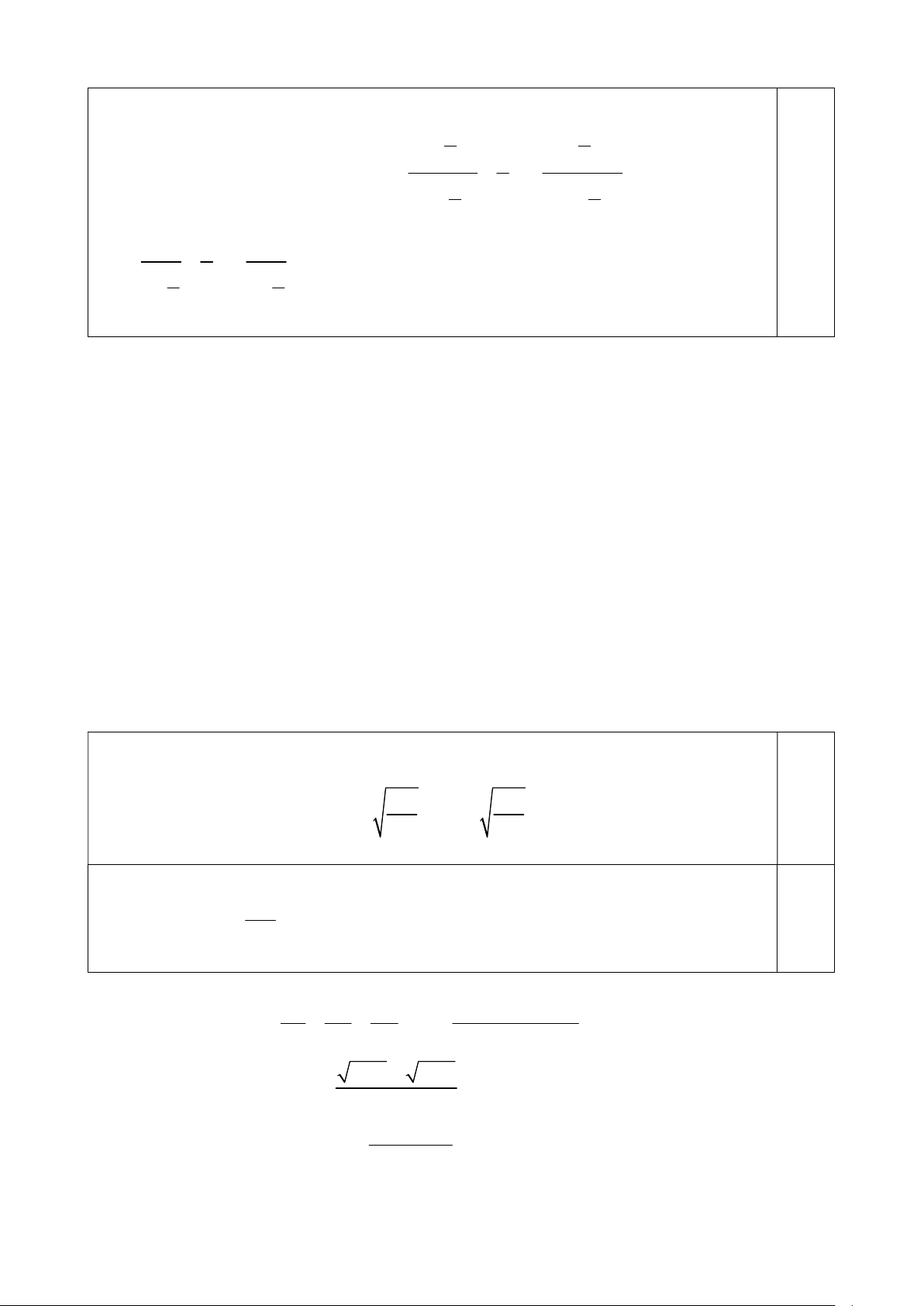
Trong mặt phẳng  ABCD , gọi P là giao điểm của BD và JK .
P  BD  (SBD) N  SM  (SBD)  ;   P  IK  (IJK )  N  IK  (IJK )
Trong mặt phẳng SBD , gọi Q là giao điểm của PN và SD .  Q  SD    SD  (IJK)    Q . Q   PN  (IJK )
Vậy Q là giao điểm của SD và IJK  . 0,5 điểm b.
Tứ giác ABCD là hình thang , đáy lớn AD  AD / / BC
Gọi E là giao điểm của AB và DC Đề thi môn Toán 11 Trang 8/2 trang EB EC BC 1 Khi đó E  BC  EAD     EA ED AD 2 EA ED  EB  ; EC 
 B,C lần lượt là trung điểm của AE; DE 2 2  B ;
D AC là đường trung tuyến trong tam giác ADE . DO 2 0,5 Mà  
O  AC  BD  O là trọng tâm của tam giác ADE   . DB 3 điểm DG 2
Gọi I là trung điểm của SC . Vì G là trọng tâm của tam giác SDC   . DI 3 DG DO 2 Xét  DGO và  DIB có   và góc D chung . DI DB 3 D  GO  D  IB  OG / / IB .  OG / / IB 0,5  Ta có : O
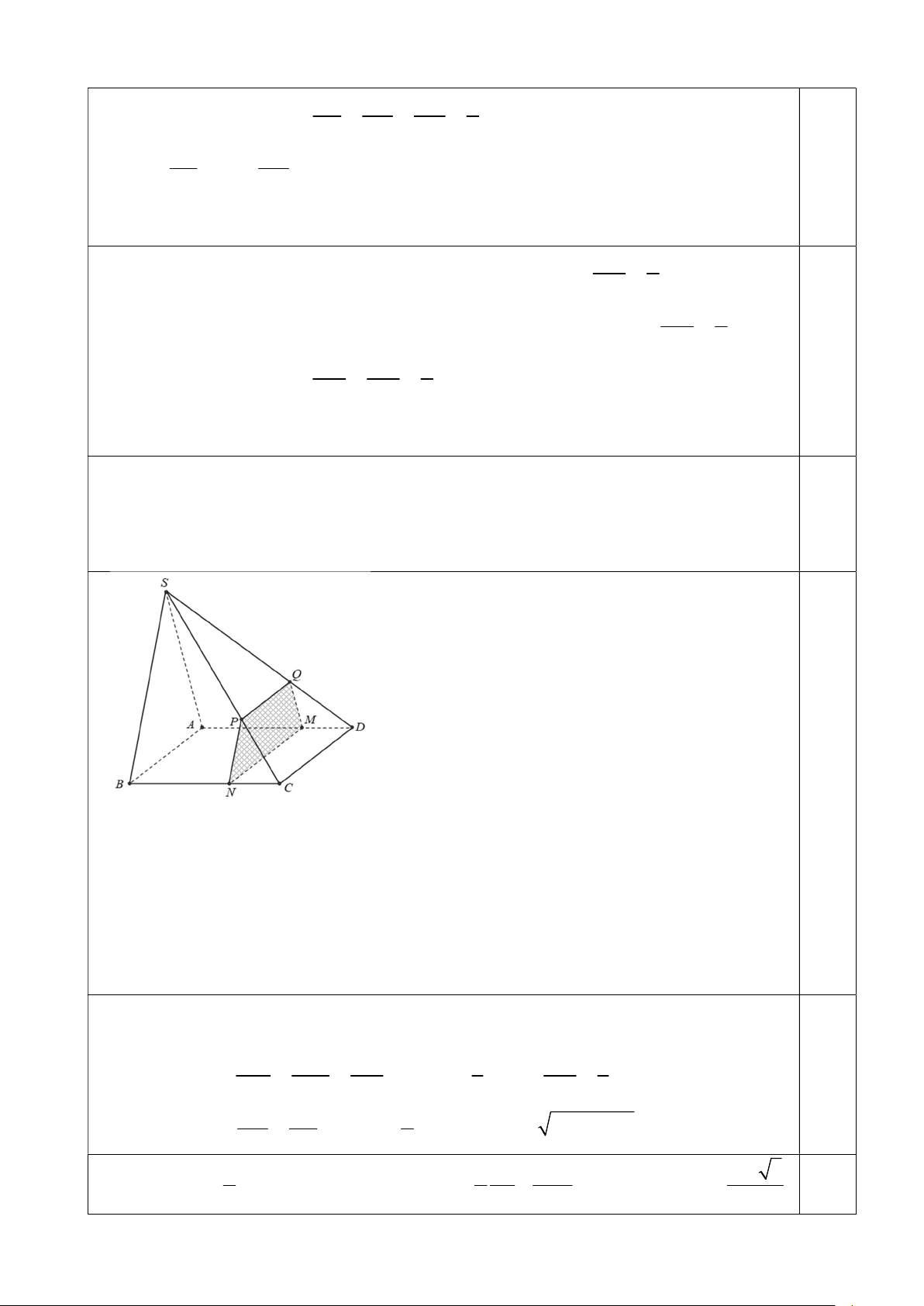
 G  (SBC)  OG / / (SBC) (đpcm). điểm  IB  (SBC)  1,0 điểm c.   P   //SAB   P     ABCD  MN Ta có:    và MN // PQ // AB M  AD,M   P   P    SCD  PQ   P   //SAB   P    SAD  MQ MQ // SA Lại có    và  M  AD,M   P   P    SBC  NP NP // SB
Từ đó suy ra P cắt hình chóp theo thiết diện là hình thang MNPQ .
Tam giác SAB vuông tại A nên SA  AB  MN  MQ 1,0
Suy ra hình thang MNPQ vuông tại M và Q . điểm MQ DM DQ 1 DQ 1 Do MQ // SA     MQ  SA và  . SA DA DS 3 DS 3 PQ SQ 2 Do PQ // CD    PQ  AB , với 2 2 AB  SB  SA  a CD SD 3 1 1 SA  2AB  2 5a 3 1,0 Ta có : S  M . Q PQ  MN  S  .  AB  S  MNPQ     2 MNPQ 2 3  3  MNPQ 18 điểm Đề thi môn Toán 11 Trang 9/2 trang 2 5a 3
Vậy diện tích thiết diện của hình chóp cắt bởi mặt phẳng P bằng . 18 Hết Đề thi môn Toán 11 Trang 10/2 trang