Đề chọn học sinh giỏi tỉnh Toán 12 năm 2020 – 2021 sở GD&ĐT Hải Dương

SỞ GIÁO DỤC VÀ ĐÀOTẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH LỚP 12 THPT HẢI DƯƠNG NĂM HỌC 2020 - 2021
Môn thi: TOÁN. Ngày thi: 21/10/2020
Thời gian làm bài: 180 phút, không kể thời gian giao đề ĐỀ CHÍNH THỨC (Đề thi có 01 trang) Câu I (2,0 điểm)
1. Tìm tất cả các giá trị của tham số m để đồ thị hàm số 4 y  x  m   2
1 x 1 có ba điểm cực trị
tạo thành một tam giác có ba góc nhọn. 1
2. Tìm tất cả các giá trị của tham số m để hàm số 3 y  x  m   2 1 x  m  3 2 x  m 1 nghịch 3 biến trên khoảng  1  ;0. Câu II (2,0 điểm) xyxy  2 2 2 1  x y  x   1  2 x  x   1
1. Giải hệ phương trình sau:  . 2 2 2x  xy x y  2   xy   2 1 x  4x  6  3  0
2. Xác định các giá trị của tham số m để phương trình sau có 2 nghiệm thực phân biệt: 4 2
5 x 1  m x 1  2 x 1  0 . Câu III (2,0 điểm)
1. Kết thúc đợt Hội học chào mừng ngày Nhà giáo Việt Nam, lớp 12A có 10 bạn được trao thưởng
trong đó có An và Bình. Phần thưởng để trao cho 10 bạn gồm 5 quyển sách Hóa, 7 quyển sách
Toán, 8 quyển sách Tiếng Anh (trong đó các quyển sách cùng môn là giống nhau). Mỗi bạn sẽ
được nhận 2 quyển sách khác loại. Tìm xác suất để An và Bình có phần thưởng giống nhau.
2. Trong mặt phẳng tọa độ Oxy , cho tam giác ABC có B  1  ;4. Gọi D , E  1  ;2 lần lượt là  3 7 
chân đường cao kẻ từ ,
A B và M là trung điểm của đoạn thẳng AB . Biết I  ;   là tâm  2 2 
đường tròn ngoại tiếp tam giác DEM . Tìm tọa độ đỉnh C của tam giác ABC . Câu IV (3,0 điểm)
1. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và góc  BAD  120 .
a) Tính thể tích khối chóp S.ABCD biết SA  SB  SC và khoảng cách từ điểm A đến mặt phẳng 3a (SCD) bằng . 4
b) Tính thể tích khối chóp S.ABC biết góc giữa 2 mặt phẳng  ABC , SBC bằng 45 và tam giác SAB vuông cân tại A.
2. Cho hình lăng trụ đứng ABC . D A B  C  D
  , đáy ABCD là hình thoi cạnh a . Gọi N là trung điểm
của DD , M nằm trên cạnh BB sao cho MB  2MB , P là giao điểm của CC và  AMN . Biết rằng góc 
ABC   và AA  a . Tìm cos để góc giữa hai đường thẳng AP và AN bằng 45 . Câu V (1,0 điểm)
Cho x, y, z là các số dương nhỏ hơn 1 thỏa mãn 43x   1  6 y  z  x y  z  x  yz .
2x  y  x  z 1 2x  z   2  x  y 1     2 2 2 2(x  3)  y  z 16
Tìm giá trị lớn nhất của biểu thức P  . 2 2 2 2x  y  z
--------------Hết--------------
Họ và tên thí sinh: ...................................................................................... Số báo danh:..................................
Cán bộ coi thi số 1:...................................................... Cán bộ coi thi số 2: ....................................................
SỞ GIÁO DỤC VÀ ĐÀOTẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH LỚP 12 THPT HẢI DƯƠNG
NĂM HỌC: 2020 - 2021. Ngày thi: 21/10/2020 Môn thi: TOÁN HƯỚNG DẪN CHẤM
(Hướng dẫn chấm gồm có 07 trang) Câu Đáp án Điểm
1. Tìm tất cả các giá trị của tham số m 4 2
để đồ thị hàm số y  x  m   1 x 1 có ba 1,0
điểm cực trị tạo thành một tam giác có ba góc nhọn. Ta có 3 y  x  m   2 4 2 1 x  2x(2x  m 1) . 0,25
Hàm số có ba cực trị  m 1  0  m  1 .  m 1 m  2 1 
Khi đó ba điểm cực trị của đồ thị hàm số là: A0;  1 , B  ;1   , 2 4    0,25  m 1 m  2 1 
  m 1 m  2    m 1 m  2 1 1  C   ;1   AB   ; , AC    ;   .  2 4        2 4 2 4    
Tam giác ABC luôn cân tại A . Do đó, tam giác ABC nhọn khi và chỉ khi góc  BAC   m 1 m  4 1 0,25
nhọn  AB  AC  0     0  m   1 m  3 1  8  0 I 2 16   (2,0 m 1 điểm)  
. Kết hợp với điều kiện, ta được m  1. 0,25 m  1 
2. Tìm tất cả các giá trị của tham số m để hàm số 1 3 1,0 y  x  m   2 1 x  m  3 2
x  m 1 nghịch biến trên khoảng  1  ;0 . 3 Ta có 2 y  x  2m  
1 x  m  3 có   m  2 2
1  m  3  m  m  4  0, m  nên y 0,25
luôn có 2 nghiệm phân biệt x , x  x  x với mọi m . 1 2  1 2
Bảng biến thiên của hàm số như sau: x  x x  1 2 y  0  0  0,25 y  y    1  0 m  4  0
Để hàm số nghịch biến trên khoảng  1  ;0 thì    0,25  y  0  0 m  3  0
 3  m  4 . Vậy tập hợp tất cả các giá trị của m là  3  ;4. 0,25 xyxy  2 2 2 1  x y  x   1  2 x  x   1
1. Giải hệ phương trình sau:  . 1,0 2 2 2x  xy x y  2   xy   2 1 x  4x  6  3  0 2 2 2 2  xy  xy   1  x y   x   1 x  x   1 (1) Hệ phương trình:  . 2 2 2x  xy x y  2   xy   2 1 x  4x  6  3  0 (2)
Từ phương trình (1) ta có: xy  x y  xy     x   x  2 2 2 1 1 1   x   1 1   (3) .
Đặt f t  t  2t  t  
1 , t   . Ta có: f t  2
 3t  2t 1  0, t   nên f t đồng 0,25 biến trên  .
Do đó (3)  xy  x 1. II
Thay vào (2), ta được x  x   2 x  x    x   2 2 1 2 3 2 x  4x  6  3  0 (2,0 0,25 x   2
 x  x  x   2 1 1 2 3
2 1 x  4x  6   0 (4) điểm) 2
a  x  2x 3  0 2 2 2 2 x  2x  3  a   b a 3 Đặt  2 2  
 b  a  2x  3  x  2 b  2 2   x  4x  6  0 x  4x  6  b 2 2 2 2 2 b  a 1 b  a 1 0,25
Phương trình (4) trở thành 1 a 1 b  0 2 2
 b  a a  ba  b  2 1  0  a  b  (do a  0, b  0 ). 3 1 Với 2 2
a  b  x  2x  3  x  4x  6  x    y  . 2 3  3 x    0,25  Vậy nghiệm của hệ là 2  . 1 y   3
2. Xác định các giá trị của tham số m để phương trình sau có 2 nghiệm thực phân biệt: 1,0 4 2
5 x 1  m x 1  2 x 1  0 . Điều kiện: x  1. x 1 x 1 0,25
Chia 2 vế cho x 1 ta được phương trình 4 5  2  m . x 1 x 1 x 1 Đặt 4 t 
là hàm số đồng biến trên 1;  . x 1 x 1 2 0,25 Ta có t  0 và 4 4 t   1  t  1. x 1 x 1
Khi đó ta có phương trình 2 m  5
 t  2t (1) với t 0; 1.
Bảng biến thiên hàm số 2
f (t)  5t  2t trên [0;1): 1 x 0 1 5 1 5 0,25 y 0 3  
Ycbt  phương trình (1) có hai nghiệm phân biệt thuộc 0; 1  1 m  0;   . 0,25  5  III
1. Kết thúc đợt hội học hội giảng chào mừng ngày Nhà giáo Việt Nam, lớp 12A có 10 (2,0
bạn được trao thưởng trong đó có An và Bình. Phần thưởng để trao cho 10 bạn gồm 5 1,0 điểm)
quyển sách Hóa, 7 quyển sách Toán, 8 quyển sách Tiếng Anh (trong đó các quyển
sách cùng môn là giống nhau). Mỗi bạn sẽ được nhận 2 quyển sách khác loại. Tìm
xác suất để An và Bình có phần thưởng giống nhau.
Gọi x, y, z lần lượt là số học sinh được nhận phần thưởng là: sách Hóa và sách Toán, x  y  5 x  2   0,25
sách Hóa và sách Tiếng Anh, sách Toán và sách Tiếng Anh  x  z  7  y  3.  y z 8    z  5  
Số phần tử của không gian mẫu là n 2 3 5  C .C .C  2520. 10 8 5 0,25
Gọi A là biến cố “An và Bình có phần thưởng giống nhau”
Có các khả năng xảy ra là:
- Khả năng 1: An và Bình cùng nhận sách Hóa và sách Toán, chọn 3 người trong 8 người
còn lại để nhận sách Hóa và sách Tiếng Anh có 3
C cách, 5 người còn lại nhận sách 8
Toán và sách Tiếng Anh có 5
C cách, nên Khả năng 1 có 3 5
C .C  56 cách chọn thỏa 5 8 5 mãn biến cố A . 0,25
- Khả năng 2: An và Bình cùng nhận sách Hóa và sách Tiếng Anh, bằng cách chọn
tương tự Khả năng 1, ta có 1 2 5 C .C .C  168 8 7 5
cách chọn thỏa mãn biến cố A .
- Khả năng 3: An và Bình cùng nhận sách Toán và sách Tiếng Anh, bằng cách chọn
tương tự Khả năng 1, ta có 3 3 2
C .C .C  560 cách chọn thỏa mãn biến cố A . 8 5 2  n A 3 5 1 2 5 3 3 2
 C .C  C .C .C  C .C .C  784 . 8 5 8 7 5 8 5 2 3 5 1 2 5 3 3 2 n A C .C  C .C .C  C .C .C 14
Vậy xác suất cần tìm là: P  A   8 5 8 7 5 8 5 2    . 0,25 n 2 3 5 C .C .C 45 10 8 5
2. Trong mặt phẳng tọa độ Oxy , cho tam giác ABC có B 1 ;4 . Gọi D , E 1;2
lần lượt là chân đường cao kẻ từ ,
A B và M là trung điểm của đoạn thẳng AB . Biết  3 7  1,0 I  ; 
 là tâm đường tròn ngoại tiếp tam giác DEM . Tìm tọa độ đỉnh C của tam  2 2  giác ABC . 0,25
Phương trình BE : x  1.
Phương trình đường thẳng AC qua E  1
 ;2 vuông góc với BE là y  2 .  c  
Gọi N là trung điểm của BC và giả sử C c;2  1 AC  N ;3   .  2 
Ta chứng minh: Tứ giác MEND nội tiếp đường tròn tâm I . Thật vậy: Ta có  MAE  
MEA vì EM là đường trung tuyến của tam giác EAB vuông tại E .  NME  
MEA vì ở vị trí so le (do MN // AC ) 0,25   MAE   NME (1)
Mặt khác D, E cùng nhìn 
AB dưới 1 góc vuông nên ABDE nội tiếp đường tròn   MAE   EDN (cùng bù với  BDE ) (2) Từ (1), (2)   NME  
EDN  MEND nội tiếp đường tròn.
Ta có tứ giác MEND nội tiếp đường tròn tâm I 2 2 2 2  c  2   1   1   3 0,25 2 2 
 IN  IE  IN  IE                2   2   2   2  c  1 C 1;2     c  5  C   5  ;2 . 0,25
1. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và góc  BAD  120 .
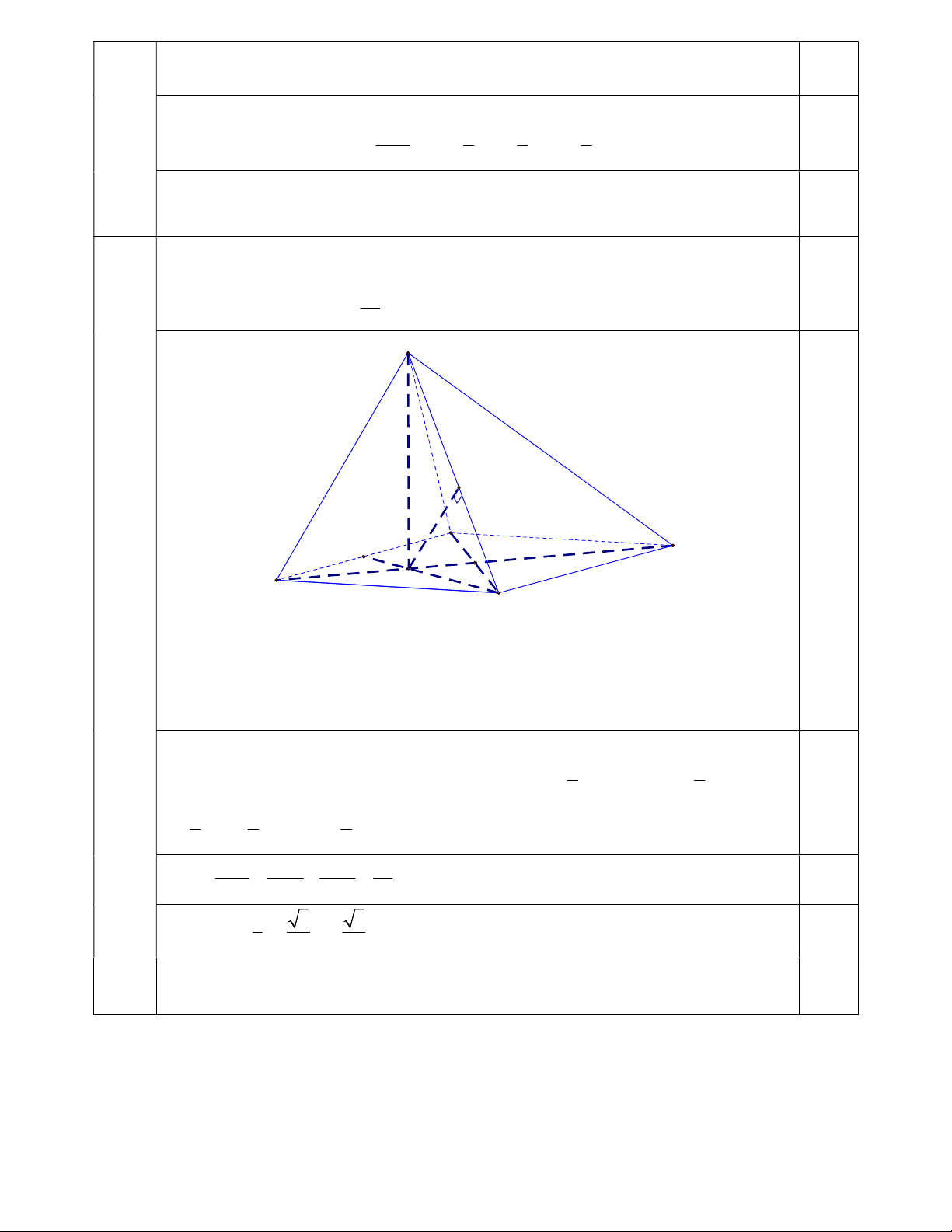
a) Tính thể tích khối chóp S.ABCD biết SA  SB  SC và khoảng cách từ điểm A đến 1,0 3a mặt phẳng (SCD) bằng . 4 S K A 0,25 M D H B IV C (2,0
Do ABCD là hình thoi canh a và có góc 
BAD  120 nên ABC đều cạnh a .
điểm) Gọi H là hình chiếu của S trên mặt phẳng  ABCD.
Do SA  SB  SC  HA  HB  HC  HC  AB  HC  C . D
Dựng HK  SC, K  SC  HK  SCD  d H,SCD  HK .
Gọi M là trung điểm của AB  M , H , C thẳng hàng. 3 3
Do AB // SCD suy ra: d  ,
A SCD  d M ,SCD  d H,SCD  HK 2 2 0,25 3 3 a  HK  a  HK  . 2 4 2 1 1 1 1 Ta có     SH  a 0,25 2 2 2 2 SH HK HC a 1 3 3 2 3  V  .a .a  a . 0,25 S.ABCD 3 2 6
b) Tính thể tích khối chóp S.ABC biết góc giữa 2 mặt phẳng  ABC , SBC bằng 45 1,0
và tam giác SAB vuông cân tại A . 0,25
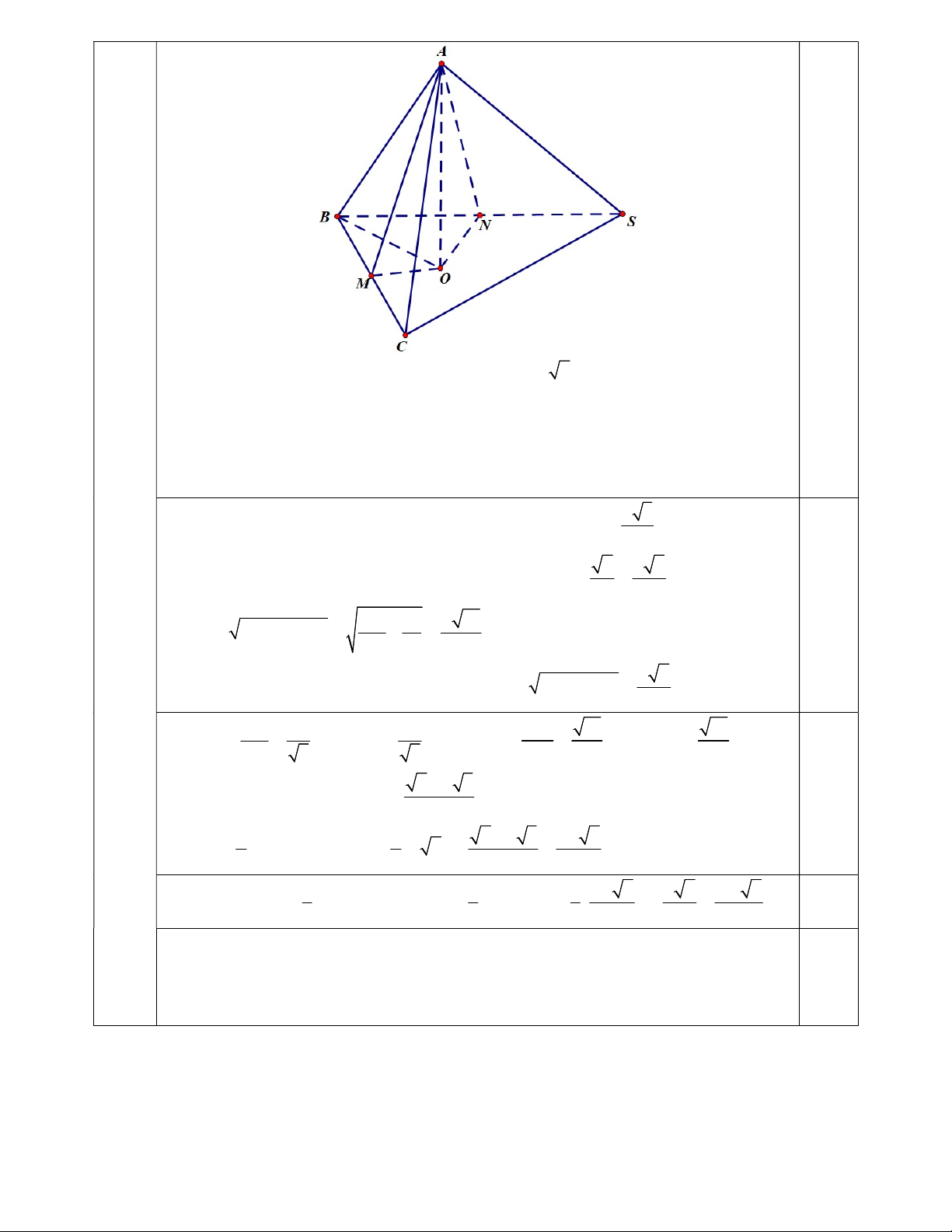
Do SAB vuông cân tại A , AB  a  SA  a, SB  a 2 . Xét hình chóp .
A SBC có SA  AB  AC , suy ra AO  (SBC) với O là tâm đường tròn
ngoại tiếp SBC  OM  BC .
Gọi M là trung điểm của BC , ABC đều suy ra AM  BC .
Suy ra góc giữa 2 mặt phẳng  ABC , SBC   bằng  AMO 45 . a 3
Xét tam giác ABC đều cạnh a có AM là đường cao  AM  . 2 2 a 6
Xét tam giác AMO vuông cân tại O nên AO  OM  AM   . 2 4 0,25 2 2 6a a a 10 2 2  OB  OM  MB    . 16 4 4 a 2
Gọi N là trung điểm của SB 2 2
 ON  SB  ON  OB  NB  . 4  ON 1 OM 15 10 SBO    2 sin , cos SBO  , sin  OBM   , cos  OBM  OB 5 5 OB 5 5    SBC   SBO    OBM  2 2 3 sin sin  0,25 5 1    S   SB  BC sin  1 2 2 3 1 6 2 SBC   a 2  a   a SBC 2 2 5 5 1 1    1 1 6 a 6 6 6 V  V   S  d , A SBC   S  AO 2 3   a   a . 0,25 S.ABC . A SBC SBC    3 3 SBC 3 5 4 60
2. Cho hình lăng trụ đứng ABCD.AB C  D
  , đáy ABCD là hình thoi cạnh a . Gọi N là
trung điểm của DD , M nằm trên cạnh BB sao cho MB  2MB , P là giao điểm 1,0
của CC  và  AMN . Biết rằng góc 
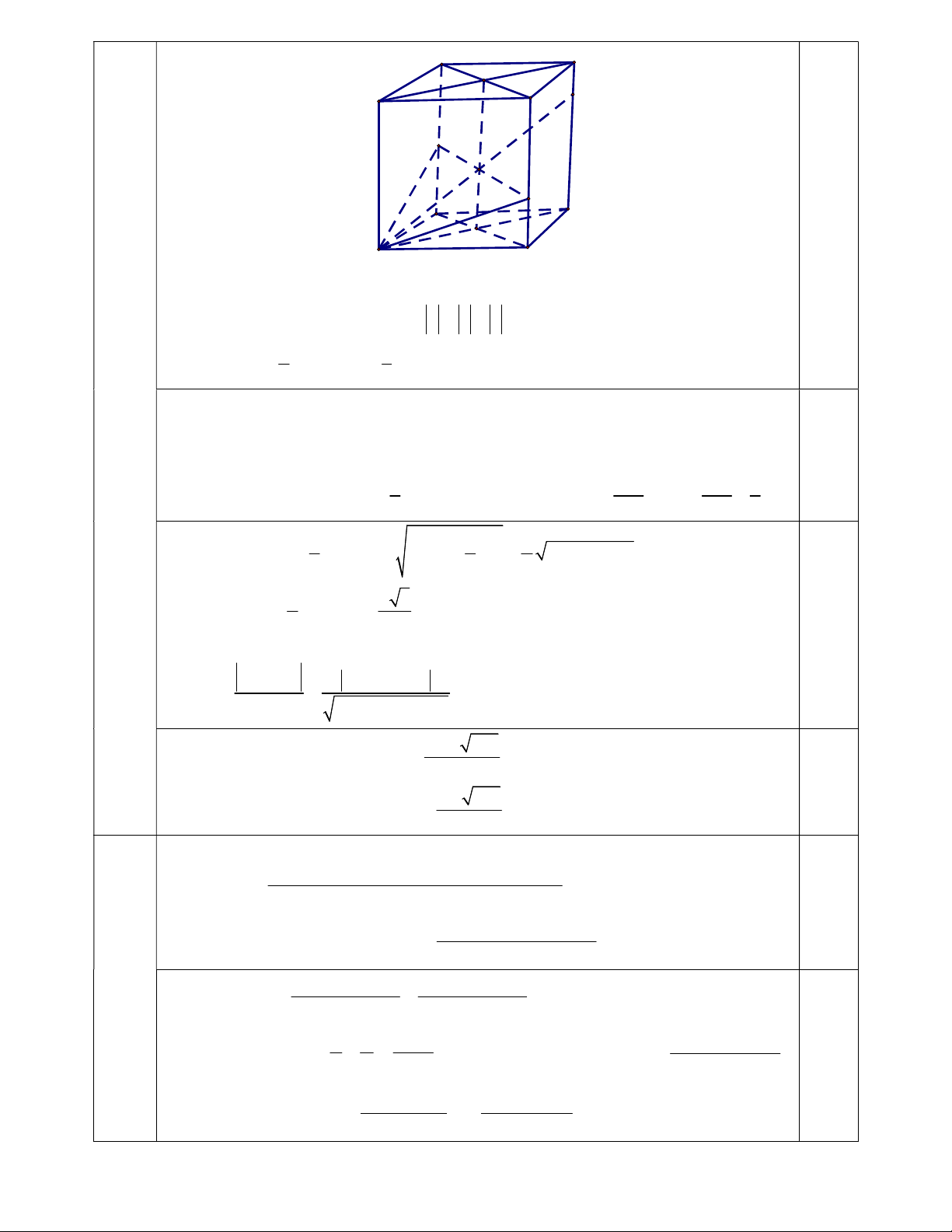
ABC   và AA  a . Tìm cos để góc giữa hai đường thẳng A P  và AN bằng 45. D' C' A' B' P N I D M C 0,25 A B
      Đặt AB  a, AD  , b AA  c,  BAD   .          Ta có 2 a c  bc  0, .
a b  a cos, a  b  c  a .
  1    1 
Ta có AN  b  c, AM  a  c . 2 3
Gọi O, O lần lượt là tâm của hai đáy ABCD, A B  C  D
  , I là giao điểm của OO và
MN , P là giao điểm của AI và CC  . Ta có P   AMN   CC và AMPN là hình bình hành. 0,25
     5 
     CP  CP 5
Ta có AP  AM  AN  a  b  c và AP  AC  CP  a  b  c . Vậy  . 6 CC CC 6 2    1     1   a Ta có: A P
  a  b  c  AP  a  b  c  73 72cos ;   6  6  6   1  a 5 AN  b  c  AN  . 2 2 0,25 Theo giả thiết, ta có:   AP  AN 1112 cos 2 cos 45  
 288cos  168cos 123  0. AP  AN 573  72cos  7 295
Giải phương trình, tìm được cos    . 24 0,25 7 295 Vậy cos o c s  0 180   cos       . 24
Cho x, y, z là các số dương nhỏ hơn 1 thỏa mãn 43x   1  6 y  z  x y  z  x  yz .
2 x  y  x  z 1 2x  z   2  x  y 1     1,0 2 2 2 2(x  3)  y  z 16
Tìm giá trị lớn nhất của biểu thức P  . 2 2 2 2x  y  z V (1,0 2 2 Từ giả thiết ta có 
 x  yx  z . điểm)
3x  2y  z 1 3x  2z  y 1 1 1 4
Sử dụng bất đẳng thức   ; x
 , y  0  x  y y  z 4  2  . 0,25 x y x  y 6x  3y  3z  2 2  x  y  x  z  2x  y  z
Mặt khác  x  y x  z  2      2  4  x  y  z2 2 8 2   t 8
. Đặt t  2x  y  z , ta được  4 6x  3y  3z  2 4 3t  2 3 2
 3t  2t  32  0  t   2
2 3t  4t 16  0  t  2  2x  y  z  2  y  z  2  2x .  y  z2 Ta có y  z     x2 2 2 2 1 2 0,25 12x  2 12x  2 6x 1 6x 1  P  1  1  1  1 . 2 2 2 2x  y  z 2x  21 x2 x  1 x2 2 2 2 2x  2x 1 6x 1 Xét hàm số f  x  với x 0;  1 . 2 2x  2x 1 x  1 0,25 2 12x  4x  8 Ta có f  x     và f  x  0  2 . 2x  2x  2 2 1 x   3
Bảng biến thiên của hàm số trên 0;  1 : 2 x 0 1 3 f  x 9 0,25 f  x 7 1
Từ bảng biến thiên, ta có f  x  9, x  0; 
1  P  1 f  x 10 . 2 1 1
Dấu bằng xảy ra khi x  , y  , z  . Vậy max P  10 . 3 3 3