Đề chọn học sinh giỏi tỉnh Toán 12 năm 2024 – 2025 sở GD&ĐT Nghệ An

Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề thi chọn học sinh giỏi cấp tỉnh môn Toán 12 năm học 2024 – 2025 sở Giáo dục và Đào tạo tỉnh Nghệ An. Đề thi có đáp án và lời giải chi tiết. Mời bạn đọc đón xem!

25 13 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung

Môn: Toán 12

Thông tin:

23 trang 1 tuần trước

Tác giả:

Profile Lê Phương
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NĂM HỌC- 2024-2025
https://www.facebook.com/groups/toanvd.vdc
Trang 1
NHÓM GIÁO VIÊN TOÁN VIỆT
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
SỞ GIÁO DỤC ĐÀO TẠO NGHỆ AN
ĐỀ THI CHỌN HSG CẤP TỈNH
Môn: Toán 12
Thời gian: 50 phút (không kể thời gian phát đề)
PHẦN I. TRẮC NGHIỆM
Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1. Cho khối chóp tứ giác đều
SABCD
có
32
,
2
AB a SA a= =
. Thể tích của khối chóp
SABCD
bằng
A.
3
2a
. B.
3
2
2
a
. C.
3
2
3
a
. D.
3
32
2
a
.
Câu 2. Giả sử một vật giao động điều hòa xung quanh vị trí cân bằng theo phương trình
. Ở đây, thời gian t tính bằng giây và
( )
xt
là li độ của vật tại thời điểm t
tính bằng centimet. Hãy cho biết trong khoảng thời gian từ 0 đến 4 giây, vật đạt li độ bằng
3
2
cm
bao nhiêu lần?
A.
6
. B.
5
. C.
3
. D. 4.
Câu 3. Một lớp có 45 học sinh, trong đó có 31 em học sinh học khá môn Toán, 24 học sinh học khá
môn Tiếng Anh, 5 học sinh không học khá cả hai môn Toán và Tiếng Anh. Chọn ngẫu nhiên
một học sinh trong lớp. Xác suất để học sinh được chọn học khá cả hai môn Toán và Tiếng
Anh là
A.
248
675
. B.
173
675
. C.
1984
6075
D.
1
3
.
Câu 4. Cho hình hộp
111 1
.ABCD A B C D
. Phát biểu nào sau đây sai?
A.
11
AC CC CB CD= +−
   
. B.
11
AC DC DD DA=+−
   
.
C.
11
AC AB AD AA=++
   
. D.
11
AC BC BB BA=++
   
.
Câu 5. Trong không gian
Oxyz
, cho hai điểm
( )
2; 1;1A −
và
( )
1; 2; 3B −
. Toạ độ của vectơ
AB

là
A.
( )
1; 3; 4−
. B.
( )
3;1; 2−
. C.
( )
1; 3; 4−−
. D.
( )
2; 2; 3−−
.
Câu 6. Bảng số liệu ghép nhóm sau cho biết chiều cao
( )
cm
của 50 học sinh lớp 10A.
Khoảng chiều cao
[
)
155;160
[
)
160;165
[
)
165;170
Số học sinh
17
25
8
Mốt của mẫu số liệu ghép nhóm trên là
A.
162,6
. B.
161,6
. C.
163, 4
. D.
160
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NĂM HỌC- 2024-2025
https://www.facebook.com/groups/toanvd.vdc
Trang 2
NHÓM GIÁO VIÊN TOÁN VIỆT
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 7. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông tâm
O
, đường thẳng
SA
vuông góc với
mặt phẳng đáy và
3
OC SA=
(tham khảo hình vẽ). Số đo góc phẳng nhị diện
[
]
,,
S BD C
bằng
A.
120
O
. B.
150
O
. C.
30
O
. D.
60
O
.
Câu 8. Cho hàm số bậc ba
( )
y fx
=
có đồ thị là đường cong như hình vẽ bên. Điểm cực tiểu của hàm
số đã cho bằng
A.
0
. B.
1
. C.
2
. D.
5
.
Câu 9. Cho hàm số
( )
22 2
22
2
xx
fx x
xx
−>
= =
−<
nÕu
nÕu
nÕu
. Phát biểu nào sau đây là đúng?
A.
( )
2
lim 2.
x
fx
−
→
=
B.
(
) ( )
2
lim 2 .
x
fx f
+
→
=
C.
( ) ( )
22
lim lim .
xx
fx fx
+−
→→
=
D. Hàm số liên tục tại
2.x
=
Câu 10. Một cấp số cộng có số hạng đầu bằng
4
và số hạng thứ
3
bằng
12
. Số hạng thứ
10
của cấp số
cộng đó bằng
A.
44.
B.
36.
C.
40.
D.
10
4.
Câu 11. Cho hàm số
( )
y fx=
có đạo hàm
( ) ( )( )
23f x xx x
′
=++
,
x∀∈
và
( ) ( ) ( ) ( )
1 2 30ff f f+ −= +
. Giá trị nhỏ nhất, giá trị lớn nhất của hàm số
( )
y fx=
trên
đoạn
[ ]
2;3−
lần lượt là
A.
( )
0f
và
( )
2.f −
B.
( )
2f −
và
( )
0.f
C.
( )
0f
và
( )
3.f
D.
(
)
3f
và
( )
0.f
Câu 12. Một vật chuyển động theo phương trình
( )
32
1
4
6
st t t t= −+
, trong đó
0t >
,
t
tính bằng giây
và
( )
st
tính bằng mét. Xét trong khoảng thời gian từ
4
giây đến
10
giây vận tốc của vật đạt
giá trị nhỏ nhất bằng
O
B
D
A
C
S
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NĂM HỌC- 2024-2025
https://www.facebook.com/groups/toanvd.vdc
Trang 3
NHÓM GIÁO VIÊN TOÁN VIỆT
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A.
16
3
(m/s). B.
32
3
(m/s). C.
4
(m/s). D.
2
(m/s).
PHẦN II. CÂU TRẮC NGHIỆM ĐÚNG SAI
Thí sinh trả lời từ câu 01 đến câu 04. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1. Cho hàm số
(
) ( )
5
log 4 1fx x
= +
.
a) Tập xác định của hàm số
( )
fx
là khoảng
1
4
;

− +∞


.
b) Bất phương trình
( )
1
0
31
x
fx−
≤
−
có đúng 2 nghiệm nguyên.
c) Đồ thị hàm số
( )
fx
đi qua trung điểm của đoạn thẳng
AB
, với
( )
34;A
và
( )
90;B
.
d) Đạo hàm của hàm số
(
)
fx
là
(
)
4
51
fx
x
′
=
+
.
Câu 2. Cho hình lăng trụ đứng
111
.ABC A B C
có đáy
ABC
là tam giác vuông cân tại
A
,
AB AC a
= =
và cạnh bên
1
2AA a
=
(tham khảo hình vẽ)
a) Thể tích của khối lăng trụ
111
.
ABC A B C
bằng
3
2
2
a
.
b) Góc giữa hai đường thẳng
1
BC
và
AC
bằng
60
°
.
c) Khoảng cách từ
A
đến mặt phẳng
( )
11
A BC
bằng
6
6
a
.
d) Gọi
,MN
lần lượt là hai điểm di động trên các đoạn thẳng
11
AC
và
1
BC
sao cho
2
a
MN =
.
Thể tích của khối chóp
1
.A A BNM
có giá trị nhỏ nhất bằng
3
72
48
a
.
Câu 3. Các học sinh lớp
12T
làm thí nghiệm gieo ba loại hạt giống
, XY
và
Z
. Xác suất để ba loại hạt
giống
, XY
và
Z
nảy mầm tương ứng là
, xy
và
( )
0,8 xy>
. Biết rằng xác suất để ít nhất một
trong ba hạt giống này mầm là
0,964
và xác suất để cả ba hạt giống đều nảy mầm là
0,224
. Giả
sử việc nảy mầm của các hạt giống
, XY
và
Z
là độc lập với nhau. Gọi
A
là biến cố: “Có ít
nhất một trong ba hạt giống nảy mầm” và
B
là biến cố: “Cả ba hạt giống đều nảy”.
a) Biến cố đối của biến cố
A
là
A
: “Cả ba hạt giống đều không nảy mầm”. mầm
b) Xác suất để xảy ra biến cố
B
là
( )
0,8P B xy=
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NĂM HỌC- 2024-2025
https://www.facebook.com/groups/toanvd.vdc
Trang 4
NHÓM GIÁO VIÊN TOÁN VIỆT
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
c) Xác suất để hạt giống
X
nảy mầm là
0, 7
.
d) Xác suất để có đúng hai hạt nảy mầm là
0,488
.
Câu 4. Cho hàm số
2
24
2
xx
y
x
++
=
+
.
a) Hàm số có giá trị cực đại lớn hơn giá trị cực tiểu.
b) Gọi
,
AB
là các điểm cực đại, cực tiểu của đồ thị hàm số. Diện tích của tam giác
OAB
bằng
8
(đơn vị diện tích), trong đó
O
là gốc tọa độ.
c) Đường thẳng đi qua hai điểm cực đại và cực tiểu của đồ thị hàm số là
22yx= +
.
d) Hàm số nghịch biến trên khoảng
(
)
4; 0
−
.
PHẦN III. CÂU TRẮC NGHIỆM TRẢ LỜI NGẮN
Thí sinh trả lời câu 1 và câu 2
Câu 1. Một doanh nghiệp tư nhân
X
chuyên kinh doanh xe gắn máy các loại. Hiện nay, doanh
nghiệp đang tập trung chiến lược kinh doanh một loại xe máy với chi phí mua vào là
38
triệu
đồng/ chiếc với giá bán ra là
43
triệu đồng/ chiếc. Với giá bán này thì số lượng xe bán ra mỗi
năm là
600
chiếc. Nhằm tiêu thụ dòng xe đang ăn khách này, doanh nghiệp dự định giảm giá
bán. Ước tính cứ giảm
1
triệu đồng/ chiếc thì số lượng xe bán ra trong năm tăng thêm
200
chiếc. Vậy doanh nghiệp phải giảm giá bán là bao nhiêu triệu đồng để thu được lợi nhuận cao
nhất trong một năm?
Câu 2. Trong ngày hội STEM, bạn An nhận được nhiệm vụ thiết kế một chiếc hộp giấy có dạng hình
hộp chữ nhật
1111
.ABCD A B C D
với độ dài các cạnh
1
,,AB a AD b AA c
và khoảng
cách giữa
AC
và
1
BC
bằng
d
( tham khảo hình vẽ). Biết rằng
,,,abcd
là các số nguyên
dương có đơn vị đo bằng decimet. Hỏi diện tích của chiếc hộp bằng bao nhiêu
2
dm
để thể tích
của chiếc hộp bạn An sẽ làm là nhỏ nhất.
HẾT
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NĂM HỌC- 2024-2025
https://www.facebook.com/groups/toanvd.vdc
Trang 5
NHÓM GIÁO VIÊN TOÁN VIỆT
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
HƯỚNG DẪN GIẢI
SỞ GIÁO DỤC ĐÀO TẠO TỈNH NGHỆ AN
ĐỀ THI CHỌN HSG CẤP TỈNH
Môn: Toán 12
Thời gian: 50 phút (không kể thời gian phát đề)
HƯỚNG DẪN GIẢI
PHẦN I. TRẮC NGHIỆM
Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Mã đề
1
2
3
4
5
6
7
8
9
10
11
12
C
D
D
C
C
B
B
C
B
C
C
C
Câu 1. Cho khối chóp tứ giác đều
SABCD
có
32
,
2
AB a SA a= =
. Thể tích của khối chóp
SABCD
bằng
A.
3
2a
. B.
3
2
2
a
. C.
3
2
3
a
. D.
3
32
2
a
.
Lời giải
Chọn C
22
23
32 2 1 2
2 . .2
2 2 33
a
SO a a V a a a

= − = ⇒= =



Câu 2. Giả sử một vật giao động điều hòa xung quanh vị trí cân bằng theo phương trình
. Ở đây, thời gian t tính bằng giây và
(
)
xt
là li độ của vật tại thời điểm t
tính bằng centimet. Hãy cho biết trong khoảng thời gian từ 0 đến 4 giây, vật đạt li độ bằng
3
2
cm
bao nhiêu lần?
A.
6
. B.
5
. C.
3
. D.4.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NĂM HỌC- 2024-2025
https://www.facebook.com/groups/toanvd.vdc
Trang 6
NHÓM GIÁO VIÊN TOÁN VIỆT
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Lời giải
Chọn D
Ta có
( )
1
42
31
33
62
3cos 4 cos 4
1
32 32
42
33
2
tk
tk
xt t t
tk
tk
ππ
π
π
π
ππ
ππ
π
π
−=+
= +
 
= −=⇔ −=⇔ ⇔
 
 
−=−+
=
Do
[ ]
27
0; 4 0; ; ; ; ;
62 3 6
tt
ππ π π
π

∈ ⇒∈


Câu 3. Một lớp có 45 học sinh, trong đó có 31 em học sinh học khá môn Toán, 24 học sinh học khá môn
Tiếng Anh, 5 học sinh không học khá cả hai môn Toán và Tiếng Anh. Chọn ngẫu nhiên một học
sinh trong lớp. Xác suất để học sinh được chọn học khá cả hai môn Toán và Tiếng Anh là
A.
248
675
. B.
173
675
. C.
1984
6075
D.
1
3
.
Lời giải
Chọn D
Số học sinh học khá Tiếng Anh hoặc Toán là 45-5=40.
Số học sinh học khá cả 2 môn Tiếng Anh và Toán là 31+24-40=15
Xác suất cần tìm là
15 1
45 3
=
Câu 4. Cho hình hộp
111 1
.ABCD A B C D
. Phát biểu nào sau đây sai?
A.
11
AC CC CB CD
= +−
   
. B.
11
AC DC DD DA=+−
   
.
C.
11
AC AB AD AA=++
   
. D.
11
AC BC BB BA
=++
   
.
Lời giải
Chọn C
11
AC AB AD AA
=++
   
theo quy tắc hình hộp.
Câu 5. Trong không gian
Oxyz
, cho hai điểm
( )
2; 1;1A −
và
( )
1; 2; 3B −
. Toạ độ của vectơ
AB

là
A.
( )
1; 3; 4−
. B.
( )
3;1; 2−
. C.
(
)
1; 3; 4−−
. D.
( )
2; 2; 3−−
.
Lời giải
Chọn C
( )
2; 1;1A −
và
(
)
1; 2; 3B
−
=> toạ độ của vectơ
( )
1; 3; 4AB =−−

.
Câu 6. Bảng số liệu ghép nhóm sau cho biết chiều cao
( )
cm
của 50 học sinh lớp 10A.
Khoảng chiều cao
[
)
155;160
[
)
160;165
[
)
165;170
Số học sinh
17
25
8
Mốt của mẫu số liệu ghép nhóm trên là
A.
162,6
. B.
161,6
. C.
163, 4
. D.
160
.
Lời giải
Chọn B
Vì nhóm
[
)
160;165
có số học sinh nhiều nhất (tần số lớn nhất) nên Mốt của mẫu số liệu đã cho
thuộc nhóm này.
Ta có
2 2 13
2, 160, 25, 17, 8, 5ja m m m h= = = = = =
. Do đó
( ) ( )
0
25 17
160 .5 161, 6
25 17 25 8
M
−
=+=
−+−
( )
cm
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NĂM HỌC- 2024-2025
https://www.facebook.com/groups/toanvd.vdc
Trang 7
NHÓM GIÁO VIÊN TOÁN VIỆT
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 7. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông tâm
O
, đường thẳng
SA
vuông góc với
mặt phẳng đáy và
3
OC SA=
(tham khảo hình vẽ). Số đo góc phẳng nhị diện
[
]
,,
S BD C
bằng
A.
120
O
. B.
150
O
. C.
30
O
. D.
60
O
.
Lời giải
Chọn B
Ta có
( )
SA ABCD SA BD⊥ ⇒⊥
mà
BD AC⊥
nên
( )
BD SAC⊥
. Do đó,
BD SO⊥
. Mặt
khác,
CO BD⊥
. Vậy góc phẳng nhị diện
[
]
,,S BD C
chính là góc
SOC
.
Ta có
00
1
tan 30 150
33
SA SA SA
SOA SOA SOC
OA OC
SA
=== =⇒=⇒=
.
Số đo góc phẳng nhị diện
[ ]
,,S BD C
bằng
0
150
.
Câu 8. Cho hàm số bậc ba
( )
y fx=
có đồ thị là đường cong như hình vẽ bên. Điểm cực tiểu của hàm
số đã cho bằng
A.
0
. B.
1
. C.
2
. D.
5
.
Lời giải
O
B
D
A
C
S
O
B
D
A
C
S
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NĂM HỌC- 2024-2025
https://www.facebook.com/groups/toanvd.vdc
Trang 8
NHÓM GIÁO VIÊN TOÁN VIỆT
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Chọn C
Dựa vào đồ thị, ta thấy điểm cực tiểu của hàm số đã cho bằng
2
.
Câu 9. Cho hàm số
(
)
22 2
22
2
xx
fx x
xx
−>
= =
−<
nÕu
nÕu
nÕu
. Phát biểu nào sau đây là đúng?
A.
( )
2
lim 2.
x
fx
−
→
=
B.
( ) ( )
2
lim 2 .
x
fx f
+
→
=
C.
( ) ( )
22
lim lim .
xx
fx fx
+−
→→
=
D. Hàm số liên tục tại
2.x =
Lời giải
Chọn B
Ta có:
( ) ( ) ( )
22
lim lim 2 2 2 2
xx
fx x f
++
→→
= −==
.
Câu 10. Một cấp số cộng có số hạng đầu bằng
4
và số hạng thứ
3
bằng
12
. Số hạng thứ
10
của cấp số
cộng đó bằng
A.
44.
B.
36.
C.
40.
D.
10
4.
Lời giải
Chọn C
Gọi
d
là công sai của cấp số cộng đã cho.
Ta có
1
4
u =
,
31
2 12uu d=+=
, suy ra
4d =
.
Vậy
10 1
9 4 9.4 40uud=+=+=
.
Câu 11. Cho hàm số
( )
y fx=
có đạo hàm
(
) ( )( )
23f x xx x
′
=++
,
x∀∈
và
( ) ( ) ( ) ( )
1 2 30ff f f+ −= +
. Giá trị nhỏ nhất, giá trị lớn nhất của hàm số
( )
y fx=
trên
đoạn
[ ]
2;3−
lần lượt là
A.
(
)
0
f
và
( )
2.f
−
B.
( )
2f −
và
( )
0.f
C.
( )
0
f
và
( )
3.f
D.
( )
3f
và
( )
0.
f
Lời giải
Chọn C
Ta có
(
)
0
03
2
x
fx x
x
=
′
=⇔=−
= −
Bảng biến thiên:
Từ bảng biến thiên ta thấy: Giá trị nhỏ nhất của hàm số
( )
y fx=
trên đoạn
[ ]
2;3−
là
( )
0f
.
Ta có:
( ) ( ) ( ) ( ) ( ) ( ) ( )
( )
1 230 103 2ff f f ff f f+ −= + ⇔ − = − −
Do
( ) ( )
10ff>
nên
( ) ( )
32ff>−
. Vậy giá trị lớn nhất của hàm số
( )
y fx=
trên đoạn
[ ]
2;3−
là
( )
3f
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NĂM HỌC- 2024-2025
https://www.facebook.com/groups/toanvd.vdc
Trang 9
NHÓM GIÁO VIÊN TOÁN VIỆT
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 12. Một vật chuyển động theo phương trình
(
)
32
1
4
6
st t t t
= −+
, trong đó
0t >
,
t
tính bằng giây
và
( )
st
tính bằng mét. Xét trong khoảng thời gian từ
4
giây đến
10
giây vận tốc của vật đạt giá
trị nhỏ nhất bằng
A.
16
3
(m/s). B.
32
3
(m/s). C.
4
(m/s). D.
2
(m/s).
Lời giải
Chọn C
Ta có
( ) (
)
2
1
24
2
vt s t t t
′
= = −+
.
( )
2vt t
′
= −
,
( )
02vt t
′
= ⇔=
.
Bảng biến thiên:
Từ bảng biến thiên ta thấy: trên đoạn
[ ]
4;10
,
( )
vt
đạt giá trị nhỏ nhất khi
4t
=
.
Vậy trong khoảng thời gian từ
4
giây đến
10
giây vận tốc của vật đạt giá trị nhỏ nhất bằng
( )
44
v
=
(m/s).
PHẦN II. CÂU TRẮC NGHIỆM ĐÚNG SAI
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1. Cho hàm số
( ) ( )
5
log 4 1fx x= +
.
a) Tập xác định của hàm số
( )
fx
là khoảng
1
4
;

− +∞


.
b) Bất phương trình
( )
1
0
31
x
fx−
≤
−
có đúng 2 nghiệm nguyên.
c) Đồ thị hàm số
( )
fx
đi qua trung điểm của đoạn thẳng
AB
, với
( )
34;A
và
( )
90;B
.
d) Đạo hàm của hàm số
( )
fx
là
( )
4
51
fx
x
′
=
+
.
Lời giải
(a) Đúng.
Điều kiện xác định:
1
4 10
4
xx+ > ⇔ >−
. Vậy tập xác định của hàm số là
1
4
;

− +∞


.
(b) Sai.
Điều kiện:
3 10 0
x
x−> ⇔ >
. Khi đó bất phương trình
(
)
1
0
31
x
fx−
≤
−
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NĂM HỌC- 2024-2025
https://www.facebook.com/groups/toanvd.vdc
Trang 10
NHÓM GIÁO VIÊN TOÁN VIỆT
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
( )
10fx⇔ −≤
(
)
1fx⇔≤
( )
5
411 415 1log x xx⇔ + ≤⇔ +≤ ⇔ ≤
.
Kết hợp điều kiện ta được tập nghiệm là
01
x
<≤
. Vậy bất phương trình đã cho có 1 nghiệm
nguyên.
(c) Đúng.
Toạ độ trung điểm
M
của đoạn
AB
là
( )
62;M
.
Toạ độ điểm
( )
62;M
thuộc đồ thị hàm số
( ) ( )
5
log 4 1y fx x= = +
.
(d) Sai.
Ta có
( )
( )
( )
( )
41
4
4 1 ln 5 4 1 ln 5
x
fx
xx
′
+
′
= =
++
.
Câu 2. Cho hình lăng trụ đứng
111
.ABC A B C
có đáy
ABC
là tam giác vuông cân tại
A
,
AB AC a
= =
và cạnh bên
1
2
AA a=
(tham khảo hình vẽ)
a) Thể tích của khối lăng trụ
111
.ABC A B C
bằng
3
2
2
a
.
b) Góc giữa hai đường thẳng
1
BC
và
AC
bằng
60°
.
c) Khoảng cách từ
A
đến mặt phẳng
( )
11
A BC
bằng
6
6
a
.
d) Gọi
,MN
lần lượt là hai điểm di động trên các đoạn thẳng
11
AC
và
1
BC
sao cho
2
a
MN =
.
Thể tích của khối chóp
1
.A A BNM
có giá trị nhỏ nhất bằng
3
72
48
a
.
Lời giải
(a) Đúng.
Thể tích của khối lăng trụ
111
.ABC A B C
bằng
3
1
12
2
22
. ...
ABC
a
V S AA aaa
∆
= = =
.
(b) Đúng.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NĂM HỌC- 2024-2025
https://www.facebook.com/groups/toanvd.vdc
Trang 11
NHÓM GIÁO VIÊN TOÁN VIỆT
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Vì
11
// AC A C
nên
( ) ( )
1 1 11 11
,,BC AC BC A C BC A= =
.
Ta có
2 2 22
2BC AB AC a a a= + = +=
;
2 2 22
11
22 2BC BC CC a a a= + = +=
;
2 2 22
11
23BA AB AA a a a= + =+=
. Ta thấy
2 22
1 11 1 11
BC AC AB AC B= + ⇒∆
vuông tại
1
A
.
Ta có
11 11
33
60
22
sin
a
BC A BC A
a
==⇒=°
.
Vậy góc giữa hai đường thẳng
1
BC
và
AC
bằng
60
°
.
(c) Sai.
Kẻ
11
BH AB
⊥
.
Ta có
( )
( )
( )
( )
11 1 11 1
,,d A A BC d B A BC B H= =
.
Xét tam giác vuông
11
ABB
, ta có
11 1
1
1
26
3
3
.
.
BA BB
aa
BH a
AB
a
= = =
.
Vậy khoảng cách từ
A
đến mặt phẳng
( )
11
A BC
bằng
6
3
a
.
(d) Đúng.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NĂM HỌC- 2024-2025
https://www.facebook.com/groups/toanvd.vdc
Trang 12
NHÓM GIÁO VIÊN TOÁN VIỆT
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Kẻ
( )
11
AK A B AK BA MN⊥⇒⊥
. Ta có
26
3
3
.aa a
AK
a
= =
.
Thể tích khối chóp
1
.A A BNM
là
11
1 16
3 33
. ..
BA MN BA MN
a
V AK S S= =
.
Thể tích khối chóp
1
.A A BNM
nhỏ nhất
1
BA MN
S
⇔
nhỏ nhất
1
C MN
S
∆
⇔
lớn nhất.
Ta có
1
11 11
13
. .sin 60 .
24
C MN
S CMCN CMCN
∆
= °=
( )
22
22
11
11
33
.
42 8
CM CN
CM CN
+
≤=+
.
Theo định lý cô sin ta có
2
2 22 22
1 1 11 1 1 11
2 . .cos 60 .
4
a
MN CM CN CMCN CM CN CMCN= + − °⇔ + = +
.
1
22
11 11 11
33 3 3
. ..
4 8 4 8 32
C MN
aa
S CMCN CMCN CMCN
∆

⇒= ≤ + ⇔ ≤


.
1
2
11
33
.
4 16
C MN
a
S CMCN
∆
⇒= ≤
. Do đó diện tích
1
C MN
S
∆
lớn nhất bằng
2
3
16
a
.
1
BA MN
S⇒
nhỏ nhất bằng
11 1
22 2
3 37 3
2 16 16
BA C C MN
aa a
SS
∆∆
− =−=
.
Khi đó thể tích khối chóp
1
.A A BNM
nhỏ nhất bằng
2
3
1 67 3 72
..
3 3 16 48
aa
Va= =
.
Câu 3. Các học sinh lớp
12T
làm thí nghiệm gieo ba loại hạt giống
, XY
và
Z
. Xác suất để ba loại hạt
giống
, XY
và
Z
nảy mầm tương ứng là
,
xy
và
( )
0,8 xy>
. Biết rằng xác suất để ít nhất một
trong ba hạt giống này mầm là
0,964
và xác suất để cả ba hạt giống đều nảy mầm là
0,224
. Giả
sử việc nảy mầm của các hạt giống
, XY
và
Z
là độc lập với nhau. Gọi
A
là biến cố: “Có ít
nhất một trong ba hạt giống nảy mầm” và
B
là biến cố: “Cả ba hạt giống đều nảy”.
a) Biến cố đối của biến cố
A
là
A
: “Cả ba hạt giống đều không nảy mầm”. mầm
b) Xác suất để xảy ra biến cố
B
là
( )
0,8P B xy=
.
c) Xác suất để hạt giống
X
nảy mầm là
0, 7
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NĂM HỌC- 2024-2025
https://www.facebook.com/groups/toanvd.vdc
Trang 13
NHÓM GIÁO VIÊN TOÁN VIỆT
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
d) Xác suất để có đúng hai hạt nảy mầm là
0,488
.
Lời giải
Chọn A
(a) Đúng.
Biến cố đối của biến cố
A
là
A
: “Cả ba hạt giống đều không nảy mầm”.
(b) Đúng.
B
là biến cố: “Cả ba hạt giống đều nảy mầm”
BXYZ⇒ = ∩∩
Xác suất để xảy ra biến cố
B
là
( ) ( )
0,8
P B P X Y Z xy= ∩∩ =
.
(c) Đúng.
Xác suất để ít nhất một trong ba hạt giống này mầm là
(
)
0,964 0,964
PX Y Z⇒ ∪∪ =
.
(
)
( )
( ) ( ) ( ) ( ) ( )
0,964PX PY PZ PX Y PX Z PY Z PX Y Z⇒ + + − ∩− ∩− ∩+ ∩∩=
0,8 0,8 0,8 0, 224 0,964 0, 2 0, 2 0, 06
x y xy x y x y xy
⇒++ − − − + = ⇒ + − =−
.
Xác suất để cả ba hạt giống đều nảy mầm là:
( )
0,224 0,224 0,8 0,224 0, 28P X Y Z xy xy⇒ ∩∩ = ⇒ = ⇒ =
.
Ta có hệ phương trình:
0,2 0, 2 0,06 1,1 0.7 0.4
0, 28 0, 28 0, 4 0, 7
x y xy x y x x
xy xy y y
+ − =− += = =

⇒ ⇒∨

= = = =

Vì
0, 7
0, 4
x
xy
y
=
>⇒
=
.
Xác suất để hạt giống
X
nảy mầm là
0, 7
.
(d) Đúng.
Xác suất để có đúng hai hạt nảy mầm là:
( )
( )
( )
PX Y Z PX Y Z PX Y Z∩∩ + ∩∩ + ∩∩
0,7.0, 4.0,2 0,7.0,6.0,8 0,3.0, 4.0,8 0, 488=++=
.
Câu 4. Cho hàm số
2
24
2
xx
y
x
++
=
+
.
a) Hàm số có giá trị cực đại lớn hơn giá trị cực tiểu.
b) Gọi
, AB
là các điểm cực đại, cực tiểu của đồ thị hàm số. Diện tích của tam giác
OAB
bằng
8
(đơn vị diện tích), trong đó
O
là gốc tọa độ.
c) Đường thẳng đi qua hai điểm cực đại và cực tiểu của đồ thị hàm số là
22yx= +
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NĂM HỌC- 2024-2025
https://www.facebook.com/groups/toanvd.vdc
Trang 14
NHÓM GIÁO VIÊN TOÁN VIỆT
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
d) Hàm số nghịch biến trên khoảng
( )
4; 0
−
.
Lời giải
Chọn A
a) Sai.
Ta có
(
)
( )
( ) ( )
2
22
22
22 2 24
24 4
2
22
x x xx
xx xx
yy
x
xx
+ +−−−
++ +
′
= ⇒= =
+
++
.
0
0
4
x
y
x
=
′
= ⇒
= −
.
Bảng biến thiên:
Vậy hàm số có giá trị cực đại nhỏ hơn giá trị cực tiểu.
b) Sai.
Gọi
, AB
là các điểm cực đại, cực tiểu của đồ thị hàm số
( ) (
)
4; 6 , 0; 2AB−−
1
.2.4 4
2
OAB
S
⇒==
(đơn vị diện tích).
c) Đúng.
(
)
( )
( )
qua 0; 2
: :2 2 0 2 2
vtcp 4;8 vtpt 2; 1
B
AB AB x y y x
AB n
⇒ −+=⇒= +
⇒−

.
Vậy đường thẳng đi qua hai điểm cực đại và cực tiểu của đồ thị hàm số là
22
yx= +
.
d) Sai.
Hàm số nghịch biến trên khoảng
( )
4; 2−−
và
(
)
2; 0
−
.
PHẦN III. CÂU TRẮC NGHIỆM TRẢ LỜI NGẮN
Thí sinh trả lời câu 1 và câu 2
Câu 1. Một doanh nghiệp tư nhân
X
chuyên kinh doanh xe gắn máy các loại. Hiện nay, doanh
nghiệp đang tập trung chiến lược kinh doanh một loại xe máy với chi phí mua vào là
38
triệu
đồng/ chiếc với giá bán ra là
43
triệu đồng/ chiếc. Với giá bán này thì số lượng xe bán ra mỗi
năm là
600
chiếc. Nhằm tiêu thụ dòng xe đang ăn khách này, doanh nghiệp dự định giảm giá
bán. Ước tính cứ giảm
1
triệu đồng/ chiếc thì số lượng xe bán ra trong năm tăng thêm
200
chiếc. Vậy doanh nghiệp phải giảm giá bán là bao nhiêu triệu đồng để thu được lợi nhuận cao
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NĂM HỌC- 2024-2025
https://www.facebook.com/groups/toanvd.vdc
Trang 15
NHÓM GIÁO VIÊN TOÁN VIỆT
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
nhất trong một năm?
Lời giải:
ĐA:
1
Gọi giá bán mới của một chiếc xe là
x
triệu đồng (
38 43x
).
Tiền lời sau khi giảm giá bán của một chiếc xe là:
38
x
triệu đồng
Số tiền giảm giá so với ban đầu là
43 x
triệu đồng.
Số xe bán được sau khi giảm là
43
600 .200
1
x


chiếc xe.
Lợi nhuận doanh nghiệp thu được trong một năm sau khi giảm giá xe là:
38 . 600 43 .200
xx




.
Xét hàm
2
38 . 600 43 .200 200 16800 349600fx x x x x




.
ta thấy
fx
đạt giá trị lớn nhất
3200
tại
42x
.
Vậy doanh nghiệp phải giảm giá bán
1
triệu đồng để thu được lợi nhuận cao nhất.
Câu 2. Trong ngày hội STEM, bạn An nhận được nhiệm vụ thiết kế một chiếc hộp giấy có dạng hình
hộp chữ nhật
1111
.ABCD A B C D
với độ dài các cạnh
1
,,
AB a AD b AA c
và khoảng
cách giữa
AC
và
1
BC
bằng
d
( tham khảo hình vẽ). Biết rằng
,,,abcd
là các số nguyên dương
có đơn vị đo bằng decimet. Hỏi diện tích của chiếc hộp bằng bao nhiêu
2
dm
để thể tích của chiếc
hộp bạn An sẽ làm là nhỏ nhất.
Lời giải:
ĐA:
90
.
Ta có:
11 11 1 11 11
// // , , ,AC AC AC BAC d AC C B d AC BAC d C BAC 
Mà
11 1 11
,,d C BAC d B BAC
, nên
1 1 11
,,d AC C B d B BAC d d

NHÓM GIÁO VIÊN TOÁN VIỆT NAM NĂM HỌC- 2024-2025
https://www.facebook.com/groups/toanvd.vdc
Trang 16
NHÓM GIÁO VIÊN TOÁN VIỆT
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Ta có
1 11
B BAC
là tứ diện vuông tại
1
B
nên
2 222
1 111
d abc

,,, abcd
Dễ thấy:
min , ,d abc
.
Không mất tính tổng quát giả sử:
0 dabc

.
TH1:
1d
thì
2cba

( vì
,,abc
), suy ra
222
1113
1
4
abc

( vô lý).
TH2:
2d
thì
3a
và
222
1111
4
abc

. Lúc này ta thấy:
Với
4a
thì
222
1111 3
4
4 16
cba
abc

( Vô lý)
Với
3
a
thay vào ta có:
222 22
1111 11 5
4 36
3 bc bc

Với
5b
thì
5cb

nên
22 22
5 11 11 2 5
36 25 36
55bc

( Vô lý)
Với
4b
thay vào ta thấy không tồn tại
c
Với
3b
ta tìm được
6c
khi đó
3.3.6 54
H
V abc
TH3:
3d
thì
4abc
nên
4.4.4 64 54
H
V abc 
Khi đó thể tích chiếc hộp nhỏ nhất bằng
54
khi
; ; 3; 3; 6abc
Do đó diện tích chiếc hộp bằng:
2
2 90S ab ac cb dm

.
HẾT
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NĂM HỌC- 2024-2025
https://www.facebook.com/groups/toanvd.vdc
Trang 1
NHÓM GIÁO VIÊN TOÁN VIỆT
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
SỞ GIÁO DỤC ĐÀO TẠO NGHỆ AN
ĐỀ THI CHỌN HSG CẤP TỈNH
Môn: Toán 12
Thời gian: 180 phút (không kể thời gian phát đề)
Câu I. (3,5 điểm)
1) Tìm các điểm cực đại và cực tiểu của hàm số
( )
3
3 6 ln 2 1
3
x
yx x
= −− −+
.
2) Một công ty bất động sản đưa ra hai phương án ký hợp đồng cho thuê căn hộ theo năm (tiền hợp đồng
thuê nhà khách hàng phải trả từ đầu năm) để làm văn phòng đại diện như sau:
Hợp đồng loại 1: Trả 220 triệu cho năm đầu tiên và sau mỗi năm tăng thêm 11 triệu đồng so với năm kề
trước.
Hợp đồng loại 2: Trả 194 triệu cho năm đầu tiên và sau mỗi năm tăng thêm
6%
so với năm kề trước.
Vào đầu năm 2024, bác Hoàng và bác Anh cùng đến thuê một căn hộ để làm văn phòng đại diện cho
công ty của mình và thuê dài hạn. Biết rằng bác Hoàng lựa chọn hợp đồng loại 1 và bác Anh lựa chọn hợp
đồng loại 2 để thuê. Hỏi từ đầu năm bao nhiêu trở đi bác Hoàng sẽ chi trả tiền thuê nhà hàng năm ít hơn
bác Anh?
Câu II. (2,0 điểm). Nuôi cấy nấm men thu sinh khối (protein, amino acid...), ứng dụng làm tế bào nhận
trong công nghệ gen để sản xuất một số chất có hoạt tính sinh học mạnh (kháng sinh...). Giả sử số lượng tế
bào của một quần thể nấm men tại môi trường nuôi cấy trong phòng thí nghiệm được mô hình hóa bằng
hàm số
( )
0,75t
m
Pt
ne
−
=
+
, trong đó thời gian
t
được tính bằng giờ. Đạo hàm của hàm số
(
)
y Pt=
biểu thị
tôc độ sinh trưởng của quần thể nấm men (tính bằng tế bào/ giờ) tại thời điểm
t
. Tại thời điểm ban đầu
0t =
, quần thể có
30
tế bào và tốc độ sinh trưởng là
15
tế bào/ giờ. Tìm số lượng tế bào của quần thể nấm
men tại thời điểm tốc độ sinh trưởng của quần thể nấm men đạt mức tối đa.
Câu III. (3,5 điểm) Các học sinh lớp
12T
làm thí nghiệm gieo ba loại hạt giống
, XY
và
Z
. Xác suất
để ba loại hạt giống
, XY
và
Z
nảy mầm tương ứng là
, xy
và
( )
0,8 xy>
. Biết rằng xác suất để ít nhất
một trong ba hạt giống này mầm là
0,964
và xác suất để cả ba hạt giống đều nảy mầm là
0,224
. Giả sử
việc nảy mầm của các hạt giống
, XY
và
Z
là độc lập với nhau. Gọi
A
là biến cố: “Có ít nhất một trong
ba hạt giống nảy mầm” và
B
là biến cố: “Cả ba hạt giống đều nảy”.
a) Biến cố đối của biến cố
A
là
A
: “Cả ba hạt giống đều không nảy mầm”. mầm
b) Xác suất để xảy ra biến cố
B
là
( )
0,8P B xy=
.
c) Xác suất để hạt giống
X
nảy mầm là
0,7
.
d) Xác suất để có đúng hai hạt nảy mầm là
0,488
.
Câu IV. (1,5 điểm) Cho hàm số
2
24
2
xx
y
x
++
=
+
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NĂM HỌC- 2024-2025
https://www.facebook.com/groups/toanvd.vdc
Trang 2
NHÓM GIÁO VIÊN TOÁN VIỆT
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
a) Hàm số có giá trị cực đại lớn hơn giá trị cực tiểu.
b) Gọi
, AB
là các điểm cực đại, cực tiểu của đồ thị hàm số. Diện tích của tam giác
OAB
bằng
8
(đơn
vị diện tích), trong đó
O
là gốc tọa độ.
c) Đường thẳng đi qua hai điểm cực đại và cực tiểu của đồ thị hàm số là
22yx= +
.
d) Hàm số nghịch biến trên khoảng
( )
4; 0
−
.
Câu V. (1,5 điểm) Cho tập
A
gồm
n
phần tử (
n
là số nguyên dương). Lấy ngẫu nhiên một bộ thứ tự
( )
,XY
với
,XY
là các tập con của tập hợp
A
. Biết xác suất để lấy được một bộ thứ tự
( )
,XY
sao cho
XYA∪=
là
81
448
. Tìm số
k
lớn nhất (
k
∈
) sao cho có thể chọn ra
k
tập hợp con khác nhau của tập hợp
A
mà hai tập con bất kì trong
k
tập đó giao nhau khác rỗng (với
XY≠
thì các bộ thứ tự
( )
,
XY
và
( )
,YX
là khác nhau).
HẾT
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NĂM HỌC- 2024-2025
https://www.facebook.com/groups/toanvd.vdc
Trang 3
NHÓM GIÁO VIÊN TOÁN VIỆT
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
HƯỚNG DẪN GIẢI
SỞ GIÁO DỤC ĐÀO TẠO TỈNH NGHỆ AN
ĐỀ THI CHỌN HSG CẤP TỈNH
Môn: Toán 12
Thời gian: 180 phút (không kể thời gian phát đề)
Câu I.
1) Tìm các điểm cực đại và cực tiểu của hàm số
( )
3
3 6 ln 2 1
3
x
yx x= −− −+
.
2) Một công ty bất động sản đưa ra hai phương án ký hợp đồng cho thuê căn hộ theo năm (tiền
hợp đồng thuê nhà khách hàng phải trả từ đầu năm) để làm văn phòng đại diện như sau:
Hợp đồng loại 1: Trả 220 triệu cho năm đầu tiên và sau mỗi năm tăng thêm 11 triệu đồng so với
năm kề trước.
Hợp đồng loại 2: Trả 194 triệu cho năm đầu tiên và sau mỗi năm tăng thêm
6%
so với năm kề
trước.
Vào đầu năm 2024, bác Hoàng và bác Anh cùng đến thuê một căn hộ để làm văn phòng đại diện
cho công ty của mình và thuê dài hạn. Biết rằng bác Hoàng lựa chọn hợp đồng loại 1 và bác Anh
lựa chọn hợp đồng loại 2 để thuê. Hỏi từ đầu năm bao nhiêu trở đi bác Hoàng sẽ chi trả tiền thuê
nhà hàng năm ít hơn bác Anh?
Lời giải
1) TXĐ:
( )
;2D = −∞
.
Ta có:
32
2
6 23
3
22
xxx
yx
xx
−+ +
′
= −+ =
−−
.
0
01
3
x
yx
xD
=
′
=⇒=−
= ∉
Bảng biến thiên:
Theo bảng biến thiên suy ra:
- Điểm cực đại của hàm số là:
1x = −
- Điểm cực tiểu của hàm số là:
0x
=
.
2) - Theo hợp đồng loại 1, số tiền thuê căn hộ mà bác Hoàng phải trả trong các năm là một cấp
số cộng với số hạng đầu
1
220u =
, công sai
11
d =
nên số tiền bác Hoàng phải trả trong năm thứ
n
là:
(
)
220 1 .11 11 209
n
An n= +− = +
(triệu đồng).
- Theo hợp đồng loại 2, số tiền thuê căn hộ mà bác Anh phải trả trong các năm là môt cấp số
nhân với số hạng đầu
1
194u =
, công bội
1 6% 1,06q =+=
nên số tiền bác Anh phải trả trong
năm thứ
n
là:
1
194.1,06
n
n
B
−
=
(triệu đồng).
Xét:
11
11 209 194.1,06 194.1,06 11 209 0 8,8
nn
nn
AB n n n
−−
<⇔+< ⇔ −−>⇔>
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NĂM HỌC- 2024-2025
https://www.facebook.com/groups/toanvd.vdc
Trang 4
NHÓM GIÁO VIÊN TOÁN VIỆT
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Vậy từ đầu năm thứ 9 trở đi thì số tiền bác Hoàng phải trả hàng năm sẽ ít hơn số tiền bác Anh
phải trả.
Câu II. Nuôi cấy nấm men thu sinh khối (protein, amino acid...), ứng dụng làm tế bào nhận trong công
nghệ gen để sản xuất một số chất có hoạt tính sinh học mạnh (kháng sinh...). Giả sử số lượng tế
bào của một quần thể nấm men tại môi trường nuôi cấy trong phòng thí nghiệm được mô hình
hóa bằng hàm số
( )
0,75t
m
Pt
ne
−
=
+
, trong đó thời gian
t
được tính bằng giờ. Đạo hàm của hàm
số
( )
y Pt=
biểu thị tôc độ sinh trưởng của quần thể nấm men (tính bằng tế bào/ giờ) tại thời
điểm
t
. Tại thời điểm ban đầu
0t =
, quần thể có
30
tế bào và tốc độ sinh trưởng là
15
tế bào/
giờ. Tìm số lượng tế bào của quần thể nấm men tại thời điểm tốc độ sinh trưởng của quần thể
nấm men đạt mức tối đa.
Lời giải
DR
=
( )
(
)
0,75
2
0,75
0,75 .
'0
t
t
me
Pt t D
ne
−
−
= > ∀∈
+
Tại thời điểm
0t =
:
(
)
0 30 30
1
m
P
n
=⇔=
+
.
Khi đó tốc độ sinh trưởng tại thời điểm
0
t =
là :
( )
( )
2
0,75.
0
1
m
P
n
′
=
+
.
Theo bài ra, ta có hệ:
( )
2
30
1
0,75.
15
1
m
n
m
n
=
+
=
+
(
)
( )
(
)
2
30 1
0,75.30. 1
15
1
mn
n
n
= +
⇔
+
=
+
45
1
2
m
n
=
⇔
=
.
Khi đó:
( )
0,75
2
0,75
0,75.45.
'
1
2
t
t
e
Pt
e
−
−
=

+


0,75
2
0,75
135
.
4
1
2
t
t
e
e
−
−
=

+


0,75
0,75
135 135
.
1
48
4. .
2
t
t
e
e
−
−
≤=
Do đó:
( )
0
135
max
8
t
Pt
≥
′
=
khi
0,75
0
1 ln 2
2 0, 75
t
e tt
−
= ⇔= =
nên
(
)
0
45
45
11
22
Pt
= =
+
Câu III. Các học sinh lớp
12T
làm thí nghiệm gieo ba loại hạt giống
, XY
và
Z
. Xác suất để ba loại hạt
giống
, XY
và
Z
nảy mầm tương ứng là
, xy
và
( )
0,8 xy>
. Biết rằng xác suất để ít nhất một
trong ba hạt giống này mầm là
0,964
và xác suất để cả ba hạt giống đều nảy mầm là
0,224
. Giả
sử việc nảy mầm của các hạt giống
, XY
và
Z
là độc lập với nhau. Gọi
A
là biến cố: “Có ít
nhất một trong ba hạt giống nảy mầm” và
B
là biến cố: “Cả ba hạt giống đều nảy”.
a) Biến cố đối của biến cố
A
là
A
: “Cả ba hạt giống đều không nảy mầm”. mầm
b) Xác suất để xảy ra biến cố
B
là
( )
0,8P B xy=
.
| 1/23
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

NHÓM GIÁO VIÊN TOÁN VIỆT NAM NĂM HỌC- 2024-2025
SỞ GIÁO DỤC ĐÀO TẠO NGHỆ AN
ĐỀ THI CHỌN HSG CẤP TỈNH Môn: Toán 12
Thời gian: 50 phút (không kể thời gian phát đề) PHẦN I. TRẮC NGHIỆM
Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. NH
Mỗi câu hỏi thí sinh chỉ chọn một phương án. ÓM G
Câu 1. Cho khối chóp tứ giác đều SABCD có 3 2
AB = a, SA =
a . Thể tích của khối chóp SABCD I 2 ÁO V bằng I 3 Ê A. 3 2a . B. 2 3 a . C. 2a . D. 3 2 3 a . N T 2 3 2 OÁ
Câu 2. Giả sử một vật giao động điều hòa xung quanh vị trí cân bằng theo phương trình  π  N V
x(t) = 3cos 4t − 
. Ở đây, thời gian t tính bằng giây và x(t) là li độ của vật tại thời điểm t 3    IỆ
tính bằng centimet. Hãy cho biết trong khoảng thời gian từ 0 đến 4 giây, vật đạt li độ bằng T N
3 cm bao nhiêu lần? AM 2 A. 6 . B. 5. C. 3. D. 4.
Câu 3. Một lớp có 45 học sinh, trong đó có 31 em học sinh học khá môn Toán, 24 học sinh học khá
môn Tiếng Anh, 5 học sinh không học khá cả hai môn Toán và Tiếng Anh. Chọn ngẫu nhiên
một học sinh trong lớp. Xác suất để học sinh được chọn học khá cả hai môn Toán và Tiếng Anh là A. 248 . B. 173 . C. 1984 D. 1 . NH 675 675 6075 3
Câu 4. Cho hình hộp ABC .
D A B C D . Phát biểu nào sau đây sai? 1 1 1 1 ÓM
   
   
A. AC = CC + CB − CD .
B. AC = DC + DD − DA. G 1 1 1 1
   
    IÁ
C. AC = AB + AD + AA .
D. AC = BC + BB + BA. 1 1 1 1 O V 
Câu 5. Trong không gian Oxyz , cho hai điểm A(2; 1; − ) 1 và B(1;2; 3
− ) . Toạ độ của vectơ AB là IÊN T A. (1; 3 − ;4). B. (3;1; 2 − ) . C. ( 1; − 3; 4 − ) . D. (2; 2; − 3 − ). OÁ
Câu 6. Bảng số liệu ghép nhóm sau cho biết chiều cao (cm) của 50 học sinh lớp 10A. N V I Khoảng chiều cao [155;160) [160;165) [165;170) ỆT Số học sinh 17 25 8
Mốt của mẫu số liệu ghép nhóm trên là A. 162,6 . B. 161,6 . C. 163,4. D. 160.
https://www.facebook.com/groups/toanvd.vdc Trang 1
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NĂM HỌC- 2024-2025
Câu 7. Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O , đường thẳng SA vuông góc với
mặt phẳng đáy và OC = 3SA (tham khảo hình vẽ). Số đo góc phẳng nhị diện [S, BD,C]bằng S D C NH O ÓM A B G A. 120O . B. 150O . C. 30O . D. 60O . IÁO V
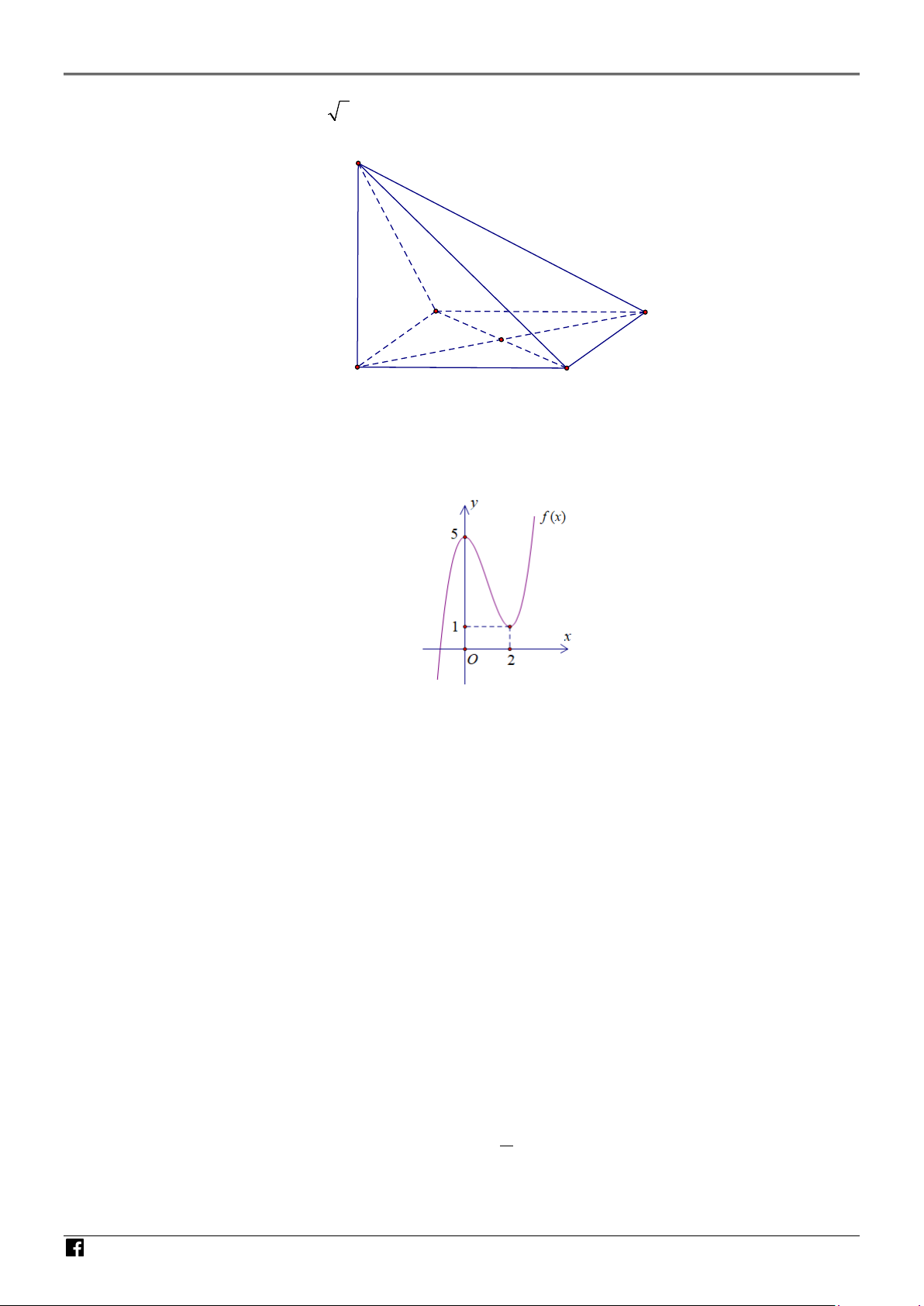
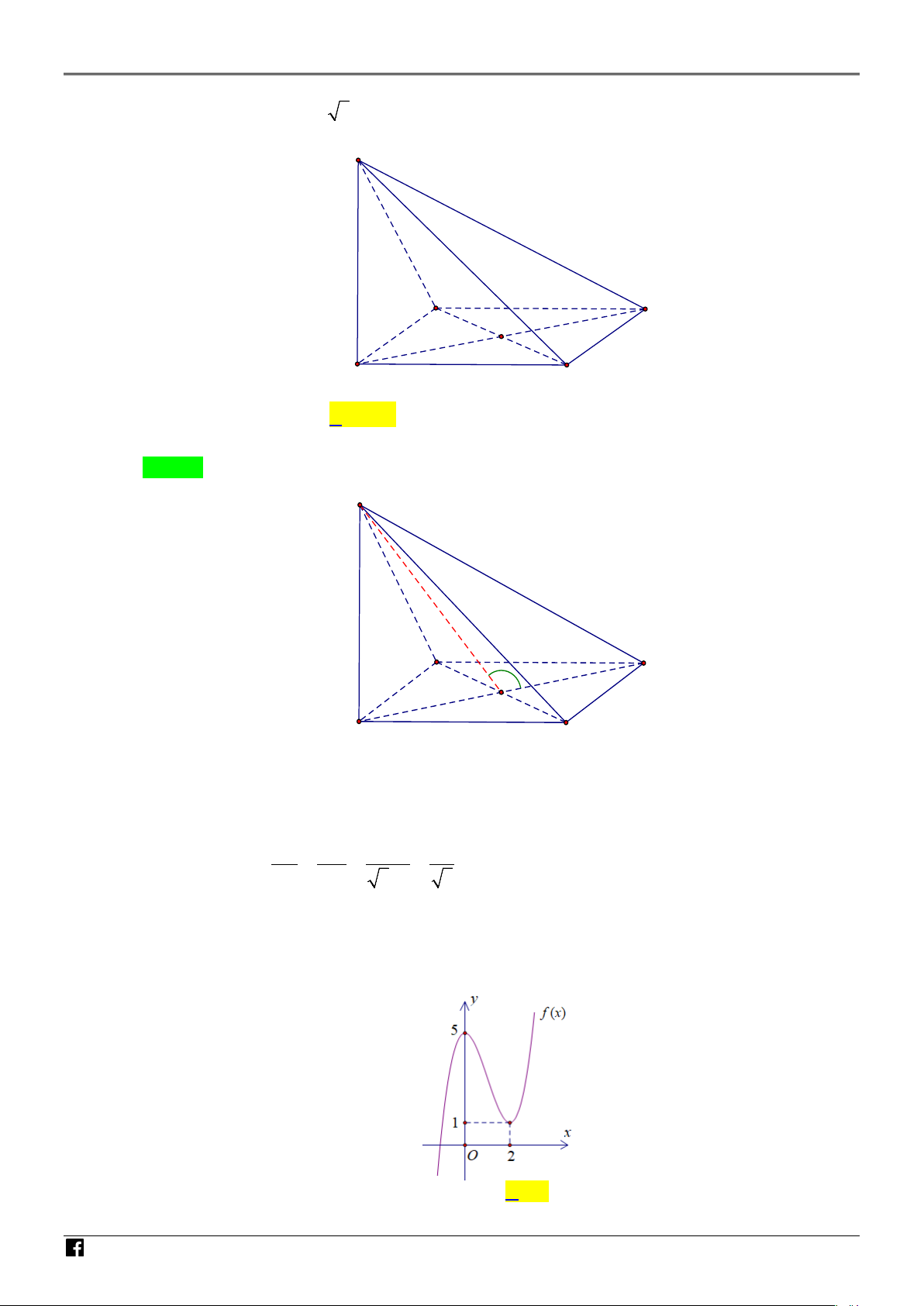
Câu 8. Cho hàm số bậc ba y = f (x) có đồ thị là đường cong như hình vẽ bên. Điểm cực tiểu của hàm I số đã cho bằng ÊN T OÁ N V IỆT N AM A. 0 . B. 1. C. 2 . D. 5.
2x − 2 nÕ x u > 2  Câu 9. Cho hàm số
f (x) = 2 nÕ x
u = 2 . Phát biểu nào sau đây là đúng?
−x nÕu x <  2
A. lim f (x) = 2.
B. lim f (x) = f (2). − + NH x→2 x→2 ÓM
C. lim f (x) = lim f (x).
D. Hàm số liên tục tại x = 2. x 2+ x 2− → →
Câu 10. Một cấp số cộng có số hạng đầu bằng 4 và số hạng thứ 3 bằng 12. Số hạng thứ 10 của cấp số GI cộng đó bằng ÁO V A. 44. B. 36. C. 40. D. 10 4 . IÊ
Câu 11. Cho hàm số y = f (x) có đạo hàm f ′(x) = x(x + 2)(x + 3) , x ∀ ∈  và N T f ( ) 1 + f ( 2
− ) = f (3) + f (0). Giá trị nhỏ nhất, giá trị lớn nhất của hàm số y = f (x) trên OÁ đoạn [ 2; − ]3 lần lượt là N V IỆ
A. f (0) và f ( 2 − ). B. f ( 2
− ) và f (0). C. f (0) và f (3).
D. f (3) và f (0). T Câu 12. 1
Một vật chuyển động theo phương trình s(t) 3 2
= t − t + 4t , trong đó t > 0, t tính bằng giây 6
và s(t) tính bằng mét. Xét trong khoảng thời gian từ 4 giây đến 10 giây vận tốc của vật đạt
giá trị nhỏ nhất bằng
https://www.facebook.com/groups/toanvd.vdc Trang 2
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NĂM HỌC- 2024-2025 A. 16 (m/s). B. 32 (m/s). C. 4 (m/s). D. 2 (m/s). 3 3
PHẦN II. CÂU TRẮC NGHIỆM ĐÚNG SAI
Thí sinh trả lời từ câu 01 đến câu 04. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1. Cho hàm số f (x) = log 4x +1 . 5 ( )  
a) Tập xác định của hàm số f (x) là khoảng 1 − ;+∞  . 4    f (x) −1
b) Bất phương trình
≤ 0 có đúng 2 nghiệm nguyên. NH 3x −1 ÓM
c) Đồ thị hàm số f (x) đi qua trung điểm của đoạn thẳng AB , với A(3;4) và B(9;0) . GI
d) Đạo hàm của hàm số f (x) là f ′(x) 4 = . Á 5x +1 O V
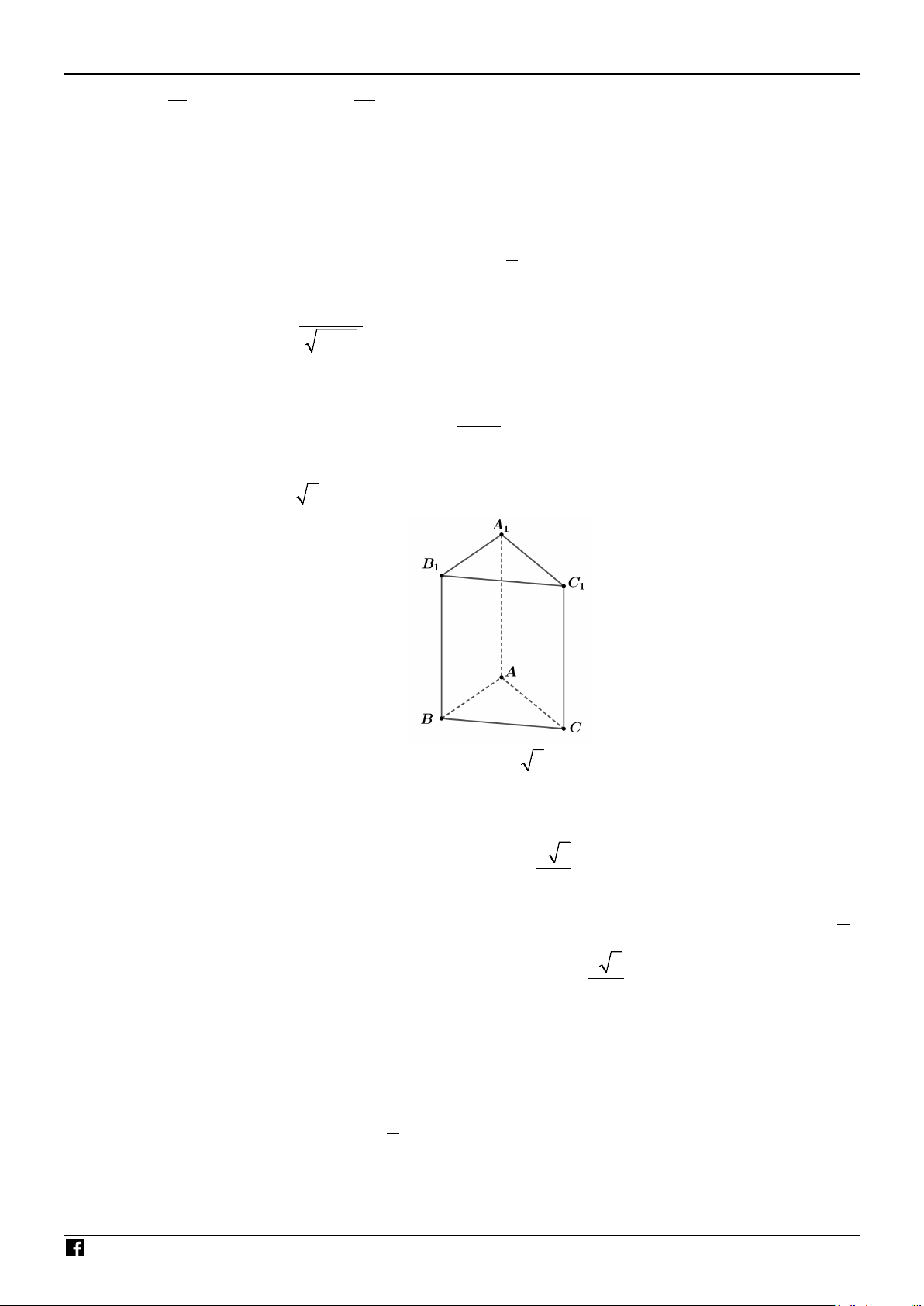
Câu 2. Cho hình lăng trụ đứng ABC.A B C có đáy ABC là tam giác vuông cân tại A , AB = AC = a 1 1 1 IÊN T
và cạnh bên AA = a 2 (tham khảo hình vẽ) 1 OÁ N V IỆT N AM 3
a) Thể tích của khối lăng trụ ABC.A B C bằng a 2 . 1 1 1 2
b) Góc giữa hai đường thẳng BC và AC bằng 60°. 1 NH a ÓM
c) Khoảng cách từ A đến mặt phẳng ( A BC bằng 6 . 1 1 ) 6 G a I
d) Gọi M , N lần lượt là hai điểm di động trên các đoạn thẳng AC và BC sao cho MN = . Á 1 1 1 2 O V 7 2 I
Thể tích của khối chóp .
A A BNM có giá trị nhỏ nhất bằng 3 a . Ê 1 48 N T
Câu 3. Các học sinh lớp 12T làm thí nghiệm gieo ba loại hạt giống X , Y và Z . Xác suất để ba loại hạt OÁ
giống X , Y và Z nảy mầm tương ứng là x, y và 0,8 (x > y) . Biết rằng xác suất để ít nhất một N V
trong ba hạt giống này mầm là 0,964 và xác suất để cả ba hạt giống đều nảy mầm là 0,224 . Giả I
sử việc nảy mầm của các hạt giống X , Y và Z là độc lập với nhau. Gọi A là biến cố: “Có ít ỆT
nhất một trong ba hạt giống nảy mầm” và B là biến cố: “Cả ba hạt giống đều nảy”.
a) Biến cố đối của biến cố A là A : “Cả ba hạt giống đều không nảy mầm”. mầm
b) Xác suất để xảy ra biến cố B là P(B) = 0,8xy .
https://www.facebook.com/groups/toanvd.vdc Trang 3
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NĂM HỌC- 2024-2025
c) Xác suất để hạt giống X nảy mầm là 0,7 .
d) Xác suất để có đúng hai hạt nảy mầm là 0,488 . 2 x + 2x + 4 y = Câu 4. Cho hàm số x + 2 .
a) Hàm số có giá trị cực đại lớn hơn giá trị cực tiểu. b) Gọi ,
A B là các điểm cực đại, cực tiểu của đồ thị hàm số. Diện tích của tam giác OAB bằng
8 (đơn vị diện tích), trong đó O là gốc tọa độ. NH
c) Đường thẳng đi qua hai điểm cực đại và cực tiểu của đồ thị hàm số là y = 2x + 2 . ÓM G
d) Hàm số nghịch biến trên khoảng ( 4; − 0) . IÁO V
PHẦN III. CÂU TRẮC NGHIỆM TRẢ LỜI NGẮN IÊN T
Thí sinh trả lời câu 1 và câu 2 OÁ
Câu 1. Một doanh nghiệp tư nhân X chuyên kinh doanh xe gắn máy các loại. Hiện nay, doanh N V
nghiệp đang tập trung chiến lược kinh doanh một loại xe máy với chi phí mua vào là 38 triệu I
đồng/ chiếc với giá bán ra là 43 triệu đồng/ chiếc. Với giá bán này thì số lượng xe bán ra mỗi ỆT N
năm là 600 chiếc. Nhằm tiêu thụ dòng xe đang ăn khách này, doanh nghiệp dự định giảm giá AM
bán. Ước tính cứ giảm 1 triệu đồng/ chiếc thì số lượng xe bán ra trong năm tăng thêm 200
chiếc. Vậy doanh nghiệp phải giảm giá bán là bao nhiêu triệu đồng để thu được lợi nhuận cao
nhất trong một năm?
Câu 2. Trong ngày hội STEM, bạn An nhận được nhiệm vụ thiết kế một chiếc hộp giấy có dạng hình
hộp chữ nhật ABCD.A B C D với độ dài các cạnh AB a,AD  ,
b AA c và khoảng 1 1 1 1 1 NH
cách giữa AC và BC bằng d ( tham khảo hình vẽ). Biết rằng a, , b ,
c d là các số nguyên 1 ÓM
dương có đơn vị đo bằng decimet. Hỏi diện tích của chiếc hộp bằng bao nhiêu 2 dm để thể tíc h
của chiếc hộp bạn An sẽ làm là nhỏ nhất. GIÁ  HẾT  O V IÊN T OÁ N V IỆT
https://www.facebook.com/groups/toanvd.vdc Trang 4
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NĂM HỌC- 2024-2025 HƯỚNG DẪN GIẢI
SỞ GIÁO DỤC ĐÀO TẠO TỈNH NGHỆ AN
ĐỀ THI CHỌN HSG CẤP TỈNH Môn: Toán 12
Thời gian: 50 phút (không kể thời gian phát đề) HƯỚNG DẪN GIẢI NH
PHẦN I. TRẮC NGHIỆM ÓM
Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. G
Mỗi câu hỏi thí sinh chỉ chọn một phương án. IÁO V Mã đề 1 2 3 4 5 6 7 8 9 10 11 12 I C D D C C B B C B C C C ÊN T OÁ
Câu 1. Cho khối chóp tứ giác đều SABCD có 3 2
AB = a, SA =
a . Thể tích của khối chóp SABCD N V 2 bằng IỆ 3 T N A. 3 2a . B. 2 3 a . C. 2a . D. 3 2 3 a . 2 3 2 AM Lời giải Chọn C NH ÓM GIÁO V I Ê 2 2 N T  3 2   a 2  1 2 2 3 SO =  a −
 = 2a ⇒ V = .a .2a = a     OÁ 2 2 3 3     N V
Câu 2. Giả sử một vật giao động điều hòa xung quanh vị trí cân bằng theo phương trình  π  IỆ
x(t) = 3cos 4t − 
 . Ở đây, thời gian t tính bằng giây và x(t) là li độ của vật tại thời điểm t T  3 
tính bằng centimet. Hãy cho biết trong khoảng thời gian từ 0 đến 4 giây, vật đạt li độ bằng 3 cm 2 bao nhiêu lần? A. 6 . B. 5. C. 3. D.4.
https://www.facebook.com/groups/toanvd.vdc Trang 5
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NĂM HỌC- 2024-2025 Lời giải Chọn D  π π  π 1 4t − = + k2π t = + kπ  π   π   Ta có x(t) 3  1 3 3 6 2 = 3cos4t − = ⇔  cos4t − = ⇔   ⇔   3  2  3  2 π π   1
4t − = − + k2π t = kπ  3 3  2  π π π π Do t [ ] 2 7 0;4 t 0; ; ; ;π;  ∈ ⇒ ∈  6 2 3 6   
Câu 3. Một lớp có 45 học sinh, trong đó có 31 em học sinh học khá môn Toán, 24 học sinh học khá môn
Tiếng Anh, 5 học sinh không học khá cả hai môn Toán và Tiếng Anh. Chọn ngẫu nhiên một học
sinh trong lớp. Xác suất để học sinh được chọn học khá cả hai môn Toán và Tiếng Anh là NH A. 248 . B. 173 . C. 1984 D. 1 . ÓM 675 675 6075 3 Lời giải G Chọn D IÁ
Số học sinh học khá Tiếng Anh hoặc Toán là 45-5=40. O V
Số học sinh học khá cả 2 môn Tiếng Anh và Toán là 31+24-40=15 IÊ
Xác suất cần tìm là 15 1 = N T 45 3 OÁ
Câu 4. Cho hình hộp ABC .
D A B C D . Phát biểu nào sau đây sai? 1 1 1 1
   
    N V
A. AC = CC + CB − CD .
B. AC = DC + DD − DA. 1 1 1 1
   
    I
C. AC = AB + AD + AA .
D. AC = BC + BB + BA. Ệ 1 1 1 1 T N Lời giải Chọn C AM
   
AC = AB + AD + AA theo quy tắc hình hộp. 1 1 
Câu 5. Trong không gian Oxyz , cho hai điểm A(2; 1; − ) 1 và B(1;2; 3
− ) . Toạ độ của vectơ AB là A. (1; 3 − ;4). B. (3;1; 2 − ) . C. ( 1; − 3; 4 − ) . D. (2; 2; − 3 − ). Lời giải Chọn C  A(2; 1; − ) 1 và B(1;2; 3
− ) => toạ độ của vectơ AB = ( 1; − 3; 4 − ) . NH
Câu 6. Bảng số liệu ghép nhóm sau cho biết chiều cao (cm) của 50 học sinh lớp 10A. ÓM Khoảng chiều cao [155;160) [160;165) [165;170) G IÁO V Số học sinh 17 25 8 I
Mốt của mẫu số liệu ghép nhóm trên là ÊN T A. 162,6 . B. 161,6 . C. 163,4. D. 160. Lời giải OÁ Chọn B N V
Vì nhóm [160;165) có số học sinh nhiều nhất (tần số lớn nhất) nên Mốt của mẫu số liệu đã cho IỆT thuộc nhóm này.
Ta có j = 2,a = 160,m = 25,m = 17,m = 8,h = 5 2 2 1 3 . Do đó 25 −17 M = 160 + .5 = 161,6 0 ( (cm) . 25 −17) + (25 − 8)
https://www.facebook.com/groups/toanvd.vdc Trang 6
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NĂM HỌC- 2024-2025
Câu 7. Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O , đường thẳng SA vuông góc với
mặt phẳng đáy và OC = 3SA (tham khảo hình vẽ). Số đo góc phẳng nhị diện [S, BD,C]bằng S D C NH O ÓM A B G A. 120O . B. 150O . C. 30O . D. 60O . IÁO V Lời giải Chọn B IÊN T S OÁ N V IỆT N AM D C O A B
Ta có SA ⊥ ( ABCD) ⇒ SA ⊥ BD mà BD ⊥ AC nên BD ⊥ (SAC) . Do đó, BD ⊥ SO . Mặt
khác, CO ⊥ BD . Vậy góc phẳng nhị diện [S, BD,C] chính là góc  SOC . NH Ta có  SA SA SA 1 = = = = ⇒  0 = ⇒  0 tan SOA SOA 30 SOC = 150 . ÓM OA OC 3SA 3 G
Số đo góc phẳng nhị diện [S, BD,C]bằng 0 150 . IÁO V
Câu 8. Cho hàm số bậc ba y = f (x) có đồ thị là đường cong như hình vẽ bên. Điểm cực tiểu của hàm I số đã cho bằng ÊN T OÁ N V IỆT A. 0 . B. 1. C. 2 . D. 5. Lời giải
https://www.facebook.com/groups/toanvd.vdc Trang 7
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NĂM HỌC- 2024-2025 Chọn C
Dựa vào đồ thị, ta thấy điểm cực tiểu của hàm số đã cho bằng 2 .
2x − 2 nÕ x u > 2  Câu 9. Cho hàm số
f (x) = 2 nÕ x
u = 2 . Phát biểu nào sau đây là đúng? −x nÕ x u <  2
A. lim f (x) = 2.
B. lim f (x) = f (2). x 2− → x 2+ →
C. lim f (x) = lim f (x).
D. Hàm số liên tục tại x = 2. x 2+ x 2− → → Lời giải Chọn B NH
Ta có: lim f (x) = lim (2x − 2) = 2 = f (2). + + ÓM x→2 x→2
Câu 10. Một cấp số cộng có số hạng đầu bằng 4 và số hạng thứ 3 bằng 12. Số hạng thứ 10 của cấp số G cộng đó bằng IÁO V A. 44. B. 36. C. 40. D. 10 4 . Lời giải IÊ Chọn C N T
Gọi d là công sai của cấp số cộng đã cho. OÁ
Ta có u = 4 u = u + 2d = 12 d = 1 , 3 1 , suy ra 4. N V
Vậy u = u + 9d = 4 + 9.4 = 40 10 1 . IỆ
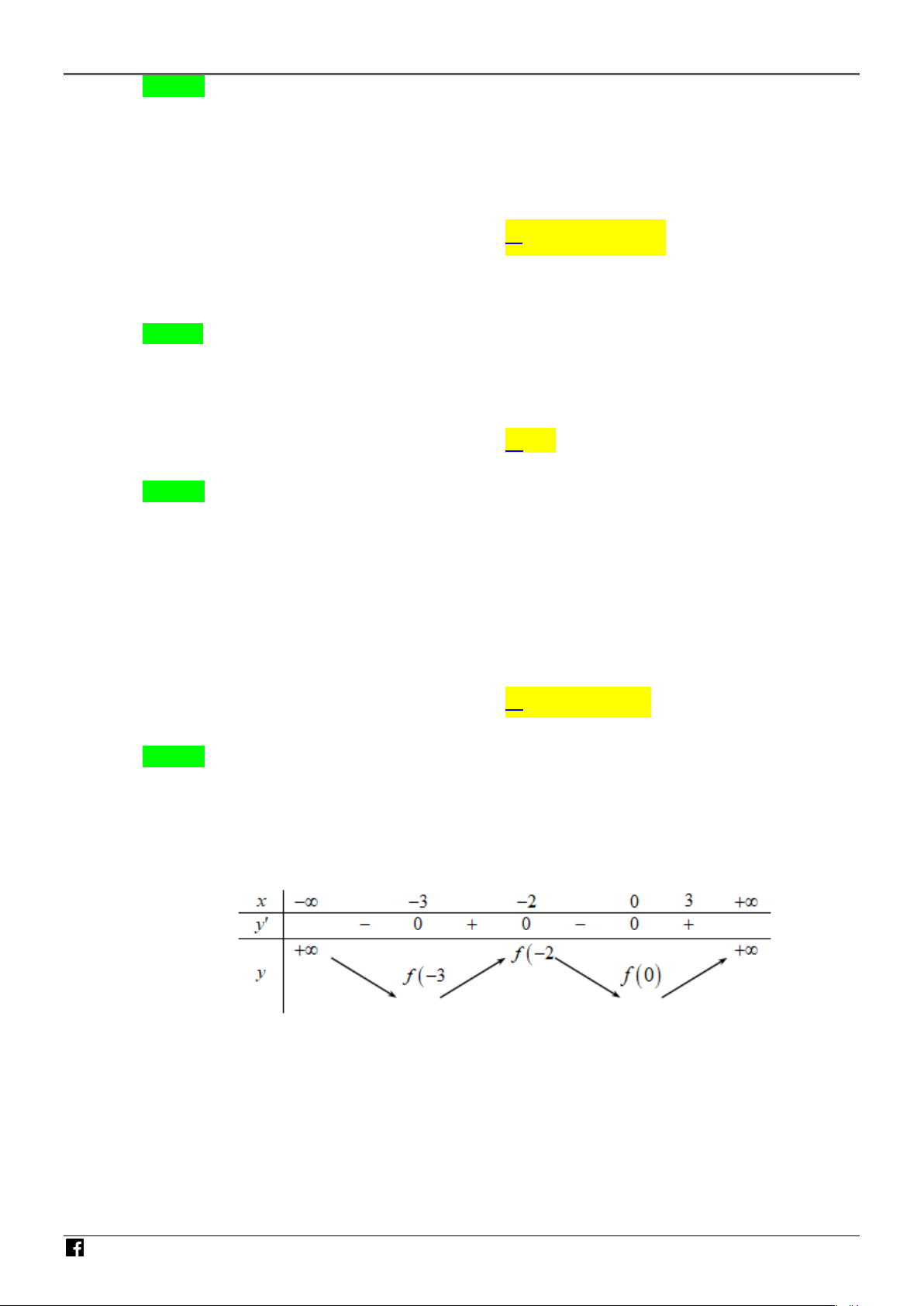
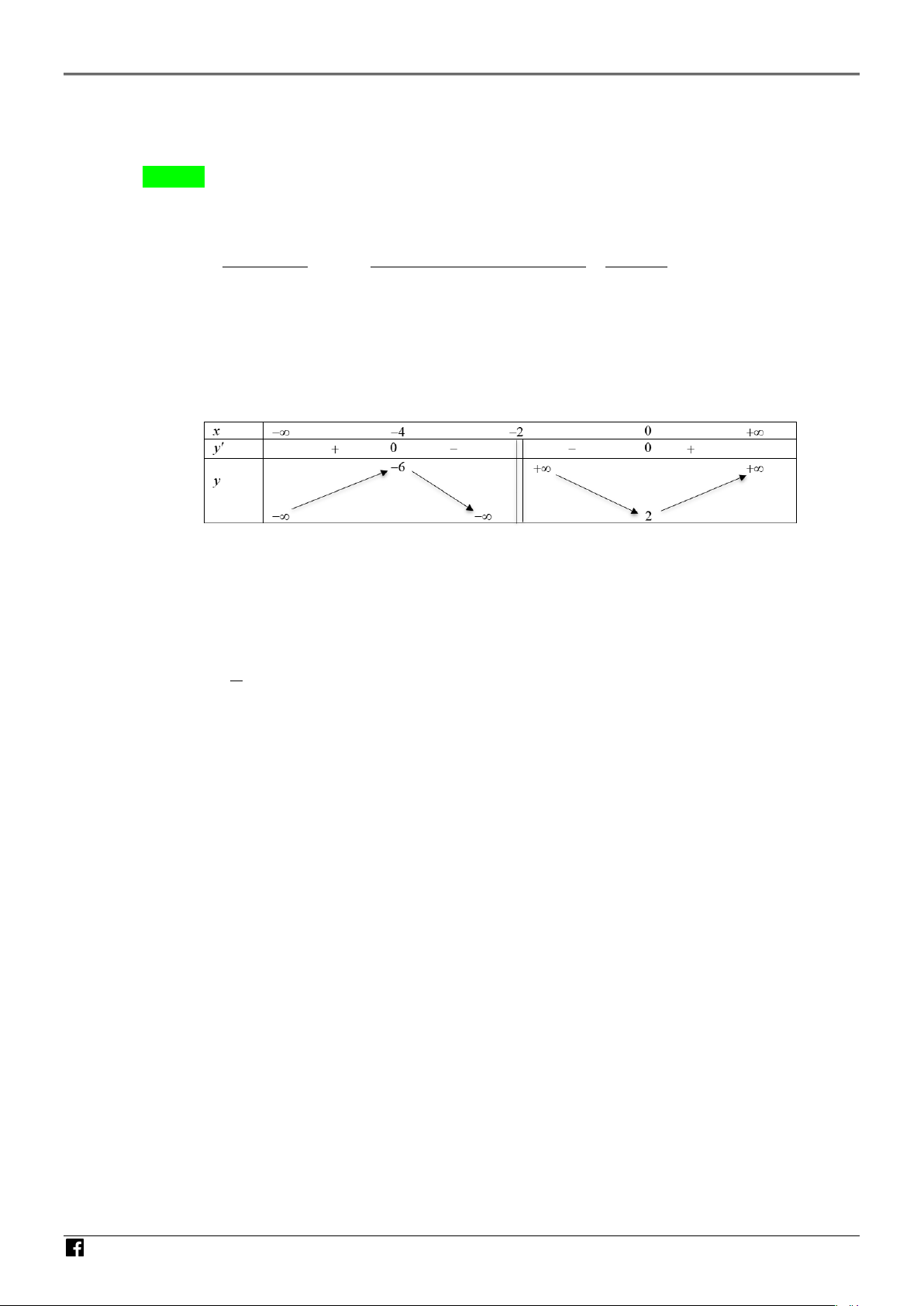
Câu 11. Cho hàm số y = f (x) có đạo hàm f ′(x) = x(x + 2)(x + 3) , x ∀ ∈  và T N f ( ) 1 + f ( 2
− ) = f (3) + f (0). Giá trị nhỏ nhất, giá trị lớn nhất của hàm số y = f (x) trên AM đoạn [ 2; − ]3 lần lượt là
A. f (0) và f ( 2 − ). B. f ( 2
− ) và f (0). C. f (0) và f (3).
D. f (3) và f (0). Lời giải Chọn C x = 0
Ta có f (x) 0  ′ = ⇔ x = 3 −  NH x = 2 −  ÓM Bảng biến thiên: GIÁO V IÊN T OÁ
Từ bảng biến thiên ta thấy: Giá trị nhỏ nhất của hàm số y = f (x) trên đoạn [ 2; − ]3 là f (0). N V Ta có: f ( ) 1 + f ( 2
− ) = f (3) + f (0) ⇔ f ( )
1 − f (0) = f (3) − f ( 2 − ) IỆ > > − = T Do f ( ) 1
f (0) nên f (3) f ( 2). Vậy giá trị lớn nhất của hàm số y f (x) trên đoạn [ 2; − ]3 là f (3).
https://www.facebook.com/groups/toanvd.vdc Trang 8
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NĂM HỌC- 2024-2025 Câu 12. 1
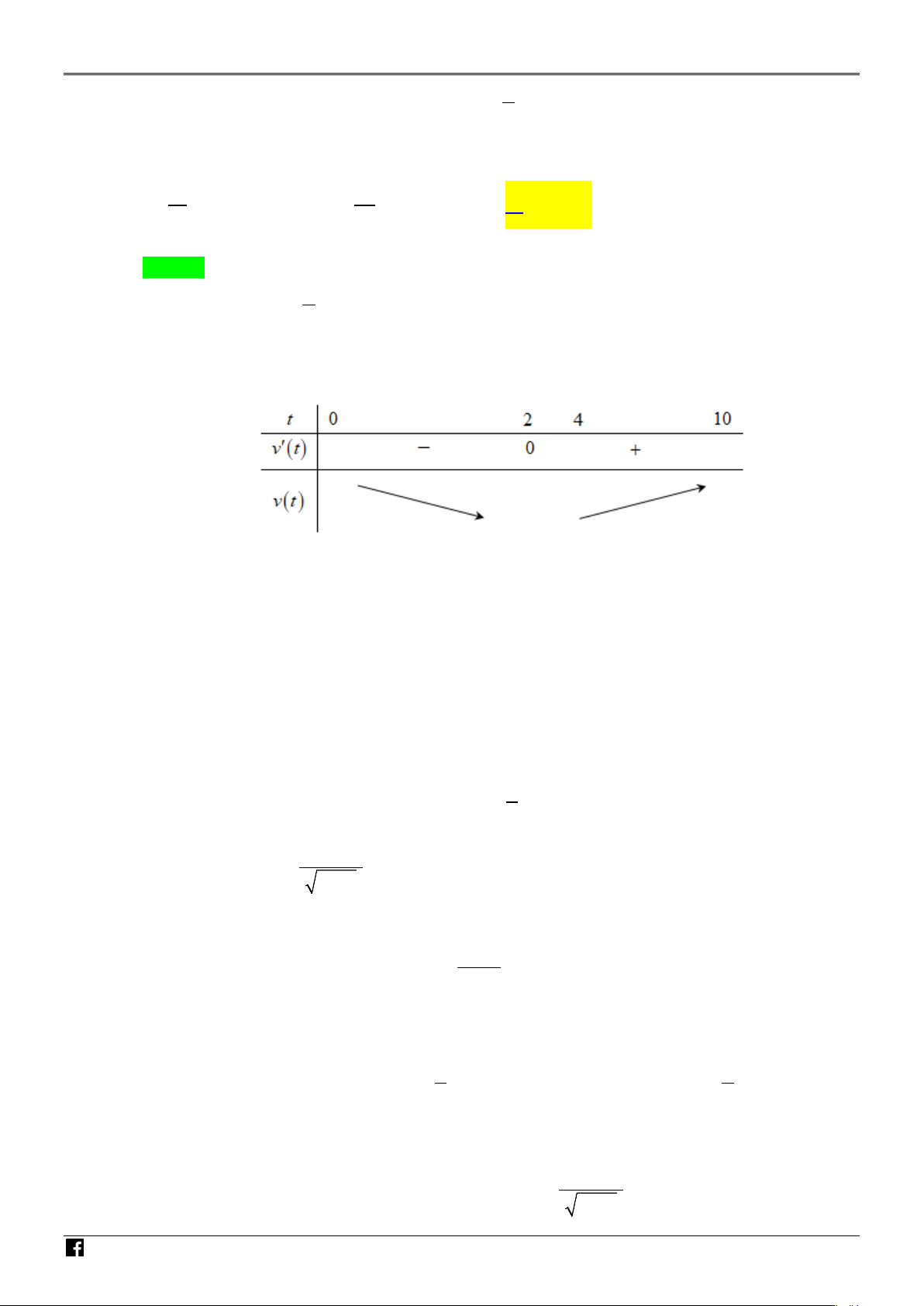
Một vật chuyển động theo phương trình s(t) 3 2
= t − t + 4t , trong đó t > 0, t tính bằng giây 6
và s(t) tính bằng mét. Xét trong khoảng thời gian từ 4 giây đến 10 giây vận tốc của vật đạt giá trị nhỏ nhất bằng A. 16 (m/s). B. 32 (m/s). C. 4 (m/s). D. 2 (m/s). 3 3 Lời giải Chọn C 1
Ta có v(t) = s′(t) 2
= t − 2t + 4 . 2 NH
v′(t) = t − 2, v′(t) = 0 ⇔ t = 2 . ÓM Bảng biến thiên: GIÁO V IÊN T OÁ N V
Từ bảng biến thiên ta thấy: trên đoạn [4;10], v(t) đạt giá trị nhỏ nhất khi t = 4. IỆ
Vậy trong khoảng thời gian từ 4 giây đến 10 giây vận tốc của vật đạt giá trị nhỏ nhất bằng T N v(4) = 4(m/s). AM
PHẦN II. CÂU TRẮC NGHIỆM ĐÚNG SAI
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1. Cho hàm số f (x) = log 4x +1 . 5 ( )  
a) Tập xác định của hàm số f (x) là khoảng 1 − ;+∞  . 4    NH f (x) −1 ÓM
b) Bất phương trình
≤ 0 có đúng 2 nghiệm nguyên. x 3 −1 G
c) Đồ thị hàm số f (x) đi qua trung điểm của đoạn thẳng AB , với A(3;4) và B(9;0) . IÁO V
d) Đạo hàm của hàm số f (x) là f ′(x) 4 = . I 5x +1 ÊN T Lời giải OÁ (a) Đúng. N V   Điều kiện xác định: 1
4x +1 > 0 ⇔ x > − . Vậy tập xác định của hàm số là 1 − ;+∞   . IỆ 4  4  T (b) Sai. f (x) −1
Điều kiện: 3x −1 > 0 ⇔ x > 0. Khi đó bất phương trình ≤ 0 3x −1
https://www.facebook.com/groups/toanvd.vdc Trang 9
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NĂM HỌC- 2024-2025
⇔ f (x) −1≤ 0 ⇔ f (x) ≤1 ⇔ log 4x +1 ≤1⇔ 4x +1≤ 5 ⇔ x ≤1. 5 ( )
Kết hợp điều kiện ta được tập nghiệm là 0 < x ≤1. Vậy bất phương trình đã cho có 1 nghiệm nguyên. (c) Đúng.
Toạ độ trung điểm M của đoạn AB là M (6;2).
Toạ độ điểm M (6;2) thuộc đồ thị hàm số y = f (x) = log 4x +1 . 5 ( ) (d) Sai. NH 4x 1 ′ + 4 ÓM Ta có f ′(x) ( ) = ( = . 4x + ) 1 ln 5 (4x + ) 1 ln 5 GI ABC. = = Á
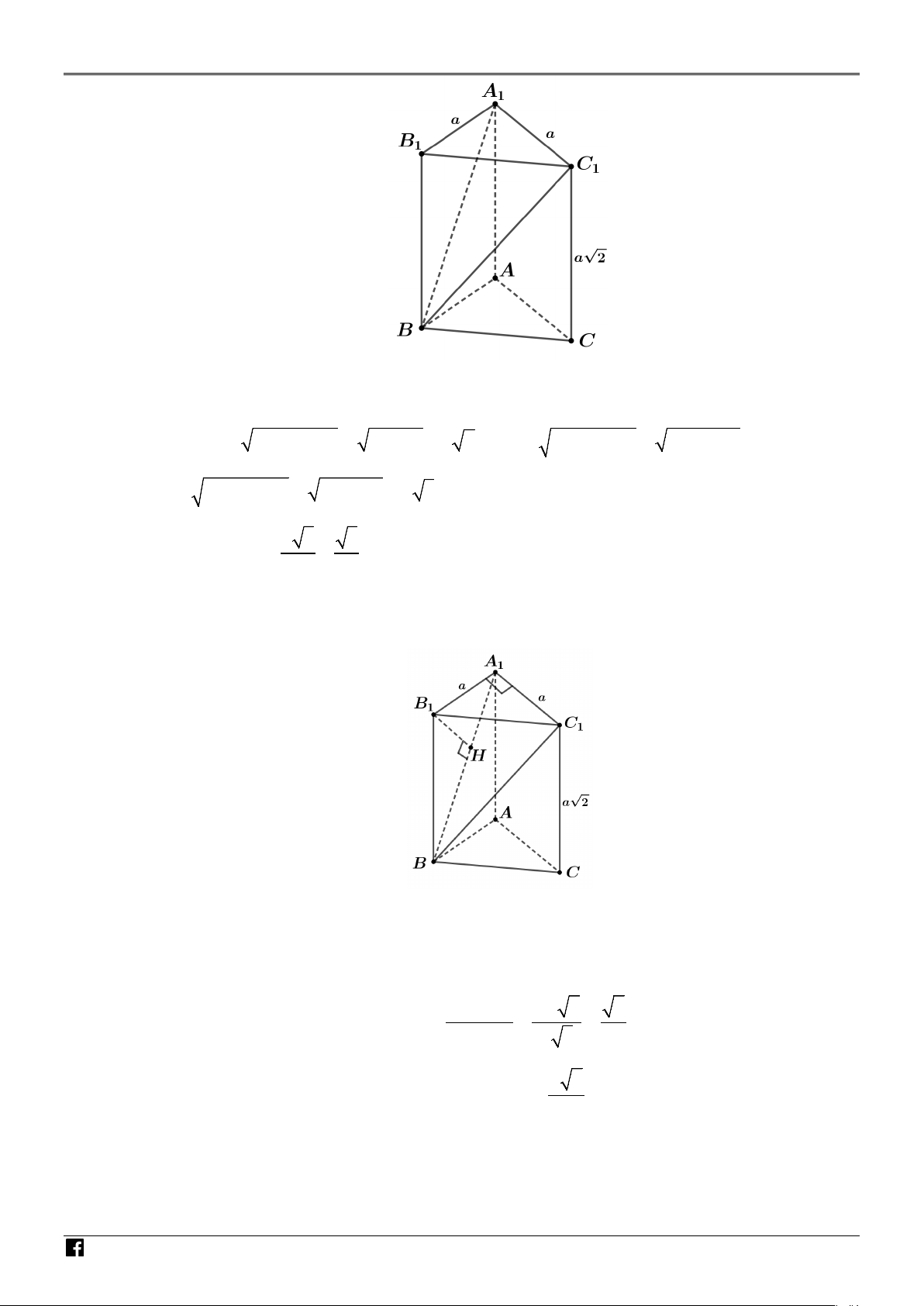
Câu 2. Cho hình lăng trụ đứng
A B C có đáy ABC là tam giác vuông cân tại A , AB AC a 1 1 1 O V
và cạnh bên AA = a 2 (tham khảo hình vẽ) 1 IÊN T OÁ N V IỆT N AM 3
a) Thể tích của khối lăng trụ ABC.A B C bằng a 2 . 1 1 1 2
b) Góc giữa hai đường thẳng BC và AC bằng 60°. 1
c) Khoảng cách từ A đến mặt phẳng A BC bằng a 6 . NH ( 1 1) 6 ÓM
d) Gọi M , N lần lượt là hai điểm di động trên các đoạn thẳng AC và BC sao cho a MN = . 1 1 1 2 G IÁ 7 2 O V
Thể tích của khối chóp .
A A BNM có giá trị nhỏ nhất bằng 3 a . 1 48 IÊ Lời giải N T (a) Đúng. OÁ 3 N V
Thể tích của khối lăng trụ ABC.A B C bằng 1 a 2 V = S .AA = . . a . a a 2 = . 1 1 1 ABC ∆ 1 2 2 IỆT (b) Đúng.
https://www.facebook.com/groups/toanvd.vdc Trang 10
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NĂM HỌC- 2024-2025 NH ÓM
Vì AC // AC nên (BC , AC = BC , AC = BC A . 1 ) ( 1 1 1)  1 1 1 1 GIÁO V Ta có 2 2 2 2
BC = AB + AC = a + a = a 2 ; 2 2 2 2
BC = BC + CC = 2a + 2a = 2a ; 1 1 IÊ 2 2 2 2
BA = AB + AA = a + 2a = a 3 . Ta thấy 2 2 2
BC = AC + A B ⇒ AC ∆
B vuông tại A . N T 1 1 1 1 1 1 1 1 1 OÁ Ta có  3 3  sin a BC A = = ⇒ BC A = 60°. N V 1 1 1 1 2a 2 I
Vậy góc giữa hai đường thẳng BC và AC bằng 60°. Ệ 1 T N (c) Sai. AM NH ÓM G
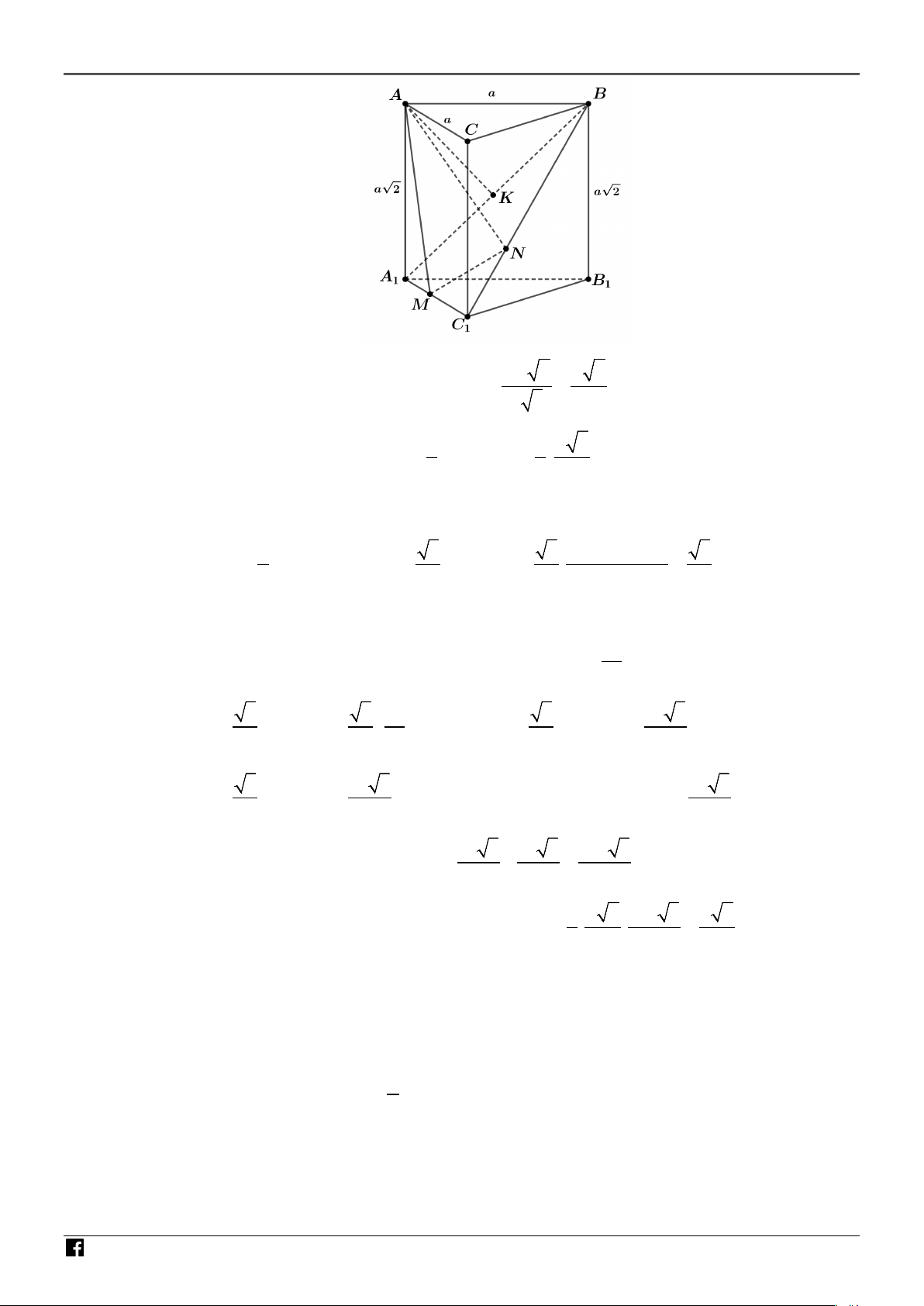
Kẻ B H ⊥ A B . 1 1 IÁO V Ta có d ( ,
A ( A BC = d B , A BC = B H . 1 1 )) ( 1 ( 1 1)) 1 IÊN T B A .B B Xét tam giác vuông a.a 2 6 A B B , ta có 1 1 1 B H = = = a . 1 1 1 OÁ A B a 3 3 1 N V a I
Vậy khoảng cách từ A đến mặt phẳng ( A BC bằng 6 . 1 1 ) Ệ 3 T (d) Đúng.
https://www.facebook.com/groups/toanvd.vdc Trang 11
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NĂM HỌC- 2024-2025 NH ÓM . Kẻ a a a
AK ⊥ A B ⇒ AK ⊥ BA MN . Ta có 2 6 AK = = . 1 ( 1 ) a 3 3 GIÁO V Thể tích khối chóp . A A BNM 1 1 a 6 V = AK.S = . .S . 1 là B 1 A MN B 1 3 3 3 A MN IÊN T Thể tích khối chóp .
A A BNM nhỏ nhất ⇔ nhỏ nhất ⇔ lớn nhất. 1 S S B 1 A MN ∆ 1 C MN OÁ 1 3 2 2 3 C M + C N 3 1 1 2 2 N V Ta có S = ° = ≤ . = (C M +C N . 1 1 ) ∆ C M C N C M C N C MN . .sin 60 . 1 1 1 1 1 2 4 4 2 8 IỆT N
Theo định lý cô sin ta có 2 AM 2 2 2 2 2 = + − 2 . .cos60 a MN C M C N C M C N
° ⇔ C M + C N = + C M.C N . 1 1 1 1 1 1 1 1 4 2 2 3 3  a  3 a 3 ⇒ S = ≤  +  ⇔ ≤ . ∆ C M C N C M C N C M C N C MN . . . 1 1 1 1 1 1 1 4 8  4  8 32 2 3 a 3 2 ⇒ S = ≤
. Do đó diện tích S
lớn nhất bằng a 3 . ∆ C M C N C MN . 1 1 1 4 16 ∆ 1 C MN 16 NH 2 2 2
a 3 a 3 7a 3 ⇒ S nhỏ nhất bằng S − = − = . ∆ S ÓM B 1 A MN B 1 A 1 C ∆ 1 C MN 2 16 16 G 2 1 a 6 7a 3 7 2 3 I
Khi đó thể tích khối chóp .
A A BNM nhỏ nhất bằng V = . . = a . Á 1 O V 3 3 16 48 I
Câu 3. Các học sinh lớp 12T làm thí nghiệm gieo ba loại hạt giống X , Y và Z . Xác suất để ba loại hạt ÊN T
giống X , Y và Z nảy mầm tương ứng là x, y và 0,8 (x > y) . Biết rằng xác suất để ít nhất một OÁ
trong ba hạt giống này mầm là 0,964 và xác suất để cả ba hạt giống đều nảy mầm là 0,224 . Giả
sử việc nảy mầm của các hạt giống X , Y và Z là độc lập với nhau. Gọi A là biến cố: “Có ít N V
nhất một trong ba hạt giống nảy mầm” và B là biến cố: “Cả ba hạt giống đều nảy”. IỆ
a) Biến cố đối của biến cố A là A : “Cả ba hạt giống đều không nảy mầm”. mầm T
b) Xác suất để xảy ra biến cố B là P(B) = 0,8xy .
c) Xác suất để hạt giống X nảy mầm là 0,7 .
https://www.facebook.com/groups/toanvd.vdc Trang 12
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NĂM HỌC- 2024-2025
d) Xác suất để có đúng hai hạt nảy mầm là 0,488 . Lời giải Chọn A (a) Đúng.
Biến cố đối của biến cố A là A : “Cả ba hạt giống đều không nảy mầm”. (b) Đúng.
B là biến cố: “Cả ba hạt giống đều nảy mầm” ⇒ B = X ∩Y ∩ Z NH
Xác suất để xảy ra biến cố B là P(B) = P( X ∩Y ∩ Z ) = 0,8xy . ÓM (c) Đúng. GIÁ
Xác suất để ít nhất một trong ba hạt giống này mầm là 0,964 ⇒ P( X ∪Y ∪ Z ) = 0,964. O V I
⇒ P( X ) + P(Y ) + P(Z ) − P( X ∩Y ) − P( X ∩ Z ) − P(Y ∩ Z ) + P( X ∩Y ∩ Z ) = 0,964 ÊN T
⇒ x + y + 0,8 − xy − 0,8x − 0,8y + 0,224 = 0,964 ⇒ 0,2x + 0,2y − xy = 0, − 06 . OÁ N V
Xác suất để cả ba hạt giống đều nảy mầm là: IỆ
0,224 ⇒ P( X ∩Y ∩ Z ) = 0,224 ⇒ 0,8xy = 0,224 ⇒ xy = 0,28 . T N Ta có hệ phương trình: AM
0, 2x + 0, 2y − xy = 0 − ,06 x + y = 1,1
x = 0.7 x = 0.4  ⇒  ⇒  ∨ xy 0, 28 xy 0, 28 y 0, 4  = = = y = 0,7 x = 0,7
Vì x > y ⇒  . y = 0, 4
Xác suất để hạt giống X nảy mầm là 0,7 . NH (d) Đúng. ÓM
Xác suất để có đúng hai hạt nảy mầm là: GIÁ
P( X ∩Y ∩ Z ) + P( X ∩Y ∩ Z ) + P( X ∩Y ∩ Z ) O V I
= 0,7.0,4.0,2 + 0,7.0,6.0,8 + 0,3.0,4.0,8 = 0,488 . ÊN T 2 x + 2x + 4 OÁ y = Câu 4. Cho hàm số x + 2 . N V
a) Hàm số có giá trị cực đại lớn hơn giá trị cực tiểu. IỆT b) Gọi ,
A B là các điểm cực đại, cực tiểu của đồ thị hàm số. Diện tích của tam giác OAB bằng
8 (đơn vị diện tích), trong đó O là gốc tọa độ.
c) Đường thẳng đi qua hai điểm cực đại và cực tiểu của đồ thị hàm số là y = 2x + 2 .
https://www.facebook.com/groups/toanvd.vdc Trang 13
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NĂM HỌC- 2024-2025
d) Hàm số nghịch biến trên khoảng ( 4; − 0) . Lời giải Chọn A a) Sai. 2 x + 2x + 4
(2x + 2)(x + 2) 2 2
− x − 2x − 4 Ta có x + 4x y = ⇒ y′ = = . x + 2 (x + 2)2 (x + 2)2 x = 0 NH y′ = 0 ⇒  . x = 4 − ÓM Bảng biến thiên: GIÁO V IÊN T OÁ
Vậy hàm số có giá trị cực đại nhỏ hơn giá trị cực tiểu. N V b) Sai. IỆT N Gọi ,
A B là các điểm cực đại, cực tiểu của đồ thị hàm số A( 4; − 6 − ), B( 0;2) AM 1 ⇒ S =
= (đơn vị diện tích). OAB .2.4 4 2 c) Đúng. qua B  ( 0;2) AB :   
⇒ AB : 2x − y + 2 = 0 ⇒ y = 2x + 2 . vtcp AB  (4;8) ⇒ vtp n( t 2;− ) 1 NH
Vậy đường thẳng đi qua hai điểm cực đại và cực tiểu của đồ thị hàm số là y = 2x + 2 . ÓM d) Sai. GI
Hàm số nghịch biến trên khoảng ( 4; − 2 − ) và ( 2; − 0) . ÁO V
PHẦN III. CÂU TRẮC NGHIỆM TRẢ LỜI NGẮN IÊN T
Thí sinh trả lời câu 1 và câu 2 OÁ
Câu 1. Một doanh nghiệp tư nhân X chuyên kinh doanh xe gắn máy các loại. Hiện nay, doanh N V
nghiệp đang tập trung chiến lược kinh doanh một loại xe máy với chi phí mua vào là 38 triệu I
đồng/ chiếc với giá bán ra là 43 triệu đồng/ chiếc. Với giá bán này thì số lượng xe bán ra mỗi ỆT
năm là 600 chiếc. Nhằm tiêu thụ dòng xe đang ăn khách này, doanh nghiệp dự định giảm giá
bán. Ước tính cứ giảm 1 triệu đồng/ chiếc thì số lượng xe bán ra trong năm tăng thêm 200
chiếc. Vậy doanh nghiệp phải giảm giá bán là bao nhiêu triệu đồng để thu được lợi nhuận cao
https://www.facebook.com/groups/toanvd.vdc Trang 14
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NĂM HỌC- 2024-2025
nhất trong một năm? Lời giải: ĐA: 1
Gọi giá bán mới của một chiếc xe là x triệu đồng ( 38  x  43 ).
Tiền lời sau khi giảm giá bán của một chiếc xe là: x  38 triệu đồng
Số tiền giảm giá so với ban đầu là 43  x triệu đồng.   
Số xe bán được sau khi giảm là 43 x 600     .200  chiếc xe.  1  NH ÓM
Lợi nhuận doanh nghiệp thu được trong một năm sau khi giảm giá xe là:  
x  38 . 600  43  x .200 G        . IÁO V
Xét hàm f x  x       x  2 38 . 600 43
.200  200x  16800x  349600   . IÊN T
ta thấy f x đạt giá trị lớn nhất 3200 tại x  42 . OÁ N V
Vậy doanh nghiệp phải giảm giá bán 1 triệu đồng để thu được lợi nhuận cao nhất. I
Câu 2. Trong ngày hội STEM, bạn An nhận được nhiệm vụ thiết kế một chiếc hộp giấy có dạng hình ỆT N
hộp chữ nhật ABCD.A B C D với độ dài các cạnh AB a,AD  ,
b AA c và khoảng 1 1 1 1 1 AM
cách giữa AC và BC bằng d ( tham khảo hình vẽ). Biết rằng a, , b ,
c d là các số nguyên dương 1
có đơn vị đo bằng decimet. Hỏi diện tích của chiếc hộp bằng bao nhiêu 2
dm để thể tích của chiếc
hộp bạn An sẽ làm là nhỏ nhất. Lời giải: ĐA: 90. NH ÓM GIÁO V IÊN T OÁ Ta có: N V
AC // AC AC // BAC d AC,C B d AC, BACd C, BAC 1 1  1 1  1    1 1   1 1 IỆT
Mà d C,BAC d B , BAC , nên d AC,C B d B , BAC d d      1   1  1 1   1 1   1  1 1
https://www.facebook.com/groups/toanvd.vdc Trang 15
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NĂM HỌC- 2024-2025 1 1 1 1
Ta có B BAC là tứ diện vuông tại B nên   
a, ,b ,cd     1 1 1 1 2 2 2 2 d a b c
Dễ thấy: d  min a, ,bc.
Không mất tính tổng quát giả sử: 0  d a b c . TH1: 1 1 1 3
d  1 thì c b a  2 ( vì a, , b c    ), suy ra 1     ( vô lý). 2 2 2 a b c 4 1 1 1 1 NH
TH2: d  2 thì a  3 và    . Lúc này ta thấy: 2 2 2 4 a b c ÓM 1 1 1 1 3 G
Với a  4 thì c b a  4      ( Vô lý) 2 2 2 I 4 a b c 16 ÁO V 1 1 1 1 1 1 5 I a        Ê Với 3 thay vào ta có: 2 2 2 2 2 N T 4 3 b c b c 36 OÁ Với 5 1 1 1 1 2 5
b  5 thì c b  5 nên       ( Vô lý) N V 2 2 2 2 36 b c 5 5 25 36 IỆT N
Với b  4 thay vào ta thấy không tồn tại c    AM
Với b  3 ta tìm được c  6 khi đó V abc  3.3.6  54 H
TH3: d  3 thì a b c  4 nên V abc  4.4.4  64  54 H
Khi đó thể tích chiếc hộp nhỏ nhất bằng 54 khi a; ; b c  3;3;6
Do đó diện tích chiếc hộp bằng: S  ab ac cb   2 2 90 dm . NH ÓM  HẾT  GIÁO V IÊN T OÁ N V IỆT
https://www.facebook.com/groups/toanvd.vdc Trang 16
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NĂM HỌC- 2024-2025
SỞ GIÁO DỤC ĐÀO TẠO NGHỆ AN
ĐỀ THI CHỌN HSG CẤP TỈNH Môn: Toán 12
Thời gian: 180 phút (không kể thời gian phát đề) Câu I. (3,5 điểm) 3
1) Tìm các điểm cực đại và cực tiểu của hàm số x y =
− 3x − 6ln (2 − x) +1. NH 3
2) Một công ty bất động sản đưa ra hai phương án ký hợp đồng cho thuê căn hộ theo năm (tiền hợp đồng ÓM
thuê nhà khách hàng phải trả từ đầu năm) để làm văn phòng đại diện như sau:
Hợp đồng loại 1: Trả 220 triệu cho năm đầu tiên và sau mỗi năm tăng thêm 11 triệu đồng so với năm kề G trước. IÁO V
Hợp đồng loại 2: Trả 194 triệu cho năm đầu tiên và sau mỗi năm tăng thêm 6% so với năm kề trước.
Vào đầu năm 2024, bác Hoàng và bác Anh cùng đến thuê một căn hộ để làm văn phòng đại diện cho IÊ
công ty của mình và thuê dài hạn. Biết rằng bác Hoàng lựa chọn hợp đồng loại 1 và bác Anh lựa chọn hợp N T
đồng loại 2 để thuê. Hỏi từ đầu năm bao nhiêu trở đi bác Hoàng sẽ chi trả tiền thuê nhà hàng năm ít hơn bác Anh? OÁ N V
Câu II. (2,0 điểm). Nuôi cấy nấm men thu sinh khối (protein, amino acid...), ứng dụng làm tế bào nhận
trong công nghệ gen để sản xuất một số chất có hoạt tính sinh học mạnh (kháng sinh...). Giả sử số lượng tế IỆ
bào của một quần thể nấm men tại môi trường nuôi cấy trong phòng thí nghiệm được mô hình hóa bằng T N m = AM hàm số P(t)
, trong đó thời gian t được tính bằng giờ. Đạo hàm của hàm số y = P(t) biểu thị 0,75t n + e−
tôc độ sinh trưởng của quần thể nấm men (tính bằng tế bào/ giờ) tại thời điểm t . Tại thời điểm ban đầu
t = 0, quần thể có 30 tế bào và tốc độ sinh trưởng là 15 tế bào/ giờ. Tìm số lượng tế bào của quần thể nấm
men tại thời điểm tốc độ sinh trưởng của quần thể nấm men đạt mức tối đa.
Câu III. (3,5 điểm) Các học sinh lớp 12T làm thí nghiệm gieo ba loại hạt giống X , Y và Z . Xác suất
để ba loại hạt giống X , Y và Z nảy mầm tương ứng là x, y và 0,8 (x > y) . Biết rằng xác suất để ít nhất NH
một trong ba hạt giống này mầm là 0,964 và xác suất để cả ba hạt giống đều nảy mầm là 0,224 . Giả sử ÓM
việc nảy mầm của các hạt giống X , Y và Z là độc lập với nhau. Gọi A là biến cố: “Có ít nhất một tr ong G
ba hạt giống nảy mầm” và B là biến cố: “Cả ba hạt giống đều nảy”. IÁO V
a) Biến cố đối của biến cố A là A : “Cả ba hạt giống đều không nảy mầm”. mầm IÊN T
b) Xác suất để xảy ra biến cố B là P(B) = 0,8xy . OÁ N V
c) Xác suất để hạt giống X nảy mầm là 0,7 . IỆ
d) Xác suất để có đúng hai hạt nảy mầm là 0,488 . T 2
Câu IV. (1,5 điểm) Cho hàm số x + 2x + 4 y = . x + 2
https://www.facebook.com/groups/toanvd.vdc Trang 1
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NĂM HỌC- 2024-2025
a) Hàm số có giá trị cực đại lớn hơn giá trị cực tiểu. b) Gọi ,
A B là các điểm cực đại, cực tiểu của đồ thị hàm số. Diện tích của tam giác OAB bằng 8 (đơn
vị diện tích), trong đó O là gốc tọa độ.
c) Đường thẳng đi qua hai điểm cực đại và cực tiểu của đồ thị hàm số là y = 2x + 2 .
d) Hàm số nghịch biến trên khoảng ( 4; − 0) .
Câu V. (1,5 điểm) Cho tập A gồm n phần tử ( n là số nguyên dương). Lấy ngẫu nhiên một bộ thứ tự NH
( X,Y ) với X,Y là các tập con của tập hợp A. Biết xác suất để lấy được một bộ thứ tự ( X,Y ) sao cho ÓM
X ∪Y = A là 81 . Tìm số k lớn nhất ( k∈ ) sao cho có thể chọn ra k tập hợp con khác nhau của tập hợp 448 G
A mà hai tập con bất kì trong k tập đó giao nhau khác rỗng (với X ≠Y thì các bộ thứ tự ( X ,Y ) và (Y, X ) IÁO V là khác nhau). IÊ  HẾT  N T OÁ N V IỆT N AM NH ÓM GIÁO V IÊN T OÁ N V IỆT
https://www.facebook.com/groups/toanvd.vdc Trang 2
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NĂM HỌC- 2024-2025 HƯỚNG DẪN GIẢI
SỞ GIÁO DỤC ĐÀO TẠO TỈNH NGHỆ AN
ĐỀ THI CHỌN HSG CẤP TỈNH Môn: Toán 12
Thời gian: 180 phút (không kể thời gian phát đề) Câu I. 3
1) Tìm các điểm cực đại và cực tiểu của hàm số x y =
− 3x − 6ln (2 − x) +1. NH 3
2) Một công ty bất động sản đưa ra hai phương án ký hợp đồng cho thuê căn hộ theo năm (tiền ÓM
hợp đồng thuê nhà khách hàng phải trả từ đầu năm) để làm văn phòng đại diện như sau:
Hợp đồng loại 1: Trả 220 triệu cho năm đầu tiên và sau mỗi năm tăng thêm 11 triệu đồng so với G năm kề trước. IÁO V
Hợp đồng loại 2: Trả 194 triệu cho năm đầu tiên và sau mỗi năm tăng thêm 6% so với năm kề trước. IÊ
Vào đầu năm 2024, bác Hoàng và bác Anh cùng đến thuê một căn hộ để làm văn phòng đại diện N T
cho công ty của mình và thuê dài hạn. Biết rằng bác Hoàng lựa chọn hợp đồng loại 1 và bác Anh
lựa chọn hợp đồng loại 2 để thuê. Hỏi từ đầu năm bao nhiêu trở đi bác Hoàng sẽ chi trả tiền thuê OÁ
nhà hàng năm ít hơn bác Anh? N V Lời giải I 1) TXĐ: D = ( ;2 −∞ ) . ỆT N 3 2 Ta có: 2 6 −x + 2x + 3 ′ = − 3 x y x + = . AM 2 − x 2 − xx = 0 y 0  ′ = ⇒ x = 1 −  x = 3∉  D Bảng biến thiên: NH ÓM GIÁO V I
Theo bảng biến thiên suy ra: ÊN T
- Điểm cực đại của hàm số là: x = 1 −
- Điểm cực tiểu của hàm số là: x = 0 . OÁ
2) - Theo hợp đồng loại 1, số tiền thuê căn hộ mà bác Hoàng phải trả trong các năm là một cấp N V
số cộng với số hạng đầu u = 220 , công sai d =11 nên số tiền bác Hoàng phải trả trong năm thứ 1 I n là: A = + n − = n + (triệu đồng). n 220 ( ) 1 .11 11 209 ỆT
- Theo hợp đồng loại 2, số tiền thuê căn hộ mà bác Anh phải trả trong các năm là môt cấp số
nhân với số hạng đầu u =194 , công bội q =1+ 6% =1,06 nên số tiền bác Anh phải trả trong 1 năm thứ n là: 1 B 194.1,06n− = (triệu đồng). n Xét: n 1 − n 1 A B n − < ⇔ + < ⇔ − n − > ⇔ n > . n n 11 209 194.1,06 194.1,06 11 209 0 8,8
https://www.facebook.com/groups/toanvd.vdc Trang 3
NHÓM GIÁO VIÊN TOÁN VIỆT NAM NĂM HỌC- 2024-2025
Vậy từ đầu năm thứ 9 trở đi thì số tiền bác Hoàng phải trả hàng năm sẽ ít hơn số tiền bác Anh phải trả.
Câu II. Nuôi cấy nấm men thu sinh khối (protein, amino acid...), ứng dụng làm tế bào nhận trong công
nghệ gen để sản xuất một số chất có hoạt tính sinh học mạnh (kháng sinh...). Giả sử số lượng tế
bào của một quần thể nấm men tại môi trường nuôi cấy trong phòng thí nghiệm được mô hình hóa bằng hàm số ( ) m P t =
, trong đó thời gian t được tính bằng giờ. Đạo hàm của hàm 0,75t n + e−
số y = P(t) biểu thị tôc độ sinh trưởng của quần thể nấm men (tính bằng tế bào/ giờ) tại thời
điểm t . Tại thời điểm ban đầut = 0, quần thể có 30 tế bào và tốc độ sinh trưởng là 15 tế bào/
giờ. Tìm số lượng tế bào của quần thể nấm men tại thời điểm tốc độ sinh trưởng của quần thể NH
nấm men đạt mức tối đa. ÓM Lời giải G D = R IÁ − O V 0,75t ( ) 0,75 . ' m e P t = > 0 t ∀ ∈ D 2 0 − ,75t I (n+e ) ÊN T m OÁ
Tại thời điểm t = 0 : P(0) = 30 ⇔ = 30 . n +1 N V I 0,75.m Ệ
Khi đó tốc độ sinh trưởng tại thời điểm t = 0 là : P′(0) = . T N (n + )2 1 AM  m  = + = 30  m 30(n ) 1 m = 45 n +1  Theo bài ra, ta có hệ:   0,75.m ⇔ 0,75.30.(n + ) 1 ⇔  1 .  = 15 = 15  n =   (n +  )2 1  2 (n + )2 1 0 − ,75t 0 − ,75t 0 − ,75t Khi đó: ( ) 0,75.45. ' e P t 135 e 135 = 135 = . e ≤ . = 2  1 2 4 4 1 − t 8 0 − ,75t  1  0,75  e  + 0 − ,75t +  e 4. .e NH 2      2  2 ÓM 135 ′ = − t 1 ln 2 45 = ⇔ = =
Do đó: max P (t) khi 0,75 e t t nên P(t = = 45 0 ) 0 G t≥0 8 2 0,75 1 1 I + Á 2 2 O V I
Câu III. Các học sinh lớp 12T làm thí nghiệm gieo ba loại hạt giống X , Y và Z . Xác suất để ba loại hạt ÊN T
giống X , Y và Z nảy mầm tương ứng là x, y và 0,8 (x > y) . Biết rằng xác suất để ít nhất một OÁ
trong ba hạt giống này mầm là 0,964 và xác suất để cả ba hạt giống đều nảy mầm là 0,224 . Giả N V
sử việc nảy mầm của các hạt giống X , Y và Z là độc lập với nhau. Gọi A là biến cố: “Có ít I
nhất một trong ba hạt giống nảy mầm” và B là biến cố: “Cả ba hạt giống đều nảy”. ỆT
a) Biến cố đối của biến cố A là A : “Cả ba hạt giống đều không nảy mầm”. mầm
b) Xác suất để xảy ra biến cố B là P(B) = 0,8xy .
https://www.facebook.com/groups/toanvd.vdc Trang 4