Đề chọn học sinh giỏi Toán 12 năm 2020 – 2021 sở GD&ĐT Gia Lai (Bảng B)

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH GIA LAI MÔN TOÁN 12 NĂM HỌC 2020-2021
(Thời gian làm bài 180 phút)
Câu 1: (4 điểm) Cho hàm số 3 y  x   m   2 2
1 x  1 m x ( m là tham số thực) có đồ thị C.
Tìm m để đường thẳng d : y  x  mcắt đồ thị C tại ba điểm phân biệt A , B và C
sao cho tổng hệ số góc của ba tiếp tuyến với C tại các điểm A , B và C nhỏ hơn 9 .
Câu 2: (4 điểm) a/ Giải phương trình sau trên tập số thực: 2 x  x  x   2 5 10 4 1 x  2x  2 .
b/ Cho 3 số thực x 1, y  1, z 1 thỏa mãn: log x y z xy yz zx . Tính M  x  y  z . xy yz zx  2 2 2 5 16  27  4    log    2   12 Câu 3. (2 điểm) Tìm hệ số của số hạng không chứa x trong khai triển n  1 1  4    , với x  0 và * n   thỏa mãn 2 2 A  nC  55n  0 .  n n    x  x 1 x  x x 1 x 1  Câu 4.
(2,0 điểm) Cho tam giác ABC thõa mãn A B C
2019sin A  2020 sin B  2021sin C  2022 cos( )  2020 cos( )  2018cos( ) (1) . Chứng 2 2 2
minh rằng tam giác ABC đều.
Câu 5: (3 điểm) Cho dãy số u thỏa mãn: u  2021 và 2 * u
 u  u 1,n   , đặt n  1 n 1  n n 1 1 1 v    . Tính lim v . n u u u n 1 2 n
Câu 6: (2 điểm) Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC cân tại A . Gọi H là trung điểm của đoạn  
BC , K là hình chiếu vuông góc của H lên AC . Biết 7 5 M ;   là trung điểm  4 4 
của đoạn HK , đường thẳng BK : x  7 y 13  0 . Gọi N là giao điểm của BK và AM . Tìm tọa độ điểm   A , biết 1 5 I ; 
 là trung điểm của đoạn AB .  2 2 
Câu 7: (2 điểm) Cho tứ diện đều ABCD có cạnh bằng .
a Gọi H là chân đường vuông góc hạ từ A
xuống mặt phẳng BCD và O là trung điểm của đoạn AH. Gọi   là mặt phẳng qua O và không đi qua các điểm , A B,C và .
D Mặt phẳng   cắt các đoạn AB, AC và AD lần lượt tại M , N và .
P Tìm giá trị nhỏ nhất của AM .AN.AP theo . a
Câu 8: (2 điểm) Cho hàm số f x   2
ln x  x 1 2021x , gọi a,b,c là các số thực dương sao cho
phương trình f a  b  c x  f 
2020 3x  0 vô nghiệm. a  b  c
Tìm GTNN của biểu thức M  . ab  bc  ac HẾT 1 HƯỚNG DẪN GIẢI Câu 1: (4 điểm) Cho hàm số 3 y  x   m   2 2
1 x  1 m x ( m là tham số thực) có đồ thị C. Tìm m để
đường thẳng d : y  x  m cắt đồ thị C tại ba điểm phân biệt A , B và C sao cho tổng
hệ số góc của ba tiếp tuyến với C tại các điểm A , B và C nhỏ hơn 9. Lời giải
Phương trình hoành độ giao điểm của d và C : 3 x   m   2 2
1 x  1 m x  x  m 3  x   m   2 2
1 x  mx  m  0   x   2 1 x  2mx  m  0 x  1    2 x  2mx  m  0    *
Theo yêu cầu bài toán :  
* phải có hai nghiệm phân biệt khác 1  . m  0, m 1 2 m  m  0      1 1 2m  m  0  m    3
Ta có A1;1 m ; Bx ; x  m ; C x ; x  m 2 2  1 1  2 y '  3x  22m   1 x 1 m y     2 ' 1 3 1  22m   1   1 1 m  2  3m y ' x  2
 3x  2 2m 1 x 1 m 1 1   1 y ' x  2
 3x  2 2m 1 x 1 m 2 2   2 x  x  2m
Áp dụng định lí Viet ta có : 1 2  x x  m  1 2
Theo yêu cầu bài toán ta có y '  1  y ' x  y ' x  9 2
 2  3m  3x  22m   2
1 x 1 m  3x  2 2m 1 x 1 m  9 1 1 2   1   2 2  3 2 2
x  x  2 2m 1 x  x  5  m  0 1 2    1 2 
 3x  x 2  6x x  2 2m 1 x  x  5  m  0 1 2 1 2   1 2    m2 3 2  6m  22m   1 .2m  5  m  0 2 2
 12m  6m 8m  4m  5 m  0 2  4m  3m  5  0 3  89   m  , 3 89 m  8 8
Giao với điều kiện ta được : 3  89  m  , 3 89 m  . 8 8 Câu 2: (4 điểm)
a/ Giải phương trình sau trên tập số thực: 2 x  x  x   2 5 10 4 1 x  2x  2 .
b/ Cho 3 số thực x 1, y  1, z 1 thỏa mãn: log x y z xy yz zx . Tính M  x  y  z . xy yz zx  2 2 2 5 16  27  4    log    2   12 Lời giải a) Giải phương trình: 2 x  x  x   2 5 10 4 1 x  2x  2   1 2 Ta có:     2 x  x    2
x  x    x   2 1 4 2 2 2 1 9 4 1 x  2x  2 x x x    2     
2 x  2x  2  x   1 2 2 2 2 1 3 2    9    2
2 x  2x  2  x   1  3   x  2   x  2     2 x  x   x   4 2 2 2 2   2 x  2x  2 2 2  x  4x  4 3  x 12x  4  0        2  x  x   x  x  4    x  4 2 2 2 4    4  x x x x x   2  2  2 2 2   8 16  3   8  0  x  2  62 6 x   3 6  2 6    x  . x  4 3   2 6 x    3
Vậy phương trình ban đầu có 2 nghiệm là 6  2 6 x  . 3
b/ Tính M  x  y  z . log 12  0
- Theo giả thiết ta có: xy  yz  zx   1 nên xyyzzx  . log xy  yz  zx  0  12  
- Áp dụng BĐT Cauchy ta có: 2 2 2 x  y  z   2 2 x  y  2 2 y  z   2 2 5 16 27 3 12 4 9 18z  2x  2 2 2 2 2 2  2 3x 1
. 2y  2 4y .9z  2 18z .2x 12xy  yz  zx Hay 2 2 2
5x 16y  27z  12xy  yz  zx , dấu “=” xảy ra khi và chỉ khi x  2y  3z . Khi đó: log  2 2 2 5x 16y  27z   log 12xy yz zx      1 log xy yz zx xy yz zx xy yz zx 12       Suy ra: log x  y  z  log xy  yz  zx   log  log xy  yz  zx xyyzzx  1 2 2 2 5 16 27  4 1 12 12 xyyzzx 12       4   log
. log xy  yz  zx    . xyyzzx  1 1 2 12 1 1 2 12     4
Dấu “=” xảy ra khi và chỉ khi  x  2 3 x  2y  3  z x  2y  3z      y  3 log . 12  log xy  yz  zx xy  yz  zx 12  xyyzzx 12        2 3 z   3 3 Vậy 11 3 M  z  y  z  . 3 n  1 1  Câu 3.
Tìm hệ số của số hạng không chứa x trong khai triển 4    , với    x  x 1 x  x x 1 x 1  x  0 và * n   thỏa mãn 2 2 A  nC  55n  0 . n n Lời giải Xét phương 2 2 A  nC  55n  0 . n n n  0 n! n! 1 2               n  . n n  55n 0 nn 1 n n  1 55n 0 n 12 2 ! 2! 2 ! 2    n  9  Vì *
n   nên ta nhận n 12. Ta biến đổi 1 1 4      x x 1 x  x x 1 x 1 1 1 4    x x x   1  x 1  x  x 1 x 1  x 1 4    x x. x 1 x 1 1 1 1 1 4 4     x   x x x 1 x 1 x 12 12 12 k 12 3  1   1 k k 6  Xét khai triển 4  x  C  
1 k  4 x   C      k k k 4 1 x . 12 12  x  k 0  x  k 0 3
Số hạng không chứa x thỏa k  6  0  k  8 . 4
Vậy hệ số của số hạng không chứa x là C  8 8 1  495 . 12 Câu 4.
(2,0 điểm) Cho tam giác ABC thõa mãn A B C
2019sin A  2020sin B  2021sin C  2022 cos( )  2020 cos( )  2018cos( ) (1) . Chứng 2 2 2
minh rằng tam giác ABC đều. Lời giải A B  C B  C B  C 1 Ta có: cos  sin  sin .cos  (sin B  sin C) 2 2 2 2 2 A
 2022cos 1011(sin B  sin C) 2 B 1 B Tương tự: cos
 (sin A  sin C)  2020cos  1010(sin A  sin C) 2 2 2 C 1 C cos
 (sin A  sin B)  2018cos 1009(sin A  sin B) 2 2 2 4
 VP(1)  (1010 1009)sin A  (10111009)sin B  (1010 1011)sin C  VP(1)  B  C cos( )  1  2   C  A
Do đó (1) xảy ra  VT (1)  VP(1)  cos( )  1 Hay A  B  C 2   A  B cos( )  1  2 Hay tam giác ABC đều. Câu 5: (4 điểm) Cho dãy số  1 1 1 u thỏa mãn: u  2021 và 2 * u
 u  u 1,n   , đặt v    . n  1 n 1  n n n u u u 1 2 n Tính lim v . n Lời giải
Ta chứng minh dãy số tăng, thật vậy u  u  u   n    .  n  n 2 * 1 0, n 1
Giả sử dãy số bị chặn trên, suy ra dãy số có giới hạn, đặt limu  x . n
Do dãy số tăng nên 2021  u  u  ...  u  x  2021. 1 2 n Ta có 2 2 u
 u  u 1  x  x  x 1  x  1vô lí. n 1  n n
Vậy dãy số tăng và không bị chặn trên hay limu   . n Ta có 2 u
 u  u 1  u 1  u u 1 , do u  2021 n 1  n n n 1  n  n  n 1 1 1 1 1 1 1        . u 1 u u 1 u 1 u u u 1 u 1 n 1  n  n  n n n n n 1  n 1 n  1 1  1 1 Suy ra            k 1  u  u u u u k k 1 1 1 1 1  k k 1   1 n 1  1 1  1 1  1 Hay v    lim v  lim    . n u 1 u 1 n 2020 u 1 2020 1 n 1   n 1   Câu 6: (2 điểm)
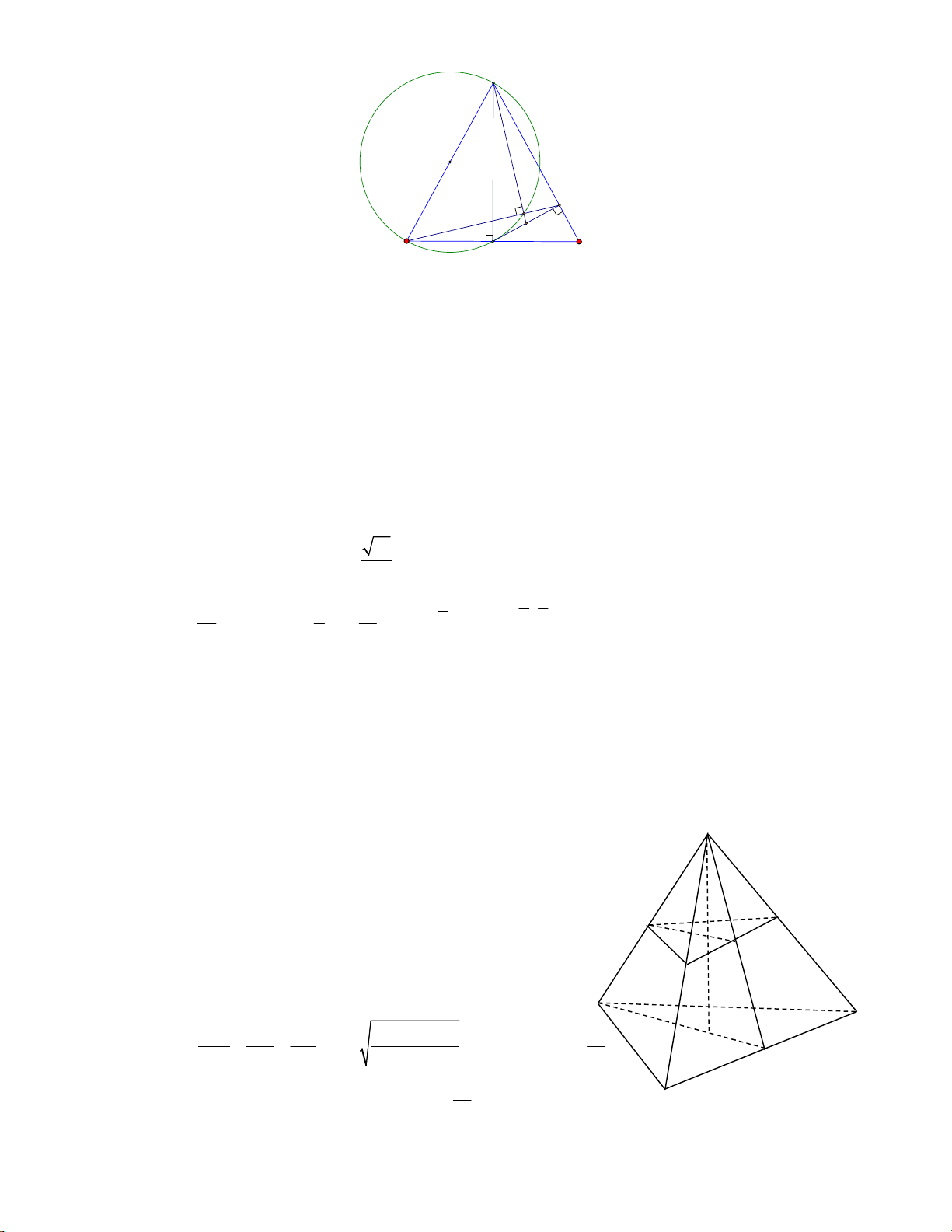
Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC cân tại A . Gọi H là trung điểm của  7 5 đoạn 
BC , K là hình chiếu vuông góc của H lên AC . Biết M ; 
 là trung điểm của đoạn  4 4 
HK , đường thẳng BK : x  7 y 13  0 . Gọi N là giao điểm của BK và AM . Tìm tọa độ điểm   A , biết 1 5 I ; 
 là trung điểm của đoạn AB .  2 2  Lời giải 5 A I N K M B H C
  
  
có 2AM  AH  AK và BK  BH  HK
     
Xét tích vô hướng: 2AM  BK  (BH  HK ) (AH  AK)
   
 BH  AK  AH.HK ; (do BH vuông góc AH , HK vuông góc AK )
      CH (CA  CK )  H . A HK
     
 CH CA  CH CK  HA HK  CH.C . A cos  HCA  CH.CK.cos  HCK  H . A H . D cos  AHD CH CK HK  CH.CA  CH.CK   H . A HK  CA CH HA 2 2 2
 CH  CK  HK  0 . Nên AM vuông góc BK tại điểm N . Ta có  9 8 
AM : 7x  y  11  N  AM  BK  ;   .  5 5 
Ta có B là giao điểm của đương thẳng BK và đường tròn tâm I bán kính IN :  B   b b 10 13 7 ; : IB  IN  2  8   9 8  2 2  25   5  10 b  B  ; ,     l   7b  b        5   5 5   2   2  4   b  2 B    1  ;2
Suy ra điểm A  2;3 .
Câu 7: Cho tứ diện đều ABCD có cạnh bằng .
a Gọi H là chân đường vuông góc hạ từ A xuống mặt
phẳng BCD và O là trung điểm của đoạn AH. Gọi   là mặt phẳng qua O và không đi qua các điểm , A B,C và .
D Mặt phẳng   cắt các đoạn AB, AC và AD lần lượt tại M , N và .
P Tìm giá trị nhỏ nhất của AM .AN.AP theo . a A Lời giải
Ta có H là trọng tâm tam giác BCD nên
     AB  AC  AD  3AH
    N  AB  AC  AD  6AO P O a  a  a    .AB  .AC  .AD  6AO AM AN AP M
Do O, M , N, P đồng phẳng nên D C 3 3 a a a a a 3     6   AM .AN.AP  . H AM AN AP AM .AN.AP 8 3 a
Vậy giá trị nhỏ nhất của AM.AN.AP  . 8 B 6 Câu 8: (2 điểm)
Cho hàm số f  x   2
ln x  x 1 2021x , gọi a,b,c là các số thực dương sao cho phương
trình f a  b  c x  f 
2020 3x  0 vô nghiệm. a  b  c
Tìm GTNN của biểu thức M  . ab  bc  ac Lời giải   2 x  x 1 f  x 1   2021   2021  0,x  .
 Hay hàm số đồng biến trên .  2 2 x  x 1 x 1 Xét   f x  ln  1 2
x  x 1 2021x  ln   2021x   ln  2
x  x 1  2021x   f x 2     x  x 1 
, hàm số đã cho là hàm số lẻ. Do đó phương trình
f a  b  c x  f 
2020 3x  0  f a bcx  f  3x  2020.
 a  b  c x  3x  2020
 a  b  c 3 x  2
 020 . Phương trình vô nghiệm  a  b  c  3  0  a  b  c  3.
 ab  bc  ca    2 2 2 2 9 a  b  c .
Áp dạng BĐT Cô-si cho 3 số: 2  a  a  a  3a  2
 b  b  b  3b  2 a  b  c  2 2 2
 a  b  c  3a  b  c  9  2 c  c  c  3c 
Hay  a  b  c    2 2 2 2 9
a  b  c   2ab  bc  ca a  b  c Vậy M 
 1, dấu bằng xảy ra khi a  b  c 1. ab  bc  ac 7
Document Outline

• de-chon-hoc-sinh-gioi-toan-12-nam-2020-2021-so-gddt-gia-lai-bang-b
• gia lai