Đề chọn học sinh giỏi Toán 12 năm 2020 – 2021 sở GD&ĐT Hải Phòng (Bảng B)

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH HẢI PHÒNG MÔN TOÁN 12 NĂM HỌC 2020 - 2021
Thời gian làm bài: 180 phút (không kể thời gian phát đề)
Câu 1: (2,0 điểm) a) Cho hàm số 3 2
y = mx + mx + (m + )
1 x − 3. Tìm tất cả các giá trị thực của tham số m để hàm
số nghịch biến trên  .
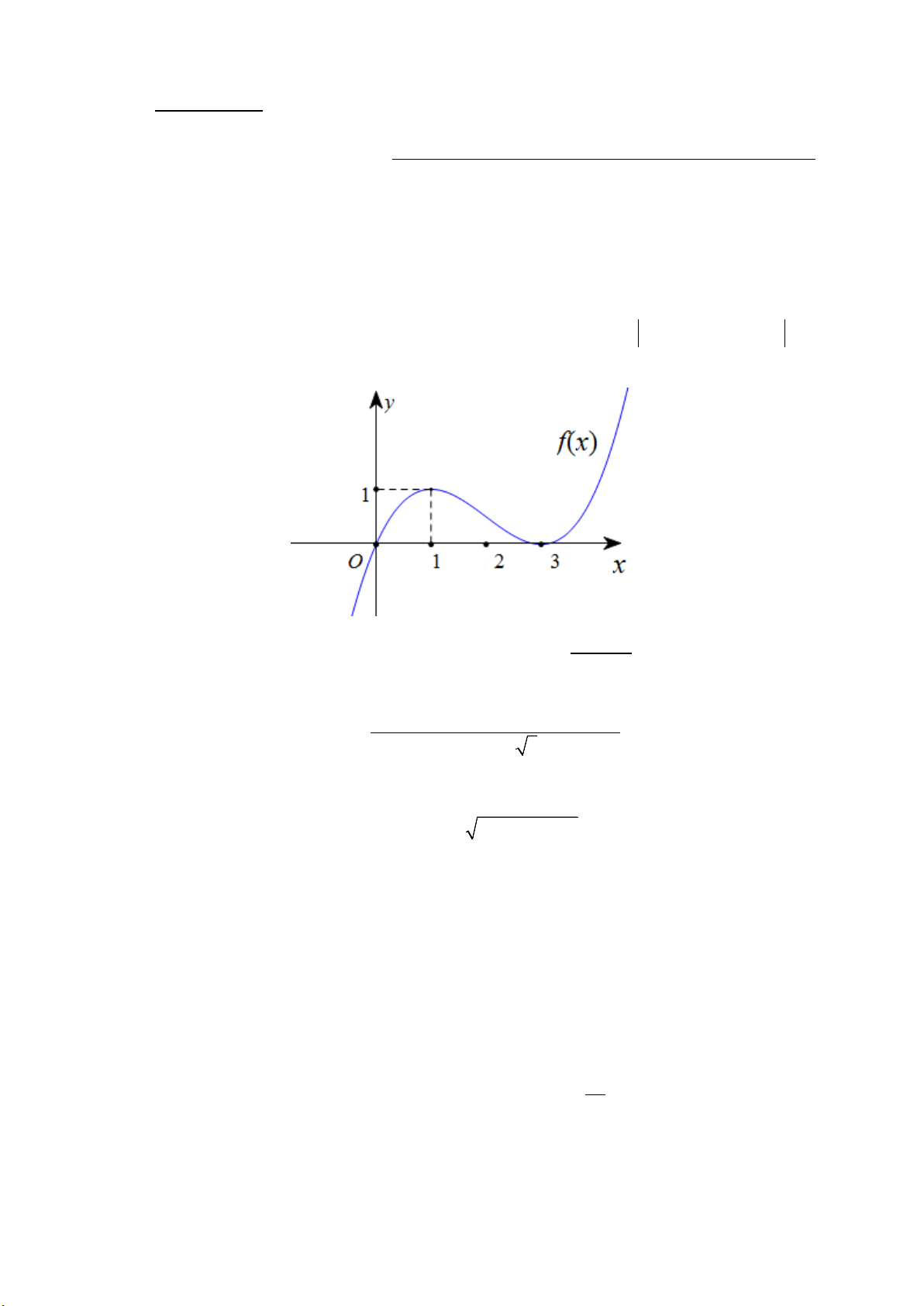
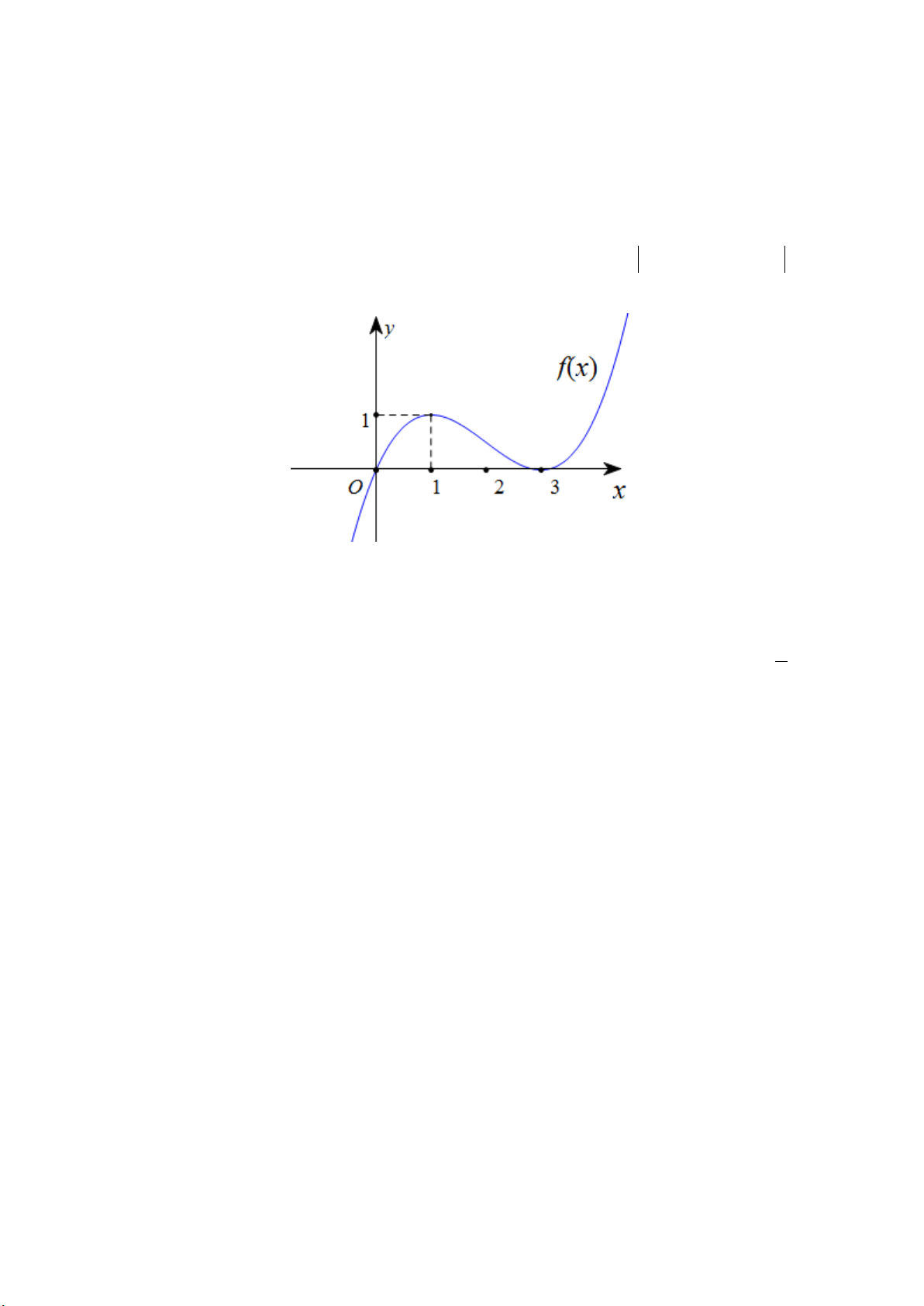
b) Cho hàm số bậc ba y = f (x) có đồ thị được biểu thị trong Hình 1. Tìm số giá trị nguyên
của tham số m trong đoạn [ 2020 −
;2020] để hàm số h(x) 2
= f (x) + 4 f (x) − m có đúng 3 điểm cực trị. +
Câu 2: (1,0 điểm) Cho log 12 = x , log 24 = y và 1 log 168 axy =
, trong đó a , b , c là các số 7 12 54 bxy + cx
nguyên. Tính giá trị biểu thức S = a + 2b + 3c . Câu 3: + x + x − x −
(1,0 điểm) Giải phương trình 4 cos 2 sin 2 sin 7cos x = 0. 2sin x + 3
Câu 4: ( 1,0 điểm) Tìm tất cả các giá trị thực của tham số m để phương trình sau có đúng ba nghiệm phân biệt 3 3 3 2
x − 5x + 3+ 2 2x − 3x + m + m = 0
Câu 5: (1,0 điểm) Một bài thi trắc nghiệm có 50 câu hỏi, mỗi câu hỏi có 4 phương án lựa chọn trong
đó chỉ có một phương án đúng. Biết rằng mỗi câu trả lời đúng được 0,2 điểm và mỗi câu trả
lời sai được 0 điểm. Một học sinh không học bài nên làm bài bằng cách chọn ngẫu nhiên mỗi
câu một phương án trả lời. Hỏi điểm số nào có xác suất xuất hiện lớn nhất?
Câu 6. ( 2,0 điểm) Cho khối tứ diện ABCD . Gọi M , N lần lượt là trung điểm của các cạnh AB,CD ; P
là điểm nằm trong đoạn BC sao cho BP  kPCk   1 .
a) Tính thể tích khối tứ diện ABCD trong trường hợp A
 CD vuông tại A , B  CD vuông cân
tại B và AB  AC  AD  a .
b) Mặt phẳng đi qua ba điểm M , N, P chia tứ diện thành hai khối đa diện có thể tích lần lượt là
V ,V ( trong đó V là thể tích của phần chứa điểm A ). Tính V2 1 2 1 V1
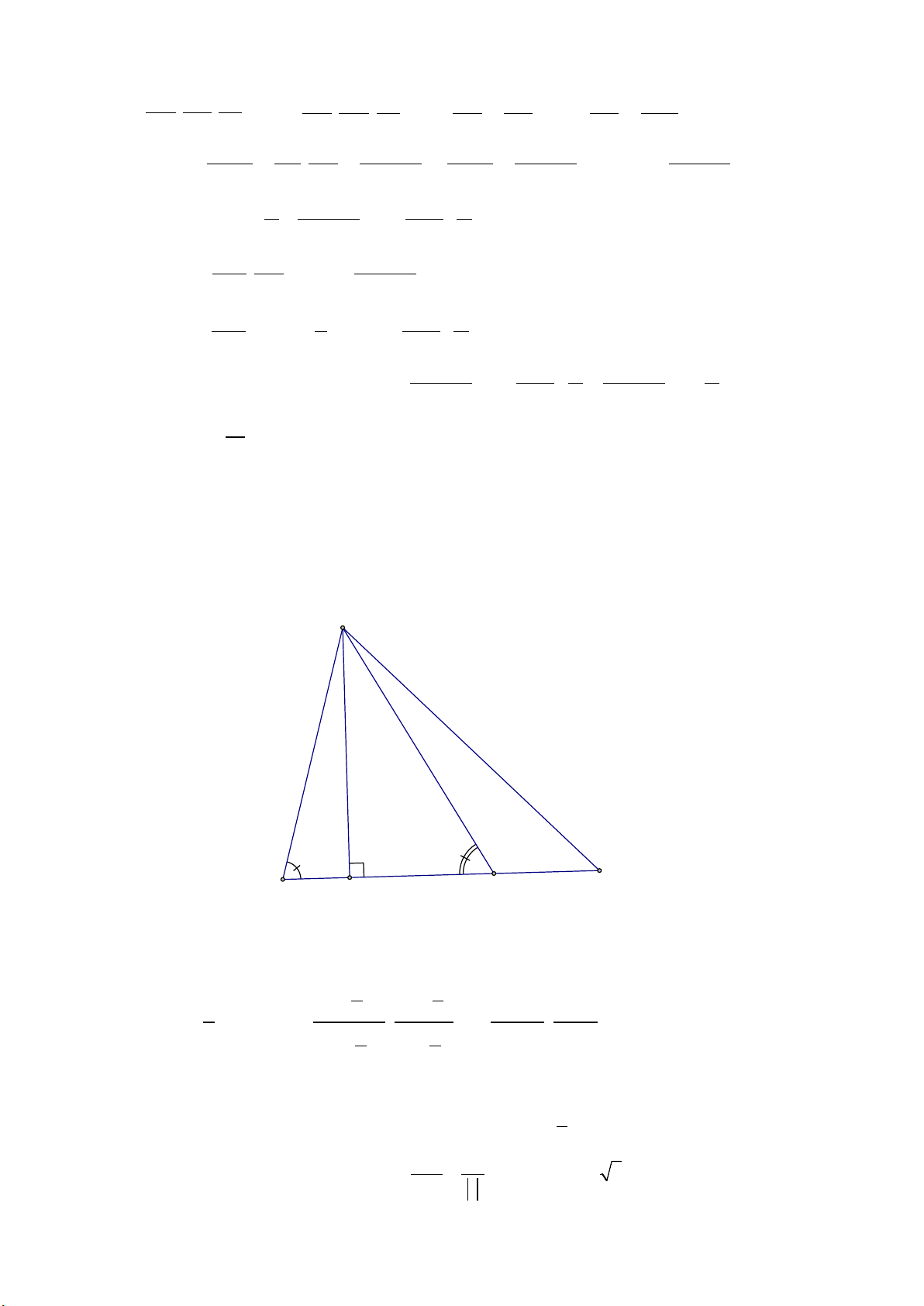
Câu 7: ( 2,0 điểm) Trong mặt phẳng tọa độ Oxy , cho tam giác ABC có 
ACB = 75°, B( 4; − 2 − ) ; D là
điểm thuộc cạnh BC sao cho DC = 2DB . Biết đường cao kẻ từ A có phương trình 2x + y = 0 và 
ADC = 60° . Tìm tọa độ điểm A biết A có hoành độ âm. 1
Câu 8. (1.0 điểm) Cho các số thực dương a,b,c thay đổi. Tìm giá trị nhỏ nhất của biểu thức 1 2 p = − . 2 2 2 2 2ab + 8ab
2a + 2b + 2c + 4ac +1
____________________ HẾT ____________________ 2 HƯỚNG DẪN GIẢI
Câu 1: (2,0 điểm) c) Cho hàm số 3 2
y = mx + mx + (m + )
1 x − 3. Tìm tất cả các giá trị thực của tham số m để hàm
số nghịch biến trên  .
d) Cho hàm số bậc ba y = f (x) có đồ thị được biểu thị trong Hình 1. Tìm số giá trị nguyên
của tham số m trong đoạn [ 2020 −
;2020] để hàm số h(x) 2
= f (x) + 4 f (x) − m có đúng 3 điểm cực trị. Lời giải
a) Nếu m = 0 ta có hàm số y = x −1 là hàm số đồng biến trên  nên không thỏa mãn. Xét m ≠ 0 ta có 2
y′ = 3mx + 2mx + m +1. Để hàm số nghịch biến trên  thì y′ ≤ 0 với mọi
a = 3m < 0 m < 0 m < 0 x∈ 3  ⇔  ⇔ ⇔ ⇔ m ≤ − . 2  
∆′ = m − 3m  (m + )1 ≤ 0 2  2
− m − 3m ≤ 0 2m + 3 ≤ 0 2
b) Ta có hàm số h(x) có tập xác định là  .
Xét hàm số g (x) 2
= f (x) + 4 f (x) − m . Khi đó:
Tập xác định D =  .
g′(x) = 2 f (x). f ′(x) + 4 f ′(x) = 2 f ′(x)  f (x) + 2   .  f ′(x) = 0
g′(x) = 0 ⇔ 2 f ′(x)  f  ( x) + 2 = 0  ⇔  .  f  ( x) = 2 − Dựa vào đồ thị ta có x = ● f ′(x) 1 = 0 ⇔  . x = 3 ● f (x) = 2
− ⇔ x = a < 0 .
● g′(2) = 2 f ′(2)  f  (2) + 2 < 0 
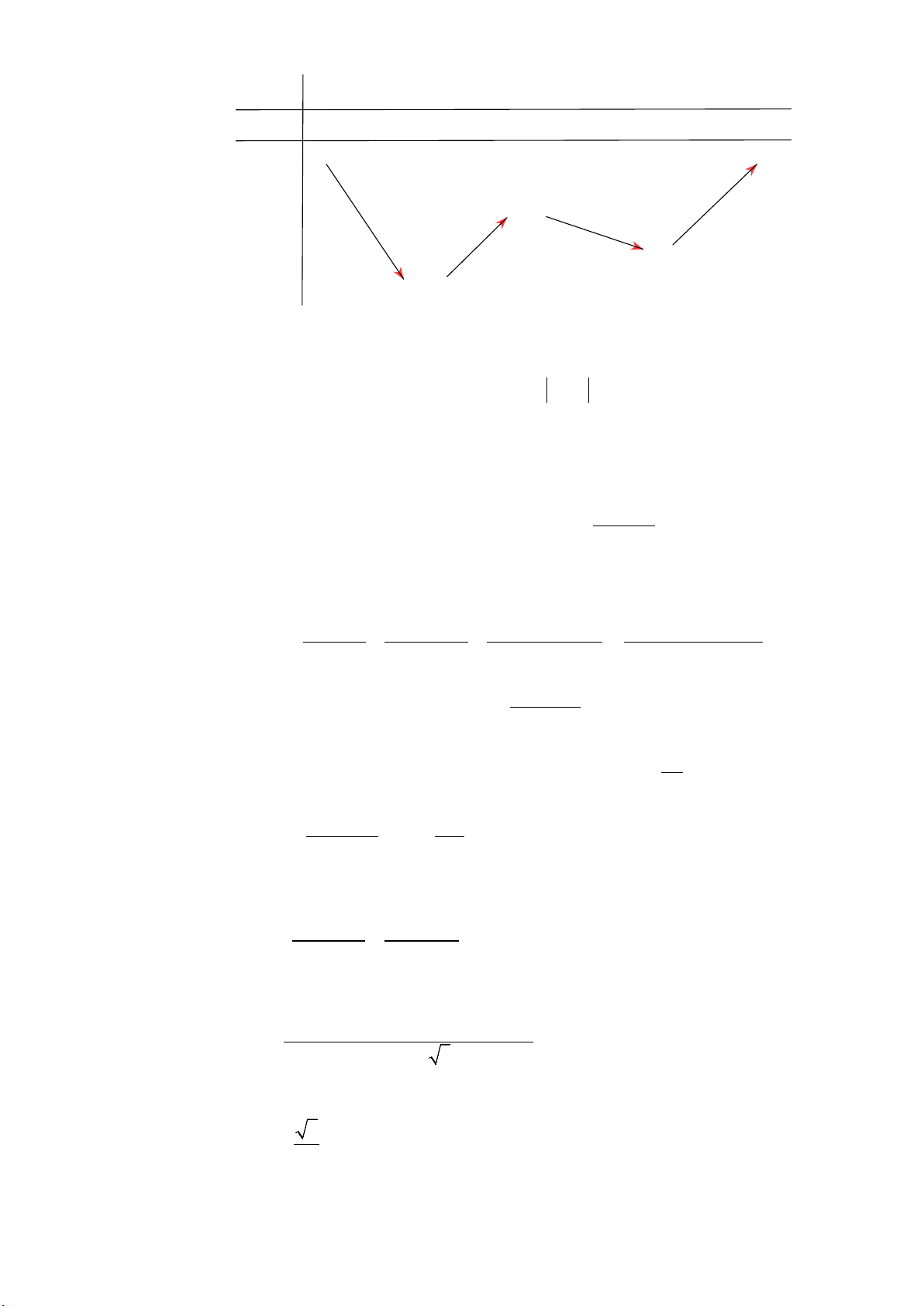
do f (2) > 0 , f ′(2) < 0 . Bảng biến thiên 3 x -∞ a 1 3 +∞ g'(x) - 0 + 0 - 0 + +∞ +∞ g(x) -m + 5 -m -m - 8
Dựa vào bảng biến thiên dễ thấy hàm số h(x) = g (x) có đúng 3 điểm cực trị khi và chỉ
khi −m −8 ≥ 0 ⇔ m ≤ 8 − .
Kết hợp với điều kiện [ 2020 −
;2020] ta có 2013 giá trị của m thỏa mãn. +
Câu 2: (1,0 điểm) Cho log 12 = x , log 24 = y và 1 log 168 axy =
, trong đó a , b , c là các 7 12 54 bxy + cx
số nguyên. Tính giá trị biểu thức S = a + 2b + 3c . Lời giải log 168 log 24.7
log 7 + log 24 log 12.log 24 +1 7 7 ( ) Ta có 7 7 log 168 = = = 7 12 = 54 log 54 log 54 log 54 log 54 7 7 7 7
Do log 54 = log 12.log 54 nên xy +1 log 168 = . 7 7 12 54 x log 54 12 Ta tính 24
log 54 = log 27.2 = log 27 + log 2 = 3log 3+ log 12 12 ( ) 12 12 12 12 12 3 Mà 3.2.12.24 12 log 3 = log = log = 3− 2log 24 12 12 12 2 12 2.12.24 24
Suy ra log 54 = 3 3− 2log 24 + log 24 −1 = 8 − 5log 24 = 8 − 5y . 12 ( 12 ) 12 12 + + Vậy xy 1 xy 1 log 168 = =
, suy ra a =1, b = 5 − , c = 8. 54 x(8 − 5y) 5 − xy + 8x
Giá trị biểu thức S = a + 2b + 3c =1+ 2( 5 − ) + 3.8 =15 . Câu 3: + x + x − x −
Giải phương trình 4 cos 2 sin 2 sin 7cos x = 0. 2sin x + 3 Lời giải Điều kiện: 3 sin x ≠ − 2 PT 2
⇔ 4 + cos 2x + sin 2x − sin x − 7cos x = 0 ⇔ 2cos x − 7cos x + 3+ 2sin x cos x − sin x = 0 4 ⇔ (2cos x − )
1 (cos x −3) + sin x(2cos x − ) 1 = 0 ⇔ (2cos x − )
1 (sin x + cos x −3) = 0  1  1 cos x = cos x  = 2  2 ⇔  .    π  3
sin x + cos x = 3 sin  x + =  (VN)   4  2 Với 1 2 1 2 3 3
cos x = ⇒ cos x = ⇒ sin x = ⇒ sin x = ± . 2 4 4 2
Kết hợp với điều kiện, suy ra phương trình đã cho vô nghiệm.
Câu 4: Tìm tất cả các giá trị thực của tham số m để phương trình sau có đúng ba nghiệm phân biệt 3 3 3 2
x − 5x + 3+ 2 2x − 3x + m + m = 0 Lời giải 3 3 3 2
x − 5x + 3+ 2 2x − 3x + m + m = 0 ( ) 1 PT ( ) 3 2 3 3 2
1 ⇔ 2x − 3x + m + 2 2x − 3x + m = (x − )3 1 + 2(x − ) 1 ⇔ f (3 3 2
2x − 3x + m ) = f (x − )1 (*)
Xét hàm số f (t) 3
= t + 2t, t ∈ . Ta có: f ′(t) 2
= 3t + 2 > 0, t ∀ ∈  .
Suy ra hàm số f liên tục và đồng biến trên  . Do đó: ( ) 3 3 2 3 2 3 2
1 ⇔ 2x − 3x + m = x −1 ⇔ 2x − 3x + m = x − 3x + 3x −1 g (x) 3
= x − 3x +1 = −m (2) .
Xét hàm số: g (x) 3 = x − 3x +1. Ta có: g′(x) 2
= 3x − 3 = 0 ⇔ x = 1
± . Suy ra hàm số g (x) có hai điểm cực trị lần lượt là x = 1 − và x =1. Phương trình ( )
1 có ba nghiệm phân biệt ⇔ phương trình (2) có ba nghiệm phân biệt ⇔ g ( )
1 < −m < g (− ) 1 ⇔ 1
− < −m < 3 ⇔ 3 − < m <1.
Câu 5: (1,0 điểm) Một bài thi trắc nghiệm có 50 câu hỏi, mỗi câu hỏi có 4 phương án lựa chọn trong
đó chỉ có một phương án đúng. Biết rằng mỗi câu trả lời đúng được 0,2 điểm và mỗi câu trả
lời sai được 0 điểm. Một học sinh không học bài nên làm bài bằng cách chọn ngẫu nhiên mỗi
câu một phương án trả lời. Hỏi điểm số nào có xác suất xuất hiện lớn nhất? Lời giải
Gọi x là số câu học sinh làm đúng (0 ≤ x ≤ 50) , lúc đó số điểm học sinh đạt được là 0,2x . x 50−x
Xác suất để học sinh đó làm đúng được x câu là x  1   3 C .  .  . 50 4  4    
Giả sử 0,2x là số điểm có xác suất lớn nhất, khi đó x 50−x x 1 + 49   1   3 −x x  x 1 +  1   3 C  .  3 1  47   .  C .  .  ≥ 50 50 ≥ 4 4 4  4 x ≥          50− x x +1 3  (x + ) 1 ≥ 50 − x  4  ⇔  ⇔  ⇔  x 50−x x 1 − 51   1   3 −x 1 3
 51− x ≥ 3x 51 x  x 1 −  1   3 C . . ≥  ≥  x ≤      C .  .  50 50    4   4   4    4   x 51− x  4
Do x nguyên nên x =12 . 5
Vậy điểm 2,4 có xác suất xuất hiện cao nhất.
Câu 6. ( 2,0 điểm) Cho khối tứ diện ABCD . Gọi M , N lần lượt là trung điểm của các cạnh AB,CD ; P
là điểm nằm trong đoạn BC sao cho BP  kPCk   1 .
a) Tính thể tích khối tứ diện ABCD trong trường hợp A
 CD vuông tại A , B  CD vuông cân
tại B và AB  AC  AD  a .
b) Mặt phẳng đi qua ba điểm M , N, P chia tứ diện thành hai khối đa diện có thể tích lần lượt là
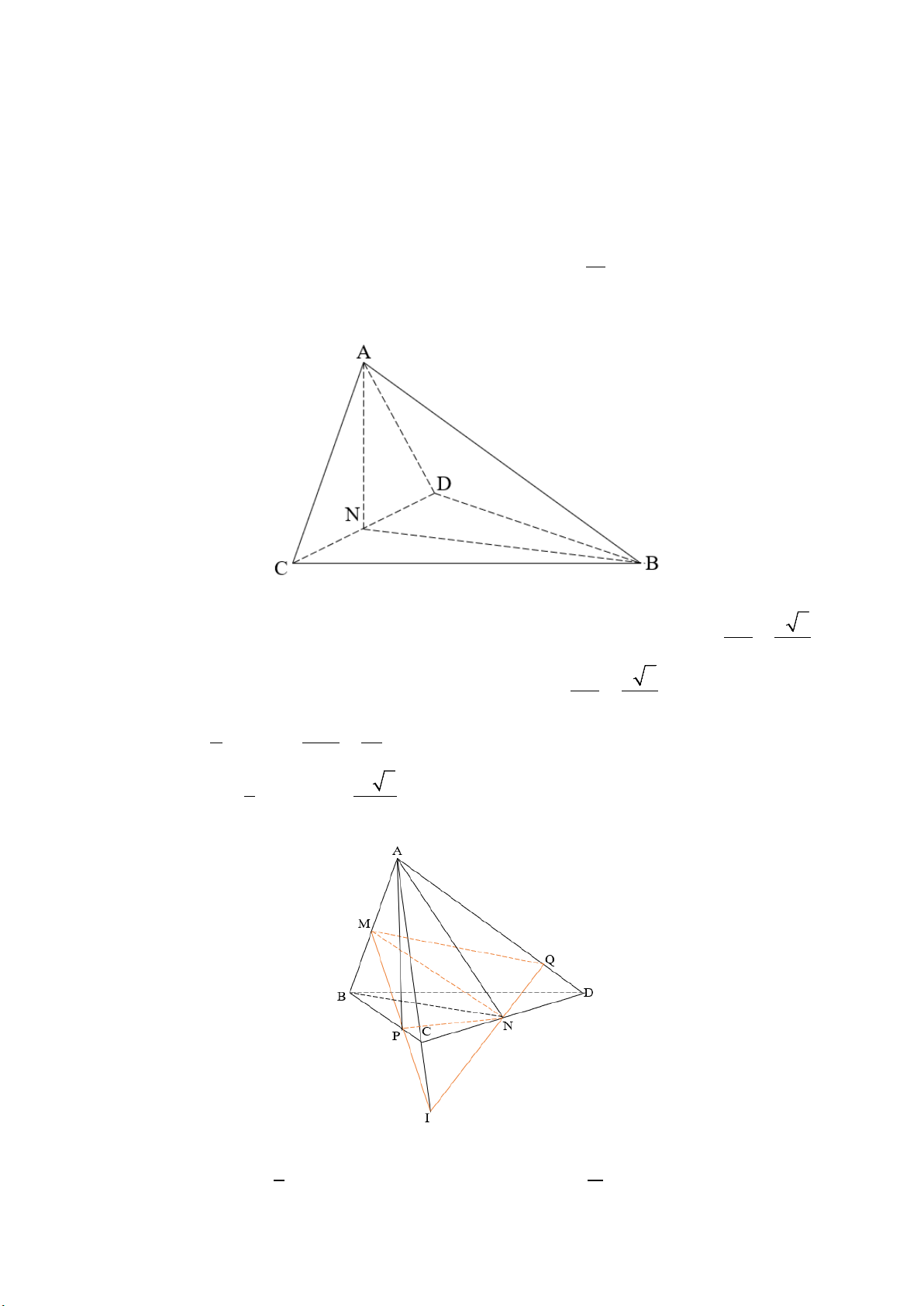
V ,V ( trong đó V là thể tích của phần chứa điểm A ). Tính V2 1 2 1 V1 Lời giải a) Vẽ hình
Có N là trung điểm của CD B CD a 2
 CD vuông cân tại B  N là tâm đường tròn ngoại tiếp B
 CD và BN   2 2 CD a 2
Lại có AB  AC  AD  a  AN BCD và AN   2 2 2 2 1 CD a S     BN CD BCD . 2 4 2 3 1 a 2 Vậy V  AN S  ABCD . . 3 BC  D 12 b) Vẽ hình
Gọi I  MP  AC,Q  IN  AD . Vậy thiết diện của tứ diện ABCD cắt bởi MNP là MPNQ Gọi 1 V V V  d A BCD S     V V ABCD  , . BCD . A BDN . A BCN 3 2 V V V V 1 . A MNQ . A MNP . A CNP 6
Áp dụng định lý Menelaus cho A  BC và A  CD , ta có:
MA . BP .IC 1 và QA . ND.IC 1 QA BP AQ k    k   MB PC IA QD NC IA QD PC AD 1 k Lại có: S CP CN V CPN 1 A CPN 1 1 .  .     V  V A CPN . S     CB CD k V k k CBD 21  A CBD 21  . 2 1 .     Suy ra V 1 k V V   V   A NP .  . .B 2 21 k k 1 2 AM AQ k V  V  A MNQ . . A BND .V . . AB AD 4k   1 AM 1  k  V V  V  V    A MNP . A BNP . A BNP  . . . . AB 2 k 1 4   Vậy k k V 1 V V V V V       V  A MNQ A MNP A CNP .V . . 1 . . . 4k   1
k 1 4 21k 2
Kết luận: V2 1 V1
Câu 7: Trong mặt phẳng tọa độ Oxy , cho tam giác ABC có 
ACB = 75°, B( 4; − 2
− ) ; D là điểm thuộc
cạnh BC sao cho DC = 2DB . Biết đường cao kẻ từ A có phương trình 2x + y = 0 và 
ADC = 60° . Tìm tọa độ điểm A biết A có hoành độ âm. Lời giải A 2x+y=0 75 B(-4;-2) 60 C H D
Ta có phương trình BC : x − 2y = 0 ⇒ H = AH ∩ BC = (0;0).
Suy ra C ∈ BC ⇒ C = (2t;t) , do  1 1 4 − + .2t 2   1 − + t   2 2   8 − + 2t 4 − +  ;   ; t DB DC D  = − ⇒ = = . 2 1 1  3 3  1+ 1   +   2 2 
Gọi tọa độ điểm A∈ AH ⇒ A = (a; 2
− a) với a < 0 . Ta tính các đoạn thẳng 2 2 AH = 5a ; 2 2 CH = 5t ; 2 5
DH = (t − 4)2 . 9 −
Xét các tỉ số lượng giác  tan AH a ACD = = = tan 75° = 2 + 3 , (1). CH t 7 − Mà  AH 3 tan a ADH = = = tan 60° = 3 ,(2). DH t − 4 −a =  (2+ 3).t 3 t − 4 t = 4 − 2 3 a = 2 − Từ (1) và (2) ta có  ⇒ 3 = . ⇔  ⇒  . − = − 2 + 3 3a 3 t 4 t t =1− 3 a = 1 − − 3 
Vậy tọa độ điểm A = ( 2; − 4) hoặc A = ( 1 − − 3;2 + 2 3) .
Câu 8. (1.0 điểm)
Cho các số thực dương a,b,c thay đổi. Tìm giá trị nhỏ nhất của biểu thức 1 2 p = − 2 2 2 2 2ab + 8ab
2a + 2b + 2c + 4ac +1 Lời giải Ta có: 2 2 2 2 2 2
2a + 2b + 2c + 4ac = 2b + 2(a + c) ≥ (b + a + c) Hay 2 − 2 − ≥ 2 2 2
2a + 2b + 2c + 4ac +1 a + b + c +1 Mặt khác ta có:
2 2ab + 8bc = 2 .
b 2a + 2 2bc = 2 .2 b a + 2 2 .
c b ≤ b + 2a + b + 2c = 2(a + b + c) 1 1 ⇒ ≥
2 2ab + 8bc 2(a + b + c) Nên 1 2 p ≥ −
; đặt t = a + b + c > 0
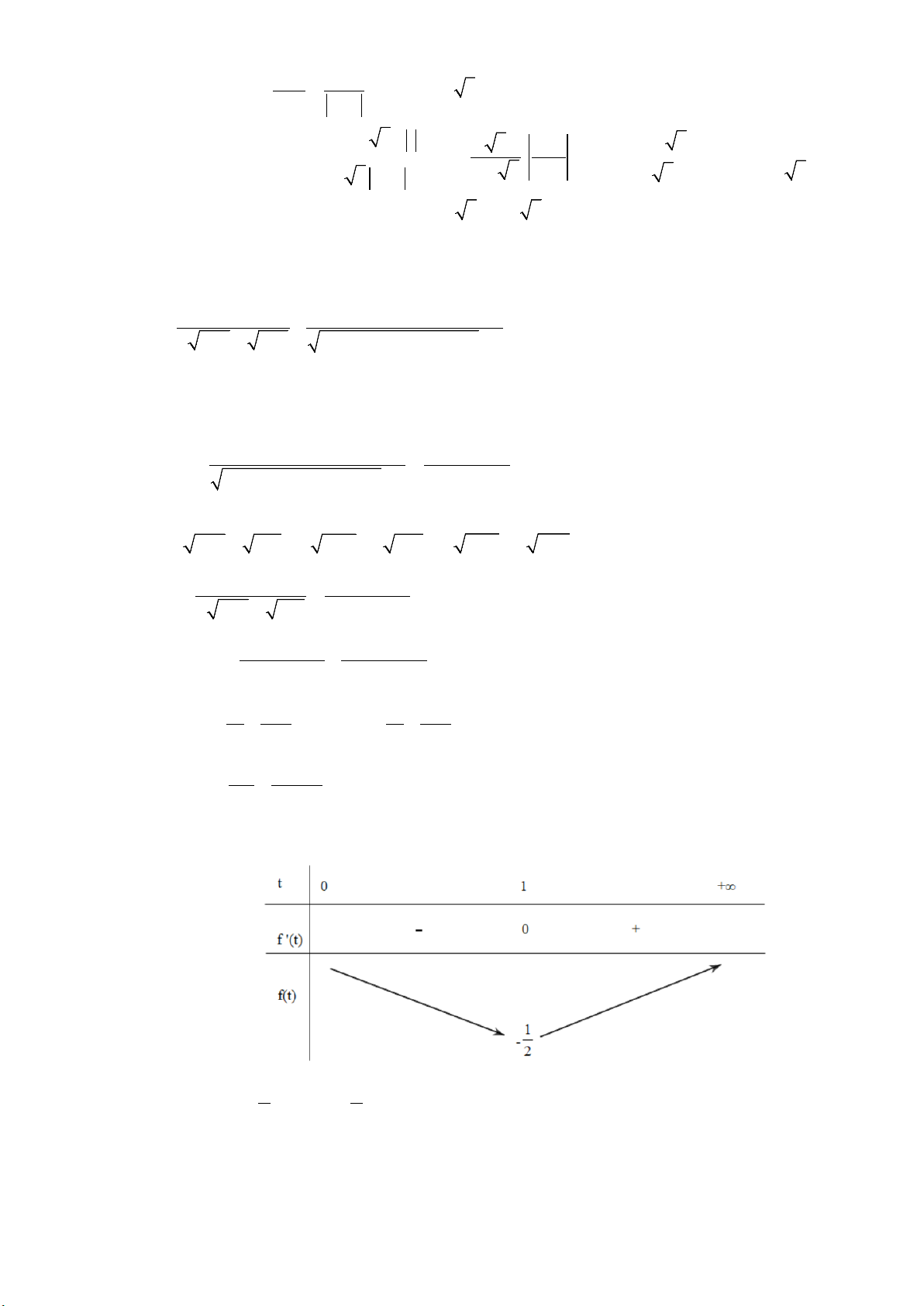
2(a + b + c) a + b + c +1 1 2 ⇒ p ≥ − ; xét 1 2 f (t) = − trên (0;+ ∞) 2t t +1 2t t +1 1 − 2 f '(t) = + = 0 ⇔ (t + )2
1 = 4t ⇔ t +1 = 2t ⇔ t =1 2 2 2t (t +1) Bảng biến thiên 1 1
⇒ f (t) ≥ − Hay p ≥ − 2 2 8  1
a + b + c =1 b = 1    2 Minp = − ⇔ b  = 2a ⇔  . 2 1 b  =  2c a = c =  4
____________________ HẾT ____________________ 9
Document Outline

• de-chon-hoc-sinh-gioi-toan-12-nam-2020-2021-so-gddt-hai-phong-bang-b
• DE-HDG-HSG-12-HAI-PHONG-BANG-B-2020-2021