Đề cuối học kì 2 Toán 11 năm 2022 – 2023 sở GD&ĐT Bắc Giang

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 11 đề kiểm tra chất lượng cuối học kì 2 môn Toán 11 THPT năm học 2022 – 2023 sở Giáo dục và Đào tạo tỉnh Bắc Giang; đề thi hình thức 50% trắc nghiệm + 50% tự luận, thời gian làm bài 90 phút (không kể thời gian giao đề)

29 15 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK2 Toán 11

Môn: Toán 11

Thông tin:

15 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
Trang 1/3 - Mã đề thi 111
SỞ GIÁO DỤC VÀ ĐÀO TẠO
BẮC GIANG
(Đề gồm có 03 trang)
ĐỀ KIỂM TRA CUỐI HỌC KÌ II
NĂM HỌC 2022 - 2023
MÔN: TOÁN LỚP 11 THPT
Thời gian làm bài: 90 phút, không kể thời gian giao đề
Mã đề: 111
I. PHẦN TRẮC NGHIỆM (5,0 điểm).
Câu 1: Số đo ba góc của một tam giác vuông tạo thành cấp số cộng. Hai góc nhọn của tam giác có số đo
(độ) là:
A.
20°
và
70 .°
B.
30
°
và
60 .°
20°
45 .°
45°
45 .
°
Câu 2: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật,
3AB a=
và
5
AC a
=
. Cạnh bên
SA
vuông góc với mặt phẳng
( )
ABCD
và
2SA a=
. Khoảng cách từ
A
đến mặt phẳng
( )
SCD
bằng
A.
4
3
a
.
B.
12 97
97
a
. C.
3 22
11
a
.
D.
12
5
a
.
Câu 3: Cho hình lăng trụ tam giác
.ABC A B C
′′′
có đáy là tam giác đều cạnh
a
. Hình chiếu vuông góc
của
A
′
trên mặt phẳng
( )
ABC
là trung điểm
H
của
BC
. Biết khoảng cách từ
H
tới
AA
′
bằng
3
4
a
. Số
đo góc
A AH
′
bằng
A.
60°
.
B.
30°
.
45°
75°
Câu 4: Cho hình lập phương
..ABCD A B C D
′′′′
Góc giữa hai đường thẳng
AC
và
BD
′′
là?
A.
60°
.
B.
90°
.
0°
45°
Câu 5: Giá trị của giới hạn
2
3
lim
23
nn
−
−+
là
A.
.−∞
B.
1.
−
C.
3
.
2
−
D. 0.
Câu 6: Cho hình chóp
.S ABC
có
3AB a=
,
4
BC a=
,
5CA a=
, các mặt bên tạo với đáy góc
60°
, gọi
H
là hình chiếu vuông góc của
S
lên mặt phẳng
(
)
ABC
(
H
thuộc miền trong của tam giác
ABC
). Độ
dài của
SH
là
A.
3
3
a
.
B.
3a
.
C.
23
3
a
.
D.
23
a
.
Câu 7: Cho dãy số
( )
n
u
, biết
23
n
un= +
với
1n ≥
. Số hạng thứ 5 của dãy số đó là
A.
13.
B.
1 1 .
35.
5.
Trang 2/3 - Mã đề thi 111
Câu 8: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông tâm
O
;
SO
vuông góc với mặt phẳng
( )
ABCD
. Khẳng định nào sau đây là Sai?
A. Hai mặt phẳng
( )
SBD
và
( )
ABCD
vuông góc.
B.
Hai mặt phẳng
( )
SAC
và
( )
ABCD
vuông góc.
C. Hai mặt phẳng
( )
SAB
và
(
)
ABCD
vuông góc.
D. Hai mặt phẳng
( )
SAC
và
( )
SBD
vuông góc.
Câu 9: Giá trị của giới hạn
2
3
1
3
lim
1
x
x
x
→
−
+
là
A.
3.−
B.
1.
1.−
2.−
Câu 10: Cho cấp số cộng
( )
n
u
có
1
3u
=
và
5.d =
Khẳng định nào sau đây đúng?
A.
( )
3 5 1.
n
un=++
B.
(
)
3 5 1.
n
un
=−−
C.
2 5.
n
un= +
D.
( )
3 5 1.
n
un
=+−
Câu 11: Một cấp số nhân có hai số hạng liên tiếp là 6 và 18. Số hạng tiếp theo là
A.
30
.
B.
12
.
54
24
Câu 12: Đạo hàm của hàm số
(
)
2
2
fx x x= −
tại điểm
3x
=
là
A.
( )
3 4.f
′
=
B.
( )
3 0.f
′
=
( )
3 1.f
′
=
( )
3 3.f
′
=
Câu 13: Giá trị của giới hạn
(
)
22
lim 2 6 5 1
x
x x x ax
→+∞
+ +− + + =−
. Khi đó giá trị của
a
là
A.
1.
B.
4.
3.
3.−
Câu 14: Giá trị của giới hạn
( )
32
lim 1
x
xx x
→−∞
− + −+
là
A.
.−∞
B.
0.
1.
.+∞
Câu 15: Cho hình chóp
.S ABCD
có
ABCD
là hình vuông và
( )
SA ABCD⊥
. Tam giác
SAC
là tam giác
gì?
A. Tam giác tù.
B. Tam giác đều.
Câu 16: Cho dãy số
( )
n
u
với
1
1
2
.
2 1, 1
nn
u
u un n
+
= −
= ++ ≥
Số hạng
2023
u
của dãy số đó là
A.
2022
2023
2025 2 .u =−+
B.
2022
2023
2023 2 .u = +
C.
2022
2023
2025 2 .u = +
D.
2022
2023
2023 2 .u
=−+
Trang 3/3 - Mã đề thi 111
Câu 17: Tìm tất cả giá trị thực của tham số
m
để hàm số
(
)
32
22
khi 1
1
2 khi 1
xx x
x
fx
x
xm x
−+−
>
−
+≤
=
liên tục tại
1.x =
A.
2.m = −
B.
1.m =
0.m =
1.m = −
Câu 18: Tính giới hạn
( )
2
lim 3 5 3 .L nn= +−
A.
5.L =
B.
.L
= −∞
3.L =
.L = +∞
Câu 19: Đạo hàm của hàm số
( )
sin 2cosfx x x= +
là
A.
( )
cos 2sin .fx x x
′
=−+
B.
( )
cos 2sin .fx x x
′
=−−
C.
( )
cos 2sin .fx x x
′
= −
D.
( )
cos 2sin .fx x x
′
= +
Câu 20: Tìm hệ số góc
k
của đường thẳng tiếp xúc với parabol
2
21yx x=++
tại điểm có hoành độ
2.x = −
A.
4.k = −
B.
0.k =
2.
k = −
1.k =
----------------------------------------------
II. PHẦN TỰ LUẬN (5,0 điểm).
Câu 1. (2,0 điểm).
a) Tính giới hạn:
2
2
14
lim
21
n
n
−
+
.
b) Cho hàm số
( )
2
2
khi 2
2
1 khi 2
xx
x
fx
x
mx
−−
=
−
−=
≠
(với
m
là tham số).
Tìm
m
để hàm số đã cho liên tục tại
2x =
.
Câu 2. (0,5 điểm). Cho hàm số
32
3 2.yx x=−+
Viết phương trình tiếp tuyến của đồ thị hàm số đã cho
biết tiếp tuyến đó song song với đường thẳng
9 7.yx= +
Câu 3. (2,5 điểm).
Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông tại
B
,
(
)
, 2,AB a AC a SA ABC= = ⊥
và
SA a=
.
a) Chứng minh rằng
( )
BC SAB⊥
.
b) Tính khoảng cách từ
A
đến mặt phẳng
( )
SBC
.
c) Tính tang của góc giữa hai mặt phẳng
( )
SBC
và
( )
SAC
.
----------- HẾT ----------
Trang 1/3 - Mã đề thi 112
SỞ GIÁO DỤC VÀ ĐÀO TẠO
BẮC GIANG
(Đề gồm có 03 trang)
ĐỀ KIỂM TRA CUỐI HỌC KÌ II
NĂM HỌC 2022 - 2023
MÔN: TOÁN LỚP 11 THPT
Thời gian làm bài: 90 phút, không kể thời gian giao đề
Mã đề: 112
I. PHẦN TRẮC NGHIỆM (5,0 điểm).
Câu 1: Số đo ba góc của một tam giác vuông tạo thành cấp số cộng. Hai góc nhọn của tam giác có số đo
(độ) là:
A.
30°
và
60 .°
B.
20
°
và
45 .°
20°
70 .°
45°
45 .
°
Câu 2: Giá trị của giới hạn
( )
32
lim 1
x
xx x
→−∞
− + −+
là
A.
.−∞
B.
0.
1.
.+∞
Câu 3: Cho dãy số
( )
n
u
với
1
1
2
.
2 1, 1
nn
u
u un n
+
= −
= ++ ≥
Số hạng
2023
u
của dãy số đó là
A.
2022
2023
2025 2 .u =−+
B.
2022
2023
2025 2 .u = +
C.
2022
2023
2023 2 .u
= +
D.
2022
2023
2023 2 .u
=−+
Câu 4: Giá trị của giới hạn
2
3
1
3
lim
1
x
x
x
→
−
+
là
A.
1.
−
B.
2.
−
3.−
1.
Câu 5: Một cấp số nhân có hai số hạng liên tiếp là 6 và 18. Số hạng tiếp theo là
A.
30
.
B.
12
.
24
54
Câu 6: Đạo hàm của hàm số
( )
sin 2cosfx x x
= +
là
A.
( )
cos 2sin .fx x x
′
= +
B.
(
)
cos 2sin .fx x x
′
=−−
C.
( )
cos 2sin .fx x x
′
= −
D.
( )
cos 2sin .fx x x
′
=−+
Câu 7: Tính giới hạn
( )
2
lim 3 5 3 .L nn= +−
A.
3.L =
B.
5.L
=
.L = −∞
.L = +∞
Câu 8: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật,
3AB a=
và
5AC a=
. Cạnh bên
SA
vuông góc với mặt phẳng
(
)
ABCD
và
2SA a=
. Khoảng cách từ
A
đến mặt phẳng
( )
SCD
bằng
A.
4
3
a
.
B.
12 97
97
a
.
C.
3 22
11
a
.
D.
12
5
a
.
Câu 9: Tìm tất cả giá trị thực của tham số
m
để hàm số
( )
32
22
khi 1
1
2 khi 1
xx x
x
fx
x
xm x
−+−
>
−
+≤
=
liên tục tại
1.
x =
A.
0.m =
B.
1.m =
1.m = −
2.m = −
Câu 10: Cho dãy số
( )
n
u
, biết
23
n
un= +
với
1n ≥
. Số hạng thứ 5 của dãy số đó là
A.
35.
B.
1 1 .
5.
13.
Câu 11: Cho hình chóp
.S ABC
có
3AB a=
,
4BC a=
,
5CA a=
, các mặt bên tạo với đáy góc
60°
, gọi
H
là hình chiếu vuông góc của
S
lên mặt phẳng
( )
ABC
(
H
thuộc miền trong của tam giác
ABC
). Độ
dài của
SH
là
A.
23a
. B.
3
a
.
C.
3
3
a
. D.
23
3
a
.
Trang 2/3 - Mã đề thi 112
Câu 12: Đạo hàm của hàm số
( )
2
2fx x x= −
tại điểm
3x =
là
A.
( )
3 3.f
′
=
B.
( )
3 0.f
′
=
( )
3 4.f
′
=
( )
3 1.f
′
=
Câu 13: Cho cấp số cộng
(
)
n
u
có
1
3u =
và
5.d =
Khẳng định nào sau đây đúng?
A.
2 5.
n
un= +
B.
(
)
3 5 1.
n
un=+−
C.
( )
3 5 1.
n
un=−−
D.
( )
3 5 1.
n
un=++
Câu 14: Giá trị của giới hạn
2
3
lim
23nn
−
−+
là
A.
3
.
2
−
B.
1.−
C. 0.
D.
.−∞
Câu 15: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông tâm
O
;
SO
vuông góc với mặt phẳng
( )
ABCD
. Khẳng định nào sau đây là Sai?
A. Hai mặt phẳng
( )
SAC
và
( )
SBD
vuông góc.
B. Hai mặt phẳng
( )
SBD
và
(
)
ABCD
vuông góc.
C.
Hai mặt phẳng
(
)
SAC
và
( )
ABCD
vuông góc.
D. Hai mặt phẳng
( )
SAB
và
(
)
ABCD
vuông góc.
Câu 16: Cho hình lăng trụ tam giác
.ABC A B C
′′′
có đáy là tam giác đều cạnh
a
. Hình chiếu vuông góc
của
A
′
trên mặt phẳng
( )
ABC
là trung điểm
H
của
BC
. Biết khoảng cách từ
H
tới
AA
′
bằng
3
4
a
. Số
đo góc
A AH
′
bằng
A.
30°
.
B.
60°
.
45°
75°
Câu 17: Cho hình lập phương
..ABCD A B C D
′′′′
Góc giữa hai đường thẳng
AC
và
BD
′′
là?
A.
90°
.
B.
60°
.
0°
45°
Trang 3/3 - Mã đề thi 112
Câu 18: Cho hình chóp
.S ABCD
có
ABCD
là hình vuông và
( )
SA ABCD⊥
. Tam giác
SAC
là tam giác
gì?
A. Tam giác đều.
B. Tam giác nhọn.
Câu 19: Tìm hệ số góc
k
của đường thẳng tiếp xúc với parabol
2
21yx x=++
tại điểm có hoành độ
2.x = −
A.
0.
k =
B.
1.
k
=
2.
k
= −
4.
k
= −
Câu 20: Giá trị của giới hạn
(
)
22
lim 2 6 5 1
x
x x x ax
→+∞
+ +− + + =−
. Khi đó giá trị của
a
là
A.
1.
B.
4.
3.−
3.
---------------------------------------------
II. PHẦN TỰ LUẬN (5,0 điểm).
Câu 1. (2,0 điểm).
a) Tính giới hạn:
2
2
14
lim
21
n
n
−
+
.
b) Cho hàm số
( )
2
2
khi 2
2
1 khi 2
xx
x
fx
x
mx
−−
=
−
−=
≠
(với
m
là tham số).
Tìm
m
để hàm số đã cho liên tục tại
2x =
.
Câu 2. (0,5 điểm). Cho hàm số
32
3 2.yx x=−+
Viết phương trình tiếp tuyến của đồ thị hàm số đã cho
biết tiếp tuyến đó song song với đường thẳng
9 7.yx
= +
Câu 3. (2,5 điểm).
Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông tại
B
,
( )
, 2,AB a AC a SA ABC= = ⊥
và
SA a
=
.
a) Chứng minh rằng
( )
BC SAB
⊥
.
b) Tính khoảng cách từ
A
đến mặt phẳng
( )
SBC
.
c) Tính tang của góc giữa hai mặt phẳng
( )
SBC
và
( )
SAC
.
----------- HẾT ----------
Trang 1/3 - Mã đề thi 113
SỞ GIÁO DỤC VÀ ĐÀO TẠO
BẮC GIANG
(Đề gồm có 03 trang)
ĐỀ KIỂM TRA CUỐI HỌC KÌ II
NĂM HỌC 2022 - 2023
MÔN: TOÁN LỚP 11 THPT
Thời gian làm bài: 90 phút, không kể thời gian giao đề
Mã đề: 113
I. PHẦN TRẮC NGHIỆM (5,0 điểm).
Câu 1: Cho hình chóp
.
S ABCD
có
ABCD
là hình vuông và
( )
SA ABCD⊥
. Tam giác
SAC
là tam giác gì?
A. Tam giác đều.
B. Tam giác tù.
Câu 2: Một cấp số nhân có hai số hạng liên tiếp là 6 và 18. Số hạng tiếp theo là
A.
12
.
B.
30
.
24
54
Câu 3: Cho hình lập phương
..ABCD A B C D
′′′′
Góc giữa hai đường thẳng
AC
và
BD
′′
là?
A.
45°
.
B.
90°
.
60°
0°
Câu 4: Đạo hàm của hàm số
( )
2
2fx x x= −
tại điểm
3x
=
là
A.
( )
3 1.f
′
=
B.
( )
3 0.f
′
=
C.
( )
3 4.f
′
=
D.
( )
3 3.f
′
=
Câu 5: Số đo ba góc của một tam giác vuông tạo thành cấp số cộng. Hai góc nhọn của tam giác có số đo
(độ) là:
A.
30°
và
60 .°
B.
20°
và
70 .°
45°
45 .°
20°
45 .°
Câu 6: Đạo hàm của hàm số
( )
sin 2cosfx x x= +
là
A.
( )
cos 2sin .fx x x
′
=−−
B.
( )
cos 2sin .fx x x
′
=−+
C.
( )
cos 2sin .fx x x
′
= −
D.
( )
cos 2sin .fx x x
′
= +
Câu 7: Cho cấp số cộng
( )
n
u
có
1
3u =
và
5.d =
Khẳng định nào sau đây đúng?
A.
( )
3 5 1.
n
un=+−
B.
( )
3 5 1.
n
un=++
C.
2 5.
n
un= +
D.
( )
3 5 1.
n
un=−−
Câu 8: Cho hình lăng trụ tam giác
.ABC A B C
′′′
có đáy là tam giác đều cạnh
a
. Hình chiếu vuông góc
của
A
′
trên mặt phẳng
( )
ABC
là trung điểm
H
của
BC
. Biết khoảng cách từ
H
tới
AA
′
bằng
3
4
a
. Số
đo góc
A AH
′
bằng
A.
75°
.
B.
45°
.
60°
30°
Trang 2/3 - Mã đề thi 113
Câu 9: Cho dãy số
(
)
n
u
với
1
1
2
.
2 1, 1
nn
u
u un n
+
= −
= ++ ≥
Số hạng
2023
u
của dãy số đó là
A.
2022
2023
2025 2 .u =−+
B.
2022
2023
2023 2 .
u
= +
C.
2022
2023
2023 2 .u =−+
D.
2022
2023
2025 2 .u = +
Câu 10: Giá trị của giới hạn
(
)
22
lim 2 6 5 1
x
x x x ax
→+∞
+ +− + + =−
. Khi đó giá trị của
a
là
A.
1.
B.
4.
3.−
3.
Câu 11: Tìm tất cả giá trị thực của tham số
m
để hàm số
( )
32
22
khi 1
1
2 khi 1
xx x
x
fx
x
xm x
−+−
>
−
+≤
=
liên tục tại
1.x =
A.
0.m =
B.
1.m = −
1.m =
2.m
= −
Câu 12: Cho dãy số
(
)
n
u
, biết
23
n
un= +
với
1n ≥
. Số hạng thứ 5 của dãy số đó là
A.
5.
B.
1 1 .
13.
35.
Câu 13: Giá trị của giới hạn
(
)
32
lim 1
x
xx x
→−∞
− + −+
là
A.
1.
B.
.+∞
.−∞
0.
Câu 14: Tìm hệ số góc
k
của đường thẳng tiếp xúc với parabol
2
21yx x=++
tại điểm có hoành độ
2.x = −
A.
2.k = −
B.
1.k
=
0.k =
4.k = −
Câu 15: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông tâm
O
;
SO
vuông góc với mặt phẳng
( )
ABCD
. Khẳng định nào sau đây là Sai?
A.
Hai mặt phẳng
( )
SBD
và
( )
ABCD
vuông góc.
B. Hai mặt phẳng
( )
SAB
và
( )
ABCD
vuông góc.
C. Hai mặt phẳng
( )
SAC
và
( )
SBD
vuông góc.
D. Hai mặt phẳng
( )
SAC
và
( )
ABCD
vuông góc.
Câu 16: Giá trị của giới hạn
2
3
lim
23nn
−
−+
là
A.
3
.
2
−
B.
1.−
C.
.−∞
D. 0.
Câu 17: Tính giới hạn
( )
2
lim 3 5 3 .L nn= +−
A.
.L = +∞
B.
.L = −∞
5.L =
3.L =
Trang 3/3 - Mã đề thi 113
Câu 18: Cho hình chóp
.S ABC
có
3AB a=
,
4BC a=
,
5CA a=
, các mặt bên tạo với đáy góc
60°
, gọi
H
là hình chiếu vuông góc của
S
lên mặt phẳng
( )
ABC
(
H
thuộc miền trong của tam giác
ABC
). Độ
dài của
SH
là
A.
23
a
. B.
3a
.
C.
3
3
a
. D.
23
3
a
.
Câu 19: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật,
3AB a=
và
5AC a=
. Cạnh bên
SA
vuông góc với mặt phẳng
( )
ABCD
và
2SA a=
. Khoảng cách từ
A
đến mặt phẳng
(
)
SCD
bằng
A.
3 22
11
a
.
B.
12
5
a
.
C.
12 97
97
a
.
D.
4
3
a
.
Câu 20: Giá trị của giới hạn
2
3
1
3
lim
1
x
x
x
→
−
+
là
A.
3.−
B.
2.−
1.
1.
−
II. PHẦN TỰ LUẬN (5,0 điểm).
Câu 1. (2,0 điểm).
a) Tính giới hạn:
2
2
14
lim
21
n
n
−
+
.
b) Cho hàm số
( )
2
2
khi 2
2
1 khi 2
xx
x
fx
x
mx
−−
=
−
−=
≠
(với
m
là tham số).
Tìm
m
để hàm số đã cho liên tục tại
2x =
.
Câu 2. (0,5 điểm). Cho hàm số
32
3 2.yx x=−+
Viết phương trình tiếp tuyến của đồ thị hàm số đã cho
biết tiếp tuyến đó song song với đường thẳng
9 7.
yx= +
Câu 3. (2,5 điểm).
Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông tại
B
,
( )
, 2,AB a AC a SA ABC
= = ⊥
và
SA a
=
.
a) Chứng minh rằng
( )
BC SAB⊥
.
b) Tính khoảng cách từ
A
đến mặt phẳng
( )
SBC
.
c) Tính tang của góc giữa hai mặt phẳng
( )
SBC
và
( )
SAC
.
----------- HẾT ----------
Trang 1/3 - Mã đề thi 114
SỞ GIÁO DỤC VÀ ĐÀO TẠO
BẮC GIANG
(Đề gồm có 03 trang)
ĐỀ KIỂM TRA CUỐI HỌC KÌ II
NĂM HỌC 2022 - 2023
MÔN: TOÁN LỚP 11 THPT
Thời gian làm bài: 90 phút, không kể thời gian giao đề
Mã đề: 114
I. PHẦN TRẮC NGHIỆM (5,0 điểm).
Câu 1: Đạo hàm của hàm số
( )
sin 2cosfx x x
= +
là
A.
( )
cos 2sin .fx x x
′
= −
B.
( )
cos 2sin .fx x x
′
= +
C.
(
)
cos 2sin .
fx x x
′
=−−
D.
( )
cos 2sin .fx x x
′
=−+
Câu 2: Số đo ba góc của một tam giác vuông tạo thành cấp số cộng. Hai góc nhọn của tam giác có số đo
(độ) là:
A.
30°
và
60 .°
B.
20°
và
70 .°
45°
45 .°
20°
45 .°
Câu 3: Giá trị của giới hạn
( )
32
lim 1
x
xx x
→−∞
− + −+
là
A.
.−∞
B.
1.
.+∞
0.
Câu 4: Tính giới hạn
( )
2
lim 3 5 3 .L nn= +−
A.
3.L
=
B.
.L = −∞
5.L =
.L = +∞
Câu 5: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông tâm
O
;
SO
vuông góc với mặt phẳng
( )
ABCD
. Khẳng định nào sau đây là Sai?
A.
Hai mặt phẳng
( )
SAB
và
( )
ABCD
vuông góc.
B. Hai mặt phẳng
( )
SAC
và
( )
ABCD
vuông góc.
C. Hai mặt phẳng
( )
SBD
và
( )
ABCD
vuông góc.
D. Hai mặt phẳng
( )
SAC
và
( )
SBD
vuông góc.
Câu 6: Cho hình lăng trụ tam giác
.ABC A B C
′′′
có đáy là tam giác đều cạnh
a
. Hình chiếu vuông góc
của
A
′
trên mặt phẳng
( )
ABC
là trung điểm
H
của
BC
. Biết khoảng cách từ
H
tới
AA
′
bằng
3
4
a
. Số
đo góc
A AH
′
bằng
A.
30°
.
B.
45°
.
75°
60°
Câu 7: Giá trị của giới hạn
2
3
1
3
lim
1
x
x
x
→
−
+
là
A.
3.−
B.
1.
1.−
2.−
Câu 8: Cho dãy số
( )
n
u
, biết
23
n
un= +
với
1n ≥
. Số hạng thứ 5 của dãy số đó là
A.
1 1 .
B.
5.
35.
13.
Trang 2/3 - Mã đề thi 114
Câu 9: Cho cấp số cộng
(
)
n
u
có
1
3
u
=
và
5.d =
Khẳng định nào sau đây đúng?
A.
2 5.
n
un= +
B.
( )
3 5 1.
n
un
=++
( )
3 5 1.
n
un=+−
( )
3 5 1.
n
un=−−
Câu 10: Giá trị của giới hạn
2
3
lim
23nn
−
−+
là
A.
3
.
2
−
B.
.−∞
C. 0.
D.
1.
−
Câu 11: Cho hình chóp
.S ABC
có
3AB a=
,
4BC a=
,
5CA a=
, các mặt bên tạo với đáy góc
60°
, gọi
H
là hình chiếu vuông góc của
S
lên mặt phẳng
( )
ABC
(
H
thuộc miền trong của tam giác
ABC
). Độ
dài của
SH
là
A.
3a
. B.
23a
.
C.
23
3
a
. D.
3
3
a
.
Câu 12: Cho hình chóp
.
S ABCD
có
ABCD
là hình vuông và
( )
SA ABCD⊥
. Tam giác
SAC
là tam giác gì?
A. Tam giác nhọn.
B. Tam giác vuông.
Câu 13: Đạo hàm của hàm số
( )
2
2fx x x
= −
tại điểm
3x =
là
A.
( )
3 1.f
′
=
B.
( )
3 4.f
′
=
( )
3 3.f
′
=
( )
3 0.f
′
=
Câu 14: Cho hình lập phương
..ABCD A B C D
′′′′
Góc giữa hai đường thẳng
AC
và
BD
′′
là?
A.
45°
.
B.
0°
.
90°
60°
Câu 15: Giá trị của giới hạn
(
)
22
lim 2 6 5 1
x
x x x ax
→+∞
+ +− + + =−
. Khi đó giá trị của
a
là
A.
4.
B.
3.
3.−
1.
Câu 16: Tìm tất cả giá trị thực của tham số
m
để hàm số
( )
32
22
khi 1
1
2 khi 1
xx x
x
fx
x
xm x
−+−
>
−
+≤
=
liên tục tại
1.x =
A.
0.m =
B.
1.m =
1.m = −
2.m = −
Câu 17: Tìm hệ số góc
k
của đường thẳng tiếp xúc với parabol
2
21yx x=++
tại điểm có hoành độ
2.x = −
A.
0.k =
B.
4.k = −
1.k =
2.k = −
Câu 18: Một cấp số nhân có hai số hạng liên tiếp là 6 và 18. Số hạng tiếp theo là
Trang 3/3 - Mã đề thi 114
A.
30
.
B.
24
.
12
54
Câu 19: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật,
3AB a=
và
5AC a=
. Cạnh bên
SA
vuông góc với mặt phẳng
( )
ABCD
và
2SA a=
. Khoảng cách từ
A
đến mặt phẳng
( )
SCD
bằng
A.
3 22
11
a
.
B.
4
3
a
. C.
12
5
a
.
D.
12 97
97
a
.
Câu 20: Cho dãy số
( )
n
u
với
1
1
2
.
2 1, 1
nn
u
u un n
+
= −
= ++ ≥
Số hạng
2023
u
của dãy số đó là
A.
2022
2023
2025 2 .
u = +
B.
2022
2023
2025 2 .u =−+
C.
2022
2023
2023 2 .
u
=−+
D.
2022
2023
2023 2 .
u
= +
-----------------------------------------------
II. PHẦN TỰ LUẬN (5,0 điểm).
Câu 1. (2,0 điểm).
a) Tính giới hạn:
2
2
14
lim
21
n
n
−
+
.
b) Cho hàm số
(
)
2
2
khi 2
2
1 khi 2
xx
x
fx
x
mx
−−
=
−
−=
≠
(với
m
là tham số).
Tìm
m
để hàm số đã cho liên tục tại
2x =
.
Câu 2. (0,5 điểm). Cho hàm số
32
3 2.yx x=−+
Viết phương trình tiếp tuyến của đồ thị hàm số đã cho
biết tiếp tuyến đó song song với đường thẳng
9 7.yx= +
Câu 3. (2,5 điểm).
Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông tại
B
,
( )
, 2,AB a AC a SA ABC= = ⊥
và
SA a=
.
a) Chứng minh rằng
( )
BC SAB⊥
.
b) Tính khoảng cách từ
A
đến mặt phẳng
( )
SBC
.
c) Tính tang của góc giữa hai mặt phẳng
( )
SBC
và
( )
SAC
.
----------- HẾT ----------
SỞ GIÁO DỤC VÀ ĐÀO TẠO
BẮC GIANG
HƯỚNG DẪN CHẤM
BÀI KIỂM TRA CHẤT LƯỢNG HỌC KÌ II
NĂM HỌC 2022 - 2023
MÔN TOÁN LỚP 11 THPT
PHẦN I. TRẮC NGHIỆM ( 5,0 điểm): Mỗi ý đúng được 0,25 điểm
MÃ ĐỀ 111
MÃ ĐỀ 112
MÃ ĐỀ 113
MÃ ĐỀ 114
Câu
Đáp án
Câu
Đáp án
Câu
Đáp án
Câu
Đáp án
1
B
1
A
1
D
1
A
2
A
2
D
2
D
2
A
3
A
3
A
3
B
3
C
4
B
4
A
4
C
4
D
5
D
5
D
5
A
5
A
6
B
6
C
6
C
6
D
7
A
7
D
7
A
7
C
8
C
8
A
8
C
8
D
9
C
9
B
9
A
9
C
10
D
10
D
10
B
10
C
11
C
11
B
11
C
11
A
12
A
12
C
12
C
12
B
13
B
13
B
13
B
13
B
14
D
14
C
14
A
14
C
15
D
15
D
15
B
15
A
16
A
16
B
16
D
16
B
17
B
17
A
17
A
17
D
18
D
18
C
18
B
18
D
19
C
19
C
19
D
19
B
20
C
20
B
20
D
20
B
PHẦN II. TỰ LUẬN ( 5,0 điểm)
Chú ý : Dưới đây chỉ là sơ lược từng bước giải và cách cho điểm từng phần của mỗi bài. Bài làm của học
sinh yêu cầu phải chi tiết, lập luận chặt chẽ. Nếu học sinh giải cách khác đúng thì chấm và cho điểm từng
phần tương ứng.
Câu
Nội dung
Điểm
1
(2 điểm)
a) Tính giới hạn:
2
2
14
lim
21
n
n
−
+
.
2
2
2
2
1
4
14
lim lim
1
21
2
n
n
n
n
−
−
=
+
+
0,5
4
2
2
−
= = −
.KL
0,5
2
b) Cho hàm số
(
)
2
2
khi 2
2
1 khi 2
xx
x
fx
x
mx
−−
=
−
−=
≠
. Tìm
m
để hàm số liên tục tại
2x =
.
Tập xác định:
;2
DD
= ∈
0,25
( )
(
)
(
)
2
22 2
12
2
lim lim lim 1 3
22
xx x
xx
xx
x
xx
→→ →
+−
−−
= = +=
−−
0,25
( )
21fm= −
0,25
Hàm số liên tục tại
2x =
khi và chỉ khi
( ) ( )
2
lim 2 3 1 4
x
fx f m m
→
= ⇔ = −⇔ =
. KL
0,25
2
(0.5 điểm)
Câu 2. Cho hàm số
32
3 2.yx x=−+
Viết phương trình tiếp tuyến của đồ thị hàm số biết
tiếp tuyến đó song song với đường thẳng
9 7.yx= +
Ta có
2
36yxx
′
= −
Vì tiếp tuyến của đồ thị hàm số song song với đường thẳng
97yx= +
nên ta
xét phương trình
22
1
3693690
3
x
xx xx
x
= −
− =⇔ − −=⇔
=
0,25
+ Với
1x
= −
ta có
2y = −
nên tiếp tuyến có phương trình là
( )
9 12 9 7y x yx= + −⇔ = +
(loại vì trùng với đường thẳng đã cho)
+ Với
3
x =
ta có
2y
=
nên tiếp tuyến có phương trình là
( )
9 3 2 9 25
y x yx= − +⇔ = −
(thỏa mãn)
KL
9 25yx= −
0,25
3
(2.5 điểm)
Câu 3. Cho khối chóp
.S ABC
có đáy
ABC
là tam giác vuông tại
B
,
(
)
, 2,AB a AC a SA ABC= = ⊥
và
SA a=
.
a) Chứng minh rằng
( )
BC SAB⊥
.
b) Tính khoảng cách từ
A
đến mặt phẳng
( )
SBC
.
c) Tính tang của góc giữa hai mặt phẳng
(
)
SBC
và
( )
SAC
.
3
a) Chứng minh rằng
( )
BC SAB⊥
.
+ Vì
( )
( )
1SA ABC SA BC⊥ ⇒⊥
0,25
Lại có
ABC∆
vuông tại
B
nên
( )
2AB BC⊥
0,25
+ Mà trong mặt phẳng
( )
SAB
ta có
{ }( )
3SA AB A∩=
0,25
Từ (1); (2); (3) suy ra
( )
BC SAB⊥
0,25
b) Tính khoảng cách từ
A
đến mặt phẳng
( )
SBC
.
Kẻ
AH SB⊥
tại
.H
Suy ra
A
đến mặt phẳng
( )
SBC
bằng
AH
.
0,5
Ta có
SABΛ
vuông cân suy ra
2
2
a
AH =
.
0,5
c)
Tính tang của góc giữa hai mặt phẳng
( )
SBC
và
( )
SAC
.
Kẻ
AK SC⊥
; chứng minh được
( )
SC AHK⊥
;
AHK∆
vuông tại
H
Chỉ ra giao tuyến của hai mặt phẳng
( )
SBC
và
( )
SAC
là
SC
Suy ra góc giữa hai mặt phẳng đó là
AKH
0,25
Tính được
22 2
1 1 1 25
5
a
AK
AK SA AC
= + ⇒=
Tính được
222
30 15
tan
10 3
a AH
HK AK AH HK AKH
HK
= − ⇒= ⇒ = =
0,25
| 1/15
| | Tải xuống

Có thể bạn quan tâm:

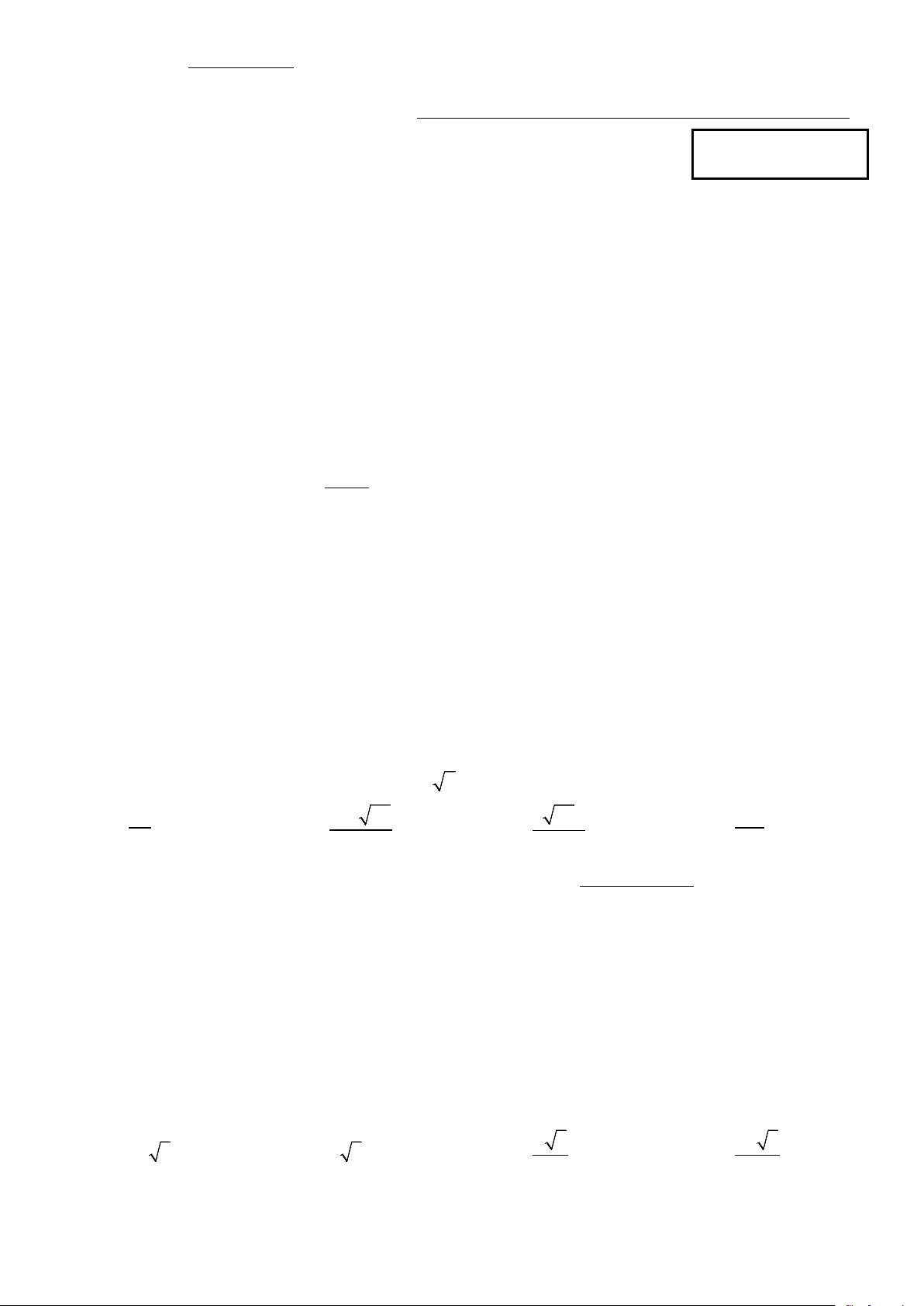
Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA CUỐI HỌC KÌ II BẮC GIANG NĂM HỌC 2022 - 2023
MÔN: TOÁN LỚP 11 THPT
Thời gian làm bài: 90 phút, không kể thời gian giao đề
(Đề gồm có 03 trang) Mã đề: 111
I. PHẦN TRẮC NGHIỆM (5,0 điểm).
Câu 1: Số đo ba góc của một tam giác vuông tạo thành cấp số cộng. Hai góc nhọn của tam giác có số đo (độ) là: A. 20° và 70 .° B. 30° và 60 .° C. 20° và 45 .° D. 45° và 45 .°
Câu 2: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = 3a và AC = 5a . Cạnh bên SA
vuông góc với mặt phẳng ( ABCD) và SA = a 2 . Khoảng cách từ A đến mặt phẳng (SCD) bằng A. 4a . a a a . 3 B. 12 97 . C. 3 22 . D. 12 97 11 5
Câu 3: Cho hình lăng trụ tam giác ABC.A′B C
′ ′ có đáy là tam giác đều cạnh a . Hình chiếu vuông góc của a
A′ trên mặt phẳng ( ABC) là trung điểm H của BC . Biết khoảng cách từ H tới AA′ bằng 3 . Số 4 đo góc  A′AH bằng A. 60°. B. 30° . C. 45°. D. 75°.
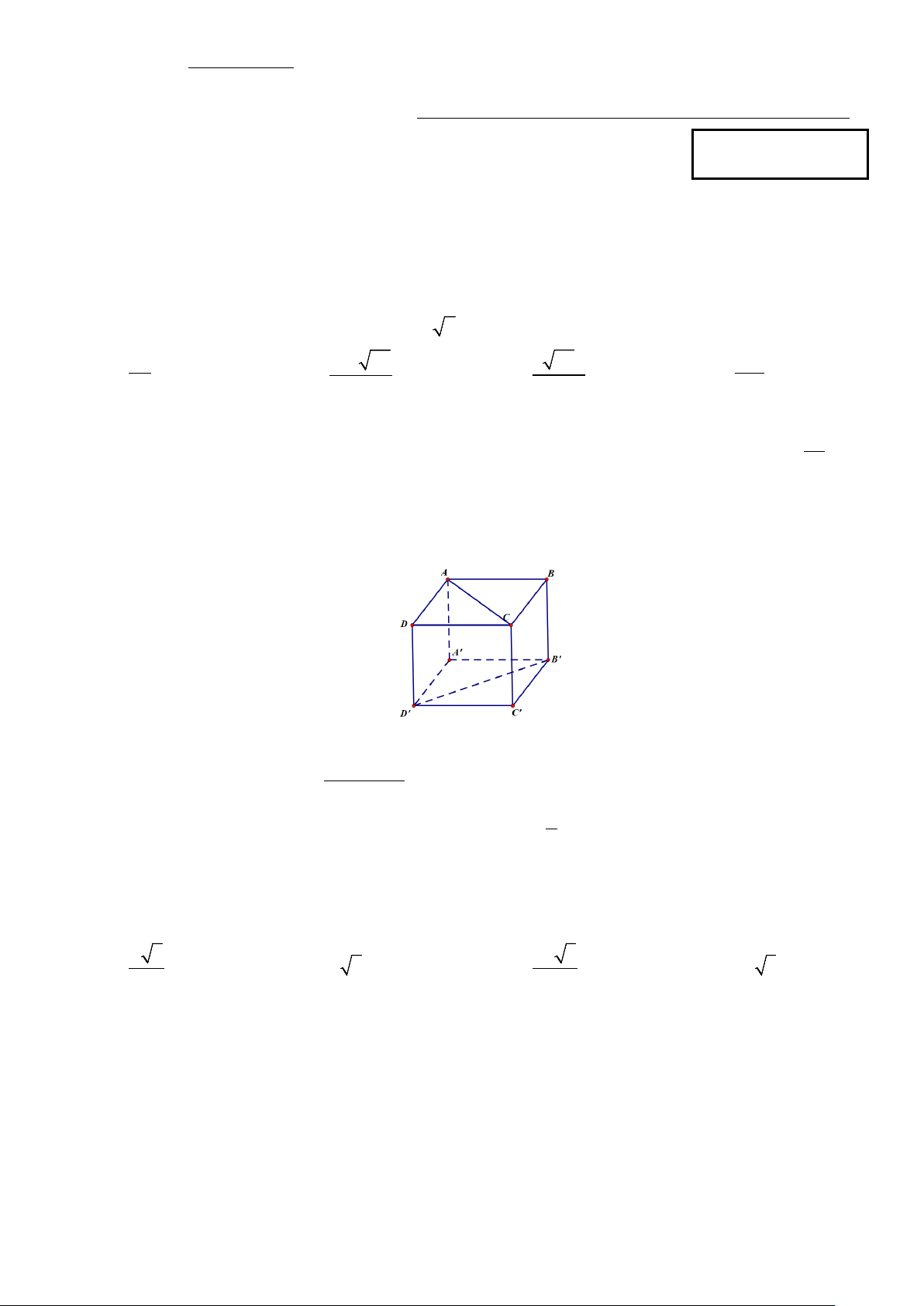
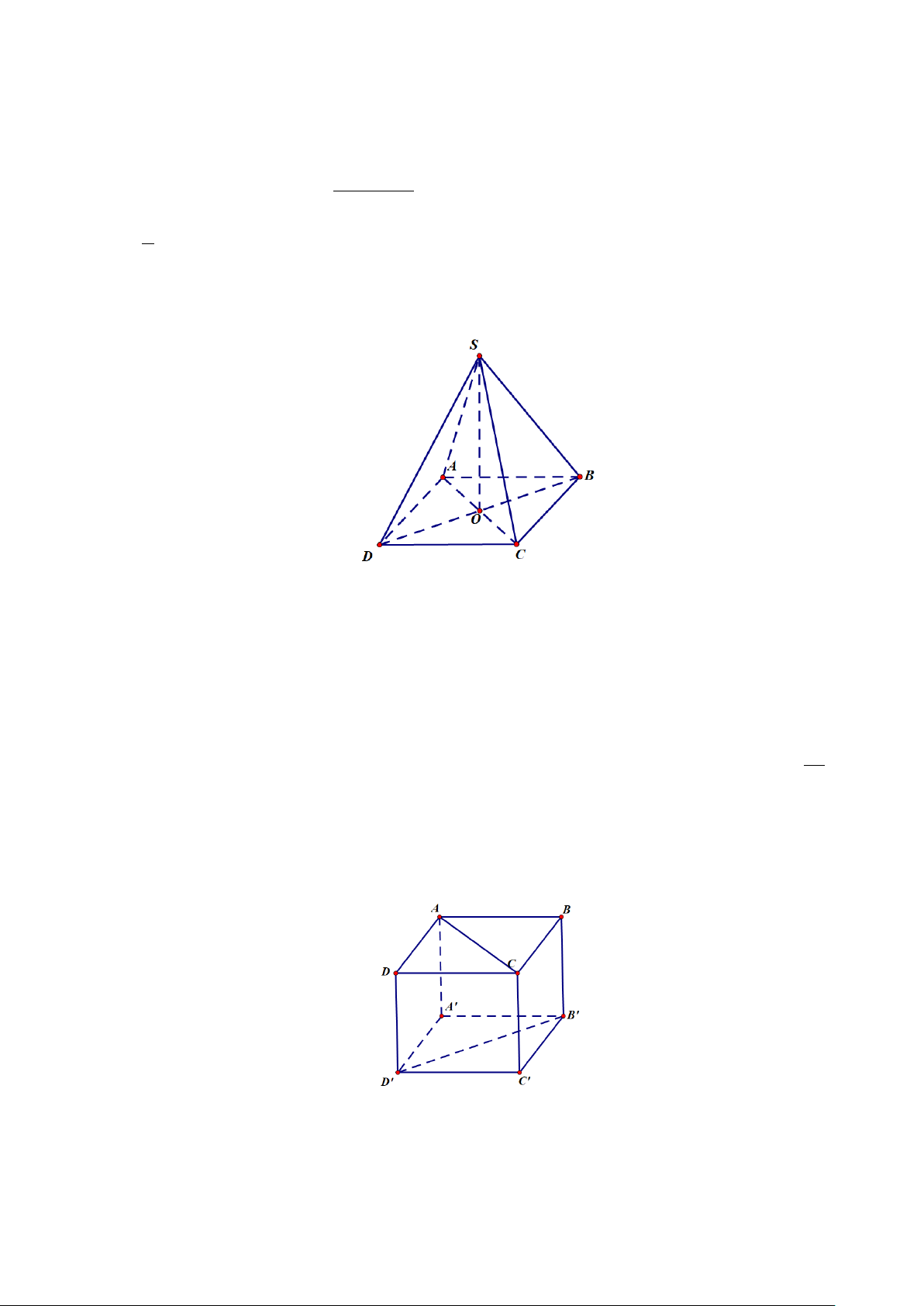
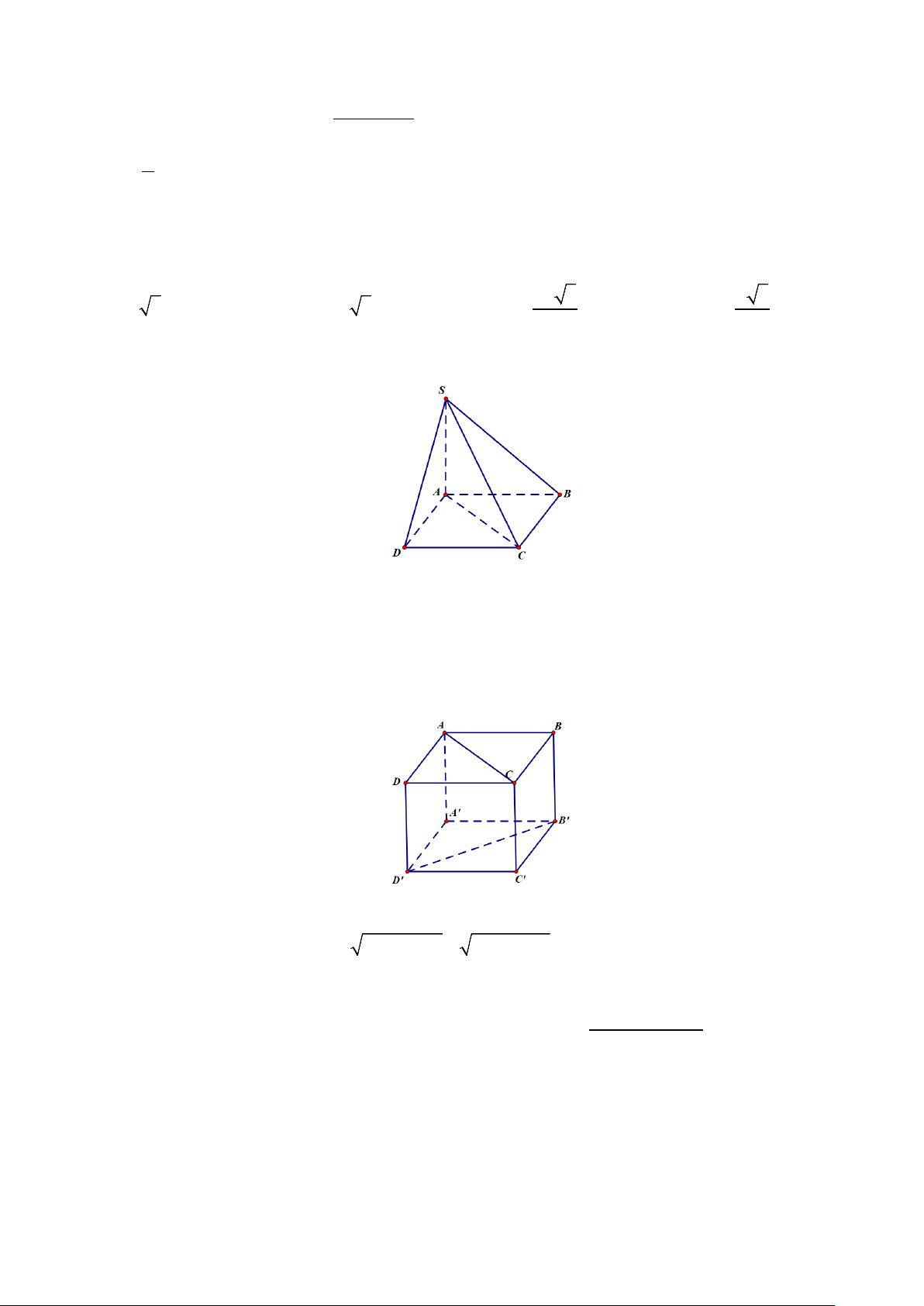
Câu 4: Cho hình lập phương ABC . D A′B C ′ D
′ .′Góc giữa hai đường thẳng AC và B D ′ ′ là? A. 60°. B. 90° . C. 0°. D. 45°.
Câu 5: Giá trị của giới hạn 3 lim − là 2 2n − n + 3 A. . −∞ B. 1. − C. 3 − . 2 D. 0.
Câu 6: Cho hình chóp S.ABC có AB = 3a , BC = 4a , CA = 5a , các mặt bên tạo với đáy góc 60°, gọi
H là hình chiếu vuông góc của S lên mặt phẳng ( ABC) ( H thuộc miền trong của tam giác ABC ). Độ dài của SH là A. a 3 . B. a 3 . C. 2a 3 . D. 2a 3 . 3 3
Câu 7: Cho dãy số (u , biết u = n + với n ≥1. Số hạng thứ 5 của dãy số đó là n 2 3 n ) A. 13. B. 1 1. C. 35. D. 5.
Trang 1/3 - Mã đề thi 111
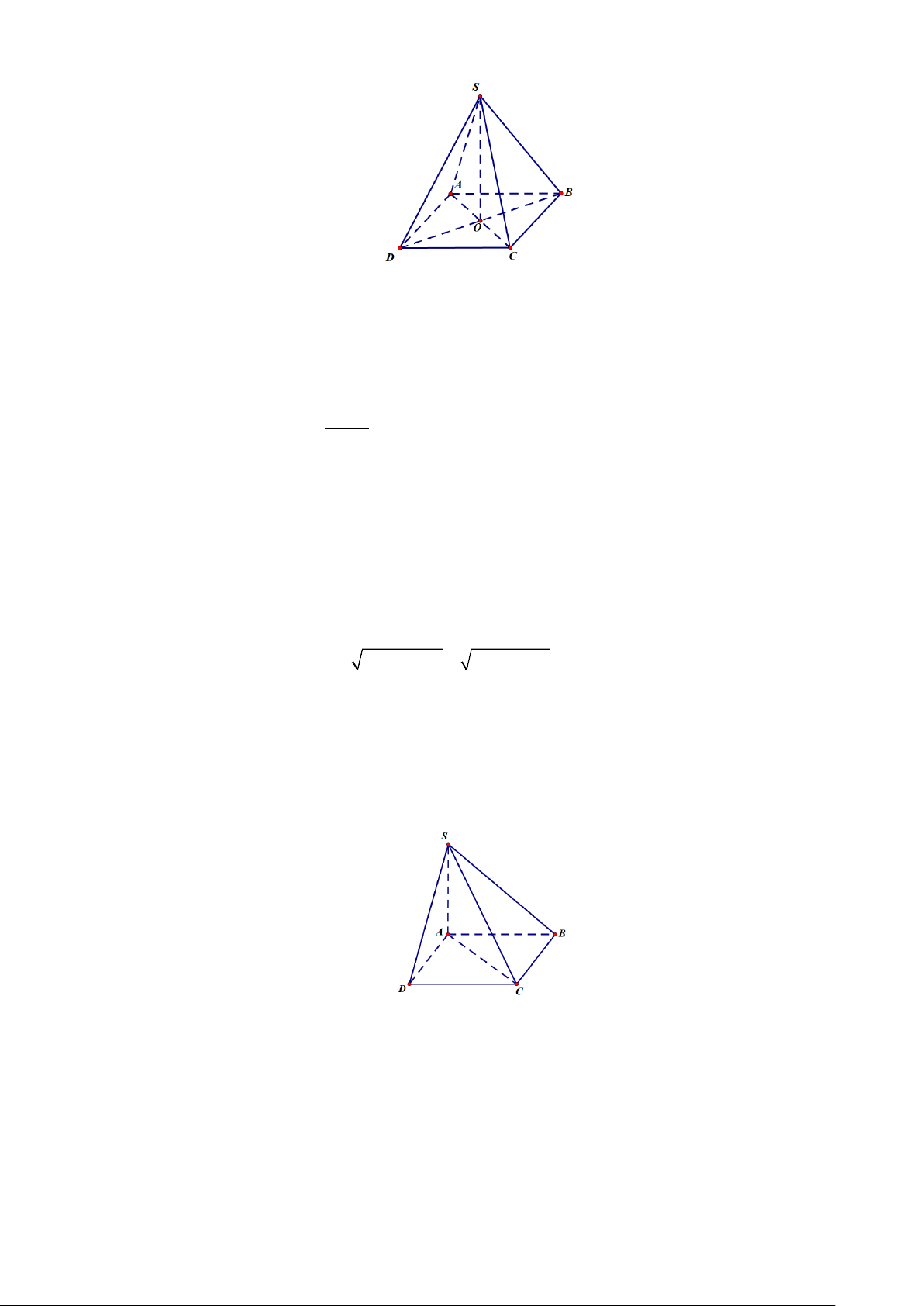
Câu 8: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O ; SO vuông góc với mặt phẳng
( ABCD) . Khẳng định nào sau đây là Sai?
A. Hai mặt phẳng (SBD)và ( ABCD) vuông góc.
B. Hai mặt phẳng (SAC) và ( ABCD) vuông góc.
C. Hai mặt phẳng (SAB) và ( ABCD) vuông góc.
D. Hai mặt phẳng (SAC)và (SBD)vuông góc. 2 Câu 9: − Giá trị của giới hạn x 3 lim là 3 x 1 → x +1 A. 3. − B. 1. C. 1. − D. 2. −
Câu 10: Cho cấp số cộng (u có u = 3 và d = 5. Khẳng định nào sau đây đúng? n ) 1
A. u = + n +
B. u = − n −
C. u = + n
D. u = + n − n 3 5( )1. n 2 5 . n 3 5( )1. n 3 5( )1.
Câu 11: Một cấp số nhân có hai số hạng liên tiếp là 6 và 18. Số hạng tiếp theo là A. 30. B. 12. C. 54. D. 24 .
Câu 12: Đạo hàm của hàm số f (x) 2
= x − 2x tại điểm x = 3 là
A. f ′(3) = 4.
B. f ′(3) = 0. C. f ′(3) =1.
D. f ′(3) = 3.
Câu 13: Giá trị của giới hạn + + − + +
= − . Khi đó giá trị của a là →+∞ ( 2 2 lim x 2x 6 x ax 5) 1 x A. 1. B. 4. C. 3. D. 3. −
Câu 14: Giá trị của giới hạn ( 3 2
lim −x + x − x + ) 1 là x→−∞ A. . −∞ B. 0. C. 1. D. . +∞
Câu 15: Cho hình chóp S.ABCD có ABCD là hình vuông và SA ⊥ ( ABCD) . Tam giác SAC là tam giác gì? A. Tam giác tù. B. Tam giác đều. C. Tam giác nhọn. D. Tam giác vuông. u  = 2 −
Câu 16: Cho dãy số (u với 1 
. Số hạng u của dãy số đó là n ) u = + + ≥  2023 + u n n n 2 n 1, 1 1 A. 2022 u = 2025 − + 2 . B. 2022 u = 2023+ 2 . 2023 2023 C. 2022 u = 2025 + 2 . D. 2022 u = 2023 − + 2 . 2023 2023
Trang 2/3 - Mã đề thi 111 3 2
x − x + 2x − 2
Câu 17: Tìm tất cả giá trị thực của tham số m để hàm số  > f (x) khi x 1 =  x −1 liên tục tại 2x + m khi x ≤1 x =1. A. m = 2. − B. m =1. C. m = 0. D. m = 1. −
Câu 18: Tính giới hạn L = ( 2
lim 3n + 5n − 3). A. L = 5. B. L = . −∞ C. L = 3. D. L = . +∞
Câu 19: Đạo hàm của hàm số f (x) = sin x + 2cos x là
A. f ′(x) = −cos x + 2sin .x
B. f ′(x) = −cos x − 2sin .x
C. f ′(x) = cos x − 2sin .x
D. f ′(x) = cos x + 2sin .x
Câu 20: Tìm hệ số góc k của đường thẳng tiếp xúc với parabol 2
y = x + 2x +1 tại điểm có hoành độ x = 2. − A. k = 4. − B. k = 0. C. k = 2. − D. k =1.
----------------------------------------------
II. PHẦN TỰ LUẬN (5,0 điểm).
Câu 1. (2,0 điểm). 2 a) Tính giới hạn: 1− 4 lim n . 2 2n +1 2
x − x − 2 b) Cho hàm số ≠ f (x)  khi x 2 =  x − 2
(với m là tham số). m−1 khi x = 2
Tìm m để hàm số đã cho liên tục tại x = 2 .
Câu 2. (0,5 điểm). Cho hàm số 3 2
y = x − 3x + 2. Viết phương trình tiếp tuyến của đồ thị hàm số đã cho
biết tiếp tuyến đó song song với đường thẳng y = 9x + 7.
Câu 3. (2,5 điểm).
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , AB = a, AC = 2a, SA ⊥ ( ABC) và SA = a .
a) Chứng minh rằng BC ⊥ (SAB) .
b) Tính khoảng cách từ A đến mặt phẳng (SBC).
c) Tính tang của góc giữa hai mặt phẳng (SBC) và (SAC). ----------- HẾT ----------
Trang 3/3 - Mã đề thi 111
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA CUỐI HỌC KÌ II BẮC GIANG NĂM HỌC 2022 - 2023
MÔN: TOÁN LỚP 11 THPT
Thời gian làm bài: 90 phút, không kể thời gian giao đề
(Đề gồm có 03 trang) Mã đề: 112
I. PHẦN TRẮC NGHIỆM (5,0 điểm).
Câu 1: Số đo ba góc của một tam giác vuông tạo thành cấp số cộng. Hai góc nhọn của tam giác có số đo (độ) là: A. 30° và 60 .° B. 20° và 45 .° C. 20° và 70 .° D. 45° và 45 .°
Câu 2: Giá trị của giới hạn ( 3 2
lim −x + x − x + ) 1 là x→−∞ A. . −∞ B. 0. C. 1. D. . +∞ u  = 2 −
Câu 3: Cho dãy số (u với 1 
. Số hạng u của dãy số đó là n ) u = + + ≥  2023 + u n n n 2 n 1, 1 1 A. 2022 u = 2025 − + 2 . B. 2022 u = 2025 + 2 . 2023 2023 C. 2022 u = 2023+ 2 . D. 2022 u = 2023 − + 2 . 2023 2023 2 Câu 4: − Giá trị của giới hạn x 3 lim là 3 x 1 → x +1 A. 1. − B. 2. − C. 3. − D. 1.
Câu 5: Một cấp số nhân có hai số hạng liên tiếp là 6 và 18. Số hạng tiếp theo là A. 30. B. 12. C. 24 . D. 54.
Câu 6: Đạo hàm của hàm số f (x) = sin x + 2cos x là
A. f ′(x) = cos x + 2sin .x
B. f ′(x) = −cos x − 2sin .x
C. f ′(x) = cos x − 2sin .x
D. f ′(x) = −cos x + 2sin .x
Câu 7: Tính giới hạn L = ( 2
lim 3n + 5n − 3). A. L = 3. B. L = 5. C. L = . −∞ D. L = . +∞
Câu 8: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = 3a và AC = 5a . Cạnh bên SA
vuông góc với mặt phẳng ( ABCD) và SA = a 2 . Khoảng cách từ A đến mặt phẳng (SCD) bằng A. 4a . a a a . 3 B. 12 97 . C. 3 22 . D. 12 97 11 5 3 2
x − x + 2x − 2
Câu 9: Tìm tất cả giá trị thực của tham số m để hàm số  > f (x) khi x 1 =  x −1 liên tục tại 2x + m khi x ≤1 x =1. A. m = 0. B. m =1. C. m = 1. − D. m = 2. −
Câu 10: Cho dãy số (u , biết u = n + với n ≥1. Số hạng thứ 5 của dãy số đó là n 2 3 n ) A. 35. B. 1 1. C. 5. D. 13.
Câu 11: Cho hình chóp S.ABC có AB = 3a , BC = 4a , CA = 5a , các mặt bên tạo với đáy góc 60°, gọi
H là hình chiếu vuông góc của S lên mặt phẳng ( ABC) ( H thuộc miền trong của tam giác ABC ). Độ dài của SH là A. 2a 3 . B. a 3 . C. a 3 . D. 2a 3 . 3 3
Trang 1/3 - Mã đề thi 112
Câu 12: Đạo hàm của hàm số f (x) 2
= x − 2x tại điểm x = 3 là
A. f ′(3) = 3.
B. f ′(3) = 0.
C. f ′(3) = 4. D. f ′(3) =1.
Câu 13: Cho cấp số cộng (u có u = 3 và d = 5. Khẳng định nào sau đây đúng? n ) 1
A. u = + n
B. u = + n −
C. u = − n −
D. u = + n + n 3 5( )1. n 3 5( )1. n 3 5( )1. n 2 5 .
Câu 14: Giá trị của giới hạn 3 lim − là 2 2n − n + 3 A. 3 − . 2 B. 1. − C. 0. D. . −∞
Câu 15: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O ; SO vuông góc với mặt phẳng
( ABCD) . Khẳng định nào sau đây là Sai?
A. Hai mặt phẳng (SAC)và (SBD)vuông góc.
B. Hai mặt phẳng (SBD)và ( ABCD) vuông góc.
C. Hai mặt phẳng (SAC) và ( ABCD) vuông góc.
D. Hai mặt phẳng (SAB) và ( ABCD) vuông góc.
Câu 16: Cho hình lăng trụ tam giác ABC.A′B C
′ ′ có đáy là tam giác đều cạnh a . Hình chiếu vuông góc của a
A′ trên mặt phẳng ( ABC) là trung điểm H của BC . Biết khoảng cách từ H tới AA′ bằng 3 . Số 4 đo góc  A′AH bằng A. 30° . B. 60°. C. 45°. D. 75°.
Câu 17: Cho hình lập phương ABC . D A′B C ′ D
′ .′Góc giữa hai đường thẳng AC và B D ′ ′ là? A. 90° . B. 60°. C. 0°. D. 45°.
Trang 2/3 - Mã đề thi 112
Câu 18: Cho hình chóp S.ABCD có ABCD là hình vuông và SA ⊥ ( ABCD) . Tam giác SAC là tam giác gì? A. Tam giác đều. B. Tam giác nhọn. C. Tam giác vuông. D. Tam giác tù.
Câu 19: Tìm hệ số góc k của đường thẳng tiếp xúc với parabol 2
y = x + 2x +1 tại điểm có hoành độ x = 2. − A. k = 0. B. k =1. C. k = 2. − D. k = 4. −
Câu 20: Giá trị của giới hạn + + − + +
= − . Khi đó giá trị của a là →+∞ ( 2 2 lim x 2x 6 x ax 5) 1 x A. 1. B. 4. C. 3. − D. 3.
---------------------------------------------
II. PHẦN TỰ LUẬN (5,0 điểm).
Câu 1. (2,0 điểm). 2 a) Tính giới hạn: 1− 4 lim n . 2 2n +1 2
x − x − 2 b) Cho hàm số ≠ f (x)  khi x 2 =  x − 2
(với m là tham số). m−1 khi x = 2
Tìm m để hàm số đã cho liên tục tại x = 2 .
Câu 2. (0,5 điểm). Cho hàm số 3 2
y = x − 3x + 2. Viết phương trình tiếp tuyến của đồ thị hàm số đã cho
biết tiếp tuyến đó song song với đường thẳng y = 9x + 7.
Câu 3. (2,5 điểm).
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , AB = a, AC = 2a, SA ⊥ ( ABC) và SA = a .
a) Chứng minh rằng BC ⊥ (SAB) .
b) Tính khoảng cách từ A đến mặt phẳng (SBC).
c) Tính tang của góc giữa hai mặt phẳng (SBC) và (SAC). ----------- HẾT ----------
Trang 3/3 - Mã đề thi 112
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA CUỐI HỌC KÌ II BẮC GIANG NĂM HỌC 2022 - 2023
MÔN: TOÁN LỚP 11 THPT
Thời gian làm bài: 90 phút, không kể thời gian giao đề
(Đề gồm có 03 trang) Mã đề: 113
I. PHẦN TRẮC NGHIỆM (5,0 điểm).
Câu 1: Cho hình chóp S.ABCD có ABCD là hình vuông và SA ⊥ ( ABCD) . Tam giác SAC là tam giác gì? A. Tam giác đều. B. Tam giác tù. C. Tam giác nhọn. D. Tam giác vuông.
Câu 2: Một cấp số nhân có hai số hạng liên tiếp là 6 và 18. Số hạng tiếp theo là A. 12. B. 30. C. 24 . D. 54.
Câu 3: Cho hình lập phương ABC . D A′B C ′ D
′ .′Góc giữa hai đường thẳng AC và B D ′ ′ là? A. 45°. B. 90° . C. 60°. D. 0°.
Câu 4: Đạo hàm của hàm số f (x) 2
= x − 2x tại điểm x = 3 là A. f ′(3) =1.
B. f ′(3) = 0.
C. f ′(3) = 4.
D. f ′(3) = 3.
Câu 5: Số đo ba góc của một tam giác vuông tạo thành cấp số cộng. Hai góc nhọn của tam giác có số đo (độ) là: A. 30° và 60 .° B. 20° và 70 .° C. 45° và 45 .° D. 20° và 45 .°
Câu 6: Đạo hàm của hàm số f (x) = sin x + 2cos x là
A. f ′(x) = −cos x − 2sin .x
B. f ′(x) = −cos x + 2sin .x
C. f ′(x) = cos x − 2sin .x
D. f ′(x) = cos x + 2sin .x
Câu 7: Cho cấp số cộng (u có u = 3 và d = 5. Khẳng định nào sau đây đúng? n ) 1
A. u = + n −
B. u = + n +
C. u = + n
D. u = − n − n 3 5( )1. n 2 5 . n 3 5( )1. n 3 5( )1.
Câu 8: Cho hình lăng trụ tam giác ABC.A′B C
′ ′ có đáy là tam giác đều cạnh a . Hình chiếu vuông góc của a
A′ trên mặt phẳng ( ABC) là trung điểm H của BC . Biết khoảng cách từ H tới AA′ bằng 3 . Số 4 đo góc  A′AH bằng A. 75°. B. 45°. C. 60°. D. 30° .
Trang 1/3 - Mã đề thi 113 u  = 2 −
Câu 9: Cho dãy số (u với 1 
. Số hạng u của dãy số đó là n ) u = + + ≥  2023 + u n n n 2 n 1, 1 1 A. 2022 u = 2025 − + 2 . B. 2022 u = 2023+ 2 . 2023 2023 C. 2022 u = 2023 − + 2 . D. 2022 u = 2025 + 2 . 2023 2023
Câu 10: Giá trị của giới hạn + + − + +
= − . Khi đó giá trị của a là →+∞ ( 2 2 lim x 2x 6 x ax 5) 1 x A. 1. B. 4. C. 3. − D. 3. 3 2
x − x + 2x − 2
Câu 11: Tìm tất cả giá trị thực của tham số m để hàm số  > f (x) khi x 1 =  x −1 liên tục tại 2x + m khi x ≤1 x =1. A. m = 0. B. m = 1. − C. m =1. D. m = 2. −
Câu 12: Cho dãy số (u , biết u = n + với n ≥1. Số hạng thứ 5 của dãy số đó là n 2 3 n ) A. 5. B. 1 1. C. 13. D. 35.
Câu 13: Giá trị của giới hạn ( 3 2
lim −x + x − x + ) 1 là x→−∞ A. 1. B. . +∞ C. . −∞ D. 0.
Câu 14: Tìm hệ số góc k của đường thẳng tiếp xúc với parabol 2
y = x + 2x +1 tại điểm có hoành độ x = 2. − A. k = 2. − B. k =1. C. k = 0. D. k = 4. −
Câu 15: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O ; SO vuông góc với mặt phẳng
( ABCD) . Khẳng định nào sau đây là Sai?
A. Hai mặt phẳng (SBD)và ( ABCD) vuông góc.
B. Hai mặt phẳng (SAB) và ( ABCD) vuông góc.
C. Hai mặt phẳng (SAC)và (SBD)vuông góc.
D. Hai mặt phẳng (SAC)và ( ABCD) vuông góc.
Câu 16: Giá trị của giới hạn 3 lim − là 2 2n − n + 3 A. 3 − . B. 1. − C. . −∞ D. 0. 2
Câu 17: Tính giới hạn L = ( 2
lim 3n + 5n − 3). A. L = . +∞ B. L = . −∞ C. L = 5. D. L = 3.
Trang 2/3 - Mã đề thi 113
Câu 18: Cho hình chóp S.ABC có AB = 3a , BC = 4a , CA = 5a , các mặt bên tạo với đáy góc 60°, gọi
H là hình chiếu vuông góc của S lên mặt phẳng ( ABC) ( H thuộc miền trong của tam giác ABC ). Độ dài của SH là A. 2a 3 . B. a 3 . C. a 3 . D. 2a 3 . 3 3
Câu 19: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = 3a và AC = 5a . Cạnh bên SA
vuông góc với mặt phẳng ( ABCD) và SA = a 2 . Khoảng cách từ A đến mặt phẳng (SCD) bằng a a A. 3 22a . B. 12 . C. 12a 97 . D. 4 . 11 5 97 3 2 Câu 20: − Giá trị của giới hạn x 3 lim là 3 x 1 → x +1 A. 3. − B. 2. − C. 1. D. 1. −
II. PHẦN TỰ LUẬN (5,0 điểm).
Câu 1. (2,0 điểm). 2 a) Tính giới hạn: 1− 4 lim n . 2 2n +1 2
x − x − 2 b) Cho hàm số ≠ f (x)  khi x 2 =  x − 2
(với m là tham số). m−1 khi x = 2
Tìm m để hàm số đã cho liên tục tại x = 2 .
Câu 2. (0,5 điểm). Cho hàm số 3 2
y = x − 3x + 2. Viết phương trình tiếp tuyến của đồ thị hàm số đã cho
biết tiếp tuyến đó song song với đường thẳng y = 9x + 7.
Câu 3. (2,5 điểm).
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , AB = a, AC = 2a, SA ⊥ ( ABC) và SA = a .
a) Chứng minh rằng BC ⊥ (SAB) .
b) Tính khoảng cách từ A đến mặt phẳng (SBC).
c) Tính tang của góc giữa hai mặt phẳng (SBC) và (SAC). ----------- HẾT ----------
Trang 3/3 - Mã đề thi 113
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA CUỐI HỌC KÌ II BẮC GIANG NĂM HỌC 2022 - 2023
MÔN: TOÁN LỚP 11 THPT
Thời gian làm bài: 90 phút, không kể thời gian giao đề
(Đề gồm có 03 trang) Mã đề: 114
I. PHẦN TRẮC NGHIỆM (5,0 điểm).
Câu 1: Đạo hàm của hàm số f (x) = sin x + 2cos x là
A. f ′(x) = cos x − 2sin .x
B. f ′(x) = cos x + 2sin .x
C. f ′(x) = −cos x − 2sin .x
D. f ′(x) = −cos x + 2sin .x
Câu 2: Số đo ba góc của một tam giác vuông tạo thành cấp số cộng. Hai góc nhọn của tam giác có số đo (độ) là: A. 30° và 60 .° B. 20° và 70 .° C. 45° và 45 .° D. 20° và 45 .°
Câu 3: Giá trị của giới hạn ( 3 2
lim −x + x − x + ) 1 là x→−∞ A. . −∞ B. 1. C. . +∞ D. 0.
Câu 4: Tính giới hạn L = ( 2
lim 3n + 5n − 3). A. L = 3. B. L = . −∞ C. L = 5. D. L = . +∞
Câu 5: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O ; SO vuông góc với mặt phẳng
( ABCD) . Khẳng định nào sau đây là Sai?
A. Hai mặt phẳng (SAB) và ( ABCD) vuông góc.
B. Hai mặt phẳng (SAC) và ( ABCD) vuông góc.
C. Hai mặt phẳng (SBD)và ( ABCD) vuông góc.
D. Hai mặt phẳng (SAC)và (SBD)vuông góc.
Câu 6: Cho hình lăng trụ tam giác ABC.A′B C
′ ′ có đáy là tam giác đều cạnh a . Hình chiếu vuông góc của a
A′ trên mặt phẳng ( ABC) là trung điểm H của BC . Biết khoảng cách từ H tới AA′ bằng 3 . Số 4 đo góc  A′AH bằng A. 30° . B. 45°. C. 75°. D. 60°. 2 Câu 7: − Giá trị của giới hạn x 3 lim là 3 x 1 → x +1 A. 3. − B. 1. C. 1. − D. 2. −
Câu 8: Cho dãy số (u , biết u = n + với n ≥1. Số hạng thứ 5 của dãy số đó là n 2 3 n ) A. 1 1. B. 5. C. 35. D. 13.
Trang 1/3 - Mã đề thi 114
Câu 9: Cho cấp số cộng (u có u = 3 và d = 5. Khẳng định nào sau đây đúng? n ) 1
A. u = + n
B. u = + n +
C. u = + n −
D. u = − n − n 3 5( )1. n 3 5( )1. n 3 5( )1. n 2 5 .
Câu 10: Giá trị của giới hạn 3 lim − là 2 2n − n + 3 A. 3 − . B. . −∞ C. 0. D. 1. − 2
Câu 11: Cho hình chóp S.ABC có AB = 3a , BC = 4a , CA = 5a , các mặt bên tạo với đáy góc 60°, gọi
H là hình chiếu vuông góc của S lên mặt phẳng ( ABC) ( H thuộc miền trong của tam giác ABC ). Độ dài của SH là A. a 3 . B. 2a 3 . C. 2a 3 . D. a 3 . 3 3
Câu 12: Cho hình chóp S.ABCD có ABCD là hình vuông và SA ⊥ ( ABCD) . Tam giác SAC là tam giác gì? A. Tam giác nhọn. B. Tam giác vuông. C. Tam giác đều. D. Tam giác tù.
Câu 13: Đạo hàm của hàm số f (x) 2
= x − 2x tại điểm x = 3 là A. f ′(3) =1.
B. f ′(3) = 4.
C. f ′(3) = 3.
D. f ′(3) = 0.
Câu 14: Cho hình lập phương ABC . D A′B C ′ D
′ .′Góc giữa hai đường thẳng AC và B D ′ ′ là? A. 45°. B. 0°. C. 90° . D. 60°.
Câu 15: Giá trị của giới hạn + + − + +
= − . Khi đó giá trị của a là →+∞ ( 2 2 lim x 2x 6 x ax 5) 1 x A. 4. B. 3. C. 3. − D. 1. 3 2
x − x + 2x − 2
Câu 16: Tìm tất cả giá trị thực của tham số m để hàm số  > f (x) khi x 1 =  x −1 liên tục tại 2x + m khi x ≤1 x =1. A. m = 0. B. m =1. C. m = 1. − D. m = 2. −
Câu 17: Tìm hệ số góc k của đường thẳng tiếp xúc với parabol 2
y = x + 2x +1 tại điểm có hoành độ x = 2. − A. k = 0. B. k = 4. − C. k =1. D. k = 2. −
Câu 18: Một cấp số nhân có hai số hạng liên tiếp là 6 và 18. Số hạng tiếp theo là
Trang 2/3 - Mã đề thi 114 A. 30. B. 24 . C. 12. D. 54.
Câu 19: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = 3a và AC = 5a . Cạnh bên SA
vuông góc với mặt phẳng ( ABCD) và SA = a 2 . Khoảng cách từ A đến mặt phẳng (SCD) bằng a a A. 3 22a . B. 4 . C. 12 . D. 12a 97 . 11 3 5 97 u  = 2 −
Câu 20: Cho dãy số (u với 1 
. Số hạng u của dãy số đó là n ) u = + + ≥  2023 + u n n n 2 n 1, 1 1 A. 2022 u = 2025 + 2 . B. 2022 u = 2025 − + 2 . 2023 2023 C. 2022 u = 2023 − + 2 . D. 2022 u = 2023+ 2 . 2023 2023
-----------------------------------------------
II. PHẦN TỰ LUẬN (5,0 điểm).
Câu 1. (2,0 điểm). 2 a) Tính giới hạn: 1− 4 lim n . 2 2n +1 2
x − x − 2 b) Cho hàm số ≠ f (x)  khi x 2 =  x − 2
(với m là tham số). m−1 khi x = 2
Tìm m để hàm số đã cho liên tục tại x = 2 .
Câu 2. (0,5 điểm). Cho hàm số 3 2
y = x − 3x + 2. Viết phương trình tiếp tuyến của đồ thị hàm số đã cho
biết tiếp tuyến đó song song với đường thẳng y = 9x + 7.
Câu 3. (2,5 điểm).
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , AB = a, AC = 2a, SA ⊥ ( ABC) và SA = a .
a) Chứng minh rằng BC ⊥ (SAB) .
b) Tính khoảng cách từ A đến mặt phẳng (SBC).
c) Tính tang của góc giữa hai mặt phẳng (SBC) và (SAC). ----------- HẾT ----------
Trang 3/3 - Mã đề thi 114
SỞ GIÁO DỤC VÀ ĐÀO TẠO HƯỚNG DẪN CHẤM BẮC GIANG
BÀI KIỂM TRA CHẤT LƯỢNG HỌC KÌ II NĂM HỌC 2022 - 2023
MÔN TOÁN LỚP 11 THPT
PHẦN I. TRẮC NGHIỆM ( 5,0 điểm): Mỗi ý đúng được 0,25 điểm MÃ ĐỀ 111 MÃ ĐỀ 112 MÃ ĐỀ 113 MÃ ĐỀ 114 Câu Đáp án Câu Đáp án Câu Đáp án Câu Đáp án 1 B 1 A 1 D 1 A 2 A 2 D 2 D 2 A 3 A 3 A 3 B 3 C 4 B 4 A 4 C 4 D 5 D 5 D 5 A 5 A 6 B 6 C 6 C 6 D 7 A 7 D 7 A 7 C 8 C 8 A 8 C 8 D 9 C 9 B 9 A 9 C 10 D 10 D 10 B 10 C 11 C 11 B 11 C 11 A 12 A 12 C 12 C 12 B 13 B 13 B 13 B 13 B 14 D 14 C 14 A 14 C 15 D 15 D 15 B 15 A 16 A 16 B 16 D 16 B 17 B 17 A 17 A 17 D 18 D 18 C 18 B 18 D 19 C 19 C 19 D 19 B 20 C 20 B 20 D 20 B
PHẦN II. TỰ LUẬN ( 5,0 điểm)
Chú ý : Dưới đây chỉ là sơ lược từng bước giải và cách cho điểm từng phần của mỗi bài. Bài làm của học
sinh yêu cầu phải chi tiết, lập luận chặt chẽ. Nếu học sinh giải cách khác đúng thì chấm và cho điểm từng
phần tương ứng. Câu Nội dung Điểm 2 a) Tính giới hạn: 1− 4 lim n . 2 2n +1 1 −4 1 2 2 1− 4 lim n = lim n 0,5 (2 điểm) 2 2n +1 1 2 + 2 n 4 − = = 2 − .KL 2 0,5 2 2
x − x − 2 b) Cho hàm số ≠ f (x)  khi x 2 =  x − 2
. Tìm m để hàm số liên tục tại x = 2 . m−1 khi x = 2
Tập xác định: D = ;2  ∈ D 0,25 2 x − x − 2 (x + )1(x − 2) lim = lim = lim(x + ) 1 = 3 0,25 x→2 x→2 x→2 x − 2 x − 2 f (2) = m −1 0,25
Hàm số liên tục tại x = 2 khi và chỉ khi
lim f (x) = f (2) ⇔ 3 = m −1⇔ m = 4 . KL 0,25 x→2 Câu 2. Cho hàm số 3 2
y = x − 3x + 2. Viết phương trình tiếp tuyến của đồ thị hàm số biết
tiếp tuyến đó song song với đường thẳng y = 9x + 7. Ta có 2
y′ = 3x − 6x
Vì tiếp tuyến của đồ thị hàm số song song với đường thẳng y = 9x + 7 nên ta 0,25 x = 1 − 2 xét phương trình 2 2
3x − 6x = 9 ⇔ 3x − 6x − 9 = 0 ⇔   x = 3
(0.5 điểm) + Với x = 1 − ta có y = 2
− nên tiếp tuyến có phương trình là y = 9(x + )
1 − 2 ⇔ y = 9x + 7 (loại vì trùng với đường thẳng đã cho)
+ Với x = 3 ta có y = 2 nên tiếp tuyến có phương trình là 0,25
y = 9(x −3) + 2 ⇔ y = 9x − 25 (thỏa mãn)
KL y = 9x − 25
Câu 3. Cho khối chóp S.ABC có đáy ABC là tam giác vuông tại B ,
AB = a, AC = 2a, SA ⊥ ( ABC) và SA = a . 3 a)
Chứng minh rằng BC ⊥ (SAB) . (2.5 điểm)
b) Tính khoảng cách từ A đến mặt phẳng (SBC). c)
Tính tang của góc giữa hai mặt phẳng (SBC) và (SAC) . 3
a) Chứng minh rằng BC ⊥ (SAB) .
+ Vì SA ⊥ ( ABC) ⇒ SA ⊥ BC ( ) 1 0,25 Lại có A
∆ BC vuông tại B nên AB ⊥ BC (2) 0,25
+ Mà trong mặt phẳng (SAB) ta có SA∩ AB = { } A (3) 0,25
Từ (1); (2); (3) suy ra BC ⊥ (SAB) 0,25
b) Tính khoảng cách từ A đến mặt phẳng (SBC) .
Kẻ AH ⊥ SB tại H. Suy ra A đến mặt phẳng (SBC) bằng AH . 0,5 Ta có a
ΛSAB vuông cân suy ra 2 AH = . 0,5 2
c) Tính tang của góc giữa hai mặt phẳng (SBC) và (SAC).
Kẻ AK ⊥ SC ; chứng minh được SC ⊥ ( AHK ); A
∆ HK vuông tại H
Chỉ ra giao tuyến của hai mặt phẳng (SBC) và (SAC) là SC 0,25
Suy ra góc giữa hai mặt phẳng đó là  AKH Tính được 1 1 1 2a 5 = + ⇒ AK = 2 2 2 AK SA AC 5 0,25 Tính được 2 2 2 a 30 = − ⇒ = ⇒  AH 15 HK AK AH HK tan AKH = = 10 HK 3
Document Outline

  • 11_HK2_11_111
    • I. PHẦN TRẮC NGHIỆM (5,0 điểm).
  • 11_HK2_11_112
    • I. PHẦN TRẮC NGHIỆM (5,0 điểm).
  • 11_HK2_11_113
    • I. PHẦN TRẮC NGHIỆM (5,0 điểm).
  • 11_HK2_11_114
    • I. PHẦN TRẮC NGHIỆM (5,0 điểm).
  • HDC Toan HK 2 lop 11 (2022-2023)